Автор: Виноградов И.М.
Теги: математика астрономия сборник статей ан ссср гаусс научное творчество геодезия и физика
Год: 1956
Текст
lOO
лет
CO дня СМЕРТИ
I855-I955
АКАДЕМИЯ НАУК СССР
ИНСТИТУТ
ИСТОРИИ ЕСТЕСТВОЗНАНИЯ и ТЕХНИКИ
Карл
Фрмдрих
ГАуСС
сборник статей
под общей редакцией
И М.ВИНОГРАДОВА
ИЗДАТЕЛЬСТВО
А КАЛ ЕМИИ НАУК СССР
Москва - 1^56
Ответственный редактор
Г. Ф.РЫБКИН
ПРЕДИСЛОВИЕ
Ученые нашей родины всегда высоко ценили и всесторонне
изучали выдающиеся труды великого немецкого математика
Карла Фридриха Гаусса (1777—1855). Неослабевающий
интерес к научному творчеству Гаусса, охватывающему не только
почти все основные области математики, но и области
астрономии, геодезии и физики, нашел свое отражение в ряде
докладов и ученых заседаний, которыми научная
общественность Советского Союза отметила столетие со дня смерти Гаусса,
исполнившееся в 1955 г.
Данью памяти великого ученого является и настоящий
сборник, в котором освещается выдающийся вклад Гаусса
в математику (теорию чисел, алгебру, геометрию, теорию
вероятностей и математический анализ), астрономию и геодезию.
В сборнике не представлены работы Гаусса по магнетизму.
Однако изданные Академией наук СССР в 1952 г. в серии
«Классики науки» избранные труды Гаусса по земному
магнетизму освещают и комментируют эту интересную и важную
часть его научного творчества.
В качестве введения к сборнику помещена речь акад.
И. М. Виноградова, произнесенная им на заседании,
организованном Всесоюзным обществом культурной связи с заграницей
и Отделением физико-математических наук АН СССР по
случаю столетия со дня смерти Гаусса.
к. Ф. г А у с г
1777 - ]855 ??.
РЕЧЬ АКАДЕМИКА И. М. ВИНОГРАДОВА ^
Сегодня мы отмечаем столетие со дня смерти великого
немецкого математика Карла Фридриха Гаусса. Гауссу
принадлежат глубокие и основополагающие исследования почти во
всех основных областях математики: в теории чисел, в
геометрии, в теории вероятностей, в анализе, в алгебре, а также
важные исследования в астрономии, в геодезии, в механике и в
теории магнетизма.
Математический гений Гаусса развивался на исследованиях
по теории целых чисел, завершившихся опубликованием в
1801 г. его знаменитой книги «Disquisitiones arithmeticae».
В дальнейшем Гаусс возвраш;ался к этим исследованиям и дал
в области теории чисел еш;е две важные работы.
В «Disquisitiones arithmeticae» Гаусс изложил всё
существенное, что было известно в теории чисел до него, но часто исходя
из более общих и более принципиальных соображений. Кроме
того, «Disquisitiones arithmeticae» в четвертом, пятом и седьмом
своих разделах заключают три крупнейших открытия самого
Гаусса: доказательство квадратичного закона взаимности,
композицию классов и родов квадратичных форм и теорию деления
круга.
Квадратичный закон взаимности является центральной
теоремой теории квадратичных вычетов, доказательство кото-
1 Произнесена на торжественном заседании, организованном
Всесоюзным обществом культурной связи с заграницей и Отделением физико-
математических наук АН СССР 23 февраля 1955 г., по случаю столетия
со дня смерти К. Ф. Гаусса.
рой долго и безуспешно пытались получить крупнейшие
математики того времени. Исследования Гаусса по квадратичному
и, позже, по биквадратичному закону взаимности послужили
исходным пунктом длинного ряда работ, приведших в конечном
итоге к отысканию общего закона взаимности, представляющего
собой одну из важных теорем теории алгебраических чисел.
Исследования Гаусса по композиции классов и родов
квадратичных форм явились важным первым этапом в труднейшем
вопросе о построении арифметики полей алгебраических чисел.
Исследования Гаусса по целым комплексным числам,
опубликованные позже (в 1832 г.), дали пример поля алгебраических
чисел, отличного от рационального, в котором действуют
законы обычной арифметики. Продолжение обоих этих
исследований привело во второй половине XIX столетия к построению
общей теории алгебраических чисел, которая является в
настоящее время одним из основных методов теории чисел.
Теория деления круга, занимающая последний, седьмой
раздел «Disquisitiones arithmeticae», содержит подробное
рассмотрение двучленного уравнения х^ = I, в котором, применяя
методы теории чисел, Гаусс сводит решение этого уравнения на
цепь уравнений низших степеней. Это исследование
представляет собой частный, но вполне завершенный случай теории,
построенной впоследствии Галуа, которая является одной из
основных теорий алгебры. Теория деления круга дала
замечательный чисто геометрический результат. К тем правильным
многоугольникам, которые умели строить при помощи циркуля и
линейки древние математики, Гаусс прибавил еще правильный
семнадцатиугольник. Более того, он нашел вообще все те
правильные многоугольники, которые можно построить при
помощи циркуля и линейки. Теорема о правильном семнадцати-
угольнике была опубликована Гауссом без доказательства,
когда он был еще 19-летним студентом и создала ему первую
известность.
В связи с теорией деления круга Гаусс рассмотрел в 1811 г.
особые тригонометрические суммы, называемые теперь
суммами Гаусса. Дальнейшее обобщение этого исследования привело
впоследствии к рассмотрению более общих тригонометрических
сумм, которые являются сейчас одним из самых сильных средств
аналитической теории чисел и способствовали доказательству
важных теорем, касающихся обыкновенных целых чисел.
О работах Гаусса, не относящихся к области теории чисел,
я скажу уже более кратко. Подобно тому, как это было у
Архимеда, Ньютона, Эйлера и, впоследствии, у Чебышева,
большинство из этих работ было вызвано задачами, которые ставили
естествознание и практическая деятельность. Так, работы по
геодезической съемке, которые были поручены Гауссу, привели
его к исследованиям по внутренней геометрии поверхностей.
Они были опубликованы в 1828 г. в знаменитом мемуаре «Dis-
quisitiones generales circa superficies curvas». В этом мемуаре
содержится также доказательство важной теоремы Гаусса
о неизменяемости кривизны при изгибании поверхностей.
Непосредственным обобщением идеи Гаусса о внутренней
геометрии поверхностей явилась впоследствии геометрия Римана,
послужившая в свою очередь основным аппаратом для общей
теории относительности.
Обширные приближенные вычисления, которые
приходилось практически производить лично Гауссу при решении
задач, относящихся к астрономии и к геодезии, привели его
к более глубокой разработке способа наименьших квадратов
и к выяснению центрального значения нормальной кривой
распределения в вопросах, связанных с теорией вероятностей.
Работы Гаусса по теории магнетизма привели его к важным
теоремам теории потенциала.
Размышляя над основными принципиальными вопросами
механики, Гаусс пришел к известному своему принципу
наименьшего действия.
Еще в самый первый период своей научной деятельности,
в связи с необходимостью обнаружить на небе потерянную
малую планету Цереру, Гаусс придумал замечательный метод
определения орбиты по трем наблюдениям. Успех этого метода,
давшего возможность снова найти Цереру, был первым
обстоятельством, которое сделало имя Гаусса всемирно известным.
Сделаю несколько общих замечаний об особенностях стиля
творчества Гаусса. Все общие математические идеи появлялись
У Гаусса в связи с решением совершенно конкретных задач.
Но эти задачи большей частью относились к важным узловым
вопросам современной ему математики. В дальнейшем, в руках
его продолжателей, идеи Гаусса привели к созданию новых
областей математики. В частности, работы Гаусса по теории
чисел предопределили развитие теории чисел более чем на
столетие; такую же роль сыграли и работы Гаусса по внутренней
геометрии поверхностей.
После Гаусса осталось обширное рукописное наследие,
которое было опубликовано много позже его смерти. В
рукописях Гаусса математики с изумлением нашли целый ряд
теорем, данных без доказательства и касающихся самых
различных отделов математики: аналитической теории чисел, теории
эллиптических и, в частности, модулярных функций,
неэвклидовой геометрии и т. д. Некоторые из этих теорем были,
задолго до обнародования посмертных рукописей Гаусса, независимо
от Гаусса, открыты и опубликованы другими математиками,
а многие не были еще известны и послужили стимулом для
работ последующих ученых.
Русские математики всегда высоко ценили и глубоко
изучали работы Гаусса. Некоторые исследования русских
математиков являлись непосредственным продолжением работ
Гаусса, например: исследования русских математиков о минимумах
определенных и неопределенных квадратичных форм, работы по
общзй теории алгебраических чисел, а в последнее время —
работы по общему закону взаимности и исследования,
переносящие гауссову внутреннюю геометрию поверхностей на случай
не аналитических поверхностей.
Я надеюсь, что указанная глубокая связь, которая всегда
существовала между немецкими и русскими математиками,
должна служить примером того дружеского сотрудничества, к
которому мы стремимся во всех областях нашей жизни и которое
принесет пользу обоим нашим великим народам.
Б.Н.Делоне
РАБОТЫ ГАУССА
ПО ТЕОРИИ
ЧИСЕА
=s:s^
1. Теория чисел до Гаусса (13).— 2. «Арифметические
исследования» Гаусса (15).— 3. О теории чисел вообще и о
современных нам ее методах (18).— 4. О теории алгебраических чисел (20).—
5. Первый, второй и третий разделы «Арифметических исследований»
Гаусса (31).— 6. Четвертый раздел «Арифметических
исследований». Первое доказательство закона взаимности (33).— 7. Целые
комплексные числа Гаусса и бпквадратичный закон взаимности
(36).— 8. О законах взаимности вообще и о задаче, которую они
решают (37).— 9. О теореме Кронекера и о теории поля классов (40).—
10. Первая часть пятого раздела «Арифметических
исследований» (41).— 11, Вторая часть пятого раздела «Арифметических
исследований». Композиция классов и композиция родов
квадратичных форм (50).— 12. Третья часть пятого раздела «Арифметических
исследований». Отступление о тройничных формах {60).— 13.
Четвертая часть пятого раздела «Арифметических исследований»,
содержащая приложение теории тройничных квадратичных форм и
исследования о числе классов (75).— 14. Шестой раздел
«Арифметических исследований». Различные приложения теорий чисел (91).—
15. Седьмой раздел «Арифметических исследований». Теория
деления круга Гаусса (92).— 16. Суммы Гаусса (102).
1. ТЕОРИЯ ЧИСЕЛ ДО ГАУССА
Важные теоремы о целых числах были доказаны уже в
древности. Так, например, в школе Пифагора (V в. до н. э.) были
найдены в бесконечном числе такие взаимно простые квадраты
целых чисел, сумма которых тоже квадрат ж^ + 2/^ = 2^. В
«Началах» Эвклида (III в. до н. э.) мы находим доказательство
бесконечности числа простых чисел. В сочинении Диофанта
(III в. н. э.) рассмотрены способы решения различных
неопределенных уравнений в рациональных числах.
13
Первый, кто в новое время начал глубокие исследования
целых чисел, был Пьер Ферма (1601-—1665) из Тулузы. Задачи,
решенные Ферма, и особенно теоремы, высказанные им, но
доказательства которых он скрыл по обычаю того времени,
произвели большое впечатление на последующих математиков.
Ферма имел особую способность проникать в самые глубокие
тайны чисел. Укажем два примера. В 1651 г. Ферма, в виде
вызова всем современным ему математикам, поставил задачу
доказать, что если Д — целое положительное число, отличное от
полного квадрата, то уравнение х^—t!^y^= 1 (которое теперь
называется уравнением Пелля) всегда имеет решения в целых
числах ж, у (уфО). Теорема эта в руках Эйлера и Лагранжа,
который первый ее доказал в 1768 г., оказалась ключом ко всему
неопределенному анализу 2-й степени. Другой пример: на
полях своего экземпляра книги Диофанта Ферма записал
утверждение, что, тогда как сумма двух квадратов целых чисел может
быть опять квадратом целого числа, сумма двух кубов или двух
одинаковых высших степеней не может быть такой же
степенью целого числа (так называемая Великая теорема Ферма).
Теорема эта в общем виде не доказана и не опровергнута до
сих пор, но уже самые попытки ее доказать привели к созданию
глубоких теорий.
Большая часть задач, оставленных Ферма последующим
поколениям математиков, была решена Эйлером (1707—1783)
и Лагранжем (1736—1813), которые также поставили и решили
многие дальнейшие собственные задачи. Эйлер, в частности,
построил теорию степенных вычетов (см. о них дальше на стр.
32); доказал (в его доказательстве, правда, есть пробел), что
уравнение х^-^- у^ = z^ не имеет решений в целых числах;
нашел на числовых примерах (однако не смог этого доказать),
что простые числа р, такие, для которых заданное целое число а
есть «квадратичный вычет» (т. е. те р, для которых существуют
такие квадраты х^, что число а отличается от них лишь на
кратности р), суть те и только те простые числа, которые
содержатся в некоторых определенных арифметических прогрессиях (так
называемый квадратичный закон взаимности в рациональном
поле), а также многое и многое другое. Лагранж глубоким и
тонким методом доказал утверждение Ферма об уравнении Пел-
14
и показал, что этот метод дает способ для полного решения
в целых числах любого неопределенного уравнения 2-й степени
о двумя неизвестными ах^ + 2te?/ + су'^ + 2йж + 2е?/ +/=0.
Кроме того, Лагранж доказал замечательную теорему, верность
которой утверждал уже Ферма, что любое целое
положительное число N есть сумма четырех квадратов целых чисел:
,V = х^ +2/^+2^+ ^^> частный случай так называемой общей
теоремы Варинга, доказанной в общем виде только в 1909 г.
Гильбертом.
Лежандр (1752—1833) опубликовал первый большой
трактат о теории чисел, в котором собрал все сделанное до него и
добавил много нового.^
Таково было положение теории чисел до Гаусса.
2. «АРИФМЕТИЧЕСКИЕ ИССЛЕДОВАНИЯ» ГАУССА
Гаусс (1777—1855) с самого раннего возраста обнаруживал
необыкновенные способности к математике. Сохранилось
предание, что он, когда ему едва минуло 3 года, присутствовал при
расчете своего отца, бывшего водопроводным мастером, с
подсобными рабочими и заметил, что расчет сделан неверно, а
верно так-то. Расчет был проверен, и присутствую,щие с
неподдельным удивлением увидели, что число, указанное трехлетним
мальчиком, правильное. Уже 18-ти лет Гаусс получил в математике
результаты величайшей важности. С 1797 г. Гаусс начал
печатать свою знаменитую книгу «Арифметические исследования»
(«Disquisitiones arithmeticae»)^. По тогдашним условиям
печатание шло медленно, и в течение этого времени Гаусс
дорабатывал разные части книги, особенно пятый ее раздел.
«Арифметические исследования» вышли в свет в 1801 г., когда Гауссу было
24 года. «Арифметические исследования» — первая книга, в
которой теория чисел, или, как говорит Гаусс, высшая
арифметика, излагается как стройная наука, причем во всех вопросах
Гаусс обращает особое внимание на принципиальную сторону
дела. Книга Гаусса оказывала решающее влияние на работы
1 С. F. Gauss. Werke, Bd. I; см. также: Gauss. Untersuchungen
Ober hohere Arithmetik. Deutsch. hrsg. von H. Maser, 1889.
IB
всех математиков мира по теории чисел в течение целого
столетия, а многие идеи, в ней заложенные, оказали влияние на всю
математику в целом. Все результаты работ в теории чисел
предыдущих ученых, таких как Ферма, Эйлер, Лагранж, Лежандр,
включены в тот или иной из семи разделов, на которые
разделено это фундаментальное сочинение, имеющее более 600 страниц,
но большей частью эти результаты изложены, исходя из более
общих, глубоких и объединяющих принципов. Кроме того,
книга содержит© четвертом, пятом и седьмом разделах три
совершенно различных первоклассных и фундаментальных для теории
чисел и алгебры новых открытия самого Гаусса: 1°
доказательство закона взаимности, 2° теорию коа^дозиции квадратичных
форм и теорию их родов и 3° теорию деления круга. Два
других крупнейших открытия Гаусса в теории чисел: 4° гауссовы
суммы и 5° арифметика целых комплексных чисел, были
сделаны уже позже, после выхода в свет «Арифметических
исследований», и опубликованы соответственно в 1811 и в 1828—1832 гг.
Относительно общего стиля «Арифметических исследований»
Гаусса надо сказать следующее. Гаусс был несравненным
вычислителем и, подобно тому, как это делали многие другие
выдающиеся арифметики, обычно получал свои новые результаты,
исходя из обширных численных вычислений, которые
позволяли ему подмечать новые, глубоко скрытые арифметические
истины, доказательства которых он получал затем нередко лишь
в результате упорной, продолжительной, иногда многолетней
работы. Книга Гаусса проникнута стремлением решить каждый
вопрос так, чтобы получить удобнейший вычислительный
алгорифм. Многие места книги поясняются численными примерами
и небольшими численными табличками, которые делают
непосредственно ясным, о чем идет дело и, так сказать, вводят в
самую практику рассматриваемых арифметических вопросов.
Когда углубляешься в изучение книги Гаусса, то прямо
недоумеваешь, как мог двадцатилетний молодой человек создать
такой грандиозный комплекс сложнейших и глубочайших
методов и теорем, так хорошо слаженный и построенный и, кроме
того, содержащий, как было указано выше, три
первоклассных открытия, каждое из которых уже одно обессмертило бы
имя любого математика. Несомненно, что умственный подвиг
16
^Ob
- «c$
%M r?4l с ? ^ t
"7^ 'T/**^/ "^!/^''^^^''*^ f^^/itty^Af^
3^J^U . -4^—™^ - - — ^-^^^^^^ ■
* и ^,fri. i "^А -i/-^'' -^f^
***<^^ /^ г
/%i\?v ¥'
'^'■^-- '--^''t /.^^'/г'^^-^-^^ь.
i t nil
4ГЙ*
ш ^^^*-^
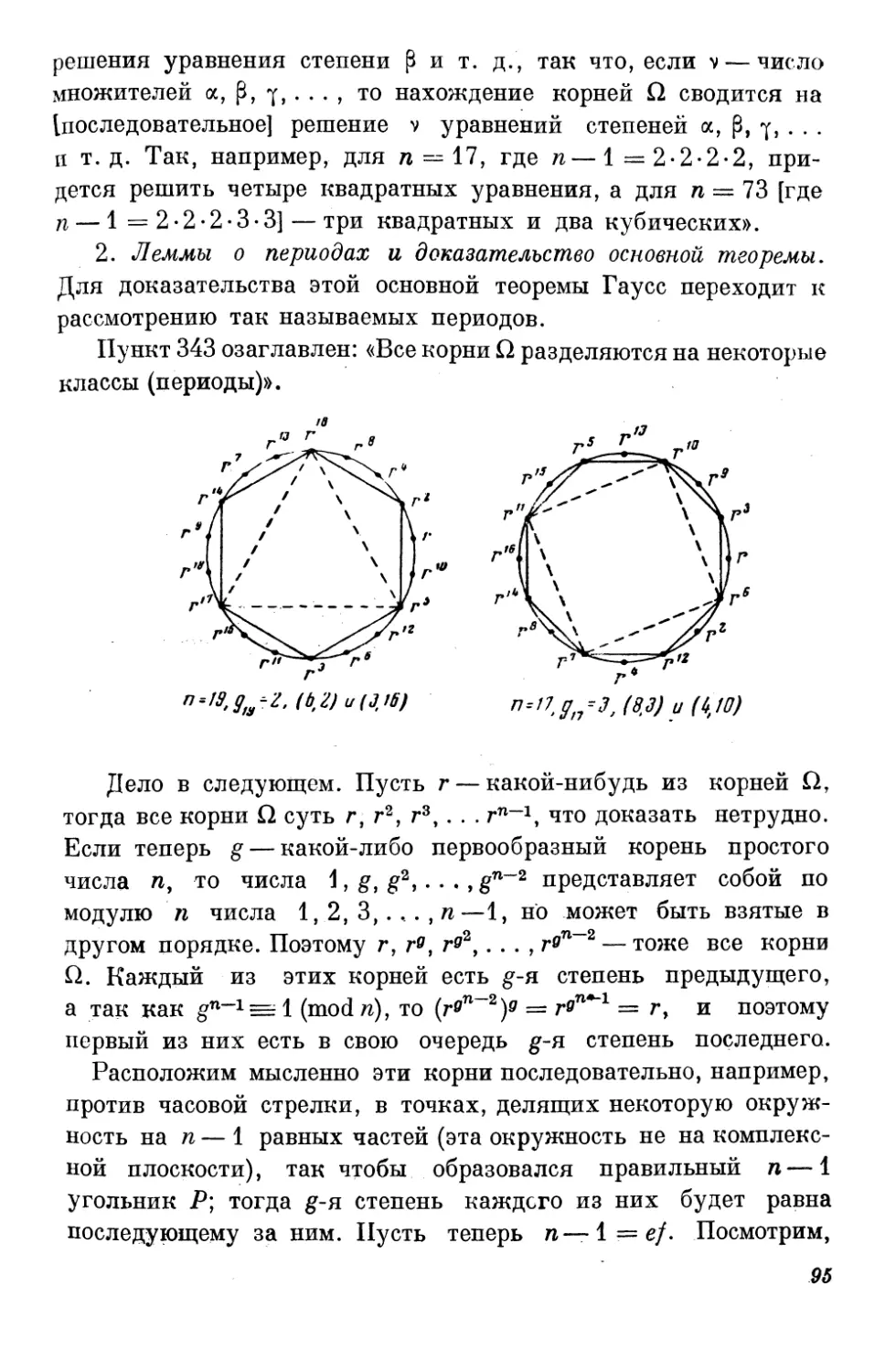
Страница из «Дневника» Гаусса (30.3—24.5, 1796)
2 к. Ф. Гаусс
молодого Гаусса, приведший к написанию «Арифметических
исследований», имеет мало себе равных в мировой науке.
Попробуем теперь по порядку рассмотреть открытия
Гаусса в теории чисел и выяснить то значение, которое каждое из
них имело для дальнейшего развития математики. Но прежде,
чем это делать, нам придется довольно много сказать о теории
чисел вообпце и о теории алгебраических чисел в частности.
3. О ТЕОРИИ ЧИСЕЛ ВООБЩЕ И О СОВРЕМЕННЫХ НАМ
ЕЕ МЕТОДАХ
Обыкновенные целые числа..., —3, —2, —1, О, 1, 2, 3,...
являются основой всей математики. В отношении сложения они
образуют весьма простую совокупность (бесконечную
циклическую абелеву группу), а именно: .,., —1—1, —1, О, 1, 1 + 1,
1 + 1 + 1, •••, единственным исходным кирпичом которой
является число 1. В отношении же к умножению тот же ряд
целых чисел имеет уже вовсе не простую структуру. А именно
тех простейших кирпичей, из которых строятся умножением
все целые числа, бесконечно много — это простые числа 2, 3, 5,
7, 11,13, 17, 19, 23, 29, 31, 37, ... Натуральные числа, большие
1, получаются из них умножением так: 2,3,2-2,5, 2*3, 7, 2-2-2,
3-3, 2-5, И, 2-2-3, 13, 2-7, 3-5, 2-2-2-2, 17, ... Для того же,
чтобы умножением получить все целые рациональные числа,
надо еще привлечь обе единицы: 1 и —1 и число 0.
Уже даже самый простой вопрос, как идут в ряду
натуральных чисел 1, 2,3,4,5,6,... простые числа, до настояш;его
времени представляет непреодолимые трудности. Со времен
Эвклида доказано, что их бесконечно много. Но только Чебы-
шеву в 1849 г. удалось -показать, что число Ti(iV) простых
чисел, меньших данного предела Л^, приблизительно равно
—^ , а затем Адамару и Валле-Пуссену — что отношение
N
Ti(A^):—^ стремится к пределу 1. Лишь совсем недавно, в 1937 г.,
И. М. Виноградову в знаменитой работе удалось доказать, что
любое достаточно большое натуральное число N есть сумма
четырех простых чисел. Но, например, до сих пор не удается
выяснить, встречаются ли сколь угодно далеко так называемые
18
«близнецы», т. е. простые числа, отличающиеся друг от друга
на число 2, как пара 101 и 103 или пара 8004119 и 8004121.
Вся трудность теории чисел состоит в том, что свойства це-
яых чисел относительно умножения (мультипликативные
свойства) с их свойствами относительно сложения (с их
аддитивными свойствами) связаны очень сложно.
Перейдем теперь к рассмотрению современных нам методов
теории чисел.
На современном нам этапе теории чисел для решения
вопросов теории обыкновенных целых рациональных чисел
используются, кроме элементарного, в основном четыре метода:
1) теория алгебраических чисел (и других алгебр);
2) теория алгебраических функций;
3) аналитическая теория чисел;
4) геометрия чисел.
Отметим тех главнейших математиков, кроме Гаусса,
которые до настояш;его времени создавали эти методы.
К использованию метода алгебраических чисел относятся
работы Вал лиса об уравнении Пелля, работы Лагранжа о
неопределенных уравнениях 2-й степени, доказательство Эйлера
теоремы Ферма для кубов, работы Эйзенштейна и Куммера о
законе взаимности, работы Дирихле о теории единиц, работы
Куммера об идеальных числах, работы Дедекинда,
Золотарева, Кронекера, Клейна по теории простых делителей,
работы Гильберта, Фуртвенглера, Такаги, Артина, Хассе
и Шевалле по теории поля классов, работы Фробениуса и
Чеботарева, обобш;ающие теорему Дирихле о прогрессии, и работы
Шафаревича об общем законе взаимности.
К обобщению этого метода на теорию квадратичных форм
с многими переменными относятся работы Венкова, Хассе,
Хекке, Зигеля, Витта, Эйхлера.
Основные сводки по этому методу принадлежат Гильберту
(1896) — по общей теории алгебраических чисел, Хассе (1924)—
по специальному вопросу теории алгебраических чисел, теории
поля классов и Эйхлеру (1952)— по применению алгебр к
арифметике квадратичных форм со многими переменными.
Использование теории алгебраических функций,
родственной теории алгебраических чисел, но имеющей свои специфиче-
2* 19
ские методы, начал Пуанкаре, затем в этом направлении
работали Морделл, А. Вейль, Хассе и др.
Аналитическая теория чисел ведет свое начало от Эйлера.
Дирихле и Чебышев продолжали развитие этих идей в
вещественной области. Новую струю влил Риман, который вышел
в комплексную плоскость и начал использовать аналитичность
функции и аналитическое продолжение. Методы
аналитической теории чисел употребляли в теории алгебраических чисел
Дирихле, Дедекинд, Кронекер, Фробениус, Чеботарев, Хекке,
Здгель, Хейльбронни др. Важный прием для аддитивных задач
придумал Вороной. Блестящее развитие та же идея, хотя, по-
видимому, и независимо от Вороного, получила в работах
Рамануджана и Харди и Литтльвуда.
Важной главой аналитической теории чисел является оценка
тригонометрических сумм, первый далеко идущий результат
в которой был получен в 1914 г. Г. Вейлем. Наиболее глубокие
новые идеи в этой области были развиты Виноградовым,
который, между прочим, получил оценки тригонометрических сумм
по простым числам.
Основателями геометрии чисел были Минковский и
Вороной. Ее методами работали у нас автор этих строк и Венков,
а также их используют многие современные математики.
Работы Гаусса по теории чисел дают первые образчики почти
во всех этих направлениях, но наибольшее значение они имеют
для развития метода алгебраических чисел и метода
тригонометрических сумм.
4. О ТЕОРИИ АЛГЕБРАИЧЕСКИХ ЧИСЕЛ
1. Основные понятия. Уже самые первые крупные
арифметики, которые пытались решать более глубокие вопросы теории
целых чисел, начали убеждаться в том, что часто для их решения
надо так или иначе привлекать некоторые вспомогательные,
так называемые алгебраические, иррациональности, т. е.
корни некоторых уравнений с рациональными коэффициентами.
Этот метод играл роль уже в работах Валлиса (1616—1703) об
уравнении Пелля, в работах Лагранжа о неопределенных
уравнениях 2-й степени, в которых |/а разлагался в непрерывную
20
гтробь. Б доказательстве невозможности уравнения х^ -{- у +
1_ 2^ = О в целых числах х, ij, z Эйлер привлекает
иррациональность V—Ъ и т. д.
Что же такое поле алгебраических чисел данной степени?
рассмотрим какое-нибудь алгебраическое уравнение п-к степени
с рациональными коэффициентами ai, ад,..., а„:
хп + ai:r^-i + азх^-з + . . . + «n-i^^ + ^п = О, (1)
неприводимое в поле рациональных чисел, т. е. такое, что его
левая часть не раскладывается на два множителя низших
степеней опять с рациональными коэффициентами, и пусть а — один
из его действительных или комплексных корней. В таком случае
число а называется алгебраическим числом n-vL степени.
Совокупность i^ всех тех чисел, которые получаются из числа а, если
соединять его само с собой любым конечным числом действий
сложения, вычитания, умножения и деления, называется полем
алгебраических чисел n-ii степени, являющимся расширением
рационального поля присоединением к нему числа а. Можно
показать, что присоединение к полю рациональных чисел
нескольких алгебраических иррациональностей равносильно
присоединению одной такой иррациональности высшей степени.
Легко далее показать, что в силу тождества а" + ^^i»^^"^+
. . . + <^п = О всякое число со поля К, являющегося
результатом присоединения числа а, можно привести к виду со = гг^а^-^^-
4- а2а^-2 _]_ _ _|. ^^ ^ где iii, щ, . . . , Un — рациональные числа,
п обратно. Если а(^), а^^), . . . , а(^) все корни уравнения (1), то
числа:
о)(1) = гг1а(1)^-1 + Waa^i)^-^ 4- . . . + w^.
которые называются сопряженными между собой, суть все
корни некоторого уравнения
хп + ь^х^'^ + Ь^х^-^ 4-. . . + bn-ix + bn = о, (2)
также с рациональными коэффициентами b^,b^,, . . ,bn, но
которое может уже быть и приводимым (степенью
неприводимого).
21
Нетрудно показать, что все те числа поля К, для которых
в уравнении (2) &i, b^, • - - , bn —целые рациональные,
называемые целыми алгебраическими, образуют в поле К так
называемое «кольцо», т. е. такую подсовокупность D чисел поля
Ку что сумма, разность и произведение ее чисел суть опять ее
же числа. Наконец, можно показать, что в этом кольце D
всех целых чисел поля К можно выбрать систему п таких его
чисел o)i, 0)2, .. . , 0)^ — базис кольца D всех целых чисел поля
К,—что любое целое число со поля К имеет вид
О) = CiCOi + СдСОз + • • • + Сп^п,
где Ci,C2, ...,Сп — целые рациональные, и обратно.
Арифметика кольца £) всех целых чисел того или иного поля
А" алгебраических чисел и играет часто роль при решении
разных вопросов теории целых рациональных чисел.
Все, что сейчас сказано, можно изложить и иначе —
геометрически.
2. Геометрическое изложение. Начнем с обыкновенных це-
лых рациональных чисел. Возьмем координатную ось и будем
называть суммой, разностью и произведением двух точек этой
оси точку, координата которой есть сумма, разность или
произведение координат этих точек. В таком случае легко видеть,
что ряд целых рациональных точек..., —2,—1, О, 1, 2, ...
'J '2 -f О f 2 3
представляет собой дискретную, неуплотняемую
совокупность точек оси — такую, что такие сумма, разность и
произведение ее точек суть ее же точки, и наоборот, если
совокупность точек оси обладает этими свойствами (и
отличается от одной точки 0), то она есть ряд целых рациональных
точек. Неуплотняемость совокупности здесь понимается в том
смысле, что нельзя к ней прибавить дальнейших точек
так, чтобы старые ее точки вместе с этими новыми опять
давали совокупность, удовлетворяюш;ую всем другим
потребованным условиям.
Такая совокупность называется неуплотняемым
дискретным кольцом точек (по отношению к введенным
покоординатным сложению^ вычитанию и умножению).
22
To же самое можно делать на плоскости, если на ней
зафиксирован некоторый заданный координатный репер Е = О, ei е^
введено покоординатное по отношению к нему сложение,
вычитание и умножение точек, так что если, например, заданы
точки (3, И) и (5, —7), то их сумма есть точка (8, 4), а
произведение—точка (15, —77). На плоскости имеется одно
очевидное, тривиальное, дискретное, пеуплотняемое
решетка всех точек с целыми рациональными
кольцо — это
координатами.
н
-1
(
i
м
т
—р-
—f—
—(
—,
1 1
1 ,
,—,
1 <
1
' г1
,
'—'
j
1
'—'
—
'—
г^
г——<
1—<
1
(
(
1 1
1 1
'—*
—.
—Н
1 (
> ■■■!
1
»
>- 1 1
> <
1 1
, ^.
Действительно,
покоординатные суммы, разность и
произведение точек этой
решетки есть, очевидно, опять
точка с целыми
рациональными координатами; эта со- —|—^—j—)—i^—| ( \—\—t-*^z/
вокупность дискретна и, как
нетрудно показать, неуплот-
няема. Но на плоскости,
кроме этого (единственного)
приводимого дискретного не-
уплотняемого кольца, есть
еще сколь угодно много других различных .колец, которые
все уже неприводимы, т. е. не имеют точек на осях координат,
кроме начала.
Как можно показать, каждое из них может быть построено
так: надо взять любое положительное целое рациональное
число Д, не делящееся на квадрат, и рассмотреть репер Е,
построенный на векторах (1, 1) и (|/"Д, —|/^Л), и решетку точек, на нем
построенную (т. е. с целыми рациональными относительно него
координатами). Если дф1 (mod 4), то сама эта решетка,
представляющая собой решетку прямоугольников, а если Д^^1 (mod 4),
то та, которая получается из нее, если добавить по точке в
центрах всех ее прямоугольников, будет двумерным
неприводимым дискретным неуплотняемым кольцом и никаких других
таких колец нет.
Можно показать, что каждое из этих колец представляет
собой не что иное, как совокупность всех целых чисел некоторого
вещественного квадратичного поля алгебраических чисел, если
каждому числу этого поля сопоставлять точку плоскости, коор-
динаты которой суть это число и ему сопряженное, и обратно.
Квадрат d площади основного параллелограмма (зашрихован
ного) такой решетки равен в первом случае 4Д, а во втором Д
^'^^V^?
Он называется дискриминантом соответственного
квадратичного поля. Итак, дискриминанты вещественных квадратичных
полей суть числа 4-2, 4-3, 5, 4-6, 4-7, 4-10, 4-11, 13, 414,
4-15,17, 4-19, 21, 4-22, 4-23, 4-26, 29,4-30, ..., причем со всяким
таким дискриминантом имеется только одно квадратичное поле.
Аналогичное имеет место для ^-мерного вещественного или
комплексного пространства, где всякое ^г-мерное неприводимое
(т. е. не имеющее точек, отличных от точки О, хоть одна из
координат которых равно нулю) неуплотняемое кольцо Г) по
отношению к покоординатным сложению, вычитанию и умножению
есть ^-мерная решетка точек, координатами которых являются
целые числа некоторого поля алгебраических чисел п-ж степени
и им сопряженные, и обратно. Таких колец £) бесконечно
много, и дискриминанты (квадраты ^-мерных объемов основ-
24
ных параллелепипедов) их суть неубывающие целые числа,
причем число различных колец Г) с одним и тем же
дискриминантом конечно (теорема Эрмпта).
Рассмотрим теперь арифметику такого кольца,Г). В отношении-
сложения и вычитания такое кольцо построено совсем просто —
всякая его точка <^=Ci(^i + C2<^2~^•••'^'^п^пу ^Д® ^ь^2'---'^п
суть концы векторов его основного репера Е, а с^, Со, ..., с^—
целые рациональные числа. Что же касается умножения, то
при п>1 уже вопрос о единицах кольца, т. е. о таких его
точках £, от умножения на каждую из которых кольцо £> переходит
само в себя, не так прост. При 72 = 1 единицы кольца две: +1
и —1. При д>1 оказывается единиц, кроме как для
квадратичных мнимых полей, бесконечно много, но все они суть
произведения степеней конечного числа так называемых основных
единиц. Теорема эта была впервые доказана для
действительных квадратичных полей Лагранжем в 1768 г., а в общем
случае Дирихле в 1841 г., причем в свое время это исследование
Дирихле считалось одним из самых трудных в теории чисел.
Далее, в £) можно выделить так называемые простые точки,
т. е. такие точки, которые уже нельзя представить в виде
произведения нескольких точек ■£), отличных от единиц.
25-
Примеры показывают, что уже при п = 2 существуют кольц5(^
£), в которых любая точка однозначно разлагается на простые
точки (если не учитывать множителей единиц), и существую^
другие кольца D, в которых это разложение, вообще говор/^,
неоднозначно. В таких «плохих» кольцах арифметика necoBeji-
шенна, и они поэтому непосредственно не могут быть успешно
использованы. Возможно, что уже и Гаусс знал об этом
обстоятельстве. Но не видно было, как от него избавиться, пока Кум-
мер (1810—1893) в 1846 г. для частных случаев полей, зависящих
от корней уравнений деления круга х^~^-\-х'^~'^-\-...-\-х-{-1 = 0,
где р — простое число, не показал, что такое кольцо £) можно
дополнить некоторыми так называемыми идеальными
элементами так, чтобы в дополненном кольце £)* (которое само уже не
является кольцом, но является мультипликативной системой,
т. е. такой, что произведение любых двух ее элементов есть ее
же элемент) разложение было уже однозначно. Позже, в начале
70-х годов, одновременно и независимо друг от друга, разными
способами показали то же самое для общего поля
алгебраических чисел Дедекинд (1831—1916) и Золотарев (1847—1878).
Еще один способ излоячить этот вопрос нашел позже Кронекер
(1823—1891). Наконец, в 1896 г. Клейн (1849—1925) для
частного случая квадратичных полей нашел очень наглядный
новый подход, который был впоследствии обобщен на любое поле
алгебраических чисел.
3. Теория идеалов Дедекинда. Изложим сначала теорию
идеалов Дедекинда. Пусть L^ и L^ — две ^-мерные подрешетки
решетки D; нетрудно доказать, что если составить все
попарные произведения их точек и затем рассмотреть все суммы и
разности полученных произведений, то получится опять
некоторая подрешетка L^ решетки D. Решетка L^ называется
произведением LiLg решеток Lj и L^. Если g такая /г-мерная
подрешетка решетки D, что Г),^ == Q, то g называется идеалом
в D. Очевидно, что если v — точка из О, отличная от нуля
(т. е. от начала), то решетка ;3 = ^^ ^^ть идеал в О, так так
Q.vD = vD, ибо DD = D ввиду того, что в D есть точка
1 = (1, 1, . . . , 1) и уже 1 D = О. Такой идеал vD называется
главным идеалом, соответствующим точке v. Дедекинд показал,
что если в D нет никаких идеалов, отличных от главных, то
26
любая точка из D однозначно, с точностью до множителей
единиц, разлагается в произведение простых его точек, т. е.
уже в самом кольце D арифметика совершенна. Если же в D
есть идеалы 3, отличные от главных, что, как это
показывают примеры, бывает очень часто (даже, повидимому,
большей частью, например, для мнимых квадратичных полей всегда,
кроме как для конечного числа таких полей), то разложение
точек D в произведение простых точек D уже неоднозначно.
Если, однако, вместо точек D рассмотреть идеалы в D, то
оказывается, что среди них имеются простые идеалы, т. е.
такие, которые нельзя представить в виде произведения
других идеалов, отличных от так называемого единичного идеала
Ю (D, очевидно, тоже идеал в D), и можно доказать основную
теорему, что.любой идеал в D однозначно разлагается в
произведение таких простых идеалов, отличных от единичного
идеала D.
Два идеала g^ и ^2 ^ D называются эквивалентными, или
подобными, если существует такая точка X в пространстве Rn,
в котором лежит D, от умножения на которую один из
идеалов переходит в другой, другими словами, если эти идеалы
3i и ^2 получаются друг из друга «растяжениями» по осям
координат. Совокупность идеалов О, подобнь1х друг другу,
образует класс идеалов в D. Все главные идеалы, очевидно,
подобны идеалу О — это главный класс. Можно показать, что
число h классов идеалов в D конечно.
4. Теория побочных решеток Клейна. Перейдем теперь
к тому дальнейшему развитию теории Дедекинда, которое
предложил Клейн. Оказывается, что если взять по представителю
^2? Зз» • • • > 3^ в каждом из неглавных классов идеалов, то
можно их домножить на такие точки из Rn, ^2» ^ з^ • • • > ^^^, что
полученные так называемые побочные решетки D', £)", . . . , D(^-i)
вместе с «главной» решеткой D образуют «нормальную фигуру»
(NormaIfigur) D*, которая уже не решетка и обладает
следующими свойствами: 1° объемы (вообш;е говоря, комплексные)
основных параллелепипедов всех решеток D, О', D", . . . , £)^^~^^
одинаковы; 2° любые две из h решеток £), D', к)\ . . . , 0^^-^)
не имеют обш;их точек, кроме точки О, обш;ей им всем; 3°
произведение любых двух точек нормальной фигуры D* есть
27
опять точка этой нормальной фигуры (но сумма двух точек
нормальной фигуры, вообще говоря, уже не есть точка
нормальной фигуры); 4° произведение любых двух решеток С^^Ю^^^
есть опять одна из этих решеток £>(^\ причем таким умножением
решетки D. . .D^^'^^ образуют абелеву группу, «единицей» которой
является D; 5° единицы s главной решетки D суть
одновременно единицы и каждой из побочных решеток в отдельности
и, следовательно, и всей нормальной фигуры £)* в целом,
причем никаких других единиц нормальная фигура не имеет;
6° всякая точка нормальной фигуры О*, с точностью до
множителей единиц, однозначно разлагается в произведение
простых точек этой нормальной фигуры.
Связь между теорией идеалов Дедекинда и теорией
нормальной фигуры D* Клейна та, что если j — какая-либо точка
нормальной фигуры (отличная от нуля) и D^^^ — решетка,
«обратная» той решетке Q^^\ в которой эта точка j лежит,
т. е. такая, что D^^^ 0^^^ = D, то jD^^) = ^ есть идеал
Дедекинда, лежащий в D, соответствующий этой точке j
нормальной фигуры D*, и обратно. Умножению точек D* соответствует
умножение соответствующих им идеалов, и обратно.
5. Причины успеха прильенения алгебраических чисел в
теории обыкновенных целых чисел. Поставим себе вопрос: на каких
обстоятельствах основан успех применения алгебраических
чисел при решении вопросов об обыкновенных целых числах?
Таковых обстоятельств три.
Во-первых, переход в подходящее поле алгебраических
чисел часто дает «линеаризацию» задачи. Вместо рассмотрения
нелинейного выражения, составленного из обыкновенных целых
чисел, рассматриваются его линейные, но иррациональные,
алгебраические множители. Пример: уравнение Пелля
х^ — Аг/2 = 1 заменяется таким {х — ]/Ау) {х + У^У) = 1» ^
далее все сводится к рассмотрению линейных выражений
X — ]/д?/ -& х-\- Y^y-
Во-вторых, при таком рассмотрении задачи происходит
так называемое «распроектирование» задачи, т. е. задачу
(которая при непосредственном к ней подходе является, скажем,
одномерной) рассматривают в пространстве высшего измерения,
где она распутывается. Возьмем тот же пример уравнения
28
Пелля. При переходе к квадратичному полю мы получаем
поскости решетку точек, соответствующих цалым числам этого
ОЛЯ, и вопрос решения уравнения х^ — А?/^ = 1 сводится
разысканию тех точек s этой решетки, которые лежат на
гиперболе ?7] = 1. Отсюда весьма несложно получается
знаменитый результат Лагранжа об уравнении Пелля.
В-третьих, заметим следуюш;ее. В любом кольце d всегда
есть точка 1 =^ (1,1, . . . , 1), а следовательно, и точки 14-1 =
= 2=(2,2,...,2), 1 + 1 + 1 = 3 = (3,3, ...,3) и т. д., так
называемые натуральные точки кольца D. Всякая точка £)*
есть делитель некоторой натуральной точки D (и всех ее
кратных, конечно). Всякая простая точка D* есть, оказывается,
делитель некоторой натуральной точки р в О, где р — натуральное
простое число, причем такая точка р разлагается не больше, чем
на п (если п—степень поля) простых множителей D*.
Поэтому для того, чтобы обозреть все простые точки D*,
достаточно знать, как разлагается каждое натуральное простое число
^' 3, 5, 7, 11, 13, 17,... в произведение простых точек D*.
Мы будем в этом случае говорить, что мы знаем, как
«опирается» арифметика того поля алгебраических чисел,
кольцом всех целых чисел которого является О, на арифметику
29
ПОЛЯ рациональных чисел. При применении некоторого поля;
алгебраических чисел к решению какой-нибудь задачи об
обыкновенных целых числах обычно очень важно бывает знать
закон этого опирания.
Важным обстоятельством является то, что для многих
полей алгебраических чисел удается найти закон этого опирания
и что во всех случаях, когда он найден, он весьма простой,
конечный; вся же трансцендентная трудность, связанная
с простыми точками £)*, остается в трансцендентной
трудности вопросов распределения обыкновенных натуральных
простых чисел р в ряду всех натуральных чисел.
Например, в квадратичном поле, задаваемом
иррациональностью |/А, где А — некоторое положительное целое
рациональное число ^1 (mod 4), не делящееся на квадрат,
натуральное простое число р есть произведение двух простых
точек D*, если оно находится в таких-то прогрессиях по модулв>
А, и оно есть само простая точка О*, если оно находится
в других прогрессиях по модулю А.
В поле деления круга на п равных частей, где п простое,
т. е. в поле, зависящем от корня неприводимого уравнения
:г^-1 -I- х^-'^ -f . . . -f- ^ + 1 = О, простое натуральное число р
разлагается на простые делители так или иначе в зависимости от
того, в какой прогрессии по модулю п лежит число /?, и т. д.
Мы описали в самых общих чертах и с современной нам точки
зрения основные обстоятельства, связанные с теорией
алгебраических чисел. Во время Гаусса все это совершенно не было еще
известно, и делом Гаусса в теории чисел, в большой его части,
было как раз глубоко и последовательно проникать во все
эти обстоятельства, исследуя частные, но уже совсем не
тривиальные относящиеся сюда вопросы, в основном связанные
с теорией квадратичных полей, которые дали важные исходные
факты для всех дальнейших исследований в этой области.
Гаусс сам, несомненно, еще не видел всей грандиозной
развернутой сейчас картины, но, очевидно, уже предугадывал
многие важные ее стороны.
После этого отступления мы можем перейти к подробному
последовательному рассмотрению содержания различных
разделов «Арифметических исследований» Гаусса.
30
ПЕРВЫЙ, ВТОРОЙ И ТРЕТИЙ РАЗДЕЛЫ «АРИФМЕТИЧЕСКИХ
^' ИССЛЕДОВАНИЙ» ГАУССА
«Арифметические исследования» разделены на 7 разделов
/глав), поделенных на мелкие пункты (параграфы), имеющие
сквозную нумерацию. Эти пункты мы будем обозначать
буквой «п». Всего в «Арифметических исследованиях» 366 пунктов.
Первые три раздела «Арифметических исследований»,
озаглавленные: 1) «О сравнениях чисел вообще», 2) «О сравнениях
первой степени», 3) «О степенных вычетах», представляют собой
как бы введение в книгу и не содержат новых открытий, но
изложение в них ведется так, что все, до того известное,
относящееся к рассматриваемым в них вопросам, приводится в
порядок, если нужно, снабжается недостающими
доказательствами и т. д.
Уже в первых строках первого раздела «Арифметических
исследований» Гаусс вводит новое важное понятие сравнения,
которое, по существу, употреблялось, конечно, и до Гаусса, но
не было еще никем сформулировано. Это понятие и всем
известный удобный значок для него: а =е 6 (mod т), обозначающий,
что числа а и b дают одинаковые остатки при делении на
«модуль» Шу вошли с тех пор в теории чисел во всеобщее
употребление, так как подчеркивают далеко идущую аналогию между
сравнениями и уравнениями.
С более современной точки зрения можно сказать, что
введением понятия сравнения положено начало рассмотрению
алгебры над конечным полем.
Во втором разделе в п. 16 доказывается однозначность
разложения натурального числа на простые множители. По этому
поводу Гаусс говорит: «То, что всякое составное число может
быть разложено на простые множители, известно из элементов;
но то, что это не может быть сделано несколькими разными
способами, неправильно большей частью принимается как само
собой разумеющееся», хотя надо сказать, что эта
однозначность уже доказана у Эвклида.
Далее рассматривается решение сравнения 1-й степени
^^ + t ^0 (mod р) и системы таких сравнений.
В п. 42 этого раздела несколько неожиданно вставлено
доказательство известной и по настоящее время так часто
31
используемой леммы Гаусса. Если многочлене целыми
рациональными коэффициентами и старшим коэффициентом 1
разлагается в произведение многочленов со старшими
коэффициентами, равными 1, и рациональными остальными коэффициентами,
то эти коэффициенты тоже целые.
В третьем разделе о степенных вычетах Гаусс, естественно,
переходя от сравнений 1-й степени к сравнениям высших
степеней, исследует сначала степенные вычеты, т. е. остатки,
которые дают степени разных чисел при делении их на данный
модуль. Особенно важен случай простого модуля р. Для
каждого числа а, не делящегося на р, существует наинизшая
степень а^, дающая остаток 1. Число d — всегда делитель числа
р — 1 и называется локазателем, «к которому принадлежит»
число а по модулю р.
В пп. 52—57 Гаусс дает способ определить число ф(б?) не
сравнимых по модулю р чисел, принадлежащих к данному
делителю d числа р — 1. А именно, он показывает, что %d)'^^{d),
где 'f — число натуральных чисел, меньших d и взаимно
простых с d. Но если d, d\ d'\.,.—все различные делители р—1,
то
6{d) + ^{d') + ^{d") + ... = p-i,
известно, что
откуда следует, что ^(d) = ?(rf), ^d') = 'i{d') и т. д. и, в
частности, что ^(р—1) = Т(р—1) Ф 0.
Таким образом, оказывается доказанным существование
первообразных корней g простого числа /?, т. е. существование
таких чисел g, которые принадлежат к показателю р — 1 по
модулю р. Это доказательство Гаусса является одним из
самых блестящих арифметических рассуждений.
Существованием первообразного корня g по простому модулю р
постоянно пользовался Эйлер, однако, повидимому, он лишь
ошибочно считал, что дал доказательство этого существования.
Степени 1, g, g"^, ..., g"^~^ имеют то свойство, что любое число,
32
не делящееся на/?, сравнимо с одной и только одной из этих
степеней по модулю р,
13 1918 г. И. М. Виноградов показал, что всегда существует
первообразный корень простого числа р меньший, чем 2^^' |/р In р,
^,д^ ]^ — число различных простых делителей р — 1.
(,. ЧКТВЕРТЫЙ РАЗДЕЛ «АРИФМЕТИЧЕСКИХ ИССЛЕДОВАНИЙ».
ПЕРВОЕ ДОКАЗАТЕЛЬСТВО ЗАКОНА ВЗАИМНОСТИ
Четвертый раздел «Арифметических исследований»
озаглавлен «О сравнениях второй степени». Он содержит знаменитое
первое доказательство предложения, называемого в настоящее
время «квадратичным законом взаимности» над полем
рациональных чисел. Закон этот эмпирически, или,как говорил Гаусс,
«индуктивно», впервые был найден Эйлером (см. его. статью
1744—1746 гг. «Theoremata circa divisores numerorum in hoc
forma pa^ + qb'^ contentorum». В форме, почти в точности
совпадающей с той, которую придает этой теореме Гаусс, теорема
эта была сформулирована Эйлером позже, в 1772 г.
(опубликована в «Opuscula Analytica» в 1783 г.). Лежандр в «Histoire de
I'Academie Royale des Sciences Annee 1785» (опубликовано
в 1788 г., стр. 465), очевидно, не зная об этих работах Эйлера,
снова нашел эту теорему. Однако доказательство этой теоремы
не поддавалось всем усилиям Эйлера и Лежандра. Лежандр
сам считал, что он ее доказал, но, как справедливо указывает
Гаусс, «доказательство» Лежандра содержит предположение о
существовании некоторых простых чисел, удовлетворяющих
некоторым условиям, доказательства которого Лежандру дать не
удалось.
В начале четвертого раздела Гаусс рассматривает вопрос
о тех числах а, которые суть так называемые квадратичные
вычеты по заданному модулю т, т. е. о тех числах а, для которых
сравнение х^ ^^ а (mod т) имеет решение. Этот вопрос легко
^"водится к рассмотрению такого же вопроса для того случая,
^огда модуль — простое число р, и затем легко решается. В
"• 107 раздела 4 Гаусс говорит: «Но обратная задача: если задано
некоторое число, найти все те модули, для которых оно —
квадратичный вычет или невычет, несравненно труднее». Эту задачу
1^. Ф. Гаусс S3
в силу выше сказанного также достаточно решить для простых
модулей р. Уже Эйлер решил вопрос для а = — 1 и 3, а Ла-
гранж— для а = 2, 5 и 7. Знаменитая теорема Эйлера о том,
что число — 1 есть квадратичный вычет простых чисел р вида
4п + 1 и невычет простых чисел р вида 4/г + 3, была той
теоремой, попытка доказательства которой, как об этом
свидетельствует сам Гаусс, безвозвратно увлекла его на путь занятия
высшей арифметикой. Гаусс решает вопрос о том, для каких
модулей данное число а есть квадратичный вычет, сначала для чисел
а = — 1, it 2, zh3, ±5, ±7, а затем переходит к
доказательству теоремы (закона взаимности), которая решает этот же
вопрос для любого числа а, причем опять достаточно рассмотреть
случай, когда заданное число а простое. Гаусс выражает эту
теорему так:
«Если р — простое число вида 4^ + 1, то +/?, если же р
вида 4п + 3, то —р есть квадратичный вычет или невычет лю~
бого простого числа, которое, взятое положительно, есть вычет
или невычет числа /?».
Гаусс делает вслед за этим следующее замечание: «Так
как почти всё, что можно высказать о квадратичных вычетах,
основано на этой теореме, то название «фундаментальная
теорема», которое мы будем дальше употреблять, не будет для нее
неподходящим».
Самое доказательство Гаусса, которое в силу его трудности
мы здесь, понятно, не можем приводить, основано на полной
индукции. Кронекер справедливо называет это доказательство
пробой сил гауссова гения. Наибольшую трудность представил
для Гаусса тот пункт этого замечательного доказательства,
в котором доказывается, что для любого простого числа а вида
8/г + 1 всегда имеются простые числа, меньшие 2]/а + 1,
для которых а — квадратичный невычет. Эта лемма как раз и
позволяет Гауссу провести полную индукцию. По словам
самого Гаусса, доказательство этой леммы мучило его целый год
и противостояло всем его усилиям («per integram annem me tor-
sit operamque enixissimam effugit»), пока, наконец, ему не
удалось решить вопроса при помощи совершенно элементарного,
но глубокого соображения, изложенного в п. 129 менее чем на
одной странице. Лишь более 100 лет после появления «Арифме-
34
тических исследований» Гаусса И. М. Виноградову удалось
]5ыяснить природу таких лемм и дать целый комплекс теорем,
J- ним относящихся.
фундаментальная теорема дает, как это показывает Гаусс
и п. 147, полное решение поставленной задачи: найти те простые
числа р, для которых заданное число А есть квадратичный
гзычет.
Действительно, пусть, например, А — некоторое заданное
]{,елос положительное число ^^1 (mod 4). Разложим А на простые
множители и припишем тем из них, которые вида 4^ + 1,
;uiaK + , а тем, которые вида in—1, знак —,и пусть они,
взятые с такими знаками, суть а, Ъ, с, d,...; тогда произведение
а Ъ с d.., равно А. Обозначим через г, г\ г",... те целые числа,
которые меньше А и взаимно простые с Л и каждое из которых —
квадратичный невычет четного числа чисел а, 5, с, rf,... Тогда,
как это легко вывести из фундаментальной теоремы,
прогрессии Ак + г, Ак + г', Ак + г", ... содержат все те и только те
простые числа р, по которым число А есть квадратичный вычет.
Для случаев других видов Л результаты совершенно
аналогичны.
В последнем п. 152 четвертого раздела Гаусс, используя
закон взаимности, дает полное решение общ;его сравнения второй
степени:
ах^ -{- Ьх-\- c=^Q (modm).
Отметим, что Лежандр еще до Гаусса ввел символ ( —)
(«символ Лежандра»), определив его так: f—1=4-1, если
а — квадратичный вычет р, и f —) = — 1, если квадратичный
невычет. При помощи этого символа фундаментальная теорема
вписывается так:
р-1 q~l
(f)(i)=<-')''^
где р и q — два нечетных простых числа. Формула эта обычно
называется законом взаимности двух простых чисел,
3* 36
7. ЦЕЛЫЕ КОМПЛЕКСНЫЕ ЧИСЛА ГА> ССА
II БИКВАДРАТИЧНЫЙ ЗАКОН ВЗАИМНОСТИ
В пятом разделе Гаусс дал второе доказательство
квадратичного закона взаимности, а впоследствии — еще 6 других его
доказательств, основанных на различающихся дуг от друга
соображениях. Затем Гаусс в течение многих лет работал над
отысканием кубического и биквадратичного законов
взаимности, т. е. над решением вопроса о том, каковы те простые числа /?,
для которых заданное число А есть вычет 3-й или 4-й степени,
т. е. сравнение х^^^ А (mod р) или х^^^ ^(mod р) имеет
решение. О кубическом законе взаимности Гаусс ничего не
опубликовал и только в 1828 г. напечатал первую свою работу о би-
квадратичных вычетах, содержащую частные результаты, а
в 1832 г.— свою знаменитую вторую работу о биквадратичных
вычетах. В этой работе он говорит, что «хотя численные примеры
дают возможность собрать богатую жатву специальных теорем
о биквадратичных вычетах, но общего связующего звена не
видно». В п. 1 первой статьи Гаусс говорит: «Теория кубических
и биквадратичных вычетов гораздо труднее, чем теория
квадратичных вычетов. Когда мы, начиная с 1805 г., начали их
исследовать..., мы быстро пришли к убеждению, что употреблявшиеся
до сих пор принципы арифметики ни в коем случае не
достаточны для построения полной теории, а что эта теория с
необходимостью требует в некотором смысле бесконечного расширения
области арифметики; а как это понимать, будет самым ясным
образом пояснено в дальнейшем ходе этих исследований». Это же
утверждение Гаусс повторяет в п. 30 второй статьи, начиная с
которого он и приступает к этому «расширению поля арифметики».
Гаусс вводит кольцо Q так называемых «целых комплекс-
пых чисел» а + Ы, где а в. b — все возможные целые
рациональные числа. Другими словами, Гаусс предлагает рассматривать
целые числа квадратичного поля, происходящего от присоеди-
нения к полю рациональных чисел числа i = Yi , т. е. корня
неприводимого квадратного уравнения а;^ -f 1 = 0.
Произведение такого числа на ему сопряженное (а -f Ы){а — Ы) ==
= а^-f 6^ называется нормой числа а + Ы, Гаусс показывает,
что единицами кольца £) являются числа 1, i, —1, —i (и только
36
они). Далее он показывает, что простыми числами этого кольца
являются: 1° числа а + Ы, нормы которых — рациональные
простые числа вида 4п + 1, и 2° сами рациональные простые
числа р вида 4п + 3. Наконец, Гаусс доказывает, что любое
число а -\- Ы рассматриваемого кольца £), с точностью до
множителей 1, i,—1, —i, однозначно раскладывается в
произведение таких простых чисел. Таким образом, в смысле
вышеизложенной теории алгебраических чисел оказывается, что в этом
кольце число классов /г == 1.
После всего этого Гауссу уже удается, опираясь на
численные примеры, сформулировать основную теорему о вычетах
4-й степени (т. е. биквадратичный закон взаимности) для чисел
рассматриваемого кольца £), причем опять достаточно это
сделать только для простых чисел этого кольца. Сам Гаусс в своем
мемуаре, однако, доказательства этой теоремы не дает, и не
известно, обладал ли он этим доказательством. Доказательство
этой теоремы непосредственно в духе идей Гаусса было дано
Бушем в начале XX в. Вообще же биквадратичный и
кубический законы взаимности были доказаны в первой половине
XIX в. Эйзенштейном (из теории комплексного умножения
специальных эллиптических функций) и Якоби (из
соображений, связанных с теорией деления круга).
Важность этого второго мемуара Гаусса о биквадратичных
вычетах заключается, конечно, не в нахождении биквадра-
тичного закона взаимности, а в, том «расширении поля
арифметики», о котором говорит Гаусс. Вся трудность была в том, чтобы
понять, что простой вид теория биквадратичных вычетов
приобретает только в поле]/"!, и показать, что в этом поле такая же
простая арифметика, как в поле рациональных чисел. Этим был
сделан суш;ественный шаг в построении метода алгебраических
чисел, хотя обе главные его трудности — общая теорема о
единицах и теория идеальных делителей — в этом простейшем
случае не были еще затронуты.
8. О ЗАКОНАХ ВЗАИМНОСТИ ВООБЩЕ И О ЗАДАЧЕ,
КОТОРУЮ ОНИ РЕШАЮТ
Что такое представляют законы взаимности с точки зрения
той схемы применения метода алгебраических чисел, которую
37
если
мы рассмотрели в параграфе 4? Начнем с самого простого
—квадратичного закона взаимности над полем рациональных чисел.
Можно показать, что в квадратичном поле с
дискриминантом rf, т. е. в поле, получаемом от присоединения к полю
рациональных чисел корня а неприводимого квадратного
уравнения х'^ + ах + b = О с рациональными коэффициентами а я Ь,
если Д—целое рациональное число, не делящееся на
квадрат, и такое, что оно отличается от числа -^ b целым или
дробным квадратным множителем в. d=^ А, если А ^ 1 (mod 4), и
с? = 4 А, если А ^5 2 или 3 (mod 4), простое число р
следующим образом раскладывается на простые делители:
1° /? разлагается на два разных простых идеальных делителя,
2° /? — само простой идеальный делитель, если ( —] = — 1;
3° р есть квадрат простого идеального делителя, если
р — множитель d, причем можно легко найти и сами
соответственные простые идеальные делители.
Таким образом, содержится или не содержится простое
число р в тех прогрессиях, которые были из квадратичного закона
взаимности выведены на стр. 35, решает вопрос об «опирании»
арифметики квадратичного поля на арифметику поля
рациональных чисел. Наоборот, можно показать, что, зная законы
разложения натуральных простых чисел в квадратичных полях,
можно из них вывести закон взаимности.
Только в свете этого обстоятельства, показывающего, что
квадратичный закон взаимности есть то главное звено, которое
делает возможным полноценное употребление квадратичного
поля для решения соответственных вопросов теории обыкновенных
целых чисел, ясно, почему Гаусс придавал ему такое большое
значение, и предложил до восьми различных его доказательств.
После Гаусса многие математики упорно занимались
отысканием законов взаимности для вычетов высших степеней. Мы уже
указывали, что кубический и биквадратичный законы
взаимности доказали Якоби и Эйзенштейн. Закон взаимности для
вычетов р-х степеней между рациональным простым числом д
р
и простым делителем поля ЩУЧ) нашел тоже Эйзенштейн.
38
Много лет работы посвятил разысканию доказательства общего
р _
.шкопа взаимности для вычетов р-х степеней в поле Щу\)
создатель теории идеальных делителей Куммер, причем в этих
исследованиях Куммер наткнулся на важность некоторой
логарифмической производной, появление которой в теории чисел
казалось совершенно необъяснимом. Долгое время закон взаим-
jiocTH Куммера считался крайним, чего удается достигнуть на
;)том пути. Но многие математики и дальше упорно занимались
разысканием еще более общих законов взаимности.
Наибольший успех был достигнут в этом вопросе знаменитым немецким
математиком Гильбертом (1862—1943) и его школой. Гильберт
показал с помощью теории поля классов (о которой будет речь
и следующем параграфе), что правая часть равенства,
записывающего закон взаимности, может быть представлена как
произведение конечного числа некоторых символов, которые он
назвал «норменными символами» и простейшие свойства которых
он установил. Однако дать прямую конструкцию этих
символов, т. е. их явное функциональное выражение через числа,
стоящие в левой части равенства, и характеристики поля ему
не удалось. Это было сделано в самые последние годы
советским математиком И. Р. Шафаревичем, который, основываясь
на новых идеях, дал, наконец, полное решение вопроса, а
именно нашел и доказал общий закон взаимности. Между прочим,
в методе Шафаревича логарифмическая производная Куммера
получила естественное объяснение. Таким образом,
знаменитый вопрос, у начала которого стоят гениальные работы
Гаусса, наконец, решен окончательно.
Каков же смысл, в свете схемы § 4, всех этих законов
взаимности? Все они суть частные случаи закона взаимности
Шафаревича, следовательно, достаточно разобрать, каков его смысл.
Закон взаимности Шафаревича решает следующий вопрос: если
задано любое поле к алгебраических чисел т-й степени,
содержащее корень /г-й степени из 1, и оно расширяется до поля К
п
присоединением к нему У(^, где о> — число поля к, узнать, как
опирается арифметика поля К на арифметику поля /с.
Квадратичный закон взаимности, как мы сейчас видели, решает этот
вопрос для того частного случая, когда к — поле рациональ-
39
иых чисел и п == 2; кубический и биквадратичный законы вза/
имности Эйзенштейна и Якоби—для частного случая, когда
к — поле деления круга на 3 или 4 равные части и ^ = 3 или 4;
закон взаимности Куммера — для частного случая, когда п =
= р я к — поле деления круга на р частей. .
9. О ТЕОРЕМЕ КРОНЕКЕРА И О ТЕОРИИ ПОЛЯ КЛАССОВ
Легко показать, что всякое квадратичное поле есть подполе
некоторого поля деления круга. Еще в 1854 г. Кронекер
наметил доказательство одной из самых замечательных теорем
всей алгебры — корень любого уравнения с рациональными
коэффициентами, группа Галуа которого абелева
(коммутативная), выражается рационально через некоторый корень из 1.
Это, несомненно, самая красивая теорема теории Галуа,
доказанная после Галуа. Таким образом, весьма просто описываются
все абелевы (т. е. с абелевыми группами Галуа) расширения
рационального поля — все они суть подполя полей деления
круга, и обратно. Ввиду того, что вопрос о том, как опирается
арифметика поля деления круга на арифметику рационального
поля, решается совсем просто, а тогда уже просто решить этот
вопрос для любого подполя поля деления круга, теорема Кро-
некера решает вопрос об опирании на арифметику
рационального поля для любых абелевых расширений поля рациональных
чисел. Рациональные простые числа р так или иначе
разлагаются в произведение простых делителей данного абелева
поля в зависимости от того, заключаются ли они или не
заключаются в таких-то прогрессиях. Теорема о разложении
натуральных простых чисел р в квадратичном поле, указанная
выше, есть просто частный случай этой общей теоремы, так как
квадратичное поле абелево.
Так как всякое абелево расширение поля рациональных
чисел р-й степени над полем корня р-й степени из 1 получается
р
присоединением одного yZi где w—число этого поля, а
арифметика таких расширений регулируется законом взаимности
Куммера, обратно из этого закона взаимности можно получить теорию
абелевых расширений рационального поля, включая теорему
Кронекера, как это было сделано в 1915 г. автором этих строк.
40
к. Ф. ГАУСС
Настоль X. Л. Шварца, 180?) i .
МулеГг Гаусоа и ПрауитвеИге
Понадобился даже, только более простой, закон взаимности
Эйзенштейна, а для циклических полей степени р^ — закон
взаимности Вестерна.
Полное доказательство теоремы Кронекера дал только Ве-
бер в 1886 г. ^ Позже, начиная с 1892 г., сначала на наиболее
простом случае относительно квадратичных полей, Гильберт
начал развивать общую теорию поля классов, т. е. теорию
классификации и теорию опирания арифметик относительно абе-
левых расширений К любого заданного поля к (а не только
рационального) алгебраических чисел. После углубленных работ
самого Гильберта, Фуртвенглера и японского математика Та-
каги такая теория была построена. Важную теорему, опираясь
на один метод, употребленный для другой цели И. Г.
Чеботаревым, дал в этой теории Артин. Более отработанное
изложение дал Хассе, а затем, из иных принципов,—
французский математик Шевалле.
Теорема Кронекера и связанная с ней теория есть частный
случай общей теории поля классов, а именно: это теория полей
классов для того случая, когда к — поле рациональных чисел.
Подобно тому, как эта частная теория поля классов может быть
получена из закона взаимности Эйзенштейна или Вестерна (как
это было указано выше), общая теория поля классов может быть
получена из общего закона взаимности Шафаревича. Это
было показано учеником И. Р. Шафаревича — А. И. Лапиным.
10. ПЕРВАЯ ЧАСТЬ ПЯТОГО РАЗДЕЛА «АРИФМЕТИЧЕСКР1Х
ИССЛЕДОВАНИЙ»
Пятый раздел «Арифметических исследований» Гаусса (ни.
153—307), озаглавленный «О формах и неопределенных
уравнениях второй степени», посвящен теории квадратичных форм.
Этот раздел самый обширный из семи разделов и необыкновенно
богат содержанием. Он, естественно, разделяется на 4 части.
Первая его часть (пп. 153—222) содержит классификацию и
теорию представления чисел двойничными квадратичными формами,
а также решение в целых числах общего неопределенного
^ Acta Math., 8.
41
уравнения 2-й степени с двумя неизвестными. Вторая его часть/
(пи. 223—265), озаглавленная «Дальнейшие исследования о фор/
мах», содержит теорию композиции классов двойничных квадра/
тичных форм и теорию их родов. Третья часть (пп. 266—285),
озаглавленная «Отступление, содержащее исследование о
тройничных формах», посвящена теории тройничных квадратичных
форм. Четвертая часть (пп. 286—307), озаглавленная
«Некоторые приложения к теории двойничных форм», содержит
доказательство теоремы о родах, теорию разложения чисел в сумму
трех квадратов или трех треугольных чисел, решение
неопределенного уравнения ах^ -\- Ъу^ -f cz^ = О, решение общего
неопределенного уравнения 2-й степени с двумя неизвестными
в рациональных числах и соображения о среднем числе
классов в роде.
Все, что изложено в первой части пятого раздела, в
принципе было уже сделано до Гаусса, в основном Лагранжем, однако
изложение Гаусса формально (но не по существу) сильно
отличается от изложения Лагранжа.
1. Сведение основных задач теории целочисленных
двойничных квадратичных форм на задачу эквивалентности двух
таких форм. Выражение вида
ах^ + 2Ьху -f- су^,
т. е. двойничную квадратичную форму, Гаусс называет формой
2-й степени, или просто формой, и обозначает (а, Ь, с).
Коэффициенты а, Ь, с предполагаются целыми рациональными. Если
существуют такие целые рациональные х = т, у~п, что
ат^ -f 2bmn + сп^ = М, то число М называется пред ставимым
формой {а,Ь,с). Число D==b^ — ас = — К называется
определителем формы. rij^cTb т, п— примитивное представление
числа М, т. е, т и п взаимно простые, и пусть jj. и v — такие
целые рациональные числа, что |j./n + v/г = 1; тогда Ь^ — ас^
^[li{mb + nc) — y{ma + nb)]^ (modlf), что следует из
тождества
{ат'^ + 2 Ьтп + сп^) (av^ — 2b\iv + cii^) =
= [\i {mb + nc) — V {ma + nb)]^ — {h^ — ac) {miJ- + n^)^.
Определитель D = b^ — ac формы есть, следовательно,
квадратичный вычет каждого представляемого ею числа М. Каж-
42
loe примитивное представление числа М, как легко показать,
независимо от выбора чисел [х и v, «принадлежит» к
некоторому определенному «значению» v выражения
1/62—ас (mod щ
После этих вводных замечаний излагается теория линейных
а линейных унимодулярных преобразований двойничной
квадратичной формы F
\\ форму F'.
Выводится формула
6'2 — а'с' -= (6- — ас) (aS — р^)',
т. е. то правило, что определитель преобразованной формы
равен определителю преобразуемой формы, помноженному на
квадрат определителя преобразования.
Формы F ж F' называются собственно эквивалентными
laSl
{proprie aequivalentes), если
y5
+ 1, и несобственно
эквивалентными (improprie aequivalentes), если| u
Лагранж не различал собственной от несобственной
эквивалентности. Он считал две формы эквивалентными, если одна
переходит в другую при помощи линейной подстановки с
определителем I U , равным -f 1 или —1, все равно.
Таким образом, класс эквивалентных форм Лагранжа
составляет два класса Гаусса, т. е. классификация Гаусса более
дробная. Если рассматривать то геометрическое толкование,
которое мы разбираем ниже, то собственно эквивалентным формам
соответствуют одинаково ориентированные основные реперы
решетки, соответствующей классу форм, а несобственно
эквивалентным — разно ориентированные, т. е. при помощи
различения этих понятий можно учитывать относительную ориентацию
реперов. Но различение Гауссом собственной и несобственной
^Жвивалентностей имело, повидимому, в основном другую,
более глубокую причину. Дело в том, что композиция
квадратичных форм, которую Гаусс вводит во второй части пятого разде-
^^а и которая имела такое капитальное значение для развития
как теории чисел, так и алгебры, как это будет нами показано,^
дает стройную теорию, только если рассматривать эквивалент-^
ность в этом более узком смысле, по Гауссу, так как только
в этом случае можно говорить не о композиции форм, а о
композиции классов.
После введения всех указанных выше понятий Гаусс ставит
две основные задачи:
1. Если даны две формы F и F' с одним и тем же
определителем D, узнать, эквивалентны ли они и притом собственно или
несобственно, а если с разными определителями, то не
содержит ли одна форма другую, и найти все собственные и несобствен--
ные преобразования одной формулы в другую.
П. Если дана форма F, узнать, представляется ли ею число
My и найти все такие представления, если они есть.
При этом Гаусс доказывает теорему: если число М
представляется формой ах'^ + 2Ьху + су^ при х = т, у = п, где т
и п взаимно простые, и если «значение» выражения |//)(modM),
к которому принадлежит это представление, равно N, то
формы F = {а, Ь,^) и G = 1М, N, ———) — собственно
эквивалентны, и F переходит в G при помощи подстановки:
x = mx' + vy', у ,= пх'-{-\iy', (1)
где р. и V находятся из уравнений:
mil -{- т = I, \i {bm -\- en) — v {am + bn) = N.
Наоборот, если F и G эквивалентны и G получается из F
подстановкой (1), то х = т, у = п есть представление числа
М формой F, принадлежащее «значению»]//) (modЛ/),
равному N.
Таким образом, решение задачи П сводится на решение
задачи I.
2. Теория приведения Faycca для случая определенной
двойничной квадратичной формы. Рассмотрим более подробно решение
первого основного вопроса, на который в конечном счете
сводятся все задачи, решаемые в первой части пятого раздела.
Подобно тому, как это делал уже и Лагранж, этот первый
вопрос Гаусс решает при помощи алгорифма последователь-
44
jioio преобразования заданных форм к эквивалентным им, так
называемым приведенным формам. Вопрос этот, естественно,
решается совсем разно для случаев, когда i)<<0 и когда
/)>0.
Однако Гаусс формально в обоих случаях прибегает к
одному и тому же средству — к вычислению последовательных
соседних справа форм, что очень красиво. Формой соседней
(права (contigua а parte prima) к форме (а, Ь, а') Гаусс
называет форму (а\ Ь', а"), которая получается из формы (а, 5, а')
подстановкой ( ^^1, где о — некоторое целое число.
Для случая i)<^0, а>0, т. е. когда форма
положительная определенная, Гаусс показывает, что если выбирать Ь
каждый раз так, чтобы V = —Ь+а^Ь заключалось между — у
м%у, т. е. чтобы было 2|&'|<a^ и строить такую форму
((а', Ь', а"), соседнюю с заданной (а, 6, а') справа, а затем,
далее, такую же форму {а!\Ь'\а'"), соседнюю с {а/Ь',а'')
справа, и т. д., то после конечного числа шагов получится
форма (Л, Л, С), эквивалентная данной, для которой
выполняются так называемые неравенства приведения:
215|<Л<С. ' (1)
Такая форма {Л, В, С) называется приведенной. Гаусс
далее показывает, что кроме двух специальных случаев две
формы эквивалентны тогда и только тогда, когда
эквивалентные им приведенные формы тождественны.
Все это становится гораздо более прозрачным, если это
рассматривать геометрически. Возможно, что уже при
писании «Арифметических исследований» и сам Гаусс
рассматривал многое в теории квадратичных форм геометрически, как
это думает, например, Бахманн, хотя геометрию
квадратичных форм, которую мы сейчас рассмотрим, Гаусс и
обнародовал гораздо позже, лишь в 1831 г.
Всякая положительная (т. е. если D =^^ Ь^—аа'<<0, а>0)
двойничная квадратичная форма (а, 6, а') с действительными
коэффициентами есть (если говорить современным языком), как
-гегко показать, скалярный квадрат линейного векторного
46
выражения, т. е.:
= \e^\4" + 2\e^\\e^\coscpxy + \е^\^у\
где \е^\, I ^21 — длины векторов е^ и eg, а ф — угол между ними.
Построим решетку Г на репере Ое^е^,, т. е. совокупность всех
точек плоскости, координаты которых относительно репера
Ое^е2 целые рациональные.
Переход к форме (а', 6', с'), эквивалентной форме (а, Ь, с),
состоит в переходе от репера Oeie^^, к другому основному
реперу 06x62^011 же решетки Г, а именно, если (а', V, с')^
== (а, 6, с), р., то ^1 = a^i + -^^2 и ^2 = ^е^ + 8^2, и обратно,
причем, если форма собственно (proprie) эквивалентна, т. о.
U == + 1, то этот новый репер Oeie^ имеет ту же
ориентацию, как заданный Ое^е^, если же несобственно (improprie)
I а 3 I
эквивалентна, т. е. и = —1> то обратную. Таким образом,
классу собственно эквивалентных форм соответствует
совокупность всех основных реперов рассматриваемой решетки Г
одной и той же ориентации. Как говорят, решетке соответствует
класс форм, и обратно. То же самое имеет место и в далее
рассматриваемой геометризации неопределенных форм, а также
в том и другом случае, если коэффициенты а, Ь, с не считать
целыми, а любыми действительными числами. Форме (а', 6', а"),
соседней справа с формой {а, Ь, а'), т. е. форме:
а {0-х' + y'f + 26 (O-rr' + у') (— х' + Ьу') + а' (— х' + Ьг/у =
= а'х'^ + 2{—Ь + а'о) х'у' + {а + 2Ьо + а'о^) у"" =
= [в1 (О-х' + У') + ^2 (-^' + by')f =
= {—е^^х' + К + 062) 2/7»
/ 01\
получаемой из нее преобразованием (_^^1 , соответствует
репер, первый вектор е^ которого равен вектору —е^,
обратному второму вектору е^ исходной формы (а, 6, а'), и второй
вектор ^2, который равен ^i + 0^2. Если, кроме того, о подобрано
так, как указано выше, т. е. чтобы было 2\Ь' \^а'у или,
I 6j I
иначе, 2 11^11 | ^21 cos ср' К | ^i | ^ или 11 ^21 cos (р' |<; —у- , то про-
46
екция второго вектора е^ на первый вх по абсолютной
величине меньше или равна половине длины |ei| первого вектора,
1. е. конец второго вектора принадлежит полоске, ограничен-
иой перпендикулярами, восставленными в серединах первого
вектора е^ и ему обратного вектора —е^.
Если, следовательно, переходить от заданной формы (а, 6, а')
к такой соседней с ней справа форме (a^ 6', а"), от нее к
такой же соседней с ней справа форме (а", 6", а") и т. д., то в
этом ряду форм, начиная с формы (а', Ь', а"), будет каждый
раз выполняться первое условие приведения 2 ] 5 1 >^ Л. Но через
конечное число шагов выполнится и второе условие приведения
^<;С, так как, если бы все время было а'>а">а'" и т. д.,
то получилось бы, что в данной решетке есть внутри круга
радиуса j/a',описанного вокруг центра О, бесконечно много
точек, все более и более близких к точке О, а этого быть не может.
Из этого геометрического рассуждения мы видим, таким
образом, что, после конечного числа шагов алгорифма Гаусса
соседних справа форм, мы от любой положительной формы
(«, 6, а!) придем, в конце концов, к собственно эквивалентной
бй приведенной форме.
47
Все полученные таким обраиом последующие реперы будут
той же ориентации, как и исходный репер, т. е. формы, им
соответствующие, будут собственно эквивалентны исходной форме.
То, что приведенная форма только одна, если у нее в
обоих случаях имеют место- неравенства, а не равенства, также
легко показать геометрически.
3. Теория приведения Гаусса для случая неопределенной
двойничной квадратичной формы. Случай i)>0, т. е. когда
(а, 6, а') — неопределенная двойничная квадратичная форма с
действительными коэффициентами, приводит к совсем
другой теории. В этом случае форма разлагается на
линейные множители с действительными коэффициентами S^, ^^^
^^1, Ъ^ где L' ' + 0: (а, Ь, а') ^ р (qrr + '^^у) -- {ri^x+ ЪУ)^ ири-
I П\ 42 I Р
чем даже бесконечным числом разных способов, так как
действительный множитель р можно выбирать произвольно.
Зафиксируем как-нибудь множитель р и рассмотрим репер Oeie^,
векторы которого относительно некоторой выбранной
декартовой координатной системы имеют координаты (q, 7]^) и (с2, ^^l-
Рассмотрим решетку, построенную на этом репере, и будем
предполагать, что она не имеет, кроме начала, точек на
координатных осях, что равносильно тому, что форма не
разлагается на множители, пропорциональные рациональным.
Неопределенную форму {А, S, С) Гаусс называет приведенной, если
она удовлетворяет условиям:
YTj — В <: i А I <; УЪ +В, В > 0. (2)
Если обратиться к рассмотренной сейчас геометрии таких
форм и геометрически истолковать эти неравенства, то
получается, что они обозначают следующее. Если называть
параллелограмм, вершина которого в рассматриваемой точке М (не
лежащей па осях 0^ и O^i), центр которого в начален стороны
которого параллельны координатным осям ОС" и 0^,то условия (2)
обозначают то, что: 1° координатные параллелограммы концов
первого и второго векторов репера, соответствующие форме
{А, В, С), скрещиваются, т. е. расположены так:
48
a не охватывают друг друга, т. е. не расположены так ~t~n|^
II 2° вдоль первой оси, т. е. оси 05, координатный
параллелограмм второго вектора длиннее, чем первого.
Легко показать (это можно сделать и геометрически),что если
от заданной неопределенной формы (а, Ь, а') переходить к
соседней с ней справа, такой, что в 6' = — 6 + а'^ число ^ берется
между]//) — \а'\ и ]/Z), то через конечное число шагов придем
к приведенной в этом смысле форме — собственно
эквивалентной форме (а, Ь, а').
Если же продолжать этот же алгорифм дальше, то будут
получаться последовательные дальнейшие приведенные формы,
госедние друг с другом, все более и более «длинные» вдоль
оси (?-:.
Аналогично тому, как это сделал уже Лагранж, Гаусс
показывает, что если коэффициенты формы — целые числа, то,
хотя различных таких приведенных вдоль оси Ос реперов
бесконечно много, различных соответствующих им форм конечное
число и они повторяются периодически. Геометрически это
происходит от того, что решетка Г, построенная на репере,
соответствующем целочисленной определенной квадратичной
форме, имеет гиперболические повороты в себя, т. е. имеет
такие множители р, что если помножить все координаты с ее
точек на р и разделить на р все координаты '^ ее точек, то решетка
Г совместится с собой.
Приведенные реперы, расположенные в одинаковых местах
различных периодов, получаются друг из друга таким
автоморфизмом решетки Г, и потому им соответствуют одинаковые
квадратичные формы.
Для того, чтобы решить задачу I, надо таким образом
вычислить полный период приведенных форм, эквивалентных
первой из заданных форм, и найти хотя бы одну приведенную
форму, эквивалентную второй заданной форме, и тогда, если она
встречается в периоде первой формы, то заданные формы
эквивалентны, если нет, то неэквивалентны.
В последних пп. 216—221 первой части пятого раздела Гаусс
прилагает теорию двойничных форм, построенную им в
предыдущих пп. 153—215 этого раздела, к решению в целых
4
Ь. Ф. Гаусс 4д
числах общего неопределенного уравнения 2-й степени с
целыми коэффициентами:
ах^ + 2Ьху + су^ + 2dx + 2ey + f = 0.
Заключительный п. 222 первой части пятого раздела
посвящен исторической справке о предшествующих
«Арифметическим исследованиям» Гаусса работах Эйлера, Лагранжа и Ле-
жандра, относящихся к тому же вопросу.
И. ВТОРАЯ ЧАСТЬ ПЯТОГО РАЗДЕЛА «АРИФМЕТИЧЕСКИХ
ИССЛЕДОВАНИЙ». КОМПОЗИЦИЯ КЛАССОВ И КОМПОЗИЦИЯ
РОДОВ КВАДРАТИЧНЫХ ФОРМ
Вторая часть пятого раздела, озаглавленная «Дальнейшие
исследования о формах» (пп. 223—265), содержит теорию
композиции классов целочисленных квадратичных двойничных
форм данного определителя, всецело принадлежащую уже
лично Гауссу.
То, что не все целочисленные двойничные квадратичные
формы данного определителя эквиваленты и что они разбиваются
на конечное число классов эквивалентных форм, было известно
уже Лагранжу, но то, что эти классы можно компонировать
друг с другом и что они образуют в смысле этой композиции
конечную коммутативную (абелеву) группу, есть
замечательное открытие Гаусса, оказавшееся как бы далекой и весьма
нетривиальной разведкой в область теории алгебраических чисел,
которая была совершена Гауссом задолго до того, как сама
эта теория была окончательно построена. Трудно гадать,
каков был путь, приведший Гаусса к открытию композиции
классов, но, во всяком случае, предвидение ее важности не
обмануло Гаусса.
1. Основные определения — определение понятия «род».
Совокупность всех целочисленных двойничных квадратичных
форм, собственно эквивалентных данной такой форме, образует
класс (собственный) форм данного определителя. Как это
непосредственно следует из теории приведения, в каждом классе
форм данного определителя есть формы, все коэффициенты
которых по абсолютной величине меньше данной функции ог
50
определителя; поэтому в случае форм с целыми коэффициентами
число классовтакихформ данного определителя конечно. В
случае отрицательного определителя D = Ь^ — ас<СО, т. е. когда
форма определенная, достаточно рассматривать лишь
положительные классы, т. е.[^ классы форм, у которых D<iO и а>0,
так как отрицательные классы получаются из них просто
изменением знаков всех коэффициентов всех форм на обратные.
Форму (а, 6, с), у которой а, 6, с не имеют общего делителя,
Гаусс называет примитивной, а если при этом а и с не оба
четные, т. е. и числа а, 2Ь, с не имеют общего делителя, то он
называет форму собственно примитивной. Тогда и все ей
эквивалентные формы тоже примитивные или собственно
примитивные. Соответственно этому рассматриваются и классы
примитивные и собственно примитивные. Два класса одного и того же
определителя Гаусс относит к одному и тому же порядку (ordo),
если (а, Ь, с) и (а', Ь\ с') — формы этих классов, и как числа
а, Ь, с в. а', Ь', с' имеют один и тот же общий наибольший
делитель, так и числа а, 2Ь, си а', 26', с' имеют один и тот же общий
наибольший делитель.
Наиболее важное значение имеет собственно примитивный
порядок, так как непримитивные формы просто связаны с
примитивными.
Совокупность классов собственно примитивного порядка
данного определителя D Гаусс далее еще разделяет на «роды»
(genera), относя в один и тот же род все те классы, формы
которых имеют один и тот же «характер». Под характером
примитивной формы, или примитивного класса форм, так как у всех
форм одного и того же класса, как легко показать, одинаковые
характерьь, Гаусс понимает следующее.
Пусть т — какой-нибудь простой делитель i), а в некоторых
случаях надо еще рассмотреть числа т = 4ит = 8, и пусть
число всех этих различных модулей т равно ^ч Можно
показать, что если Ml — один из этих ^- модулей, то для всех чисел
'^, представляемых данной собственно примитивной формой
определителя D и взаимнопростых с 2D для данного т^,
квадратичный характер (—) (символ Лежандра) имеет одно и то же
т.
значение. Выпишем эти квадратичные характеры, которые все
4* S1
равны +1 или —1, для всех X указанных модулей т^, mg,...,
Шу^, взятых в каком-либо раз навсегда выбранном порядке;
тогда для данной формы получается некоторая определенная
последовательность X чисел ±1. Эту последовательность Гаусс
называет характером (Totalcharacter) рассматриваемой
собственно примитивной формы определителя D или характером
класса, ею представляемого. Так как число всех вообще возможных
различных последовательностей, составленных из X членов,
равных +1 или —1, равно 2^, то число различных характеров
форм данного определителя, а следовательно, и число родов
никак не больше, чем 2^. Однако неясно, всякая ли такая
последовательность есть характер некоторого класса — а priori, может
быть, что число родов и меньше?
Для того, чтобы дать ответ на глубокий вопрос о том,
каково истинное число родов, Гаусс вводит особое исчисление,
в котором элементами являются не числа, а классы форм.
2. Композиция классов Гаусса и ее излож^ение по Дирихле,
Форма
F = AX^ + 2BXY + CY^
называется по Гауссу компонированной из форм
/ = ах'^ + 2Ъху + с?/2 и /' ^ а'х'^ -f Ib'x'y' -f- с'?/'^,
если она переходит в их произведение при помощи
целочисленной билинейной подстановки вида:
X =^ рхх' + р'ху' + р'ух' + р"'уу'',
Y = qxx' + q'xy' + g V + fVV'^
где числа
рр'
яд'
>
рр"
qq"
>
рр'"
qq'"
>
р'р"
q'q"
>
р'р'"
q'q'"
>
р"р'"\
q"q'"
не имеют общего им всем множителя, отличного от 1. При
этом оказывается, что класс, к которому принадлежит форма
F, вполне определяется тем, к каким классам принадлежат
компонируемые формы f ж f.
Убедиться в возможности компонирования собственно
примитивных форм одного и того же определителя проще не из
изложения, данного самим Гауссом, а при помощи того
упрощения этого изложения, которое предложил Дирихле.
52
Наметим основные пункты этого упрощенного изложения
теории Гаусса. Пусть / = ах^ + 2te?/+ с?/^ — собственно
примитивная форма, т. е. числа а, 2i, с не имеют общего им всем
делителя, отличного от 1. Заметим прежде всего, что среди
чисел, представляемых такой формой /, всегда существуют
числа, взаимно простые с любым наперед заданным числомiiC.
Действительно, если хотя бы один из крайних коэффициентов
формы /, например а, не делится на простое число р, то для
того, чтобы / не делилась на р, достаточно взять такие х и
?у, чтобы X не делилось на р, а у делилось на р. Если же
оба крайние коэффициента / делятся на р, то средний 2Ь уже
не делится на р, так как форма собственно примитивная, и
достаточно взять такие х и у^ чтобы оба они не делились на
р. Поэтому, если Pi, Р2, - - - , Рк — все различные простые
делители числа К, то для того, чтобы f = ах^-\-2bxy-{-су^ была
взаимно простой с К, достаточно так взять х, чтобы оно
делилось на одни из этих простых чисел и не делилось на
другие, и то же самое сделать с у. При этом можно еще^
очевидно, всегда выбрать х и у так, чтобы они были взаимно
простыми.
Выберем теперь по форме из компонируемых классов, и
пусть представитель второго из этих классов есть форма
{а',Ь',с'). Возьмем такие взаимно простые числа :г == а, 2/= 7»
чтобы при подстановке их в представителя первого класса
получалось число а, взаимно простое с числом а\ что, как мы
сейчас видели, всегда можно сделать. Тогда, если взять
такие ^ и о, чтобы было ао — ^^ ::^ 1^ то подстановка [ "^'^ jnepe-.
водит представителя первого класса в эквивалентную форму
(а, 6, с), первый коэффициент которой а взаимно прост с
первым коэффициентом а' представителя второго класса.
Перейдем теперь еще от этих представителей (а, 6, с) и (а', Ь\ с')
рассматриваемых классов с взаимно простыми а ж а' далее к
другим, им эквивалентным «параллельным» формам при
помощи подстановок L \^ J и (q^)- Эти формы будут иметь
прежние первые коэффициенты а и а', средние же их
коэффициенты будут а|л-f-6 и a'^i+b'. Подберем теперь так [j- и v,
53
чтобы удовлетворялось следующее неопределенное уравнение
1-й степени:
а|л + 6 — a'v + 6',
что всегда можно сделать, так как числа а и а' взаимно
простые. Обозначив a\i-{-b через В, мы получим формы {а, By с)
и (а', В у с'). Но определители этих форм равны, поэтому
В^—ас = В^ — а'с'у откуда, так как а и а' взаимно простые,
с = а'Су с' = аС. Выбранные нами, теперь окончательно,
представители рассматриваемых нами классов имеют вид:
/ = (а. By а'С\ и /' - {а'у By аС).
Определители обеих этих форм равны 5^ — aa'C=^d,
Разложим обе эти формы на линейные множители
следующим образом:
^ /■!/- . B + YI \ l^r- ' B~V~d \
f=[Vax^ -у^ у]^ [Уах + -^^_- у]^ ,
./ /i/— . , B + V~d Л Л/-7 , , B~V"J ,
f = (Vax + -y^^y) {Vax + -^^^y
Перемножая первые множители, мы получим следующее
тождество:
= Ут- {XX' - Суу-) + ^"[IJ {аху' + а'х'у + 2Вуу'), (*)
К аа
а перемножая вторые множители,—аналогичное тождество,
в котором только вместо ]/ d стоит — Yd, Перемножая оба
эти тождества, мы получаем, что форма
F = {аа'у By С)
того же определителя В^—aa'C~d переходит в
произведение форм / и /' при помощи билинейной подстановки:
Х = хх' ^ Суу'; Y = аху' + а'х'у + 2Вуу\ (1)
Коэффициенты ее
gq'g"q'"
64
€ \'ТЬ
определители
10
Оа
/100-С\
\Оаа' 2В]'
10
О а'
взаимно простые.
Если были бы выбраны не эти специальные представители
/ п /' рассматриваемых классов (называемые Дирихле «einige»—
«согласные»), а какие-либо произвольные, например,
получаемые из них подстановками:
x=^CLX + %y ^ х' =^ а'? + ^'у'
2/ =z ^Х + 02/ у' == ^Х' + ОУ,
ТО результатом их композиции можно считать ту же форму/",
но билинейная подстановка, при помощи которой она
переходит в произведение заданных форм, будет уже более
сложная, а именно та, которая получается из билинейной
подстановки (1) при помощи замены в ней х, у, х', у' по
формулам (2).
3. Свягь с умножением решеток Клейна. С той
геометрической точки зрения, которую мы рассмотрели выше, теория
Гаусса композиции классов принимает следующий вид.
Предположим для определенности, что определитель б/
положительный; если бы d было отрицательно, дальнейшее
изложение было бы совершенно аналогичное. Решетка L,
соответствующая форме /, построена (если d > 0) на векторах
(лг— -л/—. Ib + VY b — V4\ rr
(У а , у а) и I —-j=z=z— , —j:=:— , а решетка L , соответ-
У V а V а 1
ствующая форме /', построена на векторах (У а' ,]/«') и
IB + Vd B~V~d\ rr / ч
—-r=z—, —j=:— . 1ождество М показывает, что произ-
\ У а' У а' 1
ведение точки решетки L с координатами х, г/, относительно
указанного ее основного репера, на точку решетки L' с
координатами х\ у\ относительно ее указанного основного репера,
т. е. произведение любой точки решетки L на любую точку
решетки L', дает некоторую точку (с координатами (хх^ — Суу\
(^^у' + а'х^у -\- 2Вуу'))у решетки Z, соответствующей форме F.
Легко показать, что, соответственно выбирая точки решеток
L> и L' и складывая и вычитая их произведения, можно полу-
55
чить любую точку решетки X, т. е. что решетка L есть
произведение в рассматриваемом нами на стр. 26 смысле решеток
L и L'. Для этого, очевидно, достаточно показать, что концы
Л/i и М^ векторов основного репера решетки L могут быть
получены таким способом. Точка М^ с первой координатой
У аа'у очевидно, получается в результате умножения точек
(1,0) и (1, 0) решеток L и U. Для того же, чтобы получить
nj " " B + V"d
точку ilig с первой координатой — перемножим сначала
V аа'
точки (1,0) и (0,1) решеток L и L' и затем их точки (0,1) и
(1,0), тогда мы получим точки с первыми координатами
B-A-V~d ^г— B + V~I ^r-f , ^
—"7=— у а И ——Z— у а (вторые координаты будут из них
получаться заменой |/с? на —]/(i ). Складывая эти точки z^
раз первую и ещ;е Zg раз вторую, мы получим точку с первой
координатой:
\ a' у a V aa'
a так как ana' взаимно простые, то можно так выбрать z^
II Z2, чтобы было azi-{-а'Z2 ~ I, и тогда мы получим
точку М^.
Итак, с геометрической точки зрения рассмотренная нами
на стр. 52 композиция классов Гаусса есть не что иное,
как умножение решеток, соответствуюш;их этих классам, в том
смысле, как умножение решеток было рассмотрено на стр. 26.
В своих лекциях «Избранные главы теории чисел» ^ Клейн
говорит, что можно себя спросить, почему Гаусс вместо того,
чтобы говорить об умножении решеток, говорит о композиции
соответствуюш;их им квадратичных форм. Клейн думает, что
не невозможно, что уже при писании «Арифметических
исследований» Гаусс знал о связи квадратичных форм с решетками,
но не изложил вопроса так из каких-то своих личных
соображений. А между тем, это изложение при помощи решеток дает
больше, чем изложение при помощи форм, уже потому, «что
отдельный линейный множитель, задающий решетку, учиты-
1 F. Klein. Ausgewahlte Kapiteln der Zahlentheorie, Teil II. Got-
tingen, 1907, стр. 133 (литограф.).
66
вает абсолютную величину + азимут, а форма учитывает
только абсолютную величину». «Композиция форм,— говорит
Клейн,— есть, так сказать, лишь следствие, а не эквивалент
греории умножения решеток». Идея рассмотрения решеток
могла легче привести к связи с модулярными функциями. Кроме
того, идея рассмотрения при композиции не самих форм, а
линейных множителей форм, могла скорее привести к решению
самого глубокого, связанного со всеми этими исследованиями
арифметического вопроса, к построению теории делимости в полях
алгебраических чисел.
4. Связь с теорией квадратичных полей. Какой же смысл
имеет теория композиции двойничных квадратичных форм
данного определителя, созданная Гауссом, с точки зрения
теории алгебраических чисел? С той геометрической
точки зрения, на которую мы стали в § 8 в изложении теории
алгебраических чисел, дело обстоит так.
Пусть А — целое положительное число, не деляш,ееся на
квадрат; тогда, как мы видели__в § 8, кольцо D всех целых
точек квадратичного поля Л(]/Л), если Д^2 или 3(mod 4),
имеет базис (1,1)_(|/Л, — |/Д), а если Д^:1 (mod 4), имеют
базис (1,1) f 2— » 2 j' ^^^ДР^тичные формы,
построенные на этих реперах, суть {х-}-У/\у){х — |/Лг/) = z^ — Дг/^
/ I \ [Ад \ / 1 у^ \ \ д
И [Х Н- —^ 2/1 \Х Н 2 У] ==' ^^ + ^У Н 4~ У'^' ФОРМЬГ ЭТИ'
целочисленные, но «вторая из них не имеет двойки в
коэффициенте при ху. Но надо заметить, что теорию композиции
форм Гаусса можно изложить и для целочисленных двойничных
квадратичных форм вида ах'^ -f Ъху + су^, т. е. таких, у которых
при ху стоит коэффициент Ь, а не 2Ъ, как у Гаусса.
Определителем d формы тогда называется число Ъ'^ — 4ас. Вся теория
будет ровно такая же, как изложенная выше, только тождество {'^)'
надо будет заменить следующим:
\У ахА -—^-у\\у ^ ^ -\ ,- У ==
^Ут' (XX' ~ Суу') + ^±£^ [аху' + а'х'у -Ь Вуу'). (^^).
2 F аа'
57-
в случае, когда Ае^2 или 3 (mod 4), d будет равен 4Д,
а в случае Д ^ 1 (mod 4), d= i — 4-1 —7— = А. Главный класс
такого определителя d будет представляться как раз формой
х'^ — Аг/2 или соответственно формой х^ -\-ху -] -j— г/^. Этим
формам соответствует главная решетка £1. А остальным/г—1 клас,
сам примитивных форм определителя d соответствуют побочные
решетки©', D", . . . , D^ ~^\ если для каждого из них
соответственно выбрать множитель р. Выбор этих множителей, как показал
Клейн, связан с рассмотрением базиса абелевой группы классов
квадратичных форм определителя й. Композиции классов
соответствует умножение решеток D, D', D", . . . , ©^^""^^друг на друга.
Всякая точка всякой из так выбранных (в смысле выбора
множителей р) решеток D, D', D", . . . , £)^^~^^ разлагается
однозначно в произведение простых точек этих решеток с точностью
до множителей единиц г, которые все суть точки главной
решетки D, лежаш;ие на гиперболах ^ = ±i- От умножения
на любую из них каждая из решеток D, D^ . . . , £)^^~"^^ переходит
в себя, и каждая из форм соответствующего этой решетке
класса целочисленно линейно унимодулярно преобразуется в себя.
С точки же зрения теории идеалов Дедекинда дело обстоит
так. Если помножить решетку D^^^ на какую-либо точку ^
решетки (D )~^, то получается подрешетка ^ главной решетки D,
которая есть идеал решетки D i-vo класса, и обратно.
Квадратичная форма, соответствуюш;ая решетке 3, отличается от
квадратичной формы определителя d, соответствуюш;еи решетке Q^ \ целым
рациональным множителем, который есть норма идеала j
в решетке D, т. е. число показывает, во сколько раз плош;адь
основного параллелограмма решетки ^ больше, чем плош;адь
основного параллелограмма решетки D. Это число, очевидно,
равно норме по отношению к осям Ощ точки j, т. е.
произведению $7] ее координат.
Стоило Гауссу сделать в теории композиции форм еш;е один
шаг дальше, а именно, разумно подобрав множитель р (т. е.
правильно повернув решетки D', £>", . . . , D^^^""-^^ по отношению
к решетке D), начать умножать друг на друга отдельные
линейные множители квадратичных форм, лежащих в рассматри-
:ваемых классах (т. е. отдельные точки решеток-О, D', . . . , D ),
liiui ои обнаружил бы однозначность разложения и построил бы
задолго до Куммера, Дедекинда и Золотарева, арифметику|
полей алгебраических чисел.
Трудно сказать, что остановило Гаусса на этом пути. Быть
]У1ожет, одной из главных трудностей, которую, как кажется, так
и не удалось преодолеть Гауссу, была для него теорема о базисе
абслевой группы, без которой трудно сообразить, как выбирать
дпюжители р для форм, представляющих отдельные классы.
Классы форм данного определителя в смысле композиции,
рассмотренной Гауссом, образуют абелеву группу. Главный
класс является единицей этой группы. Два обратных класса,
т. е. те, которые содержат формы (а, Ь, с) и (а, —Ь, с), являются
обратными элементами и т. д. Группа классов Гаусса была
первой нетривиальной абелевой группой, которая обратила на
себя внимание математиков. Характеры классов,
рассматриваемые Гауссом в его теории родов,— первый нетривиальный
пример характеров группы, причем даже не очень простой, так как
характеры Гаусса — не числа, а последовательности чисел,
правда, очень простых, только ±1. О той роли, которую
сыграла теория композиции классов Гаусса в истории абелевых
групп, мы скажем дальше (стр. 89), где будем рассматривать
соображения Гаусса о регулярных и иррегулярных
определителях, рассмотренных им в самом конце пятого раздела, в п. 306.
5. Композиция родов и вывод неравенства g<2^~^. Вернемся
теперь снова к вопросу о числе родов целочисленных
собственно примитивных двойничных квадратичных форм данного
определителя Z), т. е. к той глубокой задаче, для решения которой
Гаусс создал свою композицию классов.
В п. 246 Гаусс рассматривает композицию родов, а именно он
отмечает, что при композиции классов характеры этих
классов перемножаются, а следовательно, род, к которому
принадлежит класс, являюш;ийся результатом композиции двух
каких-либо классов, вполне определяется тем, в каких родах
лежат эти классы, т. е., как теперь бы сказали, характеры
классов дают обычным своим умножением гомоморфное
представление группы классов.
В п. 252 Гаусс, опираясь на этот результат, естественно
приходит к тому., что в каждом роде одно и то же число
классов. Обозначая поэтому, как ранее, число классов через k^
число родов—через 7? ^ число классов в роде — через g, Гауссу
получает h ~ g^. Гаусс называет двусторонними (ambiges](
классами те классы, квадраты которых (в смысле композиций
классов) дают главный класс.
В п. 257 и следующих Гаусс доказывает, что число дву^;
сторонних классов равно -^ j^, где х ~ ^ ^^'^ь число всех
возможных различных последовательностей, состоящих из л чисел,
равных+ 1. Далее, опять, как бы мы сейчас сказали, просто
из групповых соображений, Гаусс показывает, что если
обозначить число двусторонних классов через а, а число тех классов^
которые суть квадраты некоторых классов, через 8, то h = olo.
Но все классы, которые суть квадраты некоторых классов,
принадлежат к главному роду, так как характер каждого из
таких классов есть квадрат характера того класса, квадратом
которого он является, т. е. состоит только из + 1? ^ это
характер главного рода. Поэтому 8^ g^. Учитывая это
неравенство и то, что h~g^ и /г = аВ, Гаусс в п. 261 получает, что
7^ а, т. е. число родов не более, чем 2"^""'^. Другими словами,
по крайней мере половина из всех возможных
последовательностей из >ч чисел,+1 не представляет собой характера никакого
собственного примитивного класса определителя D.
В п. 262 Гаусс из этого неравенства для числа родов
получает новое, второе доказательство квадратичного закона
взаимности, которое некоторые математики считают наиболее
глубоким из всех, данных Гауссом.
Итак, число родов 7 -^ 2^~^, но сколько именно
родов—остается и на этом месте «Арифметических исследований» все же
невыясненным. Для выяснения этого важного вопроса Гаусс
употребляет новое средство — теорию тройничных
целочисленных квадратичных форм.
12. ТРЕТЬЯ ЧАСТЬ ПЯТОГО РАЗДЕЛА «АРИФМЕТИЧЕСКИХ
ИССЛЕДОВАНИЙ». ОТСТУПЛЕНИЕ О ТРОЙНИЧНЫХ ФОРМАХ
Эта часть пятого раздела «Арифметических исследований»
озаглавлена: «Отступление, содержащее исследования о
тройничных формах» (пп. 266—285).
60
в этом «Отступлении» Гаусс рассматривает теорию форм:
f = ax^+ а'х'^ + ах"'^ + 2Ьх'х" + 2Ь'х"х + 2Ь"хх',
х^оторые он обозначает | ,„ |, где а, а', а", Ь, Ь', Ь" — целые
рациональные числа.
Число
Гаусс называет определителем такой формы и предполагает его
неравным нулю.
В этой части пятого раздела Гаусс кладет начало обширной
области исследований, посвященных арифметической теории
квадратичных форм от многих переменных, в которой
впоследствии дали важные результаты Зеебер, Эйзенштейн, Дирихле,
Арнольд Мейер, Зеллинг, Коркин и Золотарев, Смит, Минков-
ский, Вороной, Венков, Хассе, Зигель и др. Сам Гаусс построил
только самые элементы этой теории, необходимые ему для
решения вопроса о числе родов двойничных квадратичных форм.
1. Рассмотрение Гауссом параллельно с данной тройничной
формой ей союзной фор мы ^ геометрический смысл этого и
значение для кристаллографии. Рядом с заданной тройничной
формой / Гаусс рассматривает всегда так называемую союзную
с пей форму (forma adjuncta)
F =^Ах^-\- А'х'^ + А"х""^ + 2Вх'х + 2В'х"х + 2В"хх',
где:
А = Ь^ — а'а\ А' = Ь'^ — аа', А' = Ь"^ - аа']
В = аЬ — b'b\ В' - а'Ь' — bb\ В" = а"Ь" — bb'.
Сделаем в этом месте геометрическое замечание. Если форма /
положительная, т. е. все числа, ею представляемые,
положительны, то, как нетрудно показать, / = {xei + х'е^ + x"e^Y,
т. е. равна скалярному квадрату линейного векторного выра-
н^ения, причем если А =7^ О, то векторы ^i, е^, е^ не компланарны,
трехмерная «решетка» Г всех точек, имеющих целые
рациональные координаты относительно репера Oeie^e^ (совершенно подобно
^^Щ, как в случае двойничной квадратичной формы двумерная
решетка, построенная на репере Oeie<^, ей соответствующем),1
связана с формой / так, что эквивалентным с / формам, т. ej
формам, получаемым из / линейными подстановками: \
х' = а'^ + ,8V + ^'х"
х!' = а"^ + ^"1с' + -'Ч:"
с целыми рациональными коэффициентами и определителем +1,
соответствуют другие основные реперы этой же решетки Г^
т. е. решетке соответствует в этом смысле класс эквивалентных
форм, а отдельным формам класса — отдельные основные реперы
решетки.
Репером, союзным (= взаимным = полярным = обратным) к
данному реперу Ое^е^е^, называется репер Ое^е^е^, такой, что*
скалярное произведение {xei-^x'e^ + х"е^ (^'е!-]- х'*е1 + х"*е^) равно
просто XX* -{-х'х'* -\-х"х"*, т. е. такой репер, что
^* ^ [^2<?з1 g* ^ [Ч^Л ^* __ [^1^2]
Решетка Г*, построенная на союзном репере, называется
союзной с решеткой Г. Важнейшее для кристаллографии
свойство союзной решетки состоит в том, что всякий вектор
союзной решетки Г* перпендикулярен к некоторой плоской сетке
(т. е. двумерной подрешетке) заданной решетки Г и по длине
равен плош;ади ее основного параллелограмма, и обратно. Эта
обстоятельство позволяет свести изучение плоских сеток
решетки Г параллельнопереносной повторяемости кристалла
(которые играют суш;ественную роль как в вопросах о плоских
гранях кристалла, параллельных наиболее густым таким сеткам,
так и в вопросах рентгеновского, электронного и нейтронного
анализа структуры кристаллов) на изучение векторов взаимной
решетки Г*.
Рассмотрение Гауссом союзной формы было очень важным
шагом, так как эта форма или, скорее, связанная с ней
геометрическая концепция союзной {= взаимной) решетки
впоследствии стала играть (и играет сейчас) большую роль в
практической кристаллографии. Надо, однако, сказать, что
рассмотрение трехмерного репера, взаимного с данным, к
62
которому все сводится, было сделано гораздо раньше
Гаусса Лагранжем в его статье «О треугольных пирамидах»^ в
;[773 г., в которой Лагранж изучал разные геометрические
свойства тетраэдров, исходя из задания тетраэдра, имеющего
одну вершину в начале координат, девятью координатами
трех других его вершин. Эта статья Лаграижа, повидимому,
осталась мало замеченной, и француз кристаллограф Браве,
первый введший взаимную решетку в кристаллографию,
ссылается на Гаусса.
Рассмотрение Гауссом далее теории представления
тройничной формой / двойничной квадратичной формы <р (п. 280)
связано как раз с этой взаимностью, всилу которой всякому такому
представлению соответствует представление определителя D
этой формы ?, союзной с / формой F.
2. Как Гаусс решает вопрос о положительности
тройничной квадратичной формы. Отметим, между прочим, как Гаусс
в п. 271 решает вопрос о том, является ли заданная
тройничная квадратичная форма / положительной определенной или
нет. Помножив /на а, Гаусс получает форму
g - {ах + Ь''х' + b'xf ~ А'х''' + 2Вх'х" — Ах"\
а помножив форму g еш;е на А', он получает форму
h - А' {ах + U'x' + b'x"f— {А'х" — Bx'f + a^x^
и говорит: если А' и аА отрицательны, то /iпредставляет только
отрицательные числа, почему / тогда представляет только
числа, знак которых обратен знаку аЛ', т. е. числа того же знака,
как а. Таким образом, в этом случае форма / определенная и
притом положительная, если а > О, и отрицательная, если а <С 0.
Если же числа аА и Л' положительные или одно из них
положительно, а другое отрицательно (но оба не равны нулю), то
легко видеть, что соответственным подбором х, х\ х" форма h
может быть сделана как положительной, так и отрицательной,
т. е. форма / неопределенная. Далее отдельно еш;е
исследуются случаи Л'=0, а=7^0иа = 0и доказывется, что в этих
^ Solutions analytiques de quelques problemes sur les pyraraides tri-
angulaires, 1773 (Oeuvres, t. III).
63
случаях форма / неопределенная. Из всего этого Гаусс выводит
следствие, что у положительной формы числа А, А', ^'V^^,
а'А, а"А отрицательны, числа а, а ,а" положительны и число
А отрицательно.
Любопытно, что Гаусс не задается целью найти систему nev
зависимых необходимых и достаточных условий
положительности формы /. Сейчас мы знаем, что эти условия следующие:
а Ь" Ь'
Ъ" а' b
b' b а"
>0,
а Ь"
>0, а>0.
или в обозначениях Гаусса: А<0, ^"<С0, а>0. Гаусс даже не
отмечает, что девять выведенных им условий не только
необходимы,но и достаточны. То же самое замечание надо сделать
относительно рассмотренных на стр. 45 и на стр. 48 условий
приведения двойничной положительной и неопределенной
квадратичной формы. Как в тех, так и в других условиях у Гаусса к
выписанным нами прибавлено еще по одному лишнему условию,
которое есть следствие остальных.
3. Доказательство Гауссом конечности числа классов
целочисленных тройничных квадратичных форм при помощи теории
приведения таких форм, В пп. 272—275 Гаусс дает способ
приведения тройничной квадратичной формы, причем способ
такой, который одновременно годится как для случая, когда
форма / определенная, так и для случая, когда она
неопределенная. В силу уже этого обстоятельства условия приведения
Гаусса для положительной тройничной квадратичной формы
не приводят к одной приведенной форме (как это имеет место
у Зеебера). Они лишь таковы, что абсолютные величины всех
коэффициентов приведенной формы, как в случае, когда форма
определенная, так и в случае, когда она неопределенная,
могут быть ограничены в зависимости от определителя А формы /.
Поэтому, если коэффициенты а, а', а', Ь, Ь', 6" формы / целые
рациональные, число различных таких приведенных форм
определителя А конечно. Отсюда в п. 276 получается теорема
о том, что, подобно тому, как это имеет место для двойничных
целочисленных квадратичных форм, число классов
целочисленных тройничных квадратичных форм данного определителя
64
д конечно. Итак, эту основную теорему условия приведения
Гаусса дают. Но условия Гаусса приведения тройничных
квадратичных форм в том смысле несовершенны, что если даны
две эквивалентные друг другу такие формы / и /', то может
быть, что ни одна форма, приведенная в смысле Гаусса,
эквивалентная второй из них, не будет совпадать ни с одной из форм,
приведенных в смысле Гаусса, эквивалентных первой. Таким
образом, эта теория приведения Гаусса тройничных
квадратичных форм не дает возможности решить вопрос об
эквивалентности двух таких форм / и /'.
4. Сведение Гауссом представления чисел тройничной
квадратичной формы на задачу эквивалентности двух таких форм,
В п. 280 Гаусс начинает рассматривать теорию представления
тройничной квадратичной формой / определителя Д двойничной
формы
ср = р^2 ^ 2qtu + ггг2
()][[)еделителя D, если положить в форме /:
X =: mt -\- пи, х' = тЧ + п'и, х" = m"t -\- п"и.
Легко убедиться, что в этом случае форма F, союзная с /,
представляет число D, если положить в ней:
X = т'п!' — m"n\ X' = т^'п — тп^', X" — тп' — т'п.
Наоборот, оказывается, что всякое представление X, X', Х"
числа D союзной формой F таким образом получается из
некоторого представления некоторой двойничной формы <р
определителя D формой /. Геометрический смысл этого
обстоятельства мы выяснили выше на стр. 63.
Отсюда следует, что решение задачи: найти все собственные
представления числа D формой F, сводится к тому, чтобы
выписать представителей всех классов целочисленных
двойничных квадратичных форм определителя D и найти все
собственные предствления этих представителей формой /, если они есть.
Все Эти представления и дадут все представления числа D
формой F.
^ к. ф. Гаусс 65
в п. 283 предлагается следующий способ находить все
собственные представления двойничной формы:
(^ ~ pf^ j^ 2qtii -{- ru^
определителя D тройничной формой / определителя Zi..
Пусть В и В' — такие целые рациональные числа, что В^Е^а,
ВВ'^ Ь, В'^ ^ с (mod D); тогда линейную форму Вх + В'у
Гаусс называет «значением» "j/ax^ + 2bxy + су'^ (mod D). Гаусс
показывает, что всякое собственное представление формы ср формой /
принадлежит к некоторому «значению» (В, Б'), и выводит
следуюш;ее правило для нахождения всех собственных пред-
.ставлений формы ср формой /.
Надо найти все различные «значения» ]/ Д {pt^ + 2qtu + ru^)
(mod D). Если два таких «значения» обратны по знаку, надо
брать только одно из них. Чтобы найти все собственные
представления формы (р формой /, принадлежащие к данному
«значению» [В, В), надо найти тройничную форму g = i
определителя Д, в которой а =^ р^ Ь" =: g^ а' = г, аЬ — ЬЪ" = В,
а'Ь' — 66" = В', откуда уже найдутся а\ Ь, Ъ', но, вообще говоря,
в виде дробных чисел. Если либо один из коэффициентов
а", 6, Ь' выйдет нецелым, либо формы / и g не будут
эквивалентны, то представлений формы ср формой /, соответствующих
«значению» {В, В'), нет. Если же а", Ь, Ь' выйдут целые и формы /
и g эквивалентны, то каждое преобразование:
а р 7
а' ^' 7'
^" ^" Т"
формы / в форму" g дает такое представление:
х=- (/,1 + ^и, х' == а7 + [^'w, х" = (/!'t + ^р"и, I
и обратно.
В силу вышеописанной связи между представлениями числа
D формой F и представлениями двойничной формы ф формой /|
задача о представлении чисел тройничной целочисленной
квадратичной формой сводится к задаче установления
эквивалентности двух тройничных целочисленных квадратичных форм / 1
и g^ и в случае, если они эквивалентны, к нахождению всех |
66
подстановок, при помощи которых одна из них переходит в
другую, совершенно аналогично тому, как это было в вопросе
о представлении чисел двойничной целочисленной
квадратичной формой.
5. Недостаток теории приведения Гаусса тройничных
квадратичных форм. К сожалению, теория приведения Гаусса
тройничных квадратичных форм, как это было указана выше, не
дает возможности решить вопрос об эквивалентности двух
целочисленных тройничных квадратичных форм / и g, а потому и
задача представления чисел такой формой также не получает
у Гаусса полного решения. Сам Гаусс говорит об этом в п. 285
следуюп1;ее: «Относительно вопросов, которые нам ставит
решение третьей нами поставленной задачи (на которую сводятся
обе первые), а именно, если заданы две тройничные формы с
одним и тем же определителем, узнать, эквивалентны они или нет
и в первом случае найти все преобразования одной формы в
другую, можем мы на этом месте лишь очень мало сказать, так как
полное решение, которое мы привели для аналогичных задач
в случае двойничных форм, здесь связано с еще большими
трудностями. Поэтому мы ограничимся в нашем исследовании лишь
некоторыми специальными случаями, для которых, собственно,
и сделано все это отступление (т. е. изложение теории тройнич-
ных форм) от нашего исследования (т. е. от исследования
теории двойничных квадратичных форм)».
Еще раньше в п. 277, посвященном теории приведения
тройничных квадратичных форм, Гаусс прямым вычислением
показал, что -всякая целочисленная неопределенная тройничная
квадратичная форма определителя Д = -f 1 может быть
преобразована в форму х^— 2yz, Собственно, этот частный
результат о том, что существует только один класс целочисленных
тройничных неопределенных квадратичных форм с
определителем Д — +1 только и нужен Гауссу дальше из всей теории
приведения тройничных форм.
6. Работа Зеебера 1831 г. о положительных тройничных
^<^адратичных формах, аннотация Гаусса к ней и работа
Дирихле 1841 г. Возможно, как мы это уже выше говорили, что
геометрическое толкование теории квадратичных форм было
уже близко Гауссу в то время, когда он писал «Арифметические
5* ^7
исследования», хотя в них он нигде ни слова об этом не
упоминает. Опубликовано это геометрическое толкование было
Гауссом гораздо позже, в 1831 г., в его аннотации (Anzeige) к работе
Зеебера о приведении положительных тройничных
квадратичных форм^.
В первой статье Зеебер рассматривает разбиение
пространства на одинаковые параллелепипедальные молекулы, причем
рассмотрение квадрата расстояния между вершинами таких
нараллелепипедов, образующими некоторую решетку Г,
приводит его к геометрическому смыслу положительной тройнич-
€1ой квадратичной формы. В обширной (132 стр.) второй работе
Зеебер решает задачу приведения положительных тройничных
квадратичных форм так, что в каждом классе оказывается, как
у Гуасса в случае положительных двойничных форм, лишь одна
приведенная в его смысле форма. Зеебер говорит, что его при-
веда к этому решению предыдуш;ая кристаллографическая
работа. Таким образом, «Теория положительных тройничных
квадратичных форм,— говорит Зеебер,— становится полезным
или даже необходимым орудием кристаллографии». Интересно
отметить, как в этом месте при создании теории
переплетаются между собой вопросы теории чисел и кристаллографии.
В. «Anzeige»K рабрте Зеебера Гаусс дает доказательство
неравенства аа'а'<<2Д, которому удовлетворяет приведенная по
Зееберу форма. Это неравенство Зеебер нашел лишь
эмпирически, на примерах, но не дал его обш;его доказательства, а
доказал лишь, что аа'а'<;ЗД. Доказательство, которое
предлагает Гаусс, получается из одного арифметического тождества.
Впоследствии Коркиным и Золотаревым, Минковским и др.
это неравенство было обобщено на случай положительных
квадратичных форм от п переменных. Оно обозначает, что в каждой
решетке есть основной репер, «мало отличающийся от
ортогонального». Остальная часть «Anzeige» Гаусса посвящена
изложению геометризации двойничных и тройничных
квадратичных форм (положительных), рассмотренной нами выше на стр. 46
^ S е е b е г. Vcrsuch einer Erklarung des iimeren Baues der festen
Korper, 1824; Untersuchungen liber die Eigenscliaften der positiven ter-
iiaren quad rat ischen Formen, 1831.
68
II стр. 61. в самом конце Гаусс замечает, что положительная
тройничная квадратичная форма будет приведенной па Зееберу
тогда, когда параллелепипед, построенный на соответствующем
ей репере, такой, что каждое из его ребер не длиннее
диагоналей тех граней, которым они принадлежат, и не длиннее
внутренних его диагоналей. Указанное же выше неравенство Зеебера,
замечает Гаусс, означает просто то, что объем такого
параллелепипеда, помноженный на]/ 2, не меньше, чем объем
прямоугольного параллелепипеда с такими же ребрами.
Простое и весьма изяш;ное геометрическое доказательство
существования в каждой трехмерной решетке основного
параллелепипеда, удовлетворяющего условиям приведения Зеебера,
дал в 1850 г. Дирихле в работе «tjber die Reduction der positivcn
quadratischen Formen mit drei unbestimmten ganzen Zahlen»
(Crelle, 40, 1850). Эта работа Дирихле, опубликованная еще
задолго до смерти Гаусса, была, по нашему мнению, первой в
истории математики серьезной работой по геометрии чисел.
В этой работе Дирихле впервые вводит тот шестиугольник,
который сейчас принято называть областью Дирихле точки
решетки. Для других целей этот шестиугольник позже
рассматривал Эрмит в работе об обобщении непрерывных дробей,
предложенном Чебышевым. Общую теорию таких областей для
решеток любого числа измерений дал в своей знаменитой
работе «Recherches sur les paralleloedres primitifs» (1908—1909)
Г. ф. Вороной.
7. Способ задавать трехмерную решетку. Скажем еще
несколько слов о том, как задают решетку. Кристаллографы
обычно задавали решетку длинами ребер и величинами углов
какого-нибудь ее основного репера. Это во всех смыслах
неоднородное задание — даже размерность выбранных параметров
неодинакова.
Гаусс задавал основной репер решетки квадратами длин
ого ребер а, а', а" и скалярными произведениями его ребер друг
на друга Ь, Ь\ Ь" и записывал это так: (7 7 ^ 7ff ) • Задание
Гаусса однородно в смысле размерности выбранных параметров,^
Первый, кто после Гаусса сделал дальнейший шаг в вопросе
о задании решетки, был Зеллинг (Selling). В работе 1873 г.
69
(itjbcr dio binaren und ternaren quadratischen Formen» (Crelle,
74, 1873) Зеллинг предложил кроме векторов е^, е^, е^ репера
всегда рассматривать еще четвертый вектор €^= — е^ —е^ —е^.
Задание Зеллинга в некотором смысле более однородно, чем
задание Гаусса. Численно такой четырехвекторник Зеллинг
задает шестью параметрами — попарными скалярными
произведениями его векторов друг на друга (бг^з)» (^3^i)> {^1^2)^ (^lO,
(6264), (^3^4) обозначая их g , h, к, I, т,п и записывает это так:
и т п) ^^^^^ записью Зеллинг снова уничтожает
достигнутую им симметрию.
Еще более совершенна запись решетки, предложенная в
работе «Neue Begfiindung der geometrischen Kristallographie»
(Zeitschr. fiir Kristallographie, 1932) автором настоящей статьи,
при помощи символа, представляющего
пространственный тетраэдр, на ребрах
которого написаны параметры Зеллинга.
Только в этой записи непосредственно
по приведенному (по Зеллингу) символу
обнаруживаются все симметрии решетки
(группа ее «поворотов» в себя, тип ее
параллелепипеда Браве и т. д.).
8. 7 голоэдрий решеток и 32 кристаллографических класса,
14 решеток Браве и 73 арифметических класса кристаллов.
Кристаллографы много занимались вопросом о тех группах
«вращений» (вращений вокруг точки решетки и таких же
вращений плюс отражение в плоскости, проходящей через эту
точку), при которых трехмерная решетка Г совмещается с
собой. Таких групп 7— это так называемые голоэдрии. Если
рассмотреть и все их подгруппы, то получается 32 группы,
называемые кристаллографическими классами. Каждая из этих
подгрупп причисляется к наименьшей из тех голоэдрий,
которых она есть подгруппа. Так получается разбиение 32 классов
на 7 сингоний. Кристаллограф Браве в своей знаменитой
работе 1851 г. «Sur les points distribues regulierement sur le plan
et dans I'espace» вывел, кроме того, все возможные существенно
различные решетки, имеющие ту или иную голоэдрию: три —
для кубической голоэдрии, одну — для ромбоидальной, две —
для квадратной ( = тетрагональной) голоэдрии, четыре — для
(зртогональной (= ромбической) голоэдрии, две — для
моноклинной, одну — для триклинной и одну — для гексагональной
голоэдрии — всего 14 типов решеток Браве. Параллелепипедом
[Зраве данной решетки Г называется наименьший из
параллелепипедов решетки Г (т. е. параллелепипедов, вершинами
которых являются точки решетки Г), вообщ;е говоря, уже не
основной, который (как тело) имеет ту же группу «поворотов» в себя,
какую имеет сама решетка Г, или наименьший из
прямоугольных таких параллелепипедов, если такие в решетке есть.
Гексагональная решетка не имеет параллелепипеда Браве, так
как никакой параллелепипед не может иметь шестерной оси
симметрии.
Совокупность всех преобразований данной положительной
тройничной квадратичной формы в себя это не что иное, как
голоэдрия решетки, т. е. группа всех ортогональных
преобразований решетки в себя, оставляюш;их одну ее точку на месте,
записанных целочисленными унимодулярными (вообш;е говоря,
неортогональными) матрицами по отношению к некоторому
основному реперу решетки. Если преобразовать все матрицы
такой группы матриц одной и той же произвольной унимодуляр-
ной матрицей, то мы получим так называемую эквивалентную
запись голоэдрии решетки, т. е. запись ее голоэдрии по
отношению к некоторому другому основному реперу решетки. Если
считать различными такие группы целочисленных матриц,
записывающих голоэдрию решетки, которые не эквивалентны
в этом смысле, то различных таких групп оказывается 14,
каждая соответствует своей решетке Браве. Если же взять и все их
подгруппы, различные в этом же смысле, то получится всего
73 кристаллографических класса. Эту точку зрения
проводит сейчас школа известного швейцарского кристаллографа
Ниггли.
В этом смысле 7 голоэдрий можно называть «геометрическими
голоэдриями», а 14 решеток Браве — «арифметическими голо-
'^Дриями»; 32 кристаллографических класса — «геометрическими
классами», а введенные сейчас 73 кристаллографических клас-
^^ — «арифметическими классами».
9. Теория приеедения положительных квадратичных форм
^ ^ремя и с п переменными. Что касается дальнейшей истории
71
теории приведения целочисленных тройничных квадратичных
форм, то о случае определенных форм мы уже говорили, для
них весь вопрос был в высшей степени удовлетворительным
образом решен Зеебером. Дополнение к нему оставалось
сделать лишь в отношении вопроса о подстановках,
преобразующих данную форму в себя; теорию таких подстановок
разработали Эйзенштейн и Борисов. Затем Зеллинг в упомянутой
работе 1873 г., исходя из своего четырехвекторника, дал новую,
отличающуюся от зееберовой, теорию приведения тройничных
положительных форм. Автор настоящей статьи в упомянутой
выше работе 1932 г. связал теорию приведения положительной
тройничной квадратичной формы с теорией области Вороного
решетки, и довел ее до завершающей таблицы 24 сортов решеток,
законченно решающей весь этот вопрос, так что результат стал
удобен для использования в кристаллографии.
Обобщение теории приведения Зеллинга на положительные
квадратичные формы с четырьмя переменными дал Шарв (Char-
ve). Первый, кто показал, что можно и для положительной
квадратичной формы с п переменными выделить при помощи (может
быть, и бесконечного числа) линейных неравенств область
изменения их коэффициентов (основную область приведения)
такую, что: 1° никакие две формы из этой области
неэквивалентны и 2° любая положительная квадратичная форма с п
переменными имеет себе эквивалентную в этой области, был Эрмит
(Hermite); то же, что можно выделить такую область при
помощи конечного числа линейных неравенств, показал в
замечательной работе «Discontinuitatsbereich fur arithmetische Aquva-
lez» (Ges. Abh., Bd. II) Минковский. Исходя из идей Вороного,
Б. А. Венков показал в работе «О приведении положительных
квадратичных форм»^, что если д>>2,то существует континуум
различных разбиений области положительных квадратичных
форм с п переменными на фундаментальные области
приведения, каждая из которых задается конечным числом неравенств,
причем разбиение Минковского является лишь одним из таких
разбиений. Для получения разбиений Венкова надо рассмотреть
произвольную положительную форму и все ей эквивалентные
1 Известия АН СССР, 1940, № 4.
72
'j>/f','f", ...Разбиение Венкова получается, если рассмотреть
пирамиды, на которые разбивается конус положительных
форхМ, каждая из которых является областью Вороного
соответственной формы ср^^^ в смысле мероопределения Вороного.
Если ?г>2 и исходную форму ^ непрерывно изменять,
разбиение это тоже непрерывно изменяется. В
противоположность этому, как заметил еще раньше автор этих
строк, для п = 2 существует только одно такое разбиение,
так как при изменении ^ все стенки разбиения Венкова
сохраняются.
10. Теория приведения неопределенных тройничных кеад-
ратичных форм и квадратичных форм с п переменными
сигнатуры п — 2. Что касается до теории приведения
неопределенных квадратичных форм, то она гораздо труднее. Для
произвольного п и произвольной сигнатуры она не завершена еще
и теперь. Для неопределенных тройничных форм теория эта
сейчас совершенно закончена» Наиболее далеко идущий
результат принадлежит здесь также Б. А. Венкову. Поясним, в чем
дело. В случае определенной двойничной или тройничной
квадратичной формы существует одна и только одна эквивалентная
ей приведенная (в случае двойничной приведенная по Гауссу,
а в случае тройничной приведенная по Зееберу) форма и только
если решетка имеет симметрии, то несколько (конечное число)
таких приведенных форм, но они все могут быть легко найдены.
И силу этого в случае положительной двойничной или
тройничной квадратичной формы всегда можно узнать,
эквивалентна ли она другой заданной такой форме, т. е. являются
ли реперы, соответствующие этим формам, разными
реперами одной и той же решетки или нет; все равно, целые
ibiu любые действительные числа — коэффициенты этих
форм.
Совсем иные обстоятельства для неопределенных форм.
Если задана неопределенная двойничная квадратичная форма
(<^, Ь, с), то указанным на стр. 49 алгорифмом можно в конечное
число шагов придти от нее к эквивалентной ей приведенной
(в смысле стр. 48) форме и далее находить тем же алгорифмом
последовательные следующие формы цепочки приведенных форм,
ей эквивалентных. Если коэффициенты а, Ь, с не пропорциональны
73
целым числам, то все формы этой цепочки будут различные,
если же а, Ь, с целые (или пропорциональны целым числам),
то различных форм в этой (бесконечной в обе стороны) цепочке
будет лишь конечное число — они будут периодически
повторяться. Дело в том, что если а, Ь, с пропорциональны целым
числам, то решетка Г, построенная на репере, соответствуюш;ем
форме ср — (а, /^, с), будет при ее гиперболическом «вращении»
относительно асимптот Ос, Оу], получаемых, если положить
ср =гг О (т. е. при изменении числа р в ее разложении (а, Ь, с) =
^= р {с^х + ^2У) — ('^ir^ + '^2?/))i периодически совмещ;аться с собой.
г
Каждая такая решетка Г имеет свой вполне определенный
конечный наименьший гиперболический угол совмеш;ения с собой,
так называемый ее «угол Пелля» П. Если дана неопределенная
тройничная квадратичная форма f =. ах^-\~ а'х'^ + ^"^"^ + Ibx'x^^ -\-
-{-2b'x"x-\- Wxx', коэффициенты которой пропорциональны целым
числам, то, если положить /(ж, х', х^') = О, получится некоторый
конус К второго порядка, и если рассматривать целочисленные
линейные унимодулярные преобразования Л пространства {х, х', х"),
при которых этот конус совмещ;ается с собой (преобразования
Лоренца, соответствуюш;ие этой форме), и называть
эквивалентными точки, переходяш;ие друг в друга при таких
преобразованиях Л, то можно внутри К тоже выделить фундаментальную
область V такую, что: 1° каждая точка внутри К эквивалентна
точке из F; 2° две различные точки внутри V неэквивалентны.
Эта область V играет для целочисленной неопределенной
тройничной формы / ровно ту же роль, какую играет угол
Пелля П для неопределенной двойничной целочисленной формы
(а, Ь, с).
Если для данной формы / найдена эта область, то можно
решить задачу эквивалентности.
В работе Б. А. Венкова «Об арифметической группе
автоморфизмов неопределенной квадратичной формы» ^
устанавливается супцествование фундаментальной области V (удовлет-
воряюш;ей условиям 1 и 2) для неопределенных целочисленных
форме п переменными сигнатуры п — 2, состояш;ей из конечного
числа выпуклых пирамид с конечным числом граней.
1 Известия АН СССР, 1937, №2.
74
13. ЧЕТВЕРТАЯ ЧАСТЬ ПЯТОГО РАЗДЕЛА «АРИФМЕТИЧЕСКИХ
ИССЛЕДОВАНИЙ», СОДЕРЖАЩАЯ ПРИЛОЖЕНИЕ ТЕОРИИ
ТРОЙНИЧНЫХ КВАДРАТИЧНЫХ ФОРМ И ИССЛЕДОВАНИЯ
О ЧИСЛЕ КЛАССОВ
Эта часть, озаглавленная «Некоторые приложения к теории
двойничных форм», изложена в пп. 286—307.
1. Доказательство теоремы о родах: ^ = 2^~\ В п. 286 Гаусс,
используя построенную им теорию тройничных форм, доказывает
глубокую теорему: всякий класс главного рода получается
удвоением (возведением в квадрат) некоторого класса. Делает
он это так. Пусть F = {А, В, С) некоторая двойничная
квадратичная форма главного рода определителя D. Рассмотрим ей
обратную форму F' = {А, —В, С) и будем представлять эту
последнюю тройничной формой f = х'^ — 2yz. В силу
вышеизложенной теории представления двойничных форм тройничной
формой это возможно. Действительно, А = 1, поэтому надо
искать «значение» ]/(^, В, С) (mod/)), а в силу того, что форма
F — главного рода (только тут учитывается то, что F — главного
рода), можно показать, что такие «значения» имеются. Далее,
в силу специальных свойств формы /, тройничная форма g
определителя Л — 1, такая, что се коэффициенты а, а', а", Ь, Ь\ &"
удовлетворяют нужным условиям, тоже есть, причем для формы/
и коэффициенты а", Ь, Ь' формы g выходят целые, а полученная
форма g определителя А = 1 оказывается неопределенной. Но
так как выше было доказано, что имеется только один класс
неопределенных тройничных квадратичных форм определителя
А = 1 и что все они эквивалентны форме /, то форма g
эквивалентна /. Можно, следовательно, найти хотя бы одно
преобразование:
а р т
а' Р' 7'
а'^ Р" Т"
формы / в форму g. Каждое из таких преобразований дает
представление:
^^^1_^ Ргг, х' = а7 -f P'w, х'' = ol4 + B''w
75
формы F' формой /. Именно мы будем иметь:
А=^у? — 2ocV, — 5 - СХ.8 — а^8" — а"Р', С = 3^ — 2рф".
Если обозначить числа а^' — аф, аф" — а"Р', а"Р—а^'^ черс;$
а, by с, то они будут взаимно простые и мы будем иметь:
D^b^ — 2ac.
Но учитывая, как получается двойничная форма, которая
есть композит двух' двойничных квадратичных форм, можно
непосредственным вычислением проверить, что форма
F - {А, В, С) = AX^ + 2BXY + CY^
при помощи подстановки
X = 2^'хх'+ ^ху'+ ^ух'+ ^"уу'\ Y = Ъ:хх' + оса;?/' + а2/л;'+ а"?/?/'
переходит в произведение
(2аа;2— 2Ьху + су'') {lax'"" — Ibx'ij' + су'^).
т. е. в квадрат (в смысле композиции форм Гаусса) формы
(2а,--6, с),
а при помощи подстановки: р', {3, ^^^ g"j q^'^ q^^ ^^ 2ol" — в квадрат
формы
(а,-6, 2с).
Одна из этих двух форм, как легко видеть, собственна
примитивная. Таким образом, всякая форма (Л, В, С) главного
рода есть квадрат некоторой собственно примитивной формы
того же определителя.
Вернувшись к соображениям п. 261, мы видим, что раз
всякий класс главного рода есть квадрат некоторого класса,
то Ь =■ g. Теперь уже, сравнивая равенства h ^ g^ и h = Iol, мы
видим, что число родов равно числу а тех классов, квадраты
которых суть главный класс. А это число, как показал Гаусс,
равно -yX = 1^^~^- Число родов, значит, равно 2^~^.
Гаусс говорит, что если он не ошибается, этот результат
представляет собой, может быть, самое красивое, что удается
доказать о целочисленных двойничных квадратичных формах.
76
с этим нельзя не согласиться, так как таким ооразом о
таинственном числе классов h квадратичных форм с данным
определителем (или, что все равно, числе классов идеальных
делителей в данном квадратичном поле) получен глубокий и простой
результат: если определитель D делится на разные простые
хшсла п их число равно X (иногда надо еще рассматривать модули
4 и 8), то число родов в точности равно 2^~^, а следовательно,
Х1ИСЛ0 классов h есть кратное этого числа— h = g2^"~^. Каково
же число g классов в каждом роде — это неизвестно и до сих
пор. Наиболее далекий в настоящее время полученный
результат в этом вопросе состоит в том, что если D = Ь^— ас<^0, то,
какое бы ни зафиксировать положительное число s, для всех
достаточно больших (по абсолютной величине) D имеют место
неравенства
|Z)|2 '</?.<|i)|2^'
(результат Хейльбронна и Зигеля).
2. Теория родов Гауссг с точки зрения теории
алгебраических чисел. После описания того, каким образом Гаусс доказал
основную теорему о родах, стоит остановиться на том, что
такое теория родов с точки зрения современной теории
алгебраических чисел.
Дело в том, что определение понятия рода у Гаусса (см.
стр. 51) очень формальное. К одному роду Гаусс относит те классы
данного определителя, характер (Totalcharacter) которых
одинаков. Можно подойти к понятию рода гораздо более по суще-
(тву, если опираться на теорию алгебраических чисел.
Заметим прежде всего, что простые числа, которые
представляют хотя бы одной из форм данного определителя, это
тс и только те простые числа, по которым число 4D есть
квадратичный вычет, а тогда, как это следует из закона взаимности,
это те и только те простые числа, которые содержатся хотя бы
в одной из конечного числа некоторых определенных
прогрессий: 4Dt + lu Wt + ^2, ..., ^Dt + Ij, (см. стр. 35).
Известно, что аналогичное утверждение не имеет места для
отдельного класса форм. Например, для форм х'^ ~{-ху-\-6у^ с
определением 23 нельзя указать таких прогрессий: Nt + l^,
Возникает следующая задача: каким образом можно так
разбить все h классов К^, . . . ,Кп квадратичных форм данного
определителя на группы {К^_, . . .,Кг,) (i^n-fi, • • •, ^^rj • • • (... if/i)^
такие, что для того, чтобы простое число р представлялось
хотя бы одним из классов заданной группы, было бы необхо-
димо и достаточно, чтобы оно содержалось хотя бы в одной из
некоторых заданных прогрессий.
Разбиение, при котором все классы попадают в одну группу,,
этому условию удовлетворяет, а разбиение, при котором
каждый класс образует отдельную группу, вообще говоря, не
удовлетворяет. Интересно найти, конечно, разбиение на такие самые
маленькие группы, которые этому условию удовлетворяют.
Таким разбиением является разбиение на роды.
Для того чтобы доказать это обстоятельство, обратимся
к теории алгебраических чисел.
Пусть К — произвольное нормальное поле алгебраических
чисел, и оно получается от расширения поля R рациональных
чисел присоединением к нему целого алгебраического числа о.
и Р какой-нибудь простой идеальный делитель поля К, не
входящий в дискриминант числа ol, а р — то натуральное простое
число, которое делится на р. Легко показать, что существует
одна и только одна подстановка s группы Галуа ® поля К, для
которой выполняется сравнение:
~^aP(modp).
В таком случае говорят, что простой делитель р
принадлежит «в смысле Фробениуса» к автоморфизму s поля К, Другие-
простые делители числа р принадлежат, в этом смысле, к
подстановкам, сопряженным с 5, и поэтому говорят, что простое
натуральное число р принадлежит «в смысле Фробениуса» к
классу сопряженных подстановок группы @, Очевидно, что всякое
натуральное простое число /?, не входящее в дискриминант
числа а, принадлежит, в этом смысле, к одному и только одному
классу сопряженных подстановок группы ®. Поэтому все
натуральные простые числа /?, кроме конечного их числа,
разбиваются относительно поля К на классы Фробениуса, число
которых равно числу классов сопряженных элементов группы ®..
Н. г. Чеботарев доказал важную теорему о том, что к
любому классу сопряженных элементов группы ® принадлежит,
в этом смысле, бесконечно много простых чисел р.
Можно показать, что если К у тоже нормальное над /?,
подполе поля Ку то всякий класс Фробениуса поля К есть
совокупность нескольких целых классов Фробениуса поля К,
Если поле К есть поле деления круга на тп частей, то
каждый класс сопряженных подстановок его группы @ состоит-
только из одной подстановки (так как ® абелева). Простые
числа /?, принадлежащие к данной подстановке поля деления круга,,
суть, как легко показать, не что иное, как все простые числа
некоторой арифметической прогрессии mt-\-l, где / — то или,
иное из ф(т) чисел, меньших т и взаимно простых с тп, в
зависимости от того, какую из ч^{т) подстановок мы рассматриваем.
Всякое абелево над R поле алгебраических чисел есть
некоторое подполе некоторого поля деления круга (теорема
Кронекер — Вебера) и поэтому, учитывая вышесказанное,
получается, что класс Фробениуса для абелева поля есть
совокупность всех простых чисел, представляемых некоторыми
прогрессиями mt + /^, mt + 1^, ..., mt -{- l^.
При помош;и теории поля классов можно доказать следую-
ш;ую теорему.
Пусть R {У d) —квадратичное поле определителя d, И пусть,
Z—наибольшее абелево над/?(]/ d) неразветвленное его
расширение, т. е. наибольшее поле алгебраических чисел, которое
получается от присоединения к полю i?(|/c/) корня абелева,
относительного него, уравнения с коэффициентами из этого поля,
относительный дискриминант которого по отношению к полю
R[y^d) равен 1. Как это доказывается в теории поля классов,
группа Галуа G (абелева) этого поля К по отношению к полю
R{Yd) изоморфна группе классов идеалов поля i?("|/^^) и имеет,
следовательно, порядок h. Степень поля К над рациональным
полем равна 2/г; поле К относительно рационального поля тоже
иормальное поле, но группа Галуа его @ относительно
рационального поля R уже, вообш;е говоря, не абелева.
Легко видеть, что если подстановка s группы @ входит в ее-
подгруппу G, то класс сопряженных в @ с 5 подстановок состоит
из двух подстановок 5 и s~^. При помощи теории поля классов
79г
можно показать, что те простые числа р, которые
представляются данным примитивным классом квадратичных форм опреде-
лителя d (без двоек при Ь), суть те и только те простые числа,
которые в поле К принадлежат «в смысле Фробениуса» к классу
S, 5~^ сопряженных подстановок группы ®, образуемых той
подстановкой S группы G, которой соответствует рассматриваемый
класс квадратичных форм.
Из этой теоремы получается два следствия.
I. Все простые числар, представляемые формами,
принадлежащими к разным, но не обратным друг другу классам
примитивных форм данного определителя с?, различны, а представляемые
формами обратных классов одинаковы. Последнее — очевидно,
так как форме (а, 6, с) обратна форма (а, —Ь, с), а эти формы,
очевидно, представляют однаковые числа при х = т, у = п и
X " т, у = — п.
II. Всякая примитивная форма представляет бесконечно
много простых чисел — это следует из теоремы Чеботарева для
рассматриваемого поля К, но может быть, правда, доказано и
минуя теорему Чеботарева.
Перейдем теперь к разбиению классов К^, . . . , jfif/^ на группы
(iiCi, . . . , Кг,), {Кг,+ъ • • • , Кг,), ...(... Kh), о которых мы
говорили выше.
Рассмотрим наибольшее абелево над R подполе К поля К,
рассматривавшегося нами сейчас. Само поле iT (степени 2/г) тоже
может быть абелевым над/?, но может им и не быть. Во всяком
случае, квадратичное его надполе R{Vd) абелево над i?; поэтому
та подгруппа Н группы ® поля К, которой принадлежит 'К,
ость подгруппа группы G. При помош;и теории поля классов
можно показать, что ее подстановкам соответствуют классы
главного рода, а подстановкам смежных с Н в G систем — классы
других родов.
Таким образом, теория родов связана с вопросом о
наибольшем абелевом относительного R подполе, которое содержится
в так называемом абсолютном поле классов К рассматриваемого
квадратичного поля R{Vd)^
Если поле К само абелево, то Я = 1 и главный род, а
следовательно, и все роды, имеют по одному классу. Другой
крайний случай, когда наибольшее абелево подполе К есть поле
■SO
H{\^d)', тогда Н — G м все классы образуют один род. Но могут
оыть и промежуточные случаи.
Классы Фробениуса поля К суть некоторые комплексы
классов Фробениуса поля К, но какие?
Разложим группу ® поля К на смежные системы по ее
подгруппе Н\
& = H + s^H + s,H + ,. . + 5,Я;
тогда смежные системы эти своей композицией образуют группу
0 поля /{". Так как группа @ абелева, то классы, ее сопряженных
элементов совпадают с отдельными ее элементами. Так как
// ::: G, то у каждой из этих смежных систем либо все ее
элементы лежат в G, либо все не лежат в G, в зависимости от того,
лежит ли в G соответственный si- Поэтому те из этих систем,
которые лежат в G, суть просто все смежные системы G по Н.
Классы Фробениуса поля К, соответствующие классам 5, s~^
сопряженных в @ элементов, где s — подстановка G, как можно
показать, объединяются в некоторые классы Фробениуса поля К,
если объединять те из них, у которых s принадлежит одной
и той же смежной системе G по Я. Откуда, учитывая сказанное
выше, и получается, что совокупность простых чисел/?,
представляемых хотя бы одной из форм одного и того же рода, есть
не что иное, как некоторый класс Фробениуса поля X. Но так
как поле К абелево, то эта совокупность простых чисел р есть
не что иное, как совокупность всех простых чисел р,
представляемых некоторыми определенными прогрессиями.
Итак, разбиение классов на род1?1 есть одно из разбиений на
группы, о которых мы говорили выше. Можно из этих же
соображений показать, что не может быть более дробного такого
разбиения.
Совершенно иной подход к теории родов квадратичных форм
следующий.
Две целочисленные квадратичные формы f и g с п
переменными и матрицами А я В называются принадлежащими к
одному и тому же роду, если для любого целого q существует
такая матрица с рациональными элементами Г, что Т*АТ = В
и знаменатели всех элементов Т взаимно просты с д.
Этот подход к теории родов ценен тем, что он сразу
охватывает квадратичные формы с любым числом ^переменных.
^ к. Ф. Гаусс . 81
к сожалению, мы не имеем здесь возможности
останавливаться на этой теории родов.
Можно показать, что две формы принадлежат к одному и
тому же роду, если они целочисленно р-адически эквивалентны
при любом р и, кроме того, вещественно эквивалентны.
3. Дальнейшие приложения теории тройничных
квадратичных форм. Вернемся к дальнейшему описанию содержания
четвертой части пятого раздела «Арифметических исследований»,
После изложения в первых двух пунктах (пп. 286 и 287) этой
части доказательства теоремы о родах Гаусс в дальнейших
его пунктах (пп. 288—300) разбирает ряд классических задач,
которые решаются при помощи построенной им теории. Задачи
эти следующие: теория разложения чисел или двойничных
квадратичных форм на три квадрата (пп. 288—292); доказательство
теоремы, высказанной Ферма, о том, что любое натуральное
число может быть разложено на три треугольных числа или на
четыре квадрата (как известно, эта последняя знаменитая
теорема была впервые доказана Лагранжем) (п. 293). Что же
касается теоремы, высказанной также Ферма, о том, что всякое
натуральное число есть сумма пяти пятиугольных, шести
шестиугольных и т. д., то она была лишь гораздо позже доказана Коши.
Далее Гаусс дает решение неопределенного уравнения ах^-^-
+ 6у2 -Ь с^^ = О в целых числах (пп. 294—295), излагает
соображения о методе, которым Лежандр пытался доказать закон
взаимности (пп. 296—298); решает вопрос о представлении нуля
любой тройничной квадратичной формой (п. 299); наконец, дает
общее решение неопределенного уравнения 2-й степени с двумя
неизвестными в рациональных числах (п. ЗОЬ). В последни:|К
заключительных пунктах (пп. 301—307) Гаусс снова
возвращается к двойничным квадратичным формам и рассматривает
в п. 301 вопрос о среднем числе их родов, в пп. 302—304 —
вопрос о среднем ч^^сле классов и, наконец, в пп. 305—307 —
понятие о регулярных и иррегулярных определителях. Во всех
этих пунктах Гаусс старается более глубоко, чем он это сделал
до того, проникнуть в свойства группы классов
квадратичных форм данного определителя, но исследования этих
пунктов носят определенно незаконченный и фрагментарный
характер.
82 - . .
Поясним, в чем они состоят.
4, Исследования Гаусса о среднем числе классов. Ввиду того,
что число родов зависит от числа различных простых делителей
определителя Z), для ряда идущих подряд определителей dzZ>,
^z{D + 1), zh ф + 2),.., число родов скачкообразно, то
увеличивается, то опять уменьшается; однако, как замечает Гаусс,
если сложить число родов для идущих подряд определителей
-±:i9, ±(jD+1), ...±(jD+m—1) и разделить их на их число т,
то получится «среднее» число родов, которое можно оценить.
Для этого надо считать, что т берется очень большим
(например, фиксированным), а затем D берется еще гораздо большим,
чем т. Гаусс говорит, что это среднее число родов может быть
хорошо представлено формулой а log Z) + р, где а и р —
некоторые найденные им постоянные.
Аналогично Гаусс ставит вопрос о среднем числе классов
данного определителя 2), причем он получает, что «среднее»
число классов может быть хорошо представлено формулой
^УО-Ь, где т = 2^, е = 1 + 1 + 1 + 1 + Jg + • • • ,
2
а 6 = -^. В связи с этим Гаусс получает следующую прибли-
женную формулу для числа V /г (— Д) всех собственно при-
митивных классов всех отрицательных определителей, которые
по абсолютной величине меньше или равны т:
где -[ и S — числа, указанные выше.
Гаусс говорит, что он получил эту формулу «при помощи
теоретических исследований» и что она очень близко сходится
с тем, что он получил при помощи непосредственных численных
проб. Сейчас можно только гадать, как Гаусс мог найти эту
формулу, учитывающую и второй член — ^т, в то время.
Формула эта была впервые доказана в работе 1918 г.
И. М. Виноградовым со следующим остаточным членом:
Д=-1
6* 83
5. Дальнейшие исследования Гаусса о числе классов целочислен-4
них двойничных квадратичных форм. Среди посмертно (в 1876 г.)|
изданных работ Гаусса (Nachlass) имеются две статьи, озаглавь
ленные «О связи между числом классов, на которые распредеЛ
ляются двойничные квадратичные формы, и их определителеми
(De nexu inter multitudinem classium in quas formae binariaJ
secundi gradus distribuuntur earumque determinantem) и доле-!
женные Гёттингенскому королевскому обществу: первая —J
в 1834, а вторая — в 1837 г., но не напечатанные при жизнщ
Гаусса. 1
Эти статьи заключают в себе дальнейшие исследования Гауе-!
са о числе классов h целочисленных двойничных квадратичйЬгзо
форм данного определителя D. Обе эти статьи являются лишь neJ
законченными фрагментами. Однако из них видно, что Гауе
уже до Дирихле пришел к выводу тех же формул для числа
классов, которые дал затем Дирихле в знаменитой своей работ0|
1840 г.: «Recherches sur diverses applications de Г analyse infi4
nitesimale a la theorie des nombres»^.
Вывод этих замечательных формул основан на двух различ
ных способах найти некоторую «плотность». Первый спосоС
дает эту плотность как произведение числа классов h на неко
торую величину ^, которая легко вычисляется и выражается
через дискриминант D и основное решение уравнения Пелля]
х'^ — Dy^ = 1. Второй способ дает эту плотность в виде беско-]
печного ряда 21"7Г/7Г' ^^ зависяпдего (явно) от числа классов.;
п=1 ^
Сравнение этих двух выражений этой плотности дает числа
классов h.
Из статей Гаусса ясно видно, что принципы для получения:
первого йыражения искомой плотности у Гаусса и у Дирихле]
совпадают. .1
Что же касается до второго выражения искомой плотности/|
то его Гаусс получил, невидимому, уже очень давно (в декабре^
1800 г.), но к:ак он к нему пришел, из оставшихся после нега|
фрагментов не вполне ясно. Путь, который, невидимому, при-^
1 D i г i с h 1 et. Werke, Bd. I.
84
не л Гаусса к этому второму выражению, выясняет Дедекинд
]{ своих комментариях к этим работам Гаусса^.
Поясним с той точки грения, на которую мы стали на стр. 27
и стр. 28, о какой плотности идет речь и в чем состоит вывод
первой формулы для нее. Пусть, например, задано
вещественное квадратичное поле к и дискриминант его равен D, а число
его классов h. Предположим для простоты (хотя и общий
случай рассматривается совершенно аналогично), что не только
|)ешетка D вещественная, но и все ее побочные решетки Клейна
D', О", . . ., ^^^-'^) тоже вещественные (дело в том, что даже
при вещественности поля к некоторые из тех множителей Xg^
Лз, . . -,^^/1, на которые мы помножали (стр. 27) представителей
Й2> Зз> • • • > Зл идеалов неглавных классов, для того чтобы
получилось правильное расположение решеток Клейна D', D", . ..,
Г)(/г-1)^ иногда могут получаться комплексными). Предположим
также еще, что норма основной единицы Sq положительная.
Рассмотрим «угол Пелля» кольца D, т. е. угол,
образованный произвольным лучом, исходящим из начала и лежащим в
первом квадранте Ют], и тем лучом, в который он переходит
при помощи того наименьшего «гиперболического» (относительно
асимптот О?, Otj) поворота плоскости, при котором решетка D
переходит в себя. Этот поворот получается от умножения всех
гочек плоскости на основную единицу Sq.
Не только решетка D, но и каждая отдельная из решеток
D', £)", . . . , £>^^~'^\ периодична в том смысле, что она при этом
1 иперболическом 'повороте совмещается с собой. В силу этого
совокупность всех точек системы D*, лежащих в таком углу
Пелля, есть совокупность всех точек £l* с положительной
нормой, попарно не ассоциированных друг с другом, т. е.
не отличающихся друг от друга лишь множителями единицы.
Точки D*, лежащие во 2-м и 4-м квадрантах, имеют
отрицательные нормы, а точки D*, лежащие в 3-м квадранте,
ассоциированы с точками, лежащими в 1-м, цри помощи единицы —1.
Обозначим через П(0 ту часть угла Пелля, которая
отрезается от него гиперболой щ = 1 (где ^>0), и обозначим
площадь П(1) через П^; в таком случае площадь области П(^)
1 С. F. G а U S S. Werke. Bd. И, стр. 292—303,
85
равна UIi, так как область П(^) получается из области 11(1)
гомотетией с коэффициентом |/^^ относительно начала координате
Число Т точек Cl*, лежащих в области n(f), представляет
собой число всех различных идеалов поля к с положительными;
нормами, не превышающими t. \
Ввиду того, что площади основных параллелограммов всех]
решеток D, D', D", . . . , ©(^-D одинаковы и равны YD, что
решетки эти попарно не имеют общих точек, кроме начала, и
что число точек решетки с данной площадью основного
параллелограмма, принадлежащих данной области, приблизительно
равно площади этой области, деленной на площадь этого
параллелограмма, или, точно говоря (при увеличении
коэффициента гомотетии |/7), асимптотически равно этому отношению,
то число Т точек D*, лежащих в П(^), асимптотически равно
h -^. Отсюда следует, что предел
Т
lim Y = их,
тде X = jT^. Этот предел называется «плотностью» идеалов поля /с.
Это, попросту говоря, плотность точек системы Cl*, если за
^eдиницy площади принимать площадь П^.
Вывод второй формулы для этой «плотности» проводится так.
Пусть F {т) есть число различных идеалов поля к с
положительной нормой т, т. е. число точек £l*, лежащих на
гиперболе ^Y] = m в угле Пелля. Искомый предел
Но если расположить идеалы к с положительными нормами
по увеличению нормы и они суть 3i> S2> • • • » St'> . . . , а их нормы
'^i ^ ^2 ^ • ' • ^ '^т' • • • > то мы имеем очевидные неравенства:
F(l) + /^(2)-b---+/^(AiT^-l)<r</^(l)-bF(2) + ...+/'(nr),
или, если разделить на Пт», то неравенства
/'(l) + F(2)+... + /'(nj„~l) /^^ j^N ^
\ Пу, у ^ Пу, ^
<
И поэтому, так как lim (1 ) = 1, то, какое бы малое
полота-.. odV ^T'J
86
жительное S ни взять, мы будем, для всех достаточно
больших Т\ иметь их — Ь<а — <<й>« + 8, или, деля на Г', ^~ <
;7" '^ т' ' Возведя все части этого последнего неравенства
_1_ ^ Лх -f 8
в 5-ю степень, где 5>>1, умножая на (5—1) и суммируя
по всем J'^ большим некоторого достаточно большого У, мы
получим неравенства
,/,,_8).(,_1)2^Р,<(.-1)2;;^<(/^'<-8)'(^-1)2р-.-
Но известно: 1° что ряд V— при 5>>1 сходится и 2° что
Поэтому, приближая в предыдущих неравенствах s к 1, мы
получим равенство
Левая часть этого равенства является второй формулой для
искомой «плотности»; она явно не зависит от й, в ней
суммирование производится по всем идеалам поля к с
положительной нормой.
Дальнейшее преобразование левой части этого равенства
производится, во-первых, опираясь (два раза) на знаменитое
«тождество Эйлера» У ~ == Т7 zTs » ^Д^ л пробегает все
натуральные, а р — все простые числа, и которое имеет
следующее обобпцение на все идеалы ^ и все простые идеалы ^)
1 1
некоторого поля к: V = ТТ ^Гз»'^У^ ^ — значок нормы.
Ряд у\—— называется дзета-функцией Дедекинда данного
ноля к и обозначается С (5).
Во-вторых, в этом преобразовании левой части равенства (*)
учитывается закон разложения натуральных простых чисел р
на простые идеалы квадратичного поля к. Используя этот
ткон, можно получить, что:
87
1-
Р
где (—) — символ Лежандра. Отсюда величина lim {{s — 1) С (s))^
называемая вычетом дзета-функции, получается равной
.-(((-'.Г1^)П.Т71у7)'
или, если учесть, что
р р
то
lim((s-l)C(.))^limn .; ^.
Воспользовавшись снова тождеством Эйлера, но уже в
обратном направлении, мы получаем
lini((.-l)C(s)) = 2(¥)^-
ИЛИ окончательно формулу:
'^-zm■
которую уже знал Гаусс.
При помощи дальнейшего упрош;ения этой формулы
получаются следуюш;ие формулы Дирихле для числа классов h
квадратичного поля, которые содержат уже лишь конечные
суммы.
В случае
^^ = -2тЬ|1:©^ (n = i,2,...,lD\),
а в случае АУ"т, т>-0:
h = -i—]n
а
88
Ып Ып
А lb
ПИ-^"")
Ьгтг Ып^
_Ь_
2 1а2 '" / агтт агп
i дс И распространены на все квадратичные вычеты а и квадра-
щчные вычеты b{modD).
В течение 90 лет после опубликования этих формул
Дирихле математикам не удавалось избавиться от средства анализа
при выводе этих конечных формуя, выражающих искомое
натуральное число /г. Первый, кто сдвинул этот вопрос, был
Д. А. Венков. В своей работе «tjber die Klassenzahl positiver
binarer quadratischen Formen» (Math. Ztschr., 1931, 33) он вы-
1юл формулы Дирихле для т<0 для случая d^l (mod 8) иа
совсем другого принципа, а именно, применяя арифметику
кватернионов, вовсе не прибегая к средствам анализа, и тем самым
более глубоко вник в чисто арифметические свойства этого
числа.
6. Регулярные и иррегулярные определители Гаусса и исто-
1)ая теории абелевых групп. В п. 305 Гаусс называет определи-
гель D «регулярным», если в главном роде есть такой класс, что
всякий класс главного рода есть степень этого класса, т. е.
если группа классов главного рода циклическая. Если
определитель D нерегулярный, то эта группа— некоторая
нециклическая абелева группа.
В п. 306 Гаусс говорит: «Об удобнейшем расположении
системы классов, которые содержатся в главном роде в случае
нерегулярного определителя, мы не можем здесь трактовать в силу
недостатка места; мы заметим только, что так как в этом случае
одного базиса [производящего элемента] недостаточно, то в этом
< лучае надо взять два или даже несколько классов, при помощи
умножения которых получаются все остальные. В этом случае
поэтому получаются двойные и кратные индексы, которые
приносят ту же пользу, какую ординарные в случае регулярного
определителя. Этот предмет мы, однако, разберем подробно
при другом подходящем случае». Насколько, однако,
известно, не сохранилось записей Гаусса также и в его Nachlass'e,
в которых была бы дана теорема о базисе абелевой группы.
В предисловии к свой известной работе «О группах
перестановочных элементов» (1879) Фробениус и Штикельбергер
говорят: «Основания теории конечных групп перестановочных
элементов [конечных абелевых групп] были положены, с одной
стороны, Эйлером и Гауссом, а с другой,— Лагранжем
89
и Абелем, первыми в их арифметических исследованиях по теории ;
степенных вычетов, а вторыми — в их алгебраических работах,1
относящихся к решению уравнений. После этих, положивших]
начало, исследований Гаусс и Шеринг продолжили эту теорию.
Гаусс (Werke, II, 266; Nachlass, опубликованный в 1876 г.),,
дает разложение группы на примарные группы, порядки кото-i
рых взаимно простые [в прямое произведение таких групп],]
а Шеринг (Gott. Nachr., 1869, S с h е г i n g. Werke, Bd. I)?
дает ее разложение в элементарные группы, порядок каждой из
которых делится на порядок следуюш;ей». Таким образом,
теорему о базисе абелевой группы на примере гауссовой
композиции классов впервые нашел Шеринг в 1869 г. В 1870 г. Кро-
некер перенес ее на абелевы группы вообпце.
В этом месте стоит отметить, что в упоминавшейся не раз
выше теории поля классов арифметический подход Эйлера и
Гаусса и алгебраический подход Лагранжа и Абеля для
случая абелевых групп оказываются как бы соединены и
являются там двойственными описаниями одних и тех же фактов.
7. Значение собственной эквивалентности в теории
композиции классов Гаусса, Поясним в заключение этого параграфа,
какое преимуш;ество имеет для теории композиции классов
различение, делаемое Гауссом между собственной и несобственной
эквивалентностью форм. Если классом считать, по Гауссу,
совокупность собственно эквивалентных друг другу форм, то
получается группа классов, рассмотренная в теории композиции,
изложенной выше. Если же, как это делал Лагранж, относить
в один класс как собственно, так и несобственно
эквивалентные друг другу формы, то теория композиции запутывается.
Действительно, формы (а, 6, с) и (а,—6, с) несобственно
эквивалентны друг другу, вторая получается из первой подстановкой
(о S). В смысле билинейной композиции произведение этих
форм дает, как легко убедиться, главную форму (1,0, £)), т. е.
классы, соответствующие этим формам, обратные. Каждый класс
Лагранжа есть, следовательно, сумма двух взаимнообратных
классов Гаусса. Пусть имеются два класса Лагранжа а + а~^,
Ь + 6~\ где а и b — классы Гаусса. Рассмотрим произведения
аЬ, а~^Ь, аЬ~^^ а~^Ь~^, Из них аЬ и а~^Ь~^ принадлежат взаимно-
обратным классам, а а~^Ь и аЬ~^ — двум другим взаимнообрат-
90
иым классам. Поэтому произведения форм двух классов Ла-
гранжадаютне формы одного определенного класса Лагранжа,
а формы одного или другого из некоторых двух классов
Лагранжа. Поэтому композиция форм не ведет к группе композиции
классов (в смысле Лагранжа), а к некоей мультигруппе.
14. ШЕСТОЙ РАЗДЕЛ «АРИФМЕТИЧЕСКИХ ИССЛЕЛОВАНИЙ».
РАЗЛИЧНЫЕ ПРИЛОЖЕНИЯ^ТЕОРИИ ЧИСЕЛ
Раздел этот озаглавлен: «Различные применения
предыдущих исследований» (пп. 308—334).
Гаусс начинает его словами: «Как плодотворна высшая
арифметика истинами, которые полезны также и в других частях
математики, мы уже отметили во многих местах; однако мы
не считаем лишним особо рассмотреть некоторые приложения,
г^оторые заслуживают подробного рассмотрения, не для того,
чтобы исчерпать этот предмет, ибо им можно было бы
наполнить несколько томов, а для того, чтобы при помош;и
нескольких примеров выдвинуть его в более ярком свете».
Гаусс подробно рассматривает решение следующих задач.
В пп. ЗОЭ—311 рассматривается разложение дроби в сумму
более простых дробей, основанное на теорзме: если знамена-
гель 71 дроби ~ равен произведению взаимно простых чисел
а, 6, с, d, ..., то можно представить дробь в виде
В ПП. 312—318 подробно рассматривается теория обращения
обыкновенных дробей в десятичные.
В пп.' 319—322 решается сравнение х'^ ^ А (mod m). Гаусс
говорит, что, конечно, можно решать это сравнение при помощи
таблиц индексов, но что делать, если вычисления выходят за
пределы этой таблицы; поэтому Гаусс дает другой удобный спо-
<^об, который он подробно разбирает.
В пп. 323—326 предлагается близкий к предыдущему спо-
<^об для решения неопределенного уравнения тх^ -}- пу'^ = А.
В пп. 327—328 дается другой способ решения сравнения
^^ ^ А (modm) для случая, когда Л<<0.
9/
в пп. 329—334 рассматриваются два различных способа
узнавать, простое ли заданное число. Один основан на теории
квадратичных вычетов, а другой — на одном соображении^
связанном с теорией квадратичных форм.
15. СЕДЬМОЙ РАЗЛЕЛ «АРИФМЕТИЧЕСКИХ ИССЛЕДОВАНИЙ»,
ТЕОРИЯ ВЕДЕНИЯ КР^ГА ГАУССА
Этот последний раздел, озаглавленный «Об уравнениях,
от которых зависит деление круга», посвящен одной
алгебраической теории, в которой играют существенную роль
некоторые соображения теории чисел, а именно теории
уравнения о;^ = 1.
Уравнение это называется уравнением деления круга
потому, что корни его суть точки комплексной плоскости,
лежащие на окружности радиуса 1 с центром в начале и делящие эту
окружность на п равных частей.
1. Возникновение этой теории у Гаусса и основной его
результат. В рассматриваемом седьмом разделе Гаусс строит во всех
деталях для этого частного уравнения теорию, совпадающую
с теорией Галуа (1811—1832). Галуа построил свою общую
теорию алгебраических уравнений около 1830 г., т. е. через 30 лет
после выхода в свет книги Гаусса, причем эта теория была
опубликована лишь через 15 лет после смерти Галуа, в 1846 г.,
Лиувиллем, а сделалась общим достоянием алгебраистов только
в конце 50-х годов прошлого столетия, после появления в свет
курса высшей алгебры Серре. Теория Галуа имеет как бы две
стороны — алгебраическую и арифметическую. Если
подготовкой алгебраической стороны теории Галуа были работы по
теории алгебраических уравнений Лагранжа, то подготовкой ее
арифметической стороны была теория деления круга Гаусса.
Сам Галуа в своем основном мемуаре ссылается на теорию
деления круга Гаусса, которая, очевидно, послужила для него
как бы прообразом при построении его общей теории.
Исследование уравнения х^ — i дало, кроме того, Гауссу
возможность решить знаменитый вопрос о том, каково должно
быть число сторон правильного многоугольника для того, чтобы
его можно было построить циркулем и линейкой. Оказалось^
92
что кроме правильных многоугольников, у которых число
сторон равно 2^, 3*2'^, 5-2'^ или 15-2^, возможность построения
которых была известна уже древним, можно построить циркулем и
линейкой многие другие, например, правильный семнадцати-
угольник.
Это поразительное открытие Гаусс сделал еще до того, как
он начал писать «Арифметические исследования». В июне
1796 г. в «Литературной газете», издававшейся тогда в Иене,
была помещена следующая заметка:
«Н о в ы е о т к р ьт т и я
Всякому начинающему геометру известно, что можно
геометрически [т. е. циркулем и линейкой] строить разные правильные
многоугольники, а именно треугольник, пятиугольник, пятнадцати-
угольник и те, которые получаются из каждого из этих путем
последовательного удвоения числа его сторон. Это было уже известно
во времена Эвклида, и, как кажется, с тех пор было
распространено убеждение, что область элементарной геометрии дальше не
распространяется: по крайней мере, я не знаю удачной попытки
распространить ее в эту сторону. Тем более кажется мне заслуживающим
;внимания открытие, что кроме этих правильных многоугольников
может быть геометрически построено еще множество других,
например, семнадпатиугольник. Это открытие является собственно
лишь следствием одной еще не совсем законченной большой теории.
Как только она получит эту законченность, она будет предложена
публике.
К. Ф. Гаусс из Брауншвейга,
Студент-математик в Геттингене».
В рассматриваемом седьмом разделе Гаусс доказывает, что
если число п сторон правильного многоугольника имеет вид:
п — pipj. . . рг2^, где piPj, . ' ' yPi — различные простые числа
вида: /? = 2^4-1> то он может быть построен циркулем и
линейкой. (Для того чтобы число 2^^ + 1 было простым,
показатель т не должен иметь нечетных простых делителей, так как
если бы m == qiUy, где q нечетное, то число это можно было бы
написать так: 2^^ + 1 = (2^')^ + 1^, но число это делится на
2^' +1 и, следовательно, непростое. Показатель т здесь,
следовательно, может быть сам только степенью двойки,
ш = 2^^, т. е. простые числа ри Pj, • • • вида: р = 2^' + 1).
в предпоследнем п. 365 Гаусс говорит, что он имеет верный
способ доказать и обратное, а именно, что ни при каких
других /?, кроме указанных, правильный многоугольник построить
циркулем и линейкой уже нельзя. Он говорит далее: «хотя
границы нашего сочинения не позволяют привести этого,
доказательства, мы думаем, что надо все же на это указать для того,,
чтобы кто-либо не пытался искать еще других случаев, кроме
тех, которые указаны нашей теорией, например, не надеялся бы
свести на геометрические построения [т. е. на построения
циркулем и линейкой] деление на 7, И, 13, 19, ... частей и не
тратил бы зря своего времени».
Доказательство этой обратной теоремы сразу следует иа
общей теории Галуа, но оно может быть проведено и непосред-
ственно.
Перейдем теперь к изложению содержания самого седьмого
раздела. В п. 336 Гаусс сводит задачу к случаю, когда
п — простое число. В последующем изложении поэтому число
п уже везде предполагается простым. В п. 341 дается доказа-
х'^ 1
тельство того, что многочлен ——j=^x'^~'^-\-x'^~^-\- • • *-\-х-{-\=Х^
где п простое, не приводим в поле рациональных чисел.
Доказательство это сложное, сейчас найдены совершенно простые
доказательства этого факта. Совокупность корней уравнения
X = О Гаусс обозначает через D.
В п. 342 Гаусс кратко резюмирует, какую основную теорему
он будет далее доказывать. Он говорит: «Цель дальнейших
исследований состоит в том, чтобы последовательно разлагать
многочлен X на большее и большее число множителей таких,
чтобы коэффициенты их определялись при помощи решения
вспомогательных уравнений возможно более низких степеней,
пока таким образом не придем к линейным множителям, т. е.
к самим корням Q». «А именно,— говорит он,— мы покажем,
что если число п — 1 как-либо разлагается на натуральные
множители а, ,8, 7, • • • (за которые можно принять простые
числа), то л разлагается на а множителей степеней ,
коэффициенты которых определяются при помощи решения
уравнения степени а; далее, каждый из этих множителей разла-
Q о ^ п — 1
гается на р других множителей степеней —— , при помощи
94
решения уравнения степени ^ и т. д., так что, если v — число
множителей а, р, 'f, . . . , то нахождение корней Q сводится на
[последовательное] решение v уравнений степеней а, р, 'f, . . .
и т.д. Так, например, для п=^П, где п—1 = 2-2-2-2,
придется решить четыре квадратных уравнения, а для п = 73 [где
п — 1 = 2-2•2-3-3] — три квадратных и два кубических».
2. Леммы о периодах и доказательство основной теоремы.
Для доказательства этой основной теоремы Гаусс переходит к
рассмотрению так называемых периодов.
Пункт 343 озаглавлен: «Все корни Q разделяются на некоторые
классы (периоды)».
"'^9,д^г. (Ь/г) и{3,1б)
^-'^1дп^з^(з.з) u(i^,io)
Дело в следуюш;ем. Пусть г — какой-нибудь из корней fl,
тогда все корни Q суть г^т'^.т^,... г^-^, что доказать нетрудно.
Если теперь g — какой-либо первообразный корень простого
числа л, то числа 1, ^, g^,. . . jg'^"^ представляет собой по
модулю 11 числа 1, 2, 3,... , п—1, но может быть взятые в
другом порядке. Поэтому г, г^, г»^,. . . , г^'^""^ — тоже все корни
^. Каждый из этих корней есть g^-я степень предыдуш;его,
а так как g^-i=f 1 (mod n), то (г^^~^)^ == г^^*~^ = г, и поэтому
первый из них есть в свою очередь g-я степень последнего.
Расположим мысленно эти корни последовательно, например,
против часовой стрелки, в точках, делящих некоторую
окружность на ^ — 1 равных частей (эта окружность не на
комплексной плоскости), так чтобы образовался правильный п — 1
угольник Р; тогда g-я степень каждого из них будет равна
последующему за ним. Пусть теперь n—\=ef. Посмотрим,
какими свойствами обладают суммы по / этих корней такие,
что соответствующие им / вершин многоугольника Р образуют
правильный /-угольник. Эти суммы Гаусс называет «периодамш;
длины /.
Если строить такую сумму, исходя от корня г^, то она
будет равна
где h = g^, и каждое следующее ее слагаемое будет /г-й
степенью предыдущего и первое /г-й степенью последнего. Гаусс
обозначает эту сумму (/, X). Очевидно, что всё равно, с какой
из его вершин начинать такой /-угольник, т. е. что (/, \h^) ='
= (/, Х). Если положить в формуле (I) X = О (или вообще
Х^О (mod п)), то получится сумма (/, 0)=/; эту сумму Гаусс тоже
называет периодом. Но это особый период, не входящий в число
тех, которые мы выше пояснили многоугольниками.
Относительно периодов Гаусс доказывает ряд лемм.
Лемма. Произведение двух разных или одинаковых
периодов одной и той же длины выражается линейно с целыми
рациональными коэффициентами через периоды той же длины.
Например, если п = 19, т. е. п — 1 == 18, то
(6,1)2 = (6,2) + (6,8) + (6,9) + (6,12) + (6,13) + (6,19) =
= (6,2)+2 (6,8)+ 2 (6,9)+ 6.
Эта лемма очевидна, так как при умножении (/, X) на (/, ^)
надо составить сумму всех возможных произведений / корней,
выходящих в (/, X) и / корней, входящих в (/, jx); но эту
сумму можно разбить на суммы тех / произведений, в которых
расстояния цо окружности против часовой стрелки корня из
(/, |j.) от умноженного корня из (/, X) одинаковы. Каждая из
этих частных сумм произведений будет, очевидно, периодом
той же длины /, или числом /, если показатели при г при
этом получатся все делящиеся на п.
Следствие. Любая целая рациональная функция периодов
одной и той же длины с рациональнЫхМи коэффициентами равна
линейной комбинации периодов этой длины с рациональными
коэффициентами.
Получается повторным применением предыдущей леммы.
М
Лемма. Если X не делится на п, то любой период (/, |л),
где [А тоже не делится на п, имеет следующее выражение:
a + PP + TP^+'-- + V-S
где коэффициенты а, ^8, . . . , ^ рациональны, через период
(/, X), который мы обозначим тут через /?, если п—1 = е/.
При доказательстве этой леммы Гауссу приходится
использовать доказанную им в п. 341 неприводимость многочлена X.
Лемма. Всякий симметрический многочлен с
рациональными коэффициентами от / корней периода длины / выражается
линейно с рациональными коэффициентами через периоды длины /.
Доказывается при помощи предыдущих лемм.
Лемма. Пусть п — 1 = а8^ и пусть период (Р^» ^) состоит
из р более коротких периодов (у, X), (у, X'), . . .; тогда всякий
симметрический многочлен с рациональными коэффициентами
от этих более коротких периодов (у, X), (у, X'), . . . выражается
линейно с рациональными коэффициентами через периоды
длины Py-
Выводится из предыдущей леммы.
Применив эту лемму к частному случаю, когда
рассматриваются элементарные симметрические функции от периодов
(Т> ^)' (Т» ^^')' • • • ' Гаусс получает, что то уравнение степени
3, корнями которого являются эти периоды, имеет коэффициенты,
выражающиеся линейно с рациональными коэффициентами через
периоды длины ^^, откуда сейчас же и получается указанная
выше основная его теорема.
Рассмотрим пример п — 19, тогда п — 1=18 = 3-3-2 и
получается следующее разложение на периоды:
.г, г^^ (6,1), (6,2), (6,4) корни:
. г^, г^^ х^ -\- х^ — &х — 7 — 0;
(18,1) =
г12
Г",
/•17 (2,1), (2,8), (2,7) корни:
;.1б а;3_ (6,1) а;2 + [(6,1) + (6,4)J а; —
г14
г15
гЮ
(6,2) = 0;
и:
ж2 —(2,1)ж + 1 -0.
г,г^^ корни
к. Ф. Гаусс
97
Если ri=-2"'+l, т. е. п — 1=^2"\ то каждый и;^ более
длинных периодов раскладывается в сумму двух более коротких
периодов и все уравнения цепи получаются квадратные, т. е.
задача решения уравнения .х^ — 1 == О сводится на цепь
квадратных уравнений.
Например, если п = П, то п — 1 = 16 = 2-2•2-2 и
получается такое разложение на периоды:
(16,1) =
|(2,1)
(8,1) ((4.1) 1(2,13)
1(4,9) |(2,9)
1(2,15)
|(4,3) |(2,3)
(8,3) 1(2,5)
1(4,10) |(-2,10)
1(2,11)
• • '•,
..Л
• •Л
..Г2,
..'•^
..л
..г\
. . г^,
/■"
,.13
г»
,.15
,.14
,.12
,.10
,.11
(8,1), (8,3) корни:
х^ -\- X — 4 = 0;
(4,1), (4,9) корни:
а;2 —(8,1)х —1 =0;
(2,1), (2,13) корни:
х2 —(4,1)а;4-(4,3) = 0
г, г^*^ корни:
ж2 —(2,1)ж + 1 =0.
3. Связь теории деления круга Гаусса с теорией Галуа,
Стоит отметить в этом месте, какую связь имеет эта основная
теорема теории деления круга Гаусса с основной теоремой
общей теории Галуа, доказанной Галуа через 30 лет после
появления «Арифметических исследований» Гаусса.
Напомним, что Галуа начинает свою теорию с того, что если
дано алгебраическое уравнение с коэффициентами, лежащими
в некотором поле /с, то можно свести его решение на решение
некоторого другого, так называемого соответствующего ему
нормального, уравнения с коэффициентами из того же поля ку
т. е. такого: 1° которое неприводимо в поле к, и 2° все корни
которого выражаются рационально через один из его корней и
элементы поля к. Это замечание было сделано до Галуа еще
Абелем.
Для нормального уравнения Галуа следующим образом
вводит его группу. Если К — то поле, которое получается от
расширения поля к присоединением к нему корня г заданного
нормального уравнения т-й степени с коэффициентами из поля
к и если 92 W> ТзС'')? • • • > ?m W — другие его корни, то если
во всех элементах поля К заменить г через ^^{г)^ то произой-
98
дет автоморфизм поля /1, т. е. при такой :шмене элементы
ноля К перейдут в такие новые его элементы, что любое
рациональное с коэффициентами из к соотношение между его
элементами останется верным, если их заменить на те элементы,
Б которые они перешли. Эти т автоморфизмов поля К образуют
группу — так называемую группу Галуа G над полем к
рассматриваемого уравнения;
Основной результат теории Галуа состоит в следующем.
Галуа вводит понятие нормального делителя группы. Если
Я — подгруппа G, то она называется нормальным делителем G,
если для любого элемента g из G имеет место g'^Hg = //,
т. е. если // совпадает со всеми своими сопряженными.
Пусть F {х) — многочлен, стоящий в левог! части
рассматриваемого нормального уравнения, и пусть группа Галуа его
имеет нормального делителя индекса а (т. е. такого, число
элементов которого в а раз меньше числа всех элементов
группы); пусть этот нормальный делитель в свою очередь имеет
нормального делителя индекса р и т. д.; в таком случае, как
это показывает Галуа (и это его основная теорема), многочлен
F (х) разлаг8(ется на а множителей степеней ~, коэффициенты
которых выражаются рационально через корень уравнения
степени а с коэффициентами из поля к] далее, каждый из этих
множителей разлагается на ^ других множителей степеней
-^, коэффициенты которых выражаются рационально через
корень уравнения степени 3, коэффициенты которого выражаются
рационально через корень предыдущего уравнения степени ос
и элементы поля А; и т. д. Но ведь это и есть теорема Гауссаj
но для более общего случая.
Уравнение X = О Гаусса степени m = д — 1, где п —-
простое число: 1° неприводимо в поле рациональных чисел и 2*^
все его корни выражаются рационально через один, т. е. она
нормально над полем к рациональных чисел. Корни его суть
г, г^, {г^У,. . . , т. е. группа автоморфизмов циклическая. Если
порядок циклической группы равен т = а^-у . . . , то она имеет
подгруппу индекса а, которая тоже циклическая; эта
подгруппа имеет в свою очередь подгруппу индекса Р, которая
тоже циклическая, и т. д. Но любая подгруппа циклической
7* 99
группы есть се нормальный делитель. Таким образом, мы ^
видим, что основная теорема теории Галуа есть непосред- •
ственное обобщение теоремы Гаусса, о чем упоминает и сам *
Галуа. I
Что же собственно понял Галуа? Галуа понял, что успехе
теории деления круга Гаусса основан совсем не на том, что|
уравнение X— О имеет весьма специальный вид, а на том, что|
оно нормальное, и не на том, что его группа весьма специаль-1
пая (циклическая), а на том, что все ее последовательные дели-|
ТОЛИ суть нормальные делители. Как только Галуа понял эти^
истинные причины успеха Гаусса — он построил свою общую!
теорию. Для этого, кроме того, ему должна была быть близка^
идея Лагранжа о том, что истинной «философией» теории алгеб-|
раических уравнений является теория подстановок. '[
4. Вещественность всех корней всех промелсуточных у рае-:
нений, кроме последнего, если оно квадратное. В. п. 355 Гаусс^
делает еще следующее замечание.'Так как п нечетное, число
п — 1 четное. Множитель 2 числа п — 1 можно, при разложении
на периоды, всегда ставить на последнее место. Тогда
разложение это кончится двучленными периодами (2, X). Если поло-
, к 360° , . . А: 360° . к 360° . . к 360°
жить г^ = COS 1- I SI" J TO r~^ = COS I sin .
-1
Ho (2, I) = r^ + r^^S где h = g'=-g^=^ — l (mod n), т. 5.
к 360°
(2, X) = r^ -\- r~^. Поэтому (2, л) = 2 cos . Двучленные
периоды, таким образом,— действительные числа, а следовательно,
в выбранном разложении и все предыдущие им, более длинные,
из них составленные периоды — тоже действительные числа.
При таком разложении^ на периоды, т. е. когда последние
периоды, отличные от самих корней, двучленные, все
вспомогательные уравнения, кроме последнего квадратного уравнения,
дающего сами корни, имеют все корни действительные.
J, /с 360° (2, X) ,,, >v
Кроме того, получается, что cos — ^ , где (2, Л)
можно получить при помощи решения цепи уравнений с
действительными корнями.
Чтобы найти то ^^, при котором /с = 1, достаточно, очевидно,
найти наибольший положительный двучленный период (2, Ц,
Постуйая таким образом в случае п = 17, т. е. решая вспомога-
' 100
тельные уравнения: х^ + х — А =^ 0; х^ — (8,1)а: —1=0;
х^ — (4Д)а: + (4,3) — О, Гаусс находит, что
л :
+ "8 Kl7 +31/17 —V 34-2/17 ^21/34 + 2/Г?.
Эта формула содержит только квадратные корни, которые
могут быть, как известно, построены циркулем и линейкой.
Она дает поэтому возможность дать построение циркулем и
линейкой по радиусу окружности, который тут принят за 1,
отрезка, равного cos ^\ т.е. угла ^-^°, а следовательно, дает
возможность построить циркулем и линейкой правильный сем-
надцатиугольник.
5. Разрешимость всех промежуточных уравнений в
радикалах. Наконец, в п. 359 Гаусс показывает, что во всех случаях
все вспомогательные уравнения решаются в радикалах. Об
говорит: «Предыдущие исследования излагают способ находить
вспомогательные уравнения; теперь мы докажем весьма
выдающееся свойство их решения. Известно, что все усилия
величайших геометров дать общее решение уравнений, -степень
которых превосходит четвертую, или (для того, чтобы более точно
сформулировать, чего хотят) найти способ сведения смешанных
уравнений на двучленные, до сих пор были тщетны, и едва ли
можно сомневаться, что эта задача не столько превосходит
силу современного анализа, как, скорее, требует
невозможного... Тем не менее несомненно, что существует сколько
угодно смешанных, т. е. недвучлепных уравнений любой
степени, которые допускают такое сведение к двучленным
уравнениям, и мы надеемся, что не будет нежелательным геометрам,
чтобы мы показали, что наши вспомогательные уравнения всегда
относятся к таким». И далее Гаусс, используя резольвенты
Лагранжа, доказывает, что все его вспомогательные уравнения
решаются в радикалах.
Этим, по существу дела, и кончается знаменитое сочинение
Гаусса «Арифметические исследования».
W1
16. СУММЫ ГАУССА
1. Содержание работы Гаусса 1811 г. В 1811 г. Гаусс
опубликовал статью «Суммирование некоторых особых рядов» (Sum-
matio quarundam serierum singularium). Гаусс начинает п. 1
работы следующей фразой: «Среди выдающихся истин, к
которым открыло дорогу учение о делении круга, занимает не
последнее место суммирование, приведенное в п. 356
«Арифметических исследований». И это не только в силу особенной
элегантности метода этого суммирования и удивительной его
плодотворности, подробно осветить которую нам даст случай в будущем
другое исследование, но такя^е и по причине того, что строгое
и полное обоснование этого метода представляет необычные
трудности».
Дело идет о вычислении значений периодов длины
т ~ —^—, где п простое, т. е. когда совокупность всех корней
Q уравнения X =:=: О разбивается на два периода (т, 1) и (т, g).
В силу основной теоремы теории деления круга Гаусса не
представляет труда составить то квадратное уравнение с
рациональными коэффициентами, корнями которого являются эти
периоды, но как узнать, какой из этих корней есть (т, 1),
2тгг
а какой (т, g), предполагая, что /^ ~ в ^ ? Дело сводится к
определению знака zb ^ формуле для этих корней. И Гаусс
говорит, что решение многих трудных вопросов теории чисел
не взяло у него столько дней, сколько взяло лет работы
решение вопроса об этом знаке. Выяснению вопроса об этом
знаке посвящены пп. 5—32 работы; в п. 33 Гаусс показывает,
n—i
что рассмотрение этих периодов длины ^ дает также
доказательство квадратичного закона взаимности.
Итак, периоды {т, 1) и {т, g) суть, в силу основной
теоремы теории деления круга, корни некоторого квадратного
уравнения
с рациональными коэффициентами. Коэффициенты эти Гаусс в
U. 356 «Арифметических исследований» находит так. А — (т, 1) +
+ {ту g), т. е. равно сумме всех корней уравнения X ==^ х'^-^-j-
102
+ x^~^ + . . . + ж 4- 1 ~ о, т. е. равно — 1. Что же касается В,
то оно равно (т, 1)-(т, g).
Это произведение в силу леммы стр. 96 может быть
представлено в виде
(т, yV + 1) + {т, iV' + 1) + (m, Л^Ч 1) + • • • - ТУ,
где слева т слагаемых, каждое из которых равно {т, 1), (/п, g)
или (т, 0). Таким образом, В = сх.{т, 0) + p(7n, l) + ^(/n, g'),
где а, р, f — целые положительные числа, причем ol -\- ^ -\- ^ = т.
Из доказательства леммы стр. 96 сразу видно, что р = ^ и что
либо ни одно слагаемое Wне равно (/п, 0), либо такое слагаемое
только одно, т. е. что а = 1 или 0. Таким образом, либо
1 1
а —О, р = 7 = ут, либо а = 1, ^~^=z-~^[rn — 1), а так как
о п— 1
а, р, Y целые, то первое имеет место, если т = —^— четное,
т. е. п = 4/ + 1, а второе, если т нечетное, т. е. п = А1 -\-3.
д I
А так как (т, 0) = т = -^— и (т, 1) + (т, §^) = — 1, то в
1 1
первом случае (т, l)-(/n, g^) == —-^(д — 1), а во второмуд;
поэтому искомое квадратное уравнение есть
х^+х-'^{п — 1) = 0 или х^ + х + ^{n^i)^0.
Периоды {т, 1) ж {т, g) имеют вид:
(тп, 1) ^ г + г^^ + ^^* + • • • + гё^^'""'-'^;
(т, g) - г^ + rs' + гё' +'- + г^-^^~'^^\
2тгг
i де г-^€^ , т. е. они могут быть записаны и так:
2тсг 2пг
К 1) = 2'' ' ('^. б') = 1]е"
где а пробегает все квадратичные вычеты, а b — все
квадратичные невычеты по модулю п,
«Определение знака», таким образом, сводится к разысканию
2тгг
а
,:шачения суммы: Ve^ . Оно проводится Гауссом в пп. 5—32
а
103
работы при помощи преобразования суммы в произведение
(г — г"1) {г^ — г~^) • • • {г'Р-^ — г-Р+2)^ при помощи исследования
двух особых рядов:
с» оо i
/ {X, m) - 2 (- ^У (^'* /) ^ ^ (^' '^) =^ 2 ^^' ('^' /')'
где (т, /) = — J- , каждый из кото-
рых приводит Гаусса к желаемой цели.
Доказательство это принадлежит к числу трудных, поэтому
мы его здесь воспроизводить не будем.
2. Дальнейшие исследования о гауссовых суммах в XIX
столетии, В XIX в. рядом крупных математиков были
предложены другие, отличающиеся от гауссова, решения вопроса
о знаке в гауссовой сумме, основанные на разных принципах.
В. А. Лебег (1840) прибег для этой цели к эллиптическим
функциям; проще решил вопрос Коши (1840) и из тех же
соображений в 1856 г. Кронекер. Дирихле (1837) определил значение
гауссовой суммы при помощи определенного интеграла.
Кронекер (1880) вернулся к способу, ранее предложенному Коши
и основанному на основной теореме Коши о комплексном
интегрировании.
Свойства гауссовых сумм были использованы при
преобразовании ряда V f — j — в конечную сумму для вывода формул
Дирихле числа классов h квадратичного поля.
Во всяком случае, можно сказать, что в течение ровно це"
лого столетия после появления мемуара Гаусса 1811 г. совер"
шенствовались решения вопроса, поставленного Гауссом, но
никакого принципиального расширения задачи о гауссовых
суммах получено не было. В статье Бахмана (Р. В а с h ш а и п.
Uber Gausszahlentheoretische Arbeiten), появившейся в 1911 г.,
гауссовым суммам посвящены только две страницы, причем Бах-
ман, видимо, недоумевает, к чему относится замечание Гаусса
о необыкновенной важности метода его сумм. Работы XIXв.,
посвященные теории гауссовых сумм, были замкнуты в узкие
рамки.
104
3. Второй этап развития теории тригонометрических сумм
в аналитической теории чисел. В 1914 г. были сделаны две
совсем разные работы, с которых началось неожиданно мощное
дальнейшее развитие метода тригонометрических сумм в
теории чисел.
Две работы, о которых мы говорим, это работа Германа Вей-
ля (Н. Weyl) 1914 г., в которой была оценена абсолютная
величина суммы:
где а^, а^_1, ..., а^ — заданные действительные числа, причем
хотя бы одно из них иррациональное, и работа И. М.
Виноградова о распределении квадратичных вычетов. Хотя оценка
Г. Вейля лишь немного лучше тривиальной </? (которая
получается, если все слагаемые заменить 1), однако и она уже ведет
к замечательным приложениям.
Использовав ее, Харди и Литтльвуд создали первый мош,ный
аналитический метод для решения аддитивных задач теории чи-
оел. Осуп1;ествление этого метода Харди и Литтльвудом состоит
в использовании целой цепи глубоких соображений, из которых
главные: 1° применение интегрирования по контуру, 2°
применение ряда Фарея, с которым связано разбиение контура
интегрирования на большие и малые дуги (впервые примененное
к подобным вопросам Вороным в его работе 1903 г.) и 3°
использование неравенства Г. Вейля, которое позволяет
оценивать интеграл по малым дугам.
Этим методом Харди и Литтльвуду удалось, в частности,
дать более совершенное, чем у Гильберта, доказательство
теоремы Варинга: N = х\ + х%-\-,,,-\-х^, даюп1;ее
асимптотическую формулу для числа представлений суммой к п-х
степеней целых чисел любого достаточно большого целого числа,
из которой получилась хорошая оценка для числа/с слагаемых,
при которых уравнение Варинга имеет решение для любого-
такого N.
Метод Харди и Литтльвуда дал решение также ряда других
важных задач.
J о'у
Другая из двух упомянутых в начале этого пункта работ
была работа И. М. Виноградова, которую он представил в 1914 г.
на Математический факультет Петербургского университета
для того, чтобы быть «оставленным при Университете для
подготовки к профессорскому званию» (напечатана она была позже,
в 1918 г., в значительно расширенном виде). В этой работе,
используя специальным образом гауссову сумму,
Виноградов показывает, что абсолютная величина суммы символов
Лел^андра по pi подряд идущим натуральным числам,
каково бы ни было р^, не больше, чем у~р \пр, откуда,
в частности, получается, что среди натуральных чисел,
меньших ур In/?, всегда есть хотя бы один квадратичный невычет
модуля р.
Мы позволим себе привести это замечательное доказательство.
Но раньше сделаем несколько общеизвестных замечаний о
аг
гауссовых суммах. Во-первых, гауссова сумма ^е^ , где
г
г —все вычеты и а не делится на р, легко сводится на
сумму ^е^
х==о
Действительно, слагаемое этой последней суммы при х = 0
равно 1, вычеты же (mod р) квадратов 1^, 2^, . . . , (/? — 1)^ суть
все квадратичные вычеты г (mod р), но каждый взятый два
раза, так как х^ — ^1 = {^i + ^2) i^i — ^2)» и если ж^ + ^2 Д®"
лится на /?, то х^ и х^ сравнимы (mod /?), если же нет, то
несравнимы. Вычеты (mod р) двух равно отстоящих от концов
этого ряда квадратов поэтому одинаковы. Мы имеем, таким
образом, 2^^ =1 + 2^е^ . Во-вторых, если п невы-
х^=0 г
2тсг 27гг
а г — an
четы (mod /?), то 1 + ^ ^ ^ + 2^ ^' "" ^^' ^^ + ^^' ^^ +
г
11 „1 27тг 2 2^^^
-f-1 :г=: 0; поэтому у\ е^ =Ve^ — S^^ '^ ^^^^ ^^^
J06
7h + ''{j} — '
*)_i 2m , г)_1 2M
V
p-1 2!!i
Заметим еще, что модуль суммы ^е^ равен У р. Это
следует из того уравнения х^ — Ах + В = 0^ корнями которого
являются периоды (т, 1) и (т, g). Но сейчас обычно выводят
непосредственно так. Помножая сумму на ей комплексно со-
р-1 -^ах^ PZ^ ^Jllaix^-v^)
пряженную 2 ^ ^ , получаем V ^ ^ . Сделав здесь
х=0 х,у=0
подстановку х — у -^ t, так как х^ — У^ = У^ + 2^г/ -\- t^ — У^ ="
т)_1 27тг ,„ -j3_-i 27тг ^ , ^_л 2ni
= 2ty + ^2, получаем ^^^ 2^^ .Ho^e^ , если2а^
не делится на р, равно нулю. Число 2а^ делится на р только
27тг ^_.
при it = 0. Таким образом, мы получаем е ^ V 1 = 1/? = /?.
У=0
Таким образом, модуль исследуемой суммы равен YPi ^
следовательно, сама эта сумма равна s]//?, где |s| = l.
Переходим теперь к доказательству теоремы Виноградова.
т)—1 2тсг ^_л 2тгг ^,_^
771=1 m=l mi=l
откуда мы получаем
S
о]> ^ \Р
2тс1
1 ''„^ /mN ^«">
m ---1
70/
Просуммируем это равенство по а от 1 до р^, где Pi—-любое
натуральное число:
S(7)=;7?S(7)S»' ■
Перейдем к модулям (звездочками указаны ссылки на
примечания):
2кг , . , 2Tti
р_1 . -^ (Pi+1)^ ~- "г
а^1
Р-1
У Р ш^1
ni — яг — —7Ti -
'(е ^
27гг
— m
Р-1
<
** _
Р-1
2
2 у 1
V F 7п=1 sm —
in^^
Но тут о <; —'- <С Y ' ^ ^^ интервале О <; о: <^ Y
^^^2" 2 2
^ = —, т. е. sina:>> —о;. Другими словами,
sma;
>
. Tzm 2 Tzm 2т,
Р 7г"У "" р
Следовательно,
Pi
р-1
р-1
2
2(i)|<^2^-i/?S^<V?inp.
а=1 ^ ^ '^ '^ -г m=i m=i
Этот метод был распространен И. М. Виноградовым на
вопрос о распределении вычетов высших степеней и применен
Р» — am
* Если 2j ^^ рассмотреть как геометрическую прогрессию.
а=1
** Тут употребляем формулу Эйлера.
*** Тут используем свойство, что равноотстоящие от концов суммы
слагаемые равны.
JOS
к ограничению наименьшего первообразного корня g простого
числа р, Виноградов показал, что
где к — число различных простых делителей.
Период, начавшийся в 1914 г. описанными выше работами
Г. Вейля и И. М. Виноградова и по 1934 г., можно назвать
вторым этапом развития теории тригонометрических сумм в теории
чисел. По мнению И. М. Виноградова, характерными чертами
этого этапа были две: 1° отказ от нахождения точных значений
сумм и переход к их оценкам, но зато 2° освобождение от
требования, чтобы высказывания, при их помощи получаемые,
относились только к полной системе вычетов. Однако
сохранялось условие, чтобы суммирование производилось по отрезку
чисел натурального ряда, взятых подряд.
Уже в 1916 г. начали рассматривать куски полных
рациональных тригонометрических сумм, причем трудности,
возникающие при этом, не больше тех, какие имеются в теории
иррациональных сумм (т. е. таких, как суммы Г. Вейля, где а,
иррациональные), так как многочлен с иррациональными
коэффициентами все равно не периодичен по модулю р. Иногда
даже и в случае рациональной суммы выгодно брать
рациональные приближения коэффициентов, но зато с малыми
знаменателями, как это делается в случае иррациональной
суммы. В этот второй период были решены методом
тригонометрических сумм многие важные задачи. Мы уже упоминали
о знаменитых работах Харди и Литтльвуда. Были получены
важные теоремы о распределении дробных долей многочлена,
о представлении чисел в форме целого многочлена от многих
переменных:
rii-x^ + • . • + (^кХ^ + ср (a:i, . . . , хя-),
(где ср —многочлен степени не выше п — 1), о некоторых
системах диофантовых уравнений и т. д.
В 1928 г. Р. О. Кузьминым была получена следующая
весьма общая оценка тригонометрической суммы. Если f{x) на
109
отрезке а < л; < Z; — такая функция, что 6 < /' (:к)< 1 — &
/ 1 \ I ^ I 2
(где 0<е<у] и/^ (х) монотонна, то ^^^'''^^''ч ^ Т '
Тут X пробегает все целые числа между ажЪ включительно.
Геометрически это обозначает, что если имеется ломаная,
состоящая из векторов длины 1,и такая, что каждый следующий
вектор повернут относительно предыдущего на все больший и
больший угол, заключающийся между О и 1—^^, то конец этой
ломаной лежит недалеко от ее начала.
Отметим, что в настоящее время знак гауссовой суммы^
пожалуй, наиболее просто можно определить, используя
эту лемму Кузьмина. А именно, полную гауссову сумму
V в^ нетрудно свести к вычислению двух следующих сумм:
2-гЛ ^ 2^хг^ 2
Относительно W легко показать, что Re {(1 — i)W) ^~^V р^
2
где Re { } обозначает действительную часть { }. Что же
касается до Z, то, применяя лемму Кузьмина, можно показать^
что
Соединяя оба эти обстоятельства, получаем определение
знака в гауссовой сумме.
4. Третий этап развития теории тригонометрических сумм
в теории чисел. Характерной чертой третьего этапа, начавшегося
работой И. М. Виноградова 1934 г., является освобождение от
того условия, чтобы суммирование проводилось по всем
натуральным числам некоторого отрезка подряд. Так, чтобы было,,
например, возможно суммировать по простым числам или по
числам, имеющим не более, чем столько-то простых множителей
и т. д., И. М. Виноградов показал, что получаются хорошие
оценки двойных сумм:
у у ^.2-г/(х, у)
ПО
iio различным ооластяхМ, где х и у прооегают достаточно густые
независимые друг от друга последовательности целых чисел и
функция j{x, у) не разлагается в сумму двух функций, каждая
от одной переменной. Этот способ оказался очень сильным; при
помощи него И. М. Виноградов получил свою более тонкую
оценку суммы Г. Вейля и оценки сумм, при помощи которых он
доказал теорему Гольдбаха.
Конечно, мощный современный метод тригонометрических
сумм, давший в последнее десятилетие столько глубоких теорем
теории чисел, далеко ушел за рамки того, что дал Гаусс, но
все же у истоков его стоит рассматриваемая работа Гаусса
1811 г. «О суммировании некоторых особых рядов».
5. Причины успешного применения тригонометрических сумм
в теории чисел. Подобно тому, как это мы сделали в заключении
параграфа об алгебраических числах, разумной здесь поставить
такой вопрос. Во-первых, говорит И. М. Виноградов, целые
числа идут в ряду действительных чисел периодически, и
потому, очевидно, можно удобно описывать их свойства при
помощи периодической функции е^^^^. Но можно сделать и другое
замечание. Тригонометрические суммы являются тем орудием,
которое позволяет какую-нибудь искомую в теории чисел
величину выразить формулой. Например, число решений сравнения
а^л\ + Л2Х2 -)- • • • -V-ajiX^ ^z О (mod /?),
1де (li — заданные цельте числа, как нетрудно убедиться, равно
А когда искомое число записано формулой, то можно.уже
забыть задачу теории чисел и находить величину этой формулы
или оценивать эту величину — это уже совсем другая задача,
и часто, ввиду удобных свойств функции е^"^^, ее можно решить.
Это аналогично тому положению, которое имеет место в
теории дифференциальных уравнений. Решая какую-нибудь
112
задачу геометрии, механики или физики, составляют
соответствующее ей дифференциальное уравнение; а затем занимаются
второй, уже совсем другой задачей — как решить это
уравнение; эта задача основана на теоремах о дифференциальных урав--
нениях как таковых.
А.ПНорден
ГЕОМЕТРИЧЕСКИЕ
РАБОТЫ
ГАуССА
8 к. Ф. Гаусс
=s^
1. Теория поверхностей (115).—2. Теория параллельных (128).—
3. Комплексные и гиперкомплексные числа (141). — 4.
Геометрия положения (143).
В геометрии, как и в других областях математики, Гаусс
оставил неизгладимый след.
Его исследования по теории поверхностей составили эпоху
в развитии дифференциальной геометрии,превратив ее из раздела
приложений анализа в самостоятельную науку. Влияние идей
Гаусса в этой области не прекратилось и до настоящего времени.
Однако и в других разделах геометрии — в теории
параллельных, в вопросе геометрических приложений* комплексных
и гиперкомплексных чисел, в геометрии положения — Гауссу
принадлежит ряд замечательных результатов и замыслов.
Но эти результаты остались неопубликованными, а замыслы
оказали только косвенное влияние на его современников, тем
не менее это не лишает их глубокого интереса как для
истории науки, так и для характеристики творческого облика Гаусса.
1. ТЕОРИЯ ПОВЕРХНОСТЕЙ
К вопросам общей теории поверхностей Гаусс подошел в
процессе своих работ по высшей геодезии и геофизике.
В 1812—1816 гг. он занимался изучением геодезических
линий" эллиптического сфероида. В 1816 г., обобщая проблему
картографии, он приходит к общему вопросу о конформном ото-
бражепии произвольных поверхностей друг на друга и
предлагает этот вопрос как тему на соискание премии Копенгагенскому
8* 1U
ученому обществу. При содействии Шумахера, эта тема была
объявлена в 1822 г., и в этом же году Гаусс представил работу
«Общее решение задачи: отобразить часть заданной
поверхности на часть другой заданной поверхности так, чтобы
отображение было подобно отображаемому в мельчайших частях»
(Allgemeine Auflosung der Aufgabe die Telle elner gegebenen
Flache auf elner anderen gegebenen Flache so abzubilden das
die Abbildung dem Abgebildeten in den kleinsten Teilen
ahnlich wird), которая была премирована в 1823 г. (Bd. IV,
187—216)1.
В этой работе поверхность задается уравнениями,
выражающими зависимость прямоугольных координат ее точки в
функции двух независимых переменных величин t я и.
Отобразить одну поверхность на другую, значит установить
закон, согласно которому всякой точке одной поверхности
соответствует определенная точка второй. При этом можно всегда
предположить, что соответствующие точки поверхностей
определяются одинаковыми значениями величин t я и.
Квадраты линейных элементов двух поверхностей,
отображенных друг на друга, выражаются квадратичными формами ^i
О) = edf^ + 2fdtdu + gdu^,
а =- Edt^ + 2Fdtdu + Gdu^.
Условие подобия в бесконечно малом имеет вид пропорции
е ~ f ~~ g '
которая обеспечивает также сохранение углов между
соответствующими линиями.
Интегрируя уравнения
1 С. F. Gauss. Werke, Bd. IV. Gottingen, 1880.
2 Мы употребляем обозначения коэффициентов линейного элемента,
введенные Гауссом в его позднейшей работе.
116
можно придти к решениям следующего вида:
р + iq = const; р — iq = const;
Р + iQ = const; P — iQ =^ const,
где p, q, P, Q — действительные функции переменных t, и.
Общее решение поставленной задачи даст такое отображение,
которое определяется соотношениями:
P + iQ = f{p + iq)\ P-iQ = fAp-iq),
или
P + iQ = ^{p^iqy, P-iQ^^{P + 4)^
и при переходе одного отображения к другому ориентация
отображенных фигур изменяется на обратную.
Общая теория применяется к рассмотрению частных случаев
отображения плоскости, цилиндра, сферы и эллипсоида
вращения на плоскость. Для каждого из этих случаев находятся
конкретные выражения отображающей функции.
Статья содержит еще важное замечание о том, что линейный
элемент всякой поверхности может быть приведен к виду
О) =[n_{dp^ + dq^),
который теперь принято называть изотермическим.
Метод решения задачи конформного отображения,
примененный Гауссом, был ранее разработан Ламбертом^, Эйлером'^^
и Лагранжем^, в применении к частным случаям отображения
сферы или поверхности вращения (Лагранж) на плоскость.
Заслугой Гаусса является то, что он решает общую задачу
конформного отображения аналитических поверхностей.
Второй и наиболее важной работой Гаусса по теории
поверхностей является его знаменитый мемуар «Общие исследования
о кривых поверхностях» (Disquisitiones generales circa
superficies curvas), доложенный Гёттингенскому научному обществу
^1. Н. LaDibert. Anmerkungen imd Zusatze zur Entwerfung
der Land- iind Himmelskarten. Berlin, 1772.
2 L. E u 1 e r. De represaniatione superficiei sphericae super planOi—
Acta acad. sc. Petrop, t. I, 1778.
^ I. L. Lagrange. Sur la construction des cartes geographiques.—
Nouv. Mem. de I'Acad., 1779.
117
8 октября 1827 г. и вышедший в свет в 1828 г. (Bd. IV, 217—258) \
Изложим его содержание.
Суш,ествует три сцоаоба задания поверхности: уравнением
w[x,y,z) = 0, (1)
уравнениями
x = x{p,q); y-=y{p.q)', z = z{p,q), (2)
выражающими зависимость прямоу1^ольных координат точки
поверхности от двух независимых переменных /?, д, или
уравнением
z = f{x,y). (3)
Плоскость называется касательной к поверхности в ее точке
А, если все прямые, соединяющие эту точку с бесконечно
близкими точками поверхности, отклоняются бесконечно мало от
этбй плоскости. Ее положение определяется направляющими
косинусами нормали, которые определяются по формулам:
X — * , . _ :
Z — —
]/^^+wl+wl
А
Va' + в' + с^ '
в
УЖ+в' + с '
с
Va'-\-b'-\-c^
где
Выбор направления. нормали, равносильный выбору
знака у величин X, у, Z, позволяет различить внешнюю сторону
поверхности от внутренней. При первом способе задания это
различение можно произвести, учитывая, что знак выражения
w{x, у, z) будет изменяться при переходе с одной стороны
поверхности на другую.
Рассматривая направляющие косинусы нормали как
координаты точки сферы единичного радиуса, можно отобразить
^ К. Ф. Г а у с с. Общие исследования о кривых поверхностях. Пер,
М. М. Филиппова, Казань, 1895.
118
поверхность на эту сферу. При условии однозначности этого
отображения всякая замкнутая область точек поверхности перейдет
в замкнутую область точек единичной сферы. Площадь этой
последней называется полной кривизной (curvatura totale seu
Integra), соответствующей области точек поверхности, а предел
отношения полной кривизны к площади области,
стягивающейся к точке, называется мерой кривизны (mensura curvaturae)
поверхности в этой точке. Мера кривизны считается
положительной, если тройка направлений, которую определяют две линии
на поверхности и направление ее нормали, ориентирована так
же, как тройка, определенная соответствующими линиями и
внешней нормалью единичной сферы. В противоположном
случае мера кривизны считается отрицательной.
Если в различных точках мера кривизны поверхности имеет
различные знаки, то однозначность сферического отображения
нарушается, а полная кривизна определяется как
алгебраическая сумма полныхкривизн со знакопостоянной мерой кривизны,
т. е. равна интегралу ?Ы^, где к — мера кривизны, а d<^ —
элемент поверхности.
Совмещая начало координате точкой поверхности, аплоскость
хоу — с касательной плоскостью, получим, с точностью до
малых более высоких порядков,
Производя поворот осей, можно уничтожить о;^^, после чего
^^хх ^ ^1/ обратятся в кривизны главных нормальных сечений,
а кривизна произвольного нормального сечения, плоскость
которого образует угол ср с первым главным сечением,
определится по формуле Эйлера и будет равна
XX ^ ^ УУ '
Но мера кривизны поверхности, заданной уравнением (3),
выражается формулой
h — ^^ УУ ху
(1 + 4 + 4)^ '
119
которая принимает вид
к
Z" Z"
XX уу
при указанном выше выборе системы прямоугольных
координат. Таким образом, мера кривизны равна произведению
главных кривизн, а ее знак определяется тем, будут ли выпуклости
главных сечений направлены в одну или в различные стороны.
Для поверхности, заданной уравнением (1), имеет место
формула
к
'^yx^yy'^yz'^y
^х ^y'^z о
а для параметрического задания (2)
к
А2
где
и = АХу^и -f- £>Уии ~Г ^^ии] ^ = AXuv -J- i^yuv ~Г ^^их)\
D' = Axuv + Byuv + Czuv] ^ = A^ + B^ + C\
Следующие пункты работы Гаусса имеют особенно важное
значение для дальнейшего развития теории поверхностей, и
мы изложим их подробнее, позволив себе, однако, для
краткости и наглядности изложения воспользоваться современными
векторными обозначениями, не меняя ничего по существу в
ходе рассуждений Гаусса.
В рассмотрение вводятся следующие величины ^:
Е = Гр] F = Г^Га\ G = Га]
т'
т = Гг)Л
pf qqi
q^VQy
1 Здесь и в дальнейшем скалярное произведение является
сокращенным обозначением суммы парных произведений координат
соответствующих величин, встречающейся у Гаусса.
120
G помощью этих обозначений выводятся деривационные
уравнения, равносильные следующим:
nF — mG . mF — пЕ , D лт
^РР = д ^Р + д ''а + X ^'
— y^'F— m'G m'F—n'E D' д.
^va — д ^P п д ^Q 'У' ~Х ^'
_ W'F — m"G wrF~n"E D" дг
TcKi — д ''р Н д ''о' + ~д" -^^'
где N есть вектор нормали с координатами А, В, С.
Комбинируя эти уравнения, можно придти к соотношению
DD' - D'^ ^ {г^^г,, - гу ^ + E {п'' - пп") +
+ F {пт" — 2т'п' + тп') + G {т'^ — mm').
G другой стороны, легко видеть, что:
m = -jE^; m' = -jEq\ т'' = Г^ — ^Ср\
п = Fp — Y^ Eq] п' = Y ^v'y ^^ ~ Y^^
и
1 1
^VP^qq ^pq =" у-^^О'+'^РЗ у ^PP^
откуда окончательно:
4(£G-F')k = E{EqGq- 2/^pG, + G^) H-
+ F {EpGq -^ EqGp - 2EqFq + AFpFq - 2FpGp) +
+ G {EpGp - 2EpFq + Ep - 2 {EG - F^) {Eqq ~~ 2Fpq + Gpp).
Так как dx^ + dy^ + dz^ ^ Edp^ + 2Fdpdq + Gdq^ -—
линейный элемент поверхности, то последняя формула показывает,
что мера крутизны зависит только от выражения
коэффициентов линейного элемента.
Если одна из поверхностей может быть наложена или
развернута на другую поверхность, то между точками этих
поверхностей можно установить взаимнооднозначное
соответствие так, что, относя соответственным точкам этих поверхностей
одинаковые значения величин /?, ^, мы получим одновременно и
совпадение их линейных элементов, так, что в соответствующих
точках будут иметь место равенства
£ = £', F = F', G^G\
121
Отсюда вытекает следующая теорема: если поверхность
развертывается на некоторую другую поверхность, то мера при-
визны во всех ее точках и полная кривизна ее областей остается
при этом неизменной.
Отсюда же непосредственно вытекает и уравнение Монжа
характеризующее поверхности, наложимые на плоскость.
Далее следует пункт, который мы приведем дословно:
«Теорема, введенная в предыдущем пункте, приводит нас к
рассмотрению поверхностей с новой точки зрения. Если мы
будем смотреть на поверхность не как на границу тела, а как на
тело, одно из измерений которого исчезающе мало, и будем
одновременно считать поверхность гибкой, но не растяжимой,—
в таком случае свойства поверхности будут зависеть отчасти от
принятой ею формы, отчасти же будут абсолютными и
останутся неизменными, в какую бы форму мы не изогнули эту
поверхность. К этим свойствам, исследование которых открывает
новую плодотворную область геометрии, принадлежат мера
кривизны и полная кривизна, в том смысле, в каком мы понимаем
эти выражения; далее сюда же принадлежит и учение о
кратчайших линиях и нечто сверх того, рассмотрение чего мы
откладываем для дальнейшего. При этом понимании плоскость и
всякая развертывающая поверхность, например, цилиндрическая,
коническая поверхность и т. д., должны рассматриваться как
существенно тождественные».
Кратчайшую линию на поверхности можно получить,
применяя методы вариационного исчисления к интегралу:
выражающему длину дуги линии на поверхности. Выкладки
приводят к соотношениям:
pdi = Xdr\ pdri = Ydr] prfC = Zdz,
где p — радиус кривизны кратчайшей линии; dr — элемент
ее дуги, а^, 'у], С и X, F, 2 — направляющие косинусы ее
касательной и нормали к поверхности.
122
Применяя эти соотношения к пучку кратчайших линий,
исходяш;их из некоторой точки поверхности, можно придти к
следуюш;ей теореме: геометрическое место концов дуг
одинаковой длины кратчайших линий^ исходящих из одной точки
поверхности,есть линия, пересекающая все эти линии под прямым углом.
Эту теорему можно обобщить, откладывая равные дуги на
таких кратчайших линиях, которые пересекают ортогонально
произвольную кривую поверхности; концы этих дуг снова будут
лежать на ортогональной траектории кратчайших линий.
Кратчайшую линию можно задать следуюш;ей системой
уравнений:
VEG — F4^ =L. jLdE + ~ Eqdp - F^dp - J Gpdq,
. с E dp , F
^ VEG - F' dq ^ VeG~ F^
где Q — угол, под которым кратчайшая линия пересекает
линии q = const.
Если линии q = const — кратчайшие, а линии р = const—
их ортогональные траектории, то величину р можно выбрать
так, чтобы она была равна длине дуги линий q = const и
квадрат линейного элемента поверхности принял вид
dp'^ + m^dq^,
а мера ее кривизны
7 1 д'-т
Пользуясь предыдущими формулами, можно придти к сле-
дущей теореме: избыток суммы углов треугольника,
образованного кратчайшими линиями поверхности положительной
кривизны, над углом 180°, или же недостаток той же суммы
на поверхности отрицательной кривизны равен площади
сферического отображения этого треугольника.
Последние пункты мемуара посвящены вычислению
поправочных слагаемых, с точностью до которых имеют место
формулы прямолинейной тригонометрии, если их применять к
треугольнику, образованному кратчайшими линиями произвольной
поверхности. Особо отмечается, что всякому такому
треугольнику с углами А, В, С и значениями а, р, ^ меры кривизны в
123
его вершинах соответствует прямолинейный треугольник с
теми же длинами сторон, что и у данного, и с углами, которые
равны, с точностью до величин четвертого порядка относительно
сторон,
л-1(2«н-р + т)'; ^-^2(« + 2Р + т)^;
где ^ — площадь треугольника.
Трудно переоценить то влияние, которое оказали идеи
Гаусса на дальнейшее развитие дифференциальной геометрии.
Хотя понятие наложимости двух поверхностей рассматривалось
еще Эйлером, но только после выхода в свет работы Гаусса
проблема изгибания становится одной из ведущих проблем
геометрии XIX в.
Первые результаты в этом направлении были получены
учеником Гаусса Ф. Г. Миндингом (1806—1885). За ними
следуют работы Лиувилля, Бонне, Желле, Кодацци, Вейнгартена,
Бура, Эннепера, Дини, Бельтрами, Рибокура, Ли, Бианки,
Дарбу и др. Центральное место во всех этих исследованиях
занимала теорема Гаусса о сохранении меры кривизны при
изгибании, получившая название «выдающейся теоремы» (theorema
egregiumi).
Проблема изгибания имела особое значение и в истории
московской геометрической школы, основателем которой является
Карл Михайлович Петерсон (1828—1881). Петерсон окончил
в 1853 г. Дерптский университет, где слушал лекции
работавшего там с 1843 г. Миндинга. В своей кандидатской
диссертации «Об изгибании поверхностей»^ Петерсон показывает, что
поверхность определяется с точностью до положения в
пространстве заданием таких величин,которые можно выразить черезкоэф-
фициенты первой и второй квадратичных форм Гаусса, и
находит те условия, которым должны удовлетворять эти величины.
Петерсону принадлежит постановка задачи об изгибании на
главном основании. В решение этой задачи внесли свой вклад
вслед за Петерсоном ряд представителей московской математи-
^ См. Историко-математические исследования, вып. V, 1952, где
впервые диссертация была опубликована.
124
ческой школы: Д. Ф. Егоров, Б. К. Млодзеевский, СП.
Фиников и др.^
В XX в. под влиянием идей Клейна, понятие наложимости
было распространено на теорию поверхностей различных групп
преобразований (Фубини, Картан) и на другие геометрические
образы, как то: конгруэнции, комплексы и т. д.
Идеи Гаусса получили замечательное обобщение в работах
А. Д. Александрова и его школы. А. Д. Александров понимает
под поверхностью множество точек трехмерного эвклидова
пространства, обладающее следующими свойствами: 1) каждая
точка поверхности обладает окрестностью, гомеоморфной кругу;
2) любые две точки поверхности можно соединить
непрерывной кривой. Хотя изучение поверхности, определенной с такой
общностью, очевидно, не может быть проводимо методами
дифференциальной геометрии, А. Д. Александрову удается, при
дополнительном условии выпуклости, определить понятия
внутренней геометрии, кривизны, сферического отображения
и т. д. поверхности и изучить ряд весьма общих и глубоких
свойств поверхностей и их изгибания. В частности, ему
удается получить обобщение результата Гаусса о равенстве инте
тральной кривизны и площади сферического отображения 2.
Особенно плодотворным оказалось введенное Гауссом
понятие об абсолютных свойствах поверхности, определяемых
заданием квадратичной формы, выражающей квадрат линейного
элемента поверхности. Это понятие было положено Б. Риманом
в основу его знаменитой пробной лекции «О гипотезах, лежащих
в основании геометрии», которую он прочитал в Гёттингенском
университете в присутствии престарелого Гаусса 10 июня 1854 г.
Риман рассматривает многообразие, каждый элемент
которого определяется заданием значений п переменных величин a;j,
Х2, ..., х^, и называет такое многообразие п-кратно
протяженным. В это многообразие путем задания дифференциальной
квадратичной формы переменных х^, х^, ..., x^z коэффициентами,
зависящими от этих же переменных, вносится метрика, кото-
^ См. С. П. Фиников. Изгибание на главном основании и
связанные с ним геометрические задачи. М.—Л., 1937.
^А. Д. Александров. Внутренняя геометрия выпуклых
поверхностей. М.—Л., 1948.
126
рая выражает квадрат' расстояния между бесконечно близкими
точками этого многообразия. Важнейшую роль в
характеристике геометрии, определяемой этой квадратичной формой,
играет величина, связанная с направлением всякого
двумерного элемента многообразия. Следуя Гауссу, Риман назвал эту
величину мерой кривизны многообразия. Многообразие
называется плоским, если мера кривизны всякого направления равна
нулю и его линейный элемент может быть приведен, путем
выбора переменных Жь Жз? •••» ^П5 ^ сумме квадратов их
дифференциалов. Многообразие, кривизна которого постоянна, т. е. не
зависит от выбора точки и направления двумерного элемента,
обладает свойством свободной подвижности фигур. Риман
приводит выражение линейного элемента и такого многообразия;
Сопоставление идей Лобачевского с идеями Римана, которое
имело место в конце 60-х годов прошлого столетия в результате
работ Бельтрами, определило развитие неэвклидовой
геометрии в дифференциально геометрическом направлении. В
последнюю четверть века Бельтрами, Кристоффелем и Липшицем
был разработан аппарат изучения квадратичных
дифференциальных форм, получивший свое завершение в созданном Риччи
абсолютном дифференциальном исчислении, или тензорном
анализе. И здесь важнейшую роль играла теория кривизны,
исходным пунктом которой является теорема Гаусса.
Значение римановой геометрии выступило особенно ярко
после того, как Эйнштейн положил ее в основу построения
теории тяготения. Задача построения единой теории
гравитационного и электромагнитного поля привела к разработке
Вейлем, Картаном, Схоутеном и другими целой системы
геометрий с их различными модификациями, частными случаями и
обобщениями. Целый ряд таких геометрий был открыт и изучен
советскими геометрами.
Но возвратимся к мемуару Гаусса. При вычислении меры
кривизны он вводит величины D, D\ D" (стр. 100), которые
только множителем отличаются от коэффициентов второй
основной квадратичной формы поверхности, играюп];ей такую
важную роль в классической проективно-дифференциальной
геометрии поверхностей и всех геометриях подгрупп
проективной группы.
126
Гёттингецский университет. Современная гравюра
Неменьшее значение имеют и введенные Гауссом
деривационные уравнения, которые дают разложение вектора второй
производной по вектору нормали и векторам первых производных
радиуса-вектора точки поверхности. Обобщение этих
уравнений может быть положено в основу построения теории
поверхностей многомерных пространств проективной группы и ее
подгрупп ^.
Крупную роль в теории поверхностей и конгруэнции
сыграло понятие сферического отображения. Оно не потеряло своего
значения и при переходе к изучению теории гиперповерхностей
пространства проективной группы и ее подгрупп, где в
качестве его обобщения выступает понятие внутренней геометрии
второго рода 2.
В заключение остановимся на двух черновых заметках
Гаусса, опубликованных только после его смерти.
^ А. П. Н о р д е н. Пространства аффинной связности. М.—Л.,
1950; см. гл. 5.
2 Там же.
127
в первой из них, относящейся к 1822—1825 гг., он вводит
величину, которую называет боковой кривизной (Seitenkrum-
mung) кривой на поверхности и находит ее выражение через
коэффициенты первой квадратичной формы ^. Эта величина
совпадает с геодезической кривизной, открытой Миндингом в 1830 г.
Во второй заметке 1823—1827 гг. Гаусс дает уравнение
меридиана поверхности вращения, наложимой на данную
поверхность вращения. Кроме того, записав уравнение трактриссы,
он называет ее «кривой, вращение которой образует нечто
противопоставляемое (Gegenstuck) сфере» 2. Так как понятие меры
кривизны поверхности и способы ее вычисления были в это
время хорошо известны Гауссу, ТОМЫ должны придти к
заключению, что ему принадлежит и первый пример поверхности
вращения постоянной отрицательной кривизны, т. е. псевдосферы,
открытый независимо от Гаусса Миндингом в 1839 г.
'2. ТЕОРИЯ ПАРАЛЛЕЛЬНЫХ
Проблема обоснования геометрии Эвклида привлекала
внимание Гаусса с 1792 г. "(Bd. VIII, 238). Но первым
сохранившимся документом, свидетельствующим о результатах его
размышлений по теории паралле!1ьных, является следующее место из
письма 1799 г. к Фаркашу Бояи: «Я лично далеко продвинулся
в моих работах (хотя другие совершенно не связанные с этим
занятия оставляют мне для этого и мало времени); однако
дорога, которую я выбрал, ведет, скорее, не к желательной цели,
а к тому, чтобы сделать сомнительной истинность геометрии.
Правда, я достиг многого, что для большинства могло бы сойти
за доказательство, но все это не доказывает в моих глазах ровно
ничего, например, если бы кто-либо мог доказать, что возможен
такой прямолинейный треугольник, площадь которого больше
любой наперед заданной, то я был бы в состоянии строго доказать
всю геометрию. Большинство сочтет это за аксиому, я же нет.
Так могло бы быть, что площадь всегда будет ниже (infra)
некоторого данного предела, сколь бы удаленными друг от
1 С. F. G auss. Werke, Bd. VIII. Leipzig, 1900, стр. 386—395.
2 Там же, стр. 265.
128
друга в пространстве не были предположены три вершины
треугольника.
Таких положений я имею много, но ни одно из них не
нахожу удовлетворительным» (Bd. VIII, 159).
Известно, что допущение существования треугольника
сколь угодно большой площади равносильно аксиоме о
параллельных (11-й аксиоме) Эвклида, и приведенный отрывок
показывает, что, считая основной проблемой геометрии
обоснование этой аксиомы, Гаусс стал на путь изучения следствий из
ее отрицания. Однако он еще далек от мысли о возможности
неэвклидовой геометрии, как это показывают позднейшие
документы.
Так, в письме 1804 г. к Ф. Бояи мы находим следующие
слова: «Твой метод меня тоже не удовлетворяет. Я хочу со
всей возможной ясностью обнаружить тот камень
преткновения, который я еще нахожу в нем (и который принадлежит
к той же группе подводных камней, на которых терпят
крушение и мои попытки). Однако я еще надеюсь на то, что некогда,
и еще до моего конца, эти подводные камни позволят
перебраться через них» (Bd. VIII, 160).
Таким образом, еще в 1804 г. Гаусс не терял надежды на
возможность доказательства постулата Эвклид-а. Насколько
мы можем судить, он сохраняет эту надежду и в последующие
годы. Так, в черновой записи 1808 г. он определяет «линию,
параллельную прямой» как место точек, равноотстоящих от
этой прямой, добавляя: «будет ли эта линия сама прямой,
остается еще невыясненным» (Bd. VIII, 163).
В том же году Шумахер отмечает в своем дневнике, что
Гаусс свел теорию параллельных к вопросу о существовании
абсолютной меры длины, но не считает еще эту работу
достаточной (Bd. VIII, 165).
Еще в 1813 г. на черновом листке, среди других замечаний
под общим заголовком «Идеи», Гаусс пишет: «В теории
параллельных линий мы до сих пор не опередили Эвклида. Это partie
honteuse^ математики, которая, рано или поздно, должна
принять совершенно другой вид» (Bd. VIII, 166).
^ Позорная часть.
9 к. Ф. Гаусс 129
Наконец, в 1816 г., в отзыве на две попытки доказать
аксиому Эвклида, Гаусс повторяет: «Мы не продвинулись дальше
того места, где был Эвклид 2000 лет тому назад» (Bd. VIII, 170).
Поворотным пунктом в истории взглядов Гаусса на
основания геометрии мы должны считать 1817 г. В этом году в письме
к Ольберсу встречается следующая фраза: «Я все более и
более прихожу к убеждению, что необходимость нашей
геометрии не может быть доказана...» (Bd. VIII, 177).
Из этого высказывания Гаусса мы видим, что он подошел
к признанию недоказуемости аксиомы Эвклида, а
следовательно, и возможности неэвклидовой геометрии, но еще не
совершил последнего шага в этом направлении.
Чтобы Гаусс совершил этот шаг или, по крайней мере,
признался в этом, потребовался внешний толчок, которым явилось
сообщение о работах Швейкарта.
Фердинанд Карл Швейкарт (1780—1857) был профессором
права в Харькове (1812—1816), Марбурге (1816—1820) и
Кенигсберге. Он занимался математикой как любитель и в
1807 г. издал книгу «Теория параллельных с предложением
их изгнания из геометрии», в которой предлагает только
некоторую формальную перестройку изложения Эвклида.
В 1817 г. ученик Гаусса Герлинг был назначен в Кенигсберг
профессором астрономии, где он познакомился со Швейкартом.
Интересуясь проблемой параллельных и часто касаясь ее в
переписке с Гауссом, Герлинг написал ему в 1819 г. письмо, в котором
сообщил, что Швейкарт усматривает ошибки в своей «Теории
параллельных», но не оставил предмета «и в настоящее время
почти уверен, что положение Эвклида недоказуемо без каких-
либо дополнительных данных и что ему не кажется
невероятным, что наша геометрия есть глава некоторой более общей
геометрии».
К своему письму Герлинг приложил заметку Швейкарта,
датированную декабрем 1818 г. Вот наиболее существенные
положения этой небольшой заметки:
«Существует двоякая геометрия — геометрия в собственном
смысле, или эвклидова, и астральное учение о величинах.
Треугольники последнего обладают той особенностью, что
сумма их трех углов не равна двум прямым.
130
Это предположение позволяет строго до1^азать:
a) Что сумма трех углов треугольника меньше двух
прямых.
b) Что эта сумма тем меньше, чем больше площадь
треугольника.
c) Что высота равнобедренного прямоугольного
треугольника возрастает по мере возрастания его сторон, но, однако,
не может превзойти некоторую линию, которую я называю
постоянной.,.
Эвклидова геометрия имеет место только в том
предположении, что постоянная — бесконечно велика...» (Bd. VIII, 179—
181).
Категорическая форма этой заметки не позволяет, однако,
забывать, что, согласно Герлингу, Швейкарт был только «почти
убежден» в недоказуемости эвклидовой геометрии. Возможно,
что вследствие этих не преодоленных до конца сомнений Швей-
карт и не опубликовал своих исследований. Он только сообщил
о них своему племяннику Тауринусу, который хотя и
продвинулся довольно далеко в развитии неэвклидовой геометрии, но
тоже не смог до конца освободиться от мысли о безусловной
истинности геометрии Эвклртда^.
Однако вернемся к Гауссу. В ответ на письмо Герлинга
он пишет ему 16 марта 1819 г.: «Заметка господина профессора
Швейкарта доставила мне необыкновенно много удовольствия,
и я прошу выразить ему мои лучшие чувства. Почти все списано
из моей души» (Bd. VIII, 181; курсив наш.— А, Н,*), Обсуждая
далее детали заметки Швейкарта, Гаусс еще раз подчеркивает
полное совпадение его воззрений со своими.
Нам осталось отметить немногие места из позднейшей
переписки Гаусса, относящиеся к неэвклидовой геометрии.
В первом из дошедших до нас писем к Тауринусу он пишет
в 1824 г.: «Допущение, что сумма трех углов [треугольника]
меньше 180°, приводит к своеобразной, совершенно отличной
от нашей (эвклидовой) геометрии, которая обладает полной
1 Сведения о Тауринусе и отрывки из его сочинений приведены
в книге: Р. S I а с к е 1 und F. Е п g е 1. Die Theorie der Parallellinien
von Euklid bis auf Gauss. Leipzig, 1895.
9* 231
внутренней носледовательностыо и которую я развил для себя
настолько удовлетворительно, что могу решить впей всякую
задачу, предполагая определение некоторой константы, которую
нельзя охарактеризовать а priori» (Bd. VIII, 187).
В 1832г., сообщая Герлингу о получении Appendix'a Яноша
Бояи, Гаусс высказывает свое полное согласие с идеями
последнего, характеризуя его как гения первой величины (Bd. VIII,
220).
В 1841 г. Гаусс знакомится с немецким изданием «Geometri-
schp Untersuchungen» Н. И. Лобачевского и сообщает Энке о
своем желании ознакомиться с другими произведениями
русского геометра (Bd. VIII, 232).
В 1844 г. в двух письмах он сообщает Герлингу, что достал
все сочинения Лобачевского, кроме «Начал геометрии»,
напечатанных в Казанском вестнике в 1829—1830 гг. Во втором из
этих писем Гаусс вспоминает об отрицательном отзыве на «Geo-
metrische Untersuchungen» в немецком журнале «Gersdorf Re-
pertorium», (1840, Bd. 3, стр. 147). Об этом отзыве он пишет:
«Для всякого сведущего читателя ясно, что рецензия
принадлежит невежественному человеку». «С тех пор, как я имел
возможность,— пишет он далее,— прочесть эту маленькую работу
(т. е. Geomietrische Untersuchungen.— А, Я.), я имею о ней
весьма лестное суждение. Именно, она обладает значительно
большей согласованностью и точностью, чем другие большие
статьи Лобачевского, напоминающие дремучий лес, который
трудно пройти или обозреть, не ознакомившись с отдельными
деревьями» ^.
Далее Гаусс отмечает следующее место в статье Лобачевского
«Geomietrie imiaginaire», напечатанной в XVII томе журнала
Крелля за 1837 г.: «Я доказал в другом месте, опираясь на
некоторые астрономические данные, что в треугольнике, стороны
которого почти равны расстоянию Земли от Солнца, сумма
углов никогда не может отличаться от двух прямых больше,
чем на 0.0003 вшестидесятеричных секундах»^. Не будучи уве-
1 При всем уважении к творениям нашего великого геометра трудно
не согласиться с этим суждением Гаусса.
2 Н. И. Лобачевский. Поли. собр. соч., т. III. М.—Л., 1951,
стр. 147.
132
рен в том, что эта ссылка Лобачевского относится к его работе
«О началах геометрии»^, которой не было в распоряжении
Гаусса, он выражает намерение написать самому Лобачевскому
(Bd.VIII, 235—237). При этом Гаусс вспоминает, что по его
представлению Лобачевский был избран членом-корреспондентом
Гёттингенского ученого общества, а также и то, что в своем
благодарственном письме по поводу этого избрания
Лобачевский жалуется на свою большую административную нагрузку,
которая мешает его научной работе.
Последние упоминания о Лобачевском содержатся в
письмах Гаусса к Шумахеру и Струве в 1842 г. В первом из них он
отмечает, что Лобачевский шел по пути, отличному от его
собственного, и развивал свои идеи «мастерски и в подлинно
геометрическом духе» (Bd. VIII, 238—239).
До самой своей смерти Гаусс не сделал ни одного печатного
или публичного устного заявления о возможности неэвклидовой
геометрии или работах Лобачевского, Вбяи и Швейкарта. Во*
лее того, он просил Тауринуса считать свое наиболее
подробное высказывание о нёэвклидовой геометрии частным и никоим
образом не предавать его гласности (Bd. VIII, 187).
Только после смерти Гаусса все отрывки его писем и
черновики, относяш;иеся к теории параллельных, были
опубликованы и стали достоянием широкой математической
общественности.
Постараемся теперь по возможности систематически
изложить те сведения, которые позволяют судить о
достижениях Гаусса в вопросе о построении системы неэвклидовой
геометрии.
В 1831 г. Гаусс сообщает Шумахеру, что начал записывать
кое-что из своих размышлений, которые частично уж:е имеют
сорокалетнюю давность и которые он ранее никогда не
записывал (Bd. VIII, 213).
Эти записи сохранились и содержат абсолютную теорию
параллельных прямых, т. е. те положения этой теории, которые
не зависят от аксиомы Эвклида.
1 Н. И. Лобачевский. Поли. собр. соч., т. Т. М.—Л., 1946,
стр. 207—208.
JS3
Прежде всего, Гаусс вводит следующее определение
параллельных, которое, по существу, не отличается от определения,
принятого независимо друг от друга Лобачевским и Ббяи:
«Если прямые AM, BN не пересекаются, но каждая прямая,
проведенная через А между AM и АВ, напротив, пересекает BN,
то AM называется параллельной5Л^». Далее он намечает
доказательство существования параллели, основываясь на
интуитивном представлении о непрерывности, и доказывает теоремы
о независимости параллелизма от точки, о взаимности и
транзитивности параллелизма, а также теоремы о том, что прямая,
находящаяся целиком между двумя параллелями, тоже им
параллельна, и что параллельные не пересекаются при продолжении
в сторону, обратную направлению их параллелизма (Bd. VIII,
203-206).
В другом отрывке вводится определение соответственных
точек параллельных прямых как концов секущей равного
наклона к этим прямым и доказывается, что точки,
равноудаленные (в одну сторону) от соответственных, сами будут
соответственны, а также и то, что соответствие точек на трех
параллельных прямых — транзитивно (Bd. VIII, 207).
В третьем отрывке кроме повторения некоторых из этих
теорем содержится определение т/?о^ьг как такой линии, которая
является геометрическим местом соответственных точек на
пучке параллелей; эта линия рассматривалась Лобачевским
под названием предельной линии. Однако Гаусс не говорит
ничего о том, является или не является эта линия прямой, и,
следовательно, не становится здесь, как и в предыдущих
теоремах, на определенную точку зрения относительно аксиомы
Эвклида (Bd. VIII, 208, 209). Такой же абсолютный характер
носит у него определение линии, равноотстоящей от прямой
(Bd. VIII, 163).
Еще об одном шаге Гаусса в направлении развития
абсолютной геометрии мы узнаем из письма Вахтера 1816 г. Излагая
мысли, которые ему были ранее сообщены Гауссом^, Вахтер
пишет следующее: «Эвклидова геометрия неверна; но тем не
менее истинная геометрия должна начинаться с той же одиннад-
1 Вахтер виделся с Гауссом в апреле 1816 г. (Bd. VIII, 176).
134
цатой эвклидовой аксиомы или постулата о линиях и
поверхностях, которые обладают свойством, утверждаемым этой
аксиомой. Вместо прямой линии и плоскости нужно, однако,
полагать наибольшие круги того шара, который описан
бесконечным радиусом» (Bd. VIII, 175).
Из этого отрывка следует, что Гауссу было известно
свойство поверхности вращения «тропы» вокруг ее оси или свойство
предельной поверхности Лобачевского, согласно которому
внутренняя геометрия этой поверхности будет эвклидовой,
независимо от аксиомы Эвклида.
Черт. 1
Черт. 2
Положение неэвклидовой геометрии, которое было
известно Гауссу еще в 1799 г., есть положение об ограниченности
площади треугольника. Это положение развито им подробно в 1832 г.
в письме к Ф. Ббяи, написанном по поводу получения Арреп-
dix'a Я. Ббяи (Bd. VIII, 221—223). Отмечая, что «если две
прямые аЬ, ас пересекаются под углом 'f, то третья прямая de мо-
жеть быть построена (beschaffen) так, что аЬ ||| ed, ас Щ de"»,
т. е., формулируя аксиому параллельности, отрицающую
аксиому Эвклида, Гаусс предполагает, что площадь,
заключенная между этими прямыми, конечна и выражается функцией
/ (180° —^f). Рассматривая, с другой стороны, треугольник с
тремя попарно параллельными сторонами cd, hg, fe и тоже
предполагая конечность его площади ^, он выводит из черт. 1:
/(cp) + /(180°-cp) = t.
Но из черт. 2 усматривается, что
/(?) + /('Ь)+ /(180°-ср-4) = f,
135
откуда следует, что
/(? +1») = /(?) + /W-
Полученное функциональное уравнение имеет решение
/((р) = ср-const.
Наконец, из черт. 3 можно усмотреть:
а = /(Л)
180°
В
t\ ^ = /{В)
180°
Черт. 3
Т — /(^) — 180° ^*
откуда легко следует, что площадь
треугольника
180° — (А^В + С) ,
Z = ■
180°
Полученное соотношение сразу показывает, что:
1) сумма углов треугольника меньше 180°;
2) сумма эта уменьшается при возрастании плош,ади;
3) плоп];адь треугольника не может превзойти величины t.
Все эти положения были известны Гауссу значительно
ранее 1832 г. и отмечались еще в письме Герлингу в 1819 г.
(Bd. VIII, 182). Из них же следует невозможность подобных
треугольников, а следовательно, и подобных фигур вообще,
которая отмечалась Гауссом еще в 1816 г. (Bd. VIII, 169).
Перейдем теперь к вопросу о выводе основных соотношений
гиперболической тригонометрии, который справедливо
считается одним из важнейших этапов построения неэвклидовой
геометрии.
В письме 1816 г. Вахтер сообщает Гауссу, что он
«занимался разысканием подхода к Вашей трансцендентной
тригонометрии» (Bd. VIII, 176). Из контекста этого письма нельзя сделать
вполне определенных выводов о том, была ли в это время
решена или только поставлена Гауссом проблема построения
тригонометрии.
136
однако в письме 1819 г. Герлингу Гаусс приводит формул
1п2(1 -Ь К2)'
выражающую площадь, заключенную между двумя взаимнюпер-
пендикулярными прямыми и третьей прямой, которая
параллельна первым двум. Площадь эта выражается через постоянную
Швейкарта С, т. е. длину перпендикуляра, опущенного из
вершины прямого угла на эту третью прямую (Bd. VIII, 182).
Эта формула показывает, что Гауссу в это время уже было
известно основное соотношение между углом и стрелкой
параллелизма.
Следующая заметка, содержащая тригонометрические
формулы, относится к 1832 г. В своем письме того же года к Ф. Бояи
Гаусс предлагает его сыну задачу кубатуры тетраэдра
неэвклидова пространства. Указанная заметка содержит набросок
подхода Гаусса к решению этой задачи^. Он рассматривает две
грани тетраэдра, являющиеся прямоугольными
треугольниками 134 и 432 с вершинами прямых углов в точках 1 и 4, и
приводит формулу, связывающую абсолютную меру сторон этих
треугольников с их углами. Формула имеет следующий вид:
ctg2 Z 431 ctg2 / 341 — ctg2 / 234 (^llS^Y = l,
и легко выводится из основных формул гиперболической
тригонометрии. Она показывает, что Гаусс владел в это время
этими основными формулами и употреблял вместо гиперболических
функций тригонометрические функции мнимого аргумента
(Bd. VIII, 228). С той же формой записи мы встречаемся и в
другом черновике, относящемся к 1836 г. (Bd. VIII, 233).
Весьма интересным оказался черновой отрывок 40-х годов,
расшифрованный Штеккелем и содержащий вывод формул
гиперболической тригонометрии (Bd. VIII, 255—264).
Ввиду своеобразия метода Гаусса мы позволим себе изло-
1 Различные решения этой задачи были даны Лобачевским в работах
«О началах геометрии» (Полное собр. соч., т. I) и «Применение
воображаемой геометрии к вычислению некоторых интегралов» (там же, т. IIJ).
137
жить схему части его рассуждении, допустив некоторые
несущественные упрощения. Гаусс рассматривает две функции:
f / \ ds
Первая из них выражает отношение бесконечно малой дуги
окружности к соответствующему центральному углу в
функции ее радиуса, а вторая выражает отношение бесконечно малой
антибазы двупрямоугольника Сак-
кери к его базе в функции боковой
стороны ^.
Гаусс предполагает, что для
бесконечно малых фигур справедлива
тригонометрия Эвклида, т. е., точнее
говоря, ее формулы справедливы с
точностью до бесконечно малых
высшего порядка. С той же степенью
точности допускается и замена
бесконечно малой дуги хордой, а
синуса и тангенса бесконечно малого
угла — самим углом.
Чтобы установить связь между
функциями if{x) и g{x)j рассмотрим
четырехугольник ABCD с бесконечно малым основанием
АВ = а и с прямыми углами в трех первых вершинах
(черт. 4). О величине его четвертого угла а мы не будем делать
никаких предположений. Пусть перпендикуляр DE к стороне
CD пересекает сторону АВ (или ее продолжение) в точке Е,
Соотношение (**) будет приближенно справедливо и для
четырехугольника с тремя прямыми углами, так что, вводя
обозначение
BC^AD^DE = X,
мы получим
АЕ = ВЕ — ВА^ [g^ [х) — 1) а.
^ Независимость этих функций от положения фигур, естественно,
иредполагает свободную подвижность последних. Эта подвижность
принимается Гауссом без оговорок, так же как она принималась и всеми
современными ему геометрами.
Черт. 4J
U8
с* другой стороны, применяя соотношение (*) к
треугольнику ADE, мы получим
2 ^-^ f{x) ^•
Дадим теперь приращение dx боковой стороне
четырехугольника ABCD. В таком случае его сторона CD получит
приращение
FD'^ag'{x)dx,
которое с другой стороны совпадает со стороной треугольника
DFD' и будет противолежать бесконечно малому углу -^—а,
откуда следует приближенное равенство
'■<^-г
Сравнивая полученные результаты, мы придем к
соотношению
^'н = ^^. (I)
Второе соотношение мы можем получить, рассматривая
прямоугольный треугольник ABC с бесконечно малым углом
со при вершине Лис
катетом АС = X (черт. 5).
Отложив на этом катете бес- Л^-^'^^
конечно малый отрезок
Л'
с
АА' = dXj восстановим к не- /7' С
му перпендикуляр А'А" ;^ Черт. 5
^^dxoi.B точке А" гипотенузы восстановим перпендикуляр Л"С'
к А'А^^ и продолжим до точки С его пересечения с катетом
СВ, Треугольник А^С'В будет бесконечно мало отличаться от
прямоугольного треугольника с углом о при вершине Л",
вследствие чего
СС ^ df {х) О) - /' {х) dx О).
С другой стороны,
ее ^ A'A'g {х - dx) ^ A'A"g {х) ^ g {х) dxo^,
откуда
r{x) = g{x). (II)
139
Исключая функцию g {х) из соотношений (I) и (II), Гаусс
показывает, что функция у-=/{х) удовлетворяет
дифференциальному уравнению
первый интеграл которого имеет вид
(?/'2--1): 2/2=: const.
Для постоянной интегрирования Гаусс вводит обозначение
— к^ и, разделяя переменные, получает решение
кх = sltc sin к у-\-с,
причем, так как х должно стремиться к нулю вместе с у, то
С = 0,
Таким образом, оказывается, что функции, введенные Гауссом,
имеют следующее окончательное выражение:
/(^)
sin кх
g(x) = cos Аж.
Черт, б
получить
Чтобы перейти к собственно
тригонометрическим формулам, можно
проварьировать стороны а, 6, с
прямоугольного треугольника ABC и
сравнить его с измененным
треугольником АВ'С со сторонами a-\-da,
b -\- dbj с + dc.
Из черт. 6 легко видеть, что с
точностью до бесконечно малых
высшего порядка имеет место равенство
dc = dbg (а) sin В + da cos В.
Аналогичным образом можно
dc = dag {b) sin A + db cos A.
Ho гипотенуза вполне определяется заданием катетов и,
приняв во внимание взаимную независимость da ж db, а также
считая их одинаковыми в обоих уравнениях, получим следую-
140
щие соотношения:
cos JS = g {b) sin A\ cosA = g (a) sin B,
Аналогичными рассуждениями Гаусс приходит к
соотношению
Комбинируя его с предыдуш;ими и подставляя выражения
функции g{x), легко получаем уравнения, связывающие углы
и стороны прямоугольного треугольника:
cos В — cos kb sin А] cos А = cos ка sin В;
cos ка cos kb =^ cos kc,
которые совпадают с основными уравнениями сферической
тригонометрии.
Черновик Гаусса не содержит никаких указаний на то, что
эти формулы следует понимать шире, но мы уже видели, на
примере формулы, приведенной на стр. 137, что ему не мог быть
неизвестен способ перехода от формул сферической к формулам
гиперболической тригонометрии. Для этого Гауссу было
достаточно подставить мнимую единицу вместо константы/с,
действительность которой он нигде не оговаривает.
Весь вывод Гаусса, конечно, нуждается в* уточнении,
сводящемся к более строгому анализу порядка отброшенных
бесконечно малых. Этот анализ был впоследствии произведен
Кулиджем^.
Мы не будем останавливаться здесь на тех причинах,
которые обусловили длительность сомнений Гаусса в возможности
неэвклидовой геометрии и помешали ему высказать публично
свои взгляды после ее открытия.
3. КОМПЛЕКСНЫЕ И ГИПЕРКОМПЛЕКСНЫЕ ЧИСЛА
Комплексные числа использовались Гауссом почти во
всех его работах по арифметике, алгебре, теории функций,
теории поверхностей (конформное отображение) и основаниям
геометрии (тригонометрия).
^1. L. Goolidge. The elements of non-euclidian geometry.
Oxford, 1909.
141
Геометрическое истолкование комплексных чисел,
которым он владел еще в 90-х годах XVIII в., было
использовано Гауссом в решении ряда задач планиметрии и
сферической тригонометрии, о чем свидетельствуют его черновики.
Гаусс определяет положение точки на плоскости или на
сфере одним комплексным числом и характеризует соотношениями
между этими числами те или другие особенности фигуры
(Bd. VIII, 303-356).
В черновике 1840 г. Гаусс называет четверку точек
плоскости гармонической, если комплексные числа, соответству-
ющ,ие этим точкам, удовлетворяют условию
{a + b){c + d) = 2 [ab + cd),
и показывает, что эти точки расположены на одной
окружности так, что их расстояния находятся в зависимости
AC-BD = AD.BC
(Bd. VIII, 336). В этом вопросе он предвосхитил результаты
Мебиуса, опубликованные'в 1852 г.
Некоторые из черновиков свидетельствуют о
размышлениях Гаусса над вопросом о гиперкомплексных числах (Bd.
VIII, 353 и 354). Особенно интересныхми являются два
отрывка (Bd. VIII, 357—362). Второй из этих отрывков,
относящийся к 1819 г., мы приведем в дословном переводе:
«Мутации пространства трех измерений
1.
Уже с давних пор я употребляю способ выражать всякую мутацию
пространства (под которой я понимаю его сдвиг в дрз^гом пространстве,
связанный с общим увеличением или уменьшением, не нарушающим
подобия) четырьмя величинами:
а, Ь, с, d,
комплекс которых я называю шкалой мутаций (Mutationsscale).
Одновременно принимается, что некоторая точка подвижного пространства
рассматривается как неподвижная в другом пространстве и называется нулевой
точкой.
2.
Значение этих четырех величин —следующее. В неподвижном
пространстве рассматриваются три прямые 01, 02, 03, исходящие из точки б?'
и образующие между собой прямые углы.
142
Положим
Vb''-\-c^ 4-f^^ = Р,
п пусть
bed
Т' р ' 7
являются косинусами трех углов, которые образует некоторая прямая
ОР с 01, 02, 03. Эта прямая линия имеет в подвижном пространстве
такое же положение после мутации, как и до нее; полагая
Уа^ + р'- = /с
или
к = Va^ + b' + с2 -Ь d\
получим линейное увеличение в мутированном пространстве.
Наконец, если
а = /CCOS0; р = sin0,
то 20 есть вращение вокруг ОР, которое образует вместе с увеличением
к данную мутацию». ^
В другом отрывке Гаусс устанавливает следующий закон
умножения мутационных шкал:
{а, Ь, Cjd) (а,^,.^, о) — (аа — Ь^ — с^ — с?о, а^ -\~ boL — с8 + ^Т'
а^ + bo -{- COL — d^, ао — b^ + ф ~\- da),
отмечая, что это умножение не подчиняется 'переместитель-
ному закону. Он указывает также, что произведение выражает
результат последовательного выполнения двух мутаций.
Таким образом, мы видим, что Гаусс пришел к понятию
кватерниона почти за четверть века до Гамильтона, хотя и не
опубликовал свое открытие.
4. ГЕОМЕТРИЯ ПОЛОЛ^ЕНИЯ
Сарториус приводит в своих воспоминаниях следуюп],ие
слова Гаусса: «Особую надежду возлагаю я на
сформирование геометрии положения (Geometria situs), которой
принадлежат широкие, совершенно невозделанные поля,
почти совершенно не поддававшиеся нашему современному
исчислению» ^.
iSartorius V. Waltershausen. Gauss zum Gedacht-
niss. Leipzig, 1856, стр. 88.
143
в другом месте Гаусс указывает, что все имеющиеся в
геометрии положения сводятся к некоторым фрагментам
Эйлера и Вандермонда, подразумевая, очевидно, работы
Эйлера о многогранниках и статью Вандермонда 1774 г.
«Замечания о проблемах положения» (Remarques sur les ргоЫё-
mes de situation).
От собственных работ Гаусса в этой области сохранились
только фрагменты, касающиеся подсчета числа точек
самопересечения замкнутых плоских кривых (Bd.VIII, 271—285).
Хотя замыслы Гаусса в области геометрии положения и
оставались неосуществленными, тем не менее, они сыграли важную
роль в истории науки. Основоположник топологии Лестинг
(1806—1882), которому новая научная дисциплина обязана
своим названием, пишет: «Первая мысль попробовать
заняться этим предметом [геометрией положения] пришла мне во
время практической работы в Гёттингенской обсерватории
и в результате высказываний, брошенных Гауссом»^.
^ Р. S t а с к е 1. Цит. соч., стр. 54.
А.КМарщшв6ич
РАБОТЫ ГАУССА
ПО МАТЕМАТИЧЕСКОМУ
АНАЛИЗУ
10 к. Ф. Гаусс
::s:SS
Работы Гаусса в области математического анализа имели
меньшее влияние на развитие науки, чем его исследования в
области теории чисел, дифференциальной геометрии, теории
вероятностей, астрономии и теории магнетизма. Это
обстоятельство объясняется, однако, вовсе не тем, что Гаусс уделял
мало внимания вопросам анализа. Напротив, с юношеских
лет и до последних дней жизни он настойчиво занимался
систематическим изучением обпцпх принципов теории
трансцендентных функций анализа, пришел к основным идеям теории
функций комплексного переменного, развил теорию
эллиптических функций, заложил основы теории модулярных
функций, разработал теорию гипергеометрических функций.
Разработанные им методы и достигнутые результаты супдествен-
но повлияли бы на весь математический анализ первой
половины XIX в., если бы они были своевременно опубликованы.
Но хотя Гаусс многократно пытался привести в систему свои
открытия и дать их развернутое изложение, попытки его не были
осуществлены, и самые ценные и глубокие его результаты из
области математического анализа не выходили за пределы
его кабинета. Эти результаты Гаусса были переоткрыты
затем Коши, Абелем, Якоби и другими учеными и вошли в
обиход науки независимо от него.
1. Работы Гаусса но математичес1^ому анализу,
опубликованные им самим, невелики по объему и очень
немногочисленны. Это «Disquisitiones generales circa seriem infinitam
1 J_ i* ^ 4_ ^(oc+l)^P + l) ^^ , a(a-H)(a + 2).6(^+1X^ + 2) о
'"^ly"^"^ 1-2y(t+1) '''''^ 1.2.3y(T + l)(Y + 2) ^^"^
10* 147
+ etc. . . Pars prior» ^ — работа, важная для теории рядов и
теории гипергеометрических функций, опубликованная в 1813 г.,
и «Methodus nova integralium valores per approximationem
inveniendi»^, содержащая известную формулу для
приближенного вычисления интегралов, опубликованная в 1816 г. К ним
нужно присоединить те также опубликованные при жизни
Гаусса работы, в которых он занимался решением проблем
теории чисел, алгебры, геометрии, механики, физики и
астрономии, разрабатывая для этой цели соответствующие методы
анализа.
Однако правильное представление о всей совокупности
работ Гаусса в области анализа можно получить, только
привлекая дополнительно обширные материалы его научного
наследства (Nachlas?) и переписки. Публикация этих материалов
началась вскоре после смерти Гаусса и растянулась на многие
десятки лет. Расшифровка формул и скупых указаний
Гаусса потребовала большого труда группы ученых, взявшихся
под руководством Ф. Клейна за доведение до конца издания
сочинений великого математика.
В настоящей статье мы используем выводы издателей и
комментаторов работ Гаусса, в особенности Шлезингера,
самого Клейна, Фрике, Больца, а также Штекеля и Бахмана,
иногда несколько расходясь с указанными авторами в
оценке места и значения отдельных работ.
2. В своих «Лекциях о развитии математики в XIX
столетии» ^ Ф. Клейн проводит остроумное сравнение между
тематикой научного творчества Гаусса и Лежандра, отмечая
многочисленные параллели в научных интересах двух ученых и
справедливо подчеркивая преимущества глубины
проникновения в предмет в работах Гаусса. Однако если иметь в виду не
тематику, а самый характер научного творчества, то, как нам
кажется, следует сравнить Гаусса прежде всего с
Ньютоном.
Подобно Ньютону, Гаусс пришел к важнейшим своим
1 С. F. G а U S S. Werke, Bd. Ill, стр. 125—162; в дальнейшем ссылки
на сочинения Гаусса обозначаются кратко: Werke.
2 Там же, стр. 165—196.
3 Имеется русское издание части Т этих лекций, М.—Л., 1937.
148
открытиям еще в очень юном возрасте и вынашивал их долгие
годы, не спеша с опубликованием и предъявляя чрезвычайно
высокие требования к отделке своих работ. В популярных
изложениях по истории науки можно нередко встретить
суждение о том, что с Гаусса начинается поворот к «строгости»
математических доказательств, объявляемой одной из
характерных черт математики XIX в. Но сам Гаусс, мотивируя
требования строгости, предпочитал ссылаться на традиции старых
математиков, и мы не ошибемся, если скажем, что здесь он
имел в виду Ньютона и его античных предшественников.
Что касается собственно аналитических работ, то Гаусс,
подобно Ньютону, избирает в качестве основного инструмента
степенной ряд и очень быстро достигает в операциях с ним,
в особенности в операции обращ,ения степенного ряда,
такой же виртуозности, как и Ньютон. Как и Ньютон, Гаусс
применяет свои математические открытия к «натуральной
философии»—механике, астрономии, физике, почти
неизменно подчеркивая в самих заглавиях своих работ посредством
эпитета «всеобш,ий» (generalis), что речь идет не о решении частных,
хотя и важных проблем, но о построении теорий, охватываюш,их
всю совокупность изучаемых явлений. Наконец, как и Ньютон,
Гаусс чувствует себя всю жизнь одиноким творцом, которому
открытия его предшественников и современников служат лишь
свидетельством того, что существуют отдельные люди,
подымающиеся до уровня его собственного, как бы развивающегося
только из себя, творчества.
3. Проследить с достоверностью ход научных открытий
Гаусса удается только с 1796 г.— года, к которому относятся
первые указания дневника. В интересующем нас аспекте
следует остановиться на вопросах арифметико-геометриче-
ского среднего и лемнискатических функций, которые
впоследствии в работах Гаусса приводят к началам общей теории
эллиптических и модулярных функций. Здесь и в дальнейшем
мы не будем прослеживать постепенное развитие относящихся
сюда идей и результатов Гаусса, а ограничимся лишь
указанием некоторых наиболее существенных моментов.
Рассмотрим, например, работу Гаусса, относящуюся
приблизительно к 1800 г. (Werke, III, 361 и след.).
149
Отправляясь от произвольных положительных чисел а
и ^ и полагая для определенности а>6, Гаусс строит
рекуррентным путем две последовательности:
Заметив, что а^"+^Ч ^^''^ 6^^+^^ > 6^^^ О < а^"^-^ 6^^> <
<;^(^^^~^^ — 6^^"^^), он заключает, что эти последовательности
имеют общий предел М {а, Ь); этот предел и называется ариф-
метико-геометрическим средним^ чисел а я Ь. Любопытно
отметить, что Гаусс не довольствуется утверждением о
существовании общего предела, но фактически вычисляет члены
указанных последовательностей в различных частных случаях,
с весьма большим числом знаков, наблюдая, с какой
быстротой устанавливаются десятичные знаки. Именно, он проводит
вычисления для случаев:
а = 1, Ь = 0,2; а = 1, Ь = 0,6; а = 1, Ь = 0,8;
а- ]/"2, Ь=-Л,
удерживая от 10—12 до 15—20 знаков после запятой. С
помощью метода неопределенных коэффициентов он разлагает
М {1-}-X, 1) и М {1-\-X, i'-х) в ряды по целым
неотрицательным степеням х (самое существование подобных разложе-
Hiiii не вызывает сомнений у Гаусса) и получает также
разложение:
_ 1 - i 1 V Г1'3--.(2А:-1) ]2 2А-
^"^ М{1-^х, 1 — х) ~^2jL 2-4...2/с J^ •
1
Дважды дифференцируя это разложение, он находит, что
у удовлетворяет следующему дифференциальному уравнению:
^ В письме к Шумахеру, датированном 1816 г. (Werke, X, 247)
Гаусс указывает, что он занимался арифметико-геометрическим средним
еще в 1791 г., т. е. начиная с 14-летнего возраста.
150
и указывает, что общий интеграл последнего есть
и + *
М (1+х, 1 — х) ' М{1, X) '
Далее Гаусс замечает, что полный эллиптических! интеграл
тс
7Т J
Vl —х^ cos2 ф
о
имеет разложение, совпадающее с разложением у, и,
следовательно,
1 1 1 F б?ф
М(1-{-х, 1l—x) м
1 —-i^
(1, Vi — а;2) ~ тгО КГ
Иным путем эта связь между арифметико-геометрическим
средним и эллиптическим интегралом первого рода
устанавливается Гауссом в его мемуаре «Determinatio attractionis etc »,
опубликованном в 1818 г. (Werke, III, 333 и след.).
Определение векового возмущения, оказываемого одной планетой на
другую, приводит, в конечном счете, к эллиптическому
интегралу
f dT
0
Чтобы вычислить этот интеграл, Гаусс применяет
преобразование
. гг 2т sin Т'
sm 7
(т + п) cos2 Т + 2т sin'-^ Т' '
получившее впоследствии наименование преобразования
Гаусса, и находит
27Т 27Т
^ dT г dT'
J 27гГт2со82Т-г'г2 8ш2Т J 2TzVm''^co^^T'-{-n'4m^r '
о о
где т' = -у ('^ + '^) и п! =^ Утп. Неограниченно повторяя это
преобразование и полагая М {т, /г) = jj., Гаусс получает
2тг 27Т
Г dT г (Ze 1
- д2 sin2 т J
J 27Г K'm2 cos2 Т -Ь д2 sin2 Т J 27г /"^2 cos2 е + tx2 sin2 0 (X •
Jr5i
Чтобы найти значение эллиптического интеграла второго
рода
{* cos^T —sin^T
о
Гаусс устанавливает сначала соотношение
27Т
(^2 П^) \
CQs^ Т — sin^ Т
27Г кт2 cos2 Т + /г2 sin^ Т
о
27Т
dr
= V /_ ^ 2 (т'2 -— 72 2) \ ) ^
о '
и, неограниченно повторяя то же преобразование, получает
разложение искомого интеграла в весьма быстро сходящийся
ряд («per seriem infinitum citissime convergentem»)
В автореферате (Anzeige) этой работы в качестве примера
задачи, легко решаемой с помощью предложенного
алгорифма, Гаусс приводит вычисление длины эллипса. Если т —
большая полуось, ад — малая полуось эллипса, то длина
эллипса выражается суммой ряда
^ {ш'^ _ 2 (т"2 - д''2) _ 4 (т"2 _ ^-2) _ 8 (т""^ „ ^^^п^ ^ . . .}.
и*
В заключение Гаусс подчеркивает, что к изложенному
способу вычисления эллиптических интегралов он пришел
много лет назад, независимо от аналогичных исследований Ла-
гранжа и Лежандра(\Уегке, III, 360). Упоминание о Лагран-
же вызвано тем, что этот автор использовал, по сути дела,
тот же прием и для той же цели в мемуаре «Sur une nouvelle
methode de calcul integral etc.», опубликованном еще в
1784—1785 ГГ.1
1 См. Lagrange. CEuvres, II, стр. 253 и след., в особенности,
стр. 271—274. Это обстоятельство отмечено Л. Шлезингером в его
исследовании «t)ber Gauss*Arbeiten zur Funktionentheorie» (Materialen fur eine
wissenschaftliche Biographie von Gauss, Hefte III, 1912). В дальнейшем
мы часто ссылаемся на эту работу Шлезингера.
U2,
Необходимо отметить, что указанный метод вычисления
эллиптических интегралов с помощью арифметико-геометри-
ческого среднего — единственный' из результатов Гаусса,
относящихся к эллиптическим интегралам (и функциям),
опубликованный им самим.
4. Отправным пунктом в занятиях Гаусса эллиптическими
интегралами и функциями были лемнискатические функции.
Можно легко проследить по ранним работам Гаусса (начиная
с 1797 г.), как Гаусс строил теорию этих функций по аналогии
с теорией тригонометрических функций. Чтобы подчеркнуть
эту аналогию и вместе с тем реконструировать
первоначальный ход мыслей Гаусса, мы дадим здесь два параллельных
изложения начал теории тригонометрических и лемнискати-
ческих функций. Во избежание недоразумений заметим, что
у самого Гаусса такое сравнительное изложение отсутствует.
Окружность
ОАВ
-=s
(it
i-\
о
dt
Vl — t^
. (1)
YY
r = sin s =
s), (2)
= cos(-J
Лемниската
ОАВ
г
0
r = sin lemn s =
■= cos lemn i ^^ sj . (2')
1 Знак Ш применяется в книгах XVIII в. для обозначения тт.
Употребляя этот знак, Гаусс подчеркивает аналогию между лемнискатой и
окружностью (см. Л. Шлезингер. Цит. соч., стр. 18).
15Я
Если о и. s -
dp
две дуги, сумма которых постоянна, то:
do 4- ds =
dr
/1__р2 Yi^ р'
:=0.
do -\- ds ■■
dp
dr
Kl —p*
-0
p* Vl—r*
Отсюда приемами, детально разобранными во втором
отделе первой части первого тома «Institutionum calculi integra-
lis» Эйлера (глава V, где интегрируется уравнение вида
dx dy
V А + 2Вх + Са:2 ~ VA + 2Ву + Су^ '
И глава VI, где интегрируется уравнение
dx dy \
VA 4- '^Вх + С:г2 + Dx^ + Ех'^ Va + 2Ву + Су' + Dy^ + Еу'^ ]
— КНИГИ, которую молодой Гаусс штудировал, немедленно
получаются теоремы сложения:
sin (а + «?) = р l/l — г^
где р = sm а, г = sins.
(3)
Пусть а = —
тогда р = 1 и
inf-^ or.] = cos а
s = —а;
sin
Vi
откуда
sin^ a -\- cos^ a = 1
(4)
sin lemn {a -^ s) ~
1 4- r2p2
P^-
. 1^1 — r* — Г f 1
(3')
где p—sin lemn a, r^sinlemn^
(cm. Werke, III, стр. 406).
Пусть a
тогда p =
1 и
a;
sin lemn
cos lemn a :
VI
+ r'
откуда
sin lemn^ a + cos lemn^ a -f-
+ sin lemn^acoslemn^a^l. (4')
Далее из теоремы сложения следует:
sin(5-|- 2iz) = sin s. I sin lemn {s + 2т15')=:: sin lemn 5.
Чтобы определить функции чисто мнимого аргумента,
полагаем в (1), (1'): г = iv {v — действительное число). Тогда:
iv
Г dt
Vi—t^
= г
dz
о о
(у — действительное
ly
число).
0 0
{y — действительное число),
154
откуда
од'куда
sin lemn у
V ~ ^— = sh у
iv = sin {uj) == i sh у. (5)
Теперь остается только применить теорему сложения, чтобы
(5')
iv == sin lemn {Uj)= i sin lemn y.
получить
определение функции
sin {x -f iy) = и У i ~{- v^ +
где
+ w\/^i +u',
и = sinx, V = shy.
(6)
[И]
и
л комплексного аргумента
sin lemn {x + iy) ==
uVr^
uVT=-
= sin lemn
~v^ + iv V'i — u^
1 ~ uV
U2 + 1^2
~v^~— ivV'i — u*
.(6-)
:r, г; = sin lemn?/.
Сравнение формул (6) и (6') сразу вскрывает два коренных
различия между тригонометрической функцией sin z и
эллиптической (лемнискатической) функцией sin lemn z. Во-первых,
sinz — всюду конечная (целая) функция, тогда как sin lemn z
имеет бесконечное множество полюсов (в точках, где и ^ ~\~i
и г; = 4^1) и, следовательно, является мероморфной. Для
Гаусса это различие между целой и мероморфной функцией
проявляется также и в том, что первая представляется всюду
сходящимся степенным рядом, тогда как степенной ряд
второй (разложение по неотрицательным степеням z) расходится при
|z|, превышающем ближайший к началу координат полюс функ-
Щ1И (точнее говоря, Гаусс утверждает: «formula autem pro
sin lemn cp diverget, si cp ponetur >-—=r sive ^
(VVerke,
Ш, 406); там же Гаусс отмечает, что sin lemn z представляется
в виде частного двух всюду сходящихся степенных рядов Р и
Q (о них речь будет идти ниже). Во-вторых, sinz является
просто периодической функцией, тогда как из формулы (6')
немедленно вытекает, что sin lemn z есть двояко-периодическая
функция, имеющая, помимо действительного периода 2тег,
также чисто мнимый период Иъу (v не изменяется, если у
заменить на г/ -f 2ш).
155
5. Отказываясь от npocJie>KHBaHHH дальнейших аналогий
между тригонометрическими и лемнискатическими функциями,
отметим только несколько важных деталей. Из. формулы (6')
непосредственно следует, что нули sin lemn {х + iy)
удовлетворяют уравнениям: sin lemn х = sin lemn у = О, откуда х = тит,
у z^nJiJ ш X ~\- iy = oLm, п — {^ -{-1^)'^ \ аналогично, полюсы
находятся из условий: sin lemn х =^ -Л^^, sin lemn у = rt: 1 ? откуда
X -^ iy = ^^^ ^ = [(2т — 1) + i{2n — 1)] -^ {т я п —
произвольные целые числа). Обнаружив нули и полюсы sin lemn z, Гаусс
строит в виде бесконечных произведений простейшие целые
функции, имеющие нулями соответственно (х.т,п и р^п, п-
^(^) = ^n'('i-z^)' ^'(^)=П(1
771, п т, п
и утверждает, что
К
. , М (2) .„v
sm lemn z = ., ,\-. (/)
N(z) ^ ^
Эта формула дает представление лемнискатического синуса
в виде частного двух целых функций. Она имеет, однако, тот
недостаток, что функции М {z) и N (z) не являются
периодическими. Чтобы найти аналогичное представление с
периодическими целыми функциями, Гаусс вводит новое переменное:
С = sin —Z я рассматривает sin lemn z, как функцию С. Легко
видеть, что нули новой функции имеют вид:
(2П-1 — — 2п—1)—-
Ч- i р- , а полюсы: Ч т^ •
Снова строятся простейшие целые функции, обладающие
заданными нулями:
4^2
/>(z) = -jcn
1 + -
<?(z)=n
1—
12П—1) —- -(2П—1) —
156
и sin lemn z представляется в виде
sin lemn z = -p— . (8)
Q{z) ^ ^
Гаусс не считает переход к последнему равенству
самоочевидным и говорит, что он может строго доказать эту
формулу (Werke, III, стр. 415).
Полагая 2="©"^, Гаусс находит далее разложения
периодических функций Р{ът^) и Q {'от'^) в тригонометрические ряды:
Р(-ш-'^)
2^У —\е ' ''sin^^—e ' "sin3^^ + e ^ ""sinS^Tr /,
Q{-Q^)==:2 ^ К ~{l+ 2e-"cos2^u+2e-4"cos4^uH },
откуда sin lemn (uj^) =
Г 4 sin фтг— e~"^" sin Зфтг -\- e~^" sin 5ф7г •
(9)
Аналогичные формулы он получает и для cos lemn (тзгф).
Рассмотрение этих формул показывает, что функции P(z)
и Q{z) (вместе с двумя функциями j)(z) и q(z)^
соответствующими cos lemn ("сг^)) с точностью до числовых множителей
совпадают с тэта-функциями Якоби в том частном случае, когда
(в обозначениях Якоби) А=А:'=-—,/?"=iir' = -p-и д = е ^^ =^е~~^.
Так, например, функция Якоби Н {и) имеет в этом случае
разложение
Я(т7ф)=2 (е * " sin^TT —е ^ "" sin3^^ Н 1 =
а функция Якоби 0i(w) — разложение
03^ (та-ф) = 1 + 2в-" cos 2ф7г + 1е~'^'^ cos 4ф7: + • • • =
= 2^ )/ -^(?(т^Ф).
U7
He задерживаясь на лшогих других формулах, полученных
Гауссом, приведем еще разложение лемнискатического синуса
на простейшие дроби в виде (Werke, III, 417):
со
• 1 / .\ ^'^ \г\ / л\п~1 sill (2/г — 1)7гф ..^.
smlema(T^V) =—^(-i) ^^ к=Г-• (Ю)
1 2 I '>
Мы остановились с такими подробностями на открытых
Гауссом свойствах лемнискатических функций для того, чтобы
показать, что вывод этих свойств не требовал
предварительной разработки основ теории функций комплексного
переменного и, в частности, интегрирования в комплексной плоскости.
Все богатство фактов, найденных Гауссом в этой области, было
добыто средствами, обычными для аналитиков XVIII в., и не
выходило за строй привычных для них представлений. Это
относится и к рассмотрению комплексных значений аргумента,
и к получению и использованию теоремы сложения, и к
технике операций над степенными рядами (включая обращение
рядов), где широко использовался метод неопределенных
коэффициентов, и к разложению функций в бесконечные
произведения и на простейшие дроби. Вместе с тем из
изложенного явствует, что Гаусс для частного случая
лемнискатических функций разработал на исходе XVIII в. все
основное содержание позднейшей общей теории
эллиптических функций. К сожалению, Гаусс не опубликовал своих
открытий, оставив их в незавершенном, большей частью
черновом, виде. Поэтому исторически заслуга построения основ
теории эллиптических функций остается за Абелем и Якоби,
получившими свои результаты на четверть века позднее
Гаусса.
6. Если в построении теории лемнискатических функций
Гаусс исходил из аналогии с тригонометрическими
функциями, то дальше, развивая основы теории эллиптических
функций, он руководствовался аналогией с лемнискатическими
функциями. Мы ограничимся здесь кратким изложением двух
мест из Nachlass.
На листках, заполнявшихся Гауссом в ноябре 179Q г.
(Werke, X, 194 и след.), рассматривается задача обращения
158
эллиптического интеграла первого рода:
[* - dx
о
\ (1 + [l'x-^)(1 — х')
= а.
Очевидно, что этот интеграл можно считать наиболее
общим видом интеграла первого рода; случай лемнискаты
соответствует р-^ = 1. В последнем случае Гауссу было
известно, что обратная функция х = sin lemn и является двояко-
периодической функцией с периодами 2-^ и 2-07^ и что ее
можно представить по формулам (9) и (10).
Кроме того, еще 30 мая 1799 г. Гаусс фиксировал в своем
дневнике совпадение арифметико-геометрического среднего
между 1 и 1/2 и отношением — , т. е. равенство
•щ-
У1 —х^ М (1, F2)
о
В интересующих нас записях Гаусс а priori вводит два
числа:
"ОТ и —— -:г^ = 'GJ
\^М f |/ 1 + •
(здесь М {х) обозначает М(1, х)). При а =1 получаем:тгг' —ти —
полу период лемнискатпческого синуса.
Гаусс дает затем явное выражение функции s =^ S («),
которая и должна решать рассматриваемую задачу обращения.
Он называет эту функцию «универсальнейшим лемнискатиче-
ским синусом» и представляет формулой, являющейся
естественным обобщением формулы (10):
Очевидно, что sinlemn (иг'!)) получится отсюда при |а = 1
^ К этому заключению Гаусс пришел вначале эмпирическим путем;
в цитируемой записи (Werke, X, 542) отмечается, что совпадение обоих
чисел проверено им до одиннадцатого десятичного знака.
159
Далее Гаусс представляет ^'(тЕгф), снова по аналогии с лем-
нискатическим случаем, в виде отношения двух целых
функций с периодом лт:
^(^,,)^Л(^Ф) (9')
(где Г(-аг'|>) и W{jij^) отличаются от якобиевых тэта-функций
Н ж в^ множителями, не зависящими от ф) и рассматривает
основные соотношения между Т и W (аналогичные ранее
установленным им соотношениям между Р я Q).
В другой записи (Werke, VIII, 96; Фрике относит ее к
маю 1800 г.) Гаусс иным путем решает задачу обраш;ения
эллиптического интеграла первого рода. Впрочем, этот путь
также был использован им ранее, при изучении лемнискати-
ческого случая. Пусть
С dx
положим x = f{(p). Тогда для у = 1пх будем иметь:
^ = /(l-^^)(l-f^^^),
— (1 — {1:^2) — fi (1 •
Если
S^-'.
то --^ =и — t. Далее положив:
\ud(p = v,
получим
y = v
Пусть теперь
е-^ = Р{ср),
тогда
d'y (1 -
йф^
-^') = ~w
\ td(^ =w,
' — W.
е-" = Q (cp);
_ e-^ _Р(9)
•X^) (i [LX'^)
-2
+ [IX'^,
Q(9)
(11)
(12)
(13)
(14)
Дифференцируя дважды формулы (13) и используя
формулы (12), (И) и (14), легко находим дифференциальные уравне-
160
иия для функций P(<f) и Q {<f) в виде:
РР" = P'^ — Q^, QQ" = Q'^ — ixPK (15)
С помощью последних можно вычислять коэффициенты
степенных разложений функций Р я Q:
^(?) = т-т(l + |^)т' + тlo(l + 4F + ^^')?' .
Остается добавить, что эти функции P{'f) и (2(?) следует
сравнивать не с тэта-функциями Якоби, а с функциями Al^ и А1
Вейерштрасса (обозначенными так последним в честь Абеля).
В частном случае лемнискатических функций
соответствующие Р я Q функции обозначались в п. 5 через М я N\
7. Гаусс и в последующие годы занимался вопросами теории
эллиптических функций, в особенности, в связи с дальнейшим
развитием теории арифметико-геометрического среднего. Мы
приведем только некоторые результаты, содержащие начала
теории модулярных функций^. Начнем с того, что Гаусс,
по утверждению Шеринга (Werke, III, 493), еще в 1794 г.
заметил соотношения между арифметико-геометрическим
средним и степенными рядами, в которых показатели являются
квадратами чисел, образующих арифметическую прогрессию.
Речь идет о степенных рядах вида:
P{x) = i +2х + 2х^ + 2х^+ • ",
Q{x) = i — 2x + 2x^-'2x^+"-,
i_ А 3L
R{x) = 2x^ +2х^ +2х ^ -\ ( I ^ I < 1)
Последние представляют собой так называемые нулевые
тэта-ряды (они формально получаются из
тригонометрических разложений частных тэта-функций Якоби: Oi, О, Н^,
если в последних положить аргумент равным нулю и величину
К'
о = е—" к
^ Здесь, как и в предыдущих пунктах, мы используем, наряду с
сочинениями Гаусса, цитированную в сноске на стр. 152 работу Л.
Шлезингера и его замечания в Werke, X (1), 251—286.
^1 К. Ф. Гаусс 261
обозначить через х). Подобные ряды встречались до Гаусса
в работах Якова и Даниила Бернулли и Эйлера. Что именно
было известно Гауссу в 1794 г., сейчас нельзя установить.
Мы воспользуемся значительно более поздним изложением
Гаусса, написанным не ранее 1818 г. и предназначавшимся,
повидимому, для опубликования в печати. Это «Hundert
Theoreme iiber die neuen Transcendenten» (Werke, III, 461—
469). Гаусс выводит следующие тождества:
Р^ {Х) + Q^ {Х) = 2Р2 (^2)^ Q2 (^2) ^p(x)Q {Х), (16)
Р (х^) R (х^) = Y i?2 (х), Р^ (х) — Q^ {х) = i?4 (х). (17)
Из формул (16) следует, что Р^{х^) есть среднее
арифметическое между Р^{х) и Q^{x)j а Q^{x^) — среднее
геометрическое между теми же функциями. Поэтому, если положить
/>2 (д.) _ ^^ ^2 (^j _ ^^ YQ применение алгорифма арифметико-
геометрического среднего даст
откуда
М{т, /г) = lim Р^ {х^^) = lim Q^ {х^^) = 1.
Х-*- оо Х-^ оо
Если m и п — произвольные числа, m>n и М {т, п) = [х, то
естественно поставить вопрос об отыскании такого х, чтобы
было: т — р-Р^ (а;) и п = р.^^ (ж). Тогда
и вопрос сводится к решению последнего уравнения
относительно ж. Для этого замечаем, что
или, полагая —-^--^ = /г ,
, И h"
162
Но из первой формулы (17) следуем, что
далее, вторая формула (17) дает
_ R^(x) _ т^ — п^
^ "" 2* ~ 16ijl2 •
Поэтому
1
ы'^гт
1_ lem'm" \ т"') \т"") * * * ^^^^
Эта формула решает задачу. Однако в другом месте [см.,
например, Werke, Х(1), 218] Гаусс предлагает без
доказательства другую, более изящную формулу
U
х^е^'^, (20)
где ^ = М(т, п) и 1 = М{т, Ут^ — п^).
Заметим, что соотношение, установленное Гауссом между
арифметико-геометрическим средним и эллиптическим
интегралом первого рода (см. п. 3), дает:
^С dt_
т
где
\L М(т,п) 7Г J |А(1 _ ^2)(1 __ Jt2f2) '
А2
т
где
11^2) "~ 7^ J ]/"(1^|2)(1_
Поэтому
/ь^=-4
и-
X
J l^(Tiri2)(l — к*Щ
Р Л
J КП'^^/2У7|1^^2\
к
(21)
где ^Г' и К — полные эллиптические интегралы первого рода
со взаимно-дополнительными модулями.
11* т
Если рассматривать функцию, являющуюся обращением
интеграла
X
г dt
(задача решена Гауссом; см. п. 6), т. е. универсальнейший
лемнискатический синус (или функция Якоби sn гг), то 4 К
и 2iK' будут периодами этой функции. Из формул (20) и (21)
вытекает, что задача решения уравнения (18) относительно х
равносильна задаче отыскания отношения периодов
эллиптической функции Гаусса-Якоби по заданному дополнительному
модулю/с' =;;^. Последняя задача имеет прямое отношение к
теории модулярных функций. Именно, в обозначениях Якоби:
(^ (х) =:= 6 (0) = 1 — 2х + 2х^-^2х^-\ ,
Р{х) = 6i (0) - 1 + 2х + 2^4 + 2:^9 + • • •,
;г = <?~"^ ^т = ■^, Кет>о),
и
rQ(a;)l2_r 0(0)12 _
[Р{х)\ -^ [01(0) J -^
— дополнительный модуль. Эта функция комплекснОЕФ
переменного т является одной из модулярных функций.
С этой точки зрения, задача изучения всех решений уравнения
(хо) для цроизвольно заданного— совпадает с задачей
изучения поведения (распределения значений) одной из
простейших модулярных функций. И Гаусс, действительно,
занимается этой задачей. Так в отрывках, относящихся к 1827 г.
(Werke, III, 477—478) он высказывает теорему:
Если мнимые части t и — содер:жатся между — i и + /",
то действительная часть ^ полоэфсительна.
Эта формулировка сопровождается чертежом, на котором
представлена область комплексной плоскости, занимаемая
^, удовлетворяющим условиям теоремы.
161
в третьем томе сочинений чертеж Гаусса воспроизведен
неточно, так как смысл его, повидимому, не был понят
издателем (Шерингом).
1-^1
Область (Raum) для t и
С
Лишь в восьмом томе дан правильный чертеж (Werke^
VIII, 104), изображающий криволинейный треугольник с
нулевыми углами; это и есть область, удовлетворяющая
условиям теоремы (и дополнительному условию: Rei^>0).
Необходимо иметь в виду при этом, что Q(i) и P{t) обозначают
теперь значения прежних функций Q{x) 15. Р {х) при х — е~'^^
так, что формула (19) дает для одного из решений уравнения
Q4t) ^ п ,
P^t) т ' . _ И- _ М{т, п)
Как можно прийти к мысли о существовании многих,
бесконечно многих, решений уравнения (18)?
В дневцике Гаусса от 3 июня 1800 г. имеется запись о
существовании бесконечного множества различных арифме-
тико-геометрических средних между двумя заданными числа-
ми[\¥егке, Х(1), 550]. Судя по заметкам, относящимся к 1825 г,
[Werke, III, 378—379, а также Х(1), 218-219], речь идет о
том, что при вычислении средних геометрических в
алгорифме арифметико-геометрических средних можно брать то
или другое из двух значений квадратного корня. Гаусс
иллюстрирует это, полагая m = 3, ^ = 1 и беря сначала только
положительные значения квадратных корней; получается:
li = М{3, 1) = 1.8636167,
1 = М (3,1/32 _ 12) _ м (3, 2.8284270) = 2.9135822.
Затем он проводит аналогичное вычисление, беря вместо
положительного значения п' == ]/т?г — 1.7320508 отрицатель-
165
ное значение:—1.7320508, а во всех дальнейших выкладках
выбирая значение квадратного корня с положительной
действительной частью. Получается значение арифметико-
геометрического среднего, обозначаемое через (р-) и равное
0.24699625 +0.63186865/. Гаусс замечает, что
В начале отрывка стоит утверждение, что во всех случаях
1 __ 1 Aik
где к — произвольное целое число.
Шлезингер в своей неоднократно цитированной книге
высказывает различные предположения относительно того,
каким путем Гаусс мог доказать последнюю формулу
(стр. 60-63).
Нам представляется, что здесь (как и в ряде других мест)
Шлезингер придает воззрениям Гаусса в этой области большую
стройность и законченность, чем это имеет место на самом
деле. Мы полагаем, что формула
((Л)- (X "^ X
могла быть установлена Гауссом эмпирически, отправляясь
от рассмотрения частных примеров. Эмпирическим
происхождением можно объяснить и ее неполноту (Шлезингер
справедливо указывает в своей «Теории функцию) на стр. 60, что
общая формула должна иметь вид
((X)- (X "^ Xj-
Об этом свидетельствует также и то, что Гаусс два года
спустя продолжает рассматривать частные соотношения,
связывающие различные арифметико-геометрические средние.
Речь идет об отрывке, напечатанном в Werke (III, 477—478),
откуда мы привели изображенную выше фигуру. Гаусс
называет здесь простейшим средним двух чисел такое арифметико-
геометрическое среднее, при вычислении которого каждый
166
разберется значение квадратного корня У m^n",
удовлетворяющее условию
^е-—щ—>0,
И далее пишет:
«Если простейшее арифметико-геометрическое среднее
между тгг и м = |1, между т и ]/т^ — п? =-у , то ^ является ка-
яоном (Canon) отношения —, а именно БГт ~ Т^ » тогда
Tib jr (^ /
простейшее арифметико-геометрическое среднее между ш ж п
UL « ^ 1
= ^ I OV и соответствующий канон = ^ ■■ = -^ ».
— + 21
Очевидно, что здесь с помощью различных арифметико-гео-
метрических' средних устанавливается, что если t есть
решение уравнения
QVn ^ п
t
то , ^ есть решение уравнения
Q4t) ^ /г .
иными словами, решением уравнения
Р* (О '^'^
является наряду с t также и . i о-/ •
Для нас важно отметить, что из множественности значений
арифметико-геометрического среднего вытекает и
множественность решений уравнения (18). Эти решения можно теперь
записывать в виде ^' = Тхг Если опираться на общую формулу
то для 7Т\ будем иметь
W
(X)- X + tJL '
переход от (|л) к (X) есть переход от
арифметико-геометрического среднего между m и дг к арифметико-геометрическому
* В немецком издании на стр. 478 вместо этого ошибочно стоит —.
п
167
получим
/- /
среднему между п и у т^ — п?\ при этом \i заменяется
на X и X — на |л. Но, очевидно, что — и -г- должны
[JL Л
1 1
выражаться аналогичными формулами через т-т и ^ :
И- "■ (и-) + W Т ~ (X) + TJir •
Так как Z, A:, Z^, A^, Z', A:', Z^, A^ — целые числа, то отсюда
следует, что (4Z + 1) (4Zi + 1) + IBM^ = ,4:1; при
дополнительном условии:
Ref>0, Re^^>0,
здесь из двух возможных значений следует выбрать + 1.
Полагая
--t и ^^-t,
, __ (4Z,+l)^ + 4t/ci __ Pit — ф ^^.
4/ + 1 + 4i/ci — 8 + iy^ » V-^^^»
где a, p, Y, 8 — целые действительные числа, сравнимые,
соответственно, с 1, О, О и 1 по модулю 4 и удовлетворяющие
условию: ао — ^^ = 1. Можно показать^, что каждое такое fу
действительно, будет удовлетворять уравнению (18) и что
каждое решение уравнения (18) есть некоторое t\
Соответствующие утверждения формулируются самим Гауссом не вполне
точно. Так, например, в Werke (VIII, 101) находим следующее
место:
«Чтобы решить уравнение ^-j^ = А (см.2), полагают А^ = —
и ищут арифметико-геометрическое среднее между т я п\ пусть
оно равно fi. Ищут далее арифметико-геометрическое среднее
между т и |/т^—п^ или, что является тем же самым, между
т + п и т — п\ пусть оно = X. Тогда имеют: i = -~. Так по-
лучается только одно значение Z; все прочие заключаются
в формуле ^_2 г у где а, р, ^, 8 обозначают все целые числа,
удовлетворяющие уравнению: ао — 4^^ = !»•
1 Л. Шлезингер. Цит. соч., стр. 62.
2 q(t) = Q(t) и p(t) = P{t).^A. М.
168
По этому поводу Фрике, замечает (Werke, VIII, 105), что
таким путем получаются все корни более общего уравнения:
р'^ (t) т^ '
Аналогичное замечание относится к другому отрывку [Werke,
VIII, 99, или X (1), 222]. Отрывок этот гласит:
«Если
т ~" |х (1 + 2е-^" + 2е-4^" + 2е-»^" +•••?'
то вместо М можно подставить
^L_ 1
2ci
2ei 4-
1
•+17'
где йу by Cj dy е и т. д. означают произвольное нечетное
множество целых действительных чисел; или также
рМ + 2^1 _ А/ + 2 (дг — psM'^) i
где /?, д, г, 5 — любые целые действительные числа,
удовлетворяющие условию рг + 4^5 = 1».
Наконец, приведем наиболее полную, но также неточно
формулированную теорему (Werke, III, 478):
«Уравнение
P4t) "^
имеет одно и только одно решение в области:
I'
Если ао—Py'^I» a^oE^l (mod4), р и ^"~ ^^^ные,
Pit -f- ^i
., . ai -f- pi
V = i —^^ , TO
Q40_ .^QMO
РЦГ) РЦ1)
169
Здесь, как указывает Шлезингер \ вместо функции р^У-
следовало ВЗЯТЬ функцию ^
/
^1-т) -
8. В предыдущих пунктах мы, не претендуя на полноту,
рассмотрели некоторые результаты Гаусса, относящиеся к
теории эллиптических и модулярных функций. Результаты эти
выросли из его юношеских занятий арифметико-геометриче-
скими средними и лемнискатическими функциями.. Хотя
большинство результатов было получено в очень короткий
промежуток времени 1797—1801 гг. (некоторые результаты,
относящиеся к арифметико-геометрическому среднему, были
получены раньше), Гаусс продолжал заниматься этими
вопросами в течение нескольких десятилетий. Так, его заметки,
связанные с делением на 5 аргумента эллиптической функции,
относятся к 1843 г. К одним и тем же вопросам он
возвращается внозь и вновь, иногда делая попытки изложить их
систематически.
О намерении Гаусса написать большой труд по теории
трансцендентных функций и отчасти об оценке значения
такой теории говорится в письме к Шумахеру от 17 сентября
1808 г. (Werke, X, 243—245).
«В интегральном исчислении,— пишет Гаусс, — меня
значительно меньше интересует то, что относится только кпод-
ч^.тановкам, преобразованиям и т. п., короче говоря, к
известному искусно применяемому механизму, сводящему
интегралы к алгебраическим, логарифмическим или круговым
функциям, чем тщательное и глубокое исследование таких
трансцендентных функций, которые не могут быть сведены к тем
функциям. С круговыми и логарифмическими функциями
мы умеем теперь обходиться, как с единожды един, но
великолепный золотой родник, хранящий сокровенное высших
функций, остается пока почти terra incognita. Я очень много ра-
-ботал над этим прежде и со временем дам собственный
большой труд об этом, на что я намекал еще в моих «Disquisiti-
^ Л. Шлезингер. Цит. соч., стр. 68.
170
ones arithmeticae», стр. 593 ^. Приходишь в изумление от
чрезвычайного богатства новых в высшей степени
интересных истин и соотношений, доставляемых этими функциями
(к ним принадлежат, между прочим, и те, с которыми связано
спрямление- эллипса и гиперболы)...».
Намерение Гаусса не было осуш;ествлено. Ни в одном из
сохранившихся изложений мы не находим в явном виде
общих начал, которым можно было подчинить весь накопленный
Гауссом материал. Можно сказать более: каждая из
сделанных Гауссом попыток систематизации этого материала
обрывается там, где предстоит соединение в одно русло
различных течений его исследований в рассматриваемой области.
По этому поводу уместно привести сообщаемое Вейерштрас-
сом высказывание друга Гаусса Вильгельма Вебера^, что
Гаусс хотел приступить к опубликованию своих исследований
о трансцендентных функциях не раньше, чем ему удастся
привести к полному согласию различные методы, посредством
которых он подходил к их изложению. Так, относящееся к
1801 г. изложение его теории арифметико-геометрическогд
среднего (Werke, III, 360—371), о котором шла речь в п. 3,
чютанавливается на том месте, где Гаусс отмечает связь ариф-
метико-геометрического среднего с эллиптическим интегра-
,1ом. Среди многих заметок о лемнискатических функциях
некоторые можно рассматривать как попытки
систематического изложения, но все они обрываются в самом начале. Так,
тметка на латинском языке «Elegantiores integralis [ , ^ ^
J 1 —Я7
proprietates» (Werke, III, 404—406) начинается с определения
лемнискатического синуса и косинуса, далее в ней приводятся
теоремы сложения, формулы для функций кратных аргументов
разложения в степенные ряды и без всяких пояснений даются
разложения в степенные ряды еще четырех функций Р(?),
^ Werke, I, 412—413. Гаусс указывает там, что принципы излагаемой
им теории деления круга могут быть применены не только к круговым
функциям, но и к другим трансцендентным, например, зависящим от ин-
С dx
теграла \\г. i", по изучение таких функций — задача другого
<^бширного труда.
^Л. Шлезингер. Цит. соч., стр. 99—100.
111
<?(?)> P{'^)y Я{'^)у относительно которых утверждается только, что
эти ряды всюду сходятся, тогда как ряды для лемнискати-
ческих синуса и косинуса расходятся, если ср превосходит,
1 _ _
соответственно, гг= о и со. На этом заметка обрывается. Лишь
из сличения с другими заметками можно понять, что Р{^}
и Q{''f) (соответственно, /?('f) и д(?))— это функции,
построенные в виде простейших бесконечных произведений так, чтобы
их нули совпадали с нулями или полюсами sin lemn ^
(соответственно, cos lemn ^). Такой же незавершенностью
отличаются и другие сравнительно большие отрывки о лемни-
скатических функциях («Einige пене Formeln die Lemnisca-
tischen Functionen befreffend» (Werke, III, 406—412); «De
curva lemniscata» (там же, стр. 413ислед.), а также отрывки,
относяш;иеся к обраш;ению эллиптического интеграла
первого рода в обш.ем случае [Werke, III, 433—436; Х(1), 308—310].
Незаконченными остались и заметки, излагаюш,ие
определение и свойства нулевых тэта-рядов в их связи с арифметико-
геометрическим средним. Такова заметка «Hundert Theore-
ше liber neuen Transcendenten» (Werke, III, 461—469), о
которой уже шла речь в п. 7. В конце нее рассматривается
задача о решении уравнения --44^ =— , но изложение
останавливается на формуле (19); переход к основной формуле (20)
и изучение множзственности решений отсутствуют.
Почему же Гаусс так и не дал развернутого изложения
своих исследований в области теории эллиптических и
модулярных функций? Объяснение, уместное по отношению к
неэвклидовой геометрии,— боязнь крика беотийцев, здесь,
конечно, не может иметь места.
С нашей точки зрения, причина коренится в том, что Гаусс,
видя многочисленные внутренние связи и взаимные
зависимости между сделанными им открытиями, не смог все же
разработать единой и общей теории, подчиняющей себе
отдельные факты. Эту задачу удалось разрешить на протяжении
длительного времени лишь нескольким поколениям ученых,
начиная с Абеля и Якоби и кончая Вейерштрассом, Риманом,
Эрмитом и Клейном. Но не только синтетическое изложение, но
даже изложения отдельных, в известном смысле, самостоятель-
172
пых частей всей теории не давались Гауссом потому, что, ио
нашему мнению, некоторые ответственные моменты ему но
удалось обосновать в соответствии с теми высокими
требованиями, которые он неизменно предъявлял к своим
публикациям. Сказанное может относиться к трудностям обоснования
[хредставления эллиптической функции в виде частного двух
целых функций, основанного на знании нулей и полюсов
этой функции, к выявлению множества всех периодов эллипти-
ческ й функции, отправляясь от многозначности
эллиптического интеграла (трудности здесь лежат в интегрировании
функции комплексного переменного в комплексной плоскости),
к анализу отображения, осуществляемого модулярной
функцией, и т. п.
Мы уже упоминали в п. 3, что из всех своих результатов,
относящихся к эллиптическим интегралам и функциям,
Гаусс опубликовал только соотношения между арифметцко-
геометрическими средними и эллиптическими интегралами.
Как правильно указывает Шлезингере, непосредственным
поводом для этого послужило письмо, полученное Гауссом в
апреле 1816 г. от Шумахера. Последний сообщал в нем [Werke,
Х(1), 245—246], что земляк Гаусса — профессор математики
в Копенгагене — Деген уже много лет .занимается ариф-
метико-геометрическим средним, которое представляется
Шумахеру (ошибочно) отличным от гауссовского. Далее
Шумахер писал, что он сам стал заниматься тем же вопросом и
нашел связь арифметико-геометрического среднего с длиной
эллипса.
Гаусс поспешил закрепить свой приоритет сначала в
письме к Шумахеру [Werke, Х(1), 247—248], где он пишет, между
прочим: «Разве Вы в самом деле забыли, что арифметико-геомет-
рическое среднее, которым занимается г-н Деген,—
совершенно то же самое, которым я занимаюсь с 1791 г. и теперь уже
смог бы написать об этом порядочный том in quarto?», а затем
и в печати, включив свой результат в «Determinatio attracti-
onis», 1818 (см. п. 3).
С точки зрения обеспечения приоритета, выбор материала
для публикации был сделан весьма неудачно. В самом деле.
^ Л. Шлезингер. Цит. соч., стр. 102 и след.
173
он пал на результат, по существу, не новый, опубликованный
Лагранжем еще в 1784—1785 гг. (см. п. 3), тогда как все
основное богатство открытий Гаусса, предвосхищавших
работы Абеля и Якоби, продолжало оставаться под
спудом.
Наконец, осенью 1827 г. во втором томе журнала Крелля
появилась первая часть «Recherches des fonctions ellipti-
ques» Абеля. Вот что писал Гаусс Бесселю в связи с этой
работой [Werke, Х(1), 248--249]:
«К обработке исследований о трансцендентных функциях,
ведущихся уже много лет (с 1798 г.), я, пожалуй, пока не
смогу приступить, так как сначала должен буду
разделаться со многими другими вещами. Г-н Абель, как я вижу,
предупредил меня теперь и облегчил мой труд примерно на одну
треть этих вещей, тем более, что он провел все выкладки
элегантно и кратко. Он избрал совершенно тот же путь,
который я проложил в 1798 г., поэтому неудивительно большое
совпадение результатов. К моему удивлению, это
распространяется также и на форму и отчасти на выбор
обозначений, так что многие его формулы кажутся точной копией
моих. Во избежание всякого недоразумения я отмечаю, однако,
что я не помню, чтобы я когда-нибудь делился этими вещами
с кем бы то ни было».
Что касается одной третьей доли, о которой говорит здесь
Гаусс, то Шлезингере разъясняет это так, что остальные две
третьих гауссовой теории трансцендентных функций
составляют теория гипергеометрических функций и теория арифме-
тико-геометрических средних и модулярных функций. С другой
стороны, следует отметить (это и делает Шлезингер в
другом месте), что у Гаусса отсутствовала общая теория
интегралов от алгебраических функций, начала которой были
заложены Абелем. Здесь мы должны остановиться еще на одном
высказывании Гаусса. На отдельном листочке без даты
сохранилась следующая запись: «Радикальная ошибка, из-за
которой мои прежние старания воплотить дух эллиптических
функций терпели крушение, кажется, состоит в том, что я
^ Л. Шлезингер. Цит. соч,, стр. 112.
174
хотел придать интегралу
Vl — €^ sin'-*
sm-* ф
значение, как выражению конечной части шаровой
поверхности, тогда как он должен, вероятно, выражать только
бесконечно узкий шаровой сектор» [Werke, Х(1), 546]. Цитируя
эту фразу, в связи с записью в дневнике Гаусса, относяш.ей-
ся к маю 1800 г., Клейн и Шлезингер считают очевидным, что
Гаусс имеет здесь в виду изображение комплексных чисел на
сфере, под конечной частью шаровой поверхности он
подразумевает параллелограмм периодов и, наконец, что,
отказываясь от конечной части в пользу бесконечно узкого
сектора шара, Гаусс высказывает заблуждение, имевшееся у него
до 6 мая 1800 г. Заблуждение это, будто бы, заключалось в
том, что Гаусс считал при 0<е^<С1 периодами эллиптическога
интеграла два действительных числа
27Г
М(1, Vi — e')
забывая умножить второе из них на i. Все это толкование,,
перешедшее в Werke из работы Шлезингера (Цит. соч.,
стр. 40), кажется нам совершенно неправдоподобным.
Действительно, мы видели (п. 3), что Гаусс уже на первых порах
изучения лемнискатических функций должен был
обнаружить, наравне с действительным периодом, также и чисто
мнимый период лемнискатического синуса и что задачу
обращения эллиптического интеграла первого рода, более обш.его,.
чем интеграл \т7^===, он рассматривал как естественное
обобщение предыдущей задачи, что внешним образом сказалось
и в наименовании соответствующей эллиптической функции
(якобиевой функции sn и)— универсальнейшим лемнискати-
ческим синусом. Какие же имеются основания утверждать, что
Гаусс до 6 мая 1800 г. считал оба основных периода
действительными? Мы не находим таких оснований и усматриваем
в приведенном выше толковании одну из тех ошибок, в которую
может впасть исследователь, желающий увидеть в Гауссе
J7S
автора незавершенного трактата по теории эллиптических и
модулярных функций, написанного в стиле последней
четверти XIX в. Действительно, Шлезингер пишет:
«То, что Гаусс назвал здесь «вероятным», было,
следовательно, то, что этот интеграл (для е действительного и меньшего 1)
обладает действительными периодами с несоизмеримым
отношением; но это заблуждение, как молния, освеш,ает мастерскую
мысли Гаусса: мы видим, что он интерпретирует
комплексное переменное на сфере и чертит фундаментальную область,
соответствуюш,ую параллелограмму периодов; мы видим, что
он из суп];ествования двух действительных периодов заключает
о суш,ествовании бесконечно малого периода. И все это в
1800 г.!»1.
Ничего из сказанного Шлезингером мы не усматриваем
в цитированном высказывании Гаусса. Мы не находим нигде
подтверждения того, что Гаусс уже в то время при
изучении функций пользовался изображением комплексных
чисел на сфере; а если даже допустить на мгновение
возможность такого использования, то тогда остается вопрос о том,
зачем именно понадобилось изображать сеть
параллелограммов (прямоугольников) на сфере, а не на плоскости и в какой
мере такие параллелограммы, умещаюш,иеся на сфере в
бесконечном множестве, пригодны для противопоставления
конечного бесконечно малому. Что касается нашего собственного
толкования, то мы придаем этой фразе только переносный смысл:
речь идет о преувеличенном значении, которое Гаусс
придавал до известной поры эллиптическому интегралу по
отношению ко всему классу изучавшихся им трансцендентных
функций как части по отношению к целому —«сфере». Быть может,
речь идет просто о том, что полный эллиптический интеграл
первого рода должен рассматриваться лишь как бесконечно
узкий частный случай среди класса всех функций,
представляемых гипергеометрическим рядом (см. ниже).
9. Мы уже отмечали, что основные результаты Гаусса, от-
носяп],иеся к теории арифметико-геометрического среднего,
лемнискатических функций и их обобш,ений, были получе-
^ Л. Шлезингер. Цит. соч., стр. 40.
ны им в юности, в последние годы XVIII в. К этим же годам
относится выполнение им других трудов, сыгравших
исключительно большую роль в истории науки. Не останавливаясь
на знаменитых «Арифметических исследованиях»,
являющихся предметом особой статьи этого сборника, мы займемся здесь
докторской диссертацией Гаусса и связанными с ней
исследованиями. Диссертация эта, напечатанная в Гельмстеде в 1799 г.,
носит длинное название: «Новое доказательство теоремы о
том, что каждая целая рациональная алгебраическая
функция одного переменного может быть разложена на
действительные множители первой или второй степени». Мы рассмотрим
ее здесь только в отношении ее значения в истории развития
математического анализа (и теории функций).
Математики позднейших поколений склонны расценивать
теорему, избранную Гауссом в качестве предмета докторской
диссертации, прежде всего как одно из звеньев той большой
работы по критическому обоснованию математики, которая
выпала на долю XIX в. и в которой Газ^сс принял серьезное
участие.
Объективная сторона такой оценки не вызывает возражений.
Но когда этой оценке приписывается и субъективное значение
и утверждается, что Гаусс занимался этой теоремой именно в
интересах критического обоснования математики^, то здесь
нам представляется необходимым подробнее разобраться в
вопросе, чтобы избежать возможных неточностей.
Необходимо прежде всего подчеркнуть, что почти во всех
доказательствах основной теоремы высшей алгебры,
предшествовавших Гауссу, речь шла именно о возможности разложения
многочлена (с действительными коэффициентами) на
действительные множители 1-й и 2-й степени, потому что в такой
форме вопрос, естественно, возникал в математическом
анализе (например, при интегрировании рациональных функций).
Поэтому предположение Клейна о том, что Гаусс выбрал
такую формулировку теоремы, желая скрыть свои идеи о
комплексных числах и их геометрической интерпретации^
^ См., например, Клейн. Лекции о развитии математики в XIX
столетии, ч. I, стр. 35.
^ Клейн. Цит. соч., стр. 54.
12 к. Ф. Гаусс 777
представляется нам пеосновательным. Далее основная теорема,
в противоположность таким, например, предложениям,
как теорема о том, что непрерывная функция, меняющая знак,
должна обращаться в нуль, отнюдь не казалась очевидной.
Напротив, многие математики, начиная с Лейбница,
сомневались в ее справедливости и пытались строить примеры,
опровергающие эту теорему ^.
Наконец, сам Гаусс, отметив ошибки в доказательствах
своих предшественников, не смог предложить в своей
диссертации логически обоснованного во всех частях доказательства.
Этим, отчасти, объясняется то, что он два раза возвращается
к доказательству этой же теоремы и, наконец, через 50 лет
дает новый вариант первоначального доказательства. Но дело
здесь не просто в поисках доказательств, удовлетворяющих
определенным требованиям математической строгости. Гаусс
дал всего три различных по идее доказательства основной
теоремы высшей алгебры (четвертое, как уже было сказано,
является лишь другим вариантом изложения первого
доказательства), и каждое из них обогатило математическую науку:
первое и третье имели преимущественное значение для
анализа, второе — для алгебры. На первом и третьем мы и
остановимся здесь.
В начале диссертации Гаусс подвергает критическому
разбору известные ему доказательства Даламбер^а, Эйлера, Фонсе-
не и Лагранжа. Наиболее интересным, с точки зрения
математического анализа, представляется связанное с разбором
доказательства Даламбера подробное разъяснение Гауссом
того обстоятельства, что ограниченная сверху функция не
всегда достигает своей верхней грани. Собственно, само
доказательство Гаусса представляет проведение идеи Даламбера. Вопрос
о существовании корня сводится к существованию точки
пересечения двух кривых и = О ж Т = Oj где U и Т являются,
соответственно, действительной и мнимой частями
многочлена X, рассматриваемыми как функции полярных координат
г ж ^ точки плоскости. Впрочем, Гаусс нигде не использует при
^ См. об этом, например, А. И. М а р к у ш е в и ч. Очерки по
истории теории аналитических функций. М.—Л., 1951, стр. 12—15.
178
доказательстве в явном виде комплексные числа. Чтобы ив-
беялать их применения, ему приходится доказывать теоремы
вроде следующей:
Если и я Т обращаются в нуль при некоторых значениях
г и ? н г sin 'f =7^0, то соответствующий многочлен X делится на
квадратичный множитель х^—2cos<prx -\- г^, если же г sin ^=О,
го X делится на линейный множитель х—г cos ср-
«Предыдущая теорема большей частью доказывается с
помощью мнимых величин (ср. Эйлер. Введение в анализ
бесконечно малых, т. 1, стр. 110),— пишет Гаусс;— я считаю,
что стоит взять на себя труд показать, как она может быть столь
же простым способом доказана без их помощи». Далее Гаусс
сравнивает кривые U = О ж Т= О с кривыми r^cosmcp= О и
г"^ sin m'f = О, соответствующими случаю X — х'^\ и
устанавливает, что последние являются асимптотами первых. Отсюда
следует, что любая окружность достаточно большого радиуса
пересекается кривыми f/= Ои 7"= Оровно в 4 m различных точках,
расположенных так, что они попеременно принадлежат то
первой, то второй кривой. Существование точек пересечения первой
и второй кривой выводится Гауссом после этого с помощью
чертежа и пояснений, апеллирующих в конечном счете к
геометрической интуиции читателя. Гаусс указывает при этом,
что он опирается на принципы геометрии положения (geome-
tria situs), «которые обладают не меньшей доказательной
силой, чем принципы геометрии величин». В варианте того же
доказательства, относящемуся к 1849 г. («Beitrage zur Theo-
rie der Algebraischen Gleichungen»), Гаусс высказывается
несколько обстоятельнее.
«В основном, — пишет он, — существенное содержание
всей аргументации принадлежит высшей области общего
абстрактного учения о величинах, не зависящей от
пространственного, предметом которой являются связанные по
непрерывности сочетания величин — области, которая в настоящее
время мало разработана и в которой нельзя подвигаться без
языка, черпающего от пространственных образов» (Werke,
III, 79).
Следовательно, речь идет о топологии, значение которой
для математического анализа было отмечено Гауссом в самом
12* 279
начале его научной деятельности. Законным преемником
Гаусса в этом отношении был Б. Риман, расширивший
топологические средства анализа и теории функций в своей знаменитой
Диссертации «Grundlagen fur eine allgemeine Theorie der
Functionen einer Komplexen Grosse» (1851 г.).
Возвраш;аясь к диссертации Гаусса, следует отметить еш;е,
что здесь он сообш,ает (без доказательства) некоторые важные
свойства линий Г = О и ^S* = О (т. е. линий уровня двух
сопряженных гармонических полиномов), а именно, что они
пересекаются, вообще говоря, под прямым углом, что если в одной
точке встречается помногу ветвей обоих кривых, то тогда
количества тех и других должны быть одинаковы, что дугрх
одной перемежаются при этом дугами другой, причем все они
пересекаются под равными углами, и т. п. В конце Гаусс
набрасывает схематически еще один способ доказательства
основной теоремы, отчасти использующий указанные свойства. При
этом он хотя и вспоминает свое возражение против Далам-
бера, упоминавшееся нами выше, все же не замечает, что
сделанные им оговорки обеспечивают только ограниченность
изучаемой функции снизу и, следовательно, вопрос о достижении
нижней грани остается необоснованным, как и в
критиковавшемся Гауссом доказательстве Даламбера.
Правда, значительно позже (в 1840 г.) в письме к
Шумахеру [Werke, Х(1), 108] Гаусс замечает, в связи с
доказательством основной теоремы высшей алгебры, опубликованным
Клаузеном^, что оно представляет аналитическое
облачение того принципа, который он изложил в геометрической
форме в конце своей диссертации, и добавляет, что изложение Кла-
узена не удовлетворяет требованиям классической строгости,
так как в нем не обосновано, что отрицательная всегда
возрастающая величина должна достигать нулевого значения.
Гаусс объясняет здесь же, что сам он не разрабатывал дальше
свою идею именно потому, что ее изложение, выдержанное
в духе классической строгости (im Geiste des Rigor antiquus).
оказалось бы весьма пространным.
^ Th. Glausen. Beweis, dass die algebraischen Gleichungen Wur-
zeln von dep Form a + Ы haben.—Astronom. Nachrichten, 17, 1840.
180
АО, Последующие доказательства Гаусса основной теоремы
отдалены от первого промежутком в 16 лет. В этом промел^утке
несколько раз публиковались доказательства французских
математиков. Первое из них принадлежало Аргану,
включившему его в небольшое сочинение, посвященное геометрической
теории комплексных чисел («Essai sur une maniere de repre-
sonter les quantites imaginaires dans les constructions geome-
triques», 1806). Сочинение это осталось незамеченным
современниками (за исключением Лежандра).
В этой, маленькой книжке доказательство занимает меньше
двух страничек (стр. 58—59). Оно основано на замечании, что
если в некоторой точке многочлен отличен от нуля, то
найдется близкая точка, в которой модуль многочлена будет меньше,
чем в данной. Переходя от точки к точке, можно придти к
значению X, которое дает 7 — 0. Очевидно, что к этому
рассуждению применимо критическое замечание Гаусса,
приведенное в предыдущем пункте. Аналогичное доказательство
(очевидно, по Аргану) дал Лежандр во втором издании
«Теории чисел» (Theorie des Nombres, 1808). Наконец, в
связи с полемикой в Ann. de Mathem. (IV, 1813; V, 1815), в
которой Арган отстаивал свой приоритет в геометрическом
истолковании комплексных чисел, Арган вновь о'публршовал свое
доказательство. Невидимому, Гаусс не был непосредственно
знаком с этими работами. Однако косвенно он все же дал
позднее положительную оценку доказательства Аргана. Дело в том,
что то же доказательство было включено Коши в его
«Алгебраический анализ» (Analyse alg., 1821) с указанием, что
приводимое им доказательство похоже на доказательство Лежандра
и основано на тех же принципах. Значительно позже, в
августе 1834 г. в письме к Дробишу — автору руководства по
теории уравнений, включившему в свою книгу только первое
доказательство Гаусса, Гаусс указывал, что кратчайшим и
простейшим из трех принадлежащих ему доказательств он
считает третье (о нем мы будем еще говорить).
«Впрочем, я нахожу доказательство Коши в его основной
идее столь же элегантным и мог бы, если бы я должен был
ограничиться лишь одним, отдать предпочтение ему. Но
наиболее поучительным, пожалуй, было бы развитие обеих
181
основных идей, в котором фактическое рассмотрение как бы
геометрического смысла обеих идей имело бы для разума
нечто действительно усладительное» [Werke, Х(1), 107].
Оставляя в стороне второе доказательство Гаусса, целиком
принадлежащее алгебре, мы остановимся на третьем
доказательстве. Но, чтобы понять его происхождение, необходимо
будет привести здесь одно обширное высказывание Гаусса,
чрезвычайно важное само по себе, так как оно содержит в
себе краткое изложение теории интегрирования в комплексной
области. Речь идет об известном месте из письма Гаусса к
Бесселю от 18 декабря 1811 г. [Werke, Х(1), 366—368].
Непосредственным поводом для письма послужила заметка
Бесселя об интегральном логарифме hx 1^-^]. «Прежде всего
я стал бы спрашивать с того, кто хочет ввести новую функцию
в анализ, разъяснения, собирается ли он пользоваться ею
исключительно для действительных величии (действительных
значений аргухЛ1ента функции), а мнимые значения аргумента
рассматривать только как бы некий нарост (gleichsam nur als
ein Uberbein) или же он присоединяется к моему основному
принципу, что в царстве величин мнимые а -\- b V—1 — а +
-\-Ы должны рассматриваться как пользующиеся одинаковыми
с действительными величинами правами. Здесь речь идет не
о практической потребности; по-моему, анализ есть
самостоятельная наука, которая в результате пренебрежения
этими воображаемыми (fingirten) величинами теряет
исключительно много в красоте и законченности и вынуждена каждое
мгновенье присоединять в высшей степени обременительные
ограничения к истинам, которые иначе имели бы значение
всеобщих. Я, кажется, могу предположить, что Вы в
существенном согласны со мной в этом отношении, так как уже Ваше
объяснение в пункте 18 ^ показывает, что Вы никоим образом не
преграждаете пути к исследованию \\{а + Ы). Что нужно
понимать под l'^[x)dx для х== а -[- Ы? Очевидно, если хотят
исходить из ясных понятий, нужно принять, что X, отправляясь
от значения, для которого интеграл должен равняться нулю,
посредством бесконечно малых приращений (каждое вида а +
1 Речь идет об упомянутой выше заметке Бесселя.— А. М.
182
-^Ы) переходит к а;= а + Ы, и тогда сложить все ^{x)dx. Так
смысл вполне установлен. Но переход может совершиться
бесконечно многими способами; также, как совокупность всех
действительных величин можно мыслить в виде бесконечной
прямой линии, так и совокупность всех величин, действительных и
мнимых, можно сделать осязаемой (sinnlich machen)
посредством бесконечной плоскости, каждая точка которой,
определяемая абсциссой = а и ординатой = Ь, будет как бы представлять
величину а + Ы. Непрерывный переход от одного значения
X к другому а + Ы совершается поэтому по линии и,
следовательно, возможен бесконечно многими способами. Я
утверждаю теперь, что интеграл l^{x)dx при двух различных
переходах сохраняет одно и то же значение, если внутри части
плоскости, заключенной между двумя линиями,
представляющими переход, функция ^{х) нигде не равна <у^. Это прекрасная
теорема ^, нетрудное доказательство которой я дам при
удобном случае. Она связана с другими прекрасными истинами,
касающимися разложений в ряды. Переход в каждой точке
следует производить всегда так, чтобы ни разу не затронуть
места, где ф(х) =сх). Я настаиваю на том, что такие точки
следует обходить потому, что для них, очевидно, первоначальное
основное понятие интеграла J?(a::)d:r теряет ' ясность и легко
переходит к противоречиям. Вместе с тем, впрочем, отсюда
ясно, как функция, порожденная посредством l^{x)dx, может
иметь многие значения для одного и того же значения х, а
именно, в зависимости от того, будет ли при переходе допущен
однократный или многократный обход вокруг точки, в которой
?(.т) —^х)^или же такого обхода совсем не будет. Если,
например, log X определить посредством V^dx, начиная от гк = 1,
то можно прийти к log X или не огибая точку х, или
посредством однократного или многократного обхода вокруг нее;
каждый раз будет добавляться константа + 2^i или — 2^i;
отсюда совершенно ясны различные логарифмы каждого
^ При этом, собственно говоря, еще предполагается, что сама ф (х)
является однозначной (einformige) функцией от х или, по крайней мере,
'iTo для ее значений внутри всей этой части плоскости принята только
одна система значений без нарушения непрерывности.— Прим. Гаусса.
183
числа. Если же ^{х) не становится бесконечной ни для одного
конечного значения х, то интеграл всегда является только одно- j
значной функцией». /
Мы привели эту длинную выписку из письма Гаусса потому,
что из нее вытекает, что Гаусс в 1811 г. полностью владел
геометрическим представлением комплексного переменного, он
рассматривал интегралы от функций комплексного
переменного вдоль кривых, принадлежащих комплексной плоскости,
формулировал (и, повидимому, умел доказывать) основную
теорему теории функций комплексного переменного
(интегральную теорему Коши) и, наконец, умел объяснить
многозначность функций, представляемых интегралами от
однозначных функций, обходами вокруг особых точек (полюсов).
Независимо от Гаусса, но несколько позже, чем он, к
аналогичным заключениям пришел Пуассон. Однако полное
развитие всех этих идей, как известно, принадлежит Коши,
который и вошел по праву в историю науки как один из
основоположников теории аналитических функций комплексного
переменного.
Заметим, что Гаусс, так же, впрочем, как и Коши^, не
вводит условия аналитичности, ограничиваясь лишь
требованием непрерывности интегрируемой функции. Повидимому,
последнее требование нужно понимать не только в позднейшем
значении этого слова, но и в старом, эйлеровском, где функция
предполагается заданной одним и т^м же аналитическим
выражением.
Подробное изложение идей, приведенных в цитированном
письме, обрываюш;ееся, к сожалению, как раз на интересной
теореме, находится в работе Гаусса «Определение сходимости
тех рядов, в которые разлагаются периодические функции
одной переменной величины», написанной около 1850 г. fWer-
ке, Х(1), 407—416]. Из самого названия этой незаконченной
статьи можно заключить, что под «истинами, касающимися
разложений в ряды», Гаусс подразумевал не теорему о ряде
Тейлора (как это предполагал Штекель и вслед за ним и автор
настоящей статьи в своих «Очерках по истории теории аналитиче-
^ См. А. И. Маркушевич. Цит. соч., очерк второй.
184
ских функций»), а вопросы разложения в тригонометрический
ряд функций комплексного переменного. Это подтверждается
отрывком Гаусса, примыкающим к только что цитированной
статье [Werke, Х(1), 416—419], где рассматривается вопрос
о разложении в тригонометрический ряд функций f{x + iy)
с периодом 2^, определенной в полосе \у\ -< h.
11. «Третье доказательство о разложении целой
алгебраической функции на действительные множители» было
опубликовано Гауссом в 1816 г. (Werke, III, 59—64). По методам работа
эта целиком принадлежит к теории аналитических функций
комплексного переменного, хотя Гаусс с прежней тщательностью
очищает изложение от следов использования комплексных
чисел и их геометрического смысла. В результате получается
доказательство изящное, но производящее впечатление
большой искусственности.
Пусть X = х'^' + Ах"^-^ -Ь Вх^^-2 _|_ Сх"^-^ + . . ., где все
коэффициенты действительны. Гаусс вводит следующие
обозначения:
r^cos mcp + Лг^-1 cos (m — 1) ср + Br^-'^ cos (m ~ 2) ср + . . . = t,
г'" sin mcp + Л/-^" 1 sin {m — 1) cp + Br'^-^ sin (m — 2) cp + . . . = u,
du _ , dt f d-t __ „ dhi „
{t^ + 1^2) (tt" + UU'') + (tu' — Ut'f — {W + UU'f _
и показывает сначала, что при
3
г^Во=^ max
так, что t И и при этих значениях г не могут одновременно
обратиться в нуль. Все сводится теперь к тому, чтобы показать для
какого-либо /?>i?o, что существуют г и '^{0^г<^В, 0°<ср<360°)
такие, что t ^ и = О, Если допустить, что таких значений г
и '•f не существует, то у сохраняет конечное значение в
указанных для г и ^ границах; поэтому интеграл J Jz/ dr d 9 должен иметь
185
вполне определенное конечное значение О. Но
tu' — ut'
^?/(icp =
о
г (Г- + и')
в пределах от О до 360°, поэтому и О = 0. С другой стороны,
Г 7 tt' -\- ии' ^ ^
(в пределах от О до R)\ поэтому и О>>0. Из найденного
противоречия и вытекает справедливость теоремы.
Попытаемся восстановить ход идей, который привел
Гаусса к его третьему доказательству. При этом мы будем
опираться на соображения об интегралах от функций комплексного
переменного, высказанные Гауссом в приведенном выше
письме к Бесселю. Если доказывать теорему от противного и
допустить, что многочлен X нигде не обращается в нуль, то
отсюда будет следовать, что интеграл \ j"C?X, взятый по любому
замкнутому контуру, должен равняться нулю. В частности,
будем иметь
С dX
х~о.
iZHr
Этот интеграл равен разности двух значений Ln X в одной
и той же точке окружности |Х |=г.
Так как
Ln X = In j/^M^ + i Arctg ^
и In у fi -\-u^ — однозначная функция точки, то отсюда следует,
что изменение значения ^Arctg —(= ArgX) при обходе
точкой X окружности \Х\ = г равно нулю, т.е.
о о
Но,сдруго11 стороны, Гаусс еще при проведении своего
первого доказательства использовал тот факт, что многочленХ
асимптотически ведет себя, как степень х^, и, следовательно,
изменение значения Arctgy при всех достаточно больших г должно быть
186
таким же, как и для степени, т. е. равным 2-А?^г>0. Из
сопоставления этих двух фактов и следовала справедливость основной
теоремы высшей алгебры. Оставалось только построить чисто
аналитическое доказательство, свободное от ссылок на
комплексное переменное и на геометрические представления.
С этой целью Гаусс, очевидно, решил вместо рассмотрения
однократного интеграла
для которого неопределенное интегрирование приводит к много-
:5начной функции Arctg — , ввести двукратный интеграл
t
2п г
о о
Arctg-^ к/г dcp.
для которого каждое отдельное интегрирование приводит к
однозначной, рациональной относительно ^ и ^ (и их
производных) функции. Действительно, в ходе самого доказательства
выясняется, что
Но
-77^~—^ = ^— In У ^ + гг^ ^ -г- Arctg -— , -—^.—- =
д ^ . и
и, след(.»вательно,
^ ^-яТягЛ Arctg —
Р1з изложенного здесь следует, что третье доказательство
Гаусса, по сути дела, является примером применения так
называемого принципа аргумента к основной теореме высшей
алгебры.
* Шлезингер (Цит. соч., стр. 102) приводит ошибочное оыраже-
ние у:
не позволяющее раскрыть идею Гаусса.
1S7
12. Прежде чем перейти к исследованиям Гаусса по теории
гипергеометрических функций, остановимся на некоторых
отрывках, где рассматриваются вопросы теории пределов.
В незаконченной статье «Основные понятия учения о
рядах» [Grundbegriffe cler Lehre von den Reihen, Werke, X(l)y
390—394], относящейся, no определению Шлезингера, ко
времени около 1800 г., Гаусс формулирует основные понятия
теории пределов числовых последовательностей в форме,
далеко опережающей его время.
Прежде всего, Гаусс определяет понятие, ряда, вкладывая
в него смысл, выражаемый в наше время термином
последовательность. Гаусс подчеркивает, что основное в этом понятии —
принцип, по которому каждому месту соответствует
определенная величина (член ряда). Он указывает также, что если
определять ряд как совокупность значений функции одного
переменного, соответствующих натуральным значениям аргумента^
то объем понятия сузится, по крайней мере, если не придавать
термину функция более широкого содержания, чем это делалось
до сих пор (очевидно, имеется в виду функция как
аналитическое выражение, и это единственное место в отрывке, в
котором сказывается время его написания). Для пояснения
Гаусс приводит пример последовательности простых чисел, а
также чисел, обратных квадратам простых чисел.
Далее вводится понятие верхней грани X (obere Grenze)
и наименьшей верхней грани L\ которая определяется тем,
что ни один из членов последовательности не превосходит V,
и, с другой стороны, в последовательности, если только ее
достаточно далеко продолжить, найдутся члены, превышающие
всякую величину, меньшую, чем L\ Аналогично определяются
нижняя грань [J- и наибольшая нижняя грань М', Для
краткости Гаусс уславливается называть L' и М', соответственно,
верхней и нижней гранями без добавления эпитетов:
наименьшая и наибольшая. Указывается, что в последовательности
могут быть, но могут и не быть члены, равные верхней или нижней
грани. Указывается также, что существуют
последовательности, не имеющие ни верхней, ни нижней грани, имеющие
нижнюю грань, но не имеющие верхней и т. д. — всего четыре
случая. Из них последний, когда есть и верхняя и нижняя грань
188
(случай ограниченной последовательности) признается
наиболее важным.
Далее для последовательности а , а', а'",..., имеющей
верхнюю грань /У, строятся числа L", L"\ ..., представляющие
верхние грани последовательностей, получаемых из данной
отбрасыванием одного, двух и т. д. начальных членов.
Отмечается, что L'^L"^L'"^.... Аналогичное построение по
отношению к нижним граням проводится для последовательности,
имеющей нижнюю грань М', Получаются числа М", М'", ...,
причем М'^М"^М'" <^.... Если существуют одновременно
и нижняя и верхняя грани, то Af^^^<^L^^^ и последовательность
М\ М", М"\ ... имеет верхнюю грань М, а
последовательность L', L",L"', ... имеет нижнюю грань L, причем M^L.
М называется последней нижней гранью, а L—последней верхней
гранью (очевидно, что М есть нижний и L — верхний предел
последовательности). В случае, если L = М, то их общее
значение называется абсолютной границей ряда (предел
последовательности).
Отрывок заканчивается формулировкой теоремы: если по
следовательность а, а\ а", ,.. имеет абсолютную границу
А и последовательность Ь^Ъ\ &",... имеет абсолютную
границу В, то последовательность а-\-Ъ, а -\-h',а" \-Ъ", ...
имеет, абсолютную границу Л + В.
Повидимому, эта работа так и не имела продолжения. С ее
ныне столь привычными для нас понятиями и терминами
плохо вяжется архаическая терминология значительно более
поздней рукописи, написанной после 1831 г. (Шлезингер
относит ее к 40-м годам) и также незаконченной: «Сходимость рядов,
в которые разлагаются периодические функции одного
переменного» [Convergenz der Reihen, in welche die periodischen Func-
tionen einer veranderlichen Grosse entwickelt werden, Werke,
X(l), 400—405]. Под сходимостью ряда (термин ря9, очевидно,
попрежнему употребляется в смысле последовательность) Гаусс
понимает здесь стремление к нулю членов ряда. Он
указывает, что сходимость ряда отличается от сходимости «его
<^уммирования» (ihrer Summierung) к конечному пределу; из
последней следует первая, но не обратно.
Расходящимся называется ряд, в котором при достаточно
1S9
далеком продолжении встречаются члены, превосходящие
каждую наперед заданную величину.
Употребление понятий сходящегося и расходящегося
ряда в смысле, близком к этому, встречается в произведениях
Гаусса, относящихся к различному времени. Так, в своей
диссертации (1799 г.) он делает следующее замечание по поводу
асимптотических степенных разложений в Instit calc. diff.
Эйлера^: «...весьма желательно показать, ясно и строго, почему
эти ряды, которые сходятся вначале весьма сильно, потом все
слабее и слабее и, наконец, все более и более расходятся,
доставляют, несмотря на это, почти точное значение суммы, если
только берется не слишком много членов и насколько такая сумма
может быть с уверенностью принята за истинную» (Werke, III, 10).
Что касается существа поставленного здесь вопроса, то известно,
что в полном объеме он был исследован впервые Пуанкаре.
Продолжим, однако, прерванное нами изложение.
Ряды могут быть и несходящимися и нерасходящимися.
Вообще существуют следующие классы рядов
(последовательностей) : I — расходящиеся; II — не перестающие колебаться
между известными границами; III ~ ряды, сходящиеся к пределу,
отличному от нуля; IV и V — ряды, сходящиеся к нулю,
которые будут просто называться сходящимися. К классу V
относятся те из них, для которых последовательные суммы
бесконечно приближаются к определенному конечному пределу, к классу
IV — те, для которых это не имеет места. Эта классификация
распространяется и на последовательности с комплексными
членами; в отдельности определяется класс для последовательности
действительных и мнимых частей и вся данная
последовательность относится к низшему из двух классов.
Рассматривается эффект от умножения членов некоторого
ряда S на соответствующие члены геометрической прогрессии
1, /г, /г^, h^, ... Если ряд после умножения продолжает схо-
1
диться, пока/г <С—(О <Се <С 1), и перестает сходиться, если
1
h > у, то е называется показателем сходимости ряда (очевидно,
1
— ость радиус сходимости степенного ряда коэффициентами S),
1 См. Русское издание: Л. Эйлер. Дифференциальное исчисление,
ч. 2, гл. VI, 1949, стр. 302 и след.
190
Вторая половина отрывка посвящена рассуждению о
необходимости точных и притом наиболее общих определений в
математике и об отсутствии правильного понимания природы
д значения комплексных чисел до недавнего времени [здесь
делается ссылка на знаменитый автореферат исследования о
биквадратичных вычетах (1831 г.), где Гаусс изложил
геометрическое истолкование комплексных чисел, которым он
пользовался уже многие годы]. Отрывок заканчивается следующими
высказываниями о роли комплексных чисел при изучении
функций:
«Полное познание природы аналитической функции должно
включать в себя также понимание ее поведения при мнимых
значениях аргумента, и часто последнее даже необходимо
(unentbehrlich) для правильного суждения о поведении функции
в области действительного аргумента. Поэтому необходимо
также, чтобы первоначальное определение понятия функции
обязательно (mit gleicher Bundigkeit) распространялось на полную
область величин, которая охватывает собой действительные
и мнимые величины под общим именем комплексных величин».
Здесь Гаусс, как и в некоторых других местах, употребляет
термин аналитическая функция. Нет оснований понимать этот
термин в современном его значении; скорее, речь идет о функции,
определенной аналитическим выражением.
13^. Гипергеометрический ряд
1y ^ 1.2у(у + 1)
a(a+l)(a + 2)|S(6 + l)(p + 2) ,„о
-^ 1.2.3.Y(T + l)(Y + 2) ^ +■■■ ^^^)
впервые встречается в несколько более общем виде в
«Интегральном исчислении» Эйлера^, где устанавливается, в
частности, что интеграл
1
\ w^-i (1 — иу-^~^ (1 — xuydu
о
^ При составлении этого пункта мы использовали, помимо изложения
Шлезингера (цит. соч., стр. 86—100), также клейновские лекщ1И по
теории гипергеометрической функции, изданные О. Хауптом (F. Klein.
Vorlesungen tiber die hypergeometrische Function. Berlin, Springer, 1933).
^ L. E u 1 e r. Institutiones calculi integralis, TI, 1769.
191
разлагается в ряд вида
И удовлетворяет дифференциальному уравнению
х{1 —х)сРу-\- [C'-{a + b + c)x\dsdx — absdx^ -О (24)
гипергеометрическое дифференциальное уравнение).
Здесь же рассматривается и более общее
дифференциальное уравнение
х'^ {а + te^) dhj + X (с + ех'^) dy dx + {/ + gx"") ydx^=0,
решение которого также ищется в виде степенного ряда.
Последнее уравнение в более общем (неоднородном) случае
изучал учитель и друг Гаусса И. Пфафф в своих «Disquisi-
tiones analyticae» (1797). Пфафф интересовался изысканием
случаев интегрируемости уравнения в квадратурах.
Гипергеометрическому ряду в его сочинении посвящена отдельная
глава, причем здесь впервые встречается эпитет
гипергеометрический в применении именно к данному ряду.
Пфафф нашел много случаев, когда сумма ряда выражается
через элементарные функции. Любопытно отметить, что Гаусс,
представлявший свою диссертацию в Хельмштедский
университет, профессором которого был и Пфафф, употреблял тогда
(1799 г.) термин гипергеометрический в ином смысле. А именно,
желая привести пример степенного ряда, члены которого для
любого сколь угодно малого значения переменного могут
превзойти любую заданную величину, он указывает пример,
в котором коэффициенты ряда составляют
гипергеометрическую прогрессию (progressionem hypergeometricam).
Повидимому, здесь Гаусс имеет в виду последовательность
значений факториалов 1, 1-2, 1-2-3, ... или же
последовательность: 1, 2^, 3^, 4^, ..., к каждой из которых применимо
наименование сверхгеометрической. Отсюда, быть может, можно
заключить, что в это время Гаусс еще не был знаком с
исследованием своего учителя. Однако с частным и притом
нетривиальным случаем гипергеометрического ряда в смысле Пфаффа
Гаусс столкнулся в своих занятиях арифметико-геометричес-
192
КИМ средним уже около 1800 г. Именно, в п. 3 мы отмечали,
что Гаусс получил к этому времени разложение в ряд
^ M(i,Vi — X') М{1 +
1 - 1 4- у ГЬЗ...(2/с-1)12 ,
являющееся, очевидно, частным случаем геометрического ряда
(при а = р = у, 1с = 1 и замене ж на а;^ j, и заметил, что
сумма ряда удовлетворяет дифференциальному уравнению
Одновременно Гаусс обнаружил, что гипергеометрическими
рядами выражаются также коэффициенты тригонометрического
_1_
ряда, представляющего функцию (а^ + а'^ — 2аа cos ^)
(обратную величину расстояния между двумя точками),
играющую важную роль в теории планетных возмущений. В
письме к Бесселю от 3 сентября 1805 г. [Werke, Х(1), 237—248]
Гаусс мотивирует свой интерес к поискам разложений
коэффициентов ряда
— JL
(а2 + а'2 — 2аа'cos ср) ^ =
= Y Л"^ + ^' cos ср + А' cos 2ср + А" cos Зср + • • •
тем, что эти коэффициенты ему приходилось вычислять не как
обычно для одной определенной пары значений а и а', но для
больпюго числа подобных пар, достигавшего 50 в случае
Цереры; для Паллады и Юноны их потребуется еще больше.
Гаусс сообщает, что он обладает теперь искусственными
приемами, основанными частично на совсем, казалось бы,
посторонних изысканиях (вероятно, имеется в виду исследование
арифметико-геометрическбго среднего), позволяющими весьма
быстро вычислять нужные коэффициенты. Полагая ^ = /,
Гаусс приводит следующие разложения:
2^^ — i-t-2 2^^2-4 2.4^ "^2.4.6 2-4.6
13 к. Ф. Гаусс 29$
'2""^ ~'2'\ ^ 'Л-А' ^2.4 4-6' ^ 2.4.6 4-68' ^ j'
y«'^" = 2-4/^(1+ М/^+й-1:8'/* +
1.3.5 5.7.9
2.4-6 * 6.8.10^
Очевидно, что числовые коэффициенты здесь выписываются
так подробно для того, чтобы подчеркнуть закон их
составления.
Мы видим, что все найденные разложения (в скобках)
являются гипоргеометрическими рядами, в которых положено
1 13 5
а = у , ж = /^, р, соответственно, = у, у и у, 7= 1, 2 и 3.
Дальше Гаусс объясняет, почему он вместо величин
\а'А°, ^а'А', ^а'А",...,
В целях удобства и точности вычислений, вводит другие
величины, сначала
/
а затем
B^'^^d'^Y^^^ZT^^
.(/с) 2к-\-1 Б(^)
^ lk-^2 в('^-М)(1+/2) ' ^^^f
откуда получается следующее соотношение:
^iU) _ ^ __ {2к 4- ЗГ- \
^^ - ^ (2/С +3)^-1 ivU-i-i; • V^^^
Это соотношение дает возможность получить разложение
в непрерывную дробь для —-^ и, наконец, для (1 + р) N^^^^ .
Последнее быстро сходящееся разложение позволяет вычислить
N^^^\ затем с помощью выражения (26) все предыдущие N^^"^
и, наконец, при помощи уравнения (20) j^^^^^ и А^^\
Мы остановились здесь на всех этих деталях для того,
чтобы показать, как потребности астрономических вычислений
привели Гаусса не позднее, чем в 1805 г., к рассмотрению
сумм гипергеометрического ряда при одном и том же а: = /^ и
разных, но отличающихся лишь на целые числа, значениях Р
194
и 7 (переход от Л^^^ к А ^'^^^ и, следовательно, от В^^^ к А^^
сопровождается увеличением р и ^ на 1), а также к
разложению в непрерывные дроби величин N^ \ зависящих, в конечном
счете, от отношения суммы двух гипергеометрических рядов.
Все эти вопросы развивались и обобщались Гауссом в
последующие годы и получили развернутое выражение в его
«Первой части общих исследований о бесконечном ряде
, аЗ а(а + 1) Р(Р + 1) о ,
a(a + 1)(oc + 2)g(!^-1-1)^ + 2)^3 + etc.»,
^ l.Z.3.Y(Y + l)(Y-t-2) ^
напечатанной в 1813 г. (Werke, III, 125—160).
В автореферате (Werke, Ш, 196—2Э2) Гаусс отмечает
практическое и теоретическое значение изучения высших
трансцендентных функций, которые лишь в специальных случаях
связаны с простейшими трансцендентными — логарифмической и
круговыми, и сообщает, что, занимаясь многие годы этим
изучением, он в качестве введения к ряду других работ составил
эту работу, содержащую относительно небольшую часть era
результатов.
Ряд, составляющий предмет исследования, обладает
широко объемлющей общностью. Едва ли можно назвать какую-либо
изучавшуюся аналитиками трансцендентную функцию, которую^
нельзя было бы свести к этому ряду. Ограничившись
пересказом этой части автореферата, мы рассмотрим далее вкратце
содержание всей работы.
Сумму ряда автор обозначает через F {а, р, f, х)
(гипергеометрическая функция; впрочем, сам Гаусс этим термином не
пользуется), замечая при этом, что она симметрична
относительно а и j8. При а, р и Y фиксированных она является
функцией одного только X] если а — 1или р — 1 — целое
отрицательное число, то функция сводится к рациональной
алгебраической; элементу ^ нельзя придавать целые значения ^^0, так
как иначе появятся бесконечно большие члены. Из
рассмотрения отношения последующего члена ряда к предыдущему
выводится, что ряд сходится при |х1<;1, «если не с самого
начала, то после определенного места (речь, очевидно, идет о
t3* 29S
монотонной сходимости модулей членов к нулю.—^. М.) и
также (atque) приводит к определенной конечной сумме»; если
|:;с|>>1, то ряд, «если не сначала, то с определенного места
расходится, таким образом (ita) его сумма не супдествует»
(сравните п. 12). Случай х = 1 рассматривается особо (см. ниже).
Далее Гаусс дает различного вида выражения элементарных
функций, а также коэффициентов разложения в
тригонометрический ряд функции {а^ + Ь^ — 2аЬ cos ср)""^ (см. выше случай
n—-7j-) через гипергеометрические функции. Этим заканчи-
2^
вается введение. Первый, самый короткий, отдел посвяпден
выводу линейных соотношений между гипергеометрическими
функциями /^(а, р, Y, х), F{cl', р', ^', ^), F [cl\ ^\ f, х), . . . , для
которых все разности а—а', р — р', ^ — т'' ^ — '^"' ^ — Р"'
7 — 7^ • • • являются целыми числами. В основе лежат
соотношения между соседними функциями: F[ol, р, ^, ^) и /^(а', Р', ^'^ х),
для которых лишь одна из трех разностей а' — а, Р' — р и
Т' — Т равна rfclj а остальные две равны нулю.
Во втором отделе соотношения первого отдела применяются
к разложению в непрерывные дроби отношений вида
>Ча, Р, т, ^) '
где две из разностей а' — а, р' — р, ^'—^ равны -{-1, а третья
равна нулю; мы видели выше из письма к Бесселю, что именно
с этим случаем Гаусс встретился в своих астрономических
вычислениях. Гаусс не ставит вопроса о сходимости разложений,
получая их путем повторного деления степенных рядов ^.
Третий, самый обширный отдел посвяш;ен исследованию
гипергеометрического ряда при а, р и f действительных (как и во
всей работе) и х = i"^. Отметив, что все коэффициенты, начи-
^ Вопрос о сходимости был впервые поставлен и решен в более общем
случае в работе Римана «Beltrage zur Theorie der durch die Gausssche
Reihe F{ayb, c, x) darstellbaren Functionen», 1857; Риман доказал, что
непрерывные дроби сходятся к F (а, Ь, с, х) во всей комплексной
плоскости с разрезом вдоль положительной части действительной оси от 1 до со.
* Случай X комплексного по ^модулю, равного 1, совсем не
рассматривается в работе; общий случай комплексных ее, ^, у и х, \х\ = 1 был
полностью изучен в работе Вейерштрасса «Uber die Theorie der analyti-
schen Fakultaten», 1856.
196
ная с некоторого места, положительны, Гаусс «со всей
строгостью», «ради тех, кто благосклонен к строгим методам древних
геометров», высказывает следующие утверждения: 1)
коэффициенты бесконечно возрастают (если ряд не обрывается), когда
а+Р — т — 1>0; 2) коэффициенты сходятся к конечному
пределу, когда а + р — ^ — 1 — 0; 3) коэффициенты бесконечно
убывают к нулю, когда а + Р — 7^~1<0; 4) в третьем
случае для сходимости суммы нашего ряда при х ~ I нет
препятствий (summam seriei nostra pro x==l, non obstante convergen-
tia in casu tertio), если a+P — T^^ — сумма равна
бесконечности; 5) сумма, безусловно, конечна, когда а + Р — Т <^ 0.
Гаусс рассматривает более общий случай ряда
(последовательности) Л/, М\ М", М"\ . . . , для которого отношение
последующего члена к предыдущему имеет вид
t'^ + Ai^-^ 4- Bt^-^ + Ct^~^ -4- ■ •'
для t = 7V., m 4-1, //2 + 2, . . . Доказывается, что при A^a
члены последовательности бесконечно растут, при А<^а
бесконечно убывают (сходятся к нулю), при А^а они стремятся
к конечному (отличному от нуля) пределу. Далее доказывается,
что хотя при —1<$^Л — a<iO члены М, Д/', М'\ . . , и
стремятся к нулю, сумма ряда М -{- М' -\- М" -}-... «возрастает
сверх всякого предела».
Наконец, в случае, когда А — а <^ — 1, «сумма ряда
М ~\- М' + М" 4- ^"' + и т. д., продолженная в бесконечность,
наверное, будет конечной». Таким образом, Гаусс здесь
формулировал и доказал признак сходимости рядов, по праву
носящий его имя. Любопытно отметить, что сам Гаусс, повидимому,
не придал серьезного значения этому результату. По крайней
мере, он не упомянул о нем в довольно пространном немецком
автореферате работы; там говорится только, и то мимоходом,
что с геометрической строгостью доказано, что ряд при х = I
только тогда сходится к конечной сумме, когда ^ — ос — ,8^0,
Далее Гаусс высказывает следующее предложение: если в
ряде S = I + ах + Ьх^ + сх^ -\-, , , коэффициенты стремятся
к нулю, то (1—x)S~^0 при х->1. Для доказательства он
представляет (1—х) S в виде: i + {а — 1)х + {Ь — а)х^ +
197
+ (с — b) х^ + . . . и ссылается на то, что при х == I сумма
первых двух членов есть а, первых трех 6, первых четырех с
и т. д. и, следовательно, стремится к нулю; очевидно, что такое
рассуждение неявно предполагает справедливость второй
теоремы Абеля. Применяя это предложение к произведению
(1 —a:)F(a, р, f — 1, х) при ^сс — ,В > О (это условие, как Гаусс
уже доказал, обеспечивает стремление к нулю коэффициентов),
Гаусс получает из соотношения между смежными функциями
Т [т - 1 - (2т - а -^ Р - 1) X] F (а, р, т, х) +
+ (T-^)(T-P)xF(a,p,T + l,x)-
_ ^ (^ _ 1) (1 _ ^) /г (а, р, ^ - 1, ^) = О,
что
^К Р, т, 1) = ^L '^1^^в?-^(^-> Р' т + 1Д);
у (у — а — Р)
при ЭТОМ, очевидно, снова два раза неявно использована
вторая теорема Абеля. Отсюда следует, что
F(a, S V и ll(fe, y--l)n(fe,T-a-p-l)F(a,fi,y + fe,l)
^ К^у Р» Т) Ч— п(А;^у_а — 1)11(А:, у—р —1)
где
П (к, z) = 7w—r-^x—7—гтг z^*
Как раз в виде предела такого произведения при к—^оо
Эйлер определял z!, для любого z, еще в 1729 г. в письме
к Гольдбаху; при этом Эйлер ни тогда, ни позже не
обосновывал предельного перехода. Гаусс намечает такое
обоснование, записывая 1пП(/г + л, z)—1пП(/г, z) в виде
I л. , + ,_,)V-, 1-±^+-^+... + -Л^] ,27)
(мы пользуемся здесь современными нам обозначениями) и
утверждая, что легко доказать, что это приращение «всегда
остается конечным, когда п бесконечно возрастает», т. е.
стремится к конечному пределу. Учитывая, что Гаусс только
что совершал почленный предельный переход в степенном ряде,
при условии сходимости получающегося при этом ряда, как
операцию, не требующую никакого обоснования, можно не со-
198
мневаться в том, что и здесь Гаусс имел в виду лишь доказа-
тельство сходимости ряда, формально получающегося из
выражения (27) при замене каждой суммы
11 1
(h-^lf (h±2f {h + nf
соответствующим бесконечным рядом
1
П=1
{h -f пу
Как бы то ни было, Гаусс вводит функцию n(z) [=r(z— 1)]
А предел: 11
произведения
как предел: \\тИ(к^ z) и записывает ее в виде бесконечного
П(2)= ^ ^^"^^ ^''^^ ^^"^^
2 + 1 1^(2 + 2) 2'(3+z) 3^(4 + 2)
(заметим, что в упомянутом письме Эйлера, а также -в
«Дифференциальном исчислении» Эйлера встречается подобная запись:
1+т 2 -\- т 3 + т 44-т ) '
С ПОМОЩЬЮ функции n(z) окончательно получается
^ 1^, р, 7, а; — 1ц^ _ а — 1) 11 (у - р — 1) '
Оставшуюся часть статьи Гаусс посвящает изучению
функции П (z) и ее приложениям к вычислению интегралов.
Отметим, в частности, что Гаусс вводит здесь и исследует важную
функцию
Т(2) = ^1ПП{2).
В автореферате Гаусс пишет: «Эта в высшей степени
важная для всего анализа функция есть в сущности не что иное,
* Мы не можем, следовательно, полностью согласиться с
Шлезингером, который, упоминая о введении П (z) по эйлеровскому пути, говорит
далее: «при этом особо должно быть упомянуто тщатолъш е (exakte)
исследование сходимости бесконечного произведения» (Цит. соч.,
стр. 94).
199
как эйлеровская непредставимая (inexplicable) функция
n(z) = 1 •2-3-4- • -z; однако этот способ порождения, или
определения, по суждению автора, никак недопустим, так как он
имеет ясный смысл только для целых положительных
значений Z. Избранный автором способ обоснования применим в
общих условиях и сам имеет для мнимых значений z такой
же ясный смысл, как и для действительных. . .» Это место, а
также и другое место автореферата, где Гаусс из результатов,
которые он считает новыми, отмечает выражение интеграла
1
[х^~^{1—x^ydx через 11{х) (т. е. выражение эйлерова инте-
0
грала второго рода через гамма-функцию), свидетельствует
о том, что Гаусс в то время недостаточно знал результаты
Эйлера и, во всяком случае, неправильно оценивал его роль
в создании и разработке основ теории гамма-функции.
Действительно, в «Дифференциальном исчислении» Эйлера,
которое, очевидно, имел в виду Гаусс, говорится о
непредставимых функциях и в качестве примера приводится функция
1-2 •3-4... X, которая «будет непредставимой функцией от :г, ибо,
если X есть какое угодно число, то значение ее нельзя выразить
НС только алгебраически, но и с помощью какого-либо
определенного рода трансцендентных функций»^. Однако Эйлер тут же
говорит, что непредставимые функции могут быть
представлены рядами или произведениями, а несколько ниже (стр. 550—
551) дает общее выражение своей функции, отвечающее зна?1е-
нию X =оу , в виде:
ji—со 2*^ 2'^~'^*3^* 3-^'~'"'4'^ 4-^~""*^5"
S = -7-—— • -. • \/ , — • " . — и т. д.
1-f-co z-fto 34-со 5-t-w
Последнее выражение, как уже было указано выше,
совпадает с формулой, положенной Гауссом в основу его теории
гамма-функции.
В «Nachlass» Гаусса входит продолжение реферированной
выше работы, которое, однако, оставалось ненапечатанным до
выхода III тома сочинений Гаусса в 1866 г. Эта статья
называется «Определение нашего ряда посредством дифференци-
1 Л. Эйлер. Дифференциальное исчисление. М.—Л., 1949,
стр. 509.
200
ального уравнения второго порядка» (Determinatio seriei
nostrae per aequationem different!alem secundi ordinis, Werke^
III, 207-229).
^Здесь гипергеометрическое дифференциальное уравнение^
которому удовлетворяет гипергеометрическая функция,
получается сразу же как частный случай линейных соотношений
второго отдела основной статьи: если F (а, р, '[, х) — Р, jo
^ = "^/■(« + 1, р + 1, 1 + 1, х)ш
Гаусс рассматривает преобразования независимого
переменного X и функции jP, посредством которых
гипергеометрическое уравнение преобразуется само в себя (с другими
значениями а, р и f). Так, он вводит преобразование у = 1—х^
позволяющее найти наряду с F(a, р, ^^ х) второй независимый
интеграл того же уравнения:
/^(а, р, а + р + 1-Т, 1-^)
и записать общий интеграл в виде:
М/^(а, р, 7, X) + iVF(a, р, а 4- ? + 1 -ТГ 1 ~ ^),
где М и N — произвольные постоянные. Преобразование, ука-
занное Эйлером: Р = (I — xY Р\ для [i. == if — а — р, дает
Аналогичное преобразование: Р = х^ Р' при |л = 1—f при--
водит после некоторых выкладок к соотношению:
;^(а. р, а + р + 1 -Т, ^ -^) - "ilotlVn!"-"^)"'^^^°^' ^' •^' ^^ +
которое позволяет сводить вычисление суммы
гипергеометрического ряда в интервале между 0,5 и 1, где сходимость
медленная, к интервалу между О и 0,5, где она быстрее.
Но полученная формула непригодна в случае, когда
а + Р — 7 "^ целое число, так как тогда в ней будут
201
встречаться не имеющий смысла гипергеометрический ряд с це*
лым неположительным третьим элементом и бесконечные зна*^
чения функции П. В этом случае Гаусс пользуется приемом
Даламбера для получения интеграла линейного
дифференциального уравнения путем предельного перехода в линейной ком--
'бинации известных решений, и найденный результат приме-
няет к вычислению значения Р[-^ у -7-,1,1 —х\у в котором
мы узнаем —=. Получается
/.(1, |ЛЛ--.) = ~^{1П(1.)^(1, 1, 1,.) +
— соотношение, содержание которого, в терминах арифметике*
геометрического среднего, Гаусс получил ещ;е в 1799 г., когда
он не владел теорией гипергеометрических функций^.
В работе Гаусса имеются далее преобразования:
a;=^,i>=(l~2/fi>',^ = a или р;
х=^ — , Р = у^Р\ |л = а или р,
далее некоторые билинейные соотношения между
гипергеометрическими функциями и, наконец, специальные соотношения
между ними при некоторых зависимостях между а, р и f.
Шлезингере обращает внимание на то, что Гаусс, опираясь
на ранее выведенные соотношения, приходит к парадоксу:
/-(га.гр.а + р + ^т. 2/)=^(2«,2р,« + Р + {, 1-2/).
Этот парадокс тут же совершенно правильно объясняется
Гауссом ссылкой на многозначность гипергеометрической
функции, понимаемой теперь не как сумма гипергеометрического ря-
1 См. гипотетическую реконструкцию рассуждений Гаусса в работе
Шлезингера: Schlesinger. Fragmente zur Theorie des arithmetisch-
geometrischen Mitlels aus den Jaliren 1797—1799.—Malerialen fur eine
wissenschaftliche Biographie von Gauss. Gesammelt von F. Klein und
M. Brendel, Heft II, 1912.
2JI. Шлезингер. Цит. соч., стр. 98.
1i02
да, где определение ограничивается значениями I :rj <С1, а как
решение тииергеометрического уравнения. При этом Гаусс
явно ссылается на обход переменного х, принимающего как
действительные, так и мнимые значения, вокруг точек О и 1. Это
объяснение вполне согласуется с теми сведениями о функциях
комплексного переменного, которыми Гаусс делился с
Бесселем в письме от 18 декабря 1811 г.
Фактическое изучение гипергеометрических функций
/^(а, 7» ^> ^)» как функций комплексного переменного о;,
которое можно было бы проводить, опираясь на эйлеровское
интегральное представление:
Р {^^ h Т> ^) == \ 2^""' (1 - 2)^"^-"' (1 - rrz)-" dz
о
(нигде явно не используемое Гауссом), требовало, однако,
значительно более глубокой и детальной разработки основ теории
функций комплексного переменного, чем та, которой обладал
сам Гаусс. Именно поэтому систематическое исследование теории
гипоргеометрических функций не было им продолжено, и даже
вторая часть работы, которую мы только что реферировали,
не была завершена. Понадобились труды Куммера, Вейерштрас-
са, Римана, Фукса, Шварца и Клейна для того, чтобы теория
гипергеометрических функций достигла состояния,
отраженного в упоминавшихся уже лекциях Клейна о
гипергеометрической функции, где синтезирована аналитическая и
геометрическая части.
Именно в этих лекциях мы усматриваем фактическое осуш;е-
ствление замысла Гаусса дать капитальный труд, схватывающий
все его результаты и методы, относящиеся к трансцендентным
функциям.
Однако развитие теории гипергеометрических функций на
этом не закончилось. Гипергеометрические функции были
обобщены в трудах Аппеля для случая многих переменных и в
таком виде получили и продолжают получать многочисленные
применения в задачах математической физики^.
^ Р. А р р е I. Sur les fonctions hypergeometriques de plnsieurs
variables, les polynomas d'Hermite et autres fonctions spheriques dans Thy-
perespace.—Mem. Sci. Math., 1925.
20^
14- В заключение настоящей статьи мы приведем беглый
обзор ряда других работ Гаусса, имеющих непосредственное
значение для математического анализа и теории функций.
В 1813 г. Гаусс опубликовал «Theoria attractionis corporum
sphaeroidicorum ellipticorum homogeneorum methodo nova
tractata» (Werke, V, 3—22). Работа начинается с исторических
сведений.
Вопрос о притяжении точки эллипсоидом вращения по
закону Ньютона изучался самим Ньютоном, Маклореном, Ла-
гранжем и, наконец, Лежандром, в известном смысле
довершившим решение задачи.
Гораздо более трудной оказалась задача притяжения точки
трехосным эллипсоидом, но и она была доведена до конца
Лапласом; другое решение было дано Лежандром. Однако
тот и другой, как указывает Гаусс, употребляли бесконечные
ряды, не доказывая их сходимости. Кроме того, сами
доказательства были слишком длинными и трудными. В связи с этим
Лаграпж высказал еще в 1793 г. желание видеть более прямое
и более простое решение.
Гаусс сообщает в автореферате (Werke, V, 279—286), что
он нашел удивительно короткое и простое решение, суть
которого можно было бы изложить на двух страницах. Однако он
решил подробно изложить основания, на которых обо
покоится, поскольку эти основания имеют более широкое значение.
Поэтому он переходит к обоснованию шести общих теорем,
«посредством которых можно привести трехкратные
интегралы, распространенные на объем тела (korperlichen Raum),
к двухкратным интегралам, распространенным только на
поверхность тела».
Пусть Р — точка поверхности тела с координатами х, у, z,
а MX, MY, MZ — углы между РМ и осями координат, QX,
QY, QZ — углы между PQ и осями координат, QM — угол
между PQ и РМ] расстояние РМ = г.
Пусть, наконец, dli — элемент площади в плоскости а; == а,
где а меньше, чем минимальная координата х для точек
поверхности. Проведем в точке П, принадлежащей rfH,
параллель оси X, и пусть Р\ Р'\ Р'\ . . ., по порядку, —точки
пересечения ее с поверхностью. Около этих точек можно описать
204
элементы площади поверхности ds\ ds", ds"\ . . .,
проектирующиеся в dli в направлении оси х. Имеем
dZ=— ds' cos QX' = + ds" cos QX'' = — ds'" cos QX'" = . . .,
откуда:
ds' cos QX' + ds" cos QX" + ds"' cos QX'" + . . . = 0.
После этих обозначений и разъяснений формулируется и
доказывается шесть теорем, из которых мы приведем пять:
I. y^dsQ^osQ = О,
или более обще:
[ {Т cos QX + U cos QY + V cos QZ) ds,
где T зависит только от ?/, z, U — от x, z и V — от x, 2/.
II. Объем тела равен
\ dsx cos QX = \ dsy cos ^У = \ dsz cos ()Z.
III. Компоненты силы притяжения телом в точке М
выражаются (в случае ньютоновского притяжения) интегралами:
[ ds соя QX С ds cos QY Г ds cos QZ
] r ^ ] r ^ ] r
IV. Интеграл
\
ds cos MQ
равен 0, либо —2тг, либо —47:, в зависимости от того, лежит
ли точка вне тела, на его поверхности или внутри тела.
VI. Компоненты силы притяжения выражаются также
интегралами
г ^5 cos Л/Q cos МZ
И другими аналогичными.
После этого Гаусс применяет выведенные формулы к
случаю эллипсоида с полуосями Л, В и С, пользуясь при этом
параметрами р и g на поверхности эллипсоида, определяемой
205
посредством формул:
х = Acqs р, у == В sin pcosq, z = С sin р sin q,
В работе в явном виде не содержится общей теоремы,
получившей название теоремы Грина — Остроградского. Однако
доказательства всех шести теорем неизменно повторяют одну
и ту же идею, на которой основано преобразование объемного
интеграла в интеграл по поверхности, выражаемое указанной
теоремой.
Отметим, что в конце работы Гаусс указывает, что к 1809 г.
относится работа Айвори (Ivory), посвященная вопросу о
притяжении эллипсоидом^, с которой он познакомился лишь во
время печатания своей работы; но методы Айвори
существенно отличаются от его методов.
15. Опубликованная в 1814 г. работа «Methodus nova
integralium valores per approximationera inveniendi» (Werke,
[II, 165—196) посвящена выводу известной гауссовской
формулы квадратур. В основе работы лежит обобщение хода
идей, приводящего к формуле Ньютона — Котеса. Чтобы найти
1
приближенное значение интеграла \ydt, функцию г/ заме-
0
Няют интерполяционным многочленом степени п (не выше,
чем п)у который принимает одинаковые с ней значения Л, А\
А", А'", . . . при п + 1 значениях аргумента а, а!, а!\ а"\ . . .,
принадлежащих отрезку О <! ^ < 1; значение интеграла от этого
многочлена и является искомым приближением. В случае,
когда 3Ha4eHjHn аргумента являются равноотстоящими
1 2
получают классическую формулу Ньютона — Котеса. Гаусс
отказывается от требования, чтобы значения а, а\ а", . . . были
равноотстоящими, и старается подобрать их так, чтобы
погрешность приближения была возможно меньшей. Он замечает,
что интеграл от интерполяционного многочлена имеет
выражение AR -\- A^R' + A"R" + . . ., где коэффициенты /?, /?',
^ Philosophical Transactions, 1809,
206
R", . . . зависят только от n и выбора точек а, а', а", , . .. Еслд
принять сначала у = V^ и рассмотреть разность hS'^^ между
истинным значением интеграла \v^dt^= —-•--: и его ирибли-
0 '
женным значением, получится
1
Чтобы оценить разность интегралом \ydt и его прибли-.
о
женным значением, Гаусс вводит разложение у в степенной
ряд:
у^К+КЧ + КЧ^ + K'^t^ + , .., (29),
специально оговаривая (в автореферате), что он предполагает
сходимость ряда во всем промежутке интегрирования. Конечно,
при несколько ином проведении рассуждений необходимость
в этом предположении не возникла бы, и искомая оценка
(в несколько модифицированном виде) получилась бы при
одном только предположении существования производных от у
до порядка 2ai + 2 включительно. Но мы продолжаем
изложение идей Гаусса. Подставляя разложение (29) под знак
интеграла и используя формулы (28), Гаусс получает
следующее выражение погрешности:
кК + к'К' + к"К" + к'''К"' + .. .,
или (замечая, что к == к' = к" = к'" = . . . = А^") = 0):
.J,(nU)j^in) _^ ^^(п-|2)^^(п+2) _^^_ (30)
в этой формуле
Гаусс рассматривает первый член ряда (30) как его глав-,
ный член; для этого есть некоторые основания, так как иа
предположения сходимости ряда (29) при / =^ 1 следует, что
К^'^^-^0 при А1-^оо. Далее он считает, что погрешность
приближенной формулы будет тем меньше, чем выше будет
индекс первого отличного от нуля члена ряда (30). Задача
20f
состоит теперь в том, чтобы подобрать числа а, а', а", , , ,, а^Щ
так, чтобы к^'^+^\ к^'^-^^\ . . ., A^sn-i-i) обратились в нуль; тогда
вырая^ение (30) примет вид
И соответствующая приближенная формула
1
^^ydt^AR + Л'Л' + A"R" + . . . (31)
о
будет давать точные значения интеграла в случае, когда у есть
многочлен степени не выше 2/г + 1. В результате нетрудных
вычислений Гаусс находит, что все сводится к определению
чисел а^ а\ а", . . . при условии, чтобы в разложении
(^_а)(г-а'){^-а")...(г1 + 4-*""' + 4-^"' + ---)
коэффициенты при степенях Г^, Г^, . . ., M'^+i) равнялись нулю.
Остальная часть работы посвящена фактическому определению
таких чисел или, что сводится к тому же, определению
многочлена T = {t — a){t — a'){t — а"),,. Гаусс избирает для этого
путь, связанный с алгорифмом непрерывных дробей.
Кратчайший вывод (отсутствующий у Гаусса и
общеупотребительный ныне) основан на том, что приближенную
формулу (31) строят, исходя из требования, чтобы она была точной
для всех многочленов до степени 2^ + 1 включительно. Тогда
легко установить, что многочлены U {и) = 2^'^^ Т1^^^—],
которые Гаусс рассматривает одновременно с Г, имея в виду дать
формулу, удобную для промежутка интегрирования —1 «^ м ^ 1,
ортогональны в этом промежутке к любому многочлену степени
не выше п и, следовательно, являются не чем иным, как
многочленами Лежандра:
^ («) - (2п+.)(2.+1)...(.+2) • ,^ f(«^ - 1)"+^Ь
208
16 ^ Мы не будем здесь останавливаться па работах Гаусса,
относящихся прежде всего к дифферепциальной геометрии:
/(Общее решение задачи: отобразить часть задапиой
поверхности на часть другой заданной поверхности так,чтобы
отображение было подобно отображенному в мельчайших частях» (1822 г.,
впервые опубликована в 1825 г.) и его знаменитые «Общие
исследования о кривых поверхностях», так как эти работы
рассматриваются в специальной статье этого сборника. Следует
отметить только, что вторая работа имела существенное влия-
иие па развитие математического анализа и, в частности, ва-
рпациоиного исчисления. В этом отношении особо важную роль
згграют теоремы Гаусса о геодезических линиях, получившие
дальнейшее обобщение и развитие в вариационном
исчислении, в теории поля экстремалей^.
Скажем еще несколько слов о работах: «Общие принципы
теории фигуры жидкостей в состоянии равновесия» (Princi-
pia generalia theoriae figurae fluidorum. in statn aequilibrii,
1830; Werke, V, 31—77) и «Общие теоремы относительно сил
притяжения и отталкивания, действующих обратно
пропорционально квадрату расстояния» (Allgemeine Lehrsatze in
Beziehung auf die im verkehrten Verhaltnisse des Quadrats
der Entfernung wirkenden Anziehungs- un'd Abstossungs-
krafte, 1840; Werke, V, 197—242)^. Последнее сочинение
имеет большое самостоятельное значение как первое в науке
систематическое изложение основ теории потенциала.
В первой из названных работ речь идет о решении задачи из
теории каниллярности, приводящей к экстремуму двойного
][нтеграла. Если обозначить через S объем жидкости, через h —
р.ысоту центра тяжести над некоторой горизонтальной
плоскостью, через 7' — площадь части поверхности жидкости,
^ Мы пользуемся здесь работой: О. В о 1 z а, Gauss und Variations
i'echmmg [Werke, X (2), Abbandlung 5], a также русским изданием рабо-
Гаусса по магнетизму: К. Ф. Гауе с. Избранные труды по земному
магнетизму. Пер. акад. А. Н. Крылова, ред. проф. Б. М. Яновского,
' татг,и Т. Н. Розе, комментарии проф. Б. М. Яновского и Т. Н. Розе,
изд. АН СССР, 1952.
- См. об этом работу О. Больца, стр. 52—76.
^ См. также русский перевод в л^помянутом выше издании АН СССР,
'тр. 181—234.
^4 к. <[). Гаусс 209
соприкасающейся с сосудом, и через U — площадь остальной
(свободной) части поверхности, то Гаусс, пользуясь
принципом возможных перемещений, выводит, что в состоянии
равновесия выражение
Sh + (а2 — 2^2) Т + а2(7
должно иметь минимум. Здесь а^ и ^ — постоянные,
зависящие от отношения веса (удельного) к интенсивности
молекулярного притяжения частиц жидкостей друг к другу и частиц
сосуда к жидкости. Принимая упомянутую горизонтальную-
плоскость за координатную плоскость ху и обозначая
расстояние точки до нее через z, Гаусс записывает уравнение
свободной поверхности жидкости в виде z = z{x, у), а уравнение внут->
ренней поверхности сосуда в риде z == g{Xy у). Тогда задача
сводится к отысканию двойного минимума интеграла вида
w= —у^1^^~ S'^ (^' 2/)] dxdy +
+ (а2 - 2^2) ^ 1/1 + 4 + 4 ^^ "^У +
+ а2 ^ /1 + р2 + q^ dx dy,
при условии, что
^[z~g{x, ij)]dxdy-^=s.
Интегрирование распространяется здесь на проекцию Ж
свободной поверхности жидкости на ггу-плоскость. Это изо-
периметрическая двумерная задача с переменной областью
интегрирования. Как отмечает Больца (стр. 4), Гаусс впервые
в истории вариационного исчисления для задачи такого типа
вывел из условия исчезновения первой вариации не только
соответствующее уравнение с частными производными, но
также и краевые условия. При этом он применил им самим
разработанный метод для того, чтобы преодолеть две основные
трудности: вывести выражение первой вариации (трудность здесь
заключалась именно в том, что область интегрирования
переменная) и извлечь из этого выражения помимо
дифференциального уравнения также и краевое условие. Последнее было
связано с особым затруднением, неизменно останавливавшим
210
в аналогичных обстоятельствах предшественников Гаусса:
Эйлера, Лагранжа и Пуассона.
Суть вопроса легче всего может быть выяснена уже на
примере работы Эйлера^, где вообще впервые в истории
вариационного исчисления рассматривалась экстремальная проблема
для двойного интеграла с постоянной областью интегрирования.
Рассматривая интеграл вида
3 =Ц V{x, y,z, p,q,,.,)dxdij(^p=^,q=:~^,
Эйлер представил его вариацию в виде
где
и CO — бесконечно малое приращение (вариация) z.
Второй интеграл Эйлер записывает в форме
(Й+^)^^^^ = 5^^2/ + 5^с/а:;
ПО внешнему виду это формула Грина; однако понятие
криволинейного интеграла еще отсутствует у Эйлера. Вот почему
Эйлер, получив из условия оЗ= О дифференциальное уравнение
fi = О, оставляет второе условие в форме lAdy-\- \Bdx ~ О,
не видя, как можно исключить отсюда to. Как уже было
упомянуто, аналогичный вопрос не могли разрешить позднее
ни Лагранж (1811 г.), ни Пуассон (1816 г.).
В реферируемой работе Гаусса задача решается посредством
приема, вполне аналогичного тому, с помощью которого Гаусс в
1813 г. в «Theoria attractionis...» (см. выше п. 14) преобразовывал
объемный интеграл в поверхностный.
Здесь же интеграл по поверхности заменяется криволцней--
ным интегралом, взятым по ее границе. Гаусс исходит из
найденного им выражения *[ вариации площади свободной
^ L. ЕиДег. Institutiones calculi integralis, Vol. П1, АрревсИх
<ie calculo variationum. 1770, 159—174.
14* 211
поверхиости жидкости
dSx f. dh/ 'r<^ dЬzЛ
dx ^ * dx "" dxj
+ \4u[^^r, f + (I- + c.)If -,:|f] = A + B.
Здесь clU — элемент площади поверхности, с, r^ и ^ — косинусы
углов между внешней нормалью к U и тюординатнььми осями,
а ОХ', о?/, 0Z — вариации координат точек поверхности; эти
вариапии рассматриваются Гауссом как «неопределенные, но
бесконечно малые функции координат х и у» (координат
проекции точки поверхности на горизонтальную плоскость). Гаусс
преобразует выражение of/ в
W = lQ
dP + \ V dU,
где интеграл \PdQ есть криволинейный интеграл, взятый по
кривой Р, ограничивающей U {dP — элемент длины дуги Р),
Само преобразование ведется, по сути дела, тем же путем,
который в позднейших учебниках приводит к так называемой
формуле Стокса. А именно, для преобразования первого
слагаемого (А) в выражении Ш Гаусс рассматривает часть
поверхности, заключенную ме}кду двумя плоскостями с ординатами
у п у-^ dy\ между ними заключается четное число элементов
кривой Р\ dP^, dP\ dP'\ . . ., пересекающих плоскость с
ординатой у в T04iiax с абсциссами х^, х[, х", . . ., причем
dy = -^ уо dP^ = + F' dp' ^ — Y" dp" - + Y" dP'" = . . . (32)
(сравните выше в п. 14 аналогичную запись для элементов
поверхности в «Theoria Attractionis . . .^>). Здесь У^, У\ 7", . . .
означают косинусы углов касательных ь' кривой в Р,
проведенных в положительном направлении обхода кривой. Если
,гг dx dy
заменить элемент аи площади поверхности через —тг^, то часть
интеграла А, соответствующая части поверхности,
заключенной между указанными плоскостями, представится в виде
.где ицтегрирование по х распространяется на промежутки
от х^ до х', от х" до х"' и т. д. Выполняя интегрирование по
212
частям и учитывая формулы (32), Гаусс получает
— Q'bz']Y'dP' +
l!+_^^.'^iV ...
t:o
^^2/
или
2('!L+^8^_ ^by -9jz]ydP +\v,dU,'
где суммирование распространяется на все элементы dP и
интегрирование — на все элементы dU, заключенные между
плоскостями у и у -\- dy. Отсюда, наконец, для всего
интеграла А получаем
А=^\\ ^!1±-^ Ьх ~~Щ~гу^ Bzl}' dP + ^ \\ dU]
аналогично
Б ==. f Ш Ьх ~ ^^^^ rnj + T^oz] XdP + { V^ dU
и, следовательно,
Ьи =^\QdP +\V dU.
Заметим, что далее Гаусс представляет Q в симметричной
форме
^ = (УС - Z^i) Ьх + {Z\ ~ ХС) Ьу + (Хт] - Ге) 8z. •
Из сказанного здесь и в п. 14 видно, что хотя Гаусс и не дает
в своих работах 1813 и 1830 гг. общих формул,
преобразующих интегралы по объему в интегралы по поверхности
(формула Гаусса — Остроградского) или интеграл по поверхности
в криволинейный интеграл (формула Стокса и в плоском случае
формула Грина — Гаусса), однако в таких деталях и с такой
геометрической отчетливостью проводит для рассматриваемых
им специальных задач все необходимые выкладки, что всякий
213
математик, прочитавший внимательно его работы, мог без
затруднений, следуя Гауссу, шаг за шагом выполнять оба
преобразования в любой аналогичной задаче. Вот почему имя Гаусса
по праву упоминается в связи с классическими формулами
интегрального исчисления.
Преобразовав вариацию указанным путем, Гаусс без
труда получает дифференциальное уравнение свободной
поверхности жидкости:
+ °^^ [Т + 'Wj "" ^^^^^'
где R и R' — радиусы главных кривизн точки поверхности,
и краевое условие: i = А^ где i — угол между касательной
плоскостью к свободной поверхности жидкости и касательной
плоскостью к поверхности сосуда (измеряемый вне жидкости).
По поводу «Обпцих теорем относительно сил притяжения и
отталкивания» мы ограничимся здесь немногими замечаниями,
имея в виду, что издание этого труда, прокомментированное
Т. Н.Розе,выпуш;ено недавно издательством АН СССР (см. сноску
на стр. 209). Мы уже отмечали, что это первое в науке
систематическое изложение основ теории потенциала.
В изложении Гаусса последовательно используехся метод
преобразования объемных интегралов в поверхностные,
развитый им в его «Theoria attractionis...», а также специальные,
установленные им там теоремы, например, теорема IV о том,
с ds cos MQ ^ о
ЧТО значение интеграла по поверхности \ равно U,—-^тг
или — 47Г, в зависимости от расположения точки М относительно
поверхности (см. п. 14). В первой половине работы (§§ 1—18)
излагаются, как об этом сообш;ает сам Гаусс, уже известные
результаты (среди них результаты Лапласа и Пуассона),
причем Гаусс дает им новые простые и строгие доказательства.
В §§19—20 доказываются предложения, в которых, в частности,
содержится теорема Гаусса о среднем: среднее значение
потенциала по поверхности шара (внутри которого не содержится
притягиваюш;их масс) равно значению потенциала в центре
шара. В §§ 22—23 доказывается, что
214
здесь интеграл берется по поверхности, содержащей внутри
массы М, а ^ обозначает производную потенциала по
направлению внутренней нормали к поверхности. Отсюда, в
частности, следует, что когда внутри поверхности нет притягивающих
масс, то
В теореме § 25 доказывается, что потенциал, имеющий
постоянное значение на поверхности, имеет то же значение
внутри поверхности. В Nachlass Гаусса сохранились заметки
(Werke, III, 479—480), относящиеся, по указанию Шеринга,
к 1827 г. Они по содержанию тесно связаны с реферируемой
работой, но интересны тем, что рассматривается также и
двумерный случай. Приведем часть первого из них,
непосредственно относящуюся к цитированной только что теореме:
«Если внутри ограниченной фигуры всюду
а на границе V постоянно =Л, то необходимо также во всей
области V = А.
Доказательство. Пусть dM — элемент площади и
H(sr+s;+(s+^)<''-^)}«-"-
Если бы V не было постоянным, то, очевидно, интеграл
оыл бы положительным. Однако интеграл есть также
(интеграл):
распространенный по границе фигуры, и, следовательно, = 0.
Так как это противоречит предыдущему, то предположение
недопустимо. Аналогичное имеет место для трех измерений».
Начиная с § 29 и до конца работы, Гаусс занимается общей
задачей о возможности такого распределения масс на заданной
поверхности, для которого соответствующий потенциал
простого слоя
Т/ — [ J^ds
215
(где т — искомая поверхностная плотность распределения)
совпадал бы в точках этой поверхности с наперед заданной
непрерывной функцией и, в частности, сохранял бы на всей
поверхности постоянное значение. Гаусс показывает, что такое
распределение характеризуется тем, что для него интеграл
J (V—2U)ds достигает наименьшего значения. Так как этот
интеграл ограничен снизу, то Гаусс считает свое доказательство вместе
с тем и доказательством существования искомого
распределения, забывая о тех критических замечаниях, которые он сам
высказывал по аналогичному поводу еще в своей диссертации.
Известно, что такого же рода заключения (основанные на
экстремальных свойствах) после Гаусса делали В. Томсон,
Дирихле и Риман для обоснования существования решений
краевых проблем, пока критика Вейерштрасса (1870 г.) не
вынудила позднейших исследователей искать общие условия, при
которых экстремальные принципы, действительно, могут
рассматриваться как принципы существования.
Б.В.Гнеденко
О РАБОТАХ ГАуеСА
по теории
вероятностей
^s^=.
1. Гений Гаусса, проявивший себя как в создании и
развитии абстрактно-математических теорий, так и в решении
конкретных проблем естествознания, не мог пройти мимо идей
и методов теории вероятностей. Действительно, постоянный
интерес Гаусса к астрономии, а позднее и к геодезии,
неизбежно наталкивал его на необходимость рационализации методов
обработки результатов наблюдений и в связи с этим — на
создание теории ошибок измерений. Создание же этой последней
теории с неизбежностью приводило к использованию идей
II понятий теории вероятностей.
Все опубликованные при жизни Гаусса работы, связанные
в той или иной степени с теорией вероятностей, были
посвящены не развитию самой этой теории, а ее приложениям. Тем не
менее его роль в последующем развитии ряда разделов теории
вероятностей, а также математической статистики, была весьма
велика. Мы не говорим здесь о том, что теория ошибок
наблюдения до самого последнего времени излагалась почти в том
самом виде, в каком она была опубликована Гауссом. Мы имеем
в виду то, что теория ошибок наблюдений толкала
исследователей на выяснение условий применимости нормального закона
распределения (зачастую называемого также законом Гаусса).
Вместе с тем мы подчеркиваем также то, что после работ
Гаусса перед наукой с особой остротой встала задача оценки
неизвестных значений параметров нормального
распределения. Эта задача сохранила свое значение и в наши дни; более
того, она положила начало ряду разделов математической
статистики.
219
Общее число работ Гаусса, относящихся к теории
вероятностей, сравнительно невелико. Они начинаются большим^
исследованием 1809 г., посвященным в основной своей части;
задачам небесной механики и носящим название «Теория
двия^ения небесных тел, обращающихся около солнца по-
коническим орбитам» (Theoria Motus Corporum Coelestium) ^,
В заключительной части работы под названием «Определение-
орбиты, возможно точно соответствующей произвольно
большому числу наблюдений» (Determinatio orbitae observationibus
puotaenque quam proxime satisfacientos). Гаусс впервые
изложил теорию ошибок наблюдений. В следующем году в
мемуаре «Рассуждение об эллиптических элементах Палла-
ды» (Disquisitio de elemontis ellipticis Palladis. Werke, VII)
были изложены некоторые замечания к практике
обработки наблюдений. Далее последовала небольшая статья
«Определение точности наблюдений» (Bestimmung der Genauigkeit
dor Beobachtungen. Werke, IV), напечатанная в 1816 г.
Систематическое изложение теории ошибок наблюдений
было дано Гауссом в большом сочинении «Теория комбинации
наблюдений, приводящая к наименьшим ошибкам» (Theoria
combinationis observationum erroribus minimis obnoxiae.
Werke, IV), первая часть которого была сдана в печать в 1822 г.,.
а вторая — в 1823 г. Обе они вышли в свет в 1823 г. Через:
три года было закопчено добавление к этой работе под
названием «Дополнение к теории комбинации наблюдений,
приводящей к наименьшим ошибкам» (Supplementum theoria
combination observationum erroribus minimis obnoxiae. Werke, IV),.
вышло OHO в свет лишь в 1828 г. В 1855 г. этот мемуар Гаусса
вместе с pa6oToii 1816 г., соответствующими параграфами
первых двух упомянутых нами астрономических работ и еще две-
статьи, относящиеся к обработке геодезических наблюдений,
были переведены на французский язык и опубликованы
Бертраном под названием «Methode des moindres carres. MemoireS'
sur la combinaison des observations».
Большое исследование «Приложение теории вероятностей
для определения баланса вдовьих касс» (Anwendung der
1 С. F. G auss. Werke, VII.
220
V\ alirscheinliclikeitsrechnung auf die Beslimmuug dor Ijiiaiiz
(ler VVitwenkassen. Werko, IV) вместе с-приложением: «Таблицы
д;[Я определения значении времени однократной прожиточной
ренты и связанной ренты» (Tafeln znr Bestimmung Zeitwei-
tlies von Einfachen Leibrenten und von Verbindungsrenten.
Werke, IV) было написано и рассчитано Гауссом в период
1845—1851 гг. В пашем обзоре мы эту работу не
рассматриваем, так как в ней пет развития теоретико-вероятностных
методов и новых теоретико-вероятностных результатов.
Для оценки работ Гаусса в теории вероятностей
значительную роль играют его заметки, теперь опубликованные в восьмом
томе собрания его сочинений, а также письма, которыми он
обменивался со своими многочисленными корреснондептамп.
Особый интерес представляет письмо Гаусса Лапласу от 30
января 1812 г.; ниже мы посвятим этому письму особый
параграф.
2. Восемнадцатое столетие принесло точному естествозна-
аню многие, весьма совершенные средства для производства
иаблюдений и измерений. Наибольшие успехи, пожалуй, в ту
пору достались на долю астрономии. Удивительного в этом нн-
чего нет, так как к необходимости развития наблюдательных
средств астрономии приводили не только и, возможно, даже
не столько запросы самой астрономии, сколько запросы
связанных с ней задач непосредственной практической
деятельности и в первую очередь запросы мореплавания. Однако как
иы тщательно ни производились наблюдения и измерения, они
никогда не дают и не могут дать абсолютно тождественных ре-
'.ультатов. При многократном повторении измерений даже,
казалось бы, в одинаковых условиях результаты будут
отличаться один от другого. Таким образом, возникает задача о наибо-
1ге целесообразном сочетании результатов измерений для
получения по возможности надежных результатов. Необходимость
инесения поправок в непосредственные результаты наблю-
лоний для устранения влияния случайных погрешностей
была ясна астрономам уже в далекие от нас времена. Так еш;е
Тихо де Браге считал необходимым не только устранять из
результатов систематические ошибки, связанные с принятой
системой наблюдений или же с используемым прибором, но и
221
случайные ошибки наблюдений. С этой целью в особо
ответственных случаях он производил по нескольку наблюдений в
видоизмененных условиях и затем с помощью комбинации
этих наблюдений стремился избавиться от случайных ошибок.
В 1722 г. Р. Коте предложил обоснование правила
комбинирования результатов наблюдений, которое употреблялось
астрономами уже до него. Это правило состояло в
следующем: пусть величины а^ заданы и положительны, пусть далее
величины е^ получены при измерении величин а^Х, где X —
неизвестная величина. Правило для оценки х рекомендовало
принимать Х=2^г/2^г* Коте получил ЭТО правило ИЗ следующего
общего положения: наиболее вероятное значение X находится
в центре тяжести с массами а^, имеющими абсциссы -- ^.
"'г
Существенный шаг в теории обработки наблюдений был
сделан Лежандром в 1806 г. в мемуаре «Новые методы для
определения орбит комет» ^. В приложении «О методе наименьших
квадратов» (Sur la methode des moindres carres, стр. 72—80),
изложенном на нескольких страницах, им был предложен
метод наименьших квадратов в достаточно хорошо развитом
виде. Лежандр отдавал себе ясный отчет в том, что
предлагаемый им принцип использования наблюдений для оценки
неизвестной величины произволен. Но, как он писал в
указанной работе, «из всех принципов, которые можно предложить
для этой цели, не существует более простого, чем тот, которым
мы пользовались в предыдущем изложении: он состоит в том,—
чтобы обратить в минимум сумму квадратов погрешностей».
Первое печатное выступление Гаусса с теорией метода
наименьших квадратов, как мы уже говорили, относится лишь к
1809 г. Правда, в § 186 этого мемуара он отметил, что «этим
нашим принципом мы пользовались с 1795 г. К тому же он
недавно был установлен Лежандром в сочинении «Новые методы
определения кометных орбит», Париж, 1806 г., где выясняются
1 Cotes R "edge г. Aestimatio errorum in mixta mathesi. Gam-
bridge, 1722.
2 A. Legendre. Nouvelles methodes pour la determination des
orbites des cometes. Paris, 1806.
222
и некоторые другие следствия из этого принципа, которые мы
здесь ради краткости опускаем».
Примерно та же дата указывалась Гауссом в ряде его
частных писем Ольберсу (от 30 июля 1806; 5 октября 1809)^
Шумахеру (3 декабря 1831; 6 июля 1840), Лапласу (30 января
1812) и ряде других. Особенно отчетливо и убедительно об
этом говорится в письмах Ольберсу и Лапласу, поэтому мы
приведем из них небольшие отрывки. В письме от 30 июля
Ольберсу Гаусс писал: «...господин Цах писал мне еще, что Вы
предложили написать рецензию на работу Лежандра о кометных
орбитах... При беглом перелистывании показалось мне, чта
в ней содержится много остроумного. Многое из того, что я
имел в моем методе, особенно характерное для первой его
формы, нашел я снова также в этой книге. Кажется такова моя
судьба, что почти во всех моих теоретических работах я
конкурирую с Лежандром. Так было в высшей арифметике, в
исследованиях о трансцендентных функциях, связанных со
спрямлением эллипса, в первых основах геометрии и теперь снова
здесь. Так, например, принцип, которым я пользовался с
1794 г., согласно которому, чтобы наилучшим образом
представить несколько величин, неопределяемых вполне
точно, нужно сделать минимумом сумму квадратов,
используется в труде Лежандра и там как следует изложен...» (Werke,^
Vni, 139).
Еще более подробно изложена история занятий Гаусса
принципом наименьших квадратов в письме к Лапласу от 30
января 1812 г. Поскольку в этом письме достаточно точно
указаны даты занятий Гаусса теоретико-вероятностными
вопросами, мы приведем из него довольно значительную выдержку:
«Я использовал метод наименьших квадратов, начиная с
1795 г., и я нашел в моих бумагах, что в июне 1798 г. был
период, когда я его связал с принципами теории вероятностей:
одно замечание об этом находится в журнале^, который я
веду о моих математических занятиях с 1796 г. и который я
показал в эти дни господину Линдено.
^ Гаусс имеет в виду запись в дневнике от 17 июня 1798 г. под № 88
(см. Werke, X).
22а
Однако мои частые применения этого метода относятся
только к 1802 г. Начиная с этого времени, я использовал его, так
сказать, каждый день в моих астрономических расчетах,
относящихся к малым планетам. Так как мне было предложено
в это время объедпннть все методы, которые я использовал,
в большом труде (который я начал в 1805 г. и закончил этот
манускрипт на немецком в 1806 г., но затем но просьбе
господи iia Перте поревел его на латинский; печататься он начал в
1807 г., а закончился только в 1809 г.), я не стал
торопиться опубликовывать отдельный кусок; таким образом, господин
Лежандр хМеня опередил. Наконец, я сообщил об этом методе
до опубликования труда Лежандра многим лицам, среди
других господину Ольберсу, который безусловно должен об
этом помнить... Мне не пришло в голову, что г. Лежандр мо-
яшт придавать такое значение идее столь простой, что нужно
скорее удивляться тому, что ее не было еще 100 лет назад, чем
сердиться по поводу того, что я рассказывал о том, что я
пользовался ей раньше него?»...
Столь подробная информация была дана Гауссом Лапласу
в ответ на письмо от 15 ноября 1811 г., в котором тот
спрашивал, были ли у Гаусса какие-нибудь публикации о новом
методе обработки данных до появления работы Лежандра. Сам
этот вопрос явился естественной реакцией Лапласа на
возбуждение, царившее во французских математических кругах в
связи с сообщением Гаусса о том, что он владел и пользовался
методом нанменьших квадратов задолго до Лежандра. Не
остался равнодушным к этому замечанию Гаусса и Лежандр. Почти
немедленно после выхода в свет мемуара 1809 г. он обратился
к Гауссу с письмом, написанном в раздраженном тоне (письмо
Лежандра Гауссу от 30 мая 1809 г.; Gauss. Werke, X,
стр. 380): «Я не стану скрывать от Вас, что я испытал
досаду, увидев, как процитирован мой мемуар на стр. 221;
вы говорите principirum nostrum quo jam inde ab anno 1795 usi
sumus ets. He существует открытия, которое нельзя быдо бы
приписать себе, сказав, что те же вещи были найдены на
несколько лет раньше; но если не дать тому доказательство, ео-^
стоящее в,указании места, где они опубликованы, это
утверждение становится беспредметным и представляет собой только
обиду для истинного автора открытия. В математике
случается очень часто, что находят те же самые вещи, которые уже
были открыты другими и которые уже известны; подобное
случалось со мной много раз; но я никогда не упоминал о них и
никогда не называл нашим принципом принцип, который другой
опубликовал ранее меня. Вы достаточно богаты собственными
фондами, чтобы не завидовать кому бы то ни было; я, впрочем,
убежден, что мне следует огорчиться только из-за способа
выражения и ни в коем случае из-за вашего намерения...»
Кроме краткого упоминания в работе 1809 г., Гаусс никогда
и нигде в печати не делал попыток отстоять свой приоритет
в отношении метода наименьших квадратов. Мотивы такого
поведения он изложил в письме к Шумахеру, в котором
написал, что такого рода публичное выступление «означало бы
признание, будто бы мое указание, что я пользовался этим
методом с 1794 г., нуждается в оправдании, и с этим я
никак не могу согласиться...» (письмо от 3 декабря 1831;
Werke, VIII, 138).
Мы привели несколько выдержек из переписки великих
математиков прошлого не с тем, чтобы решить спор о
приоритете, тем более что спора не было и в то время. Причина для
этого была иная: эта переписка, во-первых, достаточно
определенно доказывает, что простая, по словам Гаусса, идея метода
наименьших квадратов уже тогда была высоко оценена
современниками. Во-вторых, Эта переписка показывает, как ход
развития науки приводит ученых, казалось бы, к
независимым открытиям одних и тех же результатов. Следует заметить,
что в поздних изданиях «Theorie analitique des probabilites»
Лаплас, говоря о методе наименьших квадратов и указывая на
первое по времени публикации исследование Лежандра,
отмечал, что «в отношении г. Гаусса справедливость требует
отметить, что он за несколько лет до этой публикации пришел
к той же идее, которую он и применял обычно и про которую
сообщил нескольким астрономам» (Oeuvres, VIII, 1847,
стр. 381—382).
Нам нужно добавить, что в основных чертах метод
наименьших квадратов излагается и теперь так же, как он был изло-
>кен Гауссом в работах 1821—1826 гг. Сама же идея, положен-
"•5 к. Ф. Гаусс 225:
ная в его основу, нашла применение и в других разделах
математического анализа.
3. Мы переходим теперь к краткому описанию
исследований Гаусса в области теории вероятностей. Начнем с его
работ по методу наименьших квадратов. В «Теории движения
небесных тел...» первоначальная постановка задачи была
такова: при равноточных измерениях некоторой величины
случайные ошибки имеют дифференцируемую плотность распределения
вероятностей ф(^). Требуется определить распределение ф(^),
если наиболее вероятное значение измеряемой
величины при любом числе наблюдений равно среднему
арифметическому из наблюденных значений. Несложные вычисления
привели Гаусса к хорошо известному результату, что
?(о=:-^в-''^^ (1)
Гаусс отдавал себе ясный отчет в произвольности выдвинутой
гипотезы и писал в § 179, что функция ^{t) «не может быть
определена а priori, подойдем к задаче с другой точки зрения и
найдем функцию, условившись, не оговаривая этого, принять за
основу один простой и постоянно используемый принцип.
Обычно принимают за аксиому гипотезу, что если некоторая
величина получена из многих непосредственных наблюдений,
произведенных с одинаковой тщательностью в сходных
условиях, то среднее арифметическое из наблюденных значений
будет наиболее вероятным значением этой величины, если не с
полной точностью, то во всяком случае с хорошим
приближением...».
Найдя, таким образом, распределение вероятностей ошибок
измерений, Гаусс в одном из следующих параграфов вывел в
качестве очевидного следствия следующее важное положение:
плотность вероятности данной совокупности наблюдений
достигает максимального значения при условии, что сумма
квадратов уклонений наблюденных значений от истинного значения
измеряемой величины обращается в минимум. Тут же этот
принцип был распространен на неравноточные наблюдения. Общая
теория была проиллюстрирована подробно рассмотренным
примером.
226
в работе «Рассуждения об эллиптических элементах Па ллады»
Гаусс рассмотрел численный пример определения по методу
наименьших квадратов шести поправок, связанных
двенадцатью линейными уравнениями. Здесь же вводятся и широко
используются скобки Гаусса для обозначения суммы
произведений, например
аф^ + (12^2 + • • • + cinbn = {оЬ),
Величину /г, входяш;ую в распределение (1), Гаусс назвал
мерой точности. Естественно, что оценка h по результатам
наблюдений представляет собой одну из важнейших задач
развернутой им теории. Этому в основном посвяш;ен мемуар
«Определение точности наблюдений». Начав с напоминаний о
сделанном в мемуаре 1809 г., Гаусс ввел в рассмотрение функ-
цию 6(^) = -—=\е dz, привел небольшую таблицу ее значе-
о
НИИ, ввел обозначение р = 0,4769363 для аргумента, обладаю-
щ;его свойством: 6 (р) = 0.5. Затем для функции 6 [ht) предложил
называть величину у вероятной ошибкой и обозначать ее
буквой г (ясно, что 6 (г/г) = 0.5).
Постановка основной задачи работы дана только в третьем
параграфе, который Гаусс начал словами: «предположим теперь,
что фактически полученные ошибки т наблюдений будут а,
8, -( и т. д. и найдем, какие следствия можно извлечь
относительно значений h ж г>у. Исходя из независимости
наблюдений, Гаусс нашел плотность распределения системы
наблюдений, полученных из опыта, равной
где Cm — постоянная. Максимальное значение этой функции,
как показывает легкий подсчет, достигается при
^ ^У 2(а2 + р2 + у2+ . . Y (2)
15* 227
«следовательно, наиболее вероятное значение г будет
1/2 (а^
±il±jl±i_:_0,>
Если Н есть истинное значение /г, то плотность
распределения уклонения /г, найденного по формуле (2), от Н
приближенно равна
Ке "\ где/^ = 1/^.
Остальная часть работы посвящена подсчету наиболее
вероятных значений сумм я-х степеней ошибок наблюдений и
оценкам посредством этих сумм неизвестных значений h я г. Мы
не будет останавливаться на рассмотрении полученных
Гауссом формул.
4. Наиболее полное и систематическое изложение теории
ошибок наблюдений содержится в большой работе Гаусса
«Теория комбинации наблюдений, приводящая к наименьшим
ошибкам». Изложение этой работы сделано поразительно
доступно и изящно. Оно начинается с выяснения того факта, что
фактические измерения, как бы тщательно они не производились,
всегда подвержены влиянию ошибок. Одни из них носят
характер иррегулярный, случайный; другие же можно предусмотреть,
так как они или постоянны или же изменяются в процессе
производства измерени11 вполне закономерным способом и потому
могут быть заранее рассчитаны. Такие ошибки Гаусс назвал
регулярными. Ошибки первого рода не могут быть заранее
вычислены, и они возникают как «от несовершенства наших
органов чувств», так и от «внешних иррегулярных причин, например,
от дрожания воздуха, которое приводит к менее точным
отсчетам». Гаусс далее отметил, что само подразделение ошибок на
регулярные и иррегулярные в значительной степени
условно и зависит от того, с какой реальной задачей имеют дело
измерения.
Весь мемуар посвящен изучению только закономерностей,
которым подчинено распределение иррегулярных ошибок. При
этом Гаусс стремился отойти в ней от произвольных допущений
и потому относительно плотности распределения вероятностей
228
ошибок старался возможно дольше не делать предположений,
кроме самых общих. А именно: Гаусс предполагал, что опыт
приводит к следующим заключениям относительно плотности
распределения ?(х) ошибок: ^{х)=^{~-'Х),^{х) имеет единственный
максимум при х=0, для достаточно больших значений аргумента
о{х) обращается в нуль. В этих предположениях Гаусс доказал
два интересные неравенства, которые мы здесь и
воспроизведем.
Пусть X — произвольное положительное число,
оо Хт
7722 = \ д;2^ {x)dx VL [1 ^ \ ср {х) dx,
—оо —Хт
Соотношение, связывающее X и [л, зависит от природы ср(^)-
Однако в только что высказанных предположениях
^<Р'1^3, если|л<2/д,
I< •, если fi>V3-
3 к 1 — \1
В частности, при \i = ^/^ Х не может превосходить У^/^,
т. е. вероятная ошибка не может превосходить 0.8660254 т.
Оценку величины /г, если она неизвестна, Гаусс вновь
рекомендует производить с помощью равенства (а — число
наблюдений)
= /t±i
т- ' + ^^ +
редняя квадратическая ошибка которого равна
/^
229
где а обозначает число наблюдений, а ^г^ = \ :г^ср (х) dx,
—оо
Основная задача, которой Гаусс уделил большое внимание,
состоит в следующем: предполагается, что переменные г/, ж^,
х^, . . . ,Хо связаны однородной линейной зависимостью
о
2/ = 2 ^в^8'
в которой коэффициенты ag не известны. Для их определения
из опыта находятся значения
о
2/г -= S ^3^sr, Г= 1,2, . . .,//.
Экспериментальное определение уг связано с неизбежными
ошибками, в результате которых вместо истинных значений
Уг получаются из измерений значения 7)|. = г/г + Дг- По
заданным Xsr и полученным r^f требуется определить наиболее
целесообразные приближенные значения as величин ag.
По Гауссу, olq определяются из условия
N / о \2
2 Mr— S ^sXsr =min.
Это условие приводит к системе так называемых
нормальных уравнений
о N N
2 as 2 ^^rXir = 2 ^rXir, (г =1, 2, ... , а),
s=i r=l г—]
из которых и находятся (при некоторых условиях) однозначно а^.
Полученные приближения не содержат систематической
ошибки; иными словами, математическое ожидание а|
оказывается равным искомой величине at.
230
Если ввести обозначения
N о 2
Г==1 ^ 8=1 ^
N
Ц2- f^^l
^ ~iV-a'
N а
i=l r=l ^ 8=1
TO средняя квадратическая ошибка, происходящая от замены т^
на fi^, оказывается равной
Использовав неравенства
Гаусс в § 40 получил следующие оценки для квадратической
ошибки:
5. А. Н. Колмогоров заметил ^, что верхняя оценка для
Q может быть значительно усилена и заменена следующей:
Эта оценка точна в том смысле, что она может достигаться.
Интересно отметить, что и нижняя оценка также достижима
при любых N и а, как это было показано А. И. Мальцевым ^.
^ А. Н. Колмогоров, А. А. Петров и Ю. М. Смирнов. Одна
формула Гаусса из теории метода наименьших квадратов. Изв. АН СССР,
серия математическая, т. И, 1947, стр 561—566,
^ А. И. Мальцев. Замечание к работе А. Н. Колмогорова, А.
А.'Петрова и Ю. М. Смирнова «Одна формула Гаусса из теории наименьших
квадратов».— Там же, стр. 567—568.
231
Таким образом, в результате для D{m^) теперь получены
следующие оценки:
<^W<lv—;r+ /v//^^_.^ > ecлил^<3m^
которые достигают своих крайних значений в некоторых
случаях.
Если п^ — Зт^ = О, то только что написанные формулы
дают известную для нормального распределения ошибок
формулу
^Ю = ^
Если п^^т^ и N велико сравнительно с а, то
D (т2).
N — a '
Гаусс в своем мемуаре для этого случая указал лишь
асимптотические оценки
27г* — 4т* 2w*
и
iV —а N — a*
В вырожденном случае п^=т^ величина D{m^) имеет более
высокий порядок малости:
Заметим при этом, что вырожденный случай имеет место
только для одного симметричного распределения: случайная
величина принимает лишь значения —а и +а, каждое с
вероятностью ^/2.
Замечательные результаты Гаусса по теории ошибок
измерений, как мы уже говорили, почти без изменения излагаются
232
до настоящего времени в большинстве соответствующих
учебников и при этом почти в том же объеме, в каком это было
сделано Гауссом. В то же время теперь имеются некоторые
результаты математической статистики, которые уже нельзя не
учитывать и которые должны бы были найти более широкое
отражение также в практической работе астрономов и
геодезистов. Так, если средняя KB а дратическая ошибка m неизвестна,
то для оценки возможных отклонений а^ от а^ нужно
пользоваться распределением Стьюдента с соответствующим числом
степеней свободы, а для оценки {^.^ от т^ распределением у\
Оба эти распределения были найдены лишь в начале нашего века.
Употребление же вместо этих распределений нормального
закона в качестве приближенного распределения приводит при
небольшом числе наблюдений к весьма значительной
переоценке надежности. Далее необходимо указать, что
вычислительные методы, использованные Гауссом, в настоящее время могут
быть значительно упрощены посредством широкого
использования методов и общих понятий современной линейной
алгебры, а также представлений многомерной векторной геометрии.
Такое изложение можно найти в статьях А. Н. Колмогорова
и В. В. Петрова ^.
6. В четвертом томе собрания сочинений Гаусса
напечатаны отдельные, относящиеся к теории вероятностей замечания,
сделанные им в разное время и не доведенные до опубликования.
На стр. 88—89 под названием «Прекрасная теорема по теории
вероятностей» (Schones theorem der Wahrscheinlichkeitsrecli-
nung) напечатана формула обращения для преобразования
Фурье. При этом не сделано никаких оговорок об условиях
ее применимости. Подлинная запись Гаусса состоит в
следующем: «Если [положить]
e^*^cp(f)rff|/2 7r '^(м).
1 А. Н. Колмогоров. К обоснованию метода наименьших
квадратов.— Успехи математических наук, т. I, вып. 1 (И), 1946, стр. 57—
70; В. В. Петров. О методе наименьших квадратов и его
экстремальных свойствах.— Успехи математических наук, т. IX, вып. 1 (59),
1954, стр. 41—62.
233
интегрирование распространяется от ^ = — сх) до ^ == + сю, то
[ е-^^^ф {u)du = У2^ ср (О,
интеграл берется в тех же пределах.
Основание этой теоремы содержится в формуле
Sep it + ^\ = ^ ^е-^^'^ \ ср (в) е^^«- dO,
где интегрирование предполагается распространенным от в =
= — со до в = Ч-сх) и знак S распространяется на все целые
положительные и отрицательные значения Л, в то время как
<о безгранично убывает».
Этот общий факт самим Гауссом не был использован, однако
он играет важную роль в современной математике и, в
частности, в теории вероятностей, где его можно считать одним
из первых результатов теории характеристических функций.
Точная дата, когда Гаусс сделал эту запись, не известна.
Найдена она в книге записей под названием «Opuscula ma-
thematica», 1799—1813 гг.
Второе небольшое замечание (Werke, IV, 133) сделано по
поводу распределения Бернулли. Гаусс вычислил факториаль-
ные моменты для числа р появлений события в п
независимых испытаниях, в каждом из которых событие имеет одну
и ту же вероятность р-. Вычисленные им разультаты в
современных обозначениях записываются следующим образом:
Mp = nii, Afp(p —1) = п(д —1),У, Л/р(р —1)(р—2) =
= п{п — 1){п — 2)|л^ и т. д.
Третье замечание под названием «Задача» (Werke, IV, 134—
135) посвящено формулировке и решению следующей задачи:
«Существуют р мест, на которых случайно распределяются т
предметов, причем предполагается, что каждый предмет
занимает каждое место с одной и той же вероятностью.
Вероятность того, что число занятых мест будет т—п, обозна-
1
чим через (т, п) и положим -— = х»,
234
Общего решения приведенной задачи Гаусс не привел. Он
ограничился приведением таблички решений при отдельных
значениях тип, некоторыми числовыми преобразованиями и
указанием общей формулы для математического ожидания п:
{т, 1) + 2 (т, 2) + 3 (т, 3) + . . . = а-^Г-'^-^»^)
7. Особый интерес представляет результат Гаусса,
сформулированный в письме к Лапласу от 30 января 1812 г. Этот
результат послужил одним из отправных пунктов для развития
нового интересного раздела математики — метрической теории
чисел.
Постановку задачи Гаусса мы приведем, воспользовавшись
его словами из только что упомянутого письма: «... Я
вспоминаю любопытную задачу, которой я занимался уже 12 лет
назади, но для которой я не нашел тогда удовлетворяющего
меня решения.
Быть может. Вы соблаговолите заняться ею несколько
минут: в этом случае, я убежден, вы найдете более полное решение.
Вот она. Пусть М — неизвестная величина, заключенная
между пределами О и 1, для которой все значения или
одинаково вероятны или же более или менее следуют данному
закону: предположено, что она разложена в непрерывную
дробь
м = _1
а'+±
а" + etc.
Чему равна вероятность того, что, отбросив в разложении
конечное число членов до а^^\ следующая дробь
ain+l).
а(^+2) _f, etc.
^ См. запись в дневнике от 25 октября 1800 г. за № ИЗ.
235
будет заключена в пределах между О и о:? Я обозначаю ее через
Р (п, х) и предполагаю, что для М все значения одинаково
вероятны:
Р(0, х)=^х.
Р {i,x) является трансцендентной функцией, зависящей от
функции
которую Эйлер назвал необъяснимой и которой я посвятил
многие исследования в одном из предшествующих мемуаров,
представленных нашему научному обществу, который должен в
ближайшее время быть напечатан^. Но для случая п очень
большого точное значение Р (п, х) оказывается недоступным.
Однако я нашел путем рассуждений, что ^
Щ Но усилия, которые я делал после тех моих исследований
для оценки
при очень больших значениях п, но не бесконечных, оказались
бесплодными».
Указанная проблема Гаусса была решена немногим более
чем через сто лет в работе Р. О. Кузьмина ^. Оказывается, что
^(".-)-i=^
< се-'^У'^
^ Disquisitiones cirio seriem ets. Werke, III, 123; см. особ,
стр. 154 и ел.
2 Повидимому, слова Гаусса следует понимать так, что в преположе-
нии существования предела lim P(ai, х) —Р{х) должно быть
п~*оо
log (1 4-а;)
p{x)z=z—^- X— .Однако само существование предела Гауссом не
logz
было доказано.
3 Р. О. Кузьмин. Об одной задаче Гаусса. Докл. АН СССР
(серия А), 1928, стр. 375—380.
236
где с и X — абсолютные постоянные. Доказательство этого
факта основано Кузьминым на тождестве
Р{/г + 1,а;) = 2 {/^(п,4-)-^(«. ;-^)}.{0<^<1.">0),
/С=1
известном еще Гауссу. Только Кузьмин преобразовал это
тождество путем дифференцирования в следующее:
к=--1 ^ / ^ '
(дифференцирование законно, если Р(0, х) непрерывна и
ограничена при любом х).
В 1929 г. проблема Гаусса была решена П. Леви путем
использования теоретико-вероятностных рассуждений ^. При
этом удалось получить лучшую оценку быстроты сходимости,
чем та, которая была получена Кузьминым, а именно
^(".-)-!^^'
<сГ,
где с и q — постоянные {q<Cl).
Теорема, сформулированная Гауссом и доказанная
Кузьминым, а также П. Леви, дала возможность А. Я. Хинчину ^
доказать интересные теоремы, формулировки которых мы здесь
приведем.
^ Р. Levy. Sur les lois de probabilite dont dependent les quotient
complets et incomplets d'une fraction continue. — Bull. Soc. Math., 1929,
№ 57, стр. 178—194.
2 A. К h i n t с h i n e. Metrische Kettenbruchprobleme. — Compositio
Mathematica, 1935, № 1, стр. 361—382; Zur metrischen Kettenbruchtheo-
rie. — Там же, 1936, № 3, стр. 276—285.
237
Пусть / (г) — неотрицательная функция целого полояштель-
ного аргумента г и пусть при некоторых положительных
постоянных с и о
fir)<cr' , (г==1,2,...).
Тогда для почти всех чисел отрезка (0,1)
liml 3/Ы= H/W-
Рассмотрим частные случаи.
Пусть / (г) = 1 для г = А и / (г) = О для гфк, где к —
некоторое целое положительное число. В этом случае сумма
п
представляет собой число, которое указывает, сколько раз
встречается к среди п первых элементов цепной дроби.
Отношение
*-^' = IS/w
представляет собой плотность числа к среди первых п
элементов рассматриваемой цепной дроби, а предел
d{k) = \im--%{k),
если он существует, представляет собой плотность числа к
среди всех ее элементов. Из предыдущего заключаем, что для
почти всех чисел плотность d {к) существует и равна
^(^) = l4l+W))/l'^2.
Таким образом, при разложении в цепную дробь почти
всех чисел все натуральные числа к встречаются в качестве
238
элементов цепной дроби с определенной частотой, зависящей
только от к.
Пусть теперь /(r) = lgr. Согласно теореме, для почти всех
чисел М
1 V 1 V 1 ^^ \^+ г{г-\-2)) , .
1 г=1 ^
Иными словами, среднее геометрическое первых п
элементов разложения числа М ф<^М<:^\) в непрерывную дробь для
почти всех М стремится к абсолютной постоянной:
lg2
П,{1+?17ТУ,} =2.6-
Обозначим теперь через Рп и Qn числитель и знаменатель
/г-й подходящей дроби и положим в теореме / {п) = In jr^ (или
Vn—1
Р
/(тг) = In р-^). Тогда применение общей теоремы приводит к
такому результату Хинчина: для почти всех чисел при п—>оо
где с — абсолютная постоянная. П. Леви нашел, что In с =
12 In 2*
До некоторой степени теперь разъяснилось несколько неясное
замечание, сделанное Гауссом в письме к Лапласу, о том, что
для величины М «все значения или одинаково вероятны или же
более или менее следуют данному закону». Оказывается, что
если Р (О, х) имеет ограниченную производную (а не только
в случае Р (О, х)=х, как мы рассматривали до сих пор), то все
результаты, сформулированные нами, сохраняются.
8. Мы заканчиваем наш краткий очерк, посвященный
работам Гаусса в области науки, находившейся далеко не в центре
его научных интересов. И, однако, несмотря на это
обстоятельство, мы должны признать, что ему удалось обогатить теорию
239
вероятностей многими первоклассными результатами и повлиять
на дальнейшее развитие ряда важных направлений.
Идеи Гаусса находят применение и дальнейшее развитие и в
наше время в ряде разделов теории вероятностей,
математической статистики и в смежных дисциплинах. Развитие метрической
теории непрерывных дробей является одним из убедительных
примеров, иллюстрирующих наше утверждение. Кстати, можно
предполагать,что в связи с развитием новой вычислительной
техники цепные дроби вновь вернут свое значение и при этом
вероятностные задачи, связанные с приближенным их вычисле-
еием, приобретут особый интерес.
М. Ф. вубботин
АСТРОНОМИЧЕСКИЕ
И ГЕОДЕЗИЧЕСКИЕ
РАБОТЫ ГАУССА
^6 К. Ф. Гаусс
ns^SS:
Введение (243).— 1. Общий обзор работ Гаусса по
теоретической астрономии (248).— 2. Деятельность Гаусса в области
наблюдательной астрономии (266).— 3. Деятельность Гаусса в области
геодезии (274).— 4. Theoria motus (279).— 5. Метод Гаусса для
вычисления орбит по наименьшему числу наблюдений (290).— 6.
Другие работы по теории невозмун1;енного движения (299).— 7. Метод
Гаусса для вычисления вековых возмущений (304).—
Заключение (307).
ВВЕДЕНИЕ
В творчестве Гаусса, столь широком по своему охвату и
столь глубоком по содержанию, астрономические работы
занимают очень большое место. Это вполне естественно — ведь
с 1807 г., когда Гауссу исполнилось 30 лет, и до самой своей
смерти в 1855 г., Гаусс был профессором астрономии в Гёт-
тингенском университете и директором Гёттингенской
обсерватории, уже прославленной работами Тобиаса Майера (Tobias
Mayer, 1723—1762).
Первые 20 лет после окончания университета Гаусс почти
целиком посвятил астрономии, а следующие 20 лет —
геодезии, в те времена еще только начинавшей отделяться от
астрономии.
Все астрономические работы Гаусса, как
опубликованные им самим, так и найденные в оставшихся после него
рукописях, находятся в полном собрании его сочинений,
изданном в 12 томах (1863-—1929 гг.) Гёттингенским научным
обществом.
16* 243
J3 этом монументальном памятнике, воздвигнутом немецким
народом своему великому сыну, астрономические работы
занимают целиком два тома^; два другие тома содержат работы Гаусса
по геодезии ^; дополнением к этим четырем томам служит
XI том, первая часть которого содержит дальнейшие материалы
из посмертных бумаг Гаусса, относящиеся к его
астрономическим работам^, а вторая часть — обширный мемуар Бренделя,
дающий весьма подробный анализ всех астрономических работ
Гаусса, и мемуар А. Галле, содержащий историю и описание
геодезических работ Гаусса^.
Но, несмотря на большое место, которое занимают
астрономические работы в творчестве Гаусса, им не всегда придают
должное значение, и уже одно это показывает, что
освещение деятельности Гаусса в области астрономии не является
излишним.
Такое освещение важно не для того, чтобы сравнить ценность
созданного Гауссом в астрономии с ценностью того, что он
сделал для математики или физики. Такое сравнение, если и имеет
смысл, то лишь весьма ограниченный — слишком различны
цели и методы этих наук, чтобы была достаточная база для
подобного сравнения. Оценка астрономических работ Гаусса
может быть произведена лишь путем выяснения, насколько
они отвечали насущным потребностям астрономии его времени,
1 С. F. Gauss. Werke, Bd. VI. Astronomische Abhandlungen und
Aufsatze, 1874; Bd. VII. Theoria motus und theoretisch-astronomischer
Nachlass, 1906. Bee ссылки на VII том будут относиться к изданию 1906 г.,
а не к первому изданию этого тома, вышедшему в 1871 г. и содержащему
только Theoria motus.
2 С. F. Gauss. Werke, Bd. IV. Wahrscheinlichkeitsrechnung und
Geometrie, 1880; Bd. IX. Geodasie, 1903.
3 G. F. Gauss. Werke, Bd. XI, Abteilung 1. Nachlass und Brief-
wechsel zur Physik, Astronomie und Ghronologie, 1927.
* G. F. Gauss. Werke, Bd. XI, Abteilung 2. Abhandlungen iiber
Gauss'Wissenschaftliche Tatigkeit auf den Gebieten der angewandten Ma-
thematik (Geodasie, Physik, Astronomie), 1924—1929. Abhandlung 1-
A. G a 11 e. Uber die geodasischen Arbeiten von Gauss; Abhandlung 3:
Martin В r e n d e 1. Uber die astronomischen Arbeiten von Gauss.Часть мемуара
Бренделя вышла также отдельным изданием: Materialien fur eine wis-
senschaftliche Biographie von Gauss, Heft VII, 1919.
244
насколько они прокладывали новые пути и открывали новые
горизонты.
Итак, перед нами стоит задача не только напомнить в
немногих словах о деятельности Гаусса в области тех очередных
проблем, которые стояли перед астрономией в начале XIX в.,
но и показать, какова была дальнейшая судьба работ Гаусса,
выяснить значение их для развития астрономии.
Такая задача никогда не будет исчерпана, и по мере
развития науки, к ней надо время от времени возвращаться.
Сейчас, после блестящих успехов, одержанных
теоретической астрономией за последние десятилетия, повторное
изучение научного наследия Гаусса представляется не только
оправданным, но и весьма интересным.
В своем весьма обстоятельном анализе астрономических
работ Гаусса Брендель ставит вопрос: «Почему Гаусс, главные
интересы которого были сначала направлены в сторону
глубочайших проблем чистой математики, сделался по своему
общественному положению астрономом», и отвечает так: «Он не имел
средств и должен был думать о будущем. Чистая математика
открывала путь только к месту преподавателя школы или
университета, а известно, какое отвращение питал Гаусс — с
молодости и до преклонного возраста — к преподаванию...»^.
Нисколько не отрицая возможности и таких мотивов,
позволительно думать, что тут были и другие, гораздо более
глубокие причины.
Не подлежит сомнению, что интерес к астрономии зародился
у Гаусса очень рано, может быть, еще до поступления (в 1795 г.)
в Гёттингенский университет. Известно, например, что в 1794 г.
он приобрел «Principia» Ньютона. В студенческие годы (1795—
1798) он изучал не только «Аналитическую механику» Лагранжа,
незадолго до этого появившуюся (1787) и привлекшую всеобщее
внимание, но и «Теорию Луны» Клеро, вышедшую в 1765 г.;
об этом свидетельствуют записи, сохранившиеся в универси-
i етской библиотеке. В письме, датированном 1797 г., Гаусс
^ Martin В г е п d е 1. t)ber die astronomischen Arheiten von Gauss.—
В кн.: С. F. G a n s s. Werke, Bd. XI. Abreilung 2, Abhandlimg 3, стр. 5.
245
сообщает, что болезнь помешала ему наблюдать лунное
затмение.
В письме академику Ф. И. Шуберту (1758—1825),
относящемуся к 1803 г., Гаусс, отклоняя настойчивое приглашение
перейти в Петербургскую академию наук, пишет: «Я издавна
питал особое пристрастие к Петербургу, месту, над которым
витает тень Эйлера; я уже давно имею сильную склонность
к практической астрономии; итак, что могло быть для меня
более желательно, чем лестный призыв, которым меня почтила
Академия?...»^.
Можно было бы упомянуть еще и о той настойчивости, с
которой Гаусс просил директора Зеебергской обсерватории
известного в то время астронома Цаха (F. X. s^. Zach, 1754—1832)
разрешить ему приехать для изучения практической
астрономии (1798—1799 гг.).
Но самым убедительным доказательством того, что занятия
астрономией не были для Гаусса случайностью, обусловленной
житейскими обстоятельствами, а вытекали из самой сущности
его дарования, является вся научная карьера Гаусса.
Вся его деятельность, столь плодотворная не только в
области астрономии и геодезии, но и в области физики и геофизики
(заниматься которыми никакие внешние обстоятельства его не
принуждали), свидетельствует о том, что, подобно Ньютону,
Гаусс был не только математиком, но и в неменьшей степени
естествоиспытателем, чувствовавшим потребность в
непосредственном соприкосновении с природой, с физической
реальностью.
Уже очень скоро слава Гаусса стала так велика, его научные
заслуги настолько общепризнаны, что он мог бы, если бы
захотел, ограничить свою деятельность одной математикой. Но он
этого не сделал. Более того, начиная с 1828 г., Гаусс с
энтузиазмом принимается за совершенно новую для него область —
за изучение земного магнетизма, хотя никакие внешние
обстоятельства, подобные тем, на которые указывает Брендель,
его к этому не побуждали. В течение более десяти лет Гаусс
^ «Научное наследство», т. I. Институт истории естествознания АН
СССР, 1948, стр. 787.
246
экспериментирует, изобретает новые приборы и
разрабатывает теорию земного магнетизма. Не приходится говорить, что
все это послужило стимулом и отправным пунктом для весьма
важных математических работ, изложенных в широко известном
сочинении «Общие предложения о силах притяжения и
отталкивания, действующих обратно пропорционально квадрату
расстояния». О математических работах, источником которых
были астрономические задачи, стоявшие перед Гауссом, нам
придется неоднократно говорить в дальнейшем.
Но астрономия не была для Гаусса только источником
интересных математических задач. Об этом свидетельствует вся его
жизнь от ранней молодости, когда он с таким жаром наблюдал
и вычислял, до глубокой старости, когда он охотно проводил
целые часы у рефрактора, любуясь видами Луны.
Переходя к рассмотрению того, что сделал Гаусс для развития
различных астрономических дисциплин, мы не будем
придерживаться хронологического порядка, а остановимся сначала,
и притом особенно подробно, на его работах в области
теоретической астрономии. В этой области отпечаток гения Гаусса
особенно ярок, многое из сделанного им имеет столь
законченную- форму, что без существенных изменений сохранилось
и до наших дней.
На работах Гаусса в области наблюдательной астрономии,
получившей в наше время более краткое и более удобное
наименование астрометрии, мы не будем останавливаться
подробно. Было бы бесполезно пытаться установить, имели ли эти
работы большее или меньшее значение для развития
астрономических знаний, чем его работа в области теоретической
астрономии. Но рассмотрение влияния Гаусса на выработку
методики наблюдений, методов исследования инструментов и тому
подобные вопросы требуют такого углубления в технические
детали, которое далеко выходит за рамки этой статьи. То же
самое можно сказать и про столь обширные и столь
фундаментальные работы Гаусса в области геодезии, которые иногда
довольно тесно переплетаются с его наблюдательными
астрономическими работами.
247
1. общий обзор работ гаусса по теоретической
астрономии
Хорошо известно, что начало астрономической карьеры
Гаусса тесно связано с весьма важным событием в истории
науки — с открытием малых планет, столь существенно
расширившим наши сведения о солнечной системе.
Благодаря работам Бодев 1772г. стал широко известным закон
планетных расстояний, незадолго до этого открытый Титиусом.
Этот закон, обнаруживший закономерность в расстояниях от
Солнца известных в то время шести планет, как бы
предсказывал существование еще одной планеты, которая должна
была заполнить слишком широкий интервал между Марсом
и Юпитером. Открытие Урана (1781 г.) блестяще подтвердило
закон Титиуса и сделало еще более вероятным существование
планеты между Марсом и Юпитером.
В лекциях Гаусса, записанных в 1820—1821 гг. А. Я. Куп-
фером (1799—1865), действительным членом Петербургской
академии наук с 1828 г., говорится по этому поводу следующее:
«... если расстояние Меркурия от Солнца разделить на 387
частей, то расстояния прочих планет, выраженные в этих же
частях, возрастают в следующей прогрессии:
Меркурий
Венера 387+ 293=
Земля 387+ 2-293=
Марс 387+ 4-293=
Юпитер 387+16-293=
Сатурн 397+32-293=
Уран 397+64-293=
Этот закон, сколь мало он астрономами-математиками ни
признавался, во-первых, потому, что он очень грубый, и, во-
вторых, потому, что это, собственно, не есть прогрессия (первый
член должен бы быть 387+\'2 293), дал повод г. Боде
предсказать существование новой плапоты с расстоянием 387+8-293
до Солнца.
Эта планета и была, действительно, открыта Пиацци в
Палермо, но вскоре опять, вследствие его болезни, потеряна;
но, наконец, Ольберс и Бремене, после того как ее долго и на-
248
387
680
973
1559
5 075
9 763
9139
Истинное
расстояние
387
723
1000
1524
5 208
9 541
19 082
прасно искали все европейские обсерватории, открыл ее на
основании орбиты, вычисленной Гауссом по новому способу,
пользуясь только наблюдениями, без всяких гипотез, к которым
прибег Буркхардт. Эта новая планета была названа Церерой,
и Боде издал о ней, как и об Уране, небольшое сочинение»^.
Как велик был интерес к предсказанной Боде планете,
видно из того, что в сентябре 1800 г. было решено, по
предложению Цаха, основать «специальное общество из 24 астрономов-
практиков, распределенных по всей Европе», для
систематических поисков гипотетической планеты. Но раньше, чем такое
общество сорганизовалось и начало действовать, планета была
открыта совершенно случайно во время наблюдени11,
производившихся Пиацци(0. Piazzi, 1746—1826) для составления
звездного каталога. За дату открытия принимается 1 января 1801 г.,
когда Пиацци впервые пронаблюдал звездочку немногим ярче
8-й величины (7^.6), а через несколько дней заметил ее движение.
Только 24 января Пиацци написал об открытой им «очень
маленькой комете без туманной оболочки и хвоста» директору
Берлинской обсерватории Боде (J. Е. Bode, 1747—1826),
известному парижскому астроному Лаланду (J. J. Lalande, 1732—
1807) и Ориани (В. Oriani, 1752—1832) — директору
Миланской обсерватории. Лаланд получил письмо в, феврале, но не
принял эффективных мер для обеспечения продолжения
наблюдений. Письма, посланные Боде и Ориани, достигли адресатов
лишь в апреле. Каждый из них тотчас же сообщил новость
Цаху, издававшему единственный тогда астрономический
журнал «Monatliche Correspondenz». В этом журнале и были
опубликованы 8 июня письма Пиацци с его первыми наблюдениями,
а также обстоятельная статья самого Цаха «О давно
подозреваемой между Марсом и Юпитером, а теперь, повидимому,
открытой, новой большой планете нашей солнечной системы».
Можно еще отметить, что и сам Пиацци высказал мысль
(в письме к Ориани), что открытый им объект может быть
предсказанной Боде планетой.
^К. Ф. Гаусс. Теоретическая астрономия. Лекции, читанные
в Гёттингене в 1820—1821 гг., записанные Купфером. Пер. с нем.
А. Н. Крылова, действ, члена Российской академии наук и
начальника Морской академии, Пг., 1919.
249
Между тем, за протекшие пять месяцев планета далеко ушла
от того места, где ее видел Пиацци, и давно скрылась в лучах
Солнца. Чтобы найти ее вновь, когда она достаточно отойдет
от Солнца, необходимо было вычислить ее орбиту, а по орбите
предвычислить заранее положения планеты, т. е. дать
эфемериду. Но те 19 наблюдений, которые успел сделать Пиацци
между 1 января и И февраля (когда болезнь, а затем дурная
погода заставили его прекратить наблюдения), охватывали
слишком короткую дугу орбиты, чтобы элементы орбиты можно
было вычислить при помощи употреблявшихся в то время
методов. Попытки такого рода делались, но были совершенно не
удачны. Эллиптическую орбиту вычислил известный парижский
астроном Буркхардт (J. Burckhardt, 1773—1825), основываясь
на совершенно произвольном (и оказавшимся неверным)
предположении, что планета в момент своего открытия находилась
в перигелии. Однако эта орбита была явно неудовлетворительна,
также как икруговые орбиты, вычисленные Ольберсом и Ориани.
А вычислять эллиптические орбиты, не делая какие-либо
упрощающие задачу предположения, тогда никто не умел.
Таково было положение дела, когда в руки Гаусса,
занимавшего в это время место доцента в Брауншвейге, попал
сентябрьский номер «Monatliche Correspondenz», в котором наблюдения
Пиацци были впервые полностью опубликованы (с довольно
существенными исправлениями его первых результатов).
Известие об открытии новой планеты уже раньше привлекло
внимание Гаусса. Теперь же он окончательно откладывает в сторону
все другие работы и целиком отдается задаче вычисления
орбиты новой планеты. Его «Дневник» содержит такие записи:
1801, середина сентября. Новый, наиболее простой и наиболее
эффективный метод находить элементы орбит небесных тел.
1801, октябрь. Открыл великое множество новых формул, для
теоретической астрономии весьма полезных.
В ноябре 1801 г. Гаусс решает поставленную задачу: в
декабрьском номере «Monatliche Correspondenz» мы находим
вычисленную им эллиптическую орбиту, достаточно хорошо
представлявшую наблюдения Пиацци, а также основанную на этой
орбите эфемериду.
250
1?огда при помощи эфемериды Гаусса планета была,
действительно, найдена (31 декабря 1801 г.), это вызвало всеобщий
восторг. Чтобы понять этот восторг, надо вспомнить, что
астрономы того времени не только не имели в своем распоряжении
фотографии, но их рефракторы не имели даже нитяных
микрометров. Им приходилось определять положение каждой
подозрительной звездочки относительно соседних звезд при помощи
кольцевого микрометра; только повторив такие наблюдения
на следующую ночь, можно было с полной уверенностью
отличить планету от звезды, а так как Церера выглядела в это время
как звезда почти 9-й величины, то понятно, что найти ее можно
было, лишь имея достаточно хорошую эфемериду.
Вычисленная Гауссом эфемерида оказалась ошибочной
приблизительно на полградуса по прямому восхождению и на
несколько минут по склонению. Такой результат следует признать
очень хорошим: это было, действительно, все, что можно
было извлечь из малоточных наблюдений того времени,
охватывавших, к тому же, промежуток времени всего в 41 день. Можно
еще добавить, что недостаточная точность тех (взятых из
таблиц Бувара) координат Солнца, на которые опирался Гаусс,
также заметно влияла на результаты.
Вторичное открытие Цереры сразу сделало Гаусса
знаменитостью. Известность его возросла еще больше, когда Ольберс,
усердно наблюдавший Цереру, открыл еще одну новую планету
(28 марта 1802 г.). Сенсация, вызванная открытием этой планеты,
названной Палладой, была не меньше. Гаусс, снова блестяще
справившийся со столь тогда трудной задачей вычисления
орбиты, установил, что Паллада, так же как Церера, движется
между Марсом и Юпитером. Таким образом, в этом промежутке
вместо одной планеты, как бы предсказанной законом Титиуса—
Воде, оказывалось две планеты. Последовавшие затем
открытия Юноны (1804 г.) и Весты (1807 г.) сделали еще более ясным,
что в деле изучения строения солнечной системы открылись
совсем новые перспективы, встали новые, весьма важные задачи.
Это сразу осознали ведущие астрономы того времени, а к их
числу уже принадлежал Гаусс, хотя ему было только 25 лет.
На решении новых задач, возникших, таким образом, перед
астрономией, Гаусс сразу же сосредоточил свои силы и посвя-
251
тил этим задачам свыше 15 лет упорного труда. Первая,
вставшая здесь задача заключалась в выработке возможно
простого и эффективного метода для вычисления орбиты по
минимальному количеству наблюдений. Методы, созданные Гауссом
в процессе вычисления орбит Цереры и Паллады, далеко еще не
решали эту задачу. Эти методы приводили к цели лишь путем
очень длинных вычислений, основанных па более или менее
произвольных пробах и на интерполировании между результатами
таких проб. Подобные методы были мало пригодны, поскольку
вычисление планетных орбит, перестав быть делом уникальным,
обратилось в постоянно встречающуюся задачу.
В 1805—1807гг. Гаусс создал новый метод вычисления орбит,
основанный не на интерполяционных, а на итерационных
процессах. Этот метод делал нахождение орбиты уже не столько
исследовательской работой, сколько чисто вычислительной,
и был поэтому гораздо более доступен широким кругам
астрономов. Первая задача была, таким образом, решена.
Данный Гауссом метод был настолько совершенен, что в
течении целого столетия употреблялся почти в неизменном виде.
Только в XX в., вследствие замены логарифмов
вычислительными машинами, форма метода существенно изменилась.
Вторая задача, также ставшая весьма актуальной благодаря
открытию малых планет, заключалась в создании эффективных
методов для улучшения предварительной орбиты, найденной
по первым наблюдениям. Эта задача не была столь новой, как
первая; ее решение для планетных орбит основывалось на тех
же принципах, что и для кометных орбит. Гаусс существенно
улучшил употреблявшиеся ранее методы вычислений. Но
особенно большое значение имело создание им метода наименьших
квадратов, позволившего решить вопрос о нахождении
наилучшей орбиты, соответствующей данной совокупности
наблюдений. Наблюдения не абсолютно точны. Поэтому, когда их много,
то нет такой орбиты, которая могла бы удовлетворить
совершенно точно всем наблюдениям. Какую же орбиту считать
наилучшей? С такой задачей встречались и раньше при нахождении
кометных орбит, но решали ее как бы ощупью. Гаусс, создав
метод наименьших квадратов, сделал самое понятие наилучшей
орбиты вполне определенным.
Независимо от Гаусса, к основным идеям метода
наименьших квадратов пришел Лежандр (А. М. Legendre, 1752—1834),
опубликовавший их несколько раньше. Но в то время, как
Гаусс всесторонне обосновал этот метод, Лежандр построил
его на произвольно взятом принципе, целесообразность
которого он мотивирует лишь аналогиями, заимствованными из
статики. С другой стороны, только Гаусс доработал этот метод
до конца и сделал его одним из основных орудий всех наук,
имеющих дело с обработкой наблюдений. Нужно, впрочем,
заметить, что особое развитие метод наименьших квадратов
получил у Гаусса не столько в связи с астрономическими
задачами, сколько благодаря обширным геодезическим работам,
начатым им около 1820 г. и занимавшим его свыше 20 лет.
Двум только что рассмотренным задачам Гаусс посвятил
свое знаменитое сочинение, опубликованное в 1809 г. под
длинным, но зато весьма точным названием «Теория движения
небесных тел, обращающихся вокруг Солнца по коническим
сечениям» (Theoria motus corporum. coelestium in sectionibus
conicis solem ambientium). Изучение этого сочинения, изв]естного
под сокращенным названием «Theoria motus», было в течение
целого столетия необходимой составной частью
астрономического образования. Можно судить поэтому, какое глубокое
влияние "оно оказало на формирование современной науки.
Содержание «Theoria motus» мы рассмотрим в дальнейшем
с должной подробностью; здесь же отметим только, что это
была единственная книга, опубликованная Гауссом по
астрономии. Вопросам, рассматриваемым в этой книге, т. е. методам
нахождения и исправления орбит, Гаусс посвятил еще
несколько небольших статей, о которых мы будем говорить ниже.
Третьей большой задачей, поставленной перед астрономами
открытием малых планет, было изучение их возмущенного
движения, т. е. вычисление тех возмущений, которые они
испытывают со стороны больших планет.
В первых двух задачах речь шла о движении планеты по
эллипсу, которое имело бы место, если бы на планету
действовало притяжение одного только Солнца. В третьей задаче
ставится вопрос о движении, производимом притяжением как
Солнца, так и других планет.
253
Такая задача в отношении больших планет уже решалась
Эйлером, Лагранжем и Лапласом. Но их решения
основывались целиком на специфических особенностях орбит больших
планет: расстояния между этими планетами велики,
эксцентриситеты и взаимные наклоны их орбит очень малы.
Для малых планет дело обстоит иначе. Их эксцентриситеты
и наклоны обычно на целый порядок превосходят
соответствующие величины для больших планет, А их движение вблизи
Юпитера делает возмущения со стороны этой планеты, с ее
огромной массой, очень большими и особенно трудно находимыми.
Две первые задачи, поставленные открытием малых планет,
были разрешены Гауссом за 5—6 лет с такой полнотой и
совершенством, что его методами можно было бы пользоваться в
неизмененном виде и теперь. Но 15-летняя упорная работа не
привела Гаусса к решению третьей задачи, не только в ее
общем виде, но даже в отношении тех двух планет — Цереры
и Паллады, на которых он сосредоточил свои усилия.
И это понятно — задача не была разрешена и за те 140
лет, которые прошли с того времени, когда Гаусс перестал ею
заниматься. Еще и сейчас мы, повидимому, далеки от сколько-
нибудь полного ее решения, несмотря на все усилия целого
ряда крупнейших ученых.
Конечно, многолетние усилия человека такой мощи, как
Гаусс, не могли быть и не были бесплодными. Хотя Гауссу
и не удалось дать теорию возмущенного движения ни для
Цереры, ни для Паллады, его работа над этой задачей дала весьма
ценные результаты. Важнейшие из них мы рассмотрим ниже,
а здесь ограничимся лишь указанием той
последовательности, в которой велись относящиеся сюда работы Гаусса.
Как только была вычислена орбита Цереры, стало ясно, что
эта планета должна испытывать значительные возмущения со
стороны близко от нее движущегося Юпитера. Для
приближенного нахождения этих возмущений несколькими астрономами
(и среди них академиком Ф. И. Шубертом) был использован
метод, данный Лапласом для вычисления возмущений
координат больших планет — долготы, радиуса-вектора и широты.
Гаусс, приступивший к этой работе в июне 1802 г., также
воспользовался методом Лапласа, но он внес много нового
254
в весьма существенную часть этого метода, а именно в
разложение в тригонометрические ряды частных производных
пертурбационной функции. Результаты этой работы (без изложения
метода) были им опубликованы в двух сообщениях. В первом
из них (ноябрь 1802 г.) Гаусс дает как вековые возмущения
наклона, эксцентриситета, долготы перигелия и долготы узла,
так и периодические неравенства первого порядка относительно
массы Юпитера в долготе (22 члена), в радиусе-векторе (24
члена) и в широте (9 членов). Все эти величины он находит с
учетом только первой степени эксцентриситета, отмечая, что
стремление к большей точности было бы преждевременным, так же
как и вычисление возмущений от Сатурна, поскольку имеющиеся
элементы орбиты еще мало надежны ^.
Во втором сообщении, опубликованном в марте 1803 г. 2,
даются таблицы возмущений Цереры, построенные на основе
указанных в первом сообщении формул. Гаусс считал, что
приближенные значения возмущений, находимые при помощи этих
таблиц, позволяют эффективнее использовать дальнейшие
наблюдения для уточнения исходной системы элементов Цереры,
Сам он проделал такую работу для ряда ближайших оппозиций
Цереры и получил систему элементов, которая (после учета
возмущений по только что указанным таблицам) следующим
образом представляла наблюденные оппозиции^.
Оппозиция
1802
1803
1804
1806
1807
1808
Разности между наблюденными и
вычисленными координатами Цереры
гелиоц. долгота
—0".5
+ 22.1
—34.9
-i-26.7
—26.9
4-20.8
гелиоц. широта
—1\9
1 —5.3
! —1.2
—3.6
—11.7
1 —6.0
^ См. выдержку из письма Гаусса к Цаху.— С. F. Gauss. Werke^
Bd. VI, стр. 227—230.
2 Там же, стр. 235—243.
^ См. письмо Гаусса к издателю журнала; там же, стр. 312—314.
255-
Принимая во внимание, что возмущения были найдены
только грубо приближенно, такое представление наблюдений за
6 лет следует признать очень хорошим, а полученную систему
элементов — вполне пригодной для более точного вычисления
возмущений. Но Гаусс уже не воспользовался этими элементами,
так как прекратил работу по изучению движения Цереры.
Повидимому, здесь сказались некоторые внешние
обстоятельства. В ноябре 1807 г. он переехал в Гёттинген и приступил
к работе в университете, а еще раньше, в мае этого года, Гаусс
начал окончательное оформление и печатание «Theoria motus»,
что также потребовало очень много времени^.
Но еще раньше, в 1805 г., Гаусс приступил к значительно
более точному нахождению возмущений Цереры. Поставив
себе целью найти эти возмущения с точностью до пятых степеней
эксцентриситетов Цереры и Юпитера, он решил отказаться от
аналитического метода разложения частных производных
пертурбационной функции в ряды, который он, следуя Лапласу,
употребил при первом вычислении. Вместо этого Гаусс пошел
новым путем: он создал тот метод тригонометрического
интерполирования, который очень скоро получил широкое
распространение и по настоящее время часто используется в наиболее
трудных задачах небесной механики. Этот метод подробно
изложен Гауссом в мемуаре «Theoria interpolationis methodo nova
tractata», найденном в его посмертных бумагах и впервые
опубликованном в 1866 г. 2
Вычисление возмущений Цереры вторым методом, т. е. при
помощи тригонометрического интерполирования, Гаусс только
начал.
Очень скоро он увлекся другой задачей — изучением
возмущенного движения Падлады — и к вычислению
возмущений Цереры больше не возвращался.
^ Следует отметить, что условия жизни Гаусса были в это время
очень тяжелые. В октябре 1809 г. умерла его жена, а в марте следующего
года — сын. Французскими оккупационными войсками на него была
наложена весьма значительная контрибуция.
2 С. F. G auss. Werke, Bd. III. Analysis, 1866. Zweiter Abdruck,
1876, стр. 265—330.
25B
Еще в 1802 г. Гаусс выражал желание заняться вычислением
возмущений Паллады, но указывал при этом, что к таким
вычислениям целесообразно будет приступить лишь тогда, когда
наблюдениями будут охвачены несколько обращений Паллады.
В соответствии с этим он систематически, после каждой
оппозиции Паллады, исправлял ее элементы. В первой половине
1810 г. Гаусс уже имел вполне надежные элементы Паллады,
позволившие ему установить, что влияние возмущений весьма
значительно: за 6 лет оно доходит до 3\5 в долготе и 1'.5
в широте.
План своей дальнейшей работы Гаусс излагает в письме
к Ольберсу от 24 октября 1810 г. следующим образом:
«Для Паллады я начну, однако, с того, что буду
рассматривать элементы как переменные и вычислю их возмущения за
7 лет при помощи квадратур; для этого я вывел формулы,
которые мне представляются более удобными, чем данные
Лапласом ^. В случае, если удастся (а иначе и быть не может) пронаблю-
денные до сих пор 6 оппозиций, не укладывающиеся на эллипс,
хорошо соединить, то я приступлю к вычислению возмущений
в обычной форме, т. е. как периодических возмущений долготы,
широты и радиуса-вектора, или еще лучше логарифма радиуса-
вектора, употребив для этого метод, разработанный мной 4
или 5 лет тому назад» ^.
Первая часть этого плана была очень быстро полностью
осуществлена.
1 Следует заметить, что здесь идет речь совсем не о тех <^формулах
механических квадратур Гаусса», служащих для вычисления
определенных интегралов, которые были опубликованы Гауссом в 1814 г. в
работе «Methodus nova integralium valores per approximationem inveniendi»
(cm. C. F. G a u s s. Werke, Bd. Ill, 163—196). Эти формулы не имеют
применения в астрономических вычислениях.
В письме Гаусса речь идет о формулах, устанавливающих
зависимость между суммами значений табулированной функции и значениями
ее интеграла, т. е. формулах, являющихся основой метода численного
интегрирования дифференциальных уравнений, известного под именем
«метода квадратур». Эти формулы не были Гауссом опубликованы. Р1х
опубликовал в 1834 г. Энке (J. F. Епске, 1791—1865).
2 В этом же письме (см. С. F. G а и s s. Werke, Bd. VII, 414) Гаусс
сообщает об улучшениях, внесенных им в решение нормальных
уравнений.
4 7 к. Ф. Гаусс 257
Гаусс проделал интегрирование дважды: в первом
приближении с постоянными элементами, во втором — с теми,
которые получились в первом приближении. Разности
«наблюдение — вычисление», опубликованные Гауссом^, оказались
в пределах ошибок наблюдений, как это видно из следуюндей
таблицы:
Оппозиция
Первое приближение
средняя
долгота
геолиц.
широта
Второе приближение
средняя
долгота
гелиоц.
широта
1803
1804
1805
1807
1808
1809
+ Г.З
—3.8
+3.9
—3.3
+3.2
—1.4
—1\0
+4.1
+6.0
+3.9
(-17)
—3.9
+ 7".3
-6.8
-г1.5
—3.3
—3.9
-+-5.0
+1".6
—4.0
—4.1
-3.8
(-16.9)
+3.5
По поводу этой таблицы нужно заметить, что наблюдения
в оппозицию 1808 г. были так плохи, что не позволили сколько-
нибудь надежно найти гелиоцентрическую широту. Если учесть
это обстоятельство и вообще принять во внимание точность
наблюдений того времени, то нам станет понятным
удовлетворение, какое доставили Гауссу только что указанные
результаты. Он пишет:
«Я окончил за это время свою работу над возмущениями
Паллады от Юпитера и получртл согласие с наблюдениями,
превзошедшее мои самые смелые ожидания... Но Вы
удивитесь вместе со мной, если я Вам скажу, что моя эфемерида,
помещенная в октябрьском номере «Monatliche Correspondenz»
и вычисленная без учета возмущений, теперь ошибочна больше
чем на градус...>/^.
1 В письмах, направленных редакторам «Monatliche Correspondenz»
и «Gottingische gelehrte Anzeigen» (см. С. F. Gauss. Werke, Bd. VI,
320 и 323).
2 Письмо Ольберсу от 13 декабря 1810 г. (см. С. F. G а и s s. Werke,
Bd. VII, 418).
258
к выполнению второй, наиболее трудоемкой части своего
плана — построению теории движения Паллады — Гаусс
приступил летом 1811 г. Задача заключалась в получении
аналитических выражений, позволяющих находить возмуп],ения для
любого момента времени. Трудность этой задачи
обусловливалась как близостью Паллады к Юпитеру, так и характером
ее орбиты, наклон которой равен 34.^8, а эксцентриситет равен
0.24. Сообразно с этим, Гаусс отказывается от аналитических
методов разложения в ряды, которыми пользовался Лаплас,
и везде применяет разработанный им способ
тригонометрического интерполирования, о котором уже говорилось выше.
Другой особенностью было то, что вычислялись не возмущенные
значения координат, как это всегда делалось раньше, а
значения оскулирующих элементов. Этим именно путем пошел
впоследствии Леверрье, создавший в 1850—1877 гг. свою
знаменитую теорию движения больших планет, которая до конца
XIX в. являлась основой всей астрономии.
К 1813 г. Гаусс закончил определение возмущений первого
порядка, производимых Юпитером в движении Паллады. Он
выполнил эти вычисления с очень большой точностью, приняв
во внимание все члены, пропорциональные степеням
эксцентриситета, до 11-й включительно; были также приняты во
внимание все степени отношения больших полуосей Паллады и
Юпитера, до 23-й включительно.
В процессе этих вычислений особые трудности были
связаны с наличием в движении Паллады долгопериодических
возмущений, обусловленных близкой соизмеримостью средних
суточных движений Паллады {п = 769."18) и Юпитера
(77 - 299.43).
Отношение этих средних движений выражается цепной
дробью
п' 1
^ 24-1
1 + 1
3+!
533 + .
17* 259
Первые четыре подходящие дроби .1, -1, J и - дают такие
равенства
п — 2п' = + П0^.д2; 2п--5п' =: +A2JI]
п — Ъп' = — 128121; In — 18п = — 0!08.
Отсюда видно, что 7 периодов обращения Юпитера почти
точно равны 18 периодам обращения Паллады. Вследствие
этого, поскольку период обращения Юпитера равен 11.862
годам, через каждые 83.034 года взаимное расположение планет
почти в точности повторяется. Происходящее отсюда
накопление возмущающего действия Юпитера вызывает в долготе
Паллады огромные колебания, доходящие до ±24°. С другой
стороны, эти же возмущения должны стабилизовать, как показал
Гаусс, существующее сейчас отношение 7 : 18 между
периодами обращения Юпитера и Паллады. Гаусс назвал это
явление либрацией, справедливо видя в нем аналог того, что имеет
место для Луны, где возмущающие силы поддерживают
точное равенство периода вращения Луны около оси и периода
ее обращения вокруг Земли ^.
Малая величина разности 2п—5/г' также является
источником долгопериодпческого возмущения, хотя и не столь
значительного, но все же меняющего долготу Паллады почти на
целый градус.
Работа над возмущениями первого порядка Паллады от
Юпитера была закончена в 1817 г. составлением таблиц,
облегчающих вычисление этих возмущений для заданного момента
времени. Большая часть работы по составлению этих таблиц
^ Какое большое значение сам Гаусс придавал открытию либрации
в движении Паллады, видно из того, что 25 апреля 1812 г. он сделал
в Гёттингенском научном обществе следующую шифрованную заявку:
1111 000 100 101 001,"^
ключ к которой он обещал дать «в свое время».
Гаусс ничего не опубликовал из своих исследований по теории
возмущенного движения Паллады и не дал обещанного ключа. Но из его
писем мы определенно знаем, что речь здесь шла именно о либрации,
производимой очень острой соизмеримостью 7 : 18. Можно отметить,
что числа 7 и 18 в двоичной системе изображаются так: 111 и 10010.
260
(найденных в посмертных бумагах Гаусса и впервые
опубликованных лишь в 1906 г.) была выполнена Энке.
Вычисление возмущений, производимых в движении Пал-
лады Сатурном и Марсом, было выполнено теми же самыми
методами (еще в 1813—1814 гг.) Николаи, которому Гаусс
передал эту работу.
В марте 1818 г. Гаусс произвел (при содействии Энке)
сравнение наблюдений, сделанных в оппозиции 1803—1817 гг.
с результатами всех этих вычислений и получил не только новую
уточненную систему элементов, но и поправку массы Юпитера.
Найденное им значение массы Юпитера (1/1050) весьма близко
к истинному (1/1047.4).
На этом обрываются работы Гаусса по созданию
аналитической теории движения Паллады. Гаусс ничего не
опубликовал из полученных результатов, хотя о многом сообщал в
письмах Ольберсу и Бесселю. Эти работы стали известны лишь после
опубликования в 1906 г. (во втором издании VII тома полного
собрания сочинений) всего, что было найдено в посмертных
бумагах; Гаусса по этим вопросам. Изучение опубликованных
материалов привело Георга Струве^ к заключению, что
возмущения первого порядка найдены Гауссом с большой точностью
и дают представление о наблюдениях за 107 лет настолько
хорошо, что могут служить основанием для создания полной
аналитической теории движения Паллады. Такая теория не
создана, однако, и до настоящего времени, так как уже следующий
шаг — вычисление возмущений второго порядка —
представляет весьма большие трудности.
Прекращение Гауссом в 1818 г. работы по изучению
движения Паллады объясняется прежде всего тем, что установка
новых больших инструментов Гёттингенской обсерватории,
изготовленных по его заказу, заставила Гаусса целиком
переключиться на исследование этих инструментов и наблюдения.
Начиная с 1820 г., к астрономическим наблюдениям
присоединились еще и весьма трудоемкие геодезические работы.
Рассматривая исследования Гаусса по теории движения
1 Georg S t г U л^ е. Die Darstellung der Pallasbahn durch die Gauss'-
sche Theorie fiir den Zeitraiim 1803 bis 1910. Dissertation, Berlin, Ebering,
1910, 4^ 56 стр.
261
Паллады, нельзя не упомянуть о теме, предложенной 30 марта
1804 г. Парижской академией наук на соискание премии. Эта
тема была формулирована следующим образом:
«Дать теорию возмущений планеты Паллады, открытой Оль-
берсом... Геометры и астрономы приглашаются полностью
изучить все неравенства этой теории и не пренебречь ни одним
хоть сколько-нибудь заметным; а так как эти неравенства
могут заметно измениться, если элементы орбиты окажутся не
вполне точными, то необходимо, чтобы конкуренты не
ограничились получением численных значений коэффициентов, а дали
бы для всех коэффициентов аналитические выражения, дабы
в них можно было подставить более точные значения среднего
расстояния, эксцентриситета, долготы афелия и наклона, когда
эти элементы будут лучше известны. Аналитическая форма
коэффициентов будет иметь и другое преимущество; так как
планеты Церера и Паллада находятся от Солнца на
расстояниях, столь мало различающихся, что сейчас даже трудно
сказать, которая из них дальше, а которая ближе, то полученные
формулы будут, без больших изменений, пригодны и для
Цереры, а также для всякой другой планеты, которая может быть
открыта впоследствии... Премия будет состоять из золотой
медали весом в один килограмм».
Гаусс, имевший уже опыт в деле вычисления возмущений
Цереры, сразу оценил такую постановку задачи, как
совершенно не реальную и был вполне прав — в таком общем виде
Эта задача далека от своего решения и в настоящее время.
Между тем срок представления работ на премию Парижская
академия из года в год отодвигала, так как работы не поступали.
Стало ясно, что к решению поставленной задачи должны быть
предъявлены значительно более ограниченные требования.
В связи с этим Гаусс заинтересовался возможностью
представить результаты своих исследований на соискание премии.
Сообщая в письме Ольберсу от 26 ноября 1810 г. о своих планах
развертывания работы по теории движения Паллады, он
прибавляет: «Если бы Ваши советы склонили Париж продлить
еще раз срок представления работ на премию, то это было
бы для меня еще одной побудительной причиной, чтобы
взяться за упомянутую выше работу...».
262
Срок был, действительно, продлен и притом весьма
значительно — присуждение премии было перенесено на 1816 г.,
так что работы должны были быть представлены к 1 октября
1815 г. Извещая об этом Гаусса (письмо от 25 января 1815 г.),
Ольберс выражает надежду, что Гаусс сообщит Парижской
академии созданный им метод вычисления возмущений, так как
«только ради Вас срок представления работ на премию так долго
откладывался».
Однако и на этот раз Гауссу не удалось закончить и
представить свою работу. В его бумагах было найдено в окончательно
обработанном виде только начало задуманной работы:
«Изложение нового метода для вычисления планетных возмущений
с его применением к численному нахождению возмущений в
движении Паллады»^.
Здесь он подробно изложил, между прочим, уже
упоминавшийся нами метод численного интегрирования
дифференциальных уравнений и его применение к вычислению возмущений
элементов орбиты планеты.
Чтобы дать Гауссу возможность закончить работу, срок
представления был перенесен еще на один год — до 1 октября
1816 г. Формулировка темы была теперь иная: «Дать теорию
движения планет, эксцентриситеты и наклоны орбит которых
слишком велики, чтобы их возмущения можно было вычислять
с полною точностью при помощи известных методов». При
этом не требовалось даже включать в работу численное
применение предлагаемого метода.
Но, несмотря на все это, Гауссу так и не удалось завершить
свои многолетние работы по аналитической теории движения
Паллады. Причиной была, несомненно, та необходимость
заниматься одновременно несколькими дееЯами (die Zersplitte-
rung der Zeit), на которую так часто жалуется Гаусс в своих
письхмах.
Много лет спустя, в письме Бесселю (21 марта 1843 г.) Гаусс,
благодаря его за присылку работы о массе Юпитера, замечает:
«Эта статья пробудила у меня воспоминания, всегда для меня
^ Exposition d'une nouvelle methode de calculer les perturbations
planetaires avec I'application au calcul numerique des perturbations du
mouvement de Pallas (G. F. G a u s s. Werke, Bd. VII, 439—472).
263
болезненные, о моей старой работе по возмущениям Паллады.
За истекшие почти что четверть столетия она мне стала так
чужда, что мне самому было бы теперь трудно в ней
ориентироваться...».
В 1834—1835 гг. Энке, ставший уже директором
Берлинской обсерватории, опубликовал, с согласия Гаусса, метод
численного интегрирования, употребленный при вычислении
возмущений Цереры и Паллады. С тех пор этот метод стал
основным орудием при изучении возмущенного движения планет
и комет. А в XX в. употребление этого метода вышло далеко
за пределы теоретической астрономии; он получил широкое
распространение во всех областях науки и техники, где
приходится иметь дело с дифференциальными уравнениями.
Чтобы закончить обзор деятельности Гаусса в области
теоретической астрономии, нам нужно дать представление еще
о двух его работах. Одну из них, содержавшую новый и весьма
важный метод вычисления вековых возмущений, мы рассмотрим
в дальнейшем подробно. Другую, которую Гаусс не только не
опубликовал, но о которой он даже никогда не упоминал в своей
обширной переписке, рассмотрим сейчас.
Изучение оставшихся после Гаусса рукописей показало,
что его первая астрономическая работа относилась к 1801 г. и
была посвящена теории движения Луны.
Эта проблема была тогда весьма актуальной. Несмотря на
блестящие работы Клеро (А. Clairaut, 1713—1765) и Эйлера,
теория Луны была еще настолько несовершенна, что эфемериды
Луны, столь необходимые для мореплавания, приходилось
вычислять по таблицам Тобиаса Майера^, имевшим
полуэмпирический характер. Аналитическая форма возмущений была
в них определена теоретически, а все важнейшие коэффициенты
были найдены при помощи огромного числа наблюдений. Но
начиная с 1788 г., эти таблицы пришлось подвергать все более
и более частым исправлениям, также эмпирического характера.
1 Первоначально эти таблицы были опубликованы Гёттингенским
научным обществом в 1752 г. В переработанном и улучшенном виде они
были представлены на премию, объявленную Комиссией долгот (Board
of Longitude) Британского адмиралтейства, которая их издала (Tabulae
motuum Soils et Lunae novae et correctae. London, 1770).
264
в связи с этим Парижская академия предложила в 1798 г.
на соискание премии такую тему: «Из большого числа
наилучших наблюдений Луны, как наиболее надежных старых, так
п новейших, обш;им числом не менее 500, найти средние долготы
апогея и восходящего узла орбиты Луны» .
Можно думать, что эта тема была одной из причин,
побудивших Гаусса заняться теорией движения Луны. Дошедшая
до нас рукопись^ показывает, что у Гаусса были широкие
планы — дать полную теорию движения Луны, основанную на
законе Ньютона. Но работа оборвалась в сентябре 1801 г., когда
Гаусс занялся вычислением орбиты Цереры. То
обстоятельство, что Гаусс никогда к ней больше не возвращался,
находится, возможно, в связи с появлением в 1802 г. третьего тома
«Небесной механики» Лапласа, где теория движения Луны
развита с большой полнотой и притом в направлении, очень
близком к тому, в каком ее начал развивать Гаусс. Идеи,
внесенные Гауссом, мы находим осуществленными много позднее
в работе Плана ^.
Любопытно отметить, что Гаусс, так высоко всегда
ставивший Эйлера^, не заинтересовался его работами по теории
движения Луны^. В выборе переменных, определяющих положение
Луны, и в трактовке дифференциальных уравнений движения
он пошел по пути, разработанному в мемуарах Клеро, Д'Алам-
бера и Лапласа. Между тем, именно развитие идей Эйлера
привело Хилла (G. W. Hill, 1838—1914) и Брауна (Е. W. Brown,
^ «Theorie der Bewegung des Mondes» (см. С. F. Gauss. Werke,
Bd. Vni, 613—639); эту рукопись, не имеющую даты, относят к 1801 г.
на основании сделанной в «Дневнике» в августе этого года записи: -The-
oria motus Lunae aggressi sumus».
2 Plana. Theorie du mouvement de la Lime, tomes I—III.
Turin, 1832.
^ Хорошо известны слова Гаусса: «Изучение всех работ Эйлера
навсегда останется лучшей, ничем не заменимой школой в самых
различных областях математических наук».
* L. Е U 1 е г. Opuscula varii argument!. Berlin, 1746, Theoria motus
Lunae exhibens omnes eius inaequalitates. St.-Petersburg, 1753; Theoria
motuum Lunae nova methodo pertractata. St.-Petersburg, 1772.
Последнее сочинение частично переведено на русский язык: Л. Эйлер. Новая
теория движения Луйы. Пер. с лат. акад. А. Н. Крылова, изд. АН СССР,
1934.
26^
1866—1938) к полному решению задачи о движении Луны -г
одному из величайших триумфов астрономии.
2. ДЕЯТЕЛЬНОСТЬ ГАУССА В ОБЛАСТИ НАБЛЮДАТЕЛЬНОЙ
АСТРОНОМИИ
Наблюдательной астрономии, или — как ее теперь обычно
называют — астрометрии, Гаусс посвятил не меньше времени,
чем рассмотренным нами работам по теоретическим вопросам,
но напечатал очень немного.
Остановимся прежде всего на двух небольших статьях,
опубликованных Гауссом в 1808 г.:
«Methodus peculiaris elevationem poll determinandi» (см.
С. F. Gauss. Werke, Bd. VI, 37—49).
«Uber eine Aufgabe der spharischen Astronomie» (см. там же,
стр. 129—140).
В первой из них Гаусс показывает, как, пронаблюдав
моменты, в которые две звезды имеют одинаковую высоту, можно
получить широту места наблюдения. Во второй статье
излагается метод одновременного получения широты места и поправки
часов по наблюдению моментов, в которые три звезды находятся
на одинаковой высоте.
Эти методы определения широты и времени, в наибольшей
степени освобождаюш;ие результаты от влияния
инструментальных ошибок и ошибок рефракции, хотя и излагались в широко
известных учебных руководствах, однако в течение долгого
времени не получали сколько-нибудь широкого распростране-
лия, так как требовали довольно сложных вычислений. Только
в конце XIX в. идеи Гаусса были полностью оценены и
получили должное развитие.
В 1874 г. на базе этих идей Н. Я. Цингером^ (1842—1918)
был создан общеизвестный «способ Цингера» для определения
поправки часов по наблюдению моментов, в которые две звезды
находятся на равных высотах. Им было показано, что при нали-
' В это время он был адъюнкт-астрономом Пулковской обсерватории;
впоследствии — известный военный геодезист и автор широко
распространенных учебников.
266
qHH надлежащей подготовки соответствующих «пар звезд»
производство и обработка наблюдений выполняются весьма
удобно. Этот способ, благодаря своим преимуществам, очень
скоро сделался основным методом получения долгот во всех
наших астрономо-геодезических работах и остается таковым
и по настоящее время. Недавно он был еще более
усовершенствован Д. К. Куликовым^.
Развивая эти же идеи Гаусса, другой наш военный
геодезист М. В. Певцов (1842—1902) создал (1884 г.) способ
определения широты по наблюдению двух звезд на равных высотах.
«Способ Певцова» имеет также самое широкое применение в
астрономо-геодезических работах.
С другой стороны, французскими геодезистами был создан
специальный инструмент — призменная астролябия — для
наблюдения прохождений звезд через альмукантарат,
соответствующий высоте 60°. Каждое такое наблюдение позволяет
написать условное уравнение, связывающее поправку часов
и поправку широты. Решение достаточного числа этих условных
уравнений дает географические координаты места наблюдения ^.
Таким образом, методы определения географических
координат, идущие от Гаусса, у французских геодезистов также стали
основными методами полевых работ.
.Можно еще отметить, что созданный Чендлером (S. С.
Chandler, 1846—1913)в 1885 г. альмукантар — большой обсерваторский
инструмент для решения основных задач астрометрии при
помощи наблюдения звезд на одинаковых высотах — также
является прямым потомком двух маленьких статей Гаусса,
появившихся в 1808 г.
Кроме этих статей и четырех довольно обстоятельных
описаний новых инструментов, установленных на Гёттингенской
^ Д. К. Куликов. Теория эфемерид пар Цингера и каталог
500 пар звезд в системе РКЪ на эпохи 1950.0 и 1970.0. Институт
теоретической астрономии АН СССР, 1951, 244 стр. За эту работу автору была
присуждена Сталинская премия.
2 Гаусс излагал в своих лекциях и этот способ совместного
нахождения поправок времени и широты путем решения системы условных
уравнений (см. К. Ф. Гаусс. Теоретическая астрономия, Пг., 1919,
стр. 55—62).
267
обсерватории в 1813—1819 гг., Гауссом было опубликована
следующее:
1808. «AUgemeine Tafeln fur Aberration und Nutation» (см.
С. F. Ga uss. Werke, Bd. VI, 123—128).
1811. «Tafeln fur Mittags-Verbesserung>> (см. там же,
стр. 166—171).
1820. «Tafeln zur Bestimmung der Aberration, Praecession,
Lunar- und Solarnutation fur Sternzeit eingerichtet» (см. там же,,
Bd. XI, Abteilung 1, стр. 379—381).
1822. «Refractionstafein» (см. там же, Bd. VI, 185—190).
1846. «Nadirpunkt» (см. там же, стр. 472).
В первых двух статьях и в таблицах, помеиденных в состав-
ленных Шумахером сборниках вспомогательных таблице, Гаусс
внес заметные улучшения в вычислительную практику своего
времени. Маленькая заметка об особом приеме освещать поле
зрения при наблюдении надира, напечатанная Гауссом в глубо-
кой старости, также слишком тесно связана с техническими
возможностями определенной эпохи, чтобы представлять
значительный интерес.
Переходя к обзору деятельности Гаусса как
астронома-наблюдателя, следует отметить тот по преимуществу методический
характер, который имела эта деятельность.
Гаусс никогда на ставил себе задач, связанных с
получением массового наблюдательного материала, — таких, как
создание звездных каталогов, определение фундаментальных
постоянных и тому подобных.
Его интересовали способы исследования инструментов,
определения и учета инструментальных ошибок. Он является,
вместе с Бесселем, начинателем нового течения в астрометрии.
Если раньше стремились не столько к повышению качества
наблюдений, сколько к увеличению их количества, и очень
часто полагались на регулировку инструмента, то после Гаусса
и Бесселя в основу всего кладется исследование инструмента^
^Н.С. Schumacher. Hulfstafeln zu Zeit- und Breitbestimmun-
gen, Kopenhagen, 1820.— Sammlung von Hulfstafeln, Heft I (1822),
Heft II (1825). В сборнике, вышедшем в 1822 г., Гаусс дает таблицу,
служащую для облегчения вычисления высот, азимутов и
параллактических углов, а также излагает метод получения широты из многих
зенитных расстояний, измеренных вдали от кульминации.
268
возможно полное определение его погрешностей и учет влияния
этих погрешностей на результаты наблюдений.
В связи с такими задачами Гаусс создал метод коллиматоров,
метод автоколлимации, изобрел приспособление, известное под
именем «гауссова окуляра».
Его работы по геометрической оптике также имели для
развития наблюдательной астрономии большое значение.
Во время своей жизни в Брауншвейге, т. е. от окончания
университета в 1798 г. до перехода в Гёттинген в 1807 г., Гаусс
имел в своем распоряжении только секстан, подаренный ему
Цахом, и маленький неахроматический рефрактор. Его мечтой
в это время было приобретение хотя бы небольшого, но
ахроматического рефрактора, в который можно было бы наблюдать
покрытия звезд Луной и кометы. Иногда, впрочем, ему
удавалось пользоваться несколько лучшими инструментами. Так,
его первое опубликованное наблюдение (прохождение
Меркурия по диску Солнца 3 ноября 1802 г.) было сделано при помош;и
двухфутового ахромата.
Но и при таких обстоятельствах Гаусс много занимался
астрономическими и геодезическими наблюдениями. Из его
переписки мы знаем, что он очень часто упражнялся в
определении времени при помопди своего секстана; измерял — также
с учебными целями — углы триангуляционной сети в
окрестностях Брауншвейга; делал попытки определять положения
Марса при помош;и кольцевого микрометра. Известно, что он
супцественно помог геодезистам, производившим съемку Браун-
швейгского герцогства, в трудном тогда деле обработки
наблюдений покрытий звезд Луной. В те времена эти наблюдения
употреблялись геодезистами для определения разностей долгот.
В эти же годы Гаусс, как уже упоминалось выше, пытался
посетить Готскую обсерваторию с целью усовершенствоваться
в практической астрономии. Но эта попытка не увенчалась
успехом, и Гаусс навсегда остался в области наблюдательной
астрономии, как, впрочем, и в других областях, практически
самоучкой, так как пребывание в Гёттингенском университете дало
ему очень мало.
После перехода в Гёттинген (ноябрь 1807 г.) Гаусс получил в
свое распоряжение сначала старую обсерваторию, основанную
269
в 1734 г. Сегнером (J. А. v. Segner, 1704—1777). Но еще ш
1803 г. там было начато строительство новой, широко
запланированной обсерватории. Задачей Гаусса являлось, прежде
всего, завершение этого строительства и оборудование создаваемой
обсерватории новыми, специально заказанными инструментами.
Первыми инструментами, изготовленными по заказу Гаусса^
были: 12-дюймовый повторительный круг системы Борда ш
8-дюймовый теодолит. В какой восторг привело Гаусса
получение этих первых инструментов новой обсерватории, видно из.
его писем к Ольберсу.
Характер этих инструментов (заказанных в 1811 г.,
полученных в начале 1813 г.) показывает, какое значение придавал*
Гаусс, уже в эти годы, развертыванию геодезических работ.
Как известно, в начале XIX в. во всей континентальной Европе
очень остро почувствовалась потребность в создании хороших
карт, и геодезические работы, имевшие раньше почти
исключительно научное значение, стали делом первостепенной
государственной важности.
Строительство новой обсерватории, сильно
задерживаемое политическими событиями того времени, подвигалось очень
медленно и закончилось только осенью 1816 г. А изготовление^
трех основных инструментов затянулось еще дольше. Только
в 1818 г. был установлен меридианный круг работы Репсольда,.
а в 1819 г.—пассажный инструмент и второй меридианный круг^
изготовленные Рейнхенбахом.
С большим увлечением принялся Гаусс за исследование-
этих инструментов, делавших Гёттингенскую обсерваторию
одной из наилучше оборудованных, и за пробные наблюдения.
Но начавшиеся в 1820 г. приготовления к обширным
геодезическим работам, долженствовавшим дать основу для
картографической съемки Ганноверского королевства, очень скоро
отвлекли Гаусса от обсерваторских наблюдений. В течение ряда
лет он проводил лето и осень на полевых работах по прокладке
триангуляции, а в остальное время руководил
вычислительными работами.
Помимо довольно многочисленных наблюдений малых
планет и комет, Гауссом были произведены ряды абсолютных
определений широты обсерватории и наклона эклиптики. Он регу-
270
Гёттингенская обсерватория в 1830 г.
лярно наблюдал склонения звезд, служивших для определения
широт геодезических пунктов. Иногда число наблюдений,
произведенных Гауссом, было, как показывают обсерваторские
журналы, весьма значительно. Так, например, между 21
февраля и 9 сентября 1820г. им было произведено свыше 1200
наблюдений склонений близполюсных и фундаментальных звезд.
Часть наблюдений, выполненных Гауссом, не была
своевременно обработана и опубликована. Очень часто результаты
наблюдений публиковались в форме писем, направленных
издателям астрономических журналов. Исключением является сле-
дуюш;ая работа, вполне законченная и опубликованная самим
Гауссом отдельной книгой:
J828. «Bestimmung des Breitemmterschiedcs zwischen den Stern-
warten von Gottingen und Altona durch Beobachtungen am Ramsden-
schen Zeinithsector» (см. G. F. Gauss. Werke, Bd. IX, 1—58).
Эта работа долго служила образцом как
тщательно1;€Гизучения влияния инструментальных ошибок, так и обработки
результатов наблюдений при помощи способа наименьших
271
квадратов. Но она имела очень большое значение еще и потому,
что в ней впервые было положено начало физической геодезии,
тогда как существовавшая раньше геодезия носила чисто
геометрический характер.
Установив с несомненностью, что астрономические широты
триангуляционных пунктов между Гёттингеном и Альтоной
существенно отличаются от их широт, полученных из геоде-
зических измерений, Гаусс говорит следующее (стр. 49):
«По нашему мнению, этот вопрос рассматривается с
ошибочной точки зрения, поскольку эти явления квалифицируются
как чисто местные отклонения отвесной линии, как единичные
исключения. То, что мы рассматриваем как геометрическую
поверхность Земли, есть не что иное, как та поверхность,
повсюду перпендикулярная к направлению силы тяжести, часть
которой совпадает с поверхностью океанов. Но направление
€илы тяжести в каждой точке определяется как формой твердых
частей Земли, так и их плотностью, а во внешних частях земной
коры, о которых только мы что-нибудь знаем, и форма и
плотность оказываются весьма неправильными. Эти неправильности
Б распределении плотности, могущие простираться очень
глубоко внутрь и не поддающиеся учету, лишают наши вычисления
необходимых исходных данных. Геометрическая поверхность
является результатом взаимодействия всех этих неправильно
распределенных элементов; и, вместо того, чтобы находить
странными все эти неоспоримо доказанные неправильности,
нужно, скорее, удивляться, что они так малы.
Если бы астрономические наблюдения были в десять или
в сто раз точнее, чем теперь, то подобные неправильности
обнаружились бы, без сомнения, повсеместно.
Но и при таком положении дела ничто нам не мешает
рассматривать Землю в целом как эллипсоид вращения, от
которого действительная (геометрическая) поверхность отличается
ондуляциями, то большими, то меньшими, то
распространяющимися на значительные пространства, то ограниченными. Если
бы было возможно всю Землю равномерно покрыть
тригонометрической сетью, а следовательно, найти взаимное
расположение всех точек ее поверхности, то идеальный эллипсоид
вращения был бы тот, для которого вычисленные направления
272
к. Ф. ГАУСС
1850 г.
вертикальных линии давали оы наилучшее совпадение с резуль"
татами астрономических наблюдений. Хотя мы всегда будем
далеки от этого недостижимого идеала, но все же не подлежит
сомнению, что грядущие столетия намного расширят наши
знания о фигуре Земли. Умножение числа градусных измерений
является здесь только началом, поскольку такие измерения
дают лишь небольшое число точек на изолированных Линиях.
Результаты были бы гораздо более значительны, если бы
градусные измерения, так хорошо выполняемые в отдельных
странах, были бы соединены в одну общую систему. Может быть, не
столь уж несбыточна надежда, что все европейские
обсерватории будут связаны тригонометрическими сетями...».
Поставленная в этих строках перед геодезией новая задача—
нахождение геоида, т. е. той уровенной поверхности, которая
совпадает со свободной поверхностью морей, стала, начиная
со второй половины XIX в., ее основной задачей.
Под влиянием встречи с Гумбольдтом (А. v. Humboldt,
1769—1859) в 1828 г. и дружбы с Вильгельмом Вебером
(W. Weber, 1804—1890), привлеченным, по инициативе Гаусса,
в 1831 г. в Гёттингенский университет, Гаусс увлекся
физическими проблемами. Опубликовав сначала (1829 г.) работу по
механике, в которой был дан один из наиболее, общих законов
этой науки — «принцип наименьшего принуждения», затем
(1830 г.)— теорию капиллярных явлений, Гаусс перешел потом
к изучению явлений земного магнетизма^.
В связи с этим, начиная с 1831 г., он почти полностью
прекращает свою астрономическую и геодезическую деятельность.
Но отдельные наблюдения, сделанные им, особенно наблюдения
вновь открытых малых планет и комет, встречаются и в
последующие годы. Так, с 1846 по 1851 г., т. е. в возрасте, уже
весьма преклонном, он проводит большой ряд наблюдений
фундаментальных звезд.
Наблюдение солнечного затмения 28 августа 1851 г. было
последним наблюдением, сделанным Гауссом.
1 О его работах в этой области см.: К. Ф. Г а у с с. Избранные труды
но земному магнетизму. Пер. акад. А. Н. Крылова, серия «Классики
науки», изд. АН СССР, 1953, 341 стр.
18 к. Ф. Гаусс 273
3. ДЕЯТЕЛЬНОСТЬ ГАУССА В ОБЛАСТИ ГЕОДЕЗИИ
Мы уже видели, что с самого начала своей научной
деятельности Гаусс интересовался геодезическими работами и
принимал в них участие. Если триангуляции, будучи основой
картографической съемки, имеют большое практическое значение,
то не менее важны они и для чисто научных задач, так как
точное знание формы и размеров Земли является фундаментом
всей астрономии. Эта проблема всегда интересовала Гаусса.
Еще в 1799 г. он опубликовал заметку (это было его первое
выступление в печати), посвященную выводу размеров и сжатия
Земли из только что опубликованных результатов знаменитого
измерения дуги меридиана между Дюнкерком и Барселоной,
произведенного для установления длины метра. Полученная
Гауссом величина сжатия ^/ig^ ближе к истине, чем сжатие
^/^5f^, выведенное из этой дуги французскими геодезистами.
Но, как было отмечено самим Гауссом, такая короткая дуга не
может служить для надежного определения сжатия.
В 1803—1805 гг. Гаусс живо интересовался геодезическими
работами, производившимися в Брауншвейге и Ганновере
сначала прусскими, а потом французскими военными топографами.
Это и дало ему практическое знакомство с полевыми
геодезическими работами, столь пригодившееся впоследствии.
Сделавшись в 1807 г. директором Гёттингенской
обсерватории, Гаусс с самого начала имел в виду заниматься
не только астрономией, но и геодезией. Об этом
свидетельствует, как уже было отмечено, характер заказывавшихся им
инструментов.
В 1816 г. директор Копенгагенской обсерватории Шумахер
получил от датского правительства средства на производство
градусного измерения, которое должно было охватить более
4° по меридиану и почти 5° по параллелях. Известие об этом
привело Гаусса в восторг, и, отвечая Шумахеру, он пишет: «Прежде
всего, дорогой друг, примите мое сердечное поздравление с тем
великолепным и грандиозным научным предприятием, о
котором Вы сообщаете в последнем письме. Это градусное измерение
Датского королевства даст нам, уже само по себе, весьма
ценные заключения о фигуре Земли. Но я нисколько не сомневаюсь
что в дальнейшем будет возможно продолжить Ваши измерения
274
на юг через Ганноверское королевство. Хотя в настоящий момент
я еще не могу предложить такой проект в Ганновере, так как
сейчас требуются большие средства для астрономии, но я все
же убежден, что наше правительство, которое так охотно
помогает науке, последует славному примеру Вашего превосходного
короля. Мы будем тогда иметь весьма почтенную дугу меридиана
в 6^/2 градусов и легко сможем соединить ее с триангуляционной
сетью в Баварии...» (Werke, Bd. IX, 345).
В связи с началом датского градусного измерения и
надеждой получить средства на аналогичные работы у себя в Ганновере
вопросы геодезии стали занимать Гаусса все больше и больше.
В 1820 г. был окончательно решен вопрос о съемке
Ганноверского королевства и о градусном измерении вдоль меридиана,
проходящего через Гёттингенскую обсерваторию, как основе
этой съемки. На ближайшие десять лет геодезические работы,
как нолевые, так и вычислительные, становятся главным
занятием Гаусса, который не только возглавил это большое
предприятие, но и принимал непосредственное участие в прокладке
триангуляционной сети.
В процессе этих работ Гаусс внес весьма существенные
улучшения в методику наблюдений. Он обнаружил систематические
ошибки в применявшемся при измерении углов способе
повторений и предложил новый способ. Этот способ, в несколько
измененном виде, был впоследствии введен во всеобщее
употребление учеником Гаусса немецким геодезистом О. Шрейбером и
известен под именем «способа Шрейбера». Не менее важное
значение имело изобретение Гауссом гелиотропа (1820 г.), о
котором он также ничего сам не напечатал^.
Но особенно большое значение имели его теоретические
работы но созданию методов для вполне строгой обработки как
градусных измерений, так и съемки. Оставив применявшиеся
^ Гелиотроп служит для того, чтобы направить отраженные плоским
зеркалом лучи Солнца в точку, видимую в зрительную трубу. Этот
прибор, позволивший измерять углы треугольников со сторонами,
доходившими до 160 км, имел очень большое значение для развития
геодезии. С появлением прожекторов, дающих возможность производить
наблюдения ночью (когда атмосфера более спокойна), он вышел из
употребления.
18* 275
раньше приближенные и мало обоснованные способы, он
впервые проникнул во всю глубину задачи и дал ее полное решение.
Основные идеи этого решения зародились у Гаусса уже в
самом начале его соприкосновения с геодезическими работами.
В упомянутом выше письме к Шумахеру (1816 г.) Гаусс, в связи
с намерением Копенгагенского научного общества предложить
тему на соискание премии (Preisfrage), пишет: «Мне пришла на
ум интересная задача, а именно: в самом обш;ем виде отобразить
одну заданную поверхность на другую (также заданную) так,
чтобы изображение было подобно оригиналу в бесконечно
малых частях. Частный случай, когда первая поверхность сфера,
вторая — плоскость. Здесь стереографическая и меркаторская
проекции являются частными решениями. Но нужно получить
общее решение, заключающее все частные, для любых
поверхностей...».
Отсюда видно, что еще в 1816 г. Гауссом была поставлена
задача, явившаяся отправным пунктом его столь важных
исследований по теории поверхностей.
Решение этой задачи Гаусс опубликовал в мемуаре:
1822. «AUgemeine Losiing der Aufgabe, die Telle elner gegebenen
Flache auf eine andere gegebene Flache so abzubllden, dass die Abbll-
diing dem Abgeblldeten In den klelnsten Tellen ahnllch wird» (см.
G. F. Gauss. Werke, Bd. IV, 189—216).
Развитая здесь теория конформного^ (т. е. сохраняющего
подобие бесконечно малых частей) отображения одной
поверхности на другой позволила дать точное решение двух основных
геодезических задач для эллипсоида вращения. Первая из этих
задач заключается в переносе координат: по широте и долготе
одного пункта нужно найти широту и долготу другого, зная его
расстояние (измеряемое всегда по геодезической линии) и
азимут. Во второй задаче требуется по географическим
координатам двух пунктов найти расстояние между ними (точнее
говоря, длину связывающей их геодезической линии) и взаимные
азимуты.
Обе эти задачи весьма просто решаются на поверхности
сферы при помощи основных формул сферической тригонометрии.
1 Этот термин был введен Гауссом значительно позже, в
указываемом далее мемуаре 1844 г.
276
Конформное' отображение поверхности эллипсоида вращения
на сферу позволило Гауссу свести общий случай какого угодно
сжатия к этому частному, когда сжатие равно нулю.
Так как конформное отображение эллипсоида вращения на
сферу может быть осуществлено бесконечным множеством
способов, то и для решения указанных основных задач могут быть
избраны различные пути. Три наиболее интересные с
практической точки зрения решения были опубликованы Гауссом много
позже в мемуарах:
1844. «Untersuchungen liber Gegenstande der hoheren Geodasie».
I Abhandliing (см. G. F. Gauss. Werke, Bd. IV, 259—300).
1847. «Untersuchungen liber Gegenstande der hoheren Geodasie»,
II Abhandlung (см. там же, стр. 301—340).
Первый из этих мемуаров начинается следующими словами,
как бы резюмирующими геодезическую деятельность автора:
«При выполнении, частично мной, частично под моим
руководством, триангуляционных работ, охватывающих все
Ганноверское королевство, были применены методы, отличные от
обычно употребляемых; это относится как к способам
измерений, так и, в особености, к методам математической обработки
и вывода результатов. Бывшее у меня раньше намерение по
окончании всей работы опубликовать ее результаты, вместе
с изложением методов обработки, в специальном сочинении до
сих пор не могло быть осуществлено по причинам, па которых
здесь нет надобности останавливаться; я выбираю поэтому
другой путь и хочу в ряде статей изложить то, что было мной
внесено нового в теоретические вопросы; делаю это тем охотнее,
что таким образом буду иметь возможность со всей подробностью
изложить и такие исследования, которые, хотя при обработке
измерений и не нашли себе непосредственного применения,
однако представляют самостоятельный интерес и тесно связаны
со всем остальным...».
Указанными нами тремя мемуарами ^ исчерпываются
работы по геодезии, опубликованные самим Гауссом. Но этими
тремя мемуарами, а также детальной разработкой применения
1 Перевод их на русский язык дан в сборнике: «Геодезические
исследования Гаусса, Бесселя и Ганзена». Изд. и пер. А. Тилло, СПб., 1866,
362 стр.
217
способа наименьших квадратов к геодезическим вычислениям^
он сделал для геодезии так много, что представители этой
науки с полным правом говорят о «геодезисте Гауссе».
Весьма большое значение для развития геодезии имели
также и другие работы Гаусса, им не опубликованные. Для
обработки выполненных в Ганноверском королевстве триангуляции
и производства основанных на них топографических съемок
Гауссом были введены особые координаты, позволяющие
наиболее удобно изображать части поверхности эллипсоида вра-
ш.ения на плоскости. Теория этих координат была опубликована
О. Шрейбером в 1866 г., но далеко не сразу они получили
должное распространение. Решаюпдее значение имело здесь
появление (1912 г.) капитального сочинения Л. Крюгера «Konforme
Abbildung der Erdellipsoids in der Ebene», в котором теория была
дана с некоторыми усовершенствованиями, а главное, было
убедительно показано преимущество координат Гаусса перед
другими методами обработки триангуляции и производства
топографических съемок. С 1917 г. эти координаты, под именем
«координат Гаусса-Крюгера», сделались основой всех
кадастровых съемок в Герма^нии и в Австрии. В 1918 г. они были
приняты в СССР.
Что касается непосредственных результатов
выполнявшегося Гауссом градусного измерения, то они далеко не были
столь значительны, как теоретические и технические
усовершенствования, созданные Гауссом в процессе работы. Это
градусное измерение должно было, по мысли Гаусса, явиться частью
измерения большой дуги меридиана. Но другие градусные
измерения, входившие в этот план, либо не были закончены,
либо соединение с ними не могло быть выполнено достаточно
надежно. Измерение базисов было проведено не вполне
удовлетворительно, а вынужденная обстоятельствами форма тре-
1 В этом отношении особенно большое значение имел мемуар
1828 г.: «Supplementum Theoriae Gombinationis observationum erroribis
minimis obnoxiae» (см. С. F. Gauss. Werke, Bd. IV, 55—93).
В нем рассмотрены именно те задачи уравнительных вычислений,
которые встречаются при обработке триангуляции, и даны два весьма
обстоятельно изложенных примера из геодезической практики. К работам
Гаусса по способу наименьших квадратов мы еще вернемся.
278
угольников во многих случаях не давала нужной точности
Вследствие этого ганноверское градусное измерение не внесло
существенного улучшения в определения размеров Земли и
выполненные Гауссом триангуляции могли быть использованы
лишь как основа топографической съемки. Тем не менее, по
указанным выше причинам значение этих работ для развития
геодезии было весьма велико. Неменьшую пользу они принесли
и для развития дифференциальной геометрии.
4. THEORIA MOTUS
Закончив обш.ий обзор деятельности Гаусса в области
астрономии и геодезии, мы можем теперь перейти к более детальному
рассмотрению некоторых из числа наиболее важных его
достижений в этих науках.
В широких астрономических кругах Гаусс известен прежде
всего как автор «Theoria motus».
Этот трактат, появившийся, как уже было отмечено, в 1809 г.,
сразу сделался настольной книгой астрономов и оставался
таковой до начала XX в. ^
Среди обстоятельств, способствовавших успеху сочинения
Гаусса, отметим прежде всего его исключительную
актуальность. Открытие огромного количества малых планет и все уве-
личиваюш;егося числа комет привлекало внимание весьма
многих астрономов XIX в. к вопросам вычисления орбит, а в этих
вопросах «Theoria motus» была окружена с самого начала
исключительным ореолом вследствие той роли, которую играл Гаусс
в деле открытия первых малых планет.
С другой стороны, книга Гаусса особенно тндательно
учитывала потребности астрономов-практиков. Она не только давала
все нужные формулы в совершенно готовом для вычислений
виде, но и содержала в изобилии тщательно выполненные и
подробно объясненные примеры, что так важно для первона-
1 Из переводов этого сочинения отметим: К. Ф. Гауе с. Теория
движения небесных тел, обращающихся вокруг Солнца по коническим
сечениям. Перевел с латинского студент императорского Московского
университета Догель, М., 1861; С. F. Gauss. Theorie der Bewegung
dcr Hlmmelskorper welche in Kegelschnitten die Sonne umlaufen. Ins
Deutsche ubertragen von Carl Haase, Hannover, 1865.
279
чалыюго изучения предмета. Более того, эта книга впервые дала
систематическое изложение основ вычислительной техники,
а также метода обработки наблюдений по способу наименьших
квадратов.
«Theoria motus» состоит из двух частей, или «книг» (liber),
каждая из которых разделена на четыре главы (sectio).
Рассмотрим вкратце содержание отдельных глав. Обратимся
к первой главе, в которой трактуются вопросы, относящиеся к
положению светила в орбите. Практическая целеустремленность
сочинения видна с первой же страницы. Гаусс начинает так:
«В этом сочинении мы будем изучать только те движения
небесных тел, которые производятся притягательной силой
Солнца... Сами движупдиеся тела мы будем рассматривать как
математические точд^и и будем предполагать, что движения
происходят по следующим законам, которые надо рассматривать
как основу всех исследований, излагаемых в этом сочинении.
I. Движение каждого небесного тела происходит в
неподвижной плоскости, проходящей через центр Солнца.
П. Путь, описываемый телом, есть коническое сечение,
фокус которого находится в центре Солнца.
III. Движение по этому пути совершается таким образом,
что площади секторов, описываемых вокруг Солнца в
различные промежутки времени, пропорциональны этим
промежуткам. Поэтому, разделив площадь сектора на соответствующий
промежуток времени, в частном получим постоянную величину.
IV. Квадраты этих постоянных величин, вычисленных для
различных обращающихся вокруг Солнца тел, пропорциональны
произведениям параметров описываемых ими путей на сумму
массы Солнца и массы движущегося тела».
Несколько дальше Гаусс, указав, что из этих законов может
быть выведена сила, с которой Солнце действует на
обращающиеся вокруг него тела, замечает:
«Здесь мы можем ограничиться простым указанием
перечисленных законов, а о связи их с принципом тяготения
распространяться не будем, тем более, что после великого Ньютона еще
многие другие писали об этом предмете; а Лаплас, среди них-,
в своем превосходном сочинении «Mecanique celeste» дал такое
изложение его, которое не оставляет желать ничего лучшего».
280
Законы III и rV могут быть выражены одной формулой.
Обозначим для этого через g удвоенную площадь сектора,
описанного радиусом-вектором тела за время t, через р — параметр
конического сечения, по которому тело движется, а через jn —
его массу, если масса Солнца принята за единицу. В таком
случае указанные законы равносильны формуле
^^k'pii+m), (1)
где к^ — коэффициент пропорциональности.
Чтобы найти к в употреблявшейся тогда астрономической
системе единиц (т. е. приняв за единицу длины большую
полуось земной орбиты, за единицу времени — средние солнечные
сутки, а за единицу массы-—массу. Солнца), Гаусс применил
соотношение (1) к Земле, взяв при этом t равным времени ее
полного оборота вокруг Солнца. Это ему дало
А:-0.017 202 098 95. _^ ' (2)
Современные значения массы Земли и длины года, более
точные, чем те, которыми располагал Гаусс, дали бы для к
значение, отличное от (2). Но так как менять значение (2),
являвшееся в течение всего XIX в. основой астрономических
вычислений, было бы весьма неудобно, то было решено
изменить астрономическую систему единиц. В настоящее время
она определяется единицей времени, равной продолжительности
средних солнечных суток в момент начала 1900 г., единицей
массы, равной массе Солнца, и постоянной тяготения к^, где к
имеет значение (2). Это число (2) получило название гауссовой
постоянной.
Таким образом, благодаря авторитету «Theoria motus»,
имя Гаусса оказалось связанным с системой единиц, лежащей
в основе всей астрономии.
Исходя из четырех только что указанных положений,
выражающих законы невозмущепного движения и носящих
название обобщенных законов Кеплера, Гаусс получает прежде
всего формулы, служащие для вычисления орбитальных
координат светила для заданного момента времени и позволяющие,
таким образом, находить место светила в орбите, когда элемен-
281
ты орбиты даны. Вся первая глава посвящена выводу
разнообразнейших формул, могущих служить для этой цели, и
изучению их сравнительных достоинств с точки зрения
вычислительной техники.
Во второй главе рассматриваются вопросы, связанные с
вычислением пространственных координат светила. И здесь мы
имеем столь же исчерпывающее изложение предмета. Интересно,
что в этой главе можно найти даже такие формулы, которые
только недавно, в связи с распространением арифмометров,
получили широкое применение. Но помимо разнообразных
формул для вычисления прямоугольных и сферических
координат небесного тела, Гаусс дает полную теорию как суточного
параллакса, так и аберрации. Глава заканчивается выводом
зависимостей между дифференциалами координат и
дифференциалами элементов орбиты. Изложение всех этих теперь
общеизвестных вопросов мало чем отличается от современного, но
рассматриваются и некоторые задачи, носящие специфический
отпечаток потребностей того времени. Так, например, Гаусс
двумя различными способами решает следующую задачу: найти
радиус-вектор и аргумент широты светила, если известны его
геоцентрические координаты и положение плоскости орбиты.
Третья глава, столь же обширная, как и две первые, хотя и
называется «Соотношения между многими местами в орбите»,
но почти целиком посвящена изучению зависимостей,
связывающих элементы орбиты с координатами двух положений
светила и соответствующим промежутком времени.
Многочисленные соотношения, получаемые в этой главе, подчинены одной
обшей идее: найти наиболее удобные пути для вычисления
элементов орбиты по двум гелиоцентрическим положениям светила.
Приближенное решение этой фундаментальной задачи было
дано еще Эйлером^. Легко, прежде всего, показать, что
нахождение всех элементов приводится к определению параметра
орбиты/?. С другой стороны, формула (1) показывает, что
нахождение р эквивалентно нахождению площади сектора, заключен-
^ L. Е U 1 е г. Theoria motuum planetarum et cometarum, continens
methodum facilem ex aliquot observationibus orbitas cum planetarum tum
cometarum determinandi etc. Berolini, 1744. Имеется немецкий перевод,
изданный в Вене в 1781 г.
282
ного между радиусами-векторами г^ и г^ двух рассматриваемых
положений.
Удвоенная площадь этого сектора выражается формулой
g = Cr'dv, (3)
где через г?^ и v^ обозначены соответствующие истинные
аномалии.
Взяв для интеграла (3) приближенное значение, даваемое
формулой Симпсона, Эйлер получил приближенную величину g,
а следовательно, и р.
Исключительный по своему остроумию анализ проблемы
позволил Гауссу дать ее точное решение.
Введя вместо g величину
представляющую отношение площади сектора к площади
треугольника, заключенного между теми же
радиусами-векторами, Гаусс показал, что эта величина может быть найдена
решением такой системы уравнений (в 4[ринятых теперь
обозначениях):
r^s^r^-hri~lh = 0; - (4)
h= -^ ; ^==^-1. (Ь)
Через т и I здесь обозначены величины, легко вычисляе^мые
по данным значениям г^, г2, v^,—v^ и t.2 — i^i, а функция с (х)
выражается равенством
^(^) = ^-Т + Т- 1Г{х) (*^)
через гипергеометрическую функцию
^(^)= -Г + зТб ^+ 3:5:7^ +••■ (^)
Пользуясь свойствами гипергеометрических функций, Гаусс
нашел для "ci^x) несколько разложений в цепные дроби \ гораз-
^ Здесь эти разложения даются без доказательства. Доказательство
было опубликовано позднее (1813 г.) в работе о гипергеометрическом ряде
(см. С. F. Gauss. Werke, Bd. Ill, 137).
283
до более удобные для вычислений, чем формулы (6) и (7).
Например:
2
Цх)^
35 ^"^
^ "^ 35 ^ "~ 63 ^
^~" 99 ^
70
^ —143 ^
^ "" 195 ^'
108
'^ " 255 ^
1 — etc'
При помощи этих разложений Гаусс вычислил таблицу
функции Цх) для значений х, удовлетворяюндих условию \х\ ^0.3,
что с избытком покрывает потребности практики. Такая
таблица вместе с таблицей, дающей нужный корень уравнения
(4) по аргументу /г, делает решение системы уравнений (4)
и (5) весьма простой задачей.
В четвертой главе, заканчивающей первую часть «Theoria
motus», рассматриваются «Соотношения между многими
положениями в пространстве».
Гаусс начинает с решения следующей задачи, постоянно
встречающейся при вычислении орбит: по гелиоцентрическим
координатам двух положений светила найти положение
плоскости орбиты, т. е. ее наклон i и долготу восходящего узла fi.
Но главным вопросом, рассматриваемым в четвертой главе,
является установление зависимостей, связывающих
геоцентрические расстояния трех точек, лежащих в плоскости,
проходящей через Солнце. На этих зависимостях основывается
излагаемый далее метод нахождения орбиты по трем наблюдениям,
который сам Гаусс называет важнейшей частью (pars gravis-
sima) своего сочинения. Напомним, несколько модернизируя
обозначения, какой характер имеют эти зависимости.
Обозначим через {х, у, z), {х\ 2/', z') и {х\ у\ z')
гелиоцентрические координаты светила в моменты t, f и Г. Если через
п = г'г' sin {v" — v'), п' = rr' sin {v" — v), n" = rr' sin {v' — v)
284
обозначить удвоенные площади треугольников, заключенных
между радиусами-векторами, то будут иметь место, как легко
видеть, следующие равенства:
пх — п'х' -f п"х" = О, ]
пу — п^у' + п"у" = О, i (8)
nz — n'z' + n"z' = 0.1
Эти равенства представляют условие прохождения плоскости,
определяемой тремя рассматриваемыми точками, через начало
координат.
Если обозначить, далее, через р, р', р' геоцентрические
расстояния светила, а через (X,|ji,v), (>/, |j.', v'),
{^^"уу^",^")—направляющие косинусы геоцентрических направлений на светило
в рассматриваемые моменты, то будем иметь
X = р}^ — X, y = p\i—7, 2; = pv — Z (9)
и аналогичные равенства для даух других моментов. Через
(X, У, Z), {Х\ У, Z'), {X", Y", Z") здесь обозначены
геоцентрические координаты Солнца в моменты t, f и Г.
Подстановка выражений (9) в равенства (8) дает следующие
основные уравнения:
шр — h'n'p' + Гп"р' = пХ ~ п'Х' +'п'Х\ \
\хпр — |л'/г'р' + {^-''п'р' = nY ~ п'У' + пТ", 1 (Ю)
\пр — v'n'p' + v"n"p" ~ nZ — fz'Z' + n"Z'\ J
Исключение из этих уравнений сначала одного из
геоцентрических расстояний, а затем двух дает Гауссу ряд дальнейших
соотношений. Из таких соотношений отметим здесь только
одно — то, которое получается при исключении о и о". Оно
имеет вид
Dn'p' =. ~nU + n'U' — nV\ (И)
где
i) =
= }/Ai + [x'li^ -f v'Vi,
U' =^ x% + y>., + Z4,
U"=:X'\+Y"^, + Z\A
(12)
(13)
285
если положить
Так как Гаусс вместо общеупотребительных теперь
направляющих косинусов пользуется сферическими координатами,
а вместо прямоугольных координат Солнца — его полярными
координатами, то у него все эти соотношения имеют, конечно,
гораздо более сложный вид.
Интересно отметить, что направляющими косинусами вместо
сферических координат широко пользовался (как для планеты,
так и для Солнца) еще Лагранж в мемуаре 1783 г. ^ Выгоды
их употребления при аналитических выводах были, конечно,
ясны и для Гаусса. И если он везде пользовался не
направляющими косинусами, а сферическими координатами, то это
объясняется стремлением дать формулы в наиболее удобном для
логарифмических вычислений виде. В эпоху, когда все
вычисления производились при помощи логарифмических таблиц
и даже не вошли еще в употребление логарифмы сложения и
вычитания, формулы Гаусса лучше всего отвечали потребностям
практики. Только распространение вычислительных машин
изменило положение дела.
Вторая часть «Theoria motus» состоит, как и первая, из
четырех глав. В первых двух главах излагаются созданные
Гауссом способы вычисления орбит по трем и четырем наблюдениям.
Эти способы будут нами рассмотрены отдельно с должной
обстоятельностью. Перейдем поэтому сразу к третьей главе, носящей
название «Определение орбиты, наилучше удовлетворяющей
любому количеству наблюдений». Эта глава замечательна тем,
что в ней Гаусс впервые опубликовал разработанный им
метод наименьших квадратов.
В переписке Гаусса имеются многочисленные указания па
то, что основные идеи этого исключительно важного для астро-
1 М. Ф. Субботин. Астрономические работы Лаграпжа.— В кн.:
«Жозеф Луи Лагранж (1736—1936)». Сборник статей к 200-летию со дня
рождения, изд. АН СССР, 1937.
286
номии и геодезии метода были им осознаны еще в 1794 г. под.
влиянием статьи Ламберта «Theorie der Zuverlassigkeit der
Beobachtungen und Versuche»^.
В этой статье Ламберт заменяет систему избыточных линейных
уравнений с двумя неизвестными системой двух уравнений^
которые он составляет при помощи приема, несколько
напоминающего составление нормальных уравнений в методе
наименьших квадратов.
Широкое распространение градусных измерений и
триангуляции, необходимых для точного картографирования, еще в
середине XVIII в. привлекло внимание к вопросам
уравнительных вычислений. В 1755 г. Босковичем (R. J. Boscovich, 1711 —
1787) был применен следующий принцип уравнивания:
наилучшим значением измеряемой величины считается такое, для
которого суммы положительных и отрицательных остающихся
невязок оказываются равными по абсолютной величине. Этот
принцип стал широко известен благодаря работам Лапласа, не
только применившим его к обработке градусных измерений^, но
и .обосновавшего его соображениями, взятыми из теории
вероятностей. Именно эти работы имел в виду Гаусс, делая 17 июня
1798 г. в своем «Дневнике» запись: «Calculus probabilitatis
contra Laplace defensus». Установление несовместимости метода
Лапласа, основанного ка принципе Босковича, с теорией
вероятностей явилось началом работ Гаусса по
теоретико-вероятностному обоснованию метода наименьших квадратов при помощи
принципа арифметического среднего^. Именно это
обоснование и дается в рассматриваемой нами главе.
^ J. Н. Lambert. Beitrage zum Gebraiiche der Mathematik. Ber-
liD, 1772.
2 P. S. Laplace. Sur les degres mesures des Meridiens et sur les
longueurs obser^ees du pendule etc.— Histoire de rAcodemie des Sciences,
Annee 1789, Paris, 1793.
^ Лаплас не чувствовал в эти годы особого доверия к принципу
среднего арифметического. Он считал, например, что в случае, когда три и:^-
мерения дали для неизвестной величины х значения, равные а, Ь и Ь,
причем, а< 6, то вероятнейшим значением будет а; = а + 0.860 (6 — л),
а не среднее арифметическое ^«;= а + 0.667(6—а). Позднее, в своей
«Theorie analytique des probabilites» (1812) Лаплас дал весьма глубокое
обоснование метода наименьших квадратов.
281
Но Гаусс указывает также и на возможность иного
обоснования. Он говорит («Theoria motus», art. 186):
«Впрочем, принцип, согласно которому сумма квадратов
разностей между наблюденными и вычисленными величинами
должна быть наименьшей, может быть обоснован и независимо
от исчисления вероятностей.
Если число неизвестных равно числу зависящих от них
наблюденных величин, то неизвестные можно определить так,
что наблюдения будут представлены вполне точно. Но если число
первых меньше числа вторых, то точное представление
невозможно, если только сами наблюдения не абсолютно точны. В этом
случае следует стремиться к установлению возможно лучшего
согласия, иначе говоря, к тому, чтобы остающиеся разности были
как можно меньше. Такое условие является, однако, по сути
дела, несколько неопределенным. Ибо если мы предпочтем ту
систему неизвестных, для которой все разности соответственно
меньше, чем для другой, то выбор между двумя системами
неизвестных, из которых одна лучше представляет одну часть
наблюдений, другая — другую, заключает произвол; можно
указать бесчисленное множество принципов для суждения о
выполнении нашего основного условия. Обозначивши через Д, Д',
Д",... разности между наблюдениями и вычислениями, мы
удовлетворим этому условию не только тогда, когда сумма Д^-f-
+Д'^+Д"^+... будет наименьшей (в чем состоит мой принцип),
но также и тогда, если Д^+Д'^+Д"^+..., или Д^+Д'^+Д''^-f..,,
или вообще любая сумма четных степеней будет наименьшей.
Но из всех таких принципов мой является наипростейшим,
тогда как другие приводят к очень сложным вычислениям.
Впрочем, мой принцип, которым я пользуюсь уже с 1795 г., был
недавно развит также и в сочинении Лежандра «Nouvelles тё-
thodes pour la determination des orbites des cometes», Paris,
1806; в этом сочинении рассмотрены многие другие характерные
особенности этого принципа, что я здесь краткости ради опускаю-^.
1 Метод наименьших квадратов был создан Лежандром в i805 г.
Ему принадлежит как самое название, так и приоритет в опубликовании,
на что и указывает Гаусс. Лежандр полностью отдавал себе отчет в большом
значении этого метода для обработки наблюдений. Что же касается до
288
Если выбрать четную бесконечно большую степень, то
наилучшей будет такая система неизвестных, для которой
наибольшие погрешности так малы, как это возможно».
Изложив с большой обстоятельностью метод наименьших
квадратов, Гаусс ограничивается лишь самыми краткими
указаниями относительно применения этого метода к исправлению
элементов орбит и нахождению вероятнейшей орбиты. Отметив,
что нужно сначала, путем предварительного исправления,
добиться такой малости остающихся поправок, чтобы квадратами
и произведениями их можно было пренебрегать, Гаусс излагает
только идею составления условных уравнений, служащих для
получения вероятнейшей орбите. Что же касается до
предварительных улучшений элементов, то он излагает метод вариации
геоцентрических расстояний. Большая краткость в трактовке
этих вопросов, может быть, была вызвана тем, что исправление
элементов при помощи дифференциальных поправок не было
новостью — оно давно уже вошло в употребление. Важным
нововведением здесь было применение, при таком исправлении,
нового способа уравнивания ошибок наблюдений.
В последней, очень маленькой главе Гаусс касается вопроса
о вычислении орбит с учетом возмущений. Как ни кратки три
параграфа, составляющие эту главу, в них можно найти
зародыши многих развитых впоследствии методов. Укажем,
например, на предложение использовать исправление элементов малых
планет для одновременного уточнения массы Юпитера.
Заканчивая обзор содержания «Theoria motus», следует
отметить, что две последние главы резко отличаются от
остальных шести глав своей крайней сжатостью и отсутствием при
меров. Причину этого можно искать, как иногда указывалось,
в тех трудных условиях, в которых находился Гаусс в 1805—
обоснования самого принципа, то он ограничивается следующими
замечаниями:
«Из всех принципов, которые здесь могут быть предложены, по моему
мнению, наиболее общим, наиболее правильным и наиболее удобным
в применении является тот, который обращает в минимум сумму
квадратов остающихся ошибок. Этот принцип, устанавливая в ошибках род
равновесия, удерживает наибольшие из них в должных границах и очень
пригоден для получения такого решения системы уравнений, которое
ближе всего к истине».
19 к. Ф. Гаусс 289
1806 гг., когда он иясал свою книгу. Помимо тяжелого
политического положения Германии, здесь играли роль и личные
обстоятельства. Материальное положение Гаусса, женившегося
в 1805 г., оставалось до его перехода в Гёттинген (1807 г.)
тяжелым и неопределенным.
Печатание «Theoria motus» было сопряжено с большими
трудностями. Только в 1807 г. Гаусс нашел издателя,
согласившегося печатать его книгу, но поставившего условием перевод
ее на латинский язык как обеспечивавший более широкое
распространение. Между тем, появление упомянутой выше работы
Лежандра заставляло Гаусса торопиться с опубликованием
найденного им обоснования метода наименьших квадратов.
о. МЕТОД ГАУССА ДЛЯ ВЫЧИСЛЕНИЯ ОРБИ!
ПО НАИМЕНЬШЕМУ ЧИСЛУ НАБЛЮДЕНИЙ
Совокупность вопросов, рассматриваемых в «Theoria motus»,
иначе говоря, теорию невозмуш;ешюго движения и ее
применение к нахождению орбит планет ц, комет из наблюдений,
Гаусс называет «важнейшей и прекраснейшей частью
теоретической астрономии» (Werke, Bd. VI, 60).
По особое значение он придавал изложенному в этом
сочинении новому, тш;ательно разработанному методу для
вычисления орбит по наименьшему числу наблюдений.
Движение планеты (или кометы), производимое одним только
взаимным притяжением между нею и Солнцем, определяется
тремя дифференциальными уравнениями второго порядка. Шесть
интегрирований, которые приходится выполнить для решения
этих уравнений, вводят шесть произвольных постоянных,
носящих название элементов орбиты. Чтобы найти эти шесть
элементов при помош;и наблюдений, нужно, вообш;е говоря, три
наблюдения, потому что каждое наблюдение (даюш;ее две
сферические координаты) позволяет написать два уравнения.
Только в том исключительном случае, когда светило движется в
плоскости эклиптики, нужно иметь четыре наблюдения, поскольку
в этом случае число искомых элементов равно четырем, а
каждое наблюдение (даюш;ее только одну координату — долготу
светила) позволяет написать лишь одно уравнение. Практи-
к90
чески, учитывая ограниченную точность наолюдении, к четырелт
наблюдениям приходится прибегать и в тех случаях, когда
наклон орбиты не превышает нескольких градусов. 13
дальнейшем мы ограничимся случаем вычисления орбиты по трем
наблюдениям, так как случай, когда приходится прибегать к четырем
наблюдениям, не представляет принципиальных отличий.
Шесть уравнений, даваемых тремя наблюдениями, HMejox
настолько сложную структуру, что разрешение их относительно
шести неизвестных— элементов орбиты — может быть выполнено
только численными методами.\Но вычисления, к которым
приводят такие методы, становятся, в случае системы из шести
очень сложных уравнений, практически невыполнимыми.
Раньше чем применять численные методы, нужно исключить в:\
этой системы хотя бы четыре неизвестные величины. Такой путь,
намеченный еш,е Эйлером (1744 г.), основывается на введении
вместо элементов орбиты других, надлежаш;е выбранных
неизвестных. Легко видеть, например, что за вспомогательные
неизвестные можно принять геоцентрические расстояния
светила в моменты двух наблюдений; если эти геоцентрические
расстояния р и р" будут известны, то вычисление орбиты по
координатам {х, ?/, z) и {х'\ ?/", z''), даваемым формулами
(9) для двух моментов tut", выполняется уже сравнительно
просто. Что же касается до неизвестных р и р'', к нахождению
которых приводится, таким образом, вычисление орбиты, то
их вычисляют при помощи ряда проб и интерполирования
между результатами этих проб. Этот способ, употребляемый
иногда для улучшения орбит, уже приближенно известных,
называется методом вариации геоцентрических расстояний.
В «Theoria motus» вкратце излагается десять различных
способов приведения задачи об определении орбиты к решению
системы двух уравнений с двумя неизвестнымрг вида
после чего Гаусс указывает, что эти способы «основаны на
предположении, что уже известны либо приближенные значения
расстояний небесного тела от Земли, либо приближенное
положение плоскости орбиты. Если речь идет о том, чтобы
элементы орбиты, приближенные значения которых уже известны
19* 291
( например, из ранее сделанных вычислений, основанных на
других наблюдениях), исправить при помощи наблюдений,
более удаленных друг от друга, то это не представляет,
очевидно, никаких трудностей. Но изложенные способы не
показывают, как начать первое приближение в том случае, когда
элементы орбиты еще совершенно не известны. Этот случай
рассматриваемой задачи является наиболее важным и
наиболее трудным, что можно уже видеть по аналогичной задаче
в теории комет^, которая, как известно, так долго затрудняла
геометров и была предметом столь многих тщетных изысканий.
Чтобы нашу задачу можно было считать действительно
решенной, нужно очевидно... удовлетворить нижеследующим
условиям. Во-первых, неизвестные величины х, у должны быть
выбраны так, чтобы их приближенные значения можно было найти
из самой сущности задачи, по крайней мере в том случае,когда
гелиоцентрическое движение небесного тела за время между
наблюдениями не слишком велико. Во-вторых, требуется, чтобы
малым изменениям х, у соответствовали не слишком большие
изменения вычисляемых по ним величин так, чтобы делаемые
в X ^ у ошибки не мешали считать приближенными и эти
величины. Наконец, в-третьих, нужно, чтобы вычислительные
операции, приводящие от значений х, у к значениям X и 7, были
не слишком сложны.
Эти условия дают критерий для предварительного суждения
о достоинствах того или иного метода, раньше чем частое
применение на практике сделает их вполне ясными. Тот метод,
к изложению которого мы теперь переходим и который в
известном смысле является важнейшей частью этого сочинения,
удовлетворяет этим условиям настолько, что нельзя желать
большего» («Theoria motus», art. 130).
Таким образом, Гаусс сам называет свой метод вычисления
орбит по трем наблюдениям важнейшей частью «Theoria motus».
Научным миром того времени этот метод был встречен с
единодушным восторгом как долгожданное решение труднейшей
задачи, притом такое решение, которое «не оставляет желать
^ Так во времена Гаусса называлась теория нахождения кометных
орбит из наблюдений.
292
лучшего». Если прибавить еще, что сочинение Гаусса,
явившееся результатом его обширных работ по вычислению орбит
четырех первых малых планет, в самой высокой степени
учитывало запросы практика-вычислителя, то станет понятным, почему
труды предшественников Гаусса в этой области были преданы
почти полному забвению. В течение долгого времени метод Гаусса
рассматривался не только как образец совершенства, но и как
первое практически ценное решение одной из основных задач
теоретической астрономии.
Напомним, в немногих словах, в чем состояла супдность
метода Гаусса.
Уравнения (10), выражающие условие нахождения трех
наблюденных положений светила в плоскости, проходящей
через центр Солнца, содержат пять неизвестных величин:
геоцентрические расстояния р, р', р" и отношения площадей
треугольников п/п', п"jn'. Но в случае небольших
промежутков времени между наблюдениями эти отношения с весьма
большой точностью могут быть представлены следующими
приближенными формулами, вытекающими из дифференциальных
уравнений движения:
где
il == £. А + TllV - - - f 1 4- ^^\ (14)
к {f — //); z' =:= к (Г — t)\ z' ^к{Г — О,
а через г' ^ Y^'^ ~t' У''^ + ^'^ обозначен радиус-вектор светила
в момент среднего наблюдения.
Соотношения (9), написанные для момента среднего
наблюдения, дают
г"^^^_^'2__2СгУ -\-R'\ (15)
где
С -= ):Х' + |хТ' -f >/Z'; Я'2 ^ х'2 + У"^ + Z'2
— величины известные.
Таким образом, в пределах точности, даваемой формулами
(14), уравнения (10) и (15) образуют систему четырех
уравнений с четырьмя неизвестными р, р', р" и г'. Решение этой
системы естественно начать с исключения р и р'\ что приводит
29В
я уравнениям (И) и (15), совместное решение которых (не
представляющее особых трудностей) дает р' и г'. После этого
формулы (14) и уравнения (10) легко дают р и р''.
Уравнение (11) можно написать так:
П ' — ТТ' __ ^^ + ^"^'' п-\-п"
^ " п-\-п" ' rir~'
Входящие сюда отношения площадей треугольников Гаусс
выралсает через величины Р и Q, полагая
так что это уравнение приобретает вид
Величины Р и Q Гаусс принимает за основные неизвестные.
Зная эти величины, мы можем из уравнений (15) и (17) найти
р' и г', после чего вычисление элементов орбиты не
представляет, как уже указывалось, никаких трудностей.
Сравнение равенств (14) и (16) показывает, что для
первого приближения можно взять
р = 11; Q = -cx". (18)
Когда соответствующая этим значениям Р и Q орбита
вычислена, то при помощи соотношений (4) и (5) могут быть
найдены гораздо более точные значения отношений площадей
треугольников, чем даваемые формулами (14), а следовательно,
и гораздо более точные значения Р и Q из формул (16).
Повторив решение уравнений (15) и (17) для этих новых значений
Р и Q, мы получим более точную орбиту, которая в свою
очередь позволит найти еще более точные значения Р и Q, ж т. д.
На частных примерах Гаусс показал, что такого рода
итеративный процесс быстро сходится^ и позволяет получить точ-
1 Сходимость указанного процесса была доказана лишь в самое
последнее время в работах: П. Ш. Меси с. О сходимости
последовательных приближений в способе Гаусса определения орбит.— Бюллетень
Института теоретической астрономии АН СССР, 1947, т. TV, стр. 31 —
39; Г. М. Б а ж е н о в. Исследование сходимости итерационных
процессов в задаче определения орбит.— Там же, 1949, т. IV, стр. 207—225.
294
ыую орбиту, т. е. такую, которая представляет исходные
наблюдения в пределах принятого числа знаков.
Таков, в своих основных чертах, метод Гаусса, оставивший
столь глубокий след в истории развития астрономии. Нельзя
не отметить, однако, что указанные уже нами причины,
сделавшие этот метод столь знаменитым, способствовали
установлению на него в некоторых отношениях совершенно
неправильных взглядов, получивших тем не менее довольно широкое
распространение.
Неправильным является прежде всего часто встречавшееся
и еще встречаюш;ееся иногда утверждение, что Гаусс дал
первое эффективное решение задачи об определении
эллиптической орбиты. Между тем, в трех мемуарах Лагранжа,
напечатанных в 1778 и 1783 гг. дано столь же полное решение этой
задачи. Лагранж приводит в них вычисление
геоцентрических расстояний к решению тех же самых уравнений (И) и (15),
как и Гаусс, причем для первого приближения он берет те же
самые формулы (14). Отличие метода Лагранжа от метода Гаусса
заключается только в том, что для последуюш;их приближений
вместо итеративного процесса используются разложения
отношений п/п' и п"In' в бесконечные ряды^.
Другое, общее решение задачи определения орбит было
дано в 1780 г. Лапласом ^, причем его основные уравнения
для нахождения р' и г' также очень близки к уравнениям (15)
и (17), если в это последнее подставить значения (18).
Однако все достоинства метода Лагранжа и его
эквивалентность методу Гаусса были выяснены лишь в конце XIX в.,
когда метод Гаусса давно уже сделался привычным орудием
1 См. М. Ф. Субботин. Цит. соч., стр. 53—63.
2 Р. S. de L а р 1 а с е. Memoire sur la determination des orbites des
cometes.— Memoires de rAcademie Royale de Paris, 1780 (Oeuvres, t. X).
Содержание этого мемуара изложено также в Traite de mecanique
celeste, t. I, 1799.
^ Это было сделано И. А. Бостоновым в работе «Об определении
орбит по трем наблюдениям» (Варшавские университетские известия, 1888),
Но его работа не привлекла к себе должного внимания. Метод Лагранжа
был окончательно введен в практику К. Шарлье (1911) и А. Андуайе
(1923).
295
Аналогичную судьбу имел и метод Лапласа, который только
после работ П. Харцера (1896) и, особенно, А. Лейшнера
(1902) стал применяться для вычисления орбит малых планет.
Таким образом, к моменту открытия Цереры астрономы имели
в своем распоряжении два вполне эффективных метода для
вычисления ее орбиты, но никому не припхло в голову
воспользоваться этими методами. Что это не было сделано их авторами—
Лагранжем и Лапласом, ~ понятно, так как и тот и другой
никогда сами не вычисляли. Но об этом не подумал и такой
хороший вычислитель как упоминавшийся выше Буркхардт,
много помогавший Лапласу и, несомненно, знакомый с его методом.
Ольберс, ознакомившись с присланной ему Гауссом
рукописью «Краткий обзор методов, примененных к определению
орбит двух новых главных планет» (к этой работе,
опубликованной в 1809 г., мы вернемся ниже), в письме Гауссу от 11
сентября 1802 г. отмечает: «...Впрочем, Вам известно большое
сходство Вашей основной формулы (7) с лапласовой^... Но
Ваш вывод совершенно иной, а вычисления по Вашему методу
удивительно коротки п удобны».
Можно отметить, что окончательный вид уравнения (17)
для первого приближения у Гаусса таков:
_ R^fjL 1_
тогда как Лаплас употребляет это уравнение в форме
, _ R^ /J 1_
Через Q 11 V- здесь обозначены некоторые величины,
вычисляемые по данньш наблюдений. О сравнительной легкости
вычисления их в том и другом методе и идет речь в письме
Ольберса.
Отвечая Ольберсу, Гаусс пишет^: «Формула Лапласа,
которую я видел много лет тому назад в его «Theorie du Mouv.
1 Лаплас. Небесная механика. Пер. Буркхардта, часть I,
стр. 279, или Memoires de PAcademie Royale de Paris, 1780, стр. 31.
2 Письмо от 14 сентября 1802 г. Это письмо и указанное выше письмо
Ольберса, помещены в книге: «Wilhelm Olbers, sein Leben und seine
Werke», Bd. II. Briefwechsel zwischen Olbers und Gauss, Berlin, 1900.
296
Ellipt.», совсем выпала у меня из памяти, пока я не получил,
совсем недавно, «Mecanique celeste». Мне кажется, что ее
можно очень легко получить из (7)».
Удивительный, на первый взгляд, факт недооценки и почти
полного забвения работ Лагранжа и Лапласа объясняется,
конечно, не тем, в сущности второстепенным, обстоятельством,
что в названиях этих работ шла речь только о вычислении
«орбит комет». Лагранж и Лаплас решили задачу об определении
орбиты с той же степенью общности, как и Гаусс. Причиной
здесь было то, что эти авторы ограничились лишь
математической стороной дела, тогда как Гаусс не только тщательно
обработал свое решение с точки зрения вычислительной техники,
но и учел все условия работы и все привычки астрономов-
вычислителей. Это и обеспечило методу Гаусса тот авторитет,
который заставил надолго забыть труды его предшественников.
Столь же неправильным является встречающийся иногда
взгляд на метод Гаусса как на совершенно общее решение
задачи об определении орбит. Конечно, условие малости
промежутков времени между наблюдениями, ясно
формулируемое Гауссом, вполне законно при нахождении
предварительной орбиты. Но, как впервые вскрыл замечательный по глубине
анализ метода Гаусса, сделанный В. И. Фабрициусом (1845—
1895) ^, успех этого метода целиком зависит еще и от других
условий: эксцентриситет орбиты должен быть достаточно мал,
а расстояние светила от Солнца — достаточно велико. Во всех
других случаях данный Гауссом итеративный процесс для
нахождения Р и Q либо расходится, либо сходится так медленно,
что эти величины приходится находить интерполированием.
Но тогда проще применить метод вариации геоцентрических
расстояний. Метод Гаусса оказывается неприменимым для
орбит почти параболических, так как в этом случае исходное
предположение Q='^'^'', на котором строится первое
приближение, может оказаться ошибочным не только по численной
величине, но даже по знаку.
^В. И. Фабрициус. Критические начала задачи определения
орбиты по трем наблюдениям. Киев, 1887 (оттиск из «Киевских
университетских известий» за 1887 г.).
20 к. Ф. Гаусс 297
Таким образом, метод Гаусса вовсе не является
универсальным решением задачи об определении орбит. Не следует,
впрочем, думать, что это должно рассматриваться как
недостаток: специальные методы с ясно ограниченной областью
применения обычно являются в практическом отношении гораздо
более ценными, чем те методы, которыми стремятся охватить
слишком разнородные случаи.
Метод вычисления орбит, изложенный в «Theoria motus»,
был окружен таким пиететом, что в течение долгого
времени применялся без всяких изменений. Не сразу заметили, что
этот метод «в его обосновании и некоторых деталях если и
не может быть улучшен, то все же может быть упрош;ен и
изменен» ^.
Впервые небольшие упрощ;ения и изменения были внесены
работами Энке (1854), Ганзена (1863), Оппольцера (1870) и Титье-
на (1879).
В конце XIX в. были сделаны попытки внести в метод
Гаусса гораздо более глубокие изменения. Здесь особенно
должны быть отмечены работы киевских астрономов: В. И.
Фабрициуса, появившиеся в 1877—1892 гг., и Р. Ф. Фогеля (1859—
1920), появившиеся в 1891—1894 гг. 2, а также работа Гиббса
(J. W. Gibbs), напечатанная в 1888 г.
Но лишь много позднее выработались те пути вычисления
планетных орбит, которые в настоящее время можно считать
наилучшими. Они создавались под влиянием стремления
возможно лучше приспособить метод Гаусса к условиям машинного
вычисления. С другой стороны, большую роль играло
оживление интереса к методам Лагранжа и Лапласа и стремление дать
синтез лучших сторон всех трех методов^.
1 В таких выражениях говорит о методе Гаусса Баушингер в своем
известном трактате: J. Bauschinger. Die Bahnbestimmung der
Himmelskorper 1906; 2. Aiifl., 1928.
2 Подробную библиографию этих работ можно найти в статье:
Г. М. Баженов. Обзор отечественных работ по теории определения
орбит планет и комет. Ученые записки Харьковского университета,
т. 42, 1952, стр. 17—31.
* См. М. Ф. Субботин. Курс небесной механики,, т. I. Изд. 2,
1941, главы VII и XI.
298
6. ДРУГИЕ РАБОТЫ ПО ТЕОРИИ НЕВОЗМУЩЕННОГО
ДВИЖЕНИЯ
По теории невозмущенного движения и вычисления орбит
Гаусс опубликовал, помимо «Theoria motus» и большого
количества кратких сообщений о вычисленных им орбитах или
эфемеридах, еще следующие девять статей, которые мы
расположим в хронологическом порядке:
1802. «Vorschriften, um aus der geocentrischen Lange und Breite
eines Himmelskorpers, dem Orte seines Knotens, der Neigung der
Bahn, der Lange der Sonne und ihrem Abstande von der Erde ahzulei-
ien; Des Himmelskorpers heliocentrische Lange in der Bahn, wahren
Abstand von der Sonne und wahren Abstand von der Erde» (см.
G. F. Gauss. Werke, Bd. VI, 87—93).
1804. «Einige Bemerkungen zur Vereinfachung der Rechnung
fur die geocentrischen Oerter der Planeten» (см. там же, стр. 94—105).
1804. «Uber die Grenzen der geocentrischen Oerter der Planeten»
(cm. там же, стр. 106—118).
1809. «Summarische Uebersicht der zur Bestimmung der Bahnen
der beiden neuen Hauptplaneten angewandten Methoden» (см. там
же, стр. 148—165).
1811. «Disquisitio de elementis ellipticis Palladis ex oppositio-
nibus anno rum 1803, 1804, 1805, 1807, 1808, 1809» (см. там же,
стр. 1—24).
1811. «Zur Auflosung der Aufgabe, aus zweien Radiis vectoribus
und dem eingeschlossenen Winkel die elliptischen oder hyperbolischen
Elemente zu bestimmen». Выдержка из письма Гаусса (см.
С. F. Gauss. Werke, Bd. VII, 300—301).
1813. «Observationes cometae secundi a. MDGGGXIII in obser-
vatorio Gottingensi factae adiectis nonnullis adnotationibus circa
calculum orbitarum parabolicarum» (см. G. Г. Gauss. Werke, Bd.
VI, 25-36).
1843. «Schreiben des Herrn Hofraths Gauss, Directors der Got-
tinger Sternwarte, an den Herausgeber der Astronomiscben Nachrich-
ten».—Astronomische Nachrichten, Bd. 20, Nr. 474, 1843, April 13
(cm. там же, стр. 191—193 или Bd. VII, стр. 371—373).
1848. «Uber die Zodiaken der Himmels Korper». Выдержка из
письма Гаусса (см. там же, стр. 194—196 или Bd. VII, стр. 313—316).
Не будем останавливаться на первых двух работах,
поскольку их содержание вошло в «Theoria motus». Оставим также
в стороне заметки 1804 и 1848 гг., в которых трактуется мало,
в сущности, интересный вопрос о нахождении границ той
области неба, в которой происходит движение планеты.
20* 299
Обратимся к работе 1809 г., дающей «Краткий обзор
методов, примененных при вычислении орбит обеих новых планет».
Рукопись ЭТО!! работы Гаусс послал Ольберсу вместе с письмом
от 6 августа 1802 г. в ответ на просьбу Ольберса сообщить,
какими путями им были получены столь блестящие
результаты при вычислении орбит Цереры и Паллады. После
возвращения рукописи Гауссу (ноябрь 1805 г.), она попала к Линде-
нау (v. Lindenau), который и опубликовал ее, с согласия
.Гаусса, в «Monatliche Correspondenz» (сентябрь 1809 г.). Почти
одновременное появление «Theoria motus» сделало эту статью
малоинтересной для современников Гаусса. По она
представляет немалый интерес для нас, так как помогает понять ход
мыслей, приведший Гаусса к созданию его метода вычисления
орбит.
Заметка 1811 г. содержит небольшое дополнение к «Theoria
motus». Гаусс показывает, что функцию ?(ж), определяемую
равенствами (6) и (7), можно представить в форме
1 f L
12
где
А ^ fA _ "{1 [а л ^ л^ 1-3.5.7 2 I 1-3.5-5.7.9 ^ \
Л ~ (1 X) (^J- -i"2.9^ ' 2.4.9.11^ "^ 2.4.6.9.11.13 ^ "Г ---J»
которая весьма удобна для вычислений.
Эта заметка дает хороший пример той поистине ювелирной
отделки, которой добивался Гаусс в занимавших его вопросах.
Опубликованная в том же 1811 г. работа «Исследование
эллиптических элементов Паллады по оппозициям 1803, 1804,
1805, 1808 и 1809 годов» интересна тем, что она существенно
дополняет «Theoria motus» в отношении весьма важного вопроса—
вычисления орбит по большому числу наблюдений. Гаусс
излагает в ней два метода улучшения орбиты. Первый из этих
методов предназначен для предварительного исправления
имеющейся орбиты при помощи возможно простых вычислений. Он
основан на том хорошо известном факте, что среди элементов
орбиты, найденной но небольшому числу наблюдений, наклон
300
i и долгота узла ti оказываются всегда определенными
наиболее точно. Сообразно с этим Гаусс сначала оставляет эти два
элемента без изменения и исправляет только остальные четыре
при помощи весьма своеобразных условных уравнений,
содержащих, в конечном счете, поправки только двух элементов —
долготы перигелия и угла эксцентриситета; когда их поправки
найдены, то сразу получаются исправленные значения двух
других элементов — среднего движения и средней долготы
эпохи. После этого составляются условные уравнения для
нахождения поправок Ai hAQ. Коэффициенты соответствующих
уравнений можно получить особенно просто, если используемые
наблюдения сделаны, как это обычно бывает, вблизи
оппозиции. Таким образом, в этом методе вместо системы условных
уравнений с шестью неизвестными приходится решать две
системы с двумя неизвестными каждая, что значительно легче.
С другой стороны, коэффициенты условных уравнений
вычисляются в способе Гаусса по весьма простым формулам.
Второй метод, подробно излагаемый и применяемый в
рассматриваемой работе, — это тот строгий метод
одновременного дифференциального исправления всех шести элементов,
который только упомянут в «Theoria motus».
Здесь важно отметить, что при решении нармальных
уравнений, соответствующих условным уравнениям, составленным
по второму методу, Гаусс подробно излагает тот элиминацион-
ный алгорифм, который до сих пор излагается во всех учебных
руководствах по астрономии и геодезии.
Нам нужно еще рассмотреть работы Гаусса, относящиеся
к 1813 и 1843 гг. Остановимся сначала на статье,
опубликованной в 1813 г. С несущественными сокращениями она была
напечатана Гауссом и на немецком языке:
«Beobachtungen des zweiten Gometen vom Jahre 1813, angestellt
auf der Sternwarte zu Gottingen, nebst einigen Bemerkungen fiber
die Berechnung parabolischer Bahnen», von Carl Friedrich Gauss
(vorgelegt der konigl. Gesellschaft der Wissenschaften am 10.
September 1813). Aus dem Lateinischen iibersetzt. (Zach's Monatliche Cor-
respondenz, Bd. 28).
В этой работе Гаусс, сообщив сделанные им 5 наблюдений
новой кометы, отводит все остальное место изложению тех улуч-
301
шений, которые были им внесены в метод вычисления
параболических орбит, незадолго до этого (1797) предложенный Оль-
берсом и входивший тогда во всеобщее употребление. Главным
из этих улучшении был предложенный Гауссом способ
вычислять радиусы-векторы кометы и хорду, соединяющую ее
положения, при помощи вспомогательных углов, остающихся
неизменными в последовательных приближениях. Этот способ,
хорошо учитывавший потребности логарифмического
вычисления, вошел во все руководства по вычислению орбит.
Здесь уместно напомнить, что в «Theoria motus» Гаусс
совсем не касается вопроса о вычислении кометных орбит. Это
объясняется, помимо появления знаменитой книги Ольберса,
казалось бы, исчерпывающей вопрос, еще и отсутствием личного
опыта.
Только начиная с 1805 г., Гауссу приходится вычислять
орбиты комет. Из переписки Гаусса с Ольберсом и Линденау
мы знаем, что приблизительно в то время, к которому относится
рассматриваемая работа, он много занимался относящимися
сюда вопросами. В письме к Ольберсу от 29 мая 1815 г. Гаусс
пишет: «Свои теоретические изыскания по общим вопросам
вычисления кометных орбит я склонен опубликовать в
специальном труде, как дополнение к моему Th. М. С. С. Это могло бы
составить 6—8 печатных листов, к чему я прибавил бы таблицу
параболического движения, составленную по новому принципу
и более удобную, чем таблица Баркера. Это увеличило бы объем
еще на 3 печатных листа. Начало уже положено, и в этом мне
помог господин Энке»^.
Эти замыслы Гаусса остались невыполненными. Но в
оставшихся после его смерти бумагах, а также в опубликованных
письмах мы находим много материалов, относящихся к
задуманной книге.
Сохранилась прежде всего вычисленная Гауссом таблица
параболического движения, т. е. таблица, позволяющая решать
уравнение
1 с. F.Gauss. Werke, Bd. VII, 350.
S02
определяющее истинную аномалию v в функции промежутка
времени t, отделяющего рассматриваемый момент от момента
прохождения через перигелий.
Таблица Гаусса дает г;с точностью до О".001 по аргументу
At, где
_А _£.
A^yik'q ' = [3.7005216] g ^
В небольшой заметке, напечатанной в 1843 г.,
рассматривается вопрос о решении уравнения (19) в тех случаях, когда
правая часть настолько велика, что выходит за пределы таблицы.
Здесь оказывается очень удобным тот общий прием решения
трехчленных уравнений, который был незадолго до этого
дан Гауссом в приложении к сборнику математических таблице.
Этим не исчерпываются результаты, полученные Гауссом
в отношении параболического движения. Клинкерфюс,
занимавший после Гаусса кафедру астрономии Гёттингенского
университета, опубликовал 2 данную Гауссом формулу для
отношения площадей треугольника и сектора, заключенных между
двумя радиусами-векторами г и г' и дугой параболической
орбиты, описанной за промежуток времени V—t между моментами,
соответствующими этим радиусам-векторам. Гаусс показал,
что это отношение выражается рядом
площ. треугольника ш 1 ^2 ^з 55 ^
площ. сектора 3 ^ 6 ^ 9 ^ 648 ^ * * *'
где
^~ {тЛ-т^f •
Этот ряд (или, вернее, построенная при его помощи таблица)
применяется и сейчас при вычислении параболических орбит
комет.
В заключение остановимся еще на работах Гаусса по
вычислению круговых орбит. В «Theoria motus» он этого вопроса
^ V е g а und Н и 1 s s е. Sammlung mathematischer Tafeln, 1840
(см. С. F. G auss. Werke, Bd. Ill, Zweiter Abdruck, 1876, стр. 255_
257).
2 Cm. Прибавление (Anhang, стр. 59) к уже указанному в сноске на
стр. 279 немецкому переводу «Theoria motus».
303
не затрагивает. Может быть, тут сказывался неудачный опыт
применения таких орбит: положение Цереры, предвычисленное
при помощи круговой орбиты Ольберса, оказалось ошибочным
на 9°. Но изучение оставшихся после Гаусса рукописей
показало, что он занимался и этим вопросом. Наиболее важные
результаты были им сообш;ены Клинкерфюсу, который в своем
широко известном руководстве поместил главу: «Гауссов метод
вычисления круговой орбиты», сделав к ней такое примечание:
«Автор обязан этим методом устному сообш;ению Гаусса,
сделанному в связи с поручением исследовать орбиту Эвномии»^.
7. МЕТОД ГАУССА ДЛЯ ВЫЧИСЛЕНИЯ
ВЕКОВЫХ ВОЗМУЩЕНИЙ
В 1818 г. в «Commentationes», издававшихся Гёттингенским
научным обществом, была напечатана работа Гаусса с очень
обстоятельным названием:
«Определение притяжения, которое производила бы в любой
заданной точке планета, если бы ее масса была распределена
по всей орбите пропорционально времени, в течение которого
отдельные части орбиты описываются»^.
Сформулированная в этом заглавии задача была поставлена
Гауссом в связи со следующей открытой им «теоремой
физической астрономии» ^.
^W. Klinkerfues. Theoretische Astronomie. Braunschweig,
1871; 3. Aufl., herausgegeben von H. Buchholz, Braunschweig, 1912. Эта
глава воспроизведена в сочинениях Гаусса (см. С. F. Gauss. Werke,
Bd. XI, Abt. 1, стр. 253—257).
2 «Determinatio attractionis, quam in punctum quodvis positionis
datae exerceret planeta, si eius massa per totam orhitam ratione temporis,
quo singulae partes describuntur, uniformiter esset dispertita» (см.
G. F. G a uss. Werke, Bd. Ill, 1876, стр. 331—335). Немецкий перевод
этой работы дан в Ostwald's Klassiker der exakten Wissenschaften,
Nr. 225.
^ Так BO времена Гаусса называли часть теоретической астрономии,
непосредственно занимающуюся изучением астрономических следствий
закона всемирного тяготения. Термином «небесная механика»,
введенным Лапласом, Гаусс никогда не пользовался. Во второй половине
ХТХ в., в связи с развитием астрофизики, наименование «физическая
астрономия» вышло из употребления.
304
Вековые возмущения, производимые в движении планеты Р
другой планетой Р\ не изменятся, если заменить планету Р'
материальным кольцом, распределив ее массу вдоль всей
орбиты так, чтобы часть массы, приходящаяся на каждую долю
орбиты, была пропорциональна времени, в течение которого
планета Р' описывает эту долю своей орбиты. При этом
предполагается, что средние движения планет Р и Р' несоизмеримы
между собой и что рассматриваются вековые возмущения только
первого порядка относительно возмущающих масс.
Эллиптические материальные кольца, линейная плотность
которых определяется только что указанным законом, стали
называться «гауссовыми кольцами».
Таким образом, можно сказать, что вычисление вековых
возмущений первого порядка (т. е. наиболее важных —
возмущения второго порядка уже в тысячи раз меньше) приводится
к нахождению силового поля гауссового кольца, заменяющего
возмущающую планету.
Компоненты притяжения, производимого в точке {Ху ?/, z)
гауссовым кольцом, выражаются через эллиптические интегралы
те те
sin^ Т dT
^ 2т: Vm^ cos2 Т-j-п^ sin^ Т ^ 2v: Vm^, cos^ Т + n^ sWT '
где m^ и n^ — некоторые алгебраические функции третьего
порядка координат ж, у, z.
Разработанная Гауссом (но так и неопубликованная им)
теория эллиптических интегралов позволила дать следующий
способ для вычисления указанных интегралов. При помощи
положительных чисел тяп составляется двойная
последовательность:
т
2
Общий предел, к которому сходятся
последовательности т, т', т", т'",... и д, ^', ^", д'",... и который
называется арифметически-геометрическим средним чисел m и /г,
305
обозначим через р. Тогда
M + N = -; M — N = ~-,
где
= ;;СТ [2 {т'^ ~ п'^) + 4 (т"2 - п"') + 8 (т"'^ - п'"^) +...].
т^ — п'
Имея возможность находить компоненты притяжения,
производимого кольцом, в каждой точке траектории планеты Р,
уже нетрудно вычислить вековые возмущения элементов ее
орбиты.
В своем очень кратком мемуаре Гаусс только наметил
основные линии решения, далеко не доведя его до рабочих формул.
Неудивительно поэтому, что данный им способ вычисления
вековых возмущений долго не находил применения, хотя важность
этого способа очевидна — он позволяет получать вековые
возмущения первого порядка со всей нужной точностью при
любых эксцентриситетах орбит и при любом угле между их
плоскостями. Между тем, все другие способы основаны на
разложениях по степеням эксцентриситетов и по степеням синуса угла
между плоскостями рассматриваемых орбит, а потому пригодны
лишь в тех случаях, когда эти величины достаточно малы.
Впервые методу Гаусса была придана вполне разработанная
для практических применений форма только в 1882 г. Хиллом^.
Вскоре после этого Альфану^ удалось существенно
упростить вычисление притяжения, производимого гауссовым
кольцом. Его решение этой задачи, использующее все ресурсы
теории эллиптических функций, явилось основой нескольких
способов вычисления вековых возмущений, доведенных до
конца, т. е. до сопоставления рабочих формул. Новейшим
и особенно подробно разработанным из этих способов
является способ, данный профессором Томского университета
Н. Н. Горячевым^.
1 G. W. Hill. The Collected Mathematical Works, Vol. II,
€тр. 1—46.
2 G. H. Halphen. Traite des fonctions elliptiques et de leurs
applications, t. II. Paris, 1888, стр. 310—328.
^ H. H. Горячев. Способ Halphen'a для вычисления вековых
возмущений планет и применение его к Церере. Томск, 1937.
306
Идея Гаусса заменять планету, при вычислении ее векового
влияния, соответствующим материальным кольцом была широко
использована не только для точного вычисления вековых
возмущений, но и для грубо приближенного, качественного
изучения движений небесных тел.
ЗАКЛЮЧЕНИЕ
Заканчивая этот краткий обзор деятельности Гаусса в
области астрономии и геодезии, следует отметить, что
рассмотренные нами работы еще не исчерпывают все сделанное им для
развития этих наук.
Многое в работах Гаусса по механике, особенно по теории
потенциала, представляет непосредственный интерес и для
рассматриваемой нами области знания. Таковы прежде всего
его широко известные мемуары.
1813. «Theoria attractionis corporum sphaeroidicorum ellipti-
corum homogeneormn methodo nova tractata».
1839—1840. «AUgemeine Lehrsatze in Beziehung auf die im ver-
kehrten Verhaltiiisse des Quadrats der Entfernung wirkenden Anzie-
hungs- und Abstossungskrafte»!.
Нужно вспомнить также, что влияние Гаусса на развитие
вычислительной техники далеко не исчерпывается сказанным
выше. Так, например, логарифмы сложения и вычитания,
существенно облегчившие и улучшившие астрономические
вычисления, были значительно усовершенствованы и введены в
употребление Гауссом.
Большое значение для развития науки имели не только
напечатанные Гауссом работы, или отдельные результаты его
исследований, опубликованные его учениками, не только его
преподавательская деятельность, продолжавшаяся почти
полстолетия. Весьма заметное влияние имела также обширнейшая
научная переписка, которую вел Гаусс с наиболее выдающимися
^ Оба мемуара воспроизведены в кн.: С. F. Gauss. Weike, Bd.
V. Mathematische Physik. Zweiter Abdruck, 1877. Их можно найти также
в Ostwald's Klassiker der exakten Wissenschaften, Nr. 2 und Nr. 19. Русский
перевод второго мемуара помещен в цитированной выше (стр. 273) кн.:
К. Ф. Гаусс. Избранные труды по земному магнетизму, стр. 173—234.
307
немецкими учеными того времени: с Ольберсом—в 1802—1839гг.;
с Бесселем —в 1804—1844 гг.; с Шумахером — в 1808—1850 гг.
с А. Ф. Гумбольдтом—в 1807—1854 гг.; с Герлянгом — в
1810—1850 гг.;с Николаи—в 1819—1845 гг.;сЛежен-Дирихле—
в 1826-1853 гг.; с Ф. Ббяи —в 1797—1853 гг.^
Размеры этой нерениски (почти целиком посвященной
астрономическим и геодезическим вопросам) напоминают обычаи
XVII и XVIII вв., когда, сначала при отсутствии, а потом при
крайней скудости научных журналов, переписка между учеными
имела весьма важное значение в деле распространения их идей.
Некоторые другие черты деятельности Гаусса также
больше роднят его с предшествующими поколениями ученых, чем
с последующими. Таково, например, его стремление придавать
своим сочинениям ту, так называемую «классическую», форму,
которая создалась под влиянием преклонения перед
греческими геометрами и стремления подражать им. В своих письмах
Гаусс оправдывал эту чисто синтетическую форму изложения,
иногда полностью затушевывавшую естественный ход мыслей,
тем, что «на готовом здании не должны быть видны леса и
строительные приемы». Такая форма изложения создавала большие
трудности, и сочинения Гаусса при его жизни читались мало.
Только после того, как они были изложены его учениками
в менее «классической» форме, или прокомментированы ими,
они получили должное распространение.
Напротив, лекции Гаусса, отличавшиеся, по свидетельству
одного из его учеников'
^ 1 «Wilhelm Olbers, sein Leben und seine Werke», Bd. II, Briefwech-
sel zwischen Olbers und Gauss, I und II Abt., Berlin, 1900 und 1909.
Briefwechsel zwiscben Gauss und Bessel, Leipzig, 1880.
Briefwechsel zwischen G. F. Gauss und H. C. Schumacher; Altona I
(1860), II (1860), III (1861), TV (1862), V (1863), VI (1865).
Briefe zwischen A. v. Humboldt und Gauss, Leipzig, 1877.
Briefwechsel zwischen G. F. Gauss und Ghr. L. Gerling, Berlin, 1927.
Briefe von G. F. Gauss an B. Nicolai, Karlsruhe, 1877.
Briefwechsel zwischen G. F. Gauss und P. G. Lejeune-Dirichlet, Di-
richlet's Werke, II, Berlin, 1897.
Briefwechsel zwischen G. F. Gauss und W. Bolyai, Leipzig, 1899.
2 Th. Wittstein. Gedachtnissrede auf Gar] Friedrich Gauss.
Hannover, 1877.
308
иной характер. Так, иногда он целый час объяснял, почему
не был выбран тот путь решения задачи, который, на первый
взгляд, казался наилучшим. Гаусс очень не любил, когда его
лекции записывались, он предпочитал иметь перед собой
слушателей в буквальном смысле слова.
Часто встречается утверждение, что Гаусс очень не любил
преподавание и тяготился лекциями. Однако жалобы, которые
встречаются в его письмах, говорят, скорее, о преподавании
как примере того, что разбивает время и отнимает назависи-
мость — «это основное условие действительно глубокой
умственной работы» ^.
Но особенно охотно Гаусс занимался с молодыми людьми,
уже посвятившими себя науке и приезжавшими к нему иногда
издалека для усовершенствования. Так, в 1820 г. в
астрономических и геодезических работах Гаусса принимал участие
27-летний В. Струве—наш будущий академик и создатель
Пулковской обсерватории. Среди учеников Гаусса мы
встречаем таких известных астрономов, как Бессель, Шумахер,
Энке, Виннеке и многих выдающихся геодезистов.
Говоря о влиянии Гаусса на современную ему науку,
нельзя, наконец, забывать еще об одной стороне его
деятельности. В течение многих лет он систематически помещал
в изданиях Гёттингенского научного общества
обстоятельные рецензии на новые книги. Это также позволяло ему
делать известными свои взгляды на актуальные научные
вопросы. Эти рецензии представляют очень интересный материал,
позволяющий понять многие особенности развития науки
в начале XIX в.
Если, заканчивая этот обзор, попытаться в немногих словах
резюмировать сделанное Гауссом в рассматриваемой нами
области знания, то можно сказать, что и в области теоретической
астрономии, и в области наблюдательной астрономии, и в
области геодезии Гаусс, сосредоточив свое внимание на
важнейших в его время проблемах этих наук, каждую из них
продвинул далеко вперед.
1 См. письмо к Ольбергу № 596 в указанной на стр. 308 кн.: <^Wil-
helm Olbers, sein Leben und seine Werke».
309
Данные им решения узловых проблем во многом определили
развитие науки на целое столетие вперед. Многое из созданного
Гауссом имеет столь завершенную форму и так глубоко
проникает в суш;ность веш;ей, что не только послужит материалом
для последуюш.его развития, но навсегда останется в золотом
фонде духовной культуры человечества в том виде, как оно
вышло из рук Гаусса.
СОДЕРЖАНИЕ
Предисловие 5
Речь академика И. М. Виноградова 7
Б. Н. Делоне. Работы Гаусса по теории чисел И
А. П. Н о р д е н. Геометрические работы Гаусса ИЗ
А. И. М а р к у ш е в и ч. Работы Гаусса по математическому анализу 145
Б. В. Г н е д е н к о. О работах Гаусса по теории вероятностей . 217
М. Ф. Субботин. Астрономические и геодезические работы
Гаусса 241
Утвермсдено у: печати
Институтом ист,ории естествознания и техники
Академии наук СССР
Редактор издательства Е. М. Нляус
Технический редактор Е. В. Зеленкова
Корректор Е. А. Васильева
ГИСО АН СССР № 103-16В. Сдано в набор 12/1956 г.
Оодп. в печать 18/IV 1956 г. Т-02665. Формат бум. 60x92Vi.
Печ. л 19,5+3 вкл. Уч.-изд. лист. 14,9+0,3 вкл. (15,2)
Тираж 2500.Т-02665 Изд. № 1559. Тип. зак. 76.
Цена 11 р.
Издательство Академии наук СССР
Москва, Б-64, Подсосенский пер., д. 21
2-я типография Издательства АН СССР.
Москва, Г-99, Шубпнский пер., д. 10
ИСПРАВЛЕНИЯ И ОИКЧАПП!
Страница
48
49
58
58
236
Строка
1 си.
1 св.
12 сн.
17 сн.
14 сн.
Напечатано
скрещиваются, т. с.
расположены так:
а не охватывают
друг друга, т. е. не
расположены так:
i
3
P{iux) =--
Следует читать
не охватывают друг
друга, т. е. не рас-
полоя{ены так:
а скрещиваются.
т. е расположены
так:
3
i
P{ri,x) -"
[е. Ф. iviycc