Академик И. М. ВИНОГРАДОВ
ОСНОВЫ
ТЕОРИИ ЧИСЕЛ
ИЗДАНИЕ ШЕСТОЕ,
ИСПРАВЛЕННОЕ
Допущено Министерством высшею
Чч^	образования СССР в качестве учебника
^*"-'	ёля физико-математических факультетов
_л	государственных университетов
БИБЛИОТЕКА НМУ
мАгемдтесш
ко/лсд*
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ТЕХНИКО-ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1952 ЛЕНИНГРАД

il-5-2
H Mt
1	I *10d
Редактор А. 3. Рытин.
Техн. редактор М. Д. Суховцева.	Корректор If. С. Варшавская.
Подписано к печати 26/XII 1951 г.	Бумага 84х108/з2. 2,813 Сум. л.
9,23 печ. л. 10,83 уч.-изд. л. 42,591 тип. вн. в печ. л. Т-09549.
Тираж 10 000 экз. Цена книги 3 р. 80 к. Переплёт 2 р. Заказ J* 1362
16-я типография Главполиграфиздата при Совете Министров СССР.
Москва, Трёхпрудный пер., 9.

ОГЛАВЛЕНИЕ.
Предисловие к пятомj изданию .			...	5
ГЛАВА ПЕРВАЯ.
ТЕОРИЯ ДЕЛИМОСТИ.
§ 1. Основные понятия и теоремы G). § 2. Общий наиболь-
наибольший делитель (8). § 3. Общее наименьшее кратное A2).
§ 4. Связь алгоритма Эвклида с непрерывными дробями A4).
§ 5. Простые числа A8). § 6. Единственность разложения на про-
простые сомножители B0). Вопросы к главе I B2). Численные примеры
к главе I B4).
ГЛАВА ВТОРАЯ.
ВАЖНЕЙШИЕ ФУНКЦИИ, ВСТРЕЧАЮЩИЕСЯ В ТЕОРИИ
ЧИСЕЛ.
§ 1. Функции fa;], {x} B5). § 2. Суммы, распространённые
на делители- числа B6). § 3. Функция Мёбиуса B8). § 4. Функ-
Функция Эйлера B9). Вопросы к главе II C1). Численные при-
примеры к главе II D0).
ГЛАВА ТРЕТЬЯ.
СРАВНЕНИЯ.
§ 1. Основные понятия D1). § 2. Свойства сравнений, подоб-
подобные свойствам равенств D2). § 3. Дальнейшие свойства сравне-
сравнений D4). § 4. Полная система вычетов D5). § 5. Приведённая
систему вычетов D6). § 6. Теоремы Эйлера и Ферма D7). Вопро-
Вопросы к главе III D8). Численные примеры к главе Ш E4).
ГЛАВА ЧЕТВЁРТАЯ.
СРАВНЕНИЯ С ОДНИМ НЕИЗВЕСТНЫМ.
§ 1. Основные понятия E5). § 2. Сравнения первой степени E6).
$ 3. Система сравнений первой степени E8). § 4. Сравнения лю-
любой степени по простому модулю F0). § 5. Сравнения любой
степени по составному модулю F1). Вопросы к главе IV F5).
Численные примеры к главе FV F9).

4	ОГЛАВЛЕНИЕ
ГЛАВА ПЯТАЯ.
СРАВНЕНИЯ ВТОРОЙ СТЕПЕНИ.
§ 1. Общие теоремы G1). § 2. Символ Лежандра G3). § 3. Сим-
Символ Якоби G8). § 4. Случай составного модуля (82). Вопросы
к главе V (84). Численные примеры к главе V (90).
ГЛАВА ШЕСТАЯ.
ПЕРВООБРАЗНЫЕ КОРНИ И ИНДЕКСЫ.
§ 1. Общие теоремы (92). § 2. Первообразные корни по моду-
модулям ра и 2ра (93). § 3. Разыскание первообразных корней ио
модулям ра и 2ра (95). § 4. Индексы по модулям ра и 2ра (96).
§ 5. Следствия предыдущей теории (99). § 6. Индексы по модулю
2°" A02). § 7. Индексы по любому составному модулю A04). Во-
Вопросы к главе VI A06). Численные примеры к главе VI A12).
Решения вопросов.
Решения к главе I A14).	Решения к главе II A18).
Решения к главе III A32).	Решения к главе IV A43).
Решения к главе V A49).	Решения к главе VI A59).
Ответы к численным примерам.
Ответы к главе I A70).	Ответы к главе II A70).
Ответы к .главе III A70).	Ответы к главе IV A70).
Ответы к главе V A71).	Ответы к главе VI A71).
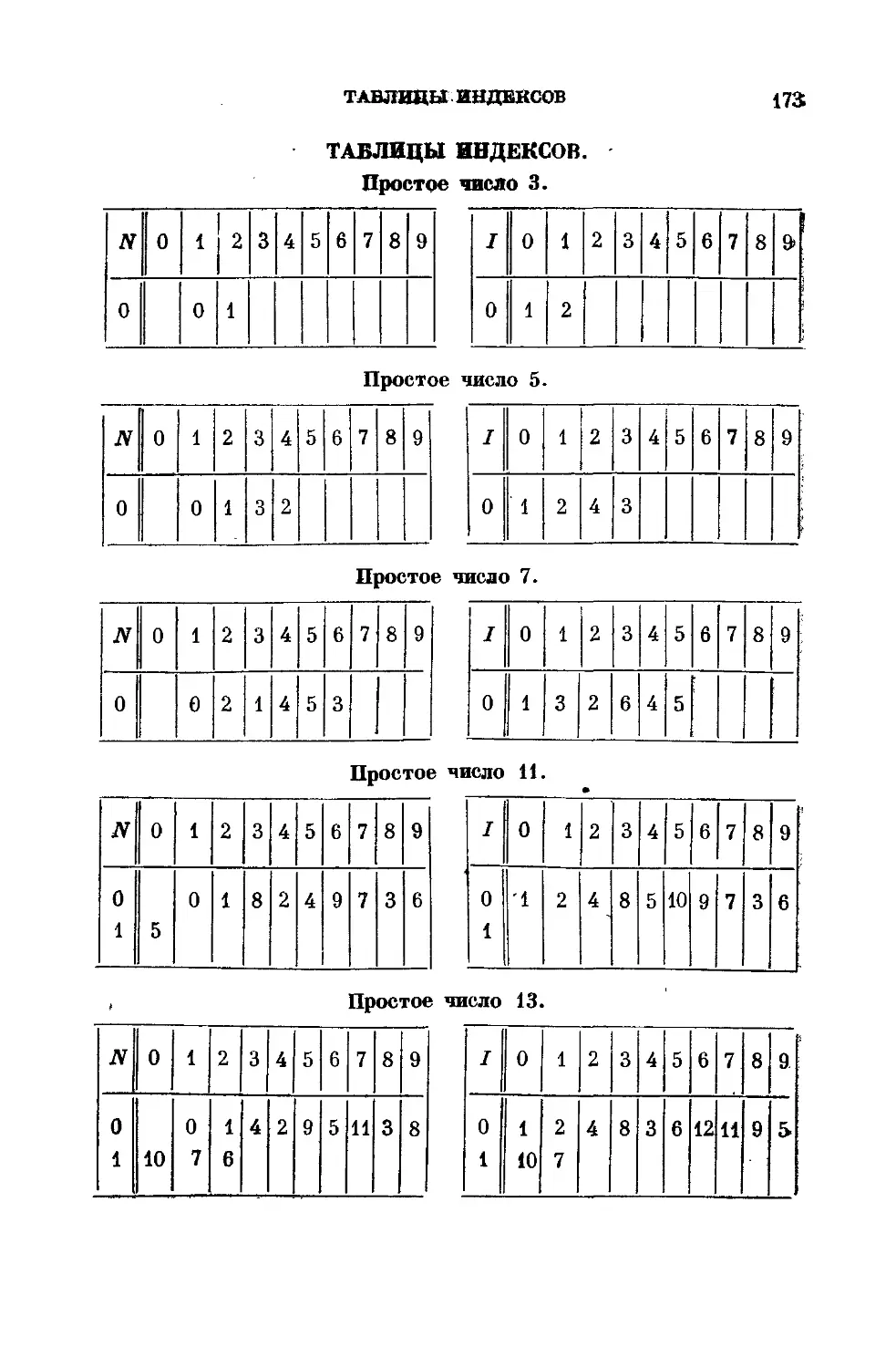
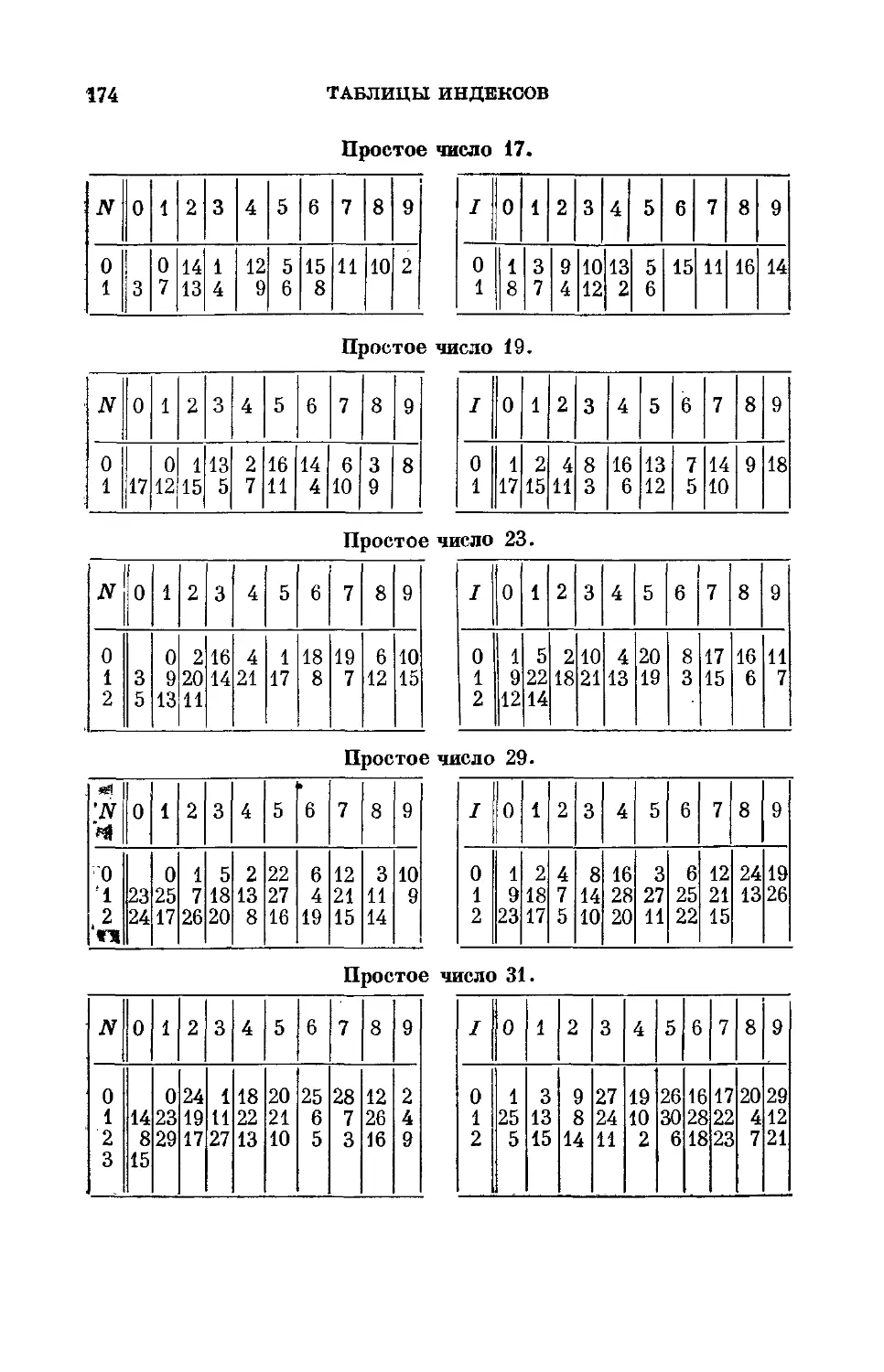
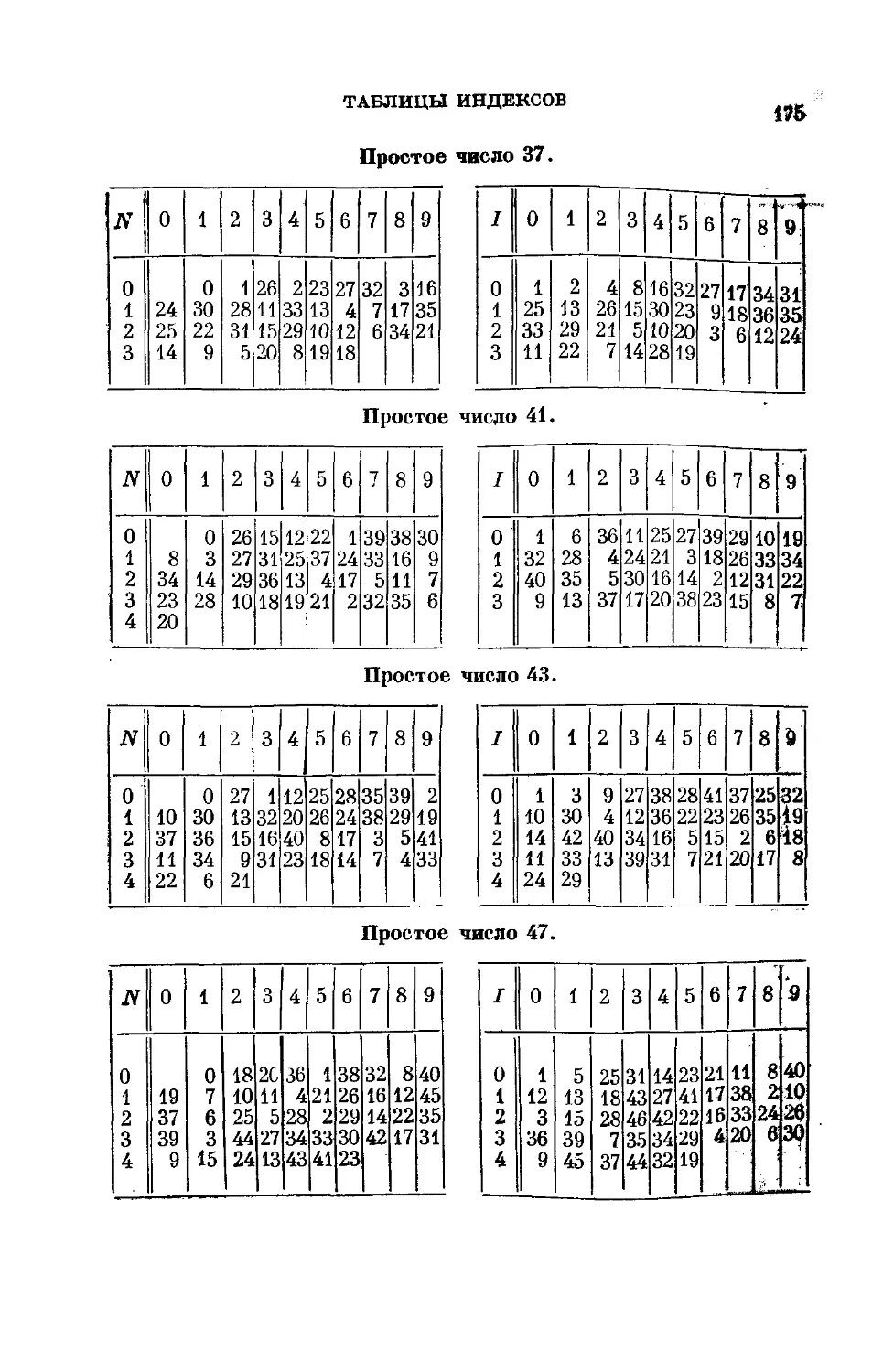
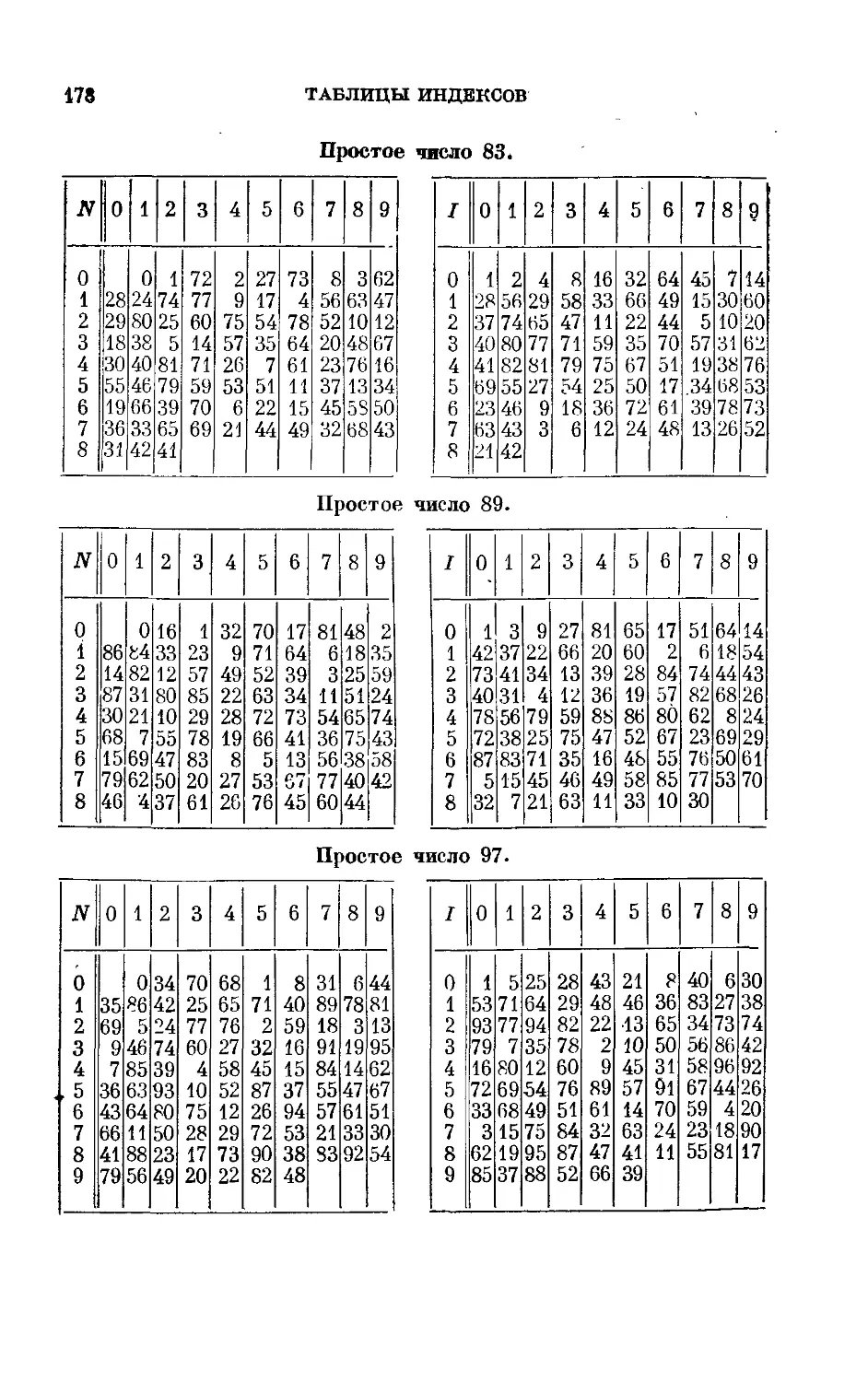
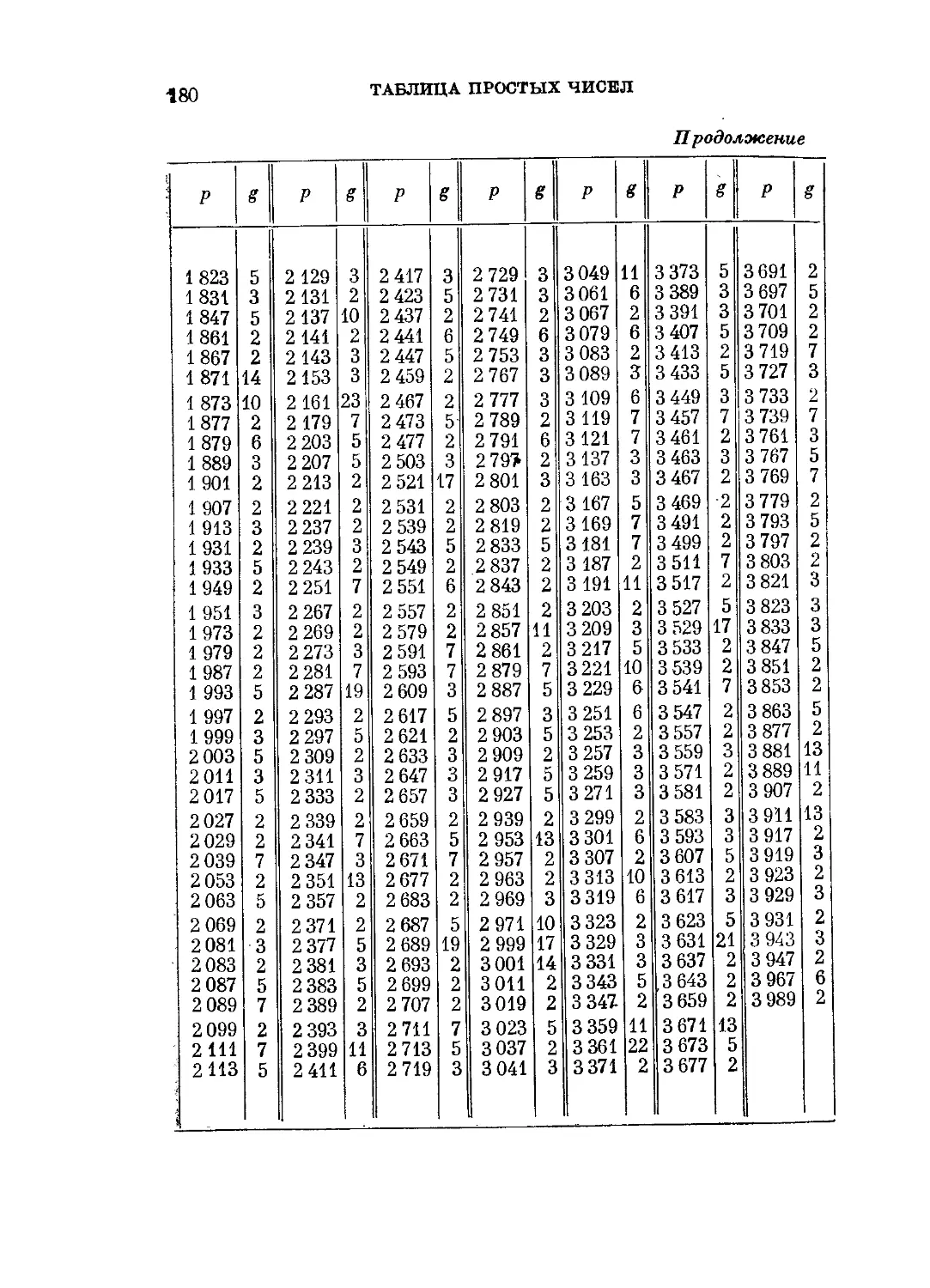
Таблицы индексов	.			173
Таблица простых чисел < 4000 и их- наименьших первооб-
первообразных корней ...		 179

ПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ.
Ряд русских математиков — Чебышев, Коркин, Золота*
рёв, Марков, Вороной и другие — занимался теорией чи-
чисел. Ознакомиться с содержанием классических работ
этих замечательных учёных можно по книжке Б. Н. Де-
Делоне «Петербургская школа теории чисел».
Советские математики, работающие в области теории
чисел, продолжая славные традиции своих предшест-
предшественников, создали новые мощные методы, позволившие
получить ряд первоклассных результатов; в разделе
теории чисел книги «Математика в СССР за 30 лет»
можно найти сведения о достижениях советских учёных
в области теории чисел, а также соответствующие библио-
библиографические данные.
В моей книге даётся систематическое изложение
основ теории чисел в объёме университетского курса.
Значительное количество задач вводит читателя в круг
некоторых новых идей в области теории чисел.
Настоящее пятое издание книги значительно отличает-
отличается от четвёртого. Ряд изменений, способствующих боль-
большей простоте изложения, внесён во все главы книги.
Особо значительными изменениями являются объедине-
объединение прежних глав IV и V в одну главу IV (благодаря
чеку число глав сократилось до шести), а также но-
новое, более простое доказательство существования пер-
первообразных корней.
Существенно переработаны вопросы, помещённые
в конце каждой главы. Порядок следования вопросов
теперь приведён в полное соответствие с порядком рас-
расположения теоретического материала. Введены некото-
некоторые новые вопросы; однако число номеров вопросов

ПРЕДИСЛОВИЕ
значительно сокращено. Последнее достигнуто путём
объединения под названиями а, Ь, с, ... ранее самостоя-
самостоятельных вопросов, близких по методу решения или по
содержанию. Пересмотрены все решения вопросов; в
ряде случаев эти решения упрощены или заменены луч-
лучшими. Особенно сильные изменения внесены в решения
вопросов, касающихся распределения вычетов и невы-
невычетов п-а степени и первообразных корней, а также
оценок соответствующих тригонометрических сумм.
И. М. Виноградов

ГЛАВА ПЕРВАЯ.
ТЕОРИЯ ДЕЛИМОСТИ.
§ 1. Основные понятия и теоремы.
а. Теория чисел занимается изучением свойств це-
целых чисел. Целыми мы будем называть не только чис-
числа натурального ряда 1, 2, 3, ... (положительные це-
целые), но также нуль и отрицательные целые —1, —2,
-3, ...
Как правило, при изложении теоретического матери-
материала мы будем обозначать буквами только целые числа.
Случаи, когда буквы могут обозначать и не целые
числа, если последнее не будет ясно само по себе, мы
будем особо оговаривать.
Сумма, разность и произведение двух целых а и b
будут также целыми, но частное от деления а на Ъ
(если Ъ не равно нулю) может быть как целым, так и
не целым.
Ь. В случае, когда частное от деления а на Ъ — це-
целое, обозначая его буквою q, имеем а = Ьд, т. е. а рав-
равно произведению Ь на целое. Мы говорим тогда, что а
делится на Ь или что Ъ делит а. При этом а называем
кратным числа Ь и Ъ — делителем числа а. То обсто-
обстоятельство, что Ь делит а, записывается так: Ь\а.
Имеют место две следующие теоремы.
1. Если а кратно т, т кратно Ь, то а кратно Ь;
Действительно, из а = а1т, m = m1b следует a = a1m1b,
где a-jnx — целое. А это и доказывает теорему.
¦ 2. Если в равенстве вида k + I + ...+n = p + q+...+s
относительно всех членов, кроме какого-либо ЬднЬго,*

t	ГЛ. I. ТЕОРИЯ ДЕЛИМОСТИ
известно, что они кратны Ь, то и этот один член
кратен Ь.
Действительно, пусть таким членом будет к. Имеем
l = ljb, ..., n = n1b, р — рф, q — qxb	s= s^b,
к — p + g+...+s — l— ...—n =
= {Pi + gi+ • ..+si-/,— ...—«!> b.
А это и доказывает теорему.
с. В общем случае, включающем, как частный, и
случай, когда а делится на Ь, имеем теорему:
Всякое целое а представляется единственным спо-
способом через положительное целое b в форме
a=bq + r\ 0<г < Ь.
Действительно, одно представление а в такой форме
получим, взяв бд равным наибольшему кратному числа
Ь, не превосходящему а. Допустив, что также a = bqi+r1,
0<Г!<6, получим 0= b(g —gi) + г — г1г откуда следует
B, Ь), что r — rl кратно Ь. Но ввиду \г — г1\ <_ b послед-
последнее возможно лишь при г — г1 — 0, т. е. при г = Г],
откуда вытекает также q = q^.
Число q называется неполным частным, а число
г — остатком от деления а на Ь.
Пример. Пусть Ъ- = 14. Имеем
177 = 14-12 + 9;	0 < 9 < 14,
-64 = 14. (-5)+ 6; 0<6<14,
154 = 14-11 + 0;	0 = 0<14.
§ 2. Общий наибольший делитель.
а. В дальнейшем мы будем рассматривать лишь поло-
положительные делители чисел. Всякое целое, делящее
одновременно целые а, Ь, .... I, называется их общим
^делителем. Наибольший из общих делителей называется
рбщим наибольшим делителем и обозначается символом
(а, Ь, ..., I). Ввиду конечности числа общих делителей
существование общего наибольшего делителя очевидно.
Если (а, Ь, ,,,, l) = i, то а, Ь, ,,,, I называются взаимно

i 2. ОБЩИЙ НАИБОЛЬШИЙ ДЕЛИТЕЛЬ	9
простыми. Если каждое из чисел а, Ь, ..., I взаимно
просто с каждым другим из них, то а, Ь, ..., / назы-
называются попарно простыми. Очевидно, числа попарно
простые всегда и взаимно простые; в случае же двух
чисел понятия «попарно простые» и «взаимно простые»
совпадают.
Примеры. Числа 6, 10, 15 ввиду F, 10, 15) = 1 —
взаимно простые. Числа 8, 13, 21 ввиду (8, 13) = (8, 21) =
= A3, 21) — 1 — попарно простые.
Ь. Сначала займёмся общими делителями двух чисел.
1.	Если а кратно Ъ, то совокупность общих делите-
делителей чисел а и Ь совпадает с совокупностью делителей
одного Ь; в частности, [а, Ъ) = Ъ.
Действительно, всякий общий делитель чисел а и 6
является делителем и одного 6. Обратно, раз а кратно Ь,
то A, Ь, § 1) всякий делитель числа Ь является также
делителем числа а, т. е. он будет общим делителем
чисел baa. Таким образом совокупность общих дели-
делителей чисел а и Ь совпадает с совокупностью делителей
одного Ь. А так как наибольший делитель числа Ь есть
само Ъ, то (а, Ь) — Ь.
2.	Если
то совокупность общих делителей чисел а и b совпадает
с совокупностью общих делителей чисел b и с; в частно-
частности, (a, b) = (b, с).
Действительно, написанное выше равенство показы-
показывает, что всякий общий делитель чисел а и b делит
также и с B, Ь, § 1) и, следовательно, является общим
делителем чисел b и с. Обратно, то же равенство пока-
показывает, что всякий общий делитель чисел бис делит а
и', следовательно, является общим делителем чисел а и Ъ.
Таким образом общие делители чисел а и b суть те же,
что и общие делители чисел b и с; в частности, должны
совпадать и наибольшие из этих делителей, т. е.
(a, b) = F, с).
с. Для разыскания общего наибольшего делителя,
а также для вывода его важнейших свойств применяется
алгоритм Эвклида. Последний состоит в нижеследующем.

10
ГЛ. I. ТЕОРИЯ ДЕЛИМОСТИ
Пусть а и 6—положительные целые. Согласно о, § 1 на-
находим ряд равенств:
a = bq1 + r2,	0<r2<b,
Ь = rzq2 + rs,	О < г3 < г2,
A)
Гп-2^ >"n~iqn-i +Гп, 0 <Гп< /•„_!
заканчивающийся, когда получаем некоторое rn+i=0.
Последнее неизбежно, так как ряд Ь, г2, г3, ... как
ряд убывающих целых не может содержать более чем b
положительных.
d. Рассматривая равенства A), идя сверху вниз,
убеждаемся (Ь), что общие делители чисел а и Ъ одина-
одинаковы с общими делителями чисел b и г2, далее одина-
одинаковы с общими делителями чисел г2 и г3, чисел г3 и г4, .. .,
чисел rn-i и гп, наконец, с делителями одного числа гп.
Одновременно с этим имеем
{a, b) = (b, r2) = {r2, /%,)= . . . =(/•„_!, гп) = гп.
Мы приходим к следующим результатам.
1.	Совокупность общих делителей чисел а и b совпа-
совпадает с совокупностью делателей их общего наибольшего
делителя.
2.	Этот общий наибольший делитель равен гп, т. е.
последнему не равному нулю остатку алгоритма Эвклида.
Пример. Применим алгоритм Эвклида к отысканию
E25, 231). Находим (вспомогательные вычисления при-
приведены слева)
42
42
63
42
21
2
231
189
42
1
525
462
63
3
231
525 =
231 =
63 =
42 =
231 • 2 +
63- 3 +
42. 1 +
21 -2.
63,
42,
21,

§ 2. ОБЩИЙ НАИБОЛЬШИЙ ДЕЛИТЕЛЬ	И
Здесь последний положительный остаток есть г4 = 21.
Значит, E25, 231) = 21.
е. 1. Обозначая буквою т любое положительное целое,
имеем (am, bm) = (а, Ь)т.
2. Обозначая буквою 8 любой общий делитель чисел
,	Га Ь\ (а, Ъ)
а и Ъ, имеем ( у, -v ) = * I в частности, имеем
(, а,. , -,—— ) = 1, т. е. частные от деления двух чисел
\(а, Ь) (а, Ь)у '	v
на их общий наибольший делитель суть числа взаимно
простые.
Действительно, умножим равенства A) почленно на т.
Получим новые равенства, где вместо а, Ь, г2, ¦ • ¦, гп
будут стоять am, bm,. r2m, . . ., гпт. Поэтому (am, bm) =
= rnm, и таким образом верно утверждение 1.
Применяя утверждение 1, находим
(a, b)={-o, To
отсюда следует утверждение 2.
f. 1. Если, (а, 6)=1, то (ас, Ь) = (с, Ь).
Действительно, (ас, Ь) делит ас и be, значит A, d),
оно делит и (ас, Ьс), ввиду 1,е равное с; но (ас, Ь)
делит и Ъ, поэтому оно делит и (с, Ь). Обратно, (с, Ь)
делит ас и Ь, поэтому оно делит и (ас, Ъ). Таким обра-
образом (ас, Ь) и (с, Ь) взаимно делят друг друга и, следо-
следовательно, равны между собою.
2.	Если (а, Ъ) = 1 и ас делится на Ь, то с делится
на Ь.
Действительно, ввиду (а, Ь) = 1 имеем (ас, 6) = (с, Ь).
Но раз ас кратно Ь, то A, Ь) имеем (ас, Ъ) = Ь, значит,
и (с, Ь) = Ь, т. е. с кратно Ъ.
3.	Если каждое аъ а2, . . ., ат взаимно просто
с каждым Ьх, Ъ2, . . ., Ьп, то и произведение а±а2 .. . ат
взаимно просто с произведением Ьф2 . . . Ьп.
Действительно (теорема 1), имеем
... ат, bk) = (а2а3 . . . ат, bk) =
= (а3 >. . ат, bk) = ... = (ат, 6j.),= 1„

12	ГЛ. I. ТЕОРИЯ ДЕЛИМОСТИ
и далее, полагая для краткости ага2 ... ат = А, точно
таким же путём найдём,
(&А&3 ••• bn, A) = (b2bs ... bn, A) =
= (Ь8 ••• Ъя,А)=...=(Ьп,А) = 1.
g. Задача отыскания общего наибольшего делителя
более чем двух чисел сводится к таковой для двух
чисел. Именно, чтобы найти общий наибольший дели-
делитель чисел аъ а2, ..., ап, составляем ряд чисел:
(«1, «г) = d2, (d2, a3) = d3, (d3, а4) = d4	(dn-i, an) •-= dn.
Число dn и будет общим наибольшим делителем всех
данных чисел.
Действительно A, d), общие делители чисел ах и а2
совпадают с делителями rf2! поэтому общие делители
чисел аъ а2 и аг совпадают с общими делителями чисел
d2 и а3, т. е. совпадают с делителями d3. Далее убе-
убедимся, что общие делители чисел аъ аг, az, я4 совпа-
совпадают с делителями rf4 и т. д. и, наконец, что общие
делители чисел аг, а2, ..., ап совпадают с делите-
делителями dn. А так как наибольший делитель dn есть
само dn, то оно будет общим наибольшим делителем
чисел аъ а2, ..., ап.
Просматривая приведённое доказательство, убеждаем-
убеждаемся, что теорема 1, d верна и для более чем двух чисел.
Верны также и теоремы 1, е и 2, е, потому что от умно-
умножения на т или разделения на 5 всех чисел аи а2, .. ., ап
точно так же и все d2, ds, .. ., dn умножатся на т
или разделятся на 8.
§ 3. Общее наименьшее кратное.
a.	Всякое целое, кратное всех данных чисел, назы-
называется их общим кратным. Наименьшее положитель-
положительное общее кратное называется общим наименьшим
кратным,
b.	Сначала займёмся общим наименьшим кратным
двух часе д. Русть М — какое-либо общее кратное целых

§ S. ОБЩИЙ НАИМЕНЬШЕЕ KVATHOE	13
а и b. Так как оно кратно а, то М = ак, где А —целое.
Но М кратно и Ь, поэтому целым должно быть и
ак_
Ъ '
что, полагая {a,b) = d, a — axd, b = btd, можно предста-
представить в виде Ц-, где (a^b^^l B, е, § 2). Поэтому
Ъ
B, f, § 2) к должно делиться на Ьъ к — bxt = -т t, где
t - целое. Отсюда
Обратно, очевидно, что всякое М такой формы кратно
как а, так и Ь, и, таким образом, эта форма даёт общий
вид всех общих кратных чисел а и Ь.
Наименьшее положительное из этих кратных, т. е.
общее наименьшее кратное, получим при t — 1. Оно будет
аЪ
Введя т, можно полученную для М формулу перепи-
переписать так:
Последнее и предпоследнее равенства приводят к тео-
теоремам:
1.	Общие кратные двух чисел совпадают с кратными
их общего наименьшего кратного.
2.	Общее наименьшее кратное двух чисел равно их
произведению, делённому на их общий наибольший де-
делитель.
, с. Пусть требуется найти общее наименьшее кратное
более чем двух чисел alt a2, ..., ап. Обозначая вообще
символом [а, Ь] общее наименьшее кратное чисел а и Ь,
составим ряд чисел:
[al!a2] = m2, [m2, а3] =т3, ..., [тп_и ап] = тп.
Полученное таким путём тп и будет общим наимень-
наименьшим кратным всех данных чисел.

14	г л. i. теория делимости
Действительно A, b), общие кратные чисел aL в а
совпадают с кратными т2, поэтому общие кратные чисел
аъ а2 и а3 совпадают с общими кратными тг и аъ, т. е.
совпадают с кратными т3. Далее убедимся, что общие
кратные чисел alt а2, а3, а4 совпадают с кратными mi
и т. д. и, наконец, что общие кратные чисел аъ а2, .. ., ап
совпадают с кратными тп, а так как наименьшее поло-
положительное кратное тп есть само тп, то оно и будет
общим наименьшим кратным чисел аг, а2, ..., ап.
Просматривая приведённое доказательство, видим, что
теорема 1, b верна и для более чем двух чисел. Кроме
того, убеждаемся в справедливости следующей теоремы:
Общее наименьшее кратное попарно простых чисел
равно их произведению.
§ 4. Связь алгоритма Эвклида с непрерывными
дробями.
а. Пусть а — любое вещественное число. Обозначим
буквою qx наибольшее целое, не превосходящее а. При
нецелом а имеем
<* = ?i + —; а2>1.
Точно так же при нецелых а2, ..., as_i имеем
I
«2 = ?2 + —; ч > 1;
ввиду чего получаем следующее разложение а в непре-
непрерывную дробь:
+	г

§ 4. связь алгоритма эвклида с непрёрывн. дробями 15
Если а иррациональное, то в ряде а, а2, ..., очевидно,
не может встретиться целых, и указанный процесс может
быть неограниченно продолжен.
Если а рациональное, как увидим далее (Ь), в ряде
а, а2, . .. непременно встретится целое, и указанный
процесс будет конечен.
Ь. Если а — рациональная несократимая дробь а — -г,
то* разложение а в непрерывную дробь тесно связано
с алгоритмом Эвклида. Действительно, имеем
a = bq+r;	| = ? +
откуда
b — r a
1-2 /n-l<7i
i-i rnqn,
a
b
b
r* q
Й = <?
i
1
¦ 4- Г«
2+ /-2'
с. Числа qx, q2, ..., участвующие в разложении числа
а в непрерывную дробь, называются неполными частными
(в случае рационального а это будут согласно b непол-
неполные частные последовательных делений алгоритма Эв-
клида), дроби же
11
называются подходящими дробями.

16
ГЛ. I. ТЕОРИЯ ДЕЛИМОСТИ
d. Весьма простой ]'~закон образования подходящих
дробей легко найдём, замечая, что о, (s > 1) получается
из 88_i заменой в буквенном выражении для 8e_i числа
gs_i на gs-i+— .
Действительно, полагая для единообразия Ро = 1,
Qo = 0, мы можем подходящие дроби последовательно
Г	АР.
представить в следующем виде (здесь равенство ~в~==/тг
пишем, желая обозначить А символом Ps, а В симво-
символом
"<?.'
92
Qu
и т. д. и вообще
Таким образом числители и знаменатели подходящих
дробей мы можем последовательно вычислять по формулам
з-2, \
I,}
B)
Эти вычисления полезно производить по следующей
схеме:
1
0
?1
1
Чг
Р*
Q*
Р*-2
Qs-2
Ps-i
Qs-i
Qs
...
Pn-i
Qn-i
In
a
b

4. СВЯЗЬ АЛГОРИТМА ЭВКЛИДА С НЕПРЕРЫВН. ДРОБЯМИ	17
Пример. Разложим в непрерывную дробь число -щ .
Здесь
105
76
~2 ~М~ +
9
8
29
27
2
4
38
29
9
~3
29
1
Поэтому указанная выше схема даёт:
Ps
Qs
1
0
2
2
1
1
3
1
3
11
4
4
47
17
2
105
38
е. Рассмотрим разность os— 3s_i соседних подходящих
дробей. При s > 1 находим
где hs = PsQs_l — QsPs_l; подставляя же вместо Ps и (?s
их 'выражения B) и делая очевидные упрощения, полу-
получим hs= — As_j. Последнее в соединении с h1 = ql • 0 —
— 1 . 1 = _ 1 даёт hs = (— l)s. Итак,
C)

13	ГЛ. I. ТЕОРИЯ ДЕЛИМОСТИ
Пример. В таблице примера, приведённого в d, имеем
105- 17-38-47 = (-1M= -1.
f.	Из C) следует, что (Ps, Qs) делит (— l)s = ^ 1
B, b, § 1). Поэтому (Ps, <2S)=1, т. е. подходящие дроби
Р„
-у~ несократимы.
g.	При 8S, не равном а (т. е. исключается случай,
когда, при рациональном a, 8S является последней подхо-
подходящей дробью), исследуем знак разности os — а. Очевидно,
os получается заменой as на qs в выражении A) для а. Но,
как видно из а, от такой замены
as уменьшится,
a^j увеличится,
as_2 уменьшится,
(при нечётном s уменьшится,
a \при чётном s увеличится.
Поэтому Ss — a < О при нечётном s и 8, — a > 0 при-'
чётном s, и следовательно, знак 8S — а совпадает со
знаком (— l)s.
h. Имеем
1ь\<
Действительно, при 8s = a это утверждение следует
(со знаком равенства) из D). При 8S, не равном а, оно
следует (со знаком неравенства) из D) и из того об-
обстоятельства, что, ввиду g, os — а и 8S_1 — а имеют разные
знаки.
§ 5. Простые числа.
а. Число 1 имеет только один положительный дели-
делитель, именно 1. В этом отношении число 1 в ряде на-
натуральных чисел стоит особо.
Всякое целое, большее 1, имеет не менее двух
делителей, именно 1 и самого себя; если этими дели-

§ 5. ПРОСТЫЕ ЧИСЛА	19
телями исчерпываются все положительные делители
целого числа, то оно называется простым. Целое > 1,
имеющее кроме 1 и самого себя другие положительные
делители, называется составным.
b.	Наименьший отличный от единицы делитель целого,
большего единицы, есть число простое.
Действительно, пусть q — наименьший отличный от
единицы делитель целого я^>1. Если бы q было состав-
составным, то оно имело бы некоторый делитель qx с условием
1 < ?i < Ч\ н0 число а, делясь на q, должно было бы
делиться и на qx (I, b, § 1), а ото противоречит нашему
предположению относительно числа q.
c.	Наименьший отличный от единицы делитель со-
составного числа а [согласно h он будет простым) не
превосходит \/ а.
Действительно, пусть q — этот делитель, тогда a~qax,
o-i~>q, откуда, перемножая и сокращая на аи получим
a><f, q <Vа-
d.	Число простых чисел бесконечно велико.
Справедливость этой теоремы следует из того, что,
каковы бы ни были различные простые ръ р2, ¦ ¦ ¦ , р^,
можно получить новое простое, среди них не заклю-
заключающееся. Таковым будет простой делитель суммы
Р1Р2 • ¦ ¦ Рк ~Ь 1, который, деля всю сумму, не может
совпадать ни с одним из простых ръ рг, ... , р^B, Ь, § 1).
e.	Для составления таблицы простых чисел, не пре-
превосходящих данного Л7, существует простой способ,
называемый решетом Эратосфена. Он состоит в ниже-
нижеследующем.
Выписываем числа
-¦ 1, 2, ...,N.	A)
Первое большее единицы число этого ряда есть 2;
оно делится только на 1 и на самого себя, следователь-
следовательно, оно простое.
Вычеркнем из ряда A) (как составные) все числа,
кратные 2, кроме самого 2. Первое следующее за 2
невычеркнутое число будет 3; оно не делится на 2
(иначе оно оказалось бы вычеркнутым),/следовательно,

20	ГЛ. I. ТЕОРИЯ ДЕЛИМОСТИ
3 делится только на 1 и на самого себя, а потому оно
также будет простым.
Вычёркиваем из ряда A) все числа, кратные 3, кроме
самого 3. Первое следующее за 3 невычеркпутое число
будет 5; оно не делится ни на 2, пи на 3 (иначе оно
оказалось бы вычеркнутым). Следовательно, 5 делится
только на 1 п на самого себя, а потому оно также
будет простым.
И т. д.
Когда указанным способом уже вычеркнуты все числа,
кратные простых, меньших простого р, то все невычер-
кнутые, меньшие р2, будут простые. Действительно,
всякое составное а, меньшее р1, нами уже вычеркнуто,
как кратное его наименьшего простого делителя, который
|/<т?. Отсюда следует:
1.	Приступая к вычёркиванию кратных простого р,
эгп,о вычёркивание следует начинать с р2.
2.	Составление таблицы простых чисел < N закон-
закончено, как только вычеркнуты все составные кратные про-
простых, не превосходящих \/~N.
§ 6. Единственность разложения на простые
сомножители.
a.	Всякое целое а или взаимно просто с данным
простым р, или оке делится на р.
Действительно, (а, р), будучи делителем р, может
быть равно или 1, или р. В первом случае а взаимно
просто с р, во втором а делится на р.
b.	Если произведение нескольких сомножителей де-
делится па р, то, по крайней мере, один из сомножите-
сомножителей делится на р.
Действительно (а), каждый сомножитель или взаимно
прост с р, или же делится на /;. Если бы все сомножи-
сомножители были взаимно просты с р, то и их произведенпе
C, f, § 2) было бы взаимно просто с р; поэтому хоть
один сомножитель делится на р.
c.	Всякое целое, большее единицы, разлагается на
произведение простых сомножителей и притом един-

6. ЕДИНСТВЕННОСТЬ РАЗЛОЖЕНИЯ НА СОМНОЖИТЕЛИ 21
ственным способом, если отвлечься от порядка следова-
следования сомножителей.
Действительно, пусть а — целое, большее единицы;
обозначая буквою р± его наименьший простой делитель,
имеем а — рхау. Если aL > 1, то, обозначая буквою р2
его наименьший простой делитель, имеем ах = р2а2. Если
а2 > 1, то подобно этому находим а2 = Рзаз и т- Д-> пока
не прпдём к какому-либо ап, равному единице. Тогда
an-i = pn. Перемножая все найденные равенства и произ-
производя сокращение, получим следующее разложение а
на простые сомножители:
а = рхр2 ... рп.
Допустим, что для того же самого а существует
и второе разложение на простые сомножители a = <7i^2 •¦• ch-
Тогда
PiPz ¦ ¦ ¦ P,i = qi<h ¦¦¦ qs-
Правая часть этого равенства делится на qx. Следо-
Следовательно (Ь), по крайней мере, один из сомножителей
левой части должен делиться на qx. Пусть, например, рх
делится на дх (порядок нумерации сомножителей в нашем
распоряжении); тогда p-l=q1 (pi кроме 1 делится только
на рх). Сокращая обе части раз^саства на /?i = <7i> имеем
РчРз • ¦ • Рп= ^2,9з ¦ ¦ • 9S- Повторяя прежнее рассуждение
применительно к этом}' равенству, получим р3 . . . рп =
= q3 . . . qs и т. д., пока, наконец, в одной части равен-
равенства, например в левой, не сократятся все сомножители.
Но одновременно должны сократиться и все сомножители
правой части, так как равенство 1 = qn-{ i • • • <7« при
?п4 1, ••• ,1$, превосходящих 1, невозможно.
Таким образом, второе разложение на простые сомно-
сомножители тождественно первому.
d. В разложении числа а на простые сомножители
некоторые из них могут повторяться. Обозначая буква-
буквами ръ р2, . . . , рк различные из них и буквами а1; а2, .. ., ак
кратность их вхождения в а, получим так называемое
каноническое разложение числа а на сомножители:
O.I nO.9	a,
a--- i ?Гг ¦ ¦ ¦ Pkk-

22	гл- I- ТЕОРИЯ ДЕЛИМОСТИ
Пример. Каноническое разложение числа 588000
будет: 588 000 =25 • 3 • 53 • 72.
е. Пусть a = pip2 ... рк — каноническое разложе-
разложение числа а. Тогда все делители а суть все числа вида
Действительно, иусть d делит а. Тогда (Ь, § 1)
a--dq н, следовательно, все простые делители d входят
в каноническое разложение а с показателями, не мень-
меньшими тех, с которыми они лходят в каноническое раз-
разложение d. Поэтому d имеет вид A).
Обратно, всякое d вида (i), очевидно, делит а.
Пример. Все делители числа 720 = 24-32-5 иолу-
чим, если в выражении 2fJl3^5^3 заставим рь р2, |3S неза-
независимо друг от друга пробегать значения C1 = 0, 1, 2, 3, 4;
3., = 0, 1, 2;,33 = 0, 1. Поэтому указанные делители будут:
1, 2, 4, 8, 16, 3, 6, 12, 24, 48, 9, 18, 36, 72, 144,,
10, 20, 40, 80, 15, 30, 60, 120, 240, 45, 90, 180, 360,
720.
Вопросы к главе I.
1.	Пусть а и Ъ — целые, не рапные одновременно нулю, и
d — ахь + by u — наименьшее положительное число вида ах + by
(х и «/ — целые). Доказать, что d = (a, Ь). Отсюда вывести тео-
теорему 1, d, § 2 и теоремы е, § 2. Обобщить эти выводы, рассма-
рассматривая числа вида ах+Ъу - ... i /м.
2.	Доказать, что из всех рациональных дробей со зцаменате-
Р
лями <;<3S подходящая дробь 8а= ~ представляет число а наи-
ч*
более точно.
3.	Пусть вещественное число а разложено в непрерывную
дробь, JV — целое положительное, к—число его десятичных зна-
знаков, п — наибольшее целое с условием Qn<iN. Доказать, что
п ^Ьк+ 1. Для доказательства выражения для Q2> <?з> Qi< ¦tQn
следует сравнить с теми, которые они имели бы, если бы все д„
были равпы 1, л сравнить далее с числами 1, (•, с2, ..., с,11'1, где
J; — положительный корень уравнения С2 — 5+1.
4.	Пусть г>1. Ряд расположенных в порядке возрастания
рациональных несократимых дробей с положительными знамена-
знаменателями, не превосходящими т, называется рядом Фарея, отве-
отвечающим т.

ВОПРОСЫ К ГЛАВЕ I	23
а. Доказать, что часть ряда Фарея, отвечающего	т, содер-
содержащая дроби а, с условием 0 jsJ а <^С 1 может быть	получена
О 1
следующим способом: пишем дроби у > -г • Если 2<-.,	то между
,	„ 0 -f 1 1
этими дробями вставим еще дробь -г—г-т=-^-, затем в полученном
0 11
ряде у > "о" > "Г межДУ каждыми двумя соседними дробями
—¦ и -j- с b1 + d1^^ вставим дробь -^—— и т. д. до тех пор,
пока это возможно. Предварительно доказать, что для любой
^ „ or. с
пары соседних дрооеи у- и — ряда, получаемого указанным
способом, имеем ad— be =—1.
r b. Рассматривая ряд Фарея, доказать теорему: пусть ^>1,
когда всякое вещественное а можно представить в форме
с. Теорему вопроса b доказать, пользуясь h, § 4.
5.	а. Доказать бесконечность числа простых чисел вида
km + 3.
b. Доказать бесконечность числа простых чисел лшда 6т + 5.
6.	Доказать бесконечность числа простых чисел, подсчиты-
подсчитывая число чисел, не превосходящих N, в каноническое разложе-
разложение которых не входят простые числа, отличные от plt p2, .... рк-
7.	Пусть К — целое положительное. Доказать, что в ряде
натуральных чисел имеется бесчисленное множество последова-
последовательностей М, М + 1, ¦.., М + К — 1, не содержащих простых
чисел.
8.	Доказать, что среди чисел, представляемых многочленом
аохп J- а1хп~1 + ... + а„, где п > 0, а0, а,, .. ., ап —целые иа0 > 0,
имеется бесчисленное множество составных.
9.	а. Доказать, что неопределённому уравнению
x3+y2 = z2, x>0,y>0, z>0, (x, у, z) = l	A)
удовлетворяют те и только те системы х, у, z, где одно из чисел
х и у имеет вид 2uv, другое — вид и2 — v2, наконец, z имеет вид
и2 -t г?2; при этом и > v > 0, (и, v) = i, uv — чётное.
b. Пользуясь тедэремой вопроса а, доказать неразрешимость
в целых положительных х, у, z уравнения х* + 1/4 = г2.
10.	Доказать теорему: если уравнение хп + а1хп~ + .. ¦ +
-:гап = 0, где п>0 и аъ ..., а„ —целые, имеет рациональный
корень, то этот корень —целое число.

24	ГЛ. I. ТЕОРИЯ ДЕЛИМОСТИ
11	1
11,	а. Пусть S = —¦ -f — 4- ... +— ; п > 1. Доказать, что ? —
ue целое.
11	1
b. Пусть S = — +—-+.-. + к—гТ'га>0- Доказать, что ,У —
о о	Ли ~г 1 ¦
не целое.
12.	Пусть я — целое, п > 0. Доказать, что все коэффициенты
разложения бинома Ньютона (а 4 Ь)п будут нечётными тогда
и только тогда, когда п имеет вид 2к — 1.
Численные примеры к главе I.
1,	а. Применяя алгоритм Эвклида, найти F188, 4709).
Ь. Найти (81 719, 52 003, 33 649, 30107).
125
2,	а. Разложив в непрерывную дрооь a = -qo~ и составив
таблицу подходящих дробей (d, § 4), найти: а) 34, В) предста-
представление а в форме, указанной в вопросе 4, Ь, считая т = 20.
, г,	*	5391
Ь. Разложив в непрерывную дробь a = w^ и составив
О и /О
таблицу подходящих дробей, найти: а) $&, §) представление a
в форме, указанной в вопросе 4, Ь, считая т = 1000.
3,	Составить ряд дробей Фарея (вопрос 4) от 0 до 1, исклю-
исключая 1, со знаменателями, не превосходящими 8.
4,	Составить таблицу простых чисел, меньших 100.
5,	а. Найти каноническое разложение числа 82 798 848.
Ь. НайтР! каноническое разложение числа 81 057 226 635 000.

ГЛАВА ВТОРАЯ.
ВАЖНЕЙШИЕ ФУНКЦИИ, ВСТРЕЧАЮЩИЕСЯ
В ТЕОРИИ ЧИСЕЛ.
§ 1. Функции [as], {ж).
a.	Важную роль в теории чисел играет функция [х\;
она определяется для ьсех вещественных х и представ-
представляет собою наибольшее целое, не превосходящее х. Эта
функция называется целой частью от х.
Примеры.
[7] = 7; [2,6] = 2; [-4,75]=-5.
Иногда рассматривается также функция {х)=х — [х\.
Эта функция называется дробной частью от х.
Примеры.
{7} = 0; {2,6)=-0,6; {-4,75} =0,25.
b.	Чтобы показать пользу введённых нами функций,
докажем теорему:
Показатель, с которым данное простое р входит в
произведение п\, равен
Действительно, число сомножителей произведения га!,
кратных р, будет — , из них кратных р2 будет \—2 ;
из этих последних кратных ps будет -^ и т. д. Сум-
Сумма указанных чисел и даст искомый показатель, так
как каждый сомножитель произведения п!, кратный

26	ГЛ. II. ВАЖНЕЙШИЕ ФУНКЦИИ В ТЕОРИИ ЧИСЕЛ
рт, но не pmAi, считается указанным путём т раз, как
кратный р, р2, ра	наконец, рт.
Пример. Показатель, с которым число 3 входит
в произведение 40!, будет следующий:
§ 2. Суммы, распространённые на делители числа.
а. Особенно важную роль в теории чисел играют муль-
мультипликативные функции. Функция 9 (а) называется муль-
мультипликативной, если выполнены следующие условия:
1.	Функция 9 (а) определена для всех целых положи-
положительных а и не обращается в нуль хотя бы при одном
таком п.
2.	Для любых положительных взаимно простых at
и я2 имеем
Пример. Нетрудно видеть, что мультипликатив-
мультипликативной будет функция 9(a) = as, где s — любое веществен-
вещественное, или комплексное, число.
b.	Из указанных свойств функции б (а), в частности,
следует, что 8A)=1. Действительно, пусть б (а0) не
равно нулю, тогда 0 (а0) = 8 A • а0) = 9 A) 9 (а0), т. е.
9A) = 1. Кроме того, получается следующее важное
свойство: если Ь1(а) и 92 (а) — функции мультипликатив
ные, то и 90 (а) — %1 (а) 92 (а) — также функция мульти-
мультипликативная. Действительно, находим
боA) = 91A)92A) = 1.
Кроме того, при (аь а2) = 1 находим
= 9Х (ах) 9Х (а2) 92 (ах) 92 (а2) =
(а2) 92 (в2) = 90 (а,) 90 (а2).
c.	Пусть 9 (а)—мультипликативная функция и а =
'—pi1 pi; ¦ . ¦ plk — каноническое разложение числа а. Тогда,
обозначая символом ^ сумму, распространённую на
4\а

§ 2. СУММЫ, РАСПРОСТРАНЁННЫЕ НА ДЕЛИТЕЛИ ЧИСЛА 27
все делители d числа а, имеем
d\a
(в случае а=1 правую часть считаем равной 1).
Чтобы доказать это тождество, раскроем скобки
в правой части. Тогда получим сумму слагаемых вида
причём ни одно такое слагаемое не будет пропущено а.
не повторится более одного раза, а это (о, § 6, гл. 1)
как раз будет то, что стоит в левой части.
d. При 9 (а) = as тождество с примет вид
d\a
11 _J_ rt s -L 2 s j_	i cti s\	I \\
В частности, при s=l левая часть A) представит
сумму делителей S(a)' числа а. Упрощая правую часть,
получим
Л W = ^Г=Т	^1Г^ ' • • Рк-1 '
Пример.
04+1 I	Q2+1 Л	К1+1	 4
5G20) = ^B* ¦ З2 • 5) = - 2_7/ • ^Ег" 5-1 =2'118-
' При s = 0 левая часть A) представит число делите-
делителей х (а) числа а, и мы получим
Пример.
¦с G20) = D+1) B+1) A + 1) = 30.

28	ГЛ. II. ВАЖНЕЙШИЕ ФУНКЦИИ В ТЕОРИИ ЧИСЕЛ
§ 3. Функция Мёбиуса.
а. Функция Мебиуса р(а) определяется для всех
целых положительных а. Она задаётся равенствами:
[х(а) = 0, если а делится на квадрат, отличный от еди-
единицы; ji(a) = (—• 1)*, если а не делится на квадрат, от-
отличный от единицы, при этом к обозначает число простых
делителей числа а; в частности, при я=1 считаем k = 0,
поэтому принимаем ,иA) = 1.
Примеры.
;.B)=-1, рF) = 1,
I* C)	1, цG)=-1, р.A1)= —1,
ft D) = 0,	р.(8) = 0,
b. Пусть % {а)— мультипликативная функция и
а = р\хр^ . . . plk
— каноническое разложение числа а. Тогда
2 [л (d) б (d) = A — б (pi)) A — б (/;2)) • ¦ ¦ A —б (рь)).
d\a
(В случае а=1 правую часть считаем равной 1.)
Действительно, функция \>-(а), очевидно, мультипли-
мультипликативная. Поэтому мультипликативной будет и функция
В1(а) = [а (а) 9 (а). Применяя к последней тождество с,
§ 2 и имея в виду, что бх (/?)=— 6 (/?); 61(/?s)=0 при
s>l, мы и убедимся в справедливости нашей теоремы.
с. В частности, полагая б(а) = 1, из b получим
= 0, если а > 1,
. = 1, если а = 1.
<2\а
Полагая же 9(d)= —, получим
	Vl	)¦•¦ М	) >' если О-~> ^ !
если а=1.

i .ФУНКЦИЯ ЭЙЛЕРА	29
Л. Пусть целым положительным
Ь = Oj, 02, . . ., Оп
отвечают любые вещественные или комплексные / = /i,
/2. • • •> fn- Тогда, обозначая символом S' сумму значений /,
отвечающих значениям о, равным 1, и символом Sd
сумму значений /, отвечающих значениям 8, кратным
d, будем иметь
где с/ пробегает все целые положительные числа, деля-
гцие хоть одно значение о.
Действительно, ввиду с имеем
S'=h 2^W + /a 2 ¦•(<*)+ ••• +/»SH-(d)-
d\62	d\in
Собирая же вместе члены с одним и тем же значением
d 11 вынося при этом \>. (d) за скобки, в скобках полу-
получим сумму тех и только тех /, у которых соответ-
соответствующие им о кратны d, а это и ость Sd.
§ 4. Функция Эйлера.
a.	Функция Эйлера ер (а) определяется для всех це-
целых положительных а и представляет собою число чи-
чисел ряда
О, 1, .... а-1	A)
взаимно простых с а.
11 р и меры.
<РA) = 1, <рD) = 2,
ерB)=1, <рE) = 4,
ФC) = 2, срF) = 2.
b.	Пусть
а = аа,	а	B)
— кагюническое разложение числа а. Тогда
f> О)

30	ГЛ. II. ВАЖНЕЙШИЕ ФУНКЦИИ В ТЕОРИИ ЧИСЕЛ
или также
ср(а) = (p*i_ р*1~1) (р^2 — Р^~1) ¦ • ¦ (Pl1'^Plk~i)' D)
в частности,
ер (ра) = р° —р°-~\ о (/?) = /> — 1.	E)
Действительно, применим теорему d, § 3. При этом
числа S и числа / определим так: пусть х пробегает
числа ряда A); каждому значению ж приведём в соот-
соответствие число о — (ж, а) и число /=1.
Тогда /5" обратится в число значений 8 = (х, а),
равных 1, т. е. в ер (я). A S& обратится в число значе-
значений Ь = (х,а), кратных d. ho (x, а) может быть крат-
кратным d лишь при условии, что d — делитель числа а.
При наличии же этого условия Sd обратится ь число
значений х, кратных d, т. е. в -г . И мы получим
ер (а) = 2.^)|,
d\a
откуда ввиду с, § 3 следует формула C), а из по-
последней ввиду B) следует формула D).
Примеры.
ер F0) = 60 (l-l) (I--!) A-4) =16;
<Р(81) = 81-27 = 54;
ср E) = 5 — 1 = 4.
с. Функция ер (а) есть функция мультипликативная.
Действительно, при (я1; я2) = 1 из Ь, очевидно, следует
ер(аь й2) = <р(а1)ер(а2).
Пример, ерD05) = ср(81)ерE) = 54- 4 = 216.
d\a

ВОПРОСЫ К ГЛ. II	.	31
В справедливости этой формулы убедимся, применяя
тождество с, § 2, которое при 6 (а) = ср (р) даёт
2
d\a
... A + <рЫ+ *(pD+ ¦¦¦+.?(/^-)).
Ввиду E) правая часть перепишется так:
A+(л-1) + (/>?-л) + ¦¦¦ + (rt-i'T1)) ¦•¦
• • • A + (Л - 1) + (Pi -Ръ)+...+ (р'к* ~ Pi" ')),
что после приведения в каждой большой скобке подоб-
подобных членов окажется равным ?/°l/?°2,*.. pakk—a.
Пример. Полагая а = 12, находим
ср A) + ср B) + ср C) + ср D) + ср F) + ? A2) =
Вопросы к глапс II.
1, а. Пусть в интервале Q^x^R функция /(х) непрерывна
и неотрицательна. Доказать, что сумма
выражает число целых точек (точек с целыми координатами)
плоской области: Q < х^Н, 0 < y^Cf(x).
Ъ. Пусть Р и Q — положительные почётные взаимно простые.
Доказать, что
	2 '
с. Пусть г > 0 и 71 — число целых точек области ж2
Доказать, что

32	ГЛ. II. ВАЖНЕЙШИЕ ФУНКЦИИ В ТЕОРИИ ЧИСЕЛ
d. Пусть п > 0 и Т—число целых точек области ж > О,
у > О, ху^.п. Доказать, что
=2 2 [т]-^»1'-
2. Пусть /1 > 0, m — целое, m>lm пробегает целые поло-
положительные числа, не делящиеся на m-ю степень целого, прево-
превосходящего 1. Доказать, что
— = п
3. Пусть положительные а и 8 таковы, что
[о*]; *=1, 2, ...; [&]; у=1, 2, ...
образуют, вместе взятые, все числа натурального ряда без
повторений. Доказать, что это имеет место тогда и только тогда,
когда а иррациональное, причём
4, а. Пусть т^>1, ? = ['] и ж(, гг2, ..., з"^ — числа 1, 2, ..., г,
расположенные в таком порядке, чтобы числа
О, {axt}, {ax^,, ..., {axt}, 1
шли не убывая. Доказать теорему вопроса 4, Ь, гл. I, рассматри-
рассматривая разности соседних чисел последнего ряда.
Ь. Пусть X, Y, ..., Z — вещественные числа, каждое из кото-
которых не меньше 1; a, fJ, ..., f — вещественные. Доказать, что суще-
существуют целые х, у, ..., z, не равные одновременно нулю, и целое и,
удовлетворяющие условиям:
\V\<Y, ..., |z|<Z,
(х, у, ...,z) =
5. Пусть а—вещественное, с — целое, с > 0. Доказать, что
6, а. Пусть а, [5, ..., X — вещественные. Доказать, что
Ь. Пусть а, 6, . .., ? — целые положительные, а + Ь + . .. + 1 — п.
Применяя Ь, § 1, доказать, что
п\
а\Ь\ ... 1\
есть целое число.

:	ВОПРОСЫ К ГЛАВЕ II	, .	&S
7.	Пусть А—целое, А > 0, р—простое и
р'*1— 1
р—1
Представляя А в форме А= ртит -f- Pm-i«m-i + ¦ • • + Pi«! + р0. где
ит — наибольшее us, не превосходящее Л, ртит — наибольшее
кратное ит, не превосходящее A, Pm-\um-i — наибольшее кратное
Mm-i> не превосходящее Л—Ртипи Рт~2ит-2 — наиболыцее кратное
ит_2, не превосходящее А— ртит — Pm-iUm^ и т. д., доказать,
что числа а с условием, что в каноническое разложение а! число />
входит с показателем А, существуют тогда и только тогда, когда
все рт, Pm-i> • ¦ •> Ри Pd меньше р, причём в этом случае указан-
указанные а суть все числа вида
а = ртРт* г + рт-хРт + ¦ ¦ ¦ + Pip2 + Pop + р',
где р' имеет значения: 0, 1, ..., р— 1.
8,	а. Пусть в интервале Qs^x^R функция /(х) имеет
вторую непрерывную производную. Полагая
г
()	{} ()
доказать, что (формула Сонина)
я
О
Ь. Пусть условие вопроса а выполняется при сколь угодно
оо
больших R, причём \ | /* (х) | dx сходится. Доказать, что
Q
оо
R)-\i ,(x)f"(x)dx,
ti
где С не зависит от R.
с. Если В принимает лишь положительные значения и отнс>
1-41"
шение -=- остаётся ограниченным сверху, то пишем.Др= О(В>

34	ГЛ. II. ВАЖНЕЙШИЕ ФУНКЦИИ В ТЕОРИИ ЧИСЕЛ
Пусть л—целое, л > 1. Доказать, что	,;
In (л!) = л In л—л+ 0 (In л).
9, а. Пусть л > 2, 9 (z, zo)= 2 *n i"> гДе P пробегает про-
стые числа. Пусть, далее, в(г) = в(г, 0) и при х > О
Л*) = в (я) + 9 (/г)
Доказать, что
ф (л) < 2л;
Ь. При л > 2 доказать, что
где р пробегает простые числа.
с. Пусть 8—произвольное положительное постоянное. Дока-
Доказать, чю в ряде натуральных чисел существует бесчисленное мно-
множество пар рп, pntl простых чисел с условием
Pn+i
d. Пусть л > 2. Доказать, что
где р пробегает простые числа и С не зависит от п.
е. Пусть л > 2. Доказать, что
п О4)-йО+»(?)>
где р пробегает простые числа и Сп не зависит от л.
10, а. Пусть в (а) —функция мультипликативная. Доказать, что
(Jj (a)— V 6 (d)—также функция мультипликативная.

ВОПРОСЫ К ГЛАВК II	¦	35
Ь. Пусть функция 0 (а) определена для всех целых положи-
положительных а и функция ф(<х) = 2 9 (<0 мультипликативная. Дока-
d\a
зать, что функция В (а) также мультипликативная.
11. Пусть при т > О тт (о) обозначает число решений неопре-
неопределённого уравнения ххх2 ... хт = а (х1г хг, ..., хт независимо друг
от друга пробегают целые положительные числа); в частности,
очевидно, с1(а)=1, ¦с2(а) = '::(а)- Доказать, что
a.	тщ (а) —функция мультипликативная.
b.	Если каноническое разложение числа о имеет вид
.. рь> то tm(a)=m*.
с. Если s произвольное положительное постоянное, то
lim imM.^0.
о-»оо а*
d- /] "^m (а) выражает число решений неравенства
х1ха ... гт ^л в целых положительных xlt х2, ..., хт.
12. Пусть R (s) обозначает вещественную часть числа s.
00
При R(s) > 1 полагаем ? (s) = ^ ~i • Пусть т > 0, т— целое.
п-1
Доказать, что
п-1
13,а. При Л(в) > 1 доказать, что
где р пробегает все простые числа.
b.	Доказать бесконечность числа простых чисел, исходя из
того, что гармонический ряд—расходящийся.
c.	Доказать бесконечность числа простых чисел, исходя
из того, что ?B)=-^—число иррациональное.
14. Пусть А(а)=1пр для а = рг, где р—простое и /—целое
положительное; Л(а)=О для других целых положительных а.

36	ГЛ. II. ВАЖНЕЙШИЕ ФУНКЦИИ В ТЕОРИИ ЧИСЕЛ
При R (s) > 1 доказать, что
оо
;'(я)	y А(п)
п=1
15.	Пусть R(s) > 1. Доказать, что
оо
р	п«=1
где р пробегает простые числа.
16,	а. Пусть п~^> 1. Применяя d, § 3, доказать, что
1= У, !»(<
Ь. Пусть If (г, г„) = ^ f (a): M W = М (х> °)"
Доказать, что
a) U (п)
с. Пусть n> I, Z —целое, / > 1, Т1 п — число целых х с усло-
условием 0 < х sZ. п, не делящихся на 1-ю степень целого, превосхо-
превосходящего 1. Применяя d, § 3, доказать, что
d-l
17, а. Пусть а—целое, а > 0, и для целых жх, хг, ..., хп
однозначно определена функция fix). Доказать, что
d\a
где jS" обозначает сумму значений / (х), распространённую
на значения х, взаимно простые с а, и Sj— сумму значений f(x),
распространённую на значения х, кратные d.
b. Пусть к > 1 и заданы системы

ВОПРОСЫ К ГЛАВК И	'	37
каждая из которых состоит из целых чисел, не равных одно-
одновременно нулю. Пусть далее для этих систем однозначно опре-
определена функция f(xlt хг, ..., Xfr). Доказать, что
где 6" обозначает сумму значений / (xlt x2, ¦¦¦, xjc), распро-
распространённую на системы взаимно простых чисел, и Sd обозначает
сумму значений f (хи х2, ..., хк), распространённую на системы
чисел, одновременно кратных d. При этом d пробегает целые
положительные числа.
с. Пусть а—целое, а > 0, и для делителей 8 числа а одно-
однозначно определена функция F(d). Полагая
d\S
доказать, что (закон обращения числовых функций)
d\a
d. Пусть целым положительным
отвечают любые вещественные, или комплексные, не равные
нулю:
/i> /г> ¦ ¦ ¦ i /п-
Доказать, что
где Р' обозначает произведение значений /, отвечающих значе-
значениям в, равным 1, Ра обозначает произведение значений /,
отвечающих значениям S, кратным d, причём d пробегает все
целые положительные числа, делящие хотя бы одно 6.
18. Пусть а-целое, а > 1, ат (п) = Iя1 + 2т + ... + пп,
%п (а)—сумма т-х степеней чисел ряда 1, 2, ..., а, взаимно про-
простых с a; Pi, Pi, ..., pjc—все простые делители числа а.
а. Применяя теорему вопроса 17, а, доказать, что
d\a
b. Доказать, что

38	ГЛ. П. ВАЖНВИШНЖ ФУНКЦИИ В ТЖОРИИ ЧИСВЛ
с. Докааать, что
4-s (в)~ (у- + (~61)>г Pip* ¦ ¦ • Р*) f («)•
19. Пусть z > 1, а —целое, а> О, 7"г—число чисел х с усло-
условиями 0<a:=SCz, (х, e) = l, s—произвольное положительное
постойнное
а. Доказать, что
b.	Доказать, что
Г« = -?¦?(«*) +О (а*).
c.	Пусть г > 1, я (г)—число простых чисел, не превосходящих г,
а—произведение простых чисел, не превосходящих \^z. Дока-
Доказать, что
d\a
20. Пусть R (s) > 1, о — целое, а > 0. Доказать, что
где в левой части п пробегает целые положительные числа,
взаимно простые с а, а в правой части р пробегает все простые
делители числа а.
21,	а. Вероятность Р того, что к целых положительных
чисел xlt х2, ... , Хк будут взаимно простыми, определим как
предел при N -* оо вероятности Рж того, что будут взаимно
простыми к чисел х1г х%, ... , х^, каждому из которых независимо
от остальных присвоено одно из значений 1, 2, ... , N, прини-
принимаемых за равновозможные. Применяя теорему вопроса 17, Ь,
доказать, что /»==(? (Л))~1.
Ь. Определяя вероятность Р несократимости дроби — анало-
if
гично тому, как в вопросе а при А=х2, доказать, что
22,	а. Пусть г>2 и Т— число целых точек (х, у) с взаимно
простыми координатами, лежащих в области х* + у* ^ га. Дока-
Доказать, что
Г=— г*+ 0 (г In г).

ВОПРОСЫ К ГЛАВЕ П	39
f b. Пусть г > 2 и Т—число целых точек (х, у, z) с взаимно
простыми координатами, лежащих в области хг -t у* + га < г'.
Доказать, что
23,	а. Первую теорему с, § 3 доказать, считая делители
числа а, не делящиеся на квадрат целого, превосходящего 1,
и имеющие 1, 2, ... простых делителей.
b.	Пусть о — целое, а > 1, d пробегает делители числа а,
имеющие не более чем пг простых делителей- доказать, что при
m чётном 2 Р1 (°0 ^ 0, а при m нечётном 2 9- W ^ 0.
c.	При условиях теоремы A, § 3, считая все / неотрицатель-
неотрицательными и заставляя d пробегать лишь числа, имеющие не более
чем m простых делителей, доказать, что
•s'^SpW-Su. j#>23i»(«0J*
в зависимости от того, будет ли m чётное или нечётное.
d.	Такие же, как в вопросе с, неравенства доказать при
условиях вопроса 17, а, считая все значения / (х) неотрицатель-
неотрицательными, а также при условиях 17, Ь, считая все значения
f(xlt xit ... , Xfr) неотрицательными.
24.	Пусть s —любое постоянное с условиями 0<з< —,
N>2, r=1njV, 0<?<iV1-6, 0<г<? (?, 0 = 1. k(N,9,Z) —
число простых чисел с условиями: р <. JV, p = qt-\-l, где t — целое.
Доказать, что
Для доказательства, полагая h=r , простые числа с ука-
указанными условиями следует рассматривать как частный случай
всех чисел с этими условиями взаимно простых с о, где а—про-
а—произведение всех простых, не превосходящих eh и не делящих д.
Следует применить теорему вопроса 23, d (условия вопроса 17, а)
с указанным о и m=2[2]nr -t-1].
25. Пусть к—чётное, к > 0, каноническое разложение числа а
имеет вид а = р1р2 ... рк и d пробегает делители числа а с усло-
условием 0 < d < У а. Доказать, qTo

40	ГЛ. И. ВАЖНЖЙШИВ ФУНКЦИИ В ТЕОРИИ ЧИСЕЛ
26. Пусть к—целое, к > 0, d пробегает числа с условием d > 0,
<s(d) = k. Доказать, что
d
27.	Пользуясь выражением для <р(а), доказать" бесконечность
числа простых чисел.
28,	а. Теорему d, § 4 доказать, установив, что число чисел
ряда 1, 2, ... , а, имеющих с а один и тот же общий наибольший
делитель в, равно ' 9 ( ~jt ) •
b. Вывести выражение для <р (а):
а) пользуясь теоремой вопроса 10, Ь;
fi) пользуясь теоремой вопроса 17, с.
29. Пусть Ii(s) > 2. Доказать, что
n=l
30. Пусть п—целое, п>2. Доказать, что
m=l
Численные примеры к главе II.
1.	а. Найти показатель, с которым 5 входит в каноническое
разложение 5258! (см. вопрос 5).
Ь. Найти каноническое разложение числа 125!
2.	а. Найти т С5600) и 5E600).
Ь. Найти -с A16 424) и 5A16 424).
3.	Составить таблицу значений функции ц(а) для всех
а=1, 2	100.
4.	Найти a) <j> E040), Р) <р A294 700).
5.	Составить таблицу значений функции ? (а) для всех
а=1, 2,..., 50, пользуясь только формулой E), §4 и тео-
теоремой с, § 4.

ГЛАВА ТРЕТЬЯ.
СРАВНЕНИЯ.
§ 1. Основные понятия.
a.	Мы будем рассматривать целые числа в связи
с остатками от деления их на данное целое положитель-
положительное т, которое назовём модулем.
Каждому целому числу отвечает определённый оста-
остаток от деления его на т (с, § 1, гл. I); если двум
целым а и Ъ отвечает один и тот же остаток г, то они
называются равноостаточными по модулю т или сравни-
сравнимыми по модулю т.
b.	Сравнимость чисел а и Ь по модулю т записы-
записывается так:
а~.Ь (modm),
что читается: а сравнимо с Ъ по модулю т.
c.	Сравнимостъ чисел а и Ь по модулю т равносильна;
1.	Возможности представить а в форме a = b + mt,
где t—цглое.
2.	Делимости а — Ь на т.
Действительно, из а = 6 (mod/к) следует
откуда
a — b = m(q—q1), a=b + mt, t^q — qy
Обратно, из а = b + rnt, представляя Ь в форме
-ВЫВОДИМ
a—mqA-r; q — qv *- t.

42	ГЛ. III. СРАВНЕНИЯ
т. е.
а = 6 (mod/га).
Поэтому верно утверждение 1.
Из i непосредственно следует утверждение 2.
§ 2. Свойства сравнений, подобные свойствам
равенств,
a.	Два числа, сравнимые с третьим, сравнимы между
собою.
Следует из а, § 1.
b.	Сравнения можно почленно складывать.
Действительно, пусть
ах = Ъх (modm), a2 = &2(modm), ..., ak~bk(mcdm). A)
Тогда A, с, § 1)
al = b1-\-mt1, a2 = b2 + mt2, ..., ak = bk + mtk, B)
откуда
ax + a2 + .. . + ak = bx + b2 + ... + bk+m (h + t2+ ... + tk),
или A, с, § i)
ax + a2 + ... + ak = bx + b2 +- .. . + bk (mod m).
Слагаемое, стоящее в какой-либо части сравнения,
можно переносить в другую часть, переменив знак на
обратный.
Действительно, складывая сравнение а 4- b = с (mod m)
с очевидным сравнением — 6 = - b(modm), получим
а = с — 6 (modm).
К каждой части сравнения можно прибавить (или
отнять от неё) любое число, кратное модуля.
Действительно, складывая сравнение а = b (modm)
с очевидным сравнением m?=;0(modm), получим
а + mk = b (mod m).
с. Сравнения можно почленно перемножать.
Действительно, рассмотрим снова сравнения (-1) и вы-
вытекающие из них равенства B). Перемножая почленно

i 2. СВОЙСТВА СРАВНЕНИЙ	43
равенства B), получим
ахал ... ак — ЬХЬ% ... bk + mN,
где IV — целое. Следовательно A, с, § 1),
ахаг ...ак = bxb2 ...Ьк(modт).
Обе части сравнения можно возвысить в одну и ту же
степень.
Это следует из предыдущего утверждения.
Обе части сравнения можно умножить на одно
и то же целое.
Действительно, перемножив сравнение а = 6(modm)
с очевидным сравнением & = &(modm), получим
ак = bk (mod т).
d. Свойства Ь и с (сложение и умножение сравне-
сравнений) обобщаются следующей теоремой.
. Если в выражении целой рациональной функции с це-
целыми коэффициентами S = 2 Ла1,... ,а.к а^1 • • • х\к заменим
Ао.х	ак, хи . .. , хк числами Bai	а.к, уъ .... ук, срав-
сравнимыми с прежними по модулю т, то новое выражение
S будет сравнимо с прежним по модулю т.
Действительно, из
хх ?2ъ-ух (mod т), . . . , xk=syk (mod m)
находим (с)
a^iisEHZ/i^modm), ... , а?*==г/?* (modm),
Aj	o.kx\i .. .х\к = ВЛ1	aft y\i ... у1к (mod m).
откуда, суммируя, получим
S-4»,	о.к x*i... хЛкк = S-6»!	о.к y\i ¦ ¦. у%к (mod m).
Если
a = 6(modm), a1^fe1(modm), ..., an = &n(modm),
x ^l xx (mod m),

44	ГЛ. III. СРАВНЕНИЯ
то
ахп + аххп~1 + ... -f ап=± bxn + btxn~l + ... +Ъп (mod m).
Это утверждение является частным случаем преды-
предыдущего.
е. Обе части сравнения можно разделить на ¦ их
общий делитель, если последний взаимно прост с моду-
модулем.
Действительно, из a = 6(modm), a — axd, b = b1d,
(d, m) = 1 следует, что разность a — b, равная (a1 — b1)d,
делится на т. Поэтому B, f, § 2, гл. I) a1 — b1 делится
на т, т. е. a1^6(d)
§ 3. Дальнейшие свойства сравнений.
a.	Обе части сравнения и модуль можно умножить
на одно и то же целое.
Действительно, из a=sb (mod т) следует
a — b + mt, ak = bk-\-mkt
и, следовательно, ak = bk(modmk).
b.	Обе части сравнения и модуль можно разделить
на любой их общий делитель.
Действительно, пусть
a = 6(modm), а = а^, b—bxd, m — mxd.
Имеем
а — b + nit, axd = bxd + mxdt, ax = bx + nixt
и, следовательно, ax^bx(mod тх).
с. Если сравнение a^fe имеет место по нескольким
модулям, то оно имеет место и по модулю, равному
общему наименьшему кратному этих модулей.
В самом деле, из a==b(modmx), a=^b(modm2), ...
... , a^±b (mod mk) следует, что разность a—b делится
на все модули т1г тг, ... , тк. Поэтому (с, § 3, гл. I)
она должна делиться и на общее наименьшее кратное т
этих модулей, т. е. ,d=fc(modm).

t 4. ПОЛНАЯ СИСТЕМА ВЫЧЕТОВ	45
d.	Если сравнение имеет место по модулю т, то оно
имеет место и по модулю d, равному любому делителю
числа т.
В самом деле, из а ^з Ь (mod m) следует, что раз-
разность а— Ъ должна делиться на т; поэтому A, Ь, § 1,
гл. I) она должна делиться и на любой делитель d
числа т, т. е. a = b(modd).
e.	Если одна часть сравнения и модуль делятся на
какое-либо число, то и другая часть сравнения должна
делиться на то же число.
Действительно, из a~b(modm) следует a=b + mt,
если а и т кратны d, то B, Ь, § 1, гл. I) и Ъ должно
быть кратным d, что и утверждалось.
f.	Если а = 6 (mod m), то (а, т) = (Ь, т).
Действительно, ввиду 2, Ь, § 2, гл. I это равенство
непосредственно следует из а = Ь -\- mt.
§ 4. Полная система вычетов.
a.	Числа равноостаточные, или, что то же самое, срав-
сравнимые по модулю т, образуют класс чисел по модулю т.
Из такого определения следует, что всем числам
класса отвечает один и тот же остаток г, и мы полу-
получим все числа класса, если в форме mq + г заставим q
пробегать все целые числа.
Соответственно т различным значениям г имеем т
классов чисел по модулю т.
b.	Любое число класса называется вычетом по мо-
модулю т по отношению ко всем числам того же класса.
Вычет, получаемый при q = 0, равный самому остатку г,
называется наименьшим неотрицательным вычетом.
Вычет с самый малый по абсолютной величине, назы-
называется абсолютно наименьшим вычетом.
Очевидно при г < у имеем р = г; приг> -j- имеем
ь—г — т; наконец, если т чётное и г = -к-, то за [>
можно принять. любое из двух чисел у и -,— m = — -~- .
Взяв от каждого класса по одному вычету, получим
полную систему вычетов по модулю т. Чаще всего в

46	ГЛ. III. СРАВНЕНИЯ
качестве полной системы вычетов употребляют наимень-
наименьшие неотрицательные вычеты 0,1,..., т — 1 или также
абсолютно наименьшие вычеты; последние, как это сле-
следует из вышеизложенного, в случае нечётного т пред-
представляются рядом
т~1	—10 1	m~i
а в случае чётного т каким-либо из двух рядов
_ ™ 4- 1	— 1 О 1	—
„ т х, . . .,	1, и, х, ...,„>
	2~'	¦••> " 1iu>1) • • • > 
c.	Любые т чисел, попарно несравнимые по модулю пг,
образуют полную систему вычетов по этому модулю.
Действительно, будучи несравнимы, эти числа тем
самым принадлежат к различным классам, а так как
их т, т. е. столько же, сколько и классов, то в каждый
класс наверно попадёт по одиому числу.
d.	Если (а, т) = 1 и х пробегает полную систему
вычетов по модулю т, то ах + Ъ, где Ь — любое целое,
тоже пробегает полную систему вычетов по модулю т.
Действительно, чисел ах -t b будет столько же, сколько
и чисел х, т. е. т. Согласно с остаётся, следовательно,
только показать, что любые два числа ахх + Ь и ах2 + Ь,
отвечающие несравнимым хх и х2, будут сами несравнимы
по модулю т.
Но допустив, что ахх 4- Ь = ах2 + b (mod m), мы при-
придём к сравнению ахх = ах2 (mod m), откуда, вследствие
(а, т) = 1, получим a;1^a;2(modm), что противоречит
предположению о несравнимости чисел хх и х2.
§ 5. Приведённая система вычетов.
а. Согласно f, § 3 числа одного и того же класса
по модулю т имеют с модулем один и тот же общий
наибольший делитель. Особенно важны классы, для
которых этот делитель равен единице, т. е. классы,
содержащие числа, взаимно простые с модулем.

I 6. ТЕОРЕМЫ 8ЙЛБРА И ФЕРМА	47
Взяв от каждого такого класса по одному вычету,
получим приведенную систему вычетов по модулю то.
Приведённую систему вычетов, следовательно, можно
составить из чисел полной системы, взаимно простых
с модулем. Обыкновенно приведённую систему вычетов
выделяют из системы наименьших неотрицательных
вычетов: 0, 1, ... , т—1. Так как среди этих чисел число
взаимно простых с т есть <?(т), то число чисел приве-
приведённой системы, равно как и число классов, содержащих
числа, взаимно простые с модулем, есть у(т).
Пример. Приведённая система вычетов по моду-
модулю 42 будет
1, ^, 11, 13, 17, 19, 23, 25, 29, 31, 37, 41.
b.	Любые <р(т) чисел, попарно несравнимые по мо-
модулю т и взаимно простые с модулем, образуют при-
приведённую систему вычетов по модулю т.
Действительно, будучи несравнимыми и взаимно про-
простыми с модулем, эти числа тем самым принадлежат
к различным классам, содержащим числа, взаимно про-
простые с модулем, а так как их ср (т.), т. е. столько же,
сколько и классов указанного вида, то в каждый класс
наверно попадёт по одному числу.
c.	Если (а, т)= 1 и х пробегает приведённую систему
вычетов по модулю т, то ах тоже пробегает приведён-
приведённую систему вычетов по модулю т.
Действительно, чисел ах будет столько же, сколько
и чисел х, т. е. у(т). Согласно Ь остаётся, следова-
следовательно, только показать, что числа ах по модулю т
несравнимы и взаимно просты с модулем. Но первое
доказано в d, § 4 для чисел более общего вида ах -t b,
второе же следует из (а, т) = 1, (х, т)= 1.
'	§ 6. Теоремы Эйлера и Ферма.
а. При т > 1 и (а, т) = 1 имеем {теорема Эйлера):
Действительно, если х пробегает приведённую си-
систему вычетов
х = ги г2, ... ,rc; c = cp(m),

48	ГЛ. 1П. СРАВНЕНИЯ
составленную из наименьших неотрицательных вычетов,
то наименьшие неотрицательные вычеты рх, \>t, ... , [>е
чисел ах будут пробегать ту же систему, но располо-
расположенную, вообще говоря, в ином порядке (с, § 5)
Перемножая почленно сравнения
)f ... , arc = рс(modm);
получим
ac/y2 ... rc== ptfa . . . pc (mod m),
откуда, деля обе части на произведение гхг2 ... гс =
= № • • • Рс. ПОЛуЧИМ
ac = l (mod m).
Ь. При р простом и а, не делящемся на р, имеем
(теорема Ферма):
ap-x=l (modjo).	A)
Эта теорема является следствием теоремы а при т — р.
Последней теореме можно придать более удобную форму.
Именно, умножая обе части сравнения A) на а, полу-
получим сравнение
справедливое уже при всех целых а, так как оно верно
и при а, кратном р.
Вопросы к главе III.
1,	а. Представляя целое число в обычной десятичной системе
исчисления, вывести признаки делимости на 3, 9, 11.
b.	Представляя целое число в системе исчисления с основа-
основанием 100, вывести признак делимости на 101.
c.	Представляя целое число в системе исчисления с основа-
основанием 1000, вывести признаки делимости на 37, 7, И, 13.
2,	а. Пусть т > 0, (о, от)=1, Ъ — целое, х пробегает полную,
а %—приведённую систему вычетов по модулю т. Доказать, что

ВОПРОСЫ К ГЛАВЕ III	49
Ь. Пусть т>0, (а, т)=1; Ь, N, t—цепые, * > О,
/ (х) —ах , / (N) > О, f(N + mt)>0. Доказать, что для тра-
т
пеции, ограниченной прямыми x = N, x = N + mt, y=0, y=f(x),
имеем
где i?—площадь трапеции, а сумма, стоящая справа, распро-
распространена на все целые точки трапеции, причём 5=1 для внут-
.1	.1
ренних точек, й=-т- для вершин, 5=-g-—для остальных точек-
контура.
с. Считая, в отличие от вопроса Ь, 5=-^- для вершин,
формулу A) доказать для треугольника с целыми вершинами.
3, а. Пусть т > 0, (о, m)=l, h^O, с — вещественное,
(х)
где ф (х) для рассматриваемых значений х принимает вначенвя
с условием с ^ ф {х) ^ с -f h. Доказать, что
S-\m
1
У
Ь. Пусть М—целое, т > 0, (а, т) — 1, Ли В—вещественные,
М+т—1
Доказать, что
с. Пусть М—целое, т > 0, (о, т) = 1,
И+т-1

50	ГЛ. Ш. СРАВНЕНИЯ
где в интервале МКх <^М+т— 1 функция f{x) имеет непре-
непрерывные производные /'(х) и /* (х), причём выполняются условия
fW) = jL + ±; (a,m) = l; | 8 | < 1, ±
где
1
Доказать, что
А- + 3
4. Пусть в разложения иррационального числа	А в непре-
непрерывную дробь все неполные частные ограничены,	М — целое,
т — целое, т > О, В — вещественное. Доказать, что
М+т-1
5, а. Пусть А> 2,А>1ив интервале Q < х sg R функция / (х)
имеет вторую непрерывную производную- удовлетворяющую
условиям
Доказать, что
Л= B/с2 (R—Q) 1пА+ 8кА) А*.
Ъ. Пусть 0<о<1, Q и R — целые. При условиях вопроса а
доказать, что число <\> (а) дробей \/(ж)>; x—Q + 1, ... , R с усло-
условием 0 <^. {/ (г)} < о выражается формулсш
6, а. Пусть Г—число целых точек (х, у) области
I2 + у2 << г2 (г !> 2). Доказать, что

ВОПРОСЫ К ГЛАЙВ Ш	51
Ь. Пусть л—целое, л > 2, Е—постоянная Эйлера. Доказать,
тA)+тB)+ ... \t(n) = n(\vin + 2E— 1) + О (га5 (In гаJ).
что
7.	Систему га целых положительных{^чисел, каждое из кото-
которых представлено в системе исчисления с основанием 2, назовём
правильной, если при всяком целом неотрицательном s число
чисел, в представление которых входит 2", будет чётным, и не^
правильной, если хотя бы при одном s это число будет нечётным.
Доказать, что неправильную систему путём уменьшения или
полного изъятия некоторого одного её плена можно сделать пра-
правильной, а правильная система от уменьшения или полного
изъятия любого её члена делается неправильной.
8,	а. Доказать, что форма
3«*„ + 3я"^л., + •.. + Ъх1 + х0,
где хп, Жл_1, ..., хг, ха независимо друг от друга пробегают
значения —1, 0, 1, представляет все числа
3»+1_ i
— Н, ..., —1, 0, 1, ..., Н\ Н = g^ ,
причём каждое число—единственным способом.
Ь. Пусть т1, т2, ..., тк—положительные попарно простые.
Пользуясь с, § 4, доказать, что полную систему вычетом
по модулю т^тъ ... т^ получим, заставляя в форме
хх -f т^хъ + тхт^х3 + ... +
числа х1г хг, ..., х/с пробегать полные системы вычетов по моду-
модулям т1, т2, ..., т^.
9. Пусть т,, т2, ..., wjt—попарно простые и
a.	Применяя с, § 4, доказать, что полную систему вычетов
по модулю mxm% ... гад. получим, заставляя в форме
Мххх + М2х2 + • • • + М кХк
числа xlt хг, ..., х^ пробегать полные системы вычетов по моду-
модулям Шх, т2, ..., т#.
b.	Применяя с, § 4, гл. II и Ь, § 5, доказать, что приведён-
приведённую систему вычетов по модулю тп^ш^... тп^ получим, заставляя
в форме
...+ Мкхк
числа xlf хг, ..., Xfr пробегать приведённые системы вычетов
по модулям Wj, mt, ..., то#.

52	ГЛ. III. СРАВНЕНИЯ
с. Доказательство теоремы вопроса b провести независима
от теоремы с, § 4, гл. II и тогда уже вывести последнюю теорему,
как следствие первой.
d. Найти элементарным путём выражение для f (рл) и, поль-
пользуясь равенством с, § 4 гл. II, вывести известное выражение
для ?(о).
10. Пусть т1г гпъ,..., т/с—попарно простые, превосходящие 1,
М
2 , цс,	^^
Пусть х1г *2, ..., xjc, х пробегают полные, a ?i,
	 ?й, ? —приведённые системы вычетов по модулям
!, т2, ..., т/с, т. Доказать, что дроби
совпадают с дробями { — V , а дроби I — + -^- + • • • + — <•
I m J	r \ т.! т2	тк j
совпадают с дробями -I — J- .
Ь. Пусть заданы к целых рациональных функций с целыми
коэффициентами от г переменных х, ..., «;(/•;> 1):
а,...,5
и пусть
а	8	«=1
ж8	w4 пробегают полные, а ?,,..., <»„ — приведённые системы
вычетов по модулю mt; х	w пробегают полные, а ?,..., ш —
приведённые системы вычетов по модулю т. Доказать, что дроби
{
i-!-i—!	'-—H- + ... + //fv 	'-—?- }• совпадают с дробями
«1	«A:	J
m /I	«i	mfc	j
совпадают с дробями < ' ''''—- \ (обобщение теорем вопроса а).
11, а. Пусть т— целое, т > 0, о — целое, х пробегает полную
систему вычетов по модулю т. Доказать, что
.ах
>п J m> если а кратно т,
(т, если а
\ О в прот
противном случае.

ВОПРОСЫ К ГЛАВЕ Ш
53
Ь. Пусть а—вещественное, М — целое, Р—целое, Р >. 0. Обо-
вначая символом (о) численное значение разности между а и бли-
ближайшим к а целым числом (расстояние а до ближайшего целого)?)
доказать, что
М+Р-1
х=М
<, min
Члтк); h>{
2 всегда
3, при (а)<-
с. Пусть от— целое, т > .1 и функции М (а) и /)(а) для зна-
значений о = 1, 2, ..., m—1 принимают целые значения с условием
Р (о) > 0. Доказать, что
т-1
2
2n.i-
М (о)
от In т	=" , при m > 12,
mlnm—m, при m!>60.
12, а. Пусть m—целое, т > 0, % пробегает приведённую
систему вычетов по модулю т. Доказать, что
b.	Пользуясь теоремой вопроса а, доказать первую из тео-
теорем с, § 3, гл. II (см. решение вопроса 28, а, гл. II).
c.	Теорему вопроса а вывести, пользуясь теоремой вопроса 17, а,
гл. II.
d.	Пусть
— целая рациональная функция с целыми коэффициентами от г
переменных х, ..., w(r > 1), а— целое, т — целое, т > 0; х, ..., w
пробегают полные, а %,..., ™ — приведённые системы вычетов
по модулю т. Вводим обозначения
'а, т.
-2-2
2л»
, Sa,m=
2т
Пусть далее т — тг ..,
превосходящие 1, и пусть
с	а
<ЧШ1 """ «
т.];, где mj, ..., mt — попарно простые,
» = Mstos. Доказать, что
т =s

54	гл. ш. сравнения
е. При обозначениях вопроса d полагаем
где а пробегает приведённую систему вычетов по модулю т.
Доказать, что
A (mj) ... А (т.]() = А (т.), А' (тох) ... А' {ти) = А' (т).
13, а. Доказать, что
2 v
07
п—0 р	ж=0
где р пробегает простые делители числа о.
Ь. Из тождества вопроса а вывести известное выражение
для ?(а).
14. Доказать, что
•c(a)=lim2s У. у. i	+ь
= 1
где 3=1 или # = 0, в зависимости от того, является ли о квадра-
квадратом целого числа или нет.
15, а. Пусть р—простое и hlt й2	ha—целые. Доказать,
что
b.	Из теоремы вопроса а вывести теорему Ферма.
c.	Из теоремы Ферма вывести теорему Эйлера.
Численные примеры к главе III.
1,	а. Найти остаток от деления
A2 3715e +34JS на т.
Ь. Делится ли на 1 0932 число 21093 — 2?
2,	а. Применяя признаки делимости вопроса 1, найти кано-
каноническое разложение числа 244 943 325.
Ь. Найти каноническое разложение числа 282 321 246 671 737.

ГЛАВА ЧЕТВЁРТАЯ.
СРАВНЕНИЯ С ОДНИМ НЕИЗВЕСТНЫМ.
§ 1. Основные понятия.
Нашей ближайшей задачей будет изучение сравне-
сравнений такого общего вида:
f(x)==0(modm); f(x) = axn + a^" + • • • + ап. A)
Если а не делится на т, то и называется степенью
сравнения.
Решить сравнение — значит найти все значения х, ему
удовлетворяющие. Два сравнения, которым удовлетво-
удовлетворяют одни и те же значения х, называются равносиль-
равносильными.
Если сравнению A) удовлетворяет какое-либо x = xlt
то (d, § 2, гл. III) тому же сравнению будут удовле-
удовлетворять и все числа, сравнимые с хх по модулю т:
x = Xi (modm). Весь этот класс чисел считается за одно
решение. При таком соглашении сравнение A) будет
иметь столько решений, сколько вычетов полной системы
ему удовлетворяет.
Пример. Сравнению
х5 + х +• 1 — 0 (mod 7)
среди чисел: 0, 1, 2, 3, 4, 5, 6 полной системы вычетос
по модулю 7 удовлетворяют два числа: х = 2 и х = 4.
Поэтому указанное сравнение имеет два решения:
х г= 2 (mod 7), z = 4(mod7).

5«	ГЛ. ГГ. «РАВНЕНИЯ С ОДНИИ НЕИЗВЕСТНЫМ
§ 2. Сравнения первой степени.
а. Сравнение первой степени перенесением свободного
члена (с обратным знаком) в правую часть можно при-
привести к виду
A)
b.	Приступая к исследованию вопроса о числе реше-
решений, мы сначала ограничим сравнение условием (а, т) = 1.
Согласно § 1 наше сравнение имеет столько решений,
сколько вычетов полной системы ему удовлетворяет. Но
когда х пробегает полную систему вычетов по модулю т,
то ах пробегает полную систему вычетов (d, § 4, гл. III).
Следовательно, в частности, при одном и только одном
значении х, взятом из полной системы, ах будет
сравнимо с Ь. Итак, при (а, т) = 1 сравнение A) имеет
одно решение.
c.	Пусть теперь (a, m) = d > I. Тогда, чтобы сравне-
сравнение A) имело решения, необходимо (е, § 3, гл. III),
чтобы Ъ делилось на d, иначе сравнение A) невозможно
ни при каком целом х. Предполагая поэтому Ь крат-
кратным d, положим a — axd, b = bxd, m^m^d. Тогда сравне-
сравнение A) будет равносильно такому (по сокращении на d):
ахх^ bx (mod TOj), в котором уже (а1г тг) = 1, и потому
оно будет иметь одно решение по модулю т1. Пусть
xv — наименьший неотрицательный вычет этого решения
по модулю пг1, тогда все числа х, образующие это реше-
решение, найдутся в форме
ZEEEEa^modmi).	B)
По модулю же m числа B) образуют не одно реше-
решение, а больше, именно столько решений, сколько
чисел B) найдётся в ряде 0, 1, 2, ..., тп — 1 наимень-
наименьших неотрицательных вычетов по модулю тп. Но сюда
попадут следующие числа B):
хъ xl + m1, x1 + 2m1,..., x1 + (d — i)m1,
т. е. всего d чисел B), следовательно, сравнение A)
имеет d решений.

I а. сравнения пврвой ствпнни	57
d.	Собирая всё доказанное, получаем теорему:
Пусть (а, m) = d. Сравнение aa; = 6(modm) невоз-
невозможно, если b не делится на d. При Ь, кратном d,
сравнение имеет d решений.
e.	Обращаясь к разысканию решений сравнения A),
мы укажем только способ, основанный на теории непре-
непрерывных дробей, п'ричём достаточно ограничиться лишь
случаем (а, т) — 1.
Разлагая в непрерывную дробь отношение т : а,
т.	1
— = ?i + ; —
и рассматривая две последние подходящие дроби:
Qn-x ' Qn а '
согласно свойствам непрерывных дробей (е, § 4, гл. I)
имеем
a- (- 1)п-1Рп_1Ь
Итак, наше сравнение имеет решение
х = (— l)n-lPn-.ib (mod m),
для разыскания которого достаточно вычислить Pn-i
согласно способу, указанному в d, § 4, гл. I.
' Пример. Решим сравнение
Ills = 75 (mod 321).	C)
Здесь A11, 321) = 3, причём 75 кратно 3. Поэтому
сравнение имеет три решения.
Деля обе части сравнения и модуль на 3, получим
сравнение
4

58
ГЛ. IV. СРАВНЕНИЯ С ОДНИМ НЕИЗВЕСТНЫМ
которое нам следует сначала решить. Имеем
107
74
37
37
33
33
33
32
Я
ps
1
2
2
1
3
8
26
4
107
Значит, в данном случае /г = 4, Р„_1=26, 6 = 25,
и мы имеем решение сравнения D) в форме
х == -26 • 25 = 99 (mod 107).
Отсюда решения сравнения C) представляются так:
х = 99; 99 + 107; 99 + 2 • 107 (mod321),
т. е.
ний
а; = 99; 206; 313 (mod 321).
§ 3. Система сравнений первой степени.
а. Мы рассмотрим лишь простейшую систему сравне-
сравней
2), ... , x = bk(modmk) A)
с одним неизвестным, но с разными и притом попарно
простыми модулями.
Ь. Решить систему A), т. е. найти все значения х, ей
удовлетворяющие, можно применяя следующую теорему:
Пусть числа Ms и M's определены из условий

i 3. СИСТЕМА СРАВНЕНИЯ ПЕРВОЙ СТЕПЕНИ	59
и пусть
х0 = M^iW + М2М'ЯЬ2 + ...+ МкМ'кЬк
Тогда совокупность значений х, удовлетворяющих системе
A), определяется сравнением
x^x0(modm1m2 . . . mk).	B)
Действительно, ввиду делимости на ms всех Mj, отлич-
отличных от Мs, при любом s= 1, 2, . . . , к имеем
х0 = MsM'sbs = bs (mod ms),
и, таким образом, системе A) удовлетворяет х — х0.
Отсюда непосредственно следует, что система A) равно-
равносильна системе
a;==a;0(modm1), x^BX0(modm2), ... , х = х0(modmk) C)
(т. е. что системам A) и C) удовлетворяют одни и те же
значения х). Системе же C), ввиду теорем с, § 3,
гл. III и d, § 3, гл. III, удовлетворяют те и только
те значения х, которые удовлетворяют сравнению B).
c.	Если blt b%, ... ,ЬЫ независимо друг от друга про-
пробегают полные системы вычетов по модулям тх, т2, . ¦. , тк,
то х0 пробегает полную систему вычетов по модулю
т1т2 ¦. ¦ тк.
Действительно, х0 пробегает тгт2. . . /га* значений,
ввиду d, § 3, гл. III, несравнимых по модулю
тхт2 ¦ ¦ ¦ тк.
d.	Пример. Решим систему
ж = Ьг (mod4), х-^b2(mod5), x = b3(mod 7).
Здесь 4 • 5 • 7 = 35 • 4 = 28 • 5 = 20 • 7, причём
'35- 3 = 1 (mod4), 28 • 2= 1 (mod5), 20 • 6 = 1 (mod7).
Поэтому
х0 = 35 ¦ 3bL + 28 • 2b2 + 20 ¦ Qb3 = 1056x + 566a + 120fe3
и, следовательно, совокупность значений х, удовлетво-
удовлетворяющих системе, может быть представлена в форме
х — 105&! + 56 b2 + 12063 (mod 140).

f%	ГЛ. IV. СРАВНЕНИЯ С ОДНИМ НЕИЗВЕСТНЫМ
Так, например, совокупность значений х, удовле-
удовлетворяющих системе
а; ==1 (mod 4), х = 3 (mod 5), х = 2 (mod 7),
будет
х = 105 • 1 + 56 • 3 +¦ 120 • 2 = 93 (mod 140),
а совокупность значений х, удовлетворяющих системе
х ==3 (mod 4), х == 2 (mod 5), х = 6 (mod 7),
будет
я; =105- 3 f 56 -2+ 120 -6 = 27(mod 140).
§ 4. Сравнения любой степени по простому модулю.
a.	Пусть р — простое. Докажем общие теоремы,
относящиеся к сравнению вида
/(a;)==0(modjB); f(x)=>axn + a1xn-i+...+an. A)
b.	Сравнение вида A) равносильно сравнению степени
не выше р — 1.
Действительно, деля / (х) на xv — x, имеем
f{x) = (x*-x)Q{x)+R{x),
где степень R (х) не выше р — 1. А так как
хР — х==0 (mod р), то f(x)==R (x) (mod /?), откуда и следует
указанная теорема.
c.	Если сравнение A) имеет более чем п решений,
то все коэффициенты f(x) кратны р.
Действительно, пусть сравнение A) имеет, по крайней
мере, га -с 1 решение. Обозначая буквами хх, х2, ... , хп, xni.t
вычеты этих решений, мы можем / (х) представить
в форме
f(x) = a(x — xx) (x — х2) ... (х — xn-z) (x — xn-i) (x — хп) +
+ b(x-Xi) (х -х2) ... (х - a:n_2) (x-xn-i) +
+ С (X — Xi) (X — Х2) ... (X - Ж„_2) +
+ к (х — хх) (х - х2) +
+ l(x-Xl) +
+ т,	B)

i 5. СРАВНЕНИЯ ПО СОСТАВНОМУ МОДУЛЮ	61
Дли этой цели, преобразовав (раскрытием скобок)
Слагаемые правой части в многочлены, выберем Ъ так,
чтобы сумма коэффициентов при хп~1 двух первых
многочленов совпала с аг; зная Ь, выберем с так, чтобы
сумма коэффициентов при хп~2 трёх первых многочле-
многочленов совпала с а2, и т. д.
Полагая в B) последовательно х = х1г х2, ... , х„, хп+\,
убеждаемся в том, что все т, I, к, ... , с, Ь, а кратны р.
Значит, и все а, аъ ... , ап кратны р (как суммы чисел,
кратных р).
d. При простом р справедливо сравнение (теорема
Вильсона)
C)
Действительно, если /> = 2, то теорема очевидна.
Если же р > 2, то рассмотрим сравнение
(х - 1) (х - 2) ... (х - (р - 1)) - (жр-1 - 1) = 0 (mod p);
оно степени не выше р — 2 и имеет р — 1 решение,
именно решения с вычетами 1, 2, ..., р — 1. Следова-
Следовательно, по теореме с все его коэффициенты кратны р;
в частности, на р делится и свободный член, равный
как раз левой части сравнения C).
Пример. Имеем1 • 2 • 3 • 4 • 5 • 6 + 1=721 ==0(mod7).
§ 5. Сравнения любой степени по составному модулю.
а. Если mlf т2, ... , тк попарно простые, то сравне-
сравнение
f(x)=iO(modmxm% ... тк)	A)
равносильно системе
/(a;)==0(modm2), ... , /(a;):==0(modmA:).
При этом, обозначая через Tlt Т2, . ¦ ¦ , Тк числа реше-
решений отдельных сравнений этой системы по соответ-
соответственным модулям и через Т—число решений сравнения
A), будем иметь
Т = ТхТг... Тк.

62	ГЛ. IV. СРАВНЕНИЯМ ОДНИМ НЕИЗВЕСТНЫМ
Действительно, первая часть теоремы следует из с
и d, § 3, гл III. Вторая часть следует из того, что
каждое сравнение
B)
выполняется тогда и только тогда, когда выполняется
одно из Ts сравнений вида
z = 6s (modms),
где bs пробегает вычеты решений сравнения B), при-
причём возможно всего 7\Т2 .. . Тк различных комбина-
комбинаций вида
х = 6i (mod ?%), x~b2 (mod m2), .. ., x == bk (mod mk),
приводящих (с, § 3) к различным классам по модулю
mxm2 ... пгк.
Пример. Сравнение
/(ж) —0(mod 35), /(а) = з;4 + 2а;3+8а; + 9 C)
равносильно системе
/(a:)==0(mod 5), /(«)== 0 (mod 7).
Легко убедимся (§ 1), что первое сравнение этой
системы имеет 2 решения: ж==1; 4 (mod 5), второе же
'сравнение имеет 3 решения: a; = 3; 5; 6 (mod 7).
Поэтому сравнение C) имеет 2-3 = 6 решений. Что-
Чтобы найти эти 6 решений, надо решить 6 систем
вида
? = 6! (mod5), x^ib2(mod7),	D)
которые получим, заставляя Ьх пробегать " значе-
значения 6Х = 1; 4, а Ь2 пробегать значения Ь2 = 3; 5; 6. Но,
ввиду
35 = 7-5 = 5-7, 7-3=5 1 (mod5), 5-3 = 1 (mod7),

§ В. СРАВНЕНИЯ ПО СОСТАВНОМУ МОДУЛЮ	63
совокупность значений х, удовлетворяющих системе D),
представится в форме (Ь, § 3)
Поэтому решения сравнения C) будут
з = 31; 26; 6; 24; 19; 34 (mod 35).
b. Ввиду теоремы а исследование и решение срав-
сравнения
f (x) = 0 (mod pi1 pi2... plk)
сводятся к исследованию и решению сравнений вида
/(a;) = 0(mod/>«);	E)
это же последнее сравнение сводится вообще, как мы
сейчас выясним, к сравнению
/(*)== О (mod/>)•	F)
Действительно, всякое х, удовлетворяющее сравне-
сравнению E), необходимо должно удовлетворять и сравие-
нию F). Пусть
х == хх (mod p)
—какое-либо решение сравнения F). Тогда Гх — %1Л- ptu
где tх — целое. Вставляя это значение х в сравнение
/ (х) = О (mod p2)
и разлагая левую часть по формуле Тейлора, найдём
(принимая во внимание, что -ту /<*) (xj) — целое,!' и от-
отбрасывая члены, кратные р2)
t
f Ы + Phf (asi) = 0 (mod р*), *-Ы + hr {Xi) _ о (mod p)
Ограничиваясь здесь случаем, когда /' (хх) не делится
на р, имеем одно решение:
hss t'i (mod p); h = t{ +ptt.

64	ГЛ. IV. СРАВНЕНИЯ С ОДНИМ НЕИЗВЕСТНЫМ
Выражение для х принимает вид
х = хх -f pt'i + /?212 = x2 4- p2 h',
вставляя его в сравнение
f(x)==0(modps),
получим
4- P2hf (z2) = 0(mod p»),
Здесь f'(x2) не делится на р, так как
2:2 = 2:! (mod p),
/'(se.) = /'(*!) (mod p),
и потому последнее сравнение имеет одно решение:
t, = ti + pt3.
В&ражение для х принимает вид
х = ж2 + у»2 «2 + у»3 *з = х3 + р313;
и т. д. Таким путём по данному решению сравнения F)
постепенно найдём сравнимое с ним решение сравне-
сравнения E). Итак, всякое решение х = х1 (mod p) сравнения F)
/' ()	д	д	д
()	р	1 ( p) р	()
при условии, что /' (г^) не делится на р, даст одно
решение сравнения E):
Пример. Решим сравнение
/(я) =^ + 7*+4. }	(';
Сравнение /(a;)==0(mod 3) имеет одно решение
z=rl(mod 3); при атом /' A)==2 (mod 3) и, следова-

ВОПРОСЫ К ГЛАВЕ IV	(J5
телыю, не делится на 3. Находим:
36=1+3*!,
/.A) + 3*i /' A) =з 0 (mod 9), 3 + Згх • 2 == 0 (mod 9),
2tx + I==0(mod3), ^ss5l(mod 3), ^ =
f D) + 9t2 /' D) == 0 (mod 27), 18 + 9ta ¦ 2 = 0 (mod 27),
2*2 + 2==0(mod3), *2 = 2(mod3), tt =
Таким образом сравнение G) имеет одно решение:
af==22(mod27).
Вопросы к главе IV.
1, а. Пусть то— целое, т > О, / (х	w) — целая рациональ-
рациональная функция с целыми коэффициентами от г переменных
х, ...,№(>> 1). Если сравнению
f(x, ..., w) = O(modm)	A)
удовлетворяет система х = х0	w = w0, то (обобщение опре-
определения § 1) систему классов чисел по модулю т:
х = х0 (mod т), ..., w = w0 (mod m)
будем считать за одно решение сравнения (II.
Пусть 71—число решений сравнения A). Доказать, что
т-\ т— 1 т—1 .а/(ж, ..., уз)
1 т. ^j ^j . . . ^j e
b. При обозначениях вопроса а и вопроса 12, е, гл. III дока-
доказать, что
Тт = тг У. А(тй).
c.	Равенство вопроса а применить к доказательству теоремы
о числе решений сравнения первой степени.
d.	Пусть т — целое, т > 0; а, ...,/, g —целые, их чи-
число равно г+1 ,(г > 0): d=(a, ..., f,m); T—число решений
сравнения
ах -f ... -f fw f g = 0 (mod m).

в&>	ГЛ. IV. СРАВНЕНИЯ О ОДНИМ НЕИЗВЕСТНЫМ
Пользуясь равенством вопроса а, доказать, что
Ы, если g кратно d,
О в противном случае.
е. Теорему вопроса d доказать, исходя из теоремы о числе
решений сравнения ах = Ъ (mod то).
2, а. Пусть то>1, (а, то) = 1. Доказать, что сравнение
ах = Ь (mod то) имеет решение х = ba^^m^~i (mod то).
b. Пусть р—простое, 0<а<р. Доказать, что сравнение
ax = b (mod p) имеет решение
с, а) Указать возможно более простой способ решения срав-
сравнения вида
2%х == Ь (mod то); B, то)=1.
Р) Указать возможно более простой способ решения сравнения
вида
3*ж = Ъ(mod то); C, п*)=1.
f) Пусть (а, то) = 1, 1 < а < то. Развивая способы, указанные
в вопросах а) и 3), доказать, что разыскание решения сравнения
aa;=&(modTO) может быть приведено к разысканию решений
сравнений вида b + mt = 0 (mod p), где р — простой делитель
числа о.
3.	Пусть то — целое, то > 1, 1<^т;<то, (я, то)=1. Пользуясь
теорией сравнений, доказать существование целых х т у с усло-
условиями
ах = у (mod то), 0<а;<':, 0 < | J/| < — .
4,	а. При (а, то)= 1 будем рассматривать символическую дробь
— по модулю то, обозначающую любой вычет решения сравне-
сравнения ахзЪ (mod то). Доказать, что (сравнения берутся по модулю то):
а) При 0 = 0!, Ь = ЬХимеем-— = — .
a aj
Р) Числитель Ъ символической дроби — можно заменить срав-
сравнимым Ьо, кратным а. Тогда символическая дробь —• сравнима
с целым числом, представляемым обычной дробью —.
.6 d __

вопросы к глав* it	вт
а с ~ас '
Ь, а) Пусть р—простое, р > 2, а—целое, О.< а < р— 1. Дока-
Доказать, что
Пусть р простое, р > 2. Доказать, что
2Р—2 .11	1
2 + з^
5, а. Пусть d—делитель числа а, не делящийся на простые,
меньшие п, и х—число различных простых делителей числа d.
Доказать, что в ряде
1-2...П, 2.3 ...(п+1), ..., o(o + l)...(a + 7i—1) A)
, -	па
чисел, кратных а, будет —у .
Ъ. Пусть рх, Рг, . ¦ •, Рк — различные простые делители числа а,
причём ни один из них не меньше чем п. Доказать, что число
чисел ряда A), взаимно пррстых с а, будет
6. Пусть mlt 2, .-.,fc — общее наименьшее кратное чисел
ти пн	т.к.
a.	Пусть d=(m1, m2). Доказать, что система
х = Ъх (mod nij), x =zb2 (mod m2)
разрешима тогда и только тогда, когда Ь2—Ьх кратно d, причём
в случае разрешимости совокупность значений х, удовлетворя-
удовлетворяющих этой системе, определяется сравнением вида
х = xlt 2 (mod mlt 2).
b.	Доказать, что в случае разрешимости системы
х = Ъх(modту), х = b2(modm2), ...,x = bjc(modm-k)
йовокупность значений х, ей удовлетворяющих, определяется срав-
сравнением вида
i,,	j\,	*>¦
7. Пусть т — целое, т > 1, а и 6—целые,

68
ГЛ. IV. СРАВНЕНИЯ С ОДНИМ НЕИЗВЕСТНЫМ
где х пробегает приведённую систему вычетов по модулю т, при-
причём х' ~l—"(mod m) (в смысле вопроса 4, а). Доказать следующие
( —— ) :
V т J
свойства символа
а) [ 	 1 вещественное.
. „ ,, . .	/ra,'bh\ /ah,b\
-[) При (h, т)—1 имеем [ —— J = ( —— J .
6) При mx, m2, ... , mj( попарно простых, полагая
mxm2 ... mj. = m, m = Msms, имеем
ml J V m2 J ' " V mk J V
...+ M.\ak, i
\
8. Пусть сравнение
aoxn + a1a-n~1+ ... +an = 0(mod
имеет я решений
я = xlt хг, ... , ж„ (mod p).
Доказать, что
«1 = — a^Sx (mod p),
я2 = Яо^г (rood р),
я3 = —«о^з (rood p),
ап = (— l)na0?n (mod p),
где Sl есть сумма всех xs; S2—сумма произведений по два,
S3~сумма произведений по три и т. д.
9,	а. Доказать теорему Вильсона, рассматривая пары х, х'
чисел ряда 2,3, ..., р—2, удовлетворяющие условию хх' = 1 (mod p).
Ь. Пусть Р — целое, Р > 1, 1 • 2 ... (Р — 1) + 1 = 0(modi)).
Доказать, что Р — простое.
10,	а. Пусть (av, т) = 1. Указать сравнение л-й степени (га > 0)
со старшим коэффициентом 1; равносильное сравнению
о0жп+ аххп~1 + ... +ап = 0 (mod w).
Ь. Доказать, что необходимое и достаточное условие того, что
сравнение / (х) = 0 (mod р); / (ж) = ж™ + а^х"'1 + ... -f an; п^,р

ЧИСЛЕННЫЕ ПРИМЕРЫ К ГЛАВЕ IV	69
имеет п решений, есть делимость на р всех коэффициентов остатка
от деления хр—х на f(x).
с. Пусть п—делитель р — 1; п > 1; (А, р)= 1. Доказать, что
необходимое и достаточное условие разрешимости сравнения
р-1
хп = A (mod р) есть А п = 1 (mod p), причём в случае разрешимо-
разрешимости указанное сравнение имеет п решений.
11. Пусть п—целое, п > О, (А, т)=1, и известно одно реше-
решение х =. х0 (mod m) сравнения хп = A (mod пг). Доказать, что все
решения этого сравнения представятся ' произведением хп на вы-
вычеты решений сравнения ун = 1 (mod m).
Численные примеры к главе IV.
1,	а. Решить сравнение 256ж = 179 (mod 337).
b. Решить сравнение 1215а: = 560 (mod 2755).
2,	а. Сравнения примеров 1, а и 1, b решить по способу
вопроса 2, с.
Ь. Сравнение 1296ж = 1105 (mod 2413) решить но способу
вопроса 2, с.
3,	Найти все пары х, у, удовлетворяющие неопределённому
уравнению 47х — Illy = 89.
4,	а. Указать общее решение для системы
х = Ъ1 (mod 13), х == Ь2 (mod 17).
Пользуясь этим общим решением, далее найти три числа
которые при делении на 13 и 17 давали бы соответственно остатки
1 и 12, 6 и 8, 11 и 4.
Ь. Указать общее решение для системы
х = 6j (mod 25), х = b2 (mod 27), х = Ь3 (mod 59).
5,	а. Решить систему сравнений (вопрос 6, а)
x==3(mod8), х =11 (mod 20), а; =1 (mod 15).
Ь. Решить систему сравнений
isl(mod3), х =4 (mod 5), х к 2 (mod 7),
же 9 (mod 11), х = 3 (mod 13)
6,	Решить систему сравнений
Зя + 4г/ — 29 = 0 (mod 143), 2а; — 9у 4-84 = 0(mod 143).
7,	а. Какому сравнению степени ниже 5 равносильно сравнение
2а;11 + а;9 + 2а^ + 4х7 + & + Зж* + а;3 + 4х2 + 2ж =
= 0 (mod 5)?

70	ГЛ. IV. СРАВНЕНИЯ С ОДНИМ НЕИЗВЕСТНЫМ
Ь. Какому сравнению степени ниже 7 равносильно сравнение
2x11 + feu + х1* + 5х12 + Зж11 + 2х10 + х* + 5х* +
+ 2Х1 + Зж» + 4с* +&х* + 4ж> + х + 4 a=,0(mad 7)?
8,	Какому сравнению со старшим коэффициентом 1 равносильно
сравнение (вопрос 10, а)
70а;6 + 78я5 + 25ж4 + 68х* + 52а;2 + 4г + 3 = 0 (mod 101)?
9,	а. Решить сравнение
/(х) = 0 (mod 27), f(x) = 7xi + 19а:+ 25,
найдя сначала помощью проб все решения сравнения
/C;) = 0(mod3).
Ь. Решить сравнение 9а;2 + 29а; + 62 s 0 (mod 64).
10,	а. Решить сравнение х3 + 2х + 2 = 0 (mod 125).
b. Решить сравнение ж1 + Ах3 -\- 2хг + 2х + 12 = 0 (mod 625).
И, а. Решить сравнение 6а;3 + 27г2 + 17а; + 20 = 0 (mod 30).
b. Решить сравнение 31а;1 + 57х3 + Жх +191 = 0 (mod 225).

ГЛАВА ПЯТАЯ
СРАВНЕНИЯ ВТОРОЙ СТЕПЕНИ.
§ 1. Общие теоремы.
a.	Из сравнений степени п > 1 в дальнейшем будут
рассматриваться лишь простейшие, а именно — двучлен-
двучленные сравнения:
xn = a(modm); (a,m) = l.	.. A)
Если сравнение A) имеет решения, то а называется
вычетом степени п, в противном случае а называется
невычетом степени п. В частности, при п = 2 вычеты
или невычеты называются квадратичными, при п = 3 —г ку-
кубическими, при п = 4 — б и квадратичными ¦
b.	В этой главе мы подробно рассмотрим случай п — 2
и в первую очередь рассмотрим" двучленные сравнения
второй степени по простому нечётному модулю р:
x2 = a(modp); (a,p)=i.	B)
c.	Если а — квадратичный вычет по модулю р, то
сравнение B) имеет два решения.	.
Действительно, если а—квадратичный вычет, то"срав-
то"сравнение B) имеет, по крайней мере, одно решение
zWa^modp). Но тогда, ввиду ( — х1J==х1, то ясе срав-
сравнение имеет и второе решение ж = — x1(modp). Это
-второе решение отлично от первого, так как Ш
jCi^z—.Xiimodp) мы имели бы 2ar1^0(modp), что fife^
возможно, ввиду. B, р) = (х1, р) = \.	'.: , ¦¦
Указанными двумя решениями и : исчерпываются!
bob решения,сравнения B), ,так -как люследневг будучи

72	¦	ГЛ. V. СРАВНЕНИЯ ВТОРОЙ СТЕПЕНИ
сравнением второй степени, более двух решений иметь
не может (с, § 4, гл. IV).
d. Приведённая система вычетов по модулю р состо-
состоит из ^y~ квадратичных вычетов, сравнимых с числами
1», 2», .... (^-1J,	C)
и ( „ J квадратичных невычетов.
Действительно, среди вычетов приведённой системы
по модулю р квадратичными вычетами являются те
и только те, которые сравнимы с квадратами чисел
(приведённая система вычетов)
т. е. с числами C). При этом числа C) по модулю р
не сравнимы, так как из №== I2 (mod р), О < к < ^
следовало бы, что сравнению ?2 = /2(mod p), вопреки с,
среди чисел D) удовлетворяют четыре: х= — I, — к, к, I.
е. Если а — квадратичный вычет по модулю р, то
а 2 ==i(modp);	E)
если а — квадратичный невычет по модулю р, то
р-1
а 2 =s —l(modp).	F)
Действительно, по теореме ферма,
дР-1===1(тоAр); (а 2 -1)(а 2 + l)
Один.и только один из сомножителей левой части по-
еледЙФго сравнения делится на р (оба сомножителя не
могут одновременно делиться на р, в противном случае
тх разность 2 должна была бы делиться на р). Поэтому
имеет место одно и только одно из сравнений E) и F).

I 2. СИМВОЛ ЛЕЖАНДРА
73
Но всякий квадратичный вычет а удовлетворяет
при некотором х сравнению
а == х2 (mod р)
G)
и, следовательно, удовлетворяет также и сравнению E),
которое можно получить почленным возведением G)
в степень ^—. При этом квадратичными вычетами
и исчерпываются все решения сравнения E), так как,
будучи сравнением степени ^—к— > оно ие может иметь
,	р—1
более чем 0 решении.
Поэтому квадратичные невычеты удовлетворяют
сравнению F).
§ 2. Символ Лежандра.
a.	Введём в рассмотрение символ Лежандра Г — )
(читается символ а по отношению к р). Этот символ
определяется для всех а, не делящихся на р; он ра-
равен 1, если а — квадратичный вычет, и —1, если а —
квадратичный невычет. Число а называется числителем,
р — знаменателем символа.
b.	Ввиду е, § 1, очевидно, имеем
с. Здесь мы выведем главнейшие свойства символа
Лежандра и в следующем параграфе — свойства обобг
ш,ения этого символа — символа Якоби, которые позво-
позволят быстро вычислять этот символ, а следовательно,
решать вопрос о возможности сравнения
d. Если a=-a1(mod р), то (— J=rf—V

74	ГЛ. V. СРАВНЕНИЯ ВТОРОЙ СЧШПЕНИ
Это свойство следует из того, что числа одного
и того же класса будут одновременно квадратичными
вычетами или невычетами.
\
Действительно, 1 = 12 и, следовательно, 1 — ква-
квадратичный вычет.
—
-1*2
Это свойство следует из b при а = — 1.
Так как _ чётное, если /? формы 4те + 1, и не-
чётное, если р формы 4т + 3, то отсюда следует, что
— 1 является квадратичным вычетом простых чисел
формы Am + 1 и квадратичным невычетом простых чи-
чисел формы 4т + 3.
Действительно, имеем
Р-1	Р—1 Р-1	Р—1
2 =
откуда и вытекает наше утверждение. Отсюда следствие:
V P J \Р
т. е. в числителе символа можно отбросить любой
квадратичный множитель.
h. Для вывода дальнейших свойств символа -Лежан-
дра мы сначала дадим ему другое истолкование. По-
р — 1
лагая />} = v ......, рассмотрим сравнения
а ¦ Issj^i (mod/?),
а ¦ 2==?2r2 (mod/?),
а ¦ pj^^rp^modp),
A)

I 2. СИМВОЛ ЛВЖАНДРА	75
где Дох—абсолютно наименьший вычет ах, гх — его
модуль, так что ах=±Л.
Числа а • 1, — о • 1, а • 2, —а «2, ..., а • ръ — а • рг
образуют приведённую систему вычетов по модулю р
(с, § 5, гл. III); их абсолютно наименьшие вычеты
суть e^i, -8^, e2r2, — s2r2, ..., sPirPi, —sPirPj.
Положительные из последних, т. е. г1; г2, ¦¦¦, гр ,
должны совпадать с числами 1, 2, ..., рх (Ь, § 4,
гл. III).
Перемножая теперь сравнения A) и сокращая на
1 • 2 ... р1=г1г2 ... rPi,
р-1
получим а 2 ^«i22 ... Эр (modp), откуда (Ь) имеем
(у) =
1*2 ••• «Р.'
i. Найденному выражению символа Лежандра при-
придадим более законченный вид. Имеем
что будет чётным или нечётным, в зависимости от
того, Зудет ли наименьший неотрицательный вычет чис-
числа ах меньше или больше -х-р, т. е. будет ли гх=\1
или зж = —1. Отсюда, очевидно,
и потому из B) находим

76	ГЛ. V. СРАВНЕНИЯ ВТОРОЙ СТЕПЕНИ
j. Предполагая а нечётным, преобразуем последнее
равенство. Имеем (а-\-р—чётное)
\*±1\
откуда
Р1 __ „2
\+-
Формула C) позволит нам вывести два весьма важных
свойства символа Лежандра.
Следует из формулы C) при а—1.
Так как, далее,
(8m.+ 1J — 1 о , , о
	=^	= от1 ± 1т четное,
а
(8т-ЬЗ)а-1 = 8m2 ± 6m + 1 нечётное,
о
то отсюда следует, что 2 будет квадратичным вычетом
простых чисел формы 8т + 1 (8т +1, 8т + 1) и ква-
квадратичным невычетом простых чисел формы
8т ±3 (8т+ 3, 8т+ 5).
1. Если р и д — простые нечётные, то (закон взаим-
взаимности квадратичных вычетов)
Так как ^-^- • Ц^- будет нечётным лишь в случае,
когда оба числа ряд будут формы 4т 4 3, и чётным,

I 2. СИМВОЛ ЛЕЖАНДРА	77
если хоть одно из этих чисел будет формы 4т-(-1, то
указанное свойство можно формулировать так:
Если оба числа р и q формы km -f- 3, то
если же хоть одно из них формы 4т+ 1, то
Для доказательства заметим, что ввиду к фор-
формула C) принимает вид
Полагая теперь ~^- = qlt рассмотрим р^х пар чисел,
2
получаемых, когда в выражениях qx, py числа х и у
независимо друг от друга пробегают системы значений
з = 1, 2, ..., Ръ у = \, 2, ..., «ft.
Никогда не может быть qx = ру, потому что из этого
равенства следовало бы, что ру кратно q, что ввиду
{Р> Я) = (У> Я) — 1 (так как ® < У < я) невозможно. Поэто-
Поэтому мы можем положить Ptfi = Si +$2> гДе ^i —число
пар с qx < ру и S2 — число пар с ру < до.
Очевидно, E1! есть также число пар с х<— у.
Здесь при данном у можно брать х — \, 2, ..., — у \ .
— 2/< — Я\ < "?" имеем — у < пх. ) Следо-
Q	Q	Ci	I О	I	у
вательно,

1%	ГЯ. V, СРАВНЕНИЯ ВТОРОЙ ОТВПВНИ
Аналогичным путём убедимся, что
Но тогда равенство D) даёт нам
поэтому
откуда и следует отмеченное свойство.
§ 3. Символ Якоби
а. Чтобы сделать вычисление символа Лежандра
более быстрым, рассматривают более общий символ
Якоби. Пусть Р — нечётное, большее единицы, и
P — PiPz ••• рг — разложение его на простые сомножители
(среди них могут быть и равные). Пусть, далее,
(а, Р) = 1. Тогда символ Якоби ( —¦ ) определяется ра-
равенством
= (л") (л") ¦'¦ (л"
Известные свойства символа Лежандра дают возмож-
возможность установить аналогичные свойства и для символа
Якоби.
Ь. Если а~аг (mod/3), то (~ J = С~Л .
Действительно,
потому что а, будучи сравнимо с ах по модулю Р,

I 8. СИМВОЛ ЯКОВИ	f|
будет сравнимо с о2 и по модулям р1г р	, р„ кото-
которые являются делителями Р.
В самом деле,
Чтобы убедиться в этом, заметим, что
' —1\ /—1\/ — 1
)~С Л X л)'" ("рГ)~
= ( _ l)~2~t~2r">T-~;
НО
Р— 1	/>iРа •¦¦ Рг—1
ввиду чего из формулы A) выводим
•¦
Действительно,
fab ... I \ _ /ttfc ... гл	fab ... 1\ _
v. i» )~\ pi )¦¦¦ к рг )~

$0	ГЛ. V. СРАВНЕНИЯ ВТОРОЙ СТЕПЕНИ
собирая символы с одинаковыми числителями, мы и
получим утверждаемое свойство. Отсюда следствие:
P2-1
Действительно,
р±±+р±1+ +plzl
= (-1) 8 + 8 - 8 .	B)
Но
8	8
8
- -g— + -g— + •. . + -g- + 2N,
ввиду чего из формулы B) выводим
Р2-1
g. Если Р и Q — положительные нечётные взаимно
простые, то
Действительно, пусть Q = q1gi ... qs есть разложение ^
на простые сомножители (среди них опять-таки могут

i з. символ якови .	81
быть равные). Имеем
2	2
Но, подобно тому, как в d, находим
a=l
ввиду чего последняя формула даёт
Пример. В качестве	примера на вычисление сим-
символа Лежандра (при этом	будем рассматривать его как
частный случай символа	Якоби) исследуем, имеет ли
решение сравнение
х2 = 219 (mod 383).
Имеем (применяя последовательно свойства g, b, след-
следствие е, g, b, e, f, g, b, d):
/ 219\	/'ЗвЗЧ _ _ /1644	Л
следовательно, рассмотренное сравнение имеет два
решения.

82	ГЛ,У. СРАВНЕНИЯ ВТОРОЙ СТЕПЕНИ
§ 4. Случай составного модуля.
a.	Сравнения второй степени по составному модулю
исследуются и решаются согласно общим указаниям
§ 5, гл. IV.
b.	Начнём со сравнения вида
x2 = a(modp°-); а > О, (а,р) = 1,	A)
где р — простое нечётное.
Полагая f(x) = x2 — a, будем иметь f'(x) = 2x,
и если х = 2=1 (mod p) есть решение сравнения
ж2^ a (mod /?),	B)
то ввиду (а, р) — 1 также (а^, /?)= 1, а так как р нечёт-
нечётное, то Bxlt р) = 1, т. е. /'(^i) не делится на р. Поэто-
Поэтому к разысканию решений сравнения A) можно приме-
применить рассуждения Ь, § 5, гл. IV, причём каждое решение
сравнения B) даст одно решение сравнения A). Из ска-
сказанного выводим, что
Сравнение A) имеет два решения или же ни одного,
в зависимости, от того, будет ли число а квадратич-
квадратичным вычетом или же невычетом по модулю р.
c.	Теперь рассмотрим сравнение
z2 = a(mod2a); a > 0, (a, 2) = 1.	C)
Здесь /' (Xi) = 2xx делится на 2, и потому рассуждения
Ь, § 5, гл. IV неприменимы; они должны быть видо-
видоизменены следующим образом:
d.	Если сравнение C) разрешимо, то ввиду (а, 2) = 1
имеем (х, 2) = 1, т. е. x = l-\-2t, где if —целое. Срав-
Сравнение C) принимает вид
Но одно из чисел t, t+i— чётное, поэтому At(t + 1)
кратно 8. Следовательно, для разрешимости последнего
сравнения, а вместе с тем и сравнения C) необходимо
a=l(mod4) при a = 2; a=l(mod8) при a>3. D)

I i. СЛУЧАВ СОСТАВНОГО ХОДУЛЯ	83
е. В случаях, когда условия D) не нарушены,
рассмотрим вопрос о разыскании решений и их числе.
Для случаев <z<3 ввиду d сравнению удовлетво-
удовлетворяют все нечётные числа. Поэтому сравнение х2 == о (mod 2)
имеет одно решение: х == 1 (mod 2), сравнение ж2 = о (mod 4)
имеет два решения: ж= 1; 3 (mod 4), сравнение х%^ a (mod 8)
имеет четыре решения: as = l; 3; 5; 7 (mod8).
Для рассмотрения случаев а = 4, 5, ... все нечётные
числа полезно объединить в две арифметические про-
прогрессии:
* = ±A + 4г,)	E)
A + 4г3 ==1 (mod 4); -_l"_4*3== -Is=3(mod4)).
Посмотрим, какие из чисел E) удовлетворяют сравне-
сравнению z3==a(mod 16). Находим
*, = *; + 2*4, х - ± A + 4t's + 8*4) = ± (jc4 + 8*4).
Посмотрим, какие из последних чисел удовлетворяют
сравнению х2 ~= a (mod 32). Находим
(z4 + 8^J==a(mod32), <4 = «i + 2*e, x = ± (as, + 16*„),
и т. д. Таким путём убедимся, что при любом а > 3
значения х, удовлетворяющие сравнению C), пред-
представятся в форме
Эти значения х образуют четыре разлр-чых решения
сравнения C)
xssxa; хл + 2л->; -хл; -хл- 2"' (mod2a) ¦
(по модулю 4 два первых сравнимы с 1, а два послед-
последних сравнимы с—1).
Пример. Сравнение
ж8 s 57 (mod 64)	(б)
ввиду 57 з& 1 (mod 8) имеет четыре решения. Представляя

84	ГЛ. V. СРАВНВНИЯ-ВТОРОЙ СТЕПЕНИ
о?* в форме¦# = ± (Г+ &3), находим ~ . ....... ;
(l + 4«3J==57(modl6), 8«3=:56(modl6),
E + 8/4J=s 57 (mod 32), 5 • 16/, == 32 (mod 32),
/4 = 0(mod2), tt=--2t5, x = ± E + 16*6),
E + 16?3J = 57 (mod 64), 5 • 32*5 == 32 (mod 64),
t5 ¦= 1 (mod 2), \ts = 1 + 2«6, x = ± B1 + 32/,).
Поэтому решения сравнения F) будут:
х===± 21; ±53 (mod 64).
f.	Из с, d и е следует:
Для сравнения
x2=.a(mod2a); (а, 2) = 1
необходимыми условиями разрешимости будут; а =
== 1 (mod 4) п./?м а = 2, а^1 (mod 8) п./?й а>3. Если эти
условия не нарушены, число решений будет: 1 п./?и а = 1;
2 при а = 2; 4 м/?м <х>3.
g.	Из b, f и a, § 5, гл. IV следует;
Для сравнения общего вида
Х2~а (mod m); m = Tj>\ij>\* . . . р^; {а, т) = 1
необходимыми условиями разрешимости будут:
при а = 2, a = l(mod8) при а>3,
\, .... Г—
нм о5но из э/тшя условий не нарушено, число реше-
решений будет: 2 гг/?м а = 0 и при а = 1; 2 + при а = 2;
2* п/)м а>3.
Вопросы к главе V.
Буквою р здесь всегда обозначаем простое нечётное- эиело.
1. Доказать, что разыскание решений сравнения вида
ахг-t Ъх f- с s 0 (mod/и), Ba, m) = i
сводится к разысканию решений сравнения вида ,яг s-?<mod m).'¦

2,	а. Пользуясь е, § 1, иайти решениа сравнения '{в- случае
его возможности)
ж* = о (mod р); р = 4т + 3.
b.	Пользуясь Ь и к, § 2, указать способ разыскания реше-
решений сравнений вида
ж2 = a (mod р); р = 8/и-|-5.
c.	Указать возможно более простой способ разыскания реше-
решений сравнений вида
хг = a (mod р); р = 8т + 1
в случае, когда известен некоторый квадратичный невычет N по
модулю р.
d.	Пользуясь теоремой Вильсона, доказать, что решения
сравнения
xs + l = 0(modp); p = 4m-fl
будут
х= ±1 ¦ 2 ... 2т (mod р)
3,	а. Доказать, что сравнение
ж2 + 1 = 0 (mod p)	A)
разрешимо тогда и только тогда, когда р имеет вид. 4та + 1;
сравнение
ж2 + 2 = 0 (mod p)	B)
разрешимо тогда и только тогда, когда р имеет вид 8/га+1 или
8то + 3; сравнение
ж2 + 3 = 0 (mod p)	C)
разрешимо тогда и только тогда, когда р имеет вид 6п»-1-1.
Ь.. Доказать бесконечность числа простых чисел вида 4m 11.
с. Доказать бесконечность числа простых чисел вида 6m t-1.
4,	Пусть, разбивая числа 1, 2, ..., р— 1 на две совокупно-
совокупности, вторая из которых содержит не менее одного числа, имеем:
произведение двух чисел одной совокупности сравнимо по мо-
модулю р с числом первой совокупности, а произведение двух зисед
различных совокупностей сравнимо по модулю р с числом второй
совокупности. Доказать, что это будет тогда и только тогда, когда
первая совокупность состоит из квадратичных вычетов, а вторая —
из квадратичных невычетов по модулю р.
•"- 5, а. Вывести теорию сравнений вида
хг = o<modp*); (а, р) = 1,
представляя а и х в системе исчисления с основанием />,

Ь. Вывести теор ню сравнений вида
х» е a (mod 2*); (л, 2) = 1,
представляя а и х в системе исчисления с основанием 2.
в. Доказать, что решения сравнения
ж* = о (mod рЛ); (в, р)=1
будут а; ¦= ± PQ' (mod рл), где
г2 = о (mod p), QQ' == 1 (mod pa).
7.	Указать способ решения сравнения х1 = 1 (mod»»), осно-
основанный на том обстоятельстве, что указанное сравнение равно-
равносильно такому: (х— 1) (х + 1) = 0 (mod m).
8.	Пусть (—) — 0 при (о, р) — р.
а. При (А, />) = 1 доказать, что
х=0
)\
Ь. Пусть каждое из чисел s и у имеет одно из значений ± 1,
Т—число пар х, х-\-\, где ж = 1, 2, .... р—2, с условием
р	д	,
Г—)=з, (^	Wtj. Доказать, что
Г = 4 (p-2-s (=-!)-,
с. Пусть (А, р) — 1,
где х ж у пробегают возрастающие последовательности, соста-
составленные соответственно из X и Y вычетов полной системы по
модулю р. Доказать, что
\S\<Y2XTp~.
Для доказательства следует воспользоваться неравенством

ВОПРОСЫ К ГЛАВЕ V	87
d. Пусть Q—целое, 1 < Q < р,
р-1	0-1
х=0	z=0
а) Доказать, что S = (p—Q)Q.
Р) Пусть X—постоянное; 0 < \ < 1. Доказать, что число Т
чисел ряда x = Q, 1, ..., р—1, для которых не выполняется усло-
условие ^х < Q°'5 + 0'5 д , удовлетворяет условию T^,pQ~x.
t) Пусть р>25, М — целое. Доказать, что в ряде
М, М + 1, ..., М+3[Ур] — 1
имеется квадратичный невычет по модулю р.
9, а. Доказать, что число представлений целого m > 1 в виде
m=z2 + 2/2, (x, г/)=1, х>0, у>0	A)
равно числу решений сравнения
z2 + l=0(modm).	B)
Для доказательства, положив т= Ym, воспользоваться пред-
представлением а = — согласно теореме вопроса 4, Ь, гл. I, и рассмо-
треть сравнение, получаемое почленным умножением B) на Q2.
Ь. Пусть а—одно из чисел 2 и 3. Доказать, что число пред-
представлений простого р с условием р > а в виде
x>0, y>0	C)
равно половине числа решений сравнения
z2 + a = O(modp).	D)
с. Пусть р имеет вид 4т+1, (к, />) = 1.
Доказать, что (Д. С. Горшков)
a) S (к)—чётное число.
При ( — ) = ^' ( — )=—^ имеем (ср. вопрос а)

88	гл. v. сравнения второй степени
10. Пусть .D—целое положительное, не являющееся квадра-
квадратом целого числа. Доказать, что:
а. Если при данном целом к уравнению
удовлетворяют две пары целых x=xlt у = ул и x = xit у=у«.
то уравнению
X2-DY*=k*
удовлетворяют целые X, Y, определяемые равенством (знак ±
выбирается произвольно)
b.	Уравнение (уравнение Пелля)
x*—Dy2 = l	A)
разрешимо в целых положительных х, у.
c.	Если ха, уй — пара положительных х, у с наименьшим х
(или, что равносильно, с наименьшим х-\-у \f D), удовлетворя-
удовлетворяющая уравнению A), то все пары положительных х, у, удовле-
удовлетворяющие этому уравнению, определяются равенством
'•==1,2, ...	B)
11, а. Пусть а—целое.
- )e p
а) При (а, />)=1 доказать, что \UatP\ = VP
Для доказательства следует сумму Ua< p умножить на сопря-
сопряжённую, получаемую заменой i на —г Обозначая буквами х,
и х переменные суммирования основной и сопряжённой сумм,
следует собрать вместе те члены произвеления, где при данном t
хх = xt (mod/)),
или же
хг = х+1 (mod p).
§) Доказать, что
" UP
\>- Пусть m > 2, (a, m)= 1,
m-i
2iti

ВОПРОСЫ К ГЛАВЕ V
а) Доказать, что Sui p= Ua< p (вопрос а).
Р) Из теорем вопросов а) и а, а) следует, что Sa p =
Доказать следующий более общий результат:
| Sa^ т | = У~т , если то = 1 (mod 2),
I ^a, m I= 0,	если те = 2 (mod 4),
| Sui m\ = yr2m, если т ~ 0 (mod 4).
Y) Пусть m>l, BA, то)=1, а = любое целое число. Дока-
Доказать, что
т—1 „ .Ах°- + ах
e
=)' т.
х=0
12, а. Пусть т—целое, превосходящее 1, М и Q—целые,
О <! Л/ < Л/ + Q<. m, 2 обозначает сумму, распространённую по
2
г на заданную совокупность целых чисел, а 21' обозначает сумму,
Z
распространённую по z лишь на числа этой совокупности, сравни-
сравнимые по модулю т с числами
М, М + 1, ..., М + Q— 1.
Пусть, далее, функция Ф (z) такова, что при некотором \ и лю-
любом о = 1, 2, ..., то — 1 имеем
>, Ф (г) е т < Д.
i —	i "
z
Доказать, что
Z	Z
1
где | 6 | < 1, д > 0 всегда, * > -«г при то > 12, д > 1 при то 5= 60.
Ь. Пусть М и Q—целые, 0 < М <
а) Доказать, что
M+Q-1

90	ГЛ. V. СРАВНЕНИЯ ВТОРОЙ СТЕПЕНИ
§) Пусть R—число квадратичных вычетов и N—число ква-
квадратичных невычетов в ряде М, M + i, .... M + Q — 1. Доказать,
что
f) Формулы вопроса Р) вывести, пользуясь теоремой вопроса
11, Ь, й) и теоремой вопроса а.
8) Пусть тга>60, B.4, /»)=1, Мо и Qo —целые, 0 < Ма < Мо +
+ Qo<?m Доказать, что
Мо-Юо-1 2га —
7, е
)'
< )' т In от.
е) Пусть /> > 60,(^4, р) = 1, Мо и Qo —целые, 0 < М0 < Л/о +
¦•¦Qo<P и 21 обозначает число чисел ряда Ах2; х~М0,
Мй + \, ..., Mu + Q0—1, сравнимых по модулю р с числами ряда
М, М-\-1, ..., М +Q — 1. Доказать, что
Р
с. Формулы вопроса b, P) вывести, рассматривая сумму
о=0«=1 х=М у^М
Численные примеры к главе V.
1,	а. Среди вычетов приведённой системы по модулю 23 ука-
указать квадратичные вычеты.
Ь. Среди вычетов приведённой системы по модулю 37 ука-
указать квадратичные невычеты.
2,	а. Применяя е, § 1, указать число решений сравнений
а) ж2 = 3 (mod 31); Р) ж2 = 2 (mod 31).
b. Указать число решений сравнений:
а) х3 = 5 (mod 73); Р) ж2 = 3 (mod 73).
3,	а. Вычисляя символ Якоби, указать число решений срав-
сравнений
а) ж2 еее-226 (mod 563); 3) х* = 429 (mod 563).

ЧИСЛЕННЫЕ ПРИМВРЫ К ГЛАВК V	91
Ь. Указать чнсло решений сравнений
а) х% == 3766 (mod 5987); §) ** = 3149 (mod 5987).
4,	а. Применяя способы вопросов 2, а; 2, Ь; 2, с, решить
сравнения:
а) х1 = 5 (mod 19); §) х" == 5 (mod 29); 7) *2 = 2 (mod 97).
b. Решить сравнения:
а) х2 = 2 (mod 311); ?) ж2 == 3 (mod 277); 7) «* = И (mod 353).
5,	а. Решить сравнение х2 = 59 (mod 125) способами
а) Ь, § 4; Р) вопроса 5, a; y) вопроса 6.
Ь. Решить сравнение хг = 91 (mod 243).
6,	а. Решить сравнение ж2 = 41 (mod 64) способами:
а) е» § 4; Р) вопроса 5, Ь.
Ь. Решить сравнение хг = 145 (mod 256).

ГЛАВА ШЕСТАЯ.
ПЕРВООБРАЗНЫЕ КОРНИ И ИНДЕКСЫ.
§ 1. Общие теоремы.
a.	При (а, т) — 1 существуют положительные у
с условием aYs? I (mod/и), например (теорема Эйлера)
у = <рG?г). Наименьшее из них называется: показатель,
которому а принадлежит по модулю т.
b.	Если а по модулю т принадлежит показате-
показателю 8, то числа 1^Еа°, о1, ..., as-1 no модулю т не-
несравнимы.
Действительно, из a1 =a*(mod7w), ()<&</< 8 сле-
следовало бы a!~*ss I (mod т); 0</ — k < h, что противоре-
противоречит определению 8.
c.	.Если a no модулю т принадлежит показателю о, то
а = a"f' (mod m) тогда и только тогда, когда у = у' (mod 8);
б частности (при у'=0), a*=l (mod m) тогда и только
тогда, когда у делится па о.
Действительно, пусть г и гх — наименьшие неотри-
неотрицательные вычеты чисел у и у' по модулю 8; тогда при
некоторых q и q1 имеем у = 8дг + >", у' = S^i-j-''i- Отсюда
и из a8 = I (mod m) следует
ат = (аг)ва/- ;=ar (modm),
Поэтому a ^ aTi (mod ги) тогда и только тогда, когда
«r = ari(modm), т. е. (Ь), когда г = гг.
d. Из a?(m)=l (modm) и из с (у' = 0) следует, что
tp(m) делится на 8. Таким образом показатели, кото-
которым числа принадлежат по модулю т., суть делители

§ 2. ЯВРВООБРАЗНЫЕ КОРНИ ПО МОДУЛЯМ р" И 2ра	93
<$(jn). Наибольший из этих делителей есть само <р(/и).
Числа, принадлежащие показателю <р(т) (если такие
существуют), называются первообразными корнями по
модулю т.
§ 2. Первообразные корни по модулям р1 и 2ра.
a.	Пусть р — простое нечётное и а>1. Докажем
существование первообразных корней по модулям ра и 2ра.
b.	Если х по модулю т принадлежит показателю
ab, то ха принадлежит показателю Ъ.
Действительно, пусть ха принадлежит показателю 5.
Тогда (хау= 1 (modm), откуда хаЪ = 1 (modm); следо-
следовательно (с, § 1) а) делится на ab, т. е. 8 делится на Ь.
С другой стороны, хаЬ= 1 (modm), откуда (#а)ь^=
= 1 (mod т); следовательно (с, § 1) b делится на S. Поэтому
8 = 6.
c.	Если х по модулю т принадлежит показателю
а, а у —показателю Ь, причём (а, Ь) = \, то ху при-
принадлежит показателю ab.
Действительно, пусть ху принадлежит показателю 8.
Тогда (ху)ъ^Еа 1 (mod/и). Отсюда хыуы~1 (modтп) и
(с, § 1) хьь~ 1 (modm). Поэтому (с, § 1) М делится
на а, и ввиду (Ь, а) — 1 8 делится на а. Так же нахо-
находим, что 8 делится на Ь. Делясь же на а и на Ь, ввиду
(а, Ь) = 1 8 делится и на ab. С другой стороны, из
(ху)аЬ == 1 (modm) следует (с, § 1), что ab делится на 6.
Поэтому Ь = аЪ.
d.	Существуют первообразные корни по модулю р.
Действительно, пусть t — общее наименьшее крат-
кратное всех тех показателей
81,82	8Г,	A)
каждому из которых по модулю ¦ р принадлежит хотя бы
одно число ряда 1,2, .. ., р— 1, ипусть х = q\lq? . . . glk —
каноническое разложение числа т; тогда при каждом s
среди чисел A) существует некоторое 8, делящееся
на.9** и тем самым представимое в форме b = aq*«. Если
ж —число, принадлежащее показателю 8, то, согласно Ь,
xs = xa принадлежит показателю д?«. Сказанное относится

94	ГЛ. VI. ПЕРВООБРАЗНЫЕ КОРНИ И ИНДЕКСЫ
к s=l, 2, ..., к; согласно о число g=»x1xa...xk при-
принадлежит показателю q^g^t ... qlk — t.
Но поскольку показатели A) суть делители числа т,
то все числа 1, 2, ..., /? —1 удовлетворяют (с, § 1)
сравнению хх =-= 1 (mod р). Значит (с, § 4, гл. IV),
р — 1 < х. Но х — делитель числа р — 1. Поэтому х = р — 1,
т. е. g — первообразный корень.
е. Пусть g — первообразный корень по модулю р.
Можно указать t с условием, что и, определяемое
равенством (§- + pt)p~1.= 1 + ри, не делится на р. Соот-
Соответствующее g + pt будет первообразным корнем по
модулю р* при любом а > 1.
Действительно, имеем
g-p-i = l + рТ0,
(g + Р^-1 = 1 + р(Т0- gP-Ч + рТ) = 1 + ри, B)
где, одновременно с t, и пробегает полную систему вычетов
по модулю р. Поэтому можно указать t с условием, что и
не делится на р. При указанном t из B) выводим также
где и2> из> • • • не делятся на р.
Пусть g + pt по модулю рЛ принадлежит показа-
показателю 5. Тогда
(g + pt)* = l (mod р*).	D)
Отсюда (g4-jwt)s=l (mod p); следовательно, 8 кратно
/7 — 1, а так как г; делит ср (рЛ) = /?*—* (/?—1), то
о == рг~г(р — 1), где г —одно из чисел 1, 2, ..., а.
Заменяя левую часть сравнения D) её выражением из
соответствующего из равенств B) и C), получим (и — иг)
Ц-р»-иг==1 (mod/?*), pr±=0(modp°-), r = a, 5*=ср(ра),
* т. е. g + pt-— первообразный корень по модулю рЛ.
f. Пусть а>1 и gx-~ первообразный корень по
модулю рЛ. Нечётное из чисел gx и gx + p* будет перво-
первообразным корнем по модулю 2ра.

S 3. РАЗЫСК. ПЕРВООБРАЗН. КОРНЕЙ ПО МОДУЛЯМ ра И 2ра 95
Действительно, всякое нечётное х, удовлетворяющее
одному из сравнений жт=;1 (mod ра) и жт== 1 (mod2/?*),
очевидно, удовлетворяет и другому. Поэтому ввиду
ср (р°-) —. ср Bjo*) всякое нечётное ж, являющееся перво-
первообразным корнем по одному из модулей рл и 2рл,
является первообразным корнем и по другому. Но из
двух первообразных корней gx и g± -f- p°- по модулю /?а
один — непременно нечётный; он, следовательно, будет
первообразным корнем и по модулю 2/?а.
§ 3. Разыскание первообразных корней
по модулям ра и 2рл.
Первообразные корни по модулям р* и 2ра, где
р — простое нечётное и а > 1, можно разыскивать, поль-
пользуясь следующей общей теоремой:
Пусть с = ср(т} и qlt q2, ..., qk — различные про-
простые делители числа с. Для того чтобы число g, взаимно
простое с т, было первообразным корнем по модулю т,
необходимо и достаточно, чтобы это g не удовлетворяло
ни одному из сравнений
g*i =l(modm), g^=l(modm), .. .,g«* = l (modm). A)
Действительно, если g — первообразный корень,
то тем самым оно принадлежит показателю с и, сле-
следовательно, ни одному из сравнений A) удовлетворять
не может.
Обратно, допустим, что g не удовлетворяет ни одному
из сравнений A). Если бы показатель 8, которому при-
принадлежит g, оказался меньше с, то, обозначая буквою q
.. с	- с
один из простых делителей -j- , мы имели бы -v- = qu,
с
с	—
— — ьи, g9 = l (modp), что противоречит нашему допу-
допущению. Значит, Ь = с и g — первообразный корень.
Пример 1. Пусть т = 41. Имеем срD1) = 40 = 23 • 5,
•д- = 8, y = 20. Следовательно, для того чтобы число gf
не делящееся на 41, было первообразным корнем по

96	ГЛ. VI. ПВРВООБРАЗНЫЕ КОРНИ И ИНДЕКСЫ
модулю 41, необходимо и достаточно, чтобы это g
не удовлетворяло ни одному из сравнений
g8==l (mod41), gM==l (mod41).	B)
Но, испытывая числа 2, 3, 4, .. ., находим (по модулю 41)
28 = 10, 38==1, 48 = 18, 58==18, 68s=i0,
22°=1,	420=1, 520=sl, 620=s40.
Отсюда видим, что числа 2, 3, 4, 5 —не первообраз-
первообразные корни, так как каждое из них удовлетворяет,
по крайней мере, одному из сравнений B). Число 6 — пер-
первообразный корень, так как оно не удовлетворяет
ни одному из сравнений B).
Пример 2. Пусть т = 1681 = 412. Первообразный
корень и здесь можно было бы найти, пользуясь общей
теоремой. Но мы найдём его проще, применяя теорему
е, § 2. Зная уже (пример 1), что первообразный
корень по модулю 41 есть 6, находим
б40 =1 + 41 C + 41/),
F + 41гL0 = 1+41 C + Ш - 639г + 41Г) = 1 + 41в.
Чтобы и не делилось на 41 достаточно взять г = 0.
Поэтому в качестве первообразного корня по модулю
1681 можно взять число 6 + 41 -0 = 6.
Пример 3. Пусть т = 3362 = 2 • 1681. Первооб-
Первообразный корень и здесь можно было бы найти, пользуясь
общей теоремой. Но мы найдём его проще, применяя
теорему f, § 2. Зная уже (пример 2), что первообразный
корень по модулю 1681 есть 6, в качестве первообраз-
первообразного корня по модулю 3362 можно взять нечётное из
чисел 6, 6 t 1681, т. е. число 1687.
§ 4. Индексы по модулям рл и 2р*.
a.	Пусть р — простое нечётное, а>1; т — одно из
чисел р* и 2ра; с = <р (т), g — первообразный корень по мо-
модулю т.
b.	Если у пробегает наименьшие неотрицательные
вычеты y = 0, 1, ..., с — 1 по модулю с, то gt пробегает
приведённую систему вычетов по модулю т.

I 4, ИНДЕКСЫ ПО МОДУЛЯМ рл И 2Р»	97
Действительно, g пробегает с чисел, взаимно про-
простых с т и, ввиду Ь, § 1, не сравнимых по модулю т.
с. Для чисел а, взаимно простых с т, введём по-
понятие об индексе, представляющее аналогию понятию
о логарифме; при этом первообразный корень играет
роль, аналогичную роли основания логарифмов.
Если
а = gt (mod m)
(считаем у>0), то у называется индексом числа а по
модулю т при основании g и обозначается символом
у = ind а (точйее у = indff a).
Ввиду Ь всякое а, взаимно простое с т, имеет не-
некоторый единственный индекс у' среди чисел ряда
Зная у', мы можем указать и все индексы числа а;
согласно с, § 1 это будут все неотрицательные числа
класса
у = у' (mode).
Непосредственно из данного здесь определения ин-
индекса следует, что числа с данным индексом у образуют
класс чисел по модулю т.
А. Имеем
ind ab . . . 1 = ind a + ind Ь + .. . + ind / (mod с)
и, в частности,
ind an = n ind a (mod с).
Действительно,
а = glnd a (mod т), Ь = gInd ь (mod m), ...
откуда, перемножая, находим
пЬ . . . /==ginda+indb + ...+ in<l! (modm).
Следовательно, inda + ind&+ ... + ind / — один из ин-
индексов произведения аЬ .. . I.

ГЛ. VI. ЙЕРВООБРАЗНЫЕ КОРНИ Й ИНДЕКСЫ
е. Ввиду практической пользы индексов для каждого
•простого модуля р (разумеется, не слишком большого)
"составлены таблицы индексов. Это две таблицы; одна —
для нахождения индекса по числу, другая — для нахо-
нахождения числа по индексу. Таблицы содержат наимень-
наименьшие неотрицательные вычеты чисел (приведённая система)
и их наименьших индексов (полная система) соответ-
соответственно по модулям р и с = <р (/>) = /? — 1 -
Пример. Построим указанные таблицы для модуля
/> = 41.. Выше было показано (пример 1, § 3), что
первообразным корнем по модулю 41 будет §" = 6; его
мы примем за основание индексов. Находим (сравнения
берутся по модулю 41):
6°==1 68 = 10 61в = 18 624=16 632 = 37
б9 = 19 б17 = 26 б25 = 14
б18 = 33
61	= 6
62	=36 б10 = 32
63=11 6" = 28
= 2
633	=17
634	= 20
= 28	6" = 34	6" = 12	636 = 38
64	= 25 612= 4	620 = 40	628 = 31	636 = 23
65	= 27 б13 = 24	б21 =5 35	629s22	б37 = 15
66	= 39 614 = 21	622= 5
= 9
67 = 29
= 3 623 =
6з8 = 8
639= 7
поэтому указанные таблицы будут
N
0
1
2
3
4
0
8
34
23
20
1
0
3
14
28
2
26
27
29
10
3
15
31
36
18
4
12
25
13
19
5
22
37
4
21
6
1
24
17
2
7
39
33
5
32
8
38
16
И
35
9
30
9
7
6
32
6 36
28
40 35
13 37
5 30
25 27
14
17 20 38 23
31
Здесь номер строки • указывает число десятков, номер
столбца — число единиц числа (индекса). В графе, общей
указанным строке и столбцу, помещается соответству-
соответствующий индекс (число).

Ь. СЛЕДСТВИЯ ПРЕДЫДУЩЕЙ ТЕОРИИ	99
Например, ind 25 найдём в графе цервой таблицы,
общей строке с номером 2 и столбцу с номером 5,
т. е. ind 25 = 4. Число, индекс которого 33, найдём
в графе второй таблицы, общей строке с номером 3
и столбцу с номером 3, т. е. 33 = ind 17.
§ 5. Следствия предыдущей теории.
a.	Пусть р — простое нечётное; а>1, т — одно из
чисел ра, 2ра, наконец, с — у(т).
b.	Пусть (п, с) = d; тогда:
1.	Сравнение
я" = a (mod m)	A)
разрешимо (и тем самым а есть вычет степени п по
модулю т) тогда и только тогда, когда ind а кратен d.
В случае разрешимости сравнение имеет d решений.
2.	В приведённой системе вычетов по модулю т число
вычетов степени п есть -j .
а
Действительно, сравнение A) равносильно такому:
п ind х = ind a (mod с),	B)
которое разрешимо тогда и только тогда, когда ind a
кратен d (d, § 2, гл. IV).
В случае разрешимости сравнения B) найдём d не-
несравнимых по модулю с значений для ind x; им отве-
отвечает d несравнимых по модулю т значений для х.
Таким образом верно утверждение 1.
Среди чисел 0, 1, .. ., с — 1, являющихся наимень-
наименьшими индексами вычетов приведённой системы по мо-
модулю т, имеется -т- кратных d. Поэтому верно утвер-
утверждение 2.
Пример 1. Для сравнения
х8 = 23 (mod 41)	C)
имеем (8, 40) = 8, причём ind 23 = 36 не делится на 8.
Поэтому сравнение C) неразрешимо.

iOft	гл. vi. Первообразные корйй и индексу
Пример 2. Для сравнения
z12 = 37(mod41)	D)
имеем A2, 40) = 4, причём ind 37 = 32 делится на 4.
Поэтому сравнение D) разрешимо, причём это сравнение
имеет 4 решения. Указанные решения найдём следу-
следующим образом.
Сравнение D) равносильно таким:
12 ind ж == 32 (mod 40), ind х ~ 6 (mod 10).
Отсюда для ind x найдём 4 несравнимых по модулю 40
значения:
ind ж = 6, 16, 26, 36,
соответственно чему найдём 4 решения сравнения D)
жзьЗЭ; 18; 2; 23 (mod 41).
Пример 3. Числа
1, 4, 10, 16, 18, 23, 25, 31, 37, 40,	E)
индексы которых кратны 4, суть все биквадратичные
вычеты (или также вычеты любой степени п = 12, 28,
36, ..., где (п, 40) = 4), имеющиеся среди наименьших
положительных вычетов по модулю 41. Число чисел
ряда E) есть 10 = -т-.
с. Одновременно с утверждением Ь, 1 полезно сле-
следующее:
Число а есть вычет степени п по модулю т тогда
и только тогда, когда
с
а?=з1 (modm).	F)
Действительно, условие ind a == 0 (mod d) равносильно
.такому: -^ ind as 0 (mod с). Последнее же равносильно
условию F).
Пример. В теореме § 3 невозможность сравнения
?;= 1 (mod m) равносильна условию, что g — невычет

$ 5. СЛЕДСТВИЯ ПРЕДЫДУЩЕЙ ТЕОРИИ.	101
степени q по модулю т. В частности, невозможность
с
сравнения g2=l(modm) равносильна условию, что
g — квадратичный невычет по модулю т (ср. е, § 1, гл. V).
d. 1. Показатель 8, которому а принадлежит по
модулю т, определяется равенством (ind а, с) = -^- ;
в частности, принадлежность а к числу первообразных
корней по модулю т определяется равенством (ind а, с) — 1.
2. В приведённой системе вычетов по модулю т число
чисел, принадлежащих показателю о, есть <р (о); в частно-
частности, число первообразных корней есть <р (с).
Действительно, о есть наименьший делитель с с усло-
условием аъ^={ (mod ?/г). Это условие равносильно
о ind a =s 0 (mod с),
или
ind a = 0 (mod -|
Значит, 5 — наименьший делитель с, при котором ~
делит ind а, отсюда -v- — наибольший делитель с, деля-
делящий ind а, т. е. -?- = (ind а, с). Поэтому верно утвер-
утверждение 1.
Среди чисел 0, 1, . . ., с — 1, являющихся наимень-
наименьшими индексами вычетов приведённой системы по мо-
модулю т, кратными -?- являются числа вида у г/, где
г/=-0, 1, ..., $ — 1. Условие С~ у, с) =у равносильно
условию (г/, о) = 1; последнему удовлетворяет <?E) зна-
значений г/. Поэтому верно утверждение 2.
Пример ]. В приведённой системе вычетов по
модулю 41 числами, принадлежащими показателю 10,
являются числа а с условием (ind a, 40) =^ = 4, т. е.
числа
4, 23, 25, 31.
Число этих чисел есть 4 = 9A0). *

102	ГЛ. VI. ПЕРВООБРАЗНЫЕ КОРНИ И ИНДЕКСЫ
Пример 2. В приведённой системе вычетов по
модулю 41 первообразными корнями являются числа а
с условием (inda, 40) = 1, т. е. числа
6, 7, И, 12, 13, 15, 17, 19, 22, 24, 26, 28, 29, 30, 34, 35.
Число этих первообразных корней есть 16 = срD0).
§ 6. Индексы по модулю 2а.
a.	Для модуля 2а предыдущая теория заменяется
несколько более сложной.
b.	Пусть а^1. Тогда 2а = 2. Имеем <рB) = 1. Перво-
Первообразным корнем по модулю 2 будет, например,
1 == — 1 (mod 2). Число 1° = (—1)° = 1 образует приве-
приведённую систему вычетов по модулю 2.
c.	Пусть а = 2. Тогда 2°= 4. Имеем срD) = 2. Пер-
Первообразным корнем по модулю 4 будет, например,
3^-1 (mod 4). Числа (—1)° = 1, (-II —3 (mod 4)
образуют приведённую систему вычетов по модулю 4.
d.	Пусть а>3. Тогда 2а>8. Имеем срB") = 2а.
Нетрудно видеть, что первообразных корней в этом
случае нет; более точно: показатель, которому принад-
принадлежит по модулю 2а нечётное число х, не превосходит
2а~2 —-х-<рBа). Действительно, имеем .
x" = lJr8t1,
xz°-* _ 1 + 2Х_2 = 1 (mod 2a).
При этом числа, принадлежащие показателю 2 ,
существуют. Таким числом будет; например, 5. Дей-
Действительно,
5 = 1 + 4,
54 = 1 + 16 + 32м2,

i 6. индексы по модулю г*	доз
откуда видим, "что ни одна из степеней 51, 5г, 5*, ..., 52*~3
не сравнима с 1 по модулю' 2*.
Нетрудно видеть, что числа двух следующих строк:
ко си ..	. t;2a-i
О , О , . . .) О	,
-5°, -51, .... _ 5aa-2-i
образуют приведённую систему вычетов по модулю 2е.
Действительно, число этих чисел будет 2 • 2a~ =±:cpBa);
числа каждой отдельно взятой строки между собой
по модулю 2а несравнимы (Ь, § 1); наконец, числа
верхней строки несравнимы с числами нижней, так как
первые по модулю 4 сравнимы с 1, а вторые с — 1.
е. Для удобства дальнейших исследований мы выра-
выразим результаты Ь, с, d в более единообразной форме,
которая будет пригодна и в случае а. — 0.
Пусть	.	_;
е = 1; со^1,	если а = 0, или а=1;
с = 2, са=2а~2, если. а>2
{таким образом всегда ссо = уBа)) и пусть у и уо неза-1
висимо друг от друга пробегают наименьшие неотри-
неотрицательные вычеты	-
у=0, ..., с—1; Yo = °> •••> со — 1.
яо модулям с и с0. Тогда (— 1)Т5Т° пробегает приведён-
приведённую систему вычетов по модулю 2а.	. .
f. С равнение
(-l)Y5V==(-l)Y'5Yo(mod2a) .. A)
имеет место тогда и только тогда, когда
Действительно, при а = 0 теорема очевидна. Поэтому
предположим, что а. > 0. Пусть наименьшие неотрица-
неотрицательные вычеты по модулям с и с0 для чисел у.и Yo
будут /• и г0, а для чисел у' и у^ будут г' и /^. Ввиду
Р(^§ 1 ( —1 принадлежит показателях с, а 5 принадле-
принадлежит показателю с0), сравнение A) имеет место тогда

104	ГЛ. VI. ПЕРВООБРАЗНЫЕ КОРНИ И ИНДЕКСЫ
и только тогда, когда ( — l)r5r° = ( — l)r'5'»(mod 2"), т. е.
(ввиду е) когда r = r', ro = r'o.
g. Если
e==-(-l)T5>(mod2"),
то система у> То называется системой индексов числа а
по модулю 2*.
Ввиду е всякое а, взаимно простое с 2* (т. е. нечёт-
нечётное), имеет единственную систему индексов y'> Yo сРеДи
сс0- <»Bа) пар значений у, у0, указанных в е.
Зная систему у'То' мы м°жем указать и все системы
индексов числа а; согласно f это будут все пары у. То-
составленные из неотрицательных чисел классов
Непосредственно из данного здесь определения си-
системы индексов следует, что числа с данной системой
индексов y, Yo образуют класс чисел до модулю 2а.
h. Индексы произведения сравнимы по модулям с и с0
с суммами индексов сомножителей.
Действительно, пусть у (а), -{0(а); ...; у (/), "@A) —
системы индексов чисел а, ..., I. Имеем
а . , . /=H(_l)T(a)+...-)Y@5Va)+"- + VI>.
Следовательно, y (a) + • • • + Y @. Yo (a) + • • • + Yo @ — ин"
дексы произведения а ... I.
§ 7. Индексы по любому составному модулю.
a.	Пусть т = 2a/)i1/?|2 • • • Pkk — каноническое разло-
разложение числа т. Пусть далее с и с0 имеют значения,
указанные в е, § 6; cs = cp(p"s); gs — наименьший перво-
первообразный корень по модулю pas.
b.	Если
a==(-l)Y5Y°(mod 2*),	)
} A)
a = gji (mod p°f)	a ~glk (mod a) J

§ ИНДЕКСЫ ПО ЛЮБОМУ СОСТАВНОМУ МОДУЛЮ	105
то система у> Yo> Yi> • ¦ • > Y* называется системой инде-
индексов числа а по модулю т.
Из такого определения следует, что у> Уо"~система
индексов числа а по модулю 2а, a Yi> •••> ул""инДексы
числа а по модулям pi1	p"kk- Поэтому (g, § 6; с,
§ 4) всякое а, взаимно простое с т (тем самым оно
взаимно простое и со всеми 2а, р\х, ..., р%к), имеет
единственную систему индексов у', Yo> Ть •••> Yt среди
cc0Ct ... ск = <? (т) систем у, уо> Yi> • • •> Y*> которые по-
получим, заставляя у. Yq> Yi> ¦•¦> Y/< независимо друг от
друга пробегать наименьшие неотрицательные вычеты
по модулям с, с0, с1( . .., ск, а все системы индексов
числа а суть все системы у> То- Yi> •••> Y*> составленные
из неотрицательных чисел классов
Y = y'(modc), Yo = Y
Числа а с данной системой индексов у> Yo- Yi> • • • > Y*
могут быть найдены путём решения системы A), а сле-
следовательно (Ь, § 3,.гл. IV), образуют класс чисел по
модулю т.
c.	Так как индексы у, Yo> Yi> • • ¦> Yt числа а по моду-
модулю иг являются индексами его соответственно по модулям
2х, Pi1, ¦¦¦, Рьк, то верна теорема:
Индексы произведения сравнимы по модулям с,с0, с1,..., ск
с суммами индексов сомножителей.
л
d.	Пусть х = срBа) при а<2 и т =-^ ср Bа) при а > 2
и пусть Л —общее наименьшее кратное чисел т, сг, ...
,.., ск. При всяком а, взаимно простом с т, сравне-
сравнение ah=l верно по всем модулям 2*, р^1, ..., р^, зна-
значит, это сравнение верно и по модулю т. Поэтому а
не может быть первообразным корнем по модулю т
в тех случаях, когда h<y(m). Но последнее имеет
место при a > 2, при /с>1, а также при. a = 2, й=1.
Поэтому для т > 1 первообразные корни могут существо
вать лишь в случаях 7П = 2, 4,-jSj1, 2/??i. Но как раз для

106	ГЛ.. VI. ПЕРВООБРАЗНЫЕ КОРНИ И ЙНДЕКШ
этих случаев существование первообразных корней было
доказано выше (§ 6, § 2). Поэтому
Все случаи, когда существуют первообразные корни
по модулю т, превосходящему 1* суть
т --- 2, 4, /Л 2/Л.
Вопросы к главе VI,
Буквою р здесь всегда обозначаем простое нечётное число, а
в вопросе'11, b также и. число 2.
1,	а. Пусть а — целое, а > 1. Доказать,, что простые нечётные
делители числа а1'—1 делят а— 1 или- имеют вид 2рх > 1.
b.	Пусть а — целое, а > 1. Доказать, что простые нечётные
делители числа а? +- 1 делят а+ 1 или имеют вид 2рх + 1.
c.	Доказать бесконечность числа простых чисел вида 2рх+1-.
d.	Пусть и—целое, п > 0. Доказать, что простые делители
числа 22" + 1 имеют вид 2п+1х-\- 1.
2.	Пусть а—целое, а > 1, и —целое, -п > 0. Доказать, что
»(ап— 1) кратно ге.
3,	а. Пусть /г—целое, п > 1. Из чисел 1, 2, . .., /г при нечёт-
нечётном п образуем перестановки
1, 3, 5, ..., и — 2, п, п — 1, 71 — 3, ..., 4, 2;
1, 5, 9, .... 7, 3
и т. д., а при чётном п образуем перестановки
1, 3, 5, ..., п— 1, 71, тг—2, ..., 4,-2;
1, 5, 9, .... 7, 3,
и т. д. Дока'зать, что k-я операция даёт исходный ряд тогда и
только тогда, когда 2г= ± 1 (mod 2п—1).
Ь. Пусть 71 — целое, п > 1, т—целое, т > 1. Будем считать
числа 1, 2, ..., п в прямом порядке от 1 до я, далее в обратном
порядке от 71 до 2, затем опять в прямом порядке от 1 до л,
далее опять в обратном порядке от п до 2 и т. д. При таком
счёте выписываем числа 1-е, (т Т 1)-е, B/л. i- l)-e и т. д., пока не
получим п чисел. С этим новым рядом п чисел повторим ту же
операцию и т. д. Доказать, что к-я операция даёт исходный ряд
тогда и только тогда, когда
тк= ±1 (mod.27i—I).	:
4.	Существование <р (8) чисел, принадлежащих показателю д,
доказать, рассматривая сравнение х& = 1 (mod p) (вопрос 1-0 с>
гл. IV) и применяя d, § 3. гл. II. „'•.	.. ,;

РОПРОСЫ К ГЛАВЕ VI	.: .	Ю?
5,	а. Доказать, что первообразный корень простого числа
вида 2м +1, п > 1 есть 3.
b.	Доказать, ято первообразный корень простого числа вида
2р+ 1 при р вида 4гс + 1 езть 2, а при р вида 4л ^ 3 есть —2.
c.	Доказать, что первообразный корень простого числа вида
Ар + 1 есть 2.
d.	Доказать, что первообразный корень простого числа вида
32п-х
2"р + 1 при п > 1 и р >	есть 3.
6,	а а) Пусть п —целое, л > 0, S=l" + 2" + ... + {р— 1)".
Доказать, что
iS1 = —I (mod p), если п кратно р— 1,
iS" = 0 (mod p)	в противном случае.
Р) При обозначениях вопроса 9, с, гл. V доказать, что
р_! |(modp).
Ь. Теорему Вильсона доказать, применяя Ь, § 4.
7.	Пусть j и ^ —первообразные корни по модулю р, a ind^ gx =
= 1 (mod p — 1).
a.	Пусть (а, /))=1. Доказать, что
ind9l a = a indj a (mod p— 1).
b.	Пусть га—делитель р—1, 1 < тг < р — 1. Числа, взаимно
простые с р, можно разбить на п совокупностей, относя к s-й
совокупности (s = 0,1, ..., п — 1) числа с условием ind я s s (mod n).
Доказать, что совокупность, имеющая при основании g номер s,
тождественна совокупности, имеющей при основании gx номер slt
где sx = as (mod n).
8.	Указать возможно более простой способ решения сравне-
сравнения ж4 = a (mod р) (удобный, если (п, р — 1) невелико) в случае,
когда известен некоторый первообразный корень g по модулю р.
/9. Пусть т, а, с, с0, сг, ..., с^, 7. To. "iv ¦•¦> Тл имеют зна-
значения, указанные в § 7. Взяв какие-либо корни Л, Ло, Rl7 .. ., R^
уравнений	^
полагаем
Если (а, т)> 1, то полагаем; ?(a)=

108	ГЛ. VI. ПЕРВООБРАЗНЫЕ КОРНИ И ИНДЕКСЫ
Определённую таким образом для всех целых а функцию
назовем характером. При R=R0 = R1 = ... = Rk = 1 характер назо-
назовём главным; он имеет значение 1 при (о, w)=l и значение 0
при {а, т) > 1.
a.	Доказать, что указанным путём мы получим ? (т) различ-
различных характеров (два характера называются различными, если
они, по крайней мере, при одном значении а не равны между
собою).
b.	Вывести следующие свойства характеров:
«О ХA) = 1,
3) 7.(aia2) = y(a1) / (я2),
Т) '/. (ai)~7.(я2), если а1 = а2 (mod т).
с. Доказать, что
т—1
т—1	С
2	1р(т) для главного характера,
0 для других характеров.
а=0	*
d. Доказать, что, суммируя при данном а по всем ?(т) харак-
характерам, имеем
у у <а)=\ f (m)' если а =
¦~ "	| 0 в противном случае
е. Рассматривая сумму
ZJ 1л
ZJ 1л ^ (а) '
где а пробегает приведённую систему вычетов по модулю т, до-
доказать, что функция ф(а), определённая для всех целых а, удо-
удовлетворяющая условиям
¦^(<г) = 0, если (а, т) > 1,
4> (а) не равна тождественно 0,
Ф (ai) — Ф (аг). если % = <г2 (mod то),
' есть характер. "	— _
f. Доказать следующие теоремы.
а) Если ул (а) и Ха(а)—характеры, то Xi (a) Za(a)—также ха-
характер.
{J) Если Хг (а)—характер и х(а) пробегает все характеры, то
7л (а) У. (а) также вробегает вее характеры

ВООЮСЫ К ГЛАВЕ VI	jQg
Tf) При (I, m) — \ имеем
V У W— f 9(т)> если а = ' (mod т.),
2л f{V)~ \ О в противном случае.
10, а. Пусть п—делитель р—1, 1 < п<^.р — 1, I—целое, не
делящееся на п. Число i?,=e " является корнем уравнения
ЯУ = 1 и, следовательно, степень е п , которой при х,
кратном р, следует приписывать значение 0, есть характер по
модулю р.
а) При (к, р) = 1 доказать, что
р— 1 „ . I ind (ж + *)-г Ind х
Л
2 Л	"=-..
Пусть Q—целое, 1 < Q < />,
а; 0	г=0
Доказать, что S —(p—Q)Q.
¦j) Пусть /) > 4я2, га > 2, Л/—целое. Доказать, что в ряде
М, М + 1, ..., М~\-2[п\^р] — 1 имеется число s-й совокупности
вопроса 7, Ь.
Ь. Пусть р > 4 ( р~~ ) 22t, Л—число различных простых
делителей р — 1, Л/ —целое. Доказать, что в ряде М, М+1, ...
. .., М + 2 -у	j- 2k YР — ^ имеется первообразный корень
по модулю г>.
11, а. Пусть а —целое, « — делитель р— 1, 1<п</> —1,
А—целое, не делящееся на га,	^
а) При (а, р)=1 доказать, что
ji) Доказать, что

НО	ГЛ. VI. НЕРЙООВРАЗНкЁ КОРИН И ИНДЕКСЫ
Y) Пусть р имеет вид im+l, •_•
р.-2 „_.ind ((?»+*)
Доказать, что (ср. вопросы 9, а и 9, с, гл. V) р = Аг + В2, где
и В —целые, определяемые равенством S = A+ Bi.
Ь. Пусть п — целое, п > 2, т> 1, (в, т»)=1,
где ж пробегает полную, а ?—приведённую систему вычетов по
модулю т (ср. вопрос 12, d, гл. III и вопрос 11, Ь, гл. V)
а) Пусть й=(п, p-^i). Доказать, что
8) Пусть (га, р)=1, s — целое, 1 < s^n. Доказать, что
7) Пусть s—целое, s > п. Доказать, что
Sa,p* — Pn~ Sa,p»-n< S'a, p« — °-
5) Доказать, что
\S9,m\<Cm n,
где С зависит только от п.
12. Пусть М и Q-целые, 0<M<M-fQ<p.
а. Пусть п—делитель р—1, 1 < га< р—1, к—целое, не де-
делящееся на п. Доказать, что
2
е
р.
Ь. Пусть У—число чисел s-й совокупности вопроса 7, Ь, за-
заключённых среди чисел М, М-\-{, ..., M + Q — 1. Доказать, что
с. Пусть к—число простых делителей р—1, Н—число пер-
первообразных корней по модулю р, заключённых среди чисел М,

ьошюсы к главе vi
'М + 1, ¦•'.., М +Q-^i. Доказать что ,"--
" p-i
d. Пусть Мх и (?!—целые, 0 <; Мг < A/x + Q, </>— 1, J—чис-
J—число чисел ряда т&М, ind(M + 1), ..., ind(lf * Q — 1), заключён-
заключённых среди чисел ряда Мх, Mx-\-i, ..., Мх^ Qx—i. Доказать, что
13.	Доказать существование постоянного р0 с условием: если
р > Ро, п—делитель р — 1, 1 < п < р—1, то наименьший из поло-
положительных невычетов степени п по модулю р будет
/г h- « In - с-2е «
14,	а. Пзгсть w > 1, (а, т)=1,
т—1 т—1	„ .ажу т-1
т-1
2
Доказать, что \\^y
Ъ, а) Пусть т > 1, (а, т)={, п—целое, п > О, К—число
решений сравнения х" = 1 (modm),
Доказать, что | S t
ji) Пусть s — произвольное положительное постоянное. При
постоянном п для числа К вопроса а) доказать, что К=О{т*)
' 15, а. Пусть (a, p)=z(b, />) = 1, п — целое, \n\ = nl, Q <п1< р,
р-1 „^ахП+Ъх
„	 ^	Р
х=1
Доказать, что

112	ГЛ. VI. ПЕРВООБРАЗНЫЕ КОРНИ И ИНДЕКСЫ
Ь. Пусть (А, р) = 1, п— це#ое, |п|=п1( 0< п, < р, Мо и
<?о—целые, 0 < М0 < М0 + Qo < р.
а) Пусть
Мо+Оо-1 , . Ах"
3 - -
Доказать, что | >У | < -y n\ pi In p.
}) Пусть М и Q—целые, 0 <. М <М +Q<p, Г—число чи-
чисел ряда Лх"; х = Ма, Мо + 1, ..., Мо + Qo — 1, сравнимых по
модулю р с числами ряда М, М+1, ..., M+Q—1.
Доказать, "то
i з
0^	3
с. Пусть (а, р) = 1, 6 и с—целые, (Ь2—4ас, р)=1.
а) Пусть Tf — целое,
р-1	. . т* •
2 + Ьх + с\ 2яг ^
)е
ж=0
с\
)
3 л
з
Доказать, что \S \ < ~к р ¦
Пусть Л/ и Q —целые, 0<Af<ilf+Q</>,
з _
Доказать, что | i11 < -y P4 In p.
Численные примеры к главе VI.
1,	а. Найти (путём возможно более простых вычислений)
•показатель, которому принадлежит 7 по модулю 43.
Ь. Найти показатель, которому принадлежит 5 по модулю 108.
2,	а. Найти первообразные корни по модулям 17, 289, 578
b.	Найти первообразные корни по модулям 23, 529, 1058.
c.	Найти наименьший первообразный корень по модулю 242.

ЧИСЛЕННЫЕ ПРИМЕРЫ К ГЛАВЕ VI	ЦЗ
3,	а. Составить таблицы индексов по модулю 17.
Ь. Составить таблицы индексов по модулю 23.
4,	а. Найти первообразный корень по модулю 71, применяя
указание примера с, § 5.
Ь. Найти первообразный корень по модулю 191.
5,	а. Пользуясь таблицей индексов, указать число решений
сравнений:
а) ж» = 79 (mod 97), g) ж" = 17 (mod 97), 7) xU = 46 (mod 97)-
b. Указать число решений сравнений
а) Зж12 = 31 (mod 41), ji) lx> = И (mod 41), 7) 5ж30 = 37 (mod 41).
6,	а. Пользуясь таблицей индексов, решить сравнения
а) ж2 = 59 (mod 67), Р) х*~° = 17 (mod 67), t) xS0 = 14 (mod 67)-
Ь. Решить сравнения
a)	23ж5 = 15 (mod 73), ^) 37жв = 69 (mod 73), 7) 44*21 = 53 (mod 73).
7,	а. Пользуясь теоремой с, § 5, определить число решений
сравнений
а) х3 = 2 (mod 37), р) ж16 = 10 (mod 37).
b. Определить число решений сравнений
а) я5 s 3 (mod 71), Э) л'21 = 5 (mod 71).
8,	а. Применяя способ вопроса 8, решить сравнения (при
решении второго сравнения воспользоваться таблицей первообраз-
первообразных корней в конце книги)
а) ж'= 37 (mod 101), S) х* = 44 (mod 101).
b. Решить сравнение
ж3 = 33 (mod 109).
9,	а. Пользуясь таблицей индексов, среди вычетов приведён-
приведённой системы по модулю 19 указать: а) квадратичные вычеты,
b)	кубические вычеты.
Ь. Среди вычетов приведённой системы по модулю 37 указать:
а) вычеты степени 15, р) вычеты степени 8.
10,	а. Среди вычетов приведённой системы по модулю 43
указать: а) числа, принадлежащие показателю 6, ji) первообраз-
первообразные корни.
' Ь. Среди вычетов приведённой системы по модулю 61 указать:
а) числа, принадлежащие показателю 10, (J) первообразные корни.

РЕШЕНИЯ ВОПРОСОВ.
Решения к главе I.
1.	Остаток от деления ах + by на d, имея видая' -f by' и будучи
меньше d, непременно равен нулю. Поэтому d—делитель всех
чисел вида ах -t by и, в частности, общий делитель чисел
о • 1 + 6 • 0 = о и а ¦ О + 6 • 1 = 6 С другой стороны, выражение
для d показывает, что всякий общий делитель чисел а п b
делит d. Поэтому d — {a, 6), и верна теорема 1, cl, § 2. Теоремы е,
§ 2 выводятся так: наименьшее положительное число вида
атх+Ъту есть атха-{-Ьту0; наименьшее положительное число
a	b	а	Ь
вида -у х + -j у есть — х0 + -у у0.
Обобщение этих результатов тривиально.
2.	Предварительно заметим, что разность двух неравных
между собою рациональных дробей -у и — (I > 0, п > 0) чи-
сленно>>
у-.
Ограничимся предположением Ss < 8,+1. Пусть
-т—несократимая дробь, не равная й8, с условием 0<6<Q,.
Не может быть 3g < -=-< 8S+1; в противном случае было бы
1
Поэтому -=- < д, или же tltl <— , В обоих случаях 5, ближе к а.
чем/т-

РЕШЕНИЯ К ГЛАВК I
3. ПрЯ га<.6 теорема очевидна; поэтому предполагаем п > 6.
Имеем
1,618...;
Отсюда
n<
0 1
4, а. Для дробей -т- и — имеем 0 ¦ 1 — 1 • 1 = —1. Вставляя
^4 С А ¦+ С
между дробями -=- и -=г- с условием Л?> — ВС =—1 дробь —
имеем Л (В 4- Z»J — 5 (А + С) =' (Л + С) D — E 4- D) С = — 1. Поэтому
верно утверждение, отмеченное в конце вопроса. Существование
к	а к с 7
дроби — с условиями -т- < -у- < -г, / < t невозможно В против-
противном случае мы имели бы
1
1 _ с a b \- d I
Й' T~~~b>~Jbd~> Ы'
b. Очевидно, достаточно рассматривать случай Osga < 1.
_	а	с	а с
Пусть -r^a<"j"> r^e "г и "j—соседние дроби ряда Фарея,
отвечающего ¦z. Возможны два случая:
a	a ± с	a f с	с
'd {Ь td)'
Поэтому верно одно из двух неравенств
1 .
6 F 1- d)'
откуда ввиду Ь {- d > x указанная теорема следует непосред-
непосредственно.
с. При а иррациональном теорема следует из h, § 4, если
Р	Р
принять за -~г подходящую дробь _!ri_, где Qa 4 <t<Q,.

116	• решения вопросов
В случае же рационального а = -г- приведённое рассуждение осуще-
осуществимо лишь при 6 > т. Но при b<;t теорема верна, так как
а
Р	, а
тогда за —у можно принять самое дробь -=- , полагая при этом
6 = 0.
5,	а. Нечётные простые числа при делении на 4 дают оста-
остаток 1 или же 3 Произведение чисел вида 4w -i- 1 имеет вид
Лт + i. Поэтому число Ap1...pk—i, где plt ..., рк — простые
иида Am 4- 3, наверно имеет простой делитель q вида 4т 4- 3.
При этом q не совпадает ни с одним из чисел рл, ..., рк. ¦
Ь. Простые числа, превосходящие 3, имеют вид 6т + 1 или
же §т -t 5. Число 6/>х ... р.—1, где р,, ...,pt, — простые вида
6т + 5, наверно имеет простой делитель q вида 6m -f 5. При этом
q не совпадает ни с одним из чисел ри ..., рк
6.	Пусть pt, ..., рк — какие-либо к простых чисел и iV—целое
с условиями 2 < JV, C in JV); < N. Число чисел а ряда 1,2, ..., N,
каноническое разложение которых имеет вида = р^1 ... р^к, ввиду
. lniV
as<-"Tn~2~ УДеТ
И
)*< C
Поэтому в ряде 1, 2, ...,N найдутся числа, в каноническое раз-
разложение которых входят простые, отличные от plt ..., рк,
7.	Например, такие последовательности получим при
М = 2 ¦ 3... (K+l)t + 2; t—1,2,...
8.	Взяв целое х„ с условием, что при ж>а;0, / (х) > 1 и
/' (х) > 0, положим f(xo) — 'X. Составными (кратными X) будут
в?е числа f (xo-t-Xt); t = 1, 2, ...
9.	а. При наличии A) одно из чисел х, у, пусть именно г,
будет чётным; из
/iiY —
"-\ 2 У ~~
, (—~- ,
где, очевидно, (—~- , —^-j = l, убеждаемся в существовании
положительных целых и и и с условиями
х	z+y „ г—у
Отсюда следует необходимость условий, указанных в вопросе
Достаточность этих условий очевидна.

ншвдшя кшш i	у7
Ь. Условимся здесь обозначать буквами лишь целые поло-
положительные числа. Допустив существование систем х, у, z, с усло-
условиями ж4 + 2/4 = г2, х > О, у > О, z > 0, (ж, ?/, z) = l, выберем из них
систему с наименьшим z. Предполагая х чётным, найдём x* = 2uv,
j/2 = «2 —и2, и>17>1, (и, V)sal, где V—чётное (при чётном и
было бы ?/2 = 4iV+l, u2 = 4JV,, v2 = 4N2 + l, AN T l = 4JVt — 4iV2— 1,
что невозможно) Отсюда u = z\, v = 2w2, у2+ Aw* = zl, 2wi = 2u1vi,
м( = т|, r1 = j/f, a;J i- ?/4 = zf, что ввиду z^ < z невозможно.
Из неразрешимости уравнения ж4 + t/4=z2 как частный случай,
очевидно, следует и неразрешимость уравнения xi + у4 = D в целых
положительных х, t/, f.
10.	Полагая х = ~; (А-, Z) = l, находим
kn + a1ktl~l 1+ ... +ап1п = 0.
Поэтому кп кратно I и, следовательно, 1 = 1.
11.	а. Пусть к—наибольшее целое с условием 2"с ^п и Р —
произведение всех нечётных чисел, не превосходящих п. Число
2*~ PS представится суммою, все слагаемые которой, кроме
2 Р— , суть целые числа.
2<
Ь. Пусть к — наибольшее целое с условием 3 <1 2ге + 1 и Р —
произведение всех взаимно простых с 6 чисел, не превосходящих
2?г + 1. Число 3*~^PSпредставится суммою, все слагаемые которой,
кроме 3t}~1P — , суть целые числа.
О
12.	При п < 8 теорема проверяется непосредственно. Поэтому
достаточно, считая при п > 8 теорему верной для биномов
a+b, (a i by, .. ., (а+ Ь)п~г, доказать справедливость теоремы
и для бинома (а 4- Ь)". Но коэффициенты разложения этого бинома
за исключением крайних, равных 1, суть числа
п п in — 1)	п (п — 1) . . . 2
Т' 1-2 "'¦'" 1 ¦ 2 ... (и—1) '
Для нечётности же всех этих чисел необходимо и достаточно,
чтобы нечётными были крайние из них, как раз равные га, и чтобы
также нечётными были числа, получаемые вычёркиванием нечётных
сомножителей из числителей и знаменателей оставшихся чисел.
Но, полагая п = 2», + 1, ати числа можно представить членами ряда
ni n\(ni—1)	п, (п, —1) ... 2
Т' Л! ' •' 1 • 2 ... («х—1)"
Последние же ввиду пг < п будут все нечётными тогда и только
тогда, когда щ имеет вид 2< — \, т. е. когда п имеет вид
*1

Ив	з>вшгаия вопросов
Решения к главе II.
1, а. На ординате точки кривой у=f (x) с абсциссою а; лежит
[/(ж)] целых точек указанной области.
Ь. Указанное равенство следует из 7'1 + 772=77, где Ти Тг, Т
обозначают числа целых точек областей
О	Р
0<x<-f, 0<у<-^-х,
Р	О
(> < У <~2 г ° <х <~р-У>
0<*<-|-, 0<у<?..
с. Указанное равенство следует из
где Tlt T2, T3, Tt обозначают числа целых точек областей
х = 0,	0<г/<г;
О < х < -4= , 0 < у < /г2—ж2;
V2
о < у < -^, о < х
d. Указанное равенство следует из Т = ТХ + 772 — Уз» ГДе
Т3 обозначают числа целых точек областей
О < к < УЛУ, 0 < у < ^-;
0<ж</л, 0<y<Yn.
2.	Число целых положительных чисел, не превосходящих л,
равно [л]. Каждое из них единственным способом представляется
в форме хкт, где к—целое положительное; при этом данному х
отвечает |/ — чисел такой формы.
3.	.Докажем необходимость указанных условий. Пусть N—це-
N—целое, N > 1. Число значений х с условием [azKJV можно пред-

РЕШЕНИЯ К ГЛАВЕ II	119
N
ставить в форме —ЬХ; 0<<X<JC, а число значений у с усло-
условием [Ту] -< iV можно представить в форме тг + ^i; O^
N	N
где С и С, не зависят от N. Из —+ Х+ -3-+X1 = JV, деля на N
а	р
1 1
и переходя к пределу при N—>оо, получим	1._=1. Послед-
Последнее равенство при рациональном <х = — (а > 6 > 0) дало бы [аЪ] =
= №(а-Ъ)).
Пусть указанные условия выполнены. Пусть с —целое, с > О,
хо=	1-? и Уо—-тт + 1) — наименьшие целые с условиями
ар	-
жо>-^-> 2/о > у- Очевидно, [ах] ^ с при ж Щ хь и [pj/]^e при
2/=?;2/о> 0<5<1, 0 < ч < 1, а? и pv) — иррациональные. Ввиду
ж0 + 2/о = с + 4 + 5 имеем S + к] = 1,— | -4=1: поэтому одно и только
а Р.
одно из чисел а? и ^ меньше 1. Следовательно, одно и только
одно из чисел [ах0] и [jii/o] равно с.
4, а. Указанные разности равны	«
{axj, {а(ж2 —Жх)}, ..., {а(ж, —я,,!», {— axf},
они неотрицательные, их сумма равна 1, их число равно f + 1;
поэтому, по крайней мере, одна из этих разностей не превосходит
11,	1
	т <— и, таким образом, существует число, меньшее — , вида
{±aQ>, гдеО<(?<т. Из ±aQ — [±aQ] +{±aQ}, полагая
± [ ± aQ] =P, находим | aQ — Р | < — ,
Р
1
Ь. Полагая Ха= [X], Y0 = [Y], ..., Z.,= [Z], рассмотрим
ряд образованный расположенными в неубывающем порядке чис-
числами вида {ах l jjy t-... + "fz1- и числом 1, предполагая, что
х, у, ..., z пробегают значения:
Получим (Х0 + 1)(У0 + 1) ... (Zn + 1) + 1 чисел, из которых соста-
составим (Хо + 1)(Yo + 1) ... (Z0 + l) разностей. По крайней мере, одна
из этих разностей не превосходит
1	1
1)...(ZI) + 1)^ XY ...Z
Отсюда уя$е легко получается указанная теорема.

120	РЕШЕНИЯ ВОПРОСОМ
5. Имеем а = сд + Г + {а}; 0<г < q,
6, а. Имеем [з + р + ... +Х] = [а] + [§] + ... -+ [X] т
а> + {{4>+ ...+vX>].
Ь. Простое р входит в и!, а\, ..., И с показателями
При этом
7. Допуская, что число а с указанными свойствами суще-
существует, представим его в форме
°<9к< Р, ° <?;<_! < Р, ¦¦¦, 0 <?1 < р, 0<9'0< р, 0<з'< р.
Согласно Ь, § 1 должно быть
Далее при любом s=l, 2, ..., т имеем
Поэтому последнее выражение для h должно полностью совпасть
с указанным в вопросе.
8, а. Пусть ж! —целое, Q<ct<§<B, хг < а < {} < хх -\ 1;
интегрированием по частям находим
р' (х) / (х) ^ =
Р
)-Р(»)/(»)-« (В)/'(Р) + « («)/'(«)+J *<*>/*
В частности, при Q^a;!, Kj + l^ff, переходя к пределу, имеем
Указанная формула теперь получается без всякого труда.

РЕШЕНИЯ К ГЛАВЕ; Ц	121
Ь. Переписав формулу вопроса а в виде
(z)dx—^ f(x)dx+f(R) f.(R)-9
- a (R) /' (R) + о (Q) /' (Q)+ ^ с (x) f" (x) dx-^в (x) f" (x) dx,
Q	R
убеждаемся в справедливости указанной формулы.
с. Применяя результат вопроса Ь, находим
In И In 2+ ... +lnn = C-rnlnn — n-t-^lnn\[^
2	J хг
п
= «1пл — п + 0Aпп).
9, а. а) Имеем (Ь, § 1)
Здесь правая часть представляет сумму значений функции in p,
распространённую на целые точки (р, s, и) с простыми р области
р>0, s > 0, 0<и<1 —. Часть этой суммы, отвечающая данным
s и и, равна 0 f I/ —J ; часть, отвечающая данному и, равна
8) Применяя при п ;> 2 результат вопроса а), имеем
Полагая Г-^-1 =т, отсюда находим {\п\ = Ъп, или [п]=2т + 1)
B1}
3 " 5 ''-
<1пBИ13>в)<71,
и»)- -и»)- * (f)+* (т)- * (т)

122	РЕШЕНИЯ ВОПРОСОВ
7) Имеем (решение вопроса Р) и результат вопроса 8, с)
т)-<т> ¦¦•¦-¦¦ -щт
= [«] In [n]-[n]-2 [i] In [-±] +2 [-J] + O(lnn) =
Далее, при s>2 находим (вопрос §))
<%Vrn всегда
=0 при s>t; i;=l -^
Поэтому
b.	Следует из равенства A), неравенства вопроса а, Р)
и равенства вопроса 8, с.
c.	Равенство вопроса b при достаточно больших т даёт
2 '
Если для всех пар рп, р с условием т < рп< р *Стг имело
бы место неравенство р >р A + е), то было бы
чю при достаточно больших m невозможно.
d. Очевидно достаточно рассматривать лишь случай, когда
п—целое.
Полагая 7(г) = —- при г простом и i(r) = 0 при. г=1, или
при г составном, имеем (вопрос Ь)
•уA) -ИB)+ ... +-((г) = 1пг + а(|-)Г"(а(г)| < С,,

РЕШЕНИЯ К ГЛАВЕ II
где Сх—постоянное. Отсюда при г > 1 (считаем аA) = 1)
21 _т j-т ¦ т — V 1п г —1пГг—1)
--Т1+Т2, Тг- 2j 	Е7
0<р in
Т — V a(r)~a(r—i)
Ji~ Zj	ПГ7
1 <r^ n
Имеем (8, b)
Tl= 2 Йп
1<г<п
где С2 — постоянное. Далее находим
Но при целом т> 1 имеем
г
сходится; при этом, если С3 его сумма, то
е. Имеем
	i_V =A-
(m + 1) ln(m + 1) J ^ " "" In то
Поэтому ряд
lnny
где С — постоянное. Отсюда, полагая С = 1пС„, мы и получим
указанное равенство.
10, а. Следует из с, § 2.
Ь. Ввиду вA)=[,A)=1 условие 1, а, § 2 для функции в (а)
выполнено. Пусть a = aja2 — одно из разложений а на два взаимно
простых сомножителя. Имеем
2

124	: РЕВДНИН ВОПРОСОВ
Бели условие 2, а, § 2 выполнено для всех произведений, мень-
меньших а, то при A^2 < а. имеем в №(/2) = 9 (^)в (с!г), и равенство A)
даёт в (а]Я2) = в (а,) 0 (а2), т. е. условие 2, а, § 2 выполняется
и для всех произведений ахаг, равных а. Но условие 2, а, § 2
выполняется для единственного произведения 1-1, равного 1.
Следовательно, оно выполняется и для всех произведений.
11, а. Пусть m > 1; для каждого данного хт, делящего а,
неопределенное уравнение х1 ... хт_1хт = а имеет ^m^i ( 	 )
V хт /
решении. Поэтому
но когда хт пробегает все делители числа а, то d=	 в обрат-
обратит
ном порядке пробегает те же делители. Следовательно,
Поэтому (вопрос 10, а) если теорема верна для функции гт_, (а),
то она верна и для функции хт (а). Но теорема верна для функ-
функции ^(а) —1. Значит, она верна всегда.
Ь. Если т > 1 и теорема верна для функции tm_j (а), то
имеем
rm (a)=zm (Pl) . . . zm (pk) =
Но теорема верна для функции 1Л (а). Значит, она верна всегда.
с. Пусть г = т~2, s2 = 2rj, a = p\i ... р^ — каноническое разло-
разложение числа а, причём />,, ... , рд. расположены в возрастающем
порядке. Для функции с2 (а) — - (а) имеем
-z (а) ^ ац + 1 at' 1	ак + 1
Каждый из сомножителей произведения, стоящего справа,
меньше —; сомножители ——	 с условием г > 2ч меньше
1\	Г«Г-11
J
^
[ 1. Поэтому, полагая C=\^-tJ .находим
т(а)	т(а) ... С .
(i	а-*со „ 2 а->» а '

РЕШЕНИЯ К ГЛАВЕ II	125
При т > 2, очевидно, имеем tm(a)<; (z(a))m. Поэтому
о-юо а
d. Системы значений хх, ... , хт, удовлетворяющие указан-
указанному неравенству, разобьём на [п] совокупностей с номерами
1, 2, ..., [л]. К совокупности с номером а отнесём системы
с условием Xi ... хт = а; число этих систем есть тт(а)-
12. При R(s)> 1 ряд. выражающий ?(.«), абсолютно сходится.
Поэтому
оо	оо
... пту
причём при данном положительном п число систем пх, ... , пт
с условием пу ... nm = n равно ^т(п).
13, а. При /?(s)> 1 произведение Р= ГТ	—абсолютно
р i~'y
1	11
сходится. Ввиду	— = 1-\—j--\—gj-+--- при N > 2 имеем
1~Т
где во второй сумме правой части п пробегает лишь числа,
не делящиеся на простые, превосходящие N. В пределе при
N -> оо левая часть обратится в Р, первая сумма правой
части — в ? (s), вторая—в нуль.
Ь. Пусть N > 2. Допустив, что простых чисел, отличных от
Pit ¦ ••> Pkt нет, находим (ср. решение вопроса а)
П1 ¦
1 ¦¦
Это неравенство ввиду расходимости гармонического ряда
1 + тг + -гг + • • • при достаточно больших N невозможно.

126	РЕШЕНИЯ ВОПРОСОВ
с. Допустив, что простых чисел, отличных от рг	рь нет,
находим (вопрос а)
Д * =;B,
ы *-—
Pi
я2
Это равенство ввиду иррациональности С B) = -^- невозможно.
14. При R{s) > 1 бесконечное произведение для ? (s) вопроса
13, а абсолютно сходится. Поэтому
р
где р пробегает все простые дисла. Дифференцируя, имеем
К' (s) __ у / In р In р _ In р _ V _ у А(п)
\ ps piS pbs •)
p	n=l
15. Пусть N > 2. Применяя теорему b, § 3, имеем
<N	0N
где во второй сумме правой части п пробегает лишь числа, боль-
большие N и не делящиеся на простые, превосходящие N. В пределе
при N ->¦ оо мы и получим указанное тождество.
16, а. Применим d, § 3 к случаю
Й=1, 2, ... ,[п], /=1, 1,... , 1.
Тогда, очевидно, <S" = 1. Далее S<j обращается в число значений й,
Гп 1
кратных а, т. е. в -т- .
Ь. о) Правая часть равенства вопроса а выражает сумму зна-
значений функции v-(d), распространённую на целые точки (d, и)
области d>0, 0<м<^—•. Часть этой суммы, отвечающая дан-
данному и, равна М ( — J .
Р) Указанное равенство получается почленным вычитанием
равенств

РЕШЕНИЯ К ГЛАВЕ И
с. Пусть п1 = [п]; 8и'82, ... ,8п определяются условием: да есть
наибольшее целое, 1-я степень которого делит s, /s=l. Тогда
S' = Tln, Sd равно числу чисел, не превосходящих п, кратных rf',
т. е. «Уй= —J- I . Отсюда получается указанное выражение для Tt n.
В частности, ввиду fB) = -g- для числа Т2п чисел, не пре-
превосходящих л и не делящихся на квадрат целого, превосходя-
превосходящего 1, имеем
17, а. Указанное равенство получим из d, § 3, если положим
3, = (я„а), /s = /(zs).
b.	Указанное равенство получим из d, § 3, если положим
°s — "• l > • • • > xk '' Is —' VI • - • • • к i •
c.	Применяя d, § 3 к случаю
где в первой строке выписаны все делители числа а, имеем
d. Указанное равенство следует из
d\5i	d\82	d\5n
P'=h	h	¦¦¦/n ¦
18, а. Применим теорему вопроса 17, а, заставляя х пробегать
числа 1, 2, ... , а и беря f(x) = x"\ Тогда
b. Имеем
d\d
Тот же результат можно получить проще. Напишем числа ря-
ряда 1, .... о, взаимно простые с а сначала в возрастающем, ватем

128	РЕШЕНИЯ ВОПРОСОВ
в убывающем порядке. Сумма членов обоих рядов, равноотстоя-
равноотстоящих от начала, равна а; число членов каждого ряда равно <р (о).
с. Имеем
d\a
19, а. Применим теорему вопроса 17, а, заставляя х пробе-
пробегать числа 1, 2, ... , [г] и беря /(ж) = 1. Тогда S'-=TZ, Sj равно
числу чисел, не превосходящих г, кратных d, т. е. Sd= -^ .
Ь. Имеем
d\a
с. Следует из равенства вопроса а.
20. Применим теорему вопроса 17, а, заставляя х пробегать
\
числа 1, 2, ... , N, где N > a, w беря / (х)=—- . Тогда найдём
Xs
2 "jr
d\a
В пределе при N -> оо получим указанное тождество.
21, а. Ьрименим теорему вопроса 17, Ь, рассматривая
указанные в определении вероятности PN системы значений
х1г х2, ... , хк и беря f(xx, хг, ... , xk) = i. Тогда Pn — -TT <
Г N Лк
i= —у- , и мы получим
N
Г N 1'<
., ел I _ I
N	N
d-1	d=l
Поэтому
*>2. Д=Л
b. Имеем С B) = -^- .
22, а. Элементарные рассуждения показывают, что число целых
точек (и, v) области и2 + «2'¦< р2; р > 0, не считая точки @, 0>,
равно лр2 + О(р). Применим теорему вопроса 17, Ь, рассматривая
координаты х, у целых точек области жа + у2 <. г8, отличных от

РЕШЕНИЯ К ГЛАВЕ II
точки @, 0), и полагая f(x, у)=1. Тогда T=S' + i, Sj равно
С Г \*
•j ) , не считая точки @,0).
Поэтому
d=l	d=l
b. Рассуждая аналогично предыдущему, получим
(
d=l
23. а. Число делителей d числа а=р\\ ... />?*, не делящихся
на квадрат целого, превосходящего 1, и имеющих х простых
делителей, равно ( J ; при этом ц (d) = (— 1)*. Поэтому
. d\o	x=0
b. Пусть а имеет тот же вид, что и в вопросе а. Достаточно
рассматривать случай т < к. Для указанной суммы имеем два
выражения
Ес'ли m чётное, то при т^-^- первое выражение > 0, а при
к	к
т > -у второе выражение >¦ 0. Если те нечётное, то при т ^ -^
к
первое выражение < 0, а при т > у второе выражение <, 0.
c.	Доказательство почти такое же, как в d, § 3, но с учётом
результата вопроса Ь.
d.	Доказательствапочти такое же, как в вопросах 17, а и 17, Ь,

130	РЕШЕНИЯ ВбПРОСОВ
24. Пусть d пробегает делители числа a, Q (d) —число простых
делителей числа d, bi (a) = s Согласно сделанному в вопросе
указанию, имеем (считаем N достаточно большим)
2(d)r<m
' г I	Zj ad '
Далее находим
n=0
п 0-7)
Наконец, обозначая буквами Сх и С2 некоторые постоянные,
имеем
' q Zj Zj d q Zj
n=m+12(d)=n ¦	n=m+i
n=m41
25. Всякому делителю d1 числа о_ с условием dx < [^a отве*
чает делитель rf2 с условиями й2 > |/а, d^^^a. При этом
=*»[j.(tf2). Поэтому
^ ^—1 \ 4 In г у
n=m+l
s
;v 2 (т) <C2v
d2	d\a

РЕШЕНИЯ К ГЛАВЕ Н	ДО
26.	Числа d, не делящиеся на квадрат целого, превосходя-
превосходящего 1, и удовлетворяющие условию 9 (d) = к, рассмотрим попарно
так, чтобы в каждую пару входило некоторое нечётное dx и чёт-
чётное 2dv. Будем иметь (x(rf,) . \i.Bd1) = О
27.	Ьусть ри ...,рк — различные простые числа. Полагая
a — Pi ••¦ Рк> имеем
<Р W =(/>!-!) ... (Pk-D-
Между тем, при отсутствии простых чисел, отличных от plt ..., рк,
мы имели бы ср (а)= 1.
28.	а. Указанные числа найдутся среди чисел sd; s —1, 2, •..,-*¦ ¦
Но (s8, a) = 5 тогда и только тогда, когда ( s, — j=l(e, §2, гл.1).
Поэтому верно утверждение, отмеченное в вопросе, и мы имеем
<)
d\a	d\a
b, i) Пусть а = ра] ... p°k — каноническое разложение числа а.
Ввиду а функция в (а) мультипликативная, причём
Р) Для целого т > О имеем
d\m
Поэтому
а
d\a
29. Имеем (р пробегает все простые числа)
П=1	Р	"	Р 1""~р8-1

i	РЕШЕНИЯ ВОПРОСОВ
30. Имеем
d\l	d\2	d\n
n
d=l
Решения к главе III.
1, а. Из
P = an lO"-1 + «„.,! 10"-2 + ...+«!,
замечая, что 10 = 1 (mod 9), имеем
P = а„ 4- an_j +...+«! (mod 9).
Следовательно, _Р кратно З тогда и только тогда, когда сумма
цифр, его изображающих, кратна 3; оно кратно 9 тогда и только
тогда, когда указанная сумма кратна 9
Замечая, что 10= —1 (mod И), имеем
Р = (а1 + а3+ ...) — (а2 + «4+ ¦ • •) (mod 11).
Следовательно, Р кратно 11 тогда и только тогда, когда разность
между суммою цифр, стоящих на нечётны* (считая справа) местах,
и суммою цифр, стоящих на чётных местах, кратна 11.
b.	Из
Р = Ъп 100я-1 + Ьп_! 100"-* + ... + Ь,
ввиду 100 = — 1 (mod 101) имеем
Р = (Ъ1 + Ь3+ .. .)-(Ь2 + ЪА+ ...) (mod 101).
Поэтому Р кратно 101 тогда и только тогда, когда (Ъх + Ь„+ .. .) —
— (Ьг + &4+ •••) кратно 101.
c.	Из
Р — сп ЮОО" + сл_х 1000"-2 + • • • + Н
ввиду 1000 = 1 (mod 37) имеем
Р = сп + сп_! +•• .+<¦•! (mod 37).
Поэтому Р кратно 37 тогда и только тогда, когда сп + cn_t
кратно 37.

РЕШЕНИЯ «ГЛАВЕ ill
Ввиду 1000 s — I(mod7 • 11 • 13) имеем
/> = (Cl+c,+ ...)-(c, + c4+...)(mod7-11-13).
Поэтому P кратно одного из чисел 7, 11, 13 тогда и только тогда,
когда (ci + cs +	)—(сг + г4 +-...) кратно этого же числа.
2, а. ->) Когда х пробегает полную систему вычетов по моду-
модулю т, то ах + Ь также пробегает полную систему; наименьший
неотрицательный вычет г числа ах t b пробегает значения
0, 1, ...,т — 1. Поэтому
m-l
l
х
\ т \
Применяя результат вопроса 18, Ь, гл. II, находим
6
b. В случае t = 1 имеем [/ (N + m)] — [/ (N)] = a,
N+m
= S
U(N + )]+[f(N)] +
N-tm	N+m
к этому случаю тривиально сводится и случай ( > 1.
с. Пусть N, М, Рл, Рг — целые, М ~> 0, Рх > 0, Р2 > 0. Тра-
Трапеция с вершинами (N, 0), (JV, Р,), (iV4-il/. 0), (JV + M, Р2)
является частным случаем рассмотренной в вопросе Ь. Поэтому
и для неё верно равенство A) Равенство A) для такой трапеции
легко пол5'чим также, рассматривая прямоугольник с вершинами
(j!V, 0), (j!V, Pi + Pt), {N+M, 0), (N+M, Pi + Pt), равновеликий
двум таким трапециям. Для этого прямоугольника равенство
аналогичное равенству A), очевидно. Отсюда ввиду 23' й = 2$3 *
S' = 2S мы и полуг.им равенство A)
Из этого результата аналогичная формула для указанного
в вопросе треугольника выводится тривиально Однако предста-
представляет интерес также следующий вывод: указанный треугольник
получается путём разбиения на два равных треугольника некото-
некоторого параллелограмма с целыми вершинами. Пусть S-^ площадь
параллелограмма и Г= 2 *. гДе суммирование распространяется

134	. РЕШЕНИЯ ВОПРОСОВ
на все целые точки параллелограмма, причём Ь определяется
аналогично, тому, как в вопросе Ь. Интересующее нас свойство
треугольника будет доказано, если мы докажем, что S=^T. Рас-
Рассмотрим квадрат с беспредельно растущей стороною А. Вся
плоскость может быть разбита на бесчисленное множество парал-
параллелограммов указанного вида. Пусть к — число параллелограммов,
полностью лежащих внутри квадрата, и R — число целых точек
внутри квадрата. Ьри А -* оо находим
lim-^=l, hm—= 1, lim^ = l.
Перемножая почленно эти равенства, получим
3, а. Пусть г—наименьший неотрицательный вычет числа
ах ¦+ [с] по модулю т. Имеем
т- 1
S= 5
где 5^Ф(г)<5 + Л; s={r} При т <; 2Л f 1 теорема очевидна
Поэтому рассмотрим лишь случай т > 2а + 1. Полагая
имеем —1-|	^й(г)<	 при r = m—[A + s], .... т — 1;
е .... Л 4-ч	„
— ^й(г)^	 в остальных случаях. Поэтому
т	т	.	-
— [А + s] -f- s <<У	г—<!A + s, i1——,
b. Имеем
m-1
z=0
Применим теорему вопроса а, полагая Л^|Х|. Тогда и получим
указанный результат.
с. Находим
т-1
2

ЙВШЕНИЯ К ГЛАВК III
135
"Применим теорему вопроса а, полагая А=1+ -=-'.¦ Тогда получим
указанный результат.
4. Разложим А в непрерывную дробь. Пусть Qn~Q'— наиболь-
наибольший из знаменателей подходящих дробей, не превосходящий т,
имеем {вопрос 4, Ь, гл I)
При этом из т < Qn^ i-<(?n vi + i)Qn --4 CQn, где С—постоянное,
которого не превосходят все ?,.+ 1, для наибольшего целого Н'
с условием H'Q' ^т следует //' < С. Применяя теорему вопроса
3, Ь, находим	,
M-IH'Q'-i
1
Пусть ml = m—H'Q'. Если пг1 > 0, то, выбирая в зависимости
от тх ппсяа Q* и Н" таким же способом, как раньше в зависи-
зависимости от т были выбраны числа Q' и #', найдём
ic.
Пусть mz = m1 — H"Q". Если m2 > 0, то подобно предыдущему
найдём
2
и т. д., пока не придём к некоторому пгд=0. Тогда получим
(H'Q'	^'k)
M+m-i
i
<~Ск.
Т1исла Q' ,• Q", ..., Q'*' удовлетворяют условиям
Поэтому (вопрос 3, гл. I), k = O (In m) и, следовательно, формула,
указанная » роиросе, верна.

36
РЕШЕНИЯ ВОПРОСОВ
5, а. Сумму, стоящую слева, обозначим буквою S. Пусть
теорема очевидна. Поэтому предполагаем
1], найдём числа аи ти йх с условиями
-; 0<т<т, («,, т1) = 1, \йг\<1.
ъ=А3. При
* > 40. Взяв
Взяв М2=М1 + т1, аналогичным путём найдём числа а2, т2, 82;
взяв М3=М2 4- w2, найдём числа а3, т3, в3; и т. д., пока не придём
К iI/s+1 = Ms + ms с условием 0<;.[Л] — Afg+1<[x]. Применяя
теорему вопроса 3, с, найдём
<
Длина интервала, для которого —
ТП TYIZ
3 1+1
~- -\	, не пре-
Ш fflz
2А „	, а
восходит — . Следовательно, с одной и той же дробью —
пы	m
2А
связано ^ —s—1-1 чисел mlt m2	ms. Пусть а1 и а2—наимень-
шее и наибольшее значения а, отвечающие данному т.
Имеем
Следовательно, с данным т связано
k(R-Q)m , , пс
чисел ту, т2, ..., пгь. Суммируя последнее выражение по всем
т» = 1, 2, .... [;], получим

0ВШЕНИЯ К ГЛАВЕ Ш
137
Ь. Имеем
2
откуда, полагая й(х) = {/(х) +1 — о} — {/(#)}> находим
<2\.
Но при {/(ж)} <о имеем 5(ж) = 1 — о, а при {/(ж)}>с имеем
«(*) = — о. Поэтому | A —о)-ф(с) —о (Л—Q—^(о)) | < 2\, откуда
и получим указанную формулу.
6, а. Применим формулу вопроса 1, с, гл. II. Полагая
2—ж2, в интервале
имеем
/'(*)=-¦
, ./"(*)=-
Поэтому (вопрос 8, а, гл. II, вопрос 5, а)
b. Имеем (вопросы 11, d и 1, d, гл. II)
Достаточно рассмотреть лишь случай п>64. Интервал X < х <^ у п ,
где Х = 2п3 , разобьём на О (Inn) интервалов вида М <х^М',
где ЛГ<2М. Полагая /(х)=—, в интервале М <х <ЛГ имеем
. . ^ 8п

±38	г РЕШЕНИЯ ВОПРОСОВ
Поэтому (вопрос 5, а)
Далее (вопрос 8, Ь, гл. II)
2 -^ = Еп+±-
Поэтому
1	1
+ 2 ¦/« { ]/гё} + О (п3 (In reJ) = n (In re + IE — 1) + 0 (re3 (In reJ').
7.	Пусть система неправильная и s — наибольшее целое
с условием, что 2s входит в нечётное число чисел системы. Одно
из последних чисел мы заменил! меньшим, содержащим лишь
степени 2s, входящие в нечётное число чисел оставшейся системы.
Пусть система —правильная. Число, меньшее одного из чисел
Т этой системы, отличается от Т, по крайней мере, одним знаком
в системе исчисления с основанием 2.
8.	а. Добавив к каждому из чисел, представляемых указанным
способом, число Я = 3П + 3П 4 ... + 3 + 1, получим числа, которые
можно получить, заставляя в той же форме хп, з-п_1, •••, х1г хл
пробегать значения О, 1, 2, т. е. получим все числа О, 1, ..., 2Н.
Ь. Указанным способом получим тхт2 ... ть чисел, не сравни-
сравнимых между собою по модулю т^^ ... год, так как из
... + тхт2 ¦.. т^^х^ =
= х[ + т^х'ъ + пь^гп^х'^ 4-... + т^т^ ... т^^х'^ (mod rn^rn^ ... ть)
последовательно находим:
хх = х[ (mod mi), x1 = x'1; mxx% = тхх'г (mod mim2), x^ = x'2;
тхт^х3 = тхтгх'ъ (mod тхтгт^), х3 = х'3,
и т. д.	.
9, а. Указанным способом получим т^гпу, ... т^ чисел, не сравни-
сравнимых по модулю тхтг ... год, так как из
М гхг + М%хг + ... + Мкхк =
s= М!*{ + Мzx't + '...+ Мкх'К {щойтгпц ... тк)

РЕШЕНИЯ К ГЛАВЕ III
следовало бы (всякое Mj, отличное от Ms, кратно т„)
^), ха s x's (mod/ns), xs = x'a.
b.	Указанным способом получим fim^ •? (т%) ... ч)(тк) =
= -p(w,w2 ... mil) чисел ввиду теоремы вопроса а, не сравнимых
по модулю/га,™,, ... mk, и ввиду (Mixl-\- М2з-2 + ... -]-Мкхк, mj =
= {MsxH, mj—l, взаимно простых с пг,пг2 ... тк.
c.	Согласно теореме вопроса а число М 1ж1 + М^х, + ... J- Ми^к,
где ж1, а;2, ..., х^ пробегают полные системы вычетов по модулям
т1, т,	т.к> пробегает полную систему вычетов по модулю
тлтг ... тк. Это число взаимно просто с тхтг ... т^ тогда и
только тогда, когда (хь m,) — (zit w2)= ... =(ж^, wt) = l. Поэтому
?(/»,w2 ... тк) =?(TOi)?(m,) ... i(mk).
d.	Чтобы получить все числа ряда 1, 2, ..., ра, взаимно про-
простые с ра, следует вычеркнуть числа этого ряда, кратные р,
т. е. числа р, 2р, ..., ра 1р. Поэтому •? (ра) = ра — pa -1. Отсюда
и из теоремы с, § 4, гл. II известное выражение для <р (а) следует
непосредственно.
iO, a. Первое утверждение следует из
—Н • ¦ • Н	У = {	 f ;
li	тк J I	т	J
второе утверждение следует из
I ml	mk J I	m	I
Ь. Дроби |A(*i>^--. Wi>+...+/*(**,^-,w»)j совпадают
с дробями
Г/, (М,а;, 4- ... + Мл-^, ..., MlWl 4- ... 4- Л/A-w>) .
... J-Mkxk, ...,
+	—	|,
т'. е, с дробями I/l(a:'---w) + ... +/Иж	W)) . Отсюда три-
виально получается первое утверждение. Второе утверждение
доказывается аналогичным способом.
11, а. При а, кратном т, имеем
„ . ах
е m=2l = W.

140	РЕШЕНИЯ ВОПРОСОВ
При а, не делящемся на т, имеем
х	е m_i
b. При нецелом а левая часть равна
s sin п (о) ^ h (о) "
с. Согласно теореме вопроса Ь левая часть не превосходит Тт<
где
m-l
Но при нечётном т
2а 4- 1 ,
о __< —mlnm,
0<a<|
а при чётном т
Гт<Т 2 1п2^1 + Т S ln2^1
Ill
При т > 6 ввиду -g	5-=-Tj- границу от In те можно уменьшить на
Zoo
Последнее выражение > -^- при те!> 12 и > т при те>60.
12, а. Пусть т = р х ... р к — каноническое разложение числа т.
Полагая р 1^=т1	р А = /п.^, при обозначениях вопроса 10, а,
имеем

РЕШЕНИЯ К ГЛАВК Ш
Но при о, = 1 находим
2 1»- v, 2*i-^
е ms=2je т« —1=
is	*s
При as > 1, полагая tf»s = />gWj, находим
m'—1
is	xs	u=0
m—1 . x
b.	Пусть m—целое, m> 1. Имеем V e m=0. Сумма сла-
слагаемых левой части этого равенства с условием (х, w) = rf согласно
теореме вопроса а равна ц ( — J .
c.	Находим
^^ 2ni — ч^-^
5	d\m
где, полагая m = mod, имеем
и=0
Последнее равно 0 при d < т и равно 1 при d=m. Отсюда и полу-
получаем теорему вопроса а.
d.	Равенства следуют из вопроса 10, Ь.
e.	Имеем
A (mi) ...
где aj, ..., а/с пробегают приведённые системы вычетов по моду-
модулям и»!, ..., т^. Отсюда (вопрос d) первое равенство вопроса
следует непосредственно.
Аналогичным путём докажем и второе равенство.
13, а. Имеем
Р-1 n-^i
( если п кратно р,
\ в противном случае,
х—О
—
p 	 ( р,
~~ \ 0

142	РЕШЕНИЯ ЙОЙРОЙОЙ
b. Раскрывая произведение, отвечающее данному п, имеем
d-i „ . пх
h e
d\a
Отсюда, суммируя по всем л = 0, 1,..., а —1, и получим известное
выражение для ср (а).
14. Часть выражения, стоящего справа, отвечающая х, деля-
делящему а, равна
!irs^KL
к — 1	1
К „ . ак
Пола1ая Ф (К)= V е	, часть, отвечающую ж, не делящему а,
4
можно представить в форме
о	,	ФC)-ФB)
Множитель, стоящий при 2з ввиду | Ф (ЛГ) | < х численно < х;
при этом lim2iX = 0. Поэтому правая часть равенства, указанного
е- О
в вопросе, равна удвоенному числу делителей числа а, мень-
меньших i а, сложенному с 8, т. е. равна -с (а).
15, а. Имеем
+ А, + А3)р s (*! + Лг)" + Л? = hf + h% + Лр3 (mod />),
и т. д.
b.	Полагая hl = hi= ... =Ла=1, из теоремы вопроса а полу-
получим теорему Ферма.
c.	Пусть (а, р) = 1. При некоторых целых Ni, N%, ...,Na
имеем
NlP)p=l + N2p\
s 1 (mod рл).

РЕШЕНИЯ К ГЛАВЕ IV	?43
Пусть m = pj1 ... ркк—каноническое разложение числа т. Имеем
аПр> ее 1 (mod р\*), ...,а9 (рк'С) = 1 (mod #),
г <т> = 1 (mod рГ1)	а9 (т) = 1 (mod />**),
Решения к главе IV.
1, а. Теорема непосредственно следует из теоремы вопроса
11, а, гл. III.
Ь. Пусть d—делитель числа то, m = mad, Hg обозначает сумму
слагаемых с условием (a,m)-=d в выражении для Тт вопроса а.
Находим
m I m~l .ар/ (ж, .... w)
„ 	 \П ^Г1	\Л	то
*-* d — / | / | ¦ • ¦ / | ^	!
а0 х = 0	ш = 0
где «о пробегает приведённую систему вычетов по модулю т0.
Отсюда выводим
mo-l m0—1
2 S--- 2 е m°
с. Пусть m > 0, (а, m) = d, a = aod, m = mQd, T—число реше-
решений сравнения ах = Ъ (mod m). Имеем
m-t m- 1	. а. tax-Ъ)
гто= ^ 2 е
а=0 х=С
т-1 т-:
= 2 2
2лг ^_'х-2п1-
mo	m
d-1
2ri^- _ Г mrf,
~\ 0 в
если b кратно а,
противном случае.

144	РЕШЕНИЯ ВОПРОСОВ'
d. Полагая (a, m)=dlt (Ъ, d,)=rfa, ..., (/, dr_1)=dn
d	rfr_1 = rfrmr, находим d = dr,
m-lm-lm-l m-1 . n (ax^-by ¦*-...-' /ic+g)
0 j/ = 0 u>=0
m-l m-l .
S-S-
V = 0 «) =0
-* 2
e. Применим метод индукции. Пусть при обозначениях во-
вопроса d теорема верна для г переменных. Рассмотрим сравнение
lv + ax+ ... 4/w + ? = 0 (modw).	B)
Пусть (I, m) = d0. Условием возможности сравнения B) будет
ах + ... 4- fw + g = 0 (.nod d0). Последнее сравнение возможно лишь
в случае, когда g кратно d', где d' = (а, ..., f,do) = (l,a, ...,/, т),
причём тогда оно имеет dft~ld' решений. Следовательно, сравне-
сравнение B) возможно лишь в случае, когда g кратно d', и тогда оно
имеет с?^ rf'( — ) da = mr d' решений. Таким образом теорема
верна и для г +1 переменных. Но теорема верна для одного пере-
переменного. Значит, она верна всегда.
2, а. Имеем a? (m)=l (.nod m), a-bdf(m)-i sb(modm).
b. Имеем
= 6.1-2 ...(a — i)(modp),
откуда, деля почленно на 1 • 2... (а—1), и получим указанную
теорему.
с. nt) Достаточно, очевидно, ограничиться случаем B, Ь) = 1.
Выбирая надлежащим образом знак, имеем 6±m = 0(nod4).
Пусть 28—наибольшая степень 2, делящая Ь±т При д!> к
имеем
Ъ±т , , ^
х = -^— (mod те).

РЕШЕНИЯ К ГЛАВЕ IV	145
Бели же д < к, то имеем
С этим сравнением повторяем аналогичную операцию, и т. д.
§) Считаем C, Ь)=1. Выбрав надлежащим образом знак, имеем
Ь i т = 0 (mod 3). Пусть 3 ->-наибольшая степень 3, делящая
Ь ± т\ При 5 ;> к имеем	ч
х = gK (mod
Если же S < к, то имеем
3е
С этим сравнением повторяем аналогичную операцию, и т. д.
¦у) Пусть р—простой делитель числа а. Найдём t из условия
b-\- mt = 0 (mod р). Пусть ps — наибольшая степень р, делящая
(a, b + mt), и пусть а = а1рь. Имеем
ЪЛ-mt .
а,х=	j—(mod m).
Р
Если ах > 1, то с этим новым сравнением повторяем аналогич-
аналогичную операцию, и т. д.
Указанный способ удобен в случае небольших простых сомно-
сомножителей числа а.
3. Полагая г = [-], пишем сравнения
а • 0 = O(modm),
а • lsj/i (mod то),
л • t = yf (mod m),
а • 0 = т (mod m).
Расположив эти сравнения в порядке возрастания правых частей
(ср. вопрос 4, а, гл. II) и вычитая почленно каждое сравнение
(кроме последнего) из следующего за ним, получим t + 1 сравнений
вида az =M(modm); 0 < |г|^,т;. При этом, по крайней мере, в
одном сравнении будет 0 < и < — . Действительно, и имеет
t + 1 > т значений, эти значения положительные, и их сумма
равна т.
4, а, а) Следует из определения символической дроби.
Р) Здесь можно положить bo = b + mt, где t определяется из
условия 6 -{-mt = 0 (mod а); тогда сравнению ах = Ь удовлетво-
удовлетворяет целое число, представляемое обычной дробью — .

146	РЕШЕНИЯ ВОПРОСОВ
¦у) Имеем F0 кратно о, d0 кратно с)
bc + ad
лс
ас
3) Имеем
Ь d _Ьа do
d0	bd
а с л с ,ас ас'
Ь, о) Имеем (сравнения берутся по модулю р)
('7>!
1-2. ..а	~ 1-2... а
Вопрос 2, b теперь проще решать так:
а ~~	1 • 2. . . {а — 1) а
3) Имеем
-¦ +
1-2
1-2.3
+••¦
5, а. Числа s, s + i, ..., s+n—1 попарно не могут иметь
общих делителей с d. Произведения s(s + l) ... (s + n — 1) могут
быть объединены в п% совокупностей по числу способов, сколькими
число d может быть разбито на п попарно простых сомножителей,
с учётом порядка последних (вопрос 11, Ь, гл. II). Пусть d=
= м1м2---мл — одно из таких разбиений. Число произведений
с условиемs =0 (аюйщ), s+1 sO(mod w2),..., s + n — 1 =0(mod м„>
равно -=¦. Поэтому искомое число равно п —г ¦
Ь. Указанное число равно
d\a
где к—число различных простых делителей числа d. Но имеем
d\a
Pi
Pa
Y
PkJ
6, а. Все значения х, удовлетворяющие первому сравнению,
даются равенством\ х = Ь1 + т1 t, где j t — целое. Чтобы выбрать
из них те,»которые удовлетворяют также и второму сравнению,
надо ограничиться лишь теми значениями t, которые удовлетво-
удовлетворяют сравнению
Wits bi—b1 (mod m2).

РЕШЕНИЯ К ГЛАВЕ IV	j'^
•Но Sto сравнение разрешимо тогда и только тогда, когда Ьл	Ъг
•кратно d.- При этом в случае разрешимости совокупность значе-
значений t, ему удовлетворяющих, определяется равенством вида
t = to+-—t', где f — целое; вместе с тем совокупность значений х,
удовлетворяющих рассматриваемой в вопросе системе, определится
равенством
х = Ь1 + т1 Qo+ ^1'Л = х1>2 + т1?а t'\ х1>2 = Ь1 + т^.
Ь. В случае разрешимости системы
х = Ъг (mod /Ил), х = 62 (mod mt)
совокупность значений х, ей удовлетворяющих, представится
сравнением вида х = хг 2 (mod 1,2)- В случае разрешимости си-
системы
х = ajj 2 (mod m.12), a; = b3 (mod m3)
совокупность значений х, ей удовлетворяющих, представится
сравнением вида а; = а;^^, (mod m1J)S). В случае разрешимости
системы
~ = *1,2,з (mod т1>23), х — Ьх (mod mt)
совокупность значений х, ей удовлетворяющих, представится
сравнением вида х = хг 23L (mod m. ,2,4,4)' и т- Д-
7, а) От замены а; на —х (вследствие чего х' заменится на—х')
величина суммы I —— 1 не изменится.
р) Когда х пробегает приведённую систему вычетов по модулю т,
то и х' пробегает приведённую систему вычетов по модулю т.
¦[) Полагая z = Az(mod m), получим
. . ahz-f bz'
2nl
Ь) Имеем
X^-s 2 •
x у
Полагая тгх'-\-rn-$'=z'', имеем
x' + rnxy') == axm\ + агт\ (mod

14$	решения вопросов
что и доказывает указанное свойство в случае двух сомножителей.
Обобщение на случайболее чем двух сомножителей тривиально.
8,	Сравнение
аохп + а^" + • • ¦ +°п—«о (*—xi) (x—xt).. .(х—хп) = 0(mod p)
имеет л решений. Оно степени ниже п. Следовательно, все его
коэффициенты кратны р, а это и выражается сравнениями, ука-
указанными в вопросе.
9,	а. При р>3 соответственно х, взятому из ряда 2, 3, ...
... , р — 2, найдём отличное от него число х' того же ряда с усло-
условием жж'= 1 (mod p); действительно, из х — х' следовало бы
(х— 1) (х + 1) =0 (mod р); х = 1 или х = р — 1. Поэтому
2-3...(р—2) = l(mod/>); 1-2...(р— 1) = -1 (mod/>)¦
b. Пусть Р > 2. Допустив, что /> имеет делитель м с усло-
условием 1 < и < Р, мы имели бы 1-2.. .(Р — 1)+ 1 = 1 (mod и).
10,	а. Находим h с условием aji == l(modm). Данное сравне
ние равносильно такому:
а;" + Oj/js" + ... + aah = 0 (mod m).
b. Пусть Q (г) — частное и Д (ж) — остаток от деления х?—х
на f(x). Все коэффициенты (? (ж) и R (х) — целые, Q (х) — степени
р—п, R (х) — степени ниже п,
Пусть сравнение / (г) = 0 (mod p) имеет п решений. Те же реше-
решения будут решениями и сравнения R (х) = 0(то&р)\ поэтому все
коэффициенты R (х) кратны р.
Обратно, пусть все коэффициенты R (х) кратны р. Тогда
f(x)Q(x) кратно р при тех же значениях х, что и х'1—х; поэтому
сумма чисел решений сравнений
/(x)=0(modp), Q (х) = 0 (mod p)
не меньше чем р. Пусть первое имеет а, а второе р решений. Из
¦<*<*, Р<Р—п, р<<х+р
выводим а=гс, р = р—п.
с. Возвышая данное сравнение почленно в степень	.,
убеждаемся в необходимости указанного условия. Пусть это усло-
р-1 р-1
вие выполнено; из хр—х = х(х?-1—А п +А п —1) следует, что
остаток от деления ж?—хввх11—А есть (А п —1)х, где А п —1
кратно р.
11. Из х"=А (modm), г^=1 (mod m) следует (хоу)п=А (mod m);
при этом произведения хау, отвечающие несравнимым (по моду-

РЕШЕНИЯ К ГЛАВЕ V	149
лю т) у, несравнимы. Из х% = A (mod т), хп з A (mod m) сле-
следует ж" == Xq (mod т), причём, определяя у условиемх = ух0 (mod m),
имеем
уп = 1 (mod m).
Решения к главе V.
1.	Указанное сравнение равносильно такому: Bах -{- бJ = б2 —
— 4ас (mod от). Соответственно каждому решению z = z0 (mod m)
сравнения z2 = 62—4ac (mod то) из гая + б^г,, (modm) найдём
одно решение указанного сравнения.
2,	а. При (—)= 1 имеем a2m+1 = 1 (mod р), (дт+1J sa(mod p),
x=±am+i(modp).
b. При^—Л=1 имеем a4m+2 = I (mod p), a2m+1 = ± l(modp),
Ввиду (—J= — 1 имеем также 24™1 = —1 (mod p). Поэтому при
некотором s, имеющем одно из значений 0; 1, получим
a2m+22Dmf 2)s ^ a(mod р)>я=± am+i2Bm+i) s (mod р).
с. Пусть p = 2kh-\-l, где &>3 и А — нечётное, Г —J=l.
Имеем
a2*-*h s ! (mod p)> a2*-2h ^ ± 1 (mod p)j ^2*-*/. = _ { (mod p)
Поэтому при некотором целом неотрицательном s2 получим
a2*-2ft/v.82*-i s j (mod p)> а2Ъ-Ч^-* _± t (mod p).
отсюда при некотором целом неотрицательном s3 получим
a2k-3hNs32*-2 s j (mod p)i a2*-*fc^.,2*-3 s ±
и т. д.; наконец, получим
2
(	p)i г = ± a
d. Имеем
1 -2 ... 2m(p—2m) ... (p — 2)(p —
A • 2 ... 2mJ +1 = 0 (mod p).
3, а. Условия разрешимости сравнений A) и B) выводятся
тривиально (f, § 2 и к. § 2). Сравнение C) разрешимо тогда и только

150
РЕШЕНИЯ ВОПРОСОВ
тогда, когда
причём
(—-) = !• Но (—-j = (-? V
/?Л_ f 1, если р имеет вид Qm+ 1,
Ъ )~~ \ —1, если р имеет вид бот+ 5.
Ь. Каковы бы ни были различные простые plt P2, • ¦ , рк вида
Am + 1, наименьший простой делитель р числа BpiP2 ... ркJ + 1
(d)
к
будет отличен от ри р2, ¦ ¦., рк и ввиду Bргр2 ... Р^J+ 1 = 0(modp)
имеет вид Am + 1.
с. Каковы бы ни были различные простые рх, р2, .... р. вида
бт + 1, наименьший простой делитель р числа Bрхр2 ... ркJ ¦+ 3
будет отличен от plt р2, ..., рк и ввиду Bр1р2 ... ркJ -. 3 = 0 (modp)
имеет вид 6т + 1.
4. Среди чисел первой совокупности будут числа, сравнимые
с 1-1, 2-2
Р-\р-\
т. е. все квадратичные вычеты пол-
2 г
ной системы: число, входящее по условию во вторую совокуп-
совокупность, будет квадратичный невычет. Но во вторую совокупность
войдут все произведения этого невычета на все вычеты, т. е.
войдут все квадратичные невычеты.
5, а. Пусть в системе исчисления с основанием р
и искомое решение (наименьший неотрицательный вычет)
x = xa_.pa~i + ... +х1р + х0.	A)
Составим таблицу:
2ж»*-а_1
2х1ха_2
2*2*а_з
Ч
2x0xi
2ххх3
X2
«3
2х„хъ
2l1?2
а2
2хох2
Х1
а,
2хах1
где в столбце под o.s стоят числа, сумма которых образует коэф-
коэффициент при р" в разложении квадрата правой части A) по сте-
степеням р. Находим х0 из условия
х% = а0 (mod p)

РЕШЕНИЯ К ГЛАВВ V
Полагая —	-ssPit находим хх из условия
рх + 2хохх а аг (mod p).
—-	Рх 4 2,ХпХ\—-di
Полагая 	= Рг. находим х3 из условия
р2 + 2хах2 + г^ = о2 (mod p),
и т. д. При данном х0 ввиду (хо,р)=1 числа а^, г2	жа_1
определятся однозначно,
Ь. Здесь
и мы будем иметь следующую
...
«4
2
таблицу:
«3
*.*
а2
Рассмотрим лишь случай а>3. Ввиду (а, 2) = 1 необходимо ао = 1.
Поэтому жо = 1. Далее необходимо о,=0, и ввиду хдхг ¦+ sf =
= Ж! -i я? = 0 (mod 2) необходимо о2 = 0. Для г, возможны два значе-
значениями 1. Числам, х31..., ха_2 определятся однозначно, а дляг,,^
возможны два значения: 0 и 1. Поэтому при а > 3 необходимо
а = 1 (mod 8), и тогда указанное сравнение имеет 4 решения.
6.	Очевидно, Р и Q — целые, причём Q по модулю р сравнимо
с числом, которое получим, заменяя о на а2, для чего достаточно
Ya заменить на г. Поэтому Q = 2а «a~1(mod p); следовательно,
(Q- р) = 1 и Q' действительно можно определить из сравнения
'QQ' = 1 (mod рл). Имеем
7«—о(?а = B+/о)а(г —/о)* = B»—a)e=0(mod/>e),
откуда
(PQ1)* ~ a (QQ')S= a (mod ря),
7.	Пусть m = 2ap?1 •¦• Pjfc — каноническое разложение числа т.
Тогда т представляется в форме m = 2.aab, где {а, Ь)=1, 2* спо-
способами

152	решения воцррео?:
Пусть а=0. Из (ж— 1) (х +1) = 0 (mod m) следует, что при неко-
некоторых а и Ь	-'¦'..
х = 1 (mod о); х = — 1 (mod 6).
Решая эту систему, получим х = х0 (mod m). Поэтому указанное
сравнение имеет 2' решений.
Пусть а=1. При некоторых а и 6
ж =1 (mod 2а); ж = — 1 (mod 26).
Решая эту систему, получим х = г0 (mod m). Поэтому указанное
сравнение имеет 2" решений.
Пусть а = 2. При некоторых а ш b
ж =1 (mod 2а); х = — 1 (mod 2Ь).
Решая эту систему, получим ж = х0 ( mod — J . Поэтому указанное
сравнение имеет 2*+ решений.
Пусть а > 3. При некоторых а и 6 должна выполняться одна
из систем
х = 1 (mod 2а);	х = — 1 (mod2a-ib);
х = 1 (modi"- а); х = — 1 (mod 26).
Решая одну из этих систем, получим х = г0 f mod -л- J . Поэтому
указанное сравнение имеет 2 решении.
8, а. Определяя х' сравнением хх' = 1 (mod p), имеем
Р-1	р-1	р-1
2^я(я:4-А)^ -^ fxx'jxx' +frx')
ж = 1
Очевидно, 1 -\ кх' пробегает все вычеты полной системы, кроме 1.
Отсюда и следует указанная теорема.
Ь. Указанное равенство следует из
x=i
с. Имеем
;... • .: J

РЕШЕНИЯ К ГЛАВВ V	153
Часть выражения, стоящего справа, отвечающая случаям yi = y,
не превосходит XpY. Рассмотрим часть, отвечающую паре не рав-
равных между собою- значений у, и у, причём для определённости
предположим, что у > 0. Полагая ху-\- к = z(mod/>), приведём
указанную часть к виду
XZ\ p , ¦
r-0
откуда убедимся (вопрос а), что она численно <|Х. Поэтому
S* < XpY + ХУ2 < 2pXY.
d, а) Имеем
P-lQ-l Q-i
Ж=0 21=0 2 = 0
При 2i=z суммирование по а; даёт р — 1. При zu не равном 2,
суммирование по х (вопрос а) даёт —1. Поэтому
Согласно теореме вопроса а) имеем
7) Полагая [l^p]=Q, применим теорему вопроса а). Допустив^
что в указанном в вопросе ряде квадратичных невычетов нет,
убедимся, что \Sx\^-Q—l при х = М, М + 1, ..., M + 2Q— 1 и,
таким образом,
что при Q !> 5 невозможно.
9, а. Если m представляется в форме A), то решение
z = 20 (mod m)	E)
сравнения x = zy (mod m) является также и решением сравнения B).
Мы будем говорить, что указанное представление связано с реше-
решением E) сравнения B).
' С каждым решением E) сравнения B) связано не менее одного
представления A). Действительно, взяв т=]/гт, имеем
=; (P,Q)=i,
w Q Q
Поэтому znQ=mP + r, где | r | < y/~m. Далее, ив B) следует, что
| г |2 -+- Q2 = 0 (mod m). Отсюда и из 0 < 1 г \г + Q2 < 2т находим
m=|/-|24Q2.	(E)

154	'	РЕШЕНИЯ ВОПРОСОВ
При этом (] г \, Q)= 1 ввиду
т
Если \г\ = г, то ввиду r = z0Q(modm) представление F) связано
с решением E). Если |г| = — г, то ввиду zlQ = zor (mod m)
Q = z0 I r \ (mod m), представление m = Q2+|r|2 связано с реше-
решением E).
С каждым решением E) связано не более одного представле-
представления A). Действительно, если два представления т = г24 У2
и т = хЦ-у\ числа т в форме A) связаны с одним и тем же ре-
решением E), то из х = zay (mod т), я, = zoyi ( nod m) следует
ху1 = хху (mod то). Поэтому xyl = x1y, откуда ввиду (х, у) =
= («1, 3/i) = l следует :» = :*:,, J/ = i/,.
b. Если m представляется в форме C), то решение
z = 20 (mod p)	G)
сравнения ж = zy (mod p) является также и решением сравне-
сравнения {V\. Мы будем говорить, что указанное представление, связано
с решением G) сравнения D).
Зная решение G) сравнения D), найдём не менее одного пред-
представления C). Действительно, взяв i=V p, имеем
Поэтому 20Q = r (mod p), где \г\ < р. Ладее из D) следует, что
| г |2 + о<22 г= 0 (mod р). Отсюда и из 0 < | г |2 + aQs < A + а) р сле-
следует, что при о = 2 должно быть или \r\" + 2Qz = p, или |г|2 +
42Q22 В по	| | ё	|| 2	Q2 + 2f
дуе, ч р	2 должно быть или \r\ + 2Q p,
4-2Q2=2p. В последнем случае | г | —чётное, |r| = 2r]( p=Q + f
При а=3 должно быть или \r\* + 3Q* = p, или |r|2 + 3Q2=2p, или
|r|' + 3Q2 = 3p Второй случай невозможен: по	4
б ил \r\ + 3Q p, ил |r| + Qp,
|r| + 3Q p. Второй случай невозможен: по модулю 4 левая,
часть сравнима с 0, а правая — с 2. В третьем случае I r | кратно
3, |rj = 3rt, p = Q3 + 3r°.
Допустив, что два представления р = я2 + аг/2 и p = a;f + aj/f
числа р в форме C) связаны с одним и тем же решением
сравнения D), найдём х = х^, у=уг. Допустив, что эти пред-
представления связаны с различными решенияму сравнения D),
найдём х = zy (mod р), х1 = — zy, (mod р), откуда хух + a?!?/ s
= 0 (mod р), что ввиду 0 < (ху1 + ж^J < (ж2 + ?/2) (ж| + у\) < ра
невоз\ ожно.
с. п) Слагаемые суммы S (к) с х = хг и х=—хх равны между
собою.
Р) Имеем

РЕШЕНИЯ К ГЛАВЕ V
-() Полагая р—1=2ри имеем
pi	pi
Pi (S (г))* + Pl (S (л)J = ^ О* <«*))* + 2
/=i	(=1
Г- ^-^^ ).
При jr. не равном х или /> — х, результат суммирования по к
будет— 2 ( — j ; при г/ = г или у = р—х он будет (р — 2) ( — ) .
_	\Р У	\ру
Поэтому
10, а. Имеем
х*-т*={х1+у1 Yd) {xi±yi Yd) fo-
b. Взяв любое %x c условием хх > 1, найдём целые а^, i/j
с условиями | Ух Y^ — Xi I < — > 0 < з/ ^ xx, откуда, умножая по-
почленно па Ух ]/ + г1<2^1 1^.0 + 1, получим | ж|—2)г/| | <2 ]/ + 1.
Взяв т2 > Tj с условием | i/i у Z)—хг | > — , найдём новые
_ тз
целые Zj, ^ с условием | x\—Dy\ \ < 2 Y-D+ 1, и т. д.
Очевидно, в интервале —2 Y-D — 1 < к < 2 VD+ I существует
такое целое, не равное нулю к, что среди nap xx, $r,; xit y2; ...
найдётся бесчисленное множество пар х, у с условием ж2 — Dy2 — k\
среди же последних наверно найдутся две пары ?,, •>), и %±, ¦»)>
с условием ?, = с ( nod | к] ),_i), = >j. (mod [ft |). Определяя целые
?o. Ъ равенством ?0 + % YD = {^x + Vi YD) (?.,— ijj YD), имеем
(вопрос а)
5§—Ь jg == I ft |2; ?„ = %1-D-fii = 0 (mod | ft |);
=0(niod|ft[).
Поэтому fo = 5|ft|, -»j0 = ^ | Ar|, где % и 7j—целые и с2 — Di?=\..
е. Числа г, г/, определяемые равенством B), удовлетворяют
(вопрос а) уравнению A).
Допустив существование пары целых положительных х, у,
удовлетворяющих уравнению A), но отличной от пар, определяе-
определяемых равенством B), мы при некотором г=1, 2, ... будем иметь

156	РЕШЕНИЯ ВОПРОСОВ
Отсюда, деля почленно на (ж0 f у0 \^в)т, получим
1< X + Y \fD<xa + yoyrD,	C)
где (вопрос а) X и Y— целые, определяемые равенством
(*о + У о
и удовлетворяющие уравнению
Но из D) следуют неравенства 0 < | JT|—\УУ?>\<1, которые
в соединении с первым неравенством C) показывают, что X
и У —положительные. Поэтому второе неравенство C) противо-
противоречит определению чисел ха и у0.
11, а, о) Имеем
I - J« p
v p J
= i x=l
При г = 1 суммирование по х даёт p—1; при f>l оно даёт
— ( — J . Поэтому
Р-1
ИЛИ
ж=0
При t = 0 суммирование по ж даёт р— 1; при t > 0 оно даёт
—е р . Поэтому
Р) При (о, р) = р теорема очевидна. При (о, р) = 1 она сле-
следует из

РЕШКНИЯ К ГЛАВВ V	157
Ь. а) Дусть г пробегает квадратичные вычеты, а п—квадра-
п—квадратичные невычеты, - заключённые в полной системе вычетов.
Имеем '
2nia-L
e p
Вычитая отсюда почленно
мы и получим указанное равенство.
Р) Имеем
m—lm—i
/=0 ж=0
2«1
При данном t суммирование по х даёт те т или 0, в зависи-
зависимости от того, делится It на т или нет. При нечётном т имеем
При чётном т = 2т1 имеем
Здесь правая часть равна нулю при нечётном Wj и равна 2т
при чётном От].
•у) При любом целом b имеем
m-l
откуда, выбирая Ъ из условия 2^46 s a (mod m), мы и получим
(вопрос Р) указанный результат.
12, а. Имеем
M+Q-lm-l	. а(г-з)
'	*1

158
РЕШЕНИЯ ВОПРОСОВ
Часть суммы, стоящей справа, отвечающая о=0, равна QS$(*)i
Z
часть, отвечающая оставшимся значениям а, численно (вопрос
И, с, гл. III)
m-1 Af-fQ-1 „ .-as
m
e
ЛтAпт —
b, a) Следует из теоремы вопроса 11, а, а) и теоремы вопроса а.
Р) Неравенство вопроса а) даёт R—If = Q У pin p. Кроме того,
очевидно, R + N —Q.
¦у) Из теоремы вопроса И, b, P) следует, что условия теоремы
вопроса а будут соблюдены, если положим т — р, Ф(г) = 1, причём
заставим z пробегать значения z=a2; ж = 0, 1, ..., р—1. Но среди
значений z имеется одно сравнимое по модулю р с 0 и по два
сравнимых по модулю р с каждым квадратичным вычетом полной
системы. Поэтому
и мы получим
Ь) Следует из теоремы вопроса 11, Ь, -у) и теоремы вопроса а.
е) Из теоремы вопроса 3) следует, что условия теоремы вопроса
а будут соблюдены, если положим то = р, Ф(г) = 1, причём заставим г
пробегать значения z — Ax*; х = М0, Мо+1, ..., Mo + Qo~ 1- По-
Поэтому
откуда и следует указанная в вопросе формула.
с. Часть суммы, содержащая слагаемые с ( — )=1, равна
piV2), оставшаяся часть равна —2pRN. Поэтому вся сумма
равна p(R — iV>8.
Часть суммы, содержащая слагаемые с о = 0, равна 0. Остав-
Оставшаяся часть численно меньше (вопрос И, с, гл. III):.
I'/
p-1 MtQ-1
2 2
2iti:
Ряедовательно, p(R — N)* < рг(In pJ, |R—N\<Vp\np.

РВШКНИЯ К ГЛАВЕ VI	159
Решения к главе VI.
1, а. Если q—простое нечётное и ap = l(mod?)f то а по мо-
модулю д принадлежит одному из показателей д = 1; р. При д=1
имеем а = l(modj), при д = р имеем д —1 = 2рж; ж—целое.
b.	Если q—простое нечётное и ар+1 = 0 (mod q), то
a2p = l(modg). Поэтому а по модулю q принадлежит одному из
показателей 8=1, 2, р, 2р. Случаи 1=1; р невозможны. При
й = 2 имеем а* = l(modq), а +¦ 1 = 0 (mod q). При 8=2р имеем
д — 1 = 2ря; х— целое.
c.	Простыми вида 2рх +1 будут, например, простые делители
числа 2Р—1. Пусть plt p2, ..., рк — какие-либо к простых чисел
вида 2рх + 1; число (pip2 ... Р^У— 1 имеет простой делитель вида
2рХ + 1, ОТЛИЧНЫЙ ОТ
d. Если q~простое и 22" 4 1 == 0 (mod ?), то 22" = 1 (mod q).
Поэтому 2 по модулю q принадлежит показателю 2n+1 и, следо-
следовательно, q — 1 = 2Пп1г; г—целое.
2.	Очевидно, а по модулю ап—1 принадлежит показателю п.
Поэтому и—делитель ?(an— 1)-
3,	а. Пусть после А--й операции снова поручается исходный
ряд. Очевидно, к-я операция равносильна следующей; в ряде
1, 2	п — 1, п, п, п— 1, ..., 2, 1, 2, ...
..., п—1, п, п, п-\, ..., 2, 1, 2, ...
берутся числа, стоящие на 1, 1 + 2й, 1 + 2-2*, ... местах. Поэтому
на 1 + 2к месте в исходном ряде должно стоять число 2. Следо-
Следовательно, указанное в вопросе условие необходимо. Но оно и
достаточно, так как при его наличии имеем следующие сравне-
сравнения по модулю 2л—1:
*****	1 = 1, 1 + 2^2, 1+2-2*^3, ...
Ь. Решение аналогично решению вопроса а.
4. Решение сравнения г5 = 1 (mod p) принадлежит показателю
вида -^т-, где д' — делитель д. При этом в' кратно d тогда и только
о
j_
тогда, когда ad =l(.nodp). Выписав все д значений д' и взяв
/ = 1, получим ^"' = 2 p(d)Sd> гДе •?' — искомое число и «?й = -|- .
\
5, а. Здесь (§ 3; пример с, § 5) должно быть (-?—J = —1.
\2 + 1 /
Это требование выполняется при g = 3.
b. Здесь не должно быть (	j =1, g8 = 1 (mod2p+1;.
Это требование выполняется при указанных вначевяях ^.

160	РЕШЕНИЯ ВОПРОСОВ
c.	Здесь не должно быть ( , j = l, g* = 1 (mod 4p + 1).
Это требование выполняется при g = 2.
d.	Здесь не должно быть (—-— —1, g2 = 1 (mod 2np + 1).
\ 2"р -|-1/
Это требование выполняется при g=S.
6, а, о) 1]ри л, кратном р — 1, теорема очевидна. Пусть п не
делится на р—1. Числа 1, 2, ..., р — 1, если отвлечься от по-
порядка их следования, по модулю р сравнимы с числами g, 2g, ...
..., (р—1) g, где g—первообразный корень по модулю р. Поэтому
Sn = gnSn(modp), ?„ = 0 (mod/>).
fj) Имеем
р-1	р-1 р-1	р-1
^(гт^)*' 2 х 2 ^+1^2 (mod^
х=1	х=1
откуда (вопрос а)) и получается указанный результат,
Ь. При р > 2 имеем
р-1
1-2 ... O-l)^1^--^-1^ 2 =-
_ „	Ind ,a	.	.	.
7,	а. Имеем jj ^x = a(modp),ind aind9g1=md
ind a = a ind a (mod p — 1).
b. Из indffa = s(modra), ind^ a = a ind0 a (mod p— 1) следует
ind a = as = sx (mod «).
8.	Пусть (n, p—1)=1. Найдя и из условия пи = l(modp—1),
получим решение х =в аи (лод. р).
Пусть п— простое, p—l — nat, a —целое положительное,
(t, n)=l. Если сравнение возможно, имеем а"а ' = 1 (mod р);
если a > 1, то, замечая, что х = gn 'r(mod р), г =0, 1	"~1,
суть все решения сравнения хп = 1 (mod p), при некотором
гг = 0, 1, ..., га-1 имеем
апа tgn i=l(modp);
если a > 2, то при некотором г2 = 0, 1, ..., п — 1 имеем
ап lg	J	2 = 1 (mod p),
и т. д.; наконец, при некотором ra_j=O, 1, ..., п—1 имеем
Найдя м и v из условия iu—пи=—1, получим га решений:
(modp); r==0, 1	/i— 1.

РЕШЕНИЯ К ГЛАВЕ VI
161
Пусть простое ni делит (л, р—1), ra = ni«a, п2 > 1. Соотве-г-
ственно каждому решению сравнения yni = a (mod р) разыскиваем
решения сравнения х 2 = jr(modp).
9, а. Указанным путём получим ссосх ... сь = ч>(т) характеров.
Пусть у двух характеров ул (о) и Ха (°) не равны между собою
значения R' и R" какого-либо из корней R, Ro, Rit ..., R^; для
числа а,, у которого все индексы равны 0, кроме лишь одного,
отвечающего указанным R' и R", равного 1, имеем
b,	а) Имеем хA) = Д° ... д? = 1.
{S) Пусть -('. •¦-, ij.; 7"' ••¦> tfc~системы индексов чисел ах и
а2; тогда ~j'+i", ¦¦-, i^ + t"^ — система индексов числа а^аг (с, § 7).
¦у) При at = а2 (mod т) индексы чисел at и а2 сравнимы ме
жду собою соответственно по модулям с, ..., с/с.
c.	Указанное свойство следует из
m—i	с—1	сА-~"'
d. Указанное свойство следует из
7.	я	«Л-
е. Пусть j (rtj) §= 0. Тогда ^@^ = ^@!) фA). Поэтому |A)=1.
Найдя а' из условия aa' = 1 (mod m), имеем ф (о) ф (а') =1. Поэтому
ф(я)^О при (а, т) = 1.
При (alt m)=l имеем
y>X(a)=y'/.(«ig)==X(ai) V
а	а	а
2' / (а)
f-~- = 0, или жо Ф(а1) = У(о,) при всех %. Но
ф (а)
а
первое предположение не может оправдываться при всех у_: тогда
было бы Н = 0, а между тем Н = у (т), так как, суммируя при
данном а по всем характерам, имеем
Sj? (о)	 J <р (т.), если а = 1 (mod т.),
ф (а) ^ 0 в противном случае.
f, а) Если Л'	Rk и Д"	Щ—значения R, ..., R
отвечающие характерам Xi (а) и Хг (а)> то Xi (а) 7.2 (а)—характер,
у которого соответствующие значения суть R'R", ..., R'jgR^-

162	РЕШЕНИЯ ВОПРОСОВ
Р) Когда R	Rk пробегают все корни соответствующих
уравнений, то R'R, ..., R^Rj. пробегают в некотором порядке
те же самые корни.
-f) Определяя V из условия IV = 1 (mod m), имеем
г
что равно у (т) или 0, в зависимости от того, будет ли а = I (mod m)
или нет.
10, а. а) Определяя х' сравнением хх' = 1 (mod p), имеем
р-1 Л ind (д+*)-1 inda; р-1 { 1 ind (l + t-я')
2j е	=2j е	= —1.
'р) Имеем
P-1Q-1 Q-1 „ . I ind(x+zi)-I ind(o;+z)
*-ssa-	5 •
ж=0 zi=0 z = 0
При zL = z суммирование по х даёт р—1, при г1( не равном z,
суммирование по х (вопрос а)) даёт —1. Поэтому
~() Пусть Qx — число чисел ряда x + z; 2 = 0, 1, ..., Q—1, не
делящихся на р, а Тп х—число чисел того же ряда, принадле-
принадлежащих s-й совокупности. Пусть, наконец,
р-1
Имеем
n-lQ-l . I (Ind (x+z)-s)	n-l , . Is
n-l
Полагая <3=[«уг/'] и допуская, что в указанном в вопросе ряде
чисел s-й совокупности нет, убедимся, что \Un х\~^>—	 при

РЕШЕНИЯ К ГЛАВЕ VI	163
= М, Af + 1, ..., Af + Q—1, и, таким образом,
что невозможно.
Ь. Пусть р0—произведение различных простых делителей
числа р—i, Qx—число чисел ряда x + z; 2 = 0, 1, ..., Q—1, не
делящихся на р, a G» —число чисел того же ряда, являющихся
лервообразными корнями по модулю р. Пусть, наконец,
Взяв /(?) = i и заставляя § пробегать значения ? = irxl (ж+ z);
2 = 0, 1, ..., Q —1, получим 5' = 2 ^(«O^i- Здесь ^"—число
0
значений ?, с условием (?, р —1)=1; поэтому S' = GX. Далее,
Sa—число значений %, кратных rf; поэтому Sd = Tdx (вопроса, f)
при s = 0. Следовательно,
wl
d\p0
Полагая Q = [P2k YP\ и допуская, что в указанном в вопросе
ряде первообразных корней нет, убедимся, что | wx \ > -*-=—
при х — М, М+1	M + Q—1 и, таким образом.
что невозможно.
11, а, я). Имеем
Ja p= у у

164	РЕШЕНИЯ ВОПРОСОВ
ji) При (а, р)=р теорема очевидна. При (о, р) = 1 она сле-
следует И8
2 j~* 'nd ° Р~' 2 i* ind Оа ах 2 i ~fc ind °
() Очевидно, ^4 и В — целые, причём! S |а =А* + В*. При неко-
некоторых в, з', е' с услоиием | s | = | s' | = | s | = 1 имеем (вопрос Щ
		2i»i^-
.?--r^-^-- v 2 2 •	*
Если гх + 2 не равно р, суммирование do x даёт нуль. Поэтому
2 = 1
b, a) При данном z сравнение ж" = z (mod/>) возможно лишь
и случае, когда ind z делится на 3, причём тогда это сравнение
имеет 5 решений. Поэтому при д=1 имеем ?о;, = 0. Если же
6 > 1, то имеем
8—1 р—1 . Jt ind г . az
*=0*=1
При А-=0 суммирование но г даёт — 1; при А > 0 оно даёт вели-
величину, модуль которой равен ]/р. Отсюда и следует результат,
указанный в вопросе.
jt) Полагая
ж = и + р*-11Р; м = 0, ..., р»-1 —1, t = 0, .. ., р — 1,
имеем
При (и, р) = 1 суммирование по v даёт нуль. Поэтому

РЕШЕНИЯ К ГЛАВЕ VI
165
f) Пусть р^ — наибольшая степень р, делящая п. Ииееи
s ^ -с + 3. Полагая
х^и + р"-1-"^; и = 0	p$-i-z — 1, v = Q, ... , р1-1,
находим
¦ ахП
"р^~
При (и, p) = i суммирование по v даёт нуль. Поэтому
хо-0
S) Пусть т = ра* ... р^1—каноническое разложение числа т.
Полагая
и определяя ах, . . ., ак из условия a = М^аг +...-)- Мк^к (mod m),
имеем (вопрос 12, d, гл. III)
а, т ¦*	<ч ¦ ¦ ¦	ал-'
ai> pj	afc, v
Но при s = 1 имеем
\Та, p*\<p-Uw
При l<s^n, (re, p) = l имеем
При 1 < s -^ га, (л, р)=р имеем
Случай s > п ввиду Го> р* = p~s+s vpn~1-5'aj p,_n = 3r'ai p«-n сводится
к случаю s s^ га, Поэтому
откуда и получается указанное в вопросе неравенство.
12, а. Следует из теоремы вопроса 11, а, а) и теоремы
вопроса 12, а, гл. V.

166	РЕШЕНИЯ ВОПРОСОВ
b. Имеем
Af4Q-ln-l .
^ 2 **
При *=0, суммируя пот, получим (J; при А>0 получим число,
модуль которого < у р In p. Отсюда и следует указанная в во-
вопросе формула.
с. Взяв f(x) = i и заставляя х пробегать значения a; = mdAf,
ind(Af+l), •••> ind(Af -Ь<?— 1), получим (вопрос 17, а, гл. II)
S' = 2j ^(d)Sa. Здесь S' — число значений х с условием
d\p-l
(х, р —1) = 1; поэтому S' = T. Далее St— число значений ж, крат-
кратных d, т. е. число вычетов степени d в рядя М, М +-1, ...
..., Af-)-<3—1. Следовательно,
#= 2 ^(Ю (J+O^/plnp^); |flrf|< 1, 8,=0.
d. Из теоремы вопроса а следует, что условия вопроса
12, а, гл. V будут соблюдены, если полошим т = р —1, Ф(г) = 1,
причём заставим z пробегать значения z=ind2;; а; = Д/, М + 1, .. .
Af + Q — 1. Тогда получим {Qv вместо Q)
13. Допустим, что невычетов, не превосходящих h, нет.
Число невычетов степени п среди чисел
1, ..., Q; <?=/рAпр)*
можно оценить двумя способами: исходя из формулы вопроса
12, b и исходя из того, что невычетами могут быть лишь числа,
делящиеся на простые, большие h. Получим
21nlnp
0<ln

РЕШЕНИЯ К ГЛАВЕ VI	167
Невозможность последнего неравенства при всех достаточно»
больших р и доказывает теорему,
14, а. Имеем
т—1 т—1 т—1	„ .axCui—у)
\s^x 2 2 2 НУх) ^~)е ** ~ •
ж = 0 1/1=0 - =0
При данных у1 и у суммирование по х даёт Хт \ р (у) |2 или нуль,
в зависимости от того, будет ли 2/i = 2/ или не1> Поэтому
| ?12 < XYm, \ S |
Ь, а) Имеем
. . оА"
1	2яг
m
где и п v пробе; ают приведённые системы вычетов по модулю т.
Отсюда
m-l т—1	.аху
b2 2	"^
2 '-^ 9(г/)= 2
Но имеем (вопрос 11, гл. IV)
т—1	т—1
х=0	у=0
Поэтому (вопрос а)
| S \ < ~~ YK'f(m) K-f (mym=K У т.
§) Пусть иг = 2ар-•-Р^* — каноническое разложение чи-
числа т. Сравнение ж" = 1 (mod m) равносильно системе
х" = 1 (mod 2а), х" = 1 (mod р), ..., ж" == 1 (mod p^k).
Пусть 7 (х) и 1„ (ж)—индексы числа х по модулю 2а (g, § 6). Сравне.
ние х" = 1 (mod 2a) равносильно системе ?if (ж) = 0 (mod с),
rcf0 (л:) = 0 (mod с-,). Первое сравнение этой системы имеет не более
2 решений; второе—не более п решений. Поэтому сравнение
х" = 1 (mod 2a) имеет не более 2п решений. Согласно Ь, § 5

168
РЕШЕНИЯ ВОПРОСОВ
каждое из сравнений х" = l(mod р*1), ..., г"=1 (mod pjfc) имеет
не более п решений. Следовательно,
in п
#<2(т(т)Iп2; К=О(т").
15, а. Имеем
р-1 Р-1 2 .a(t»-l)xn+b(t-l)x
Если f = 1 (mod р), то суммирование по ж даёт р— 1 при
t = 1 (mod р) и —1 в остальных случаях. В противном случае,
беря z (t — I) вместо х, соответствующую выбранному t часть
двойной суммы представим в форме
P-J 2^Ь-г
/н_4 \ it	\ \ —n
Поэтому
z=l
>-l +
Р-1 Р-1	2
где v (и) равно числу решений сравнения (tn — 1) (t — 1) " sit (mod p),
a \ p (v) \ не превосходит числа решений сравнения z" = v (mod p).
Поэтому ч (и) ¦< 1пи | р (v) К щ,
р-1
р-1
Применяя теорему вопроса 14, а, получим
b, а) Следует из теоремы вопроса а и теоремы вопроса
12, а, гл. V.
?S) Из теоремы вопроса а) следует, что условия теоремы
вопроса 12, а, гл. V будут соблюдены, если положим т = р,
Ф(г)=1, причём заставим s пробегать значения z = Axn; х=Мв,
Af 1, • ¦ ¦, Мй + Qo— 1- Поэтому
г	г
откуда и следует указанная в вопросе формула.

РЕШЕНИЯ К ГЛАВЕ VI	169
е, а) Пусть 1 = 4af t (mod р). Имеем (вопрос 11, а, гл. V)
р-1
ж=0
аУ + 4а&з; + 4ас\ "
ч
е
"*z=l	я=0
-2-
Z-1
з 5
Последняя же сумма (вопрос а) численно < -^ Pk •
Следует из теоремы вопроса а) и теоремы вопроса 12, а,
гл.
. V.

ОТВЕТЫ К ЧИСЛЕННЫМ ПРИМЕРАМ.
Ответы к главе I.
1,	а.	17.
Ь.	23.
о	n * 15 19 8
2,	а.	а) 34=п; ?) a=-+W7
b, a) e.= 5§; P) «=^39+739-1000 '
3. Всего получим 22 дроби.
5, а. 28 • 35 ¦ 11».
Ь. 23 • З3 • 54 • 73 • И2 • 17 • 23 • 37.
Ответы к главе II.
1.	а. 13142.
Ь. 211в • 35» • 531 • 71» • И12 • 13» • 177 • 196 ¦ 23В ¦ 29* • 31* • 37» X
X 41s • 432 • 472 • 532 • 592 • 612 • 67 • 71 ¦ 73 • 79 • 83 • 89 • 87 х
X 101 • 103 • 107 • 109 • ИЗ.
2.	а. тE600) = 36; SE600)= 15624
Ь. т A16 424) = 96; S A16 424) = 410 400
3.	Сумма всех значений равна 1.
4.	а) 1152; (О 466 400.
5.	Сумма всех значений равна 774.
Ответы к главе III.
1,	л. 70.
Ь. Делится.
2,	а. З3 • 5! • И2 • 2999.
Ь. 7 • 13 • 37 • 73 • 101 • 137 • 17 : 19 • 257.
Ответы к главе IV.
1,	а. х = 81 (mod 337).
b. x = 200; 751; 1302; 1853; 2404 (mod 2755).
2,	b. x = 1630 (mod 2413).
3,	a:=94-fillf, y=39 + 47t, где (— любое целое.

ОТВЕТЫ К ЧИСЛЕННЫМ ПРИМЕРАМ	171
4,	а. а: = 1706j + 52Ь2 (mod 221);	х = 131 (mod 221);
х = 110 (mod 221); х = 89 (mod 221).
b. x = 11151^+ И 80062+ 16 8756а (mod 39 825).
5,	а. х з 91 (mod 120).
b. x = 8479 (mod 15015).
6,	а: = 100 (mod 143); г/ = Ш (mod 143).
7,	а За:4 4- 2.г3 4 За;21 2x ~ 0 (mod 5).
b. x& 4 5а*4- За;2 4 3*4- 2 = 0 (mod 7).
8,	а;6 4- 4а;5 4 22а;* 4 7&х* + 70а;2 4- 52а; 4 39 s 0 (mod 101).
9,	а. х = 16 (mod 27).
b. ж = 22; 53 (mod 64).
10,	а. х= ИЗ (mod 125)
b. x = 43, 123, 168, 248, 293, 373, 418, 498, 543, 623 (mod 625).
11,	а. х = 2, 5, 11, 17, 20, 26 (mod 30).
b. x = 76, 22, 176, 122 (mod 225).
Ответы к главе V^
1,	а. 1, 2, 3, 4, 6, 8, 9, 12, 13, 16, 18.
b. 2, 5, 6, 8, 13, 14, 15, 17, 18, 19, 20, 22, 23, 24, 29, 31,
32, 35.
2,	a. a) 0; Р) 2.
b. a) 0; Р) 2i
3,	а. а) 0; pV2.
b. а) 0; P) 2.
4,	a. a) a; = ± 9 (mod 19); p) x = ± 11 (mod 29);
V) a; = ± 14 (mod 97).
b. а) ж = ± 66 (mod 311); P) x = ± 130 (mod 277);
•/) a; = ± 94 (mod 353).
5,	a. ж = ± 72 (mod 125).
b. x = ± 127 (mod 243).
6,	a. x = 13, 19, 45, 51 (mod 64).
b. x = 41, 87, 169, 215 (mod 256).
Ответы к главе VI.
1,	а. 6.
Ь. 18.
2,	а. 3, 3, 3.
b.	5, 5, 5.
c.	7.	••
5,	а. а) 0; Р) 1; у) 3.
Ь. а) 0; Р) 1; 7) 10.
6,	а. а) х = 40; 27 (mod 67), Р) х = 33 (mod 67),
7) a; = 8, 36, 28, 59, 31, 39 (mod 67).
Ъ. а) х= 17 (mod 73), р) х = 50, 12, 35, 23, 61, 38 (mod 73),
7) ж = 3, 24, 46 (mod 73).

172	ОТВЕТЫ К ЧИСЛВННЫЫ НРИМЕРАМ
7,	а. а) 0; В) 4.
Ъ. а) 0; р) 7.
8,	а. а) х = 54 (mod 101). В) х ¦= 53, 86, 90, 66, 8 (mod 101).
b. ж = 59, И, 39 (mod 109).
9,	а. а) 1, 4, 5, 6, 7, 9, 11, 16, 17; 8) 1, 7, 8, 11, 12, 18.
b. а) 1, 6, 8, 10, 11, 14, 23, 26, 27, 29, 31, 36;
I) 1, 7, 9,	10, 12, 16, 26, 33, 34.
О, а. а)	7, 37; ?) 3, 5, 12, 18, 19, 20, 26, 28, 29, 30, 33, 34.
Ь. а) 3,	27, 41, 52;
2, 6, 7,	10, 17, 18, 26, 30, 31, 35, 43, 44, 51, 54, 55, 59.

ТАБЛИЦЫ ИНДЕКСОВ
173
ТАБЛИЦЫ ИНДЕКСОВ.
Простое чвсло 3.
N
0
0
1
0
2
1
3
4
5
6
7
8
9
I
0
0
1
1
2
2
3
4
5
6
7
8
9»
N
0
0
1
0
2
1
3
3
4
2
5
6
Простое число 5
7
8
9
/
0
0
1
1
2
2
4
3
3
4
5
6
7
8
9
N
0
0
1
0
2
2
3
1
4
4
5
5
6
3
Простое числе
7
8
9
/
0
V.
0
1
1
3
2
2
3
6
4
4
5
5
6
7
8
9
Простое число 11.
Nl °
0
1 5
1
0
2
1
3
8
4
2
5
4
6
9
7
7
8
3
9
6
it 0
0
1
-1
1
2
2
4
3
8
4
5
5
10
6
9
7
7
8
3
9
6
Простое число 13.
N
0
1
0
10
1
0
7
2
1
6
3
4
4
2
5
9
6
5
7
11
8
3
9
8
0
1
10
1
2
7
2
4
3
8
4
3
5
6
6
12
7
11
8
9
9
5-

174
ТАБЛИЦЫ ИНДЕКСОВ
Простое число 17.
N
0
1
0
3
1
0
7
2
14
13
3
1
4
4
12
9
5
5
6
6
15
8
7
И
8
10
9
2
/
0
1
0
1
8
1
3
7
2
9
4
3
10
12
4
13
2
5
5
6
6
15
7
11
8
16
9
14
Простое число 19.
N
0
1
0
17
1
0
12
2
1
15
3
13
5
4
2
7
5
16
11
6
14
4
7
6
10
8
3
9
9
8
/
0
1
0
1
17
1
2
15
2
4
11
3
8
3
4
16
6
5
13
12
6
7
5
7
14
10
8
9
9
18
Простое число 23.
N
0
1
2
0
3
5
1
0
9
13
2
2
20
11
3
16
14
4
4
21
5
1
17
6
18
8
7
19
7
8
6
12
9
10
15
0
1
2
0
1
9
12
1
5
22
14
2
2
18
3
10
21
4
4
13
5
20
19
6
8
3
7
17
15
8
16
6
9
11
7
Простое число 29.
[N
0
I
2
rs
0
23
24
1
0
25
17
2
1
7
26
3
5
18
20
4
2
13
8
5
22
27
16
6
6
4
19
7
12
21
15
8
3
11
14
9
10
9
/
0
1
2
0
1
9
23
1
2
18
17
2
4
7
5
3
8
14
10
4
16
28
20
5
3
27
11
6
6
25
22
7
12
21
15
8
24
13
9
19
26
N
0
1
2
3
0
14
8
15
1
0
23
29
2
24
19
17
3
1
11
27
4
18
22
13
5
20
21
10
6
25
6
5
Простое число
7
28
7
3
8
12
26
16
9
2
4
9
0
1
2
31
0
1
25
5
•
1
3
13
15
2
9
8
14
3
27
24
11
4
19
10
2
5
26
30
6
6
16
28
18
7
17
22
23
8
20
4
7
9
29
12
21

ТАБЛИЦЫ ИНДЕКСОВ
Простое число 37.
176
0
1
2
3
0
24
25
14
1
0
30
22
9
2
1
28
31
5
3
26
11
15
20
4
2
33
29
8
5
23
13
10
19
6
27
4
12
18
7
32
7
6
8
3
17
34
9
16
35
21
I
0
1
2
3
0
1
25
33
11
1
2
13
29
22
2
4
26
21
7
3
8
15
5
14
4
16
30
10
28
5
32
23
20
19
6
27
9
3
7
17
18
6
8
Vi
46
9
"Н
94
0
1
2
3
4
0
8
34
23
20
1
0
3
14
28
2
26
27
29
10
3
15
31
36
18
4
12
25
13
19
5
22
37
4
21
6
1
24
17
?,
Простое число
7
39
33
5
32
8
38
16
11
35
9
30
9
7
6
I
0
1
2
3
41.
0
1
32
40
9
1
6
28
35
13
2
36
4
5
37
3
И
24
30
17
4
25
21
16
20
5
27
3
14
38
6
39
18
2
23
7
29
26
12
15
8
10
33
31
8
9
19
34
22
7
N
0
1
2
3
4
0
10
37
И
22
1
0
30
36
34
6
2
27
13
15
9
21
3
1
32
16
31
4
12
20
40
23
5
25
26
8
18
6
28
24
17
14
Простое число
7
35
38
3
7
8
39
29
5
4
9
2
19
41
33
/
0
1
2
3
4
43
0
1
10
14
И
24
1
3
30
42
33
29
2
9
4
40
13
3
27
12
34
39
4
38
36
16
31
5
28
22
5
7
6
41
23
15
21
7
37
26
2
20
8
25
35
6
17
9
32
19
18
8
Простое число 47.
N
0
1
2
3
4
0
19
37
39
9
1
0
7
6
3
15
2
18
10
25
44
24
3
2С
11
5
27
13
4
36
4
28
34
43
5
1
21
2
33
41
6
38
26
29
30
23
7
32
16
14
42
8
8
12
22
17
9
40
45
35
31
0
1
2
3
4
0
1
12
3
36
9
1
5
13
15
39
45
2
9,5
18
?,8
7
37
3
31
43
46
35
44
4
14
27
42
34
32
5
23
41
22
29
19
6
21
17
16
к
7
11
38
33
20
8
8
2
24
6
... ¦
*а
40
10
20
Л)

176
ТАБЛИЦЫ ИНДЕКСОВ
Простое число 53.
N
0
1
2
3
4
5
0
48
49
13
50
43
1
0
6
31
33
45
27
2
1
19
7
5
32
26
3
17
24
39
23
22
4
2
15
20
11
8
5
47
12
42
9
29
6
18
4
25
36
40
7
14
10
51
30
44
8
3
35
16
38
21
9
34
37
46
41
28
/|о
0
1
2
3
4
5
1
17
24
37
46
40
1
2
34
48
21
39
27
2
4
15
43
42
25
3
8
30
33
31
50
4
16
7
13
9
47
5
32
14
26
18
41
6
И
28
52
36
29
7
22
3
51
19
5
8
44
6
49
38
10
9
35
12
45
23
20
N
0
1
2
3
4
5
0
7
8
57
9
13
1
0
25
10
49
14
32
2
1
52
26
5
11
47
3
50
45
15
17
33
22
4
2
19
53
41
27
35
5
6
56
12
24
48
31
6
51
4
46
44
16
21
Простое число
7
18
40
34
55
23
30
8
3
43
20
39
54
29
9
42
38
28
37
36
59
/ || 0
0
1
2
3
4
5
1
21
28
57
17
3
1
2
42
56
55
34
6
2
4
25
53
51
9
12
3
8
50
47
43
18
24
4
16
41
35
27
36
48
5
32
23
11
54
13
37
6
5
46
22
49
26
15
7
10
33
44
39
52
30
8
20
7
29
19
45
9
40
14
58
38
31
N
0
1
2
3
4
5
6
0
23
?,4
29
25
45
30
1
0
15
55
59
54
53
2
1
8
16
5
56
42
3
6
40
57
21
43
33
4
2
50
9
48
17
19
5
22
28
44
11
34
37
6
7
4
41
14
58
52
Простое числе
7
49
47
18
39
20
32
8
3
13
51
27
10
36
9
12
26
35
46
38
31
I
0
1
2
3
4
5
61
0
1
48
47
60
13
14
1
2
35
33
59
26
28
2
4
9
5
57
52
56
3
8
18
10
53
4а
51
4
16
36
20
45
25
41
5
32
И
40
29
оО
21
6
3
22
19
58
39
42
7
6
44
38
55
17
23
8
12
27
15
49
34
46
9
24
54
30
37
7
31
N
0
1
2
'3
4
5
6
0
16
17
55
18
31
56
1
0
59
62
47
53
37
7
2
1
41
60
5
63
21
48
3
39
19
28
32
9
57
35
4
2
24
42
65
61
52
6
5
15
54
30
38
27
8
34
6
40
4
20
14
29
26
33
Простое число
7
23
64
51
22
50
49
8
3
13
25
11
43
45
9
12
10
44
58
46
36
I
0
1
2
3
4
5
6
67
0
1
19
26
25
6
47
22
1
2
38
52
50
12
27
44
2
4
9
37
33
24
54
21
3
8
18
7
66
48
41
42
4
16
36
14
65
29
15
17
5
32
5
28
63
58
30
34
6
64
10
56
59
49
60
7
61
20
45
51
31
53
8
55
40
23
35
62
39
9
43
13
46
3
57
И

N
ТАБЛИЦЫ ИНДЕКСОВ
Простое число 71.
177
26
38 39
51
30 57
33 48 43
23
17 53
12 28 32
15 44 56
14 59
36
54 24
45
29 64 20
21
19 42
63 47
118 52
49 58
13 68
22 65
50
4
6141
0
1
49
4 28 54
59
38 53
6 42
9 63
58 51
57 44 24 26 40
23
16 41
50 66 36 39 60 65
10 70 64 22
15 34 25 33
19 62
3 21
14 27 47
67
8 56
5 35
18 55
29 61
N
0
1
2
3
4
5
6
7
0
9
17
15
25
10
23
42
1
0
55
39
11
4
27
58
44
2
8
22
63
40
47
3
19
36
3
6
59
46
61
51
53
45
4
16
41
30
29
71
26
48
5
1
7
2
34
13
56
60
6
14
32
67
28
54
57
69
Простое число
7
33
21
18
64
31
68
50
8
24
20
49
70
38
43
37
9
12
62
35
65
66
5
52
0
1
?,
3
4
5
6
7
73.
0
1
50
18
24
32
67
65
38
1
5
31
17
47
14
43
33
44
2
25
9
1?,
16
70
69
19
3
52
45
60
7
58
53
22
4
41
6
8
35
71
46
37
5
59
30
40
29
63
И
39
6
3
4
54
72
23
55
49
7
15
20
51
68
42
56
26
8
2
27
36
48
64
61
57
9
10
62
34
21
28
13
66
N
0
1
2
3
4
5
6
7
0
66
70
67
74
50
71
41
1
0
68
54
56
75
22
4Ь
М
2
4
9
72
20
58
42
60
14
3
1
34
26
69
49
77
55
44
4
8
57
13
25
76
7
24
23
5
62
63
46
37
64
52
18
6
5
16
38
10
30
65
73
47 40
Простое число
7
53
21
3
19
59
33
48
43
8
12
6
61
36
17
15
29
39
9
2
32
И
35
28
31
27
0
1
?,
3
4
5
6
7
79
0
1
36
32
46
76
50
62
20
1
3
?,9
17
59
70
71
28
60
2
9
8
51
19
5?,
55
5
22
3
27
24
74
57
77
7
15
66
4
2
72
64
13
73
21
45
40
5
6
58
6
18
16
34?23
39 38
61
63
56
41
25
31
10
44
7
54
48
69
35
75
14
30
53
8
4
65
49
?,6
67
42
11
9
12
37
68
78
43
47
33

178
ТАБЛИЦЫ ИНДЕКСОВ
Простое число 83.
N
0
1
2
3
4
5
6
7
8
0
28
29
18
30
55
19
36
31
1
0
24
80
38
40
46
66
33
42
2
1
74
25
5
81
79
39
65
41
3
72
77
60
14
71
59
70
69
4
2
9
75
57
26
53
6
21
5
27
17
54
35
7
51
22
44
6
73
4
78
64
61
11
15
49
7
8
56
52
20
23
37
45
32
8
3
63
10
48
76
13
5S
68
9
62
47
12
67
16
34
50
43
I
0
1
2
3
4
5
6
7
8
0
1
28
37
40
41
69
23
63
21
1
2
56
74
80
82
55
46
43
42
2
4
29
65
77
81
27
9
3
3
8
58
47
71
79
54
18
6
4
16
33
И
59
75
25
36
12
5
32
66
22
35
67
50
72
24
6
64
49
44
70
51
17
61
48
7
45
15
5
57
19
34
39
13
8
7
30
10
31
38
68
78
26
9
14
60
20
62
76
53
73
52
N
0
1
2
3
4
5
6
7
8
0
86
14
87
30
68
15
79
46
1
0
НА
82
31
21
7
69
62
4
2
16
33
12
80
10
55
47
50
37
3
1
23
57
85
29
78
83
20
61
4
32
9
49
22
28
19
8
27
26
5
70
71
52
63
72
66
5
53
76
6
17
64
39
34
73
41
13
S7
45
Простое число
7
81
6
3
11
54
36
56
77
60
8
48
18
25
51
65
75
38
40
44
9
2
35
59
24
74
43
58
42
I
0
1
2
3
4
5
fi
7
8
89.
0
1
42
73
40
78
72
87
5
32
1
3
37
41
31
56
38
83
15
7
2
9
22
34
4
79
25
71
45
21
3
27
66
13
12
59
75
35
46
63
4
81
20
39
36
88
47
16
49
И
5
65
60
28
19
86
52
48
58
33
6
17
2
84
57
80
67
55
85
10
7
51
6
74
82
62
23
76
77
30
8
64
18
44
68
8
69
50
53
9
14
54
43
26
24
29
61
70
N
0
1
2
3
4
5
6
7
8
9
0
35
69
9
7
36
43
66
41
79
1
0
86
5
46
85
63
64
И
88
56
2
34
42
24
74
39
93
80
50
23
49
3
70
25
77
60
4
10
75
28
17
20
4
68
65
76
27
58
52
12
29
73
22
5
1
71
2
32
45
87
26
72
90
82
6
8
40
59
16
15
37
94
53
38
48
Простое число
7
31
89
18
91
84
55
57
21
83
8
6
78
3
19
14
47
61
33
92
9
44
81
13
95
62
67
51
30
54
I
0
1
2
3
4
5
6
7
8
9
97.
0
1
53
93
79
16
72
33
3
62
85
1
5
71
77
7
80
69
68
15
19
37
2
25
64
94
35
12
54
49
75
95
88
3
28
29
82
78
60
76
51
84
87
52
4
43
48
22
2
9
89
61
32
47
66
5
21
46
•13
10
45
57
14
63
41
39
6
Р
36
65
50
31
91
70
24
И
7
40
83
34
56
58
67
59
23
55
8
6
27
73
86
96
44
4
18
81
9
30
38
74
42
92
26
20
90
17

ТАБЛИЦА ПРОСТЫХ ЧИСЕЛ
179
Таблица простых чисел <4000 и их наименьших первообраз-
первообразных корней.
р
2
3
5
7
11
13
17
19
23
29
31
37
41
43
47
53
59
61
67
71
73
79
83
89
97
101
103
107
109
113
127
131
137
139
149
151
157
163
167
173
g
1
2
2
3
2
2
3
2
5
2
3
2
6
3
5
2
2
2
2
7
5
3
2
3
5
2
5
2
6
3
3
2
3
2
2
6
5
2
5
2
Р
179
181
191
193
197
199
211
223
227
229
233
239
241
251
257
263
269
271
277
2S1
283
293
307
311
313
317
331
337
347
349
353
359
367
373
379
383
389
397
401
409
g
2
2
19
с
о
2
3
2
3
2
6
3
7
7
6
3
5
2
6
5
3
3
2
5
17
10
2
3
10
2
2
3
7
6
2
2
5
2
5
3
21
I'"
419
421
431
433
439
443
449
457
461
463
467
479
487
491
499
503
509
521
523
541
547
557
563
569
571
577
587
593
599
601
607
613
617
619
631
641
643
647
653
659
g
2
2
7
5
15
2
3
13
2
3
2
13
3
2
7
5
2
3
2
2
2
2
2
3
3
5
2
3
7
7
3
2
3
2
3
3
11
5
2
2
Р
661
673
677
683
691
701
709
719
727
733
739
743
751
757
761
769
773
787
797
809
811
821
823
827
829
839
853
857
859
863
877
881
883
887
907
911
919
929
937
941
g
2
5
2
5
3
2
2
И
5
6
3
5
3
2
6
И
2
2
2
3
3
2
3
2
2
И
2
3
2
5
2
3
2
5
2
17
7
3
5
2
Р
947
953
967
971
977
9S3
991
997
1009
1013
1019
1021
1031
1033
1039
1049
1051
1061
1063
1069
1087
1091
1093
1097
1103
1109
1117
1123
1129
1151
1153
1163
1171
1181
1187
1193
1201
1213
1217
1223
g
2
3
5
6
3
5
6
7
И
3
2
10
14
5
3
3
7
2
3
6
3
2
5
3
5
2
2
2
11
17
5
5
2
7
2
3
И
2
3
5
Р
1229
1231
1237
1249
1259
1277
1279
1283
1289
1291
1297
1301
1303
1307
1319
1321
1327
1361
1367
1373
1381
1399
1409
1423
1427
1429
1433
1439
1447
1451
1453
1459
1471
1481
1483
1487
1489
1493
1499
1511
g
2
3
2
7
2
2
3
2
6
2
10
2
6
2
13
13
3
3
5
2
2
13
3
3
2
6
3
7
3
2
2
5
6
3
2
5
14
2
2
И
1523
1531
1543
1549
1553
1559
1567
1571
1579
1583
1597
1601
1607
1609
1613
1619
1621
1627
1637
1657
1663
1667
1669
1693
1697
1699
1709
1721
1723
1733
1741
1747
1753
1759
1777
1783
1787
1789
1801
1811
*
19
И
2
3
2
11
3
2
2
2
3
3
3
3
3
2
2
2
7
6
5
10
2
6
11
6

180
ТАБЛИЦА ПРОСТЫХ ЧИСЕЛ
Продолжение
р
1823
1831
1847
1861
1867
1871
1 873
1877
1879
1889
1901
1 907
1913
1931
1933
1949
1951
1973
1979
1987
1993
1997
1999
2 003
2 011
2 017
2 027
2 029
2 039
2 053
2 063
2 069
2 081
2 083
2 087
2 089
2 099
2111
2113
g
5
3
5
2
2
14
10
2
6
3
2
2
3
2
5
2
3
2
2
2
5
2
3
5
3
5
2
2
7
2
5
2
3
2
5
7
2
7
5
Р
2 129
2131
2137
2141
2143
2153
2161
2179
2 203
2 207
2 213
2 221
2 237
2 239
2 243
2 251
2 267
2 269
2 273
2 281
2 287
2 293
2 297
2 309
2 311
2 333
2 339
2 341
2 347
2 351
2 357
2 371
2 377
2 381
2 383
2 389
2 393
2 399
2 411
g
3
2
10
2
3
3
23
7
5
5
2
2
2
3
2
7
2
2
3
7
19
2
5
2
3
2
2
7
13
z
г
t
с
Z
з
И
6
р
2 417
2 423
2 437
2 441
2 447
2 459
2 467
2 473
2 477
2 503
2 521
2 531
2 539
2 543
2 549
2 551
2 557
2 579
2 591
2 593
2 609
2 617
2 621
2 633
2 647
2 657
2 659
2 663
2 671
2 677
2 683
2 687
2 689
2 693
2 699
2 707
2 711
2 713
2 719
g
3
5
2
6
5
2
2
5
2
3
17
2
2
5
2
6
2
2
7
7
3
5
2
3
3
3
2
С
7
2
2
19
С,
с
L
(
i
с
3
р
2 729
2 731
2 741
2 749
2 753
2 767
2 777
2 789
2 791
2 79?
2 801
2 803
2 819
2 833
2 837
2 843
2 851
2 857
2 861
2 879
2 887
2 897
2 903
2 909
2 917
2 927
2 939
2 953
2 957
2 963
2 969
2 971
2 999
3 001
ЗОН
3 019
3 023
3 037
3 041
3
3
2
6
3
3
3
2
6
2
3
2
2
5
2
2
2
1
2
7
5
3
5
2
5
5
2
13
2
2
з
10
17
14
с
С,
с
&
С
t
с
Z
i
Р
3 049
3 061
3 067
3 079
3 083
3 089
3 109
3 119
3121
3137
3 163
3167
3169
3181
3 187
3 191
3 203
3 209
3 217
3 221
3 229
3 251
3 253
3 257
3 259
3 271
3 299
3 301
3 307
3 313
3 319
3 323
3 329
3 331
3 343
3 347
3 359
3 361
3 371
g\
1
6
2
6
2
3
6
7
7
3
3
5
7
7
2
И
2
3
5
10
6
6
2
3
3
3
2
6
2
10
6
2
11
22
Р
3 373
3 389
3 391
3 407
3 413
3 433
3 449
3 457
3 461
3 463
3 467
3 469
3 491
3 499
3 511
3 517
3 527
3 529
3 533
3 539
3 541
3 547
3 557
3 559
3 571
3 581
3 583
3 593
3 607
3 613
3 617
3 623
3 631
3 637
3 643
3 659
3 671
3 673
3 677
g
5
3
3
5
2
5
3
7
2
3
2
2
2
2
7
2
5
17
2
2
7
2
2
3
2
2
3
3
5
2
9
21
13
Р
3 691
3 697
3 701
3 709
3 719
3 727
3 733
3 739
3 761
3 767
3 769
3 779
3 793
3 797
3 803
3 821
3 823
3 833
3 847
3 851
3 853
3 863
3 877
3 881
3 889
3 907
3 911
3 917
3 919
3 923
3 929
3 931
3 943
3 947
3 967
3 989
g
2
5
2
2
7
3
2
7
3
5
7
2
5
2
2
3
3
3
5
2
2
5
2
13
И
2
13
2
3
2
О
2
о
о
2
6
L

Замеченные опечатка
(допущены по вине типографии)
Страница
23
93
100
116
123
124
152
Зак. 1362
Строка
11 св.
13 сн.
1 сн.
15 св.
1 сн.
5 сн.
5 св.
Напечатано
когда
(ху)аЬ — l(modm)
g — =1 (mod m)
C In N) <N
/
a, 1
2
Следует читать
тогда
(xy)nb = 1 (mod m)
с
j'sl (mod m)
C In N)k < N
«2 + 1
2*