Автор: Петрушко И.М. Бараненков А.И. Богомолова Е.П.
Теги: математика высшая математика учебное пособие сборник задач 4300 задач
ISBN: 978-5-383-00199-8
Год: 2008
Текст
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
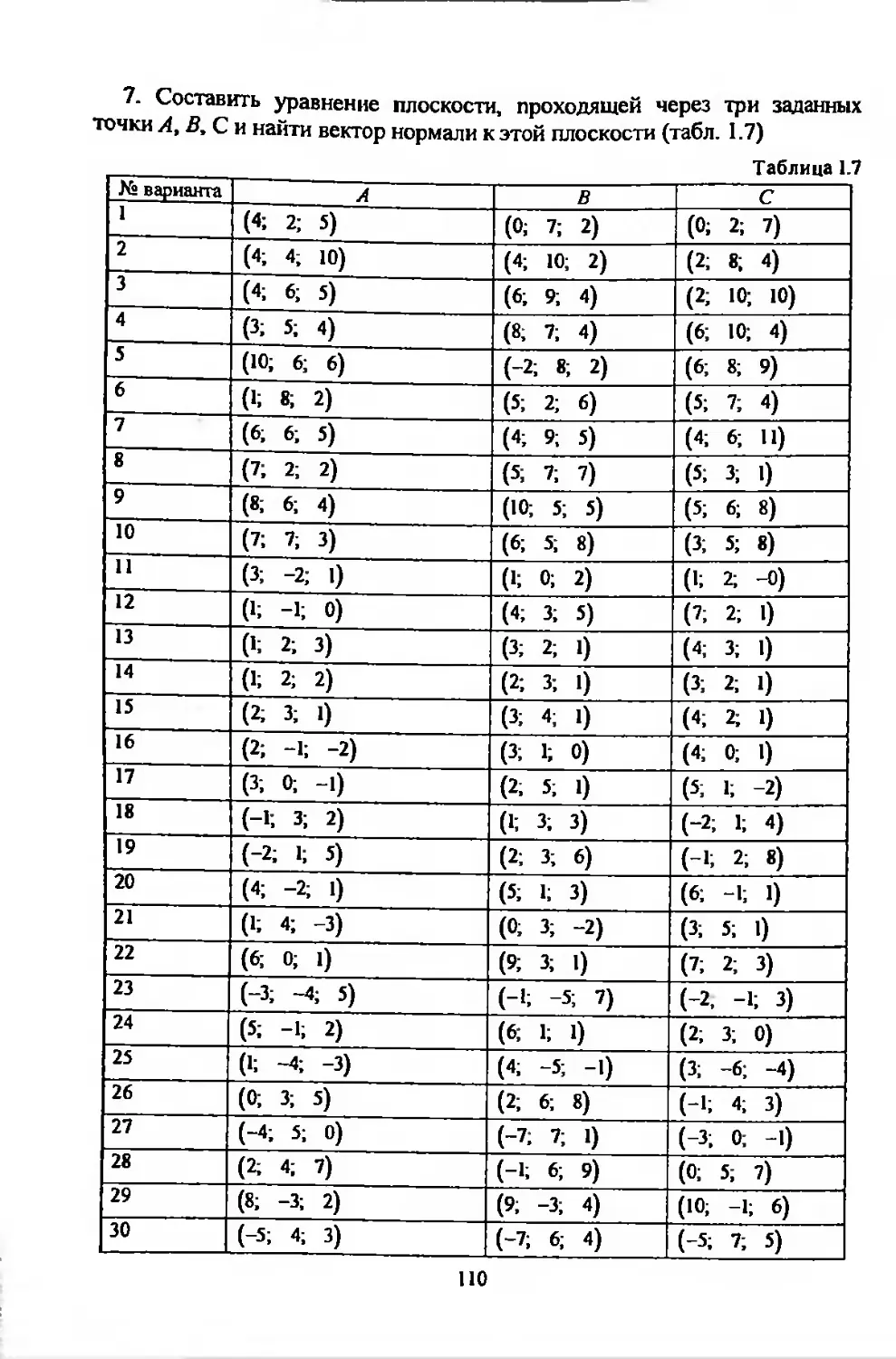
МОСКОВСКИЙ ЭНЕРГЕТИЧЕСКИЙ ИНСТИТУТ
___________(ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)
А.И. БАРАНЕНКОВ, Е.П. БОГОМОЛОВА, И.М. ПЕТРУШКО
СБОРНИК ЗАДАЧ ПО ОСНОВАМ ВЫСШЕЙ МАТЕМАТИКИ
Учебное пособие по курсу «Математика»
для студентов МЭИ (ТУ), обучающихся по всем направлениям подготовки
Москва
Издательский дом МЭИ
2008
УДК 51
Б 241
Утверждено учебным управлением МЭИ в качестве учебного пособия для студентов Подготовлено на кафедре высшей математики
Рецензент: докт. физ.-мат. наук, профессор Ю.Н. Фролов, кандидат физ.-мат. наук, доцент Г.В. Федотенков
Бараиенков А.И.
Б 241 Сборник задач по основам высшей математики: учебное пособие / А.И. Бараненков, Е.П. Богомолова, И.М. Петрушке. — М.: Издательский дом МЭИ, 2008. — 176 с.
ISBN 978-5-383-00199-8
Сборник содержит 4300 задач по курсу высшей математики. Прн составлении авторы руководствовались идеей устранить громоздкие вычисления, скрывающие основные математические понятия. Структура задачника предполагает, что разнообразие задач достаточно для решения примеров на практических занятиях с преподавателем; домашнего задания; индивидуальных типовых расчетов по каждому разделу.
Учебное пособие предназначено для студентов, обучающихся по всем направлениям подготовки в МЭИ (ТУ).
ISBN 978-5-383-00199-8
© Московский энергетический институт (технический университет), 2008
ОГЛАВЛЕНИЕ
Предисловие................................................................6
I. Элементарная математика................................................7
I. Действительные числа. Точные и приближенные вычисления. Проценты.....7
2. Алгебраические преобразования. Степени, корни, формулы сокращенного умножения...............................................................8
3. Алгебраические уравнения. Линейные уравнения. Системы линейных уравнений (метод исключения). Квадратное уравнение......................9
4. Комплексные числа и действия с ними..................................9
5. Многочлены, разложение на множители. Деление многочленов. Разложение рациональных дробей на простейшие дроби.....................10
6. Функция, аргумент и значение функции. Основные элементарные функции, их свойства и графики..................................................11
7. Элементы комбинаторики..............................................13
11. Аналитическая геометрия...............................................15
1. Декартовы прямоугольные координаты на плоскости. Полярные координаты....................................................15
2. Прямая на плоскости.................................................16
3. Кривые второго порядка..............................................18
4. Определители. Правило Крамера.......................................21
5. Векторная алгебра...................................................23
6. Плоскость а пространстве............................................29
7. Прямая в пространстве...............................................31
8. Прямая н плоскость а пространстве...................................33
9. Поверхности второго порядка.........................................35
III. Линейная алгебра.....................................................37
1. Матрицы, действия с ними. Обратная матрица..........................37
2. Ранг матрицы. Элементарные преобразования матриц...................39
3. Системы линейных уравнений. Метод Гаусса...........................40
4. Линейное пространство. Размерность н базнс. Преобразование координат вектора................................................................42
5. Скалярное произведение. Ортонормированный базис....................44
6. Линейный оператор. Матрица линейного оператора.....................45
7. Собственные векторы н собственные числа линейного оператора........46
8. Квадратичные формы. Приведение к каноническому виду................47
IV. Математический анализ................................................48
1. Предел числовой последовательности................................ 48
2. Предел функции. Простейшие методы вычисления пределов.Эквивалентные бесконечно малые для вычисления пределов...............................49
3. Производная функции и дифферешдиал. Техника дифференцирования......53
4. Касательная и нормаль к графику функции............................58
5. Исследование функций с помощью первой производной..................59
6. Исследование функций с помощью второй производной..................59
7. Правило Лопиталя для вычисления пределов...........................60
3
8. Асимптоты графиков функций..................................
9. Исследование функций н построение графиков..................
10. Непрерывность функции в точке н на отрезке.-.....~.........
11. Формула Тейлора, ее применение для исследования функций....
12. Функции нескольких переменных...............................
13. Частные производные, градиент..............................
14. Касательная плоскость н нормаль к поверхности..............
15. Исследование на экстремум функций нескольких переменных....
16. Системы линейных неравенств нескольких переменных. Графическое решение.......................................-.................
17. Простейшие задачи линейного программирования....,..........
18. Неопределенный интеграл. Основные методы интегрирования....
19. Интегралы от рациональных функций...........................
20. Интегралы от тригонометрических функций.....................
21. Интегралы от иррациональных функций.........................
22. Определенный интеграл. Формула Ньютона-Лейбница.............
23. Замена переменной и интегрирование по частям в определенном интеграле.
...61 ...62 ...63 ....65 ....66 ....67 ...69
....69
....70 ....71 ...72 ....75 ....76 ....76 ....77 ....77
24. Применение определенного интеграла для вычисления площадей и длин дуг кривых......................................................78
25. Несобственные интегралы..........................................79
V. Дифференциальные уравнения.....................................80
1. Дифференциальные уравнения. Задача Коши......-...............80
2. Дифференциальные уравнения первого порядка...................81
3. Понижение порядка дифференциального уравнения................84
4. Линейные однородные дифференциальные уравнения с постоянными коэффициентами.................................................. 85
5. Метод подбора для линейных неодиородиых дифференциальных уравнений........................................................86
VI. Ряды
1. Числовой ряд. Суммирование рядов.................................88
2. Исследование на сходимость рядов с положительными членами.......89
3. Знакопеременные ряды..............................................91
4. Функциональные ряды. Область сходимости. Равномерная сходимость...91
5. Степенные ряды..............................................-....Я
6. Ряды Фурье......................................................95
VII. Кратные интегралы................................................96
1. Повторное интегрирование........................................96
2. Двойной интеграл в декартовых координатах.......................96
3. Тройной интеграл в декартовых координатах.......................97
4. Двойной интеграл в полярных координатах..........................99
5. Тройной интеграл в цилиндрических координатах...................100
6. Тройной интеграл в сферических координатах......................101
4
VIII. Теория поля.....................................................IUZ
I. Дифференциальные операции в декартовых координатах..............
2. Интегральные операции векторного анализа........................
IX. Типовые расчеты...................................................^4
I. Аналитическая геометрия.........................................I®4
2. Линейная алгебра................................................
3. Пределы...................................................—.....^3
4. Дифференцирование...................................-..........131
5. Графики.........................................................138
6. Интегрирование..................................................1 4 1
7. Ряды.................................-.........................148
8. Функции нескольких переменных...................................' S3
9. Кратные интегралы н теория поля............................... 139
10. Дифференциальные уравнения................................... 1^8
Библиографический список ..............................................^5
ПРЕДИСЛОВИЕ
Роль математики в подготовке специалиста любой профессии часто нет оценивается. Развитие логического мышления, памяти, способности к анализу-всё это реализуется а процессе занятий математикой в течение нескольких сем< стров прн изучении математических дисциплин в высшем учебном заведении.
Математические знания обычно трудно осваиваются вследствие их мал симального абстрагирования от реальных жизненных процессов. Проблемы ов ладения математическими понятиями и методами усложняются, если вуз ставя перед собой задачу подготовки бакалавров. Количество часов на изучение мате матики в учебном плане бакалавра невелико, а требования к бакалавриату дик туют необходимость получения студентом обширных знаний природы вещей основные законы которой часто поддаются описанию с помощью базовых математических объектов и моделей.
Представляется, что занятия математикой для студентов неинжеиериых профессий должны быть направлены на освоение основных математических понятий, методов и логических связей. При этом на практических занятиях требуется на несложных в вычислительном плане задачах (причём в больших количествах) разъяснять сущность сложных математических объектов, обучать студента современным методам математики и, учитывая недостаток времени, изучать математические методы на сравнительно простых примерах.
В настоящее время ощущается дефицит полноценных задачников по математике, стимулирующих студента к успешному самостоятельному труду. Основная масса учебных материалов имеет вид пособий с достаточно большим набором разобранных задач и со скудным набором примеров для самостоятельного решения и тренировки. Данный задачник призван восполнить этот дефицит, особенно в части пособий для подготовки бакалавров.
Задачник содержит около 4300 несложных задач по стандартному курсу высшей математики для бакалавров технических и технологических, а также для бакалавров и специалистов экономических, управленческих и других специальностей.
При отборе задач авторы руководствовались идеями устранения громоздких вычислений, скрывающих основные математические понятия, и намеренного дублирования типичных примеров, облегчающего успешное выполнение домашних заданий. При необходимости усложнённых вычислений студент, освоив на простых примерах основные математические идеи, может с успехом применить для своих исследований один из многочисленных пакетов вычислительных компьютерных программ.
Структура задачника предполагает, что разнообразных задач достаточно для:
I) решения примеров на практических занятиях с преподавателем (например, чётных номеров);
2) домашнего задания (нечётные номера);
3) индивидуальных типовых расчётов (30 вариантов) по каждому разделу.
6
I. ЭЛЕМЕНТАРНАЯ МАТЕМАТИКА
1. Действительные числа. Точные и приближенные вычисления. Проценты
Написать разложение на простейшие множители чисел
1.1. 12, 65, 108, 312, 576, 2100, 37300
1.2. 30, 56,99, 256, 882, 1244, 55000
Найти НОК и НОД чисел
1.3. 18, 48, 72 1.4. 24, 45, 36 1.5 495, 2100 1.6. 363, 440, 198
Вычислить точно и приближённо ( с помощью калькулятора)
„ 1 2 „, 2 2 1
1.7. -+—+0,3 1.8. -+—--
3 15 7 21 3
, „ 2 2 4 , 7 5 11
1.9. -+ 1.10. -+
5 6 15 5 7 70 , IT 7324
III -6-J-+ 1.12. —
0,4-70,2 9
1.14. 0,1-720:745 -2—
2 \0,09 790 30
, „ 722—72 /- , , 77-7 /2 3
1.15. —j= 711
Tn-н Т35-Т5 VI5 45
Упростить
1.17. 7з7-457з5-4 Lie. о,з-71о-7б-715-о,1
1.19. ^(-3)2-2-7Г9 1.20. 7-25-^500 -7100
Сравнить числа
V8-T6 75-712 715 Тб 714-712 710 742
1.21. 7=~ И 7= V24 V20
2.4-10-4 2.8-10"4 „ .
1.23. и 0,012 1.24. -т-и 0,14
2-10-3 2-Ю-4
1.25. (ю8)2 Ю0“6 и (10‘10 1006)2
7
1.26. (о,00I3-I012) 2 (о,I2)"4 и 100
Найти указанное число процентов от указанных чисел
1.27. 10 % от 700, 16 % от 0.25, 25 % от 80, 33 % от (400:3), 60% от 10
1.28. 5 % от 75, 14 % от (200:7), 50 % от 0,001, 62 % от 8
99 % от 10 000
1.29. Увеличить число 27 на 3 %
1.31. Увеличить число 0,039 на 13 %
1.33. Уменьшить число 10 на 2 %
1.35. Уменьшить ч исло 0,15 на 70 %
Сравнить
1.37. 60% от 0,43 и 2 % от 15
1.39. 0,15%от24 н40%от0,1
1.30. Увеличить число 42 на 6 %
1.32. Увеличить число 0,225 на 5 %
1.34. Уменьшить число 100на22%
1.36. Уменьшить число 0,132 на40%
1.38. 12 % от 1024 и 7 % от 1760
1.40. 70% от 0,2 и 0,032 % от 440
2. Алгебраические преобразования. Степени, корни, формулы сокращенного умножения
Упростить выражения
2.3. 2.4.
х -у х+у х+у х-у
2.5. (у + Ю)(у-2)-4у(2-Зу) 2.6. (у + l)(y + 3)-2у(1 -Зу)
2.7. (х-3)(х+3)-[х2+2)2-х(х-3)3
2.8. (6- х)(х+2) -(х2 -1)2 - х(х + 2)3 + 3
2.9.
2.11.
2.10.
2.12.
Выделить полный квадрат
2.13. х2-4х+5
2.15. х2-Зх + 1
2.14. х2+6х-7
2.16. х2+х+3
8
2.17. 2x2+8x + I
2.19. 3xz-5x-12
2.18. 3x2+I8x + ll
2.20. 5x2-3x-16
3. Алгебраические уравнения. Линейные уравнения. Системы линейных уравнений (метод исключения). Квадратное уравнение
Решить уравнения и системы уравнений.
3.1. 4х —1 = 0
3.3. 8 = 0,5х
3.5. х + 4 = 5(0,2х + 0,1)
(2х-3у = 1
3-7
[х+5у = 2
[0,1х + 0,16у = 2
3.9. Р
(0,Зу - 3,25х = -6
3.11. х2-5х + 6 = 0
3.13. 2х2+х-3 = 0
3.15. Зх2-11х-4 = 0
X-У = 1
3.17. ,
х-2ху+8=0
2х+у = 2
3.19. , ,
4х-2ху+8/+1=5 4
3.2. 6х + 2 = 0
3.4. 3 = 0,Зх
3.6. 2(0,5+0,25х) = 7-х
{4х+у = I
2у-х=0
[5,2х-0,16у = 1
3.10. Р „
(0,2х-3,2у = -3
3.12. х2+х-6 = 0
3.14. 5xz-2x-3 = 0
3.16. 2xz+9x-5 = 0
х+у = 2
3.18. ,
/-2лу+1 = 0
х-у = -1
3.20. , ,
х1 -2ху + 6у =6
4. Комплексные числа и действия с ними
Решить уравнения
4.1. х2+9 = 0
4.3. х2-4х+5 = 0
4.5. х2+2х+2 = 0
4.7. х3-1 = 0
Вычислить
4.9. /+(2-3/)
4.11. (5+/)-(2-/)
4.13. (2-/) (4-21)
4.2. х2+4 = 0
4.4. х2-6х + 13=0
4.6. х2-2х + 5 = 0
4.8. х3 + 1 = 0
4.10. 2 + (4-/)
4.12. (4-2/)-(3+/)
4.14. (3+/)-(2-3/)
9
4.15. (0,l-i)(3+0,5ij 4.17. l + i 4.16. (0,3-2,7/j (l+i) 4.18. 2-i
4.19. 1-0,li 4.20. 3 + 1
5. Многочлены, разложение на множители. Деление многочленов. Разложение рациональных дробен на простейшие дроби
Упростить 5.1. x(x + l)2+2x-x3 53. (x-l)3-(x + l)3 5.5. (2x-l)4-(x+6)4 5.2. (x+3)(x-5)2-(x+l)[l+x2) 5.4. (x+2)3-(x-3)3 5.6. (x-2)4-(3x+6)4
Найти корни многочлена, разложив его на множители
5.7. P(x)=x3-x2 — 12x 5.9. P(x) = x4-3x3+4x 5.11. />(x)=-2x4-6x2 +8x 5.8. P(x) = x3+x2-17x+15 5.10. 7’(x) = x4+x3-30x2 5.12. />(x) = -3x4-5x2-8x
Поделить с остатком 5.13. *2- ~2x + S x-3 5.15. 2*2~4x + I x + 1 5.17 *2.+x + 1 2x—3 5 19 ^x +x ~ X2+4 5 21 *3+2x2+x+5 x-6 5.23. *-~4x + 2 x2 -4 5.14. x + 2 , ,, 3x2 -3x+5 3_!o. x-3 5.18. —— 5x + 2 5.20. -2.*.*2**3 x2 + l 5 22 *3~3*2+*~1 x+3 x3 + 2x2 -7 5.24. , x2-l
10
Разложить на простейшие дроби
5.25. 2х+5 5.26. 5х+4
х2-25 х2-9
5.27. х —1 5.28. х+2
х2+2х-3 х2+4х+3
5.29. 4х 5.30. X
х2 —5х-14 х2—2х-15
5.31. х-1 5.32. х + 4
х3 + 2х2-8х х3 +5х2 +6х
6. Функция, аргумент и значение функции. Основные элементарные функции, их свойства и графики
Вычислить значения функций в заданных точках
6.1. у = (х —З)2 (х+2), х = 2 6.2. у = (2х-1)3-(х-1), х = 0,5
6.3. у = 23’ж, х = 7 6.4. у = 5*"2, х = 5
6.5. у = /’2-2ж, х = 1 2 6.6. У = е2х1*3ж, х = -1
6.7. у = log2(xs +1), х = 1 6.8. y = log2(x3 + 5), х = 3
6.9. у = (x-4)lg(x-l), х = 1,1 6.10. y = (x2+2)lg(x + 3), х = 7
6.11. у = In(l-2x + 2e), х = е 6.12. , (, х) - у = 1п 1 + е—1, х = 3е
6.13. y = sin2x + cos2x, х = — 6 6.14. 2 . „ П y = cos x-sin2x, х = — 3
, . 2 6.15. j = smx-cosx-tg х, х =— 4 6.16. y = tgx + ctgx-sin3x, х = —
, - . л л/2 6.17. y = 2arcsinx , х = 4 2 6.18. у = 0,5arctg2x+^, х = ±
6.19. у =jshx -ch(2x + I), х = 0 6.20. y = 2ch(x-l)-sh(2x), х = 1
Построить графики функций
6.21. у = 2х-3 6.22. у = Зх+2
6.23. 2у-х=7 6.24. 5у + х = 8
6.25. Зх-7у + 21=0 6.26. 5у-4х—20 = 0
6.27. >> = х2-3
6.29. у = 5-х2+2х
6.31. у = ^4х-2
6.33. у^-у/з-Sx
6.35. y = 2sinx-I
6.37. y=2+lnx
6.39. y=5e*-3
, *-3
6.41. v=----
x+2
6.43. y = —
3-x
6.28. у=2-х2
6.30. у = х2 + 4х-2
6.32. у = у/х + 6
6.34.
6.36. у = -4cosx
6.38. у = 4-1пх
6.40. у = 1-2х
6.42. х+1 У = —5
6.44. х + 8 у=—
Упростить и построить график функции
х-3 х2-9 1 6.45. у= х х х-3 , , х2-5х I 6.47. у = 1 х+1 х-5 , , х2-4 1 х + 2 6.46. у = х х + 2 х Z Х + б Х~6 6.48. у = (х + 4)-т V ' х2-16 х-4
, .о 9х2-4 6х2-5х-6
6.49. у =----------------х
2-Зх 3-2х
6.51. у= —^- +—~4ь2-4ас 6.52. у= —р-+—кЛт Лух IOVx J ° \.2ylx 6-Jx ) 4
12
(2 + 2х 2-2х'I 4-4х
6.61. v = I------------------
^2-2x 2 + 2xJ 8X+1
6.62. ( 2х+2 2х—2^ (4X-1) (2X + 1) У [4х + 2Х+2 +1 4х—1J 4х
6.63. j' = -lnx + lne + lnx2 6.64. j' = 31nx + lnx2 + lne + lnl
6.65. 1п-Ух-1п^/х 1п^/х + 1пЧУх . з У +2 In х 6.66. у = —- In х 1Пу[х -In'^Gr InVx -InVx
6.67. y pn(4x) lg(4x)|j44xZ) Inx Igx )
6.68. Г1п(5х) lg(5x) H4?) Inx Igx J
6.69. ? = ^x1°E^2+x41O8-23yx2+x
6.70. yJx,O^3_x8,OEx45Yx2_2x + 5
6.71. y = cos4x + sin4x+2sin2xcos2x
6.72. у = sin4 x-cos4 x-sin2 x+cos2 x-2
6.73. y = sin6x+cos6x + 3sin2xcos2x 6.74. у = (tgx + ctgx)2-(tgx-ctgx)2
6.75. ,y = 2cos2| — |-sinx+2cosx 6.76. y = -2cos2 —+2sinx+cosx
6.77.
X X
у = -sin x + tg—+cosx • tg—+ tgx
6.78.
7. Элементы комбинаторики
Вычислить
7.1. 5! 7.2. 7! 7.3. 12! 7.4. 20!
6! 10! 7.7. 8! ,» 15!
7.5. 7.6. — 7.8. —
4! 7! 13! 19!
7.9. c72 7.10. C's 7.11. C?o 7.12. C,2
13
713‘ $ 7.14. С,
717- сб 7.18. Су
7.15. С,°2 7.16. С4°
7.19. сЦ 7.20. С3
Упростить
7.21.
7.25.
(л+2)!
(л-1)!
7.22.
(л+2)!-(л + 1)!
(л~2)! (л+1)|
л!
7 27 (л + 1)!+л! (л + 2)л!
72б (л-1)!-(л + 1)! и!
7.28. (л + 3)!+(л + 2)! (л+4)(л + 1)!
II. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
1. Декартовы прямоугольные координаты. Полярные координаты на плоскости
Построить в прямоугольной декартовой системе координат точки
1.1. А (2,1), В (-5,2), С (-1, -2) 1.2. А (-1,2), В (-3,1), С (-2,1)
1.3. А (0,2), В (2,0), С (-1,0) 1.4. А (3,0), В (0, -2), С (-5,0)
1.5. А (0,0,1), В (2,0,0), С (0,2,0) 1.6. А (-1,0,0), В (0, -3,0), С (0,0,-2)
1.7. А (1,2,0), В (2,-1,0), С (0,1 ,-1) 1.8. А (-2,1,0), В (0, -2,2), С (1,1,0)
1.9. А (-1,2,1), В (1, -2,-2), С (-1,-2,2) 1.10. А (1,-2,-1), В (-1,2,1), С (1ДЗ)
Построить в полярных координатах на плоскости точки
1.11.А(2,^),В(1,^),С(1,^)
1.13. А (2,^), В (1,^), С (1,^)
1.15. А (А, В (А, С (3,2л) о 2
1.12. А(1,—), В (2,—), С (3,л)
1.14. А (А, В (2 А С 6 6 4
1.16.А(1,—), В (1,—), С (1.0) б 4
Найти полярные координаты координатах
1.17. А(-2,2), В (2,-2)
1.19. А (з/з, 1),В(Мл/з, 1)
1.21. А (2,0), В (-2, 0)
Найти декартовы координаты координатах
1.23. А (А, В (А, С (1А
4 3 3
1.25. А (2,—),В(А,С(А
4 3 3
1.27. А (2, А В (А), С (3,2л)
6 2
точек, заданных в декартовых
1.18. А (1,1), В (-3,-3)
1.20. А(->/3 ,-1), В (Л,-1)
1.22. А (0,-2), В (0,2)
точек, заданных в полярных
1.24. А А), В (А С (3,я) о 2
1.26. А (А, В (А, С (А
6 6 4
1.28. А (1А, В (А, С (1,0) 6 4
Найти и изобразить в декартовых и полярных координатах точки, симметричные данным, относительно оси ох, относительно оси оу (полярная ось совпадает с положительным лучом ох)
1.29. А(-2,2), В (2, -2)
1.31. А(ТЗ, 1), В(-з/3, I)
1.33. А(2,0), В (-2, 0)
1.30. А (1,1), В (-3,-3)
1.32. А(-з/3,-1), В (7з,-1)
1.34. А (0,-2), В (0,2)
15
Найти и изобразить точки, симметричные координатным плоскостям для заданных точек
1.35. А (0,0,1), В (2,0,0), С (0,2,0)
1.36. А (-1,0,0), В (0, -3,0), С (0,0, -2)
1.37. А (1,2,0), В (2,-1,0), С (0,1,-1)
1.38. А (-2,1,0), В (0,-2,2), С (1,1,0)
1.39. А (-1,2,1), В (1, -2, -2), С (-1, -2,2)
1.40. А (1, -2,-1), В (-1,2,1), С (1,2,3)
1.41. А ( 1,2, -1), В (1, -2,2), С (-1,2,2)
1.42. А (3,1, -2), В (3, -2,2), С (-1, -2, -3)
2. Прямая иа плоскости
Определить, лежат ли на данной прямой указанные точки 2.1. у = Зх-1, А (1,2), В (0,1)
2.3. у-2 = |(х-1),А(0,1),В(2,1)
2-5’2Т’=Л71,А(1’0)’вн’')
2.7. 2х-Зу+1 = 0,А(— ,1),В(-| ,0)
2.8. Зх+2у-2=0,А(0,1),В(|,|)
2.9. = 1, А (1,1), В (-2,0)
2.2. у = —2х+3, А (1,0), В (1,-1)
2.4. у+1 = 3(х-1), А(1,-1), В (0,-4)
2.6. А (2,2), В (1,2)
2.10. ^+-^=1, А (3,2), В (0,-2)
Найти вторую координату точки, лежащей на данной прямой
2.11. у = 2х+2 ,А(х,3),В(-1,у)
2.13. Зх-2у + 1 = 0, А(х,1),В (1,у)
2.15.^ = ^р,А(х,1),В(2,у) 2-17.-^+-^=1,А(х,-1),В(2,у) 2.19. х = 3, А (х,2) , В (3,у)
2.12. у = -х + 2, А(х,-2), В(3,у)
2.14. 2х + Зу-1 = 0, А (х,1),В (2,у)
2.16.^=^у,А(х,-2),В(-1,у)
2.18. ^+^ = 1,А (х,-1),В (2,у)
2.20. у = -2, А (х,—2), В (3,у)
Составить уравнение и построить прямую, зная угловой коэффициент к и отрезок Ь, отсекаемый ею на оси оу
2.21. * = -U, 4 = 1
-Л
2.22. * = -Тз,4 = 2
16
2.23. * = -1, Ь = -2 2.24. * = —L,6 = -l V3
2.25. Л = 0, * = —1 2.26. * = -1, 6 = 0
Построить прямую и найти угловой коэффициент к и отрезок Ь,
отсекаемый ею на оси оу 2.27. 2х-3^ + 1 = 0 2.29. —+^ = 1 -2 3 2.31. ^1 = — 3 -2 2.33. х-2 = 0 2.28. Зх+2у-1 = 0 2.30.—+— = ! 3 -2 2.32.Z±1=AsL -3 2 2.34. у + 1 = 0
Составить уравнение прямой, проходящей через заданную точку, зная ее угловой коэффициент к
2.35. М (1,3), к = -1 2.37. М (-1,2) к=у/3 2.36. М (-1,-3), Л = 1 2.38. М (1,2), * = —^
2.39. М(1, —2) к=0 2.40. М (3,-1), * = °о
Составить уравнение прямой, проходящей через заданную точку параллельно данной прямой
. 2.41. М(1,3), —+—= 1 -2 3 2.43.М(2,1), х-3 = 0 2.45. М (1,3), 2х-Зу + 1 = 0 2.42. М (-1,2), |+^ = 1 2.44. М (-2,1), у+1 = 0 2.46. М (-1, -2), Зх+2у -1 = 0
Составить уравнение прямой, проходящей через заданную точку перпендикулярно данной прямой
2.47. М (1,3),—+— = 1 1 -2 3 2.49. М(2,1), х-3 = 0 2.51.М(1,3), 2х-Зу + 1 = 0 2.48. М (—1,2),—+— = 1 3 -2 2.50. М (-2,1), у + 1 = 0 2.52. М (-1, -2), Зх +2у-1 = 0
Составить уравнение и построить прямую, проходящую через две заданные точки и найти ее угловой коэффициент
2.53. А (-1,3), В (0,2) 2.55. А (1,-2), В (2,0) 2.57. А (1,1), В (1,-3) 2.54. А (1,-3), В (0,1) 2.56. А (-1,3), В (2,0) 2.58. А (-1,-1), В (2,-1)
17
Составить уравнение и построить прямую, зная отрезки, отсекаемые ею на осях координат, найти угловой коэффициент прямой
2.59. о = 1, 4 =-2 2.61. а = 0, 6 = 2 2.63. а = оо, Ь = — 1 2.60. а = 2,6 = -1 2.62. а = -2,6 = 0 2.64. а = 1, 6 = оо
Найти точки пересечения данной прямой с координатными осями
2.65. 2х-3у+ 1 = 0 2.66. Зх+2у-1 = 0
2.67. ^+Z = 1 2.68. —+—= 1
-2 3 3 -2
2.69. 2 70 =
3-2 ’ -3 2
Найти точки пересечения данных прямых
2.71. Зу-4х-1 = 0, Зх+4у-18 = 0 2.72. 2х-Зу-6 = 0, 4х-6у—5=0
2.73. у = 2х-1, у = -х+2 2.74. у = -2х + 1, у = х-2
2.75. -+^ = 1, --23’3 +-^ = 1 -2 2.76. х+2у-1 = 0, 2х+4у—2=0
2.77. - . X у = 2х-4, — ч ь^=1 2.78. у = 2х —4, — + ^ = 1
2 -1 -11
Найти угол между данными прямыми
2.79. 5х—у + 7 = 0, Зх+2у = 0
2.81. х-2у-4 = 0, 2х-4у+3=0
2.83. у = Зх+5, у = -2х+7
2.85. у = х-1, у = 0
2.87. у = >!Зх-2, х = 2
2.80. Зх-2у + 7 = 0, 2х+Зу-3=0
2.82. Зх + 2у — 1 = 0, 5х-2у+3 = 0
2.84. у = Лх, у = —Лх
2.86. у = —х + 1, у = 0
2.88. у = —УЗх + 1, х = —1
3. Кривые второго порядка
Определить, лежат ли указанные точки на данных кривых
3.1. 9х2 + 5у2-45 = 0, Лф.-З)
3.3. х2 +у2 -26х+30у+313 = 0, М(13,-6)
3.5. 1бх2-9у2 = 144, Л/(-3,75;3)
3.7. у2 = 4х-8, Л/(3,-2)
3.2. 8х2+5у2-77 = 0 , Л/(-2,3)
3.4. х2+у2 — 10х —14у-151 =0, Л/(-3,1)
3.6. 16х2 —9у2 =—144, М(2,5)
3.8. х2=7у + 2, Л/(4,2)
18
Построить окружность, определить, как расположены относительно нее указанные точки
3.9. х2+у2-4х + 6у = 0, Л/(4,0)
3.10. х2 + у2+2х-2у-7 = 0, М(0,3)
3.11. х2+у2-х+2у-1 = 0, Л/(1,5;1)
3.12. №+/ + 3x-5y-0.5 = 0, Л/(1,2)
3.13. 2х2+2у2-Зх-5у+3 = 0, М(1.2)
3.14. 2х2+2у2-5х+5у+3 = 0, М(1,1)
3.15. 0,5№+0,5/+2,5л-3,5у + 1,3 = 0, Л7(0,0)
3.16. 1,2№ + 1,2/-3,6х+4,8у-7 = 0, Л/(1,1)
Построить эллипс, определить, как расположены относительно него указанные точки
3.17. —+—= 1, Л/(0,—3) 3.18 9№+25/=1, Л/(3,0)
16 9
3.19. №+25/=25, Л/(2,1) 3.20. 25х2+/=25, Л/(0,2)
3.21. 8х2 + 5/ =77, Л/(-2,3) 3.22 8/ + 5/ =77, Л/(2,-3)
3.23. 8№ + 5/=77, Л7(-2,4) 3.24. 8х2+5/=77, Л/(-2,2)
х2 , 3.26. -—/=1, Л/(0,1)
3.28. 25л2-/ = -25, ЛГ(-1,0)
3.30. 9л2-4/=-1, Л/(0,|)
3.32. 7х2-5/=-35, ЛУСл/5,0)
Построить гиперболу, определить, принадлежат ли ей указанные точки
х2 у2
3.25. у-^- = 1, Л/(3,0)
3.27. №-25/=25, Л/(1,1)
3.29. 4№ -9/ = 1, Л/(0,|)
3.31. 5/-7/=70, Л/(6,0)
Построить параболу, определить, принадлежат ли ей указанные точки
3.33. / = 4х-8, Af(l,-2)
3.35. /=4-4х, Л/(2,4)
3.37. №=2>-4, Л/(-2,4)
3.39. х2=4-4у, Л/(-4,3)
3.34. / = 6-3х, Л/(2,0)
3.36. /=6 + 2х, Л/(5,-4)
3.38. №=3> + 6, Л/(-3,1)
3.40. №=6-3у, ЛГ(3,1)
19
Установить, какие кривые (или части кривых) определяются данным Уравнениями, и построить их
3.41. x2+/-10x + 8j> = 0 3.42. x2 +y2-8x-4y-5 = 0
3.43. j' = -3—J21-4x-x2 3.44. x = -5 + ^40-6y-y2
3.45. 5x2+9/-30x + 18^+9 = 0 3.46. 4х2 + 3/-8х + 12^-32=0
3.47. j, = l-|V-6x-x2 3.48. x = -5+|V8 + 2y-y2
3.49. I6x2-9/ -64x-54y-161 =0 3.50. 9x2-16/ +90x + 32^-367=0
3.51. y = 7-^Vx2-6x + 13 3.52. х = 5-|7/+4У-12
3.53. J' = 4x2-8x+7 3.54. x = 2/-12^ + 14
3.55. y = 3-4Vx-l 3.56. x = ~4 + 3^]y+5
3.57.—+— = o 2 8 x2 v2 3.58. -—2_ = o 2 8
3.59. x2=4 3.60. /=9
3.61. x2=0 3.62. y2=0
3.63. x2 +2y2 =-4 3.64. x2-2y2=-4
Найти точки пересечения данной кривой н прямой, построить график 3.65. х2+/-2х+4^+1 = 0,^ = х-1 З.бб. х2 +у2 + 2х-4^+1 = 0, у = -х -1
, „ X2 у2 г2 2
Зб7‘ ='’ 3*-^-2° = 0 3.68. -+21=1, х + 6у-20 = 0
2 2
з б9- —= 1, 5х-6^-1б = о 3.70. -—2L = 1 13х-10^-48=0
16 4 16 4 Л
3.71. х2 = 4у, х+^-3=0 3.72./=-9х, Зх + 4^-12 = 0
Найти точки пересечения данных кривых, построить график
3.81. х2+9/-45 = 0, х2+9/—6х-27 = 0
3.82.—+^- = 1 20 5
^-Z = i 12 3
20
X2 у2 > 3.83.—+^— = !, /=24х 100 225
х2 +у2-4х-2у-20=0
х2 у2
3.85.——— = -1, у2 = 3х
20 5 Л
3.84. 7х-> + 12 = 0,
3.86. у=х2-2х+1, х = у2-6х+7
4. Определители. Правило Крамера
Вычислить определители второго порядка
2 -1 2
4.1. 4.2.
3 4 1 3
0 1 1 0
4.3. 4.4.
2 - -2 3
х 3 -I а
4.5. 4.6.
У 2 2 ь
Вычислить определители третьего порядка
3 -2 1 I 2 0
4.7. -2 1 3 4.8. 0 1 3
2 0 -2 5 0 -1
2 0 5 2 1 3
4.9. 1 3 16 4.10. -2 3 2
0 - 10 0 2 5
2 X 0 0 а а
4.11. 1 0 3 4.12. а 0 а
0 -5 а а 0
Вычислить определители третьего порядка разложением по строке или
столбцу
1 0 0 2 -1 3
4.13. 2 2 -3 4.14. -3 0 1
-I 3 1 -4 0 2
21
2 3 0 2 0 5
4,15. -1 2 1 4.16. 1 3 16
3 2 3 0 -1 7
1 17 -7 1 2 4
4.17. -1 13 1 4.18. -2 1 3
1 7 1 3 -4 2
1 1 1 0 а Z>
4.19. X У Z 4.20. -а 0 с
X2 у2 г2 -Ь -с 0
Вычислить определители четвертого порядка
-3 0 0 3 2 -1 3 <1
2 2 0 3 0-15- 3
4.21. 4.22.
1 3 -1 0 0 0 5 - 3
-15 3 5 0 0 0 2
2 -1 1 « 2 3-34
0 12- 1 2 1-12
4.23. 4.24.
3-123 6 2 10
3 16 1 2 3 0 - 5
а Ь с d а Ь с d
b a d с d а Ь с
4.25. 4.26.
с d а Ь с d а b
d с Ь а Ь с d а
Доказать, что определитель равен нулю, не вычисляя его
1 17 -7 1 0 4
4 27. -1 13 I 4.28. -2 0 -3
0 0 0 3 0 2
2 6 3 2-13
4.29. -3 2 1 4.30. -3 0 1
-4 4 2 2-13
22
-2 4 2 2 3 2
4.31. -1 2 1 4.32. -1 2 -1
3 2 3 3 2 3
2 -I 1 0 0 -I 1 0
0 1 2 -1 3 1 2 -1
4.33. 4.34.
3 -1 2 3 -9 -1 2 3
-2 1 -I 0 -3 1 6 1
Решить систему двух линейных уравнений по правилу Крамера
4.35. 3х-5у? = 13 2х+7у = 81 4.36. 3y/-4x = l 3x + 4y = 18
4.37. 2х-3у = 6 4х-6у = 5 4.38. 2>-x=3 2x-4j/ = 4
4.39. 2х-Зу = 0 5х + у = 0 4.40. 3y + x = 0 3x-> = 0
Решить систему трех линейных уравнений по правилу Крамера
x+2y+z=4 2x-4y+9z = 28
4.41. 3x-5y+3z = l 4.42. 7x+3y-6z = -l
2x+7y-z = 8 7x + 9y-9z = 5
x + y-z = 36 x + y + z = 36
4.43. x + z-y = 13 4.44. 2x-3z=-17
y+z-x=7 6x—5z=7
2x-y+z = -2 3x-y+2z = 5
4.45. x+2y+3z = -l 4.46. • 2x—y—z=2
x-3y-2z = 3 4x-2y-2z = -3
5. Векторная алгебра
Заданы длины векторов |а| и р|, и угол между ними. Изобразить вектор с (начала всех векторов в одной точке)
_ я
=2,<р = -
5.2. |о|=1, |б|, Ф = -^-> с =а-Ь
23
5.3. |3|=1, |fe|=2, ф = р с =2a + b 5.5. |3|=1, |£|=2, <Р=~, с=-а-Ь 5.7. |3|=l, |б|=2, <р=у, с=3-24
Найти координаты вектора начала (Л) и конца (В)
5.9. >4(2,1), В(1,-2)
2 3
5.11. Д-1,-1) .
5.13. Л(1,-2,2), В(2,3,-1)
2 3 3
5.15. В(-,1,--), Л(-—,2,0)
3 4 2
5.4. |3|=1, |з|, Ф = -у-, c-2a-b
5.6. |3|=1, |?|2, <Р = ^> c=b-2S
5.8. |3|=1, |^|=2- Ф = “с-2а-Ь
а = АВ, если заданы координаты его
5.10. /(-3,2), В(0,2)
5.12. В(1;-2), Л(1,5;2,6)
5.14. Л(-3,-2,1) , В(2,-3,-2)
5.16. В(-0,6;-0,5; 0,25), А(0,6;0;-1,2)
Изобразить вектора, если заданы их координаты. Записать разложение
данных векторов по базису i,j,k
5.17. а = {1,2}, Ь = {-1,2}
5.19. а = {0,3}, К = {2,0}
5.21. а = {1,1,2}, 4 = {-1,3,2}
5.23. а = {-1,-1,0}, 4 = {-1,0-1}
5.18. а = {1,-2}, Ь = {-1,-2}
5.20. 5 = {0,-2}, 4 = {-3,0}
5.22. о = {1,-1,2}, 4 = {1,-3,1)
5.24. 5 = {0,1,-1}, 4 ={0,-1,-!}
Заданы координаты векторов а н Ь. Найти координаты вектора с и вычислить его длину
5.25. а = {1,2}, Ь = {-1,2}, с =а + Ь
5.27. 2 = {0,3}, Ь={2,0}, с = 3+24
5.29. 3 = {1,1,2}, 4 = {-1,3,2}, с = -3 - 4
5.31. 3 = {-1,-1,0}, 4={-1,0,-1}, с =а—2Ь
5.26. а = {1,-2}, 4 = {-1.-2}, с=а-Ь
5.28. 3 = {0,-2), 4 = {-3,0}, с=23+4
5.30. а = {1,-1,2), 4 = {1,-3,1), с = 4 - 2а
5.32. 3 = {0,1,-1}, 4={0,-1,-1}, с =23 — 4
24
Заданы координаты начала вектора АВ и его координаты. Найти координаты конца вектора
5.33. Л(2,1), АВ~{-1,0] -» 2 1
5.35. Л(0,-1), Л£ = {|,-}
5.37. Л(-2,1,3), Л£ = {-1,0,2}
12 1 2 11
5.39. Л(-,--,-), ЛВ =
3 5 2 3 4 3
5.34. Л(—2,2) , АВ = (0,2)
5.36. Л(1,0), Л£ = {0,75;0,3}
5.38. Л(2,-1,-1), Л£ = {1,-2,0}
5.40. Л(0,2;1;0,25), АВ={0,7;0,3;0,8)
Заданы координаты вершин треугольника. Найти координаты точек пересечения сторон и медиан треугольника
5.41. Л(2,1), £(-3,2) , С(2,0)
5.43. Л(0,0,0), £(1,2,2) , С(-1,1,2)
5.45. Л(2,—3,2), £(1,-2,1) , С(3,5,4)
5.42. Л(-2,1), £(3,2) , С(0,3)
5.44. И(-2,1,1), £(0,0,0) , С(3,-2,1)
5.46. Л(3,0,3), £(1,1,2) , С(-1,2,1)
Заданы три вершины параллелограмма. Найти координаты четвертой вершины и точки пересечения диагоналей
5.47. Л(0,0), £(1,2), С(-3,2)
5.49. Л(1,3), £(2,5), С(-4,1)
5.51. Л(0,0,0), £(-3,2,1), С(2,3,5)
5.48. Л(4,1), £(0,0) , 0(1,0)
5.50. £(-3,2), С(0,2) , 0(5,0)
5.52. £(0,0,0), С(0,-2,3) , О(-2,1,1)
Найти скалярное произведение векторов а и b
5.53. |а| = 1,|*| = 3, <р = |
5,55. |а| = 2,|*| = 2,ф=-|
5.57. |о| = 3, |*| = 1, ф = 0
5.59. |5| = 5, |б| = 2, <р = у
5.54. |о| = 2, |*| = 3, <р=^
5.56. |а| = 1, |*| = 5, <р=у
5.58. |о| = 2, |*| = 3, <р = л
5.60. |л| = 3, |*|=2, <₽ = ~
25
5.62. a = b = 2p + q
5.64. a = 3p-2q , b = p+q
1 - 1 _ - 1 -
5.66.a = -p--q , b = 3p--q
Найти скалярное произведение векторов а и b, если |р| 2, |?| _ п
угол между векторами р н q равен —
5.61. а = p + q , b = p-q
5.63. a = 2p-3q , b = p-2q
. - 1 _ U г - 1 -
5.65. a =-p+—q , b= p+—q 3 2Ч Г 4’
Найти скалярное произведение векторов а и b
5.67. а = {2,1), b = {-1,3}
5.69. а = {-1,2,1}, b = {2,0,2}
5.71. 3 = {2,3,7}, b = {-2,1,1}
5.73. а = {3,-2,|}, * = {-!,2,-|}
5.68. 5 = {0,-3}, b = {3,1}
5.70. 2 = {2,-2,1}, £ = {1,2,2}
5.72. 2 = {1,-3,5}, £ = {2,1,1}
5.74.2 = {-1,2,1},£ = {1,|,-|)
4 3 5
Выяснить, являются ли ортогональными вектора а и £
5.75. 2 = {3,1}, £ = {-1,3}
5.77. 2 = {1,3,2}, £ = {-3,1,0}
5.79. а = {!,-2,1}, £ = {2,1,3}
5.81. 2 = {-2,1,3}, £ = {2,1,1}
5.76. 2 = {0,2}, £ = {-2,0}
5.78. 2 = {2,1,-!}, £ = {1,0,2}
5.80. а = {—2,1,2}, £ = {2,3,2}
5.82. 2 = {3,1,-2), £ = {3,1,5}
Найти угол между векторами
5.83. 3 = {2,2}, £ = {3,0}
5.85. а = {0,-2}, £ = {1,73}
5.87. а = {2,-1,2), £ = {-4,2,-4}
5.89. а = {0,1,1), £ = {1,1,0}
5.91. 3 = {2,-4,4}, £ = {-3,2,6}
и b
5.84. 3 = {-1,1}, £ = {2,0}
5.86. 2 = {-2,-2-Л), £ = {1,-Л}
5.88. а={1,-7з,-Л), £={-Л,з,-з}
5.90. а = {-2,0,2}, £ = {0,2,-2)
5.92. а = {3,1,-1}, £ = {-1,3,2}
Выяснить, является ли прямоугольным треугольник АВС
5.93. И(0,0), .8(3,3), С(-4,4) 5.94. Л(-1,-2), 8(2,1), С(4,-1)
5.95. Л(-3,5,6), 8(1,-5,7), С(8,-3,-1) 5.96. 41-5,7), 8(8,-3,-1), С(4,7,-2)
5.97. Л(2,-3,2), 8(1,-2,1), С(3,5,4) 5.98. /1(3,0,3), 8(1,1,2) , С(-1,2,1)
26
Найти модуль векторного произведения векторов а и b
5.99. |о| = 1,1* ;| = 3'<₽ = i 71 5.100. |а| = 2, | - 0,1 II 6 II w | а
5.101. |а| = 2, |*| = 2, <р = - 5.102. |а| = 1, |. *| = 5, ф = у
5.103. |о| = 3, |л|=I, ф=0 5.104. |3| = 2, | &| = 3, Ф = 7Г
1-1 Зтг I-.1 - 1 /1 5тг
5.105. |5| = 5, |*|=2,ф=- 5.106. |а| = 3, |( *| = 2,ф=у
Найти площадь параллелограмма, построенного на векторах а и b, если |р| = 2, |^| = 3, угол между векторами р и q равен —
6
5.107. a-p-vq , b = p-q
5.109. a = 2p-3q , b — p-2q
5.111. a=-p+— 3 2
5.108. a = b = 2p+q
5.110. a = 3p-2q , b = p+q
5.112. a = jp-~q , b=3p-jq
4
Найти векторное произведение векторов а и Ь . Убедиться, что вектор
с =[а,Ь] ортогонален векторам а
5.113. 3 = {2,1}, * = {-1,3}
5.115. а = {-1,2,1}, * = {2,0,2}
5.117. а = {2,3.7}, * ={-2,1,1}
5.119. 5 = {3,-2,—}, *={--,2,—}
5 3 2
5.114. а = {0,-3}, *={3,1}
5.116. 3 = {2,-2,1}, *={1,2,2}
5.118. а = {1,-3,5}, * = {2,1,1}
5,120. 5 = {-—,2,1}, *={!,—,——}
Определить, коллинеарны ли данные вектора
5.121. 2 = {1,2}, * = {—2,4} 5.122. а = {-1,3}, * = {-2,6}
5.123. а = {2,1}, * = {2,2} 5.124. 5 = {-1,3}, * ={-2,3}
5.125. 5 = {1,-1,2}, * = {2,-2,4} 5.126. 5 = {1,-1,2}, * = {2,-1,1}
5.127. 5 = {-1,1,-2), * = {2,-1,1} 5.128. а = {-1,1 -2}, * = {1,-1,2}
Проверить, является ли четырехугольник ABCD параллелограммом, и вычислить его площадь
5.129. Л(0,0), 5(0,4), С(4,8), £>(4,4)
5.130. Л(—1,-4), Bf-1,1), С(2,-2), £>(2,-7)
27
5.131. /(-2,1), £(-4,6), С(1,7), 0(3,2)
5.132. Д-2,-3), 5(0,2), С(3,5), 0(1,0)
5.133. ДО,0,0), 5(-1,2,1), С(1,2,3), 0(2,0,2)
5.134. /(0,0,0), 5(2,-2,1), С(3,О,3), D(l,2,2)
5.135. Д1,-2,-3), 5(3,1,4), С(1,2,5),D(-l,-1,-2)
5.136. Д2.2.-1), 5(3,-1,4), С(5,0,5), D(4,3,0)
Вычислить площадь треугольника АВС
5.137. /(0,0), 5(3,3) , С(-4,4)
5.138. Д-1,-2), 5(2,1) , С(4,-1)
5.139. Д-3,5,6), 5(1,-5,7) , С(8,-3,-1)
5.140. Д1,-5,7), 5(8,-3,-1) , С(4,7,-2)
5.141. Д2,-3,2), 5(1,-2,1) , С(3,5,4)
5.142. /(3,0,3), 5(1,1,2) , С(1,2,1)
5.143. Д1,2,0), 5(3,0,-3) , С(5,2,6)
5.144. Д1.-1.2), 5(5,-6,2) , С(1,3,-1)
Вычислить смешанное произведение векторов d,b,c
5.145. 3 = {2,0,0}, 5={3,2,-1}, с = {1,-1,3}
5.146. 3 = {0,-3,0}, 6 = {2,4,-1}, с = {—1,—2,3}
5.147. 3 = {2,3,1}, б = {1,2,-1}, с = {2,-1,2}
5.148. 3 = {2,-1,-}, б={|,2,-1}, с = {2,-1,5}
5.149. 3 = {-1,2,1}, Ь = {2,0,2}, с = {1,2,3}
5.150. 3 = {—1,1—2}, б = {1,-1,2}, с = {2,-2,4}
Вычислить объем параллелепипеда, построенного на векторах а,Ь,с
5.151. 3 = {1,1,1}, 5 = {4,3,0}, с={1,0,3)
5.152. 3 = {2,-1—2}, b = {3,2,1}, с = {1,-2,9}
5.153. 3 = {1,-5,0}, б ={3,2,1}, с = {1,-1,3}
5.154. 3 = {1,1,0}, 5 = {-7,2,-1}, с ={1,4,3}
Вычислить объем тетраэдра с вершинами в заданных точках
5.155. Д1.-1.2), 5(2,1,2), C(l,l,4), D(6,-3,8)
5.156. Д2,—4,-3), 5(5,-6,0), С(—1,3,-3), О(-Ю,-8,7)
28
5.157. Л(-3,-5,6), £(2,1,-4), С(0,-3,-1), £>(-5,2,-8)
5.158. Л(—2,—1,—1), £(0,3,2), С(3,1,-4), £>(-4,7,3)
Определить, лежат ли данные точки в одной плоскости
5.159. Л(1,—2,-3), £(3,1,4), С(1,2,5),£>(-1,-1,-2)
5.160. Л(2,2,—1), £(3,-1,4), С(5,0,5), £>(4,3,0)
5.161. Л(1,2,2), £(2,2,2), С(1,1,1), £>(1,1,2)
5.162. Л(2,3,1), £(1,-1,7), С(5,5,5), £>(1,-6,0)
5.163. Л(2,—3,2), £(1,-2,1), С(3,5,4)
5.164. Л(3,О,3), £(1,1,2), С(-1,2,1)
Определить, является тройка векторов а,Ь,с правой или левой
5.165. а = {1,1,1), *={4,-1,0}, с = {1,0,0)
5.166. а = {1,0,0}, Ь ={0,3,0}, с = {1,0,3}
5.167. а = {2,-2,!},£ = {!,2,-1}, с = {2,1,2}
5.168. о = {1,3,1}> * = {0,2,0}, с={2,-1,2)
6. Плоскость в пространстве
Определить, какие уравнения задают плоскость в пространстве соответствующих переменных 6.1. Зх+4у+5z2-1 =0 6.3. 2Z + xu + x + 99 = 0 6.5. х2=4
6.2. х-2> = 0
6.4. 2x-2y-2z + w = 0
6.6. у2=0
6.8. z = 2x-3y
6.10. w = 2x
6.9. u=/+3u-v
6.12. Л/0(0,0,0), # = {-1,3,-2}
6.14. Л/о(3,—2,—1), # = {-1,2»-3}
6.16. Л/о(2,О,—1), N = {0,1,0}
Записать уравнение плоскости, проходящей через данную точку перпендикулярно нормальному вектору N
6.11. Л/о(1,2,0), # = {-3,2,1}
6.13. Л/о(-2,1,1), # = {3,-1.-!}
6.15. Мо(3,-2,2), # = {1,0,0}
Найти нормальный вектор и какую-либо точку данной плоскости
6.17. 2x+3y-z + l = 0
6.19. х-2у = 0
6.21. х = 2
6.18. x-2y+z-3=0
6.20. z+3x=0
6.22. у = -3
29
Записать уравнение плоскости, проходящей через точку Mq(1,2,3) параллельно данной плоскости
6.23. 2х + 3у —z + l = 0
6.25. Зх+5у = 0
6.27. у =-2
6.24. -2x + y+5z-3 = 0
6.26. 2x-3z = 0
6.28. z = -3
Плоскость отсекает на координатных осях отрезки а,Ь,с. Записал уравнение этой плоскости и преобразовать его к общему виду 6.29. а = 1, 6 = 2, с = 3 6.30. о = -1, 6 = 3, с = -2
6.31. а=—3, 6=2, с = оо 6.32. а = -1, 6 = °о, с-3
6.33. с = 2, 6 = оо, а = оо 6.34. 6=-1, а = оо, с = 0
Определить, какие отрезки отсекает на координатных осях данная плоскость
6.35. 2x + 3y-z+6 = 0 6.36. x-3y + 4z-12 = 0
6.37. z = 2 - Зу + х 6.38. z = 2х - Зу + 2
6.39. 2х+3у—1=0 6.40. 2y-3z + l = 0
6.41. х-3 = 0 6.42. z+2 = О
Найти объем тетраэдра V = — S.h, образованного координатными 3 *
плоскостями и заданной плоскостью
6.43. 2х + 3у —z+6 = 0
6.45. -x+2y + z + 3 = 0
6.47. М0(-2,1,1), Р = {3,1-1}
6.44. х—3y + 4z —12=0
6.46. 2х —y+3z + l = 0
6.48. M0(3,-2,-l), N = {-1,2,3}
Изобразить плоскость, заданную уравнением
6.49.
1 -2 3
6.51. х = 3, у = —1, у=2
6.53. х-у = 0, у = 2х
6.55. z = 2x, z = -2y
6.57. х-у+2 = 0
6.50.-+^+— = !
1 2 -4
6.52. х = -2, z = 2, z = —2
6.54. x + y = 0, у = -2х
6.56. z = -х, z = у
6.58. z + x-1 = 0
Найти уравнение плоскости, проходящей через 3 заданные точки, определить, какие отрезки она отсекает на координатных осях
6.59. м,(2,з,2), л/2(1,о,о), л/3(о,-2,о)
6.60. 1^,(0,0,-3), Л/2(3,1,-1), Л/3(0,2,0)
30
6.61. Л/|(0,0,2), Л/2(-1,1,1), Л/3(2,1,1)
6.62. Л/|(3,1,2), ЛГ2(1,0,0), Л/3(2,!2)
6.63. М,(1,-1,2), М2(0,1,-3), Л/3(—1,2,0)
6.64. Af,(0,l,-2), Л/2(—1,3,2), М3(-1,-1,0)
Найти уравнение плоскости, проходящей через данную точку параллельно двум неколлинеарным векторам
6.65. Л/о(О,О,О), а = {1,2,-1}, Ь = {1,0,1}
6.66. Л4о(О,0,0), а = {0,1,2}, £ = {3,—1,1}
6.67. Л/о(1,2,-1), 3 = {2,1,3}, £ = {0,0,2}
6.68. Л/о(О,-2,3), 3 = {-1,3,1), £ = {1,0,0}
6.69. Л40(2,1,3), 3 = {3,0,0}, £ = {0,2,0}
6.70. Л/0(!,-1,2), 3 = {0,-1,0}, £ = {1,0,0}
7. Прямая в пространстве
Найти канонические уравнения прямой, проходящей через заданную точку параллельно направляющему вектору Р. Преобразовать эти уравнения к общему виду
7.1. Л/о(2,1,3), 7* = {—4,5,6}
7.3. Л/о(О,1,2), £ = {1,-2,0}
7.5. Л/о(0,1,0), £ = {0,3,0}
7.2. Л70(-1,2,-1), Р = {2,-3,5}
7.4. Л/о(2,О,1), £ = {0,-2,3}
7.6. Л/О(-5,1,3), £ = {0,0,2}
7.10. Л/,(0,0,-3), М2(3,1,-1)
7.12. Л/|(3,1,2), Л/2(1,0,0)
7.14. Л/,(0,1,—2), Л/2(-1,3,2)
Найти канонические уравнения прямой, проходящей через две заданные точки
7.9. Л/|(2,3,2), Л/2(1,0,0)
7.11. Л/|(0,0,2), Л/2(-1,1,1)
7.13. Л/,(1,-1,2), М2(0,1,-3)
Найти какую-либо точку, лежащую на данной прямой
7.15. ] [х-3 = 0 [у+5 = 0 7.16. о о Л п + 7 N
7.17. J [ х-5 = 0 [y+2z-l=0 7.18. [х-2у + 1 = 0 [ z-2=0
31
7.19 (x~2>+1=0 (y-2z-2 = 0 7.20. < О II О m II 1 N rs + 1 к X 04
7.21 ( 2*“3y+z-l = 0 [3x+2>>-2z+5 = 0 7.22. • |x-2y + 2z + l =0 [2x+y-z-3=0
Найти какой-либо вектор, перпендикулярный двум заданным
723. о = {0,0,1}, £ = {1,2,3} 7.24. 3 = {1,0,0}, £ = {-3,2,-!}
725. я = {1,0,-1}, £ = {1,-3,2} 7.26. a = {3,-4,!}, £ = {0,-3,0}
727. я = {3,-2,7}, £ = {7,12,-5} 7.28. а = {-3,5,11}, £ = {—3,7,5}
7.29. я = (1 3,-1), £ = [1,-1,5| (2 J’ (’ 3 J 7.30. c = |l,-1.1}, £ = {-1,3,-3}
Привести к канонической форме общие уравнения прямой
73I f2x-3>-2z+6 = 0 ( x-3j>+z+3=0 7.32. J [6x—5y+3z + 8 = 0 [6x + 5y-4z + 4 = 0
7 33 f 3x+3y+z-l = 0 [2x-3y-2z+6 = 0 7.34. ] , 3x + 4y+3z + l=0 2x-4y-2z+4 = 0
735 (2x+3y-2z+6 = 0 [ x-3y+z+3=0 7.36. ] ' x-3y+z+2=0 x+3y+2z + 14 = 0
Записать в параметрической форме данные канонические уравнении
7 37 — ? = >+3 z-1 7.38. x + 1 У-2 _z+4
1 2 -3 3 1
739 - y-3 z+2 7.40. x —1 У + 2 _ z
-1 0 3 1 -2 ~0
7.41. * = >. 0 0 z-3 7 7.42. X _ ^3~ >zl= 0 z+2 0
Привести к параметрической форме общие уравнения прямой f 3x+2y + z-I =0 f-2x + 3y + 2z-l =0
{ . 7 ДА. <
[2x-3y-4z+6 = 0 [ x-3y+z+6=0
f 3x+z-l=0 ( 2y+z-2=0
[-3y-2z+l=0 |2x+y-2z + 6 = 0
32
Привести к общему виду данные уравнения прямой
7 47. £ZZ=Z±3=£Z1 7.48,- х + 1 _ y-2 _ z+4 ——
1 2 -3 -3 3 -1
7.49. с+2_у+з z+2 750 r+l_y-l z
-10 3 1 -2 "0
х=2» x = r
7.51. у = -( 7.52. y = -2t
z = f+l z = 3t
х = 0 x = -t
7.53. y = 2t 7.54. y = 0
z = 2t—\ z = t+2
х = 0 x = 3t
7.55. y = -t+2 7.56. y = 0
z = 0 z = 0
8. Прямая и плоскость в пространстве
Найти уравнение плоскости, проходящей через данную точку
перпендикулярно прямой
8 1 Л/аЛ 2 31 х+^ — У - z~[ z » Л х + 2 у z — 1 8 7 1 Г) 7^ = —=
6.1. j -у- — o.z. 2 —3
8.3. A/o(O,-2,l),^=J~ 8.4. л/о(1,2,0),у=^-=^р-
x = 0 x = -t
8.5. Afo(0,2,I), y = 2t 8.6.Мо(О,2,1), y = 0
z = 2t-\ z = Z+2
* = 0 x = 3t
8.7. Л/о(—2,2,1), y = -t+2 8.8. A/o(—2,0,1), y = 0
z = 0 z = 0
[x-2y + l = 0 [x-2y+2z+l =0
8.9. Л/о(-2,-3,1), / [y-2z-2 = 0 8.10. M0(-2,3,l) J Л [ 2x + y-z-3 = 0
33
Найти уравнение прямой, перпендикулярно плоскости
8-11. Л/о(1,2,3), 2x+3y-z+l=0
813. M0(-2,2,l), Зх+5у = 0
8-15. Wo(O,2,l),'+X+£ = 1
„ 1 -2 3
8.17. Л<Г0(-1,2,—1), х = о
проходящей через данную точг
8.12. Л/о(-2,О,1), -2x+y + 5z-3 = 0
8.14. Л/0(-2,-3,1), 2x-3z = 0
8.16. л/0(з,2,1), Y+|+q-=|
8.18. Л/о(5,3,-4), z = 3
Определить, пересекаются пересечения
ли прямая и плоскость и найти точк)
х = 0
У = 2г, х+2у+1 = 0 z = 2/-l
8.20.
x = -t
y = 0 , 2x+5z-l = 0 z = t+2
8-21.' y = 2r, -3x+z+4 = 0
8.22.
z = 3r-l
x = 0
y = t, -3x + 2y-z-2 = 0
z = 2r-2
8.23. ^1-У+3
1 2 3 ’
2x+3y-z+l=0
8.25. Z~3._z+2
-1 0 3 ’
x+2y-3z+l=0
8.24. = =
-3 3 1 ’
-2x+y + 5z-3 = 0
8.26.^=>^=*
1 —2 0’
x-y-z+4=0
Найти точку Mt, симметричную точке Mo относительно заданной плоскости
8.27. Мо(-2,О,3), 2х - 2у+10z +1 = 0
8.28. Л/о(3,3,3), 8х+6у+8z-25 = 0
8.29. Л/о(-1,0,1), 2х+4у-3 = 0 8.30. Л/0(2,-2,-3), y+z+2 = 0
8.31. Wo(-2,-3,O), х+5у+4 = 0 8.32. Л/о(3,-3,-1), 2x-4y-4z-13=0
Найти точку Л/|, симметричную точке Мо относительно заданной прямой
8.33. Л/о(О,—3,—2), 8.34. Л/о(-1,О1),
х-0,5 у+1,5 z-1,5 х-0,5 у-1 z-4
0-11 0 0 “ 2
34
8.35. Л/о(2,-2,-3), х-1 >+0,5 z + 1,5
-I - -о О
8.37. Л/о(3,3,3), х-1 >- — 1,5 z-3
-I О 1
8.36. Л/о(—1,2,0), х+О,5 > + 0,7 z-2 1 -0,2 " 2
8.38. Л/о(3,-3,-1), х-6 >-3,5 z + 0,5
5 4 “ О
9. Поверхности второго порядка
Определить координаты центра и радиус сферы, заданной уравнением 9.1. (х-1)2+(>—2)2+(z —5)2 = 1 9.2. (х-1)2+(>-2)2+(z-5)2 = 1 9.3. x2+>2+z2-6z = 0 9.4. х2+ >z+ z2-4х—2>+2z —19 = 0
9.5. х2 +>2 +z2-3x+2>-z = 0 9.6. х2 +>2 +z2 +x-5>-7z = 0
Определить, как расположена точка -4(2,-1,3) относительно заданной сферы
9.7. (х-2)2+ (>+1)2+(z—3)z = I
9.8. (х—З)2+(>+1)2+(z—I)2 =4
9.9. (х +14)2+(>-1)2+(z + 12)2 = 625
9.10. (х-6)2+(>-1)2+(z-2)2 =25
9.11. x2+>2+z2-4x + 6>-8z+22 = 0
9.12. x2+>2+z2-x + 3>-2z—3 = 0
Определить, какая кривая является линией пересечения плоскости и дайной поверхности второго порядка
9.13. x2+>2+z2-9 = 0, z = 0 9.14. х2+>2+z2-8 = 0, > = -2
9.15. х2 +>2 +z2-2х+4>+4 = 0, z = 0
9.16 х2+>2+z2 —6х + 2>-10z+22 = 0, z = 3
2 2 2 _2 ,2 ,2
О 17 X +2_ + ——= 1 х = 2 9.18. X -—+—= 1 у = 2
У. 1 / . Тб 12 4 Тб4 12 4
2 2 ^2 ,.2 ,2
О 1О *2 _У_ + —=1 г + 1 = 0 9.20. —+—=1 у —3 = 0
У.1У. 32 18 2 ’ 32" 18 2
2 2 ^2 2
0 71 X _У_ 4-6 — 0 9 22. X — = 6z 2 — 1=0
У .21. т 4 = 6z, у го - и Т" 4
35
9-23. = 2z, 3x-y+6z-14 = 0
3 6
x2 v2 z2
9.24. —+4--—= l,9x-6y + 2z-28 = 0
4 9 36
Найти точки пересечения поверхности и прямой
хг 9.25. —+ У2 г2 -г = 1 9 26 — -^=1
81 36 9 ’ ’ 16 9 4
х-3 _ у—4 z+2 х _ _У~ = z + 2
3 -6 4~ 4 ” -3 4
х2 9.27. —+ Z = z х2 О Эй л
5 3 y.zo. 9 4 ' = Z
х+1 _У-2 z+3 X У-2 _ z + *
2 -1 ” -2 3 ~ -2 ~~2~
Определить, является ли данная поверхность цилиндром или конус и построить ее
9.29. х2 +у2-2х = 0
9.31. x2+y2-z2=0
9.33. x2 + z2-2z = 0
9.35. x2-y2+z2=0
9.30. у2 + х2 + 4 у = 0
9.32. y2 + z2-x2=0
9.34. xz+ у2-z2+2z-l = 0
9.36. х2+у2+2у-0
Ш ЛИНЕЙНАЯ АЛГЕБРА
1. Матрицы, действия с ними. Обратная матрица
Найти матрицу X, выполнив указанные действия с матрицами
1.1. А=\ 2 5 4 = ° I а)Х=2А-В+Е, б) Х=А-ЗВ-5Е,
1^3 0 ) 2 -1J (О 1)
в)Л--6Я-ЗВ+1ОЕ. г)Х=А-2Е, п)Х=ЗВ+5Е,е)Х=В-2А+2Е,ж)Х=5Е>-А-В
<0-11 <1 2 1 11 01
1.2. А =1 I, В=| 1 ’ £Чо ] I а)А'=4^+6В+£.б)А'=2Л-ЗВ+Е,
в) Х= -А+6В-4Е, г) Х=3/-2£, д) Х=2В+5Е, е) Х=2В-2А+Е, ж) Х=Е-А+В
12 01 <0 -51 /1 01
1.3. Я = , 8 = , £= 1ЛХ-А-В+Е, б)Х=А+В-Е,
<0 о) <5 2) к0 1)
в) Х= —2Я—28+10£, г) Х=ЗА-2Е, д) Х=В+5Е, е) Х=4В+А-4Е, ж) Х-Е-5А-В
'2 -1 5' '8 -2 2' '1 0 О'
1.4. А = -3 4 1 , 8 = 5 1 4 , Е = 0 1 0 а)Х=2А-В+Е,
7 —4 -1 <3 -3 °, 0 0 1,
б)Х=А+В+ЗЕ
'О 2
1.5. А = 3 1 к0 -2
01 5
-3,8= О
О J (-2
0 4' Ч 0 О'
3 0 . Е = 0 1 0 а)Х=-ЗА+В+2Е,
0 7 ч0 0 1,
6)Х=4А-В-5Е
Найти указанные произведения матриц А и В:
а) АВ, б) ВА, в) А2, г) В2, д ) А2В.
1.7.
1.9.
37
'1 2 З1 '0 1 3' '-2 4 '3 -4
1.10. Л = 4 5 6 , в= 2 4 0 1.11. А= 3 -1 в = 2 -2
J 8 9 5 0 6 <7 -3 Л 1 -5
1 6 3' '0 0 1 '0 3 Г (0 0 5’
1.12. Л = 5-2 0 . в= 0 2-3 1.13. Л = 0 0 4 в= 0-2 0
4 0 0? 3 -2 4 0 0 0, 3 0 0,
Найти указанные произведения матриц
Выполнить умножение, применяя транспонирование
Найти присоединённую матрицу к матрице
38
-2 I 6'
1.33. 4-3 5
1.34.
I-4 ~5 1J
'3 -1 -2'
5 5 1
5 5 -6,
Найти обратную матрицу, сделать проверку
<2 1 А '0 4^ (2 А Г1 8 'l
1.35. 1.36. 1.37. 1.38. 1
[-7 -З) ,6 2] <5 2) 3 20)
'0 1 3' '1 1 Г
-3 6 >
1.39. I 1.40. 2 4 0 1.41. 1 0 1
5 -9j
! 0 -5 J 1 °.
'0 0 -Г '0 0 3' <5 0 А
1.42. 0 4 2 1.43. 2 1 -1 1.44. 2-5 0
J -2 6> 3 ° 0; к5 -2
'2 1-1' '12 3 '3 5 6
1.45. -4 4 4 1.46. 4 5 6 1.47. 4 5 6
2 * Ч -1 1 -1 -4 1 - -1
Решить матричные уравнения
'2 -1
1.51. 1 5
,° 0
4> <-1 2
4 Х = -2 9
2J t-6 7
'3
1.52. X- О
О
О
2
I
-9 Г
О 3
1 °,
2. Раит матрицы. Элементарные преобразования матриц
Найти ранг матрицы, вычислив её миноры
2.1.
2 -4 б']
1 -2 з)
3 1 -6
2 5-4
Г о
39
2 3 Г-1 2 0 7'1 (о 4 2 oj
2.4.
6 10 -2 14А
9 15 -3 21J
Найти ранг матрицы элементарными преобразованиями
Г1 2 О' Г 3 0 2 '
2.5. 2 3 0 2.6. -1 0 -1
4 -1 -3; 4 5 -7
'-3 7 2' ' 8 -16 12'
2.7. -2 12 2 2.8. 6 -12 9
J 5 °, -2 4 -3J
3 1 -2 ( 5 1 -2 -4'
2.9. -1 3 4 4 10 2.10. 2 117
2 7 5 18 -15 -3 5 11
1 1 4 4J [-5 -1 16 3,
'-4 -12 8 io'i [° -1 2 0 '
1 -1 -2 0
3 7 0 0
2.11. 2.12. 0 0 0 2
2 6 -4 8
-з -7 „ 10 0 0 1 1
' ^0 2 । “I
г0 1 3 Н 4 2 0 О'
2.13. 1 0 2 1 -8 2 2.14. -1 -3 1
3 2 0 2 0 7 2 3 3-1
<2 3 1 С 3J [во 0 0 -1,
3. Системы линейных уравнений. Метод Гаусса
Методом Гаусса решить систему однородных линейных уравнений, найти фундаментальную систему решений, общее решение и какое-либо частное решение системы
31 [2xj+3x2 + 5x3=0 + Зх2 + 4х3 = 0
3 2 I *' ~ Х2 + 6Ху = ° [2х, +3х2 -х3 =0
40
33 Г2х1+Х2+Х3 = °
[7xj -Зх2 +4х3 = О
35 Г4х1+х2+5хз+х4=0
(-Х| + 6х2 +4х3 = О
2х, + Зх2 + 5*з + бх4 = О
3.7. 3*| +4*2 + 6х3 + 7х4 =0
3*| +*2 +*з +4*4 =0
*1 +3*2 + 7*з +х4=0
3.9. 5*2 + 10хз+5*4=0
-2х| +7х2 +12Х3 + ПХ4 =0
2Х| +х2 +Зх3 +4х4 +5х5 =0
3.11. 6х| +3х2 -х3 +2х4 -5х5 =0
-4х, -2х2 -2х4 +2х5 =0
Х| +х2 +Х3 =0 х1-х2-х3=0
*1 +х2 +х3 — О
Х| - х2 + 5х3 + х4 = О
8xj - 5х2 - 6х3 +3х4 = О
3.8. 4Х| — х2 -Зх3 +2х4 = О 12Х| -7х2-9*з +5х4 =0
3.10.
3.12.
- Х| +3х2 +5х4 =0
2х| +х2 +7хз-3х4 =0
4Х| —х2 +11х3 — 9х4 =0
Х| - 2х2 - *з _ Зх4 + Зх5 = О 2Х| +3х2 +5х3 +х4 —х5 =0
х2 +х3 +х4 -х5 =0
Установить совместность системы, методом Гаусса решить систему неоднородных линейных уравнений, найти фундаментальную систему решений, общее решение и какое-либо частное решение системы
злз. •Г1+*2+*3 4
[Х| — х2 - х3 = 0
Зх| - х2 + х3 = 4
Х| - 7х2 - х3 = 0
{2х, +х, -х, =2 1 2 3
- Х| +3х2 +4х3 = 6
{х.-х, +5х,=0 .
1 2 з
Х| +2х2 +х3 =—3
3.17.
Х| +4х2 +Зх3 -2x4 = -б -2х| +7х2 +9х3 -1 1х4 =-18 -ЗХ| +5х2 + 8х3 -11х4 = -16
3.18.
Х| +3х2 + 5х3 = —1 6х2 + 12х3 - 6х4 = -6 -2*| - 6х2 -10х3 = 2
3.19.
5х| +х2 -2х3 -4х4 =5
10х| + 2х2 +11х3 + 7х4 = -20
3.20.
-15xj -Зх2 + 5х3 + 11х4 =-13
ЗХ| +х2 — 2х3 =9
6Х| +2х2 +4х3 +8х4 =-16
-15xj -5х2 +Зх3-7х4 = -17
41
3.21.
^+^+xJ-x4 = l 2х1+х2 + 2х3-х4 = -1 2xj + 2х2 +Зх3 - 2х4 = О
ЗХ| + 2х2 — 4х3 + 2х4 = 2 х, - 2х2 + Зх3 - Зх5 =-3 2Х|+2х3 — Зх4+5х3 =4 5х, - Зх2 + 4х3 + 2х4 - 7х5 = 2
3.23.
х, +2х2 +Зх3 -2х4 +х5 =4 Зх| + 6х2 + 5х3 - 4х4 +3х5 = 5
X! +2х2 +7х3-4х4 +х5 =11 2х, + 4д^ + 2х3 - Зх4 + Зх5 = 6
3.24.
х,-Зх2+х3+ 2х4 =4 2Х| — 5х2+4х3+3х5 =7
X] - 2х2 + Зх3 - 2х4 + Зх5 = 3
4. Линейное пространство. Размерность н базис. Преобразование координат вектора
Исследовать линейную зависимость и независимость элемент (векторов) линейного пространства
4.1. fll=(2,7,-4), а2=(1.1,-4), о, = (2,-2,-2)
4.2. о, =(1,2,3), с2=(2,—1,0), о3 =(3,1,3)
4.3. а, =(2,5,4), а2=(0,-1,1), с, =(1,5,7)
4.4. а, =(5,2,4), о2 = (0,1,4), о3 =(5,1,0)
4.5. О| =(1,2,3), а2 =(4,5,6), а3 =(7,8,9)
4.6. о, =(1,-2,-3), а2 =(-4,5,6), а3 =(7,-8,9)
4.7. О]=(2,—1,1), а; =(0,-1,2), а3 =(2,5,7), а4 =(1,-1,1)
4.8. Oj=(2,-7,3), а2=(3,-1,1), а, =(1,-13,5), о4 =(1,6,-2)
4.9. а, =(1,-1,1,1), а2 = (1,-1,1,-1), а3 =(-1,1,0,1), о4 =(1,0,-1,1)
4.10. о, =(1,1,1,1), 02 =(1,-1,-1,-1), а3 =(0,1,0,1), о4=(1,0,-1,0)
4.11. /i=l, /2=2х + х2, /3=х-1, /4=(х + 2)2
4.12. /j=x, f2 = -4x+xi, f3=x2-i, ft=2
4.13. f} =cosx, /2=cos2x, ^=cos3x, /4=cos4x
4.14. f\ =cos2x, /2=1-cos2x, ^ = cosx, /4=cos2x
4.15. /j=sinx, /2=sin2x, /3=cosx, /4=cos2x
4.16. /!=^, /2=e-’, /3=^-, /4=г
4.17. /i=<^, f2=e\ =
4.18. /1=г, f2=e-\ f3=?\ /4=e-2"
42
4.19. /,=< /2=е2х, /3=е3х, Д=е4х
4.20. fy = е* + х, /2=е2+х, fi=x, /4=sinx
4.21. f = sinx + l, f2=x-3, /3=sinx, /4=l + x + sinx
Найти координаты вектора а в данном базисе
4.22. « = (6,-3), g, =(1,3), g2 =(-1,4)
4.23. « = (-2,2), g,=(l,-4), g2=(—3,5)
4.24. a = (1,0), g,=(-2.-4), gj=(l,l)
4.25. «=(0,1), gl=H,3), g2=(-5,2)
4.26. « = (7,—4,-4), gj=(2,—1,0), g2 =(3,0,2), g3=(l,-2,l)
4.27. « = (-2,—6,6), g| =(-1,1-3), g2 =(2,0,1), g3=(0,-4,2)
Найти матрицу перехода от базиса е, =(1,0), е2 =(0,1) кбазису g,,g2 и вычислить координаты вектора а в базисе g|,g2
4.28. а = 5е{-2е2, g,=(2,-l), g2 =(7,-3)
4.29. а = -2е^е2, g, =(7.-8), g2=(7,-6)
4.30. а = в|+4е2, g|=(0,3), g2=(l,~3)
4.31. « = 7е,+12е2> g, =(2,4), g2 =(-8,-12)
Найти связь координат одного и того же вектора в базисах g1,g2,g3 и
fufbh
4.32. g, =(1,2,1), g2 =(2,3,3), g3 =(3,7,1), f =(3,1,4), /2 =(5,2,1), /з=(1.1.-6)
4.33. g, =(1,0,1), g2 =(1,2,3), g3 =(3,-1,1), f =(-2,1,1), /2=(0,-l,l), /3=(l,0,-2)
Установить, является ли линейным пространством каждое из указанных множеств и найти его подпространства для естественных операций сложения и умножения иа число
4.34 Множество натуральных чисел
4.35. Множество целых чисел
4.36. Множество чётных чисел
4.37. Множество рациональных чисел
438. Множество векторов, лежащих на оси ох
439. Множество векторов, лежащих на оси оу
4.40. Множество векторов, лежащих на плоскости хоу
4.41. Множество векторов, лежащих на плоскости xoz
4.42. Множество троек чисел вида (1 а 0)
4.43. Множество троек чисел вида (0 а 0)
4.44. Множество троек чисел вида (а а 0)
4.45. Множество многочленов степени не выше третьей
4.46. Множество квадратных трёхчленов
4.47. Множество квадратных матриц
5. Скалириое произведение. Ортонормнрованный базис
Вычислить скалярное произведение векторов
5.1.(11,6,13), (12,-14,1)
5.3. (1,0,4), (-3,1,1)
5.5. (3,2,0,-1), (3,-4,1,2)
5.7. (5,-1,6,2), (2,3,-1,1)
5.2. (7,-4,10), (-1,2,2)
5.4. (-4,-5,0), (0,4,-2)
5.6. (1,3,-4,-2), (2,-4,1,3)
5.8. (2,-2,7,4), (6,3,1,-5)
Найти норму каждого из векторов
5.9. а) (3,0,-4), 6) (0,-5,12), в) (3,5,-2) , г) (-1,3,7)
5.10. а) (3,-4,1,-1), б) (5,-1,-2,10), в) (-1,0,12,3), г) (0,-5,2,2)
Проверить, что следующие системы векторов попарно ортогональны, и дополнить их до ортогонального базиса. Нормировать полученный базис
5.11. (2,-1,1), (2,3,-1)
- Ш (и-т)
5.13.
5.12. (6,-2,1), (1,2,-2)
5.14.
-i-sfi -1^2] .3’3 ’3? 13 ’ 3 ’ 3 J
5.15 (1,-2,2,-3), (2,-3,2,4), (2,2,1,0)
5.16 (2,3,-5,-3), (0,1,3, 4), (-18,8,0,2)
44
6. Линейный оператор. Матрица линейного оператора
Установить, какие из указанных преобразований координат задают линейный оператор и составить матрицу этого оператора
6.1. ф(х) = (х2-Зх3,х,)
6.3. ф(х) = (3х2-3,х,)
6.5. ф(х) = [х23+9х1э2х,-х2)
6.7. ф(х) = (х1,11х1+2х2)
6.9. <р(х) = (6х| +х2 -х3,-5х|,7х2)
6.10. <р(х) = (х] +2х2 -Зх3,-Х| +2х2,х2 -х3)
6.11. ф(х) = (х,+Зх3,-Х|+х3.х2-х3)
6.12. ф(х) = (х3,4х, +х2-5х3,х, -2х3)
6.13. ф(х) = (2-Зх3,-х, +2х3,х2 +7х3)
6.14. ф(х) = (5Х|+х2-х3,2,х2+х3)
6.15. ф(х) = (х| +^/j^-x3,-X| +х2,х2+х3)
6.16. ф(х) = (х3,-х1+х2,х2-3/х7)
6.17. ф(х) = (х12+х2+4х3,х1+х2,-х3)
6.2. <p(x) = (6x[ +х2,-5х|,-7х2)
6.4. <р(х) = (4х,+2,х2)
6.6. ф(х) = [х/ -4х2»х, + х2)
6.8. <р(х) = (-4х| -х2,3х] + 10х2)
6.18. ф(х) = [х2+х3,х22,х2+7х3)
Найти матрицу линейного оператора, определить его ранг и дефект
6.19. ф(х) = (xi +х2 +х3,Х! +х2,х2 +х3)
6.20. ф(х) = (х| +2х2 +Зх3,Х[ +2х2,2х2 +Зх3)
6.21. ф(х) = (х| +2х2 -х3.х, +х2 +х3,-Х] +х3)
6.22. ф(х) = (-Х| +5х2 -х3,-2х| +2х2 +2х3,х( +х2 -х3)
Найти обратный оператор к оператору, матрицей,
6.23.
2
-3
-7
10
'1
6.24. И= 4
3
заданному указанной
2 3'
5 4
2 1,
Л =
45
6.25. А = ' 4 к-9 -3’ 7>
6.27. А = '-2 '1 -9> 2 4'
6.29. Л = -5 ^0 -3 1 0
6.26. А = (5
<6 ioj
'1 0 -3'
6.28. А = 2 -3 -4
0 2 2,
Г1 -2 -4’
6.30. А = 9 5 -6
1 1 о,
Т. Собственные векторы н собственные числа линейного оператора
Найти собственные векторы и собственные значения операторе заданных своими матрицами в некотором базисе
46
Найти, ие находя матрицы, собственные числа и собственные векторы операторов:
7.17. Оператора проектирования R2 на ось ох
7.18. Оператора проектирования R2 на ось оу
7.18. Оператора отражения Л2 относительно оси ох
7.19. Оператора отражения R2 относительно оси оу
7.20. Оператора проектирования R2 на плоскость хоу
7.21. Оператора проектирования R2 на ось оу
7.22. Оператора поворота Л3 на на угол 90° вокруг оси oz в положительном направлении
7.23. Оператора поворота Я3 на на угол 180° вокруг оси oz
7.24. Оператора отражения Я3 относительно плоскости хоу
7.25. Оператора дифференцирования
8. Квадратичные формы. Приведение к каноническому виду
Написать матрицу квадратичной формы и иайти её канонический вид (методом Лагранжа или методом ортогонального преобразования)
8.1. х2 + х22 + 4Х|Х2 8.2. х2 - 2х2 + 2х,х2
8.3 5х2 — Х|Х2 8.4. Х2 + 6Х|Х2
8.5. х2 + х2 + Зх2 + 4xjX2 + 2х,х3 + 2х2х3
8.6. х,х2 + х,х3 + х2х3
8.7. х2 + 5х2 - 4х3 + 2х]Х2 - 4Х]Х3
8.8. 4х^+х2+х3-4х!Х2+4хр:3-3X3X5
8.9. Зх2 + 2х2 - х2 + 2х,х2 - 4х2х3
8.10. 2х2 + Зх2 + 4х3 - 2х,х2 + 4х,х3 - Зх2х3
IV. МАТЕМАТИЧЕСКИЙ АНАЛИЗ
1. Предел числовой последовательности
Вычислить (приближённо) некоторое число членов последовательное Нанести точки на график и определить, является ли последовательное убывающей или возрастающей, а также ограниченной или имеют предел.
1.1. ол=^.п~' " Зл „ Юи+3 1.2. ап-5л
1.3. ап=^^1 " Зи 1 л -л3^1 4 °"=n+io
1.5. " 5-и2 ,, 2"2-1 *-6°л=3-л2
1 1 2я —1 1.7. а„ = — 2я 2 3я-1 >-8- °п = урГ
1.9. а„ = — " 2я 1.10. а„=-^
i.n.o„-(-i)"«zl и+6 112- Оя=(-1^
1.13. а„ =(-!)" Л -1 1.14. Ол = (-1)ЯЦ^ Л
1.16. «„=(-1)”^
1.17. ал =(-1)л 1.18. Ол = (-1Г*2
Вычислить предел последовательности
1.19. .. и-2 11П1 1.20. 2п+1 Inn
л-><с5 —л л-ко 2 — л
1.21. 7л-2 lim 1.22. ,. 3-и
Л-»ОО 3 л->«> 100000
1.23. п + 10 lim у 1.24. .. 50и-3 пт —г—
л-»» 5-п Л—>со
1.25. л2-Зл-2 lim —= "->”4и2 + 10и-3 1.26. Зл2+4л lim —z п1 + и _ j
48
1.27. lim л-юо 5л3-л2-л —2 2л3+л2 — 2 1.28. lim л—>СС 4-л3 + 7л л3 + 5л2 +3л + 6
1.29. lim (2л-1)2-(2л + 3)2 1.30. lim (л + б)2-(л-5)2
Л-ЮО л-7 2л+ 12
1.31. lim (л -1)3 - (л + З)3 1.32. lim (л + 2)3-(л-З)3
л->со л2+8 п-ьа> 2л2 + л-1
1.33. lim (л + 1)3 +(л + 7)3 1.34. lim (л + 2)3 +(л + 4)3
л-юо л2-12л л-юо л2+1
1.35. lim (л -1)3 - (2л + З)3 1.36. lim (Зл-1)3-(2л + 1)3
Л—>СО 4л3-л2+20 Л->00 21л3 + 5л2+2
1.37. lim (л-1)!-(л + 1)! 1.38. lim (л+ 1)1+л!
Л->ОО (7л+ 6) л! Л-НО (л + 2)!
1.39. lim (л + 2)!+(л + 1)! 1.40. lim (л- 1)!+(л- 2)!
л—>оо (л + 2)!—(л + 1)! Л-»ОО („_]),_(„_ 2)1
1.41. lim Ул2 + л + | 1.42. lim Ул2 + Зл + 1
л->00 Ул3+ 2 Л—>оо Ул2 + 2л
1.43. lim- Ул2 + 1 +Ул6 + 4 1.44. lim - У^Тз+УТТ^
Л—>00 л-Ул2 + 2л л-»со л-У9л4+2л
1.45. lim- 2й-3” 1.46. lim 4Л+3Л
л-юо; 3" + 2Л л-»оо 4П — зп
1.47. lim- ^л+2 . 2Л ^л~2 Qtt
1.48. lim -
П~>» 5" + 2 J л—>со; ^л । q/i+XO
2. Предел функции. Простейшие методы вычисления пределов. Эквивалентные бесконечно малые для вычисления пределов
Найти предел, разложив многочлены на множители непосредственно, или после приведения к общему знаменателю
2.1. .. х-3 lim^5 *-»Зх —4х + 3 2.2. х+5 lim х-»-5х2-х-20
2.3. .. х2-5х + 6 lim— »->2 - 4х + 4 2.4. . х2-2х + 1 lim— *->12х2+х-3
49
2.5. lim х->- х*+Зхг + 1х+5 x2-x-2 2.6. lim x->-3 x2+2x-3
x3 + 5x2 + 6x
2.7. lim 1 8?-l 6x2-5x+l 2.8. 27x3-l lim —z х_ДЗх2 + 5х-2 3
2.9. liml 1 3 1 2.10. lim 1 x—>2\ ’ 1 3 1
1-x 1-?J 2-x ' x’-sj
2.11. liml x+2 x-4 'I 2.12. lim x->2 1 1
x2-5x+4 Зх2-9х+6^ x(x-2)2 x2-3x+2
2.13. lim x->3l x2-4x+3 J 2 x-3 J 2.14. lim x—»—7 <2x2+15x+7 1 +13 k X + 1 J
2.15. lim J x-> f6x2-x-l 51 2.16. lim 7 2 C 2x2+13x+21 ! 11 [ 2x+7 +2)
[ 3x+l ' 3 J
Найти предел функции на бесконечности, вынося старшую степей за скобки
2.17. lim X-HO x2 + 2x-3 x2+2 2.18 lim X—>OC 3x2+x+l x2-l
2.19. lim X->® 4x3+2x-3 x3-x2+10 2.20. lim X—>00 2x4 + 2x3+4x x3-4x4 + 1
2.21. .. x -7x+5 lim -3 5— x-»«x +7x +3 2.22. lim X->00 2x-23 x3+30x2-10
2.23. lim X—ИЮ 6x5+2x4+2x5-x x4+x2+l 2.24. lim X—>00 -7x3+5x-3 x2+x-3
2.25. lim Х-К» f x3 xl 2.26. lim X—>00 ( 1
k4(2- x)2 4 J 7 * 1 "4 J
2.27. lim X—>« ' Зх2 (2x-l)(3x2 + x+2)' 2.28. lim X—>00 f X3 X2 1
2x + l 4X2 J k2x2-l 2x+l)
2.29. lim 2.30. lim x—>031 5x3+l 20x3 + x-4
X—>«4 x2+l 1-x 4x
50
2.32. Iim^+6W?-J
4j
2.34. lim—— fx7+S + 3x2
Найти предел, предварительно преобразовав выражение и применяя алгебраические формулы сокращённого умножения
2.35. lim-х->0 Vl + x2 -1 X 2.36. lim-x—>0 Ja+x -2 X
2.37. lim х->5 х —5 2.38. lim x->-3 Убх + х2 + 18-3 x + 3
2.39. lim-х->0 Vx2 + 1-1 х3 2.40. lim-x-»0 Jx2+9-3 x2
2.41. lim-х->0 V25 + X2 -5 2.42. Jx2+9-3
Vx2 + 16-4 x->0 . Vx2+1-1
2.43. lim- X2-yfx 2.44. lim-x->0 Ух2 + 1-1
Ух-i-i x2
2.45. lim- V25 + X-V4 + X 2.46. lim
х->0. Vx + 3 -Vx + Il x->10 Vx + 6 —4
2.47. lim-х->0 tfx2 + l-I x2 2.48. lim- x-»0 !/x2+8-2 4x2
2.49. lim-х—>0 Цх+2-^2-х 2x 2.50. lim-x-»0 !/х+Т-УГ7х
2.51. lim 2x2 2.52. lim- 3x
х->0 -j4 + x2 -2 x-»0 V25+X -5
2.53. lim 1-x 2.54. lim 5x + 5
х->1 л/3 + х -2 x—>—1 V8 + x2 -3
2.55. lim х->0 72 --Jl-bcosx 1 -cosx 2.56. 1 lim-x->0 1 — л/2 — cosx 2-2cosx
2.57. lim х->0 Vl + sinx -Vl-sinx 2sinx 2.58. lim-x—>0 j2-sinx -л/2 + sinx tgx
51
Найти пределы с помощью эквивалентных бесконечно малых фунил
2.59. lim^±£ *-*о sin5x Л7х я 2-61. lim- х-^ги-х3 2.63. l.-ni * arosin2jc Х-Я> l-cos4x e2jt—1 2.60. lim—-— x->o tg2x „ l-cos5x 2.62. lim x-»0 1 -cosx arctg6* 2.64. lim — x-to sinl2x
20-ln|l+—'i 2.65. lim i— x-»0 tg8x 2.67. lim^lt*) x-^Vl+x-l 2.69. hm- 1 х-Я) tg5x x2-l 2.71. lim 4---<-*i<lx-l 2.73. lim-^ x->x tg5x 2.75. lim-!^^1 x->e X — e | 21-lnfl+j] 2.66. lim 1 , x-»o 7x —x ln(l+3x) 2.68. lim-Tji——2 x-»o Vl + x -1 4-SX-l 2.70. lim x-»o sin5x 9x2-9 2.72. lim x-»l </x -1 „ sin3x 2.74. hm x-tn sin 8x ln2x-l 2.76. hm x_^_ 2x~e 2 X
2.77. lim —~e-x->-i 4x+4 — p 2.78. lim x->4 X-4
. 4
sin— 2.79. X-^X) gVX _ J 1 - cos— 2.80. lim x-“(4l/x_!j
l8(1+?) 2.81. lim—5—£-2 X~^ 1-cos-X ,g(,+7) 2.82. lim—— X->CO tg4 -X
Используя переход к экспоненте, найти пределы
2.83. lim(l + x)^x x->0 ' 2.84. Iim(l-2x)Vx x->0v 52
2.85. Iim(l-5x)'/2z x-»0
( i Y
2.87. lim 1+—
х-и»^ Зх)
f i Vх
2.89. lim 1——I
x-»«>^ Юху
z । .бх^-х+З
2.91. lim 1—5--------
x->»\ x +5xJ
2.86.
2.88.
2.90.
2.92.
lim(l + 10x)'/5x
3. Производная функции и дифференциал. Техника дифференцировании
Записать приращение функции Ду = у (х + Дх) - у(х) (Дх — приращение аргумента) и упростить его
3.1. у = х + 2
3.3. у = х2 + 5
3.5. у = ехр(2х + 4)
3.7. у = 231-7
3.9. у = ехр(-х2 +в)
3.2. у = 2х-3
3.4. у = 3х2
3.6. у = ехр(-х + 5)
3.8. у = 2"'+2
3.10. у = ехр(1-4х2)
_ . _ . ( 71 J
3.12. у = sin х— I z I л J
Найти отношение — для функции в заданной точке Дх
3.13. у = 2х-4 при х = | и Дх = 1
3.14. у = 2х-4 при х = 2 и Дх = -3
3.15. у = х2 + х-5 при х = -2 и Дх = -0,1
3.16. у-х2-2х прих = 0 и Дх = 0,3
3.17. у = —-— при х = 0,4 и Дх = 1
х + 2
53
Найти производную, пользуясь правилами дифференцирования
3.19. у = 7х2-3
3.21. у = 2-Jx -Зх+—4-^/3
3.23. У = (х + 4)(2х -1)
3-25-У = х(-х + 1)(5х-|)(3-х)
3.27. у = (^+^)(^_2)
3.29. у-х^^
з.з1. у=-х+| 2-7х
3.33. y=*L+'I*_
X5 ~4х
3.3S. ..-(иД)('|-д) (2-Л)1
3.37. у = х-ех
3.39. у=(Зех + 1)(2-ех)
3.41. y = —~S -8ех + 3
3.43. y=2cosx-4sinx
3.20. у = 5-8?
3.22. у = 0,8^-—+1+°1Z 0,3 6 x3
3.24. у = (-5x+3)(-x-8)
3.26. у = x2(x + l)(x-l)(l-9x)
3.28. y = (^/x+x)(VJ-l)
3.30. y = —-j2+'^x x4
, „ 4-3x
3.32. y=-----
5x + l
3.34. y=
2 + cosx
3.47. y = 2ex-cosx+5x-sinx
3.49. y = Vx-e*-t&r
3.51 y = x7-4*sinx
3.53. y = —31^х x + lnx
3.55.y = ^L!2L£
x-4x
3.57. y = 5x+4arctgx
x4 +4x
3.36. J_(7-'/x)('+^
(1-3VJ)2
3.38. y = (3-9x)ex
3.40. у = (4-ex)(5ex-2)
3.42. 4e’+9 y=—-— 3e -2
3.44. у = -3,4cosx+0,7sinx
3.46. 3-cosx y^='—:— 1 +sinx
3.48. у = -5x • cosx + ex -sinx
3.50. y = x2 ex ctgx
3.52 y = tfx-7*-cosx
3.54. y = -?~7lnx x3 + log3x
3.56. у = —2* ~x'1 |J
x 6х
3.58. у = —4x+5arcsinx
54
Представить в виде композиции
функций у = у, (у2 (Уз (••)))
3.59. у,(х) = х+2, у2(х) = 1пх, у3(х)=^х
3.60. у|(х) = 3-х, у2(х) = 2х, y3(x) = lgx
3.61. y,(x)=sinx, у2(х)=х3, у3(х) = х + 6
3.62. y,(x) = cosx, y2(x) = Vx, Уз(х) = —4х
3.63. у,(х) = ех, у2(х) = cosx, y3(x) = sinx
3.64. у|(х) = Зх, y2(x) = sinx, y3(x) = cosx
3.65. yl(x) = tgx, у2(х) = х’3, y3(x) = sinx, у4(х) = х2
3
3.66. У|(х) = 1пх, у2(х) = х 2, y3(x)=cosx, y4(x) = Vx
Разложить композицию на элементарные функции
3.67. y=2x’-7 3.68. y = -3>/x + l
3.69. y = ln(x2 + l) 3.70. y=lg(3-V7)
3.71. y = cos^5x2+1J f It.'I 3.72. y = sin 3х
3.73. y=p+-7sinxj 3.75. у = exp^2 - cos^Vx^j 3.74. у = arcsin Vcos4x
3'76‘ ™o-2sinx cose
3.77. y = —! 71+e->/x 3.78. y = ln 1+Vl+Vl + e1
Найти производную сложной функции
3.79. . 4 у = arcsin -y X 3.80.
3.81. у = cos2 (-7x) 3.82.
3.83. у = 3 cos2 x - 0,67sin5 x+cos (0,12) 3.84.
(-5) у = arctgl — I
y=]7‘g4(4*)
10
у = -sin2 х - sin5 х+sin 1
55
3.85. y = -Jl+cosx2
3.87. у = cos4(sinl00x)
3.89. y = ln(l + 34x)
3.86. j = 72-tgx5
3.88. у = sin3(ctg3x)
3.90. y = ln(l-52x)
Применяя логарифмирование, вычислить производную
3.91. у = х*г 3.92. у = х?
3.93. У - (sin х)1ех 3.94. / \sinx у = \cosx)
3.95. 3' = (1 + !пх)1п(,+Л) 3.96. , , Jn(l+x) у = (4 —ln2x)
3.97. ?,_(2*&)(И-Х3)(1+2Х) 3.98. (4-^?]0 + х)(9-9х)
(х+^)(зх+2-х) У~ (x2+V?)(2x + 2-x)
3.99. „ _ sin гх arctgx *#х6-2 3.100. cose4x arcsin- ^x9 +x
3.101. sin4(2x8) у = х3ех? sin(2x) ^(2aictgx)3 }~ tg3(-7x5)
3.102. y = (2-x)l2e Sx3cos(2 + x) ^1пбх)3
Найти производную — и вычислить её значение при заданном значе-dx
иии параметра
3.103. x = l-/2, I y=t-t\ ° 2 3.104. x = 4 + /3, 2 Z»=3 y = l-/2,
3.105. t + t X t-5' 1+z2 '°"-4 3.106. 13+1 Х = -я ,
3.107. • x = e4'sinl, n 4/ Z° = T у = e cost, J 3.108. x = e~' sin3r, a у = e~‘ cos31, 18
56
Найти дифференциал функции
3.109. y = (l + VJ)3 3.110. 1
^х + з/х
3.111. у = е~х 1пх 3.112. у=е^
3.113. y=^i 3.114. у- -
cosex arctge
Используя дифференциал, вычислить приближённо
3.115. y = V2x + l, х = 7,68 3.116. y = Vx2-x + 4, х = 1,03
3.117 у = х5, х = 2,993 3.118. У = х6, х = -1,88
3.119. у = Vx2 +1 +sinx, х = -0,05 3.120. y = ^/x3+cosx, х = 0,07
Найти вторую производную
3.121. у = х4-4х3 + 6х-9 3.122. у = х~5 +2х + з/х
3.123. у = х(х2-4)8 3.124. у = (х2 +4)4(х-3)
3.125. у=5х -(2 + х) 3.126. у = ех (1-х)
3.127. y = excos4x 3.128. y = e2xsin3x
3.129. у = (1 + х2) arctgx 3.130. у = з/1-х2 arcsin х
3.131. y = x4lg3x 3.132. у = х51п2х
Найти производную указанного и-го порядка
3.133. у = е“5х, и = 4
3.135. y = xlnx, и = 3
3.134. у = (1 + х)4?, и = 7
3.136. y = sin4x, л = 4
Доказать, что функция у = /(х) удовлетворяет уравнению
3.137. y = exsinx, у"-2у' + 2у = 0
3.138. y = e'xcosx, у' + 2у' + 2у = 0
3.139. у = е^ +е~^, ху’+^у'-^у = 0
57
3.140. у = е4х+2е"х, y*-13y'-I2y = 0
3.141. у = у2х-х2, у3у' + | = 0
3.142. у = х + з/х2+1, р+х2)у + ху'-у = 0
3-143- (2>')2 =(>-')/
3.144. у = -±^, ,/Z = ?g
1 + 5х V6 V30
4. Касательная и нормаль к графику функции
Найти угловой коэффициент касательной, проведённой к графику функции в заданной точке
4.1. у = 2,3х2+0,2х-1, х0=-О,34
4.3. у = 5х3 + х2, х0=-11
4.5. y = 'J-x‘l +х, хо=О,(П
4.2. у = -7,2х2+8,1х, х0 = 1,29
4.4. у = —7х3+2х2, х0=13
4.6. у = -Jsx1 +6, х0 = -0.5
Написать уравнения касательной и нормали к графику функции в заданной точке
4.7. у = з/х4+3, х0 = 1 4.9. у = х2—5х+4, х0=-1 4.11. y = tg2x, хо=О
4.13. у = 5х-‘, х0=3
4.15. . _! + з/27 У~1-^’ Х°~2
4.17. . _ Зх + з/х ? 2 Г~ ’ х°_ Зх - у/х
4.19. х3 + у2 +2х-6 = 0, у0 = 3
[x=z+6z2,
4.21. J Zo=-3
x = cos2z, л
4.23. J . . tg=-
ky = tg(t+n), 3
4.22.
4.24.
4.8. у = з/х5 +4, хд = 2
4.10. у = х3 +2х2-4х-3, х0 =-2
4.12. у = 1п2х, хо=О
1
4.14. у = 3‘"Л , Хр=-1
. ., 2х+з/х , 416- у=-—Зг> хо=' 2х-у]х
. - х2+3/х -
418 >=Т^Г х°=“8
4.20. xS + у5 - 2ху = О, у0 = 1
х=13-Г2 /о=-1
y = 2 + 4Z, x = sin(r-3n), д y = tg(2/-n), ° 6
58
5. Исследование функций с помощью первой производной Найти наибольшее и наименьшее значения функции на отрезке
5.1. У = ~Х+3 [-3,-1] х2+2х + 2 1 1 5.2. 4х г _ ”2’2 3+х
5.3. у = 5-7х2 + 5х, [-6,0] 5.4. У=^(х-4)2, [0,7]
5.5. у = 1 + 12х2-4х3, [0,3] 5.6. у = 10-Зх2+2х3, [-2,3]
5.7. y = cos4x+2x, [0, л] 5.8. y = sin2x-x, [-ял]
5.9. у = 716-х2, [-3,4] 5.10. у = 725-х2, [-1,3]
Показать, что указанные функции не имеют точек экстремума
5.11. у=5—v3—х 5.12. у = 3+х/2х + 7
, -Зх + З 5.13. у = 2х-2 5.14. х-2 У-9х+5
2х2-1 5.15. у- X 5.16. -Зх2+8 У = 4х
5.17. у = 4+ЗОх + Зх2 + 2х3 5.18. у = 20-х3-2х2-10х
Найти интервалы монотонности и экстремумы функций
5.19. у = 2х3-6х2 + 7 5.20. у = -х3+Зх2+9х-5
5.21. у = х2(4-х)2 5.22. у = -х2(х-9)2
5.23. у = (х-5)2 .^(х + 4)2 5.24. у=(|-х)2-$Зх+1)2
5.25. у = фх-1)(х-7)2 5.26. у = ^(х-9)(2-х)2
5.27. у = х2е*г 5.28. у = -3х2е-2х
5.29. у = 2х-!п(1 +4х2) 5.30. у = -х + 1п(1-х)
5.31. у = е6х+4е-6л 5.32. у = 2е-3х + е3х
6. Исследование функций с помощью второй производной
Исследовать характер выпуклости и найти точки перегиба функции
6.1. у=3х5 —Юх3—15х2+1 6.2. у = 3х5-5х4+Зх + 15
59
6.3. > = х+Збх2-2х3-х4 6-5- 6.4. у = хл +8х3 + 18х2-3 r, -х3
х +27 6.7. у = ^ 6.6. у- , х2+12 6.8. у = З/х + 1
69 У = Щх-2)2 6.10. y = tyx + l)2
б ”. > = xln(2x) £ 6.12. у = х2ех
6.13. у = хе”4х 6.14. у = -хе~3х
7. Правило Л о пит ал я для вычисления пределов
Найти пределы, пользуясь правилом Лопиталя
7.1. |im2^+2x-3 4
*->‘»6х3-х2+1 7.2. lim / , *-»"°х +х2+9
7-3. lim X2
х->=о X2 7.4. lim —
е х-^»ех
7.5. lim- +2
Х-ХО X2 7.6. lim —
7.7. lim х4-е~х + х3 7.8. limx2.e-10x
7-9. *Нт^х’+з).е8* Х-И-СО 7.10. lim (х5-4) е2х
Х->-00 V /
|х3+з)
7.11. lim А L п * +1
х-^-кп In X 7.12. lim
*->+»1п(х + 6)
7.13. lim —(*+3)_ Р+з)
х-*«1п(х3+2) 7.14. lim — 2- х-»+“1п(х4 +х)
7.15. lim— "(х + л)_ X~>osm(x3+2n) 7.16. lim — s(x+0,5n)
V 7 x->0cos(x2 +2,5л)
7.17. lim—~е Х~2< е*3 1 г3
х->о х - sin(x + д) 7.18. lim- 2-2L
*-»o sin6 2х
60
7.19. .. Insin 2х lim x-.olnsin3x 7.20. .. Insin х lim x-»olnsin5x
7.21. .. 2*-5* lim х-»0 7* -3х 7.22. .. 4х -3х lim х-»обх-12х
7.23. lim х3 е1^ х->0 7.24. lim х2 • е^х2 х->0
8. Асимптоты графиков функций
Найти вертикальные асимптоты графика функции
8.1. х-2 У-2х-6 8.2. х + 6 J~5x-1
8.3. _ х + 3 8.4. х2 + 1
У 2 1 У 5
х -1 х2-2
8.5. х2 - 5х + 6 У= х2—4 8.6. х2+5х + 6 У= х2—9
8.7. у = е^ 8.8. у = е",/х
8.9. у = хе~'1ж 8.10. у = х2е1^
8.11. у = (х + 4)Х<х+4>2 8.12. у = (х-3)е-'Лх-
( 1 Y
8.13. 44) 8.14. >=['+-) к х)
8.15. е1-' У~ 8.16. ех+5
У"х+5
8.17. 1 8.18. 1
ех —4 ^г-з
Найтн наклонные или горизонтальные асимптоты графиков функций
8.19. у=—— х —4 х2 8.21. у = z Зх-4 х2 8.23. у=-^ 5х2 +х-4 8.20. у=-^— х+9 8.22. у = ^- 7 х + 12 х—х2 8.24. у= * - х2+х + 8
61
х-6х3
8.25. у=—---
х2+4
8.27. у=х-е^
8.29. X
8.31. е у~
8.33. Inx у=^ 1п(х2 + 4)
8.34. V- V /
' х3
8.26. х + х2+х3
У 5х2-х-7
8.28. 2 -? у = х • е
8.30. X у=7^ е2х
8.32. У = ^Гх
8.34. 8.35. 1п(х2 + 1)
Л х2
9. Исследование функций и построение графиков
Найти интервалы знакопостоянства и корни функций
9.1. у=-х2-Зх-2
9.3. у=х3 +5х2 + 6х
9.2. у = х2—7х + 12
9.4. у = -х3 +х2 + 20х
95у=^
х -4
3х-81
9-7- У=-57-
З2 —81
9.9. у = -х-2х+5
9.11. у = -х2-1п(х2-2х + 2)
9.15. j» = sin
9.17. у
9.10. у = х-43'х
9.12. у=2х* -1п(х2 +4х + 5)
9.14. у=|х-9|-1
9.16. у = cos^“ - 2*J
9.18. y = tgf—+—|
U sj
Установить, четной или нечетной является данная функция
9.19. у=х4-|х|+5
9.21. у=х3-х
9.20. _у = х6-б|2х|
9.22. у=xs-Ух
62
9.23. у = sin х2 + tg5xctgx3
9.25. y> = sm2x + 2sinx
9.27. y = l-ln(2 + x2)
9.29. y> = x+i
X
9.24. у = cosx + sin3xtgx5
9.26. у = tg7x-7tgx
9.28. у = lg(I-x4+5x6)
9.30. y=x3---~
l + x2
Построить график функции, используя первую производную
9.31. у=2-4х3+Зх2
9.33. у = (2х~9)2(х + 5)2
9.35. у = (х-3)’(Зх + 1)3
9.37. у = 2х6-15х4-36х2+ 20
9.32. у = 15х + 6х2-х3
9.34. у = (х-7)2(Зх + 1)2
9.36. у = (4х-7)3(х + 7)3
9.38. у=11-2х6+3х'*+12х2
Провести полное исследование функции и построить её график
9.39. 1-х2 У~ 9.40. 4-х2 У=77Т
9.41. х4 9.42. х3-Зх
} х2-1
9.43. "=777 9.44. . _*2~1
* х2 + 1
9.45. y = e2x-xl 9.46. Н)/2 у = хе' "
9.47. у = хе^х 9.48. у^
9.49. у = (х-2)е^х 9.50. у=х2ё^х
9.51. 1ПХ у=— X 9.52. у=х21пх
9.53. у = х21п2х 9.54. 1пх
10. Непрерывность функции в точке и на отрезке
Найти значения параметров, при которых функция будет непрерывной
10.1. /(х) =
Зх-А, при
1-12х, при
xS-7
х>-7
4-4х, при х^б х + 12, при х>6
63
ЮЗ. /(х) = х2 - Лх, при х <-1 104/(х) Лх2+6х, при XS3 3 ns
xJ+5, при х>-1 х -26, прн х>3
х3+Лх2, при х<2
10.5. /(х) = х2 + Вх, при 2 < х < 4
-Зх+11, при х>4
10.6. /(х) =
1х3 + 2х2, при х<-1
Ахг - 5х, при -1 < х < 0 2х-В, при х>0
Найти все точки разрыва функции и определить их тип. Построил график в окрестности каждой точки разрыва
10.7. 4-х *=77? 10.8. X у~&
10.9. х + 1 10.10. х-3
У (-Ю)2
10.11. х2 —4 У=~1—’ х-8 10.12. х3-27 '=х2-9
10.13. sinx У = X 10.14. У = ^
10.15. х-5 10.16 х + 3
10.17. у,=_Ы (х + 2)< 10.18. ,=±21 (х-7)2
10.19. y = xVx 10.20. у = х^
10.21. у=х4(-)Л 10.22. yy=x431^
10.23. х-3 у= 2х-8 10.24. х + 2 9
«4
11. Формула Тейлора, ее применение дли исследования функций
Написать формулу Тейлора л-го порядка в указанной точке Хо
Н.1. У = ~----. х0=-3, л = 3 11.2. у = —-—, х0=-1, л = 3
2-х ' х + 5 °
11.3. y = yj2x + i2, х0=-5, л = 2 11.4. у = ^/2х-14, хо = 6, и = 2
11.5. у = (х+4)е'*х, х0 =1, л = 4 11.6. у = (2х-1)е1~х, х0 = -1, л = 4
11.7. у = (Зх-4)2 1пх, х0=3, л = 2
11.8. у = (2-7х)2 1п(-х), х0 = -4, л = 2
11.9. у = (х2+5х~1) 1п(з + х4), х0=1, л = 2
11.10. у = (зх2-2х + 1)21п(9 + х6), х0=-1, л = 2
11.11. у = яп^)е"*х, х0=^, л = 3
11.12. у = cos^-|^e3x, х0 =у, л = 3
Вычислить приближённо, используя несколько первых членов разложения по формуле Тейлора
11.13. у(1,98), где у = х12-х4-Зх2+2
11.14. у(2,03), где у = 10х16 + 5х5 + Зх + 2
11.15. у(1,005), где у = х100-х40 + х20
11.16. у(о,97), где y = x200+xS0 + x,°
11.17. у(0,02), где у = ех’-3х
11.18. у(-0,11), где у = ех’*5х
11.19. у(0,032), где y=ln(l+Vx)
11.20. у(0,04), где у = |п(х + з/1-х)
Исследовать поведение функции в окрестности заданной точки, написав несколько членов разложения функции по формуле Тейлора
11.2]. y = 4cos(x + 2) + 2x2 + 8x, х0=-2
65
11.23. y=x2+l-2xln(x+l), xd = О
11.24. у=2х2 -8х + 5+41пх, х0 = 1
11.25. у=2ех~2-х2+2х + \, х0 = 2
11.26. у=х2-2е~1-\ х0 = -1
12. Функции нескольких переменных Найти значения функций нескольких переменных в указанных точках
12.1. г=х2у—^, М(1,з) 12.2. z = ex+>sin(x),
X \2 2/
12.3. u = 2x-3y + z2, Л/(1,2,-1) 12.4. и = х2-Зу3+2xz, М(0,1,3)
12.5. z = (х + у) 1п(х2 + у), М(1,2)
12.6. Z = х^2-1 + ух+2, Mi(2,2), Л/2(1,3)
12.7. z = x+ysin(x + l), Л/(0,2) 12.8. z = y + cos(2-x) Л/(0,3)
12.9. u = 5x + 3y+ 2z+4sin(2z), Л/(1,2,2,0)
12.10. u = cos(2z) +х3 + 5у-4, Л/(0,1,6,3)
Найти и изобразить область определения функции
12.11. z = ^x-y-l 12.12. z = у/2х— у+ 2
12.13. z = Vy+x2+l 12.15. z = ln(2x-y+l) 12.17. z = ln(xy) 12.19. г=—, !—= Vl-x2-/ 12.21. z= 2x-y + l 12.23. z= z-? In(x2+y+l) 12.14. z = Jy-2x2-3 12.16. z = In(x + 2y-l) 12 18. z = ln(y2 - 4x + 8) 12.20. z= , 1 -— Jx2+y2-l 12.22. z = x+2y-l 12.24. z = J ln(y2-x-l)
66
13. Частные производные, градиент
Найти частные производные дифференциалы для данных функций
1-го и 2-го порядков
и полные
13.1. z = x3y + 3y2x 13.2. z = 2xy2 -3y3x2 + у
13.3. z = 3xy+— 13.4. z = 5x2y-^-
X x2
13.5. z = xcos(xy) 13.6. z = ysin(x2y3)
13.7. z=yV~2> 13.8. z = xex+y
13.9. z = !nx2/ 13.10. z = Inx/xy
13.11. z = ln(5x + 7y) 13.12. z=ln(3x + 2y)
13.13. z = xyarcsinx 13.14. z = yarctg(xy)
13.15. u = x2~3y2+2yz 13.16. u = 2y3-3xy + 5xz3
13.17. u=-+- z X2 13.18. u=4r~—
y X z
13.19. u = sin(xyz) 13.20. u = cos(xyz2)
Найти для данных функций в заданной точке
производную по направлению л
1321 и = 3х2 ~2хУ + гУ ’ л = {4,3,0}, Лф,2,0)
u = 5x-3xy + 7xyz
i3'23' л = {1,2,—2), М (3,0,1)
13 22 и = 2хг~Уг+3Ух2
' Я = {0,-4,3}, М(2,1,2)
13 24 u = 'lx2y-3xz2 + 5yz2
' л={-1,2,2), М(2,0,0)
Изобразить линии уровня функций
и найти вектор градиента для указанных
13.25. f(x,y) = x-2y
13.27. f(x,y) = 2-x-4y
13.29. f(x,y) = 7-7x + y
13.31. f(x,y) = x-y2
13.33. f(x,y) = x2+y-2
13.26. /(x,y) = 3x+y + 5
13.28. /(x,y) = 3x + 4y
13.30 ./(x,y)=-5x-10y>
13.32. /(x,y) = y + x2
13.34. /(x,y)=y2-x+3
67
Записать в явном виде функцию у = _/"(х), заданную неявно уравнена
13.35. х4 + у4=]
13.37. х’+у-2 = 1
13.39. ху = -4
13.41. 2^ = 5
13.43. 1л(х-у)-1лх = 1пЗ
13.45. (x + l)-sin(x + 2y)=cosx
13.36. х2 + у6 = 1
13.38. Зх + у-5 = 1
3
13.40. — = 17 ху
13.42. 9-v=2
13.44. 1п(х3+у) + 1п4х = 1п2
13.46. (х2 + ljtg(2xy) = cosx+siB
Найти производную — dx ^>У)=0
от функций, заданных неявно уравнею
13.47. у-х2 +2 = 0 13.48. Зу + 2х2—х = 0
13.49. х2 + у2 =9 13.50. х2-у2 =4
13.51. х2у-у2х-1=0 13.52. х2у2-х4-у"=1
13.53. х2-8у2=4 13.54. 7х3+у2=-1
13.55. у3х2 - у2 + 0,4xs =0 13.56. ху + х25 + 0,6у2 +х-0,2у=
1357. sin(jy) + cos3-^(x + 2)(5-y) =0
13.58. cos(xy) + tg9+^(х - 2)6 (1+у) = 0
13.59. е,х2+2'°’=1 13.60. е~5хх5 + 74' = 3
тт w 02 02
Наитн частные производные —, — от функций, заданных неяв ох ду
уравнением F(x,y,z) = 0
13.61. z—x2 -у2 =0
13.63. x2+y2 + z2=l
13.65. z3 -xyz = l
13.62. z + x2 -x+y = 0
13.64. х2—у2—z2=4
13.66. е2-xyz = 0
68
14. Касательная плоскость и нормаль к поверхности
Для данных поверхностей найти уравнения касательных плоскостей и нормалей в указанных точках
14.1. z = 2x2-4y2, Л/,(2,1,4), Л/2(0,1,—4)
14.2. z = xy, Л/ДМ,!), М2(-1,2,-2)
14.3. z = x2+y2, Л/,(0,0,0), Л/2(1,2,5)
14.4. z = 2x2+y2—3, Л/ДО.0,-3), Л/,(1,1,0)
14.5. x2+y2+z2=4, Л/,(0,0,2), М2(0,2,0), Л/3(2,0,0)
14.6. x2+y2-z2=0, Л/,(3,4,5), Л/2(-3,-4,5)
14.7. х2-2x + y + z2 =0, Л/2(1,—3,—2)
14.8. x3+xy-z2=O, Л/Д1.3.2), Л/2(0,3,0)
15. Исследование на экстремум функций нескольких переменных
Найти стационарные точки функций
15.1. z = 3x2+y2-2y
15.3. z = x2-2y2+2x
15.5. и = 2хг+у2+2z2-ху
15.7. z = x2 - 2xy + 2y2 - 2x - 4y
I5.9.z = x2y~x2-2xy + 2x
15.2. z=x2 -6x + y2
15.4. z = x2—y2-4y
15.6. u = 2x2 —y2 -z2 + xz
15.8. z = x2 +2xy-2y2-2x-iy
15.10. z=y2x-4xy + y2 -4y
Исследовать на экстремум функции двух переменных
15.11. z = x2-2x+y2 +4у + 5
15.13. z = x2 + ху+у2-Зх-бу
15.15. z = 3x2-X3 +у2 + 4у
15.12. z=x2 +2х-у2 +4у-3
15.14. z = xy-x2-y2 +3х
15.16. z = 3x2+l2x+3y2-y3
Найти условный экстремум функции двух переменных
15.17. z=x2+y2 , у-х + 1 = 0
15.19. z = xy , у-х = 0
15.21. z=x2-4х + у2 +4 , у = х
15.23. z = xy2 , х + 2у —1 = 0
15.18. z=x2-y2 , у-х + 1 = 0
15.20. z = xy , у + х = 0
15.22. z = x2 -4х + у2 +4 , у = х + 2
15.24. z=x3-y3 , х-у-2 = 0
69
16. Системы линейных неравенств нескольких переменных. Графическое решение
Решить графически системы неравенств и найти все угловые точки
х>2 I х<3
16.1. J 16.2. {
у<-1 1 ^>1
х>-3 х<2
16.3. J , 16.4. J
у>5 | у<-А
16.5. J x + v<3 16.6. х-у>0
х-2у>1 2х + у > 4
16.7. J х-у^0 , 16.8- х + у<2
5х-у>5 4у + х>-1
16.9. < 2х-7у<2 16.10 Зх-5у>4
у<5 Л<2
16.11. 4х+5у>0 ' 16.12. 2х + 7^<0
х + 6 <0 у + 4<0
2х + у<2 х+2у+6£0
16.13. 2х + у + 3>0 1614 х+2у<4
—4<х<2 -2£х<4
2х-3><+6>0 4х-5^+5>0
16.15. 2х^6 + 3.у 16.16. 4х<5у
0<у<4 1<^<3
х-2у-2<0 2х+у-4<0
16.17. 2x + 3j>>6 16.18. х-у>0
х-2у+2>0 2х+у+6>0
Зх+4>< + 12>0 4x-y + S>0
16.19. Зх + 4у-24<0 16.20. 4х-у-12<0
х+2у<0 х + 5у 510
70
х>у 2х<у
16.21. Зх + у<0 16.22. 4х + у£0
у + 4>0 У S3
2у>х-8 у<3 + 2х
х + 8у > 0 х+3>0
х+4у+8>0 х£7
х-Зу<3 у>0
16.23. Л 16.24.
у + 4>х у<5
у—х+4>0 х + у^8
у+6>2х х+у+120
17. Простейшие задачи линейного программировании
Методом градиента исследовать f{x,y) при указанных ограничениях на экстремум указанную функцию
17.1. /(х,у) = 2х + у 17.2. /(х,у) = -Зх-4
х<1 [Зх + у-З^О
у<1 у<х + 3
2х + 2у<3 х<2
/(х,у) = х + у + 1 /(х,у) = х + Зу-0.5
17.3. (бх + у>2 17.4. Г2х + 2у<7
[1+х + у>0 [у <4
/(х,у) = 4х + Зу + 8 /(х,у) = х + 5у-7
х+2у<6 2x+yS4
17.5. х + у<3 17.6. х + у-1<0
х2-2 у + 4£0
у>0 х>0
71
17.7.
17.9.
f(*.y) = x~y
x + y22 l-x+>20 y<4
17.8.
f(x,y) = x + y x+2y<4 x+y+320 x<8
17.11.
f(x,y)=4x-2y+3
2x+y<g
4x+2>i-5
/(x,>) = 3x + 6> + l
17.10. jx-2y<12
|б у < Зх + 5
f(x,y) = 5x+7y 3x+2y<19 х+2у<13 0<x<5
0<y<6
/(x.y) = 8-5x-2>
3x-><6
17.13. x-y^l
X + >2-l
-4<x<8
0<y
/(x,>) = 10x + 20> x+3.5><350 2x + 0.5><180 x + >210 0<x
0<y
f(x,y)=x
17.14.
x+y-l>0 y-2x<2 x + ><9 2x-><6 x>0
>20
18. Неопределенный интеграл. Основные методы интегрирования
Найти интегралы, используя таблицу интегрален и свойства линейности
18.1. J(x+l)dx 18.2. J(3x2-x + l)dx
18.3. f(8x’ -4х5 +1 lxl2)dx 18.4. Г(^-2^+А)(к
3 J 4 12 3
18.5. j(Vx+l)dx 18.6. J(^/x-3^x)dx
18.7. x3)dx 18.8. f(-2_+_2__1)dl
J r- ir ’
72
18.9. f(x « -4—)dr
2 2 3 3
18.11. J(x 3+x3+x2+x 2) dr
18.13. f-—— dr J 3x
18.15. p/EzZiir J X
18.17. [—— dr J X
3
18.19. P3~^2 dr
J 3x4
18.21. j(3e*-2-Jx) dr
18.23. J(2x3 -3x)dr
18.25. j(5sinx+2cosx)dr
. r3cos2x-5 .
18.27. j-------dr
J COS X
18.29. [(-------3cosx)dr
VT7
3 2 x
18.31. j ( -—
X
,8-33' ^+1T")dI
18.10. j(Vx-7-y+3)dx
18.12.
18.14. fx3-2x —7=^dx J V4x
3 2
18.16. r2 -*3 я J
’ x3
18.18. rx3+3x + 5 u J X
18.20. £^d/ 1 3t
18.22.
VX
18.24. J(5*-#0dr
18.26. j(3shx-7chx)dr
18.28. r5-3cos2x . J—7T *
3 sin2 X
18.30. J(2V7+y!-—-) dr
18.32.
18.34. f3 + 2x2 .
подведение под знак дифференциала,
18.35. J(3x + 2)’dr
Найти интегралы, используя преобразование подынтегрального выражения
18.36. [--—zdr
J(2x-5)6
73
18.39. f--1----dx
J^5?
18.41. |(e31+_L_)dx 3 x-3
18.43. jcos5x dx
18.45. |sin(3-2x)dx
18.47. Г—-2------dx
Jcos2(2x+5)
18.49. f—2------dx
Jx2+2x + 2
18.51. f—-1 dx Vx2 +2x+2
18.40. f 3 dx 3/3-2x
18.42. Г(-2—-e~3x)dx J zx-5
18.44. fsin—dx
3 3
18.46. |cos(2-3x)dx
18.48. f—r-2-----dx
Jsin2(4-3x)
18.50. Uj—!------dx
jx2-4x + 5
18.52. Г 1 -dx
18.54. jxcosxdx
18.56. Jxlnxdx
18.58. |ln2xdx
18.60. jx2e-*dx
Найти интегралы, используя метод интегрирования по частям
18.53. Jxexdx
18.55. Jxsinxdx
18.57 . Jx5zdx
18.59 . f^ydx
Найти интегралы, используя указанную замену переменной
18.61. (-=2-----dx, г = з/х
Зз/х(1 + х)
18.63. |хе* dx, Г = х2
18.65. P^^-dx, Z = lnx
J х
г ех
18.67. J-^-j-dx,Z = e’ + l
18.62. J—^-dx, 1 = 4^
18.64. |xcosx2dx, f = x2
18.66. [-Д-, Z = lnx
Jxln2x
18.68. p*cos(e*)dx, t = ex
74
19. Интегралы от рациональных функций
Выделить целую часть рациональной дроби
191 2х2—4х-гЗ х + 2 19.3 2>2+2х-3 х2 + 1 19.5. х-4 19.2. х-3 194 х3+2х2 + Зх-5 х-5 19.6. — ~3-~7 х2-1
Разложить правильную рациональную дробь на простейшие дроби
19.7. - - х2-25 19.9. - 3—5 х2+2х-3 19.11. ——? х-5х-14 + х — 1 19.13. -V- х3+2х2-8х х + 4 19.8. -V-^-х-9 19.10. -Зх~1 х2+4х+3 3 19.12. - х2-2х-15 19.14. - х3 + 5х2 + 6х
Вычислить интегралы от простейших рациональных дробей
19.15. Г-— dx Jx-3 19.17. f dx J(x + 5)2 19.19. f-^- dx Jx2+1 19.21. f^^dx jx2+4 19.16. f-—dx Jx+2 19.18. f—?-^-dx J(x-2)3 19.20. f^^dx Jx2+1 г2х + 5 , 19.22. dx Jx2+4
Вычислить интегралы от рациональных функций
19.23. f2*2 4x + 3dx J x+2 _. гЗх2 -3x+l . 19.24. dx J x-3
75
19.25. Г 1 Jx2- Зх+2 dx
19.27. fx3-4x + 7 3 х2-4 dx
19.29. fX3 - Зх+2 х2+1 dx
19.31. г х2 + х-1 dx
х3+2х2- 8x
19.26. !---dx
Jx2+x-6 rx3-3x2-7 ,9-28‘ I x2_—
19.30.
J x2+4
20. Интегралы от тригонометрических функций
Найти интегралы, используя указанную замену переменной
20.1. Г—-------, Z = tgf-1
J5-3cosx
20-3-1+sin х
20.5. jcos2 xsin xdx, t = cosx
20.7. jsin2xcos3xdx, t = sinx
“""Z----•' = tg
x + 3cosx
. r smx .
20.9. I------dx, t = cosx
J3-cosx
20.2. f-------
J5-4sin
20.4. f-----------j—, f = tgx
•'4sin x+cos x
20.6. jsin3xcosxdx, / =sinx
20.8. jcos3xsin2xdx, t = cosx
20.10. Jcosxecos*sinxdx, t = cosx
Найти интегралы, используя формулы понижения степени
20.11. |sin2xdx
20.13. |sin2xcos2xdx
20.15. jsin4 xcos2 xdx
20.12. jcos2xdx
20.14. |cos4xdx
20.16. jsin6xdx
21. Интегралы от иррациональных функций
Найти интегралы, используя указанную замену переменной
21.2. dx,Z = V7
Jx2+x
76
21.3. Г * ,г = ^ J^/x (^-1) 21.5. (—*—, 1+Vx+l 21.4. f - 2 21.6. j— dx, / = Vx-l
22. Определенный интеграл. Формула Ньютона—Лейбница
Вычислить интегралы
2 22.1. J(x2+l)dx 1 1 22.2. J(2x-3)dx 0
1 22.3. J(2->/x-3)dx 3 1 , 22.4. f(-j=-3x)dt 4
л 6 22.5. Jcos3xdx 0 22.7. f - Ji л 22.9. J 1 + x2 0 n 22.6. [sin—dx J 3 4 22.8. JVxdx 9 22.10. f *** -o-Jl-x2
Вычислить среднее значение функции на указанном отрезке
22.11. f(x) = x\ [1,4] 22.13. = p [1.2] 22.15. = I».*] 22.12. f(x)=x3-3x, [-1,1] 22.14./(х) = е2ж, [0,ln3] 22.16./(x) = cosx, [0,1]
23. Замена переменной и ннтегрнрование по частям в определенном интеграле
1 23.1. J(5x+3)e2xdx 0 0 23.2. J(2-3x)e’dx -1
77
о
23.3. J(2x2-8)exdx
-5
х г
23.5. |(2x-5)cos3xrfr о
23.7.
о V4-x
23.9. р?-*.
1 ^5-х2
2
23.4. J(4-3x2)e*dx
-I
23.6. j(l-2x)sin—dx о
*r(2x-l)dx
23.8. Ji---
0 -j9-x
23.10. J_6^*L_
з-710-х2
24. Применение определенного интеграла для вычисления площадей н длин дуг кривых
Вычислить площадь фигур, ограниченных кривыми, заданным! в декартовых координатах, изобразить эти фигуры
24.1. у = х2, х = 2, у = 0
24.3. у=—, х = 1, х = е, у=0 х
24.5. у = 1пх, у = 0, х-е, у=Ъ
U.I. у-х, у = х2-2
24.9. y = xlnx, у = 0, у = 4
24.2. у = 4х, у = 0, х = 1
24.4. у = е”, х = -1, X = 0, у = О
24.6. y = cosx, у = 0, х = —, х = 0
4
24.8. у=-х, у = -хг + 2х
24.10. у = хе\ у = 0, Х = 1п7
Вычислить площадь фигур,
параметрически, изобразить эти фигуры
ограниченных кривыми, заданными
24.11. J™'
[y = sin/
24.1 J Х = 3'2 (у=3/-Р
24.12.
24.14.
x = /-sin/ y = l-cosi х = ?-1 л='3-'
Вычислить длины дуг кривых
з
24.15. у = chx,x = l,x = 3 24.16. у = 2х2,х = 0,х = 4
78
24.17. (x = cos, + ,sin' [y = sin/-/cosf 24.18. (X=C°S' [у = sin Г
25. Несобственные интегралы
Вычислить интегралы с бесконечными пределами по определению или установить расходимость
00 J 25.1. 1* « J - 25.2. j(x-D2 00 J $
00 J 2SSP co 25.7. Jxdx I to J 25.6. J— 1 Vx (1 + x) CO 25.8. Jcosxdx Л 2
25.9. ’/-*Ц. -Id-») 25.10. _L xz+2x+2
Исследовать на сходимость интеграл с бесконечными пределами
25.11. /--/?• 3 2x2+7x-3 25.12. 3x3-2x2
25.13. f- 2 xz+2Vx 25.15. J 3^ +3 25.17. f-— i xi!x 25,19. 2 x3 +3x+2 4 25.14./ * {x+Vx 25.16. J- *** 2 I+Vx 25.18. /4^ 2x2 + l 25.20. 1 x-Jx +2
79
V. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
1. Дифференциальные уравнения. Задача Коши
Проверить, является ли данная функция решением соответствующего дифференциального уравнения
1.1. ху'+у=уг, У=~ 1-х
1.3. (x-y)dx + xdy = 0, у = х(5-1пх)
1.5. rv’ = v', v = r2+3
1.7. 2у = 3у2, у=—— х + 4
1.9. Г-4Г + ЗТ = 0, Г=4е' +2е3'
1.11. У+9/=0, y=xsin3x
1.13. z”-3z'+3z'-z = O, z =—е' 2
1.15. й-4й + 4и = 1, u=— 4
1.2. y'tg(x)-y = l, y=3sinx-l
1.4. dy+(2y-e’)dx = 0,
У = 5е'2х+|ех
J
1.6. (w')2=w2, w=—+ 1
1.8. У=—, y = x2lnx x
1.10. 4X’-20X' + 25X = 0,
X = 3e2’5'
1.12. у(1И)-13/ + 36у = 0, y = e’+e3x
1.14. У1Г)+8У+16>= COSX, y = icosx
1.16. w+w = chr, w = 0,5chZ
Проверить, является ли данная функция решением соответствующей задачи Коши
1.17.
у' = 2х у(0) = 0’У
1.18.
У = 3х2 yi) = o’
1.19.
/-у = 0 у(0)=1 . у = е’
,У(0) = 1
1.20.
у'+у = 0
уф = 0 . У = cosx у'ф=о
80
y" = 24x
i.21.b'+>-=A >=______i_
I y(l) = l x(l-lnx)
1.22.
>(0) = l
У(0) = 1
,/(0) = 2
y = x4+x2+x + l
Решить задачу Коши и построить интегральную кривую
1.23. У = 2х у(0) = 3 1.24. У = 3х2 ,у(0) = -1
1.25. 1.27. Ч мГц у § к 11 ч-' о V w NJ II О 11 1 и uj С* И 1.26. 1.28. -|”1 .s ° § II 11 <Л Z—. ° х е
1.29. — сч II II o' о 1.30. у(0) = 0 У(0) = 0
Для данных уравнений определить область, где существует и
единственное решение задачи Коши
1.31. у' = х2+у2
1.33. у = — У
1.35. у’= 3^
1.32. / = 71-у2
1.34.у=2±1 Х~У
1.36. y' = yjx2-y
2. Дифференциальные уравнения первого порядка
Найти общее решение или общий интеграл уравнения с разделяющимися переменными
2.1. jdx-xdy = 0
2-3. у' = ху
2.2. y2dx-x5dy = 0
, е~у
2.4. у' =-
X
81
2-5. y = cosx(l+j?)
2.7. du+w3d/ = O
2.9. у'= e*ylny
2.Ц. w' = w(x2+2x + 3)
2.13. >/l-x2d>’+>/i-yzdx = o
, ,, . 1 + u2
2.15. «=-----
1 + x2
2.17. Х' = У2°*У 2x
2.19. y, = 2x-3'
2.6. у = cos2 XI+*2)
2.8. dT = Txdx
2.10. y' = e? lnx
2.12.y’ = t(y2 + 2y+l)
2.14. y' =
2.16. % =
l+%2
2.18.
xex
2.20. yf = 2y~x
Решить задачу Коши для уравнения с разделяющимися переменными
2.21. 2.23. У'=х2у Х°) = 1 А 2а „ Vl-x2d^-— = 0 2У Х0) = 5 2.22. [У = 2у2х [ИО = -1
2.24. fdy-2e yxdx =0 L Х0) = 0
2.25. х = 2/(1+х2) х(0) = 1 ydx+xdy = 0 2.26. dx-2r(l+x2)dz = 0 r(0) = -2 ’ 7 . о , _
227. >ф = 1 [, i+'2 2.28. у dx+x dy = O X5) = 7 . ^y1 у ~
2.29. = г Зх2 х(0) = 1 2.30. 3x2 4 X-—) = 1
Зл
Найти общее решение илн общий интеграл однородного уравнения
2.31.у=2—+ 1
2.32.
X
82
2.33. у' = exp(-^) + Z х х
2.35. x’ = Jl^+-
N t2 l
m • 2 W U
2.37 u = cos —+—
x + ycos—
2.39. v' =------S.
у xcos—
2.34. y'=2^+Z + i
X___x
2.36. x'=---x2 — t
2 38 dW ,2 + w'-w2 dz i2
2 У2 2
x exp(-^) + /
2.40. y' =----г----
УХ
Решить задачу Коши для однородного уравнения
... х2 + у2 v л 7* ш и к>
2.41. f ху ?(1)=1 2.42.
2.43. .. Г-Зх t х(2) = 5 2.44. , Г+Зх X = г х(5) = 2
2.45. + см |сч О гч| к и 2 3 II 2.46. у_>/х2+/+у Я1) = 0
Найти общее решение линейного уравнения
2.47. у + ^ = 1 X 2.48. у’-^ = 1
2.49. у'-—=х X 2.50. У+^ = х X
2.51. /dx-(x+r3)d/ = 0 2.52. xdM’+(H’-x3)dx = 0
2.53. у' + 2у = е~ж 2.54. у'—2у = ех
2.55. у . V2 -2ху = 2хех 2 2.56. у +2ху=е
83
Решить задачу Кошн для линейного уравнения
2.57. 2.58. у'-— = -lnx
Xl) = 4 y(i) = i
2.59. + и и 2.60. 11* II >s| К + 4
. XI)=0 XI)=3
2.61. У+^- = х2 2x 2.62. У-^ = х3 2x
XI) = 2
3. Понижение порядка дифференциального уравнения
Найти общее решение дифференциального уравнения последовательным интегрированием
3.1. У = х 3.3. y’ = 4x 3.5. y' = cos3x 3.2. у’ = ех 3.4. У = ^ 3.6.yW=sinx
Решить задачу Коши
У = е2х y’ = i[x
3.7. у(0) = 1 3.8. Х0) = 2
У(0) = 3 У(0) = -2
Х = 1 м
ю УМ = 2
3.9. • У(0)=1 зло. Х0=з
У(0) = 0 У(1) = 2
/(!) = -!
Найти общее решение дифференциального уравнения, вводя новую неизвестную функцию z(x) =
3.11. у'х = у"
313. y'tg(x) = y'
3.15. tx"+x’ = t
3.12. 2ху" = у"
3.14. y” = y'th(x)
3.16. xw" — w” = x
84
Найтн общее решение дифференциального уравнения или, если заданы начальные условия, решить задачу Коши, вводя новую неизвестную функцию р(у) = у'
3.17. у’ = у'2
3.19. уу’ = у' + у'
?У = -1
У(1) = 1
У(1) = 1
3.21.
3.18. уу'+у'2 =0
3.20. у=уу
3.22.
у’ = е2у у(0) = 0 У(0) = 1
4. Линейные однородные дифференциальные уравнения с постоянными коэффициентами
Проверить, являются ли данные системы функций линейно независимыми в области определения
4.1 1,х
4.3. х,2х,х2
4.5. ех,хех
4.2.1,х, х2
4.4. 1,2,х
4.6. е1 cosx,е1 sin х
Вычислить определитель Вронского для данных систем функций
4.7. х,ех
4.9. е-х,хе'
4.10. sinx.cosx
Записать фундаментальную систему решений линейного однородного дифференциального уравнения, зная корни его характеристического уравнения
4.11. X, = 1,Х2 =2
4.13. X, =0,Х23 =2
4.15. Х|23 = 0
4.17. Х| =3-2i, X2=3+2i
4.19. X, = 31, Х2=-3/
4.12. Х1>2=1
4.14. Х|2 =0,Х3 =-1
4.16. Х| 2=-3, Х3=5
4.18. X, =-3-f,X2=-3+i
4.20. Xj = 0, Х2 = -1, Х3 = 1
85
Восстановить линейное однородное дифференциальное уравнение, зная его характеристическое уравнение
4.21. 9Х2—6Х + 1 = О 4.22. Х(Х + 1)(Х+2) = О
4.23. Х2+ЗХ+2 = 0 4.24. (X2+ 1)2 =0
4.25. 2Х2 - ЗХ - 5 = О 4.26. X3 = О
Составить линейное однородное дифференциальное уравнение с постоянными коэффициентами, зная фундаментальную систему решений
4.27. ех,е~х
4.29. ех,хех
4.31. sin3x,cos3x
4.28. 1,е*
4.30. 1,х,х2
4.32. ех,е2х,е3х
Найти общее решение или, если заданы начальные условия, решить задачу Коши
4.33. у'—у = 0 4.34. у'+у = 0
4.35. у" + 2у' + у = 0 4.36. у"-2У+у = 0
4.37. у’+2/-у‘-2у=0 4.38. у"-2у'+2у' = 0
4.39. у’ - Зу' + Зу' - у = 0 4.40. у" + Зу' + Зу' + у = 0
у*-4У+Зу = 0 у'-2у' + 2у = 0
4.41. И0)=6 4.42.- у(0) = 0
У(0) = 10 У(0) = 1
у’+/=0 у"+у' = 0
,,, = 1 4.43. 4.44. Х0) = °
У(0)=0 У(0) = 1
. Г(0)=1 У(0) = -1
5. Метод подбора для линейных неоднородных дифференциальных уравнений
Определить вид частного решения, зная корни характеристического уравнения и правую часть /(х) дифференциального уравнения
5.1. X) =1,х2=2, /(х) = Зх+2 5.2. X, = 1,Х2 = 0, /(х) = 2х+3
86
5.3. X, = 1Д2 = 0, /(х) = 2хе"х
5.5. Х| = 1,Х2 =О> /(x)=3sinx
5.4. X, = 1,Х2 = -1, /(х) = Зхе-Х
5.6. X] = /,Х2 =-/, /(x) = 2cosx
Определить вид частного решения, не находя неопределенных коэффициентов
5.7. у*-Зу' + 2у = Зх + 2
5.9. у’-2у'+у = х2 +1
5.11. у“ + у' = х + 5
5.13. /-у' = 3е2х
5.15. у’+у=2хех
5.17. у‘ + 2у‘ +у = 3е~х
5.19. у’+Зу + 2y = 3cosx
5.21. y' + y = sin3x
5.8. у* + у = х2-1
5.10. /+/=2х-1
5.12. у" + у = х2+х
5.14. у"+у' = (х + 1)ех
5.16. у’ + у' = хе~х
5.18. у’+2у'=хе~2х
5.20. у* + y = -3sinx
5.22. y*-y* = 2xcosx
Найти общее решение неоднородного уравнения
5.23. у’ + 2у' + у=-2
5.25. у'-4у' + 4у = х2
5.27. у’ + 4 у' + 4у = ех
5.29. у' + у = 2ех
5.31. у'-у' = exsinx
5.24. у" + у’ = |
5.26. у* + 8у' = 8х
5.28. у" + 4у'+Зу = 9е-3х
5.30. y*-y = 2cosx
5.32. у' + 2у' = 4ex(sin х+cos х)
Решить задачу Кошн
5.33.
У+у = 2(1-х)
У(О) = 2
. У(0) = -2
5.34.
у'+9у = 36е3х у(0) = 2 у'(0) = 6
5.35.
у’ + у' = е у(0) = 1 у'(0) = -1
у*+4у = sinx
5.36.
у(0) = 1
у'(0) = 1
87
VI. РЯДЫ
1. Числовой ряд. Суммирование рядов Записать развернутое выражение для данного ряда
« ] 1.1. У-л=1л 1.2. f(-l)"i Л=1 л
“ 1 1.3. У — п=|2л 1-4. Л=1 3
со | 1.5. у! п=о"! со оЛ 1.6. у±-л=о«!
1.7. Z(-I)'’—L_ 00 1 1.8. У—!—
л=1 (2м—I)! и=1(2«)!!
СО _и 1.9. Y — со „2л 1.10. у—
И=]
J н у. sin(nr) ' п=1 2л-1 1 12 у COS(2”X) л=1 (2п)3
Найти по определению сумму геометрического ряда илн установить его расходимость
СО 1 из. у± Л=о2л 1-14- Е (-1)"^ л=о 2
” Г | у со
1.15. У — ^l2.5j 1.16. У 2Л л=0
со СО |
1.17. Х(-1)”3П л=0 L18. У(-1)л-^
СО 1 1.19. У-1-^о22" 1.20. £23л л=0
1.21. f 1п2л(2) 1.22. f (—1)л1п3л(4)
л=2 л=0
88
Найти по определению сумму ряда, раскладывая общий член ряда на простейшие дроби
« 1 1.23. £—!— „1«(л + 1) « 1 1.25. Е-4— л=|4и2 —1 «° | 1.27. 2 ! ~|(Зи-2)(Зи + 1) ” 77 1.29. £-5-^ „=ол + 6л + 8 « 1 1.24. У „Т1И(и+3) СО | 1.26. £ „ti(2«-l)(2„+5) СО 1 1.28. У „=!«(« *!)(« +2) « 54 1-30. я=1 и2+5л+4
2. Исследование на сходимость рядов с положительными членами
Проверить выполнение необходимого условия сходимости ряда
2.1. п=1 Зп +2 2.3. f ^12) П=1 л Vn + 4 2.2. £^±5 „НИ +4 60 х/и +• 4 2.4. „И(л2+3)
2.5. £ л=2 « + 5 «Ю „п 2.7. £% л=1 л 2.6. „ни+3 2.8. f^±3_ „.31п(л+5)
Исследовать ряд на сходимость с помощью признаков сравнения
СО 1 2-9- г А „ниЗ” 2.11. Z«2" Л=1 «О 1 2'З.Е-Л-^|2п + 2 2.10. f „нЗ"(л + 1) 2.12. Z—3" „=1 " “ 1 2.14. У—— „=13п + 5
89
2.15. У— t' оГ 2Л7 П=|Л +1 “ C0S(л) 2.16. £ nti 3" “ и 2.18. £-/- "‘'л2 +1
2.19. У — л=1 п со 2 2.21. Z4- л=1л +3 2.20. £.ln(n + 1> л=1 11 + 3 со 2 2.22. ” ‘л2+5
2.23. f 2"sinf— л=1 UnJ 2.25. £ л2 2" 2.27 v 1,2 + 3,1+4 n=i w4 +2л-1 2 29 V + 5и) л=1 л3+3 224 f 2"tgM л=1 \3 7 « И3+4 2.26. л=1 л3Зп 2.28. Х-”^+5п-— Л=1 л +5л-3 2.30. g'^”(”+S) л=1 л3 + 4
Исследовать ряд на сходимость с помощью признака Даламбера
со -уП 2.31 0=1 л! °О «5 2.33. П=1 л! 2.35. f Сл)! л=1(2л)! 2.37. f — л=!(3л)! со оЛ 2-32. 2 — л=1(2л)! “ л4 2.34. У—Г лТ1(2л + |)! 2.36. ^1(2л + 1)! “ п” 2.38. 2^- Л=1 л!
Исследовать ряд Коши на сходимость с помощью радикального признака
2.39. f (——] лТАЗл + lJ 2-40. л=А2н + 17
90
- ( 2л2 Y 2.41. У и=|(л+1J “Г 2л2 Y 242 МзХи
со Z \Л 2-43. М- л=1 <2n + lJ " л2 2.45. У—— Л=2(1пл)" 2-44. Z«2(т^Т л=1 (2л+1> 2.46. Z-«-лТ,(л + 1)2Л
Исследовать ряд на сходимость с помощью интегрального признака Коши
СО Т 2.47. X ~2 п=2 п(\пп)2 СО ] 2-49- Z—г— л=2 flvln/7 т 1 2.48. — п=2 «(1П «) “ 1 2.50. X ! Л=2л71п’л
00 п 2.51. 2 А л=12” “ 1 2.53. У — а п=\П 00 2 2.52. Л=1 И р-4п 2-54. X V n=l 3. Знакопеременные ряды
Исследовать на сходится данный ряд сходимость, установить, условно или абсолютно
3.1.f п=1 П 3.3. f л=2 « + 5 3.5. f л=| лЗ" 3.7. Е Л=1 \2л + IJ 3.2. И=1 3-4. f (-1)"-^-л=з 1п(л + 5) 3.6. £(-1)лл2л Л=1
91
39 у(-Ц"3'' ’ ‘ £1 (2л)! з.и. Ж л=2 Л-ДпЛ 3.10. £ (2л)! 3.12. f-Ж "=2лЛп3 Л
Вычислить сумму ряда с заданной точностью а
3.13. а = 0>1 Я=1 1 + ЛЛ 3-15. а = 0.01 л=1(1 + л)3 “ /_пп 3.17. Х~. а = 0,001 п=1 2 л! 3.14. а = 0,1 3.16. f (~1)Л а = 0,01 лТ1(1 + 2л)4" « (— п" 3.18. У^-, <1 = 0,001 £1 3"л!
4. Функциональные ряды. Область сходимости. Равномерная сходимость
Найти область сходимости функционального ряда
W 1 4->-л=1Л а> 1 4-3. X-V п=1„» -3«5 СО 2 4-5- Z Ж— п=|и’ +2+3 ® ( х >" 4.7. У — ^1U+1J 4.9 Х(х2~4х+3)" П=1 СО 4-2. £х" Л=1 со 1 4-4. „=1„-х2+2х+4 “ л5 4-е z -Л— "=1ЛХ +2+3 4-8 ХЖТ л=А 2х J 4.10 f (-х2-6х-8)" Л=1
Доказать равномерную сходимость функционального ряда на (
4.11. у п=о "! 4.12. Ж иТо 10"
92
® 1 4.13. Z-т- 2 , л=ои2(1 + и2х2) 4.15. £ л=0 п » е-"2-2 4.17. Y —r- л=0 « ® 1 4-14. i Л=ол (2 + cosnx) 4.16. f л=о 2" » е-"2? 4.18. у£ л=о 3" 5. Степенные ряды
Найти область сходимости степенного ряда
СО 5.1. £х" Л=1 СО л 5.3. Е(-1)"^- л=1 3 5-5. 1^- Л=1 п <30 л 5-7-л=1 и! 5.9. £и(х-2)" П-1 5.11. ftav л-2 5.2. i(-l)nx" л-1 СО уй 5.4. У — л=15 5.6. f (-1)"<^ХД1 л=1 <п 5.8. £и!хл Л=1 5.10 f ^1 и22" 5.12. п=2 Л1П2И
Разложить функцию в ряд Тейлора в окрестности указанной точки н определить область сходимости
5.13. у = е3х, х0=0 5.15. у = sin2x, х0 =0 5-17. y=-L,xo = 0 1-х 5.14. у = 1п(1 + 4х2), хо = 0 5.16. y = xcos3x, х0=0 5.18. у = —!-,хо=0 1 + Зх
5.19. у = 1п(1-х-6х2), Хе = 0 5.20. у = 1п(1 + х-6х2), = 0
5.21. у = (2-ех)2, х0=0 5.22. у = (3-ех)2, х0 = 0
93
5.23. у = 1пх, х0 = 1 5.24. у=1,хь = 1
5.25. y = sinx, х0 =2 5.27. у = 1п(х+5) ,хо=1 5.29. у, х0 = 3 2-х 5.31. у =sin2x, xq =0 5.33. у = sin3x, xQ =2 5.26. у = cosx, Xfl = -2 5.28. y = ln(x-3), x0 = l 5.3O. y = -L-,xo = 2 x + 3 5.32. у = cos2x, x0 = 0 5.34. у = cos5x, x0 = -2
Найти сумму степенного ряда, используя его дифференцирование или интегрирование
CO л 5.35. X — л=1 n 5.37. f (n + l)x” л=0 5.39. £(и + 1)(и+2)хв n-0 5.41. X(„ + l)x"~2 л=2 5.36. f (и + Ох”-1 л=0 m 5.38. „=ои + 1 5.40. £(и + 2)х"~2 л=2 5.42. f („ + 4)х5” п=0
Вычислить приближенно с точностью 0,001
0J 2 5.43. / е“5х dx 0 0.1 5.45. Jsin(10x2)dx 0 5.47. о х 5.49. °/-П(1+2*)<1х о х 0.1 9 5.44. J е"3х dx 0 0.1 5.46. J cos(10x2)dx 0 сия °Г 1 — cos2x 5.48. J dx о х 5.50.|^±^<1х о х
94
6. Ряды Фурье
Следующие функции разложить в ряд Фурье на указанных отрезках: а) в полный ряд Фурье по синусам и косинусам, б) только по синусам, в) только по косинусам, изобразить графики сумм соответствующих рядов Фурье.
6.1. у = 5-х а) [-л, л], 6) [0,л], в) [0,л]
6.2. у = 1 + х а) [-л, л], 6) [0,л], в) [О.л]
6.3. у = 1 + 2х а) [-л, л], 6) [О.л], в) [0,л]
6.4. у = 3-2х а) [-л, л], б) [0,л], в) [0,л]
6.5. у = 9-2х2 а) [-л. л], б)[0,л], в) [0,л]
6.6. у = 4 + 3х2 а) [-л, л], б) [0, л], в) [0,л]
6.7. у = 6х а) [-л, л], б) [0,л], в) [0,л]
6.8. у = -5х а) [-л,л], б) [0,л], в) [0,л]
6.9. у = 2 + |х| а) [-л, л], б)[0,л], в) [О.л]
6.10. у = 7-|х| а)[-л,л], б) [0,л], в) [0,л]
6.11. у = 2х2+3 а) [-л, л]. б) [0,л], в) [0,л]
6.12. у = \—3х2 а) [-л, л], б) [0,л], в) [О, л]
Указанные функции разложить в ряд Фурье: а) по синусам, б) по косинусам на указанных отрезках
6.13. у = 4+х , [0,3л 6.14. у = 1-9х, J0,2л]
6.15. II 1 Г "1 о Йя 6.16. у = 5х, Ч]
6.17. У = 1-Х, [0,2] 6.18. у = 1 + х. 0,3]
6.19. у = 1+9х, [-6,0] 6.20. у = 2-7х, -1.0]
6.21. [0.{ 6.22. у = 6+3х, 0,1] 5J
6.23. у = 8, [0,4л] 6.24. у=3, 0,3 л]
95
VII. КРАТНЫЕ ИНТЕГРАЛЫ
1. Повторное интегрирование
Вычислить повторные интегралы
1 1 1.1. JdxfCx + ^dy 0 0 1 2 , 1.2. fdyf(x2+y)dx 0 0
1 X 1-3. Jdxf(x+j/)dy 0 0 1 y 1.4. fdyf(x2+y)dx 0 0
1 X 1.5. JdxJxdy 0 1 1 ? 1.6. [dp j xdx 0 2
1 1 1 1.7. JdxJdyJ(x + z)dz ООО 1 1 У 1.8. JdyjdzJ(x + z)dx 0 0 0
1.9. JdyJdxjydz ООО 1 x2 x2+p2 1.10. Jdxfdp j x2dz 0 1 0
2. Двойной интеграл в декартовых координатах Вычислить двойной интеграл по прямоугольной области
ffxydS D 21' 12x^2 D 2.2. flx2pdS D l£x<3
0<yS3 0<y<l
fl(x + y)dS 23- 0£x<;i D' 2.4. ff(x2 + y)dS D
0^ y<. 1 D:
JJ(x2+y2)dS ff(3x2-y2)d5
2'5‘ D 0^1 0^ у <,2 2.6. D 0SxS2 D-. 0^y S2
96
Вычислить двойной интеграл по произвольной области, ограниченной заданными кривыми
Я" 2.7. D 2.8. ffd5 D
D-. y-x2,y = Jx D:y = x2,y = x
JfdS 2.9. о 2.10. D
D: у = х2 ,у = х3 D.y = x,y = x3
JJxd5 2.11. D 2.12. JJydS D
D:y = x2,y-4x D:y = x2,y = x
fl(x + y)dS 2.13. D 2.14. jfydS D
D:y = x2,y = x3 D:y = x3,y = x
JJxdS 2.15. D 2.16. tfydS D
D.y = x,y = \ — x,y = 0 D:y = x,y = l-x,y=0
flxdS 2.17. D 2.18. JJydS D
D:y = x,y = l-x,x = 0 D'.y = x,y = l-x,x = 0
jj(x + y)d5 2.19. D 2.20. fl(x-y)dS D
D:y = x,y = l-x,x = 0 D-.y = 4x,y = \-x,y = 0
3. Тройной интеграл в декартовых координатах
Вычислить тройной интеграл по прямоугольной области
fJJfx + y + zJdT v
3 1. 05x51
Г:05у51
05z51
v
3.2. 05x^1
Г:05у52
05z53
97
ПК*2 +у2 +z2)dv V 3.3. O^xSl K:lsyS2 2SzS3 nJ(-*2-/+z2)d»z V 3.4. 1Sx52 V;}<. y^2 1SZS2
Ш(*+-)<1Г v У 3.5. 0 5 x 5 1 V-\<,y^e Osz^l JJJxsinydK V 0<x51 3.6. Г:0<у<у 0Szi3
Вычислить тройной интеграл по произвольной области, ограниченной заданными поверхностями
JJJdr V 3-7. 2 r~ у.У = х = z = 0,z = 3 Jfldr V 3-9. 2 з v. У = х ,y = xJ JJfdr V 3.8. 2 у.У^х -У = х z = 3,z = 0 JJJdr r 3.10. 3 у. У = х ,y = x
z = 0,z = 3-x-y JJJxdK V 3.11. 2 у.У = Х .Z = 0 z = 3,y = 4x JJJ(x + y + z)dK V 3.13. j 3 y.y = x -y = ^ z = 0,z = l z = 0,z = 2-x-y JJJydK У ЗЛ2. 2 n у.У = Х .2 = 0 y = x,z = -3 Щ(х-у-х)<1И V 3.14. 2 у.У^х -У = х z = 5,z = 6
98
fJJ(x + z)dr fff(y+z)dK
и 3.15. . У = х,у = 1-х у = 0,z = 0,z = l JJjdr V 316. ' y = x.y = 1_x y = 0,z = -l,z = l fflxdK v
3 I7' x = 0,y = 0,z = 0 x+y+z=l flf(z-y)dy У 318‘ у x = 0,y = 0,z = 0 x+y+z=2 flf(z-x)dK V
3 19 у x = 0,y = 0,z = 0 x+> + z=-l 3-20' у x = 0,y = 0,z = 0 x+y + z = -2
4. Двойной интеграл в полярных координатах
Вычислить, переходя к полярным координатам
4.1. ° 2 2 * -1 ff^x2+y2dS 4.2. ° г r.x2+>251
x^0,j<>0 JJ(l-7x2+/)d5 4.3. ° 2 2 D X +У 51 J(l-A/x2+>2)d5 4.4. D Dx +У
x>0 y>0
4.5. 1 £X2 +y2 <.4 4.6. ^x2+y2 D_\^x2 +y2 ^9
x>0.y>0 4'7' x<0,y^0 D' 2 2 x2 +y2 ^1 xiO,y>x JjV(^+/)3dS D 4'8' x^0,y^-x D- 2 2 x2 +y2 ^9
99
Вычислить площадь фигуры, ограниченной заданными кривыми
49 У2-2у+х2 = 0 у=0,у=х 4.10. У2-4х + х2 = ° х=0,у=х
4Л\.у2~4у+х2=0 У=0,У = 43х у2-8х + х2=0 4.12. х У = °-У=^
4.13. У2-^2-^ У2-4у+х2=0,у = у/Зх у2 -4х+х2 =0,у=-тг- 4.14. V3 у2 -8х + х2 =0,у = 0
5. Тройной интеграл в цилиндрических координатах
JJJ^x2+y2zdK V 5.1. x2+y2sl V:xiO, z£0 ySO.zil fff~~=r v zjx2+y2 5’3' lSx2+y254 V: xSO.ySO l<Sz£3 5.2. x2+y2<l Kzy^O.z^l yix,zSe fff~^ V y]x2 +y2 5’4' !Sx2+y2^9 Г: x>0,y£x O^zSl
Вычислить объём тела, ограниченного заданными поверхностями
y2-2y + x2 =0 5.5. x=0,y=x z = 0,z = 9 y2-4y+x2 =0 5.7. x = 0,y = ^3x z = 0,z = x2+y2 y2-4x + x2 =0 5.6. y = 0,y = x z = 0,z = 3 /-8x + x2=0 5.8. x = 0,y> = — •Л z = 0,z = -x2-y2
100
6. Тройной интеграл в сферических координатах
Вычислить объем тела, ограниченного заданными поверхностями
z>0
6Л X2+/+Z2=l
Z > у]х2 + у2
6.3. ’____
zi 71-х2-у2
65 -Jx2+y2£z^x2 + )? z2 + x2+/=l
Вычислить тройной интеграл
fl[(x2+p2+z2)dK
б7’ у.0<г^у]х2 + у1 zi^t-x2-у2
ffM^+z+z2)3^ v
5.9. Г~2 2*
v zsjxt+y2 'z^\-x2-y2
z^O
6-2. 2 2 2
x2 +y2 + z2 =4
6.4.
z^7l-x2-y2
6.6. -^x2 + yi^z^x2+y2
liz2 + x2 + y254
fff(x2+/ + z2)dr У 6-8. r-----
y.zi-^x2+y2 zsO
Hf7(x2+y2+z2)3dr 6.10. v
V: 1S x2 + y2 + Z2 <, 4
101
VIII. ТЕОРИЯ ПОЛЯ
1. Дифференциальные операции в декартовых координатах
Вычислить градиент скалярного поля в указанных точках
А 1.1. «= ,А/(1,2,3) У • , 3 4 2 1.3. и = +-,М(1,1,1) х у Z 1.5. « = х2+cosyz,Af(l,n,l) 1.7. и=хе>®,//(1,1,1) 1.9. u = yln(x + z),A/(2,3,4) 1.2. u = —,M(l,2,3) z 2 3 5 1.4. м=4— X у Z 1.6. и=у2-sinxz,//(—,5,л) 1.8. и = ре2х-',Л/(1,1,1) 1.10. u = xln(2y + 3z),//(l,l,l)
Вычислить дивергенцию векторного поля в указанных точках
1.11 " = {3x2,2y + z,z-2yJ 1.12. a = {3y2,2x + y, z3 - x}
Л/(0,1,1) //(5,1,3}
а = {cos xy.sin ху, tan z} 5 = {sinxz,cosyz,sin3z}
113‘ Л/(1,-.-) 2 4' 1.14. //(!,-,-) 2 2
1 15 S = {x + e2y*>' + «2l,z+e2’r} 1.16. а ={у+2ех,х+е2у,2г+ег}
//(1,1,1) Л/(1,1,0)
1 17 2 = {ln(2x + z),lnz,ln(x-z)} 1.18. а = {2х+>',Зг+2}’,4>,-г}
’ /*(2,5,7) Л/(0,1,0)
1.19 5сЬ'2+«2*,*2+е3*,>2+е2х} 1.20. а = {у2 + In z, х2 + In Зу, z3}
' //(0,0,0) Л/(0,1,1)
Вычислить ротор векторного поля
1.21. a = {y,-2x,z2} 1.22. а = {3z,-2y,2y}
1.23. a = {x,yz,-z} 1.24. a = {yz,2xz,xy]
102
1.25. a = {x,-3z2,y}
1.27. 3 = {-х2у2,4,х]
1.26. a = {sinx,2z2,e2r}
1.28. a={3y,-3x,x]
2. Интегральные операции векторного анализа
Вычислить поток векторного поля через замкнутую поверхность с помощью формулы Остроградского
2.1. 3 = Px^*^} S:x + y + z = l,x = 0, y = 0,z=0 2.2. a = {x,3y,e*} S:x-2y + z = 0,x = 0,y = 0,z = 0
2.3. a={z2 + 2x,-2y,2z} S:x2 + y2 = l,z = 0,z = 4 2.4. a = {ey +2x,sinz-y,5z +x2} S:x2 +y2 = z2,z = 0,z = 4
2.5. a = {z,-4y,2x} S:z=x2 + y2,z = l 2.6. a = {x+z,x-2y,x} S :x2 + y2 = l,z = x2 + y2,z = 0
2.7. a = {2x,y,-z} S:z=S-x2-y2,z = x2+y2 2.8. a={3x,y,-z} S: z=6-x2 -y^z2 = x2 +y2,z 0
Вычислить циркуляцию векторного поля вдоль замкнутого контура L, лежащего в плоскости хОу (обход против часовой стрелки)
a = {x2-y,3x} a = {3y-x,y} L: треугольник с вершинами
2.9. L: треугольник с вершинами 2.10.
A(0,0),B(I,2),C(-I,2) A(0,0),B(2,l),C(-3,2)
2.11. 5 = ^-3z2->> L: окружность x2 + y2 = 4 3 = {3x + 5,2y) 2.12. 5 = {0>-x.3'} L: окружность x2 + y2 = 9 a = {5x+3,y-2}
2.13. L: прямоугольник с вершинами 2.14. L: прямоугольник с вершинами
А(4,1),В(—4,1),С(—4,—1),D(4,-1) A(0,0),B(3,0),C(3,2),D(0,2)
103
IX. ТИПОВЫЕ РАСЧЕТЫ
1. Аналитическая геометрия
1. Найти вектор т (табл. 1.1)
Таблица 1.1
№ варианта а ь с т
1 В; -1; о) (-1; з) (0; 2; О а+2Ь-Зс
2 (о; 2; з) (-1; 2; з) (-2; з; 2) а-АЬ + Зс
3 (-2; Л з) (0; -1; О (2; з) -2а + ЗЬ+с
4 В -2; 0) В; 0; 1) (2; -2; з) Аа+ЗЬ-с
5 (2; о; з) 3; 2) (1; 0; 2) За-Ь + 2с
6 (-2; з; О (-1; з; О (о; з; •) -За + Ь + Ас
7 (-к 0; -2) (-1; 1; о) (2; з; -2) 2а+ ЗЬ-Ас
8 (о; 3; 2) (2; -и з) з. о) Аа-Ь + 2с
9 (1; 3. -2) ('= з; -1) (1; 0; 3) -За + АЬ + 2с
10 0; -1) (о. 1; -1) (3; -1; -2) 2а + АЬ-с
11 (з; 0; 2) (2; з; -О (0; -2; 3) Аа-2Ъ+Зс
12 0; -2. 3) (1; з) (3; 0. 2) -а+Ь + Ас
13 (0; -2) (з; О (3; -2; 2) 2а+Ь-Зс
14 3; 0) (з; -1; 2) (о; з; -2) За-АЬ+с
15 -2; 1) (к 0; -1) (3; 2; -2) -За+2Ь+с
16 (0; -2; -1) (з; •; -') (2; 0; 1) Аа + Ь-Зс
17 (3‘- 2; 0) (з; 2; -О (-2; -1; 0) а-ЗЬ+2с
18 (3; 1; -2) (1; -1; о) (-1; -3; о) -а + АЬ + 2с
19 (-1; 0; -1) (о. з) (2; з; 0 За + 26-4с
20 (-2; -з; 1) (о; и 2) (з; 1; 2) Аа-2Ь+с
21 В 0; -1) (-2; -2; 3) (2; 1. о) -Аа + ЗЪ + 2с
22 -з; О (-2; -1) (3; 1. о) 2а + Ъ-Ас
23 (-3; 0; -2) (-з; -2; О (з; -2; 0) Зо-4б + 5с
24 В -2; 1) В -3; 0) (-2; з; -О -Аа + ЗЬ+ 5с
25 1L. 2; 3) (-3; -1. 0) (-2; -и •) 5а + 36-4с
26 0, 3) В -О (з; -2 ; О Зй-56+4с
27 3; -2) (-з; 2; 0) (-3; -к О -Аа + Ь + Зс
28 3; 2) (->• з; -2) (о. 2. О 5а + АЬ-Зс
29 В 3; 0) (-2= -1; з) (з; 2; О а-2Ь + Ас
30 (-и А. 0; 1) в -2; 0) -2а + Ь +Ас
104
2. Найти значения неизвестных (табл. 1.2), при которых векторы а и b коллинеарны
Таблица 1.2
№ варианта а b
1 -2-7+3-j + zk x-i -6- j + 2-k
2 -3-7+7-7+* 2-7-y-J+zk
3 2-7+У-7+* i-7+7-zk
4 7-7+y-7+z-* -14-7+2-7-2*
5 2-7+y-l-ic 7+3-7-z*
6 x-T-4-J + 2-k 3-7+8-7+z-*
7 2-7-8 7 + zk Z-7-4-7+?
8 3-7-у-7+Зк z-7+2-7-*
9 7-yj+2k хи +2-J-4-k
10 3-7+yJ-k xi +2-j +3-k
11 6-7-yj + Sk 3-7-2-7+zk
12 2-i^-j-z-S 7-yl-3k
13 5-7^-7-z-k x-i +2 j +2‘k
14 -з-7-у-7+к -J-j + zk
15 -2-7t3-7-z* X’T+3j-2-k
16 Х-7+3-7-4-Л 7-y-7+3-t
17 3-7-2-7+x-* -i + y- j + 3-k
18 -7+y-7-3k -x-i +2- j+3-k
19 -7 + 3-7 + z-k 2-7-yj + 6k
20 -4-7+3-7+z* 7+y-7-k
21 1-4- j + zk -X-7+3-7+*
22 2 7-3-7 + z k 4-7+y-j~k
23 x-7 + 6-T+Z’k 2-7+3-7+*
24 4-i + y]~3k 2 7-3-7+z *
25 -z 7 + 4-7+2-Jl 3-7 + 2-7-Z к
26 Л-7+7-2* -2-7 + yJ + k
27 -7+yj-S-k x-i +3- j + k
28 x-i +2-у + 8-Г ~7+y-j-4-ic
29 -2 i + у j - 4 к 3-7-5-7+zk
30 4-/ -5-j-z-k -g-7+y7-k
105
3. Даны координаты трЕх точек Л,В,С (табл. 1.3). Найти скалярное произведение векторов АВ и АС
Таблица 1.3
№ варианта А в С
1 (3; 0; 1) (-1; -2; з) (-1; -2; 0)
2 (-2; -1; 3) (-1; 2; 3) (-2; з; 2)
3 (-2; 1; 3) (4; -1; 8) (0 -1; -з)
4 (7; 2; -5) (6. о, -3) (3 2; 7)
5 (-5; 0; 2) (-4; 4; 3) (7 9; -2)
6 (-5; 1; 0) (6; -3; -1) (4 з; 7)
7 (8; 0; -1) (-1; 5; 4) (0 4; -2)
8 (9. 9, -2) (7; И; -4) (5 6; -1)
9 (4; -з, о) (Ю; 5; -4) (2 2; -з)
10 (-6; 1; -з) (-4; 4; -2) (3 2; О
11 (-5. 4; -1) (Ю, 5; -4) (0 4; -3)
12 (4, 5; -3) (0; 7; 3) (2 -6; -2)
13 (4; -5; 0) (1; -1; О (4 51 з)
14 (-4. -6; 1) (5; -2; 0) (1 -3; 7)
15 (-5; 4; 0) (6; 0; 3) (4 8; -1)
16 О; -4; -3) (5; 0; -1) (-2; 0; 6)
17 (4; -5; 1) (4; 1; -7) (0; 1 7)
18 (-1; 3; -2) (4; 9; -1) (1; з 5)
19 (-7; 2; -2) (-9; -3; 2) (0; 1 -4)
20 (-5; -t 1) (3; -1; 8) (-3; 4; 4)
21 (°. 3; -3) ("7; 5; 1) (1; 1; 6)
22 (-4; 0; 8) (7; 1; 9) (-6; -1; о)
23 (5; 1; -О (8; -3; 1) (-3; 0, 1)
24 (0; 5; 2) (-1; 0, з) (-4; 4, 1)
25 (-1; -8; о) (-6; 1; 1) (~4; 0; -1)
26 (5; 0; 5) (-4; 1; 0) (-3; 2; 7)
27 (-5; -2) (-9; 2; 2) (-3; 0, -1)
28 (7; 7; 2) (-2; 4; -4) (0; 3; 6)
29 (-8; з; 3) (-3; -9; 0) (4; 2; -2)
30 (-7; -1; 5) (-4; 3; 8) (-3; 2; 1)
106
4. Найти косинус угла между векторами (табл. 1.4)
Таблица 1.4
№ варианта а b
1 (-1; -1; -1) з; -2)
2 (0, 4; -1) (-5; -3; 0)
3 (1; 2; 3) (-2; -з; 1)
4 (3; о; з) (з; -1; о)
5 (-4; -3; -3) (-з; -3; -2)
6 (2; 1; 4) (4; з; 2)
7 (2; -2; -2) (4; 0; 0)
8 (0; 3; 1) (-з; 0; 5)
9 (3; 5; -3) (0; 4; -3)
10 (-1; 1; -4) (5; -2; -2)
11 (1; 2; 4) (5; О
12 (3; 3; 0) (2; 2; 2)
13 (-3; 3; -1) 0; -1)
14 (2; 1; 0) (5: -1; -1)
15 (2; -1; -2) (1; -О
16 (0; -2; 3) («; -2; 2)
17 (-2; 2; -2) (0. 4; -3)
18 (4. 2; 4) (-4; -4; -1)
19 (-1; 4; -2) (4; 4; -1)
20 (0; 1; 0) (2; 2; -5)
21 (°. 4; -3) (я з; -2)
22 (21 4; 1) (5; 4; 1)
23 (-1; 1; 2) (-2; -О
24 (I; -4; 2) (-2; 0; -2)
25 (-4; -2; 2) (-4; -2; -1)
26 (-2; -2; 2) (4; 4; -2)
27 (0; 2; 1) (з; 0; 3)
28 (-4; 3; 0) (•; 3; -2)
29 (-И 3; -3) (-3; -2; О
30 (0; 1, 2) (з; з; о)
107
5. Используя векторное произведение векторов АВ и АС (табл. 1.5), найти площадь треугольника АВС
Таблица 1.5
№ варианта А В С
1 (-2; -з; О (0; 1; 2) (3 2)
2 (з; -г 1) (1; 0; -1) (3 2; -2)
3 (-1; -2; 0) (-1; 0; 1) (2 -2; 3)
4 (-1; о, -г) (-1; 1; о) (2 3. -2)
5 (3; 2; 0) (3; 2; -1) (-2; -1; 0)
6 (-2; 0; -1) (0, 1; -1) (3; -1; -2)
7 (0; -1; -2) (3; -1; 1) (з. -2; 2)
8 (•; 2; 3) (-3; -1; 0) (-2; -И О
9 (0; .2; 3) (->; 2; 3) (-2; 3; 2)
10 (з; -2; 1) (0; 3; -2) (3 2; -2)
11 (2; 0; 3) (-1; 3; 2) (1 0; 2)
12 (1; 3; -2) (1; 3; -1) (' 0; 3)
13 (3; 0; 2) (2; 3; -1) (0 -2; 3)
14 (-2; -3; 0) (-3; 1; -2) (0 -3; 2)
15 (-2; 0, 3) (-3; 1; О (3 -2; 1)
16 (-2; 3; 1) (-1; 3; 1) (о з; О
17 (0. 3; 2) (2; -1; з) (1 3; о)
18 (и -2; з) (и -1; з) (3 0; -2)
19 (-2; 0; -1) (0; 1, 3) (-2; -3; 1)
20 (-3; 0. -2) (-3; -2; I) (3. -2; 0)
21 (-3; 2; 0) (-1; 3; -2) (-2; 3; -I)
22 (-2; 1. з) (0; -1; 1) (2. 1; 3)
23 (-3; 0; -1) (-2; 2; 3) (-2; 1, 0)
24 (0; -2; -1) (3; 1; -1) (2. 0; 1)
25 (1; 2; 3) (-3; 1; -2) (-3; -1; 1)
26 (-* -3; 1) (-2; 1; -О (3; 1; 0)
27 (з; 1; -2) (1; -1; о) (-1; -3; 0)
28 (-2; -1; з) (-2; 3; 0) (3; 2. I)
29 -2; 1) (-2; -3; 0) (-2; 3; -1)
30 (3; о, 1) (-1; -2; 3) (-1; -2; 0)
108
6. Исследовать компланарность векторов а, Ь и с (табл. 1.6)
Таблица 1.6
№ варианта а ь С
1 (И 2; 3) (2; 0, 4) (2; -4; 2)
2 (4; 4; -3) (1; 0; 2) (3; 41 -5)
3 (2; >; 0) (-1; 3; 1) (5; 1; 2)
4 (5; 3; -2) (-5; -3; 0) (Я 3; -1)
5 (3; -1; 0) (3; 1; 2) (2; 5; 4)
6 (-2; 2; -2) (0; 4; -3) (-2; -2; 1)
7 (0; 2; 1) (1; 5) (3; -2; 4)
8 (2; -2; -2) (4; -1; -1) (-1; -1; -1)
9 (0; 2; 1) (3; 0; 3) (-3; 2; -2)
10 (-3; 3; -1) (-1; о, -1) (-2; 3; о)
11 (->; 2) (2; 0; 3) (1; 5; 2)
12 (0; 1; 2) (3; 3; 0) (-3; -2; 2)
13 (2; -1; 1) (1; 0; -2) (и -4; з)
14 (2; и 2) (3; -1; 0) (2; з; 2)
15 (2; 1; 0) (5; 1) (-3; 2; 1)
16 3; -3) (-3; -2; О 1(2; 5; -4)
17 (-4; -2; 2) (-4; -2; -1) (2; 1; -1)
18 (-1; 2; 2) (3; 1; 0) (X 4; 3)
19 (1; -4; 2) (-2; 0. -2) (3; -4; 4)
20 (3; 5; -3) (0; 4; -3) (-3; 1; 0)
21 (0; 4; -3) (5= 3; -2) (-5; 1; -1)
22 (0; -1; 3) (3; 1; 2) (4; 1; 5)
23 (-2; -1; -2) (-4; -4; -1) ,(0; 2; -3)
24 (0; 4, 2) (1; 3) (2; -1; з)
25 (-1; 1; -4) (5; -2; -2) (-«; 3; -2)
26 (2; и з) |(»; х 2) (0; 4; -1)
27 ('; 2; 4) (5; 1; О (-4; 1; 3)
28 (2; 4; 1) (5; 4; 1) (-1; 4; 1)
29 (2; 4; 2) (t 3; 1) (о; -1; 2)
30 (3; 4; 2) (2; 2; -1) (1; 2; 3)
109
7. Составить уравнение плоскости, проходящей через три заданных точки Я, Л, С и найти вектор нормали к этой плоскости (табл. 1.7)
Таблица 1.7
№ варианта А В С
1 (4; 2; 5) (0; 7; 2) (0; 2; 7)
2 (4; 4. '») (4; Ю; 2) (2; 8. 4)
3 (4; 6; 5) (о; 9; 4) (2; 10; 10)
4 (3; 5; 4) (8. 7; 4) (о. 10; 4)
5 (10; 6; о) (-2; 8; 2) (о; 8; 9)
6 (1; 8; 2) (з; 2; «) (5; 7; 4)
7 (6. 6; 5) (4; 9; 5) (4; 6; И)
8 (7; 2; 2) О; 7; 7) (5; 3; 1)
9 (8; 6; 4) (10; 5; 5) (s; 6; 8)
10 (7; 7; з) (о; 5; 8) (з; 5; 8)
11 (3; -2 1) ('; 0; 2) ('; 2; -0)
12 (1; -1; 0) (4; 3; 5) (’; 2; О
13 (1; 2; 3) (з; 2; О (4; з; О
14 (1; 2; 2) (2; з; 0 (з; 2; О
15 (2, 3; 0 (з; 4. 1) (4; 2; О
16 (2; -2) (з; 1; о) (4; 0; 1)
17 (3; 0; -0 (2; 5; 0 (з. 1; 2)
18 (-1-. 3 2) (1; з. з) (-2; 1; 4)
19 (-2; 1 5) (2; з; 6) (->. 2; 8)
20 (4; -2 •) (5; 1; з) (о; 1)
21 (1; 4; -з) (0; з; -2) (з; 5; •)
22 (6; 0; 0 (9; з; О (7; 2; з)
23 (-3; - 4; 5) (-1; -з; 7) (-2. з)
24 (5; -• 2) (о; 1; ') (2; 3; 0)
25 (1; -4; -з) (4. -5; -1) (з; -6; -4)
26 (0; 3; 5) (2; 6; 8) (->; 4; 3)
27 (-4; 5 0) (-7; 7; 1) (-3; 0; -1)
28 (2; 4; 7) (-•; 6; 9) (о; 5; 7)
29 (8; -3 2) (’; -3; 4) (Ю; -1; 6)
30 (-5; 4 з) (-7; 6; 4) (-5; 7; 5)
ПО
8. Найти точку пересечения прямой и плоскости (табл. 1.8)
Таблица 1.8
№ варианта Прямая Плоскость
1 л-З у+1 г-1 4 ” -3 ~ 1 2х-у+Зг + 4 = 0
2 х-4 у-5 г-10 3 6 3 х+у-г+7=0
3 х-6 у+2 z+2 5 ' 3 “ -5 2x + 3y+z + 10 = 0
4 х-7 у-4 г-8 2 " 2 ~ 11 3x+y+4z-5 = 0
5 х-9 у г-18 7 -6 18 5x-3j—z + 8 = 0
6 х-4у-1 г-11 2 8 14 х-2у + Зг-7 = 0
7 х-4 у-3 г-6 2 0 6 х + Зу+4г-11 = 0
8 х-13 у-5 г-3 12 10 “ 6 4х + 2у-Зг-3 = 0
9 х-7 у z-7 5 “-1“ 8 7х-2у+4г-8 = 0
10 х-4 у-9 z + 9 -8 “ -1 -19 2x+3j/-5z-4 = 0
11 х-1 у-2 ?+7 0 5 -8 х-2у+Зг + 10 = 0
12 х + 3 у+9 г-15 1 " -12 ” 12 2x+5j/-6z+ll = 0
13 х+8 у-8 z+5 2 4-7 х-Зу+7г + 8 = 0
14 х+б У~9 г+16 -7 = 11 -16 2x-4^+9z-10 = 0
15 х + 1 у+3 г-н -1 -5 7 3x + 5_y-z-6 = 0
16 х-1 у-3 г + 2 -4 13 -2 Зх-у+5г-25 = 0
17 х + 3 .у-2 z-1 7 6 -4 2х-Зу-г-15 = 0
18 х+2 у+1 г-5 -1 5 3 2х+2у+Зг + 8 = 0
19 х-4 у+3 z+1 5 " -3 " -2 x-4j-2z + 3 = 0
20 х-5 у-1 z-2 8-3 7 3x~2y+4z+3T = Q
111
Окончание табл. 1.8
№ варианта Прямая Плоскость
21 х у+4 г-3 -5 ~ -9 5 4x + 3y-z-37 = 0
22 х-3 у+2 z-4 Ю ‘ -7 0 3x-4y + 2z + 33 = 0
23 ;|° II Чт "1° 5x+2y+3z-39 = 0
24 х + 5 у+3 z-2 0 -6 " -3 x-5y-4z + 40 = 0
25 "I-II d'T In> II N> | N 6x + y-2z-l = 0
26 x—6 _y-4 z+2 5 ” 9 7x+4y-3z+10 = 0
27 x-8 y-3 _ z—1 7 " 5 " 4 2х+6у-4г-2 = 0
28 x-1 y-9 z+7 0 " 7 ~ -5 8x-6y+2z+8 = 0
29 x-2 y + 6 г-8 8-7 7 2x->> + 9z + 4 = 0
30 x+7 y+8 z-4 -9 ” -7 ” 6 9x+7y-6z-23 = 0
!. Линейная алгебра
1 Найти про '1 2 -Г изведение м '0 1 2 атриц А 'з о -г'] '12 3'
1. 3 0 4 4-5 0 2. 4 6 1 04-1
J 5 0> 1 1 -4 0 1 L Л 0 5>
3. '2 4 О' 3 1 1 '0 2 4' 1 3 3 4. '1 4 -2' 3 6 0 '0 1 Г 2 3 0
-1 3 5, '2 0 -2' 2 0 -1, '1 -1 0 J 1 5 '12 0' Л 4 “1 '4 0 1 '
5. 1 4 3 2 3 -2 6. 3 4-1 3 2-1
0 1 1 ? J 4 5 0 5 1 ? Л 0 2<
7. '3 4 О'] 2 2 1- 11 4' 2 0 3 8. '1 2 2' 3-10 '1 1 -5' 2 3 0
9. 1 0 5J '2 -1 О' 3 1 1 3 1 -2, '1 -5 О' 0 2 1 10. 4 0 5^ <1 4 6' 2 2 0 0 1 2> '11 О' 3 0 2
11. <° 4 2> '13 2' 0 5-1 J 3 °, '3 0 2' -15 3 12. <3 -2 4, '2 -1 О' 4 2 1 Л 2 “4> '1 5 -Г 2 0 3
13. 2 4 0, '3 2 4' 2 0-1 2 2 0 '2 -1 3' 5 2 0 14. Л 2 °, '5 0 5' 3 1 -1 Л 2 5> '-3 2 0^ 4 12
Л 1 L '-1 о Г 0 3 1? '3 6 О' 0 2 2, ' 5 6 О' J 0 3? '1 -1 3’
15. 5 3 0 1 3 4 16. -3 1 1 0 2 4
2 4 6 '5 2 1 -1 2 5J /3 0 2' <4 0 2> '1 -1 2' Л 5 6> '5 0 4'
17. 0-12 4 3 1 18. 2 3 2 3 6 0
-2 3 0 I2 1 2> <° 5 L 2 -2 3^
113
2. Найти произведение матриц
'1 3'
2 0 [1 -4 3]
1 5 (2 0 б)
.6 -з,
2
-1
'1 2 4 Г 0-162 1 -1 0 -2
-1
3
'2
О 5
4 ' -1
(1 0 2)
2
6. (2 0 -3 0)
114
7 |3 4 °' 1112
'2' 2 .-5.
я (~3 ° 1
(о 9 -1
'О -2
2 О
О 5 О
1
1
4
9.
3
О
11.
13.
15.
21.
(2
(4
10.
2
2
3
1
-1 О
2
-3
(4
-1
-3)- -1 5
4
1
6
О' 3 2
12.
3
2
О
5
( 1
9
3
4.
2
3
(5
0 4)
14.
'-1
4 О
7
О'
2 1 -2.
О -3
5 1
1
-2
-2 1 2
0 5 3
(4
16.
17.
19.
'6 2
-5 О
. 1 .
18.
2 О
3
'3 4 1 1
(4
О' 2
1 2)
'5
2
3
-1 О 7
-1
2
6, 5 1
-8
(6
(1 -1 2)- О О
20.
(3
О 6)
115
23.
24.
25.
27.
29.
26.
'O'
_‘3 О 1 4 4)
<5.
'3'
30. 2 (1 2 -4 3)
<5,
3. Вычислить определитель
2 3 1 2 2 0 5 0 2
1. 0-12 2. -2 1 0 3. 3 1 2
0 3 4 3 1 4 -1 0 1
4 5 0 1 1 2 3 2 1
4. -12 3 5. -2 0 3 6. -10 3
3 2 3 5 0 1 2 0 4
4 0-2 3-10 1 4 3
7. 5 1 0 8. 2 5 4 9. 0-2 5
3 2 1 0 1 2 1 2 0
4-12 0 1 3 2 I 0
10. 2 1 4 11. 2 0-1 12. -1 3 1
0 3 0 1 2 0 5 0 2
0 2 1 1 3 2 3 1 2
13. 3-2 4 14. 0 4-1 15. 4 0 5
1 0 5 2 0 3 0-13
116
3 0 -1 1 0 2 1 0 2
16. 1 2 1 17. 3-10 18. 3 4-5
3 2 0 2 4 1 0 6 1
2 4 0 3 1 2 2 0 3
19. 1 1 3 20. 3 0 1 21. 1 5 2
0 5 2 -2 3 0 -10 2
1 3 С -12 0 1 -1 2
22. 0 -1 2 23. 0 1 2 24. 0 3 4
2 4 С 2 4 3 2 3 0
3 -1 С 1 -2 1 -12 0
25. 2 1 2 26. 0 3 0 27. 3 1 4
0 3 2 2 2 1 2 0 1
3 0 1 2 1 0 2 2 3
28. 2 1 1 29. -12 2 30. -12 3
3 0 2 3 1 0 0 1 0
4. Вычислить определитель, разложением по элементам первой строки
а Ь с 1 т п b с a
1. 1 4 6 11. 3 -1 2 21. 2-3 0
2 3-1 2 0 4 5 1 1
X у Z р q г U V w
2. 2 3 5 12. 2 2-1 22. 3 0 -4
-10 2 0 3 5 5 1 2
к 1 т g h i ' J *
3. 1 2 -1 13. 5 0-1 23. -4 1 1
3 0 4 2 4 3 5 3 0
г s t def def
4. -2 3 1 14. -1 2 1 24. 3 2 0
1 2 2 5 5 4 -4 1 4
117
7.
-2 4
«’ j к
« 2 0-3
1 5 2
9.
' j
—4 2
О 3
17.
27.
3
-3
10.
s t
-5 1
О 3
а Ь с
18. -1 3 4
5 0 2
/ т п
19. 0 1 5
-3 2 4
9 г S
20. 1 0 -2
4 3 4
с d е
28. 1 4 -3
2 0 5
S t и
29. 2 -5 3
0 4 2
30.
У
-2
3
О
о
2
к
3
5
g
5
2
h
2
О
h
3
1
2
2
1
О 4
1
5
5. Найти матрицу, обратную данной, и сделать проверку
р 1 3 2 0 3' 2 3 Г
1. [20-1 11. 1 5 2 21. 0-12
11 2 0, -1 0 2, .0 3 4,
Г1 0 21 '1 -2 2' ' 1 12'
2. 3-10 12. 0 3 4 22. -2 0 3
.2 4 L 2 3 0, . 5 0 •>
'2 1 О' Г1 3 О' <2 2 О'
3. -1 3 1 13. 0-12 23. -2 1 0
5 2 г\ 2 4 0,
118
4.
3
1
3
О
2
2
14.
'3
2 О
О' 2
2
24.
'3
-1
2
О
1
3
2
О
О
3
4
6. Решить систему
1.
3.
*1 + *2 ~2*3 + *4 + *5 =0 2х] -*2 + *з +2*4 +*5 =0 Зт, + *2 - 6*з + 3*4 + 3*5 = О -2*1 + *2 - 3*з +*4=0
*, - 2*2 + *3 - 3*4 = О 5*! ~*2 +4*3 +2*4 =0
{*! - 2*2 + *3 + *4 - 2*5 = О 2*] +*2 -2*3 + *4 -*5 = О
{2*! — *2 +*3 -2*4-*5 =0
4*! +*2-*з-3*4+*5 =0
119
5.
7.
9.
11.
13
15.
17.
19.
21.
23.
-Эх, + Х2 “ Х3 +3x4 + 2х3 =0 6xt-2x2+3x3-x4-xs=0 xt +x2 -4x3 + x4 -3x5 = 0 3X] - 4x2 + x3 - 2x4 = 0 9xj +7x2 -x3 + 3x4 = 0 6x, - 3x2 + 2x3 - x4 = 0 8x, + 2x2 + x3 - x4 + 2x5 = 0 4Xj +2x2 -3x3 + x4 -3x5 =0 12x, - 3xj + 2x3 - 2x4 + x5 = 0 Их, -10x2 -3x3 + x4 =0 X] + x2 -10x3 +12x4 =0 -3x, + 2x2 + 6x3 - x4 = 0 9x| +4x2 -x3 + 5x4 -x5 =0 -3x| - 3x2 + 2x3 - 3x4 + 2xs = 0 6x, + x2 - 4x3 + 2x4 - xs = 0 -10X] +5x2-x3 + 2x4 = 0 5X] -x2+3x3 -x4 =0 -15x] + 2x2 - 2x3 + x4 = 0 4xj +x2 -3x3 +4x4 -2xs =0 -2xt -x2 + 2x3 -3x4 +x5 =0 6Xj + 2x2 -4x3 +x4 -3x5 = 0 4xj +2x2 + x3 -2x4 =0 14x( -6x2-3x3 + x4 =0 -X] +x2 + 2x3 -x4 =0 8x( -3x2 +x3-3x4 +2xs =0 -4Xj +x2-2x3 + x4-xj =0 12X| -2x2 +3x3 -x4 +x5 =0 6X| - 3x2 - x3 + 2x4 = 0 —4xj +x2 + 2x3 -3x4 =0 2xj -2x2 +x3 -x4 =0
3X] +x2 +x3 -3x4-x5 =0
6X| -3x2 — x3 +x4 +4x5 =0
4x, -x2 -2x3 -x4 -5xs =0 8x, +x2 + 2x3 +x4 + 2xs =0
5X] +x2 +x3 +2x4 -xs =0 10x, -3x2 -x3 -x4 +5xs =0
6Xj -x2 -3x3 -x4 -4xs =0 12x, +x2 + 2x3 +x4 -x5 =0
7x| + 2x2 - x3 + 2x4 + xs = 0
I4x| -3x2 +x3 -x4 -2xs =0
8x] -2x2 + x3 + 5x4 -3xs =0 16x! + 2x2 -2x3 +x4 -xs =0
9xj - x2 - 4x3 - x4 + 4xs = 0 18X] +3x2 +x3 +3x4 -5xs =0
20 f10il+j:2“2x3+3x4-2x5=0
[20x! + 3x2 + x3 + 2x4 - 3xs = 0
22 f*i+x2+4x3-5x4+xs=0
3xj -2x2 + 3x3 -x4 -2x5 =0
J2x| -2x2 +x3 -4x4 -5xs =0 [6xj + 3x2 - 2x3 + x4 - 3xs = 0
120
25.
27.
29.
4*1 +x2-2x3+2x4 +xs =0 -8л, - 2x2 + Зх3 - x4 - 2xs = 0 12x, + 2x2 - 3x3 + x4 + 2xs = 0 -21x, + 4x2 + x3 - 4x4 = 0 7x, + 2x2-2x3 + x4=0 14x,-3x2+3x3-x4 = 0
-Эх, + 3x2 + x3 - 4x4 - xs = 0 x, + 3x2+2x3-x4-3x5=0 2x, — 3x2 + 3x3 — x4 + 2x5 = 0
|3*i +x2-3*з -x4 +2xs = 0 26. <
[9X] -2x2 +x3 +2x4 -4xs = v
f4x, - 2x2 + x3 + 2x4 — Xj — 0 ^Oe 4
(12x, +5x2 — x3 +x4 +3x5 =0
30.
5X| + x2 + 5x3 - 2x4 + 3x5 = 0 15x, -4x2 +x3-6x4 -x5 =0
7. Решить систему
(5х, + x2 + Зх3 -2x4 +3xs = 1 [15x, +4x2 +2x3 -6x4 -xs =2
2.
С/х, + 2x2 —2x3 + 2x4 — xs = 3
[14X] + 3x2 + x3 - 3x4 - 2xs = 2
4.
{4x| + 2x2 + 2x3 + 2x4 - x5 = 4
12xj +5x2 -x3 +3x4 +3x5 = 1
6.
(6x, -x2 — 2x3 -x4 —4xs =3 |12x| +x2 + 2x3-2x4-xs =1
8.
3x] +x2 -3x3 -2x4 +x5 = 2
9x,-2x2+2x3+ x4-4xs =3
10.
[5x, +x2 + x3 +2x4 -xs =2 [10x| -3x2 -2x3 -x4 +4xs = 1
12.
{2x, - 2x2 + x3 - 3x4 - 4xs = 1 6X] +3xjj -2x3 + 2x4 -xs =4
14.
-18X| +4x2 +2x3-4x4 -xs = 1 -6x| - 2x2 - 2x3 + 3x4 + 3x5 = 2 12X| -2x2 +3x3 -x4 + x5 = 3 9x, +4x2 -2x3 +5x4 -Xj =2 -Эх, -3x2 + 2x3 -3x4 +2xs = 3 6x, +x2 —4x3 +2x4 -x5 = 1 21X] +3x2 + 2x3 -4x4 +3x5 = 3 7x, +2x2 -3x3 +x4 -2x5 =1 14x, -3xj + 2x3-x4 +xs =2 15x, -12x2 -x3 +3x4 -xs =2 x, +xj; -10x3 +x4 +5xs = 3 -3X| + 2x2 + 6x3 - 2x4 + x5 = 4 -8x] +x2 -3x3 +x4 +2xs = 3 -12X] -2x2 +x3 -2x4 -2xs =4 4x, +x2 -2x3 + x4 -xs =2 8x, +2xj+3x3 -x4 +2xs =4 4x, + 2x2-x3 + 2x4 -3xs =2 12x] - 3x2 + 2x3 - x4 + xs = 3 6x, - 3x2 - 2x3 + x4 - 3x5 = 3 -4x] +x2+x3 -3x4 +2xs =4 2x, - 2x2 + x3 - 2x4 + 5xs = 5
121
16.
(4*| ~*2 ~3*3 -*4 -5*s = 4
l8*i + *2 + 2х3 +2х4 + х5 =3
fxi + *2 + 2х3-5*4 + х5 =3
[ЗХ| -2х2 +2*3 -*4 -Зх5 = 4
18.
3*1 + *2 + 2*3-3*4-х5 = 4 .6*1 - 3*2 -х3 + 2*4 +4х5=2
20.
{Юхх+х2-2х3+Зх4-2х5=2
120*1 +3*2 +х3 +3*4 -2х5 = 4
22.
Г2*]-*2+3*з-2*4-х5=1 [4*1 + х2— 2х3 -Зх4 + *5 =3
24.
9*1+*2-3*з+*4+4х5=1
.18*| + 3*2 + х3 +2*4 -5*s =5
26.
Г*1 -2*2-*з + 2*4-2*5 =2 [2*| +*2-2*3 +*„-3*5 = 5
28.
(8*1-2*2 + *3 —4*4 -3*5 =3
[16*1 +2х2 -2*з +3*4 -х5 = 5
30.
3*! - 4х2 + 2*3 - *4 + 2х5 = 4
9х} +7х2 -2х3 +3*4 -*5 =5
6*] — 3*2 +*з -2*4 +3*5 =5
8*j — 3*2 +2*з — 3*4 +2*5 =5 -4*] +*2 -*з +2*4 -*5 =3 12*] -2*2 +3*з -2*4 +*з =4 -3*| + 4*2 - 2*з + 3*4 + *5 = 4 6*| - 2*2 + 3*з - 2*4 -*s = 5 *] +*2 -4*з +3*4 -*з =6 7*] +2*2 +3*з -2*4 +*5 =5 14*] -6*2 -3*з +*4 -2*5 = 6 -*1 +*2 +2*з -*4 +5*5 =4 —3*] +4*2 —*з +5*4 +*5 =6 б*, - 2*2 + 3*з - 2*4 - 2*5 = 4 *] +*2 -4*з +3*4 —*5 =5 4*] +*2 —*з +3*4 -2*5 =5 -2*| -*2 + 3*з -*4 +3*5 =6 6*] + 2*2 - *з + 2*4 - 3*5 = 7 *1 +*2 -2*з +3*4 +2*5 =6 2*| -*2 +*з +2*4 -*5 =7 3*] +*2 -4*з +3*4 +3*5 =5 —10*з + 5*2 - *з + 2*4 + 2*5 = 7 5*] -*2 +3*з -5*4 +*5=5 —15*з +2*2 -*з +2*4 —*5 =6
3. Пределы
1. Найти предел
_ . х3+5х + 1 1. пт „ .. Зх3+5х2-10 , ,. 7х2+5х-6
х->® Зх + 7 х-и» 7х +Х +1 х->® 2х4 — 1 lx +1
, .. -7х3+5х + 11 4. lim —т - , .. 5х2-6х+2 5. lim - , 11х2-5х + 1
х-и» 8х -6х2+1 х-и» 7х2 + 11 х-и» 2х’ + I
, Зх3-5х2-16 8 lim -6*2-3*+l Л 5х3+6х2-4
х-и» 12х2+8 х-н» 7х4 — 8х3 - 7 J. 11т *-и»9х3+Зх +1
Зх3 + 8х2-2 10. пт ,, 7х2 + 5х + 6 11. lim —= 10х2-7х + 5 12. hm х
х->® Зх + 5 х->»8х -9х-8 x-»»-Hxz + 5х + 3
,, 7х5+5х2-11 13. hm —г .. .. 4х4 + 5х3 - 6х2 +1 14. hm - .. 7х2+9х —4 15. hm —т 7
х-и» 6х +11Х+4 х-»« 17х4+5х2-13 х-и»6х5+Зх4-10
,, -Зх2+Зх-4 16. пт 7х3-8х + 9 17. lim —г Зх3 + 5х2+2 18. пт
х->» 2х -1 х-»«6х+8х + 19 х->« 2х — 6
7х2-4х+6 „ Зх4+5х3-9
19. Ilm z 20. hm 21. lim——
х-и» 8х2 + 11 х—>» -7х+9 х-н» -9x -t 5
„ Зх2-2х + 1 __ 7х2+5х—6 . Зх5-6х + 11
22. hm ; 23. hm —= 24. lim --
х-и» -х5-15 X ->«9х -6х + 5 х-и» 2х +Зх + 1
х2-2х + 4 —5х4-6х2+9 _ Зх5-11х + 12
25. hm » 26. hm г ? 27. lim »
х-и» -Зх +5 х-и» 4х +Х-3 х-и» 2х2 + 5х-8
„„ 5х2-6х + 7 6х3+4х-7 5х3—6х2 + 2
28. lim —: = 29. lim 30. lim х
х-и»3х4 -5х3 +10 х->« —2х + 5 х-и»-9х3 +Зх-4
2. Найти предел
.. Зх2-11х + 5 _ 2х2-6х+5 , Зх2+2х + 6
1. lim = 2. hm 3. lim =
х-и» -7х2+9 X->00 —9х + 11 х-и» Их2-5
. 4х2-5х + 3 , Зх5+9х+22 , ,. -Зх5+7х-8
4. lim ; 5. hm —5 6. lim
х->« 2хэ + 10 х-и» Зх2 + 12х - 4 Х-и» 14х +5х + 1
7х2 + 5х-П „ Зх5+4х3-6 „ Зх2+7х + 2
7. lim— = 8. hm 9. 11т ;
х-и» -12х-8 х->« 2х+9 х->» 9х4-12
„ 5х2+6х + 1 10. lim —= 11 г 4х4+5х2-6 11. hm —= 5 _ .. 5х3 + 7х + 1 12. lim —г х
x-><»7xz -2х + 3 х-и» Зх3 +5х2 -3 х-»~Зх’+7х2-4
123
13. lim —15*~6 -2x24-5x-6 14. hm T ,, 2x3+4x-10 15. hm —r
-3x54-12 x->® 12x +5x-6 *-»» 7x -9x+5
16. lim—,~3jf2+8 .. 3x2 4-2x4-1 17. hm —т .. 2x2+6x+1 18. hm =
»-»« 7x34-2x4-6 »-»®4x4-12x-6 3xz-ll
19. lim-*^4*2"7 -2x2 + 3x + 5 20. hm —т 2x3—3x+4 21. hm
7x* 4-11x4-6 x->« 9x -5x4-2 7X - 9
<,•5 «• 3x —2 22. lim — „ .. 2x2-5x4-2 23. lim — .. 5x2-12X+11 24. lim 5
x->»5x2 + x-l »->“x+5x2+1 »-►« -7x 4-5
25. lim A*3*3*2-6 ,, . 2x2 + 4x-9 26. hm —r -9x2 4-4x4-13 27. lim
*-»» 3x + 5 *-»«> 3x5 4-1 lx - 9 13x2 -2x4-1
28. lim —2- + 5x+7 „ 2x2+8x-9 29. lim —r 2x24-5x-4 30. lim x
*->®13x2-6x4-2 x->»7x2-2x-3 x-»« -x34-5
3. Найти предел
1. lim^17X<+5 4x + 5 2. lim- _ .. 4x3-5x24-1
»-»“ 12x7 4-15x4-6 x-»®4x2 4-1 lx —6 2x+5
4. lim - +1 lx? + 6 , .. x3+llx-7 5. hm т , 4x3-6x4-1
»-»« -2x4-7 *-»« x4 - 5x x->co 2x+4
7. lim — 7x11 x-»»3x2 4-5x-4 c .. 9x2 + 5x-6 8. hm — *-»«>llx -2x4-4 . .. -2x5-22x4-2 9. hm = x-ио 3x2 4-5X4-1
3x54-6x3-1 10. hm —— х-н»2хП4-Зх-4 .. .. -2x2-6x + 5 11. hm - .. 6x54-7x2-ll 12. hm
*->“ 3x34-ll x->«® -2x + 4
13. lim Г3*2*5*-1-1 .. .. 4x’+5x4-2 14. hm t .. 3x3-5x24-2 15. hm
*->«25x2 +3x+2 J->«17x -!2x + 5 x-><» —2x—5
16. lim - 3/+5x .. 4x5+6x4-9 17. hm —- j_ 5 v- j_ л 18. hm
»->“! Ox4 +5x’-6 *~>“2x-l 1x4-25 *->®3x4 -3x + 6
lo .. 2x2-6x4-5 19. hm .. 3x3-15x2 + 2 20. hm — - 3x24-8x-4
x-но 3x +1 *-»« x -5x -11 x->w 2xZ4-4
„ .. -3x3+5xi-6 22. hm ? .. 4xs-3x’+2 23. hm r
*-»"> 13x34-5x-i-l x->«> X -4 x->« Xs 4- 3x -12
r 7x3-5x24-9 25. hm —- 26. lim ~ 6x4-5 _ 3x2-4x4-1
x-»®9x34-6x-ll x-»«. x +5x + 6 x-к» 2x34-ll
124
28. lim —-2JC * x-»« 2x - 9 29. lim 2f 2J~3jc + 1 x-»«2x5 +6x-4 □n . 3x“-2x + l 30. hm = x->« 2x2-3
4. Найти предел
— 1 1. lim — 2. lim-- з Iim±r2L
x-*-ix +3x + 2 x->2x3-2x2+3x-6 x->3(x2-9)
x2+8x + 15 4. hm - —3(x + 3)(x + 5)2 . 6x2-5x + 1 j. hm Х-И/3 3x-l x2-9 6. lim—5-—— t-»3x2-X-6
, x2-10x + 25 7. hm т x->5 x-125 . .. x2+2x-3 8. hm z x-»l X -1 о i- *3 + 8 9. hm -= x-»-2x2-4
6x2+x-1 10. lim x-»l/3 x-1/3 .. .. 3x-21 11. hm -x x-»7x2-6x-7 x2—4 12. lim-xF — »->2x2-3x+2
,, ?-l 13. hm—т х-йх -5x + 4 .. .. x2-2x 14. hm—5 x-»03x -5x2 +x >< 8x3-l 15. hm —r x-»o,5 6x2 - 5x + 1
,, x3-!-! 16. hm —x— X-+-I xl -1 *’-8 17. hm—= x->2XZ -4 18. lim ~+— -X-X-9X +6X-27
— 9 19. lim-^—-x->3x3-27 .. x2-16 20. hm -= x-»4x -llx + 28 .. 2x2+6x 21. hm x->-3 X + 3
9x2 -1 22. lim — — x-.-l/3(3x + i)(JC_1)2 .. 3x2+5x-2 23. hm x-»-2 X + 2 _. .. 6x2+x-l 24. hm x-x-0.5 x + 0,5
,, .. x2-16 25. hm — x-»-4 x2 - 3x - 28 .. 3x2-2x-1 26. lim — x-x-l/3 (x + 1/3)2 — 4x + 3 27. lim-——— X-.3 X-3
-3x 28. lim-v—— x-»3x -6x+9 _n . 2x2 + 13x + 21 29. lim x->-3,5 2x + 7 . x2-5x-6 30. hm —z x-»-ix +2x + l
5. Найти предел
.. x4-8x2+16 2. hm —= _ x2+5x-6 3. hm
1. Iim-^J = x->2x4 -5x2 +4 x->2 X -4X + 4 X-»I x“-l
, x’-3x + 2 4. hrn-x x->l x - 4x + 3 (x2-4)2 5. lim-j x->2x -3x2-4 6. lim —2(x-2) (x+5)
125
1. lim------8
x-*-*(x + l)(x2+I6X + 64)
lim x->7
x2-4x-21 (x-7)2
9.
lim x->-l
2x3+x2+x+2 x3+l
10. lim 4----Ц-
x-»-2 y1Sx9v7
x2 — 5x
12. lim —j-----
x->5x4 -625
13. Iim-Ц-r—v*-
15. lim
16. lim
18. lim 6
19. lim — 2jf2 575 x->-5 x2 + x —20
22. lim 2~3x~?
x3-3x2+2x
20. hm —т--------
Y—bl v* _ A v Q
23. lim X—>1
(x2-2x + l)2 (2x2-x-1)2
,, ,. x2+5x-6
21. hm —----r-----
x-»-ix3+2x2-x-2
„„ x3+5x2+7x+3
24. hm —z---=------
*-»-ix +4x +5x + 2
x3
28. lim—4-
x4-8x2—425
26 hm-----—----—
x->5 (x-5)(x + 5)
27 lim
2x4-x2-1
3+2x2-x-2
29. lim x—>2
x3-3x-2 x4-16
30. lim
x2-2x + 1)2
J
6. Найти предел
x->o 3-V9-X
10. lim-9 ^81 *L x~>°5-725 + x2
.. V25 + 2X-5
13. lim----y-
x-»o 2-V4 + 3x
, 5-V25+X2
2. hm------7^ .
x->0 1-V1-X
, .. yji+x2 ->!t
5. hm-----7-
12-7144-x2
e .. 8-V64+X
8. hm----.
*^°1-71 + 5x2
.. .. V7+x - 41
11. hm---pr-
*->04-V16 + x2
.. 75 - V5 + 7x
14. hm-----r.-.
x-»0 2-V4 + X
, .. VlOO + x-lO 3. hm-----.
x->0 6 —v36+x . .. 15-7225+x 6. hm-----. —
x->0 3-V9-X
Q .. 7225 + x2-15 x->0 I-Vl+x . 12-VI44-X
12. hm----
*->0 1-Vl+x
.. 7в1-х2—9
15. hm .
x-»oV2-V2-x
126
.A KmJ1-V121-X 17 lim ^l69+X-13 ,. V7-V7 + 6X
x->0 4-V16-X *-»o 1-V1-X 18. hm— . —- x—*0 9 — у/81 + 2x
I9.[im>by2-1» 20.1™-^+^ ?1 Iim VI3 + X-V13
х-°7з-^з-2х2 x-.013-V169-x x-»o 4 - Vl 6 + x
™ л/8-Vs + x2 22. hm 23. Iim-^V 51ZL пл Um l-Vl-8x
x->0 7-V49 + X x-»0 V7 - V7 - 4x I->0s/iT-Vn-x2
,, .. V15+9X-V15 25. hm . — 26. lim ?? j. V64 + x - 8
x->u 3-V9+X x->0 >/б-л/б-х2 x-»o l-Vl-3x
is 3-V9-3X 28. hm j— x->010-V100 + x 29. lim— x->oi/5-\5-2x2 ,n .. 4-V16+3x 30. hm — x-»o l-Vl + 9x
7. Найти предел
, .. 1-cosx I. lim =— x-»0 4xz 2. lim*"2*^4* x-»0 arcsinx2 , sin3x 3. lim x-»0 tg7x
. sin5xsin3x 4. hm : x-»o sin x , .. In(l + 2x) 5. lim—s i x-»0 X , .. x(l-cos6x) 6. lim —i i x->0 tgx2
_ sin4x 7. hm x-»0cos7xsin6x „ .. 3x2-5x 8. hm x-»o arctg3x 9. lim x->o arcs in 5x • sin(x/4)
.. sin6x 10. hm—= »->08x -9x ll.lim-^4 x-»0x2 (l-cos3x) (1“e4X) 12. lim-- >- x-»o 2x +x
,, sin2x 13. lim—— 1 л lim + 2х) sin(e_bt-l)
х-и>3/1-2х-1 x-»o 1- cos(x/2) 15. lim—1 i x->0 tgX
., sin Злх 16. lim 17. lim-^-'g5* 1o .. sin4x 18. lim—
x-»0sin77tx x->01 -coslOx x->0 3Zx _ 1
19 |im !SJ 20. lim sin’(ЗА 21. lim—A—i x-»o 8x -6x
X—>o 1 - cos(-2x) x-»o sin 9x-coslOx
„ .. x-cos2x 22. lim x->oarcsinl Ijc ,, l-cos7x 23. hm z- tg(3x)2 24. lim x-»o tg9Tix
127
25. lim х—>0 Jl + 4x-l е2х—1 22х-1 26. lim -г, — х-»о<Ух-arcsinx .. cos3x-l 27. hm — x_o 49 -1
28. lim х—*0 ln(l + tg2x) sin(2x)2 29.1imteS^°-^ х-»0 tglOx cos(-3x)-l 30. hm - i— x-»0 sin9x2
8. Найти предел
2x 3x e -e 1. hm— x->01n(l-tgx) „ cos2x-cos6x 2. hm x->0 x-tgx 3. lim^S^i^ x->0 x3
ln(l+sin2(tgx)) 4. hm —— - x-»0 1-cosx 3«x-32x 5. lim- — x-»o arctg2x , .. ^i77-^/i-6x 6. hm x—*o tg2x-cosx
_ .. cosx-cos3x 7. hm — x-»o arcsin2x „ arcsin2x-sin2x 8. hm = x->0 tfl+x-1 9. lin.^OtM x-»0 cos2-1
.. arcsin4x3 10. hm —? a-»°x(53x-5x] .. .. ^\ + 2x->!\ — x 11. hm x->o sinxcos3x l-sin((n-x)/2) 12. lim — —z x->0 tg2x
13.1im^~S;n4x x-»0 4X3 .. In(cos5x) 14. hm — x-»0xarcsin4x-5x ,, -J\-x —J\+2x 15. hm ?— x—>o ln(l-7x)
,, .. cos24x-l 16. hm r— *-»0 X-tg X 46x-4x 17. lim . . x->oarctg(-5x) cos7x-cos6x 18. hm . x->0 sin^Bjrj
ln(l+/g2(sinx)) 19. lim— - ' x-»o cos xxl sin2 ((2n-x)/2) 20. lim x-»0 tg X ln(cos(-2x)) 21. lim x-»o x-tgx-2x
__ .. ЭД-7х-ЭД-Зх 22. hm x-»o sin2x-cos7x «2x Sx 23. lim-4 x->oln(l + tg3x) sin(2x)3 24. hm —г x-»° x2 • ^73x - 74x)
25 Iirnsin5x-tg5x x-»o sin2xx2 . 1-cos22x 26. hm z— x-»0 x sinJx __ cos4x-cos3x 27. hm = x-»o sin8x
28.1im-^< x x->t>tgx-^23x-2xj 29. lim —+ 6* + 4* x-»o arctg2x cos2x _ .. Vl + 2x-Vl+8x 30. hm ;— x->0 In(l-sinx)
128
9. Найти предел
lim ^;* + 2»-x-»-2arctg(3x+6)
sin(5x-n) hm--------j-----—г-
x-»« arcsin! Злх - Зл21
sin(4nx) hm —i i-x-»-3sin(3nx)
lim cos(7* + 7)s'n(5* + 5)
x-»-i 3x+3
_ sin3(x-l)
9. hm-----------------
*-»1(x-l)sin(3x-3)
cos(3x + 3)sin(2x+2)
11. hm-------5------—»-----i
x—►—i 5x + 5
sin(rar)
13. hm—/— x-»isin(3roc)
,, sin5x-sinx
15. lim ----------
x-»-n4tgx-cos2x
17 iim sin(4(x~2))arccos(4(x-2)) (2x-4)cos(x-2)
(x + 2)cos(3x + 6)
2 sin(7x + 14)
2] |. cos(6x-12)-cos(4x-8)
19. lim
2sin2(x-2) tg(7x + n)
23. lim -----------x
x->-3x arctg (x+3 n ) sin(6x-n)
25. hm------p------
2 lim5'1^3*-3)1^11*-11) (x-1)2
4. ,;msitl(3(^-0)c«s(4(x-l)) x-»l (2x-2)cos(x-l)
6. limgfo-6)-^5*-5)
x—>1 5sin(x-l)
8. lin,£°s(^-16)-cos(6x-12) 2tg2(x-2)
.. l-cos(7x-14)
10. hm —r-~ ----<
•r->2 tg|3(x-2)2J
1? sin(x-2) + sin(8x-16)
x->2 3tg(x-2)cos(x-2)
.. tg(3x- 7л)
14. hm ' \ ------>—
x-»2n arcsin (x—n)
16.1im-tg3jt-tg7x
x->n 3 • tg2x cos2x
18. lim
x-»-2 sin(-5nx)
20. |im—^~sin7x
jr->n 10-tgxcosx
.. sinx+sin3x hm ------------
л-»-5л 6 • tgx • cos 4x
24. lim - .tg* + tg4X x-»2n 8 • sin (-5x) • cosx
„ 5т(7лх)
26. lim- /
27. lim
4))
28. lim x->-2
sin(-(x+2))arccos(x + 2) (2x + 4)cos(-(x + 2))
29. lim
x-»-n 7 sin 3x cos 4x
sinx-sin3x
30. hm-------------
x-»3x5tg4x-cos8x
129
10. Найти предел
.. 1п(3 + х) 1. hm — — x->-2tg(2x + 4) , ln(l + tg2(* + l)) *->-! l-cos(2x + 2) , .. 4х-64 3. hm x->3 x-3
. .. 2 х-16 4. lim х->-4 X + 4 < I- I1”*)2 5. hm- 1-x3 .. 1/5П-2 6. hm x->3 sinror
7. lim x->io Vx-9-l 8. lim 4'-sin(2jc + 4)) x-»-2 sin(2x + 4) г еХ-£’ 9. hm . ^“>3tg(x2 -9J
1А Г 1П(Х~2) 10. lim—- L х->3 9-Х2 sin(n(x-4))cosnx 11. hm—— ’-L x->2 log2 x -1 12. hm x-»-i№+;-i
13. lim 3^ х->7 Х-1 ex-e2 14. lim - - x->2 sin(4-x2) log, X - 1 15. hm— x->3 tgTtX
.. ^2-х-1 16. hm х->1 sinror .. Inx-lnlO 17. hm , x->i«Vx-9-l Inf I +sin2(x-l)) 18. lim— x-»l l-cos(5x-5)
19. lim — /~е\. x">-3tg(x2-9) (in(x-l))2 20. hmi— x->2 8-x3 „ .. 6~x-216 21. hm x—3 x+3
,, .. 8х-64 22. hm х-»2 х-2 23. lim—^2JC-1 x-»2 sin/TX ln2(l + sin(x-2)) 24. lim Ц“ x->2 cos(2x-4)-l
25. lim х-»-2^18 + х-2 ,, .. %2 + x -1 26. lim x-x-i sin/rx In(-x)-ln2 27. hm ? ' x-»-2 Vx + 18-4
28. lim—е*~е X*>lsin(l-x2j 29. lim-!^^-' x->4 tg(n(x - 4)) (ln(5-x))2 30. limi—i x->4 64-X
4. Дифференцирование
1. Составить уравнение касательной к графику функции в точке М(х,>,у0)
1. у = х2-5х + 4, М(-1,Ю) 3. у = х2+5х-1, Л/(1,5) 5. у = х3+2х, М (1,3) 7. у=2х2—Зх + 1, Лф,0) 9. y = tg2x, М (0,0) ll.y = arccos3x, Af^O,“J 13.у = х-х3, Л/(-1,0) 15.у = х+л/х3, Л/(1,2) 2. у = х3+2х2-4х-3, М (-2,5) 4. y = gzl, w(2>2) 6. У = 4х, М(4,2) 8. у = 1[хЦ, М(1,0) lO.y = arcsin^—, Л/(1,0) 12.у=^^1, л/(2,1) 14.у = 2х2 + Зх-1, М(-2,1) 16.y = Vx2-20, М(-8,-1б)
17.у = 2х2-Зх + 1, Л/(1,0) х2-3х + 6 ( 2) 18.,= х2 , ^3,3j
19.у = 2х2+3, Л/(-1,5) 21.у = 44’ M0-’) х +1 х ( 2 А 23.у = -^-, М -2,-- х +1 к х) 25.у=-^-, Л/(1,1) х +1 Зх-2х3 1) 27.у= з , лф,-] 29.у = х2~ —- Лг(-2,-1 4 V 4) 2O.y=^iil, М(1,3) ii.y=——, м(г,Л Зх + 2 V SJ 24.y=lL^±3, М(зд) 1+Зх2 26.y=li^-, мпп х +3 х2 ( 171 28.у = —+ 3, М 2,— Ю 1 5 J ЗО.у = 8^х-7О, ЛГ(16,-54)
2. Найти производную
1. y = sin(2 + 3x)2 2. у = /з + 2х2) 3. y=2x+5cos3x
131
4 у 1 5. y = ylxex + x 6. y = ^2ex-2x+l
arctg2x
7. >> = sin(x2-5х + 1) 8. >> = cos((2x+3)6j 9. >> = sinx-(sinx+5)
10,>> = 2ctg3^ 11.3' = (l + sin2x)3 14.>=-—! arcsin 2x 12.> = (7+5x4)2
13.>> = 3x + 4cos7x lS.y = -Jx2ex +x3
16.у = >1зех—3х+ 1 17. у = cos(x2 + 2x + 5) 18.> = sin5 (3x-l)
19.>> = cosx-(cos2x + l) x2 2O._y = 5tg— 4 21.> = tg((3+7x)4)
22._y = (l + 3x3)5 23. у = 5x2 + 7 sin5 x
arccos5x
25.y = -Jx3e2x + 3x 26.y = ^2ex + 5X +3 27.> = tg(x3 + 7x-l)
28,_y = tg(5x + 7) 29. у = tgx(cosx - 4) 30.> = 7cos2^
3. Найти производную
1. > = tg25x + lg2x 2. >> = 0,5sinx2+cos2x 3. >>=sin2(x3-eI)
4. >' = 3smx-cos2x + ln3 r 1 2 x 5. > = -tg x-tgx + -> Jx 6. >>=arcsinx3+arccosx3
7. у=i(arcsinx)2-arccosx 8. y = In(arcsin5x) 9. >> = arcsin(lnx+l)
10.> = Vx2 + e2x+3x ll.>> = exp(sin2x) 12.> = 2 x
ctgl 13.> = 3 * 14.>> = lg(o,5x2+2x- "4) 15.>< = 7И“231
I6.y=—1— ln25x 17.> = 1п(1п(з-2х3) j 18.>> = 51n3(3x+l)
19.>>=xsin(lnx-10) 20. у = 0,51n^rg^ & 21. у = arcsine
. 2x + 4^ 22.y = lnl sin—-—1
132
25. у = "И 26^-31п37х 27., = ln(lg(l-2x))
28. y=21n-3(2x~l) 29.>> = 21ncos^ 30.>> = 2x3+1-х3
4. Найти производную
1 V“ — sin3 5х _ х8
1. у- ,os2(x/3) } 8М
3- >=- /гх2-2х + 1 4- у = - х з
X 3V(1+"2)
М ч-гч + СЪ 1 X
J 8х
7. у=- х4 в х3
’ ( 3-2х3)2
9. у=-5 9х + 3 (2 + х)5 10.>=_П~х2 2(х-2)4
11 sin27x х5 12 v-
Z cos2(x/4) (х-х4)<
13.;и=- х3+2х + 3 14у=~г~^
X 5^(з + х3)
15.,-=- 7 х4+х Л + х2 16->=[|4х2+1)3]{г^)
17.>=^ х6 + 2х)3 Зх2 18-у= * , (5 + х3)2
19.>=- 9х —4 + № 20 у-
6( 2х3+5) Л Г л 7^(х-2)4
133
sin43x cos(x/9) Jx* +3x + l 2x-5
25.>=^X±
7V1 + X5
134
16 у = >-0(-б)2
V (х + 2)5
18. у = х5 1-—*~,4 — V(x+l)Vx-5
20 у- (Х“4)5
(х+3)3(х+4)6
22. у = -р^+2)3 V(x+3)(x+5)5
24. у-, ^Зх + '
Ч2х+5у/2х + 2
26 >_(х+1)2(4х+1)
(х + 6)3
пв . з I х + 1
y(x-2)Vx-6
30-
6. Найти производную
1- У=(1 + х2)Л 2- > = (igx)3x 3. y = (ctg3x/
4. y = (tgx)’ 5. уг^ + Х2^ 6. y = xsin*
7. у = х“” 8. y = xarcsin* 9. у = (х-5)со”
Ю.у = (х4+5)С,£Г / э \COSX П.у = (х2+3) 12. у = (tgx)’
]3.у = у[х 14. у = х^ 15.у=х^‘"’+с0”^
16. у = (cosx)sl"x 17. у =(arctgx)* 18.у=(1 + х2)Х
19.у=(1 + х2)Х 20. у = (tgx)’2 21.y = x’2*3
135
22.y = (sinx)‘raini
ос Л 7\arccosx
25.у = ^1-х2)
2S.y = fcTi
23. у = (cosx)11™6"
26. у = (/arctgx
29.y = (tgr)arccos*
24. у = (з + x2)^*
27.y = (x2 + 4)3~5 3O.y = x16"
7. Доказать, что функция у = у (х) удовлетворяет уравнению (табл. 4.7)
Таблица 4.7
№ варианта Функция Уравнение
1 y = e* + 2xe* + e2*+xe-* у"-4 у" + 5у'~2у- (16- 12х) е х
2 у = -4+е2* + 9е-3’ + х V’ у"+у"- 6У = 20хе2х + Ие2*
3 у = Зе' sin х—е* cos х+е~2х у" + 2у* = 10ех sin х +10 ех cosx
4 у = П-7е3’+xe3*+xe-* у"-6у"+9у + 16хе“* = 0
5 J' = (0,13cosx + 0,lsinx)-ex + +е2х (cos2x+sin 2х) (У “ 4У+8J2) е~х = 0,66sinх+0,32cosx
6 у = 5 cos ж - 3 sin ж+2 (хе* +1) У“У = 10sinx+6cosx+4ex
7 У = “е3* + ^.со53ж+151пЗх+.!-е~’3’ z i 6 3 у" - 9у = -9е3х + 18sin 3x-9cos3x
8 y=“e’*-lsin8x+-e",*+l 2 8 4 6 У - 64У = -64 е8х +128 cos 8х
9 у = Зе’ sin ж + 3 - 2е-2* - е* cosж (y+2y)-0,l = exsinx + excosx
10 У = ^со59жД+Зе-’* + хе’’ y'-8iy = 81(2e’- +5т9ж)
11 У = +е'* -^(4хе*' +sin8x) у' = 64(у-е8’)+ 128cos8x
12 У = -Зе* - же* + же-’ + 5е2* У+5у' = (16- 12х) е~х + 2у + 4У
13 у = 5 cos ж + 2же’ + 4е” - 3sin ж (У - У) е~х = (I Osin х+6 cosx) е~х+4
14 у = 1+е2*-Зе-3’ + ж2е2’ (у-+у' - бу') е-* = 20же* +14е*
15 J = ~e3*+|cos3x+isin3x + e2 z -Л и у' । 9(со53ж -у' +е”)= 18sinЗж
136
Окончание табл. 4.7
№ варианта Функция Уравнение
16 >' = -0104e2xsin5x+xe2x (у* - 4у’ + 4у) ё~х = ех sin 5х
17 у = -1 + 8е3х + Зхе3х+хех у*+9у* = 4хех + бу*
18 у - е2х cos2x+0,13ех cosx+0, lex sinх у" - 4у' + 8у - О.ббе* sin х + 0,32ех cos х
19 у = (х-2) e’x.<~cos9x+/ + е-’х >" = 81(2e’x+sin9x + y)
20 y=--?x--sin8x+-?x 2 8 8 у’ = 128 (cos8x + 0,5y-0,5e8x)
21 у = -5е2х + е-3х + х2е2х+6е 0,5-у*+0,5-у*-7е2х = Юхе2х+3у'
22 у - е2х - 6хе2х - 0,04 е2х sin 5х у* = е2х sin 5х + 4 (у’ - у)
23 у = 10+Зех sin х- ех cosx - е*2* е~х (у*+2у') = 10 (sin х+cos х)
24 у=е3х + ~ cos Зх+ysin Зх е3х У 2 3 6 3 y-9(y-e3x) = 9(2sin Зх-cos Зх)
25 у = 2е3х - 4хе3х + х е"х (у” - бу*+9у') ё~х *- 4х = 0
26 у = 5cosx-3sinx+2^xex + 4exj y'* = 2-(5sinx+3cosx+2ex)+ у'
27 у = ех + 2хех+е2х + хе~х I2xe~x +у* - 4у*+5у' - 2у = 16е~х
28 у = ха’х+—cos9x + e9x+e-’x 18 y'-8iy = 162e’x+81sin9x
29 у = е~* + Зхех + е2х + хе~х у*+2у* - 7у* = 2 ( е2^ + 4хе~х - 6хех )
30 у = -5е2х + хе2х - 0,04 е2' sin 5х у' - 4у*+4 у = е2х sin 5х
5. Графики
1. Найти наибольшее и наименьшее значения функции на отрезке
1. у = 2х3-Зх2 * * 5-36х+2, [0,3]
3. у=-Зх3 + х, [0,2]
5. у =-2х3 + Зх2 + 36х - 6, [1,3]
7. у = 32з£-х2, [1,16]
9. у = 2х3+9х2+12х + 2, [0,3]
ll.y = x3/32-6-Jx, [0,4]
13.у = х3-Зх2-9х + 10, [0,-3]
I5.y = x-Vx, [0,16]
17. у = -х3 + Зх2 + 9х - 5, [-3,3]
19.у = Зх3+729/х, [1,3]
21.у = 2х3 —Зх2 — 12х + 1, [-2,3]
23. у = 4^7-х, [1,9]
25.у = 2х3-Зх2-12х + 5, [0,-2]
27.у = х2/2 + 64/х, [1,16]
29.у = 3—х—4/(х+2)2, [-1,2]
2. у = 4х£-х2/64, [0,16]
4. у = х3/96-2>/?, [0,4]
6. у = Зх3-х + 2, [-2,0]
8. у = х+4/х, [1,4]
1О.у = 2х3-24х, [1,3]
12.у=—х2/2 + 8/х+8, [-4,-1]
14. у = 4х3 - 48х—4, [-3,3]
16.у = Зх + 27/х, [2,5]
18.у = х3-27х, [1,4]
2О.у = 9л/х->/х3, [1,4]
22.у=х3-Зх2, [1,3]
24.у = 2х+32/х, [1,8]
2б.у = х2—6х, [-5,3]
28.у = 4 —х —4/х2, [1,4]
30.у = х+5/х, [1,10]
2. Провести полное исследование функции и построить график
1. у = -Зх3+2х2 2. у = -х3-Зх2+4
3- у=(х+1)2(х-1)2 4. у = -х3 + х2+5х+3
5. у=2х3-3х2-12х+13 6. у = Зх3 + 2х2-5
7. у = 0,0625 (х + 1)2(х-3)2 8. у = х3 + Зх2-4
9 У = х3-Зх2 ю. у = -х3 + Зх + 2
138
11. у = (х-3)2(х-1)2
13. у = 0,5х3-0,5х2-4х + 4
15. у = (2х +1)2 (2х -1)2
17. у = -0,0625-(х2-4)2
19 у = х3-Зх + 2
21. у=х3+6х2-15х+8
23. у=(х-3)2(х + 3)2
25. у = 2 + х—Зх3
27. у = (2х —1)2(2х—З)2
29. у = х3-9х + 8
12. у = 2х3-Зх2+5
14. у = -(1/3)х4+2х2
16. у = х3-2х2-4х + 5
18. у = -х3-х2 + х-1
20. у = х2(х-2)2
22. у = 2х3 + Зх2—5
24. у=х3-2х2 + х
26. у = х3-4х + 3
28. у = х3-6х2+9х-4
30. у = 16х2(х-1)2
3. Провести полное исследование функции и построить график
1 ’•у=^ 2‘ "=77Т _ X 3-
л *-у~4 , х4 + 1 6. X +1
X3 8 v х X2
7- >, = _3_7 х +1 (х-2)2 У=7ТГ
X3 1О.у = -т— X +1 П.у=-^-з 2-х3 12.у = х2+-X
„ 2х2+Зх-5 13.у= х-4 ,4'-ph 15.у = А±4-(х-1)2
2х-1 16.у = —у-X х2 — 4 17-3'=т-г х2 -9 18->' = 4Ц
20 v *2+8 9.
(х + 2)2 (х + 1)2
22^=4^ х +1 2х2-1 23.y=^-j-i X 24-> = ^-х +4
139
„ X3 25. у= - (х-!)2 2&.у = -£-X—4 26> (х-2)2 27у-~^ 29.,. ’’ ’V’
4. Провести полное исследование функции н построить график
1. у = 1п(х2 + 4х + 5) 2. > = (х-1)4-г 3. у=(2х2+5х+2)г
4. у = 1п(х2+6х + 12) 5. у = х-1п(х + 1) 6. у = (4х2 + 1з)-е’’2
_ Inx 7- У=~ 10.y = (l-x2)e-Jl2 8. y = (3x + 5)-e2jt 9. > = ln(Vl+x2 +xj И.у = х21пх 12.> = 10хггг
\3.у = х-еж I4.y=—ij 15. j = ln(x2 + 8x+18)
16.у = (Зх + 5)-е-3х~2 19. j> = (2x + l)-e-*2 22.у = (2х + 1)-е~х 17.> = xlnx 18.^=(х-1)-ежЧ 2О.у = 2еж2-‘Сж 21.y = xe'x 23.у = еж1~6х 24.y = ^x2 + ljex
25.у = х31пх 26.у=(х-1)е‘~ж ' ’ 27.y = x e 2
28.у = (х + 1)1п2(х + 1) 29->' , 2 30.> = x-e«l x-e
6. Интегрирование
1. Найти интегралы, используя их основные свойства
2. Найти интегралы, используя подведение под знак дифференциала н преобразование подынтегрального выражения
1-Зх
3+2х
3—2х 7+5х2
dx
3 f
141
COS X г 4?+1) 5. Je ' 'xdx 6. Jcos-idx v2
- , sin3x , '• H —dx 13 + cos3x 8. dx J2 + 3x 9. Г ydx
(x + 1)
lo.UitLdx V5x2 + 1 r larcsinx . 11.1J r- dx V 1-x2 I2.jx-7X dx
13.Jtgxdx ,. rx2 + l , 14.1 dx J x-1 IS.f-r^dx
16. Jdx , X arctg— 17J—4^ 4 + x Л U.f^-dx
19.Jctgx dx 20 r^i±5^±Zdx J x + 3 2I r^±^dx X
22-f^-dx x -5 23.j42-3*dx 24.f-^—dx V-l
25.Jcos—-sin—dx 1 4 4 26.J-^^-dx j3x2-2 27.j3 e-2' dx
28jp^+e'^ dx 29. fsin(2 + 3x)dx 30. J cos6x sin2 6x dx
3. Найти интегралы, используя метод интегрирования по частям
1. Jln9xdx 2. Jx-cosxdx 3. Jln(x-7)dx
4. Jx222jtdx 5. Jx-sin7xdx 6. Jx e2*dx
7. Jarctg5xdx 8. Je~5ixdx 9. fx2 Inxdx
10.J(3x + 5)-cosxdx H.jVx Inxdx 12.J-^-dx Sin X
13.Jarcsinxdx 14,Jx-2”'dx 15. [(4-Зх)е2^
16.J^dx 17.f(x2+l)e-8xdx 18. J6x-sinxdx
19.Jln2xdx 2O.Je'/'dx 21.Jarcsin4xdx
22. Jxln(x —l)dx 23. Jxarctgxdx 24. J(x2 - 2x+3)lnxdx
142
25. fln(x2 + l)dx
ZS.J-A-dx COS X
26.j(x2 + 7x + l)cosxdx 27. J(2-4x)-sin2xdx
29. J(x + 5)-e3jtdx 3O.f(x2-l)e9xdx
4. Найти интегралы от рациональных функций
1. [.А... J(x + l)x 2. f xdx (x2 +l)x
3. 4. J £
x2+x J(x + 7)(x + 2)
5. Г—* (x + l)2x 6. f_ Jx3-x2
7. r xdx (x + l)(x+2)(x+3) 8. f dx_ Jx2-x+3
9. ,4x2-x + 3 , 10. rx2+4x + 4 . J x(x-l)2
11. , Зх2+2х-1 . J > dx 12. r x2-5x + 9 .
J(x-1)2(x + 2) x3-5x2 +6x
13. r 3x2+8 H 5 dx Jx3+4x2+4x 14. г x + 2 ^х-ЗХх-^
15. f2x-7 , J-s dx x2+8 16. J—5-\+‘ dx x3-5x2+4x
17. f 7x-15 j J-ч 5 dx x3-2x2+5x 18. f 2x2-l 1 J 2 , dx X -X -6x
19. f x2-x + 4 J(x + l)(x-2)(x-3) 20. f 1+4 . J 3 2 x dx X +x -6x
21. [ dx (x + l)(x-5)(x + 3) 22. r *2+l j l”7 ТОХ x4+3x2
23. , x2+x + 5 Jx(x-2)(x + 3) 24. ^(x + Sjfx + e)^
r2x + 5 .
x2 + l VsXx-^
143
27. [A-±-dx
J4x3-x
29.
Jx5-16x
28.
dx
30- J-rr
5. Найти интегралы, используя указанную замену переменных
, f l+yfx j 2. Jcos32x-sin42xdx; 3 Г
2x + V4x ’ V3x-l-^3x-l
sin2x = r
x = r 3x-l=Z4
f 1 jl+4x 5- dx; xV x
4. Г dx; 6. jx3Vl-x2dx;
x = 2tgZ l+4x_(2 x = sinZ
X
7. J-7^=dx; Vx-2 8. Jcos6xsinxdx; 9- f-rJ—dx-x2'i X
Z = cosx X~2 .2
x-2 = r =r
X
io J 8-sin2x "J !> r dx
Vx-1 - J(x-rf 12.1 _ _ , 5 sin x +cos x
sin2x = Z 13.J—^i=dx; JVx^3 x-3=? x-l = t2 tgx = Z 15.J ' dx; J(2-^)j27
14.jV16-x2dx; 4sinz = x
x-t
If. r c°sx u 16 J~7- . , dx; V4 + sin x dx; <2x + l 18.Jcos6xsin3xdx;
sinx=t 2x = Z6 Z = cosx
19- J * dx; Vl+x 4-^/1 + x 20. Jcos4 3x sin3 3x dx; 2! f- i-; dx J(2 + x)Vl + x
t = cos3x
l + x = r 1 +x = t2
22.r-^Ln3x дх; ‘ l-cos3x 23j^~ldx; 1 x + 2 24 f Л
Jxj9-x2 ’
cos3x = z x-5=? x = 3sinr
144
X V X 26. J jx -2sinx + cosx’ _ X
27 d* ,
X+l , 7x+3+$/x+3
X ,gF' x + 3 = r4
28'- x = 2tgt V4+x 29. Г jx Vx(^/x+4)’ 30. J— . sin2x + 4cos2x
x = t3 tgx = f
6. Найти интегралы, используя метод интегрирования по частям
1 1. Jarctgxdx 0 2 2. Jxe-Xdx 0 Л 8 3. Jx2cos2xdx
e 12
4. Jxlnxdx 1 5- Jx2sinxdx 0 ж 6. Jxcosxdx 0
7.;^ 0 « ж 2 v 8. /—y-dx jtSin X 4 Л 2 9. f(4x-2)cosxdx Л
1 10. Jxarctgxdx 0 11. J Inxdx 1 4 12. jxsin7xdx 0
ж 4 V B-HV-dx Л 4 14. J(3x + 5)cosxdx 15.J^dx
0 cos X n 6 1 x
16. J(2x-4)sinxdx 0 17. jln(x2)dx In 2 18. J xe*dx 0
1 19. j(l-x)2exdx 0 2 2O.Jx3 Inxdx 1 In3 21. j (5+x)e3jrdx 0
22. Jx2cosxdx Л 4 4 23. Jx2ln(6x)dx 1 In 2 24. J (2x-3)e'*dx 0
145
0.5
25. J arccosxdx о
In 2
28. J x2e"3xdx о
26.Jx23x+ldx
о
2
29. J(x-l)2xdx
1
ln2
27. J (x + 2)e4xdx o
0.5
30. j arcsinxdx о
5. Найти интегралы, используя указанную замену переменных
J j 2 *
03sin x + 5cos х tgx = f
3 х
4. j dx;
оЭДх + З 8x + 3 = f3
2 Г ш___
№(^ + l)’
8x = Z3
3sinZ = x
4x = /4
J______________
o?sin2x+3cos2x tgx = /
11. J
0
cosx .
-------dx,
3-sinx
sinx-Г
,4. p"-dx;x = ?
J V4.9
17. p5ӣ-dx; p4-cosx cosx = f
15. Jcos4xsinxdx;
0
r = cosx
0.5 .
18. j--------у----dx;
i (2-x)Vl^x l-x = t2
146
1 .------
19. Jx3x/4-x2dx; о
x = 2sinr
l±i = f2 5x
dx; x=i6
25. jcos3xsin2xdx;
0
t = sinx
26. RF^dx; x = t6 6ФГ+1
dx; x = ?
29. j-J*”* dx; о V6-sin2x sinx = f
Л
21. jcos3x-sin6xdx,
0
sinx = /
4 dx___________
24 2-/2х-1-У2х-1’ 2x-l=f4
71
2 3
27. jcos2xsin xdx;
o
t = cosx
64 .
30. J ^-=?-=dx;
1 (l + ^)Vx
x = tb
8. Найти площадь фигуры, ограниченной фигуру
кривыми, изобразить эту
1. у = 6х-х2, у = 0.
3. у = х2+4х, у = 0.
5. у = 0,25х3, у=0, х = 2.
7. у = л/4-х2, х + у = 2.
9. у = х, х + у = 3, х = 0.
ll.y = sinx, у = 0,х = 0, х = л.
13.у=х2-6х, у = 0, х = 1,х = 4.
15.у = х2-4, у=-х2+4.
17.y = cosx, х = л/2, х = 0,у = 0.
19.у = х2+6х + 5, у = 0.
21.у = х2, х = -3, у = 0.
23.у = л/х, х = 4, 2у=-х.
25.х-у = 0, х = -9, у = 4-х-Т1.у = 4\-хг, у=х2.
29.ху = 9, х = 1, х = 5,у = -4.
2. у = е"х, х = 2, х=0,у=-5.
4. у = 0,25х3, у=0, х = 2, х = 0.
6. у=1пх3, у=0, х = е, х = е2.
8. у = 2х2, у = 0, х = 1, х = 2.
1О.у = 4-х2, у = хг-2х.
12.у = х2-4х+3, у=0.
14.у = 3х-1, х + у = 4.
16.у=х'*, х = 2, х=4,у=-3.
18.у = 6-х, у = 6 + х, х = 6.
2О.у=х3, х + у=2, х = 0.
22.4у = х2, у=4.
24.у = 2х2+Зх-9, у = 0.
2б.у=2-Тх, х = 1, х = 4,у = -5.
28.у = (х + 2)2, у=4-х.
ЗО.у=х3, х=0, у=-2х+12.
147
7. Ряды
1. Исследовать сходимость числового ряда
« „2 я=1 J “ я’ 2 у 100 л=1 Л "(л 4-3)! л=.(" + 1)!
4 у И ' £(2л)! СО „2 5- H-t л=1 л! б ”(2л-1)! Л=1 л!
7. „Т1(л + 4)! ро 1М8 “ л3-2” 9. лТ12л4-3
" п3 ю.£4 и=12 „4-100 л=1 л! ® 5л2 12. У л=1(2л)!
00 2" 4-1 13. £±41 л=1 п 14 У " “О л2 15-Е-4— л=12л2+4
„?13'’(л + 1)
16. л=1 3"-л СО ди 17 л?1(Я! “О и5
«1-4-7-(Зл-2) л=1 3" СО „ сП 2°-z^4-«Т1 10" « л2 о1 у п
‘*^2-7-(5л-3)
“ (л+4)! Ъ (2л)! « л1-и2 23 yZL2L л=1 8" 24 '„?13" (л 4- 40)
25 «12242-1) „Т1 7" СО 2 26. s4— лТ14”+6 27.£^ nTi 9"-л
28 У ”2 29 уН £ (4л)! зо « 1001. л,1(л4-3)!
‘ ’ ~|2-5---(Зл-1)
2. Исследовать сходимость числового ряда
СО л2 2 У "2 3- Z /<+1 у
1- Z- И=1 ' 7л + 8 + 6 ’ л=1Л|24-3 л=1 л( И3 4- 2)
со f 4- Е л=1' < \л Л ] ,4л 4-2; 5 у—^±2— ' „ti^(„3 4-6) , “ . п-п 6- £sm—- л=1 Л +1
148
27. X sin Я=1
со
30. X
Л=1
5л3 + л
Зл’ + 1
2л+ 3 У*
7n + sJ
3. Исследовать абсолютную и условную сходимость числового ряда
л=1 2 ОО | 2- л=1 2л со ( „ \Л 1 (sh)
л=| 4 5. п-'Гт-Ч-л=1 2 л—Vn 6. j(-,r А
7. Х(-|)П— л-1 7 99л + 4 « л=1 (Зл 2]. 9. £(_ 1)"_1? + 1 ’ "(п + 2)
Л=1 6л n.X(-i)"sin-L л-1 л Л=1 (2л)!
л-1 (л + 8)и я=1 л-7
149
,eS(-'r(2»t3), 17. £(-1)" (2п) „ „Т/ (Зл + 5) СО I л10 ,8„?1(’,)"sin<
>9 Z(-0"^V л=1 л^л + 2) 2O.f(-l)"^±L л=1 Л +1 21.Z(-l)n± л=1 Л
2з-2(-1)”Г5£7Г л=1 \ 5П + 1) СО Q
26.f(_iri^o; n=1 (л3+1) -11 х-г п" >/й+10
28.2(-1)Л4^ л=1 5л 29.Z(-1)"^ 30-£(-,)'’^7 Л=1 (4л)!
4. Найти интервал сходимости степенного ряда и исследовать его
сходимость на концах интервала
оз -.Л л=1 2 2 у^-О" ’ »=1 2л + 1 3. Л=1 Л
п М8 3 I * w| 3 5 у(*~~ 2)" ’ ^л-Ю”-1 со уЛ 6- Л=1 (л + 1)
со 7- “(х + 7)” 8’ л-5" 9. f л! (х + 5)" Л=1
>0. л=1 2" _ • со „Л 11. у л=| 4" л-Тл 12. л=1 л +1
13. уг^х-з)” Л=1 со ГЛ 14- Z(-l)"— л=1 п (5 » л(х+8)" лТ| 2”
16- У(-1)"7— ’ (2л-1) (2л со „Л -1)! ’7„?12', + 1 18-Z(-1)B^ л=1 2п-1
(9 ”3”(х + 2)" л=1 "! 20. л=1 Зл-1 21.^ л=1 п
22 “2"(х + 8)” л=1 я! 23. z|—— ] -Л лТЛгл+и 24.f(-l)"^ л=1 (л+1)
150
СО „п
25. У----------
£(3л-1)4п
28. „=1 2л-4
П
29. У М2
27И?.(-,Г^
ЗО.ЁЦ#
5. Разложить функцию в ряд Тейлора по степеням (х -х0)
1. у = 1п(5х + 3), х0 = 1 2. y = xcos5x, х0 = 0
3. . пх y = sin—, х0=2 4 4. y = sin(2x2), х0=0
5. У=7ГТ’ х°=2 6. f 2х31 y = cos — , Хо=О
7. У=Т^' Л°=“3 8. у = е3\ Хо=-4
9. У ~Г~Х’ ^о-0 Vx + 4 10. *S У=-Г~’ *Ь=0 \ех
11. 1 У=~1 *0=4 л/х-З 12. у = е’х4, Хо=О
13. У",- \2 * Х®“2 (3-х) 14. Л’"1-Зх2’ XU = °
15. у = ех, х0 = -1 16. у - xchx, х0 = 0
17. х2 У=—. *0 = 0 1 + х 18. У=^-^, *о = О X
19. _у = х21п(х), х0 = 1 20. у = хё~^, *(,=0
21. у = *е"2х, х0 = -2 22. Хо=О
23. . пх _ ^ = Siny, хо = 1 24. y = xln(l-x), х0 = 0
25. у = -, *Ь=-2 X 26. _у = Vl + 2x, х0 = 0
27. _у = 1п(5х), х0 = 2 28. y = xcos(4x2), *0 = 0
29. У = --Ч-. *о = ° 30. _y = cos(2x), X0 = 7t
151
6. Разложив подынтегральную функцию в ряд, проинтегрировать и вычислить с точностью до 0,01
1 1. Je-Xdx 0 rsinx 2. J-r-dx 0 VX 2 3. Jcosx2dx 0
, °>751п(1 + х1 4. J —idx 0 VX 5. Je~2?dx 1 °-8 X 6. j- -dx 0 1 +X
7 TX + 5d 7- J — 0 е 0.9|n(l+x5) 8- J-4-2^ 0 X 9. Wdx 2 x
1 . 10. jcoslx3)dx ll.Jx2e-x2dx 9 12. Jx-sinVxdx
0 0 0
13.|—dx о* +2 0 14. Jxcosx6dx i ishfx3) isj-bifc 0 X
16.|--;^ dx oVl + X4 17. Jch(x7ldx 0 18.Jxe“x dx 0
0 x 19-1 -TT-4' 0.21+V* 0.8 1 20. J Vl + x3dx 0 21. jx'°e“\fc 0
0 22. Jxncosxdx 1 „ '^1—CQSX4 j 23. 1 dx 0 x 0,9 , 24. j ^l + x6dx
25.p—_ldx 0 x °-8 x 26. f —Tdx o(l + x3) ol-cos(2x2) 27. J A —dx 1 x
1 ln(l + x4) zq-L'dx 0 VX -n l2x-sin2x . 29. j dx o w 3o 0,r541±Mi2f 0 x
8. Функции нескольких переменных
1. Найти частные производные
1. г=2хгу+Зхуг+1? 2. u = xy+y-tfz +xz 3. z = x3 +у[у-5ху
4. z = xsin(xy1 2 3 4 5 6) 5. z = exp(-x2y2) 6. z = xsin(x + y)
7. и = arctg — 1 8 г- 1 9. z = ln(x3 ч-ху + гу3)
7x2+y2 + z2
10.z = xcos(2xy) ^4x2 +y2 12,z = 3ln("M
13,z=sin—cos— У У 14.u = x3+y5-4x2z2 15.w = ln|3z + ^8x2 + у2 j f 2 Л
сч N 1 N | К <4* t + "к + и и 3 а 17.z = arccos( —| 18.z = tg 1 X J
2O.z = 7x3y-xy7 21.z = ln7x2y+9y2
22. г = exp (sin х 1[у) 23. z = J9>arcsinx2 24. и = у-Jx + yz + x4z
25.z = x-exp(x2 -у2) 26. z = arcsin 1 — J 27.u = sin(x2yz2j
28.z = cos(x2y3j 29. z = xarctg(xy2j 30.z = 53x2-3'2
2. Для функции u = u(x,y,z) найти градиент и производную по
направлению I в точке М
1. и = 2х2 + 3xy + zy, 7={3,4,0},
2. u=x2 + xy-2zy, 7={1,2,2}, Л/(1,2,1)
3. и = 3хг-4xy + 3zy, 7={0,3,4}> Af(—2,1,1)
4. и = 2х2 -3yz + 2zx, 7= {2,1,-2}, М(-1,1,4)
5. u = 2xy + zy-5xz2, 7={-4,0,3}, Л/(0,1,5)
6. и = Зху2 - 2х2 - 5zy, 7={2,-2,1}, Л/(1,-1,0)
153
7. u = x2y2+x2z2+z2y2, 7={l,4,0}> Л/(0,1,-5) 8- и = x2y—z2 +2zy2, 7={-l,2,2}, A/(l,3,-4) 9. u = xy + 2xz2-zy, 7={-3,4,-l}, w(2.1>5) 10. u = 2x2y-xz + z2y, 7={-2,4,-4}, Л/(3,1,-6) 11. u = x2-Sxy2+3zy, 7={4,0,3}, A/(2,2,l) 12. u = 4x2y-3xy + xz2, 7={-2,2,l}, A/(3,2,l) 13. u = 3xy2+3yz2-zy2, 7={l,2,0}, Af(l,2,l) 14. u = x2y-4yz + Sz2x, 7={l,-2,2}, Л/(2,1,|) 15. u = 5xy-yz2-zx2, 7={0,l,2}, W(2,2,l) 16. u = x2+5xy-zy2, 7={2,-l,2}, M(l,l,l) 17. и = 3x — 4yx2 + yz2, 7={2,2,1), Af(-3,2,1) 18. и = 5x2+3xy2-2yz, 7= {2,-2,1}, М(2Д,1) 19. u = 2x-yx2+5zy2, 7={-l,2,0), M(l,3,l) 20. u = xy2-2xy + 3zx2, 7={1,2,-1), M(3,l,l) 21. u = x2y + 3yz-xz2, 7={0,-l,2}, M(l,l,3) 22. u = xz2+2yz2-3zx2, 7={l,2,-2}, Л/(2,1,2) 23. u = x2z-5y2z+yz2, 7={-2,0,l}, Л/(3,1,3) 24. u = 2xy+yz2-2zy2, 7={l,2,-2}, M(2,2,l) 25. u = 3xy2-3yz2-3zx2, 7={l,-2,0}, M(1,2,2) 26. u = 5x2y-yz2 + zx2, 7= {2,1,-2}, Л/(1,3,2) 27. u = Sxz2+yx2-xz2, 7={0,l,-2}, Af(l,l,2) 28. u = 3xz-2xy2~2yz, 7={2,2,1}, Л/(2,2,1) 29. u = 5xy + 3yx2 + zy2, 7={2,0,-l}, M(2,3,1) 30. u = 4xy + zx2-3zy2, 7={0,3,-4}, M(l,l,3)
154
3. Найти уравнения касательной плоскости и нормали в указанной точке
1. x2+y2+z2=9, М (2,1,2)
2. x2+2x+/-z2=15, М (2,1,2)
3. 2х2 - у2-z2 =16, ЛГ(4,О,4)
4, х2 + 2j2 - 3z2 = О, М (1,1,1)
5. 2x2+/-2z = 0, М(-2,2,б)
6. х2+j2 —2j + z2 =15, Л/(0,1,4)
7. х2+4х +ji2 —z2+ 2z = 33, М(-2,6,1)
8. х2 — 2j2 — z2 =28, М (6,4,0)
9. 3x2+2/-z2 = 0, М (-1,1,1)
10. х2+2x+j2+Z2 =8, Л/(-1,0,3)
11. x2+/-2z = 0, Л4(-2,2,4)
12. x2+j>2-z2+2z = 5, М(0,2,1)
13. 3x2-/-z2=28, М(-4,2,4)
14. 2x2+/-3z2 = 0, Л/(—1,1,1)
15. z2+2/-2z = 0, Л/(-2,1,3)
16. x2+/ + z2-2z = 3, M(-2,0,l)
17. x2 + j2+2j-z2 =8, Л/(3,-1,0)
18. x2-y2-2z2=18, M(6,0,3)
19. 2x2+2/-z2=0, Af(-2,2,4)
20. x2+4/-6z = 0, M(-6,0,6)
21. x2-2x+/-2j- + z2 = 7, Af(l,l,-3)
22. x2+/-z2 = 36, M(4,6,-4)
23. x2-y2-z2=ll, Af(6,-5,0)
24. 2x2 + 2/-z2=0, A/(2,-2,4)
25. x2+y2-z2=0, W(-l,0,l)
26. 2x2+3/-4z = 0, Af(2,-2,5)
155
27. 2х2 - у2 - 4z = 0, M (2,2,1)
28. xz-3y2-3z2=21, Л/(-6,2,1)
29. x2-y2~2z = 0, M(2,4,-6)
30. x2 + 2y2 + 2z2 = 4, M (0,1,-1)
4. Провести исследование функции иа экстремум
2. z = 2xy2 -2х3 +2у2 + 24х
4. z = x3 + 2ху + 2у2 + 2х2-Збх б. z = х3 + 2ху - у2 - 7х + 2у 8. г = х3-6лу + Зу2-9х
1. z = x3-у3-Зх2+3у-24х
3. z=4xy+x2+y2-6y
5. z = x3-бху + Зу2-18х-6у
7. z = -4xy + 8x2 + 4у2-4у
9. z = x2y + 2x2-Зу2 +4у 11. z = xy2-2х3+ 2у2+8х 13. z = x2+6xy-4y3 15. z = 4xy-2x2-y3+4y 17. z = x3-y3-3x + 12y 19. z = 2xy+x + 2y2+2у 21. z = x+3y+4x2+3y2 23. z = x3-24xy-8y3 25. z = x2 + 2xy + 4y2 + 6y 27. z = x2 +2xy + 4y2 +4y 29. z = 2x3 + 6xy-y2+12x
10. z = y3-4xy-4x2-y2-27y
12. z=y3+6xy+3x2+6y2-9y
14. z = y3+3x2y-3x2-12y
16. z = 2x3+12xy-3y2 + 18x
18. z = xy-x2 + 3x-y
20. z=2x3 +2xy + y2-4x
22. z = 2x3-6xy-6x2+3y2
24. z = 8xy + 6x3+4y2-5x2
26. z = x-y-4x2-2y2
28. z=y3 + 3xy-x3
30. z = 2x-2xy + y2-4y
5. Применяя метод градиента, найти экстремум функции на заданном множестве
f(x.y) = x + y, х + 2у<0 х-2у-15<0 2x+y+7i0
f(x,y) = x + у + 1, х<6
x+2yi0
fx + 2yi0 x-2y+15i0 2х+у-6<0
156
/(*.,)') = X-.F + 1. f(x,y)=x~y-2, f(x,y) = 2x + y-3.
2х+_у-350 5. 2x-j+4>0 x>-4
х-2.у-155 0 x + 3_y+15>0 y^2
х>0 x^O x-2y^0
f(x,y)=2x-y+6, f(x.y) = x-2y-2, f(x,y) = 3x-y+3.
х58 8. Зх-^>о 9 2x-2y^7
х+у£ 9 x-2^-9^0 x+2y+9^0
2x+yi.O i2x + y~2<, 0 Lyso
f(x,y)=x-4y-4, /(х,у) = х+3у-6, f(x,y) = x + 2y+3,
4х+2_уй-1 11. X-2J- + 9S0 12 x+3y-9<0
x-2y-9i0 2x+^+2>0 2x-y+4<0
y<0 y>2x j>0
f(x,y) = x + y, f(x,y)=x-y~3> f(x,y)=x~y4-5.
x+4y£0 14. X~4 15. x+jSO
x-y-6<0 x + y^l х-4^ + 16>0
Зх+у+9^0 x+3j^0 3x+j-1250
f(x,y)=2x-y+7. /(x,j) = -2x + j>-1, f(x,y) = x+3y-7.
x+y-8i0 17. x-J+5>0 (8 xi-3
x-4y-20i0 x + 3j<+9SO 3x + ^<0
xiO xSO x+j+120
/(x,j) = 4x+j>+1, f(x,y) = x-3y+l, f(x,y)=-x + y-i.
5х+2^5б, 20. Sx-^SO 2J 4x-.y<8
1 у<л. x-2y-4<0 x+^+1^0
2x + y£0. 4x+y-16<0 j-SO
f(x,y) = x-2y-2, f(x,y)=-2x + y-3, f(x,y) = x+2y + 3,
x + 2y + 6ZO 23. x-3y+9iO M x + 4><-4<0,
x-3y-6<0 4x+y+850 x—y+6> 0,
y<0 yi3x jSl.
157
/(*.>') = х + Зу-2, f(x,y) = 3x + y-2,
25 26 Ь-2^4^0, 27
2х + 2_у-1<0 х + 2^ + 4^0,
^ + 9^0 х£8.
f(x,y) = 3x + 2y-2, f(x,y) = 2x-3y + 5.
>« [х + 2у-9^0 ZD. 29. p-'+6S() 30.
4х-_у-450 Зх + ^ + 150
х + 3^0 х^О
f(x,y) = x- Sj'+l, 2х-^-10<0
2х + _у + 5^0
f(x,y) = х-3у+4, x + j<-3<0
х-4_у-150
х + 9>0
9. Кратные интегралы
1. Вычислить двойной интеграл
1 2х
1. Jdxf xydy о х
2
2 2х
4. Jdx J x’ydy
1 2
2 1-/ r_
7. Jdy J yf^dx
-2 /
2 0
lO.Jdy J______yxdx
1
2 x—1
13 Jdy J x2dx
0 2x
2
2 У
16. J dj> J ydx
J 2.У-4
2 У2
19. Jdy J Ajrdx о о
0 7x2+I
22. J dx J_____xydy
4 >-5
25. j dy J Xyjydx
-1 о
2 2->
28. Jdy J xy3dx i о
14.Jdj J xydx 1 з>
20. J dx J xydy -2 о
i i-y2
2. f dy ] ydx
-I v2_|
3
4 2x
5. Jdx J xdj
0 —2x
I Г3
8. J dx J xydy
-2 -x
2
2 x
11. JdxJx^dj
1 i.
2
0 4+3x
23. J dx f xdj -3 x-2
9 Jy
26.fdj f >dx
1 о 9 0
29.fdy f jprdx о
3.
2 у
2
I 2>
6. jdj J ydx
о 2>-3
1 x+l —
9. fdx J y/xydy
0 2x-l
2 X2
12. Jdx J xdy 0 3x
1 y2 r-
15. | dy j -Jxydx
-I 2y
2 у/^-У
18.Jdy J xydx i 0
x+6
1 2
21. Jdx J xdy
0 2x-l
1 0 , ,
24. J dy f xy2dx
-3 j-3
3 х+3 Л
27. Jdx J x4dy
0 2x
I x2
30. J dx J ydy
-2 -i
159
2. С помощью двойного интеграла вычислить площадь фигуры, ограниченной кривыми
1. у = 2х, у = 0,5х, х = 1.
2
2. у=—, у = 0,5х, х = 4. х
3. х = 1-у2, х — у.
4. j/ = 2x + 3, у = х2.
5. у = х, х = 0,5_у, 25у54.
6. у = 1—х/гх-х2, y = t+j2x-x2, х = 0.
7. у = 2х, у = -2х, 05x50,75.
8. у = 0,5х2, у = х2-1.
9. у=43-х, у = -^3-х, xi0,75.
10. х = 0,2у2+1, х=у2, у^О.
11. х = 2у, х = 2у-3, 05x51.
12. _у = 0,5х, у = -х, х = 8.
13. y = -Jl-x, y = —Jl-x, у £-2.
2
14. х=—, у = 2х-3, 15x52.
У
15. у=4-2х,у = -2, х = 1.
16. y = -Jx, у = -х2, х = 1.
17. у = -0,5х2, у = 1-х2.
18. у = 3 + х,у = 2х, х = 0.
19. х=1, y=tfx,y=-i? .
20. у = 4, х = -у[у, х = -у5 .
21. х = у-2, х = -1, у = -3.
22. у = 0,5(х + 1),у = 2х-1, х = 0.
23. х = у-3, х = 0, у = 6.
24. у = 0,5х + 3,у = 2х-1, х = 1.
25. х = 0,5(у+1), х = 2у-1, у = 0.
160
26. y-4x,y-x-2, _у>0.
27. х = _у + 1, х = 2-у, у = -2.
28. х=2у—б, х=—у, у = — 3.
29. у=х+3, j=0, х=4.
30. _у=Зх+4,у = х-2, х = -1.
3. Вычислить тройной интеграл
1 2: у
1. Jzdz J ydyjdx о г о
I 1-> X
3- J ydy J dx j dz -1 у-1 -io
2 х2 z
5. JdxJ dz J ydy i о -2
2 , z 2y
7. fz2dzjdy j dx l о о
i у x
9. Jydy J dx Jzdz о y-1 -2
« x z
ll.jx2dxjdzJ ydy о o-i 2 - у
13. JzdzJdy j xdx
0 0-4
о у о
15. J dy J z2dzjdx -1-4 z
0 z 0
17. J dz J ydy f xdx
-2 z-l у
1 X4 у
19. JdxJydy Jzdz
-2 x2 0
2 x 2z
21,Jx2dxJdz J dy i о -i
2 2y z
2. Jydy J dzjxdx
О у 0
2 z x
4. JzdzJxdxJdy 0 £ -1
2
1 x 3y
6. Jxdxjydy j dz 0 0-4
2 10 z
8. JdyJzdzJdx о у о
3 2z X
10. Jdz j x2dxjydy
1 z 0
2 х+1 у
12.Jxdx J >dyjdz 1 x-l о
О 2x у
14. j dx J ydy J dz -1 x -3 1 y1 x
16. Jdj> j dxjdz
О 2y 0 2 x z
18. J x2dxf dz j j2dj> 0 I 0
0 y+l z
20. J dy J zdz J dx
-I у -3
2 1 z
22. Jdy j dz j xdx о >-1 -2
161
2 х2 у
23. Jxdx J dp jdz
0 3x0
I I z
25. J dyfzdzf dx
-l у -3
0 x 3=
27. J xdxjz2dz J dp
-i о -I з z »+i
29.fdzfp2dp f dx
l z I
I x+2 z
24.jdx j zdzjydy 0x0
з , 2x у
26. jx2dx J pdpjdz
2x0 2 x z+3
28. JdxJdz J ydy
i о I
2 X :2
30. JdxJzdz J dp l о z
4. С помощью тройного интеграла вычислить объём тела, ограниченного поверхностями
1. х2+р2=5, 2. z = 10-x2-p2, z>6 3. z = x2+y2,
z<x2+y2+l, zSO y<x, z<4
4. х2+р2=1. 5. x2+p2=9, x+y + z<5,z^0 6. 2z = y]x2+y2,
х2+р2=4, x+y + z<4, zZO z = yl9-x2-y2
7. 2z = x2+y2, z = 4 8. x2 + y2 = 9-z, 9. x2 +y2-z2 = 0,
y>-x, y<-x-Jl x2+y2Z4, z£0 x2+y2<4.
10. x2 + p2=6. II. x2 + >2-(z + l)2 = 0, 12. z = yjx2 +y2+l,
z<x2+y2,zZ0 22=Х2+Л x2 + >2<4 z=^3-x2-y2
13. x2+p2=4, 14. z = x2+y2, 15. 4-z = x2+y2,
z^x2+p2,zS10 z = 2(x2+y2), x2 + y2 <1 z^O x2+/<l
16. z=x2+y2, z=4 17. z=4-x2-y2, 18. x2+y2 =9,
y^x, y<Xy/3 0<z^3 x2+y2=4, z<5-x,z^0
19. z = x2+y2, l<z<4 20. z = 6-x2-y2, z^2 21. 2z = x2+y2, x2+y2<2, z£0
162
22. z = 5-x2-y2, 23. z = x2 +y2, z<4 24. x2 + y2-z2 = 0,
z>0 x2+y2<l 2z = x2 + y2.
25.3z = ?+y2, 3<z<27 26. z = x2+y2+l, 27. z = -7x2+y2,
x +y =4, z>0 z = -79-x2-/
28. 2z = x2+y2, z<18 29. x2 + y2=9, 30. x2+y2 = l,
x>0 x2+y2 = z2, 2>z>0 x2+y2=25, x + y + z<10, z>0
5. Найти поток векторного поля a = /’(x,y,z)i + g(x,y,z)y+ +7?(x,y,z)A через замкнутую поверхность с помощью формулы Остроградского.
1. l<z<2-x2-/, а = (2у+х)7+(3х + 2у)у+ 3zA
2. х2 +у2 < 1, 0 < z <-^х2 + у2, a = xi + (Зу + z)j + 5(y-z)k
3. 0<z<3,x2+y2<l 0<у <1, a = 3yi+(4x + y)j + 3zk
4. х2 + у2 = 18, 0<z<y, 0<х<у>/з a = (y + 3x)i+2xzj+ 5(x—z)k
5. z=x+y,x+y = l,z = 0,x = 0,y = 0 a = 2xi +(2y + z)j + 5(y + z)k
6. x>y2, 0<z<l-x, a = (2x+y)i+(-3y + 3z)j + 2zk
7. 0Sy<l-x, x>0, 0<z<l-x, a = 3xi-(y + z)j + (2y-3z)k
8. x2 +y2 =z,x = l,y = 0,y = 2x,z ~0
a = -^4x+y2 ji + (Зх2 + z) J + (у2 - 5z)A
9. ^x2+y2<z<l, x>0a = 2y27+(3 + 3z2p + 5(x + z)Z
10. l<x2+y2<4, 0<z<5-x,a = (x + y’)7-(5x + 2y)y-(x2-4zj/c
11. 0<z<Jx2 +y2, a = y2i + ^x2 + z)y + 5(2y + z)k
12. x2<y<l, 0<z<l, a = 6zi + (2y + z)j+^y2-3zjk
163
13.у1х2+у2 <z<4, a = (5x + 2>)7+(x-7>); + [4z-x2)* 14.1<x2+/<9, 0<z^4-x-^, a = (3x+>)7+(z2+3j-]y + [x2-7z)7
15.0<z<x2 +y2.x=l,y = 2x,y = 0, а = (4 + y)i+(х2 + 2yjj + (х+ z)k
16.0<z<l-x2-y2, a = (2x+z)l+(2-4y)j+(x? + z)k
17.0,s7x2+^ -z-2> a = (z+2y)i-(Зх2-2yjj+(x-z)k 18.10x+5> + 4z-20 = 0,
z = 0,x = 0,j> = 0, a = (4x+z)i+(z-2y)j + (x-4z)k
19.0<x2 + >2<9, —1<z<4, a = (x+2y)i-(z-3y)j+[5y2-zjk 20.0<z<T^, >' = 0,> = 9x,x = 1, a = (l + 2x)i-(4x-y)j-(2y+4z)k 21.x2<ySl, x>0, 0<z<l-x,a = (3x-l)i-(4z + 2y)j + (l + 3z)k 22.0<y<4x,x = l, 0<z<xy, a = ^2 + y3^i-^2z2 +xjj + (2y-3z)k 23.4x + 3y-6z = l2,x = 0,y = 0,z = 0
0<z, a=(2 + 3y)i-(5y + x)j'+(2x-3z)k
24.1-х<><1, x<l, 0iz<l~>,a = (> + z1)i-(2x-3>)j + (l-4z)A 25.0^x2+>2<4, 0<zi(xy)2,a = (x+y)i+(5x + 3y)j + (y-z)k 26.0<y<l-x2, 0<z<>,a = (2x+>2)7+(x2+>)y+(x2-4z)i 27.0<><l,x^0,5 0<z<1-x, a = (x + y)i~(4x + 4y)j +(3y + 2z)k 2S.5x-20y + Sz-40 = 0,x = 0,y = 0, z = 0,
a=(2 + y3^i+(5 + 2z)y+^y2 +4zjk
29.0 < z < (2xy)2, y = 0,y = 2x,x = -2,a = (z+y)i + (x-2y)y-(y-z)k 30.-(x2 +y2)^z<0, y = 3x,y = 4,x = 0,
a=(5x + l)i-6(x + y)j+(5 + 2z)k
164
6. Вычислить циркуляцию векторного поля а = Р(х,у)1 + Q(x,y)j вдоль замкнутого контура L, лежащего в плоскости хОу (обход против часовой стрелки).
1. а-(х-1)г + 2у7 параллелограмм с вершинами в точках Л(0,0),В(2,0),С(3,1),0(1,1)
2. a = (y + 3)i+xj L: треугольник с вершинами в точках Л(0,0),В(1,0),С(1,1)
3. a = 2(x-l)i + yj L : дуга ВС окружности х2 + у2 = 1 и отрезки прямых СА и АВ Л(0,0),В(1,0),с(-^у-,^у^
4. а = 2xi + (у - 1)7 L: параллелограмм с вершинами в точках Л(0,0),В(2,0),С(4,3), 0(2,3)
5. а = yi+(x-2)j L: треугольник с вершинами в точках Л(0,0),В(0,1),С(-1,0)
6. o = xi+2(y+l)7 L: прямоугольник с вершинами в точках >4(0,0), В(5,0), С(5,2), 0(0.2)
7. a = xi-(y-3)j L: параллелограмм с вершинами в точках Л(0,0),В(4,0),С(2,2),0(-2,2)
8. а = 2х/+(у + 1)7 £: дуга ВС окружности х2 + у2 = 1 и отрезки J2\
прямых СА и АВ Л(0,0),В(1,0),С1 —
9. а = Зхг-(у + 2)7 £: параллелограмм с вершинами в точках Л(0,0), В(2,0), С(0,3), О(-2,3)
10. а = (х + 3)г-2у7 £: треугольник с вершинами в точках Л(0,1),Л(1,1),С(1,3)
11. о = (х-2)г+3у7 L: прямоугольник с вершинами в точках Л(3,1),В(-3,1),С(-3,-1),О(3,-1)
12. а = Зх/ + (у+3) j L: параллелограмм с вершинами в точках
Л(0,0),В(1,3),С(-3,3),0(-4,0)
165
13. a = (x+5)7+2j L: треугольник с вершинами в точках >4(0,0),B(4,0),C(2,2)
14. a = (x-2)7-4j' L: дуга ВС окружности х2+у2 =1 иотрезки
Г л/2 уИ 'I
прямых СА и АВ >4(0,0), В| —,—— 1,С(0,1)
15. а = 2/- (у +1)/ L: параллелограмм с вершинами в точках >4(2,0),В(0,2),С(-5,2),£)(-3,0)
16. a = i+2(y-2)j L: треугольник с вершинами в точках >4(0,0), В(3,2),С(0,2)
17. a = 2xi-5yj £: прямоугольник с вершинами в точках Л(3,2),В(-1,2),С(-1,0),£)(3,0)
18. а = 3/+4уJ L: параллелограмм с вершинами в точках >4(0,0),В(1,1),С(1,4),£>(0,3)
19. а = 2xi + J L: треугольник с вершинами в точках >4(0,0),В(3,2),С(-1,2)
20. а = 2i-(у +1)7 £: дуга ВС окружности х2 + у2 = 1 и отрезки
( у^2. л/2
прямых СА и АВ >4(0,0),В——— 1,С(1,0)
21. о = (х+1)г-5у £: параллелограмм с вершинами в точках >4(0,0), В(-2, -2), С(1, -2), £>(3,0)
22. a = 3i+3y2j £: треугольник с вершинами в точках >4(0,0),В(4,2),С(0,3)
23. а = x2i + 2yJ L: прямоугольник с вершинами в точках >4(0,0), В(0,4), С(-2,4), £>(-2,0)
24. а = (х + 4) i - yj £: параллелограмм с вершинами в точках >4(0,0),В(-1,-3),С(1,-3),£>(2,0)
25. а = 4x1 - 2(у -1)/ £: треугольник с вершинами в точках >4(0,0),В(1,3),С(-2,3)
166
26. a-i-5(y + 2)j £: дуга ВС окружности х2 + у1 =1 и отрезки
прямых СА и АВ
27. а = 3х г+Зу/ £: параллелограмм с вершинами в точках Л(0,0), В(2, -2), С(0, -2), £)(-2,0)
2%.a = 2xi-(y-5)j £: треугольник с вершинами в точках Л(0,3),В(-3,0),С(0.-2)
29. a = 3(x-l)i +>2 j L: прямоугольник с вершинами в точках Л(0,0),В(0,-2),С(4,-2),£>(4,0)
3O. a = x27-Q' + 3)y £: параллелограмм с вершинами в точках у4(4,2),В(1,2),С(-1,-2),£>(2,-2)
10. Дифференциальные уравнения
1. Найти общее решение дифференциального уравнения первого порядка с разделяющимися переменными
1. x-yy'^X 2. (l + y2)dx = xdy
3. •Jl +y2dx = xydy 4. (l + y)dx-(l-x)dy = 0
5. xy + >ll-x2y' = 0 6. y'lny = y
7. (l + y2)xdx + (l + x2)dy = 0 8. у sin xdx + cos x In ydy = 0
9. ^(/+’)+(x2>->)/=0 10. x^l-y2dx + y71-x2dy = 0
11. x+yy' = 0 12. ey p + x2 jdy - 2x(l + ey jdx=0
13. (x2 -1 jdy - 2xydx = 0 14. x^/l + y2 + yy'-Jl+x2 = 0
15. p + y2)dx-xydy = 0 16. ylnydx + xdy = 0
17. tgx • sin2 у + cosx - tgy-y' = 0 18. y' = 2x+y
19. x(y + l)dx-(x2 + ijydy = 0 20. dy _ 1 + y2 dx (l + x2)xy
21. ey~2xdy = 4xdx 22. (l+y2)dx-xy(l + x2)dy = 0
23. y'sinx-ycosx = 0 24. (y + xy)dx + (x-xy)dy = 0
25. , 2 У у cos x= Inj* 26. (l + y2 jdx + 2xydy = 0
27. [Jxy + Jx}y-y=0 28. 2^ + 23x-'.y' = 0
29. (l+x)3dy-(y-2)2dx = 0 30. ydx + sin2xdy = 0
2. Найти общее решение дифференциального уравнения первого порядка, представив неизвестную функцию в виде произведения у = и v
1. х-у'+2у = х2
3. у' + 2ху = 2х
2. у'--£- = (x + 4)J
х + л v ’
4. y'-h-
Л5
168
5. y+y-tgx = secx
7. y'+2xy = 2x3
9. y'+y = e~x-cosx
Н.У+^ = х2у2 x
13.y-y-ctgx = sinx
15-У—— = x2+4x+5 x + 2
17.(x+l)-y-xy = 3
19.(l+x2)-y + xy = l
21./-2xy = -2x
23. xy'—— = x x+1
2S.y'-y = 2ex-y3
21.x-y'+y = x2 + 3x+2
29./+x2y = x2
6. (x2-ljy+(x + l)y = x-l
„ , l-2x -/
8. у---j—у = e /x
x
10. У + 2y = (x + l)y2
12. e*-у+ ex-y = x
14.2x-y'~y = 3x2
16.(4 + х2)-у+ду = 16
18. у + y- cosx = sinx-cosx
2O.(x4+x)-y + (2x3-l)> = ^^
22. у - у • tgx secx = es'cx
24.x-y'+y-ex = 0
26.(x2-x)-y-(x+l)> + 4 = 0
28.(x2-x)-y+> = 2x3-x2
3°.y—^- = ex(l + x)2
3. Найти общее решение дифференциального уравнения высшего порядка
1. y//=sinx 2. /Al X 3. у-=г (х+5)
4. У=1+5 X 5. y" = 2xex 6. У = 40х4
7. у' = хе2х 8. ул' = 20х3 9. y,y=xe3x
10. У = 60х2 11. /и = 16еГ*х 12. y = x-sin2x
13. у1У = е2х 14. y = x-cos5x 15. y’ = x2ex
16. y = -9x-sin3x 17. y’ = x-3x 18. у17 =cos2x-sin
19. y = x-cos3x 20. y,y = cos5x 21. у =—+x X
22. yW =cos3x+x 23. y,y = 40X3 + x-4 24. y' = sinx+8e2*
169
25./ = 12х3—sinx 26. y=cosx+— 27. / = 6х2 + 2х-4
28. / = x2sinx 29./F=49sin7x + 1 30. y = x-cosx+x
4. Решить задачу Кошн для уравнения второго порядка
1. / = 128/, >(0) = 1, /(0) = 8
2. У /+49 = 0, >(3) = -7, /(3) = -1
3. У+р/=х, /1) = 0, У(1) = 1
4. у’ + 50sin > • cos3 > = 0, /0) = 0, У(0) = 5
5. /•/+36 = 0, >(0) = 3, У(0) = 2
6. /-^У = -1, >(-1) = 1, У(-1) = >
7. / = 72/, >(-2) = 1, У(-2) = 6
8. / = 2sin3>-cos>, >(1) = —, У(1) = 1
9. /+^У = 0, >(1) = 0, У(1) = 1
10. У=32У, >(4) = 1, У(4) = 4
11. / У+16 = 0, >(1) = 2, У(1) = 2
12. /-> = у2, Д1)=1, У(1) = 1
13. х /=(1 + х2)у, >(1) = 0, У(1) = 1
14. / У+9 = 0, >(-!) = !, У(-1) = 3
15. /+У = х, >(0) = 0, У(0) = 1
16. у-1у=о, И-1)=0, У(-1)=1
17. / У+4 = 0, >(0) = -1, У(0) = -2
18. 2/-1у = 0, >(1) = 0, У(1)=1
19. / = 2/, >(-!) = 1, У(-1) = 1
20. У У+1=0, >(-2) = -1, У(-2) = 1
21. У = У2, >(1) = 1, У(1) = -1
ПО
22. х / = (х+1)у, у(1) = 0, у'(1) = 1
23. //+64 = 0, у(0) = 4, /(0) = 2
24. /(х-3)+/ = 0, у(4) = 0, /(4) = 1
25. y-2sin3ycosy = 0, у(1) = п/2, у(1) = —1
26. /-у3+25=0, у(2) = -5, /(2) = -1
27. /+2у /’ = 0, у(0) = 1, /(0) = 1
28. /+8siny-cos3y = 0, у(0) = 0, У(0) = 2
29. /-у3 = /, у(0) = У2, У(0) = ^
30. 2/ у = 1 + у2, у(0) = 1, у(0) = 0
5. Найти общее решение соответствующего линейного однородного дифференциального уравнения и указать вид частного решения с неопределёнными коэффициентами
1. уу+9у" = 2х2+ х-х2 е3х
2. y/|/+8y' + I6y = x3e2jr+sin2x
3. Уи+5/ + 6/= х2-е-2х-х3
4. уУ1 +2угу + /= x-l + x-cosx
5. у’7-4/= 10+х4 +x-sin(4x)
6. у"-у"+У-у = (х + 1) е* + х3-2
7. yw -1 бу" + 64у = х е2х + х е~х • sin(хУз)
8. уУ-9у" = x2 + 2x+(x + l)cos3x
9. у1’’ + 8/ +1 бу = х - е2х + (х2 + хJcos2x
10. у'1'-5у" + 6у’ = x-e”2x+2x2-cos2x
11. /7-2y/y + / = x2-x + 4cosx
12. у13' + 4/=х3 •е2х + х-sin(-T2x) +1
13. у/г+У"+у+у = (х2+4)-е-* + х + 7
14. у17 +1 бу" + 64у = х2 е~2х + Зе"х cos (*-^)
15. y/-25y = x3-9x+(x-8)-cos5x
171
16. у W - 8у" +1 бу = е2х - sin 2х+(2х+l)cos 2х 17. у"' + у" - бу' = (х - 2) • е21 + (х+9) • cos 2х 18. уУ1 - 4у” + 4у" = (х2 - х) е2х + 4 cos 2х 19. yVI -4у" =х4 +х2 • е^х + х cos(V2x) 20. уп'-2у’ + у-2у = [х2+х) е2х+1 21. уУ1 -2у"+у = хе7х+х-ех+sinx 22. у” + 9у17 = 5х2 + 4х - х • е3' + cos3x 23. уу +25У" = x + 3+(x-l)cos5x 24. у77'-у’ - бу" = х • е~2х + е3х + 2 + х cos2x 25. у17 + 16у" = х+2+х-е-4х +4x-cos4x 26. уГ/ + 125у” = х3 e~ix - 9х + (х - 8)cos5x 27. уп' - бу" = х • е2х - х3 + 2х + х • е~х - sin (6х) 28. ул'+ЗУ+У+3>' = (х3+4) е'3х+х+10 29. уп' + 5у* = х3 • е-5х - 5х + ех • sin (5х) 30. у™-18У + 81у = х2 e3x+sin9x + x
6. Найти общее решение подбора
, „ . , , . 5х 1. 2y-5y = smy
3. Зу-5у-2у=х2
5. у~10У+25у = 4е5х
7. у’+6у‘ + 25у = e-3x-cos2x
9. у-2у-8^ = 6е-2х
11. у-4У + 4у = 16х2
13. 5y-6y+5j' = e3x-cos4x
15. у"-4у'+3> = 3sinx
17. 2y+5y-3^=sin3x
дифференциального уравнения методом
2 9У-бу + у = 9е3
5 -
4. У-ЗУ+—у = е2 sin2x
6. 6у’-у'-у = 3х
8. У-12У+ 36y=sin6x
10. y'-Sy' + 25у = 9е4х sinx
12. у'+3у'-4у = е~*х
14. У-4У+4^ = 4х2-2х
16. У-2у' + 2у = 4 sinx
18. 5у'-2у' + у = ех-cos2x
172
19. y+4^ = 2sin2x-3cos3x
21. 5y’-2y'+y=ex sin2x
23. 6y-y'-y = cosy
25. y-2y+10^=ex.sinx
27. 2y-y-j/=sin2x
29. y+9j/=2sin3x
20. У+ 14У+ 13j/ = 4e 31
22. У - 8y' +16y = 4sin 4x
24. 9У - бу' + у = sin x
26. 9У - 6y' + y = 4cos—
28. У+ 8/ + 16> = cosx
30. у-ЗУ-4^ = 2е4х
7. Найти решение задачи Коши
1. 2y'-5y'-3y = eix.y(0) = 0, У(0)=|
2. 4у'+4у'+у = 2е2 ,у(0) = 1, у(0) = 1
3. 2у'-у'-у = ех.у(0) = 3, У(0) = |
4. У+У=ех+х.Х0)=|. У(0)=|
5. У-12У+36^=36х+2е6х, у(0) = -|, У(0) = 0
6. y-10y+25^ = 5sin5x, у(0) = 3, У(0) = ^
7. 2у’-у-у=х2-е 3 , у(0) = —, У(0) = 0
8.
y-8y + 16.y = 16cos4x-l, у(0) =
1
16’
у(о)=о
9. у'-4у'+4^ = 8x-4cos2x, _у(0) = 1, У(0) = -1
1О.у-12У+Зб^ = 18х3 + 1, 3'(°)=-^, У(0) = -|
1\.4у'+4у'+у = х} + 6х2, >(0) = 2, У(0) = 0
12.4у'-4у‘ + 2у = 5е2-4х, 3'(0) = 1, У(0) = 1
13./ - 2/ + 5у = -5х3 - 4х2 + 2х ,у{0) = / (0) = -3
173
I4.2/+5y-3^ = e2+6x, ?(°) = ~|- У(°)=у - “ 1
15.6y’-y'-y = e2 + e2, ^(0) = l, У(0)=-16.4у’+4У + у-2х2-4, y(o) = 4, y'(0) = 0
17.y’-Sy' +6j>=26sin2* + l, ^(0) = -j, У(0)=-1 2x
lS.9y’ + 12y' + 4y = cos——8, ^(0) = -2, У(0) = 1 19.у-8У + 16^ = 4е41, у(0) = 1, У(0) = 1
2O.y’ + 2y' +5y = 5x2-x, y(O) = l, y(0) = 0
21./-5У+6^ = Зе31 + 1, Я°) = -- У(°) = °
6
22.4У + 4У +y = Se 2 +x, y(0) = 0, y(O) = l
23.y’ + 2y' + 5y = 4e-x+sin2x. y(O) = j|. У(0) = ^ — 3 ।
24.y' + 4y' + 4y = 2e2 +x. j>(0) = —, У(0)=— 25.y-2y, + y = 4ex +x2-4x, y(0) = 2. У(0) = -2 26.у + 12у + 36_р = 2е"Лх-108х, Я°) = °- У(°) = ° 27-У-6У+ 13j> = 25sin2x, ,у(О) = у. У(0) = 1 28.у+бУ+9>' = 2е'3х-9х, 3'(0) = |, У(0) = 0 29./+ЗУ-4^ = е41 + е“*1, И°) = ^- Д°) = -^
ЗО.у'-4у=4е2х +4cos2x, _у(0) = ^, У(0) = 1
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Сборник задач по математике для втузов. Линейная алгебра и основы математического анализа / под ред. А.В. Ефимова, Б.П. Демидовича. — М.: Наука, 1993.
2. Берман Г.Н. Сборник задач по курсу математического анализа. — М.: Наука, 1977.
3. Кузнецов Л.А. Сборник заданий по аысшей математике (типовые расчеты). — М.: Высшая школа, 1994.
4. Зимина О.В., Кириллов А.И., Сальникова Т.А. Решебник. Высшая математика — М.: Физматлит, 2000.
5. Проскуряков И.В. Сборник задач по линейной алгебре.— М.: Наука, 1984.
6. Клетевнк Д.В. Сборник задач по аналитической геометрии.— М.: Наука, 1972.
7. Краснов МЛ., Киселев А.И., Макаренко Г.И. Сборник задач по обыкновенным дифференциальным уравнениям. — М.: Высшая школа, 1978.
175
Учебное издание
Бараисиков Александр Иванович, Богомолова Елена Петровна, Петрушке Игорь Мелетисвич
СБОРНИК ЗАДАНИЙ ПО ОСНОВАМ ВЫСШЕЙ МАТЕМАТИКИ
Учебное пособие
по курсу
«Математика» для студентов МЭИ (ТУ), обучающихся по всем направлениям подготовки
Редактор издательства Н.А. Хрущева________________________________________
Темллан издания МЭИ 2007, учебн. Подписано в печать 21.04.08
Печать офсетная Формат 60x84/16 Физ. печ. л. 11,0
Тираж 700 экз.___________________Изд. № 140_________Заказ 195т Цена 33 руб.
ЗАО «Издательский дом МЭИ», 111250, Москва. Красноказарменная ул., д. 14.
Отпечатано в типографии НИИ «Геодезия», 141292, Московская обл., г. Красноармейск, прося. Испытателей, д. 14