СБОРНИК ЗАДАЧ
ПО КУРСУ
ВЫСШЕЙ МАТЕМАТИКИ
Под редакцией Г. И. Кручковича
ИЗДАНИЕ ТРЕТЬЕ, ПЕРЕРАБОТАННОЕ
Допущено Министерством высшего и среднего специального образования СССР в качестве учебного пособия для студентов высших технических учебных заведений
ИЗДАТЕЛЬСТВО «ВЫСШАЯ ШКОЛА» МОСКВА—1973
Г. И. Кручкович, Н. И. Гутарпна, П. Е. Дюбюк, Г. М. Мордасова, И. Л. Панфилова, Б. С. Римский-Корсаков, X. Р. Сулейманова, И. А. Чегис
С 23 Сборник задач по курсу высшей математики. Под редакцией Г. И. Кручковича. Изд. 3, перераб. Учебное пособие для втузов. М., «Высшая школа», 1973.
576 с. с илл.
На обложке тип. л. авт.: Г. И. Кручкович, Н. И. Гу-тарина, П. Е. Дюбюк и др.
Это учебное пособие по практической части втузовского курса выси математики. В него входят все разделы основного курса — аналитическая метрия, векторная алгебра и матрицы, дифференциальное и интегралы исчисление функций одного и многих аргументов, дифференциальные урав ния, ряды, векторный анализ, теория функций комплексного переменно
Предполагается последовательное изучение и решение всех приведение задач подряд; по каждому разделу содержится необходимый для усвоен предмета минимум основных задач.
с
0=2-2-3-446
001(01)—73 °
517
Рецензент: кафедра высшей математики Московского автомеханического института.
Чувашский
ГОС, уч-»!' ; --О.ТСТ
' бюиотекд
* СБОРНИК ЗАДАЧ ПО КУРСУ ВЫСШЕЙ МАТЕМАТИКИ
Редактор А. И. Селиверстова. Ху дож. редактор Н. В. Майкова. Техн, редактор С. П. Передерий. Корректор Г. И. Кострикова.
Сдано в набор 16/V 1973 г. Подп. к печати 29/Х 1973 г. Формат 60x90’/»®.
Объем 36 печ. л. Уч.-изд. л. 35,56. Бум. тип. № Изд. № ФМ-450. Тираж 77 000 экз. Цена 1 руб. 10 коп.
План выпуска литературы издательства «Высшая школа» (вузы и техникумы) на 1973 год. Позиция № 51.
Москва, К-51, ул. Неглинная, 29/14, Издательство «Высшая школа». Зак. 762.
Ордена Трудового Красного Знамени Ленинградская типография № 1 «Печатный Двор» имени А. М. Горького Союзполиграфпрома при Государственном комитете Совета Министров СССР по делам издательств, полиграфии и книжной торговли. Ленинград, Гатчинская ул., 26,
© Издательство «Высшая школа», 1973 г.
1
4
СОДЕРЖАНИЕ
Стр,
>4 .................................................................. 6
W1 редпсловия к первому изданию...................................... 7
'в а I. Аналитическая геометрия на плоскости	8
 Декартовы координаты на плоскости ................................. 8
Прямая линия..................................................... 17
s Линии второго порядка............................................. 27
 Преобразование уравнения линии второго порядка к каноническому
*	виду............................................................. 37
1.	Полярные координаты............................................. 45
Нава II. Определители. Векторы. Матрицы............................. 51
11.	Определители................................................... 51
К.	Векторы. Линейные операции	над векторами....................... 60
В.	Декартовы прямоугольные координаты в пространстве............... 63
4.	Умножение векторов.............................................. 70
Г5.	Алгебра матриц................................................. 78
' 6.	Системы линейных уравнений	.................................... 91
| 7.	Линейные преобразования........................................ 99
лава III. Аналитическая геометрия в пространстве	108
. 1.	Плоскость. Ее уравнение....................................... 108
2.	Прямая линия................................................... 119
; 3.	Задачи на прямую и плоскость ................................. 126
4. Поверхности .................................................... 131
‘лава IV, Введение в анализ........................................ 142
1.	Понятие функции................................................. 142
2.	Графики функций ............................................... 146
3.	Числовая последовательность и ее предел ....................... 157
4.	Предел функции.................................................. 162
5.	Вычисление пределов •.......................................... 165
6.	Сравнение бесконечно малых. Эквивалентность.................... 172
7.	Непрерывность и точки разрыва функций........................   180
лава V. Производная и дифференциал................................. 185
1.	Производные простых функций .................................... 185
2.	Производные^слржных функций.................................... 187
3.	Численное значение производной. Геометрическое и механическое истолкование производной ............................................... 194
4.	Дифференциалы функций.......................................... 197
5.	Производные и дифференциалы высших порядков...................  200
6-	Дифференцирование неявных и параметрически заданных функций . .	203
1*	3
Стр.
Глава VI. Приложения дифференциального исчисления.................... 207
§ 1.	Теоремы о среднем значении. Формула Тейлора..................... 207
§ 2.	Правило Лопиталя................................................ 213
§ 3.	Приложения производных к исследованию функций и построению графиков............................................................ 219
§ 4.	Общая схема построения графиков................................. 233
§ 5.	Геометрические приложения ...................................... 242
Глава VII. Неопределенный интеграл................................... 246
§ 1.	Непосредственное интегрирование................................. 246
§ 2.	Интегрирование подстановкой................................ ...	249
§ 3.	Интегрирование по частям ....................................... 251
§ 4.	Интегрирование простейших дробей...............................  254
§ 5.	Интегрирование рациональных дробей ............................. 257
§ 6.	Интегрирование функций, рационально зависящих от тригонометрических функций...................................................... 263
§ 7.	Некоторые интегралы тригонометрических функций.................. 267
§ 8	Интегрирование некоторых алгебраических иррациональностей .... i 269
§ 9.	Смешанные задачи на интегрирование.............................. 274
Глава VIII. Определенный интеграл и его приложения .................. 276
§ I.	Основные формулы................................................ 276
§ 2.	Методы вычисления определенных интегралов....................... 280
§ 3.	Приближенное вычисление определенных интегралов................. 286
§ 4.	Несобственные интегралы......................................... 292
§ 5.	Площади плоских фигур............................'Х............. 297
§ 6.	Другие геометрические приложения................................ 301
§ 7.	Механические и физические приложения............................ 306
Глава IX. Функции нескольких переменных ............................. 313
§ 1.	Основные понятия................................................ 313
§ 2.	Частные производные и полный дифференциал....................... 321
§ 3.	Дифференцирование сложных и неявных функций..................... 386
§ 4.	Касательная плоскость и нормаль к поверхности................... ЗрО
§ 5.	Производные и дифференциалы высших порядков..................... 333
§ 6.	Экстремумы функций нескольких переменных........................ 335
Глава X. Кратные и криволинейные интегралы........................... 341
§ 1.	Двойной интеграл................................................ 341
§ 2.	Приложения двойного интеграла . . . . .......................... 351
§ 3.	Тройной интеграл................................................ 353
§ 4.	Приложения тройного интеграла................................... 366
§ 5.	Криволинейные интегралы......................................... 372
§ 6.	Поверхностные интегралы........................................
Глава XI. Элементы векторного анализа................................ 387
§ 1.	Скалярное поле. Производная по нап, явлению..................... 387
§ 2.	Градиент скалярного поля ....................................... 396
§ 3.	Векторное поле и еро поток через пог рхность ................... 392
§ 4	Дивергенция векторного поля. Теорем,. Остроградского............ 399
§ 5.	Линейный интеграл и циркуляция век орш го почя................... Ю?
§ 6.	Ротор векторного поля. Теорема Стокса........................... 40ь
§ 7.	Потенциальные и соленоида^ .ные векгеоные поля.................. 408
Глава XII. Дифференциальные уравнения................................ 413
§ 1.	Дифференциальные уравнения первого порядка...................... 413
§ 2.	Интегрирование некоторых типов дифференциальных уравнений первого порядка............................................................. 42|
Стр.
6 3. Дифференциальные уравнения высших порядков.................... 431
s 4. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами............................................. 437
§ 5.	Линейные дифференциальные уравнения n-го порядка с постоянными коэффициентами ..................................................... 443
§ 6.	Метод Лагранжа (метод вариации произвольных постоянных)......	447
§ 7.	Системы дифференциальных уравнений ........................... 449
Глава XIII. Числовые и степенные ряды.............................. 456
§ 1.	Бесконечный ряд. Его	сходимость............................... 456
§ 2.	Признаки сходимости........................................... 459
§ 3.	Функциональные ряды........................................... 468
§ 4.	Степенные ряды ............................................... 472
§ 5.	Интегрирование дифференциальных уравнений с помощью степенных рядов .............................................................. 484
§ 6.	Приложения степенных	рядов	к	приближенным вычислениям.....	487
Глава XIV. Ряды Фурье и интеграл Фурье............................  491
§ 1.	Ряды Фурье.................................................... 491
§ 2.	Интеграл Фурье................................................ 502
§ 3.	Приложения рядов Фурье и преобразования Фурье к решению простейших задач математической физики ................................ 510
Глава XV. Функции комплексного переменного ........................ 515
f 1. Комплексные числа ............................................ 515
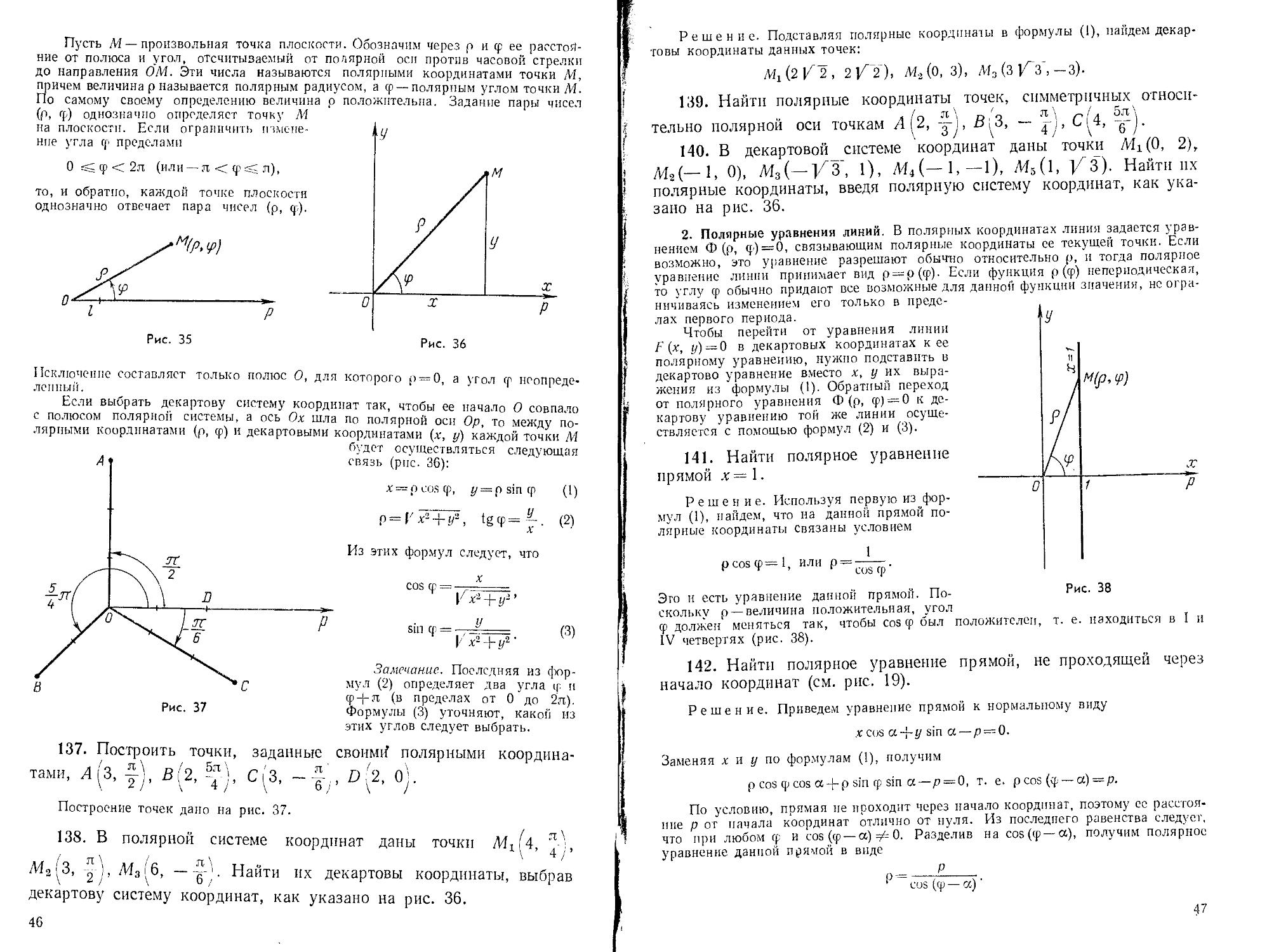
§ 2.	Элементарные функции комплексного переменного................. 522
§ 3.	Интегрирование функций комплексного переменного .............. 526
§ 4.	Ряды.......................................................... 529
§ 5.	Вычеты.	Основная теорема о вычетах............................ 537
§ 6.	Операторный метод............................................. 542
Ответы............................................................. 551
ПРЕДИСЛОВИЕ
Предлагая читателю третье издание «Сборника задач по курсу высшей математики», авторы с удовлетворением отмечают, что опыт предыдущих двух изданий подтвердил правильность избранной методической линии, изложенной в предисловии к первому изданию. Об этом свидетельствует как непосредственное использование задачника в работе со студентами, в первую очередь вечерниками и заочниками, так и многочисленные отзывы и рецензии, полученные авторами. Вместе с тем содержащиеся в откликах замечания и все увеличивающая программа втузовского курса математики привели к необходимости заново просмотреть, обновить и дополнить текст задачника. Не обошлось, конечно,, при этом без некоторого увеличения общего объема книги (число включенных в нее задач возросло примерно на 500). Естественно, что по сравнению с прежними изданиями изменилась нумерация задач, однако от двойной нумерации ввиду ее громоздкости авторы отказались.
Едва ли нужно во всех подробностях излагать те изменения, которым подвергся текст третьего издания задачника: в той или иной степени были переработаны почти все главы. Из новых разделов укажем на включение задач по алгебре матриц. В теории рядов больше внимания уделено их приложениям. В последней главе сосредоточены задачи по теории функций комплексного переменного, включая использование вычетов и операторный метод, основанный на преобразовании Лапласа. Добавлены также элементы теории преобразований Фурье и задачи на метод Фурье в уравнениях математической физики. Для того чтобы задачник более подходив для работы преподавателя с группой студентов, несколько увеличено число задач, предлагаемых для самостоятельного решения, но здесь авторы проявили известную осторожность, чтобы не вступить в противоречие с одной из главных методических установок, указанных в предисловии к первому изданию задачника.
За прошедшее время умер П. Е. Дюбюк, являющийся основным инициатором настоящей книги. Его памяти посвящают авторы свою работу.
Авторы чтут также память Р. Л. Сенкевич, много помогавшей работе над задачником.
Мы просим всех желающих высказать свои замечания по задачнику. Обращаться на кафедру высшей математики МИРЭА по адресу: Москва, Е-275, 5-я ул. Соколиной горы, д. 20.
Авторы
ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
Данный «Сборник задач» ставит своей целью помочь студенту самостоятельно овладеть методами решения задач по курсу высшей математики. Это определило структуру задачника. В каждом разделе (главе, параграфе) даны краткие теоретические сведения и приведены формулы, необходимые для решения задач, приводится значительное число подробно разобранных задач с разъяснениями методов их решения; наконец, ряд задач предлагается для самостоятельного решения, некоторые из них снабжены указаниями. Среди решенных задач немало таких, которые можно было назвать типовыми; во всяком случае ознакомление с ними позволяет студенту при самой минимальной помощи со стороны преподавателя овладеть основными методами решения задач данного раздела. Это обстоятельство особенно важно для студентов, занимающихся заочно.
Как правило, в задачнике приводятся только простые задачи. Авторы сознательно старались избежать задач повышенной трудности, так как ставили перед собой цель научить студента решать основные задачи, дать, если угодно, некоторый минимум, необходимый для усвоения студентом требований втузовской программы курса высшей математики. Вместе с тем работа с настоящим пособием не закрывает возможности более углубленного изучения предмета.
По каждой теме дается минимальное число задач в предположении, что обучающийся будет разбирать все приведенные задачи подряд. Этим объясняется некоторое уменьшение общего числа задач по сравнению с другими задачниками. Такая установка, конечно, несколько ограничивает возможность работы с данным пособием преподавателя на занятиях со студентами, но в то же время она значительно облегчает работу студента, обучающегося самостоятельно.
Следует отметить, что задачник появился в результате опыта работы в заочном институте. Все его авторы в течение ряда лет работают (или работали) на кафедре высшей математики Всесоюзного заочного энергетического института, в 1967 г. преобразованного в Московский институт радиотехники, электроники и автоматики.
При составлении настоящего «Сборника» был использован ряд задач, взятых из известных задачников по высшей математике, обычно рассматриваемых на занятиях со студентами.
Авторы
ГЛАВА I
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
§ 1. ДЕКАРТОВЫ КООРДИНАТЫ НА ПЛОСКОСТИ
1. Координаты точек. Простейшие задачи. Декартова прямоугольная система координат на плоскости определяется заданием единицы масштаба для измерения длин и двух взаимно перпендикулярных осей — оси абсцисс (Ох) и осп ординат (Оу). Их точка пересечения О называется началом координат. Оси координат
делят плоскость на четыре четверти (квадранта), нумерация которых показана на рис. 1.
Пусть М — произвольная точка плоскости. Проектируя ее на оси координат, получим точки Мх и Му. Первой координатой х точки М, ее абсциссой, называется длина отрезка 0Мх, взятая со знаком плюс, если отрезок 0Мх направлен в ту же сторону, что и ось Ох, и со знаком минус — если в противоположную. Аналогично, ординатой у точки М называется длина отрезка ОМ у, взятая со знаком плюс или минус, смотря по тому, совпадает или нет направление ОМу с направлением оси Оу. Пара чисел (х, у) полностью определяет точку М плоскости, поэтому когда в аналитической геометрии говорят «задать точку», «найти
точку», то под этим подразумевают, что задают или находят координаты этой точки. Такое аналитическое представление
точек в виде пар чисел позволяет применить к решению геометрических задач алгебраические методы. В этом состоит одна из основных идей аналитической
геометрии.
Если на плоскости даны две точки: Мг (хх, уА и Л12 (х2, (у2), то расстояние d между этими точками вычисляется по формуле
d = KU»-*i)*+(&-0i)2 •	(1)
В частности, расстояние точки М (х, у) от начала координат О (0, 0) равно ОМ = Kx2 + z/2.	(2)
Площадь треугольника определяется пэ координатам его вершин Alj (хь уг), М2 (-*2. 4/г). А13 (х3, уя) следующим образом:
•S —	| X1 U2 — 4/з)+х2 (Уз — У1)~)~хз (У1 — Уз) |-	(3)
I.	Определить координаты вершин равнобедренного треугольника О А В, изображенного на рис. 2, если его сторона равна 4 ед. ДЛИНЫ.
8
Решение. Одна из вершин треугольника совпадает с началом координат, поэтому ее координаты О (0, 0). Вершина А лежат на отрицательной части оси Ох на расстоянии 4 ед. длины от начала О, так что хА ——4, уА=0. Чтобы определить координаты вершины В, заметим, что ее проекция Вх на ось абсцисс делит отрезок О А пополам. Следовательно, хв — — 2. Значение же ув совпадает с высотой h треугольника, которую легко найти по теореме Пифагора:
ув =/г=К42-22 =/12 = 2^3'.
Итак, О (0, 0), А (-4, 0), В (-2, 2^3).
2.	В первой четверти находится точка А (а, Ь). Найти координаты точки В, симметричной А относительно биссектрисы координатного угла (рис. 3).
Решение. Пусть В (х, у), тогда x—OBv y=BBt (см. рис. 3). Треугольники OAAt и ОВ^В равны, так как они прямоугольные и имеют одинаковые гипотенузы (ОД = ОВ) и равные острые углы ( Z AOAt = L ОВВ^. Приравнивая катеты этих треугольников, получаем:
х = ОВ1 = ДД1 = Ь, у=ВВ1 = ОД1 = а, т. е. В (Ь, а).
3.	Какое соотношение выполняется между координатами точек М (х, у) биссектрис координатных углов?
Решение. По свойству биссектрисы расстояние любой ее точки до сторон угла равны. Поэтому для точек биссектрис координатных углов равны абсолютные величины их проекций на оси координат, т. е. | х | = | у |. На биссектрисе 1 и III четвертей, кроме того, равны и знаки координат: ( + , -|~) — в I чшверти и (—, —) — в III четверти. Поэтому для точек этой биссектрисы выполнено условие х=у. Аналогично, для точек биссектрисы II и IV четвертей выполняется соотношение х= —у.
4.	На оси Оу найти точку, удаленную от точки А (3, —1) на 5 ед. длины.
Решение. Пусть М (х, у) — искомая точка. Поскольку она располагается на оси Оу, то для нее х—0. Чтобы найти у, воспользуемся формулой (1), куда вместо (хь yj подставляем координаты точки А, а вместо (х3, t/2) — координаты точки М:
d=5=K(0-3)2+(y+l)2, 25=9 + (i/+l)2, (*/+1)г=16, {/+1=±4;
1/1 = 3, у2= —5.
Следовательно, условиям задачи удовлетворяют две точки: ML (0, 3) и М2 (0, —5).
9
5.	Найта площадь треугольника с вершинами А (2, 1), В (—2, 3) С (8, -1).
Решение. Подставляя координаты точек в формулу (3), найдем
$ = 1|2(3+1)-2(-1-1)+8(1-3)| = 1|-4|=2.
6.	Сторона квадрата равна 6 см. Найти координаты его вершин, если за оси координат приняты: а) диагонали квадрата, б) прямые', параллельные его сторонам и проходящие через центр.
7.	Дана точка М (а, Ь). Определить точки, симметричные точке М относительно оси Ох и оси Оу.
8.	Показать, что точки М(х, у) и М( — х, —у) симметричны относительно начала координат.
9.	Показать, что треугольник с вершинами А (2, 1), В (6, 3), С (— 1, 2) тупоугольный. Какой из его углов тупой?
Указание. В тупоугольном треугольнике квадрат стороны, лежащей против тупого угла, больше суммы квадратов двух других сторон.
10.	Доказать, что треугольник с вершинами А (4, 0), В (2, 2), С( —1, —1) прямоугольный. Какой из его углов прямой?
Указание. Использовать теорему Пифагора.
11.	Найти площади треугольников, данных в задачах 9 и 10.
12.	Найти длину высоты СК треугольника с вершинами А (—1,2) В (5, 6), С(1, 3).
Указание. Найти площадь треугольника и длину основания.
13.	На оси Ох найти точку, удаленную от точки Р(1, —8) на расстояние d — 10.
14.	На биссектрисе I и III четвертей найти точку так, чтобы ее расстояние от точки Q (— 3, 4) было равно d = 5.
Указание. Для точек этой биссектрисы х=у (см. 3).
15.	Из точки С(1, 1) проведена окружность радиуса /? = 2)/2? Найти точки пересечения этой окружности с биссектрисами координатных углов.
Указание. Искомые точки удалены ог центра С на расстояние R. Задача решается аналогично предыдущей.
2. Деление отрезка в данном отношении. Координаты точки М (х, у), делящей .	.. ..	, МХМ
направленный отрезок в заданном отношении	определяются
формулами
Xt + U2 /;_У1+?4/г х- 1+л ’ у- 1+Л
(4)
Здесь (xlt (д)—координаты начала Aft отрезка, а (х2, у2)—координаты его конца Л-12. В частности, если точка М (х, у) делит отрезок пополам, то 1 и
х
Уг+У-.
, У 2
(5)
10
16.	Отрезок AB делится точками C, D, Е на равные части (рис. 4). Зная точки Л (3, —2) и Е (6, 4), найти точки В, С, D.
АС 1
Решение. Точка С делит отрезок АЕ в отношении	~ ~2 > а точка
D — в отношении	= Ф°РмУлам (4). полагая, что (хь щ)— коор-
динаты А, а (х2, «4) —координаты точки Е, найдем:
_ 2+~-4
Ус=-------=0;С(4,0);
^2
=2: D<5- 2>’
1
3+4-6
*С =---+j—=4,
^2 3+2-6	,
i + 2	5’
Точку В можно найти по формулам (5), куда вместо (х, у) надо подставить координаты точки Е, делящей отрезок DB пополам. Считая, что точки В,
(Xi, ^—координаты точки D, а (х2, р2)—•	,
получим:	А ~ Л Е В
6=-Ц^, 4=±^_, В(7,6).
Рис. 4
17.	В треугольнике с вершинами А (2, —1), В (5,3), С( —6, 5) найти длину биссектрисы угла А.
Решение. Известно, что биссектриса делит противолежащую сторону треугольника на части, пропорциональные длинам прилежащих сторон. Иными сло-АВ
вами, точка К. (рис. 5) делит отрезок ВС в отношении	Так как по
формуле (1)
ДВ = К(2-5)2+(-1-3)а =5, ЛС = /(2+6)з+(-1-5)2=10, 5	1
то^=щ=у- Теперь по формулам (4) можно найти координаты точки К:
5+4 (-6) 4
хк	I	—з> у к “
1+г
34-5_11.„/4 Щ
" 1 > _L 3 ’ А \з ’ з )•
+ 2
Следовательно, длина биссектрисы
l/~ln 4 \2 , / ,	11 \2	-./~200	10 |2	л_. х
А/(^у ^2—g-j	j = у — = —=«4,7(ед. дл.)
18.	В какой точке прямая, проходящая через точки Л (3, —2) и В(— 1, 2), пересекает ось Оу?
Решение. Пусть М (х, у) — искомая точка. Поскольку она лежит на оси Оу, то х = 0. Из первой формулы (4) найдем отношение, в котором точка М р^лт
11
отрезок АВ, а затем вторую из этих формул используем Для определения ординаты у точки М:
х=3;	у=—гЙ~==1; Л1(0’
1 ~р* Л	1 —р о
19.	Найти вершины треугольника АВС, зная середины его сторон Р(1, 2), Q(4, 3), R (5, -4).
Указание. Считая координаты вершин неизвестными, применить к каждой из сторон формулы (5).
20.	В треугольнике с вершинами А (3, 1), В (— 3, — 1), С (5, —12) найти: а) длину медианы, проведенной из вершины С, б) точку пересечения медиан.
Указание. Медианы пересекаются в точке, делящей каждую из них в отношении 2: 1, считая от вершины.
21.	Найти центр тяжести треугольника с вершинами
М1(Х1, уг), М-2 (%2, f/г). Мз(Хз, уз).
Указание. Центр тяжести треугольника лежит в точке пересечения медиан.
22.	В треугольнике А (2, —1), В(0, 1), С( —4, —3) найти длину биссектрисы угла В.
23.	Даны три вершины параллелограмма: /1(6, 1), В(3, 2), С (— 2, 7). Найти четвертую вершину D, противолежащую вершине В.
Указание. Точка пересечения диагоналей параллелограмма делит их пополам.
3. Уравнения линий. Линия на плоскости задается при помощи уравнения F (х, р) = 0, которому удовлетворяют координаты всех точек М (х, у) данной линии и не удовлетворяют координаты ни одной точки, нс лежащей на линии. Линию можно представить себе также как траекторию движущейся («текущей») точки М. В связи с этими координаты (х, у) точки М называют часто текущими координатами. Уравнение линии, связывая текущие координаты, определяет общее свойство (геометрическое, физическое и др.), присущее всем точкам этой линии.
Существует и другой способ задания линии—параметрический. В этом случае текущие координаты (х, у) выражаются в виде функций
*=ф(0. г/=Ф(О	(6)
некоторого параметра t. Параметр t может играть роль времени, угла поворота вокруг какой-либо фиксированной точки, расстояния по кривой от некоторой начальной точки и т. д. Каждому фиксированному значению параметра t по формулам (6) соответствует определенная точка М (х, у) линии, при изменении t пробегающая всю линию. Если из двух равенств (6) исключить параметр t, то получится уравнение линии в виде F (х, f/) = 0.
В связи с изучением линий возникают два рода задач: 1) По данному уравнению изобразить соответствующую линию на плоскости и исследовать ее свойства. 2) Найти уравнение линии, заданной как геометрическое место точек, обладающих определенным общим свойством. В этом пункте будут рассмотрены примеры решения задач обоих типов. Дальнейшие задачи на эту тему будут встречаться и в других параграфах.
24.	Какие линии заданы следующими уравнениями: a)i/ = 0; б) х = 2; в) хг = уг\ г) х2+у2 = 7?2 (#>0); д) xt/=l; е)х2 + у2 = 0; ж) х2+у2 +1 =0.
Решение, а) Уравнению у = 0 удовлетворяют все точки осп Ох и только они, поэтому это уравнение оси Ох;
12
б) геометрическое место точек М (х, у), у которых абсцисса имеет одно и то же значение х=2, есть прямая, перпендикулярная оси Ох и проходящая на расстоянии двух единиц масштаба от оси Оу,
В) уравнение х2—у2 равносильно х— ± у, т. е. ему удовлетворяют как точки, у которых х=у, так и точки, у которых х ——у. В задаче 3 было показано, что такие точки расположены на биссектрисах координатных углов. Следовательно, уравнение х3 = г/2 определяет линию состоящую из двух прямых—биссектрис координатных углов;
г)	извлекая квадратный корень из обеих частей уравнения х2 + г/2 =/?2, получим |Лх2+уа=± R- Однако знак минус невозможен, поскольку величина R > 0. Следовательно, данное уравнение равносильно l'x2-ly2 — R, т. е. условию [см. формулу (4)] 0M = R. Таким образом, данному уравнению удовлетворяют все те точки М (х, у), расстояние которых от начала координат одно и то же и равно R. Очевидно, получена окружность с центром в О и радиусом R;
ч	,	1
д)	уравнение ху=1 или У— х определяет обратно пропорциональную зависимость между х и у. График обратной пропорциональности легко построить по
точкам, придавая х различные значения и вычисляя соответствующие значения у (рис. 6). Заметим, что наряду с точкой М (х, у) уравнению удовлетворяет и точка М (—х, —у). Геометрически это означает, что линия симметрична относительно начала координат (см. 8), т. е. в данном случае состоит из двух симметричных ветвей, одна из которых расположена в I четверти, а другая—в III;
е)	уравнению х2+р2=0 удовлетворяют только нулевые значения координат. Следовательно, соответствующая линия выродилась в одну точку О (0, 0). Разумеется, такого рода «линии» не представляют геометрического интереса, но поскольку речь идет об общем правиле — задании линии уравнением, возможность вырождения линии в точку следует учитывать;
ж)	уравнению x2-{-f/2-J-1 =0 не может удовлетворять ни одна пара (х, у) действительных чисел, так как его левая часть при любых х и у положительна и не может обратиться в ноль. Следовательно, данное уравнение не определяет никакого геометрического образа на плоскости. Иногда говорят, что соответствующая линия пустая или нулевая.
25.	Найти уравнение окружности радиуса R с центром в точке С (а, Ь). Получить параметрические уравнения той же окружности, приняв за параметр t угол поворота вокруг центра.
Решение. Окружность есть геометрическое место точек М (х, у) плоскости’ для которых MC—R. Используя формулу расстояния между двумя точками,
получим }' (х—а)2 + (?/ b)2 = R, или, возводя в квадрат,
(x-a)2 + (y-fe)2 = /?2.	(7)
Это и есть уравнение данной окружности, так как ему удовлетворяют координаты всех точек окружности и не удовлетворяют координаты точек, не лежащих на ней (для последних MCzfiR, а значит и Л/С2 =/= У?2).
Из рис. 7 видно, что х=а-}-СК, у=Ь+КМ, но CR=R cost, RM = = R sin t, поэтому параметрические уравнения окружности имеют вид
x—a+R cos/, y = b+R sin t. (8) Если угол / изменяется от 0 до 2л, то точка М (х, у) пробегает всю окружность против часовой стрелки.
26.	Найти геометрическое место точек М, сумма квадратов расстояний которых до двух фиксированных точек А и В есть величина постоянная, равная 2а2.
Решение. Введем систему координат так, чтобы ось Ох шла через точки А и В, а начало координат О лежало посреди между ними (рис. 8). Обозначив
АВ—2с, тогда в выбранной системе координат А (—с, 0), В (с, 0). По условию Л/Д2+Л1В2 = 2а2, но Л/Д2 = (х+с)2+({/-О)2, Л/В2 = (х—с) + (у-0)2, поэтому
(х+с)2 + «/2+(х—с)2+j/2=2а2,
откуда после несложных преобразований получим уравнение искомого геометрического места точек в виде
х2+р2=а2—с2.
Это уравнение, как мы видели (см. 24 г), определяет окружность с центром в О радиуса R=yra2—с2.
27.	Круг радиуса а катится по прямой. Каждая точка окружности описывает при этом линию, называемую циклоидой. Получить параметрические уравнения циклоиды, приняв за параметр t угол поворота точки вокруг центра круга.
14
Решение. Примем прямую, по которой катится круг, за ось Ох, а нача лом коордииат пусть будет нижнее положение рассматриваемой точки М катящейся окружности (рис. 9). По условию качения, после поворота круга на угол t имеем
ОА = MA=at. Выразим через t координаты точки М при произвольном ее положении (см. рис. 9):
x=OL=OA — LA = MA — MK=at — a sin t=a (/ — sin /), y=LM = AC— КС—a—acos/=a(l — cos/).
Итак, параметрические уравнения циклоиды имеют вид
х=а (t—sin /), у—а (1—cos/).
При изменении / от 0 до 2л точка М опишет одну арку циклоиды.
28.	На некоторой высоте шарик бросают горизонтально со скоростью v. Определить траекторию его падения, пренебрегая сопро
тивлением воздуха.
Решение. Будем считать, что начало О находится в точке бросания, ось Ох направлена горизонтально в сторону бросания, ось Оу—вертикально вниз (рис. 10). По закону инерции шарик будет перемещаться горизонтально с постоянной скоростью о и в то же время опускаться под действием силы тяжести. За время /, следовательно, он переместится по оси Ох на расстояние о/, а по оси Оу — на otf2
расстояние . Значит параметрические уравнения траектории имеют вид
или у —ах2, где
/	Я*3
x=vt, У=2~-
Исключив
а = Ji-2оа ‘ Таким
из этих равенств время /, получим
образом, траектория движения —парабола у = ах2.
29.	Какие линии определяются уравнениями а) х — а, б) у=Ь, в) ху — 0, г) у — х2 = 0, д) х2у = I, е) х2 4- г/2 = 2, ж) xs -j- ху2 = 2х, з) (*-l)2 + Q/ H)3 = 0, и) 2хг + Зу2 + 1 = 0?
15
30.	Найти геометрическое место точек, разность квадратов расстояний которых до двух фиксированных точек А и В есть величина постоянная.
Указание. См. 26.
31.	Определить геометрическое место точек, для которых расстояние от точки Р (9, 0) втрое больше расстояния от точки Q (1, 0).
32.	Отрезок АВ длины а движется так, что точка А скользит по оси Ох, а точка В — по оси Оу. При каждом фиксированном
положении этого отрезка строится прямоугольник О АР В и из точки Р опускается перпендикуляр на диагональ АВ (рис. 11, а). Геометрическое место точек М — оснований указанных перпенди-
Рис. 12
куляров — называется астроидой (рис. 11, б). Найти уравнение астроиды.
Указание. Выразить сначала х и у через угол t, указанный на рис. 11.
33.	Найти параметрические уравнения развертки круга — траектории конца раскручивающейся нити, намотанной на круг радиуса а.
Указание. Учесть, что СМ — =CA==at, x=OP-}-PQ, у=СР—СК (рис. 12).
34.	Определить траекторию тела, брошенного под углом а к горизонту со скоростью v (сопротивлением воздуха пренебречь).
16
Указание. Горизонтальное перемещение тела М (рис. 13) происходит с постоянной скоростью v cos а, а вертикальное перемещение замедляется действием силы тяжести (см. 28).
35.	Составить уравнение окружности радиуса R с центром в точке (R, 0).
Указание. Использовать свойство вписанного угла, опирающегося на диаметр.
Рис. 13
§ 2. ПРЯМАЯ ЛИНИЯ
1. Общее уравнение прямой. Уравнение с угловым коэффициентом. В декартовых координатах каждая прямая задается уравнением первой
на плоскости
степени относительно текущих координат х и у: X
О)
Ах By С = 0
и, обратно, всякое линейное уравнение (1) определяет прямую. Это уравнение называется общим уравнением прямой.
Уравнение прямой, разрешенное относительно у, называется уравнением с угловым коэффициентом:
y=kx+b.	(2)
Здесь угловой коэффициент k = tg <р, где <р—угол наклона прямой к оси Ох (рис. 14), параметр b равен величине отрезка ОВ, отсекаемого прямой от оси Оу.
В частности, прямые, параллель-
Пусть даны две прямые: (I) y=ftix+^i
ные оси Ох, включаются в формулу (2) при/?=0, а прямые, проходящие через начало О,—при Ь — 0. Прямая, параллельная оси Оу, не может быть задана уравнением вида (2), так как она не имеет углового коэффициента (для нее <р=90°). Уравнение такой прямой имеет вид х=а (см. рис. 14).
Уравнение прямой, проходящей через данную точку Ми (х0, у0) и имеющей угловой коэффициент k, находится по формуле
y-y0=k(x-x0).	(3)
Если прямая проходит через точку /Ио (хе, у0) и параллельна оси Оу, то ее уравнение записывается
в виде х=хи.
и (II) y=k2x-\-b.i. По формуле
k‘j — kt
1 +
tg©-
(4)
вычисляется тот из смежных углов между прямыми, который заметается прямой (I) при повороте ее против часовой стрелки вокруг точки пересечения прямых до совпадения с прямой (II) (рис. 15). Если в какой-либо задаче нас интересует П Ч»ашодий I FOCL	_ I
не расположение прямых, а только величина угла между ними, то удобнее использовать формулу, определяющую острый угол 6:
tge=lifeH (5)
I 1 +«1«2 1
Тупой угол дополняет острый до 180е. В формуле (5) безразлично, какую из прямых считать первой, а какую — второй.
Условие параллельности прямых:
•— k2,
условие перпендикулярности:
&ifea-f-l=0 или k2=—(6)
36. Определить точки пересечения прямой 5х + 21/ — 10 = 0 с осями координат. Построить пря-
- мую.
Рис. 15	г,	т
Решение. 1 очки, лежащие на оси
Ох, характеризуются тем, что для них у—0. Для нахождения точки А пересечения данной прямой с осью Ох надо в ее уравнении положить у = 0 и найти х: 5х-|-2-0—10 = 0, х=2. Следовательно, А (2, 0). Аналогично, полагая в данном уравнении х=0, найдем точку В (0, 5) пересечения прямой с осью Оу. Нанесем на чер-
теж вычисленные две точки и проведем через них прямую (рис. 16).
Разумеется, построить прямую можно и по двум каким-либо другим ее точкам. Например, полагая в данном уравнении х=1, найдем у= т. е. точку P^l,-g-^ прямой. Полагая х=3, найдем еще одну точку прямой Q 3, —Так что построение прямой можно было бы выполнить по точкам РИ, и Q ^3, — (см. рис. 16).
37.	Построить прямую у = 5х. Определить углы, образуемые ею с прямой задачи 36.
Решение. В уравнении у=5х отсутствует свободный член, поэтому ему удовлетворяют нулевые значения координат. Геометрически это
означает, что данная прямая проходит через на-
чало координат 0(0, 0). Найдем еще какую-либо точку этой прямой. Например, при х=1 из уравнения у=5х получим у=5, т. е. точка С(1, 5) лежит на прямой. Соединяя точки О и С, построим прямую у—5х (см. рис. 16). Коэффициент при х в этом уравнении равен угловому коэффициенту прямой /г1=5.
Чтобы определить угловой коэффициент прямой 5х+2у —10=0, разрешим
ее уравнение относительно у и возьмем коэффициент при х:
5
У ——g-*+2, k2~
18
5
2 ’
По формуле (5) определим острый угол в между данными прямыми:
tge=
4-5 1-J.5
=15
23’
О = arctg ₽« 33®. zo
Тупой же угол между ними равен 180°—0 «= 147°.
38.	Через точку MQ (1, —2) провести параллель и перпендикуляр к прямой 2% + 3# —3 = 0.
Решение. Заметим, что «провести прямую» в аналитической геометрии означает найти ее уравнение. Построение же прямой по данному уравнению осуществляется так, как только что было показано в задачах 36 и 37.
В поставленной задаче дана точка на искомой прямой, поэтому для нахождения ее уравнения можно воспользоваться формулой (3), предварительно определив угловой' коэффициент/г. Найдем сначала угловой коэффициент kA данной прямой, разрешая ее уравнение относительно у: «/== —уХ-J-l, *1=—	. Угловой
2
коэффициент параллельной прямой тот же самый: k=—	. Подставляя в (3) это
значение k и координаты точки Мо, найдем уравнение параллели к данной прямой:
у+2=— 4(x— 1), 2х + Зу + 4 = 0. О
Угловой коэффициент k2 перпендикулярной прямой определим из условия 1	3
(6): *2=—1 — 2 • Следовательно, уравнение перпендикуляра 1	Q
«/+2= 2 (х-1), Зх-2(/-7=0.
39.	Даны вершина С (—1, 3) прямого угла равнобедренного прямоугольного треугольника и его гипотенуза Зх —4г/—12 = 0. Найти уравнения катетов.
Решение. Разрешив уравнение гипотенузы относительно у, найдем ее угло-3	3
вой коэффициент: у=-^х—3,	. Катеты равнобедренного прямоугольного
треугольника наклонены к гипотенузе под углом 45°. Подставляя в формулу (5) 3
значение 6=45° и *1=^, получим уравнение для определения угловых коэф-
фициентов катетов:
tg45° =
*2-4 1+|^2
4*2 —3| 4+3*2|*
4*2 — 3.
4 -|- 3^2 *
1 =
^3 = 1, 4*2-3 = 4 + 3*2, *2 = 7;
4*2-з=-4-з*2, *;=-!.
** Otto	•
По формуле (3), зная точку С(—1, 3) на катетах, получим их уравнения: у—3 = 7(х-|-1), 7х—j/-f-10 = 0;	г/—3=—у (х+1), х^7у-20=0.
19
40.	Определить угловые коэффициенты и построить прямые
Зх — 2у-\-6 — 0, 2у — Зх —0, 5x-{-2iy-|-2 = 0.
41.	Составить уравнения прямых, проходящих через начало координат и наклоненных к осп Ох под углом 30, 45, 60, 120, 135 градусов. Построить прямые.
42.	Через точку Л40 (1, 4) провести параллель и перпендикуляр к прямой 2х + у-\-1 =0. Сделать чертеж.
43.	Провести через точку Мо (— 2, 4) прямые, параллельные осям координат.
44.	Даны сторона прямоугольника Зх —4t/-J-5 = 0 и две его вершины А (1, —3) и С (1, 2). Найти уравнения остальных сторон прямоугольника.
45.	Через точку Л40 (2, —3) провести прямые, образующие угол 45° с прямой 2х — 3//+ 6 = 0.
46.	Даны стороны треугольника х-\-у— 1 — 0, 2х — г/-(-3 = 0, 5х — у — 5 = 0. Найти величины его внутренних углов.
Указание. Прямые построить. Использовать формулу (4), выбирая kr и /?., так, чтобы поворот первой из сторон против часовой стрелки вокруг вершины заметал внутренний угол треугольника.
2. Прямая, заданная двумя точками. Уравнение, прямой, проходящей через две заданные точки (xt, гд) и Л12(х2, у2), записывается в виде
х-*1 = У~У1
Х> —Лд' </а —!/i’	U
Для того чтобы не исключать прямых, параллельных осям координат, условимся считать, что если в формуле (7) равен нулю одни из знаменателей, то следует приравнять пулю соответствующий числитель. Например, если прямая проходит через точки УЙГ (2, 3) и Л?2(3, 3), то ее уравнение
х — 2 у—3	„
трут, = 3373, т- е- У~3 = 0, пли у = 3.
Это прямая, параллельная оси Ох.
Если прямая определяется точками А (а, 0) и В (0, /?), где а и /д —величины отрезков, отсекаемых прямой па осях координат, то из (7) получается уравнение в отрезках-.
В форме (8) не могут быть записаны уравнения прямых, параллельных осям координат и проходящих через начало О.
47.	Показать, что точки Мг(2, 1), М2(—3, 3), Ма(7, — 1) лежат на одной прямой. Найти ее уравнение.
Решение. По формуле (7) найдем уравнение прямой ЛДЛ42:
=	2(х-2) = -5(у-1), 2х + 5у-9=0.
Точка Мя лежит на той же прямой, так как се координаты удовлетворяют уравнению этой прямой: 2  74-5 (—1) —9 = 0. Таким образом, всё три данные точки лежат па прямой 2х4-б(/—9 = 0.
20
48.	Дан треугольник с вершинами А (— 1, 1), С (3, —2), В (1, 5). Найти уравнения его сторон, определить внутренний угол А (рис. 17).
Решение. По формуле (7) находим уравнения сторон:
АС =ГГз=П^. 3(А--3) = -4(у + 2), Зх + 4!/-1=0;
АВ	-4(х-1) = -2(у-5), 2х~ z/ + 3 = 0;
БС	=	7(х-3) = -2(!/ + 2), 7х + 2(/- 17 = 0.
JL — □ О -[* Z
Внутренний угол Л (см. рис. 17) заметается вращением стороны АС против часовой стрелки до совпадения с АВ, поэтому, используя формулу (4), надо в ней считать за первую прямую—-АС, а за вторую —
3
АВ. Их угловые коэффициенты	, А’2 = 2,
поэтому
2 4- —
__ k2-kr =	+ 4_______И _
14* '3	2
1	4
Z A = arctg'(— 5,5)= 180° — arctg5,5 == 180° —80°= = 100°.
49.	Найти прямую, проходящую через точку М (— 2, 2) и отсекающую от одного из координатных углов треугольник с площадью S = 4,5.
Решение. Площадь указанного треуголь-	Рис. 17
ника выражается через отрезки а и b по формуле
S = -^-1 ab |. Поэтому уравнение искомой прямой следует взять в виде (8). Величины отрезков а и b будут найдены из двух условий задачи: 1) точка М (— 2, 2) лежит на прямой. Следовательно, ее координаты удовлетворяют уравнению (8), т. е.
__9	2
—-4--=1,	2a — 2b~ab;
а ' Ь	-	’
2) дана площадь треугольника S = 4,5, т. е. 4,5 = -у I ab |, | ab ] = 9 и либо а/> = 9, либо ab = —9.
Итак, для определения а и b получены две системы уравнений:
J 2a~2b — ab,	J 2a — 2b = ab,
(	ab—9,	I ab = — 9.
3	3
Первая из них имеет два решения: а, = 6, bv~ и а« = —С-, Ь2 = —6. Вторая система дает комплексные значения а и b и не определяет никакой прямой
21
Рис. 18
52. Даны прямые 2х — 31/+ 6 = 0,
Таким образом, две прямые удовлетворяют условиям поставленной задачи (рис. 18):
g+|-==1’ * + 4у —6=0;
2
-^ + ^=1, 4а:+^ + 6 = 0. ~~2
50. Дан треугольник с вершинами А (—2, — 1), В(—1, 2), С (1, 0). Найти уравнения его сторон, определить величины внутренних углов.
51. В треугольнике с вершинами А (3, 4), В(—1, 2), С (2, —1) найти: а) уравнение медианы, проведенной из вершины Л; б) уравнение средней линии, параллельной стороне ВС.
х — 4у +1 = 0. Составить для
них уравнения в отрезках.
53. Через точку' М (3, 5) провести прямую так, чтобы она отсекала от координатного угла равнобедренный треугольник.
Указание. По условию, | а \ = | Ь j.
54. Из всех прямых, параллельных данной 4х + 2у -j- 5 = 0, выделить те, которые отсекают от координатных углов треугольники с площадью S = 9.
3. Нормальное уравнение прямой. Расстояние от точки до прямой. Нормальное уравнение прямой имеет вид
х cos а + у sin а — р = 0.	(9)
Здесь р — длина перпендикуляра, опущенного из начала координат на прямую, а — угол, образованный этим перпендикуляром с положительным направлением оси Ох (рис. 19). Нормальное уравнение характеризуется тем, что сумма квадратов его
коэффициентов при х и у равна 1, а свободный член отрицательный.
Общее уравнение (1) прямой приводится к нормальному виду умножением всех членов на нормирующий множитель:
1
У ’
(10)
знак которого выбирается противоположным знаку свободного члена общего уравнения. (Если С = 0, то можно выбрать любой знак.)
22
I Расстояние d точки Л40 (x0, y(l) до прямой (9) вычисляется по формуле d= | х0 cos а + у0 sin a—p |,	(11)
или, если прямая задана общим уравнением АхБу 4-С — О, то
__I Ах0 + By о + С | /ЛЧ7^
55.	Найти расстояние р от начала координат до прямой 6х + 8у + 20 = 0.
Решение. Величину р можно определить из нормального уравнения прямой. Для приведения данного уравнения к нормальному виду найдем нормирующий множитель по формуле (10), выбирая знак минус, так как в данном случае С=20>0:
1	1	П1
(1 =--,...... =	— 77, = — 0,1.
/36 + 64	Ю
"•• Умножая данное уравнение на р, получим 0,6х — 0,8у —2 = 0, откуда р = 2.	*•
56.	Найти расстояние между параллельными прямыми 4х — Зу— — 7 = 0 и 4x-3z/4-3 = 0.
' Решение. Искомое расстояние можно найти как расстояние какой-либо . точки одной из параллелей до другой. Полагая в первом уравнении, например, ' :• х=1, получим у =—1, т. е. точка Л40 (1, —1) расположена на первой прямой, а ее расстояние до второй параллели найдем по формуле (12):
J 4 -1 —3(—1) + 3 j = ю = 2 /16 + 9	5
57.	Найти уравнения прямых, параллельных прямой 12,? +5у— X —7 = 0 и отстоящих от нее на расстоянии d = 3.
Решение. Для всякой точки М (х, у) искомой прямой согласно формуле (12) должно выполняться равенство
3 = .I.12x±^L1LL или 1 12х + 5у —7 1 = 3.13 = 39. /144 + 25	’
Отсюда либо 12х + 5у— 7 = 39, либо 12х + 5у ~ 7= — 39. В результате получены уравнения искомых прямых
12х + 5у —46 = 0 и 12х + 5у + 32 = 0.
58.	Найти уравнения биссектрис угла, образованного прямыми 2х + у~ 2 = 0 и 2х + 4у + 9 = 0. Проверить, что биссектрисы перпендикулярны.
Решение. По свойству биссектрисы расстояние любой ее точки М (х, у) до сторон угла одинаковы. Находим эти расстояния по формуле 12) и приравниваем их:
J \2х+у~2\ л _|2аг + 4(/ + 9|	I 2х+4г/ + 9|
-	2р=-—;
[2х + У-2[ = ~\2х + 4у + 2\.
Получено уравнение, которому удовлетворяет любая точка Л1 (х, у), лежащая на Искомых биссектрисах. Учитывая, что из | a j = । b | следует а = Ь или а — —Ь,
23
получим два уравнения биссектрис:
2х + у - 2	(2х + 4у - 9), 2х - 2у - 11 = 0;
2х-\-у — 2 = — g (2дг + 4//— 9), 6х 4~ 6(/ -}- 5 — 0.
Их угловые коэффициенты /г, = 1, kt=— 1 удовлетворяют условию — 1, т. е. биссектрисы перпендикулярны.
59.	Привести к нормальному виду уравнения прямых 8х — бу А-4-5 = 0, х У 3 у — 12 = 0, 12х 4~ 5г/= 0, х 4-2 = 0. Найти их расстояния от начала координат.
60.	Две стороны квадрата лежат на прямых Зх 4- 4г/ 4- 22 = 0 и Зх-|-4г/—13 = 0. Вычислить его площадь.
Указание. Показать, что прямые параллельны. Найти сторону квадрата, используя решение задачи 56.
61.	В треугольнике с вершинами Л (3, —4), В(—1, —3), С(2, 1) вычислить длину высоты, проведенной из вершины А.
Указание. Найти уравнение основания ВС и применить к вершине А формулу расстояния (12).
62.	Найти биссектрису внутреннего угла В треугольника А (—3, 0), В(3, —2), С(1, 4).
Указание. По уравнениям сторон угла найти обе биссектрисы (см. 58). С помощью чертежа выделить из них внутреннюю для данного треугольника. Имеется и другой способ решения этой задачи: найти точку К пересечения биссектрисы угла В со стороной АС (см. 17) и воспользоваться уравнением прямой заданной двумя точками.
4. Пересечение двух прямых. Если даны две прямые
Л1х + В1г/ + С1 = 0 и А.,х +Biy-lrC.i--=0, то их точка пересечения находится совместным решением двух данных уравнений. Если уравнения несовместны, то прямые не имеют общей точки, т. е. параллельны.
63.	Найти точку В, симметричную точке А (— 2, 4) относительно прямой Зх-\-у — 8 = 0.
Решение. Симметричные точки А и В расположены на одном перпендикуляре к данной прямой па одинаковом расстоянии от нее. Угловой коэффициент данной прямой /д= — 3. Угловой коэффициент перпендикулярной к ней прямой —	- -. Уравнение перпендикуляра найдем по формуле (3):
о
//-4= !.-(х4-2),	х-3//+14 = 0.
и
Найдем теперь точку пересечения данной прямой с перпендикулярной, решая совместно их уравнения:
ЗхА-У — 8 = 0, х — Зу 4-14 = 0,
х— 1, </ = 5; С (1, 5).
24
Точка С является серединой отрезка АВ. Зная точки А и С, из формул (3) § 1 находим координаты искомой точки В:
— 2А~хв
2
.	, 4+Ув
5 = —2~~
= В (4, 6).
64.	Найти прямую, пересекающую прямые Л'4-//4-3 = 0 и 2л-— у — 5 = 0 в точках А и В так, что серединой отрезка АВ является данная точка М (1, 1) (рис. 20).
Решение. Искомая прямая проходит через точку М (1, 1), поэтому ее уравнение надо записать в виде (3), где угловой коэффициент k пока неизвестен: у— 1 = k (х — 1), y=kx—
Для нахождения k используем то условие, что точка ЛГ делит отрезок АВ пополам. Так как искомая прямая пересекает данные в точках А и В, то их координаты будут найдены из следующих систем уравнений:
J* + '/ + 3 = 0, ( 2х — у — 5 = 0, ( у = kx — k + 1, (. у = kx — k + 1.
Но поскольку k неизвестно, то из этих систем координаты точек А и В выразятся через k. Достаточно выразить через k абсциссы хг и хг точек А и В. Для этого, исключая из каждой системы у, получим k—4	k—6
fc-H И k — 2 '
Рис. 20
По формуле деления отрезка пополам полусумма этих значений абсцисс должна давать абсциссу середины отрезка, т. е.
] р-4 , £-6\ ,	,	2
г^т+т+т^г1’
Таким образом, искомая прямая имеет уравнение
2
(/—1= д-(х—1), 2х — 3t/+l=0.
65.	Найти вершины треугольника, если даны его стороны %4~ А у — 5 — 0, 7х 4- 5г/4- 11 = 0, 6х 4- У —• 7 = 0.
66.	Дан треугольник с вершинами А(—8, 3), В (8, 5), С (8, —5). Найти точку пересечения его высот.
67.	Уравнение одной из сторон угла 2х — 9у — 3 = 0, а уравнение биссектрисы 4х —^4-11=0- Найти уравнение второй стороны угла.
Указание. Взять какую-либо точку А на данной стороне, симметричная ей точка В (см. 63) относительно биссектрисы будет лежать на второй стороне угла. Найти также вершину угла.
68.	Даны уравнения двух сторон параллелограмма х — 2у — В, х — у— 1=0 и точка пересечения диагоналей М (3, —1). Найти уравнения двух других сторон.
25
5. Смешанные задачи на прямую. Для усвоения изложенного материала следует уметь решать комбинированные задачи па прямую, разбивая решение па ряд шагов и выбирая нужные формулы для каждого шага. Примеры таких задач приведены здесь. К большинству из них даны указания, показывающие, по какой схеме проводится решение и как воспользоваться разобранными выше задачами.
69.	Даны две вершины Д(—2, 1) и В (3, —4) треугольника и точка Н (5, —1) пересечения его высот. Найти уравнения всех сторон треугольника.
У к а з ан ие. Уравнение АВ находится прямо по формуле (7). Уравнение ВС ищется как уравнение прямой, проходящей через точку В и перпендикулярной прямой АН (см. 38). Аналогично получается и уравнение АС.
70.	Даны две высоты треугольника 2х — Зу + 1 = 0 и х Д 2у Д 1 = 0 и координаты одной из вершин А (2, 3). Найти уравнения всех сторон треугольника.
71.	Из прямых, проходящих через точку Р(1, 5), выделить ту, для которой середина С отрезка АВ, заключенного между прямыми х — Зу — 7 = 0 и 2х — у-4-7 = 0, лежит на прямой у = %Д1.
Указание. Решая задачу аналогично задаче 64, выразить через k координаты точки С и потребовать, чгобы они удовлетворяли уравнению = Из полученного соотношения определится k.
72.	В треугольнике АВС даны уравнения стороны АВ х Д 7у — 6 = 0 и биссектрис AL хДу — 2 = 0 и ВМ х — Зу — 6 = 0. Найти координаты вершин.
Указание. Определить сначала уравнения сторон АС и ВС (см. 67).
73.	Даны уравнения сторон треугольника АВ 2хДуД5 = 0 и ДС х — Зу6 = 0 и точка Р(1, 3) пересечения его медиан. Найти уравнение стороны ВС.
Указание. Найти вершину А и, зная, что точка Р делит медиану AM в отношении 2: 1, определить координаты точки М — середины стороны ВС. Далее решение проводится также, как в задаче 64.
74.	Даны две смежные стороны параллелограмма 2х — у-4-2 = 0 и х — 2у—-2 = 0 и точка М (1, 1) пересечения диагоналей. Найти уравнения двух других сторон и диагоналей параллелограмма.
Указание. По данным уравнениям сторон определить вершину параллелограмма. Найти противоположную вершину, учитывая, что в точке М диагонали делятся пополам. Далее проводятся другие две стороны, как параллели к данным (см. 38), находятся остальные вершины и записываются по формулам (7) уравнения диагоналей.
75.	Из точки А (3, 4) на прямую х Д у Д1 = 0 падает луч света, который после отражения от этой прямой как от зеркала попадает в точку С (6, —2). Найти уравнения луча падающего и луча отраженного.
Указание. Использовать тот факт, что из точки С источник света виден «за зеркалом» в точке В, симметричной А относительно данной прямой.
26
§ 3.	ЛИНИИ ВТОРОГО ПОРЯДКА
1.	Окружность. Уравнение окружности с центром в точке С (а, 6) и радиусом R имеет вид (см. 25)
(x-a^ + {y-b^ = R\	(1)
В частности, если центр окружности лежит в начале координат, т. е. а = 6 = 0, то ее уравнение принимает простейший вид:
x2J!-y2 — R2-
Общее алгебраическое уравнение второй степени
Ах2 + 2Вху + Су2 + 2Dx -j- 2Еу + А = О
есть уравнение окружности, если Л = С, В~0. Следовательно, общее уравнение окружности имеет вид
Ax2 + Ay2 + 2Dx + ‘2EyA-F = 0-	(2)
Разделив это уравнение на А и выделив полные квадраты по х и по у, приведем его к виду (1), где
ь=_А ^=P2+_g2-dg..
а А ’ ° А ’ К А
/ р_
\ А ' тельная мнимого
Замечание. Для вещественной окружности D2JrE2~AF>0, так как при £>2_|_£2 — AF = 0 уравнение (2) определяет только одну действительную точку ------------т-1, а при D2A~E2~ AF 0 ему не удовлетворяет ни одна действи-А /
точка. В этих случаях иногда говорят об окружности нулевого или радиуса.
76.	Найти центр и радиус окружности, проходящей через точки Д(1, 5), В(—4, 0) и С (4, —4). Написать ее уравнение.
Решение. Пусть R—радиус искомой окружности, а ее центр находится в точке (а, Ь), тогда уравнение окружности можно записать в виде (1), где а, Ь, R пока неизвестны. Так как точки А, В, С лежат на окружности, то их координаты удовлетворяют уравнению (1):
или
' (1— а)2 + (5 — b)2 = R2,
< (— 4 —а)2 + (0 — b)2 = R2, (4-а)2_у(_
а2 + уг _ 2« - ЮЬ -J- 26 = R2, а2 + ьз + 8а+16 = 7?2, a2+&2-8a+8b + 32 = R2.
Вычитая из второго уравнения сначала первое, а затем последнее, получаем
( 10a + Ю&—10 = 0,	( а-\-Ь = \,
<	или <
I 16a —86 —16 = 0,	(2a—6 = 2.
Отсюда находим, что а=1, 6 = 0. Подставляя эти значения в одно из уравнений системы, получим /?а = 25, т. е. R =5.
Таким образом, искомая окружность имеет уравнение
(х-1)2+№ = 25,
ее центр С (1, 0), а радиус R-5-
27
77. Привести к виду (I) общее уравнение окружности 2х2 + 2//2 — Зх +4// +2 = 0.
Решение. Разделим все члены уравнения на 2:
х2 1/2 —%-х 4- 2г/ +1 = 0.
Сгруппируем члены, содержащие только х и только у, и квадратов:
*2Л
дополним их до полных
9
4 У 16’
откуда
1/2 + 2у =//Я-21/4-1 -!=(«/+ I)2 — 1, +'~ ~Х] ~ 16	I)2 — 1 1 = 08
/ Q ''2	□
+0/+1)* = Гб
Таким образом, уравнение окружности приведено к
Ее центр находится в точке С (-3 , — 1у, а радиус R =
78. Исследовать уравнение
х24-//‘
второй степени, с одинаковыми коэффнциеи-а члена с произведением переменных нет.
ВИДУ (1).
2ах.
Решение. Данное уравнение тами при квадратах переменных,
з , / з/ 3
4 '
Поэтому при любом значении а данное уравнение определяет окружность. Отсутствие свободного члена говорит о том, что эта окружность проходит через начало координат.
Приводим уравнение к виду (1):
х-— 2ах-^-а2— а24-г/2 = 0,	(х—а)2 + г/2 = а2.
Итак, рассматриваемая окружность имеет центр на оси Ох в точке С (а, 0) и радиус Р = |а|, т. е. касается осн Оу в начале координат (.рис. 21).
28
У
При переменном а данное уравнение определит совокупность всех окружностей, касающихся оси Оу, с центрами на оси Ох. При а > О соответствующая окружность лежит в правой полуплоскости, а при а < 0 — в левой. При а —О окружность превращается в точку (0, 0).
79. Найти точки пересечения окружности радиуса R — 2 с центром в начале координат и прямой х—2z/ + 2 = 0.
Решение. Данная окружность имеет уравнение х2 + р2 = 4. Координаты точек пересечения прямой и окружности удовлетворяют одновременно двум уравнениям
J х2 + </’- = 4,
1 х- — 2(/Д-2 = 0.
Значение х — 2у — 2 из второго уравнения подставляем в первое:
(2у—2)2 + № = 4, т. е. 5у2—8у = 0, или у (5у — 8) = 0,
о 8	о 6
откуда /ц = 0, z/2== c , тогда хх = —2, х2 = =. D	О
Искомые точки пересечения прямой и окружности:
МН-2, 0) и Л13 < А 8
у О □ /'
80.	Среди прямых, параллельных прямой 2х-{-у = 0, выделить касательные к окружности № -|- z/2 = 1.
Решение. Уравнение всякой прямой, параллельной данной, можно записать в виде
2х-|-</-|-С = 0.
Касательная к окружности имеет с ней только одну общую точку, поэтому
совместное решение уравнений прямой и окружности должно дать только один ответ. Значение у из уравнения прямой подставляем в уравнение окружности:
у — — 2х — С, х2 -р (— 2х — С)2 — 1, т. е.
5х2 + 4Сх + С2-- 1 -О.
Квадратное уравнение ах2 + Ьх + с — 0 имеет одно решение (совпавшие корни) только тогда, когда его дискриминант Ь-— 4ас равен пулю. Для данного уравнения
(4С)2 — 4-5 (С2 — 1)=0, С2 —5=0, откуда С = । J 5.
Итак, искомые касательные имеют уравнения
2х + р+| 5—0 н 2x+r/-j '5-=0.
81.	Найти геометрическое место
точек М, для каждой из которых
расстояние до точки А (3, 1) равно длине касательной МТ к окружности (% + 1 )2(z/— 2)2 = 1 (рис. 22).
Решение. Пусть Л4 (х, р)--текущая точка искомой линии. По условию, Л1Д=ЛГ/', пли, что то же, ЛМ4 -^Мг2. Из треугольника МСТ по теореме
Пифагора находим
М Т2 = Л1С2 — СТ2 = Л1С2 — R2=Л1С2 — 1,
так как радиус данной окружности равен 1. Следовательно, точка М удовлетворяет условию МА2 = МС2—1. Так как центр данной окружности имеет координаты С(—1, 2), а точка А (3, 1) дана, то, используя формулу расстояния между двумя точками (см. § 1. п. 1), получим уравнение, наложенное на текущие координаты:
(X - З)2 + (у - 1)2 = (.X + 1)2 + (у-2)2 - 1,
или после алгебраических преобразований:
4х — у—3 = 0.
Таким образом, искомое геометрическое место точек есть прямая. Проверьте самостоятельно, что эта прямая перпендикулярна прямой АС.
82.	Найти центр и радиус окружности, проходящей через точки Л (— 1, 5), В (—2, —2) и С (5, 5).
83.	Привести к виду (1) уравнение окружности
Зх2 4- Зу2 — 6х + 8у = 0.
84.	Исследовать уравнение х2-{-у2 — 2Ьу.
85.	Найти точки пересечения прямой у — х-\-2 и окружности х2 -j- у2 — 4х — 12 = 0
86.	Показать, что прямая (/ = 2x4-5 и окружность х24-у2 = 1 не пересекаются.
Указание. При совместном решении уравнений прямой и окружности должны появиться комплексные корни.
87.	Показать, что прямая р = х]/3 касается окружности (х— — 2)3 у2 = 3. Найти точку касания.
Указание. См. 80.
88.	Из точки 4(5, —I) к окружности 2х24-2у2 —4х—12р— 3 = 0 проведена касательная АТ. Найти ее длину.
Указание. См. 81.
89.	Найти геометрическое место точек, касательные из которых, проведенные к окружностям (х— 1)24-((/~ 1)2 = 1 и (х4-2)24- (у— З)2— = 1, имеют равные длины.
2.	Эллипс. Эллипсом называется геометрическое место точек плоскости, сумма расстояний которых до двух данных точек /\ и F2 (фокусов) той же плоскости есть величина постоянная. Эту постоянную обозначают 2а, расстояние между фокусами обозначают 2с, при этом а > с. Если выбрать систему координат так, чтобы ось Ох проходила через фокусы, а начало координат лежало посредине между ними, то уравнение эллипса примет (канонический) вид
у2 п2
^4-^=1 (&2 = «2-С2, а>6).
В этом случае фокусы эллипса имеют координаты (с, 0), Е2 (с, 0) (рис. 23). Начало координат О — центр симметрии эллипса (или просто его центр), а оси координат — оси симметрии эллипса. Точки	(— а, 0), А2 (а, 0),	(0, Ь),
30
Ba(0, b) называются вершинами эллипса, а длины отрезков а = 0Д2 и Ь = 0Вг — большой и малой полуосями. Величина
называется эксцентриситетом, эллипса. Эксцентриситет характеризует вытянутость эллипса, так как выражается через отношение его полуосей:
£ =	= ]Л_ (Ь\2
а а у \а
Окружность можно считать частным случаем эллипса, у которого а-~Ь, т. е. е = 0.
Если фокусы эллипса лежат на оси Оу, то его уравнение имеет вид
В этом случае координаты вершин А, (0, —а), Д2(0, а), В1(—Ь, 0), В2 (6, 0) и фокусов Рг (0, — с), F2 (0, с) (рис. 24).
90.	Найти координаты фокусов и эксцентриситет эллипса: / i
25	16"
Решение. Для данного эллипса а = 5, 6 = 4, и поэтому
с = /^б2 = /25-16 = 3.
Следовательно, фокусы имеют координаты Fl{ — 3, 0) и В2(3, 0), эксцентри-3 ситет е=-=- • о
91.	Найти полуоси, координаты фокусов и эксцентриситет эллипса 9х2 -f- 4у2 = 36.
31
Решение. Разделив на 36, приведем данное уравнение к виду
Отсюда следует, что большая полуось эллипса о = 3, а малая полуось J = 2. При этом большая ось эллипса и его фокусы расположены на оси Оу (см. рис. 24). Найдем с по формуле c = J'fl‘~ — b'-.
с = 1'9 —4 = ) 5.
Следовательно, координаты фокусов /д (0, — Г 5) и /ы (О, Jr5), а его экс-с | 5
пентриситет е —-- = ——.
92.	Составить каноническое уравнение эллипса, зная, что его большая полуось а—12, а эксцентриситет е = 0,5. Найти расстояние между фокусами эллипса.
Решение. Воспользуемся формулой, выражающей эксцентриситет через отношение полуосей:
e = J/ I , или s2=l—откуда b” = a- (1 — в2).
В данном случае Ь2 = 144 (1 —0,25) = 108.
Следовательно, каноническое уравнение эллипса
С
Так как е= -, то c = as; с= 12-0,5 = 6 и расстояние между фокусами ГХГ« ~ = 2с=12.
93.	Составить каноническое уравнение эллипса, если его большая полуось равна 10, а эксцентриситет равен 0,8.
94.	Составить каноническое уравнение эллипса, у которого малая полуось равна 2|/ 6, а расстояние между фокусами F1F2 = 8.
95.	Определить полуоси, координаты фокусов и эксцентриситет эллипса Зх2 + 4z/2 — 12 = 0.
96.	Та же задача для эллипса 2хй-\~у‘1 — 4 = 0.
97.	Определить эксцентриситет эллипса, если расстояние между фокусами равно расстоянию между вершинами большой и малой осей.
3. Гипербола. Гиперболой называется геометрическое место точек плоскости, абсолютное значение разности расстояний которых до двух данных точек F\ и Г2 (фокусов) есть величина постоянная, обозначаемая 2а. Расстояние FJ) обозначается 2с, причем с>а. Каноническое уравнение гиперболы
Х\	(Ь2 = с2 — а2).
а2 Ь-
При этом ось Ох проходит через фокусы гиперболы, а начало координат находится посредине отрезка F-J2.^ так что с есть расстояние от фокуса до начала координат О. Фокусы имеют координаты Г1(— с, 0) и F, (с, 0).
Оси координат являются осями симметрии гиперболы, а точка О —ее центром симметрии. Гипербола пересекает ось абсцисс в точках /ф (— а, 0) и А2 (а, 0), 32
которые называются ее действительными вершинами, а величина d = CM2— действительной полуосью гиперболы. Точки В1 (0, —Ь) и В2 (О, Ь) называются мни
мыми вершинами гиперсолы, а величина Ь = ОВ2— мнимой полуосью (рис. 25).
Прямоугольник с центром в начале координат и со сторонами, параллельными координатным осям и проходящими через вершины гиперболы, называется основным прямоугольником гиперболы. Его диагонали
— х а
являются асимптотами гипероолы, т. е. прямыми, к которым неограниченно приближаются ветви гиперболы.
Эксцентриситет гиперболы
Его можно выразить через полуоси гиперболы:
с ___У a2-j-Ь2
а а
так что эксцентриситет характеризует вытянутость основного прямоугольника гиперболы. Если а — Ь, то гипербола называется равносторонней. В таком случае основной прямоугольник превращается в квадрат, а эксцентриситет равен У 2,
Если фокусы гиперболы расположены на оси Оу (рис. 26), то ее уравнение имеет вид
х2 _ ^=-1 Ъ2 а2
В этом случае асимптоты гиперболы
Ъ х= ± - - у, а а
где а и Ь, как и выше, —действительная и мнимая полуоси. Вершины гиперболы (3): Hi (0, —а), Л2(0, a), Bt( — b, 0), B.,(b, 0), фокусы ?! (0, —с), F2 (0, с), где с2 = а2 ф- Ь2.
98. Начертить гиперболу 4-
д- = 1. Определить ее фокусы, вер
шины, эксцентриситет, асимптоты.
2 Кручкович и др.
33
Решение. Полуоси данной гиперболы (см. рис. 25) я —2, /> = 3, следовательно, ее вершины У11( —2, 0), Л2 (2, 0), Л, (0, —3), В2 (0, 3). Через! них про-
c.	3
водим стороны основного прямоугольника. Его диагонали у=± ^х (являются асимптотами гиперболы. Построим их. Затем через вершины Aj и А2 гиперболы проводим ее ветви, приближая их к асимптотам. По формуле с =) а~~)-Ьг находим величину с.
Отсюда следует, что ( — | 13, 0) Н Л, () 13, 0),
1,8.
99.	Определить вершины, фокусы, эксцентриситет и асимптоты ,	Л'2 Ч2 1 г'
гиперболы ]£ —g = ~ 1  Сделать чертеж.
Решение. Данная гипербола имеет фокусы на оси Оу, ее действительная 4 полуось я —3, а мнимая полуось /> —4 (ем. рис. 26). Асимптоты х=-у - у, или
3
г/ = •_»	.г. Вершины данной гиперболы /1, (0, — 3), Л.,(0, 3), Вг( —4, 0), С, (4,(1).
Далее, с— | 16+9 — 5, поэтому фокусы расположены в точках /д (0, —5), /'.,((), 5). Эксцентриситет е = -| .	z
Чертеж гиперболы сделать самостоятельно.
100.	Асимптоты гиперболы имеют уравнения 4t/±3x —0, а расстояние между фокусами равно 20. Написать ее каноническое уравнение.
Решение. Разрешим уравнения асимптот относительно у и, сравнив с общей формулой асимптот, найдем отношение Ъ к я:
Кроме того, F1F2 = 2c = 20, т. е. с — 10. Так как для гиперболы с2 — а2 + /г, то для нахождения а и b получим систему уравнении
J а ~ 4 ’ ( я2 + &2= 100, решая которую, найдем а — 8, /?—-6. Следовательно, каноническое уравнение гиперболы имеет вид
*2 _	= I
64 36 д-2	у 2
101.	Дан эллипс g + у=1. Написать уравнение гиперболы, вершины которой находятся в фокусах, а фокусы —в вершинах данного эллипса.
102.	Преобразовать к каноническому виду уравнение гиперболы 9х2 — 16у2 = 144. Найти координаты ее фокусов и вершин, эксцентриситет и уравнения асимптот. Сделать чертеж.
103.	Действительная полуось гиперболы равна 5, эксцентриситет 8=1,4. Написать каноническое уравнение гиперболы.
34
104.	Написать каноническое уравнение гиперболы, проходящей через точки А (2, 1) и В ( — 4, ф7).
У к а з а н и е. Так как точки А и В лежат на гиперболе, то их координаты удовлетворяют ее уравнению; из этого условия определяются неизвестные а и Ь.
105. Дана гипербола у
У = — 1. Найти координаты фокусов
и вершин, эксцентриситет и уравнения асимптот.
Указание. Фокусы данной гиперболы расположены на оси Оу.
4.	Парабола. Парабола есть геометрическое место точек плоскости, равноудаленных от данной точки (фокуса) и от датой прямой, не проходящей через эту точку (директрисы), расположенных в той же плоскости (рис. 27).
Каноническое уравнение параболы имеет вид
у2 — 2рх (р>0),
где р —расстояние от фокуса до директрисы. При этом система координат выбрана так, что ось Ох проходит перпендикулярно директрисе через фокус, положительное ее направление выбрано от директрисы в сторону фокуса. Ось ординат проходит параллельно директрисе, посередине между директрисой и фокусом, откуда уравнение директрисы
* = — координаты фокуса В
2	\	?
Начало координат является вершиной параболы, а ось асбцисс —ее осью сим-	рис. 27
метрии. Эксцентриситет параболы е=1.
В ряде случаев рассматривают параболы, заданные уравнениями: а) у2 — ~ — 2рх, б) х---'2ру, в) .О - - 2ру (для всех случаев р>0): В случае а) парабола симметрична относительно оси Ох и направлена в отрицательную сторону
(рис. 28, а). В случаях б) и в) осью симметрии является ось Оу (рис. 28, б, в). Координаты фокусов для этих случаев:
«) Н- V.0;, б) Л 0, в) r - о, - И.
\	2	/	\	2 !	к 2 /
2*
35
Уравнения директрис:
. р _	Р х Р
б)	У=“|, «)	2 •	\
106.	Парабола с вершиной в начале координат проходит через точку А (2, 4) и симметрична относительно оси Ох. Написать ее уравнение.
Решение. Так как парабола симметрична относительно оси Ох и проходит через точку А с положительной абсциссой, то она имеет вид, представленный на рис. 27. Подставляя координаты точки А в уравнение такой параболы у2 = 2рх, получим 16 = 2р-2, т. е. р = 4.
Следовательно, искомое уравнение
!/2 = 8x, фокус этой параболы F (2, 0), уравнение директрисы х— — 2.
107.	Парабола с вершиной в начале координат проходит через точку 4(1, —2) и симметрична относительно оси Оу. Написать ее уравнение.
Решение. Данная парабола симметрична относительно оси Оу и проходит через точку с отрицательной ординатой, поэтому опа имеет вид, представленный па рис. 28, в. Подставляя координаты точки А в уравнение х------ 2ру, получим р--=4~.	1
г 4
Следовательно, искомое уравнение ' у, или ~2х2, фокус пара-
108.	Найти фокус и уравнение директрисы параболы у3 = 24х.
109.	Парабола с вершиной в начале координат проходит через точку Л ( — 2, —3) и симметрична относительно оси Ох. Написать ее уравнение, найти фокус и директрису.
Указание. Данная парабола имеет вид, указанный на рис. 28, а.
НО. Найти точки пересечения парабол у = х2 и х = у2. Сделать чертеж.
111.	Вывести уравнение параболы, директриса которой имеет уравнение х -ф-у -ф- 1 = 0, а фокус расположен в точке F (2, 3).
Решение. Пусть М (х, у) — произвольная точка параболы. Ее расстояние d до данной директрисы определяется по формуле (12) § 2, п. 3:
d — I х 1/ ~Ь 1 !
"/2
По определению параболы, это расстояние равно MF =	— 2)г -ф- («/ — З)2. При-
равнивая эти расстояния, возводя в квадрат и делая необходимые алгебраические преобразования, получим искомое уравнение;
y^-!*+Z/+l Н1Л’*ГГ2)ЧЛ7=Ж (* + ^+ 1)2 = 2 [(х-2)2+ (i/-3)2], +	1 ф-2х«/-ф2х-ф2^ = 2 (х2 -4хА-^ + У2~бу + ^
х2 — 2ху ф- у2 — Юх — 14г/ + 25 = 0.
36
Так как система координат не является канонической для дайной параболы, получилось ее полное уравнение.
112.	Вывести уравнения парабол, имеющих указанные директрису и фокус: а) у-- — 2, F (3, 1), б) 2хф-р = 0, F( —2, —1).
§ 4.	ПРЕОБРАЗОВАНИЕ УРАВНЕНИЯ ЛИНИИ ВТОРОГО ПОРЯДКА К КАНОНИЧЕСКОМУ ВИДУ
1.	Использование параллельного переноса осей координат.
Общее уравнение линии второго порядка имеет вид
Ax2 + 2Bxy-{-Cy2-i-2Dx-i-2Etj-{-F=0,	(1)
где коэффициенты А, В и С одновременно в ноль не обращаются. С помощью преобразования системы координат уравнение линии второго порядка может быть приведено к простейшему (каноническому) виду. Если в уравнении (1) коэффи-чиент В —0, то оно имеет вид
Ах2А-Су2 + 2Ох-{-2ЕуА-Р = 0-	(2)
Это уравнение преобразуется к простейшему виду с помощью параллельного переноса осей координат по формулам
( х = х'-\-х„,
(У = У + Уо>
гДе (х0, у0) — координаты нового начала О' (в старой системе координат). Новые оси О'х' и О'у' параллельны старым. Точка О' является центром эллипса или гиперболы и вершиной в случае параболы.
Приведение уравнения (2) к простейшему виду удобно делать методом выделения полных квадратов аналогично тому, как это делалось выше для окружности.
113.	Уравнение линии второго порядка
9.т2 + 1 бу2 - 9О.г + 32z/ + 97 = О
привести к простейшему виду. Определить вид и расположение этой линии. Найти координаты фокусов. Сделать чертеж.
Решение. Группируем члены, содержащие только х и только у, вынося коэффициенты при х- и у2 за скобку:
9 (х2 - 1 Ох) + 16 (у2 + 2у) + 97 = 0.
Дополняем выражения в скобках до полных квадратов:
9 (хг-2 • 5.V + 25 - 25) 4-16 ф24-2г74-1 - 1)4-97 = 0,
9 [(х- 5)г - 25] 4-16 [Q/4-1)2 -1 ] 4-97 = 0,
9 (х —5)24-16 (у4- О3-225 — 16 4-97 = 0.
Таким образом, данное уравнение преобразовано к виду
9 (х - 5)г 4- 16 (у 4- О2 - 144 = 0.
Обозначаем
( х'~х — 5,	( х — х'А-5,
<	или {
I г/' = </+1. I у = у' — 1-
Сравнивая с уравнениями (3), видим, что эти формулы определяют параллельный перенос осей координат в точку О' (5, —1). В повой системе координат уравнение
37
запишется так:
9л'2-,-1бу'2—144 = 0.
Перенеся свободный член
вправо и разделив па него, получим
х'2 Тб
и'2
4-—-= 1
' 9
Итак, данная линия второго порядка есть эллипс с полуосями а = 4, 6 = 3. Центр эллипса находится в новом начале координат О' (5, — 1), а его фокальная ось есть ось О'х'. Расстояние фокусов от центра с = Ц4б —9 = ЦТ »=2,6, так что новые координаты правого фокуса F2: Х' = УТ, у' = 0. Старые координаты
этого же фокуса находятся из формул параллельного переноса:
х = х' + 5 = уг7 4-5,
У=у' — \ =0-1 = -1.
Аналогично, новые координаты левого фокуса 1\: х'——V 7 , у' —0. Его старые координаты: х= -ЦТ+5, у= -1.
Чтобы начертить данный эллипс, наносим на чертеж старые и новые координатные оси. По обе стороны от точки О' откладываем по оси О'х' отрезки длины а = 4, а по оси О'у' — длины 6 = 3; получив таким образом вершины эллипса, чертим сам эллипс (рис. 29).
Замечание. Для уточнения чертежа полезно найти точки пересечения данной линии со старыми координатными осями. Для этого надо в формуле (2) положить сначала р = 0, а затем х = 0 и решить получающиеся уравнения. Появление
комплексных корней будет означать, что линия соответствующую координатную
ось не пересекает.
Например, для эллипса только что разобранной задачи получаются такие уравнения:
9х2— 90x 4-97 = 0, 16р2 + 32(/4-97 = 0.
Второе из этих уравнений имеет комплексные корни, так что эллипс ось Оу не пересекает. Корни первого уравнения:
О __	о
*1=5-4/2 (^1,3), х2 = 5 + -.,-Ц2 (=«8,7).
О	о
В точках (xj, 0) и (х.>, 0) эллипс пересекает ось Ох (см. рис. 29).
114. Уравнение линии второго порядка
х2 — у2 — 4х 4- 2у 4- 7 = 0
привести к простейшему виду. Определить вид и расположение этой линии, найти координаты фокусов.
Решение. Как и в предыдущей задаче, выделяем сначала полные квадраты по х и по у:
(Х2 _ 4х) _ (у2 _ 2(/) -Н 7 = 0, <х - 2)2 - (у- 1)- 4- 4 = 0.
38
Далее,, обозначаем1
( х' — х — 2,	( х = .г'+2,
{	или !
I (/' = //•-], I У~У +1.
Геометрически это означает, что мы делаем параллельный перенос осей координат в точку О' (2, 1) [сравнить с формулой (3)]. После параллельного переноса получим
Д' 1 i fa'2 л'2- у'2+ 4 = 0, или - —	— 1,
1	4	4
т.	е. уравнение гиперболы, центр которой расположен в точке О' (2, 1). Так как ее полуоси равны (а = 6 = 2), то это равносторонняя гипербола, действительная ось которой направлена по осп О'у'. На этой оси расположены фокусы и F,
на расстоянии с= |’+ + + = 2 | 2 от центра О'.
Следовательно, новые координаты фокусов: х' = 0, у'= L 2}Л2 . Из формул параллельного переноса найдем старые координаты фокусов;
х=х' + 2 = 0 + 2 = 2,
!/ = //'	= 2 | 2 -|- 1.
В старой системе координат ([да-кусы гиперболы: ГД.2, 1—2 Г'2) и Л, (2, 1-ф2 Г 2).
Рис. 30
Для того чтобы построить данную гиперболу, проведем старые и новые координатные оси. Отложим па осях О'х' и О'у' в обе стороны от О' отрезки, равные двум единицам длины. Через полученные вершины гиперболы проведем ее основной прямоугольник (в данном случае —квадрат). Его диа
гонали являются асимптотами гиперболы. Далее, чертим ветви гиперболы, помня, что ее действительные вершины находятся на оси О'у' (рис. 30). Для уточнения расположения гиперболы найдем точки ее пересечения со старыми координатными осями. Для этого полагаем в данном уравнении сначала у = 0, а затем х = 0:
х2-4х + 7 = 0, —у2 + 2</ + 7 = 0.
Корни первого уравнения комплексные, т. е. гипербола ось Ох не пересекает. Решая второе уравнение, найдем точки пересечения гиперболы с осью Оу:
Л = 1 - 2 V2 («=-1,8), у., = 1 + 2 |Л2~ == 3,8.
115.	Привести к простейшему виду уравнение линии второго порядка Зу2 + 5х + бу + 13 = 0. Определить вид и расположение линии, найти координаты фокуса.
Решение. Так как член с х2 отсутствует, то надо выделить полный квадрат только по у.
3 (!/+1)2 + 5*+ 10 = 0.
Выносим также за скобку коэффициент при х:
3Q/ + l)2+5U + 2)=0;
39
обозначаем
xl — х 2, или
«/'==г/+1>
х~х'— 2,
У=у'-1.
Тем самым производится параллельный перенос системы координат в точку О' (—2, —1). После переноса уравнение примет вид
5 ~3Х ’
Зу'2!--5х' = 0, или у
Отсюда следует, что данная линия есть парабола (рис. 31), точка О' (—2, — 1) является ее вершиной. Парабола направлена в отрицательную сторону оси О'х' и симметрична относительно этой оси. _	5
Величина р для нее равна поэтому фокус имеет новые координаты:
, Р 5	, п
*' = -f=~T2- *=0'
Его старые координаты:
х==х,_2=_5_2 = _29
Х Х	12	12’
У = у'~- 1=0-1 = -1.
Если в данном уравнении положить у = 0 или х = 0, то обнаружим, что парабола пересекает ось Ох в точке 13
=—— а ось Оу она пе пересекает.
116.	Выяснить геометрический смысл квадратного трехчлена у ~ ах2 + Ьх 4- с (а У=0).
Решение. Выделим полный квадрат по %, преобразуя данное уравнение:
! ь \	( b b2 b2 '	I b\2 №
у=а[хг-\—х)+с,	= a х24-2+с, у = <г х + п- — —-|-с,
\ а ] а \ 2а 4а2 4а2) v \	2а] 4а 1
Переносим свободный член влево:
У~~
и обозначаем
4ас — ft2 4а
Это формулы 4ас—Ь2\
параллельного переноса системы координат в точку
40
После параллельного переноса уравнение примет вид у' = ах'2,
и, следовательно, рассматриваемая линия второго симметрии которой является ось О'у'. При этом еслиа>0, и вниз — при а<0. Вершина параболы находится в точке О', а параметр р выражается через а по формуле
порядка есть парабола, осью парабола направлена вверх,
2р =
Чтобы построить данную параболу, надо нанести на чертеж точку О', провести оси О'х' и О'у' и в новой системе координат построить параболу у' — ах'2 с вершиной в О' (рис. 32). Для уточнения расположения параболы можно найти ее точки пересечения со старыми координатными осями. Ось Оу она пересекает в точке у —с (в данном уравнении полагаем х — 0), а точки пересечения с осью Ох найдутся из квадратного уравнения
ах2~‘г Ьх~~с — 0.
Если данная парабола ось то корни этого уравнения ными.
Следующие уравнения стейшему виду. Определить ние линии второго порядка, фокусов. Сделать чертеж.
Ох не пересекает, будут комплекс-
привести к протип и расположений™ координаты
117.	7№-5г/2-14х-20г/+	120. 9х34-4/4-3(к—12//—2=0.
4-22 = 0.
118.	4х24-3/4-18//+ 15 = 0.	121. /-2х4-4у4-2-=0.
119.	5л:3-4/4-16г/-36 = 0.	122. // = -х34-2х.
2. Использование поворота осей координат. Общее уравнение второй степени (1) преобразуется к виду (2), т. е. к рассмотренному в п. 1 случаю, с помощью поворота координатных осей на угол а по формулам
х=Х cos а —У sin а, у = X sin а4- У cos а,
(4)
где X, У —новые координаты. Угол а находится из уравнения
В tg2 «4-(Д — С) tg а — 5 = 0.	(5)
Оси координат поворачиваются при этом так, чтобы новые оси Ох и ОУ были параллельны осям симметрии линии второго порядка.
Зная tg а, можно найти sin а и cos а по формулам тригонометрии
tg«	1
sin а — + --------, cos а = ± -===.
И 14-tg3 а	/1 4-tg2 а
Если угол поворота а условиться считать острым, то в этих формулах надо брать знак плюс, и для tga надо взять также положительное решение уравнения (5). В частности, при А=С систему координат нужно повернуть на угол
41
л -	л
ct ~	. Формулы поворота на угол
х = — (X— Г),
V2
имеют вид
^-(х-т.
(6)
123.	Уравнение линии второго порядка
5х2 + 4ху + 8у2 — 36 = 0
привести к простейшему виду. Установить вид и расположение этой линии.
Решение. В данном случае .1=5, В = 2*, С = 8, поэтому угол поворота ос находится из уравнения
2 tg2 а —3 tga —2 = 0.
Решения этого уравнения tga = 2 и tga= —. Ограничиваясь острым углом а, берем первое из них. Тогда
и
Х-2У
V'5
1 1
cos a = —=   - =
Kl-j-tg'-a |5
2Х+У
У = -77^--
Подставляем эти значения х и у в данное уравнение:
или
\ И5 У	Г5	Г5	\ /5 У
4	8
(Х-2У)24- (Х-2У)(2Х+У) + -° (2Х + У)2 = 36.
Раскрывая получим
скобки и приводя подобные,
9Х2 + 41/2 = 36.
Наконец, придем к
разделив иа свободный член, уравнению эллипса
Х2+Г- = 1.
4	9
Отсюда следует, что а = 3, Ь = 2, причем большая ось эллипса направлена по оси OY, а малая—по оси ОХ.
Для построения этого эллипса нанесем на чертеж повернутые оси ОХ и OY. Для этого на оси Ох отложим единицу масштаба, а на оси Оу — две. Получится точка М (1, 2), радиус которой ОМ наклонен к оси Ох под углом а, для которого tga = 2. Следовательно, через эту точку М и пройдет новая ось абсцисс. Затем отмечаем иа осях ОХ и OY вер
шины эллипса и чертим сам эллипс (рис. 33). Заметим, что данный эллипс пересекает старые координатные оси в точках, которые находятся из квадратных
Подчеркнем, что В —это половина коэффициента при ху.
42
уравнений (сели в данном уравнении положить y=t) или х = 0):
Отсюда
5х2 —30 = 0 и 8д2 —36 = 0.
х113 = :У |<7,2	± 2,7), й,2=± )Л4,5	± 2,1).
124.	Уравнение 2ху — а2 привести к простейшему виду. Уста повить вид и расположение этой линии.
Решение. В данном уравнении А = С = 0. Следовательно, нужно сделать поворот па угол а= . Заменяя в данном уравнении х и у по формулам (0), получим
. X-Y .¥ + >’	„ V9 ,	А'2 Г2 ,
2-------—!— = п2, или X2—12 = п2, т. е.-----	= 1.
I 3	|2	а- а-
Следовательно, данная линия является равносторонней гиперболой, действительная ось которой идет по оси ОХ. Ее расположение показано на рис. 34. Основной
прямоугольник гиперболы есть квадрат со стороной 2а. Очевидно, старые координатные оси совпадают с диагоналями этого квадрата и служат поэтому асимптотами гиперболы (см. рис. 34).
Итак, уравнение 2ху — а2 определяет равностороннюю гиперболу с полуосью а, симметричную относительно биссектрис координатных углов. Ее ветви расположены в I и III четвертях и асимптотически приближаются к осям Ох и Оу. Так как данное уравнение можно записать в виде
k	,	(t-
У = -х^ где ^=2--то рассматриваемая гипербола представляет собой график обратной пропорциональности с коэффициентом k.
Замечание. Аналогично рассматривается уравнение 2xj/ = — а2.
Оно определяет равностороннюю гиперболу с тем же основным прямоугольником, но расположенную во II и IV четвертях (пунктир на рис. 34).
125.	Установить геометрический смысл дробно-линейной функции
У=~гд (А = be — ad 0, с^О*).
•' сх 4- d 4	’	'	'
Р е ш е и и с.
Из
дроби
ах-гЬ cx-f-d
выделим целую часть. Для этого разделим
числитель на знаменатель по правилу деления многочленов. Получится частное
* При Д = 0 функция представляет собой константу (проверьте!), а при с = 0 получится линейная функция; и в том, и в другом случаях графиком функции служит прямая линия.
43
a	, ad be — ad A
— и остаток b-------=--------=— поэтому
c	c c c ’
A	A
ах-фА> __ a c _ a ,	<4
cx + <i	cr ex -\-d c 1 d '
Следовательно, данное
а
илп, перенося член —-
уравнение можно записать так:
влево и обозначая Д через k,
a k
с d *
Сделаем теперь параллельный перенос осей координат по формулам
f , d	, d
х'=х4- —	x — x'--,
‘ c ’	c ’
или
, a	, ft
\У=У'+--.
После этого уравнение примет вид
(/'=—, или х'у' = k.
Это уравнение рассмотрено в задаче 124.
Итак, графиком дробно-линейной функции является равносторонняя гипербола, асимптоты которой параллельны осям координат, а центр находится в точке
О'(-А “Y
\ с с)
В следующих задачах привести к простейшему виду уравнение линии второго порядка. Установить ее тип и расположение.
126.	х2 + 2х1/ + ^ = Г2х-У2л. 129. =
127.	Зх2 - Аху + 4 = 0.	130. х2+^/ = 2х.
128.	х2 + ху + у2 — 3.	131. 2ху = х + у.
3.	Случаи распадения и вырождения линии второго порядка. Если левая часть уравнения (1) распадается на произведение двух линейных множителей
(Л 1Х -ф Bpj -ф Cj) (Л2х -ф Bpj -ф С2) = 0,
то соответствующая линия второго порядка представляет собой пару прямых
AjX -ф Вру -ф Ci — 0	и Л2х -ф В$у -ф С2 ~ 0
и называется распавшейся.
Возможны случаи, когда уравнению (1) удовлетворяют координаты только одной действительной точки (х0, у0) или не удовлетворяют координаты ни одной такой точки. В первом случае говорят, что линия вырождается в точку, а во втором линию считают мнимой.
44
Например, уравнение
2(х-1)2 + (// + 2)3 = 0 определяет только одну точку х0=1, Ло=—2, а уравнение 2(х-1)2 + ((/ + 2)2=-1
не имеет ни одного действительного решения и представляет поэтому мнимую линию второго порядка.
132.	Показать, что линия второго порядка х22хуу2 = 1
распадается на пару прямых.
Решение. Левая часть уравнения представляет собой полный квадрат, т. е. (т + у)2 = I, или (x + j/)8—1 = 0.
Преобразуя разность квадратов в произведение суммы и разности, получим (% + j/ + 1) (x-j-t/—1) = 0. Значит, данная линия второго порядка состоит из пары прямых:
* + 11+1=0 и х + р —1=0.
Эти прямые параллельны, так как их угловые коэффициенты равны —1.
133.	Показать, что линия второго порядка х2 — у22х -\-2y-Q распадается на пару прямых.
Решение. Перепишем уравнение в виде х2 + 2х + (-у2+2у)^0 и разрешим его относительно х:
х= —i + ^Т^й=?г+2у)=--1 ± K(7-i?= -1 ± (У-1). откуда х~ — 2и х= —у.
Следовательно, данная линия второго порядка распалась на пару прямых х — у + 2 = 0 и х-фу = 0.
Замечание. Линия второго порядка распадается на пару прямых всегда, когда при решении ее уравнения относительно х (или относительно у) под корнем получается полный квадрат.
Что представляют собой следующие линии второго порядка?
134.	х2 — у2 — 0.
135.	x2 + ~4x^ + 4z/2 = 9.
Указание. Разложить левую часть уравнения на множители.
136.	Х2 + у2 — 4х4-2// + 5 = 0.
Указание. Выделить полные квадраты по х и по у.
§ 5. ПОЛЯРНЫЕ КООРДИНАТЫ
§ 1.	Полярная система координат. Полярная система координат на плоскости определяется заданием некоторой точки О, луча Ор, исходящего из этой точки, и единицы масштаба I (рис. 35). Точка О называется полюсом, а луч Ор —полярной осью.
45
Пусть Л4 —произвольная точка плоскости. Обозначим через р и ср ее расстояние от полюса и угол, отсчитываемый от полярной оси против часовой стрелки до направления ОМ. Эти числа называются полярными координатами точки М, причем величина р называется полярным радиусом, а ср —полярным углом точки М. По самому своему определению величина р положительна. Задание пары чисел (р, ср) однозначно определяет точку М
на плоскости. Если ограничить изменение угла ср пределами
О ср < 2л (или — л < ср т л), то, и обратно, каждой точке плоскости однозначно отвечает пара чисел (р, ср).
Исключение составляет только полюс О, для которого р = 0, а угол ср неопределенный.
Если выбрать декартову систему координат так, чтобы ее начало О совпало с полюсом полярной системы, а ось Ох шла по полярной оси Ор, то между полярными координатами (р, ср) и декартовыми координатами (х, у) каждой точки М будет осуществляться следующая /) ♦	связь (рис. 36):
х — р cos ср, z/ = psincp (1)
Р=Г х- + у2, tgcp= ^-. (2) Из этих формул следует, что
у
sin ср =
(3)
Замечание. Последняя из формул (2) определяет два угла ср и ср ф-л (в пределах от 0 до 2 л). Формулы (3) уточняют, какой из этих углов следует выбрать.
137.	Построить точки, заданные своимг/ полярными тами, А 13, В {2, Ci3, D;2, 0).
\	2 j \ ’4 j \ ’	6)'	\	]
координа-
Построение точек дано на рис. 37.
138.	В полярной системе координат даны точки ^4, М2 {з, "), М3 f 6, -	. Найти их декартовы координаты, выбрав
декартову систему координат, как указано на рис. 36.
46
Решение. Подставляя полярные координаты в формулы (1), найдем декартовы координаты данных точек:
Л1Х (2 к 2 , 2 к¥), Л1.2 (о, 3),	(3 /У, -з).
139.	Найти полярные координаты точек, симметричных относи-тельно полярной оси точкам А\2,	В\3, —	, С (Л,
140.	В декартовой системе координат даны точки МДО, 2), М2(—1, 0), М3(— УЗ, 1), М4(—1,—1), М5(1, УЗ). Найти их полярные координаты, введя полярную систему координат, как указано на рис. 36.
2. Полярные уравнения линий. В полярных координатах линия задается уравнением Ф (р, ср) = О, связывающим полярные координаты ее текущей точки. Если возможно, это уравнение разрешают обычно относительно р, и тогда полярное уравнение линии принимает вид р-=')('{)- Если функция р (ср) непериодическая, то углу ф обычно придают все возможные для данной функции значения, не огра-
ничиваясь изменением его только в пределах первого периода.
Чтобы перейти от уравнения линии F (х, у) = 0 в декартовых координатах к ее полярному уравнению, нужно подставить в декартово уравнение вместо х, у их выражения из формулы (1). Обратный переход от полярного уравнения Ф (р, ср) = 0 к декартову уравнению той же линии осуществляется с помощью формул (2) и (3).
141.	Найти полярное уравнение прямой .г=1.
Решение. Используя первую из формул (1), найдем, что на данной прямой полярные координаты связаны условием
pcos<p~l, или р = —-—. г т	r cos ср
Эго и есть уравнение данной прямой. По-
скольку р —величина положительная, угол
<р должен меняться так, чтобы cos ср был положителен, т. е. находиться в I и IV четвертях (рис. 38).
142.	Найти полярное уравнение прямой, не проходящей через начало координат (см. рис. 19).
Решение. Приведем уравнение прямой к нормальному виду
х cos а+у sin а—р = 0.
Заменяя х и у по формулам (1), получим
р cos cos а + р sin ср sin а—р = 0, т. е. р cos (ср — а) = р.
По условию, прямая не проходит через начало координат, поэтому се расстояние р от начала координат отлично от нуля. Из последнего равенства следует, что при любом ср и соз(ф —а)=^0. Разделив на соз(ф —а), получим полярное уравнение данной прямой в виде
cos (ф — а)'
47
143.	Что представляют собой линии, заданные в полярной системе координат уравнениями p = a(const) и tp = a.(const)?
Решение. Геометрическое место точек, для которых р — расстояние до полюса— постоянно, есть окружность. Поэтому уравнения р~а определяет окружность радиуса а с центром в полюсе О.
Уравнению ф=а удовлетворяют все точки полупрямой, проведенной из полюса под углом а к полярной осн. Заметим, что вся прямая, проходящая через полюс, записывается в полярной системе координат уравнениями q> = a и ф = а-}-л.
144.	Дано полярное уравнение линии р2 = 9 sin‘2<p. Построить эту л линию по точкам, задавая углу <р значения через промежуток у Найти ее декартово уравнение, расположив декартовы оси так, как показано на рис. 36.
Решение. Поскольку левая часть данного уравнения неотрицательна, то угол ф может изменяться только в тех пределах, для которых sin 2ср>= 0, т. е. л	_Зл	„	.
Ог-фйау и л=-~срг< . Для вычисления значении р (ограничиваясь точностью 0,01) составляем следующую таблицу:
Таблица 1
№ точек	Ф	2ф	sin 2ф	р = 3 У sin 2ср
1	0	0	0	0
2	л 12	Л 6^	0,50	2,12
3	л ’6	л У	0,87	2,79
4	л т	л "2”	1	3
5	л У	2л 3	0,87	2,79
6	5л 12	5л '6'	0,50	2,12
7	Я 2	Л	0	0
При изменении угла ф в пределах III чепзерзи sin 2ф будет принимать те же значения, что и в I четверти. Поэтому линия будет симметрично расположена относительно начала координат. Для ее построения проводим из полюса лучи, соответствующие выбранным значениям ф, и на каждом луче откладываем вычисленные значения полярного радиуса. Полученные точки соединяем плавной кривой (рцс. 39). Построенная линия носит название лемнискаты Бернулли.
Найдем ее уравнение в декартовой системе координат. Для этого воспользуемся формулой sin 2ф = 2 sin ф cos ср и подставим в уравнение линии р2 = 9 sin 2<р
48
= 18з1Пфсозф выражения р, sin ф и cos ф (2) п (3):
. 18..	V-—,
| х2 + Уг V xA + if
х ‘у хч-д3’ Окончательно имеем
(х2 + с/2)2=18ед.
145. Какая линия задается полярным уравнением р = аср (а^> 0)?
Решение. Поскольку р и а — положительные величины, угол ср может изменяться только в положительную сторону. При ф = 0 также и (>=- 0, т. е. данная линия выходит из полюса. При возрастании угла ф от нуля р также возрастает пропорционально. М. (р, ср) данной менпо удаляясь
by
Рис. 39

Следовательно, линии, исходя из полюса, движется вокруг от полюса. В результате точка М описывает ваемую спиралью Архимеда (рис. 40). За один оборот точка М (р, ср) перейдет в новое положение М' (р', ф'), где ср' = ср -f-2л, а
р' =пср' ~а (ср4~2л) = аф4-2ла = р + 2ло. Поэтому расстояние между точками М и М'd = р'--р = 2ло есть величина постоянная. Таким образом, спираль Архимеда рассекает каждый полярный луч па равные отрезки длины d = 2na*.
текущая точка него, одновре-спираль, назы-
146. Даны прямая и точка О, не лежащая на ней. Определить геометрическое место точек Л4, (с>0), где А — произвольная точка прямой, искомого геометрического места точек удобно запи-
для которых ОМ  О А = с
Р с ш е п и е. Уравнение сать в полярной системе координат, выбирая ее так, чтобы полюс был в точке О, а полярная ось шла перпендикулярно данной прямой. В этом случае угол а перпендикуляра к прямой с полярной осью равен пулю, и из полярного уравнения прямой (см. 142) полярный (р, ф) —полярные координаты точки
радиус точки А равен	Пусть
М. По условию задачи, р рл = с, отсюда
р — -о
соз ф — 2R cos (с, Р
Q где введено обозначение —
Не считая отрезка, примыкающего к полюсу.
49
Таким образом, полярное уравнение геометрического места точек имеет вид
р = 2R cos <р.
Это уравнение показывает, что в треугольнике OMQ (рис. 41) угол М прямой и, как известно из элементарной геометрии, точка М расположена на окружности с диаметром OQ. Тот же результат можно получить и аналитическим путем, введя соответствующую декартову систему координат. Тогда, преобразуя уравнение р = 2/?созф по формулам (1) и (2), получим:
= 2Р——-----,
I' х3 + уа
х2 ya = 2Rx, (x-R)2 + tf = R2.
Это есть уравнение окружности радиуса R с центром С (R, 0).
147. Найти полярное уравнение прямой х]/"3 + у~2 =0.
Указание. См. решение задачи 142.
148. Найти полярное уравнение окружности х2 + /у2 = 2ах.
Построить по точкам, задавая угол гр значения через про-линию p = 2cos2q>. Написать декартово уравнение этой
149.
межуток линии.
Указание. Поскольку в полярных координатах рДьО, то угол ф должен изменяться так, чтобы cos 2<р Дл 0.
150.	Построить по точкам, задавая углу <р значения через промежуток , кардиоиду
р = 2а (1 +cos <р) (а>0).
Написать декартово уравнение кардиоиды.
151.	Та же задача для линии (улитка Паскаля):
p = 2 + cos<p.
152.	Отрезок АВ постоянной длины 2а скользит своими концами по сторонам прямого угла. Из вершины прямого угла О на этот отрезок опущен перпендикуляр ОМ. Определить геометрическое место точек М.
У к а з а и и с. Ввести полярную систему координат так, чтобы полюс был в точке О, а полярная ось совпала с одной из сторон угла.
ГЛАВА II
ОПРЕДЕЛИТЕЛИ. ВЕКТОРЫ. МАТРИЦЫ
§ 1. ОПРЕДЕЛИТЕЛИ
1. Определители второго и третьего порядков. Определители второго и третьего порядков определяются следующими равенствами:
Числа a,-, bj, cj называются элементами определителя. Диагональ определителя, на которой расположены числа at, b.2 в случае (1) и alt b2,	- в случае (2),
называется главной. Элементы Ьъ а2 — в (1) и с\, Ъг, а3 — в (2) составляют побочную диагональ.
Для вычисления определителя второго порядка надо из произведения чисел, стоящих на его главной диагонали, вычесть произведение чисел, расположенных на побочной диагонали.
При вычислении определителей третьего порядка обычно пользуются правилом треугольников-, первые три слагаемых в правой части равенства (2) вычисляются по схеме I (рис. 42); они представляют собой произведения элементов,
Рис. 42
стоящих на главной диагонали и в вершинах двух треугольников, у которых одна из сторон параллельна главной диагонали. Остальные три слагаемых правой части (2) вычисляются но аналогичной схеме II, где за основу взята побочная диагональ. При этом произведения, вычисленные по второй схеме, ставятся в формулу (2) с обратным знаком.
153.	Вычислить определитель
Решение. Применяя формулу (1), получим
5 —2
15 3
= 5-3-(-2). 15=15 + 30 = 45.
51
154.	При каких значениях а обращается в ноль определитель
а + 3 5
— 1
Д =
а — 3
Решение. Вычислим сначала данный определитель:
с + 3
—1
А =
= (а + 3) (а —3) —5 (—1)=а2 —4.
Следовательно, Л = 0 при а= ± 2.
155.	Вычислить определитель третьего порядка
1
Д= 2
3
4	6
— 1 —7
5 -2
Решение. Пользуясь правилом в формулу (2) произведения:
треугольников, вычисляем входящие
по схеме I
1. (—1). (—2) = 2,
4. (..-7).3 = —84,
2 • 5 • 6 = 60,
по схеме II
6  (—1) • 3 = —18,
4 • 2 • (—2) = —16, (—7) -5.1= -35.
Произведения, вычисленные по схеме II, входят в разложение определителя (2) с обратным знаком. Поэтому
	1	4	6	
А =	2 —1 -7 3	5—2	= 2 - 84 + 60+18+16 + 35 = 4
Замечание. Для тех, кто освоил правило треугольников, нет необходимости отдельно выписыват произведения, получаемые по схемам 1 и II. Все вычисление определителя следует записывать в одну строку, подсчитывая произведения (если возможно) в уме и изменяя знаки у произведений, полученных по схеме II. Пример такой записи приведен при решении следующей задачи.
156.	Вычислить определитель
а
— 1	1
а —2
3	а
Решение, получим
Д =
Применяя для
а —1	1
2 а —2
—3	3 а
раскрытия определителя правило треугольников, = а3 + 6 —6 + 3а+2а + 6а = а3 + 11а.
Вычислить следующие определители:
	3	6		cos а	— sin а
157.			158.		
	—5	10		sina	cos а
52
159.	tga 1 — 1 tga	
	а2 — ab -I - b	а — Ь	257
160.	a2 + ab + b2 а + b '	163. 2 8 5	
		8 7 3
	а — b а	2 1	0
161.	а 4 - с а 4-	b •	164. 10	3 .
		0 5—1
	— 15 2	а а b 
162.	0 8 4	165. b 0 а .
	2 3 8	b b а
166. При каких		значениях а обращается в нуль определитель
		а 1 1
		Д= 1 al?
		1 1 а
Свойства
1) При замене всех строк, определителя на столбцы с теми же номерами величина его не изменяется (равноправность строк и столбцов), т. е.
«1 bi Ci аг b2 с2 «з b3 с3
Ь2 IQ Сг
а3 Ьз с3
2) При перестановке	)вух столбцов	(строк )	определитель меняет свой знак
например	аг bi Ci	Ь1 «1	С1
	аг b2 с2 = а3 Ь3 с3	Ь2 ^3 и3	С2 . Сз
3)	Умножение всех элементов какого-либо столбца (строки) определителя на одно и то же число 1 равносильно умножению на X определителя. Иными словами, общий множитель всех элементов данного столбца (строки) можно вынести за знак определителя, например
at Xbt а2 hb2 а3 КЬ3
bi cL
^2 Г2
Ь3 с3
4)	Если некоторый столбец (строка) определителя целиком состоит из нулей, то определитель равен нулю.
5)	Если элементы какого-либо столбца (строки) определителя пропорциональны (в частности, равны) соответствующим элементам другого столбца (строки),
53
то определитель равен нулю Так, определитель
	bi	Cl	
Хай	Мц	Xq	= 0,
а3	Ьз	с3	
так как элементы первых двух строк пропорциональны.
6)	Если каждый элемент k-ro столбца (А> =1, 2, 3) (строки) определителя представляет сумму двух слагаемых, то определитель равен сумме двух определителей, в одном из которых в том же столбце (строке) стоят первые слагаемые, а в другом— вторые. Остальные столбцы (строки) у обоих определителей одинаковые, так
°|	&1	И+*4
а, Ь2 с', + с' а3 Ь3 С;-|-с7
«1 а., а3
bi c't
Ь., с', ь3 с:.
«1
Z7.,
«3
bt сг
Ь3 с"
7)	Определитель не изменится, если к элементам какого-либо столбца (строки) прибавить соответственные элементы другого столбца (строки), умноженные на любой общий множитель, т. е.
ai	д-i	Ci
а.,	Ь,	с-,
а3	Ь3	с3
a^-^Kbi Ь^ Ci а., + М).> Ь., с., а3 -(- Хй3 Ь3 с3
Следующие два свойства определителя связаны с понятием минора и алгебраического дополнения. Минором некоторого элемента определителя называется оп ределптель, получаемый из данного вычеркиванием той строки и того столбца, в которых этот элемент расположен. Например, минором элемента at определителя (2) является определитель
Ь2 Со I
,	", минором элемента Oj —определитель
Ьз с3|
С2
а3 с3
и т. д.
Алгебраическим дополнением данного элемента определителя называется его минор, умноженный па (—l)s, где s —сумма номеров строки и столбца, на пересечении которых расположен этот элемент. Алгебраические дополнения элементов первой строки обозначаются буквами Aif Bv, С1( второй строки —Л2, В2, С2, третьей строки —Л3, В3, С3. Например, элемент аг расположен на пересечении первой строки и первого столбца, поэтому
аналогично,
Ai =(-l)1+l	bi b3	C2 Сз	= 1A'2 I ь3	c2 c3	~ ^2^3 — ^3*,
В,= (—1)1+2 | °2	ci	—	1 ai	С» 1 C31	= — (я2с3 — с2^з)>
1 а3 Ci^(-\)^	c3 a2	^2 I	1 a3 _ I a2	l>2	= #2^3	^2^3'
я3 Ь31 I а3 Ь3
Так же выписываются и остальные алгебраические дополнения. При этом полезно иметь в виду схему
где знаками плюс или минус помечены места тех элементов, для которых алгебраические дополнения равны минорам или отличаются от них знаком.
54
8)	Определитель равен сумме произведений элементов какого-либо столбца (строки) на их алгебраические дополнения, например
«I
“3
bi Ci
Ь2 с.2
Ьз сз
— Cj/lj bjBj + cjCj.
(3)
Это равенство называют разложением определителя по элементам первой строки.
9)	Сумма произведений элементов какого-либо столбца (строки) определителя на алгебраические дополнения соответственных элементов другого столбца (строки) равна нулю. Например, если элементы взять из первой строки, а алгебраические дополнения из второй, то
4- Ь2В2 4-	= 0.
Указанные свойства во многих случаях значительно облегчают вычисление определителей третьего порядка. Особое значение имеют при этом свойства 3, 7 и 8. В частности, свойство 8 сводит эту задачу к вычислению трех определителей второго порядка. Более того, если в какой-либо строке два элемента равны нулю (например, ^ = £1 = 0), то вычисление определителя Д сведется к вычислению только одного определителя второго порядка f/li в формуле (3)]. Этим замечанием часто пользуются при вычислении определителей, предварительно с помощью свойства 7 преобразуя его так, чтобы в некрторой строке (столбце) содержалось два нуля.
167. С помощью разложения числить определитель
по элементам первого столбца вы-
Д =
1
2
3
2
1
1
__2
4
Решение. Элементы первого столбца: = I, а..
2, а3 = 3. Их алгебраи-
ческие дополнения;
Аг
_о
— 1
= - (84-2) = —10,
= —24-2 = 0.
2
1
Согласно свойству 8 имеем
д = а1,414-0.,.4г4-а3713=1  54-2 (—10)4-3 • 0 = —15.
168.	Вычислить определитель
Д =
6	3	0
4	1 —3
— 2 —3	2
Решение. Замечаем, что первый столбец имеет общий множитель 2, а первая строка—3. Поэтому применяя дважды свойство 3, получим
55
В первой строке один элемент равен нулю. Чтобы сделать в ней два нуля, достаточно из элементов первого столбца вычесть соответственные элементы второго столбца. Согласно свойству 7 определитель от этого не изменится, поэтому
	0	1	0
Д = 6	1	1	-3
	2	—3	2
Так как теперь алгебраическое
в первой строке отличен от нуля только элемент bt = i, I 1 —3 1
дополнение Вг=—	1 = —8, то по формуле (3)
а его
Л = 6- 1 • (—8) = —48.
169.	Вычислить определитель Вандермонда
Д =
I
х
X2
у Z
у2 г2
1 1
Выяснить, при каких значениях х, у, г этот определитель равен нулю.
Решение. Применяя свойство 7, вычитаем первый столбец из второго и третьего:
д =	1	1	1 х	у	Z х2	у2	г2	=	еч о 1 1 N % X °* о 1	1 — CJ
К полученному определителю удобно применить разложение по первой строке
Д=1
I У~х
\ у2 — X2
г — х I I у — х	г— х	I
Отсюда видно, что определитель Вандермонда может обращаться в нуль только при равенстве двух каких-либо чисел из х, у, г. В этом случае он будет иметь два одинаковых столбца.
170. С помощью разложения по элементам первой строки вы-
числить определитель
1	2 1 —1
Д= 12	3 .
— 13	2
171. С помощью свойств 7 и 8 вычислить определитель
1 2
2 3
3 1
д =
Указание. Если к первому столону добавить удвоенный третий, а из второго — вычесть утроенный третий, то в последней строке определителя будут два пуля. После этого можно применить формулу разложения его по элементам третьей строки.
56
Вычислить следующие определители:
172. А =
sin2a sin2 (3 sin2y
1 cos2a
1 cos2p
I cos2y
Указание		К первому столбцу прибавить третий.					
173.	1 2	3		175.	cos 2а	cos2 а	sin2 а
	3 1	2			cos 2р	cos2 р	sin2 р
	2 3	1			cos 2у	cos2 у	sin2 у
174.	1	17	— 7	176.	1 1 1		
	— 1	13	1		а b с		
	1	7	1		а3 Ь3 с3		
2. Определители высших порядков. Все перечисленные выше свойства дословно переносятся на определители любого порядка. При их вычислении основную роль играют свойства 7 и 8. С помощью свойства 7 добиваются того, чтобы в некоторой выбранной строке стояли на всех местах нули, кроме, быть может, одного. Затем, применяя свойство 8, разлагают определитель по этой строке и тем самым сводят его вычисление к нахождению определителя меньшего порядка. Повторяя этот прием, в конце концов получают определитель второго или третьего порядка, который вычисляется непосредственно. Разумеется, вместо строк можно выбирать столбцы, используя свойство их равноправности.
177. Вычислить определитель четвертого порядка
2 10 2
3 2 10
—10 13
— 12 13
Решение. В данном случае удобно из тогда в ней получатся сразу три нуля:
четвертой строки вычесть третью,
2 10 2
3 2 10
10 13
0 2 0 0
Разлагая теперь определитель по четвертой строке, мы должны будем умножить ее элементы на свои алгебраические дополнения и результаты сложить. Но поскольку три из четырех этих элементов равны нулю, то из всей суммы останется
лишь второе слагаемое:
Д = 2 - (—1)2+*
2 0
п
1
1
о =2-14 = 28.
3
Выписанный минор получен из определителя А вычеркиванием вюрого элемента четвертой строки. Алгебраическое дополнение этого элемента равно минору, ум-
57
пожениому па(—l)s = (—1)2 ’*==1. Определитель третьего порядка, который Получился, вычислен непосредственно по формуле (2) (проверьте!).
178. Вычислить определитель 5-го порядка
	3	—1	2	—1	1
	5	1	—2	1	2
А =	9	—1	1	3	4
	3	0	6	—1	3
	5	2	3	—2	1
Решение. Выберем первую строку и, используя единицу, которая там стоит, сделаем нули на остальных местах. Для этого ко второму и четвертому столбцам прибавляем последний, из первого вычитаем утроенный, а из третьего— удвоенный пятый столбец. После этого разложением по первой строке сведем вычисление к определителю четвертого порядка:
	0	0	0	0	1			— 1	3	—6	3
	—1	3	—6	3	2			—3	3	—7	7
д=	—3	.3	—7	7	4	= 1	• (-1)1^ •	—6	3	0	2
	—6	3	0	2	3			2	3	1	— 1
	2	3	1	— 1	1						
В полученном определителе выносим общий множитель 3 из второго столбца и затем первую строку вычитаем из всех остальных:
	— 1	1	—6	3		— 1	1	-6	3
	—3	1	—7	7		—2	0	—1	4
Д=3-					= 3-				
	—6	1	0	2		-5	0	6	— 1
	2	1	1	— 1		3	0	7	—4
Наконец, разложением по второму столбцу сводим решение к вычислению определителя третьего порядка:
— 1	4
Д=3-1 .(—1)1 2
6 —1
7 —4
= -3(—155) = 465.
179. Вычислить определитель п-го порядка
1	2	3	4	...	п
—1	О	3	4	...	п
-1 -2	0	4 ... п
—1—2—3	0 ... п
— 1 —2 —3 —4 ... О
58
Решение. Добавляя к последней ли гель после этого по последней строке,
строке первую и раскладывая опреде-придем к формуле
Л,1 =	1 —1 — 1			2	3	4 . 4 . 4 .	.. л— 1 .. л— 1 . л— 1		п п п	;=
				0	3					
				2	0					
									
	— 1 0			2 -3 0 0 1	—4 . 0 . 2 ...	0 0 л— 1		п п	
= л(		рп \-п			—1 —1 -	0 ... _о • • •	п— 1 0		п.\	П-1»
где А,,-! — определитель тель Д„.		п		-1-го порядка		того же		типа, что и данный определи-	
Так как Д2 = л —2 раза, найдем	1 —1 ЧТО	2 0		= 2, то,	применяя полученную рекуррентную формулу				
Дп = л Д„_! = л (л — 1) Д„_2=л (л — 1) (л — 2) Д„_3 = = л (л— 1)... 3  2 = л!
Вычислить следующие определители:
= л (л — 1) (л—2)... ЗД2 =
180.	1	2	2	3	183.			1	2	2	2		
	3 -	-1 —4 —6					2	2	2	2		
	1	0	0	1					2—2	3	2		
	1	2 —	—7				2 —2 —2	4		
181.	а 6	b а		184.		1	—1	2	—2	3	
	1 2	1 0				0	1	3	-1	2	
	3 2	0 1	•			4	—2	1	3	1	
	2 С	1 2				0	5 —1	1	—	4
						5	3	5	1	2	
182.	0 л	b с		185.		а	1111			
	1 л	0 0				1	а 1 1 1			
	1 С	У о	•			1	1 а 1 1			
	1 С	0 г				1	1	1	<2	1			
						1	111а			
Вычислить определители п-го порядка										
186.	1	1 2	2 ...	2	187.		2 10 0		0	
		2 2	2 ...	2			12 10		0	
8п = 2 2 3 ... 2
0 12 1
2 2 2 ... п
О 0 0 0 ... 2
Указание. Показать, что Л.п = 2Д,1_1 — Дл_.2. Найти Д2 и Д3.
59
§ 2. ВЕКТОРЫ. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ
1. Основные понятия. Те из физических величин, которые при выбранной системе единиц характеризуются одним числом, носят название скалярных. Например, плотность, масса тела, его температура, электрический заряд и т. д. — скалярные величины.
Величины, которые характеризуются не только числом, по еще и направле
нием в пространстве, называются векторными величинами, или просто векторами. К таким величинам относятся, например, скорость, ускорение, сила, напряженность электрического или магнитного полей и т. д. Геометрически векторы изображаются направленными отрезками. Обозначать мы их будем одной жирной
буквой а или двумя буквами с черточкой Ав, где точка А есть начало вектора (его точка приложения), а В —его конец. Длина вектора называется его модулем и обозначается | а | или | АВ|. Вектор, длина которого равна нулю, называется нуль-вектором и обозначается 0 (или просто 0).
Два вектора называются равными, если: 1) равны их длины, 2) они параллельны п 3) направлены в одну сторону. Иными словами, равные векторы подучаются один из другого параллельным переносом, в пространстве, поэтому при необ-
ходимости можно тот или иной вектор параллельно перенести в любую точку.
Векторы называются коллинеарными, если они расположены на одной или на параллельных прямых, и компланарными, если они лежат иа одной или па параллельных плоскостях.
Вектор а, длина которого равна единице, называется единичным вектором, или ортом: орт обозначается а0.
2. Линейные операции над векторами. Сложение векторов производится по правилу параллелограмма: векторы а и ?’ сносятся в общую точку О, на них
строят параллелограмм ОАСВ. Тогда вектор ОС, направленный по его диагонали, называется суммой векторов а и b (рис. 43).
Поскольку вектор АС равен Ь, то можно дать другое правило нахождения суммы а-\-Ь (правило треугольника): суммой векторов а и b является вектор, идущий из начала а в конец Ь, если вектор b приложен к концу вектора а, т. с.
ОА + АС = ОС.	(1)
Это правило распространяется на любое число слагаемых: если векторы а — ОА, Ь = АВ, ... , l = KL образуют ломаную О АВ ... КВ, то суммой этих векторов является вектор ОВ, замыкающий эту ломаную, т. е.
ОА +AB + ... + KL = OL.	(2)
В частности, если ломаная замыкается, т. е. О = В, то сумма ее звеньев равна иуль-вектору 0. Сложение векторов подчиняется обычным законам сложения — переместительному и сочетательному, а также обладает обратной операцией — вычитанием.
Разностью двух векторов а и Ь, приведенных к общему началу О, является вектор, направленный из конца вычитаемого вектора Ь в конец уменьшаемого вектора а, т. е. « — Ь = ВА (см. рис. 43). Эго правило легко вытекает из формул (1): так как б В + ВД-—ОД, то
ВА — ОА — ОВ.
(3)
Векторы можно не только складывать и вычитать, но и умножать на числа (на скаляры). Вектор b равен Ва, где А —некоторое число, если: 1) b колли
60
неарен а, 2) длила вектора b отличается от длины а в |Х| раз, т. е. | Ь | = | X | | а 3) при Х>0 а и b направлены в одну сторону, при Х<0 —в разные.
Свойства произведения вектора па скаляр:
1)	1 • а = а.
2)	0-а = 0, К-0=0.
3)	X (ра) = (Хр) а.
4)	(Л + р) « = Ла~г ра.
5)	X (а + &) = Ха + ?.&.
Пусть даны ось I и вектор а —АВ. Проектируя начало и конец вектора на ось /, получим на ней вектор А'В' (рис. 44). Проекцией пр/ АВ вектора АВ на
ось I называется число, равное длине вектора А'В’, взятой со знаком плюс или минус в зависимости ог того, направлен ли вектор А'В’ в ту же сторону, что и ось Z, или в противоположную. Направление оси / можно задать с помощью какого-либо вектора I, идущего по оси и направленного в ту же сторону. Поэтому часто говорят о проекции вектора АВ на направление вектора Z или просто—на вектор I и пишут пр/ АВ.
Свойства проекций
1)	пр/ а= | а | cos ф, где ф—угол между векторами а и I.
2)	пр; (а + &) = прг а-ф-пр/ Ь.
3)	пр/ (Хв) = Х пр; а.
188.	Какому условию должны удовлетворять векторы а и Ь, чтобы
] а + b | = | а — b)?
Решение. Огнесем векторы а и b к общему началу О и построим на них параллелограммам, рис. 43). Тогда	есть длина диагонали ОС этого
параллелограмма, а | а — Ь\ — длина диагонали ВА. Из элементарной геометрии известно, что диагонали параллелограмма равны только тогда, когда параллелограмм есть прямоугольник. Следовательно; необходимым и достаточным условием выполнения равенства | а + b | = | а — b | является перпендикулярность векторов а и Ь.
61
Рис. 45
189.	По данным векторам а и b построить векторы 2а — b и л а b 2-.
Решение. См. рис. 45.
190.	В треугольнике О АВ даны векторы а —О А и Ь = ОВ. Найти векторы МА и МВ, где М — середина стороны АВ.
Решение. Согласно формуле (3)
АВ = ОВ — ОА =Ь — а.
Вектор МВ направлен в ту же сторону по той же прямой, что и АВ, но длина его в два раза меньше, поэтому
МВ = 2 АВ = А (6-а).
Вектор МА имеет ту же длину, что и МВ, но направлен в противоположную сторону. Следовательно,	$
МА = — МВ = — 4 (Ь — а) = 4 (а — &).	/
Д	Д	/ \	—&
191.	В треугольной пирамиде SABC /	\
(рис. 46) даны векторы 5Л = а, SB = b,	ь /	\ /у
SC=c. Найти вектор SA4, где М — центр	/	/\ / /
тяжести основания АВС.	/	/ Vх /
Решение. Искомый вектор SM можно / s' /М \ / найти из треугольника SAM, если будет известен вектор AM. Как известно, центр тяжести тре- В Q	С
угольника лежит в точке пересечения его медиан и, следовательно, точка М делит медиану AQ	Рис- 46
_____	2
в отношении 2:1. Отсюда следует, что AM = AQ. Из треугольника ABQ по правилу (1)
71Q = ~АВ +BQ. =~АВ + ВС,
так как Q есть середина стороны ВС. С другой стороны, по правилу (3)
А В = S В — S А = b — а, ВС = SC — S В' = с — b.
Таким образом,
___	2-91	1	1	9	1	1
ДЛ1=- Л<2=-„ (&-а) + 4(с-&) о о L	] о о о
наконец, ------------	--- 2	111
SM = SA + AM — а —а + - b + - - с = о (а + Ь -рс).
о о о <_>
62
192.	Пусть а, Ь и с —единичные векторы; составляющие с дан-д 2 д
ной осью I соответственно углы 3 , у, л. Найти проекцию на ось I вектора За + 2Ь-{-с.
Решение. Согласно свойствам 2 и 3 проекций
npz (За + 21> + с) = 3пр/й +2пр;7> -рпр/С, но по свойству 1 , л л 1 пр/О — J а 1 cos = cos - = у,
так как а — единичный вектор, т. е, \а | = 1.
Аналогично,
, 1
пр/Л> = —	пр/г ——1,
поэтому
пР/(3П+2/;-рс)=3. ’ +2^-	1 = - у.
193.	Какому условию удовлетворяют векторы а и &, если: 1) </ &>«-&, 2) а b < а -Ь '?
194.	Какому условию удовлетворяют векторы а и Ь, если вектор а-\-Ь направлен по биссектрисе угла между ними?
Указание. Параллелограмм, построенный на а и Ь, должен быть ромбом.
195.	По данным векторам а и Ь построить векторы а — 2Ь, у b — За, у а + 3 Ь.
196.	В параллелограмме ОАСВ даны векторы О А—а и ОВ = Ь. Найти векторы МО, МА, МВ и МС, где М — точка пересечения диагоналей.
197.	Точка О является центром тяжести треугольника АВС. Доказать, что О А Д- ОВ + ОС — 0.
198.	В параллелепипеде ABCDA'B'C'D' даны векторы АВ=а, AD =Ь, А А' =с, совпадающие с его ребрами. Найти векторы — диагонали AC, А'С, BD', B'D.
199.	Найти проекцию суммы векторов a, b, с, d на ось I, если «5, &	6, \с \ = 8, \d | = 12, а углы, составляемые этими век-
торами с осью I, соответственно равны 0, у л, л, у. Сделать чертеж и объяснить геометрический смысл полученного ответа.
§ 3. ДЕКАРТОВЫ ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ В ПРОСТРАНСТВЕ
1. Координаты точек. Декартова прямоугольная система координат в пространстве определяется заданием единицы масштаба для измерения длин и трех пересекающихся в точке О взаимно перпендикулярных осей, первая из которых называется осью абсцисс (Ох), вторая—осью ординат (Оу), третья—осью аппликат (Oz)\ точка О — начало координат. Положение координатных осей можно задать с помощью единичных векторов i, j, k, направленных соответственно по осям Ох, Оу, Ог\ векторы i, j, k называются основными или базисными ортами.
г----J	63
Пусть в пространстве дана точка М (рис. 47). Проектируя ее па ось Ох, получим точку Мх. Первой координатой х или абсциссой точки Л4, называется длина вектора ОМХ, взятая со знаком плюс, если ОМХ направлен в ту же сторону, что и вектор I, и со знаком минус —если в противоположную. Аналогично, проектируя точку А1 на оси Оу и Ог, определим ее ординату у и аппликату г. Тройка чисел (.г, у, г) взаимно однозначно соответствует точке .11.
Система координат называется правой, если вращение от оси Ох к оси Оу в ближайшую сторону видно с положительного направления оси Oz совершающимся против часовой стрелки, и левой, если— по часовой стрелке. Па рис. 47 изображена правая система координат,. которой п будем пользоваться в дальнейшем.
Координатные плоскости хОу, yOz, хОг делят все пространство на восемь частей — октантов (рис. 48).
200.	Как расположены относительно системы координат точки, для которых х — 0, // = 0, г = 0?
Решение, точки М равна тируя эту точку
чаем нулевой вектор ОМ. точка Л4Х совпадает с началом координат О. Следовательно, точка М лежит в плоскости, перпендикулярной оси Ох и проходящей через О. Это есть плоскость yOz. Аналогично точки, для которых у=0, расположены в плоскости хОг, а точки, для которых 2 = 0,— в плоскости хОу.
201.	Найти центр шара радиуса R = 3, который касается всех трех координатных плоскостей и расположен в четвертом октанте.
Решение. Расстояние точки Л4 до координатной плоскости yOz равно длине вектора O.W.v (см. рис. 47), т. е. модулю ее
абсциссы. Аналогично, расстояние М до плоскости хОу равно | у [, до плоскости хОу— равно | г j.
Если М — центр данного шара, то, по условию, все эти расстояния равны радиусу шара, т. е. | х | = 3, | у j = 3, |г[ = 3. Так как в IV октанте х > 0, у < 0, 2 > 0, то М (3, —3, 3).
Если абсцисса х нулю, то проек-на ось Ох, полу-т. е.
64
202.	Как расположены относительно системы координат точки А (2, 0, 0), В(0, —5, 0), С(0, 0, — 1), £)((), 2, 2), £ (5, -5, 0)?
203.	Найти координаты точек, симметричных точке А (а, Ь, с) относительно: 1) плоскости хОу, 2) плоскости уОг, 3) оси Оу, 4) начала координат.
204.	Ребра куба со стороной а идут по осям координат, а сам куб расположен в пятом октанте. Найти координаты всех его вершин.
2.	Координаты векторов. Координатами ах, ау, аг вектора а называют его проекты на координатные оси Ох, Оу, Ог и пишут а {ах, ау, ау). Координаты вектора являются коэффициентами его разложения по ортам:
а = а у + ayJ ф- a ,k.	(1)
Координаты вполне определяют вектор, т. е. у равных векторов равные координаты.
Вектор г = 0М, направленный из начала координат в точку Л1 (л-, у, г), называется радиусом-вектором точки М. Его проекции па осп координат равны координатам точки М, т. е.
r = xi-\-yJ(2)
Если даны координаты точек А (лу, yt, zt) и В (лу>, у,, г2), то координаты вектора АВ получаются вычитанием из координат его конца В координат начала А:
АВ {лу —лу, y., — yt, г2-гА, ИЛИ
АВ ~ (лу *1) I + (г/2 Ki) J + (г2 г1) fr•	(3)
При сложении (вычитании) векторов их координаты складываются (вычитаются), при умножении вектора на число все его координаты умножаются на это число, т. е. если
а {ах, ау, az} и b {bx, by, bz}, то
а	+	b = (цЛ. ± bx) i + (ау i by) j	(а: л Ьг) k,	(4)
/.« = ках i -ф 7.а(/£ ф- i.a	.	(5)
Если	векторы	а	и	b коллинеарны, то они отличаются друг	от	друга	скаляр,
ним множителем,	г.	е.	Ь--}.а. Из (5) следует, что	у коллинеарных	векторов	коор-
динаты пропорциональны:
Длина вектора а {ах, ау, аг] вычисляется по формуле
; а ! = |/ ах + ау-\-а~г.	(7)
Длина вектора АВ, заданного координатами своих концов, т. е. расстояние между точками А и В вычисляется по формуле
I ДВ I = | иу лу >' ф ((/., - У1)'2 ффг2 - гфЛ	(8)
205. Доказать, что точки Л(—3, —7, —5), В (0, —1, —2) и С (2, 3, 0) лежат на одной прямой, причем точка В расположена между А и С.
Решение. Достаточно проверить, что векторы АС и АВ расположены па одной прямой, т. е. коллинеарны, причем вектор АС длиннее вектора АВ. По
3 Кручкович и др, 1	-	65
формуле (3) найдем разложение вектора АС по ортам:
АС = (2 + 3) / + (3 + 7)./ + (0 + 5)/г = 5/ + 1 О/ + 5k.
Аналогично, находя вектор АВ и сравнивая с вектором АС, получим
3
АВ = (0 + 3) i + (-1 + 7) j + (- 2 + 5) k = 3/ + бу + 3k = 5 (5/ + 10/ + 5k).
3 - -
Следовательно, AB = AC. Отсюда следует, что векторы АВ и АС отли-
3
чаются числовым множителем X—>- и поэтому коллинеарны. Кроме того, из э
этого равенства вытекает, что | АВ | =	, АС |,
О
тора АВ, что и требовалось доказать.
т. e.
вектор AC длиннее bok-
206.	Определить, при каких значениях а и [3 векторы a — 2i\~ + +/ + А1 и & = 3/ —+ коллинеарны.
Решение. Координаты данных векторов а {2, а, 1} и b {3, —6, [)) должны быть пропорциональны:
3	—6 __ 0
2 ~ а 1 ’
3
Отсюда находим, что а = —4, [)= %. При этих значениях а и 0 векторы а и b коллинеарны.
207.	Доказать, что четырехугольник с вершинами Л (2, 1, —4), В(1, 3, 5), С (7, 2, 3), D(S, 0, —6) есть параллелограмм. Найти длины его сторон.
Решение. Для доказательства достаточно обнаружить, что векторы, совпадающие с противоположными сторонами четырехугольника, равны. Находим векторы АВ п DC по формуле (3):
AB = (I-2)Z + (3-1)j + (5 + 4)* = -/ + 2j+9*,
DC = (7 - 8) i + (2 - 0) j + (3 + 6) k = - I + 2j + 9 /г.
Таким образом, AB —DC, t. e. ABCD — параллелограмм. По формуле (7) найдем длину стороны АВ;
| АВ j = Г  1)2-|-22 + 92 = /1 +4 + 81 = /86 «= 9,3.
По формуле (8) найдем длину стороны AD параллелограмма:
| AD I = | (/—2)2 + (0 — ))2 + (—6 + 4)2 = /36 + 1+ 4	6,4.
208.	На оси ординат найти точку, равноудаленную от точек А (1, —3, 7) и В (5, 7, -5).
Решение. Искомая точка Л4 имеет координаты (0, у, 0). Ее расстояния до точек А и В:
! Л4А ! = I7 (1 - О)2 + (- 3 - у)2 -к (7 то/ = /50+(3 + г/)2',
I MB I - /(5 - О)2 + (7 - i/У + (- 5 - 0)2 = /50+ (7-///
По условию, | МА \ —, MB j, т. е.
50 + (3 + t/)2 = 50 + (7-i/)2, или (3 + i/)2 = (7 — у)2', 3+{/=± (7-у).
66
Знак минус не годится, так как приводит к противоречию. Поэтому
34-t/ = 7—у, откуда г/ = 2.
Итак, искомая точка М (0, 2, 0).
209.	Даны точки .4(1, 2, 1), В (2, —1, 3) и С(3, а, Р). При каких значениях аир точка С лежит на прямой АВ?
У к а з а и и е. Использовать условие коллинеарности векторов АВ и АС.
210.	Проверить, что точки Л (3, —1, 2), В(1, 2, —1), С(—1, 1, —3), D (3, —5, 3) служат вершинами трапеции. Найти длины ее параллельных сторон.
211.	Даны три последовательные вершины параллелограмма Л(1, 1, 4), В (2, 3, —1), С(—2, 2, 0). Найти четвертую вершину D, противоположную вершине В.
Указание. Использовать равенство АВ —DC и записать, что у равных векторов координаты равны.
212.	Доказать, что внутренние углы треугольника А (3, —2, 5), В(—2, 1, —3), С(5, 1, —1) острые.
Указание. Квадрат стороны, лежащей против острого угла, меньше суммы квадратов двух других сторон.
213.	На оси Ог найти точку, равноудаленную от Л (4, —1, 2) и В(0, 2, —1).
3.	Деление отрезка в данном отношении. Пусть точка М (х, у, г) делит отрезок между точками Лф (хр г,) и ЛЛ (х., у.,, г?) в отношении X, тогда радиvc-всктор г точки Л) выражается через радиусы-векторы и гг его концов но формуле
Отсюда получаются координатные формулы:
__М-Уу.. 'Л-ФУЛ:	Н+ЗД
I-H ’ J i+X ’ ~ ~ Гф-Л '
(Ю)
В частности, если точка Л1 делит отрезок ЛфЛД пополам, то ?.= 1 и
т. е.
+ г,
2	’
21 +
2
,-У| +Л'т
9
у
2
(О')
(Ю')
214.	Найти отношение, в котором координатная плоскость хОу делит отрезок между точками А (2, —1, 7) и В (4, 5, —2). Определить точку пересечения Л4.
Решение. Пусть прямая АВ пересекает плоскость хОу в точке /VI (х, у, 0). Из последней формулы (10) найдем Л, подставляя вместо г, и г., аппликаты точек А и В:
3
67
Зная отношение X, найдем координаты х и у точки М по остальным формулам (10):
215.	Выразить радиус-вектор центра тяжести треугольника через радиусы-векторы его вершин.
Решение. Пусть г А, Гв, г( — радиусы-векторы вершин треугольника АВС. Центр тяжести К треугольника находится в точке пересечения медиан. Следовательно, точка К делит медиану, например ,4Q, в отношении 7 = 2: 1, поэтому по формуле (9)
_ га + 2гО _ гд + 2го f+2	3	•
Поскольку точка Q есть середина стороны ВС, го согласно (9')
в с
rQ-—2—’ !4ЛИ 2го=гв+гс-
Таким образом, „	га+гв + гс
ГК- 3	-
г. е. радиус-вектор центра тяжести есть среднее арифметическое из радиусов-векторов его вершин. Из этого векторного равенства получаем:
__ ха + хв + хс _ Уд+Уц+Ус	гд + гв + гс
хк	з - У к----------з , г/<----------з •
216.	Отрезок АВ разделен точками С, D, Е, F на пять равных частей. Известны координаты точек С (3, —5, 7) и 5(—2, 4, —8). Найти остальные точки А, В, D, Е.
217.	Определить координаты центра тяжести треугольника АВС, если Л (5, 1, 12), 5(11, 3, 8), С (2, 5, 0).
218.	Выразить радус-вектор центра тяжести треугольной пирамиды через радиусы-векторы ее вершин А, В, С, D.
Указание. Центр тяжести делит отрезок DE, где Е — центр тяжести треугольника АВС, в отношении А, = 3: 1.
219.	Даны две вершины треугольника: Д(—4, — 1, 2) и 5(3, 5, —6). Найти третью вершину С(х, у, г), если известно, что середина стороны АС лежит на оси Оу, а середина ВС — на плоскости лОг.
4. Направляющие косинусы. Пусть дан вектор а ~axi +avy + агк. Ортом eci.mopa и называется единичный вектор того же направления, что и а; а*> находится ио формуле
a a,i-\-avi-l-u, k |«| у a'x+ui/F<>'i
(Н)
Пусть ось I обратит с осями координат углы а, [}, у (рис. 49). Напраил.ио-Ш’лми иссинусами оси I (или направления /) называются косинусы этих углов:
68
cos a, cosft, cosy. Если направление l задано единичным вектором е°, то направляющие косинусы служат его координатами, т. е.
с1'- <'os о: / -1-cos р/' [-cos у/<’.	(12)
Направляющие косинусы связаны меж,ту собой соотношением
cos3 a + cos2 р + cos2 у 1.	(131
Если направление I задано произвольным вектором а, то находят орт этого вектора по формуле (11) и, сравнивая с (12), получают:
av	av	а2
COS a = -	, COS Р= ' -=.	___г , cosy = ——_ :	: - . (14)
Уах + ау + аг	Ка1 + а^ + а|	У^ + ^ + аг
220.	Найти орт вектора a = 3iy4f — 12k и направляющие косинусы определяемого им направления.
Решение. Находим длину вектора а:
)а ' =	ЯИбТМ = V 169 = 13.
Следовательно, по формуле (1)
Направляющие косинусы являются координатами единичного вектора поэтому
1^ 1,4  щ-
cos a — .у , cos р
221.	Вектор а составляет с осями координат острые углы а, [3, у, причем а = 45°, р = 60°. Найти его координаты, если \at = 3.
Решение. Прежде всего из соотношения (13) найдем угол у: со:,-' 4Г)° + cos3 60J -[-cos2
' / 1 . 1 3 , , 1 1 1
- - i + i ; 4- cos" у 1, cos3 у =• 1 ---------.
'	о <{/2 I	2	4	4
(Й
Так как по условию угол у острый, то cosy = % и у - 60 .
Следовательно,
a°=cos a/-j-cos 0/-f-cosyfe= —Z-j- J~~ k.
поэю.му

2/'
222.	Найти направляющие косинусы направления I, заданного вектором АВ, где А (1, 0, — 1) и В (3, 1, —3).
223.	Может ли некоторая ось / составлять с координатными осями углы: а) а = 45°, 0=135°, у = 60°; б) а = 90°, 0=150°, у = 60°?
224.	Найти орт вектора а = — Ы -\-2J—3k.
225.	Даны векторы а— 21 — 3/Ц-6& и Ь = — I + 2/ — 2k, приложенные к общей точке. Найти орт биссектрисы угла между а и Ь.
Указан и е. Вектор c = au + &° направлен по биссектрисе угла между а и Ь.
226.	Ось / образует с осями координат равные острые углы. Найти орт этой оси.
§ 4. УМНОЖЕНИЕ ВЕКТОРОВ
1. Скалярное произведение. Скалярным произведением ab двух векторов а и b называется число, равное произведению их длин иа косинус угла между ними:
ab — \ а । ; b ' cos д.
0)
Свойства
1)	ab — ba,
2)	(a-\-b)c = ac-\-bc.
3)	(/.«) b = /. («&).
4)	Если а и b — ненулевые векторы, то ab = 0 тогда и только тогда, когда эти векторы перпендикулярны. Если ab > 0, то угол <р между а и b острый, если ей < 0, то угол <р тупой.
5)	Скалярный квадрат вектора а равен квадрату его длины, т. е. а2 = аа — = | а 2.
Первые три свойства показывают, что при скалярном перемножении суммы векторов на сумму поступают по обычному правилу умножения многочленов. Свойство 4 указывает геометрический смысл знака скалярного произведения. Из свойства 5 вытекает формула
=		(2)
Если известно скалярное произведение векторов, то по формуле (2) находятся их длины, а из формулы (1) следует
ab
costf=prw	(3)
Геометрический смысл
Скалярное произведение век юра а иа единичный вектор &° равно проекции вектора а на направление, определяемое Ьи, т. е.
ab‘1 = npfl„a.
70
В случае произвольного вектора b
пР»в = ~ураЬ-	(4)
Механический смысл
Скалярное произведение силы F на вектор х равно работе IV этой силы при перемещении материальной точки ио вектору s, т. е.
W — Fs.	(5)
Из определения скалярного произведения вытекает следующая таблица умножения ортов Z, j, /г:
ij=ji = O, ik = ki = 0, Jk = kj = 0, il= 1, // = 1, kk~ 1.	(6)
Если векторы даны своими координатами
a {ах, ау, az}, b {bx, by, b-.}, т. е.
а = axl + ayJ + агк, b = bxi + byj -\~b~k,
то, перемножая эти векторы скалярно и используя формулы (6), получим выражение скалярного произведения ab через координаты векторов:
аЬ — ахЬх + ауЬу + аЛ,.	(7)
227.	Векторы а и Ь образуют угол Зная,что \a\~3, \b\-4, найти длину вектора с = За-[-2b.
Решение. Длину вектора с можно найти по формуле (2), если будет известен его скалярный квадрат
с2 = (За + 2&)2 = 9а2 + 12аЬ ф- 462.
По определению скалярного произведения,
тт	|
а2~ | а |2 = 9, Ь- = ' Ь (2 = 16, ab = | a j J b | cos = 3 • 4 •	=6.
Следовательно, с2 = 9-9 + 12 • 6ф-4 • 16 = 217, и по формуле (2)
|с| = К2'17®=14,7.
228.	При каком условии вектор а 'г 6 перпендикулярен вектору а — Ы
Решение. Согласно свойству 4, два вектора перпендикулярны тогда п только тогда, когда скалярное произведение равно нулю. Следовательно, надо требовать, чтобы
(аф-й) (а —/») = 0, или а2 —&2 = 0.
Поскольку а2 = |а,2 и &2 = '1&|2, это условие равносильно равенству
| а ,2 = | b 3, или | а | = | b
Таким образом, векторы а-\-Ь и а — b перпендикулярны тогда и только тогда, когда а и b имеют одинаковые длины. Если заметить, что аф-6 и а — Ь представляют диагонали параллелограмма, построенного на векторах а а b (см. рис. 43), а равенство а [ = [ b \ означает, чго параллелограмм есть ромб, то доказано следующее известное из элементарной геометрии предложение. Для того чтобы диагонали параллелограмма были перпендикулярны, необходимо и достаточно, чтобы этот параллелограмм был ромбом.
71
229.	На материальную точку действуют силы
Л — 2/ -J+k,	i+j~2k.
Найти работу равнодействующей этих сил R при перемещении точки из положения А (2, —1, 0) в положение В (4, 1, —1).
Решение. Найдем равнодействующую R:
Я =/1+Л +/з = 2Z + 2/ + k.
Вектор перемещения
s = АВ = (4 - 2) t + (1 + 1) j + (— 1 - 0) 1г = 2/ + 2/ — k.
Искомую работу найдем по формулам (5) и (7):
«Z = /?s = 2-2 + 2-2+l(— 1) =4ф-4-1=7.
230.	Даны векторы а{\, —1, 2} и Ь {2, — 2, 1}. Найти проекцию вектора с = За — Ь на направление вектора Ь.
Решение. Найдем сначала координаты вектора с. Для этого надо из утроенных координат вектора а вычесть координаты вектора I):
с ~'ia — b = I — j + 5ft.
По формуле (4) получаем
М - Г» " и • I • • 2 1> +1 • ч - J •» - »
231.	Даны вершины треугольника А (3, 2, —3), В(5, 1, —1) и С(1, —2, 1). Найти внутренний угол при вершине А.
Решение. Искомый угол ф есть угол между векторами АВ и АС. По координатам концов найдем эти векторы:
Дй = 2/-/4-2й, дс = 2/-4уН-4й.
Отсюда | АВ | = К 4 4- 1 4-4 = 3, | АС \ =)-' 4 4- 16 4~ 16 = 6. По формуле (7) найдем скалярное произведение: АВ /1(?=-2(—2)-- 1 (--4)4-2-4 = — 4-f-4-f-8 = 8.
Применяя теперь формулу (3), получим:
8	4
С,К,<	3-G	9 :
4 <р= arccos -g-’3» 63°3t>'.
232.	Векторы а и b взаимно перпендикулярны, а вектор с образует с ними углы, равные . Зная, что \ a\~^\b\—-2, jrj = l, найти: 1) (2a-&)(t -a), 2) (a-\-b 4- с)*.
233.	Дано, что а [ = 3, |&i---5. При каком значении а векторы и a — ab будут перпендикулярны? Какой геометрический смысл этого условия?
234.	Даны вершины четырехугольника Л (1, 2, 3), В (7, 3, 2), С(—3, 0, G) п В (9, 2, 4). Доказать, что его диагонали взаимно перпендикулярны.
235.	Даны силы = i — j^-k и f> = 2/ +j+3k. Найти работу их равнодействующей при перемещении точки из начала координат в точку А (2, — 1, — 1).
72
236.	Даны вершины треугольника /1 (— 1, —2, 4), В(—4, —2, 0) и С (3, —2, 1). Найгп его внутренний угол срг при вершине А и внешний угол <р; при вершине В.
237.	Найти острый угол между диагоналями параллелограмма, построенного на векторах <7 {2, 1, 0} и b {0, —1, I].
238.	Найти проекцию вектора а\2, —3, 4} на ось, составляющую с координатными осями равные острые углы.
Указание. Воспользоваться решением 226 и формслой (4).
239.	Даны вершины треугольника Д (4, 1, 0), В (2, 2, 1) и С (6, 3, 1). Найти проекцию стороны АВ на сторону АС.
240.	Даны векторы
а 31 — fij — k, b — i-\-3j—bk и с 3/+ 4J + 2£.
Найти проекцию вектора йфс на вектор Ь \-с.
241.	Найти вектор х, перпендикулярный векторам a = i г к и b -2j- k. если известно, что его проекция на вектор с — i \-2jA-2k равна 1.
2.	Векторное произведение. ЛЮ./шршы.ч произведением вектора а на вектор b называется такой третий вектор длина и направление которого определяются условиями:
1)	| [а/з] п b sin <р, где тр - - угол между а и р;
2)	[«&] перпендикулярен каждому из векторов а и р;
3)	[«&[ направлен так, что кратчайший поворот от а к Ь виден с его	/<7,Л /
конца совершающимся против часо-	/
вон стрелки (рис. 50).	/
С в о й с т ь а	/	/j
1)	-Р«|.	/
2)	[(rt + Ь) г]-[«Н ИМ.	/	V
3)	[(мт) /т] - Л [«0|.	/	ц\
4)	Векторное произведение равно / нулю (пу.п>-всктору) тогда и только L------------------— ---
тогда, когда векторы а и b коллинеарны. В частности, [гтг/|— 0 дли	Рис- 50
любого вектора а.
5)	Вели векторы а и b некой.тнеарны, то модуль векторного произведении равен площади S построенного на них параллелограмма (см. рис. 50).
Из первых трс-х свойств следует, что векторное умножение суммы векторов на сумму векторов подчиняется обтачным правилам перемножен ня miioi очленов. Надо только следить за тем, чтобы порядок следования множителей не менялся. Например,
[(а - Н’) (2с - Ц) | 2 I а с Н- 2 [ 0с] -- | а<1 J -1 bd\.
М е х а н и ч с с к н й е м ы с л
Если /’—сила, приложенная к ючке Л/, то момент m^F этой силы относи
тельно точки Л равен векторному произведению векторов AM и /•', т. е.
/ил(Г)-[ЛЛ4>].
(8)
73
В частности, момент относительно начала координат т. (С) = [гС|,
где г — радиус-вектор точки приложения силы.
Основные орты перемножаются следующим образом:
[«] = «, |//] = 0, \kk\=O,
[ij]=	=	|yfe]=~|*/W- |й/| = —[/£]=/•
Если
а = аЛ./4- ayj + a Ji и b — bxl-\-t>yJ J-bzk,
то
Iab] = (atJbz — аЛу} I — (axb- — azbx) j + (axby — ауЬА к,
или в свернутой форме
(9)
(Ю)
Формула (9) получается разложением определителя (10) по первой строке.
242.	Стороны параллелограмма П1 равны диагоналям параллелограмма П2. Как связаны их площади и S2?
Решение. Пусть параллелограмм П.> построен на векторах а и Ь, тогда его диагонали aj-b и а—Ь являются, по условию, сторонами параллелограмма Ilt. По свойству 5, [(« + &) (а-&)| и 5,^1 [«&]|.
Вычислим сначала векторное произведение векторов а-\-Ь и а — Ь:
| (а + Ь) (а — Ь) | = | a a j 1 ba] — | ab\ —  [ bb\. Но
|««]^0 и |&&] = 0	(свойспзо 4),
а
jprt ]«&]	(свойство 1),
поэтому
KO-I-&) (« — &)]=—2 |«&|,
откуда
= ((« + &) (a —&)j = 2 [а&] , = 2.5г.
Следовательно, //, имеет вдвое большую площадь, чем П2.
243.	Векторы а, Ь, с удовлетворяют условию aJ-bJ-c = Q. Доказать, что [ab] = [&с] = [«г].
Решение. Умножаем данное равенство векторпо на Ь:
[ «б] + [г>б]+k&l = [0&J =0.
Отсюда
[«&] 4- |с&] = 0,
так как |&&| = 0; [с&] -=—|6с|, поэтому [«&|-—[&с| =0, или |ab| -- j be|.
Аналогично можно доказать, что [«&] = |са|, т. е. при данном условии [а&] = | bc\ = [са J.
244.	Сила F — i — 2j-\-4k приложена к точке Л-1 (1, 2, 3).
Найти момент этой силы относительно точки А (3, 2, —1).
Решение. Находим вектор AM:
HM^(l-3)j-h(2~2)/4-(3+l)/i= - 2/ + 4fe.
74
По формулам (8) и (10),
m?1(F) = [AMF] =
/	/ k
1 - 24
- 2	0 4
Раскрывая определитель по первой строке, получим
— 2 4I 114	11—2
mAF) = i — /	+*	= _8/—12/ —4fe.
- !	0 4 | 7 | — 24	| — 2 0	7
245.	Найти площадь треугольника с вершинами Л (1, 2, 0), В(3, 0, —3) и С (5, 2, 6).
Решение. Площадь треугольника АВС равна половине площади параллелограмма, построенного на векторах АВ и АС:
«д= 2 ЩВ ЛС]|.
Найдем векторы АВ и АС:
Лй=-2/-2у—Зй, ЛС = 4/Дбй.
Их векторное произведение
[ЛВ лс] =
— 2 —3
0	6
i
2
4
J k
— 2 — 3
0	6
— 3	12—2
+ fe
6	4	0
= - 12Z -24/ + 8й = 4 (— 31 — 6/
ф2й),
поэтому
| [ЛВ ЛС Г = 4 I - 3Z - 6/ + 2й ' =--4 /(- Зу + (~ бТ+У2 = 28,
и следовательно,
S л — П кв. ед.
246. Даны векторы
Найти [[а&]с] и [а[&с]].
а{1, 0, —2}, b{2, 1, 0},
с{- 1, К 1}.
Решение. Имеем:
i i
k
— 2
lftbl= 1 о
= 2z —4/4-/?,
2 1
0
|[«6] с| =
i i 2-4
— 1 1
k
-3/ — 21г.
1
Аналогично найдем (проверьте!)
[a\bc]]=—4i-5J-2k.
Отсюда следует, что [[«й| с| ^ |« |йс|], т. е. векторное произведение не обладает сочетательным законом.
247.	Упростить выражение [(2а + &) (с — a)J -}-[(& + О (# + &)]•
248.	Найти площадь параллелограмма, построенного на векторах a^pr2q и b = 2p^q, где р и q — единичные векторы, угол л
между ними <р= 3 .
249.	Доказать тождество [ab]2 + (аЬ)г = а?Ь2.
250.	Даны векторы а 'И — j— 2k и b — i r2j — к- Найти векторное произведение [(2а — Ь) (а 2&)].
75
251.	Даны векторы а = 21 — 3j Д- k, Ь ——3i + j 2k, с = i J- 2J + 3k. Найти вектор «-=[[«&] [at]].
252.	Дан Tpeyiольник с вершинами А (2, —1, 2), 73(1, 2, —1), С (3, 2, 1). Найти его площадь.
253.	Сила Л=3/'г2/— 4k приложена к точке М (2, —1, 1). Найти ее момент относительно начала координат.
254.	Даны три силы, приложенные к точке М (2, 1, 2): /3 = — /+./+£.	— 2i — 3jA~k, f>~i~-‘2jA-k. Найти момент их
равнодействующей относительно точки Л (0, —1, —1).
3. Смешанное произведение трех векторов. Смешанным произведением abe трех векторов называется их векторно-скалярное произведение
Рис. 51
Тройка некомпланарных векторов а, Ь, с называется привои, сели кратчайшее
вращение от а к b видно с конца вектора с совершающимся против часовой
стрелки (рис. 51, о), и левой — если по часовой стрелке (рис. 51, б).
Гео не г р и чес к и й с м ы с л
I. Необходимым и достаточным условием компланарности трех векторов а, 1>, с является равенство
abc = 0.
2. Если некомпланарные векторы а, Ь, с приведены к общему началу, то модуль смешанного произведения равен объему паралле-
лепипеда, построенного на векторах а, Ь, с
Рис. 52	(рис. 52). Если abc > 0, то тройка векторов
а, 1>, с правая, если abi < 0, то —левая.
Если векторы а, Ь, с заданы своими координатами
то
«{«>, «у, b{bx, by, Ьг}, е [еХ; Су, сА,
abc =
«Л- «V Щ
Д 1>ц b,
Су С,
(12)
т. е. смешанное произведение равно определителю из координат сомножителей.
76
255.	Доказать, что смешанное произведение трех векторов, из которых два коллинеарны, равно нулю. В частности, если из трех векторов два равны, то их смешанное произведение равно нулю.
Доказательство. Если, например, векторы а и b коллинеарны, то их координаты пропорциональны. Следовательно, в определителе (12) первые две строки пропорциональны, а такой определитель равен нулю (см. § 1); поэтому abc =0.
Можно рассуждать и по-другому. Если из трех векторов а, Ь, с два вектора а и b коллинеарны, то, будучи приведены к одному началу, все они расположатся в одной плоскости, так как а п I) будут направлены по одной прямой. Следовательно, а, Ь, с — компланарные векторы, и их смешанное произведение равно нулю.
256.	Доказать, что при перестановке двух любых множителей смешанное произведение меняет знак.
Доказательство. При перестановке каких-либо множителей, например и и Ь, в определителе (12) поменяются местами две строки. Следовательно, определитель изменит знак (см. § 1), а вместе с ним изменит знак и смешанно? произведение.
257.	Доказать, что векторы a = 2i. —j-C2k, b =i-\-2J— 3k, c — 37 — AJ-\-lk компланарны.
Решение. Вычислим смешанное произведение abc по формуле (12):
= 2-2-[- 1 • 16-J-2 (- 10) —0.
Определитель был раскрыт разложением по первой строке. Поскольку abc = 0, векторы а, 1> и с компланарны.
258.	Вычислить обтюм тетраэдра, вершины которого находятся в точках 0(1, 1,2), А (2, 3, — 1), В (2, — 2, 4), С (— 1,1, 3).
Решение. Введем в рассмотрение векторы а — ОА, b—ОВ, с--ОС. Объем V тетраэдра ОАВС, как известно, равен одной трети произведения площади основания на высоту. У параллелепипеда, построенного на векторах а, Ь. с (см. рис. 52), та же высота, а площадь основания в два раза больше. Следовательно,
^пяралл = у \аЬс\.
По данным точкам О, А, В, С находим координаты векторов: а = 0А {1, 2, —3}, Ь~ОВ {1, — 3, 2}, С^ОС f — 2, 0, 1), поэтому
0
259.	Доказать, что при любых А и р справедливо тождество [ab] (с + Ха + р&) = abc.
77
Указание. Воспользоваться распределительным свойством скалярного произведения и решением задачи 255.
260.	Установить, компланарны лп векторы:
1)	а-=1-\-]Д-к, b-i j k, c i-j \к,
2)	а = 31 + 5/, b=i- j-\- 2к, с 5/ 4- 3/4- 4/г.
261.	Доказать, что точки А (1, 0, 7), В (— 1, — 1,2), С (2, — 2, 2), D(0, 1, 9) лежат в одной плоскости.
Указание. Рассмотреть векторы АВ, АС, АВ-
262.	Найти объем параллелепипеда, построенного па векторах
a i — 2jA~k, b = 3/4-2/4-ft, c i-k.
Установить, какой тройкой — правой или левой — является тройка векторов а, Ь, с.
263.	Даны вершины тетраэдра О(- 5, —4, 8), А (2, 3, 1), В (4, 1, —2), С (6, 3, 7). Найти длину h высоты, опущенной из вершины О на грань АВС.
Указание. Найти объем тетраэдра и площадь S грани АВС и воспользоваться формулой Г = Sh.
§ 5. АЛГЕБРА МАТРИЦ
1.	Линейные действия с матрицами. Транспонирование. Квадратной матрицей порядка п называется таблица из п2 чисел а^, расположенных- в п строк и /1 столбцов;
/«11	«12	а1П\
д =	=	“32  а2п\	(1)
..............I
'аМ	«//2	апп
Первый индекс i у элемента о,у означает номер строки, второй индекс / — номер столбца, в которых стоит этот элемент. Диагональ аи а,г ... апп называется главной диагональю матрицы А.
Две матрицы А = (а^-) и	одного и того же порядка считаются рав-
ными, если все соответствующие их элементы равны, т. e.aij = btj (/, / = 1, 2..., п). Матрицы разных порядков не сравниваются между собою.
Линейными действиями над матрицами называются сложение матриц и умножение их на число. Оба эти действия определяются поэлементно;
Z«ii «12	... Uj/i',^	Ь12 ...	1цп', /ац~\-Ьц	а1п Д- Ь1п	\
I «21 «22	«2/1 1	, ! &21 &22 •••	^2// I = I «21 4 ’ &21	«22 + Ь,, ... а.,п + 1>.,„	'
..................,\	................I '	................................... I
\	/	''	/	\	I
\ап1 а... afl/l/ 'bni Ь„2 ...	^ani-\-bni аП2А-ЬП2 • • 
/«11	«12	«1/1 \	/^-«11	^«1‘!		/-«1/1 \
a.,L	а.12	...	a2tl j	( ла1.,!	Х«22	•  •	Xa2n j
^«//i	«//2		^ап2	...	’капп/
78
Свойства сложения матриц и умножения их и а число:
1)	А + В = В + А.
2)	(4+5)4-С = Я + (й + С).
3)	Х(Д4-В) = ХД + ХВ.	(2)
4)	(А. Д-р) А = ХА +}лД.
5)	Л (цД) = (\ц) Д.
Матрица О, целиком состоящая из нулей, называется нулевой, для нее А-|-О—- Д.
Сложение матриц имеет обратное действие — вычитание, которое также осуществляется поэлементно, например если Д = (а//), В = (&;;), то
С==А—й = («,7 —
Операция над матрицей А, при которой ее строки становятся столонами с теми же номерами, а столбцы — строками, называется транспонированием и обозначается Д'. Например, если
/аи А = I а.21
\«3i
«12
«22
«32
/«11	«21	«31\
ТО Л'= «12	«22	«32
\«13	«23	a-i3)
Операция транспонирования обладает следующими свойствами:
(Д + S)'	+ В', (АД)' = ХД', (Д')' = Д.
(3)
Матрица, у которой все элементы, не стоящие на главной диагонали, равны нулю, называется диагональной.
Матрица S называется симметрической, если опа не меняется при транспонировании, т. е. S'=S. У симметрической малицы элементы, симметричные относительно главной диагонали, равны. Матрица К называется кососимметрической, если при транспонировании опа меняет свой знак, т. е. К' — —К- У кососимметрической матрицы на главной! диагонали стоят нули, а элементы, симметричные относительно эгой диагонали, отличаются только знаком.
Определитель, составленный из элементов матрицы п-го порядка (1), называется определителем матрицы А и обозначается ! А !.
: 1
264. Пусть А =-!
С —А-'гВ + ЛУ\- В’.
Р е ш е н и е. Пользуясь женин матриц, имеем
2	/2 —4
-4.1’ В^5 ~6;.найп,
сочетательным и переместительным свойствами ело-
но
/1—3!	/2	5'
Л'—' Д В'^1 , J,
поэюму
I £	—1 \ 'Ч 1 \ и и	v '
I ! +;	I —'	з=2) I
,1 —8/ \-1 -12/ \0	20	\0 -10/
Полученная матрица С представляет пример диагональной матрицы второго порядка.
79
265. Показать, что матрица S
1	-1	3'
А =	3	3	6 !	и
2	—2	4/
Решение. Имеем
3	3 6\	/ 8 6
S-=3.4—2В= 9	9 18 Ь- — 6	2
'6 —6 12/	' —10 16
/11	3
= ( 3 11
4 10
ЗА — 2В — симметрическая, если
—4 -3 5'
В =I 3	1 1 ).
\ 5 —8 5/'
Ясно, что потученная при транспонировании.
матрица S—симметрическая, та;; как она не меняется
266. Показать,
если
что матрица К = 2Д — В — кососимметрическая,
'1	3	1	/ 2 4 —5\
.12	2 b 11 />	6 1	5 j
4—1	3	113 б'
Решение. Имеем
то матрица К является кососимметрической.
267.	Доказать, что для любой матрицы А матрица 5 = .4 + Д'— симметрическая.
Решение. Применяя свойства (3) транспонирования, получим равенство
5' --(/13-. Г)' — .4' + (.4	.4' + .4^.4 + A' = S,
т. е. S — симметрическая матрица.
268.	Показать, чю для матрицы /г-го порядка А выполняется равенство । к А \ =	, A (.
Решение. При умножении матрицы .4 на число X все ее элементы умножаются на к. Вынося этот множитель ш каждой строки за знак определителя (см. свойство 3, § 1, п.2), получим требуемое равенство.
269.	Найш С = 2Д+ЗУЗ, если А=\' I S =	’"j.
',() -3/ Д 1/
80
270.	Найти матрицу С== А — 5.S, если А = :
271.	Найти матрицу А = 2С — 3D, если
1	2	3	13 —2\
С==\' -3 —2 — 1	2 - 1 ).
\ 1	0	1	3 1	3
272. Показать, если
В = ! С
\1
что матрица Д’= В — D — кососимметрическая,
b с\	< а 0	О1,
b a j и D = I b + с	b	0 j,
1 1,	14-с 1+а 1/
273.	Показать, что матрица B — A-\-D — D' является нулевой матрицей, если
/ 0	о-1 о2 - 1 \
А ='= i 1 — а О Ь2 — с и . I — а2 с — Ьг О
/1 1 1\ I	]
D а b с j.
о2 Ь- л2''
274.	Показать, что для любой матрицы А матрица К = А — А' — кососимметрическая.
У к а з"а н и е. Ср. 267.
275.	Дана произвольная матрица А, показать, что она может быть представлена в виде суммы симметрической и кососимметрической матриц.
Указание. Рассмотреть матрицы S— (el + А') и К— 9 (4 — Д')-
276.	Выписать общий вид симметрической и кососимметрической матриц второго п третьего порядка. Найти их определители.
- 2. Умножение матриц. Произведение матрицы А на матрицу В (того же порядка) определяется следующим образом: для того чтобы получить элемент с,у — матрицы—произведения С —АВ, надо элементы i n строки матрицы А умножить на соответствующие элементы /-го столбца матрицы В и результаты сложить, т. е.
п
аЬцб/ц — 4/41/“г ~г(4) 1
cq - произведение t-й строки матрицы А на /-ii столбец матрицы В.
Свойства
1)	(АВ} С —А (ВС}.
2)	А (КВ)=АКА} В —К (АВ).
3)	(А А-В) С —АС ВС.
4)	С (А+В}-^СЛ+СВ.
5)	А1^1А--А, где
1	0	...	0\
0	1	...	О :_едИНИ1шая	матрица.
.......I
О	0	...	1/
(5)
Ы
С) АО=ОА = О, (АВ)' = В'А': I Л5' = |Л!'|5!.	(6)
Заметим, что в общем случае АВ=^ВА, т. е. умножение матриц не обладает коммутативным свойством, поэтому всегда надо строго следить за порядком множителей. Матрицы, для которых выполняется равенство АВ — ВА, называются перестановочными.
/ 2т
277.	Найти произведение строки (3 —5 4) на столбец!	2 I.
1/
Решение. Надо перемножить соответственные элементы н сложить резуль-та гы:
/ 2\
С = (3 —5 4)-( 2 =3-2 + (—5)-2-}-4-(—1) = —8.
\—1/
278.	Найти произведения АВ и ВА матриц: л /2	1\	/1 3\
\4 — 2	V 2 О
Установить, что матрицы Ап В неперестановочны.
Решение. Пусть С--АВ. Чтобы найти элемент сн, ладо умножить первую строку матрицы Л на первый столбец В:
Ч1=--(2 1)	.-2.1-|-Ь(-2)-0.
Элемент ct! произведения АВ получается умножением первой строки А на второй столбец В:
С1., = (2 1)	2 !	1-0 G.
Аналогично, умножая вторую строку А на столбцы В, найдем: / 1	3
с31-(4 —2)3	j —- 44 — 8; с.,,-(4 —2) •: , 4 • 3-2 • 0--= 12
Таким образом, О 6
С = ЛВ=-'	. Умножая теперь строки В иа столбцы Л, получим (проверьте!)
\8 12/	>
Так как ЛВ=АВА, то данные матрицы неперестаиовочны.
279.	Найти произведение АВ данных матриц третьего порядка:
/ 0	2 -1
Л-1—2 —1	2 р
\ 3 -2 — 1/
82
Решение. Умножив по очереди строки матрицы А на столбцы В, получим
/ 0-4 + 2-3-1-1
ЛВ=—2-4-1 - 3 + 2- 1
\ 3-4-2-3- 1  1
О  3 + 2 • 2 - 1  3
—2  3 - 1  2 + 2  3 3 • 3 — 2  2 — 1 -3
/ 5	1	—3\
= —9 —2	5 .
\ 5	2	—1/
0-2 + 2- 1-1 -5\
—2 -2- 1 • 1+2  5 | = 3-2 — 2- 1-1-5/
280. Найти все матрицы, перестановочные с А — j
Решение. Пусть X
I ‘ I —искомая матрица, тогда AX = i 7 о/
, и равенство АХ = ХА
соблюдается тогда и только тогда, когда у=р,
Таким образом, общий вид следующий:
матрицы перестановочной с данной матрицей А
! а.
/1 О', 0 1/
0 1\
'.1 0/'
ХА =
\ = а
281. Показать, что произведение матрицы А на транспонированную всегда является симметрической матрицей.
282. Матрица А называется ортогональной, если выполняется условие ЛЛ' —/, или Л' — Л1. Доказать, что матрица Л — ортогональная, если
/' 1/3 —2/3 - 2/3'.
Л.= ; - 2/3	1/3 —2/3 1.
.—2/3 —2/3	1/3 '
Р е ш е и и е. Из АЛ' -= + = *		симметричн ости			матрицы А следует, что		А = А',		, поэтому
		' 1 —2 2	—2 —2\		/ 1 '2 -Т2 1 2 —2 0 0\ 1 0 =/. 0 1/	”2\ 1/9 “2 = 9 ° 1/ \о	0 9 0	°\ ° 9/	
			1 —2	—2 • 1/ ,1 = 0 \о					
283. Произвести умножение примерах: 3 2\ /--2 3	'а а’Д 5,)+-4 5,1’ б) Ь					квадратных матриц /—6 di а —с/		В	следующих	
/2	5 6\	/1	—3	2\	/ 4	1	4\	/'	3	0 1\
в) ( 1	2 5 1-1	(з	—4	4	г) | -1	—2 - 1 |-	1 ~	1	2 0 t
\1	3 2;	\2	5	3/	\ 2	-1 —2/	\	0	0 2/
83
284. Показать, что матрицы А и В — перестановочны, если
	/ 3	1	—2'.	/ 2	1	0 ,
л-J	3	-2	4 1	/3-J 1	1	2
	3	5	-1/	V1	2	1/
285. Найти матрицу С~АВ — В А, если
/'1	—3	2'	/2	5	6\
.13	1	11,	/3	1	2	5 1.
2	5 3	13 2/
286. Показать, что матрицы
/cos <7. —sin а.
А ~ .	I,
since cos а
/cos В —sinp
В = ' . „	перестановочны,
sin р cosp?
Найти их произведение.
287. Найти все матрицы, перестановочные с данными:
а)	1 о	1	б)	/2	0	О'.	в)	/0	1	0	0
	1	0/ /		( °	1	1 г		1 0	0	1	0
				\о	0	1/		0	0	0	1
								'0	0	0	0<
288. рой
Найти общий вид матрицы А третьего порядка, для кото-
/0 1 о.
{ 0 0 1 ; • Л -= О.
' ,о о о, ’
289. Ненулевые матрицы А и В, для которых АВ —О, называются делителями нуля. Показать, что определитель хотя бы у одной из этих матриц равен нулю.
Указание. Использовать свойство умножения матриц (6).
290. Показать на примере матриц второго порядка, что равен-, ство АВ — В А = / невозможно.
3. Степени матриц. Многочлены от матриц. Целая неотрицательная степень матрицы определяется равенством
= Л  Я ... А = ЛР-‘ • Д = Л  /У1 и до = /.
р раз
Для произведения степеней матриц справедливо равенство АР • А'> = А'Ч  АР = АР^ч (р, q = 0, 1, 2, ...).
Если дан многочлен
Р Ц) = аох’л-|-а1хт’'1-|-... + ат .jr + am,
84
то многочленом от матрицы А называется матрица
Р (А) = а0Ат -j-ajAm 1-|-.. рат -1А Рапд•
Всякие два многочлена от матрицы А перестановочны:
P(A).Q(A) = Q(A)-P(A).
Если Р (А) — О (нулевая матрица), то матрица А называется корнем многочлена.
х 291. Найти Л" для матрицы А —
Решение. Вычисляем последовательно произведения по формуле (3):
Л 1 Г 1 1	12-	1211	13
А2 =	' :	=	Ая^ ; i =	1
01/01	01’	0101 О Г’
»	.	I 1	3'	1	1	14
А*--- А* А	1	: = . „ , ; и т. д.
,0 Г.0 1 ч0 1/
Продолжая умножение, придем к формуле
' 1 А'‘^Л"~'-Л- I .0 1 ' '
292. Матрица Р (р,,), у которой все элементы неотрицательны (Pi/P- 0), а сумма элементов каждой строки равна единице, т. е. И
^Pij == 1 (' = 1, 2, .... п), называется матрицей переходных, евро-
I1
ятностей, пли стохастической матрицей. Найти Р; и Р3 стохастической матрицы
/0 1	0 \
РАО 1/2 1/2 j.
\1/3 0 2/3j
Решение. Находим Рг и Р3 (предварительно за знак матрицы выносится г "	1 '
обшпи множитель -. :;
6 ,
0	6	0\	,0	6	О'	/0	18	18'
!	fo	3	З	-^НО	3	3	=1|6	9	21,
6 1	/ о	/	36 \	/
\2	0	4/	\2	0	4/	\8	12	16/
/0	18	18\	,0	6	О'	/36	54	126\
Р3= '	6	9	21	 1	0	3	3	42	63	HI I.
36	/6	1	21b	I
\8	12	16/	\2	0	4/	\32	84	100/
Заметим, что матрицы Р'2 и Р3 также являются стохастическими матрицами; вообще можно показать, что любая степень стохастической матрицы также является стохастической матрицей.
0 1 0
293. Найти все степени матрицы Л = 1 0 0 1 j.
\0 0 0/
85
/О О И
Решение. Имеем: Д2= О О О \о о о/
/О о О' Д3= О О О =0. \о о о/
Значит, Д1 — Д5 —... — О.
Ненулевая матрица А, для которой Л! = 0 при некотором значении /, называется нильпотентной. Наименьшее из чисел I, для которых Л' = 0, называется показателем (индексом) нильпотентности. В этом примере / = 3.
294. Найти многочлен от матрицы А, если f(x)~х2— ЗхА~5, а
/2 2 0\
А "= I 1 1 Н.
\1 0 з/
Р е ш е п и е. Искомая матрица f (Д) определяется
равенством
,2	2 0\2	,2	2	О-	,1	О	0>
/ (Д) = Д2 — ЗД+5/= 1	1 1-3-1	1	1| + 5	О	1	О
\1	оз/ \1	О	з/	\0	О	1.
6	6	2х	/6	6	°\	5	0	°\	/5	0	2-
4	3	4 "	3	3	3 4-	- 0	5	0 =	1	5	1
'5	2	9/	\3	0	9-’	0	0	5/	\2	2	5-
295. Показать, что матрица А
2—1 \
о ' — корень многочле-
на Р (х) = х2 — 5х 4- 3.
Решение. Имеем
Р(Д)
/2—12	/ 2 — Г /1 О'
3	3/	/- 3	3/+' О 1; ~
/	7—5	/ 10
\- 15 12/	15
— 5	-3 0	,0 0
15/' 1 /О З/1 ~ /О О/
т. е. Д—корень многочлена Р (х).
296. Найти А3 для следующих матриц:
1
.	1 0 t '34
а) А । б) А = -
’	3 4/ 7	2 I;1
297.	НаГти все степени матриц
/2
1 о
1 -
о"7'-
О ) 2/
—sin а\ cos а/ ’ и идем-— А. Найти общий вид инволютивной и идем-
4sin а
298.	Матрица А называется инволютивной, если Л2 = /, потентной, если А2 потентной матрицы второго порядка.
299.	Найти Р (А), если:
1
а)	Р (х) = х2 — х — 3, А =
86
о/
2	—3'
3	— 1
2	— 1
б)	Р (,r) — л-2 ~ 2л- + 1, А = \ 3	1
\1 -1
v	' /5
в)	Р (х) = х3 — 7х2 Ц-1 Зх — 5, А = ( 1 \ 2
300. Найти общий вид матриц второго порядка, квадрат которых равен нулевой матрице, т. е. А2 = О.
А второго порядка, квадрат которых
301. Найти все матрицы равен диагональной матрице
302. Найти условие, при
котором матрица А второго порядка перестановочна со всеми матрицами второго порядка.
303. Каким условиям должны удовлетворять элементы матрицы А второго порядка, для того чтобы она была перестановочна со всеми диагональными матрицами того же порядка?
4. Обратная матрица. Матрица А 1 называется обратной матрице Л, если ДД г = А~ гА — I. Для того чтобы матрица А имела обратную матрицу, необходимо и достаточно, чтобы она была невырожденной, т. е. чтобы A j 0. Обратная матрица определяется по формуле
'А„ Л,„ ... Апп!
где. Ац — алгебраические дополнения элементов ац в определителе Л [. Алгебраические дополнения для строчек матрицы А записываются в столбцы матрицы (7). Так, например, в первом столбце этой матрицы стоят алгебраические дополнения первой строки матрицы А.
С помощью обратной матрицы решаются матричные уравнения вида
АХ = В и YA = B (при | А |	0.)	(8)
Умножая первое уравнение на А 1 слева, а второе па А 1 справа, получим их решение в виде
Х = А ’!> и У = ВД-1.	(9)
Свойства
1)	=
2)	(А	=
3)	(/!’) 1 = (Д-‘Г-
4)	!ЛЛ| = |Л[-1Л—.
304. Найти обратную матрицу А 1 для матрицы А
(Ю)
/з н
(4 2.)'
Решем! не. Покажем сначала, что данная матрица невырожденная, тогда она имеет обратную матрицу. Действительно,
13 II
|Л 1= 4 2М-4 = 2*0-
87
Вычислим алгебраические дополнения элементов матрицы:
,4 ц = 2, ,1ц -= — 1, .4 с. = — 4, /1= 3.
Следовательно, матрица .1
!, обратная к /4, имеет вит.
I -4ц /1'21
-.‘dAi лг.
1; 2  1	1	12,
2 -4	З/^у-2 32,'
Проверим правильность полученного результата:
1 -12 _ - 1 О
-2	3'2 ^10 1
305. Найти матрицу, обратную для матрицы
2	5	7
.16	3	4	।.
5 —2 —3,
Решение. Так как .4 =—1=0, Вычислим алгебраические дополнения:
то данная матрица невырожденная.
Яц=(—1)’Т
3 4 I
-2 _3| = -'- ^ = ^0'
6	3
-1,з	( 1)> .	. = —27.
6 1 I
1 = 38,
5 — 3|
Аналогично находим = 1, ,422 = —41, /Тп —29, .431 = —1, Аа2 = 34, А33 =—24. Таким образом,
/ -1	1 -1\	/	1	-1 h
.4-1=—I 38 —41	34 | — —38	41 -31 .
\—27	29 —24	\	27	-29	24'
Вычислим произведение:
/2	5	7т/ 1	—1	1\	/10	0\
,4.4 1	- 6	3	4)1—38	41	—34)=	0 1	0 ,
\5	—2	-3'\ 27	—29 24'	'0 0	1/
что показывает правильность полученного результата.
-3 -.2	2 — 4\.
306.	Решить матричное уравнение X- | = ! I, или ХА ^=В.
Решение. По формуле (9) имеем Х = х. Так как
поэтому
I./2	2V-1/ 12  3) = 2.( 3
2 \б 8/ V-5 3/	2 V- 64 36/	\ 16 -9/‘
88
307.	Показать, что матрица S-1, обратная симметрической 1	2	3,
матрице S — [2	0 — 1 j, будет также симметрической.
\3 —1	4/
308. Найти матрицы, обратные для следующих:
1)Р "Л	б)	/ sinq) COS(f’'	В) / 1	3	4'	г) а	0	0
*3	4'’		\—COS ф	silKf/'	1 2	0	3 ' ’ 1	(°	ь	0
			2	1		\о	0	с,
309. Решить следующие матричные уравнения:
;4 —6,	,2	5’>	11 — 2 \ z	/—2	3	— 1	3
а)	X = |		б	JX'	1	: =		
\2	1'	\ 1	3' ’	’ \ 2	3'	—4	1/	> 4	—2 ’
		/1	2	-3		: 1	—3 0
в) АХ В и YA = В,	если	А =-- ( 3	2	—4 1	, в =	\ 10	2 7
		\2 -1	0/		\10	7 8,.
310. Показать, что	если	АВ = ВА, то	А ЛВ	-ВА	1	
311.	Как изменится обратная матрица А1, если в матрице А переставить местами две строчки?
312.	Показать, что если матрица А не имеет обратной, то п ее произведение па любую матрицу В также не имеет обратной.
313.	Две матрицы А и В называются подобными, если они связаны равенством S = T1 АТ, где Т — некоторая невырожденная матрица. Показать, что подобные матрицы имеют одинаковые определители.
5. Прямоугольные матрицы и элементарные преобразования матриц. Прямоугольная таблица чисел, расположенных в m строках и в п столбцах, называется прямоугольной матрицей размера т\п, или (щхя)-матрицей:
/й11	а12	  • а1П
д = I а21 я.,., ... а.1п
\..........................
\
'о/Л1 a,ni ... атп
(И)
Элементарными преобразованиями первого рода матрицы А называются следующие действия:
I)	умножение какой-либо строки на число Л 0;
2)	перестановка двух строк;
3)	прибавление к элементам одной строки соответственных элементов другой строки, умноженных на число X.
Элементарными преобразованиями второго рода матрицы А называются аналогичные действия со столбцами.
С помощью элементарных преобразований любую матрицу А можно привести к специальному виду:
|1	0	0	...	0	0	...	0
/О	1	0	...	0	0	...	0
Д,— 0 0 0 ... 1 о ... о
о о о ... о о ... о
о о о ... о о ... о/
89
Число г единиц, стоящих на главной диагонали, не зависит от способа приведения матрицы А к виду А, и называется рангом матрицы А.
Матрицы, получаемые друг из друга элементарными преобразованиями, называются эквивалентными и соединяются знаком со. У эквивалентных матриц одинаковые ранги.
Найти ранги следующих матриц: 314.
/1	4	10\
А =	1 7	8	18	.
'\3	7	17/
Решение. Подвергнем эту матрицу следующим элементарным преобразованиям. Ко второму столбцу прибавим первый, умноженный на (—4), а к третьему столбцу прибавим первый, умноженный на (—10), затем ко второй строке прибавим третью, умноженную па —4. После этих преобразований полученная матрица примет вид
/ i	°	0\
1—5	0	0 .
\ 3 —5 —13/
Теперь первую строку умножим на 5 и на (—3) и прибавим соответственно ко второй п третьей строкам, а затем переставим местами вторую и третью строки; тогда будем иметь матрицу
/1	0	0\
0 —5 —13 .
\0	0	о/
Далее, если умножить на (—1'5) и (—1/13) второй и третий столбцы, а затем вычесть из третьего столбца второй, то получим матрицу
/1	0	0\
А,=	0	1	0]
\0	0	о/
Следовательно, ранг г данной	матрицы равен двум, т. е. г = 2.
315.
/1	3	—1	2\
2 — 1	3	5 .
\1	10	—6	1/
Р е ш е и и е. Посредством над данной матрицей получим
последовательных элементарных преобразований следующую систему эквивалентных матриц:
[\	3—12.	/1	0	0 (К	/1	0 0	0.	,1	0 0 (К
(2 —1	3 5 оо|2 —7	5	1 оо 3 0 0	0 оо О 0 0	0) се
\1	10 —6 1/	\1	7	—5	—1/	\1	7 5	—1/	\1	7 5	—1/
/1	0	0	0\	/1	О	О	0\	,1	о	о	0.
оо 0	0	0	0	оо 0	0	0	— 1	со	О	1	0	0	.
\0	0	0	—1/	\о	0	0	о/	\о	о	о	о/
Следовательно, ранг данной матрицы равен двум.
90
316.	Найти ранги следующих матриц:
а) .’1	4\ б) '2 3 в) /1	4
\2 —1/’	\4 6/’	12 —1
\1	10
д)	/2	2	-1	Н
4	3	—1	2]
8 5 —3 4 Г
\3	3	—2	2/
— Г'\	г) /2	7	з\
4 ,	3	5	2
—6/	\9	4	1/
§ 6. СИСТЕМЫ ЛИНЕЙНЫХ уравнении
1.	Формулы Крамера. Пусть дана система линейных уравнений
' °11Х1 4" °12Х2+ •  •	— ^1.
-И ~F Й-2‘>Х2 4" • . . 4" в-2пХП ~ b-Zf	Ц)
@П1Х1 4- ^П2Х2 4“    4~ аппхп = ^п-
Определитель n-го порядка А— Д ' = ’ «/у ], составленный и?, коэффициентов при неизвестных, называется определителем системы. В зависимости от определителя системы различают следующие случаи:
а)	Если определитель А системы (1) отличен от нуля, то система имеет, и притом единственное, решение, которое может быть определено по формулам Крамера:
А„ А ’
(2)
где определитель n-го порядка A; (i = 1, 2, ... , /?) получается из А путем замены z'-го столбца свободными членами /у, /ц, ..., Ьп\
б)	если А —0, но хотя бы один из А,^0 (i — 1, 2, .... п), то система (1) несовместна;
в)	если А = 0 и А, = 0 (t = l, 2, .... п), то система (1) либо несовместна, либо имеет бесчисленное множество решений [в последнем случае хотя бы одно уравнение системы (1)—следствие других].
317.	Решить систему Г Зх + 2z/== 7,
| х-у = 4.
Решение. Определитель системы
поэтому решение ее определяется
Но
тогда
по формулам Крамера:
91
Геометрически каждое из уравнений ЗхЦ-2у = 7 и х — у = 4 определяет прямую на плоскости хОу, и поэтому решение х = 3, у — — 1 определяет точку пересечения этих прямых.
318.	Исследовать систему [ х — 2у = 5, | Зх — бу — 8.
Решение. Определитель данной системы А = 0, но определитель, 15 —2 1
А, = I	—304-16 — —11/ 0, что показывает несовместность системы.
1 | 8 —6 I
Геометрически это означает, что данные прямые не пересекаются, г. е. параллельны.
319.	Решить систему [ х — 2у =-5,
1 Зх — бу = 15.
Решение. Определители А —О, А,—О, А., —О, так как у них строки пропорциональны. Здесь оба уравнения системы определяют одну и IV же прямую и решением системы являются координаты любой точки этой прямой. Отсюда следует, что система имеет бесчисленное множество решении.
Найти все решения следующих систем:
320. 2х — 5у-—11,
I х +бу3.
321. (Зх-2у-=2,
\ 9х — бу — 6.
322. ( Зх —5г/+ 1=0, j 7х4-Зг/ + 17 = 0.
323. f2x —3«/ = 4,
| 4х — бу— 7.
324. Решить систему
х + 21/— Зг = 0, 2х — 1/4-4г = 5, . Зх -р у — г — 2.
Решение. Вычисляем определители:
		1	2	—3			0	2 _	-3	
	А =	2	— 1	4	= Ю,	А.,	—	5 -	-1	4	= 5,
		3	1	— 1			2	1 -	-1	
			1 0	-3			1	2 0		
		=	2 5	4	= 20	Дг	—	2 -	1 5	—	15.
			3 2	— 1			3	1 2		
Так как А формулам	АО, то данная Крамера:			система имеет толь		ко	одно	решен!		е. Находим его по
	ДЛ.	=	5 Го =	1 2’	А,у 20 ^~Д" - ю =	= 2, г =		А, " д		15	3 16 = 2
Решить следующие системы:
1
325.
' Зх —3// + 2г —2, 4х - 5у + 2г = 1, 5х —6г/-|-4г —3.
326.
Зх-\-2у — 4г = 8, 2х -1- 4у - 5г = 11,
1.V - .‘у-.- 2г 1.
92
327.
2ах — 361/4- сг = О, Зах — 6by + бег = 2abc, . бах — 4Ьу 2сг -= ЗаЬс.
328. [ 2xi + Зх2 + 11х3 + 5х4 = 2, | Xi 4"	4’ 5.V3 4" 2х4 — 1,
2хх+ х2 4- Зх3-(-2х4 = —3, л'14~ х2 4- Зх3 + 4xt = —3.
2. Решение системы с помощью обратной матрицы. Пусть дана система (1). Ее можно записать в матричной форме
АХ —В,	(3)
где ,4—(а;/) —матрица из коэффициентов при неизвестных, а В и X — столбцы, составленные соответственно из свободных членов и из неизвестных. Если матрица 4 —невырожденная, т. е. определитель системы А = 1 А \ 4= 0, то, умножая обе части уравнения (3) на матрицу /Г1 слева, получаем решение системы в матричной форме:
Х — А 41.	(4)
Найти решение следующих систем с помощью обратной матрицы:
329. ( х + 3// = 2,
| х — 3у = 8.
Решение. Здесь А = ‘ /1 = —6, и искомое решение имеет вид (4):
гак что матрица Д — невырожденная
Отсюда
1—3—3	2 _____ 1 . —30 _ ' 5
6 .-1	1 ' 8 ~	6 у 6; _ ;—!/'•
х = 5, у —— 1.
330.
2х-|-//+ z--2, 5х 4- у 3z = 14, 2х Ц- у 4- 2г — 5.
Решение. Определитель системы А =1 .4
4\	/ 2\
T/U4-'1  14
4 -	\ 5/
3, н тогда
откуда и следует, что
х = '2, у —-A), z = 3.
331. ( Зх-{-у=-1,
I х — у — 7.
333.
A’l-bX'l-T А’з— 1.
л'1 — х.,	2х3 = —5,
334.
2х — //4- 4г == 15,
Зх — у-[- г —о, ,—2х + у+ г-0.
4хх 4- -4 + 4х3 = —2. л-щг- 4х,-7х34-6х1 = 0, •V'! — Зх2 — 6.Y| = У,
2X14* х2 — 5л’3 4- х4 —о, 2х2— x,1-\-2xi^-~—5.
93
335.
Xi 4- 2x.> + Зх3 + 4x4 — 7, xy 4~ 2xs 4- 2xt = 5, 4xi + хч хз = o> 2xi 4_ хг + хз = 1.
3. Однородная система линейных уравнений. Система (1) называется однородной, если все свободные члены by = Ь2~... = Ьп = 0; в матричной форме однородная система имеет вид
АХ = О,	(5)
где О —нулевой столбец.
Однородная система всегда обладает тривиальным — нулевым решением:
%! = (), х2 = 0, ... , хп = 0,
т. е. она всегда совместна
Если определитель системы А I =А 0, то пулевое решение будет ее единственным решением. Для того чтобы система (5) имела ненулевое решение, необходимо и достаточно, чтобы ее определитель был равен нулю. Заметим, что система (5), имеющая одно ненулевое решение, имеет бесчисленное множество решений; если X () л АХ = О, то А (XX) = X (АХ) = КО = О при любом К 0.
Пусть, дана однородная система например, трех уравнений с тремя неизвестными
Оу, Л"| Оу >х2 +	=- 0,
/АцХх + ЯагХц+ #23X3 = 0,	(о)
<П'| Ху + Од.2Х2 П33Х3 = 0 
Здесь могут быть следующие случаи:
а)	если А 0, то нулевое решение л, -= 0, х2 = 0, лд = 0 —единственное;
б)	если А |' = 0, но один из миноров второго порядка определителя отличен от нуля, тогда одно из уравнений системы является следствием двух других сравнений и данная система сводится к системе двух уравнений с тремя неизвестными, имеющей бесчисленное множество ненулевых решений;
в)	если А|=0 и все миноры второго порядка определителя равны нулю, то система сводится к одному уравнению с тремя неизвестными, следовательно, данная система также имеет бесчисленное множество ненулевых решений.
Найти все решения следующих однородных систем:
336.
2х-|- у— г=0, 5х — у + 2z — 0, х + 2у+ z = 0.
Решен и е. Вычислим определитель системы:
—24.
Поскольку А О- 0, то данная система имеет только одно нулевое решение:
х — у — z = 0.
337.
3x4-4z/+ 2z = 0, х — у 4' 4z = 0,
5х + 2// 4- 10z —- 0,
94
Решение. Определитель этой системы
3	4
А •= 1
5
2
4
10
= 0,
поэтому система имеет ненулевые решения.
Замечаем, что миноры, содержащиеся
в первых двух строчках, отличны от нуля, например
Здесь для получения третьего уравнения надо прибавить к первому удвоенное второе (проверить!), т. е. третье уравнение — следствие первых двух, и система сводится к двум уравнениям:
Зх 4- 4у -|- 2^ — 0, х — у 4* 4z = 0.
Задавая произвольно одно из них, например г, нз этих двух уравнений найдем значения х и у. Полагая в данном случае г = /г, получим
J 3x4 4/--- —2Л,
I х — y — —-4/i, 18,	10,
откуда х =— ? /?, у— п.
Следовательно, решение системы можно записать в
18 ,	10
л——у/г, г/=у-
где Л — произвольное число.
х -j- 21/ + Зг — 0, 2х 4- 41/ + 6г = 0, . Зх 4“ 61/ 4- 9г = 0.
г = /г,
виде
338.
Решение. Нетрудно подсчитать, что здесь сам определитель и все его миноры равны нулю. Это значит, что в данной системе только одно независимое уравнение, а остальные два ему пропорциональны. Находя, например, из первого уравнения х(х = —Чу — Зг) при произвольных у ц г, получим решение данной системы. Общин вид решения можно записать так:
х ——2/1 — 3k,	y = h, z = k,
где h и // — произвольные числа.
339. / 2,25x4-31/= 0,
|	3x4-4i/ = 0.
341.
340.
3x4-21/4- г = 0, 2х 4- 5у 4- Зг = 0, Зх 4- 4у 4- 2г = 0.
342.
2х — Зу 4- г — 0, х4- 1/4- г = 0,
Зх — 21/4-2г = 0 х— 1/4- 2г = 0, 2х —21/4- 4г = 0, 5х — 51/4-Юг = 0.
95
343. При каком значении а система имеет ненулевые решения? Наш и их.
А: 4-31/4-2?--О,
ах— t/4~ z —О,
y + 4z — O.
344. (	2x4- y + 3z- t—O,
J Зх — 2у 4- z + 2/ -- О,
4x-\-3y-{-2z — 8t— О,
—Зх 4~ Ау -’г Зг — 2t = О.
4. Общий случай. Условие совместности. Пусть дана система уравнений с п неизвестными
ДХ’ = /1,	(6)
матрица А называется матрицей этой системы, а матрица
ОцЯ1г ••• а1пЬг у
а, b '
(А.В)	a‘i,: 2	1—расширенной матрицей системы.
^апиат2 •   атпЬ>п'
При этом возможны два случая:
I) ранг матрицы А системы меньше ранга расширенной матрицы (A, S), т. е.	тогда данная система несовместна и решения не существует;
2) ранги матриц А и (4, В) одинаковы, т. е. гл—г^л цр—г', тогда для данной системы существует хотя бы одно решение. При этом:
если г — п, то система имеет единственное решение;
если г<п (zn=gn), то система имеет бесконечное число решений, которые вычисляются по следующей схеме;
а)	выделяется в матрице А минор Аг r-го порядка, отличный от нуля; Аг
б)	выделяется подсистема, состоящая из уравнений, коэффициенты при неизвестных которых входят в минор Дг;
в)	полученная подсистема решается по формулам Крамера (АЛ =/= 0) при произвольных значениях (п — г) неизвестных, коэффициенты которых не входят в минор ДЛ.
345, Установить совместность системы
Xj4 Л'2 4- Л'з — 3, Х\ 4~ Xj --------- ЗЛ";> —	1 ,
2xi 4- Х-2 2л*у 1, -Vi 4- 2.V., - Зл'3 = 1.
Решение. Составим матрицу /1 системы н ее	расширенную матрицу
1 11. 11	1
/1 1 —3;	/1 1	—3 -1 \
Н2 ! _г -	,	—2	1 /’
1 2 -3Z	Ч 2	-3	1?
96
очевидно, гЛ5£3, a r,A B,^z4.				Произведем необходимые элементарные преобра-			
зования над /1	матрицей (Л, 1	1	3		Я): ,1	0	0	°,	4 0	0	0,
/1	1 —3	-1 \	/ 1	0	—4	—4 \	/' 0 1	0	0 '
\2	1 —2	1 i	СС 1 \2	— 1	—4	’ со -5 ; у0 1	-1 -if
ч	2 -3	и	ч	1	—4	—2'	-0 1	1 2Z
	/1 0	0	0\	А	0	0	0 д	о о ov
	/ 0 1	0	° \	Jo	1	0	0 !	/0	1 0 (Л
с<	\ 0 1	—1	—1 г	52 \ 0	0 -	1 со I -1 -1	10	0 1 0 j ’
	'0 1	1	2Z	о	0	1	2'	'''0	0 0 1/
откуда заключаем, что ранг расширенной матрицы г(Л В) = 4.
Таким образом, гл < 4 т. е, данная система не имеет решений.
346. Решить систему уравнений
— 2х2 — Зх3 = —3, Зл._> —	— О,
—xi + 4х2	х3 = 3,
Зхх+ х2—13х3 = —6.
Решение. Вычислим
ранг расширенной матрицы
/	1	—2	—3	—3\
	1	3	—5	° \
(A, B)-f	-1	4	1	3 / ’
\	3	1	-13	—6-
Вычитая сумму эмементов второй,	третьей		и утроенной первой строки из эле-	
ментов четвертой строки, получим				
/	1	—2	—3	—3\
	1	3	—5	° \
(А, В)<х>|	—1	4	1	3 /'
	0	0	0	о7
это показывает, что гл п •< 3 и четвертое уравнение системы —линейная комбинация первых трех ее уравнений. Далее, минор третьего порядка, расположенный на верхнем левом углу матрицы (Л, В), отличен от нуля:
Д =
1
1
—1
—2 -3
3 —5
4	1
6	0, т. е. тл> п — 3.
Но Д состоит из первых трех строк матрицы А, т. е. гА = 3.
Итак, й| = /д=3 = п, поэтому данная система имеет единственное решение, получаемое по формулам Крамера:
Дх п	Д'2	1	Аз ,
хх=д=2,	хй=д=1,	х3=А=1.
4 Кручкович и др,
97
347. Решить систему уравнений
2.г4-4 х2— х3— xt -J- х^— 1, хг — x2+ Xj+ x4 —2x3 — О, Зх4 Ц- 3x2'— 3x,3 — Зх4 -4 4%з — 2, 4xx + 5x, — 5x3 — 5xt + 7x5 = 3.
Решение. Составим расширенную матрицу данной системы:
,2	1	—1	—1	1	К
/ 1	—1	1	1	—2	0
(А’ 5)= 3	3	—3	—3	4	2
ч	5	—5	—5	7	3''
Очевидно,, ранг матрицы системы и ранг расширенной матрицы не превосходит число их строк, т. е. r^4. С другой стороны, минор второго порядка, расположенный в верхнем левом углу, отличен от нуля:
2

1
= —3 4 0,
т, е. ранг системы г -- 2. Подвергнем расширенную матрицу следующим преобразованиям: прибавим к третьей строке вторую, а затем вычтем первую, умноженную на 2; аналогично, к четвертой строке прибавим удвоенную вторую, а затем вычтем первую строку, умноженную на 3. Тогда преобразованная матрица примет вид
р. 1—1—1	1 1.
/1—1	1	1	—2 о\
\0	0	0	0	OOP
Ю 0	0	0	0 О'
i
I
откуда следует, что последние два уравнения системы являются линейными комбинациями первых двух уравнений системы, ранг = в) = 2, т. е. r<zn и система имеет бесчисленное множество решений.
Составим подсистему, состоящую из первых двух уравнений системы и перенесем в правую часть неизвестные х3, xt и х5, коэффициенты которых не входят в минор Д:
( 2xj4~^2— ХзЦ-х4— X5-4I,
I х4 — х2 = — х3 — х4 + 2х5.
Полагая х3 = с3, Xi~ci, х5 = с-,, где с3, с4, с5—произвольные постоянные, имеем ( 2л'14-х2=1 +с3 + с4—с5, \ х4 —х2 = 2с3—Сз—с4.
Решая полученную систему по формулам Крамера, имеем:
х _ Д1___1_1^+Сз + С4-“с5)	1 I L (1-4-с у
J~A “ -3	-1| ' 3 U+Cs)’
А = - У I f йс+-Л-CS) I = У(' +Зсз + 3с4-5с5).
ZA	О | 1	Сд С4)	1
Полученное решение называется общим решением системы. 98
348. Проверить, выполняется ли условие дующих систем:
а) | х — у = 8, б) Г х+ у+ z-= 2, в) \2х4~*/ = 3;	• 2х — Зу — 2 — 5,
л-4- y~z = 7;
совместности для сле-
2ху 4“ 2х3 4- х3 —-19, хг + 2х2 4~ 4х3 — 31,
4х± 4- 6.Г., 4- 9л'3 — —2;
г) 2xr- х,4- х3 - 5х4 = 4,
2х1 + 3ха-3,г34- *4 = 2, 8Xi— х34- х3— х4=1, 4хх — Зх2 4- Зхд 4- Зх4 = 2.
349. Решить следующие системы уравнений:
а)
б)
2xj 4- х2 - х3 - х4 4- хъ = 1, х4- Х34- х3+ х4-2х5 = 0,
Зад 4- Зх2 — Зх3 — Зх4 4- 4х5 = 2, 4х14- 5ха — 5х3 — 5х44- 7х5 = 3; Л
Л'1 4- 2х3 4" Х3 ~ А’-Г г X;, — — 1, 2хг 4- 5х2 4- 6х3 — 5х4 4- *5 = 0,
Xi — 2х2 4" хз— xt х5 = 3, xt 4- Зх2 + 2х3 — 2х4 4- хя = — 1, х4 — 4х2 4- х3 4- х4 — = 3.
§ 7. ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
1. Линейное преобразование и его матрица. Преобразование вектора X = 'хД *	/уЛ
) в вектор =	) в матричной форме, определяемое формулой
/У1\ [аИ а1Л\ (Xl\	V 4V	М\
=	(	, т. е. Y = АХ,	(1)
\!/з/	\а21 а2-2/ \Х2/
_	! $11	$121
называется линеиныл1 преобразованием плоскости, причем Д=	называется
,21	а22/
матрицей преобразования.
Пусть х—хУА-х-у, а у —У-^А-Уъ!, тогда этим преобразованием основные /1\	, /0\	/и11\
орты »= и J— \ переводятся соответственно в векторы/1, ==	1иЛ., = |	1.
''О/	'4/	\а21/	’ \а2«/
Преобразование (1) в координатной форме определяется формулами
У\ — а11Х1 4 <212*2, У2=а21*14-а22*2-
(2)
* Здесь нам удобно располагать координаты вектора ие в строчку, как эго делалось ранее, а в столбец и рассматривать как прямоугольную матрицу с одним столбцом; для краткости будем также вектор х, координаты которого расположены в столбце, обозначать через X.
4*
99
Аналогично, преобразование, определяемое формулами
У	1 —	+ ^12-^2 + а13^3>
У	% =	4“ <^22^2 4“
У	з~ tZ3ixl 4~ °32^2 4“ ^ЗЗ-^З	(3)
называется линейным преобразованием пространства. В матричной форме преобразование (3) имеет вид Y---AX, где
/</Д	/*А
V = [Уг , Л (ац), X = ,г2 \Уз/	W
Всякое линейное преобразование обладает следующими основными свойствами:
A (X + Y) = AX + AY,
А (аХ) = а(ДХ).
Линейное преобразование А, имеющее невырожденную матрицу преобразования А ( Л |=^0), называется невырожденным. Всякое невырожденное преобразование У = ДХ обладает единственным обратным преобразованием Х = Л1/, переводящим вектор Y обратно в вектор X; причем матрица обратного преобразования Д"1 обратна по отношению к матрице Д.
Если линейным преобразованием У — ВХ вектор X переводится в У, а преобразованием Z = AY вектор Y переводится в Z, то результат последовательного применения двух линейных преобразований В и А равносилен одному линейному преобразованию С с матрицей преобразования С=Д5; это преобразование переводит вектор X в вектор Z:
Z = CX = (AB) X.
Простейшие примеры линейных преобразований:
1)	Нулевое преобразование, которое каждому вектору X пространства (или плоскости) ставит в соответствие ноль вектор, т. е.
ОХ = 0.
Матрица О нулевого преобразования — ноль-матрица.
2)	Тождественное преобразование, которое каждому вектору X пространства (или плоскости) ставит в соответствие этот же вектор X, т. е.
/Х-Х.
Матрица тождественного преобразования—единичная матрица I.
350.	Найти матрицу преобразования суммы следующих линейных преобразований:
«1 —- Зец — 2а2,	'^Т =- 5vi + а.,
и
и-,~ 2c1 + 4c2 U’e 2сц — За..
Решение. Данные преобразования U — AV и W—BV соответственно имеют матрицы
По определению, суммы линейных преобразований t/+Wz = (H + fi) V, поэтому матрица суммы преобразований равна сумме матриц данных преобразований:
100
351.	Даны линейные преобразования U = AV и V = BW, где
/3 _2\	/ 5 —2\
Л=Д2 4/ И В = \-3 1/ НаЙ™ переводящего вектор W в вектор U.
матрицу преобразования С,
Решение. Подставив значения вектора V из второго равенства в первое, получим t/— A (BW) = (ДВ) IT, или
/3 —2\ / 5 —2\	/ 21 —8\
U= ]! Г =-•=
\2 4/ \-3 1У 2 О/
W.
Таким образом, результат последовательного применения двух линейных преобразований Л и В равносилен одному преобразованию с матрицей преобразования
„ ,	/21 —8
С = ДВ = \—2 О
352.	Показать, что поворот плоскости около начала координат на данный угол ср — линейное преобразование. Написать матрицу преобразования.
Решение. Из аналитической геометрии известно, что при повороте плоскости на угол ср произвольный вектор л: = {х1, х2} преобразуется в вектор у = {У1, Уа}> координаты которого определятся по формулам
У1 = xi cos <р — sin ср, Уч = sin ср + х2 cos ср.
(2')
Эти формулы определяют линейное преобразование плоскости с матрицей преобразования
cos ср —sin ф
sin ср cos ср
А =
Так как определитель
|А'Г-
COS ф sin ф
—sin ф cos ф
=-1 О,
то преобразование поворота —невырожденное преобразование; поэтому существует обратное преобразование, переводящее вектор у = {«/!, Уч} обратно в вектор х~ {%£, х2}:
xi = У1 cos ср + у„ sin ф,
•«2=-"— Ift sin <р + у. cos ф.
Заметим, что здесь матрица обратного преобразования Д_1 совпадает с транспонированной матрицей:
,	( cos ф sin ф\
Д"х =	==Д',
\—sm ф соэф/
т. е. матрица А является ортогональной матрицей (см. 282 и 286).
Всякое линейное преобразование (плоскости, пространства) называется ортогональным, если ее матрица ортогональная. Добавим, что обратное преобразование ортогонального преобразования и последовательное выполнение двух ортогональных преобразований также являются ортогональными преобразованиями.
101
353.	Показать, как изменяется данный вектор X при преобразовании с матрицей
/1 0 0\ 4=2 2 0 .
\3 3 з/
Решение. Закон преобразования (1) в этом случае дается равенствами
У1~ Л'1, r/a = 2xi-f-2x2, уз = 3xj + Зх2 + Зх3.
Таким образом, каждый вектор х — {хг, х2, х3} пространства преобразуется в новый вектор у={у1У у», Уз} так. что первая координата его не изменяется, вторая координата равна удвоенной сумме первых двух координат, а третья — утроенной сумме всех трех координат преобразуемого вектора х.
354.	Дано преобразование неравномерного растяжения пространства: xL = ax, th— $у, Zi~yz, где а>0, Р>0иу>0. Найти матрицу преобразования. Выяснить, как преобразуется при этом сфера х2 ф- у2 + г3 = R2-
Решение. Данная система уравнений может быть записана одним матрич-/хД	/х\	/а 0 0\
ним уравнением i/i) = D у , где диагональная матрица 0=0 £ 01 —матрица \гД	\г/	\0 0 у/
преобразования.
Разрешим данную систему относительно х, у и г:
Подставляя полученные значения в уравнение сферы, имеем
*1 . У1 . £1______рг „ „„ *i I У1 । г1 _____________________ ।
(а/?)2	ф/?)2	(у/?)2
Отсюда следует, что данное преобразование сферу переводит в эллипсоид с полуосями а = аЛ, 4 = ^. с = у7?. При а=[3 = у = К получается равномерное растяжение или сжатие пространства, переводящее сферу в сферу.
355.	Показать, что линейное преобразование
«1 = —У14-Зц2 —ц3, и2 = —Згд + 5и2 — у3, и3 = —3v1 + За, + v:i
невырожденное, и найти обратное преобразование.
Решение. Данное преобразование О = /1У имеет невырожденную мат-рицу А, так как ее определитель
-1 3 —1
| А |= —3 5—1 = 4#=0.
—3 3
Тогда преобразование U — AV невырожденное, и оно имеет обратное преобразование У~А~Ч!. Вычислим обратную матрицу:
102
искомое обратное преобразование представляется в виде
»i=y (4«i — Зн'.’.+ «з), »2 = j (3«i — 2и2 + и3), г3 = у (3ut —Зи3-|-2из)
356.	Даны линейные преобразования:
uL = 2vi 4- v2, vL = — Зда2-и
и2 = 3^! — 2v2 v2 = 2®i — 4ю2.
Найти матрицу преобразования, переводящего вектор IF — 1 I ‘	‘	>К’2/
I,	lUA в вектор и — \	|.
\иа/
357.	Найти матрицу преобразования плоскости, получающегося в результате последовательного поворота ее около начала координат сначала на угол <р, а затем на угол i|’-
358.	Найти линейное преобразование, соответствующее матрице /°0 Л
А= О 1 2 . Выяснить, как изменяются координаты преобразован-\1 2 3/ ного вектора.
359.	Найти произведение следующих линейных преобразований:
н1 = 2у1 —у2 + Зу3, и2 — 3п1 — 2с2 4" Уз- в us = 4v! ~ 3v2 — 2о3
Vi = 3®i — 2w2 + и'з, v2 = 2ffi>i — w2 4- Зда3, Уз —	— w2 — 3w3.
360.	Найти преобразование, обратное преобразованию U — AV, где
/ ° 1 0\ Л= —4 4 0 . \-2 1 2/
2. Характеристические числа и собственные векторы матрицы. Всякий ненулевой вектор X, удовлетворяющий условию
АХ = КХ (Х-У=0),
(3')
называется собственным вектором преобразования А или матрицы А, а число Л — собственным значением (характеристическим числом) А, соответствующим вектору X. Собственные значения А, матрицы А являются корнями ее характеристического уравнения
|Д-Х/|=0,	(4)
103
или в развернутом виде
Л	... nUl
ап аи-К ... а.м
М-1)" V4-(-l)n	.-%_Л+^==0 (4'),
ат
°пг
апп А
где ibt = a11-j-п22-{-...-)-апп — след матрицы, а ф„ = 1 А I.
В общем случае имеется п различных собственных значений — комплексных или вещественных корней уравнения (4), однако в отдельных случаях при наличии кратных корней их число уменьшается.
Собственный вектор %0={uJ, и2, .... ип}, соответствующий характеристическому числу л0, определяется из системы уравнений
(йц — л0)п1-|-	a12u2 Д-. •.й1Лн;1 О,
a21Ui + (u22 — Ло) и2 + •.. + а2пип = О,
алЛ+ ап1иг 4"   • + (апп ^в)ип = 0.
Собственные векторы определяются условием (3') с точностью до числового множителя, поэтому, решая систему (5), можно одну из координат вектора Хо фиксировать на каком-либо конкретном значении. В случае, если /.„—кратный корень, система (5) может определять не одно собственное направление, а множество таких направлений.
361. Найти характеристические числа и собственные векторы Л I3 4\ линейного преобразования, заданного матрицей А =	.
\ □ Л У характеристическое уравнение данного преобразования:
Р е ш е п и е. Составим
|3~Л
M-wU 5
4 I
= (3-К) (2-К)— 20 = А2 —5А — 14= О, 2 — Л
из которого получаем, что данное преобразование обладает характеристическими числами >4 = —2 и К, —7.
Собственный вектор Xv {иг, н2}, соответствующий характеристическому числу Х,1( определяется уравнениями (5):
j(3 4-2)Ul+	4и2 = 0,
I 5i(1 + (2+2) и., = 0, т. е. Гш, 4-4н2 = 0.
Полагая п1 = 4, найдем tt.,=—5 и получим АГй {4, —5}. Аналогично, собственный вектор X., {t>lt 0..J, соответствующий Характеристическому числу Л2 = 7, определяется в виде А»={1, 1) (проверьте!).
362. Найти характеристические матрицы третьего порядка
/5 2
4= 4 5
\6 4
числа и собственные векторы
~3\ —4 .
—4/
Решение. Составляем характеристическое уравнение данной матрицы:
5— А 2
| А - А/ | =
4	5-К -1	=0.
6	4	—(1 + А)
104
Раскрыв определитель |Д — V получим
I А - V I = X3 -414 11X, = 6 = 0.
Разложим полученный многочлен на линейные множители:
|A-XJ |=(Х3- 1)-6 (Ла- 1) + И (X,— 1) = (Л,— 1) (Л,—2) (X, —3) =0;
получаем, что
7.1=1, Х,2 = 2, /.3--3.
Собственный вектор X, соответствующий характеристическому числу = 1, определяется из системы уравнений
(5— 1) П] -)-	2«2 —	3«3 = 0,
4u1 + (5 — 1) «2 —	4п3=0, или
61^4«2—(4 + 1) «3 = 0,
ft — 4«i -|- 2«г — З«3 — 0, f2== 4«i 4- 4 «2 — 4и3 = 0, fe = 6«! 4- 4«2 — 5«з = 0.
Непосредственно видно, что третье уравнение — линейная комбинация первых двух уравнений 1/з = Л4- cffi\, поэтому данная система трех уравнений с тремя неизвестными приводится к системе двух уравнений
( 4(^12t/2 Зиз,
I tlL 4- и-1 = и3.
Пусть «3 = 2, тогда, решая полученную систему ( 4«i 4- 2«2 --- 6, I «14~ ^г=-2, найдем = 1, н2=1. Итак,
^ = {1, 1, 2}.
Собственный вектор Х2, соответствующий характеристическому числу Х2 = 2, определяется системой уравнений
( Зу14-2с2-Зт>3 = 0, J 4о14-2о2-4о3 = 0, ( 6о14-4уг—6v3=0.
Решая систему, находим
Х2= {1, 0, 1).
Аналогично находим, что вектор
Х3={1, 2, 2}
соответствует характеристическому числу 73 = 3.
363.	На примере матрицы Л-
361) показать, что ха-
рактеристическими числами обратной матрицы А 1 являются обратные значения характеристических чисел матрицы А.
Решение. Составим обратную матрицу А'1. Так как | А | =—14, то
/- 1	-2А
1 / 2 —4'	7	7
зГ\ 5 _3 • \ 14	14/
105
Теперь составим характеристическое уравнение матрицы Л *:
2
14
Решая квадратное уравнение, получим
-Й+-)
5	1
= ^+14^-П=°-
=2 f-A 1Л25  4VJJ_£ ЛД
(l 2\ 14 ± У 196 "Г 14/	2\ 14	14/’
откуда имеем:
1 1
R==-¥> Р2=у.
Из полученного результата можно заключить, что характеристические числа обратной матрицы Л 1 равны обратным величинам соответствующих характеристических чисел матрицы А. Заметим, что этим свойством обладают все квадратные невырожденные матрицы.
364.	Даны матрицы
/2 —1\
Н1 2 “ В
1 1
Показать, что АВ ВА, но АВ и ВА имеют одинаковые характеристические числа.
365.	Найти характеристические числа и собственные векторы симметрической матрицы
/7—2	0\
5 = 1—2 6 —2 j \ 0 —2	5/
Показать, что собственные векторы ортогональны.
366.	Показать, что число Х=1 является максимальным характе-n I 2/3 1/3\
ристическим числом для матрицы Р — \ .	„ _ и минимальным
\ 4/ / о/ ( j
для матрицы Р~г.
.0,6 0,4'.	,	/0 1\
367.	Показать, что если РХ = Р1Х и Д = ; n_ > a Zt = ( I, 0,0 О,//	\1 О/
то матрицы Р и Л имеют одинаковые максимальные характеристические числа (А.!=1), а минимальные их характеристические числа отличаются только знаком.
/2 —2	3
368.	Найти характеристические числа матриц Д —( 1	1	11
\1	3 -1/
и Л2; выяснить зависимость между их характеристическими числами.
106
369.	Найти характеристические числа матриц Л = ( О1 и Д(Л) =
= Л2 —2Л —3/. Показать на этом примере, что если матрица А имеет характеристическими числами Xj и А2, то матрица В = Р (Л) имеет характеристические числа Р (Аг) и Р (Л2).
370.	Даны матрицы
/ 2 —2 3\	/20	1\
Л 10 -4 5 ) и Т = (	13-1.
\ 5 —4 6/	\—2 1	0/
На примере матриц Л и В — ТЛГ } показать, что подобные матрицы имеют одинаковые характеристические числа.
ГЛАВА III
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
В ПРОСТРАНСТВЕ
§ 1.	ПЛОСКОСТЬ. ЕЕ УРАВНЕНИЕ
1.	Общее уравнение плоскости. Уравнение в отрезках. Всякая поверхность в пространстве задается в декартовых координатах уравнением вида
F (х, у, г) = 0.
Если F (х, у, г) —многочлен n-й степени, то соответствующая поверхность называется алгебраической поверхностью и-го порядка, или просто поверхностью н-го
порядка. Всякая поверхность первого порядка есть плоскость, т. е. всякое уравнение первой степени
Ax + By + Cz + D = 0	(1)
определяет плоскость. Уравнение (1) называется общим уравнением плоскости. Вектор N{A, В, С}, координатами которого являются коэффициенты при х, у, 2, в уравнении (1) перпендикулярен плоскости (1). Он называется нормальным вектором плоскости. Уравнение плоскости, проходящей через данную точку Л'1„ (х1Н у0, г0) перпендикулярно вектору N {А, В, С}, имеет вид
Д (х — x0) + B(t/— j/c)+C (г — го) = 0.	(2)
Если в уравнении плоскости (1) 0 = 0, то такая плоскость проходит через начало координат. Если Д=0, то плоскость параллельна оси Ох, если В —0 — параллельна оси Оу, если С =0 — параллельна оси Ог. В случае A = D = 0 плоскость проходит через ось Ох, если B = D = 0, то через ось Оу, если 0 = 0 = 0—
108
через ось Ог. Если А = В = 0,. то плоскость параллельна плоскости хОу, если В = С = 0 —параллельна плоскости yOz, если А = С = 0 —параллельна плоскости хОг. Сами координатные плоскости хОу, уОг, хОг имеют соответственно уравнения г —0, х — 0, у — 0.
Если в уравнении (1) все коэффициенты A, R, С, D отличны от нуля, то это уравнение может быть преобразовано к уравнению «в отрезках»
-- + Ч + г =1.	(3)
abc	’
Здесь а, Ь, с —величины отрезков, отсекаемых плоскостью на осях координат (рис. 53).
371.	Написать уравнение плоскости, проходящей через ось Ог и через точку Л4(1, —2, I).
Решение. В общем уравнении плоскости, проходящей через ось Ог, должно быть C = D = 0, т. е. такая плоскость задается уравнением
Дх + Ву = 0.
Точка М, по условию, лежит на этой плоскости, следовательно, ее координаты удовлетворяют уравнению плоскости
Л-14-В(—2) = 0,
откуда А = 2В. Подставляя значение А в уравнение плоскости и сокращая на В, получим искомое уравнение
2х+у=0.
372.	Составить уравнение плоскости, проходящей через точку М (2, 3, -—4) и параллельной плоскости tyOz.
Решение. Уравнение плоскости, параллельной уОг, имеет вид
Дх-рО = 0;
подставляя в него координаты точки Л4, получим
Д-2 + £> = 0, D — —2A.
Следовательно, искомое уравнение
Ах — 2А = 0, или х —2 = 0.
373.	Плоскость проходит через точку Р(3, 8, —4) и отсекает отрезки на оси абсцисс а = — 3, на оси аппликат с = 2. Составить уравнение плоскости.
Решение. Воспользуемся уравнением в отрезках (3). По условию, « = —3, с=2, поэтому
Л_ + ^_ + £ = 1
— 3^ h + 2
Точка Р лежит на плоскости, т. е. ее координаты удовлетворяют уравнению плоскости:
3 g ________4
1Гз + у + "2“=1’ откуда 6 = 2.
Следовательно, искомое уравнение
+ f+|=1. или 2х-Зу-Зг + б = 0.
109
374.	Вычислить объем пирамиды, ограниченной плоскостью х-\-2у — Зг + 2 = 0 и координатными плоскостями.
Решение. Объем пирамиды (см. рис. 53) равен у Sh, где S —площадь основания (треугольника ОЛ^Л!^, h— j ОМ3 ( — высота пирамиды. Если даны числа а, Ь, с, то
S= a J [ b (, h -= [ с !*, следовательно,
^пир ~ Iа I I I I с | = у а^с I •
Найдем отрезки, отсекаемые дайной плоскостью от координатных осей. Подставляя в се уравнение координаты точки Л4Т («, 0, 0), получим «-j-2 —0, откуда а ——2. Аналогично, подставляя в уравнение плоскости координаты точек 4
Л12 (0, Ь, 0) и М3 (0, 0, с), найдем — —1, c—i!3. Поэтому |afec| = y и г _ 2 Г ППр — g •
375.	Точка М (2, —1, 2) —основание перпендикуляра, опущенного из начала координат на плоскость. Найти уравнение плоскости.
Решение. По условию, радиус-вектор г = ОМ перпендикулярен плоскости, а его координаты равны координатам точки М (см. гл. II, § 3, п. 2), т. е. г {2, - 1, 2].
Таким образом, известны вектор {2, — 1, 2}, перпендикулярный плоскости, и точка Л1 (2, — 1, 2), лежащая на ней. По формуле (2) найдем уравнение этой плоскости:
2(х-2)-1 (t/+l) + 2(z-2) = 0, или	2х-1/ + 2г-9 = 0.
376.	Записать общее уравнение (1) плоскости в векторном виде. Какой геометрический смысл имеет свободный член D?
Решение. Пусть г {х, у, г} — радиус-вектор произвольной точки Л/(х, у, г) плоскости (рис. 54). Его скалярное произведение па нормальный вектор .V {.А, В, С} равно
Nr = Ах + By 4- Сг.
Следовательно, уравнение (1) можно записать в виде yyr_|_D = 0, или Nr = —D.	<4)
Это и есть векторная запись уравнения плоскости.
Заметим теперь, что по определению скалярного произведения
Nr = | N | | г | cos <р = | N | прд, г = | N | (± р) = ± I N ( Р,
где р —длина вектора, ОР, т. е. расстояние плоскости от начала координат (см рис 54) Причем в этой формуле знак плюс ставится тогда, когда угол между г и N острый, и минус —когда тупой. В первом случае вектор N должен быть направлен в противоположную от начала координат сторону плоскости
* Величины а, Ь, с могут быть и отрицательными, поэтому здесь нужно ставить знак модуля.
НО
(как на рис. 54), во втором случае вектор N направлен от плоскости к началу координат. Подставляя полученное выражение скалярного произведения в уравнение (4), получим
±\N\p~ — D, D=±\N\p.
Отсюда D | = | (V| р, т. е. модуль свободного члена уравнения (1) пропорционален расстоянию плоскости от начала координат. Множитель пропорциональности равен длине вектора N. Свободный член отрицателен, когда этот вектор
направлен от начала координат в сторону плоскости, и положителен, когда от плоскости к началу координат. Разумеется, все сказанное справедливо только тогда, когда плоскость не проходит через начало координат, иначе D =0.
377.	Уравнение плоскости называется нормальным, если определяющий это уравнение нормальный вектор N имеет единичную длину и направлен от начала координат в сторону плоскости. Записать нормальное уравнение. Привести общее уравнение (1) к нормальному виду.
Решение. Если вектор N единичный, то его координатами служат направляющие косинусы нормали к плоскости (см. гл. II, § 3, п. 4), т. е. N {cos а, cos р, cosy} (см. рис. 54). Поскольку |ДП = 1 и N направлен от начала координат в сторону плоскости, то из результата задачи 376 следует, что D= — р. Подставляя в уравнение (1) найденные выражения А, В, С, D, получим нормальное уравнение плоскости в виде
х cos а + у cos fj -|- z cos у — р = 0.	(5)
Чтобы превратить произвольный вектор N в единичный, достаточно разделить его на свою длину | ЛГ| (без изменения направления) или па — | IV | (с изменением направления па противоположное). Поэтому общее уравнение (1) превращается в нормальное, если все его коэффициенты умножить па величину
,, 1 1
/VI —-------------7'=^----------,	(6)
± I IV| ± у
111
причем знак здесь нужно выбрать противоположным знаку свободного члена D (в нормальном уравнении свободный член должен быть отрицательным). Если плоскость проходит через начало координат, то D = 0 и знак перед |ЛГ| выбирается произвольно. Величина М называется нормирующим множителем.
378.	Привести к нормальному виду уравнение Зх — 6// + 2г 4-14 = = 0. Определить расстояние данной плоскости от начала координат и направляющие косинусы перпендикуляра к плоскости.
Решение. Выпишем вектор У {3, —6, 2} н найдем его длину:
| N [ = /32 + (— 6)2 + 22 = /9 + 36 + 4 = 7.
377 нормирующий множитель для данного
В соответствии со сказанным в задаче уравнения М = —. Умножая на М
данное уравнение, приведем его к нормаль-
ному виду.
2
У~ J г —2 — 0.
3 , 6
7 Х + 7
Из этого уравнения получаем:
3	„ 6
р = 2, cos а = — cos р — у
2
cos у = —	,
здесь а, р, у—углы нормали с осями координат.
379.	Указать особенности в расположении относительно системы координат следующих плоскостей:
а)	4%+3// — 2г = 0;
б)	2х + Зг = 6;
в)	4г —9 — 0;
г)	8х — Бу + 1—0;
д)	бу — 5 — 0;
с) х + г/+г = 0;
ж) у — г = 0.
380.	Составить уравнение плоскости, проходящей: а) через ось Ох и через точку Q(l, —1, 3), б) через ось Оу и через точку Р(2, 1, — 1).
381.	Составить уравнение плоскости, проходящей через точку М (4, — 4, 2): а) параллельно плоскости хОг, б) параллельно плоскости хОу.
382.	Дано уравнение плоскости х — 4//Д- Зг — 2 — 0. Написать для нее уравнение в отрезках.
383.	Найти уравнение плоскости, отсекающей на осях координат равные отрезки и образующей с координатными плоскостями пирамиду, объем которой равен -д- .
Указание. См. 374.
384.	Составить уравнение плоскости, проходящей через точку Р (2, 3, 4) и отсекающей на осях Ох и Оу отрезки а=1, Ь-—1.
385.	Из точки Р(—1, —1, 4) опущен на плоскость перпендикуляр; его основание Q(2, 1, 3). Найти уравнение плоскости.
112
Указание. Данная плоскость проходит через точку Q перпендикулярно вектору PQ-
386.	Определить, являются ли следующие уравнения плоскостей нормальными:
а) * //+ |г-2 = 0, б) х - j у + | г - 2 = 0.
387.	Привести к нормальному виду уравнение плоскости бх— — бу — 7 г + 33 = 0. Найти ее расстояние от начала координат.
2.	Взаимное расположение плоскостей. Пусть даны плоскости
XiX-|-B1i/ + C1? + D1 = 0 и Д2х+В2(/+Сгг+£)2—0.
Угол между ними равен углу между перпендикулярными к ним векторами А\ { + ,	+} и N2{A2, В2, С2}. Косинус этого угла вычисляется по формуле
cos (р =	_Л; + BtB2 + СхСа
I М I ! ! Va-, +B'i+Ci VAl+Bl+Ci '
Плоскости параллельны, если векторы и TV2 коллинеарны, т. е.
+ _ + __ Ст А В2 С2'
Условие перпендикулярности плоскостей Л4Л+--0, т. е.
а1л2+в!в.,+с1с2=^о.
Если даны три плоскости своими уравнениями
AjX + Bji/+ С1г-1-D1 = 0, I
A2xA^B2yA-C2zA-D2 = 0, >
А3х4-В3у-\-C3z + D3 = 0, J
(7)
(8)
(9)
(Ю)
то их общие точки определяются из системы уравнений (10). В случае, когда перпендикулярные к этим плоскостям векторы
Nt {Дь В,, CJ, N2 {А2, В2, С2), N3 {Л,„ В.„ С.,!
некомпланариы, три плоскости имеют единственную общую точку. В самом деле,
тогда смешанное произведение
А, А 2
В,
В2 С2 У- о,

+ В3 С3
а записанный определи гель является определителем системы (10). Такая система имеет, п притом единственное, решение (см. гл. 11, § 2).
388.	Найти угол между плоскостями х-\-у —1=0 и 2х — у-\-+ ]/Зг + 1=0.
Решение. Выпишем координаты перпендикулярных к данным плоскостям векторов Л\ н N..-. TV, jl, I, 0), 7V2	— 1, |/ З}. По формуле (7),
cosip--- —-------------------------- = J [, с, (p^arccoa' да 76°.
| МИМ И 14-1 V 4+1+3	4 Y 4
113
389.	Плоскость проходит через ось Ог и составляет с плоскостью 2х4-у — ]/5z — 0 угол -д-. Найти ее уравнение.
Решение. Уравнение всякой плоскости, проходящей через ось Ог, имеет д
вид .4% + Ву = 0. Разделив на В и обозначив т — - получим тх4-у = 0. Пер-О
пенднкулярный к этой плоскости вектор N {т, 1, 0}, по условию, составляет с вектором Л\ |2, 1, —У б}, перпендикулярным плоскости 2х + у — У 5г = 0,
л. угол =
о
Следовательно,
л NN,
COS — = --4-- ,
3 |У|И1Г
т. е.
2т+1
2	И«2+1 I 4+1'+5 ’
Из полученного уравнения определяем значение mt
|'1(Г(т3 -I- 1) =- 4/n+2,	10 (trP 1) = 16m2 + 16m + 4,
6m2 + 16m — 6 = 0; ml — i-, m2 = — 3.
О
Таким образом, условию задачи удовлетворяют две плоскости:
+ = 0 11 —Зх+р = 0. О
390.	Установить, что плоскости х — у — z — 10 = 0, 4%Ц-11 z + + 43 = 0 и 7х- 5у — 31=0 имеют единственную общую точку. Найти ее.
Решение. Выпишем координаты векторов /У,, АС, У3:
М{1, -1, —1},	У2{4, 0, 11},	У3{7, -5, 0}
и вычислим их смешанное произведение:
1-1 - 1
Так как N1N2^r3^i=0, то три данные плоскости пересекаются только в одной точке. Чтобы найти ее, перепишем данные уравнения, перенеся свободные члены вправо:
г х— у— г =10,
J 4х+ Из =—43,
[ 7х— 5у =31,
и применим для решения этой системы
формулы Крамера. Ранее найдено Д-= = —2, далее Дл- = —6, Лу —4,	— 10, поэтому
- 6 „	4	. Ю ,
т = _2 = 3,	У-_2 г	5‘
Итак, данные три плоскости имеют общую точку Р (3, — 2, — 5).
Вычислить угол между следующими плоскостями:
391.	2х — у-'г 2г + 15 == 0 и 6х + 2у — Зг — 1 = 0.
392.	6,т + 2// — 4г + 5 = 0 н + Зу — 6г — 2 = 0.
114
393.	л--z/]/2z-5 = 0 и л- = 0.
394.	х-\-2у — г = 0 и 2a’4-J' + 4z4-3 = 0.
395.	Найти уравнение плоскости, проходящей через ось Ох и составляющей с плоскостью у = х угол гр = J .
396.	Установить, что плоскости 5%4-Зу4~ 10? +30 = 0, 4х — 5у4-+ 10г 4-20 = 0 и 6л' 4- 11 у4-30г = 0 имеют единственную общую точку, и найти ее.
3. Расстояние от точки до плоскости. Расстояние от точки .И,, (л'о, у(ы г0) до плоскости, заданной общим уравнением (1), определяется по формуле
d = । ^'оЧ-^Уо4~^го~[~4) !	, j ।
|/1-<4
397.	Найти расстояние между двумя параллельными плоскостями х4-2у-2г4-2 = 0, Зх4-6у-6г-4 = 0.
Решение. На одной из плоскостей возьмем какую-либо точку М, (х0, г/0, z0) и по формуле (11) определим ее расстояние до второй из параллельных плоскостей. Это и будет искомая величина. Полагая во втором из данных уравпе-4	I 4	\
нип у = 0, z = 0, найдем х =	т. е. точка Л401 =- 0, 0j лежит на второй пло-
3	\ 3	)
скости. Используя первое уравнение, по формуле (11) находим
f | 1-4-<-2.0 2-0 + 2|	|0
К 1 4- 4 4	3
398.	На оси Ох найти точку, удаленную от плоскости 2х-\-у—
2
— 2г + 4 — 0 на расстоянии d = 3 .
Решение. Поскольку искомая точка Л'1О лежит на осп Ох, то для нее уп — го = 0. Так как значение d известно, то по формуле (11)
2.v..:4	2.
з V 44-14-4 з
Отсюда или 2л-04-4 = 2, или 2л.-04~4 = —2, т. е. х„ ——1 или ха — —3. Следовательно, условию задачи удовлетворяют две точки: Л1' (—1, 0, 0) и (—3, 0, 0).
399.	Провести плоскость, параллельную данной плоскости 7х — — бу4-6г4-7 = 0 и отстоящую от нее на 2 единицы.
Решение. Пусть Л1 (х, у, г) — произвольная точка искомой плоскости. По условию, ее расстояние от данной плоскости равно 2, поэтому по формуле (Н)’
г^Т6^+6г + 7]_	i7x_6„ + 6z + 7|==2-/12T =22, 7x-6w + 6z + 7= ± 22,
J/494-36 + 36
откуда
7х —6у-|-6г—15 = 0 или 7х — 6г/4-6г-|-29 = 0.
Эти две плоскости и являются искомыми.
400.	Найти расстояние от точки Л41(2, —1, —1) до плоскости 16х — 12у 4- 15г — 4 = 0.
115
401.	На оси O.z найти точку, расстояние которой от плоскости 2х4- Зу — 6г4- 4 — 0 равно 2.
402.	Составить уравнения плоскостей, параллельных плоскости х — 2у4-2с — 2 — 0 и отстоящих от нее па расстояние </= *.
403.	На оси Оу найти точку, равноудаленную от точки А (2, 0, 1) и от плоскости х 4-2//4-2г- 5 = 0.
404.	Составить уравнения плоскостей, делящих пополам двугранные углы между плоскостями 2х — Зу— 4г — 3 = 0 и 4х — Зу — -2г —3 = 0.
Указание. Искомые плоскости представляют собой геометрическое место точек, равноудаленных от двух данных плоскостей.
405. Две из граней куба расположены на плоскостях* х 4- у 4-4-г—1=0, 2x4-21/4-2г —5 = 0. Найти его объем.
4. Основные задачи на составление уравнения плоскости.
Большинство задач па составление уравнения плоскости сводится к одной из следующих основных задач:
1) Найти уравнение плоскости, проходящей через данную точку Мп (ха, у0, г0) перпендикулярно данному вектору N {Л, В, С}.
Решение. Пусть ЛТ (х, у, г) —произволь-точка плоскости. По условию, вектор
пая
2ИОЛ4 {х л-0, у — у0, г — г0} перпендикулярен данному вектору .V (рис. 55). Следовательно скалярное. произведение этих двух векторов равно нулю, т. е. ЛСИоД1=0. Записывая это условие в координатах
А(х-х0)уВ(у — y0) + C(z-го)=О,	(12)
получим искомое уравнение.
2) Найти уравнение плоскости, проходящей через данную точку Мо (х0, уп, г0) параллельно двум данным (неколлинеарпым) векторам а [ах, av, az\ н b {bx, btJ, bz}.
Решение. Возьмем произвольную точку плоскости М (т, у, г). Векторы Л70.47 {х—х0, у — у0, z — г0), а и & будут компланарны, так как они расположены в параллельных плоскостях (рис. 56). Следовательно, их смешанное произведение МоМаЬ~О. Записывая это условие в динатах, получим уравнение искомой скости в виде х—ха ах
коо р-пло-
z —г0 аг Ьг
У~Уо
аУ Ьу определитель удобнее
= 0
(13)
раз-
Вычислять ЭТОТ ложением по первой строке.
3) Найти уравнение плоскости, проходящей через две данные точки .47, (лу, yt, zt) и .41., (лу, у2, г2) параллельно данному вектору а{а коллинеарны).
Решение.
Тогда векторы
., Оу, аг} (М1М2 и а не-
Пусть М (х, у, г)— произвольная точка плоскости (рис. 57).
ЛДМ {х—хъ y—ylt z — гА,
А71А42 {х2— xlt у2 — У1, г2 — г,} и а {ах, ау, а?}
116
располагаются в параллельных плоскостях и, следовательно, компланарны. Приравнивая нулю смешанное произведение этих векторов, получим искомое уравнение в виде
x--A-t y-tJt z-zx
Х2 —Х1 У2—У1 ?2*-Zl
a.v
ау az
= 0.
(М)
В конкретных задачах определитель левой части равенства раскрывается разложением по первой строке.
4) Найти уравнение плоскости, проходящей через три данные точки: All («1. l/i, И). А12 (х2, у2, г2), Л13 (х3, уз, г3).
Решение. Возьмем произвольную точку М (х, у, г) плоскости и соединим одну из данных точек, например М±, с точками М, М2 и Л43. Векторы МгМ2, МгМ3 компланарны, и поэтому их
Рис. 57
смешанное произведение равно нулю:
х —Xi y-y-L г — ?i
^2 —*1 У2 — У1 г2~г1 =0.
(15)
хз Х1 Уз — У1 гз— г1
Полученное уравнение (4) — искомое.
Замечание. Нетрудно увидеть, что задачи 3 и 4, в сущности, являются частным случаем задачи 2. Во всех этих задачах плоскость может быть определена точкой и двумя параллельными ей векторами, которые, в частности, могут лежать на плоскости. С другой стороны, задачу 2 можно свести к задаче 1, так как если векторы а и Ъ параллельны какой-нибудь плоскости, то их векторное произведение ,¥ = [«&] перпендикулярно этой плоскости. Так что все эти задачи можно решить единым методом. Однако на практике удобнее поступить так, как указано выше.
406.	Найти уравнение плоскости, проходящей через точку Л40(2,—3,—7) параллельно плоскости 2х — бу — Зг + 5 = 0.
Решение. Вектор N{2,—6,—3}, перпендикулярный данной плоскости, перпендикулярен и любой параллельной ей плоскости. Следовательно, искомая
плоскость проходит через точку Л4О(2,—3,—7) перпендикулярно вектору {2, —6, —3) (задача 1). Искомое уравнение найдем по формуле (1):
2 (х—2) —6(у+3) —3 (г —7) = 0, 2х —бу —3z— 43 — 0.
407.	Составить уравнение плоскости, проходящей через точку Л4О(2, —3, 5) перпендикулярно линии пересечения плоскостей 2х + у — 2z + 1 = 0 и х + У + 2 — — 5 = 0.
Решение. Перпендикулярные каждый своей плоскости векторы {2, 1, —2}
и TV2{1, 1, 1) перпендикулярны линии их пересечения и, следовательно, параллельны искомой плоскости (рис. 58). Таким образом, искомая плоскость проходит через точку Мо параллельно двум векторам н (задача 2).
117
Пусть М (х, у, г) — произвольная точка плоскости, тогда векторы Л'10Л4 {х — 2, J/ + 3, г —5}, Л\{2, 1, —2} и А3{1, 1, 1} компланарны, и поэтому их смешанное произведение равно нулю:
х — 2 г/ + 3 г — 5
2	1-2
1 1 1
= 0.
Раскрывая определитель по первой строчке, получим искомое уравнение:
(Л-2) |[ “2	(г/ + 3) | 2-2 | + (г-5)	[| = 0,
3 (х —2) —4 (г/+3) + (г —5) = 0, Зх-4г/+?-23 = 0.
408.	Найти уравнение плоскости, проходящей через точки Mi (2, 3, —1) и Л+(1, 5, 3) перпендикулярно плоскости Зх —3z-{-+ 15 = 0.
Решение. Вектор А {3, —1,3}, перпендикулярный данной плоскости, будет, очевидно, параллелей искомой. Таким образом, искомая плоскость проходит через точки Л4, и Л12 параллельно вектору А (задача 3). Надо только проверить, что векторы Д1|Л42 и N неколлинеарпы. Координаты вектора М^Л!, получатся, если из координат конца вычесть координаты начала: A4tA42 {— 1, 2, 4}. Поскольку координаты векторов МгМ2 и N непропорциональны, эти векторы неколлинеарпы.	___
Пусть М (х, у, г) — произвольная точка плоскости, тогда векторы AltAl, AljAl., N компланарны, следовательно, их смешанное произведение равно нулю:
х — 2 у — 3 г+1
— 12	4
3 —1	3
= 0.
Вычисляя определитель, получим искомое уравнение:
10х + 15г/ — 5г — 70 = 0, т. е. 2х-\-Зу — г— 14 = 0.
409.	Составить уравнение плоскости, проходящей через точки Mj (1, 2, 3), Л4г(4, —1, —2) и М3(4, 0, 3).
Решение. Пусть М (х, у, г) — произвольная точка плоскости. Тогда векторы
Л4гЛ4 {х — 1, у —2, г-3}, ЛДЛ1.,{3, —3, —5} и MtM3 {3, —2, 0}
компланарны, поэтому
х — 1
3
—3
у — 2 г —2
—3 —5 = 0.
—2	0
Раскрывая определитель, получим
— 10х—15г/ + Зг + 31=0.
Это и есть искомое уравнение.
Замечание. Для проверки правильности вычисления определителя рекомендуется в полученное уравнение подставить координаты точек, лежаших на плоскости; должно получиться тождество. В противном случае в вычислении допущена ошибка.
118
410.	Найта уравнение плоскости, проходящей через точку Д40(—2, 7, 3) параллельно плоскости х — 4у + 5г-|-1=0.
411.	Найти	уравнение	плоскости,	проходящей	через	точку
Мо (2, —3, 1) параллельно векторам а{—3, 2, —1} и &{1, 2, 3}.
412.	Найти	уравнение	плоскости,	проходящей	через	точку
Л10(2, 2, —2) перпендикулярно линии пересечения плоскостей Зх — 2у — г + 1 = 0 и х — у — г = 0.
413.	Составить уравнение плоскости, проходящей через перпендикуляры, опущенные из точки А (2, 0, 4) на плоскости х — 1у-\-4~2z = 0 и 5х-|- Зу — г = 0.
414.	Найти уравнение плоскости, проходящей через точки Mi(2, —15, 1) и Л42(3, 1, 2) перпендикулярно плоскости Зх — у — — 4z = 0.
415.	Найти уравнение плоскости, проходящей через точки Л41(1, 1, 1), М2(—1, 1, —1) параллельно прямой, определяемой точками А (5, —2, 3) и В (6, 1, 0).
416.	Составить уравнение плоскости, проходящей через точки Л/НЗ, —1, 2), М.(4,'— 1, —1), Л4;)(2, 0, 2).
417.	Найти высоту пирамиды SABC, опущенную из вершины S на грань АВС, если S (1, 4, —2), А (0, —1, 1), В (3, 5, 1), С(1, —3, —1).
Указание. Данную высоту можно найти как расстояние от точки до плоскости, определяемой точками А, В, С.
§ 2. ПРЯМАЯ ЛИНИЯ
1. Уравнения прямой. Линию L в пространстве можно определить как пересечение двух поверхностей. Рассматривая совместно уравнения этих поверхностей, получим уравнения линии L в виде
[ У7! (х, р, z) = 0,
V2(x, у, г)=0.	u
Параметрические уравнения линии L получатся, если выразить координаты ее текущей точки М (х, у, г) в виде функций некоторого параметра t, изменяющегося вдоль линии от начального значения t0 до конечного значения
х = х(/), у=у (/), г = г (t)	(2)
Линия L будет прямой, если можно выбрать такой параметр t, что уравнения (2) будут линейными, т. е.
x — a-[-mt, y=b-\-nt, z=c-\-pt	(—со < / <4-со).	(3)
Уравнения (3) называются параметрическими уравнениями прямой. Входящие в них коэффициенты а, Ь, с, т, п, р имеют следующий геометрический смысл: (а, Ь, с) — координаты некоторой точки Ми, лежащей на прямой (И., отвечает значению параметра / = 0); {/и, п, р} — координаты вектора s, параллельного прямой. Вектор s {щ, п, р] называется направляющим вектором прямой.
Исключая из уравнений (3) параметр I, приходят к каноническим уравнениям прямой:
x — uy — bz—c
----=. 2---=------ (4) nt пр-------------' '
Обратный переход от (4) к (3) легко осуществляют, приравнивая каждое из трех отношений (4) к /. При этом если знаменатель какого-либо отношения равен нулю, то надо приравнять нулю его числитель.
119
Общими уравнениями прямой называются уравнения вида ( AiXВуу-\-CiZ + Ох = 0, 1 Л2х 4~ В?у -р C2z 4~ D2 = 0.
(5)
Прямая здесь задана как пересечение двух плоскостей. Чтобы перейти от общих уравнений прямой (5) к ее каноническим уравнениям (4), надо на прямой найти какую-нибудь точку М„ (а, Ь, с) и определить ее направляющий вектор s. Точку Л1о находят так: задают произвольно значение г = с и из системы (5) находят х — а, у = Ь*
Направляющий вектор s параллелен линии пересечения плоскостей (5) и, следовательно, перпендикулярен обоим векторам {/I,, Blt Ct} и Поэтому в качестве s можно
« = [Д\лу =
Канонические уравнения
координат углы Мо(-1, о, 5).
W2M2, В2, С2} (рис. 59). взять вектор
i j k А Вх Q Д2 В, С2
(6)
прямой, проходящей через точки МД*!, г/i, zt) и М>(х2, у.
г2), имеют вид
У — Ух
Уг—Ух
г — zx
z2—
(7)
Здесь в качестве направляющего вектора s берется век-юр Л^Мг-
418. Написать ческие уравнения л 2л 4’ ?= 3
канонические и параметри-прямой, образующей с осями и проходящей через точку
а =
3 ’
Решение. В качестве направляющего вектора s можно вонь единичный вектор данной прямой. Его координатами являются направляющие косинусы:
„	.	л . ,	л . ,	2л. ,	1 . , Г 2 .	1 ,
s = cos а»4-cos fV4-cos yfr = cos 3( + cos 4/4~cos 3^2 ' + о J ~ 2 l'
По формуле (4) найдем канонические уравнения прямой:
х+ 1 _ у — 0 __ г -5 'Т	/2 - —1
2	2	2
или, умножив все знаменатели па 2, х -|- 1 у	г — 5
1 j Щ	—1
Приравняв каждое из этих отношений к t:
х ~р 1 _ у _ г — 5
= /2 “
* Если получившаяся система для определения х и у несовместна, то надо задать значение какой-либо другой координаты, например положить х--=-а и найти из (5) у = Ь, г —с.
120
получим параметрические уравнения данной прямой:
х =—1-]-/ у = }/2/, 2 = 5—I.
419. Написать канонические и параметрические уравнения прямой, проходящей через точку Л1о(1, —2, 2) параллельно осп’Оу.
Решение. Вектор j {0, 1, 0}, расположенный на оси Оу, по условию параллелен прямой, поэтому его можно считать направляющим вектором этой прямой. По формуле (4) получим ее канонические уравнения
х-1 у + 2_ г-2 0	1 “ 0 '
Переходя к параметрическим уравнениям, здесь надо учесть, что нули в знаменателях первого и третьего отношений означают, что х—1=0 и г 2 = 0. Приравнивая второе отношение к t, получим у =—2 + 7.
Следовательно, искомые параметрические уравнения имеют вид
х=1, у ——2 + 7, г=2.
420. Даны вершины треугольника А (2, 3, —1), В(1, —2, 0) и С(—3, 2, 2). Составить канонические уравнения медианы АР.
Решение. Точка Р делит сторону ВС пополам, поэтому координаты точки Р равны полусуммам координат В и С:
Следовательно, Р(—1, 0, 1). Так как медиана проходит через точки А и Р, то по формуле (7) имеем
х — 2 __ у — 3 _ г + 1
— 1 — 2 “	- Г +Т’
тем самым получены искомые канонические уравнения
х— 2 _ у — 3 _ г А-1
~ ТТУ “"2^-
421.	Привести к каноническому виду уравнения прямой
J х — 2у Д- Зг — 4 = 0, | Зх Д- 2у — 5г — 4 = 0.
Решен не. Определим координаты какой-либо точки на прямой. Для этого положим в обоих уравнениях г—0:
( х — Чу — 4 = 0,
I Зх+2г/ —4 = 0.
Отсюда определим х — 2 и :/ = —1. Таким образом, Л4П (2, —1, 0). Направляющий Вектор s найдем по формуле (G). Здесь Л\{1, —2, 3}, N.. {3, 2, —5} и
I 1 3
/ *
— 2 3
2 —5
= 47+14/+ 8*.
По формуле (4) найдем канонические уравнения:
х — 2	Z/+1 г	х — 2	:/+1 г
1 ~ 14	8’ ИЛ" 2	7	4 ’
121
Замечание. Иногда используют другой чисто формальный прием приведения общих уравнений прямой к каноническому виду. Для этого выражают одну из координат из заданных уравнений поочередно через две другие и приравнивают результаты. В данном примере, складывая уравнения, получим
у 4
4х— 2г — 8 = 0, или	.
Умножая первое уравнение на 5, а второе на 3 и складывая, найдем:
14х — 4у — 32 = 0,
_ 2у+ 16 _ у+8 7	7/2 '
Приравнивая результаты, получим канонические уравнения в виде
г/4-8 г + 4	х
W ~ ~ ’ ИЛИ 2
г + 4
4
у + 8
7
Эти уравнения отличаются от найденных выше только тем, что для их записи используется другая точка на прямой: Мв (0, —8, —4) вместо Д40 (2, —1, 0).
422.	Через точку Мп (2, —3, —4) провести прямую, параллельную прямой:
( х ~ у— 2+ 2 = 0, I х — у + 2г — 1 = 0.
Решение. Найдем, как и выше, направляющий вектор данной прямой
I
k
— 1
2
S =[?+?+]:= 1
./
1
— 1
= Z — 3J — 2k,
т. e.
s {1, —3, —2}.
Этот же вектор будет по условию параллелен и искомой прямой, поэтому ее канонические уравнения запишутся по формуле (4)
х—2 _ «/+3 _ г + 4
1 ~ —3 _ —2 '
423.	Написать канонические уравнения перпендикуляра, опущенного из начала координат на плоскость 4х — у-\- 2г — 3 = 0.
Решение. Вектор А'{4, —1, 2}, перпендикулярный данной плоскости, параллелен искомой прямой, и его можно считать направляющим вектором этой прямой. По формуле (4) имеем
+ _ J7 _ + 4	— 1	2 •
424.	Написать канонические и параметрические уравнения прямой, проходящей через точку /Чп (—1, 1, —3) параллельно вектору s {1, — 3, 4}.
425.	Написать канонические и параметрические уравнения прямой, проходящей через точки Mi (2, —1, —1) и Л12 (3, 3, —1).
426.	Написать канонические и параметрические уравнения прямой, проходящей через точку Мп (—1, —2, 2) параллельно оси Ох.
427.	Составить канонические уравнения прямой, проходящей через точку Мо(1, —5, 3) и образующей с осями координат углы а = -^-,
122
428.	Даны вершины треугольника Д(—5, 7, 1), В (2, 4, —1), С(—1, 3, 5). Найти канонические уравнения медианы, опущенной из вершины В на сторону АС.
429.	Даны вершины треугольника Д(1, —1, 3), В (3, —4, 9), С(—5, 11, 7). Найти канонические уравнения биссектрисы его внутреннего угла при вершине А.
Указание. Рассмотреть векторы АВ и АС и найти вектор S, идущий по биссектрисе угла ВАС (см. 225). Этот вектор и будет направляющим вектором искомой биссектрисы.
Привести к каноническому виду следующие уравнения прямых:
430.	( х-Зг/4-2 = 0,	432. | x-2z/ + 3z +1 =0,
\2у-г+1=0.	\ 2x4-0 —4г —8 = 0.
431.	| 2х — Зг/—Зг — 9 = 0, ( х — 2у + г 4- 3 = 0.
433. Найти канонические уравнения прямой, проходящей через точку Мо(1, —3, 5) параллельно прямой:
| Зх — у -г 2г — 7 = 0, | х 4- Зу — 2г 4- 3 = 0.
434. Найти канонические уравнения прямой, проходящей через точку Мо(2, 1, —1) перпендикулярно плоскости х —г/4-г 4-1 = 0.
2.	Взаимное расположение двух прямых. Пусть даны две прямые своими каноническими уравнениями
х —щ =	у —= г —сх х —а3	= у — Ь.2	= г—с8	.
т1	п2 р2	’ т2 пг р.г
Эти прямые заданы своими точками Л4Х (<гх, blt сх) и М.,(а2, Ь,, с3) и направляющими векторами 5Х {/щ, nlt рх} и s., {ни, п.,, р.,{. Углом ср между этими прямыми называется угол между их направляющими векторами sx и s4, и поэтому
cos ф = S|S? = "Щ'ь + 'гЩа + ЩЩ
I si s21	|/ m; + п-{ + pf m'i 4- rri + p|
Условие перпендикулярности прямых (8)
sy sy = 0 или т2т2 У пуи -|- рхр3 = 0.
Условие параллельности
«1 = Щ = Pi
пи п2 р.
Случаи (рис. 60) взаимного расположения прямых. 1) Прямые сливаются:
(Ю)
(И)
2)	Прямые параллельны:
MtM2 4 sx, но sx II s-2, г.
3)	Прямые пересекаются;
«1 Pi
"4 = «1 Pi
III., п.
123
si'i>s2. но Alj.M.,, Sj, s2 компланарны, т. e.
£> =
+—Щ ^2 +1	— !~i
«1	rtj	Pi
m2	n2	p..
(12)
4)	Прямые скрещиваются:
Л++,, 5t, s3 нскомпланарны, т. с. 0 = 0.
Рис. 60
Условие (12) выполняется и в случаях 1 и 2, тем самым оно означает, что две прямые лежат в одной плоскости.
435. Определить угол между прямыми
Зх — 4у — 22 = 0,	(4х-]-у — 6г — 2 = 0,
2x + i/-2z + l=0 Н (у —Зг —2 = 0.
Решение. По формуле
i
Si— 3
2
(6) найдем направляющие векторы этих прямых:
— 4
1
k
— 2 =10/4-2/+ lift, —2
Z j ft
4 1 —6 0 1 —3
= 3Z+12/+4ft.
Косинус угла между данными прямыми
yt.s-.,	=	10-34-2- 12 + 11 -4	= 98
[ Sj! | «а I ~ V WO + 4+Ж (/9+144 + 16" ” I95
откуда (р = 60".
436. Составить канонические уравнения прямой, лежащей в плоскости хОг, проходящей через начало координат и перпеидикуляр-„	„ х — 2	г/+1	г —5
нои к прямой —— =	= —j—.
Решение. Пусть s {т, п, р] — направляющий вектор искомой прямой. Прямая лежит в плоскости хОг, поэтому проекция вектора s на ось Оу равна нулю, т. е. п — й. Из условия перпендикулярности вектора s {/«, 0, р} направляющему вектору ху {3, —2, 1} данной прямой получим 3z/t-|-p —0. Поскольку направляющий вектор s задается с точностью до множителя, можно одну из его координат выбрать произвольно. Например, положив т =- 1, получим р — —3, следовательно, s {1, 0, —3}. Искомая прямая, кроме того, проходит через точку 124
0(0, О, 0), поэтому ее канонические уравнения =	У г
1	О -3’
тт	х—1 у + 2	г х-1-1	р+11
437. Доказать, что прямые —= — и —— — = пересекаются. Найти точку их пересечения.
Решение. Точка М1(1, —2, 0) лежит на первой прямой, а Л1»(—1, —11, —6) —на второй. Найдем смешанное произведение векторов M'tM-.i— 2, —9, —6}, S1 {2, —1, —2} и s2{l, 2, 1}:
A1^A42S|.S2—
— 2—9—6 2—1—2 1	2	1
= — 2 • 3 + 9 • 4 — 6 • 5 = 0.
Следовательно, эти векторы компланарны, и две данные прямые лежат в одной плоскости. Векторы и s2 неколлинеарны (их координаты непропорциональны), поэтому прямые не параллельны, т. е. пересекаются. Точку пересечения прямых можно иайти, например, так: привести уравнение одной из прямых к параметрическому виду и из уравнений второй прямой найти значение параметра t, отвечающее точке пересечения.
В данном примере параметрические уравнения первой прямой х=1+2/, у =—2~~t, z =—2t.
Подставляя эти выражения для х, у, г в уравнения второй прямой, получим 2 + 2/	9 — /	6—2/	„	. . *
—j— = —g—= —j—, откуда /=1 *.
Следовательно, точка пересечения
</ = — 2 — 1=— 3, г  2 • 1	- 2.
х=1 +2  1 =3,
В следующих задачах найти угол ip между прямыми: х + 2 у — 3 z + 5
1 — 1 “Кг"
( х — 2г — 5 = 0,
и 1 л
( у = 0.
взаимно перпендикулярны.
( Зх + у — 5z +1 = 0,
( 2х + 3(/-8г + 3 = 0.
438. — - = ^+2 = ~ и 1	— 1	1'2
( х + Зг-7 = 0, 439.
I У = о, Доказать, что 440. х 1	—2
прямые
г
= 3 И
( 2х + у — 4г + 2 = 0,
44» J J
( 4х — у — 5г + 4 = 0
442. Доказать, что прямые х — 2 _ у— 1 _ г ~3~ ' — 2 — 1
параллельны.
х = 1 +2(, //= — 2 + 3/ г = 1 — 6/.
х-\-у — z = 0, х — у — 5г — 8 = 0.
* Заметим, что оба уравнения дакэт одно и то же значение /. Если бы прямые не пересекались, то, проделывая аналогичные выкладки, мы получили бы v из этих уравнений разные значения /. Таким образом, можно узнать, что пря-х МЫе общей точки не имеют.
П
И
443.	Составить уравнения прямой, проходящей через точку .Wo (3, —2, 0) перпендикулярно к прямой ~ = г-^- и расположенной в плоскости хОу.
444.	Составить уравнения прямой, проходящей через точку Л40(1, 2, —1) параллельно линии пересечения плоскостей
Зх + 2z/ — 2z + 1=0 п х у z — 0.
445.	Доказать, что прямые
( х — y-\-2z — 1=0, |x + z/ + z = 0, (2x + //-z + 2 = 0 И (2х —3z = 0
скрещиваются.
446.	Доказать, что прямые
(x + z/-z + 4 = 0,	х+3 = t/ + 3 = г-1
( 2х-3//-г-5 = 0 И 4 “ 1 “ 2
пересекаются, и найти их точку пересечения.
§ 3. ЗАДАЧИ НА ПРЯМУЮ И ПЛОСКОСТЬ
1. Взаимное расположение прямой и плоскости. Пусть даны прямая
х—а и — Ь г —с	...
---= i------=------ (1) т пр
и плоскость
Xx + Bi/ + Cz + D = 0.	(2)
Углом 1|) между прямой и плоскостью называется острый угол между прямой и ее проекцией на плоскость (рис. 61). Этот угол определяется по формуле
I № |
Sin 11) =-----— =
1 Ат-\~ Вп-\-Ср!
О2 + /;-+С- 1''т2 + „2 + +'
Условие параллельности прямой плоскости:
Ns = 0, т. е. Ат-}- Вп-}-Ср = 0. (4)
Условие перпендикулярности:
АВС
W s, т. е.	(5)
т п р 4 '
Точка пересечения Р прямой и плоскости находится следующим образом: уравнения прямой приводятся к параметрическому виду
г = а + т/, y=b-}-nt, z=c-}-pt,
и затем подстановкой в уравнение (2) определяется значение параметра I, отвечающее точке пересечения Р. Если при такой подстановке уравнение (2) удовлетворяется тождественно (при любом t), то прямая (1) лежит в плоскости (2). Условием этого является соблюдение равенств
Ат-{-Вп-}-Ср = 0 и Аа -}Bb-}-Cc-}-D =0.
126
447.	Найти угол ф между прямой, проходящей через точки А(—1, 0, —5) и В(1, 2, 0), и плоскостью х —3z/ + <+5 = 0.
Решение. В качестве направляющего вектора прямой можно ваять вектор S = AB {2, 2, 5}. Так как вектор N имеет координаты {I, —3, 1}, то по формуле (3) +s|	| 1-2-3-2+1-5i	1
sin ib —____1 — 1_____________!_____। ________
1^1 И |Л1 4-9+1 F4 + 4 + 25 llJ/'З'’
Ф = arcsin —^-= «= 3°. ыКз
х' 1	и — 9 z 1
448.	Найти точку пересечения прямой —~	- = — — и плос-
кости Зх 5у — z — 2 = 0.
Решение. Приводим уравнения прямой к параметрическому виду, приравнивая к t каждое из трех данных отношений:
х=124-4/, г/ = 9 + 3/, г=1+/.
Подставляем отсюда х, у, г в уравнение плоскости: 3 (12+ 4/)+5 (9 + 3/)-(1 +0-2 = 0, откуда получаем /=—3.
Искомая точка пересечения прямой и плоскости имеет координаты х=12 + 4(—3)=0, г/ = 9 + 3 (—3)=0, г = 1-3 = — 2.
449.	Найти проекцию В точки 4(5, 2, —1) на плоскость
2х-у4-Зг + 23 = О.
Решение. Вектор 7V{2, — 1, 3}, перпендикулярный к данной плоскости, будет направляющим вектором перпендикуляра АВ (рис. 62). Поэтому канонические уравнения этого перпендикуляра имеют вид
х— 5___у — 2_г + 1
~2
Параметрические уравнения прямой АВ:
х = 5 + 2/, y = 2 — t, г = —1+3/.
Подставляя значения х, у, г из этих уравнений в данное уравнение плоскости:
2 (5 + 2/) - (2-/) +3 (-1 +3/) +23 = 0,
найдем /=—2—значение параметра, отвечающее точке В как точке пересечения прямой 4В с данной плоскостью.
Следовательно,
хв =5 + 2 (—2) = 1, г/в =2 —(—2) =4, гв =- 1 +3 (-2) =-7,
т. е. В (1, 4, — 7).
450.	Найти проекцию В точки А (4, 3, 10) на прямую
х— 1 _ у —2 _ г —3 ~2~ ~ 4 ~ “б-'
Решение. Точка В есть точка пересечения данной прямой с перпендикулярной к ней плоскостью, проходящей через точку А. Так как вектор s{2, 4, 5}
127
перпендикулярен этой плоскости, то ее уравнение [см. § 1, формула (2)j
2 (х —4) + 4(у —3)-[-5 (г—10)-=0, т. е. 2*4-4;/4-5г —70=0.
Тем же методом, что и выше, найдем точку пересечения данной прямой с найденной плоскостью: В (3, 6, 8) (проверьте!).
451.	Вычислить угол между прямой у у и плоскостью
6х — Зу 4-2г=0.
452.	Составить уравнения прямой, проходящей через точку Мп(3, —2, 4) перпендикулярно плоскости 5.x 4-Зг/ — 7г 4- 1 =0.
453.	Доказать, что прямая
2х — г/4-5 = 0,
3!_4^S-»"""”b4' + 8’+
4-6г — 3 = 0 параллельны. п		х—13 у— 1	г —4
454.	Показать, что прямая —g— =	— —g— лежит в плоскости
х + 2у — 4г 4-1 = 0.
455.	Найти проекцию точки Л (4,—3, 1) на плоскость х-\-2у— -2-3 = 0.
456.	Найти проекцию точки А (1, 2, 1) на прямую
х + 2 _ у __ г— 1
3 ~ -4 ~ 2 ’
2. Проектирующая плоскость, ями (1), то каждое из равенств
Если прямая задана каноническими уравнени-
х — а у — b	х — а г — с у — b г — с
т ~ п ’ т ~ р ’ п р
(6)
определяет плоскость, проектирующую данную прямую соответственно иа координатную плоскость хОу, xOz, уОг. Если прямая задана общими уравнениями
J Ai*4~ В}у-\- C^z 4-D\ = 0,
I А.,х 4- В^у A- Сгг -|- D^ — О,
то уравнение проектирующей плоскости на хОу получится исключением из этих двух уравнений координаты г. Аналогично, проектируя прямую на плоскость у()г (или хОг), надо исключить координату х (или у).
.у	•• *+3	17—1 г —2
457.	Написать уравнения проекции прямой -у- =	= —-
на плоскость yOz.
Решение. Уравнение плоскости, проектирующей прямую на yOz,
у—\ г —2	о , с п
~—=——• , или у — Зг-)-5 = 0.
Искомая проекция получится в пересечении этой плоскости с плоскостью уО?. (т. е. х = 0), следовательно, искомые уравнения
J У Зг + 5 — 0t I х = 0.
128
458.	Найти уравнение плоскости, проектирующей прямую
J 3,г-г/ + 2г-6 = 0, | л- +/ г + 1 ~ О на плоскость хОу.
Решение. Исключаем из двух данных уравнений координату г, для чего умножаем второе из них на 2 н складываем с первым:
5х-|-7г/-4---=0.
Это и есть уравнение искомой проектирующей плоскости.
459.	Составить уравнения проекции прямой -щ- =	— ~-
на все координатные плоскости.
460.	Найти уравнения плоскостей, проектирующих прямую
( 2х — 4т/ + г — 1 ~ 0,
| 5.г + 8у — Зг 4- 9 = 0
на все координатные плоскости.
найти уравнение проходящей через
3. Плоскость,	проходящая	через
прямую и точку. Пусть даны точка Л-1,, +>, Уо> го) и прямая, заданная урав-х —а	у—Ь	г—с	„ ,
нениями -----= ------—-------. 1 реоуется
т п р
них плоскости. (Разумеется, надо предположить, что точка Л40 не лежит на данной прямой.)
Из уравнений прямой находим, чго прямая определяется точкой Р (а, Ь, с) и направляющим вектором s {in, п, р{ (рис. 63). Пусть М (х, у, г) — произвольная точка плоскости. При любом ее выборе векторы
М„М {.с —.г0, У — Уо, г —г„}, МВР {а—х0, Ь—у0, г —с0} и s (т, п, р{
лежат в одной плоскости, и поэтом}- их смешанное произведение равно нулю:
х-~х0
а—ха
у-Уо г —г0 /> - У» с — г0
= 0.
(7)
т и р
Раскрывая определитель, получим уравнение искомой плоскости в виде (2). Совершенно так же найдем уравнение плоскости, проходящей через две параллельные пли пересекающиеся прямые: на одной из них берется любая точка Л1о (пе лежащая на другой прямой), и плоскость проводится через вторую прямую н точку Л10.
461.	Провести плоскость через прямую	= -др и
точку Л10 (2, 0, 1).
Решение. Убедимся прежде всего, что Л+ па прямой не лежит:
2-1	0+1	14-1
г от-
точка Р (1, —1, —1) лежит па данной прямой, a s {1, 2, — 1} —направляющий вектор этой прямой. Пусть М (х, у, г) —произвольная точка искомой плоскости,
б Кручкович и др.
129
тогда векторы Л10Л4 {х — 2, у, z —1}, планарны. Следовательно,
М0Р{—1, -1, —2) и s {1, 2,
—1} ком-
т. е.
л-2
—1 1
У
-1
9
г — 1
—2
—1
= 0,
1—1 —21	1-1
2 -1 ГН 1
—2
—2
Г.
— 1
1
5 (х —2) —Зу —(г —1) = 0.
Таким образом, искомая плоскость имеет уравнение
5х —Зу —г —9 = 0.
. п	х у г
462.	Провести плоскость через прямую 2 =	= — j и точку
М() (4, -3, 2).
463.	Провести	плоскость через	пару	параллельных	прямых
х — 1   у   г + 2 х + 1   у + 3  г
"г- ~ 3 ~ -Т~ и 2 — 3 ~ Г ’
...	п	х	У — 2	г +1 х + 3	у 2 г
464.	Проверить,	что прямые 0- = — =	—у и —~— —	___ =
пересекаются. Найти уравнение плоскости, в которой они лежат.
4. Смешанные задачи на прямую и плоскость. Рассмотренные выше основные задачи используются в качестве ряда последовательных этапов при решениях более сложных комбинированных задач на прямую и плоскость. Примеры задач такого рода даны в этом пункте.
465.	Через точку А (2, 0, 1) провести прямую, параллельную плоскости 2л' +3//+ 5г ---; 0 и пересекающую прямую -у— =	—
- г —1
2 '
Указание. Для нахождения направляющего вектора s искомой прямой использовать формулы (4) и из § 3 формулы (12). В полученных двух уравнениях на т, п, р одно из этих чисел можно задать произвольно и найти остальные.
466.	Найти точку А, симметричную точке Я (6, —4, —2) относительно плоскости х + у + г — 3 = 0.
Указание. Найти проекцию В точки А на плоскость. Точка В— середина отрезка АА'.
467.	Найти точку А', симметричную точке А (5, 10, 4) отпоси-., х—1	у—2	г —3
тельно прямой =	
Указание. Проекция точки А на прямую есть середина отрезка АА'.
468.	Найти точку А', симметричную точке А (3, —1, 4) относительно прямой
J 2х — 2(/ +z — 3 = 0,
1 2х + У - 2z 4-3 = 0.
469.	Составить канонические уравнения перпендикуляра, опу-
л /г о	хА-2 р—1 г
щеииого из точки А (5, 3, 1) на прямую -4— —	_ = □ •
1	Z	О
130
Указание. Искомый перпендикуляр определяется точками Л и В, где В — проекция точки А на данную прямую.
470.	Составить уравнение перпендикуляра, опущенного из начала х—5w — 2г-|-1
координат на прямую = —- =
471.	Составить уравнения прямой, проходящей через точку
А (4, 0, —1) и пересекающей две данные прямые	= —д—
х	у — 2	г + 1
и 5 ~ -1 ~ “2“'
Указание. Используя условия пересечения искомой прямой с каждой из данных, получим два уравнения, наложенных на координаты направляющего вектора s; задавая одну из его координат произвольно, найдем из этих уравнений остальные две координаты.
472.	Найти уравнение плоскости, проектирующей прямую
х — 2 у — 3	2 -р 1	I 1 О 1 *7 п
-g— = ~на плоскость х + Ay — 3z-p 7 = 0.
Указание. Вектор N, перпендикулярный данной плоскости, и направляющий вектор s данной прямой параллельны искомой плоскости.
473.	Найти канонические уравнения проекции прямой * =
=	= ^~ на плоскость х —	4-8 = 0.
Указание. Найти проектирующую плоскость (см. 472) и рассмотреть ее совместно с данной плоскостью.
474.	Найти уравнение плоскости, проходящей через прямую х—1	I/ + 2	г	.. х+1 у— 2 г —2
—я— =	параллельно прямой -Д— =	= —— .
Z	1 о	£	о	—о
§ 4. ПОВЕРХНОСТИ
1. Цилиндрические поверхности. Поверхность, описываемая прямой, остающейся параллельной некоторой данной прямой I и пересекающей данную линию L, называется цилиндрической поверхностью. Линия L называется ее направляющей,
а каждое положение движущейся прямой — образующей. Всегда можно выбрать систему координат так, чтобы прямая / совпадала с одной из координатных осей. Уравнение цилиндрической поверхности (рис. 64) с образующими, параллельными оси Ог, не содержит г, т. е. имеет вид
у) = 0.	(1)
Уравнение цилиндрической поверхности, образующие которой параллельны оси Оу или оси Ох, имеет вид
F(x, z) = 0,	(2)
или соответственно
F(y, г)=0.	(3)
б*
131
В качестве направляющей L поверхности (1) можно взять ее линию пересечения с плоскостью хОу. Уравнения этой
направляющей
L ( Нх, у) = о, I г = 0.
2
Рис. 65
Аналогично, направляющими цилиндрических поверхностей (2) п (3) являются линии
, ( F (х, г) —О, ( Г (у, г) —О, I у = 0	I х = 0
Если уравнение (1) является алгебраическим уравнением второй степени, то соответствующая цилиндрическая поверхность называется цилиндром второго порядка. На рис. 65, 66, 67 изображены эллиптический, гиперболически!! и параболический цилиндры, заданные* своими каноническими уравнениями:
tfi
г/'“^2рх.
Возможен также случай, когда уравнение (1) распадается на два линейных множшеля. В этом случае соответствующий цилиндр состоит из пары плоскостей, параллельных оси ()г.
Пусть в пространстве задана линия L как пересечение двух поверхностей L [ О(х, у, г) —О, i А2 (х, у, z) - 0.
Исключая координату г, получим уравнение вида
Ф (.V, //) —0, которое определяет цилиндрическую поверхность, проектирующую линию L на плоскость хОу. Аналогично, чтобы получить уравнение цилиндра, проекти
132
рующего линию L на плоскость хОг (или уОг), надо из уравнений (4) исключить координату у (или х).
475.	Какую поверхность определяет уравнение х2 + у2 = 2ах?
Решение. Поскольку данное уравнение не содержит г, то рассматриваемая поверхность является цилиндром с образующими, параллельными оси Ог. Направляющая этого цилиндра
( х'- + у“=2ал-,	( (х — ау + у2^^,
<	или !
I г-0,	( г-0
является окружностью с центром на оси Ох в точке (</, 0, 0) и радиусом R — 'a.
Итак, данное уравнение определяет круговой цилиндр, ось которого идет по прямой х — а, у~0.
476.	Установить вид поверхности, заданной уравнением
z2 + ‘2z~4x+ 1 = 0.
Решение. Zlaimoe уравнение не содержит у, поэтому рассматриваемая поверхность есть цилиндр с образующими, параллельными оси Оу. Его направляющая
( г22z — 4х1 = 0,	( (г1 )24х
<	пли <
I //=0	I г/ = 0
есть парабола иа плоскости хОг с вершиной в точке (0, 0, - 1), направленная в положи юльную сторону оси Ох.
Таким образом, рассматриваемая поверхность является параболическим цилиндром.
477.	Какую поверхность определяет уравнение
9z/2 - 16г2 + 64г - 18у - 199 = 0?
Решен не. Эта поверхность сеть гиперболический цилиндр с образующими, параллельными оси Ох. В самом деле, данное уравнение не содержит х, а направляющая цилиндра сеть гипербола
( !)г/2 — 16г2 64г — 18у — 199—0,	( (у~ - .(г~2^.= 1
!	или ’Io 9
I х = 0,	1
1 х=0
с центром в точке (0, 1, 2) и действительной осью, параллельной оси Оу.
478.	Какую поверхность определяет уравнение -^3—	= 0?
Решение. Левая чисть данного уравнения распадается на произведение двух линейных множи гелей
: х	У 1 х । У
'( а	b ; \ а b !
Следовательно, оно определяет пару плоскостей
пересекающихся по оси Ог.
479.	Линия L задана уравнениями x2 + z2 = /?2, у2 + z2 = г2 (R > г). Найти проекцию этой линии на плоскость хОу.
Ре нт с и не. Данная линия L представляет собой линию пересечения двух круговых цилиндров радиусов R и г. Ось Оу является осью первого из них,
133
ось Ох —второго. Чтобы получить уравнение цилиндра, проектирующего линию L на плоскость хОу, исключаем из двух данных уравнений координату г. Вычитаем из первого уравнения второе и обозначаем R2— г2 через а2:
х2 — у2 = а2.
Это есть уравнение гиперболического цилиндра, и, следовательно, проекцией линии L на плоскость хОу является равносторонняя гипербола
Какие поверхности определяются следующими уравнениями (сделать чертеж):
480.	х2 + г2==9.	484.	xz = 2.
481.	16z/2	_ 25г2 = 400.	485.	г2 + 4г - 2х + 6	= 0.
482.	у2 =	- 6г.	486.	4х2 + 9//2 - 8х	+	36г/ + 4 = 0.
483.	х2 =	г2.	487.	х2 + г/2 = 4г/.
488.	Найти проекцию на плоскость хОу линии L\
( 9у2 — бху — 2xz + 24х — 9у 4- Зг — 63 = 0,
( 2х — Зу + г — 9 = 0.
489.	Составить уравнение кругового цилиндра, ось которого параллельна оси Оу и проходит через точку Р(1, 2, —1), а радиус равен 3.
490.	Какую линию в пространстве определяет система уравнений х2 + у2 = 9, х — г = 0?
2.	Канонические уравнения поверхностей второго порядка. Поверхность второго порядка задается в декартовых координатах уравнением второй степени
Ах2 + By2 + С г2 + 2Dxy + 2Еху +	+ 26х + 2/Л/ + 2Кг + L = 0.	(4)
За счет выбора специальной системы координат это уравнение преобразуется к простейшему (каноническому) виду.
Кроме рассмотренных в п. 1 цилиндров второго порядка к поверхностям второго порядка принадлежат также (указаны простейшие уравнения) следующие:
сфера х2-'Гу2 —
д;2	g2
эллипсоид (рис. 68) - „ +	,= 1;
' а2 Ь2, с2
х2	w2	г2
двуполостный гиперболоид (рис. 69) ———_с=— 1;
^2	^«2	^2
однополостный гиперболоид (рис. 70)	---
х2 у2	г2
конус (рис. 71) -2- + -fc2--С2 =°;
X2 у2
эллиптический параболоид (рис. 72) —2- + -^2 =2г;
х2 у2 гиперболический параболоид (рис. 73)	— -2 =2г;
пара плоскостей, когда левая часть уравнения (4) распадается на два линейных множителя.
3.	Сфера. Общее уравнение сферы получается из (4) при А = В— С
D = E — F = 0:
Ах2 + А у2 + A z2 + 2Gx+2 Ну + 2/<г + L=0.
134
Рис. 73
Рис. 72
Делением на коэффициент А и выделением полных квадратов по х, у, 2, оно приводится к виду
(Л- - ау + (у - /ф Щ (г - Л ,= R2,	(5)
где R — радиус сферы, а (а, Ь, с) - -координаты центра.
В частности, простейшее уравнение сферы х2 ф-у- ф- г- = R'2 получается в том случае, когда начало координат находится в центре сферы.
491.	Сфера проходит через точку М( — 2, 3, 6), а ее центр находится в начале координат. Составить уравнение сферы.
Решение. Радиус сферы равен длине вектора ОМ { — 2, 3, 6}. Следовательно,
R = |/Л4 + 9Л 36 = И 49 = 7.
По формуле (5) находим искомое уравнение при а = Ь — с — О №-|-y2+?2 'С.
492.	Сфера с центром в точке С(1, — 2, 4) касается плоскости 2х — z/ + 2z — 3 = 0. Составить уравнение сферы.
Решение. Радиус сферы равен расстоянию центра С до касательной плоскости. По формуле (11) § 1 имеем
R 12-1~ЛлФН:2-4-3| = 9 = 3 |'4-|-1Д-4	3
По формуле (5) находим уравнение сферы
(.V- 1)'2 + (,Н-2)2 р(г-4)2 = 9.
493.	Найти центр и радиус сферы, заданной уравнением
2х'2 -1- 2z/« ф- 2г2 - 8г/ 4- 2г 4- -<*- - 0.
Решение. Разделим уравнение на 2 и выделим полные квадраты:
*2 + Л-4у-Н)4-СЧ-гф -]	। .; + Y = °,
пли
/	1 \2
x2 + (//-24 + i г-|- 2 I —4.
Сравнивая это уравнение с (5), найдем центр аферы С । 0, 2, — и ее радиус /?--2.
494.	Сфера проходит через точку М (4, 2, 2) и имеет центр в точке C(l, — I, — I). Составить ее уравнение.
495.	Сфера с центром в точке С (0, 4, 0) касается плоскости 2л" бу — Зг — 3 0. Составить уравнение сферы.
496.	Составить уравнение сферы, если известно, что точки Л (2, 5, —7) и /3(6, —I, 3) —концы одного из ее диаметров.
497.	Составить уравнение сферы радиуса R =9, проходящей через точки Л41(1, —2, —I), Л42( — 5, 10, —1), Л43( —8, —2, 2).
Указан и е. В уравнение (5) с данным радиусом подставить по очереди координаты трех точек. Из полученных трех уравнений определяются координаты центра (а, Ь, с).
136
498.	Найти центр и радиус сферы, заданной уравнением
л2 + у2 ф- г2 — 2х ф- 4у — 4г — 7 — 0.
4. Метод параллельных сечений. Если задано уравнение той или иной поверхности, то возникает задача исследования ее формы и расположения относительно координатных осей. Для решения этой задачи обычно применяют метод параллельных сечений, который состоит в том, что поверхность пересекается несколькими плоскостями, параллельными плоскостям координат. Форма и размеры полученных сечений пошоляют выяснить форму самой поверхности.
г-2	^2
499.	Исследовать сечения эллипсоида 36 + ']б + ~д =1 плоскостями г —0, ikl, И: 2, ±3, х = 0 и у = 0.
Решение. Рассмотрим сначала сечение эллипсоида плоскостями г = /г, где /г = 0, е 1, ь 2, У 3. Подставляя в уравнение эллипсоида, получим
отсюда
Л+ +
36	16 Г 9
ИЛ" 36
/Р .
9 ’
ffi
16
Вводя обозначения
получается эллипс
/Р
9 ’
Ь,:.
и-
д-, видим, что в сечении

(2
с + ah
г = 0
bh
с полуосями Л/г и Ь^. При Л —0, J: I, J. 2, ± 3 получаем:
6о = 4, 6, | = 4	= -| Г2 ^3,8,
2 = 4 У I’ = I К5” ~ ЗД Ь 13 = °’
Таким образом, наибольший эллипс получается в сечении плоскостью хОу. Если поднимать или опускать эту плоскость вдоль осп Ог параллельно плоскости хОу, то размеры сечений уменьшаются до тех пор, пока при г — J- 3 не превратятся в точку (0, 0, ± 3). При дальнейшем увеличении h плоскость эллипсоида пересекать уже не будет, так как корень, входящий в выражения для ah н станет мнимым.
В сечении плоскостями, параллельными хОг и уОг, будут также получаться эллипсы. В частности, в сечении координатными плоскостями у — 0 и х — 0 получатся наибольшие по размерам эллипсы
) 36	9	’ и J 16	9
| у —0	] х = 0.
Проведенное исследование позволяет етела1ь вывод, что эллипсоид является Овальной поверхностью (см. рис. 68).
137
500.	Исследовать форму и расположение относительно системы координат поверхности 4 —г = х2 + у2.
Решение. Применим метод сечений. Полагая в данном уравнении г =/г, получим
Х2_|_г/2 = 4_/г.
Отсюда следует, что 4 — h должно быть величиной неотрицательной. Обозначая 4 — /г = 7?2, получим в сечении плоскостью г = h линию
х2 + У2 = 7?2, 2 = h.
Эта линия, очевидно, является окружностью радиуса R с центром на оси Ог. Следовательно, данная поверхность является поверхностью вращения вокруг оси Ог. Чтобы выяснить, вращением какой линии она получается, пересечем поверхность плоскостью х = 0. В сечении получится парабола на плоскости уОг-.
у2 = 4 — г, х = 0.
Вершина ее лежит в точке (0, 0, 4), а направлена парабола в отрицательную сторону оси Ог.
Таким образом, исследуемая поверхность является параболоидом вращения, расположение которого показано на рис. 74.
501.	Показать, что уравнение
х2 и2 г2
~-----+ --2~ = 1 определяет однополо-
стями гиперболоид вращения вокруг оси Оу.
Решение. Рассмотрим сечение перпендикулярными оси Оу. В сечении
данной поверхности получим линию
плоскостями у = h,
= y = h, Где R = ~ Vb2 + h2.
Таким образом, в любом сечении, перпендикулярном осп Оу, получается окружность радиуса R, т. е. данная поверхность есть поверхность вращения
вокруг оси Оу. Осталось выяснить, вращением какой линии получена эта поверхность. Пересечем поверхность какой-либо плоскостью, проходящей через ось вращения, например плоскостью хОу. В сечении получится линия
Это есть гипербола с полуосями а, Ь. Вращаясь вокруг оси Оу, она и образует данную
вращения вокруг оси Оу (рис. 75).
поверхность, являющуюся поэтому одпополостным гиперболоидом
502.	Доказать, что уравнение г = f (x2 + у2) определяет некоторую поверхность вращения вокруг оси Ог.
138
Решение. Пусть <р —обратная функция для функции ft тогда заданное уравнение можно записать так:
x2 + */2 = <f (г).
Пересечем поверхность, определяемую этим уравнением, плоскостью г = Л, в сечении получится линия
х2 + г/2 = (р (А), г = /г.
Это есть окружность радиуса й=/<р(Л) [разумеется, для тех значений А, для которых <р (А) > 0, в противном случае плоскость г = А поверхности не пересекает, так как в сечении получится мнимое уравнение].
Итак, в сечениях плоскостями, перпендикулярными осн Ог, могут получаться только окружности, т. е. данная поверхность является поверхностью вращения вокруг оси Ог. Она получена вращением линии
z = f(x2), у=0, лежащей в плоскости хОг.
Методом сечений исследовать форму и расположение относительно системы координат следующих поверхностей (сделать чертеж);
503.	4 +4” Г = 1'	508- + + //2 = 2(г-1)2.
504.	-р + 4 ” 4 = ~ L	509. 2t/2 + z2 = 1 — х.
//2
505.	4 +	=«•	510. 3х2-у2~г2-3.
506.	4 + 4 = 2г-	511. х2-2г/2 + г2 = 1.
507.	х2 — z/2 = 2г.
512.	Показать, что если в каноническом уравнении эллипсоида (см. рис. 68) а = Ь, то это эллипсоид вращения вокруг оси Ог. Какой эллипсоид получится при а = с, Ь — с, а = Ь = с?
513.	Показать, что если в канонических уравнениях гиперболоидов (см. рис. 69, 70) а =-Ь, то это гиперболоиды вращения вокруг оси Ог.
514.	Показать, что если в каноническом уравнении параболоида (см. рис. 72) а = Ь, то это параболоид вращения вокруг оси Ог.
515.	Показать, что уравнение г2 = k2 (х2 + у2) определяет конус вращения вокруг оси Ог. Какой геометрический смысл имеет параметр /г?
516.	Установить вид поверхности, заданной уравнением;
. 1 а) г = -5—j—5, ' х2 + (/2’
б) х2 + у2 = sin2z.
Указание. См. 502.
5. Другие задачи. В случае, когда в уравнении (1) отсутствуют члены с произведениями координат (D = E = Е = 0), это уравнение приводится к каноническому виду выделением полных квадратов по х, у, г и параллельным переносом осей координат совершенно аналогично тому, как это указывалось для линий второго порядка (см. гл. I, § 4, п. 1).
Точки пересечения прямой с поверхностью второго порядка ищутся следующим образом: уравнения прямой приводятся к параметрическому виду
x = a-\-mt, y==b-\-nt,
139
затем значения х, у, z подставляют в уравнение поверхности. Из полученного квадратного уравнения для t находят значения параметра t, отвечающие точкам пересечения. Если корпн этого уравнения совпали, то прямая является касательной к поверхности, если корпи мнимые — точек пересечения пет.
517.	Какую поверхность определяет уравнение
2/2 - у2 + 2г2 + 4х 2у + 8г +1 = О?
Решение. Чтобы привести данное уравнение к каноническому виду, выделяем полные квадраты по х, у, г:
2 (л-’- -У 2х - 1) - 2 - (tf- - 2у + 1) + 1 - У 2 (г2 + 44) - 8 1 = О,
2 (л- + I )2 -(у-1 )2 2 (г + 2)-’ - 8; отсюда
_ (У-1)2 , (f±2)l _ 1 4	8 г 4	' '
Сравнивая полученное уравнение с каноническими уравнениями, видим, что что есть уравнение одцополоетного гиперболоида, центр которого смещен в точку О'(—1, I, —2). При помощи обозначений
X ----- А- + 1, Y -у—\, Z-z-l-2,
приведем уравнение к вид}'
Новые оси О'Х, O'Y, 0'7. параллельны старым. Относительно этих осей гиперболоид имеет вид, представленный на рис. 70 е заменой оси О: на ОТ, а оси Оу на OZ. По так как а --с = 2, то это однополостиый гиперболоид вращения вокруг оси ОТ.
518.	Найти точки пересечения эллипсоида ,v2 + 2у2 4г3 — 2 с прямой -~р =-= ‘ при а—-—. При каком значении а прямая касается эллипсоида?
Решение. Запишем параметрические уравнения данной прямой:
а = 1 +1, у — 1 + /, г --- ut.
Подставляя значения л', у, z в уравнение эллипсоида
(1НТ)2 + 2(1+/)2 + 4оТ2=-2,
получим квадратное уравнение для V.
(3-[-4Т) C~ + 6Z + 1=0,
из которого находим значения параметра t, отвечающие точкам пересечения прямой с эллипсоидом:
— 3 Ч 1'(Ё^’4Т
Z”~	3 + 4d2
тТ	1
При а = ~_ получатся два значения: 4 =—1, Л ——-^.Следовательно,
точки пересечения следующие:
1'2	i+
4=1 — 1=0, r/L=l — 1=0, ?( = —(—1)= —-g-;
ЛЦО, 0, -- b-'-j ,
140
14	_ i _ 4	, _ 12 / П I 2 .
5 ~ 5 ’ !/2==1	5"5'	' 2	5;r IO'
Если прямая касается эллипсоида, то должно быть — а это произойдет в том случае, если подкоренное выражение 6 — 4о2 равно нулю. Следовательно, при о । |	-g- прямая является касательной.
Какие поверхности определяются уравнениями:
519.	2х2 + у2 + 2г2 - 4х + 4у 4- 4г 4- 7 -= 0.
520.	х2 - бу2 + Зг2 4- 8х 4- 12// 4- 1 = 0.
521.	х2 4~ У2, + 2х — 2у — 2г — 2 -= 0.
_	х-4	р-|-6 z-p2
522.	В каких точках прямая	—Цу пересекает эллип-
ЛГ"' tf~“ и,*	< »-.
соид 12 . , -1?
г- л О V)	х 4	у ~р 3 4- 2
523.	В каких точках прямая	пересекает одно-
№	г/2 г2
подостный гиперболоид 1G+ g 4 = 1?
524.	Доказать, что прямая * ---=лежит на гиперболи-г-	л'2 ч3
ческом параболоиде g —4 =2.
Указание. Надо показать, что при любом значении t параметрические уравнения прямой удовлетворяют уравнению данной поверхности.
525.	Найти проекцию на плоскость хОу линии пересечения эллип-
V2 Z/2	£2
соида j64- 4 4- j = 1 и плоскости x-J-4z — 4 — 0.
У к а з а н и е. См. п. 1
52G. Наити точки пересечения прямой =	и сфе-
ры х2 4- Уг 4- г'г + 4х — ‘2у 4“ 10г — 19 — 0.
527. При каком значении а прямая ~ = Д касается сферы х2 4~У2 + г2 — 2* + 22 + 1 — Найти точку касания.
ГЛАВА IV
ВВЕДЕНИЕ В АНАЛИЗ
§ 1.	ПОНЯТИЕ ФУНКЦИИ
1.	Определения. Переменная величина у называется функцией независимой переменной величины (аргумента) х на множестве М, если каждому значению х из множества М поставлено в соответствие одно определенное значение у. Если у есть функция от х, то пишут // = ( (х), или у = 1: (х), или y — Y (х) и т. д. Символом f (ci) обозначается частное значение функции y = f (х), т. е. то значение, которое принимает функция y—f (х) при х = а. Множество М называется областью определения функции. Очень часто при задании функции аналитическим выражением y = f(x) область определения этой функции не указывается. В таком случае под областью определения функции понимают область существования аналитического выражения y~f(x), т. е. множество значений аргумента х, для которых аналитическое выражение р = /(х) имеет определенное конечное значение.
Почти все функции, с которыми мы будем иметь дело, имеют в качестве области определения либо один интервал (а, Ь), т. е. совокупность всех точек х, удовлетворяющих неравенствам а<х<Ь, либо несколько или даже бесконечное множество таких интервалов.
Интервал может быть и бесконечным, когда область определения функции является полуосью ( — со, а) или (Ь, -|-оо), или всей числовой осью ( — ос, +со). В ряде случаев области определения принадлежат и концы интервала, один или оба вместе. В последнем случае интервал называют замкнутым и обозначают [а, 6]. Замкнутый интервал иногда называют отрезком.
Функция г/ = /(х) называется чанной, если /(—x) = f(x). Например, функции y = xi, r/ = sin2x, у— |'х2 (-1 , z/ = cosx являются четными.
Функция у=-ф (х) называется нечетной, если f (— х) = — / (х). Например, функции у = х, r/ = tgx, у = | х3 являются нечетными.
Функция р = /(х) называется периодической, если существует такое положительное число Т (период функции), что при любом значении х выполняется равенство
/(хЧ-Т)=/(х).
Например, функция i/ = cosx является периодической с периодом 2л, функция p = sin 2х имеет период л.
Функция г/ = /?(х) называется сложной, если ее можно представить в виде г/ = /(ср(х)), где f (и) — функция промежуточного аргумента и, a f (ср (х)) означает что на место и ставится функция ср (х). Например, y-l sin х — сложная функция, состоящая из двух звеньев: у=\/ и , u = sinx. Подобным же образом определяется сложная функция, состоящая из большего числа звеньев. Например, у= Ig2(x4~l)— сложная функция, составленная из трех звеньев: у = иг, u = lgv, о = х-ф-1.
2.	Элементарные функции. Основными элементарными функциями являются:
1)	степенная функция у = ха. Ее область определения включает в себя при любом а всю положительную полуось (О, 4-оо). Точка х = 0 включается в область определения при </= О и исключается при а < 0. Отрицательная полуось ( — со, 0)
(	А 1 О	1	1
в одних случаях например, при /i = 0, ± 1, ± 2, ...; п= -± -- ±и т. д. : \	3’5
входит в область определения, а в других не входит (например, для функций y = V х, у=\'гх и т. д.).
142
2)	Показательная функция у — ах(а>0, </ /= 1). Область определения—вся числовая ось (— со,	со).
3)	Логарифмическая функция у = log,, х (а > 0, а=£ 1). Область определения — (О, + ос). Заметим, что десятичный логарифм (л=10) обозначается y=--lgx.
4)	Тригонометрические функции. Функции r/ = sfn х, y = cosx имеют область определения (—со, -ф сс), y = tgx— область определения содержит все х, кроме п
х = (2/г-ф 1) - где /г —любое целое число, у — etg х — область определения содержит все х, кроме х = 1гл, где k — любое целое число.
5)	Обратные тригонометрические функции. Для функций у ~ arcsin х и // arccos.’c область определения [ — 1, -|-1], r/=arctg.v, у = arcctgх — (—со, -ф л ).
Функция y = f(x) называется элем’нпшрной, если правая часть аналитического выражения г/ = /(х) составлена из основных элементарных функций е помощью применения конечного числа четырех арифметических действий и взятия функции от функции.
528.	Найти /(0), /(—.г),	если f (х) = /1 -фх2.
Решение. Имеем:
f (0)-= И -фО2 - Г 1 — 1; /(-х)=--Г1+(-л-)2^|/^1+.О;
529.	Показать, что f(x) + f (у) = f (pfj) > еслн / W = lg •
Решение.
Найдем f (у) и f
%+у\.
1+ ху) ‘

Далее, найдем f (х) -фf (у):
х + У
1 +xij х + у \^ху
р ' + Д/ Ф~ х -Р у ’ 1 + ху — X — у*
г , , । г / \	, 1 ' ф X .	1 - ф1)	, / 1 -ф X 1 -ф у\ ,
t (.V)+f (у) ~ 1g 1Л+о ;	-' i .v '1,!-
1 Л.	1 U	\ 1 Л. 1	4/ j
Сравнивая выражения, полученные для f (х)-ф/(у) и /I
действительно, f (х) ф-f (у) =f I у .
\а г ху/
1 -\-x~\-y-\-xy
1 —х — у-\-ху'
х-\-у \ 1 +ху)
видим, чго,
530.	Найти область определения функции у = ]/х2-ф2.
Решение. Выражение х2-|-2 при любом значении х положительно, поэтому извлечение корня квадратного возможно при любом значении х- Следовательно, областью определения данной функции будет вся числовая ось (--со, -фас).
531.	Найти область определения функции у~)/ 6х — х2 — 5.
Решение. Очевидно, должно выполняться неравенство бх— х- — 5 ф-0, преобразуя которое, получаем (л- — 1) (х — 5)-ос0. Последнее неравенство выполняется,
, .г 1	0.	( л- t 0,
если _ пли {
I. х — 5	0	( х — 5 -?_-0.
Из первой системы неравенств получаем
х 4s 1, х р 5, откуда 1 -гф х сс 5.
143
Из второй системы неравенств получаем х и х5, т. е. несовместимую систему.
Следовательно, областью определения данной функции будет отрезок [1; 5]-
532.	Найти область определения функции у = —2—t-----------т.
X*4 — ОХ — 4
Решение. Необходимо неравенство х2 —Зх —4 + 0, или (х |-1) (х—4) + 0.
Отсюда следует, что х+—1 и х + 4.
Следовательно, областью определения данной функции будет совокупность интервалов (—оо, —1) (—1, 4) (4, со).
533.	Найти область определения функции у = Igsin (х — 3).
Решение. Чтобы логарифм имел смысл, должно выполняться неравенство sin (х — 3) > 0. Синус положителен в I и II четвертях и имеет период 2л, поэтому последнее неравенство может быть записано в виде
2пп < х —3 < (2« + 1) л, где п = 0, ±1, ± 2, ... , или
2/ш + З < х < (2п +1) л + 3, где п = 0, т_ 1, ±2,...
Следовательно, областью определения данной функции будет совокупность интервалов
(2ЛЛ-1-3, (2«+1) л + 3), где /1 = 0, ±1, +2, ... х___________________________________________________о
534.	Найти область определения функции у = arccos .
Решение. Данная функция определена, если
Умножим все части неравенства на 2х. При этом в случае х>0 получаем
2л л 2	<’х,
а когда х < 0, то
— 2х у х— 2 У=г 2х.
Первые из этих неравенств можно представить в виде систем
Г :’v л 2. j — Зх 2,	| х 1 ,
;	или <	пли J з
1х-2т=2х,	( — х + 2,	|	_
откуда х уа -- .
Вторые неравенства можно представить в виде систем
откуда х--'. —2.
Следовательно, областью определения данной функции будет совокупность двух бесконечных интервалов (— сю, —2] | “ , + со j.
3 / г~
535. Нанги область определения функции y — Vx-}-l/ —— — -Is(2x--3).
144
X. Решение. Найдем область определения каждого слагаемого в отдельности, у Общая часть этих областей определения будет областью определения данной функции. Первое слагаемое определено на бесконечном интервале [О, ф-сс).
У Для второго слагаемого необходимо выполнение неравенства х — 2	0 или х ф- 2.
Следовательно, оно определено па совокупности двух бесконечных интервалов J (— оэ, 2) (2, +ст). Для третьего слагаемого необходимо выполнение неравенства
3	I 3	'
’ 2х— 3 > 0, или х > ф, ; его область определения — бесконечный интервал (, + ccj. Ф Сравнивая результаты, видим, что общей частью грех областей определения / 3	\
- будет совокупность интервалов - 2 I (2, + со).
д.		\	/
536.	Доказать, что произведение двух четных функций есть функция четная.
Решение. Пусть f (х) и гр (т) — четные функции. Тогда ) (— х) = f (х) и ср ( — Л') = гр(т). Отсюда, если f (х) tp (х) = F (х), то F ( —х) —f ( —х) ф ( —х) = — / (х) q-(х).	'
Следовательно, г (x) ~f (х) ф (х) — функция четная.
537.	Найти ср (х) = у [/ (х) -ф f ( — х)], если [ (х) = 2xi — Зх3 — 5ха -ф -j- 6х — 10.
538.	Найти П-2), /(-1), f (О'). /(3), если f (х) = х« - 2х'2 + 6х - 7.
539.	Найти /(0), /(-х), /(х-ф1), /(х) + 1,	если
540.	Найти /(1), [ (Ю), если f (х) == arccos (lg х).
541.	Найти [ (х), если f (х -ф 1) = х2 — Зх -ф 2.
542.	Показать, что f (х -ф 3) — 3[ (х -ф 2) -ф 3f (х -ф 1) — f (х) = 0, если f (х) = <7Х2 -ф Ьх -ф с.
543.	Показать, что f (х +у) + f (х — у) = 2f (х) f (у), если / (х) = = l(av + a-v) (а>0).
Найти область определен
544.	у= s V+5.
545.	у=-]' 2-Н х —х2.
546.	у =
фх-i—16'
54/.	____
548. у^У 1g
554. Доказать, что произ: четная.
555. Доказать, чго ирон есть функция нечетная.
1я следующих функций:
1
549.	y = 2i~x.
550.	у == ]/sin х.
551.	(/=arcsin~.
552.	у --х — arctgx.
553.	у arcsin —— lg (4 - х).
едение нечетных функций есть функция
зведение четной функции на нечетную
145
556.	Выяснить, какие из следующих функций являются четными и какие нечетными:
а)	= (ех + е'х), в) /(Ar) = lg|±~,
б)	f (х) =	г) f (х) = Г(1-2х)2.
557.	Определить, какие из перечисленных функций являются периодическими, и найти их период:
а)	/(х) = 2 sin 4х,	в) f (х) = 3cosix,
б)	/(х) =]/ctgx,	г) f (х) ==sin | х.
§ 2. ГРАФИКИ ФУНКЦИЙ
1-	Непосредственное построение графиков. Графиком функции y — f(x) называется геометрическое место точек Л1 (х, / (х)). Отметим, что i ргтфни четной функции (/ (д) —/ (—л,)) симметричен относительно оси ординат (рис. 76); график
Рис. 76
печений! функции (/ (х) ——f (—х)) (рис. 77); при построении графика ее график на любом отрезке длины
симметричен относительно начала координат периодической функции с периодом Г строят Т, а затем, пользуясь периодичностью, продолжают на всю числовую ось (рис. 78).
Две функции y--f(x) и р = <р(х) называются взаимно обратными, если для каждой пары значений а (. Ь, удовлетворяющих условию /> = / («), выполнено также условие а=ср(6) и, наоборот, для пары значений а и Ь, удовлетворяющих условию а = ф(6), выполнено условие /? = /(«). Одна из двух взаимно обратных функции (любая) может быть названа прямой, тогда другая функция называется
146
 обратной по отношению к первой. Например, функции
у-----а'' и p = logox, у -- sin х и p = Arcsinx, у = х3 и у=ргх
являются взаимно обратными. Графики взаимно обратных функций симметричны относительно биссектрисы I и Ш координатных углов (рис. 79, SO, 91).
В том случае, когда прямая функция не является монотонной, обратная функция неоднозначна. Сравните рис, 79 и 80, 91. Для многозначных функций вводится понятие однозначной ветви многозначной функции. Так, например: 1) функция p = arcsinx является однозначной ветвью функции r/ = Arcsinx (на рис. 91 функция p=arcsinx выделена жирной линией); 2) функция, обратная к функции у = х2, имеет две однозначные ветви: у = j/% и у=—^'х (Рис- 80).
Для построения графиков функций важно знать общий вид и расположение графиков основных элементарных функций, известных из школьного курса математики. Примеры графиков степенной функции при некоторых значениях показателя а даны на рис. 81, 82, 83, 84, 85. На рис. 86, 87, 88, 89 показан вид графиков показательной и логарифмической функций. Графики тригонометрических и обратных тригонометрических функций изображены на рис. 90, 91, 92, 93.
147
Рис. 84
Рис. 93
Общая схема построения графиков функции с использованием дифференциального исчисления будет даиа ниже, в гл. V!. Сейчас же будут рассмотрены те графики, построение которых основано на непосредственном исследовании функции и на применении методов аналитической геометрии (параллельный перенос, растяжение или сжатие).
К непосредственному построению графиков относятся известный из школы способ построения графика «по точкам», применение графиков основных элементарных функций, использование той или иной симметрии графика или его периодичности (если, разумеется, таковые имеются), графическое сложение графиков данных функций и другие приемы, непосредственно вытекающие из определения функции. Конечно, нужно использовать также известные из аналитической геометрии сведения о линиях первого и
второго порядка.
558. Построить график функции у = х3 — Зх.
Решение. Заметим, прежде всего, что эта функция нечетная, так что ее график симметричен относительно начала координат. Ограничиваясь неотрицательными значениями аргумента х, строим таблицу значений функции, придавая х ряд зпаче-, 1 ним через интервал п = -
Таблица 2
*1° 4 1 42 4 3
И0-1 1 ~2 -1 S’ 2 8 8 18
Рис. 94
По этим данным строим несколько точек графика (до х = 2); соединяя их плавной линией, получим вид графика на отрезке от 0 до 2. Из табл. 2 видно, что после х — 2 функция очень быстро растет. Следовательно, ее график круто уходит вверх. Используя симметрию относительно начала 0, строим график для отрицательных значений х (рис. 94).
559. Построить график функции у = \[(х)\ по известному графику функции y = f(x).
Реше и и е. По определению модуля, шла 1=3 Дх), если Дх):==0, I' W i |f (х), если (х) < 0;
поэтому там, где / (х) ; . О, т. е. где график функции // = Дх) лежит выше оси Ох, график функции y=\f(x)\ совпадает с графиком </ = Дх). Так как точки (х, —у) и (х, у) симметрично расположены относительно оси Ох, то для получения графика | f (х) | в случае f (х) < 0 надо график у==[ (х) симметрично отразить относительно оси Ох, или, что то же, повернуть его па 180° вокруг этой оси. В качестве примера па рис. 95 показано построение графика функции f/ = |logax| по графику // = log„x.
151
560.	Построить график функции у =
Решение. Нетрудно убедиться, что эта функция четная, так что достаточно построить ее график для неотрицательных х, остальная часть графика получится симметрированием относительно осп Оу.
В данном случае прибегать к построению по случайно выбранным точкам нецелесообразно. Надо использовать колебательный характер синусоиды. Поскольку — 1 < sin х tg 1, то-*-sg-5^--s£. -“• Следовательно, график данной функции
все время заключен между графиками у ——и (см. 124), а так как синусоида колеблется от —1 до -ф 1, то с увеличением х график функции у = —х , 1 1 - , , колеолется между графиками —и - - . Это и позволяет нарисовать общий вид искомого графика при х > 0 (рис. 96). Получилась картина затухающих
колебаний.
значениях
В теории пределов несколько позже будет показано, что при малых sin х ,	_
аргумента х значения------ олизки к единице. Это отражено стрелоч-
кой на рис. 96. Для уточнения
рисунка
полезно
заметить, что при
-ф2йл(й —0, 1, 2, ...) искомый график касается графика функции //	, а при
Зл	1
х — ,' - + 2А'П — графика функции </ — — —, в точках же №Л, 2л, Зл, ... он пересекает ось Ох.
561.	Символом [х] обозначается целая часть числа х, т. е. наибольшее целое число, не превосходящее х. Построим график функции у=ф].
152
Решение. По определению целой части имеем:
4, если х изменяется в пределах 4=cx<_5
3	»	»	-	»	3е; х	< 4
2	»	»	»	2 < ,t	< 3
1	»	»	»	1 • х	< 2
О	»	»	»	0 s'. х	< 1
— 1	»	»	:>	— 1 s. х'' О
Так что на каждом целочисленном промежутке график функции i/=[xj изображается отрезком прямой, параллельной оси Ох, причем левый конец отрезка принадлежит графику, а правый нег. На рис. 97 это последнее обстоятельство
_____I_Ж..________чвД......1------г------1------1------------•-
-2	--/ О I	2	J	4	5	х
Рис. 97
отмечено стрелочкой. График рассм.чтрпа.ь'мой функции не представляет сплошной линии, в каждой целочисленной точке он имеет разрыв (см. § 7).
Построить графики данных функций:
562.	и) t/^2x-.v\ б) у ---- х4 - Зх2 + 1, в)
563.	а) у ' л-2 — 1 !, б) У 1g [ х
564.	у — а Л'cos х п у — a -Vsiii,v при .v 0 (т/>1).
Указание. Применить прием, рассмотренный в 560.
565.	у —	при х У- 1 и у—1 при х—1.
Указание. Исследовать отдельно ветви графика при х > 1 и при х < 1.
566.	у — х — [-¥] (дробная доля числа у).
567.	у — 1 х -|- sin х.
Указание. Построить графики функций у~]~ух н y = sjnx, затем сложить их графически.
153
2. Параллельный перенос. Дадим способ построения графиков функций вида y=f (x — a) — b (а, 6 —любые числа),	(1)
если известен график функции у = / (х).
Запишем уравнение (1) в виде у  -b--- [ (х — а} и сделаем преобразование параллельного переноса осей координат:
Х = х — а, Y = у — Ь.
Начало новой системы будет находиться в точке (\(а, Ь). Относительно системы ХОгУ уравнение (1) примет вид
У = /(Х).
По условию, график этой функции известен.
Таким образом, способ построения графика функции вида (1) сводится
к следующему: в точку О (а, Ь) помещаем начало вспомогательной системы коор-
динат XOjY, относительно этой системы строим график функции Y= = f(X). Построенная кривая в системе хОу описывается уравнением (1) (см. также гл. I, § 4, п. 1).
568. Построить график функции у = 1g (х — 2) + 3.
Решение. Формулы параллельного переноса осей координат запишутся в виде Х = х — 2, Y=y — 3. Координаты нового начала (Д (2, 3).
В новой системе координат строится график функции V = lgX. Относительно системы хОу этот график представляет функцию у = = 1g (х —2)4-3 (рис. 98).
Построить графики функций:
569. у = (х-2)3 + 5.
570. у = 2+ехЛ
3. Сжатие и растяжение.
571.	y^2 + tgx.
572.	у — 1 + arcsin (х — 3).
Дадим способ построения графиков функций вида
(«>о. ₽ > 0)>
(2)
если известен график функции у = [(х).
Запишем функцию (2) в виде y/fi — f(x/a) и произведем замену переменных; ,z у v х
положим 1	, Х = —. или
₽ ’ а ’
х=аХ, y=$Y.	(3)
В новых переменных уравнение примет вид
Г = /(Х).
График этой функции по условию известен. Построим его и проследим, как будет он деформироваться при переходе к старым переменным х, у. Используя равенства (.3), любой точке с координатами (Хо, Ио) можно поставить в соответствие точку х(| —аХи, у0 = (ЗУ0, т. е. такую точку, у которой координата по осп абсцисс увеличилась в а раз, а координата по оси ординат — в р раз. Что же
154
касается всей кривой У — то она при этом должна растянуться в а раз по оси абсцисс и в р раз по оси ординат *.
1 X
573.	Построить график z/=2-siriy.
Решение. Имеем: ос = 3 и р= для построения графика данной функции надо растянуть график функции у = sin х в три раза по оси абсцисс и сжать
1 X
его в два раза по оси ординат. На рис. 99 построен график функции у = -%- sin •  .
Заметим, что расстояние между соседними нулями функции r/ = sinx равно л ,	1 х
а расстояние между соседними нулями функции у = 2 sm равно Зл; максимальное значение функции r/==sinx равно 1, а максимальное значение функции 1 . х 1
i/=9 sn з PaBII° 2 ’
Построить графики функций:
574.	У=[х\	576. z/ = A-tg
575.	у = 3 cos у.	577. z/ = 21g3x.
4. Более общий случай. Покажем, что, комбинируя приемы построения графиков функций вида (1) и (2), можно строить графики функций вида
=	(4)
\ U. /
где а>0, ₽ > 0, а и б —любые числа, график функции y = f(x) считается известным. Сначала по графику функции y = f(x) строится график функции уг = = MX) = M— } (п. 3). Далее, по графику функции y1 = f1(x) строится график \ а :
функции — (х— a)-pb (п. 2).
Убедимся, что построенный в результате график отвечает функции вида (4).
Подставив в формулу yi—f1{x~ а) + & выражение функции (х) = р f ( * 'j, полу
чим
yi = fi^-~a)+b = P>f [~^ + b-
'* Если а < 1 или Р <_ 1, то надо говорить не о растяжении, а о сжатии  вдоль соответствующей оси.
155
578.	Построить график функции г/ = 2 |cos 1
L \ 3 b /
Решение. Преобразуем функцию к виду (4):
получаем, что в этом случае а- - 3, [3 = 2, о = —Ь = —1, [ (х) = cos х.
На рис. 100 изображены последовательные этапы ноет роения графика. Растягивая график функции y — cosx но оси Ох в три
раза и по оси Оу в два раза, получаем график функции z/i = /r(x) = = 2cos 4. Затем в системе координат ХОгУ с началом в точке и
Oj^— 9,-1^ строим график функции У = 2 cos , который и будет / । 31 \
графиком функции у = 2 cost—3~J—I в системе хОу.
Построить графики функций:
579.	y^le-i + 3.
580.	// = (1g Цх -3 - 1).
581.	у = 2 -ф 3 sin { ф х — V \ з б)
582’ -
считать известным график функции
ГОГ>	•	2.V— 1
583. y=arcsin-=—.
J	з
584. (/ = 1 -|-2 arctg J — *''!
(считать и.лестным график функции г/ = arctg (— х)).
§ 3. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ И ЕЕ ПРЕДЕЛ
 '	1. Определения. Числовой последовательностью называется совокупность чисел
j	Oj. а2, ... , ап, ...,
(занумерованных в определенном порядке. Последовательность можно представить как функцию целочисленного аргумента: каждепгу целому положительному значению х — п отвечает определенное значение функции /(’-•) = /(/() = «„;
ап называется общим членом числовой последовательности.
ф Числовая последовательность называется монотонно возрастающей, если каж-i дый последующий член последовательности больше предыдущего. Например,
|	£ ф 3	4	_п_
<	2 ’ 3 ’ 4 ’ 5.......1’	•
fl..
§ Числовая последовательность называется монотонно убывающей, если каждый последующий член последовательности меньше предыдущего. Например,
4	1 1 1 1	1
У	’ 2 ’ 3 ’ 4 ’ ‘’ п ’ ’' ‘ ’
i
( Числовая последовательность на,ывается ограниченной сверху, если суще-ствует такое число Л), что для любого и
!|	ап Л1.
Ж Так, последовательность с общим членом
и
а'1 = ;Г£1
ограничена сверху, так как все ее члены меньше, например, 1.
Числовая последовательность называется ограниченной снизу, если существует такое число Д', что для люоого п
*	an^-N.
Например,
S	«« = --> 0-
1	п п
Числовая последовательность называется ограниченной, если она ограничена
» сверху и снизу. Тогда существует такое число .И > 0, что для любого п
Ж	—М-СапГюМ,т:.а.\аП1:нМ.
жНапример, последовательность
В	(—D,i+1
^ограниченная, так как I ап (	1 •
F 2. Пределы. Число .4 называется пределом последовательности, если для | любого е>0 существует число N => N (г) такое, что при п > N (е) выполняется Ъ-неравенство \ ап — Л i < е.
'Если число .4 есть предел последовательности, то пишут
Е '	litn «,; = /!•
№	п — -
Ф Числовая Йовательность,
последовательность не может иметь более одного предела. После-имеюшая предел, называется сходящейся. Для сходящихся после-
156
157
довательностей справедливы теоремы, вытекающие из определения предела:
Игл (ап ± &п) = Нт ап ± Нт	(1)
п-*со	п-*оо	п-»со
lim (anbn) = Нт ап • Нт Ьп;	(2)
п -* сю	«-.от	п -> со
Нт ап
lim 0,1 = -,7°°	, если Нт Ьп 0.	(3)
п^тЬп Нт Ьп п->со
585.	Найти общий член последовательности 1, 4, 9; 16, 25,...
Решение. Нетрудно видеть, что
а1=1 = 12, а2 = 4 = 22, я3=9=Зг, а4=16 = 42, а5 = 25 = 52 и т. д.
Следовательно, ап = п2.
586.	Найти общий член последовательности 1, —
и О (
J
9 ’
Решение. Имеем:
, . . , .	1 , , I II /	1 \	1	1
l°il —I1! р !«аI | з I з\/ з 2 + Р
, , I 1 I 1	1	1
,аз,-|5 |- 5~2-2+1> ,Й4Н y| 7~ 2-3+1 И Т’ Д‘
Следовательно, , , 1 1 1 10,11 2(л—1) + 1'	2п —2 + 1	2л-1’
1
где + > 0, а.2 <0, а3 > 0, а4 < 0 и т. д.
Таким образом, получаем:	‘
а _(-D"+1
°п" 2n —1 •
587.	Доказать, пользуясь определением предела последовательности, что последовательность с общим членом ап = ~^2 имеет предел равный нулю.
Решение. Запишем ряд членов последовательности:
1111111
*’ 4’ 9 ’ 16’ 25’ 36’ 49’ 64’ ”•
1 „
и положим 8= jo" Для всех членов данной последовательности, начиная с четвертого, выполняется неравенство
i (hi 9 J J ci n |	] g .
Действительно,
I 1	nl-l 1 I- 1 - 1	I 1	nl- I 1 I ' - 1
I 16	° ( I 16 I 16^ 10’	I 25	° I I 25 I	25 < 10	И T’ Д’
158
В данном случае Л' (см. определение предела последовательности) можно принять равным трем (или любому числу, большему трех), так как если порядковый номер члена последовательности п больше трех, то выполняется неравенство
\ О I I ап 1
Положим теперь е = -туу
Ясно, что для всех членов последовательности, начиная
с седьмого,
|а„-0| = Х ! <^1
теперь за N можно принять шесть (пли любое число, большее шести). Если
Е = 100 ’ то N 10 И Т' Д'
В данном случае можно найти общее выражение для числа в зависимости от е. Общий член данной последовательности ап = ^2- Задавшись произвольным положительным числом е, необходимо в соответствии с определением предела
„	-	I 1	1
потребовать, чтооы при п> N выполнялось неравенство 2— 0 < е, или < е.
г,	1
Решая неравенство относительно п, получаем п > ——. е
Итак, за W можно принять число (или любое большее число). Таким
И 8
> 0 существует такое N — что при Ге
— 0 < е, а это и доказывает, что пре-
II делом последовательности является ноль.
Отметим, что в этой задаче члены последовательности приближались к своему ! пределу, оставаясь больше этого предела, как говорят, справа.
1	588. Доказать, пользуясь определением предела последователь-
ности, что последовательность с общим членом ап — 2 — ^п имеет . предел, равный двум.
Решение. Запишем ряд членов последовательности:
I-2- I8 I26 I80
3 ’	9 ’ 27’ 81’
f образом, мы показали, что для любого е
i	1	। !
К n>N=-,~ выполняется неравенство ->	У в
Рассуждая как в предыдущей
задаче, можно показать, что


если
если
е = у о, то N 2;
1	Л,- и
е=Гоб’ То Л 4’ 11 т‘ Д"
Найдем общее выражение для числа 7V в зависимости от в. Общий член последовательности ая —2 —Для любого н > Л' имеем неравенство
данной
1 е, или < е,
159
решая которое относигсльно л, получаем
Итак, за N можно принять число — (или Л1°бое большее число). Таким
1У 8	1 g 8
образом, для любого е>0 существует такое Л' — —. что при и > N = —
выполняется неравенство |2—	— 2 j-< е, а это и доказывает, что пределом после-
довательности является число два.
Отметим, что в этой задаче члены последовательности приближались к своему пределу, оставаясь меньше этого предела, как говорят, слева.
589. Доказать, пользуясь определением предела последователь-, ( 1)"+1
пости, что последовательность с общим членом ап — -—--— имеет предел, равный пулю.
Решение. Запишем ряд членов последовательности:
_ 1	1 1 1	_ 1
2 ’ 3 ’	4’5’ b ’ ’ ’ ’
Найдем выражение для числа N в зависимости от в. Для любого п > W имеем
I ( | \Н - 1	1	1
1-----------0 < в или < е. Решая неравенство относительно п, получаем
|	п	j	’ п
и д> Итак, за N можно принять число (или любое большее число).
Таким образом, для любого г > 0 существует такое 1V—-	что при п >
> Д' — - выполняется неравенство |---------0 Это значит, что пределам
данной последовательности является число ноль.	»
В данной задаче члены последовательности приближались к своему пределу, становясь поочередно то больше, то меньше этого предела.
590. Найти предел последовательности с общим членом a,t —
5/1--|- Зи-р 2
.. 5,;2 + Зп + 2
Решение. В этой задаче треоуется наптп 1ни —--------------------
л , со 2,Р — и 1
-[-• 3// 2
выражение 2--------------- поделив почленно числитель и знаменатель
Преобразуем
па п2:
5Д=-|-Зтг + 2	..
lim -------------г-т- = lim
/г-►co
п н2 гр: п п1
2п'~ — /I + 1
Теперь общин член последовательности можно считать полеченным в результате суммирования, вычитания и деления общих членов последовательностей о.п~=5, __ 3	2	„	_ 1
“а — п , ап — ,;2 , а,1 - 2,	, ап -	.
г,	„3211
Пределы последовательноетеи ап— --, ап-	, ап— •— и ап — равны ну-
лю, а пределы последовательностей ап — 5 и ап = 2 равны соответственно 5 и 2,
160
I
j т. e. все эти последовательности сходящиеся, поэтому: 1) по формуле (1) этого * параграфа
3	9 \	3	2
Inn I 5-L	+ “ = lim 5+ lim 4- lim , = 5,
Ч--ЭТ »	»-	n-.az.n н
I
t	lim i 2— 1	- lim 2 — lim-1 -|- lim 1 =2y=0;
П — 09 , П ni /	/1—00 II — co 'г II
2) по формуле (3) этого параграфа
3 + 2> n n-
lim-------j r
и пг
.. /Z г ,	i '
lim ,5+
/1->си’,	»	'i~	5
1 П 2
lim i 2— - +	!
/1—>oo'\	l‘ n- '
Итак, предел данной последовательности равен •
591. Найти предел последовательности с общим членом а„ = /г!
— (П-Ь 1)1 —/г! 
Решение. Символом п! (читается «эн факториал») обозначают для краткости произведение п первых чисел натурального ряда;
п\ = 1  2  3 • 4 ... • п,
(„+1)1 = 1 • 2 • 3 ••/г • (п +1), очевидно, что
(//+ 1)! = п! 1). Имеем
,. п\	п\	..	/г!	1
11111 i—ттд-г= йт -г-—--п-------г= lim———:—= = Inn = 0.
п -со (« + 1)! — «I	п -со»! (//+ 1) — п\ „ -ос«1 (и-1- 1 -- I) ,,-:с»
В следующих задачах найти общий член последовательности, доказать их ограниченность:
592. 0, 1 ,	2 4 ’	3 5 ’	4 6 ’ "
593. ‘ , -	1 4 ’	1 8 ’	_ 1 16
594. 1, ‘ ,	1 5 ’	1 7 ’	1 9
Пользуясь определением предела последовательности, доказать
следующие равенства:
595. lim - = 0.		598.	lim	5/г — 1 r ,/-1-1 ^5‘
				
			Il -» -A	
596. lim Il -» с		599.	lim - Il —>	2" =Q. - ,/2
,	597. lim Il —> c	,^=o.	600.	lim I 11 -> cJ	1+^1 = 2«+l |
В следующих задачах найти предел последовательности:
on.	Зп—1	„„„	п2 — 5/г-|-1 601. а„ = =—-=.	603. а„ = —а——.
"	Гмг-1-1	11	Зп + 7
602. ап -	604. ап =	.
"	100/1-'15// •	zl п:> — 8//+ 5
". 6 Кручкович и др.	161
605.	=
/l	П3
cn„ 1.2,3,	, n—1
609. Cln -=	-V +..-)-~ .
re- 1 n2 n2	щ
606.	+, = ^±1.
607.	an
608.	an
(,i + 2)!+(„+l)l (« + 3)1
_+ + 2)l+ (»+!)!
(« + 2)1 — (и + 1)!
610. an
611. an
_ l+34-5 + ... + (2» + l) _
« + 1
_ “+_LL
-l.I.l. j. L
~~ 2	4	8 ‘ ‘	' 2" ’
§ 4. ПРЕДЕЛ ФУНКЦИИ
1. Определение предела функции. Число А называется пределом функции у — f (х) при х стремящемся к а, если для любого е > 0 существует число 6 (е) > 0 такое, что при 0 < , х — а <6 (е) выполняется неравенство I f (х) — А < е. В этом случае пишут
lim f (х) = А.
х —» а
Аналогично, число А называется пределом функции «/ —/(х) при х, стремящемся к со, если для любого е>0 существует число М (в) > 0 такое, что при [Х[> > М (е) выполняется неравенство )(х) — А | < е. В этом случае пишут
lim f(x) —А/
612.	Доказать, исходя из определения предела, что lim х2^= 4.
х->2
Решение. Пусть в—любое положительное число. Требуется доказать, -чтр можно подобрать такое б > 0, что для всех х, удовлетворяющих неравенству - х— 2 | < 6, будет выполняться неравенство
| х2 — 4 <s.
Если х-2 1<8, то | х + 2 | =+х — 2 + 4++х —2 ,+4 < 6 + 4 и |х2 — 4^ = = , х - 2 ф х 4 2 , < 6 (6 + 4) а".
Для выполнения неравенства х2— 4.<е достаточно потребовать, чтобы 6(6 + 4) —е, т. е. 62 + 4б — е — 0, откуда 6=--—2+/4 + е (второй корень — 2 — ]' 4 + е отбрасывается, так как б должно быть положительным).
Таким образом, для любого е найдено такое б, что из неравенства jx — 21 <6 следует неравенство | х2 — 4 | -< е, т. е.
lim х2---- 4.
л--> 2
613.	Доказать, исходя из определения предела, что
Решение. Пусть s — любое положительное число. Требуется доказать, что
можно подобрать такое Л-1 > 0, что для ;х|>Л1, будет выполняться неравенство
всех х, удовлетворяющих неравенству
X2	I
— 1 < е. Если I х , > Л1, то х2 + 1	|
* Для любых чисел а и b имеем: j а + b [	| а | + j b |, j ab , =, л | । b |.
162
х2 > /И2 и
|х2Д-1 I л-2-J-1ЛГ2 + 1Л42'
Следовательно, для выполнения неравенства
е достаточно Hail-
ти А1 из условия
т. е. Л1 ——-. Итак, для любого s найдено такое/VI,
что из неравенства х ।
,. х2
ЧТО 11111 ——-=|.
X — сох“ + 1
М следует неравенство
-j— 1 < е, 1, е. доказано,
В следующих задачах доказать, исходя из определения предела функции, что:
614.	lim (2х —1) —3.	616. lim
х-,3	7	х^гг* + 2
615.	lim Х.,-г-т = 4-•	617. lim ^— = 4-.
х->зЛ'- + 1	5	2х 2
2. Бесконечно малые и бесконечно большие функции. Функция а(х) называется бесконечно малой при х, стремящемся к <7, если
lim а (х) — 0. х -» а
Иными словами, функция а (х) называется бесконечно малой при х, стремящемся к а, если для любого е > 0 существует число б (е) > 0 такое, что при 0 <
< j х — а [ < б (в) выполняется неравенство j а (х) | < е.
Функция f (х) называется бесконечно большой при х, стремящемся к а, если для любого Л'> О существует число б (Л ) такое, что при 0 < | х — a j < б (/V) выполняется неравенство / (х) | > N\ это записывается так:
lim i (х) — со.
х —* а
Аналогично определяются бесконечно малые и бесконечно большие функции
при х оо. Бесконечно большие функции находятся в тесной связи с функциями бесконечно малыми. Если при данном предельном переходе функция f (х) является бесконечно большой, то функция а(х) —у-т— будет бесконечно малой при / (х)
том же предельном переходе, п обратно.
В дальнейшем в этом параграфе, формулируя то пли иное положение о бесконечно малых функциях, будем предполагать, не оговаривая этого каждый раз, что все эти функции являются бесконечно малыми при одном и том же предель-
ном переходе.
Свойства бесконечно малых функций
1)	Алгебраическая сумма любого конечного числа бесконечно малых функций есть функция бесконечно малая.
2)	Произведение конечного числа бесконечно малых функций есть функция бесконечно малая.
3)	Произведение бесконечно малой функции на функцию ограниченную есть функция бесконечно малая.
618. Доказать, пользуясь определением, что при х -> 1 функция 1 — х2 является бесконечно малой.
6*
163
Решение. Пусть е — любое положительное число. Требуется доказать, что можно подобрать такое 6 > 0, что для всех х, удовлетворяющих неравенству 0 •< J х— 1 < б, будет выполняться неравенство [ 1 —х- < в. Если
и
х-1 ;<б, то Д+1 = 'х-1+2 | ==+х-1 + 2 <6 + 2
1 — X
6 (б 4 2) *.
Для выполнения неравенства 1 --х2 \ < е достаточно потребовать, чтобы
или
6 (6-|-2) = е, т. е. б2 + 2б-е = 0
6=
(второй корень —1 — I 1-гс отбрасывается, так как б>0).
Таким образом, для любого е найдено такое 6, что из неравенства 0< < ; х—1 , < 6 следует неравенство 1—х2 ' < е. Следовательно, функция 1 —х: бесконечно мала при х —• 1.
619. Доказать, пользуясь определением, что при х—>0 функция
а'
где «>1, является бесконечно большой.
Решение. Пусть Л' — любое положительное число. Требуется доказать, что можно подобрать такое б > 0, что для всех х, удовлетворяющих неравенству
0 < ! х —-0 ' < б, или 0 < | х | < б, будет выполняться неравенство
ах~ > N.
-я 1 _ 1
п
Если
поэтому требуемое неравенство выполня-
стся при
ц6’— N, или
Таким образом,
для любого
-log„+, б=—Х=.
k tog.
+ найдено такое б, что нз неравенства
О < | х | < 6 следует является бесконечно
неравенство ах‘ > Л'. Следовательно, функция ах‘ (а>1) большой при х — 0.
В следующих
620. Функция
задачах, пользуясь определением, доказать, что: при 1.
является бесконечно большой
а х' (а> 1) является бесконечно малой
621. Функция
У Казани е. Использовать теорему о связи бесконечно малых больших функций.
И бесконечно
sin х	,
622. Функция —является бесконечно малои при х->со.
Указание. Использовать третье свойство бесконечно малых функций.
См. сноску к 612.
164
§ 5. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ
1. Применение основных теорем. При вычислении пределов функции необходимо знать следующие теоремы:
limC = C, где С — постоянная;	(1)
х —> а
lim Cf (х) = С lim f (х), где С — постоянная;	(2)
х—> а	х—^ а
если lim/(x) и lim ср (х) существуют, то
х -> а	х—а
lim [/ (х) ± ср (х)] = lim f (х) lim ср (х),	(3)
х -> а	х^> а	х-*а
lim f (х)  ср (х) = lim f (х) • lim ср (х),	(4)
х-*а	х-->а
н .	lim f(x)
lim	——, если lim ср (х) =# 0,	(5)
А._йф(х)	lim <р(х)’	х^а
х-*а
lim [f (x)]tf |'л') = Him f (x)	₽< ’	(6)
x->a	|x	I
Кроме того, надо пользоваться тем, что для всех основных элементарных функций в любой точке их области определения справедливо равенство
lim f (x)=f / lim x\.	(7)
x->a	\x—>a /
Далее следует отмстить, что:
ж	— са, если lim f(x) = O.	(8) х-> а
Действительно,	f (х) — бесконечно малая функция, следовательно,	— беско- Г ( Y)
нечно большая;	/ \л/ отсюда I-	с	1 lim j-T-r —Clim f-—--—со; х -> а 1 (х) х -> и f (х)
2) Iim ТТЙ^0’ ссли lim fW = co.	(m
х->а / Xх)	Х-*а
Действительно, [ (х) — бесконечно большая функция, следовательно, 77-т — беско-/ И/
нечно малая; отсюда
С	1
lini т-тт^-СНш ——-=^С’О — 0; x-.a/(*) x-*at(x)
3) Пш Шт0,	(10)
x-»a Y Vе)
если lini f (х) = 0 и lim <р(х) = со. Действительно, f (х) бесконечно малая функ-х-*а	х -*а
7 А "	-	1
ция, а ф (х) — оесконсчно оолыиая, но тогда —— — бесконечно малая; отсюда
165
623.	Найти lim (5x2 —бхЦ-7). x-»l
Решение. Из формул (2), (4), (1) u (3) следует, что
lim 5х2 = 5	lim х2 = 5 lim х  х = 5 lim x  lim x =	5 •	1 •	1	—5;
x-*l	.v-*l	x-*l	X~*l x~>1
lim6x' = 61im x —6-1=6;	lim 7=7;	lim (5x2 — 6x-r7)	= 5 —	6	-J-7- --6.
Л->1	x-^1	л--*1	x-*l
624.	Найти lim к-,-—Ц-.
X_o2x2-x-1
Решение. Используем формулы (4), (3) и (5):
lim (х2—1)^=—1; lim (2х2 — х — 1) = —1-* 0;
Л' -»О	Л' —* О
lim (,v2-l)
1  _ х ~~ 1	_ * -°_____________ 1	I
хУо 2х2 — х— 1 lim (2,t2 — X-— 1)	—1
х -* О
625.	Найти lim (За:)*8. х^'2
Решение. Так как lim Зх = 6 и lim .v2 = 4, то, используя формулу (6), Х-»2	х--*2
получим
lim (Зх)Л’ = 64— 1296.
626.	Найти lim sinx.
И
Решение. По формуле (7) имеем
л
lim sin х = sin , lim x =sin-F- = 1. и	л j	-
’Л	О- /
627.	Найти lim --3 ?.
Решение. Используя формулу (8), получаем, что
1-	3
lim ----тч = со,
x-.l (*~1)3
так как
lim (х— l)3 = lim [(л-—l)]:i = 0.
X -> 1	х —» 1
628. Найти lim Д-.
е-,л SX
Решение. Используя формулу (9), потучаем, что
так как
lim tgx—tg (lim ,v)==tg ф= оо. я	л
166
i
629. Найти lim
Х-Ш 11'л'
Решение. Используя формулу (10), получаем, что
так как
lim л =- 0 и lim In х ——оо.
х-.о	Л'->(>
Найти следующие пределы:
630.	,.	х2 —3 11111 -т-i—гт-г- Л-..ГЗ* +*+1	638. lim arcsin х. i х г
631.	,. х2 + 2х + 2 1ип —4——. x-l xi-1	639. lim arctg.r. /з
		х’ 3
632.	..	Зх2 + х 11 ГП 3—Д '	Н-тт; . х_,о 4х3-(-х + Ю	640. lim --х 5—гг. 1 Sin3 (х-— 1)
633.	,.	х -к 5 lim -у-,-.' - ,	. л _> _ 2 х2 4- За' + 7	641. Iim4=^=. x-,l)| tg3x
634.	lim (2л'2)’£А', х-> 1	642. lim , .. J , ,,. .х^-2 c,g (2а' + 4)
635.	lim И, А х >2 х /	643.
636.	lim 1g %.	-644. lim-4--
		x-.l>	-1. e 'x‘
637.	Нт tg,r. Л 4	645. lim |2ЛН)|
2. Раскрытие неопределенностей. Как показывают решения задач, приведенных в п. 1, в простейших случаях нахождение предела сводится к подстановке в данное выражение предельного значения аргумента. Часто, однако, подстановка предельного значения аргумента приводит к неопределенным выражениям вида , 4, 0 • со, ас —со, 0°, со0, Iе0. Нахождение предела функции в этих случаях называют раскрытием неопределенности. Для раскрытия неопределенности приходится, прежде чем перейти к пределу, проводить преобразования данного выражения.
В последующих задачах показывается, какими приемами обычно пользуются при таких преобразованиях (см. также гл. VI, § 2).
646. Найти lim —-у—46-
Л--2	х2~2х
Р е ш е н и е. Прежде всего отметим, ваться формулой (5) данного параграфа
равен пулю.
Непосредственная же подстановка в данное выражение ния аргумента приводит к неопределенному выражению вида
что для решения этой задачи пользо-нельзя, так как предел знаменателя
предельного зпаче-0 н
-Q . Следовательно,
167
прежде чем перейти к пределу, необходимо данное выражение преобразовать. Числитель и знаменатель данной дроби при х~2 обращаются в нуль, поэтому многочлены №-5л' + 6 и л'2 — 2х делятся без остатка на бином х — 2 (теорема Безу); отсюда
,. х2 — 5х + 6 ,. (х — 2) (х — 3) ,. х — 3 hm —=lim ——у—- = lim ---------.
х^2 х--2х ,v (х- 2)х х ,2 X
Теперь (в результате непосредственной подстановки в полученное выражение предельного значения аргумента) получаем
lim
л2 — ох 4- 6 х'-'- -2.V
lim
2
2 •
647. Найти lim
г,	0
Решение. Здесь также имеем неопределенность вида —; чтобы ее рас-на выражение, сопряженное числима х2 и воспользоваться теоремой
крыть, умножаем числитель и знаменатель телю. После этого можно будет сократить о пределе дроби:
lim -— х-о х-
1 .	1 -ГЛ 1
= 11111 7------- --------г----
Л- -0 (И 1 -|_Х2-|- 1) X2
1
1
lim
648. Найти lim
X2
Решение. Снова неопределенность вида менатель на неполный квадрат суммы, т. е. на
0
-Q-. Умножаем числитель и зна-
lim
х-*0
•2
= lim —
Х-.U х2
1
1+х2—1
= lim - __—.—\	. .=---- —
Д—о it (1+лг)2-Ну’1+*2-1-1 3
9 г 2 — у
649. Найти lim - lK.
Решение. В данном случае имеем неопределенность почленно на х!', где п— сте-и знаменатель на х2:
ного рода примерах числитель и знаменатель делят пень многочлена в знаменателе. Разделим числитель
2х2 — х ..
= lim
4+10
10 ‘2’
вида -
В подоб-
+ '/4+%2 -pi;
2 —
х
1	..	10 Л
так как lim  — Он нт - „ = 0. А*	V"
650.	Найта lim [|	(x-j-л) — х].
168
Решение. Имеем неопределенность вида от —от. Умножим и разделим выражение, стоящее под знаком предела, па К(х + т) (х 4- п) + х\
1 im [ |/(х + щ) (х + п) — х] = 1 im -(*—	Л =
Х-+СО	V (х + т)(х-\-п)+х
liln (т + п)х + тп = ljm	х __________ «+«
.V —* со К (* + т) (-'-' + «) 4~х	х-><х> -| Г1 I । £/г \ I j । п । I 2
Г \	% / \	‘
651.	Найти lim (]Ух~Уа — У х).
х-*-рсо
Решение. В данном примере получается неопределенность вида от — от Умножим и разделим выражение, стоящее под знаком предела, на Ух-j-a -|-4~ У х:	______ _  
,.	/.г—:— ,/—\	..	(V х + а — Ух ) (1,Лх + а+ Ух )
lim + Ух) = lim  ----------------j.	—У------!--- =
х-Н-от	лот + от	У х + а + \' х
х + а — х	,.	1
= 11m —^0=-------у-— = а lim —	---— — 0.
Л--, l-м Г X -h а + у X Х-. + ОЭ I- х-\-а-УУх
Найти следующие пределы:
652.	lim 	664. lim (|/ х2+1 — х2 — 1).
г-.— 1 х2~уЗх~у2	Х-.О0
653.	lim^z£L.	665. lim (]/'ха+f-x).
л-—>5 %—	x—> -I- co
654. lim
x2 — 5x 6
T-- -Ш-рО"'
655. lim
X -»!
2x3 — 2x2 Д- x — 1 П?^х2 + 3х -3'’
656. lim
лот — 1
2.4 + 24 --Зот-З x3 + x2 ~p x + 1
657.	lim	__!L_
x^~?> y> +8x4-21x4-18 •
658.	lim-^±£L. x-»o *4 —2x3
659.	lim ~~(a4-1) x-H<
X -> a x3 — a:>
660.	linii_1_______\
X - > I \ 1 — X 1 - - .V2 ) 
661.	iim£I+Lc£lHL X- Ol	X
662.
663.
lim -Lx2 +
л-»’> I  !G 1 ’
lim
Д-+1)
666.	]jln x (|/x2 4-1 —-t).
X-4-00
667.	lim (У x (x-j-2) — x) V-^+co ________ ________ r
668.	lim ' ;- v ' ! v-.
X-,0	x
669.	lim
ЛОТ)	ll
670.	lim^^-
Л'--*8 i- x — 2 
671.	lim
x -♦ — s 2 4- i x
672.	lim 1
.v -.t j x — i
673’2'ot (»’	4-1-
— । x3 - x2 +1).
674. lim |j (x-Н 1)2-]<(х-I)2].
675. lini(x-j- У 1 — x3)'
X. —f- ro
I x p X h
169
676.
1 — Зх
677.
678.
114^+3-
<»-И’
2х3 4- Зх + 1 ‘
1 Ox -f- 5
0,01x2 —Gx •
lim
Х-+СЭ
lim
681.	lim —44=
y.r’49 
о л 1 • 2х'^ — ох — 4
682.	lim —т=—
683.	Ит 1.4+1 .
X —* со X 4- 1
..	л-2- 5х-(-1
679. lim------------!—
х -> со Зх 4- 7
684. Ит
68°- .'1тЛти^-
3. Первый замечательный предел. При вычислении пределов трансцендентных функций часто используется формула
Рассмотрим примеры.
685. Найти lim
sin 2х х
lim
а-» О
sin а
= 1.
(11)
Решение. При х--0 а = 2х также стремится к нулю, поэтому, умножая числитель и знаменатель на 2 и применяя формулу (11), получим
sin 2х lim ----------
— 11гп
Х->0
о х
2 sin 2х „ ,,	sin 2х
—--------= 2 lim -=— =
2х ^>0 2х
686. Найти lim х sin
Решение. . 1 , sin —
..	.	1	X
lim х sin — — lim —-—=1, X	I
x~-> co	x-*co . *.
X
согласно формуле (11), так как а — - —0 при х со.
Найти следующие пределы:
sin 5х 687. Ит —=—.	694.	lim ч-р	sin2 a — sin3 [3 а2 — Р2
688. lim (х — 3) sin 2-. X - со	'	м	695.	lim Л- —0	1g ах ' X
„„„ .. sin ах
689.	lim-v-p—.
х-0 sln Р*
690.	Пт4ЦД.
д._0 Slllm X
691.	lim—. х - О х‘
692.	Ит——44==.
Л -.О Г 1 — COS X
693.	lim -^4+4^44=4.
л--О	л'
,. sin ах
696.	lirn-ч—я—.
х-0 lg Р*
697.	lim л' cig х.
л-О
1 	1? X— sin X
698.	lim -£—==-----.
х _ 0 sin3 X
699.	lim—=1£4_==.
Х-.0 j (1 — cos х)3
170
4. Пределы типа е. Известно, что
_1 lim (1 + а) " =е. о --о
(12)
Эта формула используется для вычисления пределов, которые называются «пределами типа с». При вычислении этих пределов встречаем неопределенность вида 1'.
Рассмотрим примеры (см. также § 6, п. 2, задачи 737, 738).
700.	Найти lim (1 -j- tg x)c,s x.
x->0
Решение. Так как ctgx = -r-^—. то tg.r ’
1
lim (1 -|-tgx)ctgA' — lim (1 -J-tg ,r) x =e л--о	л--. I)
согласно формуле (12), так как a = tgx—»0 при л — 0.
701.	Найти lim (	 j .
Решение. В этой задаче предел основания равен 1 (разделите числитель и знаменатель на х), а показатель степени стремится к бесконечности; имеем неопределенность вида 1е® (иногда говорят — «неопределенность типа г»). Для того чтобы раскрыть эту неопределенность, представляем основание степени в виде , ‘ 1 1 -|—<х, а в показателе выделяем множитель :
Переходя к пределу в квадратной скобке, получили число е, согласно формуле (12), так как
а —-----;--0 при х — со.
х— 1
702.	Найти lim (1+3tg2x)et"?x.
х ->о
Решение. Так как etg х — -7-, то
tg Л’
1
lim (1 -j-3 tg2x)ctK'х — lim (1 -1-3 tgs х)х = х—о	X—и
= lim (1 4-3 tga х)3
= е3.
171
Найти следующие пределы:
703.	lim (1 + sin л-)со=ес Л'.
А- -* (1
704.	lim i'y-—т;'"'.
v t<-. 2х — 3,
1
700.	lim	(1 +2№)2^
	X • 0	
707.	lim	/2х + 3\-'-|ч \ 2x4-1/
708.	lim	/х24“2'>х2 > U24-U •
705. lim
X — - со
/5х3 + 2\Ул-\ 5х3 j
§ 6. СРАВНЕНИЕ БЕСКОНЕЧНО МАЛЫХ. ЭКВИВАЛЕНТНОСТЬ
1. Сравнение порядков бесконечно малых. Бесконечно малые функции а (х) и р (х) называются бесконечно малыми одного порядка, если предел их отношения lim р равен некоторому числу С, отличному от нуля. Если же С = 0, то бесконечно малая а (х) называется бесконечно малой более высокого порядка по сравнению с Р (х).
Иногда возникает необходимость в более точном сравнении бесконечно малых функций — в выражении их порядков числами. В этом случае одну из сравниваемых бесконечно малых функций принимают за основную и относительно нее определяют порядок других бесконечно малых. Делают это, основываясь на следующем определении: если из двух бесконечно малых функций а (х) и р (х) вторая принята за основную, то бесконечно малая а (х) называется бесконечно малой порядка р по сравнению с бесконечно малой функцией р (х), если lim -.тгуттр С, IР v4 г
где С — число, отличное от нуля.
Бесконечно малые функции а (х) и Р (х) называются эквивалентными, если lim ?	= 1. Эквивалентность обозначается символом —, т. е. пишут а (х) ~ р (х).
Р W
Теоремы об эквивалентных бесконечно малых ф у и к цп я х
Теорема I. Предел отношения двух бесконечно малых функций не изменится, если эти бесконечно малые заменить им эквивалентными.
Теорема II. Для того чтобы две бесконечно малые функции были эквивалентными, необходимо и достаточно, чтобы их разность была бесконечно малой более высокого порядка по сравнению с каждой из них.
Основные эквивалентности:
sin а (x) ~	- а (л),	(1)
tg a (x)	- cz (x),	P)
aresin a (xj ~	a (л),	(3)
arctg a (x) ~	a (x),	(4)
(') _ 1	a (x),	(5)
In П 4-a(x)l —	a ( v),	(6)
„МП _!	a (x)In a.	(7)
Например, покажем, что если при х — а о. (\)  0, то tg а. (х) ~ а (л),
172
г. е. покажем, что
tga(x) .
Jim= 1.
Л-Я KW
Действительно,	пусть а (х)	— у. Тогда если при х-	a rj. (x) —* 0, то и у — 0
при х— 0, ПОЭТОМУ			
.. tg а (х)	,• tg у	sin у	1	.. sin у . .	.
lim ——ь_- =	- lim —— =	= lim	— = Jim		 lim 	— = 1-1 = 1.
х^а “(х)	</-ч У	^^(/•COSl/	;/^n cos//	и - о У
Следовательно,	tg a (х) — a	(x), если при x —a a (x)	- . 0. Eire пример. Пока-
жем, что, если при	х — а г/, (x)	• - 0, to	
т. о. покажем, что
_ а (A.),
lim
Л- -> я
Пусть а(х)=у. Тогда, если при х —> а а (х) — 0, то и // —0 при х—.а; поэтому
с.'1—L Jim-----—— = lim---------.
х-« aW ,,^о У
Обозначим e-Y— 1=г. При у —> 0 г —> 0, тогда
lim ----= lim  --—= Jim ------
,,_о У г_о>п(1+г) 2_о11!1(1+г)
In lim
— = 1.
а (х) —> 0.
Следовательно, frz(-V) — 1 а (х), сели при х —а 2х2
709. Доказать, что функции -1—-- и хг при х->0 являются бесконечно малыми одного порядка.
Решение. Найдем предел отношения двух данных функции: 2х2
1  х -|-1 ,.	2х-	_	1
lim —е—— jim _ ——^^-2 нт —-г-.о х2 х . х2(х--1) д^о х-г
Данные бесконечно малые функции есть бесконечно малые одного порядка.
710. Доказать, что порядок функции выше> чем порядок функции х~ при х->0.
Решение. Очевидно, что
т. е. функция “г~— есть бесконечно 1	3-- х
цпя х-.
711. Доказать, что функция второго порядка относительно л
малая более высокого порядка, чем функ-
1 — cos х будет бесконечно малой при х -+ 0.
173
Решение. Найдем lim------
х- о х'
п . „ х	. х
,	2 sin2 <	sin -
,.	1 — cos х	2	2	,.	. с
lim------------— lim-----------= lim--------------- lim sin — 1 -0 = 0.
x—(1 x x-.o x x_.o x x-«o 2
2
Найдем теперь lim
1 — cos x
7-
i	2 SHI2 --
1	— cos x	2
------—= lim -------------—
A’2 x—О Л-
X	. X
j sin 2 Sin „ lim --------- lim -------—
2	л._>п x д-_> n x
2	2
Следовательно, функция 1— cos x есть бесконечно малая второго порядка относительно х.
712.	Доказать, что бесконечно малые при х-*0 функции и эквивалентны.
1 + х-
Решение. Очевидно, что
х
lim
lim
х^-0
И-*2 1
Следовательно,
X	X
1 — X ljA“
при х — 0.
В двух следующих задачах определить, при каком значении постоянных С п k функция сс. (а;) эквивалентна функции р(х) = х* при х — 0.
713.	tz (х) — С In cos 4х.
Решение. Для эквивалентности функций а (х) и р С>) нужно, чтобы
1 im х->0
С In cos 4х х‘<
,. cos 4х — 1 lim--------, 
-.>о	xh
так как при х—>0 In cos 4х ~ cos 4х—1;
,, ..	— 2 sin2 2х .	„„ ,.	4х2
С lim -----------==1, или —2С 1пп ,, =1,
Л' -  U	X '	д (j X ‘
так как при х —> 0 sin 2х—2х; отсюда
— 8 С lim 1. х-^охк
Следовательно, а (х) и р (х) будут эквивалентны, если
С = —X и /г = 2.
О
174
714.	a (x) = C (cos 4x — cos 2x).
Решение. Нужно, чтобы
C(cos 4x —cos2x) Inn -----k------^ = 1.
X — 0	x
Преобразуем левую часть равенства:
—2 sin Зх sin х ,	Зх • х .	,. х'г ,
С lim------.----= 1, —2С lim —.,-=1, или -- 6С lim 1.
х-,0 X*	х^.п х'-	л--,о*
Следовательно, а (х) и [З (х) будут эквивалентны, если
С=- ! и /г = 2.
6
715.	Доказать, что функции и 1—Кх являются бесконечно малыми функциями одного порядка при х->1.
Зд4_v3
716.	Доказать, что порядок функции —.щщ- выше, чем порядок
X -р 1
функции Xя при X -> 0.
717.	Доказать, что функция tgx — sinx будет бесконечно малой третьего порядка относительно х при х—> 0.
В следующих задачах доказать эквивалентность бесконечно малых функций:
718.	g и |/Д+х-1 при х->0.
719.	e2v — ех и 2х—sinx при х-> 0.
720.	е-',пх— 1 и х при х->0.
721.	In (1 4- } х sin л-) и х при х->0.
722.	ех ~ cos х и х при х->0.
В следующих задачах определить, при каком значении постоянных С и k функция а(х) эквивалентна функции Р(х) = х* прих->0: *
723.	а (х) - С (J/T+2X5- 1).
724.	a (х) = С (2sin 2А — 1).
725.	а (х) =- С (sin Зх — 3 sin х).
726.	а (х) = С In (3 — 2 cos х).
2. Применение эквивалентных бесконечно малых к вычислению пределов. При вычислении предела отношения бесконечно малых применяют следующую теорему о замене эквивалентными: предел отношения не изменится, если числитель и знаменатель заменить на любую эквивалентную бесконечно малую функцию.
727.
3 х— 4хд- 3
Решение. При х —• 3 функция х —3 бесконечно малая и, следовательно, sin (х — 3) ~х —3.
Так как при замене бесконечно малой функции sin (х—3) эквивалентной ей функцией х —3 предел отношения не изменится, го
,. sin (х — 3)	.. х — 3	..	1	1
im -тс-——=lim -----v-;----.-= lim --? =
Л-з х2 — 4х ф 3	(х-3) (х- 1) *_3х- 1	2
175
728. Найти lini -—c°s тх х-*0 х*
Решение. Применяем сначала формулу тригонометрии
,	_ • „тх
1 — cos тх=2 sin2 g-.
При х — О
. mx mx sm -2 g- ,
. , mx 'mx\2
a sln-T^|Tj.
Заменяя в числителе бесконечно , fmx 2
2 ( -g ‘ , получим
малую 1—cosrnx эквивалентной функцией
,.	1 — cos тх
lim -------------= lim
x -<• о x x-> о
о  „тх 2sni2--
-------= liin
x2 x.u
imx'\%
'	_ m2
x2 2
_n„ T, „	cos4x — cos 2x
729. HaiiTii lim-----—.
x arcsin2 Лх
Решение. По формуле тригонометрии,
Ду-i 2y 4 г____2х
cos 4x — cos 2x=— 2 sin--~~ sin —-— = — 2 sin 3x sin x.
При x — 0
sin ЗхЗх, sin x— x, arcsin 3x 3x, t. e.
(arcsin 3x)2 ~ (3x)2, поэтому
.. cos 4x — cos 2x ,.	— 2 sin 3x sin x ,.	— 2 (3x) • x 2
11111 -—,',7------— 11П1 -----------— Inn ------------=----5-.
arcsin2 Зх A. , о arcsin2 Зх д^ц (Зх)-	3
, 7 arctg x lim_______
Л -0	•
7	7
Поскольку arclgx~ x при x — 0, a e 2t— 1-~ (—2x), to
, 7	7
arctg 4 x -4 x 7
lim —;—г = Hni —5- = — л -* 0 e *	x —* 0	°
слх_е\}х lllll -------
v ,u sin ax —sin px
Числитель и знаменатель сначала преобразуем, а потом заме
ним эквивалентными:
e(3.v	х— ]]
(а+р)х . (а —Р)х —
2 cos 2—2sin 2—	-
,,p.v
‘“‘о ,7~~(аЧ-Р).Пa. "д.'"'о '“~(а + |1)х ~ 1 ’
“ LUb 2 о	LUb о
»,\тт о j- IneosX
162. Наити inn—ъ. х
730. Найти
Реше и и с.
731. Найти
Р с ш с п п е.
lim  -----------:—pr- —Нт
v о sin — sin рх х 0
..'"(о -Р,)х
176
Решение. Для того чтобы воспользоваться формулой (6), под знаком логарифма прибавим и вычтем единицу:
In cos x = ln (1 ф-cos x — 1) ~ cos x — 1
(a = cos x — 1 —> 0 при x —0).
По теореме о замене эквивалентной получим
Решение. Так
lim
как 1 = In е, то
1	1	1п ~
In х— In е , е ..
= 11ГП ------:—=11ГП ------=11
х . Х —е Х^С Х —е X-
1П
Но при х— е функция — 1 — бесконечно малая, тогда
х
lim
In X— 1 ------— =11111
= lim --------
х -> е х &
1 Jin
734
Найти lim
Р С Hl
е и н е. При х = со функция
— бесконечно
малая. Используя фор-
мулу (7),
имеем
• х
е
lim х а
• х = 1п а.
Если х — а (<i =/= 0), то в ряде случаев, применяя теорему о замене эквивалентными, удобно сначала ввести бесконечно малую функцию а^-а — х (пли.с — а).
-ч — т 1 I* S i П 2.V
735. Наити
г „ sni Зх
Решение. Здесь числитель и знаменатель — бесконечно малые функции. Однако х не является бесконечно малой функцией (стремится не к нулю, а к л), поэтому соотношение sin 2х ~ 2х не имеет смысла.
Введем бесконечно малую а = л — х, тогда х = л — а и
sin 2х sin 2 (л - а) .. sin (2л— 2а)	— sin 2а	— 2а 2
lim .	= Inn . ,д ,------ = 11111	------T-; ^hiii ,— — 1пп —----------— — „ .
л._>л51п Зх а ^usin 3 (л —а) а.,(|sin (Зл — За) а .,0 sin За	За 3
736. Найти lim (1 — х) tg .
Решение. Сделаем предварительно замену переменного. Если ввести обозначение л—1=а, -ю а —> О при. х— 1; тогда
lim (1 — х) tg lim at»-	— lim atg -J-	_
x-> 1	-	« -»u	2	<z->o	\ 2	2 ,
= liin a etg ,, --—Inn-------Inn	—-
- oi — o < fa — о-1-'- л
ё 2	2
177
При вычислении пределов выражении вида	где при данном пре-
u (х) — I и в(х) —ос, удобно пользоваться формулой
дельном переходе
lim ua -
lim 1 —.
t
737.
Найти
Реш
е н и е.
Имеем
lim 1 - x 1
co \ t 1
lim (— /) In [ 1 —
— lira t ( —
= е.
738.
Найти lim [cos x — : s
т\х
Реш
е н и е. Имеем
lim cos — . _	, x
In 1 cos
lim
cos
= e-
— 2 lim v s!n2 —2 lim
i.v
lim
х ;
e
= PJ= 1.
тт ’’	1- I X3+ 2.V4
739. Найти hm ,4	.
x_oln (1 + 2x)
Решение. При х • 0 в числителе и нечно малые функции. Предел отношения заменить эквивалентными. При х--О
знаменателе данной дроби стоят беско-этих функций не изменится, если их
In (1 + 2х) ~ 2х, а х3 + 2х4 ~ х3.
ибо разность (х34-2х4)— х3 = 2х’ есть бесконечно малая более высокого порядка по сравнению с х34-2х4 и с х3; имеем:
2х4	1	9 г4
lim , а--; = 2 lim -г---------=0 и lim “ ,	2 lim х-0
А-их2-р2х4	1	х „ ц х3 А_о
“Г
х
(см. теорему И. § 6), поэтому
lim
х -.и
) х34-2х4	। х3 1
In (1 + 2х) А_п 2х 2
_ . „ т, „	,. sm х + х3 — х5
740. Наити lim—?—i— 
А-.о Зх —х4
Решение. По теореме II, §6, при х—0
sin х + х3 - * х5 ~ sm х,
так как разность (sin х 4-х3— х3) — sin х = х3 — х5 — бесконечно малая более высокого порядка по сравнению с sinx4~x3 —х5 и с sin х. .Аналогично, Зх — х' ~3х, поэтому
,.	sin х ф т3 — -v5 ,.	sin х 1
lim	--т----,--= lim	а—— хг	.
р-_За.' х	с>х 3
178
Найти следующие пределы:
741.
lim
sin (х + 2) 4л- + 8
752. lim ——
Sill X
742.
I;m sin <д + л) sin (а~~ *) xLo tg (a -|- x) - tg (a - x) 
15‘3. limr ~cos*
v ". О
Х“
.	, A'
1 - sm 9-
743. lim------------
,,	e — cos x
Указание.
X2
Указан п e. Заменить 1 на т 2 ’ . / л \ SIH X— _ I
1 — cos X
-+
3		знаменателе 1	вьь
Указание.	В		
нести 2 за скобку	и	1 % заменить	че-
л роз cos - , о 745. lim -Д х->1) S,n У к а ,з а н и с.	X q	1 \ tg X 1  вменить tg г	на
754. lim >1(1+^). x-0 nx
755. lim ^ДУШ-
Указание. При х — — c и 2А'бесконечно малы n In (1 -1 3Л)
756. lim -n x ~(a>C).
sin x
и привести дроии к оошему знаменателю.
746. lim ctg 2х • ctg
Л -> О	2
757. lim!4^.
X (1 П (cos P^)
У к а з а н.п с. При x — 0
In (cos ax) ~ cos ax- - 1.
758. lim {x[ln(a4 x) — Inx]}
759. lim
, Jl I
4+«x sin bx
i,
У к а з а н и с. Учесть, что ctg х ~
1 = 	11 tg X	'л '	, ctg \	— X -=tgx.
747.	2 a rc sin л-11П1 —,т	. л- .(>	3*
748.	2х — a re sin л-л-_»о ^х-|-агс1.цх
У к а	? а и и е. Вынести в числи
теле и знаменателе х за скобку.	
749.	етх— 1 11Ш	. х-0 пх
750.	lim -—.
У к а	з а и и е. Вынести в числи
теле е за	скобку.
751.	пт х-.О 3111 х
760. lim-----
761. limaX
762. lim
= a
sin px
X2
ax -\-a
a2x~a 2\'
а л a
1
X‘
a
x
x
179
763.	.. sin 5х lim ---sin 6л:	770.	i lim i —д-1 . Л-П ,C°S 2х.
У к а	за н ие. Обозначить х-л		1
icpo’> а.		771.	,. .'sin х' х~и lim ' -— .
	cos -		Л._,„ \ sin a;
764.	lim	 X- 1 1 - - 1 х	772.	lim (tg.r)'«2x.
765.	lim „ — x tgх.		4
	л 2	773.	Г, ' Л.	V|ctg2x
	1		
766.	lim [1-(у-2)1 —2.	774.	link	k x-o <5
767.	. .	А	1 Л 11ГП 1 —— ) •		,.	2tgx-x4-'-x'-
	х	\	/	775.	lim—5—7—k—•
			A-...o arctg 3x
768.	lim (sinх)1кдг.	776.	]jm I'4 (x+l)“ sin2
			Л.	arcsiii x
769.	lim (cos хУ'2. х - 0	777.	.. sin2 x — tg1 x lim Q -6	. л._0 Зл2 + 5х4
§ 7. НЕПРЕРЫВНОСТЬ И ТОЧКИ РАЗРЫВА ФУНКЦИЙ
1. Определения. Функция f (х) называется непрерывной в точке х„, если: 1) она определена в этой точке; 2) существует lim / (х); 3) этот предел равен
Л' — А‘о значению функции в точке х0, г. е. lim f (x) = f(x(<).
Л" -» Л'о
Если хотя бы одно из этих трех условий не выполняется, то функция называется разрывной в точке ха, а сама точка ха называется шовной разрыва функции.
Различают следующие виды разрывов: а) если lim [ (х) существует, ио функция f (х) в точке х„ не определена или определена, по так, что f (х0) k lim ! (х), то разрыв в точке х0 является устранимым. В этом случае для устранения разрыва надо доопределить функцию в точке х0 или изменить ее значение в этой точке так, чтобы f (х„) было равно пределу lim f (х);
А -* А' о
б) если lim f (х) не существует, по существуют оба односторонних предела А" -* Xq
в точке х0* (они не равны друг другу), то разрыв в точке х0 является разрывом первого рода, или скачком;
в) если хотя бы один из односторонних пределов не существует (в частности, равен бесконечности), а следовательно, не существует и lim '[ (х), то разрыв л-^х„ в точке х(| является разрывом второго рода. .
Разрывы первого и второго рода неустранимы.
Функция называется непрерывной на отрезке, если опа непрерывна во всех точках этого отрезка.
2. Свойства непрерывных функций. Важное значение имеют следующие теоремы;
1) Основные элементарные функции ах, х", log,, х, sinx, cos х, tgx, etgx, arcsiii х, arccos x. aretgx непрерывны во всех точках, где они определены.
* Односторонние пределы бывают правосторонними, когда х стремится к своему предельному значению, оставаясь больше пего, н левосторонними, когда х стремится к своему предельному значению, оставаясь меньше него. Правосторонний предел обозначается limf(x), а левосторонний lim/(x).
180
2) Если в точке хЛ ш прерывными являются
функции f (х) и q> (х) непрерывны, то в этой же f (х) и функции f(x)±cp(x), f (х) ср (х), а также —-'-2
точке
, если
только ср (л'о) -/ 0.
3) Если функция с/—; ср (л) непрерывна в точке хЛ, а функция у ~ [ (и) непрерывна в точке ии — ср (л-,,), то сложная функция у = f [ср (х)] непрерывна в точке х0.
Из этих теорем вытекает такое следствие: всякая функция f (х), образованная
конечным числом алгебраических действий и взятий функции от функции из основных элементарных функций, является непрерывной во всех точках, в которых
определены все составляющие ее основные элементарные функции, за исключением точек, в которых какой-либо из знаменателей обращается в нуль.
В частности, всякий многочлен есть функция, непрерывная на всей числовой оси; всякая дробно-рациональная функция (отношение двух многочленов) непре-
рывна во всех точках, в которых знаменатель не обращается в пуль.
778. Исследовать на непрерывность, найти точки разрыва, указать характер разрыва, в случае устранимого разрыва доопределить до непрерывной функцию f (X) = —— .
Решение. Поскольку sin х и х непрерывны в любой точке (теорема I), то, согласно теореме 2, непрерыв-,	sin х
иым оудет и их отношение —— во всех
Рис. 101
хах хв, отличных от пуля. В точке
Л'о = 0 данная функция не определена, и поэтому разрывна. Но существует , sin х
lim ---=1, так что разрыв в этой точке устранимый.
х-о х
Положим f (0) = 1, тогда функция
Д(л-)=	*
|	1 при х = 0
Сп-урл непрерывной в точке х = 0 (рис. 101).
779. Исследовать на непрерывность и найти точки разрыва функции
! х + 1	,	.	,
-——г—%—1,	если хф— 1,
х+1
1,	если х = — 1.
Решение. Данная функция определена для всех значений х. Если х>— 1, то
В этом случае
/ (х) = 1 • х — 1 — х — 1,
поэтому для всех значений х> — 1 функция непрерывна как многочлен первой ,	, X 1 j ,
степени. Аналогично, при х<—1,	* , р- ——1 п
[ (х) =--- — х—1
непрерывна как многочлен первой степени.
181
Исследуем точку х0 = —1. Выясним, существует ли предел функции в этой точке. Вычислим односторонние пределы при х-* —1 слева и справа. При х <.— 1 f(x)=—х—1, а при х> —1 f(x) = x— 1, поэтому '
lim / (л) lim (— х — 1) = +1 - 1 =0,
Л'—* -I—
lim f (х) = lim (х—1) = — 1 — 1	— 2.
Х-.-1+	x-.-l-t-
Следовательно, односторонние пре; ствуют, но не равны между собой; в первого рода. Ее график изображен на
1олы функции f (х) в точке х0=—1 суще-этой точке данная функция имеет разрыв рис. 102. Он состоит па двух полупрямых и точки:
г х—1 при х >—1,
f (х) —	1 при г=-1,
I — х — 1 при X < — 1.
780. Исследовать на непрерывность и найти точки разрыва функ-
1
НИИ =--------— .
1+27777
Решение. Эту функцию можно представить как сложную:
.^=Г4^.	“ =
Знаменатель первой дроби нигде в нуль не обращается.
1 1+2"
— непрерывная
функция
при любом значении и.
непрерывна для всех значений х, кроме х=1. По теореме функция непрерывна для всех х + 1 (можно было бы сразу
дениое выше следствие из теорем).
По теореме I, г/ = , ' 1
Функция и—~------]
3, данная сложная сослаться па прнве-
При х — 1 слева х—1 <0 и, следовательно,
а 2х ~ 1 —> 0,
поэтому
При х-> 1 справа х—1 >0 и, следо-
вательно,
поэтому lim --------------г— —0.
x-i+	_L_
l+2x~l
Таким образом, пределы справа и слева существуют, но не одинаковы, так что точка х„ — 1 является точкой разрыва первого рода. График данной функции представлен на рис. 103.
781. Исследовать на непрерывность и найти точки разрыва j___________
функции у = ех + 1.
182
Решение. Согласно следствию из указанных выше теорем, данная функция непрерывна везде, за исключением точки х0= — 1. Для выяснения характера разрыва в этой точке найдем пределы справа и слева:	1
1
точкой разрыва второго рода, так	|
как предел справа бесконечный (рис.	I
Ю4).	|
782. Исследовать на непре-	I
рывность и найти точки разрыва	I
функции у =	,
Решение. Эта функция является дробно-рациональной, и поэтому она непрерывна во всех точках, в которых знаменатель отличен от нуля. В точках
х= + 2 функция не определена, и поэтому разрывна. Нетрудно проверить, что в обеих этих точках односторонние пределы бесконечные:
., X	।,	х
Следовательно, х= ±2 — точки разрыва второго рода. График этой функции Дан на рис. 105.
) ЬЗ
Исследовать следующие функции на непрерывность, найти точки разрыва, в случае устранимого разрыва доопределить функцию до непрерывной:
783.	У —	tg X	п в точке х(} ~ 0. X		787.	11 —	1
					У	l+«1/v
784.		( х3+1	(л- Ф 0),	788.		2|/а —1
	У~	I -2	(х = 0).		У	21/А + 1 ’
785.		х-1		789.	1! —	1
	У	I X	 1 ,			У	х — x-s ’
786.		arctg~		790.		V л+ 15- 3
	У —		х'		У	№ — 36
ГЛАВА V
ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ
§ 1. ПРОИЗВОДНЫЕ ПРОСТЫХ ФУНКЦИЙ
1. Определение производной. Производной функции y — f (х) по аргументу х называется предел отношения приращения функции к приращению независимого переменного при условии, что это последнее стремится к нулю. Производная функции tj — f (а-) обозначается через у', или f (х). Таким образом, по определению
У’=Г (х) — lim
Дт-о
Ау
Ах
lim (х + М —/ (г)
Д.г -, О ^х
Операция отыскания производной дифференцированием, этой функции.
2. Табличные производные:
Г (у) данной функции / (л-) называется
(хг/-)' = аха 1	(1)	(tgx)' = -L-	(8)
(а, — любое действительное	число),	
		(clgx)'= -—V,	(9)
-2Т7	(2)	1
		(arcsin x)'—	 (|x.<1)	(10)
1		\ 1 — №
(1ПЛ)'=- (х>0),	(3)	
		(arccosx)'		 ('a-; < 1), (11)
(rt^)' = «я-*71И	(4)	(1- X2
(с7 =ех,	(5)	(aretgx)' =-j4~b	(!2) 1 A
(sin х)' — cos х,	(6)	1
(cosx)' = — sin л-,	(7)	(arcctg x)'= —.	(13) 1 "j" A“
Следует отметить, что формула (2) является частным случаем формулы (1) при а = '2~ • Точно так же формула (5) получается как частный случай формулы (4) при а = е.
3. Основные правила дифференцирования:
(C)' = 0,	(14)	(liv)’ = liv’ + ll'v,	(17)
(u-|-v)' = (i'4-v',	(15)	I u\’ vii' — uv'	(18)
(Си)' = Cu’,	(16)	\ v ) “ У2	
(здесь С —постоянная, а и и у —функции от л-, имеющие производные)'. 791. Найти производную от функции у = 5.v! — 2х2 -|-Зх — 4. Решение. Основываясь па формуле (15), имеем
у'= (5х3)' —(2х2)'(Зх)'— (4)'.
185
Далее, применяя формулы (16) и (14), получаем р'==5(хЗ)'--2М' + 3(л-)'.
Наконец, пользуясь формулой (I), приходим к окончательному результату: у' = 5 • Зл-’- 2 • 2х-ф 3 • 1, пли у’ = 15х2 — 4x4-3.
Разумеется, при самом небольшом навыке промежуточные выкладки могут быть сокращены.
792.	Найти у', если у -- х4 — 6х3 Д-8.
Решен и е. у' — 4х3 — 12х. „ ____________________________	3
793.	Найти у', если у = 2 х -|~ •
Решение. Переписываем заданное выражение, используя дробные и отрицательные показатели:
I у — 2х 3 + Зх '3.
Применяя те же формулы, что и в предыдущих задачах, находим у' = 2  * х ” -l 3  ( —2) х~3,
или, после очевидных преобразований, J 3) х- х3'
794.	Дано у — x3cosx. Найти у'.
Решение. По правилу дифференцирования произведения получаем 2/'= х3 (—sm х) ф-Зх2 cos х, пли у' = — х3 sin х -}- Зх2 cos х.
Попятно, что здесь применялись также формулы (1) и (7).
795.	Найти у', если // = -—КД J	J X3
Решение. Применяя правило дифференцирования дроби, а также формулы (1) и (12), находим
х3 • 1	„ — arctg х • Зх2
---------
Найти производные от следующих 796. у 2х5 - Зх3 + 4х - 6. 797. у = х3 -	х2 4- 6х 4- 7.
798. у = ах2 Ьх 4- с (а, Ь, с — постоянные).
799. у — хп 4- пха 4- 3/2 (п — постоянное).
х“ (1 -фх2) функций:
800.
Л"!
У к а з а и и е. Прежде чем находить производную, целесообразно поделить почленно числитель па знаменатель и ввести дробные и отрицательные показатели.
186
.801. у = (Vх — 2 Ух)3. У казание. Следует предвари-		806. г/—- х3 etg х. 807. у = 3-v arcsin х.		
тельно применить формулу разности.	куба	808.	У =	(14-х2) arctg х.
802. у = {—<У^.		800.	У =	tg х PT ’
803. у — х In х — х.		810.	У =	arcctg x
804. у^ех(х2-2х 4-2).		811.		arccos x
805. у ~ ех (sin х — cos х).			У	1— X- 
§ 2. ПРОИЗВОДНЫЕ СЛОЖНЫХ ФУНКЦИЙ »
1. Теорема о дифференцировании сложной функции. Приведенные в предыдущем параграфе правила и формулы дифференцирования позволяют находить производные от функции только в самых простых случаях. Знания этих правил и формул недостаточно для дифференцирования функции более сложного вида, например таких, как у | cos х, г/ = еагс1й* н т. д. В подобных случаях пользуются более общими формулами дифференцирования, основанными на теореме о производной функции от функции.
Пусть // — ([q> (х)] —сложная функция, т. е. y = f (и), а	Если для
соответствующих друг другу значений х и « существуют производные j' (и) и и' — (р' (х), то существует и производная от у по х, причем
У’ = /' (w) //'.
Пользуясь этим соотношением, можно получить таблицу формул дифференцирования:
(иа)' =- (a — любое действительное	О) число),	.. ,, 1 (tg и) = —	 и , Ь ’	COS2 и	(8)
2 I it i		(etg /()'=	Д—  и',	О)
	(2)	Sill2 и ,		V	1 (arcsin и) = —	• и , Г 1-0	(Ю)
(In uY	 u', и	(3)	(arccos II)' —	7^1z=-. - и',	(Н)
(alrY --:a" Ina - u',	(4)	у 1—11~	
	(5)	(arctg и)' = у^-2-и’,	(12)
(SHI 11)' -=cos и  и’,	(6)	1	
(cos и)' — — sin и  и',	(7)	(arcctg и) = —p-j—2--u'.	(13)
Понятно, что формула (2) частный случай формулы (4)	есть частный	случай формулы (1), а формула	(5)-
812.	Найти производную от функции у — |' х24~ Зх 1.
Решение. Вводим вспомогательную функцию и, полагая м = Xs-ф-Зх1; тогда, очевидно, можно записать
По формуле (2) имеем
у=У и, где м = №4~Зх + 1.
у' (2x4-3), 2 Г и
187
или, окончательно заменяя и его значением:
, 2х + 3 у =——- .........
2 /х2 + 3х-ф 1
813.	Найти у', если у = (х2 + 5х + 7)3.
Решение. Полагая п —х2 + 5х +7, имеем у=--и3. По формуле (1),
у'=8сУ (2л:+ 5), или окончательно у'= 8 (х2+5х + 7)7 (2хф5).
Следует заметить, что к такой подробной записи прибегают только в самой начальной стадии освоения техники дифференцирования, а обычно вспомогательная функция вводится мысленно, что и рекомендуется делать в дальнейшем.
814.	Найти у', если у = In (х3ф-7х -)-2).
Решение. Принимая в дгшном случае за и (мысленно) выражение ф -ф 7хф2 и пользуясь формулой (3), получаем
Зх2ф7
У ~х3 + 7х + 2'
815.	Найти у', если у = In (aretgx).
Решение. В данном случае роль и будет играть aretg х. Применение формулы (3) дает
, __1_  _______1_______
У 1-1-х'-	(1-|-л8), aretg х’
aretg х
816.	Найти производную от функции у — х.
Решение. Принимая aresin х за и и применяя формулу (5), имеем
817.	Найти у', если z/=sin:1x.
Решение. Следует напомнить, что обозначением кпг’х пользуются только для краткости записи и что sin3 х—(sin л):|. Таким образом, фактически имеем дело с дифференцированием функции у = (sin х)3. Принимая sin х за и и пользуясь формулой (1), получаем
у' — 3 (sin х)2 • cos х, или у' = 3 sin- х cos х.
818.	Найти у', если у = ]/ 1 — х2 aresin х.
Решение. По правилу дифференцирования произведения получаем сначала [см. формулу (17), § 1]
у'-- ]' I —х2 (aresin х)'ф-aresin х (1 - х2) •
При вычислении производной от [ 1—х2 принимаем 1 — х2 за и. Очевидно [по формуле (2)],
Таким обраюм,
,	, ?----j 1 х aresin х 	,	, х aresin х
1 1 — х-	----— пли 1/'— 1-------------------
I/1--X2	[/ 1-х2	у 1-х2
188
Найти производные от следующих функций:
819.	у = (х2 + I)10.
820.	z/ = 'У ах1 4- Ьх ф-с.
821.	у = е х.
822.	z/ = sin3x.
823.	z/ = tg5x.
824.	!/--=lntgx.
825.	x = 4cos*.
826.	у— sin (x2 4-5x4- 1).
827.	(/ = cos4x.
828.	y = In (x24~ 3x 4- 4).
829.	//--= tg(x2+ 1).
830.	y = aresin J	X
831.	y = arcctg \7 x.
832.	г/= In (1 4-V *)
833.	y = (aresin x)2.
834.	у = cos (Inx).
835.	y = \'eX_________
836.	y — V 14-arcsinx.
837.	у — e~x (x3 4- 3x2 -6x 4 6).
838.	.
Г14-Х2
839.	z/= In sinx4- 2 cos2 x-
841.	y= J/'xco.s2x.
842.	y^' A-'"+1. y x-|-1
843.	у =- * tg4 x — * tg2 x — In cos x.
844.	y=~^-.
845.	y=*^.
(У.\ - Q X
Замечание к 844 и 845. Выражение ---------------------------------------- называют гиперболическим синусом и обозначают sh х, а выражение -------------------гиперболическим косинусом и обоз
начают ch х. Легко видеть, что eh2 х — sir2 х =--1.
,.	sll X
Частное — называется гипер-ch х
бс.шческим тангенсом и обозначается через th х.
Ответы к задачам 844 и 845 показывают, что (sh х)' eh х и (ch х)' = sh х. Учитывая теорему о производной функции от функции, будем иметь:
(sh и)'--ch и • и',	(14)
(ch «)' = sh и  и'.	(15)
При решении следующих задач используются формулы (14) п (15).
846.	у = thx.
847.	у = ch2 х 4- sh2 х.
848.	x = x2chx.
849.	у = -~~. J ch х
850.	у = In th x.
851.	у = 2sllx.
2. Дифференцирование сложных функций, состоящих из нескольких звеньев. Нередко приходится иметь дело с дифференцированием функций более сложного вида, чем те, которые были рассмотрены в п. 1. Положим, например, что
</=( (4).
где и— функция переменной v: u — tf(v), причем о в свою очередь представляет собой функцию независимого переменного х: о = ф(х). При отыскании производной от у но х в таком, или еще более сложном, случае по-прежнему пользуются формулами, приведенными в и. 1, а также правилами дифференцирования, перечисленными в tj 1.
На ряде приводимых далее примеров показывается, как следует применять формулы и правила дифференцирования при решении различных более трудных задач на нахождение производных.
184
852.	Найти у', если у = In arctg
Решение. Принимаем arctg И х за вспомогательную функцию и пользуемся формулой (3):
у, (arctg К х)' arctg У х
При вычислении производной от arctg |,Л х за вспомогательную функцию принимаем теперь У х и применяем формулу (12):
1
У~х)' = 2 Кх =	1
1ф-х 1-фх 2 К х (14-х)
Подставляя найденное значение (arctg | х)' в выражение для у', получаем окончательно
, 1
у =------—-------------— .
2 \ х (1 4-х) arctg У х
При некотором навыке запись при вычислении производной может быть более компактной, как эго будет показано на следующем примере.
853.	Найти у', если у = (arcsin Ух)1.
Решение. В данном случае принимаем сначала за вспомогательную функцию arcsin р х и применяем формулу (I); затем принимаем за вспомогательную функцию У х и пользуемся формулой (10):
у' — 4 (arcsin У х)3 (arcsin |/ х)' = 4 (arcsin У х)3 •	=
У 1 — X
1
, /	.	—\з 2 / х 2 (arcsin р х)3
= 4 (arcsin у х) 	-------:---—.
I 1-х )zx-x2
854.	Найти у', если у = 2Ух‘^3х+У
Решение. Принимаем сначала за вспомогательную функцию выражение У >:'2 -|- Зх4' 4 и пользуемся формулой дифференцирования показательной функции [формула (4)]. Далее за вспомогательную функцию принимается трехчлен х2 -4-3x4-4 н применяется формула дифференцирования (2). Получаем последовательно
(/'=.2l/-v2 + 3x + 4 In 2 (|/х24-Зх"+4)' = 2/л2 + Зх+4 In 2-Jrl+j-
2 p’x24-3x + 4
При достаточной практике в решении залай на нахождение производной промежуточное звено может быть опущено и ответ записывается сразу, как эго показывается на следующем примере.
855.	Найги у', если у= lnsin5x.
Решение. Имеем
,	1 к = г -
у — ——cos 5х  о — 5 etg ох. sin 5х
19Э
856.	Найти у', если у = sin3 (х2 4~Зх + 1 )•
Решение. Учитываем прежде всего замечание, сделанное по поводу решения 817. Используем формулы (1) и (6) и правило дифференцирования многочлена:
у' --- 3 мп2 (л2 + Зх -|- 1) - cos (х2 Зх + 1) • (2х -[- 3).
857.	Найти у', если //= З1^*2'1'5*).
Решение. При вычислении производных в предыдущих задачах мы имели дело с тремя звеньями последовательно проводимых операций. Например, решая 854, сначала находили производную от показательной функции, затем производную от квадратного корпя и, наконец, производную от многочлена. В более сложных случаях число звеньев может быть и большим, но методика нахождения производной остается прежней.
В рассматриваемом примере сначала придется применить формулу дифференцирования показательной функции [формула (4)], причем за вспомогательную функцию и принимается tg4 (х24-5х), затем формулу дифференцирования степенной функции [формула (1)|, причем за вспомогательную функцию принимается tg (х2-|-5х), далее применяем формулу дифференцирования тангенса (за вспомогательную функцию принимается (х2-|-5х) и, наконец, находим производную от многочлена. При подробной записи будем иметь:
у'=-.3'еЧх'-\-5х) ln 3 {tgl (x2 + 5x)]':=3'g4(T4 : 5,г) ,п з . 4tg3 (x2 + 5x) (tg (x2-|-5x)]' =
‘ I" »•« V +w cos,(J+5t| +5,,'_
) '» |„ 3 . , ls? (.,-+5,)	ен-S-
При достаточном навыке следует писать сразу
»' ’3'8' 4 1"3 4 * Ь’+Ь) ггцллц <2‘ + 54 X
858.	Найти у , если у = arctg ,	’
Решение. Имеем
Найти производные от следующих функций:	
859. z/=lntg | .	867. у = In (х -4-]// х2 4- а~)
860. л/ = 4aictt? 1 Л3”‘.	868. у-= |/ х4~ 1 х.
	869. и = In arcsin|/ 1 — e'ix
861. z/ = (l Ч J 14-х2)5.	
862. у = tg‘ (х24- 1).	870-s-£4-
I arcsiii -	87I. {/=£з1±1+£.
863. у=--е	1'х2+1- X
864. у = tg3 2х  cos2 2х.	872. л/— In sin —. J	Хф- 1
sin3 х 865. у 	-г.	S11H X 873. У~	.
1 -1-2'	Г 14-tgx
866. у= arcsin (е*2).	874. y= In In tgx.
191
875. t/ = arctg -^--С’Ж,5 .
"	Л"* — 3V“ --  I
У к а з а и н о. Преобразуя отпет, числитель и знаменатель дроби, полученной в результате дифференцирования, следует умножить на
876.
877.
878.
879.
у =________
5 Г x2-i-3x-;-i //- sh4(x2 + 2x+ 1). у = фсII-’ Г у = In th х.
Указание. При решении 877, 878 и 879 следует учесть замечание, данное к 844 и 845.
3. Логарифмическое дифференцирование. Иногда бывает целесообразно, прежде чем находить производную от заданного выражения, предварительно преобразовать его с таким расчетом, чтобы процесс дифференцирования упрощался. В частности, если приходится вычислять производную от логарифма произведения, дроби, степени или корня, следует провести предварительное преобразова-рие, пользуясь обычными правилами логарифмирования. Во многих случаях оказывается выгодным, прежде чем дифференцировать заданную функцию, взять ее логарифм, определить затем производную от этого логарифма и по производной от логарифма отыскать производную от заданной функции. Такой прием называется способом логарифмического дифференцирования.
Метод логарифмического дифференцирования позволяет легко найти производную от сложной функции вида у = иг’, где и и v -функции аргумента .г. Действительно, логарифмируя обе части исходного равенства, получаем
In у = v 1п и.
Дифференцируя последнее соотношение, имеем
У' , , ,
= v----\~v' In и.
У и
Умножая обе части равенства на у и заменяя затем у через и!1, получаем окончательно после очевидных преобразований
у' = vuv ’ 1 и'-|-и” In и  v'.	(1G)
При отыскании производной от функции вида y = uv следует пользоваться методом логарифмического дифференцирования или применять формулу (1G), только что выведенную этим методом.
Разберем примеры, иллюстрирующие сказанное.
880. Найти у', если у = 1'т2| х.
Решение. Замечаем, что
у — j х2 р" х — ]/	= j.v5 = хG '
Д иффереп цир у я, получаем
,	5 “ У 5
у ' ~ X — — .
6	G j х
881. Найти у’, если у — У 1 Д- sin 2х.
Решение. Замечаем, что
у = | 1 + sin 2х = sin2 х 2 sin х cos х-|- cos2 х— ]Л(зш х Щсоз Л')2 sin л- Д- cos х.
Дифференцируя, находим
у' — cos х — sin х.
882. Найти у', если у = In 1/ -4=4.
192
Решение. Предварительное преобразование:
у = 1п л/ —= 3 In x-J-.l 111 (х- 1) - 1 In (.v- 4-1). ’ i	4	4	8
Далее находим , 3 ,	1	х
У "Че'1' 4(.ст—1)	/Нф-Й)’
883. Найти у', если //=-~7щ=7. )х(х-1)
Решение. Логарифмируем обе части исходного равенства:
In у-=?> In х 4 In (v2 J-1) — In x—	(x- 1) —
= ° In x - I In (x— 1) Д4 In (v- 4- 1).
Диффе1)еп'1[1РУя полученное соотношение, имеем у' 5	1	8х
4/	2 х 2 (х— 1) Н(ха+1) ’
Умножая теперь обе части последнего равенства на у и заменяя затем у .vH^+l)1
через —получаем
|v(x— 1)
, х3(х24~1)4 /5	1	, 8х \
у = . — — ।--------------------.
Ух(х — 1) \2.v	2(х — 1) х2 4~ 1 /
884. Найти у', если у = (ctgx)A'3.
Решение. Применяем метод логарифмического дифференцирования:
In у = х3 In etg х;	^ = -x3E¥rl-5-4-3x4nctgx =
= 3х2 In etg х-—--; у' = (etg х)х3 [Зх2 In etg х :—Х--\
sin х cos х	’ \	° sin х cos х j
Найти производные от следующих функций:
885.	У = ~\/ X3 V X2 ]/ X •	/54-tg - 894. у = \п	 V 5 —tg t-
886.	1/1 — cos 4х	
	У у 14~ cos 4.v'	tg-*-l 4-/2
887.	y=lnV 1 4-ctg2x.	895. У=1п—		.
		tg x— 1 _ у 2
888.	. т/№-1-3*4-1 у = In —-—. У х2у~4	5 2 896. y= / In -/+1/- + J- x
		6 x2 — x 1 J 3
889.	.	х3—9 ^=1П *3-1 '	X arctg 2x~1 . J/3 897. y = xx.
890.	1/	11!	: 1 Г -У ! 2.	
	|х2|-1--х 1 ‘2	898. y = xsinx.
891.	у = X6 (х2 + 1 )10 (Х3 4- 1).	899. у = (cos x)arc,s*.
892.	„ = 1704+!Н. У И	Sill2 X •	900. (/ = (x2 + 3)/v. 901. (/ = (1 4-x2)arcC№A.
893.	у = ех2 tgJx- arcsin х.	902. y = 'j/ arctg x.
7 Кручкович и др.
193
§ 3. ЧИСЛЕННОЕ ЗНАЧЕНИЕ ПРОИЗВОДНОЙ. ГЕОМЕТРИЧЕСКОЕ И МЕХАНИЧЕСКОЕ ИСТОЛКОВАНИЕ ПРОИЗВОДНОЙ
1. Численное значение производной. Производная от функции y = f(x) прет ставляет собою, как мы видели, также функцию от л-. При решении многих зада,, нсобходшчо бывает получить численное значение производной в данной точке, т. е. при данном значении аргумента. Обычно отыскание численного значения производной ис вызывает никаких затруднений: для решения этой задачи достаточно в общее выражение производной подставить соответствующее значение аргумента. Встречаются, однако, исключительные случаи, когда для нахождения значения производной в данной точке приходится обращаться к определению производно,; как предела отношения приращений (см. § Г); в этих случаях техника ренцирования не может быть использована.
Далее приводится несколько примеров на определение численного зплчепип производной как в простейших, так и в более трудных случаях.
903.	Найти f (1), если f (х) ^=х3 — 5х2 + 8х-4-2.
Решение. Находим производную от заданной функции:
f' (х) = 3х2 —10х-р8.
Подставляем в выражение производной вместо х единицу:
f (1) = 3 . 1 _ Ю - 1 4-8= 1.
„	тт «	г,	с , .	(	х2 sin 1	при	х ~ 0,
904.	Найти	/ (0),	если f (x)	= J *	1
( 0 при х = 0.
Решение. Выражение х2 sir: у, а также производная от этого выражшшя не имеют смысла при х = 0. Вычисляем f' (0) непосредственно, пользуясь определением производной. В соответствии с этим определением
rw-nm
Л-О о
где h — приращение аргумента. При л=-0 имеем
h 0	11
В данном случае
f (Л) = Л2 sin	f(0) = 0.
Таким образом,
/Р sin 1 — 0	.
f (0) — lira ---У------= lim /г sin -^0.
д-0	/i-о
905.	Найти f (3), если /(х) — | д-- Зг 9.
906.	Найти /'(2), если / (х) = In (1 +2-v).
907.	Найти f f"J , если f (x) = 2 sin x + 3 cos x.
908.	Найти f' i y'l, если / (x) = In sin x.
909.	Найти f (1), если /’(xp--/ -A S^nx-1 nf'n Л ""
[	0	при x = l.
194
2. Геометрический смысл производной. Пусть у = f (х) — уравнение некоторой кривой, а М (хь yt) — точка, лежащая па этой кривой (рис. 106), так что уt = = /(лу). Значение производной от функции f (х) при х=хг равно угловому коэф-
фициенту касательной к данной кривой, проходящей через точку М (хг, 1/1)- Иначе говоря, f' (*i) = tga, где а —угол между касательной к данной кривой, проведенной через точку М, и положительным направлением оси абсцисс (см. рис. 106).
Уравнение касательной к данной кривой y — f (х), проходящей через точку М (xlt yL) кривой, имеет вид
Нормалью MN к кривой в данной ее точке М (х]т у,) называется перпендикуляр к касательной, проведенный через
(2)
сывается так:

Указание на геометрический смысл производной позволяет легко решать некоторые задачи аналитической геометрии.
910.	Найти уравнение касательной и нормали к кривой у = = х34-2х в точке М (1, 3).
Решение. Для определения углового коэффициента касательной находим производную от заданной функции:
г/' = Зх2 + 2.
Значение производной в точке /И(1, 3) и дает искомый угловой коэффициент /г = 3- 14-2 = 5.
Таким образом, уравнение касательной будет
г/ —3 = 5(х—1), или 5х —г/ —2 = 0, а уравнение нормали
у — 3 = —(х~ 1)> или хф-5г/—16 = 0. и
911.	Определить, под каким углом парабола у — х?—х пересекает ось абсцисс.
Решение. Находим абсциссы точек пересечения кривой г/ = х2 —х и оси Ох, уравнение которой г/=0. Решая совместно оба уравнения, получаем х2 —х = 0, откуда заключаем, что абсциссы искомых точек будут х = 0 и х=1.
Под углом кривой с осью Ох понимается угол, который касательная к этой кривой в соответствующей точке образует с осью абсцисс. Для решения поставленной задачи следует найти угловые коэффициенты касательных к параболе в точках с абсциссами х = 0 и х=1.
Производная от функции у — х2— х будет у’ = 2х—1. Обозначая через at и а2 углы, образованные с осью абсцисс касательными к параболе, проведенными соответственно через точки (0, 0) и (1, 0), имеем
tga1=2 • 0 - 1 = — 1 и tga2 = 2 • 1 — 1 = 1, так что
оу =135° и аг = 45°.
7*
195
912.	Найти уравнение касательной к кривой z/ = x24~5x — 1 в точке М(1, 5).
913.	Найти уравнение касательной к кривой у = —• в точке Л! (1, 0).
914.	Найти уравнение нормали к кривой z/ = x24~2 в точке М (1, 3).
915.	Найти уравнение касательной и нормали к кривой = в точке (2> 2)-
916.	Найти уравнение касательной и нормали к кривой у — = 2)^2 sinx в точке М 2^.
X___ 1
917.	Определить, под каким углом кривая у = у;,..., • пересекает ось абсцисс.
918.	Определить, под каким углом синусоида у = sinx пересекает ось абсцисс в начале координат.
919.	Определить, в какой точке касательная к параболе у =-— х24~3х —5 параллельна прямой 7х —г/-|-3 = 0.
3.	Механический смысл производной. Значение производной от функции в данной точке характеризует скорость изменения функции в этой точке по сравнению со скоростью возрастания незачп-Q $ М	симого переменного. Учитывая это замечание,
........—...•	------- можно использовать понятие производной при определении скорости различных процессов.
П7	В качестве простейшего примера рассматри-
гис- 1и/	паем движение точки М по прямой, причем
через s будем обозначать расстояние от начала отсчета 0 до движущейся точки (рис. 107). Каждому моменту времени t соответствует определенное значение s, так что величина s является функцией времени: s— /(/)
Производная от s по t, т. е. s' = f'(t), есть скорость v движения точки по прямой, так что v = s'. В дальнейшем приводятся самые простые примеры, иллюстрирующие сказанное.
920.	На кривой г/ = х2 —2х-|-5 найти такую точку, в которой ордината возрастает в четыре раза быстрее, чем абсцисса.
Решение. Находим производную от заданной функции:
у' = 2х — 2.
Так как производная характеризует скорость возрастания ординаты (функции) по сравнению с возрастанием абсциссы (аргумента), то условие 2х — 2 - 1 определит абсциссу х — 3 искомой точки, а ордината находится из уравнения кривой у — хг— 2х-|-5 заменой х на 3: у = 8.
921.	Точка движется по прямой, причем расстояние s точки от начала отсчета (измеряемое в метрах) определяется по формуле s = t2 -ф-2/ 4-3, где/ —время (измеряемое в секундах). Определить скорость движения точки в конце пятой секунды.
Решение. Скорость движения точки v определяется как производная 01 пути s по времени t. В данном случае о = 2/4~2. Полученное выражение даег общую формулу для скорости движения точки.
Чтобы определить скорость движения точки в конце пятой секунды, следует в выражение для v поставить пять вместо t; получаем о5-—12 Mjceti.
196
X2
922.	При каком значении х ордината кривой У~^ будет возрастать в четыре раза быстрее, чем ордината кривой у — In х?
923.	Путь, проходимый телом, свободно падающим в пустоте, гг^2
определяется по формуле s= % . При этом предполагается, что в начальный момент времени тело находится в начале отсчета и начальная скорость равна нулю; ^—ускорение силы тяжести. Вывести закон изменения скорости свободно падающего тела.
924.	Радиус шара возрастает равномерно со скоростью 10 см/сек. С какой скоростью растет объем шара в момент, когда радиус его становится равным 100 см?
§ 4. ДИФФЕРЕНЦИАЛЫ ФУНКЦИЙ
1. Вычисление дифференциалов. Дифференциалом dy функции у-Д (х) называется произведение производной этой функции на приращение независимого переменного Дх, т. е. dy — j'(x)A.x.
Дифференциал независимого переменного dx, по определению, равен приращению независимого переменного Дх, поэтому
dy = f'(x)dx,	(1)
т. е. дифференциал функции равен произведению производной функции на дифференциал независимого переменного.
Из формулы (1) вытекает представление производной в виде частного двух дифференциалов
Этим обозначением производной постоянно пользуются наряду с обозначениями У' и /' (х).
Формула (1) показывает, что для нахождения дифференциала функции достаточно найти производную этой функции и полученное выражение умножить на dx. Таким образом, техника вычисления дифференциала может быть сведена к технике отыскания производной.
Операция нахождения дифференциала, так же как и операция нахождения производной, называется дифференцированием. Следует отметить, однако, что можно вычислить дифференциалы и непосредственно, не находя предварительно производной, а пользуясь таблицей формул и правил, подобных тем, которые Давались для производной.
В самом деле, применяя формулу (1), нетрудно составить следующую таблицу дифференциалов элементарных функций:
d (х«) = <Zxa 1 dx (а —любое действительное число),	(2)	,, , .	dx d (etg x) —	, v 2	sin2x *	(10)
й(/7)= * 2 |х	(3)	, ,		dx	. , __ d (arc sm x) = —:	; | x | < У 1 — x2	J, (И)
d (In х) = • х > 0,	(4)		
		d (arccos x) =	—==: | x [ 	< 1,
d (ах) = ах In a dx,	(5)	У 1 —x2	
d (ех) = ех dx,	(6)		(12)
d (sin х) — cos х dx,	(7)	. ,	,	,	' dx d (arctg x) —	(13)
d (cos x) = — sin x dx,	(8)	1 x*	
, ,,	dx d (tg x) =—— cos2 x ’	(9)	dx d(arcctgx)= 1+^a	. (14)
197
Основные правила нахождения дифференциалов
(они	аналогичны	основным правилам		вычисления производных)	
	rf(c)=0,		(15)	d (uv) — u dv+v du,	(18)
d (и	± о) = du ± d (си) = с du,	dv,	(16) (17)	,/ и \ vdu — u dv d 1 — 				(19)
и —функции от х, имеющие производные).
(здесь с —постоянная, а и и .	,
Положим теперь, что задастся функция от функции y = f(u), где и—функция аргумента х. По правилу дифференцирования функции от функции и по определению дифференциала,
dy = f (и) и' dx.
,.	, du	,	. du ,
Но и , поэтому dy—I (и) dx, или ах	ах
dy=f'(u)du.	(20)
Заметим, что формула (20), по которой находится дифференциал f (и), имеет совершенно такой же вид, как и формула (1), по которой определяется дифференциал f (х). Это свойство дифференциала сохранять неизменной свою форму независимо от того, задается ли функция f (х) аргумента х или функция от функции f (и), называется свойством инвариантности.
Производная (в отличие от дифференциала) не обладает свойством инвариантности. Действительно, если
t/ = f(x), то
y'=f (*).
а если
y = f(u), то
У'=Г (и) и'.
Учитывая свойство инвариантности дифференциала, можно составить				таб- (21)
лицу дифференциалов сложных	функции: d (ua)==au“-1 du			
(а —любое действительное число),				
2 F и	(22)		du	(29)
		a V-ig ii) —	sin2 и ’	
, „	, du	(23)		du	(30)
d (In «) = ~,				
d (аи) — а“ In a du,	(24)	d (arccos u) = -	du	(31)
d = du.	(25)		(z 1 — u-	
d (sin u) = cos и du,	(26)	d (arctg и)=	du ~ 1 + u2 ’	(32)
d (cos u) — — sin и du,	(27)			
, ..	.	du d (tg u) =	j- - , ' cos2 и ’	(28)	d (arcctg u) =	du 1 + U? '	(33)
В последующих примерах	требуется найгп	дифференциалы or заданных		
функций.
925. у = (1 +tgx)«.
Решение. 1-й способ. Находим производную от заданной функции:
у'= 8 (1 + 1§лГ —
X ’
198
отсюда, по определению дифференциала,
dy=8 (1 +tg хУ
2-й способ. Находим непосредственно дифференциал, используя Формулы (21) и (28):	•	'
//у
dy = 8 (1 + tg xy d (1 + tg X) = 8 (1 + tg x? .	.
926. y= In arctg (sin x).
Решение. Применяя последовательно формулы (23), (32) и (26), вычисляем дифференциал непосредственно:
d —	iarctg (sin *)] _	1 + sif‘2 x (S'n	_ cos x dx
y	arctg (sin x) arctg (sin x)	—	(1 -f- sin2 x) arctg (sin	x) '
При некотором навыке запись может быть сокращена и окончательный ответ получается сразу.
В последующих задачах рекомендуется, как и в 926, вычислять дифференциалы, не находя предварительно производных:
927.	у = arctg у.	933.	у —COS2 Ух .
928.	у (arcsin х)8.	934.	у = ]/’1 -h arctg х.
929.	У = 2‘г2 *.	935.	arctg х
			J КГ+х2
930.	у = ]/ 1 + sin2x.	936.	у = Vх (2 + cos х)2.
931.	у — хп In X.	937.	у = arccos (2х).
9.32.	г/ = etg5 (л-:! +х2).	938.	у = (1 -ф-х2) arcctgx.
2. Применение дифференциала к приближенным вычислениям. Дифференциал dy функции у--! (х) представляет собой главную часть приращения этой функции, линейную относительно Дх. Иными словами, приращение txy связано с дифференциалом соотношением
txy = y' Дх + е Дх, или Ду = Л/-|-е Дх,
где ? — 0 при Дх -> 0.
Таким образом", разность между приращением и дифференциалом функции есть бесконечно малая высшего порядка, поэтому при
Г(х)#=0 lim ^ = 1,
1 л%-+о dy
т. е. приращение функции и ее дифференциал—эквивалентные бесконечно малые. Отсюда следует, что при малых Дх имеет место приближенное равенство
Дг/ ~ dy,
ИЛИ
f (X + Дх) — / (х)	f' (х) Дх.	(34)
Соотношение (34) часто используется в приближенных вычислениях.
199
939.	Вывести приближенную формулу
Jzx + AxУ'х ч-	(35)
2 | х
при условии, что | Ах' мало по сравнению с х.
Решение. В данном случае / (л) —-= J'a, поэтому
f (л-[- Дх) = | х---Лх , f'(x) =-~;
2 У х подставляя полученные выражения в формулу (34), получим искомую прийлн-женную формулу.
940.	Показать, что ) 1-|-а?«1+-®- при малом а.
Решение. Полагаем в формуле (35) х=1 и заменяем Д.г через а.
941.	Найти приближенное значение (г26,19.
Решение. В данном случае
Нх)=У'х, Г(х) = --8/^--.
Полагая х —27, Дх ——0,81 и применяя формулу (34), получим
PU3 =	== 3/27----------= 3—	,
’	3 у' 272	3  9 ’
так что окончательно
|/'26Д9-«3-0,03 = 2,97.
942.	Вывести приближенную формулу у^х 4- Ах	yfх -|--
3 ) х2
(при условии, что | Ах I мало по сравнению с х).
943.	Вывести приближенную формулу	хЧ-Ах^-j/х -------—
п ф Х'1'1 (при условии, что | Ах | мало по сравнению с х).
944.	Показать, что 1 фасИ при малом а.
945.	Найти приближенное значение 16,64.
946.	Найти приближенное значение ]/8/76.
947.	Найти приближенное значение In0,9.
948.	Найти приближенное значение sin 29°.
Указание. Следует перейти к радианной мере угла, заменив 1° через 180- 30 через -g .
§ 5.	ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
§	1. Производные высших порядков. Производной второго порядка, или просто второй производной, заданной функции y = f(x) называется производная от ее производной у'=/'(х). Для обозначения второй производной пользуются символом у”, или [" (х). Аналогично, производной третьего порядка или третьей 200
производной данной функции называется производная от ее второй производной. Третья производная обозначается так: у'”, или f" (х).
Вообще производной n-го порядка, или n-й производной от функции, называется производная от ее (п — ))-й производной. Для производной n-го порядка принято значение у>!1>, или (х). В соответствии с этим производная четвертого порядка обозначается через у'41 или f<4' (х); производная пятого порядка — через г/15’ или (х) и т. д. (для производных первых трех порядков пользуются теми обозначениями, которые были даны вначале).
Из определения производных высших порядков следует, что для получения производной n-го порядка надо предварительно найти все предшествующие производные до (п—1)-й включительно. Например, для нахождения четвертой производной надо сначала вычислить первую производную, затем вторую, наконец третью и только после этого можно приступить к решению поставленной задачи. В отдельных исключительных случаях удается найти общую формулу для производной n-го порядка, и тогда отпадает необходимость в вычислении всех предшествующих производных.
Ниже будут приведены примеры на нахождение производных высших порядков как в тех случаях, когда необходимо вычислять все производные более низкого порядка, так и в случаях, когда удается подметить закон, по которому составляется общая формула для производной n-го порядка.
При отыскании производной n-го порядка от произведения двух функций и и v целесообразно применять формулу Лейбница
И(Л“2>	(1)
Коэффициенты в этой формуле те же, что в разложении бинома Ньютона.
При рассмотрении первой производной изучались вопросы ее геометрического и механического истолкования. Роль второй производной при построении графика функции t/ = f(x) подробно выясняется в гл. VI. Что касается механического смысла второй производной, то если первая производная истолковывается как скорость некоторого процесса, то вторая производная характеризует ускорение того же самого процесса. Обозначим, например, через s расстояние от точки, движущейся по прямой, до начала отсчета 0 (расположенного на той же прямой). Очевидно, величина s является функцией времени t, т. е. s = f (t). Скорость движения точки и равна первой производной от расстояния s по времени:
а ускорение а —второй производной:
a = d/2==f W-
2	. Дифференциалы высших порядков. Дифференциал dy функции </=7(х) является функцией от х:
dy = f'(x)dx, или dy—y'dx.
Дифференциал от него d(dy)-=d2y называется дифференциалом второго порядка. При вычислении d2y приходится дифференцировать dy, т. е. у' dx. В процессе этого дифференцирования надо учитывать, что dx=\x не зависит от х п, следовательно, при дифференцировании по х рассматривается как постоянное. Таким образом, имеем
<Py = d (dy) = d(y' dx) = d (у') dx = у" dxdx = y" (dx)2.
Выражение (rfx)2 для краткости принято записывать как dx2-, тогда окончательно
сРу = У" dx2.
201
Аналогично d (d2y) = d3y называется дифференциалом третьего порядка и вообще d (dn~*y'y== dny называется дифференциалом n-го порядка. Дифференциал n-го порядка равен произведению производной n-го порядка на п-ю степень дифференциала аргумента (dx)n dxn:
d,ly = y,n> dxn.	(2)
Например, d3y = y"' dx3.
949.	z/ = tg.r, найти у".
Решение. Находим первую производную: у'=—. Вторая производная, по определению, равна производной от первой производной, следовательно,
,, __ ( 1 V _	— 2 cos х sin х __ 2 sin х
U ~(COS2X/	COS1 X	COS3 X 
950.	у — (х-\- I)5, найти у'".
Решение. Находим последовательно первую, вторую н третью производные:
/ = 5(х+1)“, г/" = 20(х-Ы)3, у"' = 60(х+1)2.
951.	у = ах, найти производную n-го порядка.
Решение. Находим у', у”, у"'-.
у' = ах In а, у" = ах (In а)2, у'" = ах (1п а)3.
Закон образования последовательных производных определился: каждая последующая получается из предыдущей умножением на In а. Выражение для п-И производной будет
£/|Л) _ a.v ayi.
Теперь при необходимости определить какую-либо производную от av не г надобности вычислять все предшествующие, можно просто воспользоваться готовой формулой. Например, ум=ах (In а)10.
Заметим, что если у = ех, то у'п>—ех.
952.	г/= sinx* найти производную n-го порядка.
Решение. Определяем последовательно у', у", у'", уа'-_
у'— cosx. у” = —sinx, у'" = — cosx, y,l> = sinx.
Понятно теперь, что продолжать процесс последовательного вычисления производных нет надобности: yi3> будет равно у', yiS> —у" и т. д.
Очевидно, для нахождения производной какого-либо порядка от sin х достаточно поделить порядок производной на четыре, найти остаток при этом делении и отыскать производную, порядок которой равен этому остатку (если остаток равен нулю — производная равна самой функции sinx). Например,
{/<27)=^"' = —cosx, у1Ы‘ = у" — —sinx, r/‘16l = (/ = sin х.
Мы установили закон, по которому строятся последовательные производные от sin х. Но можно дать и общую формулу для n-й производной от sin х. Действительно,
,  ! , я \ у —cos х = sm I х +	,
у = cos lx + yl = sm ^х + 2-у^,
z/'" = cos ^х-ф-2 •	= sin ^x + 3 •	,
202
953.	у = х3ех, найти z/(4).
Решение. Находим последовательные производные от каждого из сомножителей отдельно:
(х3)' = 3х2, (х3)" = 6х, (х3)"' = 6, (х3)(41=0;
(ех)' = (ех) ’' = (ех) "' = (еху*' = ех.
Запишем формулу Лейбница (1) для случая п = 4:
(но)14, = н'4’у-|-4и"'у'	и"о" + 4ы'о"' + ис(41.
Применяем эту формулу в данном случае, полагая и = х3, v=ex:
у'Л} = (x3e-v) li = 4 • 6ех + 0 • 6х • e-v4-4  Зх2ехх3ех, или
у<*  = (хз +12х2 + 36х + 24) ех.
954.	z/ = arcsinx, найти у”.
xi । 1
955.	= найти у .
956.	у = угх2-[-1, найти у”.
957.	у = arctgх, найти у'".
958.	у — х3 4-2х 4-6, найти yw.
959.	г/= х6 4-5х4 4-2х3 — х2, найти z/(4).
960.	у = '\/х, найти г/(4).
961.	у = х54-2х44-6х34-5х24- h найти z/(s).
962.	y = x2sin2x, найти у”'.
963.	у = х41пх, найти yW.
Указание. При решении 962 и 963 применить формулу .Лейбница (1).
Найти выражение у1'1' от заданной функции:
964.	у = cosx.	967. z/ = sin2x.
965.	у = 1пх.	968Гу = |^.
966.	у = х!\
969.	Точка движется по прямой, причем расстояние s точки от начала отсчета (измеряемое в метрах) определяется по формуле s = — t3 — 2/24-4t — 1, где t — время (измеряемое в секундах). Определить ускорение движения точки в конце третьей секунды.
970.	Точка массы т совершает гармоническое колебание около положения равновесия О по закону x = asin2ncot, где х — расстояние точки от О в момент /, а и со — постоянные. Показать, что действующая сила пропорциональна расстоянию точки от О.
§ 6.	ДИФФЕРЕНЦИРОВАНИЕ НЕЯВНЫХ И ПАРАМЕТРИЧЕСКИ ЗАДАННЫХ ФУНКЦИИ
1.	Неявные функции. Если у как функция от х задается посредством соотношения
F (х, у)=0,	(1)
где F (х, у) — выражение, содержащее хну, то у называется неявной функцией от х. В некоторых случаях уравнение (1) удается разрешить относительно у, и
203
Тогда можно перейти от неявного способа задания функции к явному y = f (х), в других случаях такой переход оказывается неосуществимым. Независимо от возможности такого перехода производная от у по х при неявном способе задания функции может быть определена следующим образом: 1. Находим производную от левой части равенства (1), рассматривая при этом у как функцию от х, и приравниваем ее нулю.
2.	Решаем полученное уравнение относительно у'; в результате будем иметь выражение производной от неявной функции в виде
У'=Ч(х, У)-	(2)
Для определения второй производной от неявной функции дифференцируем равенство (2) (снова рассматривая у как функцию от х), а затем в правой части заменяем у' его выражением из равенства (2). Аналогично поступаем при определении производных более высоких порядков.
971.	х3у'24- Бху4-4 = 0, найти у'.
Решение. Дифференцируем заданное соотношение, рассматривая у как функцию от х:
Зх2у3 + 2х3уу' + 5у + 5ху' = 0.
Решаем полученное уравнение относительно у':
, _	ЗУ-:/’-’ -ф 5у
У 2х2у -|-5х'
972.	aretg t/ — у + х = 0, найти у”.
Решение. Дифференцируем заданное соотношение п определяем затем у':
-rr-,-v —У' + 1=0, или у' —у' —у2уЧ-1 + У2 = 0,.
А "г У
откуда
Находим далее у":
у"=-2у“3у' = -Ау«.
В правую часть последнего равенства подставляем вместо у' его значение, определяемое равенством (3),
,,„ = _ 2 Д+Л	2(++)
у У3\ У2 J	У3 -
^2, п2
973.	Дан эллипс 42 + 43 = 1. Найти уравнение касательной, проходящей через точку М (хъ гд), лежащую па эллипсе.
Решение. Переписываем уравнение эллипса в виде
a2y2^.b2x2 = a2b2.	(4)
Так как точка Л4 (xlt i/ij лежит па эллипсе, то имеет место тождество
а2у I+ Ь2х{ = а2Ь2.	(5)
Дифференцируем обе части равенства (4):
2а2уу' + 2Ь2х — 0;
определяем у':
204
Находим значение производной у' в точке (xt, у J. Это значение равно угловому коэффициенту k касательной к эллипсу, проходящей через точку Л1 (хх, yv),
Уравнение касательной, проходящей через точку Л'1 (х,, ух), запишется в виде
a у ( или после преобразований
а2ууу -J- Ь2х\х — а2у2 -|- 1>2х2.
Учитывая тождество (5), имеем
Ь2х,х + сРу^у = а2Ь2.
Поделив обе части последнего уравнения на а2Ь2, получаем окончательно
974.
975.
976.
977.
978.
в точке
979.
откуда
XlX j_ У1У _ . ’a2' 1 &2
хяу — 3x2y2 -j- 5y:i — Зх 4 = 0, найти у'.
x2y-\- aretg -0, найти у'.
ху3 + 2y — 1 = 0, найти у".
Найти значение у" в точке (1, 1), если х3 + 2ху — Зу2 = 0. Провести касательную к кривой х3 — 2х2у2 -j- 5х -ф- У — 5 •- 0 (1. J)-
Наифи уравнение касательной к гиперболе - —	= 1, про-
ходящей через точку /И (х1; г/3), лежащую на гиперболе.
980. Найти уравнение касательной к параболе у2 = 2рх, проходящей через точку М (х3, z/i), лежащую на параболе.
2. Функции, заданные параметрически.
Пусть функция у аргумента х задастся при помощи параметрических соотношений
х = а(/), р=Р (/),.	(6)
причем а (!) и |3 (t) —дифференцируемые функции t и а' (t)	0. Производная
от у по х находится путем дифференцирования равенств (6):
4х = а' (/) dt, dy-.-f>' (t) dt, dy P' (0
Вторую производную от у по х находим, дифференцируя по х соотношение (8): d(p d2y __ d [<р (/)] _ d(f (/) dt _ dt dx2 — dx dt dx ~~ dx ’ dt
(7)
(8)
981.
х = a cos3 / I „ сру > наити —.
у = a sin3/ )
Решение. Дифференцируем исходные равенства:
dx =—За cos21 sin t dt; dy = 3a sin21 cos t dt,
205
отсюда
Находим вторую производную:
d2y _ d (tg t)____d (tg О dt __ _ dt _	1
dx2 dx ~ dt dx	dx 3u sm i cos4t '
dt
982.
x=ln/ 1
} найти у .
Решение. Дифференцируем исходные соотношения:
dx=y, d//=--2cos2/ dt, отсюда
^• = 2/ cos 2t.
dx
Находим btodvio производную:
d (2t cos 2/)
d2y _ d (2t cos 2t) _ d (2t cos 2/) dt _dt_____
dx1 dx	dt dx dx
dt
= l££iZLzd!2!IL^ 2/ (cos 2t - 2.1 sin 2Q.
7’
г,	о du
В следующих задачах наити
ncQ 3at	3at2
983. x j _|_> У i -уp'1 •
984. x = -4т, у = -r^r. 985. x - | ZT\ w - { 7.
Г “у I	I ~ 1
r>	- d-y
В следующих задачах наити
986.	х = е(, у = arcsin/.
987.	х = о (sin/ — /cos/), у ~ a (cos / + / sin /).
988.	x = e'cos/, у — е* sin t.
989.	Найти уравнения касательной и нормали к циклоиде:
x — a(t~ sin/), r/ = a(l—cos/) в точке, где /= .
990.	На линии х = /2-|-1, y = 2ts — /2 найти точку Л1, в которой касательная параллельна прямой у — 2х.
ГЛАВА VI
ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
§ 1. ТЕОРЕМЫ О СРЕДНЕМ ЗНАЧЕНИИ. ФОРМУЛА ТЕЙЛОРА
1. Теоремы о среднем значении. Эти теоремы связывают значения функции на концах отрезка со значением ее производной в некоторой внутренней «средней» точки этого отрезка.
Теорема Ролля. Если функция y = f(x): 1) непрерывна на отрезке [а, й], 2) дифференцируема на интервале (а, Ь), 3)	то найдется по крайней
мере одна точка £ на интервале (а, Ь), в которой f (Е) --0.
В геометрических терминах эта теорема формулируется следующим образом: если график функции является непрерывной кривой, в каждой внутренней точке которой можно провести ка-сательную.. (график является гладкой кривой), и хорда, стягивающая концы дуги, параллельна оси Ох (рис. 108), то найдется на кривой по крайней мере одна внутренняя точка, касательная в которой параллельна оси Ох.
Теорема Лагранжа.
Если функция y = f(x)‘ 1) непрерывна на отрезке [и вале (а, !>), то на интервале {а., Ь) найдется
Л], 2) дифференцируема по
крайней мере одна которой
на интер-точка g, в
Теопема Ролля является частным случаем Ролля хорда .W.V параллельна оси Ох.
(1)
Рассмотрим геометрический смысл теоремы Лагранжа. Слева в формуле (1) стоит тангенс угла наклона хорды MN к оси Ъх tga(pnc. 109), справа — значение тангенса угла наклона касательной к графику в некоторой точке g. Теорема утверждает, что на гладкой дуге кривой всегда найдется точка, в которой касательная параллельна хорде, стягивающей концы дуги.
теоремы Лагранжа. В теореме
207
Формулу (1) иногда записывают в другом виде, обозначая Ь—х и умножая на знаменатель:
Дх)-Ш=Г (£)(*-«)	(2)
(a < £ <х).
Теорема Коши. Если две функции ср (х) и ф (х): 1) непрерывны на отрезке [н, й],
2) дифференцируемы на интервале (а, Ьф
3) ф' (я) 7^=0 на интервале (а, Ь), то на интервале (о, Ь) найдется по крайней мере одна точка в которой выполнено равенство
ф СО ~ ф (а) = Ф' (%)
Ф('')~ л|> (а)	ф'Й)'
991. Используя теорему Ролля, доказать, что для многочлена Р (х) = (х-фЗ) (х-ф-2) (х—1) на интервале (—3, 1) найдется корень уравнения Р" (х) = 0.
Решение. Многочлен Р (х) обращается в нуль в точках xL ——3, .ж --= —2, х3=1. Па каждом из интервалов (—3, —2) и (—2, 1) к функции Р (х) применима теорема Ролля, так как Р (х) всюду дифференцируема и
Р (—3) = Р (—2) = 0, Р (—2) = Р (1) = 0;
поэтому найдутся точки §£, —3<^1< — 2, 11 Е-т.
P'g1) = P'g2)=0.
К функции Р' (х) на отрезке [g1( g3] теорема Ролля найдется точка g, < g < g2, в которой P"(g)=O.
—2 < Е3 < 1 такие, что
опять применима, и потому
992. Проверить справедливость
/(х) = arcsin х на отрезке [—1,
теоремы Лагранжа для функции
1]. Найти значение при котором выполнено условие (1).
Рис. 110
Решение. Функция определена и
при —1 sg X sg 1 .
Найдем
непрерывна
Г (*)
z'w=71h’
производная конечна всюду внутри интервала (—1, 1); при х— । 1 не существует, по это не нарушает условий применимости теоремы Лагранжа. Точка g, удовлетворяющая условию (1), должна существовать. Найдем эту точку, записывая условие (1):
arcsin 1—arcsin (—1) __	1
rzrpj) yr:
лт/2 — (—л/2)  1
2	“	’
откуда
или 2	±— 4/л2 .
Итак, в данном случае условие (1) выполняется для двух точек (рис. ПО).
993. Пользуясь формулой (2), оценить значение In (1
208
Решение. Рассмотрим функцию f (х) = 1п х. Эта функция дифференцируема всюду при х>0 и /'(х) = ~-. Для отрезка [е, <?+1] пишем формулу (2):
In (1-|-е) = ln е+|(«+1) —е] •	- 1 + * ,
s ь где е < g < 1 ф-е.
Оценим выражение 1 +-— при е < £ < 1 +е:
•э
1+ 1- < 1 + так как £ > е, S
и
1 + < > 1 +“тт~ , так как Е < 1 -|-е. g 1+е’
Таким образом,
‘+т~<'п<1-М<1+-‘.
Подставляя в эту оценку е=«2,7, получаем окончательно
1,27 < In (14-е) < 1,37.
994.	Применима ли теорема Коши к функциям f (х) = cos х и <р (х) = х3 на отрезке [—л/2, л/2]?
995.	Проверить выполнение условий теоремы Лагранжа для функции f (х) = хф--“ на отрезке 2|. Найти промежуточное значение g.
996.	Пользуясь формулой (2), оценить значение arctg 1,5.
Указание. Формулу (2) применить на отрезке [1; 1,5].
997.	Проверить выполнение условий теоремы Коши для функций f(x) = cosx и <p(x) = sinx на отрезке [0, л/2]. Найти промежуточное значение F,.
2. Формула Тейлора. Обобщением формулы (2) для функций, имеющих п производных в некоторой окрестности точки х = а (включая и саму эту точку), является формула Тейлора:
,	/W=/(a)4-^/4a)-y<^^/''(a) + ...+ (£p<2/«-1((!) + ^iWi (4)
11	1	yrt ~~ 1 ) 1
где R,, (х) — остаточный член формулы Тейлора — является бесконечно малым по крайней мере я-го порядка по сравнению с разностью х— а при х—* а. В формуле Лагранжа остаточный член имеет вид
Кп^—~п“Г?,п> (g),	(5)
где g — некоторая промежуточная точка между точками а и х.
При л ! формула Тейлора совпадает с формулой (2), а при п = 2 записывается так:
/ (х) — / (а) +/' (а) (х—а)4-1?а(х), Яг (х) (х — я)2 f" (g).
998.	Представить по формуле Тейлора функцию у = sinx в окрестности точки а = 0.
209
Решение. Функция sin х имеет всюду производные,любого порядка, так что формула Тейлора для нее применима в любой точке ’ а до произвольного порядка п. Для того чтобы записать формулу Тейлора при а = 0, надо вычислить значения jin: (0). Согласно решению 952 для f(x) = sinx
(x) = sin : x4-n "j, т. e. f'nl (0) — sin п у .
Если n=2k (k — 0, 1, 2, ...), to
/<2fe> (0) = sin /гл—0,
поэтому в разложении sin х по формуле Тейлора отсутствуют члены с четными номерами. Для п нечетных и —2k—1 (/г—1, 2, 3, ...)
/>2Л-1> (0) = sin	= (— l)^ i,
так что знаки нечетных членов чередуются.
Таким образом, при /г = 2/гф-1 получим следующее разложение Тейлора функции z/ = sinx:
х3 х3 х7	(—1)*	, D , ,	...
smx = x-3,5! ~-7j+ ...	x + ^.i (*).	('Д
где
.	, 2/г+1 \
/чг*з-1> (i)	Sln . § И 2Я'	cos
р , , (Х\ — I____IP v2*+l = ___:______±____V2fe+i^(_ ns ___________
-,c- i W ” (2/г+1)!	(2/гН-1)!	V ’ (2/г~Ь 1)! ’
999.	Разложить многочлен Р (х) — 2г1 — 5ху — Зх3ф-8х + 4 по степеням (х —2).
Решение. Многочлен имеет всюду производные любого порядка. Положим (2)
в формуле (4) а —2. Вычислим коэффициенты —
Т а б л и ц а 3
п	pW (А.)	р(«)	ь п
0	Р (х) = 2х4 — 5х3 — Зх3 8х + 4	0	0
1	Р' (х) = 8х8 — 15x2-6x4-8	0	0
2	Р" (х) — 24х® — ЗОх — 6	30	15
3	Р'" (х) = 48х —30	G6	11
4	pro (Х) = 48	48	О
5	Д3> (х) = 0	0	0
	Применим формулу (4): Р (х) = 15 (х - 2)2 4- 11 (х — 2)3 4-2 (х — 2)\	(х) = 0, так как	(х)	Д).
	1000. Получить следующие разложения основных	элемент	арных
функций в окрестности точки а = 0:			
	а) е 1 4~х + 2| + si +•••+(„_ip + W> Rn	Ыу..  X’1 п’.	(7)
	г 2	уЗ б) 1п(1+х) = х--'2- + -* -... + (-	+		
	р	П'Ы-1 1	х ''!		(8)
			
210
К	„2 ,O v<!	, у2 I fl-l ’
( в) cos , _ I - Л- + » - «. + ... + (- 1)»-! |2 (t _	+ R,t w, (9)
p ___ / _ nfe C0S £ Y2k
IS	^2* —(	1)	(2/?)l x 
1001.	Разложить многочлен P (x) = x4 — 2x3 7x — 4 по степеням ;	(x-1).
1002.	Разложить многочлен P (x) = (x2 — 2x -}- З)3 по степеням x. ‘	1003. Разложить по степеням x функцию f (x) = ]/l-}-x до члена,
/ содержащего x4.
J. 1004. Разложить функцию f (x) = —1— no степеням (x — 2) до члена, r	I x
’ содержащего (x —2)4.
8‘	3. Применение формулы Тейлора. Формула Тейлора является источником
| приближенных формул. На ее основе составлены таблицы значений ряда элемен-| тарных функций. Рассмотрим некоторые относящиеся сюда задачи.
f 1005. Используя разложение (6) (см. 998), выписать три первых к многочлена Тейлора функции r/ = sinx и оценить погрешность прп-S блпженной замены функции многочленом на отрезке 0 «С х sS 0,1.
к Решение. Полагая в формуле (6) fe=l, имеем
(	sin x = x + R3 (х), 7?з (х) = — ~cos § • х3 (0<g<x).
z-ч	„	,
j‘L Отсюда выводим первую приолиженпую формулу:
sin х^х.
fc Оценивая величину остаточного члена R3 (х) на данном отрезке, получим оценку « погрешности первой приближенной формулы на отрезке:
|	|7?з(лТ=||соз^ |х;з<1(0,1)з<0,001,
так' как [ cos £ ] < 1. а х ' < 0,1 на отрезке [0; 0,1]. Далее, полагая в (6) /? — 2 п	получим вторую и третью приближенные формулы с указанными оцен-
ками погрешностей:
sin х as х —
(0J)7;
SillX«=X- g|- +
(X) | <	< (0,1)4
На рис. 111 представлены графики функции у = sin х и трех первых многочленов Тейлора. Этот пример дает наглядное представление о некоторых общих закономерностях в приближении функции многочленами Тейлора. Во-первых, отклонение многочлена от функции тем меньше, чем ближе х к а, и оно стремится к нулю при х —>а (в данном примере при х~0); во-вторых, при фиксированном х отклонение многочлена от функции тем меньше, чем выше порядок многочлена, и оно стремится к нулю при п — со.
211
I
1006. Используя разложение (7) (см. 1000), оценить абсолютную погрешность приближенной формулы
ех'zi 1 +* + 41’ на 0ТРезке [“0J; 0,13-
Ре шеи не. Формула (7) для п = 3 имеет вид
ех = 1 + х +	х3е6,
где с — внутренняя точка интервала (—0,1; 0,1).
Так же как и в 1005, точная формула отличается от приближенной величиной остаточного члена
Т?4 (х) = ^х’Л
Надо оценить | /?4 (х) [ на отрезках [0; 0,1] п [ — 0,1; 0]. В первом случае
1^4 W : = 3! !	< 0,004,
так как в данном случае 0 < £ < х 0,1; для второго отрезка
| /?4 (х) ; = ^ i | < -I (0,1)3 • < 0,002, так как — 0,1 <£< x • : ().
Сравнивая полученные оценки, заключаем, что абсолютная погрешность данной формулы на отрезке [—0,1; 0,1] не превосходит 0,004.
1007. Оценить ошибку, которую мы допускаем, вычисляя значение In 1,5 по приближенной формуле
у2	уЗ	у4
1п(1+х)^х--^+^---х4-,
т. е. используя четыре первых члена разложения (8).
Решение. Запишем формулу (8) для п = 5:
у 2 уЗ у4 1 / у \ 5
In (1 +х) =х-^2- + -3- - -4- + у	(0 < ^ < х).
Это точное равенство отличается от приближенной формулы величиной остаточного члена
1 / х ’ где 0<^<х-
Отсюда следует, что величина ошибки равна значению остаточного члена. Остаточный член может быть оценен так;
1 / 0 5 \5 0 < Т?5 < max 4 РТт) <0,007.
0<5<0,5 5 \1 + §У
Следовательно, с ошибкой не более 0,007
In (14-0,5) =«0,5 — (0,5)1 2+ 5 (0,5)3-	(0,5)4 =«0,401.
Z	О	т:
Истинное значение 1п (1+0,5) заключено, таким образом, в пределах
0,401 <1п 1,5 <0,408.
212
1008.	Оценить погрешность приближенной формулы Д-З Д*5
sinx^x —- --4--Р- на отрезке [ —л/7, л/7]. о! 01
1009.	Оценить погрешность приближенной формулы in(i+x)^z-4+4
Гп 1 1 на отрезке 0,	.
1010.	Используя разложение, полученное в 1003, вычислить значение с точностью до 0,01. Какой приближенной формулой надо при этом воспользоваться?
§ 2. ПРАВИЛО ЛОПИТАЛЯ
„	г.	0 со „
1.	Неопределенности вида — н . При отыскании предела функции часто подстановка предельного значения аргумента приводит к неопределенным выра-0 со
жениям вида	, 0-оо, оо —оо, 0°, оо°, Iе0. Нахождение предела функции
в таких случаях называют раскрытием неопределенности. Приведенная ниже тео-рема, известная под названием правила Лопиталя, является основным аппаратом для раскрытия неопределенностей.
Теорема. Если две функции <р (х) и ф (х): 1) бесконечно малые или бесконечно большие при х — а,
2)	дифференцируемы в окрестности точки х — а (в некотором интервале (а — 8, а+ 6), 6 > 0),
3)	ф' (х) ф 0 в окрестности точки х — а, за исключением, возможно, самой точки х — а, и
4)	существует конечный или бесконечный предел
Um =
х-+а ф (х)
то предел отношения этих функций равен пределу отношения их производных, т. е.
lim ТМ = lim ОЕ	(1)
х—ф (х)	х—> а ф (х)
Эта теорема справедлива также для односторонних пределов и в случае, когда х —» со.
Сформулированная теорема позволяет свести вычисление предела отношения самих функций к пределу отношения их производных, что во многих случаях представляет более простую задачу.
В следующих задачах по правилу Лопиталя вычислить данные пределы.
* Из того, что предел lim	не существует, нельзя, однако, заключить,
х—> а ф <Л)
что искомый предел не существует (см. 1039, 1040).
213
Решение. Подстановка предельного значения х—1 приводит к неопреде-
ленности вида так как Иш (д-з—1)=0 и Hm 1пх = 0. Предел отношения О	х —* 1	х -► 1
производных существует:
.. ср' (х)	.. Зх-
hm	hm—— = 3,
г—*1 Я' U) х-1 1
х
поэтому
х3-1 ..	(х3-1)
lim —,-----= hm ----------?
г—.1 1П X	Л'—>1 (И1 Л')'
г Зх2 , = lim —:— = 3.
х—1 .1. X
1012.
lim
АГ-* 1
sin олх
sin 2лх
Решение. Здесь также неопределенность
0 типа -.
Применяем к ее раскры-
тшо правило Лопиталя:
,. sin 5лх 5л cos 5лх 5 cos 5л 5
11Ш ---------- = 11Ш -------------- = — ——— =-------------—
л- — 1 sin 2лх х — 1 2л cos 2лх 2 cos 2л 2
~ — arctg х
1013.	lim —-----п-.
^ln(l + F)
Решение. Так как числитель и знаменатель при х —»-'-со бесконечно малые, то по правилу Лопптал!!
Предел отношения производных равен -|-оо (в условии 4 й=+сз), следовательно, и исходный предел равен -*-сс.
1014.	lim ^-£-,а>0.
X —-фоо х
Р е ш е н и е. Это неопределенность типа-Ц , к которой также применимо правило Лопиталя. Переходя к отношению производных, получим
lim J££= lim —
Xa x-^±ooOXa
x-*»-i-co axa
1015.	lim
X- + OO e 
Решение. Здесь для получения результата приходится применять правило Лопиталя дважды, так как и данное отношение, и отношение производных приводят к неопределенности типа--’0-. Повторные применения правила Лопиталя
214
записываются обычно в одну цепочку равенств:
lim -Xv — lim -х- = lim ...ff *1..-— lim
. „„„ ..	1—cosx
1020. lim —m-т—.
x->o 2x2
. п_	1 • su XX
1016.	11ГП —---
х->о 2--
sin 2x
3x~ ‘
sin Злх
1017.	—-.
sin 2лх
1018.	lim-Э^Ц.
Х_ояпх-х2
,О19-±ЙЧЙ'
1021. lim -tg* x
Л-.0 sin x~x
= 0.
1022. lim—2n.(1 + t'2) r—i /	.	\
x 00 In —arctg.v k	/
вида 0-оэ и co —co. Если ф (x) — 0 и tp (x) —» co при
2. Неопределенности
x—♦«, то отыскание предела lim ф (x) • ф (x) (неопределенность вида 6 • co) может x-»a
0 co
оыть сведено к одному из ранее рассмотренных случаев — или ~ при помощи
тождественных преобразований:
ф(х) • ф(х) = ^-Щ, или ip(x) • ф(х) = -9фЬ. Ф (x)	ф(х)
Если ip (x) —> oo и ф (x) —- co при x—-а, то отыскание предела lim (ф(х) —
x-— a
— ф (x)J (неопределенность вида co —co) может быть сведено к раскрытию «неопределенности вида 0 • со» путем тождественного преобразования разности функций в произведение
ф (х)-ф(х) = ф(х) • ф(х)
Иногда удобно пользоваться и другими преобразованиями:
ф(х) —ф(х)=ф(х)
[l-w]’или Ф<*)~ф(*) = ф« UQ--1]-
В следующих задачах вычислить пределы функций:
1023. Нт
Х-.П/2
Реш е н и е. а) Преобразуем функцию 2^. Очевидно,
0
ность вида - при х—>
образованной функции:
что
л \ . х —л/2 !
х — yj tg х = ctg у  I неопределен-правило Лапиталя применимо к пре-
л
X----V
lim [х — л \
'—г
lim
л
2
с tgx
lim Л Г-”2
(ctgx)' 11П^
*'* 2 sin2x

б) Можно было бы преобразовать функцию следующим образом:	X
1	tg X /	со	л \ lz
X tgx = —------ (неопределенность вида — при х-»-?-]. К преобразованной
л
х-J
215
функции правило Лопиталя опять применимо:
1
2>	2
= lim —i------------_= lim -------_---= —1.
я	(sin 2x)'	я 2 cos 2x
V->V	‘1
Сравнивая решения а и б, видим, что
решение а скорее приводит к цели.
1024. limM-
х-1 \11U
1 \
х— 1 / ’
Решение. Имеем неопределенность вида оо — оо. Преобразуем функцию: _1________________1_
1пх	X — 1
— (х-1 -In Х)= 4—
(х— 1) In X	’	(х—1) In X
1 — 1-
(х— 1— 1пх)'	..	X
=	----.—-j-^- = lim------------r .
x-1 [(x-l)lnx]'	. x-1
X
lim :;----
1 \1п х
1
х— 1 /
Удобно умножить числитель и знаменатель на х, тем самым мы избавимся от дифференцирования дроби — операции более громоздкой, чем дифференцирование произведения. Продолжая преобразования, получаем
х	(х — 1)'	1	1
-------=— = 11 m	.------Гт; = 11 m vi—. ,	.
, х— 1	1 (х In х + х—1) х j (In х)+ 1 + 1	2
"Г” X
В этом примере, как и в 1023, сложность решения в значительной степени зависит от способа преобразования функции.
1025.	lim (ех — х2).
X —*4'00
Решение. Имеем:
(см. 1015), поэтому
lim 4— х“ | = 1 и lim (ех- х3)= Пт ех 4—x24=j-oo.
Х-+&3 \ сл /	х—у ел J
1026.	lim х2е-2А‘.	1029. ПтП____________1\
.г->4-со	е.х—1/’
1027.	lim 1пх-1п(х—1).	1030. lim (Inx — J/^x).
х —»14~	4“03
1028.	lim № in у, s>0.
216
3. Неопределенности вида 0°, оо°, 1°°. При отыскании предела функции вида f(x) = <p(x)T'x> могут представиться случаи, когда нельзя подставлять в функцию предельное значение х:
1)	limcp(x)=0, limi|i(x) = 0 (0°); х ' а	х
2)	limcp (х) = со, litn ф (х) = 0 (оое); x-ха	х->п
3)	1 ini ф (х) = 1, Ишф(х) = со (Iе0). х -* а	х ха
Вычисление предела функции в любом из этих случаев можно свести [при <р(х)>0], однако, к раскрытию неопределенности вида 0 • со при помощи следующего преобразования функции:
f (х) = гр (х)4,W = c’n fP М = с’1’ <А’> ,п rp w,
н тогда, в силу непрерывности показательной функции, будем иметь
lim (л)In<р(х)
f (a) = lim ср (x)'PX1 =с х 'а	(2)
х-ха
Формулой (2) мы будем постоянно пользоваться.
В следующих задачах найти пределы функций.
1031. lim (1 — cosx)x.
х-»о
Решение. Очевидно, что имеем неопределенное выражение вида 0°. Применим формулу (2):
lim х In (1 — cos х)
lim (1 — cos x)x = e X~'>J x~* a
Вычислим отдельно предел, стоящий в показателе. Переходя от произведения к частному и применяя затем правило Лопиталя, получаем
____1___ .
,	, ,,	. [In (1 — cos х)Г 1—cosx	x2sin х
lim х • In (1 — cos х) = lim -—• /'."v—~-------------j----= — I'm----------.
x-*o	x-*o	x^o -------- 0 2 sin3 4
\x J	x2	2
Используем теперь известный прием замены бесконечно малых функций эквивалентными (sin ах ~ ах при х—> 0):
х2 sin х	х3х	_
— lim ----------= — lim —------— = 0.
2 sin2 ((-	2(4)
2	\ 2 /
Конечно, последний предел можно было бы вычислить по правилу Лопиталя, но это в данном случае нерационально. Таким образом,
lim (1—cosx)r = е° = 1.
Х-х о
1032. lim ('ln--Y.
х-ОЩ \ Х !
Решение. Имеем lim In -- = + сг-; здесь рассматривается предел справа, x-ОД- х
так как 1п— не определен для * -0. Имеем неопределенность вида сс°. Пре
217
образуем функцию по формуле (2):
In In --
, Л 1 \Л' ЛЧр. ' •,п ,п 7 х-’оу 1 lim lln—I —с ‘	=е	* ,
X - О -J- \ Х !
Сделаем замену переменной, положив / = При х —0+,	и
1 1 -L
.. П П х .. In In t .. (In In ty	1 n
lim  j—= hm —-—— lim -—.7—z-= lim ——0;
A	1	/- + 00	‘ Z- + oo‘lnf
x
окончательно,
lim Gn ДД = e° = l. x-04- \ X /
1033. lim cos .
x-0
Решение. Имеем неопределенность (1е0)- Преобразуем по формуле (2):
1.	„	1- Ineos*
hm cos2** hm —-------
*->0	*->0 sin2*
= e
lim etg2* In cos* limcos xctg2x = ex~*° c- 0
— e
(111 COS*)' lim	—7-
,v_.o (sin3*)'
2
1034.	lim Xх.
x -> 0-J-
_L
1035.	lim (1п2х)'ПА;
*—♦-}-co 1
1036.	lim (1 4~sin2x)t?2*
X-+ 0
1037.	lim (1 — х),пл’.
X —* 1 —
1
1038.	lim [ln(x + f)]* -
X-.04-
4.	Другие способы вычисления пределов. Следует отметить, что, хотя правило Лопиталя является сильным средством вычисления пределов, оно не заменяет полностью приемы вычисления пределов, рассмотренные в гл. IV.
1039.	Найти предел функции lim ~ +?s-.
Решение. Правило Лопиталя неприменимо в данном случае, так как 1 — sin х
шение производных у—------ не имеет предела при х —»оо, т. е. нарушено
1 COS X
вне 4 теоремы.
Предел данной функции, тем не менее, может быть вычислен:
отно-усло-
11m
х—со
X + COS X х + sin х
х f 1 4 lim —,-----
X-.CO x I 1
cosx\ ~ /
1,
sin x \
cosx	sinx
lim -----= 0 и lim---------= 0
r-.cn X	Г-.СО X
218
,  1
X2 sin -
1040.	Найти предел функции lim—;——. х -> 0 sin х
Решение. Имеем .  1 X2 • sin —	.
XX	1
lim —---= lim — lim x sin —- 1 -0 = 0.
,v^u sinx X_osinxx-.o x
Предел, таким образом, существует, но он не может быть вычислен по правилу „ . 1	.J	1 \ I
2х sin--х21 cos — - - -
X	\	х х*
Лопиталя, так как отношение производных ----2------— не имеет пре-
cos х	г
дела при х —» 0.
§ 3. ПРИЛОЖЕНИЯ ПРОИЗВОДНЫХ К ИССЛЕДОВАНИЮ ФУНКЦИИ и ПОСТРОЕНИЮ ГРАФИКОВ
1. Асимптоты. При построении графиков функций большую роль играют асимптоты кривых. Прямая х = а называется вертикальной асимптотой кривой, если при х — а (справа или слева) значение функции стремится к бесконечности, т. е. выполнено одно из следующих условий:
lim f(x)=±co, lim [(х)=±со.
x — a -J-	xa —
Прямая y — kx~~b является наклонной асимптотой кривой	при
х—»4~го (при х—► — со), если выполнены условия
1»	(1)
lim [/(х) — kx] — bt	(2)
соответственно
lim l^L=k, lim \f(x) — kx\ = b.
x->— oo x	x->—oo
Частным случаем наклонной асимптоты при k = 0 и b =/= со является горизонтальная асимптота. Существование горизонтальной асимптоты выявляется проще, чем существование произвольной наклонной асимптоты. Дадим специальное правило нахождения асимптоты в этом случае.
Прямая у = Ь является горизонтальной асимптотой кривой y — f(x) при х —»-}-со (при х~*—оо), если выполнено условие:
lim f(x) = b	(3)
[соответственно lim f(x) = b\. Оба определения эквивалентны, так как из ус-I	X — —J
ловия (3) следует, что k = (j
lk^= lim lim f (x) • lim — = &• O = cA
Y	' \ /	у	I
\ x->co	х->с*э X-+CO	/
и, наоборот, при k = 0 и b ф co из условия (2) следует (3). Условимся в дальнейшем асимптоту называть наклонной, если k Ф 0.
В следующих задачах найти уравнения асимптот кривых.
219
1041. у = ------н\2
J (х — 2)2
Решение. Кривая имеет вертикальную асимптоту х = 2 (рис. 112), так как
,2?3;(тК?=+'»-
Эта кривая имеет еще горизонтальную асимптоту г/ = 0 при х — -j-co и при х —. — со, так КЭК л”±Со(^2)5 = 0-
1042. z/==lnx.
Решение. Функция у = In х существует и непрерывна на интервале (0, ос). При подходе к граничной точке х = 0 функция неограниченно убывает:
lim In.v — — со. z-*0
Прямая х = 0 является, следовательно, Теперь проверим выполнение условий (1)
вертикальной асимптотой (рис. 113). п (2) при x-^-j-co:
,	In X
к= lim ---------= lim
X -J-ОО Х X -► Н
— lim — = 0.
. . х
(1ПХ)
Подставляя в (2) 4 = 0, определяем 6:
6= lim [1пх —0-х] = +со.
х -»4-00
Предел вида (2) не существует при х —>4~со, поэтому кривая z/ = In х пи наклонной, ни горизонтальной асимптот не имеет.
1043. у=-- %2 + Зх+1 х+1
Решение. Функция существует лах (—со, —1) и (—1, со). Вычислим
всюду, кроме точки х = — 1, т. е. в интерва-предел при х—1:
lim	(-!)+!]• lim -LT=_l.(+co) = -0o.
,...14.	*Н-1	,v... I -(.*-i-1
Следовательно, прямая x =—1 является вертикальной асимптотой. Проверим выполнение условий (1) и (2) прих—< ± со;
к= Ит Ш.= I го X
lim
xa + 3x-]-l X (х 4- 1)
220
b= lim [7(x) — kx] = lim —' , , -----------x-
х->.Г:о	,r--±=o	*+l
rs^vxf 2	^12 + -*.^
= lim	iim _3-----*
,v->_LCO	X + 1	x-»±oo / | t J_\
1048. у = х2е х.
1049. z/ = llIL±^.
J	X
Прямая f/ = x + 2 является наклонной асимптотой при х— »-;-со и при х ~са.
. „ .. х3 -}-1
1044.	ц = -^~.
1045.	у = х arctg х.
1-2
1046.	у = т—^-.
(х + З)2
9
1047.	г/ = 2х-|—
J	1 X— 1
2. Условия монотонности
1051. у-—- (л?4- 1) е х V x.
кции. Функция f (х) называется монотонно воз-
(рис. 114,о) выполнено условие
f (xi) sS f (хг) при а<х1<х2</?.	(4)
Функция f (х) называется монотонно убывающей на интервале (о, Ь), если для любых х± < х2 из этого интервала (рис. 114,6) выполнено условие
f (xi) f (х2) ПРИ а < хх < х2 < Ь.	(5)
Условия монотонности функций (4) и (5) обычно называют условиями монотонности в широком смысле.
Говорят, что функция [ (х) строго монотонна, если знак равенства в условиях (4) и (5) исключен. Дифференцируемая функция является монотонно возрастающей на интервале (а, &) тогда и только тогда, когда
f' (х)	0 при а < х < Ь,	(6)
и является монотонно убывающей, если
{' (х) о 0 при а < х < Ь.	(7)
221
Для дифференцируемых функций условие (4) эквивалентно условию (6), условие (5) — условию (7).
Функция f (х) постоянна на интервале (a, b) f(x) — C, тогда и только тогда, когда для всех значений х, принадлежащих (а, Ь),
Г «=о.
Геометрически формула (6) означает, что касательная к графику монотонно возрастаю щен функции образует с положительным направлением осн Ох острый
угол или параллельна ей (рис. 115,а). Касательная к графику монотонно убывающей функции образует тупой угол с положительным направлением осн Ох или параллельна ей (рис. 115,6).
Точка х = х0 называется критической точкой I рода, или просто критической, если имеет место одно из условий:
1) f‘W=0;
2)ГМ=®;
3) функция f (х) в точке х = х0 определена, но f (х0) не существует. Геометрически эти условия означают, что в критической точке касательная или параллельна оси Ох, если выполнено условие 1, или параллельна оси Оу, если выполнено условие 2, или касательной вовсе не существует (рис. 116), если имеет место условие 3.
Рис. 116
Интервал (а, Ь), во всех точках которого выполнено неравенство (6) или (7), называется интервалом монотонности функции f (х). Чтобы найти эти интервалы, надо на числовую ось нанести граничные точки области определения функции и все критические точки. Числовая ось при этом разобьется на некоторое число интервалов, на каждом из которых производная не меняет знака. Это и буд\ г интервалы монотонности. Для того чтобы узнать, возрастает или убывает функ-
222
,ция на данном интервале монотонности, достаточно выяснить, какой знак имеет производная в какой-либо точке этого интервала. Если в этой точке /' (х) > О, то функция возрастает, если f' (х) < 0, то убывает.
1052.	Определить интервалы монотонности функции
f (х) = х2 — 6х + 8.
Решение. Функция имеет производную всюду:
/' (х) = 2х — 6 = 2 (х—3).
Точка х = 3 является критической, так как в ней производная обращается в ноль. Эта точка разбивает числовую ось па два интервала монотонности (— оо, 3) и (3, +°т)- Возьмем какую-либо точку, например х = 0 из первого интервала, в ней /' (0) = — 6<0. Следовательно, на интервале (—со, 3) функция убывает. Точка х = 4 принадлежит второму интервалу, и так как /'(4)=2>0, то на нем функция возрастает.
В следующих задачах определить интервалы монотонности функций:
1053.	f (х) = 1п]/1 + т3.	1055. ZU) = y.
1054.	/ (х) = у хя -ф- ^х2 — 2х — I. 1056. f (х) = х+ cos х.
3. Локальный экстремум. Функция / (х) имеет максимум (минимум) в точке х = х0, если существует окрестность (х0 —Л, x0-~h), для всех точек которой выполнено условие / (х) </(х0) (f (х) > j (х0)). Точка максимума или минимума на-•зываегся точкой экстремума. При
нято обозначать максимум функций буквой М и минимум —буквой т. Для непрерывных функций экстремум имеет место только в критических точках. Из рис. 116 видно, однако, что это условие не является достаточным. В точках А, В, С выполнены соответственно условия 1, 2, 3, однако ни максимума, ни минимума в этих точках пег.
Первое достаточное условие экстремума. Если при переходе через критическую точку первая производная меняет знак, то данная критическая точка
является точкой экстремума.
Критическая точка х = х0 является точкой максимума (f(x0) = .'W) (рис. 117),
если
при Л > 0 /' (х0 — К) > 0 и Д (х0-фЛ) < 0,
и точкой минимума (f(x0) = m), если
при /г > 0 /'(х0 —/г)<0 и (х0-}-/;) > 0,
причем h > 0 такое, что иа интервале (x„—h, х0 + Л) имеется единственная критическая точка и всюду на этом интервале функция определена.
Если первая производная при переходе через критическую точку знака не меняет, то функция экстремума в этой точке не имеет.
При применении этого правила удобно составить таблицу изменения знаков первой производной.
223
Таблица 4
		A't < 'V < Л*2	Л 2	Л 2	Л'	.V j		Л-., < Л- < к,	Ц Т. д.
Г «		—	0	"1"	П. 0.	_L	
/(V)			///	/	Н. О.	/	
Здесь х, может быть «—со», и тогда первый столбец таблицы не заполняется; н. о. означает, что функция не определена; и. с. — производная не существует. В первой строке указываются интервалы монотонности и их граничные точки. Чтобы заполнить вторую строку, надо взять любое значение .v = o,1 из интервала монотонности, вычислить f' («]) и знак полученного числа занести в таблицу. В третьей строке под знаком «—» второй строки ставят знак «\», означающий убывание функции (см. условие 4), а под знаком «-{-» ставят «/» —знак возрастания функции (см. условие 3). В третью строку вносятся также значения максимумов М и минимумов т.
Если в критической точке выполнено условие /' (хо) = 0 и функция имеет производные высших порядков в этой точке, то можно пользоваться и другим достаточным условием наличия точек экстремума.
Второе достаточное условие. Критическая точка х~х0 является точкой экстремума функции, если первая не обращающаяся в нуль производная в этой точке имеет четный порядок. При этом, если эта производная отрицательна (положительна), то критическая точка х = х0 является точкой максимума (минимума). Например, пусть выполнены условия f' (хо) = О и [" (х0) Ф 0, тогда
если [" (х0) <0, то f (х.) = 7И;
если f" (х0) >0, то f (х0) = т.
1057. Определить экстремальные значения, указать интервалы монотонности функции f (х) = х3 — 6х2 + 9х — 3.
Решение. Так как
Г(х) = Зх2-12х-Ь9 = 3 (х-1) (х-3),
то критические точки хх=1 и х2 = 3. Исследование характера этих критических точек проведем с помощью первого достаточного условия. Для этого составим таблицу:
Таблица 5
	(“СО, 1)	Xi = I	(1, 3)	х% — 3	(3, со)
Г W	+	0	—	0	+
Кх)	7	М = 1		т = — 3	7
Таким образом, на интервалах (—со, 1) и (3, со) функция возрастает, па интервале (1, 3) — убывает. Точка хх=1 является точкой максимума, точка х2 = 3 —
224
I
.минимума. Экстремальные значения функции: максимум /И—/(]) = 1, минимум |	w=/(3) =—3. График функции представлен н.а рис. 118.
р. 1058. Определить точки ’у экстремума функции f (х) =
Решение, Функция существует всюду, кроме точки х =— 2, т. е. на интервалах (— со, — 2); (— 2, со). Определим критические точки:
2 — -	2
3 х 3 (х + 2) — х 3
'2.x + 4 — Зх 4 — х
~ I ~	’
Зх3 (х-|-2)2	Зх3'(л' + 2)2
/'(х) = 0 при л-= 4, /' (х)=со при х=0 и при х =—2.
Таким образом, хх = 4 и х3 = 0 будут критическими точками данной функции (х =—2 не является критической точкой, так как при х~— 2 функция не определена). Составим таблицу изменения знаков /'(х):
Таблица 6
	— со < ,t< — 2	х —— 2	- 2 < Л- < 0	л'^0	0 < х < 4	л — 4	1 < х < :о
Г (-V)	—	СО	—	СО	+	0	—
f(x)		Н. О.		т — 0	/	м = о	
При х~—3 /'(— 3) < 0, поэтому f' (3) < 0 на интервале (—со, —2). Аналогичным образом определяем знаки /' (х) на других интервалах. Из табл. 6 видно, что /(0) = т и /(4) = Л1. В точке минимума касательная параллельна оси Оу (минимум имеет характер точки заострения, см. рис. 116).
Найдем значения т и /И:
щ = ((0) = 0, M=f(4) = t2. О
В данном примере нельзя было воспользоваться вторым достаточным критерием для определения характера критической точки х = 0, так как в этой точке функция не дифференцируема.
1059. Определить точки экстремума функции / (х) = xsex.
Реше и и е. Найдем критические точки:
/' (х) = Зх2с~х- -- х3е-'' = хге~х (3 — х);
f(x) — 0 при Х! = 0 и х2 = 3. Точки х,—0, х3 = 3 являются критическими. Так как функция всюду дифференцируема, удобно применить второе достаточное условие экстремума. Определим f" (х):
/'' (х) = 2хе~ х (3 — х) - х2е~х (3 - х) — х2е~х = хе~х (х2 — 6х + 6);
8 Кручкович и др.	225
подставляя критические точки, получаем
f" (0) = 0, f" (3)=3е-3(9 — 18 + 6) <0.
В силу второго достаточного условия в точке х2 = 3 функция имеет максимум М=НЗ) = 27г-з.
Характер критической точки хх = 0 пока не определен, так как f" (0) = 0.
Находим (0):
Г'' W ~ ~ е': (л'3 ~ 6х2 + 6х) + е~х (3+ — 12х + 6) = е~х (— х« + 9х2 — 18х + G), Д"(0) = 6 + 0.
В точке х==0 первая отличная от нуля производная третьего (нечетного) порядка. Следовательно, критическая точка х = 0 не является точкой экстремума. Этот факт легко усмотреть непосредственно из выражения производной. Действительно, множитель хг, а вместе с ним и /' (х) не меняет знака при переходе через точку х = 0.
В следующих задачах найти точки экстремума функций:
f^\-2xS~3x2+L	1063. f(x) = ln(l+x)-x- + ^-.
1061. /(х) = ______ з	z
= In ]/ 1 + х- + arctg х. 1064. f (x) = (;._2^v+3j.
K>62.
4. Экстремум функции на отрезке и интервале. Наибольшее значение функции на отрезке а х Ь обозначается max / (х), наименьшее значение —
[а, й]
min /Дх).
[а, Ы
Непрерывная функция на отрезке [а, о] всегда достигает своего наибольшего и наименьшего значения. Для определения max f (х) надо вычислить значения [а, 6]
всех максимумов на отрезке [а, &], вычислить значения функции в концах отрезка f (а) и / (&) и взять наибольшее из полученных при этом чисел (рис. 119).
Рис. 119
Для нахождения min / (х) надо вычислить значения всех минимумов и значения на концах интервала и среди полученных чисел взять наименьшее (см. рис. 119). Надо иметь в виду, что функция, непрерывная на интервале, в частности на бесконечном интервале, может не достигать своего наибольшего или наименьшего значения.
226
Если непрерывная функция имеет па интервале единственную экстремальную точку, например минимум (максимум), то в этой точке обязательно достигается наименьшее (наибольшее) значение функции на этом интервале (рис. 120).
б)
Рис. 120
1065. Определить наибольшее и наименьшее значения функции f (х) = х?' ~ 3*2 + 1 па отрезке [—1, 4].
Решение. Определим точки максимума и минимума: /' (х) = Зх2 — 6х = Зх (х — 2), f" (х) = 6х — 6;
f (х) = 0 при х = 0 и х — 2. Точки х1 = 0 и х2 = 2 являются критическими, для них f" (0) < 0, f” (2) > 2; следовательно,
f(0) = M и /(2) = т; 7И=/(0) = 1, т = /(2) = —3.
Вычислим значения функции па концах интервала: /(-!) = -3, /(4) = 17.
Окончательно имеем:
max f (х) = max {f (— 1), /(4), Л1} = тах{—3, 17, 1} — 17,
1—1, 4]
min f (x) = min (— 1), /ф4), /ra} = min{— 3, 17, —3}=—3.
[-1. 4]
Наибольшее значение при —lex". 4 функция принимает в правом конце отрезка при х = 4. Наименьшее значение достигается в двух точках в точке минимума функции и на левом конце интервала, при х = —1.
1066. Определить наибольшее значение функции f(x) = '”x на интервале (0, сю).
Решение. Всюду на интервале (0, со) функция дифференцируема. Найдем точки максимума:
(х) = 0 при 1— 1пх = 0, откуда х = е является критической точкой; /'(х)=со при х = 0, но эта точка не является критической, так как в ней функция не
8*
227
определена;
— - - х* — 2х (1 — In х) /"(*)= —-------л--------
— Л' (3 — In х) 3 — 1п х
= х2 ’
f" (е) < 0, так что в точке х—е функция имеет максимум /И =/(<?) = — , Функция имеет единственную точку максимума на интервале (0, со), поэтому max f (х) = Л1 =—.
(О, со)	е
1067. Определить максимальную площадь равнобедренного треугольника, боковая сторона которого равна /.
Решение. Обозначим высоту треугольника х (рис. 121). Тогда АВ -~ = 2 J' Z2 —х2 и 34вс = ОС • АВ=х УР — х2. Площадь треугольника, таким образом, выражена как функция высоты этого треуголь-
Рис. 121
ника.
Первоначальная задача теперь может быть сформулирована следующим образом: определить наибольшее значение функции S (х) = х)/ Z2 —х2 па отрезке [0, ZJ. Вычислим значения функции на концах отрезка S(0) = 0, S (/) = 0. Так как площадь —величина неотрицательная, то, очевидно, функция достигает максимума внутри ин-
тервала. Найдем S' (х):
S' (х)= р /
5'(х) = 0 при х=±
2х __ Z2-2x2 .
2 У'Р^Р ~ УУ^Р ’ и S'(x)—со при х—±1.
Нас интересует только критическая точка x1=^.-z, так как точки х — —< , х = —Z лежат вне отрезка [0, Z], а значение функции в точке x = Z уже вычис-
лено: S(Z) = O.
В задачах конкретного содержания иногда удается определить характер критической точки проще, чем это делается в общем случае. Так, например, в данной задаче легко убедиться, что в точке х= функция S (х) достигает макси-
мума. Действительно, ранее отмечалось, что функцию S (х) разумно рассматривать на интервале (0, /). На этом интервале она положительна и обращается в нуль па концах его; отсюда уже следует, что функция должна достигать максимума внутри интервала, а так как имеется единственная критическая точка, то именно эта точка является точкой максимума и точкой наибольшего значения. Вычислим максимальную площадь треугольника:

1068. По двум улицам движутся к перекрестку две автомашины с постоянными скоростями и и2. Считая, что улицы пересекаются под прямым углом, и зная, что в некоторый момент времени автомашины находятся от перекрестка на расстояниях и а3, определить, через какое время расстояние между ними станет наименьшим.
228
Решение. За время t машина, двигающаяся со скоростью иъ пройдет путь u±t и будет находиться от перекрестка на расстоянии 1^ — ti-J . Вторая машина будет через время t находиться от перекрестка на расстоянии |а3 — u3/j. Выразим расстояние I между машинами как функцию времени t:
I (f) = (oj — U1t)2 + (а3 — u«t)2  Найдем
I' 1^ = 2 Kgi — “1^ (~~ц1) +	~~	(—»z)] = gi»i. + g2^ —z +
2 К(«1 — «I О2 + (fl2 — «гО2	К («г — ЩО2 + («3 —11 ity ’
в точке 4 =	^2/2- имеем I' 0i) = 0. При переходе через эту критическую
точку I' (0 меняет знак с — на +. Следовательно, в момент tx функция достигает минимума.
Отметим, что знаменатель выражения /' (г) может обратиться в ноль только 01 и1
при условии — = , что соответствует тому случаю, когда машины должны о3 X
встретиться на перекрестке. Не рассматривая здесь этот частный случай, можно утверждать, что функция I (t) па интервале (0, со) имеет единственный экстремум-минимум, В силу замечания, сделанного в начале пункта, функция достигает при этом своего наименьшего значения на интервале в точке минимума.
В следующих задачах определить наибольшее и наименьшее значения функции:
1069.	f (х) = х1 — 2х2 -ф 3 на отрезке [—2, 1].
1070.	= на отрезке [—1, 3].
1071.	f (х) = |/2х2 + 1 на отрезке [—2, 1].
1072.	Из углов квадратного листа картона размером 12x12 (спи2) нужно вырезать одинаковые квадраты так, пунктирным линиям (рис. 122), объема. Какова должна быть рона вырезаемого квадрата?
чтобы, согнув лист по коробку наибольшего
получить
сто-
1073.	Окно имеет форму прямоугольника, завершенного полукругом. Определить размеры окна при заданном периметре, имеющего наибольшую площадь (рис. 123).
1074.	Число 66 представить в виде суммы двух положительных слагаемых так, чтобы произведение этих чисел было бы наибольшим.
1075.	Определить наибольшую площадь равнобедренного треугольника, вписанного в круг радиуса R.
229
балки балки
1076.	Определить наименьшую площадь равнобедренного треугольника, описанного вокруг окружности радиуса г.
1077.	Определить максимальную площадь четырехугольника, вписанного в круг радиуса R.
Указание. Свести задачу к нахождению треугольника наибольшей площади, две вершины которого лежат на окружности, а одна в центре круга (рис. 124).
1078.	Какой из прямоугольных треугольников с заданным периметром р имеет наибольшую площадь?
1079.	Из круглого бревна диаметра d требуется вырезать балку прямоугольного сечения с основанием b и высотой h. Прочность
пропорциональна Ыг2. При каких значениях b и h прочность будет наибольшей?
1080.	Открытый бак цилиндрической формы должен вмещать V л. При какой высоте и радиусе основания бака на его изготовление уйдет наименьшее количество материала?
1081.	Из круга вырезан сектор с центральным углом а. Из оставшейся части круга свернута воронка. При каком значении угла а вместимость воронки будет наибольшей?
1082.	Полоса жести шириной 60 см должна быть согнута в виде открытого желоба так, чтобы поперечный разрез имел форму трапеции AC = CD = DB (рис. 125). Определить ширину желоба АВ, при которой вместимость его была бы наибольшей.
1083. В эллипс = 1 а? 1 IP вписать прямоугольник наибольшей площади со сторонами, параллельными осям эллипса.
А-----------------
Рис. 126
с
Рис. 125
и экс-72 = 1
1084.	В фокусы эллипса, большая полуось которого а = 2 1	’	о
центриситет е= 2 , помещены точечные заряды 71 = 2 и (рис. 126). Найти на данном эллипсе точки наибольшего и наименьшего значений потенциала этих зарядов.
Указание. Потенциал точечного заряда	где г — расстояние
от точки до заряда, (/ — величина заряда. Потенциал суммы зарядов равен сумме потенциалов.
Воспользоваться формулами t\ = a— ех, г2 = а Д-<?Л', г1-|-/-2 = 2а.
230
1085.	Как будут располагаться точки наибольшего и наименьшего значений потенциала, если в условиях 1084 считать, что <71 > 0 и 92 < 0?
1086.	На отрезке AB = d, соединяющем два источника света А (а свечей) и В (Ь свечей), найти точку М наименьшей освещенности.
Указание. Освещенность обратно пропорциональна квадрату расстояния от источника.
5. Точки перегиба. Гладкая кривая вогнута вверх в точке х = хд, если существует окрестность этой точки (т0—Л, х0 + й), в которой кривая расположена выше
касательной, проведенной в этой точке (рис. 127, а), и кривая вогнута вниз в точке х~хд, если опа лежит ниже касательной, проведенной в этой точке (рис. 127, б).
Точка х=х0 называется точкой перегиба, если касательная, проведенная в точке Л'(,, делит кривую на две части, лежащие в некоторой окрестности точки касания по разные стороны от касательной (рис. 127, в). Подобно тому как точки экстремума отделяют интервалы возрастания и убывания функции, так точки перегиба отделяют интервалы постоянного направления вогнутости кривой (рис. 127, г).
Кривая вогнута вверх (обозначают о) на интервале (а, Ь), если в каждой точке этого интервала выполнено условие
Г' (х)> 0	при	а<х<6,	(8)
и вогнута вниз (обозначают г>), если
(х) < 0	при	а<х<6.	(9)
231
Точка х —х0 называется критической точкой II рода, если в этой точке имеет место одно из следующих условий:
1) Г<Л) = 0. 2) f (х0) = со, 3) Г (л’п) не существует и при этом сама функция в точке х — хп определена.
Точки перегиба функции находятся среди критических точек II рода. Чтобы установить, является ли данная критическая точка II рода точкой перегиба кривой, надо руководствоваться правилом: если при переходе через критическую точку II рода вторая производная функции меняет знак, то данная точка является точкой перегиба. Применяя это правило, удобно составить таблицу изменения знака второй производной, аналогичную таблице изменения знака первой производной, рассмотренной в § 4.
Интервалы знакопостоянства f' (х) находятся следующим образом: на числовую ось наносят граничные точки области существования и критические точки II рода. На каждом из полученных интервалов f " (х) не может менять знак и согласно условиям 1 или 2 соответствующий участок кривой должен иметь постоянное направление вогнутости.
1087.	Определить точки перегиба и интервалы знакопостоянства f' (х) функции f (х) = х6 — 6л'5 ф- { -1 л4 ~г Зх.
Решение. Функция определена и дважды дифференцируема дла всех х. Для определения критических точек II рода найдем (л):
/' (х) = 6.0 _ 30x1 30х= 4- з,
f" (х) = ЗОх4 - 120х3 + 90х2 = 30x2 (л-2 _ 4л- _|_ 3).
Разложим f (х) на множители:
Г (х) = ЗОх2 (х — 3) (х—1).
Точки Х1 = 0, х2=1, х3 = 3 являются критическими точками II рода. Составим таблицу изменения знаков f" (х):
Таблица 7
X	— со < л* < 0	xt = 0	0 < X щ 1	Х2 =- 1	1 < х  С 5	Л'з == 3	3 •< х <: со
Г W	+	0	+	0	—	0	+
Да)	о		О	т. п.	Г-Ч	т. п.	о
Здесь т. п. означает точку перегиба.
При х = —1 f (—1) = 240 > 0. В силу условий 2 на интервале (—со, 0) функция вогнута вниз При переходе через точку хх = 0 вторая производная знака не меняет, так как множитель х2 не меняет знака. Можно убедиться в этом также, подставив значение, например, х = ~. Точка х3—0 не является точкой перегиба.
При переходе через точку х2 = 1 [" (х) меняет знак, так как множитель (х— 1) входит в выражение [" (х) в первой степени. Точка х2=1 является точкой перегиба.
Аналогично получаем, что точка х3=3 тоже является точкой перегиба.
1088.	Найти точки перегиба функции f (х) = x24~2sinx.
Решение. Определим f (х) и f (х):
f (х) = 2х + 2 cos х, f" (х) = 2 — 2 sin х = 2 (1 — sin х).
232
Очевидно, что точки xk — ‘t) 4-2Л.-Г, k — 0, ± 1, ± 2... являются критическими точками II рода. Однако пн одна из этих точек не является точкой перегиба, так как на каждом из смежных интервалов (л/2, 5л/2), (5л/2, 9л,'2) ...sinxcl, и потому f' (л) >0. Вторая производная не меняет знака при переходе nepes критические точки. Следовательно, всюду на интервале (—со, со) в силу условия 1 кривая вогнута вверх.
В следующих задачах найти точки перегиба функций:
1089.	f (х) = х5 - 5х4 + 23°- л3 + Зл- + 1.
1090.	f (х) = х ф-cosx.	1092. f (х) = е-хг ф- 2х.
1091.	/(л-) = -1!^£±Д.	1093. f (x) = j'M± l.
§ 4.	ОБЩАЯ СХЕМА ПОСТРОЕНИЯ ГРАФИКОВ
Отдельные элементы исследования функций, рассмотренные в предыдущих параграфах (см. § 2 — 3), образуют в совокупности аппарат, необходимый для построения графиков функций. Помимо этого будем использовать также непосредственное изучение функций и графики основных элементарных функции, о чем речь шла ранее (см. гл. IV, § 2).
Общая схема построения графика функции сводится к трем основным этапам:
i)	Определение общего характера графика функции. При этом следует найти область определения функции, вычислить предельные значения на ее границе, найти уравнения вертикальных, горизонтальных и наклонных асимптот, если они существуют, найти, если это несложно, точки пересечения графика с осями координат. После этого надо построить примерный ход графика, удовлетворяющего проведенному исследованию.
2)	Уточнение характера графика с использованием первой производной (исследование на экстремумы, § 3).
3)	Уточнение характера графика по второй производной (исследование иа выпуклость, вогнутость, точки перегиба, § 3).
1094. Построить график функции
у~3хех.	(!)
Решение. 1. Функция существует всюду на интервале (—сс, со). Найдем предельные значения при х —ф-со и при —»—со
lim 3.vcv = + co.	(2)
*-.-4-00	V ’
х	1
lim Зхех= 3 lim 3 lim --------------- = 0	(3)
(в первом случае оба множителя бесконечно большие, во втором —воспользовались правилом Лопиталя). Предельное условие (3) означает, что график имеет при х—* —со горизонтальную асимптоту у = 0. Предельное значение (2) указывает на неограниченное возрастание функции при х—>+со, однако наклонной асимптоты при этом не существует, так как
6 = Hm	lim Зел' = +со.
Найдем точки пересечения графика с осями координат: при х — 0 //(0)=0, т. е. график проходит через начало координат.
233
На основе проведенного исследования нельзя еще полностью построить искомый график, однако поведение его на отдельных участках уже выявлено. На рис. 128 эти участки проведены сплошными линиями; соединив их пунктирной линией, мы получим некоторую простейшую кривую, которая удовлетворяет проведенному исследованию и дает представление об общем характере графика функции. Роль дальнейшего исследования состоит в том, чтобы уточнить и частично изменить этот простейший набросок графика.
2. Найдем производную данной функции:
f' (х) = 3 (хех)' = Зех (х +1).
При х —— 1 производная равна нулю, так что эта точка критическая. Проводя обычное исследование, как указано в § 4, находим, что при х = — 1 функция достигает минимума:
m=J(— 1) = —Зе~1
128
Рис.
-1.
По результатам фик. Он не сильно нем лишь уточнено по первой производной заключается в том, что теперь доказано, что функция имеет единственный экстремум — минимум, убывает на интервале (—со, — 1) и возрастает на (—1, со ).
3. Найдем f" (х):
Г (х) = 3 [ех (х+ 1)]' = 3е* (х-ф-2).
на рис. 129 представлен уточненный гра-
этого исследования отличается от первоначального наброска (см. рис. 128), на положение точки минимума. Однако ценность исследования
Точки х = —2 является критической точкой II рода, в ней f" (—2) = 0. Применяя методы § 3, находим, что она является точкой перегиба функции.
В результате уточнено положение точки перегиба и доказано, что других точек перегиба график не имеет, т. е. на интервале (—со, —2) график является выпуклым, а на интервале (—2, со) — вогнутым, и этот характер больше нигде не меняется.
1095. Построить график функции
х2 — х - - 6
У =
Рис. 129
х-2
Решение. 1) Функция существует всюду, кроме точки х = 2, т. е. на интервалах (—со, 2), (2, со). Найдем предельные значения па границе существования:
..	х2 —х—6
lim-----«—= lim
x3i 1- ’
6
х-2
' 1	2
X 1 —
= — со,
_%_Q
lim —-—s—= lim (х2 —х —6) lim
х — 2
х— 2
2 «СО
. 1-	'
4 lim-----T
,.,2 — x —2 r—2<0
(4)
234
X2— X—6 !im -----—
^2+ X- 2
4 lim x->'2 у (X — 2)>0
I x —2
(5)
X2 — X — 6 'im --------x—
^4-co x — 2
Из условий (4) и (5) видно, что прямая тотой. Найдем k и Ь:
x = 2 является вертикальной асимп-
,	,.	X2 — X — 6	, .
k= lim —— lim х-±ю x(x — 2)	x_,±
x2 И —
2 ' х2, 1- -j
= 1,
,	,.	!x2 — x — 6
b = 1 im (-----------R—
r-»-t оз \ X — 2
,.	x2 — x — 6 — x2 4- 2x
lim ----------------=-----!---
oo	x — 2
lim
Таким образом, при x—» + co и x —— co график функции асимптотически приближается к прямой ;/ = х+1.
Найдем точки пересечения графика с осями координат. При х = 0 г/ = 3.
д"2_д.__Q
График проходит через точку Л (О, 3). Положим г/= О, тогда —-—— = 0, х2 —
— х — 6 = 0, хь2= J>~ ± ]/ 4 +6> откуда xt = 3, х2 =—2. График функции проходит через точки В(3, 0) и С ( - 2, 0).
На рис. 130 построена простейшая кривая, удовлетворяющая всем результатам исследования. Сплошными линиями, как и в 1094, проведены те участки графика, которые уже выявлены в результате исследования 1. Пунктирной линией указана простейшая возможность поведения графика.
\ л --- &
(2х—1) (х—2) —х2 + х + 6 _ (х-22)
д-2	. J.. Q
= —------. Найдем корни чис-
(х 2)
лителя: х2 — 4х 8 = 0, Xi,3 = = 2 ±	— 8 = 2 ± 21; корни ком-
плексные сопряженные, следова-
тельно, числитель ни при каких
действительных значениях х в нуль не обращается. Знаменатель равен нулю при х = 2, но в этой точке функция не определена. Отсюда следует что функция не имеет экстремумов. Это исследование не изменило первоначальный набросок графика, но доказало его правильность.
Покажем еще, что и перегибов эта функция не имеет, т. е. что возрастание и убывание происходят плавно, без изгибов.
235
„.	(2х —4) (х — 2)2 —2 (x — 2) (x*-4x + 8)	8
3) у (x) =	----------L = _ ___ . Критических
точек Ирода нет; у" (х) > 0 при х < 2, кривая вогнута вниз (ч>) на интервале (—со, 2); у" (х) < 0 при х > 2, на интервале (2, со) кривая вогнута вверх (/-).
1096. Построить график функции у = xi — 2хг -ф 3.
Решение. 1) Функция существует всюду на интервале (—со, со). Функция является четной, так как для нее выполнено условие /(—x) = f(x):
(—х)4-2(—х)2 + 3 = х4-2х2ф3.
График симметричен относительно оси ординат, поэтому достоточно вести исследование функции только для хо О. Определим значение при х—+ со:
lim (х4 — 2а'2-j~ 3) — lira х4 fl-\ 'i = -4- со.
х-> + со	х- + со \ х2 xi !
Вычислим /г:
J _ 2_ _3\
,	.. fix') ..	\	х2+х<
Й= 11Ш '-С-2 = 11ГП ------------------=-LCO.
+ “ х +	X
Следовательно, наклонной асимптоты кривая не имеет.
Найдем точки пересечения с осями координат. При х = 0 г/ = 3. График функ цип проходит через точку А (0, 3). Положим г/ = 0, тогда х4 — 2х2 + 3 = 0, х2 = и и2 —2«+3 = 0; «1,2=1 ± 1^1—-3 = 1 ± i]^2. График не пересекает ось Ох.
На рис. 131 изображена простейшая кривая, удовлетворяющая всем уело
виям проведенного исследования. мУ
2) у' (х) = 4х3 — 4х = 4х (х2 — 1). Критическими точками являются точки хх = 0, *2,3= ± И
У" W = 4 (Зх2 — 1),		(6)
подставив значения лу —0, х2=1 в у" (х), получим
(0) = — 4 < 0, t/"(l) = 8>0.
В точке хх = 0 функция достигает максимума, в точках х213 —минимума. Вычислим экстремальные значения функции Л4 —- г/(0) = 3, т = г/(±1) = 2. Очевидно, что кривая иа рис. 131 не удовлетворяет условиям исследования 2, она имеет один экстремум —минимум, график функции имеет два минимума и один максимум. На рис. 132 дан уточненный вариант графика.
236
3) Найдем Критические точки II рода, приравняв нулю правую часть выражения (6):
4(Зх2-1) = 0, а-)>5=±
„ 1
Очевидно, что при переходе через точку x4 = —= вторая производная меняет
1
знак, следовательно, точки хл- = ±—^ являются точками перегиба.
ИЗ
Кривая на рис. 132 уже удовлетворяет этим требованиям.
1097. Построить график функции у = 3'j/ х2 — 2х.
Решение. 1) Функция существует всюду на интервале (,—со, со). Определим предельные значения на границе области существования:
1>т Зг'х2 — 2х = lim — 2x11-----
х—со \	2, х /
lim 3f<?-2x = lim -2х { 1 — --Q = — со.
X— 4~со	*-».|-00	\	‘ j X /
Определим k и Ь:
,	.. Зу/Лх2 — 2х ,. о , 3	„
й = lim —------------- lim -2-!--—— = — 2,
Х—±.оо х	Л со	I X
b = lim Зрх2 —2х — (—2)-х = Нт , \2 = 4-со.
Следовательно, график не имеет асимптот при х—> ±со. Найдем точки пересечения с осями координат. При x — Oy — Q, т. е. график функции проходит через начало координат. Положим у = 0, тогда 3> х2 — 2.v = 0, х~^' (3 — 2х',3) = 0, 27
откуда х4 = 0 и x2= g-. График функции пересекает ось абсцисс в точках О (О, 0) " < «)•
На рис. 133 представлена простейшая кривая, удовлетворяющая всем условиям этого исследования.
2) у' (х) = 2х"’/а — 2 = 2—	- • при х = 1 у' (х) = 0 и у' (х) = со при х = 0.
4'' х
Точки хх = 0 и х2 = 0 являются критическими. Составим таблицу изменения знаков производной:
Таблица 8
X	— со < х С 0	л' = 0	0<х<1	х|=|	1 <Сx<Z. оо
у' W	—	СО	+	0	—
У W		т = 1	/	М=1	
При х — —1 у'=—4 < 0. Таким образом, при х4 = 0 функция имеет минимум (/и = 0) и в точке х2= 1—максимум (Л4= 1). Так как при х = 0 у' (0)=с©, то минимум имеет характер точки заострения.
График на рис. 133 требует уточнения характера точки минимума и уточнения положения точки максимума. На рис. 134 построен график, удовлетворяющий исследованиял! 1 и 2 в совокупности.
237
3	9	3
3) У'(х) = 2(х	-	X
о 1
у" <0 для всех значе-
3$'х*'
пий х, х =/= 0. График не имеет точек перегиба и всюду обращен вогнутостью
Очевидно, что график, изображенный на рис. 134, не требует дополнительных уточнений.
1098. Построить график функции =
Решение. 1) Функция существует на интервале (0, ос), так как на этом интервале существуют функции In х и Их и, кроме того, знаменатель дроби на этом интервале не обращается в нуль. Вычислим предельные значения на границе области существования:
Из условия (7) следует, что прямая х = 0 является вертикальной асимптотой, а из условия (8) —что прямая у---О является горизонтальной асимптотой при х—«--{-со. С осью ординат график не пересекается, так как при хто-0 функция пе определена. Положим у = 0,	= 0 при х=1. График функции пересекает
| х
ось абсцисс в точке А (1; 0). На рис. 135 представлен график простейшей кривой, удовлетворяющей всем условиям этого исследования.
238
1	! 1
/1	\ г	— V  ~7~=- 1П X	J 1П V
2)	км_з^ '_3.У_______________21»	_3-----__
\ V X	х	хУг
1
при 1——In х = 0, или хх = е2; хг — е2 является критической точкой. Из выражения у' (х) видно, что при х < с2 у' (х) > 0 и при х > е2 у' (х) < 0, следовательно, в критической точке хг=е2 функция достигает максимума. Уточнение графика сводится в данном случае к уточнению положения точки максимума (рис. 136).
/1 —-L- In х\ -у у  Х^xI/2 i 1- *-1пх
3)	У’’(х)=з\--= 3.-^	k 2
\ х /
X-—Уг~; у" (,х)=о при 8 —31пх = 0 х0'2
видно, что при х<е8'/3 у" <0 —кривая кривая вогнута вверх. В точке х — ег" Л2-Ч
вая но, ние ние 136
3
х3	4
или при х = е8/3. Из выражения у" (х)
У’ > 0 -
:8/3 имеется перегиб. Крина рис. 135 тоже, очевид-имеет перегиб; исследова-3 уточняет лишь положе-точки перегиба. На рис. построен график, удовлетворяющий всем условиям в совокупности.
1099. Построить график функции
у = у sin 2%4-cos х. (9)
вогнута вниз, а при х
О
е6/з
Рис. 136
Решение. 1) Функция определена всюду на интервале
у sin 2 (х + 2л) + cos (х + 2л) = у sin 2х + cos х.
(—со, со), имеет период 7’ = 2л. Действительно,
1
у’ (х)--= О
В силу периодичности достаточно построить график данной функции на любом отрезке длины 7’ = 2л, например на отрезке [ — л, л]. Вычислим значения функции (9) на концах интервала:
I I П • о , У\	~У\	=тг sin 2лcos л — — 1.
График функции проходит через точки А ( — л, —1), В (л, —1). Найдем точки пересечения графика с осями координат. При х = 0 у=1. График функции проходит через точку С (0; 1). Положим у = 0, тогда
у sin 2x-|-cos х = 0.	(10)
Преобразуем левую часть этого уравнения:
sin 2х cos х == J, • 2 sin х cos х ф- cos х = cos х (1 -ф sin х).
Уравнение (10) запишется теперь в виде cos х (1 4-sin х) =0, что эквивалентно условиям
cosx — 0	(И)
И
(1 sin х) = 0.	(12)
239
Корни уравнения (11) имеют вид хА = -‘-(2/г+1) (£—О, ±1, 12,...). Из этих корней внутрь отрезка [ — л, л] попадают точки Л'1==~ | (»ри Л—1) и х0 = as-i^^O). Так как sin х = — 1 только в тех точках, где cos .г —0, то корни уравнения (12) находятся среди корней уравнения (И)- Таким образом, график функции (9) пересекает ось Ох в точках D ( —	О') и Е ।	, о\
\	2	>	; 2	/
Как и в предыдущих задачах, построим точки .4, О, С, D, И графика и проведем простейшую кривую, проходящую через эти точки (рис. 137). Отличие этой
задачи от предыдущих заключается в том, что функция в силу периодичности нс исследуется на бесконечности и кривую достаточно строить лишь па отрезке периода.
2) у' (х) — cos2.v — sin х. Определим критические точки из уравнения cos ‘2х— sinx = 0, или, применяя формулу cos 2х — cos2 х— sin3 х— 1 — 2 sin2 х, — 1 — 2 sin2 х— sin х = 0. Обозначим sinx = ( и решим квадратное уравнение 1=0:
имеем
1 sm х — — 1 и sin х = -.
(13)
В данном случае нас интересуют только те корни уравнений (13), которые попа-,	,	л л	5 л т>
дают на отрезок [—л, л], т. е. точки х1= —	х..—  ( х8=- . Для опреде-
ления характера этих критических точек найдем у" (х):
(14)
240
В точке ,t2—~ функция достигает максимума, в точке ,г3==-^-Найдсм значения функции в точках экстремума:
минимума,
//
5 л б'
,,	1	л , л
,т М ... --- sm + cos ---=	2	3	6
ij
1	10л . 5л
=т	- sm —г.—Н cos	=
2	6	6
4
з Из" _
4 ~
Для определения характера критической точки [см. (14)]:
У"' (*) = cos 2* + sin х<
g- и а идем у (х)
л
1ЮДС1авим значение xt =—% :
у"' я == — 4 cos ( — л) + sin , —-Т i —З-Д).
В точке л'1 =—g- первая отличная ог нуля производная третьего (нечетного) порядка, поэтому в этой критической точке пег экстремума. На рис. 138 дан график функции, соответствующий результатам 1) и 2) исследований.
3) Найдем критические точки 11 рода, приравняв нулю правую час:ь выражения (14):
— 2 sin 2х — cos х = 0,
заменяя sin 2х —2 sin х cosx, получаем
— 4 sin х • cosх — cos х = 0, или cosx (1 -]-4 sin х) — 0.	(15)
Уравнение (15) распадается на уравнения cosx = 0 и 1 + 4 sinx = 0. Нас опять интересуют только корни этих уравнений, попадающие внутрь отрезка [ — л, л], т. е. точки
л
2
х5
х0 — arcsin
/	1 \	л
\	4J	12’
х,
11п
"12 ’
л
2
241
каждая из этих точек является точкой перегиба, так как выражение у" (х) = == — cos х (1+4 sin х) меняет знак при переходе через каждую из них. На рис. 139 построен график с учетом дополнений, внесенных исследованием 3. На этом же рисунке пунктирной линией показан график с рис. 138. Как видно из такого сравнения, исследование 3 в данном случае не только уточнило положение точек перегиба, существование которых было и раньше достаточно очевидно (для функции дважды дифференцируемой между всякой точкой максимума и минимума
должна иметься точка перегиба), но и выявило дополнительные точки перегиба,
.	I Л \
которые изменили характер возрастания функции на интервале I — л, -^-1.
Построить графики следующих функций.
1100. у = х3ех.
рХ 1101. У = А-:.
у х+1
1102. z/ = 2 + xa-J.
1103. г/ = 5-|-х2.
1104. г/ = ., f 4. * (1 +*)а
1105. у = -Л—-7-1 (% + 2)	(х-
1106.	у = (^\2. J \x-2j
1107.	г/ = уЛх3-Зх.
1108.	у= In (х2 — 2х-\-2).
1109.	у-(х2 + х + 2)(х2 + х-2).
1110.	у = х-\- arctgх.
1111.	г/= 2х —arcsin х.
2 _ +
1112.	у = х3 е 3 •
§ 5. ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ
1. Кривизна плоской кривой. Под кривизной кривой понимают отклонение ее от прямой линии. Кривизна К кривой в данной точке М характеризуется пределом отношения «угла смежности», т. е. угла между касательными в точках М и N (см. рис. 140) к длине дуги MN, когда N —> А4, т. е.
,. Aa do.
Л= lim -г = г д$ —>о As	as
(1)
242
Для кривых, заданных уравнением y — f(x), кривизна определяется по формуле
К-------У—-	(2)
(1 + ?/'2)2 ‘
При параметрическом задании кривой ?/ = <p(0, х = <р(1) кривизна находится по формуле
1113.	Определить кривизну окружности радиуса R.
Решение. Будем пользоваться формулой (1). Угол смежности Да, как видно на рис. 141, равен центральному углу Z.MON. Длина дуги As = /WjV, соответствующая этому центральному углу, равна Дз = РДа. Таким образом,
.... Да ,. Да 1
К— 11ГП -.— = 11Ш п—7~ = Т5-.
As—>0	As-*0^\’A$ л
Следовательно, кривизна окружности есть величина постоянная, обратная радиусу окружности.
1114.	Определить кривизну кривой у = х3-|-х2 — 5 в точке А (0, — 5).
Решение. Будем пользоваться формулой (2). Найдем у' и у"-.
у' (х) = 3х2 + 2х, i/''(x) = 6x + 2; г/'1х = о = О, г/"|х==0 = 2;
(I+0)2
У"
з
(1-Н'2)2

1115.	Определить точки наибольшей и наименьшей кривизны эллипса x = acos/, y = 6sin/(—а>6).
Указание. Функцию /< (t) исследовать на экстремум.
* Производные по параметру принято обозначать следующим образом: dx .	. dy ,	• (Ру	„
~-=х(=х,	'dP=^tt = ^ и т. д. В механике чаще употреоляются
обозначения к, к, у, у и т. д.
243
1116.	Найти кривизну кривой у = In в точке Д(1, 0).
1117.	Найти точки максимальной кривизны функции z/ = sinx.
1118.	Найти кривизну кривой х = асо83Ц у = a sin31 (астроида).
2. Радиус кривизны. В 1113 было показано, что радиус окружности есть величина, обратная ее кривизне. По аналогии с окружностью для любой кривой вводится понятие о радиусе кривизны р как величине, обратной абсолютному значению кривизны
ех
1119.	Найти выражение радиуса кривизны кривой у = ———.
Решение. Пользуясь формулами (2) и (4), получаем
Определим у' и у"-.
У' = -^ (ел‘-У" = y + e~v)> тогда
з
(4 + с2л' —2 + ^~2л')2	__ (ev + g~x)3 _
4	+ г'х)	” 4 (ел' + е~х) ~
Знак модуля опускаем, так как величина положительна для любых х.
2
1120. Найти радиус кривизны кривой «/ = --—! при х=1.
1121. Найти радиус кривизны параболы у2 — х при х = 4.
визны в точке Л/. Центр
1122. Найти выражение радиуса кривизны следующих кривых:
а) у — х3, б) х = а (cos t-^t sin f), y = = a(sint— t cos f) (эвольвента круга),
в) x — (t~ sin t), y = (l — cos /) (циклоида).
3. Центр и круг кривизны. Эволюта и эвольвента. Кругом кривизны в точке М кривой называется предельное положение круга, проходящего через точку и две другие близкие точки кривой N и Р, когда К — М и Р —< М (рис. 142). Радиус круга кривизны равен радиусу кривизны в соответствующей точке. Центр круга кривизны С называется центром кри-кривизны лежит на нормали к кривой в направлении
ее вогнутости.
Координаты центра кривизны кривой, заданной уравнением y = f(x), определяются по формулам
х ~х У'(^У'^ .	,,	„4- 14-у'2	,,,
------777---;	Ус~У4-----777~ ,	(5)
У	У
и для Кривой, мулам	заданной в параметрическом виде: у = ф(1), л' = ф (/), по фор- v	У(Уг + Уа) ,, = „_, -У (-<'2 + у2) с	Ху —Ху 'Ус J i	( )
244
Геометрическое место центров кривизны кривой называется ее эволютой. Кривая, для которой данная кривая является эволютой, называется эвольвентой.
1123.	Найти центр кривизны кривой х — t2, y = 2t3B точке А (1, —2).
Решение. Будем пользоваться формулами (6). Найдем х, х, у, у:
х = 2/, х = 2, </ = 6/2, </=12/.
Нужны значения этих производных в точке х=1, у =—2, т. е. при t — —1:
хй = — 1= 2’ х|/ = — 1 = 2,	= y\t = —1 = '2>
Подставляя найденные числа в формулу (6), получаем
у 	6 [(—2)2-j-22]	, 48	-2_l8=._10
с 1	(—2) (—12) —2 • 6 1 12	’ Ус + 12	’	3 ‘
1124.	Найти уравнение эволюты эллипса x — acost, y = bsint.
Решение. Найдем координаты центра кривизны для произвольной точки эллипса. Будем пользоваться формулами (6), предварительно вычислив значения производных .г = — a sin t, х~ = — <z cos t, y = b cos t, y~ — & sin t:
_ b cos t (a2 sin2 t + b2 cos2 t) _
Xc X ab sin2 t-^ab cos21	~	\	/
\ /
_ cos t (a2 sin2 t + b2 cos2 f)	/
Ус = x -	(°2 Sin2 *+ 62 COs2 z) •	Рис. 143
Подставляя % = <zcos t и y — b sin t, получаем параметрическое уравнение эволюты:
,	...	„ ,. Л2 „ ,	а2 — Ь2 „
xc = acost — acost(l— cos21) — ~ cosJ t или xc = —-—cos- t.
yc = b sin t — b sin f(l — sin2 0 s'n3 или Ус.~----£—sin3/.
Взаимное расположение эллипса и его эволюты дано на рис. 143.
1125.	Найти: а) координаты центра кривизны астроиды:
__ — / 1 1 \
х = V2 cos31, у = ]/2 sin31 в трчке А (у, уу;
б) уравнение эволюты параболы у — х2.
ГЛАВА VII
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 1. НЕПОСРЕДСТВЕННОЕ ИНТЕГРИРОВАНИЕ
1. Определение первообразной. Первообразной функции f (х) в данном интервале называется функция F (х), если в каждой точке этого интервала
F'(x) = f(x);	(1)
при этом все первообразные этой функции, и только они, содержатся в выражении
F(*) + C,	(2)
где С — произвольная постоянная.
Совокупность всех первообразных называется неопределенным интегралом функции fix). Неопределенный интеграл обозначается символом
j f W dx;	(3)
при этом f (х) называется подынтегральной функцией, f (х) dx— подынтегральным выражением, а — знаком интеграла. Таким образом,
j f (х) dx = F (х) С.	(4)
Отыскание неопределенного интеграла некоторой функции называется интегрированием. Интегрирование представляет собой операцию, обратную дифференцированию, поэтому каждой формуле дифференцирования (1) соответствует формула интегрирования (4).
2. Таблица основных интегралов
С	иаЛ1
\ и1 du— U ф-С (1)
1	СС —j— 1
(у/ --const, а =/=—1), (2)
(• лг»в»м интервале, в котором и =/3 0).
j е" du = eu + C,	(3)
?	du=-^—+C	(4)
J	In а	’
(a = const, а > 0, а ф 1), cos и du —sin и-{-С	(5)
\sinud« = —cosu-j-C,	(6)
Р —du—(7)
J cos3 и	1	v ’
(в любом интервале, где cos и =d= 0).
=~ctg и+с (8)
(в любом интервале, где sin и Ф 0).
+ С (— | а\ < и < | а]),	(9)
С du 1	. и , ,,
= arctg а+С>
— — 1п ; и Vи2 a -j- С.
J/u2+«
(Н)
246
Во всех формулах этой таблицы в качестве и можно брать произвольную дифференцируемую функцию и = ср(х).
Свойства неопределенного интеграла.
1) Постоянный множитель можно выносить за знак интеграла, т. е.
af (х) dx = a j f (х) dx, где а = const.	(5)
2) Интеграл от алгебраической суммы функций равен алгебраической сумме их интегралов, т. е.
$ [f (х) ± g (x)J dx = p (х) dx ± jg(x) dx.	(6)
Непосредственным интегрированием будем называть интегрирование с помощью этих двух свойств, тождественных преобразований подынтегральной функции и таблицы основных интегралов.
Во всех задачах этой главы требуется вычислить неопределенный интеграл.
1126. $(x5-3x4-7x + 5)dx.
Решение. Представляя интеграл алгебраической суммы в виде интегралов слагаемых, вынося постоянные множители за знаки интегралов и применяя формулу (1) таблицы основных интегралов, получим
(*	с с с с 1 з
\ (х5 — Зх1 — 7х -ф 5) dx=	\	х5 dx — 3 \	xi dx —7 \	х dx -ф 5 \	dx = g- х6 — у х5 —
— у х2 + 5х + С.
Заметим, что и здесь и далее произвольные постоянные, входящие, по определению, в каждый из складываемых неопределенных интегралов, объединяются в одну произвольную постоянную.
р+зрр5|Л
J фх2
Решение. Производя почленное деление и применяя формулы (1) и (2)
получим	з	5
f 2 + 3|/Г2 + 5/Г , о С ~ 2 , , о f	f dx
j ——? |/~з—— dx = 2 у х	dx + 3 J х	dx + 5 J - -- —
-f-5 In | x j -фС =---L -ф 18yx +5 In | x |-|-C.
У x
1128.
f dx
J х'ф-х2'
Решение. Прибавляя н вычитая в числителе подынтегральной функции х2, получим
dx
х ‘ х2
х2 -ф 1 — х2 ,	С dx	С dx
х2(х2+1У dX ~ J х-	J х2 -ф 1
=----— — arctg х -ф С.
С (1': _
J
х 2 dx —
Примененный здесь прием добавления в числителе подынтегральной функции взаимно уничтожающихся слагаемых иногда бывает полезен.
247
1129. \ — --- „ - dx. J sm3 x cos3 x		
Решение. Для нахождения интеграла заменим единицу в числителе подынтегральной функции выражением sin2 x-f-cos3 х и применим формулы (7) и (8) таблицы основных интегралов: С . dx	. V S'n" Хх	С dx	{ dx _	Hor-LC.		
3 sin2 х cos3 х J sin3 x cos2 x 1130.	j -v5 dx. 1131.	\ (2xs — 5x5 — 1) dx. 1132.	\ J. 1133.	{(——2dx. 1134.	{2Ji±g+6.dA._ J	* + 3 1135.	\ - - dx. -v“ x , 1136.	2~-y2 ^-. из?, j;+J *. У к а з а и и e. Представить числитель в виде 14-х2 4-1. 1138.	.//([ 4.,vi) d'<- 1139.	К* dx. 1140.	(фФ- dx. 1141.	J (x — 1 )2 x Vx dx. 1142.	f	±1- dx. J	\ x 1143. J ^x+1	J COS2 X 1148. 1149. 1150.	1 3 sin2 х ° " о   С dx J хЧ7?- f	dx. J	54- x2 P dx
		J | 7—x3 ’
	1151. 1152. 1153. 1154. 1155. 1156. 1157. 1158. 1159. 1160. 1161.	J	|/ 3 — x3 $ (2 sin x — 3 cos x) dx. ( (,—i	h -Д- i dx. J \ cos3x 1 sm2x/ (* sin 2x . \		 dx. J COS X f	dx
		j cos 2x 4- sin3 x C 2xsin2x4-l J sin2 x C cos2 x — sin x cos2 x 4-1 , \	3	:	 d.X. j	cos-	X f 1 + cos2 X , \ f	|	л	dx	, J 1	4- cos 2x C x sin 2x 4- j1 ’ x cos x J	X CCS X C xcx — X 1 \	dx. J x
1144. f L1+^+^1-.^dx.	1162.	cos2 -? dx. сазание. Выразить подын->ную функцию через cos х. § tg2 х dx. : аз а ние. Выразить подын- . 1 ную функцию через —д- •
J	V 1 -x1 1145. (l^x 4-j x)Jdx. 1146. \2xdx. 1147. ^axexdx.	У i теграль 1163. Ув тсграль	
248
§ 2.	ИНТЕГРИРОВАНИЕ ПОДСТАНОВКОЙ
1.	Подведение под знак дифференциала. По определению дифференциала функции,
ф' (.г) dx—dtf (х).
Переход в этом равенстве слева направо называют «подведением множителя q' (л) под знак дифференциала».
Пусть требуется найти интеграл вида
р (ф (*)) Ф'W	О)
Подведем в этом интеграле множитель ср' (х) под знак дифференциала, а затем произведем подстановку ф(х) = п, тогда получим формулу подстановки в неопределенном интеграле:
j f (ф (*)) ф' (*) dx = j f (ф (х)) dq> (х) = р (и) du.	(2)
Переставляя местами левую и правую части формулы (2), заменяя при этом букву и буквой х, а букву х —буквой t, получим
j / (х) dx = р (ф (/)) ф' (0 dt,	(3)
где х=<р (^—дифференцируемая функция.
Применения формулы (3) даны в последующих параграфах этой главы.
Рассмотрим примеры на интегрирование по формуле (2).
, , „ . С In2 х ,
1164.	\-----dx.
Решение. Полагая и = In,t, по формуле (1) найдем
С 1п2х , С i > л С о . и3 .	111 .V
\ ---dx == \ In2 xd In х = \ и2 du = —И С = ——j- С.
J X J	J	<3	о
lies.
Решение. Имеем
______	1	4
J*	~ J*{''"arctg xrf(arctgx) = J pu du = J и 3 du = (arctg x) 3 -j- C.
Здесь, очевидно, arctg x = u. При некотором навыке замена функции через и обычно производится устно
С cos In х .
1166. \—--------dx.
Решение. Имеем
Г cos In х . Г .	...	.	. ,	, „
\ —-— dx= \ cos In xd (In x) = sm In x -}-C.
Здесь за и принят 1пх и применена формула (5).
249
1167.	f	dx. J У sin3 x + 3
1168.	C sin3 x , \ —r— dx. j cos*’ x
У к а з тель tg3 х.	а н и e. Выделить множи
1169.	p (2x - 1) dx
	J У 1 — хф-х3
1170.	C etg x dx J COS2 X 
1171.	(* sin 2x , \ тп—^-5— dx. J 1 sm3 x
1172.	p aresin x ^===dx.
У 1 - х3
1175.	\-Qdx.
J x4~2
Указание. Представить числитель в виде (х3 + 8) — 3.
1176.	\ -1 хУ+1 dx.
J х
1177.	\	.
j sm х cos х
Указание. Представить знаменатель в виде tg х cos'2 х.
1178.	$tg3x-c?x.
Указание. Представить tg3 х в виде tgx- tg3x и выразить tg3 х че-
1173. J
< <	Г 2xdx
1	J l+x* •
Н’9. J
Н80. J
сх dx
sin х dx
УCOS X
2. Вынесение постоянного множителя. При интегрировании часто используют формулу
f (х) dx = af (х) dx,	(4)
а также тот факт, что <Др (х) = <7 [ф (х)-|-С] (C = const).
Рассмотрим примеры на интегрирование' по этой формуле.
1181.	^xe-X'dx.
Решение. Имеем
( хе~>:‘ dx = —	( ё~х2 (_-2х) dx=—	( ё~~х2 d(— х3) = —	е~х2+С.
1182.	^tgxdx.
г»	f ।	4 С sin х , С d (cos х) . .	. . _
Решение. \ tg х dx= \ ------dx = — \ —------ ~ — In cos х 4-С.
J	J COS X	J cos X	1
1183.	$^£=-dx.
J /1-х3
Решение.
X3
— Xе
||84'
_	С xdx
РеШеНИе‘ J 5 + 7^ =
х2 ,	\ Г d (х3)	1	. , ,. , „
=- dx — — |	' - = — arcsm (х3) 4- С.
3 J ’/1- (х3)3	3
rf(x3)
5 \2
-7 +(*V
г^+с.
1185.
dx
Решение.
dx
= х —In (еЛ4-1)4-С.
250
1186, $(x2 + l)32xdx.
1187. f cosxdx
3 —J— sin x
1188. Jjsin3xdx.
1189.	y^x+dx.
1190.	? Elxdl.
J COS2 X
1191.	^cosydx.
1192.	e*2 +4x +3 (x2) dx.
1193.
1194. 2x2x dx.
1195. [ZxvA-.
J V x
1 1 or С ЗЛ' dx
1196.	1_|_32at •
1197. f^C^dx.
J |<x
1198.
J J x®—-2
1199.	2 dx.
1200.	х3 У 2х4 — 3 dx.
1201.	(• х5 dx
	J Vl-x3
1202.	f dx
	,1 х — 5
1203.	У x — 1 dx.
1204.	У 4 — 3x dx.
1205.	p x3 dx
	J У^Ч-Т’
1206.	cos (x2 + 5) x dx.
1207.	"VTT dx-
1208.	P In x —3 , 1 —z=- dx. J x I In X
1209.	p x2 dx
	J У (3x3 —2)2
1210.	p exV aretg , J l-f-c2-2
1211.	f	dx
	j tg x In3 sill x
§ 3. ИНТЕГРИРОВАНИЕ ПО ЧАСТЯМ
1. Метод интегрирования по частям. Формулой интегрирования по частям называют равенство
( и dv = uv— f v du.
Применение этой формулы имеет целью заменить отыскание интеграла левой части отысканием интеграла правой, когда последний прогце. К числу интегралов, вычисляемых интегрированием по частям, относятся, Цапример, интегралы вида
j Р (х) f (х) dx,
где Р (х) — многочлен (в частности, степенная функция х'г), f (х) — одна из следующих функций: е™, sin ах, cosax, In х, aretg х, aresin х.
1212. § X2 In X dx.
Решение. Полагаем u = lnx, dv = x2dx, тогда , dx х3 * dlt= x’V-l’
* При
отыскании v по ее дифференциалу пишем
уЗ	уЗ
» = а не v = - +С, О	D
так как для применения формулы интегрирования по частям достаточно иметь какую-либо одну первообразную, а не совокупность всех первообразных, т. е. неопределенный интеграл.
251
а потому
1213. \xexdx.
Решение. Полагаем а = х, dv = ex dx, тогда
dti — dx, v = ex, а поэтому
j xe* dx—xex — ^'еЛ' dx = xex — ex~-C — ex (x— 1) + C.
Рассмотренные примеры показывают, что при интегрировании по частям и и dv нельзя выбирать как попало. Так, если в последнем примере положить и — ех, dv — xdx, то
du = exdx, v — -Q-
(*	х2 1 С
у хех dx=-%ex—% \ х2 ех dx.
В полученном интеграле степень х в подынтегральной функции возросла. Стало быть, после применения формулы интегрирования по частям получен «более сложный» интеграл, и цель не достигнута.
1214.	In я dx.	1220,	f In x , \—5- dx. J x2
1215.	j xe2x dx.	1221.	Vx\nxdx.
1216.	$ arctg x dx.	1222.	§ xn In я dx.
1217.	\ x cos x dx.	1223.	f X COS X 1 \	: o- dx. J sm3x
1218.	§ x arctg x dx.	1224.	J arcsin x dx.
1219.	f -JL-dx. \ sin2 X		
2. Повторное применение интегрирования по частям. Нередко формулу интегрирования по частям приходится применять последовательно несколько раз. Так, в следующем примере она применяется два раза.
1225.	^x3cosxdx.
Решение. Имеем
j х2 cos х dx = х2 sin х — 2 \ х sin х dx — х2 sin х +
"u a'v '	'll' dv
+ 2х cos х—2 cos х dx — х2 sin х+2х cos х — 2 sin х-|-С.
1226.	^x'le~xdx. 1228. ^xln2.rdx.
1227.	х2 sin x rfx.
3. Возвращение к исходному интегралу. Иногда повторное применение формулы интегрирования по частям приводит к уравнению искомого интеграла.
1229. § ех COS х dx.
252
Решение. Обозначая искомый интеграл буквой I и полагая u —cosx, do = ех dx, получим
I = j ех cos х dx = ех cos х + \ ех sin х dx =
и
= ех cos х + ех sin х — ех cos х dx = ех (cos х + sin х) —
Перенося I в левую часть равенства и разделив па 2, найдем
I = у ех (cos х + sin х) + С.
1230.
1231. ^e*sinxdx.
1232. ^Vl—x^dx.
1234. ^е2х sin2 xdx.
Указание. Представить sin2 х как
1235. J earcsi“ х dx.
1233. ^cos(lnx)dx.
4. Рекуррентные формулы. Иногда интегрирование по частям позволяет получить соотношение между неопределенным интегралом, содержащим степень некоторой функции, и аналогичным интегралом, ио с меньшим показателем степени той же функции. Подобные соотношения называют рекуррентными формулами. Рассмотрим важный для дальнейшего пример.
С dx
1230. Вывести рекуррентную формулу для интеграла In = \ . а
«т (X т I)
и вычислить с ее помощью \ 7-5-7775 •
j (Xs + 1 )<*
Решение. Имеем
. _ С dx _ (’ х3 + 1 — х2 , ‘п~ i (х3+1)'1 “ 3 (х2 + 1)'* dX~
= S (FF1 ~ S (Wdx=z !,l~l ~ S i'-; ;-i)4 dx'
В последнем интеграле положим
тогда
,	. С X ,	1 (• </(х2 + П 1 С di
du--dx, v-^ (л,2_н1),, dx 2	(хз+1)„	2 ) t'1 “
= 2Z ,ldt — 2-  —^-j-p4-C = —	^-—-2  ^2+1)n-i + C’
поэтому
1 х	1 С dx
Л1-Л1-1 + 2„_2 ’ (х2+1)'г i 2п-2	(х2-г1)" 1~
_ _ L ________£ . , ,_________L /
" 2и-2 (х2+1П 1 Г " 1 2п-2 "л
I х . 2п — 3
2п^2 ‘ (^+Т)«П 2п —2 ,г-1'
Таким образом, мы пришли к рекуррентной формуле
.	1	х 2п — 3
""~2п-2 ‘ (x^HF4 + 2n-2 n'L'
253
повторное применение которой в конечном счете приводит к «табличному» интегралу
С dx
' х'1 + 1 ’
Применяя рекуррентную формулу при п = 2, получим
dx	х
(?2+1)2 2 (хг-Н)
, 1 dx	х (
+ 2 J х2+1 ~ 2 (.V- + 1) +
£ arctg .г + С,
при п = 3, по той же формуле, найдем
1237.	Вывести рекуррентную формулу для интеграла 1п= xk lnrex dx (п>0, целое).
Указание. Положить и = 1пге х.
1238.	Вывести рекуррентную формулу для интеграла 1п — sinnxdx (п — целое, /г>0)
и вычислить с ее помощью ^sin4xdx.
Указание. Представить sm" х— sin™'2 х (1 — cos2 х) и положить dv = sin™‘2 х cos х dx.
§ 4.	ИНТЕГРИРОВАНИЕ ПРОСТЕЙШИХ ДРОБЕЙ
1.	Разложение на простейшие дроби. Рациональной дробью называется функция R (х), представимая в виде
где Р (х) и Q (х)— многочлены с действительными коэффициентами.
Рациональная дробь R (х) называется правильной, если степень числителя меньше степени знаменателя. Всякая правильная рациональная дробь может быть представлена в виде суммы конечного числа простейших дробей следующих четырех типов:
А	А
П	и) (х-а)”	(«> 1-натуральное число),
Till Mx-\-N .. Mx-{-N
1П) ^+77+7- IV>	(«>1-натуральное число),
п2
где ^ — q<0, т. е. корни знаменателя мнимые.
Таким образом, для интегрирования правильных рациональных дробей достаточно уметь: 1.) интегрировать простейшие дроби, 2) разлагать рациональные дроби на простейшие.
Этот параграф посвящен решению первой из этих задач.
2.	Интегрирование простейших дробей первых двух типов.
1239.	\ — dx.
У х — а,
254
Решение. Имеем
С А , л d (х~ а) й , .	, . ~
\ ----dx = А \ ------r~ = А 1 л х — a i -j- С •
J х — a	J (х — а)
С А
1240.	\ 7-—...\п dx (n> 1 — натуральное число),
j 1 л, " ’ (Л j
„	С А .	. С d(x—а)	А , _
Решение. \----------г- dx — А \  —< = — ;—-тт-;------—--С.
,) (.г —о)'1	J (х —а)’1	(п— 1) (х — а)’1 1
1241.	( —1244. ( ———•
1 J х —У £ J (Зх + 2)3'
1242 f ——	1245. ( ———
1^.	3_х.	i^a. \ (4_5а.)3 •
1243.
J 1 + 5х
3. Интегрирование этого типа
простейших дробей третьего типа. Пусть дан интеграл
С УИхУУ ,» \ тгд—1;— dx J x2-\-px-\-q
В знаменателе подынтегральной функции выделяют полный квадрат
Л-2 + рА: + 9 = х2 + 2 Р x+g = x2-|_2ix + ?- + g_?- = b+ -g-V + '\q-Р-\ Z	&	Ч	Ч \	J \	“-t /
а затем подстановкой x-^-^ — t
л Г Р2
I/ Ч~ приводят интеграл к виду
+ В Л С t dt । n С dt /2 + f’d 1^Л J /2+1+й J ^2 + i
(4 и В —некоторые числа), легко сводимому к «табличным» интегралам. Детали изложенного плана проследим на примере.
Р Qr____ 1
1246. \ 2	-.dx.
J X2 — X + 1
Решение. В знаменателе подынтегральной функции
следовательно, интегрируется простейшая дробь третьего типа. Так как
(этот прием «выделения полного квадрата» должен стать привычным инструментом изучающего), то
Делаем подстановку:
1 V3 _tv'3+i	___/з ,.
х g —t 2 I х 2 t dx 2 dt,
255
тогда
3.V--1
Л--'--Л +1
J 2~-М I ?,
\	-- “6 I'1 (У: + О + arotc'/-[-С =
3 < 4	1	2л* — 1
= о >11-, (л--л-+1) + -—— arctg — 7— -|-С =
-	'	I 3 I 3
1247.	-г—V--7-7;.
J Х--Н/Х-Н13 1248. t
J o.l" -|- IX -J- .1
'«»• \г^ё+Ъ,1х-l250' ^S^FTTT*-
4. Интегрирование простейших дробей четвертого типа. В интеграле этого типа
(•	ЛП.--1-У	/р-	\
\ ;л,—-----:—-т ах	-— а < 0, п > 1 ,
} (.г2 рх + qy>	\ 4	'	; ’
выделяют в знаменателе полный квадрат х2+аИ-<7=Л+	+
Подстановкой х+ р — t ~у приводят интеграл к виду ( Л - + 5 у._ л V ^4/ С dt
Первый интеграл правой части легко приводится к «табличном}’», а второй — находится с помощью рекуррентной формулы, полученной при решении 1236. Детали изложенного плана проследим на примере.
1251.	7-2 .VL 412^-
J (х2 + 2.с-j-З)2
Решение. В знаменателе подынтегральной функции
следовательно, интегрируется простейшая дробь четвертого типа. Учитывая, что х2 + 2х + 3 = (х+1)2 + 2, делаем подстановку.
x+l=/J-T, х=П/'2 — 1, dx=j/2’dt,
тогда
f х~{	f nz2-2	If tdt J<2 С dt
J (x2 + 2x + 3)2	' J 4(/2+l)2 ’	2 ,1 (<2 + l)2	2 ) (<2+l)2
1 (’ d(/24-l)	1' 2 C dt	1	|z2 dt
4 } (^ + 1)3	2 J (/2 + >)2	(*2 + l) 2 J (/2 + l)2’
256
В силу рекуррентной формулы (см. 1236) при п = 2 имеем
С dt t , 1 £ dt __ t , 1
J (Г2-ф1)2 “ 2 (f2+О + ~2 J Г + 1 “2(/2 + l)+ 2 g' + ’ поэтому	*
C *-l	,	1	1'2' I 2 . , , _
J (x-.r2x-r 3)'- rfA'~ 4('2 + l) 4(^+1)	4 a g +'
V2t +1	[r2 t	x + 2 Г2о . .v + 1 r
4(/- + l) ~4~ arCtg Z 1 C~ 2(x2 + 2x+3)	4 g
1252. \ t	„ dx. 1253. \ тт^к dx.
J (x2 + 2x + 2)2	J (x- — 3x-|-3)2
§ 5. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ДРОБЕЙ
1. Схема интегрирования рациональных дробей. Для интегрирования рациональных дробей
ч \А/
где Р (х) и Q (х) —многочлены с действительными коэффициентами, последовательно выполняют три шага.
Первый шаг. Если дробь неправильная, т. е. степень числителя Р (х) больше или равна степени знаменателя <2 (х), выделяют целую часть рациональной дроби R(x), деля числитель Р (х) на знаменатель Q (х) по правилу деления многочлена на многочлен. После этого рациональная дробь может быть записана в виде суммы, выделенной целой части — многочлена М (х) и правильной остаточ-
в виде суммы, выделенной целой части — многочлена М (х)
„ А Pi (х) нои дроби
(х)+—
<2 (х)
Р (х)
Второй шаг. Правильную остаточную дробь
<2 (х) шие дроби. Для этого находят корни уравнения Q(x) = 0 тель Q (х) на множители первой и второй степени с действительными коэффициентами:
<2 (х) = (х — а)к (х — Ь)1... (х2 + рх + q)m (х2 + гх4-s)n ...
разлагают на простей-и разлагают знамена-
(1)
В этом разложении знаменателя Q (х) множители первой степени соответствуют действительным корням, а множители второй степени — парам мнимых сопряженных корней. Коэффициент при наибольшей степени х в знаменателе Q (х) можно считать равным единице, ибо этого всегда можно добиться, деля на него Р (х) и Q (х). Разумеется, если знаменатель Q (х) уже представлен в виде (1), корни искать излишне.
После этого правильная остаточная дробь разлагается на простейшие по формуле
PiU) _	।	^2 ।	,	। Дг । в2_________|_	, Bi ,	,
Q(x) х — а	(х —и)2 -Г'"	(х- а)к т х — b 'г (х — б)2
, A4tx4~A^i М2Х 4- Л4 ,	.	+	,	,rn
”^х2 + рх + 7	(х24-рх + ^)2	(х2 + рх + ^)т "Г
где Xj, Л2.....MtNly ... — неопределенные (неизвестные) коэффициенты (некото-
рые из них могут равняться нулю).
9 Кручкович и др,	257
Для нахождения неопределенных коэффициентов все простейшие дроби приводят к общему знаменателю Q (х) и приравнивают числители обеих частей равенства (2). Затем сравнивают коэффициенты при одинаковых степенях х. Это приводит к системе уравнений, из которой и находятся значения интересующих нас коэффициентов.
Третий шаг. Находят интегралы выделенной целой части и всех простейших дробей (методами, рассмотренными в предшествующем параграфе), которые затем складывают.
Рассмотрим некоторые случаи.
1)	Знаменатель разлагается лишь на неповторяющиеся множители первой степени.
loti С 5х3 + 9.г2 — 22х — 8 ,
1254.	\----!—.—г--------dx.
,) х3 — 4х
Решение. Подынтегральная рациональная дробь неправильная, так как степень числителя равна степени знаменателя, поэтому выделяем целую часть:
__5х3 -ф- 9х2 — 22х — 8 I х3 — 4х
5х3	—2 Ох	|	5
9х'2— 2х--8
Таким образом,
С* 5х3+ 9х2 —22х —8 , С* /, , 9х2-2х-8\ .
J х3 — 4х	J \ х3 — 4х j
Знаменатель правильной остаточной дроби разлагается на множители следующим образом;
х3 — 4х = х(х? — 4) = х(х-—2) (x-j-2).
По формуле (2) каждому множителю знаменателя вида (х — а) в разложении .	.4
правильно!! дроби на простейшие соответствует слагаемое вида———- поэтому в данном случае получится разложение
9х2 —2х —8 _ А В С х3 — 4х х + х — 2 ' х + 2 ’
Приводя правую часть к общему знаменателю и приравнивая числители, получим тождество
9х2 —2х —8= А (х —2) (x'+2)A-Sx (х-|-2)4-Сх (х — 2).
Коэффициенты при одинаковых степенях х в обеих частях тождества должны быть равны, поэтому, отмечая за чертой слева, при каких степенях х сравниваются коэффициенты, получим систему уравнений
х2 9 = А + В + С, л-i —2 = 2В-2С, х° — 8 = — 4А.
Из третьего уравнения системы находим А = 2. Подставляя значение А в первое уравнение и сокращая второе на 2, будем иметь
В + С = 7, В —С = —1,
откуда 5 = 3, С —4.
Прием, которым найдены неизвестные А, В, С, называется способом сравнения коэффициентов.
Для определения коэффициентов часто бывает удобнее применить способ частных значений, состоящий в том, что после приравнивания числителей аргу
258
менту х придают некоторые удобные значения (таковыми являются значения корней). Так, в рассмотренном случае, отмечая за чертой слева значения, придаваемые аргументу х, получим:
х = 0 —8 =— 4А, А = 2,
х== 2 24= 8В, В=3, х = —2 32= 8С, С = 4.
Таким образом, те же значения коэффициентов получены проще. Можно при отыскании неизвестных коэффициентов комбинировать оба метода.
Заменяя под знаком интеграла остаточную дробь ее разложением на простейшие дроби (с подставленными в него найденными значениями коэффициентов) и находя нужные интегралы, последовательно получим
- С , , п С dx , „ (* dx , л С dx = 5\^^2jT + 3i^2 + 4 J ^+2 = = 5х + 2 In [ x | + 3 In | x — 2 j 4 In J x + 2 [ + C.
1255.	.........dx. 1256. x-^xi--dx.
J x3 + x2 —6x	J x3 —4x
2)	Знаменатель разлагается лишь и а множители первой степени, среди которых есть повторяющиеся.
1257' LtTW*'
Решение. Подынтегральная дробь правильная. Ее знаменатель уже представлен в виде (1). Согласно формуле (2), множителю х знаменателя в разложе-,	... А
нии подынтегральной функции будет соответствовать простейшая дробь —, а множителю (х+1)3 будет соответствовать сумма трех простейших дробей:
о_.
ЛГ-1-1 ^(х+1)2 ^(х-М)3 ’ поэтому разложение подынтегральной функции на простейшие дроби будет иметь вид
Зх+2 =А , в , С < D х(х+1)3 х +х+1 +(x+i)2+(r+l)3<
Приведя правую часть к общему знаменателю и приравнивая числители, получим Зх + 2 = 4 (х+ 1)3 + Вх (х+ l)3+ Сх (x-ф- 1) + Ох.
Комбинируя методы частных значений и сравнения коэффициентов, найдем:
2 = 4,
— 1 =— D, 0=1,
0 = 4 + В = 2 + В, В = —2,
0 = 34 + 2Д + С = 2 + С, С’=— 2;
С dx С dx п ( dx , f dx
J T — 2 j x+T
1
х= О
X3
X2
С Зх + 2	, л 1	„
з х(х+1)^Х-2	Т-2
~ 2 In I X | -2 In I х+ 1 ;+ j-j-y - 2(+q+fj2 + С = 2(х+1)2 + 2 1п | Г+Т { + с
loro С	______ 19R0 V
J (х +2)2 (л-+ 4)2-
9*
259
1950 ? Зх3ф-5х2 25л 1 ,	I960 ^Х
1259> J (хф-2) (х !)2 аХ' I2bU’
3)	Знаменатель разлагается лишь на неповторящиеся множители второй степени и, возможно, множители первой степени.
loci С Л'3 2х -3 - 2	,
126b	} (X-1)3(X2+1) “А-
Решение. Подынтегральная дробь правильная. Ее знаменатель уже представлен в виде (1). Согласно формуле (.2), множителю № ф- 1 знаменателя в разложении подынтегральной функции будет соответствовать простейшая дробь Мх J- д/
. Разложение подынтегральной функции на простейшие дроби запишется
в виде
х3--2х-!2 _ Л В Mx + N
(х - 1 f (х2 ф- 1) ~ х - 1 + (х — I)2 + х2 + 1 '
Приводя правую часть к общему знаменателю и приравнивая числители, получим х3-2хф-2 = А (х- 1) (х2ф-1)ф-В (х2 + 1) + (Л1х + Л') (х-I)2.
Комбинируя методы частных значений и сравнения коэффициентов, найдем;
х=1	1=2В, В=|,
Х“1	Р - 2/ + 2 - (Mi + Д') (/ - I)2 =- (Mi + Д/) (—21),
или, так как — I,
2 — 3i = 2M—2Ni;
отсюда, по определению равенства комплексных чисел,
( 2:--= 2М, М = 1,
хз	| —з=—гл/, w=2,
1 = А ф-Л1 = Л -|- 1, Л =0;
поэтому
3
С х3--2хф-2	1 С Их , С 2 ,
J (х——I)2 (х2ф- 1)	2 3 (х-1)2 1 3 *а+1
__	1	1 С d (х2 ф-1) , 3 С dx _
¥(Г=Т) + ¥ J ^+Т~ ~Г 2' J ~
= отЛп + 9 1п + 1) + о arctg х + С.
уЛ--1J	Z,
1262. ( 2- 3 fx+1dx.
J х3 -j-1
Решение. Подынтегральная дробь правильная. Ее знаменатель приводится к виду (1) по формуле суммы кубов. По формуле (2) имеем следующее разложение подынтегральной функции на простейшие дроби:
2х2 — Зх ф-1 х3 +1
откуда
А Мхф-N хф- 1	х2--хф- 1 ’
2х2 —Зхф-1 =А (х2 — хф- 1) ф-(Л1х-|-М) (хф- 1).
260
Комбинируя методы частных значений и сравнения коэффициентов, найдем:
х = — 1 6 = ЗА, А=2,
х2	2 = А-)-Л1 = 2-|-Л1, Л1 = 0,
х° 1 = A 4-tV = 24-tV, N =—l;
поэтому
2х2 —3x4-1 х2-Н
dx = 2
dx
x-l-1
dx
x2 + x+l
В последнем интеграле подстановка
, 1	,/3 , Уз,.
x +	2 ’ dx=" 2 dt
дает
2 С dt |/3j *2 + i
9	9	О у _L 1
^P3afdgZ+^r3arctgW
Окончательно имеем
1* 2x2 — Зх ф 1 , о 1 1 iti	± 2x H- 1 .
\--------!— dx = 2 In x + 1---, arctg —~----p C.
' x3+l	'	F3	j/3
loco C _______dx_____	1265 \ 3*3~4x4- 13 .
1263, J (x2-|-2) (x ~ I)2'	I2b5> 3 x2 (x2 — 4x4-13) dX-
c x-34-3x2 —3x-(-l ,
2b4' J (x4-l)2(x24-l) CX'
4)	Среди множителей знаменателя имеются повторяющиеся множители второй степени.
1266. С, ,
J (х-Н)(х2 + 1)2
Решение. Подынтегральная дробь правильная. Ее знаменатель уже представлен в виде (1). Согласно формуле (2), множителю (х2-|- I)2 знаменателя будет соответствовать сумма простейших дробей
jBx-j-C Dx-^-E
Х2+1 + (х24-1)2 •
Разложение подынтегральной функции на простейшие дроби будет иметь вид х34~з	__ А Вх С ( Dx Е
(х4-1) (х24-1)2 " х4-1 + х2-|-1 + (х24-1)2’
Приводя правую часть к общему знаменателю и приравнивая числители, получим х34-3 = А (x24-1)2 + (Bx + C)(x4-1)(x24-1)4-(Dx4-E) (х+1).
261
Комбинируя способы частных значений и сравнения коэффициентов, найдем:
х =—1
х = i
2 = 4Д, А =
?+3 = (Di+E) (('+1),
или, так как ,3 =— I,
3 — i = (£-D)4-z (Г 4-D), откуда, по определению равенства комплексных чисел, ( £ — 0 = 3,
I £-*-О= —1, т. е. £==1, £> = —2,
0 = Д + В = .1 + Я, В=--’ ,
3 — А + С + Е — С + 1, С = - g-.
Таким образом, 1 ,	’,3
С х'3 + 3	_ С 2 dx , С 2 *+~2 J ,
J (Х-р 1) (Х2+I)3	3x4-1+^	%2+1 dX Г
г С —2х +	dx 1 3 х dx ,3 1’ dx
+ ' (x2 + l)2	2 J x+T ~ 2 ) F+T + 2 ' x2 + 1 _
2x dx f dx 1	,	1 f d (x2 +1)
- \ (FT¥+ J (^W=’2 1п^+’|-Т \~qrr +
, 3	, C d(x2~H) , C dx
4-у aretg x (,t2 + l)2 + J(x2+1)2
= |ln;x + l ;-|lrrx2+i:+^ arctgx+^4- J
Оставшийся интеграл находится с помощью рекуррентной формулы (см. 1236 при п — 2)
С dx	х , 1	,	, „
\ (х2+1)2 ~2(х2+1) + 2 агс1§Л' + с-
подставляя его выражение, после упрощений, получим
(• i-з Д-З	*4-2	1	1
J (,+!>;+.) * - 2WT) + т >" I ’ +11 - 4 («•- + « + 2 «* « +С-
1267' § й^-Тгк2-н)гЛс‘ 1268' <а-
2. Интегрирование рациональных дробей без разложения на простейшие дроби. Недостаток рассмотренного в этом параграфе метода интегрирования рациональных дробей состоит в необходимости нахождения корней уравнения Q (х) = 0. Кроме того, изучающий должен учитывать, что указанный общий метод интегрирования рациональных дробей не следует применять, когда непосредственно виден более простой путь. Например, для нахождения интеграла
\ -.—-dx
J -х1— 1
сразу следует применить подстановку х4 —1 = /, так как
х3 dx = 4- d (х4— 1).
262
Точно также для нахождения интеграла
х dx
следует применить подстановку x* = i, а не разлагать подынтегральную функцию на простейшие дроби.
1200.
1270-
1271. (
.1 х4 (х24-1)
Указание. Представить числитель подынтегральной функции в виде (х24~1)—х2 и, разбив интеграл на сумму двух интегралов, повторить тот же прием.
§ 6. ИНТЕГРИРОВАНИЕ ФУНКЦИЙ, РАЦИОНАЛЬНО ЗАВИСЯЩИХ ОТ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
1. Универсальная подстановка. Рациональной функцией Р {и, о) двух переменных и н v называется функция, представляющая частное двух многочленов относительно этих переменных. Например, функция
п, . 5u2u —3ut» + 7о--|/3
R (и, v) = —--------у—-----—
4и2—/2ц-|~5 является рациональной функцией переменных и и у.
В этом параграфе рассматриваются способы интегрирования рациональных функций синуса и косинуса, т. е. интегралы вида
j R (sin х, cos х) dx.
Подстановка
tg g = *'
которую будем называть универсальной, рационализирует рассматриваемый интеграл, т. е. сводит его к интегралу рациональной дроби нового аргумента t\ при такой подстановке
2t	1-Z2	, 2dZ
S11^ = i+T2. cos* = r+7b dx==r+fi-
Следует, однако, учитывать, что иногда универсальная подстановка приводит к интегралу рациональной дроби, корни знаменателя которой практически невозможно найти. Это может случиться, даже если другая достаточно очевидная подстановка приводит к быстрому нахождению интеграла (см. 1275).
1272. ( —.
5 sm х
1 Решение. Подынтегральная функция рационально зависит от sin х.
Применяем универсальную подстановку:
Тогда
tg j — t,
21	, 2dt
smx^,
dx C 14-f2 2dt i‘ dt	, I x I
^=}4г-г+^=уг = 111^+с=ЧМ+с-
263
1273.	.
.) COS X
Решение. Имеем
Интегралы, полученные в 1272 и 1273, часто встречаются, их выражения полезно помнить.
P	dx
1274. \ ---------—__________
j 8 — 4 sin x 4- 7 cos x '
Решение. Применяя универсальную подстановку tg ^ = t, получим
С ________dx_________1‘	1	2 dt _
J 8 — 4 sin x 4-7 cos x J 2t I — /2 l-f ^ ° — 4 1 I 12 + 7 •.
2 dt
2 dt
(1 — 3) —(1 — 5) (/-3) (1 — 5)
JL. 1 — 3
I f_____ч
= In [ 1 — 5 | — In [ £ — 3 ; +C = ln ~t—q I l о
tgjH tg J-3
+ С.
C sin x +cosx ,
1275. \ о ,  о—dx.
J 3 4- sin 2x
Решение. Применив универсальную подстановку tg-у = t, получим 2t l-l2
3+2TT?
sin x 4- cos x ,
——7:—dx — 3 + sm 2x
1—/2
2dt	2(-^ + 2Z + l) ,,
I4-I2	314-4134~6124-414-3 ’
где корни знаменателя практически найти затруднительно, поэтому лучше сначала преобразовать знаменатель:
С sin х cos х _____ С	sin х + cos х	__
' 3 + sin2x Х~ J4 — (sin2x— 2 sin х • cos х + cos2 х) Х ~~
f sin х 4- cos х
= \	----т~.—!------тг“Л'.
J 4—(sinx — cosx)2
Теперь подстановка sinx — cosx=l, (sin x4-cos x) dx — dt дает
C sinx4-cosx ,	(‘ dt C dt
\ _____*____ zf у — \ _ __ \___________
J 34-sin2x J 4 —/2	J(2—0(24-0
1C di 1 J ( dt
4 J 24-f + 4 J 2-t
ln I 2 +1 j
1 ( (2-Q + (2 + Q
4 j (2-0 (2 + 0
J ln|2-+1 + C =
sin x — cos x 2
sin x — cos x — 2
I +
1276.
dx
5 4 sin x'
1277.	f -------—_______
J 3 sin x — 4 cos x ‘
264
1278.	Ч Г-"-Л о----------•	1280. (тТ-Л.
з 5 +sin * + 3 cos х	J 1 + tg х
1279.	\ lnx'C0S:A; ч/x.	Указание. Выразив тангенс через
' (3 + cosx)2	’	синус и косинус, представить числитель как
(sin A +cos
2.	Частные подстановки. Универсальная подстановка tg — t нередко приводит к сложным выкладкам. В указываемых ниже случаях предпочтительнее следующие частные подстановки, также рационализирующие интеграл:
1)	если функция 7? (sin х, cosx) нечетная относительно синуса, т. е. R (— sin х, cos х) = — R (sin х, cos х), то применима подстановка
cos х = t',
2)	если функция R (sin х, cosx) нечетная относительно косинуса, т. е. R (sin х, —cosx) = — 7? (sin х, cosx), то применима подстановка
sin х — t\
3)	если функция 7? (sin х, cosx) четная относительно синуса и косинуса, т. е. R (— sin х, — cos г) = R (sin х, cos х), то применима подстановка
tgx = /.
С sin3x ,
1281.	\ ---------xdx.
J cos х — 3
Решение. Здесь подынтегральная функция нечетная относительно синуса:
(— sin х)3 _ sin3 х cos х — 3 cos х — 3
Полагая cosx = 7, найдем:
sin х — 1 — /2, х = arccos t, dx —--——
|/ I—/2’ поэтому
c sin3x J	C	(pT^T2)3	dt f /2—1 C /2-9 + 8
) cosx —Зё*А’~	J /-3	' 7-3	M '	/-3	f
f	(* dt /2
= \ (/ + 3)^ + 8 \	= -1- + 3/ + 81П ; t — 3	=
= C°^ X J- 3 cos x + 8 1 n | cos x — 3 । + C.
Можно было избежать выражения sin х и dx через /, проводя следующие преобразования:
(*	sin3 х , (cos2 х—	1) d cos	х f	/-- 1 ,,
\ -----—тг- dx —	\ 2--------й-------- \	-—й- dt.
\ cos х — 3 J cos х — 3	J t — 3
1282.
J sm4 x
Решение. Здесь подынтегральная функция нечетная относительно косинуса (что непосредственно видно), поэтому применима подстановка sinx = 7. При этом
cos х = К1 — 72. х = arcsin/, dx = —7^==.
И I-/2
265
Можно было избежать выражения cosx и
dx через (, проводя такие
разевания:
преоб
1283 \_______________________________
' sin2 х — 4 sin х • cos х-[-5 cos2 x'
Решение. Подынтегральная функция четная относительно синуса и косинуса:
_____________________1_________________________ _____________1___________
(— sin х)2 — 4 (— sin х) (— cos х) 5 (— cos х)2 sin2 х — 4 sin х • cos x-j- 5 cos2 х ’
поэтому применяем подстановку tgx — t, при этом 1 1 1
COS X =	- — =: Sin X — t g X • COS X =----------,
k H-tg2x | 14-/2	J/ i-H2
x—arctg/, dx=y-^; получаем
,	г»	dt
1 _____________dx____________ _ I ________________T+72________________
I sin2 x — 4 sin x • cos x-!-5 cos2 x ~ I t2 , t	1	1
J	J -------4-	__-• .	- + О-------
1 + /2	|/1 + /2 |14-/2	H-/2
C dt C dt (* </(/ —2) __
- ) /2-4/ + 5 ~ J (/ —2)2 +1 “ J (7“ 2)2 -L l -
= arctg (/ — 2) + C = arctg (tg x — 2) + C.
Замечание. Можно было избежать выражения cosx, sin х и dx через /, про. водя следующие преобразования:
i‘	dx	___	_________dx	i‘ dt
' sin2 x—4 sin x cos x5 cos2 x j cos2 x (tg2 x — 4 tgx+ 5) j /2— 4/4-5
P //у
1284.	\
j sm° x
Решение. Хотя частные подстановки, когда они применимы, обычно приводят к более простым выкладкам, чем универсальная подстановка, однако могут быть случаи, когда универсальная подстановка обеспечивает кратчайший путь. При выборе подстановки нужна известная осмотрительность. В рассматриваемом случае подынтегральная функция нечетная относительно синуса (что непосредственно видно), поэтому применима подстановка cosx = /. При такой подстановке получим
(‘ dx ____ sin х dx ____ d (cos x) ________	(‘ dt	(‘ dt
J sin3 x J sin4 x J (1 — cos2 x)2 J (I — /2)2	' (1 — /)2 (1 4-/)2 '
Таким образом, применив частную подстановку, мы пришли к не очень простому интегралу рациональной дроби. Испробуем универсальную подстановку 266
tg у=*. тогда
2/	, 2dt
sin x = , ,' „, dx = , ,
C dx С (1-H2)3 2dt 1 С (1 + /2)'2	1 Г l+2f24-Z4
5 sirPx J 8/3	1 + /2" 4 J t3 TJ t3 a
= -4 \ +4 S т + т $ (dt = ~-^+ 2 r + “8 P + C =
=-------4-+|'n|tg-2-|+-8 fS2 i + C-
8 tg2 £	2	1	1
Выкладки были достаточно простыми, следовательно, универсальная подстановка оказалась предпочтительнее.
1285.	cos4x sin3x dx. 1288. c°s х dx.
j	j 4 sin2 x— 1
1286.	cos6x sin2xr/x. 1289.	—~~ л . , .
J	J 3 cos2 x-{-4 sin2 x
1287.	, an3* dx. 1290. C~Q—--------------------------------------5-.
J l-|-cos2%	J 19 sin2 % — 8 sm %-cos %— 3
§ 7. НЕКОТОРЫЕ ИНТЕГРАЛЫ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
1. Интегрирование произведений синусов и косинусов. Формулы тригонометрии
cos a cos р= * cos (а —р)+у	cos (а+Р),	(1)
sin а sin р = у cos (а — Р) —cos (а + Р),	(2)
sin а cos р — у sin (а — Р) + g	sin (а + Р)	(3)
позволяют представлять произведения синусов и косинусов в виде линейных комбинаций тех же функций (с другими аргументами) и могут быть использованы для интегрирования в рассматриваемом случае.
1291.	§ sin 4% sin 6x dx.
Решение. Применяя формулу (2), получим
\ sin 4х sin 6% dx= \ cos 2х dx — ~- \ cos 10% dx = 4- sin 2% — A sin 10% 4- С.
J	2	2 J	4	20	1
1292.	sin gCOSydx.	1295. sin 3x cos 10x dx.
1293.	J cos 4x cos lx dx.	1296. § sin3x sin2xdx.
1294.	sin -- sin dx.
2. Вычисление интеграла \ sin'« x cosn x dx (m или n — нечетное положительное целое число). Если показатель степени одной из тригонометрических функций— нечетное положительное целое число, то, принимая другую функцию за t, сведем рассматриваемый интеграл к табличным.
267
1297.	jj j/sin2* cos3xd.r.
Решение. Здесь показатель степени косинуса равен трем, поэтому делаем подстановку sinx=Z, cnsxdx = dt, тогда
| sin - х cos3 х dx = j ydsin2 x (1 — sin2 %) cos x dx = \ j’ 7?2 (1 — /2) dl =
/1	г	,	5_	3	H	3_______3____________
= \ t3 dt — \ t3 dt = -c- t3 — t3 + C = У sin5 x — r.- v' sin11 x-t-C.
)	j	5	11	5	r	11	r 1
1298.	sin5 x cos4 x dx. 1300. \	_jL dx.
J	J у COS4 X
3
1299.	J sin5 xcos5xdx.
3. Вычисление интеграла \ sinm x cos" x dx (tn-^-n есть четное отрицательное целое число). Если сумма показателей синуса и косинуса есть четное отрицательное число, подстановка tg.v — t сводит интеграл к табличным.
(*	d у
1301. \ —=^=.
J у cos’ х sin х
7	1
Решение. Здесь т~\~п = — %—% =— 4 есть четное отрицательное число, поэтому применяем подстановку tgx = /:
С dx _ 1* dx _ С dx __ С sec2 х d tg х _
' У COS7 X Sin X J У COS8 X tg X ' COS4 X ) Tg X ' |/tg X
-1	2 2	1	2_______ -
t 2 dt = -T t5 +2Z2+C = 4|- tg5x + 2rtgx+C. О	D
d у
1304.		
у sin3 X COS:’X
4.	Вычисление интеграла sin'« x cos" x dx (tn и n — четные неотрицательные числа). Применение формул тригонометрии
с (d + ydt= Z2t/Z+C yt ' J
1302. ( ----C^-T-.
J COS X smJ X
1303.	.
J У sin x cos3 x
1—cos 2x „ 14~cos2x sm2 x =--s, cos2 x = —!----------
2
2
позволяет повторным уменьшением вдвое показателей степеней синуса и косинуса в конечном счете, свести рассматриваемые интегралы к сумме интегралов от констант и нечетных степеней синуса и косинуса.
1305.	jj sin3 х cos4 х dx.
Решение. Имеем
sin2 х cos2 xdx = y (1 — cos 2.r) (1 ф-cos 2x)2 dx = = 4	(l-(-cos2x—cos2 2x — cos32x)dx =
1 C /. , o 1 -I- cos 4x 1 -P cos 4x n \ ,
= -g- J 1^4 4-cos 2x-—--------—---------cos 2x । dx =
— X \ (1 4- cos 2x — cos 4x — cos 4x cos 2x) dx.
268
Так как по формуле (1)
cos ix cos 2х = — cos 2x + у cos 6x, получаем
С	1 С /	1	'	1	\
\ sin2 х cos4 х dx = -j \ 1 + 2 cos 2% — cos 4x — cos 6x dx =
x , sin 2x sin 4x sin 6x , n
= 16 + “64	64	192" + C'
1306.	J cos2 x dx. 1309. § sin4 x cos2x dx.
1307.	jjcos4xcfx. 1310. jjcos(ixdx.
1308.	$sin4xrfx.
§ 8. ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ АЛГЕБРАИЧЕСКИХ ИРРАЦИОНАЛЬНОСТЕЙ
1. Интегралы вида	”x)dx* (п — натуральное число). Символ
Я (х, ') Х ) означает рациональную функцию от х и у' х. Так функция ——г—г = ——тгХ-лт;- есть (х, 'Ух). Подстановка x=fl (л—общее наимень-х2 + /х х2 -|- ( у' х)3 шее кратное показателен всех радикалов, под которыми х входит в подынтегральную функцию) рационализирует рассматриваемый интеграл, т. е. сводит его к интегралу рациональной дроби.
1311. \ —K^—dx.
J X— X2
Решение. Здесь х входит в подынтегральную функцию под радикалами с показателями 2 и 3. Общее наименьшее кратное показателей 6, поэтому делаем подстановку:
х = /°, dx = &fidt,
тогда
Vх	С	о С л	с С н-1 + i
з г ...	\	__ц dt 6 \	__। dt	6 \	dt
_6 (; (,.+1|л+б J (^р;,+1)-^-+«+з 5
_2Р+6,+ууу у
==2Z3 + 6Z-|-3 In \ t— 1 — 3 In ( Z+l i + C =
= 2/3 + 6Z + 3 1n |L-1|+C = 2 K* + 6c/-v + 3 In	—! I + C.
I ‘ + 1 I	y' x + 1 I
(•	1/x	f dx	p yd,
1312. \ .-dx. 1313. \ /, Лу-иУ- 1314. \-^-dx.
J l-|-]/x	J (l+|/x)]/x	J 1+yx
* Интегралы вида J 7? (x, xr, xs, ...)dx, где r, s, ... — рациональные числа, относятся к рассматриваемому типу, так как, если п — общий знаменатель дробей г, s, .... то подынтегральная функция оказывается рациональной функцией от х их".
269
2. Интегралы вида
dx * (и — натуральное число).
Интегралы этого вида рационализируются подстановкой
ax + b _ tn cx-\-d
yi — общее наименьшее кратное показателей всех радикалов, под которыми входит в подынтегральную функцию
ах — Ь cx + d
,з15-
1 X
Решение. Рекомендуемая подстановка -j—:— = /2 даст 1 ~X
1-^	,	, 2Р
Х 1-р/2 ’	(\+flydt’ * 1
Поэтому
(1-М2)\
4Р
1316.
1317.
_ С dt
с р'Т+Т ,
\ -—— dx.
' х
1 -р ) Зх -|~ 4
1318. г.-----yVn-yr  1/~ dx.
J (1 -х) (1-Р*)2	1 1-х
dx
3. Интегралы вида \ 1Z-	, Интегралы этого вида после выделе-
j I а X"1и х-f-с
ния полного квадрата под корнем линейными подстановками сводится к сле-
дующим:
1) если а>0 —к табличному интегралу
2) если а<0— к табличному интегралу
’ dx
J У^+А ’
С dx
1320.
dx
Г2х2-х-рЗ’
К этому типу относятся и интегралы вида
dx + b \s
где г, s, ... — рациональные числа, так как, если /г —общий знаменатель дробей г, s, .... то подынтегральная функция оказывается рациональной функцией х
I
И >
Xx + dJ
270
Решение.
,	, Р .	if* d х - 1
dx ______ 1 I _____dx________11	-___4 :
~ yi 1 f x T “ /2 -i /~7	1' 2 , 23
V ^~2 + 2	- У !*-Т; +16
.v + 3
+ C.
1321.
Решение.
1	. Зх +1
=	. arcsin —;---H C.
V3 4
C dx
1322. \ r -;^=_-=.
i X J/ 10№ —бхн-1
Решение. Данный интеграл с помощью «обратной подстановки» х — ~^~
С dx _ „ сводится к интегралу вида \ —------------.. Действительно, полагая
J ах'2 4-6% +с
1 , 1 х — , dx — — dt,
получим
р	р - dt р
1 dx _ I________________р_______I — dt
xl'W-6x4-1 “ 1 1 -/"Гб гут ~ /Тб^бГр’2
-	- 7 |/ /2 ~ Т + 1
= - \ -7— = -1пР-3 4-К10-6/4- + + С =
ЗН+Р-зр 1_________________
— In I 1—3+1/ 10- 6 + [ +с.
I х Г	X X2
1323. £
«’ 1 х-+ 1х + о
Р е ш е н и е. Замечая, что х dx= у d (xs + 4x+5)~2dx, получим
х dx _ 1 (	+ 4x + 5) g 1* _____dx
x2 + 4x + 5	2 ’ yrx2 + 4x + 5 J \fx2 + 4x + 5
__________ p dx	_________
— p x2 + 4x + 5 — 2 \ -  ...... =	У x2 + 4x + 5 —
Jp(x + 2)+l
-2 In ' x + 2 + )/'x2+4x + 5 I +C.
1324.
1325.
dx
У 5x2 + 3x + 2 dx
x У2х2 — 5x + 3
1326.
1327.
dx x/7x2 + 2x+5 ’ dx
J у2 + Зх - 2X2 '
271
1328.
(x 'r-4)rfx
] 2х2 — Зх + 5
1329.
(4х + 7) dx
4. Интегралы вида \ R (х, Уах2 + Ьх-\~с) dx. Для нахождения интегралов этого вида (к которому принадлежат и интегралы пункта 3) существует много различных приемов. Рассмотрим здесь только один — «метод тригонометрических подстановок». Выделением под знаком радикала полного квадрата (после выполнения надлежащей линейной подстановки) рассматриваемые интегралы сводятся к интегралам одного из следующих трех видов:
j 7? (х, У а2 — х2) dx, j 7? (х, f x2-'.-a2) dx, j 7? (х, Ух2 — a2) dx.
Интегралы этих трех видов «тригонометрическими подстановками» сводятся к интегралам функций, рационально зависящих от синуса и косинуса (см. § 6). Для этого достаточно в интегралах:
1)	j 7? (х, Уa2 — x2)dx сделать подстановку
x = asin7 или x = acos7; , /____________
2)	\ 7? ( х, yx2-f-a2)dx сделать подстановку
x = atg7 или x = actg7;
3)	f 7? (х, ]'х2 — a2) dx сделать подстановку
Интегралы же вида 7? (sin х, cos х} dx рационализируются, как показано в § 6. Таким образом, интегралы вида
j 7? (х, У ах2 + Ьх-\ с) dx,
в конечном счете, всегда могут быть рационализированы.
1330.
dx
(х2+ 16) )9-х2
Решение. Данный интеграл относится к интегралам вида
j R (х, У а2 — х2) dx,
поэтому делаем подстановку x = 3sin 7:
dx
(х2+16) J/'i+^x2” dt
25 sin2 7 + 16 cos21
3 cos t dt
(9 sin2 7 + 16) 3 cos 7
’	dt
cos2 7 (25 tg2 7 + 16)
d tg 7 If d tg 7
25 tg2 7-pitT “ 25 J . , , , z 4 V2
\ ° ,z
1 / \
20arCtg'(4 tg ^ + C'
Остается вернуться к аргументу х; применяя для этого формулы тригонометрии, получаем
х
, , sin 7 sin 7	3	х
tg 7 =--= —= =----------—-= —=r,
cos7 И-sm27	{ Х2 ф 9 —х2
272
поэтому
dx
* l OX , r-
- arctg---+ C.
20	4 |-'9-№
1331.
dx.
Решение. Данный интеграл относится к интегралам вида
поэтому, как указано в начале параграфа, возможна подстановка
x = tg/ или x = ctgt
Выбираем подстановку x = ctg t, которая здесь удобнее (критерием является проба!):
x'1 — x 4-1
(^+1)
= \ cos t dt — ? -т—r = sin t - In I tg 14- C =
J	J sin t	|	2 |
= sin /4-In | etg ^-|4-C.
dx= \ (etg3t — etg 7-|- 1) (—sin t) dt =
Остается получаем
вернуться к аргументу х. При помощи формул тригонометрии
sin t — —
V etg3 14-1
, t cos /+1	, ./-rrr
etg — =-----!— = x -|- У xl 1 •
2 sin t
Поэтому
? ---dx =	4- In (x4- K^TT) 4-c.
i (%34-1) Гл-4-1	/х34-1
1332.
dx
(>:34-2) |/\3 —1
Решение. Данный интеграл относится к интегралам вида
$ R (х’
У'х2 — a3) dx.
поэтому делаем подстановку
1	_	, sin t
х —-------. 1 огда dx = —vt dt
cos t	cos21
и
C	dx
' (Л--4- 2) /х3— 1
- C s'n _ ~~	3 — 2 sin3/
__ C cos t dt ____ C cos t dt
J 14~2cos3/ j 3 — 2 sin3/ f du _______ 1	dti
273
I
2 J6
du
1	C du
2	Кб ) 777 I/ — u
2 Кб’
2 V 6”
In
и
—— In
2 Г G
In
2 I 6

V 3 4-1 2 sin t p' 3 —| '2 sin t
sin t = V1 —cos21 —cos t 1/ —------1
У cos31
X
Поэтому
dx
КЧ-2) J'x2-1
—U In 2J 6
x V 3 — J 2 Kx2 — 1 !
1333. \V4-xsclx.
1334. jj-----j-.
(9 + x2)2
1335. (
’ J (5—.v-)J
1336.
J x3
1337.
(x2 + 5)J
1338. ( ——c7------------
’ J (1	+ x2):J
Указание. Замечая, что
I 2	/ |."з
1 +х + х~ — ' -X + 9 ; + у~2— у! ,
сделать подстановку
х+|- = ДД tg^.
1339.
1340.
dx
+ 4) y'ix^+l
§ 9. СМЕШАННЫЕ ЗАДАЧИ НА ИНТЕГРИРОВАНИЕ
Для овладения важнейшими элементами техники интегрирования нужно: 1) помнить таблицу основных интегралов, 2) уметь безошибочно относить заданный интеграл к одному из рассмотренных выше видов, 3) уметь, пользуясь рецептурой вычисления интегралов соответствующего вида, правильно доводить вычисления до нахождения неопределенного интеграла.
1341.	-П-dx.
х4
Решение. Интегрируем по частям, полагая
и — 1п (л + Кх2 — 1), dv =7* , du==—7~ xi' |/х3-
f In (л'+Кх2— 1) ,	1 . /	,г-~з-
‘------------dx = - -j^ln UH-kx2—0-
1
V = — 7-
х4
dx____
274
Теперь имеем интеграл, вычисляемый подстановкой
cos t ' cos* t
С dx С , , С 1+COS2/ , \ ---  — = \ cos2 t at = \ ----X----at =
,v‘J х2-1 J	J	2
t , sin 2t , ~ t , cos t sin t r = 2 +~Z~ + C= 2^-------------2--+C-
Остается вернуться к аргументу х; применяя для этого формулы тригонометрии, получаем:
1	,---------V Л2 — 1	I
cos t — —, sin t — Г 1 — cos2 t -----, t — arccos —
X ’	X	£
поэтому
' In(x-+Cx2-1E	1		•X" 0 +	1	1 , l'x2-l ,
	x*	— 3x2 •" v‘ 1 ’		6	X	6xi
1342.		1352.	f	dx
	sin7 xcos3x dx.		j i + sin x + cos x ‘
1343.	J x(x2—1)	1353.	( In aretg X , 5 i+x2 ax-
1344.	C	dx	1354.	C	dx
	' Hie+x2)3		j cos x (1 — sin x)
1345.	cos x cos 2x cos 5x dx.	1355.	
			' (x+1) Гх24-2x4-3
1346.	C	dx	1356.	cos8 x dx.
	3 /х		
1347.	f x3+x24-2 , J (x2 + 2)2 !X-	1357.	( X4 -xr4-l J \	2 T dX’
1348.	(* COS3 X , \ , dx. } sin’ X		х'3-х6
1349.	§ (x3-i- 1) In x dx.	1358.	jj sin4 x cos3 x dx.
1350.	J Их2-4x+l	1359.	
1351.	f 4-^±£±l	dx	1360.	
	J (x ~l)(xJ+x + i)		J x~
		1361.	Cex3-j-x-H (3x:2-[- 1) dx.
1
2 /6
du
,	1 C du
3”,	^2^6 J -j/'3'
2 +“	V 2
Поэтому
= 1
2 Иб
— —— In 2)6
sin t = Ki — cos21
dx
1333.	\V4-x2dx.
1334.	J—3-.
(9 + x2)2'
1335.	(
' | (5— .v-)J
1336.	\	dx.
J x3
1337.	------^-^-dx.
(л-2 + 5)Т
1 2|/6
Г in ]/ j
—in
2 |z 6
V 3 + p 2 sin /
J/ 3 — У 2 sin t
=cos/t/ i -i = F cos21	x
—Ц In
2) 6
1338.	\ —--------- -
<’ J (1 -f-x + x2):)
Указан и e. Замечая, что
1 +% + x- =: х + 1-1 + (^2~^ ,
сделать подстановку
1339.
1340.
1 2
tg/.
§ 9. СМЕШАННЫЕ ЗАДАЧИ НА ИНТЕГРИРОВАНИЕ
Для овладения важнейшими элементами техники интегрирования нужно; 1) помнить таблицу основных интегралов, 2) уметь безошибочно относить заданный интеграл к одному из рассмотренных выше видов, 3) уметь, пользуясь рецептурой вычисления интегралов соответствующего вида, правильно доводить вычисления до нахождения неопределенного интеграла.
1341. \	----0
J х*
Решение. Интегрируем по частям, полагая
и — In (х -j-V'x2 — 1), dv, du. — ————	v = —I .
X*'	l/x'3-1’	ix3’
и

Л I  I 9' I V
C In (x-j-V^x2 \ xi
—dx =
-1 1 n (x У x - — 1) + 4 \ ---^===-
274
Теперь имеем интеграл, вычисляемый подстановкой
С dx С , , .,	С 1 + cos 2/
\ -- -	— \ cos2 t dt = \ —Hr-dt —
> Xя l Л --1 J	'	2
t sin 4t „ t , cos t sin t
= 2- + —4~+c'=2-	2---+ C-
Остается вернуться к аргументу %; применяя для этого формулы тригоно-
метрии, получаем: 1		1/ ^2	1	1	
	cos t — . sin / = V 1 — cos2 t  X '	X	— , t — arccos —. ’	X f
поэтому			
С In U+ I7*2-!) ,	1 , ( , ,г~ \	Зх2	+1 Х		!-l)+	1 1 , ) , - arccos		—	p 6	X	6.V2
1342.	sin ? xcos3/ dx.	1352.	£	dx
			J 1 sin x cos x '
1343.	\-^dx. J x(x2—1)	1353.	C In arctg x , 3 l-f-X2
1344.	f	dx	1354.	C	dx
	J J/(16 + x2)3 '		J cos x (1 — sin x)
1345.	j cos x cos 2x cos 5x dx.	1355.	
			' (x-4-1) Гх24-2х + 3
1346.		1356.	cos6 x dx.
	' Vx		
1347.	С +А-Ч-2 , 3 (Г-4-2)2	1357.	2 Г dx-
1348.	I* COS2 X , \ • -Л~з- dx.		x3-x6
	J sm* x		
1349.	(x3+ 1) Inx dx.	1358.	sin4 x cos3 x dx.
1350.	( -£+L=dx. J Kx2-4x+l	1359.	5 /(Ш.1
1351.	f	*±J dx.	1360.	V^±lrlx.
	J U-l)(x2 + *+l)		
		1361.	\ exl + x+1 (3x2 +1) dx.
ГЛАВА VIII
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
§ 1. ОСНОВНЫЕ ФОРМУЛЫ
1. Определение и свойства определенного интеграла. Пусть функция f (х) определена на отрезке [а, Ь[. Разобьем этот отрезок на п частей точками
а=х0 < Xt < х2 < ... < хп = Ь.
На каждом из частичных отрезков х,] возьмем произвольную точку и составим сумму п
г = 1
которая называется интегральной суммой функции f (х) на отрезке [а, 6].
Предел интегральной суммы при условии, что число частичных отрезков неограниченно увеличивается, а длина наибольшего из них стремится к нулю, называется определенным интегралом функции f (х) в пределах от х = а до х—Ь и обозначается
Ь	п
j / (х) dx =	1 im	У, f (g,)	(1)
а	max Sx-0 j
O-o:)
Если функция непрерывна на отрезке [а, 6], то она интегрируема на этом отрезке, т. е. предел (1) существует и не зависит от способа разбиения промежутка интегрирования [а, 6] на частичные отрезки и от выбора точек при каждом таком разбиении.
Основные свойства
Ь	а
1)	Jf(x)rfx= — j/(*)*• а	b
b	b	b
2)	j (х) + C2f2 (x)J dx = C1! J ft (x) dx + Cs j h (x) dx a	a	a
(C\ и C3 — постоянные),
b	c	b
3)	f (x) dx =	(x) dx + \f (x) dx,
a	a	c
где с — некоторая точка, лежащая внутри или вне отрезка [а, Ь].
4)	Если /(x)==s<p(x) при а^х^Ь, то
Ь	Ъ
f (х) dx sg ф (х) dx.
а	а	'
276
Ь) Если т наименьшее, а М — наибольшее значения функции f (х} на отрезке а^х^Ь, то
ъ
m(b~a) (х) dx <; Л1 (Ь — а).
а
6) Если функция f (х) непрерывна на отрезке a^x^zb, то на этом отрезке найдется такая точка что
ь
р(х) dx = /(?) • (b — а).
а b
Число / (?) =	/ W назьщается средним значением функции f (х)
а
ia отрезке [а, Ь].
В следующих задачах выяснить (не вычисляя), какой из интегралов больше:
1 1362. a) \ex2dx	или	1 jj ех dx;
0		0
2		2
б) $ ех2 dx 1	или	$ ех dx, 1
Решение, а) Так	как с*2 ех	при
интеграл больше.
б) При л-т ! ех2^е\ поэтому первый интеграл
1, то, по свойству 4, второй больше.
1 _________
1363. а) $ ]Л1 +х4 dx или
- 1
I
б) х3 cos2 х dx или о
е
в) $ х In х dx или
1
В 1364 и 1365 оценить интегралы:
1	2л
1364. а) £ Kx2 + 2x"+4dx; б) ( о	о
1
х2 dx;
— 1
1
х2 cos2 х dx;
о
е
х In2 х dx.
л. 2
dx ' . С
10 -j- 2 cos х ’ В j я o'
cosa x x
dx.
Решение. Для оценки всех трех интегралов воспользуемся свойством 5. а) Функция f (х) = I' х2 + 2г + 4 монотонно возрастает на отрезке [0, 1], поэтому наибольшее и наименьшее значения она принимает на концах отрезка;
m = f(0) = 2, М=/(1) = К7 «з2,65.
Длина отрезка интегрирования 6 —а=1, и мы получаем оценку
1
2^'j/x2 + 2x + 4dx=s: 2,65;
о
б) Наибольшего значения подынтегральная функция достигает при х = я, огда косинус равен —1 и знаменатель минимален, т. е. Л4=/(л) = Т Апало-о
277
гично, при х = 0 (или х = 2п) m = f(0) = y^. Так как Ь — а=2л, То, по свойству 5,
2л
л С dx л _
6 = ' lO-f-^cosx^ 4 ’
О
в) Функции cos2 х и монотонно убывают на отрезке , Лj, монотонно убывает поэтому и их произведение, так что наибольшее и наименьшее значения подынтегральная функция принимает на концах отрезка:
Учитывая, что Ь — а — -„> получаем оценку: «5
я
'6 я 2	2	2,	___
1365. a)	б) \ 444^1 в) i^-^-dx.
Л	»'	% ~t~	J	х
О	0	я
4
2. Формула Ньютона — Лейбница. Если функция / (х) непрерывна на отрезке [а, Р] и для нее известен неопределенный интеграл
j/(x)dx = /'(x) + C,
где F (х) — какая-нибудь первообразная функции /(х) (см. гл. VII, § 1), то определенный интеграл может быть вычислен по формуле Ньютона—Лейбница
ь
jf(x)dx = F(b)—F(a),	(2)
а
т. е. определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования.
При вычислениях формулу (2) обычно пишут в виде
С	ь
\f (x}dx — F (х) , а	а
где символ справа —«подстановка от а до &» —обозначает ту же самую разность F (b) — F (а).
Применяя формулу Ньютона—Лейбница, вычислить следующие интегралы:
2
1366. jj х2 dx. — i
2
г,	С х312	2»	(-1)3 ,
Решение. \ х2 dx =	----—к  — 3.
.)	3	3	3
— 1
278
1367. $ sin3xdx. о
jt	rt	rt
2	2
Решение. 5ш3л'с/.«=^' (1 —cos4 .v) sin x dx —— J (1 — cos2 x) d cos x — О	о	6
•> \
л cos 2 I :	n , cos3 0\	2
_ cos _ +	_ cos 0 +—' = у.
1368.
dx
x К1 — (In *)a
Решение.
dx
~X -'(111
d In x
= aresin In x
= aresin In
. /-	...	.1	n ЭТ
V e — aresin In 1 = aresin A— arccos 0 — -.
2	о
1369.	( 1 + XLdx. i X" I 1	1373.	4 Г cos3 x dx ' vrsin x ЗГ r
1370.	\)У 1 -{-xdx. 0	1374.	2 I C	dx 
1371.	x d x		j x3 + 4% + 5 о
	Л (Л'2-М)* • — 1	1375.	t C	dx
1372.	(’ 1 + 111 .V , \ —	dx. J	X 1		\ у3 + 2л:-х2
В следующих задачах найти среднее значение функции на ука занном отрезке:
1376. f(x) = cos2х (0<х=ё£л).
Решение. По определению среднего Значения функции на заданном отрезке (см. п. 1, свойство 6), имеем
г,-,	1 С ,	.	1 (’ 1+cos 2л: ,	1 / sin 2лЛ l« 1
f (?) —-— \ cos4 х dx = — \ -s--dx — x H------—	— t •
jc — 0 .)	л .’	2	2n \	2 / |0	2
о	о
,377-^ = утЫ
1378. f(x)-tg2x (Q-^x^X}.
279
§ 2. МЕТОДЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
ь
1. Замена переменной. Часто для вычисления интеграла \ f (х) dx полезно а
заменить переменную интегрирования х новой переменной t при помощи подстановки х = ф(/) или / = ф(х). При этом необходимо перейти от старых пределов интегрирования а и b к новым пределам а и |3, которые определяются из уравнений
а — ф (а),	6 = ф(Р).
Замена переменной осуществляется по формуле
b.	Р
р(х) dx =jf[<p (01 ф' (0 dt. а	а
(1)
Эта формула справедлива, в частности, если f (х) — непрерывная функция, а подстановка х = ф(/) сама непрерывна и имеет непрерывную производную на отрезке [а, 0]. Подчеркнем, что при вычислении определенного интеграла методом -замены переменной в отличие от неопределенного интегрирования возврат к старой переменной не требуется.
В следующих задачах с помощью подходящих подстановок вычислить интегралы:
1379.
dx
1 + j/x
Решение. Переходим к новой переменной интегрирования, полагая х—Р (^>0). При х = 0 получаем £ = 0, а при х = 4 — / = 2; поэтому в соответствии с формулой (1) имеем
4	2	2
( -dx г = t t fl —d# = 2 —In , 14-/j) I2 ==4 —2 In 3.
J l + |/x J I +t	l + o	‘ 0
0	1 r о	0
1380. \ V4^dx. о
Решение. Положим x = 2sin/. Такая подстановка возможна (так как при любом значении t под корнем получается неотрицательная величина) и приводит к тому, что корень под знаком интеграла исчезает. При этом изменению переменной х от х=-0 до х = 1 соответствует изменение переменной t от Г = 0 до
/ =	. Применяя формулу (1), получаем
л	л
16	6
] ' 4 — х2 dx = j’ ]4 — 4 sin2 t • 2 cos t dt = 4 cos2 t dt = oo	о
JT
6	"TC	_
„ V ,. ,	o /, , sin2f\|6 л , ГЗ
= 2 J (l+cos2/)^ = 2	Q - 3 + 2 .
0
1115	_____
1381.	\	' dx.
J e г 4
0
280
Решение. Положим /-1 ‘ ех — 1, тогда
ех = /2_|_1 и ех dx — 2t dt.
При х = 0 £ = Ге°—1=0, при x = ln5 t = Ve'n5— 1 — Кб— 1 =2, поэтому
t-2tdt _ /2 + 4
= 2 it—2 arctg |2 = 2 (2 —2 arctg 1) = 4 — л.
\	2 1 (0
a	a
1382.	Доказать, что для четной функции $ f (х) dx = 2^f (х) dx,
—а	б
а
а для нечетной $ f (х) dx = 0.
~а
Решение. Разобьем отрезок интегрирования [—а, а] точкой х = 0 на две части. Тогда, по свойству 3 (см. § 1, п. 1), получим
а	0	а
j f (х) dx — j f (x) dx+^f (x) dx.	(2)
—a	—a	(J
Заменим переменную интегрирования в первом интеграле правой части этого равенства, положив х = —t. Согласно формуле (1), будем иметь
оо	о
J1 = j / W dx = р (-0 (-dt) =-\f(-t)dt.
—а	а	а
В последнем интеграле переставим пределы интегрирования (отчего интеграл изменит знак) и обозначим переменную интегрирования снова буквой х (значение интеграла не зависит от того, какой буквой обозначена переменная интегрирования), получим а	а
J1=(f(—t)dt=- j f (—х) dx. о	о
Теперь равенство (2) примет вид а	а	а	а
( / (х)	dx = j f (—х)	dx + р (х)	dx = j [f (x) + f	(—x)]	dxt
—a	0	0	0
или, учитывая,	что	для четной	функции	f(—х) = /‘(х),	а	для	нечетной f(—х) —
——f (х), имеем ’ а
2 ( f (х) dx, если f (х) четная, о
, 0,	если f (х) нечетная.
а
f (х) dx =
—а
Используя результат 1382, вычислить интегралы в 1383 и 1384.
Л.	1	________ ____________
1383. a) sinтхcosnxdx; б) $ (]7 (х + 1 )2 + р"(х — l)2)arcsinxdx; —л	—1
л
2	7
в) 5 (х5 + 5х4 —Зх34-х) dx; г) $ (cos2 х-ф-х4 sin х) dx.
*~2 —
2
281
Решение. Интегралы а) и б) равны нулю, так как подынтегральные функции нечетные (проверьте’.), а отрезки интегрирования имеют вид [—а, о] (см. предыдущую задачу); представим интеграл в) в виде суммы двух интегралов, один из которых от нечетной функции (равен нулю), а другой от четной функции легко вычисляется. Имеем
2	2	2	2
jj (х5 + 5х4 — Зх3 + х) dx = \ (№ — 3x3 + x)dx-f-5 х4 dx—10 х4 dx = 64.
-2	—2	—2	I)
Аналогично, учитывая, что функцш
рала г) получим ( (cos2x-;-x4sinx)d.' ’ Л
л
2	я
„ С 1 -4-cos2x ,	/ , sin 2х Гг
= 2 J-----2“ ^=;х + -2- о
о
9 г~
1384. ( -1^-.
} Гх-1
4
I ____________
1386. $х2]/1 — x2dx.
О
1
I* Ну 1387. \ -7—7-.
J е х-[-е х о
я
1388. I dx
j 1-f-sin x+cosx" о
х4 sin х нечетная, a cos'-x четная, для интег-
л	л	л
~2	7	2
= x4sinxdx+ j cos2xdx = 2 pos2xdx=
‘ л	л;	0
~ 2	- ~2
2 *
л
4~
1389. (	- 
J 1 +2sin2 х 0 2л
1390. а) x4sin3xr/x; ~2л
I
б) {ех -J- е-х) tg х dx-, -i
л 3
в) \ (^sin 2x + cos у 4-tgX^ dx; л
” J л *4
r>\ С x7 — Зх5 + 2х3 — х 4-4 .
Г) \ -----------~ dX’
z J	cos2 X
я ~~ —
2.	Интегрирование по частям. Если функции и (х) и v (х) обладают непрерывными производными на отрезке [а, Ь], то справедлива формула интегрирования по частям для определенного интеграла:
b
и dv iiv | — || v dUj	(3)
а	а
где символ uv Ь обозначает разность и (b) v (&) — u(a)v(a). Все сказанное в пре-~дыдущей главе по поводу применения формулы интегрирования по частям для неопределенного интеграла (см. гл. VII, § 3), относится также и к формуле (3).
Применяя формулу (3), вычислить следующие интегралы:
282
3
1391. arctg xdx. о
Решение. Положим arctgx = u, xdx — dv, тогда
, dx	х2
d« = Т-;---5 , v = х.
1 X2 ’	2
Подставляя полученные значения в формулу (3), получаем
3	з	3
С t j №	, I3 1 f х2 dx 9 х о 1 С <,	1	\ j
\ х arctg xdx = 2-arctg х |о - у р-ру = у arctg 3 —у 3 i1
о	о	о
9	1	I3	3
= arctg 3 - у (х- arctg х) =5 arctg 3 - у. Z	X	|U	£
1392. ^(1 + In х)2 dx. I
Решение. Полагаем u = (l+lnx)2, dv~dx, откуда
dx
du = 2 (1 + In x)	, v — xt
v а поэтому
4'	e	e
J = J (1 In x)2 dx — x (1 + In x)2 'j — 2 j (1 4"In x) dx.
г К последнему интегралу применим еще раз формулу (3), положив и= 1 4-1пх .	,	, dx dv = dx и du= v — x; X ’
Г	е ~
J = x(14-lnx)2 * — 2 х (14-1п х)| dx = 2е—1.
1	х
1393. \хе~х dx.	2
о	1397. \ arcsin xdx.
б
я	л
3	.	1398. ( Xs sin xdx.
1394.	$
J sin* X
JT
J
2	Л
1395. (xInxdx.	;
i	1399. 5 e2xcosxdx.
0
3 e.
1396. \ Inxdx.	1400. (sin(lnx)dx.
Указание. В двух последних задачах двукратное интегрирование по частям приводит к уравнению относительно искомого интеграла (см. гл. VII, § 3, п. 3).
3. Использование рекуррентных формул. Иногда для вычисления определенных интегралов используются рекуррентные формулы. На примере 1401 и 1402 Покажем, как это делается.
283
1401. Составить рекуррентные формулы для интегралов
Л	л
2'	~2
§ sin«x dx и jj cosnx dx
и	o'
(n 2s 0 — целое).
Решение. Заметим прежде всего, что оба эти интеграла равны. В самом деле, заменяя во втором интеграле cosxna sin — х\ и производя замену переменной ~ — x — получим
л	л	л
2*	'2	О	Т
С	с	/ л	\	с	с
Jп = \ cosnxdx = \ sin" i ~х \ dx=— \ sin"/ dt = \ sin"xdx.
J	J	\	7	J	J
оо	Ли
'2
л ~2
Теперь вычислим \ sin"xdx при	Применим формулу интегрирования по
oJ
частям, принимая и~ sin""1^, dv — sinxdx. Тогда du = (ti— 1) sin"’“2x cos x dx, и — = — cosx, и
Л	Л	Л
2	2	~2
) sin'!x dx = — sin',~1x • cos +(«—!) ) sin'! 2x c<<s2x с/х — b	о	о
л	л	и
= (rt—1) Jj sin,r’2x  (1 — sin2x) dx = (n — 1) ) sin"—xrfx —(n — 1) ) sirv’xdx, o'	II	i)
или d fl = (ft	1) dд„2	1) dn.
Решая это уравнение относительно Jп, получаем г п— 1 , dfl — ~ dn__2-	(4)
Рассмотрим два случая:
1) п=2т— четное число. Применение формулы (4) т раз дает:
г 2т— 1 ,	2т— 1 2т — 3 r 2m—1 2m —3 2т — 5
im 2^7 2m~2 2Гп 2^2' 2т~4 2ТГ“ ’ 2м^2 ’ 2^7-3	=
____	__ 2т — 1	‘2т — 3	2т — 5	3	1 2т	‘2т — 2	2m — 4	"' 4	2	°’
но
Л	л
~2	"2	Л
Jo = j sin°x dx = j dx = V • о	о
Поэтому
__ (2m—1) (2m —3) (2m —5)... 1 л
J2m ~	2m(2m-2) (2m-4) ...2	’ 2 ’
284
2) п = 2тф- 1 —нечетное число. Опять применив формулу (4) т раз, получим
2т	__ 2т 2т — 2 .	_
~ 2^+Т -mL “ Ст“М' ’ 2т — 1 ”!' 3-
_ 2ш	2т -2 2т — 4	2 ,
— 2ш+1	2т—1	2т—3'” 3 ь
или, учитывая, что л
Jt = \ sin xdx. = 1, о
2т (2т—2) (2m — 4)... 2	, .
-m+1~ (2т+1)(2т-1)(2т-3)...3’	к ’
Объединяя формулы (.5) и (6), имеем
л	л
ЗГ	2
( sin'!xrfx=^' cos"x</x=
i)	о
(rt— 1) (л— 3) (n — 5)... 1
п (n-2) («-4)... 2
(n-l)(n—3)(n-5)...2
n (n — 2) (n — 4) ... 3
• '2 ПРИ четном n, при нечетном n.
(7)
1402. Используя формулу (7) предыдущей задачи, вычислить интегралы; л	л
а) sin3xdx't б) J coslvd.r;
6	о
л	л
в) \ sin5x dx; г) cos6x dx. о	(I
Решение. Применяя формулу, указанную в условии задачи, получаем:
а)	п = 3 (нечетное!), 23 =	;
б)	!П = 4 (четное!), Л =	~ л;
4-2	8
В) П = 5, A-gTg-- 15 ;
ч й г 5 •3 • 1 л - 5
г) и —6, Л— 6.4.2 • 2	32
1403.	Составить рекуррентную формулу для интеграла
Л
Jn = cos'1 xdx.
о
1404.	Используя результат предыдущей задачи, вычислить интегралы;
Л	л
а) cos8x dx; б) cosnx dx.
о	и
285
1405.	Вывести рекуррентную формулу для интеграла
2л
Jn — \ sinn% dx и
И вычислить
2л	2л
J sin10x dx и J sin’xrfx. о	и
1406.	С помощью рекуррентной формулы, полученной в 1236, вычислить
1 f dx ' (1+Х2)*-
U
§ 3. ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
ь
1. Способ прямоугольников. Для вычисления интеграла j f (x) dx делим отре-а
зок [а, />] на п равных частей точками
х0 = а < лу < х>, < ... <хп = b и обозначаем через
!/о, Vi, Уз, > Уп-1, Уп
соответствующие значения функции у —
Полагаем приближенно
xk
j f (х) dx =» yk^xk (fe=l, 2, n)	(1)
xk-i
где
.	b—a	b —а
—x*_i = —— , xk = a + k ——
Это означает, что площадь каждой полоски, на которые разбивается криволинейная трапеция аАВЬ, заменяется площадью прямоугольника с высотой и с основанием ДхА (рис. 144).
286
зЖ^Сложив приближенные равенства (1) для fe=l, 2, п, получим формулу ^Жймоугольников
£	b	п
./= ^(x)dx^S„ =	№_1ДхА = Цр(т/0 + т/1 + ... + 1/л_1).	(2)
п	Л=1
Если /' (.г) существует и ограничена на отрезке [а, й>], то для погрешности 6п формулы (2) справедлива оценка
|б„’ = |7-5п|=е^Ц^,	(3)
где Mi — максимум модуля /'(х) на отрезке [а, 0]
,; 1407. Применяя формулу прямоугольников (при п— 10), вычис-
2
лить приближенно \ Расчет вести с тремя знаками после ’1
запятой. Оценить допускаемую погрешность.
X? Решение. Разбиваем отрезок [1, 2] на 10 равных частей точками х0=1, — 1,1, х. —— 1, 2, ...,	2*.
Таблица 9
	хк	1	1,1	1,2	1,3	1,4
	Ун	1,000	0,909	0,833	0,769	0,714
Xk	1,5	1,6	1,7	1,8	1,9	2
Ун	0,667	0,625	0,588	0,556	0,526	0,5
Находим
9
значения функции у — ~ в этих точках. Получаем У yk — 7,\&7. По формуле
/г~0
(2) найдем
2
2—1
-7,187 =» 0,719.
Оценим допущенную при этом погрешность по формуле (3). Так как f' (х) =
—) =—L то । f (х) | =-— монотонно убывает на отрезке [1, 2], поэтому X j	X	Х“
max |/'(х)| =/'(!) = ! и|б1о|=х4т = 0’05-
Поскольку допускаемая погрешность сказывается уже на втором знаке после запятой, третий знак надо округлить, п окончательно
Т = 0,72 i 0,05.
1
287
С другой стороны, по формуле Ньютона — Лейбница,
= In х =1п 2 —In 1 =1п2, i	1
Следовательно, получено приближенное значение. 1п 2:
1п 2 = 0,72 ± 0,05.
Более точно, 1п 2 = 0,6931; так что на самом деле допущена погрешность 0,03 — несколько меньшая, чем вычисленная по формуле (3).'
1408. Применяя формулу прямоугольников (/г =12), приближенно вычислить х sin х dx. Найти этот интеграл по формуле Ньютона о
— Лейбница и сравнить результаты.
2. Способ трапеций. Как и в способе прямоугольников, делим отрезок [о, 5] на п равных частей. Полагаем приближенно
f^dx^^-^'!\xk.	(4)
х k~i
Это означает, что площадь каждой плоскости, на которые разбивается криволинейная трапеция аАВЬ, заменяется площадью обычной прямолинейной трапеции
(рис. 145). Складывая приближенные равенства (4) для й=1, 2, .... п, получаем формулу трапеций
ь	it
J=^f(x)dx^ Sn= Vk-i+Vk	= A g.	+	+	+
a	k—l
+ ... + 2z/„__i + j/„).	(5)
Если f" (x) существует и ограничена на отрезке [а, 5], то погрешность 6„ формулы (5) оценивается неравенством
где М2 — максимум модуля f" (х) на отрезке [а, 5].
288
1409.	Вычислить интеграл^ — по формуле трапеций при п = 10.
1
Расчет вести с четырьмя знаками после запятой. Оценить допускаемую погрешность. Сравнить степень точности расчета данной и предыдущей задач.
Решение. Разбиваем отрезок [1, 2] на 10 равных частей и вычисляем . 1
значения функции // =— в соответствующих точках деления:
Таблица 10
*k	1,0	1,1	1,2	1,3	1,4	1,5
Ун	1,0000	0,9091	0,8333	0,7692	0,7143	0,6667
xk	1,6	1,7	1,8	1,9	2
Uk	0,6250	0,5882	0,5556	0,5263	0,5900
В соответствии с формулой (5) подсчитываем:
9
2 ^//*= 12,3754, //,,+ {/]0= 1,5000
А'=1
и окончательно получаем
2—1
(12,3754+1,5000) == 0,6938.
2
Оцепим допущенную погрешность по формуле (6). Функция = —-монотонно убывает на отрезке [1, 2], поэтому
Л-12= max I f" (x) = f (1) = 2.
В силу формулы (6) имеем
ifi |^2(2-1)3 ..
1 10i"- 12-Ю2	600
Таким образом, по формуле трапеций \ ~-- = 1п 2 = 0,694 а 0,002.
i
Сравнение оценок допускаемой погрешности в данной и предыдущей задачах показывает, что расчет по формуле трапеций дает большую степень точности по сравнению с расчетом по формуле прямоугольников (при одном и том же значении п= 10).
10
1410.	Вычислить lg10xdx по формуле трапеций (полагая п= 10).
1
10 Кручкович и др.
289
1411.	С помощью формулы трапеций вычислить
1 С dx ' 1 +х о
при п 8 и оценить допускаемую погрешность.
3. Способ парабол. Разбиваем отрезок [a, Z>] иа 2л равных частей точками х0 = а <	< х2 < ... < хм _2 < х.,п_л < л-2и = b
и обозначаем через
Уо. Уч-  - У-т-л, Ут
соответствующие значения функции \ у ==[ (х). Рассматриваем двойной частичный отрезок |лу/,,_2, лм/J и проводим дугу параболы через точки
(Тщ.г. Уч/тч), ('•'2^1, №*.1), (х2к, у-т) (рис. 146).
Заменяем площадь каждой криволинейной полоски ,42/,._2, х21-г	x2i,, Л2* площадью
соотвегс: вующей параболической полоски (полоски, ограниченной сверху дугой
параболы). Тогда для приближенного вычисления площади всей криволинейной трапеции аАВЬ получаем формулу
Ь	п
J = J	$2п ~ ~6/7"	(Учк-чА-^Учк-1А-Учк) —
а	/г = 1
= ~~&п~ f(Ут + № + № + ••• + Ут -1) +
+ 2 (t/2 + f/4 + f/e + --- + f/2n-2)]>	(7)
это так называемая параболическая формула, или формула Симпсона.
Если fl4) (х) = у141 существует и ограничена на отрезке [a, &J, то для погрешности формулы (7) справедлива следующая оценка:
|6„| = 17-52»Ы 180(2/1)^ ’	(8)
где М4~максимум модуля /,4' (х) на отрезке [а, &]. *
* Если г/'1' отыскать затруднительно, то вычисляют интеграл при каком-то значении п и потом при удвоенном значении п. Если при этом, скажем, три знака после запятой совпадают, то погрешность не превышает 0,001.
290
1412. Вычислить f е х- dx с точностью до 0,0001 по формуле Симп-
0
сона.
Решение. По условию задачи, допускаемая погрешность не должна превосходить 0,0001, поэтому число делений 2п в формуле (7) найдем, учитывая оценку (8), из неравенства
<9>
Вычислим max ! ft4) (х) | для f (х) =е~*2: 0 < Л' 1
f(4) (х) = 4(4х4-12х2 + 3)с~Л
легко видеть, что эта функция монотонно убывает на отрезке [0, 1]. В самом деле е”х“ монотонно убывает на отрезке [0, 1], (4х‘ — 12х‘--|-3)' — Юх3 —24л: = = 8х (2.V2 — 3) < 0 при 0 < х sg 1, а значит, функция t/ = 4.r4 —12х3 + 3 монотонно убывает на отрезке [0, 1]. Следовательно, тем же свойством обладает и j 11 (л), так как она отличается па константу от произведения двух монотонно убывающих функций. Па концах отрезка [0, 1]
| Г4'(0)1 = 12, Ии,(1)1 = |-2°| <12-Значит,
Л14= max [ f<4'(х) I =/'*’(0) = 12.
Подставляя значения & —а=1 и АД в неравенство (9). получаем неравенство
12	ПООО1	125
180W^°’° ’ °ТКУДа
Последнее неравенство выполняется для всех п >• 3. Берем для расчета л=5. Делим отрезок [0, I] на 10 равных частей точками хс —0, .v4- 0,1, х3 = 0,2, х8 = 0,3, ..., х31) --1 и вычисляем соответствующие значения функции f (.v) = с”х". При этом, чтобы обе.спсчять требуемую условием точность (0,0001), вычисления производим с пятью знаками после запятой, округляя окончательный результат до четырех знаков
Таблица 11
‘	Х1		'+= f (*,)	i	А'-	д=+ (х;)
0	0	1,00000	6	0,6	0,69768
1 "	0,1	0,99005	7	0,7	0,61263
2	0,2	0,96079	8	0,8	0,52729
3	0,3	0,91393	9	0,9	0,44486
4	0,4	0,85214	10	1,0	0,36788
5	0,5	0,77680			
Теперь имеем:
(/о + ^1о= 1,36788,
4 {у t + Уз + № + У1 + №) = 4 • 3,74027 = 14,96108,
2 С'/2+ '/1+.% /'.%) = 2 • 3,03790 = 6,07580.
Подставляя полученные значения в формулу (7), получаем
С	1,36788-1-6,07580 + 14,96108 n	п _„Q
\ е х dx^—..............-=—=—1 ----------= 0,/4682 =2=0,7468.
0
10*
291
1
1413.	Зная, что	= вычислить приближенно число л:
О
а) по формуле трапеций при п =10; б) по формуле Симпсона при п = 2. Вычисления вести с четырьмя знаками после запятой. Результаты вычислений сравнить между собой и с табличным значением числа л.
1414.	Вычислить по формуле Симпсона (2п=10)
л т sin (х2) dx.
6
1415.	Вычислить с точностью до 0,001 но формуле Симпсона
5
С dx ' In’x • 2
§ 4. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
1. Интегралы с бесконечными пределами. Если функция f (х) интегрируема на любом отрезке [а, Ь], где а < b <со, то полагают
со	b
\ f(x)dx-~ lim \ f (х) dx.	(1)
ii	Ь-и-о ц
СО
Интеграл ( f (х) dx называется сходящимся, если существует предел в правой части а
равенства (1), и называется расходящимся, если указанный предел не существует. Аналогично, если f (х) интегрируема на любом отрезке [а, й), где — со <. а < Ь, то полагают
&	b
\ /(v)iZ.v= Inn ' f (х) dx,	(2)
— 'j	— -а
Наконец, если f (х) интегрируема на любом отрезке [а, числовой оси, то
СО	Ь
\ f(x)dx = lim \f(x)dx.	(3)
-и	Ь-^ + со^
а —> — зо
Признаки сходимости
00
Интеграл f (х) dx (<т>0): а) сходится, если а м
и »г>1,	(4)
б) расходится, если
(5)
(здесь М и т — постоянные).
Исходя из определения несобственных интегралов с бесконечными пределами, вычислить интегралы (или установить их расходимость);
292
Решение. В силу определения (1) имеем ь
С dx /	1 Iй
lim \ -. = lim-------
л.'2 b^co\	х) 11
dx xz
lim !
b —* co \
b
Следовательно, интеграл сходится.
Решение. По формуле (2) имеем о	о
( ,	„= lim \ -утЦ = Hui (arctg 0 — arctg а) — .
1+-V-	1+%2 а—оо	2
— со	а
со
1418.	(«>1)-
3 X In X '	'
а со	Ь
„	С dx	,.	С d In х	/, г ,	, i s
Решение.	\	—:— --=	lim	\ -=---= lim (In In b — In In a) = co,
\ x In x co J In b co (1	d.
Следовательно, интеграл расходится.
1419. °$ e~x dx. 1421.
0	2	’	*
co	co
1422. j
1	—co
cc
1423. Доказать, что интеграл ( ~ (a>0) сходится при m>l и расходится при tn^l.
Используя признаки (4) и (5) сходимости несобственных интегралов, установить, сходятся или расходятся следующие интегралы:
. . п . COS X , 1424. \ —5- dx J х3 1
Решение. Так как | cos х | г' 1, то j	| sg , т. е. подынтегральная функ-
ция удовлетворяет неравенству (4) при т — 3 > 1 и М = 1. Следовательно, интеграл сходится.
1425. l^dx сух
Решение. Так как In х I при х е, то
In х 1 .
293
значит, подынтегральная функция удовлетворяет неравенству (5) при г>1=^ и М—1. Следовательно, интеграл расходится.
1
р	1
3 + arcsin —
1426.	----------^-dx.
Решение. При х 2 имеем
откуда
А _	1	,1Л
О < arcsin - - «£ arcsin -- —	< I,
х	2	6
О ,	.1
3 + arcsin — _______х	4 l-l-x^x <xi'
Следовательно, выполняется неравенство (4)
3 при /г; = -g > 1,
Л4 = 4 и
интеграл сходится.
. . _ _ I* 2 4- sin х , 1427.	dx.
Л
1430.
1 2 + arcsin --
J l + Kx
1
dx.
1428.
1429.
С dx э ’ х dx 1 /^+1'
Указание, arcsin - >0 и 1 + l'x < 2 J'zx при x - :c 1.
i‘ dx
J I' X In x+ 1 '
Указание. Использовать то, что логарифм растет медленнее любой положительной степени х.
2. Интегралы от неограниченных функций. Если функция f (х) непрерывна при а<„х- Ь и имеет бесконечный разрыв в точке х = а, т. е. lim/'(х) = со, х-*а
то полагают
Ь	Ь
j f (х) dx = 1 im	f (х) dx (е > 0).	(6)
а	Е 0 а + &
Ь
Интеграл \i(x)dx называется сходящимся, если существует предел в правой а
части равенства (6), и расходящимся, если указанный предел не существует. Аналогично определяется интеграл от функции, имеющей бесконечный разрыв в правом конце отрезка [а, (?]:
Ь	Ь — е,
\f(x)dx — lim ( f(x)dx (е>0).	(7)
а	Е-° а
Если функция f (х) непрерывна при а-ц£х<с и с<х-с& и имеет бесконечный разрыв в точке х = с, то полагают
Ь	с ~Е	ь
( / (х) dx = lim f f(x)dx4-lim f f(x)dx	(e>0).	(8)
a	E-o I	£-.o ДЕ
294
Vf:
 > .	b
Интеграл (/(л-)Лл- называется сходящимся, если оба предела в правой части' а
равенства (8) существуют, и расходящимся, если хотя бы один из указанных , пределов не существует.
На практике для решения вопроса о сходимости несобственных интегралов ..-от неограниченных функций часто используются следующие признаки сходимости:
Если функция f (х) имеет бесконечный разрыв в одном из концов интервала ь
. интегрирования (а, 6), например в точкех -- а, то несобственный интеграл f(x)dx: а
а) сходится, если
| I м
р Wp 11 т< 1'	(9)
. 6) расходится, если
Уд.	1	(10)
(здесь т и М — постоянные).
Если же f (х) имеет разрыв во внутренней точке х = с интервала (а, Ь), то • интеграл разбивают па два; от а до с и от с до Ь — и применяют указанные р признаки к каждому из полученных интегралов.
< Исходя из определения несобственных интегралов от неограничен-X. ных функций, вычислить следующие интегралы (или установить X их расходимость):
1	1432. f
J Vx
Ф;	°
X Решение. Функция непрерывна при 0 < х-<1 и имеет бесконечный Лф'	Vx
X разрыв в точке х = 0, поэтому в силу равенства (6) имеем
Й.	1	1
f-^ = lim f 4^ = lim 2 Гт I'-Пт (2-2 Ге )=2.
J V x s-»0j V x e-’O |e e-<-0
X	о	e
Значит интеграл сходится н равен 2.
1433.
J J/1-X2 о
Решение. Функция *----------------- непрерывна при 0 х < I и имеет бесконеч-
V 1 — -т2
ный разрыв в точке х=1, поэтому в силу равенства (7) имеем
1	1—е
(*	г/ у	Р dx	/	I — £ \
\ —-------= lim \	' — = lim arcsin х ] =
,) jX 1 — X2 8 -> О J pl — X2 8 -► 0 \	0	/
О	о
= lim [arcsin (1—е) — arcsin 0]= lim arcsin (1 — e) =.
0	8—>0	L
Интеграл сходится и равен у.
295
л	3
4	14ЧС
1434. ctgxdx.	' ' ' (.v — 1 '
о	0
1	(•	н
(‘ x dx	1437. V ----—----
1435. 1	}x2-7x+)i)-
J и 1 —	з
0,5 b
1438. Доказать, что интеграл , dX-^ (m>0) сходится при J и a) a
m<I и расходится при mpsl.
Используя признаки (9) и (10) сходимости несобственных интегралов от неограниченных функций, установить, сходятся или расходятся следующие интегралы:
1439.
2 + cos х Д-1)2
dx.
Решение.
Функция
2 -р cos х
имеет
бесконечный
разрыв в
точке х — 1,
2-pcosx>l при любом значении х, поэтому
2	-р cos х 	1
Д-1)2 ^’д^Гг
В силу признака (10) при Л!—1 и т = 2 интеграл расходится.
6
f ДН~2) dx
' /Д2~р2х—15)2’
3
х *4~ 2	х + 2
Решение. Подынтегральная функция	- — = —--------
< (х22л: — 15)2 у (х- 3)3Д + 5)2 терпит разрыв в точке х = 3. При 3 йт х йй 6 х-\-2 гй 8, х-р5 Эг 8 и, следовательно,
х+2	2
|/Д^З)2Д + 5)3 Д - 3)2/3 ’
т. е. удовлетворяется неравенство (9) при т=--<1 и Л4 = 2. Значит, интеграл сходится.
л	3
1441.	1443. L-гЧЙ+з-
0	2
1442. J Д — е)3	1 А А А С sin X , 1444. \ ~--.^..-:--dx J К1-Х2
е	0,5
296
§ 5.	ПЛОЩАДИ ПЛОСКИХ ФИГУР
1.	Вычисление площади в прямоугольных координатах. Если непрерывная кривая задана уравнением
«/=/(*)(/(*) 5=0,
то площадь криволинейной трапеции, ограниченной этой-кривой, двумя вертикалями в точках х = а и х — Ь и отрезком оси абсцисс (рис. 147), вычисляется по формуле
Рис. 148
Если площадь S ограничена двумя непрерывными кривыми
U=fi(x) и y=f*(x)
и двумя вертикалями х = а и х = Ь, где 0 (х) f2 (х) при a-xxxxxb (рис. 148), то
ь
(2)
а
В случае параметрического задания кривой
x=4>(t), У = №}>
площадь криволинейной трапеции, ограниченной этой кривой, двумя вертикалями х=а и х = Ь и отрезком оси абсцисс as^x^b, выражается интегралом
/3
S = j ф (0 ср' (0 dt,	(3)
где tx и t2 определяются из уравнений а=ф(У и"& = ф(0) (ф(0 2зО на отрезке 10. 0]).
1445. Вычислить площадь, мыми х = — 1 и х = 2 и осью
ограниченную параболой у = х2, абсцисс (рис. 149).
пря-
Решенис. Искомая площадь вычисляется по формуле (1):
С	X3 |2
S — \ х2 dx= =3.
J	3 |-i
— I
297
1446.	Вычислить площадь сегмента, отсекаемого прямой у = — х от параболы z/ = 2x — х2.
Решение. Методом выделения полных квадратов приведем уравнение параболы к виду
//-1=-(х-1)2;
отсюда видно, что парабола симметрична относительно прямой х = 1, ветвями направлена вниз и вершина ее лежит в точке (1, 1) (рис. 150). Совместным решением уравнений параболы у — 2х— х2 и прямой // =— х определяем абсциссы точек А и В-. хА = 0, хй = 3.
Теперь по формуле (2) вычисляем искомую площадь сегмента при fi(x) =— х,
)2(х)=-2х— х2, а = 0, Ь = 3:
з
S=^ [(2х — х2) — (— x)J dx — о
1447.	Найти - площадь фигуры, ограниченной первой аркой циклоиды x = a(t — sinQ, у = а (1 — cost) и отрезком оси абсцисс (рис. 151).
Решение. Точкам О и А соответствуют значения параметра /о = 0 и (А = 2л, поэтому по формуле (3) искомая площадь
2л	2П
S = j а (1 —cos /) [a (t — sin <)]' dt = j a2 (1 —cos t)2 dt — о	о
2n Ct	1 -1-COS 4 i\	/ 3	1	|2л
= a2\ (1 —2cos?-|-—й—— dt^--d1nt—2sin/ + -r sin 2t i — Зла2.
J \	2	]	\2	'4	/ |o
0
1448.	Вычислить площадь, ограниченную одной полуволной синусоиды у= sin х и осью Ох.
1449.	Найти площадь, ограниченную параболой у = 4х — х2 и осью Ох.
1450.	Найти площадь, ограниченную кривыми у = ех, у = е~х и прямой х= 1.
1451.	Вычислить площадь, заключенную между линиями z/=Inx и у = \п2х.
1452.	Найти площадь, ограниченную параболами у2 = 2рх и х2 — 2ру.
298
дЖу 1453. Найти площадь каждой из фигур, ограниченных окруж-^иостыо х2 +//2 6х -2(/ф-8 = 0 и параболой z/ = x2 + 6x-|- 10.
1454. Найти площадь эллипса, используя его параметрические уравнения x = acos/, y-bsint.
,	1455. Вычислить площадь фигуры
-(рис. 152), ограниченной астроидой X = «cos3£, z/ = asin3^.
Указание. Применяя формулу (3) для вычисления четверти искомой площади, лежащей в первом квадранте, нужно обра-, л ,	_
тить внимание на то, что t1= -%, а г2=ч-
5	1456. Вычислить площадь, огра-
ниченную одной ветвью трохоиды '^X = at — &sin/, у = а~ b cos t (0 < <Zb<Za), вертикальными прямыми, у проходящими через две соседние низшие точки трохоиды, и осью ~^Ох (рис. 153).
2. Вычисление площади в полярных координатах. Если кривая задана уравнением в полярных координатах р = р(<р), то площадь сектора АОВ (рис. 154), ограниченного дугой кривой и двумя полярными радиусами ОА и ОВ, соответствующими значениям угла фх=а и <р2 = р (а < Р), выразится интегралом
s=4 § tp (ф)12 d<p-
(4)
Рис. 154
1457.
внутри — a2cos
₽
а
Найти площадь, заключенную лемнискаты Бернулли р2 = 2<р (рис. 155).
299
Решение. В силу симметрии достаточно вычислить одну четверть искомой площади, а затем учетверить результат. По формуле (4) имеем
1458.	Найти площадь одного лепестка кривой p = 4sin2q> (рис. 156).
Решение. Заметим, что если полярный угол ср изменяется от ф = 0 до ф=л, то точка на кривой обходит против часовой стрелки один лепесток; поэтому по формуле (4) для искомой площади имеем
пл	л
S=-g-	16 sin4 ф </<р = 8	j dtp=2	(1 —2 cos 2q>-)-cos2 2q>) dq> =
о	о	о
пл.	л
о /	 о , I , о С 1 +cos 4® о f , sin 4ф \ I „
= 2 (ф —sin 2ф) +2 \ ——g—— б/ф = 2л-{- ( ф-|-4") = 3л-
оо	о
1459.	Вычислить площадь, ограниченную кардиоидой р = а(1 + coscp).
1460.	Найти площадь, ограниченную улиткой Паскаля р = 2 -f-+ cos ср.
1461.	Показать для архимедовой спирали р = шр, что площадь, описываемая радиусом-вектором при его первом обороте, составляет 1/3 площади круга с радиусом, равным значению радиуса-вектора в конце первого оборота (см. рис. 40). Найти площадь, содержащуюся между первым и вторым витками спирали.
1462.	Найти площадь, ограниченную трехлепестковой розой р = a cos Зср.
300
§ 6. ДРУГИЕ ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ
1. Длина дуги. Если кривая задана параметрическими уравнениями х' = х(/), y=ytf), то длина ее дуги вычисляется по формуле
С -г Г! dx\* t dy'f	...
МУ Ы+рл dt’	(I)
t,
где ft и t2 (^ </2)~значения параметра, соответствующие концам дуги.
Если кривая задана уравнением вида
«/=/(*) или x=g(y),
то, принимая за параметр соответственно х или у, вместо формулы (1) получаем
а
где а и b (а <&) — абсциссы начала и конца дуги, или
s=y l+u> ®
где end (с < d) — ординаты начала и конца дуги. Если, наконец, кривая задана уравнением в полярных координатах
Р=Р(<Р).
то, принимая за параметр угол tp и учитывая, что х=р (tp) cos <р, z/ = p (гр) sin <р, после подстановки в (1) получаем
Р _____________
s= УУ2+Г^ 2Л>	(4)
а
где а и 0 (а < 0)—значения полярного угла, соответствующие концам дуги. 1463. Вычислить длину астроиды x = acos3(, у — a sin3/. Решение. Кривая симметрична относительно обеих координатных осей (см. рис. 152), поэтому вычислим сначала длину ее четвертой части, расположенной в первом квадранте:
dx о q , . , dy —	. „ ,	,
— —За cos2 t sm t, -= За sin21 cos t. dt	dt
Tl
Параметр t изменяется от t — 0 до t = — _ Следовательно, по формуле (1) имеем
л ~2
У s — \ ]/9a2 cos4 t sin2 t + 9a2 sin4 t cos2 t dt = о л	rt_
2	  2
— 3a Vcos2 t sin2 i dt = 3a \ sin t cos t dt =
6	b
sin2 /12	3
= 3a——	= -x- a; s — ba.
2 о 2
301
1464. Вычислить длину дуги полукубической параболы у — (х:! от начала координат до точки В (4, 8).
Решение. Находим и, подставляя в формулу (2), получаем
l +	=	\ 1/ l + |xrfil+-jxj =
6	о
4 2	, 9	\3 р 8
- 9 з [1 + 4	|0 - 27 (10/10- 1).
1465. Найти длину дуги кривой х = г/2 — у In у от у — 1 до у = е.
Решение. Уравнение кривой разрешено относительно х, поэтому для вычисления длины дуги воспользуемся формулой (3):
dx у2 — 1	; dx 2	у'- J-1
dy 2уГ ’ | h \dy] ~ ~~2у~ ’
С у2+1	.	1	С /	, 1 \	,	1 /у2
s— \	--dy = -й- \ i у -- - - -1 dy—.- у-
,1 2у	3	2	\ У,	2 у 2
е2 + 1
4
1466. Найти длину дуги гиперболической спирали ptp = 1 от точки А (2, 1/2) до точки В (1/2, 2) (рис. 157).
Решение. Разрешаем уравнение спирали относительно р: р = = - . Приу—> со радиус-вектор спирали неограниченно уменьшается и витки спирали неограниченно приближа-ютсяк полюсу. Нас интересует длина дуги АВ спирали, соответствующая значениям полярного угла от ц> = = -2- до <р = 2. Из уравнения спи-
находится по формуле (4):
2
1 , - dw.
Ф
Сделаем замену переменной, положив
тогда
____г dz
(?2-l)Tl^T
Новые пределы интегрирования:
гЦ=|/г'
302
2
_ Г5 + ' ln 5±1^ _ 1 +1„ '
2	2	3-J/5	2	2
1467.	Найти длину одной арки циклоиды (см. рис. 151).
х — a (t — sin t), у = а{\ — cos t).
•Л'"”-
1468.	Найти длину дуги развертки окружности (рис. 158) х = = a (cos t-\-/sinZ), z/ = o(sin/ —ZcosZ) от /х = 0 до t2 = T.
1469.	Найти длину дуги кривой у = In х от х ==|/3 до х = ]/ 8.
1470.	Вычислить длину дуги кривой
X — In cos у, находящуюся между у = 0 и Л
У = -з-
1471.	Найти длину первых двух витков спирали Архимеда р = а<р (см. рис. 40).
1472.	Вычислить длину дуги логарифмической спирали р = аеф от ср — 0 до fP = (Po (рис- 159).
1473.	Найти всю длину кардиоиды р = а (1 4-cos ф).
а ! Х -Х'\
1474.	Найти длину дуги цепной линии у — “	концы
которой имеют абсциссы x — Q и х = а (рис. 160).
Указание. Уравнение , x сать в виде z/ = ach
— sh При интегрировании
формулу cha a — sha a = 1.
линии заии-du
тогда -j- = dx
использовать
1475. Вычислить длину дуги линии х — (t2 — 2) sin i -j- 2t cos t, у — — (2 — Г-) cos t -\-2t sin l от /х = 0 до t-, = л.
кривой у —f(x), x—b (рис. 161),
2. Объем тела вращения. Объем тела, образованного вращением вокруг оси Ох криволинейной трапеции, ограниченной отрезком оси абсцисс аух-хЬ и двумя вертикалями х — а и вычисляется по формуле
b	ь
л ) у- dx = л j /2 (х) dx.
а	а
(5)
Объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной кривой х = ф(г/), отрезком оси ординат cxyy.^.d и двумя параллелями у —с и y = d, вычисляется по формуле
d	d
Vy — л ( № dy = re <ра (у) dy. (6) с	с
1476.	Найти объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной параболой у = х2, осью Оу и прямой у=1.
Решение. По формуле (6), учитывая, что с = 0, d — 1, х2 dy — y dy, имеем
1
С j У2 I1 л
\ у dy	1 = у.
b
1477.	Найти объем тела, образованного вращением вокруг оси Ох одной арки циклоиды х = а (t — sin t), у — a(l— cos/) (см. рис. 151).
Решение. Подставляем в формулу (5) значения
y‘' — d2 (1 —cos /)2 и dx = a (1 —cos t) dt
и переходим к новым пределам интегрирования (по t). Первой арке циклоиды соответствует изменение параметра t от 1^ = 0 до —2л, поэтому для искомого
304
объема получаем
2л	2л
у	Ул- — л (' а3 (1 — cos ff dt = ла3 ( (1 — 3 cos t + 3 cos2t — cos31) dt —
b	0
/5	3	1	' \ |2л
= ла31	t — 4 sin t + -г- sin It + — sin3 t)	= 5л2а3.
\ 2	4	3	) |o
1478.	Вычислить объем тела, образованного вращением вокруг оси Ох одной полуволны синусоиды у— sinx (0 х	л).
1479.	Определить объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной линиями — = 1, У = Ь, у =—Ь.
1480.	Кубическая парабола у = х3 вращается вокруг оси ординат. Вычислить объем тела, ограниченного получаемой поверхностью вращения и двумя плоскостями, перпендикулярными к оси ординат и отстоящими от начала на расстояниях, равных восьми единицам.
1481.	Найти объем тела, образованного вращением вокруг оси Оу астроиды x = acos3£, у = а sin3£ (см. рис. 152).
3.	Площадь поверхности вращения. Если кривая задана параметрическими уравнениями
x=x(t), y = y(f) [y(t) SsOJ, то площадь поверхности, образованной вращением вокруг оси Ох дуги этой кривой, вычисляется по формуле
5 = 2л	+	К)
1	f \LO' 1	\ Lu £ /
tl
где ti и t.,	< A2) —значения параметра t, соответствующие концам дуги.
Если кривая задана уравнением вида
У = Ш,
то, принимая за параметр х, вместо формулы (7) получим
6	________
8 = 2л^(х)у l+g^2dx,	(8)
а
где а и Ь (а < !>) — абсциссы начала и конца дуги.
1482. Вычислить площадь шарового пояса, получаемого при вращении вокруг оси Ох дуги окружности х2 + у2=4 (z/>0) между точками с абсциссами х =—1 и х=1.
Решение. Составим подынтегральное выражение в соответствии с формулой (8) при у (х) — |/4 — х-:
d'J -- —= , У Cv) 1/ 1 +' f f - 2,
dx 1 4 - х- ' \dxj
и получим	।
S = 2л j 2 dx = 8л.
305
1483. Найти площадь поверхности, образованной вращением вокруг оси абсцисс астроиды x = acos3/, y = asin3/ (см. рис. 152).
Решение. Составляем подынтегральное выражение в соответствии с формулой (7):
dx „	„ , . , dy „ . „ ,	,
--- = — За cos3 t sin t, ,, = За sin3 t cos I;
dt	dt
(dx'.z idyV
Ы +U; =
a sin3 t \9а3 (cos4 t sin3 t + sin4 t cos3 t) — За3 sin4 t cos t.
Изменению параметра t от / = 0 до / = соответствует движение точки по
астроиде от А до В. Дуга АВ при вращении вокруг оси абсцисс «заметает» половину искомой площади, поэтому
з*с	л;
2	2
-5- = 2л За3 sin4 t cos t dt = &Ttcfl sin1 td sin t —
о	о
л
_ , sin® 112	6	, „ 12 „
= бла3 —=— = ла3; S = - -=- ла3.
5 [о 5	5
1484. Размеры параболического зеркала АОВ указаны на рис. 162. Требуется найти поверхность этого зеркала.
1485. Найти площадь поверхности «вере-тена», которое получается в результате вращения одной полуволны синусоиды y = sinx
вокруг оси Ох.
1486.	Найти площадь поверхности, образованной вращением вокруг оси Ох эллипса x = acos/, y=bsint (a>b).
1487.	Найти площадь поверхности тела, х образуемого вращением одной арки циклоиды x = a(t — sin/), у = а(\ — cost) вокруг ее основания (см. рис. 151).
/ X х\
1488.	Дуга цепной линии У=С^еаАге а!,
рис. иг	концы которой имеют абсциссы х = 0 их = а,
вращается вокруг оси Ох (см. рис. 160). Показать, что площадь поверхности S и объем V образуемого 2
при этом тела связаны соотношением S = V.
§ 7. МЕХАНИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ
1. Общая схема применения определенного интеграла. Пусть требуется найти некоторую механическую или физическую величину Q, имеющую определенное значение на заданном отрезке [а, 6]. Предполагается, что Q является аддитивной величиной, т. е. если отрезок [а, Ь] делится па части, то величина Q складывается из суммы значений Q, соответствующих этим частям. Из условия задачи находят «элемент» dQ величины Q, отвечающий «элементарному промежутку»
306
[х, х+</х], в виде dQ-=q(x)dx. После этого, интегрируя по отрезку [а, 6], получают величину
ъ
Q = \q (х) dx.
Е 2. Путь, пройденный точкой. Пусть точка движется по прямой с переменной ^скоростью V, являющейся известной функцией времени /: o = f(Z). Требуется определить путь, пройденный точкой от момента времени О цо момента /,. Возь-Кмем элементарный промежуток времени [/, t-/-dt]. За это время точка пройдет I путь
Г	dS = vdt = f(f) dt.
|Это и ecib «элемент» пути. Интегрируя по отрезку [/1( /,], получаем величину в пути, пройденного точкой за время [/ь /2]:
|	S = j/(/)d/.
(1)
1489. Скорость движения точки дается формулой
0 = 1/1 + / м/сек.
Шайти путь, Ежения. Чему ^времени? t Решение.
пройденный точкой за первые 10 сек от начала дви-равна средняя скорость движения на этом промежутке
з
2 I10 Г
|о
2
3
Путь, пройденный точкой за 10 сек, вычисляем по формуле (1): 10 С ,-----2
о
_ S '^Р-Щ
11 Ki Г — 1
15
2,37 м/сек.
падающим в пус-известно, что ско-где I — протекшее
ж 1490. Вычислить путь, пройденный свободно ЖТоте телом за первые Т секунд движения, если Ярость свободного падения в пустоте v = v0 + gt, «Время. g — ускорение силы тяжести, п0 —начальная скорость.
Яр 1491. Точка совершает гармонические колебания по оси Ох около
. «начала координат со скоростью и = ц, cos со/. Найти положение «Точки в момент времени /2, если известно, что в момент + она .«Находилась в точке х = лт.
'ЯК.	3. Работа силы. Пусть материальная точка движется вдоль оси Ох от точки
= а до точки х = Ь (а<Ь) под действием переменной силы /'=+ (х), причем ЗивВаправление силы совпадает с направлением движения. Найти работу, произве-Яиенную силой на этом перемещении. Возьмем элементарное перемещение Жк. х+</х]. Работа силы на этом перемещении
IK	dA = F (х) dx.
Вы получили «элемент» работы. Теперь проинтегрируем по отрезку [а, /?] и полу-|Жйм искомую работу:
|Ж.	А = j F (х) dx.
(2)
307
1492.	Какую работу нужно затратить, чтобы тело массы т поднять с поверхности Земли на высоту й? Чему равна эта работа, если тело должно быть удалено на бесконечность?
Решение. Величина силы F, производящей работу при поднятии тела с поверхности земли, равна величине силы притяжения тела Землей, т. е.
где т — масса тела, М— масса Земли, г —расстояние от тела до центра Земли, k — постоянный коэффициент. Направлена сила по радиусу от центра Земли. В этом же направлении происходит и перемещение тела из положения Г]=/? (/? —радиус Земли) в положение г2 = /?-(-/г. Работу силы F (г) на пути [Р, Р + /г] вычислим с помощью интеграла (2):
R + h	R+h
. С , тМ ,	, С dr	, .. ! 1	1 \
А = \ k —5- dr = kmM \	= ktnM -= — уг-г-г .
г2	) г2	\R	R-h
R	R
Учитывая, что на поверхности Земли (при г = Р) сила притяженпя F — tng, найдем коэффициент kt
. тМ	sR~
mS=k~j^, 0ТКУДа 6 = -^-.
И для искомой работы окончательно получим
При удалении тела на бесконечность имеем
lim А = lim mgR2 — уД-у'' = mgR, h со h -> со \	А “г' Д'
ИЛИ
1	2
1493.	Два электрических заряда ех — 10~7 к и е2 = у 10"7к находятся на расстоянии 10 см друг от друга. Разделяющей их средой служит парафин. Сначала оба заряда закреплены неподвижно. Затем заряд е2 освобождается и под действием силы отталкивания удаляется от заряда ег на расстояние 1 м. Какая работа будет при этом произведена силой отталкивания?
Указание. По закону Кулона, сила взаимодействия зарядов F (х) =
1 Г.Сл / \	\
= 4лё" ' ех2 Н ’ еСЛИ С1’ величины зарядов (к), х —расстояние между зарядами (.ч), g0= 8,854 • 10~12 Ф/.и—диэлектрическая проницаемость вакуума, е—диэлектрическая проницаемость среды (для парафина е = 2).
1494.	Какую работу нужно затратить, чтобы растянуть пружину на 6 см, если сила в 10 н растягивает ее на 1 см.
У казаки е. Согласно закону Гука, сила, растягивающая пружину,
F (х) = kx, где х —удлинение пружины, a k — коэффициент пропорциональности, который легко находится из условия задачи.
308
4. Статические моменты и центр тяжести плоской фигуры. Рассмотрим криволинейную трапецию аАВЬ (рис. 163), ограниченную сверху графиком функции у — f (х), где уу=0. Предположим, что по этой трапеции равномерно распределена
масса, так что поверхностная плотность р постоянна. Требуется определить статические моменты Мх и Mt/ трапеции относительно осей координат й центр тяжести. Возьмем элементарный отрезок [х, x-f-dxl оси Ох. В криволинейной трапеции выделится элементарная полоска, которую приближенно можно считать прямоугольником (на рис. 163 прямоугольник заштрихован). Масса полоски dm равна произведению плотности р на площадь полоски у dx, т. е.
dm — ру dx.
Считаем, что эта масса сосредоточена в центре полоски, т. е. в точке Р ^х, Тогда «элемент» статического получится, как произведение массы dm н
момента трапеции относительно оси Ох
1 ординату точки Р, т. е.
Аналогично,
dMx = dm- ^- = -^ру2 dx. dMy~dm х = рху dx.
Интегрируя эти «элементы» по отрезку [a, i], приходим к следующему результату: Ь	ь
Мх = 9 \ У2 dx; Му — р ху dx.	(3)
а	а
Теперь легко определить координаты g, г| центра тяжести фигуры. Известно, что /нг] = Л4Л., тс, —Му, где т — масса фигуры, вычисляемая по формуле
ь
т = р у dx.
а
Отсюда, принимая во внимание формулы (3), получаем
Ь
с	1
1 ху dx	2
У2 dx
"*	с	с
\у dx	\ydx
а	а
1495.	Найти статические моменты относительно осей Ох и Оу и координаты центра тяжести треугольника, ограниченного прямыми х-[-у = а, х = 0, у~0 (плотность р=1).
Решение. Здесь у = а — х. Применяя формулы (3), получаем:
..	1 С ,	, __	1 (а —х)3 |а as
Мх~ 2	dx~ 2	3 |о ~ 6 ’
о
Му =
х3 \ |а___о3
”3 / |о
309
Равенство моментов можно было установить и из соображений симметрии. Координаты центра тяжести треугольника вычисляются по формулам (4). Учиты-а3
вая, что т = 5д =имеем £ = г] = -т^—
2 °'
а
т-
1496.	Найти статические моменты прямоугольника со сторонами а а b относительно его сторон (плотность р = 1).
1497.	Вычислить статические моменты относительно осей Ох и Оу и координаты центра тяжести фигуры, ограниченной синусоидой у = = sinx и отрезком оси Ох от точки х = 0 до точки х = л (плотность р = 1).
1498.	Найти координаты центра тяжести фигуры, ограниченной эллипсом s + ^ = 1 и осями координат (Х^гО, Z/5&0).
1499.	Найти координаты центра тяжести фигуры, ограниченной первой аркой циклоиды x = a(t — sin t), y = a(l~cost) и осью Ох (см. рис. 151).
5. Давление жидкости. Пусть в жидкость вертикально погружена пластинка прямыми х — а, х=Ь и кривыми у---уу х'), у=у2(х). Предполагается, что система координат выбрана так, что ось Оу лежит на поверхности жидкости. Требуется определить полное гидростатическое давление Р, испытываемое каждой стороной пластинки. Возьмем в промежутке [а, &] элементарный отрезок [х, x-pdx], Тогда в нашей пластинке выделится элементарная полоска, которую приближенно можно считать прямоугольником с площадью dS = (j/2 — ypdx (на рис. 164 выделенная полоска заштрихована). Давление жидкости на эту полоску и будет «элементом» dP давления на всю пластину Л1В1В3Л2. Для подсчета dP воспользуемся законом Паскаля, согласно которому давление жидкости на площадку dS, расположенную на глубине х
от поверхности, равно весу цилиндрического столба жидкости высоты х, имеющего эту площадку своим основанием, т. е.
dP — ydSx, где у - удельный вес жидкости.
Или, принимая во внимание, что
dS = (y2 — yjdx, dP = yx(y2 — yl)dx.
Интегрируя по отрезку [а, Ь], получаем давление жидкости на всю фигуру: ь
Р— у x(y2 — yi)dx.	(5)
а
1500.	Найти силу давления, испытываемую каждой из сторон полукруга радиуса г, погруженного в жидкость так, что диаметр совпадает с поверхностью жидкости. Удельный вес жидкости у.
310
Решение. В рон четверти круга лат как указано на Уг(х) = Vг- - а;2:
силу симметрии достаточно найти давление на одну из сто-и удвоить полученный результат. Выбираем систему коорди-рис. 165 и вычисляем интеграл (5) при а = 0, Ь=г, уг(х)=О,
или
г'1 — х2 dx —
р=4^3-
=
о л
3
1501. Прямоугольная пластинка со сторонами а дм и b дм вертикально погружена в жидкость удельного веса у, причем сторона длиной а дм лежит на поверхности жидкости. Опре-
делить силу давления на каждую из сторон пластинки.
1502.	Вычислить силу давления воды на каждую из сторон погруженной вертикально в нее пластинку, имеющую форму равнобедренного треугольника с основанием b м и высотой h м, предполагая, что вершина треугольника лежит на свободной поверхности воды, а основание параллельно ей.
1503.	Вертикальная плотина имеет форму равнобочной трапеции. Вычислить силу давления воды на плотину, если известно, что верхнее основание плотины а = 70 м, нижнее основание Ь = 50 м, а высота плотины h — 20 м.
6. Количество электричества. Пусть по проводнику течет ток переменной силы I — I(t), гДе У(0Э=0. Определить количество электричества Q, протекшего через поперечное сечение проводника за промежуток времени [^, /2] (/2 > ^). Известно, что для постоянного тока I
Q — 1 (t2 Zj).
Для определения Q в случае переменного тока поступим согласно общей cxcmj (см. п. 1). Выделим элементарный отрезок времени [/, t-j-dt] и подсчитаем соответствующий «элемент» количества электричества dQ. Очевидно,
dQ = / (/) dt.
Далее, интегрируя по t в Пределах от 0 до t2, получим
Ц
Q=f 1(f) dt.
(6)
Замечание. Если функция / (f) на отрезке /,] меняет знак (направление тока меняется в течение данного времени), то интеграл (6) дает разность между количеством электричества, прошедшим через поперечное сечение проводника за время (t2 — G) в °ДНУ сторону, и количеством электричества, прошедшим за то же время в противоположную сторону.
1504.	При изменении температуры сопротивление металлических проводников меняется (при обычных температурах) по закону R = R0 (1 + 0,0040), где Ro — сопротивление при 0°С и О — температура по Цельсию. (Этот закон справедлив для большинства чистых
311
металлов.) Проводник, сопротивление которого при О'С равно /?о=10 ом, равномерно нагревается от &1 = 20° до = 200° в течение 10 мин. В это время по нему идет ток под напряжением U = 120 в. Сколько кулонов электричества протечет за это время через проводник?
Решение. По условию задачи, температура проводника О увеличивается с постоянной споростью
d& 200°-20°	град
clt ~~ 600 сек ~~ ’ сек '
а значит, $ изменяется по закону
fl = Ад+ 0,3/= 20+ 0,3/.
При этом сопротивление проводника
R = R0 (1 +-0,0040) = 10 [1 4-0,004 (20 + 0,3/)] = 10,8 4-0,012/,
и сила тока (по закону Ома)
120
- 10,8 + 0,012/ ’
Проинтегрировав эту функцию по промежутку [0, 600], получим искомое количество электричества
®°°	1200/	120	600
10 Я4-0 0197= 0-012-1п (10,8 + 0,012?)	=10* • (In 18 —In 10,8)	5110 («).
J 1и,0 -j-u,ulzf U,U1Z	0
1505.	Сила тока I в проводнике меняется со временем по закону I — 2 + 3/а, где I выражено в амперах и / — в сек. Найти: 1) какое количество электричества проходит через поперечное сечение проводника за время от 4 = 2 сек до 4 = 5 сек, 2) при какой силе постоянного тока через поперечное сечение проводника за это же время проходит такое же количество электричества?
1506.	Сила обычного переменного тока (городского), имеющего 50 колебаний в секунду, изменяется со временем t по закону
I = /0 sin 100 л/,
где /0 = const — наибольшее значение силы тока. Найти количество электричества, протекающее через поперечное сечение проводника за время от 4 = 0 до 4 = 0,01 сек (за половину периода).
1507.	Напряжение на клеммах электрической цепи (/=120 в. В цепь равномерно вводится сопротивление со скоростью 0,1 ом в секунду. Кроме того, в цепь включено постоянное сопротивление /?0 = 10 ом. Сколько кулонов электричества пройдет через цепь в течение двух минут?
ГЛАВА IX
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
§ 1. ОСНОВНЫЕ ПОНЯТИЯ
1. Определение. Символика. Переменная величина z называется функцией двух переменных х и у, если каждой паре значений (х, у) из данной области D соответствует вполне определенное значение г. Переменные х, у называются независимыми переменными, или аргументами. Область D называется областью определения функции. Обозначение функции двух переменных:
г = /(х, У)> или г = г(х, г/), или
z — F(x, у) и т. д.
Заметим, что по самому определению функция однозначна. Многозначных функций мы рассматривать здесь не будем.
Частным значением функции z — — f (х, у) называется ее значение, соответствующее какой-либо определенной паре значений аргументов. Если, напри-
мер, при х — а и у----Ь функция прини-
мает частное значение с, то пишут с =	Рис. 166
= f (а, Ь). Каждая пара значений аргу-
ментов {х, у) геометрически определяет точку Р на плоскости хОу, а значение функции в этой точке есть аппликата z пространственной точки М (х, у, г). Гео-
метрическое место всех точек Л1 есть поверхность, взаимно однозначно проектирующаяся в область D на плоскости хОу (рис. 166). Эта поверхность служит геометрическим изображением функции f (х, у). Иногда используют запись z = f (Р).
Рис. 167
Переменная величина и называется функцией независимых переменных х1( х2, ..., хп, если каждой системе значений (xj, х2, .... хп) этих переменных из данной области их изменения соответствует единственное значение величины и. Обозначение:
u = f (xlt х2, ..., хп), или п = п(х1, х2, ..., хп) и т. д.
В случае функции трех переменных пишут u = f (х,у, z); каждая система (х, у, г) значений аргументов определяет некоторую точку М пространства, а функция f (х, у, г) указывает некоторое число, отвечающее этой точке.
По аналогии систему значений (х1( х2, .... хп) называют «точкой» в области изменения переменных хх, х2, ... , хп и говорят о значении функции и в этой точке.
1508. Выразить объем кругового конуса V как функцию его образующей х и радиуса основания у.
Решение. Объем кругового конуса (рис. 167) равен одной трети произведения площади основания S на высоту h. Так как
5 = яг/2 и A = j/x3 — у2, то V = ™ лу2р х2 — у2.
О
Это и есть искомая функция.
313
1509. Выразить площадь треугольника с данным периметром 2р как функцию длин двух его сторон х и у.
Решение. По формуле Герона,
Sa (p -ci) (р-- b)(p <),
где а, Ъ, с —длины сторон, а р — полупернмегр. В данном случае
а=х, Ь — у, с=2р — а— Ь — 2р—х—у, поэтому
Sa = Vp (р — х) (р—у) (х+у—р).
1510. Найти частное
значение функции
f(x, у)
2ху
в точке Р (2, —1).
Решена е. Подставляя
в выражение функции х = 2, у— — 1, получим
- П_ 2'2< !>	4
1 2s + (-l)3	5-
1511. Дана функция f (х, у)=ху-\- у . Найти / (р, х), f( — x,
Р е ш е и и е. Значение
f (у, х) получается заменой аргументов х на у и у на х:
Далее,
/(г/, х) = ух-\- '
У
Н-х,
-р) = (-х)(-р) + т=4 = ^ + д’’
у обоих аргументов значения функции не меняются.
е. при замене знаков
Подставляя в выражение данной функции х=1, y = t, получим f(l, i)=l^ + 4=2i-
Полагая здесь	найдем
1512.	Дана функция
Найти ее значение в точке (0, 2, —3). Найти f^x, у,
1513.	Выразить объем правильной шестиугольной пирамиды как функцию ее высоты х и бокового ребра у.
1514.	Найти	и f(2, —1), если f (х, у) =]/гху2-[-х-[-1.
1515.	По закону Ома, сопротивление R электрической цепи выражается через силу тока I и напряжение U на ее концах по фор-
314
I муле /? = у. Каково сопротивление цепи, по которой проходит ток 2,5 а при напряжении 120 в?
1516, Составить таблицу значений функций z — Уху, давая каждому аргументу целые значения от 0 до 5.
1517. Найти /(х, —у), f (—х, у), f .	если f (х, у)=
—
у2—х ’
2. Область определения функции. Область определения функции г = /(х, у) в общем случае может быть достаточно сложной. Мы ограничимся рассмотрением только тех случаев, когда эта область есть конечная или бесконечная часть плоскости, ограниченная одной или несколькими непрерывными линиями — границами области. Не исключается и тот случай, Когда какая-то из границ превращается в одну точку. Область D называется замкнутой, если она включает в себя все свои границы. Область определения функции задается вместе с определением самой функции п обусловливается теми геометрическими, физическими и т. д. условиями, которыми эта функция определена. Если функция задана аналитическим выражением (формулой) без каких-либо дополнительных условий, то под ее областью определения понимают область существования аналитического выражения, т. е. совокупность всех тех точек, в которых данное аналитическое выражение определено и принимает только действительные значения.
Область определения функции трех переменных представляет собой некоторую пространственную область, в частности, некоторый объем. Под пространственной областью понимается часть пространства, ограниченная одной или несколькими поверхностями.
1518. Указать область определения функции, выражающей объем кругового конуса V через образующую х и радиус основания у.
Решение. Соответствующая функция была найдена в 1508. По смыслу задачи переменные х и у могут принимать только положительные значения и при этом всегда х > у, так как гипотенуза больше катета (рис. 167). Следова-f телыго, область определения D задается ;; неравенствами
х > 0, у > 0, х > у,
j. т. е. состоит из всех тех точек Р (х, у) первой четверти па плоскости хОу, кото-h рые лежат ниже биссектрисы х=--у (рис.
168). Границами области D служат пря-
у мне у = 0 и у = которые сами в область D не входят, так что эта область > незамкнутая.
?	1519. Найти область определения функции z = - z/2 ]/\2 —• z/2.
г
; Решение. Поскольку никаких дополнительных ограничений на аргументы ‘ хну не наложено, область определения D будет состоять из всех тех точек плос-й- кости, для которых данное аналитическое выражение принимает действительные t значения. Для того чтобы значения функции г были действительными числами, | подкоренное выражение должно быть неотрицательным, т. е.
х2 —У2г?0, или х-^::у2.
315
Если оставить здесь только знак равенства, то получится уравнение границы области D
х2 = у2, или х — ±у.
Эта граница состоит из двух оиссектрис х = у и х = —у координатных углов. Для внутренних точек области D должно соблюдаться неравенство х2 > у2, или I х I > | у [. Следовательно, эти точки рас-
Рис. 169
положены между биссектрисами ближе к оси Ох, так как j у | есть расстояние точки Р (х, у) до оси Ох и оно меньше расстояния | х | точки Р до оси Оу. Таким образом, область D состоит из всех точек двух углов между биссектрисами х=±(/, заключающими внутри себя ось Ох (рис. 169). Область замкнутая, так как включает в себя обе свои границы.
Замечание. Хотя аналитические выражения функции этой задачи и 1508 одинаковые, их области определения разные. На переменные х и у в 1508 были наложены дополнительные условия х > 0, у > 0, х > у, вытекающие из геометрического их определения. Поэтому и область D оказалась меньше,
чем полная область существования аналитического выражения (сравнить рис. 168 и 169).
1520. Найти область определения функции г = In (4 4-4х — у2).
Решение. Логарифм определен только при положительном значении его аргумента, поэтому
4-j-4x — у2>0, или 4-(-4х>(/2.
Никаких других ограничений на аргументы Чтобы изобразить геометрически область D, найдем сначала ее границу
4 + 4х = у2, или у2 = 4 (x-f- 1).
Полученное уравнение определяет параболу, вершина которой расположена в точке О' (—1, 0), а ось направлена в по- У ложительную сторону оси Ох. Точки пересечения параболы с осью Оу получаются из условия х = 0, откуда у2 = 4, т. е. у — ±2 (рис. 170).
Парабола делит всю плоскость на две части — внутреннюю и внешнюю по отношению к параболе. Для точек одной из этих частей выполняется неравенство у2<4-р4х, а для другой у2'>4--4х. (На самой параболе у2 = 4-|-4х.) Чтобы установить, какая из этих двух частей является областью определения данной
х, у не дано.
функции, т. е. удовлетворяет условию
y2<4-j-4x, достаточно проверить это условие для какой-нибудь одной точки, не лежащей на параболе. Например, начало координат О (0, 0) лежит внутри параболы и удовлетворяет нужному условию 0< 44-4-0.
Следовательно, рассматриваемая область D состоит из внутренних точек параболы. Сама парабола в область D входить не может, так как для точек параболы 4--4х~-у2 = 0, и логарифм не определен.
316
1521. Найти область определения функции
г = ]/х2 + У2 — 1 + In (4 — х2 — у2).
Решение. Данная функция определена и принимает действительные значения при
-2>0.
Поставив вместо знака неравенства знак равенства, мы получим уравнения границ области определения D
х3 + у- — 1 = 0 и 4 — х3 — у2 = 0,
или
xs_|_^a—1 н х3-|-(/2 —4.
Таким образом, граница области D состоит из двух окружностей с центром в начале координат и радиусами и R — 2. Эти окружности делят всю плоскость на три части (рис. 171). При этом для внутренних точек области D должны одновременно соблюдаться неравенства 0 и 4 — х2 — (/2>0.
x2 + </2-l
! 3	''
Возьмем три точки 0(0, 0), А I—, 0 ; и
\ “ /
лежащие в разных частях плоско-
сти, и проверим, соблюдаются ли для них неравенства. Точка О не удовлетворяет первому, ! а точка В — второму неравенству. Для точки А
/ Ч \2	/ 3'2
•	(jj+0-l>0 и 4-^1-0>0.
Следовательно, искомая область D есть у кольцо, заключенное между двумя данными , окружностями. При этом внутренняя окруж-
ность может быть включена в область D, так как равенство х2 + г/2— 1-- () воз-можно, а внешняя окружность в область D не входит.
у 1522. Найти область определения функции
трех переменных
<
Ее
Решение. Искомая
граница
У2
.2
пространственная
оолзсть
V определяется условием
1- , а-
№
Ь-
-	0, или
и2
Ь2
^1.
х-
Ь2
есть поверхность лежащее внутри и вся область V тая, так как включает в себя и границу.
с полуосями а, Ь, с. Так как начало координат, удовлетворяет указанному выше неравенству, то
эллипсоида эллипсоида, состоит из внутренних точек эллипсоида. Эта область замкпу-
! >
Г; и

и =
1523.	Указать область определения функции, выражающей пло->Щадь треугольника с данным периметром через длины двух его сто-1рон (см. 1509).
Указание. Использовать геометрический смысл аргументов.
317
В следующих задачах найти области определения данных функций. Выяснить, входят ли границы в эти области. Сделать чертежи.
1524.	г = -то^.	1528. z = ]/sin л (х2 + у2).
х2+г/2
1525.	z = In (х2-|-у2 — 1).	1529. z = arcsin^.
1526.	z =	+ x-y24-	1530. и = У'Ъ(1 + г-х2-г/2).
1527.	z = Vx + у In (г/2 - x2).
3. Пределы и непрерывность. Пусть Р„ (х0, уф — некоторая фиксированная точка плоскости и х-»х0, у — у„, тогда точка Р(х, у) стремится к точке Р0(х0, «/„), т. е. Р — Ро. Это равносильно стремлению к пулю расстояния РР0, которое мы будем обозначать буквой р:
Р = /(х — х„)2 4- (у — г/,,)2.
Число Л называется пределом функции z=f(P)=f(,x, у), если для любого числа е > 0 существует такое число о > 0, что из неравенства р = PPtl < о следует, неравенство
тР}-Л |<е-
Иными словами, как только расстояние переменной точки Р (х, у) от фиксирован ной точки Ро (ха, г/0) станет достаточно малым, значение функции г в точке Р будет отличаться от числа Л меньше, чем па е, где е может быть выбрано сколь, угодно малым. При этом пишут
lini f(x.y) = A, или lim f(P) = A. лто.г0 '	/>-г„
У -На
Определение предела функции можно по-другому сформулировать так: число Я называется пределом функции z = f(P) при Р --Р,., если бесконечно малому расстоянию р = РР0 отвечает бесконечно малая разность f(P) — A. Важно подчеркнуть, что, по определению, предел функции не зависит от направления движения точки Р (х, у) к точке Ро (х„, .%). Поэтому, если окажется, что при Р---Р. с разных сторон f (Р) стремится к разным предельным значениям, то функция z=./(P) предела не имеет.
Для функций двух переменных справедливы теоремы о пределе суммы, разности, произведения и частного, которые формулируются и доказываются совер шенно аналогично соответствующим теоремам для функций, зависящих от одного аргумента.
Функция z—f(P) называется непрерывной в точке Ро, если: 1) f (Р) определена как в самой точке Ро, так и в некоторой ее окрестности;
2) существует предел lim f(P);
3) этот предел равен значению функции в предельной точке
lim f(P)=f(P0).
р-р«
Из определения предела вытекает, что условия 2 и 3 можно заменить следующим равносильным требованием:
2') бесконечно малому расстоянию р — РР0 отвечает бесконечно малое приращение функции Az = f (Р) —f (Ро).
Функция непрерывна в области D, если она непрерывна во всякой точке этой области.
Точка Ро называется точкой разрыва функции z=f (Р), если для нее не выполняется хотя бы одно из трех условий в определении непрерывности. Точки раз-318
крыва данной функции могут располагаться как отдельно (изолированные точки разрыва), так и заполнять целые линии (линии разрыва).
Е Как и для функций одной переменной, сумма, разность и произведение ^непрерывных функций двух переменных в точке Ро будут непрерывными  В топ же точке; частное непрерывных функций в точке Р„ будет также непре-Яоывной в Рп функцией, если только знаменатель не обращается в пуль в этой точке. «-Справедлива также теорема о непрерывности сложной функции.
Ж Совершенно аналогично определяются предел и непрерывность функций трех К и большего числа переменных.
ж 1531. Найти предел
	lim!!itfc22+TOl.
S	...о -то <" -о-
is' Решение. Данный предел находится при условии Р (.г, у) — (0, 2). Рас-^стояние между этими точками р—Кх2+ (//--2)3, (поэтому
1- Г'рЧ7!-!	1-	(р-’ф1)-1
( lim----------'—-----== lim ——-----—lim—=
с х-.о х24-(д—2)2 р~»о р2 р -.ур2 (Гр2-!-1 +1)
й у - 2
к	г	р2	,.11
-	о — о р2 О' р2 + 1 "F О р — о 1’ Р2 1 -'г 1	2
1	1532. Найти предел
lim (х24-у2) sin--.
’	X -»о	ХУ
ь	У-гО
Решение. В данном случае Р (х, //) —» 0 (0, 0), поэтому
р = ор = Ух2+у2 и
lim (х2-фу2) sin —— = lim р2 sin = 0,
х -то	ХУ	р —► о	ХУ
1/-Ы}
так как произведение бесконечно малой величины р2 на ограниченную (\ . 1 [
sin — sS 1 I есть бесконечно малая величина.
\1 ху | j
1-	1533. Выяснить, существует ли предел
I	,. х2 — у2
k	Л-i х2 + У2
L	v-o
Решение. Предположим, что переменная точка к началу координат не произвольно, а по некоторой
так как при y = kx имеем
Р (х, прямой
У}
приближается y = kx. Вдоль
F »	.	,	X2 — у2
в-этой прямой значения функции г — фу.у/р
Ь	X2 — у2 X2 — k2X2 1 — k2
I	^+У2 ~ x2 + k2x2 " 1+*2 ’ П0ЭТ0МУ
постоянны,
х2—у2 1— k2 х2 + У2 ~~ l+k2 •
и lim р — о вдоль y = kx
[ Однако если приближаться к началу координат с разных сторон, то функция 12 ~ ~\"i ‘О будет стремиться к разным предельным значением. Действительно, Ips X “т“ у
319
величина принимает свое значение для каждого k. Например, при Р — О вдоль оси Ox (/-’== 0) значения г стремятся к 1, а при движении вдоль биссектрисы y = x(k = 1) значения г стремятся к нулю.
Следовательно, определение предела не может выполняться ни для какого числа А, т. е. данного предела не существует.
1534.	Исследовать на непрерывность функцию
х- 4- У“
Решение. В числителе и знаменателе здесь стоят многочлены, а многочлен определен и непрерывен в любой точке, плоскости. Поэтому функция ~ будет непрерывной везде, где знаменатель не обращается в нуль. В начале координат функция не определена и, следовательно, разрывна. При приближении точки Р (х, у) к началу координат знаменатель стремится к пулю, а числитель — к 1, так что функция г бесконечно возрастает.
1535.	Исследовать на непрерывность функцию
ха + 2у + 4
'	1/й-2х •
Решение. Функция г непрерывна как отношение многочленов во всех точках, где знаменатель не обращается в нуль. Точки разрыва расположены на линии г/2 —2х = 0, или у2 = 2х, т. е. на параболе. При приближении точки Р (х, у) к какой-либо точке этой параболы данная функция бесконечно возрастает.
1536.	Найти и исследовать точки разрыва функции
1 Z = COS------.
х-~У
Решение. Эта функция сложная: г = созо, где о=— -—. Функция cos о непрерывна при любом значении аргумента. Точки разрыва надо искать для . 1 функции ц=——в этих точках оудет разрывна и вся сложная функция г.
Что касается функции v = ~~, то она терпит разрыв вдоль прямой у = х, так как в точках этой прямой знаменатель обращается в нуль, и функция v бесконечно велика.
При приближении точки Р (х, у) к одной из точек прямой у = х функция г = соз-^— производит бесконечно много колебаний в пределах отрезка [—1, 1] и, следовательно, никакого предела не имеет.
1537. Вычислить
х2 + у2
предел
А — lim Г . . =— х-о V 4-— X2-— г/2-— 2
1538. Показать, что при Р (х, г/)->0(0, 0) функция
предела не имеет.
2ху х2+У2
Указание. См. 1533.
Исследовать на непрерывность следующие функции. Найти точки разрыва и выяснить, как ведет себя функция в окрестности точки разрыва.
320
1539. г
1540. z
1541. и
1
1
(х—г/)2'
1
гг-х8-г/2'
_ 1
1542. г = е
1543. г =! УТ-*2-/ ПРИ *2+1/2^1, \	0	при л-2 + ?/2>1.
§ 2. ЧАСТНЫЕ ПРОИЗВОДНЫЕ И ПОЛНЫЙ ДИФФЕРЕНЦИАЛ
1. Частные производные. Частные производные функции г = /(л', г/) определяются следующим образом:
lim Ну + Ал-, у)-/(х, у) дг _ . f(x, y+Ay)-f(x, у) 11111	.	11111	.
оЯ Дх->0	ду	Д//~*0	&у
т. е. частная производная функции z = f(x, у) по аргументу х есть производная „ ,	.	дг
этой функции по х при постоянном значении у. Аналогично есть производная функции 2 = /(.с, у) по у в предположении, что х является постоянным. Обозначаются частные производные одним из символов:
дг df 	ч dz df	ч
, д~, гг- /Д-Ч У)< 5~, д-, г,„	„(х, у).
дх’ дх’ х х х ду’ ду’ У у у ’
Частные производные функции нескольких переменных определяются как производные этой функции по одному из них при условии, что остальные переменные считаются постоянными. Например, производная функции u=f(x,y, г) по х определяется формулой
<5« = Нт + У’ У’ г)
дх дл-^о	к*
Частные производные функции г = [(х,у) сами представляют собой некоторые функции переменных х и у. Поэтому, если нас интересуют значения частных производных в какой-либо точке Р,, (лг0, уп), надо сначала по общим правилам
„ дг дг наити -.-и,-дх ду'
а затем подставить в полученные функции координаты точки Ро.
Значения частных производных в точке Ро обозначаются одним из символов:
dz\ /dz\ df (х0, у„) дх)9' \дх)р„’ дх
Гх(х0, у0),
и аналогично — для производных по у.
1544.	Найти частные производные функции z = х° + уя — Заху.
Вычислить их значения в точке Ро (1, 1).
_	„	дг
Решение. Считая у постоянным, находим^-:
~х = (дЗ+г,з _ захуух = 3Х2 .у о - Зау • 1 = Зх= - Зау.
При нахождении фиксируется аргумент х, т. о.
дг ду
= (х3 + г/3 — Заху)’у = 0 + Зу~ — Зах  1 — Зу2 — Зах.
11 Кручкович и др.
321
Значения производных в точке Ро (1, 1) следующие:
(дг} = 3—3<z, (dZ} = 3—3(7.
\дх!а	\ду,:0
1545.	Найти значения частных производных в точке Ро (0, 1) функции г
Реше н и е. Находим сначала частные производные, используя формулу дифференцирования сложной функции (е11)' = еии':
= (C-.VW)-	( _А.у)- =е-л-.у	~.'T;
=с х!1 -с~хи
Подставляя координаты точки Ри, получим
(^}	-0.
\дх;и	у)у
1546.	Найти частную производную по г от функции трех переменных
и = aretg .
Решение. По правилу дифференцирования сложной функции, считая х и у постоянными, получим
ди ( . у \	1 (У V _	1_____ У ! 1 V _
дг ~ ЛГС g xziz ~ ,,(yV\xz)z~ . . у2 x'\zjz
^[xzj	Г xV
___ x2z2 у !	1 \_ ху
~ х2г2~т~у'1 х \	г2/ х2г2 -- у2
1547.	Доказать, что функция г = In (х2 -\-ху + у2) удовлетворяет уравнению
дг , дг о
Хдх + Уду~2'
Решение. Находим частные производные:
дг	1	/9,| .у 2хф-(/
дх~~ х2 + ху + у2	+Ху + у^х х2 + ху + у2 ’
дг _	1 _____ х + 2у
ду х2ф-ху + у2 (Х ^~Ху 1	х^-ху-^у2
Подставляем и дх
dz
в данное уравнение:
2х + у	х-\-2у	=	2х2 + 2ху + 2у2
х^ + ху+у2 *~У х2 + ху-[-у2	’	х2+ху-\-у2
полученное тождество показывает, что функция действительно удовлетворяет данному уравнению.
322
Найти частные производные следующих функций:
1548.
1549.
1550.
z = 2х2у + Зху2 ф- х3.
X z =  /х24-у2
z = tg —. ь X
Г553. z = sin --cos у-у х
>554. z =
1552.
,	. Л -I- I
+ aresin ——,
ху
1555. г —1/х2
д ! 1 \ найти - -
2
! +
и =
v =
у х
найти значения частных произ-
1556.
и == j/sin2 х + sin2у -ф sin2 z; /	JT \
водных в точке Л4о; О, 0, -^-1.
1557.	tz — In (1	1/2 + z2); найти значение суммы и'х~и'и + и':,
в точке Мо(1, 1, 1).
1558.	f(x, у) = хлу — ху-значение Ф в точке Ро что
найти выражение Ф = и вычислить
I Х< I!
(1- 2).
функция и = (х — у) (у — г) (а — х) удовлетво-
1559. Показать, ряет уравнению
ди . ди . ди „ дх + ду + дг U
1560. Показать,
что
функция г = Ух sin -- удовлетворяет урав-
нению
„ дг , г, дг 2х -г 21/, -г. дх 1 J ду
2. Полный дифференциал. Пусть Р (х, у) —данная точка, а Р’ (л-(-Дх, у-'Г 4-Ду)— близкая точка, отвечающая приращениям аргументов Лх и Ду. Полным приращением функции г = /(х, у) в точке Р называется разность
Дг = ) (Р')~ f(P)=f(x + Ax, y + &y)-f(x, у).
Если приращение Дг можно представить в виде Дг=АЛх-1-ВЛу 4-е, где а — бесконечно малая более высокого порядка по р = КДх2 4* '4/2 между точками Р и Р' ^т. е. ——► 0
называется дифференцируемой, в точке Р, а главная линейная dz== /1Дх4-Ь'Ду
называется полным дифференциалом функции в точке Р. дифференциал в каждой точке некоторой области D, называется дифференцируемой в этой области.
Если функция дифференцируема, то необходимо, чтобы А=д/, B=f. дх ’ ду
Достаточным условием дифференцируемости является наличие непрерывных частных производных. Так как приращения независимых переменных совпадают
сравнению с расстоянием при р
— (И 1 то функция Z часть ее приращения
Функция, имеющая
11»
323
с их дифференциалами, т. е. &x — dx, &y = dy, то дифференциал функции 2 = = f (х, у} вычисляется по формуле
(1)
Важно подчеркнуть, что эта последняя формула остается справедливой также и в том случае, когда х и у в свою очередь являются функциями каких-либо других аргументов (свойство инвариантности полного дифференциала).
Аналогично определяется и вычисляется полный дифференциал функции любого числа переменных. Например, полный дифференциал функции u=f(x, у, г) вычисляется по формуле
, ди , , ди , , ди ,	,о.
du — dx	du -4- dz.	(2)
дх dy J дг
Теоремы и формулы для дифференциалов функций одного аргумента полностью сохраняются и для дифференциалов функций двух, трех и т. д. аргументов. Так, независимо от того, от каких аргументов зависят функции и и v, всегда справедливы равенства
d(u ± v)~ du ± dv, d (uv) = v du + и dv,
d = vdu~udv , dF (u) = F' (u) du.	(3)
1561. Найти полный дифференциал функции z = х2у — у2х.
Решение. Находим частные производные:
|| = ^У — У"х)х = 2ху — у-',	= (х'-у — у2х)у = л-2 — 2ху.
По формуле (1) имеем
dz — (2ху—у2) dx (х2 — 2ху) dy.
Полный дифференциал можно найти также и по-другому, используя правила дифференцирования (3):
dz = d (х2у — у2х) — d (х2у) — d (у2х) = yd (х2) х- dy —
— xd (у2) — у2 dx = 2ху dx х2 dy — 2ху dy — у2 dx = (2ху — у2) dx + (х2 — 2ху) dy.
Найти полные дифференциалы функций:
1562. z = ]/х2 Ц-у2.
1564.	z — In (х2 + г/2); найти значение дифференциала в точке (1, 0).
1565.	и = arctg
1566.	w = х2у sin xyz.
3. Применение дифференциала к приближенным вычислениям. Прирашение функции Дг и ее полный дифференциал dz связаны равенством
Дг = Цг + е,
где е — бесконечно малая более высокого порядка малости по сравнению с р = = УДх2+Ду2; при достаточно малых приращениях аргументов можно величиной е пренебречь и считать Дг^б/г. Это приводит к приближенному равенству
.	, дг . , дг ,
Xz =» dz — =- dx 4--=- dy, dx dy
324
или (подробно)
f(x + &x, y+Ay)—f(x, y}^df(x, у) = Ax + Ay.
Этой формулой можно пользоваться для приближенного подсчета значения f(x-f-Ax, y-j-Ay) по известным значениям функции f (х, у) и ее частных производных в данной точке Р (х, у).
1567.	Высота конуса Н~ 10 см, радиус основания R = 5 см. Как изменится объем конуса при увеличении высоты на 2 мм и уменьшении радиуса основания на 2 мм?
Решение. Объем конуса а—у лР-Н. Изменение объема приближенно заменим его дифференциалом
Av^dv= 4- я (2RHdR + R-dll).
Подставив значения (в с.и) R — 5, // = 10, dR = —0,2, dH = 0,2, получим
Av	4- л Гг • 5 • 10 (—0,2) 4- 25  0,2 1 = —5л - 15,7.
о L	J
Таким образом, объем конуса уменьшится примерно на 15,7 см?.
1568.	Вычислить приближенно число а = (1,04)2'03.
Решение. Рассмотрим функцию f (х, 1/) = х-'Л Данное число а есть приращенное значение этой функции в точке Ро(1, 2) при Ах = 0,04, Ду = 0,03. Дифференциал данной функции
df = XАл' + %	=yx'J~l Sx+xJ 1п Х
Его значение в точке Р„ (1, 2) при данных приращениях
(df)0 = 2 • 1 • 0,04 + 1 • In • 0,03 = 0,08,
поэтому по формуле (4) имеем
а = /(1,01; 2,03)яь/(1, 2)-f-(с//%= 1-|-0,08 = 1,08.
1569.	Период Т колебаний маятника вычисляется по формуле
где / — длина маятника, g —ускорение силы тяжести. Найти ошибку в определении Т, получаемую в результате небольших ошибок Д/ = а и Ag = P при измерении I и g.
Решение. При данных условиях величину Т надо рассматривать как функцию переменных / и g. Получаемую погрешность АТ заменяем приближенно дифференциалом dT этой функции:
-)-2л КI
АТ = dT = — Д/ + —Ag=2n-4=--4=A/ + dl dg &	\Гg 2^1
(- __ 1	\ Ag = « f A; - 1
\ 2g^g /	VSl \ g	/ gl g
325
При небольших ошибках Д/ = а, Ag=P получим
gVgl
1570.	Вычислить приближенно числа
а = (0,97)2,02, 6 = ]/(4,05)2±(2,93)2, с = arctg	- 1).
1571.	Одна сторона прямоугольника а = 6 см, другая 6 = 8 см. Как изменится диагональ прямоугольника, если сторону а удлинить на 4 мм, а сторону b укоротить на 1 мм?
1572.	Радиус основания конуса равен 10,2 ±0,1 см, образующая равна 44,6 ±0,1 см. Найти объем конуса и указать погрешность подсчета.
Указание. См. 1508.
§ 3.	ДИФФЕРЕНЦИРОВАНИЕ СЛОЖНЫХ И НЕЯВНЫХ ФУНКЦИЙ
1.	Сложная функция. Пусть z = f(x, у) —дифференцируемая функция своих аргументов х и у, а х и у в свою очередь являются дифференцируемыми функциями от некоторого аргумента t. Тогда сложная функция г = z (t) — f (х (/), у (/)) также дифференцируема, а ее производная находится по формуле
дг _ dz dx дг dy	.
dt дх dt ' ду "di'	' '
Если х и у зависят от нескольких переменных, например х (и, о), у (и, и), то формулы частных производных сложной функции
г —г (и, v) = f(x(u, v), у (и, г))
имеют аналогичный вид:
дг дг дх , дг ду _ дг __ дг дх дг ду
ди " дх ди " ду ди ' dv dxdv'dydv'	' '
Производные сложных функций, зависящих от большего числа аргументов, вычисляются по аналогичным правилам. Например, если u = f(x,y, г), а х, у, г сами являются функциями от каких-то переменных t, s, ... , то
ди ди дх ^глиду , ди дг
dt	дх dt 1 ду dt 1 дг dt'	'
Если х, у, г зависят только от t, то в этой формуле частные производные по t заменяются на обычные:
du _ ди dx ди dy ди dz dt дх "dt ~г ду dt'~ ду dt'
1573.	Найти если г = х2 ±ху ±у2, где x = t2, y = t3.
Решение. По формуле (1) имеем
=	+ * g = (2x + y) 2Жх + 2//) 3/а = (2/а + /з) 2/-|-
dt дх dt ду dt 4	'	’	1 '	1
+ (/а + 2/3) 3/а = 4/з 5/4	.
326
Тот же результат можно получить и иным путем: сначала выразить 2 явно через t, а затем найти производную полученной функции:
z = г (г!) = (Z2)2 + /2 • t3 + (Z3)2 = + Р +
dz
, =4Z34-5Z-’4-6f>.
dt
1574.	Найти и ^г, если г = arcsin--, где у = У"14-ха.
дх dx’	у ’
Решение. Имеем
dz /	. х \'	1	/ х \'	1	1	1
= i arcsin - -	=----—____г ( - - =___________ • — =	....
дх \ у/х 1/^1	У 'х 1/ j %3	'У2 — х2
V ~~\у) -V У2
dz
Полная производная -- вычисляется по формуле (1), где в данном случае надо
, dx
положить t — x н -.7=1: dt
dz _дг dz dy __	1
-4
х- \ м / г у \ 4-х-
У2
1 №
у2 — X2 // Iх у2 — X2 1 4-Х2
Поскольку у=\/Л-\-Х2, то у2 — х2=1 и
dz _	х2	х2 _	1
dx~ j/i j- х2 КГ+х2"- —	14-х2- 14-х2'
1575.	Найти частные производные сложной функции z = x2lny, где х = -j , y = uv.
Решение. Находим сначала частные производные данных функций;
дг _	дг _ х2. дх _ 1 _ дх _ _ и	ду _	ду _
дх~ Х П ду~ у ’ ди ~ v ’ dv —	v2’ du~~V' du~~U'
По формуле (2) находим производные от сложной функции г (и, о):
dz п ,	1 , х2 „ и , . . 1 . и2 1
= 2х In у  --Р — v = 2 — In (ио)---—j • — v =
ди	v у v	v V2 uv
= ~ [2 In («о)4-1]; д~ = 2х\пу[-~^ + Х^-и =
= —2 — 1п («о) -, +v-'B=-3 [~2 In («о)-|-1].
V ' V2 V2 UV V3
1576.	Найти производную^ сложной функции и ~ tg (3%4-2у2— х	1	1/--
—г), где у = -, г = ]/ х.
327
Решение. Применяем формулу (4), где надо считать t—x и -^-—1:
cos2 (Зх + 2у2 — г)	х2) cos2 (Зх + 2//2 —г) 2 |гх
1	/о 4г/	1	\	1	1Л-
=--------------------------— 3----------- ----, где г/= —, г=( х .
cos2 (Зх + 2 г/2 — г) \ х2 2 |х ]	х
1577.	Найти если z —е2*2-2''2, где x = cos t, у — sin/.
dt’	’
1578.	Найти —, если г = In sinгде х = 3(2, у = ]/724-1.
dt'	Vy ’
1579.	Найти —, если и = —=-1=^-, где х — R cost, y~Rsint, dt'	|V2 + +
z = H.
1580.	Найти df- если z = u71, где u = sinx, v = 2x.
dx’	’
1581.	Найти ?г и дг, если z = arctg —, где x = «.siny, « = «cosi>.
ди до ’	У
1582.	Найти и ^2, если z = ln(ev + ey), где у — х2. (JX	(л X
1583.	Показать, что если функция	дифференцируемая,
дг . дг п
то она удовлетворяет соотношению х-^+//^ = 0.
2.	Неязная функция одной переменной. Функция у называется неявной функцией от х, если она задана уравнением
Л (х, «/)=Q
(5)
не разрешенным относительно у. Это значит, что при каждом значении х = х0, при котором неявная функция определена, она принимает такое значение у0, для которого F (х0, z/o) = O.
Если Л(х, у) — дифференцируемая функция переменных х и у и F' (х, г/)^0, то определяемая уравнением (5) неявная функция имеет производную, которая вычисляется по формуле
dy______F'x{x, у)
dx ~ F'y(x, у) ’
(6)
Заметим, что эта формула выражает производную через х и у. Поэтому для „ dy
нахождения частного значения производной надо знать не только значение аргумента х=х0, но и соответствующее ему значение неявной функции у0. Последующие производные неявной функции находятся последовательным дифференцированием равенства (6), при этом учитывается, что у есть функция от х.
1584. Функция у(х) задана уравнением 1 -\-ху — In (ex-v-\-ё~хУ) = 0; dy d2y наити ~~ и dx dx2
328
Решение. В данном случае F (х, у)= 1 -\-ху—In (ехУ -\-е~хУ), поэтому
1	2/7Р“л‘^
^4-—
1	^хе~хУ
FУ = Х ~ сху^е-ху ^еХУ ~е XlJ)x= gxyj^g-xy > следовательно,
2ye~xlJ
dy F'x_	еху_^е-ху _	у
dx ~~ F’y ~ 2xe~x,J ~	х ‘
еху^_е-ху
Считая в этом равенстве у функцией от х и дифференцируя его, найдем вторую производную неявной функции. При этом используем уже найденное выражение первой производной:
dy ,	! У \
„	х~- — у-\ х — х- — у
<Ру __ dx ____________ х /	_ 2у
dx? ха	хг	х- '
1385. Найти g и g, если g + £=l.
1586.	Найти ~ и если In ]/х2 + У“ — aretg dx dx2’	r ' J ° x
1587.	Найти —, если y—l-\-yx.
1588.	Найти значение производной при х — у = а, если х3+ -\-у3 = 2аху.
3. Неявная функция двух переменных. Функция 2 называется неявной функцией от х н у, если она задается уравнением
F (х, у, г) = 0,	(7)
не разрешенным относительно 2. Это значит, что при каждых значениях аргументов х—х0 и у — у0, из области определения неявной функции, она принимает такое значение г0, для которого F (х0, Уо, го)—0. Если F (х, у, г) дифференцируемая функция грех переменных х, у, г и F'z (х, у, г) =4 0, то определяемая уравнением (7) неявная функция 2 = г (х, (/) также дифференцируема, и ее частные производные находятся по формулам
dz F'x(x, у, г) дг F'y(x, у, г)
дх~ ~ "Е;(х, у, г) ’ ду ~ ~ F'z (х, у, г) '
1589.	Найти частные производные функции г (.г, у), заданной ха . г/2 , г2 , уравнением -2-	= 1.
Решение. В данном случае
Г (х, у, z) = :v + ^ +v - Ь
,	v 1 J ' а2 о2	с2
Поэтому
Г. __2* F. _2_У F> __2z
Гх— аъ> 2 у	J2 са •
329
Следовательно, по формуле (8), 2х dz^_ -дх~ 2z ' с2
~У с"“х	dz 	b2 _ с2у
а2г ’ ду~	2г Ь2г '
с2
1590.	Найти полный дифференциал функции z(x, у), заданной уравнением z3 — Зхуг = а3.
Решение. Здесь F (х, у, z) = z3-— Зхуг —а3 и
F'x ——Зуг, F'y = —3xz, F'z = 3z2 — 3xy.
По формуле (8) найдем частные производные:
dz _ yz dz_ xz _
dx~ 'z2- -xy’ dy~ z2 — xy’ следовательно,
, dz , . dz , yz , . xz dz = т dx 4- _- dy = -----dx + -=-----dy.
dx dy z2-xy z2 — xy
Можно найти dz и другим способом. Беря дифференциалы правой и левой частей данного уравнения, получим
d (z3 — Зхуг) .-= d (о3) = 0, d (z3) — 3d (xyz) — 0, 3z2 dz —3 (xy dz-Fxz dy-j-yz dx)=0,
(z2—xy) dz—yz dx—xz dy — O.
Отсюда находим полный дифференциал dz;
Поскольку в выражении равны частным производным dz dz и для нахождения и
полного дифференциала коэффициенты при dx и dy dz dz	,
и -х- то этот способ можно использовать также dx dy’
1591.	Найти	dz дх	dz и л-	если х1 -ф у2 4- г2 — 2хг = 1.
1592.	Найти	dz,	если	xyz = x + y + z.
1593.	Найти	дг дх’	дг к И dy	dz, если cos2 х 4- cos2 у 4~ cos2 г = 1 X
1594.	Найти	dz,	если	z = yez'
§ 4. КАСАТЕЛЬНАЯ ПЛОСКОСТЬ И НОРМАЛЬ К ПОВЕРХНОСТИ
Пусть F — некоторая поверхность и Ми (х„, у0, г()) — какая-либо точка на иен. Касательной плоскостью л к поверхности F в точке /Ио называется плоскость, в которой расположены касательные к всевозможным кривым, проведенным на поверхности F через точку Мо. Нормалью п к поверхности называется прямая, проходящая через точку Л1о перпендикулярно касательной плоскости. Чтобы написать уравнение касательной плоскости л в точке Мо, надо знать вектор
330
N {А, В, С}, идущий по нормали (рис. 172). Тогда уравнение я запишется в виде (см. гл. III, § 1)
А(х— х,,) У-В (у </,,)= С (г— го)=О,	(1)
а уравнения нормали п так:
х—х„ _ у—уй _ г — г0
АВС'	' ’
Если поверхность задана уравнением, разрешенным относительно z: z = = f (х, у), то координаты нормального вектора вычисляются по формулам
А=д^’ У^, B=dl^L с=-\.	(3)
дх ’	ду ’	’ ’
В этом случае точка Л1о задается значениями х = хй и у = уй, а г0 находится из
уравнения поверхности z0 = /(x0, уа).
Если поверхность задана уравнением, не разрешенным относительно г: Fix, у, г) = 0, то координаты вектора N вычисляются по формулам
А = dF (х0, у9, г0) дх ’
_ dF (ха, у0, г0) ду
с = dF(xa, у0, г„) dz ’ v ’
а координаты заданной точки Мо должны удовлетворять уравнению поверхности, т. е. F (х„, у,„ го) = О.
Рис. 172
1595. Написать уравнение касательной плоскости и нормали к параболоиду z = x2 + y2 в точке Мо, где х0 = 1, у0 = —2.
Решен не. Находим прежде всего г0:
го = ХиА-Уо~ 1 4~( —2)2 = 5,
затем частные производные:
* „
, =--2х, дх
дг ду
— 2у.
Подставляя в них координаты точки Мо (1; —2; 5), получим, согласно формуле (3), координаты вектора N, перпендикулярного поверхности параболоида в данной точке:
А = f*') =2х0 = 2, В=(^г} = 2у0 = —4, С=-1.
•	\дх/0	\dyjo
Следовательно, касательная плоскость имеет уравнение
2 (х — 1) — 4 (г/4-2) — (г — 5) = 0, или 2х — 4г/ — г — 5 = 0; уравнение нормали
х — 1 __ у 4- 2 z — 5
2~~ —4
1596.	Найти уравнение касательной плоскости к сфере х2 + у2 -f-Н-г2=4 в точке Мо, где у0=1, г0=]/3.
331
Решение. Подставляя у0 й za в уравнение сферы, находим x0 = t>, т- ё. Л'1О (0, 1,	)• Сфера записывается уравнением
F (х, у, г,) =x2 + p24-z2 —4 = 0, откуда
F; = 2x, ^ = 2р, В’г~2г.
Согласно формуле (4), имеем
А = F’x (Мо) = 2х„ = О, В = F't/ (Мо) =2уп = 2, С = F'z (/И„) = 2г0 = 2^, поэтому уравнение касательной плоскости следующее:
0(х-0) + 2(г/-1) + 2Кз’(2-|/'3) =0, или p + J/Зг-4 =0.
Эта плоскость параллельна оси Ох.
1597.	К эллипсоиду лл-!~2//2 — Зг2 = 21 провести касательные плоскости, которые были бы параллельны плоскости х-)-4у 4-6г = 0.
Решение. В данном случае F {х, у, г) = х2 + 2р2Зг2 — 21, поэтому
^=2х, р; = 4р, f; = 6z.
Пусть Мв (х0, у0, г0) — точка, в которой касательная плоскость параллельна данной плоскости x + 4p + 6z = 0. В этом’ случае вектор N нормали к поверхности имеет координаты
А = 2х0, В — 4р0, С = 6г0.
По условию он ортогонален и заданной плоскости. Это значит, что его координаты пропорциональны коэффициентам (1, 4, 6) уравнения данной плоскости, т. е.
2х„	4;/„	6г„	п
-у-=	= g--, или уп = г„ = 2х0.
Кроме того, точка Л40 лежит на эллипсоиде, т. е.
л-'о 4” 2p<j 3z 3 = 21.
Подставляя сюда значения уп и г0, выраженные через ха, получим
Xi~\-2 (2х0)2-|-3 (2х0)2 = 21, т. е. X; = 1, х0 = ±. 1.
Следовательно, условию задачи удовлетворяют точки Л4'(1, 2, 2) и /ИД-1, -2, —2).
Для точки М’>
А = 2х„ = 2, В = 4уа = 8, С = 6.?„ = 12, уравнение касательной плоскости
2 (х — 1) + 8 (у — 2) -|-12 (г — 2) = 0, или х-|-4(/-’-6г — 21 = 0.
Аналогично, искомая касательная плоскость, проходящая через точку /Щ, имеет уравнение
х4-4«/4-6г4-21 =0.
В данной точке Мо найти уравнения касательной плоскости и нормали к следующим поверхностям:
1598.	х2у? + 2х2г-Зхуг + 2=0, Мо(1, 0, —1).
1599.	^ + ^-^ = 0 (конус), Л40(4, 3, 4).
1600,	х2 + 2у2 —4г2=5 (однополостный гиперболоид), Л40 (1, 2, 1).
332
1601.	z — x2 — у2 (гиперболический параболоид), Л40(1, 1, 0).
1602.	Показать, что конус г2 = х2 ф- у2 и сфера х2 ф- у2 ф-(г — 2)2 = 2 касаются друг друга в точке Л4о(О, 1, 1).
Указание. Показать, что у этих поверхностей в точке Л1П общая касательная плоскость.
1603.	На поверхности х2 ф-у2 — г2 — 2х — 0 найти точки, в которых касательная плоскость параллельна координатной плоскости xOz.
1604.	Доказать, что сферы (х — а)2 ф- у2 г2 = а2 и х2 ф- (у — Ь)2 ф-+ г2 = 62 ортогональны друг другу в любой точке пересечения.
Указание. Записать, что точка Мо, лежащая на линии пересечения сфер, удовлетворяет как обоим их уравнениям, так и сумме этих уравнений. Используя это, показать, что скалярное произведение нормальных векторов к сферам в точке Л10 равно нулю.
§ 5. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
Частными производными второго порядка функции z = f (х, у) называются дг дг частные производные от ее первых производных —, т. е.
й2г_ф (дг\ dx2~ дх\дх!
ф /Эг\ ду ду ’
Частные производные второго порядка обозначаются также символами
|	У), f"xy<x’ У)’	у), 1"у(х, у).
в' Аналогично определяются и обозначаются частные производные более высо-
I	-	ф	д2г д-г )
К ких порядков. Смешанные производные ^(например, и * отличающиеся Е только порядком дифференцирования, равны между собой при условии их непре-Г' рывности.
| Дифференциалы второго, третьего и т. д. порядков от функции z—f(x, у)
I определяются формулами d2z = rf(rfz), rf!z = d (d-z) и т. д. Они выражаются через J частные производные следующим образом:
», д-г	, „ , _ дгг	д2г	, „	„ д-г	, , , „ д3г	, . , ,
d~г — 3~, dx- ф- 2 г-д- dx dy - - <7>- dtp, d3z — , dx3 -- 3	, dx2dy +
dx- ' dx dy	dy-	'	дх“ dxldy
, Q д3г	<pz
--3	„ dx dy2 ф . dy ’ и t. д.
dxdy- J dy - J
|; Производные и дифференциалы высших порядков функции большего числа | переменных определяются аналогично.
I 1605. Найти вторые частные прозводные функции z = 1п (х2 ф-у2;. {убедиться, что =
1.	Решение. Находим сначала первые производные:
R'	dz	19 V
I	S - С" и+»>!.; -	+я; -	.
333
Дифференцируя каждую из полученных производных по х и по у, получим ВТО' рые частные производные:
52г д /дг\ f 2х V лЛ'2_'~^2 — х-2х_2(у2— х2)
дх2	дх \дхj	\х2 -ф у2].у	(х2 у2)2	(х2 + у2)2 ’
д (Oz\ ( 2х V___________2Л_____2t —_____
ду дх~ду \дх)	~ \х2у2‘у~	(х'-\-у2^	У~	(х2ф-ф)2	’
_ д !dz\ ! 2у \'___________2у .	=	4ху
дх ду ~ дх \ду, \х2 ф у2 'х (х2 ф у2)2	(х2 ф- у2)2 ’
&2г _ д ! dz \ _! 2у у х2+у2-у-2у _ 2 (х2 - г/2)
ду2 ~ ду \ду, 1~~\х2 ф у2;у~	(х2+у2)2	’ (.Ффф3)3 ’
_	<52г
Отсюда видно, что смешанные частные производные 
ресио отметить, что для данной функции производные
д2г	,, „
и равны. Ипте-дудх д2г д2г и отличаются <3х2 ду'
только знаком, т. е.
Это уравнение называется уравнением Лапласа. Мы доказали, что In (л--—!--//') есть одно из решений уравнения Лапласа.
1606.	Найти если z = sinw.
ду дх2 ’
Решение. Дифференцируем данную функцию дважды по х и затем еще раз по у.
дх = (sm ху)х cos ху (ху)х = у cos ху,
°дх2 = (У cos ху)х = —у2 sin ху,
д2г
дУПуу = (“у2 Sin xy^i =~2у sin ху ~ xyl cos ху-
1607.	Найти дифференциал второго порядка функции
г = Зхгу — 2ху + г/2 — 1.
Решение. Находим первые и вторые частные производные: дг с	_ дг
дх = 6ХУ ~2у’ ду = Зх ~ 2х + 2у'
д2г с	д2г „	„ д2г о
-6х— 2,	-=2.
дх2 дх ду	ду2
Следовательно по формуле (1),
d2z =6г/ rfx2 + 2 (6х — 2) dx dy-\-2dij2-
Тот же результат можно получить и другим путем. Найдем сначала первый дифференциал данной функции:
dz = 3d (х2у) — 2d (ху) -ф d (у2 — 1) --= Зх2 dy -ф вху dx — 2xdy — 2ydx-{-
-\-2у dy = (&xy—2y) dx-y (Зх2 — 2хф-2у) dy.
334
Беря дифференциал от dz, найдем d2z, при этом dx и dy надо считан, постоянными:
d2z = d [(&ху — 2у) dx -ф (Зх2 — 2х ф- 2у) dy] — (6х dy ф- бу dx — 2dy) dx ф-
+ (6xdx — 2dx-\-2dy) dy — &y dx2 -|- (12x — 4) dx dy \-2dy2.
1608.	Найти d2u, если u = xyz.
Решен иe. Для данной функции
du = d (xyz) : yz dx-'- xz dy ф-xy dz, поэтому
d2u = d (du) — d (yz) dx ф- d (xz) dy ф- d (xy) dz = (z dy ф- у dz) dx ф-ф- ( z dxф-x dz) dy ф- (у dxф-x dy) dz = 2z dx dy ф-2y dz dx ф-2x dy dz.
1609.	Найти вторые частные производные функции z= V 2ху + у3.
1610.	Найти ^4-, если z = arctg дх ду ’	° 1 — ху
1611.	Найти -^яи-. , если u = x3y5z1. дх ду dz1	и
1612. Доказать, нению Лапласа
что функция и
______j______ 1''х2ф-у2ф-г2
удовлетворяет урав-
д2и . д2и . д2и_____q
дх2 + ду2 dz2 ~~ U
1613. Доказать, что функция и
1 -W
= ——~е	удовлетворяет урав-
ди д2и
нению теплопроводности -у7 = ,-2 .
С/ V	X/ Лг
1614.	Найти d?z, если z = xlny-.
X
1615.	Найти d3z, если г = (Д'cos у.
1616.	Найти d3z, если z = х3у3-[ Зху.
§ 6. ЭКСТРЕМУМЫ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
1. Экстремум в точке. Функция z=f(x, у) имеет в точке Ро (х0, у0) максимум (соответственно, минимум), если найдется такая окрестность точки Рп, для всех точек Р (х, у) которой выполняется неравенство f (х0, z/0) > f (х, у) [соответственно f (х0, y»)<.f(x, у)]. Слова «максимум» и «минимум» можно заменить одним «экстремум». Аналогично определяется экстремум функции трех и большего числа переменных.
Всякая дифференцируемая функция нескольких переменных может достигать экстремума только в тех точках, в которых все ее частные производные обращаются в ноль. Такие точки называются стационарными.. Например, для дифференцируемой функции z = f(x, у) стационарные точки Р0(х0, у0) находятся путем решения системы уравнений
Д(г, 4/)-0,
(1) Гу(х, у)=0.
Условия (1) являются необходимыми условиями экстремума; их геометрический смысл состоит в том, что в стационарной точке касательная плоскость к поверх
335
ности z-— f(x, у) параллельна плоскости хОу. Однако не все стационарные точки обязательно являются точками экстремума. Каждая из этих точек должна быть проверена на экстремум с помощью достаточных условий экстремума. Обозначим:
r — f'xx(x0' Уо), S=f"X!/(x0, у о),	(2)
^=/^(-<0. f/o). Ь = Н-&.
Если в стационарной точке Ро (.г0, уи):
1)	А > 0 и г > 0, то Ро есть точка минимума, А > 0 и г < 0, то Рд есть точка максимума;
2)	А < 0, то в точке Ро экстремума нет;
3)	Д = 0, то требуется дополнительное исследование.
1617.	Найти экстремумы функции z = x1 + //4 — 2л1 +$ху — 2у2.
Решение. Находим частные производные: л?	dz
= 4х3 — 4х + 4у,	= 4у3 + 4х — 4у.
Приравнивая эти производные нулю, получим систему уравнений
х3-х-\-у = 0, у3-\-х—у = 0,
из которой определятся стационарные точки данной функции. Складывая эти уравнения, получим
л-3 + +~=0, т. е. у3 =—х3
и, следовательно, у =— х. Подставляя эго в первое из уравнений, найдем значения х;
х3— 2х = 0, х (№ — 2)=0.
Отсюда Д',—0, x2 —К+ х3 =—1^2, а тогда //, = 0, уг — —К2, уз~/й-Таким образом, имеются три стационарные точки:
4+10,0), М3(К2, -1/2), /И3(-К2, К2).
Проверяем эти точки на экстремум с помощью достаточных условий. Для этого найдем сначала вторые частные производные:
d2Z	. д2г . д2г 1О „ ,
л . = 12х—4, -т—~ 4,	— 12//-— 4.
дх3	дхду ау1
координаты стационарных точек, получим:
Л1г. г = — 4, s = 4, t = — 4, А=/7 —s2 = 0;
М.,: r = 20>0, 8 = 4, ( = 20, A = rt — s2 = 384 > 0;
= 20 >0, s = 4, if = 20, A = r/ —s2 = 384 >0.
0 и r > 0, так что это точки минимума функции. В этих
Подставляя сюда
1)	для точки
2)	для точки
3)	для точки М3: г
В точках /И3 и /И3 А >
точках значения функции z равны
zmi,, = 4 + 4-2-2 + 4 (- 2)—2-2 = —8.
В точке /И, А = 0, и достаточный признак ответа не дает. Дополнительным исследованием можно установить, что в начале координат функция z экстремума не имеет. В самом деле, в этой точке z = 0, а в любой окрестности начала координат имеются точки, в которых значения г могут быть как положительными, так и отрицательными. Например, вдоль осн Ох (т. е. при у = 0)
z = х* — 2№ = — х2 (2 — х2) <0
вблизи начала координат, а вдоль биссектрисы у = х
г = № + .с1 — 2.С + 4.V2 — 2х2 = 2.Д > 0.
336
1618.	Найти экстремумы функции z — 1 +6х — xs — ху — yz.
Решение. Находим частные производные:
дг „ „ дг
дх	ду	J
Стационарные точки удовлетворяют системе уравнений
6 — 2х — у —0, х-\-2у — 0.
Решение этой системы: х0 = 4, у0 =—2. Следовательно, данная функция имеет только одну стационарную точку Р0(4, —2).
Вторые частные производные данной функции постоянны:
(»	62z	д2г = _о
дх2 ' дх ду ’ ду3
поэтому в любой точке, в том числе и в точке Ро,
r — —2, S----—1, 7 = —2, S = rl — s2 — 3.
Поскольку А > О, а г <10, то точка Ро есть точка максимума данной функции. При этом
zmax = z (Ро)= 1-f-6 • 4—16 —4 (—2)—-4= 13.
Исследовать на максимум и минимум следующие функции:
1619.	z = х2 + ху + у2 — 2х — у.
1620.	z==x°y2 (6 — х — у).
1621.	г = х2 + ху + у2+ ’ + у при х>0, у>0.
1622.	z — e~xi~yt (2x2-'rz/2).
2. Экстремум в области. Рассмотренные выше экстремумы функции по самому своему определению имели локальный характер: в точке экстремума Ро функция принимает максимальное или минимальное значение среди всех ее значений в некоторой (быть может, очень малой) окрестности точки Ро. В ряде задач требуется найти глобальный экстремум, т. е. наибольшее и наименьшее значения функции z = f(x, у) в некоторой замкнутой области D. Для этого надо найти все локальные минимумы и максимумы этой функции внутри области D, а также наибольшее н наименьшее ее значения на границе области, и затем выбрать среди всех этих значений наибольшее и наименьшее.
Локальные максимумы и минимумы дифференцируемой функции z=f(x, у) находятся, как указано в предыдущем пункте. При этом надо рассматривать только те стационарные точки, которые расположены внутри области D. Важно здесь отметить, что нет надобности вычислять вторые производные и использовать достаточные условия экстремума. Поскольку все экстремумы функции z = = /(.г, у) находятся среди ее значений в стационарных точках, достаточно узнать значения функции г во всех стационарных точках и среди них выбрать наибольшее н наименьшее. Как правило, граница области D разбивается на ряд участков, каждый из которых определяется уравнением вида
у—-ф(х) (а ' х  "Ь), или х — ср (у) (с- у- rf).
Поэтому вдоль такого участка границы функция z = f(x, у) превращается в функцию только от одного х (или у)
2=f(X, ф(х)) (или Z=/(tp(y), у).
В общем случае граница области D задается параметрически:
х = ф(0.
337
В этом случае функция 2 превращается вдоль границы в функцию параметра t ф(/)) (а ==?/ ===₽).
Поэтому задача нахождения наибольшего и наименьшего значений функции z — — f (х, у) на границе области D сводится к отысканию наибольшего и наименьшего значений функции одной переменной.
1623. Найти наибольшее и наименьшее значения функции z — х-у (2—х — у) в треугольнике, ограниченном прямыми х- 0, z/= 0, ху — 6 (рис. 173).
Решение. Найдем стационарные точки, лежащие внутри данного треугольника:
dz
-д- — 4ху — Зх2у — 2ху2 = ху (4 — Зх—2у), dz
_. = 2х2 — х3 — 2х2у = х2 (2 — х — 2р).
Приравнивая производные нулю, можно на х и у сократить, так как внутри треугольника и х > 0, и у > 0, тогда
4 — Зх—2у = 0, 2 — х — 2у = 0.
Решение этой системы: x0=L Уо— Стационарная точка внутри треугольника. Значение функции г в этой точке
1 \
2 )
Ро[1,
лежит
г0=г(Р„) = 1-1^2-1-1)
4 ’
На сторонах треугольника х = 0 и у = 0 значения функции z равны нулю. Найдем ее наибольшее и наименьшее значения на стороне х-\-у = 6. На ней
у — 6 — х	(0 х 6)
и
z = z (х) — х2 (6 — х) (2 —х — 6Ц-х) = — 4x2 (6 - х).
На концах интервала z(0) = z(6)=0. Стационарные точки находим из уравнения г' (х) = 0:
—48х + 12х2 = 0, 12х(х—4) = 0.
Отсюда т = 4 (так как х = 0 — граничная точка); при этом у = 2, z = — 4- 16(6-4) =—128.
Итак, наибольшее и наименьшее значения функции г в надо искать среди следующих ее значений:
1	Л
z= — —внутри треугольника, в точке II,
данном треугольнике
П
2/’
2=0 — на сторонах х = 0 и у = 0 (в том числе и в вершинах)) Z — —128 —на стороне х-фр = 6, в точке (4, 2).
Отсюда видно, что наибольшее значение z= Данная функция принимает
внутри треугольника, в точке Ро нице, в точке (4, 2).
338
, а наименьшее z =—128—на его гра-
1624.	Найти наибольшее и наименьшее значения функции г— = х 4- у в круге х2у- 1.
Решение. Стационарных точек функция не имеет, так как
dz _ дг дх ~~ ду
= 1^0,
поэтому наибольшее и наименьшее значения она может принимать только на границе области, т. е. на окружности
х2 4- У'~ = 1 •
Параметрические уравнения этой окружности:
х — cos t, у = sin t (0 -S t s: 2л.).
На окружности z становится функцией от /;
z = z (i‘) = cos sin t.
Ищем стационарные точки этой функции:
z‘ (/) — —sin /-|-cos /— О, т. е. sin/ = cos/, отсюда
fi- 4 , h- 4 , в этих точках
[ л \ л . . я . /-г	1-^2
21=г! 4 j =- cos -4 + sin 4= ) 2, x1^yl =- 2 , /5л \ 5я . . 5л ,r=	1^2
z2 = ? 1^-4- j = COS -J- 4- sm = — v 2 , x2 = y2 = — 2~.
Тем самым доказано, что наибольшее значение z—],r2 и наименьшее г——]^2 данная функция принимает в граничных точках
//2	__/2\
\ 2’’ 2 / ” к 2 ’	2'
1625.	Из всех треугольников данного периметра 2р найти тот, который имеет наибольшую площадь.
Решение. Пусть а, Ь, с —стороны искомого треугольника. Положим а = х, Ь = у, тогда с = 2р — х — у. Как показано в 1509, площадь треугольника определяется функцией	_______________________
S = Vp(p—х) (р~у) (х+у-р).
Легко подсчитать, что
dS_ =	Р(Р~~У) (2р—2х~у) dS = Р(Р—х)(2р—х—2у)
дх 2V р(р—х)(р—у)(х+у~р)’ ду 2 У р (р—х) (р—у) (х-\-у—рУ
В треугольнике сторона не может превышать полупериметра: х<р, У<р, т. е. р — х^О и p—y^zO, поэтому равенства ^~=0 и = ® сведутся к системе
2р—2х — у = 0, 2р — х—2у = 0.
2р ..
Отсюда находим стационарную точку х0 = р0= Очевидно, при этом пло-О
щадь треугольника максимальна, так как наименьшего значения площадь тре
339
угольника с данным периметром не имеет. Всегда можно построить треугольник данного периметра сколь угодно малой площади (при х-^р, у —>р, с —0 пло-2р
щадь S—>0). Но если две стороны а = Ь=	, то третья сторона с. — 2р — а — b =
2р „
—	. Следовательно, искомым треугольник равносторонним.
1626.	Найти наибольшее и наименьшее значения функции z — х2 — у2 в круге х2 + у2^1.
1627.	Найти наибольшее и наименьшее значения функции z = — х3-ту' — Зху в прямоугольнике	—1'<-у-у2.
1628.	Найти наибольшее и наименьшее значения функции z = = х2 — 2уг 4~4ху — 6х — 1 в треугольнике, ограниченном прямыми х = 0, z/ = 0, х'-\-у = 3.
1629.	Найти прямоугольный параллелепипед данной поверхности S, имеющий наибольший объем V.
1630.	Представить положительное число а в виде произведения трех положительных сомножителей так, чтобы их сумма была наименьшей.
ГЛАВА X
КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
§ 1. ДВОЙНОЙ ИНТЕГРАЛ
1. Определение и вычисление двойного интеграла. Пусть функция г=/(Р) = = f (х, у) задана в некоторой ограниченной замкнутой области D на плоскости хОу. Разобьем эту область сеткой кривых на ячейки sb sa, sn. В каждой ячейке Si (i — 1, 2, 3, ..., п) выберем произвольную точку Р, (х;, у,) и умножим значение функции f в этой точке на площадь As,- ячейки s,. Сумма таких произведений по всем ячейкам
называется интегральной суммой.
Обозначим через d (s/) диаметр ячейки s,-, т. е. расстояние между наиболее удаленными точками этой ячейки; max d (s;) — наибольший из диаметров всех ячеек данного разбиения.
Двойным интегралом J j f (Р) ds от функции j (Р) по области D называется предел интегральных сумм при условии max d(si)0, т. е. при неограниченном увеличении числа ячеек, когда все ячейки стягиваются в точку,
Ф(Р)Л = '£)
п
Нт У
го ах d	—> 0 у __ j
f (Pi) As/-
Если такой предел существует, то функция f (Р) называется интегрируемой
в области D. Всякая непрерывная в ограниченной замкнутой области D функция f(P) интегрируема в ней. В дальнейшем мы ограничимся рассмотрением только непрерывных функций.
Простейшие свойства
1)	Если / (Р) = С/,(Р), то
^f(P)ds = Cj (P)rfs. 'D
2)	Если f {P)=-fv (P) ± /2 (P), to
И ДР) rfs = jjA (P) ds + j j f 2(P) ds.
D	'D	D
3)	Если область D состоит из двух областей Dr и О2 (рис. 174), то \\f{P)ds^\<if(P)ds+\\f{P)ds.
~Г> Dt	Ъг
341
В декартовых координатах элемент площади ds обычно записывается в виде ds—dxdy, а двойной интеграл обозначают
$ V (*, у) dx dy.
Область D на плоскости хОу назовем простой областью: 1) (относительно оси Ох) если она ограничена сверху линией у~<рз(х), снизу y — [функции од (л-) и <р»(х) непрерывны] и с боков отрезками прямых х=а и х — Ь (рис. 175);
в частных случаях один из этих отрезков (или оба вместе) могут превратиться в точку (рис. 176);
2) (относительно оси Оу), если *=1’2 (Ю [функции ^(у) и ф., (у) мых y — d и у~с (рис. 177, 178).
она ограничена слева линией х=фх (у), справа непрерывны] и сверху и снизу отрезками пря-
В случае простой области вида 1) всякая прямая, параллельная оси Оу и проходящая внутри отрезка [а, б], пересекает границу области в двух точках (см. рис. 175). Двойной интеграл по такой области вычисляется по формуле
6	<₽2 U)
И / (*, У") dx dy = j dx j f (x, y) dy.	(1)
£>	а ф, (*)
Здесь внутренний интеграл / (х, у) dy берется по у при фиксированном, но <PiW
произвольном в отрезке [а. 6] значении х от нижней границы области D до ее
342
верхней границы (т. е. по отрезку /<L). В результате получается некоторая функция от х, которая интегрируется затем по отрезку [а, й].
Если же область D есть простая область вида 2), то всякая прямая, параллельная оси Ох и проходящая внутри отрезка [с, d], пересекает границу области в двух точках (см. рис. 177). Двойной интеграл по такой области вычисляется по формуле
d 4’г (У)
J f (х, у) dx dy = \ dy f (х, у) dx.	(2)
'D
Наиболее простой вид формулы (1) области D, ограниченной прямыми »х = а, x = b, у = с, y — d (рис. 179): ь d
jj р (х, у) dx dy = $ dx \ f (x, y) dy =
(2) принимают в случае прямоугольной
и
У
У=а.
У=с
О
а
Рис. 179
X
ъ
~\dy^f (.v, y) dx.	(3)
c a
Следует заметить, что если область D не является простой областью, то ее разбивают на конечное число простых областей Dlt D2, ..., Dn и при вычислении двойного интеграла по области D используется третье свойство двойного интеграла.
Замечание. Аналогичные определения и формулы могут быть полу-
чены и тогда, когда область D лежит либо в плоскости хОг, либо в плоскости уОг. Например, если ограниченная замкнутая область D лежит в плоскости xOz и является простой относительно оси Ог, а в ней задана непрерывная функция г/ = /(х, г), то
h 7.2 (z) f (Р) ds = j f (х, г) dx dz = j dz ( f (x, г) dx
'D	D	e
И T. Д.
При изучении материала § 1—6 необходимо учитывать это замечание.
1631. Вычислить двойной интеграл	(х + у3)б1хс1у по прямоуголь-
D
ной области D, ограниченной прямыми х=1, х = 2, у = 0 и у = 2.
Решение. Вычисляем данный интеграл по формуле (3):
( j (*+Р3) dx dy = j dx j (x-|-r/3) dy.
D	I 0
Внутренний интеграл вычисляем, считая х постоянным:
р	I и1\ |2	21
(х + у3) dy = (ху + j |о = х • 2 + - - = 2х + 4. б
Полученную функцию от х интегрируем по отрезку [1, 2]:
(т+р3) dxdy= \ (2х + 4) dx=^2 -у4-
=2‘-4-4-2—1-4 = 44-8—1 — 4=7.
343
Обычно вычисление внутреннего интеграла отдельно не делают, а все выкладки записывают в одну строку следующим образом:
2	2	2
§ (х+У3) dx dy = ( dx (х + у3) dy = (ху + у-- |'dx « d	Io	i
Г	)2
=; \ (2х-|-4) dx — (х24-4х) j =4 + 8 — 1 — 1 = Z.
Такой записью мы и будем пользоваться в дальнейшем.
1632. Вычислить двойной интеграл ^^-—dydz, если область
D
D ограничена параболами z — y-и у — z2.
Решение. Область D (рис. 180) — простая относительно осн Оу. Она имеет нижнюю границу z = y2 и верхнюю границу у = г2, т. е. z = |/y (перед радикалом ставим только знак «+», так как область D находится в той части плоскости уОг, где г > 0). При любом фиксированном значении у из отрезка [0, 1] г меняется от 2 = у'2 до z — \ry, поэтому имеем
у In у dy —
1п у — 2 In у j dy — —
по
Интеграл у 1п у dy взят методом интегрирования подстановке нижнего предела использован тот факт, что lim уа1пу = 0.
0->О
частям, причем при
У
.1633. Вычислить двойной интеграл dxdy, если область D ограничена *сг
кривой х —2-4-sinz/ и прямыми х = 0, у —у — 2л.
Решение. Область D (рис. 181) является простой относительно оси Оу. Левая ее граница х = 0, а правая x = 2 + sin у. При любом фиксированном значении у из отрезка [0, 2л] х меняется от x=Q до х — 2 + sin у, поэтому по фор-
Рис. 181
34-1-
муле (2) имеем
2л 2 + sin I/	2л .	2л
\^dxdy^\dy f ±rfx = -^^|2o + s,n,/dy = ^	(2 + siny)My =
х>	о о	о	'о
2л	2л
1 i *	1 Г /	1 cos 2 у \
\ (4 + 4 sin у + sin2 у) dy =	\ 4 + 4 sin у +  --- \dy —
6	о К
2Л
1 С / 9	1	\	1/9	1 Л \ |2л
= -4 \ [у+ 4siny —cos2yUy= 4—4cosy-^-sm2yy|o =
1	9л
= |(9л-4 + 4)=
Вычислить следующие двойные интегралы:
1634.	J$ (х2 + 2у) dx dy, где область D — прямоугольник (0 х sS ^1, о^Дг).
1635.	§ §	где область D — прямоугольник (3sgxsg4,
о
1
1636.	^xydxdy, где область D — треугольник с вершинами
0(0, 0), Л (О, 1), В(1, 0).
1637.	\\2ydxdy, где область D ограничена параболой у —Ух и Ъ
прямыми t/ = 0, х+у = 2.
1638.	y2z~2 dydz, где область D ограничена прямыми у — 2
D л - 1 г~у и гиперболой 2 = у-
1639.	\^exdxdy, где область D ограничена прямыми х = 0, Ъ
у—\, у —2 и кривой х = 1пу.
2.	Перемена порядка интегрирования. Если область D является простой как вида 1), так и вида 2), то применимы обе формулы (1) и (2), следовательно,
ь <f2(x)	d фг (у)
^f(x, y)dxdy=jdx j f (x, у) dy = jdy j f (x, y) dx. 'D	a q>i(x)	c 1)4(1/)
Иными словами, повторное интегрирование не зависит от порядка интегрирования. Этим обстоятельством часто пользуются при вычислении двойного интеграла, выбирая ту из двух формул, которая приводит к более простым выкладкам.
В качестве упражнения на расстановку пределов полезна задача о перемене порядка интегрирования в повторном интеграле
Z) ф2 (х) j dx $ f (х, у) dy. а ф1 (х)
Прежде всего следует начертить область интегрирования D, которая находится в полосе между прямыми х = а и х = Ь и ограничена снизу линией r/ = tpi(x),
345
а сверху-линией у = <р2 (х). Затем область D проектируют иа ось Оу и находят уравнения прямых у = с и y==d, ограничивающих снизу и сверху полосу, в которой расположена область D, затем находят левую границу области D x = ipi ({/) и правую х — зр> (у). Если какая-либо из этих границ состоит из двух или большего числа линий, записанных разными уравнениями, то область D приходится
разбивать иа части, а интеграл--на сумму интегралов по этим частям.
Аналогично, если требуется переменить порядок интегрирования в повторном интеграле
d U’26/)
j dy j f (x, y) dx, с 4>l (//)
то, спроектировав область D на ось Ox, находят уравнения прямых х = а и х = Ь, нижнюю границу области D г/ = Ф1(х) и верхнюю у = <р2 (л)-Иногда область D приходится разбивать на части, а интеграл —на сумму интегралов по этим частям.
1640. В двойном интеграле ЭД f (х, у) dx dy D
расставить пределы для того и другого порядка интегрирования по области D, ограниченной прямыми х = 0, х = 1, у=\ и кривой у = —|/2х — х2.
Решение. Область D (рис. 182) находится в полосе между прямыми х —0 и х=1. Нижняя граница — дуга окружности у = —l/'2х— х2, верхняя — прямая у=1. Следовательно,
1.
j f(x, y)dy.
/2х —X*
Область D проектируется на ось Оу в отрезок [—1, 1]. Левая граница области имеет уравнение у-=—|/2х — х2, т. е.
х= 1 —1^1 — у2 при —и х = 0 при
Правая граница х=1. Разбивая область D на две части и О2, а интеграл — на сумму двух интегралов, получим
0	1	11
ЭД/(х, y)dxdy = j dy	fix, y)dx-\-\ dy\f(x, y)dx.
D	—1	1-Г1—y2	6	°
1641. В двойном интеграле
ЭД f (х, z) dx dz расставить пределы для того и другого порядка интег-D
рирования по области D, которая является параллелограммом с вершинами в точках А (1, 2), В (2, 4), С (2, 7) и 0(1, 5).
Решение. Найдем уравнения границ области D (рис. 183); для АВ z=2x, для ВС х = 2, для CD г=2х-|-3, для DA х=1, так как область D лежит в плоскости xOz. Область D находится в полосе между прямыми х=1 и х = 2 и
346
ограничена снизу прямой z = 2x, а сверху прямой z = 2x-|-3, поэтому
2	2*4-3
jjf(x, z)dxdz = j dx j f(x, z) dz.
D	12*
Для того чтобы расставить пределы в на гри части (см. рис. 183):
Dr j2s£z<4, 1 =Cxs£- |
D., {4sSZ<-5, 1
D3 (5^ z ss 7,	* 2];
получим
2	2x-|-3
f (x, z) dx dz = j dx (' f (x, z) dz —
D	‘1	2*
z
4	"2
= j dz j /(x, z) dx-\-2	1
5	2	7	2
f (x, z)dx~\-^dz \ f (x, z) dx.
4	1	5 z—3
2
другом порядке, разбиваем область D
1642.
Изменить порядок интегрирования в повторном интеграле
I	/2-у2
\dy Ж ?)т/г.
» у
184) расположена в плоскости yOz и между
Решение. Область D (рис.
прямыми у = 0 и у=1. Ее нижняя граница z = y, верхняя -- z—j'2 — у2 • Спроектируем область D иа ось Ог. В результате получим отрезок [О, [ 2 ) Левой границей области D является прямая у = 0, правой на участке [0, 1]— прямая y = z, а на участке [1, |2|-дуга окружности г/=р2 —z3. Поэтому область D следует разбить на две части (Dj и О2), а интеграл— на сумму интегралов:
1.	/ 2 —I/2	1 z
$ dy f (у, z) dz = j dz j f (y, z) dy-\-
О и	0	0
V2 V2—Z2
+ dz j f (y, z) dy.
1	0
Изменить порядок интегрирования в следующих повторных интегралах:
1 х2	2 2х
1643. f (xt у) dy. 1644. ^dx f(x, z)dz.
Ox3	Ox
347
1645. ^dy $ f (у, г) dz.
0 e-y
2a	V 2ax
1646. $ dx f (x, y)dy.
°	V'2ax —x2
1	2-y
1647.	\dy\ f (x, y) dx.
о у
1	3 —2г
1648.	dz f (x, z)dx.
0 Vz
1	1 — 2
1649.	dz f (y, z) dy.
0 —
2 У
1650.	§ dy jj f (x, y) dx.
1 Iny
3. Замена переменных в двойном интеграле. При вычислении двойных интегралов иногда бывает полезно сделать замену переменных. Пусть
и = и(х, у), v = v(x, у)	(4)
— функции, определенные на всей плоскости хОу или в некоторой ее области D и имеющие непрерывные частные производные в области D. Допустим также, что систему уравнений (4) можно однозначно разрешить относительно х и у.
х = х(а, и), у=у(и, о);
(5)
тогда каждой точке М (х, у) из области D будет взаимно однозначно соответствовать пара чисел (к, о), называемых криволинейными координатами этой точки. Если область D расположена в той части плоскости хОу, в которой введены криволинейные координаты и, v, то ’справедлива следующая формула:
f (х, у) dx dy—iif [х (и, о); у (и, о)] | J (и, о) [ du dv.
(6)
где О' —область изменения криволинейных координат и. и о, отвечающая области О, a J (и, о) —якобиан преобразования (5):
дх дх
ди dv _ дх ду дх ду ду ду ди dv dv ди' ди dv
В частности, в полярных координатах формулы (5) имеют вид
Рис. 185
x=pcos<p, у —о sin гр. (7)
Система (7) осуществляет переход от прямоугольных координат х и у к полярным координатам р и гр при условии, что полюс помещен в начале координат и полярная ось направлена вдоль оси Ох. В этом случае | J | = р, и формула (6) принимает вид
y)dxdy—
— \ \ f (р cos ср, р sin <р) р d<p dp.
ly
Если область D ограничена лучами, образующими с полярной осью углы ЧР1 и Фг (ф1<фг). и кривыми р = р1(ф) и Р = р2(ф) (Р1 (ф) < р2 (<р)) (рис. 185), то соответствующие этой области полярные координаты изменяются в пределах
^'{ф1=£ф^ф2>. Pi (Ф) =5 Р =5 р2 (ф)}
348
и тогда
02 (ф)
ЭД /С''. y)dxdy=^ dtp (j f (p cos ф, p sin <p) p dp.	(8)
b	<п рН<р)
Если область D охватывает начало координат, то
2л р (о>)
ЭД/ (•*> У) dx dy — J dtp 'J /(pcostp, p sin q ) о dp,	(9)
d	b 6
где p = p (q;) —полярное уравнение кривой, ограничивающей область D.
Формулы (8) и (9) удобно использовать при решении задач, когда область D есть круг или сектор круга.
Если область D лежит в плоскости хОг или в плоскости yOz, то в обоих случаях | J | = р, но' для плоскости хОг формулы перехода к полярным координатам имеют вид
х — р cos ф, z = р sin ф, а для плоскости уОг
г/ = р cos ф, г — р sin ф.
1651.	Вычислить двойной интеграл
ЭД]/1 -(x2-\-y2)dxdy,
D
если область D ограничена окружностью x2-[-z/2 = I.
Решение. Область D есть круг радиуса 1 с центром в начале координат. Введем полярные координаты. В полярных координатах х2-)-//2 = р2 [см. формулы (7)] и уравнение окружности принимает вид р=1. Тогда по формуле (9) получаем
_________2Л	1 _____
{ ( Г1 — W +1/2) dx dy = ( dtp j К1 — p2 P dp =
D	0	0
1652.	Вычислить двойной интеграл ^zdxdz, если область D
L>
ограничена половиной дуги окружности x2-]-z2 = ax и отрезком оси Ох от точки с абсциссой равной 0 до точки с абсциссой равной а.
Решение. Область D — полукруг. Введем полярные координаты:
х = рсозф, z = p sin ф.
Уравнение окружности в полярных координатах принимает вид р2 = расозф, или р = асозф.
Подынтегральная функция имеет вид г = р.втф. Угол qo меняется от 0 до
л “2
(полукруг находится в I четверти). При каждом фиксированном значении
угла ф р меняется от 0 (в начале координат) до р = цсоЗф (на окружности).
349
Тогда получаем
2 ccostp	2	acostp
^ 'z dx dz = ^ dy $ psintppdp=( sin ydy f p2dp = doo	о	о
2
sin ф •
sin (p cos3(p dy =
цЗ f*
\ cos3rpd (cos q>) =
<5 j
cos’rp V
Л
as
12 '
0
1653.	В двойном интеграле^ f(x, y)dxdy расставить пределы о
интегрирования в полярных координатах, если область D является квадратом с вершинами в точках 0(0, 0), Л(1, 0), В(1, 1), С (0, 1).
Решение. Уравнение стороны ДВ(х=1) в полярных координатах принимает вид о cos q>= 1, или р = —-—, а ВС будет о=-Д—. Угол ср меняется от 0 ' т >	' cos (р	J sin <р	т
до ” (квадрат находится в I четверти). При изменении угла от 0 до Р меня-
„1	пл
ется от 0 до р =----, а при изменении угла от до -- р меняется от 0 до
' cos Ф	4	2'
1
р = ---. Следовательно,
sin <р
Л I	л 1
4 cos ф	2	sititp
П f (а-, у) dx dy^= j dy f (p cos qp, p sin <p) p dp-j~ \ t/гр \ / (p cos ф, p sin ф) p t/p.
D	oo	'л о
7
1654.	Вычислить двойной интеграл J Jj/~ 1	— -bi- dydz, если
D I/2	22
область D ограничена эллипсом+-&2 = 1.
Решение. Для решения этой задачи удобно ввести так называемые обобщенные полярные координаты, положив r/ = apcostp, z = 6psin<p.
Найдем якобиан данного преобразования:
/ =
a cos ф — ар sin ср b sin ф bp cos ф
I cos ф = а&р sin ф
— sin ср cos ф
= abp (со52ф + sin 2ф) = abp и | J ! = abp.
Подынтегральная функция принимает вид
1—	----^3- =	— р2 СО82ф — р2 5Ш2ф = К1 — Р3 (СО52ф-|-5т2ф)=	— р2-
Теперь
имеем
И/
D
Z2
- 2 -dydz = b2
D'
350
Угол гр меняется от 0 до 2л. Уравнение эллипса принимает вид р=1, поэтому р меняется от 0 до Г, тогда
Вычислить следующие двойные интегралы:
1655.	558111 У*2 г У2 dxdy; область D ограничена окружностями л:2 Ц-г/2 = п2, х2г/2 = 4л2.
1656.	JJ (х2-|-z2) dxdz; область D ограничена окружностью х2 + z2 == 2az.
1657.	R2 ~ у2 — z2 du dz; область D ограничена окружностью о	~	_
у2--\-г2 = !^ и прямыми г = у и г = ]/3 у.
В следующих двойных интегралах, перейдя к полярным координатам, расставить пределы интегрирования по переменным <р и р:
1658.	]’Г/(х, y)dxdy; область D ограничена окружностями х24~ D
J-z/2 = 4x, x24-z/2 = 8x и прямыми у — х и у = 2х.
1659.	JJ / (х, z) dxdz; область D ограничена кривой (x24*z2)2 = = а2 (х2 — г2).
1660.	Hf(y, z)dydz; область D ограничена прямыми г = 0, у=1, D
z = y.	_____
1661.	Вычислить двойной интеграл	W^xdy, если
D
№ и*
область D ограничена кривыми +	= L ^- + 4^2- и лежит
в I квадранте.
§ 2. ПРИЛОЖЕНИЯ ДВОЙНОГО ИНТЕГРАЛА
1.	Вычисление площадей плоских областей. Площадь S плоской области D на плоскости хОу вычисляется по формуле
S = у dx dy.
1662.	Вычислить площадь плоской области D, ограниченной прямой у = 2 и параболой у — х2 — 1.
Решение. Область D (рис. 186) можно проектировать и на ось Ох и на ось Оу; спроектируем ее на ось Оу. Область D симметрична относительно оси Оу, поэтому достаточно вычислить площадь правой половины области D и результат удвоить. Правая половина области D проектируется на ось Оу в отрезок
351
[ — 1, 2] и имеет левой границей прямую .г —0, а правой—линию у=лг —1, или л-—р'у-у 1. В результате
2 /УД 2 /УМ 2	з 2
S (* I’ С	Г '----2	__
2 = \ dy \ dx= \ х dy= \ ] у-*--1 dy= — (у4-1)“	= 2р'3,
1 о -10	-1	-1
1663.	Вычислить площадь плоской области D (рис. 187), ограниченной прямыми z = 0, z = x и окружностью х2-\-г2 = 2х.
Решение. Введем полярные координаты x = pcos<p, z — p sin <р, Уравнение окружности, ограничивающей область D, имеет вид p2 = 2pcos ф,. или p=2cosq>.
Угол <р меняется от 0 до ~ и р меняется от 0 до 2costp. Тогда получаем
4	2cos<p	4
S = dtp ? pdp —
6 о	о
4
=	(1 4-cos2q))dcp = '^ф +
sin 2ф \
2 )
2созф	л
*4
йф=2^ cos2(pd<p = о	и
Т
__ л 1
- 4 + у. о
1664. Вычислить площадь
Рис. 188
плоской области D, ограниченной кривой (//2 + z2)2 = 2£zz/i (а>0).
Решение. Введем полярные координаты:
t/ = pcos<p, z = psin<p.
Уравнение кривой имеет вид р4 S 6 = 2ар3 cos3<p, или р = 2а cos3cp. Область О (рис. 188) симметрична относительно оси Оу, поэтому достаточно вычислить площадь верхней половины области D и результат удвоить. Для верхней половины области D угол <р ме-няется от 0 до -у, ар меняется от 0 до
352
2a cos3qp; поэтому
2 2a cos-’ ф
п
7
Sp2
fl
2acos3<p
7
rftp -= 2a2 \ cos°cp dtp
о	о
S
2
fl2
T
(I-|-cos 2ф)3 rfrp u
2
a?> I*
\ (1+3 cos 2(p + 3 cos2 2(p-fcos3 2<p) c/fp ~
о
a2
1
!T+2
ла2
т~
2	/
(I+cos4<p)rf<p4--l \ (1 — sifis2q-) d (sin 2<p) -u
sins2<p ( I:r ла3 Зла3 5ла3
~з~/1,)2 8 + ~ПГ“ ЛГ’
2
+
О
; sin '
\ ф Ч—
sm 2гр
.3o2 '
8 \
с 5ла2 откуда S = —g-
3 ‘2
а2 I
:in 4<p \ I л . a2 I . „
8 V
Найти площади плоских областей, ограниченных следующими
линиями:
1665.	Прямыми г/= 0, х=1 и параболой у — х3 (рис. 189).
1666.	Прямыми х = 0, z = 0, х — 2 и кривой г —ех.
1667.	Прямыми у = 0, г—1,
2 = 3 и гиперболой г = у.
1668.	Прямыми у~— 1, у~ — х и окружностью Х2+1/2 = — 2у.
Указание. Спроектировать область D на ось Оу, для вычисления интеграла использовать подстановку у 4--f- 1 = sin t.
1669.	Параболой г2 = х+2 и прямой х = 2.
[	1670. Кривой (г/2 + г2)г=
’ = 2а2 (г/2 — г2).
1671. Кривой (х2 + i/2)3 = х* + z/4.
1672. Кривой (х2 4~z2)3=4x2z2.
Указание. В 1669—1672 учесть симметрию области D.
2. Вычисление объемов. Объем ци-
 линдрического тела, ограниченного сверху поверхностью z = f(x, у) а снизу —областью D плоскости хОу (рис. 190), находится по формуле
=	У) dx dy.	(j)
Если тело не является цилиндрическим, 1 то его разбивают на цилиндрические части.
12 Кручкович и др. '
353
1673. Вычислить объем тела, ограниченного плоскостями г — О, y-\-z = 2 и цилиндром у = х2.
Решение. Данное тело (рис. 191) сверху ограничено плоскостью г = 2 — у, поэтому
(2— у) dx dy.
D
Область D есть параболический сегмент, ограниченный в плоскости хОу прямой у = 2 и параболой у = х2. Спроектируем область D на ось Оу. Тогда, с учетом симметрии тела относительно плоскости уОг, получим
1674. Вычислить объем тела, ограниченного плоскостью z/ = 0 и параболоидом у = 3 — х2 — г2.
Решение. В этой задаче удобно считать, что тело «стоит» па плоскости хОг и «сверху» (рис. 192) ограничено параболоидом у~3 — %2 —г2, поэтому
V = (3 —%2 —г2) dx dz.
D
Область D есть круг; его границу х2-(-г2 = 3 получим подстановкой </ = 0 в уравнение t/ = 3— %2 —г2. В полярных координатах уравнение этой окружности имеет вид р2 = 3, или р = Уз •
Учитывая симметрию тела относительно плоскостей хОу и уОг, найдем л _	л	/з"	л
2 /З	У	>
УГГ	1 С (3 —о2)2	9 (*	9
’4=.) (3~P2)PrfP = -у J у"2”. ЛР = 4 ) d(f = 4 <Р ио	и	о	и
Отт откуда У = ~-.
л
2'
_9л
“ 8
о
354
1675. Вычислить объем тела, вырезанного цилиндром х2 4- У2 — = Rx из сферы х2 4~ У2 + г2 = R2.
Решение. На рис. 193 изображена половина тела, объем которого находим (вторая половина, расположенная симметрично с первой, находится под плоскостью хОу). Сверху тело ограничено сферой, уравнение которой х24-у2Ч-~г г2 — R2, поэтому
V = 2 jj |/4у2-х2 —у2 dx dy.
jD
Область D есть круг, ограниченный окружностью х2 -f-у2 = Rx. С учетом Того, что половина тела симметрична относительно плоскости хОг и что уравнение окружности, ограничивающей область D,
Рис. 193
в полярных координатах имеет вид p2 = 7?pcosq), или р = /? cosip, получаем
л	л	j 7?cosq>
2 /?cos<p	2	~
*	,'	о
ио	оо
ля	л
Т	У	Т
R3 С	R3 С	R3 С
=--5- \ (sin3ср— 1) d<p = 'R- \ (1 —cos2(p) d (cos ф) + ~- \	=
о	)	о	о J
о-о	о
cos ф —
2R3	№ _ J?3 / л 2 \
9 Н' 6 ’”"3 V ’3/
Зл —4
~18-
,, 2 (Зл — 4) „ откуда У = - '  —- £>з.
Вычислить объемы тел, ограниченных следующими поверхностями:
1676. Плоскостями х = 0, у = 0, z = 0, х=4, у = 4 и параболои-
дом z = х2 + у2 + 1 (рис. 194).
1677.	Плоскостями х = О, у = О, z = О х . у , z .
и ~ + 4-+— = 1.
abc
1678.	Плоскостями х = 0, у = О, z = 0, y + z=l и параболоидом х = = У2 + z2.
1679.	Плоскостями х = 0, у = 0, z = 0,
2х + Зу — 12 = 0 и цилиндром z = ™ у2.
1680.	Плоскостями z = 0, у=1, параболоидом Z = X2+y2 и цилиндром у = х2.
1681.	Плоскостью у = 0, цилиндром х2 4- z2 = R2 и конусом х2 4- г2 = у2.
12*
355
1682.	Параболоидом х2 + z/2 — az = 0, цилиндром (x2 + z/2)3 = fl2 X X(x2 —z/2) и плоскостью z = 0 (a>0).
1683.	Параболоидом x = z/24-z2, цилиндрами z/2-|-z2 = у, z/24-z2 = = 2z/ и плоскостью x = 0.
1684.	Плоскостями z = ax, z = 0 и цилиндром x24-z/2 = 2ax.
1685.	Плоскостью y — h2 и параболоидом x24-z2 = z/.
1686.	Параболоидом 2az = x2-\-y2 и сферой x2 у2 + z2 = За2 (подразумевается объем, лежащий внутри параболоида).
У к а з а и п е. В 1681 — 1686 рекомендуется перейти к полярным координатам. Везде следует учитывать симметрию.
3. Вычисление площади поверхности. Пусть поверхность уравнением z — f (х, у), проектируется на плоскость хОу в область D (см. рис.
Тогда ее площадь S находят по формуле
а, заданная 190).
dx dy.
(2)
1687. Вычислить площадь части верхности цилиндра z2 = 4x, лежащей в I октанте, вырезанной цилиндром у2 — 4х и плоскостью х—1.
Решение. Из уравнения — 4х для I октанта имеем
dz дх
Область D (рис. 195) мент, ограниченный в
у2~-4х, пли в-2|4 и прямой х=1; тогда
ПО
поверхности г2 =
* = 0. ду
есть параболический сег-плоскостн хОу параболой
D
и
l+ lx dxdy= dx 1 + |-^= \	1+^//	=
'г/	о о	о
= 2 £ |<ГЙ|	(%+ I)2 Г	= ~	- 4	= 4 (2	К2-1).
о	|0 и о о
0
1688.	Вычислить площадь части поверхности параболоида 2у = = х2 4- г2, вырезанной цилиндром х2 ф- z2 = 1.
Решение. В этой задаче поверхность однозначно проектируется только на плоскость xOz. Поэтому ее площадь будем вычислять по формуле
Из уравнения параболоида находим:
£/ =
х2 + г'2 ду _ ~Г~ ’ дх^Х
dz
356
Область D (рис. 196) есть круг, ограниченный окружностью х24-г3=1. С учетом того, что поверхность симметрична относительно координатных плоскостей уОг и хОу и уравнение окружности, ограничивающей область D, в полярных координатах имеет вид р2=1, или р=1, получаем
л
б
2/2-1 3
2/2-1 е 2 (2/2-1)
6 л’ а д 3
Вычислить площади частей
следующих поверхностей:
1689.	Поверхности сферы х34-4- z/2 4- г2 = а2 (рис. 197), вырезанную цилиндром x24-z/2 = 7?2 IR-ba).
1690.	Плоскости х-|-^/4-г = 4, вырезанную плоскостями х = 0, // = 0, х = 2, у = 2.
. 1691. Цилиндра № Ц- у2 = 1, лежащую в I и IV октантах, вырезанную плоскостями х = 0, z = 0, у-\-z = 2.
1692. Конуса z/2 = x24-z2, вырезанную цилиндром x2-/z2 = 2z.
1693. Сферы х2 -/ у2 4- г2 = R2, вырезанную цилиндром у2 -j- г2 = Rz.
1694. Сферы х2 + «/24-г2 = 7?2, вырезанную цилиндром (х24-/2)2 = = /?2 (х2-/2).
4. Приложения двойного интеграла к механике. Пусть О —плоская пластинка, лежащая в плоскости хОу, с поверхностной плотностью массы р (х, у). Тогда:
а)	массу т. пластинки находят по формуле
т. = j j р (х, у) dx dy, b
(3)
б)	статические моменты Мх и Му пластинки относительно координатных осей Ох и Оу находят по формулам
ЛЦ=И’?/р(х, y)dxdy	(4)
D
И
Л4= j j хр, (х, у) dx dy;	(5)
357
в)	координаты центра тяжести хс и ус пластинки— по формулам М„	М,
хс=- т <6) и ^c=-^;
г)	моменты инерции 1Х, 1у и /0 пластинки соответственно относительно координатных осей Ох, Оу и начала координат находят по формулам
1х— й'2!-1 (*. У) dxdy (8), Jy~\ У) dxdy,	(9)
D	~D
/0=^ (x2 + y2) p(x, y}dxdy.	(10)
'd
Для однородных пластинок |л = const и для простоты мы в этом случае будем считать р=1.
1695.	Найти статический момент однородного прямоугольника со сторонами а и b относительно стороны а, считая, что прямоугольник лежит в плоскости хОу.
Решение. Поместим начало координат в одну из вершин прямоугольника, а ось Ох направим по стороне а (рисунок рекомендуется сделать читателю). Статический момент прямоугольника относительно стороны а будет равен статическому моменту прямоугольника относительно оси Ох. По формуле (4) имеем
а	Ь	а	а
С	С	If	16	С	62 1<*	(lb~
Ма = Мх = \ dx \ ydy=^ \	dx=^x\=-^.
"о	о	о	о
1696.	Найти статический момент однородного полукруга, лежащего в плоскости хОу, радиуса R относительно диаметра.
Решение. Поместим начало координат в середину диаметра полукруга, а ось Оу направим по диаметру (рисунок рекомендуется сделать читателю). Тогда статический момент полукруга относительно диаметра будет равен статическому моменту полукруга относительно оси Оу. С учетом того, что уравнение окружности, ограничивающей полукруг, имеет вид уг = R1-, а в полярных координатах p = R, по формуле (3) имеем
л	я
2	Я	2
Му — Му = dqp р cos фр dp = cos ф • я	0	__п
2	2
Я
R3	R3
cos ф Лр= у sin ф = 3 (1 +1) = у-.
л	~2
2
Л 2 7?3|* з А
1697.	Найти координаты центра тяжести однородной пластинки, ограниченной параболой ау = г2 и прямой у = 2 (а>0).
Решение. Пластинка лежит в плоскости уОг. В силу симметрии пластинки относительно осп Оу (читателю рекомендуется сделать рисунок) имеем гс = °.
358
Для нахождения ус найдем Л4. и /п:
2 Vau 2 г—
мг = j j у dzdy — 2 у dy dz = 2\yz \ av dy = 'D	о о	о
2 3	У	г- г-
- 2 Га у2 dt/—2V а У- Г = * Га  4 |<2 = !6 1 2 j-?-
J	О [0 и	О
0	т
2 V ау	2 г—
/п — Ц dy dz — 2 j dy 'j dz = 2 ( z ; ay dy —
'D	ob о 0
з 2 1 •-
= 2 Га if dy^ra I* =	• 2 Г2 = 8Ц’ ]-а.
)	о j(J О	и
0	2
„	M. 6
Следовательно, tir = Л .
т 5
1698.	Найти момент инерции квадрата со стороной а, поверхностная плоскость которого пропорциональна г, относительно одной из вершин, считая, что квадрат находится в плоскости xOz.
Решение. Поместим начало координат в одну из вершин квадрата, а координатные оси Ох и Oz направим по двум взаимно перпендикулярным его сторонам. Тогда искомый момент инерции будет равен моменту инерции квадрата относительно начала координат, т. е.
(x2z-f-z3) dzr=k 4- г-^ о	о '
1699.	Найти статический момент однородного круга радиуса R относительно касательной, считая, что круг лежит в плоскости xOz.
1700.	Найти координаты центра тяжести плоской однородной „	•.	„	у1 , z2 ,
пластинки, ограниченной верхней половиной эллипса -Ь = 1 и его большой осью.
1701.	Найти координаты центра тяжести плоской однородной пластинки, ограниченной окружностью х2 + */2 = /?2 и двумя радиусами р = 0 и z/ = xtga.
1702.	Найти моменты инерции прямоугольника О АС В со сторонами ОА = а и ОВ — Ь относительно вершины О и сторон О А и ОВ, если плотность его пропорциональна расстоянию до стороны ОВ, считая, что прямоугольник лежит в плоскости yOz.
1703.	Найти момент инерции круга радиуса R относительно центра н диаметра, считая, что круг лежит в плоскости хОу (р = 1).
§ 3. ТРОЙНОЙ ИНТЕГРАЛ
1. Тройной интеграл в прямоугольных координатах. Пусть функция / (М) = = f(x,y, г) задана в некоторой ограниченной замкнутой пространственной области V. Разобьем эту область на пространственные ячейки Vlt lz2, ..., Vn-В каждой ячейке V; (i = 1, 2, 3, .... п) выберем произвольно точку А1; (х,-, рг, г;) и умножим значение функции / в этой точке на объем Агу ячейки V;. Сумма таких произведений по всем ячейкам
i=; ।
называется интегральной суммой. Обозначим через d (V,) диаметр ячейки И,-, т. с. расстояние между наиболее удаленными точками этой ячейки, и max d (V,-) — наибольший из диаметров всех ячеек данного разбиения. Тройным интегралом от функции f (М) по области V называется предел интегральных
сумм при условии max J (['/) —О, т. е. при неограниченном увеличении числа ячеек, когда все ячейки стягиваются в точку:
£ НМ,) АО;.
/ (Л1) </v = lim тах</(У.)->о с
Если такой предел существует, то функция f (М) называется интегрируемой в области V; всякая непрерывная в ограниченной замкнутой области V функция f (ЛТ) интегрируема в ней. В даль-
li с боков— цилиндрической поверхностью с
нейшем мы ограничимся рассмотрением только непрерывных функций.
Тройной интеграл обладает свойствами, аналогичными свойствам двойного интеграла.
В декартовых -координатах элемент объема обычно записывают в виде dv—dxdydz, а тройной интеграл обозначают
<х’ У> dx dlJ
Пусть V проектируется в область D на плоскости хОу так, что всякая прямая, параллельная оси Ог и проходящая внутри области D, пересекает границу области V ровно в двух точках. В общем случае такая область ограничена сверху поверхностью г=ф2(х, у), снизу— поверхностью г = ф1(х, у) образующими, параллельными оси Ог
(рис. 198). В частных случаях боковая поверхность цилиндра может превратиться в линию (рис. 199). Функции тфг (х, у) и ф2 (х, у) мы будем считать непрерывными. Тройной интеграл по такой области вычисляется по формуле
’1-Э (X, У)
^f(x,y,z)dxdydz — ^dxdy j f(x,y,z)dz.	(1)
V	D 4>i (х, у)
360
Фг (.х, t/}
Здесь внутренний интеграл j fix, у, г) dz берется по г при фиксированных, (х, у)
но произвольных в D значениях х и у от нижней границы области V до ее верхней границы (т. е. по отрезку KL, см. рис. 198). В результате получается некоторая функция от х и у, которая интегрируется затем по области Ь.
Наиболее простой вид формула (1) принимает в случае, когда V есть прямоугольный параллелепипед, ограниченный плоскостями х — а, x~b, у = с, y = d, z = e, z = s-.
b d S
y, z) dx dy dz=^dx ^dy ^f (x, y, z) dz.	(2)
V	ace
Если область V имеет более сложную форму, то ее разбивают на конечное число областей |/1( V2, ... , Vn, каждая из которых удовлетворяет условиям, изложенным выше.
Замечание. Аналогичные определения и формулы могут быть получены п тогда, когда область V проектируется в область D, лежащую или в плоскости xOz, или в плоскости уОг.
1704. Вычислить тройной интеграл (x+y+z) dxdydz по об-
V
ласти V, ограниченной плоскостями х = 0, х = 1, у = 0, у—1, г = 0 и г = 1.
Решение. Вычисляем данный интеграл по формуле (2):
1	1	1
Щ (х 4~г/4~ г) dx dy dz = \ dx (j dy j (х4-(/4~г) dz.
v	0	0	0
Внутренний интеграл вычисляем, считая х и .у постоянными:
j («+#+г)^-‘^+^|;_й+адг. о
= \ Цх + 1+1/)2- U4-y)2l-
4.
2
361
Полученную функцию от х и у интегрируем по у, считая х постоянным:
I	I
§ ф m-l+^)2-(-v+y)2W = 4 jj [(*+1+у)2~(*+у)2Иу =
о	6
- ‘ 1(*+1+У? „(ЦуЮ!1	' [(x + 2)3_(.v+l)3_(x+i)3 + x3J==
л ц о	О | |0 О
= 6 [(х + 2)3-2(х+1)3+х3].
Полученную функцию от х интегрируем по х:
1	I	_
~ [(x + 2)3-2(x+l)'i + x3jc/x= ~	[(^ + 2)3-2(x+i)a + x3]a'x =
о	о
1 |(х + 2)1 (х + 1)4 ,^||1	1/81	1	1\	3
= Ъ | —4------~ + 4 ] |о ~ 6 !И + ~4	- 2 •
Обычно для сокращения записи все вычисления записывают в одну строку следующим образом:
ill	11
к ( (х+у + г) dx dy dz = dx dy (х + У + г) dz = dx \	jQrfy—
е V ’	о .о о	оо
{ [ (х+1+у)3  (x + y)3j jirfx=
3
о
о о
[(x-J-2)3 —(X-!- I)3-(х-l- I)3
О
6
Рис. 200
н и цы
и z—1—у. Переходя к
р — 2(х+ I)3 4-х3] dx =
о
I (х + 2)‘	(х+1)1
2
= 1 I___
6 L 4
3
2'
1705.	Вычислить тройной интеграл (1 — у) хг dx dydz, если об-
ласть V ограничена плоскостями л = 0, z/ = 0, г = 0 и z = l—х —у.
г —О
Решение. В этой задаче область V можно спроектировать, например, на плоскость уОг. Тогда область V (рис. 200) имеет нижнюю границу х = 0 и верхнюю границу х=1 — у — г. Область D проектируется в отрезок [0, 1] оси Оу и имеет гра-повториому интегрированию, получим
1	1 ~ и 1 — у — z
\ \ j (I — У) хг dx dy dz — $ (1 — у) dy j z dz x dx = 'v	о	oo
I	1 V	'	1 — v
=^~2 (l~y)dy гх2|‘ У ~ dz=l2-^ (\-y)dy г (1 — у—г)2 dz =
0	0	0	0
362
1 с ! cz/
= yj(l—\ [(1— У)2г— 2(1 — г/)г2ф?3] dz=. о	о
1
1 (*	Г	2-	2^	2^ I |1 —И
= 2 \ О-!/) ('-!/)!’Т-2(1-!/)'т + 7 I 'dy~ б
о
1 С 1 /1	V, А	1	о-# Р	1
2 3 12 (	‘!/)’ dy	24	’	6 [о	144	•
О
Вычислить следующие тройные интегралы:
1706.	$$$ x2y2z dx dy dz, если область V ограничена плоскостями v
х—1, х = 3, у —О, у —2, г = 2, г = 5.
1707.	(х-фуфг^ф-!)3 ’ еслп °бласть V ограничена плоскостями
*> v
х = 0, у = 0, z = 0, х + у + г=1.
1708.	^xyzdydzdx, если область V ограничена плоскостями г
х = 0, y = Q, z = 0 и сферой х2 -ф у2 -ф г2 — 1.
1709.	№ xdxdydz, если область V ограничена цилиндром х2 -\-у2 = 1 v
и плоскостями г = 0 и z = 3.
2.	Переход к цилиндрическим и сферическим координатам. При вычислении тройных интегралов иногда бывает полезно сделать замену переменных.
Пусть
и = и{х, у, г), о = ц (х, у, г), ш = аз(х, у, г)	(3)
— функции, определенные во всем пространстве хуг или в некоторой его области V и имеющие непрерывные частные производные в области V. Допустим также, что систему уравнений (3) можно однозначно разрешить относительно х, у п z:
х=х(и, v, W), у —у {и, v, w), г = г(и, о, w),	(4)
тогда каждой точке М (х, у, z) из области V будет взаимно однозначно соответствовать тройка чисел (и, о, ьа), называемых криволинейными координатами этой точки. Если область V расположена в той части пространства хуг, в которой введены криволинейные координаты и, и, w, то справедлива следующая формула:
/ (х, г/, z) dx d;/dz =	/ [х (u, v, w), у (u, о, w), г (и, v, w)]\ J \dudv dw,
где I" — область изменения криволинейных координат и, v, w, отвечающая области V, a J — якобиан преобразования (4):
	дх дх дх
	ду , до ~да)
J (и, С, W) =	дУ ди до dw
	дг дг дг
	ди до dw
363
В частности, в цилиндрических координатах формулы (4) имеют вид (рис. 201)
x = pcos<p, у = р sin ср, 2 = 2,
где 0< ф '-'2г(, 0sSp< + co, —со < г
<+со. В этом случае | J 1 = р и переход к цилиндрическим координатам ф, р, г осуществляется по формуле
от прямоугольных координат х, у, г
Рис. 201 прямоугольных координат х, у, z к вляется по формуле
f (х, у, г) dx dy dz =
= Щ / (p cos ф, p sin ф, 2) p Ap dp dz. (5)
V'
Другим важным частным случаем криволинейных координат являются сферические координаты. В сферических координатах формулы (4) имеют вид (см. рис. 201)
х = г cos ф sin 8, у— г sin ф sin 6,
2 = rCOS6,	(6)
где 0 < ф 2л, 0	0 г < -фсо.
В этом случае \ J \ = r2 sin 8 и переход от сферическим координатам ф, 8, г осущест-
У, г) dxdy dz = \\y (г cos ф sin 6, г sin ф sin 8, г cos 6) • г2 sin 6 dqdbdr. (7) j л J
1710. Вычислить тройной интеграл (х2 + г2) dx dy dz, если об-
v
ласть V ограничена плоскостью у = 2 и параболоидом х2 + г2 = 2у.
Решение. Область V (рис. 202) ограничена «снизу» параболоидом 2у = х2 + г2, а «сверху» — плоскостью у = 2. Эта область проектируется в область D плоскости xOz, ог р ан и ценную окружностью х2 +г2 = 4. Последнее уравнение получено в результате исключения у из уравнений плоскости г/ = 2 и параболоида 2у = = 4- г2.
Введем цилиндрические координаты:
х = рсозф, г = р8Шф, у = у.
Так как х2-|-г2 = р2 cos2 ф + р2 sin2 ф = = р2, то
(х2 + г2) dx dydz = §^p2p dtp dp dy.
В области V координата ф меняется от 0 до 2л, р —от 0 до 2, у —от парабо-лоида -у до плоскости у = 2.
Итак, 2л 2	2 2л 2	9
№ + г2)	^У ~ Ш Р2Р ^Ф ^Р dy ~ ^ф J Р3 ^Р \ dy = <2ф ( рпу j" 2 dp =
v	С"	й о р* о о
Т	2
364
2л	2	2л 2	2л
d<f Р3 (2“^; dP =	§ ^Р3-у Р5у! dp = ^2'p4_’l2" Р"^ |od<p =
&	о	оо	о
2я 8 (‘ ,	8	|2л	16л
=- 3- J йф-уф о - 3 .
0
1711. Вычислить тройной интеграл \\\ \/ х2 хг у'- -х z2 dxdy с!г, если область V 'v
ограничена сферой х2+у2 + г2 = г.
Решение. Область V (рис. 203) ограничена снизу и сверху сферой х2 + yi-\-z2 = z. В сферических координатах л-2 + у2г2 = г2, поэтому по формуле (7)
ЭДЭД |х2 + г/2 + г2 dx dy dz = ЭД J rr2 sin 8 dq d6 dr.
Очевидно, что в области V ф меняется от О до 2л, в — от 0 до -%, г —от 0 до cos 6, так как уравнение данной сферы принимает вид г2 —rcosQ, или г —cos 6. Тогда имеем
_____________ 2л 2	cos 5
+ у2 + г2 dx dy dz = r3 sin 6 dy dft dr = j dy sin 6 dti j r3 dr —
JVJ	’г	о b	о
я T
2л
Я
2’
_л_
2л 2
sin 0 cos4 8 d6 — —
О
2л
2л
-i- d<f cos4 8d (cos 6) —
0	’
2л	Л
1 i* COS5 0
4 '
0
I 2“ . _ 1 5—|о ':(f~20
Л
~ 20 ф|о IO'
Вычислить следующие тройные интегралы:
1712- $ЭДг/х2 + у2 dx dy dz, если об-V
ласть V ограничена плоскостями у = 0, z = 0, z = a и цилиндром х2-\-у2 = 2х (рис. 204).
1713.	^xdxdydz, если область V v
h2
ограничена конусом х2-- y2-(z2+//2) и плоскостью x — h.
365
1714.	dxdydz, если область V ограничена плоскостью у —О, цилиндром х2 + z2 = 2Rx и сферой х2 + У2 + г2 = 4/?2.
1715.	( f (  dxdydz ....... если область V ограничена плоско-
J .) J У а2 —х2 —г/2 —г2
v
стямн х = 0, z/ = 0, z = 0 и сферой х2 + у2 + z2 = а2.
Указание. Для взятия интеграла воспользоваться подстановкой r = asint.
1716.	(х24~У2) dxdydz, если область V ограничена сферами
x2 + y2 + z2 = R2 и х2+у2 + г2 = /?2
§ 4. ПРИЛОЖЕНИЯ ТРОЙНОГО ИНТЕГРАЛА
1. Вычисление объемов. Объем пространственного тела V находится по формуле
V = Щ dx dy dz.
 fr
В цилиндрических и сферических координатах имеем
V = \ Ц р d(j dp dz
и V = Щ г2 sin 6 rfrp iZO dr.
‘v?
1717. Вычислить объем тела, ограниченного цилиндрами г = = 4 — у2 и z = у2 4- 2 и плоскостями х = — 1, х = 2.
Решение. Тело, объем которого находим (рис. 205), ограничено снизу цилиндром г = у2-\-2, а сверху —цилиндром г = 4 —г/2; оно проектируется в область D плоскости хОу, ограниченную прямыми х =— I, х = 2, у—1 и у=— 1. Два последних уравнения получены в результате исключения г из уравнений цилиндров. С учетом симметрии области V относительно плоскости хОг, имеем
2	1	4-^
У — 2 j dx ( dy j dz =
— 1	й	//Н- 2
2	1	2	2	2
= 2\dx^-y2~y2-2)dy=4 С (у-У*\Ьх = 4 \ (1-	(	dx	=
1 о	.) V 3 * * * * / 0 J \	3 J 3
-1 -1	-1
__ 8 |2 _J6_ _8
“ 3 Л|-1“ 3 + 3
8.
366
1718. Вычислить объем тела, ограниченного параболоидом х = = 6 — г2 — у2 и конусом х2 = у2 + г2 (xS^O).
Решение. Объем искомого тела (рис. 206) ограничен «снизу» конусом х2 = у2г2, а «сверху» — параболоидом	х = 6 — у2 — г2	и
проектируется в область D плоскости уОг, ограниченную окружностью у2-у г2 — 4. Последнее уравнение получено в результате исключения х из уравнений конуса и параболоида. Введем цилиндра-ческие координаты:	—*
r/ = pcos<p, 2 = psin<p, х = х.
С учетом того, что данное тело симметрично относительно плоскостей хОг и хОу и что уравнения окружности, ограничивающей область D, конуса и параболоида, соответственно принимают.вид р = 2, х
Рис. 206 р и х = 6-р2, имеем
2	2	6-р2	2	2	6 _ V — 4 ( dip \ р г/р	dx = 4 ( dip ( рх 0	0	р	0	о	'р л „ С 'з 2 Р1 Р3 \ I2 ,	64 = 4^i3p2-T-Tj|o^= 3-0 '	1	2	2 • п 2	,»	р г/р = 4 \ dtp \ (6р — р3 — р-) dp — Ъ о л у"	л 64 I 2	32л 0
1719. Вычислить объем тела, ограниченного поверхностью (х2 + + у2 4- г2)3 = Зхуг.
Решение. Левая часть уравнения поверхности, ограничивающей тело, положительна при любых значениях х, у, г, значит, тело будет расположено лишь в тех октантах, где произведение хуг, стоящее в правой части уравнения поверхности, тоже положительно, т. е. в I, III, VI и VIII октантах. Очевидно, что части тела, расположенные в этих октантах, одинаковы, поэтому вычисляем лишь объем той части, которая расположена в I октанте, а полученный результат умножаем па четыре. Запишем в сферических координатах уравнение поверхности:
,	г°==3г3 sin ф cos ф sin2 0 cos О,
или	_	________ ____________
Г = )/ 3 у/ sin <р cos ф sin2 0 cos 6-
Тогда имеем
<2	2	S111 Ч-cossina6 cos0
V==4 j </ф ( sin 6 М	г2 dr—
оо	о
Л	л
2	"2”	. — . -	,
I*	(*	г3 ii/"3 у sin<pcoscpsin26cosS
= 4 \ dip \ sin 0 ---	d6 —
J	.)	3 о
О 0	'
367
л	тс	л	л
¥	¥	¥	¥
= 4 \ sin <р cos ф dtp j sin3 0 cos 0 <70 = 4 j sin <[d (sin ф) )' sin30d (sin 0) =
0	0	0	0
Л	Л
"o'	Л	2	Л
C .	, . л 12 , , .	, (* .	, , . , sin2 ф |2	1
= \ sm ф (sm4 0)	<7 (sm ф) = \ sm <pd (sm ф) =—g-2 =	.
о	6
Найти объем тел, ограниченных:
1720.	Параболоидами z = x2-\-y2, z = x2-\-2y2 и плоскостями у = х, у = 2х, х= 1.
1721.	Поверхностью г = ху и плоскостями z = x-\-y, х-\-у—\, х = 0, z/ = 0.
Указание. Проекцией тела на плоскость хОу является треугольник, ограниченный прямыми х = 0, </ = 0, х-)-у = 1; плоскость а=хф(/ располагается выше поверхности г = ху.
1722.	Параболоидом y = x2-\-z2 и плоскостью у—\.
1723.	Параболоидом y2-\-z2 = 2ax, цилиндром y2-\-z2 — 2az и плоскостью х = 0 (а>0).
1724.	Параболоидом y2-\-z2 — 3x и сферой х2 ф- у2 ф- z2 = 4 (внутренний по отношению к параболоиду).
1725.	Сферой х2 ф- у2 ф- г2 = а2, цилиндром х2 ф- z2 — ах и плоскостью у = 0 (а>0) (внутренний по отношению к цилиндру).
1726.	Поверхностью (х2 ф- у2 ф- г2)2 = а2х (а>0).
Указание. Тело расположено лишь в тех октантах, где х > 0.
1727.	Поверхностью (х2 ф- у2 ф- г2)3 = a2zs (а>0).
Указание. Тело расположено лишь в тех октантах, где г > 0.
1728. Поверхностью (х2-ф г/2-|-г2)3 = а2 (х2-\-у2)2 (а>0).
Указание. Тело расположено во всех восьми октантах.
1729. Сферой х2z/2 ф-z2 — а2 и конусом г2 = х2-\-у2 (ц>0; внешний по отношению к конусу).
д	д
У казан ие. Угол 0 меняется от 0 = У- до 0 = .
1730. Сферами х2 ф- у2 -ф z2 = 1, х2 ф- у2 ф- г2 = 16, конусом г2 = х2 ф-ф-z/2 и плоскостями х = 0, г/ = 0, г = 0 (х^эО, z/^sO, zasO).
2.	Приложения к механике. Пусть V— область пространства, занимаемая каким-либо материальным телом с плотностью ii (х, у, г). Тогда:
а)	масса этого тела т находится по формуле
т = i 9	d?'.	(1)
j
ч
б)	моменты инерции Iх, Iy, I, относительно координатных оеей Qx, Оу, Ог; Iху, Ixz, Iyz относительно координатных плоскостей хОу, xOz, yOz; /0 относи-
368
тсльно начала координат соответственно находятся:
= $ И (z2 + ?/2) И dx dy dz, /j, = J И (x2 + z2) ц dx dy dz; V	V
lz = Ц j (x2+y2) p dx dy dz;	(2)
" у
/Av = j J। \ 11г-’ dx dydz, Ixz=\\\\iy2 dx dy dz, Iyz=	dx dy dz; (3)
 V "	' V	~V
I0^^(x2 + y2-J[-z2') pdxdydz;	(4)
v
в)	координаты центра тяжести тела находятся по формулам:
j рх dx dy dz j - j шу dx dy dz j j j p.z dx dy dz
Для однородного тела (ц = const) эти формулы упрощаются, так как в этом случае можно считать, что ц=1.
1731. Найти массу тела с плотностью ц = х + г/-[~г, ограниченного плоскостями х = О, х = 1, z/ = О, у=\, 2 = 0, 2=1.
Решение. Тело, массу которого мы находим, является прямоугольным параллелепипедом. Согласно формуле (1) имеем
ill	11
т = \ dx dy	(х+у -ф г) dz = dx	dy =
'о о о	о 'о
1 1 1
= у \ dx ((х+1 +//)2-(х-|-1/)2]	Кл:+1+'/)3-
о о	; о
1
- (х +У);) j [о dx = 1 \ [(х + 2)3- (х + 1)3- (X + 1 )3 + ХЗ] dx = о
1 f(x + 2V (х+1)4 , Х41	3.
6 L 4	2	+ 4 J |о ~ 2
1732. Найти моменты инерции, однородного (ц=1) цилиндра с высотой h и радиусом основания а относительно диаметра основания и относительно оси цилиндра, считая, что ось цилиндра направлена по оси Ох.
Решение. Поместим начало координат в центр нижнего основания цилиндра. Тогда уравнение цилиндра будет иметь вид у2z2 = а2. Моменты инерции, которые мы находим, будут равны моментам инерции относительно координатных осей Ог п Ох. Следовательно, имеем
/г = J У У (х2 + у2) dx dy dz и /.v — j У j (!/2-гг2) dx dy dz.
Введем цилиндрические координаты:
z/ = pcos<p, z=psinip, x = x,
369
тогда
2ft a h	2л а $
- \ dip \ р dp \ (х2 р2 cos3 ф) dx — \ Ар р Гд -г р3 cos2 q х |о dp =
О ОО	0	0
С , С /Л3	, ,	., .Л ,	(‘ ' Н3р- h cos2 ф \ А
= \ Ар \ ', з р т A cos-фр3 j dp =	------5— р‘у |ц Ар =
о о	'б
2л	2л	2л
(• / Л3й2 , ha3 „ \ , h:sd-	I ha1 I*	.
= \ I-g- + -у cos3 Ф i Ар = —g- Ф I -h-g- (14-cosAp) Ap =
0 '	о	0
nci-h3 , tiu* ( , sin2(p\ }2л	ла2/;3 . ha* ,c. . ла2Л3 , лАЛ nifih (4/г2-|-За2)
= —+- 84 <P + -H jo =— + в’ (2л) = -з~ + -Г ----------12-----;
2л	a	li	2п	а	2л а	2п
/А.== Ар i p3dp dx— Ар Р3х'|0 а’р = ',г Р3 dp = h	4ф =
о	0	о	о	б	оо	б
2л
«4/г 1* , alh |2л aVi w'li = -Г \ ^₽= 4 Ф|О =-Г’2л=-у-.
О
1733. Определить момент инерции однородной пирамиды (ц = 1) относительно координатной плоскости хОу, если пирамида ограничена плоскостями xJry-irz= х = 0, у = 0, '.г = 0 (см. рис. 200).
Решение. Согласно формулам (3) имеем ‘	1~~х	।	1-v 1
1ху— ( I г2 dx dy dz — dx dy \ г2 dz — dx г3^ J dy —
v	boo	б V
1	1-х
= у \ dx (1 — X — у)3 dy = о о
1	I	1
1734.	Вычислить момент инерции однородного шара (ц = 1) радиуса 1 относительно его центра.
Решение. Поместим начало координат в центр шара. Тогда момент инерции шара относительно центра будет равен моменту инерции шара относительно начала координат. Согласно формуле (4) имеем
/о=£Й' (х2 + У2 + г2) dx diJ dz-г
Введя сферические координаты, получим
370
1735.	Найти координаты центра тяжести однородного тела, ограниченного параболоидом г/ = 3 —х2 —г2 и плоскостью у = 0 0/^0).
Решение. В силу симметрии тела относительно координатных плоскостей yOz и хОу (см. рпс. 192) xo = zn = 0. Для нахождения у„ найдем массу тела т. Введем цилиндрические координаты:
х=рcos ф, г = р51пф, У —у-
Согласно формуле (1) имеем
л	л
?	К3	3-р2	?	К3	л- р«
т — 4 \ с/ф \ р dp ( dy — 4 dip \ р(у) dp —
О	'О О'	б	о	1°
л.	л
2 V“ 3	2
= 4 cfrp \ р (3-~р2) с/р = 4 р2 —	р4^	3 d(p =
ио	о
л
2'	у,-
Л 9 9 \ с , п г 9л, 4/
о
2л 1^3	3 —р2
dtp \ р dp \ у dy 2л рз
б -0 о _ 2 Г, Г	_____
7о~	9л	~ 9л ) rfip \ р2 ' ]о rfp
2	°'	°
2л	рз	2л	/3
dtp jj р (3 - Р2)2 dp = - jj f/ф \ (3 - р2)2 d (3 - Р-) = о	о	о о
1736.	Найти массу тела плотности р. — х-\-у -\-г, если оно ограничено плоскостями х = 0, у -0, z = 0, х = а, у — Ь, г —с.
1737.	Найти моменты инерции конуса, высота которого h и радиус основания а, относительно диаметра и оси конуса (р==1).
1738.	Найти моменты инерции относительно координатных плоскостей тела, ограниченного конусом х2 = у2 + г2 и плоскостью x — h (/г > 0, хул0, р, == 1).
1739.	Найти момент инерции относительно начала координат тела, ограниченного параболоидом г = х2-\-у2 и плоскостью г — 4 (Н=1)- „
1740.	Найти координаты центра тяжести тела, ограниченного параболоидом x — z2-\-y2 и плоскостями г/4-г = а, х = 0, г/ = 0, z = 0 (р = 1).
371
§ 5. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
1. Криволинейный интеграл по длине дуги. Пусть /(Р)=/(х, у) есть функция, непрерывная в некоторой области на плоскости хОу, и / -некоторая плоская кусочно-гладкая * кривая, расположенная в этой области. Разобьем кривую системой точек на элементарные дуги /2, .... 1п- На каждой элементарной дуге /, (1 = 1, 2, 3, ..., и) выберем произвольную точку Pi(x/, у,) и умножим значение функции f в этой точке на длину As; элементарной дуги /;. Сумма таких произведений по всем элементар
ным дугам
Рис. 207
S f
i = 1
называется интегральной суммой. Обозначим max As; наибольшую из длин всех элементарных дуг. Криволинейным интегралом \ f (Р) ds от функции f (Р)
I
по длине дуги кривой I называется предел интегральных сумм при условии maxAs;—>0, т. е. при неограниченном увеличении числа элементарных дуг, когда все элементарные дуги стягиваются в точку:
O(P)ds= lim ^f(Pi^Si.
л	max As.-►О j-_ j
Криволинейный интеграл по длине дуги обладает следующими простейшими свойствами:
1) j (CJt ± CJ2) ds = G f fi ds ± C., f2 ds-,
I	I	I
2) если кривая l состоит из двух кривых и 12 (рис. 207), то
p(P)ds = ( f(P)ds + \f(P)ds.
I	н.	h
Заметим, что, по самому определению, криволинейный интеграл по длине дуги не зависит от направления дуги интегрирования, т. е.
f(P)ds = f f(P)ds.
Ав	BA
Для вычисления криволинейного интеграла по длине дуги пользуются одной из следующих формул:
а)	если кривая задана уравнением у —(fix) (а -'' х Р), то
ds=/ 1-Нф' WP dx
И
ь
р (Р) ds=^f [х, <р (X)] / 1 -НФ' MF dx)	(Г)
I	а
б)	если кривая задана параметрически:
x = (f(t), Р = ф(0 (a-SZsSp),
* Кривая называется гладкой, если в каждой ее точке существует касательная, непрерывно изменяющаяся вдоль кривой. Кусочно-гладкой кривой называется непрерывная кривая, состоящая из конечного числа гладких кусков.
372
то
ds = К[ф' (/)]а + [1р' (OF di и
P	P	r______________
$ f (P) ds = f [<P (/), ф (0) /It' (OP+W' (OF dt;	(2)
I	a
в)	если кривая задана уравнением р = р (<р) (ф1 =£-7 ф s== ф2), то
ds = ]^ р2 + (р')2^ф и
<Рг	_______
\ i (P) ds --- \ f (р cos <р, р sin ф) К р2 -|- (р')2 dtp.	(3)
I	<0
Аналогично определяются криволинейные интегралы от непрерывной в некоторой пространственной области функции f (M) = f (х, у, г) по длине дуги пространственной кусочно-гладкой кривой L, расположенной в этой области, т. е.
\f(M)ds =	lim У f (Mt) As;.
£	max	_ ।
Если кривая задана параметрическими уравнениями
x=x(t),	y = y(t),	z = z(t),	(asU-=rp),
TO
ds=/[x' (OF+l/ (OF + fz'WF dt
И a	_____________________
jf(M)ds = p[x(0, d(t), г (/)] /[«' (OF + I/ (OF + I*' (OF dt.	(4)
L	a
p (/s
1741. Вычислить ^=f=f=, где/ — отрезок прямой, соединяю-
щий точки 0(0, 0) и /1(1, 2).
Решение. Запишем уравнение прямой 1:у = 2х. Для данной линии ds = = \r 1 -f-22 dx — \' 5 dx. При движении от О к А х меняется от 0 до 1. По формуле (1) имеем
1	I	I
(* ds	С у 5 dx	С dx (* dx
.) Fx2 + ?/2 + 4	J J/x2 + 4x2 + 4 J Гбх2 + 4 ЛГ 4
4	V	U	U |/ Xм -----
1742. Вычислить Vу2 + г2 ds, где / — контур окружности у1 -j-i \
4- z2 = ay (a>0).
Решение. Введем полярные координаты:
1/ = рсозф, 2 = рЗШф.
Уравнение окружности принимает вид
р2 = арсоэф или р = асоэф;
тогда	____
р' = —a sin ф и ds= V a2 cos2 ф-J-a2 sin2 ф dq> = a dtp.
373
Так как окружность расположена в той части плоскости уОг, где у то угол ф меняется от —до По формуле (3) имеем
я	л	я
______	2	2	:2
( ) <z/24-z2 rfs = j pa dq> = a2 j cos ф d<p—cfl sin <p =a2 + a2 —2a2.
i	_ я	_ я	_я
2“	2'	2
1743. Вычислить (2г — Ух2 z/2) ds, где L — дуга кривой, задан-
L
ной параметрически:
x = tcost, z/ = /sin/, z~t (0^/^2л).
Решение. Так как rfs= У(х')2 + (//')2 + (г')2, dt — }'2 +t2 dt, то по формуле (4) имеем
_____ 2л	______________ _______
( (2г — Ух2 + г/2) ds = ( (2/ — У t2 cos2 t +t2 sin2t) ]'r2 +t2 dt =
L	b
2л	_3	2л Г	3	1
= jj / УГь7м/ = 1	(2+Г2)2 3	= 1 [(24-4л2)2 -2 у 2.1 =
и	'2	0
= ЦрГ(1 +2л2)2 - 1].
Вычислить следующие криволинейные интегралы по длине дуги: 1744. <\)y2ds, где/ —арка циклоиды х = о (/ — sin/), у = а(\ — cos/)
(0^С/-С2л) (см. рис. 129).
С ds	1
1745. \ где / — отрезок прямой г= 2-х —2, соединяющий
точки А (0, —2) и В (4, 0), лежащие в плоскости xOz.
1746. \yzds, где / — контур прямоугольника с вершинами в точ-i
ках О (0, 0), А (4, 0), В (4, 2), С (0, 2), лежащих в плоскости yOz. 1747. \yds, где / — дуга параболы у2 = 2рх, отсеченная парабо-i
лой х2 — 2ру.
1748.	§ (г2 4- у2)п ds, где / — окружность г2 4- у2 = а2. i ______________
1749.	§ УУ2 A-у2 ds, где / — дуга кривой x = o(cos/4-/sin /), у —
1750.	J (x2 4- z/2 4- г2) ds, где L — дуга кривой x = acost, y = asint, L
z = bt (0-с/аС2л).
2. Криволинейный интеграл по координатам. Криволинейный интеграл от
непрерывной в некоторой области плоскости хОу функции Р (х, у) по координате х вдоль дуги плоской кусочно-гладкой кривой /, расположенной в это;!
374
области, связан с рапсе рассмотренным криволинейным интегралом по длине дуги соотношением
Р (х, у) dx= \ Р (х, у) cos a ds,
где а — угол между касательной, проведенной к кривой в любой ее точке, и положительным направлением оси Ох (рис. 208). Аналогично,
Q (х, у) dy — \ Q (х, у) cos £ ds,
где fi — угол между касательной, проведенной к кривой в люоой ее точке, и
положительным направлением оси Оу (см. cos Р = sin а.
Обычно рассматривают сумму интегралов по координате х и по координате у, которая записывается в виде
\ Р (X, у) dx+Q (х, у) dy. (5) /
Криволинейные интегралы по координатам обладают теми же простейшими свойствами, что и интегралы по длине дуги. Однако в отличие от последних они зависят от выбора направления обхода кривой: если изменить направление обхода, то интеграл (5) меняет знак, т. е. (см. рис. 207)
j Р (х, у) dx+Q (х, у) dy =
Ав
= — Р (х, у) dx +Q (х, у) dy. вл
рис. 208). Очевидно, что р = ™ — а и
Рис. 208
Для вычисления интеграла (5) пользуются одной из следующих формул: а (если кривая задана уравнением у — <р (х) и при перемещении из точки А в точку В х меняется от а до Ь, то
Ь
\ Pdx + Qdy='\ {Р[х, ф(х)] +
Ав	а
+ Q[x, ф(х)]ф' (х) dx\ (6)
б) если кривая задана уравнениями х = ф(Г), (/ = ф(0 и при перемещении из точки А в точку В параметр t меняется ог а до р, то
Р dx + Qdy = \ {Р [ф (/), ф(/)] ф' (0 + Ав	а
4 <2[ф(0,	<7)
Замечание. В случае замкнутой кривой мы условимся брать направление обхода кривой I так, чтобы область, ограниченная этой кривой I, всегда оставалась слева (рис. 209).
Аналогично определяются криволинейные интегралы по координатам в случае, если кривая / лежит в плоскостях хОг или уОг и от непрерывных в некоторой пространственной области функций Р (х, у, z), Q (х, у, г), R (х, у, z) вдоль дуги пространственной кусочно-гладкой кривой L, расположенной в этой области, т. е.
) Р (х, у, z) dx-^Q (х, у, г) dy-\-R (х, у, z) dz.
L
Если кривая задана параметрическим уравнением x=x(.t), У = У(В, z — z (f) (asc/^P), то
\ P (x, y, z) rfx + Q (x, y, z) dy d-R (x, y, z) dz =
L ₽
= k (0, У (0, z (0J X' (00-Q [x (0, у (0, z (0] y' (0 +
+ 7?[x(0, y(t), z(0]z'(0}rft	(8)
1751. Вычислить (x2
— 2xz) dx + (г2 — 2xz) dz, где / — дуга болы z = x2, пробегаемая от А (— 1, 1) до точки В (1, 1) (рис. 210).
параточки
Решение. Так как г = х2, г' = 2х и при движении из точки А в точку В х меняется от —1 до 1, то по формуле (6) имеем
— 2xz) dx + (z‘2 — 2xz) dz —
= jj {(x2 — 2x • x2) + [(x2)2 -2x • x2] 2xj dx =
= j (x2 — 2X3 0- 2xs — 4x*) dx =
' хЗ _ хА	х»	4х5	\ 11 _ 1 _ [ , 1__4	J	1
\"3 ' ’2'	3~	5	2'+3	5	3	2
__ 1__4 _ 2 _ 8 __ 14
3	5 ~~ 3	5 — Т5 ’
1752.	Вычислить х dx -[-ydy 0- (х -\-у — 1) dz, где L — отрезок пря-L
мой, соединяющий точки Л(1, 1, 1) и В(2, 3, 4).
Решение. Уравнение прямой, проходящей через две данные точки, имеет вид
у 1 = — о 1 (= 0, или х=<0-1, у—2/0-1, z = 3/-|-1.
При передвижении от точки А к точке В параметр t меняется от 0 до 1; по формуле (8) имеем
I
lj х dxA-y dy-]~ (х-Hi/ — 1) dz = (/ 0- 1) Л + (2/ 0-1) 2 dt 0-
L	il
I
0-00-10-2/0-1 —1) 3 Л = (14/0-6) Л = (7/2 0-60 о
1
= 70-6= 13.
а
Вычислить следующие криволинейные интегралы по координатам:
376
1753.	\ у2 dxx2 dy, где / — верхняя половина эллипса х — 2 cost, I
y = bsint, пробегаемая по ходу часовой стрелки.
1754.	\ 2yz dy — у2 dz, если / — отрезок прямой, соединяющий /
точки 0(0, 0) и /1(2, 1), лежащие в плоскости уОг.
1755.	jj 2xz dx — х2 dz, если / — дуга параболы z = -|-x2, пробсга-/
емая от точки 0(0, 0) до точки А (2, 1), которые лежат в плоскости xOz.
1756.	2ху dx — х2 dy, если / — дуга параболы х^~-2у2, пробегаемая i
от точки 0(0, 0) до точки А (2, 1).
1757.	^2yzdy — у2 dz, если / — ломаная линия, первое звено i
которой соединяет точки 0(0, 0) и В (2, 0), а второе —точки В (2, 0) п А (2, 1), лежащие в плоскости уОг.
1758.	cos z dx — sin xdz, если /—отрезок прямой, соединяющей точки А (2, —2) и В(—2, 2), лежащие в плоскости хОг.
1759.	(j ydx+x dy, если / — четверть дуги окружности x = Rcost, i
у —7? sin/, лежащая в I квадранте и пробегаемая против хода часовой стрелки.
1760.	х“ —, если / —дуга кривой x = 7?cos3t, у — R sin3/,
‘ х3 + у3
пробегаемая от точки A(R, 0) до точки В (0, R).
1761.	^ydx — xdy, если / — дуга эллипса x = acost, y = bsint. i	_______
1762.	\yz dx-]-zVR2 — У2 dy + xy dz, если L — дуга кривой x = L
= 7? cost, у = R sin t, z = -^~, пробегаемая от точки пересечения линии с плоскостью z = 0 до точки ее пересечения с плоскостью z — a.
Указание. Интеграл J t cos 2с dt взять no частям; 0 :c" УСТ 2л.
3. Формула Грина. Пусть I — кусочно-гладкий контур на плоскости хОу, а D— ограниченная этим контуром замкнутая область. В области D заданы непрерывные функции Р (х, у) и Q (х, у), имеющие в этой области непрерывные частные производные. Тогда справедлива формула Грина
----------W^dXd!/==^ Р + у^с,у’ (9) D--------'	I
где направление на контуре / выбрано так, чтобы при движении по контуру область D все время оставалась слева.
Условием независимости криволинейного интеграла
\р (х, у) dx + Q (х, у) dy
'I
от пути интегрирования является равенство дР _ dQ ду дх ‘
(Ю)
377
Если же, кроме того, /— контур замкнутый, то
Ф Р (х, у) clx + Q (х, у) dy = 0.
I
1763. Применяя формулу Грина, вычислить 2 (х2 у-) dx -f-i
+ (х-г у)2 dy, где / — контур треугольника с вершинами в точках
2
= — j {x-yY-i
Л(1, 1), В (2, 2) и С(1, 3).
Р е ш е н и е. В данном случае Р = 2 (х2 -ф- у2), дО	дР
Q = (x+j/)3, -^-=2 (х + у), -^- = 4У- Применяя формулу Грина, получаем
§ 2 (х2 + у2) dx (х + у)2 dy =
I
=	[2	dxdy.
A ABC
Вычисляя двойной интеграл, найдем (рис. 211)
§2(x2-m rfx + (x + j/)2rfj/ = I
2 -х + 4
= 2 dx	(х — y)dy—
1	X
~	4
dx — — 4 (x — 2)2 dx —---(x —2)3
4
3 ‘
1764.	Вычислить x2 dx -j- z2 dz, где / — верхняя половина окруж-i
ности x2 + z2 = 4, пробегаемая по ходу часовой стрелки и лежащая в плоскости хОг.
дР дО
Решение. В данном случае Р = х2, Q = z2, и так как	= 0, то
результат интегрирования не зависит от пути.
Интегрирование по верхней половине окружности заменим интегрированием по отрезку оси Ох, соединяющему точки пересечения окружности Л(—2,0) и В (2, 0) с осью Ох. На этом отрезке z — О и dz — О, ах меняется от —2 до 2. Следовательно,
(*	х3
№ dx z2 dz — \ х2 dx = —
I	—2
1765.	Вычислить <^>	гДе / — окружность (х— 1)2 + (// —
Z
— 1)2 = 1, пробегаемая против хода часовой стрелки.
Р е ш е н и е. Контур / замкнутый:
п , х г, У ЙР 3Q _ 2х/у х2-\~У2 ’ х2 + «/3 ду дх '	(х2 + у2 )2 ’
поэтому по формуле Грина данный интеграл равен пулю.
378
= 8- д_ 8 = И
-2 ~ ’з + з““' з •
1766.	Применяя формулу Грина, вычислить
§ (!/2 + y+z)di/ + (i/z + !/-z)^, I
о2 Z2
где / — ЭЛЛИПС - у + /;>- = !•
а2 Ь2
1767.	Применяя формулу Грина, вычислить
ф (хг + х + г) dx (хг + х — г) dz, i
где I — окружность х3 + г3 = ах.
1768.	Доказать, что интеграл (2х-|-Зг/) dx + (3x — 4у) dy не зави-i
сит от пути интегрирования, и найти значение интеграла, интегрируя сначала по дуге параболы у = х3 от точки 0(0,0) до точки А (2, 4), а затем по прямой, соединяющей эти же точки.
1769.	Доказать, что интеграл (х^ + ^ху3) dx~l~(6xays — 5yi) dy не I
зависит от пути интегрирования, и найти значение интеграла, интег-X2 I]2 рируя сначала по дуге верхней половины гиперболы -2- — ~ = 1 от точки Л(—а, V"2b) до точки В (а, ]/2Ь), а затем по прямой, соединяющей эти точки.
4.	Приложения криволинейных интегралов. 1) Площадь области D, ограниченной замкнутым контуром /, находится по формуле
s = y х е1У—У dx,	(Н)
I
где направление обхода контура / выбрано так, что область D остается все время слева от пути интегрирования.
2) Пусть I есть плоская кривая с линейной плотностью массы р (х, у), тогда а) масса т кривой I вычисляется по формуле
т=( р (х, у) ds;	(12)
1
б) координаты центра тяжести кривой I вычисляются по формулам \ хр (х, у) ds	\ уу. (х, у) ds
х°~ й 11	= т ’	(13)
в) моменты инерции I х, 1у и /0 соответственно относительно осей Ох, Оу и начала координат равны
y)ds, /х2у (х, у) ds,	(14)
/о = \ (л“2 ч-г/2) 11 (х, у) ds.
3) Пусть F~ Р (х, у) i + Q (х, у) j есть переменная сила, совершающая работу W вдоль пути I, и функции Р (х, у) и Q (х, у) непрерывны па кривой I; тогда
1Г = ( Р (х, у) dx + Q (х, у) dy.	(15)
379
1770.	Вычислить площадь области, ограниченной эллипсом х = — a cost, y--bs\nt.
Р с ш е н и е. Из формулы (11) следует, что
2л
S — ' у х dy—y dx — -^ \ (« cos t b cos t + b sin t a sin ,') dt — о
2;r	2 л
ab I* ,	„ ab . ab , l-'л ,
— у (cos- Cf- sm-t) at =	\ dt = — /	---nab.
u	(У
1771.	Найти массу четверти эллипса x = cost, z=^2sin/, расположенной в первом квадранте плоскости xOz, если линейная плотность массы р == г.
Решение. Из формулы (12) следует, что т — \:d>,. Из уравнения кривой/
I находим
ds = ] sin2 t -1- 4 cos21 dt.
Очевидно, что параметр t меняется от 0 до  ; тогда
п
9
т — \ z ds =- \ 2 sin t I sin21 -h 4 cos2 t dt ~
I u
я	л
'ч ___________
— 2 (/ 1 + 3 cos2t d (cos /) ™ — 2 J 3 \ J/ -j- cos21 d (cos t}.
о	6J
Положив cos/ —и, получим
0	___	I _____
-2^3	4- u2 du - 2^'3 у | 4-
i	6
m-2 + iy-ln (/3 -1-2).
1772.	Найти координаты центра тяжести однородной дуги циклоиды x — a(t — sin/), у = а(\— cos/), если (Ос/ ''2л) (см. рис. 129).
Решение. В силу симметрии кривой относительно прямой х = л получаем х0 = л. Найдем теперь т, а затем у0. Из уравнения циклоиды находим, что
ds = аУ 2 у 1 — cos t dt, тогда
2л	________ 2л
т — ) ds ~ )' а рЛ2 Y1 — cos t dt = К? а С 1 — cos t dt =
I о	о
2л
i* t	t |2я
= 2а \ sin dt = — 4« cos у	= 4u -j- 4« = 8а}
О
380
2л	________
) yds ( а (1 —cos t) al^2 К1 —cos t (It
l л
m	8a
1773.	Найти моменты инерции относительно координатных осей и начала координат четверти однородной окружности у — 2 cos t, г = 2 sin t, лежащей в первом квадранте плоскости yOz.
Рушение. В силу одинакового расположения кривой по отношению координатных осей /(,==/„-. Но формулам (14) получаем
ly ~ j z-ds — 4 j sin2 tV 4 sin2 t + 4 cos2 1 dt=-i	о
Л	Л
'2	2'
c f 1 — cos 2t I. sin 2f\ n t
S \--------dt^\\t------------- 2л;
о	0
Л
/0 — \ (у- —.:-) ds -4 ( (cos2 t + sin2 t) p 4 sin21 + 4 cos2 t dt~
i	б
Л	Jt
*2	2
=8 ) dt~8t = 4л.
о	о
1774.	Вычислить работу силы F = yzi + (у + г) / при перемещении точки массы т из точки 0(0, 0) в точку /1(1, 1) по прямой г = у, лежащей в плоскости yOz.
Решение. Из формулы (15) следует, что XV — \ yz dy-'-(y\-z) dz. Так как
I
мы интегрируем по прямой z=y и при перемещении из точки О в точку А у меняется от 0 до 1, получаем
1	।
№ = $ у- у- rft/ + (t/ + y) dy = \(у" + 2у) dy= о	о
1775.	Найти площадь области, ограниченной параболой x = z2 и прямой х~1 (область лежит в плоскости xOz).
1776.	Найти площадь области, ограниченной кривой x = acos3Z, y~ws\rFt (0 t sC 2л).
1777.	Найти площадь области, ограниченной кривой x = a(2cos/ — — cos2(), У = а(2sin/ — sin2Z), если 0С/«т2л.
381
1778.	Найти массу участка линии z = lnx, лежащей в плоскости хОг между точками с абсциссами У 3 и ]/8, если плотность линии в каждой точке равна квадрату абсциссы точки.
1779.	Найти координаты центра тяжести четверти окружности радиуса а (окружность расположена в I квадранте плоскости хОу, ц = 1).
1780.	Найти моменты инерции относительно осей координат и начала координат участка однородной прямой z=—2г/+1, лежащего между осями координат в плоскости уОг.
1781.	Найти работу силы F = xyi(ху) ] при перемещении точки массы т из начала координат в точку Д(1, 1): а) по параболе y = xi, б) по ломаной, проходящей через точки 0(0, 0), В(1, 0) и Л(1, 1), звенья которой параллельны осям координат; в) по ломаной, проходящей через точки 0(0, 0), С (0, 1) и Л(1, 1), звенья которой параллельны осям координат.
§ 6. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
I. Поверхностные интегралы по площади поверхности. Пусть F (М) — F (х, у, г) есть функция, непрерывная на некоторой гладкой * поверхности а. Разобьем эту поверхность на ячейки щ, о.,, ... , В каждой ячейке о, (1=1, 2, 3, .... п) выберем произвольную точку М, (х,, у,, zy и умножим значение функции F в этой точке на площадь Дщ, ячейки щ. Сумма таких произведений по всем ячейкам
2 F (М,) Дщ
i = 1
называется интегральной суммой. Обозначим через d (о,) диаметр ячейки щ, т. е. расстояние между наиболее удаленными точками этой ячейки; max d (щ) — наибольший из диаметров всех ячеек данного разбиения. Поверхностным интегралом j ) F (/VT) do от функции F (.И) по площади поверхности о называется предел интег-п
ральных сумм при неограниченном увеличении числа ячеек, когда все ячейки стягиваются в точку
y.F(M)d<j= lim V F (Му До,.	(1)
a	max d (а,) -» 0 = t
Поверхностный интеграл по площади поверхности обладает свойствами, аналогичными свойствам криволинейного интеграла по длине дуги.
Если F (х, у, г) означает поверхностную плотность массы материальной поверхности о, то интеграл (1) определяет массу всей поверхности; и по формулам, аналогичным формулам § 4, вычисляются координаты центра тяжести и моменты инерции этой поверхности.
Предположим, что поверхность о однозначно проектируется на какую-либо координатную плоскость, например на плоскость хОу, и область D на этой плоскости является ее проекцией. Тогда элемент поверхности о определяется формулой
, dx dy
rfff — ;   7Т7ГТ ,	(2)
| cos у (M) |	’
где у (M) —угол нормали к поверхности о с осью Ог в ее текущей точке М (х, У, 2).
* Поверхность называется гладкой, если в каждой ее точке существует касательная плоскость, непрерывно изменяющаяся вдоль поверхности.
382
Если поверхность задана уравнением z=f(x, у), то
и интеграл (1) вычисляется по формуле
Я jг <’ г) * - Ц лк#2-’ L -,«.»* -
- И ' К >. / *	+ is')’ + ($)’*
D
(3)
(4)
Замечание. В более сложных случаях, когда поверхность кусочно-гладкая или неоднозначно проектируется на координатные плоскости, ее разбивают на гладкие части, однозначно проектирующиеся на одну из координатных плоскостей, а интеграл (1) разобьется на сумму интегралов по этим частям.
1782. Вычислить ( ,, , —где о —часть плоскости х + у + .) .) U т*-Гг)“
а
4-г=1, заключенная в I октанте (см. рис. 200).
Решение. Запишем уравнение данной плоскости в виде г=1— х — у. Так dz . дг	,	....
как = — 1 ,	= — 1, то по формуле (3)
da =К 1 +(— 1)а + ( — I)2 dx dy = ]^3 dxdy.
Проекцией а на плоскость хОу является треугольник D, ограниченный прямыми х + у — 1, х = 0, у=0- В этом треугольнике х меняется от 0 до 1, а при каждом фиксированном х ордината меняется от у = 0 до у=\— х. Поэтому по формуле (4) имеем
<7	D
= (С______Ез^__ = /з с =
.1 .1 (1+х+1-х — у)г .1	(2 —у)3
1>	оо
= 1 * 2—1/j0 dx = V''3	=
о	о
= /3 fin 14-х)— -i-xlP = /3 fin 2—
I	" J |0	\	" /
1783. Вычислить координаты центра тяжести С однородной полусферы радиуса R.
Решение. Выберем систему координат так, чтобы полусфера стояла на плоскости хОу, а начало координат находилось в ее центре. Тогда уравнение полусферы имеет вид л-2 — </24-z2 = /?2 (z>0). Так как поверхность однородная (постоянная плотность массы), то из соображений симметрии ее центр тяжести должен находиться на оси Ог, т. е. хс=0, ус = 0. Формула для вычисления гс однородной поверхности а имеет вид
W zda __ б о
383
В данном случае а задана уравнением x2+y2+z2 — R2 (г 3- 0), откуда z = — ГД2 — х2 — у2. Вычисляя по формуле (3) элемент поверхности сферы, получим (проверьте!)
,	/\ dx dy
da = r	.
V R2 -x2--y2
Данная полусфера проектируется в круг D радиуса R с центром в начале координат, поэтому
= л/? (О-2/?) = 2л/?2.
Для вычисления второго плоскости хОу.
Таким образом,
интеграла были применены полярные координаты на
л/?2 __ R '2ixR2 ~~ 2 '
1784. Вычислить
^4-2х+ з у} do, 1 а
где гт — часть плоскости
6хД-4т/ Д-Зг= 12, лежащая в I октанте.
1785.	Найти момент инерции однородной полусферы относительно: а) плоскости основания, б) оси симметрии.
1786.	Найти координаты центра тяжести однородной поверхности параболоида г = х2Ц-г/2, ограниченной плоскостью г=1.
1787.	Найти массу и координаты центра тяжести конической поверхности г2 = х2 + у2, 0=СггС1, если ее плотность в каждой точке пропорциональна расстоянию этой точки от оси конуса.
2.	Поверхностные интегралы по координатам. Пусть о—гладкая поверхность, на которой выбрана одна из двух сторон, определяемая направлением нормали л {cos a, cos р, cosy}. Поверхностный интеграл от непрерывной функции R (х, у, z) по координатам х и у по поверхности а R (х, у, z) dx dy выражается 'а
через рассмотренный выше поверхностный интеграл по площади поверхности следующим образом:
\ \(х, у, z)dxdy = ^ r(x, yt z) cos у da. a	a
Аналогично вводятся поверхностные интегралы по координатам х, г и у, г:
j j Q (х, у, z) dx dz—^Q(x, у, z) cos fl da a	a
384
и
ЭД Р (х, у, 2) dy dz = ЭД Р (х, у, z) cos a da.
'о	о
Обычно рассматривают сумму всех трех интегралов по координатам вида
ЭД(х, у, г) dy dz + Q (х, у, z) dx R (х, у, z)dxdy.	(5)
o’
Поверхностный интеграл ho координатам обладает всеми свойствами интеграла по площади за исключением одного: при изменении стороны поверхности интеграл (1) меняет знак.
Поверхностные интегралы по координатам вычисляются следующим образом. Предположим, что поверхность а однозначно проектируется в область DL на плоскости хОу и z=f(x, у) — ее уравнение, тогда
ЭД R (х, у, z) dxdy= ± ЭД R [х, у, f (х, у)] dx dy,	(6)
a	D\
где знак плюс берется в том случае, если на выбранной стороне поверхности cos у > 0, и знак минус — если cos у < 0. Аналогично, если о однозначно проектируется в область £>2 (или О3) на плоскости xOz (или yOz), т. е. может быть задана уравнением у = ср(х, z) [или х = ф(у, z)], то
ЭД Q f.v, У, г) dx dz = ± ЭД Q [х, <р (х, z), z] dx dz,	(7)
o’	£>2
ЭД’ Р(х, у, z)dydz=± ЭД Р [i|> (у, г) у, z] dy dz,	(8)
‘d	Ьз
в случае (7) берется тот же знак, что и у cos Р, а в случае (8) —знак cos а. Для вычисления интеграла общего вида (1) используются те же формулы
где
(2), (3) и (4), если поверхность о однозначно проектируется на все три плоскости, т. е. ее уравнение F (х, у, г) = 0 однозначно разрешимо относительно любой из координат. В более сложных случаях а разбивается на части, обладающие указанными свойствами, а интеграл (5) —на сумму интегралов по этим частям.
1788. Вычислить I — §zdxdy+
О
4- х dx dz + у dy dz, где о — т реуголь-нпк, образованный пересечением плоскости х — (/4-z=l с координатными плоскостями. Выбор нормали к поверхности о указан на рис. 212.
Решение. Будем вычислять каждый из слагаемых интегралов отдельно. В первом из них надо выразить г через х и у из уравнения плоскости z=‘l — х-\-у и применить формулу (2), причем перед интегралом по IR (т. е. по треугольнику АОВ) надо взять знак плюс, с осью Ог образует острый угол у (cosy>0):
так как выбранная нормаль п
1г — \ \ z dx dy = -\-	(1 — х + у) dx dy =
а	АОВ
1 0
dx (1 — х' + у) dy = —	.
0	х=1
13 Кручкович и др.
385
Аналогично, 1	1 —х.
/2== хг/хг/г--^ х dx dz = — х dx dz = —^v
*о	дос	о о
о 1+//
Л= ydydz = + ydydz = у dy	dz = —--.
а	ВОС	—1 о
Здесь при вычислении /2 была использована формула (3), причем знак минус взят потому, что выбранная нормаль п образует с ,осью Оу тупой угол р (cosp<0). При вычислении /3 учитывалась формула (4) и то, что cos а >0.
Таким образом,
' = ^444 = 4
1789.	Вычислить ^yz dy dz -ф xz dx dz -ф xy dx dy, где о —внеш-a
няя сторона треугольника, образованного пересечением плоскости х+у+г—а с координатными плоскостями.
1790.	Вычислить № dy dz -ф у2 dx dz -ф г2 dx dy, где о —внешняя a
сторона части сферы х2 -ф у2 -ф г2 — а2, лежащей в первом октанте.
1791.	Вычислить jj’jj х dy dz -ф у dx dz -ф z dx dy, где ст —внешняя a
сторона сферы х2 -ф у2 -ф г2 = а2.
1792.	Вычислить	(у — z) dy dz -ф (г — х) dx dz-\-(x — у) dx dy, где
a
о —внешняя сторона конической поверхности х2-}-у2 — г2 (Q^cz^h). г,	С (' /dy dz , dx dz , dx dy\
1793.	Вычислить J	—|—-—|—где о —внешняя сто-
х2 , у'1 , z2 .
рона эллипсоида и2+с2=1.
ГЛАВА XI
ЭЛЕМЕНТЫ ВЕКТОРНОГО АНАЛИЗА
§ 1.	СКАЛЯРНОЕ ПОЛЕ. ПРОИЗВОДНАЯ ПО НАПРАВЛЕНИЮ
1.	Определение скалярного поля. Поверхности уровня. Говорят, что задано скалярное поле, если указан закон, в силу которого каждой точке М. некоторой области V пространства поставлено в соответствие определенное число и(М). Если выбрана некоторая декартова система координат, то задание скалярного поля эквивалентно заданию функции трех переменных
и (М) = и (х, у, г)
(1)
в пространстве или заданию функции двух переменных
и (М) — и (х, у)
на плоскости; в этом случае поле и (.И) называется плоским полем.
Множество всех точек М из области 1/, в которых выполняется равенство и(М) = С, где С —некоторая постоянная, называется поверхностью уровня, соответствующей числу С. Семейство поверхностей уровня скалярного поля и (/VI) в декартовых координатах определяется уравнением
и (х, у, z) = C,	(3)
где С—произвольное действительное число. Заметим, что поверхностями уровня плоского-поля (2) являются цилиндрические поверхности с образующими, параллельными какой-либо координатной оси, например, оси Ог:
и(х, г/) = С.	(4)
Плоское поле (2) на любой прямой, параллельной оси 0г> принимает одинаковые значения; поэтому в дальнейшем поле (2) будет рассматриваться только на плоскости хОу, тогда уравнения (4) определяют семейство линий уровня поля (2) на плоскости хОу.
1794.	Найти поверхности уровня скалярного поля
Решение. Поверхностями уровня дан-
(2)
ного плоского поля являются цилиндрические
поверхности (рис. 213), определяемые уравнениями -----=С1, или х2 + (/2 —
yxa + z/2
13*
387
Следовательно, семейством линий уровня данного плоского поля являются концентрические окружности х2-1-у2 = С2, z = 0 (рис. 213).
1795.	Найти поверхности уровня скалярного поля
•	,4
и — arcsin .........
1^х2+у2
Решение. По формуле (3) находим уравнения поверхностей уровня:
arcsin= С, I С <-5-.
]/х2 + у2	2 ’
или
—-..— = sin С, z == J/ х2и2 sin С,
Ух2 + у2
т. е. искомые поверхности — конусы с вершиной в начале координат, осью симметрии которых служит ось Ог.
1796. Найти поверхности уровня для следующих скалярных полей: а) и(М) = ху, б) и (Л1) = |/ х2 у2 + г2.
2. Производная скалярного поля. Производная скалярного поля и (Л1) по направлению I, заданному вектором
а = ах I + а у j -\-azk,
вычисляется по формуле
ди ди , ди „ , ди
= cos а-'г э cos р+ 3 cosy,	(5)
dl дх ду дг '	х ’
где
ах о аи
cosa = ——, cosp = |-^-;, cosy = .— | a j ’	I a | ’	1	| a \ ’ .
|a| = ],/oy + ^ + aj.
Производная скалярного поля и (/И) по направлению кривой L в точке М совпадает с производной по направлению касательной X = cos oci-|-cos (3/-pees у'и. к L в точке Л4 и вычисляется по формуле (5).
.,	I ди I
Аосолютная величина - определяет скорость изменения скалярного поля в точке /И, а ее знак — характер его изменения (возрастания или убывания).
1797. Найти производную поля и (Л4) = tfz — 2xyz + г3 в точке Л/(3, 1, 1) по направлению вектора $, если s образует с координатными осями острые углы а, р, у, причем а ~	.
Установить характер изменения поля в данном направлении.
г,	_	л 1	„ л И 2
Решение. По условию задачи, cos а. = cos — у, cos р = cos. Так как cos'aa-|-cos2-P + cos2y = l, а угол у — острый, то
cos у — К1 — cos2 a —- cos2 р = j/" 1 — 4 ~" 2 = T ‘
388
Частные производные функции и (Л4) в точке Л1 (3, 1, 1) имеют значения:
= (— 2г/г) I = —2, I = (2уг — 2лг) I = — 4
дх |л;	' J ' [л/ ду |м '	I лг ’
=(^_2х^+2г) I =—3.
dz I м	i м
По формуле (5) имеем
dl 2 2	К2	2	2	’
ди .	,, „
т. е. с 0, следовательно, скалярное поле и (/И) уоывает в заданном направлении.
1798. Найти производную поля и (М) == 2 (ху + г) по винтовой линии L: х ^=2 cost, у—-2 sin/, z — 2t в точке Л10 (х0 (/), y0(i), z0 (/)), „	, З.т
соответствующей параметру t = - .
Решение. Эта линия расположена на цилиндре х2 + //2 = 4, точка М имеет координаты .г —О, у---—2, г^-Зл. Так как векторное уравнение линии L — г (/) -----2 cos ti-y‘2 sin tj -\-- '2Л1г, то касательный вектор к ней в произвольной точке М имеет вид
dr-
Т = ^ =— 2 sin Ч + 2 cos //4-2 k.
Тогда в точке Л40 (0, —2, Зл) T = 2Z4-2fe; находим орг т° вектора t:
т 214- 2k _ i 4- к
1	1/V
Таким образом, cos а = рту =	( cos [4 = 0 и cosy = —так как част'
ные производные поля и в точке М
dU\ =2у\ = —4, ^“1 =2л;| =0	=2
дх |л/0	|м0	ду |лг0 IAIO dz |л/0
то по формуле (5)
^“ = (- 4) '^-4-0.04-2^- = - 1^2.
1799.	Найти производную поля: a) U (7И) = х2 4- У2 — Зх 4- 2у в точке /И., (0, 0, 0) по направлению, идущему от этой точки к точке М'(3, 4, 0);
б)	U (М) = ху2z2 — xyz в точке М(1, 1, 2) в направлении, образующем с осями координат углы соответственно в 60°, -15 и 604
1800.	Найти скорость изменения скалярного поля U(M)^=xyz в точке /И (5, 1, —8) в направлении, идущем от этой точки к точке В (9, 4, 4).
1801.	Установить характер роста скалярного поля
U (Л'1) — bxxyz — lxy2z 4- bxyz2
в направлении вектора а = 8i — 4/-|-8fe, в точке М(1, 1, 1); найти величину скорости изменения данного поля.
3S9
§ 2. ГРАДИЕНТ СКАЛЯРНОГО ПОЛЯ
I. Определение. Дифференциальные свойства. Градиент скалярного поля и (М) есть вектор grad и, направленный по нормали к поверхности уровня поля в сторону возрастания поля и численно равный наибольшей производной по направлению. Если в пространстве выбрана некоторая декартова система коор-
динат, то grad и вычисляется по формуле , ди .	ди .	ди .	,,,
grad и — ^- t + ^-J + Л.	(1)
дх ду дг	'
Дифференциальные свойства:
grad (Cjtt! + С2«2) = Сг grad иг + С2 grad	(2)
где Ci и С2 —постоянные, grad (uv) = v grad и -f- и grad v,	(3)
grad = A (o grad и — и grad о);	(4)
grad F (u) — F' (и) grad u.	(5)
1802.	Найти величину и направление градиента скалярного поля и = х2 + у2 + г2 — 2хуг в точке Мо(1, —Г, 2). Определить, в каких точках градиент перпендикулярен к оси Ох, в каких точках он равен нулю.
Решение. Вычислим частные производные:
ди о „ ди о	ди п п
дх J ду J	дг	я
В точке Л40
ди I „ ди I „ ди I •
,	=6,	=—6, х =6;
дх |л/0 ду |лг0 дг\м,
по формуле (1),
grad и (Л40) = 6/ — 6/ + 6Л,
I grad и\= |/’б2 + (—6)24-62 = |/Той?
В произвольной точке М (х, у, г)
gtaAu(M) = 2(x — yz'}i + 2(y — xz')j-[-2(z — xy}k.
Вектор, перпендикулярный оси Ох, имеет равную нулю первую координату, поэтому
2(х-//г)=0.
Таким образом, для всех точек М, лежащих на поверхности x = yz, grad и перпендикулярен оси Ох.
Чтобы gradu(A4) = 0, нужно, чтобы
х — уг = 0, у — хг = 0, г — ху — 0.
Этой системе удовлетворяют следующие точки:
ЛМ1, 1, 1), М„(- 1, - 1, 1), М3 (1, - 1, - 1), М4(- 1, 1, -1), Л45 (0, 0,0).
Таким образом, в этих точках grad и обращается в ноль.
1803.	Найти градиент поля со (Л4) —	в точке Л10 (1,2, 2).
390
Решение. Градиент поля со (.И) определим по формуле (4), положив и(Л4) = х, о (Л4) = х2+ //2-[-г2. Так как
и (Л40)=1, о(Л40) = 9, grad и — grad v (Мо) = (2x7 + 4yJ + 2гА) \м„ = 27 4- 4/ + 4А, то по формуле (4) находим
grad со (Мо) = J2- [9Z - (2/ + 4/ + 4*)] =	.
1804.	Найти гридиент скалярного поля u — f(r), где г= V'x2 + y2 + z2.
Решение. Градиент найдем по формуле (5). Определим сначала grad г: дг ___________х_______ дг _ у	дг_______г______
dx ~ yx2 + lJ2 + z€ ’ ду ~ |/х2 + у2 + г2-’ дг ~ ]/х2 + г/2 4-г2 ’
, х . , у .	г . xi-^-yj-^-zk г
gradr = — с+ - /4---- k — —'-^1—!---= -,
г 1 г ' г	г	г '
где г —радиус-вектор точки Л4 (х, у, г).
Следовательно, по формуле (5) получим
grad f(r) = f (г) grad г = f (г) у .
1805.	Найти градиент скалярного поля и (М) — Зх2у — Зхг/3 + г/4 в точке М(1, 2, 0).
1806.	Найти градиент скалярного поля и = иУх- 4- у2 4- г2 и его длину, в произвольной точке М.
1807.	Найти угол 9 между градиентами скалярных полей и (М) — х2 4-у2 — г2 и v (М) = aresin —в точке Л4(1, 1, УТ).
У
л,	п	- л grad и grad и
Указание. Воспользоваться формулой cos 6 =	;:—г.
1 J	( grad и ( I grad v |
1808.	Показать, что функция и = in (х2 4- у2,4-г2) удовлетворяет соотношению u = 21n2 —In(gradu)2, где (grad и)2 —скалярный квадрат.
2.	Связь между производной поля и его градиентом. Между производной поля и (Л4) по направлению 7 и его градиентом в данной точке Л4 существует следующая связь:
ди
=tgrad u= | grad и | cos 0 =npx grad u,	(6)
где	t = cosa74-cosp/4-cosvft
— единичный вектор направления /, a 0 — угол между градиентом и вектором t в точке М.
Длина градиента равна наибольшей скорости изменения поля и (Л4) в точке Л4:
ди ।	, . -]/"/ди'\2	/ди\2 , /ди\2
max-7 = igradU| = y +	.	(7)
1809.	Найти наибольшую скорость возрастания поля и (Л4) = — ху — z в точке Л40 (2, 2; 4).
391
Решение. Наибольшая скорость изменения поля в данной точке определяется по формуле (7). Частные производные поля в точке Л10 (2, 2, 4) имеют значения
ди	,	0и\	„.	. . п
-	— ух1> 1	=4,	= №1пх =4 In 2,
ох \мо	Л1„ оу\м„
()и I
дг |лг„
поэтому
grad и (Л40) = 4/ + 4 In 2у — к,
а искомая наибольшая скорость возрастания поля
max = | grad и (Л1о) | = К 42 + (4 1 п 2)2 + (— 1 )2 = К17 + 16 1 п2 2.
1810.	Найти производную скалярного поля м —у, где г — ==]/x2 + z/24-z2, по направлению I {cos a, cos р, cosy}. Когда ^“ = 0?
Решение. Производную найдем по формуле (6). Так как по формуле (5)
. 1	1	, 1г г
grad у = - у grad г - - у •	= -- у
(см. 1804), то
ди ,	, 1	1 .	,	„ .	.
01= I grad у = — (х cos а + t/ cos р + г cosy).
„ Эн
Если ч,= 0, то
д1
1 1г 7=*з=0>
т. е. вектор I должен быть ортогонален радиусу-вектору г.
1811.	Найти наибольшую скорость возрастания поля и (/И) — == In (х2 + 4у2) в точке М (6, 4, 0).
1812.	Даны скалярные поля и = У\2+у2 и v — x — у + У^Зху. Найти угол 0 между градиентами этих полей в точке М (3, 4, 0).
1813.	Вычислить с помощью градиента производную поля и (М) = (х2 + z/2-|-г2)3-'2 в точке М (1, 1, 1) по направлению вектора I = 2/— k.
Указание. Для вычисления grad и (.VI,,) воспользоваться формулой (5).
1814.	Найти производную поля и(Л1) = хг/г по направлению градиента поля v (Л4) = 2х2 — 3xz Ц- z2 Д-yz в точке Л4 (1, 1, 1). Записать ответ в общем виде для произвольных скалярных полей и(Л4) и у(Л4) в М (х, у, г).
1815.	Найти градиент и, если: 1) и —г2, 2) м = у, 3) « = у.
§ 3. ВЕКТОРНОЕ ПОЛЕ И ЕГО ПОТОК ЧЕРЕЗ ПОВЕРХНОСТЬ
1. Определение потока и его вычисление методом проектирования на одну из, координатных плоскостей. В некоторой области V пространства задано векторное поле, если каждой точке Л1 (х, у, г) этой области сопоставлен вектор
а(М) = Р(х, у, z)/-|-Q(x, у, z)j + R(x, у, г) к, проекции которого —функции Р, Q и R — будем считать непрерывно дифференцируемыми в этой области.
392
Пусть в указанной области V задана двусторонняя поверхность а. Выбор стороны на этой поверхности определяется единичным вектором нормали п к поверхности а;
п = cos a i -J- cos Ру-F cos у Л.
Если поверхность а задана уравнением
2 = f(x,y),	(1)
Знак плюс соответствует выбору верхней стороны поверхности, нормаль к которой образует острый угол с осью Ог и, следовательно, cosy |т. е. коэффициент при- k в формуле (2)] положителен. Знак минус отвечает нижней стороне поверхности .
Если поверхность о задана уравнением
f (/И)=л(х, </, z)=o,	(3)
то единичный вектор нормали
grad А (Л4)	dxl + dyj + dz К
п~± | grad F (Л1) | ~ ± Г,1772 г, др г ’
причем знак в правой части берется так, чтобы получить нормальный вектор п именно к выбранной стороне поверхности.
Если поверхность состоит из нескольких частей, заданных уравнениями (1) или (3), то вектор нормали вычисляется для каждой части отдельно по тем же формулам (2) или (4), выбор знаков в которых определяется заданием одной из сторон всей составной поверхности. В случае замкнутой поверхности условимся всегда выбирать, ее внешнюю сторону.
Потоком векторного поля а через двустороннюю поверхность о называется поверхностный интеграл
П = j j а (Л1) п (Л1) dry,
'а
где и (М) — единичный вектор нормали к выбранной стороне поверхности в ее произвольной точке.
Если поверхность о взаимно однозначно проектируется на плоскость хОу в область Dxy, то вычисление потока векторного ноля а через о сводится к вычислению двойного интеграла ио области DXJ по формуле
П= \ \ ап dry — \ \ ।dx dy	г
''	J j COS Y I |г = г(л:, U)	(')
°
где cosy есть коэффициент при k в формуле (2), если уравнение поверхности задано в виде (1). Если такая поверхность о задана неявным уравнением (3), то cos у —коэффициент при k в формуле (4), а г = г(х, у) получается разрешением уравнения (3) относительно г. Аналогично, если поверхность о взаимно однозначно проектируется на плоскость уОг или гОх, поток вычисляется по формулам
11= ? I аУ dz’ U== И I dx dz- (°) J J cos a | Л-=^(Й, г)	J J cos p I (/==!/(.v, г)
D,„	D„
393
Замечание. В более сложных случаях, когда поверхность а состоит из нескольких частей аъ <т2 и т. д., имеем
П = j j an da = J J	an2 da-]-...,	(7)
a	at	aa
где nlt n.> и' т. д. соответственно нормали к поверхностям Oj, <т2 и т. д.
1816. Вычислить поток векторного поля а = (х — 2г)Г+(Зг — 4х)У+ + (5x-\-y)k через верхнюю сторону треугольника с вершинами Л(1, 0, 0), В(0, 1, 0), С(0, О, 1).
Решение. Треугольник АВС взаимно однозначно проектируется, например, на плоскость хОу, а уравнение его плоскости х-|-</-|-2 — 1 =0. Принимая
(т, у, z)=x-J-j/ + z — 1, найдем единичный вектор нормали к этой плоскости ‘
= grad/7 Z+/ + fe
1 grad F | '	/3
Здесь cosy=-|-->0, что и соответствует нормали к внешней стороне треуголь-V 3
ника. После этого находим
Г7~Г = ।/5 [(* ~2z) +(3z ~ 4х) +(5х+(/) ] I сиг> VI у о
[~ = 2х+ </-}-г.
треугольника АВС получаем 2=1 — х — у, а поэтому —аП— I .	=2х + </ + (1 — х —у) = х+ 1.
(COSYI |г=г(х, й
Так как проекция треугольника АВС на плоскость хОу есть треугольник АОВ, то по формуле (5) найдем
С С ап I  j j
\ \ т;	dxdy =
I cosy I \z=z(x, и)
t\ABC
1	1-х
= (x + 1) dx dy =	(x4-1) dx	dy =
Адов	о	6
1 (•	2
= (l—x2)dx = --.
0
1817. Найти поток векторного поля а — xi + yj + (1 — г) k через полную поверхность конуса х2 + у2 = г2	(рис.
214).
Решение. Полная поверхность а конуса состоит из двух частей <7, и <ь, соответственно заданных уравнениями F (х, у, 2) =x2 + z/2 — г2 =0 и 2 = Н. По формуле (7) имеем П = П14-П.,= )| j ап1 do + 'j \ an,, da, где «! —внешняя нор-‘а,	‘а2
маль к поверхности конуса, а п2 = /? —нормаль к плоскости 2 = //; по формуле (4) имеем
п = grad F = 2 (xi + yj — г/г) = xi + yj2k
1 i grad F |	2 |/x2 + (/2 + 22	K’2 (-<2 + г/2)
394
(z из уравнения конуса заменяется через 1/Гх24-//2). Заметим, что выбранное
направление нормали удовлетворяет условию cos у — — ——	* -
< 0 (г > 0), т. е.
Т>2 (см- Рис- 214).
По формуле (5),
тт С С j С С x2 + y2 + z2-z , , С (' 2 (х2 + г/2) -/х2 + z/2 , , П1 = i \ ««1 da= ------j-2|— dX dd = J J --------17==5------- dX dy'
rt	ГУ	ГУ	’	I J
где Dxy— круг радиуса H и х2-5гу2^:Н2. Переходя к полярным координатам, имеем
2л	Н	2л	н '
П1= dtp	—- р dp = dtp (2р2 —р) dp = 2n (2/ЗЯ3 —1/2Я2).
0	0	0	0
Аналогично, п.2 — внешняя нормаль к плоскости основания конуса: Я2 = Л; поэтому
П2 = \ J ап.,_ da — ^ j (1 — z) do = J j (1 — H) do~(l—H) j do= (1 — Я) лЯ2. (J2	^2	^2	@2
Итак,. П = Щ + П, = лЯ2 (4/ЗЯ — 1 + 1 — H) = 1 /ЗлЯ3.
1818.	Найти поток векторного поля
а = хЧ + xj + xzk
стороны параболоида в первом ок-и ограниченную плоскостью
вращения у
с положительными направлениями
через часть внешней (рис. 215), лежащую
танте
Решение. Записывая уравнение данной поверхности в виде
F (х, у, z) = x2 + z2- у = 0, найдем
— ^rat' F — 2xZ—/ H~2zfe
“ | grad F | ~ j/4x2 _|_ i 4z2 ’
Так как здесь
cos 6 = — 	*..	< 0,
 |/4x2 + l+4z2
то вектор п является внешней нормалью к данной поверхности (из рис. 215 видно, что внешняя нормаль образует острые углы осей Ох и Ог и тупой угол с положительным направлением оси Оу}. Поэтому
Г^|, = ,(х,г) = Х[2(х2 + 22)”'11
и, следовательно, по формуле (6),
п- $ S пгт, L,,.- И “2	11 л
DXZ	Dxz
395
Проекцией l>x~ является четверть круга, поэтому для вычисления полученного двойного интеграла удобно применить полярные координаты на плоскости хОг х = р cos <р, г = р sin ф:
Л/2	1 1
П = cos ф гйр (2р4 — р2) dp = lg.
О	о
1819.	Вычислить поток векторного поля
а -= (у 4- г) i - 2xj 4- (2г - х) k
через полную поверхность треугольной пирамиды с вершинами А (1, 0, 0), В(0, 1, 0), С(0, 0, 1) и 0(0, 0, 0).
1820.	Вычислить поток векторного поля а = yzl — xj — yk через полную поверхность кругового конуса х2 4~ Уг — г2 — 0, ограниченного плоскостью z = 1 (0 < г 1).
1821.	Вычислить поток векторного поля а = 2xi 4- 2yj — (2г — 1) k через замкнутую поверхность, ограниченную поверхностью параболоида у2 4~ //2 = 1 — 2г (г /0) и частью плоскости хОу.
1822.	Вычислить поток векторного поля а = х:Ч -j- ynJ4- zsk через R2
боковую поверхность конуса х2 4- У1 г2, 0	•	//; через пол-
ную поверхность конуса.
2.	Вычисление потока методом проектирования на все три координатные плоскости. Пусть поверхность о взаимно однозначно проектируется на все три координатные плоскости (ее проекции обозначим соответственно Dsx, Dxy), тогда ее уравнение
Г (у( у, г)=-0
однозначно разрешимо относительно каждого из аргументов. Если этими решениями являются функции х = х(у, г), у = у(х, г), г = г(х, у), то поток векторного поля
а = Р(х, у, z)i + Q(x, у, z\j + R(x, у, г) k
может быть вычислен по формуле
П — -j- j j Р [х (//, г), у, г] dy dz ± Q [у> У (у, г). г] dx ±
Г)уг ~	.	Йт\-
± $ Jj R [у, у, г(х, y)]dxdy,	(8)
°ху
где знак перед каждым из двойных интегралов берется соответственно таким, каков знак cos a, cos р и cosy на поверхности а.
1823.	Найти поток векторного поля
а = (у - 2z) 1 4-(у 4-3z/4-г) j 4-(5у 4-z/) fe
через треугольник, получаемый при пересечении плоскости у4~// + 4-z=l с координатными плоскостями; сторону треугольника выбрать так, чтобы нормаль к ней образовывала острые углы с осями координат.
Решение. Здесь	Л
у=1 —(</ + ?), Р[х(у, г), у, г]='1 — (у4-г) —2г= 1 —у —Зг,
—(х4~г), Q [у, уДх, г), г] = х4*3 [ 1 — (у-]-г)]-]-г = 3— 2х— 2zt
г=1 — (%4-у), R [у, у, г (у, у)] = 5х4-у.
396
По условию, все три направляющих косинуса нормали положительны, поэтому в формуле (8) надо взять все три знака плюс. Подставляя вычисленные значения Р, Q и R, получим
П j (1 —  у — Зг) dy dz + j j (3 — 2x — 2г) dz dx -ф- j	(5x+y) dx dy =
Ъуг	Ъху
I I—у	1	1 — x	1	1— у
— \dy j (1 — у — Зг) dz + j dx (3 — 2x — 2z) dz dy j (5x + y) dx = 0	0	0 I)	0	0
1824.	Найти поток векторного поля a — 2i — xjA~5zk через верхнюю сторону треугольника АВС, полученного при пересечении плоскости хА~ 2у Зг — 6 = 0 с координатными плоскостями.
1825.	Найти поток векторного поля a = 4i — 9J через внешнюю сторону поверхности параболоида вращения у = х2 -|-г2, ограниченную плоскостью у = 4, лежащую во втором октанте.
3.	Вычисление потока векторного поля с помощью криволинейных координат на поверхности. При вычислении потока векторного поля через боковую поверхность кругового цилиндра или через сферу удобно пользоваться соответственно цилиндрическими или сферическими координатами, обходясь без проектирования на координатные плоскости.
Пусть дана часть ст цилиндрической поверхности х- -фу" R2, ограниченная поверхностями
z = fi(x, у), z = f2(x, у) [fjx, г: ди, //)].
Полагая .r=/?cos<p, у = R sin q>, z —z, для данной поверхности получим
О q; з? 2л, В (R cos q>, R sin q) эт г f., (R cos <p, R sin <p), da = Rdtp dz.
Поток векторного поля а через внешнюю сторону поверхности о вычисляется по формуле
2л /2 (Кcos (р. 7?sin ф)
П — R j dtp (j andz,	(9)
б • fi (ft cos ф, R sin q) где
n== * (w-+yj}. (10) | grad (xl+yl — B2) | R J
Пусть дана часть о сферы х2 -фу2ф- г2 = R'2, ограниченная коническими поверхностями, уравнения которых в сферических координатах 0! — Z7! (ф), 0? = = /Ф (q). Воспользуемся формулами перехода
x — R cos q> sin 6,	у = R sin q> sin 0, z = Rcos6,
где <piqi «д q)2, 6j 0 sg fd, a do = R2 sin 6 d6 dtp. В этом случае поток векторного поля а через внешнюю часть сферы а вычисляется по формуле
Ч>2	6;
II = R2 , dtp j an sin 6 d6,	(11)
Ф1 8'1 где
grad (x2 + y2-|-z2 —R2)	1	, .
| grad (x2 + i/2 + z2 —R2) | - fAxi + y.)+zk).	(12)
397
7t
В случае полной поверхности сферы ф меняется от 0 до 2л, 6 от —%
до
л
2 ’
1826.	Найтк поток векторного поля а = xi -j-\- z2k через цилиндрическую поверхность х2-\-у2 = 16, ограниченную поверхностями г = 0, х-фг/-фг = 4.	_
Решение. Поток вычислим по формуле (9). Здесь /? = 4,	(х, у) = 0,
fz(x, у) — 4 — х — у — 4— 4 cos ф— 4 sin ф, 0:д;-:2л. Поэтому согласно формуле (9)
2л	4 -—4 cos ср — 4 sin ср
П = 4 d<p \	a n dz.
д	о
А так как
Xl + yJ	1 Г 9	,	1 Г,/.	.
и = —ап = 4 [х2 —(/]•.= 4-[16cos2(p-4sin<p], то
2л	4 — 4 cos ср — 4sin<p
П = 4 Лр	. Д- [16 cos2 ф — 4 sin ср] dz —
О	о
2л
— 4	(16 cos2 ф - 4 sin ф) (1 — cos ф — sin ф) Ар =
о
2л
= 16 \ (4 cos2 ф + sin2 ф — 4 cos3 ф—4 cos2 ф sin фф sin <p cos ф — sin ф) <Ар = 80л. о
1827.	Найти поток векторного поля
a = xi + (y + z)j + (z-y)k
через часть сферической поверхности х~ -ф у- -ф г2 = 9, расположенную в первом октанте.
Решенн е. Так как
grad (х2фу2фг2—9)	1 , . , . , ..
. ”""1 grad (х2фу2фг2-9)| ~ 3 ^' + у/Ф2^, ТО >
ал = у [х2фу (уфг)фг (г — у)] = * [х2ф у2фг2] = 3.
л ,	JT _ f. . л
По условию задачи, о находится в первом октанте, т, е.
В этом случае по формуле (11) л/2	л/2
С	С	|л/2	|л/2 97
П = 32 \ dtp \ 3 sin е dfl=—27ф cos 0	= л.
о	6
1828.	Найти поток векторного поля
а = (х - г) i -ф (г2 — y2)j + (* + г) k
через часть цилиндрической поверхности х2 -фу2 = R2, ограниченной плоскостями г = 0, г = Ь.
398
1829.	Найти поток векторного поля а = xi-\-2yj — zk через поверхность сферы х2 у2 ф- г2 = 4.
1830.	Найти поток векторного поля а = xyi 4- yzj4- xzk через все границы восьмой части шара х2 4- уг 4- г3 1, заключенного в первом октанте.
Указание. Искомый поток определяется по формуле П = П4 + П3 + П3П4, где П4, П3, П3 —потоки через части координатных плоскостей, а П4—поток через часть сферы.
§ 4.	ДИВЕРГЕНЦИЯ ВЕКТОРНОГО ПОЛЯ. ТЕОРЕМА ОСТРОГРАДСКОГО
1.	Дивергенция векторного поля. Дивергенцией векторного поля
а = Р(х, у, z)Z + Q(x, у, z)J + R(x, у, z)k ' <.
в точке М называется объемная плотность потока векторного поля а в этой точке:
div а (М) = lim --- \ \ an do,
О - М V i J а
где о—объем, ограниченный замкнутой поверхностью о, содержащей точку М.
В декартовой системе координат дивергенция вычисляется по формуле
л- пл fdP dQ , dR\ I	.
div a (M) = 5- +	.	(1)
\dx dy dz) |,vi
i	Свойства
1)	div [C1a1 + C3a2] = C1 div a4-|-C3 div a3, ede C1: С., —постоянные.
2)	Дивергенция постоянного вектора равна нулю. ‘
3)	Дивергенция произведения функции и (/И) на векторное поле а (/И) вычисляется по формуле
div (ua] = u div а + а grad и.	(2)
1831.	Найти дивергенцию поля b -^иа, где и = xy2z\. а = 21 4-4- 3/— к.
Решение. Дивергенцию векторного поля b найдем по формуле (2). В силу второго свойства
div а (М) = 0,
а
grad и = у2г31 -]- Zxyz-y + 3xy2z2fe,
поэтому
div & = agrad « = 2y2z34-6xyz3 —3xy2z3.
1832.	Вычислить дивергенцию единичного радиус-вектора
г° = .
г
Решение. Для вычисления дивергенции воспользуемся формулой (2), 1
положив и — —, а = г, тогда г ’
,	,1 г
grad и grad ~
(см. 810), а
дх , du , dz , , ,
div а = div г = v- + -У 4" =- = 1 4" 1 +1 =3.
дх 1 ду ‘ dz 1	'
399
Согласно формуле (2),
1833.	Вычислить дивергенцию a — f(r)r.
Решение. По формуле (2), div а = div f (г) r = f (г) div г + r grad f (г), divr = 3, grad f (r)=f'(г) grad r = /'(г) у (см. 1804) и
div а = 3f (г) + rf (г) Г = 3/ (г) + f' (г) у = 3f (г) + rf (г).	*
1834.	Найти дивергенцию напряженности магнитного поля, обра-зованного электрическим током, текущим по бесконечному прямолинейному проводу	?!
Указание. Если принять за провод ось Ог, то магнитное поле будет
#=2J (— yi + xj), (р = |".е-4-У2)-
1835.	Вычислить дивергенцию следующих векторных полей:
1) « г, 2) а=10гс, 3) a = [(r)c, 4) a = [br], где с—постоянный вектор, b = х2/’ + У2]> г = 4- м/+
2.	Теорема Остроградского. Для вычисления потока через внешнюю сторону	<
замкнутой поверхности о, ограничивающей объем v, удобно применять теорему	i
Остроградского: поток векторного поля а через любую замкнутую поверхность о у равен тройному интегралу от diva, взятому по обьему V, ограниченному поверх-ность о, т. е.	''
\ j an da = ( diva dv.	(3)	(
а	‘ V"	р
1836.	Найти поток векторного поля а = xi + .у/+ (I — г) к через полную поверхность конуса х2у2z2 (0 г И) (см. рис. 214).
Решение. Эта задача была решена выше (см. 1817) методом проектирования на координатные плоскости. Дадим еще одно решение с помощью теоремы Остроградского:
diva = -f-(x) + j) (//) + < (1-2) = 1 + 1-1 = 1,
дху ' 1 ду ' дг '	,	,
поэтому
П — j \ j d i v a dv j j j du) v	id	»
так как 0s;<ps£2jt, О Д) i/1, pT'-dd, то в цилиндрических координатах	*•
зл	п	ll	II
Г	г	(•-	С	/Н3	Ня\	лН3
П =	\ dcp	\	р dp	\ dz = 2л	\	р(Я — p)dp = 2n (-3~)	= ~3~‘
б о р	о	’
1837.	Найти поток векторного ноля а = (х Д-г) i + (z + у) k через внешнюю сторону замкнутой поверхности о‘. {хг + г/2 = 9, г==0, г = у, (zdsO)}.	|
400	В
Решение. По формуле (3), так как div а = 2,
V
Здесь V — тело, ограниченное поверхностью о. Для вычисления его объема введем цилиндрическую систему координат
x = pcos<p,	у = р sin <р,	г = г,
причем
О sg ф ££- л, 0 ел р 3,	0 г у = р sin <р,
dv = p dp dcp dz, 1 поэтому
л 3 р sirup
П = 2 jj J dv = 2 j dcp p dp ( dz = V об о
,-r	з
С	С	Iя p3 P 27
= 2 \ sin cp dcp \ (fidp = — 2 cos cp 5 -- — 4  -- = 36. .1	|o 3 |o 3
о	о
1838.	Найти поток векторного поля a = xy2iA-yz2jA-zx2k через внешнюю сторону поверхности сферы х2 -ф у2 -ф г2 = R2.
Решение. Имеем
div а = ЭР +	+^=^ + г2 + х2 = г2.
дх ду дг J
По теореме Остроградского, пользуясь сферической системой координат, получим 2л л	R
П = г2 dv = dcp sin 0 dO г4 dr = 2л (— cos 6) I • ~	~ л/?5.
V	обо
В следующих задачах с помощью теоремы Остроградского вычислить поток векторного поля а через указанную замкнутую поверхность о;
1839.	a^-x2i-\-xj\-xzk, о : {у = х2-^г2, х = 0, у=1, z = 0 (х 2s 0)}.
1840.	а = x2iz2J, а : {г2 = 1 — х — у, х = 0, y = Q, г = 0, г 2=0].
1841.	а = yzi xzjxzk, о — поверхность пирамиды с вершинам 0(0, 0, 0), А (2, 0, 0),-В(0, 1, 0), С(0, 0, 2).
1842.	a^xyi-^ yzj'A-xzk, сг :	- //- - [-г2 — 1, х = 0, г/ = 0, г = 0,
%2s0, //	0, г2з0}.
1843.	a=^2xi — yj-\-zk, о : {9 — z = х2-фу2, 0-<г=ф9}.
1844.	а = хЧ -ф z'Jk, о : {х2 -ф у2 ф- г2 — R2}.
Вычислить непосредственно и с помощью теоремы Остроград-ского поток векторного поля а через замкнутую поверхность ст:
1845.	а -~=3л7 -2zj-\- yk, о: {х-фг/-фг^2, г ;i, у (), :	(Р.
1846.	а = (х-фг) /-ф (*/-|-х)/-ф (г-ф у) к, а : {х2-фг/2 ^R2, х==--г, ?2s0}.
1847.	a — yzi — xj—ук, cs : {х2 + z2 =-^ у2, у^О, У=1(-
1848.	Вычислить поток центрально-симметрического поля а = = f(г) г через полную поверхность сферы S радиуса R с центром в точке О, где г = 0.
Указание. Воспользоваться сферическими координатами и решением 1833.
401
§ 5. ЛИНЕЙНЫЙ ИНТЕГРАЛ И ЦИРКУЛЯЦИЯ ВЕКТОРНОГО ПОЛЯ
I. Линейный интеграл и его вычисление. Пусть в некоторой области пространства задано векторное поле
а(М) = Р(х, у, z)i+Q(x, у, z)J+R(x, у, z) k
и линия L (с указанным на ней направлением). Линейным интегралом векторного поля а вдоль линии L называется криволинейный интеграл
W — ( ат ds = \ a dr = J Р (х, у, z) dx-\-Q (х, у, г) dy-\-R (х, у, z) dz, (1) l L L
где т —единичный касательный вектор к линии L, ds —дифференциал ее дуги, г —радиус-вектор точки, описывающей линию L.
Если а — поле сил, то линейный интеграл (1) представляет собой работу этого силового поля вдоль линии L.
Если линия L задана параметрическими уравнениями
х=х(0, У = г/(О> z = z(Z), причем в начальной и конечной точках пути параметр t соответственно принимает значения 1 = а, и то
Р
№ = ${P[x(0, y(f), z 0)]x'0) + Q[x(0, у (0, z(/)k'(0+	.9
+ Я[х(0, y(t), z(t)]z'(t)} dt.
Если линия L задана уравнениями • г/=г/(х), г = г(х) (а^хг^б), то линейный интеграл вычисляется й’о формуле ь
{Р[х, у(х), z(x)] + Q[x, у(х), z(x)]y'(x)+R[x, у (х), г (х))г' (х)} dx. (3) а
В случае плоской линии L формулы (2) и (3) упрощаются очевидным образом (полагают везде z = 0).
При изменении направления линии L (с концами А и В) линейный интеграл меняет знак:
adr = — 'j a dr.	(4)
АВ	ВА
1849. Вычислить работу силового поля / = — (a cos(i-^-b sin//) вдоль дуги эллипса +	2 = 0 от точки А (а, 0, 0) до точки
В(0, Ь, 0).
Решение. Параметрические уравнения данного эллипса имеют -вид х — — acost, y = bsint, z = 0, причем точке Д соответствует значение параметров JT
0 и точке В —значение	Так как
л	«	2
х' (/) = — a sin t, у'(t)=b cost, z' — 0,
то по формуле (2)
Л/2
IP — — ) [a cos t (— a sin t) -j- b sin t • b cos /] dt = о Л/2	Л/2
(•	i*	a2 — b2
= — (b2—a2) \ sin t cos t dt = (a2— b2) I sin t d (sin /) = —.
402
1-850. Вычислить линейный интеграл векторного поля + yj+ (* + Ч— О Л вдоль отрезка прямой АВ, где Л(1, В.(2, 3, 4).
Решсии с. Согласно формуле (1),
W = f х dx 4- у dy (х -I- У 1) dz.
АВ
Ct —- XL —
1, 1) И
Каноническое уравнение прямой АВ
х— 1 у — 1	2 — 1	х — 1 г/ — 1	2—1
---- — ----= ----- или -------- = —--- — ----
2—1	3-1	4-1’	1	2	3
Отсюда имеем
у = 2х — 1,	2 = Зх — 2 и dy — 2dx, dz = 3dx,
a x вдоль AB изменяется от 1 до 2. Подставив значения у, z, dy и жение для линейного интеграла и приведя подобные члены, находим 2 1*	/7	\ 12
»' = 2 \ (7х —4) dx = 2 (д х2-4xj = 13.
1851. Найти интеграл векторного поля а = yzi + г У 9 — z/2/+ xyk
вдоль дуги А винтовой линии x = 3cosR
о
у=3 siitf, г= ^-/отточки А пересечения кривой с плоскостью хОу до точки В ее пересечения с плоскостью z = 4.
Решение. Данная винтовая линия расположена на цилиндре х2 + х2 = 9 (рис. 216), причем точке А соответствует значение параметра /л = 0, а точке В—значение /в = 2п. Так как х'(0 =— 3 sin t, 2
у' (0 = 3 cos t, г' (0= то по формуле (2)
2
11-' =	3 sin t • ~ t (— 3 sin t) ~-t • У9 — 9 sin21 • 3cos
о
2л
= f f--t cos 2t — sin	dt = ~
' \ л	л / л
dz в выра-
2 t + 3 cos t • 3 sin t •
л
2л
зи
t (2 cos 2/) dt + sin 2/ dt = I 0
2л - 2л
sin 2t dt
0
= 0.
о
0
1852.	Вычислить линейный интеграл векторного поля
а = (№ + у2 — 2Rx) i R (х Д- у) j
вдоль дуги окружности (х — R)2 + У2 = R2 > г = о от точки 0(0, 0, 0) до A(R, R, 0).
403
1853.	Вычислить работу силового поля /= (2<а — у) I(у — a) j вдоль первой арки (от начала координат), циклоиды х = а{1 — sin Z), i/ = a(l — cos/), г —0.
1854.	Вычислить линейный интеграл векторного поля
а _ xi + yj + zk
I х (х- 1) + у (у- 1) + z (z+~2)
вдоль прямолинейного отрезка АВ, где А (1, 1, 1) и В (4, 4, 4).
1855.	Найти работу силового поля f x2i -\-yj 4-cos zk по одному витку дуги АВ винтовой линии x — acosi, у — a sin/, z — 2t, где з
точки Л и В соответственно получаются при I --- 0 и / — ' л.
1856.	Показать, что работа поля магнитной напряженности
Я -=	(_yz' + -V) (см. 1834) вдоль окружности x24-z/2 = /?2,
г — Н не зависит от радиуса окружности.
2. Вычисление циркуляции векторного поля. Циркуляцией векторного поля а
при пересечении параболоида скостямп (рис. 217).
называется линейный интеграл этого поля вдоль замкнутого пути L:
U.=$adr.	(5)
L
Циркуляция, как всякий линейный ин-, теграл, непосредственно вычисляется по формулам (1), (2), (3).
Замечание. Если линия L со-х стоит из нескольких частей Llt L„ и т. д., У то
Ц=( adr+'i adr+— (6) l, Ц
1857.	Найти циркуляцию векторного поля а — if-i — x2J z2k по контуру АВСА, получаемому х2 z2 = 1 — у с координатными пло-
Решение. Имеем
Ц= ф adr -= ( a dr A- j adr-\- j adr. A DCЛ	AB DC	CA
1) Ha AB: z —0 н dz~0, следовательно,
<7 = y-i — №/’•
Из уравнения параболы .v“  1—у находим
- У---1— х2 и dy-----2л- dx,
тогда
dr dxi dyj =-- dxi — 2х dxj и
adr = y2 dxy-2x's dx = [(1 — x2)2 + 2х3] dx~ [л4 -J- 2л-3 — 2x2-}-1] dx.
404
При перемещении по дуге АВ от точки А до точки В х убывает от 1 до О, поэтому
9	/1 о 9	\ i() oi
«л-	| Л-1 + 2л'3 - 2.V2 + 1 ] dx ' -5 Л-5 + 4 г* - 3 х" + х'| ( = — з() .
2) На ВС: х=0, Дг=0, а — уЧ-^к, dr = dyj + dzk. Следовательно, adr = z2dz (О ':г ;1) и
ВС	О
3) На СА: у = 0, dy = 0, а — — x-J + г'2/г, dr — dxl-\-dzk, т. е.
<idr = z- dz и
О	j
adr= \ z"dz= — -СА	1
Таким образом, ц=_31 4--1 - 1 =- 31. м 30 1 3	3	30 •
В следующих задачах вычислить циркуляцию векторного поля вдоль указанного замкнутого контура L:
1858.
1859.
1860.
1861.
1862.
a = y2i + z2j-\-x2k, L: {х-\-у + г^З, х — 0, у = 0, a=zi — xj-ryk, L : {г = х2-j-z/2 — 10, г=—!}.
а = yi -\-zj-\-xk, L : {х2 -\-у2 4~г2 = R2, xz>- 0, у 2s0, а = yi — xj + zk, L : {x2 -\-y2 + z2 = 4, x2 +y2 = z2, a = xyi + yzjH-xzk, L: {x2 + y2~l, x + у + г = 1}.
г = 0}.
г Зг 0}. г>0}.
§ 6. РОТОР ВЕКТОРНОГО ПОЛЯ. ТЕОРЕМА СТОКСА
1.	Определение ротора. Дифференциальные свойства. Векторном}’ полю а = Р(х, у, z)i + Q(x, у, z) / + R(x, у, г) к
может быть	поставлено	в соответствие другое векторное поле,	называемое рото-
ром попя a f	определяе i j к д д_ д	мое равенством _ ldR_ _ dQ \ .,[ дР__ m , (dQ \ ду dz j ''У dz дх ,	дх Свойства ротора	дР \	z1.
rot a =	дх ду дг Р Q R		- ">
1)	rot с = 0, где с — постоянный вектор.
2)	rot[C1a1 + C2a2] = C1rota1 + C2rota2,	(2)
здесь ах, аг—векторные поля, Clt С., — произвольные постоянные.
3)	rot (Ua) = U rot « + [grad U a],	(3)
здесь U — скалярная функция.
1863. Пусть а~у1-\-г]-[-хк. Найти ротор векторного поля
Л = — — У1 + ч' + хк г V х2 + у2 + Z2
405
Решение. Вычислим rot у по формуле	(3), положив ^/ = у		. Так	как
j	1	,	1 xi-Eiij-Ezk grad и = — у grad Г = — у		= - д	2* г3 ’ i k д д	а	-к,	
rot а — д дх У	ду dz Z X i	=-Z-J- i k		ТО
rot у = и rot а + [grad и «] = — ХХХХХ ц_	X Iя У	_У	 г3	г3 г	х		
_ J (/ 4Jft) — у [(xy _ Z2) i (Zy — X2) J (xz _ t/2) ft] = _	((X2 y2 xy) j J_
+ ((/2 + Z2+Z!/)7+(x2 + z2 + xz) ft].
1864. Найти ротор векторного поля a = f(r)r.
Решение. Вычислим rot а = rot f (г) г по формуле (3). Так как
grad f (r) = f' (г) grad r = f (г) у и rot г =
i j k д д д дх ду дг х у г
=0, то
б)
В)
Г)
-2.
c = 3yi — zJ-^-Sxk;
rot f (г) r = f (г) rot г + [grad f (г) г] = р' (г) у
1865. Найти ротор векторного поля а, если:
а) а — y2i — x2J + z2fe;
a — f(r)b, где & = /м + М+= const;
а = Ь 4- --7	, где b = 2xi + yi — 3zk, а
a = [gradub], где и (М) = у2 — 2хг 4-z2, a & = z4~2/ —Зй.
Теорема Стокса. Теорема. Если в некоторой области пространства содержится двусторонняя кусочно-гладкая поверхность о, ограниченная кусочно-гладким контуром L с единичным вектором нормали п, выбранным так, чтобы видимый с его конца обход контура L совершался против часовой стрелки, то
Ц=ЭД adr — ЭД rota п do,
L	а
(4)
i i i
I
т. е. циркуляция равна потоку ротора векторного поля а через поверхность о, «натянутую» на контур L.
Так как п = cos at + cos р/ + cos yk, то на основании определения (1) формула (4) может быть записана так:
Ш/ dR dQ\ . /дР dR\ „ . (dQ дР\ 1
-s— — - - cos а-Н -д-----д— cos P + i-д-----д— cos v <fo. (5)
\ ду дг)	' \дг дх )	\ дх ду j *]	' ’
а
1866. Найти циркуляцию векторного поля а —(у — x)i + + (2х — y)J+ zk вдоль замкнутой кривой L, состоящей из отрезков коор
406
динатных осей Ох, Оу и дуги окружности х = 3 cos t, у = 3 sin t, г — О, от 'точки, где параметр Z = 0, до точки, где t =
Решение. Найдем ротор поля а:
	1	/	k	
	д	д	д	
rot « =	Тх	ду	дг	= k.
	У — х	2х — у	г	
В качестве поверхности о, натянутой на контур L, может быть выбрана часть плоскости хОу, ограниченная контуром L. В качестве вектора нормали к плоскости хОу возьмем n~k, так как видимый с конца этого вектора обход контура L совершается против часовой стрелки (в соответствии с требованием теоремы Стокса).
Следовательно, по формуле (4)
Ц = (j kk do — jj do — o.
r	'a	a
В данном случае а —четверть круга радиуса 3, поэтому
1 ™ 9 а=-л/?2=-л.
9
Таким образом, Ц—у л.
1867. Найти циркуляцию векторного поля а = уЧ — x2J+z'2k по контуру АВС А, получаемому при пересечении параболоида № 4- г2 = = 1 — у с координатными плоскостями (см. рис. 217).
Решение. Эта задача была решена выше непосредственным вычислением (см. 1857). Теперь решим ее, пользуясь теоремой Стокса. В качестве поверхности, натянутой на данный контур, возьмем поверхность х2 + г2 = 1 — у. Единичный вектор нормали к этой поверхности определяется по формуле
где ^=*2+г/+г3-1;
поэтому
откуда
2x/-|-j-|-2zfe
К4х2 4- 1 + 4z2 ’
2z
cos у — —r............——- Ss 0	(г гэ 0),
К44+1+4?2
нормаль п тура L.
Ротор данного поля
обеспечивает требуемое теоремой Стокса направление обхода кон-
rot а =
I д дх
По теореме Стокса
д ду — х2
k
д_
дг
г2
= —2(х + у)/г.
о
сс Г rot ап 4 и ।-------r	dx dy,
„ LI cosy, 32=2^,40
ху
407
rota n o . , . i-----r= —2 (x-r-y),
| cos y|	'
следовательно,	'
1	1 - л-2
Ц=—2^’ (% + £/) dx dy = — 2 j dx J (x-\-y)dy = ° 0
=^р(1_,,+<цг]Л_ 0
В следующих задачах с помощью теоремы Стокса найти циркуляцию данных ,/ векторных полей а по указанному контору L:	Л
1868.	a = yi — xj-, L — замкнутая кривая, состоящая из коор&и-	!
натных осей Оу, Ох и дуги астроиды x = Rcos3t, у = R sin31 (х О,	I
y^Q, г = 0).
1869.	a = (x — 2г) i -j- (x + Зу + 2) J + (5x + У) k, Ь — контур треуголь-
ника ABC, где A (1, 0, 0), В (0, 1, 0), С (0, 0, 1).	*
1870.	a = (x — у + 3z) i 4- (у — 3x4- г) J4- (x — 3y 4- z) k, L — линия пересечения плоскости 2x4-3y4-6z —3 = 0 с координатными плоскостями.
1871.	a = yiA-zjA-xk, L —линия пересечения поверхности г =
= 2(1— х2— у2) с плоскостью г = 0.	1
В следующих задачах вычислить циркуляцию векторного поля
двумя способами (непосредственно и по теореме Стокса):
1872.	а = х2у31 +/+ zk, L : {х2 4- у2 = R2, z = 0.}
1873.	а = zi — yk, L : {х2 4-У2 = 4, хЦ-2г = 5}.
1874.	а = xyi + yzj + zxk, L: {х2А-у2=1, x.-j- у + г = 1}.	J
1875.	а = (г2 — х2) / 44х2 — У2)/+ (У2 — г2) k, L : {х2 + у2 Ц- z2 = 4,	'
х2 4- у2 = г2}.
\
§ 7.	ПОТЕНЦИАЛЬНЫЕ И СОЛЕНОИДАЛЬНЫЕ ВЕКТОРНЫЕ ПОЛЯ
1.	Потенциальное поле и его потенциал. Векторное поле а (VI) называется потенциальным, если существует такое скалярное поле и (Л4) в области I", для	£
которого
a = gradu.	(1) б
Функция и (Л1) называется потенциалом поля а*. Потенциальное поле является безвихревым, т. е.	,
rot а = 0.	(2) J
Это условие (2) является также и достаточным для потенциальности векторного I поля а (в односвязпых областях).
В случае потенциального поля линейный интеграл не зависит от формы пути, а лишь от выбора начальной и конечной точек. Потенциал этого поля определяется по формуле	i
м	I
. и (/И) = adr,	(3)
,	Ai„	1
l	Ss
* В физике обычно потенциалом называют не и (/VI), а —а (Л-1).	;Х
408
исходящему из некоторой фиксированной пути выбирают ломаную Л40, Л1Ь /И2 /И
где интеграл берется по любому пути, точки Л40. Обычно в качестве такого (рис. 218). В этом случае
и (М) = и (л-, у, г) —
= j Р (х, у0, zu) dx +
+ \ Q (х< У< го) dy-\-
Ua
+ j R (x, у, г) dz .	(4)
1876.	Показать, что вся-
кое постоянное векторное -т/ Mil^^y0^o) м2/х,у,2и)
поле « — потенциальное и	Рис
найти его потенциал.	ис’
Решение. Так как rot а = rot (ay -\-afJ -]-a3k) = 0, то поле а будет потенциальным во всем пространстве. Здесь Р (M)—aL, Q(M') = ai, R(M)=a3, поэтому по формуле (4) получим, что потенциал
х	у	z
и(х, у, z) = j Qj.dx + j a2dt/+j a3dz = (a]x~Pa2y-\-a3z) — (ЗД + a2r/0 + a3Zi>) = Xa	IJa	z„
= ar + A, где A = — (a^, -ф a2yB -ф- a3z0) = — ar0.
1877.	Дано векторное поле a — (z/ + г) /Д (х-ф- г) у-ф- (х-ф- у) к. Показать, что поле а потенциальное, и найти его потенциал.
Р е ш е н и е. Найдем rot «:
i J к , a a a rota= -v	=0.
dx dy dz УА-2 x-yz x-t-y
Следовательно, в силу условия (2) поле потенциальное. Потенциал поля найдем по формуле (4), положив в ней Л40 (Л'о, Уо, го) = ^(Р, 0, 0). Тогда
х	у	z
и (Л4) = j 0  d%+J xdy+ J (* + t/) dz = xy-\-(x-\-y) z-оно
Таким образом, и (Л4) xy-j- xz -j- yz является потенциалом поля а. Действительно, grad и -(г/-|-Д i + (х -ф- г) j -ф- (х -ф- у) k = a.
1878.	Показать, что всякое центрально-симметрическое поле— потенциальное, и вывести формулу для вычисления потенциала такого поля.
Решение. По решению 1864, rot (f (г) г) = 0, т. е. центрально-симметрическое поле f (г) г — потенциальное. По формуле (3) имеем, что потенциал
М	М	г (М)
u(M)= j adr = (j j (г) rdrj f (r) rdr = j f (r) rdr — ЛЦ	it,	r(At0)
- (p(r) r dr) |r=r	= p (r) rdr + const.
409
1879.	Показать, что данное поле а потенциально, и найти его потенциал:
1) а = 6x//Z ф-(Зх2 — 2у) J,
2) а = yzi + xzj+xyk.
1880.	Показать, что поле радиуса-вектора потенциально. Найти его потенциал.
1881.	Если поместить массу р в начале координат О, а в точку А —единичную массу, то сила притяжения единичной массы к центру О определяется формулой F = —г (поле F называется полем «ньютоновского притяжения»). Найти потенциал этого поля.
2.	Соленоидальное поле. Векторный потенциал. Векторное поле а (.И) называется соленоидальным в области V, если diva = 0 во всех точках этой области. Необходимым и достаточным условием соленоидальности поля а является равенство нулю потока этого поля через любую замкнутую поверхность области V.
Говорят, что векторное поле а (.И) обладает векторным потенциалом Н (Л1), если
a = rot (//-(-grad <р),	(5)
где ср = <р (М) —произвольное скалярное поле. Необходимым и достаточным условием существования векторного потенциала Н (.И) является соленоидальность поля а. Векторный потенциал вычисляется по формуле
1
Я (М) = $ [а (ЛГ) г (М)П Л,	(6)
и
где г — радпус-вёктор точки М, a M'(tx,.ty, /г) —точка, пробегающая отрезок ОМ, соответствующий изменению параметра t от / = 0 до / = 1, a r=xl-\-yj -\-zk, М (х, у, г).
1882.	Показать, что векторное поле a~f{f)r является солено-идальным только в том случае, если f(r) = -9-, где & —постоянная.
. Решение. Дивергенция поля а была определена в 1833: div а = 3’ (/) + //' (г).
А так как, по определению, поле соленоидально, лишь если diva = 01 то Должно выполняться условие
3f (r) + rf'(r) = 3f (r) + r^-=0.
откуда
Решим это дифференциальное уравнение:
Дф-3—= 0, /(г) г
In f (г) = — 3 In r-J-ln kt
где k —- произвольная постоянная. k Окончательно находим f (г) = - .
1883.	Показать, что векторное поле а — -~^ является потенциальным и соленоидальным, а его потенциал и является гармонической д2и д2и
функцией, т. е. удовлетворяет уравнению Лапласа	= о.
410
Решение. Найдем дивергенцию а. По формуле (2) § 4 получаем
div<i —div^., =r3 divr + rgradf5-=^-rTrgradr =
= 3 _ 3 гг = J3 _ 3 ^•3	^-4 f pi
(см. 1804).
Следовательно, поле а— соленоидальное. Определим rot а по формуле (3) § 6:
1 Г 1 1 Г г I rot«= 5 rot r+ grad г = — 3 -r г =0, ^•3	I	I I рз I *
так как
j 1 з
rot r = 0, grad - - = ~ ri r
и векторное произведение [гг] = 0.
Следовательно, поле а — потенциальное. Найдем его потенциал по формуле (3): м	м
....	С	,	Г rdr
и(М) = \ adr = 1
м0	ма
А так как гг = г2, то, дифференцируя последнее равенство, получим 2rdr — 2rdr,			
следовательно, м	м .... Г rdr С dr	1	|А1	1	, 1
и(М)= \	\	=	—- — —	1		 		 ....	. - .....		- 4-"7	.
М„	М„	г	|Aio	у х2-f-у2 + г2	г Х1 + Ув + го
„ „	д2и	д’и	д2и Найдем -r-т-,	и -t-s-: дх2 ’ ду2 дг2 ди 		х	д2и	_ 1	Зх2
дх (|/ х2 + у2 4- г2)3	дх2	(Кх24-у24-г2	(|/х2 + г/2 + г2)5’
ди	у	д2и	_ 1	Зу2
ду	(Гх2 + у2 + г2)3 ’	ду2	(1<х24-у24-г2)3	(Гх24-у2 + г2)5’
' ди	г	д2и	_ 1	Зг2
dz	(Кх2 + у24-г2 )л‘	дг2	(Ух2 + у2 + г2)л	(^24-y2-|- г2)3'
поэтому
<Э2« сРи д2и  ____________3__________3(х2 4-у2 4-г2) _ 0
дх2 + ду- + дг2 ~ (Ух2 + у2 + г2 )3	(]fx2+y2 + z2 )5 ~
1884.	Найти векторный потенциал поля а = 2zi ^Зу'-k.
П	Т А- & (2Z) I 9 (Зу2) Л
Решение. Так как div а — —ч—-  ---\	=0, то данное поле а — соле-
дх dz
нопдальное, следовательно, векторный
	i	J	k
[а (М')г(Л4)] =	2zt	0	3y2t2
	X	У	z
потенциал существует. В нашем случае
_ 3^3/2/ + (3X^2Z2 _ 2z*t) j + 2yztk\
по формуле (6) найдем векторный потенциал:
1
Н (М) = $ [ - ЗуЧЧ + (Зху2/2 - 2г2/) j + 2yztk] tdt = [~ уЧЧ + (ху2/3 - г2/2)/ + о
.	+уг^*и= — У3/ + (^а —г2)/ + угй.
411
Полученный векторный потенциал определен с точностью до градиента произвольного поля <р (,И).
1885.	Показать, что векторное поле rot а является соленоидальным.
1886.	Показать, что электромагнитное поле Н = -2( ( — yi Д- xj) является соленоидальным.
1887.	Показать, что потенциальное векторное поле а ^ (//-j-г) / Д-+ (% + г)у + (*+#) k (см. 1877) одновременно является и соленоидальным полем.
1888.	Показать, что скалярное поле и (г) = 1 -=	-	—1......
г Г(х-а)2 +(У~ЬУ- +(?-с)2 — гармоническое, за исключением точки А (а, Ь, с); поле grad и одновременно является потенциальным и соленоидальным полем.
1889.	Доказать, что поле а (Л1) = (yz — 2,v) I (xz -[-2y)J-\-xyk — потенциальное и солепоидалыюе; найти его потенциал и векторный потенциал.
1890.	Найти векторный потенциал поля магнитной индукции 2/ц
( — yiA-xJ), где / — сила тока, р() — магнитная постоянная, р = [/х2 Д-у2 - расстояние точки М до провода.
ГЛАВА XII
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
§ 1.	ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
1.	Общие понятия. Дифференциальным уравнением первого порядка называется уравнение вида
F(x, у, у')=0,	(1)
где х— аргумент, у — неизвестная функция. Чаще всего рассматривается уравнение, разрешенное относительно у':
y’=^f(x, у).	(2)
Иногда уравнение первого порядка записывается в форме
Р (х, у) dx-xQJx, y)dy = 0-	'	(3)
В этом случае за неизвестную функцию можно принять как х, так и у.
Функция у — ф (х) называется решением уравнения (1), если она обращает его в тождество, т. е.
F [у, ср (у), ф' (у)] = 0.
Решение, заданное неявно, т. е. в виде ф (у, у) = 0, называется интегралом дифференциального уравнения.
1891.	Доказать, что функция ср (х) = У 1 ~ х' есть решение уравнения
ху dx + У1 — х2 dy = 0.
,,	л	Vi —	,	— хе.'	,
Решение. Положив у = е	,наидемду =—-----—ах и, подставив
|/1 —
значения у и dy в данное уравнение, получим тождество
хе ~ х2 dx + | A1 — х3 —3’ —— ух о,
|/1— х3
1892.	Показать, что уравнение xae-v — у — 2 = 0, определяющее у как неявную функцию от х, есть интеграл дифференциального уравнения х'Ле-'’у' Ц- Зх2е-’’ — у' — 0.
Решение. Дифференцируя данное уравнение, наймем:
3x2e!J
3xV> + xWy' -у' = 0;	у’ = -	.
Подставив у' в уравнение, получим тождество
--^г(хМ-1)+з^о.
413
Проверить, являются ли данные функции решениями или интегралами соответствующих дифференциальных уравнений:
1893.	у = х2 — 4х; х dy — у dx = х2 dx.
I
1894.	у = 2е *2; у’х3 = 2у.
1895.	4х2+у2 = 2х;	4 - -у\ + 2у у' = 0.
1 J	X3 1 X J
1896.	хА-уеч =1; I -\-еу -}-еу ^1 — * 'i у' = 0.
1897.	у — х3 (Inx — 1) 4~2х2; х dy — 2ydx — x‘J Inxdx.
2. Дифференциальные уравнения семейства кривых. Однопараметрическим .семейством кривых называется совокупность'линий, определяемая уравнением
<р(х, у, С) = 0.	(4)
Фиксируя значение параметра С, получают конкретную линию данного семейства.
Так, например, уравнение у=Сх2 опреде-
ляет семейство парабол с вершиной в начале координат, симметричных относительно оси Оу. Придавая параметру С значения 1, —1, 2, получают параболы (рис. 219)
г/=х2, у = —х2, у — 2х2.
Дифференцируя уравнение семейства линий по х (считая у функцией от х):
Эф(х у, Q д^х у,q дх	ду	' '
и исключая из двух'уравнений (4) и (5) параметр С, можно прийти к дифференциальному уравнению вида F (х, у, у') = 0, которому удовлетворяет любая линия данного семейства.
1898.	Из семейства окружностей. х2 + у2 = С2 выделить ту, которая проходит через точку А (3, 4).
Решение. Чтобы выделить нужную окружность, надо найти соответствующее ей значение параметра С = С„. Так как иско
мая окружность проходит через тойку А, то координаты этой точки удовлетворяют уравнению х2-^у2=С’2. Подставляя значения х = 3, у = 4, получим С;, —25.
Уравнение искомой окружности будет
х2 + у2 = 25.
1899.	Составить дифференциальное уравнение семейства окружностей х2-\-у2 = С2 и установить дифференциальные свойства этого семейства.
Решение. Продифференцируем уравнение х2 + у'1 = С2 по х. Получим диф-
ференциальное уравнение 2х-\-2уу' = 0, или
х
7’
не содержащее парамег-
414
х
— _ следует, У проходящей через точку
pa С; оно будет искомым. Из дифференциального уравнения у' =— что угловой коэффициент касательной к окружности, М(х,у), равен—, где А> —угловой коэффициент прямой ОМ (рис. 220):
,	, „ у , , х
fe = tgf5 = T- и ^' = tga = ---
1	я । а
tg a ’ a— 2
tg₽=
проходящей
через
х2 4- у2 = 2Сх
при
водной, где.Дх, у) задана
Таким образом, общее свойство этого семейства состоит в том, что касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
1900.	Построить параболы из семейства у = х2-\-С при С = ± I; С = ±2.
- Написать уравнение, параболы этого семейства точку (—1, 4).
1901.	Построить окружности из семейства
С = ±1; С = ±4. Написать уравнение окружности этого семейства, проходящей через точку (—I, I).
1902.	Составить дифференциальное уравнение семейства парабол у = Сх2 и выяснить общее свойство кривых этого семейства.
Найти' дифференциальные уравнения следующих семейств линий: 1903. у = х + С.	1905. у2 = 2Сх.
1904. у^Сх + С2.	1906. Ji + j =1-
1907. Доказать, что для любой прямой линии, проходящей через
dy. у
начало координат, ^. = -х, и истолковать это равенство геометрически.
Указание. Составить уравнение семейства прямых, проходящих через начало координат.
3. Геометрическое истолкование дифференциального уравнения. Пусть y = q> (х) является решением дифференциального уравнения F[x, у, y') = Q. График функции у = <р(х) называется интегральной кривой уравнения F (х, у, у'')=0. Само дифференциальное уравнение устанавливает зависимость между координатами точки (х, у) и угловым коэффициентом касательной у' к интегральной кривой в той же точке.
Рассмотрим дифференциальное уравнение (2), разрешенное относительно произ-в некоторой области D на плоскости xDy. В каждой точке (х, у) области D уравнение (2) указывает направление касательной к интегральной кривой, проходящей через эту точку. Тем самым геометрически уравпе- ние (2) равносильно заданию в области D поля направлений, а интегрирование этого уравнения равносильно проведению таких линий, которые в каждой своей точке касаются направления поля, заданного в этой точке (рис. 221). Такое гео
415
метрическое истолкование дифференциального уравнения позволяет проинтегрировать его графически, т. е. представить ла чертеже приближенно общую картину хода интегральных кривых. Для этого нужно покрыть область D более или менее густой сеткой точек, и в каждой выбранной точке (х0, у„) начертить небольшую стрелку, наклоненную под углом а к осп Ох, где tga = /(.v0, уи).
Затем провести ряд интегральных кривых по направлениям, указанным стрелочками. Обычно при этом пользуются методом изоклин. Изоклиной называется линия, вдоль которой направление поля, определяемого дифференциальным уравнением (2), одно и то же. Уравнение изоклины получается из уравнения (2), если положить у' — const, т. е.
г/) = С.	(6)
Придавая в (6) параметру С ряд значений (например, С=0, ± 1, ± 3, ...), строят несколько изоклин и на каждой из них наносят ряд стрелочек (штрихов), наклоненных к оси Ох под углом а, для которого tga — С. По направлениям
этих стрелочек проводят интегральные кривые.
1908. С помощью изоклин начертить общую картину хода интегральных кривых уравнения t/' = x24-t/2~ 1.
Решение. Приравнивая правую часть данного уравнения постоянной С, получим уравнение изоклин
х2 +1/2 — 1 = С, или
х2 + ^ = С + 1.
Следовательно, изоклинами здесь являются концентрические окружности с центром в начале координат и радиусом Р = ф<С-|-1. Начертим ряд изоклин, прида-
ла	3	1
вая С значения—, 0, 1, 2, 4, 6, 8, 10 (рис. 222). На каждой изоклине прове-
дем ряд штрихов, наклоненных к оси Ох под углом а, где tg а равен значению С па этой изоклине. По направлениям штрихов проводим линии, которые приближенно представляют интегральные кривые данного дифференциального уравнения. В той области, где С > 0, интегральные кривые идут вверх, а где С <0—вниз. На изоклине, соответствующей значению С = 0, интегральные кривые имеют максимумы, минимумы или точки перегиба с горизонтальной касательной.
С помощью изоклин начертить общую картину хода интегральных кривых следующих дифференциальных уравнений:
1909. у' = ]/х2 + у2.
1911. у' = х-у2.
1910. у'=х2Ц-4у2.	1912. у' — х-[-у.
4. Задача Коши. Теорема существования и единственности решения уравнения y'=j'(x,y). Задача Коши для дифференциального уравнения первого порядка состоит в том, чтобы найти решение, которое при заданном значении аргумента х — хп принимает заданное значение у = г/0, т. с. удовлетворяет начальному условию у \х-х0 = Уо- Геометрически задача Коши формулируется следующим образом:
416
среди всех интегральных кривых данного дифференциального уравнения выделить ту, которая проходит через падинную точку (х(>, уф. Решение задачи Коши назы-
вают частным решением дифференциального уравнения.
Функция y = (f (х, б?), где С —произвольная постоянная, называется общим решением дифференциального уравнения в некоторой области D на плоскости хОу, если при соответствующем выборе значения С эта функция обращается в любое частное решение, график которого лежит в области D. Уравнение Ф (х, у, С) = 0 называется общим интегралом данного дифференциального уравнения в области D, если при соответствующем выборе значения С оно определит любую интегральную кривую, проходящую в области I). Обычно, когда находят
общее решение, довольствуются получением решения или интеграла, зависящего от произвольной постоянной С, не обращая внимания специально на область I), указанную в определении. Однако надо при этом иметь в виду, что полученное решение ие обязательно включает в себя все вообще решения данного уравнения.
Некоторые интегральные кривые могут выпасть из рассмотрения в ходе решения. Для их определения требуется специальное исследование.
Теорема существования и единственности решения задачи Коши. Если правая чисть f (х, у) дифференциального уравнения у' = f(x, у) непрерывна в области D и имеет в этой области непрерывную частную производ-
df
Ну'° ду
то через каждую точку (ха, уф этой области проходит, и притом
только одна, интегральная кривая', иными словами, при этих условиях задача Коши имеет единственное решение для любой точки (х0, уф области D.
1913.	Тело движется прямолинейно со скоростью и, пропорциональной квадрату времени. Установить зависимость между пройденным путем s и временем /, если известно, что при I = 0, s = s0.
Решение.
ds нением -„ = kt2, at
ds
Так как v= , то s (t) И t связаны дифференциальным урав-
или ds=-kt2dt. Проинтегрировав обе его части, получим общее kt3
решение дифференциального уравнения s (t) = -у-|-С. В начальный момент времени s = 5,1, поэтому, подставив в общее решение / = 0, s—s0.
найдем значение С:
Следовательно, s (/) = о-+ .s0 —искомая зависимость.
1914.	Известно, что скорость охлаждения тела в воздухе пропорциональна разности между температурой тела и температурой воздуха. Найти зависимость температуры тела Т от времени t, если за 10 мин температура тела снизилась от 100 до 60 , а температура воздуха была постоянной и равнялась 20°.
Решение. Скорость охлаждения тела температуры Т есть , где Т и I (согласно условию задачи) связаны дифференциальным уравнением
^ = /г (Г —20), или -JtL^kdt.
Проинтегрировав обе части, получим
In (Т—- 20)=И + 1п С; Т-=20-фСе,:!.
Это будет общим решением данного дифференциального уравнения.
Найдем значение С, отвечающее, данным начальным условиям. Подставляя в общее решение / = 0 и 7’=100'д получим
100 = 20 + Ce' = 20 + C, т. е. С = 80.
14 Кручкович и др.
417
Следовательно, искомая зависимость определяется частным решением: Т =4 = 20 ф 80с4'. Коэффициент пропорциональности к находим из условия, что при t— 10 мин температура тела стала равной 60°, т. е.
60 = 20 +80с10*, или с10* =
Откуда
10£ = 1п £-=— In 2 и fr = —0,1 In 2 «к — 0,07.
Таким образом, температура тела в данной задаче зависит от времени по закону
Т = 20 + 8оЛlz 1112 «= 20 + 80е~°’071.
1915.	Найти: 1) семейство кривых, для которых угловой коэффициент касательной равен ординате точки касания, 2) кривую этого семейства, проходящую через точку (2, 5).
Решение. 1) Дифференциальное уравнение искомого семейства
Проинтегрировав обе части, получим
In у —.гф1п С, откуда
У = Сех
— уравнение семейства кривых, обладающих указанным свойством.
2) Определим значение С, соответствующее начальным значениям у |Л,_а = 5>
5== Ci-, т. е. С — 5е 2, следовательно, у =	~ 5ел~2
— искомая интегральная кривая.
1916.	Материальная точка массы m движется прямолинейно под действием силы F, прямо пропорциональной времени от начала движения и обратно пропорциональной скорости движения v. Установить зависимость между скоростью и и временем /, если при 1 = 0 v = 0.
Указание.
Согласно второму закону Ньютона, Г = т
dv , dv dt \dt
— ускорение
1917.	Тело движется прямолинейно с ускорением, пропорциональным произведению скорости движения v на время I. Установить зависимость между скоростью и временем, если при t = 0 и = о0.
1918.	Замедляющее действие трения на диск, вращающийся в жидкости, пропорционально угловой скорости со. Выразить ы как функцию времени, если известно, что за 25 сек с начала движения угловая скорость снизилась со 100 до 50 об;сек.
418
1919.	Найти семейство кривых, у которых отрезок касательной, заключенный между координатными осями, делится пополам в точке касания (рис. 223). Написать уравнение кривой этого семейства,
проходящей через точку (3, 4).
Указание. Так как Д/И — МВ, то и ON — NB, где
ЛПУ
ON = x, iVB = MN etg (180° — а) = —	;
tg сс
CW =
ЛУУ tg а’
1920.	Найти кривую, проходящую через точку (4, 3), если угловой коэффициент касательной к ней в любой точке в два раза меньше углового коэффициента радиуса-вектора точки касания.
5. Метод Эйлера приближенного интегрирования дифференциального уравнения y’=f(x, у). Метод Эйлера заключается в том, что интегральную кривую, проходящую через точку (лу, р0), заменяют ломаной, каждое звено которой проведено по направлению поля, определенного уравнением у' — [ (х, у) в начальной точке этого звена. Иными словами, ы предыдущей вершины ломаной к последующей двигаются по касательной к интегральной кривой, проведенной через начальную точку каждого звена.
Предположим, что нас интересует решение, отвечающее отрезку [х0, Ь' (рис. 224). Разделим его па п равных частей:
X(j, Xi, X.,, Л'з, ••• , Xn_i, xlt—b,
тогда ломаная Эйлера определится вершинами
Мк (хк, ук)	(k = 0, 1, 2, ... , п),
где £/* =	+/г/ (•''/.л.	а h —	— —• шаг деления,
tgaA = / (MA) = f (хк, ук).
14*
419
Расчет ведется следующим образом:
Таблица 12
k	xk	Ok	о1;)	ltf k’ ок)
0	Л’о	У»	f (*о» У о)	hf(xH, y0)
1	xi = л'<> + h	Уг^Уо + hf (xn, y„)	f(Xlt У!)	hf(.xlt yj
2	х., = ^ ф /г	y-^yi + hf (xj, yj)	f(x2, у J)	hf(x.,, y.,)
							
k	Xk	У1г ~ Uk-1 "1" hf	У/г-1)	f(Xk, yk)	yk)
					
п— 1	xn^ = xn_^-h	Уп -1 = Уп~2 I + Л/(Х„..3, Уп^)	f (-Cl-b ^Я-1)	Уп-1)
п	xn = b	Уп ~ Уп-1 _f~ hf	У п-1)		
С увеличением числа делений, т. е. с уменьшением шага h, последовательность ломаных Эйлера как угодно близко приближается к искомой интегральной кри вой.
1921. Дано дифференциальное уравнение у' = х-\-у2- Построить приближенно интегральную кривую, про-ходящую через точку (0, 1), в промежутке [0; 0,5] и вычислить приближенное зиа-45- Ims	чение неизвестной функции при х —
% ' / = °-5-
1,6-
1,5,~	/	Решение. Разобьем отрезок [0; 0,5] на
/мз	5 равных частей; шаг деления й = 0,1. Согласно
12 -	приведенной выше таблице имеем: см. таблицу 13.
’ X 2	По этим данным строим ломаную Эйлера,
’ / 1	приближенно заменяющую искомую интегральную
1 мо	кривую (рис. 225).
В конечной точке Л15 х = 0,5, (/=1,90.
Для данных дифференциальных уравнений построить интегральную кривую (приближенно), проходящую через точку Л1, на указанном отрезке и вычислить приближенное значение неизвестной функции для данного значения у, шаг деления 0,1.
Z7' ' 1 1 । ।------►
0,10,2	0,5	X
1922. Уравнение у’ = 2х — у; М (0, 0); ис'	отрезок [0; 0,5]; х = 0,5.
1923. Уравнение //---.v-ф//; Л4(1, 1); отрезок [1; 1,5]; ,у=-1,5.
1924. Уравнение у'= 2 — М (1, 2); отрезок (1; 1,5); х= 1,2.
420
Таблица 13
k	А/г	«ь		hf(Xk’ l>k)^ll(xll+^k)
0	А-о = 0	У о = 1	1	0,1
1	хл = 0,1	У1=1,1	1,31	0,13
2	*2 = 0,2	у2=1,23	1,51	0,15
3	х’з — 0,3	Уз = 1,38	2,20	0,22
4	х4 = 0,4	У4=1,60	2,96	0,30
5	— 0,5	Уб = 1.90		
§ 2. ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ ТИПОВ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ ПЕРВОГО ПОРЯДКА
1. Дифференциальные уравнения с разделяющимися переменными. Если уравнение
Р (х, у) dx + Q (х, у) dy = Q	(1)
после преобразования может быть записано в виде
(-v) -/=а (у) dxH-фх (х) - ср2 (у) dy=0,	(2)
то оно называется уравнением с разделяющимися переменными. Исключим из рассмотрения точки, в которых срг (х) = 0 и f2(y) = O, тогда, разделив обе части уравнения (2) на f2 (у)	(х), получим уравнение
(3)
<Pi(*)	/2 (у)
в котором, как говорят, переменные разделены. Общим интегралом уравнения будет
J <PiW ' Му)
1925. Проинтегрировать уравнение
(ху2 у2) dx4- (х2 — х2у) dy = Q.
Решение. Преобразуем левую часть уравнения:
у2 (* + 1) rf* + *2 (1 — у) dy = 0.
Разделим переменные, поделив на г/2*2:
х ~1“ 1 . .1 *— у , п
-^-<ix + -^dy = 0. Л	у
Интегрируя, получим общин интеграл уравнения:
, 1
in X---------
x-^-dx+ ^г^=с; л	J У
х-±У^с. ху
d-y = C У
4—In у—-С\ In Х-У	У
Замечание. Непосредственной проверкой можно убедиться, что №=0 и у —0 являются решениями данного дифференциального уравнения, однако они не получаются из общего интеграла ни при каком значении С. Следовательно, в ходе
421
решения были потеряны интегральные кривые х = 0 и у = 0 (оси координат). Эта потеря произошла в том месте, где мы разделили на произведение х2у2, равное нулю вдоль этих интегральных кривых.
1926. Скорость размножения некоторых бактерий пропорциональна количеству бактерий, имеющихся в наличии в рассматриваемый момент времени t. Количество бактерий утроилось в течение 5 ч: Найти зависимость количества бактерий от времени.
Решение. Обозначим количество бактерий в момент времени I через х (/), „	dx (t)
а в начальный момент —через хо = х(0), тогда —— скорость их размножения.
По условию, х (/) удовлетворяет дифференциальному уравнению
dx t	dx , ,,
,, — kx, или — = k dt. dt	x
Проинтегрировав обе части, получим общее решение данного уравнения
In х = £Ц-|-1п С; x(f)=Cekl.
Найдем частное решение, соответствующее начальным условиям:
х । f _ о —- хт,, х„ Се , С х,,: х (/) = хиеы
— частное решение дифференциального уравнения.
Чтобы найти искомую зависимость, определим коэффициент пропорциональности k. Известно, что
х(5)=3хо, т. е. Зх0 = xoc5*, е3* —3, откуда
k= I In 3 = 0,2 in 3
5
и, следовательно,
х(0 = х/'2/1п3ззх/'®.
Проинтегрировать следующие		дифференциальные уравнения:
1927.	W + У = 0-	1931. хУ 1 -\-у2 +
1928. 1929.	х-Уху-Ууу' +х) = 0. sec2%' tg у dx-]-	+ У У 1 +хгу' = 0.
	4- sec2 у tg х dy = 0.	1932. (1 +№)(/' +
1930.	sin x  sin у dx-[-+ cos x- cos ydy — 0.	-|- У |/1 +х*--=ху.
Найти	i частное решение, или интеграл, следующих дифферен-	
циальных уравнений, удовлетворяющих соответствующим начальным условиям:
1933.	(1 г/2) dx = xydy, если £/',v=2—l-
1934.	у' == 2 У у In х, если = 1.
1935.	Определить кривую, проходящую через точку (3, 4), если угловой коэффициент касательной в любой точке кривой равен квадрату ординаты точки касания.
422
2. Однородные дифференциальные уравнения. Дифференциальное уравнение, которое можно преобразовать к виду
\ Л 1 называется однородным.
Подстановка и —	, где и (х)— новая неизвестная функция, приводит одно-
родное уравнение к уравнению с разделяющимися переменными. В самом деле,
У если и —
х
то у = их и у' = хи'-\-и. Подставляя это в уравнение (4), получим
т. е.
хи' + и = ф (н),
du , ,
Х ~ U НЛИ
du
ф (w) — и
(5)

После интегрирования (5) подставим * вместо и и получим общий интеграл данного уравнения. Надо иметь в виду, что формула (5) не охватывает тех частных решений, для которых при каком-либо значении и = и0 выполнено равенство
Ф (и,,) — «о = О, т. е. ф(и„) = ы0.
Эти частные решения имеют уравнение у-—ипх.
1936.	Проинтегрировать уравнение
2х2 dy = (х2 + у2) dx.
Решение. Разделив обе части равенства на х2 dx, получим уравнение, правая часть которого есть функция отношения - ;
Положив в нем у=их и у' — хи' + и, получим уравнение с разделяюшимися
переменными:
2хи' + 2zz = 1 +и2; 2х ^-= u2'—2и1;
1	1	dx	1	(и—I)2 х
Интегрируя и подставляя — вместо и, получим общий интеграл исходногсх..урав-нения;
_ 2х
----= 1пх + 1пС;-------------— = 1пСх; Сх=е у~\
и — 1	V-—\
X
При разделении переменных мы делили на х и на (и — 1)‘-, что возможно при х^О и и 1. Непосредственной проверкой легко убедиться, что х = 0 и п = 1,-т. е. z/ = x, являются также решениями данного уравнения, но они не входят в общий интеграл.
1937.	Найти форму зеркала, отражающего все лучи, выходящие из данной точки О параллельно данному направлению.
Решение. Рассмотрим плоское сечение зеркала. Поместим начало координат в данную точку О, а ось Оу направим параллельно данному направлению
423
(рис. 226). Тогда ОМ — луч падающий; ML — луч отраженный; МN — нормаль, МР — касательная к искомой кривой.
Так как L OMN = Z NML, то ON = ОМ, где ОМ p'I2+V> ON = OK-\-
-К KN = у--Х,	поэтому
У
V Х2 — у~--^у~К * * или ^х2 + у2 = у + х^Х-,
dx _~Ух2~Ку2 — у' dx dy х ’ dy
dx , du „ , ,
-- — и К- у. Дифференциальное dy ' dy '
примет вид
уравнение
Рис. 226
или (после преобразования и разделения переменных)
и du __ dy
J/Г^2--(1-|-u2) у’
Положив l^-ti2 = z2, 2udu = 2zdz, получим
z dz _ dy
Ц1 -z) ~ У ’
Интегрируем это уравнение:
— In (z — 1) — In У -hln C, cT	1
или Су =------г.
J г — 1
Так как z2 — 1 -|-и2 — I 4-	то,
У2 У
ной, получим
Су —	, или
V У2МХ2 — у
переходя к первоначальной
К^ + х2 —д = =сг,
перемен-
что после преобразования дает
У ‘ 2С.
— общее решение однородного дифференциального уравнения. Мы получили, что любое плоское сечение зеркала — парабола.
1938.	Найти частное решение уравнения ху' — у \ 1 -|- In уио
1
данным начальным условиям y\x.i~e 2.
К /И	х
* Из прямоугольного Lx^KM находим KN — KM ctga=r— = —, У
424
Проинтегрировать следующие дифференциальные уравнения: £
1939.	(хг у2) dx — ху dy = 0.	1942.	у'=ех + у-.
1940.	уу' = 2у — х.	1943.	х dy = (y-dlx2 + у2) dx.
1941.	ху' cos у — t/cos у_ — х.	1944.	ху' = у In £
х	х	у
1945.	Из семейства интегральных кривых дифференциального уравнения (ху' — у) arctg у = х выделить кривую, проходящую через
точку (1, 0).
1946.	Найти частное решение дифференциального уравнения у2-\-х2у'= хуу' по данным начальным условиям г/'|Д.^3 = 4.
1947.	Определить кривую, проходящую через точку М (4, 3), если подкасательная АТ любой точки ее есть среднее арифметиче-
ское координат точки касания (рис. 227).
3. Линейные дифференциальные уравнения. Уравнение вида
у' + Р (x)y=Q(x),	(6)
где Р (х) и Q (х) — непрерывные функции х, называется линейным. В частности, уравнение у' + Р (х) у = 0 называется линейным без правой части, или линейным однородным*.
В линейном однородном уравнении ^-фР(х)-у=0 переменные раз
деляются:
= — Р (х) dx,
У
и поэтому его интегрирование сводится к квадратурам (к вычислению интегралов от обеих частей равенства):
Р (х) dx С.
Для того чтобы решить уравнение (6) при Q(x)p6 0, надо искать неизвестную функцию у в виде произведения двух пока неизвестных функций от х, т. е. положить у —и (х) и (х). Тогда у' = и' (х) v (х) + и (х) о' (х). Подставив значения у и у' в уравнение (6)
и'о v'u uvP (х) = Q (х),
после группировки получим:
v • Р (x)] + u'//--Q (х).	(О')
Так как у есть произведение двух функций, то одна из них может быть выбрана произвольно, другая же должна определяться уравнением (6').
Выберем и (х) так, чтобы выражение, стоящее в квадратных скобках, обращалось в пуль, т. е. и' + иР (х) = 0; для этого достаточно, чтобы и (х) было
* Не следует смешивать однородное дифференциальное уравнение, разобранное в п. 2, с линейным однородным уравнением.
425
каким-либо частным решением * уравнения с разделяющими переменными:
du ,	_ , .	_	du л z s j
,--uP(x) = 0, или - - = — P (x) dx.
dx	и
Проинтегрировав его, найдем и(х). Подставив в уравнение (6') шачение и, получим второе дифференциальное уравнение с разделяющими переменными
,	<? М и
или dv — —~ dx и (х)	’
v'u (х) = Q (х),
общее решение которого а = о(х, С).
Следовательно, общим решением уравнения (6) будет
у = и (х) v (х, С).
В ряде случаев дифференциальное уравнение первого порядка является линейным не относительно у, а относительно х, т. е. может быть приведено к виду
d^ + F (y)x = R(y).	(7)
Cty
Метод интегрирования уравнения (7) тот же, что для уравнения (6), но переменные х и у меняют свои роли: у считается аргументом, а х = х(у)— неизвестной функцией.
1948. Проинтегрировать уравнение у' 4-2ху = 2х2е~х‘.
_	„	dy dv , du	.
Решение. Положим у = ио,	=и , -Ру подставим у и у в данное
dx dx dx ’
уравнение:
dv , du	n .,
и —ну	+ 2xuv = 2x-e л ,
dx dx >
(8) [ du , o | , dv n , ,.2
v , - + 2xu 4- и , = 2x2c .
[dx J dx
Положим d~-\-2xu = 0, или ——2^dx. Проинтегрировав, получим частное
решение (С = (J) In и —.— х2, или и = е~х2. При и = е~х~ равенство (8) обратится в уравнение
е хг 2х2й“*г; dv — 2х2 dx, dx
2 v
откуда v —	х3-|-С, и общим решением данного уравнения будет
у — uv = e~x' I з x^ + cV
1949. Проинтегрировать дифференциальное уравнение
dy_ = __________1__________
dx х cos у -\-а sin 2у '
Решение. Это уравнение не является линейным относительно у, так как у находится под знаком синуса и косинуса. Однако простыми преобразованиями оно приводится к уравнению линейному относительно х и х';
-------х cos у — a sin 2у , dy J
* Для большей простоты выкладок берем ниже частное решение, отвечающее значению С = 0.
426
Положим
Х=и (?/) V (у);
dx	dv , du
= ?/,- + i' -;
dy	dij dy
подставим эти значения в уравнение и сгруппируем члены, как мы это делали в предыдущем примере, тогда
fdu	\ , dv	. п
v -,--и cos у . 4- и — a sin 2у .
.dy	) dy
Положив du —и cos w = 0, получим дифференциальное уравнение -~ = cosydy dy ~	ч
частное решение которого
In к = sin р, или н = е51П{/.
Найдем v (у) из уравнения e41n v j^- = a sin 2р, для чего разделим переменные и проинтегрируем;
dv = 2a sin у cos ре-sln" dy; v (y) — 2a ) sin у • cos ye~"n !l dy + C.
При помощи подстановки sinp = z и применения метода интегрирования по частям получим
v (у) —— 2а (sin у+ l)e”sinv + C.
Общим решением данного дифференциального уравнения будет
х (у) = uv = e°'"'y [—2a (sin у + 1) е“	С],
или (после преобразования)
х (р) =—2a (sin 1) + Cc4in//.
1950.	Сила тока в цепи с сопротивлением R, самоиндукцией L и электродвижущей силой Е удовлетворяет дифференциальному уравнению LdJt Ц- Ri — Е. Найти зависимость силы тока от времени t, считая R и L постоянными, если электродвижущая сила возрастает пропорционально времени, т. е. E — ki\ сила тока в начальный момент равна нулю.
Решение. Дифференциальное уравнение L -^Ri — kt — линейное, где неизвестной функцией является i (/). Положим i = uv; i’ — u'v-t- uv'.
Дальнейшее решение проводится аналогично разобранным выше примерам. Общее решение данного уравнения будет
k kL -^-1
l~uv~R (^pi+Ce •
„	O kL ,	kL
Подставим начальные значения: 0 = —	откуда С =	.
Следовательно, искомая зависимость между силой тока и временем такова:
k kl 1 ~R
+ L
427
1954. / + —^ = 0.
1 х + у1
1955. 4‘	+ 2хуех'г = х • sin х.
вида
Проинтегрировать следующие дифференциальные уравнения:
1951.	у' 4-^- = х2. u 1 х
1952.	dy = (х2 + 2х — 2у) dx.
1953.	(x+V)dy-
— [2у -|- (х 4* 1 )4] dx = О-
4.	Уравнение Бернулли. Уравнение
уЧ-Р (X) y=Q(x) уп,
где Р (х) и Q (х) — непрерывные функции от х, называется уравнением Бернулли. Оно сводится к линейному подстановкой г = у1п, Уравнение Бернулли можно решить также указанным выше методом, полагая у = и(х) v (х).
1956. Проинтегрировать уравнение у'— ху = — у‘лех‘.
Решение. Это уравнение Бернулли, где п = 3. Полагая у (.с) = и (л.) и (х), у' =; u'v-\-uv', будем иметь
u'v-\-uv' — xuv = —
или
, , l'dv	\	о ч . г2
и и-\-и ! ---хс = — и3иле Л.
\dx	/
dv
Положив ~[x~~XV~^' полУчим Дифференциальное уравнение с разделяющимися переменными
X" частное решение которого (С=0) будет 1пг> —	, т. е.
х2
Подставив найденное значение v (х) в данное уравнение, получим
л2 ,	Зх2
о du	г, о —	du	.>
е2 = — и3е 2 • е А2, или — 11 -dx	dx
Разделим переменные и проинтегрируем:
du	1
24 -X + Ci
теперь находим 4 (х) =	' г. ; следовательно,
2 (^х -j-C)
есть общий интеграл данного уравнения.
Проинтегрировать следующие уравнения Бернулли: 1957. у'х4У = — ХУ2-	1959. у' == хуЦ-хяуЙ.
1958. х dy = (>Х‘у- — 2у) dx. 1960. уу' — 4х — у21 х — 0.
5.	Уравнение в полных дифференциалах. Уравнение
Р (х, у) dx + Q (х, y)dy = 0
428
называется уравнением в полных дифференциалах, если его левая часть является полным дифференциалом некоторой функции и (х, у):
Р (х, у) dx-^-Q (х, у) cly — dtt.
Для этого необходимо и достаточно, чтобы
дР (х, у) dQ(x, у) ду	дх
В этом случае и (х, у)--=С есть общий интеграл данного уравнения. Функция и (х, у) может быть найдена из системы уравнений
р);	| = Q(r,0.
Покажем на примерах, как интегрируются уравнения в полных дифференциалах.
1961. Найти общий интеграл дифференциального уравнения
ё '! dx Ц- (1 — хе~!>) dy = Q.
Решение. В данном случае Р (х, у) — е~У и Q (х, у} = \—хе~и, и так как
дР	5Q
— —еу и -?- = —е у, ду	дх
то левая часть уравнения есть полный дифференциал некоторой функции и(х, у), для которой
ди I -и =1 — хе и.
ду
ди дх
По данной частной производной
е найдем значение и (х, у) с точ-
ностью до произвольной функции
и(х, ?/)==	+ Л (г/); и (х, г/) = хе л/_[_д (у).
^Можно было бы начинать с равенства |^=1 — хе '/ и находить и (х, у) иостью до произвольной функции (х) Продифференцируем найденную
с точ-
функ-
цшо и (х, у) по у.
ди йу
— хе y +	(р).
Приравнивая уже известному нам значению =—хе W-|-l (см, выше), получим
/; (г/) = 1, откуда Д(г/) = г/ + СР
Определив функцию /х (г/), можем записать
и (х, у} = хе У-\-у + Су
и следовательно, общим интегралом уравнения будет хе~у + у + С\ = С2,
что равносильно хе~У-\-у = С (где С = С.,— Сх).
1962. Из семейства интегральных кривых дифференциального уравнения 2х cos2 у dx-\- (2у — хг sin 2у) dy 0 выбрать ту, которая проходит через начало координат.
429
Решение. Имеем
Р (х, y1 = 2xcos2y; Q (х, у) —- 2(/— х’2 sin 2у, и так как
ЭР	0Q	п . п
5— — — 4х cos if sin у и х • == — 2х sin 2г/,
ду	дх	J
то из равенства частных производных вытекает, что это уравнение в полных дифференциалах, т. е. существует такая функция и (х, у), для которой
а» (х, у) п „ ди (х, у) п , • о
---~—— = 2х cos2 у; -----— 2у — хг sin 2у.
дх	а ду J	J
Проинтегрировав второе равенство, найдем и (х, у) с точностью до произвольной функции от лч
» U, У} -= $ (2?/ — х'2- sin 2 у) dy ф Д (х); и (х, у) = у2 ф - 2у + Д, (х).
Чтобы определить Д, (х), продифференцируем найденную функцию по х: ^=AC°s2y + /:(x)
и приравняем к уже известному значению = 2xcos2y. Получим дифференциальное уравнение относительно /2 (*'):
2х cos2 у = х cos 2у + f‘, (х),
или после ряда тригонометрических преобразований:
2х cos2 у — х (cos2 у — sin2 у) -Д Д (х),
2х cos2 у = х (2 cos2 у — 1) ф Д, (х)
получим Д(х) = х. Проинтегрировав, найдем
Ф (х) = Х- +Сг;
определив f2(x)> можно записать
Следовательно, уравнение семейства интегральных кривых будет
у2 += С.
Из этого семейства кривых выделим ту, которая проходит через начало координат. Подставив значения х = 0, у = 0 в уравнение этого семейства, определим С:
С---=().
Следовательно, уравнение искомой кривой
2у2 ф х2 cos 2у ф х2 — 0.
Найти общие интегралы данных дифференциальных уравнений:
1963.	(12х ф- Бу — 9) dx ф- (5хф- 2у — 4) dy — 0.
1964.	(Злу2 — х2) dx ф- (Зх2у — 6уа — 1) dy = 0.
1965.	(In у — 2х) dx ф- {^-х- — 2у\ dy == 0.
,/sin 2х , \ ,	. / sin2x\ ,	„
966, \ Т~ + Х1 dx + [y--------)dy = o.
430
1967. Найти частный интеграл дифференциального уравнения
Зл'2е'’ + (л'3е>' — 1) у' = О,
удовлетворяющий начальным условиям у|Л._0 = 1.
6. Смешанный отдел. Проинтегрировать следующие дифферен-
циальные	уравнения первого порядка:		
1968.	У'=т + ^х’	1976.	d! - tg у dy.
1969.	у' - у = X2.	1977.	x [In x~ \ny\dy — ydx — Q.
	л	1978.	y' cos хф-у sin X 1.
1970.	(у — х2у) х dy -ф dx = 0.	1979.	у dx — x dy =- xy dx.
1971.	— у etg х = 2х sin х.	1980.	y' -2y^ ex - x.
1972. 1973.	(ху -j- 1) у dx=~- х dy. igydx -[-tgx dy — 0.	1981.	y".-v J	x cos- X
1974.	(x-\-y) -(y-x)y' --0.	1982.	(x + xy2)-(y + y.\-) y’ =0.
1975.		1983.	
§ 3. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ
1. Общие понятия. Дифференциальным уравнением n-го порядка называется уравнение вида
F (*, У, У',	••• . У"") = 0,	(1)
где х—аргумент, у — неизвестная функция. Иногда рассматривается уравнение, разрешенное относительно старшей производной
У"11 = <₽(-<, У, У', у",	, У:п~1')-	(2)
Задача Коши дифференциального уравнения н-го порядка состоит в том, чтобы найти решение данного уравнения, которое при заданном значении аргумента х=-хп принимает заданные значения у0, у’^, у", ... ,	т. е. удовлет-
воряет начальным условиям
у\х^Ха=У>>’ У".^Хо =У'>....y'!l^'
Геометрически задача Коши формулируется следующим образом: среди всех интегральных кривых данного дифференциального уравнения выделить ту, которая проходит через наперед заданную точку (х0, у0) и для которой при х = хи имеют место равенства
У (x„) = y't, у" (х„)=у'',	, У(п~и
Решение задачи Коши называют частным решением уравнения (1).
Функция y = f(x, Clt С.,, ... , Сп). где С/— произвольные постоянные, называется общим решением уравнения (1) в некоторой области D на плоскости хОу, если при соответствующем выборе значений С2, ... , С„ эта функция обращается в любое частное решение, график которого лежит в области D.
Уравнение Ф (х, у, Clt С-., .... С„) —0 называется общим интегралом данного дифференциального уравнения (1) в области D, если при соответствующем выборе значений ГД, С.,. ... , Сп оно определит любую интегральную кривую, проходящую в области 1).
431
При л = 2 дифференциальные уравнения (I) и (2) будут уравнениями второго порядка:
F (х, у, у', у") = 0; y" = tp(x, у, у').
Их общее решение зависит от двух произвольных постоянных У=Ч(х, С,, С,).
Здесь общее решение можно рассматривать
как семейство интегральных кривых данного дифференциального уравнения. зависящих от параметров С\ и С.,. Частному решению, полученному из общего, соответствует одна кривая этого семейства.
Задача Коши для дифференциального уравнения второго порядка состоит в том, чтобы найти интегральную кривую, проходящую через данную точку (х0, у0) в заданном направлении у'и (рис. 228).
1984. Проверить, будет ли з
г/ = С1Х2 4-С, общим решением уравнения 2ху" — у' в области х>0. Найти частное решение,
удовлетворяющее начальным условиям г/lv _ i = 4, y'|.v_i-=3.
Решение. Найдем:
2 С^2 >
1
,,	3 г 2
У4 (\х
Подставив значения у' и у" в дифференциальное уравнение 2ху”=у', получим тождество
„ 1 1
3	" 2’	3	2
2х-4С1.т	^-2С1Л: *
Следовательно, функция
3
У^С^2 -|-С,
есть решение данного дифференциального уравнения. Эго решение, общее в области %>0, т. е. при любом хи > 0 и заданных значениях у» и у'„ однозначно определяются соответствующие значения постоянных и С2 из системы уравнений:
3	L
У» — С1хо~ +С.,, у„ = СрГо' ,	= „- —7	, С3 = р0—у„хи.
-	d I хи	б
Найдем частное решение при заданных начальных условиях:
2 3	2
С\ =	, -2, С-, = 4- -.3-1=2.
0 1	о
Следовательно,
з
у — 2х~ +2
— искомое частное решение.
432
2.	Уравнение вида =f(x). Общее решение дифференциального уравнения вида yn=-f(x) может быть получено путем п последовательных интегрирований, а именно:
У,п~1 =p(x)dx + Ci;	{ p(x)dx + Ci} dx + C2
и т. д.
24
1985. Для данного дифференциального уравнения у = —— найти частное решение, удовлетворяющее начальным условиям I/)х _ о =-~ 1 > У	у |х_о—	!•
Решение. Имеем:
-2< (« + =)-•: Г-2» J (-Г^ + С,.	+
И? + C,JЛ +с.«+с<4
И 9	1	1	Г,г2
Д+2Р + С1Х + Са] dX==~ Д + 27 + ~ + С'-Х + Сз-
Подставив последовательно в полученные равенства начальные условия, определим Clt С2, Су.	,
6	:	' 9	1
-l=-2i+Ci,	2 = 23+Cs, 1=-^- + С3;
с — 5 с -1 с — 5
Ч- 8.	- 4 - Сз~4 -
Частным решением данного уравнения будет
1	5	L 7 4_ 5
У~ (х + 2)2	16Л	4 Л'~ 4'
Найти общее и частное (там, где даны начальные условия) решения следующих дифференциальных уравнений:
1986. у'" = 63; начальные условия: y\x_i — 2, y'\x„i = l, У" Lv -1 = 1-
1987. t/” = 4cos2x; начальные условия: y'iX_u~0, у' \х-и=^0-
1988. у" --= х sin х.
1989. (sinJ х) у'" — sin 2х.
d'^ti
1990. Кривая удовлетворяет уравнению =х-|-3.
Найти ее уравнение, если известно, что она проходит через точку (2, 4) и имеет в этой точке угловой коэффициент касательной, равный 3.
3. Уравнение вида F |х, у^п ~	= 0. Дифференциальное уравнение
л-го порядка F [х, у'п"11,	— O не содержит неизвестной функции у и ее про-
изводных до (н —2)-го порядка. Вводим новую функцию г (x) = yin"l> и, следовательно, У"	г'; получим дифференциальное уравнение первого порядка
F (х, г, г') = 0, где неизвестной функцией является функция г (х). В частном случае, когда п = 2, дифференциальное уравнение второго порядка f(x, у’, у")—0, не содержащее неизвестной функции у, подстановкой у’ — г приводится к уравнению первого порядка F (х, г, г') = 0.
433
1991.	Проинтегрировать дифференциальное уравнение второго порядка у"-\-у' tgx = sin 2х.
Решение. Это уравнение не содержит у. Положив в уравнении у' = г, получим линейное дифференциальное уравнение первого порядка относительно неизвестной функции г (х):
г' + ? tg х = sin 2х.
Интегрируем его. Полагая в уравнении Z = uv, г' — u'v ф- itv', получим div
u'u + ua' 4-ttu tg х — sin 2х, и'иф- u , v tg x' = sin 2x.
Определяем v, положив ~~f-vtgx = O:
C dv	(*	sin x ,
\	= \-------dx,
J V	J	COS X
откуда
lnt> = lncosx, ИЛИ L> = COSX.
Определим и (x): du ,, .	,	_ .	.
cos .v,—: 2 sin x  cos x; du = 2 sin x dx, dx
откуда
и (x) = — 2 cos x C; следовательно,
г = cos x (—2 cos x ф- Cp.
Возвращаясь к первоначальной переменной у, получим
= —2 cos2 х ф- С, cos х. dx
Разделим переменные и проинтегрируем:
dy — —2 cos2 х dx 4- \ Ci cos х dx -'-Су, у = —2	Jx ф- Ci sin х ф- Су
у = — x----—ф- Cx sin x ф- C.,.
Это н будет общим решением данного дифференциального уравнения.
1992.	Проинтегрировать дифференциальное уравнение у'" = (у")2.
Решение. Введем новую функцию г = у", тогда получим уравнение первого порядка относительно неизвестной функции г (х):
Разделим переменные и проинтегрируем:
dz	.	1
— — dx, --------= х 4- Cj.
2“	Z
Решим явно относительно г:
434
Вернемся к первоначальной переменной:
1
х + Ci
В результате последовательного интегрирования получаем:
/ = — 1п (д-4-Ct) -I- С2:
?У = — (х-г Ct) In (,v + Ci) Ц- x + Ci + C2.v + C3, i/ = - (Л- + C]) In (A- + C,) 4-Л- (C,. + 1) + C3 + C\.
Для большей простоты C-2 +1 можно заменить па С2, a C3+Ci на С3, и тогда общее решение примет вид
у==— (л'4-Cj) In (а + С^ + с.л' + Ся.
1993.	Если тело медленно погружается в воду, то его скорость v и ускорение w приближенно связаны уравнением w — g — kv, где g и /г — постоянные. Установить зависимость между пройденным путем s и временем I, если при / — 0 s — v = 0.
„	„	<Ps	ds
Решение. Так как ускорение = и скорость =	( то зависимость
между s и t выражается дифференциальным уравнением второго порядка d-s , ds ~dP=P~kdt'
„ ,	r-,	ds d-s dv
не содержащим неизвестно!! функции s. Положив в нем 11 dfl=dt' П°' лучим дифференциальное уравнение первого порядка с разделяющимися переменными относительно неизвестной функции о (/):
dv ,	dv
dt h	—to
Проинтегрируем обе части равенства:
— у In (g-to) = / + C1.
Определим Съ учтя, что о(0) = 0:
---J- In p = Ci.
к
Подставим найденное значение С\ в предыдущее равенство и решим его явно относительно v (/). После элементарных преобразований получим
откуда
i=in! —V-;
\g — kv j
или —а-— =ekt. g~kv
ds
V dt
f- (1 —
Разделим переменные в полученном дифференциальном уравнении первого порядка с неизвестной функцией s (/) и проинтегрируем обе части равенства:
s	(1-^)Л + Са,
435
или
НО- Л * + ,?,	+
к /г-
Из начального условия s(0) —0 определим С2:
О-Д+С.:
Подставив найденное значение Са в предыдущее равенство, получим искомую зависимость
s w=_4 i+v
Проинтегрировать уравнения:
1994.	xV'+x2/ = l.	1997. ху"' +у"-х- 1 =0.
1995.	у"х In х = у'.	1998. ху"у’ (Int/' — In х).
1996.	2ху" = у'.	1999. (1 +х2) у" + (г/)2 + 1 = 0.
4.	Уравнение вида Р(у, у', у”) == 0. В дифференциальном уравнении второго порядка F (у, у', у") —У, не содержащем в явном виде независимую переменную х, положим !/' = р(у), тогда
_ dp _ dp dy _ dp r_ dp
P dx dx dy dx dy У ~ P dy ’
получим уравнение первого порядка
F\y’ Р’ РТ^’
где неизвестной функцией является р (у), а независимой переменной у.
2000. Проинтегрировать дифференциальное уравнение
2 WY = ({/-!)У".
Решение. Полагая в этом уравнении у’~р, У"~Р^1 получим дифференциальное уравнение первого порядка
= 0.
Приравняем первый множитель нулю; р = 0, или ^ = 0. т- е- У —С. Легко проверить, что у = С (у’ = 0, р" = 0) обращает данное уравнение в тождество, следовательно, является решением.
Общее решение данного дифференциального уравнения получим, проиитег-_	,	,, dp
рировав уравнение с разделяющими переменными 2р — (у— 1)  =0:
Uy СЛ'’-1”(»-|> + 1пСГ.
Vp^C^y- 1), p = Ci(y- 1)2.
Произведя обратную замену р =	, получим дифференциальное уравнение снова
первого порядка, где неизвестной функцией является у (х):
— Cf (у—I)3.
dx 1 w '
436
Разделим переменные п проинтегрируем:
= {dx + С,; -	—р- - л- + С.;
МУ-1)’ J	G7(t/~ 1)
- ^=(х + С3)(!/-1),
или
С1 = (х + С.,) (у — 1), где С3 = —
Найти общие и частные решения (там, где указаны начальные условия):
2001. уу" = (у'У - (у')3.
2002. 2да" = 1 4-г/'2.
2003. у3у" = 1; */|л_-2=Н / 1л--2 = —1-
2004. у(1 — In у) у" -ф (1 ~г In w) у" = 0.
2005. 2уу"=у'*\ т/;л„_1 = 4, у' ,л-_1 = 1.
§ 4. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
1. Однородные уравнения. Уравнение вида
а-Р?' -фару'-фаму^-О,	(1)
где аа, О], а2 — постоянные, называется линейным однородным уравнением второго порядка с постоянными коэффициентами.
Теорема. Если щ(х) и у2 (х)— частные решения уравнения аоу"а^' -\-
4-а2у=0, причем их отношение Ф const, то у =	(х) + С2у2 (х) сети
Ifa (х)
общее решение этого уравнения.
Для определения частных решений у, (х) и у, (х) уравнения (1) следует предварительно решить характеристическое уравнение
aor24-<V4-a2 = O.	(2)
При решении квадратного уравнения (2) возможны три случая:
Таблица 14
Корни уравнения (2)	Частные решения (1)	Общее решение (1)
1. Действительные разные rf> г2	i/1 = eriX, у2~ег’х	Схе'-^+С2сГгХ
2. Равные г,—г..	у1 = ег,х, у2 — хег'х	ег'х (Сх + С2х)
3. Комплексные сопряженные а ± |3i	у1-еР-х cos 0х, у2 = ухх sin рх	еах (Сх cos рх С« sin рх)
2000. Найти общее решение дифференциального уравнения 2/' +5у' +2у = 0.
Решение. Составим характеристическое уравнение »
2г2 + 5г-f-2 = 0.
437
Корни его разные действительные: гг =—2, г2 = — о , поэтому
1 — к * !/i = c 2'> у2 — е
—	частные решения;
___р
у Су ~ С.,е 2
—	общее решение данного уравнения.
2007.	Найти частное решение дифференциального уравнения у" — 2у' Ц- у —0, удовлетворяющее начальным условиям //\._п-=4, /i.v_o = 2.
Решение. Корни характеристического уравнения г2 —2г4-1=0 действительные, равные: гг = r2= 1, поэтому частные решения будут
У-’= а
у — е' (С, + С2х)
— общее решение данного дифференциального уравнения.
Для определения частного решения в равенства
у = ех (С1 4-С.,х) п у' ~е' \С,у -j- С, С2)
подставим начальные условия. Получим систему двух уравнений
4 = Cj, 2=-Cj4-C3,
из которой определяем Сг = 4, С.2 = — 2. Подставив эти значения в общее решение, найдем частное:
У = ех (4 —2х).
2008.	Найти общее решение дифференциального уравнения
у" + 6у' + 13г/ = 0.
Решение. Корни характеристического уравнения г2 Щ 6г ф-13 = 0, комплексные сопряженные: —3 ± 21. Согласно табл. 14 (случай 3-й, а =— 3, |3 = 2), общее решение данного уравнения будет
у = (Г з-v (С] cos 2х -ф С., sin 2х).
2009.	Найти интегральную кривую дифференциального уравнения у" + 2у' 4- 2у = 0, проходящую через точку (0, 1) и касающуюся в этой точке прямой y — x-{-i.
Решение. Корни характеристического уравнения г2 + 2г-|-2 = 0 комплексные сопряженные: — 1 .1 I. Уравнение семейства интегральных кривых данного дифференциального уравнения
у = е~х (Cj cos х + С, sin х).
Чтэбы найти уравнение искомой интегральной кривой, подставим в равенства
у = е~х (Cj cos х -|- С.2 sin х) н
у' = е~х [(С2 — Cj cos х — (С„ + С,) sin х]
значения ординаты у—\ н углового коэффициента касательной y' = fe=l в точке х = 0. Получим систему уравнений
1=C1, 1=С2 —Clt
438
из которой определяем:
(?!=!, Сг = 2.
Подставив эти значения в уравнение семейства, получим искомое уравнение
у — е х (cos х + 2 sin х).
Найти общие решения следующих дифференциальных уравнений:
2014. у" — 2ау' + а2у = 0.
2015. у" — 4 г/ Ьу = 0.
2016. у"-у’~2у^0.
2017. у" - бу' /34у = 0.
2010. у" -4у = 0.
2011. у"ф-9у —0.
2012. у” + Зу'=0
2013. у” — 5у' бу = 0.
Найти частные решения следующих дифференциальных уравнений:
2018. у" -4у' + 4у = 0 при у'х~и = 3, у'1Л_0 = — 1.
2019. у" + 4у' ф-29у = 0 при у'Л_(1 = 0, у’\х .„= 15.
2020. Найти интегральную кривую уравнения у" — 4у' -ф-Зу = 0, проходящую через точку (0, 2) и касающуюся в этой точке прямой у = л:ф-2.
2. Неоднородные уравнения. Рассмотрим теперь неоднородное уравнение
ЩУ” + <ЕУ' + а.,у=ф (х)
(3)
с постоянными коэффициентами ап, а1г а., и с непрерывной правой частью /(х). Уравнение с теми же коэффициентами, но с правой частью, равной нулю:
ЩУ" + а{у' + «•>!/ = 0,
(4)
называется однородным уравнением, соответствующим неоднородному уравнению (3).
Для линейных неоднородных уравнений справедливы следующие теоремы, с помощью которых отыскиваются их общие решения.
Теорема 1. Если известно какое-нибудь частное решение у неоднородного уравнения а„у" + а1У/ + °2У = / (*)> то общее его решение у есть сумма итого частного решения и общего решения Y соответствующего однородного уравнения аау"-'гащ'-)-a.,y = 0, т. е. y~y-\-Y.
Теорема 2. Если ух — частное решение уравнения at>y" ф- ащ' + а.,у = (х), а У>— частное решение уравнения аау"-f-a2y — f.,{x), ню tji-f-y., есть частное решение уравнения а„у" -\-аху' ф-а-,у — fi (х) ф- f2 (х).
Сформулируем теоремы, при помощи которых находятся частные решения линейных неоднородных уравнений для специальных правых частей.
Теорема 3. Если правая часть линейного уравнения с постоянными коэффициентами имеет вид еах Р (х), где Р (х) — многочлен п-й степени и а не является корнем характеристического уравнения, то существует частное решение вида у=еахМ(х), где М (х) — некоторый многочлен п-й степени:
М (х) — Доф-Д ]Хф- Дгхф-... ф- Апхп.
Если же а является корнем характеристического уравнения кратности k (fe = l или fe —2), то существует частное решение вида у — хкеахМ (х).
Е частности, при а. — 0 правая часть — многочлен п-й степени, и если а = 0 не является корнем характеристического уравнения, то частное решение (х) — также некоторый многочлен той же степени. Если же а = 0 — корень кратности k, то частное решение имеет вид хкМ (х).
Теорема 4. Если правая часть линейного уравнения с постоянными коэффициентами может быть представлена в виде
смх [ рг cns рЛ- (.vjrsin fix),
(5)
где Рх (х) и Р2(х)— многочлены (п—наибольшая из их степеней) и г = а + ф не является корнем характеристического уравнения, то существует частное реше-
439
imc вида
y = e,tx [Д4 (x) cos	+ N (x) sin pv],	(6)
где	•
M (х) = 4о-р/11х-р/12х2-р...-р/1ях,г и
N (x) = Bo + BiX + B2x2 + • • • + Bnxn
— многочлены степени n. Если же a-ppi является корнем характеристического уравнения кратности k, то существует частное решение вида
у — х1,е'1х [/И (х) cos рх-рУ (х) sin рх]*.
2021. Проинтегрировать уравнение у" — 5/ + бу = 13 sin Зх.
Решение. Корнями характеристического уравнения г2 — 5г6 = 0 будут i't — 2, г., — 3, следовательно,
y = C1e2^-}-C..e3v
— общее решение уравнения у" — 5у'-р61/ = 0. Представив правую часть в виде (5)
13 sin Зх = е°Л' [0  cos Зх-Р 13 sin Зх],
видим, что а = 0, (3 = 3, Р (х)=0, Q(x)=13 (многочлены нулевой степени). И так как число ? = a-ppt = 3t не равно щ и г.2, то частное решение ищем в виде (6), положив
М (х) — /10 и N (х) = В„,
у = е»л- [ х4о cos зх .у д() sjn зх] = Л () cos Зх Во sin Зх.
Найдем:
у' = —3.4О sin Зх~рЗВ0 cos Зх; у" = —9Л0 cos Зх —9В0 sin Зх.
Подставив значения у, у', у" в данное уравнение, получим тождество
—9Л0 cos Зх — 9В0 sin Зх — 5 (—3/10 sin Зх-р 3S0 cos Зх) -ф
-р 6 (Л(> cos Зх -р Вп sin Зх) — 13 sin Зх, или
—3 (/10 -р 5В(|) cos Зх -р 3 (5Д0 — /10) sin Зх — 13 sin Зх.
Приравняем коэффициенты при sin Зх и cos Зх:
-3 (Л(,+5В„) = 0, 3 (5Л„-В„) - 13.
5	1
Решив систему, получим Ло= - -1 Во =----------. Частное решение данного неодно-
родного уравнения
~ 5	„	1 .
„ cos Зх— „-sin Зх;
о	о
общее решение
(/= Y-\-y---Cte2-''-pC2c3-v -р (5 cos Зх — sin Зх).
2022. Проинтегрировать уравнение у" ~P9z/ = e-v cos Зх.
Решение. Из характеристического уравнения г3-ф 9 = 0 находим Щ,-.— •: 31, следовательно, общее решение однородного уравнения имеет вид
У = С\ cos Зх -р С3 sin Зх.
Представим правую часть уравнения в виде (5):
ех cos Зх = ех [1 - cos Зх -р0 • sin Зх],
* Для уравнения второго порядка 1г — ).
440
где а=1, 0 = 3, г = 1-фЗ«, Р(х) = 1, Q(x) = O, и так как г =?ь »'i и г ==о гг, то частное решение иш.ем в виде (6):
•	у = е1" [Ло cos Зх-(-Д() sin Зх).
Найдем:
у' ~-е.х |(ЛС + ЗВО) • cos Зх-ф(В0 —ЗЛ0) sin Зх],
у" ^ех [(—8Л(, + 6В0) cos Зх — (8В(1 + 6Л()) sin Зх].
Подставив у, у” в данное уравнение и сократив обе части его иа ех, получим
(Л0 + 6В0)  cos Зх-ф(В0 —6Д0)  sin Зх = cos Зх + 0 sin Зх.
Приравняв коэффициенты при созЗх и sin Зх, получим систему, из которой найдем А„ и Во:
Л0-!-6В0=1, До-6Ло = О, откуда .	1	„ G
37’ ^>-37; следовательно, ~ рХ у — (cos Зх -J- 6 sin Зх),
ij Y -ф у — С] • cos Зх C2 sin Зх -ф (cos 3x -ф 6 sin 3x), или общее решение
( сУ \	/	6c"^\
У = И + У = ' С) + 37 ) cos Зх + С, -ф I sin Зх.
2023. Проинтегрировать уравнение у" — 4z/' -ф4// --хе2*.
Решение. Из характеристического уравнения г2 — 4г 4-4 = 0 находим Л,2—2, следовательно, общее решение однородного уравнения имеет впд
У = (С1х + Сг) с23
Правая часть хе2х имеет вид епх Р (х) (см. теорему 3), где Р (х) = х п а = 2 является двукратным корнем (£ = 2) характеристического уравнения. Поэтому частное решение уравнения ищем в виде
У=х2 (Ло+Лн-ИФ
у’ — е2' [2Л0х -ф (2А(| -ф ЗЛ,) х3 -ф 2Л1х3],
у” —,"гх ]2Л0-ф (8Л0-ф 6Л)) х -ф (4Л0 + 12Л,) х2 -ф 4Л;Х"].
Подставим значения у, у', у" в дифференциальное уравнение, сократим обе части на е2х и определим коэффициенты Ло, Ау.
2Л0 + (8Л0 6Аj) х + (4Л0 + 12Лj) л-2 -ф 4Л ,х:| -
— 4 ]2Лох + (2Лс.-|-.ЗЛ1) х2-|-2Л1х3]4 (Л()х2-|-Л1х‘!) = х, или
2А0А~ 6Л1х нз х, откуда следует
Ло = О, 6Л^—1, Аг=~ g-.
Частное решение данного уравнения
~	. ,v 1	1 • Ov
u = X“C-v • r х= „ х-е-х. J 6	6
441
Общее решение
У = Г+ t/ = (C1x + C2) <*>•+ ’ ^=tn'C1xXC.+-!. А О	()	!
2024. Проинтегрировать уравнение у” -ф- у = 4 cos % 4- (х2 ф- 1) ех.
Решение. Корни характеристического уравнения г2 ф-1 = 0 мнимые:
<• Общее решение уравнения у"-]-у = 0 будет
Y = Ci cos х + С, sin х.
Определим частное решение уу уравнения у” 4- у = 4 cos х:
4 cos х = с0*'[4 cos х 4-0 sin х|; а = 0; р = 1; Z = i; Р(х) = 4, Q(x)=0. Следовательно,
/И (х) = А(), Л' (х)=50,
а так как z = rlt то у} ищем в виде
г/, х [А(. cos х-\-Ва sin х], уi = An cos x 4- Bo sin x -ф x (—An sin x 4- Bo cos x), y\ = —2Др sin x4- 2Bn cos x — x (A(, cos x 4- B,, sin x).
Из тождества, которое получится после подстановки z/1( yi в уравнение у'14-у = 4 cos х, определим До и Во:
—2А0 sin x + 2Bn cos х - х (An cos х -фй(| sin х) -фх (Ао cos х ф-В0 sin х) -^= 4 cos х, откуда Ао = О, В0 = 2; следовательно,
z/r = 2х sin х.
Определим частное решение у« уравнения у" ф-г/ = (х2 4-1) ех, помня, что корни характеристического уравнения Г|,.2= :i i. В правой части имеем выражение вида (3), где Р (х) — х2-ф1; а=1, и так как а не является корнем характеристического уравнения, то частное решение ищем в виде
Уз — (Ао 4~ AiX 4-АоХ2) ех:
y.i = ex (А(| -ф Ахх 4- А2х2 4- Ai ф- 2/Lx) = ех [(А„ Aj)(Ах + 2А2) х -ф А2х2], yi = с" |(2Аа + 2Аг + Аи) -ф (4А.. -4 Ai) х4- А2х2].
Из тождества, полученного после подстановки у2 и y'i в уравнение у” -^у = = (х2 J- 1) еv, определим коэффициенты Ао, Aj, А2:
[(2А2 4- 2Ai 4- Ао)4- (4А., -ф Ах) х 4- А2х2 4- Ао4- Ахх -ф А2х2] ~ (х2 ф- 1) ext или
2А24-2Ai4-2А04- (4А34- 2Aj) х 4- 2Л,х2 - х2 -ф 1, откуда
A2"LAj4-A0= о , 2А»4-А1 = 0;
А2=у, А1 = -1, А„-= 1;
~ _ /.	,1 ф v
У‘я — । 1 — х -ф х- | е- .
Следовательно, в силу теоремы 2 общее решение данного уравнения будет
т. е. в данном случае
у — Y 4- У1 + Уг,
у = Ci cos х -фС2 sin х -ф 2х sin х -фех. 1 — хф-„- х2
442
Найти общие решения дифференциальных уравнений:
2025.	у" — 2у' 4 у = х3.	2032.	2у”45у' = 5х2-2х-1.
2026.	у" - Зу' 4 2у = ех.	2033.	z/"4y-sinx-2tTA'.
2027.	у" + 3у' + 2у = sin 2х-ф-2 cos 2х.	2034.	у” 4 2у' 4 2у — 2ех sin х.
2028.	у"+2у = х2 + 2.	2035.	У” 4- 5у' 4 бу -= е~х 4 е 2х.
2029.	у” - Зу' 2у = = Зх -'г 5 sin 2х.	2036.	у” — 9у = e3v cos х.
2030.	у” Jr4y = х sin 2х.	2037.	у" 4 2у' 4 У = х2е-А’  cos х.
2031.	у"—4у' -j-3i/ = e2vsinx.	2038.	у" -7у' -\-6у = = (х — 1) cos х4 2sin х
2039. Найти частное решение дифференциального уравнения у” — 2у' = ех (х2 -|-x — 3), удовлетворяющее начальным условиям z/)x = o = 2, у' '1=11 = 2.
2040. Найти частное решение уравнения z/"4-y =— sin 2х, удовлетворяющее начальным условиям y'.x^—l-, У' \х-^ = 1 •
2041. Найти частное решение дифференциального уравнения у" — у' =2 (1 — х), удовлетворяющее начальным условиям (/Л = о=Т, У' л ; - 1.
§ 5. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ n-ГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
1. Однородные уравнения. Уравнение вида
а^У1 п ’ + агУ ’ + а-1У п~21 + • •  +	' + ап У = 0	(О
называется линейным однородным дифференциальным уравнением с постоянными коэффициентами ав, аъ а.,, а/г. Алгебраическое уравнение
а,/'1 +	4 ам-п-*	+ апЛг + ап = 0	(2)
называется характерисишчееким уравнением дифференциального уравнения (1).
Частные решения уравнения (1) зависят от вида корней характеристического уравнения (2).
Таблица 15
Характер корпя характеристического уравнения (2)	Частные решения уравнения (J)
1. г —простой вещественный корень	ух
2. г — вещественный корень кратности k	еГХ, хе?х, х-егх, .... xk'1erx
3. а4- рг — простые комплексные сопряженные корни	еах cos Чх, е'хх sin fix
4. и. -г — комплексные сопряженные корни кратности k	e(I-vcos(3x, xc’tu\'osfix, ..х/гЩ.’и;,'созрх; en-vsinpx, xeavsinpr,	xii~1cu-vsin fix'
443
Общее решение уравнения (1)
Y ~ С1У\ 4“ С2У2. +... + Сп ^yn__i + Cnynt
где уъ уъ ,..у у}г.лу Уп~~п частных решении того же уравнения, указанные в табл. 15.
2042. Найти общее решение уравнения у'" — у” -|-4z/' — 4у = 0.
Решение. Напишем характеристическое уравнение и найдем его корни:
г3 _ г2 + 4Г_4 = о, л-з (г—1)-}-4 (г—1) = 0, (г2 + 4) (г — 1) = 0;
4=1, 4 = 21, г3=—21.
Все корпи простые, следовательно, согласно табл. 15 (см. п. 1 и 3), соответствующие частные решения будут:
t/i = ех, у2 = cos 2х, уз = sin 2х,
Y = Cj ех + С2  cos 2х С3 sin 2х
— общее решение данного дифференциального уравнения.
2043. Найти общее решение уравнения у'1' — бу" ф-9у = 0.
Решение. Напишем корни характеристического уравнения г1 — 6г2-|-9 = 0 и укажем их кратность:
(г2-3)2 = 0, 4 = ^3, fei = 2; г.2=-Кз’, /г2=2.
Корни вещественные кратности 2 (см. в табл. 15 п. 2), следовательно, частные решения:
„ _ „КЗх __ V‘3x	_..,,-/Зх.
У1	, i/o	, Уз —	’ ь'Т —	>
общее решение:
Y = Cj еУз х + С «хе *л х + С3е “ Уз х + С^е~ /з х.
2044. Найти общее решение уравнения у[й} + 9у"' =0.
Решение. Напишем характеристическое уравнение -}-9г3 = 0, где 4=0, ky — З; г«,з=3 31, /?2,3-= 1 (см. табл. 15 п. 2 и 3).
Частные решения:
y1=^eilX~\, у2 = х, у3—х-, t/4 = cos3.v, y- = sin3x; y = C1~Y С2х -f- C-Sx- ф- С4 cos Зх + С\ sin Зх
— общее решение данного дифференциального уравнения.
Найти общие и частные решения (там, где заданы начальные условия) для следующих дифференциальных уравнений:
2045.
2046.
2047.
2048.
2049.
2. Неоднородные уравнения. Уравнение вида
а3у'"' + aiy'n~1' + а^У п~2 + • • • + щ 1/' + иny=-i (х)
У'"+9/=0.
у'" - Зу' - 2у = 0.
у(4> 4~ Юу"-)-9у = 0.
У<4>+2у'"+/'=0. у'^ + 18у"4-81у = 0.
2050.	у |^с = 2,
у' |х=о = 0, у" |х=0= - 1.
2051. г/15) — г/' = 0; у--0, у' --=\, у" =0, у'" — 1, ум = 2прнх = 0. 2052. у'" + 2у" + 10у' =0, у = 2, у' = 1, у" --1 ври х = 0.
444
называется неоднородным линейным дифференциальным уравнением n-го порядка с постоянными коэффициентами alh at, а2, , ап. Решение такого уравнения находится по тон же схеме, как для уравнения второго порядка.
2053. Найти общее решение дифференциального уравнения
yw+y" = *2 +
Решен и е. Характеристическое уравнение
Л4-|-/-2 = 0, или /*2 (г2ф-1) — 0; корни его
/"1 = 0, k1 = 2', г-2,з—- I, Й2,з=1.
Общее решение соответствующего однородного уравнения
Y = Сг + С2х + С3 cos х 4- С4 sin х.
В npanoii части многочлен второй степени и характеристическое уравнение имеет корень г = 0, й = 2 (см. теорему 3, § 5), поэтому частное решение ищем в виде
У = х2 (Д,, J-Д^ф Д,х2).
Найдем производные этой функции:
у' ^ ЗДеХ-рЗАхХ2 4-4Д2х3, у" = 2Д0-ф 6Atx-|- 12А2х2;
у"' = 6Л14-24Л;х, (/'41 = 24A2
и подставим их в уравнение y‘i} -\-у" = х24~х. Из полученного тождества определим коэффициенты Ао, Дп Л2:
24Л2 + 2Л0 + 6Л1Х + 12Asx2 = ~г -Д
приравняв коэффициенты при одинаковых степенях х, получим
12Л.,= 1, BAi-l, 24Л.,-(-2Ло = О;
откуда л ।	л 1
12’’	^"б"’
следовательно,
y=_x2 + l.V3+^.
Так как общее решение линейного неоднородного дифференциального уравнения любого порядка записывается в виде
У = ¥+У
(см. теорему 1, § 5), то в данном случае
у Ci 4~ СцХ 4” б-з ^os х -j- С4 sin х — № ф- g  4— 12“
будет общим решением.
2054. Найти частное решение дифференциального уравнения
у'" — 2//' + //' = 4 (sin х + cos х),
удовлетворяющее начальным условиям:
у л=ш - 1, У' \х=м 0, у" :л=0 = - 1.
445
Решение. Найдем общее решение неоднородного уравнения. Корни характеристического уравнения г (г2 — 2г4~1) = 0:
Г1 = 0, £1 = 1; г2=1, £г=2.
Общее решение однородного уравнения имеет вид
К = С] -j- (С2 -ф С3.г) ех.
Найдем частное решение у неоднородного уравнения
4 (sin х -|- cos .v) = е" х (4 sin л- 4- 4 cos х), где а=0, [5 = 1, z = i, Р(х) = 4, Q (х) 4; положим А! (х) = А0, N (х)=В0, и так как гАуи гу4г2, то частное решение ищем в виде
у = До cos х + Во sin х\ найдем
у' — — До sin хф- б0 cos х, у" = — Лп cos х — й0 sin х,
у'" — /10 sin х — Во cos х,
после подстановки у, у", у'" в левую часть данного уравнения получим
,10 sin х — Во cos х ф- 2 (Ло cos х 4- />’о sin х) — Ло sin х 4- Л’о cos х = 2 Ло cos х 4- 2В0 sin х, т. е.
2Л0 cos х 4- 2Р0 sin х = 4 cos х4- 4 sin х,
следовательно, Ао = 2, Ве—2;
у = 2 cos х 4- 2 sin х
— частное решение неоднородного уравнения и
у = Y 4- у = Су (С2 4- С3х) ех 4- 2 cos х + 2 sin х
— общее решение неоднородного уравнения.
Найдем частное решение, соответствующее заданным начальным условиям. Продифференцируем последовательно два раза общее решение неоднородного уравнения, получим три равенства:
y = Ct 4- (С24-С3х) av4~2 cos х 4-2 sin х,
У' = [С2 4~ Сз (1 4--')] '-Л 2 (— sin х 4- cos х), у" = [С2 + С3 (2 4-х)] ех — 2 (cos хф- sin х).
Подставив в них начальные условия х = 0, у=1, у'—0, у"— — \, получим три уравнения с неизвестными Clt С.,, Ся:
1=С’14-С, + 2, 0 = Са4-С34-2, -1 =С34-2С3-2, или
Ci + C.,= -1, Са4-Сг=-2, С24-2С3=1, откуда
Сг = 4, С.,= -5, С3 = 3.
Следовательно,
у = 4 4~ (— 5 4- Зх) сЛ 4- 2 (cos х 4- sin х)
— искомое частное решение, удовлетворяющее данным начальным условиям.
446
Проинтегрировать следующие дифференциальные уравнения:
2055. у'" — Зу' -\-2у — — е-х (4х24~4х- 10).
2056. 441 — у 54 sin х.
2057.	+ 2у" у ~ х2- cos х.
2058. z/(5) + у'" = х2 — 1.
2059. y{i} — у — 5e v sin х 4 х4.
2060. yw+4y'" =ел' + + 3 sin 2х-|-1.
Найти частное решение следующих дифференциальных уравнений, удовлетворяющее начальным условиям:
2061. у'" + 2у''41/- —2е 2А; у l.v„0 = 2, у' \х^.п -= 1, у"4=о=1.
2062. у'" — Зу' = 3(2 — х2); у А-=а = 1, z/'4=j=1, /'4=u = 1.
§ 6. МЕТОД ЛАГРАНЖА (МЕТОД ВАРИАЦИИ ПРОИЗВОЛЬНЫХ ПОСТОЯННЫХ)
Выше мы применяли метод подбора частного решения при интегрировании линейных неоднородных уравнений
аиУ"г} 4 агу'п”1' 4ад"1-3' 4... 4 апу = f (х)	(1)
в случае, если функция f (х), стоящая в правой части, может быть представлена в виде
еах [ Р (х) cos [lx Q (х) sin рх]
или состоит из суммы такого рода функций.
Во всех остальных случаях пользуются методом вариации произвольных постоянных. Мы ограничимся рассмотрением этого метода на уравнениях второго порядка
аоу" 4 «1/4 а«у =f (х).	(2)
Сущность этого метода заключается в том, что для соответствующего однородного уравнения
су>у" ~\~агУ =6 записывается общее решение
Y — С1У1 4 С2у.,,
где Сг и С2 рассматриваются как функции х. Подбирают их так, чтобы
У = 4 (х) щ 4 С, (х) уг
было решением уравнения (2). Неизвестные функции <4 (х) и С3 (х) определяются из системы уравнений
4 4)4 44 (х)у2 = 0, 4 (4/44 (х)4=4(х).	(3)
2063. Проинтегрировать уравнение у" 4-у~ tg2 х.
Решение. Корни характеристического уравнения г241 =0 комплексные Сопряженные: rlj2=+i, следовательно, общее решение однородного уравнения есть
Y = <4 cos х 4 С„ sin х.
Общее решение неоднородного уравнения ищем в виде
у=С\ (х) cos х4 <4 (х) sin х.
Так как для данного примера
yL = cos х, у2 = sin х, у\ = — sin х, yi = cos х,
447
то согласно (3) имеем систему
С\ (х) cos х -f- С', (л) sin х — 0, — С\ (х) sin х С”, (.v) cos х — tg2x.
Из этой системы найдем функции С\ (х), С'., (х):
| 0 sin х I			COS X	° 1	
	1 tg2X COS X 1	_ Sin’v r (x-1 -	— sin x	tg2x 1	sin2x
с 1 и) — ।	cosx sin x I	cos2x ’	COS X	sin x 1	СОУ X ’
	— sin x cos x 1		— sin x	cos X I	
Сг (х)=-	C sin3 x ,	C sin x (1 - cos2x) dx		1	— cosx-|- Cj
	\	0 dx — } COS2 X	5	cos2x		= —	COS X	
_ , ч ( sm2x С 1—cos2x ,	, , х , л\ .	, „
С., (х) = \ ----dx = \ ------------ dx — In tg +	— sin x-J-C,.
“v } cos x	cos x	2	4	' '
Подставив найденные значения C\ (x) и C2(x), получим общее решение данного дифференциального уравнения:
у—---------------cos х-|-С1''| cosx-фГ — sinx + ln tg ' * -J-	+ sin х,
.	С OS X	'|	w	j
f x л \
//= — 1 — cos2x +Qcos x —sin2x-J-sill x In tg  9 + 4 !
/ x Л \
+ C., sin x — — 2 С,cos x у C, sin x -|- sin x tn tg 2^ 4'
2064. Найти частное решение дифференциального уравнения
удовлетворяющее начальным условиям
//^•=(>=1, Z/' 'л:—о —2.
Решелвр. Корли характеристического уравнения г2 —г = 0 вещественные разные: /у —0, г2—1;
— общее решение однородного уравнения.
Ищем общее решение неоднородного уравнения в виде
У = О U)4-C, (x)ev.
Для определения функции Сг (х) и С., (х) воспользуемся уравнениями (3); так как для данного примера //,=(), i/i, = ev, то имеем систему
с; (х) • 1 + с: (х)с*=о, с; (х) • о + c; w е* = р-р—, откуда получим:
С., (*) = • v / j л—г; >	ci (х)= ~ 1 “г т;
’ ех (1 +сЛ)	1 -|-е ’
(• dx	'
С1 W = - \ тшдт + = - X + I п (I + ^-) + с, *,
J 1 “Iе
Ci (х) — f , лд + С.. — — е л — х -f- 1п (! + сл) + С3.
С ~ГС /
* Для вычисления интеграла числитель преобразовывался:
е-
448
Следовательно, общее решение данного дифференциального уравнения будет
У = — y-f-lri (1 -(-е*) + С,-ф [ —e“v — хф-1п (1 -феу) ф-Сф, или
у= _х + ел- (С2_Л.) + (1 + РЛ-) 1П (1+ел) + СЛ
Для определения частного решения, соответствующего начальным условиям, найдем производную, т. е.
У'= — 1	[С2—хф-ln (1 + е’)I,
и подставим значения x = 0, у= 1, у' = 2 в уравнения
У = — -v-кех (С2 — л-) + (Н-ev) In (1 + е-') -ф Са
У’ = — 1 + ?Л' [С-2 — X ф In (1 + С*)].
Получим
1 =С2фСзф2 In 2, 2 = — 1 фС2ф1п 2, следовательно,
С3==3 —1п2, С3=—2 —1л2.
Искомое частное решение будет
у = -хф ех (3 - In 2 — х) 4- (1 + сх) In (1 ф- рх) - - 2 - 1 п 2.
Проинтегрировать следующие дифференциальные уравнения:
2065. у" -ф4г/ = -Дт-.	2067, У" + 4^'	2--1пх.
2066. /'-2у^-Д (М- 1)	2068.// -// =e‘-'cose\
§ 7. СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
1. Основные понятия. Метод исключения. Мы ограничимся здесь рассмотрением систем 'дифференциальных уравнений первого порядка с двумя или тремя неизвестными функциями. Переход к общему случаю не представляет каких-либо принципиальных затруднений. Для удобства геометрической и механической интерпретаций системы в этом параграфе аргумент всегда будет обозначаться буквой t, а искомые функции от / — буквами х, у, г.
В нормальной форме система двух дифференциальных уравнений первого порядка имеет вид
-J=r2(/,x, у).	(1)
Решением системы (1) называется всякий набор из двух функций
*=*(/)> у = у(/),	(2)
обращающих оба уравнения системы в тождества. Задача Коши для системы (1) состоит в том, чтобы найти такое решение (2), которое при t = t0 принимало бы заданные значения:
х(/0)=а, у(ф) = Ф	(3)
Общее решение системы (1) содержит две произвольные постоянные С,, С2, фиксируя которые находят любое частное решение в определенной области изменения начальных условий /„, а, Ь. Иногда вместо явной записи решений в виде
* 03 = 0,-1.
15 Кручкович и др.
449
(2), ограничиваются их разысканием в неявной форме:
Ф1(/, х, у) — ^, Ф2(/, х, у) = С2.	(4)
Соотношения (4) называются первыми интегралами системы.
Геометрически решение (2) определяет некоторую линию (интегральную кривую системы) на плоскости хОу. Если считать, что аргумент t играет роль времени, то указанная кривая будет служить траекторией точки, движущейся на „	„	( dx dy )
плоскости хОу. Поскольку в этом случае ( —- - ,	! определяют вектор скорости,
то с механической точки зрения система (1) означает задание поля скоростей в каждый момент времени t, а решение задачи Коши равносильно нахождению траектории точки, движущейся под воздействием этого поля и занимавшей в начальный момент времени t = t0 положение (а, Ь). Плоскость хОу, на которой рассматривается движение, называют фазовой.
Нормальный вид системы трех уравнений первого порядка:
-г, у, z),	х, у, г),	= х, у, г).	(5)
di	at	at
Все основные понятия и определения, сказанные выше для систем из двух уравнений, дословно повторяются и для системы (5) с той лишь разницей, что добавляется везде третья функция z (/), а вместо фазовой плоскости надо рассматривать фазовое пространство Oxyz. Первые интегралы системы (5) имеют вид
Ф^, X, у, г) = С1, Ф2(/, X, у, г) = с2, Ф3(<, X, у, z) = C3.	(6)
Если правые части системы (1) или (5) линейно зависят от х, у, г (но не обязательно от /!), то система называется линейной. В частности, линейная система с постоянными коэффициентами имеет в правых частях постоянные множители при х, у, г.
Для решения систем дифференциальных уравнений может быть использован обычный метод исключения неизвестных, сводящий .систему (1) к одному дифференциальному уравнению от одной неизвестной функции второго порядка,' а систему (5) —к дифференциальному уравнению третьего порядка. Если метод исключения применяется к линейной системе, то получается также линейное дифференциальное! уравнение, к решению которого можно применять методы § 4 и 5.
Заметим, что, и обратно, всякое уравнение л-го порядка
х<п>_/7(^, х> ... ( x'n-i>)
можно привести к системе уравнений первого порядка, если принять х', х", ... ... , х’"1 за новые неизвестные функции.
2069.	Решить указанную задачу Коши для системы ~^ — У + е'', ~ = х+1,- х^=о = О, г/|/=о = О.
Решение. Применяя метод исключения, выразим из первого уравнения у через х и t-.
После подстановки этого выражения во второе уравнение будем иметь _-х=^+1.
Следовательно, для нахождения неизвестной функции х получено дифференциальное уравнение второго порядка с постоянными коэффициентами. Используя методы § 4, находим его общее решение (проверьте!):
х = С1е( + С2е'-/+у?-Л
450
; Ж
А так как у было выражено через х, то теперь можно выписать и вторую неизвестную функцию:
У =	= CYef — С.^ — у е( — 1.
В результате получено общее решение данной системы. Используя начальные условия, получим для определения постоянных Q и С2 уравнения
откуда
С1 = 2 > ^'-1 ~	1 •
Таким образом, решением данной задачи Коши являются функции х = е( — е~*— t, у = е(—1.
2070.	Найти общее решение системы
x = x — 2y — z, у = y-x~\-z, z=x — z,
где x(t), y(t), г(0 — неизвестные функции, а х, у, г—их производные по аргументу t.
Решение. Исключим х, у из этих уравнений; для этого из третьего уравнения иайдем х==г+г. Продифференцируем полученное равенство по f: x — z -|-z, г
подставив значения х и х
в первое уравнение, найдем из него
•	Z
следовательно, у = — будем иметь
Подставив значения у, г/,' х во второе
уравнение,
z Z •	......
—g- = —g ~ 2 —г + г. или г — z — 2г =0.
Получили линейное однородное дифференциальное" у равнение третьего порядка. • Корни характеристического уравнения
г3 —г2 —2г=0: /-!=(), г2 = 2, rs—— 1;
.. следовательно, г (/) = -|- С,/:'1' + С:.е‘.
Чтобы определить неизвестные функции х (I) и у (t), найдем z н г из последнего равенства:
г = 2C2e2t - Сзе4, z = 4С.,е2/ + С&Г*, откуда
х (0 = г+г = -СзЖ+гС^+Сх + С^ + Сзе-ЖсжЗС^,
Общим решением данной системы будет система функций
х<0=Сх+ЗСае2г', р(0=-2С^—z (i) = Q + С,с2' + С3еЧ
15*
451
Методом исключения найти общее решение следующих систем. Выделить частное решение, отвечающее указанным начальным условиям:
2071.	dx = 4х — у, d y ~х~3г2у, х^=о = О, у\(=0=1.. LL t	dt
2'072. dx = 5x —3r/J,-2e3/, dy = x-|-// +5ez; x |,=0 = 7, z/!feo = O. dl	dt
2073. dx =2x — y, dy ==2y — x-Y§ef x'1Z=o = 0, у j^o = 0. dt	Lit
dx , dy , dz .
2o74- dt=y + z’ dt^x+z’ dt=x+y'’
x\t_(l = —l, у ^o = l, z|/_o = 0.
dx , t dy t dz
2075- dt = y+e' dt=z-e’ dt=x’
*7-o = —4, г/!/_о = 1, z\Uo = 8.
2. Метод нахождения интегрируемых комбинаций. Метод исключения имеет ряд недостатков. Во-первых, он связан с разрешением одного из уравнений системы относительно другого неизвестного, что не всегда удается сделать. Например, первое уравнение системы (1) не всегда практически допускает выражение неизвестной функции у через х. Во-вторых, полученное в результате исключения уравнение высшего порядка может быть сложным. Поэтому в ряде случаев пользуются другим методом —методом разыскания интегрируемых комбинаций, который позволяет сразу получить первые интегралы системы. Этот метод сводится к нахождению таких комбинаций уравнений системы, которые приводят к равенствам полных дифференциалов. Интегрируя эти равенства, и получают первые интегралы системы.
2076.	Решить систему
dx t — y dy x — t dt	y — x' dt	y — x'
Решение. Замечаем, что при сложении уравнений системы в правой части пропадают неизвестные х и у, то же самое происходит при сложении уравнений с множителями х и у соответственно:
Таким образом, как следствие системы получаем два равенства в полных дифференциалах:
dx-ydy=—dt, х dy-y-y dy = —tdt.
Интегрируя эти равенства (второе из них предварительно умножили на 2) и перенося член с t влево, получим первые интегралы системы в виде
х4-р4-/ = С1, х2 -|- у- -|-t2 = С2.
Отсюда нетрудно при желании выразить х и у через t, Clt С,, т. е. получить общее решение системы. Но для геометрической интерпретации решения достаточно полученных первых интегралов. В пространстве Otxy они задают окружность как пересечение сферы х2-у у2-У t2 = Сг с плоскостью x-yy-yt — C^. Проектируя эту окружность на фазовую плоскость хОу, будем, очевидно, иметь на ней эллипс. Его уравнение получится исключением t из первых интегралов (см. гл. III, § 5):
х2-уху-уу2 — Crx — Cty+ 2 (С-—Сг) = 0.
452
2077.	Записать уравнение свободных гармонических колебаний ^4-со3х = 0 в виде системы двух уравнений. Найти траектории системы на фазовой плоскости.
Решение.
рость движения уравнение будет
В качестве второй неизвестной функции введем v = ~ — ско-d v	d'*x
гармонически колеблющейся точки. Тогда -г? =-,ts- и данное at ati эквивалентно системе
dt
dx dt
= v.
Умножив первое из этих уравнений на у, второе на со2х и сложив, получим равенство в полных дифференциалах:
v do + co2x dx = 0,
откуда v2 -f-а2х2 = С. Следовательно, на фазовой плоскости xOv системы будем иметь эллипсы
7)2 Х%
С+С/ш2= b
2078.	Найти решение задачи Коши для системы (напоминаем, что точкой обозначается производная по /)
х = у-г, y = z-x, z = x-y, x|z_o = O, Н-о = 1> z^_0 = —1.
Решение. Если нахождение всех интегрируемых комбинаций затруднительно, то обычно применяют совместно метод нахождения первых интегралов и метод исключения. В данном примере один из первых интегралов находится сразу1, достаточно заметить, что сумма правых частей уравнений системы равна нулю, т. е. x-\-y+i-—0, откуда х -}-у -]-г = С1. Так как решается задача Крши, то величину Сх удобно сразу найти. Из начальных условий имеем
О-ф-1 —1==СЪ т. е. С1 = 0.
Следовательно,
x + y+z = 0, отсюда г=—х — у.
Подставляя это выражение г в первые два уравнения, сведем систему к интегрированию системы с двумя неизвестными:
х = 2у-^х, у = — у — 2х.
Решаем эту систему методом исключения:
1 . 1
У-2 х—2 х' и тогда второе уравнение дает
х Т~ Зх=0*
Интегрируя это уравнение и используя начальные условия, получим:
х = “ sin 1^3 t, у — --х-' - х cos КЗ / — Д- sin V 3 t,
/3	2	2	рЗ
z~ — х — у—— cos КЗ t----sin j/3 t.
/3
Проинтегрировать данные системы:
<ги/У- dt ~ х ’ dt ~~ у '
453
Указание. Умножить уравнения соответственно на х и у, сложить и вычесть.
опяп dx__________х. dy __ t* + x*
2080. df — t , dt ty 
Указание. Один из первых интегралов получится из первого уравнения, другой находится сложением уравнений с множителями х и у соответственно.
9ПЯ1 - У ЛУ = Х
ZU01, dt~<,y-x?' dt (у-х)*'
Указание. Сложить уравнения с множителями х и (—у), затем —.с множителями (у — 2х) и х.
2082.	, w = - •
dt у dt х
2083.	х = — х + у + ?, у = х — у-\-г, z—x-\-y-\-z.
Указание. Вычтя из первого уравнения второе, найти один из первых интегралов системы. Затем применить метод исключения.
3. Линейная однородная система с постоянными коэффициентами. Рассмотрим систему
dx , dy	.
df —аих + апУ>	— aiiX~\-a2«y,	(7)
где ajj = const. Пусть А обозначает матрицу из коэффициентов в правой части системы, a r — xiA-yj. Если считать, что координаты радиуса-вектора г расположены в столбец, то систему (7) можно записать в матричной форме:
g = 4r,	(8)
где справа стоит произведи ие матрицы А на столбец координат х, у.
Ищем частное решение системы (8) в виде r = etJp, где X — некоторое число, а р— постоянный вектор. Так как = /.е?/р, то, подставляя это решение в (8) и сокращая на е’/; получим
Ар = кр.
Следовательно, число X должно являться собственным значением матрицы А, а вектор р — собственным вектором, отвечающим значению X (см. гл. II, § 9). Ограничимся случаем вещественных различных корней характеристического уравнения матрицы А. Если Лг, Х2 —эти корни, то система (8) допускает два линейно независимых частных решения:
Г1(0 = еХ1'р1, г2(/) = емра.	(9)
Общее же решение получится по формуле
г (/) = СХГ1 (/) + С2гг (/),	(10)
где Сг и С2—произвольные постоянные.
Аналогично решается и система трех уравнений в случае различных вещественных корней Aj, Хз характеристического уравнения матрицы А третьего порядка. В этом случае к решениям (9) Добавляется г3 (/) = е?’?р3> которая с множителем С3 присоединяется к (10).
2084.	Проинтегрировать систему
g=x + 4y, Й = х-2у.
454
решение. Выпишем матрицу А и найдем корни ее характеристического уравнения;
4 =
1 4\	. Z1 4\ , /1 0\ /1-Х	4 \
1,	А—X/ =	—X =	[•
V —2/	\1 —2/ М \ 1 —2-Х/’
|А—Х/| =
= (1-Х) (—2-Х)-4 = Х24-Х-6;
Х2 + Х —6 = 0, Х1 = — 3, Х2 = 2.
Собственный вектор pt матрицы А, отвечающий значению Х = Х2 =
—3, находят
из условия
/4 4\ /at\
'о 1/ и
где {«1, /д} —координаты вектора pt. (Напомним, что собственный вектор определяется этим равенством с точностью до множителя, так что одну из координат аг или Z>! можно задать произвольно.) Производя умножение матрицы (4 — Х4) на столбец из координат вектора plt получим два уравнения:
4aj + 4<'р = 0, о, + bt = 0,
которые дают одно и тоже выражение at = —b1. Полагая /р =—1, найдем отсюда аг=1 и, следовательно,
Аналогично получаем собственный вектор, отвечающий Х = Х2 = 2:
р2 = / + 4/.
По формуле (10) запишем общее решение данной системы в векторном виде:
г	+	(Z-f-4/).
Собирая коэффициенты при ортах Z, /, получаем решение системы в скалярном виде:
х =	+ С2е2', у = —	+ 4С2е‘-\
Проинтегрировать следующие системы:
2085.	^=2х — у, = Зх — 2у. (л V	С* Р
2086.	g = 4х + 2у, Л£=-х + у.
2087.	J = 4-7x4-21/, g = Зх4-2у.
2088.	i’-x + j, g-Зх-;,.
2089.	х = — х-\-у-\-г, у = х — у4-г, z = x-^y~rz.
2090.	х = х — 2у~г, у = — x-\-y + z, i = x~z.
ГЛАВА XIII
ЧИСЛОВЫЕ И СТЕПЕННЫЕ РЯДЫ
§ 1. БЕСКОНЕЧНЫЙ РЯД, ЕГО СХОДИМОСТЬ
1. Основные понятия. Пусть задана бесконечная последовательность чисел иг, и2,	, ип, ...
Числовым рядом называется составленное из этих чисел выражение
«1+^2+•+"«+== 2 Un' п = 1
Числа Uj, иг, и3,... называются членами ряда, ип — общим членом ряда.
Конечная сумма
Sn — Щ + и2 +    + ип
называется и-й частной суммой ряда. Если существует конечный предел lim Sn, п сл,
ряд называется сходящимся, в противном случае — расходящимся. Если ряд сходится, число S= lim Sn называется суммой ряда, а разность
rn~S — Sn = ип+1 + пя+2 +   • называется остатком ряда (после n-го члена).
2091. По заданному общему члену = записать ряд и найти его сумму.
Решение. Давая п последовательно значения 1, 2, 3...получим
_L ' J_ 4--L4- I 1 - I = У —1_ Ь2Т2.3Т3-4Т "•тп(п+1)т “ п (n+ 1) ’
/2 = 1
Для нахождения суммы ряда надо найти предел при псо n-й частной суммы;
S __L4-XX, +__1___________________
Для того чтобы придать Sn более удобный вид для перехода к пределу, воспользуемся тождеством	i
1	-	1	1
fe(fe+l)	k	fc+Г
Полагая здесь	последовательно Л=1,	2,	3.п, получим;
1 _________1_ 11 1 1 _ 1 1
1  2 ~	2 ’ 2  3 ~ 2'	3 ’ 3 • 4 ~ 3	4 ’ ’ ‘' >
1 = 1________1_
п («+1) — n	n-j-1 ’
456
следовательно,
s -71- Ч ' ! 1 - Ч + Р 4+ J1 м т| + 7з'~17+ ••• + U~»+1л
Очевидно, что в этой сумме все слагаемые попарно уничтожаются, кроме первого и последнего, поэтому-
откуда
lim Sn = lim fl-—47 = 1.
/2-* co л-*со \ п~г V
т. e. ряд сходится, и его сумма равна 1.
2092. Пусть т — целое положительное число. Найти сумму следующего ряда, называемого рядом обратных факториалов:
СО
Sm = У __________1_______=
X1 п («+1)... («+///)
п — I
- 1 1 , 1 ,
1-2...(/п+1)	2-3... (/п + 2) "г 3-4...(/п+3)	•*'
Решение. Преобразуем общий член ряда ип по формуле _1 п + т — п __ 1 /	1	1	\
Лп~ т п (п +1)... (п + т) ~ т \п (п+ 1)... (п + /п— 1)	(«+ 1) ". (п-\-т);
В частности,
= J_ / 1_ __	1
U1~	т\т\	2-3...	(/п+1)
1/	1	1	\
и- т\2-3...(т+\)	3 • 4... (/п+2)/'
, = 1_ f	1______________1	\
1/3 т \3  4 ... (/« + 2)	4  5... (/п+3)/’
п /п \п(п+1)... (п+/п —1) (п + 1)... (п+/п)/’ Ясно, что _
= U1 + п2 + из +... + = Р ( Р - (	1 (п+w))
и при п — оо как предел последовательности частичных сумм получим
S<mi_ ljm 5 _—1—
тт\
2093. Показать, что гармонический ряд
1 + т+з + -+++--расходится *.
* Этот ряд называется гармоническим, так как каждый его член (кроме первого) является средним гармоническим двух членов, соседних с ним, т. е.
457
Решение. Для гармонического ряда
s„=i+y + -’- + +„•
S2rt=l + y+у + •• + ^ + ^71+ •+2^ поэтому
5 С ___1,1,	,
г>п“п+1+я+2+-" + 2/г^	2п~2’
или
s2rt > sn + g-.
Если бы гармонический ряд сходился, то последовательность Sn его частных сумм имела бы конечный предел А:
lim Srt = 4,
п -< + со
а тогда и ее подпоследовательность S.in имела бы тот же предел:
lim S2a = A,
а в предшествующем неравенстве был бы возможен предельный переход, который привел бы к соотношению
Л ‘ А g-,
что нелепо.
Следовательно, гармонический ряд расходится.
2094. Найти сумму бесконечной убывающей геометрической прогрессии
1 л 1 1 : +—1—+ =y_J—
3 ^ 6 '12^^"^ 3-2л1Т " Zj 3-2'г“1,
п = 1
Найти суммы следующих рядов:
2095. 1-73 + 274 + ^-5+ ••• +я(Л+2)
1
1
л (л+ 2) 
2096. ] з + 3_ 5 +5 7
 1 (2л-1) (2«+1)
Д«. (2л— 1) (2л-j-1)' п = 1
2097. 1 - 2 ~4'
1
2'1
1
8
2098.
Хы Л2 (л 4- 1)
, 2л-Ц
1 л2 (л-]_ I)2
3	,	5 д_
р . ”г 22• З2 1 ’
5
w	2/г+!	1	1
Указание. Использовать тождество ,, ,	= т» — ,, , ,.к.
k2(kA-i) k2 (/гр I)2
2. Необходимый признак сходимости. Если ряд сходится, то его общий член ип стремится к. нулю при л —> оо. Отсюда следует, что если ип не стремится к нулю, то ряд расходится.
458
• Указанный признак не является достаточным, т. е. если «„-О, то о схо-гшмости ряда ничего еще сказать нельзя: он может быть как сходящимся, так и 'расходящимся.
2099. Установить, выполняется ли необходимый признак сходимости для ряда
2 4- 4 Щ 6 Л- ' • 2Я ।
3 г 5	7 1 •'•-г2я+1
Решение. Общий член ряда ип =
2п
2ге+1
Так как
1-	г 2п 1-	2
lim и„= lim т;——г = lim ---------г~=1,
п-»оо „....^2/1+1	1
“ п
то необходимое условие сходимости ряда не выполняется и, следовательно, этот ряд расходится.
2100. Проверить выполнимость необходимого признака сходимости для ряда
Решение. Общий член ряда имеет вид ип =-----—. Здесь
72*
..	,. 2я—1	/2	1 \ .
lim и,,= lim ---—= lira ------5- =0.
П-.СО Я2	Я2;
Необходимое условие сходимости ряда выполняется, но, как будет видно из дальнейшего, ряд расходится (см. 2132).
Выполняется ли необходимый признак сходимости у рядов:
2101.	2104. J +{ + ! + ..,+Ц=1 + ...
п = 1 со	со
2102. У ,-4пз-	2105- Vnarctg-.
(я+1)3	Z.	ь я
п == 1	п — 1
21 OS 2_i_5. Ю \	- । 712 4~ 1 ।
2103.	-- + g+27+...+^-- + ...
§ 2. ПРИЗНАКИ СХОДИМОСТИ
1. Исследование на сходимость рядов с положительными членами
1) Признак сравнения
Если даны два ряда £ ип и £ vn с неотрицательными членами, причем члены первого ряда не превосходят соответствующих членов второго ряда:
* Достаточно, чтобы эти неравенства выполнялись начиная с некоторого номера N, т. е. для всех п -^ N.
459
to: а) из сходимости второго ряда следует сходимость первого ряда, 6) из расходимости первого ряда следует расходимость второго ряда.
Для сравнения часто используются ряды:
со '
1) 2 aq'1-1,	[ q | < 1 —сходящийся (геометрическая прогрессия),
п ~ 1
V 1	(сходящийся при а>1,
па	(расходящийся при аг^1.
п= 1
В случае а=1—гармонический (см. 2093).
Используя признак сравнения, исследовать на сходимость следующие ряды:
2106. У ----- А ..
Li. 1 п(п-1) п — 1
Решение. Общий член данного ряда
1..1	1
V и  -	__ . - Д-*	- — U И ,
/п(п-1) V	п
оо
так как с увеличением знаменателя дробь уменьшается; но ряд У А — гармо-п = 1
нический, расходящийся, следовательно, данный ряд расходится и подавно.
2107. 1 +273 + 3.32 + 4733 + ••• + „. 3«-i +• ••
Решение. Общий член данного ряда	меньше общего члена
сходящегося ряда геометрической прогрессии
1 + у + 32 + • •  + ПГТ + •  • >
поэтому данный ряд сходится.
2108.	j sin а | j sin 2а ! sin За | ,	, ' sin па 1 . 12	1	22	1 З2 1	1 Л2 1 СО
2109.	у —1— /я (1 + п2)  п — 1
2110.	1	1	1	, J	, 1п 2 "Г" 1п 3 1п 4	' In п 1 СО
2111.	У tg— п = 1
2112.	_1_ + _L_ + _L+ +	!	+ 1 - 2 1 3-’23 1 5 • 25 1	1 (2 г/ I) • 212'71
2113.	V ++ 2. i' n3  п = 1
460
Указание. Сравнить с рядом, общий член которого имеет числитель на единицу меньший.
со
2114.	V-----п—^.
Д.(^ + 3)'А
п — 1
00
Указание. Сравнить с рядом \	~.
со	со
2115.	Vsi< 2118. 2^-
п — 1	п ~ I
2116.	У -,-рД 9 .	2119. У
4^/i24-sm2na	3"
/1 — 1	п — 1
2117.	У у1 , .	2120. У ?in (М л)
А.' п + 1 — cos3 па	пI/„
п==1	п = 1	’
2) Предельная форма признака
сравнения.
Если У и„ и Y.vn — ряды с положительными членами и существует конечный, отличный от нуля
lim t?rl = /e >0, п -> оо vn
то рассматриваемые ряды одновременно сходятся или расходятся.
Пользуясь предельной формой признака сравнения, исследовать на сходимость данные ряды:
ОО
2121.
п I
Г»	1Г	..	II	V 1
Решение. Как известно, lim—।—1 > 0, но гармонический ряд / --и	г1 = ‘
расходится, следовательно, и данный ряд расходится.
ОС
2122. У1пЩ.
ti1 -ф 1
п = 1
00
VI 1
Решение. Беря для сравнения ряд У получим
,	«2 + 2
1П	--Л !
,.	Il- - - 1	. .
lim	----j-2— — Inn
л2
461
Как известно, при поэтому
In lim — n —* со
Так как ряд
х —> 0 бесконечно малая функция ln(l-y.\j эквивалентна х,
-• сходится, то и данный ряд сходится.
СО
2123. V - tg-тк п | га • п =1
Решение. При га — со бесконечно малая величина fg— эквивалентна
Г п
1	л	VI
-7=, поэтому, беря для сравнения ряд у —— , получим
i П	^п\/п .
п — 1
lim —j--------= lim У га tg— = lim | га -7—=1 >0.
п -* со 1	п -► со 1/ n п -> со I П
га '
1	3
Взятый для сравнения ряд сходится (он имеет вид у— где а = ъ->1), ^га	2
следовательно, и данный ряд сходится.
2124. ][1гу1+
п 1 Х
2125.	У 2"sin-"-.
3rt п= 1
00
2/ 2 \п
3”) ’
п === 1 со	со
2126.	NVl-cos^. 2128. V in 1 4 '2 ’ • п = 1	п — 1
со	со / ]	\2
2127.	V n3tg5-^-.	2129. У п [е^ - I )
У"3
п = 1	п — 1
Указание. Сравнить с гармоническим рядом, учитывая, что при га — со 1 -- 1 бесконечно малая функция е —1 эквивалентна — СО	со
2130. У —Lsin—.	2131. У (sin— tg— V
4у„ га	п
п = 1	« = 1
462
от п степени k, a Qi (п) — многочлен от п сте-рядов такого вида полностью исчерпывается сравне-
Здесь Ph (п) — многочлен пени I- Вопрос о сходимости нием с рядом X —- где a=l—k. Удобнее при этом использовать признак п1 п=\
сравнения в предельной форме. СО
. 2132. Исследовать на сходимость ряд
п = 1
Решение. Здесь в числителе многочлен степени й=1, степень знаменателя / = 2. Сравниваем данный ряд с гармоническим рядом:
lim
п —► оэ
/2п—1
\ П2
lim  п —* оэ
2п2- п  п2
= 2>0;
заключаем, что данный ряд расходится.
2133. Исследовать на сходимость ряд
2 (^W п = 1
Решение. Сравниваем этот ряд со сходящимся рядом	~:
.. п 1	. п3	1
lim ——=7. :	lim —гта= llm т-----гт» = 1.
n^co^+l)3 « п-со(п+1)а 4-юоЛ, I'3
\ п)
Так как предел отличен от нуля, то данный ряд также сходится.
Исследовать на сходимость следующие ряды:
оо	со
2134, 2	2137‘ 2 (5п —4) (би —5)'
п = 1	4=1
 2|35- 2,3S-4=1	4=1
ОО - 2136-(л3 — I)2 п = 1
4) Признак Коши
Если для ряда У ип с положительными членами существует lim 'у’ип = 1, то Zl —► ОО
smorn, ряд сходится при I <1 и расходится, ерли I > 1.
Замечание. Если /=1, то вопрос о поведении ряда остается открытым.
Решение. Для применения интегрального признака следует рассмотреть
	..	Р dx „
несобственный интеграл I Гак как
1
(х! — а
;---- при -7.-+1
1	- а
1п х при а— 1, то
та с СО при asc|, I j
' xa | а=Т при а> ’’
т. e. при а<1 несобственный интеграл расходится, а при а>1—сходится. Отсюда (на основании интегрального признака) заключаем, что ряд
2	1 ( сходится при а> 1, па ( расходится при asgl.
П = 1
Исследовать на сходимость следующие ряды:
2157.	со У 2	2161.	СО У 1
	3 + /Р-»=1		Ш п(1пп)2 П =2
	со		со
2158.	У	—	2162.	У —-—
	^|/3п+1 п = и		1+rt2 п~ I
	со		со
2159.	У 1	2163.	У 1
	(2//+1) (2/14-3) • и —0		win л’ п = 2
2130.	СО у е~Уп Ь Vn  п = 1		
2. Абсолютная сходимость. Теорема Лейбница о сходимости знакочередующихся рядов. В этом пункте рассматриваются ряды с членами, имеющими любой знак.
Если ряд £и,г сходится, а ряд £ \ип I расходится, то ряд называют условно сходящимся. Если ряд £ i ип сходится, то сходится и ряд £ ип, называемый в этом случае абсолютно сходящимся. Ряд
Я1 — а2 + «3 — а4 + ... + (— l)n+1art + ..., где всё а„ > 0, называется знакочередующимся.
Теорема Лейбница. 'Если члены знакочередующегося ряда удовлетворяют условиям
ах> а2> «3 >  > ап > ... и lim ап~0,
п~+оо то такой ряд сходится.
Ряд, удовлетворяющий указанным условиям, называется рядом Лейбница. Остаток
rn = ( 1)" а/1+1 + ( l)n+1 ort+2 + -
ряда Лейбница имеет знак своего первого члена и меньше его по абсолютной величине, т. е.
I rn I < 0/[+х-
466
SSko неравенство удобно использовать для оценки погрешности, получаемой при Камене суммы S ряда Лейбница ее приближенным значением
Р	= — я2+... + (—1)п+1а„.
,	2164. Исследовать на сходимость и абсолютную сходимость ряд
?	1--2- + -у + --- + (-1)я'1^ + ...
Решение. Данный знакочередующийся ряд сходится по теореме Лейб-" ннца, так как
1 >’> -'->>-1-> и -1 -0 (п-,ос). 2	3	п	п	'
Этот ряд сходится условно, так как Ряд , составленный из абсолютных • величин членов данного ряда, расходится (гармонический ряд).
2165. Исследовать на сходимость и абсолютную сходимость ряд
1 —-L-I-_L — 1. _L _L(—	... 1 --L
23 ~ 43 6зТ---Тк Ч (2га)3^’"
Найти приближенно (с точностью 0,01) сумму этого ряда.
s Решение. Очевидно, все условия теоремы Лейбница здесь выполнены: * ряд знакочередующийся, его члены по модулю монотонно убывают и стремятся к нулю. Следовательно, этот ряд сходится. Больше того, этот ряд сходится . абсолютно, так как сходится ряд из абсолютных величин членов данного ряда
1 + — + 1 4-	Н—!----1-
;	,д2з;4-'г	д(2п):1Г
 Сходимость этого последнего ряда легко обнаружить, если применить предель-V 1
ный признак сравнения со сходящимся рядом .
’ Для того чтобы найти с точностью 0,01 сумму данного ряда, надо взять столько его членов, чтобы следующий член ряда был по модулю меньше 0,01. Тогд^ весь остаток ряда, начинающийся с этого члена, будет также меньше 0,01.‘ Для данного ряда модуль четвертого члена J < 0,01, поэтому с точностью 0,01:	Н
5 = 1 ~2;1 + 43 =1	8 ^“64 = 64 = О’89'
Исследовать на сходимость и абсолютную сходимость следующие
ряды:
СО 2166. V (-!)'	.	2170.	у С-1)” In In n ' n = 3
2167. У (— 4	7 п (П • I 1)	2171.	(-1)4^2 - 1 n = 1
4168. ;-(я+(я- । / ] -)«11 1 у ।	2172.	VI (—l)n±13" Z (2n+l)” • n = 1
••• 1 ( Ч ^2«+1 у 1 ••• ОIRQ '	1	1	1	I	2173.	co У (—l),lsin-^-
21bJ> In 2 In 3 ' In 4	1 + ( -1)'1 lnU+1) +•-		
		
467
Найти приближенно (с точностью 0,01) сумму следующих рядов Лейбница:
СО	со
2174. 2 HO" 2’75- J ЦТ’-
п = 1	п = 1
Следующие ряды исследовать иа 2176. п arctg “•	2182. п=-1				сходимость: у (Зга-Н)! Z; 2" (2п—1)! п --- 1	
2177.	V П=1		2183.	2 п — 1	cos пх я3
2178.	У п 1	In 1 + °Х \ т-	2184.	2 11	]	(—1)яп lnZl ---?
2179.	2 п 1	/г — 1 ' ” 3/г л- 1 ‘ '	2185.	X1 / п-=\	е~П71 п ’ [
2180.	2 п '^1	nl 10й'	2186.	V 11=--1		_1	 п 1 + ап
2181.	5 п~ 1	п е~^п.	2187.	оо 2 п = 1	
§ 3. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
1. Область сходимости. Пусть задана последовательность функций «1 (х), »2 (х), .... ип (х)	,
имеющих общую область определения. Функциональным рядом называется составленное из этих функций выражение
«1 (х)4-и2 (х) + -•• + «„ (х) + ... = У ил(х). п 1
Для каждого значения х0 из этой области функциональный ряд обращается в числовой ряд
и1 (хо) + ^2 (хо) + • •  4" Un (*о) + • • • = 2 Ип (л’о)-/г — 1
Если последний числовой ряд сходится, точка х0 называется точкой сходимости функционального ряда. Множество всех точек сходимости называется областью сходимости функционального ряда. Область сходимости функционального ряда нередко удастся найти с помощью известных нам признаков сходимости.
2188. Найти область сходимости функционального ряда
е-х е-2х + е-пх -р . . . = е-пХ>
п~ 1
468
решение. Применяя признак Коши, будем иметь
lim е пх —е х п~^со
< 1 при х > О, > 1 при х < О,
в силу чего ряд сходится при положительных х и расходится при отрицательных. В точке х~0 данный ряд обращается в числовой ряд
1 + 1 + 1 +  • • + 1 + • • • >
очевидно, расходящийся.
Таким образом, областью сходимости данного ряда является интервал 0<х< + со.
2189. Найти область сходимости функционального ряда
у п \ X I п = 1
Решение. Члены функционального ряда определены на всей оси", за исключением точки х = 0, которая поэтому заведомо не принадлежит области сходимости рассматриваемого ряда.
X 1	__Y
Если х<0, - ! —	=—1, а поэтому при отрицательных х
i
У	У
п \ X J ш	п
п -=-1	п -= 1
Знакочередующийся ряд в правой части последнего равенства сходится по теореме Лейбница.
Если х > 0,	= а потому при положительных х
V = у 1 п \ X ] Li п' п — 1	п — 1
Ряд правой части гармонический, т. е. расходящийся. Поэтому областью сходимости рассматриваемого ряда является интервал (—со, 0).
Найти области сходимости следующих функциональных рядов:
2190. 2 (3-х2)л.
2191. 1+1 + 1 +
+ • • • + • • •
2192. У 1плх.
Л = 1
2193. У —L-.
Li х" + 1
П = 1
Указание. Применить необходимый признак сходимости (рассматривая |х|>1, \х\ <1, х=1) и признак Даламбера.
2194. у (2~х2)п.
П = 1
2195.
2. Правильная сходимость функциональных рядов. Функциональный ряд и1 W + и2 (х) + • •  + ил (•'") + • • •
469
называется правильно сходящимся на интервале (а, Ь), если его члены на этом интервале не превосходят по абсолютной величине соответствующих членов сходящегося числового ряда с неотрицательными членами:
называемого мажорантой данного функционального ряда.
2196. Найти область правильной сходимости функционального ряда
, sin 2х . sin Зх sinx + -^---1-—33-
sin пх
Пп
Решение. Для всех значений х, очевидно, имеет место неравенство
I sin пх |	1	„	,	,
——— sS —поэтому мажорантой данного функционального ряда будет число-
вой ряд	I
А , А 22 + 33
1
Пп
сходимость которого устанавливается с помощью признака Коши:
А—= Пт — =0<1.
'г)П П~+(Х> п
lim угип — lim
«-.со
Следовательно, данный ряд сходится правильно на всей числовой оси.
2197. Найти область правильной сходимости функционального ряда
1 1
; п3 + № 4
Решение. Для всех значений х имеем
_______ 1
П34-Х2	” п3
А- является мажорантой данного ряда. Мажоранта схо-
Следовательно, ряд
п~ 1
V 1	.
дится, как ряд вида у —— при а> 1.
па
Таким образом, данный ряд сходится правильно на всей оси, т. е. при
Указать области правильной сходимости рядов:
ОО.	I
2200. 2 2п У 1 + пх
п = 1
2198.
П— 1
п2
2201.
п=1
е " пЛ
470
Свойства правильно сходящихся рядов
й 1) Сумма ряда с непрерывными членами, правильно сходящегося на некотором ^интервале, непрерывна на этом интервале.
2) Если функциональный ряд с непрерывными членами правильно сходится •на отрезке [а, Ь], то его можно почленно интегрировать на этом отрезке, т. е.
в-..	b ( со 1 со b
‘	5 S (*)/dx== S 5 м« wdx-
х	a Vn — 1 J п = 1 а
Ъс ференцировать в точках
W
Ж
gj 3) Если функциональный ряд с непрерывно дифференцируемыми членами кВ сходится на данном интервале, а ряд, составленный из производных его членов, правильно сходится на этом интервале, то данный ряд можно почленно диф-
:о интервала, т. е.
00
У ип{х)
п=1
СО
2202. Показать, что функция f (х) =	непрерывна на всей
»: числовой оси.
Йй
Ш Решение. Для всех х за мажоранту данного функционального ряда можно ^Принять сходящийся числовой ряд с общим членом 1/п1. Следовательно, данный ^-функциональный ряд сходится правильно на всей числовой оси. Кроме того, |*-члены ряда функции непрерывные на всей оси, следовательно, в силу свойства 1) «/(х) непрерывна на всей оси.
К 2203. Показать, что ряд 2202 можно интегрировать в любом ^интервале и произвести интеграцию суммы ряда на отрезке [0, х].
Решение. Рассматриваемый ряд правильно сходится на всей оси, поэтому в силу свойства 2) возможно его почленное интегрирование на любом интервале:
со
„„„. л	V sin 2п пх	>	»
2204.	Убедиться, что ряд > ——- правильно сходится на всей
П — 1
' числовой оси, но что его нельзя почленно дифференцировать ни в '. одной точке.
г _		„	Sill Z ПХ 1	,	V *
Решение. Имеем ------------------- < 2"' ПРИ лю"ом х> а Ряд СХ°Д,!ТСЯ-
следовательно, данный ряд действительно сходится правильно на всей числовой оси. В то же время ряд
cos 2п пх
471
расходится при людом х, так как не выполняется необходимое условие сходимости ни при каком х,
со
2205.	Показать, что функция f (х) =	определена и не-
П = 1
прерывна при любом х.
2206.	Установить возможность почленного интегрирования ряда
2 У1-1 на отрезке ^0, и, проведя эту операцию, найти сумму
« = 1
полученного числового ряда.
Указание. Учесть, что сумма данного ряда равна -р—
2207.	Показать, что функция f (х) ==	непрерывна и имеет
п = 1
непрерывную производную на всей числовой оси.
§ 4. СТЕПЕННЫЕ РЯДЫ
1. Интервал и радиус сходимости. Степенным рядом называется ряд вида
Со+ «1 (х — а) + а2(х~а)2 + ... + а„ (х — а)п-ф... = 2 ап(х — а)п,
п = 0
где ап — числа, называемые коэффициентами степенного ряда (некоторые из них мргут быть нулями). При а = 0 степенной ряд имеет вид
со
а0 + агх + а2х2 -ф... -ф апхп -ф... = 2 апхп.
п — 0
Этот ряд всегда сходится при х = 0. Если же он сходится в точке %Ф0, то существует число R > 0 такое, что при всех | х , < R степенной ряд сходится, при всех | х | > R он расходится. Это число R называется радиусом сходимости, интервал (—R, R) — интервалом сходимости. Если степенной ряд сходится на всей числовой оси, полагают Д=-со, если же он сходится только при х = 0, полагают R = 0. В концах интервала сходимости степенной ряд может как сходиться, так и расходиться, внутри интервала сходимости степенной ряд всегда сходится абсолютно. На любом отрезке, принадлежащем интервалу сходимости, степенной ряд сходится правильно.
Одним из способов определения радиуса сходимости степенного ряда является применение признаков Даламбера и Коши.
ОО
2208. Определить радиус сходимости степенного ряда 2^-^г x'in,
П=1
Решение. Для данного ряда
/х 2n,l[ ->п /х 2«+l(n+l)t
«11 (X) = —п~ х-п; ип+1 (X) -	х-',+а.
472
В силу признака Даламбера ряд будет сходиться абсолютно для тех значений для которых
|«п+1(х)|	2n+1 (п+1)1 I X	п*
kw „Тео жк1 '^п\\х^-
л- -
\ «:
т. е. К2<у> или |х I < ]/
Следовательно, /?=^/ у.
2209. Определить радиус и интервал сходимости степенного ряда
V (х+1)"
2« («+1)0 + 2) •
п==и
Решение. Для данного ряда:
| х+ 1 \п
। Un । = 2" 0+1) (п + 2) ’
2,Н1 (п+2)(„ + 3) • |	|
В силу признака Даламбера ряд будет сходиться абсолютно при значениях х, удовлетворяющих неравенству
х7~- < 1, или [ z+1 I < 2,
которое равносильно системе неравенств
— 2 < х +1 <2, или — 3 < х < 1.
Таким образом, интервал сходимости ряда (— 3, 1), а радиус сходимости /? = 2.
2210. Определить радиус сходимости и выяснить поведение на концах интервала сходимости степенного ряда
1 д_ 2х I 4x2 I ।	2п~1х^1	,
ЗгКЗ "Г" 521Z3T "’“•••+ (2n—I)2 j/з+Д
Решение. Здесь , ч	, 2пхп
Un W - (2/1- I)2 yyFi ’ Un+1 W ~ (2n+ I)2 j з‘« ’
а потому (в силу признака Даламбера) данный степенной ряд будет сходиться абсолютно для тех значений, для которых
]jm [ ип+г (%) I _ Пт _2Мх^....... (2п-1)2/3^
„_+со \ип(х)\	п-+оо(2//+1)21/'3'г	2«'1 ! х I"’1
473
, , . 1 з т. е. для I х < —g—.
Кз"
Следовательно, радиус сходимости R=~—) а интервал сходимости
\ ? 2 /
Теперь выясним поведение ряда на концах интервала сходимости. В левом
Уз
конце, при х =---=—, данный степенной ряд превращается в числовои ряд
1- 1 Ь 1 - 1 4-
1 З2 -52	72 + •   -
/з
сходящийся по теореме Лейбница. В правом конце, при	g—> п°лучается чис-
ловой ряд
1 -L. - 1	- 1 -L. _|_!----I- .
32 г 52 -Г-• -t- (2n_ !)21  ’ также сходящийся.
Таким образом, данный степенной ряд сходится в обоих концах интервала сходимости.
2211.	Определить радиус сходимости степенного ряда Зх , з2х2 , зпхп .
У2""ГУ22"Г’"'
2212.	Определить радиус сходимости и выяснить поведение на концах интервала сходимости степенного ряда ^(Зх)'12.
п~0
Определить радиус и интервал сходимости следующих степенных рядов: СО	со
22'3- 2 (2п — Щ2П —1)1 	22'6-
п~ 1	п = 1
со	со
2214 УРЦ" —	2217 У (х~$- 
• Z\n+i;	зп ’	Z in« («+!)•
П=) со	со
2215. УЖхп.	2218. У (—	(х—1)".
Xj (2п)!	Хв' '	7 Зя2 '	1
п=1	п~1
Определить радиус, интервал сходимости  и выяснить поведение на концах интервала сходимости следующих степенных рядов:
2219. 2 п~\	/	1 \ я2 Н--Ч \ п J	2222.	СО 2	хп tg —. & п
2220.	Хп2 2" •	2223.	со 2	оП2 — 1 		гхп2. п
П==1 со 2221. 2	хп 2«-1 •	2224.	п ~ 1 со 2	sin2 ~ (х~ 1)п
П = 1			П = 1	
474
2. Ряд Тейлора. Если функция [ (х) имеет на некотором интервале, содержащем точку а, производные всех порядков, то к ней может быть применена формула Тейлора
?	/:И = /(а) + Г(а)(х — а)+Цр^-(х — а)2 + ...+
I 1 (х а)” 1 I R
 + (п-1) + а> '
7 - Ля) (?)
где Яц — ~—• (х — a)n (g — между а и х, п — любое натуральное число). Если цля некоторого значения х 7?га-^0 при п — со, то в пределе формула Тейлора превращается для этого значения х в ряд Тейлора
/W=f («) + ?' (?)(х-а) + ...+^-^(х-а)я + ...=
частности, при <7 = 0 имеем
СО
/(х) = /(0)+/'(0)х + ...+^^хя + ...= 2^<хя.
п —0
Таким образом, функция f (х) может быть разложена в ряд Тейлора для усматриваемого значения х, если:
1) она имеет производные всех порядков;
2) остаточный член Rn —> 0 при п — со для рассматриваемого значения.
2225.	Разложить в ряд по степеням х функцию f (х) =ех sinx.
Решение. Находим производные функции f (х) и их значения в точке х = 0: / (х) — ех sin х, f (0) = 0;
1' (а) = ех (cos х + sin х) =з У" 2 ех sin (^х +	, /' (0) = У 2 sin	;
' (х) = (У2 )2 ех sin (х +	, f" (0) = (|/ 2 )2 sin ~ ;
♦ •......................................................
ftn- (Х) = (р2 )п ех sin ^х+	(0) = (И 2)п sin
Теперь проверим, стремится ли остаточный член Rn Для этого оценим его абсолютную величину
хп ,	sin
(|/'2)пе|х| | х\п п\
IP Г’©
к нулю
Для ряда %ап
ип+1 .	_ »!	. /2 I х | :
“п	(п+1)!	(|/2)"e!JC| | х \п п+1
при п —* со.
.При всех х, следовательно, ряд £ ип сходится (в силу признака Даламбера), а «Го общий член ип —»0 при п—>со (в силу необходимого признака сходимости),
475
поэтому и остаточный член й (п), имеющий модуль, менЪший ип, и подавно стремится к нулю при всех х. Поэтому имеем разложение
ех sin х =	-----хп	(— со < х < +со).
2226.	Написать ряд Тейлора по степеням х— 1 функции f (х) = = 1п(х-{-2).
Решение. Находим производные функции f (х) и их значения в точке х— 1:
f (х) = 1п (х + 2),	f(l) = ln3;
х —£	о
/"(х)—1-(х + 2)Л	/"(1) = -!-;
(х) = —1 -2(х + 2ГЗ,	/"'(1) = .2L;
/<«> (х) = (- 1)«-1 (п-1)! (х + 2)-«,	/'«’	=	В1.
Следовательно, искомый ряд Тейлора функции f(x) = ln(x + 2) имеет вид
In 3 + | (x-l)--l- (* 21)2 +
1 (х-1)3
З3 3
, (-П^1 (х-1)” , ~	3"	‘ п ~
2227.	Написать ряд Тейлора для функции f(x) = ~ , приняв а = —2, и исследовать сходимость полученного степенного ряда.
2228.	Написать ряд Тейлора по степеням х— 1 для функции f (х) = 1п х и исследовать его сходимость.
2229.	Написать ряд Тейлора по степеням х — 4 для функции ^(х) = ]/х и исследовать его сходимость.
2230.	Написать ряд Тейлора по степеням х для функции f (х) —
Х*“ I х I 1
—	и найти его радиус сходимости.
(х-1) (х+2)	1 м
Указание. Разложить / (х) на элементарные дроби.
2231.	Показать, что функция f(x) = ]fx разлагается в ряд Тейлора по степеням х — 1 следующим образом:
1 + 2 (- 1)" 2'5з^~4)(х- 1)».
п — 1
2232.	Показать, что функция f (х) = разлагается в ряд Тейлора по степеням х-ф1 следующим образом:
«та=4 2 (>+»•
п = 0
476
2233.	Показать, что функция f(x) = -~=
V 34-х лора по степеням хф-2 следующим образом:
разлагается в ряд Тей-
1
V 3 + х
1 i V (- 1)” (2П— 1)1! I" Z (2га)!1
(Х + 2Г,
где (2п-1)!! = 1 • 3  5...(2n-1) и (2п)!! = 2  4 • 6.. .2п.
3. Применение таблицы простейших разложений. В предыдущих примерах для определения коэффициентов разложения функции в степенной ряд мы <: прибегли к многократному дифференцированию и нахождению значений производных в данной точке. Затем изучали, для каких значений х остаточный член —О ", при п —«4-со. Часто операции последовательного дифференцирования бывают свя-заны с громоздкими технически трудными выкладками, а исследование стремления рп к нулю представляет еше большие трудности. Эти трудности могут быть иногда обойдены на основании теоремы единственности разложения функции в степенной ряд, позволяющей утверждать, что полученное любым путем разложение функции в степенной ряд будет ее разложением в ряд Тейлора. Для обхода процесса многократного дифференцирования при разложении некоторых функций в ряд Тейлора могут быть использованы готовые разложения основных элементарных функций в комбинации с правилами сложения, вычитания, умножения рядов и теоремами об интегрировании и дифференцировании степенных рядов.
Особенно часто при этом используются разложения в ряд по степеням х следующих функций (которые поэтому полезно помнить):
уЗ	yfi
1) ^=1+х+*--(-ду +	..(-со <*< + 00),
„з „5	xin'1
2) sin х = х — Зр 4- j. , -ф- •	1)(2га 4- 1)~! + ’ ’ •
(— со < х< 4- со), -
 3) cosx=l —2| 4-4|-•+(—1)"(24ji+-"
(— СО < X <4“О0),
4) 1п(1+х) = х-^- +у-.. + (-1)л 1^ + -
(-1<х<1),
„3 v5	X2'1 1
5) arctgx = x-3 + 5 —.4- (- ir2-„+4+-
(- 1 1), ”6) (14-х)“=14-”х + к(2~1) ^4---4-
+ а(а-1)..Да-(п-П]х.,1+ (_1<х<1)>
7) гЬ=14-х4-^4-...4-^ + --(- 1 <х<1).
2234. Разложить в ряд по степеням х.
Тейлора функцию / (х) = х In (1 4-^2)
Решение. Так как
In (14-х) = х -4- *3 -  •  4- (- np-i 4-...
(-1 <Х< 1),
477
то, заменяя в последнем равенстве х на х2, будем иметь у4 уб
1п(Ц-х2)=^—2 + у + ... + (-1р 1Хя-+...(!%: <1). а поэтому 1-5	„7	,-2и ' 1
хШ(1+х2) = хЗ—2- + -3-+.„ + (-+
(’. * I < 1).
2235. Разложить в ряд Тейлора функцию / (х) = —'--ъ по степеням х-1.	х+
- Решение. Преобразуем эту функцию так, чтобы можно было использовать ,	1 ГТ
разложение функции -j—Полагая
1	а
 x-j-2 = 1 — & (х— 1) ’
из тождества 1 — & (х—1) = а (х-|-2) найдем а— , Ь — — О	□
Следовательно,
1	1 1
х-г2	3 . х—-1
1 — —3
,	1	х-1
Заменив в разложении функции	х через -—у, получим
Это разложение справедливо, когда — 3<х—1<х,	—2<х<4.
2236. Разложить f (х) = 1п 1/ в степенной ряд по степеням х.
Решение. Известно, что _ ОО 1п (1 +%)= У (- 1Г* Х”п (- 1 < X < 1), Ля*	«
П - 1 поэтому со
VI	<>"хп /	1	1 \
1п(1+2х)=	_у<х<7|,
п=1 оо
In (1 - X) = — У 1 < X < 1);
П = 1 отсюда 
= | У [(-1)пП2"-Н] =
II = 1 1 /„ з „ , 9	15 , , ,
= ТГ"2 Х +ЪХ 4Х +-)== =а- 2 *г+*3—т х4+-(”4<х<4)-
478
2237. Разложить в степенной ряд по степеням х функцию f (х) = 1
«г-	„	1
“ , Решение. Полагая — х2 = у и применяя биномиальный ряд 6) при а — —-g-,
' {[^следовательно получаем
	.	р	“
..'7W=7i^=(1+i/) f=1+'2
л	П~1
©О
,=1+2(_iPidL^j)
п — 1
~2Д 2	1/’"[
nl
У’
2я nl
(2п)1!
n = 1
п =- 1
2238. Показать, что функция f (х) = р-==^ разлагается в степен-- ной ряд по степеням х следующим образом;


В следующих задачах разложить указанные функции в ряды по степеням заданных разностей х — а.
2239. /(х)		ех — 1 X	по степеням x.
2240. /(х)	= (х — tgx) COS X	по степеням x.
2241. /(х)	X = Sln 2	по степеням x.
2242. / (х)	j—g~*2 X2	по степеням x.
2243. / (х)	= е3х	по степеням x — 1.
2244. / (х)	1 x —4	по степеням хф-2.
2245. / (х)	_ 1 — cos 2x 2	по степеням х.
2246. / (х)	x + 3 (x+1)2	по степеням х.
2247. /(х)	= (1 —x2) aretg x	по степеням х.
2248. / (х)	1 x— 1	по степеням х — 2.
2249. / (х)	= 2X	по степеням х —3.
4. Применение правила умножения рядов. Разложение в степенной ряд функции
ф(х)=/(х)ф(х)
Может быть осуществлено с помощью правила умножения рядов, если разложе-•• Ния функций / (х) и ф (х) известны.
479
Пусть в некоторой окрестности нуля имеют место разложения f (х) = а0 4- агх 4- я2х2 4-... 4- апхп 4-..., ср (х) = &о4-61х 4-V2 +.. - + ьпхп 4-..
тогда произведение f (х) ср (х) разлагается в той же окрестности нуля в степенной ряд
f (*) ф (*) = a0b0 + (П0Й1 +	X 4- (<7062 4- C7l&i 4- a2ft0) х" 4-
+  • • 4~(17</м +oi&n-t + •   + Л«^о) хп 4-- • •	(1)
В частности, при f(x) = q?(x) получается следующее правило возведения степенного ряда в квадрат;
If (Л')12 = яо 4~2яоа1Л "И (2ooa2 4*ai) х~ 4-(2с?о«з +
4-	Xs -(- (2«0«4 4- 2щп3 + a‘i) xi 4-...	(2)
2250. Разложить в степенной ряд по степеням х функцию
1п(14-х) 14-х
Решение. В интервале — 1 < х < 1 имеют место разложения
,J— =1 — х4-х2— х34-...,
у2 уЛ у4 1п(1+х)=х-у+у-у
поэтому по формуле (1)
' х- у + у - ~ 4-•  • (1 -х4-X2-X34-...) =
1 -J— X	Z О *	у
= x-G + x24-fl 4- у +	х3-{1 + А- + 1 + 1А х4у... (- 1 <х < 1).
2251. Разложить функцию f (х) = (arctg х)2 в степенной ряд по степеням х.
Решение. Так как ,	X3 , X5 х’ ,
arctgx = x-y4- g - у4-...^ то по формуле (2) 2	24	29
(arctg х)2 = х2 — у х4 4- -4д х8 — 105х8 4-... (— 1 < х < 1).
Выписать по три начальных члена разложений в степенные ряды по степеням х следующих функций:
2252. f (х) =е*1п (I +х).	2254. /(x) = sin2x.
2253. f (х) — е~х sinx.
5. Интегрирование и дифференцирование степенных рядов.
Теоремы о почленном интегрировании и дифференцировании степенных рядов.
Если пределы интегрирования а, р лежат внутри интервала сходимости СО
степенного ряда f (х) = апхп, то интеграл от суммы ряда равен сумме ряда п — 1
интегралов от членов ряда.
480
В частности, если | х | < R, то
X	СО X	со
= 2 J antndt— 2 ;^*n+1-
О	Tl^ 0 0	п — О
2. Если степенной ряд f (х) — апхп имеет радиус сходимости R, то ряд, п —О
полученный его почленным дифференцированием., имеет тот же радиус сходимости R и производная суммы ряда равна сумме производных членов ряда, т. е.
тп= 2	2
п — О	п — О
Отсюда следует, что степенной ряд можно почленно дифференцировать любое число раз, не изменяя его радиуса сходимости R'.
' 2255. Получить разложение в степенной ряд по степеням х функции
•		f (Л-) - In (x + Fl +х2).
Решение. Известно, что
X
О ~
Заменяя подынтегральную функцию ее разложением, полученным в 2238, •получим
in(x+rr+P)=x+j 2dtt
. О n = l
или, после почленного интегрирования степенного ряда,
1п(х+/Г+^) = х+2(-1Р^^--2^Г, (И<1).
4	п — 1 ,
 2256. Получить разложение
2(2п—1)11	,, ।
п =1
2257.	Получить разложение в степенной ряд по степеням х «Функции ошибок», определяемой равенством
X
и не выражающейся в конечном виде через элементарные функции.
W Кручкович и др. .	481
2258.	Получить разложения в степенные ряды по степеням д-функций:
X
С —	dt (косинус-интеграл Френеля),
)' 2л Л V t
S (х) —^Ldt (синус-интеграл Френеля).
I 2 л Л ) t
Указание. Произвести в интегралах замену переменного (Г t = и).
В 2259 — 2262 получить разложения в степенные ряды по степеням х заданных функций:
2259.	f (х) = cos е dt.	2261. f (х) = J агс^К- dt.
2260.	f (х) == у===	2262. f (х) = J Ре‘г dt.
о ' ~г	о
В 2263 — 2268, применяя почленное интегрирование, найти суммы f(x) соответствующих рядов:
2263. /(х)= 2 (2'! 'У' --
п — О
 Решение. На основании формулы производной определенного интеграла по верхнему пределу получаем
2264.	f (х) = У, пхп.	2267. f (х) = У п (п + 1) хп. п —I	П=1 со	со
2265.	f (X) = У (п + 1) х".	2268. f (х) = V п~\	п—0 со
2266.	f(x)= X (— П = 1
В 2269 — 2272, применяя почленное дифференцирование, найти суммы f (х) соответствующих рядов.
СО
2269.
n = I
482
решение. Применяя почленное дифференцирование, получим
Г(х)= у%24= у
п = 1	п == I
1).
как /(О) = о, то
J+	>
I* dt ' 1 -о
2 111 |Т^Т|

о
2270. Ш = 2 ?•

2r2rt-r2
2272. f(x)= J (- 1)я(2п + 1)^'1-
п = 0
Указание. Положить f(x) = xq>(x) и найти <р (х), как в 2269.
2273. Применяя почленное дифференцирование степенного ряда,
СО
XI Х^
азать, что функция у= / -ту лг является решением дифферен-
п — 0
иального уравнения у" — ху'—у = 0.
Решение. Почленным дифференцированием заданного ряда находим:
2/ix2't~1
(2п)1! ’
2 2«х2/г
(2п)И
п — 1
У
(2я-1)х2"-2 V (2/1+1) х2/г
(2п-2)!1 Li (2n)I!
n = 0
-Поэтому
у' — ху' — у = У
ге = 0
(2n+ 1) х2" V 2пх2П
(2п)11
(2n)!l
У2П
^=0.
00
•i|y 2274. Показать, что функция у== У
Л.	п — 0
-Дифференциального уравнения ху’'+у'^->
хп
W
)
у=о-
х'1'1
2275. Показать, что функция у = 7 —
г •	п == 0
..'дифференциального уравнения ху' = у (хЦ- 1).
СО
J 2276. Показать, что функция у= —р
п = 0
является
является
является
решением
решением
решением
4 = 1
n — 0

16*
483
§ 5.	ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ СТЕПЕННЫХ РЯДОВ
1.	Теоремы об аналитических решениях. Интегрирование линейных диффере". циальных уравнений с переменными коэффициентами (выше первого порядка;, вообще говоря, не приводится к квадратурам, а их решения не выражают; через элементарные функции. Одним из методов интегрирования таких уравнений, важных для приложений, а также некоторых других, является представление искомого решения в виде степенного ряда. Этот метод опирается на следующие теоремы теории дифференциальных уравнений.
1.	Если все коэффициенты и правая часть линейного дифференциального уравнения n-го порядка
У"" + Pl W У'п-В * * 11 + • • • + Рп W У = f (X),
с начальными условиями
У(а) = у0, у’ (a) = y1...ytn~1' (а)=уп. t
являются аналитическими функциями в точке х = а (разлагаются в степенны  ряды по степеням х—а в некоторой окрестности этой точки), то решение эта', уравнения тоже является аналитической функцией в упомянутой окрестности.
2.	Если правая часть уравнения y' = f(x, у), у(а) = Ь является аналитически, функцией переменных х и у в точке х = а, у = Ь (разлагается в степенной ряд г; > степеням х — а, у — Ь в некоторой окрестности этой точки), то существует единен! венное решение у = у(х) этого уравнения с начальным условием, являющееся ан,, литическим в точке х~а.
Диалогичное утверждение справедливо и для уравнения
у"1' =1(х, у, у', , г/1"-1)
с начальными условиями
У(а)-= yQ, у' (a)=yt, ... , у1*-'1, (а)- уп v
2.	Практическое получение решения дифференциального уравнения в виде степенного ряда. Способ последовательного дифференцирова-н и я. Искомое решение у (х) разлагается в степенной ряд по степеням х—а. Как всякий степенной ряд, он служит рядом Тейлора своей суммы, а потому разложение имеет вид
У = у(а) + -^-М (х-а)+-^2^- (х-а)а4-...^—М(х-а)я + ...
В случае уравнения и-го порядка первые п коэффициентов у (а), у'(а), ... , yin~l (и\ заданы начальными условиями. Подставляя в дифференциальное уравнение х = а. находят у{П' (а). Далее, последовательно дифференцируя уравнение и подставлял после каждого дифференцирования х = а, находят
(а), у"1'- (а), ...
Процесс или обрывается на заданном коэффициенте, или завершается нахождением общего закона построения коэффициентов.
Способ сравнения коэффициентов. Искомое решение разлагается в степенной ряд по степеням х — а:
у = а0-{-а1 (х —а)+а2 (х —а)24-...-|-ап (х — а)” + ...
Из начальных условий определяют коэффициенты:
У?	Уп i
ао = Уо, Я1 = У1, а2 = ~2р •••.
484
'у Подставляют в дифференциальное уравнение вместо у, ее производных и про-1 чих функций, входящих в уравнение, их разложения в степенные ряды по сте-. пеням х — а и приравнивают коэффициенты при одинаковых степенях х — а, опре-• ‘ ' деляя из полученных уравнений коэффициенты ряда.
2277.	Найти первые пять членов разложения решения дифференциального уравнения у" = (у')а +*У, t/(l) = 1, у' (1) = 0.
. Решение. Подставляя х=1 в дифференциальное уравнение, в силу начальных условий получаем у" (1)=1. Дважды дифференцируя уравнение, находим:
i	у”' = 2у'у’+у+ху', /"(1)=1,
5,	г/'4, = 2 (у”У+2у'у'" + 2у' + ху", yfi (1) —3.
' Таким образом,
2278.	Найти разложение в степенной ряд решения дифференциального уравнения у" =ху’ + у, у (0) = 0, у' (0)=1.
Решение. Как и в предыдущей задаче, искомое решение обладает разложением
оэ
у /?! хП' Здесь = У’ (0) = 1 и	Последовательное диффе-
п—0
лренцирование дает:
у'"— 2у’ху" у"' (0) —2
I	yi = Zy" + ху"' г^(0)=0
(/5 = 4г/'"-(-хг/4 г/5(0)=24
г/'2«> = (2п— \)ywv +ху<2п-1> у2п (0) = 0 учпц) = 2пугп~1+ху'2п> г/‘2« + 1'(0)=2-4-6 ... 2л = (2л)!1
Таким образом, СО	со
у (2/Q11	У	х^+1
у	Zl(2n+l)l	Zj	(2и + 1)1! •
п==0	я = 0
2279.	Найти решение уравнения у' = у при начальном условии 'Н0) = 1-
Решение. Запишем искомое решение в виде
у = а0 + ахх + агх2 + а3х3+ ... ,	= г/(0) = 1,
тогда
у' = «!2а2х4-За3х2-\- ...
Подстановка в данное уравнение дает
Oq -р сгх х 4" ч2 х2 4- ’ • • == 4- 2а% х 4~ Зд, х2 4- . •
Приравнивая коэффициенты при одинаковых степенях х, получим вместе с начальным условием рекуррентную систему уравнений, из которой последо-
485
вательно определяем коэффициенты ап‘
хО	aj = a0.	«о=1,
X1	2й2	>	1 “2-у2
X2	За3 = а2,	1 аз“1-2
Таким образом, л-2 Г3 !/=1+х+^+з1 + ...=-Л
В этом примере решение получилось в виде степенного ряда, изображающего ех. В большинстве случаев решение будет получаться в виде степенного ряда, сумма которого не является элементарной функцией.
2280.	Найти решение уравнения у' = у2-1гХ3 при начальном условии z/(0) = y.
Решение. Записывая искомое решение в виде степенного ряда с неизвестными коэффициентами,' последовательно находим:
у = а0+а1х+а2х2+а3х3-ф... , а0 = У (0) =, у' = аг -ф 2агх -ф За3х2-ф4а4х3 -ф...,
У2 = ah 4* 2aoajX -ф (2аоа2 -фа\) х2 -ф (2а0а3 -ф 2a1tt2) х3 -ф...
Подставляя эти разложения в данное уравнение, будем иметь
щ ф- 2«.,х -ф За3х* -ф Асцх3 -ф... = ц2 -ф 2аоа4х -ф (2aoa2 -ф а 2) х2 -ф (2aoa3 -ф 2a4a2 -ф 1) х3 -ф...
Отсюда, приравнивая коэффициенты при одинаковых степенях и присоединяя начальное условие, получаем систему уравнений для определения неизвестных
коэффициентов:
1 1 а°-у.	а°~2;
1
а1 —	4 >
2й2 =	,	#2 o'»
о
2а3 = 2аоаг-фа2,	а3 = ;
10
9
4а4 = 2а0а3-ф2а1а2-ф1, ff4 = g2.
Таким образом, искомое решение имеет вид 1.1	,1 о . 1 о , 9
'	+	* +16-*3+з2х4 + -
В следующих задачах найти разложения в степенной ряд (до указанной степени) решений следующих дифференциальных уравнений: 2281. у'^х2-у2, у(1) = 2	(до (х-1)а).
2282. у' — у-\гхеу, у (0) = 0	(до х4).
4?б
у'=х2 + у«, у (1) = 1
у'—ху-^е'', у(0) = 0 xy'-yJ-ex,
(ДО (х-1)4).
(до х4).
У	" = ху' - У -Т ех, у (0) = 1, у' (0) = 0 (до х4). у"=ху2-у', у(0) = 2, у'(0) = 1 (дох4).
y" = x+ycosy', r/(0)== 1, у' (0) = у (до х4).
У	"	У (°) Г1’ у'(°)=°- _
у'=х-Нх2 + у2; у (0) = 1 (дох3).
У	" = УУ' — х~; у (0) = 1; у' (0) = 1 (до х3).
У" =хsinуЛ; у(1) =0, у'(1) = g-.
у"=ху'-у+1; у (0) = у' (0) = 0.
"" ~ хуу', у(0) = у'(0)=1 (до х«).
= ехУ, у(0) = у'(0) = у"(0) = 1 (до хе).
= (У')2> У(0) = У'(0) = 0. У"(0)=1 (дох4).
= хуф-х2у', у (0) = 0, у'(0) =у" (0) = у"'(0) = 1 (дох7).
ж
Йч
2283.
2284.
2285.
2286.
2287.
2288.
2289. (1 +х*)у''+ху'-у = 0; у(б) = 1, у'(0) = 1 (до Xs).
2290. у'=х + х2 + уг; У(0) = 1 (до х3).
2291.
2292
2293.
2294.
2295. у'
2296. у'
2297. у1 _ .	..........„
2298. ylv = e-vy + y', у(б) = у'(б) = б,'у'Л(О) = у";(О)'= 1 (до' хе).
Найти общие решения следующих дифференциальных уравнений виде степенного ряда:
2299. у" = у.	2308. (1 +х2)у' = 1+у2.
2300. у"+2ху = 0.	2309. у"'—ху'.
2301. у" -фху' +2у = 0.	2310. у"' = х2у'+у.
2302. у"+х2у = 0.	2311. (х2 — х+ 1)у" — у.
2303. у"+у' + лгу = О. 2304. у" -4ху' + 2у = 0.	2312. у'" =ху' + 1.
	2313. yIv = x2y".
2305. у'4-х2у — х3 = 0.	2314. yIV + x4y = 0.
2306. у" = ху'.	2315. (y')2 + xy = 0.
2307. у' —еху' + У = 0. В следующих задачах, пользуясь методом неопределенных коэф-	
, найти разложение в ряд по степеням х (до указанного порядка) неявных функций, определяемых уравнениями:
2316.	хуу-ех = у	(до Xе).
2317.	tf + ху = 1	(до х3).
2318.	ех — еу = ху	(до X4).
2319.	х3-\-у3 — Зху	(до х4).
2320.	х = 24'(1+У)	(до х3).
2321.	y = sin(x + y)	(до х4).
2322.	y = tg (х + у)	(до X4).
2323.	xy + siny= 1	(до х3).
$ 6. ПРИЛОЖЕНИЯ СТЕПЕННЫХ РЯДОВ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ
1. Приближенное вычисление логарифмов. Для приближенного вычисления
2	,	2
^Логарифмов удобна формула
In (W-H) = rn W-f-2Д, + ] + 3(2Лг + 2^ + 5(2W+1)5 +”"’
Цйе N — натуральное число. Эта формула позволяет последовательно найти лога-ДЙФмы целых чисел, причем сходимость ряда тем быстрее, чем больше /V.
487
2324.	Найти приближенное значение In 2 (с точностью до 0,00001).
Решение. Число а является приближенным значением А (с точностью до 10“«), если абсолютная погрешность Д = | Д —a |==+q—. Полагая в формуле (1) У=1, будем иметь
1П 2 = 2 (у + 3 • З2 + УУ4" + + + 9 • З9 +•••)
Принимая за приближенное значение In 2 сумму первых пяти членов разложения, мы сделаем ошибку, равную величине отброшенного остаточного члена:
Г. = 2М-0	\11 - ЭИ
2 “П-311
Ч-2-+ V_A_/!+l+l+. г 13 • З13 J 11 • 311 \ З2 ' 3*
-7Т = «У<тгУ<0-0М002-
З2
Разумеется, при подобных, облегчающих оценку допускаемой ошибки, преувеличениях этой ошибки следует соблюдать известную меру, так как более грубая оценка может привести к подсчету лишних членов ряда, т. е. неэкономичности вычислительной работы. Вычисляя каждый из первых пяти членов раз ложения с точностью до 10~в, мы сделаем при их сложении ошибку, не превосходящую 5 • IO' 6. Тогда абсолютная погрешность, т. е- полная ошибка, будет
Д<5- 10-» +2- Ю“6 = 7 • 10 '6 < 0,00001
(в соответствии с заданием). Вычисляя первые пять членов разложения с указанной точностью и складывая их, получим
2	2	2	2	9
,п 2 4 +	+ His +	0,666667 + 0,024691 +
О О’О О’О / * О J ‘ о
+ 0,001646+0,000131 +0,000011=0,693146, или, округляя,
1п 2 = 0,69315 + 0,00001.
2325.	Вычислить с точностью до 0,001 In 5.
Указание. Учесть, что 1п4 = 21п2 и 1п 2 = 0,6932.
2326.	Вычислить с точностью до 0,001 In 17.
Указание. Учесть, что 1п 16 = 4 1п 2,
2. Приближенное вычисление значений тригонометрических функций.
2327. Найти приближенное значение cos 10° (с точностью до 0,0001).
Решение. Переведя градусную меру в радианную, получим
аге 10° = -^^0,1745.
Учитывая разложение косинуса в степенной ряд, получим
488
л$тот ряд является рядом Лейбница, поэтому, принимая за приближенное зна- . яеиие cos 10ч сумму первых двух членов разложения, сделаем ошибку га, по абсолютной величине меньшую третьего члена:
Таким образом,
cos 10° = 1 - у g)2 = 1 - у (0,1W
(с точностью до КТ4, с недостатком, так как третий член разложения положителен) .
Вычисляя сумму первых двух членов с точностью до 10-4 с избытком (для чего следует вычислить второй член с той же точностью с недостатком), получим абсолютную погрешность, т. е. полную ошибку, меньшую 0,0001, в соответствии с заданием (так как обе ошибки были меньше ИТ4 и имеют разные знаки). Вычисление с указанной точностью дает
cos 10° =^ 0,9948.
2328. Вычислить sin 10° с точностью до 10 5.
3. Приближенное вычисление корней. Приближенное вычисление корней производится с помощью биномиального ряда
2329. Вычислить V 130 с точностью до 0,0001.
Решение. Имеем
1 1
/13б = (5з + 5)3=5(1+1)3=5 + ^ + ^ИБГ-1 +
, 3 \ 3	/\з____;	J__________________
+	3!55	'3-5	32-5а+34.54
Полученный ряд является рядом Лейбница, н значит, погрешность от отбрасывания членов начиная с четвертого по абсолютному значению меньше ——— < <0,0001. Сохраняя поэтому только три члена разложения, будем иметь
•/130 = 5 + 0,0667 — 0,0009 = 5,0658.
2330. Вычислить )Z1027 с точностью до 0,001.
2331. Вычислить |/ 500 с точностью до 0,001.
4. Приближенное вычисление определенных интегралов. Многие практически нужные определенные интегралы не могут быть вычислены с помощью формулы Лейбница —Ньютона, ибо ее применение связано с нахождением первообразной, часто не выражаемой в элементарных функциях. Если, однако, подынтегральная функция разлагается в степенной ряд, а пределы интегрирования принадлежат интервалу сходимости этого ряда, то приближенное вычисление интеграла оказывается осуществимым с наперед заданной точностью.
1
4
2332. Вычислить ^е~х2 dx с точностью до 10'1.
о
489
Решение. Разложение подынтегральной функции в степенной ряд имеет
вид
. е 1 =1-^+	'	(—со<х<+со).
01	AM	’*’♦
П—0
Интегрируя этот ряд почленно, получим
( е *2 dx = \ У (— 1)п— r dx =	\ х2п dx =
t-i	п\	п\ .1
О	0 п=0	п—О	О
= V (- О'1	______1__________1	_ 1 _।_______L__
т	’ (2/14-1)	42,!"i	4	3 •	43 ’	215 • 45
п = 0
Полученный числовой ряд есть ряд Лейбница. Погрешность, происходящая от отбрасывания всех членов начиная с третьего, будет по абсолютной величине меньше третьего члена:
Вычисляя с точностью до 0,0001, найдем 1 ~4 ( ё~ х2 dx = 0,2448 f-L - тДт, = 0,2500 - 0,0052 'i. о
Вычислить следующие определенные интегралы с точностью до 10“3:
1
I 2333. 'i-m- ? 1 + X2 0 л 2334. Jj dx. 0 1_ io 2335. jj 1п(1+х) dx. 0	2336. ( a-^^-dx. Л х 1 2337. sinxsdx. 1 2338.	- dx  .
ГЛАВА XIV
РЯДЫ ФУРЬЕ И ИНТЕГРАЛ ФУРЬЕ
§ 1. РЯДЫ ФУРЬЕ
I. Ряды Фурье функций периода 2л. Пусть /(х) —функция периода 2л, интегрируемая на отрезке [—л, л]. Рядом Фурье функции f (х) называется ряд
? + (ап cos пх + bn sin nx)t
коэффициенты которого определяются по формулам л	л
До у f (х) dx, = ~	/ (х) cos пх dx (n—1, 2, 3, ...),
—л	—л
л
bn — - - \ f (х) sin пх dx (n= 1, 2, 3, ...).
Л j —л
Прн этом пишут так: ОО f(x)~y+ (fln cos nx-\-bri sin пх). п~ 1
Ряд Фурье. функции f (х) не всегда имеет f (х) своей суммой, если даже сходится.
4, Простейшие достаточные признаки разложимости
Зр	функции врядФурье
'Ж I. Если функция f (х) периода 2л имеет на отрезке [—л, л] не более .^.конечного числа точек разрыва и абсолютно интегрируема иа нем, то эта функ-’*? Ция разлагается в свой ряд Фурье в каждой точке, в которой она дифферен-f . цируема.
2. Если функция f(x) периода 2л удовлетворяет условию Дирихле на j отрезке [— л, л] (если этот отрезок может быть разбит иа конечное число частей *• так, что внутри каждой части функция монотонна и ограничена), то эта функ-ция разлагается в свой ряд Фурье в каждой точке непрерывности; если же х — точка разрыва, ряд Фурье сходится к числу
V	/(х 0)+/(х + 0)
2	•
2339. Разложить в ряд Фурье функцию периода 2л, определен-ную так:
<-я<х<0>'
Ц»	11	(0<х^л).
Ел -	491
№
Решение. Вычисляем коэффициенты Фурье функции f (х):
Л	0	Л п
й0=
__ 1
“ 2~>
л
—л
о
- о
а!1 —
л
cos пх dx-\- cos пх dx =0, о
о
b„ — — \ f (.v) sin пх dx=~ л '	л
у 1 sin пх dx-\- \ sm пх dx о
1 Г cos пх |° cos пх л I 2га
п.
2ля
так как
cos лп=(— I)'1,
или 3
b2k = 0 (Й = 1, 2, 3, ...),
(Л = О, 1, 2, ...).
6г/г+1 л (2^4-1)
Функция f (х) удовлетворяет условию Дирихле, а потому разлагается в свой ряд Фурье. Таким образом, в каждой точке непрерывности
> 3 У sin (2^4- 0 х Г( >	4 Н л 2А+1
*=о
2340. Разложить в ленную так (рис. 229):
ряд Фурье функцию с периодом 2л, опреде-
О
1
1_
2
0,
(О
(х = 0, х = а).
Решение. Из определения функции f (х) условиям теоремы о разложимости в ряд Фурье,
следует, что она удовлетворяет поэтому заданная функция раз-

1 С ,, . ,	1
«0 = — \ f(x)dx — ~
 латается в свой ряд Фурье. Подсчет коэффициентов Фурье дает: л	/ 0	а	л \	а
0 • dx +	1 dx +	0 • dx ) —
0	а ] о
а
492
Диалогично,
1
Z

b
П —
— л
л	а
(’ , , .	, If.	, sin пх la sin па
\ t (х) cos пх ах = — \ 1 • cos пх ах =--
,)	л J	лп |о
—Л	О
а , , . .	,	1	, cos пх!«
t (л) sin пх ах =	\ 1 • sin пх ах = — ---
л J	лп |о
о
лп
1 — cos па лп
поэтому
/ (х) =
1
Л
° !_ X1 S*n Па C0S Пх + (1 —C0S fla^ S^n Пх
2 +
п
? У; Разложить в  чдующим образом:
ряд
Фурье функции
с периодом 2л, заданные сле-
2341.
2344.
( ch л 2342.
(— Л < X (х —л).
л),
0
х' 0),
/ (*) =
(х-- л).
fw=
( 2
2345. /(л:) = 5%+2.
(0 X ^5. л).
2343. f(x) = 2x~3 на [—л, л].
2. Разложение в ряд Фурье четных функции, т. е. удовлетворяющей условию /(—x) = f(x), не содер-синусами; этот ряд имеет вид
> Фурье четной " "'ff'jKHT членов с
и
нечетных функций периода 2л. Ряд
/W
«о
2
+ ап cos пх,
Жгде *
оо =
2
Фурье
л
f (х) dx, о
нечетной функции,
2
--- ТГ ЗТ
X РЯД ..	...
у=—/(•<), не содержит свободного у%члена и членов с косинусами; этот ’..(.ряд таков;
f (х) cos пх dx (п= 1, 2, 3, ...).
о
т. е. удовлетворяющей условию / (— х) =
ffx)
«-где

У bn sin пх,
пх dx
о
(п=1, 2, 3, ...).
Рис. 230
V 2346. Разложить в ряд Фурье функцию с периодом “ 2л, определенную равенством
(рис. 230) f (х) = | х I (—л
Решение. Эта непрерывная ’Теоремы о разложимости и,
функция, очевидно, удовлетворяет условиям следовательно, разлагается в свой ряд Фурье; она
493
четная, поэтому
л
2 С 2	х2 Iя
а„ — — \ xdx — — • -х- = я> л	л	2 |о
о л	л
(*	,	2 sin пх рт 2 С .	,
\ х cos пхах =— х--\ sin пх ах —
)	л п |о лп J
6	о .
{О -при и четном
4
-----* при и нечетном; ли2
следовательно,
f W = у - ~- [cos х + у cos Эх gg cos 5х + ...	cos (2n +1) х + .
f/X)
2347. Разложить в ряд Фурье функцию, определенную равенством
[ 0 (х = л).
Решение. Эта разрывная функция (рис. 231) удовлетворяет условиям теоремы о разложимости и, следовательно, разлагается в свой ряд Фурье; функция нечетная, поэтому
,	1 х cos пх |л
х sm пх ах =----------- 4-
л п о
Рис. 231 л	;
2 (* х	1 (
Ьп — — \ -S' sin пх dx — — 1 л л ) 2	. л .
о	о
л
4- --- t cosnxdx ля ,)
о следовательно,
. sin 2х’ f (x),= sinx-+
sin Зх sin 4х .	.
+ _-J-+...+
4-  ---sin пх -I- . ..
п
2348. Разложить в ряд Фурье функцию о0 (х) периода 2л, определенную так
. 232):
о0 (х) =
л 4-х
2
о
л —х
2
(—Л sgX<0), (х = 0), (0 < х < л).
494
 рс ш e н и е. Функция &ье и нечетна, поэтому
ст0 (х) удовлетворяет условиям
разложимости в ряд
а0 (х) = У brl sin пх, п = 1
sin пх dx
cos пх |л я |о
1	|Л\	1
х-у sin пх = — ;
2па	jo J	п ’
в *
[ 2349. Разложить равенством f (х) = t 2350. Разложить
Фраз л ожить в ряд Фур Ж 2352. Разложить в lit—л, л].
W 2353. Разложить в ’К ‘ 2354. Разложить в Ж 2355. Разложить в в
3. Разложение в ряд
, . V sin пх
/1 = 1
в ряд функцию с периодом 2л, определенную (— л < х л).
в ряд Фурье функцию f(x)~ | sinx[.
Ц. 2351. Функцию периода 2л:
|	f(, \х (0<х<2л),
\ л (х = 2л)
>6.
ряд Фурье функцию периода 2л /(х) = х® на
ряд Фурье функцию f (х) — | cosx  .
ряд Фурье функцию /(x) = sin х^.
ряд Фурье функцию / (х) = cos .
<5
Фурье функций, заданных на полупериоде. Функцию,
Заданную на полупериоде (0, л), можно разложить (по желанию) в ряд синусов •®йи ряд косинусов, продолжая на *Т8Торой полупериод (— л, 0) соответственно нечетным или четным обращаем.
2356.	Функцию f (х) — — у Й|азложить в ряд косинусов на ^Интервале (0, л) (рис. 233).
Решен и е. Продолжая эту фупк-JUHO четным образом, как показано рис. 233 пунктиром, будем иметь
л
2 1‘ / л х\ ,	2 / л х2\ р 2 /л2	л2\ .
°0 ~ я 3 \ 4	2 J	4 / |о л \ 4	4 J ~' 1
0
495
я	'	л
2 (' I я х \	, /я х \ sin пх р , 1 С .	,
а,, = - \	.------л- cos пх ах = --------------------------- -4---------- \ sin пх ах --
я ,) \ 4	2 /	\ 4	2 ) п |о яп .)
О	о
cos пх |я яп2 |о
1 яп2
1 = 1
яга2 яга2
поэтому
a2k 0. ЯгЛ+1 n^k+l)2’
я х 2 V cos(2/?+l)x
4	2“ ~я (2/г 4-1)2
А=0
2357.	Разложить в ряд Фурье по синусам функцию f (х), определенную равенствами
/(х) =
Решение. Для разложения заданной функции в ряд по синусам следует продолжить ее на интервал (—я, 0) нечетным образом. Тогда коэффициенты Фурье ап будут равны нулю, а
тс	л
.	2 С .	2	|« , 2 Г ,
Ь„ = - \ х sin пх dx = — - - у cos пх 4-----\ cos пх ах =
Я )	ЯН	|о ЯП ,1
о	о
9	9	|Л	9
= (__ППЭ1------р sin ИХ =(—!)«+!
k ’ п лп2 |о	П
Продолженная функция / (х), очевидно, удовлетворяет условиям разложимости в ряд Фурье, поэтому
/(х)^2 У (-1)'-^. жвви	' L
п 1
2358.	Функцию /(х) = х2 в интервале (0, л) разложить в ряд синусов (сделать чертеж).
2359.	Функцию
( 1 при х~ 0,
/(х) = . линейную в (0, 2/г),
0	в (2/г, л)
разложить в ряд косинусов (сделать чертеж).
2360.	Разложить в ряд Фурье по синусам функцию f(x)=chx , на (0, л).
2361.	Разложить в ряд Фурье по косинусам функцию f(x) = xsinx на (0, л).
4.	Разложение в ряд Фурье функций с периодом 21. Для функции с любым периодом 21 разложение в ряд Фурье, когда оно возможно, и формулы для 496
коэффициентов Фурье таковы:
оо
а0 , V плх , », • плх f(x) = g + %cos —+ &„ sm-y-;
п = 1 I	I
1	С . , . ,	1 Г f , . плх
Оо = -у \ f (*) dx,	an = ~i~ \ г (х) cos —j— dx,
—I	—I
I
.	1 f ..	. ПЛХ ,
bn = y \ ft^n-j-dx.
-I
Если, в частности, функция fix) четная, то
. , .’ «о , V плх fW= 2 + 2, o™cos~7-;
i
2	f	2
f W dx,	f
b
Если функция fix) нечетная, то
f(x)= £ sin — ,
п — 1
I
,	2 (* с. , . плх ,
bn= L- \ f(x)sm — dx. о
2362. Разложить в ряд Фурье функцию / (х) с периодом 4; график функции на интервале-периоде (—2, 2) изображен на рис. 234.
с периодом 2/= 4, поэтому
Решение. Заданная функция нечетная
2	1
, I* . .	. плх	, С	. плх	.	2	плх р
Ь„ = \ fix) sm -х— dx - \ т sm -—о— dx =---------------х cos -	4-
11	) 'v '	2	,	2	пл	2 jo
6	о
2	пл ,	4
- - cos -то- 4——т sm
пл	2 п-л-
плх р
2
- COS пл
пл
2
4	.
—sm и-л2
пл
2
(- l)fe + 1 kn
(— 1)*	4
. (2/г + I)2 ’ л2
при n = 2k,
при гг = 2/г-|-1.
В силу очевидной разложимости f fx) в ее
ряд Фурье получим
4 пх 1	4 Зч г 1
/ (х) = я2 sin т + я sin - — Sin - 2л sin 2лх +...
497
2363.	Разложить в ряд Фурье функцию f (х) периода 21 == 4, определенную на интервале-периода ( — 2, 2) равенством /(х) = 3 — х.
2364.	Разложить в ряд Фурье функцию периода 21, равную [*'  на интервале-периоде ( — I, Г).
2365.	Функцию f (х), определенную равенством
ЛХ t'r, _	I \
cos I 0 X 2 1,

разложить в ряд по косинусам.
В следующих задачах разложить в ряд Фурье функции / (х) периода 21, заданные на интервале-периоде (— I, I) указанными равенствами:
2366. f(x) = \x\ — 5 на (—2, 2).
2367. f(x) = 5x-l на (—5, 5).
2368. /(х) = 3 —|х| на (—5, 5).
2369. f(x) = 2x —3""на (—3, 3).
5. Разложение в ряд Фурье функций с «двойной симметрией». График функции периода 2/ четной или нечетной может обладать второй симметрией относительно прямой х =-~ , или относительно точки oj . Подобные функции называют функциями с «двойной симметрией». Если функция f (к) периода 21 четная и обладает второй симметрией относительно прямой х — -% , то
L
2
Osn= j-f (%)cos	a2rt+1=0 (n—О, 1, 2...),
о
&л = 0	(п=1, 2...).
Если f (х) нечетная и симметрична относительно прямой х = -~, ее коэффи-цпенты Фурье определяются так:
ал = 0 (n = 0, 1. 2, ...), £
, л «.	4 (* , , . л (2п+1) х ,	.	. , п .
fc2„ = 0,	—	\ ^Wsm—’—Y—~d,x	(n = 0, 1, 2, ...).
о
Коэффициенты Фурье четной функции f (х) периода 21, обладающей второй симметрией относительно точки I , О ' определяются формулами
L
2
<^„ = 0, oan+i = y- f(x)cos ^2w + ^ dx [п — Ъ, 1, 2, о
&„ = 0 (п=1, 2, 3, ...)•
498
» Коэффициенты Фурье .нечетной функции периода 21, обладающей второй ю	( I \
? симметрией относительно точки ( — ( 0), определяются формулами
Г	ал = 0 (п = 0, 1, 2, ...),	&2п+1 = 0	(« = 0, 1, 2, ...),
1_ 2
62л = у \ /(A-)sin—j—dx	(n=l, 2, 3, ...).
b
2370. Разложить в ряд Фурье нечетную функцию f (х) («равнобочную трапецию») с периодом 2Z; график функции на интервале-
периоде (—/, /) изображен на рис. 235.
Решение. Вводя обозначение tga = ft, приходим к следующему выражению нечетной функции f (х) на четверти 10, -g-l интервала-периода:
на

h
Эта иечетиая функция, очевидно, удовлетворяет условиям теоремы о разложимости и, следовательно, разлагается в свой ряд Фурье. Указанное разложение используется в теоретических основах электротехники.
В силу нечетности функции коэффициент ап — 0. Так как график функции f (х) симметричен также относительно прямой х = -^ (функция обладает «двойной симметрией»), то &2т = 0, а
I
,	4 f . л(2т + 1) х ,
Ьгт +1 = у \ f (*) SItl —-dx =
0
Л	1
'k	2
4	, . л (2m-Pl) я, , 4 С , . л(2т-}-1)* ,
= у \ йл: sin —1—-j-—— dx + у l h sin —1—j—dx.
b	h
Интегрируя первое слагаемое по частям и замечая, что второй интеграл является «табличным», после упрощений получим
<,	4й/ л (2m+1) h
-т+1 - л2 (2m+l)2 Sm Ы
Искомое разложение функции f (х) в ряд Фурье будет иметь вид
ОО
/« = 2 Wt-Isin т — 0
л(2ш + 1)х	4&Z	1	(2m + 1) Л л (2т+1)а
I "“ л2- Z (2m+l)2.Sin kl S‘n I m = 0
499
Разложить в ряд Фурье функции периода 2/:
2371. f(x) =
1 на (0, 1),
О .на (1, 2),
2372. f(.r) =
на (0, 1)
на (1, 2)
(/ = 2).
2373. f(x) =
(/ = 3).
1
— 1
1
— 1
(/ = 2).
интервале-периоде (—/, /), изображенном на рис. 236 («равнобедренный треугольник»).
6. Комплексная форма ряда Фурье. Комплексной формой ряда Фурье функции f (х) периода 2л называется правая часть равенства (справедливого во всех точках разложимости f (х) в ряд Фурье) *
л
с«=2л
— л
Рис. 236	(п = 0, ±1, ±2, ...).
Комплексная форма ряда Фурье функции f (х) периода 21 такова: со	inztx	I	innx
1 , cn = ^i \ f(x)e 1 (n = 0, ± 1, ± 2, ...). — со	— I
2375. Представить рядом Фурье в комплексной форме функцию f (х) периода 2л, определенную так:
( е х (0 < х =£? л).
Решение. Коэффициенты Фурье в комплексной форме
,	л	• л
=	d L \ е-<и-г»'Чх =
fell ,)	4.1 )
О	о
_	1 е-аНЛ1Х|Я 1— (—1)пе-л 1—;П
2л 1 in |о	2л 1 -ф п2 '
Так как функция / (х) удовлетворяет условиям разложимости в ряд Фурье во всех точках непрерывности /(х), получим:

1-(-1Ге~” 1-Ш ,-пу
2л 1 + п2
* По формуле Эйлера, e"i! = cos sin <р (см. также гл. XV, § 2).
500
2376. Представить рядом Фурье в комплексной форме функцию (х) периода 21 = 2, определенную так:
Г 0 на (—1, 0),
1 на (0, 1).
Решение. Так как 1=1, коэффициенты Фурье в комплексной форме
е-Ылл- dx = _	1_ e~innx 11
2tnn о
1 С
Сп~~ 2 3 о
( 0, е-'Д” — 1 _ (—!)» — ! . _ I
п —четное,
21пл
2лп
—-——-, п — нечетное, л (2п+1)’
Так как функция f (х) удовлетворяет условиям разложимости в ряд Фурье,
W л 2 2«+ 16,1




ряда Фурье функцию
2377. Представить комплексной формой /(x) = chx на (—л, л).
2378. Представить комплексной формой f(x)=shx на (—л, л).
2379. Представить комплексной формой ряда Фурье функцию / (х) периода 21 = 4, определенную так:
_/ 1 на (-1, 1)
. ' W | 0 на (-2, 1) и (1, 2).
ряда Фурье функцию
2380. Представить комплексной формой ряда Фурье функцию периода 21 = 1, определенную на интервале-периоде	г)
равенством f (х) = е2л'.
Разложить в ряд Фурье функции на указанных
2381. ех (—1, 1).
2382. е'х^ (—1, 1).
2383.
2384.
2385.
2386. |cos х)
2387. ) sin х |
Пользуясь разложением
функции z/ = x2, найти суммы рядов:
2392. £1
п = 1
2388.
интервалах: 4).
-1 (-2. 2).
(— л, л).
(—л, л).
(— л, л).
(—л, л).
х sin х
х cos х
2389.
2390.
2391.
2393.
ряд
4 — 2 jx| (—4, (х — 2, х С 0 (х-|-0, х > 0 cos ах (— л, л)
(а нецелое).
sin ах (—л, л)
(а нецелое).
Фурье на интервале (— л, л)
(-1. 1).
в
501
00	00
2394.	(2n-l)»’	2395, 2 "(M2’
n ~ 1	n — 1
2396. Исходя из разложения в ряд Фурье на интервале (—л, л) функции у — х, почленным интегрированием получить разложения в ряд Фурье функций у — х\ у = х3, у = х\
§ 2. ИНТЕГРАЛ ФУРЬЕ
1. Двойной интеграл Фурье. Функция f (х) называется кусочно-гладкой на отрезке [а, Ь], если: 1) она непрерывна на этом отрезке или имеет конечное число точек разрыва первого рода; 2) этот отрезок можно разбить на конечное число частичных отрезков, на каждом из которых ] (х) обладает непрерывной производной, т. е. является гладкой.
Функция f (х) называется абсолютно интегрируемой на всей числовой оси, если сходится несобственный интеграл от ее модуля
у
СО
j I f (X) I dx.
Теорема разложения. Если f (х) — кусочно-гладкая функция на каждом конечном отрезке и абсолютно интегрируема на всей числовой оси *, то в каждой точке х ее непрерывности выполняется равенство
ОО
f(x)='^ (а (а) cos ах + Ь (а) sin ах] da,	(1)
где
<Х>	00
А(а)=-^-	f (Оcos rjd dt, В(а,) = -^- f{t)w\atdt,	(2)
—00	—оо
В точках разрыва левая часть формулы (1) должна быть заменена на у и (х-0)+/(х + 0)].
Интеграл в правой части формулы (1) называется интегралом Фурье. Он обладает легко усматриваемым сходством с рядом Фурье (знак суммы заменен знаком интеграла и вместо целочисленного параметра п фигурирует непрерывный параметр а).
Формула (1) после подстановки выражений (2) и применения формулы косинуса разности аргументов может быть записана в виде
00 оо
/ (х) = -1- da f (Z) cos a (t — х) dt,	(3)
б ~00
где интеграл справа называется двойным интегралом Фурье функции f (х).
2397. Представить интегралом Фурье функцию
	1 (0 < х	<1),	
/(%) =	i (х = 0	и х=1),	
	0 (х<0	и х>1).	
* Эти условия не являются необходимыми для справедливости формул (1) и (2).
502
!' Решение. Данная функция является кусочно-гладкой, так как она состоит уга трех гладких частей:
у = 0 на (—со, 0), у—1 на (0, 1) и у = 0 на (1, со)
|н имеет две точки разрыва первого рода при х = 0, х=1. Очевидно, она также ^абсолютно интегрируема на всей числовой оси, так как вне отрезка [0, I] она нравна нулю, и интеграл от нее по всей числовой оси сведется к интегралу jJiio отрезку [0, 1].
Следовательно, такая функция может быть представлена интегралом Фурье; (по формуле (3) имеем
СО СО ’	00	1
f(x) — ^yda f (t) cos a(t — x) dt — f da 1 • cos a(t — x} dt — 0	—-oo	0	6
;•	00	CO
1 l’ sin a(t — x) I1	_ 1 C sin a(l—.v) + sin ax
~ л J a |o	— л '	a	~~
,	о	о
. a a(l—2x)
(	2 C S'n 2 C0S 2	,
’	л ,) a
L	о
i' В точках x — 0 и x=l, где f (x) терпит разрыв, полученное представление ^сохраняется, так как в этих точках
I	Нх~0Щ(х + 0) .. 1
’В частности, прн х —О пблучим
а ;C0Sy
“ 2 sin
а

б
,	1 f яп« ,
da — — \ —— da, л .) a
l-что равносильно равенству
sin а , л
----da= -к
а 2
2398. Показать, что
С / sin a , sin a — a cos a .	\ ,	( X 1, X 1
\ ------cos ax H-------------5------sin ax da = <
H «	a2 / I 1, x = 1.
о	'
В следующих задачах представить интегралом Фурье соответствующие функции:
cos х на 0,
;	2399. /(%) =	0 вне I0- fl 1 на (-1, 1),
2400. f(x) =	0 вне (—1, 1)
	у при х = ±1. 503
f sin л: на ГО, л],
2401. Ж = n rL. (0 вне [0, л].
2. Интеграл Фурье для четных и нечетных функций. Если /(х) —четная функция, то п
А (а) = ~ f (/) cos at dt, В (а) = 0,	(4)
о
и ее представление интегралом Фурье имеет вид
f(x) a (a) cos ax dx,	(5)
или в виде двойного интеграла Фурье СО	оо
2	С	С
/(х) =	\ cos ах da \ f (t) cos at dt.	(6)
6	b
Если f (x) — нечетная функция, то ОО A (a) = 0, В (a) =	/ (/) sin at dt,	(7)
6
и ее представление интегралом Фурье имеет вид
/ (х) =\Ь (a) sin ах dx,	(8)
О
или в виде двойного интеграла Фурье ОО	' оо
2	С	С
f (х) = — \ sin ax da \ f (f) sin at dt.	(9)
JT	]	!
о	0
2402. Представить интегралом Фурье функцию
продолжив ее четным образом для отрицательных значений.
Решение. Заданная четная функция, очевидно, удовлетворяет указанным выше условиям представления в виде интеграла Фурье, поэтому к ней моя>но применить формулу (6), в которой интегрировать f (;) надо только по отрезку' [0, 2], так как вне этого отрезка она равна нулю. По формуле (6) имеем
оо	2
2	С	С	/	t	\
f (х) =	\ cos ax da \ (1 — cos cd dt.
b	b	'
504
Вычислим отдельно внутренний интеграл (по частям):
2	2
ГЛ * \	/ л Л О sin at 12	I (• .
\ 1 — v cos oct dt=[ 1 — —- -------- + s~ \ sin at dt
J \	2 /	\	2 / a о 2a .1
о	о
следовательно,
5 cos at p
1 —cos 2a_sin2 a
2 a2	a2
2 В частности, при x = 0
С sin2 а ' а'2 О"
sin2 a
—z— cos ax da, ni	1
т.
Г sin2 a . л e. \ —c—rfa =
J °-	2
0
о
2403. Представить интегра-‘ лом Фурье функцию
(рис. 237)
— е-
при при при
x > 0, x = 0, x < 0.
®- Решение. Эта функция явля-Ж ется кусочно-гладкой,-так как состоит  из двух гладких частей и имеет один разрыв первого рода в точке х = 0.
9 Проверим, что / (х) абсолютно ин-S тегрируема на всей числовой оси. ® Для этого убедимся, что сходится ин-Ж/ теграл:

О
«>	°	°?	10	loo
j |/(х)г/х= ) exdx±\ e~x dx — ex	— e~v =(1 —0) —(0—1) =2.
-00	—00	i)	'—co	'°
( Следовательно, функцию f (x) можно представить интегралом Фурье, а , поскольку она является нечетной, то можно воспользоваться формулой (9):
оо	оо
2	С	С
/ (х) = — \ sin ах da \ е~( sin at dt.
о	b
Интегрированием по частям найдем внутренний интеграл:
со	1со	“
f e“z sin at dt = — e~‘ sin at I 4- a f e~f cos ai dt = a V e~l cos at dt
d	1° 0J	oJ
(результат двойной подстановки равен нулю). Вторично интегрируя по частям, получим
f e z sin ai dt = a \ e 1 cos at dt = — ae * cos at
oJ '	6	1°
— а2 \ е 1 sin at dt = а — a2 f е f sin ai dt,
505
откуда
Таким образом,
СО
е~' sin at dt = о
a
1 + a3’
,. '	2 C a sin ax ,
f(x) = — \ -7-,—„-da. ' ’ л ,1 1 + a3
о
Представить интегралом Фурье следующие функции, продолжив их четным образом на отрицательную полуось:
2405. f(x) = e°A', a>0, х2=0.
( х-f-1 (0^x<l), 2406. f(x)={	„	'	.
1 ’ I 0 (1 <x<co).
2407. f(x) = e~* (0 =sg x <oo).
Представить интегралом Фурье следующие функции, продолжив их нечетным образом на отрицательную полуось:
		х —	1 (0	sSX'-C 1),
2408.		0	(х	>0-
	VI	COSX	(0^	:'ix< л),
2409. .	1	-1	/~ л		= л),
	т	К 2	(х =	
	0		<Х^	> л).
	2~3>	: (0 / 2 \3 '		'V - зг
2410.	0		<х<	
2411.	sinx	(0^	~х^	л),
	о	(л<	Х< ОО).	
3. Комплексная форма интеграла Фурье. Теорема разложения. Если функция f (х) имеет на каждом конечном интервале конечное число точек разрыва первого рода и абсолютно интегрируема на всей числовой оси, то в каждой точке х, в которой f (х) дифференцируема, выполняется равенство
СО
f (х) = j с (a) е'ах da, —00
(10)
где
00
с(а)=2’л
—00
(11)'
Функцию с (а) называют преобразованием Фурье функции f (/), или (учитывая физические соображения) спектральной плотностью функции f (/). Модуль | с (а) | называется амплитудным спектром функции f (t). Выражение f (х) по формуле (10)
506
авают комплексной формой интеграла Фурье (или обратным преобразованием
Подстановка (11) в (10) приводит к двойному интегралу Фурье в комплекс -форме: оо оо
f (х) = da ((о е'“ <х~{> dt.	(12)
—00	—оэ
2412. Найти спектральную функцию и амплитудный спектр нкции
( е~ах при х>0
?(х) = \ л	^-гх	(а>0)-
' ' (0 при х<0 v
Представить /(х) комплексной формой интеграла Фурье.
Решение. По формуле (П) находим спектральную плотность функции, лывая, что при t <0 f(t) = O;
a) = X \ e~ate~iat dt =А. f e-<a+ia>fa(	. е-w-ia> < 1°°	! . .
7 2л J	2л ,)	2.T(a-j-ia)	|о 2n(a-)-ia)’
о	о
к как подстановка верхнего предела дает нуль. В самом деле, по формулам шера,
е-< а на) t _ e-at e-iat — g-at (cos	_ j sjn	— e~at cos	_ ie-at sjn a/ _
>и Z-> + co, вследствие того что a>0, e~at — бесконечно малая функция, а lat и sin at — ограниченные функции. Следовательно, н действительная, и шмая части функции e~l’a'ria}t стремятся к нулю, значит, и
lim e-|a+‘“)Z = 0.
> Амплитудный спектр ;•	| с (а) | =
1 1
2л | а + ia | 2л / а2 + а2
1 2л (a-hi а) Комплексная форма (10) интеграла Фурье данной функции имеет вид со
f (*) = -„-	t^-eiaxda.
' 2л a+ia
1
2413. Найти спектральную плотность (преобразование Фурье) нкции
2-х3
1
О
2414. Представить функцию

при I X I
Фурье.
комплексной формой интеграла с 2415. Найти преобразование Фурье функции -	( cosx на	[0, л],
Ш = | 0	вне [о,
507
Представить следующие функции комплексной формой интеграла Фурье, найти спектральную характеристику и амплитудный спектр;
( 1 на (0, а),
2416.	= { п	.
' '	(0 вне (0, а).
( e_“*sin<o/ при />0,
2417. /(х) = п	(а>0).
(	0 при О v
4. Простейшие свойства преобразования Фурье. Преобразование Фурье можно рассматривать как оператор F [f (х)], сопоставляющий каждой функции, удов лстворяющей условиям теоремы разложимости пункта 3, другую функцию, ее спектральную плотность
СО
1/ (х)1 = С (а) = f (0 e-‘at dt,
подобно тому как оператор дифференцирования сопоставляет каждой дифферен цируемой функции другую функцию, ее производную
Z? If (x)] = f' (х), например D [sin x] = cos х.
Преобразование Фурье сводит некоторые операции математического анализа над функциями к алгебраическим операциям над их фурье-образами (спектраль иыми плотностями), т. е. сводит сложные операции к простым. Именно это делает преобразование Фурье важным для приложений-
2418.	Показать, что если функция f (х) стремится к нулю при |xj—>-оо и дифференцируема, a f (х) абсолютно интегрируема на всей числовой оси, то
F [/' (*)] = iaF [/ (х)],
т. е. операции дифференцирования функции соответствует операция умножения на ia ее преобразования Фурье.
Решение. Интегрирование по частям преобразования Фурье функции f' (х) дает
f[/'W1=-Л V'®e~iatdt = i®e~iatГ ~Za)e~,aldt =
co
= ~ § f (t) e~,at dt—iaF [f (x)],
—oo
так как результат двойной подстановки есть . нуль в силу условия f (/)—> О при ИI со-
2419.	Показать, что преобразование Фурье является линейным? т. е.
^[/1(х) + А(х)] = ^[Л(х)] + Г[/2(х)].
Указание. Привлечь определение преобразования Фурье н свойство интеграла суммы функций.
508
2420.	Показать, что если функция абсолютно интегрируема на X
всей числовой оси, a	при |х|->сю, то
о
F ^№dt _ о
-р[/«
Указание. Применить формулу интегрирования по частям.
2421.	Найти преобразование Фурье ^[(tjdt, где
о ( cos х	на [0, л],
ZW —j q	вне |д nj_
Указание. Проверить, что \ [ (/) dt -* 0 при х ; -> со. Учесть ответ 2415 О
и формулу 2420.
2422.	Показать, что если функция x"f(x) абсолютно интегрируема на всей числовой оси, то ее преобразование Фурье с (а) имеет п производных, определяемых формулой
c(/i) (а) = (—1),г	tkf (/) е !at dt, или F [х"[ (х)] = iV (а)
(k=l, 2, 3......п).
СО
I df I	I*
Указание. Учесть, что при условии < ср (х) и \ | ср (х) , dx схо-
д С	df (х, а)
дится y- \ f (х) dx = \ —----- dx.
да J '	J	да
—оо	—со
2423.	Найти преобразование Фурье функции ( х на [0, 1], ^(х)==\0 вне [0, 1],
зная преобразование Фурье функции 2414 F = 2424. Найти преобразование Фурье функции
( х2 на [0, 1], ^х) = (о вне [0, 1].
2425. Показать, что
F [/ (х - ₽)] = F [f (х)] = с (а).
Указание. Произвести в интеграле, определяющем преобразование Фурье функции f(x — Р), замену переменного х — р = «.
2426.	Показать, что F [е'"х [ (х)] = с (а — 0), где с (а) = F [f (х)].
509
2427.	Показать, что F [f (х) cos (Зх] =	( где с (а) =
-F[/(x)].
Указание. Выразить косинус по формуле Эйлера через показательную функцию и применить правила 2418 и 2426.
2428.	Показать, что F[/(x)sinPx] = ——Р) с (а Р), С(а) —
§ 3. ПРИЛОЖЕНИЯ РЯДОВ ФУРЬЕ И ПРЕОБРАЗОВАНИЯ ФУРЬЕ К РЕШЕНИЮ ПРОСТЕЙШИХ ЗАДАЧ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
1. Уравнение колебаний конечной струны. Дифференциальное уравнение свободных малых поперечных колебаний однородной струны с закрепленными концами имеет вид
д2и „д2и
dt2 дх2 с граничными условиями
и (0, =	t)=0 (— со</<со)
и начальными условиями
и (х, 0) = ф(х), u't(x, 0) = ф(х)	(0-s;xc</).
Решение этого уравнения и (х, /), дающее отклонение точек струны с абсциссой х в момент времени /, выражается рядом Фурье
-j-co
V !. knot , ,, . knat\ . knx и (x, t) — У I Ak cos—j——— ) sm—j—, a=i K
где
( 1
.	2 1	... knx ,
A^-j- \ q>(x)sin-j-rfx
°z	(*=1,2,3,...).
„	2 C . . . . knx .
о
2429. Однородная струна, закрепленная на концах х = 0 и х = 1, имеет в начальный момент времени форму параболы ср (х) = х (/ — х). Определить смещение точек струны от прямолинейного положения равновесия, предполагая, что начальные скорости отсутствуют.
Решение. Задача сводится к решению уравнения
д2и ___ 2 д-и dt2~a дх2 при граничных условиях
и (0, 0 = 0, и(/, 0=0 н начальных условиям
и(х, 0) = <р (х) = х (I—х),	= ф (х) — 0.
510
Вычисляем коэффициенты Ак и Вк: i
л 2 С ,,	», . клх .	2	йлхИ ,
Лл = Т J (/х-х ) яп —dx = -^-(/x-x2)cos —|о4-
0 , —-------------------------------------
i	I
. 2 f ,, о ч knx ,	21	. knx И , 4/ С kxx
+	(/ - 2х) cos — dx =	(/ - 2х) sin -р |о +	\ sm — dx =
--------5--------- . °
{О при k четном,
О(, 8/2	,
5 при к нечетном:
I
„	2 1'. kzix . п
Вк — -г— \ 0 • sm —:— dx = 0:
К кла .1	/	'
о
поэтому искомое решение таково:
(2п+1)ла/ . (2п+1)лх cos ->---------sin --1—-—
7	““ I
(2л+1)3
, ... 8/2 V «(*. о= лз- 2, и=0
2430. Решить уравнение колебаний конечной струны (длины 1—1) —^ = а2^г с граничными условиями и (0, t) — u(I, t) — 0 (—co<Z< <оо) и начальными условиями и (х, 0)=х2--х, щ{х, 0)=х— 1 (0==х==;1).
2431. Решить уравнение колебаний струны (длины I — 1)	—
;=а2^“ с граничными условиями «(0, t) = u(l, t) = 0 (0s£/<oo) и начальными условиями и(х, 0) = ди--- = х(1 — х) (О-^х-тс 1).
2. Уравнение колебаний бесконечной струны. Уравнение колебаний бесконечной струны имеет вид
д^и	,&и
дВ дх* с начальными условиями
и (х, 0) = <р(х), ut(x, 0) = ф(х)	(—со<х<со).
Граничные условия здесь отсутствуют, так как струна бесконечна.
Для решения задач математической физики в случае бесконечных сред часто применяют интегральное преобразование Фурье. При этом заменяют данное дифференциальное уравнение уравнением для фурье-образов его частей. Находят из этого уравнения (обычно более простого) фурье-образ искомого решения, а затем с помощью обратного преобразования Фурье получают само решение.
~ 2432. Решить уравнение колебаний бесконечной струны с начальными условиями и(х, 0) = (р(х), u't(x, 0)=0 (—oo<x<oo), применяя преобразование Фурье.
Решение. Введем для преобразований Фурье по х обозначения
F[u(x, /)] = и (а, /), F [ср (х)] = ф (а).
511
Найдем фурье-образы обеих частей уравнения колебаний. Для фурье-образа левой части, предполагая допустимым дифференцирование под знаком интеграла, получим
F Р2“1 = _L F e-iax dx =
I dt- ] 2л ,) dt2
д2 1 dt2 2я
. л -inx 1 d2u (“10 d2“ „(А f)e ,axdx
/	d2 d2	\
заменили на считая t аргументом, а а —параметром .Фурье-образ пра-
\	<9/2 dt2 ’	'	j
вой части получаем по формуле задачи 2419:
F [я2	= cflF РГ41 = (fl (,a)2 и (at) = — я2а2я.
I дх2 j I дх- |
Приравнивая фурье-образы обеих частей уравнения колебаний и начального условия, получим d2zz	.	-
-^- =—а2а2и, я (а, 0)=<р(а).
Мы пришли, таким образом, к задаче Коши для обыкновенного линейного однородного дифференциального уравнения с постоянными коэффициентами. Его характеристическое уравнение r2-j-a2a2 = 0 имеет корни r~;Lzaa, а потому общее решение имеет вид
fl-. С2е latt/, а у = iaaC1e'rtct/— iaaC2e !aat.
х	а	О l-t
С помощью начальных условий я (а, 0)=ср(а), -^ = 0 приходим к системе уравнений
С1 + С2 = (р (а), Сг — С2 = 0.
Отсюда С1 = С2 вид
1 - , , 2 <р(а).
Таким образом, фурье-образ искомого решения имеет
я = -g ср (a) е'аа/ + g' ф (“) с iaat-
Обратное преобразование Фурье с учетом формулы задачи 2426 дает искомое решение
и (х, 0 = у <Р (x—af) + у <р (x-f-aO .
ГТ	1 32Я	,
2433. Показать, что волновое уравнение ^2 = фа ^2 в области — со < х < оо при начальных условиях и (х, 0) = ср (х),	°- = ф (х)
имеет решение
и (х> t) = ф(х-С/) + ф(х + с0 + _L Y („) du.
x—ct
Указание. Применить преобразование Фурье. Совершая обратное преобразование Фурье, применить формулу задачи 2420.
512
3.	Уравнение распространения тепла в неограниченном стержне.
2434.	Найти ограниченную функцию и (х, f) (— оо < х < оо, -О С t < оо), удовлетворяющую уравнению теплопроводности ~ = а2 и начальному условию и (х, O) — f(x) (— со < х < со).
Решение. Введем для преобразований Фурье по х обозначения
F[u(x, /)] = «(«. 0. F [/«]=/'(“)•
Найдем фурье-образы обеих частей уравнения теплопроводности:
(см. решение 2432). Приравнивая фурье-образы обеих частей уравнения теплопроводности и начального условия, получим:
|“+o2aSu = 0, и (a, 0)=fta).
Мы пришли, таким образом, к задаче Коши для обыкновенного линейного Г дифференциального уравнения с постоянными коэффициентами. Решение этой t задачи Коши таково:
I1	и. (ос, t)=4(a)e~o2a2/.
Применяем теперь обратное преобразование Фурье:
СО	со
и(х, t) — ) и (ос, f)eiaxda— § f (a) e~a2a2leiax doc.
Заменяя здесь f (a) его выражением через f (х):


| и производя затем изменение порядка интегрирования (что возможно при нало-i жении на функцию f (г) должных ограничений), получим
и
e~°!a!V“*da f(^e-,aidl =
е n2r/-‘l	doc
?: Так как
e'«<v £> = cos a(x —£)-|-i sin a (х —Е,)
L и действительные части обеих частей равенства должны совпадать, находим
и(х, 0 = 2)7 §	§ е °2“!/cosa(jr-g)^.
17 Кручковнч и др.
513
Внутренний интеграл
(*-£)*
c—a2a2t cos n dec —	1/ e
2a r t	’
поэтому искомое решение
co
г;(х, /) =-L_ V	dz,.
ЪаУ'м}
2435.	Показать, что распределение температуры и (х, I) в полу-бесконечном (0 ==; х <; оо) однородном стержне с теплоизолированной боковой поверхностью, конец х = 0 которого поддерживается при нулевой температуре, выражается формулой-
«(х, /)=—y-\/(g)k	-е ]di,
2a Г nt .)
где f(x) = u(x, 0).
ГЛАВА XV
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
§ 1. КОМПЛЕКСНЫЕ ЧИСЛА
1. Действия над комплексными числами. Комплексными называются числа вида z — x-^-iy, где х и у — действительные числа, a 1 = У— 1. Числа х и у называются соответственно действительной и мнимой частями комплексного числа г. Они обозначаются x=Rez, =
Два комплексных числа считаются равными, если равны отдельно их действительные и мнимые части. Число ~ — х — iu называется сопряженным числу г=.. — x-\-iy.
Алгебраические действия над комплексными числами выполняются по фор-мулам:
И д. г-z = (-Vt -I-tt/1) L (x2-{-ZZ/2) = (x1 J x2) + i (г/1 ! Z/2),
= (-4 + ‘Ki)	+ 1у2) = (ад - - z^z/.,) + i (ха2 + xm/J,
И = 1'.Д Z-j
2436.	При каких действительных значениях х и у выполняется равенство
x(2 — i) -\-y(2i — 1) = 4 — 5t?
Решение. Раскрывая скобки в левой части уравнения и группируя действительные и мнимые части, получим
<Ъ: - - y) + i (— % + 2z/) = 4 —5z.
Приравняем действительные и мнимые части справа и слева:
2х —р = 4, —х[2у^ — 5, следовательно, х=!, г/ = —2.
2437. Вычислить (1-Н) (|/5 — 2z).
Решение. Перемножая почленно.и учитывая, что z2 = — 1, находим
(1 г) (р о — 2z ) | 5 + i I 5 — 2i Д- 2 = (I 5 2) -р i (|> 5 — 2).
। / з । ;
2438. Вычислить г = ——Выписать Re z и Im г.
2—1 I 3
Решение. Умножим числитель и знаменатель дроби на число, сопряженное знаменателю:
	(Гз-Н) (2 +г Уз) = 2 |Лз~Н2г-4-Зг — Из = Уз . 5 . г~‘(2-«Кз)(2 + г Уз)	4-рЗ	7	1 1 '
отсюда	Г,	Уз ,	5 Rez=	1шг = у.
17*
515
2439. Какие комплексные числа сопряжены своим кубам?
Решение. Так как
z3 = (х + iy)3 = (х3 — Зх//2) + i (Зх2// — у3),
а по условию задачи, z3 = l — x — iy, то, приравнивая действительные и мнимые части, получим систему уравнений для х и у.
х3 —Зх//2 = х, Зх2// — //3 = —у.
Нетрудно проверить, что эта система имеет следующие действительные решения: (х, t/) = (0, 0), (1, 0), (—1, 0), (0, 1), (0, —1). Поэтому своим кубам сопряжены следующие комплексные числа:
zx=0, z.2 = l, z3 = —1, z4 = i, z5 = — i.
2440. Найти действительные значения х и у из уравнения
(1 +0х3 + (2н-0 х — (1 — 0 «/ = 7(1 4-t).
2441.	Найти Rez и Imz, если z = ттл — ТТТТ—5Г-
2442.	Выполнить указанные действия:
а) (1 +Z)(1 -30, б) —+ 01 +0, в) ТА1Т + —.
1 К з
2443.	Показать, что ог1 — 1, если о> = — y + t—- Найти (а+&щ)х Х(а + 6оУ2).
2444.	Найти комплексные числа, сопряженные своим квадратам.
2445.	Доказать, что если z — 2, то z —действительное число.
2446.	Показать, что z + z = 2Rez, z —z = 2ilmz.
2447. Доказать тождества: zx ±: z2 = zx ± z2; zxz2 = zxz2, zn — zn,
тор, направленный из начала
2448. Пусть Р (х) — многочлен с действительными коэффициентами. Показать, что если он имеет комплексный корень г = а +10, то сопряженное число z = а — i0 также будет его корнем.
Указан-ие. Воспользоваться результатами 2445 и 2447.
2. Геометрическое изображение комплексных чисел. Каждое комплексное число z = x-j-iy можно изобразить точкой плоскости хОу, Имеющей координаты (х, у), при этом точки осн Ох изображают действительные числа, а оси Оу—чисто мнимые. Можно также числу г сопоставить век-координат О в точку z (рис. 238). Длина г этого
вектора, т. е. расстояние от точки z до начала координат О, называется модулем комплексного числа z и обозначается г =, г I:
г^\г ;==Rx2 + (/2.
Угол <р, образованный вектором z с положительным направлением осн Ох, называется аргументом числа г и обозначается Arg г. Для аргумента ф справедливы
516
формулы:
x = rcos<p, z/ = rsin<p, ^ = tg<p (r=| г ;, <p = Argz).
Значения Arg г определяются не однозначно, а с точностью до слагаемого 2л/г (k^O, ±1, ±2, ...). Фиксируя один период изменения ср в пределах — (или 0а5ф<2л), выделяют главную ветвь
аргумента, обозначаемую arg z, так что
Arg z —arg г + 2лА:	(й = 0, ±1, ±2, ...).
2449.	Изобразить на комплексной плоскости числа z = 3-(-2t и с = 3 — 21. Найти их модули и аргументы.
Решение. Точки z = 3-(-2i и г = = 3 — 2/ построены на рис. 239. Заметим, что ; z - г = К32 + 22= р'ЧЗ- Как видно на этом примере, сопряженным числам соответствуют точки комплексной плоскости, симметрично расположенные относительно действительной оси; поэтому для них arg z-
2	2	2
arg z = aretg „ , arg r = — aretg -, Arg z = aretg + 2nfe.
О	О	о
2450.	Какой геометрический смысл имеет модуль разности двух комплексных чисел?
Решение. Модуль разности двух комплексных чисел равен
Zj — z., I = ’ (*! — х2) -|- i (44 — у2У, = К(*1 — х2)2+ (</! —4'г)2
— это расстояние между точками Zj и г2.
2451.	Определить и начертить в комплексной плоскости линии, заданные уравнениями а) |г| = 1; б) \г —2‘+i| = 3.
Решение, а) По определению, | z | — расстояние от начала координат до точки г. Для данного множества точек это расстояние должно быть одним и тем же, равным 1, поэтому искомая линия является окружностью с центром в начале координат и радиусом 1.
б) Так как jZj — г2 | равен расстоянию между точками zt и г3, то из равенства |г —(2 —г)|=3 следует, что точки данной линии удалены от точки 2 —г иа расстояние, равное 3, т.
ность с центром (рис. 240).
е. данная линия —окруж-в точке 2 —г радиуса 3
2452. Определить геометрические места точек, для которых: a) Rez = 5; б) Rez2 = u‘J; в) argz = -^-.
517
Решение, а) По определению, Re г — х, поэтому уравнение можно переписать в виде х —5. Это уравнение определяет прямую, параллельную оси Оу.
б) Так как г2 = х2 — у2-^12ху, то Re г2 — х2 — у2, поэтому условие Re г2 —а2 равносильно уравнению х3—-z/2 —я2, которое, как известно, определяет равностороннюю гиперболу (рис. 241).
множеству.
str	Л
в) Уравнению arg г— у удовлетворяют точки, расположенные на луче, выходящем л
из начала координат под углом - к поло-о
жительному направлению оси Ох.
2453. Определить множества точек, удовлетворяющих неравенствам, и построить их на плоскости: a) i z — i j < 3; б) । г + 1 j >= 1; в) 1 • | z — 1 — i J < 3.
Решение, а) Неравенство \г — ( 1 <3 означает, что расстояние от точки i до точки г меньше трех. Этому условию удовлетворяют точки круга с центром в точке i радиуса 3, за исключением его границы, уравнение которой ' z— i =3.
б) Из неравенства | z +1 । тэ 1 следует, что расстояние от точки —1 до точек г дол-
жно быть не меньше 1, поэтому искомое множество лежит вне круга с центром в точке —1 радиуса 1 (рис. 242). Окружность | г +1 | = 1 принадлежит данному
Рис. 242
в) Искомое множество точек должно одновременно удовлетворять двум условиям: 1 «5 | г—1—i\ и |г—1—i I < 3. Первое из этих условий определяет внешность единичного круга, с центром в точке l-pi, второе —круг радиуса 3 с центром в той же точке 1 +1 (рис. 243). Поэтому данное множество — кольцо, ограниченное концентрическими окружностями радиусов 1 и 3 с центром в
2454. Определить, какие множества точек удовлетворяют задан-I z —I— 21	"'т	и
ным неравенствам: a) Rez<2; б) 7^2 в) — 4-<argz< 2 .
Решение, а) Так как Rez = x, то точки искомого множества должны удовлетворять неравенству х<2. Это множество — левая полуплоскость, граница множества —прямая х = 2 —ему не принадлежит.
б) Умножив обе части данного неравенства на । г — 2', получим равносильное неравенство |z-J-2jsg|z —2р Возведем обе части этого неравенства в ква
518
драт и раскроем скобки, положив ? = * + »/:
(x + 2)2+^s=(x-2)2 + i/2;
4х^_ — 4х,
Следовательно, искомое множество — левая полуплоскость, включая ее границу х = 0.
в) Для точек искомого множества значения аргументов заключены в преде- .
,лах от —
л
4
2 , поэтому данное множество —угол, ограниченный лучами
<р = —4 и <р = Сами лучи в данное множество не входят.
ДО
В 2455—2462 начертить в комплексной плоскости линии, точки которых удовлетворяют заданным уравнениям.
2459. Re г = 2.
2460. Irnz = - 3.
я
2461. arg z = — 4 .
2462. Im г2 = 2.
заданным неравенствам:
2468. Imz<—1.
2469. —1 <Rez<5.
2470. 0<1тг<1.
2471. --4-<arg2<6.
2455.	\z\ = 8.
2456.	j г-5 + 311 = 2.
2457.	\z-\-i\ = 5.
2458.	| z+ 1 । +1 2-2 ! = 5.
В следующих задачах изобразить на комплексной плоскости множества точек, удовлетворяющих
2463. |2|>2.
2464.	'iz + l. + i|<l.
2465.	2< + - 1 +21; <4.
2466.	!z - 1 j + + -3|<3.
2467.	Rez<—1.
r 3. Тригонометрическая форма комплексного числа. Тригонометрическая форма комплексного числа z--x-'-iy имеет вид
г = г (cos гр i sin (р),
(1)
где г — модуль комплексного числа г, равный
Г==/Х2 + (/2,	(2)
а ф — главное значение его аргумента, причем
tg<p=^-.	(3)
Для возведения комплексных чисел в степень п удобна формула Муавра: г” __ rn (cos п(р j sjn П(ру	(4)
Корни степени п из комплексных чисел определяются по формуле
п—;	«.— Г <р + 2л/г . . <р + 2яА |
у г (cos (р + < sin ф) = у г cos -—--Н sin -—-— (k = 0, 1, 2, .... п— 1). (5)
2472. Представить в тригонометрической форме числа 21=1+1, г2==—|/3— 1, z3 = 21 и 24 = —5.
519
Решен не. Определим модули данных чисел по формуле г = 1//х2~Ь1Л |г1| = г1 = |/1^+Р = /2, | z3 | = г3 = рЛб^=Р2^ = 2
| г21 =г2 =]/ (~ |/з)Ч(-1)2 =2, >4i = r4=K(-5)2-H02=5.
Рис. 244
Для того чтобы найти аргументы, построим точки zb z2, z3 и г4 на комплексной плоскости (рис. 244). Заметив, что точка г, лежит в первой четверти, а г2— в третьей, по формуле (3) получаем:
, 1 л,
arg Zj = 4)! = arctg j = 4 ,
.	—1	л
arg z2 = <p2 = arctg ——-л= 6
5л — л =----.
6
Точка z3 лежит на мнимой осп, следовательно, arg2i=2, а точка г4 — на отрицательной вещественной полуоси, поэтому argz4 = n. Подставим полученные значения в формулу (1):
г, — 1 -j- i = К2 cos ~
~ Г / 5л , .  ' 5л г2 = —г 3 —i = 2^cos , — -g- -f-isin , —
IL	Л 1
z3= 2 I cos -|-i sin g- I z,: = 5 [cos лi sin л].
2473. Вычислить (—| 3-г)5.
Решение. В 2472 мы нашли тригонометрическую форму числа —^3 — 1:
— И 3 — i = 2 I cos >' — 5'‘ ' + i sin ' —	') I.
L \	6 z \	6 j
Применяя формулу (4), получаем
( i/й -А5 05 Г f 25л \ I •  ! 25л \1	„0 Г ( л\ . . / л\1
(— I 3 —г)° = 2° l^cos -g— j-H sin --g— | J = 32 | cos	g ; + i sin	gjj =
| 13	1	r 
= 32 -2 — i 2 =16 КЗ—161.
1 -4- I = К2 cos -4- i sin ? I I 4	4
2474. Найти j/"l + '•
Решение. Число 1 -}-* представлено в тригонометрической форме в 2472:
Для вычисления кубических корней из данного числа используем формулу (5). Мы получим три различных значения корня:
или
1 f f	l/o	-J+2nfe _ _ |+2л*	/А . П !
T 1 ~t~1 V 1 z	ССЪ	2	1 I sin	\K — U, 1, Z),
- е ' о I	. . л	в /~п	9л. . . . 9л
z1 = y2|_cos f2 + tsini2J’ Z2 = у 2 | cos jy +1 sin — t-Д 17л	. . 17л 1
za = y 2 I cos у?- +1 sin -jTT I.
520
2475.	Найти корни уравнения z8 —2]/3 z4-j~4 = 0 и построить-их на комплексной плоскости.
Решение. Обозначим г1 — t, тогда данное уравнение превратится в квадратное уравнение относительно t:
/2 —2 НИ + 4 = 0.
Его корни ^ = 1^3 ± г, следовательно, корпи г исходного уравнения — ) К3 з г-Числа /З-Н и КЗ —г —комплексно сопряженные, поэтому модули у них одинаковые, равные 2, а аргументы отличаются знаком:
arg(|/'3 + 0 = arg (КЗ — i) = —
Используя формулу (5), находим корни четвертой степени из этих чисел:
= V рЗ г = j' 2 cos
л	п .	л . ... .
-	2nk	g + 2л/г
--------------H’sin--------i------
4	4
(k=0, 1, 2, 3),
4 ~ ,—	4
?5i6i7>il = y |/3 —i = >/2 cos
' 4-2nfe
о	. о
~---------+( SIn--------------
(fe = 0, 1, 2, 3).
Заметим, что все корни zlt z.z, ..., = |/2(й=1, ... , 8). Отсюда следует, что в начале координат радиуса ) 2. Аргу-
менты этих чисел ±	k. Это зна-
чит, что аргумент числа z3 отличается ,т
от аргумента числа zL па % ( аргумент z3 отличается от аргумента гг на л, аргу-3
мент z.j — на л. Поэтому, построив на плоскости вектор zt, получим точки г.., z3, z4, если повернем вектор гл на углы
, л, g-л соответственно. Таким образом, точки z2, z3, z, лежат в вершинах квадрата, вписанного в окружность радиуса ф'2, одна из вершин которого — точка Zj. Таким же образом строятся точки zB, z7, г8: строим точку г5 и вписываем в окружность квадрат с вершиной в этой точке, остальные его вершины
г8 имеют одинаковые модули: 'г4 = все они лежат на окружности с центром
дадут точки ze, z7, zs (рис. 245).
2476.	Представить в тригонометрической форме следующие числа:
Зг, 1 +/3 г, — 7, /3— г, 2~2i.	*
2477.	Вычислить степени, применяя формулу Муавра: (1 + i ]/3 )3, (/3 +//3)8, (-2Ф-2/)6.
2478.	Найти все корни и построить их на комплексной плоскости: У1, ]/27г, У—2 -ф 2г, V—8.
2479.	Решить уравнения: а) г2фг = 0, б) г4—16 = 0, в) г6 — — 4г3 4-8 = 0,
521
2480.	Выразить cos 5<р и sin 5<р через cos <р и sin ср.
Указание. Возвести (cos <р + < sin <р) в пятую степень по формуле Муавра и по биному Ньютона приравнять результаты и выделить из обеих частей действительные и мнимые части.
2481.	Доказать, что есл1> zY 4- z2 + z3 = 0 и | zt | = | г21 = | г31 = 1, то точки ,г2, г3 являются вершинами правильного треугольника, вписанного в единичную окружность.
2482.	Найти вершины правильного пятиугольника, если он вписан в единичную окружность с центром в начале координат и одна из его вершин лежит в точке — 1.
§ 2. ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
1. Определение функций. Основные элементарные функции комплексного ременного определяются следующими формулами (г = х+ <</):
1. Показательная функция
— ех (cos у i sjn уу
2. Тригонометрические функции:
Sinz= 21
COS Z —
, sm z , cos z
tg z =----, ctgz = -—.
cos z ’	sin z
ne-
CD
(2)
3. Гиперболические функции:
chz = —t-
, е- — е ~	,, sh z ., ch z
shz =------—, th z = -:—.	cthz — n,
2	ch z’	sh z
(3)
4. Логарифмическая- функция
Ln г = 1п j г J + < (arg г-|-2лй) (ft —любое целое число); главное значение логарифма:
In z = In ’ z 1 +< arg z.
5. Обобщенные показательная и степенная функции:
_^z Lutz ______£& Lnz
(4)
(5)
(6)
г, а и « — любые комплексные числа, а=^0.
Показательная форма комплексного числа z= i e/urgz+2^) ^ = (
3+Л1'
2483.	Вычислить значение показательной функции е 2  Решение. Исходя из определения показательной функции, получаем . nt е
cos g + i sin g = е3 [0 + i] = ie3 =» 20,09i.
2484.	Представить число J/З — i в показательной форме.
Решение. По формулам (2) и (3) § 1 находим модуль и аргумент
(7)
числа
|/3 —<| = 2, arg (|/3 —<) = —-5-, 6
522
Подставив эти значения в формулу (7), получаем
]' 3 — i = Яг '
п£
6
2485.	Вычислить значение логарифма Ln(—1).
Решение. Применяя формулу (4), находим
Ln (—l) = ln , —1 +i(arg(— 1) + 2л6) = Л1-|-2л6г = (26 +1) л< (6 = 0, ±1, ±2, ...) 2486. Вычислить sin (5 — t). Решение. По определению sinz =---------—---) следовательно,
sin (5 —i) = -f. [е'!5‘— c' ,5“'‘] —	fe1'5' — e~i~5'] =
= —g- [r (cos 5 + ( sin 5) — e"1 (cos 5 — i sin 5)] = sin 5 ch 1 — i cos 5 sh 1.
2487.	Вычислить i‘.
Решение. Полагая в формуле (6) a — i и z = i, получаем
_ 7?. -|-2л)Л
г-- = е/1.п<=еН1п|«1 + ''аге/ + /2лА] = е V2 )	(6 = 0, ±lj j
2488.	Найти корни уравнения cos г = 2 и построить их на комплексной плоскости.
Решение. Используя определение функции cosz, перепишем уравнение в виде
I 1.1г
—3—-------= 2 или е2,г —4е,г-(-1 =0.
Это квадратное уравнение относительно е'г, его корни
е/г = 2 ch КЗ-
Прологарифмируем полученное равенство:
«г = Ln (2 ± КЗ) = In' 2 ± /3 j + i arg (2 ± /З) + г2л6 = = 1п(2 ± Кз)-Н’2лА:	(6 = 0, ±1, ±2, ...).
Теперь определяем г:
г = 1- In (2 ± КЗ) + 2л6 = 2я6 — i In (2 ± КЗ) (6 = 0, +1, ...).
Мы получили две серии корней:
г:<>_2„^,1„(2 + Гз). (J_0. ±1; ±2;
г!?1 = 2.п6 — i In (2 — Кз)
Так как
In (2 -ИЗ) = In —L- = - In (2 + Г' 3), 2 -J- у 3
523
то эти числа будут располагаться на двух прямых, параллельных оси Ох и отстоящих от нее (рис. 246) на расстоянии 1п(2 + Кз).
-2Я' tin(2 + Vj)	l.ln(2-o/3) 2‘jr*ilnl2J>f3) кЛ+Пп(2*№)
	
0	
-2тг~ип(2 + \Гз)	-Un (2*fi) 2n~iln(2^l3)
Рис. 246
2489.	Вычислить значения показательных функций е , е“1+2‘, ^2/ £э2 I
2490.	Представить в показательной форме комплексные числа ф~Н> 2/, —5, —1+/, УЗ-j-i, 7.
2491.	Вычислить значение функции cos (2 — t).
2492.	Вычислить значение функции sin 2г.
2493.	Вычислить значение функции th fin 3 —
2494.	Вычислить значение функции Ln (2 — Зг).
тл	.	/1 -L i 1 -I- i
2495.	Вычислить значение функции ,
2496.	Вычислить значение функции (—3 — 4г)‘.
2497.	Решить уравнение sinz = 3i.
2498.	Доказать тождества:
ch гг = cos г, sh гг = г sin z, ch2 z — sh2 г = 1,
sin z = sin x ch tj + i cos x sh y, cos z = cos x ch у — i sin x sh y, sh z = sh x cos у + г ch x sin y, sh z = ch x cos у -j-г sh x sin y.
2. Регулярность функций комплексного переменного. Функция комплексного переменного щ=/(с) называется регулярной в точке z, если она дифференцируема в этой точке. Функция называется регулярной в области D, если она регулярна в каждой точке этой области.
Теорема Кош и—Р и м а н а. Для того чтобы функция
f(z) = u(x, y)+io(x, у)
была дифференцируема в точке z~xJ-iy, необходимо и достаточно, чтобы функции и (х, у) и v (х, у) были дифференцируемы в точке (х, у) и чтобы в этой точке выполнялись равенства
ди _ до ди __ до
дх ~ ду' ду ~ ~~ дх'
524
Производная f (г) вычисляется по формуле ди до f (z) = i—F1 л -  1 v ' дх дх
< Если функции fi (г) и f> (z) регулярны в области D, то их алгебраическая : сумма и произведение также регулярны в этой области, а частное у-.Ф- регу-. ’	12 (г)
: лярно в области D, .за исключением тех точек, в которых знаменатель обра-j щается в нуль: f2(z) = O. Однозначные элементарные функции комплексного пере-: менного регулярны всюду, где они определены.
s 2499. Показать, что функция sin2z регулярна во всей комплекс-?ной плоскости, и найти ее производную.
!. Решение. Определим действительную и мнимую части функции sin 2z. : Так как
,	pl2Z р~12г	1	, .
J	sin 2z = --~----= =* fe 2t->+2xl - e2y'2X’ ] =
2i	2i 1
— ~ [е 2у (cos 2х -J- I sin 2х) — е2и (cos 2х - i sin 2.v)] = sin 2х ch 2у + i cos 2х sh 2у,
TO
Re sin 2z = и (x, y) = sin 2x ch 2y,
Im sin 2z — v (x, y) = cos 2x sh 2y.
Вычислим частные производные этих функций:
= 2 cos 2х ch 2у,	= — 2 sin 2х sh 2у,
= 2 sin 2х sh 2у,	= 2 cos 2х ch 2у.
ду	ду
ди до ди dv
Сравнивая значения и . , т - и — видим, что они равны ‘	дх ду’ ду дх'
чениях х и у, следовательно, функция sin 2z регулярна во всей плоскости.
Производная функция sin 2г равна
при всех зна-
комплексной
(sin 2z)' = 2 cos 2х ch 2у — i2 sin 2x sh 2y = 2 cos 2z.
2500.	Доказать, что функция f (г) = z нерегулярна ни в одной точке г.
Решение. Действительная и мнимая части функции z соответственно равны:
и (х, у)~х, v (х, у) = —у.
Вычислим частные производные этих функций:
_ 1	— о	d J — о до __
дх ~ ' ду ’ дх ’ ду
ди до
Теперь ясно, что ни при каких значениях х п у частные производные и не могут быть равны, следовательно, функция z нерегулярна ни в одной точке комплексной плоскости.
2501.	Определить область регулярности функции -yт-р•
z ~t~ 1
525
Решение. Функции Д(г) = 1, f, (г) = г2 Д- 1 регулярны во всей комплексной плоскости, поэтому их отношение регулярно всюду, кроме тех точек, в которых знаменатель обращается в пуль: ггД- 1 =0, т. е. точек ?, = / и гг = — i.
2502.	Восстановить регулярную функцию f(z), если известна ее действительная часть Re f (г) = х2 — у2 4* х.
Решение. Функция и(х, у) = х- — у'2Д-у и искомая функция v (у, у) должны удовлетворять условиям Коши—Римана:
ди _ ди ди _ dv дх ду’ ду дх'
Из этих условий мы получаем
Интегрируя первое уравнение по у и считая х постоянной, получаем v(x, г/) = (2хД-1)г/Д-С(у).
,,	dv „
Но так как =2у, то должно выполняться равенство
С (у) Д- 9.у = 2г/, или С (у) = 0, откуда и находим, что C(y) = Ct, где (Д- постоянная. Следовательно, f (*+<У) = (х2~у2 + x) + i [(2х+1)г/ + С1] = 22 + г+/С1.
В задачах 2503—2506 д комплексной плоскости:
2503. гД
2504. cos (iz — 1).
В следующих задачах функций:
2507. tg2z.
сазать, что данные функции регулярны во всей
2505. г2 + 5г- 7.
2506. sh Зг.
определить области регулярности заданных
2509.	etg J .
2510.	sin-Й’ .
2511.	Восстановить регулярную функцию /(г) по ее действительной части Ref(z) = Зх2у — у3.
2512.	Восстановить регулярную функцию f(z) по ее мнимой части = 2>°-
2513.	Восстановить регулярную функцию f (г) по ее мнимой части Imf (г) =х-|-у — 3.
§ 3. ИНТЕГРИРОВАНИЕ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
Интеграл от функции комплексного переменного f (?) = “ (х, y) + iv (у, у) по дуге L вычисляется по формуле
^’/(г) clz^\и (у, у)дх—v(x, y)dy+i\v(x, y)dx + u(x, у) dy, (1)
526
оо л а ст и). Если функ-ограниченной кусочно-глад-
Рис. 247
|-  Теорема Коши (для односвязной области). Если функция f (г) к регулярна е односвязной области D, то
|	\/(г)Л = 0,
L
! где L — произвольный кусочно-гладкий замкнутый контур, лежащий в области О. Теорема Коши (для м н о г о с в я з н о й
| ция f (z) регулярна в конечной замкнутой области D,
кими контурами Lo, Llt  ,Ln (рис. 247), то
и	f (г) dz = J] f f (г) dz.
к	k = lLk
В Направление обхода контуров — против стрелки часов.
В Если функция /(г) регулярна в области D, то К для любой точки z этой области и любого замкпу-В юго кусочно-гладкого контура L, лежащего вместе В с ограниченной им областью внутри области D, и со-К держащего точку г внутри, имеют место следующие К представления:
|	и
₽ Если дуга с, начало которой в точке А и конец в точке В, лежит в области р регулярности функции / (г), то
|	р(г)^?(В)-/-(Л),
I	. с
I где F' (г) = /(г).
|	2514. Интеграл г3 dz, где L — дуга параболы х — у2 с концами
| L
| в точках /1 -- 0, В —-1 +I, выразить через криволинейные и вычис-I лить.
S Решение. Действительная и мнимая части функции г3 равны:
и (х, y) — x:s — 3xy2, v (х, у) = Зх2у — у \
поэтому формула (1) дает
z3 dz — \ (x:s — Зху-) dx — (Зх2у — у3} dy Д- i ( (Зх-у — у3) dx -|- (х3 — Зху2) dy.
i l	t
Для вычисления полученных криволинейных интегралов перейдем к параметрическому представлению кривой, положив у — I, x = t2. При этом I изменяется в пределах	получаем
I	1
z3 dz = Jj (2if’ -- 9/5 + /3) dt +1 (7/° - 5/1) dt =—1 + i  0 -1.
L i)	о
2515.	Вычислить интеграл (г Н-2г) t/г но дуге окружности \г'.= L
527
Решение. Введем на дуге окружности L: |z!==2, —g-sgarg^y параметрическое представление, положив х —2со8ф, у = 2 sin ф. На данной дуге пара-метр ср изменяется в пределах —Преооразуем подынтегральное выражение:
(г4-2г) dz = (3х— iy) (dx-j-i dy)—3x dx 4- у dy 4- i (— у dx-\-3x dy) = = [—12 cos ip sin q>-f-4 sin <p cos cp] dcp-f-c [4 sin2 <p-f- 12 cos2 cp] dcp =
.=—8 cos cp sin cp dcp-f-i [4 sin3 cp-f- 12 cos2 cp] dcp.
Вычислим интеграл: л/2	л/2
\(z-}-2z)dz— \ — 8 cos ср sin <p dcp + с \ [4 sin2 ф4-12 cos2 ф] dф = 8лi.
L	—л/2 .	— л/2
2516.	Вычислить интеграл jj (г~р5) cos zdz по произвольной ли-
L нии, соединяющей точки 0 и 21.
Решение. Подынтегральная функция регулярна во всей комплексной плоскости, поэтому интеграл равен разности значений первообразной в конечной и начальной точках пути интегрирования; следовательно,
\ (2 -]-5) cos г dz — [(г5) sin г —j sin z dz]^' = [(г + 5) sin z4-cosz]2‘ —
= (54- 2i) sin 214- cos 2« — 1 = (—2 4- 5c) sh 2 4- ch 2 — 1.
2517.	Вычислить интеграл \ dz по следующим контурам:
Lx — окружность i z | = 1, L, — окружность j z — 2 j = 1, Lj — окружность | z - 2i' = 1.
_‘	,,	~	,	COS 2
Решение. Внутри контура Lt: z == 1 функция &  регулярна, точка zo = O лежит в этом круге. По формуле Коши (2) находим
С cos z dz _ . 1 cos z I „ . 1 ai
J (z — 2)3 z	(z — 2)3Jz=o	4	2
В круге I г — 2 ] =g 1 функция регулярна, точка Zx = 2 лежит в центре этого круга. Применяя формулу Коши (3), получаем
|z-2| = 1
cos z dz z (z — 2)2
, COS 2 \'	„ . ! — 2 sin 2 — COS 2 \
----I = 2ш I
\ Z ,z=2	\
г2
_ . 2 sm 2 4- cos 2	2 sin 2 4- cos 2 .
— — 2ш------------4---------------------ц1------at.
4	2
В круге ' z — 2i I 1 функция
cos z z (z —2)2
регулярна, поэтому теорема Коши дает
|г—2i\ =
COS z zTz'-ip
dz = 0.
528
2518.	Интеграл \zzdz, где L — дуга окружности |г| = 1 (0=^ sg:arg2:C.rt), выразить через криволинейные и вычислить его зна-
чение.
2519.	Вычислить интеграл § (2 — Зг + г2) dz, где L — произвольный L
Л.	Л .
| контур, соединяющий точки 2е 3 и 2е3 .
Е 2520. Вычислить интеграл \	dz по следующим кон-
•	j (2 1) г я)
	L
турам: a) L{ — окружность | z — 1 | = ~, б) С> — окружность | г + 2/1 =
= у, в) Л3 —окружность [ г — 2t :t — -~ , г) £4— окружность [ г+ 2 , = 1.
§ 4. РЯДЫ
1. Числовые ряды с комплексными членами. Последовательность комплексных чисел
21 Х1 ‘Г	*2 4“ QAj» •••»	” Хп 4“ '^Упч  ' *
называется сходящейся, а число г — x-\-iy — ee пределом: lim zfl — z, если суще-п — го
ствуют конечные пределы lim хп — х, lim уп=у- Ряд с комплексными членами n-юо	п->со
а>1 + Ш2 + ./.-|-а>,1+ ...= У, U>n
п — 1
п
называется сходящимся, если последовательность его частичных сумм Sn— /г- 1
сходится, а число S— lim Sn называется его суммой. Ряд с комплексными чле-п -» 00 со	со
нами 2^'» называется абсолютно сходящимся, если сходится ряд 1	|»
1	1
Признаки сходимости
1.	Если для всех выполнено условие \wn\^.an, ап>0 и ряд ап
1
сходится, то рядсходится абсолютно. 1 со
2.	Если существует lirn \ = 1, то при / < 1 ряд V wn абсолютно схо-м-ccl wn I	—"
1 дится (признак Даламбера).
3.	Если существует lim y'|wni = Z, то при /<1 ряд Ус., абсолютно схо-П --СО	]
днтся (признак Коши).
г,	V cosrt-PZsinrt
2и21. Исследовать на сходимость ряд ? ------------—-.
п = 1
529
_	. ,	-	САЮ IС —Г" t ОШ IV
Решение. Модуль общего члена ряда ---...— равен
.	, I cos п i sin п I . / cos2 п + sin2 п 1
1^ = 1-------------| = У -------------=п3'-
Ряд из модулей членов исходного ряда	4г сходится, следовательно,
I	1
рассматриваемый ряд сходится абсолютно.
2/ 2___i4 п2
3“ J .
I
Решение. Извлекая корень /2-й степени из модуля /t-го члена данного ряда, получаем
А-----,	" /I /2-гW1	" /I 2-i |"2	12-i 1"	/Гб,'1	..	.
при и —оо; поэтому (на основании признака Коши) данный ряд абсолютно сходится .
Исследовать на сходимость следующие ряды:
2523. У (1±Г.	2524. У
П = 1	/1 — 1
со
2525. V
,1 = 1
2. Степенные ряды с комплексными членами. Степенным рядом называется ряд вида
+ q (г(г —«)" + ...= У сп(г-а)п,
п = О
где г —комплексное переменное, а сп и и —комплексные числа. При а—0 имеем ряд вида
сп + с1г +  • • -\~спг" +    = У1 спг” • п = О
Точки г, в которых ряд сходится, образуют область сходимости данного ряда.
Для каждого степенного ряда У с,г (г —«)'г существует круг с центром в точке и, ,1=0
в котором он сходится и вне которого он расходится. В точках границы круга сходимости степенной ряд может как сходиться, так и расходиться. Сумма степен-
ного ряда S(z) = У сп{г — а)'1 регулярна внутри круга сходимости. ,1=0
Областью сходимости степенного ряда ио отрицательным степеням г—а
bi , b, ,	1>„	, V Ьп
г — а т (Z — а)2 г (г — а)п	(г — а)п
п = 1
530
является внешность круга с центром в точке а некоторого радиуса R. Если СО	СО
ряд 2 С;	сходится в круге \z—a\<R, а ряд /<;!(г — а)~п схо-
п — 0	п --- 1
дится в области ;z —nl>r, то при 0 г < R < со областью сходимости ряда
со	со
У v- + сп(г — а)п
X. (г—«)2
П — I	п — О
является кольцо r<z\z— a\<.R\ при r>R этот ряд всюду расходится.
2526. Найти круг и радиус сходимости ряда У
п = ()
Zn
Решение. Общий член ряда = - , поэтому
I ,1 I j ? |” 'Т nl _ ! г I
I I (п+1)! + «	п+1
при и—>оо. Это значит, что (признак Даламбера) степенной ряд сходится во всех точках комплексной плоскости. Роль круга сходимости выполняет вся плоскость, радиус сходимости /? = оо.
2527. Найти круг и радиус сходимости для каждого из рядов:
а)	2 б) 2 +ЧПНУг(2-/Л
п — 0	« - 1
Решение, а) Общий член степенного ряда
wn — n\ z\ поэтому
I 1 I (,г+1)1 г " ' I niz'-J °° при г=£°,
I wn I п! г |"	' *г ! I 0 при г-=0.
Следовательно, данный степенной ряд сходится только при г = 0, круг сходимости вырождается в точку г = 0, радиус равен нулю.
б)	Общий член ряда
Wn== п2(1+1Г
поэтому
а>п+1 I 1г —( "+1 п21 1 + t ! п [ z — г | I г — t1
wn I” (п+1)2 j 1+г |"+i \z — i\n Vrt+1/ |l+/j	| 2
при n—»cc. В силу признака Даламбера степенной ряд будет сходиться при
 г < 1, или I г — I ( < |/2, /2
т. е. внутри круга радиуса V2 с центром в точке /.
2528. Найти область сходимости ряда 2 (г д•
п = 1
531
Решение. Общий член данного ряда
п
W,l~
поэтому
I wn^ I______л + 1_____| г — 1 + t I” _ „4-1___1______>	1
| wn ,2—14-1 n l n ~ n z —— 1 —]—i ~* z — 1-j-i'l при n —’ co. По признаку Даламбера этот ряд будет сходящимся, если
1
; г — 1 +« j
< 1, или ! г — 1 -|-г ! > 1.
Таким образом, область сходимости данного ряда —внешность единичного круга с центром в точке 1—i.
2529. Определить область сходимости ряда

п = 0
V	я2 4-3
L (г+ 20* ‘
Решение. Рассмотрим отдельно ряды по положительным
VI (г I 2i)n
степеням (2-4-20. Для ряда 7 А-т-т-тт общий член
2" („4-1)
п=П
= _(г + 201
п 2" („4-1)’
2
поэтому
I wn^ I = I г4-2г . 2” („4-1) _ „4-1 I ?4-2i~ I
I wn 2""l(«4-2)	\Z-\-2i у ~ п у-2
при „ —сс. Этот ряд сходится в круге ] г 4-21 [ <2.
„ v «2 +3 - » Для ряда 2, (г+20'г °0ЩИИ ЧЛен
и отрицательным
I г 4~ 2г I
2
" (г + 21'У1'
Применяя признак Даламбера, получаем
| I	О4-1)2 + 3 |z4-2»;«	(„4-1)24-3
I wn j	|?4-2i ]л+1 ’ п24-3 "	„24-3
1
___________1
,г4-21]	]z4-2i|
при п—>со, следовательно, область сходимости Таким образом, весь ряд по положительным будет сходиться в кольце 1 < । z2/ ’, < 2.
В следующих задачах найти области
ряда | z + 2i j > 1.
этого
и отрицательным степеням (z-|-2i)
сходимости рядов;
2530.
гп
2532. J
Л = 1
— гп з«
п 1
-(1.....<)В—(г + 1)я.
2531.
2533. У —
4Ы (п +1) (п + 2)
532
2534. \
п | п
п = 1
5" (Z4-1)'1
|2(3п —1)2" ‘
253в- 2ТГ+2 4'".
п — о	п — 1
2537 V (г+1-»)'' । V 2" (п + 2) Z Li 3"(п + ») L (г + 1-()«•
п=0	п — I
	3. Ряды	Тейлора и Лорана.	Функция /(z), регулярная в круге	\г — а)	< Я
разлагается в ряд	по степеням (г —а):
f(z)= V	A (z — aY1 А —	1 i f (г) dz __f'n> (a)	q i
'	’’ ,l~ 2ni J (г —а)"+1 — п! ’	°’ 1....
п=0	|г —а^=г
где 0<г<А). Этот ряд называется рядом Тейлора функции / (г). Если функция /(г) регулярна в области D, точка а принадлежит этой области, то ряд
Тейлора У Д„(г — а)" функции f (z) сходится к ней /1=0 внутри максимального круга с центром в точке а, лежащего в области D (рис. 248). Функция f (z), регулярная внутри кольца г<;г — а\ <; /? разлагается в ряд
/(г)= V An{z — a)ni
Рис. 248
4п = ^-г	7—^j~dz, п = 0, ± I,
"	2л1	,) (г —й)" 1
[г —а = р
С г < р < R. Этот ряд называется рядом ,'[орана функции / (г). Сумма
Ап(г—а)п называется главной частью ряда Лорана.
Ряды Тейлора и Лорана определяются единственным образом. Эти ряды в области сходимости можно почленно дифференцировать и интегрировать.
2538. Разложить в ряд Тейлора по степеням z функции е~ и sin г.
Решение. Функции ег н sin г регулярны во всей комплексной плоскости, поэтому пх ряды Тейлора сходятся к ним при всех г. Коэффициенты ряда для ег равны
, f'n' (°) 1
11 п\ п\ ’ так как (ег)<га> = ег; поэтому
е,-2зг"=|+‘-|4+--
П=хО
Функция sin г, по определению, равна
Ряды для функций е‘г и е",г легко получить из ряда ег: оо	оо	оо	со
2	2	2	2
п=0	п=0	п=0	п—0
533
следовательно,
1 sm г — -А-2?
v v (- о"in -3i v [i-t-D”]»'1 n\ Li n\	‘ I 2i L /1!
n =0	n — 0	J	n —11
Заметим, что при n = 2m (четном) множитель 1 — (—1)" равен нулю, а при n = 2m 4*1 (нечетном) имеем
(« [1 --(— 1)«|	2 - (/2)"11	2/(—1)”’
л! “ (2m 4-1)! “ (2m 4-1)! '
Таким образом,
(— 1)т
у >	г2т+1
(2т 4-1)!
т = о
В силу единственности разложения это ряд Тейлора функции sin г.
1 . ]
2539. Разложить в ряд по степеням г функции г2е2 и (1 4-г3) sin-z2. ।
Решение. Функции гге2 и (1 4- г3) sin нерегулярны в точке г = 0, поэтому их разложения в ряд по степеням г будут содержать как положительные, так и отрицательные степени г, т. е. они разлагаются в ряды Лорана. Так как
ew = У —-ta«; sintei = У	—Д—щ-’1 L
/1 = 0	/1=0
(см. 2538), то, полагая №= • , находим
C-L V 1 1	. 1- + -L +
Zi п\ z"	r z 2г2 г	•
п =0
1 аналогично, при ш==-;
si ’ - У <-	1 - у <- }>я 1
г2 - Li (2п4-1)! z2(2"'i’ L (2пн-1)! z*«+2 ' /1=0	/1=0
Умножая ряд для ег на г2, получаем
--— — г2 ! , _L ± J-!-L
гл-2	‘2!‘3! z 1
Этот ряд сходится в кольце 0 < I z j < со.
Ряд для sin-- умножим на (l-)-?3) и раскроем скобки:
(14 г3) sin г2 - У (2ц4-1)! г<«+2 2i (2п+1)!	+
п ~ О	11 = 0
+ У	IJ-- 1 J.+J_±_
Г L (2/14-1)1 г1" 1	‘ z2 6 z3 6 г“ т 120 2‘
и = о
Этот ряд сходится в области 0 < | z j <со.
534
f 2540. Разложить функцию .Ду п0 степеням г в областях j z\ < 3 ф 3 < | г', < оо.
’ Решение. Функция * регулярна внутри круга | г i < 3, поэтому она ^разлагается в этом круге в ряд Тейлора по степеням г. Используя формулу для ‘	<20
геометрической прогрессии
1__
1-7 ’
q \ < 1, находим
п — 0
г _ г3
9	27
Этот ряд сходится при | g |<1, т. е. при ложения это ряд Тейлора данной функции. ' . 1 „
Функция ——— регулярна в кольце 3
г | < 3. В силу единственности раз-
< | г ; < со, поэтому она разлагается
в этом кольце в ряд Лорана по степеням г. Вынесем в знаменателе г за скобку и используем формулу для суммы членов геометрической прогрессии:
1 г-3
Этот ряд сходится при |—|<1, т- е- ПРИ ' z | > 3. В силу единственности разложения это ряд Лорана данной функции.
Таким образом, функция пРеДставЛяется рядом
1 у. г" 1 г г2 3^'13 ~ 9 ~ 27
п=о
в круге j г | < 3 и рядом
1 _ V 3”	1 , 3
z —3 — zn+1 ~ г’~Гг3 г"’
п = о
в кольце 3 < | г ! < оо.
2541. Разложить в круге j г [ < 3 функцию J по степеням г.
Решение. Функция —Цт- в круге | г [ < 3 разлагается в ряд
1	v zn
г — 3 ~	Zu 3n+l
п =0
(см. 2540). Продифференцируем обе части этого равенства:
_____!_____ у 1_________________= у »
(г —З)2 ui 3«+i ’ (г-3)2 Zj 3'!+1 п — 1	п - 1
Полученный ряд и будет рядом Тейлора данной функции в круге i г | < .3.
535
2542. Разложить функцию точек г = 0 и г = — 2.
Решение. Разложим сначала тарных дробей:
(г - З)2 (г + 2) В рЯД
фУнКЦИЮ
на
окрестности
сумму элемен-
В
1	11	1111
(г_ 1)2(г + 2)	9' г + 2	9 г - 1 + 3 (г - I)2 ‘
(1)
В окрестности точки г=0, а именно в круге ! г \ < 1,
и каждое слагаемое:
элементарные дроби
1 I
9 г+2 ’
1 1
г + 2 ’ г —1
1 1 1 г—1 ’ '3 (г-1)2 ряды Тейлора:
фуНКЦИЯ (^К(1 + 2) — регулярны. Разложим
1 1 = 1 1
9 г + 2 ~ 18 г_
'2
1
9
в

= V П-1)” I 1 , 1
L [18-	9'3
п~0
1	17	27
(,l+1)F = 36 + 36Z+-
—1)2 (г + 2) нерегулярна, она регу-
В окрестности точки г = 1 функция
лярна в кольце 0< I г — 1 1 <3 (рис. 249). Разложим' ее в ряд Лорана по степеням г—1. В .правой части формулы (1) нужно разложить только слагав-
536
|«oe	Эта функция регулярна в круге | г — 1 > < 3, поэтому она разлагается
в ряд по положительным степеням г — 1:
;	-1 _____________________L_=' Vc ipll-Ji' ,, „
гф-2 г—1+3	3 , г —1	3 >	'	3"	’ ‘	* < 3>
п = 0
следовательно,
1	11	1	1 XI (— 1)"
(г—I)2 (г + 2) — 3 (г —I)2	9 г — 1 + Z 3" ' (г - 1)"-
п =о
Это и есть
ряд Лорана функции
т--ГТ»*?—в кольце 0 <
(г- 1)2(г +2)
3.
г — 1
2543.	Разложить в ряд по степеням г функции cos3z, sin (2г —1). Указание. Применить формулу sin (a + P) = sin acos р + sin Р cos a.
2544.	Разложить в ряд Тейлора по степеням г+ 2 функцию с2-1.
2545.	Разложить функцию cos (г — г) по степеням (г — /).
2546.	Разложить функцию (г+1) sin 2г по степеням (г + 1).
2547.	Разложить функцию г4 —Зг’2 + 5г по степеням г —2.
।
2548.	Разложить функцию +3 в ряд Лорана в окрестности точки г = 0.
2549.	Разложить функцию sin —^-у в ряд Лорана в окрестности точки г 1.
2550.	Разложить функцию cos —в ряд Лорана в окрестности (Z I)
точки г — /.
2551.	Разложить функцию (г + z) sin. в ряд Лорана в окрест-г+*
ности точки г = —/.
2552.	Разложить функцию уру в ряд в окрестности точек г = 0 и г = —1.
2553.	Разложить функцию ц-— 3) в Ряд в окРестности точек г = 0 и 2 = 3.
2554.	Разложить функцию ; ^9.а в ряд в окрестности точек г = 0, г = —2.
2555.	Разложить функцию —г-хД—в ряд в окрестности точек '.г+лНг + Л
г = 0, г = —2.
§ 5.	ВЫЧЕТЫ. ОСНОВНАЯ ТЕОРЕМА О ВЫЧЕТАХ
1.	Изолированные особые точки. Точка а называется изолированной особой точкой функции /(г), если /(г) регулярна в некоторой окрестности этой точки, за исключением самой точки а. Если ряд Лорана функции f (г) по степеням г —а не имеет главной части, точка а называется устранимой особой точкой, главная
часть состоит из конечного числа слагаемых
I (г)=^й'* (г — а)к =	+ -" + «'0 + а1 (г
—п
то точка а называется полюсом п-го порядка; главная часть —бесконечный ряд, точка а называется существенно особой точкой. Точка а называется нулем п-го порядка функции / (г), регулярной в некоторой ее окрестности, если
f (а) = f (а) =.. , = /<«-!> (0) = 0, f'n' («) =# 0.
Если регулярная функция f (г) имеет в точке а нуль п-го порядка, то функция 1
у—- имеет в этой точке полюс того же п-го порядка.
Нг)
Для того чтобы функция f (г) имела в точке а нуль п-го порядка, необходимо и достаточно, чтобы в некоторой окрестности точки а имело место представление
f (z) = (z—а)" <р (г),
где q (г) регулярна в окрестности точки а и q'(o);,~0- Для того чтобы точка а была устранимой особой точкой, необходимо и достаточно, чтобы существовал конечный предел
lim / (г) = с < оо.
2556. Найти все особые точки функции 4^2 и указать их характер.
Решение. Определим нули функции f (г) = г3 (z2-|-4)2. Так как
/ (г) = z3 (г + 4)2 = г3 (г Д- 2г)2 (г — 2()2,
то функция f (г) имеет три нуля: 20- -нуль третьего порядка, z2 = 2i и г3 = = —2г —нули второго порядка, что следует из разложения функции на множп-
„	ж	1
тели. Следовательно, функция	.. г
г’ (z
имеет в точке z1 = 0 полюс третьего
порядка, а в точках г2 = 2г и г3——2i— полюса второго порядка.
2557. Найти все особые точки функции и указать их характер. ,	sin 2
Решение. Определим пули функции ——. Они совпадают с нулями функ-ции sin г, т. е. с числами zft = n£, /г = 0, ±1.При k 0 это нули первого
порядка, так как
(sin г)' = cos zA = cos л k = (—1)*о ¥= 0; /г
поэтому в этих точках функция имеет простые полюса. В точке z~0 в нуль
„	'	2
обращается и числитель и знаменатель дроби , но существует предел
lim -Д- = 1,
2~.о sin г
поэтому точка г = 0— устранимая особая точка функции £
2558. Найти особые точки функции х2ег и указать их характер.
538
Решение. Функция z2ez регулярна всюду, кроме точки z = 0. В 2539 мы (заложили ее в ряд Лорана по степеням г:
указать их характер:
2559-
2560. ------С~------.
/ тт х
!2+-2J (z2 + I)2
2561. tg22z
I со
?	г2ег — V J_ *	=22„L2„(__'____-1—
е “ я! z’l~ '	'2!	3! г
/2=0
1з этого ряда видно, что точка г = 0 является существенно особой точкой функ-1
щи г2ег (бесконечная главная часть).
В следующих задачах найти все особые точки данных функций
2562.-----L_.
*" cos г— %
2563. z2 sin .
2564. (г- 1)cost—Lt. v ’	(г-1)2
2.	Вычеты. Вычетом функции f (г) в изолированной особой точке а называется коэффициент Д.! ряда Лорана этой функции, равный
res f (г) = A_i = -Lj- f (г) dz, а	с
где
три
С —замкнутый контур, лежащий в области регулярности функции f (г), которого лежит точка а и нет других особых точек этой функции.
впу-
Формулы для вычетов
В простом полюсе
res f (г) = Ит (г — a) f (г), a	z-+a
/<3(г)_ <р («) .
V Ф (г) Ф' (а) ’
(1)
(2)
в полюсе порядка п
1	dtl
(3)
Вычет
функции
в изолированной особой точке равен
нулю.
в
ее особых точках.
2565. Найти вычеты функции г3
Решение. Особые точки функции
г4(г^-\-4у
третьего порядка, z2, 3=± 2t — полюса второго порядка. Применяя формулу (3), находим:
1	1 <• Г я 1 I 1 1- Г 1 I
r“23(22+4)2~ 2 z‘Lo	г»(?2 + 4)2 J	2 ‘™о	[(г2 |-4)2]
(см. 2556), г, = 0 —полюс
1
9
lirn
z —> 0
5г2 — 4 1 (г2 + 4)»]
1
32’
4
539
Z3 (za + 4)2	1 f J ™ . dz 1(г 2‘)2 Z3 (Z _ 2i)2 (Z + 2i)2
z'™2< dz [Z3(z + 2i)d J™iL г4(г + 2<)2’ z3(z + 2i)3j 64’
- 2i гЗ(г*+4)* = 1 f 2	2/ dz [(г + 2l)" 7» (z-20a (*+20*1 =
,. d |	1	|	Г —3	2	1	!
“ г;™я</г[ гЗ(г-20« J^z2™2iL z4(z —2i)2	z3(z-2i)3J 64'
2566. Найти вычеты функции во всех ее особых точках.
z
Решение. Функция —- имеет в точке г = 0 устранимую осооую точку, в точках zk — stk (k — ± 1, ± 2, ...) простые полюса (см. 2557). Вычет в устра нимоп особой точке равен нулю, а вычеты в точках nk найдем по формуле (2), полагая <р (г) = г, ф (г) — sin г.
res— - = ———— =------------r=(— V)k nk (k = ± 1, ± 2, ...).
як sin г (sm z)rtft cos nfe
1_
2567. Найти вычет функции г2ег в нуле.
1_
Решение. Функция г':ег имеет в нуле существенно особую точку, поэтому ее вычет можно найти только из ряда Лорана. Он имеет вид (см. 2558)
^=2’“г2 + г + 2Г + ЗГг + "’
поэтому
В следующих особых точках:
I res z2 е г о
задачах найти вычеты данных функций во всех
2568. ------!—j-
sin г+ -
2571. гег~1.
Указание. Записать функцию в виде
1 1 1
zez~ 1 = (г — 1) е г — 1 4-ег — 1.
2572. sin 4,
z2
3.	Вычисления контурных интегралов. Основная теорема о вычетах. Если функция f (г) регулярна в ограниченной области D и непрерывна в замкнутой области D, за исключением конечного числа точек zs, г.г, ..., гп, лежащих в этой области, то
п
( / (z) dz = 2л( V i es f (z),
L	l< = 1 zk
где L — граница области D.
540
C dz
2573. Вычислить интеграл \	где £ —окружность
|z + 2Zj = 3.
Решение. Функция „ , , , ,.г имеет J	z3 (г2 + 4)2
(см. 2565) три полюса: г, =0— третьего и г2,з= ± 2i — второго порядков. Точки Zj = O и г3 ——2i лежат внутри контура интегрирования (рис. 250), поэтому основная теорема о вычетах дает
.ст- = 2ш res л. .	 —г +
z3 (г2 4- 4)2 I о г3 (г3 + 4)2
1	1 о • Г	1 , 1 1	ni
2S< z3 (г2 +	4)2 J	~ 2rw L	32 + 64 j	32	•
2574. Вычислить интеграл \	, L: \z\ = 4.
Решение. Функция - ? - (см. 2566) имеет в точке го = 0 устранимую особую точку, a zk — nk — ее полюса первого порядка. Внутри контура (рис. 251) лежат точки zo = 0, г1 = л, гг =—л;
I res ------------h
I. 0 sm z
tg г
поэтому
C z dz J sin z \Z\ =4 Z	2 1
+ res —----1- res —- =
—л sin Z —д sin z J = 2л1 [— л — л] = — 4лг1.
2575. Вычислить интеграл
Я
|г + 2| = 1
Решение. Функция
имеет особые точки г' = —2 и г/е = =	-|-лА(А=0, ± 1, ...). Все эти
точки —полюса первого порядка. Внутри контура интегрирования ле-г n	JT .
жат полюса — —2,	= (рис.
252); следовательно,
Л
’ г + 2
tg Z , res —4-75- 4- res .-2 z-f-2 л
2
541
Искомые вычеты найдем по формуле (2), полагая <p(z) = sinz и ф (z) = (г + 2) cos г; res = sin (~~2>	= ~ sinA = - tg 2
... 2 гф-2	[(г + 2) cos г] '. s cos (—2)
 ! я \
,	sin; —• I	.	.	„
tg z _	\	2 :	_____________—1_____,	= _ 2 .
г + 2 - [(z + 2) cos z]' „ “ _/_ я \ л \ “	4-я’
“ 2	“У \	2	/'	'	2 j
Таким образом,
7^dZ==2jIl'[_lg2”4^Tl = ”2m'[tg2+4^1-
S 2 + 2; = I
i
2576. Вычислить интеграл z2ez dz.
I Z l = I
Решение. Функция z+2 при z = 0 имеет существенно особую точку с вычетом, равным -1- (см. 2567). Точка г = 0 лежит внутри контура интегрирования, следовательно,
{ гге г dz-= 2.ш res z2e 2 =	.
J	о	6	3
; z | = 1
2577- J та
Вычислить интегралы:
dz, где L — окружность | z = 9 .
C z dz	,	(x— I)2 , y'!	,
2578. \	, где L - эллипс р-*-- +	= 1.
L
2579.	-~y, гДе L — прямоугольник с вершинами в точках
i.
Z1 = — i, z2 = 2 — i, z3 = 2 + Z, zi = i.
dz	,	I	яг |	,
-^27, где L — окружность |z- 2 | = 1.
ch 2z ,	,	।	, , ,	3
Z2(Z + 2)(Z--1) dz' где L - окружность i z + 1 [ = 2-. __
2582. dz, где L —окружность \z\^2. L
2583. (z — I)2 sin	где Л —окружность \z— li = l.
L
2580.
2581.
L
§ 6. ОПЕРАТОРНЫЙ МЕТОД
1. Преобразование Лапласа и его свойства. Оригиналом называется любая комплексная функция f (/) действительного переменного t, удовлетворяющая условиям: a) f (/) непрерывна при всех значениях /, за возможным исключением точек разрыва первого рода в конечном числе на каждом интервале конечной длины;
б) f (/) = 0 при t < 0;
542
. в) существуют числа М > 0 и s0 Уй О такие, что при всех t
Mes<‘
[s0 называется показателем роста / (/)].
Изображением функции f (t) называется функция комплексного переменного p = s-j-i'<7, определяемая равенством
g (р) = $ e-v'f (7) dt.
б
Переход от оригинала к изображению называется преобразованием Лапласа и обозначается
g(p)=Zj(O или /(/)
Функция g(p) = Lf(Q регулярна в полуплоскости Rep>s0, где s0 — показатель роста функции /(/).
Простейшие свойства преобразования Лапласа
Линейность: если А (О А £1 (Р) и & (р). то
cj 1 (0+cJi (t). - Cjg! (р) + c,g., (р).
Подобие: если f (/) .'g'(p), то 1 (at) -Л — g‘ Р-У > где а — произвольная положи-а \ а ;
тельная постоянная.
Запаздывание оригинала: если f (f) Уg (р), то для любого b > О
1 (t — t’) e~bPg(p).
Смешение изображения: если f (t) /. g(p), то для любого комплексного числа а
(t)=: g(p + “).
Дифференцирование оригинала: если функция f (/) и ее производные /' (/), f" (/), ... ,	(/) являются оригиналами и f (t) У. g (р), то
1п’ (О . Рп g (р)-р" -1 ш 0) -р"~ s f (-1- 0) -...	(+0),
где f4 (-J- 0) — предел справа в точке 0 функции fIJ> (t).
При п=1 получаем
/' (0 Pg От-
дифференцирование изображений: если f (t)g(p), то
Cg'tP), (~trf(f) g,n,(P)-
Умножение изображений: если /, (t) Д gi(p) и 1г(() Л g.>(p), то произведение gi (р)g-i (Р) является изображением интеграла
t
\/1 (^-т)/2(т)йт.
б
Этот интеграл называется сверткой функций fj (t) и (/) и обозначается Л (0 У 1г (0-
Формула Дюамеля: если ft(t) giAp), А(0 .’-^(р) 11 функция /, (/) непрерывна, а /2 (/) —непрерывно дифференцируема на [0, оз), то имеет место формула
t
pg: (Р) g-г (Р) ’. А (0 1г (+ 0) + j /, (и) f) (f - и) du.
б
543
Теорема обращения для дробно-рационального изображена я: Если изображение g (р) — правильная рациональная- дробь, та
g (р) f (0 = 2 res {g(p)eP<'>>
k = 1 >’k
где plt p2,	pm —полюсы функции g(p).
Некоторые преобразования Лапласа
Таблица 16
f (О*		g(p) = j e~Pi f (t)dt 0
1)	1	P“l
2)	е~ а>	(p + a)”1
3)	sin at	a(p2 + a^
4)	cos at	^(р2 + а2)-1
5)	sh at	a(p2-a2)“l
6)	ch at	p (p2 —а2Г3
7)	I'1	n! p^1
8)	e~al cos <ot	P + “
		(p-f-c/p-i-w2
9)	e~at sin <ot	CO
		(P + ®)2 + “2
Ю)	tne~at	(p + a)'"”1
2584. Найти изображение функции / (Z) — З/'2 — 2 — 5 sin t + 2e2Z.
Решение. Используя свойство линейности преобразования Лапласа и таблиц}' изображении, получаем
g (р) = Lf (i) = 3Lt2 - 2L1 - 5L sin t + 2Le* = 31*- - | - 5	+2	=
- 6 _ 2	5______L_
p3 p p- + 1 p — 2 '
( t (0</<2n),
2585. Найти изображение функции /(/) = <	(2л c Z)
Решение. Данный оригинал можно представить в следующем виде:
/(/)=+ —Д(/—2л)+/2(/—2л), где Д(/)=+ + 2л, /a(/) = sin I.
Применяя теорему запаздывания и таблицу изображений, находим
* Выписывается выражение оригинала только при I > 0, предполагается, что при /<0 значения — Это соглашение постоянно используется и дальше.
544
2586. Найти изображение функции f (/) = е 2- sin 2t cos ЗЛ
Решение. Сначала представим произведение sin 2/ cos 3/ в виде ра’.ности синусов:
sin2^cos3/=2 [sin 5/ — sin/],
а затем используем теорему о смещении изображений:
Le 2' sin 2/ cos 3/ = ’ Le * sin 5/ - ’ Le^ = ’ ^^'+25 ~ ~2 TpT^H ’ 2587. Найти изображение функции f (7) = tel -\-t2 sin 3t.
Решение. В силу теоремы о дифференцировании изображения имеем:
LtC' 1(Р —1) I (Р-1)2
Z./2 sin 3/ =
3 I" Г 6р
Р2 + 9 J “[	(р2 + 9)2
Зр2 —9 (Р2 + 9)3 ;
= 6
следовательно,
ог___з 1
1е< + Р sin 3/ . ‘ 18 74  2- + ----г—.
(p2 + 9)J	(р-1)2
2588. Восстановить оригинал по изображению g (р) ~.
Решение. Используя таблицу изображений и теорему запаздывания, на-. ходим
Ц	р+5 '
Ж поэтому
	е-з₽_1_•-/c“s<^3'
a	p+5  l о (/<3).
2589. Восстановить оригинал по изображению — с помощью разложения на элементарные дроби.
Решение. Знаменатель данной дроби разлагается на множители:
Рг (р2 + 5р + 4) = р2 (р +1) (р + 4),
|; поэтому для самой дроби выполняется тождество
|	_____Р + 2 А । Д , б1 D
|	Р2(р2 + 5р + 4) р2 г р ~ р+1 г р + 4’
Е где А, В, С, D — некоторые постоянные, которые нужно определить. Приведя [ правую часть к общему знаменателю и приравнивая числители справа и слева, [ находим
р + 2 = Д (р+1) (р+ 4)+ Вр (р + 1)(р + 4) + Ср2(р+4) + Ор2(р+1).
В это тождество подставим значения р=0, р = —1, р = —4, тогда А= ^,
PJ-
I 1	1
| С = О = 24’ Для того чт0®ы llaH™ подсчитаем коэффициент при
I справа и слева. Это даст
t	1	।	3
Г	0 = S + C + D, B = -C-D = -	-	;
t	о	Z4	о
18 Кручкович и др.
545
таким образом, 1 1 1
Р~(~2_______ 2 _ 8 ,	^3	,	24 , 1 z^3	._	1 e_it
р2(/,2 + 5/) + 4) р*	р  р + 1 ' р + 4 ' 2 '	8’3	г24
2590. Найти свертку функций sin t и cos/.
Реше н и е. По определению свертки,
x ,	1 I'
u) cos и du — g '
sin t X cos t =
[sin (I — 2и) + sin /] du =
1	V	1 - И	1
= „ и sin / + cos (t — 2н) = й t sin t.
2	|o	4	|o	2
2591. Восстановить оригинал по изображению g(p) с помощью свертки.
Решение. Функцию
р .	, i
Р2+1	Р2+1
Р
,Р
(Рг+П2
p
-^2~- ]p' M№KH0 рассматривать как произведение двух: sin t. По теореме умножения изображений имеем-
'sin / X cos i = I sin t
(cm. 2590).
2592. Восстановить оригинал по изображению
i \ Ря + Зр'2 -| /> -I 4
Решение. Изображение является правильной рациональной дробью с полюсами рх ——2 кратности 2, р2. з= < кратности 1. Теорема обращения в этом случае дает
рз + Эр2 + р + 4 .	рЗ + зр2 + р + 4	p:i + 3p^ + p + 4
(p + W2+B	U (Р+2)Ч/Р+!)	‘ / (p + W2 + l) +
+ ,.es£l+3P2 + P + 4 z
4 (р + 2)2(р2+1)	’
или, если учесть, что для суммы вычетов в сопряженных точках справедлива формула
res/ (р) -pres/(р) = 2 Re res/(р), если Im > 0,
Ро	/?.,	Рч
ТО
j (/) — res
Л>-'' + 3/>- + п + 4 р, 2 R р2 + Зр2+р + 4 /
(р + 2)2 ^+1)	+ К ,• (р + 2Н+ + 1)	•
Определим вычеты;
Уе2 (р + 2)2(р2+1)	2dp\ р2+1	I
 ,т (, р3 + Зр2 + р + 4	. (Зр2 + 6р + 1) (р2 + 1) - 2р (и2 + 3+ + р + 4) п.) __
р2+1	‘	(Р2+В2	J
р3 + Зр2 + р + 4 i (р + 2)Чр8 + 1)
(cos I + i sin /) = ^
Ир+йК2'-□	z и у
epi = £а+3Z2+i±i еи = __J_eii =
2i(2 + 02	2i[3 + 4i]
/2	3 х /'	2	3	\
25 cos Z + gcj sin + И - й sin ' “м cos Р >
546
тогда
и
3 . , 25 sm Л
2 Re Т {р+^+А ~ “ A C0S 1 + A Sin z
P3 + 3p2 + p + 4 .7 6	29', t _ 4
7^7+2)++++)- Ц 5 М 25.’	25
В 2593—2598 найти изображения функций.
2593. 2e^ + 5-2cos4Z.	2596. е' sin 2tе! cos 2t.
2594. sin2 3^.	2597. e2/ch/-sh2/.
2595. (/ + 2) cos/.	2598. e * sin I cos 3/.
Вычислить свертку функций f (/) н <p (/) в 2599—2603:
2599.	2601.	=
2600. /'(/) = sin 2/,		<р(/) = /3 + 2/2-5.
Ф	1.	2602.	f(t) = е!, <p(7)^cos2/.
	2603.	f (/) = ch 2/, <p (/) sin t
В 2604—2608 восстановить	оригинал с	помощью свертки:
2604.	2607.	p2
P(P-1)		(+ + 1) (+ + ?)
	2608.	P
“	(p + 3)(p2 + 4)-		(p-1) (+ + 1) '
2606. -rr\	ЛГ.		
p2(p2 — 9)		
В 2609—2612 восстановить	оригинал с	помощью разложения
на
элементарные дроби:
2609.
р3 + 1
2611. рл
р2-4р-|-13
Зр + 1
2610 ____________‘_________
UIU- (p-|- I)2 (+ + 3p + 2) •
2612< 2р2+ 8/7-|-19 ’
В 2613 — 2618 восстановить оригинал с помощью теоремы обращения:
2613.	P2+l	2616.
	(p-1) (p + 2) (р-3)’	
2614.	2p + 3 (p+I)2 P (P-+-5) 	2617.
2615.	1 (p-l)3(p2 + 3p + 2)-	2618.
(p-f-З)2 (р- 1)3'
Зр2 —2р + 1
р3 + 5р‘2 + 4р •
1
р4 —1 '
2. Решение линейных дифференциальных уравнений с постоянными коэффициентами и систем таких уравнений. Операторный метод позволяет весьма просто решать линейные дифференциальные уравнения с постоянными коэффициентами, в правых частях которых стоят оригиналы. Оператор Лапласа применяется к обеим частям такого уравнения, после чего получается алгебраическое уравнение первой степени относительно изображения неизвестной функции. Решая его, находим изображение неизвестной функции, а затем остается только восстановить оригинал но заданному изображению. Системы уравнений решаются аналогично.
2619. Найти решение уравнения х" + 4х' + 4х--sin t, удовлетворяющее начальным условиям х (0) = 1, х' (0) = —1
18*
547
Решение. Применим оператор Лапласа к обеим частям уравнения и обозначим Lx — x. Так как
Lx'—px—х (0) = рх — 1, Lx" =ргХ — рх (0) — х' (0)=рУ- р+ 1; L sin t«-Д—-
Р“ +1 то
L (х" + 4х' + 4х) {р- + 4/> + 4) X — 4 — р + 1,
и оперативное уравнение имеет вид
(р2 + 4р + 4) X — 3 —	•
Из полученного уравнения находим
V1 Г 1	, з Н „1 _ рЧ^/г-^ + 4
' (р + ?У- 1рЧ Д гР| ~ (p'4-Wp + Z)- 
Осталось восстановить оригинал х (7) по данному изображению. В 2592 оригинал определен, поэтому
,л /6 . , 29\	4	. , 3
X(Z) = (5-Z+25V	”25-C',sZ+25SlnZ-
Продифференцировав полученную функцию x(t), убеждаемся, чго она действительно удовлетворяет данному уравнению:
х' & = - {Т f + i)	+ 25 sin ' + 25 ros Л
x" ' T f ~ 23)	+24 C0S Z "235 si*‘Z’
x" 4.4x' + 4x = 'jt - Д e * + 4 cos t фД sin t - 4 ;Д t +	+
\ □	ZO/	io	i-O	О Zij
, 16 . J , 12	, , , / 6 , , 29\	16	, , 12 . ,	. ,
+ 25 Sm '+ 25 C°S ‘ + 4 l, 5 Z + 25.) e 25 C°S Z + 25 Sm Z = S,n Л
Начальные условия тоже выполнены:
29	4	28	3
^ = 25 - 25 = ’’ Д°) = -25 + 25— L
2620. Решить систему дифференциальных уравнений x' = z/Jrz, г/'=г + х, z'=x~^y
при начальных условиях; х(0)=3, //(0) — —1, г(0) = 2.
Решение. Обозначая Lx = x, Ly=y, Lz — :, находим;
Lx'—pX — 3, Ьу'^ру~\-\, Li —pi —2.
Применим оператор Лапласа к обеим частям каждого уравнения системы; получим операторную систему:
рх — 3 = г/ + ?, рУ+1 =x+c, pi — 2^x-Lff, или
px — ij--z = 3, —.v ф- ру — i —	—X — у + р’=2.
Решаем данную систему по праиплу Крамера, 1о1да
548
где
д</ =
А
р	—1	— 1
—1	р	— 1
—1	—1	Р
3	—1	— 1
—1	р	— 1
2	—1	Р
Р	3	— 1
—1	— 1	— 1
— 1	2	Р
	Р	— 1
дг=	—1	Р
	—1	— 1
3
— 1
2
А =
= р3 —Зр — 2 = (р + 1)“ (р —2)
и
/	2
= 3р2 + р —2 = 3 (р+1) [р- j
= —р2 + 5р + 6 = — (р+1) (р — 6),
— 2р'" + 2р=-2р (р + 1);
следовательно,
%
/	2 \
. 3(₽+1) \р~3/ Зр-2 _ - (р+1) (р-6)
Х~ (р+1)3(ра-2) (Р +Г) (Р 2) ’ У (р + 1)2(р-2)
Р-6
(р+ 1)(р-2)>
2р(р+1)	2р
(р+1)2 (р-2) (р + 1)(р —2)’
Восстановим оригиналы с помощью теоремы обращения:
х (1\ — res_—— —-еР^ -4- res-————-- ё~t I - -
W Le,(p+D(p-2)e ‘Т (р+1) (р-2) 3е +зС'
" « - ~ (Р2) + 7 “ (. + U-2)	1
1 W " 21 (0 + 1ИР-2) + Т (р + П^-г) “4 '+ Т Л
Легко проверить, что полученные функции удовлетворяют уравнениям системы и начальным условиям:
5	4	7	4	2	4
х (0) ~ q- + -+  = 3, у (0) =	-+~ +	= 1, z (0) = -у- + "й" = 2.
0	0	0	0	0	0
Решить в 2621 —2626 операторным методом линейные дифференциальные уравнения при заданных начальных условиях:
2621. х" + 4х = 8 sin 2/; х(0) = 3, х' (0) = —1.
2622. 2х" +5х' =29 cos/; х(0) =—Г, х'(0) = 0.
2623. х" +9х = е|‘; х(0) = 0, х'(0) = 0.
2624. х"' + х' = /, х(0) = 0, х' (0) = 0, х" (0) = 0.
2625. x" + x = cos /cos 2/; х(0) = 0, х'(0) = 0.
2626. х" — Зх'+ 2x = e'sin 2/; х (0) = 1, х'(0) = 0.
В следующих задачах решить операторным методом системы линейных уравнений при заданных начальных условиях:
2627.	х' = — 2.v - 2// - - 4г, у' = — 2х + у - 2г, г' = 5х + 2у + 7г;
х(0) = 1, у(0)-2, г(0) = —1.
549
2628.	x" — 3x'~\-2x-\~y' — y — 0, —х’ -\-x-\-y" — Ъу' -]-4у = 0; х(0) = 0, х'(0) = 0, у(0)=1, /(0) = 0.
2629.	х"-8х + ]/б/ = 0, /6 х' +у" + 2у = 0;
x(O)=l, х'(0) = 0, t/(0) = 0, у'(0) = 0.
2630.	х’ = Зу, у' = — 2г, г' == 2х + Зу — 2г;
х(0) = 2, у(0) —0, г(0) = —1.
2631.	х' + Зх + у = 0, у'— х + {/ = 0;
х(0) = 2, {/(О) = 3.
2632.	х'— 2у-\-5х = е‘, у' — х бу = е2';
х(0) = 1, у(0) = -1.
2633.	4х' — у' 4-Зх — sin t, x''+y = cos/;
х(0)==2, у(0) = —1.
2634.	х ' у -}~Х — ^, х Ц- у — 1;
х(0) = 1, х'(0) = 0, у(0) = —1, у'(0) = 2.
ОТВЕТЫ
6. а) (0, ± 3 Г2), ( ь 3 | 2, 0), б) (П 3, ±. 3). 7. (а, -Л), (-а, 6). 9. 2.САВ. 10. L АВС. 11. 5,6. 12. -4т-. 13. (—5, 0), (7, 0). 14. (0, 0), (1, 1), 15. (3, 3), I 13
(-1, -1). 19. (2, -5), (0, 9), (8, -3.) 20. а) 13, в)	. 21.
л2—~3 . 22. 8 . 23. (1, 6). 29. Прямая, параллельная осп \ и	о у 3
Оу, б) прямая, параллельная оси Ох, в) оси координат; г) парабола; д) линия, лежащая в 1 и II четвертях; е) окружность с центром в О (0, 0) и R-~['2', ж) ось Оу и окружность с центром в О (0, 0) и R — у 2 ; з) точка а2
(1, —1); и) пустая линия. 30. Пара вертикальных прямых х—у-^-.
2	2	2_
31. Окружность х2 + у2 =- 9. 32. х3+(/3=а3’ x = acos3t, у—a sin3/. 33. х~ ах3
= a sin / + а/ cos t,	у = a cos t — at sin t. 34. Парабола u = x tg a —.
r	2v2 cos2 a
35. a-2-(-y2 = 2Rx. 40. /fi== g , ^2= - /гз = ~ | • 41 • y==~$~x’ y==x<	A’>
y~—]S'3x,	42. 2x + p — 6 — 0, x — 2y -(-7 = 0. 43. x = —2, у = 4. 44.
Зх —4//—15 = 0, 4.r-|-3//-|-5 = 0, 4x + 3y—10 = 0". 45. 5x — y- 13 = 0, x + 5(/ + l3 = = 0. 46. tg A = g , tg B = и , tgC= — 3. 50. Проверить, удовлетворяют ли вершины найденным уравнениям. 51. a) lx — Зу -|- 1 = 0, б) х-\-у — 4 = 0. 53. х-[-(/—
1/V
— 8=0, х — (/<2 = 0. 54. 2х + р ± 6 = 0. 59. —0,8х + 0,6(/— 0,5=0,	х-|-
1	12	5
+ ±-V —6 = 0, - -x<	(/ = 0, — А’ —2 = 0. 60. 49. 61. 3,8. 62. х + р—1=0.
&	1 о 1 <5
65. (2, —5), (1, 1), (—3, 2). 66. (7, 3). 67. 6х + 7г/+ 25 = 0. 68. х — у— 7 = 0, х~2у — 14 = 0. 69. х —(/<1=0, 7х —2(/ —29 = 0, 2х + 3(/-|-1 = 0. 70. 2х~у~ 1 = = 0, Зл- + 2(/-12 = 0, 19л- + 22у-41=0. 71. 2х + </-7 = 0, 13х-9у<32 = 0.
/4	2 \
72. я (6, 0), (2, —4). 73. Зх- 16(/<55 = 0. 74. 2л-у-4 = 0, х-2у + + 4 = 0, х~-у—(), х+.!/ = 0. 75|_ Их —2у-25 = 0, 2х-11^-34 = 0. 82. (2, 1), R = 5. 83. (х — I)2 + ' у-\-	. 84. х2 + (г/— 5)2 = 52 — окружность касается
/1
оси Ох в начале координат; С (0, b), R — \b\. 83. (2, 4), (—2, 0). 87. (
88.	3. 89. 2х - \у + 11 = 0. 93.™+^- = 1. 94 .+ %- = 1. 95. (7=2, />=-|/X 96. а = 2, 1UU OU	Х'т
• 	г	г •	I/ 2	-	у2
£» = V2 ,(0, —| 2), Л(0, 1'2),	97- I 0,4- 101. -4-- у5- = 1- 102-
X2 /72
—	гд-5, 0), ГД5, 0).	4, 0), Д2(4, 0), /3, (0, -В), В2 (0, 3),
к	Я	1'2	7/2	у2 tj2	,-
е =	юз. 25 - 24 =L 104, -Т-‘Г=1- Ю5. Л(0, -I 10),
551
л (о, У Го), А, (о, —I), л.2(о, 1), лх (—з, 0),	(з, О) ₽= | ю, х=? Зу. ios.
Г (6, О), х — —6. 109. р2 =— g х, ; — g , 0 i, х = g . 110. (О, 0) и (1, 1). 122. к	хл
а) 6у = х2— 6хД-6, б) х2— 4хр Д-4у2 Д-20хД-Юр Д-25 = 0. 117. Гипербола —=—-О
/2
I, с=Г'12, О'(1, —2), Fj (I, -1^12-2), 0.(1, К12 — 2) (в старых
it	х,л I]
координатах.) 118. Эллипс 'Ь'4 —119, Гипербола —	= 1.
120. Эллипс i- + -?L-=l, с=|/5, O'f-ф, Гц-У, 3—F5 ;, i	у о х у	\	<3 X	j
/	5	3	\	о
Q +1Z5 (в старых координатах). 121. Парабола у'~ — 2х', у	о	Л	}
р=1, О'(—1, —2), F[^—g-; —2^ (в старых координатах). 122. Парабола
1	/ з \
у'=х'2,	О'(1, 1)>	\ (в старых координатах). 126. Парабола Y
п	X2	Y2	X2	Y2
— X2, а —	127. Гипербола ---------г~=1- 128. Эллипс -=-------=1, а
4	4	1	2	6
3 асимптоты g
=	. 129. Гипербола х'у' = 4, а = Ь = 2 У 2 , О' , 2^ ,
у —2, оси О'х' иО'у'. 130. Парабола у' = —х'2, у = у — 1, х' = х—1. 131. Гипер 11	п
бола х'2 — J/,2== 2 ’ х'~ %----, У'= > а= 4 • 134. Пару прямых х—у—-о
F £
и хД-у = 0 — биссектрисы координатных углов. 135. Пару параллельных прямых
( 5л ч хД-2уД-3 = 0 и х+2у — 3 = 0. 136. Точку х0 = 2, у„ = — 1. 139. Д'^2, B'h, С (Ч, 7^У 140. Mt У, М2(1, л), Л«з(2, -5^,
Лп/г,147. р =--------148. p=-2ocos<[. 149. (х2Д- у2)2 = 2 (х“ — у-)-
\	3	/ я \
cos^-6
150. (х2Д-у2 —2ях)2 = 4я2 (х2Д-у2). 151. (х2 Ду2 — х)2 = 4 (х2Д-у2). 152. p = asin2(f. 157. 60. 158. 1 159. -Д-. 160. 2b3. 161. — (&2Д-яс). 162. —44. 163. —202. cos2 а
164. —29. 165. b(b2- а2). 166. а=\, а = —2. 170. —20. 171. —31. 172. 0. 173. 18. 174. 180. 175. 0. 176. (аД-бД-с) (6 —а) (с —а) (с—6). 180. 12. 181. 2аД-6. 182. — (яу’Д-бхгД-сху). 183. 180. 184. 0. 185. (а— I)4 (я + 4). 186. — 2(я-1)! 187. пД-1. 193. Угол между а и b: 1) острый, 2) тупой. 194. )а)=Д&|. 196. -у(а + &), 3-(а-&), -’-(*-«), - (аД-fr). 198. а-)-» + с, a-l~»-c, b
\ с — а, Ь — с — а. 199. аД-& + сД-(4=0. 202. Точка Д лежит на оси Ох, В на оси Оу, С—на оси Ог, О —на плоскости yOz, Е — на плоскости хОу. 203. Д1 (я, Ь,	—с), Д8 (—а,	Ь, с), Д3(—я, Ь, —с),	Д4	(—а,	—Ь, —с). 204. (0, 0, 01,
(я, 0, 0),	(0, а, 0), (я,	а, 0), (0, 0, —я), (я,	0,	—а),	(0, я, —я), (я, я, —al
209. а = —4, Р = 5. 210. А В = ~ ОС, j Д fi ' = J/22, \ЪС\=2У22. 211.0(3,0,5). 213. 4, 0, 4V 216. Л(-,4- — 8> 121 в[- V-, 7> —131	> —2. 2 .
\	3/	\ о	/	\	3	у1 у о	z
£(--у, 1, -з). 4 217.	(б, 3,	218. г = | (гл + гд + гс+гд). 219.
2	1	2
С (4, —5, —2). 222. cos а =-л-- cosp= cosy — — - . 223. а) Не может; б) ми-‘	и	О	и
552
жет. 224.	6 i+ }j-~k. 225. с"= - -U i + -fL-J + -±- k. 226.
'	'	1	p 42	|42 J 42
"°^7з	232‘ n ~1'2) I3,233' а=±_5 - 235, ^=2'236-
<Pi = 90°, (b2=]35°. 237. q> = arccos=« 63°20'. 238. j/X 239. - ’ . 240. —
P 5	3 узд'
241. x = — 3-Z+ 3 /+ 3 k. 247. [ас]. 248.5=1,5. 250. 25Z + 5/ + 35fe. 251. z ч z
« = —
2) да.
42a. 252 . 3^2^22.
262. V=12, тройка
253. 21+ 11/+7*. 254. 18/ —6/ — 8Й. 260. 1) Ист, ,	/24 8>	/26 — 2Г. ’
Левая. 263. /(=11. 269. I i. 270.	I.
10 3/	\2 — 8 j
i 5	5 12\	ia b\ f 0 a\ b c\ ( 0 a b\
271.	0 —10 1 . 276. I , I J, p d e , — a 0 c
\11 —3 11/	'b c> '^a °' + e f) \—b —c 0/
283. a)
/ — 14 19-
28 37/’
/ 0 ad—be'	/29	4 27\	/ 11 2 12\	f~28 61 ~32\
6)	j, в) 17 14 19 , r) — 1 —4 —3 . 285. —14 46 —19 .
\ad-bc 0	/	^14	5 n/	\ 7	—2	—6/	12 34 —18/
, ,, n. fab c d\
/ a b\ I1* P °\ Q a b c\
287. a) I , 6) 10 b сJ, в) I	, где a, b, c, cl — произвольные числа.
\° ° &/	\0 о 0 J
/a b c\	/ 1 0\	/__29	20\	/^6
288. 0 0 0 . 296. a) ), б)	, в) 30 16 15 . 297. Л‘"г = /,
\o 0 0/	3 64/	°	39'	\15 10 11/
< f т	i.„ । о	.о	/cos na — sin na\
/М-Ч/ 442^-/	= и Tn=	298. -« / или
1	\ sin па cos па/
/а +	/ j
1 — +	] ИЛИ 1
\ b + С
/0 0\	/1 О'
, или [. 299.
+ I/	+ 0/
/+: 1 где Ьс — —а-. 301. I
\ о
О'.
।; 0 или 1 или f-1 /
1 / 1 2Ь\	/а b '
1 ,) или а(1—а) ,
2\1ьЧ	1~а,
308.	а)	/ 0,4 0,2/ 0,3 0,1/’
/1	0	0^
а		
0	1	. 309. а)
	b	
1 .8
16 /0
I 2-4/	I 5 ° 2\	/0 0 0\
а)	।; 6)	5 1 1 ; В) р 0 0 . 300.
' 12	6/	\—3 2 0/	\0 0 0/
а 0 \
1. 302. Л = Х/. 303. /1 —диагональная
± b /
/sin ср — cos ф\	/
б)	, в) 0
\COS ф sin ф/	1	„
/а р
\с —а) ’
матрица.
13	9\
5 5 , —7—6 )
О —, с/
23'/
2/ ’
°) 70 /
25 -25\
-26 —2/ ’ и)
/—4 3
+ 1 = —8 6
\-7 5
—2\
-5 , —4/
Х = Д"1В, У = ВД-!. 316. а) 2, б) 1, в) 3, г) 2, д) 4. 320. х = 3, у = — 1. 321. Координаты всех точек прямой, Зх — 2у = 2. 322. х—-—2, у = — 1. 323. Несовместна. 325. х=1, у = —1, г = 1. 326. х = 2, (/ = 3, г = 1. 327. x = bc, у=ас, z = ab. 328. xt =—2, х., = О, х3=1, х4 = — 1. 331. х =2, у — = —5. 332. х = 2, .7 = 1, г = 3. 333. Xt=l, х2 = 2, х3 = —2. 334. х^З, х2=—4, х;| = —1, Х| = 1. 335. Xi—1, х.2 = — 1, х3—0, Xj—2. 339. № 4/, // = —'it, / — произвольное число. 340. х = 0, у—-0, г — 0. 341. х — —4/, у — — I, г=-Ы, t— иро-
553
извольное число. 342. х = у— 2г, где у и z — произвольные числа. 343. При а = 0; х = /, r/==0, z = 0; при а = 2: х = 5/, у — — 8/, z=2t. 344. х = а, с/ = 2а, z = —се, t = a, а—произвольное число. 348. а) Да; б) да; в) нет; г) нет. 349. a) xt -=
1 ~г X-	1 —Зх3 Д' Зх4 — 5х3
= =
= -1- -^-. 356.
= x2-[-2xj, уя = Xi Д- 2х, Д- Зх3. 359.
3
4 — 1О'\ '. 357.
°) *1 ——2±,	*2 ——1-*з = 0, х4 =
^'cos (<р Д- ф) — sin (ср Д- ф) ' \ sin (ср Д- ф) cos (ср Д- ф) '
358. yt — хя, у2 —
п1 = 7ш1 —6ш;— Юьд, сл^бьд —5ад —бес,,
cz3 = 4w1 —За.'гД.юэ. 360. У = А~Ч/, Д~1 = 1
1 1
\ 2
т о о
L 1 /
4 2/
365. ^ = 9, Х2 = 6,
7.3 = 3. 368. для Д: А4 = — 2, Аг=1, Х3 = 3, для Д2: Х]=4, Л2=1, А3 = 9, А, (Д2) = 7. (Д)2. 369. л, —1, Х2 = 4—характеристические числа масрнцы Д; рц = — Р(1) = — 4, рг, = Р (4) = 5 — характеристические числа матрицы Р (Д). 380. а)
ЗуД-г =0, б) хД-2г = 0. 381. а) у + 4 = 0, б) г-2 = 0. 382. Х Д- —Д- А =
¥	"3
= 1. 383. хД-уД-г=±2. 384. -|-Д--¥-д. *=1. 385. Зх Д-2у- г = 5. 386. а) Да, б) нет. 387. —х^"ц	г-®“0,	р = 3.	391. <p = arccos 94- . 392.
Плоскости параллельны. 393. <р = = .	394. ср =	. 395.	у + г = 0. 306. (—10, 0, 2).
3	1
400. 1. 401. МдО, 0,-9	М2(0,	0, 3). 402.	х-2у Д 2г- 1 =0, х — 2г/Д-2z —
— 3 = 0. 403. (0, —2, 0). 404.	хД-г =	0, х —I/—1=0,	405. 3-|z3. 410. х — 4(/-
-Д 5г-|-15 = 0. 411. х + (/-гД-2 = 0. 412. х-Д2у-г-8 = 0. 413. х Д-1 \у Д-38г — — 154 = 0. 414. 9х-г/ + 7г-40 = 0. 415. 3х-4у-3г Д-4 = 0. 416. Зх^-Зу^-г — — 8 = 0. 417. й = 3. 424. -^i-1	• х==_ i+<> //= 1 -3/, г = —3 Д-
Д4/. 425. ^-_1 =	y+JL-4	2	1	У -1- 1 -ур; х = 2Д-/, у = — 1-Д4/, г = -1. 426. ^2-=
	У Д' 3 	г 2 ~ 0 - 0 ’ х — 2 у — 4 г -	х = —1Д 1- 1 429. 4 —. 432. гД-1 1 '	// = _2, г = 2. 427.	=	=	428. V2	1	1 = HJL =	430 x-±l - 'J - -1	3	8 •	3	Г- 2 • х —2 у гД1	х—1	у + 3	г —5 -Г~-2=Т“- 433, 438. <p='J. 439. <р=34Я . 443.	= ф = А
		
,,, х—1	0 —2 444. —т— = 4	—5 — # + 2	г-4 3	—7 ’ ( х —21/ —3 = 0, ( 1 г = 0	1 = 0, Збх—ПгД-23 -ДЗг —9 = 0. 465. 	,г + 1. 1 455. х Д- 2г — 1/ = 0, = 0. 462. х — 2 	9 “ ~	. 446. (1, —2, 3). 451. i|) = arcsin . 452.	= (5, -1, 0). 456. \- Д-, - L,	439. \	13 ’	13 ’	13 / 3 = 0, ( 1/-Дг = 0,	11х-41/Д6=0, 9х-гД-7 = 1 х = 0.	1 9хД-81/-6г = 0. 463. Зх-2у — 3=0. 464. хД-61/Д-=	466. Д'(8, -2, 0). 467. Д'(1, 2, 12).
468. Д'(-1, 3, 2). 469.	==^_—?- = £_1. 470.	* = JL = JL 471.
7	3	0—1	З.ч —26	2/
554
£—1 = -X ==^±L. 472. —11Л-+17//+19г —10 = 0. 473.	__
13	3/	58	u	i	4	~~
<s 1 4
=——• 474. —7х + 8у+2г-{-23 = 0. 480. Круговой цилиндр, /? — 3, с осью
Оу. 481. Гиперболический цилиндр с образующими, параллельными оси Ох. 482. Параболический цилиндр с образующими, параллельными оси Ох, направленной в отрицательную сторону оси Ог. 483. Пара плоскостей х — ± г, пересекающихся по осн Оу. 484. Гиперболический цилиндр с образующими, параллельными оси Оу. 485. Параболический цилиндр (г 4- 2)2 = 2 (х — 1). 486. Эллиптический цилиндр А А +	~ 1  487. Круговой цилиндр, ось которого совпадает с прямой
j Л_АА = 1
х = 0, р = 2. 488. Гипербола. 9	4	’ 489. (х —1)24- (г-|- 1J-- 9. 490.
I г-0.
Эллипс. 494. (х-1)2 + (у+1)'2+(г+1)г = 27.	495. х2 +(у-4)2 +г2-9. 496.
(х-4)2 + (|/-2)2 + (г-[-2)2 = 38.	497. (х + 2)2-|- (у-4)2 + (г-5)2- 81.	498.
С (1, —2, 2), R = 4. 503. При х = 0 н у = 0 — гиперболы с действительной осью Оу, при z=h — эллипсы. 504. Гиперболы с действительной осью Ог при х = 0 и у = 0, эллипсы при z — h ( Л |^2). 505. При х = 0 и у = 0 —пара прямых, проходящих через начало координат, при г = 0 —точка, при г = Л =40 —эллипсы. 506. Параболы, направленные в положительную сторону оси Ог при х = 0 и у = 0, эллипсы —при г = /|>0, точка —при г = 0. 507. При у = 0--парабола, направленная в положительную сторону оси Ог, при х = 0 —парабола, направленная в отрицательную сторону оси Ог, при г = 0 —пара прямых, при г —/гьД 9^0 — гиперболы с действительной осью, параллельной оси Ох, при h > 0 и оси Оу при /г<0. 508. Конус вращения вокруг оси Ог с вершиной в точке (0, 0, 1). 509. Эллиптический параболоид, направленный в отрицательную сторону оси Ох с вершиной в точке (1, 0, 0). 510. Двуполостный гиперболоид вращения вокруг оси Ох. 511. Однополостный гиперболоид вращения вокруг оси Оу. 515. k = tg а, где а —угол наклона образующих к плоскости хОу. 516. а) Поверхность образо-1
вана вращением линии ' у2 вокруг оси Ог. б) Поверхность образована во-[ х = 0
круг оси Ог синусоиды, идущей вдоль этой оси. 519. Эллипсоид с центром в точке (—2, 1, 0). 521. Параболоид вращения с вершиной в точке ( — 1, 1, —2). 522. Afj. (2, —3, 0). Л12 (0, 0, 2). 523.	(4, —3, 2), Л42(12, 3, 6). 525. Эллипс
f A_zA|2 л У2 = 1	> 1 о 2 \
{	4	1 г 526. (1, —1, 1), (4, 4, —3). 527. а--2,	, -	).
537. 2х4 —5х2—10. 538. —35, —16, —7, 20. 539. 1, НЛ - _А_
1 — х ’	2 + х ’	1 + х ’
J-ti. 540. я, у, 0. 541. х2 — 5x4-6. 544. (—со, 4.00). 545. [ — 1, 2].
546. (—оо, —2), (2, +оо). 547. (—со, —1) (—1, 1) (1, 4-сс). 548. [1, 4]. 549. (—со, 1), (1, 4-ос). 550. [2/г.тт, (2/г-J- 1) л], где п~6, ± 1, J. 2,_... 551. [—4, 4]. 552. (—со, 4-сс). 553. [1, 4]. 556. а) четная, б) четная, в) нечетная, г) ни чет-
Л
ная, ни нечетная. 557. а) Период у, б) период л, в) период 2л, г) непериодическая. 592.	=	593-	(	1 , 594.	601. ’5- 602'
0,01. 603. со. 604. 0. 605. 1. 606. А-. 607. 0. 608. 1. 609. -А 610. -. 611. 1. 630. 0. 631. оо. 632. 0. 633. -А 634. 1. 635. А 636. 0. 637. 1. 638.	.
5	64	0
639.	. 640. со. 641. со. 642. 0. 643. 0 при х—Н~со, со при х—— со. 644. 0.
о
555
645. 0 . 652. —2. 653. 10 . 654. A. 655. < 656. & . 657. 4. 658. -A G59. b	4	к	2
АкД 660. —А. 661. 1. 662. 4. 663. ---------------—. 664. 0. 665. 0 при л — -Осо, +'
За2	2	2 Г л-
1	2	1
при х—— со. 666.	. 667. 1. 668. п . 609. —;-------------------. 670. 12. 671. —2. 672.
2	3	3 , л.г
3	2	3	1
0-. 673. -3 . 674. 0. 675. 0. 676. —	. 677. с . 678. 0. 679. сс. 680. со. 681.
5	2 1. 682. 2. 683. 0. 684. 1. 687.	. 688.	. 689. n = m; оо, если п<т. 691. ' . 692. | 2- 693.	Ct р-. 690. 0, если п > т; 1, если 2 cos а. 694.	А , ^95, с.
696. “ . 697. 1. 698. А. 699. оо. 703. с. 704. с-’	’. 705. 1. 706. е. 707. е. 708.
723. С = 1, k = 2. 724. С = тгг-я, * = 1- 725. С = — * , fe = 3. 726. С= 1, Л = 2. 2 1п 2 ’	4 ’
741. А.	742. cos3 а. 743. 0. 744. -U.	745. 0. 746. А.	747. 2	. 748. -*	. 749.
4	|3	2	3	3
>П-. 750.	с. 751. 1. 752. 2. 753. А.	754. — .	755. 0. 756. 1	. 757. ““	. 758. m
п	2 п	а р-
759. 2/ . 760. In “ . 761.	762. In2 а. 763. —	. 764. я. 765. 1. 766. с.
b	b	р	6
767. 0. 768. 1. 769. -А_. 770. е |> . 771. cctgQ. 772. А 773. е. 774. 2 775. 1с	с	5
2	1
•л-. 776. 1. 777.	. 783. В точке х = 0 —устранимый разрыв; функция у-
О	э
—— при л-=4 0,
= <^ л- г	непрерывна в точке л- = 0. 784. В точке х=0— устранимый
[ 1 при х = 0
( х3 +1 ПРИ х
разрыв; функция у = {	непрерывна в точке х = 0. 785. В точке
[	1 при л- = 0
х=1 разрыв первого рода: lim y=l, lim у =—1. 786. В точке х=1 устрани-
ла 1ф л-1-
мый разрыв: Нщу = .я	787. В точке х = 0 разрыв первого рода: lim y = Ci,
л—*1	2	л-^О-р
lim у=1. 788. В точке х = 0 разрыв первого рода: lim y=l, lim у ——1. 789.
л'-0—	л->0ф	л—>0 —
В точках х = 0, х=1, х = — 1 разрыв второго рода: lim r/ = 4-co, lim у = л-»0+	л-»0 —
= — со, lim у = — со, lim у=ф.со, lim у = —со, lim г/=ф-со. 790.
Л-.1ф	Л—>1—	Л—>—1~Н	л—>—1 —
В точке х=6 разрыв второго рода: lim у —-[-со, lim у = —со, в точке
Л' —» 6	х —> 6 —
х = —G устранимый разрыв; функция у =
Fx + 15-З	„
х2-36 ПРИ
1
— при х =— о
непре-
рывна в точке х = — 6. 796. 10х4 — 9л'2-|-4.	797. 7х2 — 5* + 6. 798. 2ах+Ь.
799. /7х'!1 + Зпх2. 800.------А— + 2 . 801. 1 -1 “// +16 [х12 ]''х. 802.
7х2 j х2 х3
о ГлЧ—j--------------------— . 803. 111 х. 804. х2ех. 805. 2cv sin х. 806.
2	|/ х х |/ х № р х
556
x'J
sin2 х
+ 3№ctt5 х.
807. —7+==- +3* In 3 aresin х. 808. 1-(-2г aretg v. ) 1 — x!
2x -• sin v cos ,r
2x | x cos- x
10 (x2-I-I)9 2x. 820.
824. —--------------.
sin x COS X
— 4 cos3 x sin x.
810.
2ctx + b
(ax- + bx -1- <:+
— 4ros v In 4 sin
2x + 3
3( 825.
828.
+ 3x + 4 •
831.
811.
821.
826.
2v arccos л- — J I
822. 3cos3x. 823. -------
cos-
2,v
829 ------------------
cos2 (.1-2-1-1) •
„„„ 2 aresin x
830.
819.
827.
835.
839.
2(l+x) I X ’ ’ J ex 836.		2(x+ | x)' 1	J 1 - X2 -. 837. — ?'<• -	
2	2J	1+arcsinx J 1 - - x2		
COS'‘A’ 840	-	(x2+ 1) —X2 In X	841.	COS2 X
sin x ‘	x(x2-|-l)| x2 + l		2 J x
. 843.	t«3x. 844. - C	845.	—c
838. -
sh x — x eh x
x- sh
x + 2x ch x.
849.
(x+ 1)2	1 + x2 '
4 sh x ch x. 848.
834.
sill (In ,r).
842.
846.
847.
850.
851.
2sh v In 2 ch x.
859.
sin x
860.
4‘
- 1 In 4 
861.
5(1 + 1' 1 +.+)1 •
862.
8x tg3 (x2
cos- (X2 -
863.
864.
2 tg22x (3 — 2 sin2 2x).
865.
sin2 x [3 (1 + 2Л'2) cos a- — 2x  2Л'“ sin x In 2] u+^
866.
869.
871.
873.
---—,	out. 	. | 1—x'2vJ	I' X2 + <12
-----_____ .e.X....___... 870. ]!—e-x aresin | 1—e-x -----2............. l-'+THr+TI-x)2
1?’1,Р л' [4 (I + tgx) sin x cos3 x — 1]
2 (1 tg x)3' 2 cos2 x
/5 (x8 + x3 + x2 + 1)	o„„	1
«1он-1	I (x2 + 3x+ I)3
X ch (x2 + 2x+ 1) (2x + 2). 878. 4' !P r In 4  3 c+x • sh
868.
3 cos 3x (2 sin2 Зх -I 3 cos2 3x)
sin4 3x 2	, 2x + 4
872--(7WHsrTT-
2
874.	. a—r-7----•	875-
sin 2x In tg x
877.	4 sh3 (x2-;- 2x+ 1) X
886. —^-5—. 887. — etgx. 888.
cos2 2x	4(x2 + 3x+l)
„	2 /2
890. ------ . —
(I—x2)| x2 + l l/(x2 + l)xf 2x I sin2 x I 3 (a2	1)
891.	(x2 + I)20 (x3 + I)5 i
+ 3x“ 3 Ctg4 S93, еЛ'2
2x	24x2
+(+ + 4T • 889‘ < л”!	11 (,v; 1 > •
6 I 20* 1 _ 15xj-	892.
X + x2 + l + x4-l . '
/	3	.
tg3 x aresin x i 2x + -+77.^7.+
_________1_________
I 1—x2 aresin x
894. ---Ц--2—.	895. —-------. 896.
cosx + sinx	2-|-3cosx л
897.
557
Xх (1 4-In x). 898. r;nx f^+cos X In Д 899. (cos x)arctg x	 arctg?).
». ' 90l. ;
v !	x2 + 3	2 I x .	L ‘~л
3
905. y. 906.
x,——г	1	Inarcctgxl
’ arCtgA'|x-(l-f-x2)arcctgx x2 J’
+ !1£*--£^1 902.
pl—x2 J
4 In 2. 907. — -;2	908. 1. 909. 0. 912. 7x-«/-2=O. 913. x — y — 1=0. 914.
5	2
x-1-31/—10 = 0. 915. Касательная x-[-y — 4=0, нормаль x — zy = 0. 910. Касательная 2x —1/-|-2 —4 =0, нормаль x-|-2{/—4 —=0. 917. arctgяк 26'34'.
918.	 919- f2’ 5)- 922‘ 2- 923-. t, = £z- 924- Юслфлс. 927. -	928‘
929. 2tg2 A In 2 • 2 tg x —^5—. 930. sin^g^ . 931. x2(l b31nx)rfx.
1 1-As	C0!i A I' l + sin2x
1	/ • •	, - dx
932. -5 ctg4 (x2-j-x3) • -.	.;—- (3x2-|-2x) dx. 933. - 2 cos | x sin J x—=—.
' sm2 (x3y- x2) v	2 | x
934. ------------=-	935.
2(l-|-x2)| iarctg x
J^!?4£rfx.	936.
(1+x2)3’’2
2 sin x dx
3 >' 2 -}- cos x '
937. — p	938.	(2xafctgx — 1) dx.	945.	2,02. 946. 2,96. 947.	-0,1. 948.
0,485. 954. -----X .955. —.	956.------Ц=.957.	14.
(l--x2)| 1- x2 (a- I)1	(x21) | x2 + 1	0+*)’
.958. 0. 959. 120(3x2-4-1). 960.-------. 961. 5! = 120. 962. — 4 (2x2 cos 2x ;
16x’! | x
J- 6x sin 2x — 3 cos 2x). 963. 241nx-|-50.
964. z/'"> =cos [x + nyj . 965. y'n) =
=(— l)"Ji (n—1)! х~". 966. y""=n\ 967. i/f"’ = (— 1)	2 ’’ 2я-1 sin 2x-j-(n— 1)”
m
здесь
11 + I ооозначает целую часть числа	—т—
968. у"> =
2 • п\
(l-x)^i •
909. 14 м/сек2. 974.
— Зх2//-]- 6xi/2-|-3	2х3у — 2хул + у
х3 — &х2у -j- 15z/2 '	' х*х21/2 + х
12i/-’(«/2+1) 97b> (3xi/2 + 2)3	. 977.	978. 4x- 31/ - 1 =0. 979. 7,1 - 32	‘	(7-	УУ1 1 Й2 ~ 1	 980. yyi =
= p(x + xL). 983.	dy =	. 984. dy = - 1. 985. dy = dx 1—2/3	dx	2 з^Г-	986. d2y = dx2
/24-/-1	~. 987.			1	.	988. d2,J		2
о2' (1 — /2) | I — /2	dx2 at sin31	dx2 e’ (cos t — sin /)3
989. Касательная z/ = lA3 x + a.2-----, нормаль y =-----------—^4—990,
\	|'з Г  Кз згз
М (2, 1) при /=1. 995-5= 1. 996. 0,947 < arctg 1,5 < 1,025. 997. 5=^-. 1001. Р(х) = (х-1)4 + 2(х-1)3 + 5(х-1) + 2.	1002. Р (х)=х«-6х6 + 21х*-
— 44л3 + 63г-2-54л-+ 9.	1003.	’ + 4	*2 +Л *3~ ГпЪ *4-	Ю04.
4 о It) I/O
1 [,	1 -х~2\ , 1 -3/Л--2'2	1-3-5 х-2,3 , 1 . 3 - 5 - 7 , Ч— 2 «]
721	; + 2~ [~г~] - ГТ76 —; + ГТГ6-8' —; ]• 1008-
558
1 / х V 1
0,0002.1009. max !<5(х).' = max (уур-) < (ц  10,°- тах	5 (л) ,' =
о=ОС.*~	°'	0=0^5
-	1'’.«'<.Г7Тз<»Л1;
О X х -С 2
1	2	3	1
Х±^1,22. 1016. г. . 1017.	1018. 0.1019.0.1020.	.1021. -2.
4	3	2	4
1022.	— 2. 1026. 0. 1027. 0. 1028. 0. 1029. у. 1030. — со. 1034. 1. 1035. 1.
1
1036.	е. 1037. 1. 1038. е е . 1044. х = 2, х = —2, у = х при х-* + оо. 1045. у = = -5-х—1 при х—+ со и у = — '^j-x—1 ПРИ —СУ'- Ю46. х=.^ — 3, !/==1 при х—» ± со. 1047.	х~ 1,	у = 2х при х — 1 со. 1048. х — 0 при х—>0—. 1049.	х =
= —1 при х------------------------------------------------1-р,	// —0 при х—* + оо. 1050. у = 0 при х—	। со. 1051.	у =
= х + I при х -	со. 1053. Убывает при — оэ < х < 0, возрастает	при 0 < х<	; со.
1054.	Возрастает при	— сс<х< —2 и 1<х< + со, убывает	при —2 < х	< 1.
1055.	Убывает при —со < х < 1, возрастает при 1- с .	1056.
Возрастает па всей оси Ох. 1060. Л4=/(0) = 1, ш = /(1)=0. 1061. щ — [ (—I) = . тт	1
= In I 2 — , . 1062. т = [(—1) = , .	1063. Экстремумов пег. 1064. Л1 ==
4	41'
== /(1 — У 19) =а — 14, in (1 + Г 19) =а 5,5. 1069. min / (х) ^=f (И) — 2, max X г 1-1.3]	1-2. 11
X f (х) =1 (—21— 11- 1070. min / (х) -~=f (3) — — ° max f (х) = f (0) — 1. 1071. 1-1.31	IJ 1-1,3]
min f (x) = /((>)= 1,	max /(x) = /(—2) = 3.	1072. 2 cm. 1073. При
[-2,1]	[-2,1]
AC — OD. 1074. 33 + 33. 1075.	1076. 3 |-3 r2.	1077. 2/?« (квадрл).
1078. Равнобедренный боковая сторона-----------X 1079. 6 = ——, / ) '.2 ----
2+1 2.	| 3	J 3
3 /' Г	г • / 2 
1080. r = /i=-=’|/ n-. 1081. a==2n, 1 — 1/ , =» 72X 1082. AB=- =40 cm. 1083.
а У2 , b ]•' 2 .
'	4 '
~ U \	3 :
= d
-4- 1' ' r a
1084. h(x) =—----------1----——: max и (x) = и (2) = - , min //(+) =
a —ex <z -|-ex ’ [-a, p]	3	]2. 2]
$ .	1085. min ti (x) = и (— 2), max и (x) = и (2).	1086. /141 =
4	[-2,2]	1-2.2]
1089. xx = 0, x2=l, x3 = 2. 1090. xk = (2k + 1) -- (J.: = 0, ± 1,
8
± 2, ...). 1091. x1 = — 2 + e3
1092. Xi=—Lr x.,
12
-----!_ 1093. ,v1 = —4. 1100. I 2
y=0 —горизонтальная асимптота при x —— oo; tn —I (—3)=«— 1; точки перегиба Ои3±|'3. 1101. Асимптоты х.^— 1, у = 0; tn == f (0) = 1; ючек перегиба ней 1102. (— со, +со); lim у (х) — —ос; четная; tn — у (‘У}— 2, М=у(_': 1)—	;
при х=±-4= —перегиб. 1103.	(—ос,	0) (0, + сс); Inn у(х)^—оо,
lim	?с; ?/—0 при х1==2, х.,.з =—1 + ( 3 ; .41 =у (1) =2; прпх = —
х — 0 -
—1'2—ючка перегиба. 1104. (-со, -1), (-1, +оо); lim y(v)=±co, '	'	х — _L о
539
lim y(x)=± co; асимптоты x —1 и y = x — 3; m — y (0) = 0, M = y(—4) = X - — 1 I 13
— — 9 2?; точек перегиба нет. 1105. (— оо, —2) (—2, 2) (2, 4~со) четная; асимптоты х-- - 2 и у =— Г, т = у (0) = 2; точек перегиба нет. 1106. (—со, 2) (2, 4-°°)асимп-готы х = 2 и у=\; при х = 0 (/= 1 и при у = 0 х =—2; т = у (2) = 0; при х = --—4 —точка перегиба. 1107. (—оо, +оо); нечетная; lim t/(x)=±cc;
X -♦ 4* ОО
у — х — асимптота; /« = «/(!)=—ул2 ; М — у(—i) = y'2; точки перегиба (—J/~3 ,0), (0, 0); (| 3 , О). 1108. (—оо, +оо); lim у(х) = 4- оо; k = 0, b = оо; кри-i = + оо
вая вогнута вниз при больших х; при х = 0 z/ = Iri 2 и у = 0 при х=1; т — 1/(1)-^0; точки перегиба —(2, In 2), (0, In 2). 1109. (—оо, 4~со); lim у(х)-
X I со
— +«>; k = :o; кривая вогнута вверх при больших х; при x = Qy = —4 и у = 0 при *1 = - 2, х.> = 1; т =у (0)=у (-1) = -4; Л1 = у ?-) = - “. 1110. (- со, со); нечетная; lim //(х)=±оо; асимптоты у = х-\-Л при х—.4-00 и у —-
— х— 2 при х —— со; точек экстремума нет; перегиб в точке (0, 0). 1111. [—l,lj;
нечетная; т = у\ — ~	11	= !/ J “ 0,68; перегиб в точке
(0, 0). 1112. (—со, 4-сс); четная; lim i/(x) = 0; у=0—асимптота; при х —0 X —> Ч/со I
у — 0; т — у(0) = 0, Л4 = «/(±1) = е 3; при хг, ,с='з, 2 имеется перегиб. 1115. (’а, 0), (О, ' b) — вершины эллипса. 1116. К = ^Д-.	1117. хЛ- = — ”-+ 2йл
(/г — 0, ± 1, -у 2, ...). Ц18.	. 1120. 7? = Ц-1. 1121.	=
v ’	За sm 2/	2	2
1122- а) 6,x| I X ' 3	:	1/1 -, 6) at ;, в) 4 | sin 2 . 7	7„	2	1125. a) xc = yc = 2; 6) Y = Д + 5	1
4-37: . изо. _ 4	12X). x* + C. 1131. 9	л-»-	x~\-C. 1132. -- 4-C. 6	X
1133.	1 — 2 In 1 X	x,+C.	1134. y + 2x	-l-C.	1135. —1 —In x +C. 1136. x	11
2 . , ,	1	, X2 3 n X 1	3 Л 1 6	+ C. 1137. x + arctg x4-	9 С. Ц38.	+ arctg x + C. 1139.
2	/ - 4~C. 1140.	2	' - 3 x |' x +x-|-C. 1141.	j у 1 %	13	| X () x~i x -| C.
4	24 И42. -5x, x-]7	x ' (/ X5 + у >/ x:i + C.	x2 2 /- -- H43‘	2 ~ 34'x3+x+-C. 1144.
arcsin x -[ -In x'4- Г 1	+T2 ; + C. 1145. 1 x2 1 5	- - , 6 .. .0- , 18	, x2 , ,, -V + 7 A- |- X r- 13 X“ t X + 2 4- C .
9 .V	1	х
1146.	.\ +С.	1147. ,---v-r + C.	1148. arctg—4- С. 1149.
In2	In a -'г 1	j 7	]' 7
arctg—До—In | х -4 [ 5 4-х2 ,4-С- 1150. arcsin -Д—УС. 1151. 2 arcsin —— 4-
|-5 Г 5	J/7 Т	|3
~Г х2 J х 4-С. 1152. 2с’А'4-arctgх4-С. 1153. — 2 cos х-3 sin х4-С. 1154. tgx — — etgx-j С. 1155. —2cosx4~C. 1156. tgx-]-C. 1157. х2 — ctgx4 -С. 1158.sinx |-4-cos х4-tg х4-С. 1159. -ytgx+ g x4-C. 1160. —2 cos x'4-3 v'x + C. 1161. e* —
560
— х + С. 1162. * + ^ + С. 1163. tg х — х-РС. 1167. In ' sin.v+r'sin-’.v+3 -pc.
1168.	+	1169. 2 Гl-x + x2+C. 1170. A'x+ C. 1171. In (1-psin2 x)-pc.
1172. earcsill-v + C. 1173. yln2;x3+l'+C. 1174. ’ arctgx2-pC. 1175. *---x2p
-P 4x —3 In ; x-p2 |-pC. 1176.	(In x)3-pIn x-pC. 1177. ln(tgx)-pC.	Ц78.
(tg x)2-pln cos x +C. 1179. arcsin c- -pC. 1180. — 2[/cosx-pC. 1186.	_p
pC. 1187. 2 /З-psin x-pC. 1188.— ’ cos3xp-C. 1189. I ex3-'rC. 1190. —-I-3	3	cos x
+ c. 1191. 3 sin *+C. 1192. 1 йа"' +4а' + 3 + С. 1193. -U arctg ^-5. _| C. 1194. 3	2	|. 6	2
-7 ъ- + с- П95. 2e/x -l-C. 1196.	+	1197. -2 cos /х’-(-C. 1198.
In 2	In 3	'
3 In l л-< | v';' 2 )-'rC.	1199. 2c 2 +C.	1200.	|/(2x*-’3)3-pC.	1201.
— *- к 7 — x6 + C. 1202. hi ' x—5 rPC. 1203.	[ (x — 1)3 + C. 1204. - - |- (4—3x)3-r
3	ЗУ
+ c. 1205. 4F(x4+1)2 + C.	1206.	*- sin (x2 + 5) + C. 1207. In (el-P l)-pC.
О	2
1208.	0(In j x )3 -6 ИпТО" + c •	1209.	V КЗх2- 2 +c-	12Ю.
3	3
9	________ 1
J (ardg<)3 -pC. 1211.	— —------—;-C.	1214. xlnJxJ-x-pC. 1215.
3	1П j sin X I
x—p~pC. 1216. xarctgx—g In (1-px2)-pC.	1217. x sin x-pcos x-pC.
1218. * ' - arctg x - * + C. 1219. — x cig x-pln j sin x |-pC. 1220. —ln + 1
2	2	X
9	/	2 \	xn'] 1 Г	1	1
-\-C. 1221. ЗСх3 In 1 x „ +C. 1222. —-— In | x--------— ИС. 1223‘
1	3	\ 1 1	3 ) '	n +1 | 1	«+1 J
— <<	--1- etg x''. + C. 1224. x arcsin x+01—x2+C. 1226. — e~-v (x2-|-2x-|-2) i •
2	\ sin~ x	j
+ C. 1227. —x2 cos x-|-2x sin x + 2 cos х + С. 1228. x2 In2 | x [ — x2 In j x I г
Л-
+ ! X2 + C. 1230. ’ (xj/'l+x2 + ln !x+Kl +x2I) + C. 1231. e-v(sinx-cosx)+
-PC. 1232. g (x /1 — x2 + arcsin x) + C. 1233. [sin (hi x)-|-cos (In x)]4-C.
1234. C-(2-sin 2x-cos 2x)+C. 1235. earcsi11 A (x +[О — x2)+C. 1237. /„ -o	2
1	.	n ,	,	, sin'1 1 x cos x n— 1 ,
= __X	1238. /„ =------------+ ^-/,.-2-	1г41.
Injx —7;~pC. 1242. -in ,3-xl+C. 1243. ‘ ln|l+5x|+C- 1244. -07^7 d+ D	о <3 X 4)
+ c- щстуК !«’•
1248. I ln|3x2 + 2x + 5H-— - arctg ^±-L|-C. 1249. \ In j 2x2 + 2x +3 I 4-3	1	3 | 14	[14	4
j--?— arctg Ц-4-C.	1250.	5 In 1 8x2+x +1 ,-—arctg --|- C.
2 [/5 C 5	1(1 '	8 | 31 к 31
561
1252.
2х— 1
^q^w + arctg(x+l) + C.
1253.
, 26	, 2х —3 , „
т- —-7= aretg —7T-Z- + С.
3J/3	J/3
13х —24
3 (х2 — 3%4-3)
1255. -g-ln;xj + -2 In j х - 2 [+yin . * + 3 ; + С. 1256.
Л„- + + 4х-|-2 In ' х ' + 5 In ’ х — 2 J — 3 In х + 2 |-[-С. 1258. О Z
1___________4
х + 2 ~ х + 4
+21П|^1 + С- 1259.3x + y|T + 51n:x + 2i+C. 1260. -	- 2—-ly 4-
+ 3 In I—LJ + С. 1263.	*-1п(х2 + 2)--L-. aretg-Лз -	-
|х —1 |	9	9j/2 ь j 2	3(х- 1)
— у 1п|х-1 1 + С- 1264.
3	1	1
—+ у In (х24-1) — 2 aretg x-f-C. 1265. - у +
3	4 X — 9	1	9 V I 1
•]—х- In । x2 — 4x '- 13 i + a aretg —---------------j-C. 1267. ——,—F 2 In ! x — 1 i ————
Z	о	о	X — 1	‘	Л *• -|- I
-ln(x2+l) + arctgx-|-C. 1268.	.	1	  у aretg (x 1) + C. 1269. ~ ДгТ +
Л " -f- ZX -j- -	Хл - j- 1
aretg x-j-C.
1270.
-3W2)+C- I27L arctgx-3^+ !+C.	1276.
2	5tg	X 2	+ 4 1	. X tg 2 “	1 9	q	2 tg	'v — 1 1	1
„-aretg				'rC. 1277. Л In			4-C. 1278.	aretg 		-—-4-c.
3	0		tg o- 4-	1 2	1 15	1	15
1279.	—	In \ 3 4-cos x 3	_JL_ 2 4- COS X 1	-c.	1280.	1 ,  2 (sm x	— cos x) —
---F= In I tg , ' -I-. I-I-C. 1285. — 1 cos5 x 4Д-eos’x 4-C. 1286. sin3 x—
2 V' 2 I \ “	° Л	5	7	3
2	1	.1
— ,-siH3 x  _ sin’x-j-C. 1287. cos x —2 aretg (cos x) 4-C.	1288. — sinx-t-
□	/	4
. 3 , | 2 sin x — 1 -I--tn----------
^16	| 2 sin x 4-1
4-C.
1289.	aretg 2ii^ + C. 1290. 1 In I 4^“i4 | + C
2 1'3 ГЗ	lb I4tgx-|-1R
1292. —6 cos— у cos 7*-|-C. 1293. ' sin 3x J- ? sin 1 lx-|-C. 1294. 3 sin *-
1 Z I 1Z	О	ZZ	О
— rsin t-|-C. 1295. J, cos 7x—J cos 13x4-C. 1296. —у cos3x4~4 cosx-r 5	6	1	14	26	‘	6	1 4
4” 20 cos 5* + 77
1	.	, 2 cos’x cos9 x ,	5 5 ———
1298.	— 5- cos1 x -|——у------g----F^‘	1299. —- у sin8 x
5 .  _______5  _______________ 3
— -a-| sin18 x -}-k_d j' sin28 x 4-C. 1300. '-cos ° x4-3 cos
У	Zo	0
!
x + C. 1302. In , tgx; —
•-^-4—4-C. 1303. SCfgx-bC. 1304.
2 sm2 x 1	‘
л 1 I---- , z'	л , sin 2x , y.
4	tg x --C. 1306.	•
5	. sin 2x . sin 4x , „
1307. -x4-^—+ ~^- + C. 1308. о 4	32
1	1	X
x— sin 2x4-д-g sin 4x-j-C. 1309.	—
sin 2x sin 4x sin 6x „ . „
~64----------6Г- + Л9^ + С- 13I0‘
5
16
x 4- sin 2x — 4 sin3 2x 4- Д sin 4x -4 G . 4	48	64
1312. x —2 I'x 4-2 In x 4-1)4-^.	1313.	6 J x — 6 aretg x-j-С.	1314.
4|'x5-x4-y v'x3'-2 r'x 4-4|/T-41n((/T4-l)4-C.	1316.	2 J/1x-4-
562
I-In
Fh7-1
J '14-*4-1
C. 1317.-g - (3x-f-4)—-% (3x-f-4)2'3	3x4-4—in j|/'3x4-4 4~
4
>4-l!4-C.	1318.	..~ 4~C.	1319. -c -
k71	j/ ] - x2.	8.14- x
-U In ! 10/4-34-2 1'5 j7'5л24-2x4-2 l4-C-
/5
i	fi J- 5v	1
------- aresin —(=3---|-C.	1327.-------—In
F'3	7x	1'5
i ______________ 19	1	3
1328.	-2 |л2х2 - 3л- 4- 5 +	1 x - -4 -j
1	4 v — 3
1325.	——aresin—=------LC.
Г 2	5
x4-54~| 5 j- 7ла4~2л- -i- 5 5x
- -U J 7 2л-2—3л- 4- 5“ I 4-е. 1'2	|
— 4 |ЛЗ-2х-х24-3 aresin-"|1 4-C.	1333. 2 aresin * 4“А~Цг—
1324.
1326.
4-c.
1329.
1334.
V	r	12
____ | C. 1335. z__ K. 1336. .. arevos-
9J9 + л-2	5|-'5-x2	4 x
|' x- — 4 2л'2
1337. In x-J-
4- К %2 4- 5 \ -	~ 4-C.	1338. 2
|/л-24-5	3
1 ln *+i' 2£+*2) j/2	| x24-2
+ c. 1340.
2x4-1
I l-J-xg-x2
4-C.	1339. In I' I 4-л-2 ’—
4 I 15
x |- 15-{-2 Г 4x2-;-1
x \ 15—2 I z4x2 4-1
4-C. 1342.
7 • 12 12 sin x
sin 2x
~8~
26
26sin7'x4-C. 1343. In sin 4x sin 6л sin 8x . ПТГ ' IF '7Г1 c
1346.	2c1 * 4-C.
1344. 1 — X —
16 I 16-L.r2
1347.	2 In (л-2 4-2)4-
4-C, 1345.
4- — aretg-— 4-—L_ 4-C. 1348.	-	_ S^'4-С.	1349.
|'2 I 2	x2-H2	3	5	/
(X* 4-Л41П x-^-x4 C.	1350.	’ (x 4-6) I' x2 — 4x 4- Г +13 In 1 х-2-Н
\ 4	/	1 o	Z
4-1 72-4x4-1 4 C.1351. 2 In ; л-—1 14-ln ] x2 + x4-l 4-C. 1352. In I 1-i-tg * I 4-C.
1353. aretg x In aretg x ’ — aretg x-f-C-
- 1	I	I -J	I	2л'-Н3
1'2 I	x-Hl
19	s	’	‘
1357. — Fx124-3x3	_ 4X4
D
4-c. 1356. jJ
1_
- 12xl24-6 In
1354.	,	4-C.	1355.
I 1 4-Л"'
x 4- ‘ sin 2x — sin3 2x 4- Д sin 4x 4~ C  1 4	48	1 ()4
1
xl2+l X.
+ c. 1358.
5
sin7 A'

1359. -(54-x)l/'^X4-6arctgl/ J-X-4-C.	1360. InXlX9
J 1 -4- X	f 1 -f- X
-V x~ H—4-c.	1361. Х*ХС'
X
4	6
1365. a) 6	10; 6) 4 I ?	;
-|-(2]X— 1). 1371. 0. 1372.	.
О	Z
— aretg 2) = aretg 1 . 1375. "'. 1377.
75 7	 I	6
1385. 2 —In 2. 1386. £. 1387. aretg, 6
1363. а) первый; б) второй; в) первый, в) 0 <	1 .	1369. ' .	1370.
7	4
1373. А (7 1 4 - 12).	1374. (aretg 3 -
р- 1378. --—1 =0,273. 1384. 7 4-2U12. О	Я,
—у. 1388. In 2. 1389.	1390.
4	3J.3
563
о	-г ( 9 — 41Z3 ) i 3
а) 0; б) 0; в) 2; г) 8.	1393. I—.	1394.	---—+ * In Q .	13-V,
2 In 2 — ’’ . 139G. 3 In 3
4
1400.
35
1404. a) /s — 128 ,rT’
-2. 1397.
л
12
1403. /„ =
-1. 1398. л3 -6.T.
(/? — 1)(«- -3)(/? — 5) ... 1 n (n — 2) (n--4) ... 2
1399. —
J)
при четном /?.
0	при нечетном >>
/и^0.	1406. !!-!-•?. л. 1408. -6,1389. 1411).
11	48	64
—6,0656. 1411. 0,6941; > 63 s: ,'< 0,002.	141,3. а) —3,1399;	б)—3,140,
Зо4
1414. 0,157. 1415. 2,590. 1419. 1. 1420.	л2. 1421. Расходится. 1422.
1427. Сходится. 1428. Расходится. 1429. Сходится. 1430. Расходится. 1431. Ра.« I 3
ходится. 1434. Расходится. 1435. ——.	1436. Расходится. 1437. Расходится.
1441. Сходится. 1442. Расходится. 1443. Расходится. 1444. Сходится. 1448. 2.
1449. 32. 1450.	. 1451. 3-е. 1452. 4 р2. 1453.	.
3	3	9
1454. ло/>. 1455. ли2. 1456. л (2а- -Ь'-]. 1459. 0 ля2. 1460. л- 1461.
23 nW. 1462. гиГ-. 1467. 8а.	1468. 1 аТ-. 1469.	1 + In .	1470.
In (2+ 1Л3 )•	1471. а | 2л J 16л2 + Г + ? In (4л| '16л2-I-Г) | •	1472.
)<2 ц(е;/“- 1). 1473. 8«. 1474. a sh 1	1,175а. 1475. Л", 1478.	. 1479. 3 ла-1'
1480. 38,4л. 1481. '..-(А 1484. 3 ла2 (о J- 5 — 8). 1485. 2л [| 2 -f-In (| 2 + 1)]
,lrw, с ,>	2либ .	| а2 — Ь-
1486.	2ло--;—-—arcsin е, где е —------------------эксцентриситет эллипс;,.
1487. 34 ла2. 1490. г’07Ч-^:. 1491.		л' —л'[ + (s'n м/2 —sin co/j). 1493. 91 (Г5 <?,>/<.	
1494. 1,8 дж.	.	,,	ab- 1496.	Ма =	п- ,	М а	2	’	i=02'.	1497.	J	, Л4и = .л,	2 .
л	4а	4Ь	5	ab‘2
т] = _ . 1498. О	?==3л’ ^=3л'	1499. g = ла, 1] = g a.	1501. у - kJ -
О 0 1 = 9,81v 2 н.	6/г2 1502. " m = 3270/>/i2	h. 1503. -i—~ 6	: III  IO6 и. 1505.
1) 123 к, 2) 41	а. 1506. -~к. 50л	1507. 1200 In 2,2=s 946	к. 1512. - 3:
Й5+Т- 1513-	15i4- f\2 ’ ")= ,<2’ /(2, —1) = Г5
1515. 48 ом. 1517. f (х, — у} =	, f (—х, у) = у fl— -!-V-
У1 + х’	I/2 -1-х’	\ х ’ у /
=	—- . 1523. Незамкнутая область 0 < х < р, 0 <</</’
л'(х-г/2)’ f(x,y) ху--у
х-\-у>р. 1524. Вся плоскость, кроме начала координат. 1525. Внешность круга радиуса 1 с центром в начале координат. 1526. Замкнутая область l-j-x — р2:л О, 1 — Л'--SS-0. 1527. Незамкнутая область л' + 1/>0, у х > 0. 1528. Совокупность замкнутых колец: 0 ss л-2 + у- 1, 2s£x2-f-t/2si3, 4 sc №z/2 s£ 5 и т. д.
564
I; 1529. Область	кроме начала координат. 1530. Внутренность парабо-
к лоида г—Л’2-}-//* вместе с границей. 1537. —4. 1539. Точка разрыва (О, 0), в ее К окрестности функция - бесконечно велика. 1540. Линия разрыва х—у в ее В окрестности функция z бесконечно велика. 1541. Поверхность разрыва z' = .v- - Г -ф у2 (конус), в ее окрестности функция и бесконечно велика, 1542. Точка уст-| ранимого разрыва 0(0, 0): чтобы устранить разрыв, надо положить z (0, 0)=-0. Ь'	dz	dz
е 1543. Функция везде непрерывна. 1548.	. = 4ху Зу'2 + Злг®, ^=2л-2-'
. у д2 = „ У ’ ди „ у х- cos- - л- cos-052. f
dz =
di (л-2 + у2)3^
1551.
dv
dy~ '' dz _ _ dy~~~~
du __ dt
1
6л(/. 1549.
dz
dy
ди ds
ЛТ/
11 i-
_ n dz
1550. , — dx
s
-b S~ + t-  (- S2
du dz
+ //•
1553.
dx
- cos - cos
У У
у
4.v } ‘ л* ’
. л' . к sm sm
и х '
-я COS I y-y
xy—x — y
cos
V хулгх-\~У'
du (Mo) |2 dz 2
1555.
sin ‘ sin У
d ’ 1 ’’ = dx . r
1554.

где
X
VX--'гу-
155-. 2.
4
1563.
1558.
1556.
дх
(х — у) (х2 4-4а/-Н/-)
= 0,
du (AI 0) dy
= 0,
ху - р2) (х2 ~ Зр") ’ (х-2^1^ДхУ2 dx ~x‘iy d,dX
1562.
1564.
2 dx.
1565.
——г'У dx-]-x dy—dz .	1566.
У -' -г z' y1 ' J z :
+ (№ sin xyz -\-x3yz cos xyz\ dy cos xyz dz.
(2xy sin xyz -]-x2y2z cos xyz) dx
1570. a «a 0,94; b 4,998;
1572. 4730 Д. 100 cm3.
1577. —4e2 'os2/sin 2/. 1578.
с=я0,75. 1571. 1,6 лги.
.:“<L
2(1+/2)J/j	(I+I-)’
1579. 0. 1580. 2 (sin x)2v (;: etg x -(-In sin ,v). 1581. ~ = 0,
d-z=\. dv 1586. dZ- 1	1582. dZ =-. dx dy x-\-y	cx	dz	ex 4-	 2xcx‘	!585. d^^-, dx	a2y ’ yX in У	1588	d-У _	61
		ex.rftj' dx	ex_ d2y 2(x2 + ij2)		r °X‘ 1587. + (xz-		dx- i	nV' 1591. dz
	dx	x — у ’ dz	у	dx2	(x 1592 {yZ~	~y}:s — 1) dx		1— xyx l ' !) dy 1593 dZ	sin 2x	
dx~~{'	dy x — z		1 -	- xy	dx	sin 2z ’	dy
sin 2 у	sm2xdx-\-sm2ydy 15Q4 zez (z dy-’ry dx) 15gg _
sin 2z ’	sin 2z	01
z2^-xyez
1Ю9.3,+4(,_6г_0,
leoo. * + 49-b-5,	£Z±_tl_Lz!-. 1601. 2»--29-!-0, L_L =
= LL = _£_. 1603. Al, (1,1,0), A4.,(l, —1, 0). 1609.
d2z — X2 d>'z __ d2z __	x
dy1 )'(2xyу2)3 ’ дх dy dydx	]2x-\-y)V2xy -]-y2
d2z____________—y
дх2^ (2x+y) ] '2ху-\-у2'
. 1610. 0. 1611. 105№(/’z°.
1614. +
x у
1615. ev cosz/((rfx)2 — (dy)2) — 2evsin у dx dy. 1616.
565
6((dx)3J-(d//)3). = 108. 1621. В
= 0, в точках
1619. В точке Ро(1; 0) zm;n — — 1- I620- В точке Рп (3, 2) г1Пя..~ точке Pof-Д-, -Д='| гт1п = 3Г3 ' 16221 В т<чке (°. °) гтпЛ: • 3 и/	2
Pb2(0,	1) экстремума нет, в точках Р3. 4 (± 1, 0) zmax = --
1626. Наибольшее значение г-— 1 на границе круга в точках Plt!>(± 1, 0), на-именьшее значение ?-=—1 на границе круга в точках Р3. 4 (0, ± 1). 1627. Наибольшее значение z — 1.3 па границе в точке Рх (2, —1), наименьшее значение -.=—1 во внутренней точке Л>(1, 1) и в граничной точке Р3 (0, —1). 1628. Наименьшее значение г =—19 на границе в точке Pi (0, 3), наибольшее значение z-=— 1 на границе в точке Р-> (0, 0). 1629, Куб. 1630. xyz, где ,v=z/ = ? = j a.
14	О3 "	1	5	9	I
1634.	,, . 1635. In 9. . 1636. -	. 1637. - . 1638.	. 1639. 9 . 1643.
о	44	44	0	4	4
1	1	2	I/	4	2
\dy f (х, y)dx. 1644. \dy jj f (x, у) dx 4- j dy j f (x, y)dx. 1645.
о	y'4	0	j/	2	и
2	______
11	e 1	a ci — Va't — y*
\dz j f (y, zjdy-^dz j f(y, z)dy. 1646. j' dy j f(x, y)dx-t~
I I	’1 In г	0	ft’
In .
i-	z	2a
a	2a	2a 2a	lx	2
+jdy	[ (x, y) dx -j- j dy j / (x, y) dx. 1647. dx f (x, y) dy+^dx a
й	6 f	b °	1
2 — x	1	№	3	2
X \ / <Л> У) dy- 1648. dx j f (x, г) dz dx \ f (x, г) dz. 1649. n	i)	о	‘i	i>
О	II —//	1.	I-//	lll2 i-y	1	2
\ dy j f (y, z)dz-\-\dy H.V, U dz. 1650. (j dx j / (x, y)dy+\ dx j ?;
—i ft	ii ft	ft i	6i2 ’i
2	2	о 4	D3
X f(x, y) dydx [ (x, y)dy. 1655. -6л2. 1656.	1657.	1658.
Л	______
arctg2 Bcosip	4 nl ’cos2<p
( dtp \ f(pcosq>, p sin if) p dp. 1659. Ij dtp jj f (p cosq), p sin <p)pdp~-
Я 4 coscp	‘л O’
4~	" 4
5л.	_______ л
4 a]co?2cp	4	I /coscp
+ Jj dtp f(p cosip, psinq>)pdp. 1660. ij dtp f (p cos <p, p sin rp) p dp.
Зя b	() b
1661. 2 рЗ stab.	1665. -1 .	1666. 4	е2— 1.	1667. In 3. 1668. 1- +	1669- 4
10 у, 1670. 2а2	. 1671.	1672. 4	1676. 186-|-_ 1677.	1678. 1 О
1679. 16. 1680.	88	1681. 105- Ь Ь 3 '	1682. 2 . 1683. ~. 1684. леи3. 1685	
. n ла3 (б /3 — 5)	z r--------ч
-g-- 1686. ----1689. 4ла(а-/а2 -/?2 ).	1690. 4 J- 3 . 1691.
2л. 1692. 2/2 л. 1693. 2/?2 (л-2). 1694. 8/?2 (Д- + 1 - ]	1699. л7?’.
566
I700- 2/с=£,
= ^(3а2 + 2б2), /а = л/?1	2
1706. 242 у.
nh-R2	16/?3',л
“Т~- 1714. -з-\2-7. 1722-
a	27? sin а
гс —0.	1701. xc— За , yc==
ka2№ .	. kalb
4R sin2 у
2^	. 1702. /ВРрщ —
1703. /ц = /0=^
Id = !
1707.
1708.
1713.
l 1721.
F jra3
I
L ’20'’
1727.
6
Зла3 4 “ ”7»' 'J»?, 1.-1,-^-
л
2 ’
1723.
1728.
4 In 2 - " .
«Ь \	О /
1 7 I -	Л'2“2
. 171о. — .
1724. ур. 1725. “у(Зл-4).
2/2~ла3	21л (2- |/2)
3	' 173°‘	4
(2/г2 4-За2)/оси =/(/—-рр . 1738. /л,
2а	7а'2
1740. t/„^z„ = -О	«JU
pi , 3 (5 1 5
1716.
,-6. 1709. 0.
4о
15
1712. 8“2
9 '
1720. 7-
12-
1726.
1736.
it 1745.
S>; ‘д’З Г	—
-	(1 + 4л2)-’
| 5 In 2.	1746.
24.
1747.
1744.
1748. 2ла'2"’1.
1749.
«>
]. 1750.
Y J а2 4-Ь2 (За2 4- 4л2/>2). 1753.

*
1756. 2-<
1757. —4.
1758. —2 sin 2.
1759. 0.
•\cilfl	4
Ч-. 1754. }
™. «У* >
1755. 0.
—2лаЬ. 1762.
0. 1766.
0. 1767.
ita3
8 ’
1768. —4.
16
1769. 2Г-.
1761.
1775.
3/7’^TT 1776.	1777. бла2.
О
-ТТ- ™-

1778.
19
1779.
2a
*'<) — //(>--------
1780.
x9=yo=O,
(fl 1789.
О

17 , 12’ 0)
25 J
2 ’ В)
6)	1786.
О	«5
К) (5 | '5 —1) '
1790.	1791. 4ла3. 1792. 0. 1793.
О
1. 1784. 4 J 61. 1785. a)
1787. От = -Ц-^, х„ = (/„ = (), г 4'1
(а2//2а2с2 -\-Ь'2с2). 1796.
abc
4
a) xy---C - семеиегво равносторонних концентрических сфер. 1799.
гипербол, 6)
, 6) 5. 1800. -
1811. If.
№ 4- у2 + г- — С2 — семейство 92
1801. 12; возрастает.
а) - 5
1807.	•
J '2 ;	1815. j) 2г, 2) -
; grad у |
1822. 0,Зл/?2//(/?24-2//2). 1824. 24.
л. 1830. А л. 1834. 10
2 . 1840. .’4. 1841. 1. 1842.
5	10о	3
2R3. 1847.0. 1848. 4л/?3/(У?).
1805. — 12Z —/. 1806.
4-/15. 1814. о
I 1820. 0. 1821. 't
Г	64 *
ft nbR2. 1829. т g£	О
| 1839.
«1846.
1855.
1862.
7.Г
1812. arccos —-—	1813.
| 65
1819. * .
6
Л.
О. 1835. 1) 39, 2)
3 л. 1843. 81л.
16 1852.
л.
1860.
1825. - у
) ", 3) f гс, 4) 0.
л/4< 1815. 4.
49л. 1828.
12 1844. *
5
1853. ла3.
— 4
1854. 3 ) 3.
1861.
. а2(3—2а). 1858. —27. 1859. -6
- у . 1865. a) — 2(.v4-t/) k; б) [f0J; в) 2 [(/ — 5ху) i — 5(р2 — л;)/—
567
______ □
— (Зр2 — xz — Зу'2) ft], где р= I- х2-|-у2; г) i —2j-|-ft. 1868. — ^л7^5. 1869. —3.
1870. —	1871. —л. 1872. — 1 л/?". 1873. —2л.	1874. —л. 1875. 0.
4	о
1879. 1) Зх2у-у2 + С, 2) хуг^С. 1880.	-(х2+у2+ z2)-|-С. 1881.	1889.
и (Л7)=х2 + у2 + хуг + С Н W) = [y (г2-у2) + j yz] I + | (x2-z2) +1xz| j-[
f z2	4	1	2/.,
+ [ 4ЛУ2—*2) ~ 3 *4/J ft + grad <р (AI).	1890. Н(М)=-^ [z (xi + yf) - p2ft] ]
grad ф (Л4). 1900. у = х2-|-3 .	1901. х2 + у2 = —2х. 1902.y'=2^,tg(3._
-= 2 tga (Рис. 219).	1903. у'=1.	1904. у==у'х + (у')2. 1905. у = 2у'х. 1906.
—хуу' +у2 = 4. 1907. Касательная в любой точке совпадает с данной прямой, г
1916. а = 1/ (k — коэффициент пропорциональности). 1917, u = a(Je2 .
1918. w= KXte-°’°'!Z 11,2 .	1919. У=~; У=~- ,92°- Г = 4 х- 1922. У
I .
=«0,181.	1923, у == 2,44.	1924. у то 2,02.
= 1н [С(х Н)(у + 1)1- 1929. tg х tg у то С. 1930.
1927. уто-Сех 1928. х + У тоС. 1931. |'ТЬх2 + /Г+7 =
С I/ 1 х2	г _
= С. 1932. у = -- v ^=г.	1933. х2 = 2Н-2г/2.	1934.	|/ у =xlnx —
X -f- J< 1 -f- X2 113	— - х
— x-l-1.	1935. y = p 1938. У^хе 2 •	1939. z/2 = x2 (In x~Q.
1940. у   x to r;,TOz^.	1941. sin У +lnx==C. 1942. InCx =
__ ,v
= — e x. 1943. Cx-' TO/ + k'P + y2.	1944. y = xerx^. 1945. |/x2 + y2
" aretg "	1
to cx * . 1946. y==4e Зх 1947. Cy = (x—у)2; y = 3(x —у)2. 1951. y = ^.v!-(-
+ C 1952.утоСс 22+	(2x2 + 2x-l), 1953. у = C (x + l)a + ’ (x|l)‘. 1954.x-
to 2y — y2 — 2 + Ce^'J. 1955. у = С(!'~хг-\- (sin x — x cos x) e^x'. 1957. y=—== .
X i [1 О A
x2
1958. у =-----;---!-------. 1959. 1 TO 2 —x2-|- C.r 2 .	I960. х = У'- In2 i Cx '
y 1	и	4	’
* xH'Cx2	У
1963. Gx2 + 5xy + y2-9x —4y==C. 1964. Gy + 12y3 — 9x2y2 -]-2x:1 = C. 1965. xlny-— ,^-y2=-C. 1966. !1Я1£ + ^^±ХтоС. 1967. хМ-уто —1. 1968. sin
^Cx. 1969. утоСх-1-g-. 1970. y'2 4-In ^to Q. 1971. у = x3 sin x-|-C sin x. 1972. у +y = C. 1973. sinysinx = C. 1974. x2 + 2xy —у2 = C. 1975. x =--то Се ЗД + ' eZ'J. 1976.	1977. x = eyec,y. 1978. у = Ccosx +sin x.
1979. ye' -Cx. 1980. у to Cc2-v-еЧто, *, 1981. у то	xj .
1982. l+y2 = С (1 4-x2).	1983. x'2 —2СутоС'2. 1986. у = 3 In х + Ч.^ + С'-.Л' + Ч;
568
(y = 3 In +	1987. y = — cos 2(' + <?-]x-’yC.y, 4=1 —cos 2r. 19SS. у —
= - x sin a- - 2 cos x 4- ClX •+• C.. 1989. у I n sin a Cr\ ’ -|- C.,x -J- C3. 1990. у - = + ^-5x + 230. 1994.4= *+CiIn x + C2. 1995. у = (\х (In a-- 1)4-C.,. 1996. у = = yGx2 +C2. 1997. У = ^ + 2"+C1A-inx + C2A- + C3. 1998. y=	; 1 4
+ G,.	1999.	4 = (l+C'i’)ln(.v J	2001. C, !:i » 4 л c\.
2002. 4 (Cj4-l) = (CtA4-C.,)2. 2003. 2//“ - 1 =(2л' + 3)Л 2004. lni/ = l-——-J______
ClA' + C.. 
2005. 4-—2010.	4 = С1е2лЧ-С.,с 2r.	2011. 4 = C4 sin Зл'4-С, cos 3x.
2012. 4 = C1 + G/^v. 2013.	4 = Gi^-v-lc.,c2.v.	2014.	// = ?« (Ct-|-C^). 2015.
y — e2x (Cj cos x j-<4 sin x).	2016. у = Cie2A‘ + C2e •'•.	2017. 4 = e'!(Сг cos 5a- 4
-|-C2sin5x). 2018. 4 = e2v(—7x4-3). 2019. y = 3e '2x sin 5л-. 2020. у = ~ ex — — ’ e3v. 2025. 4 =чС4 4- C,x) G 4-x36x2 4-18x 4-24. 2026. 4 = Сугх-|-(Сгx)ex. 2027. 4 = Cte~x 4- Cse ix -J-cos f — 2x \ . 2028. 4 = C} cos J '2 x 4 C, sin | 2x -1-4- 2 a-2 4- ' . 2029. 4 = С1сл'-рСге2л' 4- g x 4- ' (9-J-3 cos 2x - sin 2x). 2030. у -y2	x	1
= Cl cos 2x4-Ca sin 2x —g- cos 2x-[-yg sin 2x. 2031. 4 = — c2v sin x ; <?гсА' { С.ул'\ 5 x 1	3	7
2032. 4 = C14-C2c 2 4~-q A':i—r *2 + r>cx- 2033. у = C\ cos x + C2 sin x — .j	3
—|-xcosx —e“v. 2034. 4 = [Сг sin x-j-(Cx —x) cosx] с л\ 2035.	4 = C.,,' :1A 4-
-J- e-2.v(Cj 4-x) 4- X e~x. 2036. 4 = - e3x (cos x - 6 sin x) Ct,a'' 4-C..c 3V. 2037. 4 -= - c~-v [4x sin x —x2 cos x -|-G cos x 4~ CL 4~C3x]. 2038. 4 = Cj/1 v4“C\>cv 4~-^ [(37 -f- 5x)x X cos x—(30 4-7x) sin x].	2039. y = ex(ex — x2—x-|-l).	2040. 4 = — cos x —
— 3 sinx-|--g sin 2x. 2041. 4 = eA'4-x2. 2045. 4 = Q cos 3x-}-C2 sin Зх 4-C3. 2046-4 = = C1e2A' + (C24-C3x)e' -v.	2047. 4 = Q cos x + C2 sin x4-C3 cos 3x + C4 sin 3x. 2048.
4 = Cl4-C2x4-e' A (C34-C4x). 2049. 4 = 64 cos 3x-bC2 sin 3x4-x(C3 cos 3x-|-C4 sin 3x). 2050. 4= I-)- cos x. 2051. 4 = eA-|-cos x —2.	2052. y = 2,3+ex —0,3cos3x-f-
4-3gsin3.v^. 2055. 4 = (C14-C2x) e v-4 C3c 2a4-(x24-x —l)e^A. 2056. 4 = ^' + -L C2Ga4-C3cosx4-C4 sin x — ex sin x. 2057. 4 = (C14-C2x) cosx-|- (C3 -f- C4x) sin x + + j-g—cosx sin x. 2058. 4 = g^x5—9 x3-|-C4x2 4-C2x4-C3 4-C4 cos x 4-4 С5ЯПХ. 2059. 4 = C1cA4-C2e“A4-C3 cosx-|-C4 sin x —eA sin x —x4 —24. 2060. 4 = = Cl 4- C2x 4- C3x2 + Cl cos 2x 4- C;j sin 2x -|- ex 4- x3 4- 32 x sin 2x. 2061-4 = 4~ — 3(.- A4-p“2A. 2062. 4 = eA4-r3. 2065. 4 = C4 cos 2x-|-C2 sin 2x4-cos2xlncos2x4-+ 4sin 2x- 2066- 4 = С1е1/2л'4-С2е'"|Г2х — 1 .	2067. у =1 —+ ci +
2	к
569
4- С>г е гх. 2068. 1/ = — cos ev-J-C.ie v4-C1.	2071. х =—te2!, у = (1—‘у.
2072. ' х=12е4/- е~!— 4с3', у = 4e3Z -2e“z — 2с3'. 2073. л- = —2,Бе'+0,5с-'-!-+ 4 (2 cos/ —sin/),	(/ = —2,5е' —0,5f3'-|-ez (3cos Z-|-sin/).	2074. х = —е '_
у = е~г, г = 0.	2075. х = 2с'— е 2 6 cos-L^- t 2 )z3 sin—'—/\ У
t	t	£	£	!
-J- 4 j/~3 е 2 sin tt г — 2ez+e 2 ^6 cos / — 2 J 3 sin t j . 2079. x2 + y- -=	х2-у2^С,,'2’.	2080. (х = Съ x2 + у2 = /2 + С2.	2081. x2 — y2 = Ct,
ху — х2 — t-\-C2. 2082. x-j/ = 2^ + C1, х = Сгу. 2083. x = * CiC<2/+ g C2e2'—C3e
y = — Lc1c'2/+ * C2e2'— C3c z, z = C2e2' + C3e~z. 2085. x = С/ + C^, у = С/Ц-ЗС.,^'. 2086. x = — Cxe2'— 2C.,e3', у = Cle2/ (С/. 2087. x = C,e/ + C2e3Z, 3C/+g C2e8'. 2088. x = C1c2'4-C.,c"2', j/ = C]e2Z-3C2e“2'. 2089. х = С^-‘-' J--C2e2'-J-C3e 21, y = C1e^ + C2c2'-C3c - , z = —C<z-|-2C=.e2Z. 2090. x = Cl + 3C.c’-', 1	2	3	1
// = —2C2e2Z- * C3e. z, 2 = Ct-c C2e2‘-\-Cse z. 2094.	. 2095.  4 . 2096. ' . 2097. 0.
2098. 1. 2101. Нет. 2102. Да. 2103. Да. 2104. Нет. 2105. Нет. 2108. Сходится. 2109. Сходится. 2110. Расходится. 2111. Расходится. 2112. Сходится. 2113. Расходится. 2114. Сходится. 2115. Сходится. 2116. Сходится. 2117. Расходится. 2118. Сходится. 2119. Сходится. 2120. Сходится. 2124. Расходится. 2125. Сходится. 2126. Расходится. 2127. Сходится. 2128. Сходится. 2129. Расходится. 2130. Сходится. 2131. Сходится. 2134. Сходится. 2135. Расходится. 2136. Сходится. 2137. Сходится. 2138. Расходится. 2141. Сходится. 2142. Сходится. 2143. Расходится. 2144. ('.ходится. 2145. Сходится. 2148. Сходится. 2149. Расходится. 2150. Расходится. 2151. Сходится. 2152. Сходится. 2153. Сходится. 2154. Сходится. 2155. Расходится. 2157. Сходится. 2158. Расходится. 2159. Сходится. 2160. Сходится. 2161. Сходится. 2162. Расходится. 2163. Расходится. 2166. Сходится условно. 2167. Условно сходится. 2168. Абсолютно сходится. 2169. Условно сходится. 2170. Расходится. 2171. Условно сходится. 2172. Абсолютно сходится. 2173. Условно сходится. 2174. 0,31. 2175. 0,62. 2190. (—2, —1'2) (1'2, 2). 2191. (—го, —1)(1, 4-со). 2192. ? <х<е. 2193. (—oj, — 1) (1, -.о). 2194. (--|ЛЗ, — 1) (1, | 3). 2195. ; х , < 1. 2198. —со < х <-|-сс . 2199. и л . • .	2200. —со<л-<-|со.	2201. —со < х <-}-ет.
3	| 2	1
2206. In -г , 2211.	2212. R = „ ; расходится в обоих концах интервала
2	3	,•>
сходимости. 2213. /4 = J-cc. 2214. 74 = ) Зе, (—j Зе, у Зе). 221.5. /4 = 4, (—4, 4). 2216. /4-и, (2-е, 2-|-е). 2217. /4 = -|- = . 2218. /4 == -|-сс. 2219. /4= ! ,
у j; 2220. /4 = 1, (—1, 1);' при х= >1 ряд сходится. 2221. /4 = 2, (—2, 2); при х=±2 ряд расходится. 2222. 74 = 1, (—1, 1); при л-= = —1 ряд сходится, при х= 1—расходится. 2223. /4='-, ( —	-'V при
х— — т,- ряд сходится, при х = -,2—расходится. 2224. /4 = 1, (0, 2); при х = 0 □	<5
и Л-= 2 ряд сходится. 2227. — g — g1, (л- '-г^--^ (л'7-2)’ —... —
(-4,0). 2228. J?	(0,2). 2229.	2 [1 + ij-i-.„ +
П=1
570
co
(v —4V’	1	v5 2,?+1 — (—IF	у
+ (~1)nrl П + •  ] • 223°' 1 " 2--------------2^ • xn’ R =1  2239- 1 + 21 + • •  4~
n—0
co vtl— 1	V^ ( 1 У1 X2/l+l
+чг + -’ (-°0’ +°°’- 224°-Z(^1)!2T+T’	+=°>-	224>-
li-^1 co	oo
2v2«+l	vi	X2n
+“). ««	jjpjp,<-<=.-r=>.
rt==0	n-=l
„з. V	+„). 22«. - I. V !£+Д1, (_». -1). 23«.
nt ' '	b «я	6n 1
rt=o co	co
У (-l)rt'i	(-ОЭ, -1-co). 2246. У (-l)n(2n + 3)x«, (-1, 1).	2247.
71 = 1	n
CD	CO
*+ У (-IPr^^1. (-». !)• 2248. У (—l)'t41 (x —2)'1, (1, 3). 2249. 8 + 4n2— 1	м
ri = l	11=0
У	ln‘-? ft —ЗУ1	1	1
+ 8	>	----Ц,	(—oo,	4-oo). 2252. .v+	-	.4 4-	-„	x3 + ... , x [ < i. 2253.
«1	2	3
n = l
1-x-f- 2 *•« + ..., (—co, 4-co). 2254. 4- у xH 4-	.44-...,	(—co, -(-co).
2 v' 1 r3"41	Г 2 V1	-v“+i
2257. Л V	C_.. 2258. CW_j/ ' (-»«	. S W-
«=(>	71 = 0
r?O	CO
/9 Vi	у4п-1з	vi (—IF
я i (“1),г(2п+ 1)! (4FT+3)' 2259, /w= i (6n + 1) (2n)l ’ 'Xl<
it — O	n=0
2280. /И-.+ V (	1.	« <1.	22»,. 7W
n 1
VI (—
2. n(2n-l)
n =1
f(x)= V ,C_____________
(2n + 3)/t! ’
» = o
0 0 41. 2262.
\x\< <cc. 2264.
2265. /w = £^, 1X <L 2266.	!X,<1.
2267. /(x) = 7T^-?3, lx|<l. 2268. f(x)=414-3.v>H\ 2270. f (x) V 1	)
|x|<l. 2271. 7(x) = xarctg.v. 2272. /(x) = ^~^
। x | < 1. 2281. f/ = 2 —
-3(x-l) + 7(x-l)24..-- 2282.1/=.^ -4 g 4 j+-... 2283. ?/=l+2(x-l) +
+ 4(x-l)2 + 235(.r-iy-4811 (.v-144-..-. 2284. i/=1+%22 + 2 .V“+ 2^4
2285. 0=14-	xj4-J4x4-... .	2286. y = 2+-«-	j'*’+ g **+••••
, , л , 1 , , 1 /я J 3	'	1 / 1 , л) 3 I 3, . ,
2287. у-i-r-j лг-г 4 x +	- 4--t" ij * + 2-Д 2"-r 4	+’”•
571
x*n	1	1	1.3	1.35
“ 2ж- “* 9"1+v+ 2«’+•••• и — 0
3	10	r2	2v3
2290. i/=l+* + 2 *4-31 x’-l—.. 2291. у =1 + x + 2[	3| +.. 2292. у
-- л (x__ j) -i C+_ J+ _j_	। (_+zJ).j __ (*~ *)J I 2293 и = x21 ' +
2(	} h 2!	1	3!	'	4!	5!	r"' ’	J \2! 1
,•2 v,'i i .	1.3.5	\
+ 9|+ -gr^l-r —щ—xG + ... ! . 2325‘ 1,609. 2326. 2,833. 2328.0,17365.
2330. 2,001. 2331. 7,937. 2333. 0,785. 2334. 0,758. 2335. 0,098. 2336. 40,87
2337. 0,310.	2338. 0,333.	2341. —V (—J)n cos nx
Я ' Л	’	n2+ 1
П-—1
x/x 1,1-	2 \1 cos 2nx .	, V . sin nx
2342. f x) =	+ -smx— ’ т^-7-т- 2343. /(x) = —ЗЦ-4 7 (—!)'»------------.
' ' я ‘ 2 л Xd 4(i2 +1	' v ’	Xj	n
fl-—I	)l~[
л 2 /cos x , cos3x ,	\	. sin 2x , sin 3.v	\	„	,
2344-	4 -n^ + -^ + --; + vsm^~T-+-3---r 2345- 2+
co
, V (—1)" 1 •	л2 , cos 2x cos3x .	, . ..„co.szix ,
+ 10 £; n sin nx' 2349‘ 12“~cosx-f------з------9---f-----+-(—1)" —4--
rt =1
„„„	2	4 /cos2x cos4x . cos6x ,	, cos 2fix ,	\ „	/ .
2350. -  - — —------b —+ ..  +	—, + ... . 2351. л- 2 sm x - -
л л \ 3	15	35	4rt2— 1	;	\
sin 2x sin 3,t
"1	3~
sin nx
2352.
х3 = 2я2	(— l)«+i
+ 12 2 (-1)'
sin nx
2353.	f(x)= - 7
' V ’ Я +j
n=0
(2n+l)2
2354.
/+) =
f(x)
fl sin (IX
4fi- --1 '
я2
4 (in-
I 4 3
2355. /(л) = '/ 6
sin fix. 2359.
2/i
2 V 1 —(—1)" ch я .
-- 7 ----+n—2-----(I sm (IX. 2361. f(x)”l
n ^Xd 1 + fi2	' v '
2363. 2 +
Л
-I)'1 . n.tx	I
sm ——. 2364. n 2	2
1 ял 2 Vi — !)" 2лпх n t,r, o cos ,	7 —rtos—. 2366.
2	/	я л_' 4м2 -1 I
ял-
2367. 5x — 1	—1 -/
Л 4ив'
tl^-A
1 cos fix ill 1____
9n2—1
!sin n/z\2 .
I —— sin nx
cus x ~2~
n---=2
co rn, I (2«+1)ях 4/ у | I
(2fi+D;
-4-8 У-...........
n2Zd (2fi-|-l)2
1 .
Sin -y— n b
2568.
. 2358.
2360.
cos nx
Л2—1 
. 2365. 1
Л
(2fi-’-ll ях
COS2------------
я 2
4
l+27 2 <-'i
1
2


2
I 20 V 1 /о , плх	Q . 12 V(—l)'t+1  -i/w
H—2 / To—p—лт"cos (2«+ 1)	•	2369. 2x — 3 = —3-4—- 7 ———sin--------
л2 Li (2n+1)2 v 1 ' 5	л Li n 3
n-0	n=l
co
2372‘	2 T(2T+n sin (2" + *)лх-
n--0
» cosSttlLli
2373. ‘ V -----------
11=0
2378.
/(*) =
slur у (-1)»от 
Л 1 + n2
2379.
2380. }lx)-_
/ ла	. ла	\
°i	< , 	। ; c°s -л- sin o- rj- ।
• = > (-1)"- (sh 1)1-~^-е2/я'1Л- 2399. / (x)- \ ------± cos ax+	sin ax У-
ы	1 + л2п2	' л 3 \ 1 — а2	1 — а- /
—co	*6
Xrfx, X^O. 2400.	f(x)~ 2	2401.	/(.v)-
л J а	7
о ла (л — 2х) а	_
2 12	2	, nAf.. f , .	2 ( sin a cos ха . o.Ar f/ .
= -- \ -------------z------doc, 2404. f(x) = - \ ----------------da, 2405. f(x) =
nJ 1 — а2	M a
о	о
co	co
2a C cosax ,	„.n„ £/.	2 (’ 2a sin a + cos a—1	,	. „.П7
— — \ -г------xda. 2406. f(x)= - \ -------------4:---------cos ax da, x 4= • 1  2407.
n j a2 4 a2	' ' ’ л )	a2
о	о
.. ,	2 i‘ cos ax .	...	2 a 4-sin a .	, n.nn ,
f(x) = - \ r-i—xda.	2408. f(x) =	\ —I—;----- sin ax da. 2409. I (x) =
v ' л 1 1 + а2	л j a2
о	о
a o_>	co sifl" _
-. / 2 I* a sin ла .	,	„., „	...	12 f 3	,	... o.,,
= 1/	\ ------^-smaxc/a. 2410. /(x)=--_ -\ --------— cosxada, x 4 0. 2411.
Y , r ,) 1 - a2	x ’ л j a2
о	о
/(x) . - 2	^-'n ЛСС’ sin xa da . 2413. c (a)=—S'n— I 2 cos a — -4 4 '. 2414. / (x) —
'v ’ л ,) 1 — a2	a \	a 1 a2;
0
= 1 ( ^LEe^da, x -4±l-	2415. c (a) =	1).	2416. c(a)^
л J а
£ яа
. aa sm 2
iua
cva < яа
,	,	, sin - . / о \
1 / \ 1	1	•	г / \	1 I 2 ia I x j- 1	9 117
1 c (a) = - -- sin <)!./ W —	\ --------e \	; c/a- 241/.
1 ' ’  ла j 2 | ’ л J a
C	2л (a4-ta)2 + W2 ’
__ w c"°_______c''iv___ .
.1 (а + <а2+ш2) aa-
2л | (a2 + w2)2 + a4 Jr 2a2 (n2oj'4
2421. .-,1 (е-‘Л«-1).	2423. Л
/л	л
H9-
573
J_ 2«cos ст—(2—cc2)_sina 2420_ u у [Г *+1 4 л	a3	Aj IL л«
Я=1
4	1	2	1
-I—((— l)ft—l) со5лШ-(-(—l)ft	sin nkat \ sin nkx. 2431. u(x, I)
nJk3	J	n2k2a	)
= У [__Д___ COs |/2 (2n-[-1) л^ + —-------------sin j/2(2«+l) лЛ sin (2n
—. L«J(2n+l)3	| 2л4(2«+1)4	J
~	/	7	7 \	47
+ l)n,v. 2440. (2, 1),	' j. 2441. и -	2442. a) 4-2r, 6) —
\ Z D у	О □
H- Зг, в) 0. 2443. «3 — ab-\-b'2. 2444. Zj = 0, г.,=^— Jp4-' кД гз = —у—1
2455. Окружность радиуса 8 с центром в точке г = 0. 2456. Окружность ради-
уса 2 с центром в точке г = 5—Зг. 2457. Окружность радиуса 5 с центром
/	1 2
\Х	2	г/2
в точке z = —i. 2458. Эллипс -—-------[- =1. 2459. Прямая х = 2. 2460. Пря-
4
мая х = —3. 2461. Луч х ——у, лежащий в IV четверти. 2462. Гипербола xy = i 2463. Внешность крута радиуса 2 с центром в точке г = 0. 2464. Внутреннее!' круга радиуса 1 с центром в точке г = — 1— i. 2465. Кольцо между окружении радиусов 2 и 4 с центром в точке г=1 — 21. 2466. Внутренность элл
( y_2У3
—9—-4-	= 1- 2467. Левая полуокружность относительно прямой х-
4	5
2468. Нижняя полуплоскость относительно прямой (/ =— 1. 2469. Полоса прямыми х =— 1 11 х = 5. 2470. Полоса между осью Ох и прямой у—'
Угол между прямыми х — —у и у--=*-. 2476. 3 (cos -Н'sin у , 2'С
+ I sin „ I 7 (cos л +i sm л), 2 cos , -ism . ,212, cos -.— i sm , . 24
6 У	\	6	6 , ’	\	4	4 '
!	9 rr	9 т	r !	4 J?
1296, 512i. 2478. cos V- k + i sin k , (/г = 0, 1,2),	['3 ( cosn—
\	3	3 i	\
,  	4/г-|-1 ''	io-a /	86-]-3	. .	8A4-3' .,	,, , „
4- i sm л—3— (& = (.), j, 2), j 81 cos л—---Нзшл—— (/г = 0, 1, 2,
О У	'	20	20 /
. _ / 2k -k 1	2k -I-1 '	Г
p2^cosn—g------Н япл—g—j (k — 0, 1, 2, 3, 4, 5). 2479. a) Zi = — \
I 2 I 2	| 2
+ i 2 , z2= 2	2 ’ 6) Z1 = 2,	Z2==2i'> z3 = —2’ г'1 = — 2i; B) 2,^:=
(±
= |-'2e' 12	3 ' (k = 0, 1, 2).	2480. cos 5(p = cos6 <p—10 cos3 <p sin2 cp4
4- 5 cos q> sin4 <p cos 2 -|- i sin 2 _
e ’
I 3	1
и sin 5ф = 5 cos4 ip sin ф—10 cos3 ф sin3 ip4-sin6 ф. 2489.	— i
cos 2 4- i sin 2 ( e2 [cos 1 -|- ( sin 1 ], e2 [cos 3 — i sin 3] ( C0S —J..8’0
. ЭТ , ЭТ	. 3jT . ЭТ
2490. [л2е 4, гУ2, 5ei2t, I 2c 4, 2e 3, 7ei0. 2491. cos 2 ch 1 4-1 sin 2 sh 1.
2492. i sh 2. 2493.	— i . 2494. In 13 — i arclg	4- 2aki (^ = 0, ±1, ±2,.. ,).
/Г 2 Г 2' ~ T—	л —arcb-y — 2nfe
2495.	4 (k = 0, +1, ±2, ...). 2496. e 3 x
X (cos In 5 4-i sin In 5) (fc=0±l, ...). 2497. zk1' =—	In (/ТО4-З); z^” —
574
—(2й-Ь1)л —Пп(И104-3) (fc = O, ii, lb2, ...). 2507. Вся плоскосп,, за исключением точек г* = -£ (2*+1) (/.’ = 0, ±1, j. 2508. Вся тг„то, ТЬ1 _,а •^исключением точек zn = 0, Zi = l, г.г —2. 2509. Вся плоскость, за исключением
«чек zlt = 2nk (£=0, Л1, ...) 2510. Вся плоскость, за исключением точек г„ — '	1 ± |Л1 4-4л/г —4л2/гг
•“  1, г,.-=	----------------
2я/г
2, ...). 2511. f (х, у)= Зл-ц - ,/! л
.г-« (За-//-» —л-!‘4-С1)=—izs4-»Ct. 2512. /(л-, 0 = _^ + iС- ' ; с. - -4з. /(.г, у) = х — у + Cj + i (х-Н--3) -.-(I 1 /Jz-I-C! — 31. 2518. —2. 2519.
. 2nshn .. (2f- 1)я:- л2 (14-20	, n OKOQ r
o2 | 3i. 2520. a) -gg—, 6)	, »)	]6Q	 Г) °' 2 523' Лг'1"т''а‘

2524. Сходится. 2525. Сходится. 2530. ‘	1. 2531. |z — f | < e. 2532. .?	3
4,2533. <4-r<	2534. >
I' 2 c
2537.	2 <	1|<3.
9
z'<l. 25.35. ;z+i;<-g-. 2536. 1< ? <5.
2543.
COS ?j2 —
(—1)« 32rtz2ft (W
sin (2? •-1) -=
f
4 ;s».cos
4
(__lyi
(2и Ы)!
sin 1
/7^(1
(—1}/?
(2n)1
„ v 2л(г—ej»
2544.	4г—-•
n—0
V (z"02zI
(2/1)!
tl
n =0
<?	'У (-1C Й~,П (г +и1)аЯ 1-2547. (г—2)4-) 8 (z—2)34-21 (z—2)2 + 25 (.?-2)-14.
/l-u
. -.0	CO	O°
i	•!. •»» Х'-'”даЬ5=Т)=ч 2'-1’"
rt—0	4 = 0
V (—i)«—!--------!—
л k ’ (2n+l)! (г + i)2" ’
n -- u
2552.
co
У (—l)«z'1,
n-=0
|z|<r.
;Z-H_
co
- v
< 1.	2553.
1 _ 1° __ v
9 “ Tt Л- 3""2 ’ /7 = 2
i г I < 3;
_ 110
9 ' 27
1
(- 1)пИз^-’ !?-3'<3- 2554’	’г;< : rW’
n = I
v l/г Г1 ,	„	3	2
|z + 2;<2. 2555. 2 (-1)Я^ |+ГТ+3'Т" ’	^+2 ”	“
n — u
_ 3 у (— 1J/I (г + 2)'1, z + 2;<2. 2559. Zj =—1, z2 •=—4 — полюсы первого п — о
*• порядка. 2560. z = ±/ —полюсы второго порядка, г = —у —устранимая особая
точка.
2561. гА='^-(2й+1) (А=0,
±1, ...) полюсы второго порядка. 2562. гЛ_ =
575
(ft = 0,
...) —полюсы первого
вечно особая точка.
2564. 2 = 1 — существенно
порядка. 2563. г = 0 —сущест-
. о осооая точка. 2568.
I / п •
2569. 2. 2570.
25л-
25л2 I ch 4	1
2579. —л21. 2580. —2т. 2581. — rti pAZ _|_ А д. 5 2Р 2594 1 - 1 Р 2595 ' р р2+ 16  5 2р 2 р2 + 36 	9
,	Р+1	2
А(р-Н)2 + 4'
3
2 '
. 2582. 2лЛ 2583.
-Р--—2р . . 2596. --------=,== -
(р—1)- + 4
р-2	2
2572. 0. 2577. 2л7. 2578. 0.
Я‘ . 2593.
° Р + 3
2
(рЧ-1)2
2596	-___7_____с
•	(р-1)4-4^ (Р+1Г + 4-
2597' (р —2)2 —1	>-4
2	1	13	3
2598' (Яаг+йГ"(7+3)чЛ- 2599‘	260°- 2^-¥+4cos2Z-
к f’>	5Л*	1	2	2
2601. -А-х + оЛ-^-. 2602.	(? + 2sin2/~cos/). 2603. cb 2/----cos f.
I МП • ЦИ h	4	1	'	К	К
2604. -2 + 2?. 2605. 1 e~^ +	.	2606. -	7 + ^ sh 37.
2607.
I 2 sin ) 2 7 —sin 7. 2608. - • [e'-f-sin 7 —cos 7].
2609. e‘—e 2 cos
 /3 sm 2 -
5
- ( 2
2 e 2'cos
, 7 -v i't , И ', _ H 80е W+ 1б'е
+ -3\-3/ + ^.
64^256;	^\32
2610.	—e 2/ + Г‘ 72-7+ 1+4
Y |/AHe ^sin AA' 2613-^“
2611.
3
c2/cos37.	261 *.
J 3
c~2C 2lilf r
2615. - -- e-< + t О	*
32 + 25б’е/- 2617'
4.00 у
3O7 + 1<W( 2616.
^+216(18/-
1	.	19	..
-2e^+ "e r. 2618. Jsit 7-
4	1 4	2Г
2
2623.
sin t. 2621. 3 cos 27+ 2 sin 27 — 27 cos 27.
- Го e‘ + in cos 3Z + i sin 3t- 2624’ 1 (J	1U	JU
. ' 7 sin 7 — !- cos 37 'i. 2626. 3
4 ;	4 j	2
2622. —1 4- 2e 2 + 5 sin 7 -?2 cos 7.
1 + „-72 + cos 7.	2625. -v los t
2	lb I
3- e-' + e' cos 27— e sin 27. 262?. v-
5	10	5
= 4? —3e2/, y = 2e‘, z = 3e2Z — 4eC 2628. х=Л [? + (27—1) e3/],	^ =
— {бе'— (27 + 1) c3']. 2629. x = | ch 2/ - % cos 27, у = (sh 27— sin 27). 2630.
.v = 12 еГг( — 2 cos 47 + -f - sin 47, у = — . e . cos 4/ + sin 4/, z = — <' — 5	5	5	5	5	5	5
----5 cos 47 + sin 47 .	2631. T---2c'-' — 57c 2', p = Зе'2' + 5te~2/.	2632. x =
— 3	e-4C’_ 3 1 I. e—7/_|_ _7_ _I_ . 1 c-2'	и== J 1^ e-47_g 11 g-7/_|_ 1 ./ J_ 3 fit,
10	340	+40 3 5	’ У 20	340	r40	‘ 10	’
2633. x = 4e t — 2e~3'', p = 4e 7 —6r3' + cos 7. 2634. x = — 7+ 7-’— *	у

f