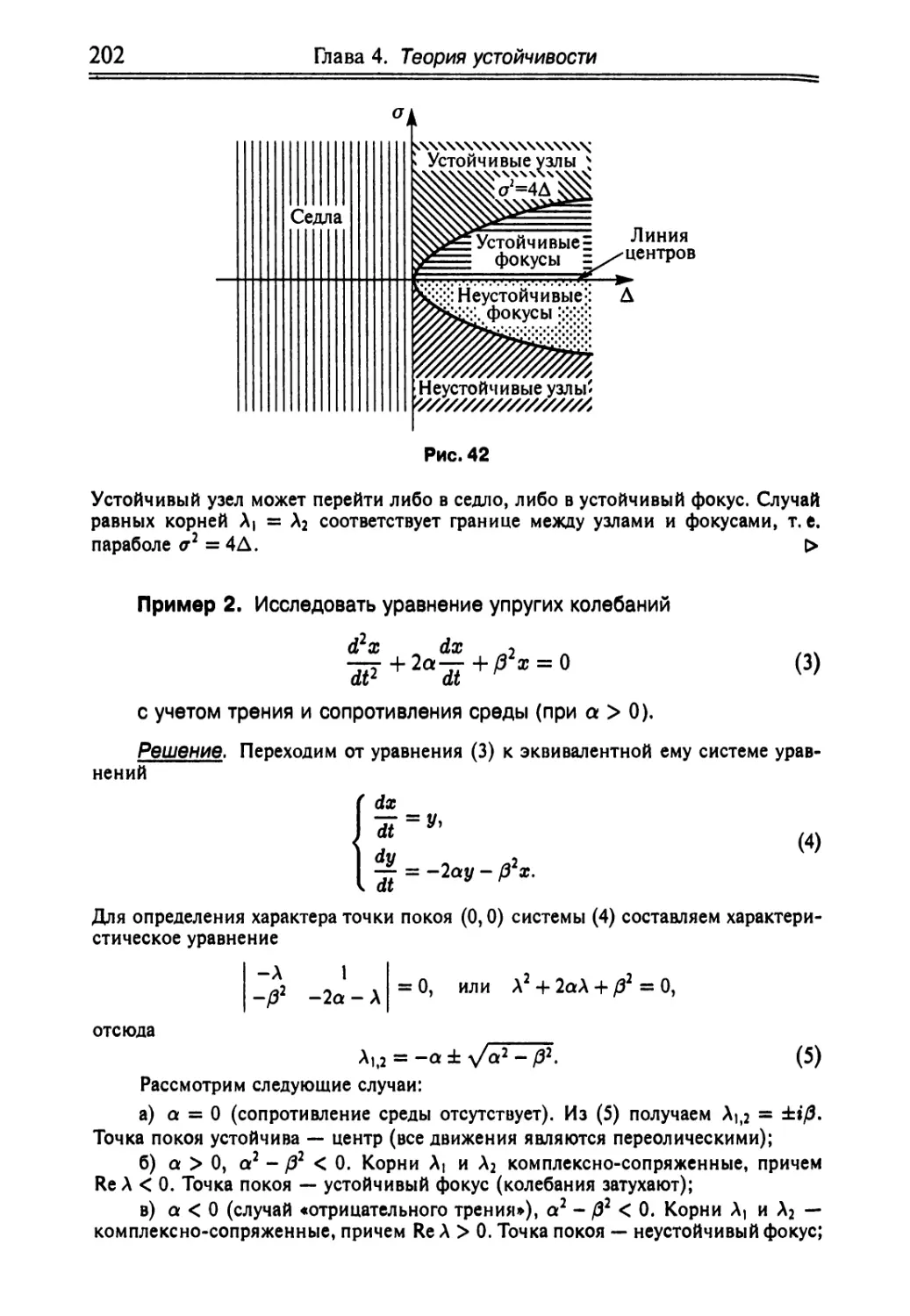
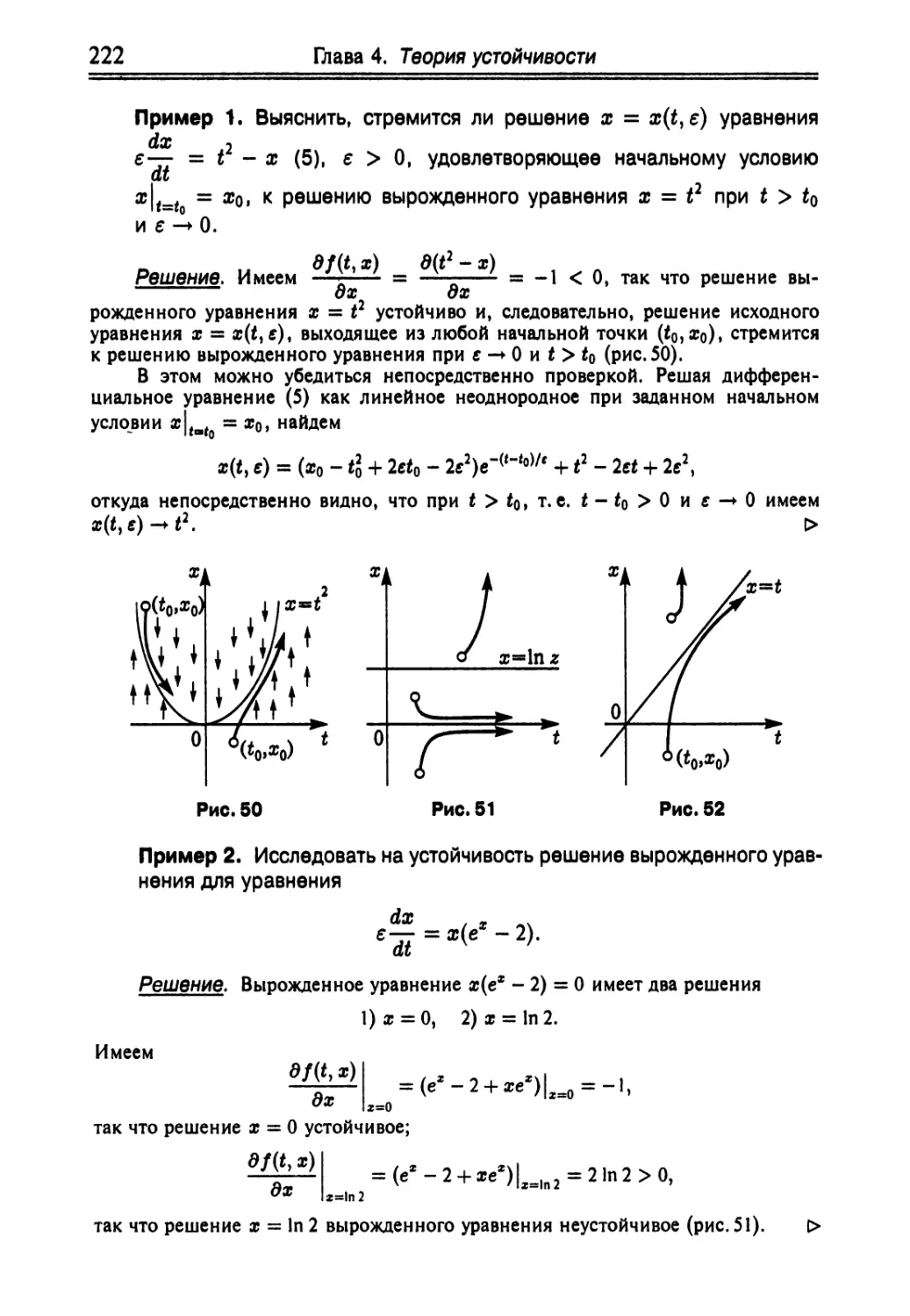
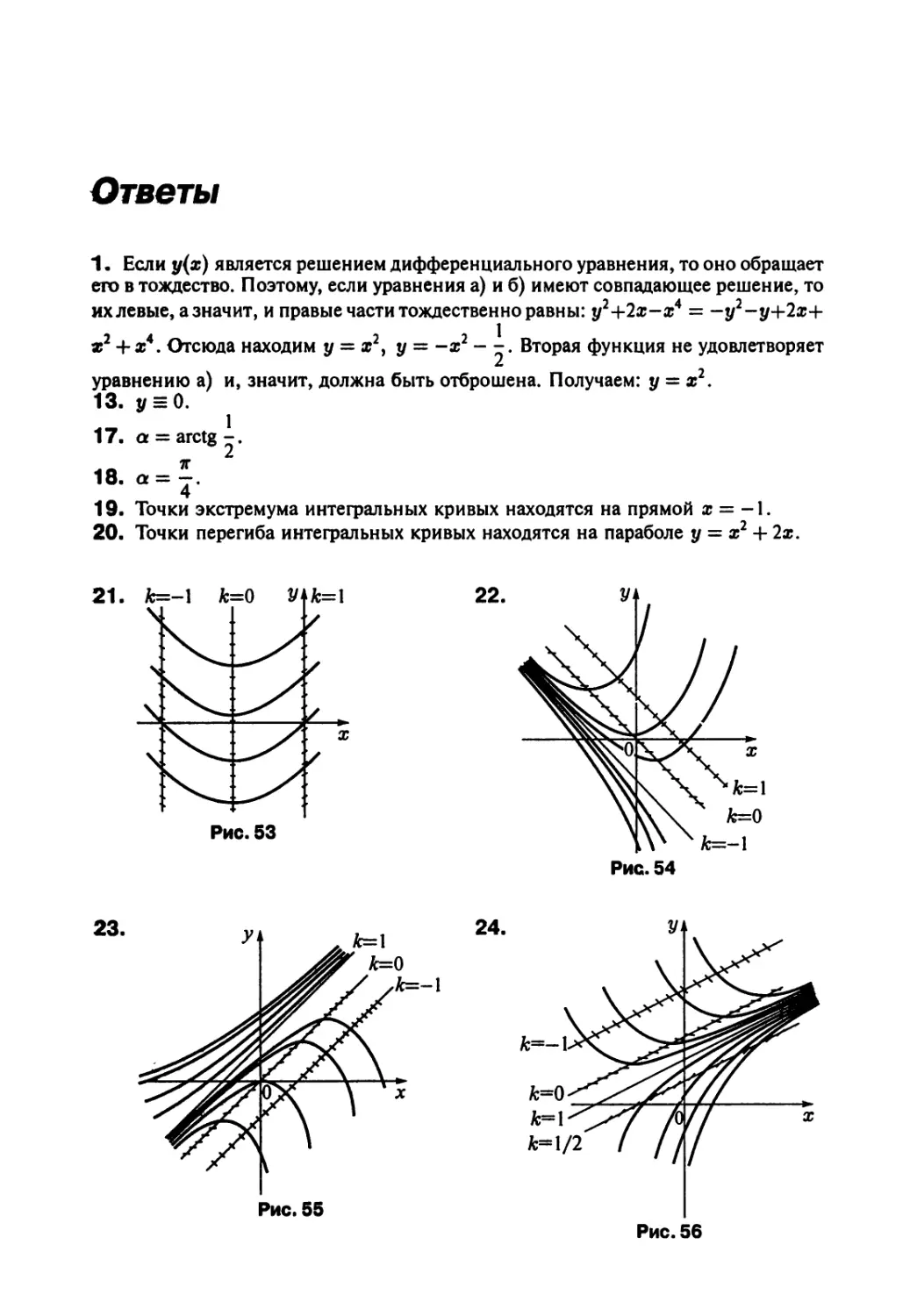
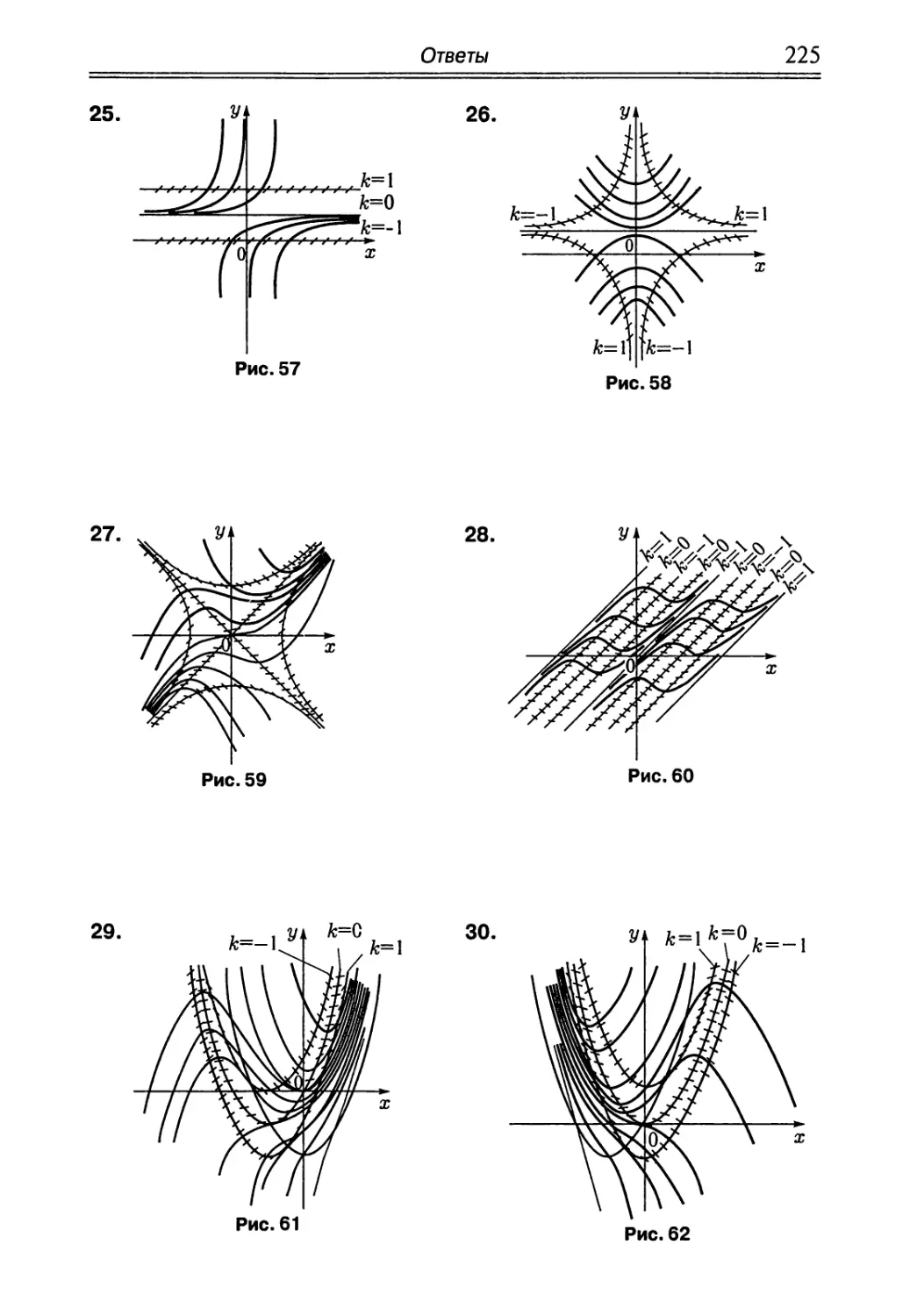
Автор: Краснов М.Л. Киселев А.И. Макаренко Г.И.
Теги: математика математический анализ математическая физика высшая математика
ISBN: 5-354-00013-0
Год: 2002
Текст
М.Л.Краснов, А.И.Киселев, Г. И. Макаренко
ОБЫКНОВЕННЫЕ
ДИФФЕРЕНЦИАЛЬНЫЕ
УРАВНЕНИЯ
ЗАДАЧИ
и
примеры с подробными решениями
Издание четвертое,
исправленное
Книга была допущена
Министерством высшего и среднего
специального образования СССР
в качестве учебного пособия
для студентов высших технических учебных заведений
УРСС
Москва • 2002
ББК22.1б1.6я73
Краснов Михаил Леонтьевич,
Киселев Александр Иванович,
Макаренко Цжгорий Иванович
Обыкновенные дифференциальные уравнения: Задачи и примеры с подробными
решениями: Учебное пособие. Изд. 4-е., испр. — М.: Едиториал УРСС,
2002. — 256 с. (Вся высшая математика в задачах.)
ISBN 5-354-00013-0
В предлагаемом сборнике задач особое внимание уделено тем вопросам,
которые недостаточно подробно освещены в имеющихся пособиях и которые,
как показывает опыт, слабо усваиваются студентами.
Детально разобраны метод изоклин для уравнений первого и второго
порядков, задачи нахождения ортогональных траекторий, линейная зависимость
и независимость систем функций.
В задачник включено большое число задач на решение линейных уравнений
с постоянными и переменными коэффициентами, задачи на устойчивость по
Ляпунову, на применение операционного метода к решению дифференциальных
уравнений и систем. Представлены также метод последовательных приближений,
особые решения дифференциальных уравнений, уравнения с малым параметром
при производной.
Приводится более 100 примеров с подробными решениями.
Издательство «Едиториал УРСС». 117312, г. Москва, пр-т 60-летия Октября, д. 9.
Лицензия ИД №05175 от 25.06.2001 г. Подписано к печати 22.01.2002 г.
Формат 60x90/16. Тираж 3000 экз. Печ. л. 16. Зак. №84.
Отпечатано в типографии ИПО «Профиэдат». 109044, г. Москва, Крутицкий вал, 18.
ИЗДАТЕЛЬСТВО У Р С^С^
НАУЧНОЙ И УЧЕБНОЙ ЛИТЕРАТУРЫ
E-mail: ure8Qursa.ru
Каталог изданий
в/ntemef: http://uree.ru
Тел./факс: 7 (095) 135-44-23
Тел7факс: 7 (095) 135-42-46
ISBN 5-354-00013-0
<D Едиториал УРСС, 2002
Все права защищены. Никакая часть настоящей книги не может быть воспроизведена
или передана в какой бы то ни было форме и какими бы то ни было средствами, будь
то электронные или механические, включая фотокопирование и запись на магнитный
носитель, если на то нет письменного разрешения Издательства.
ГЛАВА
1
Дифференциальные
уравнения
первого порядка
§ 1. Основные понятия и определения
Дифференциальным уравнением называется уравнение, связывающее
независимую переменную х, искомую функцию у = у(х) и ее
производные у',у",...,у^пК т.е. уравнение вида
Если искомая функция у = у(х) есть функция одной независимой
переменной я, дифференциальное уравнение называется обыкновенным ^;
например,
dy 11
1) f- a?y = 0, 2) у 4- у -f х = cos x} 3) (х — у ) dx — (x + y)dy = 0.
Когда искомая функция у есть функция двух и более независимых
переменных, например если у = у(х, t), то уравнение вида
ду_ <ty дту \ _
'У) дх' dt'"' dxkdtl) ~
называется уравнением в частных производных. Здесь k, I —
неотрицательные целые числа, такие, что А; + / = т; например
ду 9у _ 9у _ 02$/
Порядком дифференциального уравнения называется порядок
наивысшей производной, входящей в уравнение. Например, дифференциальное
уравнение у' + ху = е* — уравнение первого порядка, дифференциальное
уравнение у" + р(х)у = 0, где р(х) — известная функция, — уравнение
второго порядка; дифференциальное уравнение у(9) - ху" = в2 —
уравнение 9-го порядка.
Решением дифференциального уравнения n-го порядка на интервале
(а,Ь) называется функция у = <р\х), определенная на интервале (а,Ь)
вместе со своими производными до n-го порядка включительно, и такая,
что подстановка функции у = <р(х) в дифференциальное уравнение
превращает последнее в тождество по х на (а, 6). Например, функция
|} В дальнейшем будут рассматриваться только обыкновенные дифференциальные
уравнения.
4 Глава 1. Дифференциальные уравнения первого порядка
у = sin ж + cos х является решением уравнения у" + у = О на интервале
(-оо, +оо). В самом деле, дифференцируя функцию дважды, будем иметь
у' = cos х - sin ж, у" = - sin х - cos ж.
Подставляя выражения у11 и у в дифференциальное уравнение, получим
тождество
- sin х - cos ж + sin x + cos x = 0.
График решения дифференциального уравнения называется интегральной
кривой этого уравнения.
Общий вид уравнения первого порядка
F(x,y,y') = 0. (1)
Если уравнение (1) удается разрешить относительно у', то получится
»' = /(*, У) (2)
— уравнение первого порядка, разрешенное
относительно производной.
Задачей Коши называют задачу нахождения
решения у — у(х) уравнения у1 = f(xyy),
удовлетворяющего начальному условию у(хо) = уо
(другая запись у\х=Хо = у0).
Геометрически это означает, что ищется
Рис 1 интегральная кривая, проходящая через
заданную точку Мо(жо,г/о) плоскости хОу (рис. 1).
Теорема существования и единственности решения задачи
Коши. Пусть дано дифференциальное уравнение у' = /(ж, у), где функция
/(ж, у) определена в некоторой области D плоскости хОу, содержащей
точку (ж0, уо)- Если функция /(ж, у) удовлетворяет условиям
а) /(ж, у) есть непрерывная функция двух переменных ж и у
в области D;
df
б) /(ж, у) имеет частную производную —, ограниченную в обла-
ду
emu D, то найдется интервал (жо — hy xq + h), на котором существует
единственное решение у = (р(х) данного уравнения, удовлетворяющее
условию у(х0) = уо.
Теорема дает достаточные условия существования единственного
решения задачи Коши для уравнения у' — /(ж, у), но эти условия
не являются необходимыми. Именно, может существовать единственное
решение уравнения у' — /(ж,у), удовлетворяющее условию у(х0) = у0,
хотя в точке (жо,уо) не выполняются условия а) или б) или оба вместе.
Рассмотрим примеры.
1 1 Р) f о
1. у' = —. Здесь /(ж, у) = —, — = —з- в точках (жо,О) оси
Ох условия а) и б) не выполняются (функция f(xyy) и ее частная
§ 1. Основные понятия и определения
производная — разрывны на оси Ох и неограничены при у —♦ 0),
оу
но через каждую точку оси Ох проходит единственная интегральная
кривая у = у/3(х - х0) (рис. 2). >
2. у' = ху + е~у. Правая часть уравнения /(ж, у) = ху + е~у и ее
df -у
частная производная — = х - е у непрерывны по х и у во всех
оу
точках плоскости хОу. В силу теоремы существования и единственности
областью, в которой данное уравнение имеет единственное решение
является вся плоскость хОу. >
У
С /С, /С2 /С3
Рис.2
Рис.3
3- 2/' = ~vT- Правая часть уравнения /(ж, у) = -у/у*
определена и непрерывна во всех точках плоскости хОу. Частная производная
df 1
— = — обращается в бесконечность при у = 0, т.е. на оси Ож, так
что при у = 0 нарушается условие б) теоремы существования и
единственности. Следовательно, в точках оси Ох возможно нарушение един-
(х + с)3
ственности. Легко проверить, что функция у = есть решение
о
данного уравнения. Кроме этого, уравнение имеет очевидное решение
у = 0. Таким образом, через каждую точку оси Ох проходит по крайней
мере две интегральные линии и, следовательно, действительно в точках
этой оси нарушается единственность (рис.3).
Интегральными линиями данного уравнения будут также линии,
(х + с)3
составленные из кусков кубических парабол у = и отрезков оси
Ох, например, АВОС\, АВВ2С2, А2В2х и др., так что через каждую
точку оси Ох проходит бесконечное множество интегральных линий. >
Замечание. Условие ограниченности производной df/dy, фигурирующее
в теореме существования и единственности решения задачи Коши, может
быть несколько ослаблено и заменено так называемым условием Липшица.
Говорят, что функция /(ж, у), определенная в некоторой области D,
удовлетворяет в D условию Липшица по у, если существует такая
6 Глава 1. Дифференциальные уравнения первого порядка
постоянная L (постоянная Липшица), что для любых у\, yi из D
и любого жизР справедливо неравенство
df
Существование в области D ограниченной производной — до-
оу
статочно для того, чтобы функция /(ж, у) удовлетворяла в D условию
Липшица (докажите это!). Напротив, из условия Липшица не вытекает
df
условие ограниченности —; последняя может даже не существовать. На-
оу
пример, для уравнения у' = 2\у\ cos х функция /(ж, у) = 2\у\ cos x не диф-
ференцируема по у в точке (жо,О), хо Ф — + for, k = 0, ± 1,..., но условие
Липшица в окрестности этой точки выполняется. В самом деле,
= 2|cose|||jfe|-|»,||
поскольку | cosж| ^ 1, a \\y2\ - \y\\\ ^ \уг ~У\\- Таким образом, условие
Липшица выполняется с постоянной L = 2.
Теорема. Если функция /(х, у) непрерывна и удовлетворяет условию
Липшица по у в области D, то задача Коти
-£ = /(^, 2/), У\х=Хо= 2/о, (а?о> 2/о) € I?
имеет единственное решение.
Условие Липшица является существенным для единственности
решения задачи Коши. В качестве примера рассмотрим уравнение
где
О, х = у = 0.
Нетрудно видеть, что функция /(ж, у) непрерывна; с другой стороны,
Если у = ах2, Y = /9ж2, то
l/()/()l
•с
§ 1. Основные понятия и определения
и условие Липшица не удовлетворяется ни в одной области, содержащей
начало О(0,0), так как множитель при \Y - y\ оказывается
неограниченным при х -*> 0.
Данное дифференциальное уравнение допускает решение
где С — произвольная постоянная. Отсюда видно, что существует
бесконечное множество решений, удовлетворяющих начальному условию
2/(0) = 0.
Общим решением дифференциального уравнения (2) называется
функция
У = Ф, С), (3)
зависящая от одной произвольной постоянной С, и такая, что 1) она
удовлетворяет уравнению (2) при любых допустимых значениях
постоянной С; 2) каково бы ни было начальное условие
можно подобрать такое значение Со постоянной С, что решение у =
<р(х, Со) будет удовлетворять заданному начальному условию (4). При
этом предполагается, что точка (х0) уо) принадлежит области, где
выполняются условия существования и единственности решения.
Частным решением дифференциального уравнения (2) называется
решение, получаемое из общего решения (3) при каком-либо определенном
значении произвольной постоянной С.
Пример 1. Проверить, что функция у = х + С есть общее решение
дифференциального уравнения у1 = 1 и найти частное решение,
удовлетворяющее начальному условию у\х=0 = 0. Дать геометрическое
истолкование результата.
Решение. Функция у = х+С удовлетворяет данному уравнению при любых
значениях произвольной постоянной С. В самом деле, у' = (х + С)' = I.
Зададим произвольное начальное условие y\XZSXQ = Уо- Полагая х = а?0
и у = уо в равенстве у = а?+С\ найдем, что С = уо-хо. Подставив это значение С
в данную функцию, будем иметь у = х + у0 ~ хо- Эта функция удовлетворяет
заданному начальному условию: положив х =
я0, получим у = х0 + уо - х0 = у0. Итак,
функция у = х+С является общим решением
данного уравнения.
В частности, полагая х0 = 0 и уо = 0,
получим частное решение у = х.
Общее решение данного уравнения, т.е.
функция у = х + Су определяет в
плоскости хОу семейство параллельных прямых
с угловым коэффициентом к =* 1. Через
каждую точку Мо(хоУ Уо) плоскости хОу
проходит единственная интегральная линия у =
я + Уо - я0. Частное решение у = х определяет одну из интегральных кривых,
а именно прямую, проходящую через начало координат (рис.4). >
Рис.4
Глава 1. Дифференциальные уравнения первого порядка
Пример 2. Проверить, что функция у — Сех есть общее решение
уравнения у' - у = О и найти частное решение, удовлетворяющее
начальному условию У !.,._,= -1.
Решение. Имеем у = Сех, у1 = Сех.
Подставляя в данное уравнение выражения у и у',
получаем Сех - Сех = 0, т. е. функция у = Сех
удовлетворяет данному уравнению при любых
значениях постоянной С.
Зададим произвольное начальное условие
у\х=х0 = У°- п°Дставив хо и уо вместо х и у
в функцию у = Сех, будем иметь уо = Сех°, откуда
С = уов"х°. Функция у = уоех~х° удовлетворяет
начальному условию. Действительно, полагая х = #0,
получим у = уое*0"*0 = у0. Функция у = Сех есть
общее решение данного уравнения.
При х0 = 1 и уо = -1 получим частное
решение у = -ех~].
С геометрической точки зрения общее
решение определяет семейство интегральных кривых,
которыми являются графики показательных функций; частное решение есть
интегральная кривая, проходящая через точку Мо(1, -1) (рис.5). >
Соотношение вида Ф(ж, у, С) = 0, неявно определяющее общее
решение, называется общим интегралом дифференциального уравнения
первого порядка.
Соотношение, получаемое из общего интеграла при конкретном
значении постоянной С, называется частным интегралом
дифференциального уравнения.
Задача решения или интефирования дифференциального уравнения
состоит в нахождении общего решения или общего интеграла данного
дифференциального уравнения. Если дополнительно задано начальное
условие, то требуется выделить частное решение или частный интеграл,
удовлетворяющие поставленному начальному условию.
Так как с геометрической точки зрения координаты х и у равно-
dy
правны, то наряду с уравнением — = fix,у) мы будем рассматривать
ах
Рис.5
dx
уравнение — =
dy
1
— -.
f(x, у)
Задачи для самостоятельного решения
1. Найти совпадающие решения двух дифференциальных уравнений:
а) у' = у2 + 2а? - х4; б) у1 = -у2 - у + 2х + х2 + х\
В следующих задачах, пользуясь каким-либо достаточным условием
единственности, выделить области, в которых данные уравнения имеют единственные
решения.
2. у' = х2+у2. 3. у' = -. 4.у' = у + ЗУу- 5. у'= >Д^У-
§ 2. Метод изоклин
6. у'шу/х^-х. 7. у' = у/Т^. 8. у' =
х-у__
9. yf = sin у - cos ж. 10. у'= 1 - ctgt/. 11. у' = -^За; - у - 1.
12. Показать, что для уравнения у' = |у||/2 в каждой точке оси Ох нарушается
единственность решения.
13. Найти интегральную линию уравнения у' = sin (xy), проходящую через точку
0(0,0).
В следующих задачах показать, что данные функции являются решениями
указанных дифференциальных уравнений:
14. у= -^-, ху' + у = cosx. 15. у = Се"2х + -ег, у' + 2у = ех
§2. Метод изоклин
Уравнение
»' = /(*, У) (О
определяет в каждой точке (ж,у), где существует функция /(ж, у),
значение у', т.е. угловой коэффициент касательной к интегральной кривой
в этой точке.
Если в каждой точке области D задано значение некоторой
величины, то говорят, что в области D задано поле этой величины. Таким
образом, дифференциальное уравнение (I) определяет поле направлений.
Тройка чисел (ж; у; у1) определяет направление прямой, проходящей
через точку (ж, у). Совокупность отрезков этих прямых дает
геометрическую картину поля направлений.
Задача интегрирования дифференциального уравнения (1) может
быть теперь истолкована так: найти такую кривую, чтобы касательная
к ней в каждой точке имела направление, совпадающее с направлением
поля в этой точке.
Задача построения интегральной кривой часто решается введением
изоклин. Изоклиной называется геометрическое место точек, в которых
касательные к искомым интегральным кривым имеют одно и тоже
направление. Семейство изоклин дифференциального уравнения (1)
определяется уравнением
/(«,») = *, (2)
где к — параметр. Придавая параметру к близкие числовые значения,
получаем достаточно густую сеть изоклин, с помощью которых
можно приближенно построить интегральные кривые дифференциального
Уравнения (1).
Замечание 1. Нулевая изоклина /(ж, у) = 0 дает уравнение линий* на
которых могут находиться точки максимума и минимума интегральных кривых.
10
Глава 1. Дифференциальные уравнения первого порядка
Для большей точности построения интегральных кривых находят также
геометрическое место точек перегиба. Для этого находят у" в силу уравнения (1):
Of df , df
и приравнивают ее нулю. Линия, определяемая уравнением
и есть возможное геометрическое место точек перегиба.
(3)
(4)
Пример 1. С помощью изоклин построить приближенно интегральные
кривые дифференциального уравнения у' = 2х - у.
Решение. Для получения уравнения изоклин положим у1 = fe, k = const
тогда
2х - у = fc, или у = 2х-к.
Изоклинами являются параллельные прямые. При к = 0 получим изоклину
у = 2х. Эта прямая делит плоскость хОу на две части, в каждой из которых
производная у' имеет один и тот же знак (рис.6).
Интегральные кривые, пересекая прямую у = 2ж, переходят из области
убывания функции у в область возрастания, и наоборот, а значит на этой прямой
находятся точки экстремума интегральных кривых, именно точки минимума.
Возьмем еще две изоклины:
= 2я+1, А? = — 1
= 2г-1, к = 1.
Касательные, проведенные к интегральным
кривым в точках пересечения с изоклинами
к = -1 и к = 1, образуют с осью Ох углы
в 135е и 45° соответственно. Найдем далее
вторую производную у" = 2-у1 = 2-2ж + у.
Прямая у = 2а? - 2, на которой у" = 0,
является изоклиной, получаемой при к = 2,
и в то же время интегральной линией, в чем
можно убедиться подстановкой в
уравнение. Так как правая часть данного
уравнения /(ж, у) = 2х - у удовлетворяет
условиям теоремы существования и единственности
во всей плоскости хОу> то остальные
интегральные кривые не пересекают эту
изоклину. Изоклина у = 2ж, на которой находятся
точки минимума интегральных кривых,
расположена над изоклиной у = 2ж-2, а
поэтому интегральные кривые, проходящие ниже
изоклины у = 2х - 2, не имеют точек
экстремума.
Прямая у = 2х-2 делит плоскость хОу
на две части, в одной из которых
(расположенной над прямой) у11 > 0, а значит
интегральные кривые обращены вогнутостью
вверх, а в другой у" < 0 и, значит, интегральные кривые обращены
вогнутостью вниз. Интегральные кривые не пересекают прямой у = 2х - 2, значит,
Рис.6
§ 2. Метод изоклин 11
она не является геометрическим местом точек перегиба. Интегральные кривые
данного уравнения не имеют точек перегиба.
Проведенное исследование позволяет нам приближенно построить семейство
интегральных кривых уравнения (рис.6). >
Пример 2. Методом изоклин построить приближенно интегральные
кривые дифференциального уравнения у' = sin (x + у).
Решение. Полагая у' = Л, где k = const, получаем уравнение изоклин
sin (я + у) = к, причем -1 ^ к ^ 1. При к = 0 получим sin (х + у) = 0, откуда
у = -х + 1гп (п = 0,±1,±2,...). (5)
Интефальные кривые в точках пересечения с этими изоклинами имеют
горизонтальные касательные.
Определим, имеют ли интефальные кривые на изоклинах у = -х + тгп
экстремум. Для этого найдем вторую производную:
у" = (1 4- у') cos (х + у) = [1 + sin (х + у)] cos (ж + у).
При у = -х + жп имеем
у" = (1 + sin тгп) cos (тгп) = cos тгп = (-1 )п.
Если п четное, то у" > О, и, значит, в точках пересечения с изоклинами
у = -ж + тгя, п = 0,±2,±4,..., интегральные кривые имеют минимум; если же п
нечетное, то у" < О и интефальные кривые в точках пересечения с изоклинами
у = -ая- я*ж, п = ±1, ±3,..., имеют максимум. Находим изоклины:
* = -1, sin (ж + у) = -1; у = -я- - +2тгп, (6)
Л=1, sin,(z + y)=l; у = -«+ - + 2тгп, (7)
п = 0,±1,±2,... ,
Изоклинами являются параллельные прямыми с угловым коэффициентом,
равным -1,т.е. изоклины пересекают ось Ох под углом 135°. Легко убедиться в том,
что изоклины у = -х - - + 27гп, п = 0, ±1,..., являются интегральными
кривыми данного дифференциального уравнения (для этого достаточно подставить
функции у = -х- - + 2тгп в уравнение у' = sin (x + у)).
Во всех точках плоскости хОу правая часть данного уравнения, т.е.
функция f(x} у) = sin (x + у), удовлетворяет всем условиям теоремы существования
и единственности, а поэтому интегральные кривые не пересекаются, и,
следовательно, не пересекают изоклин у = -х - - + 2тгп. Производная у" обращается
в ноль при 1 + sin (х + у) = 0, т. е. на изоклинах (6), и при cos (х + у) = 0, т. е.
на изоклинах (6) и (7). При переходе (слева направо) через изоклины (7) у"
меняет знак с плюса на минус. Например, если рассмотреть полосу, заключенную
между изоклинами у = -х и у = -я+тг, то на изоклине у = -х+ — производная
у" = 0, причем под изоклиной у" > 0. Значит, интегральные кривые обращены
вогнутостью вверх, а над изоклиной у" < 0, значит, интефальные кривые
обращены вогнутостью вниз. Таким образом, изоклины (7) являются геометрическим
местом точек перегиба интегральных кривых. Полученные данные позволяют
приближенно построить семейство интегральных кривых данного уравнения. Для
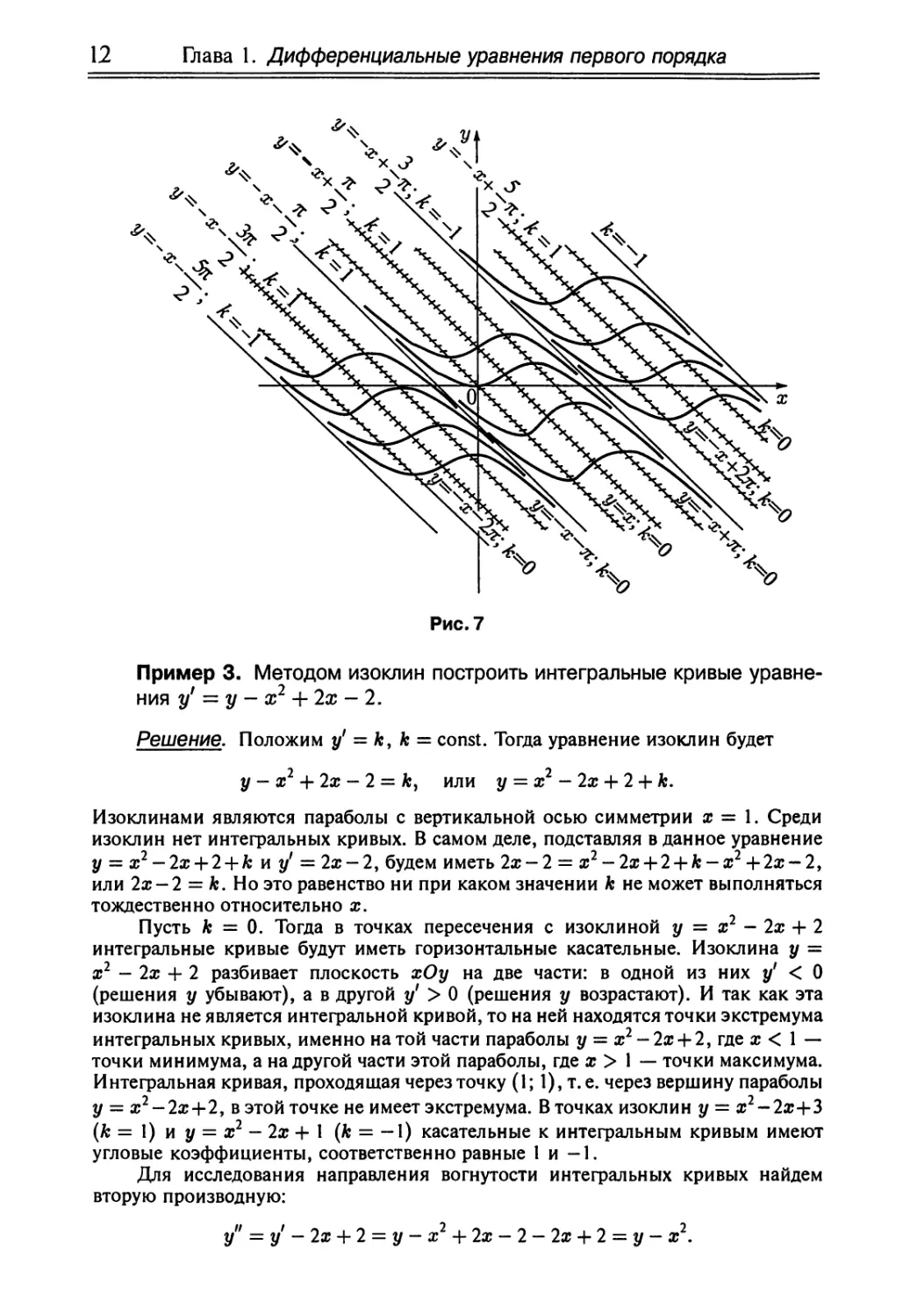
более точного построения следует нанести еще несколько изоклин (рис.7). >
12
Глава 1. Дифференциальные уравнения первого порядка
Рис.7
Пример 3. Методом изоклин построить интегральные кривые
уравнения у' = у - х2 + 2х - 2.
Решение. Положим у' = &, k = const. Тогда уравнение изоклин будет
у - х + 2х - 2 = к,
или
у = х2 - 2х + 2 + к.
Изоклинами являются параболы с вертикальной осью симметрии х = 1. Среди
изоклин нет интегральных кривых. В самом деле, подставляя в данное уравнение
у = х2-2х + 2 + к и у' = 2ж-2, будем иметь 2ж-2 = х2 -2х + 2 + к-х2 +2х-2,
или 2я-2 = к. Но это равенство ни при каком значении к не может выполняться
тождественно относительно х.
Пусть к = 0. Тогда в точках пересечения с изоклиной у = х2 — 2х + 2
интегральные кривые будут иметь горизонтальные касательные. Изоклина у =
х2 - 2х + 2 разбивает плоскость жОу на Две части: в одной из них у1 < 0
(решения у убывают), а в другой у' > 0 (решения у возрастают). И так как эта
изоклина не является интегральной кривой, то на ней находятся точки экстремума
интегральных кривых, именно на той части параболы у = х2 -2ж + 2, где х < 1 —
точки минимума, а на другой части этой параболы, где х > 1 — точки максимума.
Интегральная кривая, проходящая через точку (1; 1), т.е. через вершину параболы
у = ж2-2ж+2, в этой точке не имеет экстремума. В точках изоклин у = х2-2х-\-3
(к = 1) и у = х2 — 2х + 1 (к = — 1) касательные к интегральным кривым имеют
угловые коэффициенты, соответственно равные 1 и -1.
Для исследования направления вогнутости интегральных кривых найдем
вторую производную:
у' = у - 2х + 2 = у - х2 + 2х - 2 - 2х + 2 = у - х2.
§ 2. Метод изоклин
13
Она обращается в ноль только в точках, лежащих на параболе у = х2. В точках
плоскости хОу, координаты которых удовлетворяют условию у < х2,
интегральные кривые вогнуты вниз (у" < 0), а в точках, где у > х2, они вогнуты вверх
(у" > 0). Точки пересечения интегральных кривых с параболой у = х2 являются
точками перегиба этих кривых. Итак, парабола у = х2 есть геометрическое место
точек перегиба интегральных кривых.
Правая часть исходного уравнения f(x, у) = у — х2 + 2х - 2 во всех точках
плоскости хОу удовлетворяет условиям теоремы существования и
единственности, поэтому через каждую точку плоскости проходит единственная интегральная
кривая уравнения.
Используя полученные сведения, строим приближенно семейство
интегральных кривых данного уравнения (рис. 8). >
А;=-1
Рис.8
Замечание 2. Точки пересечения двух или нескольких изоклин могут быть
особыми точками дифференциального уравнения (1), т.е. такими точками,
в которых правая часть уравнения (1) не определена.
У
Рассмотрим уравнение у = —. Семейство изоклин определяется
у х
уравнением — = А;. Это семейство прямых, проходящих через начало
х
14
Глава 1. Дифференциальные уравнения первого порядка
координат, так что в начале координат пересекаются изоклины,
отвечающие различным наклонам касательных к интегральным кривым.
Нетрудно убедиться, что общее решение данного уравнения имеет вид у = Сх
и точка (0,0) является особой точкой дифференциального уравнения.
Здесь изоклины являются интегральными кривыми уравнения (рис.9).
Рис.9
Рис.10
Пример 4. Методом изоклин построить интегральные кривые уравне-
dy у - х
ния -г = .
dx у + х
у-х
Решение. Полагая у' = Л, k = const получаем уравнение семейства изоклин
= к. Таким образом, изоклинами являются прямые, проходящие через
начало координат 0(0,0).
При к = -I получим изоклину у = 0, при к = 0 — изоклину у = ж, при
к = 1 — изоклину х = 0.
Рассматривая «перевернутое» уравнение
dx _ у + х
dy у-х1
найдем изоклину у = -х, во всех точках которой интегральные кривые имеют
вертикальные касательные.
В точке (0,0) пересекаются все изоклины данного уравнения (особая точка
уравнения).
С помощью полученных изоклин строим интегральные кривые (рис. 10). >
Задачи для самостоятельного решения
17. Найти угол а между интегральными кривыми уравнений у' = х + у и у1 =
х - у в точке М(2,1).
18. Под каким углом а пересекают ось Ох в точке О(0,0) интегральные линии
уравнения у' = х2 + у2 + 1?
19. Найти точки экстремума интегральных уравнения у1 = х + 1.
20. Найти точки перегиба интегральных кривых уравнения у' -у-х2.
§ 3. Метод последовательных приближений 15
Методом изоклин построить интегральные кривые
ных уравнений:
21. «' = 3+1. 22. у' = х + у.
24.
27.
33.
36.
39.
у' = *2-у2.
у'=\-х.
у' = --.
г/ = у.
25.
28.
34.
37.
40.
у' = (у-О2.
у'= cos (ж-у).
у' = 2х - у.
у'=1.
у' = у2.
следующих дифференциаль-
23. у' = у-х.
26.
29.
35.
38.
у' = (у - \)х.
у' = а>2 + 2х-у.
У х-у'
у' = х2 + у.
§3. Метод последовательных приближений
Пусть требуется найти решение у = у(х) дифференциального
уравнения
V' = f(x,y), (1)
удовлетворяющее начальному условию
Будем предполагать, что в некотором прямоугольнике
D{\x - жо| < а, \у - уо| < Ь}
с центром в точке (жо>Уо) Для уравнения (1) выполнены условия а)
и б) теоремы существования и единственности решения задачи (1)-(2)
(см. с. 4).
Решение задачи (1)-(2) может быть найдено методом
последовательных приближений, который состоит в следующем.
Строим последовательность {уп(х)} функций, определяемых
рекуррентными соотношениями
х
Уп{х) = yo + J f[t, Уп-\Ш dt, n = 1, 2,.... (3)
В качестве нулевого приближения уо(х) можно взять любую функцию,
непрерывную в окрестности точки х = xq, в частности уо(х) = у0 —
начальное значение Коши (2). Можно доказать, что при сделанных
предположениях относительно уравнения (1) последовательные приближения
{Уп(х)} сходятся к точному решению уравнения (1), удовлетворяющему
условию (2), в некотором интервале хо - h < х < xq + ft, где
ft = min(a, — ), М= max |/(ж,2/)|. (4)
\ М/ (x,y)€D
16 Глава 1. Дифференциальные уравнения первого порядка
Оценка погрешности, получаемой при замене точного решения у(х) п-ы
приближением уп(х), дается неравенством
где N = max
MN
\y(X)-yn(X)\<——hn, (5)
. Применяя метод последовательных приближений,
ду
следует остановиться на таком п, для которого \уп+\ ~Уп\ не превосходит
допустимой погрешности.
Пример 1. Методом последовательных приближений найти решение
dy
уравнения — = у, удовлетворяющее начальному условию у(0) = 1.
ах
Решение. Очевидно, что для данного уравнения на всей плоскости хОу
выполнены условия теоремы существования и единственности решения задачи
Коши. Строим последовательность {уп(я)} функций, определяемых
соотношениями (3), приняв за нулевое приближение уо(х) = 1:
Уо(я) = 1,
х
У](х)=\+ fyo(t)dt=\+x,
у2(*) = 1'+ Jyi(t)dt=\+ Jl
о о
х х
Уз(х) = 1 + J y2(<) dt=\
вообще,
Ясно, что уп(х) —> е? при п —> со. Непосредственной проверкой убеждаемся,
что функция у (ж) = ех решает поставленную задачу Коши. >
Пример 2. Методом последовательных приближений найти
приближенное решение уравнения у1 = х2+у2, удовлетворяющее начальному
условию у\х=0= 0 в прямоугольнике -1^ж^1,-1^у^1.
Решение. Имеем |/(ж,у)| = х2 + у2 ^ 2, т.е. М = 2. За Л берем меньшее
6 1 1
из чисел а = 1, — = -, г. е. Л = -. Последовательные приближения согласно (4)
§ 3. Метод последовательных приближений
17
1 1
будут сходиться в интервале — - < х < -. Составляем их:
Уо(«) = О,
t = l + l,
3 + 63 + 2079 + 59535'
Абсолютная погрешность третьего приближения не превосходит величины
здесь
N = max
D
= max \2y\ = 2.
D
Замечание. Функция /(ж, у) должна удовлетворять всем условиям
теоремы существования и единственности решения задачи Коши.
Следующий пример показывает, что одной непрерывности функции
/(ж, у) недостаточно для сходимости последовательных приближений.
Пусть функция /(ж, у) определена следующим образом:
О для ж = 0, -оо < у < +оо,
2ж для 0 < ж ^ 1, -оо < у < О,
juym v/ \ u, <ч. I, 0 ^ У ^ Г*
Ж
4у
2х
для 0 < ж < 1, 0 ^ я
-2ж для 0<ж^1,ж2<у< +оо.
На множестве 0 < ж ^ 1, -оо < у < +оо функция /(ж, у) непрерывна
и ограничена постоянной М = 2. Для начальной точки (ж, у) = (0,0)
последовательные приближения при 0 ^ ж ^ 1 имеют вид:
Уо(х) = О,
х
у} (ж) - /
= ж2
= -ж2,
18 Глава 1. Дифференциальные уравнения первого порядка
и вообще
У2п-\(х) = х2, у2п(х) = -я2, п = 1, 2,....
Поэтому последовательность {уп{х)} для каждого х Ф О не имеет; предела,
т. е. последовательные приближения не сходятся. Заметим также, что
ни одна из сходящихся подпоследовательностей {у2П-\(х)} и {у2п(х)}
не сходится к решению, поскольку
у'2п-\(х) = 2х ? f(xyx2) = -2х}
у'2п(х) = -2х Ф /(*, -х2) = 2х.
Если же последовательные приближения сходятся, то полученное
решение может оказаться неединственным, как показывает следующий
пример: у' = 1/3
Возьмем начальное условие 2/(0) = 0; тогда
X
y(x) = Jy^(t)dt.
о
Беря в качестве нулевого приближения уо функцию уо(х) = 0, будем
иметь
так что все последовательные приближения равны нулю и поэтому они
сходятся к функции, тождественно равной нулю. С другой стороны,
функция у(х) = ( — J представляет собой также решение этой задачи,
существующее на полупрямой х ^ 0.
Задачи для самостоятельного решения
В следующих задачах найти три первых последовательных приближения:
41. у' = х2-у2, у\ , = 0. 42. у' = х + у2, у|я_0 = 0-
43. у' = х + у, у|1=7= 1. 44. у" = 2у - 2х2 - з" у|1=0 = 2.
45. ху' = 2х - у, у\ = 2.
§ 4. Уравнения с разделяющимися
переменными и приводящиеся к ним
Дифференциальное уравнение вида <р(у) dy = f(x) dx называется
уравнением с разделенными переменными.
Уравнение вида
<P\(x)i>\(y) dx = <p2(x)ip2(y) <ty>
§ 4. Уравнения с разделяющимися переменными 19
в котором коэффициенты при дифференциалах распадаются на
множители, зависящие только от х и только от уу называется уравнением
с разделяющимися переменными.
Путем деления на произведение *ф\(у)<Р2(х) оно приводится к
уравнению с разделенными переменными:
dx=dy.
<pi(x) My)
Общий интеграл этого уравнения имеет вид
Замечание. Деление на ty\{y)<pi{x) может привести к потере частных
решений, обращающих в ноль произведение p(){)
Дифференциальное уравнение вида
dv
^ = /(ax +
где а, Ь и с — постоянные, заменой переменных z = ax + by + с
преобразуется в уравнение с разделяющимися переменными.
Пример 1. Решить уравнение
Зех tgydx + (2- ex) sec2y dy = 0.
Решение. Разделим обе части уравнения на произведение tg у • (2 - ех):
Зех dx sec 2y dy
+ *-£ = 0.
2-е* tg у
Получили уравнение с разделенными переменными. Интегрируя его, найдем
-3ln|2-e*| + l
После потенцирования получим
|tgy|
= е '. или
tgy
= еС|.
(2-е-)3
откуда
tgy _ . с.
Обозначая ±еС| = С, будем иметь
— £ту = С или tg у - С(2 - е*)3 = 0.
Мы получили общий интеграл данного уравнения.
При делении на произведение tgy • (2 - ех) предполагалось, что ни один
из множителей не обращается в ноль. Приравняв каждый множитель нулю,
получим соответственно
20 Глава 1. Дифференциальные уравнения первого порядка
Непосредственной подстановкой в исходное уравнение убеждаемся, что у =
'&7Г и х = In 2 являются решениями этого уравнения. Они могут быть формально
получены из общего интеграла при С = 0 и С = оо. Последнее означает, что
постоянная С заменяется через —, после чего общий интеграл примет вид
tgJ/-7T(2-ex)3 = 0, или C2tgy-(2-e*)3 = 0.
Полагая в последнем равенстве С2 = 0, что соответствует С = оо, будем иметь,
что (2-е*)3 = 0, откуда и получаем решение х = In 2 исходного уравнения. Итак,
функции у — &тг, fc = 0, ±1,±2,... и х = In2 являются частными решениями
данного уравнения. Поэтому окончательный ответ будет таким:
tgy-C(2-ex)3 = 0. >
Пример 2. Найти частное решение уравнения
удовлетворяющее начальному условию у\х=0 = 1.
Решение. Имеем
Разделяй переменные, лолучаем
exdx
Интегрируя, найдем общий интеграл
^ (1)
Полагая в(1) х = 0 и у = 1 будем иметь
- '= In 2 + С, отку
Подставляя в (1) найденное значение С, получаем частное решение
- '= In 2 + С, откуда С In 2.
/1+ех\2 / /
у2 = 1+In f —— J , откуда y = ±Wl+ln (
1+ех\2
Из начального условия следует, что у > 0 (у|яг==0 = 1 > 0), поэтому перед корнем
берем знак плюс. Итак, искомое частное решение
-№}¥)'■
Пример 3. Найти частные решения уравнения
у sin х = у In 2/,
удовлетворяющие начальным условиям:
§ 4. Уравнения с разделяющимися переменными 21
Решение. Имеем
dy .
— sin х = у In у.
arc
Разделяем1 переменные
dy dx
y\ny sin x
Интегрируя, найдем общий интеграл
In | In 2/| = In
X
tg-
2
После потенцирования получим.
1пС.
lny = C-tg|, или у = еСл*(*/2\
что является общим решением исходного уравнения.
а) Положим х = -, у = е, тогда е = eClg(ir/4), откуда С = 1. Искомое
частное решение у = е'8(7г/2).
б) Полагая в общем решении ж = —, у = 1, будем иметь 1 = ec'tg(*/4\
откуда С = 0. Искомое частное решение у = 1.
Заметим, что в процессе получения общего решения постоянная С входила
под знак логарифма, и, значит, С = 0 следует рассматривать как предельное
значение. Это частное решение у = 1 содержится среди нулей произведения
у In у sin ж, на которое мы делили обе части данного уравнения. \>
Пример 4. Найти такую кривую, проходящую через точку (0, -2),
чтобы тангенс угла наклона касательной в любой ее точке равнялся
ординате этой точки, увеличенной на три единицы.
Решение. Исходя из геометрического свойства первой производной,
получаем дифференциальное уравнение семейства кривых, удовлетворяющих
требуемому в задаче свойству, а именно
Разделяя переменные и интегрируя, получаем общее решение
у = Се*-3. (2)
Так как искомая кривая должна проходить через точку (0, -2), т. е, у\х=0 — -2, то
из (2) при х = 0 получаем -2 = С-3, откуда С = 1. Искомая кривая определится
Уравнением
У = ех - 3. >
Пример 5. Найти кривую, обладающую тем свойством, что длина ее
дуги, заключенной между какими-либо двумя точками Р и Q,
пропорциональна разности расстояний точек Р и Q от неподвижной точки О.
Решение. Если фиксировать точку Р, то дуга QP будет изменяться
пропорционально разности OQ и постоянной ОР. Введем полярные координаты,
22 Глава 1. Дифференциальные уравнения первого порядка
беря точку О за полюс и ОР — за полярную ось
(рис. 11). Дифференциал дуги кривой в полярных
координатах
(ds)2 = (dr)2 + (rd<p)2.
Отсюда для нашей задачи имеем
k2(dr)2 = (dr)2 + (r dip)2, или dip = y/k2- 1 —.
Интегрируя, находим г = Сеп* (логарифмическая спираль). >
Пример 6. Допустим, что при постоянной температуре скорость
растворения твердого тела в жидкости пропорциональна количеству этого
вещества, еще могущего раствориться в жидкости до насыщения
последней (предполагается, что вещества, входящие в раствор,
химически не действуют друг на друга, и раствор далек еще от насыщения,
так как иначе линейный закон для скорости растворения неприменим).
Найти зависимость количества растворившегося вещества от времени.
Решение. Пусть Р — количество вещества, дающее насыщенный раствор,
и х — количество уже растворившегося вещества. Тогда получаем
дифференциальное уравнение
!
где к — известный из опыта коэффициент пропорциональности, at — время.
Разделяя переменные, найдем
dx
J
Интегрируя, получаем
1гф-Р| = 1пС- Art, откуда х = Р + Се~ы.
В начальный момент t = О имеем х = 0, поэтому С = -Р, так что
окончательно
я = Р(1-е-'<). >
Пример 7. В цилиндрическом сосуде объемом Vb заключен
атмосферный воздух, который адиабатически (без обмена тепла с окружающей
средой) сжимается до объема V\. Вычислить работу сжатия.
Решение. Известно, что адиабатический процесс характеризуется
уравнением Пуассона
(3)
где Vb — первоначальный объем газа, ро — первоначальное давление газа, к —
постоянная для данного газа величина. Обозначим через V и р соответственно
объем и давление газа в тот момент, когда поршень находится на высоте /i,
а через S — площадь поршня. Тогда при опускании поршня на величину dh
объем газа уменьшится на величину dV = S dh. При этом будет выполнена работа
или dW = -pdV. (4)
§ 4. Уравнения с разделяющимися переменными 23
Находя р из (3) и подставляя в (4), получаем дифференциальное уравнение
процесса
Интегрируя это уравнение, будем иметь
согласно начальному условию W|y=v = 0 из (5) получим
г- Р°у°
Таким образом, работа адиабатического сжатия (от Vo до V) будет
При V = VI получаем
Пример 8. Найти решение уравнения
a3 sin у-у' = 2. (6)
удовлетворяющее условию
7Г
2/ "♦ т при х -> оо. (7)
Решение. Разделяя переменные и интегрируя, найдем общий интеграл
уравнения (6):
cos у = -т + С.
Условие (7) дает cos - = С, т. е. С = 0, так что частный интеграл будет иметь вид
cost/ = -т. Ему соответствует бесконечное множество частных решений вида
у = ±arccos -у + 2тгп, п = 0,±1,±2,... . (8)
Среди этих решений имеется только одно, удовлетворяющее условию (7). Это
решение найдем, переходя к пределу при х -* оо в равенстве (8):
- = ± arccos 0 + 2тгп, или -=±-
откуда
24 Глава 1. Дифференциальные уравнения первого порядка
Нетрудно видеть, что уравнение (9) имеет два корня: п = 0 и п = -, причем
корень п = -, отвечающий знаку минус перед arccos ( — ), не подходит (п долж-
2 \х /
но быть целым или нулем). Таким образом, искомое частное решение
уравнения (6) будет
у = arccos -г.
х1
Задачи для самостоятельного решения
Проинтегрировать уравнения:
46. (1 + у2) da; + (1 + a;2) dy = 0.
48. у' sin х -у cos х = 0, у\х__„ = \.
50. ху/\+у2 + уу'л
52. е~у(
54. у' =
56.
58. у2 sin х dx + cos 2ж In у dy = 0.
47. (l+y2)da; + a;ydy = 0.
49. (1 +y2)dx = xdy.
51. xVl - y2 da; + у\Л - a;2 = 0,
53. у In у da; + ж dy = 0, у|xss| = 1.
55. ey(l + ж2) dy - 2ж(1 + ey) dx = 0.
57. ex sin 3y + (1 + e2x) cos у • у' = 0.
59. у' = sin (ж-у).
60. у; = аж + Ьу + с (а, Ь, с — const). 61. (ж + у)2у' = о2.
62. у + ху = а(\ + жу), 63. (а2 + у2) dж + 2х\/ах - ж2 dy = 0,
64.
, y\x=if = -.
65. Найти такую кривую, проходящую через точку (0, -2), чтобы угловой
коэффициент касательной в любой ее точке равнялся ординате этой точки,
увеличенной в три раза.
66. Найти кривую, для которой площадь Q, ограниченная кривой, осью Ох
и двумя ординатами X = 0, X = ж, является данной функцией от у: Q =
a2 In (у/а).
67. Материальная точка массой в I г движется прямолинейно под действием
силы, прямо пропорциональной времени, отсчитываемому от момента t = 0,
и обратно пропорциональной скорости движения точки. В момент t = \0 с
скорость равнялась 50 см/с, а сила — 4 дин. Какова будет скорость спустя минуту
после начала движения?
68. Доказать, что кривая, обладающая тем свойством, что все ее нормали
проходят через постоянную точку, есть окружность.
69. Пуля входит в доску толщиной h = 10 см со скоростью v0 = 200 м/с,
а вылетает из доски, пробив ее, со скоростью V\ = 80 м/с. Считая, что сила
сопротивления доски движению пули пропорциональна квадрату скорости
движения, найти время движения пули через доску.
70. Корабль замедляет свое движение под действием силы сопротивления воды,
которая пропорционально скорости корабля. Начальная скорость корабля 10 м/с,
скорость его через 5 с станет 8 м/с. Когда скорость уменьшится до 1 м/с?
§ 4. Уравнения с разделяющимися переменными 25
71. Доказать, что кривая, угловой коэффициент касательной которой в любой
точке пропорционален абсциссе точки касания, есть парабола.
72. По закону Ньютона скорость охлаждения какого-либо тела в воздухе
пропорциональна разности между температурой Т тела и температурой воздуха То.
Если температура воздуха равна 20° С и тело в течение 20 мин охлаждается от 100
до 60° С, то через сколько времени его температура понизится до 30° С?
73. Найти кривую, для которой угловой коэффициент касательной в какой-либо
точке в п раз больше углового коэффициента прямой, соединяющей ту же точку
с началом координат.
74. Определить путь 5, пройденный телом за время t, если его скорость
пропорциональна проходимому пути и если тело проходит 100 м в 10 с и 200 м
в 15 с.
75. Дно резервуара, вместимость которого 300 л, покрыто солью. Допуская,
что скорость растворения соли пропорциональна разности между концентрацией
в данный момент и концентрацией насыщенного раствора (1 кг соли на 3 л воды)
и что данное количество чистой воды растворяет 1/3 кг соли в одну минуту,
найти, сколько соли будет содержать раствор по истечении 1 ч.
76. Некоторое количество нерастворимого вещества содержит в своих порах
10 кг соли. Подвергая его действию 90 л воды, нашли, что в течение 1 ч
растворилась половина содержавшейся в нем соли. Сколько соли растворилось бы
в течение того же времени, если бы количество воды было удвоено? Скорость
растворения пропорциональна количеству еще нерастворенной соли и разности
между концентрацией раствора в данный момент и концентрацией насыщенного
раствора (1 кг на 3 л).
77. Найти кривую, обладающую тем свойством, что отрезок касательной к
кривой, заключенный между осями координат, делится в точке касания пополам.
78. Некоторое количество вещества, содержащее 3 кг влаги, было помещено
в комнате вместимостью 100 м3, воздух которой первоначально имел
влажность 25 %. Насыщенный воздух при той же температуре содержит 0,12 кг влаги
на 1 м3. Если в течение первых суток вещество потеряло половину своей влаги,
то сколько влаги в нем останется по истечении вторых суток?
Указание. Влага, содержащаяся в пористом веществе, испаряется в
окружающее пространство со скоростью, пропорциональной количеству влаги
в данном веществе, а также пропорциональной разности между влажностью
окружающего воздуха и влажностью воздуха насыщенного.
79. Некоторое количество нерастворимого вещества, содержащее в своих порах
2 кг соли, подвергается действию 30 л воды. Через 5 мин 1 кг соли
растворяется. Через сколько времени растворится 99 % первоначального количества
соли?
80. Кирпичная стена имеет толщину 30 см. Найти зависимость температуры
от расстояния точки от наружной поверхности стены, если температура
равна 20° С на внутренней и 0° С на внешней поверхности стены. Найти также
количество тепла, которое стена (на 1 см2) отдает наружу в течение суток.
Указание. В силу закона Ньютона скорость Q, с которой теплота
распространяется через площадку А, перпендикулярную оси Ох, равна Q =
dT
-kS—, где к — коэффициент теплопроводности данного вещества (к =
at
0,0015), Т — температура, t — время, S — площадь А.
81. Показать, что уравнение — = — при начальном условии y\Xzs0 = 0 имеет
бесконечное множество решений вида у = Сх. Это же уравнение при начальном
26 Глава 1. Дифференциальные уравнения первого порядка
условии y\x=Q = у0 Ф 0 не имеет ни одного решения. Построить интегральные
кривые.
dy
82. Показать, что задача — = у , у|ж=0 = 0 имеет, по крайней мере, два
решения для 0 < а < 1 и одно для а = 1 Построить интегральные кривые для
83. Найти решение уравнения —- = у\ 1пу|а, а > 0, удовлетворяющее началь-
dx
ному условию у\х=0 = 0. Для каких значений а задача имеет единственное
решение?
84. Показать, что касательные ко всем интегральным кривым
дифференциального уравнения у1 + ytgx = xtgx + 1 в точках пересечения их с осью Оу
параллельны. Определить угол, под которым интегральные кривые пересекают
ось Оу.
Проинтегрировать следующие дифференциальные уравнения:
85. cos у' = 0. 86. еу1 = 1. 87. sin у' = х. 88. In у' = х.
89. tg у' = 0. 90. еу' = я. 91. tg у1 = х.
В следующих задачах найти решения уравнений, удовлетворяющих указанным
условиям:
92. x2y'cosy+\=0, у -+ —тг, х -> +оо.
93. х2у' + cos 2у = 1, у -► —7г, х -> +оо.
94. «V-siny=l, У "♦ 5тг, х -юо.
95. (1 +s2)y'- -cos22y = 0, у -+ -тг, ж -► -оо.
96. еу = е4уу; + 1, у ограничено при х -♦ +оо.
97. (х + 1)у' = у - 1, у ограничено при х -* +оо.
98. у' = 2а?(тг + у), у ограничено при ж -► со.
99. х2у' + sin2y=l, у -+ —тг, а? -► +оо.
4
§5. Уравнения однородные
и приводящиеся к ним
1°. Однородные уравнения. Функция f{x,y) называется
однородной функцией своих аргументов измерения п, если справедливо
тождество f(tx, ty) = tnf(x, у).
Например, функция /(ж, у) = ж2 + у2 - жу есть однородная функция
второго измерения, так как f(tx, ty) = (te)2 + (ty)2 - (ta)(ty) = £2(я2 «f
2 2
§ 5. Уравнения однородные и приводящиеся к ним 27
При п = О имеем функцию нулевого измерения. Например, /(ж, у) =
х2-у2
-— г есть однородная функция нулевого измерения, так как
х1 Л-У
хЦу! = /(». у)-
dy
Дифференциальное уравнение вида — = /(а:, у) называется одно-
ax
родным относительно ж и у, если /(ж, у) есть однородная функция своих
аргументов нулевого измерения. Однородное уравнение всегда можно
представить в виде
У
Вводя новую искомую функцию и = -, уравнение (1) можно
привести к уравнению с разделяющими переменными:
du
dx ry '
Если u = щ есть корень уравнения <р(и) - tt = 0, то решение
однородного уравнения будет и = щ или у = иоя (прямая, проходящая
через начало координат).
Замечание. При решении однородных уравнений необязательно
приводить их к виду (1). Можно сразу делать подстановку у = их.
Пример 1. Решить уравнение ху1 = у/х2 -у2 + у.
Решение. Запишем уравнение в виде
так что данное уравнение оказывается однородным относительно хну. Положим
и = -, или у = их. Тогда у' = хи1 + и. Подставляя в уравнение выражения для у
. х
и у , получаем
du г
х— = V 1 - w2.
n dx
газделяя переменные:
du dx
v
Отсюда интегрированием находим
arcsin ге = In |ж| + In С, (С| > 0), или arcsin и = In C\ \х\.
Так как d|a:| = ±С\Х, то, обозначая ±С\ = С, получаем arcsin и = 1пСг, где
I In Сх\ ^ - или е~*/2 < Сж < eff/2. Заменяя и на -, будем иметь общий интеграл
*• х
У
arcsin - = In Cx.
х
°тсюда общее решение: у = a: sin In Cx.
28
Глава 1. Дифференциальные уравнения первого порядка
При разделении переменных мы делили
обе части уравнения на произведение xV\ - и2,
поэтому могли потерять решение, которые
обращают в ноль это произведение.
Положим теперь х = 0 и V\ - и2 = 0.
У
Но х Ф 0 в силу подстановки и — —, а из
соотношения V\ - и2 = 0 получаем, что 1 = 0,
х2
откуда у = ±х. Непосредственной проверкой
убеждаемся, что функция у = —х и у = х также
являются решениями данного уравнения. \>
Пример 2. Рассмотреть семейство
интегральных кривых Са однородного
уравнения
Рис.12
(2)
Показать, что касательные в соответственных точках2^ к кривым,
определяемым однородным дифференциальным уравнением (2),
параллельны между собой.
У У\
Решение. По определению соответственных точек имеем - = —, так что
X Х\
в силу самого уравнения (2)
У =У\,
где у' и у\ — угловые коэффициенты касательных к интегральным кривым Са
и Са, в точках МиМ| соответственно (рис. 12). >
Задачи для самостоятельного решения
Проинтегрировать следующие уравнения:
100. ху' = y + scos -.
X
102. ху' = y(\ny-\nx).
104. ху' =
101. (x-y)dx
103. х2 dy = (у2 -ху + х2) dx.
105. 2х2у' =
106. (4x-3y)dx + (2y-3x)dy = Q. 107. (у - x)dx + (у + х) dy = 0.
2°. Уравнения, приводящиеся к однородным.
А. Рассмотрим дифференциальное уравнение вида
dу _ / ах + by + с \
(3)
2^ Будем называть соответственными те точки на кривых CQ, которые лежат на одном
луче, выходящем из начала координат.
§ 5. Уравнения однородные и приводящиеся к ним
29
где а, Ь, с, а\, Ь\, С\ — постоянные, a f(u) — непрерывная функция
своего аргумента и.
Если с = с\ = О, то уравнение (3) является однородным и оно
интегрируется, как указано выше.
Если хотя бы одно из чисел с, С\ отлично ot нуля, то следует различать
два случая.
a b
а, 6,
Вводя новые переменные £ и rj по формулам х = £ + Л, у =
где /i и fc — пока неопределенные постоянные, приведем уравнение (3)
к виду
1) Определитель А =
* + с \
Выбирая /i и А; как решение системы линейных уравнений
+ 6А: + с = О,
bjfc + c, =0
получаем однородное уравнение
(А * 0),
(4)
Найдя его общий интеграл и заменив в нем ^ на ж - Л, а т/ на у - fe,
получаем общий интеграл уравнения (3).
Ь
2) Определитель А =
а, 6,
= 0.
Система (4) в общем случае не имеет решений и изложенный вы-
ше метод неприменим; в этом случае — = — = Л, и, следовательно,
а о
уравнение (3) имеет вид
dx
ax + by + c
Подстановка z = ax + by приводит его к уравнению с разделяющимися
переменными.
Пример 3. Решить уравнение
(х + у - 2) dx + (х - у + 4) dy = 0. (5)
Решение. Рассмотрим систему линейных алгебраических уравнений
Определитель этой системы
Д =
1 1
1 -1
= -2*0.
30 Глава 1. Дифференциальные уравнения первого порядка
Система имеет единственное решение а?0 = — 1, Уо = 3. Делаем замену х = { - 1»
у = rj + 3. Тогда уравнение (5) примет вид
0. (6)
Уравнение (6) является однородным уравнением. Полагая т} = и(, получаем
откуда
(l+2u-u2)d£ + £(1 -u)du = 0.
Разделяем переменные
d£ 1-й
-г + -—- г du = 0.
£ 1 + 2u - u2
Интегрируя, найдем
In 1(1 + 5 In 11 + 2u - u2| = In С, или £2(1 + 2u - u2) = C.
Возвращаемся к переменным ж, у:
или
ж2 + 2ху - у2 - 4ж + 8у = С (С = С| + 14). >
Пример 4. Решить уравнение (х + у +\) dx+ (2x + 2y - \)dy = 0.
Решение. Система линейных алгебраических уравнений
f х + у + 1 = О,
\ 2а? + 2у - 1 = 0
несовместна. В этом случае метод, примененный в предыдущем примере, не
подходит. Для интегрирования уравнения применяем подстановку х + у = z,
dy = dz - dx. Уравнение примет вид
(2-2)<*r + (2z-l)<te = 0.
Разделяя переменные, получаем
dx — dz = 0, отсюда х - 2z - 3 In \z - 2| = С.
Возвращаясь к переменным я, у, получаем общий интеграл данного
уравнения х + 2у + 3 In \х + у - 2| = С. >
Задачи для самостоятельного решения
Решить следующие уравнения:
108. ж + у-2 + (1-а)у' = 0.
109. (Зу - 7х + 7) dx - (За - 1у - 3) dy = 0.
110. (ж-Ь у - 2) da + (х - у + 4) dy = 0.
111. (а? + у) dx + (ж - у - 2) dy = 0.
112. 2а? + Зу-5 + (Заг + 2у - 5)у'= 0.
113. 8 '
§ 5. Уравнения однородные и приводящиеся к ним 31
114. (х - 2и - I) dx + (За - 6у + 2) dy = 0.
115. (a? + y)da? + (a? + y- l)dy = 0.
Б. Иногда уравнение можно привести к однородному заменой
переменного у = za. Это имеет место-в том случае, когда в уравнении
все члены оказываются одинакового измерения, если переменному х
приписать измерение 1, переменному у — изменение а и производной
dy
— — измерение a - 1.
ax
Пример 5. Решить уравнение
У *x = 0. (7)
Решение. Делаем подстановку у = zat dy = azQ"] dz, где а пока
произвольное число, которое мы выберем позже. Подставляя в уравнение выражения
для у и dy, получим
(x2z2a - \)aza'1 dz + 2a?z3a da? = 0,
или
(a?Va"' - zQ'])a dz + 2a?z3a da; = 0,
Заметим, что a?V°~' имеет измерение 2 +За- 1 = За-f 1, za~] имеет измерение
а-1, xzla имеет измерение 1+За. Полученное уравнение будет однородным, если
измерения всех членов одинаковы, т.е., если выполняется условие За+ 1 = а- 1,
или а = — 1.
Положим у = -; исходное уравнение принимает вид
/1 •/
или
(z2 - a?2) dz + 2*а? da? = 0.
Положим теперь z = ua?, dz = udx + xdu. Тогда это уравнение примет вид
(u2 - l)(u da? + a? du) + 2u dx = 0, откуда
u(u2 + 1) da? + a?(u2 - 1) du = Ol
Разделяем переменные в этом уравнении
dx u2 - 1 Л
— + -i du = 0.
х и2 + и
Интегрируя, найдем
/2 х{и* + О
In |а?| + In (и + 1) - In и = In С, или = С.
и
Заменяя и через —, получаем общий интеграл данного уравнения
1 + а?2у2 = Су:
Уравнение (7) имеет еще очевидное решение у = 0, которое получается
(1 н- х2у2)
из общего интеграла при С -+ оо, если интеграл записать в виде у = -— ,
а затем перейти к пределу при С -► оо. Таким образом, функция у = 0 является
частным решением исходного уравнения. >
32 Глава 1. Дифференциальные уравнения первого порядка
Задачи для самостоятельного решения
Проинтегрировать следующие уравнения:
116. 2ху'(х - у2) + у3 = 0. 117. 4у6 + х3 = 6ху5у'.
118. y(\ + y/xTyr+~i)dx + 2xdy = 0. 119. (х + у2) dx + 3(г/3 - ж)у2 dy = 0.
120. Найти кривую, обладающую тем свойством, что величина перпендикуляра,
опущенного из начала координат на касательную, равна абсциссе точки касания.
121. Определить кривую, у которой отношение отрезка, отсекаемого касательной
на Оу, к радиусу-вектору равно постоянной величине.
122. Пользуясь прямоугольными координатами, найти форму зеркала,
отражающего параллельно данному направлению все лучи, выходящие изданной точки.
123. Найти кривую, для которой длина отрезка, отсекаемого на оси ординат
нормалью, проведенной в какой-нибудь точке кривой, равна расстоянию этой
точки от начала координат.
124. Найти кривую, для которой произведение абсциссы какой-нибудь точки
на величину отрезка, отсекаемого нормалью на оси Оу, равно удвоенному
квадрату расстояния от этой точки до начала координат.
§6. Линейные уравнения первого порядка.
Уравнение Бернулли
1°. Линейные уравнения первого порядка. Линейным
дифференциальным уравнением первого порядка называется уравнение,
линейное относительно неизвестной функции и ее производной. Оно имеет вид
•^+p(x)y = q(x), 0)
ах
где р(х) и q(x) — заданные функции от ж, непрерывные в той области,
в которой требуется проинтегрировать уравнение (1).
Если q(x) = 0, то уравнение (1) называется линейным однородным.
Оно является уравнением с разделяющимися переменными и имеет общее
решение
y = Ce-fp{x)dx.
Общее решение неоднородного уравнения можно найти методом
вариации произвольной постоянной, который состоит в том, что решение
уравнения (1) ищется в виде
где С(х) — новая неизвестная функция от х.
Пример 1. Решить уравнение
*. (2)
§6. Линейные уравнения первого порядка. Уравнение Бернулли 33
Решение. Применим метод вариации постоянной. Рассмотрим однородное
уравнение
у + 2ху = О,
соответствующее данному неоднородному уравнению. Это уравнение с
разделяющимися переменными. Его общее решение имеет вид
Общее решение неоднородного уравнения ищем в виде
у = С{х)е~*\ (3)
где С(х) — неизвестная функция от х. Подставляя (3) в (2), получаем С(х) = 2х,
откуда С(х) = х2 + С. Итак, общее решение неоднородного уравнения будет
у = (х2 + С)е-*\
где С — постоянная интегрирования. >
Замечание. Может оказаться, что дифференциальное уравнение линейно
относительно х как функция от у. Нормальный вид такого уравнения
dx
— + г(у)х =
Пример 2. Решить уравнение — =
dx х cos у + sin 2y'
Решение. Данное уравнение является линейным, если рассматривать х как
функцию от у:
dx
xcosy = sin 2y. (4)
Применяем метод вариации произвольной постоянной. Сначала решаем
соответствующее однородное уравнение
dx
х cos у = О,
dy
которое является уравнением с разделяющимися переменными. Его общее
решение имеет вид
x = Ces]ny) С = const.
Общее решение уравнения (4) ищем в виде
х = С(уУп», (5)
где С(у) — неизвестная функция от у. Подставляя (5) в (4), получаем
C(y)esiny + C(y)esiny cos у - С(у)е*" cosy = sin 2y,
или
Отсюда, интегрируя по частям, будем иметь
С(у)=: f e~sinysin2ydy = 2 f e'siny cos у sin у dy =
= 2 Js\nyd(-e-siny) = 2(-s\nye-siny+[е-^у cosy dy\ =
34 Глава 1. Дифференциальные уравнения первого порядка
итак,
С(у) = -2e-sinv(l + sin у) + С. (6)
Подставляя (6) в (5), получаем общее решение уравнения (4), а значит, и данного
уравнения:
х = Cesiny - 2(1 4-siny). >
Уравнение (1) может быть проинтегрировано также следующим образом.
Полагаем
у = u(x)v(x), (7)
где и(х) и v(x) — неизвестные функции от ж, одна из которых, например и(ж),
может быть выбрана произвольно. Подставляя (7) в (1), после преобразования
получаем
vuf + (pv + v')u = q(x). (8)
Определяя v(x) из условия v' + pv = 0, найдем затем из (8) функцию и(ж),
а следовательно, и решение у = uv уравнения (1). В качестве v(x) можно взять
любое частое решение уравнения v' +pv = 0, v £ 0. >
Пример 3. Решить задачу Коши:
х{х-\)у' + у = х\2х-\), (9)
2/1**2 = 4. (10)
Решение. Ищем общее решение уравнения (9) в виде
у = и(ф(я);
имеем у' = u't> + uv'.
Подставляя выражение для у и у' в (9), будем иметь
х(х - \)(uv + uv') + uv = ж2(2ж - 1),
или
х(х - \)vu' + [х(х - l)t/ + v]u = г2(2з - 1).
Функцию v = v(x) находим из условия х(х- \)v'+v = 0. Беря любое частное
X
решение последнего уравнения, например г; = -, и подставляя его в (11),
х — 1
получаем уравнение и' = 2х— 1, из которого находим функцию и(х) = х2 -х + С.
Следовательно, общее решение уравнения (9) будет
или у=
СХ
, или уг+ж.
х — 1 ж — 1
Используя начальное условие (10), получаем для нахождения С уравнение
4 = С h 22, откуда С = 0; так что решением поставленной задачи Коши
будет
у = ж2. >
Пример 4. Известно, что между силой тока i и электродвижущей
силой Е в цепи, имеющей сопротивление R и самоиндукцию L,
существует зависимость Е = Дг + £— где R и X — постоянные. Если
§ 6. Линейные уравнения первого порядка. Уравнение Бернулли 35
считать Е функцией времени t, то получим линейное неоднородное
уравнение для силы тока г:
at L L
Найти силу тока i(t) для случая, когда Е = Ео = const и г(0) = Iq.
Решение. Имеем
d% R, Eq
It + 1|а8Т'
i(0) = /0. (13)
Общее решение уравнения (12) имеем вид
(12)
(14)
Используя начальное условие (13), получаем из (14) С = /о - —, так что искомое
решение будет
п. \ К /
Отсюда видно, что при t -> +oo сила тока i(t) стремится к постоянному
значению
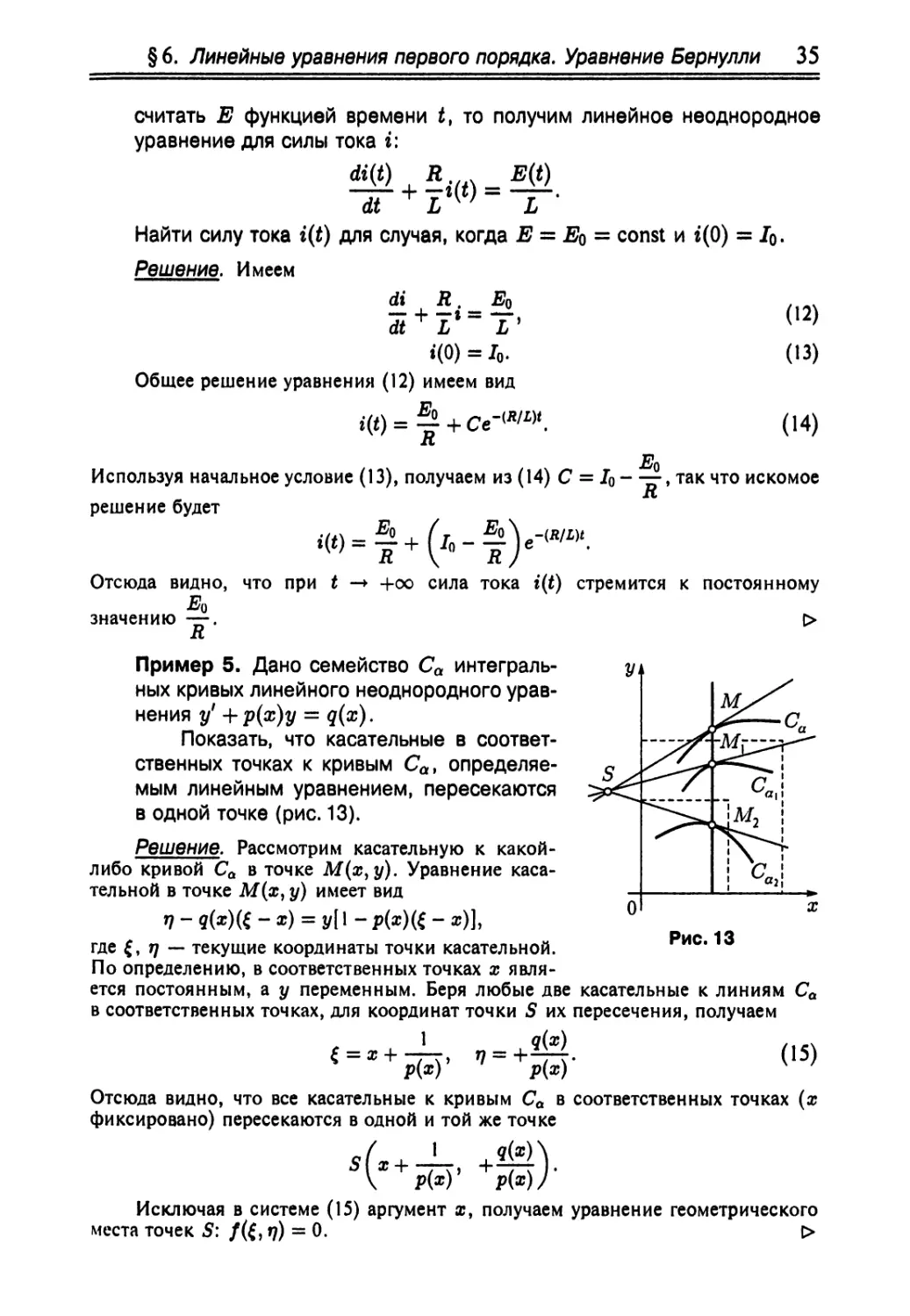
Пример 5. Дано семейство Са
интегральных кривых линейного неоднородного
уравнения у1 +р(х)у = q(x).
Показать, что касательные в
соответственных точках к кривым Са,
определяемым линейным уравнением, пересекаются
в одной точке (рис. 13).
Решение. Рассмотрим касательную к какой-
либо кривой Са в точке М(а?, у). Уравнение
касательной в точке М(ж, у) имеет вид
где {, т] — текущие координаты точки касательной. ис'
По определению, в соответственных точках х
является постоянным, а у переменным. Беря любые две касательные к линиям Са
в соответственных точках, для координат точки 5 их пересечения, получаем
> _ . ' _ . Я\х) /j^\
Отсюда видно, что все касательные к кривым Са в соответственных точках (х
фиксировано) пересекаются в одной и той же точке
V Р(*) P(x)J
Исключая в системе (15) аргумент х, получаем уравнение геометрического
места точек 5: /({, т]) = 0. >
36 Глава 1. Дифференциальные уравнения первого порядка
Пример 6. Найти решение уравнения у1 - у = cos ж - sin х,
удовлетворяющее условию: у ограничено при х —> +оо.
Решение. Общее решение данного уравнения
у = Сех + sin х.
Любое решение уравнения, получаемое из общего решения при С Ф
О, будет неограничено, так как при х —> +оо функция sin ж ограничена,
а ех —> +00. Отсюда следует, что данное уравнение имеет единственное решение
у = sin х, ограниченное при х —> +оо, которое получается из общего решения
при С = 0. >
Задачи для самостоятельного решения
Решить следующие линейные уравнения. Решить, где указано, задачу Коши:
125. у' + 1у = е-х. 126. z2 + xt/ = y, t/|x=l = 0.
127. у1 - 2ху = 2хе*2 128. у' + 2ху = е"*2.
129. yf cosx -ys'mx = 2x, y\x=Q = 0. 130. ху' -2у = хг cosx.
131. y'-ytgx= —, у|х=0 = 0. 132. y'x\nx-y = 3x2\n2x.
COS X
133. (2х - у2)у' = 2у. 134. у' + у cos х = cos ж, у|х=0 = 1.
135. у7 = ——У- . 136. (е~у2/2 -xy)dy-dx = 0.
2у\пу + у-х ч '
137. у' - уех = 2хех. 138. у' + хеху = е{]~х)еХ.
139. Найти силу тока г(£) при условии, что E(t) = Ео sin 2ттп£, г'(0) = /0» где Ео,
10 = const.
140. Конденсатор, емкость которого равна Q, включается в цепь с
напряжением Е и сопротивлением R. Определить заряд q конденсатора в момент t после
включения.
141. Точка массы m движется прямолинейно под действием силы,
пропорциональной времени (коэффициент пропорциональности fc|). Кроме того, точка
испытывает сопротивление среды, пропорциональное скорости (коэффициент
пропорциональности fc2). Найти зависимость скорости от времени, считая, что
в начальный момент скорость равна нулю.
142. Найти кривые, обладающие тем свойством, что отрезок, который
касательная в любой точке кривой отсекает на оси Оу, равен квадрату абсциссы точки
касания.
143. Найти кривую, у которой отрезок, отсекаемый касательной на оси ординат,
равен полусумме координат точки касания.
144. Найти общее решение линейного неоднородного уравнения первого
порядка у' + р(х)у = q(x), если известно одно частное решение у\(х).
145. Найти общее решение линейного неоднородного уравнения первого
порядка у' +р(х)у = q(x)y если известны два частных его решения у\{х) и уг(х).
146. Показать, что линейное уравнение остается линейным при любой замене
независимой переменной х = (pit), где <p(t) — дифференцируемая функция.
147. Показать, что линейное уравнение остается линейным при любом
линейном преобразовании искомой функции у = a(x)z + р(х), где а(х) и /3(х) —
произвольные дифференцируемые функции, причем а(х) Ф 0 в рассматриваемом
интервале.
§ 6. Линейные уравнения первого порядка. Уравнение Бернулли 37
В следующих задачах найти решения уравнений, удовлетворяющие указанным
условиям:
148. у' - y\n2 = 2smx(cosx - \)\п2, у ограничено при ж —► +оо.
149. у' - у = -2е"х, у —> О при ж —► +оо.
150. у'sinx-ycosx = —, у —> О при ж —► оо
Ж
ж2у' i
151. ж2у' cos у sin — = — I, у —И при ж —* оо.
х х
152. 2жу' - у = 1 т=' У ~~* ~1 ПРИ ж ""* +00-
153. ж2у; + у = (х2 + 1)ех, у -♦ 1 при х -> -оо.
154. ху' + у = 2х, у офаничено при ж —► 0.
155. у' sin ж + у cos х = 1, у ограничено при # —♦ 0.
156. у' cos х — у sin ж = — sin 2ж, у —► 0 при ж —♦ —.
2°. Уравнение Бернулли. Уравнение Бернулли имеет вид
где п Ф 0,1 (при п = 0 и п = 1 это уравнение является линейным).
С помощью замены переменной z = г уравнение Бернулли
уП-\
приводится к линейному уравнению и интегрируется как линейное.
Пример 7. Решить уравнение Бернулли у1 - ху = -хуъ.
Решение. Делим обе части уравнения на у3:
У1 1
-г-Ж— = -Ж.
у3 у2
Делаем замену переменной —г = z, г = z\ откуда — = —z . После
У2 У3 У3 2
подстановки последнее уравнение обратится в линейное уравнение
1 . .
~-z - xz =-х или z +2xz = 2ж,
общее решение которого
:= \+Се~х\
Отсюда получаем общий интефал данного уравнения
f Се"1' или у2 (I + Се~х2) = 1.
У2
Замечание. Уравнение Бернулли может быть проинтефировано также
методом вариации постоянной, как и линейное уравнение, и с цомощью
подстановки у(ж) = и()()
38 Глава 1. Дифференциальные уравнения первого порядка
Пример 8. Решить уравнение Бернулли
ху + у = у2 In х. (16)
Решение. Применим метод вариации произвольной постоянной. Общее
С
решение соответствующего однородного уравнения ху + у = 0 имеет вид у = —.
х
Общее решение уравнения (16) ищем в виде
X
где С(х) — новая неизвестная функция.
Подставляя (17) в (16), будем иметь
Для нахождения функции С(х) получим уравнение с разделяющимися
переменными, из которого, разделяя переменные и интегрируя, найдем
1 In х 1
Общее решение уравнения (16)
1
9 1 + Сх + In x
Некоторые нелинейные уравнения первого порядка с помощью
удачно найденной замены переменных сводятся к линейным уравнениям или
к уравнениям Бернулли.
Пример 9. Решить уравнение у1 + sin у + х cos у + х = 0.
Решение. Запишем данное уравнение в виде
у' + 2 sin - cos - + х2 cos2 - = 0.
Деля обе части уравнения на 2cos2-, получаем
2cos2(y/2)
+ tg ^ + х = 0.
2/ <k 2/'
Замена tg ^ = z, — = \. ,_ч приводит это уравнение к линейному
2 аз 2 cos * (у /2)
dz
— + z = -ж, общее решение которого
ах
Заменяя z его выражением через у, получаем общий интеграл данного уравнения
tg| = 1 - *
§ 6. Линейные уравнения первого порядка. Уравнение Бернулли 39
В некоторых уравнениях искомая функция у(х) может находиться
под знаком интеграла. В этих случаях иногда удается путем
дифференцирования свести данное уравнение к дифференциальному.
Пример 10. Решить уравнение
X X
х j y(t) dt = (x+\) f ty(t) dt, x>0.
о о
Решение. Дифференцируя обе части этого уравнения по ж, получаем
X X
J y(t) dt + ху(х) = J ty(t) dt + (x
о
или
о о
Дифференцируя еще раз по ж, будем иметь линейное однородное уравнение
относительно у(х):
у(х) = ху(х) + х2у'(х) + 2ху(х),
или
х2у'(х) + (Зх-\)у(х) = 0.
Разделяя переменные и интегрируя, найдем
Это решение, как легко проверить, удовлетворяет исходному уравнению. >
Задачи для самостоятельного решения
Решить следующие уравнения Бернулли:
157. у' + 2ху = 2ху2. 158. 2у' - у = -е*.
159. (а3 + в»)у1 = За2. 160. у1 + 2ху = у2е*2.
161. у;-2уеж = 2ууех. 162. 2y'ln*+ - = у"1 cosa.
х
163. 2у; sin х + у cos ж = у3 sin 2а?. 164. (ж2 + у2 + I) rfy + xy dx = 0.
165. у1 -у cos ж = у2 cos х.
Следующие нелинейные уравнения с помощью замены переменных свести к
линейным или уравнениям Бернулли и решить их:
166. y'-tgy = e* —. 167. у' = у(ех -fin у).
cos у
168. y'cosy + siny = a:+ I. 169. уу'+ 1 = (х - \)е'у2/2.
170. у' + х sin 2у = 2хе~х cos2y.
40 Глава 1. Дифференциальные уравнения первого порядка
С помощью дифференцирования решить следующие уравнения:
171./ ty(t) dt = х2у(х). 172. у(х) = f y(t) dt + ex.
о о
173. }ty{t)dt = x2 + y{x). 174. fy(xt)dt = ny(x).
§7. Уравнения в полных дифференциалах.
Интегрирующий множитель
1°. Уравнения в ПОЛНЫХ дифференциалах.
Дифференциальное уравнение вида
М(ж, у) dx + N(x, y)dy = O (1)
называется уравнением в полных дифференциалах, если его левая часть
представляет полный дифференциал некоторой функции и(х,у), т.е.
ди ди
М dx + N dy = du = — dx + — dy.
ox dy
Теорема. Для того, чтобы уравнение (1) являлось уравнением в полных
дифференциалах, необходимо и достаточно, чтобы в некоторой одно-
связной области D изменения переменных х и у выполнялось условие
ду ~ дх ' ()
Общий интеграл уравнения (1) имеет вид и{х,у) = С или
х У
f M(x, y)dx + J N(x, у) dy = С. (3)
хо уо
Пример 1. Решить дифференциальное уравнение
(sin ху + ху cos xy) dx + x2 cos xy dy = 0.
Решение. Проверим, что данное уравнение является уравнением в полных
дифференциалах:
дМ д . .
-— = —(sin ху + ху cos xy) =
ду оу
= х cos ху + х cos ху - х2у sin ху = 2х cos ху - х2у sin xy,
W д . 2 ч „ 2 .
—— = — (х cos ху) = 2х cos xy - х у sin sy,
так что
дМ _ dN
§ 7. Уравнения в полных дифференциалах 41
т.е. условие (2) выполнено. Таким образом, данное уравнение есть уравнение
в полных дифференциалах и
М = — = sin жу + жу cos жу, N — —- — х cos жу,
ох оу
поэтому
u(s, у) = / (sin жу + жу cos жу) йж + <р(у),
где у?(у) пока неопределенная функция.
Интегрируя, получаем
и(х, у) = х sin xy + <p(y).
du
Частная производная — найденной функции и(ж, у) должна равняться ж cos ху,
оу
что дает
ж2 cos ху + р'(у) = ж2 cos жу,
откуда <р'(у) = 0, так что (р(у) = С Таким образом
м(ж, у) = ж sin жу + С.
Общий интеграл исходного дифференциального уравнения
ж sin ху = С. >
При интегрировании некоторых дифференциальных уравнений
можно так сгруппировать члены, что получаются легко интегрируемые
комбинации.
Пример 2. Решить дифференциальное уравнение
(ж3 + ху1) dx + (х2у + у2) dy = 0. (4)
ЭМ dN
Решение. Здесь —— = 2жу, -— = 2жу, так что условие (2) выполнено и,
оу ох
следовательно, данное уравнение есть уравнение в полных дифференциалах. Это
уравнение легко привести к виду du = 0 непосредственной группировкой его
членов. С этой целью перепишем его так:
ж3 dx + жу(у dx + ж dy) + у3 dy = 0.
Очевидно,
Поэтому уравнение (4) можно записать в виде
или
Следовательно,
ж4 + 2(жу)2 + у4 = |
есть общий интеграл уравнения (4).
42 Глава 1. Дифференциальные уравнения первого порядка
Задачи для самостоятельного решения
Проинтегрировать уравнения в полных дифференциалах:
175. х(2х2 + у2) + у(х2 + 2у2)у' = 0.
176. (За2 + бху2) dx + (6х2у + 4у3) dy = 0.
V у/х2 + у2 * У/ V v^2 + У2 У У2/
178. (зх2 tg у - ^) dx + (х2 sec 2у + 4у3 + ^Л dy = 0.
179.
+)dx =
х2у ) ху2
-ЛЛ /sin2x \ / sin2
181. (Зх2 - 2х - у) dx + (2у - ж + Зу2) dy = 0.
182. ( ^pflL, + 2a?y - - ) dx + (y/\ + а;2 + х2 - In a?) dy = 0.
\vl Н-ж2 ж/
\ /
xdx + ydy | xdy-ydx а
a:2
v^ + y a
184. (sin у + у sin х + - J dx + ( х cos у - cos х + - J dy = 0.
..«*- y + sinxcos2xy / х , \ Л
185. г ^У + —з— + sm у dy = 0.
cos2xy \cos2xy /
2
187. y(x2 + у2 -h a2) dy + x(x2 + y2 - a2) dx = 0.
188. (3x2y + y3) dx + (x3 4- 3xy2) dy = 0.
2°. Интегрирующий множитель. В некоторых случаях, когда
уравнение (I) не является уравнением в полных дифференциалах, удается
подобрать функцию /х(х, у), после умножения на которую левая часть (1)
превращается в полный дифференциал
du = \iM dx + pN dy.
Такая функция fi(x) у) называется интегрирующим множителем. Из
определения интегрирующего множителя имеем
ду
или
дх ду \ ду
откуда
дх ду ву дх
§7. Уравнения в полных дифференциалах 43
Мы получили для нахождения интегрирующего множителя уравнение
в частных производных.
Отметим некоторые частные случаи, когда удается сравнительно
легко найти решение уравнения (5), т.е. найти интегрирующий множитель.
da
1. Если \i = /х(ж), то — = 0 и уравнение (5) примет вид
оу
d\np (dM/dy)-(dN/dx)
~ST = N ' (6)
Для существования интегрирующего множителя, не зависящего от у,
необходимо и достаточно, чтобы правая часть часть (6) была функцией
только х. В таком случае ln/х найдется квадратурой.
Пример 3. Решить уравнение (х + у2) dx - 2ху dy = 0.
Решение. Здесь М = х + у2, N = -2ху. Имеем
(дМ/ду) - (dN/дх) = 2у + 2у = _ 2
N -2ху " ж'
следовательно,
d\r\fi 2 1
_ = --, ln^ = -21nM, /i=?.
Уравнение
есть уравнение в полных дифференциалах. Его левую часть можно представить
в виде
dx 2xydy-y2dx Л / , , у2\
5 = 0, откуда d In \x\ =0
хх2 \ х)
и общий интеграл данного уравнения
Л л (QN дМ\ !
2. Аналогично, если I — г— 1 — есть функция только j/, то
\ ох оу / М
уравнение (1) имеет интегрирующий множитель \х = (л(у), зависящий
только от у.
Пример 4. Решить уравнение 2ху In у dx + (ж2 + у2у/у2 + 1) dy = 0.
Решение. Здесь М = 2жу In у, TV = ж2 + У2\/У2+ 1- Имеем
(flJY/gg) - (flAf/fly) _ 2а - 2a(ln у + 1) 1
М ~" 2жу1пу ""у*
следовательно,
dln/i _ 1 _ 1
44 Глава 1. Дифференциальные уравнения первого порядка
Уравнение
2xy\nydx
ж + ууУ + 1
+ dy = О
У
2/ У
является уравнением в полных дифференциалах. Его можно записать в виде
d(x2 In у) + у у/у2 + 1 dy = 0, откуда
Пример 5. Решить уравнение (Зж+2у+у2) da:+(x+4#y+5y2) dy = °»
если его интегрирующий множитель имеет вид /г = (р(х + у2).
Решение. Положим z = ж + у2, тогда // = y?(z), и, следовательно,
din// _ din /i dz _ din// din// _ din// dz _ din//
dx ~~ dz dx~ dz ' % ~ dz 5y~ ^ У"
Уравнение (5) для нахождения интегрирующего множителя будет иметь вид
/»г .,. xdln^ 0Af ^^ din// (dM/dy)-(dN/dx)
(iV_2My)__ = ___ или __ = ___ .
Так как М = Зж + 2у + у2, ЛГ = ж + 4жу + 5у2, то
(дМ/ду) - (dN/dx) _ _1 \_
N -7Му ~ х + у2 ~ z'
din// 1 2
и, значит, = -, откуда /i = z, т. е. // = ж + у . Умножая данное уравнение
dz z
на // = ж 4- у2, получим
(Зж2 + 2яу + 4жу2 + 2у3 + у4) dx + (х2 + 4х2у + бжу2 + 4жу3 + 5у4) dy = 0.
Это есть уравнение в полных дифференциалах и его общий интеграл согласно (3)
будет
X У
I (За?2 + 2а?у + 4жу2 + 2у3 + у4) dx+ (ж2, + 4х20у + 6хоу2 + 4х0у3 + 5у4) dy = С,
или . л
ж3 + ж2у + 2ж2у2 + 2жу3 + жу4 + уэ = С,
где ^
С = С + ЖоУо + 2жоУо + 2жоуо + хоуо + Уо + Xq.
После несложных преобразований будем иметь
Задачи для самостоятельного решения
Проинтегрировать следующие уравнения:
189. (I -ж2у^ж + ж2(у-ж^у = О, // = у?(ж).
190. ^2 + y^^dy = 0, // = у?(ж).
191. (ж + у2) dж - 2жу dy = 0, // = <р(х).
192. (2ж2у + 2у 4- 5) dж + (2ж3 + 2ж) dy = 0, // = <р(х).
§ 8. Уравнения, не разрешенные относительно производной 45
193. (х* In я - 2xy2) dx + Ъх2уг dy = O, ц = у(х).
194. (х + sin ж + siny) dx + cosy dy = О, /л = (р(х).
195. (2ху2 - Зу3) dx + (7 - Зжу2) <fy = О, /х = р(у).
196. (Зу2 - a?) dx + (2y3 - бжу) dy = О, // = р(я + у2).
197. (a:2 + y2+l)da?-2xydy = O, /х = у>(у2 - х2).
198. z<fo + ydy + a:(tf dy-ydz) = О, ^ = v?(x2 + y2).
§8. Дифференциальные уравнения
первого порядка, не разрешенные
относительно производной
1°. Уравнения первого порядка n-й степени
относительно у , Пусть имеем дифференциальное уравнение
Решаем это уравнение относительно у'. Пусть
У = f\{x,y), y' = fi(x,y)> .••> y' = fk(x,y) (k^n)
— вещественные решения уравнения (I).
Общий интефал уравнения (I) выразится совокупностью интегралов:
Ф, (з, у, С) = О, Ф2(х, у, С) = О, ..., Фк(х, У) С) = О,
где Ф,-(ж, г/, С) = 0 есть интефал уравнения у' = /г(ж, у) (г = 1,..., к).
Таким образом, через каждую точку области, в которой у1 принимает
вещественные значения, проходит к интегральных линий.
Пример 1, Решить уравнение у {у1)2 + (х - у)у' - х — 0.
Решение. Разрешим это уравнение относительно у':
, _ у - х ± ^(х - у)1 + 4ху , ,_ х
2у ' ' 2/'
откуда
Пример 2. Решить уравнение 2(?/)2 - 2ху' -2у + х2 =
Решение. Разрешим уравнение относительно у:
х2
Положим у' = р, где р — параметр; тогда получим
y=p-xp+j. (2)
Дифференцируя (2), найдем
dy — 2pdp-pdx-xdp-\-x dx.
46 Птава 1. Дифференциальные уравнения первого порядка
Но так как dy = р dx, то будем иметь
pdx = 2pdp -pdx - х dp + x dx,
или
Ipdp -2pdx-xdp + xdx = 0,
2p(dp - dx) - x(dp - <te) = 0,
(2p - x)(dp - dx) = 0.
Рассмотрим два случая:
1) dp - dx = 0, откуда p = ж + С, где С — произвольная постоянная.
Подставляя значение р в (2), получаем общее решение данного уравнения:
y = Cx + C2 + j. (3)
В равенстве р = х + С нельзя заменить р на у' и интегрировать полученное
уравнение у' = х+С (так как при этом появится вторая произвольная постоянная,
чего не может быть, поскольку рассматриваемое дифференциальное уравнение
является уравнением первого порядка).
х
2) 2р - х = 0, откуда р = -. Подставляя в (2), получим еще одно решение
У=Т (4)
Проверим, нарушится ли свойство единственности в каждой точке
решения (4), т.е. является ли оно особым (см. §11). Для этого возьмем на инте-
х\
гральной кривой (4) произвольную точку Мо(а?о,Уо), где у0 = -—. Будем теперь
искать решение, которое содержится в общем решении (3) и график которого
проходит через точку Мо( я0, — ). Подставляя координаты этой точки в общее
решение (3), будем иметь
Л - xl / хо\2 Л
h-т, или С+— =0,
откуда С = ——. Это значение постоянной С подставим в (3). Тогда получим
частное решение
__ X2 XqX х\ .v
2 2 4
которое не совпадает с решение (4). Для решений (4) и (5) имеем соответственно
у1 = —, у' = х ——. При х = xq обе производные совпадают. Следовательно,
в точке Мо нарушается свойство единственности, т. е. через эту точку проходят
две интегральные кривые с одной и той же касательной. Так как х0 произвольно,
то единственность нарушается в каждой точке решения (4), а это означает, что
оно является особым. >
Задачи для самостоятельного решения
Проинтегрировать следующие уравнения:
199. 4(у')2 - Эх = 0. 200. (у')2 - 2уу' = у2(е2* - I).
201. (у')2 - 2*у; - %х2 = 0. 202. х2(у')2 + Ъхуу1 + 2у2 = 0.
§ 8. Уравнения, не разрешенные относительно производной 47
203. (у')2-(2з + у)у' + а2 + *у = 0. 204. (у')3 + (* + 2)еу = 0.
205. (у')3-у(у')2-*2у' + *2У = 0. 206. (у')2-уу' + е* = 0.
207. (у')2 2
2°. Уравнения вида /(у, у') = 0 и /(ж, у1) = 0. Если
уравнения f{y)yl) = 0 и /(ж, у') = 0 легко разрешимы относительно у',
то, разрешая их, получим уравнения с разделяющимися переменными.
Рассмотрим случаи, когда эти уравнения не разрешимы
относительно у'.
А. Уравнение вида /(у, у') = 0 разрешимо относительно у:
У = <Р(У*)-
Полагаем у' = р, тогда у = <р(р). Дифференцируя это уравнение и заменяя
dy на pdxy получим
р dx = <p'(p) dp,
откуда
dx=mdp и x=
Получаем общее решение уравнения в параметрической форме
х= dp + C. у = <р(р). (6)
J р
fdy\2 /djA3
Пример 3. Решить уравнение у = а[ -^ ] + I -т^- I (а, Ь —
постовая/ \dx /
янные).
Решение. Положим -^ = р, тогда у = ар2 + Ьр3, dy = lap dp + ЗЬр2 dp,
ад?
или pdx = lap dp + ЗЬр2 dp. Отсюда dx = la dp + ЗЬр dp и ж = 2ap + -bp2 4- С
Общим решением будет
i<
Б. Если уравнение вида /(у, у') = 0 неразрешимо (или трудно
разрешимо) как относительно у, так и относительно у , но допускает
выражение у и у' через некоторый параметр t:
У = ¥>(*), Р =
48 Глава 1. Дифференциальные уравнения первого порядка
то поступаем следующим образом. Имеем dy = pdx = ip(t) dx. С другой
dx = <
стороны, dy = (p'(t) dt, так что ip(t) dx = (p'(t) dt и dx = —^ dt\ отсюда
*(*)
dt
Таким образом, получаем общее решение данного
дифференциального уравнения в параметрической форме
—— di + C, y = (p(t).
Пример 4. Решить уравнение y2^3 + (t/')2^3 *=- 1 •
Решение. Полагаем у = cos 3i, p = sin 3i,
cos2^
dy 3cosisinidi
dx = — = г-т: = -3
3i
p sin H sin 2i
Отсюда
x
общее решение
x - 3t + 3 ctg t + С, у = cos 3£.
"/(>-£)-:
В. Уравнение вида /(ж, г/;) = 0. Пусть это уравнение разрешимо
относительно х:
х = <р(у').
dy
Полагая у' = р, получим dx = <p'(p) dp. Но dx = — и, следовательно,
Р
dy
— = (р (р) dp, так что
Р
dy = р<р'(р) dp и у = / рр'(р) dp + С.
Таким образом
* = ¥>(Р), У = JP<p'(p)dp + C (7)
— общее решение уравнения в параметрической форме (р — параметр).
Замечание. В формулах (6) и (7) нельзя рассматривать р как производную.
В них р является просто параметром.
dy (dy\2
Пример 5. Решить уравнение a \-b[ — I = х.
dx \dxJ
§8. Уравнения, не разрешенные относительно производной 49
dy
Решение. Положим — = р, тогда
dx
х = ар + Ър , dx — adp + 2bp dp,
Итак,
dy = pdx = apdp + 2bp2 dp, y= %2 + -Ъръ + С.
x = ap + Ьр2, у = -p2 + -bp3 + С — общее решение.
Аналогично случаю Б можно пытаться решать уравнение /(ж, у1) = О
методом введения параметра t.
Задачи для самостоятельного решения
Проинтегрировать следующие уравнения:
208. у=(у')2еУ'. 209. у' = еу>'у.
210. х = In у'+ sin у'. 211. * = (j/')2-2i/ + 2.
212. y = y'\nyf. 213. y = (j//-l)ey'.
214. (у')> = е'/у'. 215. z(l + (у')2У/2 = а.
216. у2/5 + (у')2/5 = а2/5. 217. x = y/ + siny/.
218. y = 2//(]+y/cos2//). 219. у = arcsinj/ + In (1 + (у1)2).
3°. Уравнения Лагранжа и Клеро. Уравнение Лагранжа
имеет вид
У = ZV>(2/') + ^(i/)-
Полагая у1 = р, дифференцируя по х и заменяя dy napdx, приводим
это уравнение к линейному относительно х как функции р. Находя
решение этого последнего уравнения х = г(р, С), получаем общее решение
исходного уравнения в параметрической форме:
х = г(р, С), у = г(р, С)<р(р) + 1>(р) (р —параметр).
Кроме того, уравнение Лагранжа может иметь еще особые решения
(см. § 11) вида у = <р(с)х + ^(с), где с — корень уравнения с = <р(с).
Пример 6. Проинтегрировать уравнение у = 2ху' + In у'.
Решение. Полагаем у' = р, тогда у = 2хр + In р. Дифференцируя, находим
dp
pdx = 2pdx + 2xdp+ —,
Р
dx \ dx 2 \
откуда р— = -2х или — = —х г.
dp p dp p р2
Получили уравнение первого порядка, линейное относительно х; решая его,
находим
С 1
SO Глава 1. Дифференциальные уравнения первого порядка
Подставляя найденное значение х в выражение для у, получим окончательно
С \ . 1С .
Уравнение Клеро имеет вид
у = ху'
Метод решения тот же, что и для уравнения Лагранжа. Общее
решение уравнения Клеро имеет вид
Уравнение Клеро может иметь еще особое решение, которое
получается исключением р из уравнений у = хр + 1р(р), х + тр'(р) = 0.
а
Пример 7. Проинтегрировать уравнение у = ху + — (а = const).
Решение. Полагая у' =р, получаем
a
Дифференцируя последнее уравнение и заменяя
dy на pete, найдем
р da; = p dx + ж dp - т-^г dp,
2р2
откуда
Приравнивая нулю первый множитель,
получаем dp = 0, откуда р = С и общее решение
* а
исходного уравнения есть у = Ся+ —, однопа-
2G
раметрическое семейство прямых. Приравнивая
нулю второй множитель, будем иметь
a
Рис. 14
a 2
Исключая р из этого уравнения и из уравнения у = хр+ —, получим у = lax —
2р
это тоже решение нашего уравнения (особое решение).
С геометрической точки зрения кривая у1 = lax есть огибающая семейства
прямых, даваемых общим решением (рис. 14). >
Задачи для самостоятельного решения
Проинтегрировать следующие уравнения:
220. у = 2ху' + \т\у'. 221. у = ,
222. v = 2a?t// -h sin 2t//. 223. у = ;
§9. Уравнение Риккати 51
224. у=-ху' + еу>. 225. у = ху1 +
226. у = яу' + (у')2. 227. а(у')2 - уу' - у' + 1 = 0.
228. y = a;y4av/l+(y/)2. 229. a=^ + 7-U.
230. Найти кривую, каждая касательная к которой образует с осями координат
треугольник постоянной площади 5 = 2а2.
231. Найти кривую, для которой отрезок касательной, заключенный между
координатными осями, имеет постоянную длину а.
§9. Уравнение Риккати
Дифференциальное уравнение первого порядка вида
^ 2 = 0) (1)
где a(z), b(x), c(x) — известные функции, называется уравнением
Риккати (обобщенным). Если коэффициенты а, Ь, с в уравнении Риккати
постоянны, то уравнение допускает разделение переменных, и мы сразу
получаем общий интеграл
с,—
ау2
Как показал Лиувилль, уравнение (1) в общем случае не
интегрируется в квадратурах.
Свойства уравнения Риккати. 1. Если известно какое-нибудь частное
решение у\(х) уравнения (1), то его общее решение может быть получено
при помощи квадратур.
В самом деле, положим
У = У\(х) + г(х), (2)
где z(x) — новая неизвестная функция. Подставляя (2) в (1), найдем
+ i+о
&гi^2y]Z+z2^
откуда, в силу того что у\(х) есть решение уравнения (1) получим
или
^ 2
Уравнение (3) является частным случаем уравнения Бернулли (см. §6).
-^ + a(x)z2 + [2a(x)yl + b(x)]z = 0. (3)
ах
52 Глава 1. Дифференциальные уравнения первого порядка
Пример 1. Решить уравнение Риккати
у1 -y2 + 7exy = elx + e\ (6)
зная его частное решение у\ = ех.
Решение. Положим у = ех + z(x) и подставим в уравнение (4); получим
dz__
dx~ '
откуда
1 „
— = х - С, или z=
z
z ' C-x
Таким образом, общее решение уравнения (4)
х 1
Замечание. Вместо подстановки (2) часто бывает практически более
выгодной подстановка
которая сразу приводит уравнение Риккати (1) к линейному
и - (2оу] + b)u = a.
2. Если известны два частных решения уравнения (1), то его общий
интеграл находится одной квадратурой.
Пусть известны два частных решения у\(х) и уг(х) уравнения (1).
Используя тот факт, что имеет место тождество
— = —а(х)у\ — Ь{х)у\ — с(ж),
представим уравнение (1) в виде
1 d(v-v\)
У-У\ dx
или
d
— [In у - у\] = -а(х)(у + у\) - Ь{х). (5)
Для второго частного решения yi{x) аналогично находим
d
^ ife] = -а(ж)(» + уг) - Ь(ж). (6)
Вычитая из равенства (5) равенство (6), получаем
откуда
2/ - 2/2
§ 10. Составление дифференциальных уравнений семейств линий 53
Пример 2. Уравнение
имеет
Найти
dy га2
частные решения
1
*" = * +
его общий интеграл.
-у\
та
m =
1
X
const
m
Решение. Используя формулу (7), получаем общий интеграл исходного
уравнения
откуда *]У ~ * ~ m = С** >
уд ] = С*. >
Задачи для самостоятельного решения
Проинтегрировать следующие уравнения Риккати, зная их частные решения:
232. у'е-* + у2 - 2уех = 1 - е2х, y^ = ех.
233. у' + у2 - 2ysina; + sin2z - cos ж = 0, у\ =s\nx.
234. ху' -у2 + (2х + \)у = х2 + 2ху ух = х.
235. х2у' = х2у2 + ху + 1, у, =--.
а;
236. Найти общий интеграл уравнения Риккати, когда отношение
коэффициентов не зависит от х, т.е. а(х) : Ь(х): с(ж) = тп:п :р (m, n, p — постоянные).
237. Доказать, что уравнение Риккати сохраняет свой вид при любом
преобразовании независимой переменной х = <p(t), где (p(t) — любая непрерывно
дифференцируемая функция, определенная в интервале (£0, *i), причем <р (t) Ф 0
на (*0,*|).
§ 10. Составление дифференциальных
уравнений семейств линий.
Задачи на траектории
1°. Составление дифференциальных уравнений
семейств ЛИНИЙ. Пусть дано уравнение однопараметрического
семейства плоских кривых
у = (р(х, а) (а — параметр). (1)
Дифференцируя (1) по ж, найдем
У' = <р'х(х,а). (2)
Исключая параметр а из (1) и (2), получаем дифференциальное уравнение
F(x,y,y') = 0, (3)
54 Глава 1. Дифференциальные уравнения первого порядка
выражающее свойство, общее всем кривым семейства (1). Уравнение (3)
будет искомым дифференциальным уравнением семейства (1).
Если однопараметрическое семейство кривых определяется
уравнением
Ф(я, у, а) = О,
то дифференциальное уравнение этого семейства получим, исключая
параметр а из уравнений
Ф(ж, у, а) = О,
ЭФ дФ ,
дх ^ ду У
Пусть теперь имеем соотношение
Ф(ж,2/,а|,а2,...,ап) = О, (4)
где а,], аг,..., ап — параметры. Дифференцируя (4) п раз по а: и исключая
параметры at, а2,..., ап из (4) и полученных уравнений, приходим к
соотношению вида
F(x,y,i/y у{п))=0. (5)
Это дифференциальное уравнение заданного n-параметрического
семейства линий (4) в том смысле, что (4) есть общий интеграл уравнения (5).
Пример 1. Найти дифференциальное уравнение семейства гипербол
± £-,
а2 1
Решение. Дифференцируя это уравнение по х, получаем
2х , х ,
^ - 2уу = 0, или ? = уу .
х2
Умножим обе части на ж, тогда -г = хуу'. Подставляя в уравнение семейства
найдем хуу' - у2 = 1. >
Пример 2. Найти дифференциальное уравнение семейства линий
у = а(\ - е~*/в), где a — параметр.
Решение. Дифференцируем обе части уравнения по х:
Из выражения для у1 находим a = --—- и, подставляя это выражение для a
In у'
в уравнение семейства линий, получим
^O-y'), или
Пример 3. Составить дифференциальное уравнение семейства
прямых, отстоящих от начала координат на расстояние, равное единице.
§ 10. Составление дифференциальных уравнений семейств линий 55
Решение. Будем исходить из нормального уравнения прямой
х cos а + у sin а - 1 = 0, (6)
где а — параметр.
Дифференцируя (6) по я, найдем cos a + у'sin а = 0, откуда у' = - ctga,
следовательно,
cin /у = ; cosa = -
Подставив sin a и cos a в (6), получим
-1=0, или у = i
Задачи для самостоятельного решения
Составить дифференциальные уравнения следующих семейств линий:
238. у = -. 239. х2 - у2 = ах. 240. у = аех'а
х
241. у = Сх-С-С2. 242. у = е*(ах + Ъ). 243. у2 = 2Сх
244. у = ах2 + Ьх + с. 245. у = С\Х + — + С3. 246. (ж-а)2+(у-Ь)2 = 1.
247. у = С|Са! + С2е"*. 248. у = a sin (а? + а).
2°. Задачи на траектории. Пусть дано семейство плоских
кривых
Ф(х) у} а) = 0, (7)
зависящее от одного параметра а.
Кривая, образующая в каждой своей точке постоянный угол а с
проходящей через эту точку кривой семейства (7), называется изогональной
7Г
траекторией этого семейства; если, в частности, a = —, то —
ортогональной траекторией.
Считая семейство (7) заданным, будем разыскивать его изогональные
траектории.
А. Ортогональные траектории. Составляем дифференциальное
уравнение данного семейства кривых (см. п. Г). Пусть оно имеет вид
Дифференциальное уравнение ортогональных траекторий имеет вид
■(•■*-?)-*
56 Глава 1. Дифференциальные уравнения первого порядка
Общий интеграл этого уравнения
дает семейство ортогональных траекторий.
Пусть семейство плоских кривых задано уравнением в полярных
координатах
Ф(р,Р,а) = 0, (8)
ЭФ
где а — параметр. Исключая параметр а из (8) и — = 0, получаем
д(р
дифференциальное уравнение семейства (8): F(p)(p,p') = 0. Заменяя
в нем р' на —-, получаем дифференциальное уравнение семейства
ортогональных траекторий
*-£) =о.
Б. Изогональные траектории. Пусть траектории пересекают кривые
данного семейства под углом а, причем tga = k. Можно показать, что
дифференциальное уравнение изогональных траекторий имеет вид
Пример 4. Найти ортогональные траектории семейства линий у = кх.
Решение. Семейство линий у = кх со-
стоит из прямых, проходящих через начало
координат. Для нахождения
дифференциального уравнения данного семейства
дифференцируем по х обе части уравнения у = кх.
Имеем у1 = к. Исключая параметр к из
системы уравнений
(у =
\у'=
будем иметь дифференциальное уравнение
семейства ху' = у. Заменяя в нем у' на —-,
получаем дифференциальное уравнение
ортогональных траекторий —- = у, или уу'+х = 0.
У Рис.15
Полученное уравнение является уравнением
с разделяющимися переменными;
интегрируя его, найдем уравнение ортогональных траекторий х2 + у2 — С (С ^ 0).
Ортогональными траекториями являются окружности с центром в начале
координат (рис. 15). >
(р )
Пример 5. Найти уравнение семейства линий, ортогональных
мейству х2 + у2 = lax.
рр ур
мейству х2 + у2 = lax.
к
се§ 10. Составление дифференциальных уравнений семейств линий 57
Решение. Данное семейство линий представляет собой семейство
окружностей, центры которых находятся на оси Ох и которые касаются оси Оу.
Дифференцируя по х обе части уравнения данного семейства, найдем
х + ууг = а. Исключая параметр о из уравнений х2 + у2 = lax, х + уу1 = а,
получаем дифференциальное уравнение данного семейства х2 - у1 4- 2хуу' = 0.
Дифференциальное уравнение ортогональных траекторий есть
х2 - у2 + 2ху ( --
или у =
2ху
х2 -у2'
Это уравнение является однородным. Интегрируя его, найдем х2 + у2 = Су.
Интегральные кривые являются окружностями, центры которых расположены
на оси Оу и которые касаются оси Ох (рис. 16). >
Рис.16
Пример 6. Найти ортогональные траектории семейства парабол
у = ах .
Решение. Составляем
дифференциальное уравнение семейства парабол. Для этого
дифференцируем обе части данного уравнения
по х: у' = 2ах. Исключая параметр а, найдем
— = -, или у' = — — дифференциальное
ух х
уравнение данного семейства. Заменяя в
уравнении у' на —-, получим дифференциальное
уравнение ортогональных траекторий
; = —, ИЛИ
dx
X
Рис.17
58
Глава 1. Дифференциальные уравнения первого порядка
Интегрируя, найдем у2 = --— + С или ■—• + </2 = С, О 0. Ортогональным
семейством является семейство эллипсов (рис. 17). >
Пример 7. р2 = a cos 2y?. Найти ортогональные траектории семейства
лемнискат
Решение. Имеем
p2 = acos2y>, рр' = -a sin 2<p.
Исключая параметр а, получим
дифференциальное уравнение данного
семейства кривых
Заменяя р' на -^, найдем
дифференциальное уравнение семейства
ортогональных траекторий
Л2
откуда — ctg2<pd<p. Интегрируя, находим
уравнение ортогональных траекторий рис jg
р2 = С sin 2(p.
Ортогональными траекториями семейства лемнискат являются лемнискаты, ось
симметрии которых образуют с полярной осью угол ±45° (рис. 18). >
Задачи для самостоятельного решения
Найти ортогональные траектории для данных семейств кривых:
249. у2 + lax = 0,
250. y = axn,
a — параметр.
253. *2 + ^y2 = a2.
о > 0.
252. cosy = ае~х.
255. х" + у* = о*. 256. х2 + у2 = lay.
258. р = а(\ +cos<p). 259. у2=4(х-а).
251. y = ae",
a = const.
254. x2-y2 = a2.
257. *2-iy2 = a2.
§11. Особые решения
дифференциальных уравнений
Решение у = у?(х) дифференциального уравнения
^,2/,у') = 0 (I)
называется особым, если в каждой его точке нарушается свойство
единственности, т. е. если через каждую его точку (a?o> Уо) кроме этого решения
§11. Особые решения дифференциальных уравнений 59
проходит и другое решение, имеющее в точке (a?o> Уо) ту же касательную,
что и решение у = <р(х), но не совпадающее с ним в сколь угодно малой
окрестности (хо,уо). График особого решения будем называть особой
интегральной кривой уравнения (1). Если функция F(x,yyy') и ее частные
dF dF ,
производные — и —■ непрерывны по всем аргументам х, у, у , то
оу оу'
любое особое решение уравнения (1) удовлетворяет также уравнению
Значит, чтобы отыскать особые решения (1), надо исключить у' из
уравнений (1) и (2).
Полученное после исключения у1 из (1) и (2) уравнение
#*,») = 0 (3)
называется р-дискриминантом уравнения (1), а кривая, определяемая
уравнением (3), называется р-дискриминантной кривой (коротко ПДК).
Часто бывает так, что ПДК распадается на несколько ветвей. Тогда
нужно установить, является ли каждая в отдельности ветвь решением
уравнения (1), и если является, то будет ли оно особым решением, т.е.
нарушается ли единственность в каждой его точке.
Пример 1. Найти особые решения дифференциального уравнения
ху' + (у')2-у = 0. (4)
Решение.
а) Находим р-дискриминантную кривую. В данном случае
F(*,y,y') = ay' + (y')2-y,
и условие (2) принимает вид
отсюда у' = -"• Подставляя это выражение для у' в уравнение (4), получаем
Кривая (5) есть р-дискриминантная кривая уравнения (4): она состоит из одной
ветви — параболы.
б) Проверяем, является ли р-дискриминантная кривая решением заданного
х2
уравнения. Подставляя (5) и ее производную в (4), убеждаемся, что у = -—- есть
4
решение уравнения (4).
в) Проверяем, является ли решение (5) особым решением уравнения (4). Для
этого найдем общее решение уравнения (4). Перепишем (4) в виде у = ху' + (у')2.
Это уравнение Клеро. Его общее решение
\ (6)
60
Глава 1. Дифференциальные уравнения первого порядка
Выпишем условие касания двух кривых у = у\(х) и у = у2(х) в точке
с абсциссой х = х0:
(7)
Первое равенство выражает совпадение ординат
кривых, а второе выражает совпадение угловых
коэффициентов касательных к этим кривым
в точке с абсциссой х = х0.
х2
Полагая у, (ж) = - —, у2(х) = Сх + С\
находим, что условия (7) принимают вид
*2
4
" 2
(8)
Подставляя С = в первое из равенств (8),
получаем
4 2 4 4 4
т.е. при С = —-^ первое равенство выпол-
Рис.19
няется тождественно, так как ж0 есть абсцисса
произвольной точки.
Итак, в каждой точке кривой (5) ее касается некоторая другая кривая
х0 х2
семейства (6), а именно та, для которой С — . Значит, у = есть особое
решение уравнения (4).
г) Геометрическое истолкование.
Общее решение уравнения (4) есть семейство прямых (6), а особое
решение (5) является огибающей этого семейства прямых (рис. 19). >
Огибающей семейства кривых
(9)
называется такая кривая, которая в каждой своей точке касается
некоторой кривой семейства (9) и каждого отрезка которой касается бесконечное
множество кривых из (9)3\
Если (9) есть общий интефал уравнения (1), то огибающая семейства
кривых (9), если она существует, будет особой интефальной кривой этого
уравнения. В самом деле, в точках огибающей значения х, у, у' совпадают
со значениями х, у, у' для интефальной кривой, касающейся огибающей
в точке (ж, у), и, следовательно, в каждой точке огибающей значения х,
у9 у1 удовлетворяют уравнению F(x,y,y') = 0, т.е. огибающая является
интефальной кривой.
3* Будем говорить, что кривые Г| и Tj касаются в точке Мо, если они имеют в этой
точке общую касательную.
дФ
~дх~
^ 7
дФ
ду
§11. Особые решения дифференциальных уравнений 61
Далее, в каждой точке огибающей нарушена единственность, так как
через точки огибающей по одному направлению проходит по крайней
мере две интегральные кривые: сама огибающая и касающаяся ее в
рассматриваемой точке интегральная кривая семейства (9). Следовательно,
огибающая является особой интегральной кривой.
Из курса математического анализа известно, что огибающая
входит в состав С-дискриминантной кривой (коротко СДК), определяемой
системой уравнений
Ф(хуу,С) = 0,
8Ф(х,у,С)
дС
Некоторая ветвь СДК заведомо будет огибающей, если на ней:
1) существуют ограниченные по модулю частные производные
дФ
где М и N — постоянные;
2)
0Ф 0Ф
-*0 или -*0. (12)
Замечание. Условия 1) и 2) лишь достаточны, а потому ветви СДК,
на которых нарушено одно из этих условий, тоже могут быть огибающими.
Пример 2. Найти особые решения дифференциального уравнения
х(у')2-2уу' + 4х = 0, я>0, (13)
зная его общий интеграл
х2 = С(у-С). (14)
Решение.
а) Находим С-дискриминантную кривую. Имеем
Ф(ху у, С) = С(у - С) - х2,
так что
У
отсюда С = -. Подставляя это значение С в (14), получаем
х2 = - I v - -
откуда
(у - 2х)(у 4- 2х) = 0, или у = ±2х. (15)
Это и есть С-дискриминантная кривая: она состоит из двух прямых у = 2х
и у = -2х.
62 Глава 1. Дифференциальные уравнения первого порядка
б) Непосредственной подстановкой убеждаемся, что каждая из ветвей СДК
является решением уравнения (13).
в) Докажем, что каждое из решений (15) является особым решением
уравнения (13). В самом деле, так как
ЭФ Л 6Ф
— = -2я, — = С,
Эх ду '
то на каждой ветви СДК имеем
дФ
- = I - 2х| < 2Ь
(предполагаем, что решение у(х) уравнения (13) рассматривается на отрезке
О < а ^ х < Ь),
дФ
|С|^ЛГ; здесь JV = max|C|,
ду
С€<?
где G — область допустимых значений С.
6Ф
Заметим, что на любой из ветвей СДК — = -2х ^0 в области х > 0, так
ох
что выполняется одно из условий (12). Значит, условия (11) и (12) выполняются,
а следовательно прямые (15) являются огибающими парабол (14).
Итак, установлено, что каждое из решений (15) есть особое решение. >
В вопросах отыскания особых решений оказываются полезными
следующие символические схемы:
= О-ЗП2 = 0, (16)
= ОУ2-33 = 0. (17)
Схема (16) означает, что уравнение р-дискриминантной кривой
может распадаться на три уравнения:
1) О = 0 — уравнение огибающей;
2) 3 = 0 — уравнение геометрического места точек заострения
(возврата);
3) П = 0 — уравнение геометрического места точек прикосновения
интегральных линий, причем множитель П входит в ПДК в квадрате.
Схема (17) означает, что уравнение С-дискриминантной кривой
может распадаться на три уравнения:
1) О = 0 — уравнение огибающей;
2) У = 0 — уравнение геометрического места узловых точек, причем
множитель У входит с СДК в квадрате;
3) 3 = 0 — уравнение геометрического места точек заострения,
причем множитель 3 входит в СДК в кубе.
Не обязательно, чтобы для каждой задачи все составные части ПДК
и СДК фигурировали в соотношениях (16) и (17).
Из всех геометрических мест только огибающая есть особое решение
дифференциального уравнения. Отыскание огибающей упрощается тем,
что в схемы (16) и (17) она входит в первой степени.
§11. Особые решения дифференциальных уравнений 63
В отношении других геометрических мест (точек заострения, узловых
точек и точек прикосновения) требуется дополнительный анализ в каждом
конкретном случае. То обстоятельство, что некоторый множитель входит
в ПДК в квадрате (и совсем не входит в СДК) указывает на то, что здесь
может быть геометрическое место точек прикосновения интегральных
линий. Аналогично, если некоторый множитель входит в СДК в квадрате
(и совсем не входит в ПДК), то здесь может быть геометрическое место
узловых точек. Наконец, если множитель входит в ПДК в первой степени,
а в СДК — в третьей, то возможно наличие геометрического места точек
заострения.
Пример 3. Найти особое решение дифференциального уравнения
2у(у' + 2)-х(у')2 = 0. (18)
Решение. Особое решение, если оно существует, определяется системой
х(у) = 0,
\ 2у-2ху' = 0,
где второе уравнение (19) получено из (18) дифференцированием его по у'.
Исключив у', получим р-дискриминантную кривую
у2 + Аху = О,
которая распадается на две ветви
У = 0, ,(20)
У = -4*. ЦяТ)
Подстановкой убеждаемся, что обе функции являются решениями уравнения (18).
Чтобы установить, являются ли решения (20) и (21) особыми или нет, найдем
огибающую семейства
Су-(С-х)2 = 0, (22)
являющегося общим интегралом для (18).
Выпишем систему для определения С-дискриминантной кривой
Су-(С-х)2 = 0,
(Су-
откуда, исключая С, получаем
у2 + 4ху = 0, или у = 0 и у = -4ж,
что совпадает с (20) и (21). В силу того, что на линиях (20) и (21) условия (11) и (12)
выполняются, заключаем, что линии у = 0 и у = -4а? являются огибающими,
а значит (20) и (21) есть особые решения заданного уравнения.
Интегральные кривые (22) суть параболы у = -—•рг^, а линии у = 0,
у = -4х — огибающие этого семейства парабол (рис.20). >
64
Глава 1. Дифференциальные уравнения первого порядка
Рис. 20
Рис.21
Пример 4. Найти особые решения дифференциального уравнения
(У1)2 = 4х2.
Решение. Дифференцируем (23) по у':
2у' = 0.
(23)
(24)
Исключая у' из (23) и (24), получим х2 = 0. Дискриминантная кривая есть
ось ординат. Она не является интегральной кривой уравнения (23), но согласно
схеме (16) может быть геометрическим местом точек прикосновения интегральных
кривых.
Решениями уравнения (23) являются параболы
у = х2 + С, у = -х2 + С
и те гладкие кривые, которые можно составить из их частей (рис.21).
Из чертежа видно, что прямая х = 0 действительно есть геометрическое
место точек прикосновения интегральных кривых уравнения (23). >
Пример 5. Найти особые решения дифференциального уравнения
(у')2(2-3у)2 = 4(\-у). (25)
Решение. Найдем ПДК. Исключая у' из системы уравнений
(у')2(2-Зу)2-4(1-у) = 0,
у'(2-Зу)2 = О,
получаем
(2 - Зу)2(1 - у) = 0.
(26)
§11. Особые решения дифференциальных уравнений
65
Преобразовав уравнение (25) к виду
dxt_± 2~3У
dy 2л/1 -у'
находим его общий интеграл
Найдем СДК. Исключая С из системы уравнений
IV(l-y)-(*-C)2=0,
\ 2(х - С) = О,
будем иметь
у\\-у) = 0.
Итак, из (26) и (27) имеем
(27)
Множитель 1 - у входит в р-дискриминант и в С-дискриминант в первой
степени и дает огибающую, т. е. функция у = 1 есть особое решение
дифференциального уравнения (25). Непосредственной подстановкой убеждаемся, что
у = 1 действительно удовлетворяет уравнению.
Уравнение 2 - Зу = 0, входящее во второй степени в р-дискрИминант
и совсем не входящее в С-дискриминант, дает место точек прикосновения (Я2).
Наконец, уравнение у = 0, входящее в С-дискриминант во второй
степени и совсем не входящее в р-дискриминант, дает место узловых
точек (У2) (рис.22). >
Огибающая
Рис. 22
Пример 6. Найти особые решения дифференциального уравнения
, 2/2
X
Решение.
а) Ищем р-дискриминантную кривую. Дифференцируя (28) по у', получаем
(28)
66
Глава 1. Дифференциальные уравнения первого порядка
откуда
-
2
Подставляя (29) в (28), найдем уравнение ПДК:
ПДК = 6у - х3 = 0.
(29)
(30)
б) Ищем общий интеграл уравнения (28).
Обозначив у' через р, перепишем (28) в виде
Зу = 2хр - -р\
(31)
Дифференцируя обе части (28) по я и учитывая,
что у' = р, будем иметь
откуда
Рис. 23 Приравнивая нулю первый множитель х2-2р = О,
dp
получаем (29), а соотношение р - 2ю-£ = 0 дает
Сх=р\ (32)
Исключая параметр р из уравнений (31) и (32), найдем общее решение
уравнения (28):
(Зу + 2С)2 = 4Сх\ (33)
в) Находим С-дискриминантную кривую. Дифференцируя (33) по С, будем
иметь
(34)
1С = ж3 - Зу.
Подставляя (34) в (33), получаем уравнение СДК:
СДК = (6у - а?3)а:3 = 0.
Согласно символическим схемам (16) и (17) заключаем, что 6у-х* = 0 есть
огибающая семейства полукубических парабол (33), а х = 0 есть геометрическое
место точек заострения (множитель х входит в уравнение СДК в кубе) (рис.23).
ж3
Подстановкой в уравнение (28) убеждаемся, что у = — есть решение, а х = 0 ре-
о
шением не является (при х = 0 уравнение (28) не имеет смысла). Таким образом,
решение у = — есть особое (огибающая семейства интегральных линий). >
о
Задачи для самостоятельного решения
В следующих примерах найти особые решения, если они существуют:
260. (1+(у')2)у2-4уу'-4* = 0. 261. (у')2-4у = 0.
262. (у')3-4жууЧ8у2 = 0. 263. (у')2-у2 = 0.
§12. Разные задачи 67
264. у' = у/у*+а. При каком значении параметра а это уравнение имеет особое
решение?
265. (а?у' + у)2 + За?5(а?у' - 2у) = 0. 266. у(у - 2ху')2 = 2у'.
267. 8(у')3 - 12(у')2 = 27(у - х). 268. (у' - I)2 = у2.
С помощью С-дискриминанта найти особые решения дифференциальных
уравнений первого порядка, зная их общие интегралы.
269. у = (у')2-'+ 2
270. (а?у' + у)2 = у2у',у(С-а?)
271. 22 2 2
272. (у')2 - уу' + е* = 0, у = Се* + i.
273. За?(у')2 - 6уу' + 2у = 0, х2 + С(х - Зу) + С2 = 0.
274. у = ху1 + \Му')2 + &2» У = С* + \Л*2С
§12. Разные задачи
Проинтегрировать следующие уравнения:
275. у' = (*-у)2 + 1.
276. х sin х • у' + (sin ж - ж cos ж)у = sin x cos ж - ж.
dy
277. -р 4- у cos х = yn sin 2a?, n ^ 1.
278. $ - Ззу2) da? + (у3 - Зх2у) dy = 0.
279. (5а?у - 4у2 - 6х2) dx + (у2 - 8ау + 2,5ж2) dy = 0.
280. (Зжу2 - х2) dx + (За>2у - 6у2 - 1) dy = 0.
281. (у - ху2 In ж) <fa + х dy = 0, р ^
282. (2жуеа2 - я sin a?) da? + e*2 dy = 0.
283. у'ei
2а? - у2
284. а?2 + а?у'
285. а?уу'-у2 = а?4.
288. (а? - у + 3) da? + (За? + у + 1) dy = 0.
+
) ( у
Л„ # а? + у а? - у
289. у' + cos —г-2* = cos ""2 '
290. у'(3а?2 - 2а?) - у(6а? - 2) = 0.
291. а?уУ-у3 = ^а?4.
292. (1 +ee/y)da? + ex/^l - -) dy = 0, у|,-, = 1.
293. (a?2 + y2)da?-a?ydy = O
68 Глава 1. Дифференциальные уравнения первого порядка
294. (х - у + 2) dx + (х - у + 3) dy = 0.
295. (жу2 + у) dx - х dy = 0.
296. (ж + у~ -Ь 2ж) dx + 2y dy = 0.
297. (х - 1)(у2 - у + 1) ds = (у + \)(х2 + ж + 1) dy.
298. (ж - 2жу - у2)у; + у2 = 0.
299. у cos ж dж + (2у - sin ж) dy = 0.
300. у'-\=ех+2у.
301. 2(ж5 + 2ж3у - у2ж) dж + (у2 + 2ж2у - ж4) dy = 0.
302.
303. .
304. (ж - у2) dж + 2жу dy = 0.
305. ху' + у = у2 In ж, у|х=, = -.
2
306. sin (In ж) dж - cos (In у) dy = 0.
307-y' = yi^TJ-
309. (x + у + I) dx + (2x + 2j/ - I) dy = 0, y|x=, = 2.
310. у dж + 2(ж — жу~) dy = 0.
311. «' = :
312. Показать, что кривая, симметричная относительно центра О(0,0)
интегральной кривой уравнения 4ж2(у;)2 -у2 = жу\ также будет интегральной кривой
этого уравнения.
313. Найти интегральные линии дифференциального уравнения у'+ж(у')2—у=0,
являющиеся прямыми.
314. Найти кривую, зная, что площадь, заключенная между осями координат
этой кривой и ординатой любой точки на ней, равна кубу этой ординаты.
315. Площадь, ограниченная кривой, осями координат и ординатой какой-
либо точки кривой, численно равна длине соответствующей дуги кривой. Найти
уравнение этой кривой, если известно, что она проходит через точку М(0,1).
ГЛАВА
2
Дифференциальные
уравнения
высших порядков
§13. Основные понятия и определения
Дифференциальное уравнение n-го порядка имеет вид
f (*,»,»', у",..., »(я))= О
или, если оно разрешено относительно у^п\
yin) = f(x,y,y',...,y{n-{)). (О
Задача нахождения решения у = (р(х) уравнения (1),
удовлетворяющего начальным условиям
у\жшщ = Уо, У'\г=Хо = Уо, .... У{П-\=Х0 = У(Г\ (2)
называется задачей Коши для уравнения (1).
Теорема существования и единственности решения задачи
Коши. Если в уравнении (1) функция /(ж, уу у', у",..., у^1"^)
а) непрерывна по всем своим аргументам я, у, у1, у",..., у^п~^
в некоторой области D их изменения,
df
б) имеет ограниченные в области D частные производные —,
ду
г) f ft f ft f
0-7, 7^7, • • •, д {п_}) по аргументам у, у1, у\ ..., y{n~]), то найдется
интервал x0 - h < x < x0 + h, на котором существует единственное
решение у — <р(х) уравнения (1), удовлетворяющее условиям
У\х=Хо = 2/о, У'\х=хо = Уо, ■-., У{П~\=Х, = Уо""0»
где значения х = ж0, у — 2/о> У* = Уо, - - •, У^п~^ = З/о содержатся
в области D.
Для уравнения второго порядка у" = /(ж, у, у') начальные условия
имеют вид
где Жо, г/0» 2/о ~~ данные числа. В этом случае теорема
существования и единственности геометрически означает, что через данную точку
Мо(хо,Уо) плоскости хОу с данным тангенсом угла наклона
касательной 2/о проходит единственная кривая.
70 Глава 2. Дифференциальные уравнения высших порядков
Рассмотрим, например, уравнение у" = sin у' + е~*2у и начальные
условия
В данном случае /(я, у, у') = sin у' + е~*2у. Эта функция определена
и непрерывна при всех значениях а:, у, у'. Ее частные производные по у
и у' равны соответственно
_—.в ', -=cosy
и являются всюду непрерывными и ограниченными функциями своих
аргументов. Следовательно, каковы бы ни были начальные условия
существует единственное решение данного уравнения, удовлетворяющее
этим условиям.
Общим решением дифференциального уравнения n-го порядка (1)
называется множество всех его решений, определяемое формулой у =
(р(х, С\, Сг,... Сп), содержащей и произвольных постоянных Сь Сг,...,
С„ таких, что если заданы начальные условия (2), то найдутся такие
значения С\, Сг,..., Сп, что у = (р(х, С\, Сг,..., Сп) будет являться решением
уравнения (1), удовлетворяющим этим начальным условиям.
Любое решение, получаемое из общего решения при конкретных
значениях произвольных постоянных d, С^ ..., Сп, называется частным
решением дифференциального уравнения (1).
Уравнение вида Ф(ж, у, Cj, Сг,..., Сп) = 0, которое определяет
неявно общее решение дифференциального уравнения, называется общим
интегралом уравнения. Давая постоянным Сь Сг,..., Сп конкретные
допустимые числовые значения, получим частный интеграл
дифференциального уравнения. График частного решения или частного интеграла
называется интегральной кривой данного дифференциального уравнения.
Пример 1. Показать, что у = С\х + С2 есть общее решение
дифференциального уравнения у" = 0.
Решение. Покажем, что у = С\х + Ci удовлетворяет данному уравнению
при любых значениях постоянных С\ и Cj. В самом деле, имеем у' = С\, у" = 0.
Пусть теперь заданные произвольные начальные условия y\XSSXQ = уо>
у'\х-х = Уо« Покажем, что постоянные С\ и С2 можно подобрать так, что
у = С\х + С2 будет удовлетворять этим условиям. Имеем у = С\х + Сг, у' = С\.
Полагая я = я0, получаем систему
Г Уо = С,жо
[Уо = Си
из которой однозначно определяются С\ = yj и С2 = Уо - ^оУо- Таким образом,
решение у = у'0(х - я0) + Уо удовлетворяет поставленным начальным условиям.
§ 14. Уравнения, допускающие понижение порядка 71^
Геометрически это означает, что через каждую точку М0(х0) уо) плоскости хОу
с заданным угловым коэффициентом j/о проходит единственная прямая.
Задание одного начального условия, например у\ятх = у0, определяет
пучок прямых с центром в точке М0(х0)у0), т.е. одного начального условия
недостаточно для выделения единственного решения. >
Задачи для самостоятельного решения
316. Дифференциальное уравнение у" = 2у/у' имеет два решения у\(х) = О,
х
у2(х) = —-, удовлетворяющих начальным условиям у\хях0 = 0, у'|хв0 = 0. Почему
результат не противоречит теореме существования и единственности решения
задачи Кош и?
317. Могут ли графики двух решений данного уравнения на плоскости хОу
касаться друг друга в некоторой точке (&о,уо): а) для уравнения у' = х2 + у2;
б) для уравнения у" = х2 + у2; в) для уравнения у1" = х2 + у2?
В следующих задачах показать, что данные функции являются решениями
указанных уравнений:
318. у = «(sin х - cos ж), у" 4- у = 2(cos х + sin x).
319. у = х2 In х, хуш = 2. 320. х + С = е"у, у" = (у;)2.
С +
j
Показать, что данные функции являются общими решениями соответствующих
уравнений.
323. у = С\ sin х + С2 cos ж, у;' + у = 0.
324. у = С,ех + С2е2х + 1, у" - Зу; + 2у = 2.
Показать, что данные соотношения являются интегралами (общими или
частными) указанных уравнений.
325. (х - С,)2 + (у - С2)2 = 1, у" = (1 + (у;)2)3/2,
326. у2=1 + (1-а)2, (у'2
§ 14. Дифференциальные уравнения,
допускающие понижение порядка
Укажем некоторые виды дифференциальные уравнений,
допускающих понижение порядка.
I. Уравнение вида у^ = /(ж). После n-кратного интегрирования
получается общее решение
72 Глава 2. Дифференциальные уравнения высших порядков
II. Уравнение не содержит искомой функции и ее производных
до порядка к — 1 включительно:
Порядок такого уравнения можно понизить на к единиц заменой
х) = р(х). Тогда уравнение примет вид
Из последнего уравнения, если это возможно, определяем р =
/(ж, Ci,C2,... ,Cn_fc), а затем находим у из уравнения у^ = /(ж, Сь
С2,..., Cn-k) ^-кратным интегрированием.
III. Уравнение не содержит независимого переменного:
Подстановка у' = р позволяет понизить порядок уравнения на
единицу. При этом р рассматривается как новая неизвестная функция от у:
р = р(у). Все производные у\ у",..., у^ выражаются через производные
от новой неизвестной функции р по у:
„_p_py_ p
У ~ dx~ dydx ~Pdy'
Подставив эти выражения вместо у\ у",..., у^ в уравнение, получим
дифференциальное уравнение (п - 1)-го порядка.
IV. Уравнение F(»,у,2/',... ,2/^) = 0, однородное относительно
аргументов у, у\ у",..., у{п), т. е.
Порядок такого уравнения может быть понижен на единицу
подстановкой у — efzdx, где z — новая неизвестная функция от х: z — z(x).
V. Уравнение, записанное в дифференциалах,
F(x,y,dx,dy,d2y,...,d{n)y) =0,
в котором функция F однородна относительно своих аргументов ж, 2/, dx1
dy) d2y,..., dny, если считать х и dx — первого измерения, а у, dy, d2y
dy dry
и т. д. — измерения т. Тогда — будет иметь измерение га — 1, —j —
ах ах
измерение га - 2 и т. д.
§ 14. Уравнения, допускающие понижение порядка 73
Для понижения порядка применятся подстановка х = е\ у = uemt.
В результате получается дифференциальное уравнение между и и t,
не содержащее явно t, т. е допускающее понижение порядка не единицу
(случай III).
Рассмотрим примеры на различные случаи понижения порядка
дифференциального уравнения.
Пример 1. Найти общее решение уравнения у'" = sin x + cos ж.
Решение. Интегрируя последовательно данное уравнение, имеем:
у" = - cos х + sin x + С\,
у = -sin ж -cosz
х1
у = cos х - sin x + С] ь С2х + С3. >
Пример 2. Найти общее решение уравнения у"1 = —— и выделить
х1
решение, удовлетворяющее начальным условиям у | =| =0, у'\ =| = 1,
Л*=, = 2-
Решение. Интегрируем это уравнение последовательно три раза:
// f In х ш In ж 1 ^
У = / —dx = + С,
Уж2 я ж
у= -- In 2ж -In х + С\Х + СЪ (1)
у = -1 In 2ж + С, у + С2ж + С3.
Найдем решение, удовлетворяющее заданным начальным условиям. Подставляя
начальные данные у\х=] = 0, y'|xss| = 1, у"\х=] = 2 в (1), будем иметь
у + С2+С3 = 0, С,+С2=1, -1+С, =2.
Отсюда С| =3, С2 = -2, С3 = -. Искомым решением будет
у = -- In 2ж + -х2 - 2х + -. >
Пример 3. Решить уравнение у1" = \/\ + {у")2.
Решение. Данное уравнение не содержит искомой функции у и ее
производной, поэтому полагаем у" = р. После этого уравнение примет вид
dx
Разделяя переменные и интегрируя, найдем
е*+с\ _ е-(*+с,)
74 Глава 2. Дифференциальные уравнения высших порядков
Заменим р на у":
Интефируя последовательно, будем иметь
ex+C| _j_ e-(x+C,) ex+C, __ е-(ж+С,)
У = j + С2 И У = 2
или
у = sh (х + С,) + С2з + С3. >
Пример 4. Решить уравнение хуу - y]w = 0.
Решение. Уравнение не содержит искомой функции и ее производных
до третьего порядка включительно. Поэтому, полагая yiv =p, получаем
ж- р = 0, откуда р = С|Ж, ylv = Cj«.
Последовательно интегрируя, найдем
д.4 д.2
у' = с, —+ с2у
д.5 Ж3 ^2
у = Cl T20+ °2Т + СзТ + СаХ + С5)
или _ _ _
у = С\ХЬ + С2ж3 + С3ж2 + С4я -f C5,
гдеС,-—, С2-т, Сз-у. >
Пример 5. Решить уравнение у" + (у')2 = 2е"у-
Решение. Уравнение не содержит независимого переменного х. Полагая
у1 =р, у" =р—, получаем уравнение Бернулли
ау
Подстановкой р2 = z оно сводится к линейному уравнению
rfy
общее решение которого г = 4е"у + С\е~2у. Заменяя z на р2 = (у;)2, получаем
§ 14. Уравнения, допускающие понижение порядка 75
Разделяя переменные и интегрируя, будем иметь
откуда
Это и есть общий интеграл данного уравнения. >
Пример 6. Решить уравнение х2уу" = (у - ху')2.
Решение. Данное уравнение однородно относительно у, у\у"• Порядок
этого уравнения понижается на единицу подстановкой у = eJzdx, где z — новая
неизвестная функция от х. Имеем
y' = zeSld*, у" = (*' + * V"1-
Подставляя выражения для у, у', у" в уравнение, получаем
Сокращаем на e2fzdx\
x2(z' + z2) = (\-xz)2, или x2z' + 2xz = 1.
Это уравнение линейное. Левую часть его можно записать в виде (я2*)' = 1, откуда
2 1 С,
Гг = х + С| или z = - + -г-.
ж ж2
Находим интеграл:
Общим решением данного уравнения будет
y = e/zde = eIn|x|-C|/a+lnC2, или у = С2Же"С|/л.
Кроме того, уравнение имеет очевидное решение у = 0, которое получается
из общего при Ci = 0. >
Пример 7. Решить уравнение ж3у" = (у - яз/)2*
Решение. Покажем, что это уравнение — обобщенное однородное. Считая
х,У)У\у" величинами 1-го, m-го, (т - 1)-го и (т - 2)-го измерений
соответственно и приравнивая измерения всех членов, получаем
3 + (т - 2) = 2т, (2)
откуда m = 1. Разрешимость уравнения (2) является условием обобщенной
однородности уравнения.
Сделаем подстановку х = е', у = ие'. Так как
dy _ dy/dt _ ((fa/сй + ц)е* _ du
dx " da/eft ~" el ~ dt*U)
d^y _ (d/dt)(dy/dt) _ d2u/d<2 + du/d< _ _, /d2^ du\
da;2 " dx/dt "" e« "б V d<2 + di /'
76 Глава 2. Дифференциальные уравнения высших порядков
то данное уравнение после сокращения на множитель е2ь примет вид
du d и dp dp 2
Положив — = p, —г = p—, получим p— H-p = p . Отсюда p = 0 или
at dtl du du
dp
\-1 =p. Интефируя второе уравнение, найдем
p=l+C,ett, или — =
Общее решение этого уравнения будет
и = In —
Возвращаясь к переменным а; и у, получаем общее решение данного уравнения
\
Случай р = 0 дает и = С или у = Сх — частное решение, которое
получается из общего при С\ = е"с; С2 = 0- >
Замечание. При решении задачи Коши для уравнений высших порядков
целесообразно определять значения постоянных С,- в процессе решения,
а не после нахождения общего решения уравнения. Это ускоряет решение
задачи и, кроме того, может оказаться, что интегрирование значительно
упрощается, когда постоянные С,- принимают конкретные числовые
значения, в то время как при произвольных С,- интегрирование затруднительно,
а то и вообще невозможно в элементарных функциях.
Пример 8. Решить задачу Коши у" = 2у3; y\xss0 = 1, у'\х=0 = 1-
Решение. Полагая у1 =р, получаем
Решение. Полагая у1 =р, получаем
dP
р
откуда
Разделяя переменные, найдем
В правой части последнего равенства имеем интеграл от дифференциального
бинома. Здесь m = 0, п = 4, р = —-, т.е. неинтегрируемый случай.
Следовательно, этот интеграл не выражается в виде конечной комбинации
элементарных функций. Однако если использовать начальные условия, то полу-
dy 2
чим С] = 0. Так что — = у , откуда, учитывая начальные условия, окончательно
ах
1
находим у = . >
1 — х
§ 14, Уравнения, допускающие понижение порядка
77
Пример 9. Найти плоские кривые,
у которых радиус кривизны
пропорционален длине нормали.
Решение. Пусть у = у(х) — уравнение
искомой кривой. Ее радиус кривизны R =
(Г+(у')2)3/2
— . Длина нормали MN кривой
равна (рис.24): MN = \у\у/\ + (у')2-
Определяющее свойство кривой
выражается дифференциальным уравнением
Рис. 24
у»
(3)
где к— коэффициент пропорциональности, могущий принимать как
положительные, так и отрицательные значения. Перепишем уравнение (3) в виде
2у'у" _2у'
Интегрируя, находим
или
Разделяя переменные и интегрирую еще раз, получаем
-zr) - 1
— общий интеграл исходного уравнения (3).
Рассмотрим некоторые частные случаи.
1) к = — 1. Тогда будем иметь
х + С2
-/■
ydy
и после интегрирования —
Отсюда получаем (х + С2)2 + У2 = С\- Искомые кривые — окружности
произвольных радиусов с центрами на оси Ох.
2) к = — 2. В этом случае приходим к уравнению
Полагая у = —(1 - cost), найдем, что
78 Глава 2. Дифференциальные уравнения высших порядков
Таким образом, искомые кривые определяются в параметрической форме уран-
нениями:
* + C2=^.(*-sint), y=y(l-cos*).
Это— циклоиды, образованные качение по оси Ох окружностей произвольных
радиусов.
3) к = 1. В этом случае имеем
v
у + VУ - С]
с,
откуда
= С, / fУ = С, In
Складывая полученные равенства, будем иметь
у = £l(
2
это — цепные линии.
4) к = 2. Тогда будем иметь
С\
_ f dy
~J иг—:
или
Отсюда (я + С2)2 = 4Ci(y-C|); это — параболы, оси которых параллельны
оси Оу. >
Задачи для самостоятельного решения
Проинтегрировать следующие уравнения:
327. ylv = x. 328. у'" = х + cos ж.
329. у"(а + 2)5=1; 330. у" = хе\
331. у" = 2х In ж.
333. а?у" + у' = 0.
335. ху" = у' + х2
337. аи" = I/' In ^
332. яу" = у'.
334. яу" = (1+2ж2;
336. ж In х • у" = у'.
338. 2у" = — + -т;
339. у"' = ^!-(у")2.
341. у" = УI + (у')2.
343. /-ч/1-(у')а.
340. ay'" - у" = 0.
342. у" = (у')2.
344. у" = I + (у')2.
§ 13. Линейные дифференциальные уравнения п-го порядка 79
345. у" = у/ТТу1. 346. у" = у1 In у'; у(0) = 0, у'(0) = I.
347. у" + у' + 2 = О, 348. у" = у'(1 + у')-
у(О) = О, у'(О) = -2.
349. Зу" = (1 + (у;)2)3/2. 350. у"1 + (у")2 = 0.
351. уу" = (у')2. 352. у" = 2уу;, у(0) = у'(0) = 1.
353. Зу'у" = 2у; у(0) = у'(0) = 1. 354. 2у" = 3у2; у(-2)=1, у'(-2) = -1.
355. уу" + (у;)2 = 0. 356. уу" = у' + (у')2.
357. уу" = 1 + (у')2. 358. 2уу" = 1 + (у;)2.
359. у3у" = -1; у(1)=1, 1/(0 = 0. 360. уу" - (у')2 = уУ-
361. у" = е2у; у(0) = 0, у'(0) = I. 362. 2уу" - 3(у')2 = 4у2.
363. у'" = 3уу'; у(0) = у'(0)=1, у"(0) = \.
364. Найти плоские кривые, у которых радиус кривизны пропорционален кубу
нормали.
365. Определить форму равновесия нерастяжимой нити, на которую
действует нагрузка так, что на каждую единицу горизонтальной проекции нагрузка
одинакова (цепи цепных мостов).
366. Найти время, нужное для того, чтобы упасть на Землю с высоты 400000 км
(приблизительное расстояние Луны от центра Земли), если эта высота исчисляется
от центра Земли и если радиус Земли равен приблизительно 6400 км.
367. Найти закон движения материальной точки массы го по прямой О А под
действием отталкивающей силы, обратно пропорциональной третьей степени
расстояния точки х = ОМ от неподвижного центра О.
368. Тело массой го падает с некоторой высоты со скоростью и. При падении
тело испытывает сопротивление, пропорциональное квадрату скорости. Найти
закон движения падающего тела.
369. Найти кривую, проходящую через начало координат и такую, что площадь
треугольника, образованного касательной к кривой в некоторой точке, ординатой
этой точки и осью Ох, пропорциональна площади криволинейной трапеции,
образованной кривой, осью Ох и ординатой этой точки.
370. Определить кривую, у которой радиус кривизны равен постоянной
величине.
§ 15. Линейные дифференциальные
уравнения n-го порядка
1°. Линейная независимость функций. Определитель
Вронского. Определитель Грама. Пусть имеем конечную
систему из п функций У\(х),у2(х))..., 2/п(я)> определенных на интервале (а, 6).
Функции у\(х)} уг{х))..., уп(х) называют линейно зависимыми на
интервале (а,Ь)ч если существуют постоянные в|,а2,... ,ап, не все равные
нулю, такие, что для всех значений х из этого интервала справедливо
тождество
<*\У\(х) + а2у2(х) + ... + апУп(х) = 0.
80 Глава 2. Дифференциальные уравнения высших порядков
Если же это тождество выполняется только при с*| = а2 = ... = «п = 0,
то функции у\ (ж), з/2(я),..., уп(х) называют линейно независимыми на
интервале (а, Ь).
Пример 1. Показать, что система функций 1,ж, ж2, ж3 линейно
независима на интервале (—оо, -Ьоо),
Решение. В самом деле, равенство а]'\+а2х+а3х2+а4х3 = 0 может
выполняться для всех х £ (-оо, +оо) только при условии, что с*\ = а2 = а3 = «х* = 0.
Если же хоть одно из этих чисел не равно нулю, то в левой части равенства
будем иметь многочлен степени не выше третьей, а он может обратиться в ноль
не более, чем при трех значениях х из данного интервала. >
Пример 2. Показать, что система функций ek]X} eklX, ekyX, где k\, fc2, &з
попарно различны, линейно независима на интервале —оо < х < +оо.
Решение. Предположим обратное, т. е. что данная система функций
линейно зависима на этом интервале". Тогда
а^'х + а2е*2Х + а3е*зХ = 0 (1)
на интервале (-оо,+оо), причем, по крайней мере, одно из чисел aha2, а3
отлично от нуля, например а3 ф 0. Деля обе части тождества (1) на efc|1, будем
иметь
ai+a2e№-fc.)x + a3e№-fc,)x = 0
Дифференцируя тождество, получаем
а2(к7 - Л,)^-*'* + a3(fe3 - fc,)^3'*1'1 з 0. (2)
Делим обе части тождества (2) на е^2"*|)х:
а2(к2 - к,) + a3(fc3 " *i)e(*3"*2)x = 0. (3)
Дифференцируя (3), получаем
что невозможно, так как а3 Ф 0 по предположению, к}фк\, къф к2 по условию,
а е(к*-к2)х ф 0.
Наше предположение о линейной зависимости данной системы функций
привело к противоречию, следовательно, эта система функций линейно
независима на интервале (-оо, +ор), тте. тождество (1) будет выполняться только при
с*| = а2 = а3 = 0. >
Пример 3. Показать, что система функций еах sjn/?x, eax cos/Зж, где
/3 Ф 0, линейно независима на интервале —оо < х < +оо.
Решение. Определим значения <*i и a2, при которых будет выполняться
тождество
a,eQX sin fix + a2eax cos/3x = 0. (4)
Разделим обе его части на eQX Ф 0:
а, sin/Зж + а2 cos/Зх = 0. (5)
Подставляя в (5) значение х = 0, получаем а2 = 0 и, значит, ai sin/to = 0;
но функция sin/За: не равна тождественно нулю, поэтому с*| = 0. Тождество (5),
а следовательно, и (4) имеют место только при а\ = а2 = 0, т. е. данные функции
линейно независимы в интервале -оо < х < +оо. >
§ 15. Линейные дифференциальные уравнения п-го порядка 81
Замечание. Попутно доказана линейная независимость
тригонометрических функций sin/Зж, cos/to.
Пример 4. Доказать, что функции
smx, sin[z+-J, sin I ж--1
(6)
линейно зависимы в интервале (-оо, -f-oo).
Решение. Покажем, что существуют такие числа аг|,а2,а3, не все равные
нулю, что в интервале -оо < х < +оо справедливо тождество
/ тг\ / тг\
Sin X + а2 Sin I X + — I + Лз Sin I X 1 =0.
(7)
Предполагаем тождество (7) выполненным; положим, например, х = 0, х = —,
ТГ т 4
х = —. Тогда получим однородную систему трех уравнений с тремя неизвестными
aha2,a3:
. 7Г 7Г
a2 sin - + а3 sin - = 0,
1 Зтг тг
x-=+ol2sin у + а3 sin - = 0,
5тг Зтг
at + a2 sin — + о;3 sin —- = 0.
(8)
Определитель этой системы
Д =
1
sin
sin
sin
ТГ
"8
Зтг
5тг
T
- sin
sin
sin
ТГ
S
ТГ
8"
Зтг
8
= 0.
Следовательно, однородная система (8) имеет ненулевые решения, т. е.
существуют числа a,,a2,a3, среди которых имеется по крайней мере одно отличное
от нуля. Для нахождения такой тройки чисел aha2,a3 возьмем, например, два
первых уравнения системы (8):
тг тг
a2 sin -г ~ «з sin - = 0,
о о
-д + а2 sin -тг + а3 sin - = 0.
Из первого уравнения имеем а2 = а3, из второго <*| = -2cos— -a3. Полагая
о
а3 = 1, получим ненулевое решение системы (8):
a, = -2cos-, a2=l, а3 = 1.
82 Глава 2. Дифференциальные уравнения высших порядков
Покажем теперь, что при этих значениях а|,а2,аз тождество (7) будет
выполняться для всех х € (-оо, +оо) ]\ Имеем
ot\ sin х + а2 sin ( х + - J + а3 sin ( х - - j = -2 cos - sin x + 2 sin x cos - = 0,
каково бы ни было х. Следовательно, система функций (6) линейно зависима
на интервале -со < х < +оо. >
Замечание. Для случая двух функций можно дать более простой критерий
линейной независимости. Именно, функции у?|(а?) и <р2(х) будут линейно
независимыми на интервале (а, Ь), если их отношение не равно
тождественной постоянной ( ' . £ const) на этом интервале; если же . ч = const,
\<р2(х) ) <р2(х)
то функции будут линейно зависимыми.
Пример 5. Функции tgx и ctgz линейно независимы в интервале
тг tgx 7
0 < х < —, так как их отношение = tg x £ const в этом
2 ctgx
интервале.
Пример 6. Функции sin 2x и sin x cos x линейно зависимы в интервале
sin 2a? 2 sin х cos ж
-оо < х < +оо, так как их отношение = —: =
sin х cos х sin х cos x
sin 2x
2 = const в этом интервале (в точках разрыва функции
sin я cos ж
доопределяем это отношение по непрерывности).
Пусть п функций у\(х), У2(х), ..., уп(х) имеют производные
(п - 1)-го порядка. Определитель
2/, (х) у2(х) уп(х)
У\(х) У'2(х) у'п(х)
называется определителем Вронского для этой системы функций.
Определитель Вронского вообще является функцией от я, определенной
в некотором интервале.
Пример 7. Найти определитель Вронского для функций у\(х) = е*1*,
!) Линейную зависимость функций sin ж, sin ( х + - J, sin (х - - J можно
установить, если заметить, что sin (x+7)+sin(jr~<o)= 2 cos — sin ж, или sin f x+ - J +
sin [ x - т ) - 2 cos — sin x = 0.
8
§ 15. Линейные дифференциальные уравнения п-го порядка 83
Решение. Имеем
- *,)(*з -
- *2).
Пример 8. Найти определитель Вронского для функций: у\ (х) = sin x,
у2(«) = sin ( x + | J, з/3(ж) = sin f ж - j J .
Решение. Имеем
sins
COS Я
- sin x - i
= 0,
так как первая и последняя строки определителя пропорциональны. >
Теорема. Если система функций у\ (ж), У2(х))..., уп(х) линейно
зависима на отрезке [а, Ь], то ее определитель Вронского тождественно
равен нулю на этом отрезке.
Так, например, система функций sin x) sin ( х + — 1, sin I х - — )
линейно зависима в интервале (-оо, +оо), и определитель Вронского
этих функций равен нулю всюду в этом интервале (см. примеры 4 и 8).
Эта теорема дает необходимое условие линейной зависимости системы
функций. Обратное утверждение неверно, т.е. определитель Вронского
может тождественно обращаться в ноль и в том случае, когда
данные функции образуют линейно независимую систему на некотором
интервале.
Пример 9. Рассмотрим две функции:
2/1 (я)
у2(х) =
О, если 0 < х ^ -,
И)"
(-01.
если - < х < 1;
если 0 < х < -,
О, если -
84
Глава 2. Дифференциальные уравнения высших порядков
Графики их имеют вид, указанный на
рис.25.
Эта система функций линейно независима,
так как тождество с*\У\(х) + а2у2(ж) = О
выполняется только при с*] = а2 = 0. В самом деле,
х рассматривая его на отрезке 0, - , мы
получаем а2у2(х) = 0, откуда а2 = 0, так как у2(х) £ 0;
на отрезке же -, 1 имеем <Х\у\(х) = 0, откуда
а| =0;, так как у\(х) £ 0 на этом отрезке.
Найдем определитель Вронского W[t/i,y2] системы. На отрезке 0, -
Рис. 25
■И)
= 0,
на отрезке
И
НУ
= 0.
Таким образом, определитель Вронского W[yi,2/2] = 0 на отрезке [0,1]. 1>
Пусть имеем систему функций у\(х), 2/2(#), •••, Уп(х)> заданных
на отрезке [а, 6]. Положим
ь
(2/i, 2/j) = / Vi(x)yj(x) dx, t, j = 1, 2,..., п.
а
Определитель
(2/i,
(У2,
(2/п,
2/»)
2/.)
2/0
(2/ь
(2/2,
(2/п,
у2)
2/2)
2/2)
(2/1,
(2/2,
(2/п,
2/п)
2/п)
2/п)
называется определителем Грама системы функций {ук(х)}.
Теорема. Для того, чтобы система функций У\(х),у2(х),... ,уп(#)
была линейно зависимой, необходимо и достаточно, чтобы ее
определитель Грама равнялся нулю.
Пример 10. Показать, что функции у\ = х,
на отрезке [0,1},.
— 2х линейно зависимы
§ 15. Линейные дифференциальные уравнения п-го порядка 85
Решение. Имеем
i
f 2 1 , v / ч /* 2 2 , ч /* 2 4
(У\>У\) = / * <*ж = з' (УьУг) = (У2,У1> = / 2х Жг=-, (у2,У2) = / 4s <te = -,
О 0 0
1 2
5 5 =0,
2 4
3 3
следовательно, функции у\(х) и угС^) линейно зависимы. >
Задачи для самостоятельного решения
Исследовать, являются ли данные функции линейно независимыми в их области
определения.
371. 4, ж. 372. 1,2, а:, ж2.
373. я,2а?,аЛ 374. ех, хех, х2е\
375. sin ar, cos ж, cos 2а?. 376. 1, sin x, cos2x.
377. 5,cos2a:,sin2a\ 378. cos ж, cos (ж + l),cos(ar - 2).
379. 1, sin 2a?, (sin a: -cosa;)2. 380. a?, al8rtX (x > 0).
381. Igaa?, lgaa?2 (a? > 0). 382. 1, arcsin ж, arccos a:.
X X
383. 5, arctg a?, arcctg x. 384. 2тг, arctg —, arcctg —.
2тг 2tt
385. e-{ax2)/2,e-{ax2)/2feat2/2dt. 386. x,xf \ dt (x0 > 0).
о *o
387. Показать, что система функций
определенных на интервале (о, Ь), линейно зависима на (а, Ь).
388. Показать, что если система функций
линейно независима на интервале (а, 6), то и любая подсистема этой системы
функций также линейно независима на (а, Ь).
В следующих задачах найти определитель Вронского для указанных систем
функций:
389. 1,х. 390. *,-. 391. 1,2, ж2.
392. е-х,хе~х. 393. е*,2ех,е~х. 394. 2, cos a?, cos 2*.
395. sin ar, sin ( а? + — j. 396. arccos —, arcsin —. 397. тг, arcsin x, arccos x.
398. 4, sin ar, cos2ж. 399. ж,1паг. 400. -,ei.
401. ег^пж,ехсо5а:. 402. e"3x sin 2a?, e"3x cos 2a:.
403. cos a\ sin x. 404. sin ( x ). cos ( ar ).
\4 / \4 )
86 Глава 2. Дифференциальные уравнения высших порядков
В следующий задачах показать, что данные функции линейно независимы, а их
определитель Вронского тождественно равен нулю и построить графики этих
функций:
405. „МР
*'W ^ Л если
О, если - 1 ^ х ^ 0;
ж2, если 0 < я < 1.
0, если 0 ^ х ^ 2;
40в.
(х - 2) , если 0 ^ х ^ 2;
0, если 2 < х ^ 4.
.„ . . .ж3, если -2<ж^0;
407. у,(*)Н ' п^ ^ ,
О, если 0 < х < 1.
Г 0,
=\х2,
, если - 2 < х ^ 0;
У2(ж)=\х2 если 0<*<1.
408. у,(г) = х2, yj(e) = ф|; -1 < « < 1.
409. Пользуясь определителем Грама, показать, что системы функций задач 373,
377, 379 линейно зависимы на [—тг, тг].
2°. Линейные однородные уравнения с постоянными
коэффициентами. Рассмотрим дифференциальное уравнение
ao2/(n) + a,2/(n"1) + ... + any = O, (9)
где ао, п\} ..., ап — вещественные постоянные, по Ф 0.
Для нахождения общего решения уравнения (9) поступаем так.
Составляем характеристическое уравнение для уравнения (9):
a0An + a,An-4... + an = 0. (10)
Пусть А], Аг,..., Ап корни уравнения (10), причем среди них могут быть
и кратные.
Возможны следующие случаи:
а) А|, Аг,..., Ап — вещественные и различные.
Тогда фундаментальная система решений уравнения (9) имеет вид
А,я? А3а А„а?
с , с , . . . , с
и общим решением однородного уравнения будет
б) корни характеристического уравнения вещественные, но среди
них есть кратные. Пусть, например, А| = Аг = ... = А* = А, т. е. А
§ 15. Линейные дифференциальные уравнения п-го порядка 87
является fc-кратным корнем уравнения (10), а все остальные n-fc корней
различные. Фундаментальная система решений в этом случае имеет вид
\х \х 2 \х Л-1 \х А*+,в \пх
е , хе , х е ,..., а; е , е ,...,е ,
Ckxk']elx
а общее решение
в) среди корней характеристического уравнения есть комплексные.
Пусть для определенности Х\ = a + i/39 Л2 = а - t/J, A3 = 7 + г'^»
Л4 = j-i69 a остальные корни вещественные (так как по предположению
коэффициенты а,-, % = 0,1,2, ...,п, уравнения (9) вещественные, то
комплексные корни уравнения (10) попарно сопряженные).
Фундаментальная система решений в этом случае будет иметь вид
e^cos/ta, eQX sin/3z, e7Icos<5a:, e7*sin<fo, еАз*, еАбЯ?, ..., eKx,
а общее решение
2/о.о = С\ eax cos /Зж + C2eQX sin /Зж + С3е7* cos (5ж +
+ С4е7* sin гж + С5еА51 + ... + СпеКх;
г) в случае, если Л| = a + i/3 является fc-кратным корнем
уравнения (10) ( к ^ — 1, то Л2 = a - i/З также будет А;-кратным корнем, и
фундаментальная система решений будет иметь вид
eaxcospx) eaxs\n/3x) xeax cos /Jx, xeQX sin /3a:,
..., ^"'e^cos/Jx,..., Л0* sin/За?,..., еА"+|Ж, ..., еА«ж,
а следовательно, общее решение
2/о.о = С\ eax cos /За? + C2eax sin /За? + С3жеаа: cos fix +
+ С4жеа* sin px + ... + Сг*-!»*"^" cos/Зж +
+ C2kxk'leQX sin/3x + С2Л+,еА^|Ж + ... + CneKx.
Пример 1. Найти общее решения уравнения
2/'"-2у"-32/'= 0.
Решение. Составляем характеристическое уравнение
А3 - 2А2 - ЗА = 0.
Находим его корни: А| = О, А2 = -I, А3 = 3. Так как они действительные
и различные, то общее решение имеет вид
88. Глава 2. Дифференциальные уравнения высших порядков
Пример 2. Найти общее решение уравнения
у'" + 2у" + у' = О.
Решение. Характеристическое уравнение имеет вид
А3 + 2А2 + А = 0.
Отсюда А| = Л2 = —1, А$ = 0. Корни действительные, причем один из них,
а именно А = -1, двукратный, поэтому общее решение имеет вид
Уо.о = Схе~х + С2хе~х + С3. >
Пример 3. Найти общее решение уравнения у"' + V + \3у' = 0.
Решение. Характеристическое уравнение
А3+4А2 + 13А = 0
имеет корни А| =0, А2 = -2 - Зг, А3 = -2 + Зг.
Общее решение
Уоо = С, + С2е"2х cos Ъх + С3е~2х sin Зх. >
Пример 4. Найти общее решение уравнения
Решение. Характеристическое уравнение
А5 - 2А4 + 2А3 - 4А2 + А - 2 = 0,
или
(А-2)(А2 + 1)2 = 0
имеет корни А = 2 — однократный и А = ±i — пара двукратных мнимых корней.
Общее решение есть
Уо.о = С]е2х + (С2 + Сгх) cosх + (С4 + С5х) sin x. >
Пример 5. Решить уравнение
Решение. Составляем характеристическое уравнение
А4 + 4А3 + 8А2 + 8А + 4 = 0,
или
(А2 + 2А + 2)2 = 0.
Оно имеет двукратные комплексные корни А, = А2 = -1 - г, А3 = А4 = -1 + г и,
следовательно, общее решение будет иметь вид
уоо = С]е~х cosх + С2е~х sin х + С^хе~х cos х + С4хе~х sin ж,
или
Уо.о = е~*(С\ + С3х) cos х 4- е~х(С2 + САх) sin x. >
Задачи для самостоятельного решения
Составить линейные однородные дифференциальные уравнения, зная их
характеристические уравнения:
410. 9А2-6А+1=0. 411. А2 + ЗА + 2 = О. 412. 2А2 - ЗА - 5 = 0.
413. А(А+1)(А + 2) = 0. 414. (А2+1)2 = О. 415. А3 = 0.
§ 15. Линейные дифференциальные уравнения п-го порядка 89
Составить линейные однородные дифференциальные уравнения, если известны
корни характеристических уравнений, и написать их общие решения:
416. Л, = 1, Л2 = 2. 417. Л, = 1, А2 = 1.
418. Л,=3-2г, Л2 = 3 + 2г. 419. Л, = 1, А2 = 1, Л3 = 1.
Составить линейные однородные дифференциальные уравнения, если заданы их
фундаментальные системы решений:
420. е~\е\ 421. 1,ех. 422. е~2х>е"2а''.
423. sin За,cosЗх. 424. 1,я. 425. ех, е2*, е3х.
426. е\хех,х2ех. 427. е\хе\е2х. 428. 1,ж,ех.
429. l,sinx,cosg. 430. e2x,sina;,cosa;. 431. l,c"xsina5,e~*cosa;.
Проинтегрировать следующие уравнения и, где указано, решить задачу Коши.
432. у"-у = О. 433. Зу" - 2у'- 8у = 0.
434. у'" - Зу" + Зу' - у = 0, 435. у" + 2у' + у = 0.
у(0) = 1, у'(0) = 2, у"(0) = 3.
436. у" - 4у + Зу = О, 437. у'" + 6у" + 11у' + 6у = 0.
у(0) = 6, у'(0)=10.
438. у"-2у'-2у = 0. 43Й. yvl + 2yv + yIV = 0.
440. 4у'' - 8у + 5у = 0. 441, у" - 8у = 0.
442. ylv + 4у;/' + \0у" 4- 12у' + 5у = 0. 443. у;/ - 2у + 2у = 0,
у(0) = 0, у'(0)=1.
444. у" - 2у' + Зу = 0, 445. ylv + 2у;// + 4у;/ - 2у; - 5у = 0.
2/(0) = 1, 1/(0) = 3.
446. yv + 4yIV + 5y/;/-6y'-4y = 0. 447. у//; + 2у" - у' - 2у = 0.
448. у'" - 2у/; + 2у; = 0. 449. у" - у = 0.
450. ух = 0. 451. у1" - Зу - 2у = 0.
452. 2у//; - Зу" + у1 = 0. 453. у"1 + у;/ = 0,
у(0) = 1, у'(0) = 0, у»=1.
3°. Линейные неоднородные уравнения с постоянными
коэффициентами. А. Метод подбора. Пусть дано дифференциальное
уравнение
()
с постоянными вещественными коэффициентами ао, п\, a-i,..., ап.
Теорема. Общее решение неоднородного уравнения (11) равно сумме
общего решения соответствующего однородного уравнения и какого-
либо частного решения неоднородного уравнения.
Отыскание общего решения соответствующего однородного
уравнения осуществляется по правилам, изложенным в п. 2. Таким образом,
задача интегрирования уравнения (11) сводится к отысканию частного
решения учн неоднородного уравнения. В общем случае интегрирование
уравнения (11) может быть осуществлено методом вариации
произвольных постоянных (см. ниже п. 5°). Для правых частей специального вида
90 Глава 2. Дифференциальные уравнения высших порядков
часто решение находится проще, так называемым методом подбора.
Общий вид правой части f(x) уравнения (11), при котором возможно
применить метод подбора, следующий:
f(x) = eax[Pt(x) cos fix + Qm(x) sin /3x],
где Pi(x) и Qm(x) суть многочлены степени 2 и га соответственно. В этом
случае частное решение уч.н уравнения (11) ищется в виде
2/ч.н = х'еах[Рк(х) cos/Зх + Qk(x) sin /?я],
где к = max(ra,Z), Р*(а:) и Qk{x)— многочлены от х fc-й степени
общего вида с неопределенными коэффициентами, a s— кратность корня
А = а + г/3 характеристического уравнения (если a±i/3 не является
корнем характеристического уравнения, то s = 0).
Пример 1. Найти общее решение уравнения у'" - у"+у' - у = ж2 + х.
Решение. Характеристическое уравнение Л3-Л2+А-1 = 0 имеет различные
корни: А| = 1, Аг = -«, Аз = *, поэтому общее решение соответствующего
однородного уравнения уо.о будет
у00 = С|вх + С2 cos х + С3 sin ж.
Так как число ноль не является корнем характеристического уравнения, то частное
решение данного уравнения уч>н надо искать в виде (см. табл. 1, случай I (1)):
учм = Aix2 + А2х + Ah
где АиА2)Аз — неизвестные пока коэффициенты, подлежащие определению.
Подставляя выражение для уч.н в данное уравнение, получаем
-Ахх2 + (2А} - А2)х + (А2 - 2АХ - А3) = х2 + х,
откуда, приравнивая слева и справа коэффициенты при одинаковых степенях я,
будем иметь:
А2 - 24, - А3 = 0.
Решая эту систему, найдем А] = -1, А2 = -3, А3 = -1, следовательно, частное
решение будет
учм = -х2-Зх-\,
и общее решение уо.н данного уравнения имеет вид
уон = С\ех + С2 cos х + С3 sin ж - х2 - Зж - 1. >
Пример 2. Найти общее решение уравнения у"1 - у" = 12ж2 ч- 6ж.
Решение. Характеристическое уравнение А3 - А2 = 0 имеет корни Ai =
Л2 = 0, Аз = 1, а поэтому общее решение соответствующего однородного
уравнения будет
Уо.о = С, + С2х + Сге*.
Так как число 0 есть двукратный корень характеристического уравнения, то
частное решение надо искать в виде (см. табл. 1, случай I (2))
уч.н = х2(А\Х2 + А2х + А2) = А}хА 4- А2хг
§ 15. Линейные дифференциальные уравнения п-го порядка 91
Таблица 1
Сводная таблица видов частных решений
для различных видов правых частей*
№
I
II
III
IV
Правая часть
дифференциального
уравнения
Рт(х)
Рт(х)е°*
Pn(x)cospx +
+ Qm(x)smpx
eax[Pn(x) cos px +
+ Qn(x)s\npx]
Корни характеристического
уравнения
1. Число 0 не является
корнем характеристического
уравнения
2. Число 0 — корень
характеристического уравнения
кратности s
1. Число а не является
корнем характеристического
уравнения
2. Число а является
корнем характеристического
уравнения кратности s
1. Числа ±%р не являются
корнями
характеристического уравнения
2. Числа ± %р являются
корнями
характеристического уравнения кратности s
1. Числа a ± ip не являются
корнями
характеристического уравнения
2. Числа a ± ip являются
корнями
характеристического уравнения
кратности s
Виды частного
решения
Рт(х)
Х*Рт(х)
Рт(х)е*х
х'Рт(х)еа*
Pk(x)cospx +
+ gfc(a;)sin/3z,
к = max(m, n)
za(Pk(x)caspx +
+ Qk(x)sinpx),
к = max(m, n)
(Pk(x)cospx +
+ Qk(x)sinpx)eax,
к = max(m, n)
a^P*(z)cos/ta +
+ Q*(z)sin/3a;)eas,
к = max(m, n)
* Первые три вида правых частей являются частными случаями IV вида.
Подставляя выражение для уч>н в данное уравнение, будем иметь
-12А,я2 + (244, - 6А2)х + (6А2 - 2AZ) = 12s2
откуда
-12.4, = 12,
244, - 6А2 = 6,
6А2 - 2А2 = 0.
92 Глава 2. Дифференциальные уравнения высших порядков
Эта система имеет решение: А] = — 1, А2 = -5, Аз = —15, а значит
Уч.н = -я4 - 5ж3 - \5х2.
Общее решение данного уравнения
уон = С, + С2я + С3ех - ж4 - 5ж3 - 15ж2. >
Пример 3. Найти общее решение уравнения у" + у1 = 4х2е*.
Решение. Характеристическое уравнение А2 + А = 0 имеет корни А| = 0^
А2 = -1. Значит, общее решение уо.о соответствующего однородного уравнения
будет
Уо.о = С, + С2е'х.
Так как а = 1 не является корнем характеристического уравнения, то частное
решение уч.„ неоднородного уравнения в виде (см. табл. 1, случай II (1))
Подставляя его в исходное уравнение и сокращая обе части уравнения на е*,
будем иметь
2Ахх2 + (6А, + 2А2)х + 2А\ + ЪА2 + 2А3 = 4х2.
Приравнивая коэффициенты при одинаковых степенях х в левой и правой частях
равенства, получаем линейную систему уравнений для нахождения
коэффициентов А\у А2, Ау.
24, =4,
6АХ 4- 2А2 = 0,
2А, + ЗА2 + 2А3 = 0,
решая которую, находим А\ =2, А2 = -6, j43 = 7, так что
уч.„ = (2ж2 - 6х + 7)ех.
Общее решение данного уравнения
у(х) = С, + С2е"* + (2ж2 - 6х + 7)ев. >
Пример 4. Найти общее решение уравнения
Решение. Характеристическое уравнение А2+10А+25 = 0 имеет двукратный
корень А, = А2 = -5, поэтому
Так как а = -5 является корнем характеристического уравнения кратности
s = 2, то частное решение уч „ неоднородного уравнения ищем в виде (см. табл. 1,
случай II (2))
уч.н=В*2е-5х,
тогда
У'чм = В(2х-5х2)е-5х,
Ун.» = Б(2 - 20s + 25*2)е"5х.
Подставляя выражение для уч.„, учн, уч'н в исходное уравнение, получаем
2Ве~5х =; 4е~5*, откуда В = 2и, значит, уч.н = 2ж2е~5*. Общее решение данного
уравнения
у(х) = (С, + С2х)е~5х + 2х2е~5х. >
§ 15. Линейные дифференциальные уравнения п?го порядка 93
Пример 5. Найти общее решение уравнения
у" + Ъу + 2у = х sin х.
Решение. Первый способ. Характеристическое уравнение А2 4- ЗА +
2 = 0 имеет корни Ai = — 1, А2 = —2, поэтому
Так как число i не является корнем характеристического уравнения, то частное
решение уч.н неоднородного уравнения ищем в виде (см. табл. 1, случай III'(1))
уч.н = (А}х + А2) cos x + (B}x + В2) sin я,
тогда
Уч.н = (Л, + В2 + Б,ж) cos х + (Б, - А2 - Ахх) sin ж,
у"н = (2Б,ж -А2- А&) cos х - (24, + В2 + #,s) sin ж.
Подставляя эти выражения в исходное уравнение, будем иметь
(2В} -А2- Ахх) cos х - (24, + В2 + Б^) sin ж +
+ 2(А\Х + А2) cos х + (J9i« 4- В2) sin a? = х sin ar,
или
[(4, + ЪВх)х + ЗАХ + А2 + 2Б, + ЗБ2] cos ж +
+ [(-ЗА, + Б,)ж - 2А, - ЗА2 + ЗБ, + Б2] sin х = х sin ж.
Отсюда получаем систему линейных уравнений относительно А|,л42, БЬБ2
А,+ЗБ,=0,
ЗА, + А2 + 2Б, + ЗБ2 = 0,
1АХ -
Решая эту систему, найдем Л, = —-, А2 = •—-, Б, — --, Б2 = .—» и Частное
решение уч#н запишется так:
3 17\ /1 3
Общее решение данного уравнения
3 17\ /1 3\
- —ж+ — \ cosx+ f ~ж+ — 1 sihar.
В случае, когда правая часть f(x) содержит тригонометрические
функции sin/За: и cos/За;, оказывается удобным применять переход к
показательным функциям. Сущность этого приема покажем на примере.
Решить дифференциальное уравнение
у1 + у = х cos х.
Здесь А2+1 = 0, А( = -г, А2 = i и общее решение однородного уравнения
имеет вид
Уо.о = С\ cos х И- Сг sin x.
94 Глава 2. Дифференциальные уравнения высших порядков
Частное решение неоднородного уравнения j/4iH надо искать в виде
j/ч.н = х[(А\Х + А2) cos х + (В\Х + В2) sin x].
Поступим так. Рассмотрим уравнение
z" + z = xeia. (12)
Легко видеть, что правая часть исходного уравнения есть
вещественная часть от правой части уравнения (12):
я cos a: = Re (хе%х).
Теорема. Если дифференциальное уравнение с вещественными
коэффициентами L[y] = f\(x) + ifiix) имеет решение у = и(х) + iv(x), то
и(х) есть решение уравнения L[y] = f\(x), а v(x) — решение уравнения
Ц) = h(x).
Найдем z4.H уравнения (12):
*,.„ = (Ах + B)xeix = (Ах2 + Bx)eixy
<„ = 2Aeix + 2(2Ах + B)ieix - (Ах2 + Bx)eix.
Подставляя в уравнение (12) и сокращая обе части на е|а}, будем иметь
2А + 4Axi + 2В% = я,
% А 1
откуда 44г = I, ^4 = --, ^4 + Вг = О, В = -— = -, так что
4 г 4
/ г 2 1 \ ix ( г 2 1 V ...
z4tH = I --а? + -а? 1е'* = ( --ж + -х 1 (cos а? + г sin x) =
x cos x 4- ж2 sin x .x sin x - x2 cos x
■+i-
4
Отсюда в силу теоремы
2/ч.н =
х cos x + х2 sin x
4
Этот прием порой значительно упрощает и сокращает вычисления,
связанные с нахождением частных решений.
Решение примера 5. Второй способ. Решим этот пример путем
перехода к показательным функциям. Рассмотрим уравнение
z" + 3*' + 2z = ae'x. (13)
Легко видеть, что правая часть исходного уравнения равна мнимой части xeiz:
х sin x = lm(a?elx).
Ищем z4>H уравнения (13) в виде
*ч.„ = (Ах + Б)е'х,
§ 15. Линейные дифференциальные уравнения п-го порядка 95
тогда
г,',,, = Aeix + i(Ax + B)eix} <„ = 2iAeix - (Ax + B)eix.
Подставляя эти выражения в (13) и сокращая на е|я, получаем
2Ai - Ах - В + ЗА + ЗАгх + ЗВг + 2Ла? + 2S = я,
откуда
Г А + ЗЛг = 1,
\ 2Л* + В + ЗЛ + ЗВг = О,
так что
1 Зг i4(3-f 2г) 6 17
= Т77 "" 77» В = -•
1+Зг 10 10' 1+3»
Итак,
'1-Зг 6+17г\,я /5х + в 17-15ж
, . . v- (5х Ч- 6) cos a? -h (15ж — 17) sin ж
х (cos х + г sin х) = -j +
. (5а? + 6) sin х + (17 - 15а?) cos я?
отсюда
5я + 6 17-15»
y4lH = Im z4.H = 5Q sin x + —эд— cos »,
что совпадает с у,,.и, найденным ранее. >
Пример 6. Найти общее решение уравнения у" + 4j/ = sin 2x.
Решение. Рассмотрим уравнение г" + 4* = е2гх.
Имеем
sin 2 а? = Im e2taj,
поэтому
Уч.н = Imz4lH.
Характеристическое уравнение А2 + 4 = 0 имеет простые корни А|,2 = ±2».
Следовательно, частное решение ишем в виде (см. табл. 1, случай III (2)):
*„.„ = Axe2i\
тогда
z"M = -4Axe2ix + 4Aie2ix.
Подставляя выражения для z4tH и z"M в уравнение и сокращая на е2'35,
получаем 4А% = 1, откуда А = --, а значит
4
z,IH = --гже21а! = -o;sin2a!- i-a?cos2a?.
4 4 4
Частное решение данного неоднородного уравнения будет
уч.„ = Imz4(M = --a?cos2a\ >
96 Глава 2. Дифференциальные уравнения высших порядков
Пример 7. Найти общее решения уравнения у"-6у'+9у = 25ех sin x.
Решение. Характеристическое уравнение А2 - 6А 4 9 = 0 имеет корни
Л, = Л2 = 3; общее решение уао однородного уравнения будет
Уо.о = (С, + С2х)е3х.
Числа l±t не являются корнями характеристического уравнения, поэтому частное
решение у.,.н ищется в виде (см. табл. 1, случай IV (1))
учн = ex(a cos х 4 6 sin x).
Подставляя выражение унм в уравнение и сокращая обе части уравнения на ех,
получаем
(За - 46) cos х 4 (4а + 36) sin x = 25 sin x.
Отсюда имеем систему
Г За - 46 = О,
I 4а + 36 = 25,
решение которой есть а = 4, 6 = 3 и, следовательно,
Уч.н = е*(4 cos х 4 3 sin x).
Общее решение данного уравнения
у(х) = (С, + С2х)е3х 4 е*(4 cos х 4 3 sin x). >
Пример 8. Найти общее решение уравнения
у" + 2у +5у = е~х cos 2x.
Решение. Характеристическое уравнение Л2 + 2А 4- 5 = 0 имеет корни
Л|>2 = -1 ± 2г, так что
= (С\ cos 2х + С2 sin 2x)e~
-4- 2г является простым кс
ать в виде (см. табл. 1, случ
уцм = х(А cos 2х + В sin 2x)e~xi
Так как число а + ifi = -1 4- 2г является простым корнем характеристического
уравнения, то учн надо искать в виде (см. табл. 1, случай IV (2))
тогда
Уч.* = е~х[(А - Ах 4 2Вх) cos 2ж + (В - Bs - 2Ax) sin 2ar],
У?.н = е~*[(-2А - ЗЛх 4 4Б - 4J9a;) cos 2я 4 (-2В - ЪВх - 4А 4 4As) sin 2x].
Подставляя выражения для уцм и ее производных в исходное уравнение и
сокращая на е"*, будем иметь
-4A sin 2х 4 4Б cos 2х = cos 2ж,
откуда А = О, В = - и, значит,
4
_ 1
4
Общее решение данного уравнения будет
у(х) = (С\ cos2а; 4 С2 sin 2ат)е"х 4 ~.хе~х sin 2a;.
§ 15. Линейные дифференциальные уравнения п-го порядка 97
Задачи для самостоятельного решения
Определить вид частного решения линейного неоднородного дифференциального
уравнения, если известны корни его характеристического уравнения и правая
часть /(ж):
f(x) = ах2 + bx + с.
f(x) = ax2 + bx + с.
А2 = 2;
Л2=1;
А2 = 0;
f(x) = ах + bx + с.
f(x) = е~х(ах + 6).
f(x) = sin ж + cos x.
/(ж) = sin x + cos ж.
/(ж) = A sin 2x + Б cos 2ж.
/(ж) = Asinkx + В cos &ж.
/(a?) = e~x(A sin ж + В cos ж).
/(ж) = e~x(A sin ж + Б cos ж).
/(ж) = ах2 + Ьж + с.
/(ж) = ах2 + Ьх + с.
/(ж) = аж2 + bx + с.
/(ж) = аж2 + 6ж + с.
/(ж) = sin ж + cos ж.
454. А, = 1,
455. А, = О,
456. А, = О,
457. А, = 1, А2 = 2;
458. А, = -1, А2 = 1;
459. А, = -1, А2 = -1;
460. А, =0, А2= 1;
461. А, = -г, А2 = г;
462. А, = -2г, А2 = 2г;
463. А, = -ki, A2 = ki;
464. А, = 1, А2= 1;
465. А, = -1 -г, А2 = -1+г;
466. А, = А2 = А3 = 1;
467. А, =0, А2= 1, А3 = 2;
468. А, =А2 = 0, А3 = 1;
469. А, = А2 = А3 = 0;
470. А, =т t, А2 = -г, А3 = 1;
471. а) А, =0, А2= I,
б) А, =&, А2= 1,
в) А = А? = к
г) А, = А2 = 0, А3 = 1,
д) А| = А2 = к, Аз = 1
е) А] = А2 = А3 = А;
472. а) А, =А2= 1, А3 = 2,
б) Aj = -г, А2 = г, А3 = I
473. а) А, = 3 - 2г, А2 = 3 + 2г,
А3 = А4 = 0,
б) А, = А2 = 3 - 2i,
А3 = А4 = 3 + 2г
Для следующих линейных неоднородных дифференциальных уравнений
определить вид частного решения:
474. у" + Зу = 3. 475. у - 1у = (ж - I)2.
477. у" + 1у = е~7х.
)е4х. 479. у" - 10у' + 25у = е5х.
481. у" - 4у' = же4х.
483. у" + у = sin ж - cos ж.
476. у" + 3у' = е*.
478. у" + 8у'+16у = 0
480. 4у" - Зу; = хе3х/4.
482. у" + 25y = cos5x.
484. у"+I6y = sin(4ar
485. у"+4у'
= e
2x
98
Глава 2. Дифференциальные уравнения высших порядков
486.
488.
490.
492.
494.
496.
498.
500.
502.
504.
506.
508.
у" - 4у' + 8у = e2*(sin 2х - cos 2x)
у" + кгу = к sin (fcx + a).
у'" + у = х.
у'" + у' = 2.
ylv-y=i.
ylv-y" = 3.
ylv + 4у'" + 4у" = 1.
ylv + 2у'" + у" = е~х.
ylv + 4у" 4- 4у = sin 2x.
ylv + 4у" + 4у = х sin 2s.
ylv - 2n2y" + n4y = cos (nx + a).
y'v-4y'" + 6y"-4y' + y = ex.
. 487. у" + ву + 13y = e""3x cos 2x.
489. y'4*2y = fc,
491. y"' + 6y" + 1 ly' + 6y = 1.
493. y'" + y" = 3.
495. ylv-y' = 2.
497. ylv-y'" = 4.
499. ylv + 2y/w + yw = e4x.
501. ylv + 2y"f + y;/ = a?e"x.
503. ylv + 4y;/ + 4y = cos x.
505. ylv + 2n2y" + n4y = a sin (nx + a).
507. ylv + 4y"' + 6y/; + 4уЧ у = sin ж.
509. ylv-4yw + 6y;/-4y4y = xex.
Решить следующие линейные неоднородные уравнения:
510.
512.
514.
516.
518.
520.
y" + 2j/ + у = -2.
у" + 9у - 9 = 0.
5y'" - 7y" -3 = 0.
3ylv + y'" = 2.
y"-4y' + 4y = a2.
y"-2fcy' + *2y = ex, (** 1).
511, y'; + 2y42 = 0.
513. y'" + y"=l.
515. ylv-6y/w + 6 = 0.
517. ylv-2y/// + 2y//-2y' + y=1.
519. y" + 8y' = 8x.
521. y/; + 4y' + 4y = 8e"2x.
522.
= 9е
-3*
524. y" + 3y'= 3xe"3x.
526. y" + 2y' + 2y = 1 + x.
528. y" + 4y' - 2y = 8 sin 2x.
530. y" - 2my' + m2y = sin nx.
532. y" + o2y = 2 cos mx + 3 sin mx (m 5
533. y"-y' = -2e*sinx.
535. y" + 4y' + 5y = 10e'21 cos x.
537. y" - 3y'+ 2y = xe*.
539. y" - 3y' + 2y = (x2 + x)e3*.
541 • ylv — 2y'" + 2y;/ — 2y' + у = ex,
543. ylv + y" = x2 + x.
545. y" + 2y' + у = ж2е"х cos x.
547. ylv-2y" + y = cosz.
549. y" - 4y + 5y = e2x(sin x + 2 cos ж).
523. 7y" - y; = 14г.
525. у" + 5y' + 6y = 10(1 - ж)е"2х.
527. y" + y' -h у = (ж + a?2)ex.
529. y;/ + у = 4я cos ж.
531. у" + 2у' + 5у = е"х sin 2ж.
fee).
534. у" + 2у' = 4ex(sin x + cos ж).
536. 4у" + 8у; = х sin x.
538. у" + у' - 2у = ж2е4х.
540. у'"-у" + у'-у = х2 + х.
542. у/'-2уЧу = гс3.
544. у" + у = a?2 sin x.
546. у;" - у = sin х.
548. у"' - Зу" + Зу' - у = ех cos 2s.
Б. Принцип суперпозиции. При нахождении частных решений
линейных неоднородных уравнений удобно пользоваться следующей теоремой.
Теорема (принцип суперпозиции или наложения). Если Ук{х) есть
решение уравнения
ао(х)у{п) + al(x)y(n-|) + ... + ап(х)у = Д(х), к = 1,2,..., т,
§ IS. Линейные дифференциальные уравнения п-го порядка 99
m
то функция у(х) = £ Ук(х) является решением уравнения
ао(х)у{п) + М*)»*-1» + ... + ап(х)у = £ fk(x).
к=\
Пример 9. Решить уравнение
у"-6у' + 9у = 4е*-\6е3х. (14)
Решение. Характеристическое уравнение А2 - 6А + 9 = 0 имеет корни
Л] = А2 = 3, а поэтому общим решением уо.о соответствующего однородного
уравнения будет
3 3
Для нахождения частного решения y4iH уравнения (14) найдем частные
решения двух уравнений
4е*, (15)
-1бе3*. (16)
Уравнение (15) имеет частное решение у\ вида у\ = Аех (см. табл. 1, случай II (1)).
Подставляя выражение для у\ в уравнение (15), найдем А = 1, так что у\ = е .
Частное решение уравнения (16) ищем в виде у2 = Вх1ег* (см. табл.1,
случай II (2)). Находим у2 = -8аVх.
В силу принципа суперпозиции решений частное решение уЧаН данного
уравнения будет равно сумме частных решений у\ и у2 уравнений (15) и (16)
Уч.н = У\ + у2 = ех - 8ж2е3а:.
Общее решение уравнения (14)
у = (С, + С2х)е}* + ez- 8a?V*. >
Пример 10. Решить уравнение
у'" - 2у" -f 2yf = 4 cos я cos Зя + 6 sin 2ж. (17)
Решение. Используя известные тригонометрические тождества,
преобразуем правую часть уравнения (17) к «стандартному» виду
4 cos х cos Ъх + 6 sin 2x = 2 cos 4я - cos 2я + 3.
Исходное уравнение (17) запишется теперь так:
у'" - 2у" + 2у' = 2 cos 4а? - cos 2x + 3. (18)
Общим решением однородного уравнения у1" - 2у" + 2у' = 0 будет
Уо.о = С\ + (С2 cos ая- С3 sin а?)е*.
Для отыскания частного уравнения (18) используем принцип суперпозиции.
Для этого найдем частные решения трех уравнений:
у'" - 2у" + 2у; = - cos 2a;, (20)
у'"-2у'Ч2у' = 3. (21)
100 Глава 2. Дифференциальные уравнения высших порядков
Используя метод подбора, найдем частные решения уь у2 и у3 уравнений {19),
(20) и (21) соответственно:
1 / 7 \ 1/1 \ 3
У\ = 6^(cos4z- -sin4x I, y2 = — ( - sin 2x - cos2z I, у3 = -х.
В силу принципа суперпозиции частное решение неоднородного уравнения (8)
1 / а 1 . \ 1 /sin2a; ^ \ 3
учн = —\cosAx sin4х ] Н cos2x + -х.
65 V 4 УЮ\2 ) 2
Общее решение исходного уравнения
у = С\ + (С2 cos а: + С3 sin x)ex +
1 / . 7 . \ 1 /sin2a;
Задачи для самостоятельного решения
Определить вид частного решения линейного неоднородного дифференциального
уравнения, если известны корни его характеристического уравнения и правая
часть /(ж).
550. а) А|=-1, А2 = 1, А3 = 2,
б) А, =0, А2 = 2, А3 = 3,
\ \ \ ill
в) А, = А2 = -1, А3 = 1,
г) А, =А2 = А3 = -1,
Пользуясь принципом суперпозиции, определить вид частного решения
следующих линейных неоднородных дифференциальных уравнений:
551. у" -у'-2у = ех + е~2х. 552. у" + 4у' = х + е"4х.
553. у" - у = х + sin х. 554. у" - 2т/ + 2у = (I + sin ж)ех.
555. у" - у" = 1 + ех. 556. у" + 4у' = е2х + sin 2x.
557. у" + 4у = sin x sin 2ж. 558. у/; -4у =2 cos 24ж.
Решить следующие линейные неоднородные уравнения, используя принцип
суперпозиции для нахождения их частных решений:
559. у" - у' - 2у = Ах - 2ех.
560. у" - Зу = 18ж - 10 cos ж.
561. y"-2y4y = 2 + exsinz.
562. у" + 2у; + 2у = (5х + 4)ех + е~х.
563. у" + 2у + 5у = 4е"х + 17 sin 2x.
564. 2у/; - Зу - 2у = 5ех ch x.
565. у" + 4у = х sin 2ж.
566. ylv + 2yw + 2у/; + 2у' + у = хех + i cos x.
567. у" + у; = cos 2я + ех + ж2.
568. yv + 4yw = ex + 3 sin 2x+\.
569. у"-2у' + 5у = 10 sin ж + 17 sin 2a?.
570. у" + у' = х2 - е~х + ех.
§ 15. Линейные дифференциальные уравнения п-го порядка 101
571. у" - 2у' - Зу = 2х 4- е~х - 2е3х.
572. у"4-4у = ex4-4sin-2x + 2cos2x-I.
573. у" 4- Зу' 4- 2у = 6хе"х(1 - е~х).
574. у" 4-у = cos22x4-sin2-.
575. у1 - 4у' 4- 5у = 1 4- 8 cos x 4- е2х.
576. у" - 2у 4- 2у = ех sin 2—.
577. у" -Зу = 1 4- ех 4- cos х - sin x.
578. у" - 2у + 5у = ех(1 - 2 sin 2х) 4- 10х 4- 1.
579. у" - 4у' + 4у = 4х 4- sin x 4- sin 2x.
580. у" 4- 2у' 4- у = 1 4- 2 cos x 4- cos 2x - sin 2x.
581. у/; 4- у 4- у + 1 = sin х 4- х + х2.
582. у" + 6у' 4- 9у = 18е"3х 4- 8 sin x + 6 cos x.
583. у" + 2у' 4- 1 = 3 sin 2x 4- cos x.
584. у"' — 2у" 4- у = 2х 4- ех.
585. у" 4- у = 2 sin x sin 2x.
586. у/;/ - у" - 2у; = 4х 4- 3 sin x 4- cos x.
587. у'" - 4у' = хе2х 4- sin x 4- х2.
588. yv-ylv = xex- 1.
589. yv + у'" = х 4- 2е~х.
В. Задача Коши. Как известно, задача Коши для линейного
неоднородного уравнения
состоит в следующем: найти решение этого уравнения, удовлетворяющее
начальным условиям (данным Коши)
Пример 11. Найти частное решение уравнения
у" - у = 4ех, (22)
удовлетворяющее начальным условиям
2/(0) = 0, у'(0)=1. (23)
Решение. Находим частное решение уравнения (22)
у = С,е*4-С2е-*4-2хех. (24)
Для решения поставленной начальной задачи (22)—(23) (задачи Коши)
требуется определить значения постоянных С\ и С2 так, чтобы решение (24)
удовлетворяло начальным условиям (23). Используя условие у(0) = 0, получаем
d 4- С2 =0. Дифференцируя (24), найдем
102 Глава 2. Дифференциальные уравнения высших порядков
откуда, в силу условия у'(0) = 1, будем иметь С\ - С2 = -1. Для отыскания
С|, С2 получили систему
г с, + с2 = о,
\ С, -С2 = -1,
решая которую находим С\ = --, С2 = -. Подставляя найденные значения
произвольных постоянных в обшее решение (24), получаем решение начальной
задачи, (22)-(23):
у =--е*-f-е~х+2же* или у = 2хех - sh x. >
Пример 12. Найти частное решение уравнения
у" + 4у' + 5у = 8 cos я, (25)
ограниченное при х —♦ -оо.
Решение. Общее решение данного уравнения
у = е"2ж(С! cos a; + C2 sin ж) •+■ 2(cos x + sin ж). (26)
При х —> -ее величина е~2* —► +оо и при любых С\ и С2, не равных
одновременно нулю, первое слагаемое правой части (26) будет функцией, неограниченной
при х —> -оо, а второе слагаемое — функцией, ограниченной при всех
значениях х. Следовательно, только при С\ = С2 = 0 имеем ограниченное при х —» -оо
решение уравнения (25), именно
у = 2(coss + sina:). (27)
Более того, решение (27) уравнения (25) ограниченно при всех х:
\у\ = |2(cos х + sin г)| ^ 2(| cos х\ + \ sin x\) < 4
для всех х € (-оо, +оо). >
Пример 13. Найти частное решение уравнения
у"-3у/ + 2у = 4 + 2в"шсов«, (28)
удовлетворяющее условию у -► 2 при ж -> +оо.
Решение. Обшее решение данного уравнения
у = С\е* + С2е2х + 2 + e"x(sin x - cosx), (29)
При любых значениях постоянных С\ и С2, не равных одновременно нулю,
решение (29) является неограниченной функцией при х -+ +оо. При С\ = С2 = О
решением уравнения (28) будет функция у = 2 + e~x(sina> - cos ж) для которой,
очевидно, выполняется условие lim у = 2. Таким образом,
у = 2 4- (sin ж - cos x)e~*
будет искомым частным решением. >
§ 15. Линейные дифференциальные уравнения п-го порядка 103
Задачи для самостоятельного решения
В следующих задачах найти частные решения уравнений, удовлетворяющие
заданным начальным условиям:
590. у" + у = 2(1 - х)\ у(0) = 2, у'(0) = -2.
591. у" - 6у' + 9у = 9я2 - \2х + 2; у(0) = 1, у (0) = 3.
592. у" + 9у = 36е3х; у(0) = 2, у'(0) = 6.
593. у" - V + 4у = 2е2х; у(0) = у'(0) = 0.
594. у" - 5у' + 6у = (12* - 7)е"х; у(0) = у'(0) = 0.
595. у" + у' = е~х; у(0)=1, у'(0) = -1.
596. у" + 6у' + 9у = 10 sin a;; y(0) = у'(0) = 0.
597. у" + у = 2 cos х; у(0) = 1, у'(0) = 0.
598. у" + 4у = sin ж; у (0) = у'(0) = 1.
599. у" + у = 4х cos ж; у(0) = 0, у'(0)=1.
600. у'' - 4у' + 5у = 2zV; у(0) = 2, у'(0) = 3.
601. у" - 6у' + 9у = 16е"х + 9х - 6; у(0) = у'(0) = 1.
602. у" - у = -5e"x(sin х + cos ж); у(0) = -4, у'(0) = 5.
603. y"-2y' + 2y = 4excoss; у(тг) = тге*, у'(тг) = е*.
604. у'" - у' = -2а;; у(0) = 0, у'(0) = 1, у"(0) = 2.
605. ylv-y = 8ex; у(0) = -1, у'(0) = 0, у"(0) = 1, у» = 0.
606. у'"-у = 2х; у(0) = у;(0) = 0, у;/(0) = 2.
607. yIV-y = 8ex; у(0) = 0, у'(0) = 2, у/;(0) = 4, у» = 6.
В следующих задачах найти частные решения уравнений, удовлетворяющие
заданным условиям на бесконечности:
608. у" - 4у' + 5у = sin а?, у ограничено при х —> +оо
609. у" 4- 2у' + 5у = 4 cos 2а? + sin 2ж, у ограничено при а? -♦ -оо
610. у'1 - у = 1, у ограничено при х -♦ оо
611. у'' - у = -2 cos ж, у ограничено при а? -► оо
612. у" - 2у' + у = 4е"х, у -► 0 при х -► +оо.
613. у" + 4у' + Зу = 8ех + 9, у -> 3 при х -*- -оо.
614. у" -у'-5у а= I, у-^ -- при « -* оо.
615. у" + 4у' + 4у = 2e*(sin х + 7 cos ж), у -+ 0 при а? -+ -оо.
616. у" - 5у' + 6у = 2е"2х(9 sin 2а; + 4 cos 2а?), у -+ 0 при х -♦ +оо.
617. у" - 4у' + 4у = (9а:2 + 5а? - 12)е"х, у -► 0 при х -> +оо.
4°. Уравнения Эйлера. Линейные уравнения вида
aoxnyin) + аи^-у1"1* + ... + о».,»^ + апу = 0, (30)
где все а,- постоянные, называются уравнениями Эйлера. Эти уравнения
заменой независимого переменного х = е* преобразуются в линейные
однородные уравнения с постоянными коэффициентами:
[) \]) + ... + Ьп^у[ + bny(t) = 0. (31)
104 Глава 2. Дифференциальные уравнения высших порядков
Замечание 1. Уравнение вида
ao(ax + Ь)пу + п\(ах + Ь)п"]у + ... + ап-\(ах + Ь)у + апу = 0
также называются уравнениями Эйлера и сводятся к линейным
однородным уравнениям с постоянными коэффициентами заменой переменных
Замечание 2. Частные решения уравнения (30) можно сразу искать в
виде у = хк, при этом для А; мы получаем уравнение, которое совпадает
с характеристическим уравнением для уравнения (31).
Пример 1. Найти общее решение уравнения Эйлера х2у" + 2ху' -
6у = 0.
Решение. Первый способ. Делаем в уравнении подстановку х = е1,
тогда
, = dy = dy/dt _ _fdy
У dx dx/dt € dt'
„ _ dy' _ dy'/dt _ (d2y/dt2 - dy/d^e'1 _ _2t(d2y dy
У ~ ~dx ~ dx/dt ~ 7* ~e V^""^
и уравнение примет вид
Корни характеристического уравнения А| = -3, Л2 = 2, и общее решение
уравнения будет у = Схе~гг + C2e2t. Но так как х = е', то у = С\Х~3 + С2х2 или
у=Щ + С2х\
X
Второй способ. Будем искать решение данного уравнения в виде
у = хк, где к— неизвестное число. Находим у1 = кхк~\ у" = к(к - \)хк'2.
Подставляя в уравнение, получаем
х2к(к - \)хк-2 + 2хкхк-] - 6хк = 0,
или
хк[к(к- 1) + 2Л-6] = 0.
Но так как хк $ 0, то к(к - 1) + 2к - 6 = 0, или к2 + к - 6 = 0. Корни этого
уравнения к\ = -3, к2 = 2. Им соответствует фундаментальная система решений
у, = ж"3, у2 = х2, и общее решение по-прежнему будет
Неоднородные уравнения Эйлера вида
*=0
где Рт(и) — многочлен степени га, можно также решать методом подбора
по аналогии с решением неоднородного линейного дифференциального
уравнения с постоянными коэффициентами и с правой частью вида
еаяРт(х).
§ 15. Линейные дифференциальные уравнения п-го порядка 105
Пример 2. Решить уравнение Эйлера х2у" - ху' + 2у = х In х.
Решение. Характеристическое уравнение k(k - 1) - к + 2 = 0, или к2 -
2к 4- 2 = 0 имеет корни, к\ = 1 - г, &2 = 1 + г. Поэтому общее решение
соответствующего однородного уравнения будет
у00 = х(С\ cos In ж + С2 sin In ж).
Частное решение ищем в виде уч = ж(Л In ж + Б); имеем
Подставляя в данное уравнение, получаем
Ах - х(А In ж + А + В) + 2ж(Л In ж + В) = ж In ж,
или
Лж In ж + Вж = ж In ж,
откуда А ^= 1, Б = 0. Итак, уч = ж In ж. Общим решением будет
у = я(С| cos In ж + С2 sin In ж) + ж In ж. >
Задачи для самостоятельного решения
Проинтегрировать следующие однородные уравнения Эйлера:
618. ж2у" + жу' - у = 0. 619. ж2у" + Зжу' + у = 0.
620. ж2у" + 2жу' + 6у = 0. 621. жу" + у = 0.
622. (ж + 2)У + 3(ж + 2)у' - Зу = 0. 623. (2ж + 1)У -2(2ж+ 1)у' + 4у = 0.
624. ж2у'" - Зжу" + Зу' = 0. 625. х2у'" = 2у'.
626. (ж + 1)У" - 12у' = 0. 627. (2ж+ \)2у'" + 2(2ж + 1)у"+у' = 0.
Решить следующие неоднородные уравнений Эйлера:
628. ж2у" + жу' + у = ж(6 - In ж). 629. ж2у" - 2у = sin In ж.
630. ж2у" - жу' - Зу = _21iH. 631. ж2у" - 2жу' + 2у = ж2 - 2х + 2.
632. ж2у" + жу - у = ж771, \т\ф\. 633. ж2у" + 4жу; + 2у = 2 In 2ж + 12ж.
634. (ж + 1)У + 3(ж + 1)2у + (ж + \)у = 6 In (ж + 1).
635. (ж - 2)У - 3(ж - 2)у; + 4у = ж.
5°. Линейные дифференциальные уравнения с
переменными коэффициентами. Метод Лагранжа. Если известно
частное решение у\(х) уравнения
2/(n) +Pi(aO2/(n~I) + ••• +Рп(х)у = 0, (32)
то его порядок можно понизить на единицу (не нарушая линейности
уравнения), полагая у = y\Z, где z— новая неизвестная функция, а затем
делая замену z1 = и (можно непосредственно делать замену и = (y/y\)f).
Если известно к частных линейно независимых решений
уравнения (32), то порядок уравнения может быть понижен на к единиц.
106 Глава 2, Дифференциальные уравнения высших порядков
Общее решение уравнения
У{п) + Р\Ш»-}) + ... + Рп(х)у = f(x) (33)
есть сумма какого-нибудь его частного решения и общего решения
соответствующего однородного уравнения (32).
Если известна фундаментальная система соответствующего
однородного уравнения (32), то общее решение неоднородного уравнения (33)
может быть найдено методом вариации постоянных (метод Лагранжа).
Общее решение уравнения (32) имеет вид
У = С\ у\ + С2у2 + ... + Спуп,
где С|, С2)..., Сп — произвольные постоянные.
Будем искать решение уравнения (33) в виде
У = С, (х)у\ + С2(х)у2 + ... + Сп(х)уп, (34)
где С\(х), С2(х),..., Сп(х) — некоторые пока неизвестные функции от х.
Для их определения получаем систему
n
Разрешая эту систему относительно С-(ж), г = 1,2,..., п, получаем
откуда
— = ^(»), г = 1,2,... ,п,
Q(x) = у v?i(x)da: + Ci} г = 1,2,... ,n,
где С{ — произвольные постоянные. Внося найденные значения Q(x)
в (34), получаем общее решения уравнения (33).
В частности, для уравнения второго порядка
Уп+Р\(х)у*+P2(x)y = f(x)
система (35) имеет вид
Г У\С\+у2С'2 = 0у
\
Решая (36) относительно С\ и С'2, получаем
, _ y\f(x)
§ 15. Линейные дифференциальные уравнения п-го порядка 107
откуда находим
;
где С\ и Сг -— постоянные интегрирования.
ния ao(a;)y"+a,(a
дет выглядеть та
уА + у2с2 = о,
Замечание. Для уравнения ao(a;)y"+a,(a;)y'+a2(aj)y = /(х), где ao(x) £ 1,
ао(а?) ^ 0, система (36) будет выглядеть так:
Пример 1. Найти общее решение уравнения ху" + 2у' + ху = 0, если
sin ж
У\ = есть его частное решение.
х
_ „ sin»
Решение. Положим у = z% где z— новая неизвестная функция от х\
тогда х
' \ \ "
Подставляя в данное уравнение, получаем
(ху" + 2у[ + xyx)z + xy\z" + 2(xy\ + у()-г' = 0.
Но так как у\ = есть частное решение данного уравнения, то ху" + 2у\ +
ху\ = 0, поэтому имеем
*y,z" + 2(*yi+y,)z' = 0. (37)
. cos x sin о? . /ж„ч
Но у; = г-, а значит ху] +у\ = cosa?, и уравнение (37) примет
X X
вид
z" sin x + 2z' cos ж = 0.
Перепишем его в виде
z" Л cos ж
— +2-:—=0.
г sin х
Отсюда имеем (In l^'l -f 2 In | sin ж|)' = 0, откуда
In \z'\ + 2 In | sin x\ = In C|, или z' sin 2a? = C\.
Интегрируя это уравнение, найдем z = -С| ctga? + C2 и, следовательно, общее
решение данного уравнения будет
~ cos a; ^sina? ^ cos а? _, sin а? /Л д v
у = -С, + С2 , или у = С| + С2 (С|=-С|). >
XX XX
Пример 2. Найти общее решение уравнения у"-\—у'+у=-, (хфО).
х х
Решение. Общее решение соответствующего однородного уравнения имеет
вид (см. пример 1)
^ sin а? Л cos х
Уо.о = С| —+С2 —,
108 Глава 2. Дифференциальные уравнения высших порядков
и следовательно, его фундаментальная система решений будет
sin ж cos ж
»■ = —• * = —■
Будем искать общее решение данного уравнения методом вариации произвольных
постоянных:
Л . . sin х Л . . cos х
г/ = С,(ж)—- + С2(ж) ,
X X
где С\(х),С2(х) — постоянные неизвестные функции от ж, подлежащие
определению. Для их нахождения составим следующую систему:
... sin ж . cos х
!(z)—+ СН*)—= 0,
., ч a; cos ж - sin ж ., ч -ж sin ж - cos ж 1
Отсюда находим: С\(х) = cos ж, С'2{х) = -sin ж. Интегрируя, получаем
С\ (ж) = sin ж + С,, С2(х) — cos ж + С2.
Подставляя эти значения С\{х) и С2(х) в выражение для у, найдем общее
решение данного уравнения
~ sin ж -~ cos ж 1
СС+ >
2
ж ж ж
Пример 3. Решить уравнение у" + у =
cos ж
Решение. Соответствующее однородное уравнение будет у" + у = 0. Его
характеристическое уравнение А2 + 1 = 0 имеет мнимые корни Ai = -г, А2 = г,
и общее решение однородного уравнения имеет вид
Уо.о = С\ cos ж + С2 sin ж.
Общее решение исходного уравнения ищем в виде
у = С, (ж) cos ж + С2(х) sin ж, (38)
где С|(ж) и С2(х) — неизвестные функции от ж. Для их нахождения составим
систему
{cos ж • С\ + sin ж • С2(х) = 0,
-sinж -С\(х) + cosx-C2(x) = .
Разрешаем эту систему относительно С\(х) и С2(х):
C[(x) = -tgx, С2(ж)=1.
Интегрированием находим
С,(ж) = In | cosa?| + С,, С2(ж) = ж + С2.
Подставляя выражения С\(х) и С2(ж) в (38), получаем общее решение данного
уравнения
у = С\ cos ж + С2 sin ж + cos ж • In | cos ж| + ж sin ж.
Здесь cos ж In | cos ж| + ж sin ж есть частное решение исходного неоднородного
уравнения. >
§ 15. Линейные дифференциальные уравнения п-го порядка 109
Пример 4. Зная фундаментальную систему решений у\ = In ж, уг — х
соответствующего однородного уравнения, найти частное решение
уравнения
х2(1 - In *)/ + ху' - У = °'Па!), (39)
X
удовлетворяющее условию lim у = 0.
х—»+оо
Решение. Применяя метод вариации постоянных, находим общее решение
уравнения (39):
у = С, In х + С2х + г-—- (40)
4ж
При ж —► +оо первые два слагаемых правой части (40) стремятся к бесконечности,
причем при любых С], С2, не равных нулю одновременно, функция С\ In х + С2х
есть бесконечно большая функция при х —* +оо. Третье слагаемое правой
части (40) имеет пределом ноль при х —> +оо, что легко установить с помощью
1-21пж
правила Лопиталя. Таким образом, функция у = , которая получается
4х
из (40) при С\ =0 и С2 = 0, будет решением уравнения (39), удовлетворяющим
условию lim у = 0. >
Задачи для самостоятельного решения
Проинтегрировать следующие уравнения, если известно одно частное решение у,
однородного уравнения.
636. (2х 4- \)у" + (4х - 2)у' - 8у = 0; у, = emi.
637. (ж2 - х)у" + (2ж - 3)у; - 2у = 0; 2/i — рациональная дробь, в знаменателе
которой стоят линейные множители — делители коэффициента при у".
638. (Зж + 2х2)у" - 6(1 + х)у +6у = 6\ у, — многочлен.
639. ж2(1п х - 1)у'; - ху + у = 0; у, = ж.
640. у'' + (tg х - 2 ctg x)y + 2 ctg 2z • у = 0; у, = sin ж.
641. у" 4- tg х • у' + cos 2ж • у = 0; у\ = cos (sin ж).
642. (1 + ж2)у" + ху'-у+\=0; у, = ж.
643. х2у"-ху'-3у = 5х*; у, = 1.
644. (ж - 1)у" - Ж|/ + У = (* - 1)2е?; у, = ех.
645. у7' + у' + е"2ху = е"3х; у, = cos e'x.
646. (ж4 - «V + (^3 ~ 2х2 - х)у' - у = ^^-; 2/. = ^.
647. у" - уЧ уе2х = же2х - 1; у, = sin e*.
648. х(х - \)у" - (2аг - 1)у + 2у = х2(2х - 3); у, = х2.
649. Цепь длиной 6 м, из которых 1 м свисает со стола, начинает соскальзывать
вниз без трения. За какое время соскользнет вся цепь?
650. Найти уравнение движения точки, если ускорение в зависимости от времени
выражается формулой a = 1,2 -t и если при t = 0 расстояние 5 = 0, а при t = 5
расстояние s = 20.
110 Глава 2. Дифференциальные уравнения высших порядков
651. Тело массы m скользит по горизонтальной плоскости под действием толчка,
давшего начальную скорость v0. На тело действует сила трения, равная -km.
Найти расстояние, которое тело способно пройти.
652. Материальная точка массы m = 1 движется прямолинейно, приближаясь
к центру, отталкивающему ее с силой, равной кгх (х — расстояние точки
dx
от центра). При t = 0, х = о, — = ка. Найти закон движения.
at
Проинтегрировать методом вариации постоянных следующие уравнения:
655. у" + у= —р. 656. у" + у = ctgх.
657. у" - V + У = -£у. 658. у" + 2у' + 2у =
659. у" + у = tV- 660. у" - у' = в2* cos в*.
sin1*»
661. у'" + у" = 2^-1. 662. ху" - (1 + 2х2)у' = 4х3еш2.
663. у" -2y;tga? = 1. 664. x\nx-y"-y' = In 2я.
665. ху" + (2х - \)у' = -4а2. 666. у/; + у' tg x = cos ж ctg гг.
Найти решения следующих дифференциальных уравнений при заданных условиях
на бесконечности:
667. 4а?у" + 2у/ + у = 1, lim y=l; yi=sinv^, y2
668. 4жу" + 2уЧ у = ^^, Нш у = 0.
Я х-»+оо
669. (1 + х2)у" + 2*у' = -Lj, lim у = ^, у'|1-0 = 0.
I + X* х-»+оо о
670. (1-ж)у" + ху'-у = ({г-1)2ех, lim y = 0, y|xe0 = l; yi=«, У2 =
х-*—оо
671. 2х2(2 - In х)у" + а(4 - In х)у' - у = (2~^*) , нт у = 0;
у/Х х-»+оо
у, = In ж, у2 = V».
2 I б* е"х*
672. у'Ч-у'- у = 4ех, limy = 0, f/\ = --; у, = —, у2 = —.
х g-»-oo e а? ж
673. а?3(1па?-1)у//-ж2у/ + жу = 21na?, lim у = 0; yi = а?, у2 = 1пж.
+
674. (Ж2 _ 2а,)у" + (2 - х2)у' - 2(1 - х)у = 2(х - 1), Ит у = 1;
у, = ж2, у2 = ех
6°. Составление дифференциального уравнения по
заданной фундаментальной системе решений. Рассмотрим
линейно независимую на отрезке [а, Ь] систему функций
§ IS. Линейные дифференциальные уравнения п-го порядка 111
имеющих все производные до п-го порядка включительно. Тогда
уравнение
3/1 (я) у2(х) уп(х) у(х)
у\(х) у'2(х) ... !&(») у\х)
= 0,
где у(х) — неизвестная функция, будет линейным дифференциальным
уравнением, для которого, как нетрудно видеть, функции у\ (я), у2(х)}...,
уп(х) составляют фундаментальную систему решений. Коэффициент при
у^(х) в (42) есть определитель Вронского W[y\, у2,..., уп] системы (41).
Те точки, в которых этот определитель обращается в ноль, будут особыми
точками построенного уравнения — в этих точках обращается в ноль
коэффициент при старшей производной
Пример 1. Составить дифференциальное уравнение, для которого
У\(х) = е*, 2/2(3) = е~х образуют фундаментальную систему решений.
Решение. Применяя формулу (42), получаем
е* е"я
е -е-
У1
е- у"
= 0, или
1 1 У
1 -1 у;
1 1 у"
= 0.
(43)
Раскрывая определитель в левой части (43) по элементам третьего столбца, будем
иметь у" - у = 0. Это и есть искомое дифференциальное уравнение. >
Пример 2. Составить дифференциальное уравнение, для
которого функции фундаментальную систему решений образуют функции
Решение.
е*'
2хе*
(2 + 4а2)е*2
Составим
е"я
-2хе
(Ах2 - 2
уравнение вида
У
-*2 у'
)е~*2 у»
= 0,
(42):
или
1 1 у
2 а? -2а? у
+ 4х2 4х2 -2 у"
Раскрывая последний определитель по элементам 3-го столбца, будем иметь
ху" - у' - 4ж3у = 0. (44)
В этом примере определитель Вронского W[yby2] = -4g обращается в ноль
при х = 0. Это не противоречит обшей теории, в силу которой определитель
Вронского фундаментальной системы решений линейного однородного
дифференциального уравнения
с непрерывными на отрезке [а, Ь] коэффициентами не обращается в ноль ни в
одной точке х отрезка [а, Ь]. Записав уравнение (44) в виде
у"-1у'-4х2у = 0, (45)
видим, что коэффициент при у' терпит разрыв при х = 0, так что в точке х = 0
непрерывность коэффициентов уравнения (45) нарушается. >
112 Глава 2. Дифференциальные уравнения высших порядков
Задачи для самостоятельного решения
Составить дифференциальные уравнения, для которых данные системы функций
образуют фундаментальные системы решений:
675. y,(z)
676. у,(ж)
677. у,(*)
678. у,(а), у2() , Уз()
679. yi (ж) = х) у2(х) = sin х, уз(ж) = cos ж.
7°. Разные задачи. Пусть у\, 2/2) • • • > Уп — фундаментальная
система линейного однородного уравнения
Тогда имеет место формула Остроградского—Лиувшля
-Jpi{t)dt
W(x) = W(xo)e '<>
где W(x) = W[y\) 2/2, • • •» Уп] — определитель Вронского, а х0 — любое
значение х из отрезка [о, Ь], на котором непрерывны коэффициенты
р\ (ж), р2(х),..., рп(х) уравнения.
Пример 1. Показать, что линейное дифференциальное уравнение
ж2/"-(ж + 2)у/ + у = 0 имеет решение вида у\ = Р(х), где Р(х) —
некоторый многочлен. Показать, что второе решение у2 этого уравнения
имеет вид у2 = exQ(x), где Q(x) — также многочлен.
Решение. Будем искать решение у, (х) в виде многочлена, например, первой
степени: у{ = Ах + В. Подставляя в уравнение, найдем, что -2А + В = 0. Пусть
А = 1, тогда В = 2;.таким образом, многочлен у\ = $ + 2 будет решением
данного уравнения. Перепишем данное уравнение в виде
// х + 2 , 1
/ 0
Пусть у2(х) — второе частное решение данного уравнения, линейно независимое
с первым. Находим определитель Вронского системы решений у\ = х + 2, у2:
ж + 2 2/2
, = (х + 2)у2 - у2,
здесь х Ф -2. Применяя формулу Остроградского—Лиувилля, будем иметь
-j(t+2)/tdt
(х + 2)уз - у2 =
где ж()— любое значение ж, причем ж0 ?^ 0, х0 Ф -2, или
у2 -у2 = Ах2ех\
§ 15. Линейные дифференциальные уравнения п-го порядка 113
W(xo)e-X°
здесь А = г = const. Для нахождения у2 получили линейное дифферен-
Ч
циальное уравнение первого порядка. Деля обе части этого уравнения на (х + 2) ,
приведем его к виду
Интегрируя, найдем
= А ех; отсюда у2 = А(х - 2)ех.
х+2 х+2
Задачи для самостоятельного решения
680. Показать, что линейное дифференциальное уравнение (х2 - \)у" = 2у
имеет решением некоторый многочлен у\{х) = Р(х). Показать, что второе
решение у2(х) этого уравнения имеет вид
y2(X) p(X)\n+Q(X),
х — 1
где Q(x)— также многочлен.
681. Найти общее решение линейного однородного дифференциального
уравнения второго порядка у" + р{(х)у' + р2(х)у = О, если известно одно его частное
решение у, =у\(х).
682. Пусть у](х),у2(х) — фундаментальная система решений линейного
однородного дифференциального уравнения второго порядка
#>(*)у" +Pi(*)y' +Р2{х)У = 0.
Выразить коэффициенты Ро(х)ур\(х)1р2(х) через у\(х) и у2(х).
683. Доказать, что два решения уравнения у" +Р\(х)у' +р2(х)у = 0 с
непрерывными коэффициентами, имеющие максимум при одном и том же значении з,
линейно зависимы.
684. Доказать, что отношение двух любых линейно независимых решений
уравнения у" + Р\{х)у' + р2(х)у = 0 с непрерывными коэффициентами, не может
иметь точек локального максимума.
685. При каких значениях р\ и р2 каждое решение уравнения у" +р\у'+р2у' = 0
(P\iP2 = const) обращается в ноль на бесконечном множестве точек я?
686. Пусть функции и(х) и v(x) являются соответственно решениями уравнений
и" + р(х)и = 0 и v" + q(x)v = 0, удовлетворяющими условию и(а) = 0, v(a) = 0
(р(х) и q(x) непрерывны на отрезке [а, Ь]). Доказать, что определитель Вронского
этих решений будет равен
Z
w[u(x), ф)] = J\p(t) - q(t)Ht)v(t) dt.
а
687. Доказать, что никакие два линейно независимых решения у\(х) и у2(х)
линейного однородного уравнения у" + р(х)у' + q(x)y = 0 не могут одновременно
обращаться в ноль в одной и той же точке х0.
688. Доказать, что если у\(х) есть некоторое частное решение линейного
однородного уравнения у" + p(x)yf + q(x)y = 0, причем у\(х) £ 0, то уравнение
У\(х) = 0 не может иметь кратных корней.
114 Глава 2. Дифференциальные уравнения высших порядков
689. Показать, что подстановка у = v(x)z(x) преобразует линейное однородное
уравнение у" -\-р{х)у' + q(x)y = 0 снова в линейное однородное уравнение. Как
надо подобрать функцию v(x), чтобы в преобразованном уравнении отсутствовал
член с первой производной?
d2x
690. Доказать, что решение уравнения —-г + k x = /(£), удовлетворяющее
dtl
начальным условиям х(0) = 0, х'(0) = 0, имеет вид
x(t) = ]- [ f(u) sin k(t - u) du.
о
691. При каких значениях рис/ все решения уравнения у" + ру' + qy = О
стремятся к нулю при х -* +оо?
692. При каких значениях р и q все решения уравнения у" + ру' + qy = О
(р, q = const) являются периодическими функциями от х?
693. Пусть функция у(я), является решением уравнения (\+х2)у"-х3у' = а2+4
на отрезке [а, 6], причем это решение удовлетворяет краевым условиям у(а) = О,
у(Ь) = 0. Доказать, что для всех х из интервала (о, Ь) будет у(х) < 0.
694. Доказать, что в случае q(x) < 0 решения уравнения у" +р(х)у' + q(x)y = 0
не могут иметь положительных максимумов.
695. Доказать, что в случае q(x) > 0 для любого решения уравнения y"+q(x)y=0
отношение у'(х)/у(х) убывает при возрастании х на интервале, где у(х) Ф 0.
§ 16. Метод изоклин
для дифференциальных
уравнений второго порядка
Метод изоклин (см. § 2) применяется также к решению
некоторых уравнений второго порядка. Это те уравнения, которые могут быть
сведены к уравнению первого порядка, например, уравнения вида
d2x
■/(£..)-*
dx d2x dv
Введем новую переменную v = —. Тогда —г = v— и уравнение (1)
at dtl dx
примет вид
dv _ f(v, x)
dx"" v ' (2)
Это уравнение первого порядка, в котором х является независимым
переменным, и для его решения можно применить метод изоклин.
Будем величину х понимать как перемещение какой-либо точки системы,
dx
а — = v — как ее скорость.
at
Плоскость переменных я, v называется фазовой плоскостью. Таким
образом, уравнение (2) определяет скорость как функцию перемещения.
§ 16. Метод изоклин для уравнений второго порядка 115
Строя поле изоклин для уравнения (2), мы можем вычертить
интегральную кривую, если задана начальная точка (x0)v0). Такое графическое
изображение скорости v как функции перемещения х: v = v(x)
называют фазовой картиной (фазовый портрет). Кривые в плоскости я, v,
изображающие эту зависимость, называются фазовыми траекториями.
Мгновенные значении х и v являются координатами точки фазовой
траектории. Точка эта называется изображающей тонкой. С течением времени
изображающая точка перемещается по фазовой траектории. Заметим, что
положительная скорость вызывает возрастание перемещения со време-
dx dx
нем. В самом деле, в силу подстановки v = — при ООи — > О,
at at
что означает возрастание х при возрастании t. Таким образом, в верхней
половине фазовой плоскости, где v > О, изображающая точка должна
двигаться слева направо, а в нижней половине плоскости, где v < О
справа налево. Поэтому движение по фазовой траектории совершается
походу часовой стрелки.
Пример 1. Построить траектории в фазовой плоскости для уравнения
dv
t>—— 4- я? = 0
da '
или
dv
— =:
— — ф
V
dx
Решение. Полагаем — = v. Уравнение (3) принимает вид
at
dv x /A.
(4)
dx v v '
Уравнения изоклин для (4): -- = к. Строя изоклины, отвечающие
различным значениям Л, найдем, что фазовые траектории — окружности с центром
в точке (0,0) (рис.26).
Отметим, что замкнутые фазовые траектории соответствуют периодическим
движениям. Легко видеть, что в случае уравнения (3) мы действительно имеем
периодическое движение. Решая (3) методами, изложенными выше, находим
x(t) = С\ cos t + C2 sin t. >
Пример 2. Построить фазовые траектории для уравнения
d2x dx
dx
Решение. Полагаем v = —. тогда уравнение (5) примет вид
dt
dv v - х
dx v
v — х
Уравнение изоклин = к. Фазовые траектории имеют вид
разматывающихся спиралей (рис.27). Из фазовой картины можно усмотреть, что движение
апериодическое, с амплитудой, неограниченно возрастающей со временем. >
116 Глава 2. Дифференциальные уравнения высших порядков
Рис. 26
Рис. 27
Задачи для самостоятельного решения
Построить фазовые траектории для следующих дифференциальных уравнений:
698-
. -^г+ — +х = 0.
702. ^
705. §-|
§ 17. Краевые задачи
Рассмотрим для простоты уравнение второго порядка
у"+Р\(х)у' + Р2(х)у = 0. (I)
Коэффициенты р\(х) и Р2(х) будем считать непрерывными в некотором
интервале (a, b). Тогда каждое решение у(х) уравнения (I) будет
определено во всем этом интервале. В дальнейшем вместо уравнения (1) будем
рассматривать уравнение вида
\p(x)y']' + q(x)y = 0, p(x)>0. (2)
§ 17. Краевые задачи 117
Уравнения (1) и (2) могут быть преобразованы одно в другое. Уравнение
вида (2) называются самосопряженными.
Решение дифференциального уравнения
полностью определяется начальными условиями у(хо) = уо, 2/'(#о) = Уо-
Однако во многих физических задачах приходится искать решения,
заданные иным способом. Например, может быть поставлена задача: найти
решение уравнения (2), принимающее в точках а и Ь заданные
значения у (а) и у(Ь). Обычно в таких случаях значения решения ищутся
только для х из (а,Ь). Таким образом, заданные значения у(а) и у(Ь)
находятся на концах интервала, поэтому задачи такого рода называются
краевыми (граничными) задачами. В дальнейшем мы положим в
основу интервал (0, тг) (основной интервал), что не уменьшает общности
рассуждений.
Весьма общий вид краевых условий для уравнения второго порядка
следующий:
АоУ(О) + h}y'(0) = А, коу(ж) + *,»'(х) = Б, (3)
где /i0, h\, &о, fcj, А, В — заданные постоянные, причем 7&0, h\, fc0, к]
не равны одновременно нулю.
Если А = В = 0, то краевые условия называются однородными,
например:
1) у(0) = у(тг) = О,
2) hQy(0) = 2/'(0), у'(ic) = -fti»(ir); h0, hx > 0,
3) „'(О) - у'(тс) = 0,
4) у(0) = у(ж)} У'(О) = у'(тг).
Вообще говоря, краевые задачи не всегда разрешимы, т.е. не
всегда существует такое решение, которое принимает требуемые значения
на концах интервала. Например, краевая задача
У" = О, 2/(0) - г/(тг) = 1, г/'(0) + г/(7г) = 0
не имеет ни одного решения. Задача
»" + Ау = 0> 2/(0) = г/(тг) = 0 (4)
имеет ненулевое решение только для целочисленных значений у/Х. В
самом деле, из общего решения дифференциального уравнения (4)
вытекает, что краевые условия выполнимы в том и только в том случае,
если X = п2 есть квадрат целого числа п. Соответствующими решениями
являются функции уп = slnnx.
Как видно из этого примера, если q в уравнении (2) есть функция
параметра А, то при известных условиях существуют такие значения
параметра, для которых однородная краевая задача для уравнения (2) имеет
11.8 Глава 2. Дифференциальные уравнения высших порядков
ненулевое решение. Эти значения Л называются собственными значениями,
а соответствующие им решения краевой задачи — собственными функция-
ми. Последние определяются лишь с точностью до произвольного
постоянного множителя. Так для краевой задачи у" + Ху = 0, г/(0) = у(тт) = О,
числа I2, 22, З2,... и функции sin ж, sin 2х) ... являются соответственно
собственными значениями и собственными функциями задачи.
Наряду с простыми собственными значениями, когда одному
собственному значению отвечает одна собственная функция (с точностью
до постоянного множителя), существуют кратные собственные
значения, когда собственному значению Ло отвечают две или более линейно
независимые собственные функции.
При решении краевых задач (для линейных однородных
дифференциальных уравнений) поступают так: находят общее решение данного
дифференциального уравнения
у = С]у] (х) + С2у2{х) + ... + Спуп(х),
где у\(х)) 2/2(я)> • • •, Уп(х)— линейно независимые решения. Затем
требуют, чтобы это решение у(х) удовлетворяло заданным граничным
условиям. Это приводит к некоторой линейной системе уравнений для
определения С|,С2,... ,С„. Разрешая эту систему, если возможно, находят
решение данной краевой задачи. При этом, если возникает задача о
нахождении собственных значений, условие наличия ненулевого решения
у системы, определяющей Cj,C2,... ,С„, является условием,
определяющим собственные значения. Это бывает некоторое вообще
трансцендентное уравнение для А.
Пример 1. Решить краевую задачу
2/"-У = 0, 1/(0) = 0, 2/(1) = 1.
Решение. Общее решение данного уравнения
y(») = C,eJ + C2e-, (5)
отсюда
у'(х) = С1ех-С2е-х. (6)
Полагая х = 0 в (6) и х = 1 в (5) и учитывая краевые условия, получаем для
нахождения значений постоянных С\ и С2 неоднородную линейную систему
Определитель этой системы
Д =
1 -1
-I
е е
следовательно, она имеет единственное решение
1 1
2chl' 2~2chT
С, =
§ 17. Краевые задачи 119
Подставляя найденные значения С\ и С2 в (5), получаем решение заданной
краевой задачи
/ ч ех + е~х . . cha?
У(*) = ^ГР или у(ж)=ыГТ- >
Пример 2. Найти собственные значения и собственные функции
краевой задачи
j/" + A2j/ = 0 (A#0), (7)
1/(0) = 0, у(*) = 0. (8)
Решение. Общее решение уравнения (7)
у(я) = С, cos Аж + С2 sin Ад?, (9)
отсюда
у'(х) = -C| A sin \х + С2A cos Аж. (10)
Полагая х = ж в (9) и ж = 0 в (10) и учитывая краевые условия (8), получаем для
нахождения С\ и С2 однородную линейную систему
Г С\ cos Атг + С2 sin Атг = 0,
\ С2А = 0.
(П)
Система (II) будет иметь ненулевые решения тогда и только тогда, когда ее
определитель равен нулю; приравняв его нулю, получаем уравнение для нахождения
собственных значений данной краевой задачи:
cos Атг sin Атг
0 А
= 0, или A cos Атг = 0.
Так как по условию А Ф 0, то cos Атг = 0, а значит собственные значения
А = АП = ——' п = 0, 1,2,... .
Им соответствуют (с точностью до постоянного множителя С\% который можно
положить равным единице) собственные функции
уп(х) = cos —— х}
являющиеся решениями краевой задачи (7)-(8). >
Замечание. Собственные значения рассмотренных выше задач
образуют возрастающую числовую последовательность. Если же коэффициенты
дифференциального уравнения имеют особую точку на границе основной
области или если основная область бесконечна, например вся числовая ось,
то спектр, т.е. совокупность собственных значений, может обладать иной
структурой. В частности, могут встретиться спектры, содержащие все числа
какого-либо интервала значений А, так называемые непрерывные спектры.
Например, пусть требуется решить уравнение у" + Ау = 0 для интервала
-со < х < +оо при «краевых условиях»: у(х) ограничено на
бесконечности. Очевидно, в этом случае всякое неотрицательное число А является
собственным значением с собственными функциями sin V\x и cos /
120 Глава 2. Дифференциальные уравнения высших порядков
При решении задач математической физики, приводящих к задачам
на определение собственных значений, часто получаются
дифференциальные уравнения вида
\р(х)у']' - q(x)y + Хр(х)у = 0,
но такие, что в концевых точках основной области могут иметь место
особенности дифференциального уравнения, например, обращение в ноль
коэффициента р(х). Для этих особых точек из самого характера задачи
возникают условия, например, непрерывности или ограниченности
решения или обращение его в бесконечность не выше заданного порядка.
Эти условия играют роль краевых условий. Типичным примером является
уравнение Бесселя
(ху'У - — у + Хху = 0, (12)
х
которое появляется в задачах математической физики. Здесь р(х) = х
и сделанное выше предположение, что р(х) > 0 во всей основной
области 0 ^ х ^ 1 здесь уже не выполняется, так как р(0) = 0. Точка
х = 0 является особой точкой для уравнения Бесселя.
Требование, чтобы решение было ограничено в этой точке, будет
специального вида краевым условием для уравнения Бесселя: найти решение
уравнения (12), ограниченное при х = 0 и, например, обращающееся
в ноль при х — 1.
Пример 3. Решить краевую задачу х2у" + 2ху' - 6у = 0, у(\) - 1,
у(х) ограничено при х —> 0.
Решение. Данное уравнение является уравнение Эйлера. Его общее реше-
ние имеет вид у(х) = —+С2ж2 (см. например 1, п. 4°, § 15). По условию решение
у(х) должно быть ограниченным при х —► 0. Это требование будет выполнено,
если в общем решении положить С, = 0. Тогда будем иметь у(х) = С2х2. Краевое
условие у(1) = 1 дает С2 = 1. Следовательно, искомое решение у = х2. >
Задачи для самостоятельного решения
706. При каких значениях Л уравнение у" + Ху = 0 имеет ненулевое решение,
удовлетворяющее условиям:
а) у'(0) = у'Ог) = 0, б) »(0) = »(*), у'(0) = у'Ог)?
707. При каких значениях Л краевая задача у" + Ху = 0, у(0) = у(\) = 0 имеет
тривиальное решение у = 0?
708. Какая из следующих краевых задач разрешима:
а) у"-у = 0, »(0) = 0, у(2ж)=\,
б) 2/" + у = 0, у(0) = 0, у(2тг) = 1?
709. Решить краевую задачу у" + (А - ш2)у = 0, у(0) = у(\), у'(0) = у'(\).
Рассмотреть случаи А - ш2 > 0, А - ш2 = 0, А - ш2 < 0.
§ 18. Интегрирование уравнений при помощи рядов 121
710. Найти решение уравнения уу" + (у')2 + 1=0, проходящее через точки (0, 1)
и (1,2).
Решить следующие краевые задачи:
711. у" + у = 0, у(0) = 0, (
712. у"-у = 0, у(0) = 0, у'(1)=1.
713. у"-2у' + 2у = 0, у(0) = 0, у'(к) = е\
714. у" + ау' = 0, у(0) = еа, у'(0 = 0.
715. у" + а2у=1, у'(0) = а, у'(т) = 0 (0 < а < 1).
716. у" + у=\, у(0) = 0, y'(jr) = O.
717. у" + А2у = 0, у'(0) = 0, y'W = 0.
718. у" + А2у = 0, у(0) = 0, у'(»г) = О.
719. у'" + у" - у' - у = 0, у(0) = -1, у'(0) = 2, у(1) = 0.
720. ylv - Л4у = 0, у(0) = у"(0) = 0, у(;г) = у"(тг) = О,
721. ху" + у' = 0, у(1) = aj/O), 2/(ж) ограничено при х -» 0.
722. z2ylv + 4^2/'" + 2у" = 0, у(1) = у'(\) = 0, у(ж) ограничено при х -► 0.
723. ж3у|У + 6ж2у/;/ + бжу" = 0, у(1) = у;(1) = 0, у(х) ограничено при х -► 0.
§ 18. Интегрирование дифференциальных
уравнений при помощи рядов
1 °. Разложение решения в степенной ряд. Этот прием
является особенно удобным в применении к линейным
дифференциальным уравнениям. Проиллюстрируем его применение на примере
уравнения второго порядка. Пусть дано дифференциальное уравнение второго
порядка
y"+p(x)y' + q(x)y = Q. (1)
Предположим, что коэффициенты р(х) и q(x) представляются в виде
рядов, расположенных по целым положительным степеням ж, так что
уравнение (1) можно переписать в виде
у" + (а0 + ахх + а2х2 + .. )у + (Ьо + М + Ь2х2 + .. )у = 0. (2)
Решение этого уравнения будем искать также в виде степенного ряда
Подставляя
ОО
fc=2
ЭТО
выражение
ОО
х -t- ^
fc=0
У
У и
аЛж*
= 2^, с*х •
его производных
ОО ОО
к=\ к=0
в (2),
получаем
ОО
V"^ к
/ J CkX =
к=0
:0.
(3)
(4)
х°
х2
2
3
4
•lcjH
•2с3-
•Зс4-
Ь o0C| + Ьо<
h 2а0сг + о
Ь ЗаоСз + 2
:о = 0,
,с,+Ь0С|
а,с2 + а2с
+
60с2
0,
+ Ь,с1+Ь2со = О)
122 Глава 2. Дифференциальные уравнения высших порядков
Перемножая степенные ряды, собирая подобные члены и приравнивая
нулю коэффициенты при всех степенях х в левой части (4), получаем ряд
уравнений:
(5)
Каждое последующее из уравнений (5) содержит одним искомым
коэффициентом больше, чем предыдущее. Коэффициенты со и с\
остаются произвольными и играют роль произвольных постоянных. Первое
из уравнений (5) дает с2, второе дает сз, третье — с4 и т.д. Вообще
из (к + 0-го уравнения можно определить сд.+2, зная со, С|,..., с*+|.
Практически удобно поступать следующим образом. Определим
по описанной выше схеме два решения у\(х) и Уг{х), причем для
У\(х) выберем со = 1 и с\ = 0, а для уг{%) выберем cq = 0 и с\ = 1, что
равносильно следующим начальными условиям:
У|(0)=1, 2/1(0) = 0, у2(0) = 0, yJ(O)=l.
Всякое решение уравнения (1) будет линейной комбинацией решений
У\ (я) и у2(х).
Если начальные условия имеют вид у(0) = -4, у (0) = Б, то очевидно,
Имеет место следующая теорема.
Теорема. Если ряды
fc=0 fc=0
сходятся при \х\ < R, то построенный указанным выше способом
степенной ряд (3) будет также сходящимся при этих значениях х
и явится решением уравнения (1).
В частности, если р(х) и q(x) — многочлены от я, то ряд (3) будет
сходиться при любом значении х.
Пример 1. Найти решения уравнения
у" -ху-2у = 0
в виде степенного ряда.
Решение. Ищем у\(х) в виде ряда
k=0
§ 18. Интегрирование уравнений при помощи рядов
123
тогда
x"-2
у\(х) = J2 *<*х*-', у'Цх) = J2 *(fe - Ос»**
fc=l k=2
Подставляя у\(х), у\(х) и у"(х) в (6), получаем
f> - I)****"2 - £ кскхк - 2 £ cfca* = 0. (7)
к=2 к=\ к=0
Приводя в (7) подобные члены и приравнивая нулю коэффициенты при всех
степенях х, получаем соотношения, из которых найдем коэффициенты с0, ch ...,
Сти • • • •
Положим для определенности, что у,(0) = 1, у\(0) = 0. Тогда легко находим,
что
с0 = I, с,=0. (8)
Итак, имеем
х°
х]
х2
хг
хА
2с2 - 2с0 = 0
3
4
5
6
2с3 - 1 • с,
Зс4 - 2с2 -
4с5 - Зс3 -
5с6 - 4с4 -
- 2с, = 0,
• 2с2 = 0,
■ 2с3 = 0,
• 2с4 = 0,
отсюда
отсюда
отсюда
отсюда
отсюда
и
и
из
из
С4 =
С5 =
(8)
(8)
1
= 0,
= j
Сз = 0,
1
~3-5'
Следовательно,
Аналогично, беря
= ^2 АкХ
и начальные условия у2(0) = 0, у'2(0) = 1, получаем
i40 = 0, A, = 1.
Подставляя (10) в (6), найдем
£ *(* - f
0,
ж0
х]
х2
х>
х4
х5
2А2 =
3*2Аз
4-3^4
5-4Л5
6-5Ав
7-6А7
0, А2
- ЗА, = 0, А3
-4Л2 = 0, Л4
- 5А3 = 0, А5
- 6А4 = 0, i46
7/1 Л vl
= 0,
_ 1
" 2
1
= 0,
2-
(
4'
1
4-
з силу (11)),
6'
(9)
(10)
(11)
124 Глава 2. Дифференциальные уравнения высших порядков
Очевидно, что
итак,
х3
х3 х5 х7 ^ (х2/2)к х2/2
Общее решение уравнения (6) будет иметь вид
где 2/i (х) и У2(х) задаются формулами (9) и (12) соответственно, а А и В —
произвольные постоянные, причем у(0) = A, у'(0) = В. >
Приведем еще один способ интегрирования дифференциальных
уравнений с помощью рядов, который оказывается более простым
применительно к нелинейным дифференциальным уравнениям. Пусть дано
дифференциальное уравнение
J/n> = /(z)2,)j/,...)S,<n-|>) (13)
и начальные условия
U J/o, y'U^y'o, -.., З^и^Г0- (14)
Введем следующее определение.
Функция <р(х) называется голоморфной в некоторой окрестности
\х - жо| < Р точки х = xq, если в этой окрестности она представима
степенным рядом
00
<р(х) =
сходящимся в области \х - хо\ < р.
Аналогично, функция y>(#i, £2, • • • > жп) называется голоморфной
относительно всех своих аргументов в некоторой окрестности
точки (ж, , «2 , • • •) хп ) у если она представима степенным рядом
фих2, ...,xn) = J2 *,*,..*. (*i - ^0))*' (*г ~ 40))*2 • • • К - xf )\
сходящимся в области
Теорема. £слм правая часть уравнения (13) голоморфна относительно
всех своих аргументов ж, у, у',. • • > з/""1* ^ окрестности
§18. Интегрирование уравнений при помощи рядов
125
точки (ж0,2/о> 2/о> • • • > Уо) > wo уравнение (13) имеет единственное
решение
Jk)\
(15)
У(х) = уо + уо(х - хо) + ^-(ж - х0)
+ (?ГТ)?(Ж " ^Г1 + Е а^ж - *о)\
удовлетворяющее начальным условиям (14), w голоморфное в некоторой
окрестности точки х = х0.
Ряд (15) сходится в области
|«-я:о1<Л где р = а[1-е-6/<(п+|^];
здесь а и Ь— постоянные, удовлетворяющие условиям 0<а<Д, 0<b<R
п
Первые п + 1 коэффициентов ряда (15) определяются начальными
условиями (14) и дифференциальным уравнением (13). Следующие
коэффициенты ряда определяются в силу дифференциального уравнения (13)
путем его последовательного дифференцирования. Например,
_
ап+|"
где
у
п-1
дх
Х=Х0
ду
X=Xq
п-1
к=]
Замечание, Если уравнение (13) линейное
х=х0
у(п) + Ых)^-'» + ... + р.(*)у = Цх),
где рл(ж) (fc = 1, 2,..., п) и ^(ж) — функции, голоморфные на всей оси
то ряд (15) сходится также на всей оси.
Пример 2. Найти решение уравнения
удовлетворяющее начальным условиям
(16)
С7)
126 Глава 2. Дифференциальные уравнения высших порядков
Решение. Частное решение уравнения (16), удовлетворяющее начальным
условиям (17), ищем в виде ряда
гдеу(0)=1, 1/(0) = 0.
Из данного уравнения находим, что у"(0) = -у(0) = -1. Дифференцируя
последовательно обе части уравнения (16) и полагая в полученных равенствах
х = 0, будем иметь:
-{
О, если п = 2Л - 1,
(-.>, если „ = 2*
Найденные значения у"(0),у"'(0),... подставляем в ряд (18). Получим искомое
решение в виде степенного ряда
Очевидно, что ряд, стоящий в правой части (19), сходится на всей оси Ох
к функции у = cos ж, которая является решением поставленной задачи Ко-
ши. >
Пример 3. Найти четыре первых члена разложения в ряд Тейлора
решения у = у(х) уравнения у" = еху, удовлетворяющего начальным
условиям »|шш0= 1, у'\х=0 = 0.
Решение. Легко видеть, что правая часть уравнения, т.е. функция е*у,
разлагается в степенной ряд по степеням х и у в окрестности точки (0,0),
сходящейся в области -со < х < +оо, -оо < у < +оо (т. е. правая часть
голоморфна).
Будем искать частное решение в виде ряда
Используя само уравнение, найдем у"(0) = exy\xss0 = 1.
Дифференцируя последовательно обе части уравнения и полагая х = 0
в полученных равенствах, будем иметь
у» = [2у' + ху" + (у + ху') VU = '•
Подстаиляя вряд (20) найденные значения у"(0), у"'(0), ylv(0), получим искомое
разложение решения
X2 Z3
§ 18. Интегрирование уравнений при помощи рядов 127
Задачи для самостоятельного решения
В следующих задачах найти три первых члена разложения в степенной ряд
решения данного дифференциального уравнения для заданных начальных условий:
724. у1 = 1 - ху, у|лш0 = 0.
725. у'=У~Х -■■ -'
726. у' = sin жу, у|жв0 = 1.
727. y" + sy = 0, 3/U = °> y'Lo=L
728. у" - sin ху1 = 0, y\xs0 = 0, y'\xsiQ = 1.
729. ху" Л- у sin х = ж, y|x_ff = 1, у'|Л=ая. = 0.
730. у" In х - sin ху = 0; у^ = е~'> у'|Ляе=0.
731. у'" + ж sin у = 0, у|^в0 = —, у'|яв0 = 0, у/'|а.в0 = 0.
Проинтегрировать при помощи рядов следующие дифференциальные уравнения:
732. у'-2яу = 0, у(0)=1.
733. у" + ху' + у = 0.
734. у" - яу' + у - 1 = 0, у(0) = у'(0) = 0.
В задачах 735-738 найти шесть членов разложения у(х)\
735. у11 - (1 + *2)у = 0, у(0) = -2, у;(0) = 2.
736. у" = я2у - у', у(0) = 1, i/(0) = 0.
737. у;/ - уех - 0.
738. у1 = еу + жу, у(0) = 0.
2°. Разложение решения в обобщенный степенной ряд.
Уравнение Бесселя. Точка х0 называется обыкновенной точкой
дифференциального уравнения
y"+p(x)y' + q(x)y = 0) (21)
если коэффициенты р(х) и д(ж) голоморфны в этой точке: в противном
случае точка xq называется особой точкой дифференциального
уравнения (21).
Ряд вида
ckxk (co^O), (22)
оо
где р — заданное число, а степенной ряд ]>2 с*аг сходится в некоторой
области |х| < Д, называется обобщенным степенным рядом.
Если р есть целое неотрицательное число, то обобщенный степенной
ряд (22) обращается в обычный степенной ряд.
128 Глава 2. Дифференциальные уравнения высших порядков
Теорема. Если точка х = О есть особая точка уравнения (21),
коэффициенты р(х) и q(x) уравнения представимы в виде
00 00
£ akxk £ Ъкх"
где ряды в числителях сходятся в некоторой области \х\ < R, а
коэффициенты ао, Ьо и Ь\ не равны нулю одновременно, то уравнение (21)
имеет хотя бы одно решение в виде обобщенного степенного ряда
00
^k fo *0), (22)
который сходится, по крайней мере, в той же области \х\ < R.
Для определения показателя р и коэффициентов с* нужно подставить
ряд (22) в уравнение (21), сократить на хр и приравнять нулю
коэффициенты при всех степенях х (метод неопределенных коэффициентов).
При этом число р находится из так называемого определяющего
уравнения
\) + аор + Ъо = Оу (23)
где
ао = lim xp(x)y b0 = lim x2q(x). (24)
Пусть р\ и р2 — корни определяющего уравнения (23). Будем различать
три случая.
1. Если разность р\ - pi не равна целому числу или нулю, то можно
построить два решения вида (22)
00 00
У1 = ** Y, ъхк (со ф 0), г/2 = хр> ]£ Akxk (Ао ф 0).
2. Если разность р\ - р2 есть целое положительное число, то можно
построить, вообще говоря, лишь один ряд (решение уравнения (21))
у, =а^';£>**• (25)
*=о
3. Если уравнение (23) имеет кратный корень р\ = р2, то также,
можно построить лишь один ряд — решение (25). Понятно, что в первом
случае построенные решения у\(х) и у2(х) будут линейно независимы
(т.е. их отношение не будет постоянной величиной).
Во втором и третьем случаях мы построили только по одному
решению. Отметим, что если разность р\ - р2 есть целое положительное число
§18. Интегрирование уравнений при помощи рядов 129
или ноль, то наряду с решением (25) уравнение (21) будет иметь решение
вида
00
2/2 = Аух (х) \nx + xP2 J2 А*хк- (26)
fc=O
В этом случае уг{х) содержит добавочное слагаемое вида Ау\(х) In x, где
2/| (х) задается в виде {25).
Замечание. Постоянная А в (26) может оказаться равной нулю, и тогда
для yi получим выражение в виде обобщенного степенного ряда.
Пример 4. Решить уравнение
2х2у" + (Зх - 2х2)у' - (х + \)у = 0. (27)
Решение. Перепишем (27) в виде
или
// , 3-2х , х + 1
у +^ry--^-
Решение у(х) будем искать в виде
Yk (Co
fc=0
Для нахождения р выпишем определяющее уравнение
где
ao = lim -—— = -, Ьо = hm( —- 1 = --,
х-*о 2 2 х-.о\ 2 / 2
т.е.
(О+ 0 ^
1
2'
Согласно приведенному правилу, берем
отсюда р, = -, р2 = -1.
k=0 fc=O
Для того, чтобы найти Со, Ch ..., С„,..., надо поставить у\(х) и ее производные
у\ (х) и у"(х) в уравнение (27):
X
у,(*) = ]Гс
*=0
130 Глава 2. Дифференциальные уравнения высших порядков
Подстановка у\(х), у\(х)> у'((х) в (27) дает
2х2 £ (V - I) CuJ-W + (Зш - 2*2) fV* + IW^'» -
fc-О > ' Jfc-О >> 2'
-(*+1)£с***+(|/2)=0. (28)
fc-0
После преобразований (28) перепишется так:
Y, H2k + 3)Chxk+m - J2 2(* + 1)С***+<3/2) = 0- (29)
Так как ищется решение для х > 0, то (29) можно сократить на &|/2, что дает
l = 0. (30)
Отсюда находим соотношение для определения коэффициентов
1-5С, - 2- 1С0 = 0,
2 • 7С2 - 2 • 2С, = 0,
3)Cn-2nCn-i =0,
Полагая в первом уравнении соотношений (31) Со = 1, получим С| = -.
22 23
Из второго уравнения имеем Сг = т-г. Из третьего Сз = и т.д. Легко
заметить, что
итак,
(32)
Аналогично находим и коэффициенты Ак. Оказывается, что при Ао = 1
- 1 - 1
i - , 2 - 2J, .... * - Л!>
так что
1 гс^ ж* С*
Обшее решение уравнения (27) у(х) = Лу|(ж)+.Ву2(а), где Л и Б — произвольные
постоянные, а функции у\(х) и у2(х) задаются формулами (32) и (33). >
Пример 5. Взаимодействие двух ядер с хорошим приближением мож-
Ае'ах
но описать с помощью потенциала мезонных сил V = (притя-
X
жению соответствует А < 0). Найти в виде ряда решение волнового
§ 18. Интегрирование уравнений при помощи рядов Ш
уравнения Шредингера
^iLj = O, (34)
где а, А, Е и к = -г постоянные (ограничиться тремя ненулевыми
И
коэффициентами ряда, отвечающего большому корню определяющего
уравнения).
Решение. Ищем решение у(х) данного уравнения в виде обобщенного
степенного ряда
X
у(х) = хй ^ chxk.
ктО
Коэффициенты Aq и Во определяющего уравнения р(р- \) + Аор + Во = 0 будут
равны
Aq = lim xp(x) = 0, так как р(х) = О,
а-»0
Во = lim x2q(x) = lim x2k [E -— ] = \\т(Ех2 - Ахе~ах) = О,
так что оно принимает вид р(р - 1) = 0, откуда р\ = 1, р2 = 0.
Обобщенный степенной ряд для случая /> = 1
х
у(Ж; = X у CffX z= CqX + С\Х ■+• С2Ж + С3Ж +...J W^/
тогда
у; = со + 2с,ж + Зс2х2 + 4с3я3 + ...,
у" = 2с, + 6с2з -f 12с3а?3 + ... .
Кроме того, имеем
Подставляем в уравнение (14) ряды для у", у и е"ах\
2с, +6с2а? + 12с3а?3 + ...+
+ \кЕ - Ы^- - а 4- ^ - ^- + ... J J
Приравниваем нулю коэффициенты при степенях х:
^ J + с,а?2
х»
2С| - кАсо = 0,
6с2 + (кЕ + а)со - кАс\ = 0,
Из полученных равенств последовательно находим
Ак ЛЛс, - (кЕ + аА)со
с, = —со, с2 = g ,
132 Глава 2. Дифференциальные уравнения высших порядков
или
1 /А2к2 \
с2 = - ( — кЕ - акА 1 с0 и т. д.
Подставляя найденные значения коэффициентов в ряд (35), получаем
[Ак 1 / А2к2 \ 1
1 + —-х + - ( — кЕ - акА ) х2 + ... .
2 6 \ 2 / J
где с0— произвольная постоянная. |>
Задачи для самостоятельного решения
Проинтегрировать при помощи рядов следующие дифференциальные уравнения:
739. 4ху" + 2г/ + у = 0.
740. (1 + х)у - пу = 0.
741. 9х(\ - х)у" - Пу Л- Лу = 0.
742. Квантовый анализ эффекта Штарка (в параболической системе координат)
приводит к дифференциальному уравнению
где a,J57, Fy m — постоянные. Используя наибольший из корней определяющего
уравнения, получить решение в окрестности точки х = 0 в виде ряда (найти
первые три коэффициента).
743. В случае отсутствия азимутальной зависимости квантовомеханическое
рассмотрение молекулярного иона водорода приводит к уравнению
где a, p — постоянные. Найти решение этого уравнения в виде ряда (вычислить
первые три ненулевых коэффициента разложения).
Пример 6. Решить уравнение Бесселя
х2у" + ху' + (х2 - р2)у = 0, х > 0, (36)
где р — заданная постоянная.
Решение. Перепишем (36) в виде
X X
Здесь
р(х)=]-, q(x)=S^-,
так что
2
а0 = lim хр(х) = 1, 60 = lim x2q(x) = -р2
(см. формулы (24)). Определяющее уравнение для р:
р(р-1)+1 р-р2 = 0, или р2-р2 = 0
откуда р, = р, р2 = -р.
§ 18. Интегрирование уравнений при помощи рядов
133
Первое частное решение Бесселя (36) ищем в виде обобщенного степенного
ряда у = хр
. Подставляя у, у' и у" в уравнение (36), получаем
Jb=O
+ х Т, Ск(к+р)хк+1'-< + (х2 -р2) JT Скхк+> = О,
Л=0 *=0
или, после простых преобразований и сокращения на хр,
£[<* + Р? - Р2\СиХк +
Скхм = 0.
к=0
Отсюда, приравнивая нулю коэффициенты при всех степенях ж, будем иметь:
х"
x1
X2
x3
x4
X*
(p -p)
[(l+p)2
1(2 + P)2
1(3+P)2
[(4 + P)2
l(*+P)2
C0 = 0,
-P2]C,
-p2]c2
-P2]C3
-P2]C4
-Ack
= 0,
+ C0=0,
+ C, =0,
+ c7 = o,
+ C*-2 = 0,
(37)
Первое из соотношений (37) удовлетворяется при любом значении
коэффициента CQ. Из второго соотношения (37) получаем С\ = 0, из третьего
(2+р
-р*
22(1+P)'
из четвертого Сз = 0, из пятого
(4 + p)2_p2 24(l+p)(2+p)-b2-
Очевидно, что все коэффициенты с нечетными индексами равны нулю:
, = 0, к = 0,1, 2,... . Коэффициенты с четными индексами имеют вид:
2). Г.(р + *)■»!'
Для упрощения дальнейших выкладок примем
1,2,... .
Со=2'Г(р+\У (38)
где Г (и) — гамма-функция Эйлера. Гамма-функция Эйлера Г (и) определяется
для всех положительных значений (а также для всех комплексных значений
с положительной вещественной частью) следующим образом:
"V1 dx.
Гамма-функция обладает следующими важными свойствами:
2. Г(1) = 1.
134 Глава 2. Дифференциальные уравнения высших порядков
Если к — целое положительное число, то
3. Г(и + АЯ- 1) = (и + \)(и + 2)... (и + к)Г(и + 1).
4. Г(*+1) = *!
Пользуясь (38) и свойствами Г-функции, коэффициент С2к запишем в виде1
с = tH (-У
2к 22к(р + 1 )(р + 2)... (р + к) • к\ • 2*Т(р + 1) 22*+' ... к\ Г(р + Л + 1)'
ибо (р+ 1)(р+2)... (р+Л)Г(р+1), согласно свойству 3, равно Г(р+Л +1). Теперь
частное решение уравнения Бесселя, которое мы будем в дальнейшем обозначать
через Jpy принимает вид
2к+Р
т
Эту функцию принято называть Бесселевой функцией первого рода порядка р.
Второе частное решение уравнения Бесселя (36) ищем в виде
Jfc=O
где р — второй корень определяющего уравнения. Ясно, что это решение может
быть получено из (39) путем замены р на -р, так как уравнение (36) содержит р
в четной степени и не меняется при замене р на -р.
Итак,
т //*»\ —
Эту функцию называют Бесселевой функцией первого рода порядка -р.
Если р неравно целому числу, то решения Jp(x) и J-P(x) являются линейно
независимыми, так как их разложения в ряды начинаются с различных степеней х
и, следовательно, линейная комбинация ot\Jp(x) + a2J-p(x) может тождественно
равняться нулю лишь при at\ = а2 = 0.
Если р есть целое число, то можно установить линейную зависимость
функций Jp(x) и J-P(x), а именно оказывается, что
J-n(x) = (-1)пЛ(з) (n — целое).
Итак, при целом р вместо J-P(x) надо искать другое решение, которое было бы
линейно независимо от Jp(x). Для этого введем новую функцию
считая сначала, что р— нецелое число.
Очевидно, что так определенная функция Yp(x) является решением
уравнения (36) (в связи с тем, что она представляет линейную комбинацию частных
решений Jp(x) и J.p(x)).
Переходя к пределу в (40) при р, стремящемся к целому числу, получаем
частное решение Yp(x)t линейно независимое от Jp(x) и определенное уже и для
целых значений р.
Введенная здесь функция Yp(x) называется бесселевой функцией второго рода
порядка р. Таким образом, для всякого р, дробного или целого, мы построили
§ 18. Интегрирование уравнений при помощи рядов 135
фундаментальную систему решений уравнения Бесселя (36). Отсюда вытекает, что
общее решение уравнения (36) может быть представлено в виде
где А и В — произвольные постоянные.
В случае, когда р не является целым числом, общее решение уравнения
Бесселя можно брать в виде
где С\ и С2 — произвольные постоянные. >
Замечание 1. Часто встречающееся уравнение
х2у" + хУ' + (к2х2-р2)у = 0) (41)
где к— некоторая постоянная (к Ф 0), приводится к уравнению Бесселя
путем подстановки { = кх.
Общим решением уравнения (42) (при р, отличном от целого числа)
будет
а тогда общее решение уравнения (41) принимает вид
у = C\Jp(kx) + C2J-p(kx).
При р целом у = C\Jp(kx) + С2¥р(кх).
Замечание 2. Обширный класс уравнений вида
*2!г7 + пХТ- + (ь + схШ)У = °> (43)
ах1 ах
где а, Ь, с, ш— постоянные (с > 0, т Ф 0), приводится при помощи введения
нового переменного t и новой функции и по формулам
к уравнению Бесселя
**$+«£+<«*-л.-о,
о-1 я m 2v/c 2 (а-1)2-4Ь „
где а = —г—, ^= —, 7 = , Р = Ч . При с = 0 или т = О
2 2 m rrr
уравнение (43) является уравнением Эйлера.
Пример 7. Привести уравнение
^й"3*;!-^4-12^0 <44>
к уравнению Бесселя и найти его общее решение.
136 Глава 2. Дифференциальные уравнения высших порядков
Решение. В нашем случае коэффициенты равны a — -3, Ь = -12, с = 1,
m = 4, поэтому
о-1 т a 11
«- — —2, />=т=2, -- = ., - = -,
I 2 (а-1)2-4Ь
Введем новую независимую переменную t и функцию и по формулам
у = ( - 1 и, или у = 2ui, где и = «(£), (45)
х = ( - j , или ее = >/2*; (46)
тогда
dy d(2ut)/dt r-d г( ijidu 1/2 N
dx dx/dt dt \ dt /
Аналогично находим
d2y _ 2d2u du
dx dt dt
dy d2y
Подставив в (44) вместо х, у> —, —г их выражения через t и «, получаем
dx dx
уравнение Бесселя
общее решение которого
u = ClJ2(t) + C2Y2(t).
х2
у по формулам t = —-,
из (45) и (46), получаем общее решение данного уравнения
х2 у
Переходя к переменным ж и у по формулам t = —-, w = 3» которые получаются
Задачи для самостоятельного решения
Найти общие решения следующих уравнений Бесселя:
744. х2у" + ху' + Ux2 - 1)у = 0. 745. х2у" + ху' + (х2 - I)у = 0.
746. у" + -у + 1-у = 0. 747. у" + V + 4у = 0.
X у X
748. х2у" - 2*у' + 4(/ - \)у - 0. 749. ху" + Х-у' + ]-у = 0.
750. у" + -у' + у = 0. 751. у" + -у' + 4у = 0.
X X
§ 18. Интегрирование уравнений при помощи рядов 137
3°. Нахождение периодических решений линейных
дифференциальных уравнений. Пусть дано линейное
неоднородное дифференциальное уравнение второго порядка с постоянными
коэффициентами
3/"+Р13/+Р2У = /(&), (47)
где /(ж) — функция, периодическая с периодом 2тг, разлагающаяся в ряд
Фурье
00
/(#) = -г + X^(an cos nx + bn sin nx)'
Периодическое решение уравнения (47) ищем в виде
у(х) = —-■ + ^>2(An cos nx + Bn sin пж). (49)
n=l
Подставляем ряд (49) в уравнение (47) и подбираем его коэффициенты
так, чтобы равенство (47) удовлетворялось формально. Приравнивая
свободные члены и коэффициенты при cosnx и sinnz в левых и правых
частях полученного равенства, найдем
n=l,2,.... (50)
(p2 -7i )on -p\nan
**n = ~~7 TvT~t 2~9~>
($2 "" n ) +Р)П
Первое из равенств (50) дает необходимое условие существования
решения вида (49): если о0 Ф 0, то необходимо, чтобы pi ф 0. Подставляя (50)
в (49), получаем
\__ а° V^ [(^2 ~~п2)ап ~ V\ nbn] cos пж-h [(р2 -n2)bn - р\ пап] sin nx
2 2 ' (51)
Когда р\ = 0 и р2 = п , где п = 1, 2,..., периодическое решение будет
существовать только при условии
ап = - / /(ж) cos пж Жг = 0, Ьп = - /(ж) sin пж dx = 0. (52)
тг J тг у
о о
Коэффициенты А^ и £& при к Ф п расходятся по формулам (50),
а коэффициенты Ап и Вп остаются произвольными, так как
выражение Ап cos пж + Вп sin пж является общим решением соответствующего
однородного уравнения.
138 Глава 2. Дифференциальные уравнения высших порядков
В случае невыполнения условий (52) уравнение (47) периодических
решений не имеет (возникает резонанс). При р2 = 0 и ао = 0
коэффициент Ао остается неопределенным и уравнение (47) имеет бесконечное
множество периодических решений, отличающихся друг от друга
постоянным слагаемым.
Если правая часть f(x) уравнения (47) имеет период 21 Ф 2тг, то надо
разлагать f(x) по периоду 21 и искать решение уравнения (47) в виде
3/= у + 2^ Ип cos ~ + Бп sin "7" '
n= '
Формулы (50) при этом соответственно изменятся.
Пример 8. Найти периодические решения уравнения
00 sin nx
n=3
Решение. Имеем p, = 0, p2 = 4 = 22, a0 = 0, an = 0, Ьл = — (n = 3,4,...).
Функция
не содержит резонирующего члена a2 cos2a; + Ь2 sin 2ж, значит, уравнение имеет
периодические решения, притом бесконечное множество.
По формулам (50) находим коэффициенты
B,=0,
* ~ п )
Все периодические решения даются формулой
sin nx
у(х) = А2 cos2a; + B2 sin 2ж -
где А2 и В2 — произвольные постоянные. >
Пример 9. Найти периодические решения уравнения у" + у = cos x.
Решение. В данном случае р\ = 0, р2 = 1. Проверим выполнимость
условий (52). Имеем
2* 2*
I cos a? cos х dx = / cos 2x dx = 7г Ф 0;
о
2*
cos ж sin ж dx = 0 (здесь п = 1).
§ 18. Интегрирование уравнений при помощи рядов 139
Условия (6) существования периодического решения не выполняются.
Следовательно, данное уравнение периодических решений не имеет. В самом деле, общее
решение уравнения у" + у = cos x есть
у(х) = С\ cos х 4- С2 sin x + -я sin я,
которое, очевидно, не является периодическим из-за наличия слагаемого
1 .
-ж sin ж. >
Пример 10. Найти периодическое решение уравнения у"-у = \ sin х\.
Решение. Функция f(x) = |sina?| — периодическая с периодом тг.
Разлагаем ее в ряд Фурье в интервале (-тг, тг):
, . , 2 4 т^-ч cos2na ,
Решение данного уравнения ищем в виде
у (а?) = — + 2^J(i4n cos nx + Bn sin nx).
n=l
Имеем
Pi = o> Pi = -i; во = —, агп-i = о,
ТГ
Формулы (50) дают
4 _ _ 4 ] _
Следовательно, уравнение имеет периодическое решение вида
2 4 ^Ц cos 2nx
тг тг^16п2-Г
Задачи для самостоятельного решения
Найти периодические решения (если они существуют) следующих
дифференциальных уравнений:
752. / + 3y«1 + 2J з ■ 753. у" + у = ^
«__ . „ ^-^ч COSflX »
754. у +у = 2^—5—• '"■ У + у = cos ж cos 2ж.
756. у" + у' = f^ ^V^' 757- ^ + АУ = cos2ж-
758. у" - 4у + 4у = тг2 - х\ -тг < х < тг. 759. у11 - 4у = | cos тгя|.
760. у" - 4у' + 4у = arcsin (sin a?). 761. у" + 9у = sin 3a>.
140 Глава 2. Дифференциальные уравнения высших порядков
4°. Асимптотическое интегрирование. Пусть имеем ряд
(возможно и расходящийся)
4, + - + ^ + ... + ^ + .... (53)
X X2 Хп
Обозначим через Sn(x) сумму первых п + 1 членов ряда.
Будем говорить, что ряд (53) представляет собой асимптотическое
разложение функции /(ж) для достаточно больших \х\, если выражение
JM*) = **{/(*) - Sn(x)}
удовлетворяет условию
lim Rn(x) = 0, или Rn(x) = o( — ) (54)
|х|-»оо \х /
(га — любое фиксированное число), даже если lim |Лп(я)1 = оо (ж —
п—>оо
фиксировано). То обстоятельство, что данный ряд есть асимптотическое
разложение функции f(x) (асимптотический степенной ряд),
обозначается так:
n=0
Смысл асимптотического разложения состоит в том, что ряд (53)
может служить источником приближенных формул
А] Ап
f(x) « Aq H h ... Н——, п = 0, 1, 2,...,
так что разность f(x) - Sn(x) — рп(х) при \х\ -> оо будет бесконечно
малой порядка выше га, т.е.
lim " = 0, или lim \x\npn(x) = 0.
|*|—оо ч\х\П |х|-оо
Пример 11. Найти асимптотическое разложение функции
+00
f(x)= I Гхе*-%&, х>0. (55)
X
Решение. Применяя п раз интегрирование по частям, получаем
Обозначим un_i = и положим
хп
X X2 X3
m=0
§18. Интегрирование уравнений при помощи рядов 141
Имеем
m
= ► со при m -> оо,
так что ряд 2 um будет расходящимся для всех значений х. Однако этот ряд
го=О
может быть применен для вычисления значений f(x) при больших значениях х.
В самом деле, фиксируя некоторое значение п, получим
/(*) -jSn(x) = (-l)n+l(n + 1)! J ^j *,
отсюда, поскольку ex~l ^ I (t ^ х), будем иметь
y.f£-2 = ^. (56)
Для значений я, достаточно больших, правая часть этого неравенства может быть
сделана как угодной малой. Так, для х ^ 2п будем иметь
поэтому значение функции f(x) может быть вычислено с большой точностью для
п
больших значений ж, если взять сумму надлежащего числа членов ряда ^ um.
Из оценки (56) следует, что
Rn(x) = xn{f(x) - Sn(x)} -> 0 при z-oo
п
для всякого фиксированного п, так что ряд J2 um дает асимптотическое разло-
т=0
жение данной функции/(ж). >
Если выполняется условие (54), то для коэффициентов Ак ряда (53)
из (54) получаем
Ао = lim f(x), An = lim xn{f(x) - 5n_,(x)}, n = 1, 2,.... (57)
X—Ю0 I—>00
Отсюда следует, что если функция f(x) имеет асимптотическое
разложение, то оно единственно.
Напротив, один и тот же ряд вида (53) может служить
асимптотическим разложением для разных функций. Например, для функции
f(x) = e~x (0<х< +оо)
в силу (57) асимптотическим разложением является ряд (53), все
коэффициенты Ап которого равны нулю. Очевидно, что этот же ряд является
асимптотическим разложением и для функции f(x) = 0. Говорят, что
асимптотический ряд представляет не одну функцию, а класс
асимптотически равных функций.
142 Глава 2. Дифференциальные уравнения высших порядков
Операции над асимптотическими рядами. 1) Если
00 00
k=0 Jfc=0
ТО
f(x)±g(x)~f2Uk±Bk)x-k. (59)
2) Если имеют место асимптотические разложения (58), то
асимптотическое разложение функции f(x)g(x) может быть получено путем
формального перемножения разложений (58).
3) Если функция f(x) имеет асимптотическое разложение
§> <6°)
*=2 Х
начинающееся с члена аГ2, то имеет место асимптотическое разложение
ИЛИ
/■
х
т. е. асимптотическое разложение (60) можно формально интегрировать
почленно.
4) Формальное почленное дифференцирование асимптотического
разложения, вообще говоря, недопустимо.
В самом деле, рассмотрим функцию
f(x) = е'х sin е*, 0 < х < +оо.
ее асимптотическим разложением является ряд с коэффициентами
Ak = 0, к = 0,1,..., в то время как производная функции f'(x) =
-e~*sine* + cose* не имеет асимптотического разложения, поскольку
f(x) даже не имеет предела при х -> +оо.
Однако если функция f(x) ~ Ао + — + -j 4-... дифференцируема,
а функция f'(x) может быть разложена в асимптотический степенной
ряд, то
w,-4 А\ 2А2
§ 18. Интегрирование уравнений при помощи рядов 143
Задачи для самостоятельного решения
762. Показать, что
J т
о
где х > О вещественно.
763. Показать, что
м 1 2! 4!
dt~ - + — -...,
х х* х5
ezz'a J е-*ха
для больших положительных значений z.
764. Найти асимптотическое разложение функции
f(x) = - + е~* sin е2я, 0 < х < оо.
Показать, что производная /'(ж) не имеет асимптотического разложения.
5°. Приложения к интегрированию дифференциальных
уравнений. 1. Рассмотрим дифференциальное уравнение
Ряд
1 1! 2! п!
5 + -т + • • • + -7ГГ + • • •» (63)
а; ж2 а:3 жп+1
расходящийся при всех значениях х, формально удовлетворяет
данному уравнению, в чем нетрудно убедиться непосредственной проверкой.
Уравнению (62) удовлетворяет функция 2\
-00
причем интеграл в правой части находится при х < 0. Повторным
интегрированием по частям находим
« Л-1 tM ] 1! 2! п!
у а; х2 х3 ссп+|
е
-00
2) Функция, определяемая интегралом / — dt, называется экспоненциал-интегральной
-X
функцией и обозначается символом Ei(x).
144 Глава 2. Дифференциальные уравнения высших порядков
где
= (n+\)le-* J —2dt.
При х < 0 имеем
-00
Следовательно, взяв первые п членов ряда, мы совершим ошибку,
меньшую (п + 1)-го члена. Нетрудно видеть, что в данном случае
Rn(x) = xn{f(x) - Sn(x)} = xnpn(x) -> О при а--оо.
Поэтому построенный ряд является асимптотическим и может быть
использован для вычисления интеграла и тем самым решения
уравнения (62). >
2. Едли Jv(x) есть решение уравнения Бесселя х2у" + ху1 + (х2 -
u2)y = О, то, подставив вместо Ju функцию х~]^2у(х), обнаружим, что
у(х) будет удовлетворять уравнению
> = ». (64)
Для больших х(х > v) это уравнение естественно попытаться
заменить уравнением
»Г + У.=О, (65)
которое имеет решение
Ух = по sin х + b0 cos x.
Можно улучшить точность (для больших х) заменой постоянных uq и &о
разложениями по отрицательным степеням х:
п=0 п=0
Это означает, что решение уравнения (64) можно искать в виде
00 00
у(х) = ^^ a>nX~n sin x + ^2 bnX~n cos ж. (66)
71=0 П=0
Подставив выражение (66) в уравнение (64), получим
Г i/2-(l/4) (v2 -(\/4))(v2 -(9/4)) 1
xsing+L- , 'ас-- *,!}\2 ИЬ0 + ... cosx. (67)
L 2x 2(2cc)z J
§18. Интегрирование уравнений при помощи рядов 145
Этот процесс можно продолжить и дальше. Существенно заметить, что
эти выражения приводят к точному результату для v = ±-,±-,...
(см. Бесселевы функции полуцелого индекса). Уравнение (65) является,
как говорят, предельным уравнением для уравнения (64) (уравнение (65)
получается из (64), если в коэффициенте при у совершить предельный
переход при х —► со). Решение уравнения (65) для больших х (особенно
2k+\.
для v = ± ) достаточно хорошо определяет поведение решения
исходного уравнения (64). >
Примеры показывают, что асимптотическое поведение решений
дифференциального уравнения не всегда можно вывести из поведения
решений предельного уравнения.
Возьмем функцию
у(х) = xa sin (зР + С), а > О, Р > 0 (68)
и сконструируем дифференциальное уравнение, для которого у(х) будет
решением. Имеем
у —— we**/ о
Попробуем, чтобы а и /3 были связаны соотношением
j8(2cr + /J-l) = 0. (69)
Тогда заданная функция у(х) будет удовлетворять дифференциальному
уравнению
«-+[£♦*£*].-* С»)
Предположим, что 0 < /J < 1, например, /3 = -. Тогда из условия (69)
найдем а = - и решение
4
у(х)= Vxs\x\{y/x + C) (71)
уравнения (70) при х -> -fee будет колеблющимся. С другой стороны,
поэтому предельным уравнением, соответствующим уравнению (70),
будет
у" = 0. (72)
146 Глава 2. Дифференциальные уравнения высших порядков
Его общее решение
у = Ах + В (73)
не содержит колеблющейся части.
Итак, асимптотическое поведение решения (71) дифференциального
уравнения (70) нельзя «угадать» по поведению решения (73) предельного
уравнения (72).
Приведем некоторые относящиеся сюда результаты. Пусть дано
дифференциальное уравнение
у" + Р<(х)у'+Р2(х)у = 0, (74)
где
р2(х) = Ьо + - + 4 + • • •.
X X
так что
lim р\(х) = ао, lim р2(х) = Ьо. (76)
х—»оо х—»оо
Предельное уравнение в данном случае имеет вид
у" + ад' + bQy = 0 (77)
и является уравнением с постоянными коэффициентами. Пусть Аь А2 —
корни (которые мы для простоты предполагаем различными)
характеристического уравнения
А2 + а0А + Ьо = 0. (78)
Решения предельного уравнения — экспоненты еХ]Х1 eXlX.
Оказывается [16], что асимптотическое поведение решений
уравнения (74) аналогично не поведению линейных комбинаций экспонент
еА|*, eXlX9 а поведению линейных функций
eA'V, ex>xxa\ (79)
где показатели <т\, a-i определяются формулами
Функции (79) зависят не только от ао и Ьо» т. е. не только от предельных
значений р\(х) и р2(х) при х -► +оо, но также и от коэффициентов аь Ь\,
участвующих в правых частях равенств (75).
Теорема. Если характеристическое уравнение А2 + а0 А + Ьо = 0 имеет
различные корни \\ и \2 и если
2А| +а0 '
§18. Интегрирование уравнений при помощи рядовИ7
то уравнение
обладает линейно независимыми решениями у\(х) и уг(х), которые
можно представить асимптотическими рядами:
(81)
Если корни характеристического уравнения совпадают, то может
появиться логарифмический член. Решение у\(х) можно представить
асимптотическим рядом типа первого ряда (81), тогда как другое решение
у2 (х) теперь представимо рядом вида
У1\х) ™ Ау\ (*&) 1п ж Н- е х I Kq Н 1—г- + ... 1. (82)
\ хх1)
Коэффициенты А^ В{} К\ могут быть при этом найдены известным
способом неопределенных коэффициентов путем подстановки выражений (81)
или (82) в уравнение и приравнивания нулю коэффициентов при
степенях -. При этом формальное дифференцирование асимптотических
х
разложений, законность которого априори неясна, приводит к
правильным асимптотическим представлениям искомых функций.
Задачи для самостоятельного решения
решения вида
765. Показать, что уравнение у+(1 + — )у = 0 при х —> +оо имеет два
1ида
у}(х)= И H-Of -J J cos ж, у2(я)= (\+o(-)jxs\nx.
. Показать, что уравнение у"- (1 j Jy = 0 при х -+ +оо имеет два
766
решения вида
ГЛАВА
3
Системы
дифференциальных
уравнений
§19. Основные понятия и определения
Система обыкновенных дифференциальных уравнений
1р*(х,У11у{,...>у{Чй,У2,..-,»2*2)»---.»п,У;,...,У(*'))=0> (1)
к= 1,2, ...,п,
разрешенная относительно старших производных у\ ' , у\ ,..., 2М ,
называется канонической системой. Она имеет вид
У] =/|(Ж)У1,»1,...,У| ,У2,У2»---»У2 > — >2/п,Ут--->2/п )>
Порядком системы (1) называется число ^, равное
р = Л, -f *2 + • • • + ^п.
Пример 1. Привести к каноническому виду систему уравнений
Решение. Данная система имеет третий порядок, так как fc, = 2, fc2 = 1
и, значит, р = 3. Разрешая первое уравнение относительно у", а второе
относительно у2. получим каноническую систему
Система обыкновенных дифференциальных уравнений первого
порядка вида
Л(*,Ж|,Ж2,...,«п), fc= 1,2,...,П, (3)
где ^ — независимая переменная; Ж|, а?2,..., жп — неизвестные функции
от t, называется нормальной системой.
Число п называется порядком нормальной системы (3). Две системы
дифференциальных уравнений называются эквивалентными, если они
обладают одними и теми же решениями.
§19. Основные понятия и определения 149
Любую каноническую систему (2) можно привести к эквивалентной
ей нормальной системе (3), причем порядок этих систем будет одним
и тем же.
Пример 2. Привести к нормальной системе следующую систему
дифференциальных уравнений:
d2x
dx dx\
Решение. Положим х = Х\, — = х2, у = Жз- Тогда будем иметь = а?2,
at dt
dy dxi
— = -—--, и данная система приведется к следующей нормальной системе
at dt
третьего порядка:
dt
dx2
~dT
dt t3 '
Пример З. Привести дифференциальное уравнение
к нормальной системе.
_ „ dx dx\ d2x dxi
Решение. Положим х = ж,, — = х2, тогда -—- = х2) —г = —г-
at dt dt1 dt
Подставляя эти выражения в данное уравнение, получим
dx2
— +jp(O«2 +9(0*1=0.
Нормальная система будет иметь вид
dx\ dxi
Решением системы (3) в интервале (а, 6) называется совокупность
любых п функций
Х\=<Р\ (0) *2
определенных и непрерывно дифференцируемых в интервале (а, Ь), если
они обращают уравнения системы (3) в тождества, справедливые для всех
значений t € (а, 6).
150 Глава 3. Системы дифференциальных уравнений
Пример 4. Показать, что система функций х\ = --j, х2 = -tint,
определенных в интервале 0 < t < +оо, является решением системы
дифференциальных уравнений
^ - 7tx]
dt ~2tXu
dx2 _ x2
dt " t
dx\ 2 dxi
Решение. Имеем —— = -г, —■ = -1-ln*. Подставляя в уравнение данной
at V dt
dx\ dxi
системы вместо X\1x2i "т~ и Т" их выражения через t, получим тождества
dt dt
-j =-j =-j, -Int-1 = -ln<-1, 0<*<+oo. >
Задачи для самостоятельного решения
Проверить, являются ли данные системы функций решениями данных систем
дифференциальных уравнений.
{« _ ( dy z-\
¥-" f-Л 770. Ss—'
<& " х ' I dx У '
Задачей Коши для системы (3) называется задача нахождения решения
Я|=Ж,(*), Я2 = Я2(0, •••» Xn=Xn(t)
этой системы, удовлетворяющего начальным условиям
где <о> «?j ^2> • • •»жп — заданные числа.
Теорема существования и единственности решения задачи Коши.
Пусть имеем нормальную систему дифференциальных уравнений (3)
и пусть функции fi(t} Х\, х2)..., а?п)> * = 1,2,..., п, определены в
некоторой п+1 -мерной области D изменения переменных t, Х\, х2,..., яЛ.
существует окрестность П точки Мо($о> ®?»®2» • • • > жп)» * к°~
w функции fi а) непрерывны, 6) имеют ограниченные частные
производные по переменным х\, х2}..., хп, wo найдется интервал to - ft <
£ < £о + ft изменения t, в котором существует единственное решение
нормальной системы (3), удовлетворяющее начальным условиям (4).
§ 19. Основные понятия и определения 151
Система п дифференцируемых функций
х{ = Xi(t, С|, С2,..., Сп), г = 1,2,..., п, (5)
независимой переменной t и п произвольных постоянных C\)Ci)... ,СП
называется общим решением нормальной системы (3), если: 1) при любых
допустимых значениях Ci, Сг,..., Сп система функций (5) обращает
уравнения (3) в тождества, 2) в области, где выполняются условия
теоремы Коши, функции (5) решают любую задачу Коши.
Пример 5. Показать, что система функций
и (6)
является общим решением системы уравнений
^ = x2-4s,.
Решение. В данном примере область D есть
-00 < t < +00, -00 < Х\, Х2 < +00. (8)
Подставляя функции X\(t) и x2(t) из (6) в систему уравнений (7), получаем
тождества по J, справедливые при любых значениях постоянных С\> С2. Таким
образом, условие 1), определяющее общее решение, выполнено.
Проверим выполнение условия 2). Заметим, \гго для системы уравнений (7)
условия теоремы существования и единственности решения задачи Коши
выполняются во всей области D, определяемой соотношениями (8). Поэтому в качестве
начальных условий можно взять любую тройку чисел tOyx°ux2. Тогда
соотношения (6) дадут для определения С\, С2 систему
5
Определитель этой системы А = -4е*° Ф 0; следовательно, она однозначно
разрешима относительно Сь С2 при любых я?,^ и *о- Это равносильно тому,
что разрешима любая задача Коши. Итак, система функций (6) является общим
решением системы уравнений (7). >
Решения, получающиеся из общего при конкретных значениях
постоянных С|, Сг,..., Сп, называются частными решениями.
Пример 6. Имея общее решение (6) системы (7), найти частное
решение этой системы, удовлетворяющее начальным условиям х}(0) = О,
х2(0) = -4.
152 Глава 3. Системы дифференциальных уравнений
Решение. Задача сводится к нахождению таких значений постоянных С]
и С2, чтобы выполнялись соотношения
0 = С,+С2, -4 = 2С, -2С2.
Решая эту систему, находим С] = -1, С2 = 1. Искомое частное решение
х, (t) = -е~' + е3', *2(t) = -2е'1 - 2e3t. >
Замечание 1. Не всякую систему дифференциальных уравнений можно
свести к одному уравнению. Например, система
распадается на два независимых уравнения. Общее решение в этом случае
получается интегрированием каждого уравнения в отдельности:
х]=С]е'\ х2 = С2е1.
Замечание 2. Если число уравнений в системе равно п, а число искомых
функций N, причем N > п, то такая система является неопределенной. В этом
случае можно выбирать произвольно N - п искомых функций (лишь бы
они были нужное число раз дифференцируемыми) и в зависимости от них
находить остальные п функций.
Замечание 3. Если система состоит из п уравнений, а число искомых
функций N у причем N < п, то эта система может оказаться несовместной,
т.е. не имеющий ни одного решения.
Пусть дана (для простоты) нормальная система двух
дифференциальных уравнений
dxx
f(t)
Будем рассматривать систему значений t, x\, х2 как прямоугольные
декартовы координаты точки трехмерного пространства, отнесенного к системе
координат OtX]X2. Решение
Х\ =Ж,(£), X2 = X2(t),
принимающее при t = to значение х°и x2i изображает в этом пространстве
некоторую линию, проходящую через точку Мо(£о>#?> я2)- Эта линия
называется интегральной кривой (линией) нормальной системы (9).
Задача Коши для системы (9) получает следующую геометрическую
формулировку: в пространстве переменных (£, х\, х2) найти интегральную
кривую, проходящую через данную точку ($о, ж?, Жг)- Теорема Коши
устанавливает существование и единственность такой линии.
Нормальной системе (9) и ее решению можно дать еще такое
истолкование. Будем независимую переменную t рассматривать как время,
§19. Основные понятия и определения 153
а систему значений функций Х\,х2 как прямо-
угольные декартовы координаты точки плоско- 2
сти х\Ох2. Эту плоскость переменных х\Ох2
называют фазовой плоскостью. В фазовой
плоскости решение
x]=x{(t)1 x2=x2(t)
системы (9), принимающее при t = to
начальные значения х°их2, изображается линией АВ Рис.28
(рис.28), проходящей через точку Мо(х°их2).
Эту линию называют траекторией системы (фазовой траекторией).
Очевидно, что траектория системы (9) есть проекция интегральной кривой
на фазовую плоскость.
Система (9) определяет в каждый момент времени t в данной
точке Х\,х2 фазовой плоскости координаты скорости {/ь/2} движущейся
точки.
Пример 7. Решить систему уравнений
при начальных условиях
х(О) = хОу 2/(0) = г/0. (И)
Решение. Дифференцируя один раз по t первое уравнение системы (10)
dy
и подставляя в полученное уравнение — = -ж, сведем систему (10) к одному
at
d2x
уравнению второго порядка —-г- + х — 0, образующее решение которого
at1
х = С\ cos t + С2 sin J.
Так как у = —, то у = -Ci sin* + C2cos£; итак, общее решение системы (10):
at
у = -С, sin* + C2cos*. (12)
удовлетворяющим начальным
услових = х0 cos t + уо sin t, у = -s0 sin * + y0 cos *. (13)
ного
(14)
дста= Rcos(t + a), . K '
Частным решением системы (10), удовлетворяющим начальным
условиям (11), будет
Исключая t из уравнений (13) (путем возведения в квадрат и почленного
сложения), получаем фазовую траекторию
где R = y/xl + y2. Это окружность, проходящая через точку М0(х0, уй).
Представив уравнения (13) в виде
154
Глава 3. Системы дифференциальных уравнений
где R =
Xq + Уо sin а = —■, cos а = •—■, замечаем, что уравнения (15) выражают
R R
зависимость от времени текущих координат точки M(x(t)}y(t))t или коротко
M(t), которая начинает свое движение при t = 0 от точки MQ(xQ) у0) и движется
по окружности (14) (рис.29, а).
Направление движения точки M(t) определим с помощью заданной си-
dy
стемы (10). При х > 0, согласно уравнению — = -ж, величина у убывает
at
(как, например, в точке М,(*)), а при х < 0 величина у возрастает (как,
например, в точке Mi(t))> Таким образом, точка M(t)
движется по кривой (14) по ходу часовой
стрелки. Изменяя произвольно начальные условия (11)
(оставаясь, однако, в физически допустимых
пределах), т.е. изменяя как угодно положение начальной
точки М0(х0)у0), получаем всевозможные фазовые
траектории (14).
Дадим теперь другое истолкование
уравнений (15) (или, что то же, уравнений (13)). В
трехмерном пространстве возьмем правую декартову
систему координат Oxyz. Легко убедиться, что точка
JV(s(*),y(£),z(£)) (или коротко N(t)) с
координатами (рис. 29, б)
(16)
, z(t) =
Afft
Рис. 29
начинает свое движение при t = 0 от начальной
точки iVo(so,yo,O) и с возрастанием t поднимается
по винтовой линии (16), расположенной на
цилиндре с окружностью (14) в основании и образующими,
параллельными оси Oz.
Очевидно, что точка Nq совпадает с точкой Мо
и что при любом t точка N(t) проектируется в точку
M(t) на фазовой траектории. Так как точка M(t)
движется по ходу часовой стрелки, то
интегральная кривая, описываемая точкой N(t), есть левая
винтовая линия на цилиндре с окружностью (14)
в основании и образующими, параллельными оси Oz. При различных
положениях точки JVb(a?o» Уо>О) интегральные кривые системы (10), соответствующие
различным значением R = \/х\ + у], проектируются на плоскость хОу в
различные кривые (14), а интегральные кривые, соответствующие одному и тому же
значению Л, проектируются в одну и ту же кривую (14). >
Интегралом нормальной системы (3) называется функция itp(t)x])
£2,...,£п)> определенная и непрерывная вместе со своими частными
8Ф дФ
производными первого порядка —, -—, к = 1,2,..., п, в области D,
ut OXfi
если при подстановке в нее произвольного решения X\(t),х2(г), ..., xn(t)
системы (3) она принимает постоянное значение, т.е. функция 4ф(г)х])
&2,...,ccn) зависит только от выбора решения x\(t))x2(t))... >xn(t)9
но не от переменной t.
§19. Основные понятия и определения 155
Первым интегралом нормальной системы (3) называется равенство
1>(Ьхих2,...,хп) = С,
где ip(t)x\yx2, ••• >хп) — интеграл системы (3), а С — произвольная
постоянная ]К
Пример 8. Показать, что функция
х2
ip(t,xux2) = — -хи (17)
определенная в области D\ t Ф О, -оо < x]ix2 < +oo, является
интегралом системы уравнений
если общее решение этой системы есть
ж, =С,«, ж2 = С^2 + С2^ (19)
Решение. Подставляя (19) в (17), получаем
2t) = C]t +Clt - C,t = C2
t
в области D. Следовательно, функция (17) является в области D интегралом
системы уравнений (18), а значит первый интеграл этой системы будет Х\ — С,
где С — произвольная постоянная. >
Теорема. Для того чтобы функция ^>(£, xj, x2i..., хп) была
интегралом системы (3), необходимо и достаточно выполнения условия
в области D.
Пример 9. Показать, что функция
X^-t (21)
является интегралом системы уравнений
dx\ X\ dx2
t- «
Иногда первым интегралом системы (3) называют интеграл этой системы.
156
Глава 3. Системы дифференциальных уравнений
Решение. В данном случае
х2
х2
1
f\(t,X],X2) , /2(*,*,,*2) -
Х2 X]
Находим частные производные данной функции 11>(г,х},х2). Имеем
Мл
х2
(23)
(24)
Подставляя (23) и (24) в левую часть (20), получаем
дф дф
^+ /(* а:ж)^
ж, х] + х\
= -1 + 1=0
в области D: -со < t < +оо, Х\ ^ 0, х2 Ф 0.
Итак, функция (21) есть интеграл системы уравнений (22) и, следовательно,
первый интеграл системы (22) будет
arctg — - t = С,
х2
где С — произвольная постоянная. >
Нормальная система (3) имеет бесконечное множество систем первых
интегралов.
Интегралы ф\} fa, • •• ,ipn системы (3) называются независимыми
относительно искомых функций Ж1,Ж2,... ,жп, если между функциями
^ь V>2> • • • > 'Фп не существует соотношения вида F{il>\, ^2> • • • > *Фп) = 0
ни при каком выборе функции F> не зависящей явно от а?|, а?2,..., хп.
Теорема. Для того чтобы функции /ф\) ^2, • • • > *Фп, имеющие частные
производные -— (^, Л = 1,2,..., п),были независимыми относительно
дх
а?|, Х2,..., жп в некоторой области D, необходимо и достаточно, чтобы
якобиан этих функций был отличен от нуля в области D,
дхп
дхп
дХ) дх2
вхп
Общим интегралом нормальной системы (3) называется совокупность п
независимых первых интегралов этой системы.
§ 20. Метод исключения 157
Если известны к, где к < п, независимых первых интегралов
системы (3), то ее порядок можно понизить на А: единиц.
Задачи для самостоятельного решения
Проверить, являются ли данные функции ip первыми интегралами данных систем
дифференциальных уравнений.
dx\ X\
х2
1Г = х2-х];
772. { dt « 4> = (\ + х)е-*-е-У.
1У_ = Х_ -у.
и te '
х = у +1
773. < f~* + y' a)^ = x + y-ti
dy x — t б) ip2 = x + у +1.
~dt= x + y*
Для следующих систем дифференциальных уравнений проверить, образуют ли
данные пары функций системы независимых первых интегралов:
— - 1~у
) dt~y~x' x + y + t = Cu
'у x-t xl + vz +t=C->.
dt y-x
— - tJ*~y x~y
775. 1*~* + У' \~*
dy __ t + x t -x
~dt = x + yy t-y
§ 20. Метод исключения
(сведение системы
дифференциальных уравнений
к одному уравнению)
Частным случаем канонической системы дифференциальных
уравнений является одно уравнение n-го порядка, разрешенное относительно
старшей производной.
158
Глава 3. Системы дифференциальных уравнений
Введением новых функций
это уравнение заменяется нормальной системой п уравнений
( dx _
dx\
"dT = Ж2>
dt
Можно утверждать и обратное, что, вообще говоря, нормальная
система п уравнений первого порядка
( ^ = f(t х х х х)
dt Ч > » i» 2» ••• * п »
dxi
IT =
Ху Х\,
эквивалентна одному уравнению порядка п. На этом основан один
из методов интегрирования систем дифференциальных уравнений —
метод исключения.
Проиллюстрируем этот метод на примере системы двух уравнений:
-£ = ax + by + /(*), -| = сх + dy + g(t).
at at
(О
Здесь а,Ь,с, d — постоянные коэффициенты, a f(t) и g(t) —
заданные функции; x(t) и у(0 — искомые функции. Из первого уравнения
системы (1) находим
(2)
Подставляя во второе уравнение системы вместо у правую часть (2),
а вместо — производную от правой части (2), получаем уравнение
dt
второго порядка относительно x(t)
§ 20. Метод исключения 139
где -4, JB, С — постоянные. Отсюда находим х = х(г>С\}С2). Подставив
dx
найденное выражение для х и — в (2), найдем у.
at
Пример 1. Проинтегрировать систему уравнений
dx
+1
dx
Решение. Из первого уравнения системы (3) находим у = — - 1, тогда
dJ> = £l (4)
dt df ■ w
Подставляя (4) во второе уравнение системы (3), получаем линейное
дифференциальное уравнение с постоянными коэффициентами второго порядка
$-. —* (5)
Общее решение уравнения (5)
* = С,еЧС2е~'-1. (6)
Находя производную по t от (6), получаем
Общее решение системы (3):
х = С}е* + С2е~* - 1, у = С\е* - С2е~'- 1.
Пример 2. Решить задачу Коши для системы
dx
-77
#
-2. (8)
Решение. Из второго уравнения системы (7) находим
.-a,-*. W
откуда
*я-3^-^. (10)
dt dt dt2 K '
Подставляя (9) и (10) в первое уравнение системы (7), получаем уравнение
d2y
— - у = 0, общее решение которого
dt1
у = С,е' + С2е-(. (II)
160 Глава 3. Системы дифференциальных уравнений
Подставляя (11) в (9), найдем
x = -4C]et-2C2e~t.
Общее решение системы (7)
х = -4С^-2С2е-\ у = С,е1 + С2е~\ (12)
При начальных условиях (8) из (12) получим систему уравнений для определения
СиС2:
Г -4С, - 2С2 = 6,
I С,+С2 = -2,
решая которую, найдем С\ = — 1, С2 = -1. Подставляя эти значения С\ и С2
в (12), получаем решение поставленной задачи Коши:
ж = 4е' + 2е"', у = -еь - е"1. >
Пример 3. Решить систему уравнений
dx
t
Решение. Из первого уравнения системы находим
х dx dy x 1 dx d2x
у=1+*' такчто И = -? + 1м+^-
dy
Подставляя эти выражения для у и — во второе уравнение, получаем
at
jd2x dx dx jd2x
ь^+1ц-х=-2х+х+1И' или *V=0-
d2x
Считая t Ф 0, из последнего уравнения имеем —тг = 0 и после интегрирования
at*
получим х = С\ + Cjt. Теперь легко находим
х dx С, + C2t С,
Общее решение данной системы
Замечание. Не всякая система дифференциальных уравнений может быть
dx
сведена к одному уравнению более высокого порядка. Например, — = х,
at
dy
— = у не сводится к одному уравнению второго порядка. Ее общее решение
§21. Нахождение интегрируемых комбинаций
161
Задачи для самостоятельного решения
Методом исключения решить следующие системы дифференциальных уравнений:
776.
778.
780.
dx
dt
x(0)= 1,
y(0)=4.
dx dy
dx_
~di*y
782.
lt=y+z>
784.
786.
dx
lt
dy
Tt=x +
dz
Tt=x +
d2x dy
dt dt2
dxj dx
777.
779.
781.
783.
785.
) = *'(0)=l,
y(0) = 0.
dx
dy
dt
dx
~dt
dy
dt
dx
dy
dt
dz
= x -1.
- x + 5y,
= -x- 3y,
= -y + *,
— zy
x( ) - -
y(o)=i.
dt
d2x
= —X + Z.
= У,
£y
dt2
d]x__
dt2 ~ +
dy ,
^F = -2x-
§21. Нахождение интегрируемых
комбинаций. Симметрическая форма
системы дифференциальных уравнений
1°. Нахождение интегрируемых комбинаций. Этот метод
интефирования системы дифференциальных уравнений
ас
k= 1,2, ...,п,
(1)
состоит в следующем: с помощью проходящих арифметических операций
(сложения, вычитания, умножения, деления) из уравнений системы (1)
162
Глава 3. Системы дифференциальных уравнений
образуют так называемые интегрируемые комбинации, т.е. достаточно
просто решаемые уравнения вида
pt t)U) — j =o,
где и — некоторая функция от искомой функции x\(t))X2(t))... ,xn(t).
Каждая интегрируемая комбинация дает один первый интеграл» Если
найдено п независимых первых интефалов системы (1), то ее интегрирование
закончено; если же найдено т независимых первых интефалов, где
т < п, то система (1) сводится к системе с меньшим числом неизвестных
функций.
Пример 1. Решить систему
(2)
Решение. Складывая почленно оба уравнения, получаем
d(a?i+a?2)
dt
= (x}+x2)22t}
откуда
Я, + Х2 ~~ h X] +
Вычитая почленно оба уравнения, получаем
откуда
1
а?, -
Итак, найдены два первых интеграла данной системы
_ 2 1 _
X] + Х2
v .5 1
Х\ — Х2
которые являются независимыми, так как якобиан отличен от нуля:
1 1
D(xhx2)
«с,
(xi+x2)2 (x\+x2)2
1 1
(ж,-х2)2 (х\-х2)2
Общий интеграл системы (2)
, 1
= С2.
(3)
§21. Нахождение интегрируемых комбинаций 163
Разрешая систему (3) относительно неизвестных функций, получаем общее
решение системы (2):
с + с2 - 2*2 с2 - с,
t*y ~л 2(С,-
Пример 2. Решить систему
' dx\ X\ — а? 2
(te2 _ a?i -a?2^ ^
—- = х\ - х2 + 1.
Решение. Вычитая почленно из первого уравнения второе, получаем
—^——— = 0, откуда первый интеграл системы (4)
at
Х\ — х2 = С» (5)
Подставив (5) во второе и третье уравнения системы (4), получим систему с двумя
неизвестными функциями
(6)
-1.
Из второго уравнения системы (6) находим
Подставляя (7) в первое уравнение системы (6), будем иметь
dx2 С]
— = *. = in пл мп. л. п.
Итак,
Отсюда находим общее решение системы (4):
ж, = In |С* + С2\ + С, + С3, х2 = In |С* + С2\ + С3, а;3 = (С, + \)t + С2. >
Пример 3. Найти частное решение системы
<te _ 1
rfy _ 1
удовлетворяющее начальным условиям я|<=0= 1, 2/|<=0= *•
164 Глава 3. Системы дифференциальных уравнений
Решение. Запишем данную систему в виде
с—о*-.-
Складывая почленно последние уравнения, получаем
ydJirl+(x-t)di=0' или 7t[{x-
С\
Отсюда находим первый интеграл (х - t)y = С,. Так как х - t = —, то второе
уравнение системы примет вид — = —, откуда у = С2е*/С|. Итак,
at C\
откуда получаем общее решение
С\
Полагая / = 0 в этих равенствах, найдем 1 = —, 1 = С2, т. е. С\ = Сг — 1,
С2
и искомым частным решением будет
х = t + е~\ у = е\ >
Пример 4 (разложение вещества). Вещество А разлагается на два
вещества X и У со скоростью образования каждого из них,
пропорциональной количеству неразложившегося вещества. Найти закон
изменения количеств х и у веществ X и Y в зависимости от време-
a За
ни tt если при t = 0 имеем ж = у = 0, а через час ж = -, у = —,
о о
где a — первоначальное количество вещества А.
Решение. В момент времени t количество неразложившегося вещества А
равно a — х - у. В силу условия задачи будем иметь
dx
— = k](a-x-y),
* »< i <8)
— = к2(а -х-у).
Разделив почленно второе уравнение на первое, получим
dy к2 к2 _
- = -, откуда у=-Х + С[.
При i = 0 имеем х = у = 0, поэтому из последнего уравнения находим С\ = О,
а значит
§21. Нахождение интегрируемых комбинаций 165
Подставив (9) в первое уравнение системы, получим уравнение
dx
~di
общее решение которого
Используя начальное условие x\t=Q = 0, найдем С2 = 1- > так что
к\ ■+- к2
(10)
Подставляя (10) в (9), будем иметь
Для определения коэффициентов к] и к2 примем за единицу времени час.
п Зд
Учитывая, что х = -, у = — при t = 1, из (10) и (10') найдем
о о
откуда
Л2 = ЗЛЬ fc, +*2 = In 2,
так что к\ = —-, fc2 = - In 2, и искомое решение системы (8)
« = 2(1-2"'), »=^(|-2-*). >
Пример 5 (равновесие газов в сообщающихся сосудах). Пусть
имеются для сосуда объемов V\ и Vi соответственно, наполненные газом.
Давление газа в начальный момент времени равно Р\ в первом
сосуде и Р2 - во втором. Сосуды соединены трубкой, по которой газ
перетекает из одного сосуда в другой. Считая, что количество газа,
перетекающего в одну секунду, пропорционально разности квадратов
давлений, определить давления р\ и р2 в сосудах в момент времени t.
Решение. Пусть а — количество газа, перетекающего в единицу времени
при разности давлений, равной единице. Тогда в течение времени dt из одного
сосуда в другой протечет количество газа a(jp] - p])dt. Это количество равно
убыли газа за время dt в одном сосуде и прибыли за то же время — в другом.
Последнее выражается системой уравнений
где Ь — постоянный коэффициент.
166 Глава 3. Системы дифференциальных уравнений
Вычитая почленно уравнения системы (11), получаем
откуда
ViP,+Vtf2 = C,. (12)
Умножим обе части первого уравнения системы (11) на P\Vuz второго — на p2V2
и сложим почленно:
^y (13)
Учитывая (12) и деля обе части (13) на р], будем иметь
О,С\ Р2
- Обозначив — ?= z, получаем
Р\
dz
= к dt) откуда In
1-z
= 2*t + In C2,
или
i±i=<VM. (14)
Подставляя в (14) вместо z величину —, получаем
Pi
C2e» (15)
Pi -Р2
В начальный момент времени t = 0 имеем р\ = Р], р2 = Р2, так что
из уравнения (12) имеем
С, =P,F, +P2V2, (16)
а из уравнения (15)
Из уравнений (12) и (15) находим искомые давления p\(t) и p2(t) в любой
момент времени t> при этом постоянные С\ и С2 определяются формулами (16)
и (17). >
Задачи для самостоятельного решения
Решить следующие системы дифференциальных уравнений:
5/, *(0)=1, 17 = 2а:~^ *(0) = -1,
787. { « 788. I I
-± = -х + 2у. у(0) = 3.
ох
dx I
789. <f'TI' 790. ^*
dt " x'
§21. Нахождение интегрируемых комбинаций 167
791. i ai y 792.
dx
dt
dy
dt
dx
dt
dy
dt
X
= ?
_ У
x'
= sin x cos у
= cos x sin у
793. < « 794.
dy
— = cos 2я cos 2y + sin 2x cos 2y, sc(O) = 0,
795. { d}
dy 1
-£• = - - sin 2x sin 2y, y(0) = 0.
at 2
dx _
dt ~~
dy
dt
tdx
*Tt
tdy
6 dt
У
x -
X
X -
1
"у1
_ 1
X
У
У
i
2°. Симметрическая форма системы
дифференциальных уравнений. Для нахождения интегрируемых комбинаций при
решении системы дифференциальных уравнений (1) иногда бывает удобно
записать ее в симметричной форме
//л \ л /л \
11 f j *^ I > Х^у * * • ) Xfij J"211 j *C | j X%) • • • ) Xfi)
= ... = — — г = j. (18)
В системе дифференциальных уравнений, записанной в
симметрической форме, переменные £, zh х2,..., хп равноправны, что в некоторых
случаях упрощает нахождение интегрируемых комбинаций.
Для решения системы (18) либо берут пары отношений, допускающие
разделение переменных, либо же используют производные пропорции
п\ _ п2 _ __ ат _ Х\п\ + Агаг + ... + Amam
•... 4- Amam '
где коэффициенты Ah А2,..., Am производные и их выбирают так, чтобы
числитель был дифференциалом знаменателя, либо равен нулю.
Пример 6. Найти общее решение системы уравнений
dt dx dy
2х -\nt In t - 2x'
(20)
о dt dx
Решение. Первая интегрируемая комбинация — = . Разделяя пере-
IX |П t
менные и интегрируя, найдем первый интеграл
= С,. (21)
Вторую интегрируемую комбинацию получим, используя производные
пропорции (19). Для этого сложим числители и знаменатели дробей системы (20):
dt _ dx __ dy _ dt + dx + dy
2x ~ -\nt ~ In t - 2a? '
168 Глава 3. Системы дифференциальных уравнений
здесь А] = 1, А2 = 1, Аз = 1. Отсюда dt + dx + dy = 0, или d(t + x + у) = 0 и,
значит,
t + ж + у = С2* (22)
Первые интефалы (21) и (22) дают общий интеграл системы (20)
ж2 + t(\nt- I) = СЬ
из которого находим общее решение системы
+ t(ln*-l), y = C2-t
Пример 7. Решить систему уравнений
dt dx dy
4y-5s 5*-3j/ За:-4*'
Решение. Умножая в системе (23) числители и знаменатели дробей
соответственно на 3, 4, 5 и складывая числители и знаменатели, получаем в силу (19)
3 dt _ Adx _ 5dy _3
\2y-\5x " 20*- 12y ~ 15ж-20* ~ 0
(здесь A| =3, A2 = 4, A3 = 5). Отсюда 3 dt + 4 dx + 5 dy или d(3t + 4x + 5y) = 0,
а значит 3t + 4x + 5y = C\ — это первый интеграл системы (23).
Умножая в системе (23) числители и знаменатели дробей соответственно
на Ai = 2*, А2 = 2ж, А3 = 2у и складывая числители и знаменатели, получаем
в силу (19)
2t dt _ 2xdx _ 2у dy _ 2t dt + 2x dx + 2y dy
%yt - \0xt ~~ \0tx - 6yx ~ 6xy - Щ ~ 0 '
отсюда
2t dx + 2x dx + 2y dy = 0, или d(r + x2 + у ) = 0,
и, значит, второй первый интефал будет t2 + ж2 + у2 = С2.
Совокупность первых интефалов, которые являются независимыми, дает
общий интеграл системы (23):
3* + 4х + 5у = С,, *2 + ж2 + у2 = С2.
Итак, система (23) решена. >
Задачи для самостоятельного решения
Решить следующие системы
796. * = d* = dy
* х ty
dx dxj dp
798. — = —- = — = —
у я g
800.
802.
dt dx
t2-x2- y2 2tx
\tdy = (tx + ty + 2x
дифференциальных уравнений:
797. *=£e*.
жу y< ж^
da ^ЛЛ dx dy di
—. 799. — = — = —
p xt -yt xy
( dx 3t- 4y
dy
2ty
-1) dt
801.
воз.
I dt 2y-3x
| dy 4x-2t
{ dt " 2y - Ъх
tdt
x2 - 2xy - y2
dx
x + y
dy
x-y
§ 22. Интегрирование однородных линейных систем
169
§22. Интегрирование однородных
линейных систем с постоянными
коэффициентами. Метод Эйлера
Линейной однородной системой с постоянными коэффициентами
называется система дифференциальных уравнений вида
~^ = ^ZaikXk(t)y t=l,2,...,n, (1)
где коэффициенты а,* — постоянные, a xk(t) — искомые функции от t.
Систему (1) можно коротко записать в виде одного матричного
уравнения
dt
где
п\2
X =
fxx(t)\
X2(t)
dX
~df =
/ dx}
~dt
dx2
~dt
dxn
V dt
)
Одностолбцовая матрица
Y(t) =
Vi{t)
называется частным решением уравнения (2) в интервале (а, Ь), если
выполняется тождество
—- = AY(t) для a<t<b.
at
Система частных решений
, ..., Xn(t) =
\ хп {?) /
(здесь в записи х\ нижний индекс указывает номер решения, а верх
ний — номер функции в решении) называется фундаментальной на ин
170
Глава 3. Системы дифференциальных уравнений
тервале (а, 6), если ее определитель Вронского
для всех t G (а, Ь).
Теорема. Если система частных решений однородного уравнения (2)
является фундаментальной, то общее решение этого уравнения имеет
вид
где С\, С2,..., Сп — произвольные постоянные.
Линейные системы можно интегрировать различными способами,
рассмотренными ранее, например методом исключения, путем
нахождения интегрируемых комбинаций и т.д.
Для интефирования однородных линейных систем с постоянными
коэффициентами применяется также метод Эйлера»
Рассмотрим этот метод в применении к системе трех линейных
дифференциальных уравнений:
Г dx _
dt "aa?
dt ]
dz
— = а2х + b2y + c2z.
(3)
Решение системы (З) ищем в виде
х = Aert, у = /лег\ z = uerf,, A, /i, v и г — const. (4)
Подставляя (4) в (3) и сокращая на е'*, получаем систему уравнений
для определения A, \i и и:
а2А
(а - г)А + Ь/г + си = 0,
(с2 - r)i/ = 0.
(5)
Система (S) имеет ненулевое решение, когда ее определитель А равен
нулю,
а-г Ь с
Д = а\ Ъ\-г С\ =0. (6)
а2 Ь2 с2 — т
Уравнение (6) называется характеристическим.
§22. Интегрирование однородных линейных систем
171
А. Пусть корни Г|,г2 и гз характеристического уравнения —
вещественные и различные. Подставив в (S) вместо г число г, и решив
систему (5), получим числа А|, Ц\ и v\. Затем положим в (5) г = г2 и получим
числа Аг,/*2, ^2 и, наконец, при г = гз получим Аз,/*з и 1/3.
Соответственно трем наборам чисел A, fi и v получим три частных решения
я», =А,вГ|',
З/з = А»зеРз',
Обшее решение системы (3) имеет вид
= 1/3еГз'.
х = С,А,е
Г1<
z = C\V\6 ' -f C^vit2 4- Сз^зеГз .
Пример 1. Решить систему
Г ota _
— = -ж-К5з/ - z,
I Л* = Х " V + 3Z'
Решение. Составляем характеристическое уравнение
= 0,
3-r -I I
-I 5-r -I
I -I 3-r
или г3-11г2 + 36г-36 = 0.
Корням г, =2, г2 = 3, гз = 6 соответствуют числа
А, = 1, /ii=0, i/|=-1;
Выписываем частные решения
3'
0,
Общее решение системы:
у = С2е3( - 2С3«6',
172 Глава 3. Системы дифференциальных уравнений
Б. Рассмотрим теперь случай, когда корни характеристического
уравнения комплексные. (
Пример 2. Решить систему
dx _
dy
~di = 2x~y'
Решение. Выпишем систему для определения Аир:
r(l-r)A-5/i = 0,
\2А-(1+г)/х = 0.
Характеристическое уравнение
1 -г -5
2 -1 -г
= 0
имеет корни г} = Зг, г2 = -Зг. Подставляя г, = Зг в (8), получаем два уравнения
для определения А] и //,:
(1 - Зг)А, - 5^, = 0, 2А, - (1 + Зг)/1, = 0,
из которых одно является следствием другого (в силу того, что определитель
системы (8) равен нулю).
Возьмем А! = 5, fi\ = 1 - Зг, тогда первое частное решение запишется так:
z,=5e3", yi=(1-3.y. (9)
Аналогично, подставляя в (8) корень г2 = -Зг, найдем второе частное решение:
х2 = 5е-м, y2 = (\+3i)e-M. (10)
Перейдем к новой фундаментальной системе решений:
_ Х\ -f- а; 2 ^. д? j — д?2
2 2г (11)
2/1 -Ь 2/2 2/, — г/2
№ = -2-, Л = ^—
Пользуясь известной формулой Эйлера e±ait = cos at ± i sin at, из (9), (10) и (11)
получаем
Xi = 5 cos 3£, x2 = 5 sin 3*,
y, = cos 3£ + 3 sin 3£, г/2 = sin 3^ — 3 cos 3t.
Общим решением системы (7) будет
х = C,z, + С2х2 = 5С, cos 3* 4- 5С2 sin 3i,
у = С\ух + С2у2 = С,(cos 3* + 3 sin 3t) + C2(sin 3* - 3 cos 3t). >
Замечание. Найдя первое частное решение (9), можно было бы сразу
написать общее решение системы (7), пользуясь формулами
х = С, Rex, +C2 Imx,, гу = С, Re у, + С2 Im yu
где Re z и Imz обозначают соответственно действительную и мнимую части
комплексного числа z, т. е. если z = a + Ьг, то Re z = a, Im z = b.
§ 22. Интегрирование однородных линейных систем 173
В. Случай кратных корней.
Пример 3. Решить систему
dx
2
Решение. Характеристическое уравнение
2-г 1
-1 4-г
= 0, или г - 6г + 9 = О
имеет кратный корень rj = г2 = 3.
Решение следует искать в виде
. (13)
Подставляя (13) в первое уравнение системы (12), получаем
3(А, + /ж,*) + /i, = 2(А, + pxt) + (А2 + #ж20. (И)
Приравнивая коэффициенты при одинаковых степенях t в левой и правой
части (14), получаем:
ЗА, + /i, =2А, + А2,
3/11 =2//, + /i2,
откуда
А2 = А,+/!,, /i2 = /i|. (15)
Величины А] и /ij остаются произвольными. Обозначая их соответственно
через С] и С2, получаем общее решение системы (12):
х = (С, + С2*)е3', у = (С, + С2 + C2t)e3t. >
Замечание. Легко проверить, что если (13) подставить во второе уравнение
системы (12), то получим тот же результат (15). В самом деле, из равенства
И2 + 3(А2 + fi2t) = 4(А2 + fi2t) - (А, + /*,*)
получаем два соотношения для определения А2 и \i2 через А] и /С|:
/х2 + ЗА2 = 4А2-Аь
3/i2 = 4/i2 -Ai|,
откуда А2 = А, +/i2, Ц2=^\.
Пример 4. Решить задачу Коши для системы
dx
dy
dt
dz
< ~dt
= 82/,
- - z,
= 2x + Sy-2z
с начальными условиями х(0) = -4, y(0) = 0, z(0) = 1.
174 Глава 3. Системы дифференциальных уравнений
Решение. Характеристическое уравнение
-г 8 О
О -г -2
2 8 -2-г
= 0, или (г + 2)(г2+16) = 0. (17)
Корни уравнения (17): г1 = -2, r2 = 4t, r3 = -4i. Действительному корню
г, = -2 отвечает решение
я, = А,е"2', у = /*,е"2<, *, =i/,e~2'. (18)
Подставляя (18) в систему (16) и сокращая на е~2', получаем
-2А, = 8/1,, -2^, = -2i/,, -2i/, = 2Л, + 8/i, - 2i/,,
откуда Л| = -4/ih i/| = /ij. Полагаем, например, /i| = 1, тогда At = -4, vx = 1
и частное решение (18):
а1 = -4е-2', У)=е-2', *, = е"2'. (19)
Комплексному корню г2 = 4* отвечает решение
«2 = А2е4", у2 = /i2e4", z2 = i/2e4",
подставив которое в (16) и сокращая на е4", получим
4*А2 = 8/42, 4t/i2 = -2i/2, 4ii/2 = 2А2 + 8/i2 - 2i/2,
откуда А2 = -2i/i2> Щ = -2t/i2, так что, например, при /i2 = t имеем А2 = 2,
i/2 = 2 и частное решение
«,-2е* у2 = «е4", ,2 = ^". (20)
Корню г3 = -4t соответствует решение, комплексно сопряженное
решению (20), т.е.
*,=2е-4й, Уз = -.-е-4й, z^u*". (21)
Учитывая (19), (20), (21), получаем общее решение
х = -4С,е"2' + 2С2е4" + 2С3е"4|\
у = С, е"2' + C2te4" - Сг1е'мь} (22)
Выделим, наконец, решение с начальными условиями х(0) = -4, у(0) = 0,
z(0) = 1. Из (22) при t = 0 имеем
-4 = -4С, + 2С2 + 2С3,
0 = С, + C2i - C3i,
1 = С, + 2С2 4- 2С3,
откуда С\ = 1, С2 = -, С3 = --. Итак,
Воспользовавшись формулами Эйлера e±iat = cosa^ ± tsinai, окончательно
получим
ж = -4е~2' - 2 sin 4t, у = e~2t - cos At, z = e"2< - 2 sin 4*. >
§ 23. Методы интегрирования неоднородных линейных систем 175
Задачи для самостоятельного решения
Методом Эйлера найти общее решение данных систем и, где указано, выделить
решение, удовлетворяющее поставленным начальным условиям.
804.
806.
808.
810.
dx
dx
dx
— = Ax - 5y, x(0) = 0,
f=x, y(0)=l.
dx „
- = 2x-y + z,
dz
805.
807.
809.
811.
dx _
dy =
Г da
— =x + y, a(0) = 0,
— = 4у-2з, у(0) = -1.
d£
dy
dt
z, a;(0) = 0,
z) y(0) = 0,
§23. Методы интегрирования
неоднородных линейных систем
с постоянными коэффициентами
Пусть имеем неоднородную линейную систему с постоянными
коэффициентами
If
, г = 1, 2,..., n,
которую короче можно записать в матричном виде
где F — одностолбцовая матрица, элементами которой являются
функции fi(t).
Теорема. Общее решение X(t) неоднородной линейной системы равно
сумме общего решения X0,0(t) соответствующей однородной системы
176 Глава 3. Системы дифференциальных уравнений
dX
— = АХ и любого частного решения Хч H(t) данной неоднородной
at . . >
системы
п
X(t) = Хо.о + X4M(t) = Y^ CkXk(t) + X4M(t),
где Ci, С2,..., Cn — произвольные постоянные.
Рассмотрим некоторые методы интегрирования неоднородных
линейных систем.
1°. Метод вариации произвольных постоянных (метод
Лагранжа). Проиллюстрируем этот метод на примере системы трех
неоднородных уравнений. Пусть задана система
(l.l)
(1.2)
z + аъх + Ъ2у + e3z = /з(^). (1.3)
Будем предполагать, что общее решение соответствующей
однородной системы уже найдено:
х = С\Х\ + С2Х2 -f С3Ж3,
у = С]У] +С22/2 + С32/з, (2)
Решение неоднородной системы (1) ищем в виде
я = С, (0«1 + С2(0«2 + С3(0»з,
(3)
где С|(^), С2(£)> Сз(0 — пока неизвестные функции.
Подставим (3) в (1), тогда уравнение (1.1) примет вид
С\х\
+ С\(х\ +а\Х\ +Ъ\у\ +e\Z\)
+ С3(х'з + а,х3 + 6,2/3
Все суммы, стоящие в скобках, обратятся в ноль (в силу того, что (2) есть
решение соответствующей однородной системы), так что будем иметь
Cl]x]+Cl2x2 + C'2x3 = f](t). (5)
Аналогично из (1.2) и (КЗ) после подстановки в них (3) получим
C']z] + С&г2 + C$2:3 =/(0
§ 23. Методы интегрирования неоднородных линейных систем 177
Система уравнений (5), (6), линейных относительно С{,С2,Сз имеет
решение, так как ее определитель
Х\ 2*2 ***3
2/1 2/2 2/з
z, z2 z3
в силу линейной независимости частных решений соответствующей
однородной системы. Отыскав C\(t)y C^t), Cf3(t), затем с помощью
интегрирования найдем Ci(£), С2(*)> Сз(0> а тем самым и решение (3) неоднородной
системы (1).
Пример 1. Методом вариации постоянных решить систему
dx
— = -2х - 4у + I + 4*,
^2/ 3 2
Решение. Сначала решим соответствующую однородную систему
5
Из второго уравнения системы (8) имеем
dy dx dy d2y
* = y--, такчто Tt=Tt~^.
dx
Подставим эти выражения для х и — в первое уравнение системы (8):
at
общее решение этого уравнения
Так как х = у , то будем иметь
Общее решение однородной системы (8) есть
х = -С,е2' + 4С2е~3', у = С,е2/ + C2e'3t.
Решение неоднородной системы (7) ищем в виде
х = -C,(t)e2t + 4C2(t)e-*, у = Cx(t)e2t + С2(Ое"3<. (9)
Подставив (9) в (7) и приведя подобные члены, получим
178
Глава 3. Системы дифференциальных уравнений
откуда
Интегрируя, найдем
,
,
10
где С| и С2 — произвольные постоянные. Подставляя (10) в (9), получим общее
решение системы (7)
х = -С,е2* + 4С2е"3' +t +12, у = С,е2' + С2е"3' - 1 +1\
Задачи для самостоятельного решения
Методом вариации произвольных постоянных найти общее решение следующих
линейных неоднородных систем:
dx_ _
dt ~x + y
812.
814.
816.
at
dx
dt
dy
dt
dx
dt
dy
dt
= y + tg'i-
= tg t - x.
= y>
1
= —ж Н
cost
813.
815.
dy
dt
*(0)=1,
= -y - 2x + cos < + sin ty
У(0) = "2.
dy
_
3
2°. Метод неопределенных коэффициентов (метод
подбора). Этот метод применяется для решения неоднородной системы
линейных уравнений тогда, когда функции /,•(<), стоящие в правой
части системы, имеют специальный вид: многочлены Pk(t)9 показательные
функции eat, синусы и косинусы sin/ft, cos fit и произведения этих
функций. Проиллюстрируем этот метод на примерах.
Пример 2. Найти общее решение неоднородной системы
dx
(И)
§ 23. Методы интегрирования неоднородных линейных систем 179
Решение. Найдем сначала общее решение соответствующей однородной
системы
dx
2
(12)
Характеристическое уравнение имеет вид
1-А -2
1 4-А
: 0, или А2 - 5А + 6 = 0.
Корни этого уравнения А, = 2, А2 = 3. Корню А, = 2 соответствует частное
решение системы
*| = А*1в2*, у\ =1/|в2<.
Подставляя Х\ и у\ в (12), получаем систему уравнений для нахождения рх и i/t:
-/i, - lv\ = 0, /i, + 2i/, = 0.
Отсюда имеем, например, /j( = 2, у, = -1, так что первое частное решение
однородной системы (11) есть
х\ = 2е2<, у, = -е2'.
Корню А2 = 3 соответствует частное решение
*2 = /*2*3<, У2 = ^е3е.
Числа /i2 и i/2 находим из системы
Г -2/i2 - 2i/2 = 0,
I 0,
которой удовлетворяют, например, числа /i2 = 1, и2 = -1. Тогда второе частное
решение системы (12) есть
х2 = е3', у2 = -с3<.
Общее решение однородной системы (12):
х = 2С,е2е + С2е3', у = -С,е2' - С2е3<.
Методом неопределенных коэффициентов находим частное решение
неоднородной системы (11). Исходя из вида правых частей f\(t) = e* и f2(t) = e2it
записываем вид частного решения (см. табл. 1)
хцм = Кег + (Lt + М)е2', уч.„ =ЛГе' + (Ре + Q)e2t. (13)
Подставляя (13) в (11), будем иметь
Ке* + 2(Lt + M)e2t + Le2t = Дее -f (ie + M)e2t - 2^е' - 2(Pe + Q)e2t + e\
Nel + 2(Pe + Q)e2e + Pe2t = Ktx + (Lt + M )e2t + 4iVe* + 4(Pe + Q)e2' + e2e.
Приравнивая коэффициенты при е1, e2t и ее2< в обеих частях этих тождеств,
получаем из первого:
= K-2N+\y
2М + L = М - 2Q,
*ел 2L = L-2P,
180 Глава 3. Системы дифференциальных уравнений
из второго:
N = К + 4JV,
te2
2Р = L + 4P.
Решая эту систему уравнений, находим К — —, L = 2, М = 0, iV = -, Р = —1,
Q = -1. Значит, частное решение (13) имеет вид
хчм = -\el + 2te2t, учм = Х-е1 -
Общее решение неоднородной системы
Пример 3. Решить систему
dx
— = х + 2у,
— = х - 5 sin t.
at
Решение. Характеристическое уравнение
1 -А
1 -Л
= 0, или А2 - Л - 2 = 0.
Корни характеристического уравнения А| = -1, А2 = 2. Общее решение
соответствующей однородной системы:
x = C]e~t + 2С2е2\ у= -С,е~* + C2e2t.
Найдем частное решение неоднородной системы (14), имея в виду, что
/,(t) = 0, /2(t) = -5sint. Запишем жч.н и уч.н в виде
жч.„ = A cos t + В sin t, уч.„ = М cos t + iV sin t
и подставим в систему (14):
-A sin t + В cos t = A cos t + Б sin t + 2M cos t ^- 2iV sin t,
-M sin t.+ JV cos t = A cos t + В sin t - 5 sin t.
Приравниваем коэффициенты при sint и cost в обеих частях равенств:)
-А = В + 2Ny
В = А + 2М,
-М = В - 5,
отсюда л4 = -1, В = 3, М:р 2, JV = — 1, так что
а?ч н = — cost + 3 sin t, y,,.H = 2 cost - sin t.
§ 23. Методы интегрирования неоднородных линейных систем 181
Общее решение исходной системы:
e~l + 2C2e2t
' 2f + 2cos*-sin*.
х = х + £,,.н = С, e~l + 2C2e2t - cos t + 3 sin *,
Пример 4. Решить систему
dx 4
— =x + 2y+ \6te\
di
Решение. Характеристическое уравнение
1 -Л
= 0, или Л2 + А - 6 = 0.
Корни характеристического уравнения А| = 2, А2 = -3. Общее решение
однородной системы, соответствующей системе (15):
х = 2С, e2t + C2e"3t, у = Cbe2t - 2C2e'3t.
Частное решение неоднородной системы уравнений (15) ищем в виде
яч.н = (At + B)e\ Uhm = (Mt + N)e\ (16)
Подставим (16) в (15) и сократим на е':
At + B + A = At + B + 2Mt + 2N + 16*,
Mt + JV + M = 2At + 2B - 2M* - 2JV,
отсюда ^ = -12, В = -13, М = -8, JV = -6. Итак,
жч.н = -(12*4- 13)е*, 3/ц.н = -(W + 6)e*.
Общее решение исходной системы:
ж = ж + хчм = 2С,е2' + С2е"3< - (12* -f M)e\
У = У + 2/ч.н = Cxe2t - 2С2е"3< - (8* + 6)е*. >
Задачи для самостоятельного решения
Проинтефировать неоднородные линейные системы, с постоянными
коэффициентами.
dx
817. <( f 818.
d* ~ ] Ж'
da:
— = -y + sin*,
819. { f 820.
dy
—-= x + cost,
dt
dx
~dt
dy
dt
dx
It
dy
dt
= 3-2y,
= 2x - 2*.
= x + y +
= x + у -
182
Глава 3. Системы дифференциальных уравнений
821. <
823.
825.
, у(0) = 0.
dy
dt
dx
dt
dy
dt
— x
= 2;
= 1
x + i
822.
824.
826.
', x(O)=l,
da; dy
' dx
—
3°. Построение интегрируемых комбинаций (метод Да-
ламбера). Этот метод служит для построения интегрируемых
комбинаций при решении систем линейных уравнений с постоянными
коэффициентами. Покажем его применение для решения систем двух уравнений:
(17)
Умножим второе уравнение на некоторое число Л и сложим почленно
с первым уравнением:
d(x + Ay)
dt
= (а, + Xa2)x + (Ь, + \Ъ2)у + /, (t) + Xf2(t).
Перепишем последнее уравнение в виде
ш (в,
at
Выберем число А так, чтобы
(18)
(.9)
v f
Тогда (18) приводится к уравнению, линейному относительно х + Ху
d{x + Ху) .
-г = (^1 •
dt
§ 23. Методы интегрирования неоднородных линейных систем 183
интегрируя которое, получаем
'dt
}• (20)
Если уравнение (19) имеет различные вещественные корни Л| и Л2,
то из (20) получим два первых интеграла системы (17), и, значит,
интегрирование этой системы будет окончено.
Пример 5. Решить методом Даламбера систему
-£ = 4в + 5у+1.
at
Решение. Выберем А по формуле (19): 4 + 5А = А(5 + 4А), откуда A,t2 = ±1.
Тогда по формуле (20) для случая А = 1 будем иметь
х + у = е<5+41><{с, + /(е' + l)e-(5+4I)< dt\ =
у
- у = е(5"4)<|с2 + /V " 0е"(5"4)< dt\ = С7е* + <ее + 1.
Для А = -1 аналогично получаем
х
Итак, имеем два первых независимых интеграла системы (21):
a-C, (ш-y-te1-Oe'^Cj.
Интефирование системы закончено. >
Замечание. Если правые части нормальной системы уравнений имеют вид
аж + by + cz + Р(е)
, где а^Ь^с — постоянные, a P(t) многочлен от <, то
подстановка t = er приводит к системе с постоянными коэффициентами.
Пример в. Решить систему уравнений
№ = x
at
Решение. Сделаем замену переменного t = ег. Тогда
dx ^ dx dr _ 1 dff dy 1 dy
184 Глава 3. Системы дифференциальных уравнений
и система примет вид
-Д = -2х + 2у + е',
I (22)
dy 2т
Для решения системы (22) применим метод Даламбера. Умножим второе
уравнение системы на А и сложим почленно с первым:
^-{х + Ху) = (-2 - Х)х + (2 - 5\)у + ет + Ае2г
аг
или
^-{х + Ху) = (-2 - Х)х + (2 - 5\)у + ет + Ае2г,
аг
±(х + Ау) = (-2 - Л) [* + ^^у] + ет + Ае2г. (23)
Выберем Л так, чтобы коэффициент при у в квадратной скобке был равен Л,
т.е. = Л, или Л2 - ЗА + 2 = 0, откуда Л, = 1, А2 = 2. При А, = 1 из (23)
получаем
dr
откуда, согласно формуле (20), будем иметь
я + у = е"3г [с, Ч^(ег + е2 V'Д
После интегрирования получаем
я + у = С|е-3Ч-ег + -е2т. (24)
При А2 = 2 из (23) аналогично находим
* + 2у = С2е-4Ч^ег+^е2г. (25)
Решая систему (24)-(25) относительно а: и у, получаем общее решение систе-
,мы (22):
х =
- С2е"4г + 0,Зег + -^е2г,
у =± -С,е-Зт + С2е"4г - 0,05ег + -^е2г
Возвращаясь к переменной t (eT = f), получим общее решение данной системы
_ 2С, С2 3i i2 _ Сх С2 t It1
Задачи для самостоятельного решения
Решить методом Даламбера следующие системы уравнений:
dx ( dx ( dx
5 4 в \
5* + 4у, вх + уу
827. < * 828. i f 829.
§ 24. Применение преобразования Лапласа 185
dx
—
830. { f 831. i 7
dv t
-£=x + 3y-el. £
dt V at
§ 24. Применение преобразования
Лапласа к решению линейных
дифференциальных уравнений и систем
1°. Общие сведения о преобразовании Лапласа.
Оригинал и изображение. Функцией-оригиналом называется комплекснозначная
функция f(t) действительного переменного t, удовлетворяющая
следующим условиям:
1) f(t) = 0, если t < 0;
2) f(i) интегрируема на любом конечном интервале оси t\
3) с возрастанием t модуль функции f(t) растет не быстрее
некоторой показательной функции, т.е. существуют числа М > 0 и sq ^ 0
такие, что для всех t имеем
(1)
Изображением функции-оригинала по Лапласу называется функция
F(p) комплексного переменного р = s + га, определяемая равенством
+0
= J
f(t)e-"dt (2)
при Rep > So. Условие 3 обеспечивает существование интеграла (2).
Преобразование (2), ставящее в соответствие оригиналу f(t) его
изображение F(p), называется преобразованием Лапласа. При этом пишут
Свойства преобразования Лапласа. Всюду в дальнейшем считаем, что
/(0 = f(p), 9(t) = G{p). (3)
I. Свойство линейности. Для любых комплексных постоянных аир
<*f(t) + №) = <*F{P) + PG{p). (4)
II. Теорема подобия. Для любого постоянного а > О
III. Дифференцирование оригинала. Если f'(t) есть оригинал, то
f'(t)=pF(p)-f(O). (6)
186 Глава 3. Системы дифференциальных уравнений
Обобщение:
Если f(t) n раз непрерывно дифференцируема на (0, +оо) и если f^(t)
есть оригинал, то
f(n)(t) = pnF(p) - /"'/(О) - /-2/'(0) - ...» /(п-!)(0). (7)
IV. Дифференцирование изображения равносильно умножению
оригинала на «минус аргумент», т. е.
РЬ) .= -</(<). (8)
Обобщение:
^п(р).= Н)п*п/(0- (9)
V. Интегрирование оригинала сводится к делению изображения на р:
/ f(t) dt = -^. (10)
i p
VI. Интегрирование изображения равносильно делению на t оригинала:
00
/ F(p) dp = (11)
J t
p
00
(предполагаем, что интеграл J F(p) dp сходится).
p
VII. Теорема запаздывания. Для любого положительного числа т
II11. Теорема смещения (умножение оригинала на показательную
функцию). Для любого комплексного числа А
extf(t) = F(p - A). (13)
IX. Теорема умножения (Э. Борель). Произведение двух изображений
F(p) и G(p) также является изображением, причем
t
F(p)G(p) = J f(r)g(t - r) dr. (14)
о
Интеграл в правой части (14) называется сверткой функций f(t) и g(t)
и обозначается символом
t
= Jf(r)9(t-T)dT.
§ 24. Применение преобразования Лапласа 187
Теорема XI утверждает, что умножение изображений равносильно
свертыванию оригиналов, т. е.
f(p)G(jp) = (f*g). (15)
Отыскание оригиналов дробно-рациональных изображений. Для
нахождения оригинала f(t) по известному изображению F(p)9 где F(p) =
/ есть правильная рациональная дробь, применяют следующие при-
емы.
1) Эту дробь разлагают на сумму простейших дробей и находят для
каждой из них оригинал, пользуясь свойствами I—IX преобразования
Лапласа.
2) Находят полюсы pk) к = 1,2,..., m этой дроби и их кратности п*.
Тогда оригиналом для F(p) будет функция
где сумма берется по всем полюсам функции F(p).
В случае, если все полюсы рк функции F(p) простые, т.е. п* = 1,
к = 1, 2,..., т, последняя формула упрощается и принимает вид
•еЧ (17)
Пример 1. Найти оригинал /(<). если
р + 2
' (р+\)(р-2)(р2 + 4)'
Решение. Первый способ. Представим F(p) в виде суммы
простейших дробей
р + 2 А ,5 , Cp + D
и найдем неопределенные коэффициенты A^ByC^D. Имеем
Полагая в последнем равенстве последовательно р = -1, р = 2, р = 2i, получаем
-15Л= 1, 24В = 4
(2Ci + D)(2i + 1)(2« - 2) = 2 + 2i,
откуда i4 = -—, В= -, С = -—, J9 = --; значит,
10р2+4"
188 Глава 3. Системы дифференциальных уравнений
Находя оригиналы для каждой из простейших дробей и пользуясь свойством
линейности, получаем
Второй способ. Найдем полюсы рк функции F(p). Они совпадают
с нулями знаменателя В(р) = (р + \)(р- 2)(р2 +4)- Таким образом,
изображение F(p) имеет четыре простых полюса р, = -1, р2 = 2, рз = 2», р* = —2t.
Пользуясь формулой (17), получаем оригинал
15
15 +6 20 20
2'"
p + 2
Пример 2. Найти оригинал /(*), если F(p) = -гт -гт.
Р (р- U
Решение. Данная дробь F(p) имеет полюс р, = 0 кратности п\ = 3 и полюс
р2 = 1 кратности П2 = 2. Пользуясь формулой (16), получаем оригинал
ип, ^ [ ^ЦпРв1 + lim
2 р^о dp1 Lp3(p - IF J P-i <*P
1 d2 fp + 2
= - lim —т y-—-
^ [ ^ЦпР lim I f-jfi^y <р - 0
dp1 Lp3(p - IF J <*P LP3(P О2
1 d2 fp + 2 J
= - lim ?1 \
2
d /p + 2 „Л
J p^dp\ p3 У
2Р+16 2t(p + 5) <2(p + 2)1 Л
о^П* (p-i)3 (p-o2J /
2°. Решение задачи Коши для линейных
дифференциальных уравнений с постоянными коэффициентами. Пусть
требуется найти решение дифференциального уравнения второго
порядка с постоянными коэффициентами
(18)
удовлетворяющее начальным условиям
а(0) = *0, х'(0) = хх. (19)
Будем считать, что функция f(t) и решение x(t) вместе с его производньь
ми до второго порядка включительно являются функциями-оригиналами.
Пусть x(t) = Х(р), f(t) = F(p). По правилу дифференцирования
оригиналов с учетом (2) имеем
x(t) = рХ(р) - «о, x"(t) = р2Х(р) - рж0.- я?,.
§ 24. Применение преобразования Лапласа 189
Применяя к обеим частям (1) преобразование Лапласа и пользуясь
свойством линейности преобразования, получаем операторное уравнение
(р2 + ахр + а2)Х(р) = F(p) + хо(р + а,) + я,. (20)
Решая уравнение (20), найдем операторное решение
w i4 _
р2 + а\р+ а2
Находя оригинал для Х(р), получаем решение уравнения (18),
удовлетворяющее начальным условиям (19).
Аналогично можно решить любое уравнение n-го порядка с
постоянными коэффициентами и с начальными условиями при t = 0.
Пример 3. Решить уравнение
z' + s=l, (21)
*(0)=1. (22)
Решение. Пусть x(t) = Х(р), тогда по правилу дифференцирования
оригинала имеем
x'(t)=pX(p)-x(0)=PX(p)-\.
Известно, что I = -,, поэтому, переходя отданной задачи (21)—(22) к оператор-
Р
ному уравнению, будем иметь
рХ(р)-\+Х(р)=Х-,
откуда
(р+1)Х(р) = 1 + - или Х(р) = -
Р Р
следовательно, x(t) = 1.
Легко видеть, что функция x(t) = 1 удовлетворяет данному уравнению
и начальному условию задачи. >
Пример 4. Решить уравнение х" --5х' + 4а? = 4, х(0) = 0,- х'(0) = 2.
4 '"
Решение. Так как 4 .=' - и по условию х0 = х(0) = 0, ж, = х'(0) = 2,
Р
4
то операторное уравнение будет иметь вид (р2 - 5р + 4)Х(р) = —h 2. Отсюда
находим операторное решение
Разлагаем правую часть на элементарные дроби:
р р-\ р-4
Переходя к оригиналам, получаем искомое решение
x(t) = 1 - 2еЧ e4t.
190 Глава 3. Системы дифференциальных уравнений
Пример 5. Решить уравнение
х11 + Ах1 + Ах = 8е~2*, ж(0) = 1, х'(0) = 1.
Решение. Так как 8е"2* = г и по условию а0 = «i = 1, то операторное
р +
уравнение будет иметь вид
и, следовательно, операторное решение
Разложим правую часть на элементарные дроби:
8 3
р + 2)3 ' (р + :
1
2)2 ' Р + 2'
Переходя к оригиналам, получим решение поставленной задачи
a(f) =
• At2e"2i + lie'2
ЧеЛ >
Задачи для самостоятельного решения
Решить следующие уравнения:
832. а' + За = е~2',
833. х - За = 3<3 + 3J2 + It +
834. а'-а = cost-sin<,
835. 2а' + 6а = *е~3',
836. a' + a = 2sint,
837. а" = 0,
838. а" = 1,
839. a" = cos*,
840. а" + а' = 0,
841. а" + а' = 0,
842. а"-а'= 1,
843. J' + x^t,
844. а" + 6а' = 12*+ 2,
845. а" - 2а' + 2а = 2,
846. а" + 4а' 4- 4а = 4,
847. 2а"-2а' = (*+1)е',
848. а" + а = 2 cos t,
849. a" + 3a' + 2a = 2*2+l,
850. а" + а = 2ее,
851. a"-4a' + 4a = (t-1)e2',
852. 4а" - 4а' + а = еч\
а(0) = 0.
1, а(0) = -1,
а(0) = 0.
в(0) = -5
а(0) = 0.
а(0) = 0,
а(0) = 0,
а(0) = 0,
а(0)=1,
а(0) = -1
а(0) = 0,
а(0) = 0,
а(0) = 1,
а(0)=1,
а(0) = -1
а(0) = 4,
а(0)=1,
а(0) = 0,
а(0) = -2
а'(0) = 0.
х'(0) = 0.
а'(0) = 0.
а'(0) = 0.
ж'(0) = -1.
, а'(0) = -1.
а'(0)=1.
а'(0) = 0.
а'(0) = 0.
а'(0) = -4.
*'(0)=j.
, а'(0)=1.
а'(0) = -3.
а'(0) = 2.
а'(0)=1.
, а'(0) = 0.
§ 24. Применение преобразования Лапласа 191
853.
854.
855.
856.
857.
858.
859.
860.
861.
х"
х"
х"
х"
х"
х"
х'"
+ 3х'
-х'-
+ 4х;
-х' =
+ 9х
+ 4х
+ 2*'
-х"
+ 2х = е'1 + е"2',
- 6х = бе5' + 2е~2',
+ 4x = t2e-2',
= 2 sin t,
= I8cos3(,
= 4 cos 2t - - sin 2t,
+ 3x = <cost,
= 0,
x(0) = 2,
x(0) = 0,
x(0) = x'
x(0) = 2,
x(0) = 0,
x(0) = 0,
x(0) = -
), x(0)=l,
x(0)=l,
x'(0) = -3.
x'(0)=|
(0) = 0.
x'(0) = 0.
x'(0) = 9.
x'(0) = 1.
1 ,
a:'(0) = 3, xftl0) = 2.
862. хш - 4а?' = 1, а?(0) = 0, а;'(0) = -1, а?;/(0) = 0.
863. я'" + в" - 2* = 5е', «(0) = 0, а>'(0) = 1, х"(0) = 2.
864. х" + а: = 8\/2 sin 6 + ^)» «(0) = 0, а?;(0) = -4.
865. *" + 4aj = 2cos2t, х(0) = 0, а?'(0) = 0.
3°. Решение систем линейных дифференциальных
уравнений с постоянными коэффициентами. Пусть требуется
найти решение системы двух уравнений с постоянными коэффициентами
удовлетворяющее начальным условиям
«(О) = я?о, У(О) = 1Л). (24)
Будем предполагать, что функции /i (*)> Л(*)» ж(*)> У(*)> а также а?'(^)
и y'(t) являются функциями-оригиналами.
Пусть
По правилу дифференцирования оригиналов с учетом (24) имеем
- а?0> 2/'(0
Применяя к обеим частям каждого из уравнений системы (23)
преобразование Лапласа, получим операторную систему
Г рХ(р) =
\ рУ(р) = а2Х(р) + Ь2Г(р) + F2(p) + 2,0.
192 Глава 3. Системы дифференциальных уравнений
Эта система является линейной алгебраической системой двух
уравнений с двумя неизвестными Х(р) и Y(p). Решая ее, мы найдем Х{р)
и У(р), а затем, переходя к оригиналам, получим решение x(t), y(t)
системы (23), удовлетворяющее начальным условиям (24). Аналогично
решаются линейные системы вида
= х°к1 *=1,2,...,п.
dxk ^-ч
Пример
ак
6.
Найти
;(0> akl
решение
( dx
Tt~-
= const,
системы
удовлетворяющее начальному условию х(0) = О, у(0) = 0.
5 37
Решение. Так как 5 = -, -37t = —г и х0 = у0 = 0, то операторная
Р Р
система будет иметь вид
Решая ее, получаем
-47p - 259
Разлагаем дроби, стоящие в правых частях, на элементарные:
р
или
1. Г + 6
7
—\-
p P2 (p + 6)2 + 1
Переходя к оригиналам, получим искомое решение
x(t) = 1 - t - e~6t cos *, y(i) = 1 - It + e~6' cosi + e~6' sin <.
§ 24. Применение преобразования Лапласа
193
Задачи для самостоятельного решения
В следующих задачах решить операционным методом системы уравнений:
866.
868.
870.
872.
874.
875.
dx
— +у = 0, *(0) = 2,
^+* = 0, „(0) = 0.
«"У, *(0)=1,
dx
—
, 2/(0) =1.
е\ а(0)=1,
*> у(0)=1.
I dt -^
, у(0) = 2,
z(0) = 3.
867.
869.
871.
873.
da;
—+ x-2y = 0, x(0)=l,
ijL+x + 4y = 0, y(0)=l.
^-2x = 4, y(0) = 3.
г-S—"■
z, x(0) = 5,
J=z, y(0) = 0,
= 4'
876.
877.
——^— — i* i» /Пi ^^ 0 ** illi ^— О
—^ **^i •** 1 vJ ^^ ^* U \^/ ~" v«
-£=x-Ay, x(0) = 2, y(0) = 0,
^
878.
^ + ^ = 1, x'(0) = 2, y'(0) = -l.
194 Глава 3. Системы дифференциальных уравнений
d2a?
-^ + x + у = 5, x(0) = a; (0) = 0,
879.
^f - 4a; - 3y = -3, y(0) = y'(0) = 0.
-37 + 4y + 2a; = 4* + 1, a;(0) = 0,
dt + * У 2^ '
da;
— + у - 2a? = 0, a?(0) = 2,
881. < *
^+a?-2y = -5e'sini, y(0) = 3.
ГЛАВА Теория
4
устойчивости
§25. Устойчивость по Ляпунову.
Основные понятия и определения
Пусть имеем систему дифференциальных уравнений
dxi
— = fi(x\)x2)...>xn,t)) t = 1,2, ...,n. (1)
at
Решение v>i(0> * = '»2, ...,п, системы (1), удовлетворяющее
начальным условиям ^,-(*о) = y>i(h « = 1,2, ...,п, называется устойчивым
по Ляпунову при £ -+ оо, если для любого е > О существует 0(е) > 0 такое,
что для всякого решения я,(0, г = 1,2,... ,п, системы (1), начальные
значения которого удовлетворяют условиям
Ыго)-Ы<*> г = 1,2,... ,п, (2)
имеют место неравенства
Ыг) - <р{(г)\ < е, г=1,2,...,п, (3)
для всех t^ t0.
Если при сколь угодно малом 6 > 0 хотя бы для одного решения
£,•(*), i = 1,2,..., п, неравенства (3) не выполняются, то решение <pi(t)
называется неустойчивым.
Если кроме выполнения неравенств (3) при условии (2) выполняется
также условие
\х{(г) - Vi(t)\ = 0, г=1,2,...,п, (4)
то решение <pi(t), г = 1, 2,..., п, называется асимптотически устойчивым.
Исследование на устойчивость решения <pi(t)} г = 1,2,..., п,
системы (1) можно свести к исследованию на устойчивость нулевого
(тривиального) решения ж, = 0, г = 1, 2,..., п, некоторой системы, аналогичной
системе (1),
tier'
—- =Fi(xuX2,...,xn,t), г= 1,2, ...,п, (Г)
at
где Я(0,0,...,0,0 = 0, г= 1,2,..., п.
Говорят, что точка ж,- = 0, г = 1,2,... ,п, есть точка покоя
системы (Г).
Применительно к точке покоя определения устойчивости и
неустойчивости могут быть сформулированы так. Точка покоя Xi = О,
196
Глава 4. Теория устойчивости
г = 1, 2,..., тг, устойчива по Ляпунову, если, каково бы ни было 'е > О,
можно найти такое S > О, что для любого решения ж,-(£), t = 1, 2,..., п,
начальные данные которого ж;о = ж,(£0), * = 1,2,...,п, удовлетворят
условию
|x.-ol<«, г=1,2,...,п, (2')
выполняются неравенства
г =1,2,.
, п,
(3/)
для всех t^ to.
Для случая п = 2 геометрически это означает следующее. Каким бы
малым ни был радиус е цилиндра с осью Ot, в плоскости t = t0
найдется £-окрестность точки (0,0, *о) такая, что все интегральные кривые
Рис. 30
выходящие из этой окрестности, для всех
t ^ to будут оставаться внутри этого
цилиндра (рис. 30).
Если кроме выполнения неравенств (3),
выполняется также условие lim \xi(t)\= 0,
г = 1, 2,..., п, то устойчивость
асимптотическая.
Точка покоя Х{ = 0, г = 1,2, ...,п,
неустойчива, если при сколь угодно
малом 6 > 0 хотя бы для одного решения
Xi(t), г = 1, 2,..., 71, условие (3;) не
выполняется.
Пример 1. Исходя из определения устойчивости по Ляпунову,
исследовать на устойчивость решение уравнения
dx
удовлетворяющее начальному условию
х(0) = 0.
(5)
Решение. Уравнение (5) есть линейное неоднородное уравнение. Его общее
решение x(t) = Ce~l +1. Начальному условию х(0) = 0 удовлетворяет решение
(7)
уравнения (5). Начальному условию х(0) = х0 удовлетворяет решение
x(t) = хое~г +1.
Рассмотрим разность решений (7) и (6) уравнения (5) и запишем ее так:
x(t) - <p(t) = хое~1 + t-t = (x0- 0)e~'.
§25. Устойчивость по Ляпунову. Основные понятия и определения 197
Отсюда видно, что для всякого е > 0 существует 6 > 0 (например, 6 = е)
такое, что для всякого решения x(t) уравнения (5), начальные значения которого
удовлетворяют условию |ж0 - 0| < 6, выполняется неравенство
для всех t ^ 0. Следовательно, решение <p(t) = t является устойчивым. Более
того, поскольку
lim \x(t) - <p(t)\ = lim \x0 - 0\е~г = 0,
решение <p(t) = £ является асимптотически устойчивым.
Это решение <p(t) является неограниченным при t —> +оо. >
Приведенный пример показывает, что из устойчивости решения
дифференциального уравнения не следует ограниченности решения.
Пример 2. Исследовать на устойчивость решение уравнения
= sin 2x. (8)
dx ,
dt
Решение. Оно имеет очевидные решения
x = kn, Jb = 0,±l,±2,... . (9)
Интегрируем уравнение (8):
ctgx = C -t, или ctg х = ctg х0 - *,
откуда
s = arcctg(ctga?o-O> хфкж. (10) Рис.31
Все решения (9) и (10) ограничены на (-оо, Ч-оо). Однако решение x(t) = 0
неустойчиво при t —► +оо, так как при любом Хо € (0, тг) имеем lim x(t) = тг
(рис.31). >
Следовательно, из ограниченности решений дифференциального
уравнения, вообще говоря, не следует их устойчивости.
Это явление характерно для нелинейных уравнений и систем.
Пример 3. Исходя из определения устойчивости по Ляпунову,
показать, что решение системы
ОО
удовлетворяющее начальным условиям х(0) = 0, у(0) =; 0, устойчиво.
Решение. Решение системы (11), удовлетворяющее заданным начальным
условиям, есть x(t) = 0, y(t) = 0. Любое решение этой системы, удовлетворяющее
условиям ж(0) = Хо, у(0) = уо» имеет вид
x(t) = х0 cos t-yo sin t} y(t) = x0 sin t + y0 cos t.
dx
~dt
dy
dt
= -y
= 05,
198 Глава 4. Теория устойчивости
Возьмем произвольное е > О и покажем, что существует 6(е) > О такое, что
при \xq - 0| < £, |уо - 0| < 6 имеют место неравенства
\x(t) - 0| = |ж0 cos t - у0 sin t\ < е, \y(t) - 0| = \х0 sin t + уо cos t| < e,
для всех J ^ 0.
Это и будет означать, согласно определению, что нулевое решение x(t) = 0,
y(t) = 0 системы (11) устойчиво по Ляпунову. Имеем, очевидно,
|sosin£ + yocos*l ^ |xo sin t| + |y0 cos$| ^ |жо| + |yo|
для всех t. Поэтому, если |хо| 4- Ы < е, то и подавно
|aj0cosi-y0sini| < е, |ж0 sin* Ч- уо cosi| < e (13)
для всех t. i
Следовательно, если, например, взять 6(е) = е/2, то при |а?0| < б и \уо\ < б
в силу (12) будут иметь место неравенства (13) для всех t ^ 0, т.е.
действительно нулевое решение системы (11) устойчиво по Ляпунову, но эта устойчивость
не асимптотическая. >
Теорема. Решения системы линейных дифференциальных уравнений
либо все одновременно устойчивы, либо неустойчивы.
Это предложение не верно для нелинейных систем, некоторые решения
которых могут быть устойчивыми, а другие — неустойчивыми.
Пример 4. Исследовать на устойчивость решение нелинейного
уравнения
£■=1-«*<«). (14)
Решение. Оно имеет очевидные решения (p(t) = -1 и <p(t) = 1.
Решение <p(t) = -1 этого уравнения неустойчиво, а решение <p(t) = 1
является асимптотически устойчивым. В самом деле, при t -> +оо все решения
уравнения (14)
H:::::::i!::i <*-■>
стремятся к +1. Это означает, согласно определению, что решение <p(t) = 1
уравнения асимптотически устойчиво. >
Задачи для самостоятельного решения
Исходя из определения устойчивости по Ляпунову, исследовать на устойчивость
решения следующих уравнений и систем уравнений:
882. $ = * + *, я(0) = 1. 883. § =
at at
J = -*-2y, y(0) = 0.
§26. Простейшие типы точек покоя 199
885. §=
at
( dx
887. I
§26. Простейшие типы точек покоя
Пусть имеем систему двух линейных однородных дифференциальных
уравнений с постоянными коэффициентами
dx
— = п\\Х
i
dt
причем
A =
аи п\2
а2\ а22
Точка х = 0, у = 0, в которой правые части уравнений системы (1)
обращаются в ноль, называется тонкой покоя системы (1).
Для исследования точки покоя системы (1) надо составить
характеристическое уравнение
- Л an
2\ О>21 - А
= 0 (2)
и найти его корни Л] и Лг.
Возможны следующие случаи.
1. Корни Aj, A2 характеристического уравнения (2) вещественные и
разные:
а) А| < 0, Аг < 0. Точка покоя асимптотически устойчива
(устойчивый узел, рис.32);
б) Ai > 0, А2 > 0. Точка покоя неустойчива (неустойчивый узел,
рис.33);
в) А| > 0, Аг < 0. Точка покоя неустойчива (седло, рис. 34).
2. Корни характеристического уравнения (2) комплексные: А| = p + iq,
А2 = V - «?:
а) V < О» Я Ф 0- Точка покоя асимптотически устойчива (устойчивый
фокус, рис.35);
б) р > 0, q Ф 0. Точка покоя неустойчива (неустойчивый фокус,
рис.36);
в) р > 0, q Ф 0. Точка покоя устойчива (центр, рис. 37).
200
Глава 4. Теория устойчивости
Рис. 32
Рис. 33
Рис. 34
Рис. 35
Рис. 36
Рис. 37
Рис. 38
Рис. 39
§ 26. Простейшие типы точек покоя
201
Рис. 40
Рис.41
3. Корни Л| = Лг кратные:
а) Л| = Л2 < 0. Точка покоя асимптотически устойчива (устойчивый
узел, рис. 38, 39);
б) Aj = Л2 > 0. Точка покоя неустойчива (неустойчивый узел,
рис.40, 41).
Пример 1. Определить характер точки покоя (0,0) системы
dx
5
Решение. Составляем характеристическое уравнение
5-Л -I
2 1-Л
= 0, или Л2-6Л + 7 = 0.
Его корни Ai=3 + \/2>0, А2 = 3 - \/2 > 0 вещественные, разные,
положительные. Следовательно, точка покоя (0,0) — неустойчивый узел.
Связь между типами точек покоя и значениями корней характеристического
уравнения (2) можно представить наглядно. Для этого введём обозначения а =
~(ац + а22), А = апа22 - О|2а2ь Тогда характеристическое уравнение запишется
в виде А2 + <т\ 4- А = 0.
Рассмотрим плоскость с прямоугольными декартовыми координатами А и а
и отметим на ней области, соответствующие различным типам покоя (рис.42).
Из приведенной выше классификации следует, что условиями устойчивости точки
покоя являются Re А, < 0, ReA2 < 0. Они выполняются при А > 0 и а > 0, т. е.
для точек, которые находятся в первой четверти.
Если А, и А2 комплексные, то точка покоя будет типа фокуса. Этому
условию удовлетворяют точки, которые лежат между ветвями параболы <т2 = 4Д
и не принадлежат оси О А (а2 < 4Д, а Ф 0).
Точки полуоси а = 0, для которых А > 0, соответствуют точкам покоя типа
центра.
Точки, расположенные вне параболы а2 = 4А (а2 > 4А), соответствуют
точкам покоя типа узла.
Область плоскости ОАа, где А < 0, содержит точки покоя типа седла.
Исключая особые случаи (прохождение через начало координат),
замечаем, что седло может перейти в узел устойчивый или неустойчивый (рис. 42).
202
Глава 4. Теория устойчивости
^oSbT^L/ueHTpoB
Неустойчивые1: Л
^.фокусы #$.
Рис. 42
Устойчивый узел может перейти либо в седло, либо в устойчивый фокус. Случай
равных корней А| = А2 соответствует границе между узлами и фокусами, т.е.
параболе <т2 = 4Д. >
Пример 2. Исследовать уравнение упругих колебаний
d2x dx 2
с учетом трения и сопротивления среды (при а > 0),
(3)
Решение. Переходим от уравнения (3) к эквивалентной ему системе
уравнений
dx
(4)
Для определения характера точки покоя (0,0) системы (4) составляем
характеристическое уравнение
-А
1
-2a-A
= 0, или А2 + 2аА + /Э2 = 0,
(5)
отсюда
А,,2 = -а±
Рассмотрим следующие случаи:
а) а = 0 (сопротивление среды отсутствует). Из (5) получаем Ai,2 = ±t'/3.
Точка покоя устойчива — центр (все движения являются переолическими);
б) а > 0, а2 - /З2 < 0. Корни А| и А2 комплексно-сопряженные, причем
Re A < 0. Точка покоя — устойчивый фокус (колебания затухают);
в) а < 0 (случай «отрицательного трения»), а2 - /З2 < 0. Корни At и Л2 —
комплексно-сопряженные, причем Re A > 0. Точка покоя — неустойчивый фокус;
§ 26. Простейшие типы точек покоя 203
г) а > 0, а2-/?2 ^ 0 (сопротивлениесреды велико а ^ /3). Корни Л, и Аг —
действительные и отрицательные. Точка покоя — устойчивый узел (все движения
затухающие и неколеблющиеся);
д) а < 0, а2 -/З2 ^ 0 (случай большого «отрицательного трения»). Корни Aj
и А2 действительные и положительные. Точка покоя — неустойчивый узел. >
Задачи для самостоятельного решения
Определить характер точек покоя (0,0) для следующих систем дифференциальных
уравнений:
dx щ ( dx
+ 2
888. ( ? 889. I ? 890.
dx ( dx „ 5 ( dx
— = -2x-y, 772+Ч
891. < f 892. { f 7 893.
894. { f
895. При каких значениях а точка покоя (0,0) системы
устойчива?
Пусть имеем систему линейных однородных дифференциальных
уравнений с постоянными коэффициентами
^ i= 1,2,...,п(п^2). (6)
Для нее имеют место аналогичные типы расположения интегральных
кривых около начала координат (обобщенное седло, обобщенный узел и т. д.).
Теорема. Если все корни характеристического уравнения для
системы (6) имеют отрицательную вещественную часть, то точка покоя
системы (6) ж,- = 0, г = 1,2,..., п, асимптотически устойчива. Если
хотя бы один корень характеристического уравнения имеет
положительную вещественную часть, то точка покоя неустойчива.
204
Глава 4. Теория устойчивости
Пример 3. Будет ли устойчива точка покоя (0,0) системы
dx
—
dt
dy
~~dt
dz
, It
—
—
—x
y-
+
z
z,
" z>
Решение. Составляем характеристическое уравнение
-1-Л
0
0
-2
0
-
1
X
1
-1
-1-Л
= 0,
или (1 + Л)(Л2 -f ЗЛ + 3) = 0. Корни этого уравнения Л, = —1, Л2,з = — - ± *
имеют отрицательные вещественные части. Следовательно, точка покоя данной
системы асимптотически устойчива. >
Задачи для самостоятельного решения
§ 27. Метод функций Ляпунова
Метод функций Ляпунова состоит в непосредственном исследовании
устойчивости положения равновесия системы
dx{
— = fi(t, ж,, хъ ...,
г = 1, 2,..., п,
при помощи подходящим образом подобранной функции V($,а?|,...,
хп) — функции Ляпунова, причем делается это без предварительного
нахождения решений системы.
§ 27. Метод функций Ляпунова 205
Ограничимся рассмотрением автономных систем
d хш
-т~ = Мх\,хъ...,хп), i= 1,2,..., п, (1)
at
для которых Х{ = 0, г = 1, 2,..., п, есть точка покоя.
Функция V(a?i,aj2,... ,жп), определенная в некоторой окрестности
начала координат, называется знакоопределенноп
(определенно-положительной или определен ной-отрицательной), если она в области
ЫО, 1=1,2,...,п, (2)
где Л. — достаточно малое положительное число, может принимать
значения только одного определенного знака и обращается в ноль лишь
при х\ = х2 = ... = хп = 0. Так, в случае п = 3 функции .
V = х] + х\ + х\ и V = х} \ \
будут определенно-положительными, причем здесь величина h > О может
быть взята сколько угодно большой.
Функция V(x\y х2,..., хп) называется знакопостоянной
(положительной или отрицательной), если она в области (2) может принимать
значения только одного определенного знака, но может обращаться в ноль
и при х2 + х\ -f ... + хп Ф 0. Например, функция
будет знакопостоянной (положительной). В самом деле, функцию V(xu
х2, ж3) можно записать так: V(x\, х2) ж3) = (х\ + х2)2 + х], откуда видно,
что она обращается в ноль и при х] + х2 + х\ Ф 0, а именно при ж3 = 0
и любых Х\ и х2 таких, что х\ = -х2.
Пусть V(x\,X2,..., хп) есть дифференцируемая функция своих
аргументов и пусть Ж|, #2, • • •»жп являются некоторыми функциями времени,
удовлетворяющими системе дифференциальных уравнений (1). Тогда для
полной производной функции V по времени будем иметь:
dV
Величина —, определяемая формулой (3), называется полной производной
at
функции V по времени, составленной в силу системы уравнений (1).
Теорема 1 (теорема Ляпунова об устойчивости). Если для системы
дифференциальных уравнений (1) существует знакоопределенная функ-
dV
ция V(x\,x2i...,ж„) (функция Ляпунова), полная производная —
at
которой по времени, составленная в силу системы (1), есть функция
знакопостоянная, знака, противоположного с V, или тождественно
равная нулю, то точка покоя Х{ = 0, г = 1, 2,... ,п, системы (1)
устойчива.
206 Diaea 4. Теория устойчивости
Теорема 2 (теорема Ляпунова об асимптотической устойчивости).
Если для системы дифференциальных уравнений (1) существует знако-
определенная функция V(x\} Я2,..., хп)9 полная производная которой
по времени, составленная в силу системы (1), есть также функция зна-
коопределенная, знака противоположного с V, то тонка покоя Х{ = 0
системы (1) асимптотически устойчива.
Пример 1. Исследовать на устойчивость точку покоя системы
dx
Г
Решение. Выберем в качестве функции V(x> у) функцию V = х2 + у2. Эта
функция определенно-положительная. Производная функции V в силу
системы (4) равна
dV da л dy л
Из теоремы 1 следует, что точка покоя 0(0,0) системы (4) устойчива. Однако
асимптотической устойчивости нет: траектории системы (4) — окружности и они
не стремятся к точке О(0,0) при t -* +оо. >
Пример 2. Исследовать на устойчивость точку покоя системы
dx з
Решение. Беря опять V(x, у) = х2 + у2, найдем
^ = 2х(у - х3) + 2у(-я - Зу3) = -2(*4 + Зу4).
dV
Таким образом, — есть определенно-отрицательная функция. В силу теоремы 2
dt
точка покоя 0(0,0) системы (5) устойчива асимптотически. >
Общего метода построения функции Ляпунова нет. В простейших
случаях функцию Ляпунова можно искать в виде
V(x, у) = ах2 + by2, V(x, у) = ах4 + by4,
V(x, у) = ах4 + by2 (а > О, Ь > 0) и т. д.
Пример 3. С помощью функции Ляпунова исследовать на устойчивость
тривиальное решение х = 0, у = 0 системы
dx 22
— = -«-2|» + х»,
dy у Х*У
Ш=Х~2~ ~2~'
§ 27. Метод функций Ляпунова 207
Решение. Будем искать функцию Ляпунова в виде V = ax2 + by2, где
а > 0, Ь > 0 — произвольные параметры. Имеем
оТ dV dx OVdy
+ 2Ъу (х - ^у - 1-х*у\ = -(2аж2 + Ьу2) + (2*у - ж3у2 )(Ь - 2а).
dV
Полагая Ь — 2а, получим, что —- = -2а(х + у ) < 0. Таким образом, при вся-
dt
ком а > 0 и b = 2а функция V = аж2 + 2ау2 будет определен но-положительной,
dV
а ее производная —-, составленная в силу данной системы, является опреде-
dt
ленно-отрицательной. Из теоремы 2 Ляпунова следует, что тривиальное решение
я = 0, у = 0 данной системы устойчиво асимптотически.
Если бы в указанной выше форме функцию V(x) у) не удалось найти, то ее
следовало бы поискать в форме V = ах4 + ЬуА или V = аж4 + 6у2 и т. д. >
Теорема 3 (теорема Ляпунова о неустойчивости). Пусть для
системы дифференциальных уравнений (1) существует дифференцируемая
в окрестности начала координат функция V(x\) Xi)..., хп) такая,
dV
что V(0,0,..., 0) = 0. Если ее полная производная —» составленная
dt
в силу системы (1), есть определенно-положительная функция и сколь
угодно близко от начала координат имеются точки, в которых функция
V(x\} ж2, •.., ffn) принимает
положительные значения, то точка покоя
Xi = 0, % = 1, 2,..., п, неустойчива.
Теорема 4 (теорема Четаева о
неустойчивости). Пусть для системы
дифференциальных уравнений (1)
существует непрерывно дифференцируемая
в некоторой окрестности точки покоя ис#
Х{; = 0, г = 1, 2,..., п, функция v(x\, a?2, • • • > яп), удовлетворяющая
в некоторой замкнутой окрестности точки покоя условиям:
1) в сколь угодно малой окрестности П точки покоя ж,- = 0, г =
1, 2,..., п, существует область п\, в которой v(x\,X2>..., жп) > 0,
причем v = 0 в тех граничных точках Q\, которые являются
внутренними для П (рис. 43);
2) точка покоя О(0,0,..., 0) является граничной точкой
области п\;
dv
3) в области С1\ производная —, составленная в силу системы (1),
at
определенно-положительная.
Тогда точка покоя ж,- = 0, г = 1, 2,..., п, системы (1) неустойчива.
208 Глава 4. Теория устойчивости
Пример 4. Исследовать на устойчивость точку покоя х = 0, у = 0
системы
I,.
dx _
dy _
It ~~~У'
Решение. Возьмем функцию v(x, у) = х2 - у2. Тогда
lu = lterdiJt~dy~di = 2x +2y
есть функция определен но-положительная. Так как сколь угодно близко к началу
координат найдутся точки, в которых v > 0 (например, v == х2 > 0 вдоль прямой
у = 0), то выполнены все условия теоремы 3 и точка покоя 0(0,0) неустойчива
(седло). - ^
Пример 5. Исследовать на устойчивость точку покоя х = 0, у = О
системы
dx , ,<
Решение. Функция v = х4 - у4 удовлетворяет условиям теоремы Четаева:
1) v > 0 при |ж|> \у\;
2) — = 4(ж8 - у8) — определен но-положительная в области \х\ > \у\.
dt
Следовательно, точка покоя х = 0, у = 0 неустойчива. >
Задачи для
Исследовать на устойчивость точку покоя (0,0) систем:
dx „ Л з ( dx л
— = -Зу-2х\ — = -ху\
697. I f 898. <{ *
dx х х3
899. «! « 900. < Л""У"2"Т'
dt 2 4У
da; з ( dx 2 2 ' 5
901. ^ J ~У + Х' дог. J * "У + ХУ 4*'
d^ I Л 2
§ 28. Устойчивость по первому приближению 209
907. < f 908.
909. ^ f 910.
911. Пусть v = v(«i, ar2,..., xn) дважды непрерывно дифференцируемая
определенно-положительная функция такая, что
w дхх дхп
Исследовать на устойчивость тривиальное решение х\ = 0,... >хп = 0 системы
дифференциальных уравнений
dx\ dv
dxn dv
§28. Устойчивость по первому приближению
ных уравнений
г= 1,2,...,п, (1)
Пусть имеем систему дифференциальных уравнений
dx%
— = Л(я?|,ж
at
и пусть ж, = 0, г = 1,2,... ,п, есть точка покоя системы (1), т.е.
/,-(0,0,... ,0) = 0, г = 1,2,... ,п. Будем предполагать, что функции
fi(x\1x2)... ,хп) дифференцируемы в начале координат достаточное
число раз.
Разложим функции /, по формуле Тейлора по х в окрестности начала
координат:
fi(x\, ж2, • • • > #п) =
210 Глава 4. Теория устойчивости
0Д(О,О,...,О)
здесь uij = , а л,- — члены второго порядка малости
OXj
относительно х\, хг,..., хп.
Тогда исходная система (1) запишется так:
"37 = S а''^ + **(*!•»2i • • • >*п), г = 1,2,... ,п. (2)
Вместо системы (2) рассмотрим систему
dx- n
-JT = ]С ачх) (« = 1.2,..., п), ао« = const, (3)
называемую системой уравнений первого приближения для системы (1).
Справедливы следующие предложения.
1. Если все корни характеристического уравнения
и - А а\2 п\п
021 а22-А а2п
Oni лП2 апп - А
имеют отрицательные вещественные части, то нулевое решение я,- = О,
г = 1,2,..., п, системы (3) и системы (2) асимптотически устойчивы.
2. Если хотя бы один корень характеристического уравнения (4) имеет
положительную вещественную часть, то нулевое решение системы (3)
и системы (2) неустойчиво.
Говорят, что в случаях 1 и 2 возможно исследование на устойчивость
по первому приближению.
В критических случаях, когда вещественные части всех корней
характеристического уравнения (4) неположительны, причем вещественная
часть хотя бы одного корня равна нулю, исследование на устойчивость
по первому приближению, вообще говоря, невозможно (начинают влиять
нелинейные члены Л,-).
Пример 1. Исследовать на устойчивость по первому приближению
точку покоя х = 0, у = 0 системы
Решение. Системы первого приближения
х = 2а? 4- у у
§ 28. Устойчивость по первому приближению
211
Нелинейные члены удовлетворяют нужным условиям: их порядок больше или
равен двум. Составим характеристическое уравнение для системы (6):
2-А 1
3 1-А
= 0, или А2 - ЗА - 1 = 0.
з-\/1з
вещеКорни характеристического уравнения (7) А| = —-—, Аг = —-
ственные и Л, > 0. Следовательно, нулевое решение х = 0, у = 0 системы (5)
неустойчиво. >
Пример 2. Исследовать на устойчивость по первому приближению
точку покоя х = 0, у = 0 систем
dx з
I _ - -.з (8)
dx
(9)
Решение. Точка покоя ж = 0, у = 0 системы (8) асимптотически устойчива,
так как для этой системы функция v = х2 + у2 удовлетворяет всем условиям
теоремы Ляпунова об асимптотической устойчивости. В частности,
J = 2*(у - х3) + 2j/(-x - у3) = -2(*4 + у4) ^ 0.
В то же время точка покоя х = 0, у = 0 системы (9) неустойчива в силу теоремы
dv a
Четаева: взяв v = х + у , будем иметь — = 2(ж + у ) ^ 0.
ас
Системы (8) и (9) имеют одну и ту же систему первого приближения
dx
(10)
Характеристическое уравнение для системы (10)
= 0, или А2 + 1 = 0
-А 1
-1 -А
имеет чисто мнимые корни, так что действительные части корней
характеристического уравнения равны нулю.
Для системы первого приближения (10) начало координат является центром.
Системы (8) и (9) получаются малым возмущением правых частей системы (10)
в окрестности начала координат. Однако эти малые возмущения приводят к тому,
что замкнутые траектории превращаются в спирали, в случае (8)
приближающиеся к началу координат и образующие в точке О(0,0) устойчивый фокус,
212
Глава 4. Теория устойчивости
а в случае (9) — удаляющиеся от начала координат и образующие в точке О(0,0)
неустойчивый фокус. Таким образом, в критическом случае нелинейные чл^ны
могут влиять на устойчивость точки покоя. t>
Пример 3. Рассмотрим замкнутый контур
с линейными элементами (рис. 44);
уравнение контура
d2
ь
dx \
dx
dx
R
Рис. 44
Здесь х — заряд конденсатора и, следова-
dx
тельно, ток в цбпи; R — сопротивление; L — индуктивность;
С — емкость; д I ж, — 1 — нелинейные члены, имеющие степень
\ at /. •■ с
не ниже второй, д(0, 0) = 0.
Решение а Уравнение (II) эквивалентно системе
(12)
для которой начало координат 0(0,0), есть точка покоя.
Рассмотрим систему первого приближения
dx
dy I R
— = х v.
dt LC Ly
Характеристическое уравнение<для Системы (13) имеет в^йд
~Тс "¥"^-
-Ьб;-
Li LL>
(13)
(14)
Если —г < —, т.е. J?2 < —, то уравнение (14) имеет комплексные
L LC С
корни с отрицательной действительной частью р = и, значит, начало
координат О(0,0) для системы (13) и (12) асимптотически устойчиво.
Если R > — > то начало координат также асимптотически устойчиво
О
(все параметры R,L,C положительны).
Асимптотическая устойчивость точки покоя видна из физических
соображений: при положительном омическом сопротивлении с возрастанием t ток
неизбежно исчезает. ' ' >
§ 29. Устойчивость решений дифференциальных уравнений 213
Задачи для самостоятельного решения
Исследовать на устойчивость по первому приближению точку покоя (0,0)
следующих систем:
912
914.
у = х - Ъу + 4х .
Г х = -10s + 4ey-4cosy2,
916. < Л
\у = 2ех-2-у + х\
у = -х - 4у + 1 - cos у .
Г х = Зх - 22 sin у + х2 - у3,
915" 1 • < *2 1
^ у = sinaj-5y-fe - 1.
( х = 7s + 2 sin у - у4,
918.
920.
922.
924.
у = -у - 2з + х4 - у7.
i = ^sinz-7y(1-y)I/3 + a;3,
4
У = -я- 3ycosy- lly3.
х = 5x + ycosy- —,
917.
919.
921.
923.
у = ех - Зу - 1 + ^а2.
х = ^же* - 3JTH- sin ж2,
у = 2а? + уе"у /2 - у4 cos x.
4
• 1 • 14
У = -х - sin у + у .
у =
2y + TI-yV.
§ 29. Устойчивость решений
дифференциальных уравнений
по отношению к изменению
правых частей уравнений
Рассмотрим дифференциальные уравнения
У' = /(«, У) + ©(я,»),
(О
(2)
где функции /(ж, у) и О(ж, у) непрерывны в замкнутой области G
плоскости хОу и функция /(ж, у) имеет в этой области непрерывную
df
частную производную —.
dy
Пусть в области G выполняется неравенство |6(ж, у)\ ^ е. Если
у = ф(х) и у = ij)(x) есть решения уравнений (1) и (2) соответственно,
214 Глава 4. Теория устойчивости
удовлетворяющие одному и тому же начальному условию р|,_Жо=
\<р(х) - i>{x)\ ^ — (е |х~*01 - 1), (3)
М
где М = max —— .
(*,V)€G 9У
Из оценки (3) видно, что если возмущение в(я, у) правой части (1)
достаточно мало в области G, то на конечном интервале изменения х
разность решений уравнений (1) и (2) будет малой по абсолютной
величине. Это позволяет приближенно решать сложные дифференциальные
уравнения путем замены их разумно выбранными уравнениями,
решаемыми проще. Последнее обстоятельство может быть использовано при
решении дифференциальных уравнений, связанных с задачами физики
или техники.
Пример 1. В квадрате Q< -- ^ х < -; -- < у ^ - > найти
приближенное решение уравнения
у = sin (ху), (4)
удовлетворяющее начальному условию
2/1^ = 0,1, (5)
и оценить погрешность.
Решение. Заменим уравнение (4) уравнением
У' = ху, (6)
Уравнение (6) при начальном условии (7) имеет решение у = 0,1 • ех ^2, которое
Г 1 11 Л
для всех х € - -; - не выходит из основного квадрата Q.
В силу теоремы существования и единственности решения уравнение (4)
при начальном условии (5) имеет единственное решение у = гр(х) и в качестве
приближенного решения задачи (4)-(5) можно взять у = 0,1 • ех /2 — решение
задачи (6)-(7).
Оценим разность
1 1
Л ~ I(£(<Z/J "■ uHt2/)l> *™™" S» X S» ^«
2 2
где tp = 0,1 • ех /2 — решение задачи (6)-(7). В данном случае /(ж, у) = жу
и
21
ду
1 |*|
-. По формуле Тейлора | sin z - z\ ^ -т-, поэтому в квадрате Q
2 о
\ху\} 1 1
ху\$ < =
§ 30. Критерий Рауса—Гурвица 215
Воспользуемся оценкой (3), взяв е = —-, М = max
384 (-„ж
Нетрудно видеть, что решение хр(х) задачи (4)-(5) не выходит из основного
квадрата Q. >
Задачи для самостоятельного решения
Установить, насколько разойдутся решения данных уравнений, удовлетворяющие
одному и тому же начальному условию у\х_х = у0 на заданных интервалах
(*о = О):
925. у' = —^— + х\ у' = —^ h а?2 + 0,01 sin а? на [0,1].
926. yWsi""<1+*2\ У^е-^^Ч^ на [0,2].
927. у' = - arctg sy, у' = - arctg xy + 0,001е~*2 на [0,1].
§30. Критерий Рауса—Гурвица
Пусть имеем линейное дифференциальное уравнение с постоянными
вещественными коэффициентами:
<Wn) + а,2/(п"° + ... + апу = 0 (о0, а,,..., ап = const, а0 > 0). (1)
Нулевое решение у = 0 уравнения (1) асимптотически устойчиво,
если все корни характеристического уравнения
/(А) = а0Ап + а, А(п-° + ... ап = 0 (2)
имекзт отрицательные вещественные части.
Критерий Рауса—-Гурвица. Для того чтобы все корни уравнения (2)
имели отрицательные вещественные части, необходимо и достаточно,
чтобы были положительными все главные диагональные миноры матрицы Гур-
вица
/aia00000 0\
а3 а2 а\ по 0 0 0
О>5 О>4 из О>2 а\ а0 • • • 0
\0 0 0 0 0 0 ап/
(3)
Матрица Гурвица составляется так. По главной диагонали
выписываются коэффициенты многочлена (2), начиная с п\ и кончая ап. Столбцы
216
Глава 4. Теория устойчивости
состоят поочередно из коэффициентов только с нечетными или только
с четными индексами, причем в число последних включается
коэффициент а0. Все остальные элементы матрицы, отвечающие коэффициентам
с индексами, большими п или меньшими 0, полагаются равными нулю»
Главные диагональные миноры матрицы Гурвица имеют вид
1 а0 О
Ai=a,, A2 =
п\ по
а3 а2
А„ =
а,
а3
а5
а0
а2
а4
0
а,
а3
0
0
0
0 0 0
Таким образом, условие Гурвица гласит: для устойчивости решения
у = 0 уравнения (1) необходимо и достаточно, чтобы выполнялись
соотношения
А,>1, А2>0, ..., Ап>0. (4)
Так как Ап — unAnLY, условие Ап > 0 может быть заменено
требованием ап > 0.
Пример 1. Исследовать на устойчивость нулевое решение уравнения
»IV + 5yw + 13/+ 19у' +10» = 0. (5)
Решение. Составляем характеристическое уравнение
/(А) = Л4 + 5Л3 + 13А2 + 19Л + 10 = 0.
Здесь а0 = 1, а\ = 5, а2 = 13, а3 = 19, а4 = 10. Выписываем диагональные
миноры Гурвица
А4 =
5
19
0
0
1
13
10
0
0
5
19
0
0
1
13
10
= 4240 > 0, А3 =
5
19
0
1
13
10
о
19
= 424 > 0,
= 46 > 0, А,, = 5 > 0,
т.е. Д| > 0, Аг > 0, А3 > 0, А4 > 0,. Следовательно, тривиальное решение
у = 0 уравнения (5) асимптотически устойчиво.
Вычисление можно, например, организовать так. Составляем сначала
старший минор Гурвица Ап. По нему легко выписываются все младшие миноры
ДП_,,...,А,. Затем начинаем вычислять последовательно АЬД2 и т.д. Если
встретился отрицательный минор, решение неустойчиво и дальнейший подсчет
не нужен. >
Задачи для самостоятельного решения
Исследовать на устойчивость нулевое решение следующих уравнений:
928. у" - Зу + 2у = 0. 929. ylv + 4у'" + 1у" + 6у'+ 2у = 0.
930. у'" + 5у" + 9у' + 5г/ = 0. 931. ylv - 2у;" + у" + 2у; - 2у = 0.
932. ylv + 7у'" + 17у" + 17у; + 6у = 0. 933. у" - Зу" + 12у - Юу = 0.
§31. Критерий Михайлова
217
934. ylv + 5у'" + 18/ + 34у' + 20у = 0.
935. ylv + 7у'" -F 19у" + 23у' + 10у = 0.
936. ylv + 11у'" + 41у" + 61у' + ЗОу = 0.
937. yv + 3ylv - 5у'" - 15у" + 4у' + 12у = 0.
938. yv + 7ylv + ЗЗу'" + 88у" + 122у' + 60у = 0.
При каких значениях а будет устойчиво нулевое решение уравнений:
939. у"' + 2у" + ау' + Зу = 0.
940. ylv + ay'" + 2y" + у' + Зу = 0.
941. y'v + 2y"' + ay" + y' + y = 0.
При каких значениях а, /3 будет устойчиво нулевое решение уравнений:
942. у"' + ау"+/Зу' + у = 0.
943. ylv + Зу'" + ay" + 2у' + /Зу = 0.
§ 31. Геометрический критерий устойчивости
(критерий Михайлова)
Рассмотрим линейное дифференциальное уравнение n-го порядка
с постоянными вещественными коэффициентами
:0. (1)
(2)
Его характеристическое уравнение
/(А) = а0Лп + а, A(n-° + ... + ап = 0.
Критерий Михайлова позволяет решить
вопрос о расположении корней
характеристического уравнения (2) на комплексной
плоскости и, следовательно, решить вопрос
об устойчивости нулевого решения
уравнения (1). Полагая Л = га;, получаем
/(га;) = и(ш) + гг;(а>),
где
и(ш) = ап - ап-2со2 + ап_4а;4 -
v(u) = ап_,а; - ап_3<*>3 + •. • •
Рис.45
Величину /(га;) при заданном значении параметра ш можно изобразить
в виде вектора на комплексной плоскости u, v с началом в начале
координат.
При изменении и в интервале (-сю, +оо) конец этого вектора
опишет некоторую кривую — так называемую кривую Михайлова (рис. 45),
Так как функция и(и>) четная, то кривая Михайлова симметрична
относительно оси Ои и поэтому достаточно строить часть кривой,
чающую изменению параметра о; от 0 до +оо.
218
Глава 4. Теория устойчивости
Если многочлен /(А) степени п имеет га корней с положительной
вещественной частью и n-га корней с отрицательной, то угол <р поворота
вектора f(iu) при изменении о; от 0 до +оо равен <р = (п - 2га)-.
Ясно, что для устойчивости решения уравнения (1) необходимо
и достаточно, чтобы га = 0.
Критерий Михайлова. Для устойчивости нулевого у = 0 решения
уравнения (1) необходимо и достаточно, чтобы
1) вектор /(га;) при изменении ш отОдо Н-оо совершил поворот на угол
(р = 71— ш. е. сделал — оборотов против часовой стрелки',
2) годограф /(га;) л/ш изменении ш от 0 до оо не проходил через начало
(0,0).
Отсюда следует, что для устойчивости решения уравнения (1)
необходимо, чтобы все корни уравнений и(ш) = 0, v(u) = 0 были
вещественными и перемежающимися друг с другом, т. е. между любыми двумя
корнями одного уравнения должен находиться корень другого уравнения.
Пример 1. Исследовать на
устойчивость нулевое решение у = 0 уравнения
Решение. Составляем характеристический
многочлен
Далее,
Рис. 46
f(iw) = о;4 - iu>3 - 4а;2 + iw + I,
u(w) = а;4 - 4а;2 4- I, и(а;) = -а;3 +а; = а;(1 -а;)(1 +ш).
Построим кривую (рис.46)
Г и = и(а;),
1 _ 0 ^ а; < +оо.
ш
и
V
0
1
0
у/2-у/Ъ
0
+
1
-2
0
x/2 + v^3
0
-
lim - = 0.
7Г 7Г
Угол поворота радиуса-вектора <р = 4- = (п - 2т)-. Отсюда п - 2т = 4
и так как п = 4, то m = 0, т.е. все корни характеристического уравнения лежат
в левой полуплоскости. Значит, травиальное решение у = 0 асимптотически
устойчиво. >
§ 32. Уравнения с малым параметром при производной 219
Задачи для самостоятельного решения
Исследовать на устойчивость с помощью критерия Михайлова нулевое решение
следующих уравнений:
944. 2у'" + 7у" + 7у' + 2у = О.
945. у'" + 2у" + 2у' + у = 0.
946. 2ylv + 13у'" + 28у" + 23у' + 6у = 0.
947. 3ylv + 13у'" + 19у" + 11у' + 2у = 0.
948. 2ylv + 6у'" + 9у" + 6у' + 2у = 0.
949. ylv + Ay'" + 16y" + 24у' + 20у = 0.
950. yv + 13ylv + 43/' + 51 у" + 40у' + 12у = 0.
951. у"' + у = 0.
952. ylv + y"' + y' + y = 0.
953. yv + 3ylv + 2у'" + у" + Зу' + 2у = 0.
954. yv + ylv + y"' + y" + y' + y = 0.
955. 2ylv + 1 ly'" + 21у" + 16у' + 4у = 0.
956. yv'+yv + ylv + y" + y' + y = 0.
957. 2ylv + 9у'" + 32у" + 54у' + 20у = 0.
958. 6ylv + 29у'" + 45у" + 24у' + Ау = 0.
959. yv + ylv + 2у'" + 2у" + 2у' + 2у = 0.
960. yvl + yv + 3ylv + 2у'" + 4у" + 2у' + 2у = 0.
961. yv + 2ylv + у'" + 2у" + у' + 2у = 0.
§ 32. Уравнения с малым параметром
при производной
Возьмем дифференциальное уравнение
^ (t),e), (1)
где е — параметр.
Если функция F(t)x1 e) в некоторой замкнутой области изменения
t, ж, € непрерывна по совокупности аргументов и удовлетворяет условию
Липшица по х:
\F(t}x2,e)-F(t,xue)\£N\x2-x]\,
где N не зависит от t} x, е, то решение (1) непрерывно зависит от е.
Во многих задачах физики приходится рассматривать уравнения вида
(2)
где е — малый параметр.
Разделив обе части уравнения (2) на е, приведем его к виду
220
Глава 4. Теория устойчивости
откуда видно, что правая часть (3) терпит разрыв при е = 0, так что
теоремой о непрерывной зависимости решений от параметра е воспользоваться
в этом случае нельзя.
Вопрос ставится так: при каких условиях для малых значений \е\
dx
в уравнении (2) можно отбросить член е— ив качестве приближения
at
к решению дифференциального уравнения (2) рассматривать решение
так называемого «вырожденного уравнения»
/(*,*) = <>.
(4)
Пусть для определенности е > 0 и пусть вырожденное уравнение (4) имеет
лишь одно решение х = (p(t). В зависимости от поведения /(£, х) вблизи
решения х = (p(t) уравнения (4) решение x(t, e) дифференциального
уравнения (2) при е —* 0 стремится к решению х = (p(t) вырожденного
уравнения, либо быстро удаляется от него.
В первом случае решение х = <p(t) уравнения (4) называют
устойчивым, во втором — неустойчивым.
Именно, если при переходе через график решения х = (p(t)
вырожденного уравнения (4) функция f(t, x) с возрастанием х при
фиксированном t меняет знак с -f на -, то решение вырожденного уравнения
х = <p(t) устойчиво и им можно приближенно заменить решение ж(£,е)
уравнения (2) (рис.47).
Рис.47
Рис.48
Если же функция f(t> х) меняет знак с - на +, то решение х = <p(t)
вырожденного уравнения (4) неустойчиво и заменять решение x(t, e)
дифференциального уравнения (2) решением вырожденного уравнения (4)
нельзя (рис.48).
Достаточные условия устойчивости или неустойчивости выражаются
следующими предложениями.
-^— < 0 на решении х = tp(t) уравнения (4), то решение
дх
1. Если
дх
х = <p(t) вырожденного уравнения устойчиво.
§ 32. Уравнения с малым параметром при производной 221
df(t x)
2. Если -— > О на решении х = (p(t) уравнения (4), та решение
ах
х = (p(t) вырожденного уравнения неустойчиво.
Если вырожденное уравнение f(t> x) = 0 (4) имеет несколько
решений х = ¥>,*(£), « = 1, 2,..., т, /ио каждое из них должно быть исследовано
на устойчивость. При этом поведение интегральных кривых
дифференциального уравнения (2) при е —» О может быть различным в зависимости
от выбора начальных условий — начальной точки (£0, xq).
Возможен также полуустойчивый случай, когда функция /(£, х) при
переходе через кривую х = <p(t) не меняет знак (например, если х = (p(t)
есть корень четной кратности вырожденного уравнения (4)). В этом1
случае при малом1 е интефальные кривые уравнения (2) с одной стороны
кривой х = ip(t) стремятся к этой кривой, а с другой — удаляются от "нее:
В первом случае мы говорили, что начальная точка (to, х0)
принадлежит области притяжения полуустойчивого решения х — <p(t), а во втором
случае — области отталкивания.
В полуустойчивом случае, как правило, нельзя заменять решение
исходного уравнения (2) решением вырожденного уравнения (4).
Можно указать критерии, когда интефальные кривые уравнения (2)
при соответствующем выборе начальной точки (£о, #о) приближаются
к решению х = <p(t) вырожденного уравнения и остаются в его
окрестности при t > t0, однако это справедливо лишь при отсутствии возмущений
уравнения (2).
Приведем эти критерии. ,
Пусть в окрестности полуустойчивого решения х = <p(t)
вырожденного уравнения (4) функция /(£, х) ^ 0. Если (p'(t) > 0, то интефальные
кривые уравнения (2), приближающиеся к кривой ж,= <p(t), не могут
пересечь эту кривую и остаю-Гся в ее окрестно-
сти при t > t0 (начальная точка (£0, х0) должна
находиться в области притяжения
полуустойчивого решения ж = <p(t)', если (to, x0)
находится в области отталкивания, то
соответствующая интефальная кривая уравнения (2) быстро
удаляется от кривой х = <p(t)) (рис.49). Если
(p'(t) < 0, то интефальные кривые,
приближающиеся к фафику функции х = (p(t), пересекут рис 4д
его и с другой стороны кривой ж =; <p(t) быстро
удалятся от нее. Если <p'(t) > 0 при *о ^ * < *i и,,¥>(£) < 0 при t > t\,
то при достаточно малом е интегральные кривые, выходящие из точки
(*о>яо)> принадлежащей области притяжения корня х =,(p(t), остаются
вблизи кривой х = (p(t) при to + 6 < t < t\, 6 > 0; в ркрестности точки
t = t\ они пересекают кривую х = <p(t) и затем удаляются от нее.
Если в окрестности полуустойчивого решения х = <p(t) функция
/(£>#) < 0, то для справедливости высказанных утверждений знаки
у производной (p'(t) надо заменить противоположными.
222
Глава 4. Теория устойчивости
Пример 1. Выяснить, стремится ли решение х - я(£, е) уравнения
dx
е— = г-ж (5), е > О, удовлетворяющее начальному условию
at
\ = х°* к Решению вырожденного уравнения х = t2 при t > tQ
x\t
и е
0.
0/(*,я) 0(*s) t Л
Решение. Имеем -^—- = —^——- = -I < 0, так что решение вы-
дх дх
рожденного уравнения х = t2 устойчиво и, следовательно, решение исходного
уравнения х = &(*,£), выходящее из любой начальной точки (*о>яо)> стремится
к решению вырожденного уравнения при е —► 0 и t > to (рис.50).
В этом можно убедиться непосредственно проверкой. Решая
дифференциальное уравнение (5) как линейное неоднородное при заданном начальном
условии x\tmt = а?о» найдем
x(t} е) = («о - tl + 2etQ - 2e2)e-(t"'o)/e +12 -
откуда непосредственно видно, что при t > tOi т.е. t -10 > 0 и е -> 0 имеем
2
Рис. 50
Рис.51
Пример 2. Исследовать на устойчивость решение вырожденного
уравнения для уравнения
Решение. Вырожденное уравнение х(ех - 2) = 0 имеет два решения
От — П 1\ <г — In 1
Имеем
*/(*,*)
х=0
так что решение х = 0 устойчивое;
х=1п2
так что решение х = In 2 вырожденного уравнения неустойчивое (рис.51).
§ 32. Уравнения с малым параметром при производной 223
Пример 3. Исследовать на устойчивость решение вырожденного урав-
dx 2
нения, отвечающего уравнению е— = (х - г) .
at
Решение. Вырожденное уравнение (х -1)2 = 0 имеет корень х = t
второй кратности. Функция /(*,я) = (i-l)2>0 в окрестности этого корня,
(p(t) = t и ^'(0 = 1 > 0. Следовательно, решение х = t —
полуустойчивое, и если начальная точка to* &о лежит в полуплоскости под прямой х = t
(область притяжения корня х = £), то интегральная кривая х = £(£,£),
выходящая из точки (*о>£о)> будет при t > t0 оставаться в окрестности линии х = t
(рис.52). >
Задачи для самостоятельного решения
Исследовать на устойчивость решения вырожденных уравнений для следующих
дифференциальных уравнений:
962. £^ = х - t\ 963. е^ = x(tA + 1 - х).
at at
964. t% = (х - t)(x - е'). 965. «$ = х2 -1\
at at
966. e$ = xt. 967. e$ = (ж - *)(ln « -12 - 1).
at at
968. e$ = (t + s)2. 969. e^=x-t+\.
at at
Ответы
1. Если у(х) является решением дифференциального уравнения, то оно обращает
его в тождество. Поэтому, если уравнения а) и б) имеют совпадающее решение, то
их левые, а значит, и правые части тождественно равны: у2+2х-х4 = -у2-у+2х+
х2 + а?4. Отсюда находим у = ж2, у = —х2 — -. Вторая функция не удовлетворяет
уравнению а) и, значит, должна быть отброшена. Получаем: у = х2.
13. у = 0.
1
17. а = arctg -.
18. а=7
4
19. Точки экстремума интефальных кривых находятся на прямой х = -1.
20. Точки перегиба интефальных кривых находятся на параболе у = х2 + 2х.
22.
Рис. 53
Рис. 54
24.
Рис. 55
Рис. 56
Ответы
225
к=\
26.
Рис. 57
к=\] }к=-\
Рис. 58
28.
Рис. 60
Рис. 61
Рис. 62
226
Ответы
k=\
Рис.64
) = -^(33 - 14ж + 42ж3 - 7ж4 - 2ж7).
х2 '$
- + 20-
44.
45.
46.
47.
49.
51.
53.
55.
57.
59.
61.
63.
65.
66.
67.
69.
70.
Уо(х) = 2,
Уо(х) = 2, у\ (х) = 2х - In х, у:(х) = 2 + In 2x.
arctg х + arctg у = С, или х + у = С(1 - ху).
х2(1 + у2) = С. 48. у = sin х.
у = tg In Cx.
у=1.
1 + е" = С(\ + х2).
1
arctg е = . . ,
2 sin 2y
= 2 + х + х2 --х3 --х4.
50. \/1 + «2 + \Л + у2 = С.
52. ев = С(1 - е"у).
54. ая + а-у = С.
56. y = 2
58. у = (1 + Су + In у) cos ж.
60. Ь(аж + by + с) + а = Сеь*.
62. у = —•.
ж
64. tg| =
у' = 3у, у = -2е3*.
i -, у = (гипербола).
а а — х
^ = 20-, v = 50n/29 см/с.
dt v
dv 2
dv
dT
dt
=
, In (t7,/v0) 40 In 2,5
5 In 10
с
dT
72. — =Л(Г-
■ 60 мин.
Ответы 227
73. у' = гЛ у = Схп. 74. -£=*£, 5 = 25«2</5.
X О*
dx /1 х \
75. 18,1 кг; — = к[ - - т^г 1, Л — коэффициент пропорциональности.
at \3 300/
76. 5,2 кг; ■= = кх[Z-Z - jJ. 77. ху = С, (С * 0).
78. 0,82 кг; — = ка($ + 6). 79. 32,2 мин.
2 dT О
80. Г = |х; 864000 • 4,2 Дж; — = -^,
3 ах Аа
83. у = 0, для а < 1 решение единственно.
85. у=у(2п+1)х + С, п = 0,±1,±2,... .
86. у = С.
87. у = (-l)ft ( хarcsinx + у/\ - в2) + ятгх + С, п = 0,±1,±2,... .
88. .
89. у = птгх + С, п = 0, ±1, ±2,... .
90. у = х(1п х - 1) + С.
91. у = х arctg х - - In (I + х2) + птгх + С, п = 0, ±1, ±2,....
92. у = arcsin ( — J + 5тг. 93., у = arcctg (- ) + -^ + Зтг.
ft- Л Л 1 \ 9тг „ 1 /тг \ 7
94. у = 2arctg ( 1 - г-7 ) + -г"» 95. у = - arctg [ - +arctgx J + -тт.
96. у = 0. 97. у = 1. 98. у = -тг.
1 9 у
99. у = arcctg —- + -тт. 100. tg- = lnCx. 101. y = x(C-lnx).
ix 4 х
104. у + \/у2 - х2 = Сх2, у = х, у=-х.
105. 2х = (х - у) In Сх. 106. у2 - Зху + 2х2 = С.
107. у2 + 2ху - х2 = С. 108. у = 1 + (х - 1) In C(x - 1).
109. (х + у-1)5(х-у-1)2 = С. 110. у2-2ху-х2-8у + 4х = С.
111. у2-2ху-х2 + 4у = С. 112. у2 + 3ху + х2-5х-5у = С.
113. (4х + 2у + I)2 = 4х + С. 114. х + Зу - In |x - 2у| = С.
115. (х + у-1)2 + 2х = С.
117. Сх4 = уЧх3.
У2 5 *
119. 2 arctg 5L = In (x2 + у6) + С.
125.
127.
116.
118.
120.
122.
124.
126.
128.
у2 = х1пСу2.
х2+у2 = Сх.
у> = 2Сх + С\
хг + уг = Сх*.
у = х-х\
у = (С + х)е~*г
228
Ответы
129.
131.
133.
135.
137.
139.
140.
141.
142.
144.
148.
У =
cos ж
sin ж
У =
С
х = — +у\г\у.
у = (С + х2)ее\
R2 + (2nirL)2
130. у = Cx2 + x2 sin x.
132. у = (С + ж3)1пх.
134. y=\.
136. x = (C + y)e-y2/2.
138. y = (C + x)e{]-x)e\
[R sin 2nnt + 2nnL(e-Rt/L - cos 2n7r*)] + Ioe~Rt/L.
«2 «2
у = Cx -x2, y- xy' = ж2.
150. y =
sin x
154. v =
156.
158.
160.
162.
164.
166.
168.
170.
172.
174.
176.
178.
180.
182.
у = cos x.
y =
C-x
у In x = С + sin x.
y4 + 2x2y2 + 2y2 = C.
sin у = (x + C)ex; z = siny.
sin у = ж + Ce~x; z = sin y.
tgy=(C + z2)e"x2; z = tgy
у = (Ж + 1)ех.
у = Сх{]~п)/п.
gy y ^
«с
sin 2x x2 + y2 _
1 — — С
2
143. y =
145. y = :
149. v = '
153.
155.
sin х
159.
161.
163.
165
1 ww.
167.
169.
171.
173.
175.
177.
179.
181.
183.
y/y + 1 = Ce
y2(C - ж) sin ж = 1.
1
У\пу=е(х7с
x-2+Ce-* =
xy = C.
у = 2 - (2 + (
я4 + x2y2 + у
)ех; z =
: с j 2 :
12)е(х2"а2)/:
4 = С.
yjx2 + у2 + In \xy\ + -
У
хгу + x2 - у7
х3 + у3-хг-
/ У
у/х2 + у2 - =
Ж
= Сху.
-жу + у2 =
= С.
In у.
>
Ответы 229
184. х sin у - у cos ж + In \xy\ = С. 185. tgжy - cos ж - cosy = С.
186. у = х. 187. (ж2 + у2)2 + 2а2(у2 - х2) = С.
188. жу(ж2 + у2) = С. 189. жу2-2ж2у-2 = Сж; ц = Дг.
ж^
190. ж - - = С; // = —. 191. ж In |ж| - у2 = Сх; /х = —.
192. 5 arctg ж + 2жу = С, ж = 0; /i = г.
1 + ж2
193. у3 + ж3(1пж - 1) = Сж2; \х =—.
ж4
194. 2ех sin у + 2е*(ж - 1) + ex(sin ж - cos ж) = С; ц = ех.
195. ж2 Зжу = С; и = —.
У У2
196.
197.
198. у - 1 = Сч/ж2 + у2; ^ = (^2 + 2/2)~3/2-
199. (у-С)2 = ж3. 200. In Су = ж ± 2ех/2, у = 0.
201. у = 2ж2 + С, у = -ж2 + С. 202. жу = С, ж2у = С.
203. у = у + С, у = Сех - ж - 1. 204. 4е~у/3 = (ж + 2)4/3 + С.
2 Ж2
205. у = — + С, у = + С, у = Сех.
206. у = Сех + ^, у = ±2ех/2.
207. v = Сх + -(ж2 — С2) у = х2
— + с
208. Г -■; = ;' 209. ) _^
In J
raj lnp + sinp,
' .\y = C+p(H-sinp) + "
I -^
214. Г=*2> 215. /-1'. з
I у = С + е^(\ + -\ [у + С = -а*а t, p = tgt.
216.
у = а sin'
230
Ответы
= p + sinp,
"I
f a? + С = In |p| + si
218. ^ 2
^ у z= р+рл COSp.
217- < , h
y + C = -p + p sin p + cosp.
+ sinp + pcosp,
219.
220.
= 2arctgp- In
у = arcsin p + In (1 + p2), у = 0.
С 1
у = hlnp-2.
Р
221. { * 2}\ Р\+Св '
ly = [2(1-p) + CIe-p]
222.
223.
С cosp sinp
1С 2 cosp
у = sinp, у = 0.
P P
Cp2 + 2p - 1
x =
224.
2(p-l)2 p
225. y = Ca? + —j» 4y3 = 27aa?2. 226. у
227. у = Ca? - ^-!-, (y + I)2 = 4a?. 228. у = Са?+а\Л+С2, а?2-
229. a? = Cy + C\ 4a? = -y2. 230. xy = ±a\
maj -.2/3 I -.2/3 -2/3 лАл .. jt
&OI .a? "r W = u . &O&. У — с '
= a2.
1
233. y = sin«+
235. y = --
——.
С + x
234.
C + c*
1
a? (C - In a?)a?'
^У 2
236. В этом случае — = -[a(x)y + Ь(а?)у + c(a?)],
ax
dy
dx
dy
dx
и переменные разделяются. Имеем: С - / с(х) dx = - /
238. у + ху = 0. 239. х2 + у2 = 2а?уу\
Ответы 231
240. a?y' = ylny'. 241. у2 + у' - ху+у = 0.
242. у" - 2у + у = 0. 243. уу'2 + 2а?у' = у.
244. у/;/ = 0. 245. у" + -у" = 0.
246. у//2 = (1 + у'2)3. 247. у"-у = 0.
248. у" + у = 0. 249. 2*2 + у2 = С.
250. ж2 + пу2 = С. 251. 2х + cry2 = С.
252. sin у = Се"х.
253. у2 = Сх. 254. ау = С.
255. у = Сх, если к = 2; -^" ^ = —^, Л Ф 2.
256. ж2 + у2 = Сх. 257. жу3 = С.
258. р = С(\ - cos ^). 259. у = Се'х/2.
260. у2 = 4ж + 4. 261. у = 0.
4
262. у = 0, у = —ж . 263. Особых решений нет.
264. о = 0, у = 0. 265. 4у + х5 = 0.
266. 4ау2 + 1=0. 267. у = х - ^-.
д.2
268. Особых решений нет. 269. у = —.
270. у = 0; у = 4ж. 271. у = ±1.
272. у = ±2еж/2. 273. у = х, у = --.
274. ^ + ?г = 1. 275. у = х-—*—.
276. у = С +cosa;.
277. y]-n = 2s\nx+-^+Cein-l)«nx.
278. а?4 - 6х2у2 + у4 = С. 279. 15а?2у-24жу2-12а;3 + 2у3 = С.
ЛЛЛ ,3223 ЛЛ- 2 1
280. 6у + 12у — 9а? у + 2а? = С. 281. 2+ а?у In а; = Са?у; ц = 2 2.
282. у = Сс"ж + (sin а? - a? cos а?)е"х . 283. а; =
284. у + С = 2а; - — + 2 In It -ж|. 285. у2 =
х
286. у(у - 2ж)3 = С(у - а;)2. 287. у = С(2а? - I) + -.
х
288. х + у - I = Се{2х+т*+у-]). 289. In
290. у = С(3ж2 - 2ж). 291. у3 =
292. х + ye*lv = 1 + е. 293. In \x\
294. 1п|2а?-2у + 5|-2(ж + у-2) = С. 295.
296. а?2 + у2 = Се"х.
= C-2cos-.
232 Ответы
297. I In fi±£±J - ^(arctg * + I arctg *£
2 у2 - J/ -h 1 V V3 V3
298. z = y2(l + СеЧу). 299. sin x + 2y In |y| - Cy = 0.
300. 3e'22/ = Ce~2x - 2ex. 301. ж4 + у2 = C(x2 + у).
302. i = ^ + 4-, пФ-г.
x у2 п + 2
303. 7(3у - 4s) + (4а2 - ЗЬ2) In \1(х + у) + а2 + Ь2| = С.
304. хеу2/х = С. 305. у(\ + a? + In x) = 1.
306. y[sin (In у) + cos (In у)] = z[sin (In x) - cos (In x)] + С.
307. (ж - 1 + лЛ2 - 2х + 5)3 = С(3у - 1 + \/9у2-6у + 2).
308. (а? - у)(ж +7у - 4) = С. 309. ж + 2у + 3 In \х + у - 2| = 5.
310. у2 = Сеу2/х. 311. 2 arctg ^^ + In С(у + 2) = 0.
х ~~ j
312. При переходе от кривой к симметричной ей кривой относительно 0(0,0),
переменные ж, у, у1 заменяются на -ж, -у, у1 и данное уравнение снова
удовлетворяется.
313. Для того, чтобы прямая у = кх + Ь была интегральной линией данного
уравнения, необходимо и достаточно в силу равенства у' = к, чтобы у = кх + Ъ =
к + хк2, т. е. fc = 0 или fc= 1 и b = к. Отсюда получаем два решения: у = 0
и у = х + 1.
314. Зу2-2я = С\
315. у = спя и у = 1.
317. а) не могут; б) не могут; в) могут,
х5
327. у = — + С,я3 + С2х2 + С3я + С4.
4
328. у = — - sin х + С,ж2 + С2ж + С3.
330. у = (х-
331. у =--In ж -ж3 + С,ж + С2. 332. у = С,
3 18
333. у = С, In |ж| + С2. 334. у = С,е*2 + С2.
335. у = y + С\х2 + С2. 336. у = С|ж(1п ж - 1) + С2.
337. у = (С,* - С2)е(*/С|)+| + С2. 338. у = ^-х5/2.
339. у = C3 + C2s -sin (x + С,). 340. у = С}х3 + С2х + С).
341. у = ch (х + С,) + С2. 342. у = С2 - In |С, - я?|.
343. у = С2- cos (С, + а?). 344. у = С2 - In j cos (С, + х)\.
3
345. у=(а?^2С|)-х + С2. 346. у =
^2
347. у = -2а?. 348. у = С2 - In |1 - ех+С| |
349. (х + С,)2 + (у + С2)2 = 9.
350. у =
351. у = С2еС|г. 352. у =
Ответы
233
356. y=i-(
4, ,
y=- 1 +
4
У
'-}■
y = -ln|x-l|.
4
У =
360. С\х + С2 = In
362. ycos2(z + C,) = С2.
364. {x-Cx)2-C2y2+kC\
(х - 2)
Парабола.
d2x к
—^ = —-, где ж — расстояние тела от центра Земли; t « 122 ч.
2 Л
= 0.
at1
367. ш^ = ^; X2 = ^x{t + C2)2 + C>; a2 = ^.
ас2 xJ Ci m
368. т—-— = то -
dx
= — In chart; a =
к
369.
370.
371.
375.
379.
383.
389.
393.
396.
398.
400.
402.
404.
411.
413.
415.
416.
417.
418.
419.
420.
422.
424.
(x + C, )2 + (y + C2)2 = Д, где Д = const.
Да. 372. Нет. 373. Нет.
Да. 376. Да. 377. Нет.
Нет. 380. Нет. 381. Нет.
Нет. 384. Нет. 385. Да.
1. 390. -- (хфЪ). 391. 0.
374. Да.
378. Нет.
382. Нет.
386. Нет.
392. е"2х.
394. -8sin3x.
395. -Ti.
397. 0.
399. I - In x, x>0.
401. -е
2х
403. I.
410. 9у"-6у' + у = 0.
412. 2у" -Зу'-5у = 0.
414. 2/lv + 2y/4t/ = O.
у
у" - Зу' + 2у = 0, у = С, ех + С2е2х.
у" - 2уЧ у = 0, у = (С}+ С2х)ех.
у" - 6у' + 13у = 0, у = e3z(C, cos 2ж + С2 sin 2x).
у"' - Ъу" + Зу' - у = 0, у = е*(С, + С2х + С3х2).
у"-у = О. 421. у/;-у' = О.
у" + 4у' + 4у = 0. 423. у// + 9у = 0.
у" = 0. 425. y"'-6y"+lly'-6y = 0.
234 Ответы
426. у'" - Зу" + Зу' - у = 0. 427. у'" - 4у" 4- 5у; - 2у = 0.
428. у"'-у" = 0. 429. у'"4-у' = 0.
430. у'"-2у" + у' -2у = 0. 431. у'" 4- 2/ 4- 2у' = 0.
432. у = С,еж4-С2е-х. 433. у = С,е2х 4-С2е"4х/3.
434. у = е*(\ 4- ж). 435. у = е"х(С, + С2ж).
436. у = 4ех4-2е3х. 437. у = С
438. y = C,e(I-^ + C2e<lW4
439. у = С, 4- С2ж 4- С3ж2 4- С4ж3 4- е"х(С5 4- С6ж).
440. у = ех ( С\ cos ^ 4- С2 sin ^ J.
441. у = С,е2х + е"х(С2 cos \ftx 4- С3 sin \/Зж).
442. у = e~x(Ci 4- С2ж) 4- е~х(С3 cos 2ж 4- С4 sin 2ж).
443. у = ех sin ж.
444. у = ex(cos у/2х 4- n/2 sin У^2ж).
445. у = С]е* + С2е~х + е"х(С3 cos2ж 4- С4 sin 2ж).
446. у = С\е* + С2е"2х 4- е"х(С3 4- С4 cos ж 4- С5 sin ж).
447. у = С,ех + С2е-х + С3е-2х.
448. у = С] 4- ех(С2 cos ж 4- С3 sin ж).
449. у = С]€* + С2е~х 4- С3 cos ж 4- С4 sin ж.
450. у = С\ 4- С2ж + С3ж2 4-... 4- С|0ж9.
451. у = е"х(С, 4- С2ж) + С3е2х. 452. у = <
453. у = ж4-е"х. 454. учм =
455. уч.» = Л,ж3 4- Л2ж2 + Л3ж. 456. уч.н
457. уч.„ = е"х(А, 4- А2х). 458. учм = е"х(Л,ж + Л2ж2).
459. уч.н = e~x(i4^2 4-i42ж3). 460. уч.и = Л sin ж 4-В cos ж.
461. уч.н = х(А sin ж 4- В cos ж) 462. уч.н = х(С\ С08 2ж4-С2^п2ж).
463. уч.н = ж(С| С08Лж4-С28тЛж). 464. уч.н = е~*(С\ cos ж 4-С2 sin ж).
465. уч.н = же**х(С, cos ж 4- С2 sin ж). 466. уч.н = С\ 4- С2ж 4- С3ж2.
467. уч.н = С\х 4- С2ж2 4- С3ж3. 468. уч.н = С|Ж2 4- С2ж3 4- С3ж4.
469. уч.н = С,ж3 4- С2ж4 4- С3ж5. 470. ум.н = х(С\ cos ж 4- С2 sin ж).
471. а) уч.н = (А, 4- А2х + Агх7)ек*у б) уч.н = (С,ж 4- С2ж2 4- С3ж3)вь,
в) уч.н = (С,ж2 + С2ж3 + С3ж4)е*х, г) уч.и = (С, + С2ж + С3ж2)екх,
Д) Уч.н = (С|Ж2 4- С2ж3 4- С3ж4)е*х, е) уцм = (С,ж3 4- С2ж4 4- С3ж5)е*х.
472. а) уч.н = С\ sin ж 4- С2 cos ж, б) уч.„. = х(С\ sin ж 4- С2 cos ж).
473. а) уч.н = x(d sin 2ж 4- С2 cos 2ж)е3х, б) уч.н = ж2(С, cos 2ж 4- С2 sin 2ж)е3х.
474. уч.н = Сх. 475. уч>н = С|Ж4-С2ж2 4-С3ж3.
476. уч и = Се*. 477. уч и = Сже"*7х.
478. уч.и = (С,ж2 + С2ж3)е4х. 479. уц.н = Сж2е5ш.
480. уч.н = (С, ж 4- С2жУх/4. 481. уч.н = (С, ж 4- С2ж2)в4х.
482. уч.и = ж(С| cos 5ж 4- С2 sin 5ж). 483. уч.н = х(С\ cos ж 4- С2 sin ж).
484. уч.„ = ж(С| cos 4ж 4- С2 sin 4ж). 485. уч.н = (С\ cos 2ж4-С2 sin 2ж)е2х.
486. уч.,, = х(С\ cos 2ж 4- С2 sin 2ж)е2х.
487. уч.н = ж(С| cos 2ж + С2 sin 2ж)е"3х.
488. уч.н = х(С\ cos kx 4- С2 sin kx).
Ответы 235
489. уч.„ = С (С = const). 490. уч.н = С\ + С2х.
491. уч.„ = С (С = const). 492. уч.н = Сх.
493. уч.н = Сх2. 494. уч.н = С (С = const).
495. уч.н = Сх. 496. уч.н = Сх2.
497. уч.н = Сх3. 498. уч.н = Сх2.
499. уч.н = Се4х. 500. учн = Сх2е"х.
501. уч.н = (Cix2 4- С2х3)е"х. 502. уч.н = С\ cos 2х 4- С2 sin 2x.
503. уч.н = C| cos х + С2 sin x.
504. уч.н = (А] 4- А2х) sin 2х + (В, + В2х) cos 2x.
505. уч.„ = x2(C| cos пх 4- С2 sin пх). 506. уч.н = С, cos пх + С2 sin пх.
507. уч.„ = С, sin х + С2 cos x. 508. уч.н = CxV.
509. уч.н = (С,х4 4- С2х5)ех. 510. у = (С, + С2х)е"х - 2.
511. у = С\ + С2е"2х - х. 512. у = С) cos3x + C2sin3x-b 1.
513. у = С] 4-С2х + С3е-х + ^-. 514. у = С, + С2х 4-С3е7х/5 - -^-х2.
2 14
515. у = С, 4- С2х + С3х2 + С4ебх 4- тх3.
о
516. у = С\ 4- С2х + С3х2 + С4е~х/3 4- у
517. у = С, cosx 4- С2 sin x + (С3 4- С4х)ех + I.
518. у = (С,+Сх)е2х4-j + | + ^. 519. у = С, 4-С2е"8х + у - |.
520. у = (С, 4- С2х)е*х + ** . 521. у = (С, + С2х)е"2х 4- 4х2е"2х.
522. у = С,е"3х 4- С2е"х - ^хе"3х. 523. у = С, 4- С2ех/7 - 7х2 - 98х.
524. у = С,+С2е-3х-(у + 0е-3х.
525. у = С,е"3х + С2е"2х + (20х - 5х2)е"2х.
526. у = (C| cos х + С2 sin x)e~x н- -.
527. у = f С, cos— x + C2sin — х)е~х/ 4- -(х2-х4- 1)ех.
чоа « п л-(уЯ+2)' . г» л(\/?-2)х 16 cos 2x-f 12sin2x
ЭаО. у = С/|С •+* Сое — _.
25
529. у = C| cos х 4- С2 sin х + х cos x 4- х2 sin x.
,-лл /^ ^ v ma 2mn cos пх 4-(т2 -n2)sinnx
530. у = (С, + С2х)етх + r-j±—щ— .
531. у = (C| cos 2х 4- С2 sin 2х)е"х - T«e~* cos 2x.
_лл _ ^ . 2 cos тх 4-3 sin тх 7| , , . |Ч
532. у = C| cos ах + С2 sin ах 4- 2^ j (|а| ^ |т|).
533. у = С| 4- С2сх - (cos х + sin x)e*.
534. у = С| +С2е~2х + -(6sinx-2cosx)ex.
535. у = (C| cos х + С2 sin х)е"2х + 5хе"2х sin x.
236 Ответы
536. у = С, + С2е"2х - (± + 1) cos ж + (1 - ±) sin ж.
537. у = С,е2х + С2ех- (у+ж)ех.
538. у = С,ех + С2е-2х + ± (ж2 - ж + ^) е4х.
539. у = С,ех + С2е2х + (у -*i + Ле3*.
540. у = С,ех + C2cosa: + C3sina;- (ж2 + Зж + 1).
ж2
541. у = (С, + С2ж)ех + С3 cos ж + С4 sin ж + — ех.
542. у = (С, + С2ж)ех + ж3 + 6ж2 + 18ж + 24.
ж4 ж3 ,
543. у = С, + С2ж + С3 cos ж + С4 sin ж + — -}- — - ж .
12 о
/ ж ж3\ / ж2\
544. у= (С, + - - — ) СО8Ж+ f C2 + -T-J sin ж.
545. у = (С\ + С2х)е~х + [(6 - ж2) cos ж + 4ж sin ж]е~*.
546. у = С,ех+ ( C2cos— ж + С3 sin — ж)е"х/2 + -(cos ж - sin ж).
547. у = (С, + С2ж)ег + (С3 + С4ж)е"х + - cos ж.
548. у = (С, + С2ж + С3ж2)ех - — sin 2ж.
8
549. у = ( С\ cos ж + С2 sin ж - - cos ж + ж sin ж J е2х.
550. а) у = ж(С,ех + С2е"х), б) у = С,ех + С2е"х,
в) у = ж(С,ех + С2же"х), г) у = С,ех + С2ж3е"х
551. у,м = А]ех + А2е-2х.
552. учн = х{А\Х -ь А2) + Вхе
553. уцН = А\х + А2 +В] cosx + B2s\nx.
554. уч „ = Аех + жех(Б| cos ж + В2 sin ж).
555. уч.„ = Аж2 + Вжех.
556. уч>н = Ае2х + ж(Б, cos 2ж + В2 sin 2ж).
557. унм = А\ cos ж + В\ sin ж + А2 cos Зж + В2 sin Зж.
558. ум.н = А\Х + 5| cos 8ж ■+■ J?2 sin 8ж.
559. у = С,е"х + С2е2х - 2ж + 1 + ех.
560. у = Ci + С2е'х - Зж2 - 2ж + cos ж + 3 sin ж.
561. у = 2 + ех(С, + С2ж - sin ж).
562. у = (C| cos ж -h C2 sin ж)е"х + жех + е~х.
563. у = (C| cos 2ж + С2 sin 2ж)е"х + е~х - 4 cos 2ж + sin 2ж.
564. у = С,е2х + С2е"х/2 + ^(2же2х - 5).
4
565. у = С, cos 2ж + С2 sin 2ж + - ( I - °0S - - sin 2ж ).
8 V 4 2 /
Ответы 237
х 1 I' х \
566. у = (С, + С2ж)е~х + С3 cos х 4- С4 sin х cos х 4- - ( 1 ) ех.
8 4 \2 у
11 1 ж3
567. у = С, + С2е"х + -ех - — cos 2х + -- sin 2х + — - ж2 + 2ж.
568. у = С, + С2ж + С3ж2 4- С4 cos 2ж 4- С5 sin 2ж + —- 4- — + ———.
5 24 32
569. у = (С\ cos 2х 4- С2 sin 2х)ех 4- cos ж + 2 sin ж + 4 cos 2ж + sin 2ж.
1 х2
570. г/ = С, + С2е~* + же~х + -еж + — - х2 + 2ж.
571. у = C,e"x + С2е3* - ^х + 1 - ^ze"* - ixe3x.
572. у = С, cos 2ж + С2 sin 2ж + х ( - sin 2ж - cos 2ж ) + -ех.
\4 ) 5
573. у = С}е~х + С2е~2х + 3(ж2 - 2ж)е'х + 3(ж2 + 2ж)е"2х.
1 х
574. у = С\ cos ж -f C2 sin ж - - cos 4ж sin ж + 1.
3 4
575. у = (C| cos ж -f C2 sin ж)е2х + cos ж - sin ж + е2х + -.
/ 1 ж \
576. у = 1С] cos ж + С2 sin ж Н sin ж J ех.
I—.-. ^, ^, зг cos ж - 2 sin ж ех ж
577. у = С}+ С2е3х + у - -.
578. y=lc] cos 2ж + С2 sin 2ж + - sin 2ж ) ех 4- 2ж + 1.
579. у = (С, 4-С2ж)ех + — (4 cos ж 4- 3 sin ж) 4- - со$2ж 4- ж 4- 1.
25 8
р-лл / ч -г cos 2ж 4- 7 sin 2ж
580. у = (С, 4- С2ж)е 4- — + sin ж 4- 1.
581. у = ( С, cos — ж + С2 sin —ж J е"х/2 - cos ж 4- ж2 - ж - 2.
582. у = (С, 4- С2ж 4- 9ж2)е~3х 4- sin ж.
583. y = C,+C2e-I»
5 5 8 2
584. у = С, 4- (С2 + С3ж)ех + ж2 4- 4ж 4- ^ж2ех.
585. у = С\ cos ж 4- С2 sin ж 4- - cos Зж 4- -ж sin ж.
8 2
586. у = С, + С2е"х 4- С3е2х + ж - ж2 4- cos ж.
587. у = С, 4- С2е2х 4- С3е"2х 4-|со5Ж-^--^4- ^(2ж2 - Зж).
5 12 8 32
588. у = С,ж34-С2ж24-СзЖ + С4 4-С5ех4- гт + ( у -4ж)ех.
ж
ж2 4 С С i
4
ж
589. у = С, 4- С2ж 4- С3ж2 4- С4 cos ж 4- С5 sin ж 4- е"х.
590. у = 2-2ж. 591. у = ж24-е3х.
592. у = 2е3х. 593. у = ж2е2х.
238 Ответы
594. у = е2х - е3* + же"х. 595. у = 1 - же"х.
596. у = (ж + - Je'3* + -(48тж-3со8ж).
597. у = cos ж + ж sin ж.
598. у = cos2z+-(sin2z + sinz). 599. у = ж cos ж-f a?2 sin ж.
600. у = (cos ж - 2 sin ж)е2х + (ж - 1)V. 601. у = же3я + ж + е"х.
602. у = 2ех + (sin ж - 2 cos ж)е~* - 4.
603. у = -[тг cos ж + (тг + I - 2ж) sin ж]ех. 604. у = sh ж + ж2.
„_ _ . _, ,. ,ч , ллл . 4 _я/2 . V5
605. у = cos ж + 2 sin ж + е * + (2ж - 3)е . 606. у = 2ж —-=е ' sin —ж.
л/3 2
607. у = 2жех. 608. у = - cos ж.
609. у = ып2ж. 610. у = -1.
611. у = со8ж. 612. у = е"х.
613. у = сш + 3. 614. у = -^.
615. у = (cos ж + s\nx)ex. 616. у = е~2х cos 2ж.
617. у = (ж2 + ж)е~х. 618. у = С,ж+—.
619. у = -(С, +С21пж).
ж
620. у = -= \С\ cos (-5- In x) +C2sin ( —-\r\xj .
621. у = С\ +С21пж.
622. v = С\(х — 2) + Со(ж — 2)~3.
623! у = С,(2ж + 1) + С2(2ж + 1) In (2ж + 1).
624. у = С| + С2ж2 + С3ж4.
625. у = С, -h С2ж3 + С3 In ж.
626. у = Су+ С2(х + I)5 + С3(ж + I)"2.
вл_ _ 7_ ЧГ In (2a? + 1) . 1п(2ж+1)1
627. у = С| + (2ж + 1) С2 cos ——=—- + С3 sin ——7=—- .
L v2 v2 J
628. у = C| cos In ж + С2 sin In ж + -(7 - In ж).
•> Су 1
629. у = С,ж2 + — + -t(cos In ж - 3 sin In ж).
630. у = -(Ci + С2ж4 + In ж + 2 In 2ж).
ж
631. у = С|Ж + С2ж2 + (ж2 + 2ж)1пж+ 1.
632. у = С,ж+ — + -^-7, \т\ф\.
х ml — 1
хч ^»
633. у = — + -4 4- In 2ж - 3 In ж + 2ж + 7.
ж ж2
634. у = ^J-j-ICi + С2 In (ж + 1) + In 3(ж 4- 1)].
635. у = (ж - 2)2[С, + С2 In (ж - 2)] + ж - ^.
Ответы 239
636. y = C,(l+4a2) + C2e-2x. 637. у = С,(2ж - 3) + С2х'2.
638. у = С,ж3 + С2(х + 1) - а. 639. у = С|Ж + С2 In ж.
640. у = Ci sin а? Н- С2 sin 2ж.
641. у = С, cos (sin a?) + С2 sin (sin ж). 642. у = С)Ж + С2\/1 + ж2 + 1.
643. у = ^ + С2ж3 + ж4. 644. у = С]х+(с2-х+ у V.
645. у = С, cos (e~x) + C2 sin (c"e) + е"'. 646. у = — + С2е]/х - ^ + 1.
X X
647. у = C| cos с* + С2 sin е* + ж. 648. у = С\(2х - 1) + С2ж2 + ж3.
649. -тгг = —а? (« — длина свесившейся части цепи);
at* m
t= W-In (б + >/35) с, Л = ^, т = б.
650. § = 1,2*, S = 0,2t3-<. 651. m§ = -fcm, 5=^.
652. ^ = *2ж, ж = аеи.
653. у = (С\- ж) cos ж + (С2 + In | sin ж|) sin ж.
654. у = С,е* + С2 + (ех + I) In (I + е'х).
вн _ _ . 2
655. у = Ci cos ж + С2 sin ж
656. у = С\ cos ж
657. у = (С}+ С2х)е* - ех In у/\ +ж2 + е*ж arctg ж.
658. у = (С, - ж)е~* cos ж + (С2 + In | sin x\)e'x sin ж.
МЛ _ _ . сов2ж
659. у = C| cos ж 4- С2 sin ж Н—: .
sin ж
660. у = С,ех + С2 - cos ex.
661. у = С, 4- С2ж + С3е~х + 1 - ж + ж In |ж|.
662. у = С1ех2+С2 + (ж2-1)ех2.
663. у = С, + С2 tg ж + -(1 -f ж tg ж).
664. у = С,ж(1п ж - 1) + С2 + ж(1п 2ж - 2 In ж - 2).
665. у =
666. у = C| sin ж + С2 + (In | sin ж| - I) sin ж.
667. у=1. 668. y=i
669. y=-arctg^. 670. у= М-f ж-y
671. у = llJ^f. 672. у = (ж - 1)е*.
у/Х
673. у=-. 674. у=1.
675. y^'-J = 0. 676. (ж - 1)у" - жу' + у = 0.
240 Ответы
677. (x - \)y" - x2yf + (x2-x- \)y = 0.
678. y"' = 0.
679. xy"'-y" + xy'-y = 0.
681. y = CM+Ciy]J-2e-S»d*dx.
682. po(x) = W(x), Pl(x) = -W\x), P2(x) =
где W(x) = W(y\,y2) — определитель Вронского.
685. p] < 4p2. 689. v(x) = e
691. p > 0, g > 0. 692. p = 0, g > 0.
693. Допустим, что у(х) > 0 на (a, b). Так как решение у(х) удовлетворяет всем
условиям теоремы Ролля, то найдется точка £ € (а, Ъ), в которой у'(£) = 0 и,
значит,
Противоречие, так как в точке х = £ решение у(х) имеет максимум и должно
быть у"(£) < 0. Следовательно, у(£) < 0. Аналогично можно показать, что
и в остальных точках £, если таковые найдутся, будем иметь у(£) < 0. Отсюда
следует, что у(х) < 0 на (а,Ь).
706. а) Л = к\ * = 0,1,2,...; б) Л = 4к\ к = 0,1,2,....
707. При любых Л.
sh х
708. а) разрешима, у= ; б) неразрешима.
sh 2тг
709. 1) А - ш1 > 0, у = С, cos 2тгтгж + С2 sin 2птгж;
2) Л - о;2 = 0, у = С = const;
3) Л - и1 < 0, у = 0.
710. у = л/l +4ж - ж2. 711. у = a sin ж.
712. t/=—-. 713. y = -exsi
СП 1
714. у = еа.
O) Q<a<1 716 ,_
a2 sin атг
717. Л = п, у = cos пж, п = 1,2,... .
718. Л = п+ -, у = sin ( п+ - )ж, п = 0, 1,... .
719. 2/ = (я-1)е-*.
720. у = С sin пху п = 0, 1, 2,...; С — произвольная постоянная.
721. у = 0.
722. у = С(ж In ж - ж + 1), С — произвольная постоянная.
723. у = 0. 724. у = *-у + Д"
х2 я3
725. у=1+я-я2 + .... 726. у=1 + у + — + ..
2х4 Шж7 ^oe ж3 2ж5
727. у = ж- — + -7Г-.... 728. „ = *+- + _ +
Ответы 241
___ 1 sin I . ч2 cos 1 - sin 1 . . з
730. у=- + —(х-е)2 + — (х-е)3
тг х4' 2х6
732. у=,+*> + зг + зг + ...; ( = el2)-
(-l)nx
nx2n+1
ж2 х4 Зх6 3-5х8
734. v = 1 1 1 1-... +
У 2 4! 6! 8!
(2п+ 1)"ж2п+4
+ (2п + 4)! +'"> ГДС
, ж3 х4 7х5
735. 2/ = -2 + 2,-a:2-bT-T + —
+ 1Г +
ж2 х3 ж4 х5 13х6
х3 х4 х5 х6 29х7
+ + + +
х2 2х3 Их4 53х5 269х6
738. у = , + т + т + _ + _ + __
(у = С! cos \/х + С2 sin \/x).
*=о
m
где Со — произвольная постоянная, р = —.
1
где Со — произвольная постоянная, р= 1.
744. 2/ = CIJ1/3(2x) + C2J_1/3(2x).
745. y = C!Jl/2(x) + C2J_I/2(x).
242 Ответы
746. y = CtJ0(j
747. y = C|
748. у = z3/2 [C75/4(x2) + C2J-.V4(x2)].
749. у = ^ ]
750. у=^[С,72(») + С2У2(*)]. 751. у = £[C,J,(2*) + С2У,(2*)].
I ^ cos пж 4- sin na?
752. у = - - 2^ jfi—т:—• 753. Периодических решений нет.
. Л cosna;
• 54. v —- С\ cos х 4" CS sin *c ~™ s .
^—' n2(n2 — I)
_„ „ м __ _ л ^ cos па; 4- n sin пж
755. Периодических решений нет. 756. у = С - } rr—z—-—.
*^ц пл\п1 4- 1)
757. Периодических решений нет.
758. у=^+4У"(-1)'1^^
cos2ri7ra;
4 ^> п_, 4п cos nx 4- (4 - п2) sin пя
760. у = - ^(-1) (2n-l)V + 4)2 '
761. Периодических решений нет. 764. f(x) ~ -.
767. Да. 768. Да. 769. Нет. * 770. Нет.
771. Да. 772. Нет. 773. а) Да; б) Нет. 774. Да.
775. Нет.
\ у = С2 cos 3t 4- С\ sin 3£.
778. <Х=^~*в +.3^ '
780. J ж" 'е 2б '
(^ у = С\е + 3C2e"J + cosf.
{ж = (С, - С2) cos* 4- (С, 4- С2) sin *,
у = C| sin i - С2 cos* 4- C3ef,
z = C| cos * 4- C2 sin * 4- C3e'.
782.
* _^
783. . . .
I у = C\ e + Сге - С} sin t - C4 cos t.
Ответы
243
' х = С, + C2t + Cit\
785
786
788
\ у = 2(С2 - С, - C2t)e' + Сзе"2'.
■ (*=е; , 787. (-•'•,
[ у - е' - в". I у = -в"'.
790.
"*• {»-
= С2.
794. <
796.
798. <
С,х2
х = С
1»Р +
= с2
i/ =
g =
800. \ Х % '* '
[ у = С2х.
802.
804. {"I^f^f'
806. {J"J
808 f—^-n»,
^ у = е (cos* -2si
2sin<).
789.
791.
793.
ж + у
x-y
1 '
+1 = C2.
tg-
• C2e'.
ltg(*-y) = «.
797.
799.
801.
2С,'
803
\ а?2 - 2а?у - у2 = i
805 /х = С1+С2е2',
\ у = С, - С2е2'.
807.
809.
y = e2(-2e3(.
x=ic,e'-C
y=^C,
z=]-Cle'-C2e-21.
244 Ответы
810. { y = Qe2t-C3e\ 811. l у = 1 - e"1,
z = C,e2' - C2e3* - C3e\ { z = 2e~l - 1.
x = (1 - *)cos* - sin*,
2) cos* 4*sin*,
ж = C\ cos * 4 C2 sin * 4 tg *,
i sin * 4 C2 cos * 4 2.
\ A — ^|C — ^/2C — V^3G . Ч Л — ^C
812 /х^е^СеЧс.е-', ^ Г x = (. -
(^ у = 9e2t 4 3C,ee 4 C2e \ l У = (* - ■
{ж = C\ cos i
у = -С, sir
010. < . .
\ = -2C, - ЗС2е"4 - 3e~f In |e* - 1|.
Г ж = d cos t + C2 sin * + cos * In | cos t\ 4- * sin i,
816 <
Г ж = d cos t +
^ у = —d sin t +
C2 cos i - sin £ In | cos t\ + t cos *.
С, cos It 4 C2
cos It 4 1.
J x = C, cos * 4- C2 sin * + 1, Г ж = С, cos It 4 C2 sin 2* 4 *,
\ у = -C| sin i 4 C2 cos f. ' \ у = C| sin It - C2
в„л fs = -C|Sin*4(C2-l)cos*,
819. s л л , 820. < ,
l у = С, cos * 4 C2 sin t. i У = C, e2e - C2 - c*.
Г ж = -* Г ж = ег
821. ^ л J 822. {
I У = 0. \ у = е\
( х = -Ci sin * 4 С2 cos * 4 *,
823. < ,
(^ у = С, cos * 4 С2 sin * 4 * - 2.
[ х — —C\t + C2- 2e~l — cos * - sin *,
824. <
{
y = -0^ + C2 cos t-C3 sin t 4- *, 826. <| у = e'(,
= C2sin*4C3cos*4 1. t z = 1.
827. (* 4C'fCf' 828. ( V\(
\ у = С,е6Ч С2е'. ( у = -4С,е2' 4 4C2e7t.
( = 4C,e< 4 C2ew - g, Г x = c и c it _ j
Г ж = С,(1 4 2*)-2С2 -2cos*-3sin*,
831. ^
I y = -C,*4C24 2sin*.
832. ж = е~2' - е-3*. 833. ж = -(*3 4 2*2 4 2* 4 I).
*2 -2
834. ж = sin *. 835. ж = е"3'.
4
836. х = е"Ч sin * - cos *. 837. ж = 0.
838. ж = U2. 839. ж = 1 - cos*.
840. ж = 0. 841. х = е'ь.
Ответы
245
842.
844.
846.
848.
850.
852.
854.
856.
858.
860.
862.
864.
866.
868.
869.
871.
x = -\-t.
x = t2.
x=\- 4te~2t.
x = (* -f 1) sin* - cos*.
x = el + sin*.
.-(?♦.->>-•
ж = e' + cos* — sin *.
1
x = t ( sin 2* + - cos 2* J.
x = e2t[(\ -*)cos* + (l + *)sin*].
x = 4*(sin* - cos*).
х = e'(cos* - 2sin*),
у = e'(3sin* + cos*).
x = - - + — cos 2* - 3 sin 2*,
4 4
w = -* + 3 cos 2* H sin 2*.
2 4
я = -(sin* -l-cos*),
у = -(sin* - cos*).
22
843.
845.
847.
849.
851.
x = t.
x=\.
*2
r
x = t2 - 3* + 4.
853. x = \
855. ж
857. x
859. x
861. ж
863. x
865. x
= —e
= 3(1
1
4
= *-
= teK
+ *) sin 3*.
- l)(cos* + sin*).
1 + 2e*.
- cos 2* + * sin 2*)
867.
x = e\
У = е1.
x = 2-e\
872.
г = -2 + 5e' - <e'.
873.
875. *-2(1 6 _, )(_(
877.
879. *-««*«-1)-5«.Л«,
[ y = 7*-sh*- 17(ch*- I).
874. l у = е-\
876.
878.
у = el - sin *.
880. <j
246 Ответы
! = e'(2cos* — sin/),
881.
" у = «
882. Неустойчиво. 883. Неустойчиво.
884. Устойчиво асимптотически. 885. Устойчиво.
886. Устойчиво. 887. Устойчиво.
888. Неустойчивый фокус. 889. Седло.
890. Центр. 891. Устойчивый фокус.
892. Устойчивый узел. 893. Неустойчивый узел.
894. Неустойчивый узел (дикритический узел).
895. a<-j|.
896. а) точка покоя асимптотически устойчива; б) точка покоя неустойчива;
в) точка покоя асимптотически устойчива; г) точка покоя неустойчива; д) точка
покоя асимптотически устойчива.
897. V = 2ж2 + Зу2, асимптотически устойчиво.
898. V = х4 + у4, устойчиво. 899. V = х2 - -у2, неустойчиво.
900. V = х2 + у2, асимптотически устойчиво.
901. V = х2 + у2, неустойчиво. 902. V = 2х2 + у2, устойчиво.
903. V = х2 + у2, асимптотически устойчиво.
904. V = х2 - у2, неустойчиво. 905. V = х2 + -у2, устойчиво.
906. V = х2 + Зу2, асимптотически устойчиво.
907. 7 = ж4 - у4, неустойчиво. 908. V = ж4 + 2у2, устойчиво.
909. V = ж2 - у2, неустойчиво. 910. V = Зж2 + 2у2, устойчиво.
911. Из условий, налагаемых на функцию v(a?h ... ,жп), очевидно, что данная
система имеет тривиальное решение я, = 0,..., хп = 0. Принимая v за функцию
Ляпунова, для производной — в силу системы получим.
at
dv
Следовательно, тривиальное решение х = 0 данной системы устойчиво по Ляпу-
dv
нову при t —► + оо. Устойчивость будет асимптотической, если — представляет
at
собой отрицательно определенную функцию.
912. Неустойчиво. 913. Устойчиво. 914. Устойчиво.
915. Устойчиво. 916. Устойчиво. 917. Неустойчиво.
918. Устойчиво. 919. Неустойчиво. 920. Устойчиво.
921. Устойчиво. 922. Неустойчиво.
923. Исследование по первому приближению невозможно, так как корни
характеристического уравнения чисто мнимые. Однако сушествует функция
V = Зж2+4у2, удовлетворяющая всем условиям теоремы Ляпунова об асим-
dV
птотической устойчивости, в частности, — = -(6я + 8у ) ^ 0. Следовательно,
at
точка покоя х = 0, у = 0 асимптотически устойчива.
924. V = х2 + у2; решение х = 0 у = 0 асимптотически устойчиво.
925. Д< 0,017. 926. Д < 0,16. 927. Д< 0,0012.
Ответы
247
928.
931.
934.
937.
940.
943.
944.
947.
950.
953.
956.
959.
962.
963.
964.
965.
966.
967.
968.
Неустойчиво.
Неустойчиво.
Устойчиво.
Неустойчиво.
Всегда неустойчиво.
а> -, /?>0, 9/3-i
Устойчиво.
Устойчиво.
Устойчиво.
Неустойчиво.
Неустойчиво.
Неустойчиво.
Неустойчиво.
х = 0 неустойчиво, :
х = t устойчиво, х =
х = t при t < 0 и х •■
929. Устойчиво.
932. Устойчиво.
935. Устойчиво.
938. Устойчиво.
941. а> ^.
6а + 4<0.
945. Устойчиво.
,948. Устойчиво.
951. Неустойчиво.
954. Неустойчиво.
957. Устойчиво.
960. Неустойчиво.
г = t4 + 1 устойчиво.
= е1 неустойчиво.
= -t при t > 0 устойчивы.
х = 0 при t < 0 устойчиво.
х = t устойчиво, х =
Неустойчиво.
= ег +| неустойчиво.
969. Неустойчиво.
930. Устойчиво.
933. Неустойчиво.
936. Устойчиво.
939. а> |.
942. а>0, а/3>1+а2.
946. Устойчиво.
949. Устойчиво.
952. Неустойчиво.
955. Устойчиво.
958. Устойчиво.
961. Неустойчиво.
Приложение 1
Некоторые формулы
из дифференциальной геометрии
В декартовых координатах (рис. 65)
У = tg a
1. Подкасательная ТР = Щ.
У'
2. Поднормаль PN = уу'.
3. Длина отрезка касательной ТМ =
4. Длина отрезка нормали MN = \у\/\ +у/2|.
5. Дифференциал длины дуги кривой dS = y/dx2 + dy2.
В полярных координатах (рис. 66)
р
6. Угол р между касательной и радиусом-вектором tg /3 = —.
Р
р2
7. Полярная подкасательная ТО = -—.
. F
8. Полярная поднормаль ON = р .
9. Длина отрезка касательной ТМ =
/»;
10. Длина отрезка нормали MN = у/р2 + р'2.
11. Дифференциал длины дуги кривой dS = у/р2 + р'2 d<p.
0 Т Р N
Рис. 65
Рис. 66
Приложение 2
Основные оригиналы и их изображения
№
1
1
2
3
4
5
6
7
8
9
10
11
Оригинал f(t)
2
1
Г(п= 1,2,...)
Г (*>-0
еА<
sinu/£
cosu;t
shut
chut
sin (* - a) (a > 0)
cos (t - a) (a > 0)
tnext, n 1,2,...
Изображение F(p) = / f(t)e'ft dt
0
3
1
P
n\
рЛ+1
Г(о+1)
I
p-A
a;
p2 + a;2
p* + u2
и
p2 — c*;2
P
P2-U2
P2 + 1
p2 + \€
n!
250
Приложение 2
Продолжение таблицы
1
12
13
14
15
16
17
18
19
20
2
tQext (а>-1)
ext sin wt
ext cos ut
t sin wt
t cos wt
Jn(0, n-0,1,2,...
In*
3
(p-A)e+I
w
p-\
(pi -j- (д^2\2
(yP + 1 — p)
arcctgp
P
с = 0,57722 — постоянная Эйлера
* По определению s,(J) = / Щ* dx.
Оглавление
Глава 1. Дифференциальные уравнения первого порядка 3
■"§ 1. Основные понятия и определения 3
§2. Метод изоклин 9
§3. Метод последовательных приближений 15
Г§4. Уравнения с разделяющимися переменными
|J^ и приводящиеся к ним 18
§5. Уравнения однородные и приводящиеся к ним 26
Г. Однородные уравнения 26
2°. Уравнения, приводящиеся к однородным 28
Линейные уравнения первого порядка.
Уравнение Бернулли 32
1°. Линейные уравнения первого порядка 32
2°. Уравнение Бернулли 37
Уравнения в полных дифференциалах.
Интегрирующий множитель 40
Г. Уравнения в полных дифференциалах 40
2°. Интегрирующий множитель 42
§8. Дифференциальные уравнения первого порядка,
не разрешенные относительно производной 45
Г. Уравнения первого порядка n-й степени
относительно у' 45
2°. Уравнения вида f(yy у1) = 0 и /(я, у1) = 0 47
3°. Уравнения Лагранжа и Клеро 49
§9. Уравнение Риккати 51
§ 10. Составление дифференциальных уравнений
семейств линий. Задачи на траектории 53
Г. Составление дифференциальных уравнений
семейств линий 53
2°. Задачи на траектории 55
§11. Особые решения дифференциальных уравнений 58
§ 12. Разные задачи 67
Глава 2. Дифференциальные уравнения высших порядков 69
fL§ '3. Основные понятия и определения 69
t§ 14. Дифференциальные уравнения, допускающие
понижение порядка 71
§15. Линейные дифференциальные уравнения n-го порядка . . 79
Г. Линейная независимость функций.
Определитель Вронского. Определитель Грама 79
252 Оглавление
[2°. Линейные однородные уравнения
с постоянными коэффициентами 86
3°. Линейные неоднородные уравнения
с постоянными коэффициентами £9
4°. Уравнения Эйлера 103
5°. Линейные дифференциальные уравнения
с переменными коэффициентами. Метод Лагранжа 105
6°. Составление дифференциального уравнения
по заданной фундаментальной системе решений 110
7°. Разные задачи 112
§ 16. Метод изоклин для дифференциальных уравнений
второго порядка 114
Г § 17. Краевые задачи 116
§ 18. Интегрирование дифференциальных уравнений
при помощи рядов 121
Г. Разложение решения в степеннбй ряд 121
2°. Разложение решения в обобщенный степенной ряд.
Уравнение Бесселя 127
3°. Нахождение периодических решений
линейных дифференциальных уравнений 137
4°. Асимптотическое интегрирование 140
5°. Приложения к интегрированию
дифференциальных уравнений 143
Глава 3. Системы дифференциальных уравнений . 148
§ 19. Основные понятия и определения 148
§20. Метод исключения (сведение системы
дифференциальных уравнений к одному уравнению) .... 157
§21. Нахождение интегрируемых комбинаций. Симметрическая
форма системы дифференциальных уравнений 161
Г. Нахождение интегрируемых комбинаций 161
2°. Симметрическая форма системы
дифференциальных уравнений 167
§22. Интегрирование однородных линейных систем
с постоянными коэффициентами. Метод Эйлера 169
§23. Методы интегрирования неоднородных линейных систем
с постоянными коэффициентами 175
Г. Метод вариации произвольных постоянных
(метод Лагранжа) 176
2°. Метод неопределенных коэффициентов
(метод подбора) 178
3°. Построение интегрируемых комбинаций
(метод Даламбера) 182
§24. Применение преобразования Лапласа к решению
линейных дифференциальных уравнений и систем 185
Г. Общие сведения о преобразовании Лапласа 185
Оглавление 253
2°. Решение задачи Коши для линейных
дифференциальных уравнений
с постоянными коэффициентами 188
3°. Решение систем линейных дифференциальных
уравнений с постоянными коэффициентами 191
Глава 4. Теория устойчивости 195
§25. Устойчивость по Ляпунову.
Основные понятия и определения 195
§26. Простейшие типы точек покоя 199
§27. Метод функций Ляпунова 204
§28. Устойчивость по первому приближению 209
§29. Устойчивость решений дифференциальных уравнений
по отношению к изменению правых частей уравнений ... 213
§30. Критерий Рауса— Гурвица 215
§31. Геометрический критерий устойчивости
(критерий Михайлова) 217
§32. Уравнения с малым параметром при производной 219
Ответы 224
Приложение 1 248
Некоторые формулы из дифференциальной геометрии . . . 248
Приложение 2 249
Основные оригиналы и их изображения 249