РЕШЕБНИК
О.В. Зимина, А.И. Кириллов, Т.Д. Сальникова
ВЫСШАЯ
МАТЕМАТИКА
ИЗДАНИЕ ВТОРОЕ, ИСПРАВЛЕННОЕ
МОСКВА
ФИЗМАТЛИТ
2001

УДК 51
ББК 22.1
3 62
Зимина О.В., Кириллов А.И., Сальникова Т. А. Высшая
математика. — 2-е изд., испр. — М.: Физико-математическая литература,
2001. — 368 с. (Решебник.) — ISBN 5-9221-0126-9.
Книга содержит примеры решения почти всех типовых задач по высшей
математике. Каждой задаче отведен отдельный раздел, содержащий общую
постановку задачи, план ее решения с необходимыми теоретическими
пояснениями и решение конкретного примера. Кроме того, в раздел включены
десять задач для самостоятельного решения и ответы к ним.
Для студентов и преподавателей технических, экономических и
сельскохозяйственных вузов; может быть использована как при очной, так и
при дистанционной формах обучения.
Ил. 6.
Первое издание — 2000 г.
© ФИЗМАТЛИТ, 2000, 2001
© О.В. Зимина, А.И. Кириллов,
ISBN 5-9221-0126-9 Т.А. Сальникова, 2000, 2001

ОГЛАВЛЕНИЕ
ПРЕДИСЛОВИЕ 7
Глав а 1. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ 11
1.1. Разложение вектора по базису . . . . 11
1.2. Коллинеарность векторов 13
1.3. Угол между векторами 14
1.4. Площадь параллелограмма 15
1.5. Компланарность векторов 17
1.6. Объем и высота тетраэдра 18
1.7. Расстояние от точки до плоскости 21
1.8. Уравнение плоскости с данным нормальным вектором .... 23
1.9. Угол между плоскостями .... 24
1.10. Канонические уравнения прямой 25
1.11. Точка пересечения прямой и плоскости 28
1.12. Проекция точки на плоскость или прямую ... 31
1.13. Симметрия относительно прямой или плоскости 33
Глава2. ЛИНЕЙНАЯ АЛГЕБРА 36
2.1. Правило Крамера 36
2.2. Обратная матрица 39
2.3. Понятие линейного пространства 41
2.4. Системы линейных уравнений 44
2.5. Линейные операторы 53
2.6. Матрица, образ, ядро, ранг и дефект оператора 55
2.7. Действия с операторами и их матрицами . . . 59
2.8. Преобразование координат вектора 62
2.9. Преобразование матрицы оператора 65
2.10. Собственные значения и собственные векторы ,68
ГлаваЗ. ПРЕДЕЛЫ 71
3.1. Понятие предела последовательности 71
3.2. Вычисление hmn-too[Pk(n)/Qm{n)] 73
3.3. Вычисление limn^00[f(n)/g(n)] 75
3.4. Вычисление lim„_>00[u(n)"(n)] ... 77
3.5. Понятие предела функции 79
3.6. Понятие непрерывности функции в точке 82
3.7. Вычисление limx-ta[Pn(x)/Qm{x)] 84

4
Оглавление
3.8. Вычисление Iima;-+o[/(a0/ff(a0] 86
3.9. Вычисление lunx-+a[f(x)/g(x)] 88
3.10. Вычисление limI_^o[м(a;)"(I), ... 89
3.11. Вычисление limz_>a [u(x)vW] 92
3.12. Вычисление limx-+a F(u(x)v(x) + f(x)) 94
Глава! ДИФФЕРЕНЦИРОВАНИЕ 97
4.1. Понятие производной ........ 97
4.2. Вычисление производных 99
4.3. Уравнение касательной и нормали 102
4.4. Приближенные вычисления с помощью дифференциала .... 103
4.5. Логарифмическое дифференцирование 104
4.6. Производная функции, заданной параметрически . 106
4.7. Касательная и нормаль к кривой, заданной параметрически . 108
4.8. Производные высших порядков 110
4.9. Формула Лейбница ... 112
4.10. Вторая производная функции, заданной параметрически ... 114
Главаб. ГРАФИКИ ФУНКЦИЙ 117
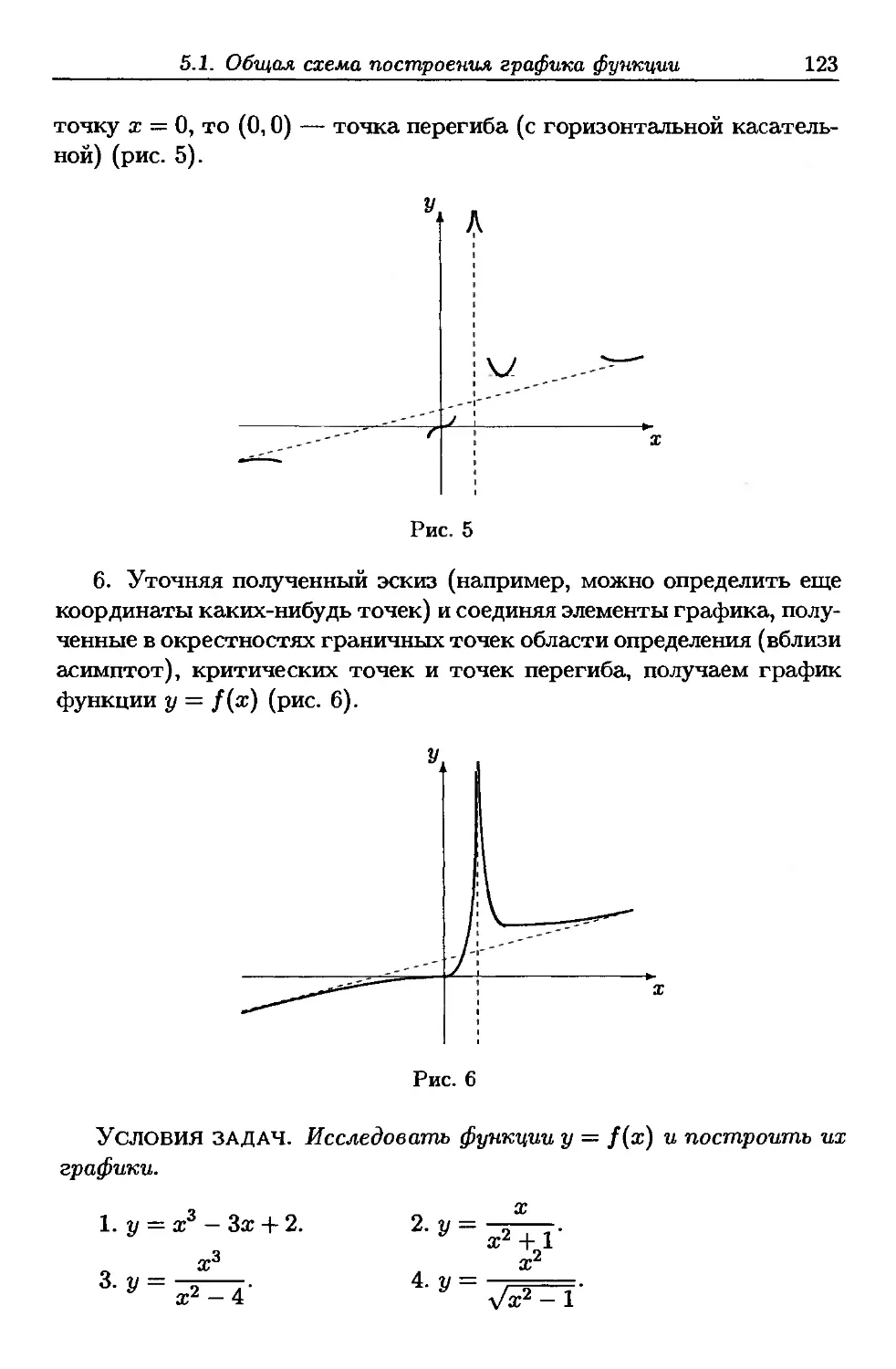
5.1. Общая схема построения графика функции 117
5.2. Наибольшее и наименьшее значения функции 124
5.3. Исследование функции с помощью производных высших
порядков . 126
Главаб. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 129
6.1. Частные производные 129
6.2. Градиент 131
6.3. Производная по направлению ... 133
6.4. Производные сложной функции . 135
6.5. Производная неявной функции 138
6.6. Касательная плоскость и нормаль к поверхности 140
6.7. Экстремум функции двух переменных 142
Г лав а 7. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 146
7.1. Интегрирование подведением под знак дифференциала ... 146
7.2. Интегрирование по частям 148
7.3. Интегрирование рациональных функций с простыми
вещественными корнями знаменателя 150
7.4. Интегрирование рациональных функций с кратными
вещественными корнями знаменателя 153
7.5. Интегрирование рациональных функций с простыми
комплексными корнями знаменателя 157
7.6. Интегрирование выражений R(sinx, cosx) 161
7.7. Интегрирование выражений sin2m x cos2n x 165

Оглавление 5
7.8. Интегрирование выражений R(х, f/ff$3, ?/ff£j, ...) . 167
7.9. Интегрирование выражений R(x, \/а2 ± х2) и .R(x, Vx2 — а2) 169
7.10. Интегрирование дифференциального бинома . 172
Глава8. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 175
8.1. Подведение под знак дифференциала 175
8.2. Интегрирование по частям 177
8.3. Интегрирование выражений R(sin х, cos х) 179
8.4. Интегрирование выражений sin2m x, cos2n x 183
8.5. Интегрирование выражений R(х, y^j. yjf+3> ■••)•■• 185
8.6. Интегрирование выражений R(x, \/а2 ± х2) и R(x, \/x2 —а2) 188
8.7. Вычисление площадей в декартовых координатах 190
8.8. Вычисление длин дуг у = /(х) 192
8.9. Вычисление длин дуг х = x(t), у = y(t) . 194
8.10. Вычисление длин дуг д = g(ip) 196
8.11. Вычисление объемов по площадям поперечных сечений ... 197
8.12. Вычисление объемов тел вращения 199
Г лав а 9. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ 202
9.1. Криволинейные интегралы первого рода 202
9.2. Криволинейные интегралы второго рода 207
Глав а 10. РЯДЫ 211
10.1. Понятие суммы ряда ... 211
10.2. Первая теорема сравнения . . 214
10.3. Вторая теорема сравнения 217
10.4. Признак Даламбера • 219
10.5. Признак Коши 222
10.6. Интегральный признак Коши 225
10.7. Признак Лейбница 227
10.8. Приближенное вычисление суммы ряда 229
10.9. Область сходимости функционального ряда .... 231
10.10. Область сходимости степенного ряда ... 234
10.11. Вычисление суммы ряда почленным интегрированием .... 237
10.12. Вычисление суммы ряда почленным дифференцированием . 241
10.13. Ряд Тейлора . 245
10.14. Приближенные вычисления с помощью рядов . 247
Глава 11. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 251
11.1. Понятие решения 251
11.2. Уравнения с разделяющимися переменными . 252
11.3. Однородные уравнения 255
11.4. Линейные уравнения 1-го порядка 257

6 Оглавление
11.5. Уравнение Бернулли 262
11.6. Уравнения в полных дифференциалах 265
11.7. Уравнения вида F(z,y(fc),j/(fc+1)) = 0 269
11.8. Уравнения вида F(y, у', у") = 0 271
11.9. Линейные уравнения с постоянными коэффициентами .... 274
11.10. Принцип суперпозиции 278
11.11. Метод Лагранжа 281
Глав а 12. КРАТНЫЕ ИНТЕГРАЛЫ 285
12.1. Изменение порядка интегрирования 285
12.2. Двойной интеграл в декартовых координатах 289
12.3. Двойной интеграл в полярных координатах 292
12.4. Интеграл в обобщенных полярных координатах 297
12.5. Вычисление объемов с помощью двойного интеграла .... 301
12.6. Вычисление площадей в декартовых координатах 304
12.7. Вычисление площадей в полярных координатах 307
12.8. Вычисление массы плоской пластины 310
12.9. Тройной интеграл в декартовых координатах 315
12.10. Тройной интеграл в цилиндрических координатах 318
12.11. Тройной интеграл в сферических координатах 321
12.12. Вычисление объемов с помощью тройного интеграла .... 325
12.13. Вычисление массы тела . 328
Г лав а 13. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ 333
13.1. Поверхностный интеграл первого рода 333
13.2. Интеграл по цилиндрической поверхности . . 336
13.3. Интеграл по сферической поверхности ............. 339
Г лав а 14. ТЕОРИЯ ПОЛЯ ... 342
14.1. Векторные линии 342
14.2. Поток векторного поля . . 344
14.3- Поток векторного поля через часть цилиндра 348
14.4. Поток векторного поля через часть сферы 351
14.5. Вычисление потока по формуле Остроградского 355
14.6. Работа силы . . 357
14.7. Циркуляция векторного поля ... 359
14.8. Вычисление циркуляции по формуле Стокса 361

ПРЕДИСЛОВИЕ
В толковом словаре русского языка под редакцией профессора
Д.Н. Ушакова сказано, что решебник — это учебное пособие,
содержащее подробные решения задач, помещенных в каком-нибудь
задачнике, ключ к задачнику. РЕШЕБНИК "Высшая математика" —ключ
сразу к нескольким основным задачникам, используемым при
изучения математики, среди которых в первую очередь следует упомянуть
изданный в сотнях тысяч экземпляров "Сборник заданий по высшей
математике (типовые расчеты)" Л. А. Кузнецова. В дополнение к
этой книге распространяется пакет программ РЕШЕБНИК.ВМ,
который помогает решать задачи, выполняя по указанию учащихся
всевозможные математические действия.
Чтобы приобрести устойчивый навык решения задач одного типа,
нужно решить три-пять таких задач. Однако, решение объективно
необходимого количества задач не предусмотрено действующими
учебными планами по двум причинам.
Во-первых, даже без повторений стандартный объем
обязательных домашних заданий превосходит все разумные пределы.
Во-вторых, в имеющихся задачниках собраны разнообразные
задачи, среди которых редко встречается несколько задач в точности
одного и того же типа.
Выходит, что студенты должны все понять решив одну-две
задачи. При этом их внимание отвлекается от сути дела на
второстепенные или уже пройденные вопросы, а также на выполнение
различных преобразований и расчетов.
Более того, чтобы научиться решать задачи, нужно
самостоятельно выполнять все действия, все "потрогать руками". Но
студенты не могут сами выполнить все действия, поскольку на
выполнение всех действий вручную требуется слишком много времени.
Студенты не могут все "потрогать руками", поскольку чтобы
познакомиться со всеми математическими действиями и ситуациями, нужно
решить столько задач, на решение которых у студентов нет времени.
По этим причинам студенты, как правило, не решают задачи
полностью и, следовательно, не до конца уясняют себе их суть. Напри-

8
Предисловие
мер, у студентов часто нет времени на графическое представление
ответов задач и их анализ, а также на анализ и проверку
промежуточных результатов. Некоторые важные и интересные задачи имеют
столь громоздкие решения, что преподаватели не могут предложить
их студентам.
В результате у студентов остаются более или менее обширные
пробелы в знаниях.
Комплекс РЕШЕБНИК "Высшая математика" предназначен для
того, чтобы устранить эти проблемы современного математического
образования. Он — первый опыт создания учебного пособия нового
типа, с которым возможно разнообразное общение: от пассивного
чтения до внесения в него изменений и получения ответов на вопросы.
Такое пособие в процессе работы адаптируется к потребностям
учащегося и помогает ему применять на практике полученные из пособия
знания.
Комплекс РЕШЕБНИК "Высшая математика" поможет
студентам учиться по-новому, т.е. без .ненужных трудностей и потерь
времени, оптимальным образом организуя взаимодействие человека и
компьютера, при котором дело человека — правильно ставить
задачи, а дело компьютера — быстро и правильно их решать.
Комплекс РЕШЕБНИК "Высшая математика" состоит из книги
РЕШЕБНИК "Высшая математика" и пакета компьютерных
программ РЕШЕБНИК.ВМ.
Книга РЕШЕБНИК "Высшая математика" содержит примеры
решения почти всех типовых задач из таких разделов высшей
математики, как аналитическая геометрия, линейная алгебра, пределы,
дифференцирование, графики, функции нескольких переменных,
неопределенные, определенные и криволинейные интегралы, ряды,
обыкновенные дифференциальные уравнения, кратные и поверхностные
интегралы, векторный анализ.
Каждой задаче отведен отдельный раздел книги, содержащий
общую постановку задачи, план ее решения с необходимыми
теоретическими пояснениями и решение конкретного примера. Кроме того,
в раздел включены задачи того же типа и ответы к ним.
Преподаватели могут предложить часть из них на аудиторных практических
занятиях, другие — в виде домашних заданий, остальные
использовать в контрольных работах, на коллоквиумах, зачетах и экзаменах.
Чтобы научиться решать задачи того или иного типа,
рекомендуется сначала изучить план решения (алгоритм) в общем виде, затем

Предисловие
9
рассмотреть пример реализации плана в конкретном случае и затем
по аналогии с ним решить несколько задач из числа предлагаемых
для самостоятельного решения.
Пакет РЕШЕБНИК.ВМ состоит из документов MS Word и
специальных компьютерных программ.
Документы MS Word в основном идентичны тем, которые
включены в книгу.
Программы пакета обеспечивают связь (интерфейс) MS Word с
системой символьной математики DERIVE фирмы Soft Warehouse
Inc. Благодаря этой связи любое математическое выражение из
документа MS Word может быть передано в DERIVE для преобразований,
результат которых затем вставляется в документ MS Word.
В пакете РЕШЕБНИК.ВМ материалы книги РЕШЕБНИК
"Высшая математика" становятся интерактивными шаблонами для
документов студентов и преподавателей. Например, если студенту нужно
решить какую-нибудь задачу, то он может:
1) найти задачу данного типа;
2) изучить план ее решения;
3) изучить пример;
4) изменить исходные данные и выполнить надлежащие действия
с ними;
5) сохранить содержание окна в каком-нибудь файле;
6) передать файл преподавателю непосредственно или
предварительно распечатав его.
Естественно, возникает вопрос: если пакет РЕШЕБНИК.ВМ
выполняет математические действия за учащихся, то как же они смогут
научиться выполнять эти действия самостоятельно? Ответ таков:
пакет Решебник ВМ выполняет за учащихся не те математические
действия, которые они изучают в данный момент, а те, которые они
уже изучили раньше. Так экономится время, внимание
концентрируется на сути изучаемого метода и математика становится проще для
понимания и интересней.
Заметим, что при использовании пакета РЕШЕБНИК.ВМ
высвобождается свыше 60% учебного времени. Это время целесообразно
уделить решению нескольких задач одного и того же типа, анализу
и обсуждению результатов, а также изучению новых тем и разделов
математики, включение которых в программу ранее не
представлялось возможным.

10
Предисловие
Подчеркнем, что для использования пакета РЕШЕБНИК.ВМ надо
уметь пользоваться только MS Word. Все остальные навыки
выработаются сами собой по мере изучения математики.
Студенты могут применять пакет и для решения задач по физике
и другим точным наукам, а также для оформления отчетов по
лабораторным и курсовым работам.
По истечении полутора-двух лет оказывается, что студенты
умеют решать всевозможные задачи самостоятельно и с использованием
мощнейшего пакета "Суперсистема символьной математики",
который сформировался на их компьютерах в процессе учебы с помощью
пакета РЕШЕБНИК.ВМ.
Преподаватели могут использовать пакет РЕШЕБНИК.ВМ при
подготовке занятий, контрольных мероприятий, методической
литературы, статей и для организации автоматического контроля знаний
студентов.
Объем пакета РЕШЕБНИК.ВМ не превосходит 500 К.
Подробная информация о пакете РЕШЕБНИК.ВМ и сам пакет
размещены на сайте Интернет www.AcademiaXXI.ru.
Авторы будут благодарны всем приславшим свои замечания о
комплексе РЕШЕБНИК "Высшая математика" и предложения по
адресу:
111250 Москва, ул. Красноказарменная, д. 14, Московский
энергетический институт (ТУ), кафедра высшей математики.
E-mail: KirillovAI@mpei.ru.

Глава 1
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
При изучении темы АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ вы
научитесь решать задачи векторной алгебры и использовать свойства
линейных операций с геометрическими векторами, скалярного,
векторного и смешанного произведений векторов для решения
геометрических задач. Вы научитесь решать задачи аналитической геометрии,
связанные с различными видами уравнений плоскости и прямой и их
взаимным расположением.
С помощью пакета РЕШЕБНИК.ВМ вы можете решить системы
уравнений, вычислить определители, выполнить все численные
расчеты и проверить правильность полученных вами результатов.
1.1. Разложение вектора по базису
Постановка задачи. Найти разложение вектора х—{х\, х2,хз}
по векторам р = {р1,р2,Рз}, <?= {вь&.вз} *t г = {ri,r2,r3}.
План решения.
1. Искомое разложение вектора х имеет вид
х = ар + /3q + 7г.
2. Это векторное уравнение относительно а, /3,7 эквивалентно
системе трех линейных уравнений с тремя неизвестными
Pi<x + qi/3 + П7 = xi,
р2а + q2l3 + Tin = х2,
Рз« + 9з/3 + Гз7 = z3.
3. Решаем эту систему уравнений относительно а, /3 и 7 и таким
образом определяем коэффициенты разложения вектора х по
векторам р, диг. Записываем ответ в виде х = ар + fiq + *уг.

12
Гл. 1. Аналитическая геометрия
Замечание. Если система уравнений не имеет решений (векторы
р, q и г лежат в одной плоскости, а вектор £ ей не принадлежит),
то вектор х нельзя разложить по векторам р, q и г. Если система
уравнений имеет бесчисленное множество решений (векторы р, q, r
и вектор х лежат в одной плоскости), то разложение вектора £ по
векторам р, qnf неоднозначно.
Пример. Найти разложение вектора £ = {3,-1,2} по векторам
р= {2,0,1}, q = {1,-1,1} иг = {1,-1,-2}.
Решение.
1. Искомое разложение вектора £ имеет вид
х = ар + /3q + jr.
2. Это векторное уравнение относительно а, /3 и 7 эквивалентно
системе трех линейных уравнений с тремя неизвестными
2а + Р+ 7= 3,
-13- 7 = -1,
а + /3-27= 2.
3. Система имеет единственное решение а = 1, /3 = 1, 7 = 0.
Ответ, x — p + q.
Условия ЗАДАЧ. Написать разложение вектора х по векторам
р, q иг.
1. I ={-2,0,9}, р={0,-1,2},
2. х ={5,-12,-1}, £ = {1,-3,0},
3. £={0,2,4},
4. £={-1,5,5},
5. £={-1,-2,3},
6. £ = {-5,2,-1},
7. £ = {1,-5,7},
8. £ = {5,1,4},
9. £ = {1,1,-1},
10. £ = {-3,7,4},
р ={3,1,-1},
р={2,1,1},
р ={2,0,1},
р ={-1,1,0},
р ={0,-1,1},
V ={2,0,2},
£ = {1,1,0},
р={-2,2,1},
9 =
q =
Q =
Q =
q =
Q =
q =
q =
Q =
q =
1,0,-1}, r={-l,2,4}.
1,-1,1}, r ={0,-1,2}.
0,-3,1}, F = {1,1,1}.
-2,0,-3}, f = {-1,2,1}.
1,2,-1}, r ={0,4,-1}.
2,-1,3}, F={1,0,1}.
2,0,1}, r ={3,-1,0}.
0,-1,1}, r ={3,-1,4}.
-1,0,1}, r={-l,0,2}.
2,0,1}, r={l,l,l}.
Ответы. 1. {2,-1,1}. 2. {4,1,-1}. 3. {-1,0,3}. 4. {-1,-1,3}.
5. {1,-3,1}. 6. {3,1,-4}. 7. {2,5,-3}. 8. {1,-2,1}. 9. {1,1,-1}.
10. {2,-1,3}.

1.2. Коллинеарность векторов
13
1.2. Коллинеарность векторов
Постановка задачи. Коллинеарны ли векторы р = Xia + А26 и
q = /iia + /i2&> го*е о = {01,02,03} и b = {61,62,63}?
План решения. Векторы коллинеарны тогда и только тогда,
когда существует число а такое, что р = aq. Иными словами, векторы
коллинеарны тогда и только тогда, когда их координаты
пропорциональны,
1. Находим координаты векторов р и q, пользуясь тем, что при
сложении векторов их координаты складываются, а при умножении
на число координаты умножаются на это число.
2. Если координаты векторов р = {рг,Р2,Рз} и Q — {въ<72>9з}
пропорциональны, т.е.
Pi _ Р2 _ Рз
9i 92 9з '
то векторы р и q коллинеарны. Если равенства
Рл_ _ Р2 _ Рз
9i 92 9з
не выполняются, то векторы р и q неколлинеарны.
ПРИМЕР. Коллинеарны ли векторы р = 4а — 36, q = 96 — 12a, где
о = {-1,2,8} и 6= {3,7,-1}?
Решение.
1. Находим координаты векторов р и q, пользуясь тем, что при
сложении векторов их координаты складываются, а при умножении
на число координаты умножаются на это число:
р = {-13,-13,35}, q = {39,39,-105}.
2. Так как
-13 _ -13 _ 35
39 ~ 39 -105 '
то координаты пропорциональны. Следовательно, векторы р и q
коллинеарны.
Ответ. Векторы р и q коллинеарны.

14
Гл. 1. Аналитическая геометрия
Условия задач. Коллинеарны ли векторы р и q ?
1. а={1,2,-3}, Ь={1,0,-1}, р = За + 6Ь, q=-a + 2b.
2. а={2,0,1}, Ь={-2,3,1}, р = 2а + 2Ь, q = 3a-2b.
3. о ={-2,2,1}, Ь ={-1,-2,2}, р=а + ЗЬ, д = 2а-Ь.
4. а={-1,2,3}, 6 ={2,1,1}, р = 2о + ЗЬ, q=a-b.
5. а={2,5,1}, Ь={5,0,2}, р=-а + Ь, д=а-ЗЬ.
6. а={1,2,-2}, 6 ={1,3,—1}, р=а + Ь, q=a + 2b.
7. о ={1,2,3}, 6 ={2,-1,0}, р = 6а-2Ь, q=-3a + a.
8. о={1,3,-1}, Ь={2,1,3}, р = 6а-ЗЬ, д=-4а + 2а.
9. а ={-1,-2,2}, Ь ={1,0,2}, р=а + ЗЬ, д=-2а-6Ь.
10. о={1,3,2}, Ь={1,-2,6}, р=а-Ь, д=-6о + 6Ь.
Ответы. 1. Нет. 2. Нет. 3. Нет. 4. Нет. 5. Нет. 6. Нет. 7. Да.
8. Да. 9. Да. 10. Да.
1.3. Угол между векторами
Постановка задачи. Даны точки A(xi,yi,zi), £B2,2/2,22) и
С(жз,2/з,2з). Найти косинус угла между векторами АВ и АС.
План решения. Косинус угла <р между векторами АВ и АС
определяется формулой
(АВ,АС)
cos w — -==— . A)
V \AB\ ■ \АС\ К '
1. Чтобы вычислить длины векторов \АВ\ и \АС\ и скалярное
произведение {АВ, АС), находим координаты векторов:
АВ- {x2-xi,y2-yi,z2 -zi}, AC = {z3-a:i,2/3-2/i,z3-zi}.
2. По формулам для длины вектора и скалярного произведения
векторов имеем
\АВ\ = у/(х2 - Х1у + B/2 - 2/iJ + (г2 - 21J,
\АС\ = у/(х3 - х{? + (уз - yiJ + (*з - ZlJ,
(АВ, ЛС) = (х2 - a:i)(a:3 - zi) + (у2 - у^уз - г/i) + (z2 - zi)(z3 - zi).
3. Вычисляем cos ip по формуле A) и записываем ответ.

1.4. Площадь параллелограмма
15
Пример. Даны точки Л(-2,4,-6), £@,2,-4) и С(-6,8,-10).
Найти косинус угла между векторами АВ и АС.
Решение.
1. Находим координаты векторов АВ — {2,-2,2} и АС = {—4,4,-4}.
2. По формулам для длины вектора и скалярного произведения
векторов имеем
\АВ\ = v/22 + (-2J + 22 = 2л/3, \АС\ = л/(~4J + 42 4- (-4J = 4л/3,
(АВ, 1С) = 2 • (-4) + (-2) • 4 + 2 • (-4) = -24.
3. Вычисляем cosy» по формуле A):
-24
COS W = ;= 7= ~ — 1 •
2v/3 • 4V^
Ответ. Косинус угла между векторами АВ и АС равен —1.
Условия ЗАДАЧ. Найти косинус угла между векторами АВ и АС.
1. ЛB,-2,3), £A,-1,2), СD,-4,5).
2. ,4@,-2,6), £(-12,-2,-3), С(-9,-2,-6).
3. ЛB,3,-1), £D,5,-2), СC,1,1).
4. Л(-1,2,-2), £C,4,-5), СA,1,0).
5. А(-2,-2,0), £A,-2,4), СE,-2,1).
6. ЛC,3,-1), £C,2,0), СD,4,-1).
7. А(-1,-7,-4), £B,-1,-1), СD,3,1).
8. ЛB,-2,6), £@,0,4), СF,-6,10).
9. А@,1,0), £C,1,4), СD,1,3).
10.^C,2,0), £A,4,-1), СD,0,2).
Ответы, l.cosv? = —1. 2.cosv? = 24/25. 3.cosy> = —4/9. 4.cosy> =0.
5. cos v? = \/2/2. 6. cos v? = 1/2. 7. cos y> = 1. 8. cos <p — — 1. 9. cos y> = 24/25.
10. cos y> = -8/9.
1.4. Площадь параллелограмма
ПОСТАНОВКА задачи. Вычислить площадь параллелограмма,
построенного на векторах а = ctip+ct2qub = P1P + P2Q, если известно,
что \р\ = ро, \о\ — Qo и угол между векторами р и q равен <р.

16
Гл. 1. Аналитическая геометрия
План решения. Площадь параллелограмма, построенного на
векторах о и Ь, равна модулю их векторного произведения:
S=\[a,b)\. A)
1. Вычисляем [о, Ь], используя свойства векторного произведения
[а,Ь] = [aip + oc2q,PiP + P2q\ =
= aiPi\p,p\ + «102 [р, q\ + a2Pi[q,p\ + a2/32[q, q\ =
= (aiP2-a2Pi)\p,q\.
2. Вычисляем модуль векторного произведения
\[a,b]\ = \аф2 - a2Pi\ \p\ \q\ siaip
(simp > 0, так как 0 < (p < it).
3. Находим площадь параллелограмма, используя формулу A)
S = |[о, Ъ]| = |а1/32 - a2/3i| \р\\q\ sin <p.
Пример. Вычислить площадь параллелограмма, построенного на
векторах о = Зр 4- 2q и b = 2р — q, если известно, что |р| = 4, \q\ — 3 и
угол между векторами р и q равен 37г/4.
Решение.
1. Вычисляем [о, Б], используя свойства векторного произведения
[а,Ь] = [Зр + 2q,2p~ q\ = 6[p,p] - 3[p,g] + 4[q,p\ - 2[q,q\ = -7[p,g].
2. Вычисляем модуль векторного произведения
|[«, Ц\ = I - 7[р,9]| = 7\p\\q\sin Ц = 42^2.
3. Находим площадь параллелограмма, используя формулу A)
5 = |[о,Ь]|=42^2.
Ответ. Площадь параллелограмма равна 42V2 (ед. длиныJ.

1.5. Компланарность векторов
17
Условия ЗАДАЧ. Вычислить площадь параллелограмма,
построенного на векторах а и b (pq — угол между векторами р и q).
1. а = р + Ш b = 2p-q, |p|=2, \q\ = 1, g = 7r/6.
2. a = 2p + q, b = p-Zq, \p\ = 2, \q\ = 2, рд=тг/4-
3. a=p-2q, b = p + 3g, |fl = 1, |g| = 2, p$ = ir/2.
4. a = 3p - 5g, 6 = p + 2?, |p| = 2, |g| = 1, p£ = 5тг/6.
5. a = p-q, b = 2p + 2q, \p\ = 1, |g| = 6, р| = Зтг/4.
6. a = p + 2g, 6 = 3p - 2g, \p\ = 3, |g] = 2, pg" = тг/3
7. a = 2p-2q, b = p + g, |p| = 2, \q\ = 3, pq=ir/2
8. a = p + q, b = p-4<f, [p| = 7, |g| = 4, pg = тг/4
9. a = 4p-4g, b = p + 3g, |p] = 2, |g| = 1, p| = тг/6
10. a = p + g, b = 2p-q, |p| = 2, \q\=Z, pq = тг/3
Ответы. 1. 5 = 7. 2. 5 = 14v/2. 3. 5 = 10. 4. 5 = 11. 5. 5 = 15v/2.
6. 5 = 24>/3. 7. 5 = 24. 8. 5 = 70^2. 9. S = 16. 10. 5 = 9>/3.
1.5. Компланарность векторов
Постановка задачи. Компланарны ли векторы а — {а\,а2,аз},
Ь= {bi,b2,h} uc= {ci,c2,c3}?
План решения. Для того чтобы три йектора были компланарны
(лежали в одной плоскости или в параллельных плоскостях),
необходимо и достаточно, чтобы их смешанное произведение (о,Ь,с) было
равно нулю.
1. Смешанное произведение векторов выражается через их
координаты формулой
(о, Ь, с)
а± а2 аз
bi &2 Ь3
С\ С2 С3
2. Если определитель в правой части этого равенства равен нулю,
то векторы компланарны, если определитель не равен нулю, то
векторы некомпланарны.
Пример. Компланарны ли векторы а — {7,4,6}, Ь = {2,1,1} и
с = {19,11,17}?

18
Гл. 1. Аналитическая геометрия
Решение.
1. Вычисляем смешанное произведение векторов:
(о, Ъ, с)
7 4 6
2 11
19 11 17
2. Так как (о,Ь,с) — 0, векторы о, Ь и с компланарны.
Ответ. Векторы о, Ь и с компланарны.
Условия ЗАДАЧ. Компланарны ли векторы о, Ь и с ?
1. а = {1,3,0},
2. а = {3,2,1},
3. а = {0,6,1}, Ь = {0,2,0},
4. а = {4,1,-2}, Ь= {3,2,1},
5. а = {2,5,0}, Ь={2,-1,2},
6. а = {1,0,-1},
7. а = {4,3,1},
8. о = {-2,4,3},
9. о ={2,5,8},
10. о = {1,5,1},
Ъ = {-1,0,-1}, с = {1,2,1}.
Ь = {5,5,5}, с = {0,-1,-2}.
с = {1,1,1}.
с = {5,5,5}.
с ={1,1,1}.
с ={3,1,-1}.
с ={2,1,-1}.
с ={2,0,-1}.
Ь= {-2,-1,0},
Ь={5,1,2},
6 = {4,7,5},
Ь = {1,-3, -7}, с = {0,5,10}.
Ь = {1,7,1}, с = {2,2,1}.
Ответы. 1. Нет. 2. Да. 3. Нет. 4. Да. 5. Нет. 6. Да. 7. Нет.
8. Да. 9. Да. 10. Нет.
1.6. Объем и высота тетраэдра
Постановка задачи. Вычислить объем тетраэдра с
вершинами в точках Ai(xi,у 1, zi), ^2B:2,2/2,22), -^3B:3,2/3,23), А4(х4,2/4,24)
и его высоту, опущенную из вершины Aj на грань А1А2А3.
План решения.
1. Из вершины А\ проведем векторы А\ Лг = {2:2—2:1,2/2— 2/i,z2—2i},
AiAz = {2:3-2:1,2/3-2/1,23-21} и А\АА = {2:4-2:1,2/4 -2/i,^4 -zi}.
В соответствии с геометрическим смыслом смешанного
произведения имеем

1.6. Объем и высота тетраэдра
19
объемы тетраэдра и параллелепипеда, построенных
где VT. и Vm
на векторах А\А2, А-^Аз и -AiAj)
С другой стороны,
Vt. — ■zS&A1A2A3 - h,
где согласно геометрическому смыслу векторного произведения
1
B)
Saabc = 2 |[-Aii42, Лйз]|-
Сравнивая формулы A) и B), получаем
ЗК
= \(А1А2,А1А3,А1А4)\
Saaxa2a3 \[АгА2, AtAsW
2. Вычисляем смешанное произведение:
Х2 -Xi 2/2 - 2/l Z2 - Zi
хз -xi уз - J/1 z3 - zi
х4 -xi 2/4 - 2/i z4 _ zi
(A1A2,A1A3,A1Ai)
и находим объем тетраэдра по формуле A).
3. Вычисляем координаты векторного произведения:
C)
[А1А2,А1Аз] =
Л
1
г
Ж2 - £Ci
Хз - Х\
2/2 - 2/1 Z2 - Zi
2/з - 2/i z3
-Z]
J
3 к
2/2 - 2/1 z2 - zi
2/з - 2/i z3 - zi
=
Х2 —Х\ Z2 - Zi
ж3 -xi г3 - zi
J
Х2-
хз-
-XI
-xi
2/2"
2/3-
-2/1
-2/1
!}•
и его модуль.
4. Находим высоту h по формуле C).
Пример. Вычислить объем тетраэдра с вершинами А\B,3,1),
ЛгD,1,—2), -А3F,3,7) и Aj(-5, — 4,8) и его высоту, опущенную из
вершины Ац на грань А1А2А3.
Решение.
1. Из вершины А\ проведем векторы А1А2 — {2, —2, —3}, А\А$ =
= {4,0,6} и :VU = {-7,-7,7}.

20
Гл. 1. Аналитическая геометрия
2. Вычисляем смешанное произведение:
{A1A2,AiA3,AiA4)
2 -2 -3
4 0 6
-7 -7 7
= 2 • 42 + 2 • 70 + (-3) • (-28) = 308
и находим объем тетраэдра по формуле A)
1 з
VT. = — ■ 308 (ед.длины) .
о
3- Вычисляем координаты векторного произведения:
[А1А2,А1А3} =
его модуль
i
2
4
3
-2
0
к
-3
6
= -12?-24j+8fc = {-12,-24,8}
[А1Аг,'А-[Щ = v/(-12J + (-24J + 82
4. Находим высоту h по формуле C):
28.
КЛхЛ^УМз.ЛхУЦ)! 308
/г = —— —— = = 11 ед.длины.
\{А^А1,ЖЩ\ 28
Ответ. VT. — (ед.длины) , h = 11 ед.длины.
о
Условия ЗАДАЧ. Вычислить объем тетраэдра с вершинами в
точках А\, А2, А3, Л4 и его высоту, опущенную из вершины Л4 на
грань Л1Л2Л3.
1. Л1B,4,7), Л2C,3,2), Л3@,1,2), Д,(-3,7,-2).
2. ^(-2,4,8), Л2D,-1,2), Л3(-8,7,10), Д,(-3,4,-2).
3. ^F,1,3), Л2F,-2,-3), Л3B,2,0), А4(-5,1,0).
4. ^@,-1,2), Л2(-3,3,-4), Л3(-9,-5,0), Л4(-8,-5,4).
5. Ах@,-4,3), Л2(-5,1,-2), Л3D,7,-2), Л4(-9,7,8).
6. ^B,1,1), Л2@,5,7), Л3C,-3,-7), Л4A,8,5).
7. ^D,1,-1), Л2A,4,-1), Л3@,1,3), Л4(-2,0,0).
8. ^E,2,1), Л2D,5,4), Л3(8,3,-3), А4(-7,12,-4).
9. ^@,2,-2), Л2A,9,3), Л3F,-6,-2), Л4C,-2,8).
10.^A2,2,3), Л2(-7,-5,0), Л3(-4,-8,-5), Л4(-4,0,-3).

1.7. Расстояние от точки до плоскости
21
Ответы.
1. V = 70/3, h = 2\/14. 2. V = 56/3, h = 4.
3. V = 43/2, /г = 43х/1б5/105. 4. V = 80/3, /г = 4.
5. V = 190, /г = 2V^8. 6. V = 15, /г = 3\/5.
7. V = 12, /г = 2л/3. 8. V = 140/3, /г = iy/Ti.
9. V = 250/3, /г = 5\/2. 10. V = 338/3, /г = V^6.
1.7. Расстояние от точки до плоскости
Постановка задачи. Найти расстояние от точки Мо(хо,уо> ^о)
до плоскости, проходящей через точки M\(x\,y\,Z\), M2{x2,y2i Z2) "
M3(x3,y3,z3).
План решения. Искомое расстояние можно найти как высоту
тетраэдра с вершинами M0(x0,yo,zo), Mi(xi,yi,zi), M2(x2,y2,Z2) и
M3(x3,y3,z3), опущенную из вершины М0(х0,Уо, *о) на грань MiM2M3
(см. задачу 1.6). Другое решение заключается в следующем.
Расстояние d от точки Мо(хо,Уо,%о) до плоскости равно длине
проекции вектора М\Мц на нормальный вектор плоскости п, т.е.
Кп.МхМо)!
d = | ПРйМхМо! = " ' . ' "" • A)
\п\
Поскольку нормальный вектор плоскости п ортогонален векторам
М\М2 и М\М3, его можно найти как их векторное произведение:
п = [М\М2,М\М3].
1. Находим координаты векторов:
М1М2 = {x2-x1,y2-yi,Z2-z1},M1M3 - {a:3-a:i,j/3-J/i,^3-zi},
Mi Mo = {xo - xltyo - 2/i, zo - zi},
и нормального вектора плоскости:
п = [MiM2,MiM3] =
г 3 *
Х2 -Х\ J/2 ~ J/l Z2 - Z!
Х3 -X! J/з - J/l Z3 - Z\
2. Вычисляем расстояние d от точки Mo(xo,yo,zo) до плоскости
по формуле A).
Пример. Найти расстояние от точки МоA,—1,2) до плоскости,
проходящей через точки Mi(l,5, -7), Мг(—3,6,3), М3(-2,7,3).

22
Гл. 1. Аналитическая геометрия
Решение.
1. Находим координаты векторов:
MiM2 = {-4,1,10}, МхМз - {-3,2,10}, MiMo = {0, -6,9},
и нормального вектора плоскости:
п = [MiM2, M1M3] =
i j k
-4 1 10
-3 2 10
= -10i+10j-5fc.
2. Вычисляем расстояние d от точки Мо до плоскости по
формуле A):
d = |nPfjM1M0| =
Кя.м^о)!
\п\
-105
V(-10J + Ю2 + (-5J
= 7.
Ответ, d = 7 ед. длины.
Условия ЗАДАЧ. Найти расстояние от точки Mq до плоскости,
проходящей через точки М\, М2 и М%.
1. Mi@,7,-4), М2D,8,-1), М3(-2,1,3), Мо(-9,10,2).
2. М1E,8,3), М2(Ю,5,6), М3(8,7,4), МоG,0,1).
3. МДМ.б), М2(-5,5,2), М3G,-1,8), М0(-3,4,3).
4. Мх @,-2,-1), М2(-3,-1,2), М3A,0,-2), М0(-3,3,1).
5. М!B,3,1), М2B,0,3), М3A,2,0), МоC,0,5).
М2D,5,2), М3E,1,4), М0(-2,-6,2).
М2D,3,0), М3A,2,9), М0F,1,-6).
М2@,5,-3), М3(-4,2,-1), М0(-4,9,-8).
М2@,-1,-3), М3D,0,0), М0(-1,4,6).
М2(-3,2,3), М3C,0,6), М0(-2,5,-4).
6. М^З.б),
7. М^.б.О),
8. MiE,i2,i),
9. Мх@,3,5),
10. М^-2,2),
Ответы. 1. d = 459/\/2265. 2. d = 5у/2. 3. d = 0. 4. d = 9/у/Ш.
5. d = \/38/38. 6. d = 5/\/29. 7. d = 2\/б. 8. d = 7. 9. d = 5/9.
10. d = 45v/l94/97.

1.8. Уравнение плоскости с данным нормальным вектором 23
1.8. Уравнение плоскости
с данным нормальным вектором
ПОСТАНОВКА ЗАДАЧИ. Написать уравнение плоскости,
проходящей через точку Мо(хо,Уо->^о) перпендикулярно вектору М\М^, где
точки М\ и Mi имеют координаты (x\,yi,Zi) и (х2,У2,22)-
План решения. Уравнение плоскости, проходящей через точку
Mo(xo,yo,zo) перпендикулярно вектору п = {А, В, С}, имеет вид
А(х - хо) + В(у - у0) + C(z - z0) = 0. A)
1. В качестве нормального вектора плоскости п выбираем вектор
MiMi - {x-z -Xi,yz -J/1,Z2- Zi}.
2. Составляем уравнение плоскости A) с нормальным вектором
MiMi, проходящей через точку М0(х0,уо,го):
(х2 - xi)(x - хо) + (г/2 - гд)(г/ - г/0) + (г2 - гх)(г - z0) = 0.
Пример. Написать уравнение плоскости, проходящей через
точку МоB,5,-3) перпендикулярно вектору М1М2, где точки Мх и Мг
имеют координаты G,8, —1) и (9,7,4).
Решение.
1. В качестве нормального вектора плоскости п выбираем вектор
МГЙ2 = {2,-.1,5}.
2. Составляем уравнение плоскости A) с нормальным вектором
п = {2, —1,5}, проходящей через точку М0B,5, —3):
2(х - 2) - 1(г/ - 5) + 5(z + 3) = 0.
Ответ. Уравнение плоскости 2х — у + 5г + 16 = 0.
Условия ЗАДАЧ. Написать уравнение плоскости, проходящей
через точку Мо перпендикулярно вектору M\Mi-
1. МоC,2,0), М№,1,5), М2B,-1,4).
2. Мо(-5,-1,0), Мг(-5,1,-4), М2(-2,2,-3).
3. М0B,-4,-2), Mii-1,-3,-7), M2(-4,-l,-5).
4. Mo(-5,3,10), Мх{0,Ь,7), М2B,7,8).

24
Гл. 1. Аналитическая, геометрия
5. МоB,-10,-4), М1@,-6,-8)> М2(-2,-5,-9).
6. М0A,9,2), М!@,4,7), М2A,-6,9).
7. Мо@,-2,7), М!(-5,-4,9), М2(-2,-2,6).
8. М0(-1,1,-4), MiC,8,-2), M2B,ll,0).
9. М0(-1,7,-6), МхC,5,-1), М2A,3,-2).
10. М0(-5,2,5), МхC, -3, -2), М2D, -1,2).
Ответы.
1. 2х + 2у + z = 0. 2. Зх + у + z - 4 = 0.
3. За; - 2у - 2z - 16 = 0. 4. 2х + 2у + z + 9 = 0.
5. 2а; - у + z - 20 = 0. 6. х + Чу + 2z - 3 = 0.
7. За; + 2у - 3z + 23 = 0. 8. а; - Зу - 2z - 8 = 0.
9. 2х + 2у + z - 16 = 0. 10. х + 2у + 4z - 5 = 0.
1.9. Угол между плоскостями
Постановка задачи. Найти угол между плоскостями
Ахх + Вгу + dz + Di =-0, Л2а; + В2у + C2z + D2 = 0.
План решения. Двугранный угол между плоскостями равен углу
между их нормальными векторами
п1 = {А1,В1,С1}, п2 = {Л2,Б2,С2}.
Поэтому угол <р между плоскостями определяется равенством
(ni,n2)
cos<p= .
|ш| • \п2\
Пример. Найти угол между плоскостями
х + 2у - 2z - 7 = 0, х + у - 35 = 0.
Решение. Двугранный угол между плоскостями равен углу
между их нормальными векторами щ = {1,2, —2} и п2 = {1,1,0}.
Поэтому угол <р между плоскостями определяется равенством
{пг,п2) 11+21-20 _ 1
C°Stf ~ |щ| • \п2\ ~~ ^12 + 22 + (-2)VI2 + l2 ~ V2 '
Таким образом, <р = arccos (l/v^2) = тг/4.
Ответ. Угол между плоскостями <р = 7г/4.

1.10. Канонические уравнения прямой
25
Условия ЗАДАЧ. Найти угол между плоскостями.
1. За; - у + 3 = О,
2. х - у + 3z - 5 = О,
3. 5z-4j/ + 3z-3 = 0,
4. 5я - Зу + 2z + 5 = О,
5. 6я + 2i/- 4z + 17 = О,
6. x-y + zy/2-5 = 0,
7. j/-3z + 5 = 0,
8. 6а; + 2i/- 3z 4-1 = О,
9. 2x + у + 2z - 5 = О,
10.5a; - у + 2z + 12 = 0,
x - 2y + 5z - 10 = 0.
a; + z - 2 = 0.
4a;-j/-z + 2 = 0.
3a; + 3j/ - 3z - 8 = 0.
9a; + 3y - 6z - 4 = 0.
x + у - z\f2 + 7 = 0.
у + 2z - 3 = 0.
x + 6y + 2z - 10 = 0.
12x + 16j/ - 15z + 2 = 0.
3x + 2j/ + z + 10 = 0.
Ответы. 1. ^? = arccos
1
2. ip = arccos
8 „ 7
—. 3. v? = arccos—.
2v/3"
7Г 27Г 7Г „ 7ГЛ 2
4. ^j = —. 5. ip = 0. 6. v5 = "s-- 7. <p — —. 8. v5 = 77- »• V = arccos —.
2 3 4 2 15
10. v5 = arccos у —.
1.10. Канонические уравнения прямой
Постановка задачи. Написать канонические уравнения
прямой, заданной как линия пересечения двух плоскостей [общими
уравнениями)
Г Агх + Вгу + Cxz + £>i = 0,
\ А2х + В2у + C2z + D2 = 0.
План решения.
1. Проверяем, что векторы п\ = {А\,В\,С\} и п2 = {А2,В2,С2}
неколлинеарны и, следовательно, плоскости пересекаются по
некоторой прямой.
Канонические уравнения прямой с направляющим вектором а =
= {/, т, п}, проходящей через данную точку Mq(xq, yo, ^о), имеют вид
х-х0 у-уо z - zo
I
п
A)
Поэтому чтобы написать уравнения прямой, необходимо найти ее
направляющий вектор и какую-нибудь точку на прямой.
2. Так как прямая принадлежит одновременно обеим плоскостям,
то ее направляющий вектор а ортогонален нормальным векторам

26
Гл. 1. Аналитическая геометрия
обеих плоскостей, т.е. а ±пх = {А\,В\,С{\ и а 1 йг = {У^Дг.Сг}-
Следовательно, направляющий вектор а находим по формуле
а= ["i,j
i j k
Ai Bt d
Ai B<i Ci
3. Теперь выберем какую-нибудь точку на прямой. Поскольку
направляющий вектор прямой непараллелен хотя бы одной из
координатных плоскостей, то прямая пересекает эту координатную
плоскость. Следовательно, в качестве точки на прямой может быть взята
точка ее пересечения с этой координатной плоскостью.
4. Подставляем найденные направляющий вектор и точку в
уравнения прямой A) и записываем ответ.
Пример. Написать канонические уравнения прямой, заданной
как линия пересечения двух плоскостей (общими уравнениями)
Г 2х + Зу + z - 8 = О,
\ x-2y-2z+l = 0.
Решение.
1. Проверим, что векторы п\ — {2,3,1} и Яг = {1, —2, —2}
неколлинеарны (см. задачу 1.2). Имеем
1 ^ -2
Векторы п\ = {2,3,1} ийг = {1,-2,-2} неколлинеарны, так как
их координаты непропорциональны. Следовательно, две плоскости
пересекаются по прямой.
2. Так как прямая принадлежит одновременно обеим плоскостям,
то ее направляющий вектор а ортогонален нормальным векторам
обеих плоскостей, т.е. а ± щ — {2,3,1} и а ± йг = {1,-2,-2}.
Следовательно, направляюющий вектор а находим по формуле
а = [п1,п7\ =
i j к
2 3 1
1 -2 -2
= -4г + 5j-7k.
3. Теперь выберем какую-нибудь точку на прямой. Поскольку
направляющий вектор прямой непараллелен ни одной из координатных
плоскостей, то прямая пересекает все три координатные плоскости.

1.10. Канонические уравнения прямой
27
Следовательно, в качестве точки на прямой может быть взята
точка ее пересечения, например, с плоскостью у = 0. Координаты этой
точки находим, решая систему трех уравнений
2х + z - 8 = 0,
х - 2г + 1 = 0,
У = 0.
Получим яо = 3, г/о = 0 и г0 = 2, т.е. МоC,0,2).
4. Подставляя найденные направляющий вектор и точку в
уравнения прямой A), получим
У
5
2-2
-4 5 -7
Ответ. Канонические уравнения прямой имеют вид
х-3 v 2-2
_3 = У
i 5
Условия ЗАДАЧ. Написать канонические уравнения прямой,
заданной как линия пересечения двух плоскостей.
7.
9.
х + у+ 2-2 = 0,
я-2/-32 + 6 = 0.
х - 2j/ + 2г - 4 = 0,
2х + 2у - 2г - 8 = 0.
2х + 3у+ 2 + 3 = 0,
х - Зу - 2г + 3 = 0.
а; + 5у + 22 + 5 = 0,
х — у— 2— 1=0.
4z + j/ - 32 + 4 = 0,
2х - у + 2г + 2 = 0.
Ответы.
а; + 2 J/-4
2.
4.
6.
8.
10.
1.
-2
2
I'
2х - 3j/ + 2г + 2 = 0,
2z + 3?/+ 2 + 14 = 0.
х + у+ 2-2 = 0,
z-j/-32 + 2 = 0.
z + y- 2-4 = 0,
x-y + 2z =0
2z + 2j/ - 22 + 1 = 0,
3z - 2y + 32 + 4 = 0.
£— J/-2 — 2=0,
i - 3j/ + 2 + 4 = 0.
2.
x + 4 _ j/ + 2
9 ~ -2
-12

28
Гл. 1. Аналитическая геометрия
z-4 y z
6- о ~1~г
х + 2 у z
5- 3 "-5 "9'
X _ J/ + 1 _ Z
 -1 2'
х + 1 _ у _ z
1 14 6"
4.
6.
8.
10.
а; у — 2 z
1 ~ -2 ~ Г
х-2 j/-3 z
1 ~ -3 -2'
х + 1 у — 1/2 _ z
1 ~ -6 -5'
х — 5 у — 3 г
2 ~ 1 ~~ 1'
1.11. Точка пересечения
прямой и плоскости
Постановка задачи. Найти точку пересечения прямой
Х-Хг _ У-У! _ Z- Z!
I т n
и плоскости
Ax + By + Cz + D = 0.
План решения.
1. Проверим, что прямая не параллельна плоскости. Это означает,
что направляющий вектор прямой а = {I, т, п} и нормальный вектор
плоскости п — {А, В, С} не ортогональны, т.е. их скалярное
произведение не равно нулю:
А1 + Вт + Спф 0.
В этом случае существует единственная точка пересечения прямой и
плоскости.
2. Для нахождения точки пересечения прямой и плоскости, вообще
говоря, надо решить систему трех уравнений с тремя неизвестными
(два уравнения прямой и одно уравнение плоскости). Однако удобнее
использовать параметрические уравнения прямой.
Положим
х-хх _ у-у\ _ z-zx _
I m n
Тогда параметрические уравнения прямой имеют вид
х — It + Х\,
y = mt + ух,
z = nt + zx.

1.11. Точка пересечения прямой и плоскости
29
3. Подставляя эти выражения для х, у и z в уравнение плоскости
и решая его относительно t, находим значение параметра t = to, при
котором происходит пересечение прямой и плоскости.
4. Найденное значение to подставляем в параметрические
уравнения прямой и получаем искомые координаты точки пересечения:
хо = Но + £i>
j/o = mt0 + г/1,
z0 = nto + z\.
Записываем ответ в таком виде: прямая и плоскость пересекаются
в точке {xo,yo,zo)-
Пример. Найти точку пересечения прямой
х — 1 _ у + 1 _ z
2 ~ 0 ~^1
и плоскости
2х - Зг/ + z - 8 = 0.
Решение.
1. Имеем
(а, п) = 2 • 2 + 0 • (-3 + (-1) -1 = 3^0.
Следовательно, направляющий вектор прямой и нормальный вектор
плоскости не ортогональны, т.е. прямая и плоскость пересекаются в
единственной точке.
2. Положим
х — 1 _у + 1 _ z _
2 ~ 0 ~^Т~ '
Тогда параметрические уравнения прямой имеют вид
3. Подставляя эти выражения для х, у и z в уравнение плоскости,
находим значение параметра t, при котором происходит пересечение
прямой и плоскости:
2B* + 1) - 3(-1) + l(-f) - 8 = 0 ==> to = 1.

30
Гл. 1. Аналитическая геометрия
4. Подставляя в параметрические уравнения прямой найденное
значение to = 1) получаем
хо = 3, j/o = -1, zo - -1.
Ответ. Прямая и плоскость пересекаются в точке C,-1,-1).
Условия ЗАДАЧ. Найти точку пересечения прямой и плоскости.
, х-2 J/-3 2 + 1 Л „
1. -у- = —j— = -34-. x + j/ + 2z-9 = 0.
х+1 _ у-3 _ z + 1
2 -4 5 '
x + 2j/-2 + 5 = 0.
3. £^I = £+*=£zI, г_з,, + г-8 = 0.
4. £zI = g = £+3, x-J/ + 4z = 0.
3 0 2
a: j/-3 z-2
5. - = »_£- = _, 3ar + »-2z = 0.
6- £±1 = L±2 = ^, * + 3l,-z-3 = 0.
x — 1 _ J/ — 2_z
2 ~ 0 ~T'
x-y + Az — 5 = 0.
a; v — 1 z + 4
9. Т = ^- = _Л_) 2x-j/ + z + 4 = 0.
10> £+2 = »zi = £+lf 2x_4j/_3, + 7 = 0.
Ответы. 1. A,2,3). 2. A,-1,4). 3. B,-1,3). 4. D,0,-1).
5. A,1,2). 6. (-1,0,-4). 7. (-1,1,-2). 8. C,2,1). 9. (-1,-1,-3).
10. (-1,2,-1).

1.12. Проекция точки на плоскость или прямую 31
1.12. Проекция точки
на плоскость или прямую
Постановка задачи. Найти координаты проекции Р' точки
Р(хр, ур, zp) на плоскость Ах + By + Cz + D = 0.
План решения. Проекция Р' точки Р на плоскость является
основанием перпендикуляра, опущенного из точки Р на зту плоскость.
1. Составляем уравнения прямой, проходящей через точку Р
перпендикулярно данной плоскости. Для этого в качестве
направляющего вектора прямой берем нормальный вектор плоскости: а = п =
= {А, В, С}. Тогда канонические уравнения прямой имеют вид
х-хр _ у-ур _ z- zp
А ~ В ~ С '
2. Находим координаты точки пересечения Р' этой прямой с
заданной плоскостью (см. задачу 1.11). Положим
х-хр _ у-ур _ z-zp _
А ~ В ~ С ~ '
Тогда параметрические уравнения прямой имеют вид
х = At + хр,
y = Bt + ур,
z-Ct + zP.
3. Подставляя x,y,z в уравнение плоскости и решая его
относительно t, находим значение параметра t — to, при котором происходит
пересечение прямой и плоскости.
4. Найденное значение to подставляем в параметрические
уравнения прямой и получаем искомые координаты точки Р1.
Замечание. Аналогично решается задача о нахождении
координат проекции точки на прямую.
Пример. Найти координаты проекции Р' точки РA,2, —1) на
плоскость За; — у + 2z — 4 = 0.
Решение.
1. Составляем уравнения прямой, проходящей через точку Р
перпендикулярно данной плоскости. Для этого в качестве
направляющего вектора прямой берем нормальный вектор плоскости: а = п =

32
Гл. 1. Аналитическая геометрия
= {3, —1,2}. Тогда канонические уравнения прямой имеют вид
х-1 _ J/-2 _ z + 1
3 -1 2 '
2. Найдем координаты точки пересечения Р' этой прямой с
заданной плоскостью. Положим
х-1 _ у-2 _ z + 1 _
3 ~ -1 ~ 2 ""'"
Тогда параметрические уравнения прямой имеют вид
х = 3t + 1,
y = -t + 2,
z-2t-l.
3. Подставляя эти выражения для х, у и z в уравнение плоскости,
находим значение параметра t, при котором происходит пересечение
прямой и плоскости:
3Ct + 1) - Ц-t + 2) + 2B* - 1) - 27 = 0 => t0 = 2.
4. Подставляя в параметрические уравнения прямой найденное
значение to = 2, получаем хо = 7, j/o = 0, zo = l.
Таким образом, точка пересечения прямой и плоскости и,
следовательно, проекция точки Р на плоскость имеет координаты G,0,1).
Ответ. Проекция Р' имеет координаты G,0,1).
УСЛОВИЯ ЗАДАЧ. Найти координаты проекции точки Р на плос-
кость
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
РA,0,1),
Р(-1,0,-1),
РB,1,0),
Р@,2,1),
Р(-1,2,0),
РB,-1,1),
РA,1,1),
РA,2,3),
Р@,-3,-2),
РA,0,-1),
4а: + 6у + 4z - 25 = 0.
2х + 6у - 2z + 11 = 0.
y + z + 2 = 0.
2х + 4у-3 = 0.
4х -5j/ -2-7 = 0.
x-y + 2z-2 = 0.
x + 4y + 3z + b = 0.
2а: + 10у + Юг -1 = 0.
2а: + 10у + 10z - 1 =0.
2j/ + 4z - 1 = 0.
Ответы. 1.B,3/2,2). 2. (-3/2,-3/2,-1/2). 3.B,-1/2,-3/2).
4. (-1/2,1,1). 5.A,-1/2,-1/2). 6.C/2,-1/2,0). 7.A/2,-1,-1/2).
8.A/2,-1/2,1/2). 9.A/2,-1/2,1/2). 10.A,1/2,0).

1.13. Симметрия относительно прямой или плоскости 33
1.13. Симметрия относительно
прямой или плоскости
Постановка задачи. Найти координаты точки Q,
симметричной точке Р(хр, ур, zp) относительно прямой
Х- Хр _ у - ур _ Z - Zp
I m n
План решения. Искомая точка Q лежит на прямой,
перпендикулярной данной и пересекающей ее в точке Р'. Поскольку точка
Р' делит отрезок PQ пополам, координаты xq, j/q и zq точки Q
определяются из условий
XP + XQ УР+VQ Zp+ZQ
хр> = ^ ' ур' = 2 ' Zf" = 2 ' О
где xp,yp,zp — координаты точки Р и xp',ypi,zp> — координаты
ее проекции Р' на данную прямую.
1. Найдем проекцию точки Р на данную прямую, т.е. точку Р'
(см. задачу 1.12). Для этого:
а) составим уравнение плоскости, проходящей через точку Р
перпендикулярно данной прямой. В качестве нормального вектора п
этой плоскости можно взять направляющий вектор данной прямой,
т.е. п = а = {/,т, п}. Получаем
1(х - хР) + т(у - уР) + n(z - zP) = 0;
б) найдем координаты точки пересечения Р' этой плоскости с
заданной прямой. Для этого запишем уравнения прямой в
параметрической форме
х = It + Хо,
у = mt + j/o,
Z = nt + Zq.
Подставляя х, у, z в уравнение плоскости и решая его относительно t,
находим значение параметра t = to, при котором происходит
пересечение прямой и плоскости;
в) найденное значение to подставляем в параметрические
уравнения прямой и получаем искомые координаты точки Р'.
2. Координаты точки Q, симметричной точке Р относительно
данной прямой, определяем из условий A). Получаем
xQ = 2хР> - хР, j/q = 2уР> - ур, zq = 2zP. - zP.

34
Гл. 1. Аналитическая геометрия
Замечание. Аналогично решается задача о нахождении
координат точки, симметричной данной, относительно плоскости.
Пример. Найти координаты точки Q, симметричной точке
РB, —1,2) относительно прямой
х — 1 у z + 1
1 = 0 = -2 '
Решение.
1. Найдем проекцию точки Р на данную прямую, т.е. точку Р'.
Для этого:
а) составим уравнение плоскости, проходящей через точку Р
перпендикулярно данной прямой. В качестве нормального вектора п
этой плоскости можно взять направляющий вектор данной прямой:
п = а = {1,0, —2}. Тогда
1(х - 2) + (% + 1) - 2(z - 2) = 0 => х - 1z + 2 = 0;
б) найдем точку пересечения заданной прямой и плоскости
х — 2z + 2 = 0. Для этого запишем уравнения прямой в
параметрической форме:
x = t + l,
У = 0,
z = -2t- 1.
Подставляя эти выражения для х, у и z в уравнение плоскости,
находим значение параметра t, при котором происходит пересечение
прямой и плоскости: to = — 1;
в) подставляя в параметрические уравнения прямой найденное
значение to = —1> получаем
хр' = 0, ур> = 0, zP, = 1.
Таким образом, точка пересечения прямой и плоскости и,
следовательно, проекция точки Р на прямую есть Р'@,0,1).
2. Координаты точки Q, симметричной точке Р относительно
данной прямой, определяются из условий A):
xq = 2хр> — хр = —2,
VQ = %УР' ~ Ур = 1»
zq = 2zp> — zp = 0.
Ответ. Точка Q имеет координаты (—2,1,0).

1.13. Симметрия относительно прямой или плоскости 35
Условия ЗАДАЧ. Найти координаты точки, симметричной
точке Р относительно заданной прямой.
1. Р@,-1,3),
2. Р(B,1,-1),
3. Р(-1,0,3),
4. РC,0,-1),
5. Р(-1,2,1),
6. РC,-1,0),
7. Р(-1,3,0),
8. РA,-1,2),
9. Р@,3,-1),
10. Р@,2,1), 2 _! з
Ответы. 1.D,-1,-1). 2.B,-1,-1). 3.A,2,-1). 4. (-1,4,-1).
5. (-1,2,-1). 6. (-1,1,2). 7. (-1,-1,4). 8. (-1,-1,2). 9.B,-1,1).
10.D,-2,-3).
х-1 у
1 -1
х-2 у
2 0
х у+1
0 2
х у-\
1 1
х + 1 у-
-1 2
х у z
1 0
х _ у _
1 ~ -1 ~
X у + 1
0 1
х +1 у
2 1
х — 4 у
Z
1
Z + 1
-1 '
Z
Z
~^1'
-2 z
! ~0'
+ 1
2
2-1
-1 '
Z-1
-2 '
z
~ 0'
+ 1 2-2

Глава 2
ЛИНЕЙНАЯ АЛГЕБРА
При изучении темы ЛИНЕЙНАЯ АЛГЕБРА вы познакомитесь на
примерах с понятиями линейного (векторного) пространства,
линейного оператора, его матрицы, образа, ядра, ранга, дефекта,
собственных векторов и собственных значений. Вы научитесь выполнять
различные операции с операторами и матрицами, исследовать и решать
системы линейных уравнений, получать всю информацию об
операторе (матрицу, образ, ядро, ранг и дефект, собственные векторы и
собственные значения) по его матрице, преобразовывать векторы и
матрицы при изменениях базисов.
С помощью пакета РЕШЕБНИК.ВМ вы можете выполнить все
действия с матрицами, привести матрицу к редуцированному
(гауссову) виду, вычислить определители, обратную матрицу, решить
системы уравнений, проверить линейность оператора, решить
характеристическое уравнение, найти собственные векторы и собственные
значения оператора, выполнить все численные расчеты и проверить
правильность полученных вами результатов.
2.1. Правило Крамера
Постановка задачи. Решить систему трех линейных
уравнений с тремя неизвестными
СцХх + С12Х2 + С13Хз — di,
С21Х1 + С22Х2 + С23Я3 = &2,
С31Я1 + С32Х2 + С33Х3 = d3
по правилу Крамера.
План решения. Если определитель матрицы системы
Д =
СЦ С\2 С\з
С21 С22 С23
С31 С32 Сзз

2.1. Правило Крамера
37
отличен от нуля, то система имеет решение и притом только одно.
Это решение определяется формулами
^, 1 = 1,2,3,
A)
где Д{ - определитель матрицы, получаемой из матрицы системы
заменой i-ого столбца столбцом свободных членов.
1. Вычисляем определитель матрицы системы
Д =
Сц Ci2 Ci3
С21 С22 С23
С31 С32 С33
и убеждаемся, что он не равен нулю. Следовательно система
уравнений имеет единственное решение.
2. Вычисляем определители
Ai =
dl С12 Схз
d2 C22 C23
<fe C32 C33
A2 =
сц di C13
C21 d2 c23
C31 <fe C33
Дз =
Сц Ci2 di
C21 c22 d2
C31 C32 ds
3. По формулам Крамера A) находим решение системы уравнений
Дх Д2 Дз
Xi =
Х2
Д ' "' Д '
Пример. Решить систему уравнений
яз
Xi + 2X2 + Хз — 4,
Zxi — 5x2 + Зхз — 1)
2хх +7х2- х3 = 8
по правилу Крамера.
Решение.
1. Вычисляем определитель матрицы системы, разлагая его по
первой строке:
2 1
-5 3
7 -1
= 1 • (-16) - 2 • (-9) + 1 • 31 = 33.
Так как он не равен нулю, то система уравнений имеет единственное
решение.

38
Гл. 2. Линейная алгебра
2. Вычисляем определители
Д1 =
До =
Ая =
4
1
8
1
3
2
1
3
2
2
-5
7
4
1
8 -
2
-5
7
1
3
-1
1
3
-1
4
1
8
4 • (-16) - 2 • 25 + 1 • 47 = 33,
= 1 • (-25) - 4 • (-9) + 1 • 22 = 33,
= 1 • (-47) - 2 • 22 + 4 • 31 = 33.
3. По формулам Крамера A) находим решение системы уравнений
Xi = 1, Х2 = 1, Хз = 1.
Ответ, xi = 1, Х2 = 1, хз = 1.
УСЛОВИЯ ЗАДАЧ.
мера.
Решить системы уравнений по правилу Кра-
1.
3.
2х
Зх
2х
Зх
5х
х
2х
5х
х
Зх
2х
х
Зх
2х
Ответы.
+ Зхг — хз = 2,
- Зх2 + 2х3 = 0, 2.
- 2х2 - хз = 4.
+ Зх2 + х3 = 1,
- 5х2 + 2х3 = -11, 4.
+ 2х2 - 2х3 = -3.
+ 5x2 + хз = —8,
- Зх2 + 5хз = 16, 6.
+ 2х2 - хз = -6.
+ 2х2+ х3 = 2,
+ 2х2 + Зх3 = 6, 8.
- 2х2 - х3 = 7.
+ Зх2 + х3 = —5,
- 4х2 + Зхз = 11, 10.
+ 4х2 - х3 = -9.
1. Xi = 1, Х2 = 0, Х3 = —1.
xi + 2x2 + хз = 5,
3xj — 5x2 + Зхз = — 7,
2xi + 7х2 - хз = 13.
xi + 4x2 + Зх3 = 5,
3xi — 2х2 + Зх3 = 9,
2xi + 4x2 - Зх3 = 1.
xi + Зхг + 2х3 = —5,
2xi — 2x2 + Зхз = —8,
3xi + 4х2 - 4х3 = 5.
Xi + 5X2 + Хз = 3,
2xi — Зхг 4- Зхз = 8,
2xi + 4x2 — хз = 0.
хх + 2х2 + Зхз = 5,
3xi - 2х2 + Зхз = -1,
2xi + Зх2 - 2х3 = 8.
2. xi = 0, х2 = 2, х3 = 1.
3. xi = —1, Х2 = 1, хз = 0. 4. xi = 2, х2 = 0, х3 = 1. 5. xj = О,
6. xi = —1, х2 = 0, хз = —2. 7. Xi = 3, х2 = О,
1, х2 = 0, хз = 2. 9. xi = О, Х2 = -2, хз = 1.
х2 = —2, х3 = 2.
хз = —1. 8. X]
10. xi = 1, х2 = 2, х3 = 0.

2.2. Обратная матрица
39
2.2. Обратная матрица
Постановка задачи. Задана квадратная матрица третьего
порядка
(СИ Ci2 C13
С21 С22 С23
С31 С32 Сзз
Устаиовштеь существование и найти обратную матрицу С-1.
План решения. Матрица С-1 называется обратной квадратной
матрице С, если
С С'1 =С1С = Е,
где £ — единичная матрица.
Если det С Ф 0 (матрица С — невырожденная), то матрица С
имеет обратную, если det С — 0, то матрица С не имеет обратной.
1. Вычисляем определитель матрицы det С Если det С Ф 0, то
матрица С имеет обратную.
2. Составляем матрицу из алгебраических дополнений
Си C\i С\з
С — I Ciy С22 С23
С31 С32 С33
3. Транспонируем матрицу С
Сц Сг\ С31
Ci2 С22 С32
С13 С23 С33
4. Разделив матрицу Ст на определитель, получаем искомую
обратную матрицу
j I Сц Ci\ C31
С~ = • I Ci2 С22 С32
det О 1 /-» /-л /~t
\ Ьхз O23 O33
5. Проверяем, что С ■ С-1 = Е и записываем ответ.
Пример. Задана квадратная матрица третьего порядка

40
Гл. 2. Линейная алгебра
Установить существование и найти обратную матрицу С
-1
Решение.
1. Вычисляем определитель матрицы detC:
detC
1 2
3 -5
2 7
= 1 • (-16) - 2 • (-9) + 1 • 31 = 33.
Так как det С ф 0, то матрица С имеет обратную.
2. Составляем матрицу из алгебраических дополнений
С =
16
9
11
9
-3
0
31
-3
-11
3. Транспонируем матрицу С
-16
9
31
9
-3
-3
11
0
-11
4. Разделив матрицу Ст на определитель, получаем искомую
обратную матрицу
С-Х =
33
-16
9
31
9
-3
-3
11
0
-11
5. Проверяем
СС
-1
Ответ. Матрица, обратная матрице С, есть

2.3. Понятие линейного пространства
41
Условия ЗАДАЧ. Найти матрицы, обратные заданным.
1.
4. О 3 1 . 5.
Ответы.
2.3. Понятие линейного пространства
Постановка задачи. Образует ли линейное пространство
заданное множество X, в котором определены "сумма" а ф 6 любых
двух элементов а и Ь и "произведение" а&а любого элемента а на
любое число а?
План решения. Исходя из определения линейного пространства,
проверяем следующие условия.
1. Являются ли введенные операции сложения и умножения на
число замкнутыми в X, т.е. верно ли, что Va, Ь £ X и Va G R
а®ЬеХ, aGaeX ?

42
Гл. 2. Линейная алгебра
Если нет, то множество X не является линейным пространством, если
да, то продолжаем проверку.
2. Находим нулевой элемент в € X такой, что Va G X
а ф 0 = a.
Если такого элемента не существует, то множество X не является
линейным пространством, если существует, то продолжаем проверку.
3. Для каждого элемента а € X определяем противоположный
элемент —a £ X такой, что
а ф -а = в.
Если такого элемента не существует, то множество X не является
линейным пространством, если существует, то продолжаем проверку.
4. Проверяем выполнение остальных аксиом линейного
пространства, т.е. Va, b, с G X и Va, 0 G К:
а ф 6 = b ф а;
(а ф 6) ф с = а ф F ф с);
а©(/б©а) = (а-/б)©а;
1 © а = а;
(а + /б)©а = а©аф/б©а;
а©(аф6) = а©афа©6.
Если хотя бы одна из аксиом нарушается, то множество X не
является линейным пространством. Если выполнены все аксиомы, то
множество X — линейное пространство.
Пример. Образует ли линейное пространство множество
положительных чисел X — К_|_, в котором операции "сложения" и
"умножения на число" определены следующим образом: Va, b € К+ и Va G К
аф6 = а-6, а&а = аа?
Решение.
1. Введенные таким образом операции являются замкнутыми в
данном множестве, так как если a, b G R+ и a G К, то
аф6=а-6>0, a©a = aQ>0,
т.е. аф6еК+ и а©аеК+.

2.3. Понятие линейного пространства
43
2. В качестве нулевого элемента нужно взять единицу (в = 1), так
как
а ■ 1 = а,
иными словами,
а® в — а.
3. В качестве элемента —а, противоположного элементу а, нужно
взять 1/а, так как
1
а- — = 1,
а
иными словами,
а ф (-а) = в.
4. Проверяем выполнение остальных аксиом линейного
пространства, т.е. Va, Ь, с G R+ и Va, C G К:
a • 6 = 6 • a => а ф 6 = 6 ф a;
(a • 6) • с = a • F - с) => (а ф Ь) ф с = а ф (Ь ф с);
(a*3)" = a"*3 => a © (/? © a) = (a - /3) © a;
a1 = a => 1 © a = a;
aQ+0 = aQ • ofi => (a + @) © a = a © a ф /б © a;
(a • 6)Q = aa • 6Q =» a © (a ф 6) = a © a ф a © b.
Все аксиомы выполнены.
Ответ. К+ — линейное пространство.
Условия задач. Образует ли линейное пространство заданное
множество X, в котором определены "сумма" любых двух
элементов а иЬ и "произведение" любого элемента а на любое число а?
1. Множество всех векторов трехмерного пространства, первая
координата которых равна 1; сумма а + Ь, произведение а ■ а.
2. Множество всех векторов трехмерного пространства; сумма
[а, Ь], произведение а ■ а.
3. Множество всех натуральных чисел; сумма а ■ Ь,
произведение аа.
4. Множество всех функций, непрерывных на отрезке [—1,1] и
таких, что /(—1) = /A) = 0; сумма f(t)+g(t), произведение a- f(t).
5. Множество всех функций, непрерывных на отрезке [—1,1] и
таких, что /(—1) = /A) = 1; сумма f(t)+g(t), произведение a-f(t).

44
Гл. 2. Линейная алгебра
6. Множество всех функций, дифференцируемых на отрезке
[-1,1] и таких, что /(-1) = /A) = 0 и /'(О) = 1; сумма f(t) + g(t),
произведение а • /(f).
7. Множество всех последовательностей а — {ип}, b — {vn},
сходящихся к нулю; сумма {и„ + v„}, произведение {аип}.
8. Множество всех последовательностей {ып}, Ь = {vn},
сходящихся к 1; сумма {ип + vn}, произведение {аип}.
9. Множество всех невырожденных матриц 3-го порядка а = (aik),
b = (bik) (г,к = 1,2,3); сумма (aik) - (Ык), произведение (ааце).
10. Множество всех диагональных матриц 3-го порядка а — (aik),
b = (bik) (i, к = 1,2,3); сумма (aik + hk), произведение (aaik).
Ответы. 1. Нет. 2. Нет. 3. Нет. 4. Да. 5. Нет. 6. Нет. 7. Да.
8. Нет. 9. Нет. 10. Да.
2.4. Системы линейных уравнений
Задача 1. Однородные системы уравнений
Постановка задачи. Найти размерность d пространства
решений, его базис (фундаментальную систему решений) и общее
решение однородной системы линейных уравнений
ацХ\ + а,\2Х2 + • • • + Gln^n = О,
а21%\ + а22%2 + • • • + а2пХп = О,
am\Xi + am2X2 + .. • + атпх„ = 0.
План решения.
1. Записываем матрицу системы:
( an a12 •■■ ain \
. _ a2i 022 • • • Й2п
\ ат\ ат2 ■ ■ ■ атп J
и с помощью элементарных преобразований строк преобразуем
матрицу А так, чтобы в максимальном числе столбцов оказалось по одной
единице (в разных строках у разных столбцов), а остальные элементы
столбцов были нулями. Очевидно, что такие столбцы линейно
независимы. Они называются базисными.

2.4. Системы линейных уравнений
45
Полученную матрицу будем называть редуцированной и
обозначать Аред.. Отметим, что редуцированная матрица эквивалентна
исходной (Лред. ~ А) и система уравнений с матрицей Аред.
эквивалентна исходной системе уравнений.
2. Так как А ~ Аред., то вычисляем ранг А как количество
базисных столбцов матрицы -Аред.:
Rg>l = Rg>lpefl. =Г.
Следовательно, размерность пространства решений есть d = п — г.
Если тг = г, то однородная система имеет единственное (нулевое)
решение, если тг > г, то фундаментальная система состоит из тг — г
линейно независимых решений.
3. Неизвестные, соответствующие базисным столбцам,
называются базисными, остальные — свободными (или параметрическими).
Запишем систему уравнений с матрицей >1ред. и перенесем п — г
свободных неизвестных в правые части уравнений системы.
Придавая свободным неизвестным тг — г наборов значений (по одной
единице, остальные — нули), для каждого такого набора решаем систему
уравнений и находим соответствующие значения базисных
неизвестных. Убедимся, что полученные решения Х\, X?,..., Xn_r линейно
независимы, составив матрицу из столбцов Х\, Xi,..., Х„-г и
вычислив ее ранг.
Записываем фундаментальную систему решений Х\, Хг,..., Хп_г
и общее решение однородной системы линейных уравнений
/*i \
С\ Xi + Ci Xi + ... + Cn-r Xn—r,
X0.o.
V*n/
где Xx, X-2,..., Xn-r — фундаментальная система решений
однородной системы линейных уравнений и С\,С^, ■ ■ ■,Сп_г — произвольные
постоянные.
Пример 1. Найти размерность d пространства решений, его базис
(фундаментальную систему решений) и общее решение однородной
системы линейных уравнений
Х2 + 2Хз — 3X4 = О,
2xi — Х2 + Зх3 + 4х5 = О,
2xi + 5хз — Зх4 + 4х5 = 0.

46
Гл. 2. Линейная алгебра
Решение.
1. Записываем матрицу системы и с помощью элементарных
преобразований строк преобразуем ее к редуцированному виду:
0
2
2
1 2
-1 3
0 5
-3 0 \
/10 5/2
0 4 ~ ( 0 1 2
-3 4/
\ 0 0 0
-3/2
-3
0
2
0
0
Очевидно, что первый и второй столбцы матрицы Аред_ (и исходной
матрицы А) линейно независимы, а остальные столбцы являются их
линейными комбинациями. Поэтому первый и второй столбцы —
базисные.
2. Так как количество линейно независимых столбцов матрицы
Лред. равно двум, то
RgA = RgApefl. = 2.
Следовательно, размерность пространства решений
d=n-r=5-2=3
и фундаментальная система решений состоит из трех линейно
независимых решений.
3. Неизвестные xi и х?, соответствующие базисным столбцам,
являются базисными, неизвестные хз,Х4,Х5 — свободными.
Запишем систему уравнений с матрицей Аред. (эта система
эквивалентна исходной) и перенесем свободные неизвестные в правые
части уравнений системы:
xi = -5/2х3 + 3/2х4
Х2 = — 2хз + 3X4.
2х5,
Для первого набора свободных неизвестных х3 = 1, Х4 = 0, xs = 0
получаем Xi = —5/2, х? = —2, т.е. первое решение имеет вид системы
*1 =
( -V2 \
-2
1
0
V о )

2.4. Системы линейных уравнений
47
Для второго набора свободных неизвестных хз = 0, хц = 1, Х5 = О
получаем х\ = 3/2, хг — 3, т.е. второе решение имеет вид системы
Х2 =
/ 3/2 \
3
О
1
О
Для третьего набора свободных неизвестных хз = 0, х^ = 0, xs = 1
получаем х\ = —2, x-i = 0, т.е. третье решение системы имеет вид
/
Хз =
V 1/
2 \
О
О
о
1
Сделаем проверку, подставив эти решения в исходную систему
уравнений, а также убедимся, что решения линейно независимы (ранг
матрицы, составленной из столбцов Х\,Хг,Хъ, равен 3).
Следовательно, решения X\,Xi,X$ образуют базис в
пространстве решений (фундаментальную систему решений).
Ответ. Размерность пространства решений есть d = 3.
Фундаментальная система решений есть
/
Xi =
5/2 \
-2
1
0
о )
, Хг =
( 3/2 \
3
0
1
1 о )
х3 =
( -2 \
О
О
о
V 1/
и общее решение однородной системы имеет вид
X -=С\Х\ + CiXi + С3Х3 = С\
/-5/2\
-2
1
0
V о )
+ С2
C/2\
3
0
1
\° )
+ с3
(-2\
0
0
0
W
где С\ Сг, и Сз — произвольные постоянные.

48
Гл.2. Линейная алгебра
Задача 2. Неоднородные системы уравнений
Постановка задачи. Найти общее решение неоднородной
системы линейных уравнений
ацхг + а12х2 + ... + а1пхп = 6Ь
a2ixi + 022X2 + ... + а2пхп = ^2,
, OmlXi + am2X2 + . • . + атпХп = Ьт.
План решения.
1. Записываем расширенную матрицу системы
(an 0,12 ... ain I 61 \
а2\ а22 ■■■ а2п \ Ь2
I 1
ami о,т2 ... атп | Ьт J
и с помощью элементарных преобразований строк преобразуем
матрицу .Арасш. к редуцированному виду.
2. Вычисляем ранги основной матрицы системы А и расширенной
матрицы Лрасш.. Если RgApacin. = Rg А, то система совместна, если
Rg Арасш. Ф Rg-^i TO система несовместна (решений не имеет).
3. Пусть Rg Лрасш. = Rg А = г. Тогда общее решение
неоднородной системы линейных уравнений определяется формулой
■Хо.н. — -Хч.н. + Cl -X"l + С2 Х2 + . . . + Сп—т Хп-Г,
где Хчв. — какое-либо частное решение неоднородной системы,
Х\,Х2,... ,ХП_Г — фундаментальная система решений
соответствующей однородной системы и Ci,C2,...,C„_r — произвольные
постоянные.
Чтобы найти фундаментальную систему решений однородной
системы уравнений Х\, Х2,..., Хп-Г, повторим операции, изложенные в
задаче 1.
4. Столбец свободных членов В расширенной матрицы есть
линейная комбинация базисных столбцов матрицы А. Добавляя к этому
выражению остальные столбцы с нулевыми коэффициентами, получаем
разложение столбца свободных членов по всем столбцам матрицы А.
Коэффициенты этого разложения образуют частное решение
неоднородной системы Хч.„..

2.4. Системы линейных уравнений
49
5. Записываем общее решение неоднородной системы линейных
уравнений:
/ *i \
= лч.в, + С\ Х\ + Сг Хг + ... + Сп—Г лп_г,
Х0.н.
\ Хп J
где Хч.в. — какое-нибудь частное решение неоднородной системы,
Xi,X2,.-.,Xn-r — фундаментальная система решений
соответствующей однородной системы уравнений и С\,Сг,. -., Сп-Г —
произвольные постоянные.
Пример 2. Найти общее решение неоднородной системы
линейных уравнений
Х2 + 2хз — 3X4 — —1>
2хх - Х2 + Зх3 + 4x5 = 5,
2xi + 5хз - 3x4 + 4x5 = 4.
Решение.
1. Записываем расширенную матрицу системы и с помощью
элементарных преобразований строк преобразуем матрицу Лрасш. к
редуцированному виду:
О 12-30|
2-13 0 4 |
2 0 5 -3 4 |
2. Так как Rg-Apacin. = Rg A = 2, то система совместна. Так как
п — г = 5 — 2 = 3, то общее решение неоднородной системы линейных
уравнений определяется формулой
Хс.н. = Хч.ы. +C\Xi + Съ Хъ + Сз Хз,
где Хч.н. — какое-нибудь частное решение неоднородной системы,
Xi,X-2,X3 — фундаментальная система решений соответствующей
однородной системы и С\,Съ,Сз — произвольные постоянные.
3. Запишем соответствующую однородную систему уравнений
Х2 + 2хз — 3X4 = 0,
- х2 + Зх3 + 4х5 = 0,
+ 5хз - Зх4 + 4x5 = 0.

50
Гл. 2. Линейная алгебра
Она совпадает с системой, приведенной в примере 1. (Если
однородная система уравнений не совпадает с системой, приведенной в
примере 1, то для нахождения фундаментальной системы решений
повторим операции, использованные при решении примера 1.)
При решении примера 1 была найдена фундаментальная система
решений однородной системы уравнений:
*! =
/
V
5/2 \
-2
1
0
о )
, х2 =
(ъ12\
3
0
1
1 о )
, *з =
( ~2\
0
0
0
1 Ч
4. Найдем какое-нибудь частное решение неоднородной системы.
Столбец свободных членов В расширенной матрицы есть линейная
комбинация базисных столбцов матрицы А, т.е. столбцов А\ и А2:
B = 2Ai-lA2.
Добавляя к этому выражению остальные столбцы с нулевыми
коэффициентами, получим
В = 2 • Аг - 1 • А2 + 0 • А3 + 0 • А4 + 0 • А5.
Коэффициенты в этом разложении образуют частное решение
неоднородной системы
/ 2\
Лч.в. —
-1
о
о
V о/
Сделаем проверку, подставив Хч.„. в исходную систему уравнений.
Ответ. Общее решение системы имеет вид
•Л0.н. —
/ 2\
-1
0
0
V Ч
+ С!
( _5/2 ^
-2
1
0
^ о )
+ с2
C/2 ^
3
0
1
^ ° )
+ С3
( -2\
0
0
0
1 1/
где С\, Сг и Сз — произвольные постоянные.

2.4. Системы линейных уравнений
51
Условия задач. Найти размерность d пространства решений
{количество линейно независимых решений), фундаментальную
систему решений {базис пространства решений) и общее решение
систем линейных уравнений.
5xi + Х2 — 7хз - 5x4 + 2x5 = О,
2xi — 2x2 — Зхз - 7х4 + 2x5 = О,
3xi + 9х2 - Зх3 + 27х4 - Зх5 = О,
Xi + 2x2 - 2хз - Зх4 = 4,
3xi + 8x2 — 4х4 = 14,
Xi + 3X2 + Х3 — Х4 = 5.
6xi + 5x2 — 2хз — х4 + 3x5 = О,
Xi — 3X2 + Хз — Х4 — Х5 = О,
2Xi + 3X2 + 2X3 + Х4 + Х5 = О,
3xi — 11^2 + бхз + х4 + 3x5 = 14,
2xi — 7x2 + 4хз + х4 =9,
Xi - 3x2 + 2хз + х4 - Зх5 = 4.
2xi — 4x2 — 22хз — 5х4 + 5xs = О,
5xi — Х2 + 8хз — 2х4 + 2x5 = О,
3xi — 3x2 - 12хз - 4х4 + 4x5 = О,
4xi + 9x2 - 5хз — 8х4 = 5,
Зхх + 7x2 _ 2хз — 4х4 = 4,
2xi + 5x2 + ^3 + Зх4 = 3.
6xi — 9x2 + 21хз — Зх4 — 12x5 = О,
8xi - 12х2 + 28х3 - 4х4 - 16х5 = О,
2хх - 3x2 + 7х3 - х4 — 4x5 = О,
-х2 + 4х3 + 8х4 - х5 = 1,
2xi - 9х2 + 2х3 + я5 = 7,
Xi — 4X2 — Хз — 4х4 + Х5 = 3.
3xi + 9x2 — хз — Зх4 = О,
Xi + 10X2 - Зхз - 2х4 - Х5 = О,
2xi + 19x2 - 4хз - 5х4 - х5 = О,
Xi + 3X2 — Хз — 2х4 = 1,
2xi + 7x2 - 4хз - Зх4 = 3,
3xi + 11х2 - 7х3 - 4х4 = 5.

52
Гл. 2. Линейная алгебра
9.
10.
4xi — 6x2 + 7хз — 6x4 + 4x5 = 0,
xi + 4x2 + 2хз + 2x4 - 5x5 = О,
6xi + 2х2 + Ихз - 2х4 - 6х5 = О,
4xi + 5x2 + 5хз + Зх4 + 2x5 = 1,
3xi + 4x2 + хз + Зх4 = 1,
2xi + 3x2 — Зхз + Зх4 — 2x5 = 1-
12xi — Х2 + 7хз + ИХ4 — Х5 = О,
23xi — 3x2 + 13хз + 23x4 — 4x5 = О,
Xi + Х2 + Хз - Х4 + 2х5 = О,
4xi — 7x2 + 5хз + 10x4 = О,
2xi - 3x2 + хз + 4х4 = 1,
3xi — 5x2 + Зхз + 7x4 = 1-
3xi + 3x2 + 4хз + 5х4 — 4x5 = О,
2xi + Х2 + Зхз + Х4 — 5X5 = О,
Xi + 3X2 — Хз + 6X4 — Х5 = О,
xi — Х2 + 4хз + Зх4 = О,
5xi _ 3x2 — 2хз — Зх4 + 4x5 = 2,
2X1 — Х2 — Зхз — 3X4 + 2X5 = 1-
3xi + 9x2 + 2хз - 2х4 + Х5 = О,
xi + 6х2 — хз + х4 + 2х5 = О,
Xi + 16X2 — 6X3 + 6X4 + 7X5 = О,
4xi — 7x2 + Зх3 + 7х4 = 1,
3Xi — 5X2 + Хз + 4X4 = 1)
2xi — 3X2 — Хз + Х4 = 1.
3xi + 5x2 — 2хз +
Xi + Х2 + 2хз —
2xi + 3X2 — Х3
Х4 — Х5 = О,
Х4 + Х5 = О,
= 0,
4xi — Их2 + 5хз + 2x4 + 3x5 =7,
3xi — 8x2 + хз + 2x4 = 5,
2xi — 5x2 — Зхз + 2x4 — 3x5 = 3.

2.5. Линейные операторы
53
Ответы *>. 1. d = 3, d = 2. 2. d = 2, d = 3. 3. d = 2, d = 2.
4. d = 4, d = 2. 5. d = 2, d = 2. 6. d = 3, d = 3. 7. d = 3,
d = 2. 8. d = 2, d = 3. 9. d = 2, d = 2. 10. d = 2, d = 3.
2.5. Линейные операторы
Постановка задачи. Пусть в некотором базисе линейного
пространства Хп задан произвольный вектор х = {х\,Х2,. • • ,х„}.
Является ли линейным оператор А : Хп ь-» Хп такой, что
Ах = {/l(xi, X2, . . . ,Х„), /2(ХЬ Х2,. . . ,ХП),. . . , /„(Х1,Х2,. • . ,ХП)},
где /i, /г,..., /п — некоторые функции п переменных?
План решения. Если х = {xi,x2,...,x„} и у = {yi,y2,• • • ,Уп} —
произвольные векторы пространства Хп, то х+у = {х\+ух, хг+уг» • • • >
х„ + Уп} и аж = {ах1,ах2,...,ах„}.
Проверяем условия линейности оператора:
Л(х + у) — Ах + Ау,
А(ах) — а Ах.
Если условия линейности выполнены, т.е.
/i(xi + У1,Х2 + у2, . . . ,Хп + уп) = /i(xi,X2,...,Xn) + /i(j/i,J/2,---,J/n),
/i(axi, ax2,..., axn) = a/i(xi,x2,.. -,x„)
при г = 1,2,..., n, то оператор Л линеен, в противном случае
оператор А нелинеен.
Пример. Пусть в некотором базисе линейного пространства Х$
задан произвольный вектор х = {хьХ2,хз}. Является ли линейным
оператор А : Xz >-» ^з такой, что
Ах = {xi - Х2,2xi + х3,3xi}?
Решение. Пусть х = {х1,Х2,хз} и у = {у1,у2,Уз} - произвольные
векторы пространства Xz- Тогда х + у — {х\ + yi,x2 + y2,xz + Уз} и
ах = {ах1,ах2,ахз}.
*' Найденные фундаментальные системы решений однородных систем
уравнений и частные решения неоднородных систем проверьте с помощью подстановки
в уравнения.

54
Гл. 2. Линейная алгебра
Проверяем условия линейности оператора:
А(х+у) = {(xi+yi)-(x2+y2),2(xi+yi) + (x3+j/3),3(x1+j/i)} =
= {хх -x2,2x1+x3,3xi} + {j/i -J/2,2yi + j/3,3j/i} = Ax + Ay,
Л(ах) = {ах1—ax2,2Qxi+ax3,3axi} = а{х\— X2,2xi+X3,3xi} = aAx.
Условия линейности выполнены. Следовательно, оператор А линеен.
Ответ. Оператор А линеен.
Условия ЗАДАЧ. Являются ли линейными операторы А, В и С?
1. Ах = {2xi - 5х2 — Зхз, —2xi — Зхг — хз, xi + Зхз},
Вх = {xi - 2x2 — 4хз, xi — х2 - Зхз, 2x2 + 3},
Сх = {х|, 2xi — Х2 — 2хз, 3X2 + Хз}.
2. Ах = {2xi — Зхг — 2хз, 2xi — Зхг, 2хг + 3},
Вх = {4xi - Зхг - яз. О, х\ + хз},
Сх = {xi - 2x2 — хз, 3xi - 2x2, Зхг + хз}.
3. Ах — {2xi — Х2 — 3X3,Xi,Xi +Х2 + Х3},
Вх — {3X1 — Х2 — Хз, 2xi, 3Xi + Х2 + Хз},
Сх = {3X1 — Х2 — Хз, 2xi, 3X1 + Х2 - 1}.
4. Ах — {2xi + Х2 + 4хз, 2хз, Xi - 2хг - Зхз},
Вх — {2xi + Х2 + 4хз, 1, xi - 2x2 + 3},
Сх = {5xi + Зх2 + х3, хз, 2xf - 2х2 - 4хз}.
5. Ах = {xi,2xi — Х2 + l,xi — Х2 - Зхз},
Вх = {xi,2Xi — Х2 — 3X3,Xi — Х2 — Зхз},
Сх — {xi, 2xi — Х2 — Зхз, Xi — Х2 — Зхз}-
6. Ах — {xi + 2х2, Зх2 - 4хз, xi - 2х\ - Зхз},
Вх = {xi + 2х2, Зх2 - 4хз, xi - 2x2 - Зхз},
Сх = {xi + 2x2, Зхг — 2, xi — 2x2 — 5}.
7. Ах — {2xi, 3xi + 2х2 + Зхз, 4хх + 5х2 + 2хз},
Вх = {2xi, 3xi + 2х2 + 3,4xi + 5х2 + 7},
Сх = {2xi, 3xi + 2х2 + Зхз, Ах\ + 5х2 + 2х3}.

2.6. Матрица, образ, ядро, ранг и дефект оператора 55
8. Ах — {х\ — 3x2 — яз, 5, х\ + 2х2 + 1},
Вх = {xi — Зх2 — хз, 0, х\ + 2x2 + Зхз},
Сх = {xi — 3X2 — Хз,Хз,Х1 + 2X2 + Зхз}.
9. Ах = {4xi - 2х2, Зхз, %\ + 2хг + ЗхЦ,
Вх = {4xi — 2x2, Зхз,Х1 + 2x2 + Зхз},
Сх = {4xi - 2х2,3,xi + 2х2 + Зх3}.
10. Ах = {5хз, %1 + 2х2 + Зхз, 2xi + Зхг + 5хз},
Вх = {5х3, xi + 2х2 + 2,2xi + Зх2 + 5},
Сх = {5хз, 0, Xj + Зхг + 5хз}.
Ответы.
1. А линейный, В нелинейный, С нелинейный.
2. А нелинейный, В нелинейный, С линейный.
3. А нелинейный, В линейный, С нелинейный.
4. А линейный, В нелинейный, С нелинейный.
5. А нелинейный, В нелинейный, С линейный.
6. А нелинейный, В линейный, С нелинейный.
7. А линейный, В нелинейный, С нелинейный.
8. А нелинейный, В нелинейный, С линейный.
9. А нелинейный, В линейный, С нелинейный.
10. А линейный, В нелинейный, С нелинейный.
2.6. Матрица, образ, ядро, ранг
и дефект оператора
Постановка задачи. Задан оператор А, осуществляющий
некоторое преобразование пространства геометрических векторов V$.
Доказать линейность, найти матрицу (б базисе i,j,k), образ, ядро,
ранг и дефект оператора А.
План решения. ^
1. По определению доказываем линейность оператора А,
используя свойства операций над геометрическими векторами в
координатной форме, т.е. проверяем, что Vx, у € V3 и Va G К
А (х + у) = Ах + Ау,
А(ах) = аАх.

56
Гл.2. Линейная алгебра
2. Строим по определению матрицу оператора А. Для этого
находим образы базисных векторов i,j,k и записываем их координаты
в базисе i,j,k. Столбцы искомой матрицы — это столбцы координат
образов базисных векторов.
3. Находим образ, ранг, ядро и дефект оператора А, исходя из их
определений.
Пример. Доказать линейность, найти матрицу (в базисе i,j,k),
образ, ядро, ранг и дефект оператора проецирования пространства
геометрических векторов V3 на плоскость XOY.
Решение.
1. Докажем по определению линейность оператора
проецирования. Пусть в базисе г, j,k имеем произвольный вектор х = {х1,Х2,хз}.
Тогда его образ (проекция) есть Рх = {xi,X2,0}.
По правилам операций с геометрическими векторами в
координатной форме Vx ='{xi,x2,x3} € V3, Vj/ = {j/i,2/2,2/3} G V3 и Va G К
имеем
Р(х + у)= {xi +J/1, х2 + 2/2,0} = {xi,x2,0} + {2/1,2/2,0} = Рх + Ру,
Р(ах) = {axi,ax2,0} = a{xi,X2,0} — аРх.
2. Так как по определению матрицы оператора ее столбцы —
это столбцы координат образов базисных векторов, найдем образы
базисных векторов i,j,k и запишем их координаты в базисе i,j, к:
Pi=i= {1,0,0}, Pj =/={0,1,0}, Pfc = 0 = {0,0,0}.
Таким образом, матрица оператора проецирования Р есть
/1 0 0\
Р= 0 1 0 .
\ о о о у
3. Находим образ, ранг, ядро и дефект оператора А, исходя из
определений.
Образ оператора проецирования Р — это множество векторов,
лежащих в плоскости XOY, следовательно, в базисе i,j,k
ImgP = {Vy: y = ai + pj, а,реЩ.
Отсюда RgP = 2.

2.6. Матрица, образ, ядро, ранг и дефект оператора 57
Ker P — это множество векторов, коллинеарных оси OZ,
следовательно, в базисе i,j,k
Ker P = {Vx : х = <yk, j € Щ.
Отсюда Def P = 1.
Заметим, что RgР + Def P = 2+1 = dimV3
Ответ. Оператор Р линеен. Его матрица в базисе i,j,k есть
/1 0 0\
Р= О 1 0 ;
\ 0 0 0 /
ImgP = {Vy: y = ai + pj, a,/3eR}, RgP = 2,
KerP = {Vx: x =-yk, 76R}, DefP = 1.
Условия задач. Доказать линейность, найти матрицу (в
базисе i,j,k), образ, ядро, ранг и дефект оператора.
1. Оператор проецирования на ось ОХ.
2. Оператор отражения относительно плоскости YOZ.
3. Оператор поворота относительно оси ОХ на угол 7г/3 в
положительном направлении.
4. Оператор отражения относительно плоскости х — z — 0.
5. Оператор проецирования на плоскость у + z = 0.
6. Оператор поворота относительно оси OZ на угол 7г/6 в
положительном направлении.
7. Оператор проецирования на плоскость х + у = 0.
8. Оператор отражения относительно плоскости у — z = 0.
9. Оператор проецирования на плоскость \/3 у + z = 0.
10. Оператор поворота относительно оси OY на угол 7г/4 в
положительном направлении.

58
Гл. 2. Линейная алгебра
Ответы.
10 0
1. Р = | 0 О О
0 0 0
ImgP = {Vj/: у = аг, a G R}, RgP = 2,
KerP = {Vx: x = /3j+fk, /3,7 6R}, DefP = 1.
-10 0
2. P= | 0 10
0 0 1
ImgP = {Vy: y = ai + /33 + fk, a,/3,7eM}, RgP = 3,
KerP = {6}, DefP = 0.
/10 0 \
3. P = 0 1/2 -y/3/2 ;
\ 0 y/2,/2 1/2 /
ImgP = {Vy: y = a? + /3j+7fc, a,/3,7€R}, RgP = 3,
KerP = {6}, DefP = 0.
0 0 1
4. P= | 0 1 0
1 0 0
ImgP = {Vy: $=оа + Рз + 1к, a,/3,7€R}, RgP = 3,
KerP = {6}, DefP = 0.
A 0 0
0 1/2 -1/2
0 -1/2 1/2
ImgP = {Vy: y = ai + Pj-l3k, a,/3eR}, RgPj=2,
KerP = {Vx: x = 7n, n = {0,1,1}, 7 e R}, Def P = 1.
1/2 -V5/2 0
6- P = ( v/3/2 1/2 0 ) ;
0 0 1

2.7. Действия с операторами и их матрицами 59
ImgP = {Vy: y = oa + P3+fkt a,/3,7€R}, RgP = 3,
KerP={6}, DefP = 0:
/ 1/2 -1/2 0\
7. P = -1/2 1/2 0 ;
V 0 0 l)
ImgP = {Vj/: y = ca-aj+Ck, а,(ЗеЩ, RgP^=2,
KerP = {Vx: x = 7n, n = {1,1,0}, 7 e K}, DefP = 1.
/10 0
8. P= I 0 0 1
\ 0 1 0
ImgP = {Vy: y = ai+l3j + 4k, a,/3OeK}, RgP = 3,
KerP = {6}, DefP = 0.
/10 0 \
9. P = 0 1/4 -\/3/4 ;
\ 0 -л/3/4 3/4 /
ImgP = {Vj7: у = аг + Cз-у/3Cк, а,(ЗеЩ, KgPj=2,
KerP = {Vx: x = v^7J+7fc, 76R}, DefP = 1.
(\/2/2 0 -л/2/2
0 1 0
\/2/2 0 \/2/2
ImgP = {Vj/: y = m+0j+fk, a,/3,4€R}, RgP = 3,
KerP = {6}, DefP = 0.
2.7. Действия с операторами
и их матрицами
Постановка задачи. В некотором базисе трехмерного
линейного пространства Хз заданы отображения
х ь-» Ах =
= {ацХ1 + Oi2X2 + Q13X3, Q21X1 + 022X2 + 023X3, 031X1 + 032X2 + 033X3},

60
■Гл.2. Линейная алгебра
х I-» Вх =
= {biiXi +bi2X2 + bisx3,621Ж1 + 622Ж2 + 623^3,631^1 +632^2+633^3},
где х = {ж1,а;2,а;з} — произвольный вектор пространства Хз-
Найти координаты вектора у = Р(А, В)х (в том же базисе), где
Р(А,В) — многочлен относительно операторов А и В.
План РЕШЕНИЯ. Так как при сложении операторов их матрицы
складываются, при умножении на число — умножаются на это число,
а матрица композиции операторов равна произведению их матриц,
то нужно найти матрицу Р(А,В), где А и В — матрицы операторов
А и В. Затем столбец координат вектора у = Р(А, В)х находим по
формуле Р(А, В) • X, где X — столбец координат вектора х.
1. Построим матрицы операторов Ли В:
«11 «12 Й13 \ / 6ц 6i2 613
А = ( a2i а22 а2з I , В — I 62i 622 623
031 азг азз / \ 631 632 бзз
2. По правилам сложения матриц, умножения матрицы на число и
умножения матриц находим матрицу Р(А, В):
Ри Р\2 Р\г
Р(А, В) = | Р21 Р22 Р23
Р31 Р32 РЗЗ
3. Находим столбец координат образа вектора х:
Ри Pi2 Р13
Р21 Р22 Р23
Р31 Р32 РЗЗ
Записываем ответ в виде Р(А, Б)х = {j/i, J/2, J/з}-
Пример. В некотором базисе трехмерного линейного
пространства Хз заданы отображения
х ■-» Ах — {xi + х2 - х3, х2 + х3, х3},
х I-» Вх = {х2 + 2х3, -жь^г},
где х — {х\, Х2,хз} — произвольный вектор пространства Хз- Найти
координаты вектора BА + А о В)х в том же базисе.

2.7. Действия с операторами и их матрицами
61
Решение.
1. Построим матрицы операторов А и. В:
2. По правилам сложения матриц, умножения матрицы на число и
умножения матриц вычисляем матрицу 2А + А- В:
1 1
О 1
О О
3. Находим столбец координат образа вектора х:
1 2 0 \ / X! \ J X! + 2Х2
BА + АоВ)х=\ -1 3 2 ] ■ \ Х2 ] = -xi+Sx2 + 2x3
О 1 2 / \ хг ) \ х2 + 2х3
Ответ. BА + АоВ)х = {хг + 2х2,-х\ + Ъх2 + 2х3,х2 + 2х3}.
Условия ЗАДАЧ. Пусть в некотором базисе заданы
отображения Ах = {xi — 2жз, Х2, Х2 - хз} и Вх = {2х3, х\, —Х2}. Найти
координаты векторов Р(А, В)х.
1. (А2 + 2В)х. 2. (А2-2В2)х.
3. (В2 + 2А)х. 4. (АВ + А2)х.
5. BЛ2 + W2)x. 6. (ЗА + 2В2)х.
7. {ВА + А?)х. 8. (В2 + ЗЛ2)аг.
9.- (АВ + В2)х. 10. (ВА-АВ)х.

62
Гл. 2. Линейная алгебра
Ответы.
1. {xi - 2х2 + 4х3,2xi + х2, -2х2 + х3}.
2. {xi + 2х2,х2 - 4х3,2xi + х3}.
3. {2xi — 2^2 - 4хз, 2x2 + 2хз, —ал + 2хг - 2х3}-
4. {Xi + 2х3, Xi + Х2, Xi + Х2 + Х3}.
5. {2xi — 10x2,2x2 + 6х3,—3xi + 2х3}.
6. {3xi — 4x2 — бхз, 3x2 + 4хз, —2xi + Зхг — Зхз}.
7. {Xi — 2х3, Xi + Х2 — 2Хз, —Х2 + Хз}.
8. {3xi — 8x2, Зхг + 2хз, —xi + Зхз}.
9. {2х3, xi + 2х3,х2}.
10. {-4хз, -2х3, —х\ — 2х2}.
2.8. Преобразование координат вектора
Постановка задачи. Вектор х в базисе ei,e2,...,e„ имеет
координаты{а\,а2,...,а„}. Найти координаты векторах в базисе
ei)e2> • • • !еш г"е
ei = сцв1 + c2ie2 + ... + c„ie„,
е'2 = ci2ei + с22е2 + ... + сп2е„,
е'п = ci„ei + С2„е2 + ... + с„„е„.
План решения. Координаты вектора при переходе от базиса
ei,е2,...,е„ к базису ei, е2,...,е'п преобразуются по формуле
Хе> = С~ Хе, A)
где Хе> и Хе — столбцы координат вектора х в базисах e'i, е2,..., е'п и
ei, ег,...,е„, С — матрица перехода от базиса ei,ег,...,е„ к базису
е1,е2).. .,е„.
1. Находим матрицу перехода С. Так как столбцы матрицы
перехода от базиса ei,e2,... ,е„ к базису е^,е2,... ,е^ — это столбцы
координат векторов е^,е2,...,е'п в базисе ei,е2,...,е„, то матрица
перехода имеет вид
/ СЦ С12 ... Ci„ \
С21 С22 ... С2п
С =
\ ст»1 сп2 • • • спп /

2.8. Преобразование координат вектора
63
2. Находим обратную матрицу С 1 и проверяем, что С 1С = Е.
3. По формуле A) находим столбец координат вектора х в базисе
е1,е2,... ,еп:
/«i
-Ле' = С -Ле =
а.
Записываем ответ в виде хе< = {а[,а'2,...,а'„}.
Пример. Вектор х в базисе е1,ег,ез имеет координаты {1,2,3}.
Найти координаты вектора х в базисе е^е^е!,, где
ei = ei + 2е3,
е'2 = е2 + е3,
е3 = —ei — е2 — 2e3.
Решение.
1. Находим матрицу перехода
С =
2. Находим обратную матрицу С методом Гаусса:
1 0 -1 | 1 0 0 \ /10 0|-1-11
01-1|010)~@10|-2 01
2 1 —2 | 0 0 1 / \ 0 0 1 | —2 —1 1
Таким образом,
Проверяем, что С гС = Е.
3. По формуле A) находим столбец координат вектора х в базисе
е1>е2>е3:
Ответ. хе' = {0,1, —1}.

64
Гл. 2. Линейная алгебра
Условия задач. Найти координаты заданного вектора х в
базисе ei,e'2,e3.
1. ei = ei + е3, 2. ei = ei,
e2 = 2ei + e2 + e3, e'2 = 2в]. + е2,
e'3 = e2, e'3 = Зег + 2е2 + e3)
xe = {3,-5,4}. xe = {1,2,7}.
3. ei = eb 4. ei = ei + e2 + e3,
e2 = ei + 2e2, e'2 = 2ег + 2e3,
e3 = ei + 2e2 + 3e3, e3 = 3e3,
xe = {6,2,0}. xe = {2,6,6}.
5. ei = 3ei + e2 + 5e3, 6. ei = 2ei + e2 + 3e3,
e'2 = 2e! + 3e2 + 3e3, e'2 = 3ei + 2e2 + 4e3,
e3 = 2ei + e2 + 4e3, e'3 = 2ei - 3e2 + e3,
xe ={0,5,5}. xe = {9,14,16}.
7. ei = 2ei + 6e2 + 5e3, 8. ei = 3ei + 2e2 + 3e3,
e2 = 5ei + 3e2 - 2e3, e2 = -4ei - Зег - 5e3,
e3 = 7ei + 4e2 - 3e3, e3 = 5ei + e2 - ез,
Xe = {1,0,-1}. Xe = {-2,0,1}.
9. ei = 2ei + 3e2 + e3, 10. ei = ei + 2e2 + 2e3,
e'2 = 7ei + 9e2 + 5e3, e'2 = 2ei + e2 - 2e3,
e3 = 3ei + 4e2 + 3e3, e3 = 2ei - 2e2 +e3,
xe ={0,3,3}. Xe ={-9,0,9}.
Ответы. l.xe- = {5,-1,-4}. 2.xe- = {4,-12,7}. 3.xe- = {5,1,0}.
4.xe, = {2,0,0}. 5.xe- = {-6,l,8}. 6.Xe, = {2,3,-2}. 7. xe-= {0,-4,3}.
8.Xe, = {5,3,-1}. 9.xe/ = {5,-4,6}. 10.xe-= {1,0,-1}.
2.9. Преобразование матрицы оператора
Постановка ЗАДАЧИ. Найти матрицу некоторого оператора А
в базисе ei, е2,...,е'п, где
ei = сцв1 + С21в2 + ... + c„ie„,
е2 = С12в1 + С22в2 + . . . + Сп2е„,
е'п = ci„ei + с2„е2 + ... + сппе„,

2.9. Преобразование матрицы оператора
65
если в базисе ei,e2,. -. ,е„ его матрица имеет вид
А* =
( оц а\2
«21 а22
\ ап1 <*п2
ain
Я2п
План решения. При переходе от базиса ei,e2,...,е„ к базису
ei,e2,... ,е'п матрица оператора преобразуется по формуле
Ае, = С^АеС,
A)
где С — матрица перехода от базиса ei,e2,...,en к базису
е1>е2)--чеп-
1. Находим матрицу перехода С. Так как столбцы матрицы
перехода от базиса в\, ег,..., еп к базису e'j, е2,.. ■, е'п — это столбцы
координат векторов е[, е2, ■ ■ •, е^, в базисе ei, ег,. - -, е„, то
/
СЦ Ci2
С21 С22
С2л
\ Cni Сп2 • ■ . Спп
2. Находим обратную матрицу С-1 и проверяем, что С~гС = Е.
3. Находим матрицу оператора А в базисе е'^е'г,...,^ по
формуле A)
А* = C-Mea
Пример. Найти матрицу оператора А в базисе e'j.e^.e^, где
ei = ei + е2 + 2е3,
е'2 = 2ei - е2)
«з = -ei + е2 + е3,
если в базисе е1,ег,ез его матрица имеет вид
Ле =

66
Гл. 2. Линейная алгебра
Решение.
1. Находим матрицу перехода
С =
2. Находим обратную матрицу С методом Гаусса:
1 2
1 -1
2 О
1 2
-1 -3
-2 -4
Таким образом,
с-1 =
Убеждаемся, что С ■ С-1 = Е:
сс-
3. Находим матрицу оператора А в базисе e'j, e2, е3 по формуле A)
-7 6 -8
11 -9 12
15 -16 19
Ответ. Ае'
-7 6 -8
11 -9 12
15 -16 19

2.9. Преобразование матрицы оператора
67
Условия задач. Найти матрицы Ле/ в базисе e'j,e2,e3, где
e'j = 2ei +3e2 +ез,
е'2 = 3ei + 4е2 + е3,
е'з = ei + 2е2 + 2ез,
если заданы матрицы Ае в базисе е1,ег,ез.
1.1= -310. 2. 1 =
4. Ае =
Ответы.
-37 -55 -27
1. Ае, = | 30 43 23 | . 2. А* = | 24 35 19
6 10 2
-26 -47 7
3. Ае< = I -13 -17 -16 | . 4. Ле- = | 13 25 -6
13 20 3
1 -1 15
5. Ле- = | -18 -28 -8 | . 6. Ае, = | -2 -1 -11
4 6 0
47
30
9
20
13
-1
27
18
-2
-67
43
12
27
-17
-2
42
-28
-4
-37
23
9
22
-16
0
13 '
-8
0

68
Гл. 2. Линейная алгебра
7. Ае, = \ 28 39 22 . 8. Д.
-43
28
10
-28
17
5
-60
39
14
-40
24
7
-34
22
7
-28
18
6
4
-1 -
0
-86
51
23
4 21
-1 -11
1 -5
-113 -
67
30
\
•
/
-60
35
18
9. Ле- = 17 24 18 . 10. А*.
2.10. Собственные значения
и собственные векторы оператора
Постановка задачи. Найти собственные значенья и
собственные векторы оператора А : Хп i-> Xn, заданного в некотором
базисе матрицей
I«и ai2 ••• a.ir
_ 021 022 • • • «2n
\a„i a„2 ... а„
План решения. Собственные значения оператора А являются
корнями его характеристического уравнения det(A — ХЕ) = 0.
1. Составляем характеристическое уравнение и находим все его
вещественные корни (среди них могут быть и кратные).
2. Для каждого собственного значения А{ найдем собственные
векторы. Для этого записываем однородную систему уравнений
(А - XtE)X = О
и находим фундаментальную систему решений Х{, Х%, ■■■, Х„_г., где
Г{ — ранг матрицы системы А — XiE. (Заметим, что Г{ < п, так как
det(A - XiE) = 0.)
3. Столбцы Х{, Х%, ■■■, Х„_г. являются столбцами координат
искомых собственных векторов е\, е2,..., е^_г.. Окончательно для Х = Xi
записываем ответ в виде
{...}, е*2 = {...}, -.-, ej,_ri ={...}
Множество собственных векторов, соо
ну значению Aj, можно записать в виде
5а=а4 = {х : x = Cie! + С2е2 + ... + C„-ri<_ri ф 0}
Замечание. Множество собственных векторов,
соответствующих собственному значению Aj, можно записать в виде

2.10. Собственные значения и собственные векторы 69
Пример. Найти собственные значения и собственные векторы
оператора А: Хз ь-> Хз, заданного в некотором базисе матрицей
А =
3
1
1
0
2
-1
0
-1
2
Решение.
1. Составляем характеристическое уравнение:
3-А
1
1
О О
2-А -1
-1 2-А
= о <=> C - А)(А2 - 4А + 3) = 0.
Поэтому Ai,2 = 3, A3 = 1.
2. Для собственного значения Ai,2 = 3 найдем собственные
векторы. Запишем однородную систему уравнений (А — 3 • Е)Х = О:
0
1
1—1
0
-1
-1
0 \
-1
-1/
/ Zl
1 х2
V х3
Г Xi
\ Xl
Х2 — Жз
Х2 - Хз
0,
0.
Очевидно, ранг матрицы этой системы равен 1 (п — г = 2 —
размерность пространства решений), следовательно, система нетривиально
совместна и ее фундаментальная система решений имеет вид
*i =
Х2 =
Итак, двукратному собственному значению Ai,2 = 3 соответствуют
два линейно независимых собственных вектора ei = {1,1,0} и ег =
= {1,0,1}. Множество всех собственных векторов Sx12=з,
соответствующих собственному значению Ai,2 = 3, имеет вид
■Sa,.2=3 = (х : х = Ciei + С2в2 ф О}.
Аналогично находим собственный вектор, соответствующий
собственному значению Аз = 1. Получим ез = {0,1,1}. Поэтому
множество всех собственных векторов S\3=i, соответствующих
собственному значению Аз = 1, имеет вид
5Аз=1 - {х : х = С3е3 ф О}.

70
Гл. 2. Линейная алгебра
Ответ.
Sa.,2=3 = {x : х = Ciei +С2е2 ф О}, где ei ={1,1,0} и е2 = {1,0,1};
5Лз=1 = {х : х = С3е3 ф О}, где е3 = {0,1,1}.
Условия ЗАДАЧ. Найти собственные значенья и собственные
векторы операторов А : Хз •->• Хз, заданных в некотором базисе
матрицами.
( 4 1 ~2\
1.1 14 2 .
V -2 2 1 /
/3-1 1\
3.-1 5-1
V 1 -1 З/
/2 1 2\
5. I 0 4 -1 .
V 0 -1 4/
( 4 0 -1\
7. 2 2-1
V -1 0 4 /
/3 1 0\
9. 13 0.
V2 1 5/
Ответы. 1. Ai = -l,ei = {l,-l,2}; Л2 = 5, е2 = {1,1,0}; Л3 = 5, е3 =
= {-2,0,1}. 2. Ai = 2, ei = {1,1,0}; Л2 = 3, е2 = {2,1,0}; Л3 = 3,
е3 = {0,0,1}. 3. А1=2,е1 = {1,0,-1}; А2 = 3, е2 = {1,1,1}; А3 = 6,
е3 = {1,-2,1}. 4. Ai=2, ei = {1,0,0}; А2 =2, е2 = {0,1,1}; А3 = 4,
е3 = {1,1,-1}. 5. Ai=2, ei = {l,0,0}; А2 =3, е2 = {3,1,1}; А3 = 5,
е3 = {1,-3,3}. 6. Ai = l, е1={2,-1,2}; А2 = 3, е2 = {1,-2,2}; А3 = 5,
ез = {0,1,0}. 7. Ах =2, ei = {0,1,0}; А2 = 3, е2 = {1,3,1}; А3 = 5,
е3 = {1,1, -1}. 8. Ах = 1, ех = {3, -3, -1}; А2 = 3, е2 = {1,1, -5};
А3=4,е3 = {0,0,1}. 9. Ах =2, е1 = {3,-3,-1}; А2 =4, е2 = {1,1,-3};
Аз = 5, е3 = {0,0,1}. 10. А1 = 1,е1 = {1,-1,-1}; А2 = 3, е2 = {1,0,-1};
Аз=4,е3 = {1,0,0}.
2.
4.
6.
10.
4
1
0
2
0
0
2
3
-1
2
1
3
4
0
0
-2
1
0
1
3
-1
0
5
0
1 0
2 0
2 4
2
2
-1
°\
°
з/
-1
-1
3
-1
-1
2
\
■
/
1
-1
2

Глава 3
ПРЕДЕЛЫ
При изучении темы ПРЕДЕЛЫ вы познакомитесь на примерах
с понятиями предела последовательности, предела и непрерывности
функции в точке, научитесь вычислять различные пределы,
используя теоремы о пределах, эквивалентные бесконечно малые и
специальные приемы.
С помощью пакета РЕШЕБНИК.ВМ вы можете решить
неравенства, выполнить численные расчеты и проверить правильность
полученных вами результатов.
3.1. Понятие предела последовательности
Постановка задачи. Пользуясь определением предела
последовательности, доказать, что
lim an — а.
План решения.
1. По определению число о называется пределом числовой
последовательности {а„}, если
Ve > О 3N(e) : п > N(e) ==> \ап - а\ < е.
Это означает, что Ve > 0 неравенство \ап — а\ < е имеет решение
п > N(e).
2. Найдем, при каких п справедливо неравенство
\ап — а\ < е,
т.е. решим это неравенство относительно п.
3. Если решение имеет вид п > N(e), то а — предел числовой
последовательности {оп}.

72
Гл. 3. Пределы
ЗАМЕЧАНИЕ. Если решение неравенства |о„ — а\ < е нельзя
представить в виде п > N(e), то число о не является пределом
последовательности {оп}.
Пример. Пользуясь определением предела последовательности,
доказать, что
2п3
lim
п—юо п°
= 2.
Решение.
1. По определению число 2 называется пределом числовой после-
довательности
Г 2п3 1
\n3-2j'
если
Ve > 0 3N{e) : п > N(e)
2п3
-2
<е.
2. Найдем, при каких п справедливо неравенство
2п3
-2
<е,
т.е. решим это неравенство относительно п.
3. Неравенство имеет решение п > N(e) = 3v/4/e + 2. Следователь-
f 2r3
но, 2 — предел числовой последовательности
Г 2п3 1
\n3-2j'
Ответ, п > ?У4/е + 2-
Условия задач. Пользуясь определением предела
последовательности, доказать, что lim,,-^ o„ = о.
1. ап =
3. оп =
5. ап =
7. о„ =
9. оп =
2п-2
Зп-1'
Зп + 2
2п + 1'
5п + 2
п+1 '
3-п3
1 + п3'
3 + 8п2
2
а=з-
3
а=2-
о = 5.
а=-1.
2. а„
4п-2
On =
1 + 4п2'
8. оп =
а— 2. 10. о„ =
2п + 3'
5п + 2
Зп + Г
4п2 + 1
п2 + 2
6п-2
2п + 1'
Зп
о = 2.
5
о = —.
3
о = 4.
о = 3.
п+1'

3.2. Вычисление Пт„-юо[-Рк(п)/<2т(п)]
73
Зе + 4 п 8-Зе „ 1 - 2е
Ответы. 1. п > — . 2. п > . 3. п > — .
9е 2е 4е
1-Зе г 3-е „ /7-2е „ з/4-е
4. п > . 5. п > . 6. п > \ . 7. п >
9е е V е
5-е „ /1-е 3-е
8. п> ——. 9. n>W —■—. 10. п> .
2е V 4е е
3.2. Вычисление \im.n^00[Pk{n)/Qm{n)]
Постановка задачи. Вычислить предел
1пп г, I ч'
n-*°° Qm(n)
где
Рк{п) = a,knk + Ofc_infc_1 + ... + а\п + о0,
<Эт(") = ЬтПт + 6m_!nm_1 + . . . + Ь1П + bo.
План РЕШЕНИЯ. Здесь Pk(n) — многочлен степени к (бесконечно
большая последовательность порядка п ) и Qm{n) — многочлен
степени m (бесконечно большая последовательность порядка пт).
1. Вынесем в числителе множитель пк, получим Рк(п) = п р(п),
где р(п) = ак + Ofc-i/n + ... + а0/пк.
2. Вынесем в знаменателе множитель пт, получим Qm{n) =nmq(n),
где q{n) = bm + 6m_i/n + ... + Ъ0/пт.
3. Имеем
lim^=lim^)
n-юо <Ут(п) n-voo nmg(fl)
4. Получаем:
. ^ r ft(")
если к> т, то lim ———г = oo;
если к < m, то hm ———r = v;
n->°° Qm\n)
если к = m, то по теореме о пределе частного
,. Рк(п) _ p(n) _ Iimn_voop(n) _ а^
n-t-oo <5m(n) n-voo g(n) ИШп-юо g(n) 6TO

74
Гл. 3. Пределы
Пример. Вычислить предел
Bп+1J-(п+1J
lim
п—юо
П2 + П + 1
Решение. Здесь Bп + IJ - (п + IJ =? Зп2 + 2п — многочлен
второй степени (бесконечно большая последовательность порядка п2) и
п2 + п + 1 — многочлен второй степени (бесконечно большая
последовательность порядка п2).
1. Вынесем в числителе множитель п2, получим
Bп + 1J - (п+1J = п2 (з+£) •
2. Вынесем в знаменателе множитель п2, получим
п2 + п + 1 = п2A + - + -П.
\ п п* J
3. Имеем
lim
п—юо
Bn + lJ-(n+lJ
п2 + п + 1
lim
n2C + 2/n)
n-Юо n2(l + 1/n + 1/n2)
4. Сокращая п2 и используя теорему о пределе частного, получаем
lim
п—юо
Bп + IJ - (п + IJ
п2 + п + 1
Цшп-ю^з + г/п)
limn_,00(l + l/n+l/n2)
= 3.
,. Bп + IJ - (п + 1J „
Ответ, lim - ^ 5__L_Z_ = з.
п-юо пг + П + 1
Условия задач. Вычислить пределы.
1. lim
E - пJ + E + пJ
п"те E - ПJ - E + ПJ '
C - пK - B - пK
2. lim
3. lim
n-юо A — nK — A 4- nK
C + nJ-B + nJ
5. lim
n-VooB + nJ-(l-7lJ'
6. lim
D - nK - B - nK
n~~(l-nJ-B + nL'
B-nJ-(l + nJ
n-^o(l + nJ-B-nJ'
(n + 2K - (n + 2J
п-Юо (n - 2K - (fl + 2K '

3.3. Вычисление limn-»oo [/(n)/sM]
75
„ ,. (l + 3nK-27n3 0 ,. C-2nJ
7. lim ^- -^-;—r-5-- 8. lim v '
n-voo A + AnJ + 2n2' ' n-voo (n - 3K - (fl + 3K '
S. Urn , £+">' ... 10. ta (- + Ч"-(• + *)•
n->oo (n + 2J - (n + lK ' ' п-юо C - nK
Ответы. 1. -оо. 2.0. 3.0. 4. -1. 5.1/3. 6. - оо. 7.9. 8. -2/9.
- 1. 10. 1.
3.3. Вычисление lim^oo [f{n)/g{n)]
Постановка задачи. Вычислить предел
lim ——,
п-юо g\n)
где f{n) — бесконечно большая последовательность порядка па и
д(п) — бесконечно большая последовательность порядка п@
(а, C е R).
План решения.
1. Вынесем в числителе множитель па, получим f(n) — natp(n),
где Итп_юо <р(п) = а, а ф 0.
2. Вынесем в знаменателе множитель п@, получим д(п) = п^ф{п),
где lim^oo ip(n) - b, 6^0.
3. Имеем
f(n) nay(n)
hm -j— = hm .
n-Yoo g[n) n-too nPlpyn)
4. Получаем:
если a> C, то lim -—- = oo;
п-юо g(n)
если a < /3, то lim ——r- = 0;
п-юо д(п)
если a = C, то по теореме о пределе частного
lim M = ^^(n) = a
п-юо д(п) lim ^(п) 6

76
Гл. 3. Пределы
Пример. Вычислить предел
,. п Ш + у~32п10 + 1
lim „ .
п~>°° (п + уЪ) Уп3 - 1
Решение. Числитель п 6v/n + %/32п10 + 1 — бесконечно большая
последовательность порядка п2 и знаменатель (п + 4/п) уп3 — 1 —
бесконечно большая последовательность порядка п2.
1. Вынесем в числителе множитель п2, получим
2. Вынесем в знаменателе множитель п2, получим
(п+^I^^г=п2A+^) уГТ.
3. Имеем
п У^ + л/32п10 + 1 = п2A/п5/6 + 2 VI + 1/п10)
"^D („ + 4/^) ^ЗТГГ ~ n52o „2(! + 1/пЗ/4) 3/1 _ 1/„3 •
4. Сокращая п2 и используя теоремы о пределах, окончательно
получаем
,. п^+^32п10 + 1 ,. 1/п5/6 + 2 yi + 1/п10
lim „ . = hm „ , = =
п-юо (п + 4/^) </п3-1 «~>°° A + 1/п3/4) У1 - 1/п3
= limn^ooCl/n5/6 + 2 yi + 1/п10) _
lim„-»oo(l + 1/п3/4) yi-1/n3
= 2.
Замечание. В данном случае было использовано свойство корня,
в силу которого linin-voo yi + 1/п10 = 1 и linin^oo yi - 1/п3 = 1.
.. п^п+V32n10+1 0
Ответ, hm _ „ . =- — 2.
п-юо (п + \fii) Vn3 - 1

3.4. Вычисление lim„->oo
77
Условия задач. Вычислить пределы.
1. ton
п\№+ V4n8 +1
п->°° (п + у/п)\/7 -п + п2
\/2п3 + 3 - \7пТ~5
л/п^Т - \/2п2 + 3
»^+~ \Vn3 + 3 + Уп5 + 2'
lim
3. lim
я-»" Vn3 + 2 - у/п- 1
4. lim
5. lim
n—юо
7. lim
y/3n + 2- \7l25n3 + i
V^+n2
Vn + 2- \/n2 + 2
y/n2 + 3 + 3n3
"■^"t» \7n12 + 2n + 1 - n2'
пу/й- у/27п6 + n4
6. lim
n-">° (n+ 4/n)v/4+~n2
\/n5 + 3 + \/n - 2
п-юо Vn4 + 1 - Vn2 - 1'
10n3 - y/n3+ 2
8. lim
9. lim
n-^o Vn4 + 2 - \jn-2
v/rT+2- V8n3 + 3
"-►°° \/4n6 + 3 — n
10. lim
n->°° V" + 5 + n
Ответы. 1. л/2. 2.0. 3. +oo. 4.3. 5.5. 6. -3. 7. -1. 8. +oo. 9.5. 10. -2.
3.4. Вычисление limn_>00 [ii(n)^n']
Постановка задачи. Вычислить предел последовательности
lim [u(n)e(n)],
n—voo
где limn-^oo u(n) — 1 и Нтп_юо v(n) = oo.
План решения.
1. Преобразуем выражение под знаком предела так, чтобы
использовать второй замечательный предел, т.е. выделим единицу:
lim \u(n)v{n)] = lim f(l +а(п)I/а^пЛ
n—voo n-too \ /
a(n)«(n)
где ct(n) — u(n) — 1 — бесконечно малая последовательность при
n —> оо. Так как а(п) -¥ 0 при п -)• оо, то
lim(l+a(n)I/a(n)=e.
n—foo
2. Если итп_юо ап — а (ап > 0, а > 0) и Ипц-юо Ьп = 6, то
lim anb" = ab.
п—юо

78
Гл.З. Пределы
Следовательно, если существует предел
lim a(n)v(n) — lim (u(n) — l)v(n),
то окончательно имеем
lim [u(n)v{n)] = e«™n-»(u(n)-i)«(n)_
Пример. Вычислить предел
/4n2+4n-l\
V4n2 + 2n + 3j
l-2n
n-voo V An2 + 2n + 3
Решение.
1. При п —>• со выражение под знаком предела представляет собой
степень, основание которой стремится к единице:
/4п2 +4п- 1\ _
n*¥L \An2 + 2n + 3j ~ '
а показатель — к минус бесконечности:
lim A — 2п) = —со.
п—*оо
Преобразуем выражение под знаком предела так, чтобы использовать
второй замечательный предел:
\4n2+2n + ZJ ~\ +
2п-4
1-2п
4п2 + 2п + 3,
('♦
2п-4
4п2 + 2п + 3
, 2п-4
4п2 + 2п + 3,
Bп - 4)A - 2п)
4п2 + 2п + 3
Так как
при п —> со, то
2п-4
4п2 + 2п + 3
2п-4
lim 1 + л , п
п-»°о V 4п2 + 2п + 3,
4п2 + 2п + 3
, 2п-4
— е.

3.5. Понятие предела функции
79
2. Так как
шп Bп:4)A'2п) = -1,
n-voo 4n2 + 2n + 3
то окончательно имеем
/4n2 + 4n-l\'
V4n2 + 2n + 3j
Вт [ ^!±i!lziy~2n = е-\
п-»оо
Ответ, lim ( 44;—г г I = е-1
п—юо
/4n2 + 4n-l\
V4n2 + 2n + 3y
Условия задач. Вычислить пределы.
п-Уоо\п — 1/ п-юо\2п + 6/
П-ЮО Y 71 ^ / П-ЮО ^271^ + 1/
5. lim c;+"^y"'. e. tafitn*".
п-юо ^nz + П — 1/ п-юо^п + О/
„ ,. f 3n2-2n \n+2 о ,. /2n2 + n + 5\3
7- llm -ТГЪ 7, ;r • 8- llm 1ГЪ 7
n-*oo \3n2 - 2n + 5/ n-voo \2n2 + n + 1/
, /n3 + 3\n_n3 ,. /n + n3n41
9. lim -=—- . 10. lim
n-юо упЛ — 2/ n-юо \П — 1J
Ответы. 1. e3. 2. у/ё. 3. е. 4. е. 5. е~2. 6. е2. 7. 1. 8. е6.
9. е-5. 10. +оо.
3.5. Понятие предела функции
Постановка задачи. Пользуясь определением предела функции
в точке, доказать, что
lim f(x) = A.

80
Гл. 3. Пределы
План решения.
1. Число А называется пределом функции f(x) в точке х = а, если
Ve > 0 36(e) > 0 : 0 < \х - а\ < 6(e) => \f(x) - А\ < е.
Это значит, что Ve > 0 неравенство \f(x) — А\ < е имеет решение
О < \х - а\ < 6(e).
2. Для того чтобы найти 6(e), сначала найдем множество М такое,
что
г£М=Ф |/(z) - А\ < е,
т.е. решим неравенство \f(x) — А\ < е. Затем найдем 6(e) такое, что
0 < \х - а\ < 6(e) => х е М.
Тогда будем иметь
0 < \х - а] < 6(e) =>1бМ=Ф |/(а;) - А\ < е.
Это означает, что
lim f(x) — A.
х-*а
Записываем ответ в виде: Ve > 0 0 < \х — а\ < 6(e)
Пример. Доказать, что
15а:2 - 2а; - 1
|/(а:)-А|<е.
lim
8.
а:-»1/3 X — 1/3
Решение.
1. Число 8 называется пределом функции f(x)
точке х = 1/3, если
1
Ve > 0 36(e) > 0 : 0 <
<<5(е)
15а:2 - 2а: - 1
а;-1/3
15а;2 - 2а; - 1
а;-1/3
8
<е.
2. Для того чтобы найти 6(e), сначала найдем множество М такое,
что
х£М
т.е. решим неравенство
15а;2 - 2а; - 1
а;-1/3
<£,
15а;2 - 2а; - 1
а;-1/3
<е.

3.5. Понятие предела функции
81
Затем найдем 6(e) такое, что
0<
х —
< E(e) =ф х е М.
Тогда будем иметь
1
0<
х —
< E(e) =яеМ
15а:2 - 2а; - 1
а;-1/3
<£.
3. Решаем неравенство:
15а;2 - 2а; - 1
а;-1/3
-8
< е <=> |15а; + 3 - 8| < е <=> --— <х<- + —
о 15 о 15
(так как в определении предела функции в точке х ф 1/3, т.е.
х —1/3 Ф О, то можно сократить дробь на множитель х —1/3). Таким
образом,
м=(Ьй'Ои(ЬЬй)
х€
Следовательно, если
15а;2 - 2а; - 1
а;-1/3
-8
<£.
ад = Е,
то
0<
1
Х_3
< E(e) => х е
U 15'з)и(з'3 + 15/
т.е.
15а;2 - 2а; - 1
I а;-1/3
- 8 < е,
15а;2 - 2а; - 1 „
lim —т-— = 8.
z-H/3 X — 1/3
Ответ Ve > 0 0 <
х —
<
15
15а;2 - 2а; - 1
а;-1/3
<£.

82
Гл. 3. Пределы
Условия ЗАДАЧ. Пользуясь определением предела функции в
точке, доказать равенства.
. ,. 2z2 + lla;+15 За;2 + 2а;-8
1. lim = —1. 2. lim = -10.
i-»-3 а; + 3 я;->-2 а;+ 2
6а;2 + 5а;-1 9а;2 + 12а: + 3 а
3. lim --— = —1. 4. hm = 6.
s-v-i/2 a;+1/2 a;-»-i/3 a;+ 1/3
3a:2 + x - 2 a:2 - x - 6 c
5. lim = —5. 6. lim = 5.
sc-»-i a; + l x-уз x - 3
„ ,. 6a;2 - 9a; + 3 0 0 ,. 4a;2 -15a; + 9 Л
7. hm = 3. 8. hm = 9.
sc->i a; — 1 а:-»з a; — 3
6a;2 + 20a; + 6 ,. 5x2 - 3x - 2
9. hm = —16. 10. Um = 7.
ж-»—з a; + 3 x-*i x — 1
Ответы. 1. E(e) = e/2. 2. E(e) = e/3. 3. E(e) - e/6. 4. E(e) = e/9.
5. E(e) = e/3. 6. 6(e) = e. 7. E(e) = e/6. 8. E(e) = e/4. 9. E(e) = e/6.
10. E(e) = e/5.
3.6. Понятие непрерывности
функции в точке
Постановка задачи. Пользуясь определением, доказать, что
функция f(x) непрерывна в точке а.
План решения.
1. Вычисляем f(a).
Функция f(x) называется непрерывной в точке х = а, если
Ve > 0 36(e) > 0 : \х - а\ < 6(e) =► \f(x) - f(a)\ < е.
Это значит, что Ve > 0 неравенство \f(x) — f(a)\ < e имеет решение
0 < \х - а\ < 6(e).
2. Для того чтобы найти 6(e), сначала найдем множество М такое,
что
х g М =» |/(аг) - f(a)\ < e,
т.е. решим неравенство |/(а;) — f(a)\ < е. Затем найдем 6(e) такое,
что
\х - а\ < 6(e) => х S М.

3.6. Понятие непрерывности функции в точке
83
Тогда будем иметь
\х-а\< 6(e) => гбМ=Ф |/(а;) - f(a)\ < е.
Это означает, что f(x) непрерывна в точке х = а.
Записываем ответ в виде: Ve>0 \x—a\ < 6(e) => |/(аг) —/(а)| <е.
ПРИМЕР. Пользуясь определением, доказать, что функция
f(x) = 5а;2 + 5 непрерывна в точке а = 8.
Решение.
1. Вычисляем /(8) = 325.
Функция f(x) называется непрерывной в точке х — 8, если
Ve > 0 36(e) > 0 : \х - 8| < 6(e) => \5х2 + 5 - 325| < е.
Это значит, что Ve > 0 неравенство \f(x) — 325)] < е имеет решение
О < |аг — 8| <6(е).
2. Для того чтобы найти 6(e), сначала найдем множество М
такое, что х £ М => |5а;2 + 5 — 325| < е, т.е. решим неравенство
|5а;2 + 5 — 325| < е, затем найдем 6(e) такое, что |ат — 8| < 6(e) =>
=> х £ М. Тогда будем иметь
\х - 8| < 6(e) => х е М ==> \Ъх2 + 5 - 325| < е.
3. Решаем неравенство (считая, что е < 320)
|5аг2 — 320| <е<=>64-^ < х2 < 64 + | <^ Л64 - | < х < д/б4+|.
Таким образом,
iGM= ( W64 - ^ , J 64 + ^ 1 =Ф |5^ + 5 - 325| < е.
Следовательно, если
«5(e) = min Is - ^64 - | , ^64 +| - в| - ^/б4 +| - 8,
то
|я - 8| < E(e) => z e (Л64 - | , Л64 + | J => |5z2 + 5 - 325| < е,

84
Гл. 3. Пределы
т.е. f(x) = 5х2 + 5 непрерывна в точке х — 8.
f
е
Ответ. Ve > 0 \х - 8| < Л64 + - - 8 => \5х2 + 5 - 325| < е
Условия ЗАДАЧ. Пользуясь определением, доказать, что
функция f(x) непрерывна в точке а.
1. f(x) = 4х2 - 1, а = 2. 2. f(x) = Зх2 - 2, а = 3.
3. /(я) = -х2 - 5, а = 1. 4. /(я) = -5я2 -7, а = 2.
5. f(x) = -Ах2 - 6, а = 3. 6. /(я) = -За:2 + 8, а = 4.
7. /(я) = 2я2 + 5, а = 2. 8. f(x) = 5z2 + 2, а = 6.
9. /(я) = 4я2 + 1, а = 8. 10. f(x) = 2х2 -\, а = 7.
Ответы. 1. E(e) = у/4 + е/4 - 2. 2. E(e) = л/9 + е/3 - 3.
3. E(e) = уТТё-1. 4. E(e) = л/4 + е/5 - 2. 5. E(e) - л/9 + е/4 - 3.
6. E(e) = Л/16 + е/3-4. 7. E(e) = у/А + е/2-2. 8. E(e) = л/Зб + е/5-6.
9. E(e) = л/64 + е/4 - 8. 10.E(е) = л/49 + е/2 - 7.
3.7. Вычисление lima;^a[Pn(a:)/Em(a:)]
Постановка задачи. Вычислить предел
bm v .,
где
Р„(а;) = ana:n 4- an_ia:n-1 + ... + ахх + а0,
Qm{x) = Ьтхт + 6m_iarm_1 + ... + hx + b0.
План решения.
1. Если Qm(a) ф 0, то функция Pn(x)/Qm(x) непрерывна в точке а
Цт Р"(Ж) = P»(Q)
"«OmW <3m(a)'
Если <5m(a) = 0 и Рп(а) ф О, то
,- Рп(х)
lim = оо.
*->а <Эт(а;)

3.7. Вычисление limI_»0[P„(x)/Qm(x)y
85
Если Qm(a) = 0 и Рп(а) = О, то, разлагая многочлены на
множители, получаем
Рп{х) _ (х - g)P„-i(a;)
Qm{x) (a:-a)<3m-i(a:)'
где Qm_i(a) ф О и P„_i(a) ^ 0.
2. Поскольку в определении предела функции при х —> а аргумент
не может принимать значение, равное а, то в последнем случае можно
сократить множитель х — а. Получаем
lim Pn{x) ^ lim (*" e)p»-i(*) _ P"-i(«)
*-+а Qm{x) *-*a {x - a)Qm-i(x) Qm-i(a) *
Замечание. Если а является кратным корнем многочленов Рп(х)
и <Эт(а:), то Р„(а;) = (а; - а)кРп-к(х), Qm{x) = (x- a)lQm-i(x) и
Рп{х) =(х- а)кРп-к(х)
Qm(x) (x-a)'Qm_i(x)'
где Qm_i(a) ^ 0 и Pn_fc(a) ф 0.
Пример. Вычислить предел
ж3 - 4а;2 - За; + 18
*-+з а;3 - 5а;2 + За; + 9 '
Решение.
1. Выражение под знаком предела (рациональная дробь) является
отношением двух бесконечно малых функций при х —>• 3.
Разложим числитель и знаменатель на множители:
а;3 - 4а;2 - За; + 18
а;3 - 5а;2 + За; + 9
(а;-3J(а; + 2)
(х - 3)Цх + 1)
2. Поскольку в определении предела функции при х —> 3
аргумент не может принимать значение, равное 3, то можно сократить
множитель (а; — ЗJ. Получаем
,. а;3 - 4а;2 - За; + 18 ,. а;+ 2 5
lim —-z -z = lim = —.
Я-+3 а;3 - 5а;2 + За; + 9 а->з х + 1 4
а;3 - 4а;2 - За; + 18 5
Ответ, lim
з а;3 - 5а;2 + За; + 9

86
Гл. 3. Пределы
Условия задач. Вычислить пределы.
х3 + За;2 + 7х + 5 „ ,. х3 + х2 - х - 1
1. hm - . 2. lim —.
x-t-i xz—x—2 x-»-i x6 — За; - 2
„ ,. х2 - 2х +1 „ ,. х4 -1
lim —д -. 4. lim
x-*i 2х2 + х — 3 а:->1 а;4 — а;3 + х — 1
х3 +4х2 + 5х + 2 „ ,. а;2 + 2а; - 3
lim =— . 6- lim
г->-1 х2 Л-2хЛ-\ ' ' *-»-з а;3 + 5а;2 + 6а;'
„ ,. а;3 - 6а;2 + 12а; - 8 „ ,. х4 + х3 + 2х + 2
7- lim ~1—7Г~5—о Г- 8- lim 5—'л •
*-»2 а;3 - 2а;2 + 2а; - 4 s-»-i a;2 - 1
а;3 — 1 а;3 — а;2 - х - 2
9. lim — -. 10. hm
>i2x2-x-l' ' х->2 х3 - 2х2 + х - 2'
Ответы. 1. 0. 2. 2/3. 3. 0. 4. 2. 5. 1. 6. -4/3. 7. 0. 8. -1/2.
9. 1. 10. 7/3.
3.8. Вычисление lim^o [f{x)/g(x)]
Постановка задачи. Вычислить предел
ж-+о (Да;)
где f(x) и д(х) — бесконечно малые функции в точке х = 0.
План решения. Бесконечно малые функции, стоящие в числителе
и знаменателе, можно заменить на им эквивалентные (табличные).
Если f(x), fi(x), g(x), gi(x) — бесконечно малые функции в точке
х = 0 такие, что f(x) ~ /i(a;) и д(х) ~ gi(x) в точке х = 0,
и существует lim^o fi(x)/gi(x), то существует Мтх^0 f(x)/g(x),
причем
Um/M = lim*M.
х->0 д(х) х-+0 д1(х)

3.8. Вычисление lim^-vo [f{x)/9{x)l
87
Пример. Вычислить предел
2х sin х
lim
ж-vO 1 — COS X
Решение. Выражение под знаком предела является отношением
двух бесконечно малых в точке х = 0, так как
lim Bа; sin х) = 0, lim A — cos x) — 0.
Бесконечно малые, стоящие в числителе и знаменателе, заменяем на
эквивалентные:
2х sin х ~ 2х • х, х —> 0,
х2
1 — cos х ~ —, х —> 0.
Таким образом,
2х sin х ,. 2а; -х
hm = hm = 4.
s-»0 1 — COS Я ж-+0 аг/2
_ ,. 2а; sin а;
Ответ, hm — 4.
ж-+о 1 — cos х
Условия задач. Вычислить пределы.
,. In(l + sin2a;) „ ,. За;2 + 6а;
1. lim —- -. 2. lim —г——.
х-уО sin За; х-уО sin За;
5х - 1 1 — cos 2a;
3. lim — т. 4. lim
х-*о ln(l -f- a;) x^o cos 5x — cos 3a;
,. l-cos2a; D .. y/9 + x - 3
lim —r-5 6. lim — —.
*-+o e2x - 1 x->o 3arctg2a;
,. tg2a; 1- v/cosa;
7. hm -5s . 8. hm \ .
ж-t-O егх — 1 a;->0 sin X
sin 2a; „„ arcsin2a;
9. lim 7-7- —. 10. hm
х-ло ln(l - 2a;)' ' x->o ln(e - 2ж) - 1 '
Ответы. 1. 2/3. 2. 2. 3. In 5. 4. -1/4. 5. 1. 6. 1/12. 7. 1.
8. 1/4. 9. -1. 10. -e.

88
Гл.З. Пределы
3.9. Вычисление lim^a [f{x)/g(x)]
Постановка задачи. Вычислить предел
х-ю g(x)
где f(x) и д(х) — бесконечно малые функции в точке х = а.
План решения.
1. Нужно заменить f(x) и д(х) на эквивалентные им бесконечно
малые функции. Но таблица эквивалентных бесконечно малых
функций составлена для точки х = 0. Поэтому сначала сделаем замену
переменной х — а — t и будем искать предел при t —> 0.
2. Преобразуем выражение под знаком предела, пользуясь
алгебраическими и тригонометрическими формулами, и заменяем в
произведении и частном бесконечно малые функции эквивалентными.
Пример. Вычислить предел
,. cos За; —cos а;
lim 5- .
х-нг tgz2a;
Решение.
1. Поскольку
lim [cos За; — cos a;] = 0, lim tg 22а; = 0,
X —>7Г X—*ЭГ
то выражение под знаком предела является отношением двух
бесконечно малых функций при х —У п. Нужно заменить эти бесконечно
малые функции эквивалентными. Для этого сначала сделаем замену
переменной х — п = t:
cos За; — cos x ,. cos 3Gг + t) — cosGr +1)
lim — = lim -
tg22a; t-»o tg22Gr-K)
2. Используя тригонометрические формулы и заменяя в
произведении и частном бесконечно малые функции эквивалентными,
получим
COS 3GT + t) — COsGT + t)
lim ^— г =
t->o tg22Gr-K)
,. cost-cos3t ,. -2sin2tsin(-t) ,. 2 • 2t ■ t
= lim 5 = lim r— = lim ——=— = 1.
t-ю tg22t t-ю tg22t t-ю At2

3.10. Вычисление limx_»o [«(a;)"'1']
_ ,. cos За; —cos a;
Ответ, hm т = 1.
ж-иг tg z2x
Условия задач. Вычислить пределы.
,. я3 - 1 „ 1 +cos5а:
1. Inn — . 2. hm = •
x->i In а; я-»» sin За;
l + cos27ra; ,. sin37ra;
3. hm 5 . 4. hm — .
x-H/2 tgz2lTX x->2 Sin87Га;
y/x2 - x - 1 - 1 tg5a;
5. hm — — . 6. hm ° .
x->2 ln(a; — 1) x-nr/2 tg 3a;
7. hm — . 8. hm - .
s-»i sin7ra; я;->1 sin эта;
tg 5a; 2* - 4
9. hm -? . 10. hm .
я-»*-sin 3a; x^2 smnx
Ответы. 1. 3. 2. 5/18. 3. 1/2. 4. 3/8. 5. 3/2. 6. 3/5. 7. З/тг.
8. -1/Dтг). 9- -5/3. 10. D In 2)/тт.
3.10. Вычисление Ищ^о [г^жI^]
Постановка задачи. Вычислить предел
где hm ы(а;) = lu hm v(x) = 00.
План решения.
1. Преобразуем выражение под знаком предела:
u(a:)"(x) =ev^)inu^\
2. Поскольку показательная функция ех непрерывна, то можно
перейти к пределу под знаком этой функции. Имеем
lim \u(x)v(x)\ = hm е*х)Ьл*х) = elim*-° К*) !"«(*)].
ж-»01 v ' x^O

90
Гл. 3. Пределы
3. Вычисляем предел показателя
lim [г)(жIпи(ж)],
х—*0
заменяя бесконечно малые функции эквивалентными.
4. Записываем окончательный ответ.
Пример. Вычислить предел
„2ох \ 1/ sil»3 x
х-ю\1 +x25xJ
Решение. При х -> 0 выражение под знаком предела
представляет собой степень, основание которой стремится к единице:
,. 1 + х22х ,
х->о 1 + х2Ьх
а показатель — к бесконечности:
1
lim
х->о sin х
1. Преобразуем выражение под знаком предела:
/l + x22*\1/six / 1 l+s22*\
\1+хЧ*) ~eXPVsin3x 1+хЧ*)-
2. Поскольку показательная функция ех непрерывна, то можно
перейти к пределу под знаком этой функции. Имеем
,. /l + x22-\1/sin3x /. 1 , 1+^2* \
hm г—- = exp lim —-— ш г—- .
х-ю \ 1 + х2Ъх ) * \х->о sin3 х 1 + х2Ьх )
3. Вычисляем предел показателя
1 , 1+ж22ж
lim —5— ш —.
х-ю sin-5 x 1 + х2Ьх

3.10. Вычисление limx_»o [^0*0]
91
Преобразуя выражение под знаком предела к виду
1
sin3x
In
• *25х(B/5)х - 1)
1 + х25х
и заменяя бесконечно малые функции эквивалентными, имеем
lira —в— In
х-*о sin x
' *25х(B/5)х - 1)
1 + ж25х
_ .. 1 х25х(B/5)х - 1) _ ,. 1 z25xzlnB/5) _ . 2
= lim
х->0 X3 1 + Х2ЪХ
4. Окончательно получаем
Лпх \ Vsi х
— lim
lim
х->0
/1 + яа2*у
\\+хЧх)
■->о ж3 1 + ж25х
plnB/5) _ 2
■ = ln-
Ответ, lim
х-уО
1+X22n1/Six 2
/1+ж22х\
Vl+x25xJ
Условия задач. Вычислить пределы
1/х2
1
х-ю \ 1 + ж2х )
/1 ■ о \ 1/sin3 х
/ 1 + Sin Ж COS ОХ \
\l+si
х-ю\1+ж24хУ
.2qx \ 1 Ag3x
3. lim . n
x->0 \ 1 + Sin X COS 2x
5. limte-S5'*1I/12.
x->0
7. lim (cos ж) ^^l
х-Ю
I/ sin x
4. lim(l-lncosxI/!
6. lim (cosжI'*
x->0
8. lim(l + sin2xI/,ncosx.
i->0
„ ,. /l + xcos2x\
9. lim I
x-*0 \ 1 + X COS Ж J
I/*3
10. limB-cosxI/InA+2x2).
x->0
Ответы. 1. 3/2. 2. 3/4. 3. e/2. 4. e1'2. 5. 1/5. 6. e^.
7. e-1'2. 8. e-2. 9. е~г'2. 10. e1^.

92
Гл. 3. Пределы
3.11. Вычисление lim^a [tt(a:)t;^]
Постановка задачи. Вычислить предел
lim [и(х)"(х)],
х—>а
где lim u(a;) = 1 и lim w(a;) = со.
х—m х—»а
План решения.
1. Чтобы использовать таблицу эквивалентных бесконечно малых,
сделаем замену переменной t = х — а (тогда t -> 0 при х —> а) и
преобразуем выражение под знаком предела:
u{x)v(x) = ui(t)*"(t) = е"'<4>1п,"<4>.
2. Поскольку показательная функция ех непрерывна, то можно
перейти к пределу под знаком этой функции. Имеем
lim [и(х)^х)] = e«n.,-oMt)ini4(t)]
3. Вычисляем предел показателя
limft;i(t)lnui(t)],
t-yO
заменяя бесконечно малые функции эквивалентными.
4. Записываем окончательный ответ.
Пример. Вычислить предел функции
<2х_1\ЩЗ+2х)/Щ2-х)
x-yl \ X )
Решение. При х —> 1 выражение под знаком предела
представляет собой степень, основание которой стремится к единице:
2а; — 1
lim = 1,
x-yl х
а показатель — к бесконечности:
,. 1пC + 2а;)
lim -г-^— г- = со.
х->1 1пB - а;)

3.11. Вычисление limx-»a [и(ж)"'х']
93
1. Чтобы использовать таблицу эквивалентных бесконечно малых,
сделаем замену переменной t = х — 1 (тогда t —> 0 при х —> 1) и
преобразуем выражение под знаком предела:
lim
х->
2х _ j\ lnC+2x)/InB-x) ,2t jv InE+2t)/ln(l-t)
/2a;-l\
= lim
t->0
№)
lim exp
t-ю
lnE + 2i) 2t+l
ln(l - t) t+1
2. Поскольку показательная функция ex непрерывна, то можно
перейти к пределу под знаком этой функции. Имеем
lira exp
t-ю
lnE + 2t), 2t+l
In
ln(l - t) t + 1
■■ exp
,. lnE + 2t), 2t + l
lmi -—r- f In
t-ю ln(l-f) t+1
3. Вычислим предел показателя, заменяя бесконечно малые
функции эквивалентными:
lira
t->o
lnE + 2t) 2t + l
ln(l -1) t + 1
= lim
t->o
lnE + 2t)
. 41 - *)
Ч-ш)
Um"°<5 + 2'>=-l-5.
t-ю -t(t + 1)
4. Окончательно получаем
Ответ, lim
x-H
' 2x - 1 \ InC+2x)/ lnB-x)
'2 _ i \ lnC+2x)/lnB-x) 1
limf^iV
(~)
Условия задач. Вычислить пределы.
tg (тгх/4)
1. lim
х->2
аМ
2. lim
X—>
/sinaA
1 \ sin 1 /
l/(x-l)

94
Гл. 3. Пределы
3. lim(H°£fI/(*-3). 4. ШB-х)*1»Ю.
х->3 \C0S3/ x->lv '
5. limCex-1-2)x/(x-1\ 6. lim (cosxI'™**.
7.' lim (tgxI/00821. 8. limC-2xI/lnB-x)
Х->7г/4 X->1
/А-тЧ^ИЗ-х) /„ч1/1пD-х)
9. limfi-E) Ю. lim(-)
x->2 \ X у x->3 \^Ж/
Ответы. 1. e2/*. 2. e^1. 3. е-**3. 4. e2^. 5. e3. 6. e/2.
7. e_1. 8. e2. 9. e. 10. e1/3.
3.12. Вычисление \imx_>a F(u(x)v(x) + /(a;))
Постановка задачи. Вычислить предел
lim F(w(x)t;(a;) + /(ж)),
X—Ю
где F(x) непрерывна на R, /(х) непрерывна в точке х — а, и(х) —
бесконечно малая функция в точке х = а и v(x) — функция,
ограниченная в некоторой окрестности точки х = а.
План решения.
1. Так как F{x) непрерывна на R, то по теореме о переходе к
пределу под знаком непрерывной функции имеем
lim F(u(x)v(x) + f(x)) = F(]im(u(x)v(x) + /(ж))).
x—»a x—»a
2. Поскольку и(х) — бесконечно малая функция в точке х = а и
v(x) — функция, ограниченная в некоторой окрестности точки х — а,
то u(x)v(x) — бесконечно малая функция в точке х — а, т.е.
lim u(x)v(x) = 0.

3.12. Вычисление limx^>a F(u(x)v(x) + f(x))
95
3. Так как /(ж) непрерывна в точке а, то
lim /(ж) = Да).
х—ю
Используя основные свойства предела функции в точке, получаем
lim F(u{x)v{x) + /(ж)) = F(/(a)).
x—>a
Пример. Вычислить предел
B+sin^)
lim .f/ж [ 2 + sin — ) + 8cosx.
x->0
Решение.
1. Так как функция у — yfx непрерывна при всех х, то, переходя
к пределу под знаком непрерывной функции, получаем
lim а х ( 2 + sin — 1 +8 cos х — \ lim х ( 2 + sin — 1 +8 cos x
х-Ю у \_ X) ух-ю[ \_ ж/
2. Так как х — бесконечно малая функция в точке х = 0, а
2 +sin A/х) — функция, ограниченная в окрестности точки х — 0, то
х B + sin A/ж)) — бесконечно малая функция в точке х — 0, т.е.
lim х
х->0
B + sin-j =0.
3. Так как cos х непрерывна в точке х = 0, то
lim cos ж = 1,
х-И)
и, используя свойства предела функции в точке, получаем
lim а х { 2 + sin - ) + 8cosх — \\ lim х ( 2 + sin - 1 + 81im cosx = 2.
х-ю у \ ж/ ух->о \ ж/ х-ю
Н-Ш)
Ответ, lim 43/ж [ 2 + sin ( - ) ) + 8cosx = 2.
х->0

96
Гл. 3. Пределы
Условия задач. Вычислить пределы.
1. lim \/9cos2х + 2хarctg —.
Х-+0 V X
,{<
2. lim л/4 sina: + Bа; — 7г) sin -
s-nr/2 V 2х - 7Г
1
3. lim \/cos х + arctgx cos2 _
х-уО V Хг
4. lim i/4cosa: + ln(l + 2а:)sin —.
х->о V ж
5. lim i/4cos2a: + (е2* — 1)arctg —„.
s->o у х*
(ех — cos a:) cos- + tg(a:+ — J
6. lim In
x-tO
x-»0
/
7. lim A/4sina: + (esin * - l)cos-.
x + 2
8. lim \/ln(a: + 2) + sinD — a:2) cos -.
x-v2 V X — 2
»tg(«
In I 3 + arctg x sin — J
9. lim tg ( arccos x + sin
*-»i V a: +
ar-1 a: + l\
cos .
x+1 x-\)
10. lim In I 3 + arctg a: sin
x-»0 l
Ответы. 1.3. 2.2. 3.1. 4.2. 5.2. 6.0. 7.2. 8. In 2.
9. 0. 10. In3.

Глава 4
ДИФФЕРЕНЦИРОВАНИЕ
При изучении темы ДИФФЕРЕНЦИРОВАНИЕ вы познакомитесь
на примерах с понятиями производной и дифференциала функции
одной переменной, научитесь вычислять производные, используя
правила дифференцирования суммы, произведения, частного и сложной
функции, научитесь дифференцировать функции, заданные
параметрически, вычислять производные высших порядков, а также
применять производные и дифференциалы в приближенных вычислениях и
при решении геометрических задач.
С помощью пакета РЕШЕБНИК.ВМ вы можете вычислить
пределы, выполнить численные расчеты, а также вычислить производные
любого порядка и проверить правильность полученных вами
результатов.
4.1. Понятие производной
Постановка задачи. Исходя из определения, найти
производную функции f(x) в точке х — 0.
План решения.
1. По определению
х->0 X
(Напомним, что при вычислении предела х —> 0, но х ф 0.)
2. Вычисляем предел
х-»0 X
3. Если предел существует и равен А, то /'@) = А, если предел не
существует, то /'@) не существует.

98
Гл. 4. Дифференцирование
Пример. Исходя из определения, найти производную функции
— cos I х sin — I,
/(*) =
1
о,
хфО,
х = 0,
в точке х — 0.
Решение.
1. По определению
т = цт /(»>-/«>) = lim l-cos(xsin(l/x))-0
х->0 X х->0 X
2. Так как sin(l/x) — ограниченная, а ж — бесконечно малая
функции при х —> 0, то по теореме о произведении бесконечно малой
функции на ограниченную xsin(l/x) —> 0 при х —> 0. Заменяя в числителе
бесконечно малую функцию эквивалентной и снова используя
упомянутую теорему, получаем
1 — cos(x sin(l/x)) — 0 ,. х2 sin2(l/x)
lim J ——— hm —— = 0.
х-Ю
x-*0
2x
3. Таким образом, предел существует и равен нулю.
Следовательно, /'@) = 0.
Ответ. /'@) = 0.
УСЛОВИЯ ЗАДАЧ. Найти производную функции /(ж) в точке х = 0.
I ж3 + х2 sin - J , ж ф 0,
1. /(ж)
/(*) =
/(*) =
0, ж = 0.
/" 2 М
ж cos —
V 9х)
tg
0, ж = 0.
+ 2ж, хф 0,
arcsin
0, ж = 0,
(XC0S^)'
хфО,

4.2. Вычисление производных
99
4. f{x) =
5. f(x) =
6. f(x) =
7. f(x) =
8. fix) =
9. fix) =
10. /(x) =
In (l-tg (x2 sin- j J , x^O,
0, ж = 0.
tg ( ж sin - J ,
0, x = 0.
хфО,
Jl+ln(l+x2sin-j -1, x^O,
О, х = 0.
sin (ex2 sinE/x> - 1V ж ^ 0,
0, x = 0.
4
x3 cos -—I- 3x, i^O,
0, x = 0.
arctg I x — x2 sin —- ) , x Ф 0,
V Зж;
0, x = 0.
sin ж cos —I- 2x, i^O,
0, ж = 0.
Ответы. 1. 0. 2. 2. 3. He существует. 4. 0. 5. He существует.
6. 0. 7. 0. 8. 3. 9. 1. 10. 2.
4.2. Вычисление производных
Постановка задачи. Найти производную функции у = /(ж).
План решения. Задача решается в несколько этапов. На каждом
этапе необходимо распознать тип функции и применить
соответствующее правило дифференцирования.
Возможны следующие типы функций.
• Функция имеет вид C\Ui + CiUi + ... + Спип, где ui(x),
И2(ж), ■ ■ ■, unix) — некоторые функции и С\,Сг,...,Сп — некоторые

100
Гл. 4. Дифференцирование
постоянные. Используем формулу производной линейной комбинации
(Ciui + С2и2 + ... + Спип)' = CWi + С2и'2 + ... + Спи'„.
• Функция имеет вид и- v. Используем формулу производной
произведения
(и ■ v)' = и' ■ v + и ■ v1'.
_ и тт
• Функция имеет вид —. Используем формулу производной част-
v
ного:
(и\' и' ■ v — и ■ v'
V/ D2
• Функция имеет вид u(v(x)). Используем формулу производной
сложной функции
u(v(x))' = u'(v) • v'(x).
• Функция имеет вид u(x)v^x\ Производная такой функции
вычисляется с помощью формулы
и(х)^х) = еуЫи.
Переход от этапа к этапу совершается до тех пор, пока под
каждым знаком производной не окажется табличная функция.
ПРИМЕР. Найти производную функции
Зх6 + 4х4 - х2 - 2
У =
Решение.
1. Функция у(х) имеет вид
15 VI + х2
15 v '
где и(х) — Зх6 + 4х4 — х2 — 2 и v(x) = \/1 + х2 . Используя формулу
для производной частного, получаем
У' =
1 (Зх6 + 4х4 - х2 - 2)'у/Г+х2 - (Зх6 + 4х4 -х2 - 2){у/Г+х2)'
15
{у/ТТх1J

4.2. Вычисление производных
101
2. Функция и(х) = Зх6 + 4х4 — х2 — 2 является линейной
комбинацией табличных функций. Поэтому
(Зх6 + 4х4 - х2 - 2)' = 18х5 + 16х3 - 2х.
3. Функция v(x) = \/l + х2 имеет вид
v(x) = ui(vi(x)),
где uj = ^/й7 и ^i(x) = 1 + х2. Используя формулу для производной
сложной функции, получаем
v'(x) = (^>(l + x2)' = -±=2x= 2X
2у/щ 2^/Т+х2'
Ответ, у' =
, A8х5 + 16х3 - 2х) у/ТТх2 - (Зх6 + 4х4 - х2 - 2) —,
= J__ 2 у/1 + х2
15 1 + х2
УСЛОВИЯ ЗАДАЧ. Найти производные заданных функций.
1. J/= 2^*. 2. J/ = ln(x +Vl + х2). 3. j/ = ln2(l-cosx).
, . /-ч г. 3x(sinx + cosxln3) „ sh2x
4. 2/ = ln(arcsin>/x). 5. у = . 6. j/ = —5—
1 + In 3 ch 2x
7. j/ = arcsin —= . 8. j/ = arctg3v^. 9. у — ln(l + Vthx).
VX
10. j/ = In sin 3
cos2x
sinx
~ ~ /*z-r ln2 1 2sinxln(l — cosx)
Ответы. 1. 2^х г =-. 2. . 3. -.
2 cos2 xvtg x V1 + x2 1 - cos x
1 cw c 2ch22x-4sh22x 1
4. —, —. 5. 31 cosx. 6. r-r— • 7. --
2 \/x - x2 arcsin v/x ' ' ch32x ' 2x y/x -1'
3^*ln2 1 cosx(l+sin2x)
A + 32^J>/х" ' 2(thx + \/thx)ch2x' ' sin2x

102
Гл. 4. Дифференцирование
4.3. Уравнение касательной и нормали
Постановка задачи. Составить уравнения касательной и
нормали к кривой у = f(x) в точке с абсциссой а.
План решения. Если функция f(x) в точке а имеет конечную
производную, то уравнение касательной имеет вид
V = № + f{a)(x-a). A)
Если /'(а) = со, то уравнение касательной имеет вид х — а.
Если /'(а) Ф 0, то уравнение нормали имеет вид
У = Яа)-1±-Лх-а). B)
Если f'(a) = 0, то уравнение нормали имеет вид х = а.
1. Находим значение /(а).
2. Находим производную /'(а).
3. Подставляя найденные значения /(а) и /'(а) в A) и B),
получаем уравнения касательной и нормали.
Пример. Составить уравнения касательной и нормали к кривой
y = 6\fc-f №
в точке с абсциссой а = 1.
Решение.
1. Находим /A) = 2/3.
2. Находим производную /'A) =2/3. Так как /'A) /Ои /'A) ^оо,
то воспользуемся уравнениями A) и B).
3. Подставляя найденные значения /(а) = 2/3 и /'(а) = 2/3 в A)
и B), получаем уравнения касательной и нормали:
Ответ. Уравнение касательной: 2х — 3j/ = 0. Уравнение нормали:
9х + 6у - 13 = 0.

4.4. Приближенные вычисления с помощью дифференциала 103
Условия задач. Составить уравнения касательной и нормали
к графику функции у — /(х) в точке с абсциссой а.
1. у — х — х2, а = 1. 2. у = х2+х-\-1, а = —1.
3. у = х3 + х, а = 1. 4. у = \/х — 2, а — А.
5. j/ = х2 + \V, а = 1. 6. ?/ = vx2 — 9, а — —27.
2 + Jx Л г-
7. г/ = -—¥=, а = 9. 8. у = 32 Ух-х, а = 16.
2-Vx
2 х2 - 2х + 2
9. у = х — х — 1, а = 1. 10. j/ = 5 1 а = 2.
Ответы. 1. х+2/-1 = 0, ж-у-1 = 0. 2. х+2/ = 0, x-j/-2 = 0.
3. 4х - 2/ - 2 = 0, х + 4j/ - 9 = 0. 4. х - Ау - 4 = 0, 4х + 2/ - 16 = 0.
5. 7x-2y-Z = 0, 2х+72/-16 = 0. 6. 2х+9у+5А = 0, 9х-2г/+243 = 0.
7. 2х - 3j/ - 33 = 0, Зх + 22/ - 17 = 0. 8. 2/ - 48 = 0, х - 16 = 0.
9. х - j/ - 2 = 0, х + 2/ = 0. 10. 22/ - 1 = 0, х - 2 = 0.
4.4. Приближенные вычисления
с помощью дифференциала
Постановка задачи. Вычислить приближенно с помощью
дифференциала значение функции у = /(х) е точке х — а.
ПЛАН РЕШЕНИЯ. Если приращение Дх — х — а аргумента х мало
по абсолютной величине, то
/(яг) = /(а + Дх) ps /(а) + /'(а) Дх. A)
1. Выбираем точку а, ближайшую к х и такую, чтобы легко
вычислялись значения /(а) и /'(а).
2. Вычисляем Дх = х — а, /(а) и /'(а).
3. По формуле A) вычисляем /(х).
ПРИМЕР. Вычислить приближенно с помощью дифференциала
значение функции у = \/х2 +5 в точке х = 1,97.

104
Гл. 4. Дифференцирование
Решение.
1. Ближайшая к 1,97 точка, в которой легко вычислить значения
/(а) и /'(а), — это точка а = 2.
2. Вычисляем:
Ах = х - а = 1,97 - 2 = -0,03,
/(а)=/B) = 3, f(x) = -74=, f{a)=y'{2) = \.
у/х* +5 о
3. По формуле A) имеем
/A,97) »3+|(-0,03) = 2,98.
Ответ. /A,97) » 2,98.
Условия задач. Вычислить приближенно с помощью
дифференциала значение функции у = f(x) в точке х = а.
1. з/ = х5, х = 2,001. 2. у = у/Ах - 3, х = 0,98.
3. J/ = ч/а?, х = 1,02. 4. j/ = х3, х = 2,999.
5. y=tyx, a; = 1,03. 6. у = у/х, х = 3,996.
7. у — у/1 + sin х, х=0,02. 8. у — \/2х + cos х, х = 0,01.
7ГХ
9. у= ?/2x-sin—, х=1,03. 10. j/ = у/4х + 1, х = 1,97.
Ответы. 1. 32,08. 2. 0,96. 3. 1,03. 4. 26,073. 5. 1,01. 6. 1,999.
7. 1,01. 8. 1,01. 9. 1,02. 10. 2,98.
4.5. Логарифмическое дифференцирование
Постановка задачи. Найти производную функции вида
у = щ(х)щ(-х)... u„(x)Vnix)wi(х)... wm(x).

4.5. Логарифмическое дифференцирование
105
План решения.
1. Логарифм данной функции имеет вид
In j/ = vi(x)lnui(x) + ... + vn(x)lnun(x) +lnwi(x) + ... + lnu;m(x).
2. Продифференцировав обе части этого равенства, получаем
y-=Ulnul + ^u>1)+...+ Ulnun + ^u'n ) + *+...+ <.
У \ Щ ) \ ип J wi wn
Поэтому
y' = y\(V^U1 + ^-u'1)+...+ UlnUn + ^u'n)+^-+...+ ^ .
3. Подставляя в последнее равенство выражение для у, получаем
ответ.
ПРИМЕР. Найти производную функции у — Xе х9.
Решение.
1. Логарифм данной функции имеет вид
In J/ = ln(xeIx9) = ex lnx + 91nx.
2. Продифференцировав обе части этого равенства, получаем
у хх
Поэтому
( ., , ех+9\
у = у ( е 1пх+ I ,
3. Подставляя в последнее равенство выражение для у, получаем
ответ.
Ответ, у' = хе" х9 (е'ЧпаЧ ] .
Условия задач. Найти производные заданных функций.
1. y = {smx)^. 2. у = ххЪ>/*.

106
Гл. 4. Дифференцирование
3. у = Xе . 4. у = (arctgx)x.
5. у = (tga;)lnx. 6. 2/ = аУ*28Й1Х.
_ oCOSX + „
7. j/ = х2 8. j/ = xtsx.
9. j/ = (sin3x)lnsin3*. 10. y = x2*3x.
Ответы.
, /lnsinx л/^СО!5а;\ « / Л , 1пЗ\
ly=y{-27x- + }L^x-)- 2^Ч1ПХ+1 + Ы-
3-»'=l'e^(^l + i)- 4..^.[lnarctgx+(i + ^arctga;].
_ . /lntgx lnx \ „ . /lnx 1 , \
5- У =У I h • 6. у =y I —-p + -=+cosa;ln2 I .
\ x sinxcosx/ \2у/х y/x )
7. j/' = j/2cosx f-sinxln2 + -). 8.y' = y (-^- + ^) .
\ х/ ^cos^x x /
9. y' = y 61nsin3xctg3x. 10. y' = у B*ln21nx + 2X- +ln3 J .
4.6. Производная функции,
заданной параметрически
Постановка задачи. Найти производную функции, заданной
параметрически.
План решения. Если зависимость у от х задана посредством
параметра t:
Г х = f(t),
\у = g(t),
то зависимость у' от х задается посредством параметра t формулами
х = /(*),
Вычисляем /'(£) и g'(t), подставляем в формулу A) и записываем
ответ.

4.6. Производнал функции, заданной параметрически 107
Пример. Найти производную у'х, если
(
х = ln(t + Vl + t2),
РЕШЕНИЕ. Вычисляем:
dx 1
dt ~ t + VT
dx _1 ( t \ _ 1
t2
A + л/1 + t2)
<и vTTT2 l + vTTT2 t2 t
Подставляя полученные результаты в формулу A), получаем
х = ln(t + у/1 + t2),
У=~Г-
х = ln(t + y/1 + t2),
Ответ. { l + t2
Условия задач. Найти производные функций, заданных
параметрически.
|i = D i/t3, f x = yfW^it,
\ j/ = sin(*3/3+3t). \j/ = ^r=n:.
Г a: = ln(£+_l), f яг=>/ГЛ,
*■ \ » = л/*гтт. 1 » = tgt.
5 Г x = ln(l-t2), 6 f * = lntgi,
^ j/ — arcsin t. \ У — 1/sin t.
j x — cos31, ( x — t — sint,
у у = sin31. \ у — 1 - cost.
{;:l^. *{
x = y/1 - *2,
j/ = arcsin t.

108
Гл. 4. Дифференцирование
Ответы
1
Г х = (t2 + 1)Л3, / х = VW^Yt,
\у' = -t4cos (t3/3 + 3t)• ' \ у' = v/^2t/C^/(t-1M).
[ x = ln(*2 + 1), r x = >/Гг*|
iV^TT. 4- I y'
з.
у1 = - ф? + 1. • \ у' = -2v/r^/cos2t.
f s = ln(l-t2), R Г * =
Г x = cos3t, Г x =
7- \y' = -tgt. 8- \y' =
= lntgt,
cos2 t/sint.
t — sin tf,
ctg(t/2).
fs = bsint, Г z = Vl-t2,
1/t.
4.7. Касательная и нормаль к кривой,
заданной параметрически
Постановка задачи. Составить уравнения касательной и
нормали к кривой
Г х = f{t),
\у = g(t)
в точке А, соответствующей значению параметра t = to-
План решения. Если функция у(х) в точке а имеет конечную
производную, то уравнение касательной имеет вид
у = у(а)+у'(а)(х-а). A)
Если у1 (а) — оо, то уравнение касательной имеет вид х = а.
Если у'(а) Ф 0, то уравнение нормали имеет вид
У = У(а) - -ггт (я - а). B)
У (а)
Если у'(а) = 0, то уравнение нормали имеет вид х = а.

4.7. Касательная и нормаль к кривой, заданной параметрически 109
1. Вычисляем координаты точки А:
{ а = /(to),
I У(а) = g(t0).
2. Находим производную у' в точке касания при t = to:
у(а) = Ж)-
3. Подставляем полученные значения в уравнения касательной A)
и нормали B) и записываем ответ.
Пример. Составить уравнения касательной и нормали к кривой
Г х = 2е\
\ у = е~ь
в точке А, соответствующей значению параметра t — 0.
Решение.
1. Вычисляем координаты точки А: а = 2, у (а) — 1.
2. Находим производную у' в точке А:
/'@) = 2e'U = 2, ,'@) = -e-'U = -1 => у'@) = Щ = -\.
Поскольку /'@) ф 0 и /'@) ф оо, то можно воспользоваться
уравнениями A) и B).
3. Подставляем полученные значения в уравнения касательной A):
и нормали B):
у = 1 + 2(х - 2).
Ответ. Уравнение касательной: х + 2у — 4 = 0. Уравнение нормали:
2х - у - 3 = 0.
Условия ЗАДАЧ. Составить уравнения касательной и нормали
к графикам функций, заданным параметрически.
.2
x = 2t + t',
f x = t-sint,
L- \y = l-cost, t0 = ir/2. ' \y = 2t-t2, t0 = l.

110
Гл. 4. Дифференцирование
„ Г х = \/3cost, . J x — t — i2,
\ y-sint, to-тт/б. \ y = t-t3, t0-l.
_ Г х = t cos t, ( x —
\ у — tsint, t0 = 7г/2. \ у =
— cos3 f,
sin31, to — it/4.
= ln(l +12),
arctg t, to = 1.
? f x = УГ^, g Г ж =
\ ?/ = arcsinf, t0 = -1. \ 2/ =
J x = In tg t, J x = f sin f 4- cos t,
9- \ 2/ = l/sin4 Ь=7г/4. 1U-\
у = sinf — f cosf, fo — тг/4.
Ответы.
1. 2х-2?/-7г + 4 = 0, 2x + 2?/- тг = 0.
2. ?/ - 1 = 0, х - 3 = 0.
3. 2х + 2у - 4 = 0, 2х - 2г/ - 2 = 0.
4. 2х - у = О, х + 2у = 0.
5. 4х + 2тгу - 7г2 = 0, 7гх — 2у + it — 0.
6. 2х + 2у - л/2 = 0, г/ - х = 0.
7. 2х - 2у - тг = 0, 2х + 2?/ + тг = 0.
8. 2х-4г/ + тг-21п2 = 0, 8х + 4г/ - тг - 81п2 = 0.
9. 2х + ?/-2 = 0, х-2?/ +4 = 0.
10. 4х - 4г/ - тг\/2 = 0, х + у- \/2 = 0.
4.8. Производные высших порядков
Постановка задачи. Найти производную п-го порядка функции
У = f(x).
План решения.
Производной п-го порядка функции у = /(х) называют
производную от производной порядка (п — 1), т.е.
yW(x)=y(n-V(x)'.
1. Дифференцируем функцию у — /(х) последовательно несколько
раз, пока не станет ясной формула для производной n-ого порядка.
2. Доказываем зту формулу методом математической индукции.
Для этого проверяем, что она справедлива при п — 1, т.е. дает
правильное значение /', и что дифференцирование выражения для /("'
эквивалентно замене п на п + 1.

4.8. Производные высших порядков
111
Пример. Найти производную n-го порядка функции у = 32х+ь.
Решение.
1. Найдем последовательно
у'{х) = C2х+1)' = 32*+1AпЗJ,
у"(х) = у'(х)' = C2*+1AпЗJ)' = 32а:+1AпЗJ22,
у'"(х) = у"{х)' = C2*+1AпЗJ22)' = 32*+1AпЗK23.
Проанализировав зти выражения, делаем предположение, что
2/(n)(x) = 32a:+1(ln3)n2".
2. Докажем эту формулу методом математической индукции.
Проверим, что она справедлива при п — 1; т.е.
у^(х) = 32х+1(\пЗJ = у'(х).
Дифференцирование /(**) эквивалентно замене п на п + 1, т.е.
2/(п)(х)' = C2ж+1AпЗ)п2п)' = 32*+1(ln3)n+12n+1 = у{п+1)(х).
Ответ. yW(x) = 32ж+1B1пЗ)".
Условия ЗАДАЧ. Найти производные п-го порядка заданных
функций.
1. у = sin2x + cos3x. 2. ?/= sinCx +1)+cos2x. 3. у = 23*.
4. у = 1пBх -I- 4). 5. у = . 6. у
х + \ 2х + 3
7. ?/ = 32*+1. 8. у = 1пCж + 1). 9. у = 52*+4.
10. у = у/х.
Ответы.
2х + — ) + Зп cos (Зх + —).
G77Г \ / 7?7Г\
Зх + 1 + —) + 2п cos Bх + —).
3. ?/(") - 23* C1п2)". 4. ?/(") = (~1)"2"(?~1)!-
у к ' У Bх + 4)"

112
Гл. 4. Дифференцирование
У (ж +1)"+1' ' У Bх + 3)"+] '
7. „м = з^+^гьз)». 8. »<»> = ()(ж1^"п~1)!-
9. „(«) = б2-4 B In 5)». 10. w(«) = ^^Llf^-
4.9. Формула Лейбница
Постановка задачи. Найти производную п-го порядка функции
у — u(x)v(x).
ПЛАН РЕШЕНИЯ. Если функции и(х) и г;(х) имеют производные
до п-го порядка включительно, то справедливы следующие формулы:
(иг;)" = u"v + 2u'v' + uv",
(uv)'" = u'"v + 3u"v' + 3u'v" + uv"',
(гш)D) = u^v + 4u"V + 6u"v" + 4uV" + wD>,
(uw)M = u(")B + nu^-^v' + "(" 21)Ц(п~2)г;// + ... + uv™ =
fc=o
где u^ = и, гД°) = г; и С„ = , w n' , ■,, — биномиальные
коэффициенты.
Формула A) для n-й производной произведения называется
формулой Лейбница.
Следовательно, для определения производной п-ro порядка
функции вида у = u(x)v(x) нужно вычислить все производные (до ri-ro
порядка включительно) каждой из функций и(х) и v(x),
биномиальные коэффициенты С* и воспользоваться формулой Лейбница.
Пример. Найти производную 4-го порядка функции
у = (х3 4- 2)е4*+3.

4.9. Формула Лейбница
113
Решение.
1. Применяем формулу Лейбница A). В данном случае
п = 4, и{х) = х3 + 2, v{x) = е4ж+3.
Имеем
и'(х) = 3х2, и"(х) = 6х, и'"(х) = 6, uD)(x) = 0,
г/(х) = 4е4*+3, v"(x) = 42е4*+3, г/"(х) = 43е4*+3, г;D)(х) = 44е4*+3.
Подставляя полученные результаты в формулу A), получим
у™ = ((х3 + 2)е4*+3)D) = 0 - е4*+3 + 4 ■ 6 ■ 4 • е4*+3 +
+i-|FxL2e4^3 + i^|Cx2L3e4^3 + f^|^(*3 + 2L4е4*+3 =
= 32е4а:+3(8х3 + 24х2 + 18х + 19).
Ответ. 2/D) = 32е4*+3(8х3 + 24х2 + 18х + 19).
Условия ЗАДАЧ. Найти производные указанного порядка
заданных функций.
1. у = (x2 + l)lnx, 2/E) =? 2. j/= (x3 + 2)cos2x, у'" =1
3. ?/ = х2 sinCx + 1), у'" = ? 4. г/ = (х2 + 1) cos3x, 2/E) =?
5. 2/ = (х3 + хIпх, 2/'"=? 6. 2/ = (х3 + 1Iп(х + 2), 2/E) =?
7. г/ = (х2 + 1J*, 2/E)=? 8. 2/ = sin2xlnx, 2/'"=?
9. у = (х2 + 1)е2х+1, 2/E)=? Ю. 2/= (х3 + 2K3ж, 2/D) =?
Ответы.
1 ,E) = £!±21
" X5 '
2. 2/"' = (8х3 - 36х + 16) sin 2х - C6х2 - 6) cos 2x.
3. у'" = A8 - 27х2) cosCx + 1) - 54xsinCx + 1).

114
Гл. 4. Дифференцирование
4. ?/5> = 810х cos Зх - 27(9х2 - 11) sin Зх.
... 6х21пх+Их2 — 1
5. у'" = ^ .
X1
„ ,« 6х3 + 60х2 + 240х + 456
" (х + 2M
7. ?/E) = 2* In3 2 [(х2 + 1) In2 2 + lOxlnx + 20].
6 cos 2x A2х2 - 2) sin 2x
8. у'" = -8cos2xlnx 5 ^ .
х-2 хЛ
9. ?/E) = 32е2*+1 (х2 + 5х + 6).
10. yW = 33*+2 In 3 [(9х3 + 18) In3 3 + 36х2 In2 3 + Збх In 3 + 8].
4.10. Вторая производная функции,
заданной параметрически
Постановка задачи. Найти производную второго порядка
функции, заданной параметрически.
План РЕШЕНИЯ. Если функция задана параметрически:
Г х = f{t),
\ у = g{t),
то ее первая производная определяется формулами
х = №,
1/ = Ш A)
Дифференцируя у' по х как сложную функцию х и используя
формулу для производной обратной функции, получим
X = /(f),
у \f'(t)J /'(*)
Пример. Найти производную второго порядка функции,
заданной параметрически:
х = In t,
у = arctg t.
{

4.10. Вторая производная функции, заданной параметрически 115
Решение.
1. Вычисляем
dx
~dl '
1
= 7'
dy_ _
dt ~
1
1-М2
и подставляем эти значения в формулу A):
( x = \nt,
l + t2'
Дифференцируя у' по х как сложную функцию х и используя
формулу для производной обратной функции, получим
х = In t,
'-Ш-
2\2
(i + П
Ответ.
х — In t,
g"=;(i-fl
Условия ЗАДАЧ. Найти производные второго порядка функций,
заданных параметрически.
= t + sin f,
cosf.
J X = COS3 f, j X = t +
\ у = sin3f. 1 J = 3-
3 f x = lntgf, 4 Г x = ln(l +t2),
\ y — l/s\n2t. ' \ у = arctg t.
5 Г x = v/T^2, 6 { x=V~t,
\ у = arcsin t. \ у = In t.
7 Г x = sin2 f, g Г x = 1/f,
(^ «/ — In cos f. \ 2/ — arctg t.
J x = l/t2, J x = arctg*,
\ »=l/(t2 + l). 1U- \ y = t2 + l.
9.

116 Гл. 4. Дифференцирование
Ответы. (Соответствующие выражения для x(i) опущены.)
1. у" = 1/C cos4t sin t). 2. у" = 1/A + cosiJ.
3. y" = 4ctg2t. 4. у" = -A + t2)Dt3).
5. y" = -y/JT~P/t3. 6. y" = -2/t.
7. 2/" = -l/cos4f. 8. y" = 2t3/{l + t2J.
9. ?/" = -2f6/(l +t2K. 10. ?/" = 6t4 + 8f2 + 2.

Глава 5
ГРАФИКИ ФУНКЦИЙ
При изучении темы ГРАФИКИ ФУНКЦИЙ вы научитесь
исследовать поведение функции: находить ее область определения,
асимптоты, промежутки возрастания и убывания, точки экстремума,
промежутки выпуклости вверх и вниз и точки перегиба, а также
воплощать полученные результаты в виде эскиза графика. Кроме того, вы
научитесь находить наименьшие и наибольшие значения функции,
непрерывной на отрезке, и исследовать локальное поведение функции
по ее производным высших порядков.
С помощью пакета РЕШЕБНИК.ВМ вы можете вычислить
производные функции (любого порядка), решить уравнения для
нахождения точек возможного экстремума и перегиба, найти значения
функции в требуемых точках, выполнить все численные расчеты и
проверить правильность полученных вами результатов.
5.1. Общая схема построения
графика функции
Постановка задачи. Исследовать функцию у = f(x) и
построить ее график.
План решения. Полученные в каждом пункте результаты
последовательно фиксируем на рисунке в качестве элементов искомого
графика и в итоге получаем эскиз графика.
1. Находим область определения D функции /(ж) и исследуем
ее поведение в граничных точках х = xi,X2,...,xn,±oo области D,
включая и х = ±оо.
а) Пусть х = Xk {k = 1,2,..., п) — конечная граничная точка
области D (т.е. f(x) не определена в этой точке). Вычисляем
односторонние пределы
lim /(ж) и/или lim f{x).
x—txic—O х—Ик+О

118
Гл. 5. Графики функций
Если хотя бы один из этих пределов бесконечен, то х — х* —
вертикальная асимптота графика /(х).
б) Исследуем поведение функции при х —> +оо:
если существуют конечные пределы
lim ^- = k и lim [f(x)-kx] = b,
X—► Ч-ОО X X—►+OO
то прямая у = kx + b — наклонная асимптота графика функции f(x)
при х —> +оо (если к — О, т.е. Ь — lim^-j+oo /(#), то у — Ь —
горизонтальная асимптота).
Аналогично исследуется поведение функции при х —> — со.
Отметим, что асимптоты при х —> +оо и при х —> —со могут быть
разными.
2. Выясняем четность и периодичность функции.
Если f(—x) = f(x), то функция f(x) называется четной. Графики
четных функций симметричны относительно оси OY. Поэтому
график четной функции достаточно построить для х > 0 и нарисовать
весь график, отразив полученную кривую относительно оси OY.
Если /(—х) = — f(x), то функция f(x) называется нечетной.
Графики нечетных функций симметричны относительно точки @,0).
Поэтому график нечетной функции достаточно построить для х > 0 и
нарисовать весь график, отразив полученную кривую относительно
точки @,0).
Если f(x + T) = f(x) при некотором Т > 0, то функция f{x)
называется периодической. График периодической функции имеет одну
и ту же форму на каждом из отрезков ..., [—2Т,—Т], [—Т,0], [0,Т],
[Т,2Т\, ... Поэтому достаточно построить график на каком-нибудь
одном таком отрезке и затем воспроизвести полученную кривую на
остальных отрезках.
3. Находим точки пересечения графика с осями координат. Для
этого вычисляем /@) и решаем уравнение f(x) = 0.
4. Находим точки максимума и минимума функции и интервалы
монотонности. Для этого:
а) вычисляем производную f'(x) и находим критические точки
функции, т.е. точки, в которых f'(x) — 0, ±со или не существует.
Отметим, что если /'(а) = 0, то касательная к графику в этой точке
горизонтальна, если /'(а) = ±со, то касательная вертикальна.
б) определяя знак производной, находим интервалы возрастания
и убывания функции: если /'(х) > 0, то функция возрастает, если
/'(х) < 0, то функция убывает;

5.1. Общая схема построения графика функции
119
в) если производная меняет знак при переходе через критическую
точку а 6 D, то а — точка экстремума:
если f'(x) > 0 при х € (а — S, а) и f'(x) < 0 при х € {а,а + <5), то
а — точка максимума;
если f'(x) < 0 при х € (в — S, а) и /'(ж) > 0 при ж € (а, а + (S), то
а — точка минимума;
если производная сохраняет знак при переходе через критическую
точку, то в этой точке экстремума нет.
5. Находим точки перегиба функции и интервалы выпуклости
вверх и вниз. Для этого:
а) вычисляем производную f"(x) и находим точки,
принадлежащие области определения функции, в которых f"{x) = 0, ±оо или
f"(x) не существует;
б) определяя знак второй производной, находим интервалы
выпуклости вверх и вниз: если f"(x) > О, функция выпукла вниз, если
f"(x) < О, функция выпукла вверх;
в) если вторая производная меняет знак при переходе через точку
а 6 D, в которой f"(x) — 0, ±оо или не существует, то а — точка
перегиба (при /'(а) = 0 график имеет горизонтальную касательную,
при /'(а) = ±оо — вертикальную касательную).
6. Уточняя полученный эскиз (например, можно определить еще
координаты каких-нибудь точек) и соединяя элементы графика,
полученные в окрестностях граничных точек области определения (вблизи
асимптот), критических точек и точек перегиба, получаем график
функции y = f(x).
х3
Пример. Исследовать функцию у = ——■ г^ и построить ее
4B — ху
график.
РЕШЕНИЕ. Полученные в каждом пункте результаты
последовательно фиксируем на рисунке в качестве элементов искомого
графика и в итоге получаем эскиз графика.
1. Находим область определения D. Очевидно, что функция
определена при всех х, кроме х — 2. Поэтому D = (—оо,2) U B, +оо).
Исследуем поведение функции в граничных точках области D.
а) Вычисляем пределы:
х3
i-»2-o 4B - жJ

120
Гл. 5. Графики функций
х->2+0 4B - жJ
+оо.
Следовательно, прямая х = 2 — вертикальная асимптота, причем
функция при приближении к ней слева и справа неограниченно
возрастает (рис. 1).
у д
Рис. 1
б) Исследуем поведение функции при х —> +оо:
lim
/(*)
lim
lim [/(ж) — kx] = lim
x-»+oo x-H-oo
x-»+oo X x-»+oo 4B — жJЖ 4
3 "•'' x(x — 1)
= lim
4B -xJ 4 J s-h-oo (ж - 2J
= 1;
и при х —> —со:
/(ж) xs 1
lim = llm Tfc \2~ = 7>
x-»-oo Ж x-»-oo 4B — X)AX 4
-.3
lim [/(ж) — kx] = lim
4B -xJ 4
ж(ж - 1)
= hm 7 rrf = 1.
x->-oo (ж — 2y
Следовательно, у = ж/4 + 1 — наклонная асимптота при ж —> ±оо.
Заметим, что при достаточно больших положительных ж /(ж) >ж/4+1,
т.е. при ж —> +оо график функции приближается к асимптоте сверху,
а при достаточно больших по абсолютной величине отрицательных ж
/(ж) < ж/4 + 1, т.е. при ж -» —оо график функции приближается к
асимптоте снизу (рис. 2).

5.1. Общая схема построения графика функции
121
А
Рис. 2
2. Функция не обладает свойствами четности и периодичности.
3. График функции пересекает оси координат в единственной
точке @,0).
4. Находим точки максимума и минимума функции и интервалы
монотонности. Для этого:
а) вычисляем первую производную: у' — х2(х — 6)/[4(ж — 2K].
Критические точки функции, принадлежащие области определения
D суть х = 0 и х = 6. Поскольку j/@) = 0 и у'F) = 0, касательная к
графику в этих точках горизонтальна (рис. 3);
У1
-*^"
)
\
X
Рис. 3
б) определяя знак производной, находим интервалы возрастания
и убывания функции: функция возрастает в интервалах (—со, 2) и
F, +оо) и убывает в интервале B,6);

122
Гл. 5. Графики функций
в) при переходе через критическую точку х = 0 производная не
меняет знак, следовательно, в этой точке экстремума нет.
При переходе через критическую точку х = 6 производная меняет
знак, следовательно, в этой точке экстремум есть.
Так как у' < 0 при х € F - 6,6) и у' > 0 при ж € F,6 + <$)), то
F,27/8) — точка минимума (рис. 4).
У
А
W.
Рис.4
5. Находим точки перегиба функции и интервалы выпуклости
вверх и вниз. Для этого:
а) вычисляем вторую производную
У
4B - жJ
6ж
(х-2У
Единственная точка, принадлежащая области определения функции,
в которой у" = 0, это точка х = 0;
б) определяя знак второй производной, находим интервалы
выпуклости вверх и вниз: функция выпукла вверх в интервале (—оо, 0)
и выпукла вниз в интервалах @,2) и B,+оо).
Отметим, что направление выпуклости соответствует
расположению графика относительно асимптот:
при х < 0 функция выпукла вверх и график приближается к
наклонной асимптоте снизу;
при х € @,2) функция выпукла вниз и график приближается к
вертикальной асимптоте х = 2 слева;
при х € B, +оо) функция выпукла вниз и график приближается к
вертикальной асимптоте х — 2 слева, а к наклонной асимптоте сверху;
в) так как вторая производная меняет знак при переходе через

5.1. Общая схема построения графика функции 123
точку х — О, то @,0) — точка перегиба (с горизонтальной
касательной) (рис. 5).
7й-
\J.
Рис. 5
6. Уточняя полученный эскиз (например, можно определить еще
координаты каких-нибудь точек) и соединяя элементы графика,
полученные в окрестностях граничных точек области определения (вблизи
асимптот), критических точек и точек перегиба, получаем график
функции у = /(ж) (рис. 6).
Рис. 6
Условия ЗАДАЧ. Исследовать функции у — /(ж) и построить их
графики.
1. у = ж3 - Зж + 2.
3- У = ~ъ 7-
т2
4. у =
ч/ж^-Т

124
Гл. 5. Графики функций
_ е
5. у = же х. 6. у = —.
х
, аг — 1 „ х
7.у = 1п + 1. S.y=-—.
х In ж
9. у = In cos x. 10. j/ = у/х2{х+ 1).
Ответы. 1. Асимптот нет. Точки: минимума A,0), максимума
(-1,4), перегиба @,2).
2. Асимптоты: горизонтальная у = 0. Точки: минимума
(-1,-1/2), максимума A,1/2), перегиба @,0), (—v/3,—v/3/4),
(v/3, v/3/4).
3. Асимптоты: вертикальные ж = —2, ж = 2, наклонная у = х.
Точки: минимума Bv3,3v3), максимума (—2v3, —ЗуЗ), перегиба
@,0).
4. Асимптоты: вертикальные ж = —2, ж = 2, наклонные у = —ж
(при ж -> —со), у = х (при ж -> +оо). Точки минимума (—у/2,2),
(А 2).
5. Асимптоты: горизонтальная у = 0 (при ж —> +оо). Точки:
максимума A,1/е), перегиба B,2/е2).
6. Асимптоты: вертикальная ж = 0, горизонтальная J/ = 0 (при
ж-> —оо). Точка минимума A,е).
7. Асимптоты: вертикальные ж = 0, ж = 1, горизонтальная
у = 1 (при ж -> ±оо).
8. Асимптоты: вертикальная ж = 1 (ж = 0 асимптотой не
является). Точки: минимума (е, е), перегиба (е2,е/2).
9. Асимптоты: вертикальные ж = 7г/2 + 7rfc. Точки максимума
BтгА;,0) (fc = 0,±l,...).
10. Асимптоты: наклонная у = ж+1/3. Точки: минимума @,0),
максимума (-2/3, y/1/Z), перегиба (-1,0).
5.2. Наибольшее и наименьшее
значения функции
Постановка задачи. Найти наибольшее и наименьшее
значения функции /(ж) на отрезке [а,Ь].
План решения. Наибольшее и наименьшее значения непрерыв-

5.2. Наибольшее и наименьшее значения функции 125
ной функции /(ж) на данном отрезке [а, Ь] достигаются в
критических точках функции (точках, в которых /'(ж) = 0, ±оо или /'(ж) не
существует) или на концах отрезка [а, Ь].
1. Проверяем, что заданная функция на данном отрезке является
непрерывной.
2. Ищем производную заданной функции.
3. Находим критические точки функции /(ж) и выбираем из них
те, которые принадлежат данному отрезку [а,Ь].
4. Вычисляем значения функции в критических точках внутри
отрезка и значения функции на концах отрезка. Сравнивая полученные
значения, находим наибольшее М и наименьшее т значения функции
на [а,Ь].
Пример. Найти наибольшее и наименьшее значения функции
_ 10ж + 10
У ~ ж2 + 2ж + 2
на отрезке [—1,2].
Решение.
1. Заданная функция является непрерывной на отрезке [—1,2], так
как является отношением непрерывных функций со знаменателем, не
равным нулю (ж2 + 2ж + 2 > 0).
2. Вычисляем производную заданной функции:
у (ж2 + 2ж + 2J"
3. Критическими точками заданной функции являются ж = 0 и
ж = —2. Данному отрезку [—1,2] принадлежит только точка х = 0.
4. Вычисляем значение функции в точке ж = 0 и значения функции
на концах заданного отрезка. Имеем
/@) = 5, /(-1) = 0, /B) = 3.
Сравнивая эти значения, заключаем, что наименьшее значение
функции т = 0 достигается в точке ж = — 1, а наибольшее
значение М = 5 — в точке ж — 0.
Ответ. Функция принимает наименьшее значение т = 0 в точке
ж = — 1, а наибольшее значение М — 5 — в точке ж = 0.

126
Гл. 5. Графики функций
УСЛОВИЯ ЗАДАЧ. Найти наибольшее и наименьшее значения
функции у — f(x) на отрезке [а,Ь].
1. у = 1- fyx2 - 2х, [0,2].
2. у = 2х-3\^, [-1,1].
3. у = х2(х-2J, [0,2].
4. у = (х3 - 9ж2)/4 + 6х - 9, [0,4].
5. j/ = 4z2/C + х2), [-1,1].
6. у = 1 + ^ж2 + 2ж, [-2,0].
7. у = 2х3 - Зх2 - 4, [0,2].
8. у = 33/{х-3J-2х + 6, [2,4].
9. j/= (/х2(х-2J, [0,2].
10. j/ = 2 - 12ж2 - 8ж3, [-2,0].
Ответы. 1. т = у@) = 2/B) = 1, М = уA) =2. 2. т = у(-1) =
= -5, М = 2/@) = 0. 3. m = 2/@) = 2/B) = 0, М = у{1) = 1.
А. т = 2/@) = -9, М = 2/B) = -4. 5. т = 2/@) = 0, М =
= J/(-l) = 2/A) = 1- 6. т = у{-2) = уA) = 1, М = 2/(-1) = 2.
7. m = 2/A) = -5, М = 2/B) = 0. 8. m = 2/C) = 0, М = 2/B) = 5.
9. m = 2/@) = 2/B) = 0, М = 2/A) = 1. 10. т = у(-1) = -2,
М = 2/(-2) = 18.
5.3. Исследование функции с помощью
производных высших порядков
Постановка задачи. Исследовать функцию у = f(x) в
окрестности точки х = а с помощью производных высших порядков.
План решения. Пусть при некотором к > 1
f (а) = /"(а) = ... = f^'Ha) = 0, /<*>(а) ф 0.

5.3. Исследование функции с помощью производных высших порядков 127
Тогда если к — четное число, то точка а является точкой экстремума,
а именно точкой максимума, если f^k'(a) < 0, и точкой минимума,
если /( '(а) > 0. Если же к — нечетное число, то точка а является
точкой перегиба.
Пример. Исследовать функцию
у = sin2(x - 1) - ж2 + 2ж
в окрестности точки а = 1 с помощью производных высших порядков.
Решение.
1. Вычисляем производные заданной функции в точке а = 1:
у' = sinBx - 2) - 2ж + 2, j/(l) = 0,
у" = 2cosBx - 2) - 2, у"A) = 0,
j/'" = -4sinBx-2), 2/"'(l) = 0,
у"" = -8cosBx - 2), у""A) = -8 < 0.
2. Так как к = 4 — четное число и у""A) < 0, то точка а = 1 есть
точка максимума функции у = sin2(x — 1) — ж2 + 2х.
Ответ. Функциия у — sin2 (ж — 1) — ж2 + 2х имеет максимум в
точке а — 1.
Условия задач. Исследовать функцию у — /(ж) в окрестности
точки х = а с помощью производных высших порядков.
1. з/ = 2ж2 + 8ж + 4соз(ж + 2), а = -2.
2. у = 41пж + 2ж2 -8ж + 5, а - 1.
3. у = 2ж — ж2+ соэ2(ж - 1), а = 1.
4. 2/ = 21п(ж-2)+ж2-8ж + 3, а = 3.
5. у = ж2 + 8ж + 8 - 2ех+3, а = -3.
6. у = 2соз(ж + 3) + ж2+6ж + 2, а = -3.
7. г/ = ж2 + 1-2ж1п(ж + 1), а = 0.
8. у = sin2 ж - ж2 + 4, а = 0.

128
Гл. 5. Графики функций
= 2.
= 0.
9. у = 2ех~2 - ж2 + 2ж + 1, а
10. у = 2ех — sin ж — ж2 — ж, а
Ответы.
1. а — — 2 — точка минимума.
3. а = 1 — точка минимума.
5. а = — 3 — точка перегиба.
7. а = 0 — точка максимума.
9. а = 2 — точка перегиба.
2. а = 1 — точка перегиба.
4. а = 3 — точка перегиба.
6. а = — 3 — точка максимума.
8. а = 0 — точка максимума.
10. а = 0 — точка перегиба.

Глава 6
ФУНКЦИИ НЕСКОЛЬКИХ
ПЕРЕМЕННЫХ
При изучении темы ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
вы на примерах познакомитесь с понятиями частных производных,
полного дифференциала, градиента, производной по направлению и
научитесь их вычислять. Вы также научитесь дифференцировать
сложные функции нескольких переменных и функции, заданные
неявно. Эти умения вы сможете применить для нахождения
касательной плоскости и нормали к поверхности и точек экстремума функции
двух переменных.
С помощью пакета РЕШЕБНИК.ВМ вы можете вычислить
частные производные, решить системы уравнений (для нахождении
стационарных точек), выполнить все численные расчеты и проверить
правильность полученных вами результатов.
6.1. Частные производные
Постановка задачи. Найти частные производные до второго
порядка включительно функции z — f{x\,X2,■ • ■ ,хп).
План решения.
1. Чтобы найти частную производную функции z — f(xi,...,xn)
по переменной Хк, фиксируем остальные переменные и
дифференцируем / как функцию одной переменной Хк-
2. Частные производные высших порядков вычисляются
аналогично последовательным дифференцированием, т.е.

130
Гл. 6. Функции нескольких переменных
Замечание. Частные производные можно обозначать также z'Xl,
zx2' • • • ' Zx„' гж1Ж1> zxix2 И Т'Д"
Пример. Найти частные производные до второго порядка
включительно функции z = ху (ж > 0).
Решение.
1. Для того чтобы найти частную производную по ж, фиксируем
у и дифференцируем функцию z = ху как функцию одной
переменной ж. Используя формулу для производной степенной функции
(ж°)' = ажа_1, получим
/ и—1
zx = yxy .
Для того чтобы найти частную производную по у, фиксируем ж
и дифференцируем функцию z — ху как функцию одной
переменной у. Используя формулу для производной показательной функции
(ах)' = ахЫа (а > 0), получим
z' = ху In ж.
2. Частную производную второго порядка z!xx вычисляем,
дифференцируя z'x по ж (при фиксированном у), т.е.
4х = (у^-'Ух = у{у -1)*».
Частную производную второго порядка zxy вычисляем,
дифференцируя z!x по у (при фиксированном ж), т.е.
z"y = (уху-% = ху~г + уху-г 1пж.
Частную производную второго порядка z" вычисляем,
дифференцируя z' по ж (при фиксированном у), т.е.
1
ж
Частную производную второго порядка z1' вычисляем,
дифференцируя z'y по у (при фиксированном ж), т.е.
^у = {хуЫх)'у = хуЫ2х.
Ответ. 4 = уху~\ z'y = ж» In ж, 4'» = 4* = ж!/_1 + ^-"Чпж,
4'х = (у&^Ух = у(у -1)^~2, <„ = ж!/ 1п2 ж-
4'х = (я^1пж)'х = уху~* 1пж + ж!/:

6.2. Градиент
131
УСЛОВИЯ ЗАДАЧ. Найти частные производные до второго
порядка включительно заданных функций.
1. z = exy. 2. z = xln(x/y).
3. z — sin(xy). 4. z = excosy.
5. z = -\/ж2 + y2. 6. z = 1п(ж2 + »).
7. z = y/2xy + y2. 8. z = In fyxy.
9. z = xcosy + ysinx. 10. z = A + xJ(l + »L.
Ответы. 1. z'x = уехУ, z'y = хехУ, 4'x = »2ex», z^ = zV»,
4» = z'yx = exy{l + ж»). 2. z£ = In ж - In» + 1, 4 = -ж/»,
4'x = V*. 4's/ = Х/У2> z"y = z'yx = -1/У- 3. z'x = ycos{xy), z'y =
= xcos(xy), 4'x = -y2sm(xy), z^y = -x2sin(xy), z£y = z%x =
= cos(xy) — xy sm(xy). 4. z'x = ex cos y, z'y = —ex sin y, zxx = ex cos y,
z'yy = -excosy, z'ly = z'^x = -exsiny. 5. z'x = x/y/x2 + y2,
z'y = y/y/^Ty^, 4X = y2/(x2 + y2fl2, z';y = ж2/(ж2 + »2K/2, 4'B =
= 4'x = -ж»/(ж2 + »2K/2. 6. 4 - 2ж/(ж2 + »), 4 = 1/(ж2 + »),
4'x - 2(»-ж2)/(ж2 + »J, zg = -1/(ж2 + »J, 4'„ = z^ =
= -2ж/(ж2 + уJ. 7. 4 = y/y/2xy + y2, z'y = (ж + y)/y/2xy + y2,
4'* = -y2/{2xy + y2)V2, z>>y = -ж2/Bж» + »2K/2, 4y = 4'x =
= ж»/Bж» + »2K/2. 8.4 = 1/C*), 4 = 1/C»), 4'x =-l/C*2),
z'yy = -C»2), 4» = 4', = °- 9- 4 = «>s» + ycosx, 4 =
= sin a; - a; sin», zxx = -jsini, z^, = -ж cos», z"^ = z£x =
= cos ж -sin». 10.4=2A + ж)A + »L, 4=4A+жJA + »K, 4'х =
= 2A+»L, г;'!/ = 12A + жJA + »J, zx;=4Jr=8(l + x)(l + »K.
6.2. Градиент
Постановка задачи. Найти градиент функции и = /(ж,», z) в
точке M(x0,y0,z0).
План решения. Градиент функции /(ж,», z) — это вектор,
координаты которого в базисе i,j,k являются частными производными
функции /(ж,», z), т.е.
grad/ = ^r+^%^fc = {^, ^, ^).
9ж 9» dz \ дх' ду' dz )

132
Гл. 6. Функции нескольких переменных
1. Находим частные производные функции f(x,y,z)
di д£ д£
dx' ду' dz
2. Вычисляем частные производные функции f(x,y,z) в точке
M{x0,yo,z0).
4. Вычисляем градиент функции м = /(ж, у, z) в точке M(xq, yo, zq):
grad/
= {fL(xo,yo,zo), f'y(xo,yo,z0), f'z(xo,yo,z0)}'
м
Записываем ответ.
Пример. Найти градиент функции
и = х2 — arctg (у + z)
в точке МB,1,1).
Решение.
1. Находим частные производные функции и = х2 — arctg (y + z):
di df l a/ l
дх ' в» l + fe + zJ' 9z l + fe + zJ'
2. Вычисляем частные производные функции и = х2 — arctg (у + z)
в точке МB,1,1):
£B,1,1) =4, #B,1,1) = -±, £B,1,1) = -±
3. Вычисляем градиент функции и = ж2 — arctg (y + z) в точке
МB,1,1):
= {£B,1,1), #2,1,1), £B,1,1)} = {4, -1, -i|.
B,1,1) I О О J
grad/
Ответ, grad /
Условия задач. Найти градиент функции и = /(ж, у, z) в
точке М.
1. и = ж + ln(z2 + у2), МB,1,1).
2. и = х2у - у/ху + z2, МA,5, -2).
3. « = sin(a; + 2у) + 2х/жр, М(тг/2,3тг/2,3).

6.3. Производная по направлению
133
4. и = х3 + у/у2 + z2, МA,1,0).
5. и = у/¥у + у/Ъ~^1?, МA,1,0).
6. и = 1пC - х2) + xy2z, M(l,3,2).
7. u = xV^-ln(z-l), M(l,l,2).
8. и = 1п(х2 + у2), МA,-1,2).
9. u = xy-x/z, М(-4,3,-1).
10. u = ln(x+y/z2 + y2), M(l,-3,4).
Ответы. 1. {1,1,1}. 2. {55/6,5/6,2/3}. 3. {3,1, тг/2}. 4. {3,1,0}.
5. {1/2,1/2,0}. 6. {17,12,9}. 7. {4,4,0}. 8. {1,-1,0}. 9. {4,-4,-4}.
10. {1/6,-1/10,2/15}.
6.3. Производная по направлению
Постановка задачи. Найти производную функции u(x,y,z) в
точке A(xi,yi,zi) no направлению к точке В(х2,У2,22).
План решения.
1. Если функция и(х,y,z) дифференцируема в точке A(xi,yi,zi),
то в этой точке существует ее производная по любому направлению I,
определяемая формулой
7ГГ =(gradu| ,&), A)
т \а
где
Г ди ди ди 1 ? I
gradu = \0x-'Zya7/' lo = J\
2. Находим координаты вектора I. В данном случае
I = АВ = {х2 - xi, ?/2 - 2/ь z2 - zi}.
3. Находим единичный вектор (орт) Iq,:
.- _ J_ _ {х2 - хь yi - ;/!, zi - zi}
° ~ \Г\ ~ у/(х2 - хО2 + B/2 - 2/iJ + Ы -Z-,J'

134
Гл. 6. Функции нескольких переменных
4. Вычисляем частные производные и градиент функции и(х, у, z)
в точке A(xi,yi,zi):
gradw
= {u'x(xi,yi,zx), u'yix^y^zi), u^(a;i,j/i,zi)}.
5. Вычисляя скалярное произведение в формуле A), получаем
ответ.
Пример. Найти производную функции
и = х2 — arctg (у + z)
в точке АB,1,1) по направлению к точке £?B,4, —3).
Решение.
1. Так как функция и = х2 — arctg (у + z) дифференцируема в
точке АB,1,1), то в этой точке существует ее производная по любому
направлению /, которая определяется формулой A).
2. Находим координаты вектора I. В данном случае
f=AB = {0,3,-4}.
3. Находим единичный вектор (орт) /0;
Г {0,3,-4}
1о
v/02 + З2 + (-4J
-Ы-8-
4. Вычисляем частные производные функции и = х2 — arctg (y + z)
в точке АB,1,1) :
ди
дх
B,1,1)
— ^Ж1B,1,1) — 4'
ди
ду
B,i,i) 1 + (У + *J
B,1,1)
1
5'
ди
~d~z
B,1,1) 1 + (У + гJ
42,1,1)
Тогда
eraduip.i.i)={4--i,~i}-
5. Подставляя полученные значения в формулу A) и вычисляя
скалярное произведение, получим
| =(grad«|Bilil))ro)=4.0+D).|+D).(-i)=^.

6-4- Производные сложной функции
135
0твет- ж
B,1,1)
_1_
25'
Условия задач. Найти производную функции и(х, у, z) в точке А
по направлению к точке В.
1. u = x+ki{z2 + y2), ЛB,1,1), 5@,2,0).
2. и = x2y - л/ху + z2, ДA,5,-2), £A,7,-4).
3. и = sin(x + 2у) + 2^/xJz, А\-,—,г\, В{- + 4, — + 3,3)
4. и = х3 + у/у1 + z2, АA,1,0), £A,2,-1).
5. и= y/xy+y/9-z2, АA,1,0), £C,3,-1).
6. и = 1пC - х2) + xy2z, A(l,3,2), £@,5,0).
7. u = x2y2z-\n(z-l), ЛA,1,2), £F,-5,2\/5 + 2).
8. и = 1п(х2 + у2), ЛA,-1,2), £B,-2,3).
9. и = ln(x + y/z2 + у2), ЛA,-3,4), £(-1,-4,5).
10.ti = x»-f, A(-4,3,-l), £A,4,-2).
Ответы. 1. -л/6/3. 2. v^/12. 3.3. А. лД/2. 5.2/3. 6.-11/3.
7. - 4/9. 8. 2л/3/3. 9. - V6/60. 10. 20\/3/9.
6.4. Производные сложной функции
Постановка задачи. Найти производные z'x и z' функции
z = z(u,v), где и — и(х,у) uv = v(x,y).
План РЕШЕНИЯ. Поскольку z является сложной функцией двух
переменных х и у, то ее производные z'x и z'y вычисляются по
формулам
dz _ dz ди dz dv
дх ди дх dv дх'
dz dz ди dz dv
dy ди ду dv dy
1. Вычисляем частные производные
dz dz du du dv dv
du' dv' dx' dy' dx' dy

136
Гл. 6. Функции нескольких переменных
2. Подставляем полученные результаты в формулы A) и B) и
записываем ответ.
Замечание. Формулы A) и B) можно обобщить на функции
любого числа переменных. Например, если дана функция f(u,v,w), где
и — и(х, у, t), v = v(x, y,t) ww = w(x, у, t), то ее частные производные
f'xi f'yi ft вычисляются по формулам
df__dj_ du df_ dv_ df_ dw
dx du dx dv dx dw dx'
dj__dj_ du dj_ dv 8f_ (hv
ду ди ду dv dy dw dy
df _ df du df dv df dw
dt du dt dv dt dw dt
Пример. Найти производные z'x и z'y функции z = u/v, где и = xy
и v = y/xy.
Решение.
1. Вычисляем частные производные
dz _ 1 dz _ и
du v' dv v2'
du _ !/_1 9ы _ dv _ у/у dv _ y/x
dx~VX ' dy ~X * dx ~ lyf? dy ~ 2y/y'
2. Подставляя полученные результаты в формулы A) и B),
получаем
dz 1 , и у/у dz 1 и у/х
— = --уху - -=• • т^р, — = - - ху Ых - — ■ ——.
dx v vA 2y/x dy v vL ly/y
Ответ.
— = I У-1 U V^
dx v v2 "ly/x
dz 1 „, и y/x
— = --ху\а.х--=■—=,
dy v vl 2y/y
где и = xy, v = y/xy.
Условия задач. Найти производные z'x и z'y функции z — z(u,v),
где и — и(х, у) и v — v(x, у).
1. z = и2 + v2, и = х + у, v — x — y.

6.4. Производные сложной функции
137
2.
3.
4.
5.
6.
7.
8.
9.
10.
z = 1п(ы2 + г;2),
z = uv,
z — u2 + 2v3,
z — arctg (u/v),
z = ln(u -v2),
z = u3 + v2,
z — tJuv,
z = euv,
. z — In {u/v),
u = xy,
и — sin x,
u — x2 — y2,
и — x sin y,
и = x2 + у2,
U = Ыл/х2 + У2,
и = 1п(ж2 + у2),
u — hix,
u = sin (ж/г/),
v = x/y.
v = cos y.
v = еж!/.
г; = х cos j/.
w = j/-
г; = arctg (y/x).
v = xy .
г; = In г/-
г; = л,/x/y.
Ответы.
1. 4 = 2ы + 2w, zj, = 2и - 2v.
. 2и 2v 1 ,
2u
2г;
z' = гш»-1
ы2 + v2 у'
гг + ir
ы2 + г;2 г/2
cos ж, z'y — u" In u- (— sin?/).
4. 4 =2ы-2ж + 6г;2-2/еа:!', z£ = 2и ■ (-2у) + 6v2 ■ хеху.
5. z' =
V . U
-o-smy „——^ • C°S2/.
Ы2 + V2 U2 + V2
. V U
zy = 2 , 2 -xcosy -resins/.
6. z!L = ^ • 2ж, z'v = — ■ 2у +
и — v
zL = Zu2 ■ -
х2 +у2
У
z'y=3u2-
" х2- Л-у
2х
2v
+ 2v
u — v*
У
9 i 9 '
xz + yz
U — V
Ф
x2 + у2
, л/« 2
2y/vl x2 + y2 2^
+ ^Ц= • 2жг/.
z' =
» 2,/г7 ж2 + ?/2 2jv~
■*■ # «141 -^
Ж
s/ 2/
1
1
1 ж
10. 4 = - • cos Tl='
и У У v 2^/ху
1 ж / ж \ 1 \/а;
ж
Z' = — • COS -
"и у
\ У2) v
2Уу/У

138
Гл. 6. Функции нескольких переменных
6.5. Производная неявной функции
Постановка задачи. Найти производную функции у = у{х),
заданной неявно уравнением
F(x,y)=0. A)
План решения. Если при каждом фиксированном ж,
принадлежащем некоторой области D, уравнение A) имеет единственное
решение у, принадлежащее некоторой области Е, то уравнение A) задает
функцию у — у (ж) с областью определения D и областью значений Е.
Если в некоторой окрестности точки (ж0, уо = у{хо)) функция
F(x,y) дифференцируема и Fy(xo,yo) ф 0, то уравнение A)
определяет функцию у — у(х), дифференцируемую в точке жо, причем ее
производная определяется формулой
у{хо) = -^(^у7У B)
1. Вычисляем частные производные F'x(x,у) и F'(x,y) в точке
(жо,?/о)> гДе Уо есть корень уравнения F(xo,y) — 0.
2. Находим у'(хо) по формуле B) и записываем ответ.
Замечание. Аналогично вычисляются частные производные
функций нескольких переменных, заданных неявно. Например, если
уравнение F(x,y,z) = 0 задает функцию z = z(x, у), то при
известных условиях функция z = z(x, у) дифференцируема в точке (жо, уо)
и ее частные производные определяются формулами
,, ч F^(x0,y0,z0) , F^(xo,yo,zo)
2ж(ж0,2/о) = -~БП Г' гу(хо,Уо) = ~-БГ, 7.
F'z (ж0) уо, zo) y F'z (ж0, уо, zo)
где 2о есть корень уравнения F(xo, yo,z) — 0-
Пример. Найти производную функции у — у(х), заданной неявно
уравнением
In у/х2 + у2 — arctg —. C)
ж
Решение.
^i
1. В данном случае F[x,y) = In y/x2 + у2 — arctg —. Вычисляем ее
частные производные:
F'
1 / у\ х + у
х2 + у2 1 + {у/хJ \ ж2 / ж2 + у2'
(Ч) = -г
\ X* / XL

6.5. Производная неявной функции
139
р, _ __2/ 1 /}_\ _ У~х
У т2 J. i,2 1 ±Л,М2 \Х ) ч-2 j. „2'
X2 + у2 1 + (у/хJ \х) Х2 + у2
Очевидно, что F(x,y), F'x и F' непрерывны при всех хфО к Р^фО
при х ф у. Следовательно, уравнение C) определяет функцию у(х),
дифференцируемую во всех точках (хо, уо) области, где х ф 0 и х ф у.
2. Находим у' по формуле B)
' = К(хр,Ур) _ {хр + Уо)/{хр + Уо) _ хр + уо
Fy{xp,уо) (ур - х0)/(х1 + yl) хо-Уо'
г. , хр+Уо
итвет. у — при всех жо, ур, удовлетворяющих
уравнено ~Ур
нию C), в области, где ж Ф 0 и ж ф у.
Условия задач. Найти производные функций у = у(х), заданных
неявно уравнениями.
1. ух = ху. 2. у = 1 + у*.
3. у — х + In у. 4. х + у = ех~у.
5. х2е2у — у2е2х —0. 6. ж — у + arctg у = 0.
7. ?/ sin ж — соз(ж — у) = 0. 8. sin^y) — еху — ж2?/ = 0.
9. 1+ж?/-1п(еа:з'-1-е-а:!') = 0. 10. ж2 - 2ху + у2 + ж + у - 2 = 0.
2.у'- у у
Ответы.
1.
3.
5.
7.
9.
у' =
у' =
У' =
у' =
у' =
ухЫ
хух~
У
v-i'
У2е2х -
х2е2у -
у-уху 1
1 — ху In ж
-хе2у
- уе2х
у cos ж + sin(a; — у)
sin (ж
-У.
X
— у) — sin ж
1 — arj/
4-2/'
6-2/ =
е1"» +1
1 + 2/2
2/2
, _ уBх + еху -cosxy)
x(cosxy — e15* — ж)
W.y>=2y-2x-\
у 2у-2х + 1

140
Гл. 6. Функции нескольких переменных
6.6. Касательная плоскость и нормаль
к поверхности
Постановка ЗАДАЧИ. Найти уравнения касательной плоскости
и нормали к поверхности, заданной уравнением
F(x, у, z) = 0,
в точке M(xo,yo,zo)-
План решения.
Нормальный вектор к поверхности, заданной уравнением
F(x,y,z)=0,
в точке M(xo,yo,zo) определяется формулой
,J (dF\ dF dF\ 1
n = gradF =S^- ,-5- . -^-\ (■
\м Удх\м дУ м дг\м)
Следовательно, уравнение касательной плоскости к данной
поверхности в точке M(xo,yo,zo) есть
F'x\M{x - х0) + F'y\M{x0,y0,z0)(y - к) + F'z\M(z -zo)=0 A)
и уравнения нормали —
х - х0 _ у -ур _ z- zp .
F'\ ~ F'\ ~ F'\
1. Находим частные производные F^., FyuF'zB точке M(xq, yo,zo).
2. Подставляем найденные значения в уравнения A) и B) и
записываем ответ.
Замечание. Если заданы только значения хо и уо, то координата
zq точки М определяется из условия, что точка М принадлежит
данной поверхности, т.е. F{xq, yo,zo) — 0.
Пример. Найти уравнения касательной плоскости и нормали к
поверхности, заданной уравнением
z = xy,
в точке МA,1).

6.6. Касательная плоскость и нормаль к поверхности 141
Решение. Запишем уравнение поверхности в виде ху — z = 0, т.е.
F = ху — z.
Координаты точки М: ж0 = 1 и j/o = 1- Координату zq
определяем из условия, что точка М принадлежит данной поверхности, т.е.
F(l, l,zo) = 0. Получаем zq = 1.
1. Находим частные производные F^., FjH^b точке МA,1,1):
-^1A,1,1)= 2/|Aдд)= 1) *!/1A,1,1)==а;1A,1,1)= ■'■» ** 1A,1,1) = _1-
2. Подставляя найденные значения в уравнения A) и B), получаем
уравнение касательной плоскости
i(x-i) + iB,-i)-iB-i) = o
и уравнения нормали
х — 1 у — 1 z— 1
1 1 -1
Ответ. Уравнение касательной плоскости: х + у — z — 1 = 0.
Уравнения нормали: х — 1=у — 1 — 1 — z.
УСЛОВИЯ ЗАДАЧ. Найти уравнения касательной плоскости и
нормали к поверхности в заданной точке М.
1. z = x2 + y2, M(l,-2,5).
2- й+т-т =0' МDА4)-
3. г = sin х cos у, М Gг/4,7г/4,1/2).
4. г^е*0082', МA,тг,1/е).
5. 2 = j/tga;, М(тг/4,1,1).
6. г = arctg(x/j/), МA,1,7г/4).
7. а:(у+ *)(*-*») =8, МB,1,3).
8. T'z + 2^2 = 8, МB,2,1).
9. х2+у2 + г2-16 = 0, MB,2,2i/2).
10. х2 + у2 - z2 = -1, МB,2,3).

142
Гл. 6. Функции нескольких переменных
Ответы.
1. 2х - 4у - z - 5 = О,
2. Зх + 4у - 6z = О,
3. х - у - 2z + 1 = О,
4. х + ez - 2 = О,
5. 2х + у - z - § = О,
6. x-y-2z+%=0,
7. 2x + 7y-5z + 4 = 0,
8. х + у - 4z = О,
9. х + у + \/2z -8 = 0,
10. 2х + 2у - Sz + 1 = О,
х- 1 _ у+ 2 _ z-5
2 ~ -4 -1 "
x-4_2/-3_z-4
3 4 -6 '
х — ж/'4 _ У — тг/4 _ z - 1/2
I = -1 = -2 '
х — 1 j/ — 7г г — 1/е
1 _ 0 ~ е '
х — 7г/4 J/ — 1 г — 1
2^ = 1 = -1 '
х — 1 у — 1 _ z — 7г/4
1 = -1 ~ -2 '
х — 2 у — 1 г — 3
2 = 7 -5 '
х-2 _у-2 _ z-1
1 ~ 1 -4 '
х-2_у-2_г- 2%/2
___________
х-2_у-2_г-3
2 2 -3 '
6.7. Экстремум функции двух переменных
Постановка задачи. Найти стационарные точки функции
z — z(x, у) и исследовать их характер.
План решения.
1. Стационарными точками функции нескольких переменных
называются точки, в которых все ее частные производные равны нулю.
Следовательно, чтобы найти стационарные точки функции z(x, у),
нужно решить систему двух уравнений с двумя неизвестными
Г z'x(x,y)=0,
\ 4(х,г/) = 0.
Решая эту систему уравнений, находим стационарные точки функции
z(x,y): M1(x1,j/i), M2(x2,j/2),---, Mn(xn,yn).

6.7. Экстремум функции двух переменных
143
2. Для того чтобы исследовать характер стационарных точек,
воспользуемся достаточными условиями экстремума функции двух
переменных.
Пусть функция z — z(x, у) определена и имеет непрерывные
частные производные второго порядка в стационарной точке М(хо,уо)
(т.е. z'x(x0, J/0) = ^у(хо,Уо) = 0). Тогда если в этой точке:
а) z"x • z'yy — (z"yJ > 0, то М — точка экстремума, причем при
z"x > 0 — точка минимума, при г!хх < 0 — точка максимума;
б) z"x " ^'j/ — (ZxyJ < 0, то М не является точкой экстремума;
в) zxx -z'yy — (zxyJ — 0, то требуется дополнительное
исследование (например, по определению).
3. Вычисляем производные второго порядка функции z(x,y).
4. В каждой стационарной точке вычисляем выражение
" ji
Л'тт * Z.
!/!/
Ю2
и определяем его знак.
Анализируем полученные результаты и записываем ответ.
Пример. Найти стационарные точки функции
z = х3 + у3 - Зху
и исследовать их характер.
Решение.
1. Вычисляем частные производные
4 = Зх2 - Зу, zy = Зу2 - Зх.
2. Для того чтобы найти стационарные точки функции, решаем
систему двух уравнений с двумя неизвестными
f Зх2 - Зу = 0,
\ Зу2 - Зх = 0.
Получаем два решения: Xi = 0, j/i = 0 и Xi — 1, yi = 1.
Следовательно, стационарные точки функции z = х3 + у3 — Зху: Mi @,0) и
М2A,1).
3. Вычисляем производные второго порядка:
z"x = 6x, z"y = -3, z'yy = 6j/.

144
Гл. 6. Функции нескольких переменных
4. В каждой стационарной точке вычисляем выражение
т" ■ 7п — (?" \2
zxx ' ^j/j/ \zxy)
и определяем его знак.
В точке М!@,0)
4^@,0)=0, 4'!/(о,о)=-з, 4,s/(o,o)=o^4'x-4's/-D'!/J=-6<o.
Следовательно, точка М\ @,0) не является точкой экстремума.
В точке М2A,1)
4'хA,1) =6, z%{\, 1) = -3, z^(l, 1) =6 => z"xx ■ z'Jy - D',J =27 > 0..
Следовательно, точка М^(\, 1) является точкой экстремума. Так как
z"x(l, 1) = 6 > 0, то МгA,1) — точка минимума.
Ответ. Функция z = х3 + у3 — Зху имеет две стационарные
точки Mi@,0) и М2A,1). В точке Мх@,0) экстремума нет, М2A,1) —
точка минимума.
УСЛОВИЯ ЗАДАЧ. Найти стационарные точки заданных функций
и исследовать их характер.
1. z — х2 — ху + у2. 2. z = х2 — ху — у2.
3. z = х2 - 2ху + 2у2 + 2х. 4. z - х3 + у3 - х2 - 2ху - у2.
5. z-x3 - 2у3 - Зх + 6у. 6. z = 4х + 2у - х2 - у2.
7. z — х3 + у3 - 15ху. 8. z = х2 + ху + у2 — Зх - 6у.
9. z = х2 + 4у2 — 2ху + 4. 10. z — х/у + 1/х + у.
Ответы.
1. М@,0) — стационарная точка. М@,0) — точка минимума,
2min=2@,0) = 0.
2. М@,0) — стационарная точка. В точке М@,0) экстремума
нет.
3. М(—2, —1) — стационарная точка. М(—2, —1) — точка
минимума, zmin = z(-2, -1) = -2.
4. Mi@,0), МгD/3,4/3) — стационарные точки. М@,0) —
точка максимума, zmax = z@,0) = 0. МD/3,4/3) —- точка минимума,
zmi„=*D/3,4/3) = -64/27.

6.7. Экстремум функции двух переменных
145
5. Mi(l,l), М2(-1,-1), М3(-1,1), М4A,-1) — стационарные
точки. В точках MiA,1), Мг(—1,-1) экстремума нет. М3(—1,1) —
точка максимума, zmax = z(—1,1) = 6. М4A, — 1) — точка
минимума, zmin = гA, -1) = -6.
6. МB,1) — стационарная точка. МB,1) — точка максимума,
zmax = 2B, 1) = 5.
7. Mi @,0), МгE,5) — стационарные точки. В точке Mi @,0)
экстремума нет. М3E,5) — точка минимума, zm\n = z(b,5) = —125.
8. М@,3) — стационарная точка. М@,3) — точка минимума,
2min = Z@, 3) = -9.
9. М@,0) — стационарная точка. М@,0) — точка минимума,
Zmin =2@,0) = 4.
10. МA,1) — стационарная точка. МA,1) — точка минимума,
Zmm = *A,1) = 3.

Глава 7
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
При изучении темы НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ вы
изучите основные приемы нахождения первообразных (подведение под
знак дифференциала, интегрирование по частям, замена
переменной), научитесь интегрировать основные классы функций
(рациональные дроби, тригонометрические и иррациональные выражения).
С помощью пакета РЕШЕБНИК.ВМ вы можете вычислить
производные, разложить многочлен на множители, разложить
рациональную функцию на элементарные дроби, решить системы уравнений
для нахождения неопределенных коэффициентов, выполнить другие
численные расчеты и проверить полученные вами результаты.
7.1. Интегрирование подведением
под знак дифференциала
Постановка задачи. Найти неопределенный интеграл
План решения. Пусть д(х) имеет очевидную первообразную
G(x), a F(x) есть функция этой первообразной, т.е. F(x) = u(G(x)).
Тогда
[ F{x)g(x) dx = f u(G(x))G'(x) dx = fu(G) dG.
Такого рода преобразование называется подведением под знак
дифференциала.
■ Если метод избран удачно, то последний интеграл оказывается
табличным или известным образом сводится к табличному.
Пример. Найти неопределенный интеграл
/ ctga; In sin ж da;.

7.1. Интегрирование подведением под знак дифференциала 147
Решение.
1. Представим подынтегральное выражение в виде произведения
двух функций F(x)g(x), где д(х) имеет очевидную первообразную
G(x), a F(x) есть функция этой первообразной, т.е. F(x) — u(G(x)).
В данном случае
,_,. . In sin x , . . . InG ._,.
F(x) = —: , g(x) — cosx, G(x) — sinx, F(x) — —— — u(G).
sinx G
2. Тогда
/lnsinx , f lnsinx , . f InG , _
—: cos a; ax = / —: dsinx = / —— dG ,
sinx J sin ж J G
где G = sin x.
3. Последний интеграл не является табличным, но к нему снова
можно применить метод подведения под знак дифференциала:
|^dG = |lnG±dG = /lnGdlnG=^+G=^^+G.
^ г , • In2 sin ж _,
Ответ. J ctgx In sin x ax = \-C.
УСЛОВИЯ ЗАДАЧ. Найти неопределенные интегралы.
3 arctg2 x /" sin 2x — cos x
!. [l^dx. 2. Г. . . ^2
J хг +1 J (cos^x + sinx)''
f x2 +1 /ГЗЬё2х
*■ У (хЗ+Зх + 1L У cos2x
5. / —; dx. 6. / , dx.
dx.
f \ dx. 6. /"
7 xylnx J
VT
X
x cos x + sin ж / arctg (x + 2)
dx.
/x cos x + sin x , „ /*
—f—.—rj— dx. 8. /
(xsinx)-5 J
9. П^йх. 10. / , ff
x2 + 4x + 5
2 arcsin x + x
dx.

148
Гл. 7. Неопределенный интеграл
Ответы.
ч 1
1. arctg3 х + С. 2. —^ + С.
cosi! х + sin х
3- -9(*з + 1 + 1)з+а 4- *8S* + C.
5. 2х/1шс + С 6. - arcsinx2 + C.
7- -^7—^—Ъ+С- 8- arctg2(x + 2) + a
2(xsinx)J
9. 1пBх\/х + х) + С. 10. arcsin2 х - y/l - х2 + С.
7.2. Интегрирование по частям
Постановка задачи. Найти неопределенный интеграл
F(x)g(x) dx.
/'
План решения. Пусть д(х) имеет очевидную первообразную
G(x), a F(x) — дифференцируемая функция, причем ее
производная f(x) — F'(x) является более простой функцией, чем F(x). Тогда
применяем формулу интегрирования по частям
J F(x)g(x) dx = F(x)G(x) - f f(x)G(x) dx.
Если метод избран удачно, то интеграл в правой части этого
равенства оказывается табличным или известным образом сводится к
табличному, например, повторным интегрированием по частям.
Пример. Найти неопределенный интеграл
xdx
/;
Решение.
1. Представим подынтегральное выражение в виде произведения
двух функций F(x)g(x), где д(х) имеет очевидную первообразную
G(x), a F(x) — дифференцируемая функция, причем ее производная
f(x) = F'(x) является более простой функцией, чем F(x).

7.2. Интегрирование по частям
149
В данном случае
F(x) = x, д(х) = ——, G(x) = tgx, f(x) = F'(x) = 1.
COS'' X
2. Применяем формулу интегрирования по частям
/xdx [ ,
—^— = х tg х — / tg x ax.
cos2 х J
3. Последний интеграл не является табличным, но к нему можно
применить метод подведения под знак дифференциала:
/tgxdx = I sinxdx = — / dcosx =
J cos ж J cos ж
■{
— lncosx + Ci при cosx>0,
— ln(— cos x) + Ci при cos x < 0.
/" xdx _ Г In cos x + Ci при cos a; > 0,
J cos2 ж \ ln(—cosx) + C2 при cosx<0.
Заметим, что если бы мы выбрали д(х) = х, то, дифференцируя
функцию F(x) — 1/ cos2 x и применяя формулу интегрирования по
частям, получили бы более сложный интеграл, чем исходный.
Условия задач. Найти неопределенные интегралы.
1. (x+l)exdx. 2. arcsiaxdx.
3. Jx^xdx. 4. J{x> + 2x + 3)cosxd*.
5. / x In xdx. 6. / —к—^x-
J J sin ж
7. / e21 cos x dx. 8. / x2 arctg x dx.
9. /dnh.*. m/xVdx.

150
Гл. 7. Неопределенный интеграл
Ответы.
1. хех + С. 2. хarcsinx + л/l - х2 + С.
3. 2xsinx — x2cosx + 2cosx + С.
4. (x+lJsinx + 2(x + l)cosx + C
х2
5. — B1nx — 1) + С. 6. — xctgx + lnsinx + C
e2x
7. -— (sin x + 2 cos x) + C.
5
x2 11
8. — arctg x - -x2 + - ln(x2 + 1) + C.
3 6 6
9. | (sin In x - cos In x) + С 10. ex(x2 -2x + 2) + C.
7.3. Интегрирование рациональных
функций с простыми
вещественными корнями знаменателя
Постановка задачи. Найти неопределенный интеграл
апхп + on_ix"_1 + ... + aix + оо
/
bmxm + bm-ix"-1 + ... + biX + b0
dx.
План решения.
1. Введем обозначения:
Рп(х) = апхп + ап-хх"-1 + ... + aix + а0,
Qm{x) = bmxm + bm_]Xm_ + ... + b\x + bo.
Сравним степени числителя Рп(х) и знаменателя Qm(x).
Если подынтегральная функция — неправильная рациональная
дробь, т.е. степень числителя п больше или равна степени
знаменателя то, то сначала выделяем целую часть рациональной функции,
поделив числитель на знаменатель:

7.3. Интегрирование рациональных функций
151
Здесь многочлен Рк{х) — остаток от деления Рп(х) на Qm(x), причем
степень Рк{х) меньше степени Qm(x).
2. Разложим правильную рациональную дробь
К{х)
Qm{x)
на элементарные дроби. Если ее знаменатель имеет простые
вещественные корни гь т2,..., rm, т.е. Qm{x) -(х- п)(х -r2)...(x- rm),
то разложение на элементарные дроби имеет вид
Рк{х) _ Ах А2 Ат
Qm{x) Х-ТХ Х-Г2 '" Х-Гт'
3. Для вычисления неопределенных коэффициентов А\, А2,..., Ат
приводим к общему знаменателю дроби в правой части тождества,
после чего приравниваем коэффициенты при одинаковых степенях х
в числителях слева и справа. Получим систему т уравнений с т
неизвестными, которая имеет единственное решение.
4. Интегрируем целую часть (если она есть) и элементарные дроби,
используя табличные интегралы, и записываем ответ
/
ед,ь.
Qm{x)
= F(x) + Аг In \x - ri| + А2 In \x - r2\ + ... + Ат In \x - rm\ + С,
где F(x) = f Mn_m(x) dx — многочлен степени п — m + 1.
Пример. Найти неопределенный интеграл
2х3 - 40х - 8
/
х(х + 1)(х-2)
dx.
Решение.
1. Подынтегральная функция — неправильная рациональная
дробь, так как п — т = 3. Выделим целую часть:
2х3 - 40х - 8 4ж2 + 24ж + 8
х(х+4)(х-2) х{х + 4)(х-2)'
2. Так как знаменатель последней дроби имеет три различных
вещественных корня х = 0, х — —4 и х — 2, то ее разложение на

152
Гл. 7. Неопределенный интеграл
элементарные дроби имеет вид
4я2 + 24я + 8 Аг А2 А3
= —L +——А +
х(х + А)(х — 2) х х + А х-2
3. Чтобы найти коэффициенты А1,А2,Аз, приводим к общему
знаменателю дроби в правой части тождества:
4х2 + 24х + 8 _ Ai{x2 + 2х - 8) + А2{х2 - 2х) + А3(х2 + Ах)
х{х + А)(х-2) х{х + А)(х-2)
Приравнивая коэффициенты при одинаковых степенях х в числителях
слева и справа, получим систему трех уравнений с тремя
неизвестными:
Ai+ А2 + А3 = 4,
2Ai - 2А2 + АА3 = 24,
-8А! = 8.
Эта система имеет единственное решение А^ — —1, А2 = —1, Аз — 6.
Следовательно, подынтегральное выражение имеет вид
2х3 - 40х - 8
V х) \ х + А)
х(х + А)(х-2) \ х) \ х + А) х-2
А. Интегрируем целую часть и элементарные дроби, используя
табличные интегралы:
Г 2х3-А0х-8 , Г [1 , Г 1 , Г 6 ,
/ —, 7Г, ^т dx= 2 да: 4- / - йх+ / - ах- / ах =
J х{х + А)(х-2) J J х J х + А J х-2
= 2х + In |x| + Ь \х + А\ - 6 In \x - 2\ + С.
I
я(я + 4)(ж - 2) (а;-2N
Условия ЗАДАЧ. Найти неопределенные интегралы
х2 + 2х + 6 , „ /" 1
/• х2 + 2х + 6 Г 1
'• У (х-1)(х-2)(х-4)ЙХ- ^ У (х-1)(х+2)(х + 3)аХ-
3' У (х2 - 1)(х2 - A) dX- 4' У x4-13x2 + 36da;-

7.4. Интегрирование рациональных функций
153
- Зх2 + 2
г Г х5 + Зх4 - За. . _ ,
5- J *=i dX-
Г 2х3 - 8х2 + 4х - 4
7- У х(х-1)(х-4) dX-
х5 + х4 - 8
■/
/• х3 + 2х2
J х(х-
■dx.
х{х-2)(х+2)
з j. о^2 _ 15х + 18
3)(х + 3)
<£х.
ч
,/
2х4 - 4х3 - 8х2 + Ъх - 10
(х-1)(х-3)(х + 2)
2х6 - 4х4 + 6х3 - 18х2 + 8
dx.
х5 — 5х3 + 4х
Ответы.
1. In
3
(х - 1K(х - 4M
(х-2O
1 (х+1L|х-2|5
In
12 (х-1L|х + 2|5
+ С.
+ С.
<£х.
1 |(х-1)(х + 3K|
2- 12 Ь (xTW
1 (х-3J|х + 2|3
60 (х + 3J|х-2|3 +
5. h х3 + Ь
4
х-1
х+ 1
6. — + — + 4х + Ь
О ^
+ с.
х2(х-2M
7. 2х + 1п
9. х2 + In
10. х2 + Ь
(х + 2K
(х-4)(х + 1J
х
\2(
(х-1J(х + 2)
х — 3
х2(х-2J(х + 1K(х-1)
(х + 2J
+ С.
+ С. 8. х + Ь
+ С.
~п +с.
(х + 3K(х - 3)
+ С.
7.4. Интегрирование рациональных
функций с кратными вещественными
корнями знаменателя
Постановка задачи. Найти неопределенный интеграл
апхп + on_iXn_1 + ... + oix + а0
I
Ьтхт + bm_ixn-! + ... + bix + b0
dx.

154
Гл. 7. Неопределенный интеграл
План решения.
1. Введем обозначения:
Рп(х) = апхп + an_ixn_1 + ... + а^х + а0,
Qm{x) = bmxm + bm_ixm_1 + ... + Ъхх + b0.
Сравним степени числителя Рп{х) и знаменателя Qm(x).
Если подынтегральная функция — неправильная рациональная
дробь, т.е. степень числителя п больше или равна степени
знаменателя т, то сначала выделяем целую часть рациональной функции,
поделив числитель на знаменатель:
Здесь многочлен Pjt(x) — остаток от деления Рп{х) на Qm(x), причем
степень Рь{х) меньше степени Qm(x).
Рк(х)
2. Разложим правильную рациональную дробь ——— на эле-
ментарные дроби. Если ее знаменатель имеет вещественные корни
г1>г2>• • •,г« кратности ni,ri2,--.,ns соответственно, т.е.
Qm(x) = (х- Г1)пЧх - г2Г • • • {х - гт)п>,
то разложение на элементарные дроби имеет вид
Рк{х) _ Ац А12 Alni
Qm{x) x-n (x-riJ '" (x-n)ni
х — г2 (х - г2у [х - Г2)П2
... + -^-+, As\n+...+ Asn°
x-rs (x-rsJ '" (x-rs)n-'
3. Чтобы найти коэффициенты Ац, Ai2,..., А8Пе, приводим к
общему знаменателю дроби в правой части тождества, после чего
приравниваем коэффициенты при одинаковых степенях х в числителях слева
и справа. Получим систему Щ+П2+- ■ .+ns уравнений с Щ+П2+- ■ -+ns
неизвестными, которая имеет единственное решение.

7.4. Интегрирование рациональных функций
155
4. Интегрируем целую часть (если она есть) и элементарные
дроби, используя табличные интегралы, и записываем ответ
/
Qm[X)
= F(x) + A11ln\x-r1\+i-^ll + ...+ *n, ,„,_,+-
Х-Гх A - ni)(X - ri)ni г
... + Asl\n\x-rs\+{-=^+...+ Ат'
X-Ts '" (l-ns^X-rsO1'-1'
где F(x) = / Mn_m(x) dx — многочлен степени п — m + 1.
ПРИМЕР. Найти неопределенный интеграл
х3 + 6х2 + 13х + 6
/;
(я-2)(я + 2K
■dx.
Решение.
1. Подынтегральная функция — правильная рациональная дробь.
2. Разложим ее на элементарные дроби. Так как знаменатель
имеет два действительных корня: г\ — 2 кратности единица и г2 — — 2
кратности три, разложение на элементарные дроби имеет вид
ж3 + 6ж2 + 13ж + 6 Ац А21 А22 А23
{х-2)(х + 2K х-2 х + 2 (ж+2J (х + 2K'
3. Чтобы найти коэффициенты Ац,... ,А23, приводим к общему
знаменателю дроби в правой части тождества:
х3 + 6ж2 + 13х + 6 _
(х - 2){х + 2K
_ Ап{х + 2K + А21{х - 2)(ж + 2J + А22{х - 2)(ж + 2) + А23{х - 2)
(х-2)(х+2K
Приравнивая коэффициенты при одинаковых степенях х в числителях
слева и справа, получим систему четырех уравнений с четырьмя
неизвестными
Ли + А2Х = 1,
6Лц + 4Л21 + А22 = 6,
12ЛП - 2Л21 + А23 = 13,
8Ai 1 - 4Ап - АА22 - 2А23 = 6.

156
Гл. 7. Неопределенный интеграл
Эта система имеет единственное решение:
An = 1, A2i = О, А22 = О, А23 = 1.
Следовательно, подынтегральное выражение имеет вид
ж3 + 6х2 + 13х + 6
1 1
+
(ж-2)(ж + 2K х-2 (х + 2K'
3. Интегрируем сумму элементарных дробей, используя
табличные интегралы:
Ответ
Jr^2dx+Jrjdwdx=4x-2l-2(xTw
х3 + 6ж2 + 13ж + 6 . . . -. 1
•/■
(x-2)(x + 2K
• dx = In \x — 2|
2{x + 2J
+ C.
+ C.
Условия ЗАДАЧ. Найти неопределенные интегралы.
х2{х + 1){х-1)
I
Г х2 + 1
J х{х-1)
Г х2 + 1
J (x-lK(z
I
dx.
■dx.
+ 3)
х2 - 2х + 3
dx.
dx.
х{х - 1J(х - 3)
J X3 — X2 — X + 1
2
4
6
8
10
х3 - 6х2 + 9х + 7
{х - 2K(х - 5)
х2 + 2
I
. [ —
J (х-1)(х+1J
■I
I
dx.
dx.
2J
5ж3 - 17ж2 + 18ж - 5
(х-1K(х-2)
х5
А я.
(х - 1K(х + 1)
dx.
Ответы.
1
3.
1 ,
- п
2
In
х —
1
х + 1
х-1
X
+ - + С.
х
2. 1п|х-5| +
2{х - 2)
+ С.
(х-1)-
+ С.
4. !b|(* + l)(*-lK| + ^
+ С.

7.5. Интегрирование рациональных функций
157
5- ;=7 In
32
х-1
6. - In
4
ж + 3
4(х - IJ 8(х - 1)
+ С.
х-2
4(х - 2) 2х
^ + С.
7. 11п1(^-1)(^-3I+^_ + а
8. 1п|(х-1J(х-2K| +
9. - In
4
10.
х+1
х-1
(х + 2J
2{х - 1)
х-1
2{х-1)'-
+ С.
+ С.
2 +-Ы(х-1K1(х + 1)|-
4(х - IJ 4(х - 1)
+ С.
7.5. Интегрирование рациональных
функций с простыми комплексными
корнями знаменателя
Постановка задачи. Найти неопределенный интеграл
апхп + an_ixn_1 + ... + а\Х + о0
/
bmxm + Ьт^х"-1 + ... + b1x + b0
dx.
План решения.
1. Введем обозначения:
Рп{х) = апхп + on_1xn_1 + ... + aix + а0,
Qm{x) = ЬтХт + Ьт-гХ™-1 + ... + blX + b0.
Сравним степени числителя Рп(^) и знаменателя Qm(x).
Если подынтегральная функция — неправильная рациональная
дробь, т.е. степень числителя п больше или равна степени
знаменателя т, то сначала выделяем целую часть рациональной функции,
поделив числитель на знаменатель:
Рп{х) -Мп_т(х) + ^Щ (к<т).
Qm{x)
Qm{x)

158
Гл. 7. Неопределенный интеграл
Здесь многочлен Рк{х) — остаток от деления Рп{х) на Qm(x), причем
степень Рк(х) меньше степени Qm(x).
2. Разложим правильную рациональную дробь
Рк(х)
на элементарные дроби. Если ее знаменатель имеет простые
комплексные корни гк = ик ± ivk, т.е.
Qm{x) = {х2 + pix + qi)(x2 + p2x + q2)...(x2 +psx + qs),
где
x2 + ркх + qk = [х - {ик + ivk)][x - (ик - ivk)],
то разложение на элементарные дроби имеет вид
Рк(х) _ А\х + В\ А2х + В2 Asx + Bs
Qm{x) x2 + pix + qx x2 + p2x + q2 '" x2 + psx + qs'
3. Для вычисления неопределенных коэффициентов А\, А2,..., As,
Bi,..., Bs приводим к общему знаменателю дроби в правой части
тождества, после чего приравниваем коэффициенты при одинаковых
степенях х в числителях слева и справа. Получим систему 2s
уравнений с 2s неизвестными, которая имеет единственное решение.
4. Интегрируем элементарные дроби вида
Ах + В
х1 +px + q
Выделяем в знаменателе полный квадрат (х + р/2J + (q — p2/4)
(поскольку q—p2/4: > 0, можно обозначить д-р2/4 — а2) и делаем замену
переменной t = х — р/2. Получим
Ах + В , Г At + Ар/2 + В ,
j i ■ at —
J xl+px + q J
t2 + a2
J t2 + a2 J t2 + a2
A , / 2 2ч AP/2 + B *
= — 1п(Г + a1) + -^ arctg -
2 a a

7.5. Интегрирование рациональных функций
159
А , , 2 ч Ар/2 + В х + р/2
= — 1п(зГ +px + q)+ i arctg -
2 4/^^74 V^VT^'
5. Складываем результаты интегрирования целой части (если она
есть) и элементарных дробей и записываем ответ.
Пример. Найти неопределенный интеграл
2х3 + Зх2 + Зх + 2
I
(х2 + х + 1)(х2 + 1)
dx.
Решение.
1. Подынтегральная функция — правильная рациональная дробь.
2. Разложим ее на элементарные дроби. Знаменатель имеет две
пары комплексно-сопряженных корней: Т\2 = —1/2 ±i\/3/2 и r^4 = ±*-
Следовательно, разложение на элементарные дроби имеет вид
2х3 + Зх2 + Зх + 2 j4ix + Bi А2х + В2
{х2 + х + 1)(х2 + 1) х2 + х + 1 х2 + 1
3. Чтобы найти коэффициенты А\, А2, В\, В2, приводим к общему
знаменателю дроби в правой части тождества:
2х3 + Зх2 + Зх + 2 _ (Ахх + Bi){x2 + 1) + (Л2х + В2)(х2 + х + 1)
(х2+х + 1)(х2 + 1) (х2+х+1)(х2 + 1)
Приравнивая коэффициенты при одинаковых степенях х в числителях
слева и справа, получим систему четырех уравнений с четырьмя
неизвестными
( А1 + А2 =2,
A2 + Bi + B2 = 3,
Ai + A2 + В2 = 3,
Bi+B2 =2.
Эта система имеет единственное решение
Аг = 1, A2 = l, Bi=l, B2 = l.
Следовательно, подынтегральное выражение имеет вид
2х3 + Зх2 + Зх + 2 х + 1 х + 1
(х2+х + 1)(х2+ 1) х2 + х+1 х2 + Г

160
Гл. 7. Неопределенный интеграл
4. Интегрируя элементарные дроби, получим
Г х + 1 , 1, , 2 ,Л 1 2ж + 1^
У x* + x + idx = 2Hx +x + 1) + 7^aicte~7T + Cu
/X + 1 1
-=—- dx = - 1п(ж2 + 1) + arctga; + С2.
а; + 1 z
/" 2а:3 + За:2 + За: + 2 ,
Ответ. / —г -гг-=—-г az =
У (а;2 + х + 1)(х2 + 1)
= - 1п(а:2 + х + 1)(а:2 + 1) + —= arctg —j=- + arctg a: + С.
2 V3 v3
Условия ЗАДАЧ. Найти неопределенные интегралы.
1 Г Х J 9 /" 2х*+х + д
*" J (x + inxz + l)™' Z- J {х + 2){х* + х+1)аХ-
3- Ix^8dx- 4" I'*-*1*"
f 7a;2 -1 _, /~ Д + 1
b" У а;4+4а;2-5ЙХ- ^ J (a;2 + l)(a;2 + 9)
Чх5-!2 У (а; + 1)(а;2+2а; + 2)
/-3a;3+a;2 + 5a;+l J /" a;4
9- У x^Tx ^ 10- j^r.
16 ^
Ответы.
1 1 1 (s+l)a
1 1 2a; +1
2. 31n|a; + 2|--ln(a;2+a;+l) + -7=arctg—p- + С
2 V3 v3
„ 1 , (a;-2J v/3 a; + l „
3- 7T7 Ь , „ ' - т7г arctg —±- + С
24 a;2 + 2a; + 4 12 \/3
4. - ln|(a;-lK(a; + l)|--arctga;+C

7.6. Интегрирование тригонометрических выражений 161
5. -In
х-1
х + 1
+^arctg^+a
„ 1, х2 + 1 1 1 х „
6- 16 1П^Т9 +8^*^-24 arCtg3+C-
„ 1 1 , (ж -1J 1 2х +1 „
7. - + -1п-^ '—- + —arctg—т=-+С-
а; 6 ж2 + ж + 1 v/З \/3
8. ж - - 1п[(ж2 + 2х + 2)(ж + IL] + 3arctg (ж + 1) + С.
9. Зж + In |ж| + 2 arctg x + С.
10. х + - In
ж + 2
- arctg - + С.
7.6. Интегрирование выражений
R(sin х, cos х)
Постановка задачи. Найти неопределенный интеграл
I
R(sinx,cosx)dx,
где R — рациональная функция двух переменных.
План решения.
1. С помощью подстановки
х
интегралы от функций R(sin x, cos x) приводятся к интегралам от
рациональных функций новой переменной t. Действительно, подставляя
в подынтегральное выражение
2t
sin a;
1 + f2'
1-f2 2
cos a; = . .„, dx — -—:—— dt,
1 + f2'
1 + f2
получаем
(It 1 — f2 \ 2
1 + 12 ' 1 + t2 J 1 + f2df = -Rl(f)df-
Подстановка t = tg(x/2) называется универсальной.

162
Гл. 7. Неопределенный интеграл
2. Применяем формулу замены переменной в неопределенном
интеграле
/Г (It 1 — t2 \ 2
Ж«ш*,со.*) dx = jR (д-^, —J _ Л.
3. Вычисляем первообразную рациональной функции t и
возвращаемся к переменной ж, подставляя t = tg (ж/2).
Замечание. Если подынтегральная функция имеет специальный
вид, то лучше применить подстановки, требующие меньше
вычислений:
а) если
R(sin х, cos x) = Ri (sin x, cos2 ж) cos ж,
то применяем подстановку t = sin ж. Действительно,
подынтегральное выражение приобретает вид
Ri (sin x, cos2 x) cos a; da; = Ri (t, 1 — £2) df;
б) если
i?(sin x, cos ж) = i?2(sin2 ж, cos ж) sin ж,
то применяем подстановку t = cos ж. Действительно,
подынтегральное выражение приобретает вид
R2(sm2 х, cosж)sinжdж = —ДгA — t2,t)df;
в) если
fi(sin ж, cos ж) = Дз (tg ж),
то применяем подстановку t = tg ж. Действительно, подынтегральное
выражение приобретает вид
Д3^ж^ж = Д3(*)—^df.
Пример 1. Найти неопределенный интеграл
sin ж
/
dж.
2 + 51ПЖ

7.6. Интегрирование тригонометрических выражений 163
Решение.
1. Сделаем подстановку t — tg(a;/2).
Подставляя в подынтегральное выражение
2* . _2_
получим
2t
sin a; , _ 1 +12 2 _ 2f
2 + sinx __ 2t TTi2df-(f2 + f + 1)(f2 + 1)df-
2. Применяем формулу замены переменной в неопределенном
интеграле
/sin а; • [ 24
2 + sinx =У (t* + t + l)(t* + l)dL
3. Вычисляем первообразную рациональной функции t:
/
2t , „ 4 2f+l „
at = 2 arctg i = arctg —-=—V С
(t2 + t + l)(*a + l) "—-"*" ,/3 Б ^
Возвращаемся к переменной x, подставляя £ = tg(a;/2):
С sina: , 4 2tg (ж/2) +1 „
I dx = x ■= arctg 6V ' + С
J 2 +sina; уД уД
f sina; , 4 ^ 2tg(a:/2) +1 _
Ответ. / dx = x = arctg = h С
J 2 +sina; уД уД
Пример 2. Найти неопределенный интеграл
' 3tg2a; - 1 ,
/
tg2a; + 5
Решение.
1. Так как подынтегральная функция имеет вид .ft(tga;), сделаем
подстановку tg x = t.
Подставляя в подынтегральное выражение
dt
tgx = t, dx= ,
1 +tz

164
Гл. 7. Неопределенный интеграл
получим
3tg2a; -1 , 3f2 - 1 1 _,
—5 т dx — -^—— r^ at.
tg2a; + 5 f2 + 5 1 + t2
2. Применяем формулу замены переменной в неопределенном
интеграле
f 3tg2a; - 1 J _ Г dt2 - 1 1 Л
J tg2a; + 5 J f2 + 5 1-Й2
4. Вычисляем первообразную рациональной функции t:
I
3*2-l 4 f
df = —arctgi 4—-parctg —= + С
(f2 + 5)(l-M2) & ' У5 &v^
Возвращаемся к переменной ж, подставляя t = tg ж:
f3te2x-l , 4 ЛкаЛ _
/ —я — аж = -х + —p=arctg I —= ) + С
/tg2a;-l , 4 AgaA Л
Ответ. / —^ аж = — x -\—^arctg I —=• I + С
Условия задач. Найти неопределенные интегралы.
dx
1. f * . 2. /
у 2 sin ж — cos ж — 1 у
3- /* £ о- 4. /
У СОБЖ + 251ПЖ + 3 J
5. /" <** 6. /"
У 4созж-Ззтж - 5' У sin2 ж cos ж + 9 cos3 ж
7. /-^V. 8. /
J 1 + sin^a; J
f dx , f cos ж ,
9. / rdx. 10. / dx.
J 51ПЖA + С05Ж) J Ц-СОБЖ
cos 2ж — sin 2ж
dx f dx
2 -sini'
2 sin ж + 3 cos ж
cos5 ж + cos ж
—3 2— "a;"
sin ж + sin ж
dx.

7.7. Интегрирование тригонометрических выражений 165
Ответы.
1. 5l»|2tgf-l
+ с.
2.
2у[2
In
tga; + l + v/2
tga; + l-v/2
+ С.
I х\ 2 Z2^!-1
3. arctg (l + tg -J + С 4. -щ arctg I -*=— | + С
5. 2C + 9tg|)_1+C. 6. ln(tg2a; + 9) + arctg^!^+a
7. —7=arctg (V^tga;) + С 8. sina; 6arctg (sinx) + С
■J 2 V / sin a;
V2
9. 'kil^+.
4 1+cosa; 2A+cos ж)
+ C.
10. x-tg- + C.
7.7. Интегрирование выражений
sin2m x cos2n x
Постановка задачи. Найти неопределенный интеграл
sin2m x cos2" xdx,
/■
где m, n — натуральные числа.
План решения.
Применяем формулы понижения степени
sin2 х = — A — cos 2x), cos2 ж = — A + cos 2x), sin x cos ж = - sin 2a;
до тех пор, пока не придем к табличным интегралам или к
интегралам, которые известным образом сводятся к табличным.
/■
Пример. Найти неопределенный интеграл
sin4 За; cos За; dx.
Решение. Применяя формулы понижения степени, имеем
/sin^3a;coS43a;da; = 2-/Bsin3a;cos3a;r^ =

166
Гл. 7. Неопределенный интеграл
= 2-4 [ sin4 6ж dx = 2_6 / A - cos 12жJ dx =
= 2_6 f dx - 2-5 A cos 12a;da; + 2_6 / cos2 12a;da;
12ж + 2~7 / A + cos 24ж) dx =
2-5
= 2~6ж - —- sin
2-5 /"
= 2_6ж sin 12ж + 2~7х + 2~7 / cos 24ж dx =
12 У
2-5 2-7
= 2~6ж - —- sin 12ж + 2~7х + —- sin 24ж + С.
12 24
Ответ
27 3-27 3-210
/31 1
sin4 За; cos4 За: dx = — х — „ ^ sin 12а: + „ ^1П sin 24а: + С.
Условия задач. Найти неопределенные интегралы.
1. / cos22xdx. 2. / cos63xdx.
3. / cos4 — dx. 4. / sin4 4a; dx.
5. /sin62xdx. 6. / sin2 8a; cos2 8a; dx.
7. I cos4 a; sin2 a; dx. 8. / cos2 ж sin4 ж dx.
9. / sin4 ж cos6 ж dx. 10. / sin6жcos4жdж.
Ответы.
ж sin4x _ „ 5ж sin6x sinl2x sin3 6a; _
L 2+"8-+a 2- 16+Ч2- + ^4--Ч4Г + а

7.8. Интегрирование иррациональных выражений 167
„ За; sin a; sin 2а: _ „ За; sin 8а: sin 16а: _
3- Т + — + -16-+С- 4 Т-Чб- + ^28-+а
_ Ъх sin 4а; 3 sin 8а: sin3 4а: _ „ х sin 32а: _
5. + + + С. 6. + С.
16 8 128 96 8 256
„a; sin 4а: sin3 2а: л х sin4x sin32x _
у I \- (^ 8 I- С
'16 64 48 ' 16 64 48
За; sin 4а: sin 8а: sin5 2а:
256 ~ 256 + 2048 + 320 + '
За; sin 4а: sin 8а: sin5 2а:
' 256 ~~ 256 + 2048 320 + '
7.8. Интегрирование выражений
I ' у сх+а1 у сх+а.1
Постановка задачи. Найти неопределенный интеграл
где R — рациональная функция иp,q,... — натуральные числа.
План решения.
1. С помощью подстановки
aX + b =tn
сх + d
где п — общий знаменатель дробей 1/р, 1/q,..., приходим к
интегралам от рациональных функций.
2. Вычисляем первообразную рациональной функции t и
возвращаемся к переменной х, подставляя t
_ nlax + b
~ V cx + d'
Пример. Найти неопределенный интеграл
4^2 - ж - у/2 + х
I
(v^T2 + Ау/Т^х){х + 2J
dx.

168
Гл. 7. Неопределенный интеграл
Решение.
1. Чтобы сделать подстановку, приводящую к интегралу от
рациональной функции, нужно преобразовать подынтегральную
функцию так, чтобы она содержала корни любой степени, но из одного
fix -4- b
и т о г о ж е выражения вида J j •
Преобразуем подынтегральное выражение, выделяя J*r~r% '•
= lv Irf
(y/x~+~U + 4у/2^~х)(х + 2J
Г 4^-У2Т¥ Г dx
1 + 4,
2. Применяем подстановку t
ГЕЕЕ.
~\2+х:
Делая замену переменной в неопределенном интеграле, получаем
/2-х
f Ч2Тх~1 Mt-1 (t2 + lJ/ 8t \
У т—/г^\—: У «л -i6- 1-(^t^j dt-
vn
1 + 4Л/^-|1(ж + 2J
3. Вычисляем первообразную рациональной функции t:
2 У U + 1 2[J \ 2) ^2] 4*+1.
4 4 lb
/2-х
Возвращаемся к переменной х, подставляя £ = */- .
- —- Wv :
(v/F+2 + ly/2^x)(x + 2J
/• 4у/2~^-У2Т¥
Ответ. / , , —;—,_ гтт ох =

7.9. Интегрирование иррациональных выражений 169
Условия задач. Найти неопределенные интегралы.
1 f da: 2 f dX
J v/2¥^l- УъГ^Т' ' J v/iTT+v^Tlj5'
3. f-fJ^. 4. / —-dx
J yft+ ^ J B-:
B-x)yfT^x'
J x2 y/2x + 3 J \ x + l
Г 5/ ж dx Г dx
J y^Tl ^' ' J У(х - 7O{x -W
9. / ^-j_dx. 10. / ^ + *<**-
У (i + 8)(l+^+8) У (i + lJ - v/iTT
Ответы.
1. A + #2ж - lJ + ln(\/2x - 1 - lJ + С 2. IzxctgsfxTl + C.
3. 6^x + 3^ + 2v/S-6b(l+ fyx) + C.
л/2ж + 3
4. - 2 arctg л/1 -ж + С. 5. - - + С.
6. ^ 1(g-2) + ^ln|g+v/ga-l| + C.
9. 6 arctg \/x + 8 - 61n \/x + 8 + 31n |1 + v^a; + 8| + C.
in i I (v^TT-1J | 2 VsTT+1 _
10. In — , = arctg = l-C.
\x + 2 + y/xTl\ V3 y/3
7.9. Интегрирование выражений
R(x, у/a2 ± x2 и R(x, \Jx2 — a2)
Постановка задачи. Найти неопределенные интегралы вида:
а) / R(x, v а2 — ж2) dx;
б) j R{x,y/a2 + x2)dx;
в) / Д(ж, \Jx2 — a2) dx;
где R — рациональная функция.

170
Гл. 7. Неопределенный интеграл
План решения.
1. Чтобы избавиться от радикала, используем
тригонометрические или гиперболические подстановки:
а) a; = asint или a; = atht;
б) a; = atgt или a; = asht;
. a
в) х — или a; = acnt.
cost
2. Применив формулу замены переменной в неопределенном
интеграле, получим интегралы вида
/
Ri (sin t, cost) dt.
3. Вычисляем последний интеграл с помощью известных
подстановок или методом понижения степени.
4. Возвращаемся к переменной х и записываем ответ.
Пример. Найти неопределенный интеграл
-2
/
dx.
ч/Э^2"
Решение.
1. Чтобы избавиться от радикала, воспользуемся подстановкой
х = 3sin£. Тогда dx = 3cost и \/9 — х2 — 3cost.
2. Сделаем замену переменной в неопределенном интеграле:
Г х2 , f9sin2t 3cost , „ Г . 2 ,
/ . dx = / . dt = 9 / sin21 dt.
J y/9^x* J V9-9sin2t J
3. Применяя формулы понижения степени, получим
/9 Г 9 9/" 9 9
sin2tdt=- (l-cos2t)dt = -t-- cos2tdt =-t--sin2t + C.
4. Возвращаемся к переменной х, подставляя t = arcsin(a;/3):
/
ч/9^
2 . 9 . x 9 . / . a;\ _
dx = - arcsin — — - sin I 2 arcsin — 1 + C.

7.9. Интегрирование иррациональных выражений 171
Замечание. Ответ можно упростить, если воспользоваться тем,
что sin 2t = 2 sin t v 1 — sin21 и sin t = x/Z:
I
Ответ
•/
x 9 xx i
. dx = - arcsin — — — у 9 — x2 + C.
y/9^x* 2 3 2 v
9
V9^,
dx = - arcsin — — — v 9 — x2 + С
3 2
y/W^x2
4dx.
dx.
>2 + x2 dx.
Условия ЗАДАЧ. Найти неопределенные интегралы.
. f у/4 - х2 dx. 2. f уД
I
J у/х2-4
/dx
x2 dx
y/B + x2K'
6.
8.
10
/dx
xy/x2 — 1
/dx
xy/4 + x2
f da
/ y/0~=
I
y/{i - x2f
dx
x3\/x2 — 1
dx.
Ответы.
x x i r -,
1. 2 arcsin — + — v 4 - x2 + С
2. ln(z + \J2 + x2) + -y/2 + x2 + С
3. |\Дс2 - 4 - 21n|z + y/x2 - 4| + С 4. arccos- + C.
5. 31n
Z-уДГ^;
+ y/9 - x2 + С 6. iln
v/4~+i2-2
+ C.

172
Гл. 7. Неопределенный интеграл
7.10. Интегрирование
дифференциального бинома
Постановка задачи. Найти неопределенный интеграл
I
xm(a + bxn)pdx, A)
где т, п и р — рациональные числа.
План решения. Выражение хт(а+ bxn)p dx называется
дифференциальным биномом. Условия его интегрируемости в
элементарных функциях получены П. Л. Чебышевым.
Условия Чебышева. Интеграл A) выражается через конечную
комбинацию элементарных функций в следующих трех случаях:
1) р — целое число; в этом случае подстановка х = zs, где s —
общий знаменатель дробей тип, приводит к интегралу от
рациональной функции.
.. т + 1 , _
2) целое число; в этом случае подстановка а + bx = z ,
п
где s — знаменатель дроби р, приводит к интегралу от рациональной
функции.
3) \- р — целое число; в этом случае подстановка ах~п + Ь —
п
= zs, где s — знаменатель дроби р, приводит к интегралу от
рациональной функции.
Пример. Найти неопределенный интеграл
5vT+17i
/
dx.
Решение. Перепишем интеграл в виде
J x Vx2 J
Подынтегральное выражение имеет вид хтA + хп)р при
7 11 т+1
т=—-, п=-, р=-, +р=-1.
5 ООП
Следовательно, имеет место третий случай интегрируемости.

7.10. Интегрирование дифференциального бинома 173
Применяя подстановку
х-1'3 + 1 = г5
и учитывая, что
х = (z5 - I), dx = -3(z5 - I)-4 5z*dz,
получаем
Условия ЗАДАЧ. Найти неопределенные интегралы.
1. /ЩД«Х. 2. /4Р*
J хг J xlyjx
Г 1 Г у/1-х4
7- I^TWdx- 8- fjS(& + i)"dx-
9. / —r-== da;. 10. / . . dx.
J х V(* + lJ У VTTi*
Ответы.

174
Гл. 7. Неопределенный интеграл
3. -1п(л/1+а;3-1)-1п|а;| + С.
. 1 . 1 + у/Т^х^ 1 у/Т^с*
4. - In = т 1— + С.
4 х2 4 а;4
i/#2 хЛ +с 6 !DV5+^-3)\Vi+^+a
4 \ х I 7 v
1 4
Bа;2-1)у/Г+^
За;3 + 2(^+l)8"r9D4/i+l)9
9. „у3 +ь/зл1ж* ч,+а
Л3/5ТТ (^Ч-!K
10. - In
1 , л4/! + ж4 + а; 1 \VTTa-4
4 #ГТ
а;4 — х
— — arctg -
+ С.

Глава 8
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
При изучении темы ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ вы
познакомитесь с формулой Ньютона-Лейбница и научитесь применять ее для
вычисления определенных интегралов, используя технику нахождения
первообразных. Вы научитесь применять определенные интегралы
для решения геометрических задач (вычисление площадей плоских
фигур, длин дуг кривых и объемов тел).
С помощью пакета РЕШЕБНИК.ВМ вы можете найти новые
пределы интегрирования (при использовании различных подстановок),
вычислить первообразные и применить формулу Ньютона-Лейбница,
выполнить все численные расчеты и проверить правильность
полученных вами результатов.
8.1. Интегрирование подведением
под знак дифференциала
Постановка задачи. Вычислить определенный интеграл
ь
I F(x)g(x)dx.
а
План решения. Пусть д(х) имеет очевидную первообразную
G(x), a F(x) есть функция этой первообразной, т.е. F(x) = u(G(x)).
Тогда
ь ь /8
Г F{x)g{x) dx= f u{G{x))G'(x) dx = f u(G) dG,
a a oc
где а = G(a), 0 = G(b).
Такого рода преобразование называется подведением под знак
дифференциала.

176
Гл. 8. Определенный интеграл
Если метод избран удачно, то последний интеграл оказывается
табличным или известным образом сводится к табличному, после
чего применяем формулу Ньютона-Лейбница.
Пример. Вычислить определенный интеграл
1
/xdx
х4 + 1'
о
Решение.
1. Представим подынтегральное выражение в виде произведения
двух функций F(x)g(x), где д(х) имеет очевидную первообразную
G(x), a F(x) есть функция этой первообразной, т.е. F(x) = u(G(x)).
В данном случае
F(g) = 5l + (»2J' 9{') = 2x, G(x)=x2, F(x) = ^r^=u(G).
2. Тогда
}jcdx__l_ Г 1 2 _ 1 [ 1
J x*+l~2j 1 + (х*)*аХ ~ 2 J 1 + GP '
0 0 0
где G = х2 и G@) = 0, G(l) = 1.
3. Последний интеграл является табличным. Применяем формулу
Ньютона-Лейбница:
о
1
_ Г xdx 7г
Ответ. / ——- = —.
J x4 + l 8
о
Условия ЗАДАЧ. Вычислить определенные интегралы.
1 тг/4
Г х , п Г sina; —™,„, ,
1. / —~ г^г яа;. 2. / ах.
J (х2 + 1J J (cosx + Г
о о
cos а;
sin а;K

8.2. Интегрирование по частям
УП
1 тг/4
3. / -г-2 ггтг dx. 4. / —х— dx.
J {x* + 4x + 2J J cos2 a;
о о
е
V2/2
5. f'-^dx. 6. Г ^=dx.
J X J л/T^lF
1 0
т/2 1
Г x cos x + sin x , f 2 arctg a; + a; ,
7. / —;—: r^— dx. 8. / ц dx.
J (x sin х)й J 1 + x*
тг/4 О
fP^dx. 10. f
J 2xy/x + x J
i 3v/a;+l , ,„ /" 2 arcsin x + x ,
9. / -—= dx. 10. / —— dx.
1 0
Ответы. 1.1/4. 2.-1/4. 3.5/56. 4.1. 5.5/4. б.тг/12. 7.14/тг
8. тг2/16 + In а/2. 9. lnB0/3). 10. (тг2 - 18л/3 + 36)/36.
8.2. Интегрирование по частям
Постановка задачи. Вычислить определенный интеграл
2
V
/ F(a;)p(a;) dx.
План решения. Пусть на отрезке [а, Ь] функция д(х) имеет
очевидную первообразную G(x), a F(x) — дифференцируемая функция,
причем ее производная f(x) — F'(x) является более простой
функцией, чем F(x). Тогда применяем формулу интегрирования по
частям
ь ь
[ F(x)g(x) dx = F(x)G(x) |* - Г f(x)G{x) dx.
о о
Если метод избран удачно, то интеграл в правой части этого
равенства оказывается табличным или известным образом сводится к
табличному, например повторным интегрированием по частям.

178
Гл. 8. Определенный интеграл
Пример. Вычислить определенный интеграл
2
/'
a; In xdx.
i
Решение.
1. Представим подынтегральное выражение в виде произведения
двух функций F(x)g(x), где д(х) имеет очевидную первообразную
G(x), a F(x) — дифференцируемая функция, причем ее производная
f(x) — F'(x) является более простой функцией, чем F(x).
В данном случае
х2 1
F(x) = In2 x, д(х) = х, G(x) = —, f(x) = F'(x) = 2]лх ■ -.
2 x
2. Применяем формулу интегрирования по частям
2 ■> 2 * 2
/х \ f х 1 f
xln2 xdx = — In2 а; — / — • 2 In x • —dx = 2 In2 2 — / a; In xdx.
2 ! ./ 2 x J
l l l
3. Последний интеграл не является табличным, но к нему можно
повторно применить формулу интегрирования по частям:
2 2,„2
Г 7* \* [Я* \ , XZ
I х In х dx = — In a; — / —- • — da; = 2 In 2
J 2 \1 J 2 x 4
2 3
= 21n2--.
i 4
2
Ответ. x\n2xdx= 21n22 - 21n2+-.
l
Условия задач. Вычислить определенные интегралы.
1 1
1. fxe-xdx. 2. J х arctg x dx.

8.3. Интегрирование тригонометрических выражений 179
2 2тг
3. / In a; da;. 4. / х2 cos x dx.
1 О
е тг/3
7. / In2 х dx. 8. /
7. / ln'xdx. 8. / ^'"^da.
i о
„"/2
9. / e^cos a; da;. 10. / cos In a; dx.
о l
Ответы. 1. (e-2)/e. 2. (тг - 2)/4. 3. 21n2-l. 4. 4тг. 5. тг/6—\/3+1.
6. тг2/4 - 2. 7. е - 2. 8. 2тг/3 - In tg Eтг/12). 9. З^ - 1)/5.
10. (е^2 - 1)/2.
8.3. Интегрирование выражений
i?(sinx,cosx)
Постановка задачи. Вычислить определенный интеграл
ь
I R(sin.x,cosx)dx,
где R — рациональная функция двух переменных.
План решения.
1. Если а и Ъ таковы, что функция tg (a;/2) определена на [а, Ь], то
с помощью подстановки
х
интегралы от функций i?(sin x, cos а;) приводятся к интегралам от
рациональных функций новой переменной t. Действительно, подставляя
в подынтегральное выражение
smx = TT¥' cosa; = TT^' dx = TT¥dt>

180
Гл. 8. Определенный интеграл
получаем
B1 1 — t2 \ 2
#(sinz,cosz) dx = R ( ^-^, —-^ J J—^ df = Rl^>dL
Подстановка t = tg (ж/2) называется универсальной.
2. Находим новые пределы интегрирования
а . 6
" = tg-, /3 = tg-.
3. Применяем формулу замены переменной в определенном
интеграле
ь /з
/д(81пж'с08Ж^ж = /д(тТ^'ТТ^) 17* *•
а а
4. Вычисляем первообразную рациональной функции t и
применяем формулу Ньютона-Лейбница.
Замечание. Если подынтегральная функция имеет специальный
вид, то лучше применить подстановки, требующие меньших
вычислений:
а) если- fi(sinx,cosx) = fii(sinx,cos2x)cosx, то применяем
подстановку t = sin x. Действительно, подынтегральное выражение
приобретает вид
Ri (sin x, cos2 x) cos xdx = Rj (t, 1 — t2) dt;
б) если fi(sin x, cos x) — /^(sin x, cos x) sin x, то применяем
подстановку t = cos x. Действительно, подынтегральное выражение
приобретает вид
Дг (sin2 х, cos x) sin ж dx = — Дг A — t2, t) dt;
в) если fi(sinx,cosx) = R^{t%x), то применяем подстановку
t = tgx (при условии, что функция tgx определена на [а, 6]).
Действительно, подынтегральное выражение приобретает вид
fi3(tgx) dx = R3(t) j-^2 dL

8.3. Интегрирование тригонометрических выражений 181
ПРИМЕР 1. Вычислить определенный интеграл
тг/2
/
sin ж
2 + sin ж
dx.
Решение.
1. Поскольку функция tg(x/2) определена на [0, тг/2], сделаем
подстановку
х
Подставляя в подынтегральное выражение
It
sin ж —
1 + t2'
dx =
1-И2
dt,
получим
It
^-dx= 1 + f2
2 + sin ж
■dt =
U
2 +
2t l+f2"- (f2 + f + l)(f2 + !)
dt.
1+i2
2. Находим новые пределы интегрирования
t@) = 0, «0 = 1-
3. Применяем формулу замены переменной в определенном
интеграле
»г/2 1
/•_8ШЖ_ Г 2*
У 2 + sinj; J (t2 + i + l)(t2 + 1
dt.
4. Вычисляем первообразную рациональной функции t и
применяем формулу Ньютона-Лейбница
/
П
(i2 +1 + l)(t2 + 1)
dt — 1 arctg t
1 4 It +1
0-7Trctg-7r
7Г 27Г
о 2 3^3'
Ответ
rr/2
-/5
sin ж 7Г 27Г
dx = —
2 + sina; 2 3\/3'

182
fir. 8. Определенный интеграл
Пример 2. Вычислить определенный интеграл
arccos(l/>/6)
/
3tg2x - 1
—~ — ах.
tg2x + 5
Решение.
1. Так как подынтегральная функция имеет вид R(tg x) и функция
tgx определена на [0, arccos(l/\/6)], сделаем подстановку tgx = t.
Подставляя в подынтегральное выражение
dt
tg x = t, ах —
1 + i2'
получаем рациональную функцию t:
3tg2x - 1 , 3t2 - 1 1 ,
—s ax = —т— ^ dr.
tg2x + 5 t2 + 5 1-M2
2. Находим новые пределы интегрирования:
tg@) = 0, tg I arccos —=. J = y/b.
3. Применяем формулу замены переменной в определенном
интеграле:
arccos(l/\/6) v/5
3tg2x - 1 Г 3t2 - 1 1
У tg2x + 5 У
tg2x + 5 У t2 + 5 1 + t2
о
dt.
4. Вычисляем первообразную рациональной функции t и
применяем формулу Ньютона-Лейбница:
v/5
J t2 + 5 1+t2
о
3t2 -1 1 ,
dt = —arctgt
^ 4 t
H—;= arctg -
о
v/5
Ответ. / —* dx = —= — arctg л/б.
У tg2x + 5 v/5
7Г /-
= -r= - arctg V5.
arccos(l/>/6)

8.4. Интегрирование тригонометрических выражений 183
Условия ЗАДАЧ. Вычислить определенные интегралы.
гг/2 гг/2
1. / dx. 2. /
J 5 + 4 sin ж + 3 cos ж у
3 + 5sinx + Зсобж
о о
dx.
гг/2 тг/2
/" COS3 Ж , f
3. / —5 dx. 4. /
У sin ж + sin ж J
COS Ж
dx.
dx.
3 + cos ж
rr/6 rr/3
rr/2 rr/2
5. f-^ j*. 6. /«?-*■
У Б1ПЖA+СОБЖ) У Sin Ж
rr/3 rr/4
rr/3 rr/4
7. /l±^£d«. 8. /_ 1 r-
У sin 2ж У 4 cos2 ж - 2 sin 2ж + sin ж
rr/4 0
rr/4 rr/4
/ 1 / 2бп1ж +Зсобж
9. / — s-da:. 10. / -7-5 —da:.
У 5 + cos-2 ж У sin ж cos ж + 9 cosd ж
о о
118 1 у/2 у/2 y/Q
Ответы. 1. -. 2. - In-. 3. 1п2 — -. 4. arctg — — arctg——.
653 2 ь 2 2 ь 6
5.| + |ьЗ. 6. J. 7.i(v/3-l + lnv/3). 8.1. 9-^arctgy|.
, 10 1
10. In— + arctg-.
8.4. Интегрирование выражений
sin2m x cos2n x
Постановка задачи. Вычислить определенный интеграл
ь
а
где тип — натуральные числа.

184
Гл. 8. Определенный интеграл
План РЕШЕНИЯ. Применяем формулы понижения степени
sin2 ж = -A —cos2x), cos2 ж = -A +cos2x), sinxcosx = -sin2x
до тех пор, пока не придем к табличным интегралам или к
интегралам, которые известным образом сводятся к табличным.
Замечание. Полезно иметь в виду, что
2гг 2л-
/ sin кх dx — О, / cos kxdx = 0 (к G N).
о о
Пример. Вычислить определенный интеграл
2тг
/ sin4 Зж cos4 Зж dx.
о
Решение. Применяя формулы понижения степени, имеем
2rr 2rr
/ sin4 Зж cos4 Зж dx — 2-4 / B sin Зж cos ЗжL dx =
о о
2гг 2л-
= 2-4 I sin4 6ж dx = 2~6 АA - cos 12жJ dx =
о о
2гг 2л- 2гг
= 2_6 dx- 2-5 / cos 12ж dx + 2-6 / cos2 12ж dx =
0 0 0
2?г
)dx ■■
о
2л- 2гг
= 2_5тг + Т1 \{\ + соб24ж) (
о
2л- 2гг
= 2-5тг + 2-7 I dx + ЧГ1 Jcos24xdx = 2-5тг + 2_6тг = -^.
о о
2тг
/Зтг
sin4 Зж cos4 Зж с?ж — -—.
64
о

8.5. Интегрирование иррациональных выражений 185
Условия ЗАДАЧ. Вычислить определенные интегралы.
о о
тг т/2
3. / sin2 - cos2 - dx. 4. / 25 cos6 ж dx.
о о
тг/2 тг/2
5. / 25 sin6 ж с?ж. 6. / 28 sin4 x cos4 x dx.
о о
тг/2 гг/2
7. / sin2 ж cos6 ж с?ж. 8. / :
8. / sinznxdx.
о о
гг/2 гг/2
9. I cos2mxdx. 10. J sin2nxcos2mxdx.
о о
Ответы. 1. 7г. 2. 7г. 3. 7г. 4. 57г. 5. 57г. 6. Зэт. 7. 7г.
Bп - 1)!! тг Bт - 1)!! тг Bп - 1)!! Bт-1)!! тг
Bп)!! ' Bт)!! 2' ' Bп + 2т)!! 2'
8.5. Интегрирование выражений
р ( ™ plax+b glax+b
Постановка задачи. Вычислить определенный интеграл
а.
где R — рациональная функция и р, q,... — натуральные числа.

186
Гл. 8. Определенный интеграл
План решения. С помощью подстановки
ах + Ь
сх + d
— tn
где п — общий знаменатель дробей 1/р, 1/q,..., приходим к
интегралам от рациональных функций.
ПРИМЕР. Вычислить определенный интеграл
2
Г 1у/2^х - у/Т+х
I —. . ах.
J (У^Т2 + 4л/2^¥)(ж + 2J
о
Решение.
1. Чтобы сделать подстановку, приводящую к интегралу от
рациональной функции, нужно преобразовать подынтегральную
функцию так, чтобы она содержала корни любой степени, но из одного
и т о г о ж е выражения вида ах ~J_j. Поэтому преобразуем
подынтегральное выражение, выделяя Jr. , f :
J (v/Ff2 + 4%/2^)(z + 2J J
^ dx= I L-Li dx
° о f 1 + 4*/- (z + 2J
vbl)
2. Применяем подстановку —
2-х
+ x
= t7
4 8t
х=щ-[-2, <b = -jp-^dt, t@) = l, tB)=0.
Делая замену переменной в определенном интеграле, получаем
J ( РГГх-\, оЧ, J 4t+l 16 V *2 + lV

8.5. Интегрирование иррациональных выражений 187
Вычисляем первообразную рациональной функции и применяем
формулу Ньютона-Лейбница:
1 >£(«-!) 1^
2 J 4t + 1 4
1
0
1
-?
+ -ln|4t + l|
In 5
б""
Ответ.
/
4y/2 - x - yJ2 + x
{Vx + 2 + 4y/2^x)(x + 2J
dx
ln5
"ie"'
Условия задач. Вычислить определенные интегралы.
f_Vx_
J л/5-1
dx.
2.
[ ^_ '
J у/х + 1+ л
у/х + \ + \/{х + IK
dx.
4 Х /
3. / dx. 4. / х —^-dx.
J l + v/2TTT У V2 + x
(^H-^ldx. 6. /
x+ \/з?+ fyx
' + л/жТТ "' 7 x(l+ З/х
1
63
dx.
7-!xerridx- 87
6-v/iTT-i- #яТТ
v/(x + lK - 7(x + 1) - 6 У (a: + lK
29
/
3+(/(x-2J
dx. 10.
/
4-^/2 - x - v/3x - 2
(ч/3х~^2 + 4v'2^~x')Cx - 2J
dx.
dx.
Ответы. 1. 7 + 21n2. 2. тг/6. 3. 2-ln2. 4. 3(^9-1)/8.
5. [y/2 - 1 - ln(l + \/2)]/2. 6. 9/2 - Зтг/2 + 6arctg2. 7. lnB + \/3)/2.
8. lnA6/81). 9. 8 + Зл/32тг/2. 10. 1п5/16.

188
Гл. 8. Определенный интеграл
8.6. Интегрирование выражений
R(x, (a2 ± х2I'2) и R(x, {x2 - а2I'2)
Постановка задачи. Вычислить определенные интегралы вида:
/3
a) / R(x, у/а2 — ж2) dx;
а
/3
а
/3
в) / R(x, у/х2 — a2) dx;
где R — рациональная функция.
План решения.
1. Чтобы избавиться от радикала, используем
тригонометрические или гиперболические подстановки:
а) x = asint или х = atht;
б) х — atgt или х — asht;
. a .
в) х = или х = acht.
cost
2. Применив формулу замены переменной в определенном
интеграле, получим интегралы вида
I Ri(sint,cost)dt или / Ri(sht,cht)dt.
t, t,
3. Вычисляем полученные интегралы с помощью известных
подстановок или методом понижения степени.
ПРИМЕР. Вычислить определенный интеграл
3/2
/
„2
X
-dx.
у/Г-
о
Решение.
1. Чтобы избавиться от радикала, используем подстановку

8.6. Интегрирование иррациональных выражений 189
х — 3 sin t. Тогда
dx = 3 cos t dt, t@) = arcsinO = 0, Mo)— arcsin - = —
\2/ 2 6
и л/9 — x2 = |3cost| = 3cost, поскольку cost>0 при t£[0,7r/6].
2. Сделаем замену переменной в определенном интеграле:
3/2 jr/6 jt/6
/ ж2 /" 9(sintJ-3cost , Л Г . 2 ,
/ dx= / V ; ==■ dt = 9 / sin2tdi.
У л/JT^2 У v/9-9(sintJ У
о о v о
3. Применяя формулы понижения степени, получим
ГГ/6 7Г/6 7г/б
9 / sin2 tdt = - / A - cos2t) dt= -ж- - I cos2tdt =
oo о
3 9 . Г/6 З 9ч/3
= -7Г Sin2t = -7Г •
3/2
4 4 |0 4 8
х2 ^ 3 9ч/3
Ответ. / . dx — —ж —-.
v/9^^ 4 8
о
Условия ЗАДАЧ. Вычислить определенные интегралы.
1 3
1. / л/1 - ж2 dx. 2. /x2\/9-x2dx.
/^ - /
3. I^ZI*,. 4. /^Пй.
1 1
У x2 dx" 6' у д/A + *2K
1/2 О
3 . 5
у/{9 ~ х2K
Г*9-***,. 8. А-*
J х6 У x2Vx*^>
: dx.
9
1 3
n/3 , 1
/" v/l + X2 Г 1
9. / V , dx. 10. / ■=
J x2 J x+VT
1 0

190
Гл. 8. Определенный интеграл
ъ - "" 817Г „ \/3 I- 7Г /- 7Г \/2
Ответы. 1. -. 2. —. 3. т. 4. v/3- -. 5. л/5- -. 6. -.
7Г
128у/2 4 3y/2-2y/3 , , 2 + у/з
7. ———. 8.-—. 9. hln —. 10. t
45 45 3 1 + л/2 4
8.7. Вычисление площадей
в декартовых координатах
Постановка задачи. Вычислить площадь области,
ограниченной графиками функций у = /i(x) и у = /г(х) (/i(x) > fi{x) или
/i(x) < /г(х) для всех точек области) и, возможно, прямыми х = а
их = Ь.
План решения. Если область D задана системой неравенств
{
а < х < Ь,
и(х) <у< v(x),
то площадь области D вычисляется по формуле
SD= J (v(x) - и{х)) dx. A)
Jo
Если неравенства, определяющие область D, неизвестны, т.е.
неизвестны а и Ь и неизвестно, какая из функций /i(x) и fi{x) больше
другой на (а, Ь), то выполняем следующие операции.
1. Находим а и Ь как абсциссы точек пересечения графиков
функций /i(x) и /г(х), т.е. решаем уравнение
Д(х) = /2(х).
2. Исследуем знак разности /i(x) — /г(х) на [а,Ь]. Для этого
достаточно вычислить значение /i(x) — /г(х) в какой-нибудь точке из
(а,Ь). Если оно положительно, то /i(x) > /г(х) и, следовательно,
и(х) — /г(х) и г;(х) = /i(x). Если оно отрицательно, то /i(x) < /2(х)
и, следовательно, и(х) = /i(x) и г;(х) = /г(х).
3. Применяем формулу A) и находим Sp.
Записываем ответ, не забывая о размерности.

8.7. Вычисление площадей в декартовых координатах 191
Пример. Вычислить площадь области, ограниченной графиками
функций
у - х2 - 4х + 3, у = -х2 + 2х + 3.
Решение.
1. Находим абсциссы а и 6 точек пересечения графиков. Для этого
решаем уравнение
х2 - 4х + 3 = -х2 + 2х + 3.
Получаем а = 0, 6 = 3.
2. Исследуем знак функции ip = х2 — 4х + 3 — (—х2 + 2х + 3) на
отрезке [а, 6] — [0,3]. Для этого придадим х любое значение из @,3),
например х = 1. Получаем, что <рA) = —4. Следовательно, f < 0 при
х £ @,3). Поэтому х2 — 4х + 3 < —х2 + 2х + 3 при х G [0,3] и область
D определяется системой неравенств
{
0 < х < 3,
г2 - 4х + 3 < у < -х2 + 2х + 3.
3. Применяем формулу A) при г;(х) = —х2 + 2х + 3, и(х) =
= х2 - 4х + 3, а = 0 и 6 = 3:
SD= (-х2 + 2х + 3 - х2 + 4х - 3) dx = / (-2х2 + 6х) dx = 9.
JO JO
Ответ. 5 = 9 (ед. длиныJ.
УСЛОВИЯ ЗАДАЧ. Вычислить площади областей, ограниченных
графиками заданных функций.
1. у = 32-х2, у = -4х.
2. у = Зл/х, у — 3/х, х = 4.
3. х = 5 - у2, х = —Ау.
4. у = \/ех - 1, у —0, х = 1п4.
5. j/ = sinx, y — cosx, х = 0 (х > 0).
6. у — v/x, У — 1/х, х -16.

192
Гл. 8. Определенный интеграл
7. х = 27-у2, х= -6у.
8. y = sinx, y = cosx, х = 0 (я < 0).
9. у = у/9 - х2, у = 0, х = 0, х = 3/2.
10. у = 2/х, у = 5ех, у = 2, у = 5.
Ответы. 1.288. 2. 14-31п4. 3.36. 4. F\/3 - 2тг)/3. 5. л/2-1.
6. 42 - In 16. 7. 288. 8. 1 + у/2. 9. (Зтг + \/3)/4. 10. 3.
8.8. Вычисление длин дуг у — f(x)
Постановка ЗАДАЧИ. Вычислить длину кривой, заданной
уравнением
У = f{x)
и ограниченной точками с абсциссами х — а и х = Ь.
План решения. Длина I кусочно гладкой кривой у = f(x),
ограниченной точками с абсциссами х = а и х = Ь, равна
ь
I = j \/l + (y'Jdx. A)
а
1. Находим у1 — f'(x).
2. Вычисляем дифференциал длины дуги
dl = y/l + (y'Jdx.
3. Находим длину дуги, вычисляя определенный интеграл A).
Записываем ответ, не забывая о размерности.
Пример. Вычислить длину дуги кривой
1 _ е* _ е-х
У= 0<*<3.

8.8. Вычисление длин дуг у = f(x)
193
Решение.
1. Дифференцируя уравнение кривой, получим
, -ех + е~х
У = = -shx.
2. Вычисляем дифференциал длины дуги:
dl — y/l + (у1J dx = v 1 + sh2xdx = chxdx.
3. Находим длину дуги, вычисляя определенный интеграл A):
Г3 з
1=1 chxdx = shx|0 = sh3.
JO
Ответ. I = sh 3 ед. длины.
Условия ЗАДАЧ. Вычислить длины дуг заданных кривых.
1. у = 1пх, 2v/2<x<2v/6.
2. j/ = lncosx, 0 < х < 7г/6.
3. у = ех, 1п\/3<х<1пл/8-
4. у — In sin х, 7г/3 < х < 7г/2.
5. у = 2у/х, 1/3 < х < 1/8.
6. у = chx, 0 < х < 1.
7. у = х2/2, 0 < х < 1.
8. у = 1-1пх, уД<х<у/8.
9. у = 1 - chx, 0 <х< 3.
10. у — \/1 -x2+arcsinx, 0 < х < 1/2.
Л , 2 ЬЗ „ 1, 3 , 1пЗ r n , 3
Ответы. 1. 2 + 1п—. 2.-—. 3.1 +-In-. 4.-—. 5. 2 +In-.
6.shl. 7 v^ + ln(l + v^) 8.l + |b|. 9.sh3. 10.2(v/3-v/2).

194
Гл. 8. Определенный интеграл
8.9. Вычисление длин дуг х = :г(£), у = y(t)
Постановка задачи. Вычислить длину дуги кривой, заданной
параметрически
{Х=Х£Ь «<t<p.
\ y = y(t),
План решения. Если кривая задана уравнениями в
параметрической форме
\ y = y{t),
где х = x(t) и у = y(i) — кусочно-гладкие функции, то длина I дуги
кривой определяется формулой
/3
1 = JV(*iJ + (!/02*, (l)
Q
где а и Р — значения параметра, соответствующие граничным
точкам дуги.
1. Находим х[ и y't.
2. Вычисляем дифференциал длины дуги
dl = y/{x'tJ + {y'tJdt.
3. Находим длину дуги, вычисляя определенный интеграл A).
Записываем ответ, не забывая о размерности.
Пример. Вычислить длину дуги кривой, заданной
параметрически
f х = (t2 - 2) sin* + It cost,
\ y = {2-t2)cost + 2tsint, U<t_7r.
Решение.
1. Находим х\ и у[ :
x't = t2 cos t, y't = t2 sin t.
2. Вычисляем дифференциал длины дуги:
dl = y/(x'tJ + (y'tJ dt = V't4 cos4 t + t4 sin4 tdt = t2 dt.

8.9. Вычисление длин дуг х = x(t), у = y(t)
195
3. Находим длину дуги, вычисляя определенный интеграл A):
7Г
Vdt
7Г°
У
Ответ. / = 7г3/3 ед. длины.
Условия ЗАДАЧ. Вычислить длины дуг заданных кривых.
1.
3.
5.
6.
7.
8.
9.
10.
Г х — t — sin t,
\ у = 1 — cos t,
j x = 2 cos t,
\ j/ = 2sin«,
( X — COS3 t,
\ j/ = sin3*,
{x = 2 cos t —
у = 2sin£ -
{x — e* cost,
у = e'sint,
{
{
J x = cos £ +
^ у = sin t —
0<t<2n.
0<t< тг/3.
0 < t < тт.
— cos 2£,
x = e* sin i,
у = elcost,
x — 3cos£,
у — 3 sin i,
sin 2t,
0<t<l.
0<t<7T.
0<t<2n.
t sin t,
t cos £,
x — 4 cos3£,
у = 4 sin3 £,
{
Г x = 2(< - sin*),
\ у = 2A -cost),
0 < t < тг/6.
0 < t < тг/3.
0 < t < тг/6.
7Г < t < 7Г/2.
Ответы. 1. 8. 2. 2тг/3. 3. 3. 4. 16. 5. \/2(e - 1). 6. v^(e* - 1).
7. тг/2. 8. тг2/18. 9. 3. 10. 8 - 4v/2.

196
Гл. 8. Определенный интеграл
8.10. Вычисление длин дуг g — д{ф)
Постановка задачи. Вычислить длину дуги кривой, заданной
уравнением в полярных координатах
Q = Q(<p), a<(p<C.
План решения.
Если кусочно гладкая кривая задана уравнением в полярных
координатах q = g((p), то длина дуги равна
/3
1 = JVQ(VJ + Q'(vJdv, A)
Q
где а и /3 — значения tp, соответствующие граничным точкам дуги.
1. Находим (>'(ф).
2. Вычисляем дифференциал длины дуги
dl = \ZQ{fJ + Q'{fJd<fi.
3. Находим длину дуги, вычисляя определенный интеграл A).
Записываем ответ, не забывая о размерности.
ПРИМЕР. Вычислить длину дуги кривой, заданной уравнением в
полярных координатах
Q = 6sm<p, 0 < tfi < 7г/3.
Решение.
1. Находим д'(<р):
g'if) = 6 cos ip.
2. Вычисляем дифференциал длины дуги:
dl = л/д(<рJ + g'{<pJ dtp — y36sin2 (p + 36 cos2 <pd<p = 6dip.
3. Находим длину дуги, вычисляя определенный интеграл A):
тг/З
о
Ответ. I = 2п ед. длины.
1= f 6d<p= 6у>|о/3 = 2тг.

8.11. Вычисление объемов по площадям поперечных сечений 197
Условия ЗАДАЧ. Вычислить длины дуг заданных кривой.
7Г
1. Q = If, 0 < (f < 1. 2. Q=COStfi, 0<ip<—.
7Г
3. g — 2smip, — < <р < п. 4. q=\ — costp, 0 < ip < 7г.
5. g=l + cos<p, 0<tp<n. 6. о = е2*, 0<ip<27r.
7Г 7Г 7Г Зя"
7. e=l + sinv, -_<^<_. 8. e=l-sm^, - < <p < —.
9. £ = 3siny>, 0 < (p < —. 10. g = 3cosv?, 0 < у < —.
6 о
Ответы. 1. [v/2 + ln(l + v/2)]/2. 2. тг/2. 3. тг. 4. 2. 5. 2.
6. Vb(e47r -1)/2. 7. 2. 8. 2. 9. тг/2. 10. ж.
8.11. Вычисление объемов
по площадям поперечных сечений
Постановка задачи. Вычислить объем тела, если известны
площади его поперечных сечений.
План решения. Если 5 = S(x) — площадь сечения тела
плоскостью, перпендикулярной к оси ОХ и пересекающей ее в точке с
абсциссой х, то объем части тела, заключенной между плоскостями
х = х\ и х = Х2, определяется формулой
Х2
/ S(x) dx. A)
Xl
1. Находим S{x).
2. Подставляем S(x) в формулу A) и вычисляем определенный
интеграл.
Записываем ответ, не забывая о размерности.
Замечание. Аналогично решается задача, если известны
площади сечений плоскостями, перпендикулярными оси OY {S(y)) или
оси OZ (S(z)).

198
Гл. 8. Определенный интеграл
Пример. Вычислить объем тела, ограниченного поверхностями
я2 у2 z2
Решение. Если S — S(z) — площадь сечения тела плоскостью,
перпендикулярной к оси OZ и пересекающей ее в точке с аппликатой
z, то объем части тела, заключенной между плоскостями z — z\ и
z = z2, определяется формулой
V
= IS{z)dz. B)
*1
1. Сечение заданного тела плоскостью z = const определяется
неравенством
х2 у2 „ z2
— + — < 1 ,
16 9 _ 196'
т.е. при \z\ < 14 является эллипсом
196х2 196у2
16A96 - z2) 9A96 - z2)
с полуосями
4-^196 - z2 , 3V196 - z2
14 ' 14
Площадь этого эллипса равна
5 = тгаЬ=^-A96-22).
Таким образом, при 0 < z < 7
S(z) = gA96-z2).
2. Подставляем S(z) в формулу B) и вычисляем определенный
интеграл:
7
\3
V = -£- A96 - z2) dz = 77тг (ед. длиныK
о
Ответ. 777Г (ед. длины) .

8.12. Вычисление объемов тел вращения
199
Условия задач. Вычислить объемы тел, ограниченных
указанными поверхностями.
1. z = Ах2 + 9у2, 2 = 6.
2. z = 9х2 + 4у2, 2 = 6.
3. 2 = 2х2 + 8у2, 2 = 4.
v2 z2
4. х2 + ^- + — = 1, 2 = 0, 2 = 2.
X2 22
5- ^+У2 + —= 1, 2 = 0, 2 = 3.
X
2
„2 Q.2
6. — + У* - 3Z* = 1, 2=0, 2=1.
7. х2 + У- - 2z2 = 1, 2 = 0, 2 = 1.
Ответы. 1. Зтг. 2. Зтг. 3. 2тг. 4. 4тг. 5. 8тг. 6. бтг. 7. 5тг.
8. 42тг. 9. 8тг. 10. 50тг.
8.12. Вычисление объемов тел вращения
Постановка задачи. Вычислить объем тела, образованного
вращением области, ограниченной графиками функций у — /i(x) и
у — /г(х) и, возможно, прямыми х — а и х — Ь, вокруг оси ОХ.
План решения. Объем тела, образованного вращением области,
ограниченной кривыми у = и(х) и у = v(x) и прямыми х — а, х — Ь,
где и(х) < v(x), т.е. области, определяемой системой неравенств
Г а < х < Ь,
1 и(х) < у < v(x),

200
Гл. 8. Определенный интеграл
вычисляется по формуле
V = тг [ (v{xJ - u{xJ) dx. A)
1. Определяем область D. Если неравенства, определяющие
область D, неизвестны, т.е. неизвестны а и Ъ и/или неизвестно, какая
из функций Д(х) и /г(х) больше другой на отрезке [а, Ь], то
выполняем следующие операции.
а) находим а и Ъ как абсциссы точек пересечения графиков
функций /i(x) и /2(х), т.е. решаем уравнение
Л (я) = /2B);
б) исследуем знак разности Д(х) — /г(х) на [а, Ь]. Для этого
достаточно вычислить значение Д(х) — /г(х) в какой-нибудь точке из (а, Ь).
Если оно положительно, то /i(x) > /г(х) и, следовательно, и(х) —
= /г(х) и г;(х) = /i(x). Если оно отрицательно, то Д(х) < /г(х) и,
следовательно, и(х) = Д(х) и г;(х) = /г(х).
2. Вычисляем объем по формуле A).
Записываем ответ, не забывая о размерности.
Замечание. Аналогично решается задача, если тело образовано
вращением области вокруг оси OY или оси OZ.
Пример. Вычислить объем тела, образованного вращением
области, ограниченной графиками функций
у = х3 у = \/х,
вокруг оси ОХ.
Решение.
1. Определяем область D:
а) находим абсциссы а и Ь точек пересечения графиков. Для этого
решаем уравнение
х3 = у/х.
Получаем
а = 0, Ь = 1;
б) на отрезке [0,1] \[х > х3. Следовательно, и(х) =х3 и г;(х) = у/х.

8.12. Вычисление объемов тел вращения
201
2. Вычисляем объем по формуле A):
V = 7Г / [(у/БJ - (X3J]dx = 7Г / (х - X6)dx = ^.
Jo Jo l^
Ответ. 57г/14 (ед. длины) .
Условия ЗАДАЧ. Вычислить объемы тел, образованных
вращением вокруг оси ОХ областей, ограниченных графиками заданных
функций.
1. у = -х2 + 1, у — О. 2. у — sm{nx/2), у = х.
3. j/ = х2, j/ = у/х. 4. у-х2, у = 2х.
5. j/ = cosx, j/ = sinx, x = 0 @ < х < 7г/4).
6. j/ = sin2 х, j/ = 0, х = тг/2 @ < х < тг/2).
7. 2/ = ех, у = 1, х = 1.
8. j/ = lnx, 3/=0, х = е.
2
9. у=-, J/ = l, x = l.
х
10. j/ = cos2 х, j/ = 0 (-эт/2 < х < тг/2).
Ответы. 1. 16тг/15. 2. Eтг2 - 48)/Fтг). 3. Зтг/10. 4. 16тг/15.
5. тг2/4 - 1/2. 6. Зтг2/16. 7. тг(е2 - 4е + 5)/2. 8. тг(е - 2).
9. тгC-41п2). 10. Зтг2/8.

Глава 9
КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
При изучении темы КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ вы
познакомитесь с понятиями криволинейных интегралов первого рода
(по длине дуги) и второго рода (по координатам) от функций двух и
трех переменных и научитесь вычислять их вдоль различных плоских
и пространственных кривых, заданных параметрически, в
декартовых и в полярных координатах, приводя криволинейные интегралы к
определенным.
С помощью пакета РЕП1ЕБНИК.ВМ вы можете вычислить
производные функций, задающих кривую, решить системы уравнений,
определяющие граничные значения параметра, вычислить
полученные вами определенные интегралы и проверить правильность
полученных вами результатов.
9.1. Криволинейные интегралы
первого рода
Постановка задачи. Вычислить криволинейный интеграл
/ f{x,y,z)dl,
ь
где L — часть гладкой кривой, заданной параметрически
х = x(t),
у = y{t), h <t< t2,
z = z(t),
и dl — дифференциал длины дуги.

9.1. Криволинейные интегралы первого рода
203
ПЛАН РЕШЕНИЯ. Криволинейный интеграл первого рода по
кривой L определяется формулой
«2
J /(х, y,z)dl = J f{x{t), y(t), z(t)) y/xW + y'(tJ + z>(t)*dt. A)
L ti
Подчеркнем, что криволинейный интеграл первого рода не зависит
от направления обхода кривой и всегда ti < t2.
1. Вычисляем x'{t), y'(t), z'(i) и dl = ■sfx'itJ + j/'(fJ + z'(tJdt.
2. Вычисляем криволинейный интеграл по формуле A) и
записываем ответ.
Замечание 1. Если граничные точки кривой L M(xi,yi,zi) и
N(x2, J/2, z2) заданы в декартовых координатах, то f i и t2 определяем,
решая системы уравнений
2i = x(U), ( х2 = x(t2),
J/i = y(h), < J/2 = y(t2),
z\ = z{ti); { z2 = z(t2).
Замечание 2. Если кривая задана как линия пересечения двух
поверхностей:
Г Fi(x,y,z) = 0,
\ F2(x,y,z)=0,
то ее необходимо параметризовать.
Замечание 3. Если плоская кривая задана уравнением у — у{х)
(а < х < Ь), то дифференциал длины дуги равен dl = ^/1 + у'(хJ dx
и формула A) имеет вид
ь
j f{x, у) dl = j f(x, y{x)) v/1 + y'{xJ dx. A')
L a
Если плоская кривая задана в полярных координатах (я = gcosip,
у = gsinip) уравнением g = g((f) (a < ip < b), то дифференциал длины
дуги равен

204
Гл. 9. Криволинейные интегралы
и формула A) имеет вид
ь
I f(x,y)dl = / f(g(<p)costp,g(tp)simp) y/g{(pJ + g'{<pJd<p. A")
L a
Пример 1. Вычислить криволинейный интеграл
■Л
I
z
dl,
х2 + у2
L
где L — первый виток винтовой линии
х = cosf,
у — sint, 0 < t < 2-я.
z = t,
Решение.
1. Вычисляем: x'{t) = —sinf, y'{t) = cost, z'(t) — 1, dl — \/2dt и
f(x,y) = z2/(x2+y2)=t2.
2. Подставляем эти результаты в формулу A) и вычисляем
определенный интеграл:
2т
8%/2тг3
/^TF'fl = /i!^ =
L
Ответ.
'•/
х2 + у2 3
L
Пример 2. Вычислить криволинейный интеграл
(х-у)dl,
ь
где L — отрезок прямой от точки А@,0) до точки ВD., 3).
Решение.
1. В данном случае уравнение прямой есть у — Зх/4 @ < х < 4)
и, следовательно, у'(х) — 3/4 и dl = Ъ/idt.

9.1. Криволинейные интегралы первого рода
205
2. Подставляем эти результаты в формулу A') и вычисляем
определенный интеграл:
I (x-y)dl= I (х- -х) ^dx=-.
L 0
Ответ. I (х — y)dl — -.
ь
Пример 3. Вычислить криволинейный интеграл
Г у
/ arctg — dl,
L
где L — часть спирали Архимеда g = ip @ <ip < 7г/2).
Решение.
1. Вычисляем: д'((р) — 1, dl — у/(р2 + 1 dip и f{x,y) — ip, так как
arctg (tg ip) = ip при 0 < ip < -njl.
2. Подставляем эти результаты в формулу A") и вычисляем
определенный интеграл:
/Mrtg i Л - 'fr&Ti* =^+if \""= f+42f -8.
L 0 °
Г « (тг2 + 4K/2-8
Ответ. / arctg — dl = .
J x 24
L
Условия ЗАДАЧ. Вычислить криволинейные интегралы.
1. /у» Л, L - пасть кривой x = t- sin, у = 1 - cos*
@ < f < 27г) (арка ииклоиды).
. /*а7,
L — •часть кривой х = tcost, у — tsint, z = t
L
@ < t < 7г) (первый виток конической винтовой линии).

206
Пг. 9. Криволинейные интегралы
3. /(** + у- + *2) dl, L - част, кривой х = cost, у = sin.,
L
z = It @ < t < 7г) (первый виток винтовой линии).
4. / yJ2ydl, L — часть кривой х = t, у — t2/2, z = f3/3
L
(О < t < 1).
5. / y/ydl, L — часть параболы у = x2 от точки А@,0) <?о
точки ВB,4).
6. I xdl, L — отрезок прямой от точки ЛA,0) до точки
B@,2)L
7. / (я + ?/)а7, L — граница треугольника с вершинами @,0),
A,0) и @,1).
8. fj*T?a, L-окружность х> +у* = 2х.
L
9. / \Jx2 + y2dl, L — кардиоида g=l — cosip.
10.
L
I \y\dl, L — лемниската Бернулли g = y/oo~PZip.
, 64 n B + 7Г2K/2 - 2л/2 „ 2тгч/5C+1б7г2)
Ответы. 1. —. 2. - . 3. *— .
3 3 3
32
8. 8. 9. —. 10. 2B - л/2).
О

9.2. Криволинейные интегралы второго рода
207
9.2. Криволинейные интегралы
второго рода
Постановка задачи. Вычислить криволинейный интеграл
/ Р(х, у, z) dx + Q(x, у, z) dy + R(x, у, z) dz
L
где L — •часть гладкой кривой, заданной параметрически
х — x(i),
У = y(t), h<t< t2,
z = z(t).
План решения. Криволинейный интеграл второго рода по
кривой L определяется формулой
/ Р(х, у, z) dx + Q(x, у, z) dy + R(x, у, z) dz =
У'[Р(а;@,»(*)»г(*))*'(*) + в(а;(*).»(*),г(*))»'(*)+Я(а!(*).»(*).г(*))г'(*)]Л.
t,
1. Вычисляем x'(t), y'(t) и z'(t).
2. Вычисляем криволинейный интеграл по формуле A) и
записываем ответ.
Замечание 1. Если граничные точки кривой L M(xi,yi,zi) и
N(xi, j/2, Z2) заданы в декартовых координатах, то t\ и ti определяем,
решая системы уравнений
Xi = X(fi), ( Х2= X{t2),
J/i = y(h), I У2 = y(t2),
zi = z(ti); { z2 = z[t2).
ЗАМЕЧАНИЕ 2. Если кривая задана как линия пересечения двух
поверхностей:
Г Fl{x,y,z) = 0,
\ F2(x,y,z) = 0,
то ее необходимо параметризовать.

208
Гл. 9. Криволинейные интегралы
Пример 1. Вычислить криволинейный интеграл
/
dx — Зх dy + х dz
по части кривой L, заданной параметрически
х = 2 cost,
у = 2 sin t,
z — 1 — 2cosf — 2smt.
0<*<-,
Решение.
1. Вычисляем: x'(t) = —2sinf, y'(t) = 2cosf и z'(t) = 2sin£ —2cosf.
2. Вычисляем криволинейный интеграл по формуле A):
/
dx — Зх dy + x dz —
тг/2
= / -sinf(—2sinf) — 6cosiBcosf) +2cosfBsinf — 2cosf)
о
dt
о 13
= 2--,.
/13
y/3 dx — 3x dy + x dz = 2 ——тг.
Пример 2. Вычислить криволинейный интеграл
J(x-y)dx+dy + zdz
от точки МB,0,4) до точки N(—2,0,4) (j/ > 0) по кривой L,
образованной пересечением параболоида 2=х2 + у2 и плоскости 2 = 4,
Решение. В сечении получается окружность
х2 + у2 = 4,
2 = 4.

9.2. Криволинейные интегралы второго рода 209
Поэтому параметрические уравнения кривой L имеют вид
х = 2cosf,
у = 2sinf,
2 = 4.
1. Вычисляем: x'(t) — —2sinf, y'(t) = 2cosf и z'(t) = 0.
Определяем 11 и i2 из условий
2 = 2cosfb Г -2 = 2cosf2,
0 = 2sinfb \ 0 = 2sinf2,
4 = 4; ^4=4.
Учитывая, что у > 0, получаем 11 = 0 и f2 = тт.
2. Вычисляем криволинейный интеграл по формуле A):
/ (х -y)dx + dy + zdz — I [Bcosf - 2sinf)(-2sinf) +2cosf]<tt = 2-я.
l 0
Ответ. / (x — y)dx + dy + zdz = 2ж.
L
Условия ЗАДАЧ. Вычислить криволинейные интегралы.
j(y2-z2)
dx + 2yz dy — x dz, L — часть кривой х = t,y = t2,
L
z = t3 от точки М@,0,0) до точки NA,1,1).
2. / B — y)dx + xdy, L — арка циклоиды х = t — sinf,
L
y=l-cost @<*<2тг).
3. / ydx+zdy + xdz, L — первый виток винтовой линии
L
-cost, у — sint, z — t.
4. /(x + y)dx + (x - y)dy, L - окружность (x - 1)* + {y - 1)* = 4.
L
/(x + y)dx — (x — y)dy , 9 ,
-—x—^ —, L — окружность x + J/ = 1.
xz + yz
L

210
Гл. 9. Криволинейные интегралы
6. / Dа; 4- у) dx + (х + 4у) dy, L — часть параболы у — х4 от
точки МA,1) до точки N(—1,1).
7. / 2ху dx + х2 dy, L - отрезок прямой от точки М@,0) до
L
точки N{\, 1).
8. I ydx + xdy + (х + у + z) dz, L — отрезок прямой от точки
МB,3,4) до точки 7VC,4,5).
9. / zdx + xdy + у dz, L — линия пересечения цилиндра х2 +у2=А
и плоскости z — 0.
10. fydx - xdy + zdz, L - линия пересечения сферы x2+y4z2=4
L
и конуса х2 + у2 = z2 (z > 0).
Ответы. 1. 1/35. 2. -2тг. 3. -it. 4.0. 5. -2тг. 6.-2. 7.1.
8. 33/2. 9. 4тг. 10. - 4тг.

Глава 10
РЯДЫ
При изучении темы РЯДЫ вы познакомитесь с понятиями
сходимости, суммы и остатка ряда, научитесь исследовать сходимость
числовых рядов, применяя теоремы сравнения и различные признаки
сходимости. Вы познакомитесь с понятиями функционального и
степенного рядов, научитесь находить их области сходимости и суммы.
Вы узнаете, что такое ряд Тейлора, научитесь находить разложения
функций в ряд Тейлора и применять полученные разложения в
приближенных вычислениях.
С помощью пакета РЕШЕБНИК.ВМ вы можете вычислить
пределы, выполнить приближенные вычисления и проверить полученные
вами результаты.
10.1. Понятие суммы ряда
Постановка задачи. Найти сумму ряда
у d ,
^-J n2 + рп + q'
где A,p,q — целые числа.
ОО
План решения. Суммой ряда 52 ап называется предел 5 после-
п=1
довательности его частичных сумм {5„}, т.е.
5 = lim 5„, A)
п—юо
где Sn — а\ + а2 + .. ■ + а„.
1. По условию задачи
А
пА +pn + q

212
Гл. 10. Ряды
Если корни знаменателя различаются на целое число, т.е. n2+pn+q =
= (п 4- а)(п + а + к), где к — натуральное число, то члены после-
оо
довательности частичных сумм ряда 52 ап легко найти, так как в
п=1
выражении Sn — «i 4- ai +... + ап многие слагаемые взаимно
уничтожаются.
2. Разлагаем общий член ряда на элементарные дроби:
А _ 1 /_А А \
n2+pn + q к \п + a n + a + kj '
и выписываем несколько членов ряда так, чтобы было видно, какие
слагаемые сокращаются при вычислении частичных сумм ряда.
3. Находим n-ю частичную сумму ряда:
Sn = 0,1 + а2 + ■ ■ ■ + ап,
сократив соответствующие слагаемые.
4. Вычисляем сумму ряда по формуле A)
5= lim Sn
п—>оо
и записываем ответ.
Пример. Найти сумму ряда
^ п2 + Ъп + 4"
Решение.
1. Корни знаменателя п = — 1 и п = — 4 различаются на целое
число, т.е. п2 + Ъп + 4 = (п + 1)(п + 1 + 3). Следовательно, члены по-
следовательности частичных сумм ряда 52 °п легко найти, так как
п=1
в выражении Sn — аг + а-ь + ... + ап многие слагаемые взаимно
уничтожаются.
2. Разлагаем общий член ряда на элементарные дроби
- 72 _ 24 24
п2+5п + 4 п + 1 п + 4
и выписываем несколько членов ряда:
24 24 24 24 24 24

20.2. Понятие суммы ряда
213
24 24 24
^""Т1 °5 = "б""
24 24
Оп-5 — . , ,
п — 4 п — 1
24 24
°п-з — 0 ■; 1»
24 24 24
" 9 ' °6 " У ~ 10'
24 24
«п-4 = „■ ,
п — 3 п
24 24
О-п-1 — л , 0.
п-2 п + 1' " ' п-1 п + 2'
_ 24 24 24 24
п п+3 п+1п+4
3. Сокращая все слагаемые, какие возможно, находим n-ю
частичную сумму ряда:
5п = «1 + о,1 + ... + ап =
24 24 24 24 24 24 „„ 24 24 24
= тг + ^г + -: г ^ : = 26
2 3 4 п+2 п+3 п+4 п+2 п+3 п+4
4. Вычисляем сумму ряда по формуле A):
/ 24 24 24 \
5 = lim 5„ = lim ( 26 ) =
n-юо п-юо у п + 2 п + 3 п + 4/
26.
Ответ. 5 = 26.
Условия ЗАДАЧ. Найти суммы рядов.
2
1. у 6—
*-^ п2 + Ъп +
.. . — . 6
п=1
30
£
, 25п2 + 5п-б"
п=1
^ 18
•^п2 + 3п'
п=1
°° 3
•^9п2-Зп-2' ' ^_, 16п2-8п-3'
п=1 п=1
f « . 10. f. <*>
Z-* этЛп -I- 1V« J-9^ ■£-'
v
n=6
T
^4n2-
n=l
oo
3
■5n + 6'
-1"
90
^-i 4n2 + 8n - 5"
n—l
oo
16
' £rJn(n+l)(n + 2)" ' ^Bn+l)Bn + 3)(-2n + 5)"
Ответы. 1. 5 = 2. 2. 5 = 1. 3. 5 = 2. 4. 5 = 2. 5. 5 = 11.
6.5 = 23. 7.5 = 1. 8.5 = 4. 9.5 = 2. 10.5 = 1.

214
Гл. 10. Ряды
10.2. Первая теорема сравнения
Постановка задачи. Исследовать сходимость ряда с
неотрицательными членами
п=1
где ап = f(n,ui(n),U2{n),...) и Ui(n),U2(n),... — функции с
известными наименьшими и наибольшими значениями (например, синус,
косинус и т.п.), причем функция f монотонно зависит от щ,и2, ■ • •
План решения.
1. Проверяем, что lin^^oo о„ = 0 (если Ишп^оо ап ф О, то ряд
расходится, так как не выполнено необходимое условие сходимости
ряда).
2. Поскольку о„ > 0, применяем первую теорему сравнения.
Пусть даны два ряда с неотрицательными членами 52„=1 ап и
ЕГ=1 Ьп-
Если ап < Ьп, то из сходимости ряда 52^Li bn следует
сходимость ряда 52^Li an-
Если ап > Ьп, то из расходимости ряда Yl^Li bn следует
расходимость ряда 52^=i ап-
3. Чтобы сделать вывод о сходимости (расходимости) данного
ряда, мы должны установить справедливость одной из двух гипотез
(проверяем их в любом порядке).
I. Исходный ряд 52^Li ап сходится.
П. Исходный ряд 52^Li °n расходится.
I. Проверяем первую гипотезу. Чтобы установить, что исходный
ряд 52^Li °" сходится, нужно найти сходящийся ряд 52^Li &n
такой, что
ап < Ьп- A)
В качестве эталонного ряда 52^Li ^n используем один из следующих
рядов:
сходящийся гармонический ряд 2^п=1 — при р > 1;

10.2. Первая теорема сравнения
215
б) сходящийся геометрический ряд 52^Li сЧп ПРИ 0 < q < 1
(с — некоторое положительное число).
Если существует сходящийся ряд Y^=\ bn такой, что
выполняется неравенство A), то по первой теореме сравнения исходный ряд
S^Li °n сходится. В противном случае, проверяем вторую гипотезу.
II. Чтобы установить, что исходный ряд J^n=1 °« расходится, надо
найти расходящийся ряд 2^n=1 On такой, что
ап>Ьп. B)
В качестве эталонного ряда 52^Li bn используем один из следующих
рядов:
а) расходящийся гармонический ряд 2^п=1 — при р < 1;
б) расходящийся геометрический ряд 52n=i сЧп ПРИ 9^1
(с — некоторое положительное число).
Если существует расходящийся ряд Xl^Li ^n такой, что
выполняется неравенство B), то по первой теореме сравнения исходный ряд
„=1 ап расходится.
Замечание. Для оценки общего члена ряда используем
неравенства:
—1 < cosn < 1, — 1 < sinn < 1,
1 < Inn < np (Vp > 0), — < arctgn < — и т. п.
Пример. Исследовать сходимость ряда
Vn3 + 1
^ n2B +sinn)
Решение.
1. Имеем
lim „._ :—г = 0,
«-too пг{2 + sinn)
т.е. необходимое условие сходимости ряда выполнено.

216
Гл. 10. Ряды
2. Так как — 1 < sin п < 1 и 1 < 2 + sin п < 3 при всех п > 1 и
^^ >0,
n2B + sinn)
то можно применить первую теорему сравнения.
3. Чтобы сделать вывод о сходимости (расходимости) данного
ряда, мы должны установить справедливость одной из двух гипотез
(проверяем в любом порядке).
I. Исходный ряд ^Z^Lj an сходится.
Поскольку —1 < sinn < 1, имеем 1 < 2+sinn < 3, \/п3 + 1 < 2п3/2,
и, следовательно,
v/^TT 2n3/2
n2B + sinn) n2 п1/2
Так как ряд
00 2
Z^^TT2
n=l
расходится как гармонический с р = 1/2 < 1, то гипотеза о
сходимости исходного ряда не подтвердилась.
Проверяем вторую гипотезу.
И. Исходный ряд JZ^l.! ап расходится.
Поскольку — 1 < sinn < 1, имеем 1 < 2 + sinn < 3, \/nz + 1 > vn3,
и, следовательно,
Vtf n3/2_ 1 „х
n2B + sinn) - Зп2 Зп1/2'
Так как ряд
ОО j
^Зп^Т2
п=1
расходится как гармонический с р = 1/2 < 1, то в силу неравенства
C) по первой теореме сравнения расходится и исходный ряд.
Vn3 + 2
Ответ. Ряд 22n=i im , • Т расходится.
n^B + smn)

10.3. Вторая теорема сравнения
217
Условия задач. Исследовать сходимость рядов.
i ^ arctg(n3) ^4 — 2 sin n
■" п — Inn
n=l
°° 21
En Inn
n3-2'
n=2
2 + sm n
3.
5.
7.
9.
^n(n + 2)(n + 3)
^ 2 + cos n
^ n2 + 3 '
n=l
^ 5 — 2 cos n
oo .
^-^ Inn
oo .
^ Inn
^n(n2 + 3)'
n=l x
s- E
OO о
coszn
oo
io. £
n2 + l'
Inn
Ответы. 1. Ряд сходится. 2. Ряд расходится. 3. Ряд
сходится. 4. Ряд расходится. 5. Ряд расходится. 6. Ряд
сходится. 7. Ряд сходится. 8. Ряд сходится. 9. Ряд сходится.
10. Ряд расходится.
10.3. Вторая теорема сравнения
Постановка задачи. Исследовать сходимость ряда с
положительными членами
оо
]Г ап.
п=1
План решения.
1. Проверяем, что Пши^оойп = 0 (если Нп^-юоС,, ^ 0, то ряд
расходится, так как не выполнено необходимое условие сходимости
ряда).
2. Проверяем, что о„ > 0 для всех п > 1.
3. Делаем вывод о сходимости или расходимости данного ряда,
используя вторую (предельную) теорему сравнения.

218
Гл. 10. Ряды
Пусть даны два ряда Y^n°=i °") S^Li ^«> причем существует
номер N такой, что при всех п>N ап >0 и Ьп >0.
Если существует конечный и отличный от нуля предел
,. On
lim —,
n-юо оп
то ряды Y^n°=i an u Y^H=i bn либо оба сходятся, либо оба расходятся.
В качестве эталонного ряда ^Z^Lj bn используем гармонический
ряд Xl^Li —i который сходится при р > 1 и расходится при р < 1,
или геометрический ряд 52^Li cqn (q > 0), который сходится при
q < 1 и расходится при g > 1. Таким образом, нужно найти
последовательность А/пр (или Bqn) такую, что
А
ап ~ — (или ап ~ Bqn) при п —> оо.
■п?
Вывод: по второй теореме сравнения исходный ряд сходится, если
р > 1 (q < 1), и расходится, если р < 1 (q > 1).
Пример. Исследовать сходимость ряда
оо __
оо
arcsin ■
Решение.
1. Имеем
(п2 + 3M/2 '
п—1 у '
lim arcsin —-—-т^т = 0.
moo (n2 + ЗM'2
2. Проверяем, что члены данного ряда положительны.
Действительно,
п г.
arcsin ———-T7Z > 0
(п2 -I- ЗM/2
при всех п > 1, так как п/(п2 + ЗM/2 € @,1).
3. Делаем вывод о сходимости или расходимости данного ряда,
используя вторую (предельную) теорему сравнения.
Имеем
п 1
arcsin —-—„.-,„ ~ —г при п -> оо.
(п2 + ЗM/2 п4
Ряд
п=1

10.4. Признак Даламбера
219
сходится как гармонический с р = 4 > 1. Следовательно, в силу
второй (предельной) теоремы сравнения исходный ряд также сходится.
Ответ. Ряд Y^Li arcsin —;——— сходится.
(nz + 6H'-i
Условия ЗАДАЧ. Исследовать сходимость рядов.
n=l n=l
ОО
"" 1 . 1
3. У л/n^arctg—г. 4. y^n2sin-77=.
п=1 n=l v
оо 4 I о °° i о
_ v-4 1 п +3 с \^ • п + 3
5. > nln—: . 6. > Sill
n4 + 2' " ^ n(n + 2K'
n=l n=\ v '
00 on i °° 2 i i
V^ 3 + П о V^ 3/- . П + 1
7. > —-. 8. > ymxcsxa. —.—-.
•^ 7" + 2n ^ n4 - 2
П=1 П=1
oo oo
9. ^(e^-l). 10. £ntg2^.
n=l n=l
Ответы. 1. Ряд сходится. 2. Ряд сходится. 3. Ряд сходится.
4. Ряд расходится. 5. Ряд сходится. 6. Ряд сходится. 7. Ряд
сходится. 8. Ряд сходится. 9. Ряд расходится. 10. Ряд сходится.
10.4. Признак Даламбера
Постановка задачи. Исследовать сходимость ряда с
положительными членами
ОО
п=1
где ап ~ Ьп и Ьп содержит произведения многих сомножителей
{например, факториалы).
План решения. Если при вычислении предела

220
Гл. 10. Ряды
можно сократить многие множители в числителе и знаменателе дроби
Ьп-и/Ьп, то обычно применяют признак Даламбера.
Пусть дан ряд с положительными членами
оо
п=1
Если существует предел
hm —— = g,
то при g < 1 ряд сходится, при g > 1 расходится. (Если g = 1, то
признак Даламбера ответа не дает.)
1. Проверяем, что ап > 0 при всех п > 1.
2. Упрощаем, если требуется, выражение для ап, т.е. будем
исследовать сходимость ряда $^^Li Ьп такого, что а„ ~ Ь„ при п —> со, а
затем воспользуемся второй теоремой сравнения.
3. Вычисляем bn+i.
4. Вычисляем предел
lim %± = е. A)
5. Применяем признак Даламбера и вторую теорему сравнения.
Если g < 1, ряд X^^Li^n сходится. Следовательно, по второй
теореме сравнения сходится и исходный ряд $3^1 j a«-
Если g > 1, ряд X^^Li bn расходится. Следовательно, по второй
теореме сравнения расходится и исходный ряд J^nLi a«-
Пример. Исследовать сходимость ряда
v^ 1 ■ 4 ■ 7 ■... • (Зп - 2) . 1
£ п\ 81П2^Г-
n=l
Решение.
1. Проверяем, что члены ряда положительны. Действительно,
1-4-7-...-(Зп-2) . 1
ап = ; sm „ ., > U
п\ 2n+1
при всех п > 1.

10.4. Признак Даламбера
221
2. Поскольку sin ж ~ х при х —> 0, можно упростить выражение
для ап:
1 - 4 • 7 •... • (Зп - 2) . 1 1 • 4 • 7 •... • (Зп - 2)
~\ sm2^+T~ 2»+1n!
т.е. будем исследовать сходимость ряда J^nLi &»»> гДе
_ 1 • 4 • 7 •... • (Зп - 2)
2»+1п!
и затем воспользуемся второй теоремой сравнения.
Поскольку Ь„ содержит произведения сомножителей типа
факториалов, следует применить признак Даламбера.
3. Вычисляем bn+i:
_ 1 • 4 • 7 •... • (Зп - 2) • (Зп + 1)
п+1 ~ 2»+2(п + 1)!
4. Вычисляем д по формуле A)
,. Ьп+1
q = lim —— =
п-+оо 6„
1 ■ 4 ■ 7 ■... • (Зп - 2) ■ (Зп + 1) 2п+1п!
2"+2(п + 1)! 1 • 4 • 7 •... ■ (Зп - 2)
Зп +1 3
= lim — г = —.
п-+оо 2(п + 1) 2
5. Применяем признак Даламбера и вторую теорему сравнения.
Так как д = 3/2 > 1, то ряд
2L, 2n+1n
1 • 4 • 7 •... • (Зп - 2)
i
п=1
расходится. Следовательно, по второй теореме сравнения расходится
и исходный ряд.
^ 1 • 4 • 7 •... ■ (Зп - 2) . 1
Ответ. Ряд 2^, 1 sm 5^+Г расходится.
п=1

222
Гл. 10. Ряды
Условия задач. Исследовать сходимость рядов.
00 on , о °° сп
^ (Зп + 2)! у>2"(п5-1)
^2"Bп + 5)!' '^ п!
П=1 Х ' П=1
-ЧBп)!' ^3» +
Й B")!
„=!" 2
f>n!Bn + 2)! f>2"n!
^- (Зп)! ' ^Bп)!'
п=1 '
п-\
J2. 2nnl J2. Q"„l
9. yfJL. ю. yfJL.
n=l n=l
Ответы. 1. Ряд сходится (g = 0). 2. Ряд сходится (g = 0).
3. Ряд расходится (g = +oo). 4. Ряд сходится (g = 0). 5. Ряд
сходится (д — 0). 6. Ряд расходится (д = +оо). 7. Ряд сходится
(д = 4/9). 8. Ряд сходится (д = 0). 9. Ряд сходится (д — 2/е).
10. Ряд расходится {д — 3/е).
10.5. Признак Коши
Постановка задачи. Исследовать сходимость ряда с
положительными членами
оо
Х]а„,
п=1
где ап~Ъп и Птп_юо y/b^ существует и легко вычисляется.
План решения. Если Ьп имеет, например, вид g(n) /(n)n , где /
и 9 — рациональные функции п, то Птп_юо y/b^ существует и легко
вычисляется. В таком случае применяем радикальный признак Коши.
Пусть дан ряд с положительными членами
оо
£<>«■
п=1

10.5. Признак Когии
223
Если существует предел
lim Ук = д, A)
п-юо
то при д < 1 ряд сходится, при q > 1 расходится. (Если g — 1, то
признак Коши ответа не дает.)
1. Проверяем, что ап > 0 при всех п > 1.
2. Упрощаем, если требуется, выражение для ап, т.е. будем
исследовать сходимость ряда Y^=i bn такого, что ап ~ Ьп при п —> оо, а
затем воспользуемся второй теоремой сравнения.
3. Вычисляем предел
lim v/б^ = g.
П—УОО
4. Применяем радикальный признак Коши и вторую теорему
сравнения.
Если g < 1, ряд Yl^Li bn сходится. Следовательно, по второй
теореме сравнения сходится и исходный ряд 2^п=1 ап.
Если g > 1, ряд X^^Li bn расходится. Следовательно, по второй
теореме сравнения расходится и исходный ряд 2^n=i а«-
Замечание. Полезно иметь в виду, что
lim ^И=1, lim #1п~^=1, lim y/P{n) = 1,
п-юо п—юо п-юо
где Р(п) — многочлен относительно п.
Пример. Исследовать сходимость ряда
оо
Vn4 arctg2"-^.
*-? 4п
п=1
Решение.
1. Проверяем, что члены ряда положительны. Действительно,
ап = п4 arctg2" — > О
in
при всех п > 1.
2. Поскольку arctg ж ~ ж при а; —> 0, упрощаем выражение для ап:
п arctg -~n {-) ,

224
Гл. 10. Ряды
т.е. будем исследовать сходимость ряда 52^LX &»»> гДе
л ( *_Y
и затем воспользуемся второй теоремой сравнения.
Очевидно, что Птп_юо \/Ъ^ существует и легко вычисляется. В
таком случае применяем радикальный признак Коши.
3. Вычисляем g по формуле A), учитывая, что lim,,.»,» \/п = 1:
q = lim
П—УОО
n4(fJnl1/n=iimn4/«(fJ = 0<i.
\4п/ п->оо \4п/
4. Применяем радикальный признак Коши и вторую теорему
сравнения.
Так как g = 0 < 1, то ряд
Х>4 (*Г
п=1
сходится. Следовательно, по второй теореме сравнения сходится и
исходный ряд.
Ответ. Ряд YJn4 arctg2n— сходится.
4п
п=1
Условия ЗАДАЧ. Исследовать сходимость рядов.
^\2п2 + 1>/ ' ^V3n»-iy "
n=l ч ' п=1 ч '
00 / "л _ Ч \  °° / \ 
5- Е(^м] • 6- Х>Ч^тзГ
п=1 ч ' п=1 ч '
оо / \2п °° / л i\ n/2
- Е^^ ■ s. е £^ .
n=l ч ' п=1 ч
п=1 п=1

10.6. Интегральный признак Коши
225
Ответы. 1. Ряд расходится (д = +оо). 2. Ряд сходится (д = 0).
3. Ряд сходится (д — 0). 4. Ряд сходится {д = 0). 5. Ряд сходится
(д = 0). 6. Ряд сходится (д = 3/5). 7. Ряд сходится (д — 1/4).
8. Ряд сходится (д = 2/3). 9. Ряд сходится (д — 3/5). 10. Ряд
расходится (д = 3/е).
10.6. Интегральный признак Коши
Постановка задачи. Исследовать сходимость ряда с
положительными членами
оо
п=1
где ап ~ Ьп — /(п), причем первообразная функции f(x) легко
вычисляется.
План решения. Если Ьп — /(п), причем первообразная функции
f(x) легко вычисляется, то применяем интегральный признак Коши.
Если функция f(x), принимающая в точках х — п (п G N) значения
/(п) — Ъп > 0, убывает в некотором промежутке Ь < х < +оо
(Ь > 1), то ряд Yln°=i bn u несобственный интеграл fb f(x) dx либо
оба сходятся, либо оба расходятся.
1. Упрощаем, если требуется, выражение для ап, т.е. будем
исследовать сходимость ряда $^^Li Ьп такого, что ап ~ Ьп при п —> оо
и Ьп — /(п) выбраны так, чтобы функция f(x) имела очевидную
первообразную F(x). Затем используем вторую теорему сравнения.
2. Исследуем сходимость несобственного интеграла по
определению:
г+оо
/ f(x)dx= lim F(b)-F{a).
Jb b-y+oo
3. Применяем интегральный признак Коши к ряду
оо
п=1
и затем делаем вывод о сходимости или расходимости исходного ряда
X^^Li an, используя вторую теорему сравнения.

226
Гл. 10. Ряды
Замечание. Интегральный признак Коши применяется, в
частности, к рядам вида X^^Li —/(Inn).
Пример. Исследовать сходимость ряда
Зп
£
=2(n2-2)lnBn)-
Решение.
1. Упрощаем выражение для а„
Зп
(n2-2)lnBn) nlnn
и будем исследовать сходимость ряда Т)~ , —:— с помощью ин-
nlnn
3
тегрального признака Коши, так как функция f(x) = —— имеет
очевидную первообразную F(x) = 3 In In ж. Затем используем вторую
теорему сравнения.
2. Исследуем сходимость несобственного интеграла по
определению:
Г+°° 3dx Гь Zdx
/ = lira / — =3 lira [lnlnb - lnln2] = +oo.
J2 xmx 6->+ooJ2 xmx 6-n-oo
Интеграл расходится.
3. Применяем интегральный признак Коши:
3
Функция f(x) = —— непрерывна в промежутке [2, +оо) и убыва-
1Ш1
ет в нем к нулю. Следовательно, из расходимости интеграла следует
расходимость ряда
оо „
Y-.
*—' nlnn
п=2
По второй теореме сравнения расходится и исходный ряд.
Ответ. Ряд V —х— , , расходится.
*-^ (п* — 2) 1пBп)

10.7. Признак Лейбница
227
УСЛОВИЯ ЗАДАЧ. Исследовать сходимость рядов.
оо
L ^Bn + 3)lnBn)' 2' ^(n + l)ln2n'
^JCn-2)vTnBn + l)" ' ^nlns(n + l)'
ОО - ОО -
5. V L_^. 6. V ,
„=2 Bп + !) VЬ n ~ 2n^/ln3Cn + 1)
оо оо
7 V 8 V п
^пу/Щп + 3)' ' ^2(n2 + l)ln2n'
3
^9(»3 + 2)ln2n' ^(-2)lnrT
n=2 v ' n=2 ч '
Ответы. 1. Ряд расходится. 2. Ряд сходится. 3. Ряд расходится.
4. Ряд сходится. 5. Ряд расходится. 6. Ряд сходится. 7. Ряд
расходится. 8. Ряд сходится. 9. Ряд сходится. 10. Ряд расходится.
10.7. Признак Лейбница
Постановка задачи. Исследовать сходимость
знакочередующегося ряда
оо
Y, (-l)nan, an > 0.
п=1
План решения.
1. Проверяем, что limn-^ooO,, = 0 (если итп_юоа„ ф 0, то ряд
расходится, так как не выполнено необходимое условие сходимости
ряда).
2. Исследуем сходимость ряда, составленного из модулей,
X^Q"'
п=1
используя теоремы сравнения и признаки сходимости для рядов с
положительными членами.

228
Гл. 10. Ряды
Если ряд из модулей сходится, то исходный ряд сходится
абсолютно.
3. Если ряд из модулей расходится, то остается еще возможность
того, что исходный ряд сходится условно.
Чтобы исследовать эту возможность, применяем признак
Лейбница.
Если члены знакочередующегося ряда убывают по абсолютной
величине и стремятся к нулю при п —> со, то ряд сходится (по
крайней мере, условно).
В данном случае, если условия признака Лейбница выполнены, то
исходный ряд сходится условно (так как уже выяснено, что
абсолютно он не сходится).
Пример. Исследовать сходимость ряда
t,-ir(i-„£).
Решение.
1. Проверим выполнение необходимого условия сходимости:
lira (-1)" ( 1 - cos 4= I = 0.
п-+оо у y/nj
2. Исследуем сходимость ряда, составленного из модулей:
g|(-ir(i—- £)|-g('—£)■
Так как при п —> со
l_cosJ_^ J_
yfn In
то по второй (предельной) теореме сравнения ряд из модулей
расходится.
3. Проверяем условия признака Лейбница:
а) ряд знакочередующийся с а„ = 1 - cos —=;
б) члены ряда убывают по абсолютной величине:

10.8. Приближенное вычисление суммы ряда
229
в) члены ряда стремятся к нулю при п —> со (см. п. 1).
Следовательно, по признаку Лейбница исходный ряд сходится.
Ответ. Ряд 2J (—1)" ( 1 — cos-r= } сходится условно.
Условия задач. Исследовать сходимость рядов.
1. £(_1)«+1_*!±1 2. у (_!)»_ 2
7.
n(n + 2)' ' ^-J n5 + n2 + 1 '
n=l v ' n=l
n=l ч ' n=l ч '
$>iVW£. io. у
oo
COS7Tn
n=l
3n ^ y/ri + 2
Ответы. 1. Ряд сходится условно. 2. Ряд сходится абсолютно.
3. Ряд сходится условно. 4. Ряд сходится абсолютно. 5. Ряд
сходится условно. 6. Ряд сходится условно. 7. Ряд сходится абсолютно.
8. Ряд расходится. 9. Ряд сходится абсолютно. 10. Ряд сходится
условно.
10.8. Приближенное вычисление
суммы ряда
Постановка задачи. Вычислить сумму знакочередующегося
числового ряда
оо
^(-1)п_1вп, ап>0,
с заданной точностью а.

230
Гл. 10. Ряды
План решения.
1. Если ап+\ < ап и Нтп_юоап = 0, то для остатка ряда Rn
справедливо неравенство
\Rn\ < ап+1-
2. Если ап+\ < а, то и |i?n| < а. Поэтому, решая неравенство
a„+i < а,
находим количество членов ряда, которое необходимо взять для
вычисления суммы ряда с заданной точностью а.
3. Непосредственно вычисляем n-ю частичную сумму и
записываем ответ:
S к 5„ = а\ — а,2 + - ■. + (—1)п_ а„.
Пример. Вычислить сумму ряда
оо
A + п3J
с точностью а — 0,001.
Решение.
1. Данный ряд знакочередующийся и сходящийся (абсолютно).
Члены ряда убывают по абсолютной величине:
п + 1 п
< Т. ZTK Vn > 1.
A + (п + 1KJ A + П3J
Следовательно, справедливо неравенство
п + 1
\Rn\ < О-п+1
A + (п+1KJ'
2. Если an+i < а, то и |ДП| < а. Поэтому, решая неравенство
п+1 1
<
A + (п + 1KJ 1000'
находим количество членов ряда, которое необходимо взять для
вычисления суммы ряда с заданной точностью а. Получаем п > 3, т.е.
достаточно взять первые три члена ряда.

10.9. Область сходимости функционального ряда 231
3. Вычисляем:
Ответ: S и -0,229 ± 0,001.
Условия ЗАДАЧ. Вычислить суммы знакочередующихся рядов с
заданной точностью а.
оо
1. ГЦ-, а = 0,01. 2. У2{ > , а = 0,001.
n=l n=l
n=l v ' n=l v '
°° (—1)п °° (—1)"
5- Ет^Г' а-0,0001. 6. 5ZVt' а = 0,001.
*—' Bп)!п ^—' 2пп!
п=1 ч п=1
°° Г—1)" °° (—1)п
7- Екг* а=0'01- 8- ЕУ-- -=o,oi.
n=0 n=l v '
Ответы. 1. S ~ 0,84. 2. 5 ~ 0,896. 3. 5 ~ -0,275. 4. 5 ~
~ -0,332. 5. S ~ -0,4796. 6. 5 ~ -0,393. 7. 5 ~ 0,13. 8. 5 ~
~-0,45. 9. S ~ 0,36. 10. 5 ~ 0,04.
10.9. Область сходимости
функционального ряда
Постановка задачи. Найти область сходимости
функционального ряда
оо
£/-(*)■
п=1

232
Гл. 10. Ряды
План решения. При каждом допустимом значении х
рассматриваем данный ряд как числовой и исследуем его сходимость, применяя
теоремы сравнения, признаки Коши, Даламбера и др. Таким образом
находим те значения х, при которых данный ряд сходится.
Совокупность таких значений х образует область сходимости ряда.
При использовании признаков Даламбера или Коши поступаем
следующим образом.
1. Находим q(x) по одной из формул (если пределы существуют)
в(х) = lim |{п+;(?,I или в(х) = lim VJAWJ,
п-*°° |/п(я)| n_>°°
где fn(x) — общий член ряда.
2. Так как по признакам Даламбера или Коши ряд сходится при
q < 1 и расходится при g > 1, находим интервал сходимости, решая
неравенство д(х) < 1.
3. Исследуем поведение ряда в граничных точках интервала
сходимости.
Записываем ответ.
Пример 1. Найти область сходимости ряда
^-J {п2 + у/п+1)х
n—l v '
+ 1'
Решение.
1. Для каждого фиксированного х все члены данного ряда
положительны:
> 0 Vn > 1.
п (п2 + V" + l)x+1
2. Используем вторую (предельную) теорему сравнения. Имеем
п3 1
(п2 + д/п + 1)х+1 п2^1)
Так как при 2(х + 1) — 3 > 1 ряд
°° 1
2—/ п2(х+1)-3
п=1
при п —> оо.

10.9. Область сходимости функционального ряда 233
сходится, а при 2(х + 1) — 3 < 1 расходится (как обобщенный
гармонический), то по второй теореме сравнения ряд
n=l v v '
сходится при всех х > 1.
Ответ. Область сходимости ряда — A,оо).
Пример 2. Найти область сходимости ряда
Т •
^ п3(х2 -4ж + 7)п
n=l v '
Решение.
1. Для того чтобы применить признак Даламбера, находим д(х)
по формуле
4n+1
, ч .. |/n+i| ,. (n + lK|x2-4x + 7|»+i 4
gix) = hm , , , = hm - ——-rj; ! = 7-5 — .
n3|x2 -4x + 7|n
2. Так как по признаку Даламбера ряд сходится при д < 1 и
расходится при д > 1, находим интервал сходимости, решая
неравенство д(х) < 1:
4
\х2 - Ах + 7\
Получаем х £ (—со, 1) U C, со).
3. Исследуем сходимость ряда в граничных точках:
при х — 1 ряд
Е^
jL^, п3
п=1
сходится (как обобщенный гармонический с р = 3 > 1);
при х = 3 ряд
оо
Е^
Z-, П3
п=1
также сходится.
Ответ. Область сходимости ряда — (—со, 1] U [3, +со).

234
Гл. 10. Ряды
Условия ЗАДАЧ. Найти области сходимости функциональных
рядов.
оо со on
1 V 2 V
*-" (¥п + 1)*+3' ' ^ п(х2 -6х + 10)"'
п—1 v v ' п=1 х '
ОО Л ОО
3 У П 4 У
3"
nx2+4x + з z-' п(х2 - Ъх + 9)"'
n=l n=l v '
4"
Z-^ nx2-2 + j Z^
n=l rt=l
+ 1 ^ П2(Х2 + 3)
n=l v '
5"
oo 2 °°
7 ^ n 8 V
-^ (n + л/")* ' ^ "(a;2 - 4a; + 8)"'
~ П2 + 1 ^ 6"
9- 2^ „З+Зх-х2 • 10- 2^
n=l
n3+3x-x2- • Z^n2(a.2_2a; + 6)n'
n=l v 7
Ответы. 1. C,+oo). 2. (-oo, 2) U D,+oo). 3. (-oo,-5) U (l,+oo).
4. (-oo,2)UC,+oo). 5. (-oo,-2)UB,+oo). 6. (-oo,-l] U[l,+oo).
7. C, +oo). 8. (-oo, 1) U C, +oo). 9. @,3). 10. (-oo, 0] U [2, +oo).
10.10. Область сходимости степенного ряда
Постановка задачи. Найти область сходимости степенного
ряда
ОО
У^Сп(ж-Жо)П.
п=1
План решения.
1. Если существуют пределы
hm 1 г или
"-*00 |с„+1| limn.
юо V I п
то можно найти радиус сходимости степенного ряда по формуле Да-
ламбера
R = lim J^L (l)
n-*°° |c„+i|

10.10. Область сходимости степенного ряда
235
R = ==. B)
lim^ooVICnl
или по формуле Коши
Тогда интервал сходимости ряда есть — R < х — xq < R.
Замечание. Формулы A) и B) применимы лишь тогда, когда все
коэффициенты степенного ряда сп отличны от нуля. В противном
случае находим д(х) по одной из формул
в(х) = lim l("+l(!|)l и™ в(х) = lim У[Щ1,
где /п(#) — общий член ряда (см. задачу 10.9). По признакам Далам-
бера или Коши ряд сходится при g < 1 и расходится при g > 1.
Следовательно, находим интервал сходимости, решая неравенство д(х) < 1.
2. Исследуем поведение степенного ряда в граничных точках
интервала сходимости х = хо ± R-
Записываем ответ.
Пример 1. Найти область сходимости ряда
£!г±£(ж+1)..
i-J О-п Л- 1 V '
Решение.
. 2п+1
а=1
(п +1M
1. В данном случае сп = — -ф 0 при всех п. Поэтому можно
применить формулы A) или B) для радиуса сходимости степенного
ряда.
По формуле Даламбера
Д= lim
n—too
Cn+1
п-юо 2n + 1 / 2n + 3
Следовательно, интервал сходимости определяется неравенствами
— 1<ж + 1<1и имеет вид (—2,0).
2. Исследуем сходимость ряда в граничных точках интервала
сходимости. В точке х = — 2 степенной ряд принимает вид
£;kt£<-ir
^ 2n + l v ;
п=1

236
Гл. 10. Ряды
и в точке х = О степенной ряд принимает вид
^ 2п+1К '
п=1
Оба ряда расходятся, так как не удовлетворяют необходимому
условию сходимости рядов:
Um%±il!(±1)n^0.
п-+оо 2n + l V ' Г
Следовательно, в этих точках ряд расходится.
Ответ. Область сходимости степенного ряда — (—2,0).
Пример 2. Найти область сходимости ряда
°° 1
71=1
Решение.
1. В данном случае сп = 0 при всех нечетных п. Поэтому нельзя
применять формулы для радиуса сходимости степенного ряда.
Используем признак Коши, для чего вычислим
в(х)= lim пуЩЩ,
п—юо
где/п(х) = —|—(х-2Jп.
Находим q{x):
q(x) = lim nJ-±-(x-2)^ = {x- 2J.
n-+oo V П + 1
По признаку Коши ряд сходится при g < 1 и расходится при
q > 1. Следовательно, интервал сходимости определяется
неравенством (х — 2J < 1 и имеет вид A,3).
2. Исследуем сходимость ряда в граничных точках интервала
сходимости. В точке х — 1 ряд
У -i-(-l)"
п=1

10.11. Вычисление, суммы ряда почленным интегрированием 237
сходится условно по признаку Лейбница.
В точке х = 3 ряд
1
y^_i_(l)n.
п=1
расходится.
Ответ. Область сходимости степенного ряда — [1,3).
Условия задач. Найти области сходимости степенных рядов.
1 f- (*-2)" 2 vMx-3J"*1
, n9n
П=1
у^(х + 5J" ^ (»+1)"
^ 4П ' ' 2^ (n + iJn •
' n=l v '
п=1
(х-2)" а ^ (Ж_з)
2п-1
2-^ (п + 1K"' ' 2— Bп3 + ЗпLп'
ОО 1— ОО
7- Е-^Т^ + ЗГ- 8. V7 ^—-A + 2)".
^-^n2 + lv ' -<Wn + lJ3"v '
n=l n=l v '
.3
n=l v ' n=lv 7
Ответы. 1. (-7,11). 2.B,4). 3. (-7,-3). 4. [-2,1). 5. [-1,5).
6. [1,5]. 7. [-4,-2]. 8. [-5,1). 9. (-6,-2]. 10. (-oo,+oo).
10.11. Вычисление суммы ряда
почленным интегрированием
Постановка задачи. Найти сумму функционального ряда вида
" /(*)"
£
п
п—к
и указать область сходимости ряда к этой сумме.

238
Гл. 10. Ряды
План решения.
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется
неравенством
Если f(x) = 1, ряд расходится. Если f(x) — — 1, ряд сходится условно
(по признаку Лейбница). Следовательно, область сходимости
определяется неравенствами — 1 < f(x) < 1.
2. Делаем в исходном ряде замену f(x) = t, получим степенной
ряд
ос г
Ет (ч
1 п
п=1
с областью сходимости [—1,1).
3. Известна формула для вычисления суммы членов бесконечно
убывающей геометрической прогрессии
Е'п = ггг |t|<L B)
п=к
4. Кроме того, имеем очевидное равенство
Г*
%=к п=к
00 fn °° ft
£- = £/o"n-1^ *€(-i,i).
5. Учитывая, что степенной ряд можно почленно интегрировать
на любом отрезке [0,t], целиком принадлежащем интервалу
сходимости, и используя формулу B), получаем
°° fn rt °° ft к
S(t) = £-= / S«n-1d«= -. du, te(-i,i). C)
„=fc n ■'o n=fc Jo l-u
Заметим, что так как ряд A) сходится в граничной точке t = — 1,
то сумма ряда непрерывна в этой точке (справа). Следовательно,
5(-1)= ton S(t).
t-f-1+0
6. Вычисляем интеграл, делаем замену t на f(x) и записываем
ответ: сумму ряда и область его сходимости.

10.11. Вычисление суммы ряда почленным интегрированием 239
Замечание. Если ряд имеет вид
fix)"
£
п=к(п + а)(п + ЬУ
то применяем теорему о почленном интегрировании степенного ряда
дважды или разлагаем дробь на элементарные:
I = р U—,
(п + а)(п + Ь) \п + а n + bj b - а'
и вычисляем сумму каждого ряда почленным интегрированием.
Пример. Найти сумму ряда
£
sin х
п
п=1
и указать область сходимости ряда к этой сумме.
Решение.
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется
неравенством |sinx| < 1.
В граничных точках при х = 7г/2 + 2жк ряд расходится, при х =
= Зя-/2 + 2-кк ряд сходится условно.
Следовательно, данный ряд сходится при всех х ф ж/2 + 2жк
(*: = 0>±11...)-
2. Сделаем замену sin a; = t. Получим геометрический ряд A) с
областью сходимости [—1,1).
3. Используем формулу для вычисления суммы членов бесконечно
убывающей геометрической прогрессии
°° 1
Е*п_1 = тз7' 1*1 <L D)
п=1
4. Кроме того, имеем очевидное равенство
n=l n=lJ0

240
Гл. 10. Ряды
5. Учитывая, что степенной ряд можно почленно интегрировать
на любом отрезке [0, t], целиком принадлежащем интервалу
сходимости, и используя формулу D), получаем
°° in ft oo Г1 Л
£-=/ J2"n-ldu= du=-ln(l-t), \t\<l. E)
„=1 П J0 „=1 JO L U
Заметим, что так как ряд A) сходится в граничной точке t=—l,
то его сумма непрерывна в этой точке (справа). Следовательно,
формула E) справедлива при всех t G [—1,1).
6. Заменяя t на sinx, получаем при х ф тт/2 + 2-кк
S(x) = — InA — sinx).
Ответ. S(x) = - In A-sinx), хфтг/2 + 2-кк.
УСЛОВИЯ ЗАДАЧ. Найти суммы функциональных рядов и указать
области их сходимости к этим суммам.
°° сп„п °° „п+2
1. JT—. 2. JT Х
оо
Е
п=0
ОО
п=0
оо
Е:
п=1
ОО
п
A
(п
- 16х4)"
п + 1
2"
+ 1)х2"'
3"
п(п+1)х"'
(-
-1)п4"х2п
^ п(п + 1)'
п=1 х '
t—1 nxn_1
n=l
Е2
^n(n + l)'
(-l)nx2n+1
ОО
t-' 2n + l
п=0
9. у1'^ . ю. г
^—' 9г> -1- 1 ^—>
(-l)"-^2"
2п +1 " — z_/ nBn - 1)
n=l n=l x '
Ответы.
1. S=-ln(l-6x), x G [-1/6,1/6).
2. S=(x-x2)ln(l-x) + x2, are [-1,1].

10.12. Вычисление суммы ряда почленным дифференцированием 241
3. S = -81n
8х4-1
8х4
, xG (-l/v^l/v^)
4. S=-|ln- , xG (-oo, -3]UC,+oo).
т»2 «2 __ о
5. 5=-—In 5—. xG (-оо,-\/2)и(\/2,+оо).
I х*
6. 5 = A - 2х) ln(l - 2х) + 2х, х G [-1/2,1/2].
7. 5 = —^ In—^ + |, xG(-oo,-3]u[3,+oo).
8. 5=arctgx, x G [—1,1].
9- S=-^p-l xG[-l/2,l/2].
10. S = 2xarctgx-ln(l + x2), are [-1,1].
10.12. Вычисление суммы ряда
почленным дифференцированием
Постановка задачи. Найти сумму функционального ряда вида
оо
Х> + 6)/(х)"
п—к
и указать область сходимости ряда к этой сумме.
План решения.
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется
неравенством
Если /(х) = ±1, ряд расходится (не выполнено необходимое условие
сходимости). Следовательно, область сходимости определяется
неравенствами —1 < /(х) < 1.

242
Гл. 10. Ряды
2. Делаем в исходном ряде замену /(х) = t и записываем его в
виде суммы двух рядов
Ё™*"+&£*""
п—к п—к
Следовательно, достаточно найти суммы рядов
оо оо
п=к п=к
3. Известна формула для суммы членов бесконечно убывающей
геометрической прогрессии
£<п = тЬ' |t|<L A)
i
n=fc
4. Кроме того, имеем очевидное равенство
оо оо оо ,
n=fc n=k п—к
5. Учитывая, что степенной ряд можно почленно
дифференцировать в любой точке интервала сходимости, и используя формулу A),
получаем
°° J °° j j.k
£»'"='!£'" ='lib «еи-ч-
п=к п=к
6. Вычисляем производную и делаем замену t на /(х).
Записываем ответ: сумму ряда и область его сходимости.
Замечание. Если ряд имеет вид
оо
J2(n2 + bn + c)f(x)n,
п=к
то вычисляем сумму трех рядов, причем при вычислении суммы ряда
оо
п=к

10.12. Вычисление суммы ряда почленным дифференцированием 243
применяем теорему о почленном дифференцировании степенного
ряда дважды.
Пример. Найти сумму ряда
оо
£(п + 6)х
7п
71 -Г V)X
п=0
и указать область сходимости ряда к этой сумме.
Решение.
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется
неравенством |х7| < 1. Отсюда —1 < х < 1. В граничных точках х = ±1 ряд
расходится, так как не выполнено необходимое условие сходимости.
Следовательно, ряд сходится в интервале (—1,1).
2. Делаем в исходном ряде замену х7 = t и записываем его в виде
суммы двух рядов
оо оо
S(t) = 6 £V + ]Г Tit" = 65lW + 52(*)-
n=0 n=0
Следовательно, достаточно найти суммы рядов
оо оо
п—0 п=1
3. Используем формулу для вычисления суммы членов бесконечно
убывающей геометрической прогрессии:
оо
Е*п = гт? |t|<L B)
п=0
Следовательно, Si(t) = при всех t G (—1,1).
4. Кроме того, имеем очевидное равенство
оо оо оо ,
Е»*п='1;»*я-1='£!*"•
n=l n=l n=l

244
Гл. 10. Ряды
5. Учитывая, что степенной ряд можно почленно
дифференцировать в любой точке интервала сходимости, и используя формулу B),
получаем
d A .„ d t t
n=l n=l ч '
Таким образом,
S(t) = 65l(«) + &(*) = JL + -L^ = ^L 4 € (_i, l).
Заменяя t наг, получим
£(n + 6)x7" = ^-^ VxG(-l,l).
6 — 5x7
Ответ. S(x) = — =^, x G (-1,1).
(l — a:'J*
УСЛОВИЯ ЗАДАЧ. Найти суммы функциональных рядов и указать
области их сходимости к этим суммам.
оо
1. ^nxn+1. 2. ^n2nxn.
П=1 П=1
JUL ~ Г-П»»-1птп-1
з. 5>+u«**«. 4- E( V" -
n=0 n=l
5. £(п+1)^+2)а^. e. £>v-i.
n=0 n=l
oo oo
7. JZ Bn2 - 2n + l)xn. 8. ^ (-l)n-xn(n + l)xn.
n=0 n=l
oo oo
9. ^n(n + 2)xn. 10. J^n^ + l)"-1.
n=l n=l

10.13. Ряд Тейлора
245
Ответы.
3-S= A^5M. ^(-1,1). 4-S=(^5. «(-3,3).
16 14-х
5' S = B^3- * е <'2>- 6' S = A^K. ' * ("'• ')•
O-r х^ 1
9-5=A-хK' XG(-1'1)- 10-5 = ^6' «€(-^2,0).
10.13. Ряд Тейлора
ПОСТАНОВКА ЗАДАЧИ. Разложить функцию /(х) в ряд Тейлора
по степеням х (хо = 0).
План решения.
1. Преобразуем функцию /(х) к виду, допускающему
использование табличных разложений ех, sinx, cosx, A + x)m, ln(l -1- x).
2. Находим разложение функции в ряд Тейлора, используя
табличные разложения, сложение (вычитание) рядов, умножение ряда на
число.
3. Определяем область сходимости полученного ряда к
функции /(х).
Замечание. Если необходимо разложить функцию в ряд Тейлора
по степеням х — хо, сначала делаем замену переменной t = х — хо,
находим разложение по степеням t и возвращаемся к переменной х.
Пример. Разложить функцию
3
/(*) =
2 - х - х2
в ряд Тейлора по степеням х (хо = 0).

246
Гл. 10. Ряды
Решение.
1. Чтобы использовать табличные разложения, разложим данную
функцию на элементарные дроби:
3 1 1
+
2 — х — х2 1-х х + 2
2. Используя табличное разложение
1 °°
—- = 1 + t + t2 + ... + tn + ... = 52 *"» * G (-1,1),
n=0
:m 1 °°
= $>", xG(-l,l),
1-х ■*—*
n=0
oo
4-х- 2 l+x/2~2^-; 2" ~^ 2"+! ' tl ' h
2 + a: 21+x/2 _ „
' n=0 n=0
Таким образом,
2 - x - x2
n=0
?>»"
3. Областью сходимости полученного ряда является пересечение
вышеуказанных областей сходимости, т.е. (—1,1) П (—2,2) = (—1,1).
Ответ. - = y(l + t^-)xn VxG(-l,l).
2 - х - х2 t-' V 2n+1 J v
n=0 v '
УСЛОВИЯ ЗАДАЧ. Разложить функции в ряды Тейлора (хо = 0).
2. 1пA-х-20а:2).
4. *
1.
3.
5.
7.
5
6 — х — х2
sin(x + -)
X
3 + 2х'
хе2*2+1.
v/эТх2'
6. #16 + х.
8. 1
#27-х'
9. 1пA2х2 + 7х + 1). 10. cos23x.

10.14. Приближенные вычисления с помощью рядов 247
Ответы.
Е (з^Г + Ут) *". *€(-2,2).
п=0
оо
гг+1 2n+1
(-l)n_14n - 5"
n=l
5'5У
2. V- х", xG
2n+1 + ^E^2n- xe(-oo,+oo).
я ^v- (-i)n r.
2 ^Bn + 1)!*
1 ^(-1)"
2
n=0
Bn)!
«• l+£^fe#^. «(-.»>•
5- Т.ЧГ
n! 2n 32
(-JT^ +1
3»г+1 Ж ' X fe
■1)
. 2 + ^ + f-(_irI3-7-116 D"-5)жп, x€ [-16,16].
32 t—' ' 26n_1n!
n=2
— V
7. e У"^—rx2n+1, xG(-oo,+oo).
n=0
1 ^l-4-7...Cn-2) .
8- *+Z^ -io4»4.i ж ' «e (-27,27).
3 ' ^ n!34n+1
n=l
9- £(-D
n-t4" + 3-
n=l
Ю-1 + Ё
n
\nc2n
x", a; G
V 4'4
(-1)2 2n
v ' x , x G (-cx),+cx)).
- 2Bn)!
10.14. Приближенные вычисления
с помощью степенных рядов
Постановка задачи. Вычислить интеграл
ь
f(x)dx
о
о
/■
с точностью а, где /(х) разложима в степенной ряд, имеющий
радиус сходимости R> b.

248
Гл. 10. Ряды
ПЛАН РЕШЕНИЯ. Практические вычисления обычно сводятся к
суммированию того или иного числового ряда. В данном случае
такой ряд получается, если разложить подынтегральное выражение в
степенной ряд и проинтегрировать его почленно.
1. Разлагаем подынтегральную функцию в степенной ряд по
степеням х
/(Х) = ЦС«Х"'
п=0
и определяем его область сходимости.
2. Степенной ряд можно интегрировать почленно по любому
отрезку, принадлежащему интервалу сходимости. Поэтому,
интегрируя почленно полученный ряд и используя формулу
Ньютона-Лейбница, получаем
О О
/ f(x)dx= / ]Рспхпdx=Y2c" —ГТ
3. Вычисляем сумму числового ряда с заданной точностью
(оценивая остаток ряда).
Замечание. Если разложить подынтегральную функцию в ряд
не по степеням х, а по степеням х — 6/2, то ряд будет сходится
быстрее, т.е. для обеспечения заданной точности может потребоваться
меньше слагаемых, однако в итоге вычисления оказываются более
сложными.
Пример. Вычислить интеграл
0,1
/ cosA00x2) dx
о
с точностью а = 0,001.
Решение.
1. Разлагаем подынтегральную функцию в ряд Тейлора по степе-

10.14. Приближенные вычисления с помощью рядов 249
ням х:
.,„ 2л , (Ю2х2J A02х2L A02х2N
coSA00x2) = i-i-^ + L_J__L_ri. + ...=
-v2^2-\2n _j^ Ю4пх4п
МЛ2т212п „
Bп)! ^v ' Bп)! '
п=0 v ' п=0 v '
Разложение справедливо при всех х.
2. Интегрируем почленно полученный ряд:
0,1 0,1 „ 0,1
/Г °° if|4n_4n °° 1П4п /"
cosA02x2)dx = /^(-ir^rdx = 5:(-irH_/x4"dx =
о о п_0 п_0 о
у^( 1ГЮ4" *4"+1 01. I у> (-1)"
^ К > Bп)! 4п + 1 0 10 ^ Dп + 1)Bп)!'
3. Оценим остаток ряда. Так как ряд знакочередующийся,
1 1
°" = Т^Гл , ,w» м > ап+1 —
10Dп+1)Bп)! """ 10Dп + 5)Bп + 2)!
и Итп_юо ап = О, то справедливо неравенство
1
\Rn\ < On+l =
10Dn + 5)Bn + 2)!'
Для вычисления интеграла с заданной точностью достаточно
взять два члена ряда, так как
В.! < < 0,001.
1 - 10 • 9 • 4!
4. Производя вычисления, получаем
0,1
J cosA00x2) dx S -L - iQ * 2j * 0,090.
о
0,1
Ответ. J cosA00z2) dx =* 0,090 ± 0,001.

250
Гл. 10. Ряды
Условия задач. Вычислить интегралы с точностью а — 0,001.
1 1
1. / е~х dx. 2. / sinx2dx.
о о
0,5 0,5
3. / 7dx. 4. / л/l + х3 dx.
J 1+x4 J V
о о
0,5 2/3
5. [e~x2/4dx. 6. f 4; l dx.
J J tyT+rf
о о
1 1
7. / dx. 8. / \/xcosxdx.
J y/TT^ J
о о
•v/3/3 1
9. / x3 arctgxdx. 10. / „, dx.
J J e/8T^
о о
Ответы. 1.5 SO, 747. 2.5^0,310. 3.5^0,494. 4.5^0,190.
5.5 = 0,508. 6. 5 SO, 490. 7.5^0,662. 8. 5 SO,608. 9. 5 SO,012.
10. 5 S 0,495.

Глава 11
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
При изучении темы ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ вы
познакомитесь с различными типами уравнений первого и второго
порядков и освоите методы их решения. Вы изучите линейные
уравнения с постоянными коэффициентами, структуру их общего
решения и методы его нахождения (метод Эйлера, метод подбора частных
решений, метод Лагранжа).
С помощью пакета РЕШЕБНИК.ВМ вы можете вычислить
интегралы, решить системы уравнений, продифференцировать найденные
решения и выполнить численные расчеты (например, при решении
задачи Коши), а также проверить полученные вами результаты.
11.1. Понятие решения
Постановка задачи. Доказать, что функция у — у(х)
удовлетворяет дифференциальному уравнению F(x, у, у') = 0.
План решения.
Для доказательства того, что функция у = у(х) удовлетворяет
уравнению F(x,y,y') — 0, достаточно вычислить производную у'{х),
подставить у(х) и у'(х) в это уравнение и убедиться в том, что
получается тождество, т.е. F(x, у(х), у'(х)) = 0 для всех допустимых х.
Пример. Доказать, что функция у = —\/х4 — х2 удовлетворяет
уравнению
яуу' ~ У2 = я4.
Решение. Имеем
,_ хBх2 - 1)
У ~~ v/ic47^'
Подставим у и у' в левую часть уравнения и проведем необходимые

252
Гл. 11. Дифференциальные уравнения
преобразования:
(-у/х^^) (-^£=U) -(х4-х2) = хBх*-х)-х4+х2 =
^ ' V, Vx4 — х2 )
х\
Получаем тождество х = ж4.
Ответ. Функция у = —у/х4 — х2 удовлетворяет заданному
уравнению.
Условия задач. Доказать, что функция у = у(х)
удовлетворяет дифференциальному уравнению f(x, у, у') = 0.
1. у = хе~х I2, ху1 = A — х2)у.
2. у = Ъе-2х + ^, у' + 2у = ех.
3. у = ху/1 — х2, уу' = х — 2х3.
4. у = у/х2 — сх, (х2 + y2)dx — 2xydy = 0.
5. у = etg(x/2), у' sin x = у In у.
Ь-\- X . 2 /\
6. у= , , Ьж> у-ху =ЬA+х у).
7. у = -v/2/x2 - 1, 1+у2+хуу'=0.
8- У= —, у-жу =аA + ж у ).
аа; + 1
9. у = ех+*2 +2ех, у' -у = 2хех+х2.
10. у = 2 + сл/1-ж2, A - ж2)?/ + жу = 2ж.
11.2. Уравнения
с разделяющимися переменными
Постановка задачи. Найти интегральные кривые
дифференциального уравнения вида
E(x)F(y)dx = G(x)H(y)dy. A)

11.2. Уравнения с разделяющимися переменными 253
План решения.
1. В области, где G(x) ф О и F(y) ф О разделяем переменные, т.е.
представляем уравнение A) в виде
G{x)dX F(y)dy-
2. Вычислим интегралы в уравнении
J G(x) J
F(y) *
и преобразуем его к виду ip(x, у) = С.
3. Ответ записываем в таком виде: интегральные кривые
определяются уравнением ip(x,y) = С при всевозможных значениях С.
Замечание. Если одно или оба уравнения G(x) — О и F(y) = О
имеют решения xi, Х2,- ■■ nyi, у2,---,то равенства х — х\, х — Х2,- ..и
У = 2/1 > У = 2/2, • • • нужно присоединить к ответу, так как они являются
интегральными кривыми дифференциального уравнения A).
Пример. Найти интегральные кривые дифференциального
уравнения
6х dx — 6ydy — 2х у dy — Зху dx.
Решение.
1. Перепишем исходное уравнение в виде
ЗжB + у2) dx = 2у(х2 + 3) dy. B)
Поскольку х2 + 3 > 0 и 2 + у2 > О, разделяем переменные, т.е.
представляем уравнение B) в виде
Зж 2у
dx — ——=■ dy-
х2 + 3 2 + у2
2. Вычислим интегралы в уравнении
/Ъх [ 2у
^Тъйх = J 2Ty-*dy-
I
2у
— ах= I —
-3 У 2
Ат- = — \г\(т
аг2+3
Имеем
:dz = -m(a;2 + 3)-l-Ci,
оД? . О , / о

254
En. 11. Дифференциальные уравнения
2» .,.._._/о , 2л
2 + 2/
Следовательно,
/^=г-2<1у = \п{2+у')+С2.
3,
|1п(^2 + 3)-1пB + у2)+Со,
где С0 = С2 - Сх.
3. Упростив это равенство, получим
(*2 + 3K
B + ?/2)
Ответ. Интегральные кривые определяются уравнением
(х2 + 3K
B +У2)
при всевозможных значениях С.
= С
УСЛОВИЯ ЗАДАЧ. Найти интегральные кривые
дифференциальных уравнений.
1. ydx + A + x2)dy = 0. 2. «/'= tg a; tg«/.
3. у'у = —2xsecy. 4. у' + sin(x + у) = sin(x — у).
5. y(l + x2)j/' + x(l + «/2) =0. 6. exdx-(l+ey)ydy = 0.
7. j/ = 2excosa;. 8- y' — ylny.
2т 1
9. j/' - -^. 10. y' =
1 + x2' 'a VS2^!"
Ответы.
1. ln|j/| +arctgx = C. 2. sin j/cos a; = C.
3. x2 + ysiny + cosy = C. 4. ln|tg(j//2)| + 2sinx = C.
5. (z2 + l)(l + y2)=C. 6. 21n(l + e*)-y2 = C.
7. j/ = e^cosa; + sinx) +C. 8. In | In y| - a; = С
9. у = 1пA+ж2) + С. 10. y = ln\x + y/x2-l\+C.

11.3. Однородные уравнения
255
11.3. Однородные уравнения
Постановка задачи. Найти интегральные кривые однородного
дифференциального уравнения первого порядка, т.е.
дифференциального уравнения вида
P(x,y)dx + Q(x,y)dy = 0, (I)
где Р(х, у) и Q(x, у) — однородные функции одинакового порядка,
т.е. P{tx,ty) = tnP(x,y) и Q{tx,ty) = tnQ{x,y).
План решения.
1. Преобразуем уравнение A) к виду
2. Делаем подстановку у(х) — х z(x), где z(x) — новая неизвестная
функция. Тогда у' = z + xz' и уравнение A') приводится к виду
т.е. к уравнению с разделяющимися переменными.
Заметим, что подстановку у(х) = xz(x) можно делать сразу в
уравнении A), не приводя его к виду A').
3. Разделяем переменные в области, где f(z) — z ф 0:
dz dx
f(z) - z x
4. Интегрируем полученное уравнение с разделенными
переменными и делаем замену z(x) — y(x)/x. Записываем ответ.
Замечания.
1. Если z = zq — корень уравнения f(z) — z — 0, то решением
уравнения A) будет также у = zqx.
2. Интегральные кривые однородного уравнения можно искать и
в полярных координатах.
Пример. Найти интегральные кривые дифференциального
уравнения
, х2 + 2ху — Ъу1
у — .
2х2 —бху

256
Гл. 11. Дифференциальные уравнения
Решение.
1. Преобразуем заданное уравнение к виду
I _ X \XJ
У — у
2-6-
х
(мы разделили числитель и знаменатель правой части заданного
уравнения на ж2).
2. Делаем подстановку у = xz(x), где z(x) — новая неизвестная
функция. Тогда у' = z + xz' и уравнение приводится к виду
, l+2z-5z2
ZX + Z= 2-6. '
т.е. к уравнению с разделяющимися переменными.
В результате простых преобразований получаем
dz 1 + z2
■ х =
dx 2 — 6z
3. Разделяем переменные A + z2 ф О и х ф 0):
2 — 6г , dx
^dz= —.
1 +Z2 X
4. Интегрируя, получаем
2arctg z - 3 ln(l + z2) = In |ж| + С.
Заменяя z на у/х, получаем
2arctg - - 31n A + ^ ) - In \x\ = C.
x \ ar/
Ответ. Интегральные кривые определяются уравнением
2arctg^_ln(£l±p! = c
х \х\°
при всевозможных значениях С.

11.4. Линейные уравнения 1-го порядка
257
Условия задач. Найти интегральные кривые
дифференциальных уравнений.
1. у' = еу/х + -. 2. у1 = - - 1. 3. жУ = ху + у2е~х/У.
X X
4. xcos—dy + [х— ycos — ) dx = 0. 5. (x2 + 2ху) dx + ху dy— 0.
х V х/
6. xy'ln ( — J =ж + у1п ( — J . 7. ydx + By/xy - x)dy — 0.
8. (Ay2+x2)y' =xy. 9.xy,sin(-\+x = ysm(-J.
10. xy + y2 = Bж2 + ху) у'.
Ответы.
1. е~у/х + In |z| = С. 2. xеУ1х = С.
3. ех1У + In |ж| = С. 4. ln|x|+sin^=C.
ж
5. 1п|ж + у| + —^-=С 6. Ina:-^fln--0 = С.
х + у х V х )
7. ./£ + 1п|у|=С. 8. ]п\у\ = ^+С.
\ х о у
9. Сж = ecos(!//x). 10. j/2 = Cxe~vlx.
11.4. Линейные уравнения 1-го порядка
Постановка задачи. Решить задачу Коши для уравнения
У + Р{х)у = q{x) A)
с начальным условием
у(хо) = Уо- A')
План решения.
1-й способ.
1. Запишем соответствующее однородное линейное уравнение:
у'+р(х)у = 0. B)

258
Гл. 11. Дифференциальные уравнения
Это уравнение с разделяющимися переменными.
2. Разделяя переменные и интегрируя, получим общее решение
однородного уравнения B)
\ - / Р(х)dx \
у = Сехр < — / р(х) dx > . C)
3. Применяем метод вариации произвольной постоянной:
а) ищем решение неоднородного уравнения A) в виде C), считая
С неизвестной функцией х, т.е. полагая С = С(х);
б) подставляем в уравнение A) у и у1, определяемые из
соотношения C), где С = С(х). Из полученного дифференциального уравнения
определяем функцию С(х).
4. Таким образом, общее решение неоднородного уравнения A)
получаем в виде
у = С{х) ехр \ - I р(х) dx 1. C')
Здесь С(х) содержит произвольную постоянную Со-
5. Используя начальные условия A'), находим значение Со и
получаем решение поставленной задачи Коши.
Записываем ответ в виде у = <р(х).
2-й способ.
1. Ищем решение уравнения A) в виде
у = u(x)v(x), D)
где и и v — неизвестные функции х.
2. Уравнение A) принимает вид
u'v + uv + p(x)uv = q(x). E)
3. Поскольку теперь мы имеем две неизвестные функции, а
уравнение, которому они должны удовлетворять, только одно, то еще одно
уравнение мы можем принять произвольно, лишь бы оно не сужало
множество решений у.
Пусть одна из функций (например, и(х)) удовлетворяет
уравнению
и'+р(х)и = 0. F)

11.4. Линейные уравнения 1-го порядка
259
Тогда уравнение E) примет вид
v'u - q(x). G)
Решая уравнение F) (с разделяющимися переменными), находим и, не
равное тождественно нулю, чтобы не сужать множество решений у.
4. Подставляем и(х) в уравнение G) и решаем его относительно v.
5. Записываем общее решение уравнения в виде у(х) — u(x)v(x).
6. Используя начальные условия A'), получаем решение
поставленной задачи Коши.
Записываем ответ в виде у = ip(x).
Пример. Найти решение задачи Коши для уравнения
!/'--»=— (8)
х х*
с начальным условием
2/A) = 1.
Решение.
1-й способ.
1. Записываем соответствующее однородное линейное уравнение:
г/--у = о.
х
Это уравнение с разделяющимися переменными.
2. Разделяя переменные и интегрируя, получаем общее решение
однородного уравнения
у = Сх.
3. Применяем метод вариации произвольной постоянной:
а) ищем решение неоднородного уравнения (8) в виде
у = С(х)х,
где С(х) — неизвестная функция х;
б) подставляя в уравнение (8)
у = С(х)х и у' = С'(х)х + С(х),

260
Гл. 11. Дифференциальные уравнения
получаем дифференциальное уравнение относительно С(х)
С'{х)х = ~.
х*
Это уравнение с разделяющимися переменными.
Разделяя переменные
2
dC = —г dx
Xй
и интегрируя, получаем
X*
где Со — произвольная постоянная.
4. Таким образом, общее решение неоднородного уравнения (8)
имеет вид
у=G?+с°)*■ (9)
5. Используя начальное условие уA) = 1, получаем
находим Со = 0 и подставляем в общее решение (9).
Ответ, у = 1/х.
2-й способ.
1. Ищем решение уравнения (8) в виде
у — u(x)v(x),
где и w.v — неизвестные функции х.
2. Уравнение (8) принимает вид
1 2
u'v + ш/ uv = —-. A0)
х аг
3. Поскольку теперь мы имеем две неизвестные функции, а
уравнение, которому они должны удовлетворять, только одно, то еще одно
уравнение мы можем принять произвольно, лишь бы оно не сужало
множество решений у.

11.4. Линейные уравнения 1-го порядка
261
Пусть одна из функций (например, и(х)) удовлетворяет
уравнению
и' - -и = 0. A1)
X
Тогда уравнение A0) принимает вид
t/u=~- A2)
аг
Решая уравнение A1) (с разделяющимися переменными), находим
и(х) — Ах,
где А — произвольная постоянная (А ф 0, чтобы не сужать
множество решений).
4. Подставляем и(х) в уравнение A2) и решаем его
относительно V.
' 2 v=*+B,
Ах3 Ах2
где В — произвольная постоянная.
5. Записываем общее решение уравнения (8) в виде
у(х) — u(x)v(x) — —Ь Сх,
х
где С = АВ — произвольная постоянная.
6. Используя начальное условие 2/A) = 1, находим С = 0.
Ответ, у = 1/х.
УСЛОВИЯ ЗАДАЧ. Найти решения задач Коши для
дифференциальных уравнений.
1. ху' + у - ех = 0, j/@) = 1.
2. 2/'-2/tgai= , j/@) = 0.
cos a;
3. у'cos2 х + у - \,gx, y{Q)-Q.

262
Гл. 11. Дифференциальные уравнения
4- у' - J/thai = ch2a;, j/@)=0.
* i У i
5. у — = a;lna;,
а; ш. а;
6. y'sinx — ycosx = 1,
7- J/' — ytgx — cosa;,
8. j/' - 2xy = Zx2 - 2x4,
9. xy' -2y = 2a;4,
10. j/' + j/cosa; = esina:,
Ответы.
1. J/ = 2. j/ =
2/(e) =
/■^4
2/@) =
2/@) =
2/A) =
2/@) =
e2
2
= 0.
:0.
= 0.
= 0.
= 0.
x cosa;
3. j/ = e~t&x + tga; — 1. 4. y = cha;sha;.
ж2
5. у — — In a;. 6. у = — cos a;.
ar3.
/a; sin2a;\ 1
7- 2/ = U + —7- • 8. у =
\2 4 / cosa;
9. у = x4 — x2. 10. y = xe~
11.5. Уравнение Бернулли
Постановка задачи. Найти решение задачи Коши для
уравнения Бернулли
y' + 9{?)y = f(x)ya {ее ф 0,1) A)
с начальным условием
У(хо) = 2/0- A')
План решения.
1. С помощью подстановки
уравнение приводится к линейному
z' + p{x)z = q{x), B)

11.5. Уравнение Бернулли
263
где р - A - а)д и q - A - a)f.
2. Решаем линейное уравнение B) и делаем замену z = у1-0.
3. Используя начальное условие A'), находим решение
поставленной задачи Коши.
Записываем ответ в виде у — <р(х).
Замечание. При решения уравнения Бернулли можно не
приводить его к линейному, а искать решение в виде у = u(x)v(x) или
применять метод вариации произвольной постоянной.
Пример. Найти решение задачи Коши
ху' + у = ху2 C)
с начальным условием
УA) - 1.
Решение.
Преобразовав уравнение к виду
/ 1 2
У +-У = У ,
х
убеждаемся, что это уравнение Бернулли с а — 2.
1. С помощью подстановки
у = z1-** = z-1
уравнение C) приводится к линейному
z' - - г = -1. D)
х
2. Решаем уравнение D) методом вариации произвольной
постоянной:
а) решаем однородное уравнение
z' - - z = О,
х
получаем z — Сх;
б) ищем решение неоднородного уравнения в виде
z = С(х)х;

264
Гл. 11. Дифференциальные уравнения
в) подставляя в уравнение D)
г = С{х)х, z' = С'(х)х + С{х),
получаем уравнение с разделяющимися переменными
С'{х)х = -1.
Разделяя переменные и интегрируя, получаем
С{х) = С0-1пх.
Таким образом, общее решение неоднородного уравнения D) имеет
вид
z — х(Со —In ж),
или, после замены z — у-1,
У
х(Со — In ж)
3. Используя начальное условие 2/A) = 1:
1
1(С0 - 0)
получаем Со = 1.
Ответ, у
1,
хA — In х)
Условия задач. Найти решения задач Коши для
дифференциальных уравнений.
1. ху' = 4у = х2у/у, 2/A) = 0.
3. ху' + у=-х2у2, j/(l) = 1.

11.6. Уравнения е полных дифференциалах
265
4. ху' + у = у2 In х, j/(l) = 1.
5. {х+1)у' +у = -у2(х + 1), j/@) = 1.
6. у' + 2у = еху2, 2/@) = 1.
7. у'+у = ху2, 2/@) = 1.
а • + *-■?£, ,(,0 = 1
ж cos-^a; 7r2
/ 1 1 sh2a: о ,„ч 1
9. 2/sha; + 2/cha; = —— у', 2/@) = ^у.
10. у' - 2/tg х + у2 cos ж = 0, 2/@) = 1-
Ответы.
1.2/ = —г In2 |ж|. 2. у = A + a:2)arctg4a:. 3. у = —т.
4 аг
4>|,= ЬП^- 5-y=(l + x)(l + b|l + xl)- 6-|' = e""
1 „ /l + blcosxl \2 1
7-у=ттх- 8-у={—г-1**') ■ 9-у=а
10.2/
sha;
(ж + 1) cos ж
11.6. Уравнения в полных дифференциалах
Постановка задачи. Найти интегральные кривые
дифференциального уравнения
P{x,y)dx + Q{x,y)dy = 0. (I)
План решения.
1. Если в некоторой области D Р(х, у) и Q(x, у) имеют
непрерывные частные производные и выполнено условие
ду ~ дх'
то Р(х, у) dx + Q{x, у) dy — дифференциал некоторой функции
U(x, у). Тогда уравнение A) называется уравнением в полных диффе-

266
Гл. 11. Дифференциальные уравнения
ренциалах и может быть записано в виде
dU(x,y) = 0, (V)
где U(x, у) — дважды непрерывно дифференцируемая неизвестная
функция.
Из A') следует, что интегральные кривые определяются
уравнением U(x, у) = С при всевозможных значениях С.
Для отыскания U заметим, что
g =*>(«, у), f = Q(*,V). B)
2. Интегрируя первое равенство в B) по х, получим
U = J P{x,y)dx + <p{y),
где tp(y) — неизвестная функция, которую еще предстоит найти.
3. Дифференцируя U по у, имеем
-ду- = д-у1Р{х'У)АХ + 1рМ-
Используя второе равенство в B), получим уравнение
— P(x,y)dx + <p'(y) = Q(x,y).
4. Находим <р(у) и затем U(x, у).
Ответ. Интегральные кривые определяются уравнением U(x,y)=C
при всевозможных значениях С.
Пример. Найти интегральные кривые дифференциального
уравнения
а , а , xdy-ydx
xdx + ydy-] 5~;—5~~ =0- C)
аг + у*
Решение.
1. Преобразуем уравнение C):
{X-A^)dX+{y+x^)dy = °-

11.6. Уравнения в полных дифференциалах
267
В данном случае
р(ж'у) = (х~ *Т?) • Q^y) = {у + *Т?) ■
Эти функции непрерывно дифференцируемы в области х2 + у2 > 0.
Кроме того,
1У{х-^)^1(у+^тт) (*2-^2>°)-
Поэтому Р(х, у) dx + Q(x, у) dy — дифференциал некоторой функции
U(x, у) в любой односвязной области D, не содержащей точку х = 0,
у = 0. Следовательно, уравнение C) является уравнением в полных
дифференциалах и может быть записано в виде
dU(x, у) — 0 при (ж, у) е D.
При этом
dU__ у &U__ х
дх~Х х2 + у2' ду~У+х2 + у2' {)
2. Интегрируя первое равенство в D) по х, получим, что при у Ф 0
u = I{x-x^)<b = Y~aTCtel + ,p{y)'
где >р(у) — неизвестная функция, которую еще предстоит найти.
3. Дифференцируя U по у, имеем
8U х
+ <р'{у)-
ду х2 + у2
Используя второе равенство в B), получим
+ Ч> Ы = У +
х2 + у2 х2 + у2
После преобразований имеем
Ч>' {У) = У-

268
Гл. 11. Дифференциальные уравнения
4. Отсюда
и, следовательно,
У2
<р(у) = Y + С,
х -f- у х
U(x, у) — — arctg —Ь С, у > 0 или у < 0.
2 У
Ответ. Интегральные кривые в области у > 0 или в области у < 0
определяются уравнением
^-arctg^=C
2 У
при всевозможных значениях С.
Условия задач. Найти интегральные кривые
дифференциальных уравнений.
1. (х + у) dx + (х + 2у) dy = 0.
2. Ca;2+6a;j/2)da;+Fa;2j/ + 4j/3)dj/=0.
3. Bх + 5у) dx + {Ъх + 3j/2) dy = 0.
4. Ba;j/ + 3j/2)da; + (a;2+6a;j/-3j/2)dj/ = 0.
5. Cj/2 + 2xy + 2x) dx + Fxy + x2 + 3) dy = 0.
6. (ж2 + у2 + 2x) dx + 2xy dy = 0.
7. (ж3 - Зжу2 + 2) йж - (Зж2у - у2) dy = 0.
8. (ж ch у + shy) dx + (ж ch ж 4- sh ж) dj/ = 0.
9. 2жA + у/х2 - у) dx - у/х2 -ydy = 0.

11.7. Уравнения вида F(x,y(k),yik+1)) = 0 269
Ответы.
х2
1. — + ху + у2 = С. 2. х3 + Ъх2у2 + у4 = С.
3. ж2 + Ъху + у3 = С. 4. ж2!/ + Зху2 -у3 = С.
х3
5. Зху2 + х2у + Ъу + х2 = С. 6. — + ху2 + х2 = С.
О
х4 3 W3
7. — - -ж2!/2 + 2х + У- = С. 8. yshx + xshy = C.
9. х2 + \{х2 + у2K'2 = С. 10. -2L- + In - = С.
3 х-у у
11.7. Уравнения вида F(rc,y^,2/^+1)) = 0
Постановка задачи. Найти общее решение дифференциального
уравнения
F(x,i/<*>,i/<*+1>) = 0
План решения.
1. Полагая у№ = р{х), получим дифференциальное уравнение
первого порядка
F(x,p,p') = 0.
2. Определяя тип этого уравнения и применяя соответствующий
метод решения, находим р — f(x,Ci), где С\ — произвольная
постоянная.
3. Так как р = у^к\х), имеем
У1к) = f{x,d).
Последовательно интегрируя к раз (при каждом интегрировании не
забывая о произвольной постоянной), получим ответ
y = ifi(x,Ci,C2,.-.,Cn), n = k+l,
C"i, Сг,..., Сп — произвольные постоянные.
Пример. Найти общее решение дифференциального уравнения
A + х2)у" + 2ху' = 12ж3.

270
Гл.11. Дифференциальные уравнения
Решение.
1. Поскольку дифференциальное уравнение не содержит у, то
полагая у' = р(ж), имеем у" — р'(ж). Получаем дифференциальное
уравнение первого порядка
A + ж2)р' + 2жр = 12ж3.
2. Уравнение
2ж 12ж3
1 + х1 1 + х1
линейное относительно р и р'. Решая его, например, методом
вариации произвольной постоянной, находим
Зж4 + С
3. Так как р = у'(ж), имеем
, _ Зж4 + С
У 1 + ж2 '
Интегрируя, получим общее решение у = (С + 3) arctg ж + ж3 — Зх + С2.
Ответ, у = С\ arctg ж + ж3 — Зж + С2.
Условия задач. Найти общие решения дифференциальных
уравнений.
1.у" = 1-у'2. 2. ху" + у' = 0.
3. A + х2)у" + у'2 + 1 = 0. 4. х2у" + ху' = 1.
5. ху'" + у" = 1 + ж. 6. у"'2 + у = 1.
7.у'A+у'2) = гЛ 8. у" = -х/у'.
9. ж у" + у' + х = 0. 10. у' = 4у".
Ответы.
1. у = 1п\е2х + С1\-х + С2. 2. y^d+Csln^l.
3. у = A+С2Iп\х + С1\-С1х + С2.
4. y^icinHf+dlnN+d.

11.8. Уравнения вида F(y,y',y") = 0
271
3 2
5. i/ = ^ +Y+Cixln|x| + C2X + C3.
6. у = sin(Ci +х) + С2х + С3.
7. x-Ci = ln|sin(j/-C2)|-
8. у = Cix2 Anx - D + C2x + C3.
9. y = Ciln|x|-^ + C2.
10. y=i(C1+xL + C2x + C3.
11.8. Уравнения вида F(y,y',y") — 0
Постановка задачи. Найти решение задачи Коти для
дифференциального уравнения
F{y,y',y")=0
с начальными условиями
У(хо) = 2Л>, у'(з:о) = у'0.
План решения.
1. Поскольку дифференциальное уравнение не содержит явно
независимой переменной х, полагаем
у' = р{у),
где р(у) — новая неизвестная функция. Тогда по формуле для
производной сложной функции имеем
" — Л. ' = — () = ^..^к.= fjP
dx dx dy dx dy
Получим уравнение первого порядка относительно р(у)
F(y'p'pi)=a
2. Определяя тип этого уравнения и применяя соответствующий
метод решения, находим р = f(y,C), где С — произвольная посто
янная.

272
Гл. 11. Дифференциальные уравнения
3. Используя начальные условия (оба), находим С — С\.
4. Подставляя С\, получаем дифференциальное уравнение с
разделяющимися переменными
Разделяя переменные в области, где f(y,Ci) ф О, получаем
dy
f(y,Ci)
= dx
и, интегрируя, находим ж = ip(y,СьСг).
Проверяем, не является ли решение f(y, C\) = 0 особым решением
исходного уравнения, удовлетворяющим начальным условиям.
5. Используем начальные условия для нахождения второй
постоянной Ci (значение С\ уже было найдено в п. 3) и получаем решение
задачи Коши.
Ответ записываем в виде у = у(х) или ж = х(у).
Пример. Найти решение задачи Коши для дифференциального
уравнения
у"у3 + 1=0
с начальными условиями
1/A) = -1, 1/A) = -1.
Решение.
1. Поскольку дифференциальное уравнение не содержит явно
независимой переменной ж, полагаем
у' = р(у),
где р(у) — новая неизвестная функция. Тогда по формуле для
производной сложной функции имеем
#/ _ J*_ # _ _fL / ч _ 4Р dy. = dP.
У ~ dxV ~ dxP(V) ~ dy ' dx ~~ Vdy'
Получим уравнение первого порядка относительно р(у)
dp з ,
-ГРУ =-1-
dy

11.8. Уравнения вида F(y,y',y") = 0
273
2. Разделяя переменные и интегрируя, находим
У2
т.е.
(знак минус мы выбрали из начального условия у'A) = —1 < 0.)
3. Из начальных условий (обоих) имеем у' = —1 при у = —1.
Отсюда, С\ = 0. Учитывая, что в силу первого начального условия
у < 0 и, следовательно, \у\ — —у, получаем
, 1
У = -■
У
4. Разделяя переменные и интегрируя, находим
У2
5. Из начального условия уA) = —1 получим Сч — 1/2.
Следовательно,
у = -у/2х - 1.
(Знак минус мы выбрали из начального условия уA) — — 1 < 0.)
Ответ, у = —\/2ж — 1.
Условия задач. Найти решения задач Коши для
дифференциальных уравнений.
i/V = i,
уу"+у'2 = 1,
у"-у'2 + у'{у-1) = о,
у2 + у'2-2уу" = 0,
Зу'у" = У + У'3 + 1.
!/A/2) = 1,
1/@) = 1,
!/@) = 2,
1/@) = 1,
1/@) = -2,
|/A/2) = 1.
1/@) = I-
1/@) = 2-
1/@) = 1.
|/@) = 0.

274
Гл. 11. Дифференциальные уравнения
6. у' у2 + у у" -у'2 = 0, у(О) =
7. 2уу"-3у'2 = 4у2, y@) =
8- A + уу')у" = A + у'2)у', у@) =
9. 2уу" + у2-у'2=0, 2/@) =
10. г/2/' + 2/'2 + 2/2/"=0, у@) =
Ответы.
2/'@) = 2.
У'@) = 0.
2,'@) = 1.
2/@) = 1.
У'(О) =
е- 1
1. 2г,2 - 4х2
1.
5.г/ = -|(г/ + 2J/3.
8.2, = е*
2.2, = ж+1.
Зе3ж
6. у =
2 + е:
Зж '
3. у = 2ех. 4.2, = ех.
7. у = sec2 ж.
9.2, = sin х + 1. 10. у =
е — е "
е-1
11.9. Линейные уравнения
с постоянными коэффициентами
Постановка задачи. Найти общее решение линейного
дифференциального уравнения второго порядка с постоянными
коэффициентами
у" + ТУ' + ЧУ = еах[Рп(х) cosbx + Qm{x) sinbx],
где Рп(х) — многочлен степени п, Qm(x) — многочлен степени т
up,q,a,b — действительные числа.
План решения.
Общее решение неоднородного линейного уравнения n-го порядка
имеет следующую структуру:
2/о.н. = Уо.о. + Уч.». = Ci2/i + С22/2 + • • • + С„2/„ + 2/ч.н.,
A)
где 2/1,2/2 > Уп — фундаментальная система решений и 2/0.0. — общее
решение соответствующего однородного уравнения, 2/ч.н. —
какое-нибудь частное решение неоднородного уравнения.

11.9. Линейные уравнения с постоянными коэффициентами 275
1. Записываем соответствующее однородное уравнение
y"+py' + qy = 0 B)
и ищем его решение в виде у = еАх, где Л — неизвестное число.
Подставляя у = еАх, у' — АеАх и у" = Л2еАх в уравнение B) и
сокращая е , получаем так называемое характеристическое
уравнение
X2+pX + q = 0. C)
2. Решаем характеристическое уравнение. Обозначим корни
характеристического уравнения Ai и А2. Тогда фундаментальная
система решений и общее решение уравнения B) записываются в одном
из следующих трех видов:
а) если Ах и А2 вещественны и Ai ф А2, то фундаментальная
система решений — это у\ — eXlx, у2 — е*2Х и общее решение имеет
вид
Уо.о. =CieAia:+C2eA2X;
б) если Ai и А2 вещественны и Ai = А2, то фундаментальная
система решений — это yi = eAlX, yi = xeAlX и общее решение имеет
вид
Усе. = CieAlX + C2xeAlX;
в) если Ai и А2 комплексные, т.е. AiJ = a±iC, то фундаментальная
система решений — это yi = eax cos f3x, y2 = еах sin/Зж и общее
решение имеет вид
Уо.о. = еах(С\ cos (Зх + С2 sin (Зх).
3. Ищем какое-либо частное решение неоднородного уравнения.
Поскольку правая часть уравнения имеет вид
eax[Pn(x)cosbx + Qm(x)smbx], D)
можно применить метод подбора частных решений:
если а ± %Ь не является корнем характеристического
уравнения C), то
2/ч.н. = еах[Р*(ж) cos Ьх + Qk(x) sin bx],
где Pk(x) и Qfc(x) — многочлены степени k = max{n, m} с
неопределенными коэффициентами;

276
Гл. 11. Дифференциальные уравнения
если а ± гЬ есть корень характеристического уравнения(З)
кратности s, то
Уч.н. = xseax[Pk{x) cosbx + Qk{x) siabx],
где Pfc(x) и Qk(x) — многочлены степени к — max{n, m} с
неопределенными коэффициентами.
4. Находим неопределенные коэффициенты, подставляя уч.н. в
исходное уравнение.
Записываем ответ по формуле A).
Замечание. Аналогично решаются линейные дифференциальные
уравнения с постоянными коэффициентами любого порядка.
Пример. Найти общее решение линейного дифференциального
уравнения
у" + у = х sin х. E)
Решение.
1. Записываем соответствующее однородное уравнение
у" + у = 0 F)
и ищем его решение в виде у = еХх, где Л — неизвестное число.
Подставляя у — еХх, у' = ЛеАх и у" — А2еАж в уравнение F) и
сокращая еЛш, получаем характеристическое уравнение
Л2 + 1 = 0.
2. Характеристическое уравнение имеет два комплексно
сопряженных корня Ai,2 = ±г.
Имеем фундаментальную систему решений
Ух = cos ж, г/2 = sin х
и общее решение однородного уравнения F)
Уо.о. — С\ cos х + Ci sin x.
3. Ищем какое-либо частное решение неоднородного уравнения
E). В нашем случае правая часть неоднородного уравнения имеет
вид D) с а = 0, Ь — 1, п = 0, m = 1.

11.9. Линейные уравнения с постоянными коэффициентами 277
Так как характеристическое уравнение имеет комплексные корни
а ± ib — ±г кратности s = 1 и max{n,m} = 1, то частное решение
ищем в виде
Уч.н. = x[(Aix + А2) cosx + (Bix + В2) sinx],
где А\, А2, Вх, В2 — неизвестные числа (неопределенные
коэффициенты).
4. Находим неопределенные коэффициенты, дифференцируя уч.„.
два раза и подставляя в уравнение E).
Приравнивая коэффициенты в обеих частях равенства при cos ж,
х cos х, sin ж, ж sin ж, получаем четыре уравнения
{ 2ЛХ + 2В2 = О,
4Bi = О,
-2А2 + 2ВХ = О,
-4Л! = 1,
из которых определяем Ах = —1/4, А2 = О, В\ = О, В2 — 1/4. Таким
образом,
Ж14 X .
уч „ = cos ж н— smx.
4 4
По формуле A) находим общее решение неоднородного уравнения
о
X X
у = С\ cos х + С2 sin ж —— cos ж 4- — sin ж.
о
Ж Ж .
Ответ, у — Сл cos ж + С? sin ж — cos ж + — sin ж.
4 4
Условия задач. Найти общие решения дифференциальных
уравнений.
1. у" +у = cosx. 2. у" + у' - 2у = 8Бт2ж.
3. у" - 2у' + Ъу = ех cos 2ж. 4. у" + у = 3 sin x.
5- у" + У — 4ж cos ж. 6. у" - 9у = е3х cos ж.
7. у" — 4у = е2ш sin 2ж. 8. у" — 2у = 2ж e^cos ж — sin ж).
9- J/"— j/= 2 sin ж —4 cos ж. 10. у" - 6у'+ 25у = 28шж + Зсо8ж.

278
Гл. 11. Дифференциальные уравнения
Ответы.
ж
1. у = С\ cosx + C^sinx + — sinx.
2
2. у = Ciex + C2e-2a: - - Csin2x + cos2x).
5
ж
3. у = (Ci cos 2x + C2 sin 2x) ex + — ex sin 2x.
3
4. у — Cicosx + C2sinx— -xcosx.
5. у = Ci cos ж + C2 sin x + x cos ж + ж2 sin ж.
6. у = Ci e3x + C2e~3x + ^- e3lFsinx - сое ж).
2x
7. у = d e~2x + C2 e2x - ^— (sin 2ж + 2 cos 2ж).
8. y = Ci e~Xy/2~ + C2exv/2 + ж ex sin ж + ех cos ж.
9. у = C\ex + C2e~x + 2собж — smx.
10. у = (Ci cos 4ж + C2 sin 4ж) е3х + —— A4 cos ж + 5 sin ж).
11.10. Принцип суперпозиции
Постановка задачи. Найти общее решение линейного
дифференциального уравнения п - го порядка с постоянными
коэффициентами
у(») + piy(n-i) + ... + рп1у> + pnj/ = jP(x)) A)
где f (ж) - Л (ж) + /2(ж) + ... + Д(ж).
План решения.
Принцип суперпозиции. Если правая часть уравнения A)
есть сумма нескольких функций
F{x) = /ж(аг) + /2(ж) + ... + Д(ж)
и У* (г = 1,2,..., к) — какое-нибудь частное решение каждого
уравнения
У{п)+Р1У{п-1) + ...+Рп-1У,+РпУ = Ш (» = 1,2,...,*), B)

11.10. Принцип суперпозиции
279
то в силу линейности уравнения A) его общее решение имеет вид
y = y0 + Y1+Y2 + ... + Yk, C)
где 2/о — общее решение однородного уравнения
У
(п)
+ Pi2/(n-1) + ...+Pn-iy'+ РпУ = 0.
1. Находим фундаментальную систему решений и общее решение
г/о однородного уравнения.
2. Для каждого неоднородного уравнения B) (г — 1,2,...,к)
находим частное решение Yi (используя, например, метод подбора или
метод вариации произвольных постоянных).
Записываем ответ в виде C).
Пример. Найти общее решение линейного дифференциального
уравнения
у'" - 1002/' =■ 20е10х + 100 cos Юж.
Решение.
1. Записываем соответствующее однородное уравнение
у'" - 1002/' = 0 D)
и ищем его решение в виде у — еХх, где Л — неизвестное число.
Подставляя у = еАх, у' = АеАх и у" = Х2еХх в уравнение D) и
сокращая е , получаем характеристическое уравнение
Л3 - 100А = 0.
Характеристическое уравнение имеет три корня Ai = 0, А2 = 10 и
Аз = -Ю.
Таким образом, имеем фундаментальную систему решений
2/1 = 1, 2/2 = е10х, 2/з = е-10ж
и общее решение однородного уравнения
2/о = Сх + С2е10ж + С3е~10х.
2. Решаем неоднородное уравнение, используя принцип
суперпозиции:
а) ищем частное решение Y\ неоднородного уравнения
у'" - 1002/' = 20е10а: E)

280
Гл.11. Дифференциальные уравнения
в виде У] = хАе10х, где А — неопределенный коэффициент (так
как а + ib = 10 — корень характеристического уравнения кратности
Я = 1).
Дифференцируя Ух три раза и подставляя в уравнение E),
находим А = 1/10. Таким образом,
Xl 10 '
б) ищем частное решение Y2 неоднородного уравнения
у'" - 100?/' = 100 cos Юх F)
в виде Уг = В\ cos Юх 4- В2 sin Юх, где Bi и В2 — неопределенные
коэффициенты (так как а ± ib = ±10г не являются корнями
характеристического уравнения, то множитель х отсутствует).
Дифференцируя У2 три раза и подставляя в уравнение F),
находим В\ = 0 и В2 = -1/20. Таким образом,
У2 = -— sinlOx.
Используя принцип суперпозиции C), получаем
y = yo + Y1+Y2 = C1+ С2е10х + С3е~10х + ^ е10х - ^ sin Юх.
Ответ. y = Ci+ С2е10х + C3e"lte + ^ е10х - ^ sin Юх.
Условия ЗАДАЧ. Найти общие решения дифференциальных
уравнений.
1. у" +у' = 5х + 2ех. 2. 2/"+2j/+2/ = e_xcosx-l-xe~x.
3. у" -Zy1 = x + cosх. 4. у" - 2у' + Юг/ = sin3x -I- ex.
5. 2/"+4?/ = 2sin2x-3cos2x-l-l. 6. у" +9у = хеЪх + 2xsinx.
7. 2/"+2/ = 2xcosxcos2x. 8. у'" -by" +8у' -4г/ = 2е3х + 3е2х.
9. у'"+у" = x* + l+Zxex. 10. уп+2у"+у = ех+sinx + sm2x.

11.11. Метод Лагранжа
281
Ответы.
1. у = С1+С2е-х+ех + ^х2-5х.
г3
2. y = {Ci+C2x+ — -cosx)e-x.
6
1 2
3. г/ = С*1 + С2е3х - — (cosx + 3sinx)-^- - ^.
10 6 9
1 ех
4. г/ = (Ci cos Зх 4- С2 sin Зх) ех Н (sin3x + 6cos3x) H .
о/ У
X 1
5. у — С\ cos 2х + Сг sin2х — — C sin2х + 2cos2х) 4- -.
4 4
6. г/ = CiCOs3x + C2sin3x + -xsinx - — cosx4- — (Зх — 1)е3х.
4 16 54
7. у — Ci cos x 4-С2 sin x 4- — cosx+ —-sinx — — cos 3x+ — sin3x.
4 4 о о2
8. у = Cxex + (C2 + C3x) e2x + e3x + | x2e2*.
9. y = C1e-x+C2+C3x + ^x2-±x3 + ±x*+(^x-'^)ex.
10. г/ =(Cix + C2)cosx+(C3X+C4)sinx + -ex —-x2sinx + -sin2x.
4 8 9
11.11. Метод Лагранжа
Постановка задачи. Найти решение задачи Коши для
линейного неоднородного уравнения с постоянными коэффициентами
y"+Piy'+P2y = f(x) A)
с начальными условиями
у(хо) = 2/0, у'(х0) = у'0. (!')
План решения.
1. Записываем соответствующее однородное уравнение с
постоянными коэффициентами
y"+Piy'+p2y = 0. B)

282
Гл. 11. Дифференциальные уравнения
Находим фундаментальную систему решений yi(x) и у2{х) и общее
решение однородного уравнения
У = Ciyi(x) + С2у2(х).
2. Применяем метод Лагранжа (метод вариации произвольных
постоянных).
Если известна фундаментальная система решений yi(x), у2(х)
однородного уравнения B), то общее решение соответствующего
неоднородного уравнения A) может быть найдено по формуле
у = Ci(x) yx(x) + С2(х) у2(х),
где функции С[(х) и С'2(х) определяются из системы линейных
алгебраических уравнений
Г С'1(х)у1(х) + С'2(х)у2(х) = 0,
\ C'1(x)y'1(x) + C2(x)y2(x) = f(x).
Интегрируя, находим функции С\(х) и С2(х) и записываем общее
решение неоднородного уравнения.
3. Используя начальные условия A'), находим решение задачи
Коши.
Записываем ответ в виде у — у(х).
Пример. Найти решение задачи Коши
1
у" + у = —-
COSX
с начальными условиями у@) = 1, у'@) = 0.
Решение.
1. Записываем соответствующее однородное уравнение:
у" + У - 0.
Находим фундаментальную систему решений уд = cos x и у2 — sin x и
общее решение однородного уравнения
у — С\ cos х + С2 sinx.
2. Применяем метод Лагранжа (метод вариации произвольных
постоянных):

11.11. Метод Лагранжа
283
а) ищем решение данного неоднородного уравнения в виде
у = С\{х) cosx 4- С2(х) sin я;
б) записываем систему уравнений для определения функций С[(х)
и С2(х):
С[ (х) cos х + С'2(х) sin х = О,
C'i(x)(— sinx) + C'2{x)cosx = 1/cosx.
{
Решая ее (так как решение ищем в окрестности точки х = 0, то
cosx > 0), получим
C[(x) = -tgx, C2(x) = l.
Интегрируя, находим
Ci(x) — lncosx + Cj, C2(x) =x + C2;
в) записываем полученное общее решение данного неоднородного
уравнения
у — (lncosx + Cj)cosx + (x + C£)sinx.
3. Используя начальные условия, определяем константы С\ и С2.
Так как
у@) = (IncosO + С*!*) cosO + @ + С*2*) sinO = 0,
то С\ = 1. Так как
у'@) = (In cos 0 + С?) sin 0 + (-^^)cosO + sinO + @ + C£)cosO = 0,
то С% - 0.
Ответ, у = cos x(ln cos х + 1) + х sin x.
Условия задач. Найти решения задач Коши для,
дифференциальных уравнений.
1. у» + 2у' + у = —, 2/A) = 0, i/(l) =0.
х

284
Гл. 11. Дифференциальные уравнения
2. у" + у
1
sin x
3. y" + 4y = 2tgx,
1
4. y" + ly
cos2x
5. у" + у- tg х,
6. у"-2у' + у=—,
7. y"-?/ = thx,
8. y"-2?/ = 4xV2,
2/@) = 0,
2/@) = О,
2/@) = 2,
2/A) = е,
2/'@) = -2-
2/'@) = 0.
2/'@) = 1.
2/'A) = Зе.
7Г
9. 2/"-2/ =
4х2 + 1
х2 + 2х + 2
1/@) = 2 + -, 2/'@) = 1.
2/@) = 3, з/'@) = 0.
2/A) = е - 4, i/(l) - е - 2.
10. у" - 22/ + 2/ =
Ответы.
1.2/ = A — а: + xlnx) е~х.
7Г . . . .
2. у — — cosx + sinx — xcos£ + sinxln|sina:|.
3. у = —х cos 2x — — sin2x + sin2xIn | cosx|.
1 х
4.2/ = — cos 2x In | cos 2x\ + — sin 2x.
, 2/(-l) = --l, y'(_i) = __i.
e e
7.2/ = (ex + e_x)(l + arctge*).
5.2/ = cos a; 4- sin x 4- cos In
6. у — xex A +lnx).
8. у = ехуД + е~хуД + ex*. 9. j/ = ex - 4y/x. I0.y = ex + -.
x

Глава 12
КРАТНЫЕ ИНТЕГРАЛЫ
При изучении темы КРАТНЫЕ ИНТЕГРАЛЫ вы научитесь
записывать области (на плоскости и в пространстве) с помощью
неравенств в декартовых, полярных, цилиндрических и сферических
координатах, расставлять пределы интегрирования и сводить кратные
интегралы к повторным. Вы научитесь также решать задачи
геометрии и механики с использованием двойных и тройных интегралов
(в декартовых, полярных, обобщенных полярных, цилиндрических и
сферических координатах).
С помощью пакета РЕШЕБНИК.ВМ вы можете решить
неравенства, вычислить полученные повторные интегралы, выполнить все
численные расчеты и проверить правильность полученных вами
результатов.
12.1. Изменение порядка интегрирования
Постановка задачи. Изменить порядок интегрирования
Ь х2(у) d 2:4B/)
I - dy / f(x,y)dx+ dy / f{x,y)dx.
° 2:1C/) с x3(y)
План решения.
1. Область интегрирования состоит из двух областей D\ и Di-
Зададим их неравенствами
П_Г/ \ а <У <Ь, 1
ДМ: *i(v) < х < х2(у) /'
г» f/ \ c<y<d, \
D2={(x,y): ХЗЫ < х < х4Ы J'

286
Гл. 12. Кратные интегралы
2. Решаем системы неравенств, определяющих области D\ и Ог,
относительно у и получаем
У?\х) < у < $\х), у?\х) < у < у22\х).
3. Определяем границы изменения х, решая неравенства
уРЫ^уРМ, У{^(х)<у22)(х).
Получаем h < х < mi и 1^ < х < тг.
4. Области Di и £>г можно представить в виде
г. \ ( \ h<x<m\, \
п \( \ h<x<m2, \
D2 = \(x'y): №*)<у<№{*)!■
5. Записываем интегралы J с измененным порядком
интегрирования:
1= dx / f(x,y)dy+ dx f(x,y)dy.
6. Если lx = l2 = l, гп\ = тг = m и y2 (x) = y\ '(x) или
2/г (x) = 2/i (x)i TO I можно представить одним интегралом
УB2Чх) m У^'С*)
I = dx / f(x,y)dy или I = dx / f(x,y)dy.
Записываем ответ.
Пример. Изменить порядок интегрирования
1 л/j/ V v/2-!/2
I = dy f(x, y)dx+ dy / /(x, ?/) dx.
0 0 10

12.1. Изменение порядка интегрирования
287
Решение.
1. Область интегрирования состоит из двух областей Di и £>2-
Зададим их неравенствами
*={<**■■ Si: &}•
ч<^о<:^}-
2. Решаем системы неравенств, определяющих области D\ и 1?2,
относительно у и получаем
х2 <у<1, 1<у< \/2 - х2.
3. Определяем границы изменения х, решая неравенства
< 1, 1 < V2
аг < 1, 1 < yj'1-x'.
Учитывая, что х > 0, в обоих случаях получаем 0 < х < 1.
4. Области Di и Di можно представить в виде
5. Записываем интегралы J с измененным порядком
интегрирования:
11 1 \Л2-я2
1= dx f(x, y)dy+ I dx I f(x, y) dy.
0 x2 0 1
6. Пользуясь линейностью и аддитивностью интегралов, получаем
1 ( 1 \/1-х2 "J 1 у/2-х2
I- I dxl / /(х, j/) dy + / /(х, y)dy\= I dx J f(x, у)
dy.
о
1 \/4—X'
Ответ. I = I dx I f(x, y) dy.

288
Гл. 12. Кратные интегралы
Условия задач. Изменить порядок интегрирования.
2 2/х
1 2х
1. dx f(x,y)dy+ dx f(x,y)dy.
0 1 11
14 2 4
2- аУ f(x> V)dx+ dy f(x, y) dy.
1/4 1/j,
1 „2
-3 V36-»2 0 y/-y2-12y
3. dy / f(x,y)dx+ dy / f(x,y)dy.
-6 о
16 0
-3 о
32 0
4- dy f(x' y)dx+ I dy I f(x, y) dx.
0 -y/4
V6 ^fe5
16 -ч/35^
2л/3 V12-X2
5. dx f(x,y)dy+ dx f(x,y)dy.
о о
1 0
2 0
6- dy f(x' y)dx+ dy / f{x, y) dx.
0 -у2 1 -v^=7
1 V* 2 2-х
7. dx f(x, y)dy+ dx / f(x, y) dy.
0 0 10
0 V1-»2 1 %/lzr!/
8. dy / /(x, y)dx+ dy / /(x, ?/) dx.
-10 0 0
1 ev e e/j/
9- / dy / /(x, y) dx + M«/ / /(x, y) dx.
0 1 11
-10 0 0
10. dx f(x,y)dy+ dx f(x,y)dy.
-2 -2-х
-1 x3

12.2. Двойной интеграл в декартовых координатах 289
Ответы.
2 2/у 4 y/i
1- /dy / f{x,y)dx. 2. dx f(x,y)dy.
1 log2y 1 1/x
3v/3 -6+V36-X2 О 32-х2
3. dx / f(x,y)dy. 4. dx f(x,y)dy.
0 -v/36^  -4x
^g y/Vi-y2 О l+vT^s5"
5- / d«/ / Дх, ?/) dx. 6. dx / /(x, ?/) dy.
1 2-y 1 1-х2
7- / dy / /(s> 2/)da;- 8. / dx / /(x, y) dy.
0 у2 о -yr^2"
e e/x 0 vi/
9. fdxff(x,y)dy. 10. /dy f f(x,y)dx.
1 lnx -1 -2-y
12.2. Двойной интеграл
в декартовых координатах
Постановка задачи. Вычислить двойной интеграл
// f(x,y)dxdy,
D
где область D ограничена линиями fi{x,y) = 0, /г(х, у) = 0 (и,
возможно, прямыми х = а и х = Ь или у = с и у = d).
План решения.
1. Зададим область D неравенствами. Для этого выясним, каким
из неравенств
h(x,y)<0, h(x,y)>0, f2(x,y)<0 или f2(x,y)>0
удовлетворяют координаты точек области D.

290
Гл. 12. Кратные интегралы
Пусть, например, такими неравенствами оказались /i(x,j/) < 0 и
/2(x,j/)<0. Тогда
V-\[x,y). /a(a.|y)<0 ]■
Решаем неравенства, определяющие D, относительно х и у. Получаем
п - /1 \ а<х<Ь, \
и-\^у): У1(х)<у<у2{х) /
или
D=\(x,J/): *!(»)<* <*2(у) )•
2. Переходим от двойного интеграла к повторному:
6 1/2 (я)
f(x,y)dxdy= dx / f(x,y)dy
D а и(х)
или
d *2(l/)
// f(x,y)dxdy= dy f(x,y)dx.
D с !,(!,)
3. Последовательно интегрируем, используя свойства
определенного интеграла.
Записываем ответ.
Замечание. Если необходимо, разбиваем область на части и
используем свойство аддитивности интеграла.
ПРИМЕР. Вычислить двойной интеграл
[[(Ь4х2у2 + 150x4j/4) dxdy,
D
где область D ограничена линиями х =1, у = х3 и у = —Jx.
Решение.
1. Зададим область D неравенствами. Очевидно, что —Jx < х3.
Поэтому — у/х < у < х3. Поскольку х фигурирует под знаком
квадратного корня, х > 0. Для х возможны неравенства 0 < х < 1 или
1 < х. Во втором случае область неограничена, что неприемлемо.

12.2. Двойной интеграл в декартовых координатах 291
Итак,
Н(-): -°М^Л
2. Переходим от двойного интеграла к повторному:
1 х3
ff(Mx2y2 + 150а: V) dxdy= f dx f E4xV + 150хУ) dy.
D 0 _^/i
3. Используя свойства определенного интеграла, последовательно
интегрируем сначала по у (считая х постоянной), затем по х:
1 х
f dx f E4хV + 150xV) dy =
О -Vi
-3 х3
,.2 J.. _i_ 1 cnj / „,4 ,
/" 54x2 f y2dy+ 150x4 /" j/4 dy
— ijx —ijx
dx —
x3 x3
= / |54x2^| +150x4^|
/
dx
j.
= Al8xn + 18x7'2 + 30x19 + ЗОх13'2] dx = ll.
//<
Ответ. / / E4хУ + 150x4j/4) dxdj/ = 11.
D
Условия ЗАДАЧ. Вычислить двойные интегралы по областям D,
ограниченным заданными линиями.
1. Bx-y)dxdy,. y = x2, у = \/х.
D
2. {x-y)dxdy, г/ = 2-х2, у = 2х - 1.
D

292
Гл. 12. Кратные интегралы
3. (y\nx)dxdy, 2/=-, у = у/х, х = 2.
D
4. IJ (cos2x + siny) dxdy, у = — — х, у —0, х = 0.
D
5. sin(x+ y)dxdy, у = х, у = -, х = 0.
о
/Yx2 1
6. / / -J dxdj/, j/ = -, у = х, х = 2.
8. 11 Bх — y)dxdy, у = х2, у = х, ж=1, х = 2.
о
9. / / \/l - х2 - j/2 dx dy, у = y/l- x2, у = 0, х = 0.
о
10. / / x2y2y/l — x3 — у3dxdy, у = у 1 -13, J/= 0, x = 0.
Ответы. 1. J = 1/10. 2. J = 64/15. 3. J = 5B1n2 - l)/8.
4. / = (тг + 1 - 2V§)/4. 5. J = 1. 6. / = 9/4. 7. J = 33/140.
8. 1 = 9/10. 9. / = тг/6. 10. J = 4/135.
12.3. Двойной интеграл
в полярных координатах
Постановка задачи. Вычислить двойной интеграл
// f(x,y)dxdy,
D
где область D ограничена двумя окружностями
У2 + о.\у + Ьхх + х2 = 0, у2 + а-2.у + Ъ^х + х2 = 0

12.3. Двойной интеграл в полярных координатах 293
(d =0, а2 = 0, bib2 > 0 или b\ = О, 62 = 0, а\а2 > 0)
и двумя прямыми
т\у + к\х = 0, (т2 + к\ ф 0), m2j/ + fc2x = 0, (т2 4- к\ ф 0).
План решения.
1. Зададим область D неравенствами в декартовой системе
координат.
Для этого заметим, что окружности у2 + aij/ + bix + х2 = Ои
у2 + а2у + Ь2х + х2 — 0 проходят через начало координат и их центры
расположены на оси ОХ (при а.\ = 0, а2 = 0) или на оси OY (при
Ь\ = 0, Ь2 = 0) по одну сторону от начала координат (так как Ь\Ь2> 0
или а.\а.2 > 0). Поэтому та из окружностей, которая имеет меньший
радиус, расположена внутри другой. Пусть, например, это
окружность у2 + а\у + Ь\Х + х2 —0. Область D находится между
окружностями, поэтому координаты точек области D удовлетворяют
неравенствам
У2 + а\у + hx + х2 > 0, у2 + а2у + Ьгя + х2 < 0.
Прямые т\у + к\х = 0 и m2j/ -t- к2х = 0 проходят через начало
координат. Область D расположена между ними. Учитывая, в
какой полуплоскости находятся окружности и, следовательно, область
D, определяем, каким из следующих пар неравенств удовлетворяют
координаты точек области D:
"гпгУ + kix > 0, т2у + к2х > 0,
"ИЗ/ + к\Х < 0, т2у 4- к2х > 0,
mi3/ + к\х > 0, т2у + fc2x < 0,
r«i3/ + k\x < 0, m2y + k2x<0.
2. Так как область D ограничена окружностями и прямыми,
проходящими через начало координат, поставленную задачу проще
решать в полярных координатах
{
х = Qcastp,
У = QSlTUp.
При этом (g, (p) G D', а искомый интеграл определяется формулой
/ / /(х> y)dxdy = I I f(g cos <p, g sin tp) g dg dip.

294
Гл. 12. Кратные интегралы
3. Чтобы найти область D', заменяем в неравенствах,
определяющих область D, х на gcasip и у на gsimp. Затем разрешаем
полученные неравенства относительно gvup. Таким образом получим
jy=i(xv). <Pl<f<<P2, \
V ]' Qi(<P)<Q<Q2(v) Г
4. Переходим от двойного интеграла к повторному:
V2 £2(v)
S = I dip J f(g cos ip, g sin ip) g dg
vi ei(v)
и последовательно интегрируем, используя свойства определенного
интеграла.
Записываем ответ.
Пример. Вычислить двойной интеграл
х dx dy,
II •
D
где область D ограничена линиями
у2 - Ау + х2 = 0, у2 - 8у + х2 = 0, y = x/V3, x = 0.
Решение.
1. Зададим область D неравенствами в декартовой системе
координат. Для этого заметим, что, выделяя полные квадраты в
уравнениях окружностей у2 — 4j/ + х2 — 0 и у2 — 8у + х2 = 0, их можно
привести к виду
(j/-2J + x2 = 4, A)
(j/-4J+x2 = 16. B)
Очевидно, что обе окружности проходят через начало координат
и их центры расположены на оси OY в точках @,2) и @,4).
Окружность A) имеет радиус 2 и, следовательно, лежит внутри
окружности B), имеющей радиус 4. Поскольку область D находится между
окружностями, координаты ее точек удовлетворяют неравенствам
(у - 2J + х2 > 4, (у - 4J + х2 < 16.

12.3. Двойной интеграл в полярных координатах 295
Прямые у = х/л/3 и х = 0 проходят через начало координат.
Область D расположена между ними. Учитывая, что окружности, а
следовательно, и область D находятся в верхней полуплоскости,
заключаем, что область D находится над прямой у = x/V3 и справа от
прямой х = 0. Поэтому координаты точек области D удовлетворяют
неравенствам
у > х/\/3, х > 0.
Итак,
£>= <
(j/-2J+x2>4,
(х,у): B/-4J+х2<16,
у > x/y/Z, х > 0
> .
2. Так как область D ограничена окружностями и прямыми,
проходящими через начало координат, поставленную задачу проще
решать в полярных координатах
{
х = gcos(f,
у- gsinip.
При этом (g, <p) € D1, а искомый интеграл определяется формулой
// xdxdy— II дcosipgdgdip.
3. Чтобы найти область D1, заменяем в неравенствах,
определяющих область D, х на gcosip и у на gsimp:
(gsin<p — 2J + д2cos2 ip > 4,
(д sin <p — 4J + д2 cos2 f < 16,
QCOSip
gsmtp >
V3
-, gcos<p~>0.
Решая эти неравенства относительно д и (р, получаем
7г/6 < (Р < 7г/2,
D'={{g,<p)
4 sin (p < д < 8 sin <p

296
Гл. 12. Кратные интегралы
4. Переходим от двойного интеграла к повторному:
7г/2 8sinv?
11 xdxdy = II g cos <pgdgd<p = I cos <p dtp I g2 dg.
D D' ir/6 Isirup
Последовательно интегрируя, получаем
тг/2 8sinv? т/2
/ costpdip I g2dg = I costpdip —
тг/6
4sinv» тг/6
8 sin <p
4 simp
ж/2
448 f • 3
= —- I sin ipcostpdip
112
• sin v7
7Г/2
= 35.
тг/6
tt/6
Ответ. / / xdxdy — 35.
Условия задач. Вычислить двойные интегралы по областям
D, ограниченным заданными линиями.
1. Ijydxdy, у2 - 2у + х2 = 0, у2 - Ау + х2 = О,
D
X
у= V3x.
2. / / xdxdy, у'-бу+х' = 0, г/^-ву+х* =0, у = х, х = 0.
3. [[ 'У dxdy, y2-Ay+x2=0, y2-8y+x2=0, y = x,
J J y/x2+y2
D
Х = 0.
4. // Х =dxdy, у2 - Ау + х2 = 0, ?/2 - 6j/ + х2 = 0,
J J yJX1 + у1
у = х, х = 0.
5. ff-^-^dxdy, у2-6у + х2 = 0, у2-10у + х2=0,
D
у = х, х — 0.

12.4. Интеграл в обобщенных полярных координатах 297
6- // ,Х о dxdy, j/2-2x + x2 = 0, у2 - 4z + х2 = О,
J J х2+у2
D
У = -^. У = \/Зх.
7- // J* „dxdy, j/2-4x + x2=0, j/2-6x + x2=0,
J J x2 + j/2
j/ = -=, у = \/3x.
8- l(-=T—?dxdy, j/2-4x + x2 = 0, j/2-8x + x2 = 0,
J J x2 + yz
D
у = 0, j/ = \/Зя.
9. // У =dxdy, j/2-2x + x2=0, j/2-6x + x2 = 0,
J J y/x2+y2
y = ^y = o-
10. // —=Х dxdy, j/2-2x + x2 = 0, j/2 - lOx + x2 = 0,
ii v/x2 + j/2
j/ = \/3x, j/ = 0.
Ответы. 1. J = —Bтг - у/3). 2. I = 18-. 3. I = 10\/2.
4. / = |D-v/2). 5. J = l + |. 6. / = ^. 7. / = 1Bтг - x/3).
12.4. Двойной интеграл в обобщенных
полярных координатах
Постановка задачи. Вычислить двойной интеграл
/ / f(x,y)dxdy,
D
где область D задана неравенствами
х2 v2
°* - ^ + Ь ~ °2 (° > °> Ь > °> ci ^ °' с2 > °)>

298
Гл. 12. Кратные интегралы
rrny + kix>0 (ml + kj^O), т2у + к2х>0 (т\ + к\фО).
План решения.
1. Область D задана неравенствами в декартовой системе
координат, т.е.
х
..
(х,у)
ГП\У + к\Х > О,
m2j/ + к2х > О
> .
2. Так как область D ограничена эллипсами и прямыми,
проходящими через начало координат, поставленную задачу проще решать в
обобщенных полярных координатах
j x — ад cos ip,
\ у = bgsmip.
При этом (д, <р) £ D1, а искомый интеграл определяется формулой
/ / f(x,y)dxdy = II f(ag cos ip, bg sin <p) abg dg dip.
D D'
3. Чтобы найти область D1, заменяем в неравенствах,
определяющих область D, х на ад cos tp и у на bgsimp. Затем разрешаем
полученные неравенства относительно д и ip. Таким образом, получаем
"={м" 1VA?}-
4. Переходим от двойного интеграла к повторному:
// f{x,y)dxdy = ab I dip I f(agcosip,bgsmip)gdg',
и последовательно интегрируем, используя свойства определенного
интеграла.
Записываем ответ.
Пример. Вычислить двойной интеграл
//
х
-rdxdy,

12.4. Интеграл в обобщенных полярных координатах 299
где область D задана неравенствами
х
1<^+2/2<3,
х
х> 0.
Решение.
1. Область D задана неравенствами в декартовой системе
координат:
D
х"
(х,у)
1<^+2/2<3,
X
4
2. Так как область D ограничена эллипсами и прямыми,
проходящими через начало координат, поставленную задачу проще решать в
обобщенных полярных координатах
{::
х — Ag cos <р,
у = gsimp.
При этом (g, <р) € D1, а искомый интеграл определяется формулой
// -zdxdy= // . - Agdgdip.
J J У5 J J g5sirf<p
D
3. Чтобы найти область D', заменяем в неравенствах,
определяющих область D, х на agcostp и у на bgsinip:
1 <
1б£> COS2 <p
16
+ д2 sin2 <р < 3,
Agcosip
gsmip> , gcos<p>0
Решая эти неравенства относительно д и (р, получаем
I я/4 < Ч> < тг/2 I
4. Переходя от двойного интеграла к повторному и
последовательно интегрируя, получаем
Ц ^dxdy= II igj^ Agdgd<p
£>°Sin ip
*/2 V3
тг/4
, „ _•» COS(p ,
16p 3 =*- dg =
sin y>

300
Гл. 12. Кратные интегралы
чтР>*--1<-^к)Сш
V3
= 4.
тг/4
Ответ. / / — dx dy = 4.
D
х
УСЛОВИЯ ЗАДАЧ. Вычислить двойные интегралы.
1. // —dxdy,
2. I I —dxdy,
JJ У
D
3. 11 —dxdy,
JJ У
D
D
5. 11 —dxdy,
41
da; dj/,
10.
//?
D =
D
D =
D =
J/
/ / х3У dx dy, D =
D
D =
dx dy, D =
dx dy, D
D
9. ff^dxdy, D
D
dx dy, D =
x2 y2 „ 2x\
l<¥ + ^<2, y>0, „<T|.
1<^4<4, ,>0, ,>|}.
1<Тб + У-4<4,х>0,у>-\.
x2 у2 \
}■
}•
1<^+2/2<25, х>0, 2/>||-
1<ж2 + |^<9, j/>0, 2/<4х|.
1<^ + У2<4, ^°> ^f}"
ж2 и2 Зх 1
1<Т + у<36, z>0, j/> —|-
X2 V2
1<-Г + Т7<5, х>0, у>2х
4 16
х2 ь2 2х
i<-g- + ^<5, ж^0' y^Y
Ответы. 1. J = ln2. 2. J = 31n2. 3. J = 121n2. 4. 1 = 6.
5. J = 41n2. 6. J = 91n2. 7. J = 21n5. 8. J = 81n3. 9. J = ln2.
10. J = 21n6.

12.5. Вычисление объемов с помощью двойного интеграла 301
12.5. Вычисление объемов
с помощью двойного интеграла
Постановка задачи. Найти объем тела, ограниченного
поверхностями
9i(x,y)=0 (г = 1,2,...), z = f!(x,y), z = f2{x,y) (fa(x,y) > fi(x,y)).
План решения.
1. Объем цилиндрического бруса, ограниченного заданными
поверхностями, определяется формулой
V = ff\h{x,у) - fi(x,у)} dxdy, (l)
D
где D — проекция тела на плоскость XOY.
2. Чтобы найти D, задаем тело с помощью неравенств и
исключаем из них z.
Допустим, например, что координаты точек тела удовлетворяют
неравенствам 0 < z < f(x,y), gi(x,y) > 0 и g?(x,у) < 0. Тогда тело
определяется системой неравенств
5i (х, у) >0,
52 (х, у) <0,
0<z<f(x,y).
Исключая z, получим
(gi(x,y) >0,
(х,у): 52(ж,2/)<0,
0<f(x,y)
3. Вычисляем двойной интеграл по формуле A) при /2 = f(x,y) и
/i=0.
Записываем ответ, не забывая о размерности.
Пример 1. Найти объем тела, ограниченного поверхностями
г=17у/2у, х = 2у/Ъ/, z = l/2-j/, z-0.

302
Гл. 12. Кратные интегралы
Решение.
1. По формуле A) с /г = 1/2 — у и /i = 0 искомый объем равен
//(N
где jD — проекция тела на плоскость XOY.
2. Чтобы найти D, задаем тело с помощью неравенств и
исключаем из них z. В данном случае тело определяется системой
неравенств
( х < 17у/2у,
x>2yfly,
0 < z < 1/2 - у
Поэтому
Г 2уЩ) <Х< \lyffi>, \
Здесь неравенство у > 0 необходимо, так как j/ стоит под знаком
квадратного корня.
3. Вычисляем двойной интеграл:
V= (--yjdxdy= dy / l--yjdx =
d о 2v/25
1/2
= \ЬуЯ f (\-y\y/ydy=l.
0
Ответ. V = 1 ед. объема.
Пример 2. Найти объем тела, ограниченного поверхностями
х2 + у2 + 2х = 0, z = — -y2, 2 = 0.
Решение.
1. По формуле A) с fc = 25/4 — у2 и /i = 0 искомый объем равен
V = IJ(j-y2-(^dxdy,
D

12.5. Вычисление объемов с помощью двойного интеграла 303
где D — проекция тела на плоскость XOY.
2. Чтобы найти D, задаем тело с помощью неравенств и
исключаем из них z. В данном случае тело определяется неравенствами
Г (z+lJ+2/2<l,
\ 0<z<25/4-2/2
Из первого неравенства очевидно, что \у\ < 1 и, следовательно, второе
неравенство выполняется автоматически (геометрически это
означает, что проекция поверхности z = 25/4 — у2 на плоскость XOY
охватывает круг (х + IJ + у2 < 1). Поэтому
D = {(x,y): (х + 1J+у2<1).
3. Так как область D ограничена окружностями и прямыми,
проходящими через начало координат, поставленную задачу проще
решать в полярных координатах
{
X = Q COS If,
у- Qsirnp.
При этом (g, <р) € 1У, а искомый объем определяется формулой
V = II [-Г-У2) dxdy= [-Г -£2sin2v?J gdydg.
D D'
4. Чтобы найти область D1, заменяем в неравенстве,
определяющем область D, х на g cos ip и у на q sin ip:
(gcosip + lJ + q2sin2 ip < 1.
Получаем
D'JM.. 0<в<-2ooeV,l
\KU,V) n/2<<p<3n/2 J
Заметим, что из неравенств 0 < q < —2 cos у следует тг/2 < лр < Зп/2.
5. Переходим от двойного интеграла к повторному:
37г/2 —2 cos if
V = / / I — g2sin2 ip I q dg dip = I dip I I — q2 sin2 ip J q dg.
D' Л-/2 0

304
Гл. 12. Кратные интегралы
Последовательно интегрируя, получаем
Зтг/2 -2cosv
V = I dtp I ( —— д2 sin2 ip J д dg =
тг/2
Зтг/2
' п2 „4
тг/2
Зтг/2
—2cosv>
dy> =
О
Г BЪд2 д4 . 2 \
Зтг/2
/ (~<Г 'cos2 V — 4 cos4 v? sin2 y> J dy> = бтг.
тг/2
Ответ. V = бтг ед. объема.
УСЛОВИЯ ЗАДАЧ. Найти объемы тел, ограниченных заданными
поверхностями.
1. х = у/у, х = 2у/у, z = \-y, 2 = 0.
2. у = у/х, у = 2^/х, z = 6 - х, 2 = 0.
3. у — у/х, у = 0, х=1, 2 = х + у + 1, 2 = 0.
4. у = х2, у = 1, 2 = а;2 + J/2, 2 = 0.
5. у = 6 — Зх/2, у = 6 — Зх, у = 0, z — 6 — х — у, 2 = 0.
6. я2 + у2 = 4, z = ху, 2 = 0 (х > 0, у > 0).
7. j/ = у/х~/2, У = 0 2 = 4-а;-2j/, 2 = 0.
8. х2 + у2 - 4j/ = 0, 2 = 4 - ж2, 2 = 0.
9. х2 +у2 -2х = 0,
10. ж2 + у2 - 2х = 0,
z = x2+y2,
2 = 2х,
2 = 0.
2 = 4х
Ответы. 1. V = 4/15. 2.V = 48л/б/5. 3. V = 79/60. 4. V = 40/3.
5. V = 12. 6. V = 4. .7. V = 17/5. 8. V = 12тг. 9. V = Зтг/2.
10. V = 2тг.
12.6. Вычисление площадей
в декартовых координатах
Постановка задачи. Найти площадь области D, ограниченной
линиями fi(x,y) — 0, $2{х,у) = 0 (и, возможно, прямыми х = а и
х = Ь или у = с иу = d).

12.6. Вычисление площадей в декартовых координатах 305
План решения.
Из определения двойного интеграла следует, что искомая площадь
S численно равна
ffldxdy. A)
D
1. Зададим область D неравенствами. Для этого выясним, какие
из неравенств
fi(x,y) < 0, fi(x,y) > 0, h(x,y) < 0 или f2(x,y) > 0
выполняются для координат точек области D.
Пусть, например, такими неравенствами оказались fi(x,y) < 0 и
/2(z,j/)<0. Тогда
п J, . h(x,y)<0,\
D=yX>y): Мх,у)<0 J'
Решаем неравенства, определяющие D, относительно х и у. Получаем
{а < х <Ь, 1
{Х,У): щ(х)<у<Уя(х) )
2. Переходим от двойного интеграла к повторному:
Ь 3/2 (г)
ffdxdy = jdx J dy
или
а г/1 (г)
d x2{.y)
JJdxdy = Jdy J dx.
D с Xl(y)
3. Последовательно интегрируем, используя свойства
определенного интеграла.
Записываем ответ, не забывая о размерности.
Замечание. Если необходимо, разбиваем область на части и
используем свойство аддитивности интеграла.

306
Гл. 12. Кратные интегралы
Пример. Найти площадь области D, ограниченной линиями
х2 + у2 = 12, xV6 = y2 (ж > 0).
Решение.
1. Зададим область D неравенствами. Область не может
находиться вне круга, так как тогда она неограничена. Область не может
находиться слева от параболы, так как в этом случае ее точки могут
иметь отрицательные абсциссы, что исключено условием х > 0.
Следовательно,
D
\{X'V)- х>у2/^ )
Решаем неравенства, определяющие D, относительно х и у. Получаем
4= < х < у/\2 - у2.
V6
Следовательно, у2/у/& < у/\2 — у2. Отсюда — л/б <у< л/б- Итак,
2. Вычисляем площадь области D по формуле A). Переходя от
двойного интеграла к повторному, получим
v/6 >/l2=
S = I I dxdy — I dy I dx.
-v/6 y2/v/6
3. Используя свойства определенного интеграла, последовательно
интегрируем:
^6 \Л2-а2 у/ё
S= f dy f dx= f (y/\2 -y2- -^= J dy = Зтг + 2.
-v/6 y2/v/6 -v/6
Ответ. S = C7Г + 2) (ед. длиныJ.

12.7. Вычисление площадей в полярных координатах 307
Условия ЗАДАЧ. Найти площади фигур, ограниченных
заданными линиями.
1. у = 2/х, у = 4ех, у = 2, у = 4.
2. у = 1/х, у = 2ех, j/ = l, у = 2.
3. у — 2/х, у = 2у/х, х = 4.
4. х2 + у2 = 2, у = -х2 (у<0).
5. j/ = у/х, у = 0, х = 4.
6. х = 2 — у2, х — —у.
7. у = sin х, y = cosx, x = 0, x — ir/4.
8. j/ = 2x2 — 1, j/ = ж.
9. ж = у/А - у2, х = у2/3.
10. y — lnx, у — е/х, х = 1.
Ответы. 1. 5 = 2. 2. 5 = 1. 3. 5 = 28/3 - In 16. 4. 5 =
= тг/2 + 1/3. 5. 5 = 16/3. 6. 5 = 7/6. 7. 5 = \/2 - 1. 8. 5 = 27/24.
9. 5 = 2тг/3 - \/3/6. 10. 5 = е - 1.
12.7. Вычисление площадей
в полярных координатах
Постановка задачи. Найти площадь области D, ограниченной
двумя окружностями
У2 + а\У + hx + х2 = 0, у2 + а2у + Ь2х + х2 - 0,
(ai =0, a2 = 0, b\b2 > 0 или b\ —0, 62 = 0, aia2 > 0)
и двумя прямыми
fniy + kix = 0, (ml + k\ ф 0), т2у + к2х = 0, (т\ Л-к\ф 0).

308
Гл. 12. Кратные интегралы
План решения. Из определения двойного интеграла следует, что
искомая площадь S численно равна
ffldxdy. A)
5
D
1. Так как область D ограничена окружностями и прямыми,
проходящими через начало координат, поставленную задачу проще
решать, переходя к полярным координатам
{х = pcostp,
y = psimp
и записывая уравнения границ в полярных координатах.
При этом область D перейдет в область ТУ, а искомая площадь
будет равна
S = I I pdpdip.
D'
2. Зададим неравенствами область ГУ в полярных координатах:
2/= /(„,„): Ъ<<Р<Ч*, \
[ Р\{Ф) <Р< Р2{Ф) J
3. Переходим от двойного интеграла к повторному:
¥>2 Рг(¥>)
S = I dtp I pdp
и вычисляем его, пользуясь свойствами определенного интеграла.
Записываем ответ, не забывая о размерности.
Пример. Найти площадь фигуры, ограниченной данными
линиями
у2 - 4у + х2 = 0, у2 - 8у + х2 = 0, 2/="^. * = О-
Решение.
1. Так как область D ограничена окружностями и прямыми,
проходящими через начало координат, поставленную задачу проще
решать, переходя к полярным координатам
J X = р COS if,
\ y = psimp.

12.7. Вычисление площадей в полярных координатах 309
При этом область D перейдет в область V, ограниченную линиями
о I
А искомая площадь будет равна
S = II gdodip.
D'
2. Зададим неравенствами область ТУ в полярных координатах:
I 4siny> < g < 8sin^i I
3. Переходим от двойного интеграла к повторному:
7г/2 8 sin <р
S = I dip / gdg.
7г/6 4sinv>
Последовательно интегрируя, получим
7г/2 8 sin и тг/2 - . тг/2
'- - * - 2 |8sin^j '-
dip / Qdg= /у dip = 24 sin2 y>dy> = 4тг + 3\/3.
^ ^ I4sinc£ ^
14 sin v?
7I-/6 4sinv 7г/6 7Г/6
2
Ответ. S = D7Г + 3\/3) (ед. длины)
Условия ЗАДАЧ. Найти площади фигур, ограниченных
заданными линиями.
1. у2 - Зу + х2 = 0, у1 - Ъу + х2 = О, J/ = ж/\/3, ж = 0.
2 J/2 + Ъу + ж2 = 0, у2 + Ъу + х2 = 0, у = х, х = 0.
3. j/2 - Зу + х2 = 0, у2 - 7у + х2 = 0, j/ = \/Зж, х = 0.
4. j/2 + 3j/ + ж2 = 0, j/2 + 5j/ + ж2 = 0, j/ = ж, у — х/у/З.
5. j/2 - Зу + х2 = 0, у2 - Ъу + х2 = 0, j/ = ж/\/3, ж = \/Зж.

310
Гл. 12. Кратные интегралы
6. у2 - Ъх + х2 = 0, у2 - 7х + х2 = 0, у = х/у/Ъ, у = 0.
7. у2 + 4х + х2 = 0, у2 + 6х + х2 = 0, у = х/лД, у = \/Зх.
8. у2 - Зх + х2 = 0, у2 - 5х + х2 = 0, у = \/Зх, у = 0.
9. у2 + 2х + х2 — 0, у2 + 4х + х2 = 0, у = я, у = 0.
10. у2 + 2х + х2 = 0, у2 + 10х + х2 = 0, у = уДх, у = 0.
Ответы. 1. 5 = 4тг/3 + %/3. 2. S = тг + 2. 3. 5 = 5тг/3 + 5%/3/2.
4. S = тг/3 - 2 + у/3. 5. 5 = 2тг/3. 6. 5 = тг + 3%/3/2. 7. 5 = 5тг/6.
8. 5 - 4тг/3 + д/5. 9. 5 = Зтг/4 + 3/2. 10. 5 = 8тг + 6ч/з.
12.8. Вычисление массы плоской пластины
ПОСТАНОВКА ЗАДАЧИ. Найти массу плоской пластины D с
поверхностной плотностью ц = ц(х,у), ограниченной заданными
кривыми.
План решения.
1. Масса пластины D с поверхностной плотностью /х(х,у)
определяется формулой
т = 11 fi(x, у) dx dy.
D
2. Вычисляем полученный двойной интеграл. Записываем ответ,
не забывая о размерности.
Пример 1. Найти массу пластины D с поверхностной плотностью
ц — 16х + 9у2/2, ограниченной кривыми
х=\, У = 0, У2 = 16х (у>0).
Решение.
1. Масса пластины D с поверхностной плотностью ц = 16х+9у2/2
определяется формулой
,, ,.„ ^
т
= [[Aвх+%-) dxdv-
D

12.8. Вычисление массы плоской пластины
311
2. Вычисляем полученный двойной интеграл в декартовых
координатах:
а) зададим область D системой неравенств:
I
О < х < 1/4,
О < у < 4-v/i.
Неравенство 0 < х следует из того, что у2 = 16х, т.е. х
неотрицательно;
б) перейдем от двойного интеграла к повторному:
1/4 4у/х
J J (lftr + ^|Л dxdy = j dx f Ых + ЩЛ dy;
в) последовательно интегрируем, используя свойства
определенного интеграла:
1/4 4v/£
т
о о
= f dx f Лбх+^|-) dy =
1/4
= I A6x1/ + \ ) dx = 160 j x3/2 dx = 2.
X'4 - - 4^ 1/4
0
Ответ, т = 2 ед. массы.
Пример 2. Найти массу пластины D с поверхностной плотностью
/i = х2 /{х2 + у2), ограниченной кривыми
у2 - Ау + х2 = 0, у2 - 8у + х2 = 0, 2/=4=, а; = 0.
Решение.
1. Масса пластины D с поверхностной плотностью ц = х2/(х2+у2)
определяется формулой
m = JJ-r^dxdy-
У2
D
2. Вычисляем полученный двойной интеграл:

312
Гл. 12. Кратные интегралы
а) так как область D ограничена окружностями и прямыми,
проходящими через начало координат, поставленную задачу проще
решать в полярных координатах
Г х = д cos ц>,
\ y = gs\rup.
При этом область D перейдет в область £>', ограниченную линиями
g = 4smtp, g — asmip, tp=—, tp ■
2'
а искомая масса определяется формулой
т= II —5 xdxdy= I/ cos2ipgdgdip.
J J x2 + y2 J J
D D'
Зададим неравенствами область £>' в полярных координатах:
Г 7I-/6 < ip < -к 12, 1
^ 4 sin tp < q < 8 sin tp J
б) перейдем от двойного интеграла к повторному
Я-/2 8 sin <p
11 cos2ipgdgdip — I cos2ipdip j gdg;
m ■■
D' jr/6 4 sin v
в) последовательно интегрируя, получим
m
jt/2 8sinv т/2
= / cos2 ip dip j gdg= j cos2 ip
7Г/6
4 sin v>
тг/2
8 sin v>
dy> =
5Г/6
4 sin ^7
= 24 / sin2 y>cos2ipdip = I 3y> — — sin4y> j
jr/6
jt/2
= 7Г +
3%/3
5Г/6
Ответ, тп = 7г + 3v3/8 ед. массы.

12.8. Вычисление массы плоской пластины
313
Пример 3. Найти массу пластины D с поверхностной плотностью
ц — х/у5, ограниченной кривыми
2 2
X 9 X 9 X I X \
Тб+У =1« 16+2/ =3' У=4' Х = ° (^4'Х-°)-
Решение.
1. Масса пластины D с поверхностной плотностью ц = х/у5
определяется формулой
т = / / -g dx dy.
2. Вычисляем полученный двойной интеграл:
а) зададим область D неравенствами в декартовой системе
координат
{К — + у2 < 3,
{х,у): -16 У ~
2/>х/4, х>0
Так как область D ограничена эллипсами и прямыми, проходящими
через начало координат, поставленную задачу проще решать в
обобщенных полярных координатах
х — Agcosip,
у = д sin ц>.
\ 2/ =
При этом (д, if) € D', а искомая масса определяется формулой
т= -gdxdy= // . 5 Agdgdip.
D D'
Чтобы найти область D', заменяем в неравенствах, определяющих
область £>, х на Ад cos f и у на ^ sin уз:
16й2 COS2 W 9.9
1< 16 *+g2sin2y<3,
^ sin v? > 4р cos уз/4, р cos у > 0.
Решая эти неравенства относительно д и tp, получаем
1 < Q < \/3,
£>' = { @, ¥>) : тг тг

314
Гл. 12. Кратные интегралы
б) переходим от двойного интеграла к повторному:
т/2 -УЗ
Г Г Agcosip . , , f , f,. _3 cosw ,
m = / / — г— Ад ад dtp — I dtp I log • —t— dg;
J J g5sin ip J J sin y;
D' jr/4 1
в) последовательно интегрируя, получаем
тг/4 1
Ответ, т = 4 ед. массы.
Условия задач. Найти массу пластины D с поверхностной
плотностью ц, где D ограничена заданными линиями.
1. ц = 2х + у2, х = 4, у = О, у = у/х.
2. ц = х2 + у, х = 1, у = 0, у = 2-v/x.
3. ^ = х2 + 2у, х-0, у - 4, у = я2 (х > 0).
4. /i = x + 2/2, х = 0, у = 1, у = х2/А (х > 0).
5- М- zT^a» х = 0' У = 0' а;2 + 2/2=4, х2 + у2 = 9
х^ + 2Г
(х > 0, у < 0).
6. ц = 2j/, * х = 0, 2/ = 0, х2+2/2=3, х2+2/2 = 5
х2 + 2/2'
(х<0, 2/>0).
7- /х=4т^2-' х = 0' У = 0' *2 + 2/2=4. х2 + 2/2 = 16
х^ + 2/
(х<0, 2/>0).
2 2
8. ц(х,у) = у, у=0, у = ху/3, х2 + ^- = 1, х2 + ^-=9
B/>0, 1/<а:^3).

12.9. Тройной интеграл в декартовых координатах 315
9. »(х,у) = \, 2/ = 0, у = х, ^-+2/2 = 1, ?L+y* = 4
хА 4 4
(у > 0, у < х).
10.ф,у) = ^, х = 0, у = х, ^ + ^- = 1, ?L + ^=25
(х > О, у > х).
Ответы. 1. т = 448/15. 2. m = 11/7. 3. т = 448/15. 4. m = 11/7.
5. m = 2. 6. m = 3(л/5-\/3). 7. m = 4. 8. m = 52/3. 9. m = (\/2-l)/2.
10. m = 18(\/2 - 1).
12.9. Тройной интеграл
в декартовых координатах
Постановка задачи. Вычислить тройной интеграл
III f{x,y,z)dxdydz,
п
где область fi ограничена некоторыми поверхностями.
План решения.
1. Зададим область Q системой неравенств, например,
а < х < Ь,
Уг(х) <у <У2(х),
z\\x,y) <z< z2{x,y).
2. Перейдем от тройного интеграла к повторному:
Ъ 3/г(а:) z2[x,y)
f(x,y,z)dxdydz= dx dV f(x,y,z)dz.
fi a yi(x) гг(х,у)
3. Используя свойства определенного интеграла, последовательно
интегрируем сначала по z (считая х и у постоянными), затем по у
(считая х постоянной), затем по х.
Записываем ответ.

316
Гл. 12. Кратные интегралы
ПРИМЕР. Вычислить тройной интеграл
/ / / х2 sh (xy) dx dy dz,
где Q ограничена плоскостями
х = 2, у = -, у = О, z = О, z = 1.
Решение.
1. Зададим область fi неравенствами. Очевидно, что 0 < z < 1.
Для у возможны неравенства 0 < у < х/2 или х/2 < у < 0. Если
0 < у < х/2, то х > 0 и для х имеем 0 < х < 2. Если же х/2 < у < 0, то
х < 0 и область не примыкает к плоскости х = 2. Значит, мы должны
принять, что 0 < у < х/2 и определить О. системой неравенств
' 0 < х < 2,
0 < у < х/2,
0 < z < 1.
2. Перейдем от тройного интеграла к повторному:
2 х/2 1
/ / / х2 sh. (xy)dxdydz = I dx I dy I x2sh(xy)dz.
n ooo
3. Используя свойства определенного интеграла, последовательно
интегрируем сначала по z (считая х и у постоянными), затем по у
(считая х постоянной), затем по х:
2 х/2 1
/ / / х2 sh (xy) dx dydz = I dx I dy I x2 sh (xy) dz =
n ooo
2 x/2 12 x/2
= I dx I x2sh (xy) dy I dz = I dx I x2 sh (xy) dy =
о о
2
2 ch (xy)
0 0 0
2
= у x2fhMp dx=zjx^_ ch0) dx :

12.9. Тройной интеграл в декартовых координатах 317
= sh-
2= sh2-2.
Ответ. / / / х2 sh (ху) dx dydz = sh 2 - 2.
Условия задач. Вычислить тройной интеграл по области fl,
ограниченной заданными поверхностями.
1. / / / 4y2zexydxdydz, x = 0, у = 1, у = х, z = 0, z = 1.
п
2. [zy*z*e-xydxdydz, х = 0, у =-2, у = 4х, z = 0, z = 1.
п
3. I 3x*z*exy/*dxdydz, x = 0, у = 2, у = 2х, z = 0, z =-1.
п
4. / / / 2?/2xcosGrx2/)dxdydz, x = 0, у = 1, у = 2х, z = 0, z = ir2.
о.
5. / / У x22;sinGrx2/)dxdydz, x = 1, у = 2х, у = 0, z = 0, z = 47r.
n
6. / / / y2zch(xy)dxdydz, x = 0, у = — 1, У — x, z = 0, z = 2.
n
7. / / / 2/z3 cos(xy) dx dy dz, x = l, y = n, z = 2, x=0, y=0, z=0.
n
8. / / / x2zshCxy)dxdydz, x = 1, у — 2х, у = 0, z = 0, z = 1.
n
III Zxz2 sm(xy)dxdydz, x = 2, y = n, z = l, x = 0, y=0, z=0.
10
Ответы. 1. / = e-2. 2. / = 2e~\ 3.1 = 4e-8. 4. / = 4. 5. / = 16тг2.
6./ = 2chl-2. 7.1 = 8. 8./ = (sh6-6)/72. 9./ = ch2-l. 10. / = 2.

318
Гл. 12. Кратные интегралы
12.10. Тройной интеграл
в цилиндрических координатах
Постановка задачи. Вычислить тройной интеграл
/ / / f(x,y,z)dxdydz,
п
где область П ограничена поверхностями
z = gi(x2 +y2), z = g2(x2+y2).
План решения.
1. Поскольку 17 — тело вращения вокруг оси OZ, удобно перейти
к цилиндрическим координатам
х = gcostp,
у = gsinip,
z = z.
При этом (g, ip, z) £ f2', а искомый интеграл определяется формулой
/ / / f(x,y,z)dxdydz = III f (g cos ip,g simp, z) gdg dip dz.
n n'
2. Зададим область Г2' неравенствами. Для этого сначала
заменим в уравнениях поверхностей х на g cos ip и у на g sin ip. Тогда 17'
определяется неравенствами gi(g2)<z<g^(g2) или gi(g2)<z<gi(g2).
Чтобы выбрать правильные неравенства, решаем уравнение
gi(g2) = 52(е2) относительно д. Если оно имеет два решения д\ и
02 @ < pi < 02), то исследуем, какая из функций gi(g2) или <fr(g2)
больше другой на промежутке д\ < д < д%. Предположим для
определенности, что gi{g2) < дг(д2) при gi < д < gi- Тогда область 17'
определяется системой неравенств
17'= <
Q\ < Q < Q2,
(g,ip,z): gi(Q2) < z < д2(д2),
0 < ip < 2тг
Если уравнение gi(g2) — gz(g2) имеет единственное положительное
решение д = gi, то неравенства для д имеют вид 0 < д < gi.

12.10. Тройной интеграл в цилиндрических координатах 319
3. Переходим от тройного интеграла к повторному:
/// f(x,y,z)dxdydz = / / / f(gcostp, gsiatp, z) gdgdtpdz
27Г q2 »г(е)
I dtp J gdg J f(gcostp,gsmtp,z)dz,
0 ei gi(e)
и последовательно интегрируем, используя свойства определенного
интеграла.
Записываем ответ.
Пример. Вычислить тройной интеграл
III^hdxdydz'
где область fi ограничена поверхностями
z= -\/x2 + 2/2, z = — -x2 -у2.
Решение.
1. Поскольку П — тело вращения вокруг оси OZ, удобно перейти
к цилиндрическим координатам
х = g cos tp,
у = gsintp,
z = z.
При этом (g, tp, z) £ fi', а искомый интеграл определяется формулой
/ / / ~~2 ^dxdydz — III cos2 tp gdgdtpdz.
2. Зададим область Г2' неравенствами. Для этого сначала заменим
в уравнениях поверхностей х на g cos tp и у на g sin tp. Тогда fi'
определяется неравенствами 9g/2 < z < 11/2 —д2 или 11/2 — д2 < z < 9д/2.
Чтобы выбрать правильные неравенства, решаем уравнение
9 11 2
2е = Т~е-

320
Гл. 12. Кратные интегралы
Это уравнение имеет единственное положительное решение д = 1.
Следовательно, 0 < д < 1. При 0 < д < 1
9 . 11 2
2*<Т-0.
Таким образом, область JV определяется системой неравенств:
0< Q< 1,
9/2^ < z < 11/2 - £2,
0 < <р < 2тг
3. Переходим от тройного интеграла к повторному:
о2 cos2 <
gz cos2 <р + £2 sin'' v?
/ / / 2 , 2dxdydz= III — 2 gdgd<pdz =
J J J x1 + y2 J J J g2 cos2 w + g2 sin'' y>
n
2тг 1 U/2-e2
= / cos2 ipdip I gdg I dz.
0 0 9e/2
Последовательно интегрируя, получаем
2тг 1 "/2-е2 1
cos2 <pd<p gdg / dz = тг / ( — - g2 - -g\ gdg = ж.
0 0 ge/2 0
Ответ. / / / —2^ ^dxdydz — 7r.
n
УСЛОВИЯ ЗАДАЧ. Вычислить тройной интеграл по области ft,
ограниченной заданными поверхностями.
JJJ х2+у2
l- I I „2 , ,.i dxdydz, х2 + у2 + Ах = 0, z = 8 - у2, z = 0.
п
_ri Л'.- Ло1 А-, о-2 -L OI2 _ Aii — Г\ -г — К _ -г-2 •>- — i
■у I 9
х-2 + У2
1- 111 ^2~Г^2 dxdydz, х2 + у2 - Ау = 0, z = 6 - х'2, z = 0.

12.11. Тройной интеграл в сферических координатах 321
3. / / / У dxdydz, х2 + у2 - 4у = 0, z = 4 - х2, z = О.
7 7 7 ^/х2 + у2
4. / / / . Х dxdydz, х2 + у2 - 4х = О, z = 10 - у2, z = 0.
777 ^/х2 + у2
5. / / / -^—^ dxdydz, х2 + у2 - 4х = 0, z = 12 - у2, z = 0.
■У
и
6- / / / ~1 2 dxdydz, z = у/36 -х2 - у2, z =
п
7' lflx^dXdydZ' Z = Л/1-*2-»2,
х2 + у2
9 '
2 2 2(х2 + у2)
3
8- //Ыт?***- г=^^. -^
п
10- ///-jF=== dxdydz, z=y--x2-y2, z = x2+y2-
44 2 32 32 2
Ответы. 1. ——тт. 2. 10-7Г. 3. 32—. 4. 96—. 5. 22-тг.
3 3 35 35 3
3 19
6. 42-тг. 7. —тг. 8. 0. 9. 0. 10. 0.
4 96
12.11. Тройной интеграл
в сферических координатах
Постановка задачи. Вычислить тройной интеграл
III f(x,у,z)dxdydz,
n
где область Q ограничена поверхностями
x2+y2+z2 = R2, z = ±^±y2
,2

322
Гл. 12. Кратные интегралы
План решения.
1. Поскольку Q ограничена сферой и круглым конусом, удобно
перейти к сферическим координатам
х = £cosy?sin#,
у = gsin<psm6,
Z = QCOS0.
Возможные границы изменения сферических координат суть
О < £ < оо, 0<в < тг, 0 < у < 2тг.
При этом (д, в, <р) G fl', а искомый интеграл определяется формулой
/ / / /fa. J/.z) dx dy dz =
n
-///■
f(g cos <p sin в, q sin <p sin в, g cos в) д sin Odg d6 d<p.
w
2. Заменяем в уравнениях поверхностей х на £ cosy? sin 0, у на
£ sin у? sin 0 и z на gcos6. Получаем
g = R, tg0 = ±|a|.
3. Зададим область ft' с помощью системы неравенств:
О < д < R,
в\<6< 02,
О < у < 2тг,
где границы изменения в находим, решая уравнение tg# = ±|a| и
учитывая, что в может изменяться только от 0 до 7г.
Замечание. Если ft ограничена также плоскостями у = kix и
у = fox, проходящими через ось OZ, уравнения которых в
сферических координатах имеют вид tg <р = ki и tg <p = &2, находим границы
изменения tp, решая эти уравнения.
4. Переходим от тройного интеграла к повторному:
/(х, у, z) dx dy dz =
///

12.11. Тройной интеграл в сферических координатах 323
— I I I f(gcos<psin6,g sin <p sin 6, g cos 6) g2 sin 6 dgd6 d<p —
2тг в2 R
= d<p sinOde / f(gcos <psin6,gsin y? sin в, gcos 0) £2 dg,
0 0!
и последовательно интегрируем, используя свойства определенного
интеграла.
Записываем ответ.
Пример. Вычислить тройной интеграл
и
где область Q ограничена поверхностями
= V36-x2-y2, z = yj-
х2 + у2
3
Решение.
1. Поскольку Q — область, ограниченная верхней полусферой и
верхним полуконусом, удобно перейти к сферическим координатам
х = gcos<psin6,
у = £sin<£sin#,
z = gcosG.
При этом (#, в, <р) 6 £У, а искомый интеграл определяется
формулой
/ / / ~~2 2 dxdydz = III cos2 y>£2 sin в dgdOdy.
2. Заменяем в уравнениях поверхностей х на £ cosy? sin 0, у на
0sin у? sin0 и 2 на gcosd. Получаем
0 = 6, tg 0 = л/3.
3. Зададим область П' с помощью системы неравенств:
П'= «
О < 0 < 6,
@,0,у>): 0<е<тг/3,
О < <р < 2тг.

324
Гл. 12. Кратные интегралы
4. Переходя от тройного интеграла к повторному и
последовательно интегрируя, получаем
/ / / ~2 2 dxdydz = III cos2 <pg2smOdgdOdtp —
2тг т/3 6
= / cos2<pd<p I sin6d6 / g2 dg = 367r.
X2
Ответ. / / / —^—^dxdydz — 367Г.
J J J x2 + y2
и
Условия ЗАДАЧ. Вычислить тройной интеграл по области Q,
ограниченной заданными поверхностями.
х2 +у2
1///^2Ty2dXdj/dZ' z=V25-x2-j/2, z=yj- g9
n
х2 + у2
27//l?T7<fa*<b' * = ^зб-*»-л , = / 63
п
*-Iff*T7dxdvdz' г = ^1б-х2-у2, * = У^
п
4' ni^J+y2~dxdydz' г=^-^2-Г7. * = /
х2 +у2
~80~
п
X2 + J/2
57//^7dXd2/d2' г = ^-*2-у2, * = / 35 •
n v
6' JJJ'^Tij*dxdydZ^ * = лЛ - *2 ~ У2. z=y^~[^--
п

12.12. Вычисление объемов с помощью тройного интеграла 325
///ТЭТ?***1 > = ^/5гT^■ ' - F¥-
' 2х + 3у
ЧПт0В^ -j*^. -fW-
n
15"
ШШ??Т?***- '-^^^7- > = \ЩУ
Ответы. 1. 75тг/2. 2. 63тг. 3. 0. 4. 0. 5. 0. 6. 2тг. 7. бтг.
8. 0. 9. 0. 10. 0.
12.12. Вычисление объемов
с помощью тройного интеграла
Постановка задачи. Найти объем тела £}, ограниченного
заданными поверхностями.
План решения. Искомый объем равен
[[[ldxdydz. A)
V
' п
1. Зададим область fi неравенствами.
2. Вычисляем тройной интеграл, сводя его к повторному, и
записываем ответ, не забывая о размерности.
Пример 1. Найти объем тела П, ограниченного поверхностями
х = 17-/2у, x = 2-v/2y, г=2_У' Z = °"
Решение.
1. Зададим область Q неравенствами. Поскольку 17\/2у > 2-^/2у,
для х имеем неравенства 2^/2у < х < 17^/2у. Поскольку у фигурирует
под знаком квадратного корня, у > 0. Для z возможны неравенства
0 < z < 1/2 - у или 1/2 - у < z < 0. В первом случае 0 < у < 1/2. Во
втором случае у > 1/2, т.е. область неограничена, что неприемлемо.

326
Гл. 12. Кратные интегралы
Итак,
П= <
2у/Ъ) <х< 17у/2у, 1
(х,у,г): 0<у<1/2,
О < z < 1/2 - у
> .
2. Вычисляем объем по формуле A), сводя тройной интеграл к
повторному:
1/2 17^2Т 1/2-!/
/
2у/2у
V= f[fldxdydz= f dy f dx f dz=\
n о
Ответ. V = 1 ед. объема.
Пример 2. Найти объем тела ft, ограниченного поверхностями
^ / о , о 11 2 2
Решение.
1. Поскольку £1 — тело вращения вокруг оси OZ, удобно
использовать цилиндрические координаты
х = q cos <р,
у - gsm<p,
Z — Z.
При этом (д, <p,z) G ft', а искомый объем определяется формулой
V = Г f f QdQdydz, B)
где область Q! ограничена поверхностями
Z = ~Q,
И 2
2. Зададим область £1 неравенствами. Возможны два случая: либо
^£/2 < z < 11/2-е2, либо 11/2-е2 < z < 9д/2. В первом случае q < 1,
во втором случае # > 1, т.е. область неограличена, что неприемлемо.
Итак,
0<£<1,
(Q,<p,z): 9q/2<z<U/2-q2,
О < V < 2тг
£У = -

12.12. Вычисление объемов с помощью тройного интеграла 327
3. Вычисляем объем по формуле B), сводя тройной интеграл к
повторному:
2тг 1 U/2-e2
V — I dip I gdg I dz = 2it.
о о эе/2
Ответ. V = 27г ед. объема.
Пример 3. Найти объем тела ft, ограниченного поверхностями
z = y/2,Q -х2- у2, z=J -—.
Решение.
1. Поскольку Q — область, ограниченная верхней полусферой и
верхним полуконусом, удобно перейти к сферическим координатам
х — £cos<£sin0,
у ■= £siny>sin#,
z — gcosO.
При этом (д, в, <р) € ft', а искомый объем определяется формулой
V= [ff g2 s\n6 dgd6 d<p. C)
Заменяем в уравнениях поверхностей х на д cos <p sin в, у на д sin <p sin в
и z на gcos6. После преобразований получаем
2 = 6, tg 6> = л/3.
Область Q' ограничена этими поверхностями.
2. Зададим область ft' системой неравенств
fl' = {
О < д < 6,
{д,в,<р): О<0<тг/3,
О < <р < 2тг
3. Вычисляем объем по формуле C), сводя тройной интеграл к
повторному:
2тг тг/3 6
V= f d4> f sin6de fg2dg = 72ir.

328
Гл. 12. Кратные интегралы
Ответ. V = 727Г ед. объема.
Условия задач. Найти объемы тел, ограниченных поверхностями
1. х = 2у/у, х = у/у,
2. у- 2у/х, у = у/х,
3. х2 + у2 = 5, у = 2^Д,
4. х2 + у2 - 2х = 0, z = О,
5. х2 + у2-2у = 0, 2 = 0,
6. z = v/4 - х2 - у2, г = v/3(x2 + у2).
2 = 0,
2 = 0,
2 = 0,
2 = 4-
2 = 4-
-у2.
-X2.
2 = 1 - у.
2 = 1 — X.
2 = 2х.
7. 2= v/9-x2-y2, z = 0, х2 + у2 = 1 (х2 + у2 < 1).
8. 2=^9-х2-у2, z = ]j^±yl.
9. 2 = ^/4-х2-у2, 2 = У"
24 '
10. 2 = X2 + у2, 2 = v/x2+y2.
Ответы. 1. V = 4/15. 2. V = 4/15. 3. V = 8/5. 4. V = 15тт/4.
5. У = 15тг/4. 6. У = 2тг(8/3-5\/3/4). 7. V = 2тг(9 - 16л/2/3).
8. V = 9тг. 9. V = 64тг/5. 10. V = тг/6.
12.13. Вычисление массы тела
Постановка задачи. Найти массу тела Q с плотностью
fj,(x,y,z), ограниченного заданными поверхностями.
План решения.
1. Масса тела ft с плотностью д(х, у, г) определяется формулой
= / / / ц(х, у, z) dx dy dz.
m ■■
' n
2. Зададим область ft неравенствами.
3. Вычисляем тройной интеграл, сводя его к повторному, и
записываем ответ, не забывая о размерности.

12.13. Вычисление массы тела
329
Пример 1. Найти массу тела ft с плотностью у = 2х,
ограниченного поверхностями
х = 2у/2у, х = у/2у, z = 1 - у, z-0.
Решение.
1. Масса тела Q с плотностью у = 2х определяется формулой
= 111
т= HI 2xdxdydz.
2. Зададим область Q неравенствами. Поскольку 2у/2у > у/2у,
для х имеем неравенства \/2у < х < 2^/2у. Поскольку у фигурирует
под знаком квадратного корня, у > 0. Для z возможны неравенства
0 < z < 1 — у или 1 — у < z <0. В первом случае 0 < у < 1. Во втором
случае у > 1, т.е. область неограничена, что неприемлемо.
Итак,
' уДу < х < 2v/2y",
(x,y,z): 0<у<1,
0<z<1-у
fl = <
3. Вычисляем m, сводя тройной интеграл к повторному:
1 2-v/2j 1-у
т= In 2xdxdydz— / dy / 2xdx / dz—1.
n о v^ о
Ответ, m — 1 ед. массы.
Пример 2. Найти массу тела ft с плотностью у = z,
ограниченного поверхностями
х2 + у2 = 4, z = 0, z=X +2V .
Решение.
1. Масса тела fl с плотностью у = z определяется формулой
т= HI zdxdydz.
n

330
Гл. 12. Кратные интегралы
Поскольку Г2 — тело вращения вокруг оси OZ, удобно перейти к
цилиндрическим координатам
х = q cos <f,
y = gsimp,
z = z.
При этом (q, (p, z) £ il', а искомая масса определяется формулой
V — I I I zgdgdipdz.
Заменяем в уравнениях поверхностей х на gcosif и у на д sirup.
Получим
д = 2, z = 0, z = —.
2. Зададим область £2' системой неравенств
£2' = I
0<д<2,
(q,V,z): 0<z<g2/2,
0 < у < 2тг
3. Вычисляем т, сводя тройной интеграл к повторному:
2тг 2 е2/2
IdipI6deI
о о
Ответ. V = 87г/3 ед. массы.
Пример 3. Найти массу тела £1 с плотностью /z = 20z,
ограниченного поверхностями
z= yjl-x2 - у2,
2 _l„2
Za +
Решение.
1. Масса тела £2 с плотностью ц = 20z определяется формулой
m = /// 20z cfo: dj/ dz.

12.13. Вычисление массы тела
331
Поскольку Я — область, ограниченная верхней полусферой и
верхним полуконусом, удобно перейти к сферическим координатам:
х = QCOS(psm6,
у = Qsimpshie,
z = gcosB.
При этом (д, в, ф) € Я', а искомая масса определяется формулой
-///'
т= I I I 20длsinOcosOdipdBdg.
П'
Заменяем в уравнениях поверхностей х на д cos ip sin в, упад sin ip sin в
и z на д cos 0. Получаем
д = 1, tg0 = 2.
Область Л' ограничена этими поверхностями.
2. Зададим область О! системой неравенств
П'= <
О < д < 1,
(ftfl.v): O<0<arctg2,
О < V < 2тг
m
3. Вычисляем т, сводя тройной интеграл к повторному:
27г arctg 2 1
sin Й ms ftdft I n3dn = 4Птг — -
Lit artbg .£ l
= 20 I dip / smBcosede g3dg = 40n
oo о
Здесь мы воспользовались формулой
tg20
о
= 47Г.
sin20
=arctg2 1 + tg2^
e=arctg 2
4
5'
Ответ, m = 4n ед. массы.

332
Гл. 12. Кратные интегралы
УСЛОВИЯ ЗАДАЧ. Найти массу тела с плотностью ц,
ограниченного заданными поверхностями.
1. /х = 2у2еху, х = 0, у = 1, у = х, z = 0, 2 = 1.
2. ц = у2е~хУ, х = 0, у = -2, у = Ах, z = 0, z = 1.
3. /i = у2ехУ/2, х = 0, у = 2, у = 2ж, z = 0, z = -1.
а;
,2
4- ^ = _2~;—2» х + У ~АУ = °> г = 4-ж2, z = 0.
ж-4 4- у*
v2
5. ц = -^г—5"» ж2 + у2 - 4ж = О, z = 10-j/2, z = О.
х* + jr
X2 /ZZ s о X2 + у2
6- М = ~2~, 2 ' Z = \/36-Ж2 -J/2, Z =
X2 + у2 ' V " ' 9 '
7 У2 Л 2 2 2(Х2 + У2)
7- ^ = ^Т^2' г=^1-^2-2/2. * = з
8. /z = 32z, z = у/1 - х2 - у2, z=y/x2 + у2.
9. fi = 5z, z = у/16 - х2 - у2, z = y—-—
лА2 + У2
10. /z = 10z, z = ^/4 — ж2 — j/2, z =
Ответы. 1. m = e-2. 2. m = 2e_1. 3. m = 4e - 8. А.т-5тг/2.
5. m = 17тг/2. 6. m = 171тт/4. 7. m = 19тг/96. 8. m = 4тг. 9. m = 288тг.
10. m = 32тг.

Глава 13
ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
При изучении темы ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ вы
познакомитесь с понятием интеграла по поверхности от функции трех
переменных и научитесь сводить его к двойному (а затем — к
повторному), проецируя заданную поверхность на одну из
координатных плоскостей. Кроме того, вы научитесь вычислять интегралы по
части цилиндрической и сферической поверхностей.
С помощью пакета РЕШЕБНИК.ВМ вы можете найти
координаты единичного нормального вектора поверхности (вычислить
частные производные и длину вектора), вычислить полученные вами
повторные интегралы, выполнить все численные расчеты и проверить
правильность полученных вами результатов.
13.1. Поверхностный интеграл
первого рода
Постановка задачи. Вычислить поверхностный интеграл
f(x,y,z)do,
где £ — часть поверхности, описываемая уравнением F(x, у, z) = О
и некоторыми неравенствами.
ПЛАН РЕШЕНИЯ. Поверхностный интеграл сводится к двойному
проецированием £ на координатную плоскость XOY по формуле
// f(x,y,z)da= II f(x,y,z(x,y)) ,* ,, С1)
£ D
где D — проекция £ на плоскость XOY, 7 — угол между нормалью
к поверхности Е и осью OZ\ z(x, у) определяем из уравнения
поверхности F(x, у, z) = 0.
//

334
Гл. 13. Поверхностные интегралы
Замечание. Если уравнение F(x,y,z) — О не определяет
однозначно функцию z = z(x, у), то проецируем Е на другую
координатную плоскость или используем криволинейные координаты (можно
также разбить поверхность на части и воспользоваться
аддитивностью интеграла).
1. Единичные нормальные векторы щ = {cos a, cos /3, cos 7} к
поверхности, заданной уравнением F(x, у, z) = 0, определяются
формулой
_ _ gradF
2. Проекцию D поверхности Е на плоскость XOY находим,
исключая z из условий, определяющих Е.
3. Находим z = z(x,y), решая уравнение F(x,y,z) = 0.
4. Переходим от поверхностного интеграла к двойному по
формуле A) и вычисляем двойной интеграл, сводя его к повторному.
Записываем ответ.
ПРИМЕР. Вычислить поверхностный интеграл
(-х + 3у + 4z) da,
//<
где Е — часть плоскости
х + 2у + Zz = 1,
расположенная в первом октанте (т.е. х > 0, у > 0, z > 0).
Решение.
1. Единичные нормальные векторы По = {cos a, cos /3, cos7} к
поверхности, заданной уравнением F(x, у, z) = 0, определяются
формулой
gradF
|gradF|'
В данном случае F(x, у, z) = х + Чу + Зг — 1. Следовательно,
- .О^з} з
П0 = ±-7!Г' |cos7l = 7n-
2. Поверхность Е определяется условиями
„ J, , x + 2y + Zz = l, \
Z={(x,y,z): x>0,y>0,z>0j

13.1. Поверхностный интеграл первого рода
335
Ее проекцию D на плоскость XOY находим, исключая z из условии,
определяющих Е:
Г z = (l-x-2y)/Z, \
(. х>0, у>0, z>0)
=>D={(x,y): }
Г 0<(l-x-2i,)/3 J
Отсюда
Г 0 < у < 12, 1
\К ,Ю 0<х<1-2у f
3. Иэ уравнения x + 2y + Zz — 1 = 0 находим z(x, у) = (l — x — 2y)/Z.
4. Переходим от поверхностного интеграла к двойному по
формуле A) и вычисляем двойной интеграл, сводя его к повторному:
Г (-х + 4у + Zz) do= J (-x + Ay+ Zz)
Vu
dxdy =
z=(l-x-2y)/3
1/2 l-2j/
18~'
о о
Hi -2x + 2y)dxdy = ^у- I dy I (l-2x + 2y)dx =
D
Ответ. {-x + 4y + Zz) da =
л/5
18 '
Условия ЗАДАЧ. Вычислить поверхностные интегралы.
Г Г Г х -\- v -\- z — 1 I
1-llxyzdo-, T,= l(x,y,z): ж > 0, j/> 0,'z > О (•
/•/• Г a; + j/ + z = l, I
2. Hy + z)da, V={(x,y,z): \.
J J [ x>0, j/>0, z>0 J

336
Гл. 13. Поверхностные интегралы
ff ( 2 \ Г ж +J//2 + z/З = 1, \
3. // Cx + -z) dc, E={{z,y,z): \.
J J \ 3/ [ x>0, y>0, z>0 )
ff ( x+2y + Zz=l, ]
.. (x+18y + 24z)dc, S= (i,y,z): V.
J J [ x>0, y>0, z>0)
ff \ x2 + y2+z2 = 1, \
JJzdc, E=|(«,»,z): ^Q J.
/Y Г ж + j/ + z = 1, 1
.JJ(x + y + z)dcr, £=|(W): ^0|y>0>z>0}-
.//zoV, E=|(*,y,z): ' <7< i ^ _ ^ } "
в.уу^ + Л*. Е=|(х,9,2):о<г<1 ■!.
E V - - У
/"/" Г x2 + j/2-z2 =0, 1
• (xy + yz + zx) da, E = < (ж, j/, z) : > .
Jj I 0 < z < 1 I
e к - - j
ff , Г x2 + у2 - 4z2 = 0, I
Vx2 + y2do, E=Uzty,z): }.
J J { 0 < z < 1/2 J
4,
E
5.
E
6
~E
7.
9
E
10.
E
Ответы. 1. N/3/120. 2. v^/3. 3. 35/6. 4. л/П/2. 5. 2тг.
6. \/3/2. 7. 12A + 6л/3)тг/15. 8. v/2tt/2. 9. 0. 10. у/Ъж/З.
13.2. Интеграл
по цилиндрической поверхности
Постановка задачи. Вычислить поверхностный интеграл
// f{x,y,z)da,
Е
где £ — часть поверхности х2 + у2 — г2, вырезаемая плоскостями
z = 0 и z = h.

13.2. Интеграл по цилиндрической поверхности 337
План решения.
1. Вводим на заданной поверхности (цилиндре) криволинейные
координаты
х — q cos ip,
y = Qsimp,
z — z.
В этих координатах поверхность задается условиями
£= <
2. Так как
то
Q = r,
(q,<P,z): 0<^<2тг,
0<z<h
da — rdipdz,
2тг h
> .
// f(x,y,z)da — г I dip I f(r cos ip,rsinip,z)dz.
£ 0 0
3. Вычисляем повторный интеграл и записываем ответ.
Пример. Вычислить поверхностный интеграл
jj(x2 + y2)dcr,
где Е — часть поверхности х2 + у2 = 1, вырезаемая плоскостями
z = О, z = 2.
Решение.
1. Вводим на заданной поверхности (цилиндре) криволинейные
координаты
х = q cos <р,
у = gsimp,
z — z.
В этих координатах поверхность задается условиями
0=1,
Е= <(e,V.*): °<¥><2тг,
0<z<2

338
Гл. 13. Поверхностные интегралы
2. Так как da = 1 ■ d ip dz и х2 + у2 = 1, то имеем
2тг 2
/У (ж2 + y2)da= j dV j dz.
Е 0 0
3. Вычисляем повторный интеграл:
2тг 2
(х2 +y2)da - dip dz = 47Г.
Е
||(х2 + 2/2)(
Е 0 0
Ответ. I (xz + yz) da - 4тг
Е
Условия задач. Вычислить поверхностные интегралы,
1. 11 xdcr, £= < (x,j/,z)
ж2+г/2 = 1,
z = 0, z = 2
Е
/" /" I х2 + v2 = 4
2. JJ(x + y)da, Е= U1'^1 z = 0 z = 4
Е *•
3. (x + y + z)da, £= <(i,j/,z) :
Е *•
4. J J (у2-1) da, E=Ux,y,z):
x2 + y2 = l,
z = 0, z = 1
z = 0,z = l
/" /" Г ж2 + и2 = 1
5. JJB-x2-y2)da, E=l(x,y,z)
z = 0, z = 2
x2 + J/2 = 1,
z = 0, z = 3
E v
6. Ij(x2 + z)da, T,= <(x,y,z) :
7. // y/x2 +y2da, T,= hx,y,z)
x2 + y2 = 4,
z = 0, z = 1

13.3. Интеграл по сферической поверхности
339
8. JJ(ху + z2) da, Е = | (х, y,z): * +* ^ =^ I
9. /7 3/9-x2-j/2dcr, Е = | (х, у, z) : * +* Д1 j 1
/ х2+у2 = 2, 1
10. ff y/z + x2+ у2 da, E
Е
Ответы. 1. 0. 2. 0. 3. 2тг. 4. 0. 5. 4тг. 6. 12тг. 7. 8тг.
8. 2тг/3. 9. 4тг. 10. 32тг(\/2 - 1)/3.
13.3. Интеграл
по сферической поверхности
Постановка задачи. Вычислить поверхностный интеграл
// f(x,y,z)da,
где Е — верхняя полусфера
х2 + у2 + z2 = г2, z>0.
План решения.
1. Вводим на заданной поверхности (сфере) криволинейные
координаты
х = QCos(fsm6,
у = q sin (p sin в,
Z = QCOS0.
В этих координатах поверхность задается условиями
Е= <
(g,e,V): О<0<тг/2,
0 < V < 2тг

340
Гл. 13. Поверхностные интегралы
2. Так как da = r2 smOdOdtp, имеем
2тг »г/2
// f{x-,y->z)d° = T I dip I f(r cos tp sin в, г sin tp sin в, г cos в) sin в йв.
Е 0 0
3. Вычисляем повторный интеграл и записываем ответ.
ПРИМЕР. Вычислить поверхностный интеграл
JJ(x2 + y2)do,
где Е — верхняя полусфера
х2 + у2 + z2 = 9, z > 0.
Решение.
1. Вводим на заданной поверхности (сфере) криволинейные
координаты
х = q cos <p sin в,
y = gsm<p sin в,
z = qcosO.
В этих координатах поверхность задается условиями
£= <
(е,0,у>): О<0<тг/2,
0 < v? < 2тг
> .
2. Так как d а = 9 sin 0 dB dtp и /(х, у) = х2 + у2 — 9 sin2 в, имеем
2к т/2
ll(x2 + y2)do= fd(p J 9sm26-9sm6d6.
E 0 0
3. Вычисляем повторный интеграл:
2тг к/2 тг/2
/dv? A 9sin20-9sin0d0=-1627r A(l-cos20)d
cos0 = 1O8tt.
Ответ. / / (х2 + у2) da = 108тг.

13.3. Интеграл по сферической поверхности
341
Условия задач. Вычислить поверхностные интегралы.
{х2 + у2 + z2 = 7, z> 0}.
{х2 + у2 + z2 = 4, z > 0}.
{х2 + у2 + z2 = 5, г > 0}.
{х2 + у2 + z2 = 2, z > 0}.
{х2 + у2 + z2 = 1, г > 0}.
{x2+j/2 + z2 = 1, z>0}.
{х2 + у2 + z2 = 9, z > 0}.
{х2 + у2 + z2 = 3, z > 0}.
{х2 + у2 + z2 = 10, z > 0}.
{х2 + у2 + z2 = 1, z > 0}.
1. // xda,
Е
2. //,<*,,
Е
3. J J Bx - 5j/) da,
2
4. jj{z2 + \)da,
Е
5. ffz4da,
Е
6. ff^x2 + y2da,
7. ff(x2 + y2-2z)do,
E
8. ff(x2 + y2-2)d<x,
E
9. /УB1х - 21j/ + z) da,
E
10. (xy + z2)da,
E =
E =
E =
E =
E =
E =
E =
E =
E =
E =
Ответы. 1. 0. 2. 8тт. 3. 0. 4. 20тг/3. 5. 2тг/5. 6. тг2/2.
7. 54тг. 8. 0. 9. IOv/IOtt. Ю. 2тг/3.

Глава 14
ТЕОРИЯ ПОЛЯ
При изучении темы ТЕОРИЯ ПОЛЯ (ВЕКТОРНЫЙ АНАЛИЗ)
вы познакомитесь с понятиями векторного поля, векторных линий,
потока векторного поля через поверхность, циркуляции векторного
поля, дивергенции и ротора векторного поля. Вы научитесь
вычислять поток векторного поля как поверхностный интеграл, а также
использовать формулу Остроградского для вычисления потока через
замкнутую поверхность. Вы научитесь вычислять работу векторного
поля как криволинейный интеграл второго рода, а также применять
формулу Стокса для вычисления циркуляции.
С помощью пакета РЕШЕБНИК.ВМ вы можете вычислить
производные, единичный нормальный вектор поверхности, дивергенцию и
ротор векторного поля, определенные и повторные интегралы,
выполнить все численные расчеты и проверить правильность полученных
вами результатов.
14.1. Векторные линии
Постановка задачи. Найти векторные линии векторных полей
a = P(x,y)i + Q(x,y)j,
или
а = Р(х, z)i + R(x, z)k,
или
a = Q(y,z)j + R(y,z)k.
План решения.
1. Запишем дифференциальные уравнения векторных линий
dx _ dy _
Р(х, У) Q(x, У)

14.1. Векторные линии
343
dx dz
при у = С,
Р(х, у) R{x, у, z)
dy dz
при х = С.
Q{x,y) R{x,y,z)
Мы учли, что в первом случае dz = 0, во втором случае dy = 0 и
в третьем случае dx = О, поскольку равна нулю соответствующая
координата векторного поля.
2. Решая соответствующее дифференциальное уравнение,
получим, что векторные линии (в пространстве) определяются системами
уравнений
Г F(x,y) = C1,
\z = C2,
или
Г F(x,z) = d,
\у = с2,
или
Г F(y,z) = Ci,
\ х = С2.
Пример. Найти векторные линии векторного поля
о = 9zj — Ayk.
Решение.
1. Так как первая координата поля Р(х, у, z) = 0, то dx = 0 и,
следовательно, х — С. Поэтому запишем дифференциальное уравнение
векторных линий в виде:
dy dz
— = при х — С.
9г 4j/ F
2. Решая дифференциальное уравнение, получим
Г 9z2 + Ay2 = d,
\ х = С2.
Ответ. Векторные линии определяются системой уравнений
Г 9z2+4j/2 = Cb
1 х = С2.

344
Гл. 14. Теория поля
Условия задач. Найти векторные линии векторных полей.
1. a = 2yi + 6xj. 2. a = 2xi + 3j/j. 3. a = 2yi — 4xj.
5. a = 2yj + 3zk. 6. a = zi — Azk.
8. a = 3xi + 6j/j. 9. a = 3j/i — 2xj.
4.
7.
10
a ;
a ■■
. a-
— zi — xfc.
= 2zj + 9j/fc.
= yj + zk.
Ответы.
1.
4.
7.
1С
{
{
{
-{
3x2-j/2=Cb
x2 + г2 = Си
У = С2.
9y2 - 2z2 = d,
x = C2.
* = Cx/y,
x = C2.
5. <
8. i
2.
5.
1 8.
Г у = С^1\ Г 2x2 +
" \ г = C2. \ г = С
/ z = C1ffi'2, . / 4x2 +
• \ x = C2. \ » = С
Г j/ = C1x2, f 2x2 + 3
\ z = C2. I z = C2.
2=Cb
C2.
*2 = Ci,
c2.
3j/2 = Cb
14.2. Поток векторного поля
Постановка задачи. Найти поток векторного поля
а = P(x,y,zjt+ Q{x,y,z)j+ R{x,y,z)k
через поверхность Е, описываемую уравнением F(x,y,z)=0 и
некоторыми неравенствами (нормаль образует острый угол с осью OZ).
План решения. По определению поток П векторного поля а
через поверхность Е с полем единичных нормалей щ определяется
формулой
П= ff{a,n0)d(x. A)
1. Поле единичных нормалей к поверхности, заданной уравнением
F(x, у, z) = 0, определяется формулой
gradF
по = ±т тт^ - ±{cosa,cos/y,cos7}-
gradF

14.2. Поток векторного поля
345
Учитывая что нормали должны образовывать острый угол с осью OZ,
т.е. что cos 7 > 0, выбираем в этой формуле знак плюс или минус.
Имеем
no = cos ai + cos 0j + cos'yk, cos 7 > 0.
2. Находим скалярное произведение
(а, пЬ) = P(x, у, z) cos a + Q(x, y, z) cos C + R{x, y, z) cos 7 = f(x, y, z).
3. В силу формулы A), поток определяется поверхностным
интегралом:
П= ll{a,n0)do= II f(x,y,z)da.
4. Переходим от поверхностного интеграла первого рода к
двойному, проецируя Е на плоскость XOY:
п= // f{x,V,z)do= // f{x,y,z{x,y))
dxdy
I cos 7I'
E D
где D — проекция Е на плоскость XOY; z(x, у) определяем из
уравнения поверхности F(x, у, z) = 0.
Замечание. Если уравнение F(x, у, z) = 0 не определяет
однозначно функцию z = z(x, у), то проецируем Е на другую
координатную плоскость или используем криволинейные координаты (можно
также разбить поверхность на части и воспользоваться
аддитивностью интеграла).
5. Вычисляем двойной интеграл, сводя его к повторному.
Записываем ответ, не забывая о размерности.
Пример. Найти поток векторного поля
а = — xi + 2yj + zk
через часть плоскости
x + 2y + 3z = l,
расположенную в первом октанте (нормаль образует острый угол с
осью OZ).

346
Гл. 14. Теория поля
Решение.
1. Поле единичных нормалей к поверхности, заданной уравнением
F(x, у, z) = 0, определяется формулой
- = _grad_F_
|gradF|'
В данном случае F(x, у, z) = х + 2у + 3z — 1 и, следовательно,
{1,2,3}
п0 = ±-
л/14
Учитывая что нормали должны образовывать острый угол с осью
OZ, т.е. что cos 7 = ±3/\/l4 > 0, выбираем в этой формуле знак
плюс. Имеем
- _/J L 3 I
n°~lv/l4' у/й' JTi]'
2. Находим скалярное произведение:
(S, по) = —7=(-х + Ау + 3z).
V14
3. Согласно формуле A), поток определяется поверхностным
интегралом:
П= [Г-==(-х + 4у + Зг)<1а.
4. Переходим от поверхностного интеграла к двойному,
проецируя Е на плоскость XOY:
/"/" 1 „ . dxdy
= // -7=(-x + 4y + 3z) Sr,
где D — проекция Е на плоскость XOY и cos 7 = 3/y/Ti.
Поверхность Е определяется условиями
Г x + 2y + 3z = l, \
I я>0, у>0, z>0J

14.2. Поток векторного поля
347
Ее проекцию D на плоскость XOY находим, исключая z из условий,
определяющих Е:
Г z=(l-x-2y)/3, \
£= \{x,y,z): i =>
I х>0, ?/>0, z>0J
„ Г, ч 2г > 0, у > 0, 1
=>С=|(х,„): 0<A_х_2у)/3]-
Отсюда
D f(l)f)!os,<iA l
\V tf/ 0<x<l-2j/ J
5. Вычисляем двойной интеграл, сводя его к повторному:
dxdy
-//<
-х + 4?/ + 3.г)
cos7|
£> lz=(l-x-2j/)/3
1/2 l-2j,
= ^j[(l-2x + 2y)dxdy=^Jdy J (l-2x + 2y)dx = j^.
D 0 0
Ответ. П = 1/18 ед. потока.
Условия задач. Найти поток векторного поля а через часть
плоскости, расположенную в первом октанте (нормаль образует
острый угол с осью OZ).
1. а = xi + yj, х + у + z = 1.
2. а = 2xi + zk, х + у + z = 1.
3. а = yj + zk, 2x + у + z = 1.
4. а = xi + yj, х + у + 2z = 1.
5. а = j/j 4- zfc, 2х + 2у + z = 1.
6. о = хг + yj, 2х + у + 2z = 1.

348
Гл. 14. Теория поля
7. а = хг + 2yj, х + у + z = 1.
8- а = yj + zk, 2x + 2y + z= 1.
9. a = xt + 2yj + zk, x/2 + у + z/З = 1.
10. a = xi + yj + 2zk, x/3 + y/2 + z=l.
Ответы. 1. 1/3 ед. потока. 2. 1/2 ед. потока. 3. 1/6 ед. потока.
4. 1/6 ед. потока. 5. 1/8 ед. потока. 6. 1/8 ед. потока. 7. 1/2 ед.
потока. 8. 1/8 ед. потока. 9. 4 ед. потока. 10. 4 ед. потока.
14.3. Поток векторного поля
через часть цилиндра
Постановка задачи. Найти поток векторного поля
а - Р(х, у, z)i + Q{x, у, z)j + Щх, у, z)k
через часть поверхности
2,2 2
xL + yz = rz,
вырезаемую плоскостями z = 0 и z = h (нормаль внешняя к
замкнутой поверхности, образуемой данными поверхностями).
План решения. По определению поток П векторного поля а через
поверхность Е с полем единичных нормалей по определяется
формулой
П= fl{a,n0)do. A)
1. Поле единичных нормалей к поверхности, заданной уравнением
F(x, у, z) = 0, определяется формулой
gradF
п0 -±;
|gradF|'
В данном случае F(x, у, z) = х2 + у2 — г2 и, следовательно,
{х,у,0}
По = ±—,

14.3. Поток векторного поля через часть цилиндра 349
Учитывая, что нормали должны образовывать острый угол с осью
ОХ при х > 0, т.е. cos а > О при х > О, и тупой угол с осью ОХ при
х < 0, т.е. cos а < О при х < 0, выбираем в этой формуле знак плюс.
2. Находим скалярное произведение
,^ ^ P(x,y,z)x + Q{x,y,z)y
{а,по) = . , , = f(x,y,z).
Vх + У
3. Согласно формуле A) поток определяется поверхностным
интегралом:
П= Па,п0) da = // f(x,y,z)da.
4. Вводим на заданной поверхности (цилиндре) криволинейные
координаты
х = gcosip,
у- Qsirnp,
z = z.
В этих координатах поверхность задается условиями
g = r,
О < v? < 2тг,
О < z < h.
Поскольку do = rdipdz, имеем
2я- h
И —г I dip I /(rcos(p,rsinц>,z)dz.
о о
5. Вычисляем повторный интеграл и записываем ответ, не
забывая о размерности.
Пример. Найти поток векторного поля
а — xi + yj + zk
через часть поверхности
*2+j/2 = l,
вырезаемую плоскостями z = 0 и z = 2. (нормаль внешняя к
замкнутой поверхности, образуемой данными поверхностями).

350
Гл. 14. Теория поля
Решение.
1. Поле единичных нормалей к поверхности, заданной уравнением
F(x, у, z) — 0, определяется формулой
gradF
По = ±1
■|gradF|"
В данном случае F(x, у, z) = х2 + у2 — 1 и, следовательно,
{х,у,0}
п0 - ±
\/х2 + у2'
Учитывая что нормали должны образовывать острый угол с осью
ОХ при х > 0, т.е. cos а > 0 при х > 0, и тупой угол с осью ОХ при
х < 0, т.е. cos а < 0 при х < 0, выбираем в этой формуле знак плюс.
2. Находим скалярное произведение
,_ ... P{x,y,z)x + Q{x,y,z)y г-г- j
(а, п0) = = у/х2 + у2.
V ж + 2Г
3. Согласно формуле A) поток определяется поверхностным
интегралом:
П = / / (a, rib) dcr = / / у/х2 + у2 da.
S S
4. Вводим на заданной поверхности (цилиндре) криволинейные
координаты
х — q cos tp,
у = gsintp,
z = z.
В этих координатах поверхность задается условиями
0=1,
0 < v? < 2тг,
0 < z < 2.
Поскольку dcr = 1 • dtpdz и х2 +у2 = 1, имеем
2тг 2
dz.
о о
^7Г Z
П = /^/

14.4. Поток векторного поля через часть сферы 351
5. Вычисляем повторный интеграл
2тг 2
dz — Air.
о о
Ответ. П = 47Г ед. потока.
Условия ЗАДАЧ. Найти поток векторного поля а через часть
цилиндрической поверхности Е, вырезаемую заданными
плоскостями.
1. а = хг + yj + 2z4k, Е = {ж2 + у2 = 1}, z = 0, z = 3.
2. а — хг + yj + x2yzk, Е = {ж2 + ?/2 = 4}, z = 2, z = 5.
3. а = (ж + z?/)?-(жг - y)j + xk, Е = {ж2 + ?/2 = 4}, z = 0, z — 2.
4. а = xi + yj + xz2k, E = {ж2 + у2 — 9}, z = 0, z = 3.
5. a = xi + yj-2zk, E = {ж2 + у2 = 4}, z = 0, z=^2.
6. S-xT+yj + yz3k, E = {ж2 + ?/2 = 3}, z = 0, z = 2.
7. а = (ж-3?/)г + (Зж + 2/O + г2Л, Е = {ж2+?/2 = 5}, z = 0, z = 2.
8. а = хг + у] + sin2 zfc, E = {ж2 + у2 = 4}, z = 1, z = 3.
9. а = жг + 2/3' + ж2Л, Е = {ж2 + у2 = 3}, z = 2, z = 4.
10. а = Si + уз +zk, E = {ж2 + у2 = 2}, z = 2, z = 4.
Ответы. 1. бэт ед. потока. 2. 24-л- ед. потока. 3. 32-7Г ед. потока.
4. 54-7Г ед. потока. 5. 16-7Г ед. потока. 6. 12-л- ед. потока. 7. 20ir ед.
потока. 8. 16-7Г ед. потока. 9. 12-л- ед. потока. 10. Air ед. потока.
14.4. Поток векторного поля
через часть сферы
Постановка задачи. Найти поток векторного поля
а - Р(х, у, г)г + Q(x, у, z)j + R(x, у, z)k
через часть сферы
2 I 2 , 2 2
ж^ + у + z =г',

352
Гл. 14. Теория полл
вырезаемую плоскостью z = О (z > 0) (нормаль внешняя к
замкнутой поверхности, образуемой данными поверхностями).
План решения. По определению поток П векторного поля а через
поверхность Е с полем единичных нормалей по определяется
формулой
П= ll(a,no)d(T. A)
s
1. Поле единичных нормалей к поверхности, заданной уравнением
F(x, у, z) = 0, определяется формулой
gradF
п0 = ±7
|gradF|'
У сферы, очевидно, внешняя нормаль в каждой точке совпадает с
радиусом-вектором этой точки, т.е.
{х,у,z}
п0 =
у/х1 + у2 + z2
2. Находим скалярное произведение:
,- -. Р{х, у, z)x + Q(x, у, z)y + R(x, у, z)z
{а,П0) = , , ,: = f(x,y,z).
у/Х2 + y2+Z2
3. Согласно формуле A) поток определяется поверхностным
интегралом:
П= (a,n0)da= // f(x,y,z)da.
s s
4. Вводим на заданной поверхности (сфере) криволинейные
координаты
х = £>cosv?sin#,
у — QsimpsmO,
Z = QCOsd.
В этих координатах поверхность задается условиями
Q = r,
О < <р < 2тг,
О < в < -к J2.

14.4. Поток векторного поля через часть сферы 353
Поскольку da — г2 sinOdtpdO, имеем
2тт т/2
II —г2 I dip I f(rcostpsm6,rsinipsin6,rcos6)sin6d6.
о о
5. Вычисляем повторный интеграл и записываем ответ, не
забывая о размерности.
Пример. Найти поток векторного поля
а = хг + (у + z)j + (z- y)k
через часть поверхности
х2 + у2 + z2 = 9,
вырезаемую плоскостью z = 0 (z > 0) (нормаль внешняя к
замкнутой поверхности, образуемой данными поверхностями).
Решение.
1. Внешняя нормаль в каждой точке сферы х2 + у2 + z2 = 9
совпадает с радиусом-вектором, т.е.
{х, у, z}
yjx1 + yz + zl
2. Находим скалярное произведение
,^ -ч х2 + у(у + z) + z(z - у) I
(а, п0) = '- = у/х2 + у2 + z2.
у/Х2 +yZ + Z1
3. Согласно формуле A) поток определяется поверхностным
интегралом:
П = И {a, no) da = Ц у/х2 +у2 + z2da.
S S
4. Вводим на заданной поверхности (сфере) криволинейные
координаты
х = QCostpsmO,
у = q sin if sin 0,
Z — QCOS0.

354
Гл. 14. Теория поля
В этих координатах поверхность задается условиями
0 = 3,
О < <р < 2тг.
О<0<?.
Поскольку da = 9 sin6d<pd6, имеем
2тт тг/2
n4dvf
9-3sm6d6 = b4-K.
о о
Ответ. П = 54-7Г ед. потока.
Условия задач. Найти поток векторного поля а через часть
сферы, вырезаемую плоскостью z = О (z > 0).
1. а = (х + x2z)i + yj + (z - x3)k,
2. a = xi + {y + y2z2)j + (z-zy3)k,
3. a — (x + z)i + yj + (z - x)k,
4. a = (x + x2y)i + (y — x3)j + zk,
5. a = (x + yz)i + yj + (z- xy)k,
6. a = xi + (y + xyz)j + (z — xy2)k,
7. a = (x - xy2)i + (x2y + y)j + zk,
8. a = (x + yz2)i + yj + (z- xyz)k,
9. a — (x + yz)i + (y — xz)j + zk,
x2 +y2 +z2 = 4.
x2 + y2 + z2 = 4.
x2 + y2 + z2 = 4.
x2 + y2 + z2 = 1.
x2 + y2 + z2 = 1.
x2 + y2 + z2 = 1.
x2 + y2 + z2 - 1.
x2 +y2 + z2 = 9.
x2 + y2 +z2 = 4.
10. a = (x + xy2z)i + (y — x2yz)j + zk, x2 + y2 + z2 — 9.
Ответы. 1. 167Г ед. потока. 2. 167Г ед. потока. 3. 167Г ед. потока.
4. 27Г ед. потока. 5. 1-к ед. потока. 6. 2-к ед. потока. 7. 2-к ед.
потока. 8. 54-7Г ед. потока. 9. 16-7Г ед. потока. 10. 54-7Г ед. потока.

14.5. Вычисление потока по формуле Остроградского 355
14.5. Вычисление потока по формуле
Остроградского
Постановка задачи. Найти поток векторного поля
а = Р(х, y,z)i + Q{x, y,z)j + R(x, y,z)k
через замкнутую поверхность Е (нормаль внешняя).
План РЕШЕНИЯ. Поток векторного поля через замкнутую
поверхность Е в направлении внешней нормали вычисляется по формуле
Остроградского
11= I I I div a dxdydz, A)
Q
где Q — область, ограниченная поверхностью Е, и
,. , дР dQ dR
div а = — + — + —
ох • оу oz
—■ дивергенция векторного поля а.
1. Вычисляем дивергенцию diva.
2. Задаем область П неравенствами.
3. Вычисляем поток по формуле A) как тройной интеграл
Записываем ответ, не забывая о размерности.
Пример. Найти поток векторного поля
а = (у2 + г2)г+ (ху + y2)j + (xz + z)k
через замкнутую поверхность Е, являющуюся полной
поверхностью цилиндра
х2 + у2 - 1, z = 0, z - 1.
(нормаль внешняя).

356
Гл. 14. Теория поля
Решение.
1. Вычисляем дивергенцию векторного поля:
.. - д(у2 + *2) , д(ху + у2) , d(xz + z)
div a — 1 Н — 2х + 2у + 1.
дх
ду
dz
2. Задаем область О. неравенствами.
Поверхность Е, ограничивающая область Q, состоит из трех
поверхностей и может быть записана в виде
\ 0<z<l J U \x2 + y2<lj U \x2 + y2<lj
Из этих условий находим систему неравенств, определяющих
область П:
0 Г, , х2+У2<1,
S2 = < (x.y.z) :
|v "" ' 0<z<l
Форма области £1 такова, что удобно перейти к цилиндрическим
координатам. Имеем
0 < <р < 2тг, '
n={{Q,V,z): 0<q<1, >.
0<z< 1
3. Вычисляем поток по формуле A) как тройной интеграл:
П= Bх + 2у + 1) dx dy dz.
Q
Переходя к цилиндрическим координатам, получаем
1 2тг 1
П = I dz I dtp I qBgcostp + 2qsintp + \)dg = 2-я.
0 0 0
Ответ. П = 27г ед. потока.

14.6. Работа силы
357
Условия задач. Найти поток векторного поля а через
замкнутую поверхность, образованную заданными поверхностями (нормаль
внешняя).
1. а= (xy2 + yz)i + (x2y + z2)j + (x2 + z3/S)k, х2 + у2 + z2 = 1,
z = О {z > 0).
2. a = (?/ + z2)i'+(a;2 + 22/z)J,+ B/2 + 2z2)fc, x2 + ?/2 = l-z, z = 0.
3. a=Bxy + y2z)i + Bxy + x2z)j + (xy + z2)k, x2 + y2 + z2 = y/2,
z = 0 (z > 0).
4. a- (x2 + y2+z2)i + (xy + z)j + (x + 3z)k, x2 + y2=z2, z = 4.
5. а = Ca;2 + y)?+ (a;2 - 2x2y + zjj + (x2 - y2)k, x2 + y2 = 1,
z = 0, z = 1.
6. a = (x2 + yz)i + xj + yk, z = 1 — x — y, x = 0, у = 0, z = 0.
7. а = (z2 +а;г)^+ (ху -z2)j + yzk, x2 + y2 = l, z = 0,z = y/2.
8. a = (a;2 + a;?/ + z2)i* + (a;2 + ?/2 + yz)j + (y2 + z2 + xz)k,
x2 + y2 + z2 = 1, x2 + y2 = z2 (z > 0).
9. a = (a;z+?/2z)?+(a;2z-2j/)J+a;?/fc, a;2+?/2+z2 = 1, z = 0 (z > 0).
10. a = (a;?/ + ?/2 + z)i*+ (a:2z + ?/z)J + (a;2 + a;z)fc, x2 + y2 = 4,
z = 0, z = 1.
Ответы. 1. 2-7г/5 ед. потока. 2. 7г ед. потока. 3. -л- ед. потока.
4. 647Г ед. потока. 5. — тт/2 ед. потока. 6. 1/12 ед. потока.
7. 7г ед. потока. 8. 3-7г/8 ед. потока. 9. — 13-7г/12 ед. потока.
10. 27г ед. потока.
14.6. Работа силы
Постановка задачи. Найти работу силы
F = P{x,y)i + Q{x,y)j
при перемещении вдоль кривой L от точки М(х\,у\) к точке
N(x2,y2).

358
Гл. 14. Теория поля
План решения.
1. Работа А силового поля равна криволинейному интегралу
второго рода по кривой L:
А = f(F,dr) = JР(х,у) dx + Q(x,у) dy.
2. Вычисляем криволинейный интеграл.
Записываем ответ, не забывая о размерности.
Пример. Найти работу силы
F - (х - у)г + j
при перемещении вдоль кривой L
х2 + у2 = А {у>0)
от точки МB,0) к точке N(—2,0).
Решение.
1. Работа А силового поля равна криволинейному интегралу
второго рода по кривой L:
A-f&df>-fi,-,)*. + *.
2. Вычисляем криволинейный интеграл. Для этого:
а) поскольку L — верхняя полуокружность, ее параметрические
уравнения записываем в виде
fz = 2cos*, 0<1<ж
[ у = 2smt, ~ ~
Вычисляем dx — — 2 sin tdt и dy = 2 cos tdt;
б) переходим от криволинейного интеграла к определенному:
A- j(x-y)dx + dy- [Bcost -2sint)(-2sint) + 2cost]dt -2ж.
l о
Ответ. А = 27г ед.работы.

14.7. Циркуляция векторного поля
359
Условия задач. Найти работу силы F при перемещении вдоль
заданной кривой от точки М к точке N.
1. F = xi + yj, х2+у2 = 4 (у>0), МB,0), N(-2,0).
2.Р = хЧ, х2 + у2 = 4 (у > О, х > 0), МB,0), N@,2).
3. F = (х2 + y)i+ (х2 - y)j, у = х2, М(-1,1), NA,1).
4. F = 2xyi + x2j, y = 2x3, МA,2), NB,16).
5. F = yi + 2yj, x2+y2 = l(y>0), МA,0), N(-1,0).
6. F = xi~yj, x2+y2=2(y>0), М(у/2,0), Щ-у/2,0).
7. F = 2yj, х2+у2 = 1(у>0,х> 0), М(\,0), N@,1).
8. F = x2yi, x2+y2=A(y>0, х>0), МB,0), N@,2).
9. F = (у - x2)i + xj, y = 2x2, M@,0), NA,2).
10. F = yi-xl у = х3, М@,0), Щ2,8).
Ответы. 1. 0 ед.работы. 2. —4 ед.работы. 3. 4/3 ед.работы.
4. 62 ед.работы. 5. — 7г ед.работы. 6. 0 ед.работы. 7. 1 ед.работы.
8. — я- ед.работы. 9. 5/3 ед.работы. 10. —8 ед.работы.
14.7. Циркуляция векторного поля
Постановка задачи. Найти циркуляцию векторного поля
а = Р(х, у, z)i + Q(x, у, z)j+R(x, у, z)k
вдоль замкнутого контура Г
х = x(t),
y = y(t), te[t!,t2].
z = z(t),

360
Гл. 14. Теория поля
План решения.
1. По определению циркуляция векторного поля равна
криволинейному интегралу второго рода вдоль кривой Г:
А — J>(a,dr) — Ф P(x,y,z)dx + Q(x,y,z)dy + R(x,y,z)dz.
г г
2. Вычисляем криволинейный интеграл, сводя его к
определенному:
А
г
= 4>{a,df) =
- j[P{x(t), y{t), z(t)) x'(t) + Q{x{t), y(t), z(t)) y'(t)+
ti
+ R{x{t),y{t),z{t)) z'{t)]dt.
Записываем ответ.
Пример. Найти циркуляцию векторного поля
_ У- - -
а = -гЗ — 3xj + хк
О
вдоль замкнутого контура Г
х — 2 cos t,
j/ = 2sint, *е[0,2тг].
z = l— 2 cost — 2sint,
Решение.
1. По определению циркуляция векторного поля равна
криволинейному интегралу второго рода вдоль кривой Г:
А = d>(a,dr) — Ф — dx — Зх dy + х dz.
г г
2. Вычисляем криволинейный интеграл, сводя его к
определенному:
А= Ф -dx — 3xdyЛ-xdz —
г

14.8. Вычисление циркуляции по формуле Стокса 361
2тг
Я 4 . 2 ,„ 2 . • "\ , 52тг
— sin t — locos t + 4sintcost I at — ——.
о
Ответ. А = -52tt/3.
УСЛОВИЯ ЗАДАЧ. Найти циркуляцию векторного поля а вдоль
заданного замкнутого контура (i 6 [0,27г]).
1. а = yi — z2j + x2yk, x = 2cost, у = suit, z = 1.
2. Й = — x2yi + 4j + x2zk, x = 2 cos t, у — 2 sin f, г = 4.
3. a = ж3г — z2j + yk, x = cost, j/ = 2sint, z = 2cost.
4. a = — Izi — x2j + zk, x = 1 cos t, у — 2 sin t, г = sin t.
5. a = j/2i — zj + yk, x = 5cost, у = 2sint, z — 2A — cost).
6. a — x3i — y2j + yk, x — cost, у — 3sint, z — cost — sint.
7. a = yi + xj + yAk, x = 2cost, у = sint, z = 5sint.
8. a — zi — xj + yzk, x — cost, y — 6sint, z — 3.
9. a = — x2i + 5j + j/fc, x = cos t, j/ = 5 sin t, z = 3 cos t.
10. a = 4j/i + xj 4- j/fc, a; = cost, у — sint, г = 2 — cost — sint.
Ответы. 1. -2тт. 2. 18тг. 3. -4тг. 4. 4тг. 5. -8тг. 6. -Зтг. 7. тт.
8. -бтг. 9. -15тг. 10. -8тг.
14.8. Вычисление циркуляции
по формуле Стокса
Постановка задачи. Найти модуль циркуляции векторного
поля
а = Р(х, у, г)г + Q(x, у, z)j+ R(x, у, z)k

362
Гл. 14. Теория поля
вдоль замкнутого контура
-{
{x,y,z):
Fi{x,y,z)
F2{x,y,z)
•п
План РЕШЕНИЯ. Циркуляция А векторного поля а = {Р, Q, R} по
замкнутому кусочно-гладкому контуру Г, расположенному в области
G, в которой функции P,Q,R имеют непрерывные частные
производные, равна потоку ротора этого векторного поля через любую
кусочно-гладкую поверхность Е, натянутую на контур Г и
расположенную внутри области G, т.е. справедлива формула Стокса
= //(rota,
по) da.
A)
Предполагается, что ориентация единичных нормалей
rio = {cos a, cos /3, cos 7}
к поверхности Е согласована с ориентацией контура Г так, чтобы
из конца каждой нормали обход контура в выбранном направлении
выглядел как обход против часовой стрелки.
1. Возможны два противоположных направления обхода Г.
Циркуляция при этих обходах отличается только знаком. Поскольку
требуется найти только модуль циркуляции, выбираем направление
обхода произвольно, а в ответе запишем модуль результата.
2. Выбираем поверхность Е, натянутую на контур Г.
3. Определяем нормали по к поверхности Е.
4. Находим rot a:
rota =
5. Вычисляем скалярное произведение (rota,rio).
6. Применяем формулу Стокса A):
г
д
дх
Р
3
д
ду
Q
к
д
дг
R
и (rot a, n0)
da.

14.8. Вычисление циркуляции по формуле Стокса 363
7. Вычисляем поверхностный интеграл.
Записываем ответ, не забывая про модуль.
Пример. Найти модуль циркуляции векторного поля
а = yi — xzj + xyk
вдоль замкнутого контура
Г
Uz,y-z) :
х2 + у2 + z2
х2 + у1 = 9
Ч-
Решение.
1. В данном случае очевидно, что Г — окружность х2 + у2 = 9,
лежащая в плоскости z — 0. Выбираем направление обхода контура
Г против часовой стрелки, если смотреть из конца вектора к.
2. Выбираем поверхность Е, натянутую на контур Г.
Естественно в качестве Е взять круг:
= {(х,у,*)- ^+°;2<9 }•
3. Согласно выбранной ориентации контура нормаль rio к Е одна
и та же в каждой точке и равна к.
5. Находим rot a:
rota ■■
i
д
дх
У
3
д
ду
—XZ
к
д
dz
ху
2xi — yj + (—1 — z)k.
5. Вычисляем скалярное произведение:
(rot а, по) — Bхг — yj + (—l — z)k, к) = — 1 — z.
6. Находим циркуляцию по формуле Стокса A):
"//<-
z)ch.
7. Вычисляем поверхностный интеграл, сводя его к двойному:
А = и (-1 -z)da= П (-1 - z)\z=0 dxdy = -9тг.
х2+у2<9

364
Гл. 14. Теория тюля
Ответ: \А\ = 9тг.
УСЛОВИЯ ЗАДАЧ. Найти модуль циркуляции векторного поля а
вдоль замкнутого контура Г.
1. а = (xz + y)i + (yz - x)j, Г =
2. a = x2zi-yj+yk, Г-
3. a = xzi + 2xzj + x3yk, Г =
4. a = (x — y)i + xj — zk, Г =
5. a = yi — xj + xzk,
6. a — 4yi + xj + yk,
7. a = yi — xj + zk,
8. a = xyi + yzj + xzk,
9. a = yi + A — x)j — zfc,
10. a = xi — z2j + yk,
Г =
Г =
r =
r =
r =
r =
a;2 + y2 = 1, 1
z = 3 J '
z = 3(z2 + j/2) -1,1
z = 2 J '
a;2 + y2 + z2 = 9, \
x2 + y2 = l (z>0) }
x2 + y2 = l, \
z = 2 J'
z = 2(x2 + y2) + l, \
z = 3 J "
x2 + j/2 = l, 1
ar + y + z = 1 J "
x2 + y2 + z2 = 1, 1
a; = г J '
+ j/2=4, 1
+y+z=l J"
a;'
2a;
a;2 + у2 + г2 = 9, \
x2 + y2=4 (z>0) J
a;2 + 2/2 = 4, 1
4aj-3j/-z = 3 J'
Ответы. 1. 2тт. 2. 0. 3. 4\/2тг. 4. 2тг. 5. 2тг. 6. 2тг. 7. \/2тг.
8. 8тг. 9. 8тг. 10. 60тг.

Учебное издание
ЗИМИНА Ольга Всеволодовна
КИРИЛЛОВ Андрей Игоревич
САЛЬНИКОВА Татьяна Анатольевна
РЕШЕБНИК
ВЫСШАЯ МАТЕМАТИКА
Редактор Е.Ю. Ходан
Компьютерный набор Т.А. Сальниковой
Компьютерная верстка О. В. Зиминой
ЛР JV« 071930 от 06.07.99. Подписано в печать 02.04.01.
Формат 60x90/16. Бумага офсетная. Печать офсетная.
Усл.печ.л. 23. Уч.-изд.л. 22. Тираж 5000 экз. Заказ №1490
Издательская фирма «Физико-математическая литература»
МАИК «Наука/Интерпериодика»
117864 Москва, ул. Профсоюзная, 90
Отпечатано с готовых диапозитивов
в ППП «Типография «Наука»
121099 Москва, Шубинский пер., 6

THE SOLVER
O.V. ZIMINA, A.I. KIRILLOV, T.A. SALNIKOVA
HIGHER MATHEMATICS
PHYSICS AND MATHEMATICS PUBLISHERS
International Academic Publishing Company "Nauka"
Russian Academy of Sciences
Moscow, 2001, 368 pages
The authors have extensive experience in teaching mathematics at the
Moscow Institute of Power Engineering (Technical University) and other
technical universities in Russia and abroad.
A well-known expert in higher education and a member of the Presidium
of the Scientific Methods Council on Mathematics of the Russian Ministry of
Education, Professor A. I. Kirillov is a coauthor of every single mathematics
curriculum developed and used in Russia during the last twenty years. He is the
recipient of several state awards for his successes in teaching higher mathematics
to students in technical universities and in using computers in education. He has
presented his ideas on mathematical education at many international congresses
and conferences and in lectures at many universities around the world and is
also known in scientific circles for his significant papers on infinite-dimensional
analysis, stochastic processes, and quantum field theory.
THE SOLVER is a part of a new educational project EduXXI initiated by
A. I. Kirillov and O. V. Zimina in 1999. The project aim is to make the student's
studies effective, interesting, and arousing creative activity. The main means
for achieving the project aim are new tutorial complexes consisting of especially
written textbooks and software. THE SOLVER is the common name of the
family of such complexes.
THE SOLVER "Higher Mathematics" is the first complex realized by the
project EduXXI. It is designed for computer-based mathematical education and
consists of this book and the software package THE SOLVER.HM.
The complex gives a solution to the fundamental problem of modern
education: how can students manage with the enormous information the professors
have to give thern?

They cannot now. Therefore, the modern students learn almost the same
mathematics as the students at the end of the 19th century. Moreover, they
solve only one or two problems of each kind whereas they should solve from
three to five problems of each kind to really understand and acquire the solution
methods.
There are no books containing the necessary number of problems of one
kind. On the other hand, the students do not have the time to solve the large
number of problems required.
THE SOLVER "Higher Mathematics" contains this book with nine to ten
problems of each kind and software that enables students to quickly solve all
these problems.
The complex opens a new way for learning mathematics—without
unnecessary difficulties and waste a time. It establishes an optimal student-computer
cooperation, where the student's task is to formulate the problems properly and
the computer's task is to perform the routine operations.
Using the complex, the students can deeply understand how to solve the
basic problems of higher mathematics because they solve many problems and
their attention is concentrated on the new and the essential.
The complex frees about half of time devoted to higher mathematics in the
curricula. This free time can be used for teaching the students the ideas and
methods of mathematics of the 20th century.
THE SOLVER "Higher Mathematics" can be used at colleges, technical
universities, and for extension education. It enables the students to study
independently. This is important because this increases the educational possibilities
for people living far from universities and for those who cannot leave their homes
for some reason.
This book contains 14 chapters:
Analytic Geometry Definite Integrals
Linear Algebra Line Integrals
Limits Series
Differential Calculus Differential Equations
Graphs Multiple Integrals
Functions of Several Variables Surface Integrals
Indefinite Integrals Field Theory
The chapters are divided into sections. Each section deals with one basic
problem and contains a general formulation of the problem, a solution plan
with short theoretical comments, a solution example, nine to ten problems of
the same kind, and the answers to these problems.
The package SOLVER.HM consists of special computer programs and a
hypertext book.

The programs establish a so-called Word-CAS interface, i.e., an interface
between Microsoft Word and a computer algebra system (CAS) such as
DERIVE, Maple V, MuPAD, etc. according to the user choice. The Word-CAS
interface is better than the original CAS interfaces because Microsoft Word
provides more tools for the text editing, viewing, and printing than the original
CAS interfaces.
The Word-CAS interface can be easily customized. This is important in
teaching, where all unnecessary menu items must be hidden because they divert
the attention of students or even frighten them with unknown mathematical
terms.
Obeying a student command, the Word-CAS interface takes a selected
formula from the Word document and activates the CAS, sending the formula to
the CAS for the required mathematical operations with the selected formula.
Then the Word-CAS interface inserts the CAS result in the Word document.
All mathematical formulas can be treated in this way. It is important that only
standard mathematical notation is used in the dialog between the student and
computer.
THE SOLVER. HM hypertext book is a collection of Microsoft Word
documents with a navigation tool. The documents are almost identical to those
in the book. The navigation tool enables the students to quickly find a
template for the mathematical problem they have to solve. Context-sensitive help
is available.
The Word documents are used as templates for correct and comprehensive
solutions of basic mathematical problems. Having a problem to solve, a student
can easily find an analogous problem in the Word documents, study the plan of
its solution, study the solution example, change the document, use the Word-
CAS interface for doing the required mathematical operations, save the results
of the work, and present the file to the professor.
THE SOLVER.HM helps a student to concentrate on the new and essential
while the computer does all the operations that are already known to the
student. The package size is about 500 kilobytes. It is sold at a low price. Every
student can and should have it.
THE SOLVER "Higher Mathematics" is the first tutorial complex of new
type. Analogous tutorial complexes are in preparation for teaching special
chapters of higher mathematics: functions of a complex variable, operational
calculus, Fourier series, equations in partial derivatives, probability theory and
statistics, and financial mathematics.
THE SOLVERs "Mechanics", "Physics", "Electricity", etc. for colleges and
universities as well as appropriate packages for high schools will be created by
the project EduXXI.
Information about THE SOLVER "Higher Mathematics" can be found on
the Internet site www.AcademiaXXI.ru.