ВЫСШАЯ
МАТЕМАТИКА
М.Л.Краснов
А.И.Киселев
Г.И.Макаренко
Е.В.Шикин
В.И.Заляпин
С.К.Соболев
Рекомендовано
Министерством образования
Российской Федерации
в качестве учебника для студентов
высших технических учебных заведений
Эдиториал УРСС • Москва • 2001

ББК22.1я73
Краснов Михаил Леонтьевич, Киселев Александр Иванович,
Макаренко Цшгорий Иванович, Шикин Евгений Викторович,
Заляпин Владимир Ильич, Соболев Сергей Константинович
Вся высшая математика: Учебник. Т. 3. -- М.: Эдиториал УРСС, 2001. — 240 с.
ISBN 5-8360-0153-7
Предлагаемый учебник впервые вышел в свет в виде двухтомника сначала на английском и
испанском языках в 1990 году, а затем на французском. Он пользуется большим спросом за рубежом.
В 1999 году книга стала лауреатом конкурса по созданию новых учебников Министерства
образования России.
Этот учебник адресован студентам высших учебных заведений (в первую очередь будущим
инженерам и экономистам) и охватывает практически все разделы математики, но при этом представляет
собой не набор разрозненных глав, а единое целое.
В третий том вошел материал по некоторым разделам математического анализа (числовые,
степенные, функциональные ряды, ряды Фурье) и обыкновенным дифференциальным уравнениям.
Директор — Доминго Марин Рикой
Заместители директора — Наталья Финогенова, Ирина Макеева
Администратор — Леонид Иосилевич
Главный редактор — Елена Кудряшова
Компьютерный дизайн — Виктор Романов, Василий Подобед
Верстка — Василий Подобед, Наталия Бекетова
Редакция — Василий Подобед
Корректурные работы — Лариса Кирдяшкина, Марина Косарева
Указатель — Василий Подобед, Андрей Стулов
Обработка графики — Василий Подобед
Дизайн обложки — Ирина Макеева
Техническая поддержка — Наталья Аринчева
Набор — Анна Тюрина, Марина Круцко
Менеджер по продажам — Алексей Петяев
Издательство «Эдиториал УРСС». 113208, г. Москва, ул. Чертановская, д. 2/11, к. п.
Лицензия ИД №03216 от 10.11.2000 г. Гигиенический сертификат на выпуск книжной
продукции № 77.ФЦ.8.953.П.270.3.99 от 30.03.99 г. Подписано к печати 21.12.2000 г.
Формат 70 х 100/16. Тираж 2500 экз. Печ. л. 15. Зак. Nfe 179 .
Отпечатано в АООТ «Политех-4». 129110, г. Москва, ул. Б. Переяславская, 46.
ISBN 5-8360-0150-2 (Полное произведение)
ISBN 5-8360-0153-7 (Том 3)
7 8 5 8 3 6 "0 0 1 5 3 7 »> <£> Эдиториал УРСС, 2000
Все права защищены. Никакая часть настоящей книги не может быть воспроизведена или передана
в какой бы то ни было форме и какими бы то ни было средствами, будь то электронные или
механические, включая фотокопирование и запись на магнитный носитель, если на то нет письменного
разрешения Издательства.
Эдиториал УРСС ЙВЕИК»
E-mail: unt9um.ru
научная И учебная литература Каталог изданий в Internet: http://um.ru

Глава XVII
ЧИСЛОВЫЕ РЯДЫ
§1. Числовой ряд. Сумма ряда
Пусть дана бесконечная числовая последовательность
ai,a2,... ,an,... .
Числовым рядом называется выражение вида
<М + а2 + ... + ап + ...,
(О
которое короче записывается так
Числа ai, иг,... называются членами ряда, а число ап — общим (п-м) члером ряда.
Сумма Sn первых п членов ряда называется n-й частичной суммой ряда
Sn = а>\ + <*2 + • • • + aw = /] ак-
*=i
Рассмотрим последовательность {Sn} частичных сумм ряда (1)
S\=a\, 52 = ai-fa2, ..., Sn = а\ -f a2-f... + an, ....
Определение. Если последовательность {5П} имеет конечный предел,
lim Sn = S,
П-+0О
oo
т. е. последовательность {Sn} сходится, то этот предел называют суммой ряда Yl an,
n=l
пишут ]Г) an = 5 и говорят, что ряд сходится. Если же предел
п=1
lim 5n
не существует, т.е. последовательность {5„} расходится, то говорят, что ряд ]Г) ап
расходится (и суммы не имеет).

Замечание. Символ
00
п=1
принято использовать для обозначения как самого ряда, так и его суммы.
Примеры.
1. Покажем, что ряд
^Г^Щь!)рЩ1тщр
111 l ^1
З"1" 15 "^ 35 "^ "' * ^ 4п*-\+'" ~^4п2-1
сходится.
<4 Рассмотрим n-ю частичную сумму ряда
1 1 J^ 1
5я"3 + Т5 + 35+ •+4п^1*
Используя очевидное равенство
4п2
преобразуем сумму Sn :
1 l l
1 _ 1 =Ч ' \\
-1 (2п-1)(2п-Н) 2\2п-1 ..Зп;+.1/'
1-3 3-5 5-7 •" (2п-1)(2п+1)
2 V 3 J + 2 \3 " 5 J + 2 \5 ~ 7) + ''' + 2 \2n-l ~ 2n+lJ = 2 У J^+lJ;
2
Переходя к пределу при п -* оо, получим
lim 5n = -.
n-»oo 2
В силу определения данный ряд сходится, и его сумма S = ~:
^4п2-1 2*
2. Рассмотрим ряд, составленный из членов геометрической прогрессии со знаменателем q {q Ф 0),
оо
a + aq + aq2 + ... + aqn'x + .... = У\ Щ*~Х-
•4 Сумма первых п членов этого ряда равна1'
Sn = а + aq + eg2 + ..
Если |?| < 1, то lim gn = 0, и поэтому
5я=а + ая + ая2 + ... ч-ад""1 = * ag = -^- - ^—-, q ф 1.
1-g 1-g 1-g
/а аяп \ а
Urn Sn ;= Urn -—- - -JL_ -
П-00 и rt-oo^l-g l-qj 1-0
т. е. данный ряд сходится и его сумма
Если \q\ > 1, то lim qn = оо и, значит, lim 5n = оо, т. е. ряд расходится.
я—»оо п—»оо
'' Напомним, как получить сумму геометрической прогрессии:
Sn = Sn + agn - agn = a + (a? + aq2 + ... + agn~' + agn) - aqn =
= (a - aqn) + g(a + ag + ... + agn"2 + agn_1) = a(l - tfn) + tfS„.
Рассматривая начало и конец цепочки как уравнение относительно Sn .получаем искомое:
«о-л

12.
При q = -1 получим расходящийся ряд
а-а+а-а + .
Его n-я частичная сумма равна
i нечетно,
t четно,
_ Г в, если п i
*п "~ \ О, если л •
сущестЕ
При g = 1 получим ряд
откуда видно, что Шп 5„ не существует.
а + а + а + ... ,
» = па и, следовательно, 1
Итак, ряд
сходится при \q\ < 1, причем его сумма равна ~-, и расходится при \q\ ^ 1. ►
для которого Sn = па и, следовательно, lim Sn= lim na = оо, т. е. этот ряд расходится.
а + aq + aq2 +... + eg11"1 +...
§2. Простейшие действия над рядами
Над числовыми радами можносовершать некоторые действия, допустимость которых
обосновывается следующими теоремами.
Теорема 1. Если ряд
00
<М + «2 +... + an + ... = ^2 ап (1)
п=\
сходится, то сходится и ряд, полученный из него изменением (в частности,
отбрасыванием) любого конечного числа членов. Обратно, из сходимости ряда, полученного из ряда (1)
изменением (в частности, отбрасыванием) конечного числа членов, вытекает сходимость
ряда{\).
< Для простоты рассмотрим случай, когда изменяются первые к членов ряда (1).
Обозначим через Sn n-ю частичную сумму нового ряда
Si + а2 4-... + ак 4- ак+{ +... 4- ап +... . (4)
Разность _ _
sn - sn = Sk - Sk
при n > к постоянна (не зависит от п). Тем самым, последовательность Sn и Sn
сходятся или расходятся одновременно и, значит, из сходимости ряда (1) следует
сходимость ряда (2). Верно и обратное, из сходимости ряда (2) следует сходимость
ряда(1). ►
Теорема 2. Пусть имеется сходящийся ряд
00
ai 4- <*2 +... 4- ап 4-... = ^Г а»
и некоторое число \Ф О. Тогда ряд
Ха{ 4- Ла2 4-... 4- Ла„ 4-... =У^Лап
п=1

. Глава XVIL Числение
будет сходящимся, причем
оо оо
п=1 п=1
ОО 00
< Составим n-е частичные суммы рядов Y2 ап и ]|Г) \ап. Имеем
п=1 п=1
5п = ах 4- а2 4-... 4- ап, 5п = \ах 4- Аа2 4- ... 4- Аап.
~ 00
Очевидно, что 5п = \Sn. Так как по условию ряд Y2 ап сходится, т.е. существует
п=1 _
предел lim 5„, то в силу последнего равенства существует предел lim Sn, причем
n-юо п-юо
lim Sn = lim A5n = A lim 5n,
n->oo n->oo n-*oo
ИЛИ
^Aan = A^an. ►
n=l
Теорема З. Пусть ряды
00 00
n=l n=l
сходятся. Тогда их сумма и разность, т. е. ряды
00 00
53(а" + ь») w 53 (Лп" ь»)>
буду/и сходиться, причем
00 00 00
п=1 п=1 п=1
<* Пусть
5„ = ai +02 + ... 4-ап,
^п = &i 4-^2 + ... +bny
°п = (ai 4- Ъх) 4- (а2 4- h) + . •. + (ап 4- Ь„)
— n-е частичные суммы соответственно рядов
00 00 00
53 а»> 53 Ьп> 53(а*+ь»)-
п=1 п=1 п=1
Очевидно, что
0"п = Sn +Sn-

§2. Простейшие действия над рядами __ 7
00 00
Так как по условию ряды £ ап и J2 ьп сходятся, т. е. существуют пределы lim Sn
n=l n=l п-кх>
и lim Sn, то из последнего равенства, справедливого для всех п, следует существование
п-юо
предела lim an, причем
п-юо
lim <тп = lim (Sn + Sn) = lim Sn + lim 5n,
п-юо п-юо п-юо п-юо
что равносильно равенству
00 00 00
п=1 п=1 п=1
оо
Аналогично доказывается сходимость ряда 5^(ап - ^п)« ►
п=1
Введем понятие остатка ряда.
Определение. Если в сходящемся ряде
00
ах + а2 + ... + ап + an+i + an+2 + ... = /Zan
n=l
отбросить первые п членов, то получим сходящийся ряд
an+i + ап+2 + ... + an+* + ...,
который называют п-м остатком данного ряда и обозначают
Rn= Yl ak
(здесь п фиксировано). Тогда исходный ряд можно записать в виде
00
Y^an = Sn+Rn.
00
Если S — сумма ряда ]И an, то остаток ряда Rn = S-Sn для любого п = 1, 2,..,
п=1
Пример, п-м остатком ряда
00
п=1
является ряд
00
/с,» = aq + eg + ... + aq + ... = 2^ <*q ,
который сходится при Ы < 1 •

8 Глава XVII. Числовые рады
§3. Критерий Коши сходимости ряда
Из критерия Коши для сходимости последовательности вытекает самый общий
критерий сходимости числового ряда.
оо
Теорема 4 (критерий Коши). Для того чтобы числовой ряд Y1 *п сходился, необходимо и
достаточно, чтобы для любого числа е > О существовал номер N = N(e) такой, что при
любом п> N неравенство
К + Оп+1 + • • • + Оп+р\ < £ 0)
выполнялось для всех р = О, 1, 2,... .
00
Используя частичные суммы Sn+P и Sn-\ рассматриваемого ряда ^2 ап, неравен-
п=1
ство (1) можно записать в виде
Из критерия Коши вытекает необходимый признак сходимости числового ряда.
Теорема 5. Если ряд
00
n=l
сходится, то
lim ап = 0.
П-+00
< Полагая р = 0 в теореме 4, получим неравенство
которое выполняется для всех п > N(e). В силу произвольности числа е > О это
означает, что
lim ап = 0. ►
П-+00
Следствие. Если lim an отличен от нуля или не существует, то ряд
п-юо
00
п-\
расходится.

§3. Критерий Коши сходимости ряда.
Пример 1. Числовой ряд
расходится, так как
Пример 2. Ряд
расходится, так как
, 1 \/2 тг ^ тг
-1 + 0 + - + — + cos - +... = V cos -
22 5 Й Л
lim en = lim cos — = cos 0 = 1 Ф 0.
П-»00 П-»00 XI
i-i + i-i + ...=£(-i)'
п=1
lim an= lim(-l)n
п+1
не существует.
Замечание. Теорема 5 дает необходимое условие сходимости ряда, но оно не является достаточным, т. е.
00
условие lim ап = 0 может выполняться и для расходящегося ряда £ вп.
п-°° n=i
Пример 3. Рассмотрим числовой ряд
который называется гармоническим рядом. Для гармонического ряда выполнено необходимое условие
сходимости, так как
lim an = lim - = 0.
n-»oo n-»oo fj
Воспользовавшись критерием Коши, покажем, что этот ряд расходится. Положим р = п. Тогда
1
п
+
1
п+1
1 111
п + 2+'" + 2п>п+1 + п + 2+"
1 11
' +2п~П' 2п~ 2'
1 1 1
. + — > + + ..
2п п + п п + п
1
• + 2^ =
Полученное неравенство выполняется для любого как угодно большого п. Отсюда следует, что для
£ ^ \ и Р = п неравенство (1) не выполняется. Тем самым, в силу критерия Коши гармонический ряд
расходится.
Важное замечание. В известном смысле ряд является обобщением конечной суммы. Однако в отличие
от последней, слагаемые в которой можно совершенно произвольно группировать и переставлять
местами, отчего сумма, как известно, не меняется, действия с членами произвольного ряда нужно
проводить осмотрительно — последствия могут быть не всегда предсказуемыми.
Если в расходящемся ряде
1-1 + 1-1 + 1-1 + ...
(не выполнен необходимый признак сходимости) попарно сгруппировать соседние группы
(1-1) + (1-1) + (1-1) + ...,
то получится сходящийся ряд
0+0+0+
Члены сходящегося ряда
11111
'-2+3-4+5-6+-
(см. пример из § 8) можно переставить так, что он будет сходиться к любому числу и даже расходиться.
В частности, ряд
J.J. !_!_! I_J__ J_
1~2~4 + 3 6~8 + 5~10~12+'"'
полученный перестановкой его членов, сходится к полусумме исходного (пример из § 9). То, что в этих
примерах члены ряда имеют разные знаки, существенно.

10 —- , , fr Глава XVI». Числовые рады
§4. Признак сравнения
для рядов с положительными членами
Приведем признаки, дающие возможность установить сходимость или расходимость
некоторых числовых рядов путем сравнения их с другими рядами, сходимость или
расходимость которых известна заранее.
Теорема 6 (признак сравнения). Пусть даны два ряда
00
а\ + а2 +... + ап + ... = ]Р ап, (1)
п=1
00
bi+b2 + ... +Ьп + ... =Х1Ь»> (2)
п=\
члены которых ап и Ьп положительны. Если для всех номеров п выполняется неравенство
ап^ЪПу (3)
00 00
то из сходимости ряда Y1 &п следует сходимость ряда ]Г) ап, а из расходимости ряда
п=\ п-\
00 00
]Г} ап следует расходимость ряда Y1 К-
п=\ п=\
< Составим частичные суммы рядов (1) и (2)
Sn = а\ + а2 +... + an, Sn = Ь{+Ь2 +... +Ъп.
Из условия (3) теоремы следует, что Sn < Sn для всех п = 1,2,... .
1) Предположим, что ряд (2) сходится, т. е. существует предел его n-х частичных
сумм
lim Sn = S.
п—юо
Так как все члены данных рядов положительны, то
О < Sn < S,
откуда в силу неравенства (3) следует, что
0<5П <5 дляп= 1,2,... .
Таким образом, все частичные суммы Sn ряда (1) ограничены и возрастают при
возрастании п, так как ап > 0. Следовательно, последовательность частичных сумм {Sn}
00
является сходящейся, что означает сходимость ряда ]Г} ап. При этом при переходе
~ п=1
к пределу в неравенстве 0 ^ Sn ^ S при п —> оо, получим, что
О ^ S ^ S,
т. е. сумма 5 ряда (1) не превосходит суммы 5 сходящегося ряда (2).
00
2) Пусть ряд Y!, ап расходится. Так как все ап > 0, то последовательность Sn
возрастает и, следовательно,
lim Sn = + оо.
П-+00

§4, Признак сравнения для рядов с положительными членами 11
В силу неравенства Sn > Sn (n = 1,2,...) получим
lim Sn = -f oo,
п-*со
00
т. е. ряд 52 К расходится. ►
п=1
Замечание. Теорема 6 остается справедливой и в случае, когда неравенство ап ^ Ъп выполняется не для
всех п, а начиная лишь с некоторого номера к, т. е. для всех п ^ Л, так как изменение конечного числа
членов ряда не нарушает его сходимости.
Примеры. Исследовать на сходимость следующие ряды:
S^ (3)
•4 Имеем
Так как числовой ряд
сходится, то по признаку сравнения исходный ряд (3) также сходится. ►
00 t
£к- »
4 Из неравенства In n < п следует неравенство j~ > £ для п = 2,3,... . Так как гармонический
ряд
00 t
n=l
n
(5)
00 j
расходится (как и ряд £ -), то по признаку сравнения исходный ряд (4) также расходится. ►
Замечание. Теорема 6 остается справедливой и в случае более общего неравенства ап ^ \Ъп (п = 1,2,...),
где А > 0.
Пример 3. Исследовать на сходимость ряд
4 Используя неравенство sin ж ^ ж, справедливое для всех ж ^ 0, найдем, что
0< l-cos~r = 2smz-~- ^2(r-rr) =-=-•■=■
2n 2-2n \ 2 • 2n / 2 4n
для n = 1,2,... . Так как ряд
00 t
L~i 411
л=1
сходится, то по признаку сравнения (здесь А = у) сходится и данный ряд (5). ►
Следствие. Если существует конечный отличный от нуля предел
lim -^ = L, О < L < +00,
п-*оо Оп
то ряды (1) и (2) сходятся или расходятся одновременно.

12 ГлаааХУМ.
Ч Из существования указанного выше предела вытекает, что для любого числа € > О,
найдется номер N такой, что для всех п> N будет выполняться неравенство
\ъп I
или
ап
L-e< — <L + e.
On
Отсюда
(L - е)Ьп <an<(L + e)bni n>N.
Если ряд (2) сходится, то сходится и ряд
00
п=1
Но так как
an<(L + e)bny n>Ny
то в силу теоремы 6 будет сходиться иряд(1). Если же ряд (2) расходится, то расходится
и ряд
п=1
(е считаем столь малым, что L - е > 0).
Так как
(L - ё)Ьп < On для всех п> N,
то по теореме 6 ряд (1) расходится. ►
Замечание. Условие леммы равносильно тому, что последовательности ап и Lbn при 0 < L < +оо
эквивалентны
или, что то же
km -— = 1.
В случае L = 0 из сходимости ряда (2) вытекает сходимость ряда (1). Обратное неверно*
В случае L = +оо из расходимости ряда (1) следует расходимость ряда (2). Обратное неверно.
Примеры. Исследовать на сходимость следующие числовые ряды:
оо ж
1. £ sin-.
п=1 п
4 Сравним этот ряд с гармоническим рядом
Имеем
00 j
en sin - sin -
lim —- = lim —у*- = lim ж —у*" = ж Ф 0
n-»oo 5n n-»oo ! n-»oo i
(Z/ = *). Так как гармонический ряд расходится, то расходится и данный ряд. ►

§5,1Чж»иак Даламбера.
-4 Возьмем для сравнения сходящийся ряд
£(Г
Тогда
а —~ 2П 1
lim -2. = iim J^IL - цт _ = цт = 1^0
2* 2
(L = 1), так как
Исходный ряд сходится. ►
§5. Признак Даламбера
п-»оо 2П
00
Теорема 7 (признак Даламбера). Пусть дан ряд £) ап, где все а„ > 0. £е/ш существует
предел
п—юо dn
/wo я/ш 0 ^ A < 1 /wd сходится, а при A > 1 ряд расходится.
< Пусть существует предел
hm = Л,
п->оо а„
где 0 ^ Л < 1. Возьмем q такое, что А < q < 1. Тогда для любого числа е > О,
например, для е = q - А, найдется номер N такой, что для всех п ^ N будет выполняться
неравенство
- Л < q- \.
В частности, будем иметь
ап+\ . . .
А < g - А,
или
откуда an+i < anq для всех n ^ JV. Из этого неравенства, придавая п последовательно
значения JV, JV + 1, JV + 2,..., получим
а#+1 < aNq,
a>N+2 < o>n+\<1 < a>N<l ,
з
aN+i < aN+2q < *nQ i
Члены ряда
ujv+i -f &N+2 + а#+з + ...
не превосходят соответствующих членов ряда
a>N4 + a>NQ2 + a^g3 + ... ,

14 Глава XVII. Числовые ряды
который сходится как ряд, составленный из членов геометрической прогрессии со
знаменателем д, 0 < q < 1. По признаку сравнения ряд
aN+\ + aN+2 + aN+i + ...
00
сходится, а значит, сходится и исходный ряд ]Г) ап-
п=1
В случае Л > 1, начиная с некоторого номера N, будет выполняться неравенство
> 1, или aN+\ > aN > 0.
00
Следовательно, lim an ^ 0, и ряд ]Г] an расходится, так как не выполнен НеобхОДИ-
n-oo п=1
мый признак сходимости. ►
Замечание. Если
hm = 1,
»-«> ап
или не существует, то признак Даламбера ответа о сходимости или расходимости ряда не дает.
Примеры. Исследовать на сходимость следующие ряды:
оо 2
< Для данного ряда имеем
п2 (п+1)2
2n' "n+' 2n+1 '
Тогда
a«+i r (n+l)2>2B 1Л 1\2 1 ,
lim = hm —ггтг-o— = Ьш - 1 + - 1 == - < 1.
По признаку Даламбера ряд сходится. ►
00 пп
2. V—.
Я*
4 Имеем
_ пп _ (n+l)**1 _ (п + 1)л
fln - п!, ап+] - (п+1)! - ы ;
г an+i г (п+1)п-п! / 1\"
hm —— = hm ~ = hm 1 + - = е > 1.
п-*оо ап п-+оо fiJ fjn п-*оо \ п I
Данный ряд расходится. ►
§6. Признак Коши
Теорема 8 (признак Коши). Пусть дан ряд
00
^]an, an>0, n=l,2,... . (1)
n=l
Если существует конечный предел
lim v^n = A,
то 1) я/ш 0 ^ А < 1 ряд сходится; 2) при А > 1 ряд расходится.

§&. Признак Коши.
.15
< 1) Пусть Л < 1. Возьмем число q такое, что А < q < 1. Так как существует предел
lim ф^ = Л,
п-юо
где Л < q, то, начиная с некоторого номера N, будет выполняться неравенство
фТц < q, В самом деле, из предельного равенства вытекает, что для любого е, в том
числе и для е = q - Л, найдется такой номер N, начиная с которого будет выполняться
неравенство
|vfi£-A| <e = q- A,
откуда v^ - Л < g - Л или, что то же,
л/ё£<д.
Отсюда получаем
ап < qn для п ^ JV. .
Таким образом, все члены ряда, начиная с aN+\, меньше соответствующих членов
00
сходящегося ряда J2 gn. По признаку сравнения ряд
00
n=iV+l
сходится, а значит сходится и ряд (1).
2) Пусть А > 1. Тогда, начиная с некоторого номера N для всех п > JV, будет
выполняться неравенство tya^ > 1, или
ап> 1.
Следовательно,
lim an ^ О
п-»оо
и ряд (1) расходится. ►
Замечание. Если А = 1, то ряд (1) может как сходиться, так и расходиться.
Примеры. Исследовать на сходимость следующие ряды:
* 2П
1.
;дтп(п + 1)*
<4 Имеем
Ряд сходится. ►
2.
< Здесь
Ряд расходится. ►
lnn(n+l)'
№ы =
lim УвГ= lim
П-»00 П-»ОС
1п(п+1)'
:0<1.
»-♦«> 1п(1 + п)
А 1 / 1\*2
1 / 1\n e
im ^ = lim - 1 + - ) = г > 1.
-оо v п-оо 2 V п) 2
lim
п-»оо

16.
-ritttaXVU.
§7. Интегральный признак сходимости ряда
Теорема 9 (интефальный признак сходимости). Пусть функция f(x) определена, непрерывна,
положительна и не возрастает на луне х ^ 1. Тогда:
00
1) числовой ряд ]£ /(те) сходится, если сходится несобственный интеграл
п=1
+00
f(x) dx;
0)
2) Р*д Z) f(n) расходится, если расходится несобственный интеграл (1).
п=1
< Возьмем на графике функции f(x) точ- у \
ки с абсциссами
«1 = 1, х2 = 2, х3 = 3, ...,i| = n
и построим две ступенчатые фигуры,
состоящие из выступающих и входящих
прямоугольников так, как показано на
рис. 1. Площадь Q криволинейной
трапеции, ограниченной прямыми х = 1,
х = те, у = 0 и кривой jf = /(ж) равна
п
= j f(x)dx.
Рис.1
Возьмем п-ю частичную сумму ряда £) /(я):
п=1
S. = /(!) +/(2)+ /(3) + ...+/(п).
Тогда площадь Q+ выступающей фигуры будет равна
Q+ = /0) + /(2) + /(3) +... + /(п - 1) = 5„-,.
а площадь Q_ входящей фигуры равна
<?_ = /(2) + /(3) +... + /(n) = Sn - /(1).
Из построения и свойств функции f(x) следует, что Q_ < Q < Q+, т. е.
п
Sn-f(l)<ff(x)dx<Sn-h
1
Так как Sn_i < Sn (в силу условия /(те) > 0), то
п
Sn-f(l)<f f(x)dx<Sn> n = l,2,....
(2)

$7^Иитирмы1Ый wpwmwc оходимости рада 17
1) Пусть интеграл Щ сходится. Тогда существует предел
п
f f(x)dx~Ay
Urn
n-»oo
1
так как
+00
J f(x)dx^A= [ f(x)dx
l l
(в силу условия /(ж) > 0 для ж € [1, -f оо)), то из неравенства (2) следует, что
п
Sn < /О) + / /(*) dx ^ /(1) + А = М = const,
1
т. е. О < Sn < М для п = 1,2,... . Тем самым, последовательность {Sn} ограничена,
и при возрастании п сумма Sn возрастает, так как /(п) > 0 для п = 1, 2,... . Поэтому
она имеет предел
lim Sn = S,
n-*oo
00
что означает сходимость ряда £) /(п).
2) Пусть интеграл (1) расходится. Так как по условию /(ж) > 0 для ж ^ 1, то
+00
Из неравенства
следует, что
//(ж)dx = lim / fix)dx = -f оо.
п-юо J
l l
n
Sn> f f(x)dxy 11=1,2,... ,
l
lim 5n = +oo,
00
т. е. ряд ]j£ /(n) расходится, ►
n=l
Пример 1. Исследовать на сходимость ряд
00 1
Si-
4 Здесь /(n) = ^. Известно, что несобственный интеграл
I
сходится при р > 1 и расходится при р ^ 1. Следовательно, данный ряд сходится при р > 1 и
расходится при р ^ 1. В частности, при р = 1 получим гармонический ряд
,11 1 Д1

18.
. Глава XVII. Числовые ряды
Пример 2. Исследовать на сходимость ряд
w I
< В данном случае функция f(x) — -^щ и
г dx ^ t dx \Ь . 7Г 7Г 7Г
/ -з—г = lim / "1—г = um arctgar I = ton (arctg b - arctg 1) = - - - = -,
J x2 + \ &-+00.7 ж2-И &-»+«> ° li 6-H-oo '244
i
+00
r dx
J X*J1
1
т. е. интеграл
сходится, а значит, сходится и ряд. ►
Пример 3. Исследовать на сходимость ряд
4 Так как общий член данного ряда имеет вид /(п)
Несобственный интеграл
+оо . Ь
^щ, то выбираем функцию f(x) = ^щ.
г xdx с xdx f. 1 f . 2 ,4!ft
/ -^—7= hm Is—г= hm xN* +1),= "m
У Ж2 + 1 ft-Ч-ооУ Ж2 + 1 &-+оо 2 ll &-+ос
iln(62 + l)-iln2
1 1
расходится, следовательно, ряд тоже расходится. ►
Замечание. Нижний предел интегрирования в несобственном интеграле
+00
J f(x)dx
1
можно взять произвольным, например, равным а, где а ^ 1 — любое число.
Пример 4. Исследовать сходимость ряда
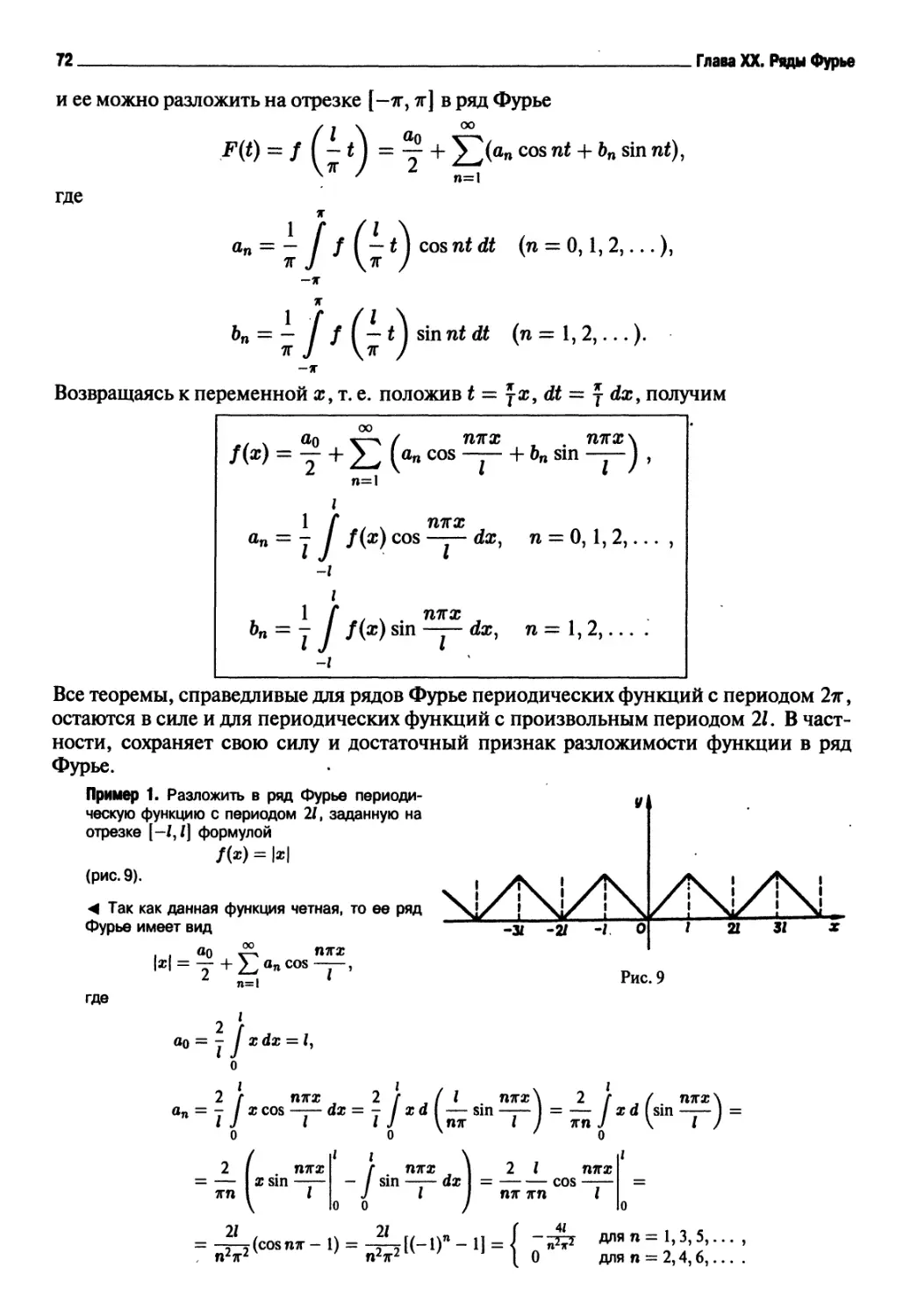
00 |
2(ri-2)ln2<n-2)-
= +оо
<4 Так как общий член ряда
то в качестве функции f(x) возьмем
/(■)=
Тогда
dx
. (х-2
_ 1
fln " (^^In1^^)'
1
(ж-2)1п2(ж-2)
ь
, где х ^ 4.
У (ж-2)1п2(ж-2) &-+W (ж - 2) 1п2(ж - 2) ft-J+W
d[]n(x - 2)]
ln2(s-2)
1
6-i+°oo [ 1п(ж - 2)
: lim
&-++00
1
In 2 ln(6-2)J
Jl_
In2*
Так как несобственный интеграл
/dx
(х - 2) 1п2(ж - 2)
4
сходится, то сходится и исходный ряд. ►

§7. Интегральный признак сходимости рада.
.19
В случае сходимости ряда £ /(те) метод, примененный при доказательстве инте-
п=1
трального признака сходимости, позволяет получить оценку погрешности,
возникающей при замене суммы ряда частичной суммой.
Пусть функция f(x) удовлетворяет условиям теоремы 9, ряд
£/(«)
я=1
сходится и его сумма равна 5. Можно показать, что в этом случае будет сходиться и
несобственный интеграл
+оо
/
f(x) dx.
Пользуясь неравенством
к
/(*)< J /(*)&>,
*-1
оценим остаток R„ заданного ряда. Имеем
оо оо * у»
Rn = S-Sn= ]Г /(*)^ ]Г у f(x)dx= J f(x)dx
*=n+l
fc=s,l+l*-l
Итак,
Таким образом, погрешность, получаемая при замене суммы S сходящегося ряда
00 +00
53 /(те) его п-й частичной суммой 5П, не превосходит интеграла / f(x) dx.
n=l n
Пример 5. Установить сходимость ряда
и оценить погрешность при замене его суммы S частичной суммой S$.
4 Здесь
/(«) =
+00 6
(*2+1)2=ЛоУ (*2 + 1)2 =6-
lim
+00
(*2 + 1)2'
1 ]
[ 2(s2 + l)J
= lim
- 6-++00
"1 1 1
4 2(62+l)j
В силу интегрального признака ряд сходится. Обозначим сумму этого ряда через S и будем считать,
что S& Ss- Тогда
5« 55 = - + - + — + — + — = 0,25 + 0,08 + 0,03 + 0,013841 + 0,007396 = 0,381237.
Оценим погрешность R$. Имеем
/xdx _ 1
(*2 + 1)2 = ~2(*2 + 1)
и 0,019231. ►

20 ■ - ^K ■•••'•-*:- Глава ХУН.Числолы#ряды
Замечание. Обозначение
1
2<*2 + 1)
понимается так:
\Ь
1
:»55о("2^П))
2(*2+1)|
Пример 6. Оценить n-й остаток сходящегося ряда
1 1 г 1 1
52 2 ft-»+oo ж2 + 1 52
00 J
гдер> 1.
< Имеем
+00 +00
^lv.-h-'-^
р)хР-
<Р-1И"1
§8. Знакочередующиеся ряды. Признак Лейбница
Определение. Числовой ряд
а, - а2 + а3 - ... + (-1)п"1ап + ...,
где все числа ап положительны, называется знакочередующимся.
Пример. Ряд
является знакочередующимся, а ряд
111
!-2 + 3-4+-
, 11111
знакочередующимся не является.
Для знакочередующихся рядов имеет место следующий признак сходимости,
который носит название признака Лейбница.
Теорема 10 (признак Лейбница). Пусть в знакочередующемся ряде
а\ — й2 4- а>ъ"~ • • •
числовая последовательность {ап} убывает, а\ > а^ > а^ > ... и lim an ~ 0. Тогда
п-юо
этот ряд сходится, причем его сумма S положительна и не превосходит первого члена:
0<5^а,.

(8. Знаючетуюурес* РВДУ. Признак Лейбница 21
4 Возьмем четную частичную сумму 52п этого ряда и запишем ее в виде
Sm = («1 ~ а2) + (а3 - а4) +... + (a2n-i - a2„).
Из условия теоремы следует, что разности в скобках положительны и, значит, S2n > О,
причем с возрастанием п частичная сумма S2n возрастает. Эту сумму можно записать
итак:
Sin - ai - (a2 - a3) - (a4 - a5) - ... - (a2n_2 - a2n-\) - a2n.
Здесь каждая скобка положительна, откуда следует, что
S2„<a, (n=l,2,...).
Итак, последовательность {52п} монотонно возрастает и ограничена. Следовательно,
она имеет предел
lim 52n = 5,
п-юо
причем 0 < S < ai.
Для нечетной частичной суммы 52n+i будем иметь
52n+i = #2п + a2n+i (n = 1,2,...).
По доказанному
а по условию теоремы
Поэтому существует предел
lim
п-юо
Таким образом, доказано, что
lim 52п = Sy
п-юо
lim a2n+1 = 0.
lim £2*1+1 = lim 52n + lim a2n+i = 5.
n—юо n—»oo n-+oo
lim Sn = Sy
п-юо
т. е. данный ряд сходится. Из неравенства 0 < S < ах следует, в частности,
положительность суммы ряда. ►
Теорема остается справедливой в части сходимости, если условие монотонности
последовательности {ап} будет выполняться для всех номеров п, начиная с некоторого номера N.
Пример. Знакочередующийся ряд
сходится, так как
Теорема 10 позволяет оценить n-й остаток
Rn = ±(оп+\ - an+2 +...)
рассматриваемого рада, который также является знакочередующимся рядом. По
абсолютной величине остаток будет не больше абсолютной величины первого своего
члена, |Я„| < а„+1. Так как Rn = S - 5П, то
5+I-J+-
1 1
>2>3>
(_!)п-1
.. + -—-— + .
п
и lim - = 0.
n-oo n
\S - Sn\ ^ an+b

23U _ , , Глава XVII. Числовые ряды
т. е. абсолютная погрешность, получающаяся при замене суэдмы знакочередующегося^
ряда его n-й частичной суммой, не превосходит абсолютной величины первого из
отброшенных членов ряда (an+1).
Пример. Вычислить приближенно сумму ряда
ill ИГ"1
ограничившись четырьмя членами, и оценить погрешность.
4 Сходимость ряда очевидна. Положим приближенно
S«S4 = l-i + i-l=0,625.
Тогда
1 41^5! 120
Абсолютная погрешность не превосходит -^ « 0,0083, ►
§9. Знакопеременные ряды.
Абсолютно и условно сходящиеся ряды
Числовой ряд
00
членами которого являются действительные числа любого знака, называется
знакопеременным. Знакопеременными рядами будут, например, ряды
1 + cos 1 + cos 2 + ... + cos п + ...,
11111
1-2-3 + 4-5"6+.-
(плюс, два минуса, плюс, два минуса и т. д.).
Наряду со знакопеременным рядом
а\ + щ + ...
рассмотрим ряд, составленный из абсолютных величин его членов, т. е.
1«и| + |а2| + ... ,
и докажем следующую теорему.
Теорема 11. Если сходится ряд
то сходится и ряд
^2 la"l'
00
п=\

§9. Знакопеременные ряды. Абсолютно и условно сходящиеся ряды 23
«« Из двойного неравенства -|an| ^ ап < |ап| получаем
О < ап + \ап\ < 210*1 для п = 1,2,... .
Пусть ряд
п=1
сходится. Тогда ряд
00
п=1
также будет сходиться, а по признаку сравнения будет сходящимся и ряд
00
5>. + h.l).
п=1
00
Но ряд ^2 ап есть разность двух сходящихся рядов
п=1
00 00 00
X)(«n+io»f) - X) KI=X) в»>
п=1 п=1 п=1
поэтому он также будет сходящимся. ►
Следствие. Если ряд
Х>»|
п=1
сходится, то справедливо неравенство
00 00
п=1 п=1
< Для любого натурального числа к имеет место неравенство
к к
т.е.
n=l n=l n=l
Переходя к пределу при к —* оо, получим
00 00 00
п=1 п=1 п=1
ИЛИ
00 00
|Еа»|<Е !*»!•►
п=1 п=1

24 Глава XVH. Числовые раду
При исследовании ряда
Х>»|
на сходимость можно применять все достаточные признаки сходимости,
установленные для знакоположительных рядов.
Замечание. Из сходимости рада
сходимости ряда
00
п=1
вообще говоря, не следует, т. е. доказанная теорема дает лишь достаточное условие сходимости
знакопеременного ряда.
Пример 1. Ряд
111
!-2 + 3-4+-
сходится по признаку Лейбница, но ряд, составленный из абсолютных величин его членов,
1 1 1 1
— это гармонический ряд, который расходится.
Определение. Знакопеременный числовой ряд
00
называется абсолютно сходящимся, если сходится ряд
Х>»|-
п=1
Ряд
оо
называется условно сходящимся, если он сходится, а ряд
00
£|«»|
расходится.
12. Числовой ряд
i_±-± ±_
22 32 + 42 *••
(плюс, два минуса, плюс, два минуса и т. д.) является абсолютно сходящимся, так как ряд, составленный
из абсолютных величин его членов,
сходится. Ряд из примера 1 является условно сходящимся.
Отметим следующие свойства абсолютно сходящихся и условно сходящихся рядов.
Теорема 12. Абсолютно сходящийся ряд при любой перестановке его членов остается
абсолютно сходящимся, и его сумма не изменяется.

§& Знакопвреишшые рады. Абсолютно и условно сходящиеся ряды 25
Замечание. Утверждение теоремы справедливо для любого сходящегося знакопостоянного ряда.
Условно сходящиеся ряды этим свойством не обладают.
Теорема 13. Если ряд сходится условно, то, каково бы ни было наперед взятое число А,
можно так переставить члены этого ряда, что преобразованный ряд будет иметь своей
суммой число А.
Более того, члены условно сходящегося ряда можно переставить так, что
полученный после перестановки ряд будет расходящимся.
Пример. Рассмотрим условно сходящийся ряд
,11111
сумму которого обозначим через S. Переставим члены ряда так, чтобы за каждым положительным
членом следовали два очередных отрицательных. Тогда получим ряд
1_i i_i_i i_ J L
2 4 + 3 6 8 + 5 10 \2+'"'
Покажем, что он сходится и его сумма равна jS- Рассмотрим подпоследовательность его
частичных сумм #з* •
Нетрудно убедиться в том, что она сходится к ^S. А из того, что
1
£з*+1 = Sn - ■
#3*+2 = #3* -
4*-2
1 1
4* - 2 4*
получаем, что lim Sn существует и он равен ^S.
Таким образом, при указанной перестановке членов ряда, мы получили сходящийся ряд, сумма
которого в два раза меньше суммы исходного ряда.
Упражнения
Напишите формулу общего члена для следующих рядов:
18 27 149 16 Л„345
,.- + - + _ + .... 2.,_ + _ + _ + _-. + .... 3.2+; + - + -+....
12 3 4 т 2 6 24 120
42 + 5+10 + 17+"-- 5-3 + 8 + В + "24 +- *
Найдите сумму Sn первых п членов ряда и докажите его сходимость, используя определение
сходимости ряда:
00 1 00 1 00 ^П+1 00 Or» _1_ 1
6. У —-—. 7. У . 8. У —. 9. У +

26 Глава XVII. Числовые ряды
Используя признаки сравнения, а также необходимый признак, исследуйте на сходимость
следующие ряды:
00 001 °° / 4Г \ °°1Р
14. У)в-*5. 15. V Ц-. 16. £(l-cosf ). 17. Vtg-.
18. f>(l+2-n). 19. f: sin ^.
Пользуясь признаком Даламбера, исследуйте на сходимость следующие ряды:
оо _3 оо ^п оо _4 оо пп
iifn;- »•£"'<•?• »-£>«£т- »•££ «х-*».
n=l n=l n=l n=l
С помощью признака Коши исследуйте сходимость следующих рядов:
а|Ш' а§Ш" »£—:•
*■££• »£*-(^)' »£^.
П=1 ^ П=1 \ Я / п=1 "
Применяя интегральный признак, исследуйте на сходимость следующие ряды:
00 00 1 1 00 1
34. Е-г^=- 35. ЕЛ*»-- зб. У —=.
00 .2 °° ten °° 1 ,-
37. V пе"V. 38. V -^т- 39. V -^2"^.
Комбинируя различные признаки, исследуйте на сходимость следующие ряды:
оо _2 | _ | 1 оо 1 оо I
40 У " +w+1 41 V 42 У '
00 4
43. £ ln4fa+1)« Указание. Воспользуйтесь неравенством ln(l+s)^s,-l<s< +oo.
00 00 _
44. У^—5 5—• 45. V'sin-^—-.
Исследуйте на сходимость и абсолютную сходимость следующие ряды:
оо „ оо / i\n+l оо / i\n+l
»»-T'J. «Е^г- *ЕЙЬ-
П=1 П=1 * П=/
00 /_i\n-l^n 00 / f\n+l_ 00 in
"■5ет W-S^- s'-£<->~'^
Ответы
1. an = ^. 2. ow = fr. 3. an = cos*. 4. an = ^. 5. an = ^. 6. Sn = ^. 7. 5n = £у.
8.5n = 6[l-(§) ]. 9.Sn = fflp. 10.Расходится. 11.Расходится. 12.Сходится. 13.Сходится.
14. Расходится. 15. Сходится. 16. Сходится. 17. Расходится. 18. Сходится. 19. Расходится.
20. Сходится. 21. Расходится. 22. Сходится. 23. Расходится. 24. Расходится. 25. Сходится.

§9. Знакопеременные ряды. Абсолютно и условно сходящиеся ряды
,27
26.* Сходится. 27. Сходится; 28. Сходится. 29. Сходится. 30. Сходится. 31. Расходится.
32. Расходится. 33. Сходится. 34. Расходится. 35. Сходится. 36. Расходится. 37. Сходится.
38. Сходится. 39. Сходится. 40. Сходится. 41. Сходится. 42. Сходится. 43. Расходится.
44. Сходится. 45. Сходится. 46. Абсолютно сходится. 47. Условно сходится. 48. Условно
сходится. 49. Абсолютно сходится. 50. Расходится. 51. Расходится.

Глава XVIII
ФУНКЦИОНАЛЬНЫЕ РЯДЫ
§ 1. Область сходимости
Функциональным рядом называется ряд
00 |
(1)
/i(x) + /2(x) + ..
• + /»(*) + •.
п=1
членами которого являются функции fn(x), п = 1,2,..., определенные на некотором
множестве Е числовой оси. Например, члены ряда
1 + х + х2 + ...
определены на интервале -оо < х < +оо, а члены ряда
1 + arcsin х + arcsin2 x +...
определены на отрезке -1 ^ х ^ 1.
Функциональный ряд (1) называется сходящимся в точке х0 е Е9 если сходится
оо
числовой ряд ]Г) /n(so). Если ряд (1) сходится в каждой точке х множества D С Е
и расходится в каждой точке, множеству D не принадлежащей, то говорят, что ряд
сходится на множестве D, и называют I) областью сходимости ряда.
Рад (1) называется абсолютно сходящимся на множестве D, если на этом множестве
сходится ряд
El/n(x)|.
В случае сходимости ряда (1) на множестве D его сумма 5 будет являться функцией,
определенной на D,
S = 5(ж), xeD.
Область сходимости некоторых функциональных рядов можно найти с помощью
известных достаточных признаков, установленных для рядов с положительными
членами, например, признака Даламбера, признака Коши.
Пример 1. Найти область сходимости ряда

§ 1. Область сходимости
29
4 Так как числовой ряд
пР
сходится при р > 1 и расходится при р ^ 1, то, полагая р -\gx, получим данный ряд, который будет
сходиться при ]gx > Ц т. е. если х > 10, и расходиться при Igs ^ 1, т.е. при 0 < х ^ 10. Таким
образом, областью сходимости ряда является луч
4 10 < х < +оо. ►
Пример 2. Найти область сходимости ряда
ЕМГ'пе-
<4 Рассмотрим ряд
£\(-1Г1пе"*\ = £пе**.
п=1 п—\
Члены этого ряда положительны при всех значениях х. Применим к нему признак Даламбера. Имеем
п-»оо пе n-юо ц
При ех < 1, т.е. при а: < 0, этот ряд будет сходиться. Следовательно, заданный ряд сходится
абсолютно на интервале -оо < х < 0.
При х > 0 ряд расходится, так как А = е* > 1. Расходимость ряда при 2 = 0 очевидна. ►
Пример 3. Найти область сходимости ряда
S10+*2)""
4 Члены данного ряда определены и непрерывны на множестве -оо < х < +оо. Применяя признак
Коши, найдем
I п* п
А = lim ?/ j- =т- = lim =■ = +oo
n-юо у (1 -J- x2)n *-*<* 1 4- x2
для любого х € (-оо, +оо). Следовательно, ряд расходится при всех значениях х. ►
Обозначим через 5П($) n-ю частичную сумму функционального ряда (1). Если
этот ряд сходится на множестве!) и его сумма равна S(x), то ее можно представить
в виде
S(x)^Sn(x) + Rn(x)}
где Rn(x) есть сумма сходящегося на множестве D ряда
/п+1(*) + Л+2(*) + ... = J2 /*(*),
*=n+l
который называется п-м остатком функционального ряда (1). Для всех значений
х Е D ийеет место соотношение
lim Sn(x) = S(x)}
п—юо
И ПОЭТОМУ,
lim Rn(x) = lim [Sn(x) - S(x)] = 0,
т. е. остаток Rn(x) сходящегося ряда £} fn(x) стремится к нулю при п —► оо, каково
бы ни было ж Е 22.

30 Глава XVIII. Функциональные ряды
§2. Равномерная сходимость
Среди всех сходящихся функциональных рядов важную роль играют так называемые
равномерно сходящиеся ряды.
Пусть дан сходящийся на множестве D функциональный ряд
сумма которого равна S(x). Возьмем его n-ю частичную сумму
п
Определение. Функциональный ряд
£/»(*)
п=1
называется равномерно сходящимся на множестве П С D, если для любого числа е > 0
найдется число N > 0 такое, что неравенство
\S(x) - Sn(x)\ = |^(x)| < е
будет выполняться для всех номеров п > N и для всех х из множества П.
Замечание. Здесь число N является одним и тем же для всех х € Ю, т. е. не зависит от х, однако зависит
от выбора числа €, так что пишут N =. N(e).
00
Равномерную сходимость функционального ряда J^ /n(&) к функции S (х) на
множестве П часто обозначают так:
00 I
]Г fn(x) z* 5(ж) на П.
п=1
00
Определение равномерной сходимости ряда X) /п(ж) на множестве П можно за-
писать короче с помощью логических символов:
00
(£/n(s) =*$(*) на п)«»
«* (Ve > 0 ЭЩе) е N : Vn > JV(c) Va G ft =► |S„(s) - S(x)\ < e).
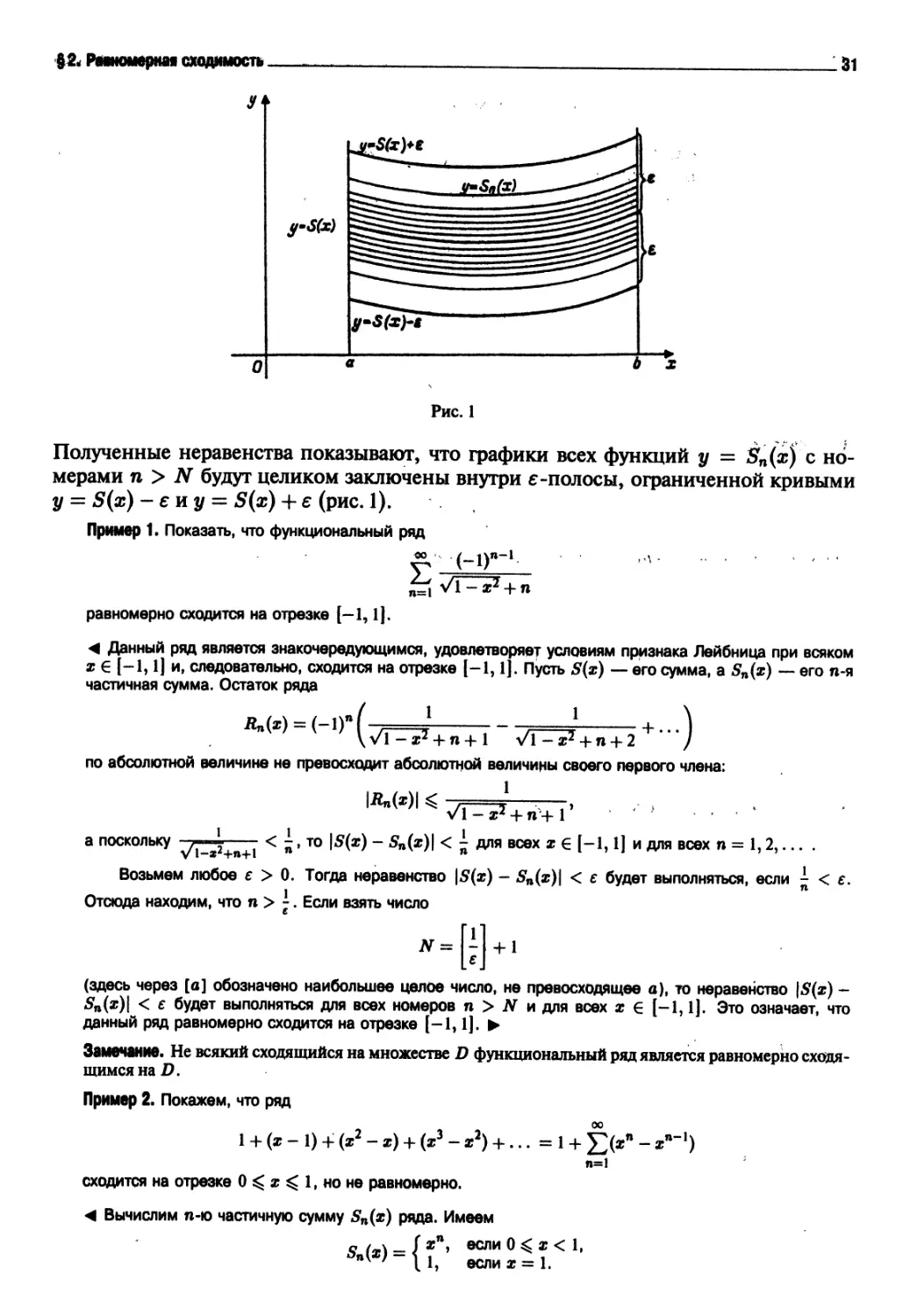
Поясним геометрически смысл равномерной сходимости функционального ряда.
Возьмем в качестве множества П отрезок [а, Ь] и построим графики функций у = S(x),
у = S(a) - е, у = S(a) + е (е > 0), у = Sn(x). Неравенство \S(x) - 5п(ж)| < е,
выполняющееся для номеров п > N и для всех ж G [а, Ь], можно записать в следующем
виде
5(a) - е < Sn(x) < S(x) + е.

Рис.1
Полученные неравенства показывают, что графики всех функций у = Sn(x) с
номерами п > N будут целиком заключены внутри е -полосы, ограниченной кривыми
у = S(x) - е и у = S(x) + е (рис. 1).
Пример 1. Показать, что функциональный ряд
« '" '(-1)п""1. "' - •• •
VT-
1Р + п
равномерно сходится на отрезке [—1,1}.
Л Данный ряд является знакочередующимся, удовлетворяет условиям признака Лейбница при всяком
х е [-1,1] и, следовательно, сходится на отрезке [-1,1]. Пусть S(x) — его сумма, a Sn(x) — его п-я
частичная сумма. Остаток ряда
1М*) = Н)ш(-7=^ г~-/т=г ; + •••)
\Vl-:r2 + n+l Vl - х2 + п + 2 /
по абсолютной величине не превосходит абсолютной величины своего первого члена:
№.(*)! ^ h ! , ,, . ,- ,
vl-a:2 + n+l
а поскольку ^^ < ^. т<> №) - $»(*)! < £ для всех я: е [—1,1] и для всех п = 1,2,... .
Возьмем любое с > 0. Тогда неравенство \S(x) - Sn(x)\ < e будет выполняться, если
Отсюда находим, что п > \. Если взять число
< е.
*-И
+ 1
(здесь через [а] обозначено наибольшее целое число, не превосходящее а), то неравенство \S(x) -
Sn(x)\ < е будет выполняться для всех номеров п > N и для всех х е [-1,1]. Это означает, что
данный ряд равномерно сходится на отрезке [-1,1]. ►
Замечание. Не всякий сходящийся на множестве D функциональный ряд является равномерно
сходящимся на D.
Пример 2. Покажем, что ряд
1 + (*-1) + (»а-*) + (»3-*а) + ... =l + f>л--:rй-,)
сходится на отрезке 0 ^ х ^ 1, но не равномерно.
< Вычислим п-ю частичную сумму Sn(x) ряда. Имеем
с /-\ _ / жп> если 0 ^ х < 1,
**w""\l, если ж = 1.

32 ГлаааХУШ.
Откуда '
n-»oo x ' 11, если ж = 1.
Данный ряд сходится на отрезке [0,1] и его сумма
<?/„л j, / °> если 0 < ж < L»
dW^\l, если ж «1.
Абсолютная величина разности S(x) - Sn(x) (остатка ряда) равна
Возьмем число £ такое, что 0 < е < 1. Пусть
|S(e)-A«i(*)l'<.#•< е-
Разрешим неравенство 0 < жп < е относительно п. Имеем п1пж < 1п£, откуда
line
п > г—
In а?
(так как 0 < ж < 1, то In х < О, и при делении на In ж знак неравенства меняется на обратный).
Неравенство \S(x) - Sn(x)\ <e будет выполняться при
»>*<.,,>. Fjsj
+i.
Но
JV(£, Ж) -> +00 ПрИ Ж -♦ 1 - 0.
Поэтому такого не зависящего от х числа N(e), чтобы неравенство
|5(жЬ$;(ж)|<жл<<г £
выполнялось для каждого n > N(e) сразу для всех х из отрезка, 0 ^ ж С 1, не существует.
Если же заменить отрезок 0 < ж ^ 1 меньшим отрезком Q ^ ж < 1 - £, где 0 < 0 < 1,1088
последнем данный ряд будет сходиться к функции 5(ж) = 0 равномерно. В самом деле,
1п£ jne ,■
ЬТж ^ 1п(1-Л)
при 0 ^ ж ^ 1 - б, и поэтому
|5(ж)-5я(ж)|=жп<е прип>й^5
сразу для всех ж € [0,1 - б]. ►
§3. Признак Вейерштрасса
Достаточный признак равномерной сходимости функционального ряда дается
теоремой Вейерштрасса.
Теорема 1 (признак Вейерштрасса). Пусть для всех х из множества Q члены функционального
ряда
£/»(*) (1)
по абсолютной величине не превосходят соответствующих членов сходящегося числового
ряда
i>- (2)
с положительными членами, т. е.
1/»(*)1 < о», п=1,2,..., (3)
для всех х € П. Тогда функциональный ряд (I) на множестве ft сходится абсолютно и
равномерно.

03. Признак Вейерштрасса.
4 1ак как по условию терремы члены ряда (1) удовлетворяют условию (3) на всем
00
множестве П, то по признаку сравнения ряд J2 1/п(#)1 сходится при любом х Е П, и,
следовательно, ряд (1) сходится на П абсолютно.
Докажем равномерную сходимость ряда (1). Пусть
00 00
п=1 п=\
Обозначим через Sn(x) и <тп частичные суммы рядов (1) и (2) соответственно. Имеем
\S(x) - Sn(x)\ = \fn+t(x) + /n+2(a) + ... | <
^ |/n+i(ar)| + |/n+2(s)| +... ^ an+i + a„_2 +... < <r - <rn
для всех x G ft.
Возьмем любое (сколь угодно малое) число е > 0. Тогда из сходимости числового
ряда (2) следует существование номера N = N(e) такого, что а - <тп < е и,
следовательно, \S(x) - Sn(x)\ < е для всех номеров п > N(e) и для всех х G П, т. е. ряд (1)
сходится равномерно на множестве П. ►
Замечание. Числовой ряд (2) часто называют мажорирующим, или мажорантным, для функционального
ряда(1).
Пример 1. Исследовать на равномерную сходимость ряд
^ч cos па?
п*
<4 Неравенство
|cosnjc| 1
выполняется для всех п = 1,2,... «для всех х € (-оо, -foo). Числовой ряд
00 1
Si
сходится. В силу признака Вейерштрасса рассматриваемый функциональный ряд сходится абсолютно
и равномерно на всей оси. ►
Пример 2. Исследовать на равномерную сходимость ряд
^ sin пх
Ч Члены ряда определены и непрерывны на отрезке [-2,2]. Так как
(4~х2)п/2 = (^4^2)%0
на отрезке [-2,2] для любого натурального п, то
| sin nx\ 1 1
|п2 + (4-ж2)»/2
Таким образом, неравенство
^
п2 + (4 - ж2)»/2 ^ п2 + (4 - ж2)»/2 п2'
1
<;?
|п2 + (4-ж2)п/2|
выполняется для п = 1,2,... и для всех ж € [—2,2]. Так как числовой ряд
00 1
2 Зак. 179

34 Глава XVHL Функциональные ряды
сходится, то по признаку Вейерштрасса исходный функциональный ряд сходится абсолютно и
равномерно на отрезке [-2,2).
Замечание. Функциональный ряд (1) может сходится равномерно на множестве Пив том случае,
когда не существует числового мажорантного ряда (2), т.е. признак Вейерштрасса является лишь
достаточным признаком для равномерной сходимости, но не является необходимым.
Пример. Как было показано выше (пример 1 в § 2), ряд
f» НУ1
Sn + vT^1
равномерно сходится на отрезке [-1,1]. Однако для него мажорантного сходящегося числового ряда (2)
не существует. В самом деле, для всех натуральных п и для всех а? € [—1,1J выполняется неравенство
п + л/1-х2
<$■
причем равенство достигается при х = — 1 и х — 1. Поэтому члены искомого мажорантного ряда (2)
непременно должны удовлетворять условию
но числовой ряд
00 1
Е
71=1
п
расходится. Значит, будет расходиться и ряд £ ап.
п=1
§4. Свойства равномерно сходящихся
функциональных рядов
Равномерно сходящиеся функциональные ряды обладают рядом важных свойств.
Теорема 2. Если все члены ряда
00
п=1
равномерно сходящегося на отрезке [а, Ъ], умножить на одну и ту же функцию д(х),
ограниченную на [а, Ь], то полученный функциональный ряд
00
п=\
будет равномерно сходиться на [а, Ь].
00
< Пусть на отрезке [а, Ь] ряд J2 /п(ж) равномерно сходится к функции S(x), а функ-
ция д(х) ограничена, т. е. существует постоянная С > 0 такая, что
\д(х)\^С Уже[а,&].
По определению равномерной сходимости ряда для любого числа е > 0 существует
номер N такой, что для всех п> N и для всех х G [а, Ь] будет выполняться неравенство
\Sn(x)-S(x)\<^,

§4. Саойства равномерно сходящихся функциональных рядов 35
где Sn(x) — частичная сумма рассматриваемого ряда. Поэтому будем иметь
\g(x)Sn(x)-g(x)S(x)\ = \g(x)\\Sn(x) - S(x)\ < С £ =е
для п> N и для любого х € [а, Ъ], т. е. ряд
J2g(x)fn(x)
равномерно сходится на [а, Ь] к функции ^(ж)5(ж). ►
Теорема 3. Пусть все члены /п(з) функционального ряда
00
п=1
непрерывны и ряд сходится равномерно на отрезке [а, Ь]. Тогда сумма S(x) ряда
непрерывна на этом отрезке.
Ч Возьмем на отрезке [а, Ь] две произвольные точки х н х + Ах. Так как данный
ряд сходится на отрезке [а, Ь] равномерно, то для любого числа е > О найдется номер
N = N(e) такой, что для всех п> N будут выполняться неравенства
\S(x)-Sn(x)\<e-1
\S(x + Ax) - Sn(x + Ax)\ < -,
00
где5„(ж) —частичные суммы ряда J2 /»»(#)• Эти частичные суммы Sn (x) непрерывны
на отрезке [а, Ь] как суммы конечного числа непрерывных на [а, Ь] функций fn(x).
Поэтому для фиксированного номера n0 > N(e) и взятого числа е найдется число
6 = 6(e) > О такое, что для приращения Аж, удовлетворяющего условию \Ах\ < 6,
будет иметь место неравенство
\Sno(x + Ax)-Sno(x)\<8-. (2)
Приращение AS суммы S(x) можно представить в следующем виде:
AS = S(x + Ax) - S(x) =
= [S(x + Ах) - Sno(x + Ах)] + [SnQ(x + Ах) - Sno(x)] + [Sno(x) - S(x)],
откуда
\AS\ ^ \S(x + Ax) - Sno(x + Ax)\ + \Sno(x + Ax) - Sno(x)\ + \S(x) - SnQ(x)\.
Учитывая неравенства (1) и (2), для приращений Ах, удовлетворяющих условию
\Ах\ < 6, получим
3 3 3
Это означает, что lim AS = 0, т.е. сумма S(x) непрерывна в точке х. Так как х
Дж-»0
является произвольной точкой отрезка [а, 6], то S(x) непрерывна на [а, Ь]. ►

Замечание. Функциональный ряд
. Глава XVIII. Функциональные ряды
п=1
члены которого непрерывны на отрезке [а, Ь], но который сходится на [а,Ь] неравномерно, может
иметь суммой разрывную функцию.
Пример 1. Рассмотрим функциональный ряд
(1 - х) + х(1 - х) + х2(\ - х) +... + жп-1(1 - х) +...
на отрезке [0,1]. Вычислим его n-ю частичную сумму
Sn(x) = (\-x) + x(l-x) + x2(l-x) + ... + хп~1(1-х) =
= (1 - х)(\ + х + х2 +... + ж»-1) = (1 - х) ^- = 1 - хп.
1-х
Поэтому
Km С /*Л — / 1 ДЛЯ 0 < Ж < 1,
&*W = io для* = 1,
т. е. сумма ряда
S(x) = [l0 *»0<«<1.
, 0 для х = 1.
Она разрывна на отрезке [0,1], хотя члены ряда непрерывны на нем. В силу доказанной теоремы
данный ряд не является равномерно сходящимся на отрезке [0,1].
Пример 2. Рассмотрим ряд
00 1
л—.
Как было показано выше, этот ряд сходится при х > 1. Для х ^ 1 + а, где а > О, ряд будет сходиться
равномерно по признаку Вейерштрасса, так как
-L<J_
и числовой ряд
00 j
2-rf nl+a
п=1 П
сходится. Следовательно, для любого х > 1 сумма этого ряда непрерывна.
Замечание. Функция
««)=£: 4 «>»,
п=1 п
называется функцией Римана (эта функция играет большую роль в теории чисел).
Теорема 4 (о почленном интегрировании функционального ряда). Пусть все члены fn(x) ряда
00
непрерывны, и ряд сходится равномерно на отрезке [a, b] к функции S(x). ТЬгда справед-
ливо равенство
XX X
J S(t) dt = f [E /.<*)] dt = Hj /"<*) *'
/и. е. данный ряд можно почленно интегрировать в пределах от Жо до х при любых х и
xq Е [а, 6]. Полученный ряд будет сходиться равномерно по х на отрезке [а, Ь], каково
бы ни было xq € [а, Ь].

§4/Шйстваравн(Ш^^ : 37
< В силу непрерывности функций fn(x) и разномерной сходимости данного ряда на
отрезке [а, Ь] его сумма S(x) непрерывна и, следовательно, интефируема на [а, Ь].
Рассмотрим разность
XX X
j S(t) dt- f Sn(t) dt = j [Sit)- Sn(t)] dt,
Xq Xq Xq
гдеж,ж0 € [а,Ъ\.
Из равномерной сходимости ряда на [а, Ь] следует, что для любого е > О найдется
число N(e) > О такое, что для всех номеров n > N(e) и для всех х € [а, Ь] будет
выполняться неравенство
\S(x)-S*(z)\< E
Ъ- а
Но тогда
XXX X
\f S(t)dt~ f Sn(t\dt\ < \J |5(f) - 5„(0| л| < \f -^— dt
XQ Xq Xq Xq
~ \x - ж0| < |ft ~ a| = -^ = e.
b — a b — a b — a
Итак,
/ 5(0 dt - f Sn(t) dt
<e
Xq Xq
для любого п > N(e). Иными словами,
т.е.
n n
f S(t)dt= lim f S„{t)dt= lim /fy>(<)l «= Hm V) f fk(t)dt,
XQ XQ Xq k~* k~X XQ
} °° r
/ S(t)dt = Y^ h{i)dt.>
XQ K~l XQ
00
Если ряд Y2 /n(0 не является равномерно сходящимся, то его, вообще говоря,
нельзя почленно интефировать, т. е.
х со х
j s(t)dt^Y,J'/»(')«•
xq ft=1 х0
Теорема 5 (о почленном дифференцировании функционального ряда). Пусть все члены fn(x)
сходящегося ряда
£/»(*)
п=\

. Глава XVIII. Функциональные ряды
имеют непрерывные производные и ряд
составленный из этих производных, равномерно сходится на отрезке [а, Ь]. Тогда в любой
точке х Е [а, Ь] справедливо равенство
00 00
п=1
т. е. данный ряд можно почленно дифференцировать.
Ч Положим
00 00
Y^Mx) = S(x), *£f'n(x) = <r(x).
п=1 п=1
Возьмем две любые точки х и xq Е [а, Ь]. Тогда в силу теоремы 4 будем иметь
00 00
|a(t)dt = f[EfUt)]dt = J2JfUt)dt =
хо г0 n=1 B=,*o
= Ё [/•<*) - /•<*»)] = Е /»<«) - Е /»(««) = 5(*) - SM-
n=l n=l
Функция а(ж) непрерывна как сумма равномерно сходящегося ряда непрерывных
функций. Поэтому, дифференцируя равенство
х
f a(t)dt = S(x)-S(xo),
XQ
получим
т.е. а(х) = S'(ж), или
[|(т(<)л]' = 5'(0,
[Е/.(»)]'=Е/.(«).
п=1 п=1
Упражнения
Найдите области сходимости данных функциональных рядов:
1-EJ- «-Е~ з.Ее- 4.Е^. 5.ЕШ-Х.
П=1 ^ П=1 " 71=1 71=1 Z П=1
00 ^ м! О0/»00 00
б.Е'п"(1+х2). т.е^. i^i,i. э.£п- ю-Е - J
п=1 п=1 Л n=l * n=I n=0 z

§4. Свойства равномерно сходящихся функциональных рядов 39
Пользуясь признаком Вейерштрасса, докажите равномерную сходимость данных
функциональных рядов на указанных интервалах:
. sin пх
11. > —, -00 < X < +00. 12. > 7=-, -00 < X < +00.
00 1 °° / х \
Snln2n + (4-x2)2 ^ V п >
Ответы
1. -1 < х < 1. 2. -оо < а? < +00. 3. -оо < х < 0. 4. О < ж < +оо. 5. е"1 < х < е.
6. -Ve- 1 < ar < Ve- 1. 7. Всюду расходится. 8. -2 < а? < 2. 9.0 < х < е. 10. -оо < х < +оо.

Глава XIX
СТЕПЕННЫЕ РЯДЫ
§1. Теорема Абеля.
Интервал и радиус сходимости степенного ряда
Степенным рядом называется функциональный ряд вида
СО + С\Х + С2Х* + . . . + СпХП + . . . =^2 СпХП
п=0
или вида
со + сх(х - ж0) + с2(ж - ж0)2 + ...' + Сп(х - ж0)п +... =53 ^ "" ж°)п>
п=0
(1)
(2)
где коэффициенты со, с\, сг,..., с„,... — постоянные.
Ряд (2) формальной заменой ж - жо на х сводится к ряду (1). Степенной ряд (1)
всегда сходится в точке ж = 0, а рад (2) — в точке ж0, и их сумма в этих точках равна со.
Пример. Ряды
х + х3 +... + х2п 1 +..
(* + 2)2 + (* + 2)4 + ... +(ж + 2)2п + ...
являются степенными рядами.
Выясним вид области сходимости степенного ряда.
Теорема 1 (Абель). Если степенной ряд
СпХ
п=0
сходится при ж = х\ Ф О, то он сходится абсолютно для всех ж таких, что \х\ < \х\\\
если степенной ряд расходится при ж = хг,то он расходится при любом х, для которого
1*1 > 1*21.

§ 1. Теорема Абеля. Интервал и радиус сходимости степеннбго ряда 41
<*1 Пусть степенной ряд
Е^"
сходится при ж = х\ Ф О, т. ё. сходится числовой ряд
Отсюда следует, что
lim Спх\ = О,
п->оо
а значит, существует число М > О такое, что |с„ж"| < М для всех п.
Рассмотрим ряд ^ ,
. Е i%a
п=0
где |ж| < \х\ |, и оценим его общий член. Имеем
К*Ч = |**?|- Iff <J*V,
гДе0 = Ш < 1- Но ряд
00
Ем«п
п=0
составлен из членов геометрической прогрессии со знаменателем д, где 0 ^ q < 1, и
00
значит, сходится. На основании признака сравнения ряд ]£ |с„хп| сходится в любой
■'-■■ ■•■ -; <> -' ■' п==о
точке ж, для которой |ж| < \х\\. Следовательно, степенной ряд £) СпХп абсолютно
сходится для |ж| <\х\\.
Пусть теперь степенной ряд
00
расходится при ж = ж2. Допустим, что этот ряд сходится для |ж| > \х2\. По
доказанному он должен сходиться и при х = жз, так как |ж21 < |ж|, что противоречит условию
расходимости ряда при х = ж2. ►
Теорема Абеля дает возможность установить характер области сходимости
степенного ряда
00
Е^п-
Пусть в точке х\ Ф О ряд сходится. Тогда ряд будет абсолютно сходиться в
интервале (-\х\ |, |ж! |). Если в некоторой точке ж2 (здесь |ж2| > |ж! |) ряд расходится, то
он будет расходиться и в бесконечных интервалах (-оо, -|ж2|) и (|ж2|, +оо). В этих
условиях на оси Ох существуют две точки (симметричные относительно начальной

42
Глава XIX, Степенные ряды
точки О), которые отделяют интервалы расходимости от интервала сходимости. Имеет
место следующая теорема.
Теорема 2. Пусть степенной ряд
]CnXn
п=0
сходится в точке х Ф 0. Тогда либо этот ряд абсолютно сходится в каждой точке
числовой прямой, либо существует число R > 0 такое, что ряд сходится абсолютно при
\х\ < R и расходится при \х\ > R.
Расходится [ -R ! Абс. сходится j # \ Расходится
hU—*—4- V • и >
-W -|х.| 0 |xf| fe|
Рис.1
Определение. Интервалом сходимости степенного ряда
00
п=0
называется интервал (-R, R), где Я > 0, такой, что в каждой точке х Е (~R}R)
ряд абсолютно сходится, а в точках ж таких, что \х\ > R, ряд расходится. Число R
называется радиусом сходимости степенного ряда.
Замечание. Что касается концов интервала сходимости (-Л, Л), то возможны следующие три случая:
1) степенной ряд сходится как в точке х = -Л, так и в точке х = Л, 2) степенной ряд расходится
в обеих точках, 3) степенной ряд сходится в одном конце интервала сходимости и расходится в другом.
Замечание. Степенной ряд
00
J2cn(x-x0)n,
n=0 v /
где хо Ф О, имеет тот же радиус сходимости, что и ряд
00
п=0
но его интервалом сходимости является интервал (xq — Л, хо 4- Л).
При условии существования конечного предела
lim ^~ =Ly 0<L< +oo,
n-+oo \Cn\
оо оо
радиус сходимости степенного ряда $^ с^х" (или ряда ^ £»»(# ~ жо)п, #o Ф 0) можно
п=0 п=0
найти по формуле
jR = lim
|Cn+l
(3)

§ 1. Теорема Абеля. Интервал и радиус сходимости стеленного ряда 43
Для доказательства формулы (3) рассмотрим ряд, составленный из абсолютных
величин членов данного ряда
00
Ы + \схх\ + |с2я2| + ... + \спхп\ + ...=£ \спхп\. (4)
п=0
Применяя к этому ряду признак Даламбера, находим
hm — -г- = hm —— = hm -—r\x\ = ж bm -—r = \x\L.
Отсюда следует, что ряд (4) будет сходиться, если \x\L < 1, и расходиться, если \x\L > 1,
т. е. степенной ряд сходится абсолютно для всех х таких, что \х\ < ^, и расходится
при \х\ > £. По определению радиуса сходимости получаем, что R = ^, т. е.
Л = j или R = hm
Радиус сходимости степенного ряда можно находить также по формуле
R= lim
n-°° l/W*
(5)
если существует конечный предел
lim \/jcJ = X, 0 < L < -boo.
n->oo
Формулу (5) легко получить, используя признак Коши.
Если степенной ряд
00
сходится только в точке х = 0, то говорят, что его радиус сходимости R = 0 (это
возможно, например, при lim %*Д = оо или lim \/\с^\ = оо).
П-+00 • п| П-КЭО
Если степенной ряд сходится во всех точках числовой оси, то полагают R = + оо
(это имеет место, например, при lim %^ = 0 или lim уЛс^\ = 0).
Областью сходимости степенного ряда
^2 Сп(х - Х0)П
п=0
может оказаться либо интервал (х0 - R, х0 + R), либо отрезок [х0 - R, xQ + R], либо
один из полуинтервалов (х0 - Д, х0 + R] или [ж0 - R,x0 + R). Если Д = -f оо, то
областью сходимости ряда будет вся числовая ось, т. е. интервал (-оо, + оо).
Для отыскания области сходимости степенного ряда
00
^2сп(х-Х0)П
п=0
нужно сначала вычислить его радиус сходимости R (например, по одной из
приведенных выше формул) и тем самым найти интервал сходимости (х0 - R1 x0 -f R),

44 „ м—__ Глава XIX, Стеоенные ряды
в котором рад абсолютно сходится*зате^-**: иоеледашат^сход^мость рада в донцах
интервала сходимости — в точках х = хо - R, х = х0 + R.
Пример 1. Найти область сходимости степенного ряда
00
£<-1Г'»х\ (6)
п=1
<4 1) Для нахождения радиуса сходимости R данного ряда удобно применить формулу (3). Так как
сп = (-1)п_1п и сп+\ = (-1)п(п + 1), то будем иметь
р .. \Сп\ .. |(-1)П-!п| П
R = lim г = lim ,. <Хп/ -гт = lim = 1.
»-*« |cn+i| n-»oo |(-l)n(fl + 1)| n-»oo n + 1
Ряд сходится абсолютно на интервале -1 < х < 1.
2) Исследуем сходимость ряда (6) в концах интервала сходимости. Положив х = -1, получим
числовой ряд
fx-0-y-D" = й-Г'. = Е(-п),
n=l n=l n=s?l
расходимость которого очевидна (не выполнен необходимый признак сходимости: lim (—п) / 0).
п—»оо
При х = 1 получим числовой ряд
для которого
lim(-l)n-,n
не существует, а значит, этот ряд расходится.
Итак, область сходимости ряда (6) есть интервал — 1 < х < 1. ►
Пример 2. Найти область сходимости ряда
e4^-(*+2)B- (7)
•4 1) Радиус сходимости находим по формуле (3). Имеем
(-о"-' . _ (-о-
сп — ~~ZZ » Сп+1
1ЫГ'
п2п > -»+i -(n+i)2«+iJ
И
л= Иш 1^; I = lim (n + yf+l = lim 2(1 + ^ =2.
|(п+"1)ГИ-Ч V '
Ряд (7) сходится абсолютно на интервале |ж + 2| < 2, или -2 < ж + 2 < 2, откуда -4 < х < 0.
2) При х = -4 получим числовой ряд
оо / i\n-l оо / |\2п-1 оо |
n=i n=i n=l
который расходится (гармонический ряд).
При х = О будем иметь числовой ряд
f (-о-1
сходящийся условно.
Таким образом, ряд (7) сходится в области -4 < х ^ 0. ►
Пример 3. Найти интервал сходимости ряда
А(-1)"(х-2)"

$2. Равномерная сходимость степенного ряда и непрерывность его суммы 45
4 Так как Сп = ^-, то для нахождения радиуса сходимости применим формулу (5):
R = lim пл—г = lim , = lim n = +оо.
*-°° VW п^°° п/|(-1)»| »->«>
V^
Это означает, что данный ряд сходится при всех значениях х, т.е. областью сходимости является
интервал (-оо, +оо). ►
Пример 4. Найти интервал сходимости ряда
$>!*", 0!=1. (8)
4 Так как Сп = п!, сп+\ = (п + 1)! = п\(п + 1), то получим
Л= lim r^7= lim "! ,. = lim -Ц-=0.
»-»°° |сЛ+11 »-»«> п! (П + 1) »-°° П + 1
Равенство R = О означает, что ряд (8) сходится только в точке х = 0, т. е. область сходимости данного
степенного ряда состоит из одной точки х = 0. ►
§2. Равномерная сходимость степенного ряда
и непрерывность его суммы
Теорема 1. Степенной ряд
Е
п=0
СпХП
сходится абсолютно и равномерно на любом отрезке [-а, а], а > 0, содержащемся в
интервале сходимости ряда (-R,R), R > 0.
4 Пусть 0 < а < R. Тогда для всех х, удовлетворяющих условию |ж| ^ а, и для
00
любого п = 0,1,2,... будем иметь \спХп\ ^ |с„ап|. Но так как числовой ряд X) |с„ап|
п=0
сходится, то по признаку Вейерштрасса данный степенной ряд сходится на отрезке
[-а, а] абсолютно и равномерно. ►
Теорема 2. Сумма степенного ряда
00
*(*) = £ «W*!1
непрерывна в каждой точке х его интервала сходимости (-R, R), R > 0.
^ Любую точку х из интервала сходимости (-Д, Д) можно заключить в некоторый
отрезок [-а, а], 0 < \х\ < а < R, на котором данный ряд сходится равномерно. Так
как члены ряда непрерывны, то его сумма S(x) будет непрерывной на отрезке [-а, а],
а значит, и в точке х. ►

46 Глава ХИС. Степенные ряды
§3. Интегрирование степенных рядов
Теорема 3 (о почленном интегрировании степенного ряда). Степенной ряд
00
п=0
можно интегрировать почленно в его интервале сходимости (-Л, R), R > 0, причем
радиус сходимости ряда, полученного почленным интегрированием, также равен R. В
частности, для любого х из интервала (-Д, R) справедлива формула
J/OO v 00
~ хп=0 ' п=0
xn+i.
<4 Любую точку х из интервала сходимости (-Д, R) можно заключить в некоторый
отрезок [-а, а], где 0 < \х\ < а < R. На этом отрезке данный ряд будет сходиться
равномерно, а так как члены ряда непрерывны, то его можно почленно интегрировать,
например, в пределах от 0 до х. Тогда, согласно теореме 4 главы XVIII,
^00 00 ^ 00 fi+1
JQ n=0 n=0 JQ n=0 "Г
Найдем радиус сходимости Д' полученного ряда
00 00
п=0 п=0
где
с„ = , п=1,2,... и Cq = 0,
п
при дополнительном условии существования конечного предела hm Д-^Ч = R. Име-
n-юо |Сп+н
ем
D, г |Cnl .. /п+1 \Сп-\\\ П+1 \Сп-\\ , „ „
jR = hm ——- = hm I ■—- J = hm lim ——— = 1 • it = it.
n->oo \Cn+l\ n-+oo\ П \Cn\ / n-*oo 71 n->oo |Cn|
Итак, радиус сходимости степенного ряда при интегрировании не меняется. ►
Замечание. Утверждение теоремы остается справедливым и при R = +оо.
§4. Дифференцирование степенных рядов
Теорема 4 (о почленном дифференцировании степенного ряда). Степенной ряд
00
п=0

§4, Дифференцирование степенных рядов 47
можно дифференцировать почленно в любой точке х его интервала сходимости (-R, R),
R > О, при этом выполняется равенство
00 00
$'(*) = (£<v*n) = Еис**п~
п=0
<4 Пусть R — радиус сходимости ряда
!>*", о)
п=0
а Л' — радиус сходимости ряда
00
п=0
Предположим, что существует (конечный или бесконечный) предел
n-oo Ic+il
Найдем радиус R1 ряда
где
Имеем
c4 = (n-hl)c^+i.
# = hm 7-1—г = hm I И • г = 1 • R = R.
Тем самым, радиусы сходимости рядов (1) и (2) равны. Обозначим сумму ряда (2)
через <г(х):
а(х) = ]С пСпхП
п=\
Ряды (1) и (2) равномерно сходятся на любом отрезке [-а, а], где 0 < а < R. При
этом все члены ряда (2) непрерывны и являются производными соответствующих
членов ряда (1). Поэтому, согласно теореме 5 главы XVIII, на отрезке [-а, а] выполняется
равенство а(х) = S'(x). В силу произвольности а последнее равенство выполнено и
на интервале (-Д, R). ►
Следствие. Степенной ряд
00
п=0
можно почленно дифференцировать сколько угодно раз в любой точке х его интервала
сходимости (-Л, R), причем радиусы сходимости всех получаемых рядов будут равны R.

48 Глава XIX. Степенные ряды l
§5. Ряд Тейлора
00
Определение. Будем говорить, что функция f(x) разлагается в степенной ряд £) Спя"
п=0
на интервале (-JR, R), если на этом интервале указанный ряд сходится и его сумма
равна/(ж):
00
f(x) = Y,CnXn, xe(-R,R). (1)
n=0
Докажем сначала, что функция f(x) не может иметь двух различных разложений
в степенной ряд вида (1).
Теорема 5. Если функция f(x) на интервале (--R, R) разлагается в степенной ряд (1), то
это разложение единственно, т. е. коэффициенты ряда (1) по его сумме определяются
однозначно.
< Пусть функция f(x) в интервале (-Я, R) разложена в сходящийся степенной ряд
f(x) = Co + С\Х + С2Х2 + . . . + СпХП + . . . .
Дифференцируя этот ряд почленно п раз, найдем
/(n)(s) = l-2-3-... -(n-l)fMV,+2-3-... •(n-l)n(n+l)ivl+1e + ... .
При х — О получаем
/(П)(0)=Ь23.... (п-1)псп,
или
/(п)(0)=п»сп, п = 0,1,2,... ,
откуда
/М(0)
Сп =
п\
(2)
(здась/<°)(0) = /(0),0! = 1).
Таким образом, коэффициенты с„ (п = 0,1, 2,...) степенного ряда (1)
формулой (2) определяются однозначно. ►
Замечание. Если функция f(x) разложена в степенной ряд по степеням разности х-хо,
00
/(*) = £ сп(х - *о)п, х € (х0 - Я, xQ + Я),
п=0
то коэффициенты сп этого ряда определяются формулами
сп :
:^, П = 0,1,2,... (/0>Ы = /Ы).
(3)
Пусть функция f(x) при ж = Хо имеет производные всех порядков /'(a?o), /"(жо)>
... , /^(хо),... , т. е. является бесконечно дифференцируемой в точке жо- Составим
для этой функции формальный степенной ряд
00
]Г Сп(х - Ж0)П,
п=0
вычислив его коэффициенты по формуле (3).

§5. Ряд Тейлора 49
Определение. Рядом Тейлора функции f(x) относительно точки х0 называется степенной
ряд вида
/Ы + /'Ы(* - хо) + Ц^(х - х0)2 + ^р*-(х - х0)3 + ... +
, /(П)Ы {Т -, _ f> /(П)Ы . ,п
(здесь 0! = 1, f^(xo) = /fao)). Коэффициенты этого ряда
со = /(я0), с, = -ур-, с2 = 2| , ... , Сп = —~—, • •.
называются коэффициентами Тейлора функции f(x).
При хо = 0 ряд Тейлора
/(0) + /(0)* + —* + ... + -^j-* + ••• =2^—^Г"ж
называют рядом Маклорена.
Из теоремы 5 вытекает следующее утверждение.
Теорема в. Если на интервале (хо - R, xQ + R), R > 0, функция f(x) разлагается в
степенной ряд
00
]Г Сп(х ~ Ж0)П,
п=0
то этот ряд является рядом Тейлора функции f(x).
Пример 1. Рассмотрим функцию
f(x) = { е-1/*2 Для х Ф О,
I 0 для ж = О,
и найдем ее производные.
< Для ж ^ 0 эта функция имеет производные всех порядков, которые находятся по обычным Правилам
и, вообще,
/*\x)=P3n(iy-i,x2 (n='l,2,...),
где -Рзп(^) — многочлен степени Зп относительно £.
Покажем теперь, что в точке ж = 0 данная функция также имеет производные любого порядка,
причем все они равны нулю. Исходя из определения производной, имеем
/(o)=UmmiiM=UmM=Umf^=Um4T=um4z4=u«^-,/i2=o
а-»0 X х-*0 X *-»0 X ж-»0 е1/* г-»0 _4_ е1/г2 *-»0 2
*3
(при вычислении предела мы применили правило Лопиталя). Аналогичным образом можно доказать,
что
/"(0) = /'"(0) = ... = /<п)(0) = ... = 0.

50 Глава XIX. Степенные рады
Тем самым, заданная функция имеет на числовой оси производные врех порядков,
Построим формальный ряд Тейлора исходной функции относительно точки хо = 0. Имеем
0 + 0-s + 0-s2 + ... +0-sn + ... .
Очевидно, что сумма S(x) этого ряда тождественно равна нулю, в то время как сама функция f(x)
тождественно равной нулю не является. ►
Про этот пример стоит вспомнить при обсуждении комплексного анализа
(аналитичности): функция, внешне совершенно благопристойная, проявляет на
действительной оси капризный характер, являющийся следствием неприятностей на мнимой
оси.
Формально построенный в примере для заданной бесконечно дифференцируемой
функции ряд сходится, но его сумма не совпадает со значениями этой функции при
х Ф 0. В связи с этом возникает естественный вопрос: каким условиям должна
удовлетворять функция f(x) на интервале (xq - Л, xq + R), чтобы ее можно было
разложить в сходящийся к ней ряд Тейлора?
Условия разложимости функции в ряд Тейлора
Для простоты будем рассматривать степенной ряд вида
т. е. ряд Маклорена.
Теорема 7. Для того чтобы функцию f(x) можно было разложить в степенной ряд
00
на интервале (-#, R), необходимо и достаточно, чтобы на этом интервале функция f(x)
имела производные всех порядков и чтобы в ее формуле Тейлора
/(*) = /(0) + /'(0)* + ^ а;2 +... + ^- хп + *.(*) (1)
остаточный член Rn(x) стремился к нулю при п —> оо для всех х Е (--R, R).
< Необходимость. Пусть на интервале (-R,R), R > 0, функция f(x) разложима в
степенной ряд
00
Е**". (2)
п=0
т. е. ряд (2) сходится и его сумма равна f(x). Тогда по теореме 4 и следствию из нее
функция f(x) имеет на интервале (-Д, R) производные f^(x) всех порядков. По
теореме 5 (формула (2)) коэффициенты ряда (2) имеют вид
т. е. мы можем написать равенство
/(*) = /(0) + /'(0)х + ^*2 + ...+^а:п + .... (3)

§5. Ряд Тейлора —^_j 51
В силу сходимости этого ряда на интервале (-Л, R) его ocrafbK
к=п+\
к
стремится к нулю при п -* оо для всех х € (-Л, R).
Достаточность. Пусть функция f(x) на интервале (-Я, R) имеет производные всех
порядков и в ее формуле Тейлора остаточный член Rn(x) —► 0 при и —► оо для любого
х £ (-Д, Д). Поскольку
*,(*) = /(*) - [/(0) + /(0)* + ^х2 + ... + ^*я],
ТО
/"(°Ь, , /(п)(о)_п1
/(х) - [/(0) + /'(0) х + Ш** + _ + £_У ^ j = |Д,(«)|-^ 0 (4)
при п —^ оо. Поскольку в квадратных скобках записана n-я частичная сумма ряда
Тейлора, то формула (4) означает, что ряд Тейлора функции f(x) сходится на интервале
(-Д, R) и его суммой является функция f(x). ►
Достаточные условия разложимости функции в степенной ряд, удобные для
практического применения, описываются следующей теоремой.
Теорема 8. Для того, чтобы функцию f(x) на интервале (-Д, R) можно было разложить
в степенной ряд
00
достаточно, чтобы функция f(x) имела на этом интервале производные всех порядков и
чтобы существовала постоянная М > 0 такая, что
l/(n)(x)| *S M
для всех п = 0,1, 2,... и для всех х € (-Д, R).
Ч Пусть функция f(x) имеет на интервале (-Д, R) производные всех порядков. Тогда
для нее можно формально написать ряд Тейлора
f:^x- («=1,/«<о)=/<о)).
п=0
Докажем, что он сходится к функции /(ж). Для этого достаточно показать, что
остаточный член
в формуле Тейлора (1) стремится к нулю при п -* оо для всех х € (-R, R). В самом
деле, учитывая, что -R< х < R и |/(п+1)(<?а;)1 < М (Ох 6 (-R, R)), будем иметь
л<|пуги -|/("+1)(0*)гп+1| 1/(п+1)(0*)|-|*Г' ,мд"+1
°^|л»(ж)|-|-0Гй)Гх Г (^ТТ)! <КП)! (5)

52 : - Глш XIX. Стиинме рады
для п = О,1,... и для всех х € (-R, R). Числовой ряд
сходится в силу признака Даламбера:
MRn+2
п->оо МД"+* n-оо П + 2
ют
Поэтому
мдп+1 л
lim 7 7Т7 = °
n-оо (П + 1)!
в силу необходимого признака сходимости. Из неравенства (3) получаем
lim Rn(x) = О
для всех х € (-Д, Л). ►
[отя функция
янной М, or
<р(п) = тах|/(л)(а?)| -+ оо
Продолжение примера 1. Хотя функция из примера 1 и имеет на числовой оси производные всех
порядков, универсальной постоянной М, ограничивающей их абсолютные величины, не существует,
при п -* оо.
§6. Ряды Тейлора элементарных функций
Рассмотрим разложения в ряд
п=0
основных элементарных функций.
6.1. f(x) = ех
Эта функция имеет производные всех порядков на интервале (-а, а), где а > 0 —
любое число, причем
|/w(*)| = ех < е\ « = 0,1,2,....
Следовательно, показательная функция ех разлагается в ряд Тейлора на любом
интервале (-а, а) и, тем самым, на всей оси Ох, Так как /^(0) = е° = 1 (п = 0,1,2,...),
то получаем ряд
х2 хп А хп
е* = \+х + — + ...+ — + ..- =У,-т
2! n! *—f n!
п=0
(О
Радиус сходимости этого ряда R = +оо.

д|6. Рады Тейлора амммтярных функций.
.53
Если в разложении (1) заменить х иа -ж, то будем иметь
х2 х3
е-* = 1-* + ^ + ...+(-1)^ + ...=£И>П^Г
п=0
О')
6.2. fix) = sin x
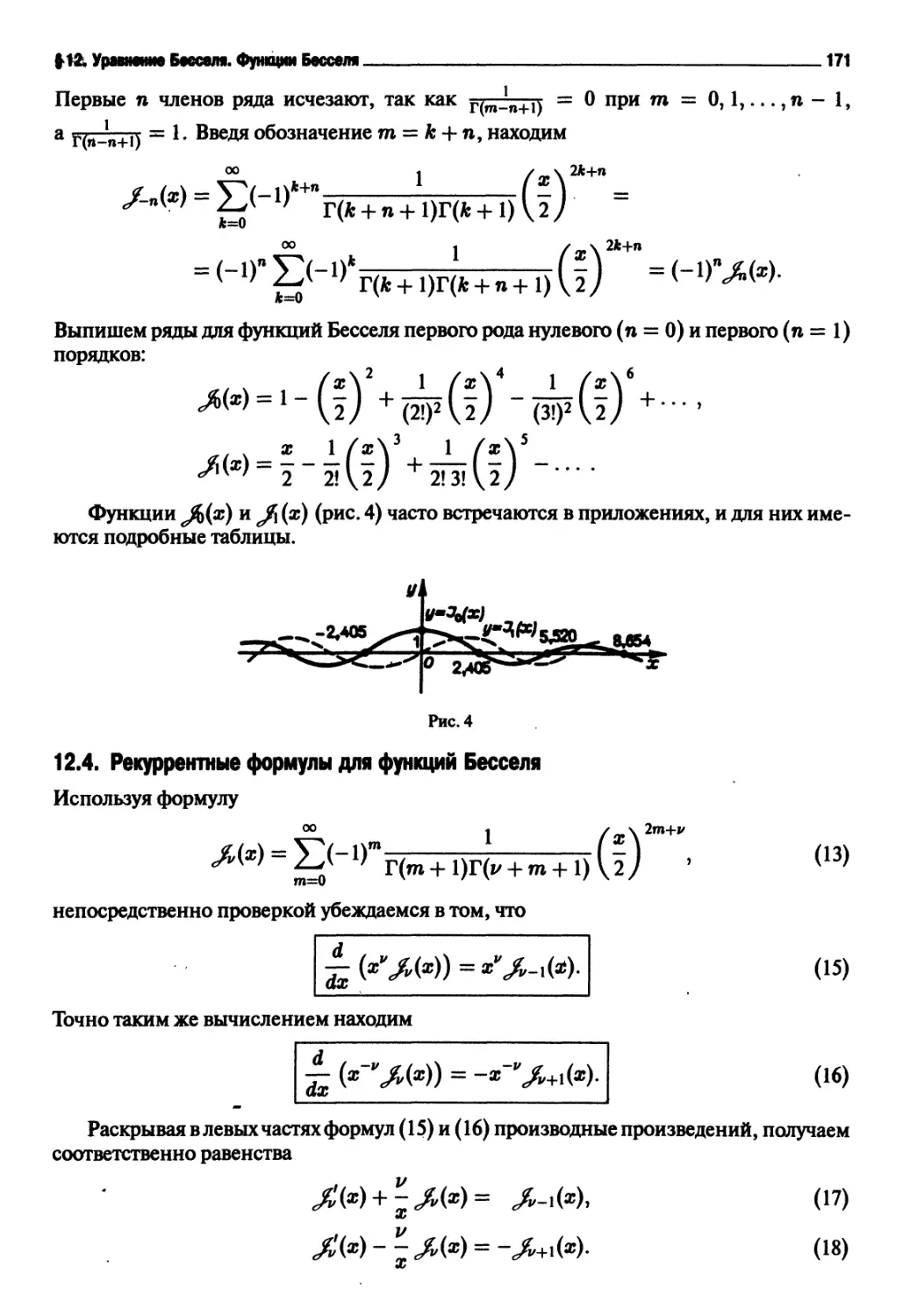
Данная функция имеет производные любого порядка, причем
|(sina)(n)|= sin(a + n|) ^ 1
для п = 0,1,2,... и ж € (-оо, Н-оо). Тем самым, по теореме 8 функция sin ж
разлагается в сходящийся к ней на интервале (-оо, +оо) ряд Тейлора. Так как
,<п)/лч . птг /0 дляга = 0,2,4,... ,
дляп = 1,3,5,.
то этот ряд имеет следующий вид
-2п+1
S1II X — X -
хъ х5 х2*+{ JZ* т2п+
1)!'
(2)
Радиус сходимости ряда R *= -f оо.
6.3. fix) = cos х
Аналогично получаем, что
х2 хА х2п J^ х2п
(3)
6.4. fix) = (1 + х)а, где х > —1, а — любое действительное число
Эта функция удовлетворяет соотношению
(1+*)/'(*) = «/(*) (4)
и условию /(0) = 1.
Будем искать степенной ряд, сумма которого S(x) удовлетворяет соотношению (4)
и условию 5(0) = 1. Положим
S(x) = 1 + схх + с2х2 + с3ж3 +... + с„жп + ... .
Отсюда находим
S'(х) = с, + 2с2ж + Зс3ж2 + ... 4- пСпХп'х + ... .
Подставляя соотношения (5) и (6) в формулу (4), будем иметь
(1 + ж)(с, + 2с2ж + Зс3ж2 +... + пспхп~х + ...) =
= а(1 + С1Ж + с2ж2 + с3ж3 + ... +<*,&" + ...)>
(5)
(6)
или
с, + (с, + 2с2)ж + (2с2 + Зс3)ж2 + ... + [псп + (га + 1)с„+1]жп + ... =
= а + ас\х + ас2х + ... + аСпХп + ... .

54 Глава XIX. Степенные ряды
Приравнивая коэффициенты при одинаковых степенях х в левой и правой частях
равенства, получим 1
с, =<*,
с\ + 2с2 = ас\,
2с2 + Зс3 = ас2,
(n-l)cn_,+ncn = Qfcn_,,
откуда находим
с, =а,
а(а-1)
с2 =
с3 =
Сп =
2! '
а(а - 1)(а - 2)
3!
>
а(а - 1)(а - 2)... (а - п + 1)
(7)
п!
Подставляя эти значения коэффициентов в соотношение (5), получим ряд
5(a;) = l + «a; + ^li)x4a(a-^a-2)x4...+
, а(а-1)(а-2)...(а-п+1) _„ ,
"I : х -f- .. . .
n!
Найдем радиус сходимости ряда (7) в случае, когда а не является натуральным
числом. Имеем
n-»oo
JC+,1 n-«i ja(a-l)...(a-n-fl)(a-n)j n—oo |cr — n| n->oo|£-l|
Итак, ряд (7) сходится при |ж| < 1, т. е. на интервале (-1,1).
Докажем, что сумма S(x) ряда (7) на интервале (-1,1) равна (1 + х)а. Для этого
рассмотрим отношение
цЫ _5(*)_ g(»)
Так как 5(a) удовлетворяет соотношению (4), т. е.
S'(x) = j^-S(x),
1 + X
то для производной функции tp(x) получаем:
S'(x)f(x) - f'(x)S(x) (1 + x)aS'(x) - a(l + x)e-'S(x) _
(/(x))2 (1+xp
(l + x)5'(x)-a5(x) (1 + x^Sfx) - aS(x) 0
(1 + x)«+' (1 + x)«+1 (1 + x)e+'

§6. Ряды Тейлора элементарных функций.
.55
для х £ (-1,1). Отсюда следует, что
(р(х) = С = const
на (-1,1). В частности, при х = 0 имеем
с-*»-*!».,.
и значит, fgi = у,(ж) = 1, т. е.
5(х) = (! + *)-,
или
/,, л« ....... <»(«-!) _2 , . а(а-1)...(а-я+1)_. ,
(1 + х) = 1 + ах н — х +... Н — = х +... ,
2!
п!
(8)
где -1 < х < 1.
Полученный ряд называется биномиальным, а его коэффициенты — биномиальными
коэффициентами.
Замечание. В случае, если а — натуральное число (а = п), функция (1 + х)а будет многочленом п-й
степени, и Rn(x) = 0 для всех п> а.
Отметим еще два разложения. При а = -1 будем иметь
1 7 з
= 1-ж + ж -ж^ + ... , -1<ж< 1.
1+ж
Заменив ж на -ж в последнем равенстве, получим
1 о з
= 1 + ж + ж^ + ж^ + ... , -1<ж< 1.
1 -ж
(9)
(10)
6.5. fix) = ln(l + х), х > -1
- получения разложения этой функции в ряд Тейлора по степеням х проинтегрируем
t ...енство (9) в пределах от 0 до х, где х € (-1,1). Имеем
/ш=/<1-'+'!-,!+->"1-
или
ряд
, *2 *3 а;4 (-1)п-'хп
1„(1 + х) = х-т + т-т + ...+—— + ....|
) справедливо в интервале -1 < ж < 1. Заменяя в нем ж на
_,2 3 _,4 _,п
Hi-)—- T-T-T---T-"
(11)
(12)
где -1 < ж < 1.
Можно доказать, что равенство (11) справедливо и для ж = 1:

56.
. Глава XIX. Стеленные ряды
Таблица разложений в степенной ряд (ряд Маклорена) основных элементарных функций.
аг х"
ех = \ + х + — + ... + — + ...,
2! га!
хъ Xs
„2п+1
81пЖ=Ж-3! + 5!--+(-1)П(2^Т)!
+ ...,
х2 х4
-2п
„.,= ,__ + __...+<_!)■_ + ...,
2!
3!
, a(g-l)(g-2)...(«-«+!)_„ ,
п ; я> ■+■•••)
n!
1+х
= 1-х+х"-агЧ...+(-1) "ж" + ...,
х2 х3
щ(1+х) = х- - + --...+(-!)"- - + ...,
2 3 га
-оо < х < -hop;
-оо<ж<+оо;
-оо<ж<+оо;
-1<я<1;
-1 <ж< 1;
Пользуясь этой таблицей, можно получать разложения в степенной ряд более
сложных функций. Покажем на примерах, как это делается.
Пример 1. Разложить функцию
1
4-ж
в степенной ряд в окрестности точки жо = 2, т. е. по степеням разности х — 2.
<4 Преобразуем данную функцию так, чтобы можно было использовать ряд (10) для функции ^ •
Имеем ,
1 _ 1 1 ""! 1 Т ; :' • ' ' J
4-х"-4~((х~2) + 2)'"2-(х~2)33'2 1-(^)'
Заменяя в формуле (10) х на —-, получим
1 1
4-ж 2
1 +
ж-2 /ж-2\2 /ж-2\3
или
1 1 ж-2 (ж-2)2 (ж-2)3
= ~ +
4-ж 2 22 23 24
Это разложение справедливо, когда выполнено любое из эквивалентных неравенств
|ж-1|
< 1, |ж-1|<2, -2<ж-2<2, 0<ж<4. ►
Пример 2. Разложить по степеням х функцию
ж2-Зж + 2'
используя формулу (10).
<4 Разлагая знаменатель на множители, представим данную рациональную функцию в виде разности
двух простейших дробей. Имеем
1 _ 1 _ 1 1_
х2 - Зж + 2 ~ (х - 1) (ж - 2) ~ х - 2 ж - 1'

(6. Ряды Тейлора элементарных функций_
.57
После простых преобразований получим
1
1
1 1
(13)
1 < -•< ; " <*■**-3* +2 1-я 2 1-(§)'
К каждому слагаемому в правой части равенства (13) применяем формулу (10), в результате чего
получим стеленные ряды
1 7 1
= 1+ж + ж2 + ж3 + ... , (14)
1 — х
, 3
,_• -■ , ■ i,i ■ i,i +•• О5)
V'+HfNi)3
Ряд (14) сходится для |ж| < 1, а ряд (15) сходится для U < 1, т.е. \х\ < 2. Оба ряда (14) и (15) будут
сходиться одновременно для |х| < 1. Так как в интервале (-1,1) ряды (14) и (15) сходятся, то их можно
почленно вычитать. В результате мы получим искомый степенной ряд
j jг ~ /~\2 /_\3
g»-te + 2as(1 + S + *a + g3 + -)"2 ! +
И)Ч)'--1
0п+\
2+ 22
•*+■
- аГ + ... + •
■ «-+...,
23 "' '' •"• r 2n+1
радиус сходимости которого равен R = 1. Этот ряд сходится абсолютно для |х| < 1. »>
)3. Разложить в ряд Тейлора в окрестности точки xq = 0 функцию arcsinx.
4 Известно, что
(arcsinx)' = -^J^ = (i + (-х2))",/2. •
Применим к функции (l + (-ж2)) формулу (8), заменяя в ней а; на -ж2. В результате для | -х2\ =
ж2 < 1, т. е. для -1 < х < 1, получаем
1 2 -2-Й"1) 4 -К-5-0Н-2) 6
(arcsinO, = l + ^2 + -2i~ Уж4_ 2V 2 ^Л 2 Ужб+ =
1 2 13 4 ЬЗ-5 6
~ 2 * "*" 2! 22 * + 3! 23 Х * "" '
Интефируя обе части последнего равенства от нуля до х (почленное интефирование законно, так как
степенной ряд равномерно сходится на любом отрезке с концами в точках 0 и х, лежащем в интервале
(-1,1)), найдем
/(arcsinx)'d< = /(l + y + ^<4-^<6 + ...)^
I» \х 1 *3 Г 1-з <*
arcsin<|o=<|o + -T|o + ^2T
1-3-5 V
3' 23 7
0 J'z ' lo
Тем самым, окончательно получаем, что
1
1-3
arcsin х = х + —- ж + ^т^
2-3 2! 23 • 5
аг +
1-3-5
3!23-7
*'+...,
где -1<ж<1 (Д = 1). ►
Разложение в степенные ряды можно использовать для вычисления интегралов, не
выражающихся в конечном виде через элементарные функции.
Приведем несколько примеров.
Пример 4. Вычислить интеграл (интегральный синус)
Si
ix = /
sin*
dL

58
Глава XIX. Степенные ряды
Ч Известно, что первообразная для функции ^ не выражается через элементарные функции.
Разложим подынтегральную функцию в степенной ряд, пользуясь тем, что
t3 t5 t1
sin* = *__ + ___ + .... (16)
Из равенства (16) находим
sin*
tl f t*
:1-<й+5!-7!+'
(17)
Заметим, что деление ряда (16) на t при t Ф О законно. Равенство (17) сохраняется и при t = О,
если считать, что при t = О отношение 2~ = 1. Тем самым, ряд (17) сходится при всех значениях t
{R == +оо), Интегрируя его почленно, получим
Six
fsmt м
3! 3 + 5! 5 7! 7 + *
Полученный ряд — знакочередующийся, так что погрешность при замене его суммы частичной суммой
оценивается просто. ►
Пример 5. Вычислить интеграл
/.-<*
< Здесь первообразная для подынтегральной функции е г также не является элементарной функцией.
Для вычисления интеграла заменим в формуле
х2 хг
е* = 1+*+~ + ¥ + ...
х на —г. Получим
Проинтегрируем обе части этого равенства в пределах от 0 до х:
-*2 2 t4 t6
6 =1-<+2Гз!+"
0
* t5
* t7
3'-7
X3 X5 X7
0+-=*-Т + 2!75-ЗЬ7+"Ч
Этот ряд сходится при любых $ (его радиус сходимости R = +оо) и является знакочередующимся
при х > 0. ►
Упражнения
Найдите область сходимости степенных рядов:
00 И 00 ^П
i-E-V- 2-Е-^-т*"-
4. £>V.
'о-Е
rt П2+1
^Ш(1+п)-
11. £^(.-2)-.
п=0
5»
б.Е^х,
11=0
п+1

§в. Риды Тейлора элементарных функций 59
Разложите следующие функции в ряд Маклорена и укажите области сходимости полученных
рядов:
13. —i—. 14. -^-. 15. shx. 16. спя.
2 + Ъх х-\
17. v^l+x3. 18. * . 19. arctgs. 20. hi(x + \/1 + аЛ
V 8 4- х v '
21. ах, 0<а^1. 22. sinf ж "" т)- 23- cosfox - j J. 24. sin2 я.
Указание. Воспользуйтесь таблицей.
Пользуясь таблицей, разложите заданные функции в ряд Тейлора по степеням х - х0 и
укажите интервалы сходимости полученных рядов.
1 1 ж +1
25.-, ж0 = -3. 26-Т-ГТ> ж° = 1. ^ 7» *о = -1.
х
2х + 3' *0-1- х-Г
«С Ч~ 1 7Г 7Г
28. -, х0 = !• 29. sin», «о = г- 30. cos ж, жо=х-
х + 2 2 2
31. 1п(3х - 2), «о = 2. 32. 1п(2х - 1), х0 = 1. 33. е"', х0 = -1.
34. Vx + 1, х0 = 1.
Ответы
1. -2 < х < 2. 2. -i < х < ±. 3. -1 < х < 1. 4. х = 0. 5. -1 < х < 1. 6. -1 < х < 1.
7. -3 < х ^ -1. 8. -6 < х < 0. 9. -е-1 - К х < е-1 - 1. 10. -К х < 3.11. х = 2. 12. х = 1.
13.±-£х+£х2-..., -|<х<|.14.-х-х2-х3...,-1<х<1. M.»+si + sf+...,
-оо < х < +оо. 16.1 + *[ + *£+..., -оо < * < +оо. 17.1 + ± х3 - ^ х6 +±$ х9 -..., -1<
х < 1. 18. i x-jij х2+5гз^5 х3 + з^ х4+...,-К х < 1. 19. х-^ + ^-^,-1 < х < 1.
20.х-^ + ^х5-...+(-1Г5^^х2»+Ч...,-1<х^1.21.1 + |1^х»,-оо<
х < +оо. 22.3fi(-i+«+£-ff-$f+...), -оо < х < +оо. 23. ^(l+2x-f *2-| х3-Ц х4+
£x5-...),-oo<x<+oo.24.|x2-£x4+f x6-...+(-l)^gf*2n+...,-oo<x<+oo.
25.-i[l + ^ + ^i + ^ + ...])-6<x<0.26.i-H*-0 + ^(*-l)2-^(*-03+...)
-§<«<!• 27. -*±!-^-^-...,-3<х< 1. 28. | + ^1-^ + 1*^+...,
-2 < х < 4. 29.1~V 2! + 41 ~ 6! '~°° < * < +00- 30.-(х-|)+^ 3,2' -
(*5Г +• • •' -°° < * < +0°- 31-21п2+! (»-2)-дг (*-2)2+^т (х-2)3-..., | < х < f.
32.2(x-l)-2^ + %^-...,-i<*<5-33.e[l-(x+l) + ^-^ + ...],
-оо < х < +00. 34. v^[l + *£■ - ^ (х - I)2 + $ (х - I)3 - ... ], -К х < 3.

Глава XX. н ,,,_ L ^ , ,_ih
РЯДЫ ФУРЬЕ
§1. Тригонометрические ряды
Определение. Функция /(ж), определенная на неограниченном множестве D,
называется периодической, если существует число Т ФО такое, что дая каждого х £ D
выполняется условие
/(ж±Т) = /(ж), где ж±ГЕ1).
Наименьшее из таких чисел Т называется периодом функции /(ж).
> 1. Функция
/(х) = sin х,
определенная на интервале (-оо, +оо), является периодической, так как существует число Т = 2*г Ф О
такое, что для всех х £ (-оо, +оо) выполняется условие
sin(x + 2ir) = sin ж, х + 2ir G (-00, -f 00).
Таким образом, функция sin х имеет период Т = 2*.
То же самое относится и к функции
f(x) = cos ж.
Пример 2. Функция
/(ar) = tgx,
определенная на множестве D чисел
**£ + пж (n = 0,±i,±2,...),
является периодической, так как существует число Т Ф 0, а именно, Г = 7г, такое, что для х € D
имеем tg(x + я-) = tgж, где а: + я* € jD.
Определение. Функциональный ряд вида
— + a\ cos х + bi sin ж + аз cos 2ж + b2 sin 2ж + ... +
00
+ an cos nx + bn sin гаж +... = — + У^(«п cos гаж + bn sin гаж) (1)
называется тригонометрическим рядом, а постоянные ao, On, 6n (n = 1,2,...)
называются коэффициентами тригонометрического ряда (1).
Частичные суммы 5п(ж) тригонометрического ряда (1) являются линейными
комбинациями функций из системы функций
1, cos ж, sin ж, соз2ж, sin2z, ... ,

§ 2. Ортогональность тригонометрической системы
61
которая называется тригонометрической системой. Так как членами этого ряда
являются периодические функции с периодом 2тг, то в случае сходимости ряда (1) его
сумма S(x) будет периодической функцией с периодом Т — 2ir:
I S(x + 2*) =5 S(x), х € (-оо, +оо). I
Определение. Разложить периодическую функцию f(x) с периодом Т = 2ir в
тригонометрический ряд (1) означает найти сходящийся тригонометрический ряд, сумма
которого равна функции f(x).
§2. Ортогональность тригонометрической системы
Определение. Функции f(x) и д(х), непрерывные на отрезке [а, Ь], называются
ортогональными на этом отрезке, если выполнено условие
ь
] f(x)g(x)dx = 0.
а
Например, функции f(x) = х и д(х) = х ортогональны на отрезке [-1,1], так как
1 1
/ х • x2dx = I x3dx = 0.
Определение. Конечная или бесконечная система функций
pi(s), Ы*)> • • • , ¥>*»(*), ♦ • • , где tpn(x) £ О
(п = 1,2,...), интегрируемых на отрезке [a, ft], называется ортогональной системой
на отрезке [a, ft], если для любых номеров тип таких, что т Ф п, выполняется
равенство
ь
I <Рт{х)ч>п{х) dx = 0.
а
Теореме 1. Тригонометрическая система
1, cos a:, sing, cos2x, sin 2s, ... , cosnx, sinnx, ...
ортогональна на отрезке [-7Г, ж].

62.
Глава XX. Ряды
< При любом целом п Ф О имеем
sin nx
I
1 • cos nx dx =
п
■=о, /
1 • sin nx dx = -
cos па?
= 0.
-tf -1Г
С помощью известных формул тригонометрии
cos(a - в) + cos(a + в) Л cos(a - в) - cos(a + 0)
cosacos/? = — Ц- —, sinasin/? = —
2 2
для любых натуральных тип9тфп, находим:
ж ж
I cos mx cos nx dx = - / [cos(ra - п)ж + cos(ra + n)x] dx =
= o,
sin(m - n)x
rn-n
sin(m -f n)x I
ra + n
-к -к
I sin ш sin nx dx = - / [cos(ra - n)x - cos(ra + n)x] dx =
-H
1 fsin(ra - n)x
га -п
sin(ra -h n)x
га
' + Ф\Ж 1 =0
+ * |_J
Наконец, в силу формулы
sin a cos /3 =
для любых целых тип получаем
sin(a - /3) + sin(a + /3)
ж ж
I sin mx cos nx dx = - / [sin(ra - п)х + sin(ra + n)x] dx =
1 Г cos(ra - n)x
га-п
cos(m + п)х
m + n
= 0.
При т = п имеем
ж
I
sin nx cos nx dx
/ cos nxdx = /
-яг -*
/ sin2 nxdx = I
—ж
ж
•I
cos 2nx 1
dx = -
2 2
* sin 2nx "
* 2n
J-
1 - cos 2nx
dx = 7Г,
sin 2nx cos 2nx
—-— dx = -
2n
= <).►

§3, Тригонометрический ряд Фурье „ 63
§3. Тригонометрический ряд Фурье
Поставим себе задачей вычислить коэффициенты ао, а„, Ьп (п = 1,2,... )
тригонометрического ряда (1), зная функцию f(x).
Теорема 2. Пусть равенство
f(x) = -у + Х^а" cos ЛЖ + &n sin nx) 0)
2 п=1
имеет место для всех значений х, причем ряд в правой части равенства сходится
равномерно на отрезке [~тг, тт]. Тогда справедливы формулы
ж
ап = — / /(ж) cos nxdx (n = 0,1,2,...),
ж
Ьп = — / /(ж) sin nx dx (п = 1,2,...).
(2)
Ч Из равномерной сходимости ряда (1) вытекает непрерывность, а значит, и
интегрируемость функции /(ж). Поэтому равенства (2) имеют смысл. Более того, ряд (1)
можно почленно интегрировать. Имеем
/ f(x) dx= — I dx + ^2 I an I cos nx dx + bn I sin nx dx J,
-ж -ж n=1 ^ -ж -ж '
-ж
или
ж
I f(x) dx = oo^r,
откуда и следует первая из формул (2) для п = 0.
Умножим теперь обе части равенства (1) на функцию cos mx, где т —
произвольное натуральное число:
00
f(x) cos mx = -— cos mx + jT^ (a„ cos mx cos nx + 6n cos mx sin пж). (3)
2
n=l
Ряд (З), как и ряд (1), сходится равномерно. Поэтому его можно интегрировать
почленно,
ж ж
I f(x) cos mx dx = — /cos mx dx +
-Ж ~* 00 / * * \
+ ^ I an I cos mx cos nx dx + bn I cos mx sin nxdx\.
n=1 ^ -* -* '

64.
. Глава XX. Ряды Фурье
Все интегралы в правой части, кроме одного, который получается при п = т, равны
нулю в силу ортогональности тригонометрической системы. Поэтому
ж ж
I f(x) cos mx dx = ат I <
I cos mx dx = am I cos mx dx = атжу
-ж
откуда
<hn
ж
cosmxdx, m = 1,2,...
Аналогично, умножая обе части равенства (1) на sinmx и интегрируя от -ж до ж,
получим
ж ж
I f(x) sin mx dx = Ьт I sin2 mx dx = Ьтжу
откуда
ж
= i//(x)si
sin mar dx, m = 1,2,... . ►
Пусть дана произвольная периодическая функция /(ж) периода 2тг, интегрируемая
на отрезке [-тг, ж]. Можно ли ее представить в виде суммы некоторого
сходящегося тригонометрического ряда, заранее неизвестно. Однако по формулам (2) можно
вычислить постоянные ап и Ьп.
Определение. Тригонометрический ряд
во
+ ^(вп cos nx + &n sin пж),
п=1
коэффициенты ао,ап, Ьп которого определяются через функцию f(x) по формулам
ж
ап = — I /(ж) cos nx dx, n = 0,1,2,... ,
-ж
ж
bn = — I f(x) sin nx dx, n = 1,2,... ,
называется тригонометрическим рядам Фурье функции /(ж), а коэффициенты о„, Ь„,
определяемые по этим формулам, называются коэффициентами Фурье функции f(x).
Каждой интегрируемой на отрезке [-тг, ж] функции f(x) можно поставить в
соответствие ее ряд Фурье
ои
f(x) ~ — + 5^(лп cos nx + Ьп sin пж),
п=\

§4. Достаточные условия разложимости функции в ряд Фурье
65
т.е. тригонометрический ряд, коэффициенты которого определяются по
формулам (2). Однако если от функции f(x) не требовать ничего, кроме интегрируемости
на отрезке [-тг, тг], то знак соответствия в последнем соотношении, вообще говоря,
нельзя заменить знаком равенства.
Замечание. Часто требуется разложить в тригонометрический ряд функцию f(x), определенную толькб
на отрезке [—л-, л-] и, следовательно, не являющуюся периодической. Так как в формулах (2) для
коэффициентов Фурье интегралы вычисляются по отрезку [—л-, л-], то для такой функции тоже можно
написать тригонометрический ряд Фурье. Вместе с тем, если продолжить функцию f(x) периодически
на всю ось Ох, то получим функцию F(x), периодическую с периодом 2л-, совпадающую с f(x) на
интервале (—л-, л-):
F(*) = /(*)V* €(-*,*).
Эту функцию F(x) называют периодическим продолжением функции f(x). При этом функция F(x) не
имеет однозначного определения в точках х = ±7г, ±3тг, ±57г,....
Ряд Фурье для функции F(x) тождествен ряду Фурье для функции f(x). K тому же, если ряд
Фурье для функции f(x) сходится к ней, то его сумма, являясь периодической функцией, дает
периодическое продолжение функции f(x) с отрезка [-л-, ж] на всю ось Ох. В этом смысле говорить о ряде
Фурье для функции fix), определенной на отрезке [-л-, л-], равносильно тому, что говорить о ряде
Фурье для функции F(x), являющейся периодическим продолжением функции f(x) на всю ось Ох.
Отсюда следует, что признаки сходимости рядов Фурье достаточно сформулировать для периодических
функций.
§4. Достаточные условия
разложимости функции в ряд Фурье
Приведем достаточный признак
сходимости ряда Фурье, т. е. сформулируем
условия на заданную функцию, при
выполнении которых построенный по ней ряд
Фурье сходится, и выясним, как при этом
ведет себя сумма этого ряда. Важно
подчеркнуть, что хотя приведенный ниже класс
кусочно-монотонных функций и является
достаточно широким, функции, ряд
Фурье для которых сходится, им не
исчерпываются.
Определение. Функция f(x) называется кусочно-монотонной на отрезке [а, Ь], если этот
отрезок можно разбить конечным числом точек a < Х\ < Х2 < ... < жп-1 < Ь на
интервалы (а, х\), (х\у ж2),... , (хп, Ь), на каждом из которых f(x) монотонна, т.е.
либо не убывает, либо не возрастает (см. рис. 1).
Пример 1. Функция
f(x) = x2
является кусочно-монотонной на интервале (-оо,оо), так как этот интервал можно разбить на два
интервала (-оо, 0) и (0, +оо), на первом из которых она убывает (и значит, не возрастает), а на втором
возрастает (и значит, не убывает).
Пример 2. Функция
f(x) = cos х
кусочно-монотонна на отрезке [—л-, я-], так как этот отрезок можно разбить на два интервала (—л-, 0) и
(О, л-), на первом из которых cos а: возрастает от -1 до +1, а на втором убывает от +1 до — 1.
х, «^ ж, я; 6 х
Риг 1
3 Зак. 179

66
Глава XX. Ряды Фурье
Теорема 3. Функция f(x), кусочно-монотонная и ограниченная на отрезке [а, Ь], может
иметь на нем только точки разрыва первого рода.
М Пусть, например, х = с, с Е (а, 6) — точка разрыва функции f(x). Тогда в силу
ограниченности функции f(x) и монотонности по обе стороны отточки с существуют
конечные односторонние пределы
Шп /(*) = /(с - 0), Ит /(*) = /(с + 0).
х<с х>с
Это означает, что точка с есть точка разрыва первого рода (рис. 2). ►
Теорема 4. Если периодическая функция f(x) с периодом 2тг кусочно-монотонна и
ограничена на отрезке [—я-, ir], то ее ряд Фурье сходится в каждой точке х этого отрезка,
причем для суммы
по
S(x) = — + ^(ап cos пх + Ьп sin nx)
п=1
этого ряда выполняются равенства:
1) S(x) = f(x), если -ir < х <ir и х является точкой непрерывности f(x),
2) S(x) = \ [/(ж+0)-т-/(ж-0)], если -ir < х < тг их является точкой разрыва f(x),
3) S(-tt) = S(ir) = ^[/(-тг + 0) + /Or - 0)].
л!
-Зя
-2ir
fl
-ir о
1
IN
L 1
[4 1
n
Ъг
IN.
I \
1 ^
3*
X
Рис.2
Рис.3
ПримерЗ. Функция f(x) периода 2л-, определяемая на интервале (—7г, 7г) равенством
f(x) = л- - х
(рис. 3), удовлетворяет условиям теоремы. Поэтому ее можно разложить в ряд Фурье. Находим для i
коэффициенты Фурье:
(п-х)2>-
ао
= ;/(»-«)& = -
2п
= 2*г,
1 7/ ч * 7/ xj/8"1*1^ Ь ч sinnsl* 1 г .
ап = - / (я- - ж) cos пж dх = - / (л- - х) d ( 1 = -(п - а?) + — / sin nx dx ■
Я" J IT J \ П / 1С П |_х ПП J
-г --к -*
cos nx F cos(-nfl-) - cos тот
= 0, n = l,2,.

§4. Достаточные условия разложимости функции в ряд Фурье.
-67
Ьп = — / (п - х) sin nx dx = - (ж — x)d I 1 =
= (л-- ж) cos па: I*, I cos nxdx =
лтГ * тгп J
-1С
1 1 2 (-1)"
= —2л- cos(-mr) =■ sin пж|* = - cos птг = 2 п = 1,2,... .
л-n пи2 п п
Ряд Фурье для данной функции имеет вид
~ * sin nx
У\
*-* = * + 2£(-i)w-
-7Г < Ж < Л\
п=1
Пример 4. Разложить функцию
f(x) - I °> _7Г < ж < °'
/W-\ ж, 0^ж<тг,
в ряд Фурье (рис. 4) на интервале (-л-, я-).
Д-Д
^ -2яг -1
■я О jT" Sr W ■
Рис.4
4 Данная функция удовлетворяет условиям теоремы. Найдем коэффициенты Фурье. Используя
свойство аддитивности определенного интеграла, будем иметь
aQ = -J f(x)dx=-[ j f(x)dx + Jf(x)dx\=-\ Jo-dx + J
xdx\=X-X-
1 f
x cos nx dx
— * f я ts*n nx ^ — * fx sin r
~" 7Г У Vn/ Л-! П
0 V
H)"-i J-A
= = = < 1СП2
л-n2 (О
-;;
sin nx dx \ =
COS П7Г - 1
1ГП'
для n = 1,3,5,... ,
для n = 2,4,6,... ,
If If / cosnx\
0 0
1 I xcosnxl I } \ cosmr (-l)n+1 f ^
= _ + _ / Cos nx dx = = -— , n = l,2,.
7Г l П \ П J J П П
\ 10 0 /
Следовательно, ряд Фурье имеет следующий вид:
ж ( 2 cos х sin x sin 2x 2 cos Ъх sin Зж sin 4ж 2 cos 5ж \
/(ж)=4 + (^— + — - — -*— + -Ъ Т~-« — + '-) =
-1 . V^ | 2cos(2n-l)s +1sinna;
~а+2^| „ (2n-l)2 +l *' п
-1Г <Х <1Г.
На концах отрезка [-л-, я-], т. е. в точках х = -п и я = л-, которые являются точками разрыва первого
рода, будем иметь
*t ч */ ч 0 + 7Г 7Г
/(-*■) = /(*)= — = 2*
Замечание. Если в найденном ряде Фурье положить х = 0, то получим
л * 2(l l l \
откуда

68.
. Глава XX. Ряды Фурье
§5. Разложение в ряд Фурье четных и нечетных функций
Функция f(x), определенная на отрезке [-J, I], где I > 0, называется четной, если
f(-x) = f(x) для всех х Е [-J,1].
График четной функции симметричен относительно оси ординат.
Функция f(x), определенная на отрезке [-J, I], где I > О, называется нечетной,
если
/(-ж) = -f(x) для всех х е [-1,1].
График нечетной функции симметричен относительно начала координат.
Пример.
а) Функция
/(ж) = cos ж
является четной на отрезке [—л-, тг], так как
cos(-a;) = cos(a;)
ДЛЯ ВСеХ X е [—7Г, 7Г].
б) Функция
f(x) = sin ж,
где —я* ^ х ^ л-, является нечетной, так как
sin(—х) = - sin х
для всех х € [—тг,тг].
в) Функция
f(x) = ж2 - ж,
где -л- ^ х ^ 7Г, не принадлежит ни к четным, ни к нечетным функциям, так как
/(—ж) = ж + ж, /(-ж) ^ ж — ж, /(—ж)^=ж-ж для ж € [—я*, л-], ж Ф 0.
Пусть функция /(ж), удовлетворяющая условиям теоремы 1, является четной на
отрезке [-тт, 7г]. Тогда
f(-x) cos(-na:) = /(ж) cos пж,
/(-ж) sin(-nx) = -/(ж) sin пж
для всех ж Е [-тт, тт],
т. е. /(ж) cos пх является четной функцией, а /(ж) sin пж — нечетной. Поэтому
коэффициенты Фурье четной функции /(ж) будут равны
ап
— — I /(ж) cos пх dx = — / /(ж) cos пж (*ж, п = 0,1, 2,... ,
7Г J IT J
-к 0
ж
bn = — I /(ж) sin пж (*ж = 0, п = 1, 2,... .
Следовательно, ряд Фурье четной функции имеет вид
f(x) = -j + ]T)an cos пж.
2 п=1

§5. Разложение в ряд Фурье четных и нечетных функций 69
Если f(x) — нечетная функция на отрезке [-тг, ir], то произведение f(x) cosnx
будет нечетной функцией, а произведение f(x) sin nx — четной функцией. Поэтому
будем иметь
ап = — I f(x) cos nxdx = 0 для n = 0,1, 2,... ,
•к ж
bn = — I f(x) sin nxdx = — I f(x) sin nx dx для n = 1, 2,... .
я* J я J
-* 0
Таким образом, ряд Фурье нечетной функции имеет вид
f(x) = ^2 bn sin nx.
n=\
Пример 1. Разложить в ряд Фурье на отрезке -тг ^ х ^ л- функцию
f(x) = x2.
<4 Так как эта функция четная и удовлетворяет условиям теоремы 1, то ее ряд Фурье имеет вид
2 _ а0 ~
2 «*и , v-л
X = — + 2^ fln COS ПХ.
Находим коэффициенты Фурье. Имеем
2 } 2 2*3Г 2 2
о l0
Применяя дважды интегрирование по частям, получим, что
2 г о .2
IX cosnxdx = — х d i J =
о о
2 sin па; 2 с \ 4 ? /cos na; \
х / х sin nx dx \ = — I xd\ =
n n J I nir J \ n J
10 0 /0
4 ( г / A ■
= —~— x cosnx — / cos nxdx = —
П27Г \ 10 J In
4
n27T
Значит, ряд Фурье данной функции выглядит так:
или, в развернутом виде,
х =Т+4^(_1) ~пГ
) тг л /cosж cos2x cos За;
....).
I2 22 ' З2
Это равенство справедливо для любого х € [-л-, л-], так как в точках х = ±7г сумма ряда совпадает со
значениями функции /(ж) = х2, поскольку
/(-») + /(») _7Г2+7Г2 ,
2 ~ —2— ~ '' ' М_л>
Графики функции f(x) = х2 и суммы полученного ряда даны на рис. 5. ►
Замечание. Этот ряд Фурье позволяет найти сумму одного из сходящихся числовых рядов, а именно,
при х = 0 получаем, что

70
Глава XX, Ряды Фурье
Пример 2. Разложить в ряд Фурье на
интервале (-tf,7r) функцию
/(«) = *.
4 Функция /(ж) удовлетворяет условиям
теоремы 1, следовательно ее можно
разложить в ряд Фурье, который в силу
нечетности этой функции будет иметь вид
00
х = ^2 Ьп sin nx.
п=1
Интегрируя по частям, находим
коэффициенты Фурье
о *
Ьп = — / х sir
7Г J
z sin nx dx =
Рис.5
2 } / cosns\ 2 / I* / j \
= - xdl J = ( x cos пж - / cos nx dx J =
о V о /
n = l,2,....
2 2 (-Пп+1
= -i com* = --(-1)" = 2^—,
Следовательно, ряд Фурье данной функции
имеет вид
-»v^/ i4n+isinna; *Л sin2a; \
* = 2£(-1) ~jr"=2Vsinx 2" + "Г
Это равенство имеет место для всех х €
(-тт,*). В точках х = ±п сумма ряда
Фурье не совпадает со значениями функции
/(я) = х, так как она равна
5 [/<-»> + /<»>]-^=о.
Вне отрезка [-7Г, ж] сумма ряда является
периодическим продолжением функции f(x) = x; ее график изображен на рис.6.
Рис.6
§6. Разложение функции, заданной на отрезке,
в ряд по синусам или по косинусам
Пусть ограниченная кусочно-монотонная функция f(x) задана на отрезке [0, тг].
Значения этой функции на отрезке [-тг, 0] можно доопределить различным образом.
Например, можно определить функцию f(x) на отрезке [-тг, тг] так, чтобы f(x) = f(-x).
В этом случае говорят, что f(x) «продолжена на отрезок [-тг, 0] четным образом»; ее
ряд Фурье будет содержать только косинусы. Если же функцию f(x) определить на
отрезке [-тг, тг] так, чтобы f(x) = -f(-x), то получится нечетная функция, и тогда
говорят, что f(x) «продолжена на отрезок [-7Г, 0] нечетным образом»; в этом случае
ее ряд Фурье будет содержать только синусы.
Итак, каждую ограниченную кусочно-монотонную функцию f(x), определенную
на отрезке [0, тг], можно разложить в ряд Фурье и по синусам, и по косинусам.
Пример 1. Функцию
f(x) = 7г-ж, О^ж^л",
разложить в ряд Фурье: а) по косинусам; 6) по синусам.

§7. Ряд Фурье для функции с произвольным периодом.
.71
4 Данная функция при ее четном и нечетном
продолжениях в отрезок [—7г, 0J будет
ограниченной и кусочно-монотонной.
а) Продолжим /(ж) в отрезок [—7г, 0]
У\
а) Продолжим f{x) в отрезок [-7г,0] ук ук Л. ук л
четным образом (рис. 7), тогда ее ряд Фурье / • \^ / \ \^ /1 N. /1 N. / \
будет иметь вид ! XX 1 XX XX 1 XX [
oo±f
7Г - X = — + 2^ «n COS ПЖ,
2 п=1
где коэффициенты Фурье равны соответственно
-2Я -Я О!
Рис.7
2fr 3tr
ао = - (ж-х)йх = —(я- — яг)
о
2 / 2 / /sinnxx 2 I sinns!" 1 г.
ап = - / (я-- ж) cos пж <*ж = - (w-x)d ( J = - Н7г-ж) + - / sinnxdx
2 Iя" 2 2 Г 4
= -СОвПЖ = r(l ~COSfl7r) = T [1 ~ (-1)П1 = < irn1
тгп2 L irn2v ' тгп2 l V ' J \ 0
7ГП
Следовательно,
lo irn'
7Г-Ж = - +
к
cos ж cos Зж cos 5ж
+ -V5— + —7T- +
б) Продолжим /(ж) в отрезок [-7г,0]
нечетным образом (рис. 8). Тогда ее ряд
Фурье
где
7Г-ж = £)6nsinns,
n=l
К = - / (я- - ж) sin пж <fcc =
Рис.8
7Г J
С
2
7Г
и поэтому
ДЛЯ 0 < X ^ 7Г.
, ч cos пж
7Г-
►
п У"
* *
/cos пж йж
п J
0 0 J
я /sinж sii
_ 2 тг _ 2
7Г П fl'
12ж sin Зж
—+ —+-
п=1,2,... ,
для п= 1,3,5,... ,
для п = 2,4,6,... .
§7. Ряд Фурье для функции с произвольным периодом
Пусть функция f(x) является периодической с периодом 21, I ^ 0. Для разложения
ее в ряд Фурье на отрезке [-J,1], где I > 0, сделаем замену переменной, положив
х = ft. Тогда функция F(t) = / (^t) будет периодической функцией аргумента t с
периодом 2тг,т.к.
F(« + 2») = /[i(« + 2»)]=/(i« + 2l) =/(i«) =
*W,

72.
и ее можно разложить на отрезке [-7Г, тг] в ряд Фурье
^(0 =м~0=т+ 5^an cos nt + bn sin nt^
. Глава XX, Ряды Фурье
п=\
где
/Ф)
cos n£ iff (n = 0,1, 2,...),
Ъп = - J f (-Asinntdt (n= 1,2,...).
Возвращаясь к переменной ж, т. е. положив t = jx, dt = j dx, получим
/(*) =
«n =
Ьп =
: у у /(Ж) COS
у У /(«) sin
cos
717Г2
П7ГЖ
~7~
ПЖХ
- da:,
dx,
+ ъп
n -
n =
sin—),
= 0,1,2,...,
= i,2,...:
Все теоремы, справедливые для рядов Фурье периодических функций с периодом 2ж,
остаются в силе и для периодических функций с произвольным периодом 2Z. В
частности, сохраняет свою силу и достаточный признак разложимости функции в ряд
Фурье.
Пример 1. Разложить в ряд Фурье
периодическую функцию с периодом 21, заданную на
отрезке [-/,/] формулой
f(x) = \x\
(рис. 9).
-4 Так как данная функция четная, то ее ряд
Фурье имеет вид
«о
V*
-Л -2/ -I. 0\
i X!
/ 22 31
Рис.9
где
'ж1 = у + 2L,ancos—,
n=l
I
а° = 7 / х **х =''
о
2 г П7гж 2 / / / . пя-аЛ 2 г / шх\
a» = iJXC0S-rdx=iJxd{™sm—) = ™Jxd(sm-r) =
п 0 х ' 0
/• . П7ГЖ ^ \ 2 1 ПТС2
- / sin —— ах = cos ——
J I I П7Г 7ГП f
2 / П7ГЖ
— he sin ——
7ГП l /
* (cosn7r-l) = -^[(-l)n-l] = J -да ДЛЯ n= 1,3,5,...,
i2tt2V ' n27r2lv ' \0 для n = 2,4,6,... .

§7. Ряд Фурье для функции с произвольным периодом.
.73
Подставляя в ряд Фурье найденные значения коэффициентов Фурье, получим
м
cos =? cos ^ cos -5,rz
/ 41 f wva -j- wo —j
52
■ + .
••)
для -I ^ x ^ I. ►
Отметим одно важное свойство периодических функций.
Теорема 5. Если функция f(x) имеет период Т и интегрируема, то для любого числа а
выполняется равенство
а+Т
j f(x) dx= I f(x) dxy
m. е. интеграл по отрезку, длина которого равна периоду Т, имеет одно и то же значение
независимо от положения этого отрезка на числовой оси.
< В самом деле,
а+Т Т а+Т
I f(x) dx= j f(x) dx+ f(x) dx.
a a T
Делаем замену переменной во втором интеграле, полагая х = t + T, dx — dt. Это дает
а+Т а а а
f f(x)dx= f f(t + T)dt= f f(t)dt= f f(x)dxy
и следовательно,
а+Т Т
I f(x) dx= I f(x) dx+ f(x) dx= f(x) dx+ f(x) dx = / f(x) dx.
Геометрически это свойство
означает, что в случае f(x) ^ 0 площади
заштрихованных на рис. 10 областей
равны между собой. ►
В частности, для функции f(x) с периодом
Т = 27Г получим при а = —ж
j f(x)dx = Jf(x)dx.
-к 0
Пример 2. Функция
f(x) = sin7 х рис ш
является периодической с периодом
Т = 2ж. В силу нечетности данной функции без вычисления интегралов можно утверждать, что при
любом а
а+2тг 2тг
/ sin7 х dx = /sin x dx = / sin7 x dx = 0.

74
Глава XX. Ряды Фурье
Доказанное свойство, в частности, показывает, что коэффициенты Фурье
периодической функции f(x) с периодом 21 можно вычислять по формулам
1 Г тпгх
ап = - f(x)cos — dx (n = 0,1,2,...),
а
а+2/
1 Г 71ТГХ
Ьп = у / /(ж) sin — dx (n=l,2,...).
(О
(2)
где а — произвольное действительное число (отметим, что функции cos ^ и sin ■
имеют период 21).
Пример 3. Разложить в ряд Фурье заданную на интервале 0 < х < 2ж функцию
'<■> = {'."*• м<х<*-
если ж < х < 27Г,
с периодом 27Г (рис. 11).
4?
■N-Nr
-4* -3« -2« -t
Nr-N^-N
It 3«
Рис.11
4 Найдем коэффициенты Фурье данной функции. Положив в формулах (1) и (2) а = 0, I = ж, найдем,
что
2тг
а0-.
1
2тг |- л- 2тг
/ /(ж) dx = - /(я- - х) dx + / da;
7Г + 2
Lo
x) cos пж da: + / cos nx dx
/7Г
2ir
/sir
(я- - ж) sin nxdx+ / sin na; da;
1 / ж-х I* 1 -cosn7r\ 1
— _ cos na; ) = —
ж\ n |Q n у 7Г
i Г
— / (я- - x) cos na; da: = < n ж
*{ l о
1 Г r . ( cosnx\ cosn
для n= 1,3,...
для n = 2,4,...
2tm
* , (-')"-'
П П
= ±[, + (-1)»-!]
П7Г
"{?
Т5Г Апяп=1,3
для n = 2,4, — .
Следовательно, ряд Фурье будет выглядеть так:
7Г + 2 2 cos а: 7Г - 2 sin a: sin 2а: 2 cos За: 7Г — 2 sin За: sin 4a:
ДЛЯ 0 < X < 27Г.

§ 8. Комплексная запись ряда Фурье
75
В точке х = тг (точка разрыва первого рода) имеем
... _ /(7Г-0) + /(7Г + 0) _ 0+ 1 _ 1
№- 2 - 2 -г>
§8. Комплексная запись ряда Фурье
V
В этом параграфе используются некоторые элементы комплексного анализа (см.
главу XXX, где все, производимые здесь действия с комплексными выражениями, строго
обоснованы).
Пусть функция f(x) удовлетворяет достаточным условиям разложимости в ряд
Фурье. Тогда на отрезке [-тг, тг] ее можно представить рядом вида
f(x) — — 4- Jj(an cos nx 4- bn sin nx).
n=l
Используя формулы Эйлера (см. ***)
e — cos nx 4- г sin nx, e = cos nx - г sin nx,
найдем, что
cos nx =
егпх + e-tnx
sin nx
= г
2 2i 2
Подставляя эти выражения в ряд (1) вместо cos nx и sin nx, будем иметь
/<*>=?+
t(-
егпх + е-гпх ^ е"Ш - еШ
+ ibn-
)
ао , <А fa>n-ibninx ап + ibn inx\
= 7 + 1д—2~e +-^—e )■
Введем следующие обозначения
Яо _ fln - tt>n _ an -f- ibn _
Тогда ряд (2) примет вид
f(x) = co + J2(cneinX + c-»e~inX)-
П=\
Преобразуем правую часть этого равенства следующим образом
00 00 00 -00
/(*) = со + Е се«- + J2 с-»*'™* = <* + Е ^ + Е ^^
п=1 п=\ п=\ п=-\
-1 00 -1 00
= Е «■*•'"■+*»+X>e'"* = Е с«е<пх+Ес»е,'пх-
п=1
п=0
(О
(2)

76.
. Глава XX. Ряды Фурье
Последнее равенство можно записать так:
/(*)= ^се'"
(3)
Таким образом, ряд Фурье (1) представлен в комплексной форме (3).
Найдем выражения коэффициентов Сп и с_п через интегралы. Имеем
Сп =
ап - ibn 1
= — I / f(x) cos nx dx -i I f(x) sin nx dx
= — / f(x)(cosnx - i sinnx) dx = — / f(x)e~mx dx.
Аналогачно находим
c-„ = ±ff(x)ein*dx.
Окончательно формулы для Сп, c_n и cq можно записать так:
где n = 0, ±1,±2,... .
Коэффициенты Сп называются комплексными коэффициентами Фурье функции
Для периодической функции f(x) с периодом Т = 21 (I > 0) комплексная форма
ряда Фурье примет вид
(4)
где коэффициенты с„ вычисляются по формулам
1 f , . _; П1СХ
Сп= д I f(x)e ~ dx, п = 0,±1,±2,... .
-/
Сходимость рядов (3) и (4) понимается так: ряды (3) и (4) называются сходящимися
для данного значения ж, если существуют пределы
п п
lim У^ cketkx и lim У^ с*е*
fc=-n fc=-n
Пример. Разложить в комплексный ряд Фурье функцию периода 2ж
I .
/W~\ 1, 0<Ж<7Г.

§ 9. Ряды Фурье по общим ортогональным системам функций 77
Ч Данная функция удовлетворяет достаточным условиям разложимости в ряд Фурье. Пусть
+00
'/<*)= £ се'».
П=-00
Найдем комплексные коэффициенты Фурье этой функции. Имеем
*-i//««-*-*-5F/e-"* = s(-Se"*"D = -
27ГШ
1 - cos(-n?r) + i sin(—П7г) 1 — cos пж . (-l)n - 1 J —-г- для нечетных п,
s»^,(-ir-l_f -fn
%i 27гп 1 о
или,короче,
27гт 2тгт zwn у о для четных п,
C2n-1 = "^i)' С2п=0-
Подставляя значения сп в ряд (3), окончательно получим
t- +оо e»(2n-l)z
/(*) = — £ ,„ , » -«■<«'< 0, 0<ж<тг.
Заметим, что этот ряд можно записать и так:
^ +оо ei(2n+l)z
= -• ►
* «П** 2п + 1 2
§9. Ряды Фурье
по общим ортогональным системам функций
9.1. Ортогональные системы функций
Обозначим через L2 [а, ft] множество всех (действительных) функций, определенных
и интегрируемых на отрезке [а, ft] с квадратом, т. е. таких, для которых существует
интеграл1)
ь
)dx < -f-oo.
а
В частности, все функции /(ж), непрерывные на отрезке [a, ft], принадлежат /^[а, ft],
а
непрерыв]
и значения их интегралов Лебега совпадают со значениями интегралов Римана.
Определение. Система функций {у?п(ж)}, где <рп(х) Е -ЬгК &]»называется ортогональной
на отрезке [a, ft], если
ь
(<Рт, Vn) = f Ы*Ш*) dx = J °к > 0 ^ ш ^ n.' (!)
Условие (1) предполагает, в частности, что ни одна из функций (рп(х) не равна
тождественно нулю.
Интеграл понимается в смысле Лебега.

78.
. Глава XX. Ряды Фурье
Введем обозначение
\ш\2 --
ь
= (<Рп,<Рп)= 1 <pl(x)dx
а
и назовем величину ||^„|| ^ 0 нормой функции <рп(х).
Если в ортогональной системе {<рп(х)} для всякого п имеем ||^„|| = 1, то система
функций {<Рп(х)} называется ортонормированной.
Если система {<рп(х)} ортогональна, то система I |^Цг > ортонормирована.
Пример 1. Тригонометрическая система
1, cos ж, sin ж, cos2je, sin2«, ...,cosnx, sinnx,
ортогональна на отрезке [—7г, 7г]. Система функций
1 cos ж sin ж cosnx sin пх
~3тж* 717' 717' '"' \/2тг ' Vbr ' ""
является ортонормированной системой функций на [—7г, 7г].
Пример 2. Косинус-система
7ГЖ 27ГЖ П7ГЗ
1, cos—, cos——, ..., cos ——
и синус-система
. 7ГЖ 27ГЖ
sin —, sin ——,
/
являются ортогональными на отрезке [0, I], но не ортонормированными (при I Ф 2), так как их нормы
1пжх II || . шх || /7
cos— 1тт \ = п*и
Пример 3. Многочлены, определяемые равенством
Рп(х) =
1 d"(x2-l)n
n!2n dxn
(2)
(n = 0,1,2,...), называются многочленами (полиномами) Лежандра. При п = О имеем
Р0(х) = 1,
при п = 1 получаем
при п = 2 имеем
и т. д.
Можно доказать, что функции
*е> = шг(в,-1)=''
/ v 3 2 1
Р2(*)=-/--2
<pn(*) = f^-Pn(x), n = 0,l,2,...
образуют ортонормированную систему функций на отрезке [-1, 1].

§ 9. Ряды Фурье по общим ортогональным системам функций.
.79
Покажем, например, ортогональность полиномов Лежандра. Пусть т > п. В этом случае,
интегрируя п раз по частям, находим
fp(x)P(z)dz- ' *П(Х2-1)П 'V-^dx-
Jp* Wp« Wd* ~ 2гп2птЫ\ J dx- dx™ dX ~
m\n\2m+n
dm-l(x2-\)m dn+V-l)"
dxm~x
dxn+x
}dm-\x1-\)m dn+\x2-l)n
dxm~x
dxn+\
-j
-1
1 \dm-\x2-\)m dn+x(x2-\)n
~ m\n\2m+n J dxm~x ' dxn+l X ~
-l
_ (-1)* } dm'n(x2 - l)m d2n(x2 - l)w _ (-l)n(2n)! } <Г~п(х2 - 1)
dx
■i
dx =
■Г
■ dx = 0,
m\n\2m+n J dxm~n dx2n ~ m\n\2m+n J dxm~n
-i -i
поскольку для функции Um = (ж2 - 1)то все производные до порядка m - 1 включительно обращаются
в нуль на концах отрезка [-1,1].
Определение. Система функций {<рп(х)} называется ортогональной на интервале (а, Ь)
с весом р(х), если:
1) для всех п = 1, 2,... существуют интегралы
ь
р(х)<р2п(х) dx;
/■
2)
b
/ р(х)<рт(х)<рп(х) dx = I ^
для тфп,
> 0 для т — п.
Здесь предполагается, что весовая функция р(х) определена и положительна всюду на
интервале (а, Ь) за возможным исключением конечного числа точек, где р(х) может
обращаться в нуль.
Пример 4. Система функций Бесселя {^(/^ж)}._ ортогональна на интервале (0,1) с весом р(х) = х,
т. е.
1
о
для i^j. Здесь ji,- (i = 1, 2,...) — нули функции Бесселя ^(х).
Пример 5. Рассмотрим многочлены Чебышева—Эрмита, которые могут быть определены при помощи
равенства
tf„(z) = (-l)V
.2 <Ге~
dxn
(11 = 0,1,2,...).
(3)
Выполнив дифференцирование в формуле (3), находим
Щ(х) = 1, Я, (ж) = 2ж, Н2(х) = 4х2 - 2, ... .
Можно показать, что многочлены Чебышева—Эрмита ортогональны на интервале (-оо, +оо) с весом
р(х) = е~х , т. е.
/ е~х Hm(x)Hn(x) dx = 0 для тфп.

. Глава XX. Рады Фурье
9.2. Ряд Фурье по ортогональной системе
Пусть {<рп(х)}п=1 — ортогональная система функций в интервале (а, Ь) и йусть ряд
сХ(рх(х) + с2(р2(х) + ... 4- Сп<рп(х) 4-... (4)
(с, = const) сходится на этом интервале к функции f(x):
f(x) = cX(pi(x) 4- с2(р2(х) 4-... 4- Сп<Рп(х) 4-... .
Умножая обе части последнего равенства на (pk(x) (к — фиксировано) и интегрируя
по х от а до Ь, в силу ортогональности системы {<рп(х)} получим, что
1
ск =
J <pftx) dx a
о
J f(x)<pk(x)dx,
(5)
или
_ (/ИР*) к_
Эта операция имеет, вообще говоря, чисто формальный характер. Тем не менее,
в некоторых случаях, например, когда ряд (4) сходится равномерно, все функции
ipk(x) непрерывны и интервал (а, Ь) конечен, эта операция законна. Но для нас сейчас
важна именно формальная трактовка. Итак, пусть задана функция f(x) G L2[a, b].
Образуем числа ск по формуле (5) и напишем
f(x) ~ cxipx(x) 4- с2<р2(х) 4-... 4- Cn<Pn(x) 4-... .
(6)
Ряд, стоящий в правой части, называется рядом Фурье функции f(x) относительно
системы {<Рп(х)}. Числа с„ называются коэффициентами Фурье функции f(x) по этой
системе. Знак ~ в формуле (6) означает лишь, что числа Сп связаны с функцией f(x)
формулой (5) (при этом не предполагается, что ряд справа вообще сходится, а тем более
сходится к функции f(x)). Поэтому естественно возникает вопрос: каковы свойства
этого ряда? В каком смысле он «представляет» функцию /(ж)?
9.3. Сходимость в среднем
Определение. Последовательность {fn(x)}, fn(x) G L2[a, b], сходится к элементу fn G
Ь2[а, b] в среднем, если
ь
ton f[f(x)-fn(x)]2dx = 0,
П-КХ) J
a
или, что то же, ||/ - /„|| —► 0, где || • || — норма в пространстве L2[a, b].
Теорема 6. Если последовательность {/п(#)} сходится равномерно, то она сходится и
в среднем.

§9. Рады Фурье по общим ортогональным системам функций 81
4 Пусть последовательность {/„(я)} сходится равномерно на отрезке [а, 6] к
функции f(x). Это означает, что для всякого е > О при всех достаточно больших п имеем
1/(*)-/»(*)!<* V*€[a,b].
Следовательно,
J[№-fn(x)]2dx<e2(b-a),
откуда вытекает наше утверждение. ►
Обратное утверждение неверно: последовательность {/„(ж)} может сходиться
в среднем к f(x), но не быть равномерно сходящейся.
Пример. Рассмотрим последовательность
пх
Легко видеть, что
limofn(x) = 0 Уж 6 [0,1].
Но эта сходимость не равномерна:
существует е, например, е = -^, такое,
что сколь бы большим ни было п, на
отрезке [0,1] найдется точка,
именно, точка х = £, в которой значение
функции fn(x) равно \: /п(^) = \-
Таким образом, за счет увеличения п
сделать неравенство |/л(ж) - 0| < ^
справедливым сразу для всех
значений х от 0 до 1 никак нельзя. Иными
словами, уже для е = j не
существует номера N, который годился бы для
всех х 6 [0,1] одновременно (здесь характерен горб высоты \ (рис. 12), «передвигающийся» справа
налево с возрастанием п).
С другой стороны,
/[/„(.) -Ofdx = / ^g^ dx = -^Ljj + JL arctgn^O,
0 0
так что последовательность {fn{x)} сходится в среднем к функции f(x) = 0.
9.4. Минимальное свойство коэффициентов Фурье.
Неравенство Бесселя. Равенство Парсеваля
Пусть {ipn(x)}9 <Рп(х) £ -М^Ь] — ортонормированная система функций на
отрезке [а, Ь],
Рис.12
/ <Рт(х)<Рп(х) dx = { l\
УТЬ = 71,
и пусть f(x) e Ьг[а,Ъ]. Обозначим через ск коэффициенты Фурье функции f(x)
по ортонормированной системе {<рп(%)}'-
ск = J /(*)*>*(») dx (к =1,2,...).

82.
. Глава XX. Рады Фурье
Рассмотрим линейную комбинацию
Тп(х) = ai(pi(x) + а2<р2(х) + ... + ап<рп(х),
где п ^ 1 — фиксированное целое число, и найдем значения постоянных а\, а2,...,
ап, при которых интеграл
J[f(x)-Tn(x)]2dx
а
принимает минимальное значение. Запишем его подробнее
ь ь
f [/(*) - Тп(х)] 2dx = f [f\x) - 2f(x)Tn(x) + Tl{x)} dx.
a a
Интефируя почленно, в силу ортонормированности системы {<рп(х)} получим
/ [f(x) - Т„(х)] 2dx = / f\x) dx - 2 ]Г скак + J2 «* =
(*)
*=1
*=1
= f\X)dx-Y,c\+Y<^-ck)2'
Jn k=\ *=1
(7)
Первые два слагаемых в правой части равенства (7) не зависят от а*, а третье слагаемое
неотрицательно. Поэтому интеграл (*) принимает минимальное значение при а* = с*
(к = 1,2,...). Интеграл
J[f(x)-Tn(x)]2dx
называют средним квадратичным приближением функции f(x) линейной
комбинацией Тп(х). Таким образом, среднее квадратичное приближение функции f(x) Е L2[a, Ь]
принимает минимальное значение, когда а* = с*, (к = 1, 2,...), т. е. когда Тп(х)
есть п-я частичная сумма ряда Фурье функции f(x) по системе {<рп(х)}: Тп(х) =
Sn(x). Полагая а* = с*, из (7) получаем
ь ь
или
(8)
(9)
Равенство (9) называется тождеством Бесселя. Так как его левая часть неотрицательна,
то из него следует неравенство Бесселя

§9. Ряды Фурье по общим ортогональным системам функций.
.83
Поскольку п здесь произвольно, то неравенство Бесселя можно представить в
усиленной форме
00 .
(10)
т. е. для всякой функции f(x) £ L2[a, b] ряд из квадратов коэффициентов Фурье этой
функции по ортонормированной системе {<рп(х)} сходится.
Так как система
1 cos a; sin a; cos2a; sin2a;
V^' V^J v^Sr' л/2тг ' л/2тг ' ""
ортонормирована на отрезке [-7Г, тг], то неравенство (10) в переводе на привычную
запись тригонометрического ряда Фурье дает соотношение
00
справедливое для любой функции f(x) с интегрируемым квадратом.
Если /2 (х) интегрируема, то в силу необходимого условия сходимости ряда в левой
части неравенства (11) получаем, что а* —► 0, 6fe —* 0 при к —* оо.
Равенство Парсеваля
Для некоторых систем {<рп(х)} знак неравенства в формуле (10) может быть заменен
(для всех функций f(x) £ L2[a, b]) знаком равенства. Получаемое равенство
(12)
называется равенством Парсеваля—Стеклова (условием полноты).
Тождество Бесселя (9) позволяет записать условие (12) в равносильной форме
lim||/-Sn||=0.
Тем самым выполнение условия полноты означает, что частичные суммы Sn(x) ряда
Фурье функции f(x) сходятся к функции f(x) в среднем, т.е. по норме
пространства^ [а, 6].
Определение. Ортонормированная система {<рп(х)} называется полной в L2K Ъ], если
всякую функцию
f(x)€L2[a,b]
можно с любой точностью приблизить в среднем линейной комбинацией вида
Yl a*Ms)
с достаточно большим числом слагаемых, т. е. если для всякой функции f(x) £ L2[a, b]
и для любого е > 0 найдется натуральное число Щ и числа а\, а2> • • • > <*щ такие, что
J ~ Yl <W*(s)
k=\
<е.

84 Глава XX. Ряды Фурье
Из приведенных рассуждений следует
Теорема 7. Если ортонормированная система {<рп(я)} полна в пространстве /^[а, Ь], то
ряд Фурье всякой функции f(x) Е Ь2[а, b] no этой системе сходится к f(x) в среднем,
т. е. по норме L2[a, 6].
Можно показать, что тригонометрическая система
1 cos х sin x cos na; sin па;
\/2tFj л/2тг' V2wy ""' Vbr ' VSr'"'
полна в пространстве Ь2[-ж, я*]. Отсюда следует утверждение.
Теорет 8. Если функция f(x) Е L2[-ir, я*Ь то ее тригонометрический ряд Фурье сходится
к ней в среднем.
9.5. Замкнутые системы. Полнота и замкнутость систем
Определение. Ортонормированная система функций {<рп(х)}, <рп(х) £ L2[a, Ь],
называется замкнутой, если в пространстве L2 [а> &] не существует отличной от нуля функции,
ортогональной ко всем функциям <рп(х).
В пространстве L2[a, b] понятия полноты и замкнутости ортонормированных
систем совпадают.
Упражнения
1. Разложите в ряд Фурье в интервале (-тг, тг) функцию
/<*) = {
1 при -тг < х < О,
О при 0 < х < тг.
2. Разложите в ряд Фурье в интервале (-тг, тг) функцию
/(*) = {
2 при -тг < х < О,
1 при 0 < х < тг.
3. Разложите в ряд Фурье в интервале (-тг, тг) функцию
/<*) = {
О при -тг < х ^ О,
4а? при 0 ^ х < тг.
4. Разложите в ряд Фурье в интервале (-тг, тг) функцию
/<*) = {
-2х при -тг < х ^ О,
За: при 0 ^ х < тг.
5. Разложите в ряд Фурье в интервале (-тг, тг) функцию f(x) = тг + х.
6. Разложите в ряд Фурье в интервале (-тг, тг) функцию
при -тг < х < О,
f ( \ _ / ° ПРИ -7Г < х < '
/ W "~ | тг - а? при 0 < ж < тг.
7. Разложите в ряд Фурье в интервале (-тг, тг) функцию f(x) = sin2 x.
8. Разложите в ряд Фурье в интервале (-тг, тг) функцию f(x) = п ~23ж .

§9. Ряды Фурье по общим ортогональным системам функций 85
9. Разложите в ряд Фурье в интервале (—тг, 7г) функцию f(x) = | sin a?|.
10. Разложите в ряд Фурье в интервале (—тг, тг) функцию f(x) = §.
11. Разложите в ряд Фурье в интервале (-тг, тг) функцию f(x) = sin §.
12. Разложите в ряд Фурье функцию f(x) — тг - 2х, заданную в интервале (0, тг), продолжив
ее в интервал (-7Г, 0); а) четным образом; б) нечетным образом.
13. Разл9жите в ряд Фурье по синусам функцию f(x) = х2, заданную в интервале (0, тг).
14. Разложите в ряд Фурье функцию f(x) = 3 - ж, заданную в интервале (-2,2).
15. Разложите в ряд Фурье функцию f(x) = \х\, заданную в интервале (—1,1).
16. Разложите в ряд Фурье по синусам функцию f(x) = 2х, заданную в интервале (0,1).
Ответы
1- /(•) = \ - \ £ **£?=. s(o) = i, s(±n) = i. 2. /(.) = | - \ E «£?*, s(±n) = §,
n=l n=l
S(0) = §. 3. /(*) = *-£ E *$^ + 4 EH)""1*?5, S(±w) = 2*. 4. /(x) = f* -
n=l v ' n=l
7 S т£# + ЁНГ1*?5, *(±») = §*. 5. /(x) = r + 2 £(_i)-«-sm, 5(±») = ir.
n=l v ' n=l n=l
6. f(x) = | - | E =££#= + Ё **, »(±») = |. 7. /(») = I - Icos2x.
n=l v ' n=l
8. /(x) = £(-l)-'«p. 9. /(«) = 1 - i E S^. Ю. f{x) = f(-i)-'fta-; 5(±x) = 0.
n=l n=l n=l
11. fix) = f ЕНГ1^ • 12. a) /(*) = i E ^r#; 6) /(x) = 2 E *?=. 13. /(«) =
n=l n=l x ' n=l
2^Ё(-1)"-'^-| Ё E^^.14./(x) = 2+i Е(-1)п^.15./(х)=Ь^ёп^П^-
n=l n=l v ' n=l n=l v '
1б./(х) = 1-| Ё51^-
n=l

Глава XXI
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
ПЕРВОГО ПОРЯДКА
§ 1. Общие понятия. Примеры
Обыкновенным дифференциальным уравнением называется уравнение вида
(1)
&{х,у,у,,...,у{п))=0,
связывающее независимую переменную ж, искомую функцию у = у(х) и ее
производные у1 (ж), у"(х),..., у^п\х) (наличие хотя бы одной производной обязательно).
Здесь & — заданная функция своих аргументов.
Замечание. Обозначения зависимой и независимой переменных через х и у, используемые в
приведенном определении, не являются жесткими; часто в качестве независимой удобно брать переменную J,
иными буквами обозначают и зависимую переменную (см. ниже пример 2).
В обыкновенном дифференциальном уравнении искомая функция у — у(х) есть
функция одной независимой переменной х. Если искомая функция есть функция двух
(и более) независимых переменных, то имеем дифференциальное уравнение с
частными производными. В этой и двух следующих главах мы будем рассматривать только
обыкновенные дифференциальные уравнения.
Простейшим дифференциальным уравнением является уравнение вида
у=т, (2)
где f(x) — известная непрерывная на некотором интервале (а, Ь) функция,
а у = у(х) — искомая функция. С таким уравнением мы уже встречались в
интегральном исчислении, когда поданной функции f(x) требовалось найти ее первообразную
F(x). Как известно, всякая функция, удовлетворяющая уравнению (2), имеет вид
y = F(x) + C,
где F(x) — какая-нибудь первообразная для функции f(x) на интервале (а, Ь), а С —
произвольная постоянная. Таким образом, искомая функция у — у(х) определяется
из уравнения (2) неоднозначно.
Порядком дифференциального уравнения называется порядок наивысшей
производной, входящей в уравнение. Например,
/ 100
у =ху
— дифференциальное уравнение 1-го порядка;
у" + sin у = 0

§ 1. Общие понятия. Примеры
87
— дифференциальное уравнение 2-го порядка;
уv + у" + у = х + 1
— дифференциальное уравнение пятого порядка.
Решением дифференциальногоуравнения n-го порядка на интервале (а, Ь) называется
всякая функция у = <р(х)9 имеющая на этом интервале производные до n-го порядка
включительно и такая, что подстановка функции у = <р(х) и ее производных в
дифференциальное уравнение обращает последнее в тождество по х на интервале (а, Ь).
Например, функция у = sin ж является решением дифференциального уравнения второго порядка
на интервале (-оо, +оо). В самом деле, у' = cos ж, у" = -sin ж. Подставив в данное уравнение
найденные значения уму", получим - sin ж + sin ж = 0 Уж 6 (-оо, +оо)..
Задача. Найти совпадающие решения двух дифференциальных уравнений (не решая самих уравнений):
а) у' = у2 4- 2х - ж4 и б) у' = -у2 - у 4- 2ж 4- ж2 4- ж4.
График решения дифференциального уравнения называется интегральной кривой
этого уравнения.
Процесс нахождения решения дифференциального уравнения называется
интегрированием дифференциального уравнения. К составлению и интегрированию
дифференциальных уравнений приводят многочисленные задачи как самой математики, так
и других наук (физики, химии, биологии и т. п.).
Пример 1. Найти такую кривую, чтобы тангенс угла наклона касательной в каждой ее точке численно
равнялся ординате точки касания.
<4 Пусть
У = У{*)
— уравнение искомой кривой. Как известно, tg a = у'(х) и, значит, определяющее свойство кривой
есть
у'(х) = у(х)
— дифференциальное уравнение первого порядка. Нетрудно видеть, что функция
У = е*
,ть решение этого уравнения. Оно также имеет очевидное решение у = 0. Кроме того, решениями
будут функции
у = Сех,
где С — произвольная постоянная, так что уравнение имеет бесконечное множество решений. ►
Пример 2. Найти закон прямолинейного движения материальной точки, движущейся с постоянным
ускорением а.
< Требуется найти формулу з = s(t), выражающую пройденный путь как функцию времени. По условию
имеем
w=a
— дифференциальное уравнение второго порядка. Последовательно находим:
ds at2
— = at л-Си s(t)=— +C,*4-C2. (*)
Произвольные постоянные можно определить, если положить
ds\
= v0.
\t=tQ
В самом деле, полагая t = to в первом из соотношений (*), получаем vo = at0 + C\, откуда С\ =
vo - at0. Из второго соотношения (*) при t = to имеем
ац atn
so = — + Cit0 -f C2, или 50 = — + (v0 - at0)to 4- C2,
*U = So> Tt

откуда
C2 = Sq- V0t0 +
. Глава XXI. Дифференциальные уравнения первого порядка
atl
2
Подставляя найденные значения С\ и Сг в выражение для функции s(t), приходим к известному
закону движения материальной точки с постоянным ускорением:
ч «(* ~ *о)2
s(t) = s0 + v0(t -10) + . ►
§2. Эквивалентные дифференциальные уравнения.
Задача Коши
Пусть имеем дифференциальное уравнение первого порядка
&(х,у,у') = 0.
Если в этом уравнении удается выразить производную у' через а; и у, то получаем
уравнение
y' = f(x,y)A (1)
разрешенное относительно производной. Здесь / — заданная функция своих
аргументов.
Наряду с уравнением (1) рассматривают эквивалентное ему дифференциальное
уравнение
dy-f(x,y)dx = 0A (!')
или уравнение более общего вида
М(х, у) dx + N(x, у) dy = 0A (l")
получаемое из (Г) путем умножения на некоторую функцию N(x> у) £ 0 (М(ж, у),
N(x, у) — известные функции своих аргументов).
Два дифференциальных уравнения
9i(x,y,y') = 0, 9i(x,y,y') = Q
называются эквивалентными в некоторой области D изменения величин х,у,у', если
всякое решение у(х) G D одного из этих уравнений является решением другого
уравнения и наоборот. При преобразовании дифференциальных уравнений надо следить
за тем, чтобы преобразованное уравнение было эквивалентным исходному.
Если дифференциальное уравнение имеет решение, то, как правило, множество
его решений оказывается бесконечным. Впрочем, дифференциальное уравнение
(у'-1)2 + (х2-у2)2 = 0
имеет только одно решение
у = х,
а уравнение
у'2 4-1 = О
вообще не имеет действительных решений.

§3. Теорема существования и единственности решения задачи Коши для уравнения у' = f{x,y) 89
Чтобы выделить определенное решение уравнения (1), надо задать начальное
условие, которое заключается в том, что при некотором значении xq независимой
переменной х заранее дано значение уо искомой функции у(х):
У
X—XQ
уо> или у(х0) = у0.
(2)
Геометрически это означает, что задается точка Мо(жо,Уо), через которую должна
проходить искомая интегральная кривая.
Задачу отыскания решения у(х) уравнения (1), удовлетворяющего начальному
условию (2), называют задачей Коши (начальной задачей) для уравнения (1).
§3. Теорема существования и единственности
решения задачи Коши для уравнения у' = f(x,y)
Рис.1
Теорема 1 (существования и единственности решения). Пусть имеем дифференциальное
уравнение
У=/(х,у) (1)
и пусть функция f(x,y) определена в некоторой
области D на плоскости хОу. Выберем
произвольную точку Мо(хо> уо) £ D. Если
существует окрестность Q этой точки, в которой функция
/(я, у)
1) непрерывна по совокупности аргументов;
2) имеет ограниченную частную производную Ц,
то найдется интервал (хо - ho, хо + hQ) оси Ох,
на котором существует, и притом единственная,
функция у = <р(х), являющаяся решением
уравнения (\)и принимающая при х = хо значение yQ (рис. 1).
Геометрически это означает, что через точку Мо(жо, Уо) проходит одна и только
одна интегральная кривая уравнения (1).
Теорема 1 имеет локальный характер: она гарантирует существование
единственного решения у = <р(х) уравнения (1) лишь в достаточно малой окрестности точки ж0.
Из теоремы 1 вытекает, что уравнение (1) имеет бесконечное множество различных
решений (например, одно решение, график которого проходит через точку (xq, y0);
другое решение, когда график проходит через точку (a?o, У\) и т. д.).
Пример 1. В уравнении
у' = х + у
функция
f(x,y) = x + y
определена и непрерывна во всех точках плоскости хОу и имеет всюду -£• — 1. В силу теоремы 1 через
каждую точку (жо, Уо) плоскости хОу проходит единственная интегральная кривая этого уравнения.
Пример 2. В уравнении
функция
f(x,y) = ly2'3

90.
. Глава XXI. Дифференциальные уравнения первого порядка
определена и непрерывна на всей плоскости хОу. Здесь
BJ_ __2 ^
так что второе условие теоремы 1 нарушается в точках оси Ох. Нетрудно проверить, что функция
У = (х + С)\
где С — любая постоянная, является решением данного уравнения. Кроме того, уравнение имее\
очевидное решение
Если искать решения этого уравнения, соответствующие условию у(0) = 0, то таких решений найдется
бесчисленное множество, й частности, следующие (рис. 2):
ж^О, [ж3, ж<0,
ж>0, ^"1 0, 00,
Таким образом, через каждую точку оси Ох проходят по
крайней мере две интегральные кривые и, следовательно, в точках этой
оси нарушается единственность.
Если взять точку М|(1,1), то в достаточно малой ее
окрестности выполнены все условия теоремы 1. Следовательно, через
данную точку в малом квадрате П проходит единственная
интегральная кривая
У = 0,
(0, ^0, \х\
У~\х\ *>0, У~\ 0,
У-
у = х
х>0,
уравнения у' = Зу з. Если квадрат О, взять достаточно большим
(подумайте, каким), то в нем единственность решения уже не будет
иметь места. Это подтверждает локальный характер теоремы 1.
Рис.2
Теорема 1 дает достаточные условия существования
единственного решения уравнения у' = /(ж, у). Это
означает, что может существовать единственное решение у = у(х) уравнения у1 =
/(ж, у), удовлетворяющее условию y\x=xQ = 2fo> хотя в точке (жо, Уо) не выполняются
условия 1) или 2) теоремы или оба вместе.
Пример 3. Для уравнения
имеем
В точках оси Ох функции / и Ц- разрывны, причем
ду ~ у3 у-о
Но через каждую точку (жо, 0) оси Ох проходит единственная
интегральная кривая
у= ^3(х - *о)
(рис.3).
Рис. 3
Замечание. Если отказаться от ограниченности -ф-, то получается следующая теорема существования
решения.
Теорема 2. Если функция /(ж, у) непрерывна в некоторой окрестности точки (жо, Уо), то
уравнение у' = /(ж, у) имеет в этой окрестности по крайней мере одно решение у = <р(х),
принимающее при х = xq значение уо.

§ 3. Теорема существований и единственности решения задачи Коши для уравнения у = / ( х, у) 91
Задача. Найти интегральную кривую уравнения
у' = sin(zy),
проходящую через точку 0(0,0).
Задача. Найти решение задачи Коши
•^ = sgny, у(х0) = у0.
Определение 1. Общим решением дифференциального уравнения
»' = /(*,») (1)
в некоторой области О, существования и единственности решения задачи Коши
называется однопараметрическое семейство S функций у — <р(х, С), зависящих от пере-
менной х и одной произвольной постоянной С (параметра), такое, что
1) при любом допустимом значении постоянной С функция у = у?(ж, С) Е S
является решением уравнения (1):
(р'я(х, С) = /(ж, <р(х, С)), хе (х0 - Л, х0 + Л);
2) каково бы ни было начальное условие у\х=х0 = 2/<ь можно подобрать такое
значение Со постоянной С, что решение у = у?(ж, С0) будет удовлетворять начальному
условию
(p(x0i Со) = 2/0-
При этом предполагается, что точка (жо, уо) принадлежит области ft существования
и единственности решения задачи Коши.
Пример 4. Показать, что общим решением дифференциального уравнения
!/ = 1
является функция
У = х + С,
где С — произвольная постоянная.
<4 В данном случае /(ж, у) = 1, и условия теоремы 1 выполняются всюду. Следовательно, через каждую
точку (а?о, уо) плоскости хОу проходит единственная интегральная кривая данного уравнения.
Проверим, что функция
у = х + С
удовлетворяет условиям 1) и 2), содержащимся в определении общего решения. Действительно,
при любом С имеем
• = (* + С)' = 1,
так что у = ж + С есть решение данного уравнения. Потребовав, чтобы при х = хо решение принимало
значение уо, приходим к соотношению у0 = х0 + С0, откуда
Со = Уо — хо-
Решение у = х + у0 - жо. или
у - Уо = х - ж0,
удовлетворяет поставленному начальному условию. ►
Частным решением дифференциального уравнения (1) называется решение,
получаемое из общего при каком-либо конкретном значении произвольной постоянной С
(включая ±оо). Таким образом, общее решение этого дифференциального уравнения
можно определить как множество всех частных решений уравнения.
В процессе интегрирования дифференциального уравнения мы часто приходим
к уравнению
Ф(*,»,С) = 0, (2)

92 Глава XXI. Дифференциальные уравнения первого порядка
неявно задающему общее решение уравнения. Уравнение (2) называют общим
интегралом дифференциального уравнения (1).
Уравнение
|ф(ж,з/,С0) = 0,|
где Со — некоторое конкретное значение постоянной С, называется частным
интегралом.
Замечание. Название происходит от того, что для простейшего дифференциального уравнения вида
!/' = /(*)
его общее решение действительно записывается при помощи обычного неопределенного интеграла
У = J /(*) dx.
Пример. Общий интеграл уравнения
у' = cos х
имеет следующий вид
у = sin х + С
или
у — sin х — С = 0.
В дальнейшем для краткости мы будем иногда говорить, что решение уравнения
проходит через некоторую точку Мо(ж0,2/о), если точка М0 лежит на графике этого
решения.
Определение 2. Решение
У = Щх)
дифференциального уравнения (1) называется особым, если в каждой его точке
нарушается свойство единственности, т. е. если через каждую его точку (жо, Уо) кроме
этого решения проходит и другое решение уравнения (1), не совпадающее с у = Ф(ж)
в сколь угодно малой окрестности точки (ж0, уо).
График особого решения называют особой интегральной кривой уравнения.
Геометрически это — огибающая семейства интегральных кривых дифференциального
уравнения, определяемых его общим интегралом 1\
Если для дифференциального уравнения (1) в некоторой области D на
плоскости хОу выполнены условия теоремы 1, то через каждую точку (жо, Уо) € D проходит
единственная интегральная кривая у = <р(х) уравнения. Эта кривая входит в однопа-
раметрическое семейство кривых
Ф(ж,2/,С) = 0,
образующих общий интеграл уравнения (1), и получается из этого семейства при
конкретном значении параметра С, т.е. является частным интегралом уравнения (1).
Никаких других решений, проходящих через точку (ж0, уо), здесь быть не может.
Следовательно, для существования особого решения у уравнения (1) необходимо, чтобы
не выполнялись условия теоремы 1. В частности, если правая часть уравнения (1)
непрерывна в рассматриваемой области D, то особые решения могут проходить только
через те точки, где производная ^ становится бесконечной.
') Напомним, что огибающей семейства кривых Ф(х, у, С) = 0 называется такая кривая, которая в
каждой своей точке касается некоторой кривой семейства и каждого отрезка которой касается бесконечное
множество кривых из этого семейства.

§4. Приближенные методы интегрирования уравнения у' = f(x,y) 93
Например, для уравнения
у' = зз/2/3 (з)
функция / = Зу2/3 непрерывна всюду, но производная щ обращается в бесконечность при у = 0, т. е.
на оси Ох плоскости хОу. Уравнение (3) имеет общее решение
у = (х + С)3
— семейство кубических парабол — и очевидное решение
У = 0,
проходящее через те точки, где производная -g- не ограничена. Решение у = 0 — особое, так как
через каждую его точку проходит и кубическая парабола, и сама эта прямая у = О (см. рис. 2). Таким
образом, в каждой точке решения у = 0 нарушается свойство единственности. Особое решение у = О
не получается из решения у = (ж + С)3 ни при каком числовом значении параметра С (включая ±оо).
Из теоремы 1 можно вывести только необходимые условия для особого решения.
Множество тех точек, где производная Ц не ограничена, если оно является
кривой, может и не быть особым решением уже потому, что эта кривая, вообще говоря,
не является интегральной кривой уравнения (1).
Если, например, вместо уравнения (3) взять уравнение
у' = 3у2/3 + а, а = const, а ф О, (4)
то в точках прямой у = 0 по-прежнему нарушается условие ограниченности производной J-, но эта
прямая, очевидно, не является интегральной кривой уравнения (4).
Итак, чтобы найти особые решения уравнения (1), надо
1) найти множество точек, где производная ^ обращается в бесконечность;
2) если это множество точек образует одну или несколько кривых, проверить,
являются ли они интегральными кривыми уравнения (1);
3) если это интегральные кривые, проверить, нарушается ли в каждой их точке
свойство единственности.
При выполнении всех этих условий найденная кривая представляет собой особое
решение уравнения (1).
Задача. Найти особые решения уравнения
Сделать рисунок.
§4. Приближенные методы интегрирования
уравнения у9 = /(ж, у)
4.1. Метод изоклин
Пусть имеем дифференциальное уравнение
»' = /(*,»), (1)
где функция /(ж, у) в некоторой области D на плоскости хОу удовлетворяет условиям
теоремы 1. Это уравнение определяет в каждой точке (ж, у) области D значение у',
т. е. угловой коэффициент касательной к интегральной кривой в этой точке. Говорят,
что уравнение (1) определяет в области D поле направлений. Чтобы его построить, надо
в каждой точке (ж0, уо) £ D представить с помощью некоторого отрезка направление
касательной к интегральной кривой в этой точке, определяемое значением /(жо, уо).

94
Глава XXI. Дифференциальные уравнения первого порядка
Совокупность этих отрезков дает геометрическую картину поля направлений.
Задача интегрирования дифференциального уравнения (1) может быть теперь
сформулирована так: найти такую кривую, чтобы касательная к ней в каждой точке имела
направление, совпадающее с направлением поля в этой точке. Такое истолкование
дифференциального уравнения и его интегрирования дает графический способ
решения уравнения.
Для построения интегральных кривых пользуются изоклинами. Изоклиной
называется множество всех точек плоскости хОу, в которых касательные к искомым
интегральным кривым имеют одно и то же направление (у1 = const).
Из этого определения следует, что семейство изоклин дифференциального
уравнения (1) задается уравнением
/(ж, у) = fc,
где к — числовой параметр. Если придать параметру к близкие числовые значения,
можно найти достаточно густую сеть изоклин и приближенно построить интегральные
кривые дифференциального уравнения.
Пример 1. Проинтегрировать уравнение
у =х
по способу изоклин.
<4 Семейство изоклин данного уравнения определяется уравнением
х = к.
Полагая к = О, +1, -1,..., получаем изоклины
ж =0, х = 1, х = —1, ... ,
по которым строим интегральные кривые уравнения (рис. 4). ►
Нулевая изоклина
/(*, у) = 0
Рис.4
определяет множество возможных точек экстремума интегральных кривых (прямая
х = 0 в примере 1).
Для большей точности построения интегральных кривых определяют направление
вогнутости и точки перегиба этих кривых (если такие точки существуют). Для этого
находят у" в силу уравнения (1):
у" = /. + М = К(*, у) + /J(*, »)/(*, у)-
Знак правой части определяет знак у", т. е. направление вогнутости интегральных
кривых. Линия, заданная уравнением
/i(«, У)+ /i(*. »)/(*.») = 0,
есть множество всех возможных точек перегиба интегральных кривых.
В примере 1 имеем
поэтому все интегральные кривые обращены вогнутостью вверх, и точек перегиба интегральных кривых

§4. Приближенные методы интегрирования уравнения у' — f(x,y)
4.2. Метод последовательных приближений
Пусть имеем дифференциальное уравнение
95
(1)
где функция /(ж, у) в некоторой области D изменения х, у удовлетворяет условиям
теоремы 1, и пусть точка (ж0, уо) € D.
Решение задачи Коши
2 =/(*.»)> (2)
2/Ы = 2/о (3)
равносильно решению некоторого интегрального уравнения, т. е. уравнения, в
которое неизвестная функция входит под знаком интеграла. В самом деле, пусть
У = 2/0*0
— решение уравнения (2), заданное в некоторой окрестности (хо - ho, хо 4- h0) точки ж0
и удовлетворяющее начальному условию (3). Тогда при х € (xq - h0i xq -f ho) имеет
место тождество
£=/<-.*»•
Проинтегрируем это тождество по ж
»(«) = с +у/(*,»(*)) л.
«о
Отсюда учитывая (3), получаем
х
у(х) = 2/о 4- / /(*, 2/(0) Л, ж е (х0 - fto, х0 + fto)>
«о
так что решение у(х) задачи Коши удовлетворяет интегральному уравнению
2/ = Уо +
]f(t,y(t))dt.
XQ
(4)
Обратно: если непрерывная функция у(х), ж Е (ж0 - /&о, #о + Ло), удовлетворяет
интегральному уравнению (4), то, как легко проверить, у(х) является решением задачи
Коши (2)-(3).
Решение у = <р(х) интегрального уравнения (4) для всех ж, достаточно близких
к ж0, может быть построено методом последовательных приближений по формуле
(р(х) = lim ipn(x),
где
Pn+i(s) = 2/о + / /(*, ^п(')) *» п = 0,1, 2,... ,
«о

96 Глава XXI. Дифференциальные уравнения первого порядка
причем в качестве <po(t) можно взять любую непрерывную на отрезке [ж<> - ^о, #о + Ло]
функцию, в частности, <po(t) =yo = const.
Пример 2. Методом последовательных приближений решить задачу Коши
<4 Сводим данную задачу к интегральному уравнению
х
y(x)=\+Jy(t)dt.
о
Выбирая за нулевое приближение функцию
<р0(х) = 1,
последовательно находим:
X
tp\(x) = 1 + J <p0(t)dt=l + x,
о
xx 2
<p2(x) = l + J<pl(t)dt=l + J(l + t)dt = l + x + ^i
о о
/ ч , Х *2 Х"
1! 2! n! n_f0°
Легко видеть, что функция у = ех есть решение задачи. ►
4.3. Численные методы решения задачи Коши
Метод Эйлера
Пусть требуется найти приближенное решение дифференциального уравнения
£ = /(*. у). 0)
удовлетворяющее начальному условию
у(х0) = 2/о. (2)
Будем предполагать, что в некотором прямоугольнике!) = {|ж-жо| ^ А, \у~Уо\ ^ В}
функция /(ж, у) непрерывна и имеет непрерывные частные производные достаточно
высокого порядка по всем аргументам, так что решение задачи Коши (1)-(2)
существует, единственно и является функцией, дифференцируемой достаточное число раз.
Численное решение задачи (1)-(2) состоит в построении таблицы приближенных
значений У\,У2,---,Уп решения задачи в точках хх, ж2,..., хп. Чаще всего выбирают
хк = xq + kh (к = 0,1,..., п). Точки хк называют узлами сетки, а величину h > 0 —
шагом сетки. Так как по определению производная $L есть предел разностного
отношения у^х+ £~у\х) при h —»• 0, то, заменяя производную этим отношением, вместо
дифференциального уравнения (1) получим разностное уравнение (разностную схему
Эйлера)
^±i~- = f(xk,yk), _ * = 0,1,2 (3)
ИЛИ
0*+i = Ук + ft/(s*, 2/fc), * = 0,1, 2r... . (4)
Отсюда последовательно находим значения ук = y(xk), учитывая, что у0 = у(х0) —
заданная величина.

§4. Приближенные методы интегрирования уравнения у = f(x,y)
.97
Рис.5
В результате вместо решения у = у(х) мы у|
находим функцию
Ук = у(хк)
дискретного аргумента хк (сеточную
функцию), дающую приближенное решение
задачи (1 )-(2). Геометрически искомая
интегральная кривая у = у (ж), проходящая через
точку Мо(жо, Уо)> заменяется ломаной Эйлера
М0М\М2 ... с вершинами в точках Mk(xkl yk)
(см. рис. 5).
Метод Эйлера относится к группе одно-
шаговых методов, в которых для вычисления
точки (ж*+1,2/*+i) требуется знание только предыдущей вычисленной точки (хк, Ун)-
Для оценки погрешности метода на одном шаге сетки разложим точное решение
у = у(х) в окрестности узла х = хк по формуле Тейлора
У&ш) = У(хк + ft) = У(хк) + 2/Wft + 0(ft2) = y(xk) + fc/(s», №) + 0(h2). (5)
Сравнение формул (4) и (5) показывает, что они совпадают до членов первого порядка
по ft включительно, а погрешность формулы (4) равна 0(ft2). Поэтому говорят, что
метод Эйлера имеет первый порядок.
Пример. Методом Эйлера решить задачу Коши
dx
= у-х, у(0) = 2
на отрезке [0; 0,5] с шагом Л = 0,1.
«* В данном случае /(ж, у) = у~х, ж0 = 0, уо = 2. Пользуясь формулой (4),
Ук+i =yk + hf(xh,yk\
последовательно находим
У\ = Уо + hf(x0i уо) = 2 + 0,1(2 - 0) = 2,2,
» = Я+Л/(«ьУ|) = 2,2 + 0,1(2,2 -0,1) = 2,41,
и т. д. Результаты вычислений сведем в таблицу
к
0
1
2
3
4
5
я*
0
0,1
0,2
0,3
0,4
0,5
Ук
2,0000
2,2000
2,4100
2,6310
2,8641
3,1105
/(*к,Ук)
2,0000
2,1000
2,2100
2,3310
2,4641
Ч*к,Ук)
2,0000
0,2100
0,2210
0,2331
0,2464
Точное решение
у = ех + х + 1
2,0000
2,2052
2,4214
2,6499
2,8918
3,1487
Замечание. Если рассмотреть задачу Коши
Тх=у-Х>
У(0) = 1
на любом отрезке [0, а] с любым шагом h > 0, тс* получим у\ = 1 + Л, уг — 1 + 2Л, уз = 1 + ЗЛ и т.д.,
так что в этом случае ломаная Эйлера «распрямляется» и совпадает с прямой у = х + 1 — точным
решением поставленной задачи Коши.
4 Зак. 179

. Глава XXI. Дифференциальные уравнения первого порядка
Понятие о методе Рунге—Кутта
Метод Эйлера весьма прост, но имеет низкую точность. Точность решения можно
повысить путем усложнения разностной схемы. Весьма распространенными на практике
являются схемы Рунге—Кутта.
Пусть опять требуется решить задачу Коши (1)-(2). Будем строить таблицу
приближенных значений уь у2)..., уп решения у = у(х) уравнения (1) в точках хь х2, • • • >ж„
(узлах сетки).
Рассмотрим схему равноотстоящих узлов ж* = хо + kh9 где h > 0 — шаг сетки.
В методе Рунге—Кутта величины 2/t+i вычисляются по следующей схеме
»+i = У% + g (*i + 2Л2 + 2fc3 + «ы).
где
*Т"
*2:
fc3:
Л?4 :
= /(*•> 3/0,
= /(*.
= /(*.
= /(*,•
• 2»
+ ft,
* + ^)J
» + ^).
» + ft*3).
§5. Некоторые виды уравнений,
интегрируемых в квадратурах
В общем случае, даже зная, что решение уравнения существует, отыскать его довольно
трудно. Однако существуют некоторые виды дифференциальных уравнений, методы
получения решений которых особенно просты (при помощи интегралов от
элементарных функций). Рассмотрим некоторые из них.
5.1. Уравнения с разделяющимися переменными
Уравнение вида
f\(y)dy = f2(x)dx
(1)
называется дифференциальным уравнением с разделенными переменными. Здесь f\(y),
/2 (ж) — известные непрерывные функции своих аргументов.
Покажем, как найти решение этого уравнения. Пусть F\(y) и F2(x) —
первообразные функции f\(y) и f2(x) соответственно. Равенство (1) равносильно тому, что
дифференциалы этих функций должны совпадать
dFx(x) = dF2{x).
Отсюда следует, что
Fl(y)=Fb(x) + Ct (2)
где С — произвольная постоянная.
Разрешая последнее уравнение (2) относительно у, получим функцию (может
быть, и не одну)
У = Ф),
которая обращает уравнение (1) в тождество и значит, является его решением.

§5. Некоторые виды уравнений, интегрируемых в квадратурах
99
Например,
х 4х + у dy = О
— уравнение с разделенными переменными. Записав его в виде
ydy = —х dx
и интегрируя обе части, найдем общий интеграл данного уравнения:
х2 + у2 = С.
Уравнение вида
f\(x)<P\(y) dx = f2(x)(p2(y) ^ (3)
в котором коэффициенты при дифференциалах распадаются на множители,
зависящие только от ж и только от у, называется дифференциальным уравнением с
разделяющимися переменными, так как путем деления на 4>\(y)h{x) £ 0 оно приводится
к уравнению с разделенными переменными
lMdx = fMdy
h(x) tpx(y)
Пример 1. Проинтегрировать уравнение
(\+y2)xdx = (\+x2)ydy.
4 Деля обе части уравнения на (1 + у2)(\ + х2) Ф О, приведем его к виду
xdx ydy
1 + х2 ~~ 1 + у2'
Интегрируя обе части полученного равенства, найдем
1п(1 + ж2)=1п(1 + у2) + 1пС.
откуда
(1+х2)
О+У2)
= С. ►
Заметим, что деление на <P\(y)f2(x) может привести к потере решений,
обращающих в нуль произведение <р\ (y)f2(x).
Например, разделяя переменные в уравнении
xdy = y dx,
получаем
dy dx
у ~~ х '
а после интегрирования —
In |у| = In |х| + In |С|,
откуда
у = Сх
(здесь С может принимать как положительные, так и отрицательные значения, но С Ф 0). При делении
на у потеряно решение
которое может быть включено в общее решение у = Сх, если постоянной С разрешить принимать
значение С = 0.
Если считать переменные х и у равноправными, то уравнение
<ty = I
dx х1
теряющее смысл при х = 0, надо дополнить уравнением
dx _ х
которое имеет очевидное решение х = 0.
4*

100.
. Глава XXI. Дифференциальные уравнения первого порядка
В общем случае наряду с дифференциальным уравнением
dy
dx
= /(«, у)
следует рассматривать уравнение
dx * / \
dy
(4)
(4')
где f\ (ж, у) = jA-x, используя уравнение (4') там, где уравнение (4) не имеет смысла,
а уравнение (4') имеет смысл.
Некоторые дифференциальные уравнения путем замены переменных могут быть
приведены к уравнениям с разделяющимися переменными. Например, уравнение
вида
dy
— = /(аж + Ьу + с),
(5)
где f(z) — непрерывная функция своего аргумента, а, Ь, с — постоянные числа,
подстановкой z = ax + by + c преобразуется в дифференциальное уравнение с
разделяющимися переменными:
dz dv
откуда
а + bf(z)
dz = dx.
После интегрирования получаем
/
dz
= ж + С.
a + bf(z)
Заменяя в последнем соотношении z на ах + by -f с, найдем общий интеграл
уравнения (5).
Пример 2. Проинтегрировать уравнение
dx
4 Положим z = х + у, тогда
откуда
Интегрируя, находим
= (* + *).
dz
dz dy uz 2
di = 1+^' или ^ = 1+*'
dz
ds.
1 + z2
arctg z = ж + С,
г = tg(z + С).
Подставляя вместо z величину х + у, получаем общее решение данного уравнения
у = tg(x + С) - х. ►
Пример 3. Известно, что скорость радиоактивного распада пропорциональна количеству х еще не
распавшегося вещества. Найти зависимость х от времени t, если в начальный момент t = to имелось
х = х0 вещества.

§ 5. Некоторые виды уравнений, интегрируемых в квадратурах 101
А Дифференциальное уравнение процесса
dx
dt
—
-kx.l
<*)
Здесь к > 0 — постоянная распада — предполагается известной, знак «-» указывает на уменьшение х
при возрастании t. Разделяя переменные в уравнении (*) и интегрируя, получаем
In \х\ = -Ы + In |С|, откуда х = Се~
Учитывая начальное условие ж|*=*0 = хо, находим, что С = xoekt°, поэтому
x(t) = x0e"kit-tb). ►
(**)
Любой процесс (не только радиоактивный распад), при котором скорость распада пропорциональна
количеству еще не прореагировавшего вещества, описывается уравнением (*).
Уравнение
dx
— = кх, к > 0, (***)
отличающееся лишь знаком правой части от уравнения (*), описывает лавинообразный процесс
размножения, например «размножение» нейтронов в цепных ядерных реакциях или размножение бактерий
в предположении, что скорость их размножения пропорциональна наличному числу бактерий. Решение
уравнения (***), удовлетворяющее условию х\ = а?о. имеет вид
x(t) = xQek{t-to)
и в отличие от решения уравнения (**) возрастает с возрастанием t.
Уравнения (*) и (***) можно объединить в одно
dt
ку, к = const,
(****)
которое дает простейшую математическую модель динамики популяций (совокупности особей того или
иного вида растительных или животных Организмов). Пусть y(t) — число членов популяции в момент
времени t. Если предположить, что скорость изменения популяции пропорциональна величине
популяции, то мы приходим к уравнению (****). Положим к = т — п, где т — коэффициент относительной
скорости рождаемости, an — коэффициент относительной скорости умирания. Тогда к > 0 при т> п
и к < 0 при т <п. Если в момент t = 0 величина популяции равна уо, то уравнение (****) приводит
к экспоненциальному закону изменения популяции
y(t) = yoekt;
при к < 0 имеем уф)'-* 0 при\t ** Ч-оо, при к > 0 имеем y(i) -* +co при i--+ +co.
Предположение, что величины тип являются постоянными, не выполняется для больших
популяций. Действительно, большое число членов популяции приводит к уменьшению соответствующих
ресурсов, что снижает скорость рождаемости и увеличивает скорость умирания. Это можно задать
простейшими законами
m = b\ - b2y, n = ft3 + Ъьу,
где Ь{ — положительные постоянные (t = 1,2,3,4). Тогда
к = т-п
■Ъ]-Ь3-(Ь2 + Ъ4)у = (Ь2+Ь4)№^-у\=а(А-у),
где а = &2 + &4. А =
Уравнение динамики популяции в этой модели имеет вид
-=а(А-у)у.
Это так называемое логистическое уравнение — фундаментальное уравнение в демографии и в
математической теории экологии. Оно применяется в математической теории распространения слухов,
болезней и других проблемах физиологии и социологии. Разделяя переменные в последнем
уравнении, получаем
(А-у)у
adt,
откуда
У-А У
- — =Aadt

102 Глава XXI. Дифференциальные уравнения первого порядка
и далее
In \y-A\- In \y\ = Aat + In С.
Потенцируя
У
и выражая у через t, окончательно получаем
Aat
_ АСе
У ~~ 1 + Се'1"''
Считая, что у(0) = уо, найдем уравнение логистической кривой
При а > 0 и А > 0 получаем, что y(t) -* А при $ -* +оо. Логистическая кривая содержит два
параметра Л и а. Для их определения надо иметь два дополнительных значения y(t) при каких-то t\
и *2-
5.2. Уравнения, однородные относительно ж и у
Функция /(ж, у) называется однородной функцией п-го измерения относительно
переменных х иу9 если при любом допустимом t справедливо тождество
f{tx,ty) = tnf{x,y).
Например, для функции
f(x,y) = x2-xy + y2
f(tx, ty) = t2x2 - t2xy + t2y2 = t2(x2 -xy + y2) = t2f(x, y),
так что /(ж, у) = х2 - ху + у2 — однородная функция относительно переменных х и у второго
измерения.
Для функции
имеем
так что /(ж, у) = | есть однородная функция нулевого измерения.
Дифференциальное уравнение первого порядка
называется однородным относительно х и у, если функция f(x,y) есть однородная
функция нулевого измерения относительно переменных х и у.
Пусть имеем дифференциальное уравнение
ЛУ *i \
£ = /<*.»>■
однородное относительно переменных х и у. Положив t = £ в тождестве /(£ж, £у) =
/(ж, у), получим
/(«,f) = /(i,|),
т. е. однородная функция нулевого измерения зависит только от отношения
аргументов. Обозначая / (1, |) через (р (|), видим, что однородное относительно
переменных хиу дифференциальное уравнение всегда можно представить в виде

§5. Некоторые виды уравнений, интегрируемых в квадратурах
При произвольной непрерывной функции (р переменные не разделяются.
Введем новую искомую функцию и(х) формулой и = J, откуда у = хи. Подставляя
выражение % = и + х% в уравнение (6), получаем
м + #—= y?(w), или ж du = [v>(«) - м] dx.
dx
Деля обе части последнего равенства на х[(р(и) -и]и интегрируя, находим
du
I
■=1гф|+1п|С|.
(р(и) - и
Заменяя здесь и на его значение |, получаем общий интеграл уравнения (6).
Пример 4. Проинтегрировать уравнение
dx
Y+«2
ху
4 Имеем
*а = 1 + -
dx х у'
Положим |=t». Тогда $L = « + х ||, и уравнение преобразуется к виду
du 1
и + х —-=«+-,
dx «
«du:
dx
Интегрируя, найдем и2 = In Сж2, или
у2 = х2 In Ca:2. ►
Пример 5. Найти форму зеркала, собирающего пучок параллельно падающих на него лучей в одну точку.
4 Прежде всего, зеркало должйо иметь форму поверхности вращения, так как только для поверхности
вращения все нормали к поверхности проходят через ось вращения.
Выберем прямоугольную декартову систему
координат так, чтобы лучи были параллельны оси Ох и
чтобы точкой, в которой собирались бы отраженные лучи,
явилось бы начало координат. Найдем форму сечения
зеркала плоскостью хОу. Пусть уравнение сечения есть
у = <р(х) (рис.6). В точке М(х,у) падения луча L
на зеркало проведем касательную BN к сечению и
обозначим ее угол с осью Ох через а. Пусть N — точка
пересечения этой касательной с осью Ох. По закону
отражения углы NMO и BML равны. Нетрудно видеть,
что угол МОР равен 2а. Так как tga = у , tg2a = |
и tg 2a = 2tgf , то во всякой точке кривой у = ip(x)
° 1 -цр a
выполняется соотношение
Рис.6
2у'
— дифференциальное уравнение, определяющее требуемый ход луча. Разрешая это уравнение
относительно производной, получаем два однородных уравнения:
•Ф
x + dxz + yz
ф
х2 + у2
Первое из них путем замены | = и преобразуется к виду
и + хи
-l + v/T+tt2"

104.
Глава XXI. Дифференциальные уравнении первого порядка
или
udu
dx
1 + и2 - v/1 + и2
udu r d(y/\ + и2 - 1)
интегрируя, найдем
/ udu r di\/\ + ul-\) , / г г ч
J 1+и2-\ДТи? J Vi + и2 - 1 vv у
Потенцируя последнее соотношение и заменяя « через |, после несложных преобразований имеем
у2 = 2Сх + С2,
К>
у1 = 2С
Полученное уравнение в плоскости хОу определяет семейство парабол, симметричных относительно
оси Ох. фокусы всех этих парабол совпадают с началом координат. Фиксируя С и вращая параболу
вокруг оси Ох, получаем параболоид вращения
y2 + z2=2c(x+^y
Таким образом, зеркало в виде параболоида вращения решает поставленную задачу. Это свойство
используется в прожекторах. ►
Замечание. Если
то уравнение (6) имеет вид
<р(и) - и = 0,
dy У
dx x
и интегрируется разделением переменных. Его общее решение
у р: Сх.
Если (р(и) — и обращается в нуль при значении и = «о = const, то существует также решение и = «о,
или
у = иох
(прямая, проходящая через начало координат).
Рассмотрим уравнения, приводящиеся к однородным. Уравнение
dy ax + by -fс
dx а\Х + Ъ\у + с\*
(7)
где а, Ь, с, а\, Ь\, с\ — постоянные числа, при с = с\ = 0 является однородным. Пусть
теперь по крайней мере одно из чисел с, с\ отлично от нуля. Здесь следует различать
два случая.
I а Ь
1. Определитель I w " I отличен от нуля. Введем новые переменные £ и г\
по формулам
x = £ + hy y = Tf + ky
где h,k — пока не определенные постоянные. Тогда dx = d£,dy = drj. Уравнение (7)
преобразуется при этом в уравнение
dtf at + brj + ah + bk + c
d£ ~~ а>\£ + М 4- u\h + ftifc -f c\'
Если выбрать /i и к как решения системы линейных алгебраических уравнений
a/i-f Ь& + с = 0,
ai/i-f M + ci =0, ' '

f 6. Некоторые виды уравнений, интегрируемых в квадратурах _
.105
то получим однородное относительно £, rj уравнение
drj a£ + Щ
d£ "" <ц£ + Ь\ч\
Заменяя в его общем интеграле £ на ж - Л, 17 на у - fc, найдем общий интеграл
уравнения (7).
I а Ь
2. Определитель
си Ь\
равен нулю. Система (8) в общем случае не имеет
решения и изложенный выше метод неприменим. Но в этом случае ^ = ^J- = Л,
т. е. уравнение (7) имеет вид
dy ах + Ъу + с
dx Х(ах + by) + с\
и приводится к уравнению с разделяющимися переменными подстановкой z = ax+by.
Аналогичными приемами интегрируется уравнение
dy / ax + by + c \
dx \aix + b\y + c{j '
где f(w) — непрерывная функция своего аргумента.
5.3. Линейные дифференциальные уравнения
Линейным дифференциальным уравнением первого порядка называется уравнение,
линейное относительно неизвестной функции и ее производной. В общем случае оно имеет
вид
A{x)^+B{x)y = f{x),
(9)
где коэффициенты уравнения А(х) и В(х) и его правая часть f(x) считаются
известными функциями, заданными на некотором интервале (а, /3).
Если f(x) = 0 на (а, /3), то это уравнение называется однородным, в противном
случае оно называется неоднородным. Считая А(х) ф 0 на (а, /3) и деля обе части
уравнения (9) на -4(a), приведем (9) к виду
dy
— +p(x)y = q(x)y
(10)
TOjK*) = ag. «<*> = $•
Теорема 3. Если функции р(х) и q(x) непрерывны на отрезке [а, Ь] С (а, (3), то
уравнение (10) всегда имеет единственное решение, удовлетворяющее начальному условию
у\х=х = ЗЛь где точка (жо, 2/о) принадлежит полосе а < х <Ь, -оо < у < + оо.

106 Глава XXI. Дифференциальные уравнения первого порядка
-4 Разрешая уравнение (10) относительно у', приведем его к виду
у = -р(х)у + q(x),
где правая часть
/(ж, У) = ~Р(х)у + q(x)
удовлетворяет всем условиям теоремы 1: она непрерывна по совокупности
переменных ж и у и имеет ограниченную частную производную
в указанной полосе. Отсюда следует справедливость утверждения. ►
Линейное однородное уравнение, соответствующее уравнению (10), имеет вид
dy
— +р(х)у = 0.
(»)
Оно интегрируется разделением переменных:
— = -р(х) dx>
У
откуда
In
или
\y\ = -fp(z)dx + ln\C\,
\у = Се
■ Jp(x)dx
(12)
При делении на у потеряно решение у = 0, однако оно может быть включено в
найденное семейство решений (12), если считать, что С может принимать значение, равное
нулю. Формула (12) дает общее решение уравнения (И) в указанной выше полосе
а < х < 6, -оо < у < 4-оо.
Для интегрирования неоднородного линейного уравнения
dy
— +p(x)y = q(x)
может быть применен так называемый метод вариации постоянной. Он основан на том,
что общее решение уравнения (10) равно сумме общего решения уравнения (11) и
какого-либо частного решения уравнения (10)
2/о.н. = Уо.о. "г 2/ч.н. •
Подставляя в левую часть (11) вместо у сумму 2/0.о. + 2/ч.н., получим
a°Y УЧН' +Р(х)(Уо.о. + 2/ч.н.) = -~ +Р(х)Уо.о. + -~~1 +Р(х)Уч.н. =
CLX CLX CLX
= 0 + -^ 4- р(х)уч.И. = q(x).
С другой стороны, разность двух частных решений jjf4.H. и #ч.н. уравнения (10) является
решением однородного уравнения (11)
4H'dx УЧН' +Р(ж)(&.н. " 2/ч.н.) = ~^Г +Р(Х)УЧ.Н. - 1^- +р(х)Уч.н.) =
= «(*) - Ф) = О-

§ 5. Некоторые виды уравнений, интегрируемых в квадратурах.
.107
Поэтому сначала интегрируем соответствующее однородное уравнение
dy
— +р{х)у = 0,
общее решение которого имеет вид
где С — произвольная постоянная. Решение неоднородного уравнения (10) ищем
в виде
y = C(x)e-fpix)dx,
(13)
где С(х) — новая неизвестная функция.
Вычисляя производную з| и подставляя значения д| и у в исходное уравнение (10),
получаем
Ш=ф)€1р^х,
dx
откуда
С(х)= f q(x)efp{x)dxdx + C,
где С — новая произвольная постоянная интегрирования. Следовательно,
y = C(x)e-SpMd* = Ce-fpix)dx + e-fp{x)dx fq(x)efp{x)dx dx.
(14)
Это есть общее решение линейного неоднородного дифференциального
уравнения (10).
В формуле (14) общего решения неопределенные интегралы можно заменить
определенными интегралами с переменным верхним пределом:
-fp(t)dt * Jp(t)dt
у(х) = е *° С+ q(x)e** dx
Здесь С = 2/(жо) = Уо, поэтому общее решение уравнения (10) можно записать в виде
(15)
где роль произвольной постоянной играет начальное значение уо искомой
функции^»).
Формула (15) является общим решением уравнения (10) в форме Коши. Отсюда
следует, что если р(х) и q(x) определены и непрерывны в интервале -оо < х < + оо,
то и решение у(х) уравнения (10) с любыми начальными данными у(х$) = у0 будет
непрерывным и даже непрерывно дифференцируемым при всех конечных значениях ж,
так что интегральная кривая, проходящая через любую точку («о, Уо), будет гладкой
кривой в интервале -оо < х < + оо.

i Глава XXI. Дифференциальные уравнения первого порядка
Пример 6. Проинтегрировать уравнение .
dy
—- +ycosx = 2 cos х. (*)
ах
< Однородное уравнение
dy
— + ycosz~0,
dx
соответствующее данному, проинтегрируем, разделяя переменные:
Уо.о. = Се-*пх.
Решение исходного уравнения будем искать в виде
у = С(х)е-«а*, (**)
где С(х) — неизвестная функция. Находя ^| и подставляя -£ и у в (*), последовательно получаем:
dx dx
<Щ*±€-™* _ с(а.)е-яп* CQSX + c(l)e-sinx CQsx = 2cos«,
dx
dC(x)
dx
C(*) = 2esinx + C,
где С — постоянная интегрирования. Из формулы (**) находим общее решение уравнения (*)
y(x) = y0.H.=Ce-sinx + 2.+
Частное решение уЧшП. = 2 неоднородного уравнения (*) легко усматривается. Вообще, если
удается «угадать» частное решение линейного неоднородного уравнения, то разыскание его общего решения
значительно упрощается.
Пример 7. Рассмотрим дифференциальное уравнение, описывающее изменение силы тока при
замыкании цепи постоянного электрического тока.
< Если R — сопротивление цепи, Е — внешняя ЭДС, то сила тока I = I(t) постепенно возрастает
Е
от значения, равного нулю, до конечного стационарного значения д.
Пусть L — коэффициент самоиндукции цепи, роль которой такова, что при всяком изменении си-
r dl
лы тока в цепи появляется электродвижущая сила, равная L-^ и направленная противоположно
внешней ЭДС. На основании закона Ома, по которому в каждый момент t произведение силы тока на
сопротивление равно фактически действующей ЭДС, получаем
IR = E-Ld±,
ИЛИ
dl R Е
— + -/=- (Я,Ь,Д = const). (*)
Уравнение (*) есть линейное неоднородное уравнение относительно I(t). Нетрудно видеть, что его
частным решением является функция
W0 = §•
Общее, решение соответствующего однородного уравнения
/o.o.(*) = Ce-WL>(,
откуда общее решение неоднородного уравнения (*):
При t = 0 имеем 1(0) = 0, поэтому С = - ^, так что окончательно
'«>=!(
Я/,_е-<вд<у
Отсюда видно, что сила тока при включении асимптотически приближается при t -* +oo к своему
стационарному значению д. ►

§5. Некоторые виды уравнений, интегрируемых в квадратурах 109
Линейное неоднородное дифференциальное уравнение
dv
JL+p(x)y = q(x) (Ю)
может быть проинтегрировано также следующим приемом.
Будем искать решение у(х) уравнения (10) в виде
у(х) = u(x)v(x), (16)
где и(х) и v(x) — неизвестные функции, одна из которых, например v(x), может
быть выбрана произвольно. Подставляя у(х) в форме (16) в уравнение (10), после
элементарных преобразований получим
и • v -f (г/ -f p(x)v)u = q(x). (17)
Выберем в качестве v(x) любое частное решение v(x) ^ 0 уравнения
г/ + p(x)v = 0.
Тогда в силу (17) для и(х) получим уравнение
du
v-=q(x),
которое без труда интегрируется в квадратурах. Зная v(x) и и(х), найдем решение у (х)
уравнения (10).
Пример. Найти общее решение уравнения
2
у + 2ху = хе~х .
< Будем искать решение у(х) данного линейного неоднородного уравнения в виде
y(x) = u(x)-v(x).
Подставляя у = и • v в исходное уравнение, получим
u'v + uv' + 2xuv = хе~х ,
или
u'v + (v' + 2xv)u = xe~* . (17')
Определим функцию v(x) как решение уравнения
v' + 2xv = 0.
Разделяя переменные, найдем
dv __2
— = -2ж dx, v = Се х .
v
Выберем любое частное решение, например, отвечающее С = 1. Тогда из (17') получим
е-х\' = хе-х\
откуда я' = ж, I* = у + С.
Для общего решения исходного уравнения получаем выражение
у(«) = u(x)v(x) = ( у + с) е'х\ ►
Преимущество метода вариации постоянной заключается в том, что он
переносится на линейные неоднородные дифференциальные уравнения высшего порядка.

110.
. Глава XXI. Дифференциальные уравнения первого порядка
5.4. Уравнение Бернулли
Некоторые дифференциальные уравнения дутем замены переменных могут быть
сведены к линейным. К числу таких уравнений относится уравнение Бернулли
dx
+ Р(Х)У = Я(х)уа> а = const •
Уравнение это предложено Я. Бернулли в 1695 г., метод решения опубликовал И.
Бернулли в 1697 г.
При а = 1 получаем однородное линейное уравнение
dy
dx
+ [p(x)-q(x)]y = 0.
При а = 0 — неоднородное линейное уравнение
dy
dx
+ p(x)y = q(x).
Поэтому будем предполагать, что аф0,аф 1 (для а нецелого считаем, что у > 0).
Подстановкой z = y~a+] уравнение Бернулли приводится к линейному уравнению
относительно функции z{x).
Однако уравнение Бернулли можно проинтегрировать сразу методом вариации
постоянной. Это делается так. Сначала интегрируем уравнение
^-+р(х)у = 0.
Его общее решение
y = Ce-Jp{x)dx.
Решение уравнения Бернулли будем искать в виде
3, = Оде"/><*>'*, (♦)
где С(х) — новая неизвестная функция. Подставляя это выражение для у(х) в
уравнение Бернулли, получаем
C'(x) = q(x)(C(x))ae{{-a)fp{x)dx
— уравнение с разделяющимися переменными относительно С(х). Интегрируя это
уравнение, находим
(с(х)у-а = г q{x)e«-a)fpw*dx + C)
1 — a J
где С — постоянная интефирования. Тогда из формулы (*) получаем общий интеграл
уравнения Бернулли
2,'-» = (1 - в)^-')/**)* 17 ф)^'-")/'«d* dx + C
Замечание. При а > 0 уравнение Бернулли имеет очевидное решение у = 0.
Для интефирования уравнения Бернулли
dy
dx
+ р(х)у = q(x)ya

§5. Некоторые «иды уравнений, интегрируемых в квадратурах 111
можно также воспользоваться подстановкой
у(х) = u(x)v(x)y
где в качестве v(x) берется любое нетривиальное решение уравнения
v(x) + p(x)v = 0,
а функция и(х) определяется как решение уравнения
— = q(x)(v(x))a~\x)ua.
у' -ytgx = -y2cosx.
dx
Пример. Найти решение уравнения Бернулли
у'
<4 Ищем решение у(х) уравнения в виде
у(х) = u(x)v(x):
Подставляя у — и • v в исходное уравнение, получим
u'v + tit/ - uv tg x = ~u2v2 cos x,
или
u'v + (t/ — v tg x)u — — и v cos x.
Выберем в качестве v(x) какое-нибудь ненулевое решение уравнения
v' - v tg x — О
и проинтегрируем его,
dv _ sin ж _ С
v cos ж ' cos ж*
Поскольку нас интересует какое угодно частное решение, положим С = 1, т. е. возьмем v = ^^.
Тогда для «(ж) получим уравнение
«' = -«2,
интегрируя которое, найдем
ж + С
Общее решение у(ж) исходного уравнения определится формулой
1
у(х) = «(ж)я(ж) =
5.5. Уравнения в полных дифференциалах
Уравнение
(ж + С) cos ж'
М(ж, у) dx + iV(z, у) dy = 0 (18)
называется уравнением в полных дифференциалах, если левая часть уравнения
представляет собой полный дифференциал некоторой функции и(х> у) двух независимых
переменных х и у, т. е.
М(ж, у) dx + iV(#, у) dj/ = du = —- dx + — dj/.
аж ду
В этом случае и(ж, у) = С будет общим интегралом дифференциального уравнения (18).
Будем предполагать, что функции М(ж, у) и iV(fc, у) имеют непрерывные
частные производные соответственно по у и по х в некоторой односвязной области D
на плоскости хОу.

112
Глава XXI. Дифференциальные уравнения первого порядка
Теорема 4. Для того чтобы левая часть М(х1 у) dx + N(x, у) dy уравнения (18) была
полным дифференциалом некоторой функции и(х, у) двух независимых переменных х и у,
необходимо и достаточно, чтобы выполнялось тождество
ду дх v '
< Необходимость. Предположим, что левая часть уравнения (18) есть полный
дифференциал некоторой функции и(ху у), т. е.
ди ди
М(ху у) dx + N(x, y)dy = du=—dx + — dy,
ox ay
тогда M = ^, N = щ. Дифференцируем первое соотношение по у, а второе по х:
8М д2и 8N д2и
ду дудх' дх дхду
Отсюда, в силу равенства смешанных производных, вытекает тождество
дМ _ dN
~ду = ~дх'
Необходимость (19) доказана.
Достаточность. Покажем, что условие (19) является и достаточным, а именно,
предполагая его выполненным, найдем функцию и(х> у) такую, что du=M(x, у) dx +
N(xy у) dy, или, что то же,
ди ди
— = М(х,у), —=Щх,у). (20)
Найдем сначала функцию и(х, у), удовлетворяющую первому условию (20).
Интегрируя это равенство по х (считаем у постоянной), получаем
и = / М(ж, у) dx + (p(y), (21)
где (р(у) — произвольная функция от у.
Подберем <р{у) так, чтобы частная производная по у от функции и, определяемой
формулой (21), была равна N(xyy). Такой выбор функции (р(у) при условии (19)
всегда возможен. В самом деле, из (21) имеем
dy' = dy'JM{x>y)dx + (p{y)-
Приравняв правую часть полученного равенства к N(x, у), найдем
ip'(у) = N(x, y)~-^J M{x, у) dx. (22)
Левая часть последнего равенства не зависит от х. Убедимся в том, что при условии (20)
в его правую часть также не входит х. Для этого покажем, что частная производная
по а; от правой части (22) тождественно равна нулю. Имеем
• и • /„J™ • г* /„j« • г» tMim
дх [ ду J \ дх дх [ду J J дх ду [дх J

§5. Некоторые виды уравнений, интегрируемых в квадратурах ИЗ
Но
— / М(ху у) dx = М (ж, у)
и, следовательно,
д Г д f 1 dN дМ
-7Г\Я-— I Mdx\=~- — = 0.
Эх [ ду J J дх ду
Теперь, интефируя равенство (22) по у, получим, что
<р{у) = j\^N-^J Mdv^dy + C,
где С — постоянная интефирования. Подставляя найденное значение для <р(у) в
формулу (21), получим искомую функцию
и(хуу)= I Mdx+ J \n- — J Mdx\ dy + Cy
полный дифференциал которой, как нетрудно проверить, равен
du(xy у) = М(х, у) dx + N(xy у) dy. ►
Приведенный прием построения функции и(ху у) составляет метод
интефирования уравнения (18), левая часть которого есть полный дифференциал.
Пример 8. Проверить, что уравнение
e-ydx-(2y + xe-y)dy = 0 (*)
является уравнением в полных дифференциалах, и проинтегрировать его.
4 В данном случае
М = е~у, i\r = -(2y + xe~y).
bJL - _ -у ^L - _ -у
ду - е ' дх " е '
откуда
дМ _ dN
~ду ~ ~дх'
Следовательно, уравнение (*) есть уравнение в полных дифференциалах.
Теперь находим и (см. (21)):
и - J М(х, у) dx + ip(y) = f е~у dx + ip(y),
или
и = хе~у + (р(у). (**)
нивая ^ функции N(x,
хе~у + (р(у) = -2у - хе~у,
Находя ^ от функции и из (**) и приравнивая ^ функции N(x,y) = -2у - хе у, получаем
откуда <р'(у) = -2у и, следовательно,
ч>(у) - -у2 + ci с =const •
Подставив найденное выражение для <р(у) в (**), найдем
и = хе~у -у2 + С.
Таким образом,
хе-у-у2 = С
— общий интеграл исходного уравнения. ►
Иногда можно найти такую функцию (i(x, у), что
fiM dx + fiN dy

1И „ Глава XXI. Дифференциальные уравнении первого порядка
будет полным дифференциалом, хотя М dx + N dy может им и не быть. Такую
функцию ц(х, у) называют интегрирующим множителем.
Можно показать, что для уравнения первого порядка
М(ж, у) dx + N(xy у) dy = 0
при определенныхусловияхна функции М(ж, у) hN(x> у) интегрирующий множитель
всегда существует, но отыскание его из условия
д(иМ) _ d(fiN)
ду "" дх
в общем случае сводится к интегрированию уравнения в частных производных, что
составляет, как правило, задачу еще более трудную.
Задача. Найти интегрирующий множитель для линейного дифференциального уравнения
Указание. Искать множитель в виде ц = р(х).
§6. Уравнение Риккати
Уравнение
I dn ~ I
(О
dy о
— =q(x)+p(x)y + r(x)y ,
где q(x), p(x), r(x) — известные функции, называется уравнением Риккати. Если р,
q,r — постоянные, то оно интегрируется разделением переменных:
/
dV =x + C.
q+py + ry2
В случае, когда г(х) = 0, уравнение (1) оказывается линейным, в случае q(x) = 0 —
уравнением Бернулли. В общем случае уравнение (1) не интегрируется в квадратурах.
Укажем некоторые свойства уравнения Риккати.
Теорема 5. Если известно одно частное решение уравнения Риккати, то его общее решение
может быть получено с помощью квадратур.
< Пусть известно частное решение у = у\ (х) уравнения (1), тогда
у\ (х) = q(x) + р(х)у{ (х) + г(х)у]{х). (2)
Полагая у = у\(х) + z(x), где z(x) — новая искомая функция, в силу тождества (2)
получаем
(р(х) + 2r(x)yl(x))z = r(x)z2
уравнение Бернулли, которое интегрируется в квадратурах. ►
Пример. Проинтегрировать уравнение Риккати
если известно его частное решение
у,-у2 + 2еху = е2х + ех,
У\ =е .

§ & Уравнение Риккати
Ц Полагая
для функции z(x) получаем
откуда
.115
У = е + *,
dz _ 2
С-*'
решением исходного уравнения будет функция
у(х) = ех +
1
(С-*)
Частным случаем уравнения (1) является специальное уравнение Риккати:
^+ау2 = Ъха, х>0,
ах
(3)
где a, b, a — постоянные.
При а = О имеем
и уравнение интефируется разделением переменных.
При а = -2 получаем
do: ж2'
Полагая у = ~, где z — новая неизвестная функция, находим
откуда
1 dz a &
z2 dx z2 х2'
do; Vsc/
Это уравнение однородное относительно xyz. Оно интефируется в квадратурах.
Кроме а = 0иа: = -2 существует еще бесконечное множество других значений а,
при которых уравнение Риккати (3) интефируется в квадратурах. Они задаются
формулой
4k
а ==
-2А: + 1
* = ±1,±2,... .
При всех других значениях а решение уравнения Риккати (3) не выражается в
квадратурах.
Замечание. Если же положить в уравнении (3)
и
где и — и(х) — новая неизвестная функция, то придем к уравнению второго порядка
dx2
- abxau = О,
решение которого может быть выражено в функциях Бесселя.

116
Глава XXI. Дифференциальные уравнения первого порядка
§7. Дифференциальные уравнения,
не разрешенные относительно производной
Рассмотрим теперь общий случай уравнения первого порядка
Щх,у,у,) = 0, (1)
не разрешенного относительно производной.
Уравнения, относящиеся к этому классу, весьма разнообразны, и поэтому в
общем случае становится невозможным делать выводы о существовании и
единственности решения, даже накладывая достаточно сильные офаничения на участвующие
в уравнении функции (ограниченность, гладкость, монотонность и т. п.). Например,
уравнение
у2 + 1 = О
вообще не имеет действительных решений. Для уравнения
va = \
решения суть прямые у = ±х+С, так что через каждую точку плоскости хОу проходят
две взаимно перпендикулярные интегральные линии. Поле интефальных кривых
уравнения у'2 = 1 получается наложением полей уравнений у' = 1 и у1 = -1. Если
уравнение
удается разрешить относительно производной у', то получаются уравнения вида
У =fi(x,y), « = 1,2,... ,
которые иногда могут быть проинтефированы изложенными выше методами.
Введем понятие общего решения (интефала) для уравнения (1). Допустим, что
это уравнение в окрестности точки (жо, У о) может быть разрешено относительно
производной, т. е. распадается на уравнения
У =Л(«,У), « = 1,2,...,т,
и пусть каждое из этих уравнений имеет общее решение
у = <р{(х,С)у г =1,2,..., га, (2)
или общий интефал
Ф<(*,3/,С) = 0, г=1,2,...,га. (3)
Совокупность общих решений (2) (или общих интефалов (3)) будем называть
общим решением (общим интегралом) уравнения (1).
Так, уравнение
распадается на два:
j/ = l, »' = -1.
Их общие решения у = х + С, у — —х + С в совокупности составляют общее решение исходного
уравнения у12 = 1. Общий интеграл этого уравнения часто записывают в виде
(у-х- С)(у + х- С) = 0.
Однако не всегда уравнение (1) легко разрешимо относительно у* и еще реже
полученные после этого уравнения у' =; /,(ж, у) интефируются в квадратурах. Рассмотрим
некоторые методы интефирования уравнения (1).

§7v Дифференциальные уравнения, не разрешенные относительно производной .
1. Пусть уравнение (1) имеет вид
.117
<г(г/) = о,
(4)
причем существует по крайней мере один действительный корень у' = &,- этого
уравнения. Так как это уравнение не содержит х и у, то &,- — постоянная. Интегрируя
уравнение у' = к$, получаем
у = к{Х + С,
или
*,- =
(У-С)
Но ki является корнем уравнения; следовательно,
И-
— интеграл рассматриваемого уравнения.
Например, уравнение
(з/)7-(!/)5 + р'-3 = 0
имеет интеграл
(¥)Ч¥)!^--°-
2. Пусть уравнение (1) имеет вид
ЗГ(у,у') = 0.
(5)
Если это уравнение трудно разрешить относительно у', то бывает целесообразно ввести
параметр t и заменить уравнение (5) двумя:
» = ¥>(*)> »' = *(*)> t0^t^tu
такими,что S*"(у?(£), tp(t)) = 0, £ £ (£<>, *i). Таккак dy = y'dx,то
*« * = *$*,
if № '
откуда
ж= / t^-dt + C.
•I
№
Следовательно, искомые интегральные кривые определяются уравнениями в
параметрической форме
Чтл+« у=т
Пример 1. Проинтегрировать уравнение
у2/3 + (»')2/3 = 1-
4 Полагаем у — cos31, у' = sin31, тогда
dy -3 cos2 J sin J cos2*
dx= —r = Г-Т7 «* = -3 -ГТ7 **•
y' sin31 sur J

118
. Глава XXI. Дифференциальные уравнения первого порадка
Далее находим
/cos t
-7-TT^ = 3« + 3ctg« + C
sinzt
и параметрические уравнения искомых интегральных кривых:
% - ЪЬ + 3ctg* + С,г- у = cos31. ►
Если уравнение (5) легко разрешимо относительно у, то обычно за параметр
берут у'. Действительно, если у = <р(у'), то, полагая у' = р, получаем у = у>(р), так
что
Же = — = dp,
У* V
откуда
Параметрические уравнения интегральных кривых:
<р'(р)
= J*JEldP + c, у = ф).
Исключая параметр р, получаем общий интеграл
Ф(а:,з/,С) = 0
уравнения (5).
Пример 2. Проинтегрировать уравнение
4 Разрешим уравнение относительно у:
1-у
#.-*--
У1 2(р-1р/2'
1 +с.
Положим у' =р, тогда
Далее имеем:
/Р-
Таким образом, находим параметрические уравнения интегральных кривых
Параметр р здесь легко исключить. В самом деле, из первого уравнения системы находим
Первую часть второго уравнения преобразуем следующим образом:
2-р I р-1 1 г—
откуда
,= vh~^
у = -т=т -\/р-1=х-С-
VP~ 1 v ж-С
— общее решение данного дифференциального уравнения. ►

§ 7, Дифференциальные уравнения, не разрешенные относительно производной 119
3. Пусть уравнение (1) имеет вид
Щх>У') = 0.\ (6)
Если это уравнение трудно разрешить относительно у', то, как и в предыдущем случае,
целесообразно ввести параметр t и заменить уравнение (6) двумя:
x = <p(t), y' = i>{t\ t0^t^U.
тогда
dy = y'dx = i>(t)<p'(t) dt, y= f tp{t)(p'(t) dt + C. ^
Следовательно, интефальные кривые уравнения (6) определяются в параметрической
форме уравнениями
x = <p(t), y = J\l>(t)4>\t)dt + C.
Если уравнение (6) легко разрешимо относительно х:
* = (р(у)у
то в качестве параметра удобно выбрать у' = р. Тогда х = <р(р), dy = y'dx = p<p'(p) dp,
откуда
У = / V4>ip) dp + С.
Пример 3. Решить уравнение
<4 Положим у' = р. Тогда
Далее имеем:
х = (у'?-у'-\.
х = р3-р-1.
4 2
dy = y'dx = p(3p2-l)dp, у = 3^--^- + С.
В параметрической форме семейство интегральных кривых данного уравнения определяют уравнения
з / Р2
4. Уравнение Лагранжа. Уравнением Лагранжа называется дифференциальное уравнение
вида
» = *¥>(»')+ ^(»')э (?)
линейное относительно хиу. Здесь <p,i> — известные функции.
Введя параметр gj = p, получаем
3/ = яу?(р) + <ф(р) (8)
— соотношение, связывающее переменные х, у и параметр р. Чтобы получить второе
соотношение, нужное для определения хиу как функций параметра р,
продифференцируем (8) по ж:
/ ч t, х dp , dp
р = у?(р) + Х(р (р) — + i> (р) —,
откуда
p-p(p)=[V(p)+v'(p)]£, (9)

120 Глава XXI. Дифференциальные уравнения первого порядка
или
dx
[р ~ <р(р)] ^ = xip'ip) + *>'(р). (Ю)
Уравнение (10) линейно относительно х и 0 и, следовательно, легко
интегрируется, например, методом вариации постоянной. Получив общее решение
х = ш(ру С)
уравнения (10) и присоединив к нему уравнение
У = х<р(р) + ^(р)>
получим параметрические уравнения искомых интегральных кривых.
При переходе от уравнения (9) к (10) пришлось делить на ^. При этом теряются
решения, для которых р постоянно, а значит,
^ = о.
dx
Считая р постоянным, замечаем, что уравнение (9) удовлетворяется лишь в том случае,
если р является корнем уравнения
v - <р(р) = о.
Итак, если уравнение р-<р(р) = 0 имеет действительные корни р = р,, то к найденным
выше решениям уравнения Лагранжа надо еще добавить решения
у = х(р(р) + <ф{р),
(у = х<р{
\р = Ри
или
у = х(р(р{) + tyipi)
— это прямые линии.
5. Уравнение Клеро. Уравнением Клеро называется дифференциальное уравнение вида
у = *V+ «(•). (И)
Полагая у' = р, получаем
у = хр + <ф{р).
Дифференцируя по ж, имеем
dp dp
P = V + Xlfa+^^~dx~'
или
откуда или ^ = 0 и, значит, р = С, или
х + i/>'(p) = 0.
В первом случае, исключая р, найдем семейство прямых
у = Сх + i>(C)

§7. Дифференциальные уравнения, не разрешенные относительно производной . 121
— общее решение уравнения Клеро. Оно находится без квадратур и представляет собой
однопараметрическое семейство прямых. Во втором случае решение определяется
уравнениями
2/ = жр + ^(р), ж = -^'(р). (12)
Можно показать, что, как правило, интегральная кривая (12) является огибающей
найденного семейства прямых.
Пример 4. Решить уравнение Клеро
<4 Общее решение данного уравнения видно сразу:
у-Сх- С2.
Другое (особое) решение определяется уравнениями
-.2
у = хр-р, х-.
Исключая параметр р, находим
х2
:2Р.
Рис.7
— огибающую прямых у = Сх-С2 (рис.7). ►
Для уравнения вида
ЗГ(я,2/,2/') = 0
через некоторую точку (жп, уо), вообще говоря, проходит не одна, а несколько
интегральных кривых, так как, разрешая уравнение ^(ж, у, у') = О относительно у\ мы,
как правило, получаем не одно, а несколько действительных значений
У = /»(я> 2/), t = l,2,...,m,
и если каждое из уравнений у1 = /, (ж, у) в окрестности точки (ж0, уо) удовлетворяет
условиям теоремы существования и единственности решения, то для каждого из этих
уравнений найдется единственное решение, удовлетворяющее условию
у(хо) = Уо-
Поэтому свойство единственности решения уравнения ^"(ж, уу у') = 0,
удовлетворяющего условию у(ж0) = уо, обычно понимается в том смысле, что через данную
точку (жо, Уо) по данному направлению проходит не более одной интефальной кривой
уравнения ^~(ж, у, у') = 0.
Например, для решений уравнения
»'2-1 = 0
свойство единственности в этом смысле всюду выполнено, поскольку через каждую точку (х0, уо)
плоскости хОу проходят две интегральные кривые, но по различным направлениям. Для уравнения Клеро
у = ху' - у2
(см. пример 4) через точку (0,0) проходят также две интегральные линии: прямая
У = 0,
входящая в общее решение этого уравнения, и парабола
г2
У-
х
Т'
причем эти линии имеют в точке (0,0) одно и то же направление:
У' = о.
Таким образом, в точке (0,0) свойство единственности нарушается.

Глава XXI. Дифференциальные уравнения первого порядка
Теорема 6. Пусть имеем уравнение
Щх,у,у') = 0
и пусть в некоторой окрестности точки (xq, 2/о> Уо), где у'0 — один из действительных
корней уравнения
@~(хо, 2/о, у') = 0,
функция ^"(ж, у, у') удовлетворяет условиям:
1) ^"(ж, у, у') непрерывна по всем аргументам;
2) производная -щг существует и отлична от нуля;
3) существует ограниченная производная Щ-:
двг
<N.
ду
Тогда найдется отрезок [xq - Л0, жо + ho], на котором существует единственное
решение у = у(х) уравнения ^"(ж, у, у') = 0, удовлетворяющее условию у(хо) = уо,
для которого у'(хо) = уг0.
§8. Геометрические вопросы, связанные
с дифференциальными уравнениями 1-го порядка.
Ортогональные траектории
Общее решение у = ^>(ж, С) дифференциального уравнения 1-го порядка определяет
семейство плоских кривых, зависящее от одного параметра С.
Поставим теперь в некотором смысле обратную задачу: дано однопараметрическое
семейство кривых
у = tp(x, С),
и требуется составить дифференциальное уравнение, для которого у — tp(x, С) будет
общим решением.
Итак, пусть дано соотношение
у = <р(х1С)1 (1)
где С — параметр. Дифференцируя (1) по ж, получим
у' = <р'х(х,С). (2)
Если правая часть (2) уже не содержит С, то формула (2) будет представлять
дифференциальное уравнение семейства кривых (1). Например, если у = ж + С, то у' = 1
будет дифференциальным уравнением семейства прямых у = х + С.
Пусть теперь правая часть (2) содержит С. Разрешая соотношение (1)
относительно С, определим С как функцию ж и у:
С = #*,»). (3)
Подставляя это выражение для С в формулу (2), получим дифференциальное
уравнение 1-го порядка
y' = <p'(x,1>(x,y)). (4)

§8, Геометрические вопросы, связанные с дифференциальными уравнениями 1-го порядка 123
Нетрудно убедиться в том, что у = у>(ж, С) представляет собой общее решение
уравнения (4).
Если соотношение между величинами х,у и С задано в виде
Ф(х,у,С) = 0, (5)
то, дифференцируя его по ж, получим
Ф; + Ф;У=0. (6)
Исключая С из соотношений (5) и (6), приходим к уравнению
&-(х,у,у') = 0. (7)
Можно показать, что (5) является общим интегралом уравнения (7).
Ортогональные траектории
В ряде прикладных вопросов встречается следующая задача. Дано семейство кривых
Ф(ж,г/,С) = 0.
Требуется найти такое семейство
Ф(ж,у,С) = 0,
чтобы каждая кривая семейства Ф(ж, у, С) — О, про- у к
ходящая через точку (ж,у), пересекалась в этой I
точке кривой семейства Ф(ж, у} С) = О под пря- I
мым углом, т. е. чтобы касательные к кривым се- I
мейства Ф = 0иФ = 0в точке (ж, у) были
ортогональны (рис.8). Семейство Ф(ж,у,С) = О
называется семейством ортогональных траекторий
к Ф(ж, у, С) = О (и наоборот). Если, например,
кривые семейства Ф = 0 — силовые линии
некоторого силового поля, то ортогональные траектории —
эквипотенциальные линии. I
Аналитически это означает следующее. Если °\
&Г(х,у1у') = 0
есть дифференциальное уравнение семейства
Ф(ж,у,С) = 0,
тодифференциальноеуравнениетраекторий,ортогональныхксемействуФ = 0, имеет
вид
к('-'--?)-81
(угловые коэффициенты касательных к кривым семейств Ф = 0иФ = 0в каждой
точке должны быть связаны условием ортогональности к\ • &2 = -1 )•
Таким образом, чтобы найти ортогональные траектории к семейству Ф(ж, у, С) =
О, надо составить дифференциальное уравнение ^"(ж, у, у') = О этого семейства и
заменить в нем у' на (-Л). Интегрируя полученное таким образом уравнение, найдем
семейство ортогональных траекторий.

124.
. Глава XXI. Дифференциальные уравнения первого поридаа
Пример. Найти ортогональные траектории семейства
х2 + у2 = С2 (8)
окружностей с центром в начале координат.
< Составляем дифференциальное уравнение
семейства (8). Дифференцируя (8) по х, получим
2х + 2уу = О,
или
х + уу = О,
откуда
Это дифференциальное уравнение данного семейства.
Заменив в нем у' на (-^г)> найдем дифференциальное
уравнение семейства ортогональных траекторий:
1 х
У
У
У
Рис.9
Интегрируя последнее уравнение, получаем, что искомыми ортогональными траекториями будут
полупрямые (рис. 9)
у = Сх (хфО),
х = О (у ф 0). ►
Упражнения
Методом изоклин постройте кривые дифференциальных уравнений:
\.\f = х + у. 2. s/ = (у - 1)ж.
3. Методом последовательных приближений решите задачу Коши:
у' = 2ху, у(0) = 1.
Проинтегрируйте дифференциальные уравнения:
4.2xydy + (\+y2)dx = 0.
6.*^=у + *еу/ж, у(1) = 1п2.
ах
5. eysin xdx + cos xdy = 0.
y-x-4
Ю.у -yctgx = 2xsinx1 yl-J = \.
2x-y2
U.xyy' = 2y2-3x2.
\b.x2yy' + y2x=\.
18. (y2 + —1^-) dx + (2xy+tgx)dy = 0.
\ COS X /
7.xy' = y + y/y2-x2.
9.y' + 2xy = xe~x .
U.x2y' + 2xy = ex, y(l) = L
13. xy' + y = y2kix.
\b.(xy + x2y*)dy = dx.
17.(2x-l-J)dx-(2!,-i)dy=0.
19.2у = гу' + у'1пу'.
20. Найдите ортогональные траектории семейства гипербол
(а — числовой параметр).
2 2 2
х -у =а

§8. Геометрические вопросы, связанные с дифференциальными уравнениями 1-го порядка 125
Ответы
1. Рис.10. 2. Рис.11. 3. у = ех\ 4. х(1 + у2) = С. 5. tgs - х - ^ = С. 6. е~у/х =
In f. 7. С*2 = у + v/y2~=rSI. 8. ж2 + 2*у - у2 - 4х + 8у = С. 9. у = (^ + с)е'х2.
10.y=jWl-£)sin*. Il.y^b^l. Ц« = Се*+4 + ! + $. 13.у=^1^.
14. VlFTi7 = Сх\ 15. х = CeV/2+y2_2. 16. у2 = ^. 17. х2 - х + J - у2 = С.
, f ж =Ср-1пр-2;
18. sy2 + y tg« = С. 19. < =с£_ 20. жу = С.
Рис.10 ' Рис. И

Глава XXII
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
ВЫСШИХ ПОРЯДКОВ
§1. Задача Коши
Пусть имеем дифференциальное уравнение n-го порядка, разрешенное относительно
старшей производной у^:
y{n) = f(x>y,y'>...,y(n-l)).
(1)
Возникает вопрос: какие надо задать условия, чтобы выделить определенное, частное
решение уравнения (1)? Для дифференциального уравнения первого порядка
У = /(», у)
достаточно задать значение уо частного решения при каком-то значении жо
независимой переменной ж, т.е. задать точку (жо,уо)> через которую должна проходить
интефальная кривая этого уравнения. Для уравнений высшего порядка этого уже
недостаточно. Например, уравнение
у" = о
имеет решениями функции
2/ = С,ж + С2,
где С\, Ci — произвольные постоянные. Уравнение
у = Схх + С2
определяет двухпараметрическое семейство прямых на плоскости хОу, и, чтобы
выделить определенную прямую, мало задать точку (ж0, уо), через которую прямая должна
проходить, — надо еще задать угловой коэффициент прямой
В общем случае дифференциального уравнения n-го порядка (1) для выделения
частного решения надо задать п условий:
4=*„ = иь y'L, =2/о, ..., у{п:\=х=у(Г1)
X=XQ
X=XQ
X=XQ
(2)
где уо, 2/о> • • •»У о — некоторые числа. Совокупность этих условий называется
начальными условиями для дифференциального уравнения (1). Задача Коши для этого

§1. Задача Коши
127
Рие.1
уравнения ставится так: найти решение дифференциального уравнения (1),
удовлетворяющее заданным начальным условиям (2). \
Сформулируем теорему существования и единственности решения задачи Коши.
Теорема 1 (существования и единственное™ решения задачи Коши),
ПутьшлёёмШффёренцйаАьное уравнение п-го порядка,
разрешенное относительно старшей производной,
У{п) = /(х,У,У,...,У(п-1)).
Если правая часть этого уравнения непрерывна как
функция п + 1 аргументов ж, у, у1]..., у^п~ ^ в некоторой
окрестности Q точки Мо(ж0, уо, Уо> • • > Уо ) (на Рис- * ДЯЯ
п = 2), то найдется интервал Xq - ho < х < Хо + ho
оси Ох, на котором существует по крайней мере одно ре-
шение у = <р(х) уравнения (I), удовлетворяющее начальным
условиям
Если, кроме того, функция /(ж, у, у\ ..., у^п~1^) имеет ограниченные частные
производные з£, ^7,..., ^ф^' в указанной окрестности О, то такое решение единственно.
Так, для уравнения
2
у" = е"х у -f sin у'
правая часть
/ = e~z y + sin у',
рассматриваемая как функция трех независимых переменных х,у, у', непрерывна всюду и имеет
ограниченные всюду производные
Of -,2 Of
тГе , ^=cosy.
Поэтому, какова бы ни была тройка чисел (х(ьУ<ьУо)> существует единственное решение этого
уравнения, удовлетворяющее начальным условиям
\X=XQ \X-XQ
Определение. Общим решением дифференциального уравнения n-го порядка
y{n) = f(x,y,y',...,y{n-l))
в некоторой области ft существования и единственности решения задачи^Соши^назы^
вается п-параметрическое семейство S функций у = ip(x, Сь С2>..., Сп), зависящих
от х и п произвольных постоянных С], С2,..., Сп, такое, что:
1) при любых допустимых значениях постоянных Сь С2,..., Сп функция
y = <p(x,CuC2,...,Cn)eS
является решением дифференциального уравнения (1), т. е.
<р{п)(х, Си Съ ..., Сп) = f(x, ф, Си С2,..., Сп),..., <р{п~1)(х, Си С2,..., С»)),
ж € (х0 - Л, ж0 + h);

t28 Глава XXII. Дифференциальные уравнения высших порядков
2) каковы бы ни были начальные условия
v\ass90 = 2/о, У'\Х=Х0 = 2/0, • • • , У(П~Х=Х0 = 2/01"0
(лишь бы точка (а?о, 2fo, 2/о> • • •, Уо ) принадлежала области Q существования и
единственности решения задачи Коши для уравнения (1)), можно так подобрать значения
Ci^C^..., CjJ постоянных, чтобы решение
удовлетворяло заданным начальным условиям.
Решение, получаемое из общего при конкретных значениях постоянных С\, Сг,...,
Сп, называется частным решением. Его график — кривую на плоскости хОу —
называют интегральной кривой данного дифференциального уравнения.
Соотношение Ф(ж, у, Ci, Сг,..., Сп) = 0, неявно определяющее общее решение,
называют общим интегралом дифференциального уравнения (1).
Задача. Показать, что функция
у = С\ cos х + Ci sin x
является общим решением уравнения
/
§2. Уравнения высших порядков,
допускающие понижение порядка
1. Уравнение вида
у{п) = /Ш (О
где f(x) — известная непрерывная функция, интегрируется в квадратурах. Учитывая,
что у^ = (у^п~^) , и интегрируя по х левую и правую части уравнения, получаем
У("~° = ff(x)dx + Cu
т. е. приходим к уравнению такого же вида, что и исходное; далее находим
у(п-2) = fff f(x) dx) dx + Cxx + C2.
Через п шагов получим общее решение уравнения (1):
y(x) = J
Пример 1.
[(... f f(x)dx..A dx
Найти общее решение уравнения
/ = 2х.
• +с„.\
Ч Последовательно интегрируя дважды, получаем искомое общее решение
у' = f 2xdx = х2 + Си у = у + Схх + С2. ►

§2. Уравнения высших порядков, допускающие понижение порядка.
.129
2. Бели уравнение не содержит искомой функции и ее производных до порядка к - \
включительно, т. е. имеет вид
^(*,y(*W*+,),...,y(n))=o,
(2)
то порядок уравнения может быть снижен до порядка п-к заменой у^ = р(х). После
такой замены уравнение принимает вид
^(а^,...,р<п-*>)=0.
Пусть удалось проинтегрировать полученное уравнение:
р = ф(я?>СьС2,...,С„-к).
Замечая, что р = у^(х), приходим к уравнению
/> = Ф(х,СьС2,...,Сп.|Ь),
из которого у(х) находится fc-кратным интегрированием.
Пример 2. Найти общее решение уравнения
= 0.
<4 Положим у" = р(х), тогда
и данное уравнение примет вид
У'"=р'(х)
dx х
Разделяя переменные в последнем уравнении, найдем р = С\х, или
у" = Схх,
откуда легко получаем общее решение исходного уравнения:
С\ з
у = — ж + С2х + С3. ►
о
3. Пусть дифференциальное уравнение не содержит явно независимой переменной х,
т. е. имеет вид
F(y,y',...,y^)=0.
(3)
Порядок этого уравнения можно понизить на единицу подстановкой у' = р(у), где р =
р(у) рассматривается как новая неизвестная функция, а у принимается за независимую
переменную. В этом случае все производные £j£, к = 1, 2,..., п, надо выразить через
производные от функции р по у:
djy
dx2
da;3
_ j^ /dy \ _ d_ dy _ dp
dx\dx) dymy}> dx P dy'
~ dx \dx2) ~ dy \P dy) dx~P \dv) +P
ld*P
dy2
и т.д.
5 Зак. 179

130 Глава XXII. Дифференциальные уравнения высших порядков
Мы видим, что любая производная £f, к = 1,2,..., п, выражается через
производные от р по у порядка не выше к -1, что приводит к понижению порядка уравнения
на единицу.
Пример 3. Проинтегрировать уравнение
»»" + (у')2 = о. (*)
■4 Положим у' =р(у), тогда
У Pdy
и данное уравнение принимает вид
dV 2 Л
УР-+Р =0.
Сокращая на р, р Ф 0, и разделяя переменные, найдем
откуда
или
Случай р — 0 дает решение
У2 ~
у = y/Cix + C2. (**)
содержащееся в (**). ►
Всегда следует посмотреть, не является ли левая часть данного уравнения полным
дифференциалом некоторого выражения. Так, уравнение (*) можно переписать в виде
£(уу') = о,
откуда находим:
Часто встречающееся уравнение
у" = /(у)
можно легко проинтефировать в квадратурах, если умножить обе его части на у'
(проделайте это!).
Замечание 1. Рассмотрим уравнение второго порядка
y"+Pi(x)y' + P2(s)y = 0, (4)
линейное относительно искомой функции у(х) и ее производных у' и у". Положим
у(х) = и(х) ф), (5)
где ф) , ф) — новые функции, из которых одну мы можем выбирать произвольно. Подставляя у(х)
в форме (5) в исходное уравнение (4), для функции и(х) получаем уравнение
и + l2-+piJu+( — ]« = 0. (6)
Если известно одно решение у\(х) £ 0 исходного уравнения (4), то можно взять v = У\(х). В
уравнении (6) тогда исчезнет слагаемое, содержащее функцию и(х) (если v = у\ (х), то
v" +pxv' + p2v = 0,

§2. Уравнения высших порядков, допускающие понижение порядка 131
так как, по предположению, у\ (х) — решение уравнения (4)). Уравнение (6) примет тогда вид
U" + (2^+PlW = 0
и легко интегрируется. В результате мы найдем общее решение исходного уравнения (4).
Если положить
»(*) = е-5/"<*>*, (7)
то в уравнении (6) исчезнет слагаемое с первой производной, и уравнение примет вид
и" + q(x) и = 0.
Такое преобразование полезно для качественного анализа уравнения и при использовании
приближенных методов решения.
Рассмотрим, например, дифференциальное уравнение Бесселя
х2у" + ху' + (х2 -и2) у = 0, v — числовой параметр, (8)
(его решения — функции Бесселя — играют важную роль во многих задачах физики); представим его
в виде
' /- + i-/+(i-5)»-a.
Здесь р\ (х) — -, так что в силу (7) имеем
_' rtl _'
v(x) = е 5J » =j 2, х>0.
Полагая у(х) = x~lt2u(x), получаем для и(х) уравнение
«"+(i-^i)u=o,
весьма удобное для изучения поведения функций Бесселя при больших значениях х.
Замечание 2. При решении задачи Коши для уравнений высших порядков бывает целесообразно
определять значения постоянных С,- в процессе решения, а не после нахождения общего решения
уравнения. Это связано с тем, что интегрирование порой значительно упрощается, когда постоянные С,
принимают конкретные числовые значения, в то время как при произвольных С,- интегрирование
затруднительно, а то и вообще невозможно в элементарных функциях.
Рассмотрим, например, следующую задачу Коши:
У" = 2у\ yU=o = I, •l,-o = l.
Полагая у' = р(у), получаем
р -£. = 2у »
откуда р2 =у* + С\, или
Разделяя переменные, найдем
x + C2 = j(yA + CxTxl2dy.
В правой части последнего равенства имеем интеграл от дифференциального бинома. Здесь т = 0,
п = 4, р = — j, так что этот интеграл не выражается в виде конечной комбинации элементарных
функций. Однако если использовать начальные условия, то С\ =0. Это сразу дает
dx у '
откуда, учитывая начальные условия, находим
У-
(1-х)

132 Глава XXII. Дифференциальные уравнения высших порядков
Задача. Найти два решения задачи Коши для уравнения
с начальными условиями у(0) — у'(0) = 0. Не противоречит ли этот факт теореме существования
и единственности решения задачи Коши?
§3. Линейные однородные
дифференциальные уравнения n-го порядка
Линейным дифференциальным уравнением п-го порядка называется уравнение, линейное
относительно неизвестной функции и всех ее производных. Оно имеет вид
а0(х)у(п) + а, (х)у{п 1) + ... + ап(х)у = д(х),
где ао(ж), а\(х),..., ап(х), д(х) — заданные на некотором интервале (a, f$) функции.
Если д(х) = 0 на этом интервале, то уравнение называется линейным однородным,
в противном случае уравнение называется неоднородным.
Пусть имеем линейное однородное дифференциальное уравнение
ao(x)yin) + ax(x)yln'l) + ...+ ап(х)у = 0.
Если ао(х) Ф 0 на некотором интервале, то разделив все члены данного уравнения
на коэффициент а^(х), получим
У{п) +Pi(x)yin-l) + ... +Рп(х)у = 0, (1)
или
»W = -Pi(e)»(""!)-... -Рп(х)у.\ (2)
Если коэффициенты Рк(х)9 к = 1, 2,..., п, уравнения (1) непрерывны на отрезке
[а, ft], то правая часть уравнения (2) непрерывна по х, а ^ х ^ ft, и по j/, у\ ..., у^п~1^
для любых значений у, у\ ..., у^п~1^ и, кроме того, имеет частные производные по у^к\
равные -pn-k(x), ограниченные на [a, ft]. Поэтому в силу теоремы 1 получаем:
если коэффициенты pk(x), k= 1,2,..., п, уравнения (1) непрерывнына [a, ft], то, каковы
бы ни были начальные условия
I i\ i («-1)1 («-О
3/|Ж==Ж0= З/о, 2/|ж=Жо=2/о, .-., Ук 'U*0=2/o ',
х0 е (а, ft), -оо < уР < +оо, к = О,1,..., п - 1,
существует единственное решение уравнения (1), удовлетворяющее этим начальным
условиям.

§3. Линейные однородные дифференциальные уравнения n-го порядка
133
Напомним следующее понятие. Говорят, что на множестве Е задан оператор Л
со значениями в множестве F, если каждому элементу у Е Е по некоторому закону
поставлен в соответствие определенный элемент/ = Лу Е F. Множество 2? называют
областью определения оператора Л.
Пусть Е — линейное пространство. Оператор Л, заданный на Е, называется
линейным, если он аддитивен и однороден, т. е.
1) А{У\ + у2) = Лу\ + Ау2, Vj/j , Vj/2 Е E\
2) А(ау) = аЛу Vy Е E, Va, где а — число.
Представим линейное однородное уравнение (1) в виде
1^Ы = 0,|
где
1 С[у] = у{п) +Мх)у{п-1) + ... +Рп(х)у. |
Нетрудно видеть, что С есть линейный дифференциальный оператор,
определенный на линейном пространстве функций у(х), непрерывных на интервале (a, b)%
вместе со всеми производными до n-го порядка включительно. Дифференциальный
характер оператора очевиден. Покажем его линейность, т. е. что
1)£[У1+У2] = £[у\] + £[У2];
2) С[Су] = СС[у], где С — постоянная.
< Имеем
С[у\ + у2] = (l/i + 2/2)(n) + P\ (x)(yi + у2){п~1) + • • • + Рп(х)(у{ + у2) =
= ЫП^Р1(^п-,) + ...+рп(о:)2/1) +
+ (i4")+pi(*)i4""1)+--- +*.<*)»)=*ы+4»]
и
£[Су] = (Су)(п) + Р1(*)(Сз,)(п-'> +... +р„(х)Су =
= С(у(п) +р,(х)у(п-,> +... +р„(х)у) = С£[у]. ►
Как следствие получаем
С
т
= ^Р C{C[yi], где С,- — постоянные.
»=i 1
Установим некоторые свойства решений линейного однородного уравнения.
Теорема 2. Если функция уо(х) является решением линейного однородного
дифференциального уравнения
С[у] = о,
то функция Суо(х), где С — произвольная постоянная, тоже является решением этого
уравнения.

134 Глава XXII. Дифференциальные уравнения высших порядков
<4 По условию,
С[уо] = 0.
Надо доказать, что
С[Суо] = 0.
Пользуясь свойством однородности оператора С[у], имеем
С[Су0] = СС[у0] = 0.
Это означает, что функция Су0(х) есть решение уравнения С[у] = 0. ►
Теорема 3. Если функции у\(х) и уг{я) являются решениями линейного однородного
уравнения
то сумма функций у\(х) + У2(х) тоже является решением этого уравнения.
<4 По условию, С[у\] = 0 и С[у2] = 0. Надо доказать, что
Последнее сразу вытекает из свойства аддитивности оператора С[у]:
Следствие. Линейная комбинация с произвольными постоянными коэффициентами
т
решений у\(х), уг(х),..., ут(х) линейного однородного дифференциального уравнения
С[у] = 0
является решением того же уравнения.
Линейное однородное дифференциальное уравнение С[у] = 0 всегда имеет
тривиальное решение у = 0. Изтеорем2иЗ получаем: совокупность решений линейного
однородного дифференциального уравнения С[у] = 0 образует линейное
пространство, нулем которого является функция у = 0.
Теорема 4. Если линейное однородное уравнение
£[у] = 0
с действительными коэффициентами pk(x), к = 1,2,..., п, имеет комплексное решение
у(х) = u(x) + iv(x)}
то действительная часть этого решения и(х) и его мнимая часть v(x) в отдельности
являются решениями того же однородного уравнения.

$4. Линейно зависимые и линейно независимые системы функций
135
< Дано, что
С[и + iv] = 0.
Надо доказать, что
С[и] = 0 и C[v] = 0.
Пользуясь свойствами линейности оператора С, получаем
С[и + iv] = С[и] + iC[v] = 0.
Отсюда следует, что £[м] = 0 и C[v] = 0, так как комплекснозначная функция
действительного аргумента обращается тождественно в нуль тогда и только тогда, когда
ее действительная и мнимая части тождественно равны нулю. ►
§4. Линейно зависимые и линейно независимые
системы функций
Пусть имеем систему функций у\(х),у2(х),...,уп(х), определенных на некотором
интервале (a, ft).
Определение. Будем говорить, что система функций у\(х), у2(х),..., уп(я) линейно
зависима на интервале а < х < ft, если существуют постоянные ai, а2,..., ап такие, что
на этом интервале выполняется тождество по х:
<*\У\(х) + а2у2(х) + ... + апуп(х) = 0,
причем хотя бы одно из чисел а,- отлично от нуля.
Если это тождество имеет место только при а\ = а2 = ... = а„ = 0, то семейство
функций у\ (х)у У2(х),..., уп(х) называется линейно независимым на интервале (a, ft).
Рассмотрим примеры линейно зависимых и линейно независимых систем
функций.
1. Функции
У\(х) = х и уг(х) = 2х
линейно зависимы на любом интервале (а, Ъ), так как имеет место, например, тождество
2у\ -У2 = 2х-2х = 0,
где ot\ =2, ai = — 1.
2. Функции
1, «, х\ ..., хп
линейно независимы на любом интервале (а, Ъ), так как тождество
a0-l + aia; + ... +апжл = 0, ж € (а,6),
возможно лишь в случае, если а,- = 0, i = 0,1,2,..., п.
<4 Если хоть одно из чисел а, было бы отлично от нуля, то в левой части тождества стоял бы многочлен
степени не выше п, который может иметь не более п различных корней и, следовательно, обращается
в нуль не более чем в п точках рассматриваемого интервала. ►
3. Функции
к\х *2* р*»*
где ki Ф kj при t Ф j, линейно независимы на любом интервале (a, b).
4 Для простоты ограничимся случаем п = 3. Допустим, что функции е*1*, е*2Х, е*3* являются линейно
зависимыми. Тогда имеет место тождество
a,e*,x + a2e*2X+a3<?M=0,

136.
. Глава XXII. Дифференциальные уравнения высших порядков
причем хотя бы одно из а,- не равно нулю. Пусть для определенности аз ф 0. Разделив тождество
на е*|Х и продифференцировав, получим тождество
а2(к2 - *,)е<*2-*,)ж + а3(*3 - *i)e(*3-*,)a: = 0,
деля которое на е
(k2-ki)x
и дифференцируя результат по х, найдем
аз(*з-Л1)(Лз-*2)е(*3"*2)ж=0,
что невозможно, так как аз ф 0 по предположению и &,- Ф kj при t Ф j. Значит, наше допущение
неверно, и рассматриваемые функции являются линейно независимыми. ►
Замечание. Линейная зависимость пары функций означает, что одна из функций получается из другой
умножением на постоянную:
у2(х) = Ру\ (ж), р = const.
Вообще, если функции у\(х), у2(х), • • • >Уп(х) линейно зависимы на (а, 6), то по крайней мере
одна из них есть линейная комбинация остальных.
Задача. Показать, что если система функций
У\(х),у2(х),...,уп(х)
линейно независима на интервале (о, Ь), то и любая подсистема этой системы функций также линейно
независима на (а, 6).
Теорема 5 (необходимое условие линейной зависимости функций). Если функции
У\(х),У2(х)у...,Уп(х),
имеющие производные до порядка п - 1 включительно, Линейно зависимы на интервале
(а, ft), то на этом интервале определитель
У\(х) у2(х) ... уп(х)
У\(х) у'2(х) ... Уп(х)
W(x) =
>-о
,("-1)7
»Г"<*) уГ'(*)
й"'-в|)й
называемый определителем Вронского системы функций у\(х), г/2(я), • • •, уп(х),
тождественно равен нулю:
W(x) = 0 на (а, ft).
<4 Ограничимся случаем п = 3. Пусть дважды дифференцируемые функции у\(х),
у2(х), Уз(х) линейно зависимы на интервале (a, ft). Значит, на (a, ft) выполняется
тождество
«i2/i (х) + а2у2(х) + а3у3(х) = 0,
причем не все числа щ (г = 1,2,3) равны нулю. Для определенности будем считать,
что ai Ф 0. Разрешим тождество относительно у\(х) и дважды продифференцируем
его:
У\(х) = —- уг{х) - — уз(х),
«1 «1
а2
<*з
а2
<*з
У\(х) = -=i у'2(х) - ^ 4(х), У'1{х) = -=i rf(x) - ^ rf(x).
Составим определитель Вронского системы функций у\ (ж), Уг(х), у$(х):
I У\{х) уг(х) у3(х)
W(x) = \y\(x) у'2(х) у',(х)
\у"(х) У"(х) уЧ(х)
(1)
(2)

§4. Линейно зависимые и линейно независимые системы функций.
или, с учетом формул (1) и (2),
.137
W(x) =
У2(х) - — УЗ(х) у2(х) Уъ{х)
CL\ OL\
—- Уг{х) - — Уъ(х) y'i{x) у'ъ{х)
а2
а3
1 it/ \ 3 "/ \ и/ \ и/ \
У2(х) 2/з (х) У2(х) Уз(х)
Первый столбец определителя является линейной комбинацией двух других при любом
х Е (а,Ь). Такой определитель, как известно, равен нулю; следовательно, W(x) = О
Рассуждением от противного легко доказывается следующая теорема.
Теорема 6. Если определитель Вронского W(x) системы п функций неравен тождественно
нулю в некотором интервале (a, b), то эти функции линейно независимы в этом
интервале.
Для произвольной системы п - 1 раз
дифференцируемых на (а, Ь) функций теорема, обратная теореме 5,
неверна. Чтобы убедиться в этом, рассмотрим пример.
Для функций (рис. 2)
U
-1<ж<0,
0<ж< 1,
-1<ж<0,
определитель Вронского на интервале (-1,1) тождественно равен нулю:
W[x) = \*) Щ
v ' \Ч>\ 4>г\
х2
2х
0
0
0
0
*2|
2х\
= 0, -1<ж<0,
= 0, 0<г<1.
Однако, как легко видеть, функции <р\(х) и <рг(х) на интервале (-1,1) линейно независимы. Заметим,
что в интервалах (-1,0) и (0,1) функции <р\(х) и <рг(х) уже линейно зависимы.
Можно несколько обобщить рассмотренный пример, взяв систему функций
ж<0,
О о.
ж<0,
х>0.
(тп > 1, целое).
Эти функции линейно независимы в любом интервале, содержащем внутри себя точку х = 0, а вместе
с тем их определитель Вронского тождественно равен нулю. При этом, скажем, функция $г(х) имеет
всюду непрерывные производные, до порядка m - 1 включительно, и лишь производная m-го порядка
терпит разрыв с конечным скачком в точке х = 0. Выбирая m достаточно большим, получаем систему
функций, обладающих непрерывными производными любого нужного порядка.
Задача. Что можно сказать об определителе Вронского системы функций
У\(х),Уг(*),.--,Уп(х),
если только известно, что эти функции а) линейно зависимы; б) линейно независимы?

138
Глава XXII. Дифференциальные уравнения высших порядков
Теорема 7 (необходимое условие линейной независимости решений), Если линейно независимые,
наинтервале (а, ft) функции у\(х), у2{х),..., уп(х) являются решениями линейного
однородного дифференциального уравнения
У(п) + Pi(x)y{n-l).+ ...+ Рп(х)у = О (3)
с непрерывными на [а, ft] коэффициентами Рк(х), то определитель Вронского этой
системы решений
I У\(х) Уг{*) ••• Уп(х) I
„w ч У'\(*) У2(х) •-. Уп{х)
\у<Г\х) yt%) ... У{Г\х)
не может обратиться в нуль ни в одной точке интервала (а, ft).
Л Ограничимся рассмотрением случая п = 3. Допустим, что в некоторой точке
хо Е (а, ft) определитель Вронского равен нулю:
W(x0)=0, х0е(а,Ъ).
Составим систему трех линейных однородных алгебраических уравнений
относительно а\,а\9ау.
(<х\У\(хо) + а2у2(х0) + а3у3(х0) = О,
(Х\у'\(х0) + а2у2(х0) + а3у3(х0) = 0, (4)
<*\У\(хо) + «22/2(^0) + <*зЗ/з (&<>) = 0.
Определитель этой системы W(xo) в силу допущения равен нулю, поэтому система
имеет ненулевое решение а\9 а2, аз, т. е. по крайней мере одно из чисел а, отлично
от нуля.
Рассмотрим функцию
У = «i2/i (я) + а2у2(х) + а3у3(х). (5)
Она является линейной комбинацией решений у\(х), у2(х), Уз(х) уравнения (3), и,
значит, сама есть решение этого уравнения. Это решение в силу уравнений (4)
удовлетворяет нулевым начальным условиям
у(х0) = &1ух(хо) + а2у2(х0) + а3у3(х0) = 0,
у(х0) = аху\ (х0) + а2у2(х0) + а3у'3(х0) = 0, (6)
у"(х0) = &\у"(х0) + а2у"(х0) + а3у"(х0) = 0.
Таким начальным условиям, очевидно, удовлетворяет тривиальное решение у = 0
уравнения (3) и, по теореме о единственности решения, только это решение.
Следовательно,
«\У\(я) + а2у2(х) + а3у3(х) = 0 на (о, ft),
причем хотя бы одно из а, отлично от нуля. Таким образом, решения У\(х)9 у2(х),
у3(х) оказываются вопреки условию теоремы линейно зависимыми. Противоречие
возникло в связи с допущением, что W(x) обращается в нуль в точке хо € (а, ft).
Значит, наше допущение неверно, и W(x) Ф 0 всюду в интервале (a, ft). ►
Из теорем 5 и 7 как следствие получаем следующую важную теорему.

§ 5i Структура общего решения линейного однородного дифференциального уравнения 139
Теорема 8. Для того, чтобы частные решения у\(х), 2/2(ж), • • • > Уп(х) линейного
однородного дифференциального уравнения (3) с непрерывными на отрезке [а, Ь] коэффициентами
были линейно независимыми на интервале (а, Ь), необходимо и достаточно, чтобы
определитель Вронского W(x) системы решений был отличен от нуля.
<4 Необходимость условия прямо следует из теоремы 7.
Достаточность условия вытекает из того, что при линейной зависимости функций
У\ (ж), У2(х))..., Уп(х)9 согласно теореме 5, имеем W(x) = 0. Поэтому если W(x) Ф 0,
то функции у\(х), Уг{х), - - -> Уп(х) не могут быть линейно зависимыми^, е. онивэтом
случае линейно независимы. ►
Задача. Доказать, что два решения уравнения
у"+рЛ*)у'+Р2(*)у = о
с непрерывными коэффициентами, имеющие максимум при одном и том же значении х, линейно
зависимы.
Задача. Доказать, что отношение двух любых линейно независимых решений уравнения
у"+Р\(х)у+Р2(х)у = 0
с непрерывными коэффициентами не может иметь точек максимума.
Задача. Показать, что два линейно независимых решения у\(х) и уг(х) уравнения
у"+Р\(х)у' + Р2(х)У = 0
с непрерывными на отрезке [а, Ь] коэффициентами не могут обращаться в нуль при одном и том же
значении х0 € (а, 6).
§5. Структура общего решения
линейного однородного
дифференциального уравнения
Теорема 9 (о структуре общего решения линейного однородного дифференциального уравнения).
Общим решением в области а < х < Ь, |j/fc'| < +оо, к = 0,1,2,..., п - 1, линейного
однородного дифференциального уравнения
У{п) + Pi(x)y{n-l) + ...+ Рп(х)у = 0 (1)
с непрерывными на отрезке [а, Ь] коэффициентами Pk(x), к — 1,2,..., п, является
линейная комбинация
п
» = £<Ы*) (2)
1=1
п линейно независимых на интервале (а, Ь) частных решений y%{x),i= 1,2,..., п, этого
уравнения (С\у Сг,..., Сп — произвольные постоянные).

140
Глава XXII. Дифференциальные уравнения высших порядков
< Будем исходить из определения общего решения и просто проверим, что семейство
ФУНКЦИЙ
п
У = 5Z CiVi(x)
удовлетворяет условиям 1), 2) этого определения.
Функция у(х)9 определенная формулой (2), является решением
дифференциального уравнения (1) при любых значениях постоянных Сь С2,..., Сп. Это следует
из того, что, как было установлено выше, любая линейная комбинация частных
решений линейного однородного уравнения есть снова решение этого уравнения.
Для уравнения (1) при х G [а, ft] выполнены условия теоремй 1 существования
и единственности решения задачи Коши; поэтому остается показать, что
постоянные С\} С2>..., Сп всегда можно подобрать так, чтобы удовлетворялись произвольно
заданные начальные условия
!fU*=«b 3>'L*0=2/o, ..., У{п~1)\х=Х0=У(Г{\
гдеж0 G (a, ft).
Ограничимся случаем, когда п = 3. Потребовав, чтобы решение
у(х) = Сху\(х) + С2у2(х) + С3уз(х)
удовлетворяло поставленным начальным условиям, получим систему трех линейных
алгебраических уравнений относительно С\, С2, Сз:
С\у\(х0) + С2у2(хо) + С3уз(х0) = y0l
Сху\ (х0) + С2у'2(х0) + С3узЫ = 2/о, ' (3)
Сц/!(х0) + С21Д(х0) +СзйЫ = У'о-
Определитель этой системы есть определитель Вронского W(xo) линейно
независимой системы решений однородного уравнения (1), и, следовательно, отличен от нуля
при любом х G (a, ft), в частности при х == хо. Поэтому система уравнений (3)
однозначно разрешима относительно С\, С2, С$ при любом хо G (a, ft) и при любых
правых частях, т. е. при любых уо, у'0, у$. А это и означает возможность выбора таких
значений С?\УС%,С%У чтобы частное решение
У(х) = С\ух{х) + С%у2(х) + С°зУз(х)
удовлетворяло поставленным начальным условиям, каковы бы они ни были. ►
Из теоремы 9 следует, что если известно п линейно независимых частных
решений линейного однородного дифференциального уравнения n-го порядка, то всякое
другое решение этого уравнения представляется в виде линейной комбинации этих
частных решений и, значит, линейно зависимо с ними. Отсюда вытекает, что
максимальное число линейно независимых решений однородного линейного
дифференциального уравнения равно его порядку.
Таким образом,
совокупность решений линейного однородного дифференциального уравнения образует
линейное пространство, размерность которого равна порядку дифференциального
уравнения.
Введем понятие фундаментальной системы решений.

§5. Структура общего решения линейного однородного дифференциального уравнения 141
Определение. Совокупность любых п линейно независимых частных решений
линейного однородного дифференциального уравнения n-го порядка называется его
фундаментальной системой решений.
Теорема 10. У каждого линейного однородного уравнения (1) с непрерывными
коэффициентами Pk(x) существует фундаментальная система решений (и даже бесконечное
множество фундаментальных систем решений).
< В самом деле, рассмотрим, например, однородное уравнение второго порядка
у" + р} (х)у + р2(х)у = 0 (4)
с непрерывными на отрезке {а, Ь] коэффициентами. Пусть «о € (<*, Ь). По теореме 1
уравнение (4) имеет решения
У = У\(х), У = У2(х), (5)
удовлетворяющие при х = х0 начальным условиям
»i(«o) = l, УЫ = 0; Ы*о) = 0, y'2(x0) = L (5')
Определитель Вронского в точке xq системы решений (5) отличен от нуля,
W(x0) =
1 0
0 1
*о.
Следовательно, система решений (5) для уравнения (4) фундаментальна. Выбор
начальных условий (5') обеспечил построение одной фундаментальной системы. За
начальные данные в точке хо можно взять любую систему чисел:
У\(х0) = а1и у[(х0) = а2и Ыжо) = а12, у2(х0) = а2Ъ
лишь бы определитель Вронского
W(x0) =
а2\ а22
был отличен от нуля. Очевидно, таких систем чисел можно подобрать бесконечно
много и построить бесконечно много фундаментальных систем решений для
уравнения (4). ►
Задача. Составить общее решение уравнения
у'+р(х)У = 0,
если известно ненулевое частное решение у\(х) этого уравнения.
Теорема-11. Если два уравнения вида
yin)+Pi(x)yin-l) + ...+pn(x)y = 0
y{n)+qi(x)yin-]) + ... +qn(x)y = 0,
где функции pi(x) и q%{x), t = 1,2,..., п, непрерывны на отрезке [а, Ь], имеют общую
фундаментальную систему решений У\(х), у2(х),..., уп(х), то эти уравнения
совпадают, т. е. Pi(x) = Qi(x) на отрезке [а, Ь\.

142.
. Глава XXII. Дифференциальные уравнения высших лоралде
Таким образом, фундаментальная система решений вполне определяет
линейное однородное уравнение (1), т.е. полностью определяет коэффициенты Pi(x),
i = 1,2,..., п, этого уравнения. Следовательно, можно поставить задачу о
нахождении уравнения вида (1), имеющего заданную фундаментальную систему решений
У\(х), уг(х),..., у„(х). Представим дифференциальное уравнение с левой частью в
виде определителя:
У\(х)
У\{х)
Уг(х)
Уг(х)
Уп(х)
у'Лх)
У(х)
уЧх)
уГ\х)
У*Г\х)
У(ГЧ*)
Л)
У?'(х) у<">(х)
У{Г\х)
= 0,
(6)
где у(х) — искомая функция, а у\(х), уг{х),..., уп(х) — заданная фундаментальная
система решений. Уравнение (6) имеет в качестве решений функции
У\{х),у2{х), ...,Уп(я),
так как при подстановке вместо у (х) каждой из этих п функций два столбца
определителя становятся тождественно равными и определитель обращается в нуль
тождественно по ж £ (а, Ь). Разлагая определитель по элементам последнего Столбца, получаем
из (6) уравнение вида
W(x)y{n) - Wx(x)y{n"x) + ... ± Wn(x)y = 0,
где W(x) — определитель Вронского системы функций у\ (ж), у2(я),..., уп(х), а
(7)
Wi(x)
У\(х)
У\(х)
Уг{х)
У2(х)
Уп(х)
У'Лх)
yt%)
yt%)
У(2П\*)
yt%)
у{:Чх)
Разделив все члены уравнения (7) на
+ Рп(х)у = 0,
Определитель Вронского W(x) фундаментальной системы решений
у](х),у2(х)1 ...,у„(ж)
отличен от нуля во всем интервале (а, Ь).
W(x) Ф 0, приведем это уравнение к виду (1)
у{п)+Р](х)у{п-]) + .
где, в частности, р{(х) = -р^.
Можно показать, что если элементы atJ- определителя Д n-го порядка есть
дифференцируемые функции аргумента х:
dij = uij{x),
то производная определителя Д = А(х) равна сумме п определителей:
Д' = Д',+Д'2 + ... + К,
где Д^, к = 1,2,..., п, — определитель, получающийся из данного заменой
элементов его fc-ой строки производными от этих элементов. Например, для определителя
Вронского системы функций У\(х), уг{я) имеем
_1
dx
У\{х)у2{х)
У\(х)у'2(х)
У\{х)у'2{х)
У\(х)У2(х)
+
У\{х)у2{х)
у"{х)у'1(х)
У\(х)У2(х)
У"{х)у'1{х)

§ 6j Линейные однородные дифференциальные уравнения с постоянными коэффициентами 143
Нетрудно проверить, что W\ (x) = J™; следовательно,
Интегрируя последнее равенство по ж от «о до ж, получим формулу Остроградского—
Лиувилля:
- fp\(x)dx
W(x) = W(x0)e x«
Задача. Составить линейное дифференциальное уравнение второго порядка, имеющее решения
У\ = *, у2 = х2.
Показать, что функции х, х2 линейно независимы на интервале (-оо, +оо). Убедиться в том, что
определитель Вронского для этих функций равен нулю в точке х = 0. Почему это не противоречит
необходимому условию линейной независимости системы решений линейного однородного дифференциального
уравнения?
§ б. Линейные однородные дифференциальные уравнения
с постоянными коэффициентами
6.1. Частный случай: уравнение второго порядка
Пусть имеем линейное однородное дифференциальное уравнение второго порядка
у" + Р\У' + РгУ = 0,
(1)
где р\, рг — действительные числа. Чтобы найти общее решение этого уравнения,
надо найти два его линейно независимых частных решения. Следуя Эйлеру, будем
искать их в виде
' ^ (2)
У-е
~Хх
где Л = const; тогда
у' = \еХх, у" = Х2еХх.
Подставляя эти выражения для у и ее производных в уравнение (1), получаем
eA*(A2+J>iA + j>2) = 0.
Так как еХх ф 0, то должно выполняться равенство
A2+i?iA + i?2 = 0.
Следовательно, функция у = еХх будет решением уравнения (1), т. е. будет обращать
его в тождество по х, если А будет удовлетворять алгебраическому уравнению
\2+р}\ + р2 = 0.
(3)
Уравнение (3) называется характеристическим уравнением по отношению к
уравнению (1), а его левая часть (р( А) = А2 + р\ А + р2 называется характеристическим
многочленом.
Уравнение (3) есть квадратное уравнение. Обозначим его корни через Х\ и Х2; они
могут быть

144
Глава XXII. Дифференциальные уравнения высших порядков
1) действительными и разными;
2) комплексными;
3) действительными и равными.
Рассмотрим каждый случай в отдельности.
1. Если корни Ль Х2 характеристического уравнения действительные и разные, то
частными решениями уравнения (1) будут функции
У\ =е
Х\х
У 2
0*2*
Эти решения линейно независимы (Л1 Ф Л2) и, следовательно, образуют
фундаментальную систему решений уравнения. Общее решение уравнения имеет вид
у = C\eXlX + C2eXlx (С\,С2 — произвольные постоянные).
Пример 1. Найти общее решение уравнения
у"-3з/ + 2у = 0.
•4 Составляем характеристическое уравнение:
Оно имеет корни
Отсюда получаем искомое общее решение
У - ЗА + 2 = 0.
A, = l, A2t=2.
у = С\е* + С2е
2х
2. Пусть корни характеристического уравнения комплексные. Так как
коэффициенты р\, р2 Характеристического уравнения действительные, комплексные корни входят
попарно сопряженными. Положим, что
Aj = а + ip и \2 = а - if3.
Частные решения дифференциального уравнения (1) можно записать в виде
У,=е<"+'^,
У2
J<*-ip)x
Это комплекснозначные функции действительного аргумента х, а мы будем
заниматься лишь действительными решениями. С помощью формул Эйлера
e,/3z = cos fix + i sin /Зх, e~,/3z = cos fix - i sin /3x
частные решения у\ и у2 уравнения (1) можно представить в виде
У\ = eaz(cos fix + г sin /Зх), у2 = eaz(cos fix - i sin fix).
Воспользовавшись теоремой 4, получим, что частными решениями уравнения (1) будут
также функции
ух = еах cos /Зх, у2 =; еах sin /Зх.
Эти решения линейно независимы, так как
У2(х)
У\(х)
tg j3x £ const,

§6. Линейные однородные дифференциальные уравнения с постоянными коэффициентами 145
и, значит, составляют фундаментальную систему решений. Общее решение
уравнения (1) в рассматриваемом случае, имеет вид
у = С\еах cos fix + C2eax sin fix.
Пример 2. Найти общее решение уравнения
А2 + 2А + 5 = 0.
<4 Составляем характеристическое уравнение:
Оно имеет корни
Ai=-l+2t, A2 = -l-2t,
поэтому а — -1, (3 = 2; искомое общее решение
у = С\в~х cos2x + Сг*Гх sin2s. ►
3. Пусть теперь корни характеристического уравнения действительные и равные. Одно
частное решение
У. = еЛ"
получаем сразу. Второе частное решение, линейно независимое с первым, будем
искать в виде
у2 = еХхХч{х),
где и(х) — новая неизвестная функция. Дифференцируя, находим:
у'2 = A,eAl*t* + еА' V, у\ = Х]ех*хи + 2A,eAl V + еА'V.
Подставляя полученные выражения в (1), получаем
ex'x[u" + (2Xl+pl)u, + (X]+plXl+p2)u] = 0. (4)
Так как Х\ — корень характеристического уравнения, то
A?+j>iA,+p2 = 0,
а так как Ai — двукратный корень, то и
2А1+1?! =0.
Следовательно, соотношение (4) примет вид
и" = 0.
Отсюда
и = Ах + В,
где А и В — постоянные. Можно, в частности, положить А = 1, В = 0; тогда
и = ж.
Таким образом, в качестве второго частного решения уравнения можно взять
у2 = хех*х.
Это решение линейно независимо с первым, так как
Уг(я)
—— = х щ const.
У\(х)

146 Глава XXII* Дифференциальные уравнения высших порядков
Решения ух = eAl*, у2 = хеХхХ образуют фундаментальную систему решений уравнен
ния (1), общее решение которого в этом случае имеет вид
или
y = eXl*(Cx+C2x).
Пример 3. Найти общее решение уравнения
у" + 2у + у = 0.
А2 + 2Л+1 = 0
<4 Характеристическое уравнение
имеет кратные корни
А,=А2 = -1.
Поэтому общее решение исходного дифференциального уравнения:
y = de-x + C2xe~x. ►
Замечание. Пусть имеем линейное однородное дифференциальное уравнение (вообще, с переменными
коэффициентами)
С\у\ = У(я) +P,(x)j,<"-|> + ... + рп(х)у = 0. (5)
Пусть у\ (ж) — частное решение уравнения. Введем новую искомую функцию и(х) соотношением
У = у\(х)и(х)
(разрешимым относительно и(х) в тех интервалах, где у\(х) не обращается в нуль). Из этого
соотношения найдем производные от у:
У =У\и' + УлЩ
y" = yiu" + 2yW+y"u,
y(n) = yiti(n) + ^W(n-° + ...+y{n)ti
и подставим их в уравнение (5):
»,(*)«<"> + [пу\ +?,»,]«<"-'> + ...+[...]„'+ [, W +piy(ri) + ... +РпШ]и = 0.
Для функции и(х) получаем опять уравнение порядка п, но коэффициент при и(х) есть С[у\\.
Он тождественно равен нулю, так как у\ (х) есть решение уравнения (5). Следовательно, в полученном
уравнении порядок понизится, если ввести новую искомую функцию z(x) = u'(x). Разделив, кроме
того, все члены последнего уравнения на у\ (х) Ф 0, приведем его к виду
*<*"'> + д,(ф(я-2> + ... + *.,(«)* = 0.
Итак, если известно частное решение уравнения (5), то задача интегрирования этого уравнения
приводится к интегрированию линейного однородного уравнения порядка п - 1. Можно показать,
что если известны два частных линейно независимых решения, то порядок уравнения может быть
понижен на две единицы. Вообще, если известно г частных линейно независимых решений линейного
однородного дифференциального уравнения, то порядок этого уравнения может быть понижен на г
единиц.
6.2. Физические приложения: уравнение колебаний
Линейные дифференциальные уравнения с постоянными коэффициентами
возникают в задачах о механических и электрических колебаниях. Рассмотрим уравнение
свободных механических колебаний, причем независимой переменной будем считать
время t:
d v dv , v
mw+h£+k*=b (6)

§6. Линейные однородные дифференциальные уравнения с постоянными коэффициентами 147
где у — отклонение колеблющейся точки от положения равновесия, ni — масса
точки, h — коэффициент трения (считаем, что сила трения пропорциональна
скорости), к > О — коэффициент упругости восстанавливающей силы (считаем, что эта
сила пропорциональна отклонению). Характеристическое уравнение для (6)
т\2 + h\ + k = Q
имеет корни
Если трение достаточно велико, h2 > 4тк, то эти корни действительные и
отрицательные. Общее решение уравнения (6) в этом случае имеет вид
y = C]eXlt + C2eX2t. (7)
Так как Л1 < 0, Аг < 0, то из (7) заключаем, что при большом трении отклонение точки
от положения равновесия с возрастанием t стремится к нулю, не совершая колебаний.
Если трение мало, h2 < 4mfc, то характеристическое уравнение имеет комплексно
сопряженные корни -a±i/39 где а = ^ > 0, р = J^-jjy. Общее решение
уравнения (6) в этом случае определяется формулой
у = С\ е'* cos pt + C2e~at sin pt (a > 0)
или
у = Ae~at sin {pt + 6) (А, б = const).
Отсюда видно, что в случае малого трения происходят затухающие колебания.
Пусть теперь трение отсутствует, т. е. h = 0. В этом случае характеристическое
уравнение гаА2 + к = 0 имеет чисто мнимые корни Aif2 = ±iy^. Решение
уравнения (6) имеет вид
у = С\ cos u)t + Ci sin u)t = A sin(u)t + 6),
где и) = J ^, т. е. в этом случае происходят незатухающие гармонические колебания
с частотой ш = \1 ^ и произвольными амплитудой А и начальной фазой б.
Задача. При каких р\, рг (р\, р2 = const)
1) все решения уравнения
у" +Р\У +Р2У = 0
стремятся к нулю при х —►Ч-оо;
2) каждое решение уравнения
У"+Р\У+Р2У = 0
обращается в нуль на бесконечном множестве точек х?
6.3. Общий случай: уравнение произвольного порядка
Рассмотрим теперь линейное однородное дифференциальное уравнение произвольного
порядка п(п^ 1) с постоянными коэффициентами
С[у] = у{п) + Piyin~l) + ... + РпУ = 0, (8)
гдерьрг, • • • ,Рп — действительные числа. Общее решение дифференциального
уравнения (8) находим так же, как и в случае уравнения второго порядка.

148 Глава XXII. Дифференциальные уравнения высших порядков
1. Ищем решение в виде
У = еХх.
Подставляя вместо у величину еАяг в уравнение (8), получаем
£[eA*] = eAV(A) = 0,
что приводит к характеристическому уравнению
' (9)
<p(\) = \n+Pl\n-l + ... +рп = 0.
2. Находим корни
Ai, A2,..., Ап
характеристического уравнения.
3. По характеру корней выписываем частные линейно независимые решения
уравнения (8), руководствуясь тем, что:
а) Каждому действительному однократному корню А характеристического
уравнения соответствует частное решение
еХх -
уравнения (8).
б) Каждой паре однократных комплексно сопряженных корней
А! = а + ip и Х2 = a-i/3
соответствуют два линейно независимых частных решения
еах cos /Зх и еах sin fix
уравнения (8).
в) Каждому действительному корню А кратности г соответствует г линейно
независимых частных решений
с j Же ^ • • . у X с
уравнения (8).
Л Рассмотрим случай в) подробнее. Пусть число А есть корень кратности г
характеристического уравнения (р(Х) = 0. Функцию у = еХх будем рассматривать как
функцию двух аргументов: ж и А. Она имеет непрерывные производные по ж и по А
всех порядков, причем
&
т
:(еХх)=хтеХх.
дХ»
Поэтому частные производные функции у = еХх по ж и по А не зависят от порядка
дифференцирования (операции дифференцирования функции у по ж и по А
перестановочны), так что
\дтуЛ дт г ,
* 7К= = 1^М-
[дХт} д\п
Воспользовавшись этой перестановочностью, а также тем, что
£[eA*]=eAV(A), (10)

16. Линейные однородные дифференциальные уравнения с постоянными коэффициентами.
получаем
= xeAV(A) + eAV(A),
= х2еХх<р(\) + 2жеАУ (А) + еАу (А),
г-1 Xxl ° /А*.
.148
Ф е 1 = ^73Т (eAV(A)) =
(П)
0А
= аГ'еА*у>(А) + ^^ аГ2еАУ(А) +... + еА>(г_1)(А).
Если А есть г-кратный корень характеристического уравнения <р(\) = 0, то
ф) = <р'(\) = ...= <р{т-1)(Х) = О, />(А) ф О
и, стало быть, правые части (10) и (11) тождественно по х равны нулю:
С[еХх] = 0, С[хеХх] = 0, ..., С[хг~1еХх] = 0.
Это означает, что функции еАж, жеА*,..., хг~хеХх являются в этом случае решениями
уравнения (8). Легко проверить, что функции еА*, жеАж,..., хг~хеХх линейно
независимы на любом интервале (а, Ь) изменения х. ►
г) Приведенные в пункте в) рассуждения сохраняют силу и для комплексных
корней. Поэтому каждой паре комплексно сопряженных корней \ = a + if3n\ = a-i/3
кратности fi отвечает 2\i частных решений уравнения (8):
ах л ах а /1—1 ах л
е cos /Зх, xe cos fix, ..., ar e cos /3x,
ax • л ax • a
e sin/Зж, xe sin/to,
•i«-i-e*
sin/ta.
4. Число построенных таким образом частных решений уравнения (8) равно порядку п
этого уравнения. Можно показать, что все эти решения линейно независимы в
совокупности. Имея п линейно независимых частных решений у\(х), уг{х)>..., уп(х)
уравнения (8), получаем общее решение этого уравнения,
У = С\ух{х) + С2у2(х) + ... + Спуп(х),
где Ci, Сг,..., Сп — произвольные постоянные.
Пример 4. Найти общее решение уравнения
/■-/ = 0.
< 1. Составляем характеристическое уравнение:
Аб-А2=0, или А2(А4-1)=0.
2. Находим корни характеристического уравнения:
А, = А2 = 0, Аз = 1, А4 = -1, А5 = t, Аб = -i.
3. По характеру корней выписываем частные линейно независимые решения дифференциального
уравнения:
У\ = 1, Уг = х, уз = ех, у4 = е~х, у5 = cos s, y6 = sin x. /
4. Общее решение дифференциального уравнения имеет вид
у = С\ + С2х + С3е* + С4е~* + С5cosx + Сбsinx. ►

150.
. Глава XXII. Дифференциальные уравнения высших порядков
Схема решения линейного дифференциального уравнения с постоянными коэффициентами
Дифференциальное уравнение
С[у] = у{п)(х) +Plyin-])(x) +... +Рпу(х) = 0
(Р\, P2i • • •) Рп — действительные числа).
Характеристическое уравнение
(p(\) = \n+Pl\n-l + ... +рп = 0.
Корни
Ai, A2, ..., Ап
характеристического уравнения
¥>(Л) = 0.
Частные линейно независимые решения
У\{х), Уг(х), ..., у»(х)
дифференциального уравнения
С[у] = 0.
Общее решение уравнения С[у] = 0:
у(х) = Схух{х) + С2у2{х) + ... + Спуп(х)
(С\, Сг,..., Сп — произвольные
постоянные).
§7. Уравнения, приводящие к уравнениям
с постоянными коэффициентами
Существуют линейные дифференциальные уравнения с переменными
коэффициентами, которые с помощью замены переменных преобразуются в уравнения с
постоянными коэффициентами. К их числу принадлежит уравнение Эйлера
Х^+*Х d^+'+Pn-lXdi+PnV = 0>

f 7. сравнения, приводящие к уравнениям с постоянными коэффициентами 151
где риР2г < ♦ - t Pn — постоянные числа. Ограничимся рассмотрением уравнения
Эйлера 2-го порядка (оно встречается в задачах математической физики):
2 d у dy
х —j + p\x — + р2у = 0 (р,, р2 = const).
(1)
Положим х = е*; тогда
dy __dy dt __ _tdy
dx dt dx dx
йж2 dx \dx) dt\dxjdx dt2 dt'
Подставляя выражения для х, — и —г в (1), получим дифференциальное уравнение
аж oar
с постоянными коэффициентами
§ + ^■-1)^+^ = 0. (2)
Последнее интегрируется обычным приемом: составляем характеристическое
уравнение
A2 + (j>i-l)A+p2 = 0, (3)
находим его корни и по характеру корней выписываем общее решение уравнения (2),
после чего возвращаемся к старой переменной х.
Пример. Найти общее решение уравнения
id2y
Ч Замена переменной х = е* приводит к уравнению
с уравнению
d2y dy
характеристическое уравнение которого
А2 + 2А + 1 = О
имеет корни Л] = А2 = -1. Общее решение преобразованного уравнения равно
y(t) = Cle-t + C2te-t.
Учитывая, что х — ег, для общего решения исходного уравнения получаем выражение
у(х) = _ f а?>0. ►
Замечание 1. Для преобразованного уравнения (2) в случае действительных и различных корней
характеристического уравнения (3) частные решения имеют вид
е" = («<)* = **.
Поэтому можно сразу задаться этим видом частного решения. Подставляя у = хк (х > 0) в
уравнение (1), получим для к уравнение
*2 + (pi-l)*+p2 = 0, (4)
совпадающее с (3). Каждому простому действительному корню уравнения (4) отвечает частное решение
у = хк
уравнения (1); двукратному корню отвечают два решения
У\= *к, У2=хк\пх

152 Глава XXII. Дифференциальные уравнения высших порядков
уравнения (1). Паре комплексных сопряженных корней а ± %р уравнения (4) будут соответствовать
два решения
Ух = ха cos(/? In ж), у2 = ха sin{/3 In х)
уравнения (1).
Замечание 2. Уравнение
(ах + Ъ)2^+р1(ах + Ъ)(^+р2у = 0
(в, Ьу р\, р2 — постоянные числа) подстановкой ах + Ь = е1 также приводится к уравнению с
постоянными коэффициентами.
§8. Линейные неоднородные
дифференциальные уравнения
Линейное неоднородное дифференциальное уравнение п-го порядка имеет вид
оо(х)у<п) + а, (*)/-'> +... + ап(х)у = д(х). (1)
Здесь а0(х),at(x),... ,ап(х),д(х) — заданные на некотором интервале (а,/3)
функции. Если а0(х) Ф О на (а, /3), то после деления на оо(ж) получим уравнение
у<»> + Pl(x)yln-» + ...+ рп(х)у = /(*), (2)
где
Из теоремы 1 существования и единственности решения задачи Коши получаем:
если на отрезке [а, Ь] коэффициенты рн (х) и правая часть f(x) уравнения (2) непрерывны,
то это уравнение имеет единственное решение, удовлетворяющее условиям
у\х=Хо = Уо, У'\х=Хо = Уо, •••, y{n~X=X0 = yt~X\
где х0 е (а, Ь), -оо < % < +°°> к = 0,1,..., п - 1.
Уравнение (2) можно записать в виде
С[у] = /(*), (3)
где, как и выше,
С[у] = у{п) +Pi(x)y{n~l)'+... +рп(х)у.
Теорема 12. Если у(х) есть решение неоднородного уравнения
С[у) = /(*),
я Уо(х) есть решение соответствующего однородного уравнения
с[у] = о,
то сумма уо(х) + у(х) есть решение неоднородного уравнения.

§8. Линейные неоднородные дифференциальные уравнения 153
<« По условию, С[у] = /(ж), С[уо] = 0. В силу линейности оператора С имеем
С[уо + у] = С[у0] + С[у] = f(x).
Это означает, что функция уо(х) + у(х) есть решение уравнения С[у] = /(ж). ►
Теорема 13. Если у\(х) есть решение уравнения
С[у] = Мх),
а уг{х) есть решение уравнения
C[y] = f2(x),
та функция у\(х) + Уг(я) есть решение уравнения
£ly] = fi(x) + fi(x)-
<« По условию, С[у\] = f\(x), С[у2] = h{x)\ используя линейность оператора £,
получаем
С[У\ + У2] = ^Ы + £[»J = /i(x) + /2(ж).
Последнее означает, что функция у\ (х)+yi(x) есть решение уравнения £[у] = f\ (x) +
Л(«). ►
Теорема выражает так называемый принцип суперпозиции (наложения).
Теорема 14. Если уравнение
C[y] = U(x} + iV(x),
где все коэффициенты Pk(x), к = 1,2,..., п, и функции U(x) и V(x) действительные,
имеет решение у = и(х) + iv(x), то действительная часть решения и(х) и его мнимая
часть v(x) являются соответственно решениями уравнений
C[u] = U(x), C[v] = V(x).
<« По условию имеем
С[и + iv] = U(x) + %V(x),
или
С[и] + iC[v] = U(x) + iV(x).
Отсюда получаем:
С[и] = U(x), C[v] = V(x). ►
Теорема 15 (о структуре общего решения линейного неоднородного дифференциального уравнения).
Общее решение в области а<х <Ь, \у^ \ < +оо, к = 0,1,2,..., п - 1, уравнения
С[у] = у{п) + рх(х)у{п-]) + ... + рп(х)у = f(x) (2)
с непрерывными на отрезке [а, Ь] коэффициентами Pk(x), к = 1,2,..., п, и правой
частью f(x) равно сумме общего решения
п
J2Qyi(x)
«=1
соответствующего однородного уравнения и какого-нибудь частного решения у(х)
неоднородного уравнения, т. е.
Уо.н. =z Уо.о. г Уч.н.'

154
Глава XXII. Дифференциальные уравнения высших порядков
< Надо доказать, что
п
y(x) = Y^,cM(x) + y(x)> (4)
1=1
где Ci, C2l..., Сп — произвольные постоянные, а у\(х), у2,..., уп(х) — линейно
независимые решения соответствующего однородного уравнения С[у] = 0, является
общим решением неоднородного уравнения
C[y] = f(x).
Будем исходить из определения общего решения и просто проверим* что семейство
функций у(х), определяемое формулой (4), удовлетворяет условиям 1) и 2),
содержащимся в этом определении.
В самом деле, функция у(х), определяемая формулой (4), является решением
уравнения (2) при любых значениях постоянных, поскольку сумма какого-либо
решения неоднородного уравнения и любого решения соответствующего однородного
уравнения есть решение неоднородного уравнения С[у] = f(x).
Так как для уравнения (2) при х Е [а, Ь] выполнены условия теоремы 1
существования и единственности решения задачи Коши, то остается показать, что подбором
постоянных С\, С2, k.., Сп в (4) можно удовлетворить произвольно заданным
начальным условиям
v\9ss9Q = Vo, 2/'L,0 = 2/d, •••> 2/(n"1)L=,0=^1)j (5)
где ж0 Е (а,Ь), т.е. можно решить любую задачу Коши. Ограничимся случаем,
когда п = 3. Потребовав, чтобы решение (4) удовлетворяло начальным условиям (5),
приходим к системе уравнений для отыскания С\, С2, Сз:
( Схух (х0) + С2у2(хо) + Сзуз(жо) + у(х0) = yQi
< Cjyi(so) + С22/2Ы + С3уз(хо) + 2/'(жо) = 2/о, (6)
I СчД(хо) + C2j£(x0) + С3уи3(хо) + Г(х0) = yl
Эта линейная по отношению к С\, С2, Сз система трех уравнений с тремя
неизвестными допускает единственное решение относительно С\, С2, Сз при произвольных
правых частях, так как определитель этой системы есть определитель Вронского W(x$)
для линейно независимой системы решений соответствующего однородного
уравнения и, следовательно, отличен от нуля в любой точке х Е (а, Ь), в частности в точке
х = жр. Значит, какова бы ни была тройка чисел уо, у'0, у%, найдется решение С?\,С%,
Су системы (6) такое, что функция
у = CiVi (х) + С%у2(х) + С1уъ(х) + Ц(х)
будет решением дифференциального уравнения (2), удовлетворяющим начальным
условиям
у\х=Х0 = 2/о, 2/'U*0 = Уо, 2/"|*=*0 = 2/0- ►
Из этой теоремы следует, что задача нахождения общего решения линейного не*
однородного уравнения сводится к отысканию какого-либо частного решения этого
неоднородного уравнения и общего решения соответствующего однородного
уравнения.

f 9. Интегрирование линейного неоднородного дифференциального уравнения методом вариации постоянных 155
Пример 1. Найти общее решение уравнения
у" + у = х.
Ч Нетрудно заметить, что функция
является частным решением данного неоднородного уравнения. Чтобы найти общее решение этого
уравнения, остается отыскать общее решение соответствующего однородного уравнения
у" + у = о. (♦)
Это уравнение есть линейное однородное уравнение с постоянными коэффициентами.
Характеристическое уравнение, соответствующее уравнению (*), есть
А2 + 1 = 0;
корни его Aj = t, A2 = —t. Поэтому общее решение уравнения (*) имеет вид
Уо.о. = С\ cos х + С2 sin x.
Общее решение исходного неоднородного уравнения:
Уом. = С\ cos х + С2 sin x + х. ►
§9. Интегрирование линейного неоднородного
дифференциального уравнения
методом вариации постоянных
9.1. Частный случай: уравнение второго порядка
Начнем для простоты со случая уравнения второго порядка. Пусть имеем
дифференциальное уравнение
У" + Р\ (*)У + Pi(x)y = f(x) (l)
(функции р\ (х), Р2(х), f(x) непрерывны на [а, Ь]) и пусть известна фундаментальная
система у\(х), У2(х) решений соответствующего однородного уравнения
у"+Р\(х)у+Р2(х)у = 0, (2)
тогда
У = С\у\ (х) + С2уг{х) (С\, С2 — постоянные)
— общее решение уравнения (2).
Заметим, что это предположение является весьма стеснительным, так как общего метода отыскания
решений линейных однородных уравнений порядка n ^ 2 с переменными коэффициентами не
существует.
Для интегрирования неоднородного уравнения (1) применим метод вариации
постоянных (метод Лагранжа), который состоит в следующем. Будем искать решение
неоднородного уравнения (1) в виде
У = Ci(x)yi(x) + С2(х)у2(х)) (3)
где С\ (х), С2(х) — новые неизвестные функции от х. Для их нахождения необходимы
два уравнения, содержащие эти функции. Естественно, что функции С\(х), С2(х)
должны удовлетворять тому уравнению, которое получится, если в исходное уравнение
подставить вместо у(х) выражение С\(х)у\(х) + С2(х)у2(х).

156 Глава XXII. Дифференциальные уравнения высших порядков
Наложим на функции С\(х), С2(х) еще одно дополнительное условие.
Продифференцируем (3),
У = Сх{х)у\ + С2(х)у'2 + С\{х)ух + С,2{х)уъ
и в качестве дополнительного условия, налагаемого на С\, C2i возьмем следующее
(целесообразность этого будет видна из дальнейшего):
С\(х)ух(х) + С'2(х)у2(х) = 0;\ (4)
тогда
У=Сх(х)у'х+С2(х)у'ъ (5)
у" = Сху'{ + С2уЧ + С[у\ + С'2у*2. (6)
Подставляя выражения для у, у1, у" из (3), (5), (6) в исходное уравнение (1), после
элементарной группировки слагаемых получаем
С\(х) [y"+pi(x)y\ +р2(х)ух] +С2(х) [у"+рх(х)у'2+р2(х)у2] +С[(х)у[ +С,2(х)у2 = f(x).
Выражения в квадратных скобках тождественно равны нулю, поскольку ух(х) и у2(х)
есть решения однородного уравнения (2). Следовательно, результат подстановки у,
у', у" в (1) таков:
С[{х)у\(х) + С'2(х)у'2(х) = /(*). (7)
Значит, функция у = Сх(х)ух(х) + С2(х)у2(х) будет решением неоднородного
дифференциального уравнения (1), если функции Сх (х) и С2(х) будут удовлетворять
одновременно уравнениям (4) и (7), т. е. системе
С'х(х)ух(х) + С'2(х)у2(х) = 0,
C'x(x)y\(x) + C'2(x)y'2(x) = f(x), U
определитель которой есть определитель Вронского линейно независимых решений
ух(х), у2(х) уравнения (2) и, следовательно, отличен от нуля всюду в интервале (а, Ь).
Решаем эту систему как линейную алгебраическую систему относительно С\ (х), С2 (х):
С\ (х) = <рх (ж), С2(х) = <р2(х)
(здесь <рх(х), <р2(х) — известные функции) и интегрируем:
Сх(х) = / (рх(х) dx + Cu С2(х) = f (frix) dx + С2
(здесь Сх, С2 — постоянные интегрирования). Подставляя эти выражения для Сх(х)9
С2(х) в (3), найдем общее решение неоднородного дифференциального уравнения (1):
{
У = Схух(х) + С2у2(х) + ух(х) / (рх(х) dx + у2(х) / (р2(х) dx
(Сх, С2 — произвольные постоянные).
Итак,
если известна фундаментальная система решений соответствующего однородного
уравнения, то общее решение неоднородного уравнения может быть найдено с помощью
квадратур.

f 9. Интегрирование линейного неоднородного дифференциального уравнения методом вариации постоянных 157
Пример. Найти общее решение уравнения
у" + у = ^-.
sin я
<4 Рассмотрим однородное уравнение, соответствующее данному неоднородному.
/ + У = 0
— это есть линейное уравнение с постоянными коэффициентами. Функции
ух (х) = sin ж, у2(х) = cos x
образуют его фундаментальную систему решений. Будем искать решение исходного уравнения в виде
у = С\(х)$тх + С2(х)со&х. • (*)
Система (8) для определения С[(х), С2(х) в данном случае примет вид
(С\(х) sin ж + С'2(х) cos х = О,
С\(х) cosх - С2(х) sinх = -—.
sin я
Решая эту систему относительно С\(х), С'2(х), получаем:
CiW=^7> C2(x) = -l;
Sffl X
С\(х) = In | sina?| + Си С2(х) = -х + С2.
Подставляя найденные выражения для С\(х), С2(х) в (*), найдем общее решение данного уравнения:
у = С\ sin х + С2 cos х + sin x In | sin x\ - х cos x. ►
9.2. Общий случай: уравнение произвольного порядка
Для интегрирования линейного неоднородного дифференциального уравнения п-го
порядка (п ^ 1)
У{п) + Vx (х)у{п~1) +... + Рп(х)у = f(x) (9)
поступаем аналогично.
Пусть у\ (ж), уг{х)>..., уп(х) — известная фундаментальная система решений
соответствующего однородного уравнения. Будем искать решение уравнения (9) в виде
У = Сг(х)ух(х) + С2(х)у2(х) + ...+ Сп(х)уп(х), (10)
где С\(х), С2(х)>..., Сп(х) — новые неизвестные функции.
Чтобы найти п функций С\(х), Сг(х),..., Сп(х), надо составить систему из п
уравнений, содержащих эти функции. При составлении такой системы уравнений
можно п - 1 уравнений взять произвольно и затем составить n-е уравнение,
исходя из требования, чтобы функция у(х), ойределенная формулой (10), удовлетворяла
уравнению (9). В качестве первых п - 1 уравнений возьмем следующие:
С[(х)ух + С'2(х)у2 + ...+ С'п(х)Уп = 0,
С[{х)у\ + С£(*)|й +... + Ci(*)i£ = 0,
С[(х)у{Г2) + C'2(x)yt2) + ...+ C'n(x)yt2) = 0.
Тогда, чтобы функция у (ж), определенная формулой (10), удовлетворяла
уравнению (9), надо на функции С,-(ж) наложить условие
Clrf-') + C'2(x)ytl) + ■■■+ Сп(х)у^П = /(*).

158.
. Глава XXII. Дифференциальные уравнения высших порядков
Для определения С'{(х), г = 1,2,..., п, получаем систему
C\yi+C'2y2 + ... +С'пУп = 0,
el»? + c5»i +... + cii4 = о,
с!у!п"Пс^-2) + ...+^2-2) = о,
(11)
vj»-1), wJ»-0
1с1уГ1> + с'2уГ1, + --.+с'пУГ1) = №
'>-о_
Определитель этой системы есть определитель Вронского фундаментальной
системы решений однородного уравнения и, следовательно, отличен от нуля всюду в
интервале (а, Ь). Поэтому система (11) однозначно разрешима относительно СЦх),
г = 1, 2,..., п. Решая ее, находим С[(х) = у>,(ж), где <fi(x) — известные функции,
откуда
?i(x) = j <fi(x)
dx + Q, i = 1,2,... , п.
Подставляя найденные выражения для Q(x) в (10), получаем общее решение у(х)
исходного уравнения (9):
где С\, Сг,..., Сп — произвольные постоянные.
§10. Неоднородные
линейные дифференциальные уравнения
с постоянными коэффициентами
В предыдущем параграфе был рассмотрен общий метод решения неоднородного
линейного дифференциального уравнения — метод вариации постоянных. В случае
дифференциального уравнения с постоянными коэффициентами частное решение
неоднородного уравнения иногда бывает возможно найти проще — методом подбора.
Рассмотрим некоторые виды уравнений, допускающие применение этого метода:
1. Уравнение вида
С[у] s у{п) + рху^х) + ... + Рпу = Рт(х),
(1)
где pi, р2> рз, • •, Рп ~ действительные числа, Рт(х) — данный многочлен m-й
степени,
Рт(х) = А0хт + Аххт~х +...+Ат, А0*0.
Характеристическое уравнение для соответствующего (1) однородного уравнения
имеет вид
»п-1
или
¥>(А) = 0,

§ 10. Неоднородные линейные дифференциальные уравнения с постоянными коэффициентами 159
где
(p(\) = \n+Pl\n-l + ... +Pn
— характеристический многочлен.
Если коэффициент рп отличен от нуля, т. е. А = 0 не является корнем
характеристического уравнения <р(\) = 0, то существует частное решение у(х) уравнения (1),
имеющее тоже вид многочлена степени т. Действительно, беря у(х) в виде
у(х) = В0хт + Вххт~1 +... + Вт
(Б0, Ви. • •, Вт — неопределенные коэффициенты), подставляя его в уравнение (1)
и сравнивая коэффициенты при одинаковых степенях х в левой и правой частях,
получаем для определения коэффициентов Б,- систему линейных алгебраических
уравнений, которая всегда разрешима, если рп ф 0. В самом деле, приравнивая
коэффициенты при жт, хт~\ ... 9 имеем:
рпВ0 = А0, откуда
трп-хВо + РпВ\ = Аи откуда
Д> =
В,=
Ло
Рп'
6lz
-mpn_
\Вр
Рп
Итак,
если А = 0 не является корнем характеристического уравнения (р(Х) = 0, то существует
частное решение у(х) уравнения (1), имеющее вид многочлена, степень которого равна
степени многочлена, стоящего в правой части уравнения (1):
у(х) = В0хт + Вххт~1 +...+Вт. (2)
Предположим теперь, что рп = 0, причем для большей общности допустим, что и
Рп-\ = Рп-2 = • • • = Рп-г+1 =0, HO pn-r ^ 0,
т.е. Л = 0 является г-кратным корнем (г ^ 1) характеристического уравнения
у?(Л) = 0. При этом уравнение (1) имеет вид
У{п) + РхУ{п~Х) + • • • + Рп-гУ{г) = Р»(*). (3)
Полагая j/r* = z, приходим к предыдущему случаю; следовательно, существует
частное решение уравнения (3), имеющее вид
у{г)(х) = Д*т + Вххт~х + ... + Вт.
Отсюда получаем, что у(х) является многочленом степени т + г, причем члены,
содержащие ж в степени г - 1 и ниже, будут иметь произвольные постоянные
коэффициенты, которые могут быть, в частности, выбраны равными нулю. Тогда частное
решение примет вид
у(х) = хг(В0хт + Вххт~х +...+Вт).
Итак,
если А = 0 есть корень кратности г ^ 1 характеристического уравнения <р(\) = 0,
то частное решение у(х) уравнения (1) надо искать в виде произведения хг на многочлен
Qm(x) степени т с неопределенными коэффициентами:
у(х) = xrQm(x).

160 Глава XXII. Дифференциальные уравнения высших порядков
Пример 1. Найти частное решение уравнения
/ + j/ = 2s + 3.
Ч Характеристическое уравнение
А2 + А = 0
имеет корни Х\ = 0, Аг = -1, поэтому А = 0 есть простой корень (г = 1) этого уравнения. В правой
части многочлен первой степени (т = 1), поэтому частное решение неоднородного дифференциального
уравнения следует искать в виде
jftx) = х(В0х + В\).
Подставляя у(х) в уравнение и сравнивая коэффициенты при одинаковых степенях х, найдем, что
Во = 1, В\ = 1; поэтому искомое частное решение будет
д(х) = х2+х. ►
2. Уравнение вида
С[у] = у{п) + РхУ{п~Х) + ... + РпУ = еахРт{х), а = const. (4)
Частное решение у(х) этого уравнения будем искать в виде
у(х) = eaxz(x),
где z = z(x) — функция от ж, которая должна быть определена из условия
C[eaxz] = eaxPm(x). (5)
Тогда имеем:
У = еахг,
tf = ea*(az + z'),...,
fM = е- (.', + £ а-У + ^^ .'-V + • • • + *<'>) , • • •,
y(n) = e°* (a"z + не»" V + ^Г^ а»"2*" +... + z(n)) .
Умножим функции у, у',..., §W соответственно на рп.Рп-ь ..'., 1 и сложим
полученные результаты, группируя слагаемые по столбцам:
£[Л] = е"{*>(ф + ^ *' + ... + ^ *« + ... + *<">}.
Здесь у?(а) есть результат подстановки в характеристический многочлен <р(\) значения
А = а. Отсюда следует, что для получения тождества (5) надо определить функцию
z(x) как решение уравнения
z(n) + + <£!£) z(r) + + pf(e)z,+^(ф=р^(ж) (6)
г!
Это линейное неоднородное уравнение с постоянными коэффициентами, его
правая часть — многочлен. Поэтому частное решение уравнения (6) надо искать в виде
многочлена Qm(x) степени т, если (р(а) Ф 0, т.е. когда число а не есть корень
характеристического уравнения (р(Х) = 0. Если же число а окажется корнем
характеристического уравнения кратности г ^ 1, то
р(а) = у/(а) = ... = ^(г-°(а) = 0, />(а) Ф 0
и решение уравнения (6) надо искать в виде xrQm(x). Поэтому

§ 10. Неоднородные линейные дифференциальные уравнения с постоянными коэффициентами 161
частное решение у(х) исходного уравнения (4) надо искать в виде
у(х) = ea*Qm(x), (7)
если число а не есть корень характеристического уравнения <р(Х) = 0, и в виде
y(x) = xrea*Qm(x), (8)
если число а есть корень характеристического уравнения кратности г ^ 1.
Здесь Qm(x) — многочлен степени т с неопределенными коэффициентами,
Qm(x) = В0хт + Вххт~х + ... + Вт.
Пример 2. Найти частное решение уравнения
у" + у, = 2ех.
< Характеристическое уравнение
А2 + А = 0
имеет корни Ai = 0, Аг = -1. Правая часть уравнения представляет собой произведение е*, а = 1,
на многочлен нулевой степени (т = 0). Так как число а, равное единице, не является корнем
характеристического уравнения, частное решение у{х) уравнения надо искать в виде
Ц(х) = Вех.
Подставляя у(х) в уравнение, сокращая на ех, найдем В = 1, откуда
$(х) = е*.*>
Пример 3. Указать вид частного решения уравнения
у"-2у' + у = хех.
А2 - 2А + 1 = 0
4 Характеристическое уравнение
имеет корни Aj = A2 = 1. В данном случае
Рт(х) = х,
т.е. т = 1 и число а, равное единице, является двукратным корнем (г = 2) характеристического
уравнения. Поэтому частное решение у(х) следует искать в виде
у(х) = х2ех(В0х + В1). ►
3. Приведенные выше рассуждения остаются справедливыми и при комплексном а.
Поэтому, если правая часть линейного дифференциального уравнения
С[у] = у{п) +р,^1) +... +Рпу = №
(9)
имеет вид
f(x) = eQX [Pm(x) cos px + Qs(x) sin fix] Л (10)
где Рт(х)9 Qs(x) — многочлены степеней т и s соответственно, то поступим так.
Преобразуем тригонометрические функции по формулам Эйлера к показательным:
eipx + e-ipx eipx _ е-фх
cos дх — , sin 0x = ,
6 Зак. 179

162 Глава XXII. Дифференциальные уравнения высших порядков
тогда
Р*РХ л- Р~*РХ Р*Р* - р"*Рх
/(*) = е"Рт(х) у + ea'Q,(x) J =
В квадратных скобках стоят многочлены, имеющие степень, равную наивысшей
степени многочленов Рт(х) и Qs{x). Обозначив эти многочлены через М(х) и N(x)9
получим в правой части дифференциального уравнения выражение вида
М(х)е{а+*)х + ЭДе(в-'Л*. (11)
Для каждого слагаемого правой части можно применить указанное правило: если
а ± i/З не являются корнями характеристического уравнения, то частное решение
дифференциального уравнения можно искать в виде (11); если же числа a±i/3
являются корнями характеристического уравнения кратности г ^ 1, то частное решение
приобретает еще множитель хг.
Если опять вернуться к тригонометрическим функциям, то это правило можно
сформулировать так:
а) если числа а ± i/З не являются корнями характеристического уравнения, то частное^
решение у(х) дифференциального уравнения (9) надо искать в виде
у(х) = еах [U(x) cos fix + V(x) sin рх], (12)
где U(x), V(x) — многочлены с неопределенными коэффициентами, степень каждого
из которых равна наивысшей из степеней многочленов Рт(х), Q8(x).
Чтобы найти коэффициенты этих многочленов, надо подставить функцию у(х)
в дифференциальное уравнение и приравнять коэффициенты при одинаковых
степенях х в левых и правых частях. При этом надо приравнять друг другу соответствующие
коэффициенты тех многочленов, которые стоят множителями при cos/fo, и
отдельно — коэффициенты многочленов при sin рх;
б) если a±i/3 являются г -кратными корнями характеристического уравнения
(резонансный случай), то частное решение у(х) надо искать в виде
у(х) = xreax [17(a) cos fix + V(x) sin рх]. (13)
Замечание. Указанные виды частных решений (12) и (13) сохраняются и в том случае, когда в правой
части уравнения один из многочленов Qs(x) или Рт(х) тождественно равен нулю, т.е. когда правая
часть имеет вид
ea*Pm(x)cosPx или eaxQs(x) sin fix.
Пример 4. Найти частное решение уравнения
у" + 2у' + y = coss.
4 Характеристическое уравнение
А2 + А + 1 = О
имеет корни Ai = A2 = -1. В данном случае a = 0, р — 1, поэтому числа a ± ifi - ±i не являются
корнями характеристического уравнения;
Pm(*) = l, Q,(x) = О,

f 10/ Неоднородные линейные дифференциальные уравнения с постоянными коэффициентами.
.163
значит, частное решение уравнения следует искать в виде
у(х) = A cos х + В sin ж, А, В = const.
Подставляя функцию у(х) в уравнение, получаем А = 0, В = ^ и, следовательно,
у(ж)= ^ sin*. ►
Пример 5 (явление резонанса). Рассмотрим уравнение упругих колебаний без сопротивления при
наличии периодической внешней силы
у" + w2y = a sin/ft
(*)
(независимой переменной считаем время t).
<4 Общим решением однородного уравнения является функция
Уо.о. = С\ cos vt + Ci sin b)t — A sin(w£ 4- 6).
Если р Ф ш, т.е. если частота внешней силы не совпадает с частотой о/ собственных колебаний
системы, то частное решение неоднородного уравнения имеет вид
9(t) = M co&pt + Nsmpt, Af,JV = const.
Подставляя это выражение в уравнение (*), найдем, что М = 0, N = т^гЬш- Общее решение
уравнения (*) имеет в этом случае вид
у0.н. = Asin(a/* + 6) + ц2__02 sin/ft,
т. е. результирующее движение слагается из собственных колебаний с частотой из и вынужденных
колебаний с частотой р.
Если р = ш, т.е. частота внешней силы совпадает с
частотой собственных колебаний системы, то частное решение
неоднородного уравнения (*) надо искать в виде
g(t) = t(M coswt + N sin uft).
Подставляя ij(t) в (*), находим, что
М =
а а
-~~, N = 0, откуда fj(t) = ---t cos u>L
2d/ 2d/
Общее решение уравнения (*) будет иметь вид
а
у = A sin(w£ +6) - -r-t cos art.
2uj
(**)
Рис.3
Второе слагаемое в правой части (**) показывает, что в этом
случае амплитуда колебаний неограниченно возрастает при
неограниченном возрастании времени t (рис. 3). Это явление,
возникающее при совпадении частоты внешней силы с частотой собственных колебаний системы,
называется резонансом. ►
Удобным для отыскания частных решений является следующий прием. Пусть
имеем линейное неоднородное дифференциальное уравнение с действительными
постоянными коэффициентами
С[у] = у(п) + W*-0 + • • •'+ РпУ = eaxPm(x) cos pz,
(14)
где Pm(x) — заданный многочлен степени m с действительными коэффициентами,
а и /3 — действительные числа. Составим вспомогательное неоднородное уравнение
с той же левой частью, что и у уравнения (14), и правой частью в виде комплексно-
значной функции действительного переменного х:
C[z] = z{n) + pizln'l) + ... + pnz = eaxPm(x) cos0x + ieaxPm(x) sin /3x. (15)
Правая часть уравнения (14) есть действительная часть правой части уравнения (15),
и поэтому в силу теоремы 14 действительная часть и(х) решения z(x) = и(х) + iv(x)
6*

164
Глава XXII. Дифференциальные уравнения высших порядков
уравнения (15) будет решением исходного уравнения (14). Таким образом вопрос
сводится к отысканию частного решения уравнения (15), которое можно переписать
в виде
ф] = е<в+*Крт(х). (16)
Из приведенных выше рассмотрений следует:
1) если число аЛ-ip не является корнем характеристического уравнения
у>(А) = Ап+р1Ап-1 + ...+Л= О,
то частное решение уравнения (16) следует искать в виде
f(x) = e<e+<">*Qm(s), (17)
где Qm(z) — многочлен степени т с неопределенными коэффициентами,
Qm(x) = В0хт + Вххт-] + ... + Вт;
2) если a+i/З является корнем кратности г характеристического уравнения, то частное
решение уравнения (16) имеет вид
z(x) = xre(°+if,»Qm(x). (18)
Замена тригонометрических функций показательной упрощает вычисления, так
как после подстановки z(x) в уравнение (16) обе части уравнения можно сократить
на е*Л+,^ж. Комплексные коэффициенты Во, В\,..., Вп многочлена Qm(x)
определяются путем подстановки решений (17) или (18) в уравнение (16) и приравнивания
коэффициентов при одинаковых степенях х в левой и правой частях полученного
равенства. Отделив действительную часть и(х) решений (17) или (18), найдем частное
решение уравнения (14). В случае уравнения вида
C[y] = eaxPm(x)sm/3x (19)
поступаем аналогично: 1) переходим к вспомогательному уравнению (16); 2) находим
частное решение z(x) = u(x) + iv(x) этого уравнения. Мнимая часть v(x) решения
будет частным решением уравнения (19).
Пример 6. Найти частное решение уравнения
у" -\-у — 5хе~* cos х. (*)
< Составляем вспомогательное уравнение
*" + * = 5*е<-,+,>. (•*)
Поскольку число -1 + i не является корнем характеристического уравнения
А2 + 1 = О,
частное решение уравнения (**) ищем в виде
2(x) = (B0x + Bx)e{-l+i)x.
Подставляя 2(х) и
f(x) = 2(-1 + t)B0eH+,> + (-1 + i)2(B0x + Б,)е<-1+,>
в уравнение (**) и сокращая на е(~1+<)х, получаем
(-2 + 2t)B0 + (-2i + l)(B0x + B{) = 5x.

§11. Применение степенных и <>6о6Щённь1Хстепенных радов км 165
Приравнивая коэффициенты при одинаковых степенях х В левой и правой частях последнего равенства,
найдем:
В0(1 - 2i) = 5, откуда В0 = 1 + 2i;
B,(l-2i) + (-2 + 2i)Bo=0, откуда В\ = (24^14|).
Поэтому для z(s) имеем формулу
z(a?) = (1 + 2i)x + - + -— t e~*(cos x + i sin ж).
Отсюда получаем частное решение данного уравнения:
ti(s) = Re2(x) = e~* fs + - J cos ж- [2х+ --Jsmar . ►
§11. Применение степенных
и обобщенных степенных рядов
к интегрированию дифференциальных уравнений
Пусть имеем дифференциальное уравнение
y" = f(x,y,y')\ (1)
и требуется найти решение этого уравнения, удовлетворяющее начальным условиям
у(хо) = Jfo; у'(х0) = yi (2)
Предположим, что функция / аналитична в окрестности точки (а?о, уо, у'0), т. е.
представляется стейенным рядом по степеням х - ж0, у - Уо, у1 - у^ Тогда решение у(х)
задачи Коши (1), (2) можно получить в виде ряда
у(^;ы+^(х-«.)+^(х-^+...+^(«-,,)ч....
(3)
В самом деле, зная х0, Уо, Уо, в силу самого уравнения (1) найдем з/'(жо) — /(#о> Уо> #а)<
Дифференцируем уравнение (1) по ж:
. y'" = ti + f'yy' + fh"- • (4)
Подставляя в правую часть (4) значения жо, Уо» Уо и только что найденное значение
/(жо), найдем з/"(ж0) и т.д.
Если ряд (3) сходится в некотором интервале (х0 - Л, хо + Л), то он определяет там
решение задачи (1), (2).
Пример 1. Найти решение задачи Коши
У" = У, (*)
1(0) = 1, у'(0) = 1. (**)
•4 В силу (*), (**) имеем
9"(0) = 1.
Дифференцируя (*), найдем

166 Глава XXII. Дифференциальные уравнения высших порядков
откуда у'"(0) = у'(0) = 1, и вообще
у<*>(0) = 1, п = 0,1,2,...;
отсюда
хх2 хп
Рассмотрим линейное дифференциальное уравнение
Ро(х)у" + Р\ (х)у + р2(х)у = 0. (5)
Теорема 16 (об аналитичности решения). Если ро(х), р\(х), р2(х) являются аналитическими
функциями в окрестности точки х = х0 и р(х0) ф 0, то решения уравнения (5)
также являются аналитическими функциями в некоторой окрестности точки х = х0 и,
следовательно, эти решения можно искать в виде ряда
у = а0 + ах(х - Xq) + а2(х - х0)2 + ... + ап(х - х0)п + ... . (6)
Пример 2. Найти решение задачи
У" + У = 0, у(0) = 0, у'(0) = 1.
4 Решение будем искать в виде ряда
у(х) = а0 + ахх + а2х2 + а3х3 + ... 4- апхп + ... .
Имеем:
у'(х) = ах+ 2а2х + Ъаъх2 + ... + па»:!;*"1 + ... ,
у\х) = 1 • 2а2 + 2 • За3« +... + п(п - 1)о«жл~2 +,.. .
Подставим у(ж) и у"(я) в данное уравнение и приравняем нулю коэффициенты при степенях х:
•° ' оо + Ь2а2=0, откуда а2 = -тЛ»
а1+2-За3=0, откуда «з^-уТз»
«п-2 + я(п - 1)«п = 0, откуда а» = Л 2
(n-l)n'
В силу начальных условий имеем ао = 0, а\ — 1, поэтому а2 = 0 \л вообще
«2*=0, Лг = 1,2,... .
Далее имеем а\ = 1, а3 = -|3» а5 = — Ц = i.2.3-4-5 ' и во°бще
(-о*
«2*+! =
(2*+1)Г
ж2*+1
Окончательно получаем
ф) = П " ЗГ+ • • •+ Н)* ci+lj!+' • • = sln *' *
Пусть теперь коэффициент ро(#) обращается в нуль в точке xq .
Определение. Точка зд называется нулем порядка (кратности) т (га — целое
положительное число) функции f(x)9 если /(ж) представима в виде f(x) = (х - #o)m/i(#)>
где/1(ж0)^0.

§ 12. Уравнение Бесселя. Функции Бессел* :—: 167
Теорема 17 (о разложимости решения в обобщенный степенной ряд). Если в уравнении
Ро(х)у" + Р\{х)у + р2(х)у = О
(5)
коэффициенты ро(х), р\(х), р2(х) суть аналитические функции в окрестности точки х$,
причем х = xq является нулем порядка т функции Pq(x), нулем порядка т - 1 или выше
функции р\ (х) (если т> I) и нулем порядка га - 2 или выше функции р2(х) (если т > 2),
то существует по крайней мере одно нетривиальное решение уравнения (5) в виде суммы
обобщенного степенного ряда
у(х) = ао(ж - хоу + ai(x- xo)ff+l +... +ап(х- х0)п+а + ... ,
где а — некоторое действительное число, вообще говоря, не целое.
§12. Уравнение Бесселя. Функции Бесселя
12.1. Дифференциальное уравнение Бесселя
Дифференциальным уравнением Бесселя называется уравнение вида
х2у" + ху' + (х2 - v2)y = О,
(7)
где I/ —-действительное число. Это уравнение имеет особую точку ж = 0 (коэффициент
при старшей производной в (7) обращается в нуль при х = 0). Сравнивая (5) и (7),
заключаем, что для уравнения Бесселя
р0(х) = ж2, рх(х) = х, р2(х) = х2 - i/2,
так что х = 0 является нулем второго порядка (га = 2) функции ро(х), нулем первого
порядка функции р\(х) и не является нулем функции р2(х) (если v Ф 0). Поэтому
в силу теоремы 17 существует решение уравнения (7) в виде обобщенного степенного
ряда
у(х) = ха ]Г akxk, a0 ф 0,
*=о
(8)
где а — характеристический показатель, подлежащий определению. Перепишем
выражение (8) в виде
00
и найдем производные:
ОО 00
2,' = ]T(fc + a)akxk^~\ у" = ]П(* + <r)(* + а - \)akJ*-\
Подставим эти выражения в уравнение (7),
00 00 00
х2 J2(k + *)(* + °- 0«***+"2 + х ]T(k + *)ahxk+*-1 + (x2 - i/2) JT akxk+* = 0,
*=0
*=o
*=o

1«.
. Глава XXII. Дифференциальные уравнения высших порядков
и приравнивая нулю коэффициенты при х в степени а, аг +1,..., а + к,..., получим
систему уравнений
V -*2]ао = 0,
[(cr+l)2-v2]ai=0,
[((г + 2)2-1/2]а2+ао = 0,
^+2
,.*+*
(9)
[(сг + к)2 - р2]ак + а*_2 = 0, k = 2, 3,... .
Так как оо Ф 0, то из первого уравнения (9) следует, что а2 - i/2 = 0, или
(7 = ±1/.
Теперь из второго уравнения (9) будем иметь
а, =0.
Рассмотрим сначала случай а = v > 0. Перепишем k-e (k > 1) уравнение
системы (9) в виде
(а + к + i/)(tr + к - */)а* + а*_2 = 0,
откуда получаем рекуррентную формулу для определения а* через ац~г\
а* = -
я*-2
(сг + к + 1/)(<г + к - v)'
Учитывая, что ai = 0, получаем отсюда аз = 0 и вообще агт+\ = 0- С другой стороны,
каждый четный коэффициент может быть выражен через предыдущий по формуле
«2m = ~
I U2m-2
(а + 2т + */)(сг + 2т - v)'
или, с учетом a = v,
0>2т
dim-!
22т(т +1/)"
Последовательное применение этой формулы позволяет найти выражение а2т
через оо:
a,Q й2 ао
Л2=;
22l(i/+l)'
а4
22 • 2(i/ + 2) 24b2(i/+l)(*v + 2)'
вообще
Подставим найденные значения коэффициентов в формулу (8),
л — ( \\т а°
zro V ' 22"»m!(i/+l)(i/ + 2).
.;(i/ + m)#;
3/,(ж) = аож'
■('+D-
\ m=l
„2m
i)"
г^т! (i/ + 1)С" + 2) ... (и + т)
)
(Ю)
Нетрудно проверить, что ряд в правой части (10) сходится на полуоси х > 0 и опреде
ляет там функцию у\ (х) — частное решение уравнения Бесселя.

§ 12. Уравнение Бесселя. Функции Бесселя.
Рассмотрим теперь второй случай, когда а = -i/. Если v не равно
положительному целому числу, то можно написать второе частное решение, которое получается
из выражения (10) заменой v на -i/ (в уравнение (7) v входит четным образом),
у2(х) = OqX
Jim
О"
22mm! (-v + !)(-!/ + 2) ... (-1/ + га)
)
(Vt)
(Если v равно целому положительному числу, то решение (10') теряет силу, так как
начиная с некоторого числа один из множителей в знаменателе членов разложения (10')
будет равен нулю.) Ряд в правой части (10') также сходится при всех значениях х > 0.
Решения у\(х) и уг(х) линейно независимы. Действительно, их отношение
У2(Х) -21/
У\(х)
= X
1"?(^И) + ---
1
гЧу+\)
+ ..
не является постоянным.
12.2. Г-функция Эйлера и ее свойства
Для дальнейшего нам понадобятся некоторые свойства Г-функции Эйлера. Она
определяется следующим образом:
+00
Г(р) = |а
^""'е-* dx, Rep>0.
Интегрированием по частям получаем основное функциональное уравнение для Г-
функции:
(И)
Г(р+1)=рГ(р).
Так как Г(1) = 1, то Г(2) = 1 • Г(1) = 1, Г(3) = 2Г(2) = 2! и вообще
Можно показать еще, что
Г(п + 1) = n!, n = 0,1,2,.
(О-
V5F.
С помощью функционального уравнения (11) можно определить гамма-функцию
для отрицательных значений аргумента. Записав уравнение (11) в виде Т(р) = г^ >
замечаем, что для малых р выполняется соотношение Г(р) « £.
Аналогично, если m — положительное целое число, то ддя значений р, близких
к числу -га, имеем
г(р)
1
(-О"
га! p + m'
Можно показать, что Г(р) Ф 0 при всяком р, поэтому функция щ будет непрерывной
для всех значений р, если положить
1
Г(-т)
0, т = 0,1, 2,.

170
Глава XXII. Дифференциальные уравнения высших порядков
12.3. Функции Бесселя
Возвратимся к решению уравнения Бесселя (7). Коэффициент ао до сих пор оставался
произвольным. Если v Ф -п, где п > 0 —- целое число, то, полагая
а0
1
2vT(v+ 1)'
найдем
= (-1)"
1
22ro+"m!(i/ + l)(i/ + 2)... (i/ + т)Г(1/ + 1)
1
22го+*Т(т+1)Г(1/ + т+1)*
Подставляя это выражение ддя коэффициентов в (9), получаем
Ух
^ = ^~^mr(m+ l)T(v + m+ 1) \2j
(12)
Ряд (12) определяет функцию
оо - / Ж \ 2m+I/
^ = 5/~1)ror(m+l)r(i/ + m+l)V2) *
(13)
которая является решением уравнения Бесселя и называется функцией Бесселя первого
рода v -го порядка.
Ряд
1
/_1/(Ж) = ]^~1)тт(т+1)Г(-и + т+1)
:(f)
2т-v
отвечает случаю а = -v (у — нецелое) и определяет второе решение уравнения (7),
линейно независимое с функцией ^(ж).
Итак, если v не равно целому числу (у Ф О, ±1, ±2,...), то функции Jv(x)
и f-v(&) образуют фундаментальную систему решений уравнения Бесселя (7) и его
общее решение имеет в этом случае вид
y = Cxfv{x) + C2f-v{x).
При v целом выполняется линейная зависимость
/_„(*) = (-1)"^(х).
(14)
В самом деле, имеем
оо j / \
ЛП(Х) = £(~1ГГ(т + 1)Г(т - . + 1) Ы
2т-п

lt& Уравнение Бесселя. Функции Бесселя 171
Первые п членов ряда исчезают, так как Г(т1п+л = 0 при т = 0,1,..., п - 1,
a wn]n+\\ = 1. Введя обозначение т = к + п, находим
оо ^ /х\2к+п
/_"(а:) = 2("1)t+"r(* + n + l)r(ife + l) \2) =
оо j /ж\2*+п
=(-iyg(-o'r(t+,)r(t+,,.M)G) -нл*«.
*=0
Выпишем ряды для функций Бесселя первого рода нулевого (п = 0) и первого (п = 1)
порядков:
^)=i-(f)2+^(f)4-^(f)6+...,
Функции ^(ж) и J\ (ж) (рис. 4) часто встречаются в приложениях, и для них
имеются подробные таблицы.
Р 2>
Рис.4
12.4. Рекуррентные формулы для функций Бесселя
Используя формулу
^(Ж)~2( 1)тГ(т+1)Г(|/ + т + 1)(2У
2m+i/
непосредственно проверкой убеждаемся в том, что
dx
{х"£{*))=*"Л-М-
Точно таким же вычислением находим
dx
{x-v £{*)) = -*-" Л+М-
(13)
(15)
(16)
Раскрывая в левых частях формул (15) и (16) производные произведений, получаем
соответственно равенства
X
X
(17)
(18)

172 Глава XXII. Дифференциальные уравнении высших порядков
Складывая и вычитая (17) и (18), получим две важные рекуррентные формулы
(19)
<20)
Формула (19) показывает, что производные функций Бесселя выражаются через
бесселевыже функции. Из формулы (20) вытекает, что, зная Jv(x) и Jv-\(x), можно
найти </и+\(х). В частности, все функции Бесселя целых номеров выражаются через
две функции Js(x) nj\(x). Здесь оказывается полезным соотношение (14). При1/ = 1
из (20) находим, например,
12.5. Функции Бесселя полуцелого индекса
Рассмотрим специальный класс бесселевых функций с индексом, равным половине
нечетного целого числа. Этот класс встречается в приложениях и замечателен тем, что
в рассматриваемом случае бесселевы функции могут быть выражены через
элементарные. Так, при v = \ путем несложных преобразований находим
Аналогично, при v = —\ получаем
/-I/2(*)=v^
Обе эти формулы можно записать в виде
sin ж.
cos ж.
^/ ч Г2~ / 1/7Г 7Г\ 1
(21)
sin ж
COS
•)
По рекуррентной формуле (20) подсчитываем, например,
М(*) = \ М*) - /-mi*) = у Тх (~
и т. д.
12.6. Нули бесселевых функций
При решении многих прикладных вопросов необходимо иметь представление о
распределении нулей функций Бесселя. Нули функций J\ii(x) и JL\/2(x) совпадают
с нулями sin ж и cos ж соответственно. Можно показать, что для больших значений х
имеет место асимптотическое представление1^ (сравните с (21))
лм = ^вЧж~т-5)+°(я
-3/2
).
+00,
(22)
*) Символ f(x) — 0((р(х)) означает, что отношение jgj остается ограниченным при х -»• оо (см.
главу VIII).

§ 12. Уравнение Бесселя. Функции Бесселя Ш
справедливое как для целых, так и для дробных i/. Формула (22) показывает, как
ведет себя функция Бесселя при возрастании аргумента. Это колеблющаяся функция,
бесчисленное множество раз обращающаяся в нуль, причем амплитуда колебаний
стремится к нулю при ж -* +оо.
Распределение нулей функции Бесселя с целым положительным индексом, т. е.
корней уравнения
М*) = 0 (п = 0,1,2,...)
устанавливается следующей теоремой.
Теорема 18. Функция Jn{x) (п = 0,1,2,...) не имеет комплексных нулей, но имеет
бесконечное множество действительных нулей, расположенных симметрично относительно
точки ж = О, которая в случае п = 1,2,... принадлежит к их числу. Все нули
функции простые за исключением точки ж = О, которая при п = 1,2,... является нулем
кратности п соответственно.
12.7. Ортогональность и норма функций Бесселя
Ортогональность функций Бесселя
Рассмотрим дифференциальное уравнение
х2у" + ху' + (А V - i/2) у = 0, (23)
где Л — некоторый числовой параметр, отличный от нуля. Нетрудно проверить, что
уравнению (23) удовлетворяет функция Бесселя ^(Аж).
Перепишем уравнение (23) в виде
у"+1у'+{х2-^)у=0 <24>
и обозначим у\ = Jv{\\x), уг = ^(Агж), где Ai, Л2 — какие-либо значения
параметра Л. Тогда будем иметь тождества
Уг
Умножая первое тождество на у2 (ж), второе — на у\(х) и вычитая одно из другого,
получим
У\У2 - у\у" + - (у\У2 - ут) + (а? - xl)ym = о.
X
Умножив все члены последнего тождества на ж, замечаем, что его можно записать
в виде
J- ЫУ\У2 - 011Й)] = (Лг - X2\)xyiy2.
Интегрируя последнее тождество по ж в пределах от 0 до 1, будем иметь
1
13=1 /
[я (У\У2 - Ут)] \9=0 = (*2 - А?) I ху1(х)у2(х) dx,

174.
. Глава XXII. Дифференциальные уравнения высших порядке!
или
(25)
1. Пусть Ai Ф А2. Тогда из равенства (25) следует, что если Ai, А2 есть нули функции
Jv(x), то левая часть (25), а значит, и правая, равны нулю, так что
Это означает, согласно определению, что функции ^(Ajx), ^(A2a;) ортогональны
с весом р(х) = х на отрезке [0,1].
Бесселева функция Jv (x) имеет счетное множество нулей
О < Ai < А2 < ... < Ап < ...
и, следовательно, система функций
fv{\\x), ^(А2ж), ..., Ju(Xnx), ... (у — фиксировано)
есть ортогональная на отрезке [0,1] система с весом р(х) = ж,
(26)
1
/
xjrl,(\ix)t/j/(\jx) dx = 0 при i Ф j.
(27)
2. Если Aj, А2 являются корнями уравнения
/М = о,
то в этом случае при Ai ф А2 из (25) также имеем
J xfv{\xx)fv{\2x)dx = U.
(28)
Следовательно, система функций {ju(Kx) }™=l, где Ап — корни уравнения^'(ж) = О,
ортогональна на отрезке [0,1] с весом р(х) = х.
3. Пусть Ai, А2 являются корнями уравнения
*&*) ... и
М*) '
где h — некоторое фиксированное число. Уравнение (28) встречается в
математической физике и при v > -1 имеет бесконечное множество положительных корней,
но не имеет комплексных корней (исключая случай (-Л + v) < О, когда есть два чисто
мнимых корня). Записав левую часть равенства (25) в виде
"Ai^(A,) А2/ДА2)1
А1/ЛА1ША2) - ^ХМ/иМ = МЪШЪ)
МЪ) МЪ)

fr12. Уравнение Бесселя. Функции Бесселя _
Ш
убеждаемся в ортогональности бесселевых функций по нулям линейной комбинации
xcfv(x) ~~ Ь</Лй) = 0 функции Бесселя и ее производной:
1
/
x/v(Xix)/v(Xjx) dx = 0 при i Ф j,
где Xk (к = 1,2,...) — корни уравнения (28).
Норма функций Бесселя
Величина
\\fv(\x)\\ = (Jx/?(\x)dx)
1/2
называется нормой функции Бесселя Jv{Xx).
Пользуясь равенством (25), можно показать, что
IU(A-)||2 = |
Дй(А)+(1-£)^2(А)].
(29)
В частности, для Jis{Xx), где Л — нуль бесселевой функции, имеем
IU(A*)||2 = \ Л\\) = \ f?(\) U(A) = -^(А)).
12.8. Функции Неймана (Вебера)
Всякое нетривиальное решение уравнения Бесселя
жУ + жуЧ(ж2-1/2)у = 0 (7)
называют цилиндрической функцией. При v нецелом функции^ (х) и J~v (x) образуют
функциональную систему решений уравнения Бесселя (7). При v = n — целом имеет
место линейная зависимость
/_„(*) = (-1)»^(х).
Чтобы к решению Jn(x) подыскать такое, которое ему не пропорционально,
поступаем так: при нецелом v составляем функцию
JK(x) =
f1/(x)cosin/-cf-1,(x)
sm7ri/
(30)
Она является линейной комбинацией решений линейного однородного уравнения (7)
и, следовательно, сама есть решение этого уравнения! Переходя в (30) к пределу
при 1/-*пи пользуясь правилом Лопиталя, будем иметь
Л£(*) =
(-1)-»
Характерное свойство функций J/"n(x) (функций Бесселя 2-го рода) — наличие
особенности в начале координат (рис. 5)
Л{х)~1\п(^\, 7=1,781...,
(п-1)! /2\"
^i(»)~-i '-[-) , п = 1,2,...
7Г \Х /
о+о,

176
Глава XXII. Дифференциальные уравнения высших порядков
Найденное решение *Жп (х) уравнения
Бесселя (7) при v = n вместе с Jn(&) составляет
фундаментальную систему решений уравнения
х2у" + ху + (ж2 - п2)у = 0.
Функцию Jfn{x) называют также функцией
Неймана или функцией Вебера.
При достаточно больших х
^(*)~V^cos(*-^-J),
^(x)~V^sin(x-T-^)-
►+оо,
Рис.5
Таким образом, на больших расстояниях от начала координат цилиндрические
функции 1 -го и 2-го рода относятся друг к другу как косинус и синус, но затухают с ростом х
благодаря множителю 4%. Эти функции удобны для представления стоячих
цилиндрических волн.
По аналогии с показательными функциями (формулы Эйлера) можно построить
линейную комбинацию функций Jv(x) и J/y(x), дающую функции, связанные с
бегущими волнами. Так мы приходим к бесселевым функциям 3-го рода или функциям
Ханкеля, определяемым соотношениями
(x)=f„(x)-i^rv(x).
НИИ
Упражнения
Найдите общее решение уравнений:
l.(l + x2)y" + 2xy' = x3. 2.j,,vth* = j,"'. З.уу" = уа. 4.уу" + у'2 = 1.
Найдите решение задачи Коши:
5. у" + 18 sin у cos3 у = 0, у(0) = 0, у'(0) = 3. б.у" = 18у3, у(1) = 1, у'(1) = 3.
7.!>У' = 4(!,4-1), »(0) = А j/(0) = V2.
Проинтегрируйте уравнения, найдя, где указано, частные решения:
В.у"-4у' + 4у = 0. 9. у" - 2у'- Зу = 0. 10. у" + 2у' + 5у = 0.
11.у"-3у' + 2у = 0, у(0) = 0, у'(0)=1. 12.у'"-у' = 0.
13. у'" - у = 0, у(1) = у'(1) = У"(1) = 0- 14.ylv-y = 0.
15. ylv + у = 0. 16. yv = 0.
Найдите общие решения следующих линейных неоднородных дифференциальных уравне-
17. у" + у = 1. 18.у"-2у' + у = ж + 1. 19. у" - у = 4хех.
20. у" - 2у' + у = 2ех. 21. у" + у + у = sin х. 22.у" + у = cos*- 2sinx.
23. у" + Ay - Ъх sin х. 24. у" + Ay = 2 sin2 x.

§ 12. Уравнение Бесселя. Функции Бесселя
177
Виды частных решений неоднородных линейных уравнений с постоянными коэффициентами
для различных правых частей
Правая часть*)
дифференциальных
уравнений
1- Рт(х)
2. еахРт(х)
3. Pm(x)cospx +
+ Qs(x)sinpx
4. eax[Pm(x)cospx +
+ Qs(x)sinpx]
Корни характеристического уравнения
Число 0 не является корнем
характеристического уравнения
Число 0 — корень характеристического
уравнения кратности г ^ 1
Число а не является корнем
характеристического уравнения
Число а является корнем
характеристического уравнения
кратности г ^ 1
Числа ±ip не являются корнями
характеристического уравнения
Числа ±ip являются корнями
характеристического уравнения
кратности г
Числа а ± гр не являются корнями
характеристического уравнения
Числа а ± гр являются корнями
характеристического уравнения
кратности г
Виды частного решения
Рт(х)
ХГ?т(х)
€аХРт(х)
хгеахРт(х)
Рк(х) cos px +
+ Qk(x)sinpx,
к = max{m, s]
xr (Pk(x) cosрх-\-
+ Qk(x)sinpx)
eax(Pk(x)cospx +
+ Qk(x)sinpxy
к = max{m, s}
xreax(Pk(x)cospx +
+ Qk(x)sinpx)
*) Первые три вида правых частей являются частными случаями четвертого.
Укажите вид частных решений следующих линейных неоднородных уравнений:
25. у" - у = 3 + хех + ж2 sinх. 26. у" + у' = 2 + х + х2ех + х sinx.
27. у" - у" = 1 + хех + 2х cos ж. 28. у" + у" = х + хех + х sin ж.
29. у" - у = 1 + хех + ех cos ж.
Методом вариации постоянных проинтегрируйте следующие уравнения:
30. у" + у= —. 31. у" -у' = е2х sin е*.
cos ж
Проинтегрируйте следующие уравнения Эйлера:
32. х2у" - ху - Зу = 0. 33. жУ + жу' + у = 0.
Ответы
ж3 ж
1.у = т^-т+С1 arctga?+C2. 2.у = Сх chhx+C2x2+C3x+C4. З.у = C2ec,z. 4. у2 = (ж+С2)2+
С,. 5.у = агс1ё3ж. б.у= ^. 7.у = л/Г+1^. 8. у = Схе2х + С2же2х. 9. у = С,е"х + С2е3*.

178 : Глава XXII. Дифференциальные уравнения высших порядков
10. у = Схе~* cos2x+C2e-x вт2ж. 11. у = е2х-ех. 12. у = С, +С2е~* + С3е*. 13. у = 0. 14. у =
v^ /г v^ at ; ^ V5 j^
Ciez-fC2e х+Сзсо8ЖН-С48тж. 15.у = deTxcos Y^+^e 2 *sin ^ ж+С3е~*2-* cos Ц ж+
C4e 2 x sin Y ж- 16. у = Cx + С2ж + С3ж2 + С4ж3 + С5ж4. 17. у = Ci cos ж + С2 sin ж + 1.
18. у = С^е* + С2хех + ж + 3. 19. у = Схех + С2е~х + (ж2 - х)ех. 20. у = С,е* + С2же* + ж2е*.
21. у = Cie~z/2cos ^ж + С2е~2 sin ^ ж-cos ж. 22. у = С\ совж + С2 sin ж + ж(со$ ж-f -sin ж).
2 1 ж
23. у = С\ cos 2ж + С2 sin 2ж + ж sin ж - - cos ж. 24. у = Сх cos 2ж + С2 sin 2ж + - - т sul 2s.
3 4 4
25. у = Лж+ж(Л1Ж+В1)ех+(А2ж2+В2ж+1>2) cos ж+(Л3ж2+В3ж+1>з) sin ж. 26. у = ж(Лж+Б)+
(Л1Ж2+В,ж+1>1)еа:+ж[(Л2Ж+В2)со8Ж + (АзЖ+Вз)8Шж]. 27.у = Лж^ж^ж+БОе^ + ^жЧ-
^созж+О^зж+Вз^тж. 28. у = (Лж+В)ж2+(А1Ж+В1)еаг+(Л2ж+В2)со8Ж+(ЛзЖ+Вз)8тж.
29. у = А + (Л хх + 2?i)e2z + ех(Л2 cos ж + В2 sin ж). 30. у = Сх cos ж + С2 sin ж + cos ж In | cos ж| +
ж sin ж. 31. у = С, +C2ez-sinez. 32. у = С,ж3 + —. 33. у = С, cos(ln ж) + С2 sin(ln ж), ж > 0,

Глава XXIII
СИСТЕМЫ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
§ 1. Основные понятия и определения
К системе дифференциальных уравнений приводит уже простейшая задача динамики
точки: даны силы, действующие на материальную точку; найти закон движения, т. е.
найти функции х = x(t), у = y(t), z = z(t), выражающие зависимость координат
движущейся точки от времени. Система, которая при этом получается, в общем
случае имеет вид
[ ^х _ ( dx dy dz\
J d2y ( dx dy dz\
I d2z ( dx dy dz\
1^ = /^,*,^,-,-,^).
Здесь ж, у, z — координаты движущейся точки, t — время, f,g,h — известные
функции своих аргументов.
Система вида (1) называется канонической. Обращаясь к общему случаю системы т
дифференциальных уравнений с т неизвестными функциями x\(t), x2(t),... , xm(t)
аргумента t, назовем канонической систему вида
**} = Л(*. *ь *ь .... «i*1"0,...,»«,««,..., «2""°). *=l,2,...,m,
(2)
разрешенную относительно старших производных. Система уравнений первого
порядка, разрешенных относительно производных от искомых функций,
Х{ = /;(*, XU Ж2, . . . , Яп), t = 1, 2, . . . , П, (3)
называется нормальной.
Если ж|, ж",..., х\ '"' в (2) принять за новые вспомогательные функции, то
общую каноническую систему (2) можно заменить эквивалентной ей нормальной
системой, состоящей из N = к\ + &2 + • • • + кт уравнений. Поэтому достаточно
рассматривать лишь нормальные системы.
Например, одно уравнение
d2x

180 Глава XXIII. Системы дифференциальных уравнений
является частным случаем канонической системы. Положив -^ = у, в силу исходного уравнения будем
иметь
* = -..
В результате получаем нормальную систему уравнений
At
dy- *
эквивалентную исходному уравнению.
Определение 1. Решением нормальной системы (3) на интервале (а,Ъ) изменения
аргумента t называется всякая система п функций
Х\ = Ж,(0, Х2 = Ж2(*), . . . , «п = Xn(t), (4)
дифференцируемых на интервале а < t < b, обращающая уравнения системы (3)
в тождества по t на интервале (а, Ь).
Задача Коши для системы (3) формулируется так: найти решение (4) системы,
удовлетворяющее при t — t0 начальным условиям
Х\ \t=t0 = ЖЬ «2^ = «2, • • • , Xn\t=t0 = X°n- (5)
Теорема 1 (существования и единственности решения задачи Коши). Пусть имеем нормальную
систему дифференциальных уравнений
dx{
— = /,-(<, жь ж2,..., ж„), г = 1, 2,..., п,
и пусть функции /,•($, Х\, x2l..., жп) (Ч# = 1,2,..., п^ определены в некоторой (п + 1)-
мерной области D изменения переменных t, x]f х2, ..., хп. Если существует
окрестность П тонки Мо(*о, s?, «J» • • • > жп)> * которой функции /,- непрерывны по совокупности
аргументов и имеют ограниченные частные производные по переменным Х\, хг, ... ,хп,
то найдется интервал *о - /i0 < t < to + h0 изменения t, на котором существует
единственное решение нормальной системы (3), удовлетворяющее начальным условиям
I 0 I 0 10
ХАыо = ЖЬ «2||s|0 = «2, • - • , ««Ц, = Жп.
Определение 2. Система гг функций
ж, = Xi(t, С\,С2,..., С„), г = 1,2,..., гс, (6)
зависящих от * и п произвольных постоянных С\, Сг,..., Сп, называется общим
решением нормальной системы (3) в некоторой области П существования и единственности
решения задачи Коши, если
1) при любых допустимых значениях Сь С2,..., С„ система функций (6) обращает
уравнения (3) в тождества,
2) в области ft функции (6) решают любую задачу Коши.

§2. Методы интегрирования систем дифференциальных уравнений
181
Решения, получающиеся до общего при конкретных значениях постоянных С\,
Сг,... , Сп, называются частными решениями.
Обратимся для наглядности к нормальной системе двух уравнений,
dx\
f\(t,xux2),
dx2
-fl=f2(t,XbX2).
(7)
Рис.1
Будем рассматривать систему значений*, х\, хг как
прямоугольные декартовы координаты точки трехмерного
пространства, отнесенного к системе координат Otx\X2.
Решение
хх =ж,(0,
х2 = x2(t)
системы (7), принимающее при t — Ц значения ж?, х2,
определяет в пространстве некоторую линию,
проходящую через точку Мо(2о, х°ь х2). Эта линия называется ш*-
тегральной кривой нормальной системы (7). Задача Ко-
ши для системы (7) получает следующую геометрическую
формулировку: в пространстве переменных t,x\,x2
найти интегральную кривую, проходящую через данную точку
Мо(*о, хи х\) (рис. 1). Теорема 1 устанавливает
существование и единственность такой кривой.
Нормальной системе (7) и ее решению можно придать
еще такое истолкование: будем независимую переменную t
рассматривать как параметр, а решение
Х\ =Xl(t),
х2 = x2(t)
системы — как параметрические уравнения кривой на
плоскости х\Ох2. Эту плоскость переменных х\х2
называют фазовой плоскостью. В фазовой плоскости
решение х\ = x\(t), x2 = x2(t) системы (7), принимающее
при t = to начальные значения х°]9 х\, изображается кривой АВ, проходящей через
точку Мо(х°и х2) (рис. 2). Эту кривую называют траекторией системы (фазовой
траекторией). Траектория системы (7) есть проекция интегральной кривой на фазовую
плоскость. По интегральной кривой фазовая траектория определяется однозначно,
но не наоборот.
4
0
1
А
У
*,
Рис.2
§2. Методы интегрирования
систем дифференциальных уравнений
2.1. Метод исключения
Один из методов интегрирования — метод исключения. Частным случаем
канонической системы является одно уравнение n-го порядка, разрешенное относительно

182.
. Глава XXIII. Системы дифференциальных уравнений
старшей производной,
x^ = f(t,x,x',...,x^l\
Введя новые функции х\ = x'(t), х2 = x"(t),
уравнение следующей нормальной системой п уравнений:
dx
, жп_1 = х^п l\t), заменим это
dt
dx\
~dT
dx„-2
= Ж|,
= Ж2,
(1)
dt
dxn-\
= «n-l>
dt
= f(t,x, xi,...,x„_i),
т. е. одно уравнение п-го порядка эквивалентно нормальной системе (1).
Можно утверждать и обратное, что, вообще говоря, нормальная система п
уравнений первого порядка эквивалентна одному уравнению порядка п. На этом и основан
метод исключения для интегрирования систем дифференциальных уравнений.
Делается это так. Пусть имеем нормальную систему дифференциальных уравнений
— = fx(t,xux2, ...,жп),
dx* * и \
— = f2{t,xbx2l...,xn),
dxn
I dt
fn{t,Xi,X2,.. . ,Жп).
(2)
Продифференцируем первое из уравнений (2) по t. Имеем
d2xx dfi dfi dxi df\ dx2
~dt+dxi dt + 8x2 dt
dt2
fl/i dxn
dxn dt
Заменяя в правой части производные -^ их выражениями /,(£, хи х2,...> хп),
получим
dlxx 0/, fl/, fl/, 5/,
или, короче,
d2xi
ей2
= J,2(<,a:i,X2)...,xn).
(3)
Уравнение (3) снова дифференцируем по t. Принимая во внимание систему (2),
получим
IF'Ht^ дх/] + " '+ dxnfn>
или
d?xx
F3(t1xux2,...1xn).

§2. Методы интегрирования систем дифференциальных уравнений
Продолжая этот процесс, найдем
<?Х\
.183
= F4(t,x\,x2,... ,ж„),
dt4
dT-lx{
dt
dTxl
dtn
= Fn(t,xux2,...,xn).
Предположим, что определитель
D(fuF2,...,Fn-i)
D(xbxh...,xn)
0/.
дх2
8F2
Шх~2
dFn.x
дхъ
dF2
дхз
OFn-i
dx„
dF2
dxn
dFn-t
дх2 дхз i dxn
(якобиан системы функций f\, F2y... , Fn-\) отличей от нуля при рассматриваемых
значениях х2у жз, • • • > хп,
D(fuF2,...,Fn-l)
D(x2, ж3,..., хп)
т^О.
(4)
Тогда система уравнений, составленная из первого уравнения системы (2) и уравнений
— =F2(*,xi,...,3n),
<Г~1х
dV
—r=Fn-l(t,xuxb...ixn)
будет разрешима относительно неизвестных ж2, а?з,..., жп. При этом ж2, ж3,..., жп
выразятся через t, Х\, -^-, ...,
dtn
^г
Внося найденные выражения в уравнение
(Гх\
-^r=Fn{t,xux2y...,xn)}
получим одно уравнение n-го порядка
(5)
Из самого способа его построения следует, что если x\(t), x2(t),..., xn(t) есть решения
системы (2), то функция хх (t) будет решением уравнения (5).
Обратно, пусть х \ (t) — решение уравнения (5). Дифференцируя это решение по t,
dxx
вычислим -^,...,
d»-
dtn-
и подставим найденные значения как известные функции

184.
. Глава XXIII. Системы дифференциальных уравнений
от t в систему уравнений
dx\
~dT
d2x{
dt2
dtn~x
= /,(*, жьж2, ...,ж„),
~F2(t,xuxb ...,arn),
= Fn-i(t1xux2j ...,ж„).
По предположению эту систему можно разрешить относительно х2, жз»..., хп, т. е,
найти #2, £з> • • • * а?п как функции от t.
Можно показать, что так построенная система функций
Ж!=Ж,(0, X2 = X2(t), ..., Xn = Xn(t)
составляет решение системы дифференциальных уравнений (2).
Пример. Требуется проинтегрировать систему
dx dy
dt=y' ¥ = "x-
<4 Дифференцируя первое уравнение системы, имеем
d2x _ dy
~d£~~di'
(6)
откуда, используя второе уравнение, получаем
dt2
+ x = Q
— линейное дифференциальное уравнение второго порядка с постоянными коэффициентами с одной
неизвестной функцией. Его общее решение имеет вид
x(t) = C\ cost + C2 sint.
В силу первого уравнения системы находим функцию
y(t) = -C\ sin 14- Сг cos t.
Найденные функции x(t), y(t), как легко проверить, при любых значениях С\ и С2 удовлетворяют
заданной системе.
Функции x(t), y(t) можно представить в виде
х = A sin(< 4- а), у = Acos(t + а), (7)
откуда видно, что интегральные кривые системы (6) — винтовые линии
с шагом h = 2к и с общей осью х = у = 0, которая также является
интегральной кривой (рис. 3).
Исключая в формулах (7) параметр t, получаем уравнение
*.2_l«2 - А2
х 4-у = А ,
так что фазовые траектории данной системы суть окружности с центром
в начале координат — проекции винтовых линий на плоскость хОу.
При А = О фазовая траектория состоит из одной точки х = 0, у = О,
называемой точкой покоя системы. ►
Рис.3
е. Может оказаться, что функции х2, хз,..., хп нельзя
выразить через t, х\, -gJ-,..., *'. Тогда уравнения и-го порядка,
эквивалентного исходной системе, мы не получим. Вот простой пример.
Систему уравнений
dx\
dt
dxj
It
= xu
= Ж2
нельзя заменить эквивалентным уравнением второго порядка относительно х\ или х2. Эта система
составлена из пары уравнений 1-го порядка, каждое из которых интегрируется независимо, что дает
х\ = С\е\ х2 = С2еК

§2. Методы интегрирования систем дифференциальных уравнений 185
2.2. Метод интегрируемых комбинаций
Интегрирование нормальных систем дифференциальных уравнений
-£ = Л0, *ь *2, • • • > *п), * = 1, 2,..., п, (8)
иногда осуществляется методом интегрируемых комбинаций.
Интегрируемой комбинацией называется дифференциальное уравнение,
являющееся следствием уравнений (8), но уже легко интегрирующееся.
Пример. Проинтегрировать систему
dx dy
««Складывая почленно данные уравнения, находим одну интегрируемую комбинацию:
ft±*..+fc
откуда
Вычитая почленно из первого уравнения системы второе, получаем вторую интегрируемую комбинацию:
dt
-(* - У),
х-у = С2е~
откуда
Мы нашли два конечных уравнения
х + у = С\е\ х-у.
из которых легко определяется общее решение системы:
С2е~
x(t) = i (Cie* + С2е~% y(t) = \ (С,е* - С2еГ% ►
Одна интегрируемая комбинация дает возможность получить одно уравнение
Ф1(*,Х1,Х2,...,Хя) = Сь
связывающее независимую переменную t и неизвестные функции a?i, £2, • •., хп.
Такое конечное уравнение называется первым интегралом системы (8). Иначе: первым
интегралом системы дифференциальных уравнений (8) называется
дифференцируемая функция Ф(£, х\, Ж2, • • •, хп), не равная тождественно постоянной, но
сохраняющая постоянное значение на любой интегральной кривой этой системы.
Если найдено п первых интегралов системы (8) и все они независимы, т. е. якобиан
системы функций Ф1}..., Ф„ отличен от нуля:
дФ\ дФ{ дФ{
дх\ дх2 дхп
/о,
0Ф„ &К дФ^
дх\ дх2 дхп
то задача интегрирования системы (8) решена (так как из системы
[ Ф,(*,ЖЬЖ2, ...,ЖП) = СЬ
Фг(*, si, я2,..., жп) = С2,
{ Фп(*, ЖЬ Ж2, . . . , Ж„) = Сп
определяются все неизвестные функции x\(t), жг(0> • • • > xn(t))-

186.
. Глава XXIII. Системы дифференциальных уравнений
§ 3. Системы линейных дифференциальных уравнений
Система дифференциальных уравнений называется линейной, если она линейна
относительно неизвестных функций и их производных, входящих в уравнение. Система п
линейных уравнений первого порядка, записанная в нормальной форме, имеет вид
^ = ЕМ')ч + Л(0; « = if2,...,n,
.7=1
или, в матричной форме,
§=AX + F,
(1)
(2)
где
Х =
х,(0\
x2(t)
*n{t)J
, F =
/i(0
/2(0
fn{t)t
an(t) an(t)
A= . a2i(t) a22(t)
,an\(t) an2(t)
a2n(t)
ann(t) t
Теорема 2. Если все функции a{j(t) и fi(t), t, j = 1,2,..., n, непрерывны на отрезке
a^t ^.b, то в достаточно малой окрестности каждой точки Mo(to, ж?, х2,..., х%), где
t0 € (а, Ь), выполнены условия теоремы существования и единственности решения задачи
Кошии, следовательно, через каждую такую точку проходит единственной интегральная
кривая системы (1).
< Действительно, в таком случае правые части системы (1) непрерывны по
совокупности аргументов J, х\, х2у..., хп и их частные производные по Xj, j = 1,2, ..., n,
ограничены, так как эти производные равны непрерывным на отрезке [а, Ь)
коэффициентам Oij(t). ►
Введем линейный оператор
£ =
dt
Тогда система (2) запишется в виде
С[Х]
(3)
Если матрица F — нулевая, т. е. /<(£) = 0, t = 1,2,..., п, на интервале (о, ft), то
система (2) называется линейной однородной и имеет вид
С[Х] = 0.
(4)
Приведем некоторые теоремы, устанавливающие свойства решений линейных
систем.
Теорема 3. Если X(t) является решением линейной однородной системы
£[Х] = 0,
то cX(t), где с — произвольная постоянная, является решением той же системы.

§3. Системы линейных дифференциальных уравнений
187
Теорема 4. Сумма
Xi(t) + X2(t)
двух решений X\(t) и Хгф однородной линейной системы уравнений является решением
той же системы.
Следствие. Линейная комбинация
т
с произвольными постоянными коэффициентами с,- решений X\(t),... ,Xm(t) линейной
однородной системы дифференциальных уравнений
С[Х] = О
является решением той же системы.
Теорема 5. Если X(t) есть решение линейной неоднородной системы
£[Х] = F,
я Хо(0 —решение соответствующей однородной системы
С[Х) = 0,
то сумма
Х(*) + Хо(«)
будет решением неоднородной системы С[Х] = F.
4 Действительно, по условию,
£[X] = F, £[Xo] = 0.
Пользуясь свойством аддитивности оператора £, получаем
£[X + X0] = £[X] + £[X0] = F.
Это означает, что сумма X(t) + Xo(t) есть решение неоднородной системы уравнений
С[Х] = F. ►
Определение. Векторы
Х,(«), Х2(«), ...,ХП(0,
где
*„«>
называются линейно зависимыми на интервале а < £ < Ь, если существуют постоянные
числа ai, а2,..., а„ такие, что
а,Х,(0 + а2Х2(«) + ... + а„Хп(0'= 0 (5)

. Глава XXIII. Системы дифференциальных уравнений
при t G (а, Ь), причем по крайней мере одно из чисел а,- не равно нулю. Если
тождество (5) справедливо только при ot\ = а2 — ... = ап = 0, то векторы Xi(i), Хг(£)>••• >
Хп(£) называются линейно независимыми на (а, Ь).
Заметим, что одно векторное тождество (5) эквивалентно п тождествам:
п п п
]Г) akxlk(t) = О, ]Г) akx2k(t) = 0, ..., ^2 a^nk(t) = 0.
Определитель
W(t)
xn(t) xn(t) ... arln(0
S2l(*) ^22(0 ••• Ж2«(0
l«iil(0 Xn2(t) ... Snn(*)
называется определителем Вронского системы векторов Х\ (£), Х2(1)у..., Хп(£).
Определение. Пусть имеем линейную однородную систему
^=A(t)X, (6)
где А(£) — п х п -матрица с элементами atJ(£). Система п решений
Xi(«), х2(«), ...,х„(0
линейной однородной системы (6), линейно независимых на интервале a < t < Ь,
называется фундаментальной.
Теорема 6. Определитель Вронского W(t) фундаментальной ни интервале а < t < Ь
системы решений линейной однородной системы (6) с непрерывными на отрезке a^t^b
коэффициентами a>ij(t) отличен от нуля во всех точках интервала (а, Ь).
Теорема 7 (о структуре общего реиюния линейной однородной системы). Общим решением в
области а < t < Ь, \хк\ < +оо, к = 1, 2,..., п, линейной однородной системы
£-А«Х
с непрерывными на отрезке а ^ t ^ Ь коэффициентами atJ(£) является линейная
комбинация п линейно независимых на интервале а < t < b решений X\(t), X2(t), • • •» Хп(£)
системы (6):
п
Хо.о. = Х>х,(0
.7=1
(с\, с2,..., Сп — произвольные постоянные числа).

§3. Системы линейных дифференциальных уравнений.
Пример. Система
имеет, как нетрудно проверить, решения
= *2,
-Х\
x-w=(-"?)• **»=(««)•
Эти решения линейно независимы, так как определитель Вронского отличен от нуля:
cos t sin t\
- sin t cos t\
тшг/*\ I cost sint 1 i
Общее решение системы имеет вид
Х(*) = с,Х,(*) + саХ2(*),
или
з, (*) = с\ cos * 4- ci sin <, ж2(0 = -с\ sin * 4- с2 cos t
(с\, С2 — произвольные постоянные). ►
3.1. Фундаментальная матрица
Квадратная матрица
Х(*) =
x\\(t) xn(t) ... xXn(t)
X2\(t) x22(t) ... x2„(t)
^xni(t) xn2(t) ... xnn(t)4
столбцами которой являются линейно независимые решения Xi(J), X2(t),..., Xn(t)
системы (6), называется фундаментальной матрицей этой системы. Нетрудно
проверить, что фундаментальная матрица удовлетворяет матричному уравнению
dX
~dt
= А(*)Х(*).
Если X(t) — фундаментальная матрица системы (6), то общее решение системы
можно представить в виде
' ' (7)
X(t) = X(t)C,
где
С =
— постоянная матрица-столбец с произвольными элементами. Полагая в (7) t = to,
имеем
Х(*о) = Х(*0)С,
откуда
следовательно,
С = Х-1(*о)Х(<о);
х(0 = х(*)х-Ч*о)х(<0).
Матрица X(t)X 1(to) = K(t,<0) называется матрицей Коши. С ее помощью решение
системы (6) можно представить так:
Х(*) = К(Мо)Х(*о).

190
Глава XXIII. Системы дифференциальных уравнений
Теорема 8 (о структуре общего решения линейной неоднородной системы дифференциальных
уравнений). Общее решение в области а < t < Ь, \хи\ < +00, к = 1, 2,..., п, линейной
неоднородной системы дифференциальных уравнений
^ = A(t)X + f(t) (2)
с непрерывными на отрезке a ^t ^ Ь коэффициентами а,;(£) и правыми частями fi(t)
равно сумме общего решения
п
соответствующей однородной системы и какого-нибудь частного решения X(t)
неоднородной системы (2):
^о.н. == ^о.о. ~г Хч.н..
3.2. Метод вариации постоянных
Если известно общее решение линейной однородной системы (6), то частное решение
неоднородной системы можно находить методом вариации постоянных (метод Лаг-
ранжа).
< Пусть
п
х(0 = 1>Х*(*)
есть общее решение однородной системы (6), тогда
--±=A(t)Xk(t)y te(a,b), *=1,2,...,п,
причем решения Xk(t) линейно независимы.
Будем искать частное решение неоднородной системы
dX
_=A(0X + F(0
в виде
п
X(*) = EC*(W)> (9)
*=1
где Ck(t)9 к = 1,2,..., п, — неизвестные функции от t. Дифференцируя X(t) по t,
имеем _
dX J^ ,dXk
Подставляя X(t) и ^ в (2), получаем

§4, Системы линейных дифференциальных уравнений с постоянными коэффициентами.
Так как
.191
dt
А(*)Х*(*) = 0,
то для определения c'k(t) получаем систему
•£<4<*)x»(*) = f(*),
*=1
или, в развернутом виде,
c\(t)xu(t) + c2(t)xn(t) + ...+ <i(t)xln(t) = /,(<),
(Ю)
c\(t)xnl(t) + d2(t)xn2(t) +... +<i(t)xnn(t) = /„(«).
Система (10) есть линейная алгебраическая система относительно c'h(t),
определителем которой является определитель Вронского W(t) фундаментальной системы
решений Xj (f), Хг(0) • • •) Хп(£). Этот определитель отличен от нуля всюду на интервале
а < t < b, так что система (10) имеет единственное решение
<4(') = Ы*)| * = 1,2,...,п,
где <pk(t) — известные непрерывные функции. Интегрируя последние соотношения,
находим
<*(*) = У<Pk(t)dt, *=1,2,...,п.
Подставляя эти значения ck(t) в (9), находим частное решение системы (2):
п Г
х(0 = Х>(')/Ы0<й
(здесь под символом / <Pk(t) dt понимается одна из первообразных для функции
§4. Системы линейных дифференциальных уравнений
с постоянными коэффициентами
Рассмотрим линейную систему дифференциальных уравнений
dx% %■ -\
-rr = 2-j aiixJ + Л(')> * = 1, 2,..., п,
в которой все коэффициенты а,у(«, j — 1, 2,..., п) — постоянные. Чаще всего такая
система интегрируется сведением ее к одному уравнению более высокого порядка,
причем это уравнение будет также линейным с постоянными коэффициентами.
Другой эффективный метод интегрирования систем с постоянными коэффициентами —
метод преобразования Лапласа.
Мы рассмотрим еще метод Эйлера интегрирования линейных однородных систем
дифференциальных уравнений с постоянными коэффициентами. Он состоит в
следующем.

192.
. Глава XXIII. Системы дифференциальных уравнений
4.1. Метод Эйлера
Будем искать решение системы
dt
dx2
"dt
dxn
= aux\ + a\2x2 + ... + aXnxn,
= a2\xx + a22X2 + ... + a>2nXn,
(1)
dt
= a,n\Xi + an2x2 + ... + annxn
в виде
x\ = a\ext, x2 = a2ext,
, xn — ocne
xt
(2)
где A, t*i, t*2,..., an — постоянные. Подставляя ж* в форме (2) в систему (1),
сокращая на ext и перенося все члены в одну часть равенства, получаем систему
{ (ац ~ А) а, + а12а2 + ... + а1пап = О,
a2iai + (а22 - А) а2 + ... + а2па„ = О,
[ anlai + ап2а2 + ... + (апп - А) ап = 0.
Для того, чтобы эта система (3) линейных однородных алгебраических уравнений с п
неизвестными ai, a2,..., a„ имела нетривиальное решение, необходимо и
достаточно, чтобы ее определитель был равен нулю:
ац-А а12
a2i а22 — А
<*>2п
<*>пг
= 0.
(4)
Уравнение (4) называется характеристическим. В его левой части стоит
многочлен относительно А степени п. Из этого уравнения определяются те значения А,
при которых система (3) имеет нетривиальные решения а\, а2,..., ап. Если все кор-
ни A,*, t = 1, 2,..., п, характеристического уравнения (4) различны, то, подставляя
их по очереди в систему (3), находим соответствующие им нетривиальные решения
«н> «2») • • • > «ni> * = 1, 2,..., п, этой системы и, следовательно, находим п решений
исходной системы дифференциальных уравнений (1) в виде
М
Л'
л,*
хн = аие\ x2i = a2iet, ..., xni = anie » , *=l,2,...,n,
(5)
где второй индекс указывает номер решения, а первый — номер неизвестной функции.
Построенные таким образом п частных решений линейной однородной системы (1)
(6)
образуют, как можно проверить, фундаментальную систему решений этой системы.

§4. Системы линейных дифференциальных уравнений с постоянными коэффициентами 193
Следовательно, общее решение однородной системы дифференциальных
уравнений (1) имеет вид
Х(«) = с,Х,(«) + c2X2(t) + ... + СпХп®,
или
X\(t) = C{XU(t) + C2Xl2(t) + . . . + СпХщЦ),
x2(t) = c{x2\(t) + с2ж22(0 + ... + cnx2n(t),
xn(t) = cxxnl(t) + c2xn2(t) + ... + с„жпп(0,
где ci, c2,..., Cn — произвольные постоянные.
Случай, когда характеристическое уравнение имеет кратные корни, мы
рассматривать не будем.
1. Решить систему
<4 Ищем решение в виде
Характеристическое уравнение
dx\
— = -*,+2*2,
d*7 -
— =2.,- s2.
«1 —a\ext^ х2 = a2ext.
|-1~А 2 1-0
I 2 -1~А|-и'
или
А2 + 2А - 3 = 0,
имеет корни Л] = 1, Л2 = -3.
Система (3) для определения а\, а2 выглядит так:
Г(-1-А)а,+2а2=0,
\2а,+(-1-А)а2=0.
Подставляя в (*) А = 1, получаем
f-2an+2a2, =0,
\ 2а,,-2а2, = 0,
откуда a2i = ац. Следовательно,
х\\ -а\\е , ж21 =аце .
Полагая в (*) А = -3, находим а22 ='-а\2, поэтому
Общее решение данной системы:
(*)
Х\2=а\2е ', х22 = -а\2еи.
x](t) = clauet +c2al2e 2\
x2(t) = ciauel - c2al2e~3t,
или
zl(t) = Clet + C2e-*,
x2(t) = Clet-C2e-it.^
4.2. Матричный метод
Изложим еще матричный метод интегрирования однородной системы (1). Запишем
систему (1) в виде
dX
7 Зак. 179 — = АХ, (7)
at

194.
. Глава ХХШ. Системы дифференциальных уравнений
где
Х(*) =
х,(*)\
x2(t)
,xn(t)J
А = (a*j)"j=i ~nx n-матрица с постоянными действительными элементами а,у.
Напомним некоторые понятия из линейной алгебры. Вектор g Ф О называется
собственным вектором матрицы А, если
Ag = Ag.
Число Л называется собственным значением матрицы А, отвечающим собственному
вектору g, и является корнем характеристического уравнения
det(A - AI) = О,
где I — единичная матрица.
Будем предполагать, что все собственные значения Ai, Л2,..., Лп матрицы А
различны. В этом случае собственные векторы gi, g2,..., gn линейно независимы и
существует п х п-матрица Т, приводящая матрицу А к диагональному виду, т. е. такая,
что
\х О
Л2
(8)
Л = Т^АТ:
О Ап,
Столбцами матрицы Т являются координаты собственных векторов gi, g2> • > > > gn
матрицы А.
Введем еще следующие понятия. Пусть B(t) —• n x n-матрица, элементы b{j(t)
которой суть функции аргумента t, определенные на множестве П. Матрица B(t)
называется непрерывной на Q, если непрерывны на П все ее элементы b{j(t).
Матрица B(t) называется дифференцируемой на Q,, если дифференцируемы на П все элементы
bij(t) этой матрицы. При этом производной -Jp- матрицы B(t) называется матрица,
элементами которой являются производные % соответствующих элементов
матрицы B(t).
Пусть B(t) — п х п-матрица,
| x2(t) *
Х(*)= .
\xn(t)J
— вектор-столбец. Учитывая правила алгебры матриц, непосредственной проверкой
убеждаемся в справедливости формулы
£<вдвд>-«*ад.+.»£.
(»
В частности, если В — постоянная матрица, то
так как ^ есть нуль-матрица.

§4. Системы линейных дифференциальных уравнений с постоянными коэффициентами 195
Теорема 9. Если собственные значения \\, А2)..., Ап матрицы А различны, то общее
решение системы (7) имеет вид
Щ = c,eA,'g, + c2eA2'g2 + ... + c^'fa, (10)
^е gi, g2, • •., gn — собственные векторы-столбцы матрицы А, л Cj, сг,..., <v, —
произвольные постоянные числа.
< Введем новый неизвестный вектор-столбец Y(£) по формуле
X(*) = TY(«), (11)
где Т — матрица, приводящая матрицу А к диагональному виду. Подставляя X(t)
из (11) в (7), получим систему
T¥ = ATY-
Умножая обе части последнего соотношения слева на Т ] и учитывая, что Т l AT = Л,
придем к системе
= AY,
или
<
Г dyx
\ ЛУ2 Л
dyn
[-м=КУп\
(12)
Мы получили систему из п независимых уравнений, которая без труда интегрируется:
V\=c{eXl\
2/2 = с2е
а2*
Уп = Сг»е
Ап*
Здесь с\, С2,..., Сп — произвольные постоянные числа.
Вводя единичные п -мерные векторы-столбцы
(1\
' о 1
о
в! =
о
W
о
е2 =
0
W
е„ =
/°\
0
0
о
Vi/
решение Y(£) можно представить в виде
Х2*с
Щ = c,eA,'e, + с2еА2'е2 + ... + c„eAnlen.
вАП*с
(13)
В силу (11) X(t) = TY(£). Так как столбцы матрицы Т есть собственные векторы
матрицы А, то Те* = g*, где g* — k-й собственный вектор матрицы А. Поэтому,
подставляя (13) в (11), получим формулу (10):
А2'с
-Anf
Х(0 = c,eA,,g, + c2eA2lg2 + ... + CneAntgn.
7*

196
Глава XXIII. Системы дифференциальных уравнений
Таким образом, если матрица А системы дифференциальных уравнений (7) имеет
различные собственные значения, для получения общего решения этой системы:
1) находим собственные значения Ab А2,..., А„ матрицы как корни
алгебраического уравнения
det(A - Л1) = 0;
2) находим все собственные векторы gi, g2,..., g„;
3) выписываем общее решение системы дифференциальных уравнений (7) по
формуле (10).
Пример 2. Решить систему
<4 Матрица А системы имеет вид
dx
-а о-
1) Составляем характеристическое уравнение
det(A-AI) = |32A 21A| = 0,
А2-5А + 4 = 0.
Корни характеристического уравнения Ai = 4, Аг = 1.
2) Находим собственные векторы
-(И)- *-(£)■
Для А = 4 получаем систему
откуда git =012, так что
Аналогично для А = 1 находим
{
-011+012 = 0,
20Ц -012 = 0,
-(-S)-
3) Пользуясь формулой (10), получаем общее решение системы дифференциальных уравнений
«!)-<*(!)-''(-!)■
или
x(t) = c\eAt + сге*,
у(0 = с,е4<-2с2е<. ►
Корни характеристического уравнения могут быть действительными и
комплексными. Так как по предположению коэффициенты aij системы (7) действительные, то
характеристическое уравнение
det(A - Л1) = 0
будет иметь действительные коэффициенты. Поэтому наряду с комплексным
корнем Л оно будет иметь и корень Л*, комплексно сопряженный с Л. Нетрудно прказать,
что если g — собственный вектор, отвечающий собственному значению Л, то Л* —
тоже собственное значение, которому отвечает собственный вектор g*, комплексно
сопряженный с g.

§4. Системы линейных дифференциальных уравнений с постоянными коэффициентами.
.197
При комплексном Л решение
V ЛА*
Х = е g
системы (7) также будет комплексным. Действительная часть
X, = Re(eA'g)
и мнимая часть
Х2 = Im(eA'g)
этого решения являются решениями системы (7). Собственному значению Л* будет
отвечать пара действительных решений Xi и -Хг, т. е. та же пара, что и для
собственного значения Л. Таким образом, паре Л, Л* комплексно сопряженных собственных
значений отвечает пара действительных решений системы (7) дифференциальных
уравнений.
Пусть Л], Лг,..., Л* — действительные собственные значения, Aj.+i, A^+j, Ад.+2>
K+2i • • • — комплексные собственные значения. Тогда всякое действительное
решение системы (7) имеет вид
Х(0 = c,eA''gl + c2eA2'g2 + ... + c*eA*'g*+
+ сш Re(eA*+«*gfc+l) + ск+2 Im(eA*+l'ak+1) + ... ,
где С{ — произвольные постоянные.
» 3. Решить систему
dx
dt
= х-Ъу,
А Матрица системы
^ = 3х+ „.
-О D-
1) Характеристическое уравнение системы
II-А -3 I
3 1-А
= 0,
Его корни Ai = 1 + 3t, Аг = 1 — 3t.
2) Собственные векторы матрицы
3) Решение системы
(1-А)2+ 9 = 0.
* = (-!). *=(!)•
где а\, а2 — произвольные комплексные постоянные.
Найдем действительные решения системы. Пользуясь формулой Эйлера
-cos<p + t sin <р,
получаем
е \-i ) ~ \smlt ) +г \-со*ЪЬ) '
Следовательно, всякое действительное решение системы имеет вид
W(t))=Cie Uin3«J+C2e (,-cos3*J'

198
Глава XXIII. Системы дифференциальных уравнений
x(t) = с\еь cos 3t -f с2е sin 32,
y(t) = c\el sin 3t — c2e' cos 32,
где с\, с2 — произвольные действительные числа. ►
Упражнения
Методом исключения проинтегрируйте системы:
1. <
dx
~dt
dy
^ dt
= -х + 2у,
= 2х-
2. {
dx^
dt
dy
I dt
= Зж - 2y,
2ж-
Методом интефируемых комбинаций проинтегрируйте системы:
dx
4. <
dy
5. <
dt
= x + y + t.
( dx
It
dy
dt
Матричным способом проинтефируйте системы:
dx ( dx
6. < 7. <
| = 3Ж + 4У. 11=- + ».
Ответы
1. х = с,е' + с2е~~3', у = qe' - с2е~3'. 2. ж = (ci + f )e' + с2*е', у = cxel + с2*е'.
3. ж = cie*+c2e~*+c3 sin£+c4cos£, у = с\<£+,съе~% — с^ sinf-c4cosi. 4. х = Ci+c2e2' — j — | — |,
у = -с, +с2е2Ч £ -1 - \. 5. а? = y/c2(2t + cv), у = у^Щ^. 6, «•= с,еЧс2е5', у = -с,еЧЗс2е5'.
7. х = Cie'cos£ + c2e'sin£, у = Cje'sinJ - c2e'cos£.

Глава XXIV
ТЕОРИЯ УСТОЙЧИВОСТИ
§ 1. Предварительные замечания
Рассмотрим вопрос о зависимости решения задачи Коши от начальных данных.
Пусть дана задача Коши
x(to) = Xq.
(i)
(2)
Если функция /(*, х) непрерывна по совокупности аргументов и имеет ограниченную
производную ^ в некоторой области П изменения t, ж, содержащей точку (£0, х0), то
решение задачи Коши (1)-(2) существует и единственно. Если изменять значения t0
и хо, то будет меняться и решение. Возникает важный в приложениях вопрос: как оно
будет меняться? Вопрос этот имеет и большое принципиальное значение.
Действительно, если какая-либо физическая задача приводит.к задаче Коши, то начальные
значения находятся из опыта и за абсолютную точность измерения ручаться нельзя,
И если сколь угодно малые изменения начальных данных способны сильно изменять
решение, то математическая модель окажется малопригодной для описания реального
процесса.
* Справедлива следующая теорема о непрерывной зависимости решения от
начальных условий.
Теорема 1. Если правая часть /(£, х) дифференциального уравнения
непрерывна по совокупности переменных и имеет ограниченную частную производную ^
в некоторой области G изменения t, x, то решение
ж(*) = ж(*;*о,я0),
удовлетворяющее начальному условию x(to) = хо, где (*о, х0) G G, непрерывно зависит
от начальных данных.

200 Глава XXIV. Теория устойчивости
Иными словами, пусть через точку (t0j ж0) проходит решение x(t) уравнения (1),
определенное наугрезке a ^.t ^ /3,t0 е (а,/3). Тогда для любого е > 0 найдется такое
б > 0, что при \i0 - *ol < ^, 1#о - х0\ < 6 решение x(t) уравнения (1), проходящее
через точку (?о, #o)> существует на отрезке [а, /3] и отличается там от x(t) меньше чем
на е:
\\x(t)-x(t)\<e Vt€ [q,/?].*]
Аналогичная теорема справедлива и для системы дифференциальных уравнений
dx{
— = /,(*,хихь...,хп), г = 1, 2,...,п.
При выполнении условий теоремы (1) решение задачи Коши существует,
единственно и непрерывно зависит от начальных данных. В этом случае говорят, что задача
Коши поставлена корректно. Существенным является то обстоятельство, что отрезок
[а, Ь] изменения t конечен. Однако во многих задачах нас интересует зависимость
решения от начальных данных в бесконечном промежутке to ^ t < оо. Переход
от конечного промежутка, в котором рассматривается непрерывная зависимость
решения от начальных значений, к бесконечному существенно меняет характер задачи
и методы исследования. Эта проблема относится к теории устойчивости, созданной
А. М.Ляпуновым.
Остановимся вкратце на понятии о продолжаемости решения. Пусть имеем
систему дифференциальных уравнений
dx'
-^ = /.(*> хи «2, • • •, яп), г = 1, 2,..., п, (3)
где t — независимая переменная (время); x\(t), х2(*)>••• > xn(t) — искомые
функции; /,(*, Х\) Х2у • • • > Хп ) — функции, определенные для t е (а, +оо) и х\, ж2,..., хп
из некоторой области Del". Если функции
/•(*, хи Ж2,..., хп), % = 1, 2,..., п,
в их области определения непрерывны по совокупности аргументов и имеют
ограниченные частные производные по x\yx2l... ухп, то для системы (3) справедлива
локальная теорема существования:
для каждой системы значений
(t0, х°и х2у..., ж°), *0 € (а, + оо), (х°и х°ъ..., х°п) G D,
существует единственное решение
x\(t),x2(t),..,,xn{t)
системы (3), определенное в некотором интервале (to-ho, ^о+^о) С (а, +оо) изменения t
и удовлетворяющее начальным условиям
Xi(t0) = xl г = 1,2,..., п. (4)

§2. Устойчивость по Ляпунову. Основные понятия и определения 201
Введем следующее понятие. Пусть
xl(t),x2(t)1...,xn(t)
—- решение задачи Коши (3)-(4), определенное на некотором интервале I = (£ь t2).
Это решение может быть продолжено, вообще говоря, на больший интервал времени.
Решение
»1(*)»Ы*)»« ••»»«(*)
называется продолжением решения x\(t), x2(t),..., xn(t), если оно определено на
большем интервале /ь I\ Э /, и совпадает с x\(t)9 x2(t)9 ... , xn(t) при t Е I. Решение
называется неограниченно продолжаемым (неограниченно продолжаемым вправо или
влево), если его можно продолжить на всю ось -оо < t < +00 (на полуось to ^t < +00
или -оо < t < £0 соответственно).
Для дальнейших рассмотрений важен вопрос о существовании решения £,(£),
г = 1, 2,..., п, для to ^ t < +00 (глобальная теорема существования). Этим
свойством обладает линейная система
dx{ х~"* / ч / ч
"й" = Z-f M')*i + /«Of « = 1,2,..., n,
7=1
где atj(£) и /,-($) — непрерывные функции на [t0, +оо). Для нее каждое решение
Xi(t)9 г = 1,2,..., п, существует на [*о, +оо) (неограниченно продолжаемо вправо)
и единственно.
Не все системы обладают таким свойством. Например, для скалярного уравнения
dx 2
*=* <5>
функция
f(t,x) = x2
непрерывна и имеет производные всех порядков по х. Нетрудно проверить, что функция
а
является решением задачи
dx -у
— = х\ х(0) = a, a > 0.
Однако это решение существует только в интервале (-оо, - J, зависящем от начального условия, и не-
продолжаемо на полуинтервал (-оо, -1.
Уравнение (5) есть уравнение сверхбыстрого размножения, когда прирост пропорционален числу
всевозможных пар. Его решение показывает, что при таком законе прироста населения количество
населения становится бесконечным за конечное время (в то время как обычный закон прироста —
экспоненциальный).
Задача. Показать, что решения уравнения
dx 2 ,
нельзя продолжить неограниченно ни вправо, ни влево.
§2. Устойчивость по Ляпунову.
Основные понятия и определения
Рассмотрим дифференциальное уравнение первого порядка
(О
dx

202.
. Глава XXIV. Теория устойчивости
где функция /(£, х) определена и непрерывна для t € (а, +оо) и х ,из некоторой
области D и имеет ограниченную частную производную ^. Пусть функция
х = <p(t)
есть решение уравнения (1), удовлетворяющее начальному условию
Пусть, далее, функция
ж = x(t)
есть решение того же уравнения, удовлетворяющее другому начальному условию
x\t=tQ=x(t0).
Предполагается, что решения <p(t) и x(t) определены для всех t ^ to, т.е.
неограниченно продолжаемы вправо.
Определение 1. Решение х = у>(£) уравнения (1) называется устойчивым по Ляпунову
при £ —► -hoo, если для любого е > О существует 0 = £(е) > 0 такое, что для всякого
решения х = x(t) этого уравнения из неравенства
1*(<о) " р(*о)1 < * (2)
следует неравенство
\x(t)-<p(t)\<e (3)
для всех t^ to (всегда можно считать, что 6 ^ е).
Это значит, что решения, близкие по
начальным значениям к решению х = <p(t)9 остаются
близкими и при всех t ^ to. Геометрически это
означает следующее. Решение
х = <p(t)
уравнения (1) устойчиво, если, какой бы
узкой ни была е -полоска, содержащая кривую
х = <p(t), все достаточно близкие к ней в
начальный момент t =■ to интегральные кривые
х — x(t) уравнения целиком содержатся в
указанной £-полоске при всех t^to (рис. 1).
Если при сколь угодно малом 6 > О хотя
бы для одного решения х — x(t) уравнения (1)
неравенство (3) не выполняется, то решение
х = (p(t) этого уравнения называется неустойчивым. Неустойчивым следует считать
и решение, не продолжаемое вправо при t —► со.
Определение 2. Решение х = <p(t) уравнения (1) называется асимптотически
устойчивым, если
1) решение х = <p(t) устойчиво;
2) существует б\ > О такое, что для любого решения х = x(t) уравнения (1),
удовлетворяющего условию |ж(£0) - ¥>(*о)1 < *i > имеем
ton \x(t)-(p(t)\ = 0.
t-++oo
Рис. 1

§2. Устойчивость по Ляпунову. Основные понятия и определения.
.203
Это означает, что все решения х = x(t), близкие по начальным условиям к
асимптотически устойчивому решению х = (p(t), не только остаются близкими к нему
при О *о > но и неограниченно сближаются с ним при t -* +00.
Вот простая физическая модель. Пусть шарик лежит на дне полусферической
лунки (находится в положении равновесия). Если малым возмущением вывести шарик
из этого положения, то он будет колебаться около него. При отсутствии трения
положение равновесия будет устойчивым, при наличии трения колебания шарика будут
уменьшаться с возрастанием времени, т. е. положение равновесия будет
асимптотически устойчивым.
1. Исследовать на устойчивость тривиальное решение
х = 0
уравнения
dx
~dt
= 0.
(*)
< Решение х = 0, очевидно, удовлетворяет
начальному условию xh
\t=t0
Решение уравнения (*), удовлетворяющее
начальному условию
1<=<о
:3(Ь
'x=Jtf///////////////////////y
Рис.2
Рис.3
имеет вид
х = х0.
Легко видеть (рис. 2), что, какова бы ни была е-полоска вокруг интегральной кривой х — 0, существует
б > 0, например, б = е, такое, что любая интегральная кривая х — xq, для которой |жо-0| < б, целиком
содержится в указанной £-полоске для всех t ^ to. Следовательно, решение х = 0 устойчиво.
Асимптотической устойчивости нет, поскольку решение х = хо при t -* +00 не стремится к прямой х = 0. ►
Пример 2. Исследовать на устойчивость тривиальное
решение х = 0 уравнения xf
dx • 2
-=-ог (а — const). (**)
dt
А Решение уравнения (**), удовлетворяющее
начальному условию
имеет вид
х = хое
Возьмем любое е > 0 и рассмотрим разность решений x(t) и (p(t) = 0:
x(t) - <p(t) = x0e-a2(t-to) -0 = (x0- 0)e-e2('-4 (***)
Поскольку e~a ^~'°) ^ 1 для всех t ^ to, из выражения (***) следует, что существует б > 0, например,
б = е, такое, что при \хо - 0| < б = е имеем
\x(t) - <p(t)\ = x0e-a2(t-to) < е Vt^to.
Согласно определению (1) это означает, что решение <p(t) = 0 уравнения (**) устойчиво. Кроме того,
имеем
lim \x(t)-<p(t)\= lim |zok"e2('"'o) = 0,
поэтому решение <p(t) = 0 асимптотически устойчиво (рис. 3). ►
Пример 3. Показать, что решение
?(*) = 0
. - <гп*-а <М>>

204
Глава XXIV. Теория устойчивости
уравнения
dx
~dt
неустойчиво.
4 В самом деле, при сколь угодно малом \xq\ решение
x(t) = s0ee2('-'o)
этого уравнения не удовлетворяет условию
\x(t) - 0| = |z0|ee2('-'o) < e
при достаточно больших t > to. Более того, при любых xq Ф 0 имеем
|*(*)||-»+оо — +00
(рис.4). ►
Рассмотрим теперь систему дифференциальных уравнений
dxi
~dt
= fi(t, ж,, ж2,..., хп) г = 1, 2,..., п,
Рис.4
(4)
где функции /, определены для а < t < +оо и жь ж2, • • • > #п из некоторой
области D изменения жь ж2, • • •, #п и удовлетворяют условиям теоремы существования
и единственности решения задачи Коши. Предположим, что все решения системы (4)
неограниченно продолжаемы вправо при t^t0> а.
Определение 3. Решение
(Pi(t), i = l,2,...,n,
системы (4) называется устойчивым по Ляпунову при t —► +оо, если для любого е > О
существует 6 = 6(e) > О такое, что для всякого решения £,(£)>* = 1, 2,..., п, той же
системы, начальные значения которого удовлетворяют условию
\xi(to) - (Pi(t)\ < 6} i=l,2,...,n,
выполняются неравенства
!*•(*) - ¥>.-(01 < *» *=1,2,...,п> (5)
для всех £ ^ *о j т. е. близкие по начальным значениям решения остаются близкими
для всех t ^ tQ.
Если при сколь угодно малом б > О, хотя бы для одного решения ж,(£),
г = 1, 2,..., п, не все неравенства (5) выполняются, то решение (pi(t) называется
неустойчивым.
Определение 4. Решение
¥>,-(*), i = 1,2,...,п,
системы (4) называется асимптотически устойчивым, если:
1) решение это устойчиво;
2) существует #, > 0 такое, что всякое решение ж,(£), г — 1,2,.
для которого
М*о) - У>.(*о)1 < *ь * = 1, 2,..., п,
удовлетворяет условию
ton \xi(t)-<pi(t)\ = 0, i = l, 2,..., n.
г—►Ч-оо
., п, системы,

§2. Устойчивость по Ляпунову. Основные понятия и определения 205
Пример 4. Исходя из определения устойчивости по Ляпунову, показать, что решение системы
dx dy
удовлетворяющее начальным условиям
*(0) = 0, у(0) = 0, (**)
устойчиво.
<4 Решение системы (*), удовлетворяющее начальным условиям (**), есть
x(t) = 0, y(t) = Q.
Решение этой системы, удовлетворяющее условиям х(0) — х0, у(0) = у0, имеет вид
x(t) - хо cos t + уо sin *, y(t) = -х0 sin t + yo cos t.
Возьмем произвольное е > 0 и покажем, что существует 6(e) > 0 такое, что при |ж0-0| < 6 и \уо~0\ < 6
выполняются неравенства
|з(0 - 0| = |ж0 cos t + уо sin t\ < е, \y(t) - 0| = | - х0 sin t + у0 cos t\ < е
для всех t ^ 0. Это и будет означать, согласно определению, что нулевое решение x(t) = 0, y(t) = 0
системы (*) устойчиво по Ляпунову. Очевидно, имеем:
|ж0 cos t + уо sin t\ ^ |ж0 cos t\ + \у0 sin t\ ^ |ж0| 4- \yol
\-xos\nt + yocost\ ^ |ж0sint\ + |y0cost\ ^ |sol +W-
Если взять
«M-§,
то при |ж0| < tf и |yol < * будут иметь место неравенства
\х0 cos t + уо sin t\ < е, | - ж0 sin * + yo cos t\ < e
для всех t ^ 0, т.е. действительно нулевое решение системы устойчиво по Ляпунову, но эта
устойчивость не асимптотическая. ►
Из устойчивости нетривиального решения дифференциального уравнения не
следует ограниченности этого решения.
Рассмотрим, например, уравнение
dt
Решением этого уравнения, удовлетворяющим условию х(0) = 0,
является функция
<p(t)=t.
Решение, удовлетворяющее начальному условию х(0) — xq, имеет вид
x(t) = t + x0.
Геометрически очевидно (рис.5), что для всякого е > 0 существует
6 > 0, например 6 = е такое, что любое решение x(t) уравнения,
для которого верно неравенство |ж0 - 0| < 6, удовлетворяет условию
\x(t) - t\ < e Vt ^ 0. Последнее означает, что решение tp(t) = t
устойчиво по Ляпунову, однако это решение является неограниченным р 5
при t —► +оо.
Из ограниченности решений дифференциального уравнения не следует
устойчивости решений.
Рассмотрим уравнение
dx 2
-=sinx. (6)
Оно имеет очевидные решения
ж = *тг, * = 0,±1,±2,... . (7)
Интегрируя уравнение (6), находим
ctg х = ctg хо - *,
или
х = arcctg(ctgzo - t), хо Ф **• (8)

206.
Все решения (7) и (8) ограничены на (-оо, +оо). Однако
решение <p(t) = 0 неустойчиво при t —► +оо, так как при любом
х Е (0, ж) имеем
. Глава XXIV. Теория устойчивости
lim x(t) = ж
(рис.6).
Таким образом, ограниченность и устойчивость
решений являются понятиями, независимыми друг
от друга.
Замечание. Исследуемое на устойчивость решение Рис. 6
4>i(t), f = l,2,...,n,
системы (4) всегда можно преобразовать в тривиальное решение
Уг=0
другой системы заменой
Уг = x{(t) - <pi(t), i= 1,2,..., п.
В самом деле, пусть имеем (для простоты) одно дифференциальное уравнение
!=/(«,«>, м
и пусть требуется исследовать на устойчивость какое-либо решение tp(t) этого уравнения. Положим,
что
y(t) = x(t)-<p(t)
(величину x(t) - <p(t) называют возмущением). Тогда
x(t) = y(t) + <p(t)1
и подстановка в (*) приводит к равенству
dt dt
Но (p(t) — решение уравнения (*), поэтому
dtp
dy + d4=f(tMt)+v(t)).
(•*>
1='М<».
и из (**) имеем
§ =/(*,*(*) + !»(*))-/(*, !»(*))•
Обозначив здесь правую часть через F(t, у), получим
Это уравнение имеет решение у = 0, так как при у = 0 его левая и правая части тождественно по t
равны нулю:
f(t,0) = f(t,<p(t))-f(t,4>(tj)=0.
Таким образом, вопрос об устойчивости решения <p(t) уравнения (*) приводится к вопросу об
устойчивости тривиального решения у = 0 уравнения (***), к которому сводится (*). Поэтому в дальнейшем
мы будем, как правило, считать, что на устойчивость исследуется тривиальное решение.
§3. Устойчивость автономных систем.
Простейшие типы точек покоя
Нормальная система дифференциальных уравнений называется автономной, если ее
правые части /, не зависят явно от t, т. е. если она имеет вид
— = fi(xux2, ...,ж„), г= 1,2, ...,п.

§3. Устойчивость автономных систем. Простейшие типы точек покоя _
.207
Это значит, что закон изменения неизвестных функций, описываемый автономной
системой, не меняется со временем, как это бывает с физическими законами. Пусть
имеем автономную систему
dx'
-jr = fi(x\,x2,..., х„), i = 1,2,..., п,
0)
и пусть (а\, аг,..., ап) — такая совокупность чисел, что
fi(au аъ ..., ап) = 0, г = 1, 2,..., п.
Тогда система функций
Xi(t) = aiy i=l,2,...,n,
будет решением системы (1). Точку (аьа2,... ,ап) фазового пространства (хи
ж2,..., хп) называют тонкой покоя (положением равновесия) данной системы.
Рассмотрим автономную систему (1), для которой
/,(0,0,...,0) = 0, г=1,2,...,п,
так что точка
Xi =0, i= 1,2, ...,n,
есть точка покоя этой системы. Обозначим через S(R) шар
и будем считать, что для рассматриваемой системы в шаре S(R) выполнены условия
теоремы существования и единственности решения задачи Коши.
Определение. Будем говорить, что точка покоя
х{=0, t= l,2,...,n,
системы (1) устойчива, если для любого е > 0
(0 < е < R) существует такое 6 = 6(e) > 0, что
любая траектория системы, начинающаяся в
начальный момент t = to в точке Mq E S(6), все
время затем остается в шаре S(e). Точка покоя
асимптотически устойчива, если:
1) она устойчива;
2) существует такое 6\ > 0, что каждая
траектория системы, начинающаясявточке Mq области
S(6]), стремится к началу координат, когда время t
неограниченно растет (рис. 7).
Поясним это определение примерами.
Пример 1. Рассмотрим систему
dx dy
dt yi dt
Траектории здесь — концентрические окружности
x2+y2 = h2
с центром в начале координат — единственной точкой покоя системы. Если взять 6 — е, то любая
траектория, начинающаяся в круге S(6), остается все время внутри S(6), а следовательно, и внутри S(e), так
Рис.7

208.
. Глава XXIV. Теория устойчивости
что имеет место устойчивость. Однако траектории не приближаются к началу координат при t
и точка покоя не является асимптотически устойчивой.
Пример 2. Пусть дана система
dx dy
- -X, — = -у.
+00
Ее решения:
Отсюда имеем
dt
dt
х-Ае\ у = Be
У В
- = — =к = const,
х А
поэтому траекториями являются лучи, входящие в начало
координат (рис.8). Можно снова выбрать 6 = е. Любая точка
траектории, находившаяся в начальный момент внутри S(6), остается
все время в круге S(e) и, кроме того, неограниченно
приближается к началу координат при t -► +оо. Следовательно, наблюдается
асимптотическая устойчивость.
Be'.
Пример 3. Возьмем,
Ее решение
Здесь также
наконец, систему
dx
х — Ае*,
dy
dt
У =
Рис.8
= к
и траекториями являются лучи, исходящие из начала координат, но в отличие от примера 2 движение
по лучам происходит в направлении от центра. Точка покоя неустойчива. ►
Простейшие типы точек покоя
Исследуем расположение траекторий в окрестности точки покоя х = 0, у = 0 системы
двух линейных однородных уравнений с постоянными коэффициентами:
dx dy
— =aux + ai2y, —
dy dt
а2\х + а22У,
(2)
где
Решение будем искать в виде
а\\ а12
021 ^22
*0.
х = аех\ у = /3ext.
Для определения А получаем характеристическое уравнение
= 0.
а,\\ — А а\2
«21 022 ~ А
(3)
Величины a, J3 с точностью до постоянного множителя определяются из системы
(ап - \)а + апр = 0, а2\а + (а22 - А)/? = 0.
Возможны следующие случаи.
А. Корни Ai, A2 характеристического уравнения (3) — действительные и различные.
Общее решение системы (2) имеет вид
„А2*
Ait
x(t) = СхахеА* + С2а2еЛ2\ y(t) = СфхеА* + С2/32еЛ2\
оХ2*
(4)

§3. Устойчивость автономных систем. Простейшие типы точек покоя.
.209
1. Пусть Ai < 0, А2 < 0. Точкапокоя (0,0) в этом случае асимптотически устойчива, так
как из-за наличия множителей еЛ,<, е*2' все точки каждой траекторий, находившиеся
в начальный момент t — to в произвольной £-окрестности начала координат, при
достаточно большом t переходят в точки, лежащие в сколь угодно малой е-окрестности
начала координат, а при t —► +00 стремятся к этому началу. Такая 'точка покоя
называется устойчивым узлом.
При Сг = 0 из (4) получаем у к
откуда
|« = Cia1eAllf y = Ci/JieA|lf|
у = — ж,
«1
и траекториями являются два луча, входящие в
начало координат с угловым коэффициентом
*,=*.
Рис.9
«1
Аналогично, при С\ = 0 получаем еще два луча, входящие в начало координат
с угловым коэффициентом
«2
Пусть теперь С\ Ф 0 и Ci ф 0 и (для определенности) |Ai | > |А2|. Тогда в силу (4)
dy flflAie^ + CSi/^c*2' A . . ^
т. е. все траектории (исключая лучи у = §*-ж) в окрестности точки покоя О(0,0) имеют
направление луча
«1
А
2/= —ж
а2
(рис.9).
2. Если Ai > 0, А2 > 0, то расположение траекторий такое же, как и в предыдущем
случае, но точки движутся по траекториям в противоположном направлении. Точка
покоя рассматриваемого типа называется неустойчивым узлом (рис. 10).
Пример. Рассмотрим систему
ds _
Для нее точка О(0,0) — точка покоя. Характеристическое
уравнение
I 1_А ° 1-0
I 0 • 2-А |~и
имеет корни Ai = 1, А2 = 2, так что налицо неустойчивый
узел. Перейдем от данной системы к одному уравнению
dy = 2у
dx х '
или
xdy-2ydx = 0.
О За к. 179
i-*-
Рис.10

210.
. Глава XXIV. Теория устойчивости
Оно имеет решения / ?, >■ ,^
* у = 0, х = 0 и y = CsV ■ -w v
так что траекториями системы будут лучи, совпадающие с
координатными полуосями» ^ремвйство парабол, касающихся оси Ojc в начале,
ксюрдинар(рир*1*Ц. вЧ5 t> .,.Л , .j ...,,,.tM t.,^ v ,
3. Пусть Teiilp^^^A2 < 0 5 т()Гда точка Покоя неустойчива.
При С2 = 9 гфлу^ещ>ешение
ar'^dareA|', у = С,/^'.
С возрастанием щ точка этой траекторий Движется по лучу
У= —х
в направлении от начала (Ai > 0), неограниченно удаляясь от негб. npnCi = 0имеем:
Рис.11
х = С2а2еХг\ у = С2р2е
x2t
Отсюда видно, что при возрастании t точка
движется по лучу Ч л
А
у- —#
а2
в направлении к началу координат (А2 < 0).
Если С\ ф0цС2фЪ,7о как при t —► Н-оо, так
и при £ -* -оо траектория покидает окрестность
точки покоя. Точка покоя рассматриваемого
типа называется седлом (рис. 12).
Пример. Исследуем характер точки покоя О(0г0)
системы
dx dy
S = -«, Tt=V- (5)
4 Характеристическое уравнение системы
А2 - 1 = О
имеет корни Ai = 1, А2 = -1. Перейдем к одному уравнению
dx х '
Рис. 12
(6)
xdy + ydx = 0,
интегрируя которое получаем
ху = С.
Уравнение (6) имеет также решения у = 0 и х = 0.
Таким образом, интегральные кривые этого уравнения (траектории системы (5)) — равнобочные
гиперболы и лучи, совпадающие с координатными полуосями. ►
Б. Корни Ai, А2 характеристического уравнения — комплексные: А^ =p±iq9q^ 0.
Общее решение системы (2) можно представить в виде
x(t) = а?*{Сх cos qt + C2 sin qt), y(t) = е**(С* cos qt + C2 sin qt),
(7)
где С\ и C2 — произвольные постоянные, а С*, С2 — некоторые линейные
комбинации этих постоянных.

§3. Устойчивость автономны* систем. Простейшие типы точек покоя.
.211
1. Пусть Ai)2 =7 р + iq, р < О, q Ф 0; в этом
случае множитесь f?x стремится к нулю при t -* 4-оо,
а вторые множители в (7) — одщниченцые дорио-
дическир функции. Траектории — спирали,
асимптотически приближающиеся к началу координат
при t —> -т^бо, ТЪчка покоя х = 0, у = 0
асимптотически устойчива. Она называется устойчивым
фокусом (рис. 13). ч
2. Если Ai,2 = р ± *<?, р > 0, q Ф 0, то этот случай
переходит в предыдущий при замену *. на -£.
Траектории не отличаются от траекторий предыдущего
случая, но движение по ним при возрастании t
происходит в противоположном направлении. Точка
покоя неустойчива г- неустойчивый фокус.
3. Если же Aj)2 = ±Щ, qф0,to решения системы (2) —
периодические функции. Траекториями являются
замкнутые кривые, содержащие внутри себя точку покоя,
называемую в этом (Шучае центром (рис. 14). Центр
является устойчивой точкой покоя, однако
асимптотической устойчивости нет, так как решение
x(t) = C\CO&qt + C2 sin qt, y(t) = С* cos qt + C\ sin qt
не стремится к нулю при t -+ +oo.
Пример. Рассмотрим систему уравнений
dx
dy
—- =х + ау (а = const).
dt
(8)
Характеристическое уравнение системы
(в-А)2 + 1=0
имеет комплексные корни \\^ = а ± i.
Перейдем от системы к одному уравнению
dy (х + ау)
и введем полярные координаты
и
Следовательно,
Используя уравнение (9),
х — р
dx (ах - у)
cos (р, у = р sin у. Тогда
/>2 = ж2 + у2> tgp =
dp dy 2 d<P
dp _ х + уу*
dtp ~ xy'-y'
.находим, что
dp
-*р=а*
_ У
X
dx
-у
Рис.13
Рис.14
,(9)
откуда
Эти интегральные кривые являются логарифмическими спиралями, навивающимися на начало
координат, которое достигается в пределе при <р -+ +оо или <р -» -оо в зависимости от того, будет ли а < 0
или а > 0. Налицо точка покоя типа фокуса. В частном случае, когда а = 0, уравнение (9) принимает
вид
dx у'

212
__ Глава XXIV. Теория устойчивости
Интегральные кривые этого уравнения — окружности с центром в начале координат, которое при а = О
является точкой покоя системы (8) типа центра.
В. Корни Ai, A2 характеристического уравнения кратные: Ai = A2. Случай этот —
скорее искдючение, а не правило, так как сколь угодно малое изменение коэффициентов
системы разрущает его. Применяя метод исключения, находим, что общее решение
системы уравнений (2) имеет вид
*(*) = (С, + С2*)еА|', V(t) = (С? + Cj*)eAlf
(Cf, С\ — некоторые линейные комбинации С\, Сг)
1.ЕслиЛ1 == \г < 0, то из-за наличия множителя
е^1 \ Af < 0, решения x(t), у (t) стремятся к нулю
при t —> +00. Точка покоя х = 0, у = 0
асимптотически устойчива. Ее называют
устойчивым вырожденным узлом (рис. 15). Он отличается
от узла в случае А. 1 (там одна из траекторий
имела касательную, отличную от всех остальных).
Возможен также дикритическийузел (см. рис. 8).
2. При Ai = A2 > 0 замена t на -t приводит
К предыдущему случаю, но движение по
траекториям происходит в противоположном
направлении. Точка покоя в этом случае называется
неустойчивым вырожденным узлом.
Пример, Для системы уравнений
Рис.15
dx
dy
dt y
характеристическое уравнение
(А-1)2 = 0
имеет кратные корни \\ = А2 = 1. Деля второе уравнение системы на первое, найдем
У
откуда
В этом случае
s = I+-.-
у = ж(1гф| + с).
ton у(х) = О, ton у'(х) = ton (l + С + In |ж|) = -оо
Поэтому все интегральные кривые проходят через начало координат, и все они имеют там ось Оу
общей касательной.
Мы перебрали и исчерпали все возможности, поскольку случай Ai = 0 (или Аг = 0)
исключен условием
«21 Л22
Ф0.
Пример. Исследовать уравнение малых колебаний маятника с учетом трения.
4 Уравнение малых колебаний маятника в этом случае имеет вид
d2x
dx
7F = -x-kH>
W

§3. Устойчивость автономных систем. Простейшие типы точек покоя.
.213
где ж —угол малого отклонения маятника от вертикали, X; -— коэффициент трения. Заменим
уравнение (*) эквивалентной системой
dx
dx\
""ЗГ
Х= -9:Г- kV\
ы
Характеристическое уравнение для Системы^*)
I "А 1
I -1 -А?-А
или
#* *Л+ !*?*),
имеет корни
= 0,
Если 0 < к < 2, то эти корни будут комплексными с отрицательной действительной частью, так что
нижнее положение равновесия маятника х - х^ —0 будет устойчивым фокусом. Решением уравнения (*)
является функция
x(t)±A* ^sto(ci/<4*e),
где
■~.f$
— частота колебаний, а величины А, а определяются из начальных условий.
График решения и фазовая кривая х.
при 0 < к < 2 имеют вид, изображенный
на рис.16. При к -+ 0, ъе. о
уменьшением коэффициента трения, фокус
превращается в центр: маятник будет
совершать незатухающие периодические
колебания. ►
Сформулируем результаты,
касающиеся устойчивости решений
системы п линейных однородных
дифференциальных уравнений первого
порядка с постоянными
коэффициентами
dx{ ^—\ .
= 2^a«i«i, t = l,2,...,n, aij = const.
Рис.16
dt
(10)
Рассмотрим для системы (10) характеристическое уравнение
«и -А а\2 ... а\п
а2\ а22 - А ... а2п
Справедливы следующие предложения:
Onn - A
= 0.
1) если все корни характеристического уравнения имеют отрицательную
действительную часть, то все решения системы (10) асимптотически устойчивы. Действительно,
в этом случае все слагаемые общего решения содержат множители е**Л*', стремящиеся
к нулю при t —► +оо;
2) если хотя бы один корень А* характеристического уравнения имеет положительную
действительную часть, то все решения системы неустойчивы;

214
Глава XXIV. Теория устойчивости
3) если характеристическое уравнение имеет простые корни с путевой действительной
частью (т. е. чисто мнимые или равные нулю корни), а остальные корни, если они есть,
имеют отрицательную действительную часть, тавсе решения устойчивы, но
асимптотической устойчивости нет.
Эти результаты относятся и к одцому линейному дифференциальному уравнению
с постоянными крэффициецтами.
Следует обратить внимание на то, что для линейной системы все решения либо
устойчивы, либо неустойчивы одновременно.
Теорема 2. Решения Системы линейных дифференциальных уравнений
л п
-^ = £ *u(*)*j + Л(«). * = 1,2,..., пэ . (11)
либо все одновременно устойчивы, либо неустойчивы.
< Преобразуем произвольное частное решение
^1 9i(f), * = 1,2,...,п,
системы (11) в тривиальное с помощью замены
Vi = Xi(t) - (pi(t).
Система (11) преобразуется при этом в линейную однородную систему относительно
| = ЕМ*)«, «=1,2,..., п. (12)
i=i
Следовательно, все частные решения системы (11) в смысле устойчивости ведут себя
одинаково, а именно как тривиальное решение однородной системы (12).
В самом деле, пусть тривиальное решение
|й(*)==0, t=I,2,...,n,
системы (12) устойчиво, Это значит, что для любого е > О существует 6 = ё(е) > О
такое, что для всякого другого решения системы у,-(<), г = 1,2,..., п, из условия
М*о)1 < в, t = 1,2,... „ п, следует, что
|»(*)|<е, i=l,2,...,n, Vt^to.
Замечая, что у,-($) = X{(t) - (pi(t), получаем, что из условия
Wo)-W(«o)l<*,. i=l,2,...,n,
следует
\xi(t) - <pi(t)\ < е, i = 1,2,..., n, V« > «о
для всякого решения ж,(£), i = 1, 2,..., п, исходной системы (11). Согласно
определению, это означает устойчивость решения y>f(0>* = 1,2,..., n, этой системы. ►
Это предложение не имеет места для нелинейных систем, некоторые решения
которых могут быть устойчивыми, а другие — неустойчивыми.
Пример. Рассмотрим нелинейное уравнение

§4. Метод функций Ляпунова.
.215
Оно имеет очевидные решения
Решение x(t) - -*1 неустойчиво, а решение x(t) « \ является асимптотически устойчивым. В самом
деле, при t -+ +оо все решения
стремятся к -1-1. Это означает, согласно определению, что решение1 x(t) - 1 асимгггбтичеЧ^ устойчиво.
е. Как и в случае п = 2, можно ис^едов^тъ расположение траекторий ъ окрестности точки
покоя О(0,0,0) системы (10). Для п = 3 возможны так называемые узлофокусы (рис. 17), седлофокусы
(рис. 18) и т. д.
Рис.17
Рис.18
§4. Метод функций Ляпунова
Метод функций Ляпунова состоит в исследовании устойчивости точки покоя системы
дифференциальных уравнений с помощью подходящим образом выбранной,
функции v(ty х\, «2,..., хп) —- так называемой функции Ляпунова, причем делается это без
предварительного построения решения системы; в этом неоценимое преимущество
метода.
Ограничимся рассмотрением автономных систем
d>X\
—£ = fi(x\y *г,---,Хп), i=l,2, ...,n,
(1)
для которых Xi; = 0, i = 1,2,..., п, есть точка покоя.
Идея метода состоит в следующем. Предположим, что на устойчивость исследуется
точка покоя ж,- = 0, i = 1,2,..., п, системы (1). Если бы с возрастанием t точки
всех траекторий приближались к началу координат или хотя бы не удалялись от него,
то рассматриваемая точка покоя была бы устойчивой. Проверка выполнения этого
условия не требует знания решений системы. Действительно, если р — расстояние
от точки траектории Xi = ж,*(£), i = 1,2,;.., п, до начала координат
р = \ГЕхШ),
1=1

Глава XXIV. Teopm устойчивости
'''$«В|^'*ё"-^Л<*й^Л^««)^ ;- v(2)
(производная вдоль траектории): Правая часть в (2) есть известная функция от хь
х2,..., хп, и можно исследовать ее знак. Если окажется, что ^f ^ 0, то точки навсё^
тг^зк^1$щ^у;|^ О,
i = 1,2,..., п, устойчива. Однако точка покоя может быть устойчивой и при немощь
т^нно^^ (например, щслунае,
когда траектории — эллипсы). Поэтому А. М.Ляпунов вместо функции р
рассматривал функции v(x\, х2)..., хп), являющиеся в некотором смысле «обобщенным
расстоянием» от начала координат. ?
Определение 1. Функция v(x\y ж2> • • • > хп)» определенная в некоторой окрестности
начала координат, называется знакодпределенной (знакоположительной илизнакоотрица-
теяьной), если в области G
|ж,-Ю, i = l,2,...,n,
где h — достаточно малое положительное число, она может принимать значения
только одного определенного знака и обращается в нуль лишь при
Х\ = а?2 = • • • = жп = 0.
Так, в случае п = 3 функции
V = ж? -|- х\ + Яз
И 2 2 2
будут знакоположительными, причем здесь величина h > 0 может быть взята сколь угодно большой.
Определение 2. Функция v(a:b ж2,..., жп) называется знакопостоянной (положительной
или отрицательной), если она в области 6 может принимать значения только одного
определенного знака, но может обращаться в нудь и при
х\ч-х\ + ..; +х2пфЪ,
Например, функция
будет знакопостоянной (положительной). В самом деле, функцию v(x\, x2, а?з) можно представить так:
•(*ь «2, *з) = (*1 + х2)2 + «з;
отсюда видно, что она неотрицательна всюду, но обращается в нуль и при х\ -f х\ + х\ Ф 0, а именно
при жз = 0 и любых «1, Х2 таких, что si = -$2-
Пусть vfci, а?2» яп) — дифференцируемая функция своих аргументов, и пусть
являются некоторыми функциями времени, удовлетворяющими системе
дифференциальных уравнений (1). Тогда для полной производной функции v по времени имеем
dv ^—v dv dxi x-^ ^v
216.

§4. Метод функций Ляпунова
217
Определение 3. Величина $f, определяемая формулой (3), называется полной
производной функции v по времени, составленнойув силу системы уравнений {\).
Определение 4 Функцию v(a?b##v /., а?л)^ладающугос1юйств8Нйи:
нат;
hv(0,0,.:.,0)^0; °
3) полная производная ^ функции v(x\, жг,!.., жп), составленная в С1Щ^ш?гр-
мы(1),
всюду в Q, называют функцией Ляпунова.
Теорема 3 (теорема Ляпунова об устойчивости). Если для системы дифференцйальныхуравнений
dX'
-£ = М*и*2, •-.,**), t=l,2,...,n, (1)
существуетдифференцируемаязнакоопределеннаяфункцияу(хи ж2,..., xn)f полная
производная % которой по времени, составленная в силу системы (I), есть знакопостоянная
функция (знака, противоположного с v) или тождественно обращается в ноль, то тонка
покоя Х{ = 0 (i = 1,2, ...,п,) системы (1) устойчива.
< Приведем идею доказательства. Пусть для определенности v(xu я?2,..., хп) есть
знакоположительная функция, для которой % < 0. Т^к как
и(ж,,Ж2,...,жп)^0,
причем v = 0 лишь при х\ = х% = ... = хп =р 0, то начало координат есть
точка строгого минимума функции t;(zi, ar2, • • • > жп)« В окрестности начала координат
поверхности уровня
ф,,ж2,...,жп) = С
функции г/ являются, как можно показать, замкнутыми поверхностями, внутри
которых находится начало координат. Чтобы картина стала нагляднее, остановимся
на случае п = 2. Так как v < 0 для малых х\, х2 и v = 0 только для a?i = хг = 0, то
поверхность
г = ф,,ж2)
в общих чертах напоминает параболоид, вогнутый вверх (рис. 19).

,218
Глава XXIV. Теория устойчивости
Рис. 19 Рис. 20
Линии уровня v(x\y хг) = С представляют собой семейство замкнутых кривых,
окружающих начало координат. При этом если С\ < Сг, то линия уровня v = С\
целиком лежит внутри области, ограниченной линией v = С2. Зададим е > 0. При
достаточно малом С > 0 линия уровня v = С целиком лежит в е -окрестности начала
координат, т*о rte проходит через начало. Следовательно, можно выбрать 6 > 0 такое,
что ^-окрестность начала координат целиком лежит внутри области, ограниченной
линией v = С, причем в этой окрестности v < С (рис. 20).
Рассмотрим траекторию системы (1), выходящую в начальный момент времени
t = to из какой-нибудь точки Mo(x\(to), «2(^0)) в tf-окресщрсти начала координат.
Эта траектория при возрастании t никогда не пересечет ни одной из линий v(x\> X2)
изнутри наружу. В самом деле, если бы такое пересечение было возможным в какой-
нибудь точке, то в этой точке или в ее окрестности функция v (si (£), жг(£)) необходимо
имела бы положительную производную ^, тйк как при переходе от какой-нибудь
линии v =с С к другой линии этого семейства, охватывающей первую, функция v(x\>X2)
возрастает. Но это невозможно в сйл^ того, что по условию ^ ^ 0. Значит, если в
начальный момент времени какая-нибудь траектория находилась внутри области,
ограниченной линией v = С, тоона и в дальнейшем будет все время оставаться внутри этой
области. Отсюда ясно, что для всякого е > 0 существует 6 > 0 такое, что любая
траектория системы, выходящая в начальный момент времени t = *0 из ^-окрестности
начала координат, для всех t ^ t0 будет содержаться в е -окрестности начала. Это
и означает устойчивость точки покоя ж,= 0, г = 1, 2,..., п, системы (1). ►
Теорема 4 (теорема Ляпунова об асимптотической устойчивости). Если для системы
дифференциальных уравнений
dx*
-тг = fi(x\,x2l..., жп), г = 1,2,..., п, (1)
at
существует дифференцируемая знакоопределенная функция v(xux2>..., хп), полная
производная которой по времени, составленная в силу системы, есть также знакоопреде-
ленная функция знака, противоположного с v, то тонка покоя ж, = 0, t = 1,2,..., п,
системы (1) асимптотически устойчива.

it 4 Штод функций Ляпунова _ 2J9
Пример. Исследовать на устойчивость точку покоя 0(0,0) системы
dx dy
<4 Выберем в качестве функция v(x,y) функцию
2 2
t; = х1 + у \
Эта функция знакоположительная. В силу системы (*) найдем
dv . dn dx dv dy ^
Из теоремы 3 следует4, что точка покоя 0(0,0) системы {*) устойчива (центр). Асимптотической
устойчивости нет, так как траектория системы (*) — окружности. ►
Пример 2. Исследовать на устойчивость точку покоя 0(0,0) системы
dx 2 dy 2
<4 Беря опять
*(*,у)=*2 + у2,
найдем
J = 2х(у - х3) •+ *(-* - у3) = -2(*4 + И).
Таким образом, ^ есть знакоотрицательная функция. В силу теоремы 4 точка покоя 0(0,0)
системы (**) устойчива асимптотически. ►
Теорема 5 (о неустойчивости). Пусть для системы дифференциальных уравнений
dx*
-^ = fi(xuxb...yxn) (Л(0,0,...,0) = 0), t=l,2,...,n, (4)
существует дифференцируемая в окрестности начала координат функция v(x\, Х2,... >хп)
такая, что v(0,0,..., 0) = 0. Если ее полная производная %, составленная в силу
системы (4), есть знакоположительная функция и сколь угодно близко от начала координат
имеются точки, в которых функция v(xh ж2,..., хп) принимает положительные
значения, то точка покоя Х{ =s 0, % = 1,2,,.., п, системы (4) неустойчива.
Пример 3. Исследовать на устойчивость точку покоя О(0,0) системы
dx dy
А Возьмем функцию
= Ху = —«.
dt ' dt y
v(x,y) = x2-y2.
Для нее функция
dv dv dx Ov dy . 2 2*
dt dx dt^ dy dt v ^y '
знакоположительная. Так как сколь угодно близко к началу координат найдутся точки, в которых v > О
(например, v = х2 >0 вдоль прямой у = 0), то выполнены все условия теоремы 5 и точка покоя 0(0,0)
неустойчива (седло). ► ,
Метод функций Ляпунова оказывается универсальным и эффективным для
широкого круга проблем теории устойчивости. Недостаток же метода в том, что достаточно
общего конструктивного способа построения функций Ляпунова пока нет. В
простейших случаях функцию Ляпунова можно искать в виде
v(xy у) = ах2 + by2, v(x, у) — ах4 + Ьу*у а > О, Ь > О и т. д.

§5. Устойчивость по первому (линейному) приближению
Пусть имеем систему дифференциальных уравцедий
UXi ' Н *
-^ = /,-(£,, s2,...,s„), i = l,2,...,n, (1)
и пусть Xi = 0, i = 1,2,..., п, есп*4Ъчка покоя системы; т. е.
Будем предполагать* чтфузнктеи^
начала координат достаточное число раз. Применяя формулу Тейлора, разложим
Фунюши^то^
,' У^гХь.,^^ШХ•"•'.",0) + i£ ^'''^x-±Ri(xux2,...,жп),
или, учитывай (2),
■-■' "*:-.*■ <-:-^' * ^:; ■*'. .о;,- <,- * ^ .-,-,•.
/t(^i> Д?2, • • > а?п) = >J flijagj + Д|(жь ж2, • • •, Д?п),
>-i -*'^* • * - -* ; "> ■
где
<*и = V ^ = const,
а слагаемые Ri содержат члены не ниже второго порядка малости относительно
х\у а?2,..., хп. Система дифференциальных уравнений (1) примет вид
dx* \, >
-дГ = 2-f а«^ +*(*ь *2, -.--', *>»)> t = 1,2,..., п, а0 = const. (3)
Так как понятие устойчивости точки покоя О(0,0,..., 0) связано с малой
окрестностью начала координат в фазовом пространстве, то естественно ожидать, что
поведение решения (1) будет определяться главными линейными членами разложения
функций /,- по х. Поэтому наряду с системой (3) рассмотрим систему
d,X{ чг-^\ . / ч
— = 2^ачх*> i=l,2,...,n, (4)
j=\
называемую системой уравнений первого (линейного) приближения для системы (3).
Вообще говоря, строгой связи между системами (3) и (4) нет.
Рассмотрим, например, уравнение
Здесь f(x) = 0; линеаризированное уравнение для уравнения (5) имеет вид
dt
Решение x(t) = 0 уравнения (6) является устойчивым. Оно же, будучи решением исходного
уравнения (5), не является для него устойчивым. В самом деле, каждое действительное решение
уравнения (5), удовлетворяющее начальному условию х\ = х0 > 0, имеет вид х = ,{*°х , и перестает
существовать при t = — (решение непродолжаемо вправо).

§5. Устойчивость по первому (линейному) приближению
221
Теорема 6. Если все корни характеристического уравнения
Дц-А аХ2 ... а«п
й2\ 022 - А . . . <*2п
Оп\
а>пг
&пп -А
(7)
имеют отрицательные действительные части, то точка покоя ж,- = 0, * = 1,2,..., п,
системы (4) и системы (3) асимптотически устойчива,
1, ■ , Г , ; 1 '.II -> .-"I' '■ ■ ,:'.'„ ,м'' I|il 1И. '■■■ Г У.
При выполнений условий теоремы возможно исследование на устойчивость по
первому приближению.
Теорема 7. Если хотя бы один корень характеристического уравнения (7) имеет
положительную действительную часть, то точка покоя ж,- = 0 системы (4) и систшы (3)
неустойчива.
В этом случае также возможно исследование на устойчивость по первому
приближению.
Наметим идею доказательства теорем 6 и 7.
< Пусть для простоты корни Ai, А2,..., Ап характеристического уравнения (7)
—действительные и различные. В этом случае существует такая невырожденная матрица Т
с постоянными элементами, что матрица Т~ * AT будет диагональной:
Т"'АТ =
Л, О О
О А2 О
О
о
0 0 0
У\
г =
где А = (aij)"j=l — матрица из коэффициентов системы (4). Положим
X = TY, где Х =
Тогда
и система (4) преобразуется к виду
«I
хг
dX_ <*Y
dt~ dt'
*£=-•
Отсюда получаем
или, в силу выбора матрицы Т,
dt
—
dt
г-1
= T"'ATY(
= AfK, « = 1,2,..
,n.

'222 _ •ъ1л?^.г^мы;ч+--*ыаыг- Глава XXIV. Творив устойчивости
Система (3) при том же преобразовании перейдет в систему
-^r^XiVi + Riiyi,2/2, ••!%), (8)
причем в ifcj опять входят члейк не ниже fctdpdro йоряйка малости отнбскггёйьно у,-
приу; -►О.
Рассмотрим следующие возможности:
si. Все корни А* -** отрицательные.* Положим *
V=|/?+J/2 + -.. +»2,
тогда производная ^ в силусистемы ($)^
-J = 2(А,2/? + А22/2 + • • - + »2) + ^(2/ь 2/2,... г 2/«),
где S(y\, 2/2, .., Уп) при 5^ у} -> 0 — малая более высокого порядка, чем квадратичная
форма ^ W-
Таким образом, в достаточно малой окрестности П точки О(0,0,..., 0) функция
v(2/i, 2/2,.., 2/п) знакоположительна, а производная ^ — знакоотрицательна, и,
значит, точка покоя 0(О> 0,..., 0} асимптотически устойчива.
2. Некоторые из корней А* (например, Ai, Аг,...,Am, m < п) положительные,
а остальные — отрицательные. Положим
» = »? + 02 + • • • + Ут ~ Ут+\ - • • . - 2/п>
тогда
''** n 'ill
= 2(A,2/f + ... + Amym - Am+i0m+1 - \nyn) + S(yu y2}..., 0n).
dt
Отсюда видно, что сколь угодно близко к началу координат найдутся точки (например,
такие, у которых ут+\ = ... = уп = 0), где v > 0. Что касается производной %L,
то, поскольку ATO+i,..., Ап отрицательны, производная ^ — знакоположительная
функция. В силу теоремы 5 точка покоя О(0,0,..., 0) неустойчива.
В критическом случае, когда все действительные части корней
характеристического уравнения неположительны, причем действительная часть хотя бы одного корня
равна нулю, на устойчивость тривиального решения системы (3) начинают влиять
нелинейные члены R+ и исследование на устойчивость по первому приближению
становится невозможным. ►
Пример 1. Исследовать на устойчивость по первому приближению точку покоя х = О, у = О системы
- = -х + 2у-5у\ -=2х-у+Т. <*)
< Система первого приближения имеет вид
dx dv . .
Нелинейные члены удовлетворяют нужным условиям: их порядок не меньше 2. Составляем
характеристическое уравнение для системы (**):
I-1_А 2 1-о
2 -1-А - '

fб; Устойчивость по первому (линейному) приближению „. Jdffl
ИЛИ • . ' Ч • / '. п- ' > •;
А2 + 2А - 3 = 0.
Корни характеристического уравнения Л) = 1, Аг = -3. Поскольку Ai> > 0, нулевое решение х = 0,
у = 0 системы (*) неустойчиво. ►
ь Пример 2. Исследуем наустр^
dx 3 #у 3 " " ./ ч
<4 Точка покоя ж = 0, у = 0 системы (*) асимптотически устойчив», так как для этой системы функция
Ляпунова
удовлетворяет условиям теоремы Ляпунова об асимптотической устойчивости. В частности,
^ = 2*(у - я3) + 2у(-х - у3) = -2(*4 + y*)<ih
В то же время точка покоя х = 0, у = 0 системы
da; з dtf з / ч
. ., *=»+',' ,*-,:-' ... ..., ,^,Г(Г}
неустойчива.
В самом деле, для функции v(x,y) = х2 + у2 в силу системы (**) имеем
dv dv dx dv dy „ . 3v ^ / 3v ^ a 4v ^ ^ ;
^ = TxTt+^I = 2x(v + x) + 2v(-x+y) = 2(x+v);
т.е. •£ — функция знакоположительная. Сколь угодно близко от начала координат О(0,0) имеются
точки, в которых v(x, у) > 0.
В силу теоремы 5 заключаем о неустойчивости точки покоя О(0,0) системы (**).
Для системы (*) и (**) система первого приближения одна и та же:
dx dy
Характеристическое уравнение
А2 + 1 = 0
для системы (***) имеет чисто мнимые корни — критический случай (действительные части корней
характеристического уравнения равны нулю). Для системы первого приближения (***) начало координат
является устойчивой точкой покоя — центром. Системы (*) и (**) получаются малым возмущением
правых частей (***) в окрестности начала координат. Однако эти малые возмущения приводят к тому,
что для системы (*) точка покоя О(в,0) становится, асимптотически устойчивой, а для системы (**)-—
неустойчивой. ►
Этот пример показывает, что в критическом случае нелинейные члены могут
влиять на устойчивость точки покоя.
Задача. Исследовать на устойчивость точку покоя О(0,0) системы
-|= У-«/(*,!/), ^ = -ж-у/(ж,у),
где функция /(ж, у) разлагается в сходящийся степенной ряд и /(0,0) = 0.
Упражнения
Пользуясь определением, исследуйте на устойчивость решения уравнений:
dx dx dx
1.-+х=1, x(0)=l. 2.--* = l, s(0) = -l. 3.-=2, *(0)=0.
Установите характер точки покоя О(0,0) системы и нарисуйте расположение траекторий
в окрестности этой точки:
dx
— = х + 2у,
dt б
dy
л=2х+У.
dx * ( dx
«—+*» 7 \*=*+2*>
±—2.-,. ' |<U-s.-,.
I dt " ( dt *

224.
. Глава XXIV. Теория устойчивости
Методом функций Ляпунова исследуйте на устойчивость точку покоя О(0,0) систем:
' dх _ , ( dx > , ( dx
8. <
— = -2ж + у + ху ,
at
^ = -7х-2у-7х2у.
9. I
dt
dt
= -у + *У,
«=^*у.
ю.
dt
= » + «
Исследуйте на устойчивость по первому (линейному) приближению точку покоя 0(0,0)
систем: '• .- ■ ' - " - -1,,_ •. . * х"
—- = -2s + sm у,
at
11.
,#
12.
-р 5=2*-у cos у,
l^5^^:f^';l
dy л
r^^^x^ty-Qty \
Ответы
1. Асимптотически устойчиво. 2. Неустойчиво. 3. Устойчиво. 4. Устойчивый узел. 5. Седло.
6. Устойчивый фокус. 7. Центр. 8. Асимптотически устойчива, v = 7х2 + у2. 9. Устойчива,
v = х2 + у2. 10. Неустойчива, ж2 - у2. 11. Асимптотически устойчива. 12. Неустойчива.

Глава XXV
НЕКОТОРЫЕ
СПЕЦИАЛЬНЫЕ ВОПРОСЫ
ТЕОРИИ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
§ 1. Асимптотическое поведение
решений дифференциальных уравнений
при х —► оо
Пусть в дифференциальном уравнении
y" + q(*)y = о (1)
функция q(x) имеет положительный предел при х —► +оо, который без ограничения
общности можно считать равным единице. Тогда
q(x) = l + a(x),
где а(х) —> 0, и уравнение (1) примет вид
X—»+0О
у" + У + а(х)у = 0. (2)
При х —► +00 мы получаем «предельное» уравнение
У" + У = 0, (3)
все решения которого
у = A cos х + В sin ж
ограничены для ж Е (-оо, +оо). Поэтому естественно ожидать, что решения
дифференциального уравнения (2) также ограничены при х -* + оо.
Теорема 1. Если а(х) — непрерывно дифференцируемая функция, причем
а
N*)|<£, |a'(*)|<£ (4)
ж ж-6
для всех достаточно больших х, где а — положительная постоянная, то всякое решение
дифференциального уравнения (2) ограничено при х —► +оо.

226 Глава XXV. Некоторые специальные вопросы теории дифференциальных уравнений
<* Умножим все члены уравнения (2) на у' и проинтегрируем результаты по ж от
некоторого положительного числа жо, которое надлежащим образом будет выбрано позже,
дож:
(/)!::;+V)G+2 / «(»Wdx=°-
XQ
Интегрируя по частям последнее слагаемоелевой части, получаем
X
уп(х) - уй(х0) + у\х) - у2(х0) + (ау2) Со - J a>(x)y2(x)dx = О,
откуда
У2(х) < г/'2(ж) + г/2(ж) < С(х0) + |а(ж)|у2(ж) + J \a'(x)\y2(x) dx, (5)
«о
где С(хо) 5? О — выражение, зависящее только от жо.
Обозначим через М наибольшее значение функции \у(х) | на отрезке [ж<>, ж]. Пусть
оно достигается в некоторой тс?чке£ € [ж0, ж]. Используянеравенства(4)и(5),найдем
М2 ^ С(х0) + ^ + М2а (l--j\; М2 (l - ~) < С(»о).
Если выбрать ж0 5? 2а, то получим
М2 ^ 2С(ж0),
что и доказывает утверждение, так как величина 2С(жо) не зависит от ж. ►
Задача. Показать, что все решения уравнения
ограничены на [0, +оо].
Если на а(х) наложить более сильные условия убывания:
а(х) = О (^j , ж -> +оо, (6)
то большая близость уравнения (2) к предельному уравнению (3) повлечет за собой
не только ограниченность решений, но и асимптотическое их приближение к
тригонометрическим функциям — решениям предельного уравнения. Можно показать, что
для всякого решения у(х) уравнения (2) в этом случае имеет место асимптотическая
формула
у(х) = А 8ш(ж + 60) + О
где а\,6о — некоторые постоянные.
Так, уравнение
У-

$2. Лйжпие о иетоде возмущений
_227
а(х) = ±
ji >
удовлетворяет условию (6). Решение этого уравнения связано с функцией Бесселя Jv(x) равенством
у(х) = Vx/vix),
что приводит к асимптотической формуле для функций Бесселя
(здесь А = ^, 60 = -~ + |).
Примеры показывают, что асимптотическое доведение решений
дифференциального уравнения не всегда можно вывести из поведения решений предельного
уравнения.
Рассмотрим, например, два уравнения:
у"-2у' + у = 0, (7)
у"+\у' + У = 0- (8)
Предельным уравнением при х -> +оо для каждого из них является уравнение
У" + У = 0. (9)
Все решения уравнения (9) ограничены на [1,+оо]. Уравнение (7) имеет фундаментальную систему
решений
у\ (х) = sin х -х cos ж, у2(ж) = cos х + х sin ж,
откуда видно, что все нетривиальные решения этого уравнения при х -+ +оо неограничены. С другой
стороны, уравнение (8) имеет фундаментальную систему решений
. ч sin ж . . cos я;
У1(х)=—-, у2(х)=—-;
X X
следовательно, все его решения ограничены на [1, +оо] и даже стремятся к нулю при х —► +оо.
§2. Понятие о методе возмущений
Одним из мощных методов прикладной математики является метод малого параметра
(метод возмущений). Он состоит в следующем. Пусть формулировка некоторой задачи
помимо основных неизвестных величин содержит некоторый параметр е, причем эта
задача может быть решена точно или сравнительно легко при е = ео. Не нарушая
общности, можно считать ео = 0. Тогда решение задачи при е9 близких к нулю, во многих
случаях может быть получено в виде некоторого разложения по степеням е. При этом
первый член разложения, не содержащий е, получается при е = 0и дает так
называемое невозмущенное решение; дальнейшие члены дают поправки на «возмущение»
решения.
Проиллюстрируем этот метод на примере.
Пусть требуется решить задачу Коши
dv х
- f(0) = 0. (1)
dx 1+0,1жу
Рассмотрим более общую задачу
»(0) = 0, (2)
dx 1+txy'
из которой задача (1) получается при е = 0,1. При е = 0 задача (2) легко решается; ее решение -
х2

22ft _ . . Глава XXV. Некоторые специальные вопросы теории дифференциальных уравнений
(невозмущенное решение). Решение задачи (2) при е = 0 будем искать в виде ряда по степеням ?:
у (ж, е) = у0(х) + еух (х) + е2уг{х) +... , (3)
откуда
у'(х, е) = Уо<*) + еу\ (х) + e2yfi(x) +... .
Подставим у(х, е) и у'(ж, е) в (2) и умножим на знаменатель:
[у(х) + fyi(x) + e2J/2(«) + .-.]• [l + «Фо(*) + £2xyi(x) + £2жу2(*) + ...]- ж = 0. (4)
Из начального условия j/(0) = 0, применительно к (3) имеем
Уо(О) + еуЛ0) + е2У2(0) + ... = 0,
откуда в силу произвольности е получаем
!fo(0) = Q, yi(0) = 0, y2(0) = 0, .... (5)
Поскольку уравнение (4) должно удовлетворяться для всех достаточно малых \е\, а последовательность
степеней е линейно независима, коэффициент при каждой степени е обращается в нуль независимо.
Раскрываем скобки в (4) и приравниваем нулю коэффициенты при степенях е:
Уо = х (невозмущенное уравнение),
е
Уг + ху0у\ + xy'Qyi = 0
Из первого уравнения (6) с учетом (5) находим
х2
Уо = ~2'
Подставляя t/o и у'о во второе уравнение из (6), получаем
* = 1о-
Из третьего уравнения теперь определится
7х1
12 =
и т. д. Тем самым, формула (3) принимает вид
У2 160
, . х1 л* 21*
^f) = T-£io+eT6o+-
В частности, для уравнения (1) получим (е = 0,1)
" • 7xs
У 2 100 + 16000
причем ряд в правой части при |ж| < 1 быстро сходится.
Опишем более общую ситуацию. Рассмотрим задачу Коши для уравнения
£ = /(*, У, е), У(0) = у°, . (7)
где е > 0 — малый параметр.
Можно показать, что
если:
1) функция f(x)ye) непрерывна и имеет непрерывные и равномерно ограниченные
производные любого порядка по совокупности аргументов при 0 ^х ^а, -оо <у < + оо,
0 < е ^ ео, и
2) задача Коши (7) при е = 0
^ = /(*,У,0), у(0) = У°, (8)
имеет единственное решение у = <р(х),

№1*тттеомтоюмтк№т#±
.229
то на некотором отрезке 0 ^ х ^ х0 задана Коши (7) имеет решение у = у{х,е),
для которого справедливо представление
У(*,е) = "]>2екУк(х).
(9)
*=а
При этом для любого N ^ 1 имеем асимптотическую формулу
где zN+\(x, е) —► 0 при "б -* 0, 0 ^ ж < ж0, 2jv+i(s, г) = 0(eN+x) при JV
фиксированном и е —► 0 (см. [17]).
Процедура отыскания функций у*(ж), fc = 0,1,2,... , такова. Подставляем
выражение для у в виде формального ряда
в уравнение (7):
dyo
dx
y = yo(x) + eyi(x) + ...
+ е -£ + • • • = /(*,Уо(х) + еу}(х) + ...,*).
(10)
(Н)
Разлагая правую часть (11) также формально по степеням е, получаем:
* + .* + ...-Лм*.Н
«/(*,»>, о) , df(x,yQ,o) t
ey\ H — е +.
ду
А*
Из начального условия в силу (9) имеем
УоФ) + еу\(0) + ... = 2/°
Приравняем члены с одинаковыми степенями е,
dyo
dx
dy\ Of(x, 2/o, 0)
~ = f(x, 2/o, 0), 2/o(0) = 2/°,
dx
02/
2/1 + gg , 2/1 (0) = 0,
Для 2/о(ж) получаем задачу Коши (8), которая, по предположению, имеет
единственное решение у = (р(х)9 поэтому 2/о = ^(ж). Для функции yi(aj) получаем задачу
Коши
(12)
Уравнение (12) есть линейное дифференциальное уравнение первого порядка
относительно 2/i (х), которое интегрируется явно. Для последующих приближений
Ыз), 2/з(з),... мы опять получаемлинейныедифференциальныеуравнения(у,(0) = 0,
г = 2,3,...), которые также интегрируются явно.
1 dyi df(x, ф), 0) df{x, ф), 0)
1 *г = —щ—yt{x)+—fe—•
lh(0) = 0.

230 Глава XXV. Некоторые специальные вопросы теории диффеденциальндодомемий
§3. Осцилляция решений дифференциальных уравнений
С точки зрения физических приложений, а также и с теоретической точки зрения
очень важно уметь решать вопрос о наличии нулей решения у(х) уравнения
Ро(х)у" + Р\ (Ф* + Р2(х)у = 0 (1)
в интервале (а, 6), т. е. тех значений х £ (а, Ь), при которых решение у(х) обращается
в нуль.
Рассмотрим простейшее уравнение второго порядка с постоянными
коэффициентами
у" + 02/- 0, q~ const.
Если q ^ 0, то каждое решение этого уравнения может на всем интервале - оо < х < +оо
обратиться в нуль не более чем в одной точке. При q > 0 каждое решение
у = С\ cos y/qx -f Сг sin sfqx = A bm{yfqx + 6)
имеет бесчисленное множество нулей, расстояние между которыми равно -^,
т. е. тем меньше, чем больше q.
Определение. Решением у(х) дифференциального уравнения называется неосциллиру-
ющим в данном интервале, если оно имеет в этом интервале не более одного нуля;
в противном случае решение называется осциллирующим.
Таким образом, уравнение вида
У1 ЧУ = ° (? = const)
имеет неосциллирующие в любом интервале решения, если q ^ 0, и осциллирующие
в достаточно большом интервале, если q > 0.
Обобщим этот результат на уравнение второго порядка с переменными
коэффициентами. Предположим, что коэффициенты уравнения действительные, и изучим
только действительные решения таких уравнений. Рассмотрим уравнение вида
*" + *(*)* = 0, (2)
к которому приводится любое уравнение (1).
Теорема 2. Если q(x) ^ 0 всюду в интервале (а, Ь), то все решении уравнения
у" + я(х)у = о
— неосциллирующие в интервале (а, 6).
Дадим геометрическое пояснение теоремы.
Предположим, что некоторое решение
У\(х)2 0
уравнения (2) имеет по крайней мере два нуля на
интервале (а, Ь). Пусть это будут х0 и х\,х0 < жь
и пусть на интервале (жо, х\) функция у\ (х) не имеет
других нулей (рис. 1). Тогда у\(х) как непрерывная
функция сохраняет постоянный знак в интервале
Рис.1

ьуЯ&ЩШт решений дифференциальных уравнений _—■ : 281
(&o;ef):; Пусть для определенности у\(х) > 0 в (ж0, х\) (в противном случае мы
взяли бы решение -у\(х)). В некоторой точке £ £ (ж0, Х\) функция у\(х) будет иметь
положительный максимум; следовательно, в некоторой окрестности точки-£ будем
иметь
А*1< О-
С другой стороны, если q(x) < 0 на (а, Ь), то из уравнения (2) следует, что
у'Цх) > О
всюду в (а, Ь). Полученное противоречие говорит о том, что наше предположение
неверно и все решения уравнения неосциллирующие.
Теорема 3 (Штурма). Если х0 и х\ — два последовательных нуля решения у\(х)
дифференциального уравнения
у" + q(x)y = о,
то всякое другое линейно независимое решение jfe(#) того же уравнения имеет в точности
один нуль между Xq и х\; другими словами, нули двух линейно независимых решений
уравнения (2) взаимно разделяют друг друга,
А Предположим, что во всем интервале (а?о> х\) решение уг(х) не имеет нулей. В силу
линейной независимости рещений у\{х) и уг(х) решение yi(x) не обращается в нуль
при а?о и х\. Составим определитель Вронского:
W(x) = у\(х)у2{х) - у2(х)ух(х). (3)
Так как W(x) не обращается в нуль, то он сохраняет постоянный знак. Пусть для
определенности W(x) > 0. Деля обе части тождества (3) на у\(х), получаем
У\(х)У\(х) - y'2(x)yi(x) W(x)
У№ У\(х)\
W(x)
dx \ 2/г(ж) /
УК*)'
В силу допущения, что уг(х) Ф 0 в [хо, *|], мы имеем в правой части непрерывную
функцию от х. Интегрируя последнее тождество по х от хо до х\, получим
у\х) |—1 _ У W(x) ^
1х=х\ Г
Х=Х0 J
у2(х)\х=х0 J y\(x)
хо
Левая часть равна нулю в силу условий у\(хо) = у\(х\) = 0, а в правой части
стоит интеграл от положительной функции, т. е. положительная величина.
Противоречие доказывает, что между двумя последовательностями нулями у\(х) существует
по крайней мере один нуль уг(х). Если бы нулей было два:
У2(Х3) = У2(Х4) =0, Хо<Хз<Х4<Хи
то, меняя ролями у\(х) и У2(х), мы доказали бы существование нуля функции у\(х)
между жз и ж4 и, следовательно, между xq и хх. А это противоречит условию, что у\ (х)
не имеет нулей между а?о и х\. ►

232
Глава XXV. Некоторые специальные вопросы теории дифференциальных уравнений
Например, для уравнения
у" + у = о
функции
#i = sin ж, у2 = cos х
являются двумя линейно независимыми решениями. Их нули взаимно разделяют друг друга. Уравнение
у" + у = 0 имеет также комплекснозначное решение
у — cos х + i sin x.
Это последнее не имеет нулей ни в одном интервале действительной оси.
Задача. Показать, что если на интервале (а, Ь) одно решение уравнения
имеет более двух нулей, то все решения — осциллирующие.
Теорема 4 (сравнения). Пусть имеем два уравнения:
У" + Я\(х)у = 0 (4)
и
z" + q2(x)z = 0. (5)
Если 42(2?) ^ Ч\(х) в интервале (а, Ь), то между каждыми нулями любого решения у(х)
уравнения (4) заключен по крайней мере один нуль каждого решения z(x) уравнения (5).
Теорему сравнения обычно применяют, беря в качестве одного из уравнений (4)
или (5) уравнение с постоянными коэффициентами.
Пусть имеем уравнение
/ + # = 0, (6)
в котором q(x) > 0 на отрезке [о, Ь] и функция q(x) непрерывна на нем, и пусть
М = max д(ж), т = min д(ж).
Предположим, что М > то, так что q(x) =£ const на [о, Ь]. Принимая за
уравнение (4) уравнение у" + ту = 0, а за уравнение (5) — данное уравнение (6), получаем
следующий результат: расстояние между двумя последовательными нулями решения
уравнения (6) меньше чем 4L-. Принимая затем данное уравнение (6) за уравнение (4),
а в качестве уравнения (5) беря уравнение
у" + My = 0,
заключаем, что расстояние между двумя последовательными нулями решения
уравнения (6) не меньше чем ^jj-.
Эта теорема дает оценку сверху и снизу расстояния между нулями осциллирующих
решений дифференциальных уравнений. Можно также показать, что если
lim q(x) = q > 0,
х-юо
то любое решение уравнения (6) — бесконечно осциллирующее, причем расстояние
между соседними нулями стремится к -т- .
Например, для уравнения Бесселя
х2у" + ху' + (х2 - v2) = 0, х > 0,
полагая у = x~l^2z, получаем

3. Осцилляция решений дифференциальных уравнений 233
При достаточно большом х выражение
1 J"1
и ••■■■■<жл'1 \ 'ь--;' , ■ "-:■.-„.■*■■ < ' 3
может быть сделано как угодно близким к единице. Поэтому при достаточно больших значениях х
расстояние между последовательными нулями решений уравнения Бесселя как угодно близко к л*.
Задача. Показать, что при неограниченном возрастании х последовательные нули всякого решения
уравнения Эйри
' jf + ху = 0, х > О
неограниченно сближаются. (Уравнение Эйри встречается в различных приложениях, например в
квантовой механике, и не поддается интегрированию элементарными методами.)
Упражнения
1. Покажите, что на [0, +со) ограничены все решения уравнения
«г + (| + ТТ?)' = а
2. Получите асцмгдтотическую формулу с остаточным членом 0(е2) для решения у{х, е)
задачи Коши для уравнения Риккати
(у-=2ху + е-*2 +еху\ у(0) = 0.
ах
3. Рассмотрите задачу Коши
у+у = еу\ у(о) = 1;
(а) найдите три члена разложения решения для малого е > 0;
(б) покажите, что точное решение имеет вид
У =
1+е(е-*-1)'
(в) разложите это точное решение для малого е > 0 и сравните с результатом п. 1.
Ответы
2. у = хе*2 + fe*2 [l 4- е*\х2 - 1)] + 0(е2).

Предметный указатель
А И
Абеля теорема 40-41
Б
Бернулли уравнение ПО
Бесселя неравенство 82
— тождество 82
— уравнение дифференциальное 131,167
— функции 79,131
, норма 175
1-го рода 170
2-го рода 175
3-го рода 176
в
Вебера функция 176
Вейерштрасса признак сходимости
функционального ряда 32-33
векторы линейно зависимые на интервале 187
независимые на интервале 188
возмущение 206
Вронского определитель системы векторов 188
функций 136
Д
Даламбера признак сходимости числового ряда
13-14
3
задача Коши для обыкновенного
дифференциального уравнения 89
для нормальной системы дифференциальных
уравнений 180
для дифференциального уравнения n-го
порядка, разрешенного относительно старшей
производной 126
изоклина 94
интеграл дифференциального уравнения 1-го
порядка общий 92,116
частный 92
n-го порядка общий 128
— первый нормальной системы
дифференциальных уравнений 185
интегральный синус 57
интегрирование дифференциального уравнения 87
интервал сходимости степенного ряда 42
к
Клеро уравнение 120
комбинация интегрируемая 185
Коши критерий сходимости числового ряда 8
— матрица 189
— признак сходимости числового ряда 14-15
коэффициенты биномиальные 55
— Тейлора 49
— тригонометрического ряда 60
— Фурье 64,80
комплексные 76
кривая интегральная 87
дифференциального уравнения n-го порядка
128
— — нормальной системы дифференциальных
уравнений 181
особая 92
критерий Коши сходимости числового ряда 8
л
Лагранжа метод отыскания частного решения
линейной неоднородной системы
дифференциальных уравнений 190-191
— уравнение 119
Лежандра многочлены (полиномы) 78
Лейбница признак сходимости
знакочередующегося числового ряда 20-21
ломаная Эйлера 97

Предметный указатель
М
Маклорена ряд 49
матрица, дифференцируемая на множестве 194
-Коши 189 Jf; f >■■?/*
— непрерывная на множестве 194 р
— , собственное значение 194
— , собственный вектор 194
— фундаментальная однородной линейной
системы дифференциальных уравнений 189
метод вариации постоянной интефирования
неоднородного линейного уравнения 106-109
постоянных отыскания частного решения
линейной неоднородной системы
дифференциальных уравнений 190-191
— возмущений (малого параметра) 227
— изоклин интефирования дифференциального
уравнения 1-го порядка 93-94
— интегрируемых комбинаций интефирования
нормальной системы дифференциальных
.уравнений 185
— исключения интефирования системы
дифференциальных уравнений 181-184
— Лагранжа отыскания частного решения
линейной неоднородной системы
дифференциальных уравнений 190-191
— малого параметра (возмущений) 227
— матричный интегрирования однородной
линейной системы дифференциальных уравнений
193-198
— последовательных приближений для
нахождения приближенного решения
дифференциального уравнения 95-96
— преобразования Лапласа интефирования
линейной системы дифференциальных
уравнений с постоянными коэффициентами 191
— Рунге—Кутта приближенного решения
дифференциального уравнения 98
— Эйлера интефирования линейной однородной
системы дифференциальных уравнений с
постоянными коэффициентами 191-193
приближенного решения
дифференциального уравнения 96-97
многочлен характеристический 143
многочлены Лежандра 78
— Чебышева—Эрмита 79
множитель интегрирующий 114
н
Неймана функция 176
неравенство Бесселя 82
норма функции 78
Бесселя 175
нуль порядка (кратности) т 166
о
область определения оператора 133
— сходимости функционального ряда 28
огибающая семейства кривых 92
235
оператор 133
— линейный 133
определитель Вронского системы векторов 188
функций 136
остаток функционального ряда 29
— числового ряда 7
Острофадского—Лиувилля формула 143
п
Парсеваля (Парсеваля—Стеклова) равенство 83
период функции 60
плоскость фазовая 181
поле направлений 93
полиномы Лежандра 78
— Чебышева—Эрмита 79
положение равновесия системы
дифференциальных уравнений 207
порядок дифференциального уравнения 86
приближение функции линейной комбинацией
среднее квадратичное 82
признак сравнения для числовых рядов с
положительными членами 10-11
— сходимости Вейерппрасса функционального
ряда 32-33
Лейбница знакочередующегося числового
ряда 20-21
Даламбера числового ряда 13-14
интефальный числового ряда 16-17
Коши числового ряда 14-15
необходимый числового ряда 8
принцип суперпозиции 153
продолжение решения 201
— функции периодическое 65
р
равенство Парсеваля (Парсеваля—Стеклова) 83
радиус сходимости степенного ряда 42
разложение функции в степенной ряд 48
в тригонометрический ряд 61
резонанс 163
решение дифференциального уравнения 87
1-го порядка, не разрешенного
относительно производной, общее 116
линейного неоднородного в форме
Коши 107
п-го порядка общее 127
частное 128
неосциллирующее 230
неустойчивое 202
осциллирующее 230
общее 91
особое 92
— устойчивое по Ляпунову 202
асимптотически 202
частное 91
— задачи Коши неофаниченно продолжаемое 201
влево 201
вправо 201

236
— линейной системы дифференциальных
уравнений 186
t свойства 186-187
— нормальной системы дифференциальных
уравнений 180
общее 180
частное 181
— системы дифференциальных уравнений
неустойчивое 204
устойчивое по Ляпунову 204
асимптотически 204
Риккати уравнение 114
специальное 115
Римана функция 36
Рунге—Кутта метод приближенного решения
дифференциального уравнения 98
ряд биномиальный 55
— Маклорена 49
— степенной 40
— Тейлора 49
— тригонометрический 60
— Фурье тригонометрический 64
в комплексной форме 76
сходящийся 76
по ортогональным системам функций 80
— функциональный 28
сходящийся в точке 28
на множестве 28
абсолютно 28
равномерно 30
— числовой 3
гармонический 9
знакопеременный 22
сходящийся абсолютно 24
условно 24
знакочередующийся 20
мажорирующий (мажорантный) для
функционального ряда 33
расходящийся 3
сходящийся 3
с
седло 210
семейство ортогональных траекторий 123
синус интегральный 57
система дифференциальных уравнений
автономная 206
каноническая 179
линейная 186
однородная 186
1-го порядка нормальная 179
— решений фундаментальная линейного
однородного дифференциального уравнения n-го
порядка 141
линейной однородной системы
дифференциальных уравнений 188
— функций линейно зависимая 135
независимая 135
ортогональная 61
на интервале с весом р 79
на отрезке 77
Предметный указатель
ортонормированная 78
замкнутая 84
полная 83
тригонометрическая 61
— дифференциальных уравнений первого
(линейного) приближения 220
собственное значение матрицы 194 м
собственный вектор матрицы 194
сумма числового ряда 3
частичная 3
схема разностная Эйлера 96
сходимость последовательности функций в
среднем 80
т
Тейлора коэффициенты 49
— ряд 49
теорема Абеля 40-41
— о единственности разложения функции в
степенной ряд 48
— о почленном дифференцировании степенного
ряда 46-47
функционального ряда 37-38
интегрировании степенного ряда 46
функционального ряда 36-37
— о разложимости решения однородного
линейного дифференциального уравнения 2-го
порядка в обобщенный степенной ряд 167
— о структуре общего решения линейного
неоднородного дифференциального уравнения
153-154
однородного дифференциального
уравнения 139-140
линейной однородной системы
дифференциальных уравнений 188,190
— об аналитичности решения однородного
линейного дифференциального уравнения 2-го
порядка 166
— об ортогональности тригонометрической
системы функций 61-62
— существования и единственности решения
задачи Коши 89
для дифференциального
уравнения n-го порядка 127
для системы дифференциальных
уравнений 180
тождество Бесселя 82
точка покоя системы дифференциальных
уравнений 184,207
9 типы 206-215
устойчивая 207
асимптотически 207
траектория фазовая системы дифференциальных
уравнений 181
у
узелдикритический 212
— неустойчивый 209
вырожденный 212

Предметный указатель
237
— сетки 96
— устойчивый 209
вырожденный 212
уравнение Бернулли ПО
— Бесселя дифференциальное131,167
— в полных дифференциалах 111
— дифференциальное, интегрирумое в
квадратурах 98
линейное 1-го порядка 105
неоднородное 105
однородное 105
п-го порядка 132
неоднородное 132
однородное 132
обыкновенное 86
однородное 102
с разделенными переменными 98
с разделяющимися переменными 99
— Клеро 120
— Лагранжа 119
— логистическое 101
— Риккати 114
специальное 115
— характеристическое для линейного однородного
дифференциального уравнения 143
для системы линейных дифференциальных
уравнений с постоянными
коэффициентами 192
— Эйлера 150
условие линейной зависимости функций
необходимое 136-137
независимости решений необходимое 138
и достаточное 139
— полноты 83
— разложимости функции в ряд Тейлора
достаточное 51-52
необходимое и достаточное 50-51
— начальное для дифференциального уравнения
1-го порядка 88
п-го порядка 126
для системы дифференциальных уравнений
180
Ф
фокус неустойчивый 211
— устойчивый 211
формула Остроградского—Лиувилля 143
формулы рекуррентные для функций Бесселя 172
фундаментальная система решений линейного
однородного дифференциального уравнения п-го
порядка 141
линейной однородной системы
дифференциальных уравнений 188
функции Бесселя 79,131
, норма 175
1-го рода 170
2-го рода 175
3-го рода 176
— ортогональные 61
— Ханкеля 176
функция Ляпунова 215, 217
— Вебера176 . к
— знакоопределенная (знакоположительная, 'зна-
коотрицательная) 216
— знакопостоянная (положительная,
отрицательная) 216
— кусочно-монотонная на отрезке 65
— Неймана 176
— нечетная(58, , . ,,, , ,... .,,.. , , ?
— однородная п-го измерения относительно
двух переменных 102
— периодическая 60
— Римана36
— сеточная 97
— цилиндрическая 175
— четная 68 ., ,
Г -функция Эйлера 169
Фурье ряд по ортогональным системам функций 80
, коэффициенты 80
тригонометрический 64
, коэффициенты
в комплексной форме ]6
, коэффициенты 76
сходящийся 76
х
Ханкеля функции 176
Ч
центр 211
ч
Чебышева—Эрмита многочлены (полиномы) 79
член числового ряда 3
общий 3
ш
шаг сетки 96
э
Эйлера ломаная 97
— метод интегрирования линейной однородной
системы дифференциальных уравнений с
постоянными коэффициентами 191-193
приближенного решения
дифференциального уравнения 96-97
— разностная схема 96
— уравнение 150
— Г-функция 169
эквивалентность дифференциальных уравнений 88
я
якобиан системы функций 183

■ I . П HI II ill I. *
Оглавление
Глава XVII. Числовые ряды 3
Глава XVIII. Функциональные ряды 28
Глава ХЕХ. Степенные ряды с 40
Глава XX. Ряды Фурье 60
Глава XXI. Дифференциальные уравнения первого порядка 86
Глава XXII. Дифференциальные уравнения высших порядков 126
Глава XXIII. Системы дифференциальных уравнений 179
Глава XXIV. Теория устойчивости „ 199
Глава XXV. Некоторые специальные вопросы теории дифференциальных уравнений . . . , 225
Предметный указатель 234

i
Издательство УРСС
специализируется на выпуске учебной и научной литературы, в том числе
монографии, журналов, трудов ученых Российской Академии наук,
научно-исследовательских инстизу|<>в и учебных заведений.
Уважаемые читатели! Уважаемые авторы!
Ос^^ьщясь на щидакон ц.плодотворном сртрудщществе,я Российским
фондом фундаментальных исследований и Российским гуманитарным научным
фондом, мы предлагаем авторам свои услуги на выгодных экономических условиях
При этом мы берем на себя всю работу по подготовке издания — от набора,
редактирования и верстки до тиражирования и распространения.
Среди недавно вышедших книг мы предлагаем Вам следующие.
Пригожий Я, Стенгерс И. Время, хаос, квант. К решению парадокса времени.
Пригожим Я, Стенгерс Я Порядок из хаоса. Новый диалог человека с природой.
Самарский А. А. и др. Задачи и упражнения по численным методам.
Боровков А. А. Теория вероятностей.
Гнеденко Б. В. Курс теории вероятностей.
Гнеденко Б. В. О математике.
Шикин Е. В. От игр к играм.
Дубровин Б. А., Новиков С. Я, Фоменко А. Т. Современная геометрия. Методы и
приложения. 5-е издание, исправленное. Т. 1-3.
Арнольд В. И. Математические методы классической механики.
Волобуев И. Я., Кубышин Ю.А. Дифференциальная геометрия и алгебры Ли и их
приложения в теории поля.
Табор М. Хаос и интегрируемость в нелинейной динамике.
Малинецкий Г. Г., Потапов А. Б. Современные проблемы нелинейной динамики.
Капица С. Я, Курдюмов С. Я, Малинецкий Г. Г. Синергетика и прогнозы будущего.
Эбелинг В., Энтелъ А, Файстель Р. Физика процессов эволюции.
Кириллов В. М. и др. Решение задач по физике.
Шепелев А. В. Оптика. Готовимся к экзаменам, зачетам, коллоквиумам.
Колоколов Я. В., Кузнецов Е.А. и др. Задачи по математическим методам физики.
Рубеков В. А. Классические калибровочные поля.
Ельяшевич М.А. Атомная и молекулярная спектроскопия.
Морозов А, Д. и др. Инвариантные множества динамических систем в Windows.
Волсинов А. В., Фоменко А. Т. Геометрия и топология интегрируемых геодезических
потоков на поверхностях.
Коноплева Н. Я, Попов В. Н. Калибровочные поля.
Темчин А. Н. Уравнения Эйнштейна на многообразии.
Неретин Ю.А. Категории симметрии и бесконечномерные группы.
Пытьев Ю. И Возможность. Элементы теории и применения.
Гейзенберг В. Собрание научных трудов.
Низовцев В. В. Время и место физики XX века.
1
Ш
ЕЙ
■1
■
По всем вопросам Вы можете обратиться к нам:
тел./факс (095) 135-44-23, тел. 135-42-46
или электронной почтой urss@urss.ru.
Полный каталог изданий представлен
в Интернет-магазине: http://arss.ni
Издательство УРСС
Научная и учебная
литература
Ш
ж