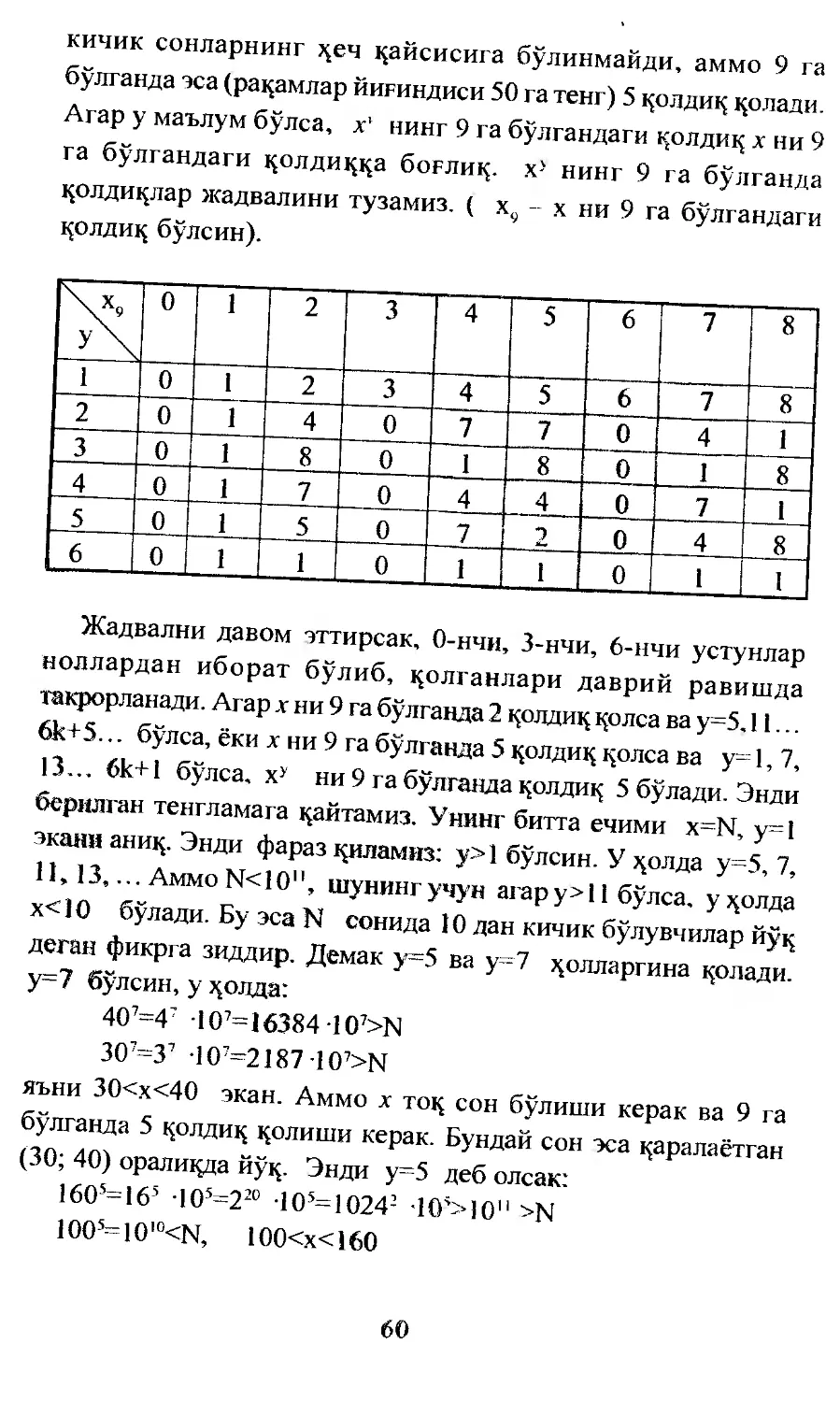
Текст
УМИД исмоилов
МАТЕМАТИКАДАН
ОЛИМПИАДА МАСАЛАЛАРИ
УМИД исмоилов
МАТЕМАТИКАДАН
ОЛИМПИАДА
МАСАЛАЛАРИ
У.л/1 май урта таълим мактаблари уцувчилари, академик лицей,
каеб-уупар коллежлари талабалари ва укитувчила1>и учун ^улланма
Тошкент
“Янги аср авлоди”
2007
'<«<•> Ц1 । i.,ij uu i ni/' Ланн uuOa 9-1 l-синфлар буйича
u.ii'i, <iu «"uu «,</«< ini, тки фан nip олимпиадаларида берилган
<«>. .. 1.1 (,i/' <m >i ши. an in h</>. парча па, a in nip ечилиш усуллари ёки ечиш
i-пн up. .nun.i i.ipi'u taniirpui.-au l\\ rum иадаолимпиадаларда берилган
in.. ni in/'^.iii t.i и nauwa tap i, iniiipii i. aii булиб, уларнинг 20 таси ечилиш
।. । । i.i/'ii n.। W ih.i. и 'H iinahiup ка iiiinu берилган уолда мустацил ечиш
14» Н Ifltlfh ни ЧП и
/\i । шина г и г пин \рта пин, т и мактаблари, академик лицей ва касб-
I wap к,, i и- * inpii гц гнчн uipii \амда уцитувчиларига мулжалланган.
Та^ризчилар:
Мадра^имов Рузимбой,
' р. анч Дан иип университеты «Функциялар назарияси»
nii/n-Opai ii мудири, физика-математика
фаи ицт номзоди, доцент.
Ьобожонов \амид,
\ р.-апч ша \piuHi.-u 2-сон академик лицейининг
и,пн,-танина финн буйича алий тоифали уцитувчиси
||1 > ' И I I | I Ш1 I ..Il
II • !• >11 h '|| I 1ч................... > ,14 ' 110111114 14 M4I .1'1.11111)111
‘In <= , «в • «н нн Hu i
СУЗ БОШИ
Ицтидорли уцувчиларнинг фанлардан эгаллаган билимлари
цаичалик чукур ва мустаукамлиги, уларнинг тафаккур доираси
кенглиги, куввайи уофизасининг кучлилиги ва мантикий
фикрлашларининг кенг камровли эканлигини аникрювчи мезонлардан
бири фан олимпиад аларидир.
Фан олимпиадаларида катнашишни орзу цилган уар бирукувчи
ёки талаба чуцур масъулиятни уис этган уолда, мактаб, лицей ва
коллежларда берилаётган билим билан чегараланиб колмайдилар.
Чунки олимпиадаларга тайёргарлик куриш укитувчидан уам,
ёцувчидан уам купрок изланишни, цушимча адабиётларни купрок
ёцишни ва урганшини талаб килади.
Математикадан олимпиадаларга тайёрланувчилар учун
мулмсалланган ушбу методик цулланма узбек тилида ёзилган худди
шундай цулланмаларнинг камлигини эътиборга олиб уамда вилоят
ва республика олимпиадаларида берилган тест намуналари билан
тулдирилган уолда натр килинмокда.
Цулланмадаги барча масалалар ечилишлари билан, айрим
уолларда ечиш учун курсатмалар билан баён килинган.
Масалаларпинг биринчи 56 таси 9-синфларга, 57 109 гача 10-
синфларга ва 110-161 гача 11-синфларга мулжаллангандир.
Геометрияга дойр масалалар эса алоуида баён цилинди.
Олимпиадаларда берилган тест намуналаридан 20 таси
ечилишлари билан берилган булиб, 50 таси мустацил ечиш учун
тавсия килинмокда. Мустацил ечишга мулжалланган тест
намуналарининг жавоблар калити берилган.
7
Мустацил ечиш учун берилган тест намуналари Урганч
шауридаги 2-сон академик лицейнинг .математика фа ни буйича
алий тоифали уцитувчиси Бобожонов томонидан тавсия
цилинган.
Булланманинг цулёзма нусхаси билан танишиб, узларининг
цимматли масла^атларини берган доцент Р.Мадра^имовга,
Х.Бобожоновга уз миннатдорчилигимизни билдирамиз.
Мамлакатимизда ицтидорли уцувчиларни тарбиялашга,
уларнинг билим ва куникмаларини янада мустаукамлатга жуда
катта эътибор берила'ётганини назарда тутган %олда, ушбу
цулланма математика уцитувчиларига ицтидорли уцувчиларни
тарбиялашда, уларга математиканинг ажойиб сир-асрорларини
ургатишда, шунингдек, математикадан олимпиадаларга
тайёрланувчи уцувчиларга ёрдамчи цулланмалардан бири булади,
деган умиддамиз.
Муаллиф
АЛГЕБРАИК МАСАЛАЛАР
I. Бешта номанфий соннинг йиг-индиси бирга тенг. Бу сон-
ларнинг жуфт-жуфт айирмалари абсолют г^ийматларининг йи-
гиндиси ^андай энг капа ^ийматга эта булиши мумкин?
2. Бешта копдан биринчиси ва иккинчиси биргаликда 12 фунт,
иккинчиси ва учинчиси биргаликда 13,5 фунт, учинчи ва туртин-
чиси биргаликда 11,5 фунт, туртинчи ва бешинчиси биргаликда
К фунт, биринчи, учинчи ва бешинчи биргаликда 16 фунтдан
келади. .\ар бир коп ^анчадан келади?
3. Учта бутун мусбат сон берилган. Уларнинг энг капа уму-
мий булувчиси I га тенг. ихтиёрий иккитасининг йигиндиси
»са учинчига булинади. Шу сонларни топинг.
4. п-1 нинг 15 га ва 1001 нинг п+1 га булиниши маълум
булса, (п)ни топинг.
5. Натурал сонлардан тузилган арифметик прогрессияда
охирги разами 3 билан тугаган гуади бор булиб. аммо охирги
раками 5 билан тугаган >,ади йу^. Бу арифметик прогрессияда
охирги раками 7 билан тугаган ?уад борми?
6. Аниг^ квадрат буладиган ва унт томонига 1 разами ёзил-
ганда яна квадрат (анигу буладиган бутун сонларнинг чексиз
куп эканлигини исботлапг.
7. Каримнинг ёши 1959 йилда гутилган йили ра^амларининг
йш индисига тенг булди. Агар унинг XX асрда тугилганлиги
маълум булса, тугилган йилини топинг.
8. Ёзилиш тартибида арифметик прогрессиянинг тагикил
^илувчи ва - yfztui’ шартни цаноголангирувчи , zl, uv
икки хонали сонларни топинг.
9. Квадратларининг йигиндиси 16000 га тент булган барча
натурал сонлар жуфтликларини топинг.
10. Биринчи разами 2 булган уч хонали сон 1992 марта кет-
ма-кет ёзилди, натижада 91 га булинувчи сон ^осил булди. Шу
сонни топинг.
11. Ушбу 2ху+х+у=83 тенгламани каноатлантирувчи х ва у
нинг барча бутун адйматларини топинг.
12. xy+l=z тенгламани туб сонларда ечинг.
13. х ва у бутун сонлар булиб, 6х+11у сони 31 га булинса,
х+7у сонининг ^ам 31 га булинишини исботланг.
14. х2+ах+1=Ь тенгламанинг илдизлари натурал сонлардан
иборат булса, а2+Ь2 нинг мураккаб сон булишини исботланг.
15. Агар х5+у5=2х2у2 тенгламани х ва у рационал сонлар к;ано-
атлантирса, 1-ху ифоданинг рационал соннинг квадрати були-
шини исботланг.
16. Агар х. у, z лар .\ар хил натурал сонлар булиб, улардан
исталган иккитасининг купайтмаси учинчсига булинса, x-y+z
=1 тенгламанинг чексиз куп илдизга зга булишини исботланг.
17. Тенгламалар системасини бутун сонларда ечинг:
xz - 2 у! = 3
xt + yz - 1
18. Агар -J^yz - (х + y)yz булса, х, у, z ларни топинг.
19 Агар -yj^yz = Zy/x + у булса, х, у, z ларни топинг.
20. Куп ^аднинг энг кичик кийматини топинг:
х6+2х4+2х3+х2+2х-1
21. Тенгламани натурал сонлар тупламида чексиз куп ечим-
га зга эканлини исботланг:
x2+y3+z5 =t7
22. р ва q нинг т^андай кийматларида x2+px+q’0 тенглама-
нинг илдизлари р ва q сонлар булади?
23. Соддалаштиринг:
2 + Л 2-Л
V2 + ^2 + V3
6
Ill 7 7 T
24. Агар x + у + z — 1 ва- + — + - = О булса, х + у + z
х у z
пн 1ОПИПГ.
25. р ва q туб сонлар экани маълум булиб, x4-px3+q=0 тенг-
na ма бутун илдизларга эт а булса, р ва q ни топинт.
2(>. Тенгламалар системасини ечинг:
X] + X] • х2 = 1
х2 + х2 • х3 = 1
х3 + х3 • х4 =1
х99 + х99 • х)00 =
.*100 + *100 ‘*1 =
27. х3 — 9х2 + 27 х = 19 тенгламани ечинг.
28. Ифоданинг энг кичик тртйматини топинт:
2х2 - 2ху + 5у2 + 2х + 2у
29. Тенгламалар системасини ечинг.
х2 + ху + у2 = 7
• х2 + xz + z2 + 21
у1 + yz + z2 = 28
30. N натурал сон 12 та булинувчига эга (1 ва N ни ^ам т^исоб-
га олганда). Уларни усиб бориш тартибида номерлаймиз:
d^d^d^...<d|2d4-l булувчининг(d+d,+d3)d8купайтмагатенг-
лиги маълум булса, N ни топинт.
31. Тенгламани ечинг:
7-^ - +х2 -4 = 0.
7
32. Агар а ва b лар натурал сонлар булса, учта турли усул-
лар билан 1 За+73Ь куринишда ёзиш мумкин булган знг кичик
сонни топинг.
33. x2+px+q-0 тенгламанинг илдизи х, ва x ' px- q~0 тен-
гламанинг илдизи х, булса, х2+2рх+ 2q=0 тенгламанинг илдизи
х) ва х2 лар орасида ётишини исботланг.
34. п нинг ^ар ^андай натурал кийматларида ^ам ушбу
n4+3n3+2n2+2n ифода бирорта соннинг квадрата була олмасли-
гини исботланг.
35. п нинг ь^андай натурал кийматларида ir+З сони n+З га
булинади?
36. Тенгламалар системасининг мусбат ечимларини топинг:
xv’(x + и) = 6
yz(y + z) = 12
zx(z + х) = 30
37. Агар «Ьс= 1 ва а + ь + с = ~ ~ экани маълум булса,
а,Ь,с лардан камида биттасининг 1 га тенг булишини исбот-
ланг.
38. Кайей катта :
а) 2300 ёки З200 б) 291 ёки 535
39. Тенгламани ечинг:
х + 2 Y ( х - 2 Y 5 х2 - 4 л
---- + ------ -------;-- = 0
х +1 / V х -1 / 2 х" -1
40. Агар xyz= 1 булса.
1 + х + ху 1 + у + yz 1 + z + zx
тенгламанинг тугрилигини исботланг.
41. Ушбу 1989 1990 1991 1992+1 соннинг туда квадрат
эканини исботланг.
42. йигиндини топинг:
1 -3+3 -5+5 -7 т...+999 1001
8
43. Агар л ва у мусбат сонлари х+у>2,6 ва х2+у2<4 тенг-
си «ликларни ^аноатлантирса, ху>1 тенгсизликнинг турри ака-
пнии исботланг.
44. Исталган t учун тенгсизликнинг туррилигини исбот-
лапг:
/' -/+—>0
2
45. Агар а>0, Ь>0, с>0 булса,
<rbce > (a+b-c)(a+c-b)(b+c-a) тенгсизликнинг тугрилиги ис-
ботланг.
46. Тенгламани ечинг:
з 2 1
X + г + х =— •
3
47. 2р+р2 соннинг туб сон буладиган Р нинг барча туб ^ий-
ма тларини топинг.
48. а) шундай иккита х ва у натурал сонларни топингки, на-
тижада ху+х ва ху+у лар турли натурал сонларнинг квадратла-
ри булсин;
б) 988 дан 1991 сонлари орасида юцоридаги шаргни ^ано-
111 лантирувчи х ва у ни топиш мумкинми?
49. х - тенглама (бу ерда п натурал сон) натурал сон-
лар тупламида ягона х ва у ечимга зга булиши учун п нинг туб
сон булиши зарур ва етарли эканлигини исботланг.
50. Утган куни мен 14 ёшга тулган эдим, келгуси Йили эса
17 ёшга ^араб кетаман, деди Шерзод.
Шерзоднинг айтгани тугрими?
51. Берилган (1-х)( 1 +х+х2+...+х,99Э) ифодада ^авсларни очинг
па соддалаштиринг.
52. Тирга кираётиб, уйинчи кассага 100 сум ташлайди. ?^ар
би it а нишонга тугри урганда унинг пули 10% га ортади ва ^ар
бигга нишонга теккиза олмагани учун 10% га камаяди. Нишонга
бпр неча марта отгандан кейин унинг пули 80 сум 19 тийин
булиб ^олиши мумкинми?
9
53. А сони ра^амлари йириндисининг квадрати А2 нинг
рацамлари йигиндисигатенг булган барча икки хонали сонларни
топинг.
54. а, в, с лар учбурчакнинг томонлари булса, а’+в’+3авс>с’
тенгсизликнинг туррилигини исботланг.
55. Ушбу х*-2у2=1 тенгламани ^аноатлантирувчи х ва у нинг
барча бутун 1(ийматларини топинг.
56. Бешта соннинг купайтмаси нолга тенг эмас. >^ар битта
сонни биттага камайтириб, купайтирганда ^ам купайтма
узгармайди. Шундай сонларга мисоллар келтиринг.
57. Тенгламалар системасини бутун сонларда ечинг:
ab + cd = -1
- ac + bd = -1
ad + be = -2
58. Тенгламалар системасини бутун сонларда ечинг:
x2+y2+z2=x+y+z=2
59. Тенгламани ечинг:
д/х + 2 + Зл/2х —5 + у1х~2~^2х — 5 = 2у[2
60. Тенгламалар системасини ечинг:
X - у[у - 1
у-yfz =1
Z-\[x - 1
61. х’"'+у'«9,=х'992+у1992 тенгламанинг рационал сонларда
чексиз куп ечимга эга эканлигини исботланг.
62. Тенгламалар системсини ечинг.
sin х + sin у = л/2 sin а
<
cos х + cos у - у/2 cos а
10
63. Тенгламалар системасини ечинг:
х,+2х2 +...+9х,+10х1О=55
х2 +2х, +.„+9х|0+х1 =55
«
x10 +2Xj +...+9х8 1 Ох, =55
64. Тснгламани ечинг:
4х2-4х-3=4
2
1 1 1 = 1
65. Агар х, у, z сонлари x+y+z=a ва х + у + z а шарт-
ларни ^аноатлантирса, х,у, z сонларидан камида биттаси а га
тенгбулишини исботланг.
66. Тенгламни бутун сонларда ечинг:
(14-1)^'=(1 + _2_)|’«
т 1992
67. х3+113 =у’тенгламанинг натурал сонларда ечимийу^и-
гини исботланг.
68. Тенгламани ечинг: ^2-х + \lx-i = 1
69. Тенгламалар системасини ечинг:
х2 - yz = у - X
< у~ - xz = z — у
Z2 -ху = х- Z
11 1 _ 1
70. Агар Х'+7Г хг+~~Хз+“ =Х',+Т шарт бажарилса,
х2 X, х4 X,
ёки х^Хз^-.Хд, ёки |х, х, ... х„|< I булишини исботланг.
71. Тенгламани ечинг:
(16х200 +1)( j200 +1) = 1 б(ху)'00
11
ci с а а + с с
72. Агар — < — (бу ерда Ь>0 ва d>0 ) булса, - < -—- < —
b a b b+d d
тенгсизликнинг турри булишини исботланг.
сизликни исботланг.
74. а,Ь,с номанфий сонлари учун ушбу тенгсизликнинг тугри-
лигини исботланг:
75. Агар х5+у5=х-у ва х>у>0 булса, х4+у4< 1 тенгсизлик-
нинг тугрилигини исботланг.
76. Тенгсизликни исботланг:
1 1 11
з , , з Г' + зд i-+ -----з---(а,Л,с>0)
a +b +abc b +с +abc с +а +abc abc
77. а,Ь,с номанфий сонлар учун
a) a4 + b4 +с4 < 2(аЬ2 + а2с2 +Ь2с2) тенгсизликдан
a2 +b2 +с2 <2(ab+ac+bc) тенгсизликнинг келиб чи^ишини
исботланг;
б) иккинчи тенгсизликдан биринчи тенгсизлик келиб чи^а-
дими?
78. а, р ва у сонлари 0 < а < у, 0 < Р <у. 0</<у ва
tga tgp + tgy tgP + tga-tgy <1 шартларни ^аноатлантирса,
a + p + y<— булишини исботланг.
79. Ихтиёрий натурал сон учун ь^уйидаги тенгсизликнинг
тугрилигини исботланг:
|sin l| + |sin 2| +... + |sin(3« -1 )| + [sin Зл|
80. Саккизинчи синф у^увчиси Карим 1£атнашадиган мате-
матика тугарагига ^атнашувчиларнинг 93% дан купроги
ту^изинчи синф укувчиларидир. Бу тугарак аъзоларининг
мумкин булган >пг кам сони нечта булиши мумкин?
12
КI. \адлари мусбат сонлардан иборат ва махражи q га
।chi булган чексиз камаювчи геометрик прогрессиянинг иккин-
чп \адидан бошлаб \ар бир ^ади, узидан олдинги ^адларининг
ЙШ'индисидан катта экани маълум булса, q цандай ^ийматлар-
HII 1£|бул к;илиши мумкин?
К2. f(x) функция учун f(x)=(x2+5x-8)100 х5 (1)
формула билан берилган. Агар (1) формуланинг унг томонида
курсагилаган амалларни бажариб, сунгра ухшаш ^адларни их-
чамласак, f(x) функция ^уйидаги куринишдаги куп^ад доли-
та ке лад и:
f(x)=fl0x205+ «,х204+....+ я,04х+ а,05 (2)
бу ерда а0, а,,а2,.... ,а2т куп ^аднинг коэффициентлари.
а) куп ^аднинг барча коэффициентларининг йигиндиси:
S=fl|+a2+ ....+ а2О5 ни топинг;
б) куп ^аднинг то^ даражали х узгарувчилари олдидаги ко-
•ффицентларининг йигиндиси:
S=a0+ а2+а4+ «204 ни топинг;
с) Sm=«(+a3+o5+....+«,05 йигиндинитопинг (бу ерда а{, а,,
...., a№f ларжуфт даража курсаткичли узгарувчилар олдидаги
ко >ффициентлардир).
83. Сонлар у^ида анш^ланган ^ар ^андай функциянинг жуфт
на 1 о^ функцияларнинг йигиндиси куринишида ифодалаш мум-
киплигини исботланг.
84. Икки натурал сон урта арифметигининг уларнинг урта
геометригига нисбати натурал сон эканлиги маълум булса, бу
еопларнинг тенглигини исботланг.
85. л нинг ^андай натурал ^ийматларида —туб сон булади?
86. Бешинчи даражаси олти хонали сон булган ва 4 разами
билан тугалланган барча натурал сонларни топинг.
87. k't3 нинг к2+1 га булинадиган к нинг барча бутан
ципматларини топинг.
13
88. К^андайдир соннинг куби ~п*******~1 га тенг экани маъ-
лум. Шу сонни топинг.
89. 989 1001 1007+320 сонни туб купайтувчиларгаажратинг.
90. х1,х2,....,хп,.... кетма-кетликнинг^адларихп+|=хп3-Зхп2+Зхп
шартни ^аноатлантиради. Кетма-кетликнинг х100 ва х]000 ^адлари
тенг булиши учун х( ^андай булиши керак?
91. Агар а+4Ь=2 булса, аЪ купайтманинг энг катта ^ийма-
тини топинг.
92. li'«-42"w+3im+...+n,m йигиндининг-пнинг^ар^ан-
дай натурал ^ийматида ^ам п+2 га булинмаслигини исботланг.
93. Умумий ^ади а=1+22+33+....+пп га тенг булган кетма-
кетликда тоц мураккаб сонларнинг чексиз куп эканлигини ис-
ботланг.
94. а ва d лар номанфий сонлар ^амда b ва с лар мусбат
сонлар булиб, b+c>a+d шартни ^анотлантирса, ушбу
6 с
ифоданинг энг кичик ^иймати нимага тенг булиши
мумкин?
95. К^уйидаги шартларни ^анотлантирувчи а ва b сонлари
мавжудми?
а) а+Ъ рационал сон, а'+Ь" эса п>2 булган барча натурал
п ларда иррационал сон;
б) а+Ь иррационал сон, а"+Ьп эса, п>2 булган барча
натурал п ларда рационал сон.
96. 2"+4n (n°N) сонлар таркибида нечта соннинг квадрата
бор?
97. 2n+4k (n°N, k°N) сонлар таркибида нечта соннинг квадра-
та бор?
98. а, Ь, с, d натурал сонлар a+b=c+d=1000 тенгликни
а b
цаноатлантиради ~+~j йигиндининг энг катта ^ийматини
топинг.
99. К^айси бири катта: 7^ ми ёки 5^ ми?
14
100. ,ич^1992! > ,9,$1993! тенгсизлик тугрими?
101. Сонларнинг бутун ^исмини топинг:
б+7б+>/б+...+7б + V6+V6+V6+ +V6
102. Кайси катта: 1g211 ёки 1g 12 ?
103. Куйидаги функцияларнинг графикларини ясанг:
б) у~^(у!х + 2у/х-\-у1х-2у!х-\)
104. Йигиндини топинг:
а) 1 2+2 -3+3 -4+,.,+п {п+1)
в) 1 -2 -3+2 -3 -4+.. .+п <п+1) <п+2)
с) 1 -3 -5+2 -4 -6+3 -5 7+...+П ( п+2) fn+4)
105. Тенгламалар системасини ечинг:
Зх-у „
х + —----г = 3
х +-у
106. Стол устида шилли^ курт узгармас тезлик билан ^ара-
ка г цилмо^да. У ^ар 15 минутда 90 градусга бурилади ва бури-
лишлар ораси ту₽ри чизи^ буйича ^аракат ^илади. Унинг чиь;-
цан жойига цайтиб келиши учун бутун соатлар сарф булишини
исботланг.
107. (1-х)2 (1+2х+2х2+...+1994х|993)ифоданисоддалаштиринг.
108. \арбиттаси илдизга эга булган, исталган иккитасининг
йигипдиси илдизга эга булмайдиган учта квадрат уч^ад
мавжудми?
15
109. а, в, с мусбат сонлар учун —+-+->а+6+с
а b с
тенгсизлик уринли экани маълум булса, a+b+с > ЗаЬс
тенгсизликнинг уринли булишини исботланг.
ПО. Агар учбурчак бурчакларининг тангенслари нотугри
сонлардан иборат булса, уларнинг нимага тенг булишини
топинг.
111. у=х2+пх+Ь куринишдаги ва координата у^арини учта
^ар хил ну^таларда кесиб утувчи параболаларнинг мумкин
булган барча ^олларини ^араймиз. >^ар бир ана шундай пара-
бола учун бу учта Hyifra ортали утувчи айлана чизинг ва бу
айланаларнинг барчаси умумий ну^тага эга булишини исбот-
ланг.
112. Агар п<Ь<с эканлиги маълум булса,
1 I 1
----+----- +----= 0 тенглама а<х,<Ь<х,<с шартни^аноат-
х-ах-ох-с-------1 1
лантирувчи иккита х( ва х2 илдизларга эга булишини исбот-
ланг.
113. у=х2 парабола Оху текисликнинг ^айси нучугаларидан
тугри бурчак остида куринади?
114. а нинг исталган ^ийматида 10ax4-4ax3+a2x2+6x-2=0 тенг-
лама [0; I] кесмада камида битта илдизга эга булишини исбот-
ланг.
115. Тенгламани ечинг:
а) ^2+^У +(л/2-л/3)л=2
b) (72+V3y +(л/2->/ЗГ =2'
116. ху=48261724457 тенгламани бутун сонларда ечинг.
117. (х-у)2=х+у тенгламанинг |х| <100, ]_}'] <100 шартлар-
ни ^аноатлантирувчи бутун ечимларини топинг.
118. х, у ва а ^а^и^ий сонлари х+у=а-1 ва ху=о2-7а+14
шартларини ^аноатлантирса, а нинг ^андай цийматида х2+у2 йи-
ринди энг катта ^ийматга эга булади?
16
II') 1 chi ламалар системасини ечинг:
X3 = 1х + 2у
_у3 = 2х + 1у
I 20 Тенгламалар системасини ечинг:
х = у2 +ау + Ь
<
у = х2 +ах + Ь
121. Бир нечта сонлар берилган булиб, уларнинг йигиндиси
1 । а на кнадратлари йигиндиси 1 га тенг. Бу сонлар ичида йи-
I'liiiMiicH 1 дан кичик булмаган учта сон топилишини исботланг.
122. Шундай барча натурал сонларни топингки, уларнинг
(•Улувчилари сонининг квадрати натурал соннинг узига тенг
Булсин.
123. Тенгламани ечинг:
4 ।
sin X + cos х = —
2
124. а ва b ларнинг кандай цийматларида
у](ах + b)~ + i](ax - />)2 + yja2x2 — b2 = \[b
। chi лама ягона ечимга эта булади.
125. Тенгламани ечинг:
-Г+ 2xsinxy + I =0
п/ _ х + а
126. х = а + 2 cos- тенглама нечта илдизга зга?
2
127. К^уйидаги тенглама илдизларининг та1{рибий ^иймат-
ларини 0.1 гача аншулик билан топинг:
0,001х3+х2-1=0
128. Xs < 4х2+4 куп ^адни туртинчи даражали иккита куп^ад-
IIHIII купайтмаси куринишида тасвирланг.
17
129. хр х,, х3,... кетма-кетлик х,=1/2, xn,1=x2i+xii
1 1 1
(п=1,2,3,...) шарт билан берилган булса, Л
соннинг бутун КИСМИНИ топинг.
130. Агар хр х,, х3,...х1 лар йигиндиси 1 га тент булган
номанфийсонларбулса, х, х,+х, х3+...+хп, хп ифоданингэнг
катта г;ийматини топинг.
131. Агар х, у z лар мусбат сонлар булиб, xyz(x+y+z)=l
тенглик бажарилса, (x4 y)(y+z) ифоданинг энг кичик ^иймати-
ни топинг.
132. х>0, у>0, z>0 булиб, улар учун x2+y2+z2=l
тенглик бажарилса,
ху xz yz
4 4 йигиндининг энг кичик
1$ийматини топинг.
133. «ваЬ мусбат сонлар квадратларининг йигиндиси бир-
га тент булса, а1 °+Ь1 °< 1 тенгсизликнинг бажарилишини исбот-
ланг.
134. Агар «+Ь+с= 1 шарт бажарилса, а2+Ь2+с2> 1/3 тенгсиз-
ликнинг 5Ф>инли булишини исботланг.
135. 1х| + |jj + |z| < 1 тенгсизлик фазода ^андай фигурадан ибо-
рат булади?
136. а ва b лар узаро туб сонлар булсин, у ^олда п>Ь
шартни ^аноатлантирувчи и нинг барча натурал ^ийматларида
а"-1 ифода b га булинишини исботланг.
137. Тенгликни исботланг:
^20 +14-72 + V20-14V2 = 4
138. Ихтиёрий мусбат а2, ... , ап сонлари учун
я, a,+a. а,1-а.+а, и,+а,+...+а„ а, а, а. а„
тенгсизликнинг бажарилишини исботланг.
139. Тенгламани ечинг:
4 sin12 х + 4(sin6 х + l)cos6 х + 3sin' 2x = 4
140. 7з + сони илдиз була оладиган, бутун коэффициент-
ли куп^адни топинг (иккинчи даражали булиши шарт эмас).
18
Ill Исгалгап мусбат а ва b сонлари учун
'J-I • ‘'Xlab тснгсизликнинг тугрилигини исботланг.
II? Arap x, у, z>0 ва arctgx+arctgy+arctgz< яг шартла-
рн урин'in булса, xyz<x+y+z тенгсизликнинг бажарилишини
in bin наш.
I-В Исгалгап п натурал сон учун
2 г- ГТ Г- Г- 4л+3 г-
—п\!п < vl + у2 + ...+ -ул <-V»
3 6
iciii гнзликнингтугрилигини исботланг.
I I I. л ва у мусбат сонлар учун ху+ух=хх+уу тенглик
VpiiiiHii булганда х=у булишини исботланг.
, , •> , 2
|-|5 Агар a+b~+с~+d~-ab-bc-cd-d + — = O
пони । маълум булса, a. b, с. d сонларни топинг.
146. Йигиндини топинг: ПТГззТГ
147 Тенгликни исботланг: (п>2)
tgx tg2x + /g2x )g3x + ... + fg(/7- l).x-/gnx = - n
tgx
I4X. Агар а ва p иррационал сонлар булса, ар
рационал сон булишини исботланг.
149 п нинг цандай натурал ^ийматларида 321Г,‘~22"*‘-6"
н<|>одаиин1 киймати мураккаб сон була олади?
150. Ифодаларни соддалаштиринг:
a) log /g|" + Iog1/g21’ Iog;,/g88" +-Iogurg89"
b) logi( sin60L’ • log(, sin61e log,, sin 119° logn sin 120°
в) log, 3 - log. 4 - log,, г(и-1)- log,, , n
151. Исботланг:
л 2л 1
cos — + cos — = —
5 5 2
19
152. Исботланг:
sin 18° = —-—-
153. Тенгламани ечинг:
zgx-2[rgx]-3 = O
(квадрат ^авсдаги ифода соннинг бутун ^исмини билдиради).
154. 19 дан 80 гача булган иккихонали сонларни кегма-кегёзиш-
дан ^осил булган 19202122...787980 сони 1980 га булинадими?
155. Шахматчилар туриирида жами 55 партия уйналди. Му-
соба^адан икки уйинчи чтнуиб кетди. Ундан бири 10 партия, ик-
кинчиси эса бир партия уйнаган эди. Бу шахматчилар узаро уч-
рашганмиди?
156. Вуйидаги учта тасди^дан иккитаси тугри. битгаси нотуг-
ри эканлиги маълум булса, тасдшуаан m натурал сонни топинг.
а) ш+37 анш$ квадрат булса;
б) m сонининг охирги разами 5 булса:
в) т-52 сони аншу квадрат булса.
157. 7(ар бипаси иккиза турли хакикий илдизга зга булган,
аммо исталган иккитасининг йигиндиси ^а^и^ий илдизга эга
булмаган учта уч^ад мавжудми?
158. Геометрик прогрессиянинг биринчи, унинчи вауттизинчи
^адлари натурал сонлар булса, прогрессиянинг йигирманчи ^ади
^ам натурал сон буладими?
Э Э > •» 1 •>
_ х х z* A" z" у
159. Агар х, у z мусбат сонлар учун —
тенглик бажарилса, х, у, z сонлардан камида иккитасининг
тенглигини исботланг.
10000001 20000001
160. Ушбу сонлардан каиси капа: ---------ёки—- —
J 1 10000002 20000002
20
ГЕОМЕТРИК МАСАЛАЛАР
I ABCD тугри туртбурчакнинг АВ, ВС, CD, DA томонла-
рндл учларидан фар^ли ^илиб, К, L, М, N нуцталар олинган.
А / || A//V ва КМ _L NL экани маълум. КМ, LM кесмалар-
IIIIHI кесишиш ну^талари тугри туртбурчакнинг BD диагона-
1Н1ДП ёгишини исботланг.
? АВС учбурчакнинг АВ ва ВС томонларида мос равиш-
да М на N нуцталар AM:MB=BN:NC муносабат уринли
(•Уладиган ^илиб олинган. AN ва СМ тугри чизи^ларнинг
кесишиш нуцтаси Q булсин. MBNQ тугри туртбурчак юзи
А( 'Q учбурчакнинг юзига тенглигини исботланг.
Г А, В, С, D ну^талар ABCD цавари^ туртбурчакнинг кет-
мп-кет келган учлари булсин. Агар AB+BD<AC+CD шартурин-
ип булганда, АВ<АС булишини исботланг.
4. Уткир бурчакли учбурчакнинг турли учларидан медиана
биссектриса ва баландлик утказилди. Уларнинг кесишиш ну^-
111 лари тенг томонли учбурчакнинг учлари бу лиши мумкинми?
5. АВС мунтазам учбурчакка таищи чизилган айланадан
бпрорта М нуцта олинган. Агар учбурчакнинг томони а га тенг
<>Vncii, шу М ну^тадан учбурчак учларигача булган масофалар
ь ипдратларининг йигиндисини топинг.
6 D, Е ва F ну^талар АВС учбурчакнинг мос равишда
В( АС ва АВ томонларида ётади. AD, BE ва CF кесмалар
,, л ЕО FO R DO
О иуктада кесишади. Агар ~- = сгва — = Р булса, — ни
t-ti г С DA
IOIII1IU.
21
7. Трапеция асосларининг урталари, диагоналларининг кеси-
шиш нукаем, ён томонларининг давомини кесишиш ну^таси
бир тугри чизивда ётишини исботланг.
8. Мунтазам учбурчакнинг исталган ички ёки чегаравий
ну1$тасидан томонларигача булган масофаларнинг йигиндиси
шу учбурчак баландлигининг узунлигига тенг эканини исбот-
ланг.
9. АВС учбурчакка О марказли ички айлана чизилган. Т
ну^ада у ВС томонига уринади. Бунда ZBOT: Z.COT = 3:4- Агар
ички чизилган айлана радиуси 3 ва Z_A = 30° булса, ВС томон-
ни топинг.
10. ABCD квадратнинг ВС BaCD томонларида мос равиш-
да Е ва F нуьдалар ЕС=2ЕВ ва FC=FD тенгликлар бажарила-
диган ^илиб олинган. АЕВ бурчак AEF бурчакка тенглигини
исботланг.
11. Исталган учбурчак учун 1 = _L +—+— тенгликнинг
г Л, h, h,
бажарилишини исботланг. Бу ерда г - учбурчакка ички чи-
зилган айлана радиуси, ha, hb, h. лар учбурчакнинг баландликла-
ридир.
12. АВС тугри бурчакли учбурчакда ( /£ = 90° ) CD ба-
ландлик утказилган.
а) агар ACD ва BCD учбурчакларга ички чизилган айлана-
ларнинг радиуси мос равишда г( ва г, булса, АВС учбурчак-
ка ички чизилган айлананинг радиусини топинг;
б) агар ACD ва BCD учбурчакларнинг периметрлари мос
равишда Pt ва Р, булса, АВС учбурчакнинг периметрини топинг.
13. Берилган учбурчакнинг томонини кесувчи ва асосига
параллел ^илиб шундай турри чизиь; утказингки, бунда учбур-
чак ён томонларига утказилган тугри чизи^ билан асос оралиги-
даги кесмаларнинг узунликлари йигиндиси асос узунлигига тенг
булсин.
14.. К^авариг; туртбурчакнинг томонларини диаметр цилиб
чизилган доиралар туртбурчакни ^оплашини исботланг.
22
IS Гугри бурчакли учбурчаккаайлана ички чизилган. Гепотену-
uiitiiin шу айланага уриниш нуьрасидан ажратилган кесмаларининг
h Vi mil гмаси учбурчакнинг юзига тенг булишини исботланг.
I (> а) Цавари^ туртбурчакнинг диагоналлари уни туртга уч-
бурчнкка ажратади. Агар АОВ, ВОС, COD, AOD учбурчак-
impiiiiiu юзлари мос равишда Sp S2, S3, S4 булса, S, S2 =S3 S4
виииши исботланг;
(») ABCD трапецияда диагоналлар утказилган булиб, S =8,
SMI|, S„ чкани маълум булса, ABO (бу ерда О диагоналлар ке-
। IIIHI1III пу^гаси) учбурчакнинг юзини топинг.
17. Ихтиёрий учбурчакнинг a, fl, У бурчаклари учун
ушбу геигсизликнинг тугрилигини исботланг:
sin<z sin/? sin у ,1 I . ,1 1, . „ 1 1
4 ---+----) < ( h —)Sin« + (—+—)Sin/?+ (— + —)Sin у
а P у P у ay pa
IK Уткир бурчакли ABC учбурчакка тайней айлана чизил-
iiiii Айланага А ва С нуцталардан утказилган уринмалар В
иу|у111дан утказилган уринмани мос равишда М ва N нуцталар-
1(п кесади. АВС учбурчакда BP ( Р ну^та АС томонда ётади)
би инн дли к утказилган. ВР тугри чизи^нинг MPN бурчакниш
(ИНССК1 рисаси булишини исботланг.
19. Агар а, Ь, с лар учбурчак томонларининг узунликлари
оуниб, « I Ьгс=1 булса, a2+b2+c2+4abc<l/2 тенгсизликни ис-
Гн>| Ilnur.
.’О ABCD ^авариц учбурчакнинг АВ ва CD томонларида
moi равишда К ва М ну^талар олинган. AM ва КД кесмалар-
HIHII кссишиш ну^таси L, КС ва ВМ кесмаларнинг кесишиш
куцнки N булсин:
л) ai ар К ва М ну^талар АВ ва CD гомонларнинг урталари
ОУига, эканини исботланг;
3
6) агар AK:KB=CM:MD=m:n булса, <—-------
пг+nri '
ihiiiiiiiiii исботланг.
23
21. АВС уткир бурчакка тапщи чизилган айлананинг марка-
зи D булсин. А, В ва D ну^талар ортали утувчи айлана АС ва
ВС томонларни мос равишда М ва N ну^таларда кесади. ABD
ва MNC учбурчакларга танп^и чизилган айланаларнинг тенгли-
гини исботланг.
22. Трапеция асосларидаги бурчакларнинг йигиндиси 90°
га тенг. Асосларининг урталарини туташтирувчи кесманинг
узунлиги диагоналларнинг урталарини туташтирувчи кесманинг
узунлигига тенглигини исботланг.
23. АВС учбурчакнинг А, В, С бурчаклари мос равишда
а, Р, у га тенг. Мос бурчаклар царшисида ётган томонлар а,
Ь, с га тенг булса,
a) acosa + bcos, /3 < с эканини исботланг;
. а .В .у
б) sm—-sm—sm— купайтманинг энг катта цийматини то-
пинг. Учбурчак ^андай булганда бу ифода узининг энг катта
^ийматига эришади?
24. А, В, С ну^талар бир тугри чизш^да ётиб, В ну^та А
ва С ну^талар орасида жойлашган. Шундай М нукта олинган-
ки, бунда АМВ ва ВМС учбурчакларга таш^и чизилган айла-
налар тенг булса, М ну^танинг геометрик урнини топинг.
25. Агар АВС учбурчакнинг А учидан утказилган биссек-
трисаси AD булса, AD2=AB AC-BD • CD тенгликнинг бажари-
лишинии исботланг.
26. Агар ^авари^ туртбурчакнинг иккита ^арама-^арши то
монларининг урталарини туташтирувчи кесманинг узунлиги
долган икки томон узунликлари йигиндисининг ярмига тенг
булса, у >^олда бу туртбурчакнинг трапеция булишини исбот-
ланг.
27. а нинг исталган ^иймати учун томонлари
J+l, Vo2 + o + l, у^Л+З лардан иборат булган учбур
чакнинг мавжудлигини ва унинг юзи а га богли^ булмаслиги-
ни исботланг.
24
.’К Гомоплари а, Ь, с ва ar bt, ct булган иккита учбурчак
VIVII 7""i JW’, +4сс1 = yj(at +bt +ct)(a + b + c) тенглик бажарил-
< и, vimpiiHiu ухшаш булишини исботланг.
Айлапага ички чизилган учбурчакнинг бир учидан айла-
iiiii а V । ка пин ан уринма царю и томога перпендикуляр булса, у
V'l/in учбурчакнинг томонлари орасидаги богланишни топинг.
«О К^авари^ туртбурчакда иккита ^арама-^арши томон урта-
i и лип у I I ан турри чизик;, туртбурчакнинг диагонали билан тенг
Оурчнклар \осил ^илади. Диагоналларнинг тенглигини исбот-
ИП111
« 1. ABCD квадратнинг АВ ва AD томонларида мос равиш-
да К на N нукталар АК AN=2BK DN шартни ^аноатлантира-
Д11111Н цнлиб олинган. СК ва CN кесмалар BD диагонални Lea
М пу^галарда кесиб утади, К, L, М, N ва А ну^таларнинг
Опии айланада ётишини исботланг.
«.’.АВС учбурчакда ВР ва СТ биссект рисалар О нук;тада
мтишади. Агар А, Р, О ва Т ну^таларнинг битта айланада ётиши
мн 1.лум булса. А бурчакнинг катталигини топинг.
«V Фазода учта мунтазам ABCDE, ALNMB ваАЕКРЕ беш-
Пурчаклар жойлашган. AC. .AN ва АК тугри чизикларниш узаро
нсрисндикулярликларини исботланг.
«4. Гетраэдрнинг асоси тенг томонли учбурчак,ён ёгртари-
IIHIII юзлари узаро тенг. Агар асосининг томони а. ён тдтрра-
нпрдаи бирининг узунлиги h га тенг булса. долган иккита ён
Кирраларининг узунлигини топинг.
«5. АВС учбурчакнинг ВС томонида шундай D нуктани
। inulin ки, бунда ABD ва ACD учбурчакларга ички чизилган
iillniiiianap бир-бирига уринсин.
«<• A BCD параллелограммнинг АВ ва CD томонларида Р
ни <2 нукталар олинган булиб. бунда AP=CQ N эса AD томон-
HIIIII исталган нуктаси булсин. PQ. BN ва CN турри чизи^лар
пириллслограммни учта учбурчакга ва учта туртбурчакга ажра-
। или 1>ир учбурчак юзининг долган иккита учбурчак юзларининг
11|||'||||дисига ва биртуртбурчак юзининг долган иккита туртбур-
чпкпар юзларининг йигиндисига тенг эканлигини исботланг.
25
37. Трапециянинг диагоналлари уни туртта учбурчакка аж-
ратади, S трапециянинг юзи, S! ва S, лар трапеция асосларига
ёпишган учбурчакларнинг юзлари булса, -Js = + ^5?
булишини исботланг.
38. Доирага ички чизилган бешбурчакда биртомонига ёпиш-
маган исталган иккита бурчагининг йигиндиси 180е дан катта
булишини исботланг.
39. Асоси тугри бурчакли учбурчак ва учидаги текис бур-
чаклари тугри булган учбурчакли пирамида мавжудми?
40. ABCD параллелограмм томонларига параллел икки жуфт
тугри чизшргар билан туг^изта параллелограммга ажратилган.
Агар S берилган параллели раммнинг юзи ва Q марказий фи-
гура (штрихланган A‘B‘C‘D‘ ) нингюзи булса, MMKL туртбур-
чакнинг юзини топинг (шаклга ь^араиг).
1- L 1 L _L
41. Исталган тетраэдр учун ушбу + + + тенг-
ликнинг бажарилишини исботланг.
42. Кубнинг иккита ^ушни ён ё^лари кесишмайдиган диа-
гоналлари орасидаги масофа Р га тенг. Кубнинг ^ажмини то-
пинг.
43. М нугута ABCD тугри туртбурчак ичида жойлашган
булиб, S унинг юзи булсин. Ушбу S<AM • СМ+ВМ -DM тенг-
сизликни исботланг.
44 Айлана ичида иккита айлана берилган булиб, улар таш-
№ айланага А ва В нуг^таларда уринади ва узаро кесишади.
Агар айланаларнинг кесишиш ну^аларидан бирортаси АВ кес-
26
мп.та i'ica, у ,\олда кичик айланалар радиусларининг йигиндиси
iuii i.i айлана радиусигатенгбулишини исботланг. Тескариси >^ам
VpiinniiMii?
IЛВС тугри бурчакли учбурчакнингуткир бурчаклари-
uiii он и аси 30° га тенг. М ну^та АВ гипотенузанинг уртаси, О
.... чнтилган айлананинг маркази булса, ОМС бурчакнимага
inn *
•1(>. .1/? диаметрли айлана берилган. Маркази А ну^тада
(•yniaii иккинчи айлана АВ кесмани С нуцтада келиб утади,
буи ча А('< - АВ. Иккита айлананинг умумий уринмаси биринчи
пйпанага D ну^тада уринади. CD тугри чизи^нинг АВ га
। м-pi к- ид и кулярлигини исботланг.
I/. АВС учбурчакда AD ва DE медианалар М ну^тада
мч Н111ади. Агар АМВ бурчак:
л) । угри бурчак булса;
б) уткир бурчак булса,
АС । ВС > ЗАВ тенгсизликнинг бажарилишини исботланг.
48. АВС учбурчакда АК биссектриса, BN медиана ва СМ
бппандлик утказилган. KNM учбурчак эса тенг томонли. АВС
учбурчакнинг тенг томонли эканини исботланг.
49. Айланага АВС тугри бурчакли учбурчак ички чизилган.
-I// гипотенуза. К ну^та ВС ёйнинг уртаси булсин ва А ну^та
Н(' 1‘йда ётмасин. N ну^та АС кесманинг уртаси ва М ну^та зса
KN нурнинг айлана билан кесишган нуграси булсин. А ва С
пущалар ортали айланага утказилган уринмалар Е ну града
M’ciiiHca, Z ЕМК = 90° булишини исботланг.
SO. АВС тугри бурчакли учбурчакнинг АВ гипотенузасида
М па N ну^талар олиниб, АС=АМ ва BC=BN шартлари бажа-
punia. /MCN =45° булишини исботланг.
s I ABCD ^авари^ купбурчакда Е ва F ну^талар мос рави-
...да ВС ва CD томонларнинг урталарди. АЕ, AF, BF кесмалар
19рн»урчакни шундай туртта учбурчакка ажратадики, бу учбур-
чпк паркинг излари кетма-кет келган натурал сонларга тенг була-
ап ABD учбурчакнинг юзи ^андай энг катта цийматни ^абул
цппиши мумкин?
27
ЖАВОБ ВА КУРСАТМАЛАР
1. Фараз ^иламиз: х,; х2; х3; х4; х5 лар талаб ^илинган
сонлар булиб, ани^лик учун х, < х,< х3< х4< х5 булсин. У ^олда
x2-xt; х3-х,; .... х5-х4; куринишдаги 10 та айирма ^осил булиб.
уларнинг йигиндиси:
4х5+2х4-2х,-4х1
ифодага тенг булади.
4х 5+2х4-2х,-4х , <4(х 5+х4+х3+х ,+х t )=4
Агар х5=1 ва х4=х3=х2=х1= 0 булса, натижа 4 га тенг булади.
2. Е^опларнинг массаларини мос равишда х(; х,; х3; х4; х5 деб
белгилаб олайлик. Масаланинг шартига кура, ушбу системани
тузамиз:
Х]+х,= 12; х,+х3=13,5; х3+х4=11,5; х4+х5=8;
x^Xj+x^ie
Тенгламаларни ^адлаб 1$ушиб, ушбу тенгламани ^осил 1$ила-
миз:
гх^х^+зхз+гх/^х^б 1
„ 61-(12 + 8) „
Ьундан х, =--------= / ни ^осил ^иламиз. Энди долган
номаълумларни топиш осон.
Жавоб: Х[=5,5; х2=6,5; х3=7; х4=4,5; х}=3,5
3. х,; х,; х3 - берилган сонлар булиб, х, < х2 <х3 булсин
дейлик. У ^олда х,+ х,< 2х3 бундан ёки Х]+ х,= х3, ёки х+
х2=2х3. Охирги ифода фа^ат х( = х2=х3 булгандагина уринли-
дир, у ^олда уларни узаро тублигидан Xj = х2= х3 =1. Энди х(+
х2= х3 булсин. Бу э^олда Х]+ х3=2х,+х, ифода х, га булиниши
керак, демак, 2х булиниши керак, х, га аммо 2х1<2х,, бундан
ёки xt=x,, ёки 2х1=х, экани келиб чи^ади. Биринчи ^олда х,=
2х, ва уларнинг узаро тублигидан { х(; х,; х}}={1; 1; 3}
28
Иккинчи ^олда х3=Зх| ва { х(; х2; х3}={1; 2; 3}
Жавоб: {1; 1; 1}; {1; 1; 3}; {1; 2: 3}
•I Курсатма: 1001=7 11 13 Шунингучун 1001 нинг барча
нуиупчилари 1, 7, 11, 13, 77,91,143, 1001 сонларидан иборат-
пир
Жавоб: 76
SФараз циламиз: а,, а,, я,,... берилган арифметик про-
। рсч сня булиб, ап ^ади 3 разами билан тугасин. ^ад эса 7
рпцами билан тугасин дейлик. Агар m>n булиб, дейлик
и и । к, к>0 булса, ап+2к зуад эса 1 разами билан тугайди.
</ , 1( ,\ад эса 5 разами билан тугайди.Бу эса шартга зиддир.
Ai пр п1<п булиб, п<т+е, е>0 булса, у ^олда от12с >^ад 9
<|||>111и гугайди, Апи3г ^ад 5 разами билан тугайди. Бу >^ам
пшрп а шддир. Демак, бу арифметик прогрессияда 7 разами
(iiuiaii тугаган хад йу^ экан.
<>. Виз 10m2+l=k2 шартни ^аноатлантирувчи (т, к) натурал
сонлар жуфтлигининг чексиз куп эканини курсатишимиз керак.
Ьирннчи ана шундай жуфтликка m=6, k= 19 сонларкиради (Тан-
ино гопдик хаци^атан зуам, 62=36, 192=361). Бундан ташцари.
шар 10nr+l=k2 булса, у ^олда:
I <X2mk)2+1 ;40(mk)2+ l=40m2( 1 OmT 1 )Н =400m4 >40in2+1Т 20m Т1):
Шунинг учун ки^оридаги шартни цаноатлантирувчи (гл, к)
ж уф глик ёрдамида (2тк, 2т+1) жуфтликни ^ам хгосил ^или-
1Ш1МИЗ мумкин. Бу эса галаб ^илинган жуфтликдан чексиз куп
1КИПЛИГИНИ курсатади.
7. Курсатма: Карим 1900+10х+у йилда гугилган булсин. У
\1»ица масаланинг шартига кура, у XX асрда тутилгани учун:
59-(10х+у)=1 i-9+х+у
59-10х-у=10+х+у
11х+2у=49
u ni ламани ечиш керак
Жаноб: 1938
К. XT a. zt ~ b, UV дейлик.
V уолда a = Jzt+ . <,2=1006 + с, Ib^a-^c булади Бунда
,1 S0</ 4- 51с булгани учун а (о-50) сони мусбат ва 51 га були-
29
нади, булинмада эса икки хонали сон ^осил булади. Демак., а
сони 68 ёки 84. с нинг унга мос ^ийматлари 24 ва 56, бундан b
нинг ^иймати 46 ва 70 булиши мумкинлиги келиб чикади.
Жавоб: (68;46;24) (84;70;56)
9. Маълумки, х.ар т^андай жуфт соннинг квадрати 4 га були-
нади ва тоц соннинг квадратини 4 га булганда 1 ^олдиц ^олади.
Шунинг учун, агар х2+у2= 16000 булса, у^олда х=2т, у=2п
булиши керак.
Фикримизга кура:
(2т)2+(2п)2= 16000
т2+п?-4000
^осил булади ва худди ю^оридагидай m 2mf, n=2n( десак
т^+п 2=1000 булади. Бу жараённи яна бир марта
т1=2т,, п)=2п, деб давом вршсак. т?+п,2=250=4 -62+2 келиб
читали. Демак, т2 ^ам, п, хам ток; сон экан. Агар т,>п, деб
олсак, 125>т22<250 булиши керак Аммо бу орачи^да го, нинг
фа^ат иккита ^иймати бор, яъни m,=13 ва т,15 булиши мум-
кин. Бундан эса ор^ага цайтиб х-104, у=72 вах -120, у=40
булиши мумкинлигини курамиз.
Жавоб: 104=4 72М20:-<-402=1600
10. Агар суралган сон аЬсаЬс куринишга эга булса, у 1001
га булинади, демак у 91 га ^ам булинади. Шунинг учун ^осил
булган соннинг 91 га булиниши учун уч хонали сон 91 га були-
ниши керак. 91 га булинадиган уч хонали сонлар орасида фа-
f^ar 273 гина масала шартини ^аноатлантиради. Бундан излан-
ган сон экани келиб чикади.
1992 мирта
11. Тенгламанинг иккала томонига 2 ни купайтириб ва 1 ни
^ушиб, ушбуни хосил ^иламиз:
4ху+ 2х+2у+1=167
2х(2у+1)+(2у+1)=167
(2х+1)(2уН>=167
Бу генгламанинг куйидагича туртта ечими мавжуд:
(О;УЗ), (83;0), (-1 ;-84), (-84;-!)
30
12. Arap x жуфт сон булса z то^ сон ва аксинча х тоц сон
булса z жуфт сон булади. x<z экани аншу х=2 булсин, агар у
1оц сон булса, 2у+1 сони 3 га булинади (узингиз исботлашга
царакат дилинг) ва у=3 да23+1~9>3, аммо z туб сон булиши
керак, демак, у-жуфт сон экан, яъни у=2, у ^олда z=5 булади.
Жавоб: (2;2;5)
13. 6(х+7у)=(6х+11у)+31у
11 Зартга кура, ифода 31 га булинади. Йигинди 31 га булин-
1П11И учун 6(х+7у) хам 31 га булинади.
14. х, ва х2 берилган тенгламанинг илдизи булсин.
Виет теоремасига кура системани ^осил ^иламиз:
х, + х2 = -а
х, • х, = 1 - b
бундан ушбу:
I (х, + х2)2 = сг
1(1- X, -х2)2 =Z>2
Системадаги тенгламаларни г^ушиб, ^уйидагини ^осил сила-
ми»:
ч I b2 = (xt + х2)2 +(1 -xt -х,)2 = х, + 2х,х, + х2 +1 - 2xtx, + (х,х, )2 =
V,’’ + х; +1 + х2х2 = (х2 +1) + х2 (х2 +1) = (х2 +1 )(х; +1).
л ~ +1 ва х| +1 йигиндилар бирдан катта сонлардир.
15. х5+у5=2х2у2 тенгликнинг иккала томонини квадратга
кутарамиз, тенгликнинг иккала томонига - 4х5у5 ни фтпамиз:
х"’г2х5у5+у|0=4х4у4
х'°-2х5у5+у|0=4хУ-4х5у5
( X у5)2=4 х4 у*( 1 -ху) (ху 0)
1-ху = (
2х'у2
Шу ни исботлаш талаб ^илинган эди.
16. х mn, y=nk, z=mk булсин, бу ерда т, п, к лар натурал
«онпар. х, у, z ларнинг ^ийматларини берилган тенгламага
31
Хуйиб n(k-tn)=mk-l тенгламани хосил киламиз. к-т=1 деб,
тенгламани хуйидаги куринишдаги чексиз куп илдизларини то-
памиз:
x=m(m2+m-1); у= (m+1)(т ?+т-1); z= т(т+1)
17. Курсатма: Берилган системадан хуйидагини косил хиламиз
(xz-2yt)2+2(xt+yz)2=(x2+2y2)(z2+2t2)=ll
Бундан, ёки
х2+2у2=1, (х2=1; у=0)
ёки
z?+2t2=l
Жавоб: (1;0;3;1), (-1;0;-3;1), (-1;0-3;-1), (3;1;1;0)
18. Берилгантенгликдан (+ + (.v + _y)'r = lO.vv + s.
ёки ((х + у)2 - l)z = 1 Оху.
Агар ху учга булинмаса, у холда х+у хам учга булинмай-
ди. Демак. (х+у)2 ни учга булганда 1 холдих холади. Аммо бу
Холда тенгликнинг чаи гомони эса учга булинади. Демак, бич
зиддйятга учрадик. ху хам, х+у хам » z хам учга булинар
экан. Агар х+у ифода 12, 15, 18 хийматларни хабул хилса.
10 ху сони мос равишда 143 га, 224 га, 323 га булинади, у холда
ху хам 143 га, 224 га, 323 га булиниши керак. Бу холнинг эса
булиши мумкин эмас. Чунки, ху икки хонали сон. х+у=3 булса,
8z=10 ху тенглик хосил булади. Бу холнинг хам булиши мум-
кин эмас, чунки, z бирлар хонасидаги рахам булиб, ху эса
икки хонали сондир. х+у=6 булса, 7z=2 ху =20х+2у= 18х+12
булиб, бу ерда z нинг 6 га булиниши куриниб турибди, яъни
z=6, 30=18х бу холнинг хам булиши мумкин эмас. х+у=9 булса.
8х= ху =9х+9. Бундан z=9, х=7 ва у=2 булади. Шундай хилиб,
масала шартини каноатлантирувчи рахамларнинг ягона учли-
ги х=7, у=2, z=9 лардан иборат.
Жавоб: х=7, у=2, z=9
19. Берилган тенглама ушбу z2(x+y)=10 ху +z ёки
z2(x+y)-10 ху=г тенгламага тенг кучлидир. Агар z учгабулин-
мша, /’ ни учга булганда 1 г^олдгщ цолади. Ушолда тенгликнинг
•uni гомони ( х+у ва Юху ларни учга булганда бир хил
цондшуиар долгами учун) учга булинади. Бу ^арама-^аршилик-
tuii / пинг учга булинишидан ху ва х+у ларни ^ам учга були-
1ППНН келиб чи^ади. Демак, xyz ~ z2(x + y) сон 27 га були-
1Н1ДП. Бунда булинманинг мумкин булган ^ийматлари 17, 18,
1’>. 27, 28, 29 булиши мумкин. Чунки фак,ат мана шу доллар-
пи ина кунайтманинг охирги раками 3 га булинади. Бу сонлар-
IIH 1скшириб куриб, фа^ат ^уйидаги х=7, у=2, z=9 сонларни-
। IHUI масала шартини каноатлантиришини курамиз.
Жавоб: х=7, у=2, z=9
20. х*’+2 х4+2 х’+ х2+2х-1=( х’<-х+1)2~2
Бу ерда берилган куп^адда х’+х+1-О булганда унинг
1\пйма । и >нг кичик (-2) булиши куриниб турибди.
21 1 анлаш усули билан тенгламанинг битта ечимини топамиз:
х 10. у=3, z~l, t=2
( унгра л, у, z, / ларнинг топилган кийматларини мос ра-
шнпда и10', п7°, п43 ва nK‘(n°N) ларга купайтирамиз. ''шоу
< онларгуртлиги:
{ 10 п,п\ З п’°. п42 , 2-п’° } n°N
нс гайтан п да жавоб булади
,, I/Г 4-р2 4-9 = 0
22 /> на с) илдиз булгани учун { системани
|92 + Р9-гд=0
\ih ini цила.миз. Системани ечиб, жавобни оламиз.
. у; v4-t2vz3 x'-S г I /т х/З —I
.4 V? I V’- 7=- ва у2-v3 =--~-
V2 22 /2
Бупарни берилган ифодага куйиб, маълум шакл алмашти-
1«1пнп.|рда11 кейин натижага эриша.миз.
Жавоб: х/З
1 1 1
2-1 Масала шартига кура ~ ~ г ~ дан ху * yzJ xz--0
Moinii ксчиб читали.
33
x+y+z=l дан x2+y2+z2+2(xy+yz+xz)=l булади.
Демак, x2+y2+z2=l экан.
25. а берилган тенгламани бутун илдизи булсин дейлик. У
солдат/4 pn3+q=O дан q-~a3(p-a). q туб сонбулганиучун л3=1,
яъни а=1, демак, q-p-1. р ва q нинг туб сонлар эканини
эътиборга олсак, р=3 ва q=2 экани келиб чикади.
Жавоб: р=3, q=2
26. Агар х,= х,-...= х|00булса, системадаги тенгламалар
х)2+х|-1=0куринишигакелади. Бутенгламаниечиб, =
ни ^осил циламиз. Энди системанинг бош^а ечимлари йу^лиги-
ни курсатамиз. Тенгламаларни ь^йлаги куринишда ёзиб оламиз:
i I 1
V( _---. _............. Х(, _ —. —.
I+.V, I TV 1+Xj
xr x„... xw ^адларнинг^ийматлариниохиргитен!ла.магакуйиб:
1+JT,
узлуксиз касрни ^осил циламиз. Тенгликнинг унг томонида
С1Х- + Ь
шакл узгартиришлар ^илиб, уни -vi - куринишга кел-
тириб оламиз.
Бу эса квадрат тенгламага тенг кучлидир. Демак, х, учун
иккитадан куп ^иймат мавжуд булиши мумкин эмас. Биз бун-
дай иккита ^ийматни биламиз:
-1+J5
2
Демак, х, улардан биттасига тенг. Бундан фойдаланиб, х|М,
х99, ...х, ларнитопамиз,натижадах| = х,= ... =хэд=х|00 келиб
чикади
34
Жавоб: х, = х, =.... = х,„ = х|0„ = —-—
27. Курсатма х=1 тенгликни цаноатлантиргани учун х3-
9x’i27x-l9 куп^адни купайтувчиларга ажратинг:
х' 9х2+27х-19 = (х-1)( х2-8х+19)
Жавоб: х=1
28. Курсатма. Ифодани хуйидаги куринишга келтиринг:
1(2х-у + 1)2+|(Зу + 1)2-1
2
пфоданинг энг кичик ^иймати (-1) булиб, у бунга х = -— ва
1
>• - булганда эришади.
Жавоб: -1
29. Курсатма. Биринчи тенгламани ( х - у ) га, икинчисини
( / х ) га, учинчисини ( у - z ) га купайтириб 1(ушамиз. Ушбу
1С1П лама:
7(х-у)+21 (z-x)+28(y-z)=0
\осил булади. Бундан z=3y-2x ни иккинчи ва учинчи тенгла-
маларга 1(уйиб, у=0 ёки у=2х ни ^осил ^иламиз.
Жавоб: (ТУ; 0; -277). (-Т7;0; 277), (1; 2 4), (-1;-2;-4)
30. Жавоб: 1989
32. N=13o1+73b|=13o2+73b,=13o}+73bJ ва а< сц <а}
оулсин. У ?(олда 13(o,-o1)=73(b,-bl) булиб o,-o, сон 73 га
булинади.
13(a,-o|)=73(b3-b|) дан эса a}-af нинг 73 га булиниши
кслиб чи^ади. Демак, д3>«,+73>(а|+73)+73>1+73+73=147
бУлганидан:
N=13«3+73b >13 -147+73=1984
1»у идаи 1984 ни талаб ^илинганидай, учта турли куринишда тас-
IIUрлаin мумкин, деган хулоса келиб читали. Бу ерда:
о=1, а,=74, о=147,
Ь,=27, Ь2=14, Ь=1,
35
33. Масаланинг шартига кура, = рх2 + д,х[ = -рхл -q
jxj + 2рх2 +2q = 3.v{
Шунинг учун 1Af + 2pAi+2<7 = _^
Бундан куринадики, х, ва х, лардан биттаси (ёки иккаласи
^ам) тенгламанинг илдизи булади. Ёки тенгламанинг чан го-
мони х, ва х, цийматларни ^абул ^илганда турли ишораларга
эга булади. У ^олда булар орасида x2+2px+2q=0 тенгламанинг
илдизи ётади.
34. (n2+n)2=n4+2n3+n2< n4+2n’+2n2+2n+l< n4+2n’+3n2+2n+1=
= (n2+n+l)2
35. n3+3=(n3+27)-24=(n+3)(n2-3n+9)-24.
Демак, n+3 сони 24 нинг булувчиси булиши керак. У холда
п ушбу 1, 3, 5, 9, 21 кийматларни кабул килиши мумкин.
Жавоб: {1,3,5,9,21}
36. Системадаги барча тенгламаларни ^ушиб,
х2у+ у2х+ y2z+ z2y+ z2x+ x2z=48
тенгламани ^осил ^ламиз. Уларни купайтириб, фавела рн и очиб,
юцоридаги ^осил булган тенгламани ^исобга олган ^олда ушбу:
(xyz)2( 48+2xyz)=2160
тенгламани ^осил ^иламиз. Агар xyz=t деб олсак, 2t’+48t2-
2160=Q, t’+24t2-1080=0 кубиктенглама^осилбулади.Бу тен-
глама1, =6ва1,= - 15±3л/з илдизларга эга. Куринибтурибдики,
масаланинг шартини фа^ат биринчи илдиз ^аноатлантиради.
_6 _ 6 _6
Демак, xyz=6 дан xz ~ у' булганда,
ушбу:
X + у = Z
у+ z = 2x
x + z = 5у
тенгламалар системасини >$осил ^иламиз.
Буни ечиб жавоб х=2, у=1, z=3 эканини топамиз.
37. а+Ь+с = - + - тенгликнингунгтомонини abc га купаи-
тирамиз, сунгра тенгликнинг иккала томонига 1 ни ^ушамиз.
36
ч । b । с-лЬ+лс+Ьс
< /bc । a+b+c=«b+«c+bc+1
< /bc-<zb-flc-bc+«+b+c-1 =0
< /b(c-1 )-«(c-1 )-b(c-1 )+(c-1)=0
(c-1 )(ab-«-b+l)=0
(t-l)[«(b-l)-(b-l)]=0
(c-1 )(«-l)(b-l)=0
Дсмак, a, b, с лардан камида биттаси 1 га тенг экан.
а) 2300=(23)|00 -8100 33°o=(32)ioo=9i0o
Бундан 9100 >8|0°, демак, 3200>2300
6) 29|=(213)7
5,s-(55)7
2' -52 ёки 2'°>54, демак, 2|3=23-2|0>5-54=55
<9. Курсатма:
х + 2 2 х-2 , 5 ,х-2 х + 2
---г) +(--г) --•(---г) (--г)
+1 х-1 2 х-1 х +1
х + 2 х-2
----= и, -------= V
х + 1 х-1
дес» счиш керак.
Жавоб:
±3±У7
2
40.
I + х + ху I + у + yz \ + z + zx
Z XZ 1
——.......—• Ч------------1--------
z(\+x + xy) xz(\+y + yz) \ + z + zx
z + zx + xyz xz + xyz + z xyz \ +z + zx
1 + z + zx J
I + Z + ZX
37
41. 1989=п булсин. У ^олда:
1989 1990 -1991 -1992+1 =n(n+1 )(n+2)(n+3)+1 =(n2+3n)( n2+3n+2)+ i
n2+3n-»-l=m деб белгилаб олсак:
(n2+3n)(n2+3n+2)+1 =(m-1 )(m+1)+1 =m2-1+1 ~m2
(к +2)3 -к3 -8
42. к(к+2) =-----—-------- тенгликдан фойдаланиб, йи-
6
гиндини фшидаги куринишда ёзиб оламиз:
I-3 + 3-5 + 5-7 + ...+999-1001 =
З3—I3—8 53 -33 -8 73-53-8 10013-9993-8
--------+----------+----------+... +------------
6 6 6 6
I0013
-1-500-8
----------= 167166э00.
6
43. (х+у)4 >(2,6)2,
х2 +2ху + у~ > 6,76
дан х2+у2<4 ни айирсак, 2ху>2,76; ху>1,38 бундан ху>1 эканк
келиб чи^ади. Шуни исботлаш суралганди.
44. /4-/ + ^ = (/2-|)2+(/-|)2>0.
45. (Ь-с)2>0 дан а2+(Ь-с)2>«2. а2>а~ -(b-с)2 тенгсизлик-
ни ^осил ^иламиз.
Худди шундай, b2>b2 -(а-с)2 ва с2>с2 -(д-b)2 тенгсизлик-
ларни ^ам келтириб чи^ариш мумкин. Учала тенгсизликни купай-
тириб, зарур амалларни бажариб:
(obc)2>(rz+b-c)2(o+c-b)2(b+c-fl)2,
(obc)>(fl+b-c) (fl+c-b) (b+c-o)
тенгсизликни келтириб чи^арамиз. Исботи тугади.
46. Тенгламани ь^уйидаги куринишда ёзиб оламиз:
Зх3+Зх2+Зх+1=О
(х+1 )3+2х3=0 тенгламадан
х +1 = -х V2,
1
1 + V2 ткани келиб чикади.
38
47. Агар р=2 булса, 22+-22=8 мураккаб сон ^осил булади.
A nip р 3 булса, 17 ^осил булади. Энди р>3 дейлик, у ^олда
р Ik । I булса (бу ерда к ^андайдир натурал сон):
। р’ = (3-1 )’UI + (ЗА±1)2 = (ЗЛ/ -1) + (ЗА' + 1) = 3(Л/ +.V)
\осил булади. Демак, масаланинг шаргини ^аноатлантирувчи
/I ниш ягона гутймати 3 ткан.
48. а) х=1, у=8
6) Мумкин эмас. Фараз гутламиз: ху+х ва ху +у лар
iypjin натурал сонларнинг квадратлари булиб. бунда у>х
Пенсии. У ^олда:
х’- хуЪг<ху+у
(ху । у )-(ху+х)-у-х>(х+1 )2-х2=2х+1
бу ерда у>Зх+1
III 11
49 ------= _ тенгламадан ’ > , яъни х<п булиши
л г и х п
хсппб чикади. Шунинг учун агар n 1 булса, тенглама натурал
гониарда ечимга эга була олмайди. n I дейлик. у холда х п
I । । и( п — к)
к. О- к-n ва - = - . бундан ----------------- Демак,
/7-1 п г J
uu । Урал сонлар гупламида тенгламанинг битта ечими доимо мав-
жуц. бу к I булганда х- п-I. г =- п(п-1) куринишда булади.
>п ди н губ сон ва к>1 булсин. деб фараз килайлик. У холда п
на к лар узаро туб. шунингдек, к ва п к хам узаро туб сон
ГЦ пади. Ьундай булса, п(л- к) ва к \ам узаро туб сон булади.
Шунинг учун. агар п туб сон ва к>1 булса, у=л-'
к
бунлцн. Демак, п губ сон булса. к- I булиши зарур экан ва тенг-
Ш1МП янша ечимга эга булади. Агар п мураккаб сон булса,
и п, и. булиб. k n. дейлик, у ^олда х-n I. у n(n-l) ечим-
>нн| коника яна битта х=п п . у=п (п-п ) ечим борлиги келиб чи-
цндн I>у эса масала шаргини туда тасди^лайди.
39
5О .Су^бат 1989 йил 1 январда булиб утган. Шерзод 14 ёшга
1988 йил 30 декабрда тулган. Шунинг учун хам 1990 йил 3!
декабрда ун еттига ^араб кетади.
51 (1 - х)(1 + х + х2 +К + х1953) =
= (1-х)(1 + х) + х2(1-х) + х3 •
•(1 - х) +К + х,993(1 ~ х) = 1 - х1994
52. Масалани ечишда 8019 ни купайтувчиларга ажратиб.
муло^аза юритган маъ^ул. Бунда, агар уйинчи нишонга урганда
унинг пулини 1,1 га купайтириш ва нишонга теккизолмаса, 0,9
га купайтиришни эътиборга олиш зарур:
8019=93 11, яъни 8019=100 1,1 0,93.
Бундан, агар у бир марта нишонга уриб, уч марта нишонга
уролмаса, шу ^ол юз бериши мумкин эканлиги келиб чгщади,
53. А икки хонали сон учун А:...992 = 9801<9999 тенгсизлик
уринли. Шунинг учун А2 нинг ракамлари йигиндиси 9 4=36
дан кичик. У ^олда А нинг рацамлари йигиндиси эса </36 = 6
дан кичик булиши ани^, яъни, ёки 5 га тенг, ёки 5 дан кичик.
Демак, 10, 11, 12, 13, 14, 20, 21, 22, 23. 30. 31, 32, 40, 41, 50 дан
иборат 15 та х^олни ^араш талаб ^илинади. Булардан 9 гаси - 10.
И, 12, 13, 20, 21, 22, 30, 31 ларгина масала шартини
^аноатлантиришини текшириб куриш мумкин.
54. Берилган тенгсизликни исботлаш учун
а + Ъ>с ва а2 - ab + Ь2 > 0 лардан фойдаланамиз:
а3 + Ь3 + abc = (a + b)(a2 -ab + b2) + ЗаЬс>
>с(а2 -ab + Ь2 )+ЪаЬс - а2с - abc + Ь2с + ЪаЬс -
- с(а2 + 2аЬ + Ь2) = с(а + Ь)2 >с • с2 ==с ’.
55. хва у ларнинг ишораларини ихтиёрий танлаш мумкин.
шунинг учун номанфий ечимларни ^идирамиз. Тенгламаниш
берилишидан маълумки, х то^сон, х=2/+1. Бундан фойдаланиб.
тенгламани (^уйидаги куринишда ёзамиз:
х4 -1 = 2у2. х4 -1 = (х2 - 1)(х2 +1) = (х- I)(x + 1)(х2 +1) =
40
- 2/ • (2/ + 2)(Ф2 + 4/ + 2) = 2у2, куринибтурибдики, у-жуфт
сон экан, яъни у =24.
У ^олда /(/+l)(2f(f+l)+l)=tr
сонлари жуфт-жуфт узаро туб сонлардир, уларнинг
кУнайтмаси эса туда квадратдир. Бундан келиб чи^адики,
уларнинг ^ар бири тула квадратдан иборат экан. Бу ^ол фа^ат
I 0 булганда мумкин. У ^олда и= 0 булиб, х- ± 1, у = 0 булади.
56. Жавоб: 5,6,7,8, -1
Бонща мисол ^ам топиш мумкин. Биринчи туртта ра^ам 2
лпрдан иборат булсин. Бешинчи сонни х деб тенглама тузамиз.
1
16 v л -1 Бундан л' = -—
57. Биршгчи тенгламадан иккинчисини айирамиз:
(b-c)(tf-d)=0
Дсмак, fl=d ёки Ь=с худди шундай а=с ёки b=d ни
келтириб чи^арамиз. Куриниб турибдики, туртта сондан учтаси
геш. Фараз ^иламиз: b=c=d булсин. У ^олда тенгламалар
системаси
ab + b~ = -1
ah + b~ = -1
ab + Ьг = -1
куринишга келади.
!>(</• Ь)=-1 ёкиЬ—1 ва с+Ь=1 ёки а+Ь=-1 ва Ь=1 бундан
л. Ь, с. d лардан биттаси ± 2 га, цолганлари р. 1 га тенг
ноши келиб чи^ади.
58. х=1 + а, У=1+/? деболсак z=-( а+/?)буладивабиринчи
I пн лама ( а+ 1)’+(/? + !)’-( а +/?)’=2 куринишга келади.
( оддалаштиришдан кейин:
а2+Д2+а+/?=а >9(а+^)
ёки
а + /?=( а + Д+2)(а+^-а /7)
41
булиб, а + р йиринди (Х + /7+2 га булиниши керак. Бундан
куринадики, а + Р йиринди О, -1. 3. -4 ^ийматларни кабуч
финиши мумкин: а +P=Q булсин. У ^олда кейинги тенгликдан
о=2-(-а Р), а/7=о, а=о ёки /7=о а-г/7—1 булса,-]—i-aР-
а /7=0, а=0 ёки /7=0. Агар а+/7—3 булса, -3—1 (-3- а /7).
3=-3-а Р, а /7—6, а=-6/ р. Агар а + /7=-4булса -4=-2(-4-
а/7), 2=-4-а р, а/7 =-6, а=-6.'/7. Агар а=о, /7=0
булса, х=1, у=1, z=0 булади. Худди шундай х=0, у=1, z=l ва
у=0, z=l, х=1 ^оллари булиши мумкин. Булардан х, у, z
узгарувчилардан биттаси нолга тенг, ^олганлари эса ! га теш
экан, деган хулоса келиб чикади.
59. Курсатма: у = д/2х-5 деб белгилаб олинг. У ^олда
у > 0 ва (у+3)+| у-1|=4. Бундан 0<у<1
Жавоб: — < у < 3
2
60. х^1, у> 1, z>l экани ани!$. Фараз ^илайлик: х
уларнинг энг каттаси булсин: х>у, x>z. у=(х-1)2, x=(z-l’)
ва x=(z-l)2 булгани учун х>у дан (z-l)2>(x-l)2 экани
келиб чикади. Бундан z>x, аммо шартга кура x>z эди.
демак, x=z экан. Худди шундай х=у булишини ^ам курсатиш
мумкин. Демак, x=y=z экан. Бундан фойдаланиб тенгламала;
системасини ечсак, жавоб:
3 + V5
—-— булади.
61. ~ - а бу ерда a - исталган рационал сон. У ^олда
у 1991 ц 1991 _|_ у!991— у!992 ц 1992_|_ у 1992
1W941 1+с?991
y~l+a^9^>2, x~a'\+d992
Булардан фойдаланиб, берилган тенгламанинг хо^лаганча
рационал ечимларини топиш мумкин.
42
62-Тенгламаларни квадратга кутариб ^ушамиз, натижада
ios(x у)=0 тенгламани ^осил ^иламиз. Бундан
я _
Х*У _ + к л , ke.Z, х=гз---------гЪт,когни
2 ' 2
ю^оридаг и тенгламалардан биттасига ^уйиб, у ни топамиз.
7Г 7Г
Жавоб: {±о + — + 2тя, + 2 а + — + 2пл}, m.neZ
4 4
63. Тенгламалар системаларини ^ушиб
55х, <-55х2<-....+ 55х1О=550 (1) тенгламани хосил рила-
ми г Системадаги иккинчи тенгиамадан биринчисини оламиз:
9х, х2-...-х|О=О (2)
(2) ни (1) га ^ушсак, 10x^10. х,=1 келиб чи^ади. Худди
шу усулданфойдаланиб, х,,х3,.... х10 номаълумларнитопамиз.
Жавоб: х, = х,=....=х|0=18
2х-1
64. Курсатма: 1 - —~— деб белгилаш киритиб, тенгламани
I' I (t| куринишга келтирамиз. Бунда t<l ва t>2 булганда
ICII1J1HK уринли булмайди. У холда 1 < t < 2 булиши керак.
Бунда |tHI булиб, t-^2 тенглама хосил булади.
2-72 + 1
Жавоб: --------
( V + г + Z )(ху + yz + xz) ~ X)’Z
( V + ) + z)(.vy + yz + xz) - X}'Z - 0
(v + у + z)(xy + yz + xz) - xyz -- (x + у )(x + z)(y + z) = 0
43
Бундан ёки х+у=О, ёки x+z=O, ёки y+z=O булиши
керак, x+y+z=rz булиши учун эса х. у, z лардан камида
биттаси а га тенг булиши керак.
1992
66.
1992
дан
т
( ffl + H (1993
t т J 11992 /
19931442 (w+ !)""'
=-----— ни хосил циламиз.
Бу ердаги касрлар кисцармас касрлар булгани учун:
1992|992=т""'
Агар т>1992 булса, у холда т",’|>19921992 булади.
Агар 0<т<1992 булса, у холда тП1‘|<1992|99: булади. Агар
т<-1 булса, у х.олда п=-(т+1) булганда I992i992=n
бундан п=1992 экани келиб чикади.
Жавоб: т-1993
67 . Курсатма: берилган тенгламани:
(х-у)(х2+ху+у2)=11 ’
куринишга келтириб ечинг.
68 .Тенгламани ечиш учун янги узгарувчи киритамиз:
y = V2-x, ? = Vx -1,
_rJ + x = 2, z2 +1 = x. у + ~ = 1
булардан y’+z2=l, y+z=l, z=l-y ни биринчи тенгламаг;
1$уйиб, y’-ty2-2y=O тенгламани >$рсил ^иламиз. Бу ердаг
У°{0; 1; -2}
Демак, берилган тенгламанинг илдизлари 1; 2; 10 сонларг
булар экан.
69 .Системадаги тенгламаларни х.адлаб 1$ушамиз:
х2+у2+z2 -yz-xz-xy=y-x+z-y t-x-z
х21 y‘+ z2-yz-xz-xy=0
2 x2+2 y2+2 z2~2xy-2xz-2yz=0
(x-y/+(x-z)2+(y-z)2=0
44
бундан x=y=z экани келиб читали.
70. Масаланинг шартидан
v,-x2 =
х2 - X,
х2-х.
-X,
л
х,-х2
Агар х'=х2 булса, х2=х3=...=х" булади. Агар х2*х2
б^лса, х2 Ф х3 ф ... Ф х" Ф х1 булиб, бу ^олда берилган барча
тспгликни купайтириб, сунгра (х‘-х2)(х2-х3)...(хп-х') га
цис^артириб, (х1 х2 х3 ... х") 2=1 ни з^осил ^иламиз.
71. Курсатма: тенгламанинг иккала томонини 4(ху)100 га
буламиз:
(4х'°0 + J. )( у ’00 JL) = 4
' 4yiooA'x 100 7
з^ар бир з^авс ичида ифода 2 дан кичик булмагани учун
4х"’°=1, у|00=1
Жавоб: х = ±й^’ 'V = ±1
а с
72. т<-7 Дан ad<bc экани келиб чикади.
b а
<id'«b<bc+ab (иккала томонига ob ни фтпдик). a(b+d)<b(a+c)
а а + с
Иккала томонини b(b+d) га булсак, т<Т—7 булади.
b Ь + а
Иккинчидан «d<bc га de ни ^ушеак
«d • dc<bc+dc d(a+c)<c(b+d)
а + с с
иккала томонини d(b+d) га булсак, +j <~J булади.
а а + с с
Демик, — < ~ экан. Шуни исбог ь^атиш талаб ^иинган эди.
45
73. Тенгсизликнинг иккала томонини xyz га буламиз:
тенгсизлик исботланди.
74. Тенгсизликни исботлаш учун иккита номанфий соннин
урта арифметиги ва урта геометриги ха^идаги тенгсизликдаг
фойдаланамиз:
сГ +bc > 2a^lbc,
b + ас > 2bjac.
с~ +ab > 2су[аЬ.
ab + ас
2
> ayfbc.
ab + Ьс , г—
---------> by,!ас.
ас + he г-у
----- > cyab
Бу олтита тенгсизликни ^ушиб, берилган тенгсизликнин.
тугрилигига ишонч хосил ^иламиз.
75. -Vs -у5 < -г5 + у5 _ ]
X - у X + у
-------= х + у +х у + хг +х’г’" < 1
х-у
булгани учун бундан х4+у4< 1 экани келиб чи^ади.
76. а>0, b>0, <z3+b3>ob(tz+b) тенгсизлик уринли булгани учун
1 1 __________________ 1
a}+b}+abc ab(a + b) + abc ab(a + b+c)
1 1 _ 1
b3+c'+abc bc(c + b) + abc bc\a + b + c)
1 1 __________________ 1
a3 +c' +abc ac(a + c) + abc ac(a+b + e)
Бу учала тенгсизликни ^ушиб. исбот килиш керак булган
46
тенгсизликни оламиз:
1.11 1
- ------i- ——— ---j— -------<------------j_
a' +b' +abc c’+b'+abc a +c+abc ab(a + b+c)
1 1 I
4--------•--1-----—---—---
cb(a + b + c) ac(a + b + c) abc
77.а) Биринчи тенгсизликнинг унг ва чаи томонлари
йЙирмасини топиб, шакл алмаштириш бажарамиз:
D=2(a2b2+ «2с3+ с2Ь2) -( а4 +Ь4+с4)=
-4 а2Ь2—(а2 +Ь2)2+2с2(а2 +Ь2)-с4=(2 аЬ)Ч а2 +Ь2-с2)2
Агар D>0 булса, у ^олда 2аЬ > | а2 +Ь2-с2|, а, Ь, с лар
берилган муносабатда симметриклик шартини ^аноатлаютргани
учун а>Ь>с деб олсак булади.У ^олда а2+Ь2+с2= |«? +Ъ2-
с'| 12c2<2tfb+2c2<2(ab-t-bc+ac)
б) жавоб йук (масалан. а=4. Ь=с=1 булса, иккинчи шарт
бу «клади).
78. tg rz tg/?+tg/? tg/+tgtz tg/<l
ншртдан фойдаланамиз:
tger tg J3+ tg/ (tg/? +tgcz)<l
‘g X • (tg p +tg a )<l-tg • tg p
---------< । ^осил булади.
\~tgaigP
Ширк а кура 1 -tg а tg Р>0, демак,
‘g/tg( а + р}<\
tgy< ctg(a + /?)
<g/ < tg(f a~P)
л
У 2-a-p
n
a ' //' У< ~
47
79. Берилган тенгсизликнинг тугрилигини исботлаш учун
исталган ^аь^ш^ий сон учун:
|sinx|+|sin(x+l)|+|sin(x+2)|> |
Тенгсизликнинг тугрилигини исботлаш етарли.
f(x)= |sinx|+|sin(x+1 )|+|sin(x+2)|
Фукнция даври л булган даврий функция булгани учун тенг-
сизликнинг барча х°[0; л ] лар учун исбот ^илиш етарли. Олдин
х°[0;р]да f(x)>2sinl эканини курсатайлик. 0<х< л-1 булсин
У ^олда f(x)=sinx+sm(x+1 p-sin(x+2)=2cos 1 sin(x+1 )rsin(x+1)
1 <x+l < я-1 булганида sin(x+l)>sinl, sin2>sinl шуниш
учун f(x) > sin2+sin 1 >2sin 1
Ушбу л-2 < x <л-1 ва я-1< х <л булган доллар ^ам
худди шундай царалади.
ЯО.Тугаракка х у^увчи аъзо булсин дейлик; масаланинг
шартига кура, тугарак аъзоларининг 7% дан камроги саккизинчи
синф уку'вчиларидир. Иккинчи томондан, камида бир саккизинчи
синф укувчиси (Карим) тугаракда шугулланмо^да. Шунинг учун
1<0,07х, х>14,2. Демак, тугаракда камида 15 та аъзо бор
экан.
81. Шартга кура a>at, а>а2+а}, .... , а>ап +а^+...+а1
а2=а, q, a=a.q2, ... ап= a, q"'1
булгани учун q>l, q2>q+l, ... , q">q" 1+...-rq-rl экани келиб
чикади.
48
Бундан
/-1
---Г’9>1
9-1
экани аниг$, q”+l -2q"+l>0,
q"(q -2)+1>0
Агар q>2 булса, охирги тенгсизлик ихтиёрий п учун
тугри булади, агар 1 < q < 2 булса, шундай п топиладики,
1
2-9
тенгсизлик бажарилмайди.
82. а) (2) формулада S=f(l) ни ^илоблаш керак.
(I ) формуладан эса f(l)=2100 булиши келиб читали. Демак,
S 2100
б) (2) формуладан Г(-1)=-оД я|-л,+...+«,04-а,05 эканидан
ю^оридаги (а) шартга асосан:
5, = "(/(»- /(-1)) = +12|М) = 2V> (I + 6"’“)
в) S-ST=Sx 8ж=2|00-299(1+610с>-2"(1-6100)
83. y=f(x) функция сонлар у^ида ани^ланган булса, у =f(-x)
функция \ам сонлар ут^ида ани^лангандир. и (х) ва
функциялари шундай танлаб олайликки, сонлар у^ида биттаси
жуфт. иккинчиси тог; булсин:
1 '(')= -(./ 1 (') + /Х~л)) жуфт функция ва
А<25А2+15А + 3
(х) = ^ (-/ (х)~ J (-х)) тог; функциядир.
У ^олда х нинг исталган ^ийматида f(x)-M(x)+v(x) уринли
булади
_ Л1 . / а
84. а - - о - д/х, v2 булсин. Шартга кура т - «
2 ' b
дин и =nb, демак, b - рационал сон ва. демак. натурал ^ам.
х^х, сонлари х ’ 2i/xib -0 тенгламани ^аноатлантиради.
Шунинг учун улар а±уЦ5 га тенг.
1) 4а: 4b2=4b2(n: 1)
49
Arap n--l булгандагина D квадрат була олади. Демак, D 1
ва х,=х, экан.
85. Фараз г^иламиз п масала шартини г^аноатлантирсин. п}-
нинг 5 га булинишидан п сони ёки 1 разами билан ёки 6 раг^ам >
билан тугаши керак, яъни 5k+ 1 куринишда булиши керак
«’-! (5A+1V-1
У г^олда: —— = ---------= 254’ +15Г+34 = А(25Г+154+3)
Э 5
4<2542+15к+3 булгани учун, ^осил булган купайтма фа^ат к=1
яъни п=6 булгандагина туб сон булади.
86. >£ар ^андай натурал соннинг бешинчи даражаси шу
соннинг узи цандай ра^ам билан тугалланган булса, шу ра^ам
билан тугалланади. Демак, ахтарилаётган сон 4 разами билан
тугашидан унинг 14 экани келиб чикади. Чунки 205 егти хонали
сондир. 105 эса олти хонали сон, демак, суралган сон фа^ат 14.
булиши мумкин. Бевосита текшириш билан 14 хаки^атдан ^ам
масаланинг шартини ₽;аноатлантиришини курамиз.
87. k5+3=(k’-k)(k2+1 )+k+3
Куриниб турибдики, k’+З нинг к2+ 1 га булиниши учун
к+3=0, яъни к=-3 булиши керак жан. Худди шундай к--1. О,
1, 2 гргйматларда х.ам кЧЗнинг к2+1 га булиниши курсатиш
мумкин.
Жавоб: { -3; -1; 0; 1; 2}
88. Берилган сон 8000000000=8 -109 га яг$ин булиши учун ва
(2000)3=8 109 булганидан суралган соннинг 2000 дан кичик
экани келиб чикади. Аммо берилган соннинг 7 билан тугаши
эса суралган сонинг 3 разами билан тугашидан далолат беради.
Демак, биз суралган сонни 1993, 1983, 1973 сонлари ичидан
ахтаришимиз керак.
19933>19903=103(200-Г)’=103(8 106-3-4- 104+6 102-1 )>
>10’(800- 12)=788 - 107
Бу епда иккинчи раг^ам 8 булгани учун 1993 3>х’,
19733=(2 103-27)3=8 109- 81-4-106+6 - 272 103 -273<
<106(8000-324)+5 -10М06 • 7681
50
Бундан 19733<х3 булардан суралган сон 1983 экан деган
хулоса келиб читали.
Жавоб: 1983
89. Агар f(x)=(x-a)(x~b)(x-c) булса, у ^олда:
f(x)+f(-x)=-2(a+b+c)x2+2f(0) яъни, агар а+Ь+с=0 булса.
f(x)i-f(-x)=2f(O)= abc узгармас булади. Берилган мисолда
1{х) (х-10)(х+2)(х+8) деб олиш мумкин, у ^олда берилган сон:
f(999)-2f(0)==-f(-999)=1009 997-991
Булар эса туб сонлардир.
Жавоб: 1009 997 -991
90. хп+=(хп-1)3+1 бундан хпИ-1=(хп-1)\ Шунинг учун
тенглик ва m Ф п шартдан
(х,-1) =(х|-1)3 экани келиб чикади, бу эса Xpl^O, хп~хп
ёки х(-1= + 1 булганда уринли булади.
Жавоб: 0; 1; 2
91. Биринчи усу л: а ва b лар ёки ^ар хил ишорали ёки
иккаласи ^ам мусбат булиши мумкин. Биринчи ^ол булиши
мумкин эмас, чунки купайтма манфий ишорали булади. Демак,
а ва b ларнинг иккаласи ^ам мусбат ишора булиши керак.
Мусбат сонларнинг урта арифметиги ва урта геометриги
^а^идаги тенгсизликка асосан 2-а + 4Ь>2->[а-4Ь-л4аЬ
г~^ 1 г а<- 1
Jab < - бундан ab < -
Бу ерда агар а = 4Ь булганда, яъни Ь = — ва а=1 булганда
4
тенглик уринли булади. Демак, ab купайтманинг энг катта
^иймати булиши мумкин экан.
Иккинчиусул: «+4/> = 2.
а —2 — 4Ь,
ab = b(2-4b) = 2b(\-2b)
квадрат функция ^осил булади. Бу функциянинг энг катта
^иймати масаланинг жавоби була олади.
51
1
Жавоб: —
4
92. ап=,993+2,993+....+п1993 дейлик. Ушолда
2cz =2 • 1|993+2 • 2|993+...+2 п'993
п
=2+2+2,993+31993+з ,993-+- ч~п
ГЭ’993 1 М,993Ч . . /v»1993 . -),993\ О 1 А
2+ <124 44 4)4+2"4~Q?4 4+3 3) = 2 + /’,
Бу ерда Ьл йигинди п+2 га булинади, Ь+2 эса п+2 г?
булинмайди. Демак, берилган йигинди ^ам п+2 га булинмас экан
93. Курсатма: п=4к+1 булса, ап то^ сон булади. ап ни 6 га
булгандаги ^оддшдги текшириб, ап ?^адп=36р+17 булганда 3 га
булинишига ишонч ^осил jgunriu мумкин.
94. Курсатма: n+b >c + d деб олиш мумкин. У ^олда
,1 Ь с b + с 1 1 1
/> + с>- (а+Ь+с+фва------~ +-т =-т-с(----
2 c + d a + b c + d c + d a + d 2
a+b+c+d . ... 1 1 . 1 a + b c + d 1 rr- 1
------ (c + d)(-)=------+-------> V2--
c + d-----------------------------------c + d a + b 2 c+d a+b 2-2
Arap n = V2 +1. b=V2-l. c=2. d=0 булса, берилган ифода
A 1 .
v 2 - — ^ииматни ^абул ^илади.
Жавоб: >/2-|
95.а) Жавоб: мавжуд. а-2 + V2, b = -Л
б) Мавжуд эмас.
а ва b сонлари масаланинг шартини ^аноатлантирсин дейлик.
У^олдаа^О, Ь^О а~Ь~
~(а2 +Ь2)2(а4-Ь4) айниятдан
а2Ь2нинграционалэканива a5 +b5 =(cd +/»’)(<73 +b2)-a2b2(a + b)
айниятдан эса а+b нинг ^ам рационал экани келиб чи^ади. Бу эса
масала шаргига зид.
52
96. 2n+4'-2n(2''+l). Агар бу сон бирор соннинг квадрата
булса, у ^олда унинг жуфт купайтувчиси 2" ?^ам бирорта соннинг
квадрата булиши керак. Бу эса и жуфт булса уринлидир. Шунинг
билан бирга 2П+ 1 то^ купайтувчи хам бирорта соннинг
квадратига тенг булиши керак. Аммо п жуфт булганда 2!’+1
ни 3 га булганда 2 ^олди^ ^олади ва у бирорта соннинг квадрата
була олмайди. Демак, ^аралаётган сонлар тупламида бирорта
соннинг ^ам квадрата йу^.
97. n=2k+3 деб олсак, 2n+4k=22k+3+4k=22k -9=(2k -З)2 Демак,
берилган тупламда чексиз куп сонларнинг квадрати бор.
98.Фараз ^илайлик:
булсин деб. У холда
a a + b b
-------, яъни — < 1 а < 998 булсин, унда
с c+d d d — - J
— <998. — + -у <998 булади. Агар — = 999 (я = 999. с = Г) булса
с а
a b О Ь
- + — > 999. Шундай ^илиб. ~ ~ йигинди ^ушилувчилардан
бирортаси 999 га тенг булса, энг катта буларкан.
99. (7''V5 -75 = 16807 >15625-5fc >(5v’’)v5
демак 7'’’ > 5 х 7
100.
'4п\ > ny[(n + i)\
(и!Г‘>((« + !)!)",
(и!)""1 >(«!)" (« + 1)я
«!> (« + 1)"
Нотугри хулосага келдик. Демак, берилган тенгсизлик
уринли эмас.
53
101. Биринчи цушилувчининг охирги ра^амини 9 билан в.:
иккинчи ^ушилувчининг охирги ра^амини 8 билав
алмаштирайлик:
\[б+ т/б + ... + л/б + ^6 +д/б + ... + \/б < \6 + +
+ ^6 + >/б + .... + Ш =3 + 2 = 5
Демак, берилган йиринди 5 дан кичик экан. Иккинчидан:
Аммо -/б >2,4; ^6>1,6 демак 2,4 <7б+7б+....+Тб
ва 1,6<^/б +^6 + ... + ^Ж Булардан куринадики,
4 < у[б + у/б +... + + -^6+ у/б +... + \/б < 5
Шундай ^илиб,берилган сонинг бутун ^исми 4 га тенг экан.
102. 1g1 211 = (1 +lgl,l)2 > 1 + 21g 1.1 = 1 + lgl,21 = Igl2.1 > Igl 2
4>У
103.
б) функциянинг аншрганиш со^аси [1; ос) ,
1 [ х ~ 1, агар х < 2 булса,
—(А-— j Л-— 2 I) = ч
2 [1, агар х > 2 булса.
Энди ушбу
агар 1<х<2 булса
1, агар х > 2 булса
У =
Функциянинг графигини ясаймиз:
54
2
-2 12 4 6
104. Курсатма: а) ок=к(к+1) дейлик, у ^олда:
к(к+1 )(к+2)-(к-1 )к(к+1 )=3к(к+1 )=3ак
К^уйидаги п та тенгликни ёзамиз:
1-2-3 . 2-3-4 1-2-3
U. ~-------U. Q —.....................
1 3 3 3
А(£-ь1)(Л-ь2) (А-1)А:(А + 1)
" 3 з .........
Il(n+ 1)(/7 -I- 2) (п~ 1)/7(И + 1)
___ а — ———--------------------------
п(п + 1)(и + 2)
Бу тенгликларни ($ушиб + а2 +.....+ а„ ------------- ни
^осил ^иламиз.
б) худди ю^оридагига ухшаш:
ж IV91 - *<А + № + 2^к + 3> - -’)*(* + № + 2>
К1.К + 1ДК + — - — ",
4 4
тенгликдан фойдаланиб топилади.
в) бунда n(n+2)(n+4)=n(n+1 )(n+2)+3n(n+1 )+Зп ва кщоридаги
(а) ва (б) мисолларнинг натижасидан фойдаланилади.
w . е _п(« + 1)(л + 2)
Жавоб: а) ------------------
е и(« + 1)(«+2)(и + 3)
б) 5„=---------------
и(« + 1)(« + 4)(/7 + 5)
в) S„=-------------------
105. Системадаги биринчи тенгламани у га, иккинчи
тенгламани .г га купайтириб, хосил булган тенгламани ($ушиб,
ушбуни ^осил ^иламиз:
55
Х~ + у~
ёки 2ху-1=3у бу ерда у ^tO булганидан
2 2у-
Бу муносабатни берилган системадаги иккинчи тенгламага ^уйиб:
’ 3 !
У (г+ч~
_ 2 2у
^±)-Зу = О
2 2у
тенгламани ^осил тдтламиз. Бундан:
4у4-Зу2-1=0
тенглама келиб читали.
Бу тенгламани ечиб, х=1, х,=2, у,—1, у2=1 эканини
топамиз.
Жавоб: (2;1)
106. Шиллик i^ypr ^ар 15 минут да юрган йулининг узунлигини
бир бугин дейлик. Шилли^ ^уртнинг бошлангич пунктдан
узшрташидиган горизонтал бугинлари сони уни бошланрич
пунктга я^инлашувчи бугинлари сонига тенг. Демак, барча
буринлар сони жуфтдир. Худди шунга ухшаш муло^аза билан
вертикал бугинларнинг ^.ам жуфтлигини курамиз. Бундан барча
бугинлар сони 4 га каррали экани келиб читали.
У ^олда: (2л + 2«) • 15 • — = п соат
Шуни исботлаш талаб ^илинган эди.
107. Жавоб: 1 - 99 х’00 + 100 х101
Изо^: Иккинчи ^авс ичидаги куп^адни (1 - х)га икки марта
купайтиринг.
108. Мисол учун, (х2, (х-1)2 ва (х-2)2 куп^адларнинг j^ap
битгаси илдизга эга, аммо исталган иккитасининг йигиндиси х
нинг j^ap ^андай цийматида нолдан каттадир. Демак, мавжуд экан.
1,1 д.
109. Берилган ~^ + ~^ + ~^~а + ^ + с тенгсизликни умумий
махражга келтириб, унга тенг кучли булган ушбу
Ьс + ас + ab > {а + b + c)abc тенгсизликни ^осил ^ламиз.
56
Энди ушбу (a+b + c)2 >3(ab+bc+ac) ёрдамчи генгсизликни
исботлаймиз:
(а-b)2 + (а-с)2 + (Ь-с)2 >0, ^авсларни очиб,
2(а‘ +Ь2 + с2) > 2(ab + Ьс + ас) ни ёки
сг + Ь2 + с2 >ah + bc + ac эга буламиз. Тенгсизликнинг иккала
гомонига 2(ab + Ьс + ас) ни ^ушамиз.
а2 +Ь2 + с1 + 2(ab + bc + ac)> 3(ab + Ьс + ас). Бундан:
! а + Ь + с)2 > 3(аЬ 4 Ьс + ас) булиб,
! а + b + с)2 > 3(ab + Ьс + ас) > (а + b + c)abc. яъни:
ta + b+c)2 >3(a + b + c)abc « a + b+c>3abc исботланиши
арур булган тенгсизлик келиб читали.
НО. Учбурчакнинг бурчакларини деб белгилаб
лайлик ва и < р<у булсин. У ^олда ()<fZ < 5. бунга кура
3’
•<tga < у/З.
tga натурал сон булгани учун, tga = I, яъни а -
тс
~ булади.
4
^олда
“ булиб, бу ердан,
rg/? + zgy tgy -1. (if'P -1 )(ft7 -1) = 2
I -
енгликнингунгтомонида 2-туб сон тургани учун tgP- 1 -• 1 ва
-1 = 2 (ёки аксинча) булиши керак. Бу ердан tgfi - 2, tgy = 3
чани келиб чикади.
II1. х'+дх+Ь 0 квадрат тенглама х., х, илдизларга эга
' теин. у-х:< лх< Ь парабола Ох у^ини А(х(; 0) ва В(х,: 0)
чцталарда кесиб утади. Оу у^ини С (0; Ь) ну^тада кесиб
.ади: OA OB=OC OD
О Hyifra координата боши булгани учун А, В, С ну^талардан
>\ нчи айлана D(0, 1) ну^адан ^ам утади.
57
112. Тенгламани ф'йидаги куринишда ёзиб оламиз:
f(x)=(x-b)(x-c)+(x-«)(x-c)+(x-«)(x-b)=O
Шартга кура
f(a)=(a-b)(a-c)>0
f(b)=(b-a)(b-c)<0
f(c)=(c-n)(c-b)>0
Булардан куринадики, тенглама [а; Ь] ва [Ь; с] кесмаларда
биттадан илдизга эга. f(x) -квадрат уч^ад булгани учун унинг
иккитадан куп илдизи булиши мумкин эмас.
113. у=х1 2 функция графигининг (с, с2) ну^гасидан утувчи
уринма у=2с(х-с)+с2=2сх-с2 куринишида булади. Текисликнинг
^андайдир ну^аси ортали иккита у=2сх-с2 ва y=2bx-b2 уринма
етказилган булсин; аниь^лик учун (х0; у(1) нукуани олсак:
у0=2сх0-с2 ва y0-2bx0-b? булади. Бу уринмалар узаро
перпендикуляр булса, 2с -2Ь=-1 булади. Бундан Ьс=- экани
4
маълум булади:
2cx0-c2=2bx0-b2
2cx0-2bx0=c2-b2
2x0(c-b)=(c-b)(c+b), (с Ь)
Ь+с з
хо ~ • буни ус=2сх0-с* га ^уямиз.
~ Ь + с 2 , 1
к -2с---------с -be- —
2 4
(х0; у0) ну^тадан у=х2 парабола утказилган уринмаларнинг
1
перпендикулярлигидан Уо = экани келиб читали. Демак,
1
У() = - - тугри чизиь; ну уталаридан у=х~ парабола тугри бурчак
остида куринар экан.
114. Биринчи усул:
Р(х)=10ах4-4ах3+а3х2+6х-2 деб олайлик
Р(0;=-2<0,
58
(1 \ I 1
Р - = -а + -а2 + 1>0.
uJ 8 4
1
Демак, [0; — ] кесмада тенгламанинг а нинг ^ар ^андай
^ийматида битта илдизи мавжуд.
Иккинчи усул:
'г_, . , 10а 4а а2 6 „ а2 , .
Р(х)сД =-----------+ — ч----2 = — + ач-1 >0
/ 5 4 3 2 3
Демак, Р(х) функция [0; 1] кесмада ^амиша манфий
^ийматга эга була олмайди. Аммо Р(0)<0, демак, функция
[0; 1 ] да ишорасини узгартиради. Бундан берилган тенгламанинг
[0; 1 ] да илдизи мавжудлиги келиб читали.
115. Курсатма: а) (2 + д/з )(2 - -Уз) = I булганини эътиборга
олиб, (72 + л/3)г =t деб белгилаб, ушбу тенгламани ^осил
1
^иламиз: t ч- ~=2
б) берилган тенгламани ^уйидагича ёзиб оламиз:
= 1
Тенгликнинг чап томонида иккита монотон камаювчи
курсаткичли функциялар турибди. Шунинг учун чап
томонининг узи камаювчи функциядир. Аммо монотон
функциялар ?^ар бир цийматни бир марта цабул ^илади.
Демак, берилган тенглама биттадан орти^ илдизга эга эмас.
116. Берилган тенгламанинг унг томонини N билан
белгилаймиз. Бевосита текшириш шуни курсатадики, N 2 га
^ам, 3 га ^ам, 5 га >^ам, 7 га ^ам булинмайди. Демак, 10 дан
59
кичик сонларнинг \еч ^айсисига булинмайди, аммо 9 га
булганда эса (ра^амлар йигиндиси 50 га тенг) 5 ^олди^ ^олади.
Агар у маълум булса, х' нинг 9 га булгандаги цолди^ х ни 9
га булгандаги ^олдиеда богли^. х-' нинг 9 га булганда
^олди^лар жадвалини тузамиз. ( х9 - х ни 9 га булгандаги
ь;олди^ булсин).
\х9 у\ 0 1 2 3 4 5 6 7 8
1 0 1 2 3 4 5 6 7 ос
2 0 1 4 0 7 7 0 4 1
3 0 1 8 0 1 8 0 1 8
4 0 1 7 0 4 4 0 7 1
5 0 1 5 0 7 э 0 4 8
6 0 1 1 0 1 1 0 1 1
Жадвални давом эттирсак, 0-нчи, 3-нчи, 6-нчи устунлар
ноллардан иборат булиб, ^олганлари даврий равишда
такрорланади. Агар х ни 9 га булганда 2 ^олди^ ^олса ва у=5. И...
6к+5... булса, ёки х ни 9 га булганда 5 ^олди^ ^олса ва у= 1, 7,
13... 6k+1 булса, ху ни 9 га булганда ^олди^ 5 булади. Энди
берилган тенгламага ^айтамиз. Унинг битта ечими x=N, у=1
экани аниц. Энди фараз ^иламиз: у>1 булсин. У ^олда у=5, 7,
11,13,... Аммо N<10", шунингучун агару> 11 булса. у^олда
х<10 булади. Бу эса N сонида 10 дан кичик булувчилар йу^
деган фикрга зиддир. Демак у=5 ва у=7 \олларгина ^олади.
у=7 булсин, у ^олда:
407=4' 107=16384 107>N
307=37 107=2187 107>N
яъни 30<х<40 экан. Аммо х тоц сон булиши керак ва 9 га
булганда 5 ^олди^ ^олиши керак. Бундай сон эса ^аралаётган
(30; 40) ораливда fiyiy Энди у=5 деб олсак:
160М65 -105=220 10М0242 1(Г>]0" >N
1005=10'°<N, 100<х<160
60
N сони toi^ ва 9 га булганда ^олди^да 2 булиши керак. Бундай
сонлардан (100; 160) орали^да туртта - 101, 119, 137, 155.
Аммо 119 сони 7 га, 155 сони 5 га булиниши учун улар биз учун
яро^сиз. 101 сонини цараймиз. Агар х сони 1 разами билан тугаса,
ху сони ^ам 1 разами билан тугаши керак. Демак, ягона ^ол
х=137 экан.
137’=43261724457
Жавоб: (137; 5)
117. (х-у)=п булсин, у ^олда х+у=п2
И(И+1) «(«-!)
бундан т = —-—• У = —~—
Булар и нинг ^ар ^андай ^ийматида бутун сондир. Демак,
fn(n+l) n(n-l)) „
тенгламанинг бутун ечимлари I——.....у- j куринишда булар
экан. ]х|<100 ва |у|<100 ни ^аноатлантирувчи ечимлари эса
|n|< 13 булганда бажарилади.
118. х2 + у- = (х + Я2 - 2лт = {а - I)2 - 2(а2 - 7а + 14) =
= а2 - 2а +1 - 2а2 +14а - 28 = -а2 +12а - 27
Охирги ифода а нинг функцияси булган квадрат уч^аддар.
Бу уч^ад учун масаланинг шартини ^аноатлантирувчи х ва у
лар мавжуд. х ва у нинг ^ийматлари ушбу системадан топилади:
f х + у = а -1
рт = а2 — 7а+14
Демак, х ва у лар ^уйидаги квадрат тенгламани
^аноатлантиради:
Г + а2 -7а+ 14 = 0
D = -За2 + 26а - 55
Л
Дискриминант а нинг — < а < 5
булган ^ийматларида
манфий эмас. Бундан танщари а нинг [f;5J кесмадаги
^ийматлари учунгина х ва у нинг ^а^и^ий ^ийматлари мавжуд.
61
Масаланинг шарти шундан иборатки, Пр 5 кесмада шундай а
ни топиш керакки, -а2+12а-27 уч^ад эш катта цнйматга эга
булсин. b=-tr+12a-27 парабола учининг абсциссаси а=6, бу
эса
Я _1
кесмага тегишли эмас. Демак, -а-+12я-27 уч^ад
узининг кесмадаги энг катта ^ийматига а=5 булгандагина
эришар экан.
119. Курсатма: системадаги тенгламаларни ^адлаб
1$ушиб,сунгра айириб, ^осил булган янги тенгламалар
системасидан фойдаланинг:
Жавоб:{(0; 0), (3; 3), (-3; - 3),(x/5;-Vs), (~>/5;>/5),
(-'fa+'fi -Ун-Уз
[ 2 ’ 2
120. Курсатма: системадаги биринчи тенгламадан
иккинчисини олиб, куйидаги тенгламани ^осил циламиз:
х - У = (у2 - V2) + а(у- х)
(у2 - х2) + а(у - х)+ (у -х) = 0
(у - х)(у + х + о + 1) = 0
Бундан ёки у-х=0 ёки у+х+а+1=0
121. Фараз ^иламиз: х( > х, > х5> ... > хл берилган сонлар
булсин. У ^олда:
х, +х2 +х, >х, +х2 +х. -(х, -х5Х1-х,)-(х,-х.)(1-х,)-
= Х|2 +х2 +х5(3-х, — х2) = х,2 +х2 +х.(х. +х4 +... + х„)>
> х2 +х2 +... + Х2 = 1
122. Жавоб: 1 ва 9
123. Курсатма:
62
sin4 x + cos4 x - (sin2 x + cos2 x) -2sin2 x-cos2 x =
i ' • 2 о
= 1—sin 2x
2
эканидан фойдаланинг.
Д’ кл
Жавоб: —+— k&Z
4 2
124. Тенгламанинг чап ^исми жуфт функция булгани учун
тенгламанинг ягона ечими О булади. х-0 булса:
= y[h2 хосил булиб, бунда ёки Ь=0, ёки b=i булиши
мумкин. Фараз ^илайлик: Ь=0 булсин. У холда берилган тенглама
у[(ах)2 + у/(ах)2 + у[а2х2 - О
куринишга келади ва а 0 булт анда ягона х-0 ечимга эга
булади. Энди Ь=1 булсин, у холда берилган тенглама:
д/(«х + 1)2 + ij(ax-\)2 +\[а2х2 -1=1
куринишга келади. Vax+l=w деб ва <fax--V деб олсак,
и2 + vz + uv = 1
ушбу ] 7, -
и -v ~ 2
яъни
W + V2 + UV - 1
<
(м - v)(w~ + v2 + uv) - 2
тенгламалар системаси ^осил булади. Бу системами ечиб, Y?--1
ва и=1 эканини топам из. сх+1=1 ва сх- 1=1 тенгликлардан эса
а 0 булганда, х=0 ягона ечимлиги келиб читали Шундай
1^либ, берилган тенглама а О, Ь=0 ва а 0, b= 1 булганда
ягона ечимга эга булар экан.
63
125. D = 4sin2 xy-4 - 4(sin2 xy-l)
булгани учун тенглама фа^ат sin2xy-l, яъни sinxy=+l
булгандагина ечимга эга. Бундан эса х= ± 1,
я
у = — + 7ГП,
2
keZ
экани келиб чи^ади.
X 4- (I
126. f(x)-x-a + 2cos---------- деб белгилаб.
Цх)
функцияни ^арайлик. У ^олда исталган x°R учун
Z'» / \ 1 • A I С«
.1 (х) = 1 - sin —> 0 булади. Шунинг учун f(x) функция
. х + а ,
sin-у— = 1 тенгламанинг илдизлари орасидаги исталган
оралиеда усади. f(x)функциянинг узлуксизлигидан эса у
сонлар тупламида усувчидир. Демак, берилган тенглама биттадан
ортиг$ илдизга эга булиши мумкин эмас, иккинчидан f(«-3)<0, f
(«+3)>0 булгани учун, урта ^иймал ^а^идаги теоремага асосан
[а 3; а+3] кесманинг камида битта нуграсида функция 0 га
айланади.
127. f(x)=0,001x3+x2-l дейлик ва ff (х )=0,001 х \ f,(x)=x2 1
деб белгилаб олсак, f(x>=f|(x)+f,(x) булади.
f,(x)=O десак, бу тенгламанинг илдизлари 1 ва 1 булади
ва |х|<2 булса, ^(х^О.ОО! булгани учун f(x) нинг иккита
илдизи х,=+1, х,=-1 булиб, f( 1 )=0,001 >0, f(0,9)<0 бундан
0,9<х[<1 экани келиб читали. Худди шундай: -1,1 <х,<1 эканини
топамиз. Энди 0,001х3+х2=О тенгламанинг илдизи м 1000 булади
ва f(-1000)=- КО ва Я -999,9)>0.
Демак, -1000<х3<-999,9
Жавоб: 0,9<х(<1, -1,1<х,<1, -1000<х,<м999,9
128. xs+4x2+4=( х8+4х2+4)Ц4х6+8х4+4х2)м(4х6+8х4+4х2)=
=(х8+4х4+4+4х6+4х4+8х2)м4х2(х4+2х24-1) =
=(х4+2х2+2)2(2х(х2+1))2=
-(х4+2х2+2+2х3+2х)(х4 ь2х2+2 -2х' -2х)
129.
1 _ 1 1 J_____________1
-v„+l х„ х„(х„+1) х„ х.„,
64
1 L
булгани учун ^аралаётган ииринди х Л1ю X|w га тенг
3 (3 Y 3
булади. хп кетма-кетлик усувчи хг = —,х} =1 - I + д>| демак,
х n > 1 у холда 1 < 2---< 2 экани келиб чикади.
100 * • у
Л1(Х)
Жавоб: 1
130. х + х3+ х5+.. .= а ва =х2+х4+...=Ь. У ^олда шартта кура
о+Ь=1 ва х1х,+ х,х3+...+ хп|хп<(х + х3+х5+..-Хх.2+х4+х6+...)=
1(1 Y I
=аЬ=л(1-о) = -4
1
Агар -Ti--T2-—,
х, = х4 =... = х„ = 0 десак, у ^олда
хсх2+ х2 • х4 + К + х„_,х„ = --
1
Жавоб: ~
4
131. a=y+z, b=x+z, с=х+у деб томонлари а, Ь, с
булган учбурчакни ^арайлик. Бундай учбурчак мавжуд. Бу
учбурчакнинг периметри 2P=o+b+c=2(x+y+z)
х=Р -а .у
у=Р-Ь г
z=P-e А
x+y+z=P ч У\"
унинг юзи эса Герои формуласидан
S’ = y]P-(P—a)(P~b)(P—c) = у](х + у + z)xyz = I
Иккинчи томондан 2S-bcsinft (бу ерда а бурчак b ва с
томонлар орасидаги бурчавдир), шунинг учун:
(x+z)(x+y)=bc>2S=2
65
Бу ерда тенглик учбурчак тугри бурчакли булганда
бажарилади, яъни:
а2=Ь2+с2 шартда. Бу шарт эса x(x+y+z)=yz гатенгкучлидир
(хусусий ^олда, яъни x + y = x + z = y/2. y+z=2, яъни y=z= 1
булганда (x+y)(x+z)=2 булади).
Тенгликнинг ^ачон уринли эканлигини билган ^олда
p+q>2-Jpq тенгсизликдан фойдаланиб, ^ис^а алгебраик
усулда 1$уйидагича исбот т^илиш мумкин:
(х + у Xх + 2) - х(х + У + z) + У= 2-Jxyz(x + y + z) > 2
Жавоб: 2
132. Курсатма: S2 ифодани ^аранг ва икки соннинг урта
арифметиги ^а^идаги тенгсизликни уч марта >$лланг.
Жавоб: д/з
133. Шартга кура а2+Ь2=1 дан куринадики:
0<а<1 ва 0<Ь<1
У ^олда а'°<а2, b'°<b2 муносабатлардан а'°+Ь|0< а2+Ь2
экани келиб чи^ади.
134. Курсатма: З^10»-10 = 10 3,g3 < 10^3 < 27 = З3
(1g 3 < — дан фойдаланилди).
135. Курсатма:суралган фигуранинг z=0 (хОу) текислик
билан кесишиши |х|+|у|< 1 тенгсизлик билан берилган
фигурадир. Худди шундай, бу фигурани бош^а координата
текисликлари ^ам кесиб утишидан фойдаланиш керак.
Жавоб: учлари(1; 0; 0), (0; 1; 0), (0; 0; 1), (-1; 0; 0),
(0; -1; 0), (0; 0; -1) ну угадан иборат октаэдр.
136. Курсатма: а, а2, ... аь сонлардан бирортаси >^ам b
га булинмайди. Аммо ^андайдир ак ва д' куринишдаги иккита
сон топиладики, уларни b га булганда бир хил ^олди^ ^олади.
У ^олда «kaL айирма албатта b га булинади.
137. Тенгликнинг чап ^исмини х билан белгилаб, иккала
томонини кубга кутарамиз. Сунгра (л+Ь)3=«3+Ь’+За(о+Ь)
формуладан фойдаланиб, ушбуни э^осил киламиз.
66
x3 = 20 + 14>/2 + 20-14>/2+3xv202 -2 • 142 = 6х + 40
х’=6х+40 тенгламанинг ягона илдизи х=4 дир.
138. av а,... ап сонларни усиш тартибида bv b2, Ь},
... Ьп деб ёзиб олайлик. 1 дан п гача булган исталган п
z < i
УЧУН а, + а2 +... + а, + Ь2 +... + bt
11 111 1
пя —— Ч----Ь...Ч-= 1----Ь...Ч-
а, а2 а„ />, Ь2 Ь„
12 " /1 1 И
булгани учун ушбу + - + b^bi~+^ * WV"'* Й
тенсизликни b сонлари учун исботлаш етарли. Чап томондаги
(9'шилувчиларни ба^олаймиз:
2 2 1 и+1
--------------= — КЯ 2 < k < -
bi+b2 />,+/), Л, ва ~ ~ 2
шартни ^аноатлантирувчи исталган к учун:
2ЬЧ______< 2Л -1 2А - 1 2
bt +b, +... + Ьи , ~Ь,+...+£,*_! kb, , bk l’
2к < 2к < 2^ 2
by+Ьг+... + Ь2к ЬЬ1+К +Ь2к кЬк Ьк
булардан фойдаланиб, зарур тенгсизликни ^осил ^иламиз.
b, by +b, Ь, + b2 + by by + Ь2 + b. + by
Шуни исбот цилиш талаб ^илинган эди.
139. cos!,x ва sin22x ни sinx ортали ифодалаб.
^уйидагини хосил ^иламиз:
4sin12 x + 4(sinb ,v +1)(1 - sin2 х) +3 - 4sin2 х(1 - sin2 х) = 4
Соддалаштиришдан кейин sin10 х - sin8 х = 0 ёки
67
* 8 'У
sm x-cos"x = 0 тенглама келиб чикади. Бу тенгламанинг
илдизлари х = — п, weZ булади.
Жавоб: х = —п.
не я
140. Курсатма: (ps + Z?)2 -ю] нинг бутун эканлигини
курсатиш етарли.
Жавоб: (х2-10)2-84
141. Илдиздан фггилиш учун x^fcl5,y = «K' деб олайлик, у
^олда берилган тенгсизлик ^уйидаги куринишга келади:
Зх5+2у5-5х3у2>0
Тенгсизликннг иккала томони у5 га булиб ва -=' деб
белгилаб, 3ts-5t3+2>0 тенгсизликни ^осил ^иламиз. Бу
тенгсизликни купайтувчиларга ажратамиз.
(t- 1 )’(3t3+6t2+4t+2)>0
t>0 булганда иккала купайтувчи ^ам манфий эмас. демак,
тенгсизлик тугри экан. Агар Р=1, яъни йМ>2 булганда тенгсизлик
бажарилади. Берилган тенгсизликга урта арифметик ва геометрик
^агдгдаги тенгсизликни г^уллаб г^ам исботлаш мумкин. Масалан:
3-S/i'= \lb + \[b+tfb\ 2-Ja - 4а + 4а
Бу бешта сон учун:
Демак, 3VK + 24а > s4ab тенгсизлик исботланди.
142. arctgx= a, arctgy= fl, arctgz-/ деб белгилаб олсак,
x=tga, y=tg/?, z=tg/ булади. У ?^олда:
х + у + г - xyz = tga + tg/? + tgy - tgtttgyStgy =
_ sin(« + ff) _ cos(o +/?) _ sin(g -r /Qeosy -r sin ycos(a’ г fl) _
cos a cos/? cos a cos fl cos «cos fl cos у
= sin<g Д+ X) ->0
cos a coscos у
68
0< а + Р + У < п ва махраждаги барча купайтувчилар мусбат
булгани учун cos(arctgt)>0, чунки ~—<arctgt< — исталган /
учун уринли.
143. [0; я] кесмада y = *Jx функциянинг графигини
^арайлик. У = уГх эгри чизи^, Ох уки ва х=п тугри
чизи^лари ^осил ^илган эди.
Чизи^ли учбурчакнинг юзини S
дейлик.
. 3
У ^олда
булади.
S„ = + 72 +...+yjn булсин. Бунда Sn шаклда тасвирланган
зинапоясимон фигуранинг юзи булади. Куриниб турибдики:
sn>s
Иккинчи томондан ушбу шаклдаги фигуранинг юзи,
Л+Л+...+7ГТ+^=
2
=(7i+^+.
булади. Бу эса S дан кичик.
Шундай ^илиб S„ > S > Sn -
Шу ни исботлаш суралган эди.
69
144. Фараз ^илайлик:
х>у деб, у ^олда
х' -х‘ = уг - уу => х‘ (хv ' -1) - у v(yт ‘ -1) =>
Бу эса зидликдир. Худди шундай х<у деб олганда ^ам
зиддият келиб чицади. Демак, х=у экан.
145. Тенгламада шакл алмаштиришларни бажариб,
ьуйидаги куринишга келтирамиз:
1 А В С D
1--------------------------= — +-----+-------1-----
^(А_ + 1)(А’ + 2)(Л + 3) к к + 1 к+ 2 к+3
деб А, В, С, D ларни топамиз. Натижада ушбу тенгликни
э^осил ^иламиз:
_________1_______-Ifl______2_+ J_______О
А-(А + 1)(А+2)(А ч-З)” бЦ А + 14 А + 2 А + 3 J
Шундай чучлиб изланган йигинди:
If I 3 3 13
61.47 W + 1 п + 2 п + 3)
га тенг.
147. Курсатма:
айниятдан фойдаланинг.
148. а = ^2, /? = log^3 булсин. Бу ерда /? сони
иррационал сондир. ^ачдщатдан ^ам, агар log 3 = — булсин
<7
десак, ( бу ерда р ва q натурал сонлар )
70
3 = (v'2)t 3’=(72У, 9’=2' тенглик уринли булиши
керак. Бу эса мумкин эмас, чунки 9Ч го^ ва 2Р жуфт сондир.
Иккинчидан эса:
Демак, а ва ft иррационал булса, ар иррационал сон
булолмас экан.
149. 32"+| -22я+| -6” = (з” - 2яХз"+‘ + 2"+1)
Демак, берилган куринишдаги сон п>1 булганда мураккаб
сон булади. п=1 да эса 13-туб сон з^осил булади.
150. a) log,, /gl3 + log,, /g2' t log, zg.3“ +... + log, tgXl" r
+ log,, Zg881' + log,, zg891’ =
~ log„(/£lu 4g2" tg3" -...4089'’) =
-- log ,[ugl‘7g89u X/g2'7g88,,)...(zg44i,fg46,iRg45"l =
“log [(/gl'c/gl1'I(zg2!,c7g2‘'.(Zg44!’cZg 141')Zg-l5"] ~0
6 ) log,, sin 60t! log,, sin 61° log , sin 62°....log, sin 120° - 0 ,
чунки log,, sin 90° - log , I = 0
в) log, 3 log. 4 log4 5...log,, ,(/7- l)log„, n =• = log, n
log, 2
. , , , П ,T , . Д’ ЭЯ .IK .Ln
151. 2-лп cos +2sin cos sin sin i sin
5 _5 5 5_ ______________________5'
2sm 2sin
5 5
sin] zf “ . |
, .t
2 sin
Зя 2я 2л
152. cos ~ -- cos(tt - —) - - cos — булгани учун олдинги
мисолдан фойдаланиб:
71
п Зя 1 я 2я 1
cos—+cos — = — дан cos----cos — = — хосил киламиз.
5 5 2 5 5 2
cos36°-cos72° = —
2
cos 36°-sin 18°=-
2
1 — 2 sin218° — sin 18° = -
2
4sin218°2sinI8l'-l =0 дан
sin 18° = x деб4х2+2х-1=0 квадрат тенгламани хосил хиламиз.
X = sin 18° > 0 эканини эътиборга олиб ва тенгламани ечиб
ни sin 18° =
хосил циламиз.
153. tgx - 2[/gx] + 3. tgx - бутун сон.
Бундан [tgx]=igx, tgx=2tgx+3, tgx=-3
Жавоб: x=-arc(g3+k Л, k°Z -
154. 1980=99-20 булгани учун (99 ва 20 умумий
булувчиларга эга эмас). А= 192021... 7980 сони 20 га ва 99 га
булинишини курсатиш етарли. Берилган соннинг 20 га
булиниши аних Энди унинг 99 га булинишини курсатиш холди.
100 нинг \ар хандай даражасини 99 га булганда 1 цолдиц колади.
Шунинг учун А=19 1006t+20 10060+...+79 -100+80 ни 99 га
булганда ханча холДИ1( холса’ В= 19+20 + ... + 79+80
ни хам 99 га булганда шунча ^олдик холади.
Аммо:
5 = 19+20+...+ 79+ 80 = ^|^-62 = 99-31 булиб. В сони
99 га булинар экан. Демак, А сони хам 99 га булинади. бундан
берилган соннинг ! 980 га булинар экан, деган хулоса келиб чихади.
155. Агар турнир иштирокчилари х булса, турнир тугагунча
уйнаган шахматчиларнинг сони х-2 та булади. Шахматчилар
72
узаро fc- _3) та партия уйнашган булади. Мусобакадан
2
чи^иб кетган иккита уйинчи 10 та ёки 11 та учрашувда ^атнашган
булиб, бу уларнинг узаро учрашувига боглиг;. Ю^оридагиларга
асосланиб:
(х-2Хх-3) (х-2Хх-3)
+ । и - ээ ва >• 11 — 5 j
2----------------------------2
тенгламаларни тузамиз. Бу тенгламалардан кайсиси бутун мусбат
ечимга эга булса, фа^ат шугина масала шартини
^аноатлантиради. Биринчи тенгламанинг ечими х=12 булади.
Демак, шахматчилар узаро уйнашган экан.
156. m натурал сон 52 дан катта булиб, т+37 ва т-52
лардан бири то^, иккинчиси жуфт сондир. Айтайлик а ва б
тасди^лар тугри булсин, у ^олда ^уйидаги тенгламалар
системасига эга буламиз:
от+ 37 = х3
от - 52 = у~
Бу системанинг натурал сонлардати ечимлари х-45, у=44
булади. Бундан, пт= 1988 экани келиб читали. Демак, б тасдик
хато экан. Худди шундай а ва б \амда б ва г тасли^лар
биргаликда уринли була олмаслигини исботлаймиз а ваб учун:
от + 37 = х'
от = 10А +15,бундан х2=10(к+4)+2
Бу ^олнинг булиши мумкин эмас, чунки натурал соннинг
квадрата 2 билан тугамайди; б ва г учун
f т ~ 10Z +5
[от - 52 = г .бундан у2= 10(к-3)+3
Бунда ^ам натурал соннинг квадрати 3 билан тугамайди.
Жавоб: 1988
157. Хар биттаси турли 2 та хак;иь;ий илдизларга эга булган
куп^адларга (х-10)2-1, х2-1 ва(х+10):-1 лар мисол була олади.
Аммо уларнинг исталган иккитасининг йигиндиси ^акикий
7.3
илдизга эга эмас. Демак, масала шартини цаноатлантирувчи
уч^адлар мавжуд экан.
158. а2,... ап - берилган геометрик прогрессия, q - махражи
булсин. Шартга кура, «10 = a^q9 ва а50 = а -q19 натурал
сонлардир. Шунинг учун q9 ва q29 лар мусбат рационал
сонлардир. Бундан келиб чи^адики, Q - ТТСГ мусбат рационал
\Ч /
сон ва <7 = ^ам мусбат рационал сондир.
Фараз ^иламиз: ч = — булиб, бу ерда т ва п - узаро туб
24
<Г ,0 /И
натурал сонлар булсин. У ^олда - натурал
сон булиб, /и29 ва /г9 лар узаро туб, бундан келиб чи^адики, я,
1« w19
^ад л29 га булинади. Бундан о,0 = at -q'9 -at — — хам натурал
сон экани келиб чикади.
159. Берилган тенгликда махраждан ^утулиб, ^уйидаги
куринишга келамиз:
x3z - х3у + z3y - z3x + yJx- y3z = О
Чап томонни купайтувчиларга ажратамиз:
(х - - zXz - х)(х + у + z) = О
х, у, z ларнинг шартга кура мусбатлигидан охирги каве
мусбатдир. Куриниб турибдики, агар х, у, z лар ^ар хил сонлар
булса, тенглик бажарилмайди. Бу эса зиддиятдир.
160. 10000002 = х, 20000002 = у деб белгилаб, берилган
1-х 1-у
сонларни ---- ва —~ куринишда ёзиб оламиз. у > х булгани
1 1 )-х_. 1 , 1 _ 1 - V
vhvh ва----------—-----------
х у X х у у
„ 20000001 10000001
Демак, ------->-----—.
20000002 10000002
74
ГЕОМЕТРИК МАСАЛАЛАР:
ЖАВОБ ВА КУРСАТМАЛАР
1. Биринчи усул:
О ну^та КМ ва LN кесмаларнинг кесишиш ну^талари
булсин. Z.NDM + Z.MON = 180° булгани учун MDNO
тургбурчакка тапщи чизилган айлана чизиш мумкин. Шунинг
учун ZNOD = Z.NMD
Худди шундай Z.LOB = Z.LKB. LK || MN, КВ j| MD
булгани учун zLNKID - /.LKB ва Z.NOD = Z.LOB булиб,
D, О. В нукталар бир тугри чизи^да ётади:
2. Курсатма: SA№=SAM<. муносабатдан фойдаланинг:
mn $лмс , , । ^аи< бу ерда 4 =------
к +1 мв
75
3. Фараз ^илайлик: АВ>ВС булсин. У ^олда /ВСА > ЛСВА
ва, демак, /BCD> /CBD. Бундан ВО>СБва AB+BD>AC+CD
бу эса масала шартига зиддир:
4. АВС учбурчакнинг АН - баландлигини, ВМ -
медианасини ва СК - биссектрисасини утказайлик. Уларнинг
кесишишидан ^осил булган XYZ учбурчак тенг томонли
булсин дейлик. У ^олда ХНС учбурчакдан ЛХСН = 30" экани
келиб чи^ади. СК биссектриса булгани учун
/АСВ = 2 /ХСН = 60° В YH учбурчакдан эса
ЛХВН = /СВМ = 30° Демак, /ВМС = 90° булиб, ВМ -
медиана ^ам баландлик булиб додали ( АВС учбурчак учун).
Бундан АВ=ВС, яъни АВС учбурчак тенг ёнли булади.
Асосидаги бурчаги 60° булгани учун АВС учбурчак тенг
томонли ^амдир. У ^олда X, Y, Z ну^талар устма-уст тушиши
керак. Бу эса зидликдир:
76
5. МА=х, МВ=у, MC=z дейлик Z.MAB = АМСВ = а, У
^олда /_МОВ = 2а булади. Энди косинуслар теоремасини
МАО, МОВ, МОС учбурчаклар учун щЬшаймиз:
х2 =2Я2 --2Д2 cos(Z »7Ш),
у2 = 2/?: -- 2 ~ cost ZLMOB}.
z2 = 2R2 - 2R2 co^ZMOC),
ZWJ= 120“-2а, ZMOB=2a. ва R = ~^.
Z.MOC = 120" + 2а
эканини эътиборга олиб, ю^оридаги учта тенгликни ^ушиб,
^уйидагини ^осил циламиз: х2 + у2 + z2 = 2а2
Жавоб: 2а2
6. Курсатма:
$овс = OD S^^OE SAOII _ OF
^лвс AD SAhc BE SAnc B(
тенгликлардан:
OP OE OF
AD+ BE + FC
экани келиб чицади.
Жавоб: \-d-p
7. ВС ва AD трапециянинг асослари булиб, М ва N уларнинг
урталари, диагоналларнинг кесишган ну^таси О ва ён томонлари
давомининг кесишиш ну^гаси F булсин. Бунда FBC учбурчакни
77
FAB учбурчакка утказувчи ухшаш алмаш-
тиришни ^арасак, М ну^та N ну^тага утади. Шунинг учун F.
М, N ну^галар бир туги чизи^да стали:
8. Учбурчакнинг ихтиёрий бирорта ички ну^гасини олайлик
ва уни М дейлик. hp h2, h3 лар М ну^гадан учбурчак
томонларигача булган масофалар булсин. а ва h мунтазам
учбурчакнинг мос равишда томони ва баландлиги булсин. У
холда:
2 ’ 2 ’ 2 83 $ ~ + ‘'Ч/яс + $.ш<.
aht ah, ah. ah
эканидан ~2~+~2~+~2^~~Y > бундан hM^+h^+h, экани келиб
чикади. Агар М ну^та учбурчак томонларида ётиб ^олса, у
холда хам шунга ухшаш исботланади:
9. Масаланинг шартидан ОТ ± ВС ^амда ВО ва СО лар
биссектрисалардир. /ВОТ - а, /.СОТ - /? дейлик.
Шартга кура:
78
a _ 3
?~4’
AACB = x, ЛАВС = у, деб олсак
Системани ечиб, АО ВТ = 45° ва АОСТ = 30° эканини
топамиз. Булардан фойдаланиб, ВС 3+ д/З эканини топиш
жуда осон.
Жавоб: ВС - 3 + З-Тз
10. Квадратнинг томонини бир бирликка тенг деб олиб, СВ
кесма давомида ВМ = - ^илиб М ну^тани оламиз.
ЕС = -
3
5 5
Т булгани учун EF = -~. МЕ = ~. AM А!
2. 6 6
булади. Шундай ^илиб MEFA туртбурчакда ME=EF, МА=АЕ
Демак, V АМЕ- VAEF бундан АЛЕВ = АЛЕЕ экани келиб
читали:
М В Е
79
1-_L _L J_
11- r~ h + fa + h тенгликнинг иккала томонини
учбурчакнинг юзи - S га купайтирамиз.
5 5 5 5 5 5 1 5 1,51
— = — + — + ~ = Р, — = —а, —~-Ь. — = —с
г К, К А. г /7„ 2 h„ 2 hc 2
_ a + b+c
лардан п ------
2
12.АВ=с, ВС=а, АС=Ь дейлик VABC<® VACDua VABCoo
VBCD (учбурчакларнинг иккита бурчаги буйича ухшашлик
аломатидан). Булардан ухшашлик коэффициента мос равишда
b а
— ва — эканини топамиз.
С с
а) агар АВС учбурчакка ички чизилган айлананинг радиусини
г десак. г, ва г, пар мос равишда ACD ва BCD
учбурчакларга ички чизилган айланаларнинг радиуслари булса,
г, =— ва г =-— булади. Шунинг учун
С " с
, , (br V (ar V b2 + а2 , 2
/•.* + г2* = — + — =----;--/•* = г демак,
\ с ) \ с ) е'
г ~ 4- г22 экан;
б) АВС учбурчакнинг периметри Р булсин. Р( ва Р, лар
ACD ва BCD учбурчакларнинг (мос равишда) периметрлари
булса,
80
ЬР
— ва
аР
--- булади.
ьр\
аР
Ь2 + а2
булар экан.
CDE бурчакларнинг
Жавоб: а) г - у]г? + б) Р-
13. Фараз к£илайлик: DE суралган
кесма булсин. ВС томонидан CD
га тенг CF кесмани ажратамиз.
BC=BE+CD булиши учун CF=CD
деб олганимиздан BE=BF
булиши керак. Демак BEF ва
CDF учбурчаклар тенг ёнли экани
ва ED||BC булганидан EF ва
DF лар мос равишда BEF ва
биссектрисалари булиши келиб чикади. Шунинг учун F нукта
АВ, АС ва ED кесмалардан бир хил узо^ликда ётади. Бундан
эса F ну^танинг АВС учбурчакнинг А бурчагидан чик^ан
биссектрисада ётиши келиб чикади. F ну^тани топгандан кейин
эса тугри чизи^ни ^аердан утказишни билиш фшин эмас.
14. М ну^та ABCD туртбурчакнинг ичида жойлашган булиб,
у доиралар билан коиланмасин. У ^олда АМВ, ВМС, CMD
ва DMA бурчаклар 90° булиши керак. Бу ^олнинг булиши
мумкин эмас.
15. а ва b берилган учбурчакнинг катетлари, с эса
гипотенузаси булсин. Ар В, ва С, ички чизилган айлананинг
учбурчак томонларига уриниш ну^алари булсин. Айланага
битта нуцтадан утказилган уринмаларнинг тенглиги ^а^идаги
теоремаларга асосан:
АС=АВ, ВС,= ВА| СВ= СА(
с c + ,,, с + а-Ь
Бундан: ИС, =— й(,=—-—.
81
Шунинг учун:
AC, -BC = —(c + b-a)(c-(b-a)) = —(c2-(b-a)2) =
4 4
~а'~ -b2 +2ab) = ~ = S,l)
4 2
(бу ерда Пифагор теоремасидан фойдаланилди). Исталган АВС
учбурчак учун эса 5'w -АС,- ВС, c/gl -
формуланинг
тугрилигини исботлаш мумкин.
16. а) АОВ ваВОС учбурчакларнинг В учидан утказилган
баландликлари умумий. Шунинг учун улар юзларининг нисбати
асослари узунликларининг нисбати кабидир.
5, АО
S, ~ СО'
S4 АО
Худди шундай: - со
булади.
Бундан ’
5, • S', = S2-S4 экан.
б) $аво=$асо (Асослар ва баландликлар бирхил). Шунинг
учун SCDO=SADO=S говоридаги масалага асосан:
S-S'=S-S2, №=5,-5,, S = JS,-S2
Бу масалани ВОС ва AOD учбурчакларнинг ухшашлигидан
фойдаланиб ^ам исботлаш мумкин.
17. Исбот цилишда учбурчакда бурчак ортганда шу бурчак
мос синуснинг ^иймати ^ам ортишидан ва
а > р булса, (а - Р )(sin а -sin р )>0 ёки
-----— |(sin а - sin /7) > 0.
Р а)
тенгсизликдан фойдаланамиз. Ани^лик учун а > Р > Y деб
олайлик. Берилган тенгсизликда унг томонидаги ифодани
тенгсизликнинг чап томонига утказиб, баъзи шакл
алмаштиришлардан кейин ушбуни ^осил циламиз:
Бундан
| ---- |(sin а - sin р)+1 — - — |(sin а - sin/)+1 — - — |(sin /?—sin /) > О
V/? а) а) Р)
экани келиб читали.
18. АВ=с, ВС=я, ZBAC = a, Z-BCA-y булсин.
АМВ тенг ёнли учбурчакда AM уринма билан АВ ватар
орасидаги МАВ бурчак АВ ёйнинг ярмига тенг. АСВ бурчак
^ам ички чизилган бурчак булгани учун АВ ёйнинг ярмига
тенг. Демак:
^МАВ = /. /.МАР = у + а, AM =---------
2 cos у
83
(АМВ учбурчакда). Худди шунга ухшаш
ANCB - a, Z.NCP -у+а, CN - ---------эканини курсатиш
2 cos о-
мумкин. Булардан ташкари, AP=ccosd, PC=acos/. Шундай
1$илиб, АРМ ва CPN учбурчакларда Z.MAP = A.NCP ва
АР СР „
~уГ7 - "ДТ ~ 2 cos a cos/. Демак, VAPM со yCPN. Бундан
келиб чи^адики, Z.MPB = ANPB
Шуни исбот з^илиш талаб ^илинган эди.
19. Курсатма: томонлари а, Ь.
с булган учбурчакнинг юзини S
деб, Герои формуласидан
фойдаланинг.
20. б) ABCD туртбурчакнинг
юзини S билан, ABC, BCD, CDA,
DAB учбурчакларнинг юзларини
мос равишда b, с, d, а билан
белгилайлик. АМВ ва DKC учбурчакларнинг юзларини мос
равишда S, ваБ, деб, AKMD туртбурчакларнинг юзларини
эса мос равишда S3 ва S4 деб олайлик. » = булсин.
У ^олда = аа + (1 - a)b, S2 = ас + (1 - a)d,
S', = aS' + (1 - a)d. S4 - aS2 + (1 - a)b
S S 5*| S'-
ларни ^осил оламиз SKIM = ва siw = aQ
s s
лардан фойдаланиб, =a^~a^^s^S
„ O(l-o) „
ни топамиз: < -----
l-o + o-
o(l-o) „ j -X
kiak <тенгсизлик 11 -a + a' IS.S, < S,S,
1 - О + О ’ ' Г-12 3 4
тенгсизликка тенг кучлидир. S),S„S},S4 лар урнига уларнинг
84
a, b, c, d ортали ифодаланган ^ийматларни ^уйиб,
a(ab + cd-ac)+(\-a/b2 + d2 +bd-ad~bc)>0 тенгсизликни
^осил ^иламиз.
ab + cd > Sminla.c). ad + bc£Smax(b.d) = max(b.d)b2 +d~ < b: +d +bd
эканлигини эътиборга олган ^олда, ab+cd-cc>0 ва
b2+d2+bd>ad+bc ларнинг тугрилигини курсатиш етарли.
Агар б ^олда m=n=l булса, а шартнинг тугрилиги келиб
читали.
а
21 .Синуслар теоремасига кура: « =
ABD ва MNB учбурчаклар битта айланага ички чизилган,
MNB ва MNC учбураклар эса умумий MN томонга эга булгани
учун Z.MCN = Z.MBN эканини DB~DC=DA булганидан
Z.MAD = dMCD ва Z.DBN = Z.DCN, шунингдек,
Z.MAD = Z.MBD, булардан эса Z.MCN = Z.MBN :
экани келиб чи^ади.
22.Трапецияни ён томонлари кесишгунча давом ^илдирам из.
Уносил булган ADK тугри бурчакли учбурчакнинг медианасини
утказамиз. Трапециянинг асослари а ва b булиб, а>Ъ булсин.
ADK тугри бурчакли учбурчакда KN медианаси булгани учун
а-Ь
булади. Худди шундай, EF кесманинг узунлигини
а-Ь
^ам — га тенг эканини курсатиш мумкин.
85
23,а) курсатма: n=2Rsina, b=2Rsin/?, c=2Rsin / ва
sin( a + /3 )=sin Y формуладан фойдаланинг. Бу ерда R ташци
чизилган айлананинг радиуси;
Худди шундай: sinTr-~7= ва
' ' z 2-Jac
Sin — <---;=
2 2-jah
Шундай ф1либ:
. а . р . у
sm-— sin- sin — <
2 2
Демак, берилган ифоданинг энг катта ^иймати
га тенг
булиб,бунга у фаг;ат учбурчак тенг томонли булганда эришади.
24. Z.MCB = YLMAB, чунки бу
бурчаклар ички чизилган ва тенг
ёйларга мос бурчаклардир. Шунинг
учун МАС учбурчак тенг ёнли .
Демак, М ну^та АС кесманинг
уртасидан уткзилган перпендикулярда
ётар экан.
25. Курсатма: косинуслар теоремасидан ва учбурчак
бурчакларининг биссектрисаси хоссасидан фойдаланинг.
26. М ва N ну^талар ВС ва AD томонларнинг уртаси
булсин, МР кесма АВ га параллел ва МР=АВ. Худди шундай
MQ кесма CD га парраллел ва MQ=CD. ANP ва DNQ
86
учбурчакларни ^араймиз. Бу
учбурчакларда AN=ND, АР ва QD
кесмалар тенг ва параллел булгани
учун PN=NQ. Демак, MN кесма
MPQ учбурчакнинг медианасидир.
РК кесма MQ кесмага параллел булгани учун PK=MQ, яъни
MPKQ параллелограмм экан. Масаланинг шартига кура,
в
м
MN = -(АВ + CD), шунинг учун
MK=2MN=AB+CI>MP+-MQ=MPrPK.
Бундан Р, М ва К ну^таларнинг бир тугри чизи^да ётиши
келиб чи^ади. Бу эса АВ ва CD кесмалар узаро параллел
демакдир.
27. Учбурчакнинг мавжудлигини исботлашучун ю^оридаги
катталиклардан энг каттасини долган иккитасининг
йигиндисидан кичик эканини курсатиш етарли:
^4а2 +3 -а + 1 + Ja2 +а + I
Иккала томонни квадратга кутариб, ^уйидаги тенгсизликни
косил ^иламиз:
2а2 + 3 < 2у1ал + «2 +1
Бунинг \ам иккала томонини квадратга кутарамиз
4я4 + 4а2 +1 < 4«4 + 4«2 + 4
3>0 тугрилиги исботланди. Энди косинуслар теоремасидан
энг катта бурчакнинг косинусини топамиз:
2а2 +1 2а2+1
cos <р = —. I - = 1 • ;
2Уо2-<? +17а2+<? +1 2-vo4+«2+1
Сунгра шу бурчакнинг синусини топамиз:
7з
sm<р = —. ..-. —
2т/«4 + а‘ +1
Шундай килиб, учбурчакнинг юзи:
5 = —-Ja2 + a + lja2 -a + lsind> = ^-
2 4
87
28. Берилган тенгликнинг иккала томонини квадратга
кутариб, соддалаштиришдан кейин ушбу:
а _ b с
тенглик э^осил булиб, бундан 7г = ~ экани келиб чи^ади
"i и ci
Демак, АВС ва А^С, учбурчаклар ухшаш экан.
29. АВС учбурчакда АВ=с, ВС=о
булсин. АВС учбурчакнинг С учидан
тапир! чизилган айланага уткзилган уринма
АВ томонига перпендикуляр булсин.
Сунгра, ВМ=х, СМ=у, дейлик, АСМ ва
ВСМ учбурчаклар ухшаш (чунки улар тугри
бурчакли з^амда АСАМ = АВСМ) булгани
учун зууйидагиларга эга буламиз:
х у у х +с _ о2с abc
— = ~ ва —~ булардан Х~Т1 Т’ У~Т5 Т
a b a b Ь -с b -а
ВМС тугри бурчакли учбурчакдан х2+у2=а2 бунга х ва у
ларнинг ю^оридаги з^ийматларини ^уйсак:
а1 с ] ( abc Y _ 2
^2 _ci J _с2 J ~а з^осил булади ва ушбу ифода
(а2+Ъ2)с2=(Ъ2-с2)2 келиб чи^ади. Бу эса талаб ^илинган
богланишдир.
30. М, N, ва К ну^талар ABCD
* м в туртбурчакнинг АВ, CD ва ВС
томонларининг урталари булсин.
с ^-'2' -XZ \ Масала шартига кура, MN тугри
'iA чизи^ диагоналлари билан тенг
бурчаклар з^осил ^илади. МК ва
KN лар АВС ва BCD учбурчакларнинг урта чизицлари
булгани учун ю^оридаги шартдан AKMN = AKNM ва
KM=KN, демак, AC=BD уринли экан.
88
Зтг
31. Олдин АВКС + ADNC = — эканини курсатайлик. Агар
квадратнинг томонини бир бирликка тенг деб олиб:
В С
ctg(ABKC) = ВК = а,
ctg(ADNC) = DN = p
белгиласак, ушбуни ^осил ^иламиз:
а-р ВК-1)\\ л L . ' |
2а • Р = 2ВК DN = АК• AN = (1 - ВК)(\ -DN) = (1 -а)(А - Р\
{\-а)(\- Р) = 2а-р
Бундан: tg(ABKC + ADNC) = =
-\ + аР
Демак:
Зл-
ABLK ----ABKL = ADNC = АВСМ = АВАМ. Шунинг учун
4
AKLM -i АКАМ = я. Демак, А, К, L, М ну^талар битта
айланада ётар экан.
Худди шундай: Н, А, М, L ну^талар хам битта шу айланада
ётишини курсатиш мумкин.
ЛТАР
32. Курсатма: исталган учбурчакда ATOP = 90" +——
булади. А. Р. О ва Т ну^таларнинг битта айланада ётиш
шартидан: А ТАР + А ТОР - 180°
Бундан АА = 60° экани келиб чикади.
Жавоб: 60°
89
33. АЕ томонга перпендикуляр ва унинг уртасидан утувчи
текисликка нисбатан ABCDE ва AEKPL бешбурчаклар узаро
симметрия булади. Бундан DK=BL. Аммо BL=AD. Шундай
тршиб, D нуцта А ва К нукзалардан баравар узо^ликда ётади.
Аммо АЕ=ЕК булгани учун LE ± АК булиб ва АК нинг
уртасидан утувчи ва унга перпендикуляр булган текисликда
ётади. DE^AC булганидан эса АС±АК булади. Худди
шундай бош^а томонлар жуфтликларининг ^ам
перпендикулярлигини исбот ^илиш мумкин.
34. Курсатма: масаланинг шартидан ён ё^ларининг
баландликлари тенг. Демак, баландликларнинг асос
текислигидаги проекциялари .^ам тенг булади. Тетраэдр учининг
асос текислигига проекцияси эса асосга ички ёки таш^и
чизилган айлананинг маркази билан усма-уст тушади.
Агар Лл/3>а булса, жавоб: {b,b };
Агар Ь>0 булса, жавоб: ^,^2а2 +Ь2 };
Агар Ь>а-у[3 булса. жавоб: \jb2~-2az, ^jb2 -2а2 }
булади.
35. Курсатма: айланага битта ну^тадан утказилган
уринмаларнинг шу нуцтадан уриниш нуцтасигача булган
кесмаларнинг тенглигидан фойдаланинг.
D Ну^ани АВС учбурчакка ички чизилган айлананинг ВС
томонига уриниш ну^таси булишини исботлаш мумкин.
ВС + АВ-АС
Жавоб: -
2
36. EHF у чбурчак юзининг
ВРЕ ва CFQ учбурчаклар
юзларининг йивиндисига тенг
эканини исботлайлик.
BNC учбурчакнинг юзи
параллелограмм юзининг
ярмига тенг ва PBCQ тарпециянинг юзи хам параллелограмм
юзининг ярмига тенг булгани учун:
90
$ЕМ-' — Si™ +^BEF< ^(T()
Демак: SKNI, - Sт1.:
Шуни исботлаш талаб ^илинган эди. Энди BEFC
туртбурчакнинг юзи APEN ва FNDQ туртбурчаклар юзларининг
йигиндисига тенг эканини исботлаш керак:
8црн + + S<io ~ 2^ab,i> $
WO.'i •
SBEFC ~ APEN + ^NFQZ
булади.
Бу шарт ^ам исботланди.
37. Трапеция асослари а ва b булиб, уларга ёпишган
учбурчакларнинг баландликлари мос равишда ha ва hb булсин.
С a+b И, , с ahu е bh2
У ^олда 5 = ——(ha + hb).s, =—-,S, =-—
° _
Д AOD оо ВОС булгани учун
ни ю^оридаги формулаларга щ?ямиз.
а _
' десак, Л, = thb
_bt+b
—
2
)2^
2
S -_bt + th» -
*2 2
„ bb„ rz
5, = —- ; JS =
2
'S + JS =
'S
Масала исботланди.
91
ZT + Z01800.
38. А В C D Е бешбурчакда
ZA + ZC > 180° эканини исботлайлик.
Бунинг учун AD диагонални утказамиз,
у.\олда ABCD туртбурчакайланагаички
чизилган булгани учун
ZBAD + Z.C -180е булади. Аммо
ZBAE > ZBAD шунинг учун
39. Шундай пирамида мавжуд булсин деб фараз ^илайлик.
Агар пирамида ён ^ирраларининг узунликлари х, у, z ва асос
томонларини а, Ь, с деб олсак, г^уйидаги система ^осил булади:
Биринчиваиккинчитенгламаницушиб, 2х' + у' + г~ = а~ +Ь2
тенгламани, иккинчи ва туртинчи тенгламалардан 2х~ + с2 = с2
тенгламани .\осил ^иламиз. Охирги тенгликдан х~=0 экани келиб
чи^ади. Аммо масала шартига кура х мусбат сон булиши
керак. Бу эса масала шартига зид. Демак. ю^оридаги масалани
^аноатлантирувчи пирамида мавжуд эмас экан.
40. MNKL гуртбурчак AMDL, AMBN. BNCK, CKDL
параллелограммларнинг яримлари ва ABCD параллелограмм
юзларининг йигиндисига тенг. Шунинг учун:
41 .Тенгликнинг иккала томонини 3V ( V тетраэдр .\ажми)га
ЗЕ ЗЕ ЗЕ ЗЕ ЗЕ
купайтириб, ^'7Г + У+Т+7Г ни ^осил ^иламиз.
92
- ~Sr = -S,r формулага асосан юцоридаги тенгликнинг иккала
цисми цам тетраэдрнинг туда сиртини беради. (S -
тетраэдрнинг тула сирти, S, - ён ёгининг юзи).
42. Кубнинг циррасини х деб олиб, С f D
ва BfC диагоналларини царайлик.
В^ЦАрваСрЦВ^ булгани
учун A(CtD ва АВ(С текисликлар цам
узаро параллел булади. В,С ва C(D тугри
чизицлар ай цат тугри чизицлар булиб,
улар орасидаги масофа ва АВ,С
текислик орасидаги масофага тенг булиб, шартга кура, EF=P
булади. A j С, D ва АВ, С текисликлар BD диагоналга перпендикуляр
булгани учун Р масофа диагонал узунлиги билан D^.^D
пирамида баландлигининг узунлиги иккиланганининг айирмасига
1 X -v
тенг булади. Пирамида хажми -х’, A^D асосинингюзи
, у цолда пирамида баландлиги Щ
булади. Демак,
ВО,=лл/з. В='=яъни x = Р = №=3р’>/3
43. Тугри туртбурчакнинг юзи AMD ва ВМС
учбурчакларнинг юзидан 2 марта капа экани аниц. AD томонда
ВМС учбурчакка тенг учбурчак ясаймиз. Бунда AN-CM,
DN;BM у цолда:
5 = 2(.Уш/1+5,п„ )=25|„,п = 2.S'4W+2S,W. <AM I\+DXDM^
= AM CM + ИМ DM
Шуни исботлаш талаб цилинган эди.
93
44. О, Ор О2 берилган айланалар марказлари г, гр г, мос
равишда радиуслари булсин. О( ва О, лар мос равишда ОА ва
ОВ да ётади. У ^олда ОАВ, С^АС, О,ВС учбурчаклар тенг
ёнли ва улар ухшаш учбурчаклар булади. Бундан ОО,СО2
нинг параллелограмм экани келиб читали. Демак,
r=OA=OO +О, А=О,С+О, А=г2+г,
Масаланинг тескариси ^ам уринлидир.
Агарг=г+г, булса, АВ кесма, албатта, ички
айланаларнинг кесишиш нут^тасидан утади.
Исбот 1$илиш учун OOjCO,
параллелограмм ясаймиз. Унинг С ва О,
учлари АВваОВ кесмаларда ётади. О, АС
ва О ,ВС учбурчаклар тенг ёнли учбурчакка
ухшаш шунинг учун О С‘=О А=г демак, С ну^га марказли
айланага тегишли ва О,‘В=О,‘С‘=ОО|=ОА-О1А=г, бундан
О,‘=О, ва С‘ ну^та О, марказли айланага ^ам тегишли экан.
45. Z4 = 30° булсин (шартга кура) у ^олда:
АОСМ = АОСА - АМСА = 15°= АОАМ
(ёки ХАОС = ААМС = 120° )
Демак, А, М, О ну^талар битта
айланага тегишли.
Бундан АОМС = АОАС = 15° экани келиб
читали.
46. Исботни щгйидагича баён ^иламиз:
Уринманинг иккинчи айлана билан
уриниш нур^таси Е ва биринчи айлананинг
марказини О дейлик. AOD учбурчак тенг А
ёнли, шунинг учун Z ODA = Z OAD. OD
Р ЕА булгани учун Z DAE = Z ODA.
Булардан V DEA = V DC А (икки томони ва улар орасидаги
бурчак буйича).
Бундан Z DC А = Z DEA = 90° экани келиб читали. яъни DC
± АВ экан.
47. АВС учбурчакнинг AD ва BE медианаларининг кесишиш
нукталари М булиб, АМВ учбурчакнинг ?^ам AF ва ВК
медианиларини утказамиз. AF ва ВК ларнинг кесишиш нуь^таси
94
N булсин. BE ва AD медианалар кесишган с
М ну^та BE томонни 2:1 нисбатда булгани //
учун MF = ^-BM = MF уринли булади. L
KAMF < 90° булган учун А учдан BE /
кесмага туширилган перпендикулярнинг
асоси МВ нурда ётади.
Шунинг учун AF < АЕ (бу ерда тенглик ZAMB = 90°
булганда уринли булади) булганидан
2 2 1
AN =-AF<-AE = -AC.
3 3 3
Худди шундай: BN < - ВС булишини ^ам курсатиш мумкин.
3
Энди учбурчак теигсизлигини ф'ллаб, AC+ ВС> 3(AN + NB)>3AB
^осил ^иламиз.
48, Берилишига кура, АМС учбурчак д’
тугри бурчакли ва MN унинг медианаси / \
булгани учун MN = AN =NC. / \
Шартга кура, МК = KN = MN булгани
учун KN = MN - AN = NC. АКС учбурчакда / \
^ам KN медиана булиб, KN = AN = NC \/
булгани учун АКС бурчак тугри бурчакдир.
Демак, АВС учбурчакда АКбиссектриса баландлик ^амдир.
Бундан келиб чи^адики, АВС учбурчак тенг ёнли ва АК эса
медианадир, яъни ВК = КС.
Демак, МК кесма ВМС учбурчакнинг медианаси булади.
Шунинг учун ВС = 2МК = 2KN = АС. Шундай ^илиб, АВ = ВС
-АС. Шуни исботлаш талаб ^илинган эди.
49. О ну^та айлананинг маркази булсин. е
АВС учбурчак тугри бурчакли учбурчак
булгани учун О ну^та АВ гипотенузанинг
уртаси билан устма-уст тушади. 11 XX
NOK бурчак тугри бурчак, чунки ABC —ХС
учбурчакнинг урта чизиги NO ^аршисида ВС V'' XX—-чв
томонга параллел. ОК тугри чизиц ВОС тенг \ )
томонли учбурчакнинг баландлигини уз ичига
95
олади (ОК тугри чизи^ ВОС бурчакнинг биссектрисасидир).
Е, N ва О ну^талар унчалик ^ийин эмас. ^а^и^атан ^ам, ECO
ва ЕАО учбурчаклар битта катети ва гипотенузаси буйича узаро
тенг, шунта кура ЕОАЕС бурчакнинг биссектрисасидир. Иккинчи
томондан, АЕС учбурчак тенг ёнли. EN кесма ЛЕС учбурчакнинг
медианаси ва бир ва^тда биссектриса ^амдир. Шунинг учун
EN ва ЕО нурлар АЕС бурчакнинг биссектрисаси сифатида
устма-уст тушади. у.есо= /еао=90° булганидан А, Е, С ва О
ну^талар битта айланада ётади. Айланадаги узаро кесишувчи
ватарлар ^а^идаги теоремага асосан: .4Л= ENND (1)
Шу теоремани АС ва МК ватарларга ^ам ^улласак
AN NC = MN NK (2) ^амда (1) ва (2) муносабатлардан
ME NK = EN ND экани келиб читали.
Узаро кесишувчи ватарлар ^а^идаги теоремага - тескари
теоремага асосан М, К, Е ва О ну^талар ^ам битта айланада
ётади.
ЕМК ва ЕОК бурчаклар битта ёйни тортиб турган бурчаклар
(М, К, Е, О ну^талардан утувчи айланада) булгани учун узаро
тенг. Аммо Z.EOK - 90°, демак, АЕМК = 90°
50. MCN учбурчакнинг бурчакларини
Z.MCN = х, Z.CMN = у, Z.CNM = z деб белгилаб олайлик. У ^олда
х + у + z = 180°. АСМ ва BCN учбурчаклар тенг ёнли, Z АСМ
у, /- МСВ = z-x ва, демак, у + z - х = 90°
Jx + y + z = 180°
[у + z - х = 90 с
Биринчи тенгламадан /|\\
иккинчисини ^адлаб айириб, / / \
натижага эришамиз, яъни: / / \
2х = 90°, х = 45° / \ \
51. Фараз ^иламиз -----bf---£д_----------—
учбурчакларнинг юзлари п,
п+1, п+2, л+3 ларга тенг булсин. У ^олда АВСЕ) туртбурчакнинг
юзи 4л+6 га тенг булади. BCD учбурчакнинг юзи ЕСЕ учбурчак
юзининг турт бараварига тенг. Бундан:
96
$АН1> ~$АВСГ> ‘S'WP - + 6)
Arap ECF учбурчакнинг юзи курсатилган туртта учбурчаклар
юзларининг энг кичиги булса, тенглик уринли булади. Энди 6
цийматнинг 1<;абул ^илиниши мумкинлигини курсатайлик. Бунга
мисол ^илиб, асослари AD=6, ВС~4 ва баландлиги 2 га тенг
булган тенг ёнли трапецияни олиш мумкин (шаклдаги рацамлар
мос учбурчакларнинг юзларини билдиради).
ТЕСТЛАРДАН НАМУНАЛАР
(ечилишлари билан)
1. Йиринди 255 га тенг булиши учун 3 дан бошлаб нечта
кетма-кет то^ сонни ^ушиш керак?
А) 14 В) 13 С) 15 D) 16 Е) 17
Ечилиши. Бу масала арифметик прогрессияга тушади.
S =255, а=3, d=2
Sn = • п формуладан:
п2=2п-255=0
D=4+1020=1024, и, - —+_3? = 15
2
3 дан бошлаб, 15 та то^ натурал сонни т^ушиш керак.
Жавоб: С
2. Трапециянинг изи а2 дан орти^. Унинг урта чизири m
баландлигидан 4 марта катта. Трапециянинг урта чизирини
бахоланг.
А) /и = 2 |а| В) т <2 |а| С) т > 2 |«| D) ба^олаб булмайди.
Е) Тугри жавоб берилмаган
Ечилиши:
MN = т
се-7’
S>a2.
2 ">
„ т т т 7 т . , . .
S„,=m — = —• —>а'; —>\а т>2\а\
mi 44’4 2 1 1 11
98
Жавоб: С
3. 7 + 77 + ... + 777 + ... + 77777777 йигиндини ^исобланг.
А)86491746 В)864119746 С)86791446 D)8641947
Е) Тугри жавоб йуц.
Ечилиши
77777777
7777777
777777
77777
7777
777
77
Жавоб: В
4. Трапециянинг асослари а ва в (в > а). Бу трапеция урта
чизигининг диагоналлари орасида жойлашган фгсмини топинг.
(Ь-а) (b-а) (Ь1-а2) (Ь + а)
А) —, В) —, С) ——, D) —.
Е) Тугри жавоб йу^
Ечилиши. Бу ерда ВС = a, AD=e, в>0, KF - х деб
белгилаймиз. ABCD трапецияда CD ён томонга параллел BE
тугри чизи^ чизамиз.
У ^олда ED=a, С ва F ну^таларни туташтирамиз. АСЕ тугри
чизи^ утказамиз. Трапеция урта чизигининг хоссасига кура KF
кесма АСЕ учбурчакнинг урта чизигидир. АЕ = в-а,
„„ АЕ Ь-а
KF =-—;х = ;
2 2
Жавоб: А.
99
а нинг нечта цийматида
И+Ы = о’
х2 + у2 = 1
тенгламалар
системаси 4 та ечимга эга?
А) 2 В) 1 Е) О D) чексиз куп Е) тугри жавоб йуц
Ечилиши:
|х| + |_у| = а, х2 + у2 + 2 |ху| = а2
х2+у2 = 1. [х2+у2=1
ёки 2|х_р| = а -1, j2 = a-l. (а = 3 fa = 3
2 |ху| = (о - 1)(о +1). [Ы = ° +1 11*И = 4 1Л =У1=2-
х =1; у,=4, х3=4; у3=1
|2=о+1, (a = l. ja-1
I |ху| = o-l ||ху| = 0. [х = v = 0.
Демак, а нинг 2 та куийматида система 4 та ечимга эга.
Жавоб: А
6. 12' + 5'= 13' тенгламанинг нечта ечими бор?
А) 4 В) 2 С) ечими йуц: D) 3 Е) 1.
Жавоб: Битта ечими бор х = 2
Жавоб: Е
7. а + в + с < 0 ва ах2 + ex + с = 0 тенглама ^а^и^ий ечимга
эга эмас. а ва с ларнинг ишорасини топинг.
А) а <0. с < О В) а > 0, с< О С) а < 0, с > О D) я > О, О О
Ечилиши: а + в + с < 0, ах2 + вх + с = О, D = в2 - 4 ас, D < О
булиши керак. в2 < 4 ас, в2 > 0, 4 > 0 => а < 0, с <0. Жавоб: А
8. а нинг цандай цийматларида тенгламалар системаси
ечимга эга булади?
х2 + ах + 1=0
х2 + х +а = О
А) а = -1 В) а = 1 С) а = 2 D) а = -2
Ечилиши. Берилган тенгламалар системаси ечимга эга
булиши учун D = 0 булиши керак. Демак:
100
D = a2—4,
D = \-4a.
a2—4 = 0,
l-4cz = 0
a = ±2,
анинг бу
^ийматларини тенгламалар системасига цуйиб текшириб
курамиз:
1) а=2 да
2) а= -2 да
№ + 2х +1 = О,
X2 + х + 2 = О.
х2 - 2х +1 = О, х = 1
х2+х-2 = 0, х = 1,х = 2.
1 ч
3)
Булардан куриниб турибдики, фа^ат а = -2 булганда
тенгламалар системаси ечимга эга булди.
Жавоб: D
9. х: + рх + q = 0 тенгламанинг ечимларидан бири 1 + ва
р, q лар рационал сонлар булса, р ва q ни топинг.
А) р = 2 q = -2. В) р = -2 q = 2. С) р = 2 q = -2. D) р = 2, q
= 2
Ечилиши: х2 + рх + q = 0 тенгламада х, = I + >/з булса,
х,= 1 -у/з булади. У ^олда Виет теоремасига кура:
Х}+Х2= -р,
х, -х2 =q
экани дан:
101
\ + у[з + 1-у[з~~р, fp = -2
(1 + -7з^1 — л/з j = q. (g = —2.
Жавоб: A
10. Параллелограммнинг томонлари 46 см ва 22 см,
диагоналларининг нисбати эса 2:3 каби. Диагоиаллар
узунликларининг йигиндисини топинг.
А) 90 см В) 100 см С) ПО см D) 120 см
Ечилиши:
4х2 + 9х2=2 462 + 2 222
13 х2 = 5200, х2 = 400, х = 20
5 х = 5 20 = 100 см
Жавоб: В
11. Учбурчакнинг иккита баландлиги бу баландлик
туширилган томопдан кичик эмас. Учбурчак баландликларини
топинг.
А) 45°, 45°, 90° В) 30°, 60°, 90° С) 30°, 30°, 120° D) 60°, 60°, 60°
Ечилиши. Фараз ^и лай ли к, учбурчак ихтиёрий булсин:
а=Д+/, Д=180°-(а+/),/ = а+Д
/=а-180°+а+/,2а=180°; а-90с
Бундан учбурчакнинг тугри бурчакли экани келиб чикади.
Шартга кура, иккита баландлик ?$ам шу баландлик туширилган
томондан кичик эмаслигидан, учбурчакнинг тенг ёнли экани
келиб чикдди. Демак, учбурчакнинг бурчаклари 45°, 45°, 90 дан
иборат экан.
Жавоб: А
12. Текисликда ихтиёрий учтаси бир тугри чизи^да
ётмайдиган 101 та ну^танинг \ар бопща ну^талар билан бири
бирлаштирилган. Бу тугри чизшрзар сонини аницланг.
А) 5050 В) 5151 С) 5150 D) 5000
п(п-З)
Ечилиши. Масалани ечиш учун —-— формуладан
фойдаланамиз.
— (10П-3)+101 = 191^ + 101 =101 (49+0 = 5050.
2 2
102
Жавоб: А
13. Ра^амлари йигиндиси 25 га тенг булган ва 11 га
булинадиган нечта уч хонали сон бор?
А) 1 В) 2 С) 3 D) 4 Е) 5
Ечилиши: Ра^амлари йигиндиси 25 га тенг булган уч хонали
сондан олтитаси мавжуд булиб, 988, 898, 889, 799, 979, 997
булардан фа^ат 979 сони 11 га булинади.
Жавоб: А.
14. Координаталари х2 + (|у| -1)2 < I тенгсизликни
^аноатлантирувчи (х; у) нутдгалардан тузилган фигура юзини
топинг.
А) 2 л- В) л С) 1 D) я-х/2 Е) 4 л
Ечилиши: х2 + (У ± I)2 -1 • Бу радиуси R = 1, булган айлана
билан чегараланган дойра булиб, унинг юзи S = 2FIR-
формуладан 5 = 2/7 экани келиб чи^ади.
Жавоб: А.
„ п ’ -1 ,
15. п нинг нечта натурал ^ииматида —— ифоданинг
^иймати туб сон булади?
А) 1. В) 2. С) 3 D) 4 Е) чексиз куп
Ечилиши: +w+l.) ифода туб сон булиши учун
натурал сон булиши керак ва л - 1 = 7 булиши керак. Агар п -
1 7 булса, п - 1 = 7 к (каМ) булади ва суратдаги ифода мураккаб
сон булади. Шунга кура п = 8 булсагина масала шарти
бажарилади.
Жавоб: А.
16.Агар sin l°-sin 2°-sin 3°К sinl79°=c булса,
cos Г-cos 2°-cos 3°-К -cos 89° ни а ортали ифодаланг.
A) 71 -а В) a C) 71-«2 D) 4a E) a2
103
Ечилиши:
sinl° = sin (90°-89°) = cos89°
sin 2° = sin (90°-88°) = cos 88°
sin 89° = sin (90° - 89°) = cos 1 °.
sin 90° = I
sin 91 ° = cos 1 °
sin 179° = sin (90° + 89°) = cos 89°
>£осил булган ифодада тенгликнинг унг ва чап томонларини
^адма-^ад купайтириб sin Г • sin 2° sin 3°-К. sin 179°=
(cos l°-cos 2°-cos 3°-K cos89°)2o; cos 1°cos 2° cos 3°K cos89°=s/a
булишини топамиз.
Жавоб: D.
17. x2 + 4x + a = 0 тенгламанинг илдизлари x, ва x,, y2 + 8 у +
в = 0 тенгламанинг илдизлари yt ва у,. Агар ур хр у,, х,
арифметик прогрессия булса, у :\олда в - а ни топинг.
А) 4 В) 8 С) 12 D) 16 Е) 20
Ечилиши: у, х, у, х, арифметик прогрессияни ташкил
^илгани учун х,- х, 2d, х, = у( +d, у, = х, + d, у, = у( + 2d.
Энди биринчи тенгламадан Виет теоремасига кура:
х( + х, = м4, х, +х( + 2d = —4, х( + d = -2, у, = -2
Иккинчи тенгламадан Виет теоремасига кура
У, + У, = -8, у, + у, + 2d = -8, у, + d = -4, х, = 4
х, = -4 ва у = -2 эканидан у = 6 ва х, = 0 экани келиб чикади
(арифметик прогрессия булгани учун). У ^олда х, х, = а дан а =
0, у, у, = в дан в = 12 булади ва ушбу 6-0=12-0=12 жавобни
оламиз.
Жавоб: С.
18. 5 '=sin/rx тенгламани ечинг.
А) ±5 В) 0,5 С) -0,5 D) 0 Е) Ечимга эга эмас.
Ечилиши. Берилган тенглама ушбу:
104
5M = 1
- sin 7ГХ = 1
1 - 4х2 > 0 тенгламалар системасига тенг кучли. У ^олда:
5'"4х2 = 1
sin ЛХ = 1
х = 2k + — .kez.
2
2
х-2кл—;kez.
2
Охирги система к = 0 да ечимга эта.
Жавоб: В.
19. Урта чизири 5 га тенг булган тенг ёнли трапециянинг
диагоналлари асос билан 45° ли бурчак ташкил ^илади.
Трапециянинг юзини топинг.
А) 5 В) 10 С) 15 D) 20 Е) 25
Ечилиши. Тенг ёнли трапециянинг кичик асоси учидан капа
асосига туширилган баландлик катта асосни икки ^исмга
булади. Улардан каттаси трапециянинг урта чизигига тенг
булади. Агар трапеция диагоналлари асос билан 45° ли бурчак
^осил ь^илса (бу >^олда диагоналлар узаро перпендикуляр булади),
урта чизи^ трапециянинг баландлигига тенг булади. Шундай экан,
берилган тенг ёнли трапециянинг юзи:
5 = MN-h = MN-MN = 5-5 = 25.
Жавоб: Е.
2О. Тенг ёнли трапециянинг ён
томони ва кичик асоси 5 га,
баландлиги эса 4 га тенг.
Трапециянинг юзи 20 дан цанча
куп?
А) 19 В) 22 С) 18 D 24 Е) 12
Ечилиши: Шаклдан муло^аза юритиб, .S' = -4 = 16• 2 = 32
12 та куп эканини топамиз.
Жавоб: Е
105
МУСТАЦИЛ ЕЧИШ УЧУН
ТЕСТЛАРДАН НАМУНАЛАР
1. Тенгсизликни ечинг: (х2 + х + 1) < 1
А)(-оо;1) ВХ-оо;-1) C)(l; оо) D)0
\Ja
2. Агар а = п булса, “7=- ни ^исобланг.
1 5/7-3 6а - 5
А)- В)2я С) - D)—-—
а 6 3
3. Тенгламани ечинг:
ig*2 + !g*3 + Jg*4 + = 8
(1g х)2 (lg х)3 (1g х) 4
А)10-х/Г0~ В)2л/пГ С)10ч/2 D)3
4. а параметрнинг ^андай ^ийматларида тенглама ягона
мусбат ечимга эга булади?
А)1 В)2 С)3 D)4
5. ^исобланг:
.1 .1 .3
arcsin — + arcsm —= + arcsin —=
3 Зл/П V11
л л тс тс
А)? В)- О- О)-
6. '16^ сонлардан (1), (3,5), (7,9,11)... каби гуру^лар тузилган.
100-гуру,хдаги сонлар йигиндисини топинг.
А)9702998 В)922368 QIOOOOOO D)10000000
7. ^исобланг:
sin
4
7т . 4 Зтг . л 5тг
— + sm — + sin — + sin
8 8 8
1л
8
106
3 1 3
А)~ В)- О-
D)6,5
8. х2+тх + п — 0 тенгламани ечмасдан илдизлари
кубларининг йириндисини топинг.
А.)т(3п - т2) В)т(2т+п) С)т3+п3 D)m(m2-3n)
9. —— +---— + — +---1— - ? булса, sin2 2а ни
ctg~a surer cos’ а
топинг.
13 4 8
В) С) - D) 7
10. Тенг ёнли трапециянинг диагоналлари узаро
перпендикуляр ва урта чизиги к га тенг. Трапециянинг юзини
топинг.
А)2А B)3F С)к2 0)3/.
х2 + 2 _
11. а нинг кандай кийматида г~.; у - а тенгсизлик урин-
X X’ + 1
ли булади?
А)3 В)2 С)9 0)7
12. V2 + V5 + ^2-^5 = т айният булса, т ни топинг.
А)1 В)2 С)-2 D)4
I___
i3' (5-уЗ)5
махражни иррационалликдан фткаринг.
5 +7з А> 5 5 - 7з 5 + /з 5 + В) 5= С) 2? 0)--—
14. Касрнинг махражини иррационалликдан ^т^аринг:
_____1______
V 4 4- V6 + V9
А) - \[2 В) -1/9 С) V3 - 1 О) 1 - V3
И.'7
15.
1 1 1
~ +— + ~
х ху у
тенглама нечта бутун мусбат ечимга
эга?
А) 4 В) чексиз куп С)0 D) 1
16. а нинг^андай цийматларида х2 — 4х - log2 а — 0 тенг-
ламанинг илдизлари ^а1$иций булади?
А) [24; оо) В) [2 4; оо) С) (0; оо) D) 0
17. Агар а>Ь>0 ва a2+b2=6ab булса, lg(a + Б) - lg(a - b)
нимага тенг?
A)lg3 B)0,5Mlg2 C)lg4 D)0,5Mln2
18. | x | + | у | <100 тенгсизлик бутун сонларда нечта ечимга
эга?
А)19601 В)19701 С)19801 D)10
19. 3333+1 сонини 5 га булгандаги ^олдшрзи топинг.
А)4 В)2 QI ” D)3
20. 16л -34у= 7 тенглама бутун сонларда нечта ечимга эга?
А)2 В)3 С)4 6)5
куп^аддан квадрат ил-
диз чи^аринг.
, 1 2 1 1
А)Х'+—-4 В)х +— QX + --4 D)-2
Х~ X X
2 Х
22. У — lgx ' ctgx + cos функциянинг цийматлар со^а-
сини топинг.
А)(1; 2)0(2; 3) В)(2;3) 0(1; 2)0(2; 4] D)(l;3)
23. Агар х-’+/лх+/н-’+а=О тенгламанинг илдизлари а ва /?
булса, а2 afi + ft1 + а нинг ^ийматини топинг.
А)1 В)0 02 D)4
108
24. 30х4-17х’- 228х2+17х+30=0 тенгламанинг илдизлари
купайтмасини топинг.
А)2 В)-2 С)1 D)-l
25.
^акикий сонлар тупламида нечта илдизга тенг?
А)1 В)2 С)4 D)5
тенглама
26. Агар иккита соннинг айирмаси, квадратларининг айир-
маси, кубларининг айирмаси 1:3:7 каби нисбатда эканлиги маъ-
лум булса, шу сонларнинг урта арифметигини топинг.
27. Уч хонали сонни хоналари тескари тартибда ёзилса, 99
га камаяди. Ра^амлари йигиндиси 14 га тенг ва уртада турган
ра^ам долган ра^амлари йигиндисига тенг. Шу соннинг
ра^амлари купайтмасини топинг.
А)48 В)84 С)120 D)68
28. Соддалаштиринг:
1 1 1 1
log2 3 log| 3 log’ 3 log’ 3
A)101og,3 B)91og,3 Q101og32 D)91og32
29. Тенгламани ечинг: fn' . m3 . w5 . . w2r_| — n , бунда
in >1.
IgW. i--------- ,-------- /lg«
A)Vlg« QVlgwlgn D^Igw
109
30. п нинг ^андай ^а^и^ий ^ийматларида
х2 - гач-1
х2 + х +1
тенгсизлик х нинг барча ^ийматларида уринли булади?
А)-5< и <1 В) и >5
С)-5л<1 D)-5<n<-l
о/2 2ч / ч т + и
31. Хисобланг: S ~(т —п ) + (т + п) Ч +... Бун-
т - п
да: т- п > 1.
(т - и)2(т + п)
т — п — \
(т-п)(т + п)2
т — п — \
(т - п)(т + и)
D)---------;—
т + п +1
(т - п)(т + п)2
т-п+\
32. «Математика» сузидан нечта анаграмма тузиш мумкин?
А) 152200 В)151200 С) 152300 D) 150300
33. Тенгламалар системасининг ечими (х; у) булса, х : у ни
топинг.
log,. X 9
lx -у-х2
log4 у- logy(j-3x) = l
А)2 В)3 С)4 D)5
34. Vx - 2 + л/З-х > д/х-1 - л/б-х тенгсизлик нечта
бутун ечимга эга?
А)2 В)4 С)3 D)6
35. Агар х ~ ^7+ 5^2 ~ булса, х3 + 3 ' -14
нимага тенг?
ПО
А)0 В)1 С)2 D)3
36. Тенгламанинг илдизи 10 дан ^анча кам?
А)4 В)8 С)6
D)10
37. Тенгламанинг илдизлари йигиндисини топинг:
X
y + z
У z
--------------- х + у + 2
Х + Z + 1 х + у-1
А) 1,5 В)2,5 С)0,5 D)0,8
38. (/л - 1)(/и - 2)(т - 3)(т - 4) + 10 ифоданинг энг ки-
чик ^ийматини топинг.
А)5 В)4 С)0,5 D)9
39. К^авсларни очгандан сунг хосил булган кущаднинг ко-
эффициентлари йигиндисини топинг.
(7х7 -бх6 + 5х5 -4х4 + х’ - 2)2007
А)1 В)2 С)2007 D)2006
40. arctg — + arctg — = arctgx тенглама нечта ечимга эга?
2 л
А)2 В)3 С)4 D)5
41. Йигиндини ^исобланг:
lg(2rgl°) + lg(23#3°) + ... + lg(289Zg89°)
A)2 ’025 В) 21025 С) 24025 D) 22025
42. k нинг ^андай ^ийматларида x| X — 2к | -1 - к = 0 генг-
лама ягона ечимга эга булади?
А)[-0
1 г Л
~2
С)0
111
43. sin x = 0,001 тенглама [— я"; 5я] кесмада нечта ечимга
эга?
А)4 В)3 С)6 D)2
44. Соат 1700. Неча минутдан кейин соат курсаткичи минут
курсаткичи билан устма-уст тушади?
А)27 В)28 С)27,5 D)27,6
45. Агар 2Р -5А =20 ва 2х 5Г = 5000 булса, Р+К ни
топинг.
А)6 В)4 С)5 D)8
46. (0,027)°’<3) = х — 2,7 тенгламани ечинг.
А)4 В)3 С)5 D)8
47. nj3 - т-1 = 0 булса, щ1 нитопинг.
А) 2т2 + 2т +1 В) т +1 С) tn2 + 2т + 3
D)(w-1)2
48. Zg258° = т булса, c(g24° ни топинг.
т1 -1 т2 - 1
А)------- В)--------------C)2m D)5zn+1
4 т
49. 4юоо + д27 + сони тула квадрат буладиган т нинг
энг катта бутун ^ийматини топинг.
А) 1972 В) 1980 С)2006 D)2008
50.
, 2х >4-’
тенгсизликлар системасини каноатланти-
-5>х>10
рувчи бутун сонлар нечта?
А) 10 В)7 С)9
D)6
112
МУСТАВИЛ ЕЧИШ УЧУН БЕРИЛГАН ТЕСТ
НАМУНАСИНИНГ ЖАВОБЛАР КАЛИТИ
0 1 2 3 4 5 6 7 8 9
В с А D С С А А D
1 С В А С А С в В С А
2 D D А в С А А В С D
3 D А В с А А В с D А
4 В D В с В С в А D А
5 С
МУНДАРИЖА
СУЗ БОШИ...............................3
АЛГЕБРАИК МАСАЛАЛАР....................5
ГЕОМЕТРИК МАСАЛАЛАР...................21
ЖАВОБ ВАКУ PC АТМАЛАР ............... 28
ГЕОМЕТРИК МАСАЛАЛАР: ЖАВОБ В А КУРСАТМАЛАР 75
ТЕСТЛАРДАН НАМУНАЛАР..................98
МУСТАКДИ ЕЧИШ УЧУН
ТЕСТЛАРДАН НАМУНАЛАР.................106
МУ СТАВИЛ ЕЧИШ УЧУН БЕРИЛГАН ТЕСТ
НАМУНАСИНИНГ ЖАВОБЛАР КАЛИГИ ........113
Умид ИСМОИЛОВ
МАТЕМАТИКАДАН
ОЛИМПИАДА МАСАЛАЛАРИ
Му^аррир
Гав^ар Мирзаева
Бадиий му\аррир
Ба^риддин Бозоров
Техник му^аррир
Елена Демченко
Мусах^и^
Ил^ом Цосимов
Са^ифаловчя
Андреи Маточенко
Оригинал макет “El-Press" МЧЖда тайёрлапди
Босишга 21.05.2007 й.да рухсат этилди.
Гарнитура Times Uzb 95 Бичими 84х 108 1 /32.
Босматобоги 3,625. Шартли босма тобоги 6,09.
Адади 2000 нусха. Буюргма № 141
Бахоси келишилган нархда.
«Янги аср авлоди» нашриёт-матбаа марказида тайёрланди.
«Ёшлар матбуоти» босмахонасида босилди.
700113. Тошкент, Чилонзор -8, Кат о pro л кучаси, 60.
Мурожаат учун телефонлар:
Нашрбулими: 278-36-89; маркетинг булими' 128-78-43
Факс: 173-00-14: e-mail: vangiasravlodi^mail.ru
УМИД КАРИМОВИЧ исмоилов
Математикадан «Нестандарт
масала ларни ечиш» ва «Олий
У КУ в юрт ларига кирувчилар учун
математикадан кУлланма» мето-
дик кулланмалари муаллисри,
Узбекистан Республикаси халк таъ-
лими аълочиси.
Халк таълимини ривожланти-
риш ва математика сранини Укитиш
методикаси буйича матбуотда
куплаб илмий-методик маколала-
ри чоп килинган. 2006 йилда лотин
алисрбосида «Эртакларда мате
матика», « Математик жумбок-
лар», «Уйнаб топ ва уйлаб топ»
китоблари нашр этилди.
ISBN 978-9943-08-108-6