Методологические основы внешнего проектирования целенаправленных процессов и целеустремленных систем - Петухов Г.Б., Якунин В.И.

1.2. Основные принципы исследования операций и теории эффективности целенаправленных процессов
1.2.3. Общая характеристика элементов операционного комплекса
Глава 2. Методологические основы теории эффективности целенаправленных процессов
2.2.2. Критерии оценивания качества объектов
2.3. Основные принципы исследования эффективности целенаправленных процессов
2.3.2. Показатели качества результатов операции
2.3.3. Показатель эффективности операции
2.3.4. Схема оценивания эффективности операции
2.3.5. Задачи исследования эффективности операций
2.5. Постановка задачи исследования качества ЦУТС
2.6. О принципах выбора показателей результативности ЦНПФС и формулирования целей операций
3.1.2. Законы распределения стохастических супериндикаторов
3.1.3. Квантили распределений стохастических супериндикаторов
3.1.4. Числовые характеристики стохастических супериндикаторов
3.2. Математическая формулировка задачи оценивания эффективности целенаправленного процесса
3.2.2. Гарантируемая вероятность достижения цели операции
3.3. Методы свёртывания векторных показателей качества результатов целенаправленных процессов
3.4. Методы вычисления показателей эффективности целенаправленных процессов
3.4.2. Метод статистического имитационного моделирования
3.4.3. Анализ схем имитационных испытаний
3.5. О вырожденных задачах оценивания эффективности целенаправленных процессов
Глава 4. Методы исследования эффективности целенаправленных процессов
4.1.2. Характеристики чувствительности показателей эффективности операции
4.1.3. Характеристики влияния параметров моделей ЦУТС и ЦНПФС на эффективность операции
4.1.4. О неформальном анализе эффективности операции
4.2. Методы синтеза эффективных целенаправленных процессов
4.2.2. Формулировка задачи синтеза операционной системы по критерию оптимальности
4.2.3. 0 приближённом синтезе операционной системы
4.3.2. О корректности постановки задачи оптимального синтеза операционной системы
4.4. Об экономическом анализе ЦУТС и ЦНПФС
4.4.2. Структура экономических затрат на программу
Глава 5. Методы построения математических моделей элементов операционного комплекса
5.2. Схема построения моделей элементов операционного комплекса
5.2.2. Структурная схема вероятностных моделей элементов операционного комплекса
5.3.2. Классификация операционных ресурсов
5.3.4. Основные свойства моделей операционных функционалов и общая схема их построения
5.4. Методы построения математических моделей показателей качества результатов целенаправленного процесса
5.4.2. Методика построения математической модели показателя виртуального качества результатов операции
5.4.3. Методика построения математической модели показателя требуемого качества результатов операции
6.1.2. Построение агрегированной математической модели операционной системы
6.1.4. Анализ эффективности ЦНПФС и качества ЦУТС
6.1.5. Синтез эффективного ЦНПФС и качественной ЦУТС
6.2. Нелинейные функционально-стохастические модели непрерывных целенаправленных процессов
6.2.2. Функционально-стохастическая модель непрерывного директивного ЦНП
6.2.3. Функционально-стохастическая модель непрерывного нормативно-директивного ЦНП
6.3. Функционально-стохастическая модель циклического целенаправленного процесса
6.3.2. Построение агрегированной математической модели операционной системы
Глава 7. Специализированные модели целенаправленных процессов
7.2. Постановка задачи исследования эффективности Т-процессов массового обслуживания
7.2.2. Показатели эффективности ОПМО и математическая формулировка задачи его анализа
7.2.3. Методы определения закона обслуживания
7.2.4. Методы определения закона обслуженности
7.2.5. О методах решения задач оптимального синтеза КМО и ОПМО
7.2.6. О характеристиках оперативности ОПМО
7.2.7. Об экспертном оценивании оперативности ОПМО
7.3. Определение и классификация моделей циклических ОПМО
7.3.3. Математическая формулировка задач исследования ЦОПО
7.3.4. Классификация моделей ЦОПО и задач его синтеза
7.4. Модель процесса функционирования восстанавливаемой ЦУТС
7.4.2. Построение агрегированной математической модели ЦОПО
7.4.4. Анализ эффективности ЦНПФС и качества ЦУТС
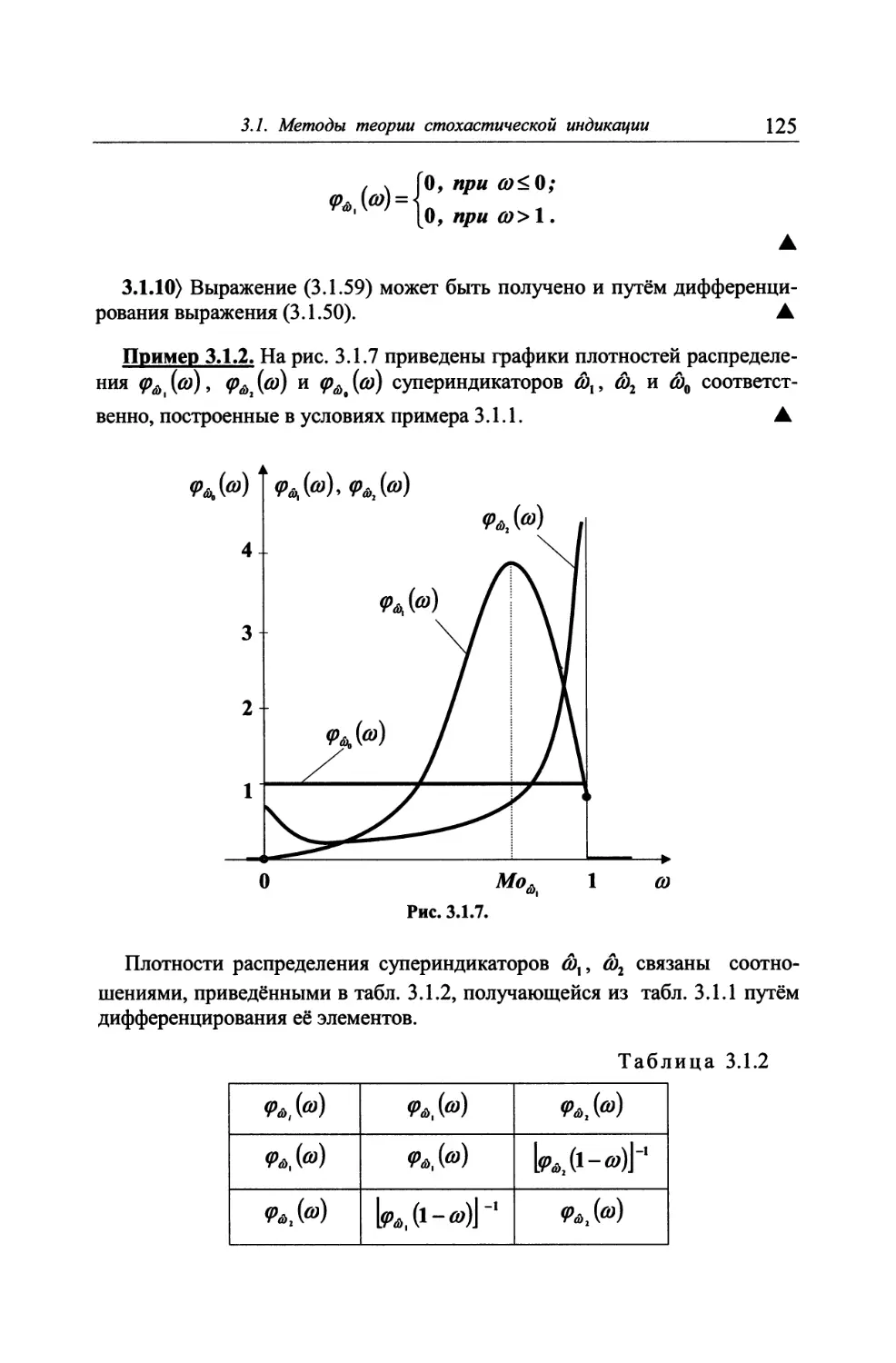
Автор: Петухов Г.Б. Якунин В.И.
Теги: исследование операций кибернетика монография методология исследования концепция цнп-операции
ISBN: 5-17-034652-2
Год: 2006
Похожие
Основы исследования операций в военной технике
Основы проектирования интегральных схем и систем
Принятие решений на основе нечетких моделей. Примеры использования
Информатика и программирование. Основы информатики
Текст
                    Г.Б. ПЕТУХОВ, В.И. ЯКУНИН
МЕТОДОЛОГИЧЕСКИЕ ОСНОВЫ
ВНЕШНЕГО ПРОЕКТИРОВАНИЯ
ЦЕЛЕНАПРАВЛЕННЫХ ПРОЦЕССОВ
И ЦЕЛЕУСТРЕМЛЁННЫХ СИСТЕМ
*С1
ИЗДАТЕЛЬСТВО
МОСКВА
2006

УДК 519.8(075.8)
ББК 32.817
П29
Авторы:
заслуженный деятель науки Российской Федерации,
доктор технических наук,
профессор Петухов Георгий Борисович;
кандидат технических наук, доцент
Якунин Владимир Иванович.
Рецензенты:
доктор технических наук, профессор В.В. Панов;
доктор технических наук, профессор В.К. Дедков
Петухов, Г.Б., Якунин, В.И.
П29 Методологические основы внешнего проектирования целенаправленных
процессов и целеустремленных систем / Г.Б. Петухов, В.И. Якунин.—М:
ACT, 2006. —504 с.
ISBN 5-17-034652-2
В монографии дается последовательное и полное освещение основополагающих
концепций, методологии и методов комплексного (системного) исследования эффектив-
ности целенаправленных процессов (ЦНП-операций) любой природы, а также методов
и методик анализа и оптимального синтеза целеустремленных технических систем
(ЦУТС) и процессов их целевого функционирования (ЦНПФС) на этапах их внешнего
проектирования (ВНЕПР).
Монография предназначена для научных сотрудников и системных инженеров
(системотехников), деятельность которых связана с проблемами исследования качества
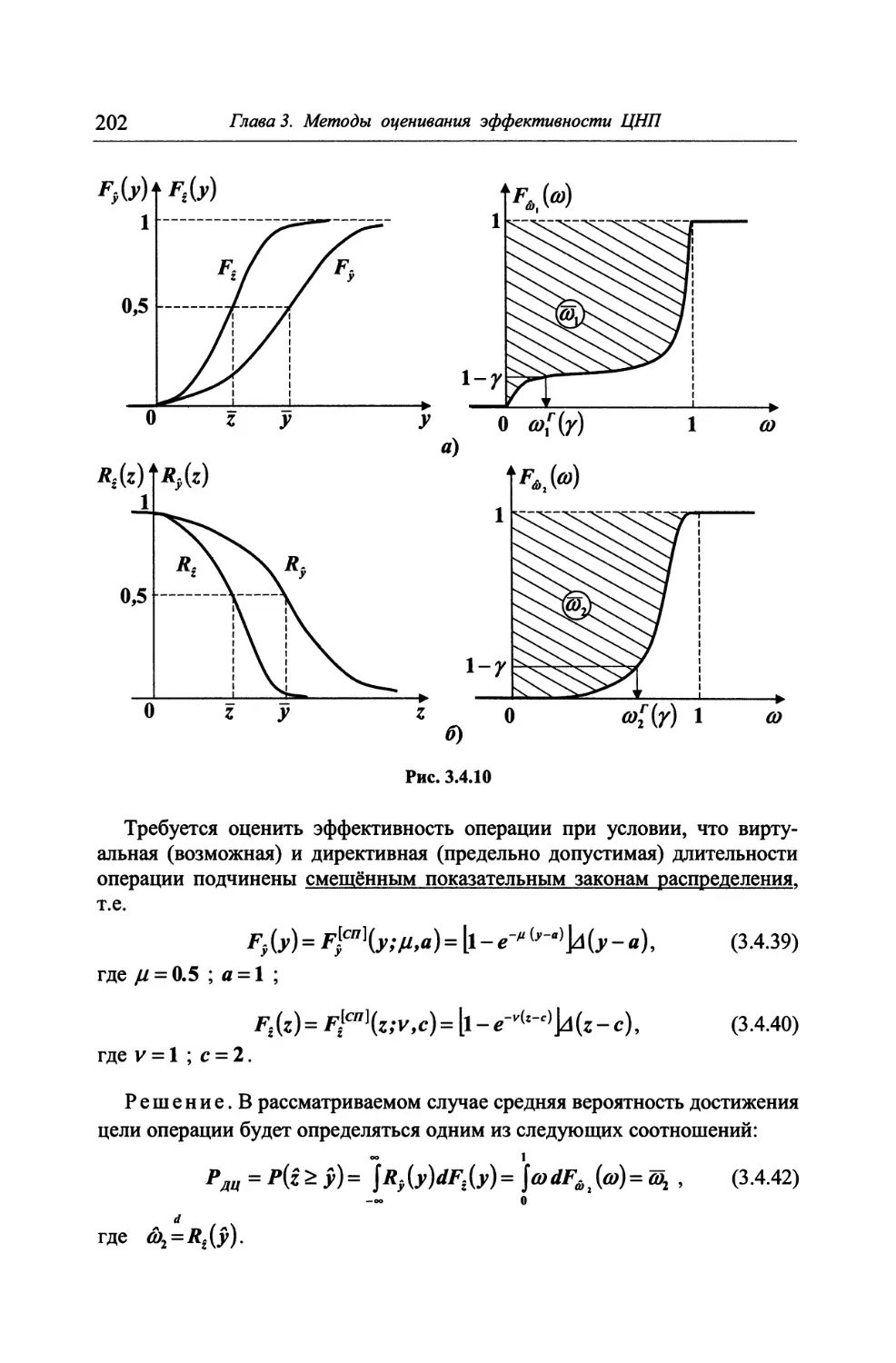
ЦУТС и эффективности ЦНПФС, а также для студентов и преподавателей ВТУЗов.
УДК 519.8(075.8)
ББК 32.817
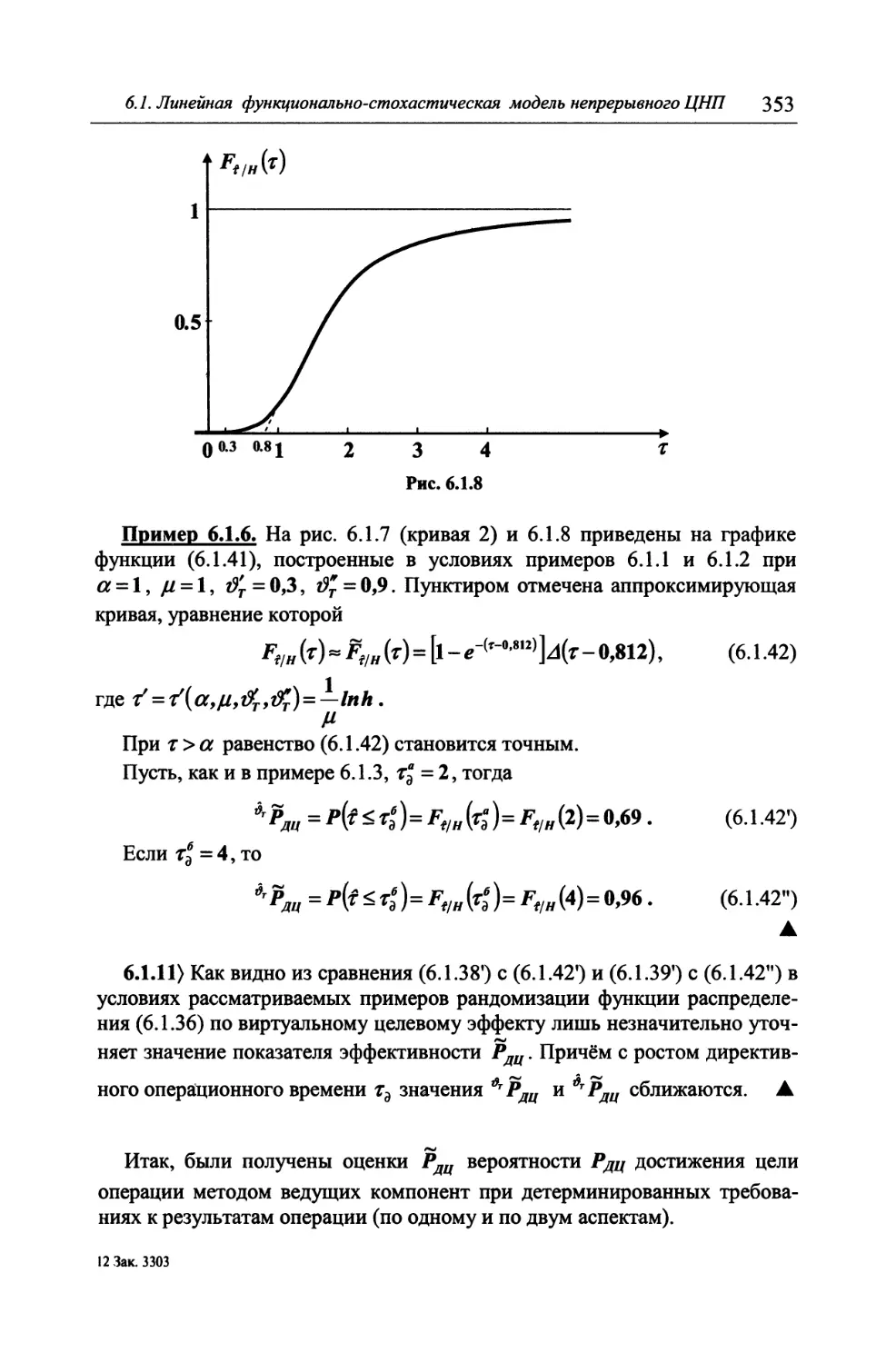
ISBN 985-13-5638-7
(ООО «Харвесг»)
© Петухов Г.Б., Якунин В.И., 2004
© Оформление.
ООО «Издательство ACT», 2006

ОГЛАВЛЕНИЕ
Предисловие 8
Введение 11
Раздел I. МЕТОДОЛОГИЯ
Глава 1. Концептуальные основы системных исследований
1.1. Системный подход и системные направления в науке 21
1.2. Основные принципы исследования операций и теории эффек-
тивности целенаправленных процессов 27
1.2.1. Основные понятия 27
1.2.2. Терминология 30
1.2.3. Общая характеристика элементов операционного ком-
плекса 33
1.3. Комментарии 38
Глава 2. Методологические основы теории эффективности
целенаправленных процессов
2.1. Семантические аспекты теории эффективности 40
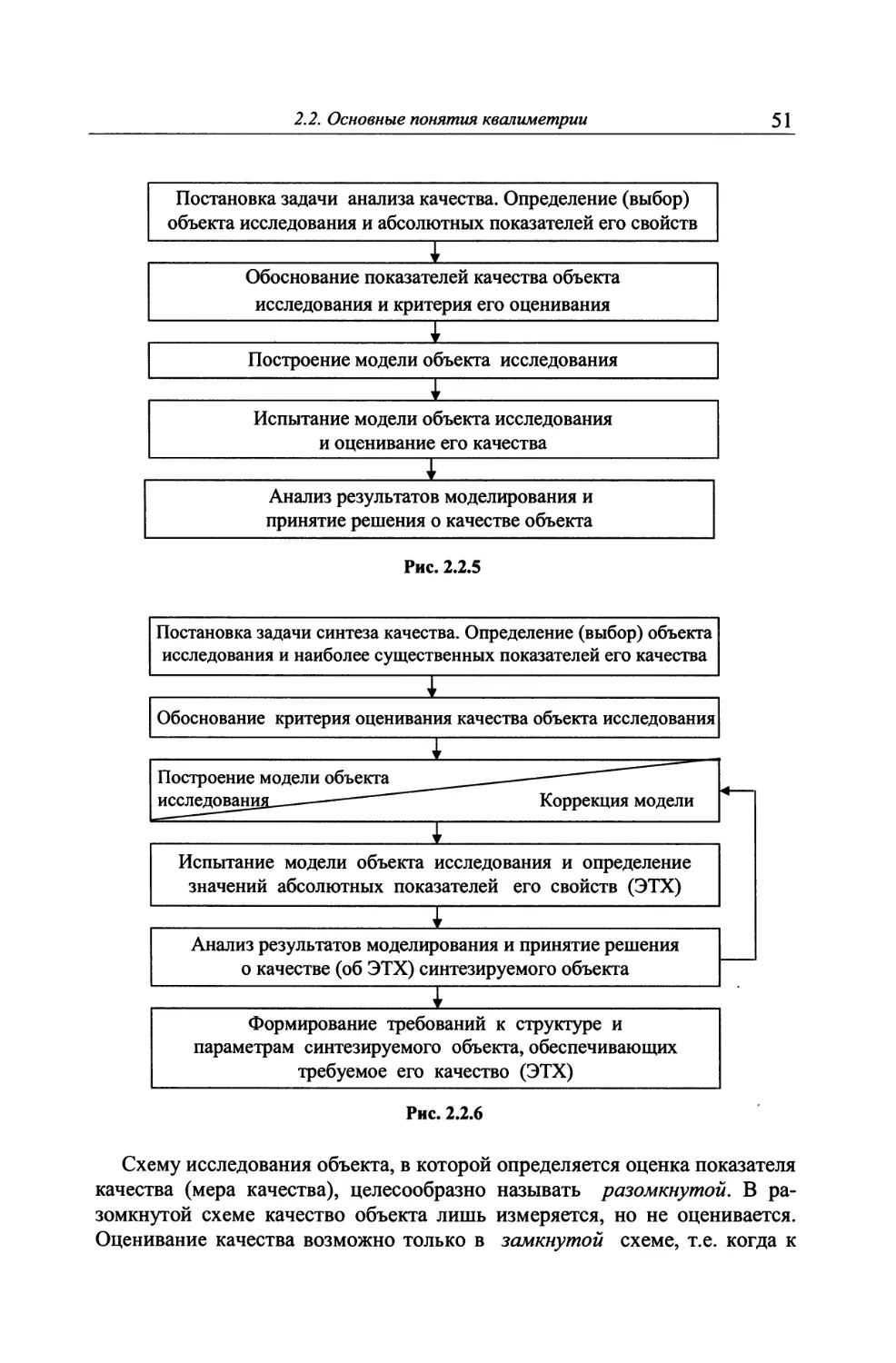
2.2. Основные понятия квалиметрии 42
2.2.1. Основные принципы и концепции квалиметрии 42
2.2.2. Критерии оценивания качества объектов 44
2.2.3. К проблеме оценивания 50
2.3. Основные принципы исследования эффективности целена-
правленных процессов 56
2.3.1. Общие предпосылки 56
2.3.2. Показатели качества результатов операции 58
2.3.3. Показатель эффективности операции 62
2.3.4. Схема оценивания эффективности операции 66
2.3.5. Задачи исследования эффективности операций 69
2.4. Целевые и критериальные функции 71
2.5. Постановка задачи исследования качества ЦУТС 78
2.6. О принципах выбора показателей результативности ЦНПФС и
формулирования целей операций 82
2.6.1. Классификация показателей результативности операций . 82
2.6.2. О формулировании целей операций 84
2.7. Комментарии 88

4
Оглавление
Раздел II. МЕТОДЫ
Глава 3. Методы оценивания эффективности
целенаправленных процессов
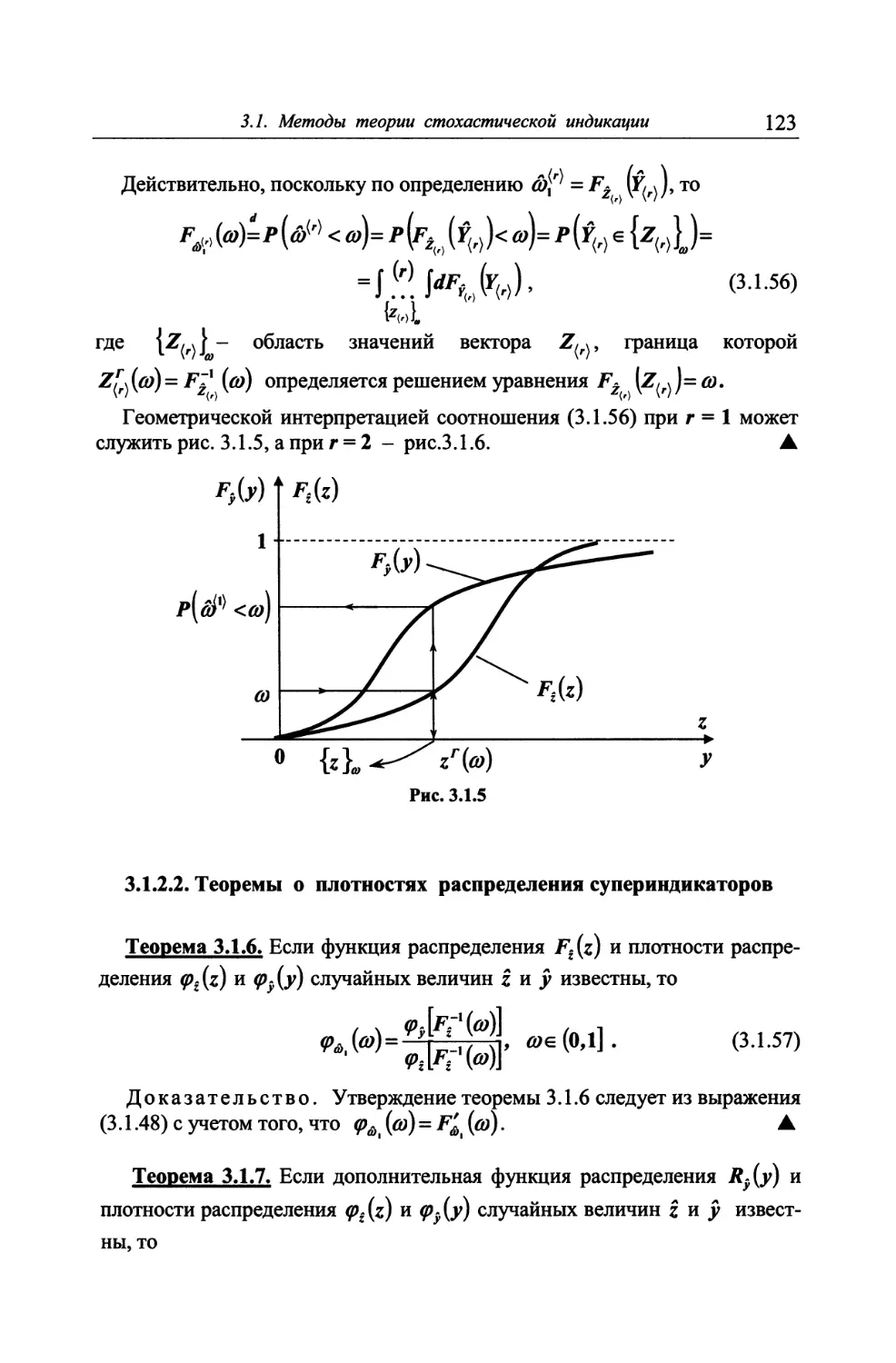
3.1. Методы теории стохастической индикации 102
3.1.1. Семантические аспекты теории стохастической индика-
ции. Терминология и символика 104
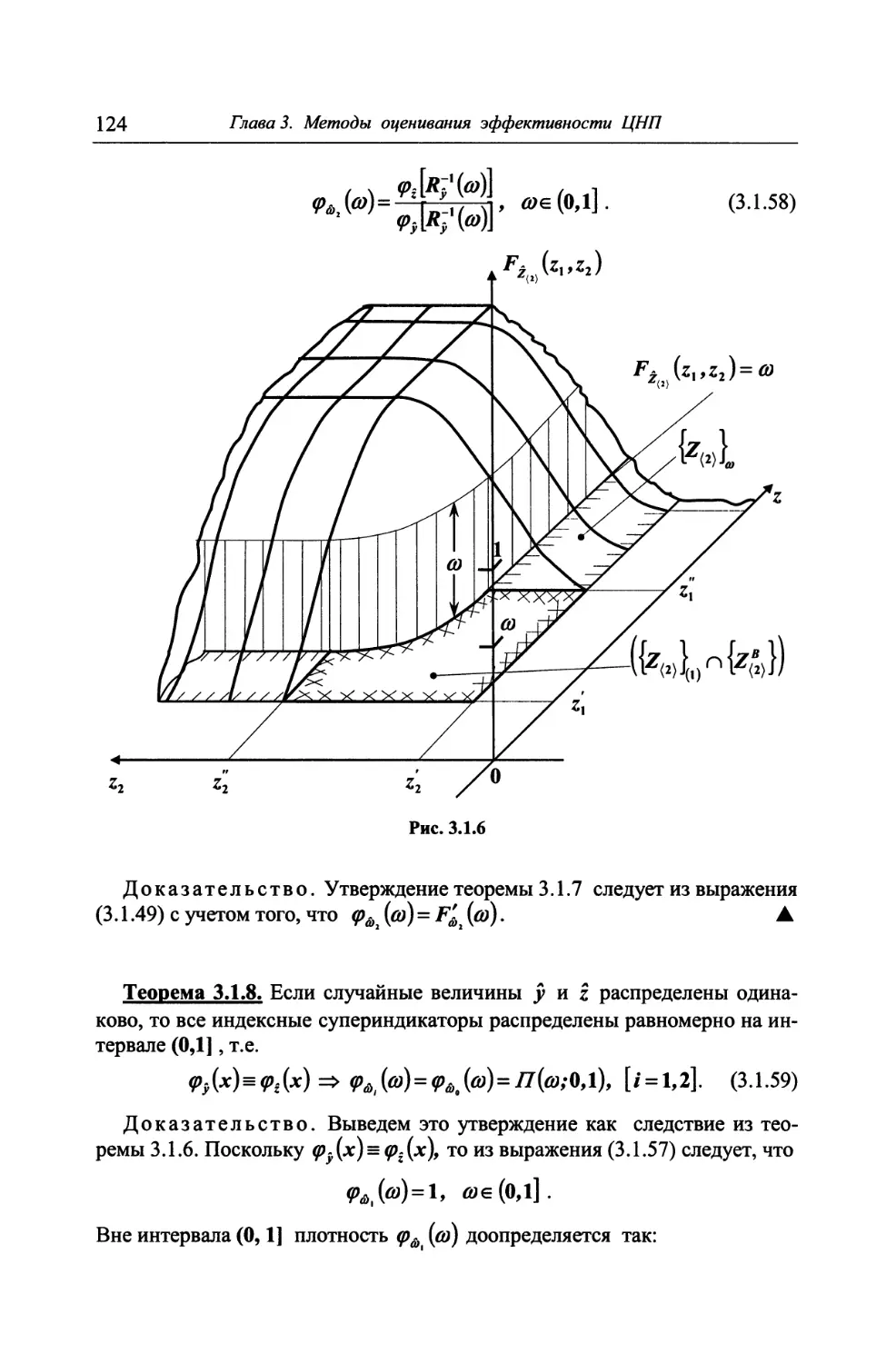
3.1.2. Законы распределения стохастических супериндикаторов 117
3.1.3. Квантили распределений стохастических супериндикато-
ров 128
3.1.4. Числовые характеристики стохастических супериндика-
торов 132
3.2. Математическая формулировка задачи оценивания эффектив-
ности целенаправленного процесса 138
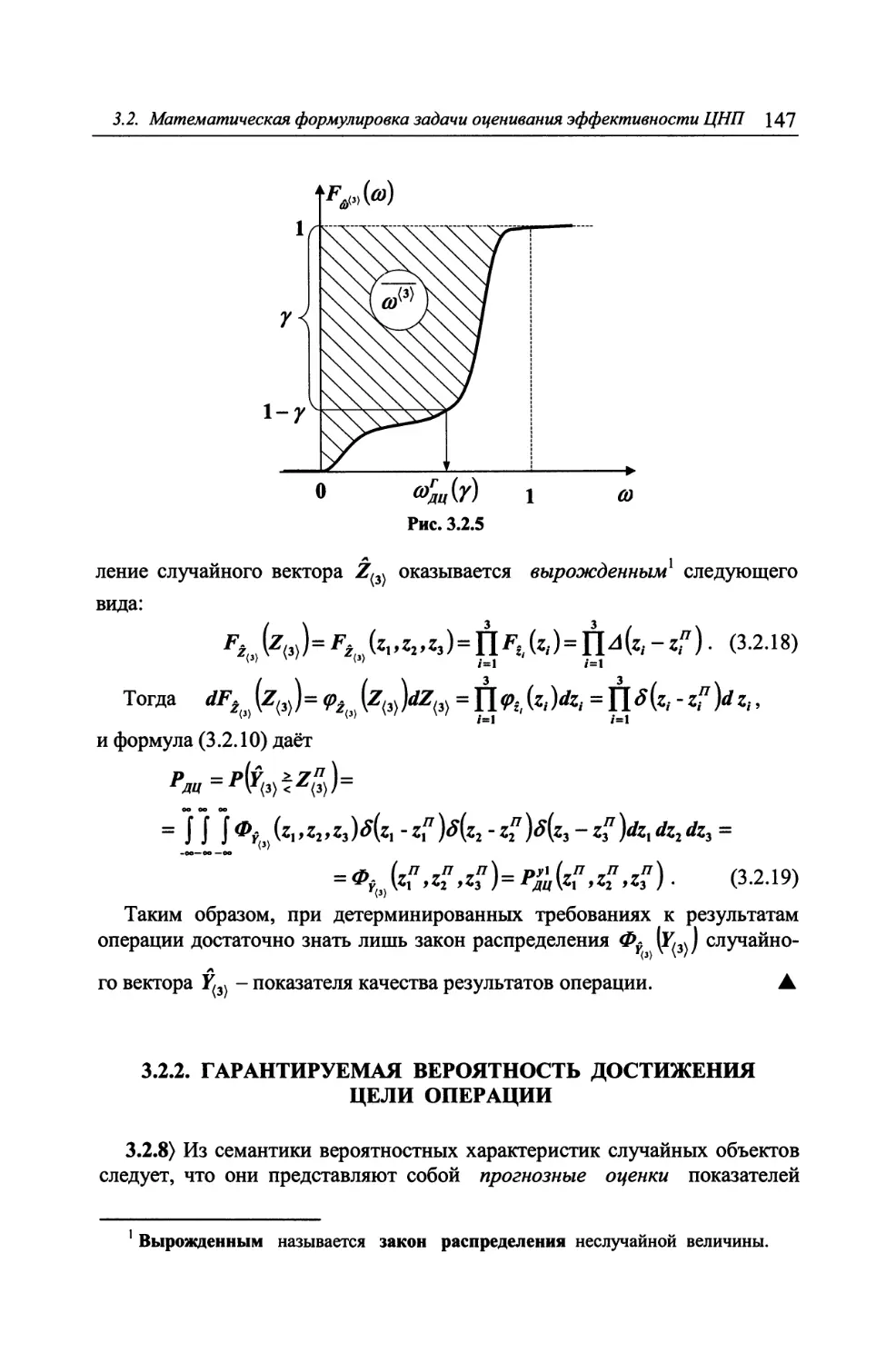
3.2.1. Средняя вероятность достижения цели операции 140
3.2.2. Гарантируемая вероятность достижения цели операции ... 147
3.3. Методы свёртывания векторных показателей качества резуль-
татов целенаправленных процессов 151
3.3.1. Состояние вопроса 151
3.3.2. Метод главной компоненты 157
3.3.3. Метод ведущих компонент 159
3.3.4. Эффект поглощения 165
3.4. Методы вычисления показателей эффективности целенаправ-
ленных процессов 175
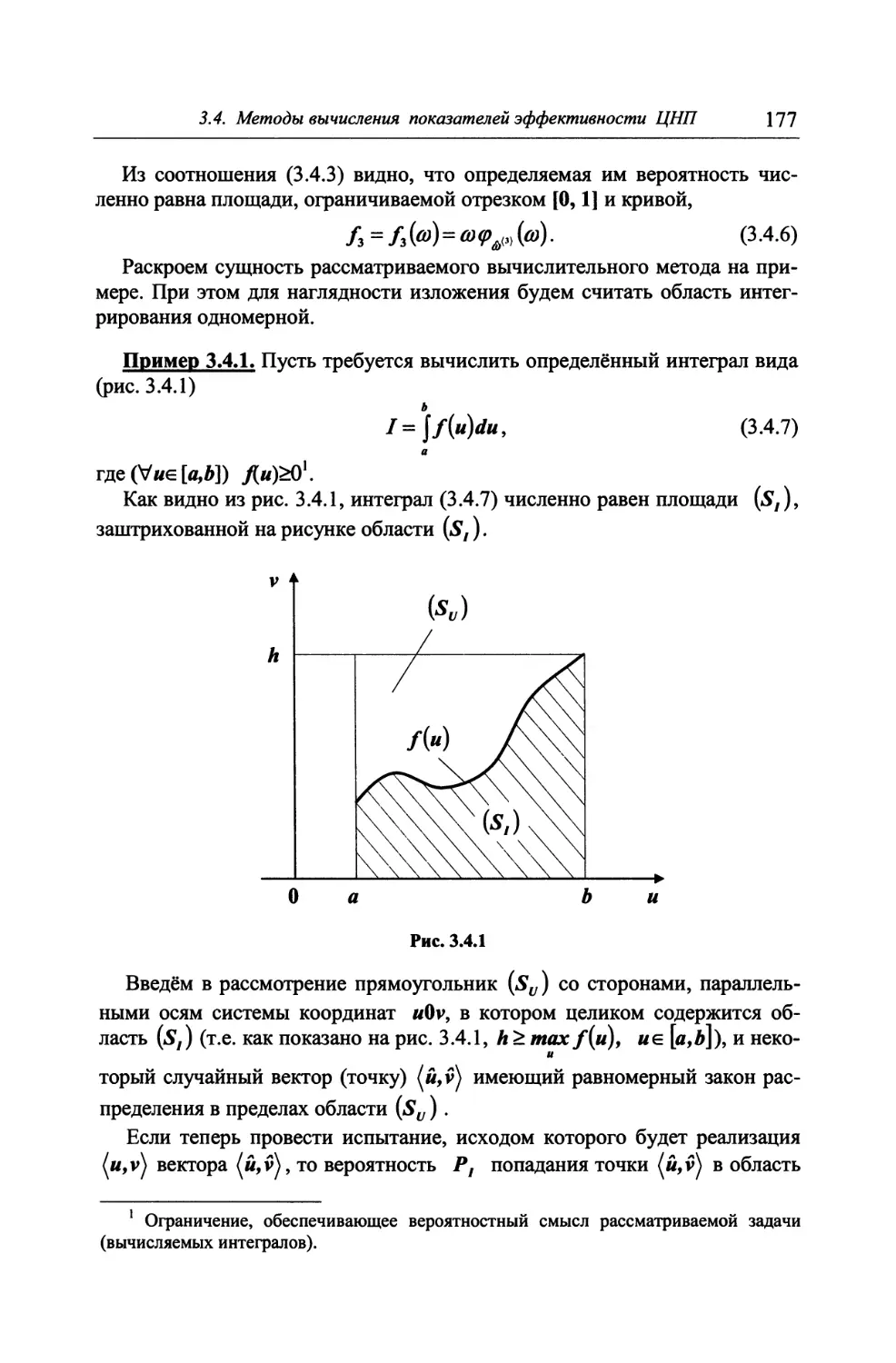
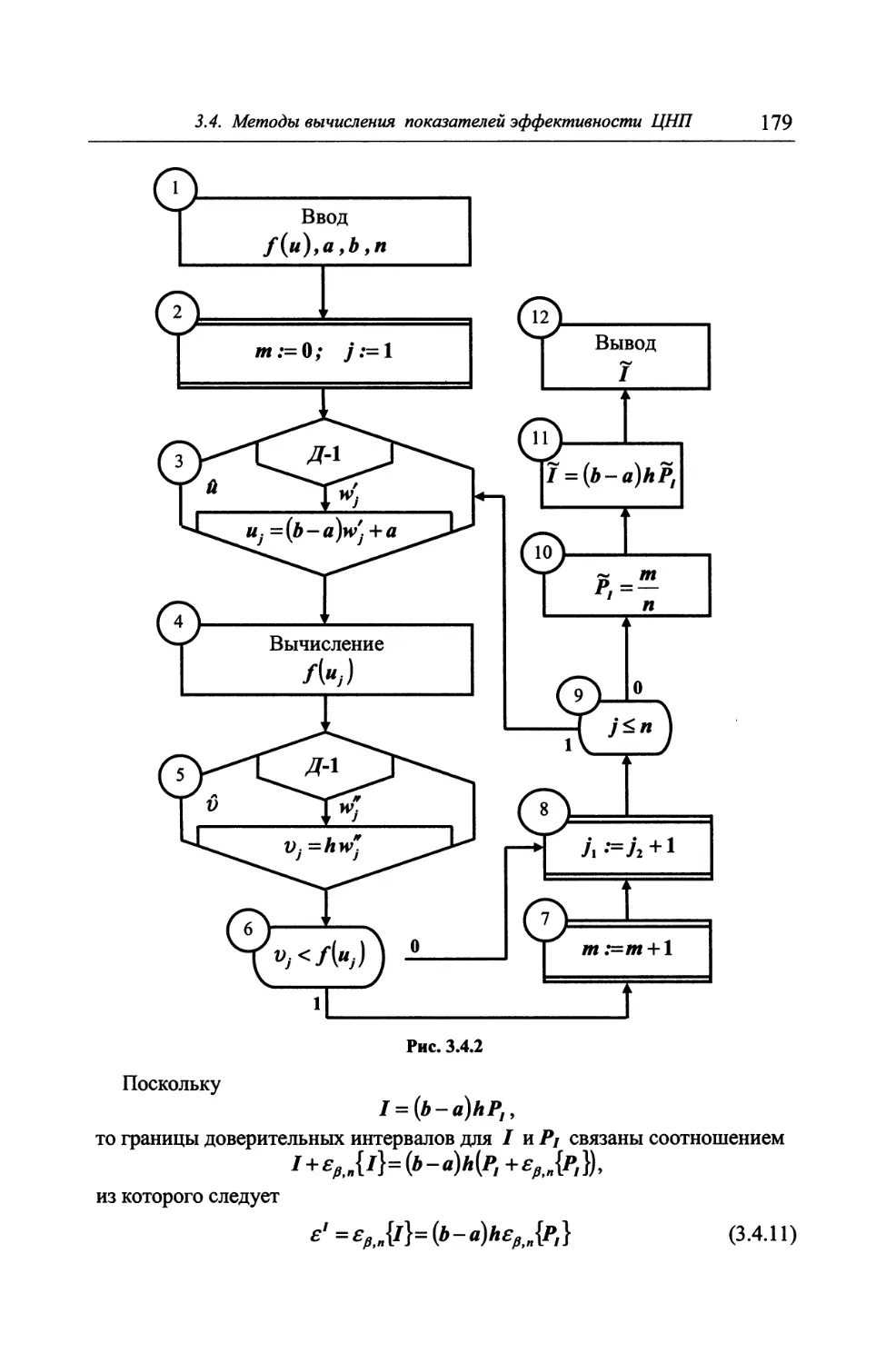
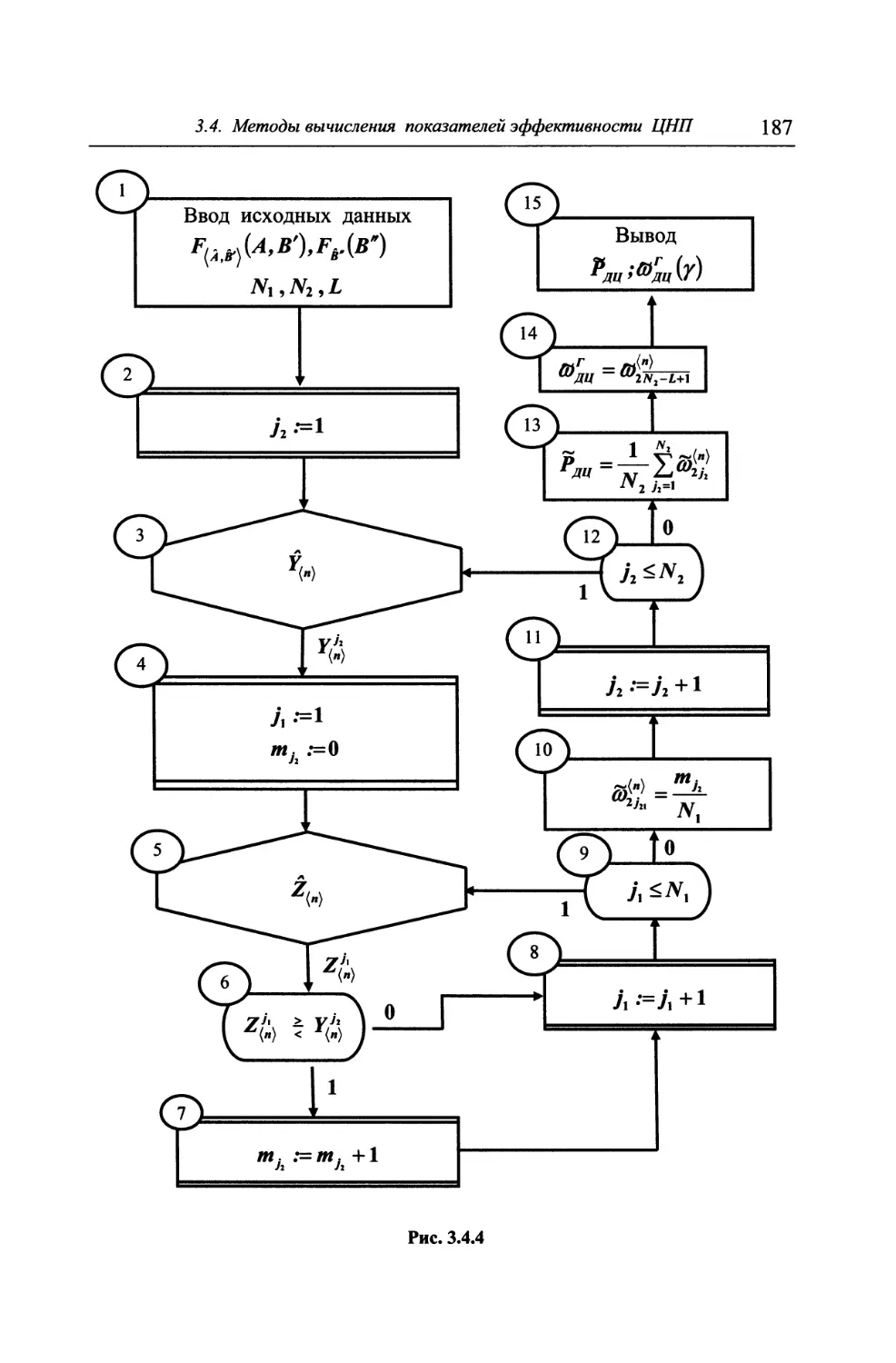
3.4.1. Аналитические и численные методы 175
3.4.2. Метод статистического имитационного моделирования ... 181
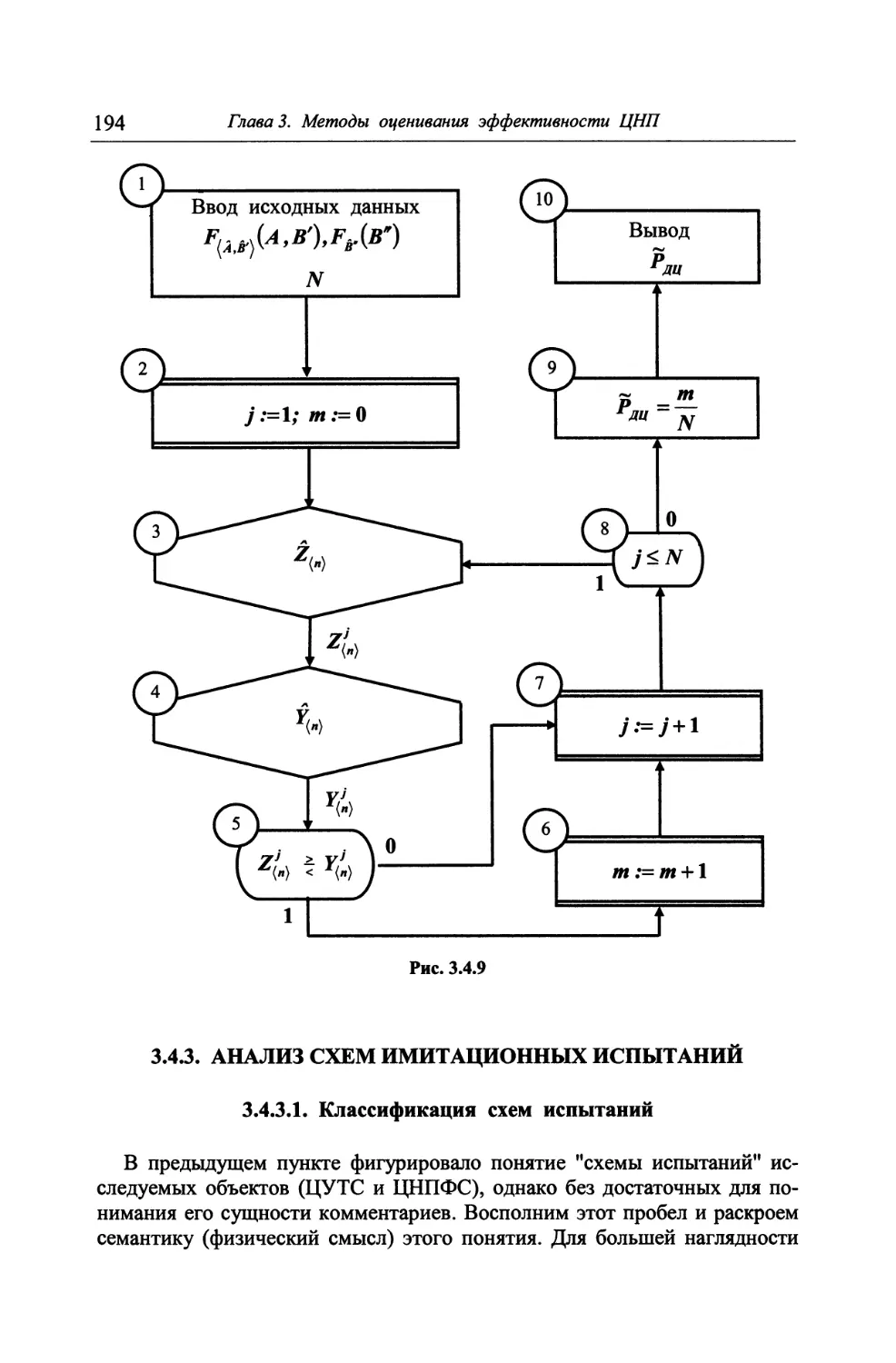
3.4.3. Анализ схем имитационных испытаний 194
3.5. О вырожденных задачах оценивания эффективности целена-
правленных процессов 205
3.6. Комментарии 219
Глава 4. Методы исследования эффективности
целенаправленных процессов
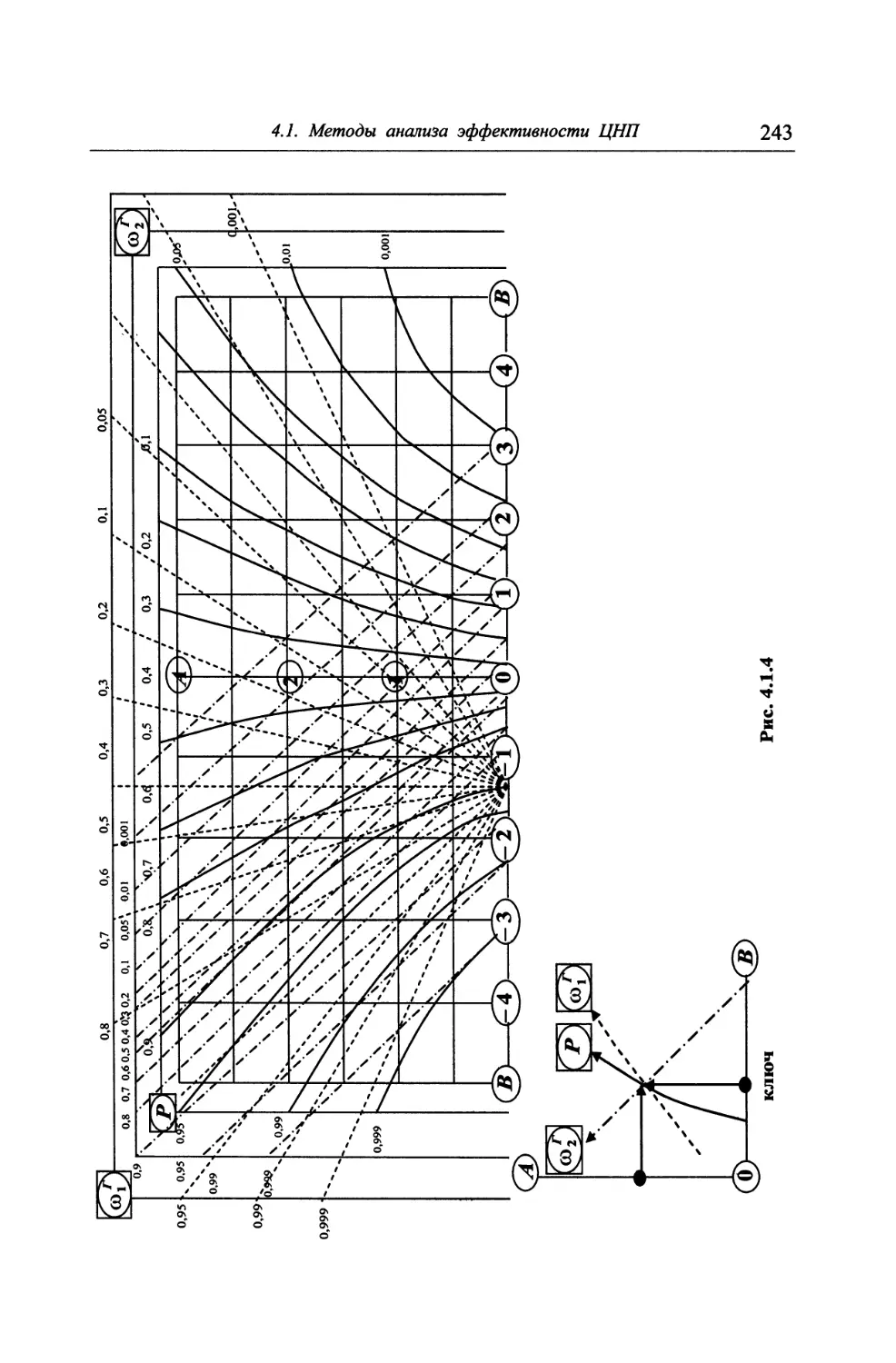
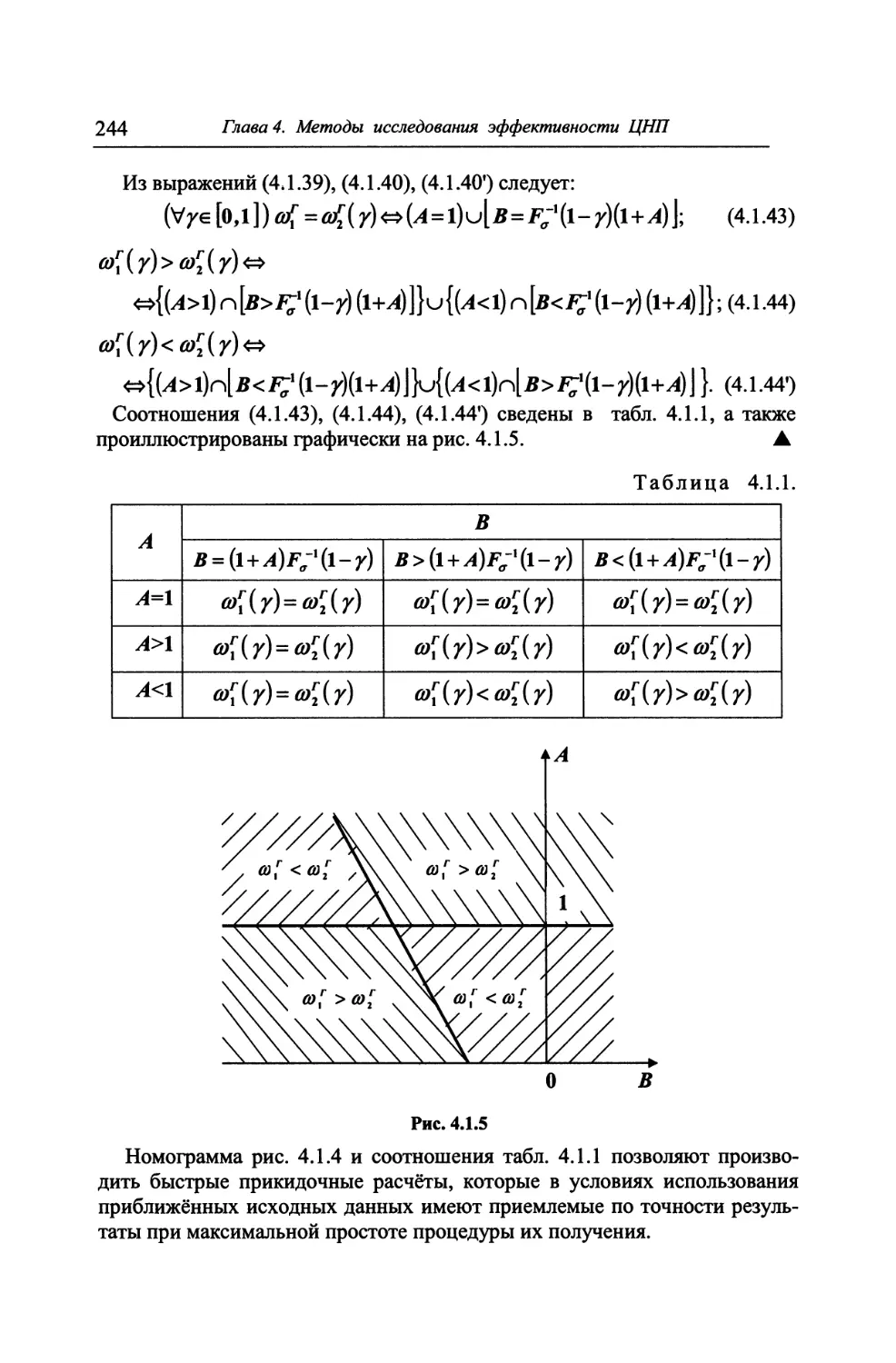
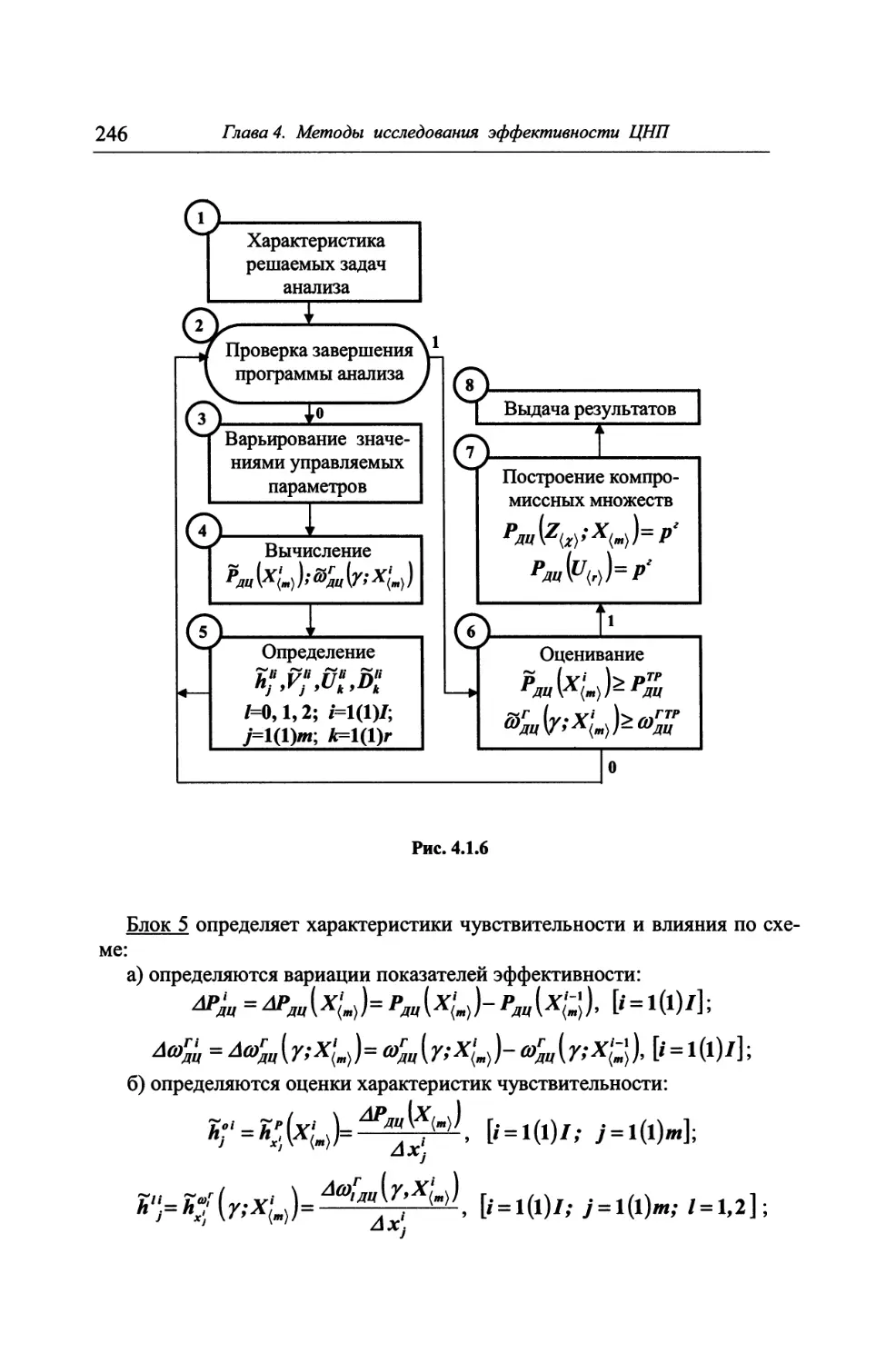
4.1. Методы анализа эффективности целенаправленных процессов ... 222
4.1.1. Формулировка задачи анализа эффективности операции ... 222
4.1.2. Характеристики чувствительности показателей эффек-
тивности операции 224
4.1.3. Характеристики влияния параметров моделей ЦУТС и
ЦНПФС на эффективность операции 229
4.1.4. О неформальном анализе эффективности операции 235

Оглавление 5
4.2. Методы синтеза эффективных целенаправленных процессов ... 248
4.2.1. Формулировка задачи синтеза операционной системы по
критерию пригодности 248
4.2.2. Формулировка задачи синтеза операционной системы
по критерию оптимальности 254
4.2.3.0 приближённом синтезе операционной системы 256
4.3. Дополнения 261
4.3.1. О детерминированных и квазирегулярных моделях опе-
рационных систем и комплексов 261
4.3.2. О корректности постановки задачи оптимального синтеза
операционной системы 266
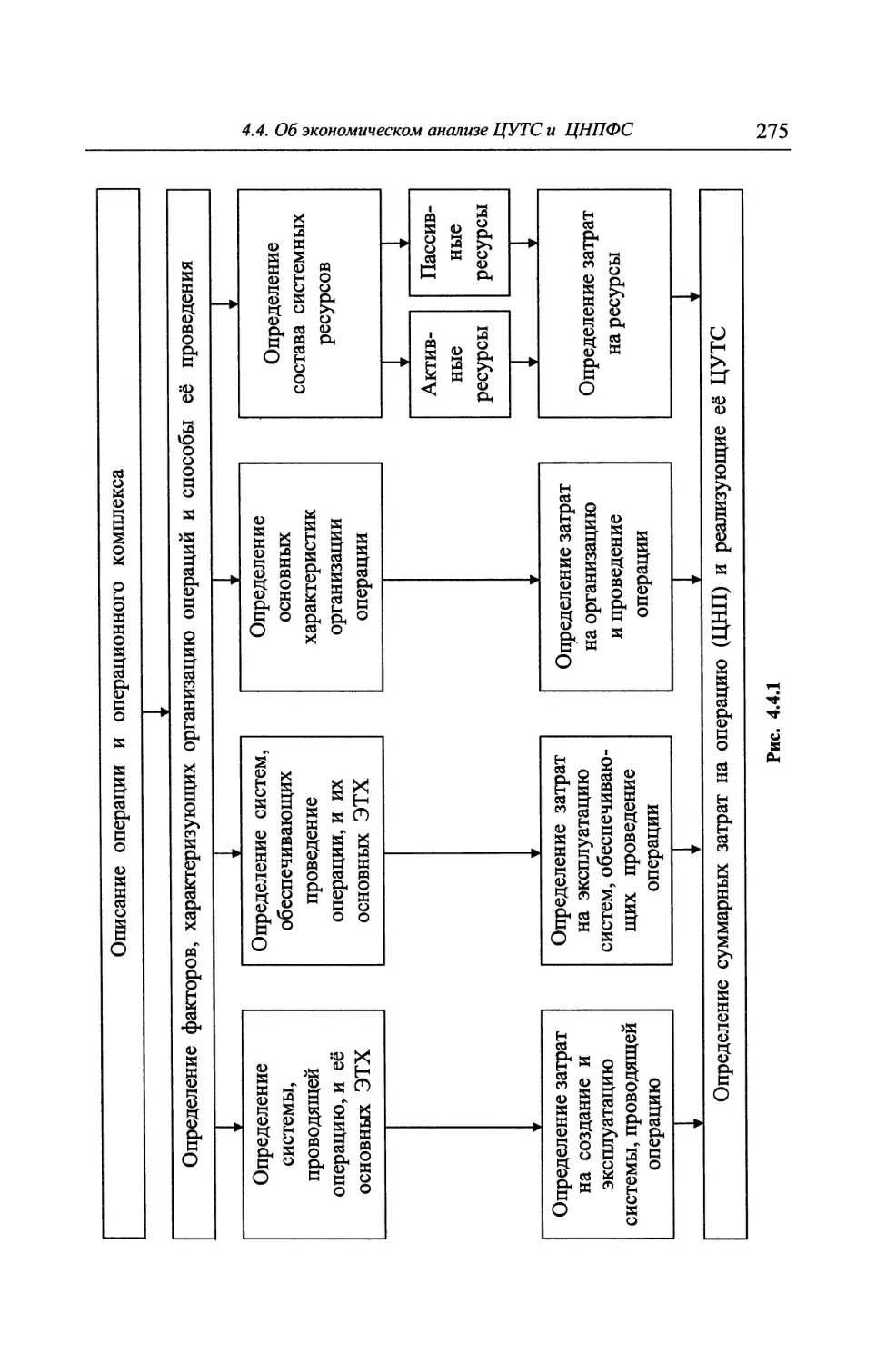
4.4. Об экономическом анализе ЦУТС и ЦНПФС 270
4.4.1. Сущность и задачи экономического анализа 270
4.4.2. Структура экономических затрат на программу 274
4.4.3. Методы определения затрат 279
4.5. Комментарии 283
Глава 5. Методы построения математических моделей
элементов операционного комплекса
5.1. Общие предпосылки 285
5.2. Схема построения моделей элементов операционного
комплекса 287
5.2.1. Алгоритм построения математических моделей элемен-
тов операционного комплекса 287
5.2.2. Структурная схема вероятностных моделей элементов
операционного комплекса 293
5.3. Операционный функционал 296
5.3.1. Понятие операционного функционала 296
5.3.2. Классификация операционных ресурсов 300
5.3.3. Примеры операционных функций 303
5.3.4. Основные свойства моделей операционных функциона-
лов и общая схема их построения 309
5.4. Методы построения математических моделей показателей ка-
чества результатов целенаправленного процесса 313
5.4.1. Теоретические основы 313
5.4.2. Методика построения математической модели показателя
виртуального качества результатов операции 320
5.4.3. Методика построения математической модели показателя
требуемого качества результатов операции 323
5.5. Комментарии 328

6
Оглавление
Раздел III. МОДЕЛИ
Глава 6. Комплексные функциональные модели
целенаправленных процессов
6.1. Линейная функционально-стохастическая модель непрерывно-
го целенаправленного процесса 332
6.1.1. Содержательная (вербальная) постановка задачи 332
6.1.2. Построение агрегированной математической модели опе-
рационной системы 333
6.1.3. Оценивание эффективности ЦНПФС 345
6.1.4. Анализ эффективности ЦНПФС и качества ЦУТС 356
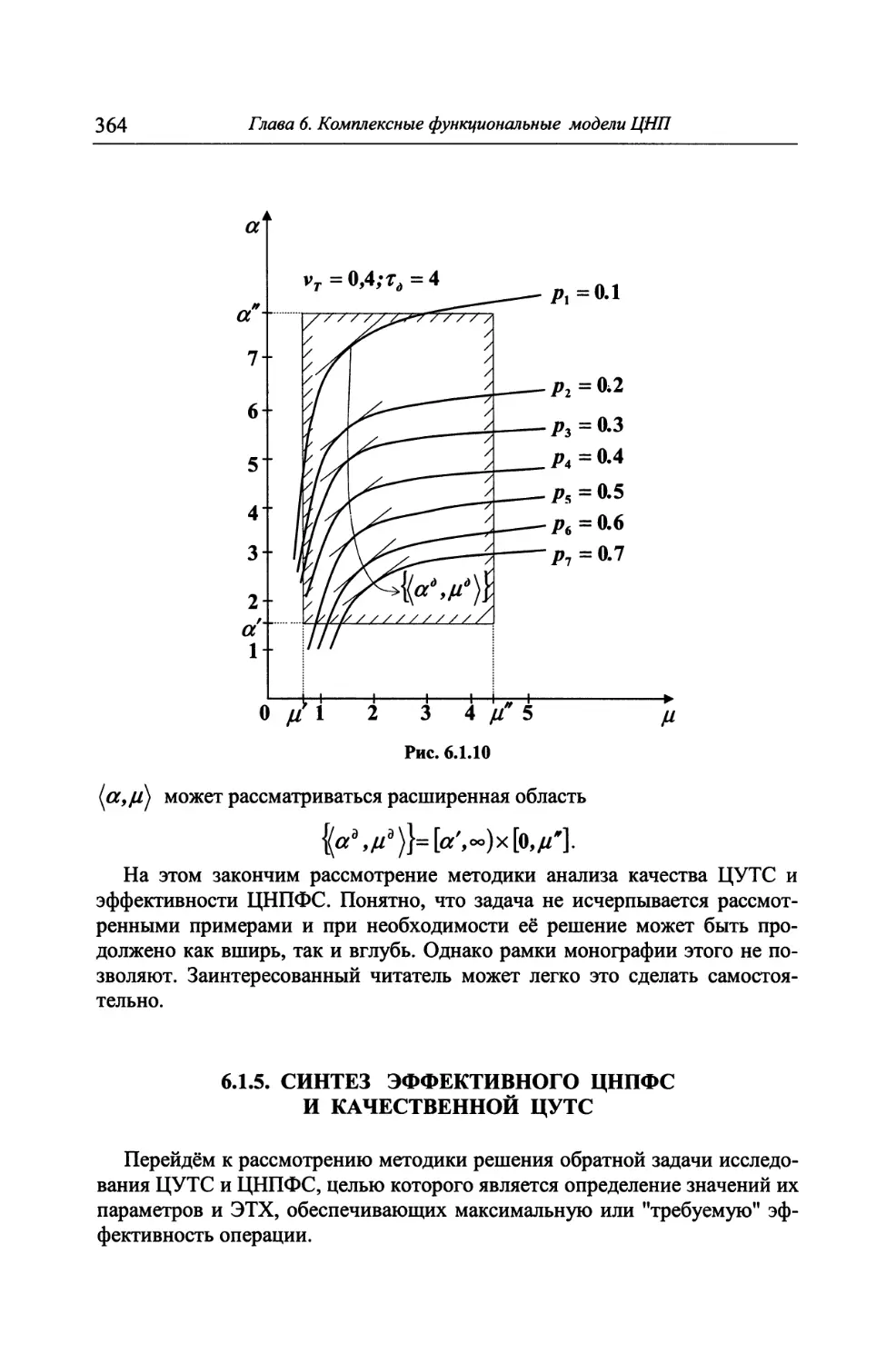
6.1.5. Синтез эффективного ЦНПФС и качественной ЦУТС .... 364
6.2. Нелинейные функционально-стохастические модели непре-
рывных целенаправленных процессов 367
6.2.1. Функционально-стохастическая модель непрерывного
нормативного ЦНП 367
6.2.2. Функционально-стохастическая модель непрерывного
директивного ЦНП 372
6.2.3. Функционально-стохастическая модель непрерывного
нормативно-директивного ЦНП 376
6.3. Функционально-стохастическая модель циклического целена-
правленного процесса 385
6.3.1. Содержательная (вербальная) постановка задачи 385
6.3.2. Построение агрегированной математической модели опе-
рационной системы 386
6.4. Комментарии 403
Глава 7. Специализированные модели
целенаправленных процессов
7.1. Определение и классификация Г-процессов 406
7.1.1. Г-процесс и его характеристики 406
7.1.2. Классификация Г-процессов 407
7.2. Постановка задачи исследования эффективности Г-процессов
массового обслуживания 408
7.2.1. Оперативный Г-процесс как модель ПМО 408
7.2.2. Показатели эффективности ОПМО и математическая
формулировка задачи его анализа 411
7.2.3. Методы определения закона обслуживания 413
7.2.4. Методы определения закона обслуженное™ 419
7.2.5. О методах решения задач оптимального синтеза КМО и
ОПМО 421

Оглавление 7
7.2.6. О характеристиках оперативности ОПМО 423
7.2.7. Об экспертном оценивании оперативности ОПМО 426
7.3. Определение и классификация моделей циклических ОПМО .... 429
7.3.1. Циклический ОПМО и его математическая модель 429
7.3.2. Модель абстрактного КМО 433
7.3.3. Математическая формулировка задач исследования
ЦОПО 440
7.3.4. Классификация моделей ЦОПО и задач его синтеза 442
7.4. Модель процесса функционирования восстанавливаемой ЦУТС 446
7.4.1. Содержательная (вербальная) постановка задачи 446
7.4.2. Построение агрегированной математической модели
ЦОПО 446
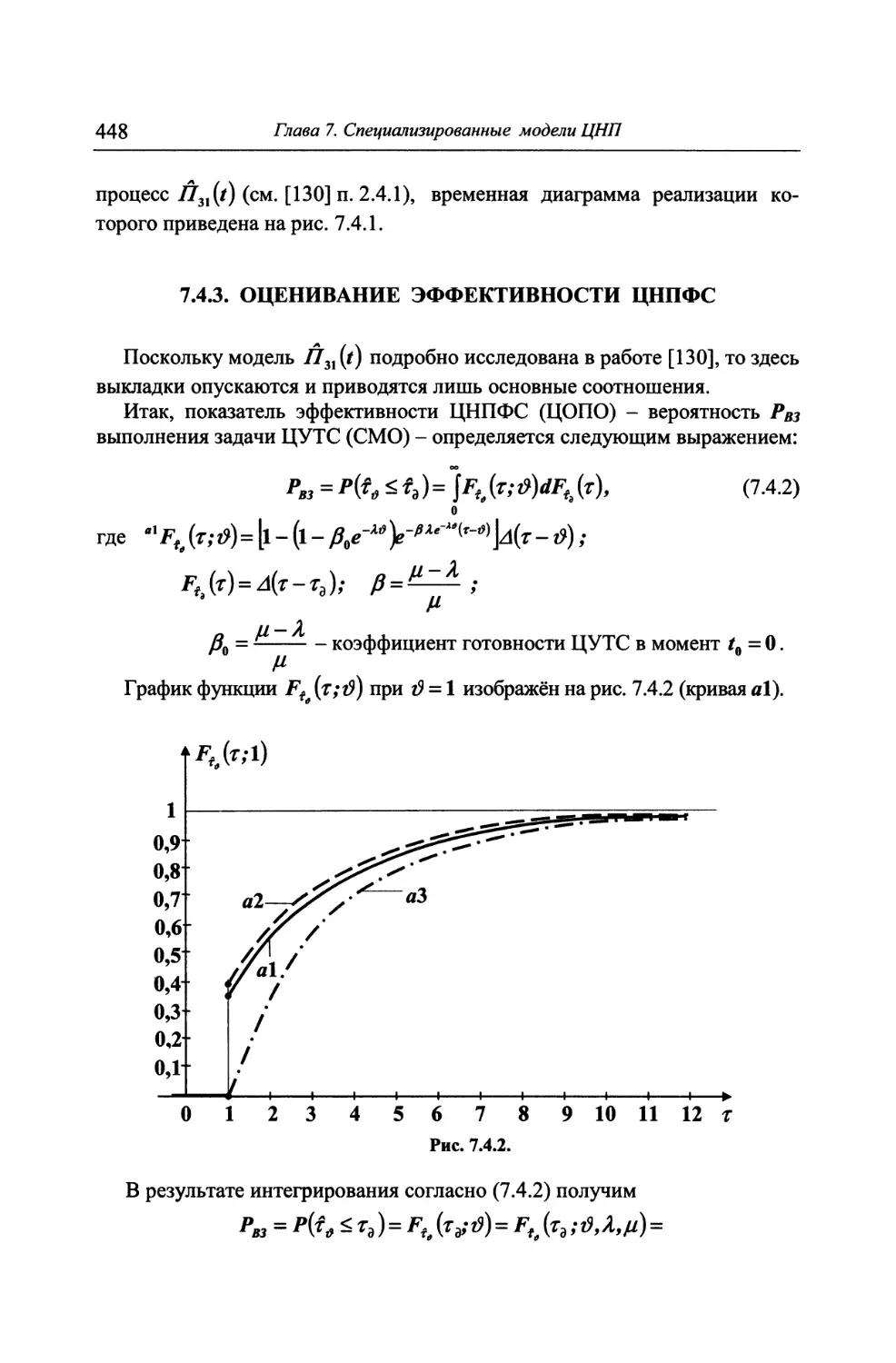
7.4.3. Оценивание эффективности ЦНПФС 448
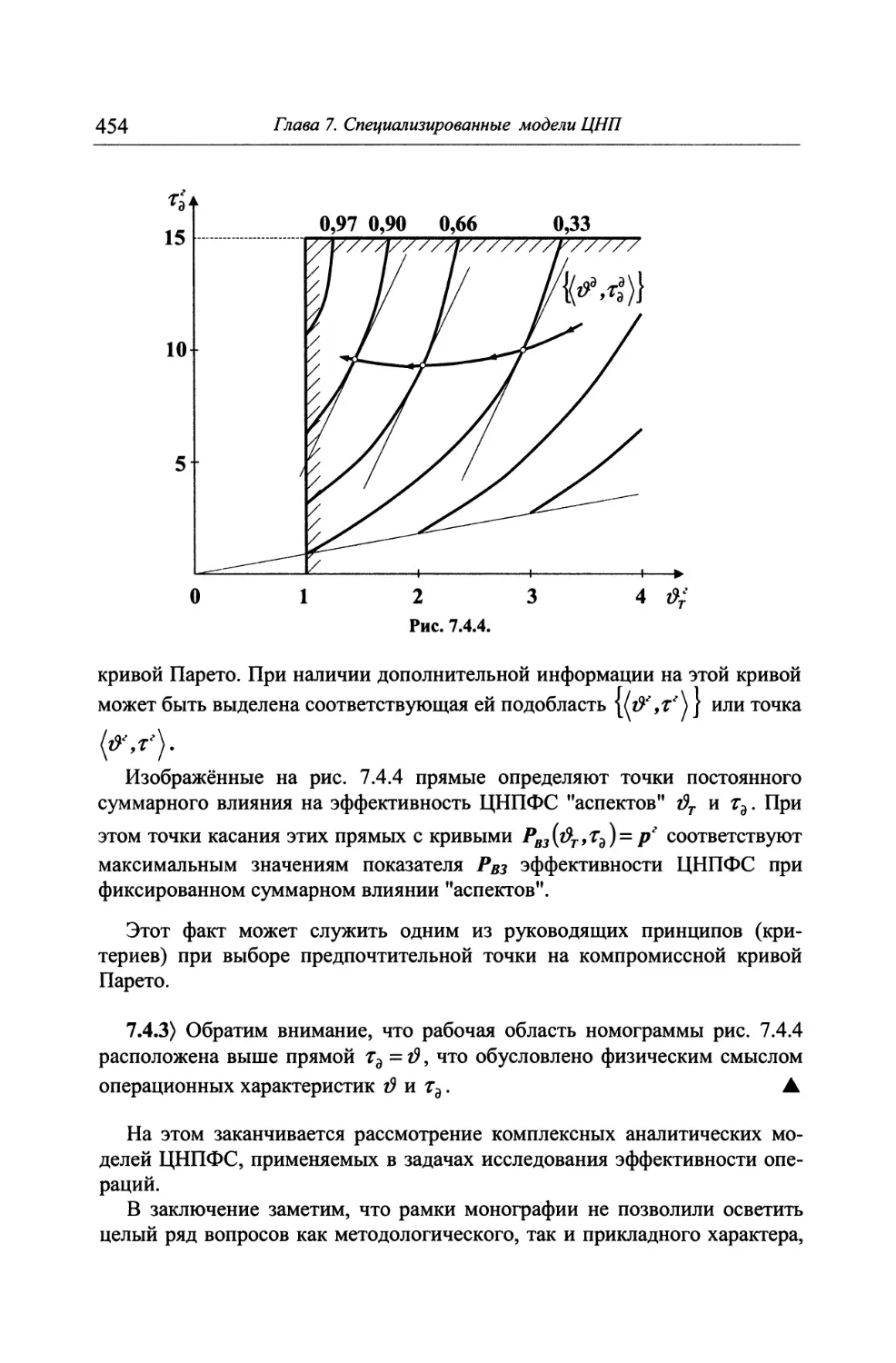
7.4.4. Анализ эффективности ЦНПФС и качества ЦУТС 450
7.5. Комментарии 455
Заключение 460
Приложения: П. 1. Основные обозначения 465
П.2. Аббревиатуры 474
П.З. Предметный указатель 478
Библиография
492

ПРЕДИСЛОВИЕ
Настоящая монография представляет собой оригинальное посо-
бие по методологии и методам внешнего проектирования (ВНЕПР)
целенаправленных процессов (ЦНП) и целеустремлённых систем
(ЦУС), составляющих основу ряда дисциплин системного направле-
ния: «Исследование операций», «Прикладная кибернетика», «Систе-
мотехника», «Теория управления», «Анализ систем» и др. В книге, с
одной стороны, прокомментированы и обобщены все наиболее со-
держательные работы [3, 6, 9, 10, 12, 26, 30, 31, 32, 33, 34, 39, 40, 42,
43, 48, 50, 51, 61, 65, 75, 63, 88, 95, 96, 97, 112, 123, 124, 125, 128, 130,
144, 156, 164, 165, 166, 167, 190], связанные с проблемами количест-
венного исследования качества целеустремлённых технических сис-
тем (ЦУТС) и эффективности процессов их целевого функционирова-
ния (ЦНПФС), а с другой - обоснованы и изложены концепции и об-
щие принципы системного подхода к комплексному исследованию
эффективности ЦНПФС, лежащие в основе единой методологии их
внешнего проектирования.
Повышение эффективности общественного производства является
общей закономерностью экономического роста, развития экономики.
В современных условиях реконструкции народного хозяйства на ос-
нове научно-технического прогресса оно приобретает особое значе-
ние. Для этого надо прежде всего изменить структурную и инвести-
ционную политику. Суть перемен - в перенесении центра внимания с
количественных показателей на качество и эффективность, с проме-
жуточных результатов - на конечные.
Проблема разработки и внедрения в практику научных методов ис-
следования качества продукции и эффективности производства при-
обретает особую актуальность.
Для решения этих задач необходимо, чтобы инженерные и
управленческие кадры, в том числе сотрудники и выпускники
ВТУЗов, овладели основами современной теории эффективности,
научились применять её методы в своей практической деятельно-
сти по обучению и воспитанию личного состава, эксплуатации и
целевому применению техники и вооружения.
Для понимания материала достаточна математическая подго-
товка в объёме, предусмотренном программой ВТУЗа, однако для
его усвоения необходимы прочные теоретико-вероятностные зна-
ния, обеспечивающие глубокое вероятностное мышление и чёткое
понимание сущности рассматриваемых объектов и явлений.

Предисловие
9
Книга такого содержания (целиком ориентированная на проблему
внешнего проектирования ЦНП и ЦУС на основе исследования эф-
фективности ЦНПФС) выходит впервые. Поэтому для её усвоения аб-
солютно необходима вдумчивая систематическая проработка всего
(без пропусков) приведённого материала, и прежде всего при пер-
вом прочтении, с целью осознания всего комплекса (системы) кон-
цептуальных и методологических особенностей методов и моделей,
используемых в теории эффективности ЦНП.
В силу сложности проблемы, а также большого многообразия как
аспектов её изучения, так и взглядов по ним и обусловленной этим
сложности первоначального восприятия рассматриваемых в моногра-
фии понятий, принципов и концепций возникает постоянная необхо-
димость обсуждения и подчёркивания их семантики (смысла) с целью
раскрытия их глубинной сущности ("тонкостей") и правильной фи-
зически обоснованной интерпретации. Это приводит к неизбежным
повторениям уже сказанного. Поэтому все обсуждения семантических
аспектов используемых понятий оформлены в виде замечаний (по
тексту) и комментариев (в конце каждой главы), на которые затем
лишь делаются ссылки.
Замечания позволяют решать две методические задачи:
- адресовать читателя по мере необходимости к соответствующим
замечаниям без дублирования их в тексте;
- освобождать читателя от чтения всех замечаний при обращении к
монографии за справкой по конкретному вопросу.
Этой же цели служат и комментарии, но в отличие от замечаний их
содержание менее связано с контекстом и посвящено всей совокупно-
сти рассматриваемых в главе вопросов, поэтому они носят более об-
зорный характер и помещены в конце главы.
При первом чтении текста монографии замечания и комментарии
пропускать не следует. При повторном чтении их иногда можно
опускать, однако для правильного понимания и интерпретации изла-
гаемого материала иметь их в виду необходимо. В целом содержание
книги требует внимательного и вдумчивого изучения.
Для облегчения работы с книгой в поисках справок введена под-
робная рубрикация её элементов (пунктов, определений, теорем,
формул, рисунков, таблиц, примеров) на основе их тройной нумера-
ции. При этом первая цифра N означает номер главы, вторая М -
номер параграфа, третья I (или J, или К) - номер элемента (пункта,
определения и т.д.). Аналогично пронумерованы и приводимые за-
мечания и комментарии. Номера замечаний отмечены угловой скоб-
кой - ), номера комментариев - фигурной скобкой - }. При ссылках
номера формул даются в круглых скобках (N.M.I), номера замеча-
ний- в угловых - (N.M.J), номера комментариев - в фигурных -

10
Предисловие
{N.M.K}. Ссылки на подстрочные примечания даются в виде (ПП
R/S), что означает: R-e подстрочное примечание на S-й странице.
Ссылки на литературу даны в квадратных скобках. Символ А означа-
ет окончание определения, теоремы, примера, замечания, коммента-
рия. Подобная рубрикация даёт возможность более гибко использо-
вать материал монографии при его проработке.
Используемая в монографии символика находится в полном соот-
ветствии с руководствами [127], [169].
Монография включает в себя три раздела, посвященные, соответ-
ственно, методологии ВНЕПР, методам исследования ЦНП и ЦУТС
и их обобщённым моделям, описанным в терминах теории эффектив-
ности ЦНПФС.
В Прил. 1 приведены основные обозначения, в Прил. 2 дан список
принятых сокращений (аббревиатур).
Предметный указатель, содержащий перечень наиболее важных и
употребительных понятий теории эффективности ЦНП и призванный
играть роль терминологического словаря, дан в Прил. 3. Предметный
указатель позволит быстро найти интересующий читателя термин.
Жирным шрифтом прописными буквами в предметном указателе вы-
делены основные термины предметной области ВНЕПР, определения
которых выделены и пронумерованы в тексте книги. Прописными бу-
квами в предметном указателе выделены термины, определения кото-
рых приведены в тексте. Для остальных терминов в предметном ука-
зателе приведены страницы, на которых читатель найдёт определе-
ния, разъяснения и обсуждения этих терминов.
Приведённый список литературы представляет собой достаточно
полный перечень работ, так или иначе связанных с тематикой моно-
графии, призванный играть роль справочника, расширяющего пред-
ставления читателя об этой научной области (рекомендуемые для бо-
лее глубокой проработки источники отмечены звёздочками). Однако
поскольку лежащие в основе многих из этих работ концепции не все-
гда отвечают требованиям методологической обоснованности исполь-
зуемых принципов, то их следует читать критически и лучше после
проработки материала монографии.

Наука только тогда достигает совер-
шенства, когда ей удаётся пользоваться
математикой
К. Маркс
ВВЕДЕНИЕ
Предлагаемая вниманию читателей монография «Методологические ос-
новы внешнего проектирования (ВНЕПР) целенаправленных процессов
(ЦНП) и целеустремлённых систем (ЦУС)» призвана осветить концепту-
альные основы методологии ВНЕПР, а также методы решения конкретных
прикладных задач.
По определению:
- проект - это план, замысел [159];
- проектирование - разработка проекта [159].
Из приведённых определений следует, что проектирование составляет
основу любой целенаправленной деятельности. При этом выработка за-
мысла этой деятельности осуществляется на априорном представлении
проектируемого объекта (проекта ЦУС; организации ЦНП; стратегии опе-
рации; плана, алгоритма, программы, технологии целевого функциониро-
вания ЦУС и управления ЦНП), называемом его концептуальной моделью.
Представляется очевидным, что основным требованием к качеству та-
кой модели является её адекватность как объекту исследования (проек-
тирования), так и проблеме (задаче), в рамках которой проектируется объ-
ект.
Следует обратить внимание, что в общем случае процесс проектирова-
ния распадается на две ярко выраженные стадии (фазы):
- обоснование функций, стратегий и макроструктуры проектируемого
объекта;
- конструирование функциональных элементов и разработка алгорит-
мов и программ их целевого функционирования.
Первую фазу принято называть [42] внешним (или макро) проектиро-
ванием (ВНЕПР), а вторую - внутренним (или микро) проектированием
(ВНУПР).
Поскольку любая деятельность целенаправленна и требует для своей
реализации расхода ресурсов (различных видов) и времени, то при разра-
ботке её замысла естественно стремление сделать расходы ресурсов целе-
сообразными (рациональными) относительно цели деятельности, а делае-
мые для этого усилия - эффективными.
Из сказанного следует, что основу методов проектирования, и в первую
очередь ВНЕПР [42], должна составлять "Теория эффективности ЦНП"
(ТЭЦНП) [133], положения которой и представляют основу монографии.

12
Введение
Термин "эффективность" ныне стал одним из наиболее употребитель-
ных, вошёл "в моду". Однако излишне частое употребление слов, терми-
нов, словосочетаний и фраз имеет и негативную сторону: возникает опас-
ность искажения смысла слова (его своеобразная "девальвация"), отрыва
его от выражаемой им сущности, от реального предмета или явления. Что-
бы показать, что эта опасность отнюдь не иллюзорна, приведём определе-
ние эффективности, данное в научной статье1:
«Эффективность - это научная категория для обозначения единства
соответствий, порождаемых действием функционально-целевой детер-
минации объективных реальностей. ...Эффективность эффективна при-
менимостью сравнимо измеряемого, ... критериальной объективностью и
... оптимизацией».
Как говорится, "нарочно не придумаешь". Подобному определению
скорее место в фельетоне, а не в научной статье. Однако к сожалению, это
далеко не единичный пример. Опасность терминологической, а следова-
тельно, и понятийной путаницы можно уменьшить, если разобраться в
сущности понятия "эффективности", выяснить, насколько оно является
конструктивным, какие практические задачи (например, в области народ-
ного хозяйства или военного дела) позволяет решать "Теория эффективно-
сти".
Как научная дисциплина "Теория эффективности" возникла вскоре по
окончании Второй мировой войны (лет 55-60 тому назад), однако осно-
вополагающие результаты получены в ней сравнительно недавно (лет 20 -
25 назад), что обусловлено целым рядом объективных причин.
Современная научно-техническая революция привела к колоссальному
росту производительных сил общества, видоизменила орудия производст-
ва, материалы, технологии, как самих производственных процессов, так и
управления ими. Она потребовала гигантских и всё увеличивающихся
вложений в обновление и совершенствование производственного аппарата
и экономики, в создание больших сложных и дорогостоящих систем и объ-
ектов народного хозяйства и вооружённых сил, в научные поиски и прак-
тическое применение их результатов. Если учесть, что ресурсы общества
ограничены, то возникает проблема поиска средств для подобного рода за-
трат. Ответ на этот вопрос в современных условиях один: эти средства на-
ходятся в самом народном хозяйстве, и путь их мобилизации - повышение
эффективности производства отдачи (производительности) расходуемых
на него ресурсов (рабочего времени, оборудования, сырья, энергии и т.п.).
Повышение эффективности выступает как объективное условие расши-
ренного воспроизводства [1]. При ограниченных ресурсах (всех видов) не-
обходимо стремиться к использованию этих ресурсов наиболее рацио-
нально, наилучшим образом. Здесь сразу возникает вопрос: "что значит
1 Гулько В. Некоторые вопросы методологии теории эффективности. Труды II
Всесоюзного симпозиума по АСУ. - Л., 1972.

Введение
13
наилучшим образом!" ("что такое - лучше?"). Чтобы ответить на этот во-
прос, необходимо научиться оценивать результаты целенаправленной дея-
тельности, научиться сопоставлять их с поставленными задачами и сопут-
ствующими их решению затратами. Но чтобы сравнивать, надо научиться
измерять, т.е. иметь некоторую количественную меру, характеризующую
результат функционирования объекта, а также "инструмент" ("мерило"),
позволяющий этот результат оценивать. В связи с этим возникают естест-
венные вопросы: что измерять? чем измерять? как измерять? как оцени-
вать? Поскольку проблема состоит в выборе лучшего из сравниваемых
объектов, то измерять нужно их качества.
Качество любого объекта в полной мере проявляется лишь в процессе
его использования по назначению (в процессе его целевого функциониро-
вания). Поэтому наиболее объективным является оценивание качества
объекта по эффективности его применения. Таким образом, для обосно-
ванного выбора предпочтительного объекта необходимо измерять эффек-
тивности целевого функционирования сравниваемых его вариантов.
В принципе с этим утверждением никто не спорит, однако в публикаци-
ях даются различные определения эффективности (или определения вооб-
ще не даются). Более того, часто понятие эффективности связывается с
различными по сути объектами (операциями, действиями [3, 26, 123], сис-
темами [38, 114, 120], устройствами [123, 191], средствами [123, 190], тех-
никой [125], решениями [116] и т.д. [50, 88, 109, 123]), причём подобные
разночтения часто фигурируют в одной и той же публикации. Вследствие
подобного разнобоя понятие эффективности приобретает множество смы-
слов, порождаемых как многообразием его определений, так и ещё боль-
шим многообразием его количественных характеристик - показателей эф-
фективности. При этом последние, как правило, постулируются без обос-
нования их структуры и анализа основных свойств, обусловливающих
правомерность их применения. О необходимости такого обоснования мо-
жет свидетельствовать ставший уже классическим приведённый ниже при-
мер времён Второй мировой войны [190].
Решался вопрос об оснащении транспортных судов союзников зенитными
орудиями. Когда в качестве критерия для принятия решения фигурировало соот-
ношение расходов и ущерба, наносимого зенитными орудиями атакующим са-
молетам противника, следовал вывод о нецелесообразности установки орудий,
поскольку связанные с этим расходы значительно превосходили потери авиации
противника. Когда же расходы по установке и обслуживанию орудий были соот-
несены с предотвращённым с их помощью ущербом транспортного флота, по-
следовал противоположный вывод. Поскольку орудия предназначались для за-
щиты судов, а не для собственно борьбы с авиацией противника, то было приня-
то решение о целесообразности установки орудий, правильность которого под-
твердила последующая практика. Перечень подобных примеров может быть
продолжен.

14
Введение
Из приведённого примера видно, что правильность решения по органи-
зации операции существенно зависит от цспользуемого показателя её ка-
чества {эффективности).
В настоящее время нет такой области человеческой деятельности, в ко-
торой не приходилось бы сталкиваться с необходимостью решения про-
блемы повышения эффективности этой деятельности.
Повышение эффективности общественного производства и перевода
экономики страны на новый, более высокий уровень является общей зако-
номерностью экономического роста, развития экономики. В современных
условиях решение этой проблемы приобретает особое значение.
Ускорение социально-экономического развития страны - настоятельное
требование времени. Оно позволит всесторонне удовлетворить растущие
материальные и духовные потребности людей, создать условия для всесто-
роннего развития человека.
Необходимым условием ускорения является внедрение новейших дос-
тижений науки и техники на основе кардинального ускорения научно-
технического прогресса. Научно-технический прогресс означает прежде
всего прогресс научной мысли по пути её сближения с практикой, разра-
ботки действенных методов исследования, прогрессивных технологий и
технических решений народнохозяйственных и военно-прикладных задач.
Решение этих задач непосредственно связано с повышением уровня ру-
ководства народным хозяйством, вооруженными силами, совершенствова-
нием методов планирования и управления. Поэтому становится очевид-
ным, сколь важной является проблема повышения эффективности всех це-
ленаправленных процессов (ЦНП) человеческой деятельности. Также оче-
видно, что научно обоснованное решение этой проблемы возможно лишь
на основе количественных методов, разработкой которых, в частности, и
занимается современная "Теория эффективности". Ведь для того, чтобы
выявить пути повышения эффективности той или иной деятельности, ме-
роприятий, действий, необходимо уметь количественно оценивать их эф-
фективность.
Количественное определение эффективности целенаправленного про-
цесса даёт возможность действительно на научной основе, с привлечением
самых современных математических методов решать проблему повышения
его эффективности. По мнению одного из видных учёных в области "Сис-
темотехники" Р.Э. Макола: "Сама идея количественного определения эф-
фективности... с полным правом может рассматриваться как поворотный
пункт истории науки, сравнимый по своей важности с некоторыми круп-
нейшими открытиями в физике" [42].
Эффективность любой целенаправленной деятельности в значительной
степени определяется качеством решений, принимаемых управляющими
органами разных уровней. В связи с этим важное значение приобретает за-
дача совершенствования принципов и критериев принятия решений.

Введение
15
Проектирование, организация, планирование и в целом управление свя-
заны с рассмотрением более или менее отдалённого будущего и поэтому
всегда содержат элемент неопределённости. Кроме того, должны учи-
тываться и другие особенности управленческих задач, такие как необхо-
димая оперативность решения, недостаточно полная информация для при-
нятия решения, необходимость учёта социально-психологических факто-
ров. В отмеченных выше условиях в основе решения задач проектирова-
ния, организации, планирования и управления должен лежать так назы-
ваемый системный подход. Он органически вытекает из материалистиче-
ской диалектики и предполагает рассмотрение явлений в их взаимосвязи и
взаимообусловленности. Широко известны слова В.И. Ленина: "Чтобы
действительно знать предмет, надо охватить, изучить все его стороны, все
связи и "опосредования"".
Системный подход означает также, что интересующий нас объект рас-
сматривается не только во взаимосвязи с другими объектами, но и как сис-
тема. Изучение объекта во внешних взаимосвязях позволяет определить
цели его функционирования, а анализ внутренней структуры - оценить пу-
ти достижения поставленной цели. При решении любой из отмеченных
выше управленческих задач (проектирование, организация, планирование,
управления) основной является проблема выбора (определения) наилучше-
го (наиболее рационального) решения, называемого оптимальным.
Когда идёт речь о чем-то наилучшем, оптимальном, то предполагается,
что имеется целое множество вариантов выбора синтезируемого объекта
(систем, проектов, вариантов организации, планов, способов действий,
стратегий управления и т.п.), из которых желательно выбрать наиболее
предпочтительный (наилучший, оптимальный). Очевидно, что выбор мо-
жет производиться только путём сравнения различных конкурирующих
вариантов (альтернатив). Сравнение может производиться одним из двух
способов.
Первый способ связан с созданием и испытанием реальных конкури-
рующих объектов (система процессов, организаций, управлений, ...), в хо-
де которых производится их экспериментальное сравнение. Однако пред-
ставляется совершенно очевидным, что применительно к уникальным,
сложным, дорогостоящим объектам (системам и процессам) такой путь не-
реален, так как в условиях научно-технической революции, с одной сторо-
ны, резко возрастает многовариантность технических, проектных, эконо-
мических, организационных, управленческих и других решений, а с другой
стороны, весьма возросла цена неверного, ошибочного решения. В сущно-
сти, проблема состоит в том, чтобы сделать выбор еще до создания реаль-
ного объекта, так как после его создания выбирать уже поздно.
Остаётся практически реализуемым лишь второй способ, основанный
на построении достаточно адекватных (близких к оригиналу) математиче-
ских моделей (аналитических или имитационных) реальных объектов и

16
Введение
процессов их функционирования и сравнения результатов исследования
этих моделей.
"Теория эффективности целенаправленных процессов" (ТЭЦНП) и со-
ставляет методологическую и математическую основы модельного экспе-
риментирования со сложными объектами (системами и процессами) на ба-
зе такого комплексного (системного) операционного свойства целенаправ-
ленного процесса функционирования объектов (систем), как его эффектив-
ность, количественной меры этого свойства - показателя эффективности и
принципа его оценивания - критерия эффективности.
В дальнейшем речь будет идти в основном о целеустремлённых техни-
ческих системах (ЦУТС) и процессах их целенаправленного функ-
ционирования (ЦНПФС). При этом, по определению (см. п. 1.2.2), ЦНПФС
представляет собой операцию, т.е. упорядоченную совокупность взаимо-
связанных действий, направленных на достижение определённой цели. Та-
ким образом, может быть сформулировано следующее содержательное оп-
ределение.
Теория эффективности целенаправленных процессов (ТЭЦНП) -
это прикладная дисциплина, в рамках которой разрабатываются и иссле-
дуются принципы и методы количественного оценивания и анализа ре-
зультатов целевого функционирования ЦУТС и степени их соответствия
целям операции (стоящим перед ЦУТС задачам), а также методы оптими-
зации проектируемых ЦУТС и организуемых ЦНПФС (операций).
Предметом изучения ТЭЦНП является наиболее общее комплексное
свойство ЦНПФС - его эффективность. ТЭЦНП формирует и раскрывает
содержательный смысл этого понятия, рассматривает факторы, обусловли-
вающие эффективность ЦНПФС, принципы и способы обоснования и оп-
ределения количественной меры эффективности ЦНПФС - показателя эф-
фективности, принципы суждения об эффективности ЦНПФС - критерии
эффективности, формулирует проблемы и задачи, требующие решения, и
разрабатывает необходимые для этого методы.
Как научное направление "Теория эффективности" зародилась в воен-
ном деле и, в частности, в теории стрельбы, предметом которой является
оценивание действенности применения огнестрельного оружия.
Бурное развитие "Теории эффективности" происходит в годы Великой
Отечественной войны и особенно в послевоенные годы в связи с необхо-
димостью создания новых видов вооружения и разработки новых способов
его боевого применения. В этот период "Теория эффективности" (ТЭ) раз-
вивалась в основном в недрах "Исследования операций", представляюще-
го собой научное направление, предмет которого - анализ и оптимальная
организация операций (ЦНПФС) на этапе принятия организационных и
управленческих решений.

Введение
17
Наиболее выдающимся трудом того времени явилась статья акаде-
мика А.Н. Колмогорова "Число попаданий при нескольких выстрелах и
общие принципы оценивания эффективности стрельбы", опубликован-
ная в трудах Математического института им. В.А. Стеклова в 1945 г.
В этой статье А.Н. Колмогоров предложил оценивать эффективность
стрельбы не на основе частных показателей, а по степени объективной
возможности выполнения той основной задачи, ради которой эта
стрельба производится. С этого времени в ТЭ прочно вошёл наиболее
объективный и информативный показатель эффективности применения
оружия - вероятность выполнения боевой задачи (т.е. вероятность дос-
тижения цели операции).
В настоящее время ТЭЦНП, непрерывно развиваясь и совершенствуясь,
способна решать все более сложные задачи теории и практики "Исследо-
вания операций" и "Системотехники". Её методы получили всеобщее при-
знание и находят широкое применение при решении различных задач, свя-
занных с разработкой как новых образцов вооружения и военной техники,
так и способов их целевого (боевого) применения.
Следует отметить, что бурное развитие ТЭЦНП представляет собой за-
кономерный процесс, обусловленный возрастанием роли науки во всех
областях общественной жизни и деятельности человека. Пожалуй, наибо-
лее заметно это проявляется в военной области, так как для современного
и перспективного вооружения характерны особенности, существенно от-
личающие его от вооружения, применявшегося в прошлых войнах, в том
числе и во Второй мировой войне.
Во-первых, исключительно высокая поражающая способность. Залп со-
временной ракетной части по мощности намного превосходит мощность
всех огневых средств любой из воюющих сторон во Второй мировой вой-
не. Отсюда вытекает очень высокая ответственность лиц, принимающих
решение о применении оружия и организующих это применение.
Во-вторых, большая и всё возрастающая сложность, а вместе с тем и
стоимость вооружения. Как никогда ранее, мощь вооружённых сил зависит
от экономики. Сейчас особенно злободневно звучат слова Ф.Энгельса: "В
настоящее время армия и военный флот... стоят чертовски много денег"
("Анти-Дюринг"). Указанные особенности предъявляют к современному
вооружению высокие требования. С одной стороны, необходимо, чтобы
вооружение, создаваемое на выделенные средства, и способы его боевого
применения были наиболее действенными (эффективными), а с другой -
чтобы вооружение было относительно экономичным (материальные затра-
ты - приемлемыми).
Достижение в интересах общества наибольших результатов при допус-
тимых затратах, т.е. достижение максимальной эффективности целевого
функционирования всех отраслей народного хозяйства есть непреложный
закон государственного строительства.

18
Введение
Изучение ТЭЦНП для системного инженера имеет чрезвычайно важное
значение по следующему ряду причин.
1. ТЭЦНП является представителем научных дисциплин так называемо-
го системотехнического цикла ("Общая теория систем", "Анализ сис-
тем", "Системотехника", "Кибернетика", "Исследование операций",
"Теория принятия решений", "Теория полезности" и т.д.). Она разви-
вает у будущего инженера системное мышление, прививает навыки
комплексного подхода к исследованию процессов целевого функцио-
нирования сложных ЦУТС на всех этапах их жизненных циклов от
разработки и проектирования до эксплуатации и применения на осно-
ве анализа наиболее общего комплексного свойства ЦНПФС - эффек-
тивности, а не только частных свойств ЦУТС (надёжности, живучести
и т.п.), хотя и важных, но отражающих лишь отдельные аспекты про-
блемы их оптимального проектирования и организации. Только на ос-
нове всесторонней, комплексной оценки конкурирующих вариантов
можно выработать решение, компромиссное по отношению к различ-
ным аспектам проблемы, но максимально соответствующее целям ис-
следуемой программы в целом. Другими словами, ТЭЦНП формирует
у системных инженеров способность "видеть за деревьями лес".
2. ТЭЦНП объединяет, интегрирует знания, сведения, результаты, полу-
ченные в других дисциплинах, являясь связующим звеном между об-
щеинженерными и специальными дисциплинами, с одной стороны, и
системно-специальными - с другой, так как в ТЭЦНП наиболее тесно
совместно используются оперативно-тактические и эксплуатационно-
технические характеристики систем и проводимых ими операций.
3. Принципиальной особенностью ТЭЦНП является то, что выработка и
реализация решений, получаемых её методами, не мыслится без при-
менения вычислительной техники (ЭВМ). При этом ЭВМ использует-
ся не только, как иногда считают, с целью облегчения трудоёмких
расчётов и освобождения человека от громоздкой рутинной работы.
Существенным является то, что современные средства вычислитель-
ной техники придают выработанным решениям новое качество. Они
способны производить такие расчёты и в такие сроки, которые други-
ми средствами принципиально недостижимы. Комплексы ЭВМ, снаб-
жённых математическим обеспечением (комплексами алгоритмов и
программ), позволяющие решать различные задачи проектирования,
планирования, выработки решений и управления, получили название
"искусственного интеллекта", что свидетельствует о высоком уровне
сложности этих задач.
Из всего сказанного следует, что дисциплина «Внешнее проектирование
целенаправленных процессов и целеустремлённых систем» (ВНЕПР ЦНП
и ЦУС) (основным инструментом которой является "Теория эффективно-
сти целенаправленных процессов") играет важную роль в подготовке сие-

Введение
19
темного инженера, так как, с одной стороны, она вбирает в себя знания,
получаемые в таких курсах, как "Философия", "Высшая математика",
"Теория вероятностей и математическая статистика" и др., а с другой -
обеспечивает более глубокое понимание и сознательное изучение всех
системно-специальных дисциплин и должна служить руководством в его
практической деятельности по вопросам, связанным с оптимальной (ра-
циональной) организацией процессов целевого функционирования экс-
плуатируемых ЦУТС (реализуемых ЦУТС операций).
Ещё раз обратим внимание, что для правильного и глубокого понима-
ния концептуальных и методологических основ ТЭЦНП текст монографии
должен быть проработан полностью, со всеми замечаниями и коммента-
риями.

Раздел I
МЕТОДОЛОГИЯ
Претендовать на достоверность полу-
ченных результатов, конечно, трудно. Как и в
других областях естественнонаучного знания,
следует ожидать, что завтра мы будем луч-
ше понимать предмет, чем сегодня. Теория в
отличие от теоремы подвержена постоян-
ным изменениям, но даже чтобы называться
теорией, любая гипотеза должна пройти
много проверок. Стоит, по-видимому, напом-
нить, что только при опровержении гипоте-
зы человечество имеет возможность узнать
что-нибудь новое.
М.Х. Холстед. "Начала науки о программах"
Глава 1
КОНЦЕПТУАЛЬНЫЕ ОСНОВЫ
СИСТЕМНЫХ ИССЛЕДОВАНИЙ
Как и у всякой научной дисциплины, атрибутами теории ВНЕПР ЦНП и
ЦУС являются:
- объект и предмет исследования;
- цель и задачи исследования;
- концептуально-методологические принципы;
- естественнонаучные - гносеологические основы;
- система исходных понятий, терминов и определений, образующих
язык - тезаурус дисциплины;
- система основных производных понятий, постулатов, аксиом и тео-
рем, образующих методологические основы теории;
- принципы построения адекватных моделей объектов исследования;
- методы исследования;
- экспериментально-информационная база;
- научно обоснованная сфера приложения методов.
Задачи данной главы:
- введение в предмет ТЭЦНП;
- определение объекта и предмета исследования ТЭЦНП;

1.1. Системный подход и системные направления в науке 21
- формулирование основных принципов и концепций ТЭЦНП;
- определение целей и задач ТЭЦНП;
~ определение места ТЭЦНП среди дисциплин системного направле-
ния.
1.1. СИСТЕМНЫЙ ПОДХОД И СИСТЕМНЫЕ
НАПРАВЛЕНИЯ В НАУКЕ
Системный подход - это методология комплексного исследования
сложных объектов природы, техники и общества как систем, т.е. как объе-
динений элементов, связанных комплексом (системой) отношений и вы-
ступающих по отношению к внешней среде как единое целое. А
Как методология системный подход требует проводить исследования
сложных систем (СС) и процессов их функционирования (ПФС) с учётом
(и во взаимосвязи) следующих аспектов:
- системно-компонентного (исследование состава системы);
- системно-структурного (исследование структуры и строения систе-
мы);
~ системно-функционального (исследование функций и функциональ-
ных связей элементов системы);
- системно-агрегативного (исследование системообразующих факто-
ров);
- системно-ситуационного (исследование взаимодействия системы с
внешней средой);
- системно-эволюционного (исследование динамики поведения и раз-
вития системы).
Для учёта перечисленных аспектов системный подход (базируется на
следующих принципах:
1. Любая исследуемая система должна рассматриваться как совокуп-
ность взаимосвязанных элементов, подсистем (субсистем).
2. Любая система должна рассматриваться, с одной стороны, как под-
система в системе более высокого уровня (надсистеме, суперсисте-
ме), а с другой, - как совокупность образующих её (входящих в неё)
подсистем (субсистем) и элементов.
3. Исследование любой системы требует анализа всех её свойств и
взаимосвязей.
4. При исследовании системы описание её элементов не должно носить
самодовлеющего характера, а должно вытекать из задач самой сис-
темы и задач её исследования.

22 Глава 1. Концептуальные основы системных исследований
Именно для системного подхода специфична проблема порождения
свойств системы свойствами её элементов, и наоборот, поведения элемен-
тов поведением системы. По существу, системный подход сводится к тре-
бованию всесторонности, комплексности исследования любого объекта
или явления. При этом комплексность системного подхода проявляется в
том, что наряду с рассмотрением системы как единого целого (комплекс-
но) учитываются как положительные, так и отрицательные её свойства
(комплекс свойств), все её связи и взаимодействия с окружающей средой
(комплекс связей и взаимодействий), а также все возможные последствия
её целевого функционирования (комплекс результатов), как положитель-
ные (позитивные), так и отрицательные (негативные).
Таким образом, системный подход - это общенаучная методология,
которая не содержит конкретных средств исследования объектов, а обос-
новывает и разрабатывает принципы таких исследований.
Следствием развития и практического применения системного подхода
явилось возникновение междисциплинарных научных направлений в изу-
чении сложных явлений, систем и процессов. К таким направлениям отно-
сятся:
1) общая теория систем (ОТС);
2) анализ систем (АНС);
3) системотехника (СИТ);
4) прикладная кибернетика
(ПРК);
5) исследование операций
(ИСО);
6) теория эффективности
целенаправленных процессов
(ТЭЦНП);
7) теория полезности (ТПО);
8) теория принятия решений
(ТПР);
9) квалиметрия (КВМ) и т.д.
На рис. 1.1.1 приведена схемати-
Рис. 1.1.1 ческая диаграмма, иллюстрирующая
отношения перечисленных научных
направлений.
Из рис. 1.1.1 видно, что, с одной стороны, все они взаимосвязаны (ме-
тодологией системного подхода), а с другой - у каждого из направлений
есть своя специфика и проблематика.
В последнее время получили развитие такие направления, как технико-
экономический анализ (ТЭА) и функционально-экономический анализ
(ФЭА), в частности военно-экономический анализ (ВЭА).

1.1. Системный подход и системные направления в науке 23
Основная задача всех перечисленных направлений - оптимальный
синтез, т.е.:
- проектирование (организация) оптимальных (в каком-то смысле)
целеустремлённых систем;
- организация (проектирование) оптимальных (в каком-то смысле) це-
ленаправленных процессов.
Отличия системных направлений заключаются в следующем:
- в объектах и предметах исследований;
- в перечнях этапов системного анализа1, реализуемых в рамках кон-
кретного системного направления;
- в количестве и характере априорной информации и обусловленных
этим методах исследования;
- глубине и характере проработки исследуемого вопроса.
На рис. 1.1.2. приведена структурная схема, иллюстрирующая взаимо-
связь АНС, ИСО и ТЭЦНП.
Из рис. 1.1.2. видно, что ИСО представляет собой этап АНС, а ТЭЦНП-
этап ИСО.
Таким образом, ТЭЦНП служит инструментом ИСО, а последняя - ин-
струментом АНС [42].
Аналогичные связи можно выявить и между остальными направления-
ми. В частности, как отмечено в монографии [42], многие проблемы и ме-
тоды исследования являются общими как для ИСО, так и для СИТ (проек-
тирование больших систем), так как предмет исследования у них общий:
ЦУТС и ЦНПФС. Общими являются и цели исследования - синтез опти-
мального ЦНПФС. В рамках ИСО эта задача решается с помощью выра-
ботки организационных решений по синтезу ЦНПФС, а в рамках СИТ -
путём выработки проектных решений по синтезу ЦУТС, реализующей этот
ЦНПФС.
Таким образом, различными являются объекты и этапы системных ис-
следований. Так, в ИСО - это операция, проводимая системой, облик кото-
рой уже определён (замоделирован), а в СИТ - это сложная система
(ЦУТС), у которой определена (замоделирована) организация её ЦНПФС.
Иллюстрацией взаимодействия ИСО и СИТ может служить тот же
рис. 1.1.2, где роль АНС играет СИТ. Из сказанного следует, что ТЭЦНП
находит применение практически во всех системных направлениях науч-
ных исследований, будучи инструментом ИСО.
Как отмечено в фундаментальной монографии [42] по "Системотехни-
ке"2, процесс синтеза (проектирования, организации) любого сложного
объекта (системы, операции) имеет два чётко выраженных этапа, называе-
Системный анализ - это метод исследования (не смешивать с анализом систем
(АНС) - научной дисциплиной).
2 С которой читателю рекомендуется ознакомиться подробнее.

24 Глава 1. Концептуальные основы системных исследований
мых соответственно внешним и внутренним проектированием (синте-
зом). Исходя из физического смысла решаемых на этих этапах задач их
ещё целесообразно называть этапами системно-агрегативного и
структурно-параметрического синтеза (проектирования).
v
Постановка задачи
и формулирование
целей исследования
Исследование
ресурсов
Перебор вариан-
тов решения
Построение вербальной, эври-
стической модели объекта ис-
следования, установление наи-
более важных зависимостей (со-
держательное моделирование)
Оценивание
вариантов
Выбор варианта
(принятие
решения)
Реализация
решения
Контроль
г>\
X
Построение агрегативной
математической модели
(абстрагирование)
i
Обоснование показателей качества
системы, эффективности её функ-
ционирования и критериев их оце-
нивания (формализация задачи)
*
Реализация модели и исследова-
ние влияния её управляемых
параметров на показатели
качества системы и операции
X
Сопоставление результатов ана-
лиза с моделируемым объектом
(проверка качества модели)
j | Определение оптимального
решения
«
S
Я
<
Он
ы
с
о
W
S
в
<
т
о
ч
щ
ч
и
о
S
V
Рис. 1.1.2
Внешнее (системно-агрегативное) проектирование (ВНЕПР) - это
первый этап синтеза объекта, на котором:
- изучается проблема - цели создания и будущего применения (функ-
ционирования) объекта;
- исследуются проблемная ситуация - фон и окружение проблемы,
т.е. её предметная область, прецеденты и прототипы;
- обосновываются показатели качества СС (ЦУТС) и эффективности
её ЦНПФ (ЦНПФС), а также критерии их оценивания;
~ строятся агрегированные и агрегативные модели синтезируемых
объектов (ЦУТС и ЦНПФС);
- организуются и проводятся эксперименты по сбору информации, не-
обходимой для построения и уточнения моделей.

1.1. Системный подход и системные направления в науке 25
Таким образом, на этапе внешнего проектирования выявляются требо-
вания к ЦУТС и ЦНПФС, обусловленные их окружением, т.е. внешней
средой и целевым предназначением.
Внутреннее (структурно-параметрическое) проектирование
(ВНУПР) - это второй этап синтеза объекта, на котором:
- прорабатывается предварительный проект структуры и эксплуата-
ционно-технических свойств {характеристик - ЭТХ) системы в
единичном акте её функционирования;
- прорабатывается проект системы, рассчитанной на полную загрузку
в условиях воздействия случайных факторов;
- анализируется ЦНПФС в условиях воздействия антагонистических
факторов (противника, конкурента).
Таким образом, на этапе внутреннего проектирования вырабатывается
проектное задание на ЦУТС и ЦНПФС. При этом все его подэтапы осуще-
ствляются одновременно в течение всего процесса проектировании, реали-
зуя тем самым комплексный подход в замкнутой схеме.
На рис. 1.1.3 приведены структурные схемы процесса проектирования
сложных больших систем (ЦУТС) на различных его фазах:
а) начальной фазе;
б) организационной фазе;
в) фазе предварительного структурно-параметрического проектирова-
ния.
Как видно из рис. 1.1.3, в), результаты ВНУПР используются для уточ-
нения моделей ЦУТС и ЦНПФС. Следовательно, оба этапа (ВНЕПР и
ВНУПР) тесно связаны между собой.
Таким образом, в процессе ВНЕПР разрабатывается (проектируется,
синтезируется) концептуальная модель [93] (? облик") ЦУТС (её орга-
низация и системно-агрегативные свойства), наилучшим (в каком-то
смысле) образом соответствующий её задачам (целям ПФС); в процес-
се ВНУПР уточняются ЭТХ ЦУТС (её структурно-параметрические и экс-
плуатационные свойства). В основе ВНЕПР лежат методы ИСО (методоло-
гия и математические модели), основу которых, в свою очередь, составля-
ют методы ТЭЦНП, базирующиеся на концепциях "Квалиметрии". По-
скольку задачи ИСО решаются в условиях принципиальной априорной не-
определённости, то основным орудием ВНЕПР являются "Теория вероят-
ностей" и "Математическая статистика" [42].
Итак, ТЭЦНП - это прикладная математическая дисциплина, служащая
инструментом ИСО, СИТ, ПРК, АНС в задачах измерения (оценивания) и
анализа эффективности ЦНП, а также оптимального синтеза ЦУТС и
ЦНПФС.

26 Глава 1. Концептуальные основы системных исследований
ВНЕПР
ВНУПР
Формулировка задачи
ВНЕПР
Формулировка
задачи
х
Агрегативная мате-
матическая модель
Планирование
экспериментов
а)
б)
Предлагаемое решение
ВНУПР
i—>-
Проектирование еди-
ничного канала ЦУТС
Проектирование ЦУТС
для большой нагрузки
Проектирование ЦУТС
для конфликтной
ситуации
ВНЕПР
ВНУПР
Формули-
ровка
задачи
Агрегатив-
ная матема-
тическая
модель
Планирова-
ние экспе-
риментов
Испытания
модели опе-
рационного
комплекса
Проектиро-
вание еди-
ничного ка-
нала ЦУТС
Проектиро-
вание ЦУТС
|для большой)
нагрузки
Проектиро-1
вание ЦУТС)
для конф-
ликтной си-
туации
Входы h
Связь Н
Логическое
управление
Рефлек-
сивное
управление
Средства
отобра-
жения
Выходы
Анализ h
Опыты с
критичес-
кой аппа-
ратурой
в)
Рис. 1.1.3

1.2. Основные принципы исследования операций и теории эффективности 27
Определения не имеют значения для
науки, поскольку они всегда оказываются
неудовлетворительными. Единственно ре-
альным определением оказывается разви-
тие самой сути дела, и оно уже не есть оп-
ределение.
...Но для практического применения
краткое указание наиболее общих и в то же
время наиболее характерных признаков в
так называемом определении часто бывает
полезно и необходимо, и оно не может по-
вредить, если только от него не требуют,
чтобы оно давало больше, чем оно может
выражать.
Ф. Энгельс. "Анти-Дюринг"
1.2. ОСНОВНЫЕ ПРИНЦИПЫ ИССЛЕДОВАНИЯ
ОПЕРАЦИЙ И ТЕОРИИ ЭФФЕКТИВНОСТИ
ЦЕЛЕНАПРАВЛЕННЫХ ПРОЦЕССОВ
Поскольку методы ТЭЦНП применяются при решении задач ИСО, то
представляется необходимым знать её основные методологические прин-
ципы и терминологию.
1.2.1. ОСНОВНЫЕ ПОНЯТИЯ
Существует множество определений предмета "Исследования опера-
ций" [26, 40, 82, 109, 123, 190]. В каждом из них подчёркивается та или
иная характерная черта этого научного направления, чёткие границы кото-
рого до настоящего времени ещё не определены и которое, как уже отме-
чалось, в значительной степени перекликается с другими системными дис-
циплинами как по решаемым проблемам, так и по методам их решения.
Приведём ряд определений различных авторов, данных на вербальном
(содержательном, неформальном) уровне:
- исследование операций - это совокупность конкретных практических
приёмов решения задач и управления, методов исследования кон-
кретных социальных (в том числе военных) процессов, так или иначе
связанных с принятием решений, планированием и управлением;
- исследование операций - это совокупность методов оптимизации
решений, принимаемых людьми, в сложных ситуациях, основанных
на точном, формализованном описании ситуации и количественном

28 Глава 1. Концептуальные основы системных исследований
анализе факторов, определяющих возможности достижения постав-
ленных целей;
- исследование операций - это приложение научных методов к про-
блемам принятия решений, связанным с эффективным обслуживани-
ем и управлением в реальных системах, состоящих из машин и лю-
дей, и с распределением материально-денежных ресурсов;
- исследование операций - это совокупность математических методов,
применяемых при исследовании целенаправленных процессов воо-
ружённой борьбы;
- исследование операций - это количественное выражение здравого
смысла.
Последнее определение нельзя считать строгим, однако оно достаточно
ёмко характеризует сущность "Исследования операций".
Из приведённых определений следует:
- объект исследования ИСО - операция (ЦНПФС);
- предмет исследования ИСО - организация операции (ЦНПФС);
- задача ИСО - разработка рациональных способов организации и
проведения операций (ЦНПФС), в каком-то смысле оптимальных.
Как было отмечено, организация ЦНПФС начинается уже в период про-
ектирования ЦУТС, призванной проводить операцию. Таким образом, син-
тез ЦУТС и синтез ЦНПФС - это две фазы (две стадии, две этапа) синтеза
операции.
Поскольку проблема заключается в выборе лучшего из сравниваемых вариан-
тов исследуемого объекта (ЦУТС или ЦНПФС), то она, в свою очередь, порож-
дает проблему измерения качества объекта и управления его качеством.
Качество любого объекта в полной мере проявляется лишь в процессе
его использования по назначению (в процессе его целевого функциониро-
вания), поэтому наиболее объективным является оценивание качества объ-
екта по эффективности его целевого применения.
Как отмечалось, понятие эффективности получило научно-практическое
применение в рамках ИСО при оценивании качества организации опера-
ции (ЦНПФС). Концептуальные, методологические и методические осно-
вы такого оценивания в результате их эволюции сформировались в "Те*>
рии эффективности", объектом исследования которой является (как и в
ИСО) операция (ЦНП), а предметом исследования - качество (эффектив-
ность) операции.
Поскольку, как было отмечено, понятие эффективности часто связыва-
ется с множеством объектов различной природы (вопреки словарному тол-
кованию [159]), то возникает необходимость в уточнении предмета рас-
сматриваемой в монографии дисциплины.
Итак, это "Теория эффективности целенаправленных процессов". При-
менительно к целям данной монографии ей может быть дано следующее
определение.

1.2. Основные принципы исследования операций и теории эффективности 29
Теория эффективности целенаправленных процессов (ТЭЦНП) -
это научно-прикладная дисциплина, в рамках которой разрабатываются и
исследуются принципы и методы количественного оценивания и анализа
качества результатов целевого функционирования ЦУТС и степени их со-
ответствия целям операции (стоящим перед ЦУТС задачам), а также мето-
ды оптимизации проектируемых ЦУТС и организуемых ЦНПФС (опера-
ций). А
При решении задач ИСО и ТЭЦНП должны соблюдаться следующие
основные принципы:
1. Анализ условий задачи с общей для всей ситуации единой точки
зрения. Это в первую очередь проявляется при определении (форму-
лировании) критериев оценивания эффективности операции, по-
скольку оптимизироваться должны параметры ЦУТС и ЦНПФС, су-
щественные для операции в целом.
2. Реализация системного, комплексного подхода, как к постановке, так
и к решению задачи. В этом проявляется тесная связь ИСО с ОТС,
АНС, СИТ и ПРК.
3. Рассмотрение не объектов как таковых, а их агрегированных матема-
тических моделей.
Это одна из основных особенностей системного метода. При этом сис-
темный подход позволяет совершенно различные по физической природе
ситуации и процессы рассматривать как стандартные условия задачи вы-
бора оптимальной альтернативы, оптимального распределения ресурсов,
оптимального процесса (модельного) достижения цели и т.п. Это означает,
что в задачах ИСО и ТЭЦНП главное внимание уделяется не содержанию
решения, а способу его получения, структуре и общим свойствам алгорит-
мов решения. Единство способа, а не объектов исследования - суть мето-
дов математического моделирования вообще и операционных исследова-
ний в частности.
4. Абстрагирование, формализация и математизация проблемной си-
туации со строгим количественным описанием связей агрегирован-
ных характеристик модели с ЭТХ ЦУТС и ЦНПФС. Единственные
допускаемые эксперименты - это мысленные эксперименты на ана-
литической модели или машинные эксперименты на имитационной
модели.
5. Конкретность целей исследования на основе научных методов.
Методы ИСО и ТЭЦНП отличаются строгой практической направлен-
ностью. Это сугубо прикладные методы. Кроме того, это синтетические
методы, направленные на воссоздание целостной картины проблемной си-
туации.

30 Глава 1. Концептуальные основы системных исследований
1.2.2. ТЕРМИНОЛОГИЯ
Как в любой научной дисциплине, в ИСО и ТЭЦНП для обозначения
используемых понятий применяется специальная терминология. Хотя мно-
гие фигурировавшие уже понятия ИСО и ТЭЦНП известны из литературы,
однако, чтобы избежать возможных разночтений, представляется целесо-
образным уточнить определения используемых в дальнейшем понятий в
соответствии с наиболее авторитетными источниками.
Базовыми понятиями ИСО и ТЭЦНП являются:
- операция;
- цель операции;
- система;
- задача системы;
- стратегия;
- операционная система;
- операционный комплекс и т.д.
Дадим их определения.
Определение 1.2.1. Система - это целостное множество (совокупность)
взаимосвязанных объектов (предметов - элементов системы). А
1.2.1) Сложная система (СС) - это система, характеризующаяся мно-
жеством возможных состояний, каждое из которых описывается набором
значений её конкретных параметров. СС характеризуется сложным строе-
нием и сложным поведением.
Все рассматриваемые в дальнейшем системы - сложные.
Сложная система военного назначения - это человеко-машинная {эрга-
тическая) система, называемая военно-технической системой (ВТС). А
Определение 1.2.2. Целеустремлённая техническая система
(ЦУТС) - это множество взаимосвязанных материальных объектов (тех-
нических средств и обслуживающих их групп людей), непосредственно
участвующих в проведении операции и объединённых общей целью. А
Для выделения системы из множества объектов используется понятие
операции.
Определение 1.2.3. Операция - это упорядоченная совокупность (сис-
тема) взаимосвязанных действий, направленных на достижение опреде-
лённой цели. А
Применительно к СС (ЦУТС) операция - это целенаправленный процесс
(ЦНП) функционирования системы (ЦНПФС). Именно наличие общей це-
ли объединяет множество объектов в систему (ЦУТС).

1.2. Основные принципы исследования операций и теории эффективности 31
1.2.2) Необходимо подчеркнуть, что нераздельным атрибутом опера-
ции является конечная её длительность, называемая операционным вре-
менем. А
Определение 1.2.4. Цель - это требуемый (желаемый) исход опера-
ции. А
Сложные системы могут быть расчленены на подсистемы и элементы с
определённой иерархической структурой связей между ними.
Определение 1.2.5. Подсистема (субсистема) - это сложная система
меньшего масштаба, чем исходная, организационно входящая в послед-
нюю, реализующая самостоятельную операцию, цель которой подчинена
цели операции, проводимой исходной системой, являющейся по отноше-
нию к подсистеме надсистемой (суперсистемой). А
Определение 1.2.6. Элемент системы - это объект, входящий в состав
системы, но не имеющий в рамках конкретной операции самостоятельной
цели и не подлежащий расчленению на части. А
Понятия подсистемы и элемента сугубо модельные и, в этом смысле,
условные. Так, одна и та же совокупность объектов может в рамках одной
операции являться элементом, в рамках другой - подсистемой (субсисте-
мой), в рамках третьей - системой или даже надсистемой (суперсистемой).
Элементы сложной системы функционируют во взаимодействии, в ре-
зультате чего свойства СС определяются не только (и не столько) свойст-
вами её элементов и подсистем, но и характером взаимодействия между
ними, т.е. новыми, так называемыми системными свойствами.
Определение 1.2.7. Комплекс - это совокупность объектов (систем,
подсистем, элементов) различной физической природы, объединённых
общей целью, но с менее жёсткими, чем в системе, организационными свя-
зями. А
1.2.3) Под военно-техническим комплексом (ВТК) понимается объ-
единение военно-технических систем, каждая из которых проводит само-
стоятельную операцию. А
Как следует из определений 1.2.3 и 1.2.4, пока нет цели, нет и операции.
В рамках ИСО и ТЭЦНП предполагается (и это принципиально), что цель
операции - единственная. Операция, преследующая несколько целей, - это
совокупность одноцелевых операций. При этом эффективности отдельных
таких операций могут быть (и, как правило, являются) различными. Если
цели этих операций взаимосвязаны, то иногда их совокупность может рас-
сматриваться как одна обобщённая (сложная, групповая) цель.

32 Глава 1. Концептуальные основы системных исследований
Цель считается достигнутой, если путём преобразования (расходования)
функционирующей ЦУТС некоторых (в каждой операции своих) ресурсов
(сырья, энергии, информации, времени и т.д.) получен соответствующий
(требуемый, потребный) ей результат (исход операции).
Определение 1.2.8. Задача системы - это достижение требуемого ис-
хода операции в результате функционирования ЦУТС при заданном рас-
ходе ресурсов, за заданное время и характеризуемого заданным набором
количественных данных. А
Другими словами, задача - это конкретизированная цель. По существу,
цель операции становится задачей системы, если конкретизированы коли-
чественные характеристики требуемого результата и отпускаемых на его
получение ресурсов и времени. Практически цель операции достигается
путём выполнения системой последовательности задач.
Если цель операции сформулирована (задача системы поставлена), то
может быть начата разработка альтернативных способов (стратегий, пла-
нов, программ) достижения цели (выполнения задачи). Из набора альтер-
нативных планов наилучший выбирается на основе тех или иных принци-
пов и вытекающих из них концепций, которые формально выражаются в
форме критериев {правил суждения).
Определение 1.2.9. Стратегия — это определённая организация и спо-
соб проведения операции (применения системы). А
1.2.4) Крупномасштабные операции всегда реализуются как совокупно-
сти более мелких частных операций. А
Определение 1.2.10. Результаты операции - это совокупность всех её
эффектов (последствий). А
Определение 1.2.11. Целевой эффект операции - это результат, ради
получения которого проводится операция. А
Определение 1.2.12. Ресурсы - это запасы материи (сырья), энергии,
информации, времени, а также технические и людские ресурсы, необходи-
мые для проведения операции и получения требуемого целевого эффекта.
А
Определение 1.2.13. Свойство - это объективная особенность объекта,
зависящая от его.строения и характеризующая отдельную его сторону (ас-
пект). А
Определение 1.2.14. Качество - это совокупность свойств объекта, от-
личающих его от других объектов и характеризующих его соответствие
назначению. А

1.2. Основные принципы исследования операций и теории эффективности 33
Определение 1.2.15. Операционная система (ОС) - это совокупность
объектов (как материальных, так и нематериальных: информация, время и
т.д.), в результате взаимодействия которых реализуется операция. А
Определение 1.2.16. Операционный комплекс (ОК) - это совокуп-
ность объектов, включающая в себя в качестве элементов операционную
систему, суперсистему и окружающую среду. А
Определение 1.2.17. Окружающая среда (ОКС) - это совокупность
объектов, не входящих в операционную систему, непосредственного уча-
стия в операции не принимающих, но обусловливающих операционную
ситуацию и оказывающих влияние на ЦНПФС и его исход. А
В дальнейшем окружающая (внешняя) среда интерпретируется как ус-
ловия проведения операции (УПО), представляющие собой, в свою оче-
редь, совокупность условий функционирования (УФС) и условий примене-
ния (УПС) системы (ЦУТС).
Определение 1.2.18. Операционная ситуация (ОСТ) - это состояние
объектов окружающей среды, определяющих условия применения систе-
мы (ЦУТС). А
1.2.5) В принципе состояние ОС, зависящее от условий функциониро-
вания ЦУТС, также влияет на ситуацию, однако представляется целесооб-
разным под ОСТ понимать состояние объектов окружающей среды, яв-
ляющихся по отношению к ЦУТС и ОС внешними и обусловливающих
требования, которым должны удовлетворять результаты операции для дос-
тижения её цели. А
Более детально семантика введённых понятий раскрывается по мере об-
ращения к ним в последующих главах.
1.2.3. ОБЩАЯ ХАРАКТЕРИСТИКА
ЭЛЕМЕНТОВ ОПЕРАЦИОННОГО КОМПЛЕКСА
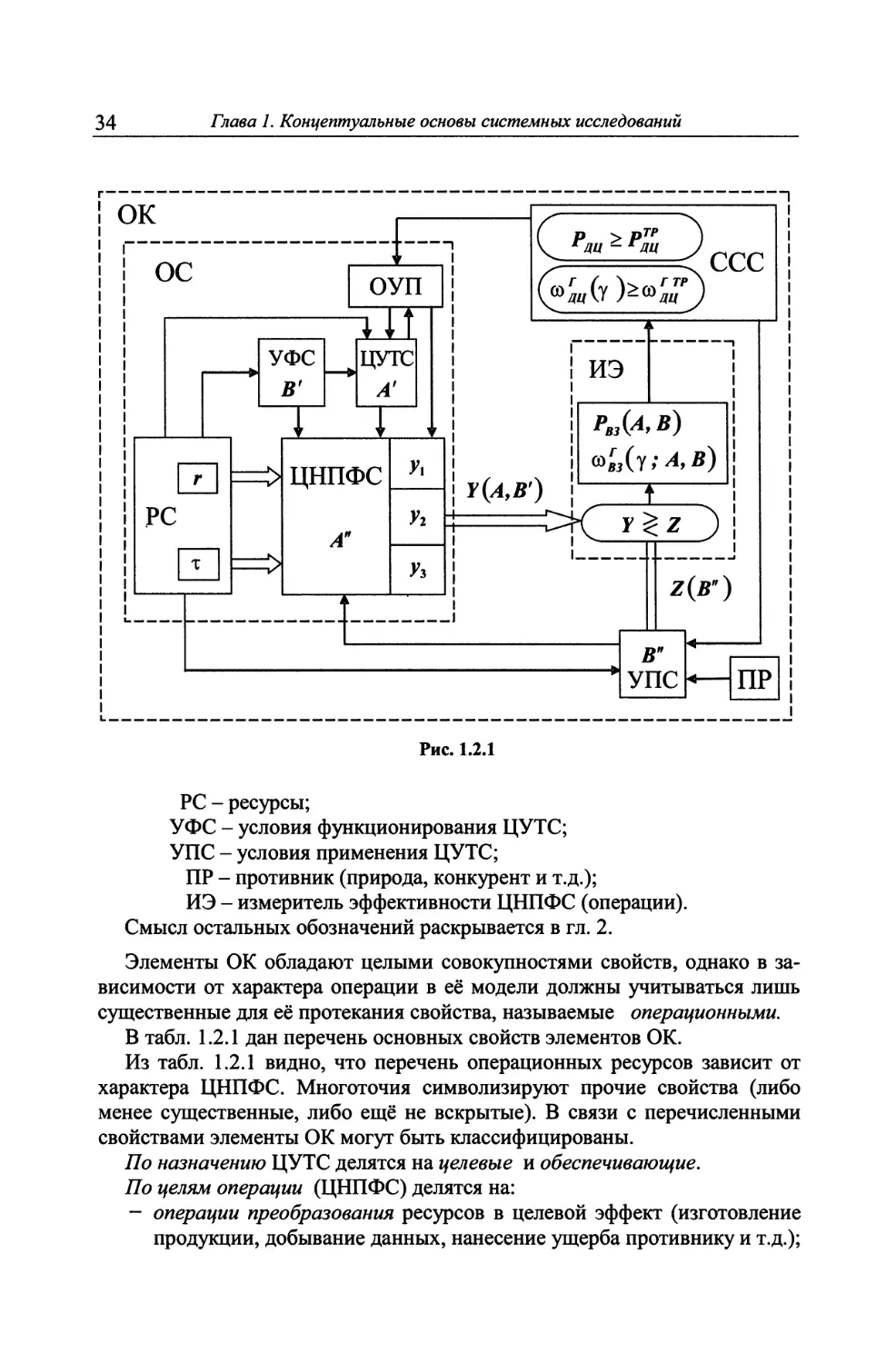
На рис. 1.2.1. приведена обобщённая структурная схема ОК, где обозна-
чены:
ОК - операционный комплекс;
ОС - операционная система;
ССС - суперсистема;
ОУП - орган управления;
ЦУТС - целеустремлённая техническая система;
ЦНПФС - целенаправленный процесс функционирования ЦУТС;
2 Зак. 3303

34 Глава 1. Концептуальные основы системных исследований
ок
ос
ОУП
УФС
В'
L
ЦУТС
Л'
(<(тк;)
ссс
иэ
к
?2
Уз
У(л,Д')
РВЗ(А,В)
I J
Z(B")
В"
УПС
ПР
Рис. 1.2.1
PC - ресурсы;
УФС - условия функционирования ЦУТС;
УПС - условия применения ЦУТС;
ПР - противник (природа, конкурент и т.д.);
ИЭ - измеритель эффективности ЦНПФС (операции).
Смысл остальных обозначений раскрывается в гл. 2.
Элементы ОК обладают целыми совокупностями свойств, однако в за-
висимости от характера операции в её модели должны учитываться лишь
существенные для её протекания свойства, называемые операционными.
В табл. 1.2.1 дан перечень основных свойств элементов ОК.
Из табл. 1.2.1 видно, что перечень операционных ресурсов зависит от
характера ЦНПФС. Многоточия символизируют прочие свойства (либо
менее существенные, либо ещё не вскрытые). В связи с перечисленными
свойствами элементы ОК могут быть классифицированы.
По назначению ЦУТС делятся на целевые и обеспечивающие.
По целям операции (ЦНПФС) делятся на:
~ операции преобразования ресурсов в целевой эффект (изготовление
продукции, добывание данных, нанесение ущерба противнику и т.д.);

1.2. Основные принципы исследования операций и теории эффективности 35
- операции распределения и перемещения (транспортные перевозки,
передача информации и т.д.).
По характеру протекания во времени операции делятся на непрерыв-
ные и дискретные (циклические).
1.2.6) Строго говоря, все операции дискретны, так как отдельные их
этапы (стадии, фазы) разнесены во времени, однако некоторые фазы
ЦНПФС могут протекать непрерывно. А
Таблица 1.2.1.
Элементы ОК
ЦУТС
ЦНПФС
Основные свойства
Характеристики строения
- состав;
- структура (габариты, веса);
- масштабы (сложность);
- надёжность;
Характеристики поведения
- мощность;
- мобильность;
- манёвренность;
- производительность;
- быстродействие;
- готовность;
- работоспособность;
- точность;
- живучесть;
- долговечность;
- экономичность;
Общие
- масштабность;
- продолжительность;
- устойчивость (помехоустойчивость);
Операционные
- результативность;
- ресурсоёмкое^;
- оперативность;
- эффективность;

36 Глава 1. Концептуальные основы системных исследований
Продолжение табл. 1.2.1.
Элементы ОК
Результаты ЦНПФС
Ресурсы
Основные свойства
Прямые - целевые
- объём (величина) целевого эффекта;
- качество целевого эффекта: точность,
достоверность, информативность,
содержательность, полнота,
своевременность и т.д.
Косвенные - побочные
- расход операционных ресурсов;
- расход операционного времени;
- потери и ущербы;
- объём (количество);
- состав (структура);
- качество;
- динамичность;
- активность;
По характеру повторяемости операции делятся на:
- массовые (плановые транспортные перевозки, решения задач управ-
ления, сбор метеоинформации, сбор разведданных и т.д.);
- единичные - уникальные (запуск космического аппарата; стыковка
космических аппаратов на орбите; вскрытие мероприятия, проводи-
мого противником; нанесение удара по цели и т.д.).
На рис. 1.2.2. приведена классификация результатов операций, соглас-
но которой следует различать результаты:
- положительные и отрицательные',
- прямые и косвенные (побочные).
Кроме того, в рамках каждого из блоков схемы рис. 1.2.2. результаты
могут быть однородными и неоднородными.
Ресурсы могут быть классифицированы по структуре и по динамике
превращения в целевой эффект.
По структуре ресурсы делятся на однородные и неоднородные.
1.2.7) Однородность ресурсов существенно упрощает исследование
операции и её эффективности, однако подобные операции крайне редки
(если вообще существуют). Выражение всех ресурсов в их стоимостном
"эквиваленте" приводит к вырождению задачи до некорректной. ▲

1.2. Основные принципы исследования операций и теории эффективности 37
Результаты операции (ЦНП)
т
Положительные
(позитивные)
If—>•
1—>►
Целевые эффекты
(прямые
результаты)
Побочные
положительные
эффекты
т
Отрицательные
(негативные)
Расходы ресурсов
(прямые
результаты)
Побочные
отрицательные
эффекты
<—1
Рис. 1.2.2
По динамике превращения в целевой эффект различают ресурсы:
- активные и пассивные;
- динамические и статические.
Активными (А) называются ресурсы, непосредственно превращающие-
ся в целевой эффект.
Пассивными (П) называются ресурсы, участвующие в получении целе-
вого эффекта, но непосредственно в него не превращающиеся.
Динамическими (Д) называются ресурсы, расходуемые на получение
целевого эффекта в ходе операции.
Статическими (С) называются ресурсы, расходуемые при создании
ЦУТС и организации ЦНПФС и участвующие в нём опосредованно в ка-
честве технического ресурса средств, уровня технологии, параметров и
ЭТХ ЦУТС и ЦНПФС и т.д. Это капитальные затраты. В ходе операции
эти ресурсы расходуются, но весьма медленно, так что в пределах одной
операции они практически не изменяются, но их наличие абсолютно необ-
ходимо.
Типичными являются операции, в ходе которых расходуются (исполь-
зуются) ресурсы различных видов:
- ресурс сырьевой (А, Д);
- ресурс энергетический (А, Д);
- ресурс структурный ЦУТС (П, Д);
- ресурс технический (П, С);
- ресурс технологический (П, С);
- ресурс информационный (П, Д);
- ресурс управленческий - организационный (П, Д);
- ресурс временной (П, Д);
- ресурс трудовой - людской (П, Д) и т.д.

38 Глава 1. Концептуальные основы системных исследований
Более подробно роли ресурсов различных видов выявляются в после-
дующих главах.
1.3. КОММЕНТАРИИ
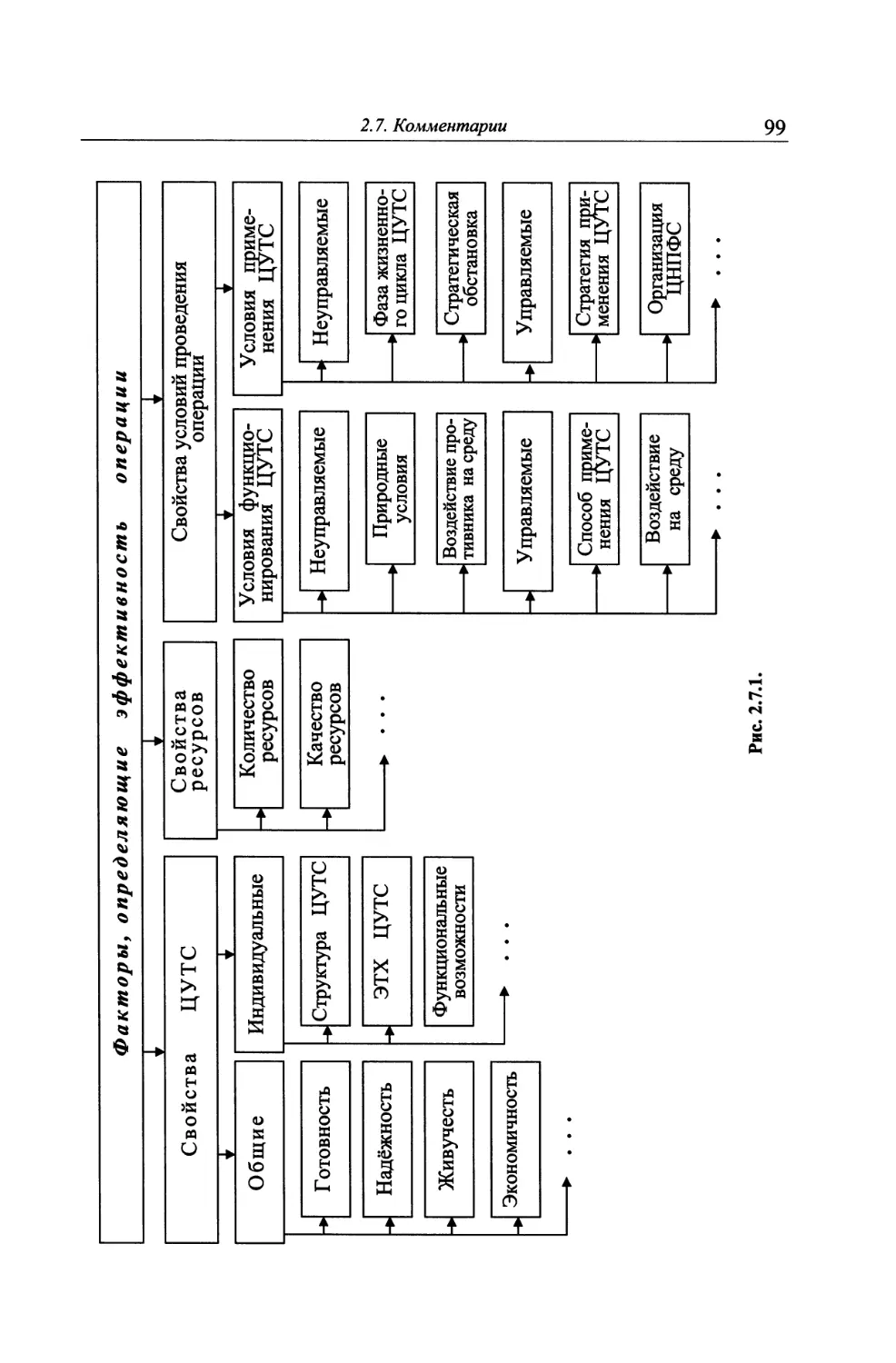
1.3.1} Цель данной главы - введение в предмет ТЭЦНП, формулировка
основных её концепций и определение её места среди дисциплин систем-
но-технического цикла. Поэтому сами эти дисциплины практически лишь
упоминаются. Заинтересованного читателя адресуем к посвященной этим
дисциплинам литературе (см. библиографию). А
1.3.2} В дополнение к сказанному в конце п. 1.1 обратим внимание на
следующее принципиальное обстоятельство, не нашедшее в литературе
достаточного отражения.
Как было отмечено выше, этапу внешнего проектирования сопутствует
большая неопределенность, обусловленная множеством самых различных
факторов технического, экономического, социального, политического, ...
характера. Поэтому (см. [42]) основным орудием внешнего проектирова-
ния, а следовательно, и его инструментария - ИСО и ТЭЦНП является
"Теория вероятностей". Но "Теория вероятностей" - это теория матема-
тического моделирования стохастических (неопределённых) ситуаций
(случайных явлений) и прогнозирования поведения случайных объектов -
характеристик таких ситуаций (событий, величин, векторов, функций). Та-
ким образом, как в ИСО, так и в ТЭЦНП строятся априорные (прогнозные)
модели ЦУТС и ЦНПФС и исследуются их прогнозные свойства, которые
в силу неопределённости исходных данных также содержат элемент неоп-
ределённости. Поэтому когда в задачах ИСО и ТЭЦНП рассматривается
ЦУТС или ЦНПФС, то речь идёт не о конкретном объекте исследования
(ЦУТС, ЦНПФС), а о целом классе таких объектов, функциональные свой-
ства которых имеют некоторый разброс относительно зафиксированных в
модели номинальных значений.
Действительно, хорошо известно, что в любой партии однотипных из-
делий не существует идентичных или что невозможно абсолютно точно
повторить какую-либо последовательность действий.
Таким образом, когда априори говорится о качестве объекта, то речь
идёт о качестве его проекта, модели, а не конкретного образца (которого
ещё нет). Аналогично под эффективностью операции (ЦНПФС) следует
понимать эффективность класса операций с "одинаковой" организацией
(стратегией), в рамках которой отдельные элементы этого класса могут об-
ладать различными по качеству результатами. А

Одна из основных опасностей, подсте-
регающих исследователя, который решает
практические задачи с помощью моделиро-
вания, - это неправильно выбранный кри-
терий эффективности. Это, в свою оче-
редь, в большинстве случаев объясняется
необоснованным перенесением на новые
системы методов, выбранных для других
систем.
Д. Хорафакс. "Системы и моделирование"
Глава 2
МЕТОДОЛОГИЧЕСКИЕ ОСНОВЫ
ТЕОРИИ ЭФФЕКТИВНОСТИ
ЦЕЛЕНАПРАВЛЕННЫХ ПРОЦЕССОВ
В гл. 1 были даны определения ключевых (базовых) понятий, лежащих
в основе системных исследований и используемых в рамках системных
научных направлений. При этом было отмечено, что для системного под-
хода специфична проблема порождения свойств (поведения) целого из
свойств (поведения) его элементов, и наоборот, порождения свойств (по-
ведения) частей из свойств (поведения) целого. Принципы системного
подхода выражаются в требовании всесторонности, комплексности иссле-
дования любого объекта или явления. Комплексность системного подхо-
да проявляется в том, что наряду с рассмотрением сложного объекта ис-
следования (ЦУТС, ЦНПФС) как единого целого - комплексно, должен
учитываться весь комплекс его существенных свойств (как положитель-
ных, так и отрицательных), а также все возможные (положительные и от-
рицательные) последствия его целевого применения - комплекс результа-
тов функционирования объекта.
Целями данной главы являются, с одной стороны, раскрытие семантики
(физического смысла) этих понятий, а с другой - их формализация, т.е. ма-
тематическая формулировка, обладающая достаточной общностью и при-
годная для описания широкого класса объектов исследования (ЦУТС и
ЦНПФС).

40 Глава 2. Методологические основы теории эффективности
2.1. СЕМАНТИЧЕСКИЕ АСПЕКТЫ
ТЕОРИИ ЭФФЕКТИВНОСТИ
Как отмечалось ранее, основным объектом исследования теории эффек-
тивности является операция, т.е. целенаправленный процесс функциони-
рования ЦУТС (ЦНПФС). При этом цель исследования - выявление фак-
торов, обусловливающих основные (существенные для анализа) свойства
ЦНПФС, анализ влияния этих факторов на качество ЦНПФС, т.е. на его
соответствие целям операции, определение принципов, путей и методов
организации (планирования и обеспечения) и последующего управления
ЦНПФС, обеспечивающих его наивысшее качество.
В гл. 1 было показано, что основу разрешения всех проблем системных
исследований составляет поиск наилучших (оптимальных) вариантов ис-
следуемых объектов: ЦУТС и ЦНПФС. При этом оптимальность решения
(варианта) тождественна наибольшему (наилучшему) соответствию синте-
зируемого (проектируемого, организуемого) объекта его целевому назна-
чению. Другими словами, во всех системных исследованиях первичным
является целевое назначение объекта, точнее, достигаемая с его помощью
(путём его применения по назначению) цель. Вспомним её определение.
Определение 2.1 Л. Цель1 - это желаемый исход операции (ЦНПФС).А
Определение 2.1.2. Операция (ЦНПФС) - это совокупность или по-
следовательность согласованных действий, направленных на достижение
некоторой конкретной цели. ▲
Так как операция протекает во времени, то это процесс, а поскольку
операция имеет цель, то это целенаправленный процесс (ЦНП). Любой
процесс есть следствие развития некоторой материальной системы. Если
назначением системы является реализация (проведение) этого процесса, то
процесс ее функционирования будет целенаправленным. Таким образом,
операция - это целенаправленный процесс функционирования некоторой
системы (в частности, ЦУТС), т.е. любой ЦНПФС представляет собой опе-
рацию. Однако поскольку не все процессы целенаправленны, то необхо-
димо сформулировать отличительные признаки операций, выделяющие их
в самостоятельный класс процессов.
Представляется очевидным, что поскольку операция организуется и
проводится с определённой целью, то об её качестве следует судить по
степени достижения этой цели. Поэтому мера (показатель) качества опера-
ции должна учитывать как целевые эффекты, ради которых проводится
операция, так и "усилия", необходимые для получения этих эффектов.
1 Существует множество определений понятия "цели", отличных от приведённого,
содержащих гораздо больше слов, но при этом теряющих чёткость определения [26,40,
138].

2.1. Семантические аспекты теории эффективности 41
Из множества свойств, присущих любому процессу (стационарность,
последействие, устойчивость и т.п. [129]), для характеристики целенаправ-
ленного процесса существенны так называемые операционные свойства1,
которые и определяют его качество как объекта исследования. Операцион-
ные свойства ЦНПФС в совокупности и во взаимосвязи порождают его
обобщённое свойство - эффективность, определяющее качество ЦНПФС и
присущее только операциям. Раскроем семантику понятия эффективности.
Вообще термин "эффект" многозначен. Из всех его значений нашим
целям отвечает лишь одно: эффект - это действие, производимое чем-
либо, результат такого действия. Отсюда эффективный - это дающий
эффект, результативный, действенный (от латинского "производитель-
ный") [159, 160]. Таким образом, эффективность - это свойство дейст-
вия (операции - ЦНПФС) давать эффект.
2.1.1) В общем случае по отношению к цели рассматриваемого действия
эффект качественно может быть как положительным (позитивным), так и
отрицательным (негативным), однако при определении показателя качест-
ва результатов операции речь идёт всегда о положительном (по смыслу, а
не по значению) эффекте. Поэтому эффективность - это не просто спо-
собность давать эффект, а именно действенность такой способности, т.е.
результативность, соотнесённая с затратами ресурсов всех видов (матери-
альных, энергетических, информационных, временных, людских и т.п.). А
2.1.2) Поскольку эффективность - это свойство действия, то распро-
странённое словосочетание "эффективность системы (ЦУТС)" семантиче-
ски некорректно (неточно). Если оно и может использоваться, то только
лишь в смысле характеристики потенциальных возможностей ЦУТС, оп-
ределяемых её качеством. Таким образом, не следует смешивать понятия
"качество ЦУТС" и "качество ЦНПФС", относящиеся к существенно раз-
личным объектам исследования. А
2.1.3) При исследовании эффективности операций вводится понятие
операционной системы, включающей в себя в качестве элементов (подсис-
тем) и ЦУТС, и реализуемый ею ЦНПФС. Применительно к этой системе
(и только к ней) можно говорить об её эффективности, да и то лишь о по-
тенциальной [185]. Однако поскольку это условие зачастую не выполняет-
ся, то правильнее говорить об эффективности ЦНПФС (т.е. операции). А
Обобщив всё ранее сказанное, дадим определение понятию эффектив-
ности.
1 Таким образом, операционные свойства ЦНП - это его атрибуты2.
2 Атрибут - это существенный признак, свойство, неотъемлемая принадлежность
предмета (объекта исследования) [159,160].

42 Глава 2. Методологические основы теории эффективности
Определение 2.1.3. Эффективность - это комплексное операционное
свойство ("качество" - "атрибут") ЦНПФС, характеризующее его при-
способленность к достижению цели реализуемой ЦУТС операции (к вы-
полнению стоящей перед ЦУТС задачи). ▲
Из данного определения следует, что поскольку эффективность - это
качество (свойство) операции, то методы её исследования должны опи-
раться на основные положения науки о качестве, получившей название
"Квалиметрия". Для чёткого понимания сущности современной методоло-
гии, теории эффективности необходимо уяснить лежащие в её основе по-
нятия «квалиметрии» и «теории оценивания».
Измерять, что измеримо, делать изме-
римым то, что ещё не измеримо.
Г. Галилей
2.2. ОСНОВНЫЕ ПОНЯТИЯ КВАЛИМЕТРИИ
Квалиметрия - это научная область, в которой разрабатываются мето-
дологические основы, методы и методики количественного оценивания и
анализа качества объектов. А
Для более глубокого изучения принципов и методов квалиметрии заин-
тересованному читателю следует обратиться к специальной литературе [4].
Здесь же приведена выборка основных её понятий и концепций, имеющих
непосредственное отношение к проблеме исследования эффективности
ЦНПФС. При этом формулировки ряда понятий уточнены.
2.2.1. ОСНОВНЫЕ ПРИНЦИПЫ И КОНЦЕПЦИИ КВАЛИМЕТРИИ
Прежде всего следует обратить внимание на неоднозначность понятия
качества. Необходимо различать его философскую и потребительскую ин-
терпретации, в связи с которыми оно имеет следующие определения:
- «качество»1 - это наличие существенных признаков, свойств, особен-
ностей (атрибутов), отличающих один предмет или явление от дру-
гих [159]; именно в этом смысле эффективность характеризует "ка-
чество" целенаправленного процесса (см. определение 2.1.3);
- качество - это то или иное свойство, достоинство, степень пригодно-
сти кого-нибудь или чего-нибудь [159].
При употреблении термина «качество» в философской концепции он заключается
в кавычки.

2.2. Основные понятия квалиметрии
43
Легко заметить, что оба определения недостаточно чёткие, поскольку
содержат последовательности неоднородных "синонимов": признаки -
свойства - особенности в первом случае, свойство - достоинство - степень
пригодности - во втором. Причём понятие свойства входит в оба опреде-
ления. Понятно, что в каждом из определений оно имеет свой «оттенок»,
соответствующий сущности понятия качества. В дальнейшем (в рамках
квалиметрии) речь будет идти о качестве потребительском (без кавычек).
В основе последующих построений лежат три постулата.
ПОСТУЛАТ 2.2.1. Каждый исследуемый объект обладает определён-
ными свойствами, обусловливающими его качество. А
Определение 2.2.1. Качество - это свойство или совокупность
свойств объекта, обусловливающих его пригодность для использования по
назначению. А
ПОСТУЛАТ 2.2.2. Каждое из свойств объекта может быть описано ко-
личественно с помощью некоторой переменной, значение которой характе-
ризует меру (интенсивность) его качества относительно этого свойства. А
Эту меру называют показателем свойства или единичным, частным
показателем качества объекта.
Уровень качества объекта характеризуется значениями совокупности
показателей его существенных - атрибутивных свойств (АС), т.е.
свойств, необходимых для соответствия объекта его назначению. Эта со-
вокупность называется показателем качества. Поясним понятие "сущест-
венные свойства" на примерах.
Пример 2.2.1. Пусть объект исследования - радиоприёмник. Из его
возможных свойств (полоса частот, чувствительность, вес, габариты, на-
дёжность, ремонтопригодность, долговечность, эстетичность - внешнее
оформление, стоимость и т.д.) совокупности существенных свойств будут
определяться назначением и условиями целевого применения (условиями
эксплуатации) этого приёмника. Так, для переносных вариантов важными
свойствами будут вес и габариты, для стационарных - полоса частот и чувст-
вительность, для бытовых - внешнее оформление, стоимость и т.д. А
Пример 2.2.2. Пусть объектом исследования является трава на лугу. Её
"качество" обусловливается множеством свойств (физических, химиче-
ских, биологических и т.п.). Однако пока трава не используется, она не об-
ладает качеством потребительским. Такое качество возникает при намере-
нии использовать траву. При этом в зависимости от целей использования
травы в число существенных будут входить различные её свойства (для
выпаса стада - одни, для заготовки кормов - другие, для прогулки и отды-
ха - третьи, для игры в футбол - четвёртые и т.д.). А

44 Глава 2. Методологические основы теории эффективности
Определение 2.2.2. Показатель качества объекта - это вектор, ком-
поненты которого суть показатели его отдельных свойств, представляю-
щие собой частные, единичные показатели качества объекта. ▲
Размерность этого вектора определяется числом существенных свойств
(атрибутов) объекта.
2.2.1) Следует особо подчеркнуть тот факт, что показатель качества -
вектор (т.е. комплексное понятие), а не простое множество показателей
свойств объекта, поскольку между отдельными его свойствами могут суще-
ствовать связи, которые в терминах теории множеств не описываются. А
ПОСТУЛАТ 2.2.3. Требуемое качество объекта задаётся условиями,
которым должны удовлетворять виртуальные (возможные) значения пока-
зателей его существенных свойств - атрибутов (АС). А
Эти условия называются критериями оценивания качества объекта, а
проверка их выполнения называется оцениванием качества объекта.
Определение 2.2.3. Критерий1 оценивания качества - это руково-
дящее правило (условие или совокупность условий), вытекающее из
принятых (положенных в основу исследования) концепций и принципов
оценивания, реализуемое при принятии того или иного решения (проект-
ного, организационного, управленческого и т.п.) о качестве исследуемого
объекта. А
2.2.2. КРИТЕРИИ ОЦЕНИВАНИЯ КАЧЕСТВА ОБЪЕКТОВ
При оценивании качества любого объекта, описываемого я-мерным
векторным показателем, реализуется совокупность критериев, каждый из
которых в общем случае может принадлежать одному из трёх классов:
- классу {G} критериев пригодности;
- классу {О} критериев оптимальности;
- классу {£} критериев превосходства.
Приведём их математические формулировки [112].
Пусть у\, [# = l(l)#i; y = l(l)iw J - показатель /-го свойствау'-го объ-
екта, т.е. показатель качествау-го объекта есть вектор FA = ( j/>J>2>"M.Fwb
{j??j- множество (область) допустимых значений показателя у\ или
1 Критерий - это мерило (но не мера!) оценки, суждения [159]. Критерий - отли-
чительный признак, "пробный камень", мерило; критерий истины - то, что удостоверя-
ет объективную истину [160].

2.2. Основные понятия квалиметрии
45
в векторной форме |гЛ j={(j>i%J>^--vJwj- Тогда критерии перечислен-
ных выше классов имеют следующие определения.
Критерий пригодности:
G- Ш*Ш = "> [j = l{l)m], (2.2.1)
1=1
где (/-достоверное событие (истинное высказывание);
п - символ булева пересечения событий {конъюнкции высказываний).
В векторной форме критерий (2.2.1) принимает следующий вид:
G: (¥^е{¥^}П")=и, [y = l(l)m], (2.2.11)
где {К'\ } - область допустимых значений показателя качества пригодно-
го объекта.
По определению, объекты, для которых выполняются условия (2.2.1),
(2.2. Г), пригодны для использования по назначению. При этом все они об-
ладают одинаковым качеством.
Пример 2.2.3. Критерий (2.2. Г) иллюстрируется рис. 2.2.1 для случая
W = 2; w = 5; {г^}ПР = [у\,у[ ]х[у2,/2 ].
Как видно из рис. 2.2.1, в приведённом примере объекты 1-й, 2-й, 3-й и
5-й пригодны, а 4-й не пригоден, т.е.
1Т(2) J = 1У(2> > Y(2) > Y(2) > Y(2) J ' ^
Критерий оптимальности:
О: ПЫеМЬ ПЫ=*Г")=".к = 1(1)я; У = 1(1)«], (2.2.2)
*=l ke{k\n
ОПТ i
где yk - оптимальное значение показателя ft-го свойства;
/i0 - объём множества {к}^ номеров (число) оптимизируемых
свойств объекта.
В векторной форме критерий (2.2.2) принимает вид
О: (% s {Y{:}})n(У(А = У«")з (% е {Y^h U,\j = l{l )*], (2.2.2')
где \Y>dn\\ - область допустимых значений показателя качества опти-
мального объекта.
По определению, объект, для которого выполняются условия (2.2.2'),
называется оптимальным по А-му свойству, т.е. по я0 свойствам. Понятно,
что такой объект должен быть и пригодным.

46 Глава 2. Методологические основы теории эффективности
Пример 2.2.4. Критерий (2.2.21) иллюстрируется рис. 2.2.2, построен-
ным в условиях примера 2.2.3 для случая
щ=\; k = l; {г{2)}ОПТ={уГЫу'»У;}-
Как видно из рис. 2.2.2, в приведенном примере 1-й и 3-й объекты оп-
тимальны по первому свойству (по показателю у{), т.е.
У г k
ОПТ »
Ух Ух Ух
Ух Ух Ух
Рис. 2.2.1 Рис. 2.2.2
Критерий превосходства:
S: Г)Г\{у]е{у!})пГ\Г)(у'>у>)=и, [/ = l(l)«i], (2-23)
у=1 /=1 /=1 J*i
где / - номер превосходного объекта.
В векторной форме критерий (2.2.3) принимает вид
7=1
где (Ца)*%%Ш*У1)'>
/=1
|гЛ] - область допустимых значений показателя качества пре-
восходного объекта.
По определению, объект, для которого выполняются условия (2.2.3),
превосходит по качеству все остальные объекты. Если [){у1. = yj)=U, то
/=i
качества /-го и у-го объектов признаются одинаковыми. Если же хотя бы

2.2. Основные понятия квалиметрии
47
одно из условий (2.2.3) не выполняется, то это означает, что заданная со-
вокупность показателей свойств не позволяет выявить объект, превосхо-
дящий по качеству все остальные из числа исследуемых.
Пример 2.2.5. Критерий (2.2.3') иллюстрируется рис. 2.2.3, построен-
ным в условиях примеров 2.2.3 и 2.2.4, т.е.
Как следует из рис. 2.2.3, на заданной совокупности объектов 3-й объект
i&}~
ЩТ - i
ОПТ "
Ух Ух Ух
Рис. 2.2.3
является превосходным, несмотря на то что имеет место соотношение
Уг > У г у поскольку 4-й объект не пригоден и, следовательно, не конкурен-
тоспособен по сравнению с остальными. А
2.2.2) Легко заметить, что критерий оптимальности является частным
случаем критерия пригодности, поскольку выражение (2.2.2) означает, что
bihbrh **{*}„>
или в векторной форме
{%ГГ=КТ}ХП[^^]- (2-2.4)
В условиях примеров 2.2.1, 2.2.2 выражение (2.2.4) принимает вид
Иллюстрацией соотношения (2.2.5) может служить рис. 2.2.2, из которо-
го видно, что в критерии оптимальности область {гД ] , превращаясь в об-
Ivd \°ПТ ~ ,
ласть щ2к j , вырождается в отрезок прямой (а на конечной совокупно-

48 Глава 2. Методологические основы теории эффективности
сти т исследуемых объектов-в двухточечное множество |к!2ч,ГД]).
В свою очередь, критерий превосходства представляет собой частный
случай критерия оптимальности, поскольку выражение (2.2.3) означает
ШУ'^У{)*Ш=УГ) (2-2.6)
или в векторной форме
{%Гв=ПЬ'Г}. (2.2.6')
В условиях примеров 2.2.1 - 2.2.3 выражение (2.2.61) принимает вид
НТЕВ =№ПТ ИуГЫу™} • (2.2.7)
▲
Пример 2.2,6. Иллюстрацией соотношения (2.2.7) служит рис. 2.2.3, из
которого видно, что в рамках критерия превосходства область |кД}, пре-
вращаясь в область {к! } , вырождается в точку {(у*,yl) }. А
Таким образом, при оценивании качества объекта критерий G пригод-
ности является доминирующим и универсальным и определяется выраже-
нием
G^: Y{H)e{Y{ff] = U, (2.2.8)
где [К] = ПР, ОПТ, ПРЕВ - индекс класса критерия ;
*М ~ допустимое значение вектора Y,\ для критерия К-то класса;
{у*М][*]1{у*М.(у -¥М)=(ОБЪЕКТ ПРИГОДЕН)} - область
d
допустимых значений показателя качества объекта, соответст-
вующая задаче его исследования, т.е. выявлению его пригодно-
сти, оптимальности или превосходства. А
2.2.3) Приведённые выше формулировки (2.2.1) - (2.2.3) критериев
предназначены для сравнительного оценивания качества объектов и опти-
мизации их свойств (качеств) на дискретно-непрерывных множествах
|{j>/ j |от значений показателей качества объектов. Однако поскольку на
этапах отработки и испытания объекта конкурируют его гипотетические
варианты одного класса (определяемые конкретными значениями показа-
телей свойств), число т которых в принципе не ограничено, то оптимиза-
ция показателей его качеств (свойств) производится на континуальных
множествах \yf }=[^,JI' J , [i = l(l)#i]. Очевидно, что в этом случае ин-
В дальнейшем индекс К класса критерия будет опускаться.

2.2. Основные понятия квалиметрии
49
деке у при показателе у\ свойства у. у-го объекта теряет смысл. Поэтому
в дальнейшем в обозначениях показателей качества он опущен.
Сказанное может быть проиллюстрировано рис. 2.2.4, построенным в
условиях примеров 2.2.3 - 2.2.5, где совокупности допустимых значений
У г k
Уг
Уг
О
V77777777T77777T7,
CZ
Х////////////////Л
К\
Уг
Уг Уг
Рис. 2.2.4
показателей качества исследуемых объектов интерпретируются следую-
щим образом:
- вся область
- область оптимальных значений
fcr=W}x[^X];
- область превосходных значений
fej}™={rfMrfM<rf,rf>}. а
2.2.4) Поскольку, по определению, качество объекта характеризуется
совокупностью его свойств, то оно, в свою очередь, также представляет
собой обобщённое (комплексное) свойство объекта, которое само по себе
ещё не характеризует степени его соответствия назначению. Этой цели
служат показатели качества и критерии его оценивания. Таким образом,
качество и его показатель ~ различные понятия. А
2.2.5) Не следует смешивать понятия "показатель качества" и "крите-
рий оценивания качества", первое из которых означает числовую характе-

50 Глава 2. Методологические основы теории эффективности
ристику или функцию {меру качества), а второе - совокупность высказы-
ваний и предикатов [т.е. условия (2.2.1) - (2.2.3), (2.2.8)]. А
2.2.6) Наконец, сделаем замечание более общего характера. При опре-
делении любого объекта перечисляются его отличительные признаки, т.е.
его особенности и свойства. Для обозначения конкретного свойства ис-
пользуется некоторый символ, имеющий смысл "имени свойства". Для
обозначения меры (интенсивности) этого свойства должен использоваться
символ (показатель), отличный от символа - имени. Значение, принимае-
мое показателем при измерении, не тождественно самому показателю и
должно иметь отличное от него обозначение. Указанные принципиальные
отличия характеристик исследуемого объекта обычно не учитываются. Из
контекста, как правило, бывает ясно, о чём идет речь, тем не менее для
чёткого понимания сущности рассматриваемой проблемы семантическое
разделение указанных понятий абсолютно необходимо. А
Следует различать прямые и обратные задачи квалиметрии, т.е. соот-
ветственно задачи анализа качества объектов и задачи синтеза объектов
с требуемыми (заданными) качествами. Общие схемы (алгоритмы) реше-
ния прямой и обратной задач исследования качества объектов изображе-
ны на рис. 2.2.5 и 2.2.6, из которых видно, что основу прямой задачи со-
ставляет измерение качества объекта, а основу обратной задачи - управ-
ление качеством объекта с целью придания ему необходимых свойств.
2.2.3. К ПРОБЛЕМЕ ОЦЕНИВАНИЯ
В данной монографии большинство понятий вводится по ходу изложе-
ния. Однако представляется необходимым терминам, определяющим фун-
даментальные понятия, правильное понимание которых имеет принципи-
альнее значение, уделить особое внимание и обсудить их отдельно.
Начнём с ряда распространённых в литературе неточностей в слово-
употреблении, которые вредны, с одной стороны, в семантическом смысле,
так как неправильное (неграмотное) словоупотребление приводит к разно-
чтениям и неверному пониманию сущности предмета обсуждения, а с дру-
гой - в терминологическом, поскольку они сокращают число терминов,
имеющих самостоятельный смысл и призванных отражать специфические
особенности исследуемых объектов.
Прежде всего следует различать понятия оценки качества и оценивания
качества.
Оценка качества - числовая характеристика показателя качества, по-
лучаемая опытным путём или с помощью расчётов (при косвенных изме-
рениях) с использованием модели показателя качества.
Оценивание качества - процедура принятия решения о качестве объекта.

2.2. Основные понятия квалиметрии
51
Постановка задачи анализа качества. Определение (выбор)
объекта исследования и абсолютных показателей его свойств
I
Обоснование показателей качества объекта
исследования и критерия его оценивания
Построение модели объекта исследования
i
Испытание модели объекта исследования
и оценивание его качества
Анализ результатов моделирования и
принятие решения о качестве объекта
Рис. 2.2.5
Постановка задачи синтеза качества. Определение (выбор) объекта
исследования и наиболее существенных показателей его качества
У
Обоснование критерия оценивания качества объекта исследования
У ^_J3T~
Построение модели объекта —■— I
исследований Коррекция модели Г I
~~ i
Испытание модели объекта исследования и определение
значений абсолютных показателей его свойств (ЭТХ)
Анализ результатов моделирования и принятие решения
о качестве (об ЭТХ) синтезируемого объекта
У '
Формирование требований к структуре и
параметрам синтезируемого объекта, обеспечивающих
требуемое его качество (ЭТХ)
Рис. 2.2.6
Схему исследования объекта, в которой определяется оценка показателя
качества (мера качества), целесообразно называть разомкнутой, В ра-
зомкнутой схеме качество объекта лишь измеряется, но не оценивается.
Оценивание качества возможно только в замкнутой схеме, т.е. когда к

52 Глава 2. Методологические основы теории эффективности
качеству объекта предъявлены требования. Именно они (требования) "за-
мыкают" схему оценивания. Эта задача решается с помощью критериев
оценивания качества.
Один из важнейших этапов оценивания - этап измерения. Это первый
этап, на котором определяется мера (количественная или качественная)
оцениваемой характеристики исследуемого объекта. Измерение1 осущест-
вляется путём сравнения показателя (количественного или качественного)
измеряемой характеристики с эталонной шкалой, проградуированной в оп-
ределённых единицах измерения. Поскольку процесс измерения подвер-
жен воздействию целого ряда неконтролируемых (а потому неопределён-
ных, случайных) факторов, то получаемый в его результате "отсчет" в об-
щем случае отличается от истинного значения измеряемой характеристики
(которое, таким образом, остаётся неизвестным) и называется его оценкой.
Таким образом, оценка - это приближённое значение оцениваемой ха-
рактеристики (параметра).
В общем случае, когда оцениваемый показатель не может быть измерен
непосредственно (ненаблюдаем), реализуется процедура так называемых
косвенных измерений. В её рамках непосредственно измеряется некоторый
(некоторые) наблюдаемый показатель (показатели), связанный функцио-
нально с оцениваемым, значение которого затем вычисляется.
Поскольку до настоящего времени в научно-технической литературе
семантическим аспектам используемой терминологии (а также символики)
уделялось недостаточно внимания, то представляется необходимым кратко
обсудить вопросы соотношения понятий количественного и качественного
оценивания.
С общепринятой точки зрения измерение - это количественное оцени-
вание значения показателя конкретного свойства исследуемого объекта.
При этом под качественным оцениванием понимается процедура принятия
решения по бинарной схеме, т.е. процедура выбора одной из двух альтер-
натив: "дя" - "не/w"; годен - не годен; хороший - плохой; задача выполне-
на - не выполнена; цель достигнута - не достигнута и т.п. Однако, как
показывает практика, качественное оценивание является более гибким и в
бинарную схему вписывается далеко не всегда. Примерами значений, при-
нимаемых оценками качественных показателей в полинарной (полиадиче-
ской) схеме, могут служить следующие "возрастающие" последовательно-
сти:
а) очень плохой - плохой - посредственный - удовлетворительный - хо-
роший - отличный - превосходный;
б) чрезвычайно мало - очень мало - мало - сравнительно мало (малова-
то) - немного - достаточно - порядочно - многовато - много -
очень много - чрезвычайно много;
1 С теорией измерений можно познакомиться в специальной литературе (см. также
Д1в[112])

2.2. Основные понятия квалиметрии
53
в) задача не выполнена - задача недовыполнена - задача почти выпол-
нена - задача выполнена - задача перевыполнена и т.п.
Приведённые оценки естественно называть "нечёткими". Понятно, что
за каждой из них скрыты количественные показатели рассмотренных ха-
рактеристик объекта (количества, качества степени выполнения задачи).
Таким образом, в принципе можно говорить как о качественных харак-
теристиках количественной меры, так и о количественных характеристи-
ках качественной меры.
Рассмотрение приведённых выше последовательностей "нечётких" оце-
нок наводит на мысль, что различие между количественным и качествен-
ным лишь в квантифицированности (в степени определённости) эталон-
ных шкал измерительных "приборов"1. Так, в бинарной схеме качествен-
ная шкала может быть заменена количественной шкалой, содержащей
лишь два возможных значения {0,1} измеряемого показателя.
В общем случае, т.е. в многоальтернативной - полинарной схеме, про-
вести подобную квантификацию весьма трудно, так как каждому значению
нечёткой оценки измеряемого показателя соответствует диапазон значений
количественной характеристики исследуемого объекта, и наоборот, каж-
дому значению количественной характеристики может соответствовать
целое множество значений качественной оценки. При этом относительные
размеры диапазонов и их взаимное расположение на шкале также нечетки.
Тем не менее в этом направлении ведутся обширные исследования и в на-
стоящее время уже имеются заслуживающие внимания результаты, полу-
ченные на базе теории нечётких понятий [58, 81, 121, 122].
Пример 2.2.7. При оценивании ответов на экзамене как "удовлетвори-
тельных" истинные знания экзаменуемого могут варьироваться в доста-
точно широком диапазоне, что зависит и от "удачи", и от требований экза-
менатора и т.п. При этом даже при одинаковых оценках ответов различных
экзаменуемых эти вариации могут быть весьма значительными. Аналогич-
но обстоит дело и при выставлении за ответ экзаменуемого оценки "3". Те-
перь соответствующие ей знания расцениваются как "удовлетворитель-
ные", а прежде они считались "посредственными" (и это, по-видимому,
ближе к истине). А
Поскольку в результате измерения определяется оценка значения неко-
торого показателя, то естественно считать целью этого процесса оценива-
ние. Однако легко убедиться, что получение количественной оценки прак-
тически никогда не является самоцелью. Цель процесса оценивания состо-
ит в выработке суждения об исследуемом объекте (об его пригодности, оп-
тимальности, превосходстве), количественная характеристика (показатель)
1 Термин "прибор" понимается в самом широком смысле; в том числе это и вычис-
лительная процедура, дающая оценку показателя при косвенных измерениях.

54 Глава 2. Методологические основы теории эффективности
которого приняла измеренное значение. Такое суждение вырабатывается
на основе определённых (принятых, положенных в основу исследования)
принципов и правил, формулируемых в форме критериев оценивания.
Результатом применения этих критериев также являются оценки, но по-
следние уже носят качественный характер. При этом чаще всего (хотя и не
всегда) такие оценки вырабатываются по бинарной схеме и отображаются
на множество {0,1} [104]. Примером качественного оценивания в поли-
нарной схеме может служить ранжирование объектов по качеству [прису-
ждение мест конкурирующим (соревнующимся) объектам при их эксперт-
ном (балльном) оценивании и т.п.].
Таким образом, не следует смешивать понятия «показатель» и «крите-
рий» оценивания, первое из которых означает числовую характеристику,
т.е. меру (количественную или качественную), а второе - совокупность ус-
ловий, т.е. высказываний и предикатов, реализующих принятые принципы
[см. (2.2.1) - (2.2.3), (2.2.8) и определения 2.2.2 и 2.2.3].
Итак, при внимательном анализе процесса оценивания объекта обнару-
живается, что он реализуется в два этапа. На первом этапе производится
измерение характеристики объекта, т.е. определение или вычисление её
показателя (количественного или качественного), а на втором - собственно
оценивание объекта (его качества) по принятому критерию, принадлежа-
щее одному из трёх классов (пригодности, оптимальности, превосходства),
определение которых дано в п. 2.2.2.
2.2.7) Вообще говоря, формально измерение может рассматриваться как
оценивание по критерию равенства измеренного значения показателя од-
ной из отметок эталонной шкалы. Однако поскольку на этапе выработки
суждения об исследуемом объекте результат измерения представляет со-
бой исходную информацию (часть ее), то схему оценивания на первом эта-
пе логично называть разомкнутой, а на втором - замкнутой. А
В заключение кратко обсудим некоторые свойства показателей, т.е. мер
(количественных и качественных) характеристик объектов и критериев их
оценивания. Как известно, показатели бывают прямыми и косвенными, а
также абсолютными и относительными. В соответствии с этим и оцени-
вание бывает прямым и косвенным, абсолютным и относительным.
Понятно, что косвенное оценивание реализуется в условиях, когда пря-
мое оценивание невозможно, и, разумеется, уступает последнему по ин-
формативности, а следовательно, и по объективности (точности и досто-
верности).
Что касается соотношения абсолютного и относительного оценива-
ния, то оно сложнее и конкретный его вид диктуется целями исследования.
Отметим двоякий смысл термина "относительный". С одной стороны,
показатель может быть относительным по структуре (по форме), т.е. пред-
ставлять собой отношение некоторых величин, с другой - он может быть

2.2. Основные понятия квалиметрии
55
относительным по содержанию, когда используется для сравнительного
(относительного) оценивания различных объектов [112].
При абсолютном оценивании показатель должен характеризовать аб-
солютную меру свойства объекта1.
Поскольку сравнительное оценивание объектов может осуществляться
и с использованием их абсолютных показателей, то последние являются
наиболее информативными и универсальными.
2.2.8) Поскольку при оценивании качества объекта наблюдаются лишь
его существенные свойства (атрибуты), то каждому значению показателя
его качества соответствует целая совокупность "значений" его истинного
качества, обусловленная неконтролируемыми "несущественными" свойст-
вами. Кроме того, в рамках критерия пригодности (лежащего в основе ана-
лиза качества) объекты, значения показателей качества которых различны,
но принадлежат области их допустимых значений, считаются одинаковы-
ми по качеству. Поэтому, строго говоря, при оценивании качества объекта
истинное его "значение" остаётся неизвестным (как и при любом оценива-
нии) и, следовательно, в сущности, оценивается целый класс объектов по-
тенциально "одинакового" (по определению) качества. Понятно, что в пре-
делах "класса" качества различных объектов различны (хотя и все прием-
лемы по критерию пригодности). Это объективный факт, сопутствующий
априорному (до применения по назначению) оцениванию качества объек-
та, с которым следует считаться при принятии решений. ▲
На этом общее рассмотрение основных терминологических и методоло-
гических "тонкостей", требующих учета в рамках теории эффективности
целенаправленных процессов на этапе их ВНЕПР, закончим. Однако с це-
лью более глубокого их уяснения по мере необходимости будем возвра-
щаться к их обсуждению в замечаниях и комментариях.
Здесь термин "абсолютный" используется в значении "совершенный", "полный" (а
не в смысле абсолютной величины) [159].

56 Глава 2. Методологические основы теории эффективности
Если мы требуем победы и не знаем,
что подразумеваем под этим, мы встре-
тимся с призраком, стучащимся в дверь.
Н. Винер. "Кибернетика"
2.3. ОСНОВНЫЕ ПРИНЦИПЫ ИССЛЕДОВАНИЯ
ЭФФЕКТИВНОСТИ ЦЕЛЕНАПРАВЛЕННЫХ
ПРОЦЕССОВ
До сих пор, в пределах гл. 2, понятие объекта исследования не было
конкретизировано. В дальнейшем такими объектами будут ЦУТС и
ЦНПФС. Однако в рамках данной книги рассмотрение ЦУТС и её качества
необходимы лишь для выявления факторов, обусловливающих основные
свойства и качества ЦНПФС. Поэтому объектом дальнейшего изучения
является ЦНПФС, т.е. операция, реализуемая ЦУТС.
2.3.1. ОБЩИЕ ПРЕДПОСЫЛКИ
Как отмечалось в п. 2.1, из множества свойств, присущих любому про-
цессу, для характеристики ЦНПФС существенными являются лишь его
операционные свойства (атрибуты), которые и определяют качество дан-
ного ЦНП как объекта исследования.
Большинство этих свойств характеризуются результатами операции, т.е.
даваемыми ею эффектами, и, следовательно, являются косвенными харак-
теристиками её качества. Конкретный физический смысл таких показате-
лей определяется характером и целями операции, а также свойствами и ус-
ловиями применения реализующей её ЦУТС. Примером прямого показа-
теля свойства операции может служить её длительность, т.е. время, по-
требное для достижения цели операции.
Таким образом, в общем случае качество операции включает в себя собст-
венную и несобственную составляющие, компонентами первой из которых
являются длительность операции и уровень достижения её цели, а компонен-
тами второй - качество различных характеристик её результатов (эффектов).
Поэтому следует различать др&уровня оценивания качества операции:
1. Оценивание качества результатов операции.
2. Оценивание качества самой операции, называемого её эффектив-
ностью1.
Второй уровень оценивания качества операции - доминирующий (глав-
ный), поскольку операция может считаться качественной (эффективной)
тогда и только тогда, когда требуемыми качествами обладают все (без ис-
1 Таким образом, эффективность непосредственно не наблюдаема и определяется
(измеряется) косвенными методами.

2.3. Основные принципы исследования эффективности
57
ключения) её результаты. При этом критерии оценивания качеств опера-
ции и её результатов должны выбираться независимо друг от друга.
Как указывалось выше, в ходе операции на достижение её цели расхо-
дуются ресурсы (материальные, временные и т.п.). Способность (точнее,
приспособленность) операции наилучшим образом преобразовывать рас-
ходуемые ресурсы в выходные эффекты является её основным (присущим
только операциям) свойством.
Вообще говоря, собственно результатом операции является получаемый
в ходе неё целевой эффект (т.е. результат, ради которого проводилась опе-
рация). Однако с формальной точки зрения соответствующий этому эф-
фекту расход ресурсов также следует рассматривать как результат опера-
ции [или как её побочный эффект (см. п. 2.3.2)]. Таким образом, свойства
результатов операции (а также ЦУТС), определяющие их качества, целесо-
образно разбить на две группы:
- целевые {функциональные);
- обеспечивающие {эксплуатационно-технические) .
Эта классификация в какой-то мере условна, поскольку целью одной
операции может быть обеспечение проведения другой операции более
крупного масштаба или более высокого уровня (супероперации). К тому
же цели операции могут изменяться в ходе её проведения. Однако с мето-
дической точки зрения такая классификация всегда полезна, так как позво-
ляет провести структуризацию задачи исследования и выделить факторы,
оказывающие решающее влияние на успех операции (на качество её ре-
зультатов - эффектов).
Пример 2.3Л. Пусть, например, цель операции - нанесение плацдарму
противника определённого ущерба. Тогда очевидно, что показателем целе-
вого свойства результатов операции (ее результативности) будет количест-
венная мера наносимого ущерба (абсолютного или относительного). В ка-
честве обеспечивающих могут выступать такие свойства ЦУТС и ЦНПФС
(операции), как готовность, надёжность, живучесть, мобильность, быстро-
действие, точность, устойчивость, оперативность (своевременность) и др.
При этом для подсистем ЦУТС, обеспечивающих поддержание на задан-
ных уровнях этих свойств, последние будут целевыми.
Если теперь перейти к исследованию операции более крупного масшта-
ба (более высокого уровня), необходимым (но не достаточным) условием
достижения цели которой является нанесение плацдарму противника
ущерба, не менее требуемого, то свойство первой операции - способность
наносить ущерб плацдарму противника - станет обеспечивающим. А
Из приведённого примера видно, что наряду с иерархией ЦУТС суще-
ствует соответствующая ей иерархия целей реализуемых ими операций.
При этом, поскольку ЦУТС, функционируя, выполняет задачу, поставлен-
ную перед ней суперсистемой, то её цели подчинены целям последней.

58 Глава 2. Методологические основы теории эффективности
2.3.2. ПОКАЗАТЕЛИ КАЧЕСТВА РЕЗУЛЬТАТОВ ОПЕРАЦИИ
По определению (см. п. 2.2), качество - это свойство или совокупность
существенных свойств объекта, обусловливающих его пригодность для
использования по назначению. Применительно к ЦНП подобные его свой-
ства - атрибуты называются операционными.
К ним относятся:
- результативность ЦНП;
- ресурсоёмкость ЦНП;
- оперативность ЦНП.
В совокупности эти свойства порождают комплексное свойство ЦНП -
эффективность, присущее только операциям.
Во избежание неточностей в понимании проблемы оценивания качества
операции представляется необходимым кратко обсудить семантику (смы-
словое содержание) операционных свойств ЦНП.
Результативность ЦНП характеризуется получаемым в его результа-
те целевым эффектом. Она обусловливается способностью операции да-
вать целевой эффект (т.е. результат, ради которого проводится операция).
2.3.1) В военных приложениях, в частности в "Теории стрельбы", это
свойство операции (процесса ведения стрельбы) называется действитель-
ностью1, т.е. действительность стрельбы - это её способность пора-
жать цель. А
Ресурсоёмкость ЦНП характеризуется расходом операционных ресур-
сов всех видов (материально-технических, энергетических, информацион-
ных, временных, финансовых, людских и т.п.), потребных для проведения
операции и получения целевого эффекта.
Оперативность ЦНП характеризуется расходом операционного време-
ни, т.е. времени, потребного для достижения цели операции.
2.3.2) Из всего сказанного следует, что качество операции не может
быть охарактеризовано ни одним из перечисленных частных (единичных)
свойств ее результатов в отдельности, а определяется их совокупностью -
комплексом, включающим в себя три группы компонент2 (минимум три
компоненты). А
Введём следующие обозначения:
Ул\ = V,\ - показатель (вектор) виртуального операционного целевого
(позитивного) эффекта операции;
Действительный - это производящий, оказывающий действие [159].
2 Такие группы показателей свойств, характеризующие сложные агрегативные
свойства, иногда [177] называются аспектами.

2.3. Основные принципы исследования эффективности
59
yP\=R, к - показатель (вектор) виртуальных затрат операционных
ресурсов (побочных, негативных эффектов) на получение
целевых эффектов;
YP\ —Т,„\ - показатель (вектор) виртуальных затрат операционного
времени (побочных, негативных эффектов) на получение
целевых эффектов.
Тогда показатель результатов (точнее, показатель качества результа-
тов) операции будет представлять собой я-мерный (и = w1 +#i2 +я3) век-
тор, содержащий три группы компонент (векторов) - показателей "качест-
ва" операционных свойств ЦНПФС, в одной из двух форм:
- в комплексной канонической форме (ККФ):
у[ШФ]_у[Шф]_/у{1) у(2) y(3)\_/V р Т \. О 1 П
- в развёрнутой форме (РФ)1:
г^ф] = (у^^\..,/:!; у?\у?,...,у*; *(3)^3Uj><?)=
=(^2,...,уЛ1; г,,г2,...,гЛ2; т19т29...9т„з). (2.3.2)
С учетом (2.3.1) и (2.3.2) критерий пригодности операции по её резуль-
татам (оценивающий качество её результатов) получит следующее выра-
жение:
«Ф1-- ^fyJ'W. (2-3-3)
Здесь
ШК]4У{%:(У{,)=Г(^ЦОД(ЗСВ)},
где \У(дк)1 ~ область допустимых значений показателя YiK\ качества
результатов операции в комплексной канонической фор-
ме по критерию [К];
ЦОД - "цель операции (ЦНПФС) достигнута";
ЗСВ - "задача ЦУТС выполнена",
G1*}: Y{n)e{Y{n)}[K] = U, (2.3.4)
где { ГЛ ] - область допустимых значений показателя К» качества ре-
зультатов операции в развёрнутой форме,
{%Г = {% •• (г<.> = *&)* ЦОД (зев)].
Соотношения (2.3.3), (2.3.4) представляют собой математические
формулировки цели операции - ЦНПФС (задачи ЦУТС).
1 Поскольку из контекста ясно, о какой форме идёт речь, то верхние индексы [ККФ]
или [РФ] будут опускаться.

60 Глава 2. Методологические основы теории эффективности
Часто внутри групп компонент вектора Км (внутри показателей К/Д,
[/ = 1,2,3 ]) может быть произведено свёртывание частных (единичных)
показателей результатов операции (одним из известных методов) путём
введения обобщённых показателей.
Например: v = ^aivi ;
T = 2^rk или r = max:{r1,r2,...,ril3} и т.п.
В таких случаях я, = п2 = пъ = 1 и поскольку п = я, + п2 + пъ, то будут
выполняться равенства я = /г= 3 и соотношения (2.3.1) - (2.3.4) примут
симплексную каноническую форму (СКФ):
¥(ш) =Г(з) =(Л>Л>ЛН^,Т), С2-3-5)
где ^ = j;(l); j;2 = j;(2)/ j3 = У(3);
СЦР: Y{3)e{Y{3)\=U, (2.3.6)
где \Y,t) - область допустимых значений показателя K3v качества резуль-
татов операции в симплексной канонической форме1.
Соотношения (2.3.5), (2.3.6) для к— п = 2 иллюстрируются рис. 2.3.1.
Если требования, предъявляемые к результатам уи у г, взаимно незави-
симы, то
и рис. 2.3.1 трансформируется в рис. 2.3.2.
2.3.3) Из вышесказанного следует, что компоненты показателя Y^\ це-
левых эффектов (их качества) представляют собой количественные харак-
теристики лишь количественных результатов операции. Однако такая их
трактовка правомерна только в предположении, что "качества целевых эф-
фектов" заведомо удовлетворяют предъявляемым к ним требованиям, т.е.
качество результатов обеспечивается (гарантируется) ещё до проведения
операции. В общем же случае показатели собственно качеств результатов
операции (не зависящие от их количества) могут также входить в состав
вектора Yr\. В этом случае "качество целевых эффектов" оценивается со-
вместно с оцениванием качеств всех результатов (целевых и побочных эф-
фектов) операции.
1 В дальнейшем подобные уточнения делаться не будут, так как из контекста ясно, о
какой форме показателя качества результатов операции идёт речь.

2.3. Основные принципы исследования эффективности
61
•М
Ч /1 / П / П П ) 11 ПА
ZJ
te)
Г(2>
Ух Ух
Рис. 2.3.2
Ух Ух
Аналогичное замечание можно сделать и относительно качества расхо-
дуемых ресурсов. Поскольку от качества ресурсов зависят потребные их
количества, а также качество целевых эффектов и расходуемое на их полу-
чение операционное время (определяемое зависящей от качества ресурсов
производительностью ЦУТС), то к нему могут предъявляться самостоя-
тельные конкретные требования. А
2.3.4) Вообще говоря, время, затрачиваемое на проведение операции, -
это тоже расходуемый ресурс и в ряде случаев возможна "перекачка" (вза-
имный обмен в соответствующем соотношении за счёт изменения техно-
логии ЦНПФС по принципу: "быстрее - дороже", "дешевле - медленнее" и
т.п.) одних ресурсов в другие, однако функциональная значимость {суб-
станциальность) времени при исследовании любых процессов требует
раздельного рассмотрения векторов
%') и
у(з)
2.3.5) Термин "операционное свойство" призван подчеркнуть его непо-
средственное отношение к операции. Так, наряду с операционным целе-
вым эффектом конкретного ЦНП могут быть получены и побочные для не-
го положительные эффекты, являющиеся целевыми для ЦНП высшего
уровня иерархии (супер ЦНП). Подобные эффекты не являются операци-
онными.
То же самое можно сказать и о расходуемых ресурсах. Наряду с опера-
ционными динамическими, активными ресурсами yP\ в ходе операции
опосредованно расходуются и статические, пассивные ресурсы, затрачи-
ваемые на этапах разработки, создания и эксплуатации (технического об-
служивания) ЦУТС, а также в ходе организации и обеспечения ЦНПФС.

62 Глава 2. Методологические основы теории эффективности
Такие ресурсы в показатель yP\ не входят, а учитываются зависящим от
них вектором Акх параметров и ЭТХ ЦУТС и ЦНПФС. Кроме того, в ходе
операции могут возникать и отрицательные эффекты - последствия раз-
личного характера (технического, геофизического, экологического, орга-
низационного и т.п.), ликвидация (устранение влияния) которых связана с
затратами ресурсов, являющимися по отношению к операционным ресур-
сам побочными расходами (см. рис. 1.2.2 и п. 5.3.2).
Наконец, операционное время yP\ в общем случае не совпадает с те-
кущим (календарным) временем. Так, например, когда ЦНП может преры-
ваться и протекать циклически, то отдельные компоненты вектора yP\
(длительности этапов, фаз, стадий, циклов операции) могут "накладывать-
ся друг на друга". А
2.3.6) При свёртывании разнородных показателей обобщённый показа-
тель теряет физический смысл. Поэтому при комплексном многокомпо-
нентном исследовании качества ЦНП (операции) свёртывание допустимо
лишь внутри групп показателей его результатов. Свёртывание компонент
показателя качества результатов ЦНП из различных групп некорректно. ▲
2.3.3. ПОКАЗАТЕЛЬ ЭФФЕКТИВНОСТИ ОПЕРАЦИИ
Как уже отмечалось (и будет ещё неоднократно комментироваться), к
настоящему времени предложено множество показателей (зачастую назы-
ваемых "критериями") эффективности операций, однако без достаточного
обоснования как их структуры, так и обусловленных ею свойств. Многие
показатели с аддитивной или мультипликативной структурой не без осно-
вания подвергались критике [26], но без конкретных предложений показа-
телей, свободных от указываемых недостатков. В то же время существует
совокупность общих требований, которым должен удовлетворять любой
показатель эффективности операции, чтобы соответствовать своему на-
значению. Важнейшими из таких требований являются [190]:
- представительность (адекватность);
- критичность (чувствительность);
- комплексность (полнота);
- стохастичность;
- "простота".
Представительный показатель позволяет оценивать эффективность
операции по достижению её основной (а не второстепенных) цели. Цель
операции должна находить своё прямое отображение в показателе её эф-
фективности.
Критичный показатель чувствителен к изменениям исследуемых ха-
рактеристик ЦУТС и ЦНПФС. Чем чувствительность выше, тем лучше.

2.3. Основные принципы исследования эффективности
63
Комплексный (единый) показатель позволяет решать задачу исследова-
ния эффективности операции без привлечения других ее характеристик.
Стохастичный (вероятностный) показатель позволяет учитывать не-
определённость условий проведения операции, обусловленную воздейст-
вием случайных факторов и всегда сопутствующую исследованию опера-
ции и её эффективности, проводимому на первых этапах ВНЕПР.
Показатель эффективности должен быть достаточно «простым» (при
необходимой комплексности), чтобы его вычисление и последующий ана-
лиз эффективности операции могли быть реализованы в приемлемые сроки
и имели бы наглядную интерпретацию.
Обратим внимание, что рассматриваемый ниже показатель эффективно-
сти операции удовлетворяет всем перечисленным требованиям.
По определению (см. п. 2.1), эффективность - это комплексное опера-
ционное свойство ^качество") ЦНПФС, характеризующее его приспо-
собленность к достижению цели реализуемой ЦУТС операции (к выполне-
нию стоящей перед ЦУТС задачи).
Следует ещё раз подчеркнуть, что для комплексного (многокомпонент-
ного, "многокритериального") исследования эффективности ЦНП (опера-
ции) показатель К» качества его результатов (короче, показатель резуль-
татов или эффектов) должен определяться в канонической форме и
включать в себя три группы компонент - три аспекта:
У£?)'У<"^ характеризующих соответственно вир-
туальные целевые эффекты {результативность, действительность опе-
рации), затраты ресурсов (ресурсоёмкость операции) и затраты времени
(оперативность операции), т.е. как минимум три компоненты1.
2.3.7) Поскольку качество операции (её результатов) определяется не
только получаемым целевым эффектом, но и затрачиваемыми на это ре-
сурсами, то эффективность ЦНП - это, по сути, эффективность усилий
(действий) по переводу ресурсов в целевой эффект или, другими словами,
эффективность расходования ресурсов. А
Как отмечалось (см. п. 2.3.2), /i-мерный вектор L результатов опера-
ции путём свёртывания показателей частных (единичных) результатов
(эффектов) внутри групп (аспектов) может быть сведён к трёхмерному
(точнее, трёхкомпонентному) и представлен в СК-форме: К , = K3v. В
дальнейшем для большей наглядности будем рассматривать в основном
такую форму показателя Ум с периодическим её обобщением. Понятно,
что поскольку форма вектора К л остаётся канонической, то общность по-
становок задач исследования ЦУТС и ЦНПФС при этом не снижается.
1 Следует иметь в виду, что это операционные характеристики результатов
ЦНПФС.

64 Глава 2. Методологические основы теории эффективности
Итак, пусть качество результатов операции описывается вектором
Г<з> = (/W) = (Л,Л»Л) = far) ■ (2-3.7)
Каждая из компонент вектора Е3\ зависит от характеристик ЦУТС и
ЦНПФС (от их параметров и ЭТХ), условий её функционирования, а также
от организации ЦНПФС, т.е.
Y(3) = *(з)\^*')> \")> B(v)> B(r))- Y{3)\A{k)9B(i)) > (2.3.8)
где AL* = Л'*Д B[r)9 B(r)) -характеристики (параметры и ЭТХ) ЦУТС;
А?к,л =Л?кЛв!гу В7ГА - характеристики организации (параметры и
ЭТХ) ЦНПФС;
BLk - характеристики условий функционирования ЦУТС;
JB/L - характеристики условий применения ЦУТС;
Л — Л ^г Л •
2.3.8) Следует обратить внимание, что характеристики BL* и В?гл ус-
ловий функционирования ЦУТС (УФС) и условий применения ЦУТС
(УПС) влияют как на ЭТХ А!кл и Л?к„к> так и на вид функции
F/3\ \A/k\ 9 Btt\ ), т.е. являются её параметрами. А
В свою очередь, компоненты вектора КД допустимых значений резуль-
татов операции зависят от условий применения ЦУТС и связанных с ними
требований, предъявляемых суперсистемой к ЦНПФС, т.е.
% = %(*<;.>), (23.9)
где itfL - характеристики условий применения ЦУТС (см. п. 2.7).
2.3.9) Поскольку эффективность - это операционное свойство ЦНПФС,
а операция отличается от всех других процессов наличием цели, то её мера
(показатель) должна характеризовать степень достижения цели операции.
А
Содержательно цель операции может определяться по-разному, однако
во всех случаях она заключается в получении требуемых результатов, со-
ответствующих цели операции, что формально означает выполнение усло-
вия (2.3.3), т.е.
G^.-F^e {%}=*/. (2.3.10)
Соотношение (2.3.10) равносильно пригодности операции по результа-
там для использования по назначению с требуемой целью, и, таким обра-
зом, представляет собой формальное выражение цели операции.

2.3. Основные принципы исследования эффективности
65
Для сложных ЦУТС типичной является ситуация, когда на их ЭТХ и
параметры, на условия их функционирования и применения, а также на па-
раметры и ЭТХ ЦНПФС воздействует целый ряд априори неизвестных, а
потому случайных факторов. Поэтому до проведения операции (а именно
в этот период исследование её эффективности представляет наи-
больший практический интерес) векторы А,к^ и й,л, а следовательно, и
вектор F/3j оказываются случайными. Более того, априори случайными яв-
ляются и допустимые значения КД вектора К3\, зависящие от условий
применения ЦУТС, характеризуемых вектором В?гу поскольку до прове-
дения операции неизвестно, какими должны быть её результаты, чтобы по-
ставленная цель операции была достигнута. Таким образом:
*(з) = ¥(з)\А(к)>'&(v)> B"i'V ' (2.3.11)
В результате в реальных условиях критерий (2.3.10) пригодности опе-
рации (её результатов) к достижению её цели принимает вид:
СЦР:¥{3)е{¥^\=и. (2.3.13)
Как видно из выражения (2.3.13), пригодность операции есть случайное
событие, по которому непосредственно судить о качестве операции (об её
эффективности) нельзя. Поэтому характеристикой качества ЦНПФС, т.е.
степени его приспособленности к достижению цели в условиях реального
воздействия случайных факторов, может служить только вероятность слу-
чайного события (2.3.13), характеризующая, как известно [29], степень его
объективной возможности (возможности его наступления) при заданном
комплексе условий:
РДц =P(Y{3)e {¥^\)=Рдц(х{т)), (2.3.14)
где вектор Х.к = (х^ х^Х^Л = (А,куВ>Л не случаен, так как в отличие
от (2.3.11), (2.3.12) здесь компоненты векторов А,^ и В,л либо являются
неслучайными компонентами соответственно случайных векторов А,к^ и
В,* из (2.3.11), (2.3.12), либо представляют собой вероятностные характе-
ристики их случайных компонент1.
1 Специальные обозначения для этих векторов не вводятся для разгрузки символи-
ки. Их физический смысл ясен из контекста задачи.
3 Зак. 3303

66 Глава 2. Методологические основы теории эффективности
Вероятность РДЦ называется вероятностью достижения цели опе-
рации (или вероятностью выполнения задачи ЦУТС) и является пока-
зателем эффективности ЦНПФС (массового характера1), т.е. мерой степени
достижения его цели.
2.3.10) Следует обратить особое внимание на то, что допустимые зна-
чения YL результатов операции обусловлены характеристиками Щ,л си-
туации (условий применения ЦУТС), в которой ЦУТС реально придётся
выполнять задачу и которая априори (до операции) неизвестна и не может
быть задана исследователем (ЛПР - лицом, принимающим решения). Есте-
ственно характеристики 2Г1 (как, впрочем, и Ц.*) назвать объективными
факторами. Как будет показано, наряду с объективными факторами на ха-
рактеристики области \YL\ могут оказывать влияние и субъективные
факторы, т.е. решения о требованиях к виртуальным результатам К3ч
операции, принимаемые ЛПР на этапе планирования и организации опе-
рации с учётом функциональных возможностей ЦУТС и прогнозируемых
ЛПР условий её применения (см. {2.7.15}). ▲
2.3.11) Выше речь шла об оценивании качества результатов ЦНП. Пред-
ставляется достаточно очевидным, что аналогичная ситуация возникает
при оценивании качества любого объекта. Действительно, априори, т.е. на
этапах разработки и создания, а также перед применением объекта, как его
качество, так и требования к нему, обуславливаемые ситуацией, в которой
объект будет выполнять свои функции, случайны и, следовательно, при-
годность объекта для использования по назначению - случайное событие.
Поэтому наиболее объективной и информативной априорной оценкой ка-
чества объекта является вероятность его пригодности. ▲
2.3.4. СХЕМА ОЦЕНИВАНИЯ ЭФФЕКТИВНОСТИ ОПЕРАЦИИ
Поскольку, как было показано в п. 2.3.3, по качеству результатов опера-
ции непосредственно судить о её качестве нельзя, то необходима вероят-
ностная формулировка задачи, в соответствии с которой оценивание эф-
фективности ("качества") операции должно проводиться на двух уровнях и
реализоваться в два этапа.
1 Об эффективности уникальных ЦНП говорится в п. 3.2.

2.3. Основные принципы исследования эффективности
67
На первом уровне (1-й этап):
1.1) определяется (формулируется, обосновывается, устанавливает-
ся) показатель виртуального качества результатов операции
(ЦНПФС)— вектор К3) показателей v, Я, f его частных результатов
(эффектов);
1.2) определяются (обосновываются, задаются, предъявляются) требо-
вания к качеству результатов операции (ЦНПФС) - область \У?ЪА допус-
тимых значений vd, fd, тд показателей v, r, f качества ее результатов;
1.3) формулируется (обосновывается, строится) критерий оценива-
ния качества результатов операции (ЦНПФС) - 2я-местный (6-
местный) предикат
ОЦР:¥{3)е{¥{3)\=и. (2.3.15)
На втором уровне (2-й этап):
2.1) определяется (вычисляется, "оценивается") показатель эффек-
тивности операции (ЦНПФС) - вероятность достижения её цели (вероят-
ность выполнения задачи ЦУТС):
РДЦ=Рвз = р(г{3)е{г;)\); (2.3.16)
2.2) определяются (обосновываются, задаются, предъявляются) тре-
бования к эффективности операции (ЦНПФС) - потребное (минималь-
но-допустимое) или оптимальное (максимальное) значение [Рдц (Рвз)
или РдцТ (Pg"T) ] вероятности Рдц (Рвз) достижения цели операции
(выполнения задачи ЦУТС);
2.3) формулируется (обосновывается, строится) и реализуется один
из "выбранных" (обоснованных) критериев оценивания эффективности
операции (ЦНПФС) - одноместных предикатов:
- критерий пригодности
[р > рТР .
e-' \Pm~>PZ' <"•">
\?вз - гвз •
- критерий оптимальности
Р™-Р™> (2.3.18)
р _ рОПТ
гвз — гвз •
2.4) производится собственно оценивание эффективности операции
(ЦНПФС).
Структурная схема алгоритма оценивания эффективности операции
приведена на рис. 2.3.3.

68 Глава 2. Методологические основы теории эффективности
Этапы (уровни) оценивания эффективности операции (ЦНП)
►
Оценивание качества результатов операции (ЦНП)
Щ
£)
Ф
CHJ
©
©
(Н)
|(3
Определение показателя качества результатов
операции (ЦНПФС)
Определение требований к качеству результатов
операции (ЦНПФС)
Формулировка критерия оценивания качества
результатов операции (ЦНПФС)
Оценивание эффективности операции (ЦНП)
Определение показателя эффективности
операции (ЦНПФС)
Определение требований к эффективности
операции (ЦНПФС)
Формулировка критерия оценивания эффективности
операции (ЦНПФС)
1
Оценивание эффективности операции (ЦНПФС)
Рис. 2.3.3

2.3. Основные принципы исследования эффективности
69
2.3.5. ЗАДАЧИ ИССЛЕДОВАНИЯ ЭФФЕКТИВНОСТИ ОПЕРАЦИЙ
Исследование эффективности операции (ЦНПФС) представляет собой
триединую задачу:
- задачу оценивания {измерения) эффективности операции;
- задачу анализа эффективности операции;
- задачу оптимального синтеза эффективной операции.
Первые две задачи часто объединяются под общим названием прямой
задачи, а третья называется обратной задачей.
Примерная схема классификации задач исследования эффективности
операций показана на рис. 2.3.4. Общие схемы (алгоритмы) их решения
аналогичны схемам решения задач оценивания качества объектов произ-
вольной природы, изображенным на рис. 2.2.5 и 2.2.6 соответственно.
Хотя прямая и обратная задачи имеют самостоятельные значения, ко-
нечная цель их решений, как правило, состоит в оптимальном проектиро-
вании ЦУТС и организации ЦНПФС, обеспечивающих достижение цели
операции с наибольшей вероятностью, т.е. в решении задачи синтеза. Тем
не менее первые их звенья составляют задачи оценивания и анализа эф-
фективности операции, цели которых достигаются путём:
- построения математических моделей исследуемых объектов, т.е.
ЦУТС и ЦНПФС;
- определения (обоснования) показателей качества ЦУТС и эффектив-
ности ЦНПФС;
- оценивания эффективности ЦНПФС;
- анализа влияния на эффективность ЦНПФС и качество ЦУТС их па-
раметров и ЭТХ.
Окончательные результаты решения задачи анализа являются инстру-
ментом (средством), используемым при решении задач синтеза ЦУТС и
ЦНПФС (см. рис. 2.2.5 и 2.2.6).
В силу огромного многообразия ЦУТС и реализуемых ими ЦНПФС,
различающихся не только целями, но и используемыми для их достижения
средствами и ресурсами, существует множество постановок задач исследо-
вания эффективности операций с использованием как детерминированных,
так и квазирегулярных или стохастических моделей.
Отметим, однако, что поскольку все операции проводятся и протекают в
условиях воздействия множества априори неизвестных, а следовательно,
случайных факторов, то их достаточно адекватное описание может быть
дано только на базе стохастических моделей. Что же касается моделей де-
терминированных и квазирегулярных, то их следует рассматривать лишь
как некоторые приближения стохастических моделей и правомерность их
применения должна обосновываться в каждом конкретном случае. К обсу-
ждению этого вопроса будем ещё неоднократно возвращаться (см. пп. 2.4,
2.7, 3.2).

70
Глава 2. Методологические основы теории эффективности
3
!5Г|
3
«о
5
•9-1
at
Д
X
э
8-
С
о
се
со
О
н
и
Д
о
Д
и*
се
э
со
S
9
О
I
Он
О
Д
I
Он
аГ
С
о
ее
со
Д
9
S
IS
Д
I
<L>
(D
д
9
PQ
о
&
Д д
£д
<L>
и*
О
4
PQ
PQ
Д
Д PQ
Sb
(-и М
О ев
Sa
с* Я
o> 2
Д w
s§
a|
I"
•e-g
О 53
Дм
is
PQ
ft я
gg
с д
W ни
:0
Й&
IB
В»
О
д д
55 ce
в!?
о о
vo
О
д
5
о
2
>Д
о
о
О
д s
Й9
§&
О
д
д
<D
О
О
О
С
О
К
Я
О
ч
опреде
ристик
SH
д £
ss
3&
cLx
<t> .
8й
ой
одели
мальн
so
25 *о
Л
С
°
К
\V
ь
>>
ЕГ
\х^\
^н
од
д
МО
«>д
Д Я
Я «
So
« 2
о&*
Ко я
и^
овани
(пара
X
<->
о
Ю
О
§1=1
о
8*8
Й&
11
(D Д
s н
х U
2^
д л
о
О
ю
Д
I
о
2
)Д
о
S3 9
В|
н х
се о
ев
й
PL,
О
<L> X
Ч Я"
йЯ
S3»
« о
о
в
О
Д
в
5
S
PQ
к>
ь
>>
Рй
и*
х§н
н?а
ание влияни
ффективнос!
PQ CD
о
йл
Ом
о
о
к
и
е
с
S
S
В
}Д 2
3 о
ж о
&&
PQ
о
д
о
О
ю
О
^
ь
>.
.Я
^ в
Но
э8.
X
£3
R 1
о Д
Д£
л S
Ss
5 со
н
Д &
«.$
«н
PQ О
к^Д
со
Д
5
д
<
^F У

2.4. Целевые и критериальные функции
71
Если хочешь добиться математиче-
ской достоверности в вещах, не допус-
кающих этого, нельзя не впасть в неле-
пость или варварство.
Ф. Энгельс. "Анти-Дюринг"
2Л. ЦЕЛЕВЫЕ И КРИТЕРИАЛЬНЫЕ ФУНКЦИИ
Как было показано, наиболее информативным комплексным показате-
лем эффективности ЦНП является вероятность РДЦ достижения цели опе-
рации (выполнения задачи ЦУТС). Наряду с этим при исследовании опе-
раций (ЦНПФС) и систем (ЦУТС) широкое распространение получили
другие показатели, называемые обычно целевыми или критериальными
функциями и обозначаемые чаще всего через W.
2.4.1) Следует обратить внимание, что оба приведённые названия не-
точны, так как в этих функциях - показателях ни цель операции, ни крите-
рий оценивания её эффективности отражения не находят. Однако посколь-
ку эти функции могут использоваться при сравнительном анализе ЦУТС и
ЦНПФС в качестве операндов критериев сравнительного оценивания их
качества, то термин "критериальные функции" представляется более при-
емлемым. А
Поскольку любая операция характеризуется множеством эффектов (как
положительных, так и отрицательных), часть которых находится в проти-
воречии с целью операции, то, естественно, объективно оценить её резуль-
таты одним числовым показателем не представляется возможным. В то же
время совокупность противоречивых показателей частных (единичных) ре-
зультатов операции также не позволяет однозначно оценивать эффектив-
ность ЦНПФС. В связи с этим, сознавая необходимость комплексного
(многокомпонентного, "многокритериального"1) оценивания и анализа ка-
чества операций, исследователи вводят в рассмотрение различные функ-
ции - "свёртки" компонент вектора Y,, [показателя результатов операции
(ЦНПФС)], называя их "показателями эффективности" (см. {2.7.2}).
Так, при исследовании операции определяется "критериальная функ-
ция результатов операции" (КФР):
Термин неточен, так как в его рамках критериями называются единичные (част-
ные) показатели качества объектов исследования.

72 Глава 2. Методологические основы теории эффективности
- в развернутой форме:
W = W/ {Y(n))=WPp (¥{я); Х'^
= Wf {yx, уг,..., у„; х\, *;,..., хт); (2.4.1)
- в комплексной канонической форме:
^=^(^^=<(^^)=<(^)ЦЙЦЗ^М); (2А2)
- в симплексной канонической форме:
w="7W=»7( V*V>)=К(у»у»у»'х\».'))' (2-4-3)
В приведённых выражениях вектор X'л = (Л'Ал> ^Ly tfts) игРает Роль
параметра зависимости W = W(y) (cm. {2.3.6}).
При решении задач проектирования и анализа систем (ЦУТС) в качест-
ве критериальных используются функции от параметров и ЭТХ ЦУТС и
ЦНПФС - "критериальные функции параметров системы" (КФП).
Поскольку
г«=r<.)l*W= F«Kr 4r 4>J' (2А4)
то выражения (2.4.1) - (2.4.3) можно привести к виду
w=wP[Y{n))=wP[Y{n)[x{n{))\=wn (;rj=^(4>'4v4>)- (2А5>
2.4.2) Подчеркнём, что в выражениях (2.4.1) - (2.4.5) все входящие в
них переменные детерминированные (неслучайные). А
Приведём в качестве примеров ряд наиболее распространённых крите-
риальных функций.
Пример 2.4.1. Аддитивные критериальные функции:
- функция целевого эффекта операции
Wt=WlP{Y{1))=yi=3; (2.4.6)
- сепарабелъная функция результатов операции
W1 = Wif(Y{B))= t a2i fM , (2.4.7)
1=1
если функции f2i (у.)могут быть линеаризованы, то
W3=fV3P(Y{n))=±a3iyi; (2.4.8)
/=1
- сепарабелъная функция параметров и ЭТХ ЦУТС и ЦНПФС
Ъ = W3n(xU)= t «4y g*j W, (2-4.9)

2.4. Целевые и критериальные функции
1Ъ
если функции gA\x'j) линеаризуются, то
ws = »U*V>)= £ «W- (2А10>
Наряду с приведенными "аддитивными" критериальными функциями
(2.4.6) - (2.4.10) находят применение и "мультипликативные" критери-
альные функции:
- функция целевого эффекта операции и расходуемых на его получе-
ние ресурсов [116]
W6 = W6P(Y{1))=Z- = ?-; (2.4.11)
W Уг г
- функции результатов операции:
^7 = ^Л1ы)=П/7ЛЫ ; (2-4.12)
^ = M*w)=i-n и-лЫ!*; (2.4.13)
- функции параметров и ЭТХ ЦУТС и ЦНПФС:
Ъ = *«(*V>)=fWM; (2-4.14)
7=1
^., = ^(^M)=l-nb-A.yW]",i • (2-4Л5>
у=1
Наконец, иногда используются "функции от целевых функций":
Wn=Wx^Wk)=W\Jk ; (2.4.16)
*п = *п№)="\_1. , (2-4.17)
"* "А
где W^ - значение, принятое Л-й целевой (критериальной) функцией (из
числа приведённых выше) в результате проведения операции;
Wk - значение, принимаемое Л-й целевой функцией без проведения
операции;
Wku - значение, принимаемое Л-й целевой функцией при проведении
операции в идеальных условиях (при идеальной ее организа-
ции). А
Поскольку, как было отмечено выше, в общем случае результаты (эф-
фекты) операции случайны (см. п. 2.3.3), то используются аналогичные
приведённым функции от математических ожиданий аргументов критери-
альных функций. Получаемые при таком подходе математические модели

74 Глава 2. Методологические основы теории эффективности
ЦУТС и ЦНПФС называются квазирегулярными. Произведя подобную
подстановку в соотношениях (2.4.6) - (2.4.17), получим соответствующие
им выражения квазирегулярных критериальных функций.
Пример 2.4.2. Аддитивные квазирегулярные критериальные функции:
Wx=Wxp{¥{x))=k=3 = Wx, (2.4.6')
#г =Г„(7{Я))=± СЬ/Лу,) ; (2.4.7')
W3 = WiP(Y{n))= £ a3i у, = W3 ; (2.4.81)
&4 = W4n(x\m))= £ a4J g^x'j); (2.4.91)
7=1
Мультипликативные квазирегулярные функции:
W6=W6P(Y{n))=*- = l ; (2.4.11-)
* 2
Wn = W1P(Y{n))= П ЛЛ(й) J (2-4.12')
*=1
Ws = WiP(¥{n))=l-f[ [!-/«(Ji)]*'; (2-4.13*)
1=1
y=l
^• = ^1.я(^=1-П[1-А.у(*гу)]^/- (2А15')
7=
Квазирегулярные функции от целевых функций:
^n = ^nFJ=-^r^; (2A16')
wk
;о
Wn = wM=*_* , (2.4.17-)
где — (черта над символом) - знак математического ожидания отме-
ченного им случайного объекта (величины, вектора, функции);
~ (тильда над символом) - знак приближённого значения (оценки)
отмеченной им величины.

2.4. Целевые и критериальные функции
75
2.4.3) Нетрудно заметить, что если функции (2.4.11), (2.4.12), (2.4.14)
или (2.4.12'), (2.4.14!) прологарифмировать, то они примут аддитивную
форму. ▲
2.4.4) Раскрывая семантику целевых (критериальных) функций, можно
дать им следующую интерпретацию:
- функции результатов - это взвешенные "валовые" показатели ре-
зультатов ЦНПФС;
- функции параметров - это взвешенные показатели качества ЦУТС и
организации ЦНПФС. ▲
2.4.5) Из определений элементов (операндов) соотношений (2.4.16),
(2.4.17) или (2.4.16'), (2.4.17') следует, что показатели Wn, Wn или Wu,
Wn призваны характеризовать действенность операций в обеспечении
операций более высокого уровня (суперопераций). Другими словами, это
показатели вклада подопераций в "эффективность" надопераций. Таким
образом, указанные показатели - это типичные несобственные показатели
качества подопераций (субопераций), характеризующие его косвенно, но
не дающие его абсолютной оценки. ▲
2.4.6) В различных источниках отдаётся предпочтение тем или иным
критериальным функциям с указанием (не всегда) их преимуществ перед
другими. Однако следует отметить, что все функции типов (2.4.6) - (2.4.17)
или (2.4.6') - (2.4.17') имеют больше недостатков, чем достоинств. Чтобы
убедиться в этом, прокомментируем приведённые примеры критериальных
функций.
Как уже отмечалось (см. (2.4.1)), во всех приведённых функциях
(2.4.6) - (2.4.17) не находит отражения цель операции, поскольку в них не
предъявляется требований к результатам (эффектам) у. [i = l(l)n] опера-
ции. В выражениях (2.4.1) - (2.4.5) это обстоятельство находит отражение
в структуре вектора Х!« = (A^yA^yBL,\ характеристик ЦУТС, ЦНПФС
и условий функционирования ЦУТС, в который не входят характеристики
В?Г} условий проведения операции, определяющих требования к ее ре-
зультатам [см. (2.3.9)]. Необходимо подчеркнуть, что на уровне средних
значений у. [#=l(l)#i] результатов операции предъявлять к ним требова-
ния нельзя в принципе, так как не известно, при каком среднем результате
истинный (случайный) результат (его реализация) будет достаточен для
достижения цели операции.
Таким образом, при оценивании "эффективности" (точнее, качества)
ЦНПФС по значениям показателей Wk, Wk [A: = l(l)l2] реализуется pa-

76 Глава 2. Методологические основы теории эффективности
зомкнутая схема, позволяющая лишь измерять свойство, но не позволяю-
щая его оценивать. А
2.4.7) При решении задач оптимального синтеза ЦНПФС или ЦУТС ис-
пользуется критерий оптимальности, согласно которому показатели Wk
или Wk максимизируются. При этом схема оценивания качества операции
замыкается, так как к его показателю Wk (Wk) предъявляется требование
maxWk {maxWk), но вне связи с требованиями, диктуемыми целями опе-
рации, поскольку допустимым считается лишь максимальное значение по-
казателя Wk (fVk). Другими словами, при подобной постановке задачи оп-
тимального синтеза цель операции (задача ЦУТС) отождествляется с мак-
симизацией критериальной функции [84]. Однако, с одной стороны, это
(максимальное) значение критериальной функции может не обеспечивать
достижения цели операции, так как в принципе нельзя определить, при ка-
ком значении Wk, Wk [k = l(l)l2 ] она достигается, поскольку все показа-
тели Wk (Wk\ кроме Wx (Wx\ лишены физического смысла, связанного с
целью операции, а с другой - оно в общем случае может находиться вне
области {Wk } его допустимых значений, обеспечивающих достижение
цели операции (выполнение задачи ЦУТС). Добавим, что поскольку ис-
тинная цель операции может быть достигнута не обязательно при предель-
но допустимых значениях эффектов Y.x или параметров X',* то макси-
мизация функций от них представляется совершенно необоснованной. А
2.4.8) Использование функций (2.4.7) - (2.4.17) или (2.4.7') - (2.4.17'),
имеющих искусственные размерности (или не имеющие их), затушёвывает
физическую сущность задач исследования ЦУТС и ЦНПФС и затрудняет
анализ и осмысление результатов. А
2.4.9) Показатели (2.4.11), (2.4.11') не учитывают временных затрат, а
показатели (2.4.6), (2.4.9), (2.4.10), (2.4.14) - (2.4.17); (2.4.9'), (2.4.10'),
(2.4.14') - (2.4.17') вообще не учитывают расхода ресурсов, что при ком-
плексном исследовании эффективности неприемлемо в принципе (см.
п. 2.3.2). А
2.4.10) Для функций типа (2.4.6) - (2.4.17) к отмеченным недостаткам
добавляется ещё их детерминированность, плохо соответствующая реаль-
ным практическим задачам. А
2.4.11) Показатели W2, W4, Wk [# = 6(l)l2] не являются математиче-
скими ожиданиями соответствующих показателей W29 W4, Wk
[А: = 6(l)l2] и в общем случае могут существенно от них отличаться.

2.4. Целевые и критериальные функции
11
К сожалению, это обстоятельство, как правило, не учитывается и даже не
исследуется влияние такой замены (подмены). А
2.4.12) К указанным недостаткам показателей Wk, Wk [A = l(l)l2] до-
бавляется их неопределённость, поскольку одна и та же величина отноше-
ния может быть достигнута при различных значениях входящих в него ве-
личин [26]. А
2.4.13) Резюмируя сказанное, следует отметить, что необходимо разли-
чать показатели эффективности и показатели эффектов операции. По-
следние, оценивая в какой-то мере качество ЦНПФС и ЦУТС, характеризуют
эффективность операции лишь косвенно, как потенциально возможную, без
учета её цели, т.е. в разомкнутой схеме. Поэтому подобные показатели при-
годны лишь для сравнительного оценивания качества различных операций и
только после достаточного обоснования их структуры (что, как правило, не
производится) и не пригодны для оценивания (ни абсолютного, ни относи-
тельного) их эффективности (см. п. 2.2.3 и {2.7.1}). А
2.4.14) В приведённых критериальных функциях не учитывается взаим-
ная зависимость компонент вектора F,v (целевой эффект есть функция за-
трат ресурсов и времени) и они "работают" в используемых формулах мно-
гократно (сами по себе и совместно с зависимой компонентой без учёта
действительной степени их влияния на качество ЦУТС и ЦНПФС) в отли-
чие от независимых компонент (которые в составе вектора Y,, также су-
ществуют). Понятно, что подобное влияние зависимых компонент на пока-
затель Wk искажает даваемую им оценку качества ЦНПФС или ЦУТС. А
2.4.15) В заключение обратим внимание на следующее важное обстоя-
тельство. В общем случае как между показателями у. [i = l(l)#i] качества
результатов операции (ЦНПФС), так и между параметрами (ЭТХ) ау.
[j = l{l)k] ЦУТС и ЦНПФС могут существовать связи. Если эти связи
выявлены, то множества аргументов критериальных функций (2.4.1) -
(2.4.5) естественным образом сокращаются, и некоторые из характеристик
у. или ttj перестают фигурировать в соответствующих выражениях. Мо-
жет показаться, что этот факт на решении задачи исследования качества
ЦНПФС или ЦУТС не сказывается, поскольку "исчезнувшие" параметры
учтены через зависимые от них переменные. Однако следует иметь в виду,
что при решении задач оптимального синтеза ЦУТС и ЦНПФС требования
предъявляются к каждой из характеристик в отдельности и их исключение
из критериальных функций приводит к вырождению задачи и невозможно-
сти её решения. А

78 Глава 2. Методологические основы теории эффективности
1
§1
а:
§
съ
«б
I
а»
§
i
i
53
5
PQ
(D
S
Он
« о
g Х\
" PQ
8 I
lij
§•©1
S
X
8-
Он
. w
5
3
3
Д
о>
PQ
О
О
ее
PQ
н
се s
* я
теля
пера
се о
СО
§ о
2 н
С ее
н
Л Л
о Я
Я £
о- Л
01
азм
Г"
<d
3
я
S*
о
Й
0>
PQ
;
к
<i>
3
я
*
и
J
3
я
щен
"8
Ю
О
а>
3
В
о!
се
ЕГ
к
Я
с
я
я
W
3
В
о
ю
о
U
S
О*

2.4. Целевые и критериальные функции
79
Из содержания данного параграфа и приведённых замечаний - коммен-
тариев следует, что "критериальной" функцией1, пригодной для измерения
эффективности операции в замкнутой схеме, т.е. с учетом объективных
требований к её результатам, выполнение которых равносильно выполне-
нию задачи ЦУТС, является вероятность Рдц достижения цели реализуе-
мой (проводимой) ЦУТС операции (ЦНПФС), т.е.
где А^ = \А(к,},А^J, А^ = А^[В^);
B(') = \B(iVB(i"))>
X{m) = \\)'B(i))-
На рис. 2.4.1 приведена схема классификации показателей качества и
эффективности операций (ЦНПФС) и критериев их оценивания. Элемен-
ты схемы описаны достаточно подробно и специальных комментариев не
требуют, тем не менее в последующих параграфах их семантика раскрыва-
ется более полно.
2.5. ПОСТАНОВКА ЗАДАЧИ ИССЛЕДОВАНИЯ
КАЧЕСТВА ЦУТС
В предыдущих параграфах была достаточно полно рассмотрена про-
блема исследования качества ЦНПФС (точнее, качества результатов
ЦНПФС и его эффективности), т.е. её математическая формулировка и
принципы, лежащие в основе методов её решения (см. также пункты 2.6,
2.7). Поскольку в данной монографии объектом исследования является
ЦНПФС (операция), то реализующая его ЦУТС рассматривается лишь как
элемент операционной системы и операционного комплекса, так как в
рамках исследования операций структура, параметры и ЭТХ ЦУТС счита-
ются заданными или варьируемыми (кроме структуры) в ограниченных
пределах. Однако в других дисциплинах системного цикла ("Общая теория
систем", "Анализ систем", "Системотехника" и т.д.) объектом исследова-
ния является ЦУТС, и проблемой исследования - её синтез, т.е. разработка
и создание ЦУТС, обладающей требуемым качеством. Поэтому представ-
Эта (и только эта!) функция может называться ещё и целевой.

80 Глава 2. Методологические основы теории эффективности
ляется необходимым рассмотреть общую постановку задачи такого иссле-
дования на языке ТЭЦНП.
Качество любого объекта в полной мере проявляется лишь в процессе
его использования по назначению. Поэтому наиболее информативным и
объективным является оценивание качества объекта по эффективности его
целевого применения. Для такого оценивания объект должен быть под-
вергнут испытаниям, в ходе которых и выявляется его качество. Это отно-
сится как к качеству продукции вообще, так и к качеству ЦУТС в частно-
сти. Однако, с одной стороны, далеко не все объекты (ЦУТС) могут быть
испытаны в условиях, достаточно близких к тем, в которых им придется
функционировать по назначению, с другой - наибольший практический
интерес представляет априорная оценка качества объекта (ЦУТС), т.е. еще
до его применения. Так, для управления качеством продукции его необхо-
димо оценивать в процессе производства и даже ещё раньше - на этапе
разработки образцов продукции.
Это же относится и к ЦУТС, прогноз качества которой необходим на
этапах её проектирования и разработки, а оценка качества - на этапе при-
ёмных испытаний, предшествующем её применению в реальных условиях.
Априорное оценивание качества любого объекта (контроль продукции
ОТК, приемка ЦУТС) без прямого его применения по назначению возмож-
но, если известно соотношение, связывающее его характеристики (струк-
туру, организацию, параметры, ЭТХ и т.п.) с выходными эффектами его
целевого применения (функционирования по назначению).
Итак, пусть объект исследования ЦУТС и пусть F,v - вектор выходных
эффектов ЦНПФС (показатель виртуального качества его результатов),
A',k* - вектор виртуальных значений параметров и ЭТХ ЦУТС (структур-
ных, организационных, эксплуатационных, технических, параметрических
и т.п.), А?к* - вектор виртуальных значений характеристик организации
ЦНПФС, 2Г'7м - вектор характеристик условий функционирования ЦУТС.
Кроме того, пусть известно соотношение (см. (2.3.8»
Y(n) = ^(n)l^V> ,#^"(*'>'^\г)>' (2.5.1)
устанавливающее зависимость выходных эффектов (результатов) ЦНПФС
от параметров, ЭТХ и условий функционирования ЦУТС и характеристик
ЦНПФС. Тогда, если через { ГЛ ] обозначить область допустимых значе-
ний ГЛ вектора F,v, т.е. таких, при которых ЦУТС выполняет свои зада-
чи, то критерий пригодности ЦУТС для целевого применения (критерий
целевой пригодности) будет иметь следующее выражение:
GVP--Y{n)e{Y^\=U. (2.5.2)

2.5. Постановка задачи исследования качества ЦУТС
81
Если для оператора (2.5.1) существует обратный оператор по вектору
А[ку
А\к')= А\к') \У(т)9^'\кт) >В'{1'))~ Y{k') \Y{n)>'A"{k") >В'(Г) ) > (2.5.3)
позволяющий выразить зависимость виртуальных "значений" параметров и
ЭТХ ЦУТС от выходных эффектов, характеристик ЦНПФС и условий
функционирования ЦУТС, то может быть определена область ( А'Л j до-
пустимых значений А'Л вектора А,к,к параметров и ЭТХ ЦУТС, при кото-
рых она может выполнить свои функции, соответствующая области { УЛ ]
допустимых значений ГЛ результатов Y.k ЦНПФС, т.е.
К !=> К-> }= ко •• ^4V4r*'(")= К) 1. <2-5-4>
где А*?"к - номинальные (расчётные) значения характеристик ЦНПФС;
BIS - номинальные (расчётные) значения характеристик условий
функционирования ЦУТС, создаваемых в ходе приемных ис-
пытаний.
Тогда критерий параметрической пригодности ЦУТС будет иметь вид
Таким образом, для контроля, проверки и приемки ЦУТС (и любой дру-
гой продукции) реализуется критерий (2.5.5), позволяющий управлять её
качеством, не подвергая целевому применению.
2.5.1) Понятно, что в пределах области {Д'Д ] качества ЦУТС (систем),
удовлетворяющих критерию (2.5.5), различны, однако в его (критерия)
рамках оно (качество ЦУТС) считается одинаковым. А
2.5.2) В принципе в выражениях (2.5.2) и (2.5.5) области {уЛ ] и \А'Л j
могут иметь размерности меньшие, чем соответственно я и Л', и даже мо-
гут быть точками, что определяется классом К руководящего ("выбранно-
го") критерия, координаты которых определяют оптимальные или превос-
ходные значения выходных эффектов Y, v и соответствующих им парамет-
ров А'{к,} ЦУТС (см. (2.2.1». А
2.5.3) На практике допустимые значения A',L параметров А!к* опреде-
ляются, как правило, экспериментально с применением испытаний ЦУТС
(стендовых, полигонных и т.п.). А

82 Глава 2. Методологические основы теории эффективности
2.6. О ПРИНЦИПАХ ВЫБОРА ПОКАЗАТЕЛЕЙ
РЕЗУЛЬТАТИВНОСТИ ЦНПФС И
ФОРМУЛИРОВАНИИ ЦЕЛЕЙ ОПЕРАЦИЙ
2.6.1. КЛАССИФИКАЦИЯ ПОКАЗАТЕЛЕЙ
РЕЗУЛЬТАТИВНОСТИ ОПЕРАЦИЙ
Наряду с приведённой на рис. 2.4.1 классификацией применяемых пока-
зателей эффективности операций и критериев ее оценивания целесообраз-
но рассмотреть и классификацию показателей результативности ЦНПФС,
отражающую специфику широкого и весьма универсального класса целе-
направленных процессов, а именно процессов массового обслуживания
(ПМО), при оценивании эффективности которых применяются специфиче-
ские показатели их результатов (целевых и побочных эффектов). Схема
классификации таких показателей по пяти основным аспектам показана на
рис. 2.6.1. Кратко рассмотрим методологические основы (принципы) этой
классификации.
1. Прежде всего следует различать функциональную (целевую) и эко-
номическую (ресурсную) компоненты вектора результатов ЦНП. Под
"функциональной эффективностью" (см. {2.7.12}) понимается приспособ-
ленность исследуемого объекта - ЦУТС (правильнее, процесса его целево-
го функционирования - ЦНПФС) к выполнению возложенных на него
функций (поставленной перед ним задачи - цели). Это свойство, как отме-
чалось в п. 2.3.2, называется результативностью (или действительностью)
ЦНП, реализуемого объектом (ЦУТС). В то же время "экономическая эф-
фективность" (см. {2.7.12}) отражает либо такие свойства ЦНПФС, как
доходность, рентабельность и т.д. (для народнохозяйственных ОК), либо
стоимостные показатели процессов проектирования, изготовления, испы-
таний и эксплуатации (боевого применения) военно-технических ОК
(ВТК).
2. В рассматриваемой схеме (рис. 2.6.1) термины "прямые и косвенные
показатели" призваны отразить степень их информативности по отноше-
нию к задаче исследования. Так, прямые показатели непосредственно от-
вечают на вопросы: насколько результативен ЦНПФС и насколько ОК
(ОС) приспособлен к выполнению поставленных перед ним задач. Однако,
к сожалению, не всегда удаётся четко сформулировать задачи ОК, что, как
правило, обусловлено наличием нескольких, подчас противоречивых за-
дач. В таких случаях целесообразно использовать косвенные показатели
результативности ЦНП, дающие исследователю представление о наиболее
важных характеристиках ЦНПФС. Окончательное суждение о его эффек-
тивности вырабатывается эвристически с учётом целого ряда неформали-
зуемых дополнительных данных и сведений.

2.6. О принципах выбора показателей результативности ЦНПФС 83
(D
§
ST
К
нам
| 5
/■■^
-
<->
S
(зав
S
Он

84 Глава 2. Методологические основы теории эффективности
3. По третьему аспекту показатели результативности ЦНП делятся на
индивидуальные и групповые. Такая классификация в первую очередь от-
носится к процессам массового обслуживания, протекающим в КМО и
СМО. При этом, если индивидуальные показатели в основном характери-
зуют "качество"1 процесса обслуживания отдельного (но произвольного)
требования (среднестатистического "представителя" потока требований),
то групповые показатели характеризуют (в среднем) "качество" процесса
обслуживания всех поступающих в СМО требований [129].
4. По четвертому аспекту показатели делятся на локальные (точечные)
и интегральные (интервальные), т.е. на показатели, определяющие ре-
зультативность ПМО соответственно в некоторый произвольный момент
времени и за некоторый период (интервал) времени.
5. По признаку зависимости от времени следует различать статисти-
ческие и динамические показатели результативности. Строго говоря, все
показатели результативности ЦНПФС зависят от времени, причём в выра-
жения для локальных показателей эта переменная (время) входит непо-
средственно (как аргумент), а в интегральных показателях она определяет
начальный момент периода функционирования ЦУТС - СМО (начало
ЦНПФС - ПМО) и играет роль параметра. Однако в установившемся, ста-
ционарном режиме работы ЦУТС (СМО) (если он существует) указанная
зависимость исчезает, локальные показатели становятся постоянными
(константами), а интегральные зависят только от длительности периода
функционирования ЦУТС (СМО) и не зависят от его положения на вре-
менной оси.
2.6.2. О ФОРМУЛИРОВАНИИ ЦЕЛЕЙ ОПЕРАЦИЙ
Как уже отмечалось ранее, ключевой проблемой при исследовании эф-
фективности операций (ЦНПФС) является корректная (правильная, обос-
нованная) формулировка задач, стоящих перед ЦУТС, от которой зависит
правильность выводов об эффективности реализуемых ими операций и
пригодности последних для достижения целей, поставленных суперсисте-
мой.
Из содержания п. 2.3 следует, что поскольку математическое выражение
цели операции - это критерий оценивания качества её результатов (эффек-
тов) [(2.3.3) или (2.3.4)], то формулирование цели операции начинается с
определения спецификации существенных эффектов ЦНПФС и требований
к ним, количественные меры которых образуют векторы F, * и ГЛ, а закан-
чиваются установлением отношений между компонентами этих векторов,
обеспечивающих достижение цели операции (равносильных ему).
Здесь речь идёт о "качестве массового обслуживания", а не о качестве, характери-
зуемом эффектом обслуживания.

2.6. О принципах выбора показателей результативности ЦНПФС 85
В состав операционных систем, проводящих сложные (большие) опера-
ции, часто входят несколько ЦУТС, собственные цели которых могут не
совпадать (как, например, в моделях двусторонних боевых действий). Не-
обходимость учёта этого обстоятельства делает задачу формирования цели
операции в значительной степени неопределенной и поэтому весьма слож-
ной. Успех её решения в значительной мере зависит от компетентности и
опыта управляющего органа ОС (суперсистемы).
Универсальных формальных методов решения таких задач не сущест-
вует. Однако представляется полезным обсудить основные принципы, ле-
жащие в основе процесса формирования показателя качества результатов
операции и формулирования ее цели.
Из вышесказанного следует, что операционные комплексы (ОК) разли-
чаются как по структуре операционных систем (ОС), так и по форме и сте-
пени участия их элементов в проведении операций (ЦНПФС). В связи с
этим следует различать сплочённые и разобщённые операционные
комплексы (СОК и РОК).
В сплочённых ОК все их элементы в полной мере "заинтересованы" в
оптимальности одних и тех же результатов (эффектов) операции, вследст-
вие чего совокупность "существенных" их показателей включает в себя как
целевые (функциональные) эффекты, так и расходуемые на их достижение
ресурсы (материально-технические и временные).
Что касается разобщённых ОК, то их исследование существенно зави-
сит от причин разобщения "интересов" их элементов. Такими причинами
могут быть либо антагонизм, либо индифферентность.
В первом случае состав показателей существенных результатов (ПСР)
операции зависит от состава элементов ОК, сплочённых с суперсистемой.
Во втором случае, если индифферентность интересов элементов ОК
полная, то состав ПСР зависит лишь от постановки задачи исследования.
При частичной индифферентности состав ПСР должен назначаться с
учётом элементов ОК, интересы которых наиболее чувствительны к реше-
нию задачи. Поясним сказанное на ряде примеров из теории (точнее, из
практики) массового обслуживания.
Пример 2.6.1. Пусть ЦУТС (есть ВТС) - система ПВО, рассматривае-
мая как система массового обслуживания (СМО), "клиентами" которой яв-
ляются самолеты противника, также образующие ЦУТС (самостоятель-
ную). Понятно, что соответствующий такому случаю ОК будет разобщён-
ным по интересам ЦУТС - ПВО и ЦУТС - самолеты противника, обра-
зующие поток заявок (требований) на обслуживание в СМО. Понятно так-
же, что причиной разобщения является антагонизм СМО и ее "клиента". В
рассматриваемом примере состав ПСР, очевидно, зависит от того, чья
ПВО (своя или противника) рассматривается.
В первом случае ЦНПФС - обстрел самолетов противника. Поэтому в
качестве целевых эффектов операции могут фигурировать либо число
сбитых самолетов, либо предотвращённый ущерб, либо оба показателя в
отдельности, либо некоторая функция от них.

86 Глава 2. Методологические основы теории эффективности
Во втором случае ЦНПФС - преодоление самолетами ПВО противника
и нанесения ему ущерба. Теперь в качестве целевых эффектов могут рас-
сматриваться либо ущерб, нанесённый противнику, либо относительное
число (доля) самолетов, преодолевших ПВО, либо ущерб, соотнесённый с
потерями самолетов, либо некоторая функция от этих показателей. А
2.6.1) В связи с приведённым примером необходимо обратить внимание
на следующее обстоятельство. Иногда потери (своих самолетов или нане-
сение самолетами противника) рассматриваются как расход ресурсов. Од-
нако такой подход представляется не совсем правомерным, так как подоб-
ные потери изменяют характеристики Alk,s ЦУТС, а не ресурсов. Действи-
тельно, это так, поскольку, во-первых, цель операции может быть достиг-
нута и без потерь (в принципе), а во-вторых, и с изменившейся в резуль-
тате потерь структурой (а следовательно, с изменившимися ЭТХ) ЦУТС
может (в принципе) выполнить задачу в последующей операции (см.
п. 5.3.2). А
2.6.2) Применение относительных показателей целевого эффекта (нане-
сённый ущерб / потерянные самолеты и т.д.) нежелательно, поскольку их
размерность, лишённая чёткого физического смысла, не позволяет предъ-
являть к ним осмысленные требования. А
Пример 2.6.2. Пусть СМО - ателье бытового обслуживания. Основной
задачей такой системы является качественное и массовое обслуживание
"клиентов". Одним из важнейших показателей "качества результатов" та-
кого ЦНПФС (ПМО) является длительность выполнения заказа (побочный
эффект операции). Однако число обслуживающих каналов (приборов, уст-
ройств, мастеров и т.п.) и их быстродействие ограничены условиями "эко-
номической эффективности" [рентабельности (см. {2.7.12.})] работы ате-
лье, в значительной мере предопределяющей его индифферентность ("без-
различие") к интересам "клиентов", вынужденных в ожидании обслужива-
ния выстаивать большие очереди.
В подобных условиях одним из путей улучшения "качества массового
обслуживания" "клиентов" (повышения эффективности этого процесса в
интересах "клиентов") является введение "штрафов", налагаемых на СМО,
если время ожидания "клиентом" начала обслуживания или время его пре-
бывания в СМО превзойдет предельно допустимое значение и "клиент"
покинет СМО необслуженным.
Понятно, что введение штрафов целесообразно лишь в случае, когда в
интересах клиентов отражаются интересы ОК, т.е. суперсистемы. Таким
образом, в состав ПСР наряду с показателем качества целевого обслужи-
вания "клиентов" должны входить и время его ожидания начала обслужи-
вания или пребывания в СМО, и характеристики связанных с этим потерь
на уровне ОК. А

2.6. О принципах выбора показателей результативности ЦНПФС 87
Наконец, встречаются ОК, "разобщенные в малом" [т.е. на уровне от-
дельных СМО (ЦУТС): ателье, автобазы, предприятия и т.п.] и "сплочён-
ные в большом" (на уровне отрасли, министерства, региона, народного хо-
зяйства и т.п.), в которых недостаточный учёт интересов "клиентов" в од-
них СМО (ЦУТС) компенсируется соответствующим их учётом в других
СМО (ЦУТС). Так, например, попытка ликвидировать "очереди" перед
СМО определённого типа путём улучшения её технического оснащения
или увеличения "обслуживающего персонала" могла бы привести к увели-
чению "очередей" перед СМО других типов, что, в свою очередь, могло бы
отрицательно сказаться как на "качестве массового обслуживания" "клиен-
тов", так и на "экономической эффективности" процесса функционирова-
ния всей сети массового обслуживания в целом.
Для учёта указанных факторов должны использоваться векторные пока-
затели F/v и ГЛ качества результатов операции и требований к ним, от-
дельные компоненты которых и призваны описывать количественно не
только целевые (функциональные), но и наиболее существенные побочные
эффекты, также характеризующие приспособленность ЦНПФС к достиже-
нию цели операции. Так, в примере 2.6.2 "целевой эффект" - качество
функционального обслуживания ("выполнение заказа"), а один из важней-
ших побочных эффектов - длительность обслуживания1. При этом доми-
нирующими являются интересы (цели) суперсистемы, организующей опе-
рацию, которые включают в себя и которым должны быть подчинены ин-
тересы (подцели) всех сплочённых с ней элементов ОК. Однако следует
помнить, что принципы комплексного исследования эффективности опе-
раций требуют включения в состав векторов Y.k и ГЛ компонент трёх
групп, характеризующих наряду с целевыми (и на равных с ними правах) и
побочные эффекты операции - расходы ресурсов и времени. Отмеченные
обстоятельства должны учитываться также при определении остальных
элементов критерия ОцР оценивания качества результатов операции и при-
способленности ЦНПФС к её достижению.
Таким образом, формулирование цели операции - это один из важней-
ших и ответственных этапов исследования эффективности ЦНПФС, в зна-
чительной степени предопределяющий правильность окончательных вы-
водов.
В рамках "Теории массового обслуживания" исследуются лишь временные ха-
рактеристики ПМО. При этом качественность функционального обслуживания посту-
лируется.

88 Глава 2. Методологические основы теории эффективности
2.7. КОММЕНТАРИИ
Подведём некоторый итог и прокомментируем рассмотренные в данной
главе понятия, принципы и концепции, лежащие в основе теории эффек-
тивности ЦНП, в понимании которых до настоящего времени существуют
различия, делающие само понятие "эффективности" расплывчатым [38, 50,
88, 116, 125, 190, 191] и затрудняющие его формализацию и построение
теории, обладающей достаточной общностью и необходимой для практики
содержательностью и конструктивностью (см. также все замечания).
2.7.1} Прежде всего необходимо уточнить понятия уровней и этапов
оценивания эффективности ЦНП. Как было отмечено в пункте 2.2.3, про-
цедура оценивания качества объекта реализуется в два этапа на двух уров-
нях:
- первый этап - количественное оценивание (называемое измерением)
качества реализуется в разомкнутой схеме;
- второй этап - качественное оценивание (собственно оценивание) ка-
чества реализуется в замкнутой схеме.
Следует подчеркнуть, что указанные этапы оценивания реализуются
при прямых измерениях, т.е. когда непосредственно наблюдается и изме-
ряется показатель исследуемого свойства.
Поскольку эффективность - это "качество" операции (ЦНПФС), то для
его оценивания в замкнутой схеме необходимо реализовать оба этапа. В то
же время эффективность, будучи комплексным свойством ("качеством")
операции, непосредственно не наблюдается, а определяется через качество
результатов ЦНПФС, т.е. посредством косвенных "измерений" по описан-
ной выше схеме в два этапа (на двух уровнях). При этом на каждом этапе
(на каждом уровне) реализуются замкнутые схемы оценивания (см.
п. 2.3.4): на первом - качества результатов операции (подэтапы 1.1 - 1.3),
на втором - эффективности операции (подэтапы 2.1 - 2.3). Таким образом,
всего реализуются четыре этапа, на двух из которых производится измере-
ние (подэтапы 1.1, 2.1), а на двух других - собственно оценивание (подэта-
пы 1.3, 2.3) соответственно качества результатов и степени (вероятности)
достижения цели операции.
Выше были рассмотрены методологические основы комплексного ис-
следования эффективности одноцелевой операции. Если операция "много-
целевая"1, то её эффективность по достижении каждой из целей должна
оцениваться самостоятельно по описанной выше схеме (см. п. 2.3.4,
(3.3.23), (3.3.24». А
Строго говоря, согласно определению такую операцию необходимо рассматривать
как совокупность одноцелевых операций (см. определение 1.2.3).

2.7. Комментарии
89
2.7.2} Как было установлено, показатель эффективности операции - это
комплексный показатель "качества" ЦНПФС как объекта исследования, а
критерии оценивания качества результатов ЦНПФС и его эффективности
суть математические формулировки цели операции и требуемой степени её
достижения.
Таким образом, не следует смешивать понятия:
- эффективность - свойство операции,
- показатель эффективности - количественная мера этого свойства;
- критерий оценивания эффективности - совокупность условий, оп-
ределяющих цели операции и в соответствии с ними пригодность, опти-
мальность или превосходство исследуемой операции (целенаправленной
системы действий). А
2.7.3} В принципе понятия "цель операции" и "задача ЦУТС" сходны.
Однако в общем случае отождествлять их не следует. Как отмечалось в
п. 1.2, цель операции достигается путём выполнения последовательности
(или одной) задач. Действительно, если цель операции достигнута, то это
означает, что ЦУТС свои задачи (задачу) выполнила. В то же время не-
трудно представить ситуацию, когда задача ЦУТС выполнена, а цель опе-
рации не достигнута. Применительно к изображенной на рис. 2.4.11 клас-
сификации показателей эффективности вероятность Рдц достижения цели
операции является собственным (внутренним) показателем для операци-
онного комплекса (для суперсистемы), а вероятность Рвз выполнения за-
дачи ЦУТС - несобственным (внешним) показателем для операционной
системы (для ЦУТС) (см. рис. 1.2.1). При этом если операцию реализует
одна ЦУТС, цель которой совпадает с целью суперсистемы, то должно вы-
полняться равенство Рдц = Рвз.
Хотя в целях простоты изложения в рамках монографии указанное раз-
личие в основном не учитывается, тем не менее, поскольку вероятность
Рдц есть показатель эффективности операции (ЦНПФС), то её целесооб-
разно называть вероятностью достижения цели операции в отличие от
распространённого в литературе словосочетания "вероятность выполнения
задачи ЦУТС". А
2.7.4} Физически достижение цели операции (ЦНПФС) - это наступле-
ние некоторого события, математически - это выполнение необходимых
условий, которые в формализованной, конструктивной форме представля-
ют собой предикаты, т.е. системы отношений (принадлежности, включе-
ния, равенств, неравенств и т.п.), заданных на множествах значений пока-
зателей качества результатов операции и ее эффективности. Следует под-
черкнуть, что это не условия функционирования или применения ЦУТС, а
Фигурирующее на рис. 2.4.1 понятие "ведущих компонент" раскрывается в п. 3.3.

90 Глава 2. Методологические основы теории эффективности
также не ограничения, накладываемые на параметры и ЭТХ ЦУТС и
ЦНПФС, а условия выполнения задачи ЦУТС, т.е. условия, при выполне-
нии которых цель операции может считаться достигнутой.
Таким образом, как отмечалось в п. 2.3.2, критерий оценивания качест-
ва результатов операции представляет собой математическую формули-
ровку её цели, А
2.7.5} При описанном подходе к оцениванию качества результатов и
эффективности операции все целенаправленные процессы оказываются
сравнимыми по эффективности, имеющей единую меру - вероятность РДЦ
достижения цели операции. Подчеркнём, что в рамках этого подхода пока-
затель эффективности не только единый, но и единственный, тогда как при
других подходах рассматриваются множества "показателей эффективно-
сти" (см. п. 2.4), которые, в сущности, таковыми не являются. А
2.7.6} Вероятность Рдц, по существу, является одновременно относи-
тельным и абсолютным показателем эффективности операции. Действи-
тельно, с одной стороны, поскольку в общем случае целевой эффект связан
с затратами ресурсов (побочными эффектами), то, как следует из выраже-
ний (2.3.7) и (2.3.16), вероятность Рдц характеризует эффективность опе-
рации с учётом соотношения целевого (основного) и побочных эффектов.
С другой стороны, для фиксированного комплекса условий вероятность
случайного события есть абсолютная характеристика (мера) степени объ-
ективной возможности его реализации (появления, осуществления, насту-
пления). Говоря строже, ее значение и в этом случае относительно, но по
сравнению с единицей, т.е. с абсолютной мерой (единицей измерения) сте-
пени объективной возможности достоверного события. В связи с этим для
объективного оценивания эффективности операции, характеризующей
степень достижения её цели, достаточно знать его вероятность Рдц. Такой
показатель эффективности операции позволяет производить как относи-
тельное (сравнительное), так и абсолютное оценивание по эффективности
различных по организации ЦНП. Другие распространённые "показатели
эффективности" [несмотря на их обилие (см. п. 2.4)] этим важным свойст-
вом (абсолютного оценивания) не обладают. А
2.7.7} Компоненты вектора ГЛ, как правило, взаимно независимы, по-
скольку требования к результатам ЦНП из различных их групп вытекают
из различных не взаимосвязанных предпосылок. Так, требуемый целевой
эффект yP\* диктуется собственно целью операции, допустимый расход
ресурсов YP\d обусловлен их наличием и качеством, директивный срок

2.7. Комментарии
91
достижения цели операции К^г обусловлен ситуацией и динамикой ее
развития.
Представляется, что в общем случае указанные предпосылки не связаны
друг с другом, хотя возможны и исключения, о которых, в частности, бу-
дет говориться в п. 5.2. ▲
2.7.8} Следует подчеркнуть, что допущение о независимости компо-
нент вектора Y,^ неправомерно в принципе, так как, с одной стороны, це-
левой эффект ух получается за счёт расходования ресурсов, образующих
побочные эффекты j;2 и j;3, а, с другой стороны, наличие избыточности
ресурсов позволяет (в определённых пределах) осуществлять их взаимные
обмены (см. п. 2.3.2), так что побочные эффекты в общем случае связаны
друг с другом. А
2.7.9} Как отмечалось в п. 2.3.1, характеристики (свойства) ЦУТС и
ЦНПФС (их параметры и ЭТХ, а также организация и результаты) можно
разделить на целевые и обеспечивающие. Многообразие целевых характе-
ристик практически неисчерпаемо (как и многообразие целей операций),
поэтому здесь обсуждаться не будет. Что касается обеспечивающих харак-
теристик, то представляется необходимым кратко рассмотреть их.
К обеспечивающим в первую очередь относятся основные эксплуатаци-
онно-технические характеристики ЦУТС и ЦНПФС, такие как готов-
ность и эксплуатационно-техническая надёжность1.
Рассуждая аналогично {2.7.7}, предположим, что требования к готовно-
сти, эксплуатационно-технической надёжности ЦУТС и результатам
ЦНПФС взаимно независимы2. Тогда область { Yff't ] допустимых значе-
ний обобщённых характеристик ЦУТС и результатов ЦНПФС может быть
представлена в следующем виде:
l^'M^M^)И*<:;>}. k+«.+*n="j. (2-7.1)
где { Г/Л J - область допустимых значений "характеристик готовности"
ЦНП, т.е. результатов ЦНПФС, обусловленных техниче-
ской готовностью ЦУТС;
{ Y(":\ \ - область допустимых значений "характеристик надёжности"
(^живучести") ЦНП, т.е. результатов ЦНПФС, обуслов-
ленных эксплуатационно-технической надёжностью
ЦУТС;
1 Семантику этого понятия обсудим в {2.7.10}.
2 В общем случае этот постулат неправомерен.

92 Глава 2. Методологические основы теории эффективности
i *М J ~ область допустимых значений "целевых (операционных)
характеристик" ЦНП, т.е. результатов ЦНПФС [целевых
эффектов и расходуемых ресурсов (т.е. пц =п)]9 обеспе-
чивающих достижение цели операции.
Введем обозначения:
у/* - вектор обобщённых характеристик ЦУТС и результатов
\Поб)
ЦНПФС;
Y/ х - вектор "характеристик готовности" ЦНП;
\пг)
Y/'n\ - вектор "характеристик надёжности" ЦНП;
К * v - вектор "целевых характеристик" ЦНП.
Тогда критерий пригодности ЦНП будет определяться следующим пре-
дикатом:
» AnВпС= (Y;g)e{ifo \Н^ц)еЦ** \)= DnC=U, (2.7.2)
где К* ч = Г/ \ + К \ _ вектор "обеспечивающих характеристик"
ЦНП1;
I ^М J= I ^(О Jx I ^(О J ~ °бласть допустимых значений вектора F/\.
Теперь показатель эффективности ЦНПФС примет одно из следующих
выражений:
рДМКА £> }М(&> е1 % 1W^l> eU:5 }W%, el % ))l=
=ЛКг)e 1 ч; > )M*<:.>e I fo> I) рЦ:„)e Ц:;> ))=^ ^ ^> <2-7-3)
где Рг = Р(г/ v e { F/'t )) - вероятность того, что в момент начала опе-
рации (ЦНПФС) ЦУТС будет готова к
функционированию (к применению) - веро-
ятность события А;
Рн = Р\¥,нп v e{ У£\ \) - условная вероятность того, что в ходе опе-
рации (ЦНПФС) параметры ЭТХ ЦУТС бу-
дут находиться в пределах, обеспечиваю-
щих выполнение её задачи - вероятность
события В при условии А;
1 Следует различать векторы Y^ v и Y? \, т.е. обобщённые и обеспечивающие ха-
рактеристики.

2.7. Комментарии
93
Рц = P\Y,4n \ е [КД^ }) - условная вероятность того, что цель прово-
димой операции будет достигнута - вероят-
ность события С при условии Аг\В,
или
= '(%)*№)№%)*[*£)])= рл*б . (2-7.4)
где Рд = р(к* v€ |к*Л })= Рг Рн - вероятность того, что в ходе операции
ЦУТС будет находиться в дееспособном1 (работоспособном)
состоянии, т.е. вероятность качественного эксплуатационно-
технического обеспечения операции (ЦНПФС).
Обратим внимание, что поскольку С с: An В, т.е.
то вероятность РДЦ - есть безусловная (априорная) вероятность случайно-
го события С = ^К* че|кЛ*ч j) , которое, таким образом, характеризует
достижение цели операции исчерпывающе.
В заключение ещё одно замечание семантического характера. При рас-
смотрении процесса достижения цели операции (ЦНПФС) в динамике, т.е.
в последовательности реализации его фаз (этапов, стадий), представляется
целесообразным терминологическое уточнение рассмотренных выше ха-
рактеристик. Так, вероятность Рн целесообразно обозначить через РБ и
называть показателем безотказности ЦУТС, а вероятность Рц-Р3 - ус-
ловной вероятностью выполнения задачи ЦУТС. При этом, исходя из фи-
зического смысла сомножителей РГ9 РБ и Р3 в выражении
Рдц = Р,РБР3 [см. (2.7.3)], их целесообразно соответственно называть:
- вероятность Рг - показателем эксплуатационно-технической го-
товности ЦУТС;
- произведение РГРБ - показателем функционально-технической
(оперативной) готовности ("живучести") ЦУТС (см. {2.7.10});
- вероятность Р3 - показателем функциональной способности ЦУТС.
Применительно к боевым военно-техническим системам (ВТС), с уче-
том существующей терминологии, последние два показателя имеют
смысл:
- произведение РГРБ - показатель боеготовности ВТС;
- вероятность Р3 - показатель боеспособности ВТС. ▲
Дееспособность - это обобщение понятия работоспособности на сложные и боль-
шие системы.

94 Глава 2. Методологические основы теории эффективности
2.7.10} Существует множество работ (как правило, по "Теории на-
дёжности" [113], [147], [187]), в которых эффективность ЦНПФС, "по-
нимаемая" как эффективность системы (ЦУТС), отождествляется с её
надежностью или даже ещё уже, с безотказностью. Другими словами,
предполагается (постулируется), что если система (ЦУТС) не откажет в
течение периода времени, необходимого для выполнения задачи систе-
мы (ЦУТС), то цель операции (ЦНПФС) будет достигнута. Представля-
ется совершенно очевидной несостоятельность (необоснованность) по-
добной концепции, так как, во-первых, "безотказность" работы системы
(ЦУТС) и достижение цели операции (ЦНПФС) не тождественны (см.
{2.7.3} и {2.7.7}), во-вторых, в общем случае время функционирования
системы и время, необходимое для получения требуемого целевого эф-
фекта (операционное время), не равны, в-третьих, операционное время
принципиально случайно, т.е. случаен момент достижения цели опера-
ции и, следовательно, заранее не известно, сколько времени должна без-
отказно профункционировать система (ЦУТС). Подобные ситуации ле-
жат за рамками проблем современной "Теории надёжности". Другими
словами, в ней рассматриваются не реальные, а идеализированные (вы-
ше допустимого) условия применения системы (ЦУТС), уводящие ис-
следования от существующей в действительности проблемы в сторону
её необоснованного упрощения. В рамках рассматриваемой здесь мето-
дологии этого не происходит.
Вернёмся к термину "эксплуатационно-техническая надёжность". По
определению [159], надёжный - это внушающий доверие, верный, проч-
ный.
Из приведённого определения следует, что термин "надёжность" может
характеризовать свойства существенно различной физической природы,
такие как степень доверия, прочность и верность. Однако в определении не
уточнён смысл термина "верный", которым, с одной стороны, характеризу-
ется степень соответствия (точность, правильность), а с другой - предан-
ность. К сожалению, в технической литературе не уделяется достаточно
внимания уточнению смысла употребляемых терминов, что часто является
причиной разночтений и нечёткости в понимании рассматриваемой про-
блемы. Так, в "Теории надёжности" надёжность элементов систем имеет
смысл их "безотказности" или, другими словами, "прочности". В качестве
мер этого свойства используются вероятностные характеристики времени
безотказной работы (дополнительная функция распределения, математиче-
ское ожидание и т.п.).
Например, "функция надёжности" есть вероятность того, что элемент
системы (техническое устройство) проработает безотказно в течение неко-
торого (неслучайного) времени и, следовательно, характеризует степень
"доверия", оказываемого элементу. Однако поскольку безотказная работа
(прочность) элемента системы (ЦУТС) зависит не только от его свойств,

2.7. Комментарии
95
но и от условий его функционирования, то бытующее понимание термина
"надёжность" не в полной мере отвечает его назначению.
Теперь о термине "живучесть". По определению [159], живучий - это
1) жизнеспособный; 2) прочно сохраняющийся, устойчивый. Здесь, в отли-
чие от определения понятия "надёжный", разночтений меньше и обе ин-
терпретации (толкования) термина сходны по смыслу.
Если процитировать определения понятия "надёжность", приводимые в
различных источниках [25, 114, 137, 197], то можно заметить, что, по су-
ществу, всюду речь идет о "живучести", а не о "прочности" элементов (уст-
ройств, блоков, агрегатов) систем (ЦУТС). Поэтому встречающееся
словосочетание "методы создания надёжных систем из ненадёжных эле-
ментов" [имеются в виду методы резервирования элементов, блоков, агре-
гатов и подсистем, а также другие приемы создания в системе (ЦУТС) раз-
личного рода "избыточности" (элементной, структурной, временной и
т.п.)] следует понимать как "методы создания живучих систем из ненадёж-
ных элементов". В последнем словосочетании термин "ненадёжный" по-
нимается как не внушающий доверия по прочности (непрочный).
Вообще, термин "надёжность" в смысле "прочность" к сложным и
большим системам неприменим, так как для них не определено понятие
отказа. Действительно, в отличие от простых технических устройств, вы-
ходящих из строя при отказе любого из их элементов, сложные и большие
системы благодаря различного рода избыточности могут функциониро-
вать при отказе (выходе из строя) многих из элементов и даже подсистем.
Закрепление термина "живучесть" для характеристики способности
ЦУТС сохранять свои функции при воздействии противника представляет-
ся необоснованным, поскольку эта способность (это свойство) ЦУТС име-
ет единый смысл (см. выше), ее интенсивность зависит только от характера
воздействия и не зависит от того, кто (или что) воздействует на ЦУТС.
Из сказанного следует, что под "Теорией надёжности" следует понимать
"Теорию живучести", а собственно теорией надёжности является "Теория
физической надёжности" [101], которой до настоящего времени уделяется
явно недостаточное внимание.
Обобщая всё сказанное, отметим, что использованный выше термин
"эксплуатационно-техническая надёжность" есть синоним понятия "живу-
честь" (в указанном выше общем смысле), т.е. способность системы
(ЦУТС) сохранять свои функции при любых воздействиях на нее окру-
жающей среды (понимаемой в широком смысле, включая противника). Что
касается меры живучести как свойства системы (ЦУТС), то она может
быть только вероятностной и иметь смысл "степени доверия к системе
(ЦУТС)".
Наконец, о термине "устойчивость". По определению [159], устойчи-
вый - это 1) стоящий твердо, не колеблясь, не падая; 2) не поддающийся,
не подверженный колебаниям, стойкий, твёрдый.

96 Глава 2. Методологические основы теории эффективности
Очевидно, что применительно к задачам исследования операций и тео-
рии эффективности ЦНП имеет отношение лишь вторая трактовка этого
термина. Возникает вопрос: к какому объекту он относится? Приходится
встречать словосочетания "устойчивая система", "устойчивый процесс".
Понятно, что смысл этих словосочетаний различен и речь в них идет о
свойствах существенно различных объектов (системы и процесса) и, сле-
довательно, о различных свойствах. Поэтому представляется необходимым
уточнение этих понятий.
Применительно к системе (ЦУТС) понятие "устойчивость" - синоним
понятия "живучесть" (см. выше) и термин "устойчивость системы", ничего
не уточняя, лишь запутывает дело. Поэтому представляется целесообраз-
ным употреблять лишь термин "устойчивость ЦНПФС", понимая его как
способность ЦНПФС сохранять свои функциональные (целевые) свойства
в условиях воздействия различных факторов (окружающей среды, условий
проведения операции, противника). ▲
2.7.11} В соответствии с принятой в настоящее время терминологией
используемые на практике "показатели эффективности" (прямые и косвен-
ные) можно подразделить на два класса:
I класс - показатели результатов (эффектов) операции (показатели ре-
зультативности, действительности ЦНПФС);
II класс - показатели функциональной (целевой) надёжности (достовер-
ности) результатов операции (показатели эффективности
ЦНПФС).
Ранее было отмечено, что на этапе планирования и организации опера-
ций условия функционирования и применения ЦУТС содержат элемент
неопределённости (случайности) [см. (2.3.11), (2.3.12)]. Более того, все ко-
личественные характеристики ЦУТС и ЦНПФС (параметры и ЭТХ - ДА\),
фигурирующие в математической модели операции, в принципе также яв-
ляются случайными. Поэтому все показатели эффективности операций
должны носцть вероятностный характер [48, 190]. Так, показатели I класса
характеризуют средний или гарантируемый (с какой-то вероятностью) це-
левой эффект операции, а показатели II класса характеризуют вероятность
достижения требуемого результата (цели) операции, т.е. вероятность
выполнения задачи ЦУТС.
Из физической сущности этих характеристик следует, что показатели
I класса [см. (2.4.61) - (2.4.17')] слабо связаны (явно вообще не связаны) с
целью операции (с задачей ЦУТС) и поэтому являются косвенными пока-
зателями её эффективности. Показатели же II класса являются прямыми,
поскольку непосредственно отвечают на вопрос, в какой степени (вероят-
ностной мере) будет достигнута цель операции (будет выполнена задача
ЦУТС). Таким образом, при исследовании уникальных (единичных, не
массовых) операций для оценивания эффективности пригодны лишь пока-

2.7. Комментарии
97
затели их функциональной (целевой) надёжности. Использование для этой
цели показателей среднего, или средневзвешенного [(2.4.61) или (2.4.8')],
или гарантированного результата некорректно. Однако следует заметить,
что информативность, а следовательно, и объективность последнего пока-
зателя выше, поскольку его определение опирается на закон распределения
целевого эффекта операции. А
2.7.12} В литературе часто встречаются термины "целевая эффектив-
ность", "боевая эффективность", "функциональная эффективность",
"техническая эффективность" системы и т.п. Строго говоря, эффектив-
ность одна (это комплексное операционное свойство ЦНП) и эти термины
относятся к компонентам показателя качества результатов операции, т.е. к
ее эффектам. Так, "функциональная эффективность" характеризуется
прямым (целевым) эффектом, полученным при выполнении ЦУТС своих
прямых функций; "экономическая эффективность" - экономическим (т.е.
косвенным, побочным) эффектом, выражающимся в затратах, прибылях,
предотвращённых потерях и т.д.
Следует подчеркнуть, что эффективность как свойство операции одна, и
в этом смысле операция может быть либо эффективной (когда этого свой-
ства в ней достаточно), либо неэффективной. Причём в соответствии с
требованиями комплексного исследования эффективности её измерение и
оценивание должны проводиться с учётом всех существующих эффектов
операции (функциональных, технических, экономических, боевых и т.п.).
Так, "функциональная эффективность" характеризуется прямым (целевым)
эффектом операции, получаемым при выполнении ЦУТС своих прямых
функций; "экономическая эффективность" - экономическим (т.е. косвен-
ным, побочным по отношению к цели операции) эффектом, выражающим-
ся в затратах, прибылях, предотвращённых потерях (если это не цель опе-
рации) и т.п.
Следует ещё раз подчеркнуть, что понятия "прямой" и "косвенный" эф-
фекты относительны и применимы лишь в рамках конкретных операций.
Например, существуют операции, основной целью которых является полу-
чение "экономического эффекта" (прибыли), а "функциональный эффект"
(если это не чисто финансовая операция) либо учитывается косвенно, либо
не учитывается вообще. Как правило, именно так поступают при исследо-
вании "экономической эффективности". Поэтому за множеством "различ-
ных эффективностей" обычно скрывается некомплексный подход, при ко-
тором изолированно рассматриваются отдельные эффекты операции. При
этом, по-видимому, допускаются ситуации, когда операция эффективна
экономически, но неэффективна в целевом отношении. Понятно, что по-
добные допущения абсурдны, так как если цель операции не достигнута,
то она не удовлетворяет критерию пригодности и, следовательно, обсуж-
дение каких бы то ни было "других эффективностей" лишено смысла.
4 Зак. 3303

98 Глава 2. Методологические основы теории эффективности
Представляется, что отмеченное выше словоупотребление имеет прак-
тический смысл лишь при желании терминологически выделить ведущие
компоненты показателя К* качества результатов операции (см. п. 3.3.3). А
2.7.13} Поскольку функциональный (целевой) и экономический (побоч-
ный - расход ресурсов) эффекты находятся в противоречии (увеличение
одного из них влечёт за собой снижение другого), то одной из фундамен-
тальных проблем "Исследования операций" и "Теории эффективности" яв-
ляется проблема "эффективность-стоимость". Эта проблема возникла
в сфере "военно-экономического" и "технико-экономического" анализа до-
рогостоящих технических проектов и программ, т.е. крупных мероприя-
тий, связанных со значительными затратами на решение вопросов, обу-
славливающих принятие ответственных решений.
Подчеркнём, что при формулировании задачи исследования эффектив-
ности операции в замкнутой схеме, определяемой формулами (2.3.15) -
(2.3.18), проблема "эффективность - стоимость" решается автоматически1.
В дальнейшем это будет показано на примерах. ▲
2.7.14} Практика исследования эффективности ЦНПФС показывает, что
наиболее сложным его этапом является этап формулирования цели опера-
ции, от которого зависит правильность выводов и принимаемых решений.
Следует помнить, что критерии оценивания качества результатов операции
должны иметь свою иерархию, строго соответствующую иерархии ЦУТС,
реализующей эти операции. А
2.7.15} На рис. 2.7.1 приведена схема классификации основных факто-
ров, обусловливающих эффективность ЦНПФС (операции). Фигурирую-
щие на рис. 2.7.1. многоточия обозначают прочие свойства ЦУТС, ресур-
сов и условий проведения операции либо менее существенные, либо ещё
не выявленные. Стратегическая обстановка, отнесённая на рис. 2.7.1 к не-
управляемым условиям применения ЦУТС, в общем случае может быть
обусловлена как естественным развитием операции, так и действиями кон-
курента (противника).
Представляется необходимым раскрыть семантику фигурирующих на
рис. 2.7.1 и в выражениях (2.3.8), (2.3.9) понятий "условия функциониро-
вания ЦУТС" и "условия применения ЦУТС".
Когда мерой стоимости служит расход операционных ресурсов.

2.7. Комментарии
99
5
§
so
s
■Si
3"
s
s
H
m
н
о
о
«
U
H
К
&
Ю
О
о
о
и
ffl
i
g
О
i
о
о
I

100 Глава 2. Методологические основы теории эффективности
Условия функционирования ЦУТС (УФС) - это совокупность фак-
торов (как правило, природного происхождения), оказывающих влияние на
параметры и ЭТХ ЦУТС (Л'Лл), а также на характеристики ЦНПФС (Л**\)
и через них обусловливающие виртуальные результаты операции [см.
(2.3.8)].
Условия применения ЦУТС (УПС) - это совокупность факторов (как
правило, организационно-ситуационного происхождения), влияющих на
ситуацию, в которой ЦУТС придётся выполнять задачу, и тем самым обу-
славливающие допустимые (требуемые) результаты операции [см. (2.3.9) и
(2.3.5)]. А
Пример 2.7.1. Пусть операция - ЦНПФ ЦУТС, функционирующей как
в мирное, так и в военное время. Тогда если противник воздействия на
ЦУТС не оказывает, то условия её функционирования как в мирное, так и в
военное время будут одинаковыми. Однако представляется очевидным,
что требования к результатам ЦНПФС в военное время будут жёстче. Это
означает, что условия применения ЦУТС в мирное и в военное время су-
щественно различны. А
Пример 2.7.2. Пусть операция проводится в Антарктиде с применением
вездехода. Условия функционирования вездехода (низкие температуры и
бездорожье) требуют повышенного расхода топлива. Условия же приме-
нения вездехода (большая удалённость места проведения операции от ис-
точников топлива и сложность его доставки) требуют его повышенной
экономичности по расходу топлива. Оба эти обстоятельства должны учи-
тываться при проектировании и создании как вездехода, так и любых дру-
гих технических средств, предназначенных для работы в Антарктиде. А
Аналогичные примеры можно привести и применительно к другим от-
далённым районам со сложными условиями проведения операции, т.е.
условиями функционирования и применения технических средств.
Пример 2.7.3. Пусть операция - участие спортивной команды в сорев-
нованиях. Тогда, с одной стороны, такие факторы, как время проведения
соревнований (время года, время суток, поясное время места соревнова-
ний), климатические и погодные условия в месте соревнований и т.п. бу-
дут влиять на "условия функционирования команды", а следовательно, на
физическое состояние спортсменов, и тем самым будут предопределять
(обусловливать) их возможные (виртуальные) спортивные результаты. С
другой стороны, прибывший на соревнования контингент спортсменов-
противников будет обусловливать спортивные результаты команды, необ-
ходимые (потребные) для победы в соревнованиях. Последние факторы и
определяют "условия применения команды". А

2.7. Комментарии
101
2.7.16} В зависимости от задач исследования любой объект или явление
может рассматриваться применительно либо к его прошлому, либо к на-
стоящему, либо к будущему.
Следует уяснить, что в рамках ТЭЦНП речь идёт о будущей эффектив-
ности будущего ЦНПФС либо существующей, либо будущей ЦУТС. В
первом случае имеет место проблема организации ЦНПФС, во втором -
проблема проектирования ЦУТС. Если и ЦУТС, и организация (стратегия)
ЦНПФС определены (синтезированы), то возникает (имеет место) пробле-
ма управления ЦНПФС и ЦУТС (см. {1.4.2}). А
2.7.17} В данной главе были рассмотрены общая проблема и методоло-
гические основы исследования эффективности ЦНПФС (операций). Из ее
содержания видно, что целями таких исследований являются:
- оценивание эффективности ЦНПФС;
- анализ влияния на эффективность ЦНПФС его организации и пара-
метров и ЭТХ ЦУТС;
- синтез ЦУТС и ЦНПФС, обеспечивающих достижение цели опера-
ции.
Таким образом, исследование эффективности ЦНПФС представляет со-
бой двуединую квалиметрическую задачу его анализа и оптимального син-
теза. ▲

Раздел II
МЕТОДЫ
Так как во всяком учении о природе
имеется науки в собственном смысле
лишь столько, сколько имеется в ней ап-
риорного познания, то учение о природе
будет содержать науку в собственном
смысле лишь в той мере, в какой может
быть применена в нём математика.
И. Кант
Глава 3
МЕТОДЫ ОЦЕНИВАНИЯ ЭФФЕКТИВНОСТИ
ЦЕЛЕНАПРАВЛЕННЫХ ПРОЦЕССОВ
В гл. 2 были рассмотрены методологические аспекты теории эффек-
тивности ЦНП, а также содержание и общая формулировка задач исследо-
вания качества ЦУТС и эффективности ЦНПФС. Как было отмечено,
исследование эффективности ЦНПФС представляет собой двуединую
задачу её анализа и оптимального синтеза. При этом первым этапом
решения задачи анализа является этап оценивания эффективности,
который из-за огромного много- и разнообразия ЦУТС и реализуемых ими
ЦНПФС и обусловленного этим многообразия их моделей, требующих
индивидуального подхода, оказывается главным этапом анализа.
Цель данной главы - рассмотрение теоретических основ и методов оце-
нивания эффективности ЦНП, а также связанных с этим проблем.
3.1. МЕТОДЫ ТЕОРИИ СТОХАСТИЧЕСКОЙ ИНДИКАЦИИх
В данном параграфе излагаются элементы (основы, начала) "Теории
стохастической индикации" (ТСИ) - нового раздела "Теории вероятно-
стей", родившегося из задач научно-исследовательской практики и
имеющего ярко выраженную прикладную направленность. Концепции и
Более подробное изложение дано в монографии [128].

3.1. Методы теории стохастической индикации
103
методы ТСИ находят применение в самых различных областях систем-
ных научных исследований: "Анализе систем", "Прикладной киберне-
тике", "Исследовании операций", "Теории эффективности ЦНП", "Тео-
рии планирования испытаний", "Теории принятия решений", "Непара-
метрической статистике". Нет сомнения, что действительная сфера её
применимости приведенным перечнем не исчерпывается и, прежде всего
потому, что ТСИ является разделом "Теории вероятностей", без приме-
нения методов которой сейчас не мыслится ни одно серьёзное научное
исследование.
В последние годы получили широкое развитие и внедрение в научную
практику концепции "Теории нечетких понятий" (переменных, множеств,
отношений и т.п. [58, 81, 121, 122]). Однако следует отметить, что до на-
стоящего времени как методы этой теории, так и получаемые с их помо-
щью решения не имеют достаточно содержательной и наглядной интер-
претации, что, несомненно, снижает их практическую ценность. В то же
время в работе [121] раскрыта несомненная связь между "Теорией нечет-
ких множеств" и "Теорией случайных множеств", которая может быть
описана математически. А поскольку основной объект ТСИ - стохастиче-
ский индикатор представляет собой индикатор (характеристическую
функцию [28]) случайного множества, то (в других терминах) ТСИ также
представляет собой "Теорию случайных множеств", и притом в наиболее
конструктивном варианте1, так как ТСИ - теория вероятностная и, следо-
вательно, получаемые на её основе решения имеют чёткую частотную ин-
терпретацию (в отличие от "Теории нечётких множеств") и не вызывают
затруднений в их осмыслении и практическом использовании.
Как будет показано, ТСИ служит основой для разработки методов оце-
нивания эффективности операций и в первую очередь уникальных (еди-
ничных), для исследования которых известные вероятностные методы ма-
ло пригодны. В то же время, поскольку исследование эффективности ЦНП
является важнейшим этапом решения задач "Анализа систем", "Исследо-
вания операций", "Военно-прикладной кибернетики", то концепции и ме-
тоды ТСИ находят применение при решении задач проектирования ЦУТС,
планирования и организации ЦНПФС, а также задач принятия решений в
условиях неопределённости.
В настоящее время ТСИ представляет собой достаточно развитую тео-
рию, и освещение её в полном объеме вышло бы за рамки монографии.
Поэтому здесь излагаются лишь её элементы. Тем не менее семантическим
аспектам ТСИ, без уяснения которых нельзя усвоить её концепций, уделе-
но достаточно много внимания. Для глубокого изучения ТСИ рекомендуем
читателю пособие [128].
Советуем читателю путём вдумчивой проработки материала этого параграфа убе-
диться в этом.

104 Глава 3. Методы оценивания эффективности ЦНП
3.1.1. СЕМАНТИЧЕСКИЕ АСПЕКТЫ ТЕОРИИ СТОХАСТИЧЕСКОЙ
ИНДИКАЦИИ. ТЕРМИНОЛОГИЯ И СИМВОЛИКА
3.1.1.1. Общие предпосылки
Весьма плодотворным математическим понятием, широко используе-
мым в теории функций, функциональном анализе [79], теории меры [79],
теории вероятностей [183], алгебре логики и т.д., является понятие индика-
тора множества1, определяемого следующим образом.
Определение 3.1.1. Индикатором множества А называется функция
d Г 1, яге А;
1А=1А{х) = \ (3.1.1)
А
Каждому множеству соответствует его индикатор, и наоборот, каждая
функция, принимающая лишь одно из двух значений {ОД }, может интер-
претироваться как индикатор некоторого множества.
Если f(x) - произвольная функция, принимающая отличные от нуля
значения лишь на некотором множестве А значений аргумента х , то с по-
мощью индикатора множества А она может быть определена (задана)
линейным выражением вида
/ ч / \ [ f(x)f xe А;
[ 0, дгй А.
Пусть теперь С - пересечение, a D - объединение двух множеств А и В,
т.е. C=AnB, D=AkjB. Очевидно, что тогда
Ic = inf{lA,IB}=min{lA9IB}; (3.1.3)
ID=sup{lA,IB}=max{lA,IB}, (3.1.4)
т.е. значение индикатора 1с или ID множества С или D равно соответст-
венно наименьшему или наибольшему из значений индикаторов 1А и 1В.
Поэтому для обозначения наименьшего или наибольшего из значений двух
функций f(x) и g(jt) часто используются теоретико-множественные обо-
значения2 [183]:
inf{f{x),g{x)*£fng{x); (3.1.5)
sup{f{x),g(x)£fvg{x). (3.1.6)
1 Другое его название "характеристическая функция множества" в вероятностных
приложениях неудобно из-за возможности смешения с другим понятием.
2 Иногда для этих целей вместо символов Пии используются соответственно
символы л и V [74].

3.1. Методы теории стохастической индикации
105
В качестве примеров индикаторов — селекторов множеств могут слу-
жить широко используемые в прикладной математике кусочно-единичные
^селектирующие") функции [108, 169]:
-"селектор луча"
/ Л 0, jc<0;
А(х)=\ (3.1.7)
- "селектор интервала"1
П(х;а,Ь)=А(х-а)-А(х-Ь)=А{х-а)-А(Ь-х); (3.1.8)
- "селектор точки"
е(х;а)=А{х-а)-А(а-х). (3.1.9)
Нетрудно видеть, что
А{х) = 1А{х), А = [0,оо); (3.1.10)
П{х;а,Ь)=1с(х), C = AnB, A = [a,<*>)9 B = (-oo,b); (3.1.11)
е(х;а) = 1{а}(х), {а}=а , (3.1.12)
т.е. "селектор луча" ("единичная функция Хевисайда") - А (х) - суть инди-
катор полубесконечного интервала [0,°о); "селектор интервала" ("единич-
ный прямоугольный импульс") - П(х;а,Ь) - индикатор интервала [a,by,
"селектор точки" ("функция эквивалентности") - е(х;а) - индикатор од-
ноточечного множества {а }. Если, кроме того, воспользоваться обозначе-
нием (3.1.5), то
n(x;a,b) = fng{x), (3.1.13)
где f(x)=A(x-a); g(x) = A(a-x);
e{x;a)=f{x)ng{x), (3.1.14)
где f(x) = A(x-a); g(x)=A(a-x).
3.1.1.2. Понятие стохастического индикатора
Пусть теперь множество AczU является случайным событием (где
U - универсальное множество [74], множество логических возможностей
[74], пространство элементарных событий [183], достоверное событие
1 В вероятностных приложениях удобнее определения функций (3.1.7), (3.1.8), дан-
ные в списке обозначений, которые и используются в дальнейшем.

106 Глава 3. Методы оценивания эффективности ЦНП
[28, 29]). Тогда его индикатор 1А будет представлять собой случайную
величину со следующими свойствами1:
d Л d [ \ у если А произойдёт;
0, если А не произойдёт (произойдёт —А).
h=®A={ Л Л „л. / .... л (3-Ы5)
В отличие от индикаторов множеств индикаторы 6)А случайных собы-
тий называются стохастическими. Плотность распределения2 и функция
распределения стохастического индикатора й)А соответственно имеют сле-
дующие выражения:
<р»А{о)) = д-3{о))+р-3{а)-1); (3.1.16)
^>) = г4^)+/>-^-1)> (ЗЛ.17)
где р = р(А); q = l-Р = р(-тА).
Переход от случайных событий к их индикаторам - случайным величи-
нам весьма плодотворен, поскольку математический аппарат и методы ис-
следования вероятностных свойств случайных величин обладают большей
гибкостью и универсальностью.
Итак, из соотношения (3.1.15) с учетом (3.1.16), (3.1.17) следует
р(а)=Р = Р{Аа=1) = М[Аа]=1Ва. (3.1.18)
Раскроем семантику (смысловое содержание) равенства (3.1.18), для че-
го воспользуемся содержательной трактовкой понятия случайного собы-
тия, используемой в "элементарной" теории вероятностей. Под событием
понимается исход опыта, состоящего в реализации вполне определенного
комплекса N условий. Тогда случайное событие есть не что иное, как ис-
ход опыта, проходящего при воздействии на комплекс К не поддающихся
учёту случайных факторов, т.е. в условиях X некоторой неопределённо-
сти. Указанная неопределённость приводит к тому, что конкретное собы-
тие А происходит не при каждой реализации комплекса X, а лишь иногда
и, следовательно, связь между событием А и предопределяющим его ком-
плексом К условий носит стохастический (случайный) характер. Для ко-
личественного оценивания этой связи вводится понятие вероятности Р[А)
случайного события А, которая, таким образом, характеризует степень
объективной возможности появления события А в условиях N [28].
1 Для дальнейшего изложения обозначение (ЬА более удобно, чем IA.
2 Здесь и всюду в дальнейшем плотность распределения понимается в обобщённом
смысле [169].
3 Будем ог
уточнения увела бы нас в сторону от обсуждаемого вопроса
3 Будем опираться на интуитивное восприятие понятия "возможность". Попытка его

3.1. Методы теории стохастической индикации
107
В аналогичной связи находятся высказывание А и ситуация К, в кото-
рой это высказывание истинно [74]. Указанная аналогия фундаментальна.
Действительно, при решении конкретных прикладных задач описание любо-
го из исследуемых событий (исходов опыта) даётся в форме некоторого вы-
сказывания. Очевидно, что истинность такого высказывания адекватна дос-
товерности соответствующего ему события. При этом аналогом множества
элементарных событий, из которых состоит событие А, является множество
логических возможностей (при реализации которых высказывание А истин-
но), называемое множеством истинности1 высказывания А [74]. При такой
трактовке событий появляется возможность вести содержательное описание
методов теории вероятностей в терминах алгебры высказываний, которое
применительно к некоторым вероятностным задачам обладает большей на-
глядностью, чем описание на языке алгебры событий [28].
Если для множества истинности высказывания А определить индика-
тор 1А(л:), то принимаемые им значения будут равны значениям истинно-
сти высказывания А на множестве U всех логических возможностей, т.е.
, ч [1, хеА, AcU,
1А{х) = \ (3.1.19)
Продолжая проводить аналогии между алгебрами высказываний и со-
бытий, легко установить, что истинность и ложность высказывания А эк-
вивалентны соответственно достоверности и невозможности события А , а
неопределённость ситуации К, в которой высказывание А истинно, экви-
валентна неопределённости комплекса К условий, определяющих слу-
чайный эксперимент (опыт). Из всего сказанного следует, что каждая из
алгебр - высказываний и событий - является булевой и изоморфна алгебре
их индикаторов. Следовательно, эти алгебры изоморфны между собой, т.е.
с формальной точки зрения описания стохастической ситуации на языке
любой из них адекватны. Приведённые соображения лежат в основе веро-
ятностной логики [74].
Итак, что же такое вероятность случайного события? Из равенства
(3.1.18) следует, что, с одной стороны, - это вероятность того, что случай-
ное событие А произойдёт, т.е. станет достоверным, а с другой - это ве-
роятность того, что соответствующее высказывание А окажется истин-
ным''. В обоих случаях она равна вероятности P(cbA = l) того, что стохасти-
ческий индикатор &А примет значение 1, которое на языке алгебры собы-
тий есть вероятность достоверного события, а на языке алгебры высказыва-
Высказывание и множество его истинности будем обозначать одной и той же бук-
вой по аналогии с событием и множеством образующих его элементарных событий.
2 Для краткости обычно говорят просто "вероятность события" и "вероятность вы-
сказывания".

108 Глава 3. Методы оценивания эффективности ЦНП
ний есть значение истинности заведомо истинного высказывания. Тогда из
эквивалентности понятий "достоверность события" и "истинность высказы-
вания" следует эквивалентность понятий "вероятность случайного события"
и "степень достоверности случайного события", а также понятий "вероят-
ность высказывания" и "степень истинности высказывания". Но тогда при-
обретают вполне определённое (и, как будет показано, весьма глубокое) со-
держание высказывания: "достоверность (точнее, степень достоверности)
события U равна 1"; "достоверность невозможного события Нравна 0";
"достоверность случайного события А равна его вероятности р(л)", a
также высказывания: "истинность (точнее, степень истинности) истинного
высказывания U равна 1"; "истинность ложного высказывания V равна 0";
"истинность произвольного высказывания А равна его вероятности Р^)".
Таким образом, вероятность случайного события А - это степень объ-
ективной возможности точного воспроизведения комплекса К условий,
при которых событие А достоверно, или, другими словами, - это степень
объективной возможности ситуации К, в которой соответствующее собы-
тию А высказывание А истинно. Эта семантическая двойственность поня-
тия вероятности будет в дальнейшем использована при формулировке ос-
новных концепций теории стохастической индикации.
3.1.1.3. Количественные характеристики неопределённости
стохастической ситуации
При исследовании процессов функционирования сложных систем
(ЦУТС) принято различать три составляющие этих процессов [15]: детер-
минированную, случайную и неопределённую.
Детерминированными называются процессы, вызванные действием
полностью известных причин Х0. Эти процессы изучаются методами фи-
зики и других естественных наук.
Случайные процессы возникают при воздействии на известные причи-
ны Х0 не поддающихся учету случайных факторов К,, делающих причи-
ны К = Я0 и К j, обусловливающие основные свойства процесса, случай-
ными. Изучение случайных процессов основано на наблюдениях и анализе
их вероятностных свойств по проявлениям этих свойств в прошлом.
Неопределённая составляющая исследуемого процесса обусловлена не-
достаточностью или отсутствием наблюдений, необходимых для опреде-
ления её вероятностных свойств. Для их выявления используются эксперт-
ные оценки, в основе которых лежат понятия "полезность", "предпочти-
тельность" и "субъективная вероятность".

3.1. Методы теории стохастической индикации
109
3.1.1) Не вдаваясь в сколько-нибудь подробный сравнительный анализ
понятий "случайность" и "неопределённость", а также связанных с ними
понятий "объективная" и "субъективная" вероятности, отметим, что в
принципе различия между ними чисто условны. Действительно, с одной
стороны, при наблюдениях реальных процессов их случайность и неопре-
делённость проявляются одинаково - как невозможность точного предска-
зания их поведения; с другой стороны, "объективные" вероятностные ха-
рактеристики случайных процессов не могут быть полностью свободными
от "субъективных" взглядов их исследователей. В то же время задаваемые
экспертами "субъективные" вероятности в значительной мере являются
"объективными", поскольку основаны на опыте изучения экспертами ок-
ружающей их объективной реальности и не являются чисто умозритель-
ными. ▲
В дальнейшем используются оба термина "случайность" и "неопреде-
лённость", однако их не следует полностью отождествлять с понятиями,
упомянутыми в замечании.
Итак, как было установлено в п. 3.1.1.2, степень случайности1 выска-
зывания характеризуется его вероятностью Р\А)=р. Если высказыва-
ние^ окажется истинным, то его вероятность станет равной 1, а если оно
окажется ложным, то - 0. Поскольку априори неизвестно, истинным или
ложным окажется высказывание А, то, следовательно, неизвестно, какое
из значений (1 или 0) примет его вероятность, которая, таким образом, яв-
ляется случайной величиной, подчиненной закону распределения Бернул-
ли с параметром р. Именно так распределён стохастический индикатор &А
[см.(3.1.16), (3.1.17)] и, следовательно, он имеет смысл апостериорной ве-
роятности высказывания А в неопределённой ситуации X (условной ве-
роятности высказывания А относительно ситуации X). Таким образом, в
приведённой трактовке неопределённость ситуации X характеризуется на-
бором {0,l} возможных значений стохастического2 индикатора &Л, а
случайность высказывания А характеризуется его вероятностью р .
Приведённые выше рассуждения относительно ситуации К в значи-
тельной мере носят качественный характер, затрудняющий применение
математических методов исследования. Для получения возможности ко-
личественного анализа таких ситуаций необходима их формализация, т.е.
построение адекватных им математических моделей.
Пусть U - множество действительных чисел3 (действительная
прямая);
Точнее, степень достоверности или, что то же самое, - степень истинности.
2 В дальнейшем это слово часто будет опускаться.
3 В общем случае это может быть векторное пространство.

ПО Глава 3. Методы оценивания эффективности ЦНП
d
U1 = U х U - двумерное множество действительных чисел
(действительная плоскость);
а, Ъ - константы (возможно векторные);
у, z - переменные (возможно векторные);
<,>,<,> - отношения порядка.
Тогда: а<Ъ, а>Ъ, а<Ь, а>Ъ- высказывания;
z<a, z> a, z^b, z^b - одноместные предикаты1;
z<y, z>y, z^y, z^.y - двухместные предикаты.
3.1.2) Известно [194], что всякий двухместный предикат можно пред-
ставить как одноместный на множестве наборов (пар) (j;, z)eU2, однако,
как будет показано, при решении вероятностных задач такой переход мо-
жет привести к существенной потере информации. А
Проанализируем приведённые выше выражения трёх различных клас-
сов. Легко заметить, что константы а, Ъ фиксируют вполне определённую
ситуацию, в которой соответствующее высказывание (например, а < Ь) ли-
бо истинно (если а<Ь\ либо ложно (если а > Ь). Что касается переменных
у, z, то они определяют целые множества возможных их значений, фикса-
ция которых превращает соответствующий предикат (например, z < а) ли-
бо в истинное (если ze (-°° , а) ), либо в ложное (если ге [ а , «>) ) высказы-
вание.
Если заранее не известно, в какое из указанных множеств попадают пе-
ременные у, z или (у у z), то возникает неопределённая ситуация (случай-
ное явление), в которой можно говорить лишь о вероятности (или степени
истинности) высказывания, получаемого из соответствующего предиката.
Если переменная z является случайной величиной, то одноместный
предикат z < а будет представлять собой "неопределённое" высказывание
или, другими словами, случайное событие А. При этом, как нетрудно ви-
деть, неопределённость ситуации заложена в неопределённости перемен-
ной z, и для определения вероятности этого высказывания достаточно
знать закон распределения случайной величины z, т.е.
p = p(A)=P{z<a)= )dFi{z) = Fi{a). (3.1.20)
Пусть IA (z) = cbA - стохастический индикатор множества А=(-оо9 а).
Тогда из выражений (3.1.18), (3.1.20) следует, что Р{фА =l) = F-(a), и вы-
ражения (3.1.16), (3.1.17) примут вид:
1 В некоторых источниках [194] предикаты называются высказывательными фор-
мами.

3.1. Методы теории стохастической индикации
111
<р&л{а) = К.г{а)5{а>)+Р.{а)д{а>-\); (3.1.21)
F&A{co)=Ri{a)-A{(o)+Fi{a)-A{a>-\). (3.1.22)
Найдём числовые характеристики индикатора cbA, который в дальней-
шем будем называть константным. Начальный момент Л-го порядка рас-
пределения индикатора &А определяется соотношением
vk[<&A]=M[a>kA]=ri = )atdFtA(a>)=Ft(a), [* = l(l)...] (3.1.23)
и, следовательно,
M^=^ = F£(a); (3.1.24)
^=^ = ^-SUF^e)-Fl,(e)=Fl(a).JIl(a). (3.1.25)
Таким образом, как видно из равенства (3.1.24), вероятность случайного
события А равна математическому ожиданию его индикатора &А.
Известно, что дисперсия случайной величины характеризует степень
"рассеяния" возможных её значений относительно математического ожи-
дания ("среднего значения") этой величины. Поскольку возможными зна-
чениями стохастического индикатора служат возможные степени досто-
верности случайного события А, т.е. степени истинности неопределённого
высказывания z < а, являющиеся значениями его апостериорной вероятно-
сти, то в рассматриваемом случае дисперсия D& характеризует степень
неопределённости предиката (£ < а) ~ (d)A = l). При этом, как нетрудно по-
нять, максимальная неопределённость будет иметь место при а = Mei.
Пусть теперь z < у - двухместный предикат. Ситуация, в которой соот-
ветствующее этому предикату высказывание истинно, может быть неопре-
делённой как по одной (любой), так и по двум переменным. Рассмотрим
оба случая.
Допустим, что случайной является переменная £. Тогда будет иметь
место неопределённый предикат z< у, т.е. случайное событие А 9 завися-
щее от неслучайной переменной у. Поэтому
p = p(y) = p{Ay)=P(z<y)= ]dF.(z) = F.(y)=P[a>A{y) = l], (3.1.26)
где cbA(y) - стохастический индикатор множества А = (-°°,у).
Из выражения (3.1.26) видно, что в данном случае
cbA=d)A(y) = A(y-z) (рис.3.1.1), т.е. формально индикатор случайного
события Ау представляет собой случайную функцию, одномерные

112 Глава 3. Методы оценивания эффективности ЦНП
<оа{у)
i ».
О z У
Рис. 3.1.1.
законы распределения которой имеют следующие выражения:
<pK{m;y)=Ri{y)-d{o>)+Fi{y)-S{(o-\); (3.1.27)
F^ {a>;y)=R.(y)-A{co)+ F.{y)-A{co-l). (3.1.28)
Стохастический индикатор d>A(y) будем называть функциональным.
Его числовые характеристики определяются следующими равенствами:
м№Ау)]=Жу)= ]»^(»;jO=*iGO; (3-1.29)
—оо
M[&A{y)]=mA{y)=Fi{y); (3.1.30)
о[&М=Шу)=^а{у)-К{у)=Ф)ФУ (3.1.31)
Наконец, пусть переменная у также случайна. Тогда имеет место пре-
дикат z < у и, следовательно, случайное событие А~ ~(z< у), в свою оче-
редь, зависит от случайной величины у, т.е. предикат z < у становится
уже дважды неопределенным. Вновь поставим задачу: определить вероят-
ность случайного события А..
Если переменная z, определяющая ситуацию, связана с переменной у,
то для решения поставленной задачи необходимо знать закон совместного
распределения случайного вектора (уЛ)- Допустим, что известна плот-
ность распределения ^/а 2\0%z). Тогда решение может быть представлено
в одной из следующих форм:
p(A})=P{z<y)=P[{y,z)e (H)]= \\<p{hi){y,z)dydz, (3.1.32)
(И)
где {H)~{(y,z):z<y};
p(A.)=P{z<y)=P{u<0)=)<pu{u)du, где u = z-y, (3.1.33)
p(AP)=P{z<y)=p(S>o)=)<Pt{0)d#, (3.1.34)
0
где tf = j>-£.

3.1. Методы теории стохастической индикации
113
Выражения (3.1.32) - (3.1.34) реализуют различные способы перехода
от двухместного предиката z < у к одному из одноместных предикатов:
(y,z)e (#), или и < 0, или г?> 0. Однако, как будет видно из дальнейше-
го, при таком решении задачи теряется большое (точнее, большее) количе-
ство информации об исследуемом явлении. Поэтому в основу дальнейших
рассуждений положено соотношение, отличное от приведенных выше. Для
его получения преобразуем выражение (3.1.32):
(я)
z<y
\<Pz/Az;y)dz
= \Fvy{y;y)dF9{y) ;
dy =
(3.1.35)
(tf)
y>z
\<Pz/yiy;z)dy
= JRy/z(z;z)dF,(z).
dz =
(3.1.36)
Как видно из соотношений (3.1.35) и (3.1.36), в данном случае для опре-
деления искомой вероятности р = P(z < у) имеются уже два пути, кото-
рые приводят, естественно, к одним и тем же результатам, но обеспечива-
ют различную его надёжность (см. п. 3.4.3, 3.4.4).
Наиболее распространённым на практике является случай, когда слу-
чайные величины у и z взаимно независимы. Именно этот случай лежит в
основе наиболее содержательных приложений рассматриваемой здесь тео-
рии.
Итак, если у и z взаимно независимы, то соотношения (3.1.35) и
(3.1.36) соответственно примут вид:
P(i<y)=iFt(y)dF,{y);
/»(j>>f)=]*,(z)rfF,(z).
Введём следующие обозначения:
a>x=o)l(y)=Fi{y);
Л,=в»,(г)=Л,(г).
Тогда, как видно из (3.1.37) и (3.1.38),
P{z<y) = M[d>l]=mi ]
Р{у>г)=М[&г]=Ш2\
0)\ =СОг.
(3.1.37)
(3.1.38)
(3.1.39)
(3.1.40)
(3.1.41)

114 Глава 3. Методы оценивания эффективности ЦНП
Случайные величины &х и <Ь2 называются стохастическими супер-
индикаторами. Поскольку каждому двухместному дважды неопределён-
ному предикату соответствуют два супериндикатора, то для отличия их
друг от друга они снабжены индексами (номерами). Поэтому в дальней-
шем они также будут называться индексными.
Из соотношения (3.1.41) следует, что
Р{2<у) = Щ = )(DdF&x{a)) = CD2 = )codF&i(co), (3.1.42)
о о
где F&(co), F&i(co) - соответственно функции распределения суперинди-
каторов &х и <Ь2.
Проведём сравнение основных свойств стохастических индикаторов
трёх рассмотренных классов. Из выражений (3.1.21) и (3.1.27) видно, что
константный (<ЬА) и функциональный [tf^M] индикаторы, определяющие
соответственно апостериорные вероятности случайных событий А и А ,
могут принимать лишь одно из двух значений (0 или 1), тогда как супер-
индикаторы &х и d)2 могут принимать бесконечное множество значений
из интервала (ОД], т.е. апостериорные вероятности случайного события
А} являются случайными величинами более общего типа.
Из всего сказанного можно сделать вывод, что безусловная (априорная)
вероятность любого случайного события равна математическому ожида-
нию его условной (апостериорной) вероятности или, другими словами, это
его средневзвешенная достоверность. При этом, если достоверность собы-
тий А и А принимает лишь одно из двух значений: 0 или 1 с весами (ве-
роятностями) q, p соответственно, то достоверность события А* распре-
делена на интервале (ОД] с плотностью фЛ (со) или фй (со).
Далее, как следует из равенств (3.1.20) и (3.1.26),
ША=Р(АА=1); coA(y) = P[d>A(y) = ll
но
GJx±P(d>x=l) ; Ш2ФР(&2=1).
Это различие является следствием того, что в последнем случае не
только ситуация неопределённа (случайна), но и степень истинности соот-
ветствующего высказывания (степень достоверности события) случайна и
может принимать значения, отличные от 0 и 1.
Таким образом, супериндикаторы cbx и 6)2 совмещают в себе свойства
и функции со(у) случайного аргумента и случайной функции &(у) [см.
(3.1.39), (3.1.40)], т.е. представляют собой случайные функции случайных
аргументов. При неслучайных аргументах эти функции превращаются в
функциональные индикаторы d)A (у), &в (z), а при фиксации значений

3.1. Методы теории стохастической индикации
115
этих аргументов превращаются соответственно в константные индикато-
ры &А и &в, где А = {z :z < а }, В = {у:у > Ъ].
Физический смысл таких свойств стохастических индикаторов заклю-
чается в следующем. Если переменная £ случайна, то в предикате z<a
константа а определяет границу детерминированного множества
А = (-<*>, а), а в предикате £ < у переменная у определяет границу пере-
менного множества А = (- °°,у)9 при попадании в которое случайной ве-
личины £ индикаторы &А и &А {у) принимают значение 1 (т.е. достовер-
ности событий А = (z < а) и А = (z < у) равны 1). В предикате £ < у пе-
ременная у определяет границу "неопределённого" ("случайного") мно-
жества Ар = {-°°,у), при попадании в которое случайной величины £ ин-
дикаторы *й,, а>2 могут принять уже любые значения из интервала (0, 1].
Это объясняется тем, что в данном случае как "размеры", так и "располо-
жение" множества А- в пределах пространства U элементарных собы-
тий случайны и вероятность попадания £ в такое множество оказывается
также случайной.
Подведём некоторый итог сказанному. Итак, при вычислении вероятно-
стей случайных событий по формулам (3.1.20), (3.1.26), (3.1.32) - (3.1.34),
(3.1.37), (3.1.38), в сущности, вычисляются математические ожидания со-
ответствующих стохастических индикаторов. Однако известно, что любой
конечный набор числовых характеристик случайной величины менее ин-
формативен, чем закон её распределения, т.е. при использовании только
перечисленных выше формул теряется значительная часть информации,
которая может оказаться полезной в самых различных исследованиях.
3.1.3) Из сравнения формулы (3.1.32) с формулами (3.1.33) и (3.1.34)
следует, что в последних двух выражениях искомая вероятность
p = P(z<y) вычисляется путём перехода от распределения <P/pAy>z)
случайного вектора (y,z) к распределению <рй{и) или <р$(у) случайной ве-
личины и или v соответственно. При этом, как нетрудно видеть, физиче-
ские размерности величин й, v и компонент вектора (уЛ) совпадают.
Если теперь сравнить выражения (3.1.37) и (3.1.36) с (3.1.42), то здесь
также можно усмотреть переход от распределений F.(y), Ft(z) компо-
нент вектора (y,z) к распределениям FA {y)f F& (z) индексных суперин-
дикаторов. Однако в этом случае независимо от размерностей случайных
величин у и £ случайные величины &х и &2 безразмерны (как вероятно-
сти). Указанный переход называется трансформацией
распределений F^(y) и Ft(z) соответственно в распределения FA (у) и
F&{z). Причём по аналогии с другими интегральными преобразования-

116 Глава 3. Методы оценивания эффективности ЦНП
ми интегрируемые в выражениях (3.1.37) и (3.1.38) функции распреде-
ления ("ядра") называются трансформирующими, а интегрирующие
функции распределения - трансформируемыми, А
Пусть теперь в отличие от (3.1.39), (3.1.40) исходные переменные у и z
являются r-мерными векторами К* и Z.k соответственно. Тогда
А(Г>=«.У=^(Д)); (3-1.43)
4>=^(^))=^()(z(r)). (3.1.44)
Если положить (z(r) < Y^)=П(гу < yt),
то P(z{r)<f{r))= р^^<г)Ц^^=«('> = }вД^,(в); (3.1.45)
*&>>*«)= f'-J^^wKJ^^^^^H^^' (зл-46)
где
^ММ"пи<о
*<„ V"{.
*«>«)М
П(А<я)
/=1
dX{r)=dxxdx2-dxr9 (*,-= #,£,).
Число г называется рангом индексного стохастического супериндика-
тора.
Наконец, могут возникнуть задачи, требующие рассмотрения предика-
тов вида fy < d)j (где &й, &j - индексные супериндикаторы), вычисления
вероятности Р(а>. <&.) и анализа её стохастических свойств, аналогично-
го приведенному выше применительно к вероятности P(z < у). Для реше-
ния таких задач потребуется трансформировать распределения суперинди-
каторов d)n d)j, которые в этом случае будут называться индикаторами
первого порядка, в индикаторы d>\j , cbjfJ второго порядка и реализовать
следующие процедуры:
Р(щ «&,)= \F&i{a>)dF&i{a>)= \a>dFM=a>f;
0 0
/>(<&,. ><&,)= \R&/ {a>)dF&i (а) = \(0dF^ И=^.
(3.1.47)
Очевидно, что повторное применение описанного приема повышает по-
рядок исследуемых супериндикаторов.

3.1. Методы теории стохастической индикации
117
3.1.4) Для обозначения характеристик двух признаков классификации
стохастических супериндикаторов - их ранга и порядка - применяются
верхние индексы соответственно в угловых ( ) и квадратных [ ] скобках.
Понятно, что поскольку применительно к каждому супериндикатору мож-
но говорить как о ранге, так и о порядке, то в его обозначении должны
присутствовать оба индекса. Однако для разгрузки символики в контексте
это требование нарушено и индекс порядка супериндикатора всюду опу-
щен. Поскольку в рамках излагаемых здесь методов фигурируют лишь су-
периндикаторы первого порядка, то отмеченное упрощение символики
вполне оправданно. ▲
3.1.2. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СТОХАСТИЧЕСКИХ
СУПЕРИНДИКАТОРОВ
Из вышеизложенного следует, что для практического применения ма-
тематического аппарата стохастических супериндикаторов необходимо
знать законы их распределения. Для теоретического обоснования методов
определения этих законов в данном пункте приведён ряд теорем. Все дока-
зательства проводятся в предположении, что случайные величины у и z
взаимно независимые, скалярные и непрерывные. Ограничения эти не
принципиальны и имеют целью избежать громоздких выкладок и рассуж-
дений, неизбежных при рассмотрении общего случая (см. [128]). Кроме то-
го, для практических приложений наиболее интересен именно непрерыв-
ный случай.
3.1.2.1. Теоремы о функциях распределения супериндикаторов
Теорема 3.1.1. Если функции распределения F-(y) и F~(z) случайных
величин у и z известны, то
F&i{a>) = F.\F?{a>)}. (3.1.48)
Доказательство. Введём обозначения:
d
^t=Fiiy); 0) = io{y) = Ft[y); y = y{(o) = F:l{(D).
Тогда, поскольку функция Ft (z) неубывающая, то
F^ {a>)=P{a>, <а>)= P{F.(y)< F^(«)]}= P\y<y{a>)]=

118 Глава 3. Методы оценивания эффективности ЦНП
Теорема 3.1.2. Если дополнительные функции распределения R~y(y) и
Л|(г) случайных величин у и z известны, то
^И=Л.[л:,И]. (3.1.49)
Доказательство. Введём обозначения:
d>2=Ry(z); eo = a)(y)=Ry{z); z = z{o)) = R:l{a)).
Тогда, поскольку функция Ry(y) невозрастающая, то
^И=Р(»2<й;)=р{л.(г)<лЛгИ]}=Р[£>гИ]=
= Л|[гИ]=/гг[л:,И], ое(0,1]. ▲
3.1.5) Супериндикаторы cbx и 6)г называются ещё индикаторами рас-
пределений Fy(y) и R2(z) соответственно (см. (3.1.6), (3.1.9)). ▲
Из доказанных теорем вытекает очень важное для практики следствие -
теорема 3.1.3.
Теорема 3.1.3. Если случайные величины у и z распределены одина-
ково, то все индексные супериндикаторы распределены равномерно на ин-
тервале (0,1], т.е.
Рр{х)^Р2(х)^Р£{х) ^ F&i{cd) = Fk(g)) =
= О)Л(а);0,1)+А(а)-1), [/ = 1,2] . (3.1.50)
Доказательство. Выведем это утверждение как следствие из тео-
ремы 3.1.1. Пусть у- f(x) и х = f~l(y) - взаимно обратные функции.
Тогда, как известно, /|/"1Ск)]= у- Поэтому при Fy(x) = Ft(x) = F.(x) из
соотношения (3.1.48) следует
FAH = FjFj-V)]=a>, а>б(0,1].
При со < 0 или со > 1 функция F& (со) доопределяется естественным
образом:
, v [0, при (О<0;
*Л } \\,при со>\.
А
3.1.6) Супериндикатор со0 называется собственным индикатором
распределения F~(x) [R-(x)]. A
3.1.7) Теорема 3.1.3 лежит в основе алгоритмов статистического моде-
лирования случайных величин с заданным законом распределения "мето-
дом обратной функции" [64, 163,173]. А

3.1. Методы теории стохастической индикации
119
Пример 3.1.1. На рис. 3.1.2 приведены графики функций распределения
F&{fo); Fuj{a>) и FA(co) супериндикаторов щ\ а>2 и сой соответственно,
построенные для случая, когда случайные величины у и г подчинены
нормальным законам распределения с параметрами: у = 2, <7-=1, г = 1,
о, = 2, т.е.
F,{y)=F,b;y,<r,)=Fa
fy-y)
\ °'У J
= F„
F.W-F^W,)^/'"^
у °i j
= F„
У-2
1
г-1
При этом
Fui{a) = Fp[Fri{(o)]=FcrlAF;l(a))+B]n(6),%l)+A(6)-i);
Р^со) = кХщ1{(о)]=1-РМ~х{Р;\\-о})-в)}п{т^,\)+Л{о)-\),
где А = ^-; В = ^^-.
а- о-
У У
Следует подчеркнуть, что график функции распределения F& {со) имеет
вид рис. 3.1.2,6 как при х = у, <Ji=o,}, так и при x = z, ak=av A
Рис. 3.1.2.
3.1.8) При построении функций распределения супериндикаторов весь-
ма эффективен графический метод, в основе которого лежат теоремы
3.1.1-3.1.3. Ключ к реализации этого метода дан на рис. 3.1.3. А
При доказательстве следующих теорем будет использована лемма 3.1.1.

120 Глава 3. Методы оценивания эффективности ЦНП
z 0 со 1 со
Рис. 3.1.3.
Лемма 3.1.1. Если для каждой из функций /,, /2, ...,fk соответствен-
но существуют обратные функции J\x, /2"!,..., f^, то
у=fi(A(4fА*))-)) => *=/Г,(/й(-(/Г,Ы)-)). (3-1.51)
Доказательство. По определению
* = /(*) => лг = Г'Ы. (3.1.52)
Последовательно применяя соотношение (3.1.52), будем иметь:
*=/.(/*(...(/;(*))•••)) => /,to(.~(/*(*)).~))=/,'Ы =>
/stoUUMMbyr'Or'M) => - =>
/*W=/;-,,fc(-U-,U-,W))...)) => «-/r'taU/r'W)-)). а
Теперь докажем теорему, устанавливающую характер связи законов
распределения индексных супериндикаторов &х, й2.

3.1. Методы теории стохастической индикации
121
(3.1.53)
(3.1.54)
Теорема 3.1.4. Функции распределения индексных супериндикаторов
&х, &г связаны следующими соотношениями:
F&i{(o)=\-F^{\-a>), e»e(0,l];l
F,»=l-F,-;(l-<»), a>e(0,l].J
Доказательство. Согласно лемме 3.1.1
^,M=^h",M]=7 => ^f-^^f.If;1^)];
^|И = Л|[й>-*И]=»7 => <o = F£(7j) = R}[r:1(ti)].
Поскольку, кроме того,
17 = ^Л(дс) = 1-ЛЛ(де) => x = F?{fi)=R?(l-fi),
то с учётом соотношений (3.1.54) получим:
^,H=^h",H]=i-^k,(i-«)]=i-^I,(i-«)>
FAiH=^[«;,(e»)]=i-F£[F;,(i-»)]=i-F;i,(i-e»). A
Подобными соотношениями связаны и дополнительные функции рас-
пределения индексных супериндикаторов. Все они сведены в табл. 3.1.1.
Таблица 3.1.1
*■*»
*■*»
л*, И
л*, И
**»
^»
1-^-'(1-й>)
1-^,И
<(!-«)
*■*»
l-Fj(l-a>)
*"*»
КМ-а»)
i-f,»
^,и
1-<И
1-<И
^,и
**»
**»
1-<И
i-*d»
<и
*«>)
Приведём без доказательства (которое можно найти в [128]) важную
теорему о функции распределения супериндикатора r-го ранга.
Теорема 3.1.5. Если компоненты случайного вектора
X, v =(jc,,jc2,...,jcr) взаимно независимы, то супериндикатор r-го ранга
щ$ = F£ \X/r\) имеет функцию распределения вида
^^^М^ЕИГ"' ^^-П{ео;ИЛ)+Л{со-\), (3.1.55)
[/ = 1,2].

122 Глава 3. Методы оценивания эффективности ЦНП
На рис. 3.1.4 приведён график функции F.{r)(a)) распределения собст-
венного индикатора Щ' произвольного факторизованного1 г-мерного
распределения F% [Х,\) при г = 2.
FA®)
Рис. 3.1.4
3.1.9) Как можно было заметить, приведённые выше теоремы в основ-
ном касались функций распределения супериндикаторов 1-го ранга. Ис-
ключение составила лишь теорема 3.1.5, посвященная частному случаю,
когда компоненты случайного вектора Х.к взаимно независимы и при
этом трансформируемое и трансформирующее распределения одинаковы,
и, следовательно, &^ = Щ' = F% \Х,\
Что касается общего случая:
<аи=р.
(U
где Fj [Xtry)*F£ (^/r\)> то Для него получить выражения, аналогичные
выражениям (3.1.48) - (3.1.55), не удаётся.
Соотношения того же назначения получены в монографии [128], но из-
за сложности и малой наглядности здесь они не приводятся. Тем не менее
имеется возможность получить наглядное выражение для функции распре-
деления супериндикатора r-го ранга путём обобщения соотношений
(3.1.48), (3.1.49), основанного на геометрической интерпретации стохасти-
ческой ситуации, порождающей понятие супериндикатора.
Факторизованным называется распределение системы взаимно независимых слу-
чайных величин.

3.1. Методы теории стохастической индикации
123
Действительно, поскольку по определению щ' = F% (*м)>то
^,>)=р(<&<'> < а>)= />Ц Д>)< a>)= P(f{r) e {z{r)}J=
=j!:!KA>b (3l56)
где i^(r\) ~ область значений вектора Z,y граница которой
ZfrAa)) = F~£ (со) определяется решением уравнения F% \z,A=a).
Геометрической интерпретацией соотношения (3.1.56) при г = 1 может
служить рис. 3.1.5, а при г = 2 - рис.3.1.6. А
p(Sl) <(о)
Рис. 3.1.5
3.1.2.2. Теоремы о плотностях распределения супериндикаторов
Теорема 3.1.6. Если функция распределения F-(z) и плотности распре-
деления <pt(z) и <р${у) случайных величин z и у известны, то
*«-2Ш-м.
(3.1.57)
Доказательство. Утверждение теоремы 3.1.6 следует из выражения
(3.1.48) с учетом того, что фА (со) = F^ (cd) . A
Теорема 3.1.7. Если дополнительная функция распределения R^(y) и
плотности распределения <pt(z) и <Р}(у) случайных величин z и у извест-
ны, то

124 Глава 3. Методы оценивания эффективности ЦНП
*^-10т' -м-
(3.1.58)
LFtJ*l>b)
FzJ^,Z2)=0)
(K)i,nk)})
Доказательство. Утверждение теоремы 3.1.7 следует из выражения
(3.1.49) с учетом того, что фй (со) = F'& (со). А
Теорема 3.1.8. Если случайные величины у и z распределены одина-
ково, то все индексные супериндикаторы распределены равномерно на ин-
тервале (ОД], т.е.
Фр(х)=ф2(х) => ^|И = ^.И=/7(т;вД), [/ = 1,2]. (3.1.59)
Доказательство. Выведем это утверждение как следствие из тео-
ремы 3.1.6. Поскольку ф${х) = ф£(х\ то из выражения (3.1.57) следует, что
ФЛ1(й>) = 1, юе(0Д].
Вне интервала (0,1] плотность фй (со) доопределяется так:

3.1. Методы теории стохастической индикации
125
^,И =
О, при со<0;
О, при со>\.
3.1.10) Выражение (3.1.59) может быть получено и путём дифференци-
рования выражения (3.1.50). А
Пример 3.1.2. На рис. 3.1.7 приведены графики плотностей распределе-
ния фй (со), ф& (со) и фл (со) супериндикаторов сох, 6ог и со0 соответст-
венно, построенные в условиях примера 3.1.1. А
4
3
2
1
—-и
'^И.^И
ч><№)
*чН 1
>^
9л,
И .
►
МоА
со
Рис. 3.1.7.
Плотности распределения супериндикаторов $,, со2 связаны соотно-
шениями, приведёнными в табл. 3.1.2, получающейся из табл. 3.1.1 путём
дифференцирования её элементов.
Таблица 3.1.2
9*№)
я»,И
9л№)
Я»,М
^,н
к (1-*)]-
9*№)
к (*-*>)]"'
я»,М

126 Глава 3. Методы оценивания эффективности ЦНП
Теорема 3.1.9. Если компоненты случайного вектора
Х.х =(jc,,jc2,...,jcr) взаимно независимы, то супериндикатор r-го ранга
Щь =F% \Х,А имеет плотность распределения вида
In
Доказательство. Вьфажение (3.1.60) получается путём дифферен-
цирования выражения (3.1.55). ▲
На рис. 3.1.8 приведён гра-
фик плотности распределения
<р&(г)(со) собственного индика-
тора щ' произвольного фак-
торизованного r-мерного рас-
пределения (рк \Х(Г}).
Рис. 3.1.8.
3.1.11) Супериндикаторы r-го ранга щ$=Fk \Х,А и Щ^=ЯЛ №г\)
называются собственными индикаторами распределений F% \Х/Г\) и
Rk ytir\) соответственно. При этом, как видно из соотношений (3.1.55) и
(3.1.60), если компоненты случайного вектора Х.к взаимно независимы, то
оба собственных индикатора щ? и т£ подчинены одному и тому же ло-
гарифмическому закону распределения r-го порядка. В общем случае рас-
пределения случайных величин щ$ и щ{ различны. Исключение состав-
ляют собственные индикаторы одномерных распределений. Независимо от
характера исходных распределений F~(x) и Я£(х) их собственные инди-
каторы супериндикаторы 1-го ранга cbl0 = Ff(jc) и &20 = Я.(х) имеют оди-
наковые равномерные распределения на интервале (0, 1] [см. (3.1.50) и
(3.1.59)]. А

3.1. Методы теории стохастической индикации
127
3.1.2.3. Обратные теоремы
В приложениях ТСИ при решении задач синтеза ЦУТС и ЦНПФС нахо-
дят применение (см. п. 4.2) и теоремы, обратные к доказанным выше. При-
ведём основные из них [128].
Теорема 3.1.10. Если известны функции распределения F^ (со) и Ft (z)
супериндикатора &А и случайной величины z соответственно, то
РМ = Ъ,[Ф)1 (3-1.61)
Доказательство. Введём обозначения:
&x=F.(y); a> = a>(y)=F.{y). (3.1.62)
С учётом (3.1.61) из соотношения (3.1.48) следует
Согласно определению обратной функции
Ft-%[FM=y => F,{y) = F^[Ft{y)]- A
Теорема 3.1.11. Если известны функции распределений F&((o) и
Rf{y) супериндикатора &2 и случайной величины у соответственно, то
*t(z) = Ft\R,{z)\. (3.1.63)
Доказательство. Введём обозначения:
a>2 = RP(z); o) = a){z) = R^{z). (3.1.64)
С учётом (3.1.64) из соотношения (3.1.49) следует
*■*, М= ^>(г)] = F^ [й,(г)]= К,{Щ%{г)]}.
Согласно определению обратной функции
Из доказанных теорем вытекает важное следствие - теорема 3.1.12.
Теорема 3.1.12. Если функции распределений F&(cci) и F.(z) или
R${y) соответственно супериндикатора щ и случайных величин £ или у
известны и при этом
F&i{a)) = F&t{a))=coI7{a);0,i)+A{eo-l), [/ = 1,2], (3.1.65)
т.е. супериндикатор щ, [ * = 1, 2] распределён равномерно на интервале
(0,1], то
F,(y)*Ft(z) (3.1.66)

128 Глава 3. Методы оценивания эффективности ЦНП
или Д£(г) = дДг) (3.1.67)
Доказательство. Поскольку согласно (3.1.65)
F&i{o)) = a), <В€(0Д], [/ = 1,2],
то из соотношения (3.1.61) следует (3.1.66), а из (3.1.63) следует (3.1.67). ▲
3.1.3. КВАНТИЛИ РАСПРЕДЕЛЕНИЙ СТОХАСТИЧЕСКИХ
СУПЕРИНДИКАТОРОВ
Как будет видно из дальнейшего, теоремы п. 3.1.2 служат для обоснова-
ния методов решения так называемой прямой задачи оценивания вероят-
ностей изучаемых случайных событий. Не менее важной для практики яв-
ляется обратная задача оценивания, т.е. задача определения толерантных
границ для этих вероятностей, характеризующих точность и надёжность
их оценок. Основой методов решения обратной задачи является совокуп-
ность теорем о квантилях распределений супериндикаторов.
Теорема 3.1.13. Если функции распределений F~(y) и F~(z) случайных
величин у и z известны, то 100/7-процентный квантиль cox{rj) распреде-
ления F& (со) супериндикатора 6)х имеет следующее выражение:
Щ{П)=Ф?(П)]> 176 [0,1]. (3.1.68)
Доказательство. По определению
щ(п)=Р£{п)- (3.1.69)
Согласно лемме 3.1.1
Fti(a) = F,[Ffl{to)] => Fffyj) = Ft\F?(Tl)]. (3-1.70)
Из выражений (3.1.69) и (3.1.70) следует (3.1.68). А
Теорема 3.1.14. Если дополнительные функции распределений Rp(y)
hjR£(z) случайных величин у и £ известны, то 100 ^-процентный квантиль
0)2(tj) распределения F& (со) супериндикатора а>2 имеет следующее выра-
жение:
^(//ЬдДдг'У, 17е[0,1]. (3.1.71)
Доказательство. По определению
^г(п)=Р^(п). (3.1.72)

3.1. Методы теории стохастической индикации
129
Согласно лемме 3.1.1
^»=Яг[д:'И] => F^Tj^R^irj)]. (3.1.73)
Из соотношений (3.1.72) и (3.1.73) следует (3.1.71). ▲
Пример 3.1.3. На рис. 3.1.9 обозначены квантили сох{г]) и ct)2(rj) одина-
кового уровня 7] для распределений F& (со) и FA (а>) соответственно, по-
строечные в условиях примера 3.1.1. ▲
Рис. 3.1.9
Поскольку функции распределения F2(z) и R^z) произвольной слу-
чайной величины z связаны соотношениями:
F^l-R^z); (3.1.74)
Frl{n)=R:l(l-n), (3-1.75)
то в каждом из равенств (3.1.68) и (3.1.71) трансформируемые законы рас-
пределения могут быть заменены на дополнительные. В результате будет
получена система соотношений, приведенных в табл. 3.1.3, где выражения
для квантилей (ofa) [i = 1, 2] находятся в столбцах порождающих их зако-
нов распределения.
3.1.12) При построении квантилей распределений супериндикаторов
весьма эффективен графический метод, в основе которого лежат теоремы
3.1.13 и 3.1.14. Ключ к реализации этого метода дан на рис. 3.1.10. А
5 Зак. 3303

130 Глава 3. Методы оценивания эффективности ЦНП
щ(п)
a>Av)
юМ
щ{л)
Таблица 3.1.3.
>* 1
Z
Ft{z)
F^irj)]
l-F^il-rj)]
Fy(y)
рА&Ь-ч)]
^[^(1-7)]
*>Ы
Л,(«)
1-ф?{г1)]
i-^к'У
F,{y)
1-^[^'(1-17)]|
Ф?(ч)]
*>00
У
Рис. 3.1.10

3.1. Методы теории стохастической индикации
131
Поскольку индексные стохастические индикаторы (супериндикаторы
[128]) образуют систему зависимых случайных величин, законы распреде-
ления которых связаны равенствами, доказанными выше, то квантили этих
распределений также связаны соотношениями, являющимися следствиями
из указанных равенств. Выведение этих следствий основывается на рас-
смотренных ваше свойствах индексных супериндикаторов и законов их
распределений. Здесь оно не проводится, но результаты вывода, представ-
ленные в табл. 3.1.4, будут использованы в дальнейшем.
Таблица 3.1.4.
&&)
а>М
ЮгЬ)
fM
FJ{V)
l-FJl-77)
fM
l-F&i{\-tl)
f;xM
R^ifi>)
*£(i-n)
**(i-v)
ДЙ,И
^(l-»7)
<(1-^)
Поскольку квантили распределения супериндикатора представляют со-
бой функциональные преобразования исходных распределений F-(z) и
Fy(y) tCM- (3.1.68) и (3.1.71)], то для каждой из посвященных им теорем
существует обратная. Приведём их.
Теорема 3.1.15. Если известны функции распределений F& (а)) и Ft(z)
случайных величин &х и ъ соответственно, то 100/7 -процентный квантиль
yv распределения F- (у) определяется следующим выражением:
уч =F:,{rJ)=F.-1[F£(t])\ , qe[0, l] . (3.1.76)
Доказательство. На основании леммы 3.1.1 из (3.1.61) следует
(3.1.76), т. е.
Р>(у)=РА[Ш]=> yn=F^{TjhFt-iF^(rj)\. ▲
Теорема 3.1.16. Если известны функции распределений F& (со) и Rp{y)
случайных величин &2 и у соответственно, то 100^-процентный кван-
тиль zn распределения F-(z) определяется следующим выражением:
z,=Fr4r,)=R:*[F£{l-Tj)l (3.1.77)
Доказательство. Поскольку F-"1 (rj) = Rf (l-tj) , то согласно лемме
3.1.1 из (3.1.63) следует (3.1.77), т. е.
RtizhF^RM^z^il-nhRAF^l-Tjt A

132 Глава 3. Методы оценивания эффективности ЦНП
3.1.4. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ
СТОХАСТИЧЕСКИХ СУПЕРИНДИКАТОРОВ
В предыдущих пунктах были изучены свойства законов распределения
супериндикаторов, которые исчерпывающим образом характеризуют их
вероятностные свойства. Однако, как известно, многие практические зада-
чи могут быть решены на базе числовых характеристик случайных вели-
чин, которые по назначению делятся на два класса:
- характеристики положения - математическое ожидание, мода, ме-
диана, квантили распределения и т.п.;
- характеристики рассеяния - дисперсия, среднее квадратическое от-
клонение, размах распределения, интерквантильные разности и т.п.
В силу особой практической важности квантилей распределения сто-
хастических супериндикаторов они были рассмотрены в отдельном пунк-
те. Здесь будут рассмотрены методы определения некоторых из названных
числовых характеристик супериндикаторов.
3.1.4.1. Математические ожидания
Универсальными выражениями для определения математических ожи-
даний супериндикаторов являются интегралы вида (3.1.37), (3.1.38) и
(3.1.45), (3.1.46), т.е. для супериндикаторов 1-го ранга
Щ^М^ \Ftiy)iF9{y);
4=M&i = ~\Rp{z)dF.{z);
для супериндикаторов r-го ранга
-»
При этом имеют место следующие соотношения (см. п. 3.1.1)
Ш1=Ш2;
*><'>=*><'>.
(3.1.78)
(3.1.79)
(3.1.80)
(3.1.81)
Таким образом, если известны трансформируемые законы распределе-
ния F.(y), F£(z) или Ff (У(г\)> F£ \Z,r\), то математические ожидания ин-
дексных индикаторов могут быть определены соответственно по форму-
лам (3.1.78) или (3.1.79). Если же известны законы распределения F {1)(а>),

3.1. Методы теории стохастической индикации
133
[/ = 1,2 ; r = l(l)...] самих супериндикаторов, то задача решается по об-
щим формулам, т.е. для супериндикаторов любого ранга
l$ = M4,=M[dP]=)(UdF4M* [/ = l,2;r = l(l)...] (3.1.82)
О
(см. рис. 3.1.9, где Й7, и Ш2 численно равны заштрихованным площадям).
Из сравнения выражений (3.1.78), (3.1.79) и (3.1.82) видно, что послед-
нее значительно проще, однако для его реализации необходимо знать за-
кон распределения F&{r)(o)) супериндикатора щ\ что, в свою очередь,
требует выполнения подчас достаточно сложных и громоздких математи-
ческих выкладок (см. п. 3.1.2). Поэтому могут оказаться полезными оце-
ночные соотношения, которые дают представление о порядке исследуемых
величин. Приведём некоторые из них.
Известно (неравенство Чебышева), что если случайная величина f не-
отрицательная и имеет конечное математическое ожидание f < ©о 9 то при
любом т0 > О имеет место неравенство
P{f>T0)<—. (3.1.83)
Поскольку супериндикаторы щ неотрицательны и всегда 2JJ < ©о, то со-
гласно (3.1.83)
Э;.>л0Яа,к), [/ = 1,2]. (3.1.84)
Из неравенства (3.1.84), в частности, следует:
Л4(0.25)<4Щ.; 1
Я^{0.50)<2Щ ; L (3.1.85)
Д^(0.75)<1.33й5>. .J
Вообще неравенства (3.1.85) являются достаточно грубыми, однако с их
помощью можно, зная лишь среднее значение c5t супериндикатора &п
оценить порядок значений функции его распределения в точках, интере-
сующих исследователя в первую очередь.
Начиная с этого абзаца, будем предполагать, что случайные величины z
и у являются ограниченными, т.е. существуют такие числа а , b и с , d,
что
P(a<£<*) = P(c<j><</) = l, (3.1.86)
и при этом \а\ , \Ь\ , |с| , |rf|<°o. Поскольку на практике встречаются только
такие случаи, то сделанное допущение не сужает сферы приложений при-
водимых ниже результатов. Приведём без доказательств (за которыми ад-
ресуем читателя к монографии [128]) ряд теорем о математических ожида-
ниях стохастических супериндикаторов. Итак, пусть условия (3.1.86) вы-
полняются. Тогда имеют место следующие теоремы.

134 Глава 3. Методы оценивания эффективности ЦНП
Теорема 3.1.17. Если случайные величины z и у имеют произвольные,
но симметричные распределения F-(z) и F~(y) и при этом z = у, то
2^=2^=0.5. (3.1.87)
А
Следствие 3.1.1. Если распределения F£(z) и F^(y) симметричны, то
(z<y) => {щ > 0.5)п(ш2> 0.5) ;
(z>y) => (щ < 0.5)п (й72 < 0.5).
А
3.1.13) Если распределения F£(z) и F-(y) одинаковы, то независимо от
их симметричности
^,=^=0,5. (3.1.89)
Равенство (3.1.89) является следствием теорем 3.1.3 и 3.1.8 и дополни-
тельных обоснований не требует. А
Теорема 3.1.18. Если функция распределения F£(z) случайной величи-
ны £ в пределах области [c,d] возможных значений (носителя распреде-
ления) случайной величины у выпукла и при этом [c,rf]c \a9b\, то
S,>F-(j;). (3.1.90)
А
Теорема 3.1.19. Если функция распределения F~(z) случайной вели-
чины z в пределах области [c,d] возможных значений (носителя распре-
деления) случайной величины у вогнута и при этом [c,rf]c [a,b], то
m^F-iy). (3.1.91)
А
Теорема 3.1.20. Если дополнительная функция распределения Rp(y)
случайной величины у в пределах области [а, Ь\ возможных значений (но-
сителя распределения) случайной величины z выпукла и при этом
[a, b]c[c,d], то
m2>R9(z). (3.1.92)
▲
Теорема 3.1.21. Если дополнительная функция распределения И${у)
случайной величины у в пределах области [a,b] возможных значений (но-
сителя распределения) случайной величины ъ вогнута и при этом
[a,b]c[c,d], то
Щ<Щ{1). (3.1.93)
▲
(3.1.88)

3.1. Методы теории стохастической индикации
135
Следствие 3.1.2. Пусть [а,й]= [c,d]. Тогда:
1) если F£(z) - выпукла, a R^{y) - вогнута, то
F^y)<Wx=W2<R-{z);
2) если F-(z) - вогнута, a R^{y) - выпукла, то
(3.1.94)
(3.1.95)
А
3.1.14) Если трансформирующая функция распределения строго (в пре-
делах всего носителя распределения) выпукла или вогнута, то все доказан-
ные (приведённые) неравенства становятся строгими. А
3.1.15) Если трансформирующая функция распределения в пределах но-
сителя трансформируемого распределения линейна, то все доказанные
(приведённые) соотношения превращаются в равенства. А
3.1.16) Если трансформируемое распределение вырождено1, то все до-
казанные соотношения превращаются в равенства. А
3.1.4.2. Дисперсии
Универсальные выражения для определения дисперсий супериндикато-
ров имеют вид:
(3.1.96)
м[Й")!] = И'- v =|:!]Ц,](уи)-й,«]Ц.,W; ]
I— -J — оо —ее J
где щ' [/ = 1,2; г = l(l)...] вычислены по формулам (3.1.79).
При г=1 соотношения (3.1.96) упрощаются:
~%=В&1 = )Щу)-щ]гйР.(у);
$=2^ = ][яДг)-й>2]2^£(г),
где Щ [/ = 1,2] вычислены по формулам (3.1.78).
Если же известны законы распределения F {г) (со), [/ = 1,2 ; г = 1 (l)..J,
(О,
самих супериндикаторов щ', то задача решается по общим формулам, т.е.
для супериндикаторов любого ранга
(3.1.97)
Вырожденным называется "распределение" неслучайной величины.

136 Глава 3. Методы оценивания эффективности ЦНП
(uf)2 = D^ = 2>[<8fr>]= ){a>-af) V,,>{со), [i = 1,2 ; г = l(l)..J, (3.1.98)
О
где щ' [/ = 1,2; r = l(l)...] вычислены по формулам (3.1.81).
Приведём ряд оценочных соотношений для дисперсий супериндикато-
ров, которые могут оказаться полезными для прикидочных расчётов.
Поскольку всегда 0 < щ < 1, то со] < Щ и, следовательно,
\ (3.1.99)
Так как из всех распределений, сосредоточенных на интервале (0,l],
наибольшую дисперсию, равную p{l-p), имеет двухточечное распреде-
ление Бернулли [45] при р = 0.5, то всегда выполняются неравенства
Z>^<^.(l-fi>,.)<0.25; 1
^<#^)<0.5, [/ = 1,2].}
(3.1.100)
3.1.17) Наряду с рассмотренными основными числовыми характеристи-
ками супериндикаторов Щг\ [# = 1,2; r = l(l)...] могут найти практиче-
ское применение и моменты их распределений более высоких порядков
как начальные щ ) у так и центральные Щ ) , [/ = 1,2; r = l(l)...;
k = 2(l)... ]. Для ознакомления с определяющими их формулами адресуем
читателя к монографии [128]. А
3.1.18) Можно показать [128], что число параметров распределения су-
периндикатора равно сумме их чисел для трансформируемого и трансфор-
мирующего распределений. Собственные индикаторы распределений со-
ставляют исключение из сформулированного правила. Их распределения
имеют неизменные числа параметров, определяемые их рангом и свойст-
вами трансформирующих распределений. А
3.1.19) В заключение ещё раз прокомментируем семантический аспект
данного параграфа, в котором были рассмотрены основы (начала) теории
стохастической индикации, призванной служить инструментом вероятно-
стного анализа случайных явлений второго порядка (уровня, ступени). В
принципе поскольку согласно одному из основных положений материали-
стической философии (диалектического материализма) процесс познания
действительности бесконечен и, следовательно, на любой период времени
знания исследователя содержат элемент неопределённости,, то число сту-
пеней (уровней) анализа может неограниченно расти. Действительно, все

3.1. Методы теории стохастической индикации
137
вероятностные модели случайных явлений строятся в предположении, что
основные условия эксперимента1 известны. Так, в "элементарной" теории
вероятностей [29] - это комплекс М условий "эксперимента", в аксиомати-
ческой теории - это пространство U элементарных событий, в матема-
тической статистике - это генеральная совокупность.
Как известно [29], вероятности случайных событий характеризуют сте-
пени объективной возможности их реализации (появления, наступления) в
этих условиях (на этом пространстве элементарных событий или на этой
генеральной совокупности) и являются по определению неслучайными ве-
личинами. Однако, если условия К эксперимента до его проведения неиз-
вестны (полностью), то задача определения вероятностей исходов такого
эксперимента становится неопределённой. Первым шагом на пути преодо-
ления этой неопределённости является применение формулы полной веро-
ятности (или полного математического ожидания [78]) в дискретной или
непрерывной (интегральной) форме:
р(а)=^р{Й)р{а/н) (3.1.101)
или
Р(Л)= ]p(A/x)dF-{x), (3.1.102)
где Р\Н.) - вероятность гипотезы Н. [/ = l(l)w ];
Р\А/ Н.) - условная вероятность случайного события А относительно
гипотезы Н. (реализованной - неслучайной);
d Fk (х) - вероятность гипотезы (х < х < х + dx);
Р\А/Н.) - условная вероятность случайного события А относительно
гипотезы (jc < х < х + dx).
Нетрудно видеть, что вычисленная по формуле (3.1.101) или (3.1.102)
вероятность Р\А) случайного события А представляет собой математиче-
ское ожидание ("среднее значение") его условной вероятности Р\А/ Й)
или Р[А/х), принимающей соответственно значения РуА/Н.) или
Р\А/х) с вероятностями Р\Н§) или dF.(x) [29].
Как известно [29], любой конечный набор числовых характеристик (па-
раметров распределения) содержит о случайной величине меньше инфор-
мации, нежели закон её распределения. Поэтому исследование закона рас-
пределения условной вероятности РуА/Й) или Р\А/х), несомненно,
представляет большой практический интерес. Эту задачу, как можно было
Следует иметь в виду, что в рамках теории вероятностей все "эксперименты" мыс-
ленные, тогда как в рамках математической статистики все эксперименты реальные.

138 Глава 3. Методы оценивания эффективности ЦНП
заметить, и призвана решать теория стохастической индикации. Для этого,
как было показано, необходимо знать распределение вероятностей Р\Н.)
или dFk(x) гипотез и условные вероятности Р[А/Н.) или Р\А/ х) слу-
чайного события А относительно каждой из них. Однако в распределени-
ях Р[Н.) или dF~(x) также может содержаться неопределённость (напри-
мер, когда они определены статистически или экспертно). Тогда полная
вероятность Р\А) случайного события А, в свою очередь, окажется слу-
чайной и вновь возникнет задача определения её вероятностных характе-
ристик. Эта задача тоже может быть решена в рамках теории стохастиче-
ской индикации, но при этом объектом исследования будут уже индексные
супериндикаторы второго порядка [см. п. 3.1.1 и (3.1.47)].
Очевидно, что описанная схема может быть неоднократно последова-
тельно реализована, однако с каждым шагом будет усложняться как реше-
ние задачи, так и содержательная трактовка получаемых результатов. По-
этому на данной ступени развития методов теории стохастической инди-
кации наиболее эффективен математический аппарат рассмотренных здесь
супериндикаторов первого порядка (см. (3.1.4), [126]). А
...приписывать неопределённым по са-
мой своей сути величинам какую-то особую
точность бесполезно и нечестно, и, каков
бы ни был предмет, применение точных
формул к этим слишком вольно определён-
ным величинам есть не что иное, как обман
и пустая трата времени.
Н. Винер. Творец и робот
3.2. МАТЕМАТИЧЕСКАЯ ФОРМУЛИРОВКА ЗАДАЧИ
ОЦЕНИВАНИЯ ЭФФЕКТИВНОСТИ
ЦЕЛЕНАПРАВЛЕННОГО ПРОЦЕССА
Как отмечалось, методы теории эффективности целенаправленных
процессов (операций) являются инструментом системных дисциплин
("Исследование операций", "Прикладная кибернетика" и т.д.), предна-

3.2. Математическая формулировка задачи оценивания эффективности ЦНП 139
значенным для формализации одного из важнейших этапов системного
анализа - этапа оценивания эффективности операции (ЦНП) и качества
проводящей её системы (ЦУТС) (см. рис. 1.1.2), поэтому приводимая
ниже математическая формулировка задачи оценивания эффективности
ЦНП имеет принципиальное значение и призвана обеспечить (и обеспе-
чивает) необходимые общность и универсальность рассматриваемой
здесь методологии.
3.2.1) Как отмечено в [178] и как подтверждают теория и практика ре-
шения оптимизационных задач (а все системные исследования в конечном
счёте проводятся с целью поиска оптимальных решений: проектных, орга-
низационных, управленческих и т.п.), практически могут быть реализова-
ны лишь вычислительные схемы решения "однокритериальных" (одно-
компонентных - скалярных) "детерминированных" оптимизационных за-
дач, т.е. задач поиска оптимума скалярной детерминированной "критери-
альной" функции от детерминированных аргументов (возможно вектор-
ных). Все другие оптимизационные процедуры неизбежно содержат в себе
элементы субъективизма и произвола, обусловленные формулировкой
принципа (критерия) оптимальности. Поэтому весьма актуальными оста-
ются так называемые проблемы "скаляризации" и "детерминизации" зада-
чи исследования или, точнее, выходных характеристик математической
модели объекта исследования (ЦУТС или ЦНПФС), определяющих её ре-
шение. В связи со сделанным замечанием следует подчеркнуть, что в рам-
ках изложенной в гл. 2 методологии обе указанные проблемы решаются
автоматически. А
Как было показано в п. 2.3.4, оценивание эффективности операции
должно проводиться на двух уровнях, в два этапа, первый из которых за-
вершается оцениванием качества её результатов, точнее, формулировкой
(формализованным описанием) её цели в виде критерия пригодности GU3,
а второй - оцениванием её эффективности по одному из принятых (обос-
нованных) критериев GU3 или Оцэ. При этом на первом этапе решается
задача скаляризации путём перехода от вектора Г, v к единственному кри-
терию Y, v е \yA] , а на втором этапе - задача детерминизации путем пе-
рехода от случайного события (Y^e \Y/*\\ ) к его вероятности РДЦ или
Рвз. Так обстоит дело на уровне идей. Для материализации этих идей их
необходимо формализовать с помощью математических моделей иссле-
дуемых объектов (ЦУТС и ЦНПФС) и на основе последних построить ме-
тоды и методики, позволяющие решать конкретные практические задачи.
Этим целям и призван служить данный параграф.

140 Глава 3. Методы оценивания эффективности ЦНП
3.2.1. СРЕДНЯЯ ВЕРОЯТНОСТЬ ДОСТИЖЕНИЯ ЦЕЛИ ОПЕРАЦИИ
Как было показано в п. 2.3, оценивание эффективности ЦНП заключа-
ется в определении (вычислении) показателя эффективности РДЦ (Рвз) и
его сравнении с требуемым (или оптимальным) значением РТДЦ (Р^) (или
РдцТ (Р£?т)1 ). Таким образом, первый этап оценивания эффективности -
это её измерение, заключающееся в определении (оценивании) значения
Рдц показателя эффективности2.
Итак, согласно выражению (2.3.16)
P„=P(twe{t{$, (3.2.1)
где К3\ - показатель качества результатов операции (в симплексной ка-
нонической форме);
\YL\ _ область допустимых значений показателя K3v - (см. рис. 2.3.1,
2.3.2).
Из (3.2.1) следует, что для вычисления показателя РДЦ эффективности
операции должны быть заданы законы распределения случайного вектора
К3ч и случайной области {fAj (в общем случае L и {кД }). Универсаль-
ной формой первого, как известно, является функция распределения
Ff( Ч(Г{Э))^[(И *л)п(& <у2)п(у3<у3)] . (3.2.2)
Однако, как будет показано, применительно к рассматриваемой проблеме
чаще более удобной оказывается следующая форма интегрального закона
распределения:
Ф^Г{3))=Р[(У1*у,)п{уг<у2)п{у3<у3)], (3.2.3)
которая и используется в дальнейшем.
3.2.2) Если перейти к рассмотрению отрицательного целевого эффекта
("~-.Pi)> то соотношения (3.2.2) и (3.2.3) поменяются местами. Таким обра-
зом, распределения F^(y) и ФДг), моделирующие показатель качества
результатов операции, отличаются лишь направлением оси Оух в системе
координат Оухугуъ. А
1 В дальнейшем для разгрузки текста символ Рвз будет опускаться, но будет
подразумеваться.
В дальнейшем показатель и принимаемое им значение обозначаются одинаково.
Смысл символа конкретизируется контекстом.

3.2. Математическая формулировка задачи оценивания эффективности ЦНП 141
Определением закона распределения фДг) вектора Y (показателя ка-
чества результатов операции) завершается процедура построения матема-
тической модели ЦНПФС в задаче исследования его эффективности. Од-
нако на базе такой модели может быть реализована только разомкнутая
схема анализа эффективности операции, основанная лишь на измерении
эффектов (результатов операции) без их оценивания.
Для замыкания схемы необходимо знать закон распределения области
|кЛ| допустимых значений ГЛ показателя K3v результатов операции,
свойства и характеристики которой зависят от условий применения ЦУТС,
описываемых параметрами В?*. В общем случае с их помощью могут
учитываться и условия, создаваемые искусственно (воздействия противни-
ка и т.п.). Закон распределения случайной области |кД } может быть задан
аналитически лишь в простых случаях, когда она может быть описана ко-
нечным множеством случайных параметров. Например, указанная область
может представлять собой куб со случайными координатами вершин и
длинами ребер или шар со случайными координатами центра и радиусом и
т.п.
Если ограничения на компоненты вектора YL взаимно независимы, то
область \Y^\\ представляет собой параллелепипед (в общем случае п-
мерный гиперпараллелепипед) со сторонами, параллельными осям систе-
мы координат Оуху2у3, т.е. прямое (декартово) произведение отрезков
\yn yl\ , определяющих области допустимых значений yf результатов у. ,
[/ = 1,2,3]:
{%}=[JU^^^ . (3.2.4)
При Х=2 соотношение (3.2.4) иллюстрируется рис. 2.3.2. Как было от-
мечено (см. {2.7.7}), предположение о независимости ограничений, нала-
гаемых на различные эффекты (результаты) операции - компоненты век-
тора K3v, как правило, правомерно, поскольку они обусловливаются не
связанными между собой факторами1.
До сих пор рассматривался самый общий случай предъявления требо-
ваний к результатам операции. Применительно к показателям операцион-
ных свойств ЦНП эти требования носят односторонний характер. Так,
виртуальный целевой эффект у[ должен быть не менее требуемого {ми-
нимально допустимого) - у[, виртуальные затраты у2 ресурсов должны
быть не выше максимально допустимых - у2 , называемых предельными,
Об исключениях говорится в п. 5.2.

142 Глава 3. Методы оценивания эффективности ЦНП
цель операции должна быть достигнута за виртуальное время у3, не пре-
вышающее максимально допустимого - у*, называемого директивным
временем [130].
3.2.3) Следует особо подчеркнуть, что односторонность требований к
характеристикам операционных свойств ЦНП носит принципиальный ха-
рактер и обусловлена спецификой этих свойств. В отличие от любых дру-
гих управляемых параметров ЦУТС (включая её ЭТХ) и ЦНПФС, которые
для обеспечения требуемых свойств (требуемых качеств) ЦУТС и ЦНПФС
должны находиться в определённых пределах (двусторонних), для опера-
ционных свойств ЦНП подобных пределов (обусловленных объективной
необходимостью) не существует. А если ограничения всё-таки есть, то они
обусловлены физическими особенностями этих свойств, но не целями опе-
рации. Так, если целевой эффект характеризуется позитивным свойством
результата операции (а это всегда так), то "чем его больше - тем лучше".
Верхний его предел (если он существует) будет обусловлен возможностя-
ми ЦУТС и ЦНПФС, т.е. физическими свойствами показателя ух. Расход
ресурсов (всех видов) - это негативное свойство результата операции и,
следовательно, "чем его меньше - тем лучше". Нижний его предел (в част-
ности, нулевое значение) обусловлен также физическим смыслом ресурсов
j>2, j>3, а не целями операции. Если же пойти по пути максимального
обобщения, то отрицательный расход ресурсов можно трактовать как их
прирост. Так, применительно к операционному времени уъ это означало
бы, что цель операции достигнута до её начала (т.е. до t0 = 0). Аналогично
бесконечно большие расходы ресурсов могут быть истолкованы как факт
невозможности достижения цели операции. А
Введём следующие обозначения:
d d d
Ух =«i/ Уг =«2/Л=«з •
Тогда область \YjiA допустимых значений результатов операции (пока-
зателей их качества) будет представлять собой октант (в общем случае
я-мерный гипероктант)
{%}=[г.»~)х(-~Л ]х(-о-,|,] (3.2.5)
с вершиной в точке Z/3) -{^хЛгЛъ)* Возможные реализации вектора iL
и области |г,1 } приведены на рис. 3.2.1.
При #=2
Y(2) = (Ух>Уг)> {^(2>|=Ьи00)х(-00^2], Z{2)=(Zl,Z2),
что иллюстрируется рис. 3.2.2.

3.2. Математическая формулировка задачи оценивания эффективности ЦНП 143
«з1л
/.
/
//
$—
Ъ7-,П—ъ
/ i /
1г\Уг
Ужму*' а *
2
/J Y
г|?Г
Рис. 3.2.1 Рис. 3.2.2
С учётом сказанного критерий пригодности результатов операции
(2.3.13) примет вид
СЦР : (Г(3)е {%})«(к(з>^^з>Ь[0>1 * *)п(л < £2)п& ^ £3)1>
где согласно (2.3.11) и (2.3.12)
Теперь вероятностное описание области \YL \ не представляет трудно-
сти, так как оно сводится к определению закона распределения случайного
вектора 2,ъу
Применительно к рассматриваемой задаче целесообразно использовать
две формы интегрального закона распределения следующего вида:
Fi(3)(z(3))=P[fo <zt)n(z2 <z2)n(z3 < г,)]; (3.2.9)
фф(3У=р[& uZl)n{z2 >z2)n{z3 >z3)]. (3.2.9')
Если законы распределения случайных векторов К3> и ^/3)известны>то
по формуле полной вероятности (в интегральной форме) вероятность
достижения цели операции будет определяться одним из следующих вы-
ражений:
Шфк5)(^з)К3)Цз))Л3.2.10)
РдЦ=Л%Ац])=Л%гА^=\
Ш<^Л)Ц>(3>), (3.2.10')

144 Глава 3. Методы оценивания эффективности ЦНП
d\(YJ=%MJdY(>) ; dY^dyidyidy3.
По структуре выражений (3.2.10) видно, что вероятность РДЦ представ-
ляет собой математическое ожидание ^среднее" значение) одной из слу-
чайных величин:
43)Ц3)Цз>); (3-2.il)
^ЦД>) . (3-2.12)
называемых соответственно первым и вторым стохастическими суперин-
дикаторами третьего ранга1 (см. п. 3.1 и [128]).
3.2.4) Рассматривая соотношения (3.2.10) как формулы полных вероят-
ностей, легко понять, что случайные величины щ3-Ф$ \2,ЪА представ-
ляют собой условные вероятности достижения цели операции относи-
тельно событий \Zi3x = Z/3J и [Уф = К3\) соответственно
<и1<3>=<р^Цз>)=^Йг(г.»г1»*з);
Поскольку реализации этих событий предшествует вычисление услов-
ных вероятностей, то эти вероятности еще называются апостериорными
(послеопытными).
Известно, что наиболее информативной исчерпывающей вероятностной
характеристикой случайной величины является закон её распределения.
Это в полной мере относится и к супериндикаторам щ' и щ'. Как пока-
зано в п. 3.1, функция распределения супериндикатора определяется соот-
ношением
F&w(<»)=P(<b{i)<a>)=p(z{3)e{Y{3)}J= Д dF,Jz{3)), (3.2.13)
где Н(з)| - область значений вектора К3\, граница которой
Y£A(d) = Ф$х (со) определяется решением уравнения
•*>«J-«. (3-2-14)
В дальнейшем они часто называются просто индикаторами.

3.2. Математическая формулировка задачи оценивания эффективности ЦНП 145
Пример 3.2.1. Пусть #=1 и при этом Кк* = кФ = ух. Тогда согласно
(3.2.14)
Rhiy) = a> => у[(а>)=к£{а>)
(см. рис.3.2.3,а)) и формула (3.2.13) дает
^■>И = ^И = ^,к,И] • (3-2.15)
А
Пример 3.2.2. Пусть tf-l и при этом Кк. = кФ = j>2. Тогда, согласно
(3.2.14)
Fh{y)=a> => ^н=^;'И
(см. рис.3.2.3,б)) и формула (3.2.13) дает
FMM = FM = FdFy>)] ■ (3-2-16)
▲
Л
(«S-w.
m^itr"
а)
Рис. 3.2.3
б)
3.2.5) При К>1 решение задачи усложняется и выражений типа (3.2.15)
или (3.2.16) в общем случае получить не удается. Однако геометрической
интерпретацией области { Y,^ } при tf=2 может служить рис. 3.2.4. А
Если закон распределения (3.2.13) известен, то
РДЦ=^ = М^=м[4]]=)^Р&М, [i = hll (3.2.17)
' о '
Таким образом, как следует из выражения (3.2.17), вероятность дости-
жения цели операции представляет собой математическое ожидание его
условной вероятности &f*. В связи с этим вероятность Рдц имеет смысл
средней условной вероятности достижения цели операции.

146 Глава 3. Методы оценивания эффективности ЦНП
Рис. 3.2.4
Поскольку случайная величина бй£ъ>, [/ = 1,2] неотрицательная, то веро-
ятность РДЦ=а)1 численно равна площади заштрихованной на рис. 3.2.5
области [29].
3.2.6) Поскольку вероятность Рдц вычисляется путём рандомизации ус-
ловной вероятности Ф$ \^(з)/ или ®z гш > т,е- е^ взвешенного усредне-
ния по всем возможным реализациям условий [значениям вектора Z^ в
(3.2.10) или Г(3) В (3.2.10')], то она от этих условий уже не зависит и поэто-
му называется безусловной вероятностью, а поскольку она определяется
до реализации условий, то она ещё называется априорной (доопытной).
А
3.2.7) Поскольку определение закона распределения F% [z^) вектора
Z^ требуемых результатов операции является прерогативой суперсисте-
мы и функция F^ [Z,3x) часто оказывается неизвестной, то в таких случаях
предельно допустимые значения Z^ результатов Г^ операции полагают-
d
ся детерминированными и заданными, т.е. Z^=Z^. При этом распреде-

3.2. Математическая формулировка задачи оценивания эффективности ЦНП 147
\f*M
1-у
ление случайного вектора Z^ оказывается вырожденным1 следующего
вида:
^wW=F*„(«i^^)eUnfe)=n^fc-«f)- (з-2-18)
Тогда dFtw(z{i))= <p^(z{^dZ(3) = П*у,(г,)*, =№(*, -$ К>
и формула (3.2.10) даёт
Рдц =PV(3)<Z(3))=
= *,w(«f ,«f,гзя)=^(г,я,г2я,г3я). (3.2.19)
Таким образом, при детерминированных требованиях к результатам
операции достаточно знать лишь закон распределения Ф$ (K3J случайно-
го вектора Y^ - показателя качества результатов операции. А
3.2.2. ГАРАНТИРУЕМАЯ ВЕРОЯТНОСТЬ ДОСТИЖЕНИЯ
ЦЕЛИ ОПЕРАЦИИ
3.2.8) Из семантики вероятностных характеристик случайных объектов
следует, что они представляют собой прогнозные оценки показателей
Вырожденным называется закон распределения неслучайной величины.

148 Глава 3. Методы оценивания эффективности ЦНП
различных свойств этих объектов. Так, математическое ожидание и на-
чальные моменты распределения случайной величины характеризуют
("априори") положение центра её рассеяния на числовой оси; дисперсия и
центральные моменты распределения характеризуют рассеяние возмож-
ных значений случайной величины относительно этого центра и т.п. При
этом наиболее полной и исчерпывающей априорной характеристикой слу-
чайной величины является закон её распределения, учитывающий все её
вероятностные свойства в совокупности и во взаимосвязи.
Следует обратить внимание на существенное различие прогнозирую-
щих свойств и возможностей указанных характеристик. Так, числовые ха-
рактеристики (и моменты распределения) случайных величин дают про-
гнозы лишь средних результатов будущих массовых опытов, тогда как за-
коны их распределений позволяют прогнозировать результаты единичных
опытов. Поэтому при наличии закона распределения случайной величины
использование лишь числовых характеристик обедняет анализ её свойств и
используемую математическую модель исследуемого объекта (явления)
[29]. А
Итак, если известны законы распределения F {3) (со) и F {3) (со) суперин-
дикаторов щ' и щ соответственно (рис. 3.2.5), то могут быть определе-
ны ещё два очень важных показателя эффективности операции, называе-
мые гарантируемыми вероятностями достижения её цели:
\af{r)=R&М=Р^(1-Г); (3.2.20)
[a)r2(r)=R^ (у) = F^} (1 - у\ (3.2.20')
где у- уровень гарантии {гарантийная вероятность).
Поскольку при определении гарантируемой вероятности (оГдц\у) ис-
пользуется закон распределения супериндикатора щ' или Щ , то этот по-
казатель позволяет оценивать эффективность уникальных (единичных)
операций в отличие от вероятности РДЦ9 достаточно полно характери-
зующей эффективность лишь массовых операций.
В силу естественных аналогий свойств случайных величин щ' и щ
(см. п. 3.1) в дальнейшем часто рассматривается лишь один из суперинди-
каторов, который при этом конкретизируется контекстом и обозначается
через cor '.
3.2.9) При исследовании эффективности операций в условиях неопреде-
лённости, вызываемой воздействием случайных факторов, полное её уст-
ранение невозможно в принципе. Поэтому в любом решении о качестве ре-
зультатов ЦНП будет присутствовать элемент неопределённости (недосто-

3.2. Математическая формулировка задачи оценивания эффективности ЦНП 149
верности), т.е. непредсказуемого несоответствия их действительному
уровню. Если операция будет повторяться многократно, то эти несоответ-
ствия будут "в среднем" сглаживаться. Однако при немногократном и осо-
бенно при одноразовом применении ЦУТС отклонения показателей щ\
щ эффективности ЦНПФС от их среднего значения РДЦ могут оказаться
существенными, и тогда надо считаться с возможностью появления не-
ожиданностей в каждом отдельном случае. А
3.2.10) Как видно из рис. 3.2.5, гарантируемая вероятность (огдц\у)
достижения цели операции есть невозрастающая функция аргумента у, т.е.
чем выше уровень ^гарантии, тем ниже гарантируемое на этом уровне
значение (одц\у) условной вероятности достижения цели операции. По-
этому в общем случае гарантируемая вероятность (одц{у) значительно ни-
же средней вероятности Рдц. Отклонение от этого правила может возник-
нуть лишь в случаях, когда уровень гарантии ниже средней вероятности
Рдц (т.е. когда У<РДЦ). Поэтому при исследовании эффективности уни-
кальных ЦНП следует "не пугаться" малых значений согдц\у) и помнить,
что основным назначением этого показателя является сравнительный ана-
лиз и оптимизация операций (ЦНПФС и проводящих их ЦУТС), а не абсо-
лютное оценивание их эффективности. А
3.2.11) В определении показателя эффективности операции (огдц\у) фи-
гурируют две вероятности: гарантируемая - сог и гарантийная - у Для
уяснения их различия представляется целесообразным дать их частотные
трактовки.
Поскольку соДцУу) — это наименьшее (с вероятностью у) из значений ус-
ловной вероятности dr"'=Ф$ \Z,A, принимаемых ею при фиксации ус-
ловий применения ЦУТС, т.е. при фиксации значения Z^ вектора Z,,, то
(одцху) имеет смысл минимально возможной (с вероятностью $ доли реа-
лизации условий применения ЦУТС, в которых цель операции достигается
с вероятностью Sr' > 0)дц(у).
В свою очередь, при многократной реализации операции гарантийная
вероятность у приближенно равна доле проведённых операций, в которых
условная вероятность taff (j - номер операции) достижения цели опера-
ции удовлетворяет неравенству or' > содц(у) (см. п. 3.4, 3.5).
Для лучшего уяснения сказанного следует ознакомиться с п. 3.4.2 и
рис. 3.4.3, 3.4.4. А

150 Глава 3. Методы оценивания эффективности ЦЦП
3.2.12) Напомним, что сокращение размерностей nk, \k^ 1,2,3] компо-
нент Yr\ и Zr\ векторов L и Z, х - показателей результатов операции
и требований к ним л, = п2 = пъ = 1 имело целью лишь повысить нагляд-
ность и упростить изложение, а следовательно, и понимание логических
построений. С формальной же точки зрения все сказанное справедливо для
любых nk и все элементы рассматриваемых моделей легко обобщаются на
случай иЛ>1, [* = 1,2,3]. А
3.2.13) Если требования Z/^, предъявляемые к результатам Y,3. опера-
ции, детерминированные (неслучайные), т.е. вектор Z3v имеет вырожден-
ное распределение
^W-^W-ft^b-^).
где Z^L =(z,y7,zf ,z?) - заданное предельно допустимое значение вектора
К3\, то, как следует из определений (3.2.11) и (3.2.12), супериндикаторы
(з) (з)
(0\' и щ' становятся неслучайными:
их распределения оказываются вырожденными (см. рис. 3.2.6):
F^{a))=F&M = A(a)-G)r)
1-у v
Рис. 3.2.6

3.2. Математическая формулировка задачи оценивания эффективности ЦНП 151
и, следовательно,
Как известно, у вырожденного распределения квантили всех уровней
равны заданному значению "случайной" величины, поэтому
Таким образом, при детерминированных требованиях к результатам
операции все показатели её эффективности равны между собой при любом
уровне у гарантии, т.е.
Рт = ^ = ^-<4f(rW М-«г, (3-2.21)
где о)г - гарантированное значение вероятности достижения цели.
Все сказанное в (3.2.13) применительно к n=N=3 справедливо для про-
извольного п< °°. А
3.3. МЕТОДЫ СВЁРТЫВАНИЯ ВЕКТОРНЫХ
ПОКАЗАТЕЛЕЙ КАЧЕСТВА РЕЗУЛЬТАТОВ
ЦЕЛЕНАПРАВЛЕННЫХ ПРОЦЕССОВ
3.3.1. СОСТОЯНИЕ ВОПРОСА
Представляется достаточно очевидным, что качество ни одного сколь-
ко-нибудь сложного объекта не может быть охарактеризовано лишь одним
свойством, и, следовательно, показатель качества такого объекта есть век-
тор (см. п. 2.2.1). Сказанное в полной мере относится к таким действитель-
но сложным объектам, как ЦУТС и ЦНПФС. При этом, как было показано,
показатель качества результатов ЦНП включает в себя не менее трех ком-
понент (симплексная каноническая форма). Понятно, что в таких условиях
при сравнительном оценивании качества различных объектов возможно
возникновение противоречий из-за неоднозначности ситуации принятия
решения, поскольку по одним свойствам более качественным может ока-
заться один объект, а по другим - другой. Задачи принятия решений в по-
добных ситуациях принято называть "многокритериальными" [177, 178].
3.3.1) Используемый термин ("многокритериальная задача") нельзя счи-
тать удачным, поскольку в нём под критериями понимаются показатели
отдельных (единичных) свойств объекта. Что касается собственно крите-
риев выработки решений, то они в рамках указанных задач вообще никак
не называются. Подобная терминология приводит к смешению понятий и
затрудняет как понимание сущности проблемы, так и её формулировку и
решение. Поэтому семантически правильнее указанные задачи называть

152 Глава 3. Методы оценивания эффективности ЦНП
"многокомпонентными" или, ещё лучше, "задачами с векторными пока-
зателями качества" исследуемых объектов (решений)" (см. (2.2.1),
(2.2.4), {2.7.2}, {2.7.4}). Как нам представляется, других задач практически
не существует, так как качество сложного объекта одним показателем
(скаляром) описать нельзя. Указанная ситуация и порождает проблему
скаляризации, о которой говорилось в (3.2.1). А
Понятно, что из-за неоднозначности формулировки многокомпонент-
ных задач их решения оказываются также неоднозначными. Это обстоя-
тельство без введения дополнительных условий и ограничений (как на са-
ми показатели качества исследуемого объекта, так и на характер взаимо-
связи этих показателей) делает задачу принятия решения (оптимального
(3.2.1)) некорректной (неразрешимой). Поэтому все предлагаемые методы
решения таких задач посвящены поискам компромиссных решений путём
построения так называемых "обобщённых показателей" качества, называе-
мых ещё "целевыми" или "критериальными" функциями (см. п. 2.4).
Как отмечалось в п. 2.4, обобщённые показатели представляют собой
различные функции от частных (единичных) показателей. Вид этих функ-
ций (как правило, постулируемый без достаточных обоснований) и опре-
деляет дополнительные условия, позволяющие свести задачу с векторным
оптимизируемым показателем к одной или нескольким последовательно
решаемым задачам, каждая из которых имеет скалярный оптимизируемый
показатель качества объекта (решения). Для указанных методов использу-
ются названия, отражающие заложенные в них принципы поиска компро-
миссных решений: "Метод главной компоненты" [26], "Метод компро-
миссов", "Метод последовательных уступок", "Лексикографический ме-
тод" [134] и т.п.
3.3.2) Заметим, что ни один из перечисленных методов не даёт доста-
точно обоснованных решений и, что самое главное, во всех этих методах
задача решается в детерминированной постановке, мало соответствующей
реальным практическим ситуациям. В связи с этим возникает отмеченная в
(3.2.1) проблема обоснованной детерминизации.
Как отмечалось в п. 2.4, для учёта случайности (реально всегда сущест-
вующей) аргументов критериальных функций рассматриваются квазирегу-
лярные модели, в рамках которых в этих функциях фигурируют математи-
ческие ожидания их аргументов. Однако при этом, несмотря на кажущийся
учет неопределённости (случайности) факторов, влияющих на исследуе-
мый объект (ЦУТС, ЦНПФС), модель остаётся детерминированной. Не-
достатки таких моделей прокомментированы в (2.4.5) - (2.4.14). ▲
В различных источниках предлагаются различные подходы к свёртыва-
нию частных показателей качества в обобщённые, причём часто все по-
добные подходы подвергаются аргументированной критике [26, 84]. Тем

3.3. Методы свёртывания векторных показателей качества результатов ЦНП 153
не менее они получили распространение на практике и поэтому заслужи-
вают обсуждения.
Все способы свёртывания можно "условно" разбить на четыре класса
[84].
3.3.1.1. Формирование критериальной функции качественного типа
Под "качественной целевой функцией" понимается функция, прини-
мающая лишь одно из двух значений {0,1} (см. п. 2.2.3). При её определе-
нии все результаты операции (все возможные значения показателя их ка-
чества), приводящие к достижению её цели, считаются одинаково пригод-
ными, а все результаты, не приводящие к достижению цели операции, счи-
таются одинаково непригодными.
Свёртывание единичных показателей качества результатов операции в
обобщённый осуществляется путем разбиения множеств значений показа-
телей единичных (частных) свойств на подмножества допустимых и недо-
пустимых их значений. С этой целью назначаются некоторые числа zn
[j = l(l)/f], и допустимыми считаются лишь значения yn [i = l(l)#i] пока-
зателей, удовлетворяющие условиям (отношениям порядка)
Л*г, , [/ = 1(1)л], (3.3.1)
d
где конкретный вид отношений ^={>,>,<,<} определяется физической
сущностью показателя у. и его предельно допустимого значения zr При
этом мультипликативная критериальная функция принимает вид
Wp = tlA(y?-z?)> (3-3.2)
1=1
где yf, Z? - приведенные значения переменных у., zt, преобразующие
отношения ^ к единому виду >.
Аналогично может быть определена и критериальная функция парамет-
ров
Wn=f[n(x.;x'j,x';), (3.3.3)
7=1
где [jCy, jcJ J - множество допустимых значений параметра х..
3.3.3) В работе [84] описанный подход назван "способом формирования
цели качественного типа". Данный термин представляется весьма неудач-
ным, поскольку из него следует, что, с одной стороны, значение критери-
альной функции отождествляется с целью операции [84], а с другой - что

154 Глава 5. Методы оценивания эффективности ЦНП
существуют "цели количественного типа". Однако, как было показано в п.
2.3.2, формулировка цели операции носит всегда качественный характер
[см.(2.3.3), (2.3.4)], а степень (мера) её достижения - количественный ха-
рактер. А
3.3.4) Данный мультипликативный способ формирования критериаль-
ной функции (3.3.2) или (3.3.3) обладает большой семантической (смысло-
вой) наглядностью и понятностью для ЛПР. Однако детерминированность
его формулировки и сложность определения граничных значений zi9
[i = l(l)n] и хр jcJ, [y = l(l)iw] показателей у. и х. делают реализую-
щую его процедуру достаточно противоречивой [84]. А
3.3.1.2. Логическое свёртывание
Такое название получили методы, реализуемые в предположении, что
сами показатели w. единичных свойств объекта (ЦУТС, ЦНПФС) носят
"качественный" характер, т.е. принимают лишь одно из двух значений
{ОД }. В этом случае их свёртывание производится по аналогии с логиче-
скими операциями.
Так, если для достижения цели операции все её результаты должны
быть качественными (т.е. показатели wt всех её результатов должны быть
равны 1), то мультипликативная критериальная функция называется
конъюнкцией и имеет вид
W^flw,. (3.3.4)
Если же для достижения цели операции достаточно хотя бы одного ка-
чественного результата, то аддитивная критериальная функция называется
дизъюнкцией и имеет вид
Wp = l-f[{\-Wi). (3.3.41)
1=1
3.3.5) Следует обратить внимание, что, строго говоря, цитированные
термины [84] неточны, так как "конъюнкцией" и "дизъюнкцией" называ-
ются логические операции над высказываниями и предикатами [типа
(3.3.1)], а не над значениями их истинности. Об этом свидетельствует и
фигурирующий в (3.3.4) и (3.3.4') оператор JJ произведения, а не опера-
тор п пересечения (конъюнкции). А
3.3.6) Как было показано в п. 3.1, значение истинности высказывания
имеет смысл его условной (апостериорной) вероятности. Поэтому крите-

3.3. Методы свёртывания векторных показателей качества результатов ЦНП 155
риальные функции вида (3.3.2), (3.3.3) и (3.3.4), (3.3.4*) можно трактовать
как условные вероятности достижения цели операции при различных её
формулировках. Так, если ввести понятие "частной цели" операции1, под
которой понимать выполнение i-го условия у? > zj7, то формально при
критериальных функциях вида (3.3.2), (3.3.3) и (3.3.4) цель операции трак-
туется как пересечение (булево произведение) её "частных целей", а при
критериальной функции вида (3.3.4') - как их объединение (булева сумма)
[40, 84]. А
3.3.7) С семантической точки зрения для более осмысленного формули-
рования цели операции и более содержательного определения критериаль-
ной функции представляется целесообразным избегать показателей
и>.е [ОД] и заменять их индикаторами А (у/7 - z/7)^ [ОД], где yf, zf - чи-
словые переменные. Другими словами, вместо функции (3.3.4) рекоменду-
ется пользоваться функцией (3.3.2) или (3.3.3). При этом формулы (3.3.4) и
(3.3.41) соответственно примут вид:
^n^fe7-*/7); (3-3.5)
#=1
^l-ntl-^U77-*/7)]. (3-3.5')
1=1
А
3.3.8) Поскольку при использовании критериальной функции (3.3.5')
допускается достижение хотя бы одной "частной цели" операции, то доста-
точно содержательным её обобщением могла бы явиться аддитивная кри-
териальная функция вида
Wp=±±A{y?-zf1). (3.3.6)
Легко заметить, что функция (3.3.6) численно равна доле достигнутых
"частных целей" операции от их общего числа я.
Если "частные цели" операции не равнозначны (не равноважны) и для
них определены весовые коэффициенты (коэффициенты важности) лг, ,
[0 <Kt < 1, [i = l(l)/i], ^/rf. = 1], то критериальная функция (3.3.6) примет
/=1
вид
Wp = t^{yf-z?). (3-3.7)
/=1
Напомним, что в рамках реализуемой здесь методологии каждая операция имеет
одну цель.

156 Глава 3. Методы оценивания эффективности ЦНП
Обратим внимание, что выражения (3.3.6) и (3.3.7) могут трактоваться
как формулы полных вероятностей достижения цели операции. При этом
роль вероятностей гипотез выполняют индикаторы Л [yf7 - zf),
[/ = l(l)n] , а роль условных вероятностей - весовые коэффициенты — в
п
(3.3.6) и к. , [j = l(l)ii] в (3.3.7). Вместе с тем следует подчеркнуть, что
поскольку в рамках критериальных функций (3.3.6) и (3.3.7) достижения
частных целей предполагаются несовместными, то тем самым не учиты-
ваются возможные кумулятивные эффекты, получаемые в ходе операции
при совместном достижении различных комбинаций (совокупностей) тре-
буемых частных эффектов. ▲
3.3.1.3. Обобщенное логическое свёртывание
В качестве другого (по сравнению с (3.3.8)) обобщения "логических"
критериальных функций рассматриваются следующие соотношения:
Wp=min{Kxwx,K2w2,...,Knyi>n}\ (3.3.8)
Wp = max {к, wx, K2w2,...,Knwn). (3.3.9)
В выражениях (3.3.8) и (3.3.9) переменные wn [/ = 1 (l)w] могут быть
как количественными, так и качественными. Однако в первом случае не
учитываются предъявляемые к ним требования w]p, [ i = 1 (l)#i ].
Нетрудно понять, что если все w.€ [ОД] и к. =1, [i = l(l)n], то вы-
ражения (3.3.8) и (3.3.9) превращаются в (3.3.4) и (3.3.4') соответственно.
3.3.1.4. Линейное свёртывание
При этом способе аддитивную критериальную функцию представляют
в виде линейной комбинации функций от показателей wl9 [i = 1 (l)/i ] ча-
стных свойств объекта (результатов ЦНПФС, параметров и ЭТХ ЦУТС и
ЦНПФС):
wp = t*i/M > (З.З.Ю)
называемой сепарабельной критериальной функцией.
В зависимости от содержания (физического смысла) показателей и>.,
[j = l(l)#i] на коэффициенты к. и функции /(и>.) могут накладываться

3.3. Методы свёртывания векторных показателей качества результатов ЦНП 157
различные ограничения. Например, к. >0 , [i = l(l)/i] или 0</г/<1 ,
[i = l(l)/i] и £к.=1 ;/,(*>,)=*, и т.п. (см. п. 2.4).
Иногда данный способ свёртывания называют "экономическим". Это
бывает в случаях, когда в качестве коэффициентов к. фигурируют цены
на товар, а функция Wp приобретает смысл суммарной прибыли [84].
В заключение отметим, что, несмотря на достаточную необоснован-
ность и искусственность рассмотренных способов свёртывания, обуслов-
ленных стремлением к простоте аналитических свойств получаемых кри-
териальных функций, их применение связано со значительными трудно-
стями как семантического, так и технического характера [84].
3.3.9) Рассмотренные способы свёртывания показателей частных
свойств объектов приводили к обобщённым скалярным, детерминирован-
ным критериальным функциям, различающимся как формулировками цели
операции, так и обусловленной этим структурой их математических выра-
жений. При этом фигурирующие в них весовые коэффициенты призваны
отражать относительные "важности" отдельных частных (единичных)
свойств результатов операции для достижения её цели. Определение весо-
вых коэффициентов, производимое на балльных шкалах [112], представля-
ет собой достаточно сложную (методологически) задачу, решение которой
в значительной мере подвержено влиянию субъективных факторов. По-
скольку ранжирование свойств на порядковой шкале [112] гораздо проще
их "взвешивания", то широкое применение находят методы последова-
тельного (пошагового) решения оптимизационных задач, в которых на ка-
ждом шаге оптимизируется лишь одно свойство объекта, считающееся на
этом шаге наиболее важным, а свойства "высших рангов" поддерживаются
на заданном уровне (в заданных диапазонах). Понятно, что при таком под-
ходе оптимизация каждого из свойств осуществляется за счёт свойств бо-
лее "низких рангов". Этим обусловлены и названия соответствующих ме-
тодов (см. (3.3.1), (3.3.2)). Из сущности этих методов (которые можно на-
звать "циклическими" или "каскадными") следует, что в них как таковое
свёртывание показателей частных свойств заменяется последовательным
(циклическим, каскадным) синтезом. А
3.3.2. МЕТОД ГЛАВНОЙ КОМПОНЕНТЫ
Данный метод [26, 112] представляет собой частную и наиболее про-
стую разновидность "каскадного метода". Здесь он выделен для более на-
глядной иллюстрации сущности подобных методов.

158 Глава 3. Методы оценивания эффективности ЦНП
Пусть wn [i = l(l)ii] - показатель 1-го эффекта (результата) опера-
ции. Тогда в детерминированной модели w. = yn [i = l(l)/f ]; в квазире-
гулярной модели w.-yn [j = 1 (l)n ] ; в стохастической модели
w. =/>(j>^£.). И пусть главным из всех является показатель н>,, т.е.
операция считается успешной (пригодной для реализации), если пока-
затель и>, достигает требуемого уровня [максимального (минимально-
го) или не менее (не более) заданного], а остальные показатели н>.,
[i = l(l)#i] удовлетворяют некоторой системе ограничений (т.е. крите-
рию пригодности):
г \опт
WitWi,w"\ [i = 2(l )n; wnw"e (- 00,00) ]#
При такой постановке задачи все решения, не удовлетворяющие соот-
ношениям (3.3.11), отбрасываются как неконкурентоспособные.
Нетрудно заметить, что соотношения (3.3.11) реализуют критерий оп-
тимальности при л0 = 1, т.е. когда оптимизируется одно качество (свойст-
во) результата операции, а остальные свойства удовлетворяют критерию
пригодности. Таким образом, "метод главной компоненты" следует из рас-
смотренной выше "каскадной" формулировки задачи как её частный слу-
чай (см. (2.2.1), <2.2.2».
3.3.10) Описанный подход не лишён серьёзных недостатков, как, впро-
чем, и другие рассмотренные в п. 3.3.1 способы свёртывания показателей
частных свойств, поскольку в нём не учитывается их возможная взаимная
зависимость, с одной стороны, и практическая сложность выделения глав-
ной компоненты - с другой. Кроме того, независимо от конкретного вида
показателей wn [i = l(l)/i] подход является принципиально детермини-
рованным. А
3.3.11) Применение метода главной компоненты обычно аргументиру-
ется сложностью обоснования обобщённого показателя качества результа-
тов операции и отыскания с его помощью компромиссного решения. Од-
нако несомненные сложности создаёт и большая размерность п векторов
Y.k и Z/v. Причём эти сложности не только (и даже не столько) техниче-
ского, а в большей степени эвристического характера, так как при больших
п задача (модель операции) становится труднообозримой и плохо подда-
ётся осмыслению и анализу. А
(3.3.11)

3.3. Методы свёртывания векторных показателей качества результатов ЦНП 159
3.3.3. МЕТОД ВЕДУЩИХ КОМПОНЕНТ
При больших размерностях п векторов К, и Z/v непосредственное
использование формулы (3.2.9) или (3.2.10) становится затруднительным.
Как было показано в п. 3.3.1, для преодоления возникающих трудностей
используются различные методы свёртывания показателей yn [ i = 1 (l)n ]
частных свойств результатов операции в обобщённые. При этом в зависи-
мости от желания (произвола) исследователя показателям w. присваива-
ются различные свойства, описываемые количественно или качественно,
что делает саму формулировку задачи оценивания эффективности опера-
ции неоднозначной.
Всюду в дальнейшем (как и ранее) показатели виртуального (У,Л и
требуемого (Z, О качества результатов операции рассматриваются как чи-
словые векторы, включающие в себя три группы компонент. Как было от-
мечено в п. 2.3.2, показатели yn [i = l(l)/i] качества частных (единич-
ных) результатов операции могут свёртываться в обобщённые показатели
операционных свойств ЦНП - "аспектов". Однако такое свёртывание
допустимо лишь внутри группы компонент, относящихся к одному, обще-
му для всей группы аспекту. Реализация этого метода часто позволяет со-
кратить размерность п вектора Y, к (а следовательно, и вектора Z, ^) до
трёх и привести его к симплексной канонической форме (см. п. 2.3.2). Тем
не менее и в этом случае исследование эффективности ЦНПФС часто на-
талкивается на некоторые технические и вычислительные трудности.
В значительной мере преодолеть трудности позволяет метод ведущих
компонент. Раскроем его сущность.
Прежде всего подчеркнём, что в рамках этого метода ни одна из компо-
нент вектора Y. v (показателя качества результатов операции) не считается
главнее остальных, поскольку в соответствии с требованиями комплексно-
го подхода вектор Y, v включает в себя лишь показатели результатов опе-
рации, существенных для оценивания её эффективности в равной мере.
Вместо главной выделяются ведущие компоненты вектора Y, v.
3.3.12) Так, например, в наступательных операциях ведущая компонен-
та вектора Гм - показатель наносимого противнику ущерба, в оборони-
тельных операциях - показатель предотвращённого ущерба, в народнохо-
зяйственных операциях - показатель выпуска продукта, в экономических
операциях - показатель дохода (прибыли), в оперативных ЦНП - время,
потребное для достижения цели операции, и т.п. ▲

160 Глава 3. Методы оценивания эффективности ЦНП
Определение 3.3.1. Ведущими называются компоненты F/n, показа-
теля Y, v качества результатов операции, которые наиболее полно отра-
жают физическую сущность её цели. А
Остальные компоненты Y?*\ вектора L называются ведомыми. На
ведомые компоненты априори накладываются ограничения, и в дальней-
шем анализе они в явном виде не фигурируют, но участвуют через пара-
метры законов их распределений.
3.3.13) Следует подчеркнуть, что в соответствии с рассматриваемой по-
становкой задачи исследования эффективности операции ограничения, на-
лагаемые на ведомые компоненты Y,^ вектора К», задаются ведомыми
компонентами Zf ~ вектора Z,v требований к результатам (к их качеству)
операции, так что в отличие от задач математического программирования
и метода главной компоненты здесь ограничения стохастические (случай-
ные). ▲
Пусть, например, ведущие компоненты вектора F v образуют вектор
КЛч, а ведомые - вектор КЛч. Тогда интегральный закон апостериорного
(условного)распределения случайного вектора F/,v, относительно события2
будет определяться соотношением
где
^^ = %,г,^уУ'.,)=^К^К->^) (3-3.13)
- условный интегральный закон распределения случайного вектора Yf*
относительно события3
1 г»
В рамках конкретного исследования.
2
При условии его наступления.
Когда оно не случайно, а достоверно.

3.3. Методы свёртывания векторных показателей качества результатов ЦНП 161
3.3.14) Легко заметить, что соотношение (3.3.12) реализует формулу
полной вероятности в интегральной форме, где
dF^Z") - P(Z" = Z")= Р{Н2.) ;
ФггАГ;Г)=р{лг/нг)АЙ^) ;
Точка с запятой в равенстве (3.3.13) символизирует, что в этом выра-
жении вектор Y,~ играет роль параметра, а не аргумента, так что функции
(3.3.12) и (3.3.13) должны обладать всеми свойствами функций распреде-
ления [с учетом их определений (3.2.3)].
Напомним, что согласно используемой здесь символике [127, 169]
d
Ру1/у1(У\>'Уг)=Р(У1^У\/У1=Уг)>'
Рк7Н{Ух;Уг)=Р{у^Уг/ Уг^Уг);
Ру1±у,{у<;Уг)=Р{у1 ^ Уг /Уг * Уг)'
Поскольку в определении функций фДк) участвуют отношения <, >
двух типов, то в обозначении условного закона распределения
&ripft'>Y") используется символ ±. ▲
3.3.15) Выражение (3.3.12) получено на основе соотношения (3.2.10),
т.е. применительно к комплексно-симплексной (К-С) схеме исследования
эффективности операции (см. п. 3.4.3, [128]). Понятно, что аналогичное
(3.3.12) выражение может быть получено и на основе соотношения
(3.2.107), т.е. применительно к симплексно-комплексной (С-К) схеме ис-
следования. В этом случае подынтегральная функция будет определяться
равенством
и будет представлять собой условный интегральный закон распределения
случайного вектора Z',« относительно события H-\ff~^Z?*A-Hz.
Следует обратить внимание на различие отношений в (3.3.13) и (3.3.14).
▲
3.3.16) В дальнейшем в основном рассматривается К-С-схема исследо-
вания эффективности операций. В качестве упражнения рекомендуем чи-
тателю проанализировать и С-К-схему. ▲
6 Зак. 3303

162 Глава 3. Методы оценивания эффективности ЦНП
Если закон распределения ведущих компонент УЛ* показателя L ка-
чества результатов операции известен, то априорная вероятность достиже-
ния её цели будет определяться равенством
^=р{К'гЛ'))= ]••• ]^ЖМ' fcO <3-3-15)
или
Frm = J^ = M&W =м[а>{п')]= )<odF&M, (3.3.16)
О
а гарантируемая вероятность достижения цели операции - равенством
<г =^(1-у) = ^(у)- (3-3.17)
Здесь &'=d>^ = 0WH(z');
(п)
F^)^P{d)'<(o') = p(z^{Y%)= l{...JdF,,(Z% (3.3.18)
где {F'}^ - область значений вектора У' соответствующая значению (о\
граница которой Y/^(a/) = 0f}/н(а/) определяется решением уравнения
(см.п.З.2.1) Ф^^'^со'.
3.3.17) Если требуемые (предельно допустимые) значения ведомых
d
компонент детерминированы и заданы, т.е. Z^=Z^Jl, то
^Ы=П^ = П^(<-*Г)=> dF, (z;.})=f[S(z:-zr)
и формула (3.3.12) примет вид
Ф (Г)-Ф (i" .^я)-*'<->Ц?;2<^ G319^
где jfr«(fo*Z$).
Если, кроме того, заданы и требуемые значения ведущих компонент,
^, W-n^w-ft^ fe-*;77) => ^,(^))=п^;-г;я)
и согласно соотношению (3.3.15)

3.3. Методы свёртывания векторных показателей качества результатов ЦНП 163
Если ведущая компонента одна, т.е. я' = 1, то выражения (3.3.12),
(3.3.19) и (3.3.20) соответственно примут вид
f^_t)\ (л-1>/
¥(«-i) = № > у г у-> у i-x > Ум >•»> у,);
Алг /ллг луг /»лг /»>г ллг\
& („_l) — \^1 9 Z2 f»f Zi_x 9 Zi+l y*9 Z„ J 9
bM=*^jyt*tii=y \l{::\; (3.3.22)
РдЦ = р(у'^п)=Ф//н(г'п)=
. . Ф( {z'n;Z"")
*(-o
Пусть вектор К» задан в симплексной канонической форме KKv = F,3v и
при этом ведущая компонента ух. Тогда формулы (3.3.21), (3.3.22) и
(3.3.23) соответственно примут следующий вид:
со оо ф. (y;z19Z<s)
*A/-W- J J p (7 r \ dF^>Z3), (3.3.24)
где £«[(& **,)n(&££,)];
Ф'П/Н{У) = Ф^7Л^^)= <? ( , , (3.3.25)
где H-[(y2<z?)n(y3<z?)];
/^ = р(й>г,я)=1гЛ/„(г,я)=
-*>.гкМ^)- ^>z?) ■ (3.3.2а,
Поскольку распределение (3.3.24) одномерно и при этом
ф.Ух/н{у)=Р{у^у/н)=щ1/И{у),

164 Глава 3. Методы оценивания эффективности ЦНП
то согласно данным п. 3.1 и с учетом обозначения R-x/H(y)=Rh(y) фор-
мулы (3.2.10), (3.2.10'), (3.2.11), (3.2.12), (3.2.15), (3.2.16), (3.2.17), (3.2.20),
(3.2.20') соответственно примут следующие выражения:
р;„=/>&>£)=
где
\Rh{z)dF.x{z); (3.3.27)
foGOrfF^M, (3-3.271)
Rhb>)=Rh/Hiy); Fyiiy)=Fh/H{y)=l-R}x/H{y);
Fa>)=*>:>)J,fi;e(0,l|;
F^(<o)= Fh[Frl(a>)],a>e (0,1],•
Р;ц=Щ = Му=М[сЬЛ=)а><1Ру{<о), (/ = 1,2); (3.3.32)
0
\<»f(r)=**> W=Fj(i- r); (з.з.зз)
(3.3.28)
(3.3.29)
(3.3.30)
(3.3.31)
<M=
tf(r) = q(r)=FJ(l-r).
(3.3.33')
A
Рекомендуем читателю в качестве упражнения вывести аналогичные
формулы для случаев, когда ведущими компонентами являются у2 или
j>3 ] (см. пример 3.2.2).
3.3.18) Следует обратить внимание, что вероятности достижения цели
операции, определяемые соответственно соотношениями (3.2.10) и
(3.3.15), (3.2.19) и (3.3.26), (3.2.20) и (3.3.33), численно не равны. При этом,
поскольку в методе ведущих компонент эффективность ЦНП исследуется
при условии, что по ведомым компонентам цель операции уже достигнута
(в среднем), то получаемые в рамках этого метода оценки эффективности
операции представляют собой "потенциальные" условные вероятности
достижения её цели и, следовательно, принимают более высокие, чем пол-
ные его вероятности значения. Это обстоятельство необходимо учитывать
при абсолютном оценивании эффективности операции (т.е. при сравнении
1 Исследованию специального случая, когда ведущей компонентой является уъ,
посвящена монография [130].

3.3. Методы свёртывания векторных показателей качества результатов ЦНП 165
РДЦ с 1 ). Однако на решении задач её анализа и оптимального синтеза
ЦНПФС это не отражается, поскольку все вероятностные характеристики
(параметры распределения) ведомых компонент ГЛх и Zf ,v векторов
F/v и Z/v входят в выражения для показателей Р'дц, ф^ (^) "потенци-
альной" эффективности ЦНПФС. А
3.3.19) Если требования, предъявляемые к результатам (к их ведущим
компонентам) F/* операции детерминированные (неслучайные), т.е.
^Ц^,то(см.<ЗЗЛ2»
РдЦ=Ц = 0)'дгц(Г)=0)'г9 (/ = 1,2 ;7e [0,l]). (3.3.34)
А
3.3.4. ЭФФЕКТ ПОГЛОЩЕНИЯ
Как было показано, в общем случае вероятность достижения цели опе-
рации в симплексной канонической форме определяется соотношением
Рдц =Р%)Щ3^Р[{у1 >£,)n(j>2 <z2)n{y3 <z3)]. (3.3.35)
При этом, поскольку для получения эффекта j>, требуются ресурсы у2, и
время j>3, то компоненты вектора Е3\ связаны между собой очевидными
соотношениями
*.=*&»&)»• (3-3-36)
y3=siyi;yi), (3.3.37)
называемыми операционным функционалом (см. п.5.3).
До сих пор предполагалось , что векторы Гм и Z/ * взаимно независи-
мы. В действительности, как правило, так оно и есть. Однако в так назы-
ваемых "сплочённых операционных комплексах" (см. п. 2.6.2) все их эле-
менты "стремятся" к достижению одной и той же цели. При этом требова-
ния к некоторым результатам ЦНП заранее обусловлены его технологией,
возможностями ЦУТС и условиями проведения операции и заведомо
удовлетворяются. В таких случаях достижение цели операции по некото-
рым отдельным её результатам или "аспектам" оказывается достоверным
фактом, а соответствующий операнд в критерии пригодности результатов
операции "исчезает", поглощается остальными операндами. В результате
Интуитивно, согласно здравому смыслу.

166 Глава 3. Методы оценивания эффективности ЦНП
число п или К компонент показателя Y, » или F,Kv качества результатов
операции сокращается, т.е. происходит их "автоматическое" свёртывание,
и задача исследования эффективности ЦНП упрощается. Для большей на-
глядности проиллюстрируем проявление эффекта поглощения на ряде
примеров.
Пример 3.3.1. Пусть ЦНП организован так, что получаемый в его ре-
зультате целевой эффект всегда равен требуемому. Это означает, что орга-
низатор ЦНП (суперсистема) довольствуется получаемым эффектом, т.е.
zJ = у{. Формально это равносильно выполнению условия [ух = £,)~ U. В
этом случае критерий пригодности результатов операции (ее формализо-
ванная цель) принимает вид1
Gp: [foa$>fo£*)nfo^MK£3)n&£3)], (3.3.38)
где ] 1П ( \? \ - операционный функционал (см. п. 5.3). (3.3.381)
Соотношения (3.3.38) и (3.3.38') означают, что расходы ресурсов у\ и
времени у'ъ обусловлены требуемым целевым эффектом ъ[ и для дости-
жения цели операции необходимо и достаточно, чтобы эти расходы не
превзошли допустимых ($г и гъ соответственно). В результате уг и уъ
становятся ведущими компонентами вектора
*<э> = (*Г> Ут (%)> Уз/г (£))•
Закон их совместного распределения будет определяться соотношением
(см. <3.3.13>, (3.3.14»
оо
<\/я(Л'Л)= 1\,К(Уг>Уз}ь№*;(г1)=РХц(Уг>У3)> (3-3-39)
где Й~{у'х=г');
\,х{Уг*У*;ъ£ф'г * УгЫУг ± уМ%= «,)]=
При этом вероятность достижения цели операции
рдц = ] )фу;г)/н^3)<1ГЩг){г2г3)= } ]ргди{гг,гъ)йР^{1г,гъ), (3.3.40)
1 Вспомним, что AnU=A.

3.3. Методы свёртывания векторных показателей качества результатов ЦНП 167
где P*u(z2,Z3)= lP^{zlfz2,z3)dFri(zl) - условная вероятность достижения
цели операции при (z2 = z2 )П [z3 = z3). А
3.3.20) Совпадение обозначений функций (3.3.12) и (3.3.39) говорит о
том, что они имеют одинаковый смысл и, следовательно, в рассматривае-
мом случае также может быть определена гарантируемая вероятность
0)дЦ (у) достижения цели операции. Для упражнения рекомендуем сделать
это читателю. А
3.3.21) Отсутствие штриха в обозначении Рдц в (3.3.40) [см. (3.3.15),
(3.3.16)] говорит о том, что это выражение точное (значение Рдц не завы-
шено (3.3.18)), поскольку в отличие от (3.3.15) здесь условие Н - (j>, = zx)
достоверно. А
Пример 3.3.2.' Пусть ЦНП организован так, что расходуются все
имеющиеся ресурсы, т.е. (у2 = z2)~ U, где %г = у\. В этом случае
Gp: fa*il)n&Zll)nfoztt)]«\iytb%)n(%Zg$, (3.3.41)
где Л) Х/1 (\\\ " операционный функционал (см. п. 5.3). (3.3.4Г)
В результате
оо
фг(1}/н(У1>Уз)= \фцг)г/г{Ух>Уъ^г)^Г1{гг), (3.3.42)
где i *(# = £)?
%,Л{У1>Уг;*г)=Ф\ * УШ% * УМК = Z2)] =
у(%{у'^2,у3) ,
При этом
Рдц = ] ]^1)/я(*1^з)^,)(*1**з)= J ]P^(^z3)dFrJzl9z3\ (3.3.43)
где РдЦ(ь>ь)= \Pw{zx9z2yZ3)dFh{z2) - условная вероятность дос-
тижения цели операции при (£,' = zx) п (£3 = z3) . А
В этом и последующих примерах пояснения, аналогичные сделанным в примере
3.3.1, опускаются.

168 Глава 3. Методы оценивания эффективности ЦНП
Пример 3.3.3. Пусть ЦНП организован так, что операционное время
равно директивному (плановому), т.е. (у3 =z3)~U, где £3 = у*. В этом
случае
Gp: [(y^it)n(y2<z2)n(y3<z3)M(y[>C^(y^z2)], (3.3.44)
где
!:=',/з£Н (3.3.44-)
Уг = yi/3\Z3) )
- операционный функционал (см. п.5.3).
В результате
фу(2)/н(Уг>Уг)= )%/n(yi>yi;z3)dFi3{z3) , (3.3.45)
где й*(у'3=г;у,
%/n(yl,y2;zS=P[(y'l*y1)n(y2<y2)/(y'3 = z3)]=
При этом
рт = "\ ]%/я(г.»г2)^(2)(г„г2)= ] p^UpzJrfF^fe^), (3.3.46)
где РУДЦ (г,, г2) = |Рвд (г,, г2, г3 У^ (г3) - условная вероятность достижения
цели операции при (z[ = zx )п (г2 = г2). А
Пример 3.3.4. Пусть ЦНП организован так, что получаемый в его ре-
зультате целевой эффект всегда равен требуемому, но при этом расходу-
ются все имеющиеся ресурсы, т.е.
[(U=z,)n(j>z=z2)]=t/,
где £, = yf, z2 = у". В этом случае
GP: [&>zx)n(j2<z2)n(y3<z3)] = {y'3<z3), (3.3.47)
где
- операционный функционал (см. п. 5.3).
В результате
оо оо
Фу,1н{Уъ)=Гу31н(У>)= \ iFy^iys'-Zi'Zi^Fz-Jb'h), (3-3.48)
где Н = [{у" = гГ) п (у2 = £)];

3.3. Методы свёртывания векторных показателей качества результатов ЦНП 169
*>/*£, Cf3»**i»«2)= рШ ^ Уз)/{у"= г,)п(Х= Zl)]=
При этом
Рдц = ]^;/«(гэУ^(г3)= fcfe)^, (z3)> (3-3-49)
где /^(z3)= J J^iflCz^ZjjZj)^. (г,,г2) - условная вероятность дости-
—ее— оо
жения цели операции при (z3 = z3). A
Пример 3.3.5. Пусть ЦНП организован так, что получаемый в его ре-
зультате целевой эффект всегда равен требуемому, но при этом расходу-
ются все имеющиеся ресурсы, т.е.
где zx = j>f, z3 = $ • В этом случае
Gp : [(J), > zjnfa < z2)n{y3 < z3)\={y'2 < z2) , (3.3.50)
где
Уг=УцА?х>%) (3.3.50')
- операционный функционал (см. п. 5.3).
В результате
^/яОъЬ^/яОъЬ ] J^GvVSa)^,^) , (3-3-51)
где ^£[(j>r=zf)n(K=l3')];
d
= J^tt—г**-
- ^2)U„z3J
При этом
*w = К/я(г2)^(г2)= ]^(г2)^2(г2), (3.3.52)
—во —ев
во ев
где /да(г2)= J J^fa^^V^zfafa'^) - условная вероятность дости-
жения цели операции при (z2 = z2) • ^
Пример 3.3.6. Пусть ЦНП организован так, что расходуются все имею-
щиеся ресурсы и все плановое время, т.е. [(у2 = z2)r*{y3 = z3)] = U,

170 Глава 3. Методы оценивания эффективности ЦНП
где £2= Я> *з=.Уз- В этом случае
Gp: [(3>1>£Оп(3>2<^)п(Л<^)]=(^>^), (3.3.53)
где
у[ = УхпА%Л") (3.3.53')
- операционный функционал (см. п.5.3).
В результате
ФК/н{у1)=«К/н(Уг)= ] ]^;/%и;г2,гз)^Г)(г2,г3), (3.3.54)
где # = [(# = g)n{у" = %)];
При этом
^ = ]*k/«(z,)^;(z,)= P&fc^fe) , (3.3.55)
оо оо
где jP^(z,) = J \P^(zlfz29z3)dF^ (z2,z3) - условная вероятность дости-
жения цели операции при (£,' = z,) . ▲
Рассмотренные примеры охватывают все возможные варианты прояв-
ления эффекта поглощения при симплексной форме показателя К3\ каче-
ства результатов операции.
3.3,22) Следует заметить, что соотношения (3.3.39), (3.3.42), (3.3.45),
(3.3.48), (3.3.51), (3.3.54) носят весьма общий и потому в значительной ме-
ре условный характер, поскольку в конкретных случаях подынтегральные
функции этих выражений не обязательно имеют смысл условных законов
распределения (как в приведённых формулах), а могут иметь специфиче-
ские формы вероятностных характеристик ведущих компонент вектора
Y . Это обусловлено в первую очередь тем, что наряду с зависимостью ве-
дущих компонент Y виртуальных результатов Y ЦНП от ведомых ком-
понент Z требуемых его результатов Z и обусловленным этим вероятно-
стным поведением случайного вектора ж могут существовать независи-
мые от Z случайные факторы, также влияющие на стохастические
свойства ведущих компонент Y вектора Г.
Более подробно этот вопрос рассматривается в гл. 5, здесь же для иллю-
страции сказанного приведём ряд примеров. ▲

3.3. Методы свёртывания векторных показателей качества результатов ЦНП 171
Пример 3.3.7. Пусть в условиях примера 3.3.2 математическая модель
показателя К3, виртуального качества результатов ЦНП исчерпывающе
описывается соотношениями (3.3.4Г) (т.е. единственным источником слу-
чайности является предельно допустимый г"г уровень расхода ресурсов).
Тогда1
%1иЬ»Уг)=Фх *Ух)^{уг ^У3)]= Р[Ь>1/2(%>лЬМ&йУз)\ =
-J
\dFr(Zl). (3.3.57)
Пределы интегрирования в (3.3.57) обусловлены вытекающим из
(3.3.56) очевидным требованием
Ут («з) * З'Г/г (г,) => г3 ^ л/2Ь^ (г< Я • А
Пример 3.3.8. Пусть в условиях примера 3.3.6 математическая модель
показателя Е3, виртуального качества результатов ЦНП исчерпывающе
описывается соотношением (3.3.53') (т.е. случайных факторов, отличных
от (f*,Ij*), нет).
Тогда
= Р[{%,$е к,г3}„ J= JJ ^if,(*»*) ; (3.3.58)
Ъг = J
.V.3 ^ '*»
Я k *%(*»»*)
к
*■«(«.)•
(3.3.59)
Из (3.3.59) видно, что в данном случае равенства, аналогичного (3.3.57),
получить нельзя и, следовательно, для каждого конкретного случая реше-
ние будет иметь своё выражение. Пусть, например, ведущие компоненты
(*2»2з) вектора Z,3, связаны между собой имеющим достаточно ясную
1 Формулы (3.3.56) и (3.3.57) представляют собой варианты формул (3.3.42) и
(3.3.43) соответственно.

172 Глава 3. Методы оценивания эффективности ЦНП
интерпретацию соотношением z2= flz3 (т.е. предельно допустимые расхо-
ды ресурса и операционного времени пропорциональны) и пусть, кроме
того, j>,=jty2(«2)=az2-
Тогда ух =az2 = otj3z3 и, следовательно,
= P(afiz;>yi) = P\z"3>-Z
=*rJ-^h (3-3-60)
a>0j z\afi
p« = K(^)rfFri(«.)- (3.3.61)
A
Рекомендуем читателю найти аналогичные интерпретации в условиях
остальных приведённых выше примеров.
3.3.23) В замечаниях п. 3.3.1 практически все рассмотренные там спосо-
бы свёртывания компонент показателя качества результатов операции кри-
тиковались. Эта критика обусловлена в первую очередь тем, что свёрты-
ваемые "показатели эффективности" таковыми не являлись, так как опре-
делялись в разомкнутой схеме. Однако в принципе свёртывание действи-
тельных показателей эффективности операций представляется вполне кор-
ректным.
Ранее было постулировано, что в рамках рассматриваемой методологии
исследуемые операции одноцелевые. При этом многоцелевую операцию
(супероперацию) рекомендуется рассматривать как совокупность одноце-
левых операций (подопераций, субопераций), эффективности которых в
общем случае могут существенно различаться.
Если исследуется супероперация, направленная на достижение R целей,
то комплексный показатель её эффективности может быть определен соот-
ношением
^]? = 1>,/>й (3.3.62)
или
<?} = 2Х<%,)> (3.3.63)
где Р^ц - средняя (априорная) вероятность достижения r-й цели
операции;
Юдц&г) ~ гарантируемая с вероятностью уг условная (апостериорная)
вероятность достижения r-й цели операции;
v — коэффициент важности (вес) r-й цели операции.

3.3. Методы свёртывания векторных показателей качества результатов ЦНП 173
Чтобы показатели (3.3.62) и (3.3.63) имели смысл взвешенных вероят-
ностей, коэффициенты vr, должны удовлетворять условиям vr > О,
[г = l(l)if] и ]£ vr = 1, т.е. должны быть нормированными.
Легко заметить, что выражения (3.3.62) и (3.3.63) могут интерпретиро-
ваться как формулы полных вероятностей {средней и гарантируемой) дос-
тижения обобщённой цели (состоящей из R подцелей) супероперации.
При этом коэффициент vr имеет смысл вероятности гипотезы о том, что
супероперация имеет лишь одну r-ю цель, а вероятность Руц - смысл ус-
ловной вероятности достижения цели супероперации относительно этой
гипотезы. Понятно, что при такой трактовке достижения различных под-
целей супероперации считаются (подразумеваются, трактуются) несовме-
стными событиями (принцип суперпозиции).
Следует подчеркнуть, что ранжирование (взвешивание) целей супер-
операции семантически проще, чем ранжирование показателей качества
результатов операции или параметров и ЭТХ ЦУТС и ЦНПФС, так как бо-
лее ясны роли отдельных подопераций относительно всей их совокупно-
сти, чем влияние отдельных результатов операции или ЭТХ ЦУТС и
ЦНПФС на её эффективность. А
3.3.24) Отмеченная в (3.3.23) интерпретация структуры супероперации
(несовместность подопераций, реализующая принцип суперпозиции) при
использовании показателей (3.3.62) и (3.3.63) может быть отнесена к их
недостаткам, так как в принципе наряду с неравной важностью подцелей
супероперации наверняка различные комбинации (сочетания) достигнутых
подцелей вносят в достижение суперцели неодинаковый вклад.
Для учета этого обстоятельства комплексный показатель эффективно-
сти супероперации может быть определён соотношением
s=\
«Й*-!*,»^. (3-3-65)
s=l
вероятность достижения 5-й комбинации подцелей суперопера-
ции;
степень (например, условная средневзвешенная вероятность)
достижения суперцели при достижении 5-й комбинации подце-
лей супероперации;
оценка гарантируемой вероятности достижения суперцели при
достижении 5-й комбинации подцелей супероперации.
или
где Кс -
шдц

174 Глава 3. Методы оценивания эффективности ЦНП
Элементы формул (3.3.64) и (3.3.65) определяются следующими равен-
ствами:
tf _ p(rsi )p(rsi/rsi) pVSKs Л" ,Г« ""'r*(*,-«)J /ъ о f.f\
^Б^^ДЦ ГДЦ %,%ГДЦ ' \Э.ЭЛ)Ч)
где Рдц "'"' s{*s-l)) _ условная вероятность Л-й подцели в 5-й комбина-
ции относительно совместного достижения (Л-1)
предшествующих подцелей;
ГДЦ-1аУгвГДЦ >
vrj>0, г,=1(1)Л5; £v„=l
(3.3.67)
Показатель соДц' чёткой вероятностной интерпретации не имеет и мо-
жет определяться по-разному. Например:
*>=К<НО> (3-3-68)
где Rs - число подцелей в 5-й их комбинации, или
«№=-ф, k <ifJk )is. (3-3.69)
(3.3.70)
где {r5} - множество номеров rs подцелей супероперации, входящих в
5-ю комбинацию.
Заметим, что при определении Xs по (3.3.66) может не выполняться усло-
2R
вие ]£Х5 = 1 и соотношение (3.3.65) не будет интерпретироваться как фор-
мула полной вероятности. Однако, с одной стороны, это не обязательно, по-
скольку и в случае, когда показатели (3.3.64), (3.3.65) не могут трактоваться
как вероятности, они могут использоваться для сравнительного (относитель-
ного) оценивания эффективности супероперации, а с другой - этот недостаток
может быть устранён путём нормирования коэффициентов Х^ по формуле
Х,=-^-. (3.3.71)
Приведённые выражения (3.3.62) - (3.3.71) были определены эвристи-
чески и интерпретированы в вероятностных терминах. При более строгом
подходе для гарантированного от ошибок их применения необходимо бо-
лее детальное изучение их свойств. Тем не менее представляется, что при-
ведённая интерпретация обобщённых показателей (3.3.62) - (3.3.65) дос-
таточно аргументированна и их применение в задачах исследования эф-
фективности многоцелевых операций (суперопераций) правомерно. А

3.4. Методы вычисления показателей эффективности ЦНП 175
Знание людей заслуживает имени нау-
ки в зависимости от того, какую роль иг-
рает в нём число.
Э. Бор ель. "Вероятность и достоверность"
3.4. МЕТОДЫ ВЫЧИСЛЕНИЯ
ПОКАЗАТЕЛЕЙ ЭФФЕКТИВНОСТИ
ЦЕЛЕНАПРАВЛЕННЫХ ПРОЦЕССОВ
3.4.1. АНАЛИТИЧЕСКИЕ И ЧИСЛЕННЫЕ МЕТОДЫ
В предыдущих параграфах была дана математическая формулировка
задачи оценивания эффективности операции и приведены соотношения,
определяющие её показатели РДЦ и соГдц (у), однако ничего не говорилось
о вычислительных аспектах задачи оценивания эффективности. Понятно,
что они образуют самостоятельную проблему, соизмеримую по сложности
с концептуально-методологической, но носящую методико-технический
характер.
Итак, для вычисления показателей эффективности операции необходи-
мо реализовать формулы (3.2.10), (3.2.13), (3.2.17), (3.2.20)1 или (3.3.12),
(3.3.15), (3.3.16), (3.3.17) [см. (3.2.8), (3.3.15)]. На современном уровне раз-
вития прикладной математики это можно сделать одним из четырёх мето-
дов: аналитическим, численным, статистических испытаний (СИ), стати-
стического имитационного моделирования (СИМ)2. Кратко прокомменти-
руем их.
3.4.1.1. Аналитический метод
Аналитический метод основан на непосредственном интегрировании по
формулам (3.2.10), (3.2.13) и (3.2.17). Для реализации этого метода, естест-
венно, необходимо знать явные выражения для интегрируемой и интегри-
рующей функции фДк) и F^(z), а также необходимо, чтобы интегралы
имели выражения через элементарные функции (т.е. чтобы интегралы
"брались"). Методика решения задачи этим методом будет описана и про-
иллюстрирована на примере в п. 6.13.
В дальнейшем в силу аналогии будут рассматриваться лишь эти формулы.
2 В силу большой практической важности метода СИМ в задачах ВНЕПР его
рассмотрению посвящен отдельный п. 3.4.2.
3 См. также примеры 3.4.4, 3.4.5.

176 Глава 3. Методы оценивания эффективности ЦНП
3.4.1.2. Численный метод
Численный метод основан на численном интегрировании выражений
(3.2.10), (3.2.13) и (3.2.17). Понятно, что его реализация возможна лишь
при наличии ЭВМ. При этом поскольку, как известно, точность и время
решения задачи зависят от шага разбиения области интегрирования, то при
большой размерности п (или п*) вектора К л (или F/л) затраты вычисли-
тельных ресурсов (времени, памяти ЭВМ) могут оказаться значительными.
Следует заметить, что для определения гарантируемой вероятности
0)дц(у) достижения цели операции по формуле (3.2.20) полученное по
(3.2.13) выражение для функции распределения F w (со) может быть пред-
варительно аппроксимировано "подходящей" элементарной функцией.
При этом может оказаться, что интеграл (3.2.17) может быть вычислен
аналитически.
3.4.1.3. Метод статистических испытаний
Метод статистических испытаний основан на геометрическом способе
определения вероятности случайного события и её частотной интерпрета-
ции [63, 163, 173]. Для его реализации выражения (3.2.10), (3.2.13) и
(3.2.17) преобразуются соответственно к виду:
PM = \<09tl»{a>)da>. (3.4.3)
0
Из соотношений (3.4.1), (3.4.2), (3.4.3) видно, что эти интегралы чис-
ленно равны соответствующим гиперобъёмам тел, ограниченных областя-
ми интегрирования и поверхностями, описываемыми подынтегральными
функциями. Так, в (3.4.1) носителем \Z^\ распределения (областью воз-
можных значений) случайного вектора Z,^ и поверхностью, уравнение
которой
/.=/W=\^KW. (3-4.4)
в (3.4.2) - областью {У,3А и поверхностью распределения случайного век-
тора JL\ и поверхностью, уравнение которой

3.4. Методы вычисления показателей эффективности ЦНП 177
Из соотношения (3.4.3) видно, что определяемая им вероятность чис-
ленно равна площади, ограничиваемой отрезком [0,1] и кривой,
/з = /зИ=а>9&) И- (3.4.6)
Раскроем сущность рассматриваемого вычислительного метода на при-
мере. При этом для наглядности изложения будем считать область интег-
рирования одномерной.
Пример 3.4.1, Пусть требуется вычислить определённый интеграл вида
(рис. 3.4.1)
I=Sf{u)du,
(3.4.7)
где(Уи€[а,Л]) Ди)^)1.
Как видно из рис. 3.4.1, интеграл (3.4.7) численно равен площади (£,),
заштрихованной на рисунке области (S,).
Рис. 3.4.1
Введём в рассмотрение прямоугольник (Sv) со сторонами, параллель-
ными осям системы координат hOv, в котором целиком содержится об-
ласть (Sj) (т.е. как показано на рис. 3.4.1, h > maxf(u), ue [а,Л]), и неко-
и
торый случайный вектор (точку) (u,v) имеющий равномерный закон рас-
пределения в пределах области (Su).
Если теперь провести испытание, исходом которого будет реализация
(u,v) вектора (u,v), то вероятность Р, попадания точки (u,v) в область
Ограничение, обеспечивающее вероятностный смысл рассматриваемой задачи
(вычисляемых интегралов).

178 Глава 3. Методы оценивания эффективности ЦНП
(Sj) будет (согласно геометрическому определению вероятности) опреде-
ляться равенством [29]
Р,^~Ш = £-=', (3.4.8)
mes [Su) Sv (b-a)h
где mes(S) - мера области (*S);
откуда
1 = {Ь-а)кРЙ. (3.4.9)
Описанное испытание повторяется достаточно большое число п раз1.
После подсчета числа m{SI) попаданий точек /иу.,уу.\, [/=1(1)л , j - номер
испытания] в область (S,) определяется оценка Pt =m(Sl)/n вероятности
Pj и затем приближённое значение / интеграла / по формуле
I = {b-a)hPI~{b-a)hPI=I. (3.4.10)
Структурная схема алгоритма вычисления интеграла (3.4.7) методом
статистических испытаний приведена на рис. 3.4.2, где через ДЛ обозна-
чен датчик случайных чисел и>, равномерно распределённых на интервале
(0,1].
Поскольку стороны прямоугольника (5^) параллельны осям системы
координат и uOv (см. рис. 3.4.1), то компоненты случайного вектора («,v)
взаимно независимы и для их раздельного моделирования в приведенном
алгоритме реализован "метод обратной функции" [63, 163, 173]. При этом
блок 3 алгоритма (рис. 3.4.2) вырабатывает реализации и. случайной ве-
личины й, равномерно распределенной в интервале (а, Ь] , а блок 5 - реа-
лизации vj случайной величины v, равномерно распределенной в ин-
тервале (0, Н]. Блоки 2 и 8 ограничивают цикл моделирования, повто-
ряющийся п раз. Остальные блоки специальных пояснений не требуют.
Более подробно рассмотренный метод описан в книгах [63,163,173].
3.4.1) Поскольку описанный метод основан на статистическом оцени-
вании вероятности случайного события по его частоте (частости), то точ-
ность вычисления интеграла / этим способом зависит от числа п стати-
стических испытаний, а так как частота события априори является случай-
ной, то оценка этой точности должна быть вероятностной.
Пусть €pfH{l}= e1 - максимально допустимая с вероятностью /3 абсо-
лютная погрешность вычисления интеграла / при п испытаниях, т.е. в
терминах математической статистики е! - это половина длины довери-
тельного интервала для интеграла / при доверительной вероятности J3 и
объёме выборки п.
Обеспечивающее требуемые точность и надёжность оценки [173].

3.4. Методы вычисления показателей эффективности ЦНП 179
Вычисление
Вывод
7
1/=(*-а)А/>
В -0L
'- п
Рис. 3.4.2
Поскольку
/ = (*-а)йР7,
то границы доверительных интервалов для / и Р/ связаны соотношением
1+ер>п{1}={ь-а№.+ерЛр,})>
из которого следует
е' =ePMXb-a)hep,n{p,} (3-4.11)

180 Глава 3. Методы оценивания эффективности ЦНП
или
е'
*'^><}=(^)А- (ЗА12)
Поэтому для вычисления (оценивания) интеграла с точностью не
ниже е' при доверительной вероятности /3 необходимо число п1 испыта-
ний, определяемое следующим соотношением [169]:
где tp -табличная функция [169].
Как видно из (3.4.13), для определения потребного объема п! испыта-
ний необходимо знать Р, (или, что то же самое, / ). Однако именно эти
величины и вычисляются и, следовательно, формула (3.4.13) непосредст-
венно неприменима. Поэтому вначале "на глаз" определяется приближён-
ное значение
Pj = mes yS, J/mes ySy J,
где mes(S) - мера области S.
По значению Pt находится первое приближение числа п':
и* •
которое затем уточняется по результатам испытаний [Pt). Если окажется, что
п' >п', то никаких уточнений п' не требуется и используется число п'.
Подробно вопросы статистического оценивания освещены в пособиях
[170] и [173]. А
Изучив (уяснив) приведённый пример, не представляет труда обобщить
реализованную в нем методику вычисления интеграла на рассматриваемые
случаи (3.4.1), (3.4.2), (3.4.3). Так, в формуле (3.4.3) элементы примера
3.4.1 имеют следующие выражения: (a,b]= (0,l]; /3(«)= и0^<з> («) (блок 3).
Поэтому блок 2 алгоритма (рис. 3.4.2) моделирует случайную величину й
по формуле иj = w., а блок 5 проверяет условие v. < и. <p&{i) (ny), [/=1(1)л].
В формуле (3.4.1) роль интервала (a,b] играет носитель \ZfLj распре-
деления случайного вектора Z/3v, на котором равномерно распределён слу-
чайный вектор U,3x, моделируемый блоком 2. Блок 3 вычисляет значения
а блок 5 сравнивает их со значениями v., выработанными блоком 4.

3.4. Методы вычисления показателей эффективности ЦНП 181
Напомним, что должно выполняться условие h > тахв л/гу^Ш-
В формуле (3.4.2) роль интервала (a,b\ играет область \У/г\\ , в которой
равномерно распределён вектор UJZ), моделируемый блоком 2. Блок 3 вы-
числяет значения
а блок 5 сравнивает их со значениями v., выработанными блоком 4.
Остальные блоки алгоритма работают, как показано на рис. 3.4.2.
В данном пункте была рассмотрена сущность аналитического и числен-
ного методов оценивания эффективности операций. С деталями соответст-
вующих методик читатели могут ознакомиться по специальной литературе
[63, 179].
3.4.2. МЕТОД СТАТИСТИЧЕСКОГО ИМИТАЦИОННОГО
МОДЕЛИРОВАНИЯ
Как нетрудно было заметить, для реализации рассмотренных в п. 3.4.1
методов необходимо знать явные выражения подынтегральных функций
или, другими словами, законов распределения фДг), F%{z) и F&{(o) век-
торов K3v, Z/3s и супериндикатора &F'. Подобная необходимость сущест-
венно ограничивает сферу применимости этих методов, что обусловлено
причинами двух типов:
а) необходимостью постулирования (принятия) целого ряда допущений,
без которых аналитическая модель не может быть построена и которые,
как правило, достаточно трудно строго обосновать. Единственным руково-
дящим принципом при построении моделей в этих случаях является
"принцип аналогий и правдоподобности рассуждений" [135], правомер-
ность которого существенно зависит от компетентности и опыта исследо-
вателя и ЛПР. В связи с этим вопрос об адекватности математической мо-
дели исследуемому объекту (ЦУТС и ЦНПФС) часто не получает удовле-
творительного решения и остаётся открытым;
б) сравнительной технической сложностью решения задачи (в том чис-
ле и при допущениях), требующей от исследователя высокой математиче-
ской подготовки.
3.4.2) Следует подчеркнуть, что хотя "принцип правдоподобности рас-
суждений" может показаться недостаточно убедительным для обоснования
адекватности модели, тем не менее он лежит в основе всех научных иссле-

182 Глава 3. Методы оценивания эффективности ЦНП
дований, во всяком случае, на первой их стадии, когда объективных - экс-
периментальных данных об исследуемом явлении еще недостаточно и мо-
дель явления строится на основе прошлого опыта и научной интуиции ис-
следователя. Понятно, какое большое значение на этом этапе имеет компе-
тентность исследователя и ЛПР, обусловливающая основанную на их опы-
те объективность эвристических (экспертных) данных, используемых при
построении исходных вариантов моделей. А
Известно, что критерием истины является опыт, т.е. эксперимент над
исследуемым объектом (ЦУТС, ЦНПФС), позволяющий наиболее полно
изучить его свойства и оценить качество (см. п. 2.5). Однако проведение
подобных экспериментов наталкивается на препятствия принципиального
характера двух существенно различных типов:
а) необходимостью априорного оценивания качества объекта, так как
наибольший интерес качество объекта (ЦУТС, ЦНПФС) представляет на
этапах его проектирования (планирования) и создания (организации), т.е.
когда объекта ещё нет, но прогноз его качества уже необходим;
б) трудностью экспериментальных исследований качества сложных, до-
рогостоящих и особенно уникальных (единичных) объектов, так как они
зачастую не могут быть подвергнуты испытаниям, проводимым в услови-
ях, близких к реальным (в которых объект призван выполнять свои функ-
ции), и сохраняющим в то же время проектное качество объектов.
По этим причинам широкое применение нашли методы исследования
объектов на их моделях. Различают модели аналитические и имитаци-
онные.
Модели первого типа представляют собой совокупности математиче-
ских зависимостей и соотношений, описывающих основные свойства объ-
екта, взаимосвязи этих свойств и взаимодействия объекта со средой, т.е. с
условиями его функционирования и целевого применения. Таким образом,
это модели математические (см. п. 3.4.1).
Модели второго типа делятся на "физические", "математические" и
"смешанные" и согласно их названию призваны имитировать процесс це-
левого функционирования объекта.
Физические имитационные модели представляют собой либо образец
исследуемого объекта, либо его копию (часто выполненную в меньшем
масштабе), исследуемые свойства которой подобны (адекватны) аналогич-
ным свойствам моделируемого объекта.
Математические имитационные модели строятся с применением вычис-
лительной техники (аналоговой или цифровой). Они, как правило, совер-
шенно не похожи на моделируемые объекты, но, как и у физических моде-
лей, количественные характеристики их динамических свойств (свойств,
проявляющихся при целевом применении объекта) подобны (адекватны)
соответствующим свойствам моделируемого объекта.

3.4. Методы вычисления показателей эффективности ЦНП 183
Смешанные имитационные модели представляют собой комплексы,
элементы которых являются либо физическими, либо математическими
моделями, имитирующими функционирование (работу) элементов (агрега-
тов, подсистем) моделируемых объектов.
Поскольку по отмеченным выше причинам физическое моделирование
сложных объектов (ЦУТС, ЦНПФС) не всегда возможно, особенно на
этапах проектирования ЦУТС и планирования ЦНПФС, то наиболее дей-
ственным методом их исследования является метод математического ими-
тационного моделирования. Как было отмечено, для решения задач опти-
мального проектирования и построения ЦУТС, а также планирования и ор-
ганизации ЦНПФС необходимо прогнозировать их качество и эффектив-
ность в условиях значительной неопределённости, обусловленной недоста-
точностью на этих этапах информации об условиях функционирования и
применения ЦУТС. Эти обстоятельства приводят к необходимости, в це-
лях обеспечения модели достаточной адекватности, имитировать и реально
существующую неопределённость, обусловленную воздействием на пара-
метры и ЭТХ ЦУТС и ЦНПФС случайных факторов. Способ, позволяю-
щий исследовать операции (ЦНПФС) с учётом воздействия таких факто-
ров, получил название метода статистического имитационного моде-
лирования.
В дальнейшем предполагается, что читатель знаком с сущностью как
метода статистических испытаний (СИ) (см. п. 3.4.1.3), так и метода стати-
стического имитационного моделирования (СИМ) [63, 94, 136, 163, 173].
Поэтому здесь рассматривается методика применения метода СИМ лишь к
решению задач исследования эффективности операций (ЦНПФС).
Для реализации метода СИМ строится так называемая имитационная
модель ЦНПФС, отображающая его в формализованной форме с помощью
алгоритмического описания (которая, как правило, реализуется на ЭВМ).
Таким образом, имитационная модель - это алгоритм работы ЭВМ, моде-
лирующий, т.е. приближенно воспроизводящий, ЦНПФС (его протекание
во времени) или его отдельные этапы, стадии, фазы, циклы. При этом эле-
ментарные явления, образующие ЦНПФС, т.е. этапы ЦНП и происходящие
в его ходе события имитируются с сохранением их логических связей и
последовательности протекания во времени, а также характера и состава
информации о последовательных соотношениях и событиях процесса.
Влияние случайных факторов на ЦНПФС имитируется путём моделирова-
ния случайных объектов (событий, величин, векторов, функций, полей) с
обусловленными характером протекания процесса вероятностными харак-
теристиками. Эти характеристики, в свою очередь, определяются в процес-
се "функционирования" имитационной модели ЦНПФС. При реализации
моделирующего алгоритма на ЭВМ вырабатывается информация, описы-
вающая элементарные события и этапы процесса с учётом их связей и вза-
имных влияний. Затем эта информация используется для определения

184 Глава 3. Методы оценивания эффективности ЦНП
(оценивания) исследуемых характеристик ЦУТС и ЦНПФС. Весьма глубо-
ко и детально сущность метода СИМ раскрыта в пособиях [63, 173]. По-
этому здесь мы ограничимся сказанным и перейдём к рассмотрению мето-
дики оценивания эффективности ЦНПФС (операции).
Итак, требуется разработать алгоритм, моделирующий ЦНПФС и по-
зволяющий определять (вычислять) показатели РДЦ и 0)дЦ(у) его эффек-
тивности.
Поскольку показатели эффективности операции представляют собой
вероятности некоторых случайных событий, то их оценками, обладающи-
ми всеми необходимыми свойствами (состоятельность, несмещённость,
"эффективность" [170, 173]), являются частоты (частости) появления этих
событий в "длинных" сериях однородных опытов (испытаний). Как было
показано в п. 3.4.1.3, такие оценки могут быть получены методом стати-
стических испытаний. Однако при реализации метода СИМ испытаниям
подвергаются не абстрактные модели стохастических экспериментов, у ко-
торых лишь некоторые параметры численно равны оцениваемым характе-
ристикам исследуемого объекта [или связаны с ними известными зависи-
мостями (см. пример 3.4.1)], а модели конкретных ЦУТС и ЦНПФС, во
всех существенных деталях количественно адекватные реальным или соз-
даваемым (организуемым) ЦУТС (ЦНПФС).
Как видно из (3.2.10), вероятность Рдц может вычисляться двумя путя-
ми (способами) и, следовательно, статистически может оцениваться по
двум схемам (алгоритмам), называемым соответственно комплексно-
симплексной (К-С) и симплексно-комплексной (С-К) схемами1. Структур-
ные схемы алгоритмов статистического имитационного моделирования
ЦНПФС по К-С и С-К схемам приведены соответственно на рис. 3.4.3 и
3.4.4. При описании работы алгоритмов ограничимся рассмотрением лишь
К-С схемы (рис. 3.4.3). В целях активизации процесса изучения предмета
рекомендуем читателю "параллельно" провести аналогичные рассуждения
применительно к С-К схеме (рис. 3.4.4).
Как видно из рис. 3.4.3, алгоритм включает в себя два цикла:
- внешний цикл - по у, (у, - номер испытания во внешнем цикле),
повторяющийся Nx раз;
- внутренний цикл - по у2 (у2 - номер испытания во внутреннем
цикле), повторяющийся в каждом у, -м внешнем цикле N2 раз.
Рассмотрим последовательность работы блоков алгоритма.
Блок 1 осуществляет ввод исходных данных, необходимых для стати-
стического имитационного моделирования ЦНПФС и статистического
оценивания показателей его эффективности.
Смысл этих терминов раскрывается в п. 3.4.3.

3.4. Методы вычисления показателей эффективности ЦНП 185
О
Ввод исходных данных
NUN2,L
Q=
ix •=!
О
Iff i •=ttt. +1
©
Вывод
Вывод
Рдц&тЬ)
©
u/ nit — "Л,
ЛДО wlNt-L+\
0—L_
гдц M lsw\jx
У1-=Л+1
Рис. 3.4.3

186 Глава 3. Методы оценивания эффективности ЦНП
Набор этих данных зависит от этапа жизненного цикла ЦУТС, на котором
проводится исследование ЦНПФС, и обусловленного этим характера имею-
щейся у исследователя информации (детерминированная, случайная, неопре-
делённая, вероятностная и т.п.).
Блок 2 (вспомогательный) организует начало внешнего цикла, засылая в
счётчик циклов единицу.
Блок 3 (стохастический) моделирует вектор Ж.к требуемых (предельно
допустимых) значений результатов L операции.
Блок 4 (вспомогательный) организует начало внутреннего цикла, засылая в
счётчик циклов единицу и очищая счётчик числа т^ "успешных" испытаний
(в которых при фиксированных требованиях Z/\ к результатам операции бы-
ла достигнута её цель) внутреннего цикла (полное число которых равно N2).
Блок 5 (стохастический) моделирует вектор L виртуальных результатов
операции.
Блок 6 (логический) реализует критерий пригодности результатов опера-
ции для использования по назначению. Выполнение проверяемых блоком 6
условий означает достижение цели операции [см. (2.3.3), (2.3.4), (2.3.15),
(3.2.6)].
Блок 7 (счётчик) подсчитывает число т. "успешных" испытаний внутрен-
него цикла.
Блок 8 (счётчик) подсчитывает число у2 пройденных испытаний внутрен-
него цикла (нумерует текущее испытание внутреннего цикла).
Блок 9 (логический) устанавливает факт окончания внутреннего цикла ис-
пытаний.
Блок 10 (арифметический) вычисляет оценку щ") значения условной (апо-
стериорной) вероятности щ"' достижения цели операции в у, -м испытании
внешнего цикла.
Блок 11 (счётчик) подсчитывает число jx пройденных испытаний внешне-
го цикла (нумерует текущее испытание внешнего цикла).
Блок 12 (логический) устанавливает факт окончания внешнего цикла испы-
таний.
Блок 13 (арифметический) вычисляет значение оценки РДЦ средней (апри-
орной) вероятности достижения цели операции.
Блок 14 (логический) определяет значение оценки б)[дц (у) гарантируемой
вероятности достижения цели операции.
Блок 15 осуществляет вывод полученных в ходе статистического имитаци-
онного моделирования оценок Рдц, 8)[дц(у) показателей Рдц, со[дц(у)
эффективности операции.

3.4. Методы вычисления показателей эффективности ЦНП 187
0
Ввод исходных данных
NlyN2,L
0
Л-1
«л .-=0
Ф
Iff , .*= Iff , +1
О
Вывод
0
а'=ф
ДЦ W2N2-L+1
X
0 L_
р =—ys(,,>
iV2 Л=1
0
Л--Л + 1
0
2л- iv,
тТ^М
0
У1--У1+1
Рис. 3.4.4

188 Глава 3. Методы оценивания эффективности ЦНП
Приведённого описания алгоритма, моделирующего ЦНПФС, вполне
достаточно для уяснения общей идеи метода СИМ, однако для практиче-
ской её реализации необходимо раскрыть содержание блоков 3, 5 (пред-
ставляющих собой самостоятельные моделирующие алгоритмы) и блока
14 (являющегося логическим блоком с одним выходом), реализуемых спе-
циальными подпрограммами.
В зависимости от этапа жизненного цикла ЦУТС, на котором оценива-
ется эффективность ЦНПФС, а также от класса ОК (сплочённый или ра-
зобщённый, см. п. 2.6.2) вероятностное описание требований Z.k , предъ-
являемых к результатам Y, ч операции, может задаваться в различных
формах. В частности, оно может быть задано в форме закона распределе-
ния F% \Z,A случайного вектора Z, v или закона распределения
F& \В(Г}) случайного вектора Bfa характеристик условий применения
ЦУТС, компоненты которого могут быть как количественными, так и "ка-
чественными" (например, иметь лишь несколько градаций без указания
"расстояния" между ними либо только две градации - {0,1} и т.п.). При
этом должны быть заданы зависимости (не обязательно аналитические),
связывающие векторы В,* и Z, v [см. (2.3.12), (3.2.8)]. Если, кроме того,
требования к результатам ЦНПФС предъявляются с учетом возможностей
ЦУТС в сплочённых ОК (см. п. 2.6.2), то должны быть описаны как связи
вектора Z.x с A,k, - ЭТХ ЦУТС и ЦНПФС, так и взаимосвязи его компо-
нент между собой, которые в этом случае имеют место (см. {2.7.7},
{2.7.8}). Если указанные описания есть, то структурная схема алгоритма,
моделирующего случайный вектор Z. ч, будет иметь вид рис. 3.4.5, где
вектор Bif* моделируется подблоком 3.1 с помощью известных методов
[63,170,171,173].
Если условия В,гк проведения операции неуправляемы, то обусловлен-
ный ими вектор Z, ч описывает объективные (не зависящие от ЛПР) тре-
бования к её результатам, которые для достижения цели операции должны
быть выполнены. Поскольку требования к различным операционным
свойствам (аспектам) результата операции обусловлены не связанными
между собой факторами (см. {2.7.7}), то компоненты вектора Z,, ока-
зываются взаимно независимыми. В этом случае, если законы распределе-
ния Ft(z), [* = l(l)#i] компонент zt случайного вектора Z,x известны, то
алгоритм блока 3 примет вид рис. 3.4.6, где ДА - датчик случайных чисел,

3.4. Методы вычисления показателей эффективности ЦНП 189
Рис. 3.4.5
распределённых равномерно на интервале (0,l]. Работа остальных подбло-
ков блока 3 наглядно описывается их начертанием [169].
3.4.3) Выше было сделано предположение о том, что вероятностное
описание вектора Z.k задаётся в форме закона распределения, однако ни-
чего не говорилось о том, как этот закон распределения определять. Мето-
дика определения закона распределения существенно зависит от этапа
жизненного цикла ЦУТС, на котором оценивается эффективность
ЦНПФС, и от обусловленной этим информации, которой располагает ис-
следователь. Рассмотрению подобной методики (её сущности) посвящен
п. 5.5. А
Теперь раскроем содержание блока 5. Функцией этого блока является
моделирование случайного вектора Г, ч, т.е. показателя качества результа-
тов, получаемых вследствие расходования на них ресурсов. Насколько ра-
ционально (действенно, эффективно) в ходе операции ресурсы превраща-
ются в целевой эффект, настолько эффективен ЦНПФС. Поэтому исход-
ными данными для алгоритма, реализуемого блоком 5, являются все пара-
метры и ЭТХ ЦУТС и ЦНПФС, влияющие на процесс преобразования ре-
сурсов в целевой эффект, а его ядро ("тело") образуют соотношения, опи-
сывающие взаимные связи всех элементов операционной системы (см. п.
1.2), т.е. связи ЭТХ ЦУТС и ЦНПФС как между собой, так и с операцион-
ными свойствами ЦНПФС, а также связи ресурсов с целевым эффектом и

190 Глава 3. Методы оценивания эффективности ЦНП
Рис. 3.4.6
между собой. Последние зависимости называются "операционным функ-
ционалом"1.
На рис. 3.4.7 приведена структурная схема алгоритма, реализуемого
блоком 5. Из рис. 3.4.7 видно, что подблок 5.1 моделирует условия функ-
ционирования ЦУТС, характеристики которых описываются случайным
вектором BL. Подблок 5.2 моделирует влияние условий функционирова-
ния на параметры и ЭТХ ЦУТС и ЦНПФС. Подблок 5.3 моделирует влия-
ние на результат операции ЭТХ ЦУТС и ЦНПФС и условий функциониро-
вания ЦУТС, а также взаимное влияние расходуемых в ходе операции ре-
сурсов и зависимость от них получаемого целевого эффекта.
Подробно об этом говорится в п. 5.3.

3.4. Методы вычисления показателей эффективности ЦНП 191
3.4.4) Строго говоря, именно блок 5 моделирует ЦНПФС и поэтому яв-
ляется "главным" блоком алгоритма рис. 3.4.3. А
Рис. 3.4.7
Теперь о блоке 14, который выше был назван логическим. Как известно
(см. п. 3.1), по определению супериндикатор
представляет собой условную вероятность достижения цели операции от-
носительно случайного события \Z,n\-Z,\ при реализации (наступле-
нии) которого она принимает значение
При реализации К-С алгоритма (К-С схемы, рис. 3.4.3) во внешнем
цикле фиксируется значение ZK вектора Z,, и по частоте дйг") появления

192 Глава 3. Методы оценивания эффективности ЦНП
событий (f/2v^Z/\) оценивается значение условной вероятности щт\ вы-
числяемой блоком 10. В результате реализации внешнего цикла TV, раз
вырабатывается последовательность
-P'(Y^Z^)=^l=^-. (3.4.14)
Пусть у - гарантийная вероятность (уровень гарантии), определяемая
равенством
Г=р[Ми) * *>r(r)]= *^ W{y)\. (3.4.15)
Приближённо её можно оценить по частоте события [coy. >0)г(у)] в
серии TV, испытаний, т.е.
y~p-[6t:l>a>r(r)]=±=f,
где L - число испытаний, в которых произошло событие [щ] ^ &г{у)\\
/"-частотасобытия [u)\j > CDr(y)] (см. рис. 3.4.8).
Потребуем выполнения неравенства
у = — >у.
TV, '
Тогда L = E(yNl)+l9 где Е(и) - целая часть и. При этом в образующей
вариационный ряд упорядоченной последовательности щ"' ,[r = l(l)TV,],
такой, что (off <(o\^ (где г -ранг порядковой статистики [170, 173]), по-
рядковая статистика йг„_ш, занимающая в вариационном ряде по величи-
не (TV, - L + l)-e место (имеющая (TV, - L + 1)-й ранг), будет иметь не левее
себя L членов вариационного ряда ш\^\щ\...9а)^\, т.е. их — = у-ю
часть (см. рис. 3.4.8). Таким образом, порядковая статистика ю„_ы может
служить оценкой наименьшей вероятности о>дЦ{у) достижения цели опе-
рации, гарантируемой с вероятностью у, т.е.
<(r) = ^M=«fei- (34.17)
Поскольку для определения оценки 8)дЦхУ) необходимо упорядочение
выборки a){j , [/, =l(l)TVj и определение её конкретного члена, то реали-
зующий эту процедуру блок 14 является логическим блоком.

3.4. Методы вычисления показателей эффективности ЦНП 193
*.<»
N-L + X
N
О Щ оу2
N-L+1
Рис. 3.4.8.
3.4.5) В принципе рассмотренный алгоритм, моделирующий ЦНПФС,
может быть реализован и в случае, когда законы распределения фДк) и
F^(z) случайных векторов L и Z.x известны и их моделирование про-
изводится обычными методами [63, 163, 173], минуя моделирование соб-
ственно операции, либо по алгоритму типа рис. 3.4.6, либо по алгоритму,
учитывающему стохастическую зависимость компонент векторов L и
Z/v. В этом случае, строго говоря, модель ЦНПФС и реализующий её ал-
горитм перестают быть имитационными и становятся просто статистиче-
скими, поскольку моделироваться будут лишь виртуальные и требуемые
результаты операции, а не сам ЦНПФС и реализующая его ЦУТС, описы-
ваемые характеристикамиАк,9 В,*. Другими словами, в этом случае будет
реализоваться метод статистических испытаний и с его помощью будут
оцениваться вероятности РДЦ и содц(у) по соответствующим частотам
3.4.6) Если ЦНПФС носит массовый характер (операция многоразового
применения) и при этом число N будущих операций велико, то удовле-
творительной мерой его эффективности может служить лишь априорная
(средняя) вероятность Рдц = аг' достижения цели операции. В этом слу-
чае гарантируемая вероятность й)дц(у) может не оцениваться, модели-
рующий алгоритм упрощается и принимает вид рис. 3.4.9, который специ-
альных пояснений не требует. А
7 Зак. 3303

194 Глава 3. Методы оценивания эффективности ЦНП
О
Ввод исходных данных
0
Л^у
N
j:=l; m:=0
0
О
©
Вывод
1 ДЦ
р =
гдц
т
D
/.•=;+!
hi := w +1
Рис. 3.4.9
3.4.3. АНАЛИЗ СХЕМ ИМИТАЦИОННЫХ ИСПЫТАНИЙ
3.4.3.1. Классификация схем испытаний
В предыдущем пункте фигурировало понятие "схемы испытаний" ис-
следуемых объектов (ЦУТС и ЦНПФС), однако без достаточных для по-
нимания его сущности комментариев. Восполним этот пробел и раскроем
семантику (физический смысл) этого понятия. Для большей наглядности

3.4. Методы вычисления показателей эффективности ЦНП 195
рассуждений будем полагать, что показатель качества результатов опера-
ции скалярный1, т.е. L = у, Z,^ = z. Обратимся вновь к показателю эф-
фективности операции. В рассматриваемом (одномерном) случае он будет
иметь следующее выражение:
Рдц=ННг)> (3.4.18)
где у - значение характеристики виртуального результата (достижимого
качества) операции;
z - значение характеристики необходимого результата (требуемого
качества) операции.
Структура выражения (3.4.18) призвана подчеркнуть, что в зависимости
от физического смысла операции для достижения её цели виртуальный ре-
зультат у должен быть не меньше или не больше некоторого необходи-
мого (требуемого - предельно допустимого) значения z, т.е. при проведе-
нии операции может реализоваться соответственно один из двух принци-
пов: "чем больше, тем лучше" или "чем меньше, тем лучше". В первом
случае выражение (3.4.18) имеет вид
Pm=P{y>z), (3.4.19)
во втором случае -
Рдц=Р(у<г), (3.4.20)
Таким образом, величина z определяет уровень результата операции,
преодоление которого величиной у означает достижение её цели.
В общем случае любая из величин у, z (или обе) может оказаться как
детерминированной, так и случайной, поэтому оценивание результата опе-
рации будет сводиться к проверке выполнения одного из четырёх нера-
венств, приведённых в обобщённой форме в табл. 3.4.1. Эти неравенства
определяют четыре2 схемы3 оценивания качества результата операции:
- симплексно-симплексная (С-С) схема определяет оценку качества ре-
зультатов операции, проводимой ЦУТС с детерминированными (неслу-
чайными) характеристиками (ЭТХ), т.е. в детерминированных условиях
функционирования, при детерминированных (неслучайных) требовани-
ях к результатам ЦНПФС, т.е. при детерминированных условиях приме-
нения ЦУТС;
1 Реализован метод ведущих компонент (см. п. 3.3.3).
2 В предложении, что все компоненты вектора К v или Z, v обладают однотипны-
ми вероятностными свойствами.
3 В обозначении схемы первая компонента относится к виртуальному результату,
вторая - к требуемому.

196 Глава 3. Методы оценивания эффективности ЦНП
- симплексно-комплексная (С-К) схема определяет оценку качества ре-
зультатов операции, проводимой ЦУТС с детерминированными (неслу-
чайными) характеристиками, при неопределённых (случайных) требова-
ниях к её результатам (в неопределённых условиях применения ЦУТС);
- комплексно-симплексная (К-С) схема определяет оценку качества ре-
зультатов операции, проводимой ЦУТС, свойства (ЭТХ) которой под-
вержены воздействию случайных факторов (в неопределённых условиях
функционирования ЦУТС), при детерминированных (неслучайных) тре-
бованиях к её результатам;
- комплексно-комплексная (К-К) схема определяет оценку качества ре-
зультатов операции, проводимой ЦУТС, свойства (ЭТХ) которой под-
вержены воздействию случайных факторов (в неопределённых условиях
функционирования ЦУТС), при неопределённых (случайных) требова-
ниях к её результатам (в неопределённых условиях применения ЦУТС).
Схема К-К является самой общей, так как с наибольшей полнотой от-
ражает действительные условия, в которых проводится операция, и апри-
орное оценивание её эффективности как на этапах планирования и органи-
зации, так и на этапе проведения операции. Три остальные схемы пред-
ставляют собой различные варианты её идеализации и упрощения.

3.4. Методы вычисления показателей эффективности ЦНП 197
3.4.3.2. Выбор схемы имитационных испытаний
В п. 3.2.1 рассматривалось аналитическое решение задачи оценивания
эффективности операции. При этом в рамках соотношений (3.2.10) реали-
зуется К-К схема оценивания. Однако, как было отмечено, из-за сложно-
сти определения законов распределения фДк) и F^(z) аналитическое
решение не всегда возможно. В таких случаях оценивание эффективности
операции осуществляется методом статистических испытаний или мето-
дом статистического имитационного моделирования ЦНПФС.
В зависимости от объема и характера исходных данных, а также имею-
щихся у исследователя средств (математических - формулы, методики и
т.п., технических - ЭВМ, вычислительные устройства и т.п.) может воз-
никнуть ряд типичных ситуаций. Рассмотрим некоторые из них, для опре-
деленности полагая, что достижение цели операции равносильно выполне-
нию неравенства (наступлению события) у < z, а в качестве показателя её
эффективности используется средняя (априорная, безусловная) вероят-
ность достижения цели
P„=P{y*z)= fF,(*)rfF£(«)=24 ,
d
где Wx=F-y(z)
или
РДЦ = Р(2>у)= )ъ(у)<1Р,{у)=щ,
где m2=F.{z).
1. Пусть поставлена задача: оценить эффективность проводимой
ЦУТС операции, подверженной воздействию случайных факторов (в слу-
чайных условиях функционирования - Щг\)9 в детерминированных усло-
виях применения ЦУТС - Bt!L.
Как было показано в п. 3.4.2, при определении вероятности достижения
цели операции методом статистического имитационного моделирования
(СИМ) моделируются параметры и ЭТХ ЦУТС и частота, оценивающая
вероятность, находится как отношение "числа систем", выполнивших за-
дачу, к полному "числу смоделированных систем". При этом определяется
оценка й>, значения сох апостериорной (условной) вероятности а\ дости-
жения цели операции. Согласно определению (см. п. 3.4.3), описанная
процедура реализует К-С схему имитационных испытаний.
(3.4.21)
(3.4.22)

198 Глава 3. Методы оценивания эффективности ЦНП
Пример 3.4.2. Примеры задач, приводящих к К-С схеме испытаний:
а) оценивание эффективности массового применения боевого средст-
ва определённого образца по типовой цели (по цели со стандартными ха-
рактеристиками);
б) оценивание эффективности массового применения однотипных
ЦУТС военного назначения в определённых условиях и в конкретный пе-
риод боевых действий;
в) оценивание эффективности массового (многоразового) применения
конкретной ЦУТС, параметры и ЭТХ которой подвержены воздействию
случайных факторов, в определённых условиях и в конкретный период
боевых действий и т.п. ▲
2. Пусть поставлена задача: оценить эффективность операции, прово-
димой конкретной ЦУТС, в детерминированных условиях функциониро-
вания - jBL, но в случайных (неопределённых) условиях применения -
EL, т.е. при неопределённых требованиях к результатам операции.
Как было показано в п. 3.4.2, при определении вероятности достижения
цели операции методом статистического имитационного моделирования
(СИМ) моделируются требования £ результатам операции, зависящие от
условий применения ЦУТС, и частота, оценивающая вероятность, нахо-
дится как отношение "числа операций", в которых цель была достигнута, к
полному "числу смоделированных операций". При этом определяется
оценка д)2 значения со2 апостериорной (условной) вероятности &2 дости-
жения цели операции. Согласно определению (см. п. 3.4.3), описанная про-
цедура реализует С-К схему имитационных испытаний.
Пример 3.4.3. Примеры задач, приводящих к С-К схеме испытаний:
а) оценивание эффективности применения боевого средства по целям
одного класса, характеристики которых (живучесть, защищённость, ориен-
тация и т.п.) априори неизвестны (случайны);
б) оценивание эффективности применения конкретной ЦУТС военного
назначения в различные, априори неизвестные периоды боевых действий;
в) оценивание эффективности применения конкретной ЦУТС в услови-
ях возможного, но априори неизвестного противодействия противника. А
Понятно, что получаемые в приведённых выше схемах имитационных
испытаний оценки эффективности операции не позволяют выработать
окончательное суждение о степени её приспособленности к достижению
поставленной цели, так как не учитывают возможные случайные отклоне-
ния условий применения ЦУТС в К-С схеме и условий функционирования
ЦУТС в С-К схеме, т.е. не учитывают одновременного (наиболее реально-
го) воздействия случайных факторов как на условия функционирования,

3.4. Методы вычисления показателей эффективности ЦНП 199
так и на условия применения ЦУТС. Поэтому схемы С-К и К-С следует
рассматривать как промежуточные на пути от С-С схемы к К-К схеме, ко-
торая дает исчерпывающую характеристику эффективности операции.
Легко заметить, что если реализована одна из схем С-К или К-С, то тем
самым определён один из законов распределения Ft(y) или F-(y) соответ-
ственно. В этом случае для реализации К-К схемы необходимо либо ис-
пользовать эти функции в формулах (3.4.21) или (3.4.22), либо (если
трансформирующие распределения соответственно F*(y) или F-(y) неиз-
вестны) вновь воспользоваться статистическим моделированием.
Пусть известно распределение F*(y). Тогда, реализуя стохастическую
модель условий применения ЦУТС и подставляя получаемые значения
zj% - предъявляемых к результатам операции требований в зыражение для
F.(y), получают последовательность значений супериндикатора а\, т.е.
<°^=FAhX t/i=l(lW. (3.4.23)
и по ней находят оценки средней (априорной) и гарантируемой (апостери-
орной) вероятностей достижения цели операции (см. п. 3.4,2):
*£rM = ".S^«- (3-4.25)
Если же известно распределение Щ(у)9 то, реализуя стохастическую
модель условий функционирования ЦУТС и подставляя получаемые зна-
чения yh виртуальных результатов операции в выражение для Я£(г), по-
лучают последовательность значений супериндикатора &г, т.е.
<»*л=*«Ы' [/2=l(lM. (3A26)
и по ней находят оценки средней (априорной) и гарантируемой (апостери-
орной) вероятностей достижения цели операции (см. п. 3.4.2):
*л*=4-£«ь; (ЗА27)
««00 = »,^ ■ (3-4.28)
Попутно по выборкам (3.4.23) и (3.4.26) могут быть построены стати-
стические функции распределения F^ (со) и F^ (со) супериндикаторов &х
и ^соответственно.
Отметим, что на рис. 3.4.3 и 3.4.4 изображены структурные схемы алго-
ритмов, реализующих соответственно схемы С-С-»К-С->К-К и
С-С -> С-К -> К-К.

200 Глава 3. Методы оценивания эффективности ЦНП
Как было показано в п. 3.1, распределения супериндикаторов а\ и &2 в
общем случае существенно различны. Так, различны их моды, одноимён-
ные квантили, дисперсии и т.д., вследствие чего при одном и том же уров-
не гарантии у гарантируемые вероятности а)[ДЦ (у) и (о[дц (у) достижения
цели операции различны.
Таким образом, можно сделать вывод, что процедуры оценивания эф-
фективности операции по схемам С-С->К-С->К-К и С-С->С-К->К-К
не в равной мере надёжны и, следовательно, в зависимости от параметров
распределений F.(y) или Ft{z) следует отдавать предпочтение той или
иной схеме испытаний. Проиллюстрируем сказанное на конкретных при-
мерах.
Пример 3.4.4. Планируется нанесение удара по площадной "цели". Для
вывода "цели" из строя ей должен быть нанесен относительный ущерб не
менее z. Выделяемые для этого боевые средства могут нанести относи-
тельный ущерб, равный у. Цель операции - выведение "цели" из строя.
Требуется: оценить эффективность операции при условии, что вирту-
альный (возможный) и необходимый (требуемый) ущербы подчинены
нормальным законам распределения (см. [169]), т.е.
(\. тЛ
(3.4.29)
°у J
Ft(y)=Fl%;y,v,)=Fjy-^
где J; = 0.7; <т-=0.1;
*-Н (3.4.30)
V °i )
где z = 0.6; <7- =0.5.
Решение. В рассматриваемом случае средняя вероятность достижения
цели операции будет определяться одним из следующих соотношений:
Pm = P(z<y)= )Ft{y)dFt{y)=)adFui{a) = Wi, (3.4.31)
-оо 0
d
где <q=F2(j>),iura
Рдц = Р{у > z) = ] R,(z)dFu(z) = )<DdF&i {со) = Ш2, (3.4.32)
-оо 0
d
где d)2=R-{z).
Согласно (3.1.48) и (3.1.49) функции распределения F& (со) и F& (а)} оп-
ределяются следующими выражениями1:
Не следует смешивать "агрегаты" А и В с параметрами А,кк и В,

3.4. Методы вычисления показателей эффективности ЦНП 201
F&t{w) = F\F7'{o))\=Fa[AF;\o>)+B\=FaWsF;x-\\; (3.4.33)
F^H = ^[^M]=fJ1^1M+^J = fJ2I^-2] , (3.4.34)
где А = -*- = 0.5 ; В =
=lzZ=_
=-i.
°>
После подстановки (3.4.33) в (3.4.31), (3.4.34) в (3.4.32) и последующего
интегрирования (с учетом заданных значений параметров распределений
случайных величин у и z) получим
col=a)2=F0
-В
^л/ГТ^
Согласно (3.1.65) и (3.1.68), с учетом заданных значений параметров
распределений F.(y) или F-(z), при уровне гарантии у = 0.9 имеют место
следующие равенства:
>Ло.1)+1
f;x(i-y)-b
А
= F,
0,5
со
2ДЦ
= 0.29; (3.4.36)
(r)=<w=^:(i-r)=^J^;,(i-r)-^]=
= F<r[0.5F;,(0.l)+l]=0.64 . (3.4.37)
Из равенств (3.4.36) и (3.4.37) следует, что при уровне гарантии у = 0.9
й>2г(0.9)><(0.9) (3.4.38)
и, таким образом, "более целесообразна" схема испытаний
С-С—»С-К—>К-К, поскольку она обеспечивает более высокий гарантиро-
ванный результат (гарантируемую вероятность достижения цели опера-
ции). На рис. 3.4.10 приведены графики функций распределения F& (a)j и
F& (o)j супериндикаторов &х и &2 соответственно, построенные при за-
данных значениях параметров распределений F-(y) и Ft(z) случайных ве-
личин у и z, иллюстрирующие полученное решение. А
Пример 3.4.5. Планируется операция, которая должна быть завершена
не позднее директивного момента времени z. Параметры и ЭТХ ЦУТС и
реализуемого ею ЦНПФС позволяют завершить операцию к моменту вре-
мени у.

202 Глава 3. Методы оценивания эффективности ЦНП
Рис. 3.4.10
Требуется оценить эффективность операции при условии, что вирту-
альная (возможная) и директивная (предельно допустимая) длительности
операции подчинены смещённым показательным законам распределения,
т.е.
F9{y)=Flcn](y;jufa) = [l-e-fl{"-")U(y-a), (3.4.39)
где ju = 0.5 ; а = 1 ;
*i(*) = F}cn]{z;v,c)= [l-e-^Uiz-c), (3.4.40)
где v = 1 ; с = 2.
Решение. В рассматриваемом случае средняя вероятность достижения
цели операции будет определяться одним из следующих соотношений:
Pm = P{z>y)= )R,(y)dFt(y)= )a>dF&i{a>)=mt , (3.4.42)
0
d
где й>2=Д2(.р)-

3.4. Методы вычисления показателей эффективности ЦНП 203
Согласно (3.1.48) и (3.1.49) функции распределения Fa(cd) и F&(co)
определяются следующими выражениями:
/?*/e>)=FjF/4a»)]=[i-^(e^i-^V(»;^W,i)+^(a>-i)=
= [l-e(l-й))2\п{а>;0.39,1) + Л{бО-1) ; (3.4.43)
F&i{a>)= R}[R:t(o))]=e/l{"c)uy;n{(o;0,l)+A(o}-1) =
= 0.606а>*#(ю;0,1)+Л(ю-1). (3.4.44)
После подстановки (3.4.43) в (3.4.41), (3.4.44) в (3.4.42) и последующего
интегрирования (с учётом заданных значений параметров распределений
случайных величин у и z ) получим
ж = со2 = 1 У—е^а-с) = 0.596 . (3.4.45)
v + //
Согласно (3.1.65) и (3.1.68), с учётом заданных значений параметров
распределений F^{y) и F^{z)9 при уровне гарантии у = 0.9 имеют место
следующие равенства:
<да(г) = ^ГЫ = ^//(1-г) = 1-Г ИЛ-с) = 1-(0.9)Ь^ =0.424 ; (3.4.46)
<цМ= <»fW= Fftl- Г)= (l- r)^v (а"с) = (М) V"> = 0.027 .
(3.4.47)
Из равенств (3.4.46) и (3.4.47) следует, что при уровне гарантии у = 0,9
^(0.9)>^2(0.9) (3.4.48)
и, таким образом, "более целесообразна" схема испытаний
С-С—»К-С—>К-К, поскольку она обеспечивает более высокий гарантиро-
ванный результат (гарантируемую вероятность достижения цели опера-
ции). На рис. 3.4.11 приведены графики функций распределения F& {со) и
F& {со) супериндикаторов &х и &2 соответственно, построенные при за-
данных значениях параметров распределений F~{y) и Fi{z) случайных ве-
личин у и z, иллюстрирующие полученное решение. А
3.4.7) Обратим внимание на реальный смысл выводов, сделанных по
результатам примеров 3.4.4 и 3.4.5.
В принципе объективно существует одна гарантируемая вероятность
соГДЦ {у) достижения цели операции (выполнения задачи ЦУТС), и две раз-
личные её оценки со[{у) и со[{у) свидетельствуют о наличии неадекват-
ности лежащих в основе этих оценок вероятностных моделей исследуемо-
му случайному явлению. Однако эта неадекватность кажущаяся. На самом

204 Глава 3. Методы оценивания эффективности ЦНП
0 а
у О F^cfafiy) 1
а)
со
деле она отражает позицию исследователя, анализирующего операцию, т.е.
ситуацию, в которой он оказывается при установлении мест (ролей) "неоп-
ределённости" и "случайности" в построенной им вероятностной модели
(см. (3.1.1)). Напомним, что трансформируемое распределение характери-
зует "случайность", а трансформирующее - "неопределённость". На какую
же из вероятностей 0)[(у) или oo^iy) следует ориентироваться? Ответ на
этот вопрос зависит от концепций исследователя и его возможностей по
выбору схемы испытаний. Если выбор ограничен, то вопрос теряет смысл.
Если же могут быть реализованы обе схемы, то при анализе эффективно-
сти операции полезно знать обе вероятности 0)[(у) и (О^У)- Что касается
синтеза операции, то, с одной стороны, для экономии средств (ресурсов) и
усилий следует ориентироваться на большую из этих вероятностей, но, с
другой стороны, для большей гарантии успеха операции надо отправляться
от меньшей из них. Поэтому в зависимости от реальных условий проведе-
ния операции и возможностей её оптимизации должно приниматься неко-
торое компромиссное решение. А

3.5. О вырожденных задачах оценивания эффективности ЦНП 205
3.5. О ВЫРОЖДЕННЫХ ЗАДАЧАХ ОЦЕНИВАНИЯ
ЭФФЕКТИВНОСТИ ЦЕЛЕНАПРАВЛЕННЫХ ПРОЦЕССОВ
Как указывалось выше, в основе методологии комплексного исследова-
ния операции, как при оценивании её результатов, так и при оценивании
эффективности, лежат критерии пригодности и оптимальности [см. п.2.2.2,
формулы (2.2.1), (2.2.2), (2.2.3)]. При этом все операции, показатели каче-
ства результатов и показатели эффективности которых удовлетворяют
этим критериям, считаются одинаково эффективными. Это обстоятельство
порождает ряд возражений против оценивания эффективности операции
по вероятности РДЦ или согдц (у) достижения её цели. Приведём наиболее
типичные из таких возражений.
1. Цель операции может быть достигнута при различных результатах
(эффектах), а при таком подходе это якобы не учитывается. Причём выска-
зывается мнение, что квазирегулярные модели (см. п. 2.4) позволяют про-
изводить такой учёт.
2. По некоторым эффектам (как правило, побочным) цель операции за-
ведомо достигается, и, следовательно, задача ЦУТС состоит в достижении
требуемого целевого эффекта. Поэтому нет необходимости вводить в рас-
смотрение векторный показатель Км качества результатов операции.
3. В детерминированной постановке задачи вероятность Рдц достиже-
ния цели операции может принимать лишь одно из двух значений: 1, если
Ум g [У?\], и 0, если L £ \Уи\\ > и> следовательно, вероятностный пока-
затель не позволяет сравнивать между собой конкурирующие варианты
операций (их организации) по их эффективности.
4. Если ресурсы всех видов не ограничены и требуемый целевой эф-
фект достигается наверняка, то Рдц = 1 и, следовательно, операции, даю-
щие различные эффекты, по этому показателю неразличимы. Если же ре-
сурсы ограничены настолько, что требуемый целевой эффект наверняка не
достигается, то Рдц = 0 и, следовательно, все операции, обладающие та-
кой "эффективностью", также неразличимы.
Постановки задач исследования операций, в рамках которых высказы-
ваются приведённые выше замечания, получили распространение в лите-
ратуре и находят практическое применение. Однако представляется целе-
сообразным подобные задачи называть вырожденными (чтобы не сказать
"надуманными"), если вообще их можно считать реальными задачами.
Прокомментируем их в той же последовательности.
3.5.1) Приспособленность операции к достижению цели выражается в ее
результатах (F/„\)5 имеющих вполне определённый закон распределения, в

206 Глава 3. Методы оценивания эффективности ЦНП
котором проявляется специализация операции (ЦНПФС) по достижению
тех или иных отдельных эффектов (по аспектам). Так что при фиксиро-
ванных требованиях (Z?\) к результатам операция, дающая больший эф-
фект определённого вида при одинаковых остальных эффектах, будет
иметь большую вероятность РДЦ достижения цели, так как на последнюю
оказывает влияние и характер рассеяния эффектов (см. п. 4.2). Таким обра-
зом, квазирегулярные, а тем более детерминированные модели этого не
учитывают. А
3.5.2) Если по каким-либо эффектам цель операции заведомо достигает-
ся, то соответствующие им показатели не должны входить в состав вектора
Y, х, так как его образуют лишь показатели существенных эффектов. Если
же к таким эффектам относятся затраты ресурсов и времени, то задача вы-
рождается до некорректной и в принципе в рамках теории эффективности
не должна рассматриваться. Действительно, если ресурсы не ограничены и
получение требуемого целевого эффекта "не к спеху", то никакой пробле-
мы нет, нечего анализировать и оптимизировать, так как за неограничен-
ное время при неограниченных ресурсах может быть получен любой напе-
рёд заданный результат. А
3.5.3) Как уже неоднократно подчёркивалось, детерминированная мо-
дель не является адекватной ни одной реальной операционной системе и
должна рассматриваться лишь как весьма грубая ее аппроксимация.
При Рдц = 0 сравнение результатов различных операций (различных
вариантов организации ЦНПФС) бессмысленно, потому что операции не-
пригодны для реализации, поскольку не достигают цели. Если же есть та-
кие возражения, что, мол, хотя цель операции и не достигается, но опера-
ция должна проводиться и желательно, чтобы при этом ее результаты были
бы "получше", то это означает, что цель операции была сформулирована
неправильно.
Действительно, если можно довольствоваться результатами операции
ниже требуемых (а желание их сравнивать при нулевой вероятности Рдц
свидетельствует именно об этом), то это означает, что при таких снижен-
ных результатах также достигается цель операции, хотя и ограниченная.
Это обстоятельство легко учитывается в стохастической модели путём за-
мены детерминированных требований - ZK к результатам - Ум операции
случайными {рандомизированными ) требованиями - Z,, > область (носи-
тель) распределения которых - \Z^} располагается в окрестности точки
Путём введения искусственного рассеяния.

3.5. О вырожденных задачах оценивания эффективности ЦНП 207
Zf. так, чтобы по компонентам вектора К* результатов операции, не
удовлетворяющим заданным требованиям - Z\, последние были бы "в
среднем" снижены.
Сформулированные рекомендации для случая я=2 иллюстрируются
рис. 3.5.1, на котором обозначено: ух — показатель целевого эффекта; у2 -
показатель расхода ресурсов; ZL- заданное значение показателя требуе-
мых (предельно допустимых) результатов (эффектов) операции; \Zf% j -
область возможных значений (носитель распределения) рандомизирован-
>р
<2>
ного вектора ZL - показателя результатов операции; zf, zf"[i = 1,2]
границы носителей распределений компонент if, if/f рандомизирован-
ного вектора ZL. При этом верхние индексы (/ ) показателей У$ вирту-
альных результатов операции обозначают вариант ее организации. Рандо-
мизация требований к результатам операции должна проводиться по зако-
ну распределения F%P \Z,2A, наиболее полно учитывающему относитель-
ную "важность" ("весомость") отдельных её эффектов ух и у2. Легко по-
нять, что в рассматриваемом случае
рДЦ=р[г[2)е(ц")\,
где (ц(/)) - подобласти области {z^f}, при попадании в которые вектора
ZL цель операции достигается.
Всё сказанное в полной мере относится и к случаю Рдц = 1 с тем раз-
личием, что рандомизация требований - ZL должна проводиться в сторо-
ну их "повышения". Этот случай иллюстрируется рис. 3.5.2. А
3.5.4) Последний случай практически сводится к предыдущему, с тем
различием, что результаты - К2* операции здесь случайны. При этом
предполагается, что операции, для которых РДЦ =1 (или Рдц = 0), "эф-
фективны" не в равной степени, более "эффективна" та, у которой выше
показатель W = Wp\y,A. Ещё раз подчеркнём, что подобная точка зрения -
заблуждение вследствие неправильной постановки задачи. Действительно,
ведь если результаты различных операций сравниваются не только по це-
левому эффекту, но и по затратам ресурсов и времени, то это означает, что
ресурсы и время надо экономить. Их экономия приведёт к снижению веро-
ятности Рдц достижения цели операции.

208 Глава 3. Методы оценивания эффективности ЦНП
Р{1) =0
ГДЦ и
г2 '
*-г
0
0
у(»)
- у> w
z<y
Г
! ?
F J« *,
Г(2)
Рис. 3.5.1
Таким образом, неограниченность ресурсов, как, впрочем, и чрезмерное
их ограничение - это абстракции от конкретных реальных задач. При кор-
ректной постановке задачи в рассматриваемом случае, как и в предыду-
щем, требования - Z,2v к результатам операции как по целевому эффекту,
так и по расходу ресурсов должны быть повышены (или понижены) до ре-
альных пределов. При этом вероятности Р^ц снизятся (или повысятся) и
различие вариантов операции в их результативности и ресурсоёмкое™
проявится в различии их эффективностей, т.е. в различии вероятностей
р(0
гдц-

3.5. О вырожденных задачах оценивания эффективности ЦНП 209
V
^
*2
У?
0
'Л
" "7
р(|)=1
73
/
А
w/////
у
К i У
ГУ 1 *
/>(2)=1
у(»)
Z2 — Z2
«Г'^
p(D ф л
Рис. 3.5.2
Сказанное иллюстрируется рис. 3.5.3 и 3.5.4, на которых обозначено:
\Y$] - область возможных значений (носитель распределения) показателя
Y$ результатов 1-го варианта операции (/ = 1, 2); \Zt, ) - область воз-
можных значений (носитель распределения) показателя Z,^ требуемых
(предельно допустимых) результатов операции; \Z^ j - область возмож-
ных значений (носитель распределителя) рандомизированного показателя
ZL требуемых результатов операции. ▲

210 Глава 3. Методы оценивания эффективности ЦНП
If
Уг'
Уг
(О
у2 ^iD = i
шшщ
--щшй
!*&}
1«°}
-
ГТШ
-Щтжг
т
г, yt
,'(0
Ух
*(»)
Ух
\?>»»»»Л
Zi I - - к^щс^^Д
»(г)
Уг
yf
Уг
/>(2)=1
Ш
Ух
,Ф)
tirl
Ух
Ух
,'(»)
р(1) ф 1
/г(г)
z?=y\{l)
Рис. 3.5.3
3.5.5) В заключение ещё раз отметим, что закон распределения, рандо-
мизирующий вектор Z;\, должен задаваться с учётом важности (весомо-
сти) компонент векторов Y$. При этом естественно, что области {К^|,
{z^ j , \Zf%j возможных значений (носители распределений) случайных
векторов F/7 , Z/v, Z, \ соответственно в общем случае могут иметь про-
извольные конфигурации, учитывающие возможные связи их компонент.
На рис. 3.5.1-3.5.4 эти области прямоугольные лишь для большей нагляд-
ности. А

3.5. О вырожденных задачах оценивания эффективности ЦНП 211
*?'=*(2)
<*о
4-jP
4=# У1{1) К(2) г( = У?г) «.
Рис. 3.5.4
3.5.6) В общем случае за счёт степени повышения (или снижения) тре-
бований по различным компонентам вектора L может быть учтена их от-
носительная "важность". Однако, как указывалось ранее, при комплексном
исследовании эффективности операции в состав вектора L должны вхо-
дить лишь показатели существенных и потому одинаково важных её ре-
зультатов. Таким образом, в качестве границ области \Z£? j, "смягчаю-
щих" ("ужесточающих") требования к результатам К» ЦНПФС, лучше
брать их предельно допустимые значения (на рис. 3.5.1-3.5.4 они обозна-
чены штрихами). Отметим, что в общем случае совпадение величин zf
it" с у\'К [i = l(l)«; / = 1,2] (рис. 3.5.1, 3.5.2) или с у^'К у{(,)
[i = l(l)« ; / = 1,2] (рис. 3.5.3,3.5.4) не обязательно. А

212 Глава 3. Методы оценивания эффективности ЦНП
3.5.7) При вырождении задачи, т.е. когда РДЦ = 1 или Рдц = 0 (как
при детерминированной постановке задачи, так и при вероятностной), ран-
домизации может быть подвергнут не только вектор Z,y но и векторы
y№- Однако, чтобы получаемые при этом результаты были сравнимы, в
основу рандомизации должны быть положены принципы, обеспечивающие
одинаковую её степень для всех сравниваемых вариантов операции. А
Проиллюстрируем общую методику решения вырожденных задач ис-
следования эффективности операций на ряде примеров.
Пример 3.5.1. Пусть Z(32>=(zf,z2J> = (2,5,3); Г$ = (^(,),^2)> = (l,8,3);
У(2? = (уР'У?) = (4>3>5) (см. рис. 3.5.1). Тогда
т.е. обе операции неэффективны. Однако требуется выбрать из них "более
предпочтительную".
Решение. Решение задачи зависит от выбранного показателя качества
операции (критериальной функции):
а) если руководствоваться показателем целевого эффекта (2.4.6), то
»f = ,<'>= 1.5; 1
\ (3.5.2)
^>=*(2)=4, j
т.е. более результативна операция О® и, следовательно, О^ < 0^г\
где -< - знак доминирования (превосходства);
б) если руководствоваться показателем (2.4.7), то
6 W 3.5
(3.5.3)
т.е. менее ресурсоёмка операция 0(|), и, следовательно, и 0(|) >- 0(2);
в) если положить #31 = 1, а32 = -1, и воспользоваться показателем
(2.4.8), то
W^^a^+a^ = 1.5-1 = 0.5; 1
W® = а31 у® + ad? = 4 - 3.5 = 0.5 J
и, следовательно, операции О^ и О^ по показателю W3 неразличимы.

3.5. О вырожденных задачах оценивания эффективности ЦНП 213
Понятно, что результаты (3.5.2) - (3.5.4) не позволяют с уверенностью
отдать предпочтение ни одной из сравниваемых операций (ни одному из
вариантов ЦНПФС) О^ или 0^2К Это происходит потому, что использо-
ванные детерминированные показатели JVl9 W39 W6 не оценивают эффек-
тивности операций О^ и О^ поскольку никак не учитывают их цели, а
лишь измеряют некоторые операционные свойства их результатов, такие,
как результативность операции - Wx, производительность (отдача) ресур-
сов - W6 (или ресурсоёмкость целевого эффекта - W^x); обобщённый эф-
фект операции - \¥ъ ;
г) проведём рандомизацию требований - ZL, предъявляемых к результа-
там - Коопераций 0(,) и 0(2). Как отмечалось (см. (3.5.1), (3.5.2)), в основу
рандомизации могут быть положены различные принципы (например, учёт
сравнительной "важности" эффектов у$'\ у^). Однако наиболее простое (из
разумных) решение даёт подход, при котором полностью учитываются дос-
тоинства и в равной мере (хотя, быть может, и частично) недостатки конку-
рирующих вариантов О^ и О^ операции. Этот подход иллюстрируется
рис. 3.5.1, где "максимальные" требования zP/ , гР2; обусловлены лучшими
эффектами JY ,j>2 операций О^ и О^ соответственно, а "минимальные"
требования zP/', zP// - худшими из допустимых эффектов miny\ , таху\ .
.р/
Пусть miny^ =0.6; таху2=4Л. Тогда zt =0.6; zt = 4; z2 =1;
zP// = 4.1 и, следовательно,
(3.5.5)
*3=?l W2) * zh W2) * *f )]=p\K)e №)l
Будем считать, что вектор ZL распределён в пределах области \Z[%}
равномерно. Тогда из соотношений (3.5.5) имеем:
1 \(Ц{1))\
PilhJi^fMzM1dz2=1r-^l\dz1dz2
|K<2)j|(tf(")
(«
та
-1Я
.(».
«f'X
*"-*,"
L(l.5-0.6)(4.1-l)_
(гГ-гГДгГ-гГ)" (4-0.б)(4.1-1)
(2)^ Я^А^К^тт—гг JJ&,*,
= 0.26;
(3.5.6)
'Д4
(ц«)
1^1
_ (zr-zrhr -^)_(4-0.6)(4.1-3.5)_
~и'#-х."К'-*ГГ (4-0.6)(4.1-l) ~0Л9' (3-57)

214 Глава 3. Методы оценивания эффективности ЦНП
где \Ц^)\ , {^(2? Л ~ меры (площади) областей \Ц ) и \Z^j соответст-
венно.
Из сравнения результатов (3.5.6) и (3.5.7) следует, что операция О^
более эффективна, чем операция О^ т.е. О^ У О®. В частотной трактов-
ке понятия вероятности это означает, что при возможных отклонениях
требований - Z,2v к результатам операции от заданных - ZL при много-
кратной реализации ЦНПФС типа О'1' цель операции будет достигаться
чаще, чем при реализации ЦНПФС типа О® (и это несмотря на то, что
,««,«). А
В последующих примерах будут приведены лишь математические вы-
кладки. Сопутствующие им рассуждения аналогичны приведённым в при-
мере 3.5.1. Рекомендуем читателю провести их самостоятельно.
Пример 3.5.2. Пусть Z3{2) = (zf,z23) = (2, 3); Г$ = (у®,у®)= (4,2,5);
(см. рис. 3.5.2). Тогда
^5MW^^)nW)<z25)]=l;l
Требуется выбрать из операций О^ и О^ "более предпочтительную".
Решение. В зависимости от показателя качества операции (критери-
альной функции)получим:
(3.5.8)
а) по формуле (2.4.6)
т.е. 0(х)<0(1);
б) по формуле (2.4. W)
»f = ,<2)=4,
(3.5.9)
Ъ
(o-if-A-2.
1.5
(3.5.10)
W® = \r = ^- = 1.6,
T.e.O(Vo(1);
в) по формуле (2.4.8) при а31 = 1, а31 = -1
»f = «з,Al) + ajp = 3 -1.5 = 1.5 ;
»f = a3ly\2) + ad? = 4 - 2.5 = 1.5,
т.е. О^ = 0^г\ где = - знак "равносильности";
(3.5.11)

3.5. О вырожденных задачах оценивания эффективности ЦНП 215
73
положив zf/= zf,
г) проведём рандомизацию требований
zP2;/ =Ух\ zP2'=у^\ zP//=zl и, считая, что в пределах области \Z?£\
вектор ZL распределён равномерно. Тогда
(4м) \\Z{2)i\(4(,))
\(Ц{1))\ Ul)-7P/)(7P// -7P/\ 3-2
|VM >[ = ¥1 h-Jgi hA =i L = о so . G5 12")
И
<> = />[z{'2) e (д«)]= JJ f>i& fe.*»)*. A, = -гЛтг 1/4,4, =
J to")
т.е. 0<o V0W-
РЩ
.(гГ-гГХгГ-^), 3-2.5
(«."-*.")&'-«.") 3-i.s
= 0.33; (3.5.12')
3.5.8) В приведённых примерах к выводу о превосходстве операции О^
над операцией О^ приводят как показатель РДЦ, так и показатель W6.
Однако это совпадение чисто случайно и обусловлено лишь исходными
данными примеров. Действительно, если в условиях примера 3.5.1 поло-
житьГ$ = (^,,«) = <4,3),то
W^ = \ = - = 1.33
6 У? 3
и по показателю Wt по-прежнему Or' >Ок'- В то же время
(0
»ю.
„W
Р(2)_гГ-^_ 4.1-3,
ГДЦ р// р/
Z2 -Z2
= 0.35
4.1-1
и, следовательно, по показателю Рдц О^ •< 0^2\ т.е. операция 0^ стала
(оказалась) более эффективной, чем операция О^. Именно такой вывод
должен быть сделан по их сравнительному оцениванию.
Всё сказанное в равной мере относится и к примеру 3.5.2. Рекомендуем
читателю убедиться в этом самостоятельно путём варьирования исходных
данных. ▲
Пример 3.5.3. Пусть случайные векторы кУ, К(22Л Z,^ распределены
равномерно соответственно в пределах областей \F/f\^j , {F^2*} , \%?Л
(см. рис.3.5.3), вершины которых имеют следующие координаты: z[ = 0.5;

216 Глава 3. Методы оценивания эффективности ЦНП
zf =1.7; zi=3;4=4; *'<'> = 2 ; <<'> = 3.5; ^ = 0.5 ; ^ = 1.5 ;
у?* = 3 ; rf « = 4.2 ; у'® = 1 ; у^ = 2.5 .
Из рис. 3.5.3 видно, что
р0) _ р(2) _ t
и, следовательно, обе операции О^ и О*2) "абсолютно эффективны". Это
является результатом некорректной формулировки задачи, обусловленной
занижением требований к результатам (эффектам) операции. Требуется
выбрать "предпочтительный вариант" операции (ЦНПФС).
Решение. При различных показателях качества операции (критери-
альных функциях) получим:
а) по формуле (2.4.6')
= 2.75
,Г(0_?(0_^/(1)^Г(1)_2 + 3.5_
1 Ух 2 2
,ч И2) + i//(2) 1 + 4 2
^(2) = ^(2) = УХ +Л = 3+±f = 3.60
1 Jx 2 2
(3.5.13)
т.е. 0(1)<0(2)
б) по формуле (2.4.1 Г)
«W
^(,) = |; = ^ = 2.75;
~(2)=^=з:бо = 10
* J2(2) 1.75
(3.5.14)
(3.5.15)
т.е. 0(,)хО«.
в) по формуле (2.4.80 ПРИ &з\ = *> азг = ~*
^з(1) = «з,У11) + <*пА1) = 2.75 -1 = 1.75 ;
Из(2) = «3iJi(2) + «и У® = 3.60 -1.75 = 1.85
т.е. 0{1) <0{2);
г) введём дополнительную рандомизацию вектора Z/2v требований к ре-
зультатам операций, положив
7Р/ = _/ _/>// = v//(2). Я/ = /(1). Р// _ //
и считая, что в пределах области случайный вектор \Z^} вновь распределён
равномерно. Тогда
*Й = РЫ] * гТ)п (jf * #)]= Я ф*'!(^К'„fe'*)' 1
Urol -<2> w
^ = *!2) * Zh№ * «Г)]= Я <М**)^*& (*.*);
lZ(2) /
(3.5.16)

3.5. О вырожденных задачах оценивания эффективности ЦНП 217
где
= JR,,oU)F,,o0'2), (/ = W);
F1&(r,,%)=P|fe' <Z|)n(£2" <*2)]=i»fe' <*>(# <z2)=F,,(Zl)F£,(Z2).
Поскольку при равномерном распределении
^(г) = |-^я(г;а,*)+Л(г-А);
Ъ-а
Ri{z)=A{a-z)+^n{z;a,b),
b —a
(3.5.17)
то с учётом того, что
и, следовательно,
ft(z) =!?(*) =
n{z;a,b)
b-a
jv(\ M( \j n{z;a,b)dz
dF.[z) = <pt{z)dz = —*- '—,
b — a
формулы (3.5.16) принимают вид
г?" г"
Pfu= ]*^<,,(г>1Г(г,К J l>(z,)p£f («,)*,=
z, z,
\dz\
ijf -Л 2 2
(/ = 1,2).
В результате интегрирования вьфажения (3.5.18) по формулам
'Ил( Wb-ZT7l *\1 * "г * ,*r [b-z)dz 2{a-c)+{b-a) }
dz2,
(3.5.18)
</-c aJ(*-a)(rf-c) i</-c 2(</-c) 'J
(3.5.19)
имеем

218 Глава 3. Методы оценивания эффективности ЦНП
рм _ Ш> -z?htim -№)№" -yFMz? -yi{,))] /._! 2)
(3.5.20)
Подставив в формулу (3.5.20) числовые данные примера, получим
(|)_[2(2-0.5)+(3.5-2)][(1.5-0.5) + 2(4-1.5)]_
т~ 4(4.2-0.5)(4-0.5)
(2)_[2(3-0.5) + (4.2-3)][(2,5-1) + 2(4-15)]_
т~ 4(4.2-0.5)(4-0.5) "
(3.5.21)
Сравнение результатов (3.5.21) показывает, что О^<0^г\ т.е. опера-
ция О™ эффективнее операции О^1' (хотя и незначительно). Заметим, что
из выражений (3.5.14) следуют противоположные выводы. ▲
Пример 3.5.4. Пусть случайные векторы Щ), кФ, Z,2> распределены
равномерно соответственно в пределах областей JF/f\(,)j , |кД(2)) , \^н)\
(рис. 3.5.4), вершины которых имеют следующие координаты: г,'= 2.5;
z"2=4.2; г; = 1.5; г? = 2.5; Х(,) = 0Л; tf(,) = 1.8; ^(,)=0.5; ^(,) = 2;
Х« = 3; y;V = 4.5;y'V = 3;/V = 4.
Из рис. 3.5.4 видно, что
р(0 _»(»)_ л
Л ли Л ли v »
1 дц - Лдц
и, следовательно, обе операции О^ и О*2* "абсолютно неэффективны", т.е.
поставленная цель операции никогда не достигается. Однако это может
быть обусловлено чрезмерным завышением требований к результатам
(эффектам) операции. Тем не менее необходимо выбрать "предпочтитель-
ный вариант" операции.
Решение. Предоставляем читателю провести его в качестве упражне-
ния по схеме (алгоритму), реализованной в примере 3.5.3. А
Примеры 3.5.1 - 3.5.4 ещё раз убеждают нас в том, что распространён-
ные на практике показатели W\9 W3, We и т.п. не позволяют проводить
сравнительный анализ операций по их эффективности в замкнутой схеме,
так как они не характеризуют в достаточной мере это комплексное свойст-
во ЦПФС и, следовательно, непригодны для их оптимального синтеза. Эта
задача может быть корректно решена только на базе стохастических моде-
лей элементов операционного комплекса, лежащих в основе методов, рас-
сматриваемых в данной монографии (см. п. 4.2).

3.6. Комментарии
219
3.6. КОММЕНТАРИИ
В силу сугубо практической направленности рассматриваемой пробле-
мы в монографии большое внимание уделяется обсуждению ее семантиче-
ских и методологических аспектов, четкое понимание которых абсолютно
необходимо для корректного формулирования задач исследования и по-
строения адекватных математических моделей изучаемых объектов
(ЦУТС и ЦНПФС). С этой целью прокомментируем принципиальные по-
ложения, составляющие основу данной главы.
3.6.1} Как было отмечено в (2.2.6), при априорном (до применения по
назначению) оценивании качества объекта, по существу, оценивается
"класс объектов", в пределах которого истинные качества их образцов (эк-
земпляров) имеют разброс, обусловленный, с одной стороны, размерами
области {УД ] допустимых значений показателя качества F/\, а с другой -
возможным разбросом "несущественных" свойств объекта, не учитывае-
мых при оценивании его качества.
При оценивании эффективности ЦНП это обстоятельство также прояв-
ляется в полной мере. Кроме того, к отмеченным выше факторам добавля-
ется априорная неопределённость и обусловленный ею разброс требова-
ний, предъявляемых к качеству результатов операции (см. (2.3.7)). Поэто-
му при априорном оценивании эффективности ЦНПФС, в сущности, оце-
нивается его потенциальная эффективность, присущая "классу ЦНП", оп-
ределяемому его организацией, т.е. стратегией его целевого применения, а
не отдельной реализации этой стратегии, проявляющейся в конкретной
операции. А
3.6.2} Как отмечалось ранее, согласно комплексному, системному под-
ходу при исследовании операции и оценивании ее эффективности исполь-
зуются специфичные агрегированные модели ЦУТС и ЦНПФС, при-
званные отражать с требуемой адекватностью результаты ЦНПФС, дина-
мику их получения в ходе операции и их связи с параметрами и ЭТХ
ЦУТС и ЦНПФС, без детального описания всех элементов ОК и элемен-
тарных актов их функционирования.
При необходимости анализа влияния характеристик конкретного эле-
мента ОС или ОК на эффективность ЦНПФС эти элементы в модели "вы-
свечиваются" путём выделения их параметров из агрегированных характе-
ристик ЦНПФС или ЦУТС. ▲
3.6.3} При наличии существенно неопределённых характеристик ЦУТС
и ЦНПФС, а также условий функционирования и применения ЦУТС (т.е.
условий проведения операции) используется понятие "гарантированной"

220 Глава 3. Методы оценивания эффективности ЦНП
вероятности1 РДЦ достижения цели операции, представляющей собой
пессимистическую оценку вероятности Рдц, получаемую при наи-
худших (наиболее неблагоприятных) значениях неопределённых характе-
ристик, для которых известен лишь их возможный диапазон. А
3.6.4} Иногда высказывается утверждение о том, что рассматриваемый
здесь подход к оцениванию эффективности операции не имеет преиму-
ществ перед методом, основанным на использовании критериальных
функций (см. п. 2.4), поскольку в случаях, когда модели ЦНПФС недоста-
точно адекватны реальным операциям, получаемые на их основе значения
вероятности Рдц достижения цели операции не равны истинным значени-
ям Рдц показателя её эффективности. Однако следует иметь в виду, что
даже в этом случае в рассматриваемой методологии "веса" аспектов (опе-
рационных свойств результата операции) реализуются (проявляются) в
замкнутой схеме, т.е. с предъявлением требований к результатам операции,
в отличие от метода критериальных функций, в рамках которого они (веса)
определяются эвристически (интуитивно), практически ни на чем не осно-
вываясь. ▲
3.6.5} Рассмотренный в п. 3.5 метод рандомизации показателей вир-
туального и требуемого результатов операции - это один из способов
"взвешивания" его существенных операционных свойств (аспектов - атри-
бутов), причём методологически наиболее обоснованный, поскольку про-
водится в замкнутой схеме, на основе объективных исходных данных (ус-
ловий задачи). ▲
3.6.6} В вырожденных задачах оценивания эффективности операций
снижение показателей РДЦ их эффективности в результате рандомизации
условий функционирования и применения ЦУТС (см. (3.6.5)) пропорцио-
нально для всех сравниваемых вариантов ЦНПФС, однако воздействует
оно на Р^ц через аспекты качества ЦНП селективно (индивидуально). А
3.6.7} При оценивании эффективности ЦНПФС не следует "пугаться"
малых значений вероятности РДЦ достижения цели операции, так как, не-
смотря на психологическое неприятие малой вероятности Рдц, она более
адекватно отражает реальную ситуацию, чем детерминированный показа-
тель W, поскольку в отличие от него определяется в замкнутой схеме (см.
также (3.2.10». ▲
1 Не следует смешивать это понятие с понятиями «гарантируемой» и «гарантий-
ной» вероятностей (см. (3.2.11)).

3.6. Комментарии
221
3.6.8} Следует обратить внимание, что в рамках факторизованной моде-
ли показателя L виртуального качества результатов операции (см. п.
3.5.2) применение метода ведущих компонент приводит к вырождению за-
дачи, так как если компоненты вектора L взаимно независимы, то выде-
ление из них ведущих компонент равносильно исключению ведомых ком-
понент из рассмотрения. Понятно, что в этом случае возможно оценивание
пригодности операции лишь по некоторым аспектам качества её результа-
тов. Оценивание комплексного качества операции - её эффективности при
этом невозможно. А

Глава 4
МЕТОДЫ ИССЛЕДОВАНИЯ ЭФФЕКТИВНОСТИ
ЦЕЛЕНАПРАВЛЕННЫХ ПРОЦЕССОВ
Как было отмечено в п. 2.3.5, исследование эффективности ЦНП пред-
ставляет собой триединую задачу (оценивания, анализа и синтеза), причём
решения первых двух задач - это этапы прямой задачи, а решение треть-
ей - этап обратной задачи исследования эффективности ЦНП.
В силу методологической важности и концептуальной особенности, а
также большого многообразия аспектов, связанных с решением задач оце-
нивания эффективности ЦНП, её рассмотрению посвящена гл. 3. В данной
главе рассматриваются методы исследования эффективности ЦНП, т.е. ме-
тоды её анализа и оптимального синтеза.
4.1. МЕТОДЫ АНАЛИЗА ЭФФЕКТИВНОСТИ
ЦЕЛЕНАПРАВЛЕННЫХ ПРОЦЕССОВ
Как отмечалось (см. п. 2.3.5), основу всех методов "Исследования опе-
раций" и "Теории эффективности целенаправленных процессов" составля-
ет их математическое моделирование (аналитическое или имитационное).
Поэтому решение прямой задачи исследования эффективности ЦНП за-
ключается в анализе свойств (параметров и ЭТХ) его модели. О методах
построения моделей ЦНП речь будет идти в гл. 5, здесь же будем предпо-
лагать, что такие модели уже построены, и рассмотрим задачи и методы их
анализа.
4.1.1. ФОРМУЛИРОВКА ЗАДАЧИ АНАЛИЗА
ЭФФЕКТИВНОСТИ ОПЕРАЦИИ
На рис. 2.3.5 приведена схема примерной классификации прямых и об-
ратных задач исследования эффективности операции. Как нетрудно ви-
деть, задачи анализа операции и её эффективности реализуются при по-
строении математических моделей ЦУТС и ЦНПФС, используемых и при
решении задач их оптимального синтеза (см. рис. 2.2.5 и 2.2.6).
Собственно задачами анализа эффективности операции являются:
- вычисление показателей эффективности операции при заданных па-
раметрах и ЭТХ ЦУТС и ЦНПФС (характеристиках А',к« и AL*), а также

4.1. Методы анализа эффективности ЦНП
223
при заданных условиях проведения операции (характеристиках J5L и
В[г))\
- оценивание эффективности операции по соответствующему задаче
исследования критерию;
- анализ чувствительности показателей эффективности операции к из-
менениям параметров А,к, ЦУТС и ЦНПФС и условий В,* проведения
операции;
- исследование характера и степени влияния характеристик А', А", В\
В" на эффективность операции и отбор значимых факторов, т.е. факторов,
оказывающих наиболее существенное влияние на эффективность ЦНПФС;
- выявление параметров Л'£\, ^ГА' Щ)* Щг\ > наиболее пригодных для
управления эффективностью операции (см. рис. 5.2.1).
Вычисление показателей РДЦ, <огдц (у) эффективности операции произ-
водится по формулам (3.2.10), (3.2.10'); (3.2.17'); (3.2.20), (3.2.20'). Что ка-
сается оценивания эффективности операции, то, как известно, в его основе
лежат критерии пригодности и оптимальности, которые в задачах её ана-
лиза принимают вид:
п • р > р7
с;
о.
дц -' дц>
о>[(у)><о%(г);
гдц ~ гдц >
0'э:а>[(г) = <огдцОПТ(г);
о;:а>Хг)=<»дцОПТ(г)-
(4.1.1)
(4.1.2)
Как было показано [см. формулу (2.3.14)], значения показателей эффек-
тивности операции зависят от значений характеристик ЦУТС, ЦНПФС и
условий проведения операции, т.е.
Рт,,, = Рдц \А,к) , А л ]= Рдц [Х,т));
дц
со
(у)=
| а>х ir) = (о[(у;А{к),В{1))=(о[(у;Х{т));
[а>[{у)= а>[(у;А{к),В{1))=а)[^;Х{т)),
ГДе \к) ~ \^(*') » ^(*') / = ^(т,) '
В(1)={В(г)'В(0/ = ХМ;
Л<*>-Г>,>'ЛЫ/-
(4.1.3)
(4.1.4)
(4.1.4')

224 Глава 4. Методы исследования эффективности ЦНП
При этом в отличие от (2.3.11), (2.3.12) компоненты вектора Х.к не
случайны, так как либо являются неслучайными компонентами векторов
Л*)' A*)' ™6° представляют собой вероятностные характеристики их слу-
чайных компонент.
Для действенного управления ЦНПФС необходимо знать наиболее зна-
чимые факторы (характеристики А,кк и В^), а также характер и степень их
влияния на эффективность операции. Эта задача решается методами "Тео-
рии чувствительности" [119, 151].
4.1.2. ХАРАКТЕРИСТИКИ ЧУВСТВИТЕЛЬНОСТИ
ПОКАЗАТЕЛЕЙ ЭФФЕКТИВНОСТИ ОПЕРАЦИИ
При решении многих задач1 "Исследования операций" и "Теории эф-
фективности ЦНП" возникает вопрос о степени влияния на результат па-
раметров, определяющих условия задачи. Это в первую очередь задачи
анализа и синтеза сложных систем (ЦУТС) и процессов их целевого функ-
ционирования (ЦНПФС), задачи принятия решений (проектных, организа-
ционных, управленческих и т.п.), задачи непараметрической статистики
[170] и т.д. В основе характеристик такого влияния лежат так называемые
функции и коэффициенты чувствительности. Методы получения и иссле-
дования этих характеристик разрабатываются в "Теории чувствительно-
сти" [151] и здесь рассматриваться не будут, однако для понимания мате-
риала прикладных разделов монографии необходимо знакомство с основ-
ными начальными понятиями этой теории. К таким понятиям в первую
очередь относится понятие функции чувствительности. Дадим её опреде-
ление применительно к задачам теории эффективности ЦНП.
Пусть решение задачи оценивания эффективности операции имеет вид
*| = *#Ц.);г)> [/ = 0,l,2;m = l(l)...], (4.1.5)
где wt - 1-й показатель эффективности операции (ЦНП)
[w,(x)=Pm{x), w1(X;r)=a[{r;X), w2(X;r)=af{y;X)[,
Х.х = (А,куВ,Л - вектор параметров задачи исследования эффективности
операции, от которых зависят параметры распределений
0f \У,„\) и F% \Z/„\), а следовательно, и параметры
распределений F&{H) (со) супериндикаторов &;'
[/ = 1,2; /i = l(l)...];
Примеры таких задач будут рассмотрены ниже.

4.1. Методы анализа эффективности ЦНП 225
у - гарантийная вероятность, играющая в задачах анализа
эффективности операции роль параметра.
Определение 4.1.1. Функцией чувствительности показателя w.
эффективности ЦНП к параметру х. (к его изменению) называется част-
ная производная функция и>Дх ч;у) по аргументу xJ9 т.е.
йдЛ(«)'//-яхЛЛ(«)'^- Лг
dXj
,[/ = 0Д,2; j = 1(1)ж], (4.1.6)
где Х\ =(xf, Jcf,..., jc' ) = (af,ef,..., af, Af,A* ,..., bf) - вектор базовых
(номинальных, расчётных) значений параметров Xj, [/ = 1 (l)»»] • А
4.1.1) В матричной форме система равенств (4.1.6) примет следующий
вид [111,119]:
(">"/" «<.,
*<«)-*£)
(4.1.7)
где
^>(^Ь;У)=к(*м;г)»*5^>»-уЙ(^г.)/г)1 [/=i(iM; (4.1.7)
Из определений (4.1.7) и (4.1.7й) следует:
- #/зДХ^\;?') - 3-мерный вектор-столбец, называемый вектор-
функцией чувствительности показателя W,^ = (w0, wl, w2) =
= \Рдц9^(у)9(о[(у)) эффективности операции к параметру ху.;
- Н!Ах?,;у) - m-мерный вектор-строка, называемый вектор-
функцией чувствительности показателя wt эффективности операции к па-
раметру Х(м). А
Если показатель wt от переменной у не зависит (как, например,
w0 = Рдц) или исследуется при фиксированном её значении у0, то
^ = ^{ту'Го)=^{Х{т)), [/ = 0,1,2] (4.1.8)
и выражение (4.1.7) примет вид
<m>/ «w
Х(т)-Х(т)
8 Зак. 3303

226 Глава 4. Методы исследования эффективности ЦНП
где
«М-скУ-^
**,
\Х{»ГХ(»)
, [/=0,1,2;/ = l(l)m]. (4.1.10)
Числа hlj[X?A [/=0,1,2; /' = l(l)w], называются коэффициентами
чувствительности.
4.1.2) В принципе значение х* параметра х} в выражении (4.1.6) может
быть произвольным, т.е. вместо вектора X,, в нем может фигурировать
вектор
где nf/ = 0(l)nf; т" = т-т';
ЛГЛч - вектор фиксируемых (номинальных) значений параметров ХТтк;
ЛГЛгч - вектор варьируемых значений параметров Х?у
Очевидно, что в этом случае функция (4.1.5), а следовательно, и функ-
ция чувствительности (4.1.6) будут функциями т" + \ аргументов и их ис-
следование существенно усложнится. Однако наибольший практический
интерес представляет чувствительность показателей wn [/ = 0,1,2] к ва-
риациям параметров х. именно в окрестности их номинальных значений
х% [/ = l(l)m]. A
Более детально функции чувствительности показателей РДЦ9 Ci)[(y)9
&[ (у) применительно к конкретным распределениям F^(y) и Ft(z) слу-
чайных величин у и z рассмотрены в монографии [128], с которой реко-
мендуем читателю ознакомиться более подробно.
Для иллюстрации рассмотренных выше понятий приведём ряд приме-
ров.
Пример 4.1.1. Найдём характеристики чувствительности показателей
эффективности операции в условиях примера 3.4.4.
Решение. Как было показано, при нормальных распределениях вир-
туального (у) и требуемого (£) целевых эффектов показатели эффектив-
ности операции определяются следующими выражениями:
и>п
,0(x{J=w0(AfB)=P^(AfB)=Fo
wl(x{m);y)= wl(A,B;y)=a)[(y;A,B)=F0
*>2{х{т);у)= w2(A,B;y)=a)[(y;A,B)=Fa
-В
41 +A2 J
F;l(i-y)-B
(4.1.11)
(4Л.12)
AF;l(l-r)-B\9 (4.1.12»)

4.1. Методы анализа эффективности ЦНП
227
гкХ{т) = Х(2}=(А,В);
А, В-обобщённые (агрегированные) параметры ("агрегаты") задачи;
у - гарантийная вероятность.
В результате дифференцирования соотношений (4.1.11), (4.1.12) и
(4.1.12') при Л = 0.5, В = -1 и 7=0,9 получим
^А(А,в) = -^-Т<р,
В
Л
(1 + Аг){ Чл/Г^?
VI+ А2 {л11 + А2
f;x{\-y)-b
;c^,io=*-f;'(1A
А1
= 0,096;
= -0.240;
= 0,387;
(4.1.13)
-1
к«{у;А,В)=-±<р{
F;l{i-r)-B
= -0,678;
hf(r;A,B)=F;,(i-r)<p<T[AF;l{i-r)-B]=-o,m;
hf {y;A,B) = -<pAaf;1{1 - у)- в] = -0,374.
(4.1.14)
(4.1.14')
A
Из числовых данных примера видно, что как величины, так и знаки ха-
рактеристик чувствительности показателей эффективности к параметрам А
и В зависят от величин и знаков этих параметров [128].
Пример 4.1.2. Найдём характеристики чувствительности показателей
эффективности операции в условиях примера 3.4.5.
Решение. Как было показано, при смещённых показательных распре-
делениях виртуальной (у) и директивной (г) длительностей операции по-
казатели её эффективности определяются следующими выражениями:
w.
(х,т))=ь>9{м,а,У,с)=РДЦ{м,а,У,с) = 1 У—е»^; (4.1.15)
JU + V
W,
".(*<„>>t)= wj,fi,a,v,c;y)= af{y;n,a,v,c) = 1-у'е*™*; (4.1.16)
wi\x{m)>y)= w2(fi,a,v,c;y)=a>[{y;ju,a,v,c)=(l-y)Mev{a-c), (4.1.16')
rfleX<m) = X(4)=(//,a,v,c);
ju, a,v, с -параметры ("агрегаты") задачи;
у - гарантийная вероятность.

228 Глава 4. Методы исследования эффективности ЦНП
В результате дифференцирования соотношений (4.1.15), (4.1.16) и
(4.1.16') при ju = 0,5, а = 1, v = 1, с = 2 и у = 0,9 получим:
V"+v)
hZ(M,a,v,c) = ^^e>'{-c) = -0,202;
/л-v
^(//,a,v,c) = 7-^r^(-c) =-0,135;
h^{n,a,v,c) = -^-e"{tt-c) =0,202;
h?(y;ii,a,v,c) =
-Iny
-a + c \у*е»(а-с) = 0,636;
** ^//)a)v,c)-//r'/M) = -0,778;
A<(r;/M,v,c) = 4r*A(e~c) =0,778;
v
A* (r;//,«,v,c) = fir e"("~e) = 0,778;
^(^,a,v,c)=^%^(l-r)L"^ = -2,303;
M
hf (y;n,a,v,c)=-v{l - yfev^ = -0,027;
ln{l-y)
hf {y;n,a,v,c) = v(l - yfev{c-a) = 0,027.
h?{y;n,a,v,c) = \ myi 7, + c-a \{\-y)i>ev(c-a) =-0,098;
Как видно из примера, при одних и тех же номинальных значениях па-
раметров ju, a, v, с характеристики чувствительности показателей эф-
фективности операции принимают самые различные значения и предска-
зать их поведение только по выражению показателя эффективности нельзя
[128].

4.1. Методы анализа эффективности ЦНП
229
4.1.3. ХАРАКТЕРИСТИКИ ВЛИЯНИЯ ПАРАМЕТРОВ МОДЕЛЕЙ
ЦУТС И ЦНПФС НА ЭФФЕКТИВНОСТЬ ОПЕРАЦИИ
Достаточно очевидно, что рассмотренные характеристики чувствитель-
ности представляют несомненный практический интерес, так как позволя-
ют анализировать характер изменения эффективности операции при изме-
нении значений параметров моделей ЦУТС и ЦНПФС, являющихся агре-
гированными комплексами их параметров и ЭТХ (ДА\). Однако сущест-
венным недостатком этих характеристик является различие их размерно-
стей, не позволяющее проводить их сравнительный анализ. Для осуществ-
ления такого анализа вводится в рассмотрение ряд характеристик, произ-
водных от характеристик чувствительности (либо безразмерных, либо
имеющих одинаковые размерности):
- коэффициент (показатель) влияния параметра х} на показатель эф-
фективности и>7 (/ = 0,1,2)
У\=У:;=К\Х;\ (4-1.19)
- коэффициент (показатель) нестабильности показателя wt по па-
раметру х., [/ = l(l)#fi]
^'=*;'=<'<V (4Л.20)
- потенциал управления показателем и>7 по управляемому параметру
ик, [к = 1 (l)r] (г - число управляемых параметров)
и[=и::=\Кк\\Лик\, (4.1.21)
где Л ик - диапазон возможного изменения параметра ик;
- потенциал оптимизации [коэффициент (показатель) действенно-
сти управления] показателя wt по параметру uk, [k = l(l)r]
i \\^uk\
Dl=D"' = А"' ' -, (4.1.22)
где Аик - диапазон возможного прогрессивного (способствующего по-
вышению эффективности) изменения параметра ик;
£ Ск - затраты, необходимые для изменения параметра ик в диапазо-
не £ик.
4.1.3) В отличие от показателей Vj 9 N1., U[, которые для всех j и к
имеют одинаковые размерности, совпадающие с размерностью показате-
лей wt (поскольку в рассматриваемом случае wn [/ = 0,1,2] - это вероят-
ности и, следовательно, безразмерны, то безразмерны и характеристики

230 Глава 4. Методы исследования эффективности ЦНП
Vj, Nj9 U[) и потому пригодны для сравнительного анализа, показатели
D'k9 [k = l(l)r\ имеют размерности, обратные размерностям затрат Ск на
управление параметрами wA, [A = l(l)r]. Поэтому для сравнимости этих
характеристик для различных параметров затраты СЛ, [# = l(l)r] следует
выражать в одних единицах. ▲
Некоторые из приведённых характеристик имеют широкое применение
в "Теории производственных функций" и "Теории операционных функ-
ционалов" (см. гл. 5 и [59]), хотя иногда и под другими названиями.
При широком толковании понятия "ресурс" можно говорить о ресурсе
конкретного свойства объекта, понимая под этим "интенсивность" этого
свойства [4, 158]. А поскольку параметры объекта характеризуют количе-
ственно его свойства, то их значения характеризуют запасы ("ресурс") это-
го свойства у объекта. Опираясь на такое толкование понятия ресурса, рас-
смотрим ещё ряд характеристик, позволяющих проводить углублённый
анализ свойств исследуемых объектов ЦУТС и ЦНПФС, а также их каче-
ства й эффективности.
Характеристики производительности "параметрическихресурсов" 1:
- показатель предельной производительности параметра х.
lt=h'>> (41-23)
- показатель средней производительности параметра х.
Щ
XJ
= *;' . (4.1.24)
Характеристики замещения "параметрическихресурсов"
- коэффициент (показатель) эластичности показателя wl по парамет-
ру Xj
dw, x. h\ ,
p—L = 1± = 3; (4.1.25)
dxj w, hj
- показатель предельной нормы замещения параметра х} парамет-
ром х,
дХ; h\
- показатель эластичности замещения параметра Xj параметром х,
' Подробно эти характеристики анализируются в [59].

4.1. Методы анализа эффективности ЦНП
231
d(Xi/Xj) 3lj _ia>
-коэффициент (показатель) эластичности показателя w,
= Э'и; (4.1.27)
т т 7)иу х
4.1.4) В зависимости от задач анализа коэффициент Эу' может тракто-
ваться либо как параметроёмкость показателя wt по параметру xj9 ли-
бо как параметровооружённостъ ЦУТС и ЦНПФС параметром х. (см.
п. 5.3.2). А
В основном из приведённых определений достаточно ясен физический
смысл соответствующих характеристик, тем не менее некоторые из них
требуют пояснения. Так, коэффициент эластичности показателя wt харак-
теризует степень его относительного изменения при относительном изме-
нении параметра х. на единицу. Показатель эластичности замещения па-
раметров характеризует относительное изменение отношения параметров
при относительном изменении предельной нормы замещения параметров
на единицу, т.е. характеризует возможности по управлению показателем
wt за счет взаимного изменения значений параметров jc, и х}.
Для иллюстрации сказанного рассмотрим плоскость двух параметров щ
и и. (рис.4.1.1) и построим на ней линии уровня (равных значений
и>, = Pk) показателя wr Такие линии называются изоквантами. Прямые,
в точках, которых суммы взвешенных (с весами, равными коэффициентам
чувствительности) значений параметров (суммы коэффициентов влияния
параметров) щ и и. постоянны, называются изокостами. Нетрудно по-
нять, что величина Э/у показывает, на сколько процентов должно изме-
ниться отношение значений параметров при движении вдоль изокванты,
чтобы при этом величина З'и изменилась на один процент.
Таким образом, изокванты - это линии одинаковой эффективности
("изоэффы"), а изокосты - линии одинаковых суммарных "затрат пара-
метрических ресурсов". Точки касания изоквант и изокост соответствуют
наименьшим суммарным "затратам параметрических ресурсов", обеспечи-
вающим соответствующие этим точкам значения показателя эффективно-
сти. Очевидно, что для управления эффективностью операции с целью её
увеличения целесообразно (если нет дополнительных ограничений) под-
держивать значения параметров «Л, [* = l(l)r] на линии, образованной
точками касания изоквант и изокост. Эта линия называется траекторией
оптимального (по параметрам) управления.

232 Глава 4. Методы исследования эффективности ЦНП
<Рг<Р>
Рг
Рг
О и\
Рис. 4.1.1
С помощью приведённых характеристик может решаться целый ряд со-
держательных в практическом отношении задач анализа:
- выделение параметров и ЭТХ ЦУТС и ЦНПФС, а также условий про-
ведения операции, к изменениям которых наиболее чувствительны показа-
тели её эффективности;
- определение точки Х\ или области {Х*Л, в которых показатели
эффективности операции нечувствительны к изменению параметров Х,т);
- сравнительный анализ влияния различных параметров и ЭТХ на эф-
фективность операции и выбор из них наиболее пригодных для управления
организацией ЦНПФС и качеством ЦУТС;
- анализ критичности операции к требованиям, предъявляемым к ре-
зультатам операции, и выделение из их операционных свойств (аспектов)
наиболее важных;
- содержательное (неформальное) решение некоторых задач оптималь-
ного синтеза ЦУТС и ЦНПФС.
Проиллюстрируем сказанное на примерах.
Пример 4.1.3, Провести анализ эффективности операции в условиях
примеров 3.4.4 и 4.1.1.
Решение. Подставив результаты (4.1.13) в (4.1.19), получим:
и.

4.1. Методы анализа эффективности ЦНП
233
у;=ка=
А2В
<Ро
В
3 Т0\ I
(1 + А*)г 41 +А
= 0,048;
(
\
v'-*-^b'hb)
= -0,240;
(4.1.29)
vf .к'д^К(17)~д]--°'<78;
(4.1.30)
Vf = hfA = AF;1{1- у)(ра(АРЛ- Г)-В)= -0,240;1
Vf = hfB = -B90(af;1(1 -у)-в)= -0,374. J
(4.1.30')
Пусть A = jc, , В = хг. Тогда предельные нормы замещения параметра
А параметром В для различных показателей и>0 = РДЦ, и>, = о>[, w1=a>[
примут следующие значения:
иг
(4.1.31)
(4.1.32)
(4.1.32')
ир
12 ""*:"
12 ~~tf
12 " !.<
= 2,50;
= 1,76;
= -0,78
Соответствующие показатели эластичности замещения параметров А и
В примут значения:
^B)J^
11 d3*n А/В
^B)J^
d3, А/В
г _d(A/B) 3f2 _ ,
^И — л! .. / n — >'
d3ln А/В
56.
(4.1.33)
(4.1.34)
(4.1.34')
Наконец, коэффициенты эластичности показателей w, по параметрам
А и В примут значения:

234 Глава 4. Методы исследования эффективности ЦНП
Э1в=А1в/А1в=А1°-^- = 0,059;
°ДЦ
Э\ = h\ /h2° = h\ — = -0,294;
"дц
Э,1 = h\ /h\ =hl^r = 0,667;
Э21=А]/А21=А]^г = -2,338/
Э2 = А? /*? = А2 -4- = -0,375;
Э22 = Л2 /А2 = hi ^г = -0,584,
2 2 2 W
(4.1.35)
(4.1.36)
(4.1.36')
Из результатов (4.1.29) - (4.1.36) следует:
а) характеристики чувствительности и влияния могут существенно от-
личаться друг от друга, как по величине, так и по знаку [см. (4.1.13) -
(4.1.14') и (4.1.29)-(4.1.30')];
б) при управлении эффективностью операции путём варьирования па-
раметров А и В, параметр А требует большого изменения: при управле-
нии показателем Рдц = н>0 - в 2,5 раза, при управлении показателем
а)[ =wx - в 1,76 раза, при управлении показателем со[ = w2- в 0,78 раза
(т.е. в последнем случае параметр В требует большего увеличения, чем
параметр А [см. (4.1.31) -(4.1.32')]);
в) при управлении показателем Рдц для изменения предельной нормы
замещения 3,°2 параметра А параметром В на 1% отношение А/В долж-
но измениться на 5%, при управлении показателем (о[ - на 3,52%, при
управлении показателем (о[- на 1,56% (в сторону уменьшения);
г) при управлении показателем Рдц, его процентное изменение за счёт
изменения параметра В почти в 5 раз выше, чем за счёт изменения пара-
метра А, при управлении показателем (о[ - в 3,5 раза, при управлении по-
казателем со[ - в 1,5 раза. А
Представляется весьма очевидной практическая ценность подобного
анализа как на этапе проектирования ЦУТС, так и на этапах организации и
управления ЦНПФС.
Понятно, что проведённый краткий анализ далеко не исчерпывает воз-
можности аппарата рассмотренных характеристик, так как многие из них в
рамках примера не использовались. Рекомендуем читателю для приобре-

4.L Методы анализа эффективности ЦНП
235
тения навыков решения задач анализа в качестве упражнения провести
анализ эффективности операции в условиях примеров 3.4.5 и 4.1.2.
4.1.4. О НЕФОРМАЛЬНОМ АНАЛИЗЕ ЭФФЕКТИВНОСТИ ОПЕРАЦИИ
Под неформальным здесь понимается эвристический содержательный
анализ зависимостей, проводимый, как правило, по их графикам и нося-
щий в основном качественный характер. Поскольку при таком анализе не
используются "формальные характеристики", определяемые при целом ря-
де предположений и допущений (не всегда достаточно обоснованных), то
содержательный, качественный анализ в ряде случаев может оказаться бо-
лее предпочтительным. Из рассмотрения распространенных практических
методов анализа следует, что среди них содержательный анализ занимает
весьма существенное место. Строгой классификации таких методов не су-
ществует, да, по-видимому, и не может существовать из-за их много- и
разнообразия. Тем не менее представляется целесообразным условно раз-
бить их на две группы: графоаналитические методы и имитационные ме-
тоды. Рассмотрим их.
4.1.4.1. Графоаналитические методы
Среди графоаналитических методов анализа качества объектов особое
место занимает "Метод компромисса", в основе которого лежит построе-
ние компромиссных множеств ("множеств Парето").
Понятие компромиссного множества возникает в так называемых "мно-
гокритериальных" (см. (3.3.1)) задачах принятия решений [36, 55, 177,
178]. Сразу заметим, что в известной литературе этот метод фигурирует
как принципиально детерминированный. Кроме того, он применяется в тех
случаях, когда не удаётся построить единую (обобщённую) критериальную
функцию и компоненты у. показателя Y,n) качества объекта (ЦНПФС и
ЦУТС), будучи его атрибутами, фигурируют как таковые в полной их со-
вокупности. В этом случае рассматривается пространство |уЛ ] векторов
F/\ =(у?,У2,Уз), называемое [162] "пространством критериев"1; в кото-
ром выделяются так называемые "эффективные" точки Г/?, определяе-
мые с помощью отношения Парето р [177] и обладающие следующими
свойствами:
Точнее, "пространство аспектов".

236 Глава 4. Методы исследования эффективности ЦНП
т.е. объект, показатель качества которого (Г/£?) определяет "эффективную"
точку, по всем компонентам не хуже остальных объектов и хотя бы (по
меньшей мере) по одной компоненте заведомо лучше их. Качество объек-
та, соответствующее эффективной точке, называется доминирующим.
Множество {г/? ) "эффективных" точек образует "компромиссное множе-
ство" (множество Парето), а соответствующие им объекты называются
"оптимальными по Парето".
4.1.5) В литературе [162] в рамках рассмотренной модели вводится ещё
целый ряд понятий, таких как:
- пространство параметров;
- параметрические ограничения;
- пространство критериев;
- критериальные ограничения;
-множество допустимых точек;
- множество управлений и т.п.
В рамках рассматриваемой методологии параметры объектов образуют
векторы (^ALyA^yBf,ryB^rA = X,,9 пространство параметров - множест-
во [Х, Л, параметрические ограничения - Х,.е \Х?т\\ (где {-Х?да\| -
множество допустимых точек), пространство "критериев" (аспектов)
|кЛ], критериальные ограничения -Y/t^e \Y/^\ (или Y^^Zfs); множе-
ство допустимых управлений - \U?r\ ].
Приведённые понятия иллюстрируются рис. 4.1.2, построенным для
случая конечного числа 5=12 объектов х = 2, на котором "эффективные"
точки выделены двойными кружками1. А
4.1.6) Обратим внимание, что приведённое определение компромиссно-
го множества основано (и это принципиально) на предположении о равно-
значности рассматриваемых аспектов ("критериев"). Поэтому множество
"оптимальных по Парето" объектов точнее было бы назвать множеством
"несравнимых по Парето" объектов, поскольку для каждого из них суще-
ствуют объекты, превосходящие их по одним аспектам ("критериям") и
уступающие - по другим. Таким образом, при наличии "компромиссного
множества" объектов проблема выбора из них оптимального не снимается
и для её решения должна привлекаться дополнительная информация о
1 Аспекты ух и у2 имеют определённый в формуле (2.3.5) физический смысл
(ух - целевой эффект; у2 - расход ресурсов).

4.1. Методы анализа эффективности ЦНП
237
предпочтениях или ограничениях на множестве \У,ХЛ компонент вектора
К*. Наличие дополнительной информации об относительной (сравни-
тельной) значимости (важности) аспектов существенно повлияло бы на
структуру компромиссного множества. Впрочем, это произошло бы только
в случае оставшейся (после ранжирования в соответствии с дополнитель-
ными данными "эффективных" точек) их несравнимости по каким-то "рав-
нозначным" аспектам. ▲
Уг\
0
i
II
1
I
|
i
' |
!
|
j
|
1
4
i
i
' 'С'
<
>
A
Ъ
►••
f\
V
Г"
>
4
щ>
i
-4
........<!
> 1
j
i
1
1
ft
у
Ух
Рис. 4.1.2
В рамках рассматриваемой методологии указанной "дополнительной"
информацией является уровень рг "изоэффы", т.е. гарантийная вероят-
ность Р*ДЦ = рг обеспечения требуемого качества результатов операции
или параметров и ЭТХ ЦУТС и ЦНПФС. При этом наличие единого ком-
плексного показателя качества исследуемого объекта (ЦУТС и ЦНПФС) -
показателя Рдц (или 0)дц(у)) эффективности операции приводит к новой
концепции и вытекающим из нее принципам решения многокритериаль-
ных задач, основанным на понятии "гарантированного компромиссного
множества".
Определение 4.1.2. Множество \Zf v} (или {хг* j) значений показателя
требуемого качества объекта (результатов операции или параметров ЦУТС
и ЦНПФС), гарантируемых с вероятностью не менее р\ называется
компромиссным множеством уровня р (КМУ). А

238 Глава 4. Методы исследования эффективности ЦНП
Легко понять, что в пространстве \z, А (или {Xv j) КМУ представляет
собой изоэффу (изокванту), пометка рг которой - Уровень гарантии ка-
чества объекта" называется "гарантийной вероятностью"*.
Пусть требования Z, *, предъявляемые к качеству результатов опера-
*
ции, строго определены (заданы предельными значениями), т.е. Z^^Z^,
тогда, как известно (см. п.2.4), "критериальная функция" будет иметь вид
*,(*£> )= рт = <\,К) )= <\,(Z(z)'XH )• <4Л-38)
Для отличия от функции Wp\p,A виртуальных результатов Y,, крите-
риальная функция WA\Z?s\ называется директивной.
Пусть (для простоты и наглядности) х = 2. Тогда компромиссные мно-
жества будут иметь вид кривых, изображённых на рис. 4.1.3, где г,я/,
z"п - предельно допустимые (наиболее "мягкие") требуемые значения
показателей у19 у2 качества результатов операции, JP^J, (/ = 1,2,3) -веро-
ятность достижения цели /-го варианта операции, определяемого вектором
4.1Л) Легко заметить, что кривые на рис. 4.1.3 являются изоэффами, а
их совокупности, совмещённые на одном поле - "декартовом абаке" [186],
представляют собой "сетчатую номограмму".
Сетчатая номограмма (рис. 4.1.3) позволяет на качественном уровне ре-
шать целый ряд задач как анализа ЦУТС и ЦНПФС, так и их "рациональ-
ного" (субоптимального) синтеза. Так, если реализуется критерий пригод-
ности - РДЦ > РТдЦ, то на рис. 4.1.3 определяется компромиссная кривая:
a) PW(Z{X))=PZ<> или б) *тК))=Р*> ИЛИ В) РЛ2Ъ)>ии)=рт и
соответствующее ей гарантируемое значение ZP1 показателя Z,. ка-
чества результатов операции (ГУЕМР), или гарантирующее требуемую
эффективность операции значение иГЦ* управляемых параметров U,r)
(ГУЮЩП), или значение (zf^fU^) комплексного показателя \Z,)9U,i)
(ГУЕМРЮЩП) - задачи синтеза ЦУТС и ЦНПФС.
1 Не следует смешивать вероятности рг и у, имеющие аналогичные названия, но
относящиеся к различным характеристикам.

4.1. Методы анализа эффективности ЦНП
239
■(*)
«)
С)
i
pW >> р(*)
Z?" *,W
б)
р(*) _ р ly(k) Jj(k) \
•)
■(*)
>
(*)
»(*)
*5
р(») _ в (т<*) 7/(*) )
Рис. 4.1.3

240 Глава 4. Методы исследования эффективности ЦНП
При реализации критерия оптимальности РДЦ = Р™ компромиссная
кривая отвечает уравнению Рдц [ Z,,) = Ф$ [ Z, *) = Р%£, или
Рдц[и(г))=Рщ, или Pm(z{x),U{r))=0f (z{x);uJ=P™, а соотвегсг-
'(X)
вующее ей искомое значение вектора
Z[K)^argmaxPm{z^ ,
Z/"s€
ш
или
К)=^тр*«К))>
{ZU'K)) = t «*"■« P^Z^t/J.
Если пометки Р1ДЦ компромиссных кривых снабдить значениями пара-
метра Z,y или 17/v, или (Z/v,17/Л, то, исследуя рис. 4.1.3, можно осу-
ществлять качественный анализ влияния параметров Z!L, или V,^, или
(Z£v,J7/rv) на эффективность ЦНПФС, а, следовательно, и на качество
ЦУТС. А
4.1.8) Обратим внимание, что в общем случае как
Р Ык) -ХМ)± Р (7(к) •Х&А
так и
Р Ы*'} • X(l) ) ± Р (Z(*>} • X® ) А
4.1.9) Аналогично решаются задачи анализа эффективности ЦНПФС и в
случае, когда в качестве показателя эффективности фигурирует гаранти-
руемая вероятность С0дЦ(у) достижения цели операции, с той разницей,
что в пометках компромиссных кривых к параметрам Z/L, J7/rv,
(Z/L,£/,v) добавляется гарантийная вероятность у. А
4.1.10) Следует обратить внимание, что рассмотренная методика по
сравнению с известными [36, 162, 178] обладает несомненными преиму-
ществами, поскольку кроме "критериальных ограничений" учитывает и ог-
раничения по эффективности (её минимально допустимое значение). При-
чём, как уже отмечалось, этот глобальный обобщённый показатель качест-
ва исследуемого объекта (ЦУТС, ЦНПФС) определяется без необоснован-
ного постулирования [36, 84, 178] структуры критериальной функции, зна-

4.1. Методы анализа эффективности ЦНП
241
чений её весовых коэффициентов и т.п. (см. п.2.4, (2.4.13), (2.4.14), п.3.3,
(3.3.8), (3.3.9)). А
4.1.11) Подчеркнём, что в общем случае при решении задачи оценива-
ния качества объекта в разомкнутой схеме, т.е. только по показателю К \
(без учёта эффективности операции), компромиссные множества будут от-
личаться от изображённых на рис. 4.1.3 и будут иметь отличный от них
смысл. А
4.1.12) Ещё раз подчеркнём, что если замкнутая схема исследования
эффективности реализована в полном объёме, т.е. при рандомизированных
по всем аспектам требованиях Z, v к результатам операции, то компро-
миссное по требованиям ZJL множество "размывается" (исчезает) и каче-
ство анализируемого объекта (ЦУТС или ЦНПФС) определяется единст-
венным комплексным показателем РДЦ\х,т)) [или согдц\у;Х,к)] - веро-
ятностью достижения цели операции. В этом случае вероятность Рдц
[о)дЦ(у)] будет зависеть только от параметров Х,ту (или U,,) и компро-
миссное множество Парето будет подмножеством пространства допусти-
мых значений параметров, т.е.
t*wM*<->)шш К>1сК>1- А
4.1.13) Из рассмотрения рис. 3.1.9 следует, что хотя в общем случае яв-
ной функциональной зависимости между средней вероятностью Рдц (на-
помним, что /дц =й>1 =<й2) и гарантируемой вероятностью 0)гдц(у)
(ю'лб(у)~F&*(l"~У)) достижения цели операции нет, тем не менее их не-
явная связь имеет вполне определенную тенденцию, которую можно оха-
рактеризовать следующими неравенствами:
ЬРДЦ ' Ъу
Как можно было заметить, графоаналитические методы, по существу,
являются номографическими, так как основаны на применении номограмм,
т.е. специальным образом построенных семейств кривых. Проиллюстриру-
ем сказанное на примере.
Пример 4.1.4. Пусть качество результатов операции характеризуется
одним показателем - аспектом ("эффект поглощения", см. п. 3.3.4). Причём

242 Глава 4. Методы исследования эффективности ЦНП
виртуальный и требуемый целевые эффекты j>, и £, подчинены нормаль-
ным законам распределения с параметрами y,OpViz,<7i соответственно.
Тогда, как показано в примере 3.4.4, показатели эффективности опера-
ции определяются следующими выражениями:
°>м=<
Рдц=Рм{А>В)=К
a>;(r)=G>[(y;A,B)=F0
В
.VI
+ Аг
F;l(i-r)-B'
[<Dl(y)=<o[(r;A,B) = F<r[AF;1(l-y)-B
(4.1.39)
(4.1.40)
(4.1.40')
где АиВ- агрегированные обобщённые параметры операции (ЦНПФС),
А =
В
<У.у
Для уравнений (4.1.39), (4.1.40), (4.1.40') могут быть построены сетча-
тые номограммы (абак Декарта [128, 186]). Это целесообразно сделать в
системе координат BOA , т.е. интерпретируя агрегаты АиВ как аспекты.
Разрешив уравнения (4.1.39), (4.1.40), (4.1.40' ) относительно агрегата А,
получим:
А = .
В2
W('-r)J
-1;
F?{l-y)-Bu
F-Ai-r) '
(4.1.41)
(4.1.42)
(4.1.421)
Соответствующие равенствам (4.1.41), (4.1.42), (4.1.42') изоэффы для
компактности совмещены на одном поле (абаке) и приведены на рис. 4.1.4,
Ключ к номограмме рис. 4.1.4 дан в его правом нижнем углу.
С помощью приведённой номограммы может быть решён целый ряд за-
дач анализа эффективности операции. В частности, может быть проанали-
зирована зависимость соотношения гарантируемых вероятностей 0)[ и
со[ достижения её цели от значений параметров АиВ .

4.1. Методы анализа эффективности ЦНП
243

244 Глава 4. Методы исследования эффективности ЦНП
Из выражений (4.1.39), (4.1.40), (4.1.40') следует:
{Vre[0A])af = ar2(r)**{A=l)u[B=F;,{l-y){l+A)\; (4.1.43)
а>гАг) ><(/)«*
^{Й>1)п[Б>^1(1-г)(М]}^{Й<1)п[5<^,(1-г)(1+^)]}; (4-1.44)
<t>rt(r)<o>i{r)**
^{(^>i)n[^<^:1(i-r)(i+4]WU<i)n[i?>/^,(i-r)(i+^)] }• (4.1.44-)
Соотношения (4.1.43), (4.1.44), (4.1.44') сведены в табл. 4.1.1, а также
проиллюстрированы графически на рис. 4.1.5. А
Таблица 4.1.1.
А
А=\
А>\
А<\
В
b={\+a)f;x{\-y)
<огАг)=о>гг{у)
(0ГАг)=о)Г1{г)
<»ГЫ=<»£Ы
B>(l + A)Fa-l(l-r)
<»ГЛг)=<»г(г)
а>ГАг)>а>Гг{у)
(оГЛу)<а)Гг{г)
B<(l + A)Fa-l(l-y)
(0ГЛу) = (0Г1{у)
tf(r)<<»2(r)
<»гАг)><*>гАг)
о в
Рис. 4.1.5
Номограмма рис. 4.1.4 и соотношения табл. 4.1.1 позволяют произво-
дить быстрые прикидочные расчёты, которые в условиях использования
приближённых исходных данных имеют приемлемые по точности резуль-
таты при максимальной простоте процедуры их получения.

4.1. Методы анализа эффективности ЦНП
245
4.1.4.2. Имитационные методы
В настоящее время благодаря высокому уровню развития вычисли-
тельной техники всё более широкое применение получают методы иссле-
дования (анализа и синтеза) объектов (ЦУТС и ЦНПФС) с помощью их
имитационного моделирования на ЭВМ. Поскольку, как отмечалось, ана-
лиз качества объекта представляет собой второй этап (фазу, стадию) реше-
ния прямой задачи его исследования, то основу его алгоритма составляет
алгоритм оценивания качества. Применительно к задачам исследования
эффективности ЦНПФС такой алгоритм был достаточно подробно рас-
смотрен в п. 3.4.2. При анализе качества ЦУТС и эффективности ЦНПФС
он выполняет роль подалгоритма в алгоритме их исследования более вы-
сокого уровня. Общая структура такого алгоритма приведена на рис. 4.1.6
(см. п. 2.3.5 и рис. 2.2.5 и 2.2.6). В зависимости от решаемой задачи анали-
за (определяемой блоком 1) содержание работы отдельных блоков может
несколько варьироваться, однако основное их назначение остаётся неиз-
менным. Кратко поясним сказанное.
Блок 1 описывает класс решаемых задач анализа [определение характе-
ристик чувствительности и влияния, построения "изоэфф" (компромисс-
ных множеств), оценивание эффективности операции по заданному крите-
рию и т.п.].
Блок 2 контролирует (проверяет) выполнение программы анализа и ус-
танавливает факт её завершения.
Блок 3 в соответствии с программой варьирует значения синтезируе-
мых [Х,т)) или управляемых \р,г)) параметров и ЭТХ ЦУТС и ЦНПФС и
определяет их приращения (вариации) по формулам
Щт) = Х[т)-Х^, [1 = 1(1)7],
где Х!т) - 1-й вариант значений параметров X, , = \А,куВЛ\
X! ^ - исходное (номинальное, расчетное) значение параметров Х,т);
/ - число запланированных вариаций;
АХ[т)={Ах[,Ах11,...,Ах,т).
Блок 4 вычисляет для новых значений Х'т = Х]~\ +ЛХ',^ параметров
Х(т\ оценки РДЦ
И»))» ®дц\г>'хи) показателей Рдц{Х{т)), а>гдц\у;Х{т))
эффективности операции по алгоритму рис. 3.4.3, или 3.4.4, или 3.4.9.

246 Глава 4. Методы исследования эффективности ЦНП
о
Характеристика
решаемых задач
анализа
Проверка завершения
программы анализа
ж
Варьирование значе-
ниями управляемых
параметров
0
Вычисление
©
Определение
hf,Vf,Ut,Dt
1=0,1,2; /=1(1)7;
y=l(l)in; А=1(1)г
Выдача результатов
Построение компро-
миссных множеств
РДЦ\2{Х)>Х(т))=Рг
/»д><,>)=/>'
3!
Оценивание
рдц\х(т))- рдц
Рис. 4.1.6
ме:
Блок 5 определяет характеристики чувствительности и влияния по схе-
а) определяются вариации показателей эффективности:
ЛР'ц=ЛРдц{х[т))=Рдц(х[т))-Рдц{х^), [/ = 1(1)/];
б) определяются оценки характеристик чувствительности:
^'=^k))=^#^' moo" ;=i(iH;
hl)=h« (у;XQ=
. \ Лф[дц(г,х!т))
Ах)
, [i = l(l)/;/ = l(l)in;/ = l,2];

4.1. Методы анализа эффективности ЦНП
247
в) определяются оценки характеристик влияния:
V]1 = h'/x), [I = 0,1,2; i = 1(1)/; у = l(l)m];
Я';=Ц'а*}, [/ = 0,1,2; / = 1(1)/; j = l(l)m\;
0? =№Uik\, [/ = 0,1,2; / = 1(1)/; * = l(l)r];
%' = \Щт^1> [/ = 0Д,2; / = 1(1)/; * = l(l)r].
"А
Блок 6 оценивает пригодность операции по эффективности путём про-
верки условий:
Рдц^Рдц' ММ'];
^(rXF(rl [/=i(i)4
Блок 7 определяет элементы компромиссных множеств ("эффективные
точки" пространства аспектов).
Блок 8 выдаёт результаты.
4.1.14) При необходимости программой работы блока 5 может быть
предусмотрено и определение характеристик производительности и заме-
щения параметров. А
После выдачи результатов проводится их анализ и принимается реше-
ние об эффективности ЦНПФС и качестве ЦУТС. В принципе последняя
процедура также может быть формализована и реализована на ЭВМ.
Рекомендуем читателю внимательно ознакомиться с приведённым опи-
санием алгоритма анализа качества исследуемого объекта (ЦУТС и
ЦНПФС) и, уяснив принципы его работы, сформулировать другие воз-
можные задачи анализа и необходимые для его реализации процедуры.
4.1.15) В соответствии с физическим смыслом решаемых задач (про-
странств JZ/ v ), JJ7/V ) или UZi \>U,k )\ анализ соответственно называ-
ется аспектным, параметрическим или аспектно-параметрическим. ▲

248 Глава 4. Методы исследования эффективности ЦНП
4.2. МЕТОДЫ СИНТЕЗА ЭФФЕКТИВНЫХ
ЦЕЛЕНАПРАВЛЕННЫХ ПРОЦЕССОВ
Как отмечалось, задача синтеза объектов, обладающих требуемым или
оптимальным качеством, является по отношению к задачам его оценивания
и анализа обратной. Поэтому она также решается с помощью моделей объ-
ектов. Однако в отличие от задачи анализа, в рамках которой структура и
характеристики модели предполагаются заданными и исследуется их
влияние на качество объекта (его модели), задача синтеза состоит именно в
определении структуры и характеристик объекта (его модели), обеспечи-
вающих требуемое его качество (заданное или оптимальное). Данный па-
раграф посвящен рассмотрению (обзору) основных, наиболее перспектив-
ных подходов к решению этой важной практической задачи.
В классификационной схеме рис. 2.3.4 задачи синтеза операций (обрат-
ные задачи) до некоторой степени условно подразделяются на инженерно-
технические и организационные. Основное содержание этих задач ясно из
самой схемы. Поэтому здесь мы не будем рассматривать содержание каж-
дой из этих задач (перечень которых, приведённый на схеме, не исчерпы-
вает всего их многообразия), а кратко обсудим основные варианты их
формулировок и методов решения.
4.2.1. ФОРМУЛИРОВКА ЗАДАЧИ СИНТЕЗА ОПЕРАЦИОННОЙ
СИСТЕМЫ ПО КРИТЕРИЮ ПРИГОДНОСТИ
Под синтезом операционной системы (ОС) понимается определение оп-
тимальных значений её характеристик, обеспечивающих достижение цели
операции в максимально возможной степени. К таким характеристикам
относятся: структура, параметры и ЭТХ ЦУТС, а также организация и
управление ЦНПФС (операции).
4.2.1.1. Формальное решение
При реализации критерия пригодности задача синтеза объекта не имеет
однозначного (единственного) решения, так как в соответствии с этим кри-
терием качества сравниваемые объекты считаются одинаковыми для неко-
торых диапазонов значений показателей их свойств (характеристик - па-
раметров и ЭТХ). Общих методов решения таким образом сформулиро-
ванных задач синтеза не существует, и в основе применяемых на практике
алгоритмов лежат методы прямого или направленного перебора вариантов
и поиска компромиссного решения. Покажем это.

4.2. Методы синтеза эффективных ЦНП
249
Как известно [см. (2.3.17)], критерии пригодности операции по эффек-
тивности имеют выражения:
(Гэ:РДЦ(и{г))>Р^; (4.2.1)
<?э •• <r(r;U{r})> а>гдТц"(г), (4.2.2)
где t//v - вектор управляемых характеристик, параметров и ЭТХ ЦУТС и
ЦНПФС.
Поскольку для увеличения эффективности прогрессивное изменение
dtUix (увеличение положительных и уменьшение отрицательных) харак-
теристик U,, синтезируемого объекта (ЦУТС и ЦНПФС) требует опреде-
лённых дополнительных затрат Л С, то желательно эти затраты свести к
минимуму. Как видно из соотношений (4.2.1) и (4.2.2), минимум затрат бу-
дет обеспечиваться в случае равенства возможных и требуемых (мини-
мально допустимых) значений показателей эффективности ЦНПФС, т.е.
когда
PjmK))=P£i> (4-23)
<,(riU{r))=a№(r). (4.2.4)
Легко понять, что наиболее рациональные (наиболее "экономичные" по
критерию пригодности) значения {/,\ характеристик СЛ* определяются
решениями уравнений (4.2.3) и (4.2.4), т.е.
U(r)(pZ)=arg{pm(u{r))=PZ\; (4.2.5)
ЩгНТц{ г))=«У {а>дц(у;и{г))= <"( у)\. (4.2.6)
Поскольку U, к - вектор, то уравнения (4.2.3) и (4.2.4) описывают не
единственные точки, а поверхности в (г + 1)-мерных пространствах векто-
ров (их,и2,...,иг,Рдц} и (иА,и2,...,иг,(Огдц{у^. Для г = 2 сказанное иллюст-
рируется рис. 4.2.1. Из рис. 4.2.1 видно, что кривая
^гш~Рдц№(г))~Рдц =® представляет собой изокванту - изоэффу (см.
п. 4.1.3), во всех точках которой эффективность операции одинакова и ха-
рактеризуется требуемой средней вероятностью достижения цели - Р™ц.
Руководствуясь, кроме критерия (4.2.3), "дополнительными соображе-
ниями", на кривой j\fJi2\) выбирается наиболее рациональная точка UL.
Пример 4.2Л. Пусть в условиях примера 4.1.1 Р™ц = 0.9.
Требуется определить значения параметров А и В, обеспечивающие
требуемую эффективность операции.

250 Глава 4. Методы исследования эффективности ЦНП
j(u*2))=0
Рис. 4.2.1
Решение. По номограмме рис. 4.1.4 находится изоэффа уровня
/;г=0.9 (кривая, помеченная штриховкой). Любая точка (аэ,Вэ) этой
кривой обеспечивает пригодность операции, т.е. её требуемую эффектив-
ность. Для однозначности решения необходимы "дополнительные дан-
ные".
Пусть, например, известно, что Аэ =1. Тогда, как видно из рис. 4.1.4,
для выполнения условия (4.2.3) должно выполняться равенство Вэ =-1.8,
т. е. (аэ ,ВЭ) = (1,-1.8), а для выполнения условия (4.2.1) должны выпол-
няться неравенства (а<Аэ)п(в<Вэ) ,т.е. (А,В)<(аэ,ВэУ А
4.2.1.2. Неформальное решение
Фигурировавшие выше соотношения
РДЦ=РДЦ[и{г)), (4.2.7)
<0гдц{у)=а>дц{г;и{г)) (4.2.8)
могут быть получены в случае, когда требования Z, v , предъявляемые к
результатам Е* операции, случайны и закон их распределения известен.
Если же они детерминированы и заданы вектором ZlL, то выражения
(4.2.7) и (4.2.8) примут вид:

4.2. Методы синтеза эффективных ЦНП
251
<,ir) = ^(r;Z^uJ=w,(u{r);Z^tr), (# = 1,2), (4.2.10)
т.е. вероятность достижения цели будет функцией не только управляемых
характеристик £Лд, но и заданных требований Z/L к результатам опера-
ции. В этом случае операционная система может синтезироваться как по
параметрам U,y так и по требованиям Z?.. При этом синтез может осу-
ществляться в трёх постановках:
- определение значений Г/Л характеристик £Лд, обеспечивающих при
заданных требованиях ZJL требуемую эффективность Р™ц или а?дЦ
операции;
- определение требований Zf v, которые можно предъявить к результа-
там Y, v операции при заданных значениях UL характеристик 1Лд, обес-
печивающих эффективность операции не ниже требуемой [Рщ или
0)дцР{у)]> т.е. определение гарантированных значений аспектов (см.
п. 4.1.4.1);
- определение значений £/,\ и Z? v векторов U,x и Z, v, при которых
обеспечивается требуемая эффективность [PJJJ или fljJ^OOl операции.
Представляется очевидным, что чем больше аргументов в выражениях
(4.2.9) и (4.2.10), тем больше требуется дополнительных данных (устра-
няющих неопределённости) для решения сформулированных задач син-
теза.
Пример 4.2.2. Пусть организуется (планируется) операция, качество ре-
зультатов которой характеризуется одним (вследствие эффекта поглоще-
ния) целевым эффектом у, подчинённым нормальному закону распреде-
ления, т.е.
г
Fy{y)=FlHb;y>*y)=Fo
l-^l (4.2.11)
ч °у )
а потребный (минимально допустимый) целевой эффект детерминирован
(неслучаен) и задан значением z11, т.е.
Fi{z) = A(z-z1)^ (4.2.12)
Тогда, как известно (см. (3.2.13)),
( - п -Л
PM=p(y>zn)=Ry(zn)=l-Fp(zn)=l-F0
V °у J
(4.2.13)

252 Глава 4. Методы исследования эффективности ЦНП
Фигурирующие в (4.2.13) параметры у и ау представляют собой агре-
гаты (как и переменная zn), значения которых определяются значениями
параметров и ЭТХ ЦУТС и ЦНПФС, а также условиями проведения опе-
рации, т.е.
В условиях примера синтез ОС заключается в отыскании значений уэ,
а\ и ъг параметров у, оу и zn, обеспечивающих требуемую эффектив-
pM(y,<r;,z')=i-F0
,у „ „ ~r- Г J •> -у
ность операции при гарантируемом качестве её результатов, т.е. выполне-
ния равенства
Г г__-э\
''-' ' ~*\Ч^ГР"' {42Л5)
V У )
где z* - гарантируемое значение потребного целевого эффекта.
Используя дополнительные данные, фиксирующие значения двух (лю-
бых) параметров, можно найти значение третьего.
Уменьшим число параметров задачи, введя в рассмотрение коэффици-
ент вариации г?- = oyjy распределения виртуального целевого эффекта
у. Тогда соотношение (4.2.15) может быть приведено к виду
Рдц(*" >*,)=!-Ъ
zH'-\
_ рТР
~~ ГДЦ>
(4.2.16)
где zHe = —— необходимое гарантируемое значение.
У
На рис. 4.2.2 изображена поверхность
Р =1-F
и изоэффа
/(z"%tf,)=l-Fe
-Ртр =0
Из физических соображений у>0 и, следовательно, должно выпол-
няться условие
(;р>3<т-)=>(0<г?.<1/3).
Резонно также предположить, что
(zn<y + 3ay)^ (г"*<1 + 3г?-).
Указанные допущения нашли отражение на рис. 4.2.2.

4.2. Методы синтеза эффективных ЦНП
253
Решение задачи синтеза ОС определяется точкой (г?^,г*), лежащей на
изоэффе. Фиксация одного из параметров Щ или V однозначно опреде-
ляет значение другого V или Щ соответственно [см. рис. 4.2.2, где
дzHd9&1)}= [ ги/Ди//]х[г^,г^] - область допустимых значений (множест-
во допустимых управлений) управляемых параметров гнг и г?^ , обеспечи-
вающих выполнение условия (4.2.16)]. А
4.2.1) Исследование в условиях примера применительно к показателю
О)дц(у) аналогично приведённому выше с отличием, отмеченным в
(4.1.9)), (см. также (3.2.13)). А
4.2.2) Как было отмечено, неформальное решение задачи синтеза ОС
аналогично подобному решению задачи её анализа (см. п. 4.1.4). Более то-
го, поскольку в основном исследование эффективности операции прово-
дится с целью синтеза (желательно оптимального) ЦУТС и ЦНПФС, то обе
эти задачи (прямая и обратная) практически решаются совместно (пооче-
редно, итерационно). А
Рис. 4.2.2

254 Глава 4: Методы исследования эффективности ЦНП
4.2.3) В отличие от рассмотренной задача синтеза ОС по критерию пре-
восходства либо имеет единственное решение, либо вовсе его не имеет.
Однако в основе алгоритмов, реализующих этот критерий, также лежит
метод перебора вариантов с целью поиска единственного, превосходящего
все остальные. А
4.2.2. ФОРМУЛИРОВКА ЗАДАЧИ СИНТЕЗА ОПЕРАЦИОННОЙ
СИСТЕМЫ ПО КРИТЕРИЮ ОПТИМАЛЬНОСТИ
Наиболее сложными и в то же время наиболее разработанными являют-
ся методы решения задач синтеза исследуемых объектов (ОС, ОК, ЦУТС,
ЦНПФС), основанные на критерии оптимальности. Алгоритм решения за-
дачи синтеза зависит от "степени аналитичности" операторов:
Pm=Pm{U(r))=w\U(r)); (4.2.17)
o>rm{y)=(Orm\r;U{r))=^(u(r);r), (/ = 1,2), (4.2.18)
где U,, -lAlyBli\ (ky + ly=r)- вектор управляемых характеристик
(параметров и ЭТХ ОС, ОК, ЦУТС и ЦНПФС);
wo(^m)> w№(r)>Y)" критериальные функции (см. п. 2.4).
Если операторы (4.2.17), (4.2.18) не имеют существенных особенностей,
усложняющих их математический анализ, то решение задачи оптимально-
го синтеза дают решения U??T следующих систем уравнений:
*»№,))
Ж-
= 0,,; (4.2.19)
^j^-tw. (, = 1,2), (4.2.20)
dU(r)
где О-» - r-мерныйнуль-вектор.
Легко заметить, что уравнения (4.2.19), (4.2.20) равносильны следую-
щим [см. (4.1.7")]:
Н(г)К)>'Г)=%> (/ = 1>2), (4-2-22)
т.е. в оптимальной точке U??T показатели эффективности ЦНПФС нечув-
ствительны к изменениям параметров ОС и ОК (ЦУТС и ЦНПФС). Это об-
стоятельство позволяет решать целый ряд задач оптимального синтеза
объектов методами теории чувствительности [128,151].

4.2. Методы синтеза эффективных ЦНП
255
4.2.4) Сформулированный подход к решению задачи синтеза объекта
исследования иногда называют "классическим". Принципиальным обстоя-
тельством, допускающим такой подход, является отсутствие ограничений
на управляемые характеристики U,r). Другими словами, \Utr\}= \Pir) J> T-e-
множество допустимых управлений не ограничено. В реальных практиче-
ских условиях такое предположение неправомерно, так как по физическим
соображениям область (множество) Щг\\ (или {j+J7/vj) допустимых
управлений всегда ограничена предельно допустимыми значениями управ-
ляемых характеристик uk, [k = l(l)r], обусловленными рядом факторов
(технических, технологических, информационных, стоимостных и др.). А
Если на пространство \U,r\\ (или |/4+£Л \ |) налагаются ограничения, то
в ряде случаев задача оптимального синтеза может быть решена методами
"математического программирования" [65]. При этом она имеет следую-
щую математическую формулировку: найти значения V9JT, параметров
£Лд, доставляющие максимум показателю и>Д£Л J, (/ = 0,1,2) эффектив-
ности операции при ограничениях U??T е {{/Л/с |#лл| > где \UfrA - об-
ласть допустимых значений U\ параметров U,r) (множество допустимых
управлений).
Формализованные формулировки этих задач имеют следующие выра-
жения:
U™ =argmax\РДЦ(и{г))\'> (4-2.23)
U™ =argmaxU(r;U{r))\9 (/ = 1,2), (4.2.24)
"<о6 Wo/
где {tf/'vjc \U,A - область допустимых значений управляемых парамет-
ров 1Л », граница которой задается уравнениями
G{s)(u{r)) ± G$(u{r}). (4.2.25)
В общем случае в силу сложности исследуемых объектов (ОС, ОК,
ЦУТС, ЦНПФС) аналитические выражения показателей Рдц\и,А и
0)дц[у;и,\) оказываются такими, что непосредственное применение раз-
работанных методов математического программирования оказывается за-
труднительным. Однако в ряде случаев возможно приемлемое по точности
приближённое решение задачи путем её приведения к каноническим фор-
мам задач математического программирования (линейного, нелинейного,
динамического и т.п.).

256 Глава 4. Методы исследования эффективности ЦНП
4.2.3.0 ПРИБЛИЖЁННОМ СИНТЕЗЕ ОПЕРАЦИОННОЙ СИСТЕМЫ
В принципе область \Ud} допустимых управлений, описываемая сис-
темой ограничений (4.2.25) - равенств и неравенств, не произвольна, а
представляет собой некоторую окрестность номинальных (расчётных) зна-
чений UFx параметров U,y Если в пределах этой области нелинейность
функции (4.2.17), (4.2.18) и (4.2.25) по параметрам незначительна, то воз-
можна аппроксимация этих функций, например, путем разложения их в
ряды Тейлора в окрестности точки 1УД с оставлением в разложении огра-
ниченного числа членов: только линейных, линейных и квадратичных и
т.д. В первом случае задача будет сведена к задаче линейного программи-
рования, а во втором - к задаче квадратичного программирования и может
решаться разработанными для этих задач методами.
4.2.5) Линеаризация функций w<\Uir\) и и>Д1Лд;у), (/ = 1,2) равно-
сильна замене описываемых ими гиперповерхностей гиперплоскостями, а
линеаризация вектор-функции GS[U,A - замене ограничивающей область
\Ufr\ J гиперповерхности гипермногогранником. Для правомерности таких
замен необходимо, чтобы в пределах области \Ufv) допустимых значений
параметров U,, функции и>ДгЛд), и>Д(7/л;у), GS[U,,) отличались от ли-
нейных незначительно. А
Для иллюстрации сказанного рассмотрим методику приближённого
синтеза ОС путем линеаризации критериальных функций wt[u,x),
(/ = 0,1,2). Чтобы не повторяться, ограничимся рассмотрением лишь од-
ной критериальной функции. Пусть это будет w0[U,A= РДЦ\U.A. Тогда
Рдц=Рдц{и{г))= "№(,))-%Au{r)k
=".Ю+i к: (*%)(«* -О, (4.2.26)
где Г/Л - базовое (расчётное, номинальное) значение характеристик СЛ*;
К' \U(r))~~ коэффициент чувствительности показателя w0 к параметру uJ9
/ г \d Эи>0Шм)|
и*4 жтБ I- °v \г)'\
Если показатель Рдц эффективности операции определяется при детер-
минированных требованиях Z?\ к её результатам, то выражение (4.2.26)

4.2. Методы синтеза эффективных ЦНП
257
примет вид
Рдц = Pm{u{r);Z3{x))= w0(u{r);Z3x))~ ф{г);г3{х))=
= w9(u^;Z3x))+ ±K; (u?r);Z3x))(uk -«f) (4.2.26')
ИЛИ
Рдц = Pw{u{r);Z{x))= w0(u{r);Z{x))~ w0(u{r);Z{x))=
=»Hyzi»)+%к (Чу 4))(u> - «*)+
+ iK(u^Zlx))(zi-zf). (4.2.26")
4.2.6) Обратим внимание, что в отличие от (4.2.26'), где Z?\ является
параметром, в (4.2.26") вектор Z, ч становится аргументом, равноправным
с вектором U, к (см. пп. 4.1.4.1) и совместно с ним фигурирует в решении
задачи синтеза (см. (4.1.7) - (4.1.9)). А
Итак, если в пределах области \UtA функция (4.2.26) мало отличается
от функции Рдц - w0[U,x), то она может использоваться в качестве крите-
риальной в задаче линейного программирования.
Что касается ограничений, то их линеаризация сводится к линеаризации
компонент qj\Uir\) вектор-функции G.Au.Ayio формуле
fуК>)"?,К>)= *;(<> К t«5.(^(5)U - <') , (4-2-27)
А=1
™е 9jk\U(rj
"»-"'i
Uu(- "центр" линеаризации у'-й ограничивающей функции ?Д£//Г\) •
4.2.7) В принципе точка U?! может быть любой (в том числе и Ufr\ од-
цако с практической точки зрения желательно, чтобы U?! е \U?A и при-
том лежала ближе к "середине" области {l/fx }. А
4.2.8) Если в пределах области {#?r\j функция qj\JJ,A существенно не-
линейна, то область \U?A разбивается на непересекающиеся подобласти
\и?к} такие, что (J { U?A = { UfA , и в пределах каждой из них функция
9 Зак. 3303

258 Глава 4. Методы исследования эффективности ЦНП
ц\и,А линеаризуется аналогично (4.2.27). В результате описанной проце-
дуры размерность вектор-функции G, v [U, \) возрастёт до S = ^ L}.
Аналогично линеаризуются и функции q3fd\U,A, и после их переноса в
левую часть (4.2.25) может быть получена каноническая форма ограниче-
ний задачи линейного программирования (ЗЛП) [65]. А
Нетрудно было заметить, что рассмотренные критериальные функции
представляют собой функции параметров, т.е. w\U, J= Wr [U,\) (см. п. 2.4).
Однако, как было показано в п. 4.1.4, несомненный практический инте-
рес представляют и директивные критериальные функции (см. (3.2.13)):
или
где Г/* - вектор ведущих компонент показателя Y!* качества результа-
тов операции, используемый в задачах неформального анализа эффектив-
ности ЦНПФС [см. (4.1.38)].
В зависимости от задачи исследования в качестве "центра линеариза-
ции" могут выступать различные точки пространства \Z, v) (или \Z',X*}) -
носителя распределения требуемых результатов Z,. (или \Zf ,v j) опера-
ции. Так, если требуемые результаты Zf^ операции задаются в окрестно-
сти её среднего виртуального результата У? м, то приближённая дирек-
тивная критериальная функция будет иметь следующее выражение:
wjz£,})= *л.(3?))= <\,/я(^')+ ЕМИ^К^ - 5V ),(4.2.30)
где ф>;Х')^ф!^
57/r5U'>
Хр = ЛГЛ - расчётные (номинальные) значения параметров А7\.
Критериальная функция (4.2.30) соответствует случаю "среднего экс-
пертного компромисса" (ЛПР-компромисса) (см. п.5.2), при котором в
наибольшей степени учитываются средние возможности ОС (ЦУТС и
ЦНПФС) в получении результатов У,\ операции, и при этом требования
Z/'^л не выходят за пределы области {5^ +^К/м}, в которой функция
\¥Д[£'(*')/ мало отличается от линейной.

4.2. Методы синтеза эффективных ЦНП
259
Если требуемые результаты Z? * операции задаются в окрестности их
среднего значения Z,,,, то приближённая директивная критериальная
функция принимает вид
+ th^;Xp)(z^-Z[,), (/ = 1,2,3). (4.2.31)
Критериальная функция (4.2.31) соответствует случаю среднего "экс-
пертного - ЛПР - компромисса", при котором в наибольшей степени учи-
тываются средние требования к ОС (ЦУТС и ЦНПФС) по достижению ре-
зультатов Y! а операции и предъявляемые к ним требования Z',3* не вы-
ходят за пределы области \ЩХ>\ + AZ!,A, в которой функция WAT\Z,,3A
мало отличается от линейной.
Если требуемые результаты операции строго директивны, то их дирек-
тивные значения Ztj* определяют "центр линеаризации" и приближённая
директивная критериальная функция примет вид
+ |I<(^^*<:>)(Я?-<Z^I,). (*' = U,3). (4.2.32)
Критериальная функция (4.2.32) соответствует случаю наименьшего
"экспертного - ЛПР - компромисса", при котором в наибольшей степени
учитываются директивные требования к ОС (ЦУТС и ЦНПФС) по дости-
жению результатов К* операции и предъявляемые к ним требования
Z!\ не выходят за пределы области \Щ"\ +AZ'll,A , в которой функция
WMT\Z',3,x) мало отличается от линейной.
4.2,9) Несомненный практический интерес могут представлять прибли-
жённые директивные критериальные функции, у которых в качестве "цен-
тров линеаризации" служат гарантированные, т.е. наихудшие
Y{x.) =(Й >У" 'у")> или наилУ4™16 Y(z)={y" >Уг>Уъ)> или наиболее ве-
роятные значения F/? = \У?° ,у¥° уУ^/ виртуальных результатов Y,,
операции. Получаемые при этом оценки и>, показателей wn (/ = 0,1,2)
эффективности операции соответственно называются пессимистическими,
или оптимистическими, или модальными. А

260 Глава 4. Методы исследования эффективности ЦНП
4.2.10) Из сравнения выражений (2.4.10), (2.4.11) с (4.2.26) и (2.4.8), (2.4.9) с
(4.2.30) - (4.2.32) становится ясен физический смысл весовых коэффициентов
критериальных функций. А
4.2.11) Рассмотренный метод линеаризации директивных критериальных
функций применим и при решении задач анализа эффективности операции. В
этом случае компромиссные множества будут представлять собой плоскости
(в симплексной канонической форме показателя K3v) или гиперплоскости (в
комплексной канонической форме - Y, % или в развернутой форме У,Л\ при
X = п = 2 это будут прямые (см. рис. 4.1.3).
Как видно из рис. 4.2.2, в рабочей области аргументов (zn,&-) поверх-
ность Рдц = Pav\Zn,&.) мало отличается от плоскости, а изоэффа
J[Zn ,&- )= 0 - от прямой и может быть линеаризована с достаточной точно-
стью. Понятно, что при этом анализ эффективности операции в техническом
отношении упрощается. ▲
4.2.12) Если в выражениях директивных критериальных функций
WA[Z?\,U,\) (не обязательно линеаризованных) в качестве аргументов рас-
сматривать не только директивные требования Z? к к результатам операции,
но и управляемые параметры U,^, то может решаться задача комплексного
синтеза ОС (ЦУТС и ЦНПФС), целью которого является определение как оп-
тимальных значений U??T параметров и ЭТХ ЦУТС и ЦНПФС, так и наибо-
лее соответствующих им значений Z?"J требований ZL\ к результатам Y,,
операции, обеспечивающих совместно максимальную её эффективность. А
4.2.13) Из всего вышеизложенного следует, что операция (ЦНПФС) синте-
зируется как непосредственно путём её организации, т.е. определения и реали-
зации (на этапе целевого применения ЦУТС) оптимальных (или пригодных)
значений А?% (или AZS) его параметров и ЭТХ - А£,,, так и опосредованно
путём синтеза ЦУТС, т.е. определения и реализации (на этапе разработки и
создания ЦУТС) оптимальных (или пригодных) значений А!°,\ (или А'Л) его
параметров и ЭТХ - А^9 обеспечивающих требуемую эффективность
ЦНПФС (см. п. 2.5). А
4.2.14) Заметим, что в принципе задачи анализа и синтеза объектов (ЦУТС
и ЦНПФС) исследования тесно связаны между собой и всегда цели первой из
них подчинены целям второй. Таким образом, задача синтеза ОС (ЦУТС и
ЦНПФС) решается и в ходе анализа эффективности операции, целью которого
является поиск путей оптимизации ЦУТС и ЦНПФС, т.е. путей их синтеза. А

4.3. Дополнения
261
4.3. ДОПОЛНЕНИЯ
4.3.1. О ДЕТЕРМИНИРОВАННЫХ И КВАЗИРЕГУЛЯРНЫХ
МОДЕЛЯХ ОПЕРАЦИОННЫХ СИСТЕМ И КОМПЛЕКСОВ
Вернёмся к п. 2.4 и вспомним приведённые там выражения (2.4.1) -
(2.4.17) широко распространённых в литературе функций результатов опе-
рации (2.4.6) - (2.4.9), (2.4.12), (2.4.13) и функций параметров ЦУТС и
ЦНПФС (2.4.10), (2.4.11), (2.4.14), (2.4.15), используемых в качестве пока-
зателей эффективности ЦНПФС.
В отличие от детерминированных моделей ОС, в рамках которых ис-
пользуются показатели (2.4.6) - (2.4.17), в квазирегулярных моделях дела-
ется попытка учесть случайность результатов операции и параметров
ЦУТС и ЦНПФС, обусловленную случайностью условий BLx функциони-
рования ЦУТС, путём оперирования с их математическими ожиданиями
[см. (2.4.6) - (2.4.17)]. Однако, как уже отмечалось (см. (2.4.5) - (2.4.13»,
такой учет случайности не может считаться удовлетворительным, и осо-
бенно тогда, когда показатели L качества результатов операции и пара-
метры ААл ЦУТС и ЦНПФС имеют несимметричные относительно их
средних значений К v и А,к, распределения.
Кроме того, при обоих подходах никак не учитываются истинные цели
операции, поскольку в задачах анализа к её результатам не предъявляется
никаких требований. Таким образом, строятся модели лишь операционной
системы (а не операционного комплекса), позволяющие реализовать ра-
зомкнутую схему анализа эффективности операции, в рамках которой мо-
гут сравниваться и отбираться "лучшие" (что не доказывается, а постули-
руется) из вариантов ОС без ответа на вопрос, насколько они вообще хо-
роши.
Несколько иначе обстоит дело при решении задач оптимального синтеза
ОС, когда схема замыкается путём предъявления к показателям (2.4.6) -
(2.4.17) требования их максимальности. Однако вновь, даже при достиже-
нии этими показателями максимумов, вопрос о том, достигнута или нет
цель операции, остаётся открытым.
При решении задач оптимального синтеза ЦНПФС и ЦУТС или ОС в
целом обычно рассматриваются две их постановки:
- обеспечение максимального целевого эффекта - max yx при заданных
ограничениях у2 < z2 на расход ресурсов у2 (принцип максимизации
целевого эффекта);

262 Глава 4. Методы исследования эффективности ЦНП
- обеспечение минимального расхода ресурсов - nun у2 при заданных
ограничениях ух > zx на получаемый целевой эффект yt (принцип
экономии ресурсов).
Сформулированные постановки задачи оптимального синтеза операций
и систем, называемые соответственно задачами "с открытой экономикой" и
"с закрытой экономикой", реализуют их детерминированные модели.
В квазирегулярных моделях вместо детерминированных значений ух,
у2 целевого эффекта и расхода ресурсов фигурируют математические
ожидания ух, у2 их стохастических аналогов ух, у2. Однако при этом ог-
раничения z2 (в первом случае) и zx (во втором случае) остаются детер-
минированными и наперёд заданными. Прокомментируем сформулиро-
ванные постановки задач.
Понятно, что при таком подходе не учитывается неопределённость, все-
гда сопутствующая формулированию цели операции и не позволяющая
однозначно определять требуемый (минимально допустимый) уровень zx
целевого эффекта ух и предельный (максимально допустимый) уровень z2
расхода потребных ресурсов у2. Если же обратиться к квазирегулярной
модели, то к отмеченным недостаткам добавится ещё один (не менее су-
щественный). Он состоит в том, что предъявление требований к средним
величинам ух, у2 целевого эффекта и расходуемых ресурсов сопровожда-
ется неучитываемой недостоверностью получаемых решений, обусловлен-
ной случайностью истинных реализуемых в ходе операции значений ух и
у2 эффекта и расхода ресурсов.
Кратко обсудим показатель W6=yx/y2, выдвинутый в монографии
[116] в качестве основного и нашедший применение в ряде других работ
[26,190].
Поскольку целевой эффект ух связан с расходом ресурсов у2 функцио-
нальной зависимостью (рис. 4.3.1)
Уг=*{Уг)> (4-ЗЛ)
то значение показателя
^6=Л = *Ы (43.2)
Уг Уг
в точке у2 = у\ имеет физический смысл "скорости изменения" наиболь-
шего значения у" = у™** целевого эффекта при условии, что зависимость
(4.3.1) заменена линейной вида
>_*к),
Л =*(*)-*(л)=^Л. (4-3.3)
•^ 2

4.3. Дополнения
263
Как видно из рис. 4.3.1, в общем случае при заданном уровне z2 допус-
тимого расхода ресурсов
у°2 = argmaxW6(y2)* argmax 9t(y2)= y\
y*£z2 y2£z2
и, следовательно, максимизация показателя W6 не обеспечивает достиже-
ния максимального целевого эффекта. Таким образом, данное в работе
[116] "обоснование" допустимости применения на практике показателя W6
нельзя считать убедительным.
0 y2=argmaxW2 y2=z2
Рис. 4.3.1
Уг
О = argmax W2 =y°2 y2= z2
Рис. 4.3.2
Уг
Приведённая в работе [116] кривая зависимости yl=(R{y2) целевого
эффекта от расхода ресурсов, называемая "логистической", обосновывает-
ся как единственно возможная форма связи величин у1 и у2. Однако при-
ведённые там рассуждения противоречат практике (см. (5.3.13)) и не могут
служить доказательством единственности такой формы РЭ-функции. Дей-

264 Глава 4. Методы исследования эффективности ЦНП
ствительно, эффект "насыщения", т.е. замедления роста целевого эффекта
при неограниченном увеличении расхода ресурсов, имеет место и под-
тверждается практикой. Что касается начального участка кривой
Уг = ^1^2 /' то он может иметь самый различный характер, в частности
экспоненциальный (рис. 4.3.2). При этом, как нетрудно видеть,
yl=argmaxW6(y2)=0 => у°хПТ = <ф2°)=0. (4.3.4)
Из выражения (4.3.4) следует, что в случае, когда РЭ-функция
У\ =(&\Уг)> показатель W6 для решения оптимизационных задач непри-
годен.
4.3.1) Самым существенным недостатком показателя W6 является его
независимость от времени у3, расходуемого на достижение целевого эф-
фекта ух, учёт которого при комплексном исследовании эффективности
ЦНПФС абсолютно необходим. ▲
4.3.2) Как было показано, отношение ух/у2 = Wb не может служить по-
казателем эффективности операции, тем не менее оно обладает достаточно
содержательными характеристическими свойствами, широко используе-
мыми на практике. Так, в математических моделях экономики [59] соглас-
но физическому смыслу отношение ух/у2 называется средней произво-
дительностью ресурса [ср. с (4.1.24)]. Обратную величину у2/ух естест-
венно назвать средней ресурсоёмкостью целевого эффекта. Соответст-
вующие этим характеристикам производные dyx/dy2 и dy2/dyx называют-
ся предельными производительностью и ресурсоёмкостью.
Следует обратить внимание, что вследствие соотношения (4.3.1) пока-
затель W6 =W6(y2) представляет собой функцию расходуемых ресурсов,
однако это обстоятельство, как правило, никак не учитывается. А
В дополнение к замечаниям (2.4.1) - (2.4.14) отметим следующее. Если
для вычисления показателей Wx, W2, W3 по формулам (2.4.6'), (2.4.8х),
(2.4.10'), достаточно знать математические ожидания у. компонент уп
[i = l(l)/f] вектора Г{м)9 то в случаях (2.4.7'), (2.4.9'), (2.4.11'), (2.4.12')
этого недостаточно и для вычисления показателей Wk, [A: = 2,4,6(l)l0]'
необходимо знать закон распределения случайного вектора Y, v. Наконец,
во всех случаях (2.4.6') - (2.4.15') показатели Wk, [k = 2(l)l0] не учитыва-
ют связи между компонентами уп у., [/,/ = l(l)/i; iФ j] и её влияния на
результаты ЦНПФС и на его эффективность.

4.3. Дополнения
265
Итак, для объективного комплексного оценивания и анализа эффек-
тивности ЦНПФС показатели Wk (функции средних эффектов) непри-
годны. Спрашивается, пригодны ли они для оптимального синтеза
ЦНПФС и ЦУТС? Чтобы ответить на этот вопрос, необходимо устано-
вить и проанализировать характер связи показателей Wk с вероятно-
стью Рдц достижения цели операции (см. п. 4.5).
Поскольку коэффициенты аи в соотношениях (2.4.7) - (2.4.15) про-
извольны, то исчерпывающий ответ на поставленный выше вопрос по-
лучить практически невозможно. Однако общее представление о харак-
тере такой зависимости может быть получено при рассмотрении ряда
частных случаев.
Пусть в общей постановке задачи исследования эффективности
ЦНПФС реализован метод ведущей компоненты и получен условный за-
кон распределения F-/H(y) ведущей компоненты у = ух вектора Y, *
относительно события Й = №\^Z?*}). Тогда согласно выражению
(3.3.27) вероятность достижения цели операции
Рдц = Р{у> £)= J*,(z)dF£(z) • (4.3.5)
При этом в случае (2.4.6')'
Wx =W{yl) = y, (4.3.6)
и, следовательно,
Wt =Щ =w{yl) = y,=M[y/H] , (4.3.7)
т.е. показатель Wx никак не учитывает требования zx к целевому эффек-
ту JV
Предлагаемое иногда включение расходуемых временных ресурсов
уъ в состав показателя у2 неправомерно, поскольку, как отмечалось
ранее, ограничения £3 на СР0К Уз достижения цели операции задаются
независимо от ограничений £,, z2 на остальные компоненты уг, у2 век-
тора F(3) (см. (2.7.7».
Наконец, ещё раз подчеркнём, что максимизация целевого эффекта
или минимизация расхода ресурсов в общем случае не максимизирует
вероятности Рдц или согдц{у) достижения цели операции (см. п.4.3.2) и,
следовательно, получаемые при этом решения задачи синтеза ОС (ЦУТС
и ЦНПФС) не являются оптимальными, тем более что истинная цель
операции, выражаемая критерием (2.3.3) или (2.3.4) её пригодности, в
1 Практически это случай (2.4.8) при OC3i=l, OC3i=0, [l=2(l)/i].

266 Глава 4. Методы исследования эффективности ЦНП
принципе может быть достигнута не только при максимальном уровне
целевого эффекта или минимальном расходе ресурсов. Более того, в си-
лу противоречивости требований ix и £2, £3 > предъявляемых соответст-
венно к компонентам ух и у2, уъ вектора К3*, оптимальное решение, как пра-
вило, является компромиссным, т.е. таким, что ни один из показателей ух, у2,
j>3 не достигает экстремального значения.
Из всего сказанного следует вывод, что только стохастические и притом
замкнутые модели ОС и ОК позволяют проводить комплексные исследо-
вания эффективности операций как в рамках задач их анализа, так и в рам-
ках задач синтеза. Именно о таких моделях здесь и идёт речь.
4.3.2. О КОРРЕКТНОСТИ ПОСТАНОВКИ ЗАДАЧИ
ОПТИМАЛЬНОГО СИНТЕЗА ОПЕРАЦИОННОЙ СИСТЕМЫ
Вновь обратимся к наиболее распространённым критериальным функ-
циям Wk,[k= 1,2,3], определяемым соотношениями (2.4.60- (2.4.8')1.
Из сказанного ранее следует, что, строго говоря, величины W2 и \¥ъ
являются показателями средневзвешенных эффектов операции и, посколь-
ку в них не входят требования к её результатам, то мерой эффективности
операции они служить не могут. Более того, поскольку показатели W2 и
W3 не имеют физического смысла, то они непригодны для оценивания эф-
фективности ЦНПФС в замкнутой схеме, т.е. с предъявлением требований
к их значениям.
Теперь рассмотрим показатель W1=Wl=yl, т.е. математическое ожи-
дание целевого эффекта уг, получивший широкое распространение в каче-
стве критериальной функции и называемый часто "показателем (и даже
"критерием" [26, 190]) эффективности ЦНП" в задачах оценивания дейст-
вительности ударов по военным целям, оценивания валового продукта, и
т.п., и установим характер его связи с действительным показателем РДЦ
эффективности операции.
Пусть случайные величины у и z распределены нормально и имеют
соответственно числовые характеристики у, о~у и г, ov т.е.
Л. *Л
FP{y) = FlH]{y;y,(Tp) = F\
У-У
V °у J
По ходу изложения речь будет идти о том или ином показателе этой группы.

4.3. Дополнения
267
F.z{z) = F}»\z;z,^=F0
где Fa{x) - табличная функция [169], и пусть цель операции выражается
неравенством у > £. Тогда, как показано в примере 3.4.4,
F&{a))=R.[R:l(<0)]=Fc
Рдц = р{у>1)=тг = Р0
У-z
\Щ^,\
У-Z
9
<Оди(г)=0>2{г)=Р0
<±е;%-г)-1^-
°У
°>
(4.3.8)
(4.3.9)
(4.3.10)
В общем случае требования z , предъявляемые к целевому эффекту
операции, могут зависеть от принимаемых им значений у (см. п. 5.2.2).
Однако в рамках рассматриваемой задачи представляется целесообразным
полагать целевой эффект у и предъявляемые к нему требования z стохас-
тически независимыми (т.е. z = const, <7- = const).
Известно, что параметры законов распределения случайных объектов
(величин, векторов, функций) взаимно независимы (между собой). Следо-
вательно, при нормальном законе распределения взаимно независимы ве-
личины у и о-. Однако при оптимизации ЦНП по критерию максимума
среднего целевого эффекта (результата) y = Wl операции с целью измене-
ния (в частности, увеличения) у изменяются параметры и ЭТХ ЦУТС -
л(;гицнпфс
А?к~, а также условия функционирования ЦУТС - В[е),
щ
(О'
что может повлиять (и, как правило, влияет) и на величину рассеяния ау
значений у целевого эффекта операции. При этом естественно предполо-
жить, что с увеличением среднего результата у рассеяние о'- виртуально-
го целевого эффекта у имеет тенденцию к увеличению.
С учётом сказанного выражения (4.3.9) и (4.3.10) могут быть представ-
лены в следующем виде:
Лу
Pw=P{Ay)=F0
corM{y)=a)[(y;Ay)=F0
Jf?W)
+ С7?
о.
-^{1-у)+-
АУ
f,(Ay) ' v " f,(Ay)
где А у = у - z; //(*) - неубывающая функция аргумента х.
(4.3.11)
(4.3.12)

268 Глава 4. Методы исследования эффективности ЦНП
Будем полагать, что при изменении среднего результата (целевого эф-
фекта) у распределение его виртуального значения у остаётся нормаль-
ным, и проанализируем характер связи показателей РДЦ, согдц {у) и Wx=y
при различных зависимостях а у от Ау.
На рис. 4.3.3 и 4.3.4 соответственно показаны кривые зависимостей
(4.3.11) и (4.3.12) при
причём
f,(Ay)=<r,+\dy\',[i=o(i)3],
d)a, = ft{Ay) = a9+\dy];
a)a.=f2(Ay) = a0+\Ay\2;
(4.3.13)
(4.3.14)
ЪШ
-1Аух 0 Ауг\
4 Ау
Рис. 4.3.3
Как видно из рис. 4.3.3, если выполняется условие
(VAy) Af,{Ay)<C\Ay\ (С = const), (4.3.15)
т.е. среднее квадратическое отклонение о~у растёт не быстрее линейной за-
висимости от \Ау\, то с увеличением среднего целевого эффекта (результа-
та) у, {Ау) вероятность Рдц достижения цели операции (выполнения за-
дачи системы) монотонно возрастает. Если же
(ЗАу) Af,(Ay)>C\Ay\
(4.3.16)

4.3. Дополнения
269
то в зависимости от диапазона изменения среднего результата у, (А у) при
его увеличении вероятность Рдц может как расти, так и падать, проходя
через две экстремальные точки (А У, min Рдц}, (А у" > max Рдц}.
Рис. 4.3.4.
Понятно, что в случаях [(4.3.14), в), г)] увеличение А у более чем на
А у" приводит к снижению эффективности ЦНПФС. К сожалению, при
решении оптимизационных задач отмеченное обстоятельство не учиты-
вается, в результате чего "оптимальные" решения фактически таковыми
не являются1.
Итак, был рассмотрен случай зависимости от среднего результата у
операции характеристики его рассеяния. Однако в подобной зависимо-
сти могут находиться характеристики (моменты) распределения вирту-
ального целевого эффекта у более высоких порядков (асимметрия, экс-
цесс и т.п.). В этом случае с изменением среднего эффекта у будет из-
меняться вид (класс, семейство) закона распределения случайной вели-
чины у, что также приведёт к изменению вероятности Рдц достижения
цели операции. Для выявления точного характера указанной зависимо-
сти необходимы специальные исследования. Совершенно очевидно, что
без проведения таких исследований оптимизация ЦНПФС и ЦУТС по
критерию максимума среднего целевого эффекта является некорректной
(необоснованной).
1 Анализ зависимости (4.3.12) и рис. 4.3.4 рекомендуем провести читателю.

270 Глава 4. Методы исследования эффективности ЦНП
Понятно, что всё сказанное в ещё большей степени относится к много-
компонентному (комплексному) анализу эффективности ЦНП, когда реа-
лизуется соотношение (2.4.7) или (2.4.8), а не (2.4.6). В этом случае при
максимизации показателя W2 или W3 за счёт изменения параметров А,к.
и будут изменяться параметры распределения всех компонент случайного
вектора L. Поскольку же требования к результатам операции (ЦНПФС)
по различным аспектам, как правило, противоречивы (желательно иметь
целевой эффект побольше, а затраты ресурсов всех видов поменьше, тогда
как для получения большего целевого эффекта необходимы большие за-
траты), то при максимизации показателя \¥ъ или W4 вероятности РДЦ9
С0дЦ(у) достижения цели операции могут как расти, так и убывать. Понят-
но, что лишь в первом случае допустима оптимизация ЦНП по критерию
maxWk, однако общих методов его выявления не существует.
4.4. ОБ ЭКОНОМИЧЕСКОМ АНАЛИЗЕ ЦУТС И ЦНПФС
В принципе экономический анализ (ЭА) - это типичное междисципли-
нарное направление системных исследований, о которых говорится в гл. 1.
Однако ознакомлению с основами экономического анализа ЦУТС и
ЦНПФС должно предшествовать изучение общей методологии ТЭЦНП.
Поэтому данный параграф рекомендуется читать после изучения первых
двух разделов монографии.
4.4.1. СУЩНОСТЬ И ЗАДАЧИ ЭКОНОМИЧЕСКОГО АНАЛИЗА
По мере развития и совершенствования техники, а также роста масшта-
бов её производства и внедрения как в народнохозяйственной, так и в во-
енной областях весьма острой становится проблема обоснования её эконо-
мической целесообразности или, как принято говорить, "экономической
эффективности" (см. {2.7.12}, {2.7.13}).
В основу исследования "экономической эффективности" разрабатывае-
мой сложной (большой) системы с учётом всех этапов (фаз) её жизненного
цикла (ЖЦС): проектирования (разработки), создания (изготовления), экс-
плуатации (целевого применения) - кладётся анализ соотношения "эффек-
тивность - стоимость" [75, 116]. При этом если стоимость обычно из-
меряется в денежных единицах, то с эффективностью дело обстоит слож-
нее и, как отмечалось в п. 1.1.1, разные авторы вкладывают в этот термин

4.4. Об экономическом анализе ЦУТС и ЦНПФС
271
самый различный смысл. Это и "полезный эффект", под которым понима-
ется "степень достижения цели" [51, 111], и "прибыль" [16, 68], и "стои-
мость произведённой продукции" [180], и "наносимый или предотвращён-
ный ущерб" [26, 48], и "значение технического параметра или функции от
него" [62, 84], и "полезность" [45, 140] и т.д. В качестве показателей "эко-
номической эффективности" обычно используются отношения количест-
венных мер отмеченных характеристик к стоимостям соответствующих
проектов (программ). Хотя каждый из авторов пытается обосновывать
предлагаемый показатель, однако их обилие и разнообразие свидетельст-
вует о том, что общей точки зрения по этому вопросу пока не существует.
Тем не менее с целью установления экономической целесообразности про-
екта (программы) на этапе проектирования ЦУТС и организации ЦНПФС
экономический анализ должен проводиться.
4.4.1) Сразу отметим, что применительно к ударным (боевым) военно-
техническим системам (ВТС) и комплексам (ВТК) в силу принципиальной
сложности определения стоимости целевого эффекта ЦНПФС (операции)
формальный экономический анализ весьма затруднителен как в техниче-
ском, так и в семантическом отношении хотя бы уже потому, что, во-
первых, наносимый или предотвращаемый ущерб далеко не всегда может
быть выражен в денежных единицах, а во-вторых, не всегда ясно, к стои-
мости чего этот ущерб следует отнести. А
В ходе экономического анализа наряду с расчётами затрат на разработ-
ку, создание и эксплуатацию ЦУТС основную роль играют экспертное
оценивание полученного при этом целевого эффекта и анализ его соответ-
ствия затратам.
Следует особо подчеркнуть, что в рамках ЭА как эффекты, так и затра-
ты на их получение рассматриваются на уровне суперсистемы, т.е. на
уровне ОК, а не ОС. Это означает, что в основном здесь речь идет о стати-
ческих ресурсах (и их стоимости), расходуемых на этапах разработки и
создания ЦУТС и организации ЦНПФС, в то время как в рамках ИО и
ТЭЦНП рассматриваются динамические ресурсы (называемые операцион-
ными), расходуемые в ходе операции на получение её операционного це-
левого эффекта. Исключение составляют эксплуатационные затраты, свя-
занные с расходом динамических ресурсов, однако это ресурсы надопе-
рационные, так как расходуются они в обеспечивающих подсистемах ОК и
непосредственно в образовании целевого эффекта операции не участвуют.
Подробнее об этом говорится в п. 5.3.2.
Как отмечалось в п. 1.2 (а также в п. 5.3.2), по функциональным свой-
ствам следует различать ресурсы: статические (динамические), активные
(пассивные), операционные. Из вышесказанного следует, что наряду с
этим существуют и "квазистатические", "квазиактивные", "надоперацион-

272 Глава 4. Методы исследования эффективности ЦНП
ные" ресурсы, которые расходуются на создание и эксплуатацию ЦУТС, а
также на организацию и управление ЦНПФС и участвуют в операции не
явно, а опосредованно через агрегированные эксплуатационно-
технические характеристики (ЭТХ) ЦУТС и ЦНПФС.
В дальнейшем в пределах данного параграфа говорится о системных
(надоперационных - программных, проектных) целевых эффектах и сис-
темных затратах ресурсов и денежных средств.
Введём обозначения:
А',к.к - вектор параметров и ЭТХ ЦУТС;
А?к* - вектор параметров и ЭТХ ЦНПФС;
В,, v - вектор характеристик условий проведения операции;
С, (А') - системные затраты на придание ЭТХ ЦУТС значений AL*;
С2(А") - системные затраты на придание ЭТХ ЦНПФС значений А?к.\;
Y^l - показатель целевых эффектов операции;
F/2v - показатель расхода операционных ресурсов;
YP\ - показатель расхода операционного времени;
Г,(ДС - показатель системного (надоперационного) целевого эффекта от
реализации проекта (программы);
F/Д с - показатель расхода системных (надоперационных) ресурсов;
F/3C\C - показатель расхода системного (надоперационного) времени
(длительность жизненного цикла ЦУТС).
В принципе имеют место следующие соотношения:
y(i)_y(i)(y(2) у«.д ) Г44П
где F(i=y(iHo'4o;i?('>/;
y(3) _ у(3) ( л> л* . R )
уО) С _ у(\)С ( у(2)С у(Ъ)С . » ) (л л ?ч
гтте y(2)c-y(2)c(yW yW yW.J? )•
y(3)C _y(3)c(y(l) y(2) y(3)#o \
V) -*(nf) \ж(*)'жЫ'жЫ'"(1с)>>
и, следовательно,
УЙС =Сил]{сМ%Сг{Л"% (4.4.3)
т.е. системный целевой эффект от применения ЦУТС (суммарный эффект
операций, проведённых ЦУТС за период её жизненного цикла) зависит от

4.4. Об экономическом анализе ЦУТС и ЦНПФС
273
системных затрат на создание и эксплуатацию ЦУТС, а также на организа-
цию ЦНПФС и управление им.
4.4.2) Обратим внимание, что векторы yP\ и y№? также описывают за-
траты на проведение операции и реализацию проекта (программы) соот-
ветственно, однако в отличие от затрат С{(А') и С2(А"), выражаемых в
денежных единицах, это затраты конкретных ресурсов, расходуемых в хо-
де операции, а также на её обеспечение и эксплуатацию ЦУТС. А
Поскольку ЭА проводится на самом первом этапе жизненного цикла
ЦУТС, т.е. на этапе её внешнего проектирования, то ему сопутствует су-
щественная неопределённость как всех перечисленных выше характери-
стик, так и характеристик Z)x\? 9 Z,(2\c, ZJ3)C? требований, которым должны
удовлетворять системные характеристики У/Дс, Y$\ > Y/{%C результатов
реализации проекта (программы). Поэтому мера качества проекта (про-
граммы) носит вероятностный характер и имеет следующее выражение
[см. (2.3.14), (3.2.6), (3.2.10)]:
= p[to<*^ , (4.4.4)
V) -*>f} *■?<*) -~к>/■■?(*) -*>0
1 дц ~ итг*агги
где РдЦ - вероятность достижения цели программы (реализации проекта);
/Iе = ncx + #i2c + псъ .
4.4.3) Как видно, соотношение (4.4.4) имеет структуру выражений
(2.3.14), (3.2.10), однако смысл входящих в них операндов несколько раз-
личен. Поскольку источники неопределённости на первом этапе системно-
го исследования проекта (программы) в рамках АНС и на этапе исследова-
ния операции в рамках ТЭЦНП имеют различную природу, то их описания
носят различный характер. Так, в ТЭЦНП широко используются принципы
аналогий и прототипов. В АНС возможности их применения значительно
уже. Поэтому здесь многие оценки носят экспертный характер и вероят-
ность Рсдц может трактоваться как субъективная.
С учётом (4.4.1) - (4.4.3) из (4.4.4) следует
РСдц=РСМ<\СгШ- (4А5)
А
Свойства компонент Z)x]?, ZJ2\C9 z!3c\c соотношения (4.4.4) выявляют-
ся в ходе системного анализа проблемной ситуации.
Характеристики F/'c\c, YrAc определяются на основе моделирования
\»i; \*>;
ЦУТС и ЦНПФС в рамках ИСО.

274 Глава 4. Методы исследования эффективности ЦНП
Определение показателя У/Дс, выявление его связи с С,(у4'), С2(А") и
составляет предмет ЭА.
В зависимости от цели анализа и используемой при этом информации
различают:
- военно-экономический анализ (ВЭА), в общем случае функционально-
экономический (стоимостной) анализ (ФЭА);
- технико-экономический анализ (ТЭА).
Задача ВЭА - анализ зависимости y№Ic от У(я1\с9 Y$\C и через них от
Сх(А')> С2(А")9 т.е. исследование взаимосвязи затрат на подготовку и про-
ведение операции с показателями её качества:
у(1)С_у(1)с(у(2)С у(з)С.дС )
=* сД4^)=с2Кг'^^в4гд(о)- <4A6>
Задача ТЭА - анализ зависимости показателя качества ЦУТС от затрат
на её разработку и создание:
4'>=4'>1с-'4')) => c.l4'))=ctl4'>'4')i- <4А7>
Общая схема проведения системного экономического анализа приведе-
на на рис. 4.4.1.
4.4.2. СТРУКТУРА ЭКОНОМИЧЕСКИХ ЗАТРАТ НА ПРОГРАММУ
Затраты, сопутствующие реализации программы (проекта), делятся на
[112]:
- статические (осуществляемые до проведения операции);
- динамические (осуществляемые в ходе проведения операции).
Обобщённая структурная схема затрат на программу приведена на
рис. 4.4.2.
При анализе затрат на ЦУТС их принято рассматривать применительно
к жизненному циклу ЦУТС.
Определение 4.4.1. Жизненный цикл ЦУТС (ЖЦС) - это период
времени от момента начала проектирования системы до момента её снятия
с эксплуатации в связи с физическим или моральным устареванием (изно-
сом). ▲
ЖЦС включает в себя три этапа (фазы):
- проектирование ЦУТС;
- создание ЦУТС;
- эксплуатация и целевое применение ЦУТС.

4.4. Об экономическом анализе ЦУТС и ЦНПФС
275
Описание операции и операционного комплекса
—>
Определение факторов, характеризующих организацию операций и способы её проведения
—►
Определение
состава системных
ресурсов
Определение
основных
характеристик
организации
операции
Определение систем,
обеспечивающих
проведение
операции, и их
основных ЭТХ
Определение
системы,
проводящей
операцию, и её
основных ЭТХ
Пассив-
ные
ресурсы
Актив-
ные
ресурсы
w
Определение затрат
на ресурсы
Определение затрат
на организацию
и проведение
операции
Определение затрат
на эксплуатацию
систем, обеспечиваю-
щих проведение
операции
Определение затрат
на создание и
эксплуатацию
системы, проводящей
операцию
—н
—*-
Определение суммарных затрат на операцию (ЦНП) и реализующие её ЦУТС

276 Глава 4. Методы исследования эффективности ЦНП
Затраты на операцию (ЦНП)
Статические
Затраты на разработку
проекта и создание ЦУТС
Затраты на создание, модер-
низацию и совершенствова-
ние ЦУТС, обеспечивающих
проведение операции
Затраты на создание запасов
ресурсов, расходуемых в
ходе операции
Затраты на организацию
операции
Динамические
Расходы ресурсов
в ходе операций
Эксплутационные расходы
на ЦУТС, проводящую
операцию
Эксплутационные расходы
на ЦУТС, обеспечивающие
проведение операции
Расходы на проведение
операции (на планирование
и управление ЦНПФС)
Рис. 4.4.2.
По степени отношения к результатам операции затраты можно разде-
лить на непосредственные и опосредованные, а в зависимости от их на-
значения и этапа ЖЦС - на основные, сопряжённые и сопутствующие.
Примерная схема классификации затрат по второму признаку приведена
на рис. 4.4.3. Кратко1 прокомментируем рис. 4.4.3 в соответствии с его
рубрикацией.
Основные затраты имеют отношение к получению целевого эффекта
ЦНПФС на всех этапах ЖЦС, но в различной степени: от непосредствен-
ного до весьма опосредованного, в связи с чем они делятся на прямые и
косвенные.
Прямые затраты идут на создание (проектирование и изготовление),
содержание в готовном состоянии (техническое обслуживание и эксплуа-
тацию) и целевое применение ЦУТС:
Более подробно эти вопросы освещены в пособии [111].

4.4. Об экономическом анализе ЦУТСи ЦНПФС
277
Затраты на ЦУТС
Основные
Сопряжённые
Сопутствующие
Прямые
Косвенные
Рис. 4.4.3.
а) на этапе проектирования ЦУТС это расходы:
- на производственные потребности конструкторских бюро (проек-
танта);
- на потребности внешних научно-исследовательских организаций;
б) на этапе изготовления ЦУТС это расходы:
- на материалы, полуфабрикаты, покупные изделия;
- на заработную плату производственных рабочих;
- на контрагентские поставки и работы смежников;
в) на этапе эксплуатации ЦУТС это расходы:
- на материально-техническое снабжение;
- на все виды энергии;
- на сырьё (расходные материалы);
- на ремонт;
- на содержание обслуживающего ЦУТС персонала;
г) на этапе целевого применения ЦУТС это расходы операционных ре-
сурсов всех видов (см. п. 1.2.3).
Косвенные затраты обусловлены накладными расходами на содержа-
ние административно-управленческого аппарата КБ, НИИ, предприятий-
изготовителей, на содержание, амортизацию, техническое обслуживание и
ремонт оборудования и т.д.
Сопряжённые затраты идут на создание, эксплуатацию и материаль-
но-техническое обеспечение комплексов базирования и обеспечения
ЦУТС, а также на совершенствование, модернизацию и создание новых
систем, обеспечивающих организацию и проведение операции (улучшение
помещений, развитие систем энергоснабжения, связи и т.д.).
Сопутствующие затраты возникают в смежных областях науки, произ-
водства и экономики, связанных с обеспечением программы (в других от-
раслях промышленности, транспортных системах, в добывающей про-
мышленности и т.д.).
Введём обозначения:
СХ=СП - затраты на этапе проектирования ЦУТС;
С2=СИ - затраты на этапе изготовления ЦУТС;

278 Глава 4. Методы исследования эффективности ЦНП
С3=СЭ - затраты на этапе эксплуатации и применения ЦУТС;
суммарные косвенные затраты;
'сопр ~ суммарные сопряженные затраты;
Ссопут ~ суммарные сопутствующие затраты;
C.(t) - интенсивность затрат на *-м этапе ЖЦС.
Суммарная интенсивность затрат на всём ЖЦС определяется выраже-
нием
Ф)=1с,(')-
Тогда полные затраты Спр на реализацию программы (проекта) будут
определяться соотношением
СПР ='}с1(г)Л + '}с2(/)Л + '}Сз(<)Л + с£в + с£, +с£уг , (4.4.8)
'#/ 'я 'о
где tH- момент начала ЖЦС;
t0 - момент ввода ЦУТС в эксплуатацию;
tK - момент снятия ЦУТС с эксплуатации - момент окончания ЖЦС.
На рис. 4.4.4 приведён график, иллюстрирующий примерный характер
зависимости интенсивности C(t) затрат от момента t ЖЦС. Из рис. 4.4.4
видно, что на каждом из этапов ЖЦС функция C(t) имеет экстремум и
уменьшается по мере их завершения.
сЛ')1
ct(t),c2(*)A(t)
Рис. 4.4.4
Исключение составляет этап эксплуатации ЦУТС, к концу которого ин-
тенсивность затрат вновь возрастает, что связано со старением ЦУТС,
ухудшением её ЭТХ и обусловленным этим увеличением эксплуатацион-
ных расходов.

4.4. Об экономическом анализе ЦУТС и ЦНПФС
279
4.4.4) При анализе сопряжённых и сопутствующих затрат на создание,
модернизацию и совершенствование обеспечивающих систем необходим^
учитывать существенную их особенность, состоящую в том, что они чаще
всего участвуют во многих операциях, т.е. обеспечивают функционирова-
ние целого ряда различных операционных систем. Так, например, данные
радиолокационных станций (РЛС) ПВО используются зенитной артилле-
рией, системой зенитных управляемых ракет (ЗУР), истребительной авиа-
цией; данные космической навигационной системы используются подвиж-
ными средствами систем различного назначения; данные спутниковой ме-
теорологической системы используются как в народнохозяйственных, так
и в военных комплексах и т.д. В связи с этим затраты данных видов рас-
пределяются между ЦУТС, в интересах которых функционируют обеспе-
чивающие системы. А
4.4.5) При оценивании затрат на создание запасов эксплуатационных и
операционных ресурсов необходимо учитывать, что из-за их физической
конкретности возникают ограничения при обеспечении ими различных
операций, так как недостаток ресурсов одних видов не может быть ском-
пенсирован избытком (резервом) ресурсов других видов. Поэтому затраты
на ресурсы, обладающие указанными свойствами, должны оцениваться
раздельно. А
4.4.6) Под затратами на организацию операции понимаются расходы,
связанные с выбором оптимального способа и плана проведения операции
и последующим управлением ею. А
4.4.3. МЕТОДЫ ОПРЕДЕЛЕНИЯ ЗАТРАТ
Определение затрат на ЦУТС и ЦНПФС производится в соответствии с
общими принципами оценивания и включает в себя два этапа.
1. Формулирование критерия оценивания:
- спецификация номенклатуры затрат;
- определение показателей затрат данной номенклатуры;
- формулирование (обоснование) требований (нормирующих условий)
к значениям показателей затрат.
2. Оценивание затрат:
- измерение уровней показателей затрат (получение их оценок);
- сопоставление измеренных значений затрат с нормирующими усло-
виями (реализация критериев оценивания).
Например, при определении затрат на военно-техническую систему
(ВТС) её структура и общий облик считаются известными. В качестве ос-
новного типового элемента структуры ВТС принимается комплекс воо-

280 Глава 4. Методы исследования эффективности ЦНП
ружения (KB), включающий в себя целевую подсистему (оружие) и обес-
печивающую подсистему (технологическое оборудование).
Экономический анализ ведётся применительно к сроку (периоду) реали-
зации программы вооружения с данным КВ. При этом используются сле-
дующие показатели:
Спрг- средняя суммарная стоимость программы вооружения с данным
_ KB;
СБЗ - средняя стоимость выполнения боевой задачи;
СТЗ - средняя стоимость выполнения типовой боевой задачи;
С по ~ средняя стоимость применения единицы оружия;
С^- средние годовые эксплуатационные расходы;
Сэк - средняя стоимость элемента KB (ЭКВ);
Сгэо - средние годовые эксплуатационные расходы с учётом отвлече-
ния средств из народного хозяйства.
При этом
С„0=-^-, (4.4.9)
™ ПРГ
где N прг - число единиц оружия, предусмотренное программой;
СБЗ=СП0МБЗ, (4.4.10)
где Na - число единиц оружия, необходимых для выполнения боевой за-
дачи; _ _ _
С«=С/Э + ^СЯЛ., (4.4.11)
где КуСпрг - ущерб, наносимый народному хозяйству из-за отвлечения
средств.
Период реализации программы вооружения начинается с утверждения
ТТЗ на KB, а заканчивается снятием его с вооружения. Средняя стоимость
программы определяется следующей суммой:
^прг ~ ^рс ~*~ ^пр "*" ^то "*" ^сс ~*~ ^эс> (4.4.12)
где СРС - средние расходы на разработку вооружения системы (ЦУТС);
Спр - средние расходы на производство оружия;
Сто - средние расходы на производство технологического оборудова-
ния;
С ее ~ средние расходы на строительство сооружений;
Сэс- средние расходы на эксплуатацию вооружения системы (ЦУТС).
Более подробно содержание слагаемых в (4.4.12) раскрывается в [38,
116,125].

4.4. Об экономическом анализе ЦУТС и ЦНПФС
281
При экономическом анализе ЦУТС на этапе её проектирования необхо-
димо знать соотношения между её качеством и стоимостью, т.е. зависимо-
сти стоимостей элементов KB от их параметров и ЭТХ:
СЭК = СЭК(А*«), (4.4.13)
где А^л - вектор параметров и ЭТХ элемента КВ.
Зависимость (4.4.13) называется функцией стоимости (ФС). Основ-
ными методами определения ФС являются:
- методы калькуляции;
- методы производственных функций [функций затрат - ЭР-функций
(см. п. 5.3.1)];
- статистические методы.
В рамках калькуляционных методов могут использоваться различные
исходные данные:
- данные о стоимостях реализованных прототипов KB;
- данные о стоимостях ЭКВ реализованных прототипов KB;
- данные о стоимостях элементов KB, получаемые путем укрупнённых
расчётов по сметной и базисной статьям калькуляции, по удель-
ным затратам, с использованием базисных коэффициентов.
Таким образом, совокупность калькуляционных методов расчёта стои-
мости ЭК может быть разбита на две группы:
- методы прототипов;
- методы укрупнённых расчётов.
Методы укрупнённых расчётов, в свою очередь, имеют ряд разновидно-
стей:
- метод сметной калькуляции;
-метод базисной статьи калькуляции;
- метод удельных затрат;
-метод базисных коэффициентов.
Более подробно все отмеченные методы рассматриваются в пособии [112].
В основе методов производственных функций лежит математиче-
ский аппарат регрессионного и корреляционного анализов. При этом наи-
большее распространение получили линейные регрессионные модели, а
также модели парных и множественных корреляций. Качество моделей
оценивается по дисперсиям оценок их параметров (коэффициентов регрес-
сии и корреляции).
Основное влияние на качество моделей производственных функций
[операционных ЭР-функций и РЭ-функций (см. п. 5.3)] оказывает выбор
(определение) состава факторов (параметров и ЭТХ ЦУТС и ЦНПФС),
обусловливающих организацию и протекание операции. Первоначальный
перечень факторов определяется эмпирически, после чего методами фак-
торного анализа производится отбор из них наиболее существенных (наи-
более значимых).

282 Глава 4. Методы исследования эффективности ЦНП
В основе построения РЭ-функций лежит функционально-стоимостный
анализ (ФЭА) соотношений (4.4.6), в результате которого определяются
зависимости затрат от факторов YP\9 а затем и от параметров и ЭТХ А,к,
ЦУТС и ЦНПФС, т.е. из соотношения:
следует
откуда
Здесь
YM -*(nt)\YM;AW J-G(nx)\A(kyY{n2) b
СЭк = СэАс{к)(А^)\. (4.4.14)
у(»)р|у(»)э I _s АЭК^\ ЛЭКЪ \
где \Г/^\Э ] - область допустимых значений целевых эффектов операции.
Зависимости C\A?kKA [i = l(l)&] - компоненты вектор-функции
С,кх[А^л) могут иметь различный характер, однако, как правило, их приво-
дят к линейным или степенным функциям, т.е.
C9K, = C,(a,)=Ch + C;,[i = l(l)*\,
C3K=tcfi> + tcU (4-4.15)
ИЛИ
СЭК,=С,{а,) = С^-+С„ [/ = 1(1)*];
C3K=tcti' +tcU (4-4.16)
где
c;=^M,[i=i(i)k).
В основе статистических методов лежит определение, по экспери-
ментальным данным, собранным на реализованных прототипах, вероятно-
стных характеристик затрат на ЦУТС на различных этапах ЖЦС в форме
условных законов их распределений относительно условий протекания
каждого из этапов.
Достоинство этого метода состоит в учёте неопределённости, всегда со-
путствующей экономическому анализу, однако недостаточная изученность
механизма воздействия неопределённых (случайных) факторов сущест-
венно затрудняет его практическое использование, поскольку этот метод
принципиально опирается на ретроспективные данные.

4.4. Об экономическом анализе ЦУТС и ЦНПФС
283
4.4.7) Рассмотренные выше методы ЭА, основанные на средних стоимо-
стях элементов KB (ЭКВ) и компонентов программы вооружения, облада-
ют существенным недостатком - малой надёжностью (достоверностью),
так как при реализации проекта (программы) реальные стоимости могут
существенно отличаться от их средних значений. Поэтому методы ВЭА
(ФЭА) и ТЭА требуют дальнейшего совершенствования в направлении бо-
лее адекватного реальной ситуации учёта неопределённости стоимостных
данных. А
4.4.8) Как можно было заметить, методы экономического анализа ЦУТС
и ЦНПФС обладают большим много- и разнообразием и требуют отдель-
ного изучения. Поскольку тематика монографии принадлежит смежной
области системных исследований, то здесь были лишь обозначены конту-
ры этого научно-прикладного направления. Заинтересованный читатель
может расширить свои познания по работам [9, 11, 14, 16, 38,41,43, 53, 59,
63, 68, 76, 80, 85, 88, 97,98, 108, 116, 120, 125,132, 133, 149, 164, 180]. А
4.5. КОММЕНТАРИИ
Продолжая обсуждение проблемы исследования эффективности опера-
ции и обусловливающего её качества ЦУТС и ЦНПФС, прокомментируем
ряд ключевых концептуальных и методологических вопросов. Заметим,
что возможные повторы сказанного ранее обусловлены различием уровней
и ракурсов (точек зрения) рассмотрения методологических аспектов про-
блемы, которые необходимо уяснить в новом контексте.
4.5.1} Прежде всего следует подчеркнуть, что детерминированные мо-
дели учитывают лишь потенциальные характеристики ОС, ОК и их эле-
ментов, относящиеся к некоторым вариантам ЦУТС и ЦНПФС, которые в
силу воздействия случайных факторов будут реализовываться с нулевой
вероятностью.
Квазирегулярные модели имеют незначительные преимущества, так как
ориентированы на средние значения моделируемых случайных характери-
стик, реализуемые также с нулевой вероятностью и не обязательно с мак-
симальным элементом вероятности. При этом свойства самой критериаль-
ной функции в общем случае остаются неизвестными (см. (2.4.10)). А
4.5.2} В известных методиках [84, 177, 178] исследования операций
наиболее сложным и необоснованным этапом является определение пока-
зателей, называемых критериями или функциями ценности, полезности и
т.п. [36, 45]. Лежащие в их основе постулаты носят умозрительный харак-
тер, и реализующие их практические процедуры не определены. А

284 Глава 4. Методы исследования эффективности ЦНП
4.5.3} Ещё раз подчеркнём принципиальное различие критериальных
функций Wp и Wn результатов Y,n) операции и параметров X',,, ЦУТС и
ЦНПФС соответственно (см. п. 2.4): первые - это операционные характе-
ристики ЦНПФС, а вторые - эксплуатационно-технические характеристи-
ки ЦУТС и ЦНПФС.
Обратим внимание, что требования (ограничения) к качеству результа-
тов операции всегда односторонние, тогда как требования к параметрам и
ЭТХ ЦУТС и ЦНПФС могут быть как одно-, так и двусторонними. Не сле-
дует эти ограничения смешивать. А
4.5.4} Если при исследовании эффективности операции данных для оп-
ределения закона распределения F% \Z/n\) предельно допустимых (тре-
буемых) значений Z,^ показателя К v качества её результатов недоста-
точно, то весьма полезными могут оказаться гарантированные - пессими-
стическая и оптимистическая оценки РДЦ и Рдц показателя Рдц эффек-
тивности ЦНПФС при крайних значениях параметров и ЭТХ ЦУТС и
ЦНПФС. Малость диапазона 1/^ ,/^/J значений показателя Рдц может
служить обоснованием правомерности предъявления к результатам К*
операции детерминированных требований Z\. A

Глава 5
МЕТОДЫ ПОСТРОЕНИЯ МАТЕМАТИЧЕСКИХ
МОДЕЛЕЙ ЭЛЕМЕНТОВ ОПЕРАЦИОННОГО
КОМПЛЕКСА
5.1. ОБЩИЕ ПРЕДПОСЫЛКИ
Как известно [16, 20 - 22, 44, 52, 59, 70, 74, 82, 84, 85, 89, 94, 108, 171,
178, 181], математической моделью сложного объекта называется сово-
купность соотношений, описывающих его строение (состав, структуру, ор-
ганизацию), поведение и взаимодействие с другими объектами и с окру-
жающей средой и позволяющих изучать объект в развитии. В зависимости
от задач исследования объекта степень детальности модели может быть
различной (от учёта каждого его элемента до представления в виде "черно-
го ящика"). Однако следует отметить, что методологическим аспектам
проблемы построения математических моделей сложных объектов (ЦУТС
и ЦНПФС) в известной литературе уделено недостаточно внимания. Точ-
нее сказать, мало обсуждаются принципы и методики построения моделей
и основные требования, которым они должны удовлетворять. Другими
словами, в основном говорится, что такое математические модели, и при-
водятся их примеры и не говорится о том, как эти модели построить и ка-
кими они должны быть, чтобы их можно было использовать в конкретных
исследованиях. Мало говорится о специфике моделей в исследовании опе-
раций вообще и в рамках задачи исследования их эффективности в частно-
сти. Тем не менее общие концептуальные основы в этих работах освеще-
ны. Рекомендуем читателю ознакомиться с ними.
Для уяснения основных принципов математического моделирования
процитируем их из работ [74] и [84].
В основе методологии научного исследования лежит следующая схема:
- формулируется проблема;
- строится математическая модель исследуемого объекта;
- формулируется теория рассматриваемого явления;
- выводятся некоторые следствия из этой теории;
~ даётся интерпретация полученных результатов.
Описанная схема иллюстрирует весь цикл научного метода, за исклю-
чением этапа сбора фактов. Этот этап начинается с набора уже известных
фактов, их использования в рамках правдоподобных рассуждений [135],
затем идёт экспериментальная верификация (проверка адекватности) и за-

286 Глава 5. Методы построения математических, моделей элементов ОК
канчивается готовностью использовать предсказания теории для решения
конкретных практических задач. После построения математической моде-
ли, её "экспериментальной" проверки по ограниченным исходным данным
и её достаточной детализации представляется экспериментальное доказа-
тельство возможной неадекватности первоначальной модели, но сам факт
неадекватности предполагает возможность создания улучшенного (более
адекватного) варианта модели (см. рис. 2.2.6).
К сказанному необходимо добавить следующее [178]. При построении
математических (как правило, аналитических) моделей зачастую делаются
(постулируются) предположения (допущения), позволяющие упростить
описывающие модель аналитические зависимости (детерминизация, ска-
ляризация, линеаризация и т.п.) с целью повышения возможностей её ана-
литического исследования, а также наглядности и иллюстрируемости по-
лучаемых результатов. При этом, естественно, адекватность модели сни-
жается. Тем не менее, если сделанные при построении модели допущения
принципиально не противоречат физическому смыслу рассматриваемого
явления и упрощенная модель отражает основные тенденции в строении и
поведении исследуемого объекта, то получаемое с её помощью решение
позволяет сделать многие полезные выводы и дать рекомендации. Важно,
чтобы интерпретация результатов соответствовала реальным фактам, про-
веряемым экспериментально (возможно, и на имитационных моделях). По-
этому подобные модели широко используются в теоретических и приклад-
ных исследованиях и расчётах.
5.1.1) Применительно к задачам исследования эффективности операций
вышесказанное означает, что среди всех свойств моделей исследуемых
объектов (ЦУТС и ЦНПФС) первостепенное значение имеет правильное
описание ими влияния параметров и ЭТХ ЦУТС и ЦНПФС на эффектив-
ность. Что касается точности абсолютного измерения (оценивания) эффек-
тивности операции, то её уровень должен обеспечивать правильное срав-
нительное оценивание и ранжирование по эффективности альтернативных
вариантов ЦУТС и ЦНПФС (см. п. 2.3.3). Именно наличием таких свойств
у критериальных функций (см. п. 2.4) может быть оправдано их практиче-
ское использование. Однако при их определении обоснованию наличия
этих свойств должного внимания, как правило, не уделяется. А
5.1.2) Следует подчеркнуть, что модели ЦУТС и ЦНПФС в задачах ис-
следования их качества и эффективности достаточно специфичны и прежде
всего своей агрегированностъю, т.е. комплексностью учёта в рамках моде-
ли реальных параметров и ЭТХ объектов исследования. Кроме того, это
модели не конкретной ЦУТС или ЦНПФС, а модели соответственно клас-
са ЦУТС, определяемого её проектом, и класса ЦНПФС, определяемого
его организацией. Еще раз напомним, что в задачах исследования опера-

5.7. Общие предпосылки
287
ций и теории эффективности целенаправленных процессов моделируются
не существующие, а вновь создаваемые (гипотетические) объекты. А
5.2. СХЕМА ПОСТРОЕНИЯ МОДЕЛЕЙ ЭЛЕМЕНТОВ
ОПЕРАЦИОННОГО КОМПЛЕКСА
Во всём предшествующем изложении для обозначения исследуемых
объектов и формулирования задач исследования широко использовалась
математическая символика. При этом одни символы призваны описывать
структуру и основные свойства объектов, а другие - их поведение. Сово-
купности всех этих символов и образуют математические модели объек-
тов. Применявшиеся до сих пор символы носили весьма общий и абст-
рактный характер (за исключением некоторых примеров). Причём практи-
чески ничего не говорилось о том, как эти модели строить, т.е. как и где
брать необходимые для этого данные и что с ними делать, чтобы модель
объекта была как можно более адекватной ему. Настало время обсудить
основные аспекты этой проблемы.
5.2.1. АЛГОРИТМ ПОСТРОЕНИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ
ЭЛЕМЕНТОВ ОПЕРАЦИОННОГО КОМПЛЕКСА
Процесс построения математической модели любой операции (любого
ЦНПФС) включает в себя две фазы и реализуется в два этапа:
- на первом этапе строится модель операционной системы, включаю-
щей в себя в качестве подмоделей: модель ЦУТС, модель условий
функционирования ЦУТС и модель ЦНПФС;
- на втором этапе строится модель операционной ситуации, т.е. модель
условий применения ЦУТС.
На рис. 5.2.1 приведена обобщённая структурная схема алгоритма по-
строения математической модели операционного комплекса и его элемен-
тов. Кратко прокомментируем функции отдельных блоков схемы.
Блоки 1-3 определяют спецификации:
- существенных эффектов (атрибутов) операции, определяющих вир-
туальное качество её результатов - вектора К*;
- параметров и ЭТХ ЦУТС и ЦНПФС - векторов Alk* и Л?к~ (управ-
ляемых Ж х и неуправляемых А!к Л\

288 Глава 5. Методы построения математических моделей элементов ОК
ттт ттт ттт «
! ^
о
! £
!'—
и и
1 О
L*
mm ттт ттт
У|Л
^Г
f-x
•ч
<
«К
•ч
«г
•ч
1
II
ттт ттт ттт ттт т
! н
<->
о
Is
1
~*
<м
«3
*
•«к
II
•*
X
ттГ
1."
и
J <*>
1 r-i
—
-►
--
иг
*-
—
<Г>
V
•ч 1
%
•ч \
•ч 1
•ч J
*» 1
II
<^
«fl
--
иг
:—■
••ч
II
с2
J «ч
1 ,"н
—
"*
- —
"
U-
—
^
'"""rU
•ч 1
л 1
Ч|
II
—
--
"
:—г
II
I 1-Н
1 f—*
—
-►
■ —
"
*-
—
ir>
. „
&\
II
О «Г
—
- —
1..
I—Г
L-^—-*.
•ч
•ч
* —
<5
•*ч
<5
1 *ч
■о
1 •*
*^
II
1 * .*>
J о
1 тН
—
-*
—
Wmm
V
—
*
*~~X '
•ч
"ST"
II
S'?
• —
"
^
«Г
**>
••ч
ГЧ»
Я
••ч
•ч
II
On
—' Г""
! |
—■ i
so
—- 3 J
"^ ■*•♦. «г
^г «Г
Ч" ^
.. N^ «ас
•2» »*^ >-^
3 ^ и
—
j
■*
—
—-
Г—
«г
и
и
00
А
г^
»г
♦•ч
II
--.
Ц|
—'|

5.2. Схема построения моделей элементов операционного комплекса 289
- характеристик условий функционирования ЦУТС - вектора 1?L,
влияющих на параметры AL* и А?к«.
Блок 4 представляет собой операционную модель ЦУТС, описывающую
зависимость параметров А,кх = (А',к«, А?^) от ЭТХ и условий функциони-
рования ЦУТС и от организации ЦНПФС.
Блоки 5-7 определяют операционный функционал со всеми его пара-
метрами - агрегатами (см. п. 5.4), а также закон распределения показателя
F/v виртуального качества результатов операции и представляют собой
математическую модель ЦНПФС.
Блок 8 определяет подвектор (U'{/) = (Afo,Bfa))с(X'{mf) = {A{k),B'{r)J)
управляемых компонент вектора Х',« (параметров и ЭТХ ЦУТС и
ЦНПФС), а также стратегии (способы) управления ими и, таким образом,
моделирует работу органа управления качеством ЦУТС и эффективностью
ЦНПФС.
Блоки 9 и 10 определяют спецификацию показателя Z, v требуемого ка-
чества результатов операции и характеристик В7гх условий применения
ЦУТС.
Блоки 11 и 12 определяют зависимость требований Z.y предъявляемых
к результатам L операции, от условий щ* применения ЦУТС, а также
закон распределения случайного вектора Zv и, таким образом, совместно
с блоками 9 и 10 реализуют априорную модель ситуации (стратегической и
оперативной обстановки), в которой проводится операция и достигается её
цель.
Блок 13 определяет подвектор Ufi = UT* сX?* = BJL управляемых
компонент вектора X?* (характеристик условий применения ЦУТС), а
также стратегии (способы) управления ими и совместно с блоком 8 моде-
лирует работу органа управления требуемым качеством результатов опе-
рации.
Блок 14 определяет соотношения ^ между компонентами векторов L
и Z/v, обеспечивающие достижение цели операции и, таким образом, мо-
делирует процедуру оценивания качества результатов операции.
Из сказанного следует, что блоки 1-8 образуют модель операционной
системы (МОС), блоки 9-13 образуют модель операционной ситуации
(МОСТ), а блоки 1-14 образуют .модель операционного комплекса (МОК)
в целом.
10 Зак. 3303

290 Глава 5. Методы построения математических моделей элементов ОК
5.2.1) Следует обратить особое внимание на специфику математических
моделей, строящихся по рассмотренному алгоритму, которая обусловлена
их назначением. Указанная специфика раскрывается в дальнейшем. При
этом необходимо иметь в виду, что схема, изображенная на рис. 5.2.1, но-
сит весьма общий характер и называется "алгоритмом" условно, поскольку
в конкретных случаях в зависимости от имеющихся данных о ЦУТС и
ЦНПФС, а также от возможностей и процедур их добывания последова-
тельность реализации блоков этого "алгоритма" может отличаться от по-
следовательности, приведённой на рис. 5.2.1. А
При изучении физических явлений объектом моделирования являются
связи между их различными характеристиками. При исследовании техни-
ческих устройств, систем и протекающих в них процессов моделируются
связи их состояний (понимаемых в широком смысле, т.е. включая и свой-
ства объектов) с внешними воздействиями (как естественными, так и спе-
циально организованными), а также с другими элементами и подсистема-
ми (точнее, с их состояниями) исследуемого объекта (ЦУТС или ЦНПФС).
Для пояснения сказанного процитируем определение понятия матема-
тической модели: "математическая модель реальной системы - это
совокупность соотношений (формул, уравнений, неравенств, логических
условий, операторов и т.д.), определяющих характеристики состояния
системы (а через них и выходные сигналы) в зависимости от пара-
метров системы, входных сигналов, начальных условий и времени" [74, 93,
178].
Понятию "соотношение" в этом определении придаётся весьма широ-
кий смысл: в одних случаях - это явные функции от параметров системы,
входных сигналов, начальных условий и времени, в других - это совокуп-
ность уравнений (алгебраических, дифференциальных, функциональных и
т.д.) относительно характеристик состояний системы и её выходных сиг-
налов. При этом параметры системы входят в коэффициенты уравнений, а
входные сигналы - в их правые части.
Однако при исследовании реальных систем не всегда удаётся построить
математические модели в виде явных функций или уравнений. Подтвер-
ждением сказанного служат модели конкретных сложных систем и про-
цессов, построенные с учётом воздействия на них различных случайных
факторов. Рекомендуем читателю ознакомиться с монографией [178] более
подробно.
Операционный комплекс - это сложная (большая) система, поэтому
приведённая выше цитата относится к нему в полной мере. Это, в частно-
сти, иллюстрируется и приведёнными на рис. 5.2.1 соотношениями общего
характера, конкретные выражения которых могут принимать самые раз-
личные формы. Тем не менее ОК и ОС имеют специфические особенности,
присущие только им и обусловленные задачами исследования.

5.2. Схема построения моделей элементов операционного комплекса 291
Прежде всего следует отметить, что в общем случае характеризующие
математическую модель параметры и ЭТХ ЦУТС и ЦНПФС Х,к являют-
ся функциями времени, т.е. X,s=X,mAf). Это означает, что от времени за-
висят как показатели К,, Z,k качества результатов (виртуальных и тре-
буемых) операций, т.е. Г(||> = Y{n){X[mf){t)), Z{n) = Z{ll)[x^(t))9 так и пока-
затели её эффективности, т.е. РДЦ = Pm[x{m){t)), (0Гдц{у)^(0Гдц{г;Х{т){()),
Поэтому состояния ОС и ОК могут характеризоваться любой из приве-
денных функций времени.
5.2.2) До сих пор для большей простоты и наглядности изложения из-
менение характеристик Х,к ЦУТС и ЦНПФС во времени явно не подчёр-
кивалось. В дальнейшем символ / , как правило, также опускается, но при
существенной зависимости характеристик исследуемых объектов (ЦУТС и
ЦНПФС) от времени он должен фигурировать в модели в явном виде.1 ▲
Интерпретируя приведённое выше определение математической моде-
ли, заметим, что под "состояниями" ЦУТС и ЦНПФС следует понимать
значения A'^Ai) и A^kAt) их параметров и ЭТХ, под "выходными сигна-
лами" - значения Y,\t) показателя Y.x качества результатов операции,
под "входными сигналами" - значения (^A%At),AyAt)) = Utry их управ-
ляемых параметров и ЭТХ, под "начальными условиями" - значения
Щгк(tQ) и YP\(t0) характеристик условий функционирования ЦУТС и за-
пасов ресурсов в начале операции.
5.2.3) При некотором воображении, в рамках задачи синтеза к входным
(управляющим) "сигналам" можно отнести и значения показателя Y^l
расходуемых ресурсов, характеристик В^ условий применения ЦУТС и
показателя Z, v требуемого качества результатов операции. А
5.2.4) В приведённых обозначениях элементов математических моделей
символ t в общем случае может обозначать различные моменты времени.
Так, в выражениях показателей Y,At), Z,At)9 РДЦЬ) и ctfMU{y;t) - это
момент оценивания эффективности операции и принятия решения о её ка-
честве и пригодности, в выражениях B',rAt0) , YP\(tQ) - это момент начала
операции, в остальных выражениях - это текущее время, принимающее
1 Не следует смешивать текущее время t с операционным временем Т.

292 Глава 5. Методы построения математических моделей элементов ОК
значения из интервала [*0,*я]. Следует заметить, что хотя в принципе все
характеристики X,St), Y,At)9 Z,ndt) модели с течением времени изме-
няются, однако многие из них в ходе одной (единичной) операции (в тече-
ние времени г ) в силу малости изменений целесообразно считать посто-
янными. В то же время применительно ко всему жизненному циклу ЦУТС
подобное допущение неправомерно и изменение её характеристик от вре-
мени должно учитываться. А
Другая особенность моделей ОС и ОК заключается в том, что имею-
щиеся в ОС запасы ресурсов и времени, с одной стороны, играют роль
"входных сигналов", а с другой - будучи израсходованными, характери-
зуют качество результатов операции ("цену" целевого эффекта) и играют
уже роль "выходных сигналов". Именно это свойство математической мо-
дели операции и позволяет оценивать её результаты комплексно, т.е. во
взаимосвязи и сопоставлении (соотнесении) целевого эффекта с израсхо-
дованными на его получение ресурсами и временем и с учётом предъяв-
ляемых к совокупным результатам (с учётом потерь - расхода ресурсов и
времени) операции требований, т.е. в замкнутой схеме.
Третья особенность модели ОС состоит в том, что поскольку количе-
ства Г/2!, Г/3} израсходованных ресурсов и времени отражены в показате-
ле F/v, то основной её функцией является адекватное описание этого пока-
зателя. При этом в рамках задачи оценивания эффективности операции в
её показатели параметры X, v в явном виде могут и не входить. Что же ка-
сается задач анализа и синтеза (см. гл. 4), то в выражения, описывающие
модель ОС, явно должны входить лишь управляемые агрегированные па-
раметры U, у Другими словами, при оценивании эффективности опера-
ции модель ОС может рассматриваться как "чёрный ящик", на вход кото-
рого поступают ресурсы г/2!, г/3!, а на выходе появляются результаты
Y, v =(Гл1,к/л,Гл{). При решении задач анализа и синтеза в "чёрном
ящике" "высвечивается окно", в котором "просматриваются" управляемые
параметры U.x.
Наконец, одной из важнейших и принципиальных особенностей мате-
матических моделей ОС и ОК является их стохастичность, т.е., другими
словами, эти модели принципиально вероятностные.
Подведём итог. Особенность математических моделей ОС и ОК (и их
элементов) заключается в том, что они описывают процесс функциониро-
вания и применения ЦУТС не как процесс изменения её состояний во вре-
мени, а как процесс преобразования имеющихся в системе ресурсов к/2!,
yP\ в обусловленный задачей ЦНПФС необходимый целевой эффект yP\ .

5.2. Схема построения моделей элементов операционного комплекса 293
5.2.2. СТРУКТУРНАЯ СХЕМА ВЕРОЯТНОСТНЫХ МОДЕЛЕЙ
ЭЛЕМЕНТОВ ОПЕРАЦИОННОГО КОМПЛЕКСА
Теперь, когда выявлены основные особенности математических моде-
лей ОС и ОК, раскроем основные свойства моделей их элементов, описы-
ваемых вероятностными моделями показателей качества результатов
ЦНП и его эффективности.
Элементами модели показателя эффективности ЦНП (МПЭЦНП) яв-
ляются:
(1) - модель виртуальной результативности операции - показателя
виртуального целевого эффекта;
(2) - модель виртуальной ресурсоёмкости операции - показателя вир-
туального расхода операционных ресурсов;
(3) - модель виртуальной оперативности операции - показателя вирту-
ального расхода операционного времени;
(4) - модель операционной функции, связывающей целевой эффект с
расходуемыми операционными ресурсами;
(5) -модель функции связи (балансных соотношений) различных ресур-
сов между собой;
(6) - модель виртуальных результатов операции - показателя Fv вир-
туального качества совокупных результатов (как позитивных, так и нега-
тивных) операции;
(7) - модель требуемой результативности операции - показателя z£\
требуемого (минимально допустимого) целевого эффекта операции;
(8) - модель предельной ресурсоёмкости операции - показателя zFK
предельного (максимально допустимого) расхода операционных ресурсов;
(9) - модель требуемой оперативности операции - показателя Z^\ ди-
рективного (максимально допустимого) расхода операционного времени;
(10) - модель {функционал) организационного (экспертного) компро-
мисса по расходу операционных ресурсов (ФЭКР);
(11) - модель {функционал) организационного (экспертного) компро-
мисса по расходу операционного времени (ФЭКО);
(12) -модель требуемых результатов операции - показателя Z,, тре-
буемого качества совокупных результатов операции;
(13) - модели комплексного качества (эффективности) операции -
показателей РДЦ и соГдц{у) эффективности операции;
МПВКРО - модель показателя виртуального качества результатов
операции;
МПТКРО - модель показателя требуемого качества результатов опе-
рации;

294 Глава 5. Методы построения математических моделей элементов ОК
МПЭЦНП - модель показателя эффективности ЦНП.
Поскольку исследование эффективности операций вообще и построение
моделей ОС и ОК в частности происходит в условиях априорной неопре-
делённости, проявляющейся как случайность моделируемых элементов
операционного комплекса и описывающих их характеристик (величин,
векторов, функций, параметров), то в принципе все перечисленные модели
должны быть вероятностными. Другими словами, это - совокупность за-
конов распределения случайных величин (векторов, функций), а также
функциональных, регрессионных, корреляционных, дисперсионных, фак-
торных и других подобных зависимостей [170], призванных описывать
взаимосвязи и взаимодействия (в динамических моделях) между элемен-
тами ОК, т.е. между моделями его элементов.
На рис. 5.2.2 приведена структурная схема совокупности перечислен-
ных выше моделей элементов ОК, где стрелки указывают направление и
последовательность построения и использования моделей. Кратко про-
комментируем приведённую схему.
Как видно из рис. 5.2.2, конечной целью моделирования ОК является
определение (построение моделей) показателей эффективности операции.
5.2.5) Выше отмечалось (см. {2.7.8}), что в общем случае компоненты
вектора К , существенно зависимы между собой. Эта зависимость моде-
лируется (описывается) операционным функционалом, представляющим
собой совокупность операционной функции и функции связи (блоки (4) и
(5)). Как известно [29], для определения закона распределения случайного
вектора недостаточно знать безусловные (маргинальные) распределения их
компонент, а необходимо знать характер и степень их взаимной зависимо-
сти. Именно эту задачу и решает модель операционного функционала1. За-
метим, что X[mf)={A{kyB[nY A
5.2.6) Ранее также говорилось (см. {2.7.7}), что компоненты вектора
Z, ч, как правило, взаимно независимы. Кроме того, поскольку они при-
званы отражать ситуацию, в которой протекает операция (условия приме-
нения ЦУТС) и которая априори неопределённа (случайна), то естественно
полагать их независимыми от компонент вектора Y,k . Однако в "сплочён-
ных" ОК (см. п. 2.6.2) возможности ЦУТС по получению целевого эффекта
в соответствии с ресурсоёмкостью и оперативностью её ЦНПФС могут (и
должны) учитываться при предъявлении требований к качеству результа-
О том, как это делается, говорится в п. 5.3.

5.2. Схема построения моделей элементов операционного комплекса 295
I
о
В
•л
«2
и
<а
<э
(а
NT
II
NT
<э
NT
*С5
3 «г
о
Си,
бш
®
<а
«г
ST
I!
037
(3f_2
2* is
N.
*r
<3
•
<a
i
■*
"5*
$£
ft*
II
S

296 Глава 5. Методы построения математических моделей элементов ОК
тов операции. Так, с одной стороны, количество отпускаемых на операцию
ресурсов должно согласовываться как с требуемым целевым эффектом, так
и с требуемой оперативностью, а с другой, - должны согласовываться ме-
жду собой требуемая оперативность и допустимая ресурсоёмкость
ЦНПФС. Такая согласованность обеспечивается с помощью "экспертного
компромисса" (ФЭК, блоки (10) и (11)). При этом компоненты вектора
Z/v становятся зависимыми как между собой, так и от компонент вектора
fix (от параметров их распределений и от операционного функционала).
Всё сказанное будет в дальнейшем проиллюстрировано на примерах. ▲
5.3. ОПЕРАЦИОННЫЙ ФУНКЦИОНАЛ
Ранее неоднократно употреблялся (на интуитивном уровне) термин
"операционный функционал" без чёткого определения и раскрытия семан-
тики этого нового понятия. Рассмотрим его подробнее.
5.3.1. ПОНЯТИЕ ОПЕРАЦИОННОГО ФУНКЦИОНАЛА
Как было показано, компоненты показателя Y,n) качества результатов
операции зависят от характеристик (параметров и ЭТХ) ЦУТС - вектора
А',,* и ЦНПФС - вектора А?к*, а также от условий функционирования
ЦУТС - вектора В',г), а поскольку эти характеристики влияют на все ком-
поненты вектора Y., одновременно, то последние оказываются взаимосвя-
занными. Поэтому для построения математической модели виртуальных
результатов операции необходимо иметь модели указанных зависимостей
и связей. Эту задачу решает операционный функционал (ОФЛ).
Определение 5.3.1. Операционный функционал (ОФЛ) - это сово-
купность операционной функции и функций связи. А
Определение 5.3.2. Операционной функцией (ОФ) называется со-
отношение, описывающее зависимость целевого эффекта от расходуемых
операционных ресурсов и времени. А
Определение 5.3.3. Функцией связи (ФСВ) называются балансные
соотношения между различными характеристиками результатов опера-
ции (в частности, между ресурсами различных видов). А

5.3. Операционный функционал
297
5.3.1) Как следует из определений 5.3.1 - 5.3.3, понятие "операционная
функция" представляет собой обобщённый аналог используемого в эконо-
мической кибернетике понятия "производственная функция", описываю-
щий зависимость результата ("продукта") функционирования сложной
системы (ЦУТС) от расходуемых на его получение ресурсов [59, 85, 179].
А
Операционная функция может определяться одним из двух способов:
ИЛИ
Функция (5.3.1) называется РЭ-функцией (РЭФ) или "функцией выпус-
ка" [59], а функция (5.3.2) - ЭР-функцией (ЭРФ) или "функцией затрат"
[59].
5.3.2) Символы РЭ и ЭР соответственно означают: "ресурс-эффект" и
"эффект-ресурс", т.е. в РЭ-функции аргументом является ресурс, а в ЭР-
функции - эффект. В связи с этим использованные в [59] названия следо-
вало бы поменять местами. А
В зависимости от имеющихся данных о соответствующих расходах
операционных ресурсов и времени функции связи также могут опреде-
ляться с помощью различных взаимно обратных соотношений. В частно-
сти, материально-технические и временные ресурсы связаны соотноше-
ниями
Г(!3 = У{{М1)= S31(Yti;A{k),B>{r)), (5.3.3)
ИЛИ
Y^ = Y^(Y^S^;A{k)tB'{t)). (5.3.4)
Таким образом, операционный функционал представляет собой одну из
следующих "пар соотношений"1:
у(')_дг (у(Л у(ъ)-А Я' )• 1
Fw=^/(Fw^w^</o)^ ['Л = 1>2; М = 2,з].}
В симплексной канонической форме соотношения (5.3.1) - (5.3.5) соот-
ветственно примут вид
Ух =Уг(Уг,У3) = %г(Уг>У3;А,В') (5.3.6)
или
Уг = л(*,л)=*и(к»лМ,л/); (5-3.7)
Действительное число соотношений, естественно, может быть и больше двух.

298 Глава 5. Методы построения математических моделей элементов ОК
У3=уМ=Я32{Уг;А,В') (5.3.8)
ИЛИ
л = зЖэ)=*»(лМ,л'); (5.3.9)
*=%,{уРУъ;А>#)> [/,7 = 1,2]/
y^SufoA,*), [M = 2,3].|
(5.3.10)
5.3.3) Как было отмечено, в отличие от соотношений (5.3.8), (5.3.9) со-
отношения (5.3.3), (5.3.4) описывают частный случай связи ресурсов (ма-
териально-технических и временных), поскольку между компонентами по-
казателя Г/2? материально-технических операционных ресурсов также су-
ществуют связи, требующие описания при построении модели операцион-
ного комплекса. ▲
5.3.4) В приведённых выражениях векторы А,кк = А и В'.^ = В' играют
роль параметров. Однако на этапе проектирования ЦУТС и организации
ЦНПФС они согласно (2.3.11) являются аргументами и обусловливают ка-
чество результатов операции. Поэтому в дополнение к операционному
функционалу, моделирующему (описывающему) "динамику" превращения
операционных ресурсов в целевой эффект, должны быть определены соот-
ношения (2.3.11), (2.3.12), моделирующие его "статику", т.е. возможности
ЦУТС и ЦНПФС по такому превращению, закладываемые в них при раз-
работке и создании ЦУТС и организации и управления ЦНПФС. А
Раскроем физический смысл приведённых соотношений на примере
конкретного ОФЛ, для наглядности ограничившись симплексной канони-
ческой формой показателя Y., качества результатов операции. Начнём с
замечания. Как отмечается в [59, 179], применяемые в настоящее время
"производственные функции" (РЭ и ЭР) строятся, как правило, в предпо-
ложении о мгновенной превращаемости ресурсов в целевой эффект, почти
неограниченной взаимозаменяемости ресурсов различных видов, полном
предвидении (детерминированности) хода операции и т.п. Кроме того, эти
функции практически не отражают прогресса в технологии (в стратегии)
проведения операции, что также следует отнести к их недостаткам. Хотя
независимо от сложности приводимого примера он может иллюстрировать
лишь некоторый частный случай, естественно, не охватывающий всего
многообразия РЭ-функций (РЭФ) и ЭР-функций (ЭРФ), тем не менее
представляется, что он обладает достаточной общностью и в значительной
мере лишён отмеченных недостатков производственных функций.

5.3. Операционный функционал
299
Пример 5.3.1. Пусть в ходе операции целевой эффект ух образуется по
следующему закону:
Ух =«.аи.л) = аи)л(0* = а1аЛ(у,)=ам5аи), (5.3.11)
о
где ап - размерный коэффициент, характеризующий удельную ресурсо-
ёмкость целевого эффекта ух операции;
y2(f) - темп (скорость) освоения расходуемых материально-
технических ресурсов,
у2- количество освоенных (израсходованных) в ходе операции ре-
сурсов;
уъ- длительность операции (периода освоения ресурсов у2 и пре-
вращения их в целевой эффект ух)- операционное время.
Соотношение (5.3.11) описывает (моделирует) процесс освоения ресур-
сов в ходе операции.
Как было отмечено в (5.3.4), в общем случае существуют зависимости1
ап = aii\4k)>B(i'))>
К = Уъ{\к)>в[,>))>
(5.3.12)
а следовательно, и зависимость
Ух =л( Уг>Уъ>\)'К) У (5.3.13)
Поэтому стохастический вариант выражения (5.3.11) имеет вид
Л=<*12 }л(0*' = <*12Л(?з)- (5.3.14)
о
Понятно, что в каждое из выражений (5.3.12) и (5.3.13) могут входить
как некоторые, так и все компоненты векторов А,кх и щ*. А
5.3.5) Понятно, что, когда РЭФ описывается соотношением типа (5.3.4),
задание соотношений (5.3.1) - (5.3.10) в явном виде становится затрудни-
тельным (или невозможным), однако, как будет показано, их явное задание
требуется не всегда (см. гл. 6, 7, 8). А
1 Из (5.3.12) следует, что коэффициент ОСХ1 представляет собой агрегированный па-
раметр модели ОФЛ, называемый далее "агрегатом" или "комплексом".

300 Глава 5. Методы построения математических моделей элементов ОК
5.3,2. КЛАССИФИКАЦИЯ ОПЕРАЦИОННЫХ РЕСУРСОВ
Анализ задачи построения математической модели ОФ приводит к вы-
воду, что по характеру участия расходуемых в ходе операции ресурсов в
процессе их превращения в целевой эффект следует различать ресурсы
статические и динамические, а также пассивные и активные.
1.а) Статические (С) ресурсы расходуются на этапах создания ЦУТС
и организации ЦНПФС и в ходе операции участвуют опосредованно в
форме технического ресурса участвующих в операции средств, уровня
технологии и т.п. - это, как правило, капитальные затраты (вложения), т.е.
надоперационные ресурсы.
1.6) Динамические (Д) ресурсы расходуются в ходе операции на по-
лучение целевого эффекта - это операционные ресурсы.
2.а) Пассивные (П) ресурсы участвуют в процессе получения целево-
го эффекта, но непосредственно в него не превращаются.
2.6) Активные (А) ресурсы непосредственно превращаются в целе-
вой эффект.
Как следует из приведённых определений, соответствующие первой и
второй парам свойства ресурсов не исключают друг друга, а проявляются
совместно, т.е. как статические, так и динамические ресурсы могут быть, в
свою очередь, как пассивными, так и активными.
Типичной является операция (ЦНПФС), в ходе которой участвуют ре-
сурсы различных видов, различающиеся как по степени участия в опера-
ции, так и по скорости их расходования1. В связи с этим следует разли-
чать2:
- ресурс сырьевой (АД);
- ресурс энергетический (АД);
- ресурс структурно-параметрический (ПД) (см. (2.6.1));
- ресурс технический (ПД);
- ресурс технологический (ЦД);
- ресурс трудовой (людской) (ЦД);
- ресурс информационный (ПД);
- ресурс временной (ПД) и т.д.
Прокомментируем приведённые термины.
Сырьевой ресурс. На первый взгляд наиболее очевидным представ-
ляется понятие сырьевого ресурса. Именно сырье должно превращаться в
продукцию ЦНПФС, т.е. в его целевой эффект. Однако не в любой опера-
ции этот вид ресурса легко определяется. Действительно, если ЦНПФС -
это боевая операция, то в качестве целевого эффекта может выступать не
количество "произведённой продукции", а, например, величина наносимо-
1 В общем случае не все используемые в операции ресурсы расходуются.
2 Символы в скобках означают признаки классификации ресурсов.

5.3. Операционный функционал
301
го противнику ущерба. Ясно, что на получение требуемого эффекта
(ущерба) расходуются боевые средства (снаряды, бомбы и т.п.), которые и
играют роль "сырья". Однако специфичность формы превращения расхо-
дуемых средств в целевой эффект затрудняет их отождествление с сырьём.
Тем не менее в соответствии с ролью сырьевого ресурса в операции он яв-
ляется активным динамическим (АД) ресурсом.
Энергетический ресурс. То, что энергетический ресурс является ди-
намическим, представляется вполне очевидным. Менее очевидно его отне-
сение к активным ресурсам. Однако поскольку превращение сырья в "про-
дукт" возможно лишь за счёт расходования энергии, то это активный ре-
сурс.
Структурно-параметрический ресурс (см. (2.6.1)). Может показаться
странным понятие структурного ресурса. Однако в целом ряде операций
для достижения её цели необходимы вполне определённые характеристики
ЦУТС, которые могут изменяться и в ходе конкретной операции участво-
вать в различной мере. К таким характеристикам в первую очередь отно-
сятся различного рода "накопители": объёмы памяти ЭВМ, размеры склад-
ских помещений, протяжённость маневровых и запасных путей железно-
дорожных узлов, число и размеры причалов в портах и т.п., а также такие
структурные характеристики, как наличный состав транспортных средств,
находящийся в строю личный состав ЦУТС и т.п. Хотя в ходе операции
подобный ресурс в буквальном смысле и не расходуется, тем не менее по-
скольку для получения целевого эффекта он абсолютно необходим, то это
ресурс динамический, хотя и пассивный. В математических моделях ОС и
ОК ресурсы этого вида фигурируют в виде параметров и ЭТХ ЦУТС и
ЦНПФС. Этим и объясняется их название.
Технический ресурс. Технический ресурс средств, участвующих в
операции, - это ресурс параметров и ЭТХ ЦУТС. В принципе это ресурс
динамический и, безусловно, активный, поскольку он в ходе операции рас-
ходуется (параметры и ЭТХ ЦУТС при её эксплуатации ухудшаются). Од-
нако поскольку в течение одной операции он расходуется сравнительно
медленно, то его можно отнести к пассивным ресурсам.
Технологический ресурс. Под технологическим ресурсом понимают-
ся капитальные вложения, затраченные на разработку и внедрение техно-
логии данного уровня, от которого зависит как оперативность ЦНПФС,
обусловленная производительностью и надёжностью ["живучестью" (см.
{2.7.10})] оборудования, так и качество целевого эффекта ("продукции").
Понятно, что это ресурс активный, но статический.
Трудовой ресурс. Под трудовым ресурсом понимается число людей, с
учётом их квалификации, способных участвовать в проведении операции
(непрерывно или периодически - поэтапно) в соответствии с технологией
ЦНПФС. Это, естественно, динамический и в определённой степени ак-
тивный (аналогично энергетическому) ресурс. Однако поскольку этот ре-

302 Глава 5. Методы построения математических моделей элементов ОК
суре, как правило, в ходе операции не расходуется, то он отнесён к числу
пассивных.
Информационный ресурс. Информационный ресурс может быть клас-
сифицирован во всех вариантах. Действительно, информация, использо-
ванная на этапе создания ЦУТС и организации ЦНПФС, может быть отне-
сена к статическим ресурсам, тогда как информация, используемая в ходе
операции, представляет собой динамический ресурс. Что касается второго
признака классификации, то в зависимости от характера целевого эффекта
информационный ресурс может быть как активным, так и пассивным.
Временной ресурс. Временной ресурс - это время, которое должно и
может быть израсходовано для получения соответствующего целевого эф-
фекта. Это время называется операционным (см. п. 2.3.2).
5.3.6) Представляются возможными операции, в ходе которых расходу-
ются ресурсы, отличные от рассмотренных, но, несмотря на их специфич-
ность, могущие быть классифицированы по рассмотренной схеме. Напри-
мер, в боевых операциях в качестве ресурсов выступают боевые средства,
как расходуемые на достижение целевого эффекта - ущерба, наносимого
противнику, так и расходуемые в результате действий противника. Пред-
ставляется, что, несмотря на специфичность подобных ресурсов, они могут
быть классифицированы по рассмотренной схеме. Так, расходуемые сна-
ряды, бомбы и т.п. могут рассматриваться как сырьевые ресурсы, а теряе-
мые средства вооружения - как структурные ресурсы, так как в результате
расходования последних изменяется структура ЦУТС, участвующей в сле-
дующей операции без восполнения потерь. А
5.3.7) Следует обратить внимание, что даже если в ходе операции па-
раметры ЦУТС остаются неизменными (т.е. не расходуются в буквальном
смысле), тем не менее без наличия определённого уровня "параметриче-
ского ресурса" (см. (4.1.3), (4.1.4)) ЦУТС не может выполнять свои функ-
ции. Другими словами, "параметрический ресурс" в некотором смысле
аналогичен информационному ресурсу, который потребляется, не убывая.
А
5.3.8) Может возникнуть естественный вопрос: для чего вообще нужна
подобная терминология и классификация? Ведь обычно все потребные на
операцию ресурсы исчисляются в единых единицах (например, в рублях -
"финансовый ресурс"), что существенно упрощает как модель ЦНПФС, так
и его последующий анализ.
Следует особо подчеркнуть, что подобная "простота" обусловлена под-
меной реальной задачи искусственной, не адекватной реальной ситуации.
Действительно, как было показано в п. 2.3.2, показатель YW = Яп\ качест-
ва результатов операции по второму аспекту, характеризующий её ресур-
соемкость, включает в себя показатели виртуальных расходов ресурсов

5.3. Операционный функционал
303
различных видов (материально-сырьевых, энергетических, технических,
информационных и т.д.). При этом определяемые вектором zF\ = Rf1 \
предельно допустимые их расходы задаются дифференцированно ("персо-
нально") для каждого вида ресурса, а не интегрально для всех их видов в
форме ограничения на валовый одноразмерный (например, стоимостный)
показатель.
Ещё раз обратим внимание на то, что указанная особенность рассматри-
ваемой методологии обусловлена физической сущностью задачи оценива-
ния качества результатов операции и не может (не должна) рассматривать-
ся как один из возможных подходов к её решению, так как реальные огра-
ничения на расходы ресурсов для каждого их вида персональны (индиви-
дуальны). Действительно, весьма типичными для практики являются си-
туации, в которых при наличии запаса денежных ресурсов цель операции
не может быть достигнута из-за дефицита (нехватки) ресурса некоторого
конкретного вида. Подобные возможности (ситуации) должны учитывать-
ся самой моделью ЦНПФС. Это может быть достигнуто лишь при диффе-
ренциации ресурсов различных видов в показателях Г/2| и Z^\ их опера-
ционных свойств. ▲
5.3.3. ПРИМЕРЫ ОПЕРАЦИОННЫХ ФУНКЦИЙ
Для иллюстрации сказанного в п. 5.3.2 приведём ряд примеров "произ-
водственных функций", используемых в экономической кибернетике и мо-
гущих служить прототипами операционных функций.
Одной из наиболее распространённых является степенная РЭФ вида [59,
179]
Уг=*1гУ&У&™&> С5-3-15)
где otn,fi. - "агрегаты", причём ап - коэффициент производительности
(отдачи) ресурсов, а яг"1 - коэффициент ресурсоёмкое™ единицы целевого
эффекта,
IM
^12 "" ги ' ^12 ~~
1=1
При п2 = 2 РЭФ (5.3.15) принимает вид
yt=<x»)fiy2- (5-3-16)
Функция (5.3.16) называется производственной функцией Кобба -Ду-
гласа. При этом часто входящие в (5.3.15) и (5.3.16) переменные yl9 y2i

304 Глава 5. Методы построения математических моделей элементов ОК
[i = l(l )п2 ] выражаются в относительных единицах, т.е. yx,y2i e [0,l],
где уЛ = -^— ; V, = -^- .
itm<Uf max
«Fi Ун
5.3.9) Часто предполагаются возможными операции [59], в которых це-
левой эффект ух растёт пропорционально расходуемым ресурсам (обоб-
щённым одноразмерным) и времени. В этом случае РЭФ примет вид
Л= «и Уп Уп- (5.3.17)
Однако следует иметь в виду, что РЭФ вида (5.3.11), согласно которой
Уг = уХУъ)^агъУгУъ-> более адекватна реальному ЦНПФС и её варианты
(5.3.15) - (5.3.17) должны рассматриваться лишь как исключения, требую-
щие специальных обоснований. А
Представляется очевидным, что входящие в выражения (5.3.15) и
(5.3.16) переменные являются функциями операционного времени уЗУ т.е.
Я=яОО;Л/=Л/(Л/Ь U^OO^] [см. (5.3Л l)] и, следовательно,
ух =»B(F«,F«)=aiaft^(^) , (5.3.18)
1=1
где ап =ап[А,куВ^л ); Д = fi.[A,kyBL). При комплексном исследова-
нии эффективности ЦНПФС это обстоятельство должно учитываться.
Производственные функции вида (5.3.15) - (5.3.18) называются муль-
типликативными. Наряду с ними находят применение и аддитивные
функции вида [59]
У, -afeW! )=£<*, Jtf (уЛ (5-3.19)
где a2i = a2i[A{k)9B[v) j, Д = Д [A{k),B[f)).
В частном случае, когда Д = 1, [# = 1 (l)«2 ], аддитивная производст-
венная функция становится линейной вида
^iX^U,). (5.3.19-)
i=l
Находят применение и производственные функции с постоянными про-
порциями, определяемые следующим соотношением [59]:
у, =Xu(Y$,Y$)=auMin{ уЛуЛуМ^У^М}' (5-3-20)
где у^Уз)- 1/ \ ; Уп(Уз)~ о / \ ~ нормированные показатели каче-
лЬз) УгЛУз)
ства результатов операции;

5.3. Операционный функционал
305
У г,(Уз) ~ удельные затраты ресурса i-го вида, необходимые для полу-
чения целевого эффекта ух (у3)=аХ2 ух (у3).
5.3.10) Как видно из (5.3.20), при фиксированном расходе некоторого
ресурса увеличение расходов других ресурсов к увеличению целевого эф-
фекта не приводит. А
Обобщением приведённых примеров производственных функций, ис-
пользуемых в экономическом анализе, может служить так называемая
функция с постоянной эластичностью замещения (см. п. 4.1.3) следующего
вида:
Ух=аА±аг1у;?{у3)\ fi, (5.3.21)
где у - показатель однородности, численно равный показателю Э1 эла-
стичности показателя ух или эластичности производства [59].
Подробно свойства приведённых производственных функций (5.3.15) -
(5.3.21) рассмотрены в монографии [59], к которой мы отсылаем заинтере-
сованного читателя. Здесь же отметим, что, несмотря на широкое приме-
нение в экономической практике рассмотренных производственных функ-
ций (5.3.15) - (5.3.21), возможность их использования в качестве операци-
онных функций представляется достаточно ограниченной из-за недоста-
точной адекватности реальным ЦНПФС. В этом отношении наиболее аде-
кватной структурой операционной функции представляется соотношение,
аналогичное выражению (5.3.11), т.е.
(ч Угх (я2) У*пг / \
,., С'СЛ') )= I - К>(ГЫ;Х;,> К,, (5.3.22)
о о
которое лишь в частных случаях может аппроксимироваться выражениями
типов (5.3.15) - (5.3.21). Проиллюстрируем сказанное на примере.
Пример 5.3.2. Пусть операционная функция имеет вид (5.3.11), т.е.
Уз
Ух = %2(У2х^Уз ) = <*! Угх (Уз) = <*1 \hx {^Уп'Угъ )** >
о
где угх- сырьевой ресурс;
у22- энергетический ресурс;
угъ - технологический ресурс (характеризующий уровень технологии);
У2i (') ~ скорость освоения сырьевых ресурсов;
yn(t) - скорость расходования энергии.
Рассмотрим простейший случай:
У и М = Угх Ьгг ('/Лэ )] = ЪУп (*} Угз У>

306 Глава 5. Методы построения математических моделей элементов ОК
Тогда У21{у3) = а2а3у23у3 и, следовательно,
у^аха2а3у23у3,
где а, = а, ЦЛ), #('г) ), [i = 1, 2, 3 ] - "агрегаты". А
5.3.11) Легко понять, что в общем случае связь между расходуемыми в
ходе операции ресурсами различных видов носит более сложный характер,
т.е.
У г = Уп ±Уп ^»^Угпг > (5.3.23)
где J_ - символ некоторого соотношения ("закона композиции"). А
5.3.12) При наличии функций связи ("балансных соотношений") (см.
п. 5.3.1) операционная функция может быть представлена несколькими
способами, вытекающими из следующих соотношений (представленных
для наглядности в симплексной канонической форме):
^,=»U^3) = »i2U^3iU)) = 9li3(*23UU). (5.3.24)
где S32(y2)= y3{y2);S23(y3)= y2(y3). А
5.3.13) Следует особо подчеркнуть, что при построении математических
моделей операционных функционалов должны учитываться все особенно-
сти операции и прежде всего динамика превращения ресурсов в целевой
эффект. Так, например, если какие-то ресурсы поступают в ЦУТС в ходе
операции (поставки смежников, дозаправка топливом, подвоз снарядов,
поступление информации об операционной ситуации и т.п.), то для адек-
ватности модели должно учитываться соотношение между темпами (ско-
ростями) введения и освоения ресурсов различных видов, как по величине,
так и по характеру их временной зависимости. А
Проиллюстрируем сказанное на примере.
Пример 5.3.3. Пусть в условиях примера 5.3.1 темп освоения ресурса
у2Х есть у2Х (t) = * и пусть количество введённых за время 0 ре-
сурсов - у2Х (б) определяется соотношением
tf.(*) = ]#.(')*. (5-3.25)
о
где у2Х (t) = 21 - темп введения (ввода) ресурса у2Х в операцию. При
dt
этом, естественно, Уг\^)-Уг\(^\ув[^)* 0 = & [A(k)>B(r) )•
Если y2X(t)*const и у2Х^)фconst, т.е. ylx{t)*1b и y2X{t)^0 то> как

5.3. Операционный функционал
307
легко заметить, выражения (5.3.11) и (5.3.25) в какой-то степени учитыва-
ют инерционность процесса превращения ресурсов в целевой эффект, а
также изменение технологии (её прогресс или регресс) проведения опера-
ции.
Пусть т - операционное время, отсчитываемое от момента начала опе-
рации, а у\х {©) и у21 (т) - соответственно количества ресурсов, введённых
за время 0 > т и освоенных за время т. Тогда очевидно, что
УпКУ*)-*] В(„\ / ч в(Гк\ (5.3.26)
Понятно, что соотношения (5.3.26) справедливы лишь в предположении
о полном освоении введённых ресурсов, так как из-за возможных потерь
(объём которых случаен), как правило, угх{р)<у1х{$)-
Для конкретности положим
y2l(t)=a2e-»'A(t); 1
yBlt{t) = rA(t)=const,]
а количество ресурсов, введённых к началу операции (имеющихся в
ЦУТС), равно г0. Примерные графики функций уи (т) и y't (т) приведены
на рис. 5.3.1, из которого видно, что
(5.3.27)
yM = ^(l-e-^r)Hro + rr)n(r;0,Tj+^{l-e^)-d
А{т-тг),
(5.3.28)
Рис. 5.3.1

308 Глава 5. Методы построения математических моделей элементов ОК
где d = J3~l\а2 - firQ -r(l-Inr + lna2)]9 a максимально возможное количе-
ство осваиваемых ресурсов равно а2 //?.
Понятно, что время уъ = г освоения ресурсов (операционное время) за-
висит как от имеющегося их количества у21, так и от скорости y2l (t) их
освоения, и в условиях рассматриваемого примера определяется следую-
щим соотношением:
Уз=-р-Чп
\ /3(гв + г0)
а,
Я (<9 ; 0, г,) + 6>/7(б> ,т,, г2)-
-р~Чп
t /3(r0+ro+d)'
а,
А{0-тг).
(5.3.29)
Интегрирование (5.3.11) с учётом (5.3.27) и (5.3.29) даёт
}л(у3-т2)\9
IP .
(5.3.30)
или
yi=a&ro+rO)n(0;O,T2)+{ro-d + r0)A(0-T2)]. (5.3.31)
Выражение (5.3.11) совместно с (5.3.25), (5.3.27) - (5.3.30) и определяет
операционный функционал рассматриваемого ЦНПФС. А
5.3.14) Фигурирующие в приведённых выражениях параметры аХ9 сс29
J3, rQ9 г, d, т19 т29 & зависят от компонент векторов А,куВ,^ (или совпа-
дают с ними) и представляют собой "агрегаты" ("комплексы"), учитываю-
щие как качество ЦУТС (через А!кл)9 реализующей операцию, и организа-
цию ЦНПФС (через Л**), так и условия функционирования ЦУТС (через
2J,' ). Понятно, что в общем случае любой из этих параметров (а возможно,
и все) может оказаться случайным, так что компоненты ух, у2, уъ показа-
теля К3) качества результатов ЦНПФС будут функциями случайных аргу-
ментов, т.е. случайными величинами, а поскольку многие из их аргументов
являются общими (совпадают), то эти случайные величины существенно
взаимно зависимы. Задача определения закона их совместного распределе-
ния Ф. (f,3J и составляет основу построения математической модели
операционной системы (ОС). А

5.3. Операционный функционал
309
5.3.4. ОСНОВНЫЕ СВОЙСТВА МОДЕЛЕЙ ОПЕРАЦИОННЫХ
ФУНКЦИОНАЛОВ И ОБЩАЯ СХЕМА ИХ ПОСТРОЕНИЯ
Как уже было отмечено, операционный функционал представляет собой
"сердцевину" математической модели ЦНПФС, от качества которой зави-
сит адекватность модели, а следовательно, и объективность, точность и
достоверность окончательных выводов о качестве ЦУТС и реализуемого
ею ЦНПФС.
При построении модели операционного функционала должны быть ре-
шены следующие задачи:
- анализ структуры операционного комплекса и определение функ-
циональных и эксплуатационно-технических характеристик ЦУТС и
установление и описание всех связей между ними;
- анализ существенных свойств (атрибутов) результатов ЦНПФС, т.е.
целевых эффектов и расходуемых операционных ресурсов, обуслов-
ливающих эффективность операции;
- построение математической модели операционного функционала,
т.е. определение соотношений для операционной функции и функ-
ций связи.
Рассматриваемые в 3-м разделе монографии методики построения опе-
рационных функционалов конкретных ЦНПФС, как правило (в основном),
реализуют эту схему.
Выше были рассмотрены примеры производственных функций, исполь-
зуемых в качестве математических моделей процессов преобразования ре-
сурсов в целевой эффект. Адекватность подобных моделей должна обос-
новываться в каждом конкретном случае самостоятельно. Однако сущест-
вует ряд общих требований, которым должны удовлетворять функции,
описывающие такие модели. В основу этих требований положен практиче-
ский опыт и здравый смысл; формулируются они в форме постулатов,
выражающих основные принципы, которыми следует руководствоваться
при "конструировании" (построении) операционных функций и функций
связи [59].
ПОСТУЛАТ 5,3.1. "Операционная функция" есть функция неубываю-
щая (рис. 5.3.2), т.е.
или
(у>Уг) => *{у'г>У>)Ъ*{Уг>Уг)> (5-3-321)
{/3>У3) => ХЫ,У;>Х{У„У*), (5-3.32")
Ы>/*№>/,)=> *G£rf)**GkjO. (5.3.32»)
А

310 Глава 5. Методы построения математических моделей элементов ОК
5.3.15) Сформулированный постулат представляется очевидным, так
#ак основан на естественном предположении, что при увеличении затрат
операционных ресурсов целевой эффект операции не может уменьшаться.
Однако это справедливо не всегда. Так, если при увеличении расхода ре-
сурсов технология ЦНПФС ухудшается, то целевой результат (эффект)
операции также может ухудшаться (уменьшаться).
Рис. 5.3.2
Другим примером ЦНПФС, операционная функция которого не удовле-
творяет соотношениям (5.3.32") или (5.3.32"'), может служить операция по
добыванию данных, целевой эффект которой - собранная информация, в
силу старения последней с течением времени падает, и если скорость ста-
рения информации превосходит скорость её добывания, то соотношения
(5.3.32") и (5.3.32 "') выполняться не будут.
Хотя при построении операционных функций этот постулат, как прави-
ло, принимается, тем не менее в особых конкретных случаях (информаци-
онные и другие подобные ЦНПФС) он должен отвергаться и должны стро-
иться более адекватные реальному ЦНПФС операционные функционалы
(и входящие в них операционные функции). А
ПОСТУЛАТ 5.3.2. Операционная РЭ-функция - вогнутая, а ЭР-
функция - выпуклая (рис. 5.3.2), т.е. при 0 < а < 1
^(«^2,+(1-^22^э)^«^(^21/Л)+(1"^)^и2^з)- (5.3.33)
5.3.16) Соотношение (5.3.33) означает, что при увеличении расхода од-
ного ресурса и постоянных расходах других ресурсов производительность
(ресурсоотдача) этого ресурса падает. Кроме того, из неравенства (5.3.33)
следует, что операционная функция не имеет перегибов и описываемая ею
поверхность расположена по одну сторону от гиперплоскости

5.3. Операционный функционал
311
Ух =а*{У21;Уз)+(1-<х)К{у22;у3). (5.3.34)
А
5.3.17) Заметим, что лежащее в основе работы [116] концепции проти-
воречат постулату 5.3.2 и представляются необоснованными. А
Определение 5.3.4. При расширении (увеличении) расхода ресурсов их
отдача:
- постоянна, если
^З^Ь*9*®^!)' <5-3-35>
-возрастает, если
*из>-*$)> a^rM'rS))' <5-з-зб>
-убывает, если
^(aY^;Y^)<a^;Y^). (5.3.37)
А
ПОСТУЛАТ 5.3.3. "Операционная функция" характеризуется посто-
янной отдачей ресурсов при расширении "производства" (масштабов опе-
рации) [59], т.е.
^(аУ^;У^)=а^;^). (5.3.38)
А
5.3.18) Соотношение (5.3.38) означает, что при расширении масштаба
производства (операции), т.е. при увеличении затрат ресурсов, целевой
эффект возрастает в той же пропорции. Понятно, что это условие выполня-
ется не всегда. Причём чем больше операционная функция отличается от
линейной, тем сомнительнее правомерность постулата (5.3.38). Так, на-
пример, если операция проводится с целью нанесения ущерба противнику,
то навряд ли можно предположить, что при удвоении расхода снарядов
наносимый цели ущерб также удвоится. Поэтому, хотя постулат 5.3.3 и
применяется в рамках теории производственных функций [59, 179], в зада-
чах теории эффективности целенаправленных процессов характер "отдачи
ресурсов" должен исследоваться специально. А
Определение 5.3.5. Скалярная функция ^(^j/^j) называется одно-
родной функцией степени у, если она удовлетворяет соотношению
*Ц^ . (5.3.39)
А
5.3.19) При у = 1 функция ^(^\/^1з)) называется линейно однородной
и характеризуется постоянной отдачей ресурсов при расширении масшта-
бов производства (операции) [см. (5.3.35)]; при у>\ - отдача ресурсов

312 Глава 5. Методы построения математических моделей элементов ОК
возрастающая [см. (5.3.36)]; при у <1 - отдача ресурсов убывающая [см.
(5.3.37)]. ▲
5.3.20) В монографии [59] проводится достаточно подробный анализ
основных производственных функций, существенных при исследовании
экономических аспектов производства, для чего вводится целый ряд спе-
циальных терминов и специфических понятий, таких как предельная про-
изводительность ресурса, норма замещения ресурса, эластичность выпус-
ка, эластичность производства, эластичность замещения, отдача от расши-
рения масштаба производства и т. п. Некоторые из перечисленных поня-
тий, имеющие отношение к проблеме исследования эффективности
ЦНПФС, обсуждались, однако более полное их использование выходит за
рамки основного предмета монографии. А
ПОСТУЛАТ 5.3.4. Операционная РЭ-функция удовлетворяет соотно-
шению
1$*9ф$;1$), (5.3.40)
а ЭР-функция - соотношениям
гй^»^И;ГЙ); (5.3.41)
Yftz^frftsYft). (5.3.42)
А
5.3.21) Неравенство (5.3.40) означает, что при определённом расходе
ресурсов получаемый целевой эффект может быть либо соответствующим
проектной технологии и определяемым в (5.3.40) равенством, либо мень-
ше.
Аналогично неравенства (5.3.41) и (5.3.42) означают, что для получения
определённого целевого эффекта требуются либо соответствующие про-
ектной технологии и определяемые в (5.3.41) и (5.3.42) равенствами коли-
чества ресурсов, либо больше.
В принципе соотношения (5.3.40) - (5.3.42) следуют из постулата 5.3.2,
однако ввиду их принципиальной важности они постулированы в более
наглядной (содержательной) форме.
Иллюстрацией соотношений (5.3.40) и (5.3.41) могут служить заштри-
хованные на рис. 5.3.2 и 5.3.3 области, которые называются областями
операционных (производственных) возможностей (ООВ). А
5.3.22) Несмотря на полную практическую очевидность постулата 5.3.4,
определяемые им свойства ОФ зачастую не учитываются, что приводит к
недопустимым искажениям реальных зависимостей получаемых целевых
эффектов от расходуемых ресурсов. А

5.3. Операционный функционал
313
5.3.23) Легко понять, что границы ООВ представляют собой компро-
миссные множества Парето (см. п. 4.1.4), элементами которых являются
"эффективные" точки пространства \УЛ ) возможных виртуальных резуль-
Рис. 5.3.3
татов L операции, реализуемые при полном (без потерь) использовании
ресурсов. В этом случае, естественно, во всех соотношениях (5.3.40) -
(5.3.42) будут иметь место (будут выполняться) равенства. При этом заме-
тим, что, когда целевой эффект - скаляр, т.е. yF\ = Y$=yl9 то каждой
точке у(„\^(„\) пространства затрат ресурсов соответствует наибольшее
значение целевого эффекта ух. А
5.4. МЕТОДЫ ПОСТРОЕНИЯ МАТЕМАТИЧЕСКИХ
МОДЕЛЕЙ ПОКАЗАТЕЛЕЙ КАЧЕСТВА РЕЗУЛЬТАТОВ
ЦЕЛЕНАПРАВЛЕННОГО ПРОЦЕССА
5.4.1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ
Основные свойства законов распределения систем случайных величин -
случайных векторов и их компонент рассматриваются в любом учебном
пособии по теории вероятностей [28, 29, 142]. Известно, что проще всего
они определяются в случае, когда компоненты уп [i = l(l)/i] случайного
вектора К v взаимно независимы. В этом случае плотность и функция рас-
пределения случайного вектора Y.x определяются через безусловные (ап-

314 Глава 5. Методы построения математических моделей элементов ОК
риорные, маргинальные) законы распределения его компонент уг, j>2,...,
уп следующими выражениями:
^J^-))=faU)-^W^>J. (5.42)
'<•>
Если между случайными величинами у19 у29...9 у„ существует стохас-
тическая зависимость, то она описывается с помощью условных (апосте-
риорных) законов распределения этих величин и соотношения (5.4.1),
(5.4.2) соответственно принимают вид [28]:
хР9Аы)Ьъ}У1>Уг)---Г^^^ (5-4-4)
где символы у2 / j>, и у2/ ух имеют различный смысл (см. (3.3.14)), а
или
уЫ у(з)
Г/') -co -oo -co -~
5.4.1) Формулы (5.4.3) и (5.4.4) носят универсальный характер и "рабо-
тают" при любом виде и степени взаимной зависимости компонент вектора
У(„\' Формулы же (5.4.1) и (5.4.2) соответственно представляют собой их
частные случаи и имеют узкую область применения. В частности, они не-
пригодны для определения закона распределения показателя Y.k качества
результатов операции, поскольку, как отмечалось (см. (2.2.1), (2.4.14),
{2.7.8}), его компоненты существенно взаимно зависимы. А
Как было показано (см. п.3.2.1 и рис. 5.2.2), основу математической мо-
дели результатов операции составляет интегральный закон распределения
(функция распределения) показателя L (или Y, * ) их качества, опреде-
ляемый в комплексной канонической форме выражением [см. (5.4.6)]

5.4. Методы построения математических моделей ПК результатов ЦНП 315
или в симплексной канонической форме выражением
ФфиУ^Уз)=Р[(у^УгМУг^Уг)П{у3^У3)1 (5-4.8)
С учётом (5.4.4), (5.4.6) функции распределения (5.4.7), (5.4.8) можно
представить в виде (см. (3.3.14))
*'«ТС'Г(3,Уы)= Ry&TOK<4Ur<-) ¥{£)>'r№))x
ИЛИ
Функция распределения Ф^ (К \ ) может определяться либо аналитиче-
ски, либо экспериментально.
В первом случае, как отмечалось, необходимо знать все "операнды" вы-
ражений (5.4.9) или (5.4.10), т.е. безусловные и условные1 законы распре-
деления компонент у., [ i = l(l)n ] случайного вектора L.
Во втором случае необходимо наблюдать реализации УЛ, [/ = 1 (l)/v]
вектора К* в длинной серии однородных операций (экспериментов), про-
водимых в одинаковых условиях - В'^ = const, по результатам которых
может быть построена статистическая функция распределения Ф*> \У/„\)
или кумулята Ф^ (К\) распределения случайного вектора Y.x [170,173].
Следует заметить, что поскольку исследование эффективности ЦНПФС,
как правило, проводится до его реализации2, то указанные выше операции
могут быть лишь модельными и имитируются на ЭВМ (см. п. 3.4.2). При
этом для обеспечения достаточной точности и надёжности оценочной
функции распределения Ф^ \Y, * J машинный эксперимент может оказать-
ся весьма трудоёмким, длительным и дорогостоящим.
5.4.2) Как отмечалось в п. 3.4.2, имитационное моделирование ЦНПФС
может проводиться и без использования явного аналитического выражения
функции распределения Ф^(у). В этом одно из достоинств данного ме-
тода. А
1 Относительно совокупностей (систем) предшествующих компонент.
2 В этом специфика задач исследования операций и теории эффективности.

316 Глава 5. Методы построения математических моделей элементов ОК
Аналитическое построение функции распределения Ф~ (к*) показате-
ля L в общем случае также достаточно сложно и трудоёмко. Кроме того,
оно требует от исследователя высокой математической (теоретико-
вероятностной) подготовки. Однако оказывается, что наличие функцио-
нальных связей между компонентами вектора У,, упрощает задачу оты-
скания закона его распределения, так как в этом случае достаточно знать
безусловный (априорный, маргинальный) закон распределения лишь части
его компонент, называемых доминирующими (ДК), или базисными (БК),
или генеральными (ГК).
Пусть генеральная компонента уу - скалярная и все компоненты векто-
ра Y,k связаны с ней функционально, т.е.
д=^(уг).[/,=1(1)',]; (5А11>
д=илЫ' La=i(iKL (5.4.1 г)
где г?У| (уу) - монотонно возрастающие функции;
и]г\уу) - монотонно убывающие функции, для которых соответствен-
но существуют обратные функции:
JV,=#U).fo=i(i)*i];
jv=<W,L/w(ik].
Тогда справедливо следующее утверждение.
Теорема 5.4.1. Если известна функция распределения F^ (у) генераль-
ной компоненты уу , то функция распределения Ф^ \У,,) случайного век-
тора К v определяется соотношением:
^l//(^,...,^;K,...,^)J-^lvU,...,^;/,...,^)J • (5.4.12)
Здесь I^efy;}; {у^ПЬ^>уЛ
Км - возможные значения вектора У, к ;
\УЛ ] - носитель распределения случайного вектора L;
у[1,у[г - границы множества (отрезка) [j'/s.vf2] возможных значений
у? компоненты у. , определяемые равенствами

5.4. Методы построения математических моделей ПК результатов ЦНП 317
лг'=«%(??) или j>f'=",Gvr');l
У?'=#Ш или у?>=и&),\ (5А13)
$, [*' = 1 (l)fi'] - компоненты вектора К., ограниченные "снизу";
JV» [*" = 1 (l)""] - компоненты вектора К ,, ограниченные "сверху";
м(у'и'-Угг ;у1*~,у'г)=**»{(«?! to,)),. >(#л (у})},:\;
j^ - аргумент функции Ф^ (F/,v,F/*rJ, соответствующий компо-
ненте y'j,, связанной с ГК уу возрастающей функцией г?У) (у);
Ууг - аргумент функции Ф^ (УЛ,К^]5 соответствующий компо-
ненте yh, связанной с ГК уу убывающей функцией Uj (у);
у". - аргумент функции Ф^ (К/м,КЛЛ соответствующий компо-
ненте у"*, связанной с ГК уу возрастающей функцией г?^ (у);
у"* - аргумент функции Ф^ (K^,K^J, соответствующий компо-
ненте j>J*, связанной с ГК уу убывающей функцией Uj (у);
Ш1,
- выборки (последовательности) значений обратных
функций tfr1 и «Т1 объёмов /,', /*, 1'2,1" соответст-
венно [169], где /1, + /2/=я,5 /*+/* = л", n' + n" = n.
5.4.3) Поскольку ду{уу)= иу(уу)=уу9 то из уу е {^{следует уе {у,'},,,
т.е. уу является аргументом функции у(У/л ), [n = l[ + /*], а из jr е { jyj
следует у € {/^, т.е. является аргументом функции ju (кЛх j, \n№ -1\л- /*].
▲
Доказательство. Проведём его в предположении, что все функции
связи yj = 0j{yr)9 [/ = 1(1)Л] монотонно возрастающие.
а) Вначале с учётом (5.4.3) положим уу е {у'у\, т.е. в выражении (5.4.12)
ГК уу ограничена снизу. Тогда плотность распределения <р^ (К J слу-
чайного вектора К* согласно (5.4.3) будет иметь следующее выражение:

318 Глава 5. Методы построения математических моделей элементов ОК
9t{e) [у[*™>У7*-~>У*9У^-М= <Руу {yr)v>y[/yr U># JV)-
где £(у- г?) - дельта функция Дирака (см. прил. 1 и [169]).
Интегрирование (5.4.14) даёт
(5.4.14)
у, у* —
= k(/J
'ее * Уг
П J *t//-«VW)*/fl f S(y"r-t»r(yy))dyr
l=i У/
.1*7
У-1-e.
♦r =
=kW
=k>;
л*>'0*)
y"*y
у"=1
/-I
-^
y'=l
tf,-'GV)
= F,r |><(rf,~,.£)]- F,r [у{у\,.,уг,..,у'Л, (5.4.15)
где л ^,(j£)=mi^«£,(j£)^»«#(jC')b
/-1
б) Пусть теперь ууе {у"~\9 т.е. в выражении (5.4.12) ГК уу ограничена
сверху. Тогда выражение для плотности распределения q>^ (к ч ) случай-
ного вектора L примет вид
/-1
У*'*/
а его интегрирование даёт

5.4. Методы построения математических моделей ПК результатов ЦНП 319
•>')- '"У)*
%\ЧгчУи \- \чНгЧ-))аЧ')ач-)=
Ух У»' —
dy" =
n4#M)-y'r)iiM-»M))
/=i
#
ft^-^V/))ft4^W-^)
/=>
JrVy
/«=1
"".o-.r^ LA1 J L/-1
= F-r [// (jWr,,.^)J~ РУг [v Wr..,^)] • (5.4.17)
Из сравнения выражений (5.4.15) и (5.4.17) с (5.4.12) видно, что они
совпадают с точностью до обозначений входящих в них операндов. Таким
образом, теорема доказана. А
5.4.4) Аналогично доказывается теорема и в случае, когда все функции
связи монотонно убывающие, а также когда среди них имеются как воз-
растающие, так и убывающие функции. Единственным необходимым ус-
ловием является их монотонность и существование обратных функций. В
реальных условиях эти требования практически всегда выполняются. ▲
5.4.5) Следует заметить, что в соответствии с постулатами теории опе-
рационных функционалов первый из рассмотренных случаев (возрастаю-
щие функции связи) на практике встречается чаще, так как для получения
большего целевого эффекта (ограниченные "снизу" компоненты у.,,
[// = l(l)n/] вектора L требуются и большие расходы ресурсов (огра-
ниченные "сверху" компоненты j)J., [/" = l(l)#i"] вектора Y,y Однако, по-
скольку, как отмечалось в (2.3.2), иногда возможна "перекачка" - взаим-
ный обмен ресурсов, то связывающие такие ресурсы функции могут ока-
заться убывающими. Если при этом функции связи остаются монотонны-
ми, то доказанная теорема может применяться непосредственно. Если же
функции связи оказываются немонотонными, то функцию распределения
Ф^ (kJ необходимо (легче) определять по общей схеме (5.4.3) => (5.4.6).
'<•>
Этот подход реализуется в п. 6.1.

320 Глава 5. Методы построения математических моделей элементов ОК
5.4.6) Если функции, определяющие ОФЛ, в явном виде не известны, то
в ряде случаев могут использоваться аппроксимирующие их уравнения
регрессии с последующей рандомизацией [183] полученных соотношений,
если дисперсии компонент у\ вектора У, к относительно линий (поверхно-
сти) регрессии существенны. Если же их рассеянием можно пренебречь, то
регрессионные зависимости могут быть использованы в качестве функций
связи и г?У1 (у) или «у (у) непосредственно. ▲
5.4.7) В рамках доказанной теоремы 5.4.1 генеральная компонента уу
была скалярной. Однако это предположение было принято лишь для на-
глядности доказательства теоремы и "прозрачности" её физического смыс-
ла. Понятно, что в общем случае ГК - вектор УУ\, компоненты которого
либо взаимно независимые, либо связанные стохастически случайные ве-
личины, являющиеся аргументами функций связи, определяющих осталь-
ные компоненты вектора У, , т.е.
5.4.8) В заключение заметим, что при наиболее общем (абстрактном)
взгляде на проблему построения математической модели показателя К,
качества результатов операции операционный функционал можно тракто-
вать как совокупность данных о связях компонент вектора У, к (в том чис-
ле и не формализованных в явном виде с помощью функциональных зави-
симостей), носящих стохастический характер и учитываемых, как правило,
эвристически при определении условных законов распределения компо-
нент случайного вектора У к в выражениях (5.4.3), (5.4.4) и (5.4.9) (см.
п. 6.1). А
5.4.2. МЕТОДИКА ПОСТРОЕНИЯ МАТЕМАТИЧЕСКОЙ
МОДЕЛИ ПОКАЗАТЕЛЯ ВИРТУАЛЬНОГО КАЧЕСТВА
РЕЗУЛЬТАТОВ ОПЕРАЦИИ
Как следует из схемы рис. 5.2.2, для построения математической моде-
ли - Ф^ (У/„\) показателя К* виртуального качества результатов опера-
ции должны быть реализованы её блоки 1-6.
Как уже отмечалось (см. п. 5.4.1), в зависимости от имеющейся исход-
ной информации о свойствах, параметрах и ЭТХ ЦУТС [А1кл) и ЦНПФС

5.4. Методы построения математических моделей ПК результатов ЦНП 321
[Л7к^), а также об условиях [BL,) функционирования ЦУТС могут быть
применены аналитические или статистические методы построения мате-
матической модели показателя Y, v качества результатов операции. При
этом последние могут опираться либо на реальный - физический, либо на
имитационный - машинный, либо на смешанный эксперимент (включая
физическое имитационное моделирование). Принципы различных типов
моделирования достаточно освещены в литературе [74, 178] и предпола-
гаются известными читателю. Поэтому здесь рассматривается лишь мето-
дика аналитического решения задачи, основанная на применении теоремы
5.4.1, которая для большей наглядности демонстрируется на конкретном
примере.
Пример 5.4.1. Пусть показатель Y,x виртуального качества результатов
операции задан в симплексной канонической форме, т.е.
(*) = (х) = (з> ~(У\>Уг>Уъ)> а его компоненты связаны монотонными за-
висимостями
*=*«(?,); (5А18)
y3=S32(y2), (5.4.19)
где У1'12(у)> 0; S'32(y)^0. Закон распределения F^ (у) случайной величины
у2 известен, т.е. у2 = уу является генеральной (доминирующей) компонен-
той вектора K3v.
Требуется построить вероятностную модель вектора K3v, т.е. найти
функцию Ф^ (K3v) его распределения, определяемую соотношением
*Г„Ь»Уг>У>) = Фх **)П& ^Уг)Шг *Л)]. (5-4.20)
Решение. Поскольку по условию задачи S'32 (у )f 0, то следует разли-
чать два случая: 532 {у) > 0 и 532 (у) < 0.
А. Пусть S32 (у) > 0. Тогда
и поскольку 9?{2 (у) > 0, т.е.
*вО0=*,(л).
то выполняются условия теоремы 5.4.1, б) и, следовательно,
=F-i[i»i«U,^,U)B-^Ik,U)] •
Конкретизируем пример, положив
11 Зак. 3303

322 Глава 5. Методы построения математических моделей элементов ОК
о —а
где Рх > О, 03 > О. С учётом (5.4.22) выражение (5.4.21) примет вид
(5.4.21)
(5.4.22)
Ф,
+ А(тт{уг,Р;х{уг -a3)}-b)-
КЧу\-<*%)-* ЛУ%-Щ .. Л
П
А
-;а,А
Ь-а
-4А (К-«,)-*), (5А23)
(л»Л»Л>е h + М ^ + Д*]х[а,А]х[а3 + М а3 + А*Ыг<зВ>}
Б. Пусть теперь S31 (уг) < 0. Тогда
и поскольку !Ки (уг) > 0, т.е.
то условия теоремы 5.4.1 выполняются [хотя и вне рассмотренных случаев
а) и б)] и согласно (5.4.12)
&у{1) {yi,y2>yihFh\ju{y2)]-Fh Ии,Л)] =
= Fh(yl)-Fh[max№{ylW(y3)}]- (5.424)
Конкретизируем пример, положив в (5.4.22) Д > 0, a yS3 < 0. Тогда
Ф^{ух,Уг,У>) = ^П{уг;а,Ъ)+А(уг-Ь)-
о — а
'<*>
IftOXl
*-« I I A A J J
-(«^{Д-'и-ог,^^-^)}-*). (5А25)
(у1>Уг>у>)* к +А«» «i +А*М«» *]xk + Аз*» «з + Аз«]={^f)}.
где |^f\] - множество возможных значений - носитель распределения
случайного вектора Y,3) [см. также (5.4.23)].

5.4. Методы построения математических моделей ПК результатов ЦНП 323
Исчерпывающе подробные представления выражений (5.4.23) и (5.4.25)
весьма громоздки и здесь не приводятся (см. задачи 8.51 - 8.54 в [156]). А
5.4.9) Ряд других методик построения математической модели показа-
теля Y, v качества результатов операции рассматривается в следующем
разделе. А
5.4.3. МЕТОДИКА ПОСТРОЕНИЯ МАТЕМАТИЧЕСКОЙ
МОДЕЛИ ПОКАЗАТЕЛЯ ТРЕБУЕМОГО КАЧЕСТВА
РЕЗУЛЬТАТОВ ОПЕРАЦИИ
В п. 5.4.2 была рассмотрена методика построения модели показателя
Л.
L виртуального качества результатов операции, исчерпывающе характе-
ризующего в рамках задачи исследования эффективности ЦНПФС опера-
ционную систему, модель которой (МОС) образуют блоки 1-7 (см.
рис. 5.2.1). Как видно из рис. 5.2.1, для построения модели операционного
комплекса (МОК) МОС должна быть дополнена моделью операционной
ситуации (МОСТ), замыкающей МОК и делающей её пригодной для ре-
шения задач исследования эффективности операции.
Как известно (см. пп. 2.2.3, 2.2.4; (2.2.7)), для замыкания схемы оцени-
вания результатов операции к ним должны быть предъявлены обоснован-
ные требования, описываемые вектором Z,k , значения которого зависят от
условий применения ЦУТС, характеризуемых вектором JKL.
Поскольку вектор Z,, случаен (см. пп. 2.3.3, 3.2.1), то исчерпывающей
его моделью является закон распределения F% [Z/„\)> Для построения ко-
торого должны быть реализованы блоки 7-12 (см. рис. 5.2.2).
В общем случае определение закона распределения F$ [Z/„\) показате-
ля Z/ч требуемого качества результатов операции является прерогативой
суперсистемы. Тем не менее представляется необходимым кратко обсу-
дить основные методы решения этой задачи. В основе построения закона
распределения F$ [Z/„\) лежат методы экспертного оценивания и
статистических испытаний. Раскроем их сущность.
Прежде всего напомним (см. (2.7.7», что в отличие от компонент векто-
ра К, компоненты вектора Z, *, как правило, взаимно независимы. По-
этому

324 Глава 5. Методы построения математических моделей элементов ОК
Аналогичную структуру будет иметь и эмпирическая функция распре-
деления случайного вектора Z,,, т.е.
/7pw экспертном оценивании
F£i(z) = F^(z) = ZytM\
0<g.<l; ±g,=\
, (5.4.28)
7=1
где F£* (z) - функция распределения i-й компоненты £. вектора Z,v, за-
даваемая (определяемая) у-м экспертом;
gj - весовые коэффициенты, выражающие относительную сте-
пень объективности (компетентности, опытности, автори-
тетности) мнения у-го эксперта;
тэ - число опрошенных экспертов.
Если даваемые экспертами оценки компонент z, вектора Z.k детерми-
нированы (не случайны), то их распределения будут (формально) вырож-
денными и, следовательно,
^(«)=^э(*)=2^(*-*#)» (5А29>
где Zy - предельно допустимое значение i-й компоненты вектора К v, на-
значаемое у-м экспертом.
Возможны случаи, когда одни эксперты задают законы распределения
F?(z), а другие - конкретные значения г? компонент zf вектора Z.y
Тогда, как нетрудно понять, будет иметь место "смесь" выражений (5.4.28)
и (5.4.29), т.е.
JW=F»(*)=2>yF»(«)+ £ 8jA(z-z]), (5.4.30)
у=1 /=тЭ1 +1
где тЭ1 + тЭ2 = тэ; смысл остальных элементов соотношения (5.4.30)
ясен из ранее сказанного.
При оценивании методом статистических испытаний
F-(z)=<(z) = — 2^(z-z;), (5.4.31)
где г» - предельное значение результата у., потребовавшееся в у -м
предшествовавшем опыте (эксперименте);
т0 - число проведённых опытов (испытаний - операций).

5.4. Методы построения математических моделей ПК результатов ЦНП 325
Если объём т0 выборки велик, то вместо статистической функции рас-
пределения F?(z) строится кумулята распределения [170,173]
/=i
р;л (г_^+1)+р;4^-г n(z;zUzL)
, (5.4.32)
где zf ,zf+l - границы /-го разряда статистического ряда распределения
случайной величины £;;
Pi - частота попадания варианта ц в 1-й разряд;
г - число разрядов статистического ряда.
Экспериментальное определение законов распределения Ft (z) должно
опираться на опыт проведения операций, аналогичных исследуемой (по
стратегии и организации), и осуществляться методами математической
статистики.
Если имеются результаты экспертного оценивания и эксперименталь-
ные данные, то применяется метод вкладов [170], согласно которому
FiM) = g3F?(z)+g0Fi°(z), [0*g9,go*i;g3 + go = l]> (5-4.33)
где F°(z) = F~(z) или F^(z) = F^(z) - опытная (экспериментальная) ста-
тистическая функция распределения случайной величины z,-; g3, g0 - ве-
совые коэффициенты, выражающие (учитывающие) степень доверия соот-
ветственно к экспертным и опытным оценкам. Соотношение между весами
8э и So должно отражать соотношение между объёмами экспертных и
опытных данных, а также уровень знаний рассматриваемых явлений и
уровень развития техники в настоящем и в прошлом.
Наконец, закон распределения F% \Zin\) случайного вектора Z, v mo-
*<»>
жет быть построен методом статистического моделирования. Для этого
разрабатывается имитационная статистическая модель ОК, которая затем
испытывается на ЭВМ. Результаты г~, [/ = 1(1)тя] испытаний, где ти -
число проимитированных операций, обрабатываются методами математи-
ческой статистики; по ним вновь строятся статистические функции F?(z)
или кумуляты F^(z) распределений случайных величин £,., [i = l(l)it].
Для удобства последующего использования полученные одним из опи-
санных выше способов оценочные функции распределения F-(z) могут
быть выровнены (аппроксимированы) соответствующей теоретической
функцией распределения по методу моментов, с помощью распределений
Пирсона, Грамма - Шарлье, рядов Эджворта и др.

326 Глава 5. Методы построения математических моделей элементов ОК
5.4.10) Итак, выше были рассмотрены общие методы построения мате-
матической модели показателя Z v, требуемого качества результатов опе-
рации в случае, когда его компоненты zt, [/ = 1 (l)wj взаимно независимы.
Однако в "жёстко организованных" ЦНПФС, подобных производственным
процессам, в которых реализуется "программно-целевое" планирование и
управление [138], между предельно допустимыми (требуемыми) значе-
ниями Z,(4, Z,(4, zJ4 показателей кЭД, F/2j, yF\ операционных свойств
(качества результатов) ЦНПФС (см. п. 2,3.2) существует естественная за-
висимость. Так, при увеличении планового задания, определяемого векто-
ром Z?\ , естественно, должен быть увеличен предельный (предельно до-
г(2)
быть отодвинуты директивные сроки Zr\ выполнения планового задания
(см. п. 5.3.4). Если же при увеличении задания Zr\ директивный срок Z^\
пустимый) расход Z)K ресурсов (сырья, энергии и т.п.), а также должны
г(з)
h)
(месяц, квартал, год, пятилетка и т.п.) остаётся неизменным, то для его вы-
полнения необходимы дополнительные затраты ресурсов (как сырьевых и
энергетических, так и технологических и структурных), которые должны
быть введены в операцию в сроки, обеспечивающие их эффективное ис-
пользование.
Для описания указанных связей в математическую модель показателя
Z/ v требуемого качества результатов ЦНПФС вводятся функционалы
ZM=K^AZ^))uZt) = K{SZt^ (CM- РИС- 522)' называемые функ-
циями организационного (или экспертного) компромисса (ФОК).
По формальным свойствам эти функции аналогичны операционному
функционалу МПВКРО (т.е. РЭ-функции и функции связи), и поэтому все
сказанное о свойствах ОФ МВК справедливо и для ФОК МПТКРО. В ча-
стности, если ФОК - монотонные и непрерывные функции, то согласно
теореме 5.4.1 для определения закона распределения случайного вектора
Z л достаточно знать закон распределения генеральной (доминирующей)
компоненты Z^\ (скалярной или векторной). При этом если для оценива-
ния эффективности ЦНПФС используется выражение (3.2.10), т.е. функция
распределения случайного вектора Z, v определяется в форме (3.2.9), то
поскольку в этом случае все компоненты £., [j = l(l)#i] вектора Z ч ог-
раничены сверху, т.е. Zf-z^, формула (5.4.12) упрощается и принимает
вид

5.4. Методы построения математических моделей ПК результатов ЦНП 327
Fiw(z(»))=Fi,,^"^'-z»)=jP
не**)
.'=1
=^>(гг,г;,..,г;.)]-^иг;,г;,..,г;-)], (5аз4)
где zr = vr{zr); zu =vJi{zr), [/, =l(l)/,];
у, - номер компоненты г,, связанной с ГК ir возрастающей ФОК ь} (г);
у'г - номер компоненты г,, связанной с ГК zY возрастающей ФОК ил (г);
ц (г,*,..., г*,..., г*)=minfa* (г,,),..., vj (zu),..., гу,...,«,;' (г,,)};
Ц (г*,.», <,.», <)=max {«"' (г,, ),..., и:1 (гл),.«, и,;1 (г,2)}. А
Пример 5.4.2. Пусть в условиях примера 5.4.1 показатель Z,» требуе-
мого качества результатов операции задан в симплексной канонической
форме, т.е., Z,n\ =%ы\ =%(з) ~{^\ЛгЛ3), а его компоненты связаны моно-
тонными зависимостями:
Zl = K2l{Zl); (5.4.35)
z3=K31{Zl), (5.4.36)
где K2l (z) > О, К'ъх (z) > 0. Известен закон распределения F- (z) случайной
величины zx (планового задания).
Требуется построить вероятностную модель вектора Z/3\, т.е. опреде-
лить функцию его распределения F% (z,3v ), определяемую соотношением
Fi{){zlz1,z3)=P[{zl<zl)n(z1<z1)n{z3<z3)]. (5.4.37)
Решение. Поскольку по условию задачи К2Х (z) > 0 и J5T31 (*)> * >т-е-
то согласно (5.4.34)
Конкретизируем пример, положив
F-M = ^n{z;c,d)+A{z-d);
а —с
v2{z) = e2+S2z => v2(z) =
vAz) = e3+S3z^v-l{z)^
z-e2
z-e%
(5.4.39)
где Л>0и^>0.

328 Глава 5. Методы построения математических моделей элементов ОК
С учётом (5.4.39) выражение (5.4.38) примет вид
F (r т . \*m{zl,S?{z2-e2),S;l{z3-£3)}-c
*z{3)\zi>z2>h)- dc х
xn(min{Zl,S;l{z2 -e2), S;l{z3 -£3)};c, d)+
+ A (min{zlA1(z2-e2U;1(z,-e3)}-d)9 (5.4.40)
(z^z2,z3)e [c,d]x[e2 +S2c, e2 + S2d]x[e3 + 83c, e3 + S3d] = {zB3)\,
где {^(3)} - множество возможных значений (носитель распределения)
случайного вектора Z,3\ • ^
Рекомендуем читателю в качестве упражнения получить соотношение
(5.4.40) в развёрнутом виде с учётом свойств функции распределения слу-
чайного вектора (см. задачи 8.51 - 8.54 в [156]).
5.4.11) Вспомнив {2.7.7}, подчеркнём, что наличие "жёсткой" функцио-
нальной зависимости между компонентами вектора Z,^ всё-таки скорее
исключение из правил. Значительно чаще эта зависимость (если она суще-
ствует) носит стохастический характер. В случаях же, когда на условия
jff^v применения ЦУТС существенное влияние оказывает малоизученная
среда (в частности, противник), то диктуемые операционной ситуацией
требования Z?\, 2?\9 z£\ к результатам yF[9 г/21, fP\ операции по
различным аспектам (результативности, ресурсоёмкое™, оперативности)
оказываются взаимно независимыми.
Напомним, что в рамках любой вероятностной задачи все фигурирую-
щие в ней неслучайные величины (скаляры, векторы, функции) взаимно
независимы (как между собой, так и со всеми случайными объектами). По-
этому в случаях, когда требования Z?\, z№)> %ил Детерминированные
(см. (3.2.7)), их взаимная независимость самоочевидна. А
5.5. КОММЕНТАРИИ
5.5.1} В данной главе были рассмотрены общие вопросы, связанные с
проблемой построения математических моделей (ММ) операционных ком-
плексов в свете основополагающих принципов и концепций излагаемой
здесь методологии. Понятно, что из-за огромного много- и разнообразия
конкретных ОК (как существующих, так и вновь создаваемых) не пред-

5.5. Комментарии
329
ставляется возможным рассмотреть в приводимых примерах методики по-
строения ММ каждого из них. Тем не менее в следующем разделе на ряде
примеров, носящих достаточно общий характер, будут рассмотрены ос-
новные этапы и особенности подобных методик. А
5.5.2} Подчеркнём, что в силу высокой априорной неопределённости
операционной ситуации математические модели ЦУТС и ЦНПФС носят
приближённый характер. Поэтому среди предъявляемых к ним требований
основным является их внутренняя сбалансированность, т.е. правильный
учёт относительного влияния параметров и ЭТХ ЦУТС и ЦНПФС на эф-
фективность операции, обеспечивающий адекватный (правильный) срав-
нительный анализ её альтернативных вариантов. А
5.5.3} Следует особо подчеркнуть, что в задачах исследования эффек-
тивности ЦНП математические модели совершенно не похожи на модели-
руемые объекты ни по структуре, ни по поведению и представляют собой
вероятностные описания их атрибутивных свойств, обусловливающих ка-
чество результатов операции. В частности, для ОС такими свойствами яв-
ляются результаты ЦНП, а их показателями - показатели виртуального ка-
чества результатов ЦНП. А
5.5.4} Напомним (см. {3.6.2}), что в задачах исследования эффективно-
сти операций математические модели элементов ОК носят агрегированный
характер и их параметры, называемые "агрегатами" или "комплексами",
представляют собой функции (функционалы) от реальных параметров и
ЭТХ ЦУТС и ЦНПФС, т.е. от AL* и А?к,\, а также от условий функциони-
рования и применения ЦУТС, т.е. от В',^ и B'L.. В следующем разделе при
рассмотрении конкретных моделей ОК эта связь будет комментироваться.
А
5.5.5} Ещё раз обратим внимание, что поскольку "агрегаты" ММ могут
принимать произвольные (из некоторого диапазона) значения, то матема-
тическая модель описывает не конкретный объект (ЦУТС или ЦНПФС), а
класс аналогичных (но не идентичных) объектов (проектов ЦУТС, страте-
гий и способов реализации ЦНПФС и т.п.), элементы которого в общем
случае отличны друг от друга. Причём эти отличия носят принципиально
случайный характер. Поэтому получаемые на моделях ЦУТС и ЦНПФС
оценки их качества и эффективности являются принципиально прогноз-
ными, а потому вероятностными. Важно понять, что качество существую-
щей ЦУТС и эффективность реализованного ЦНПФС не оцениваются, а
потребляются в виде результатов проведённой операции. При этом сужде-
ние о них носит качественный характер и выносится в форме высказыва-
ний типа "годен - негоден", "хороший - плохой" и т.п. (см. п. 2.2.3). А

330 Глава 5. Методы построения математических моделей элементов ОК
5.5.6} Ещё раз подчеркнём, что при исследовании эффективности
ЦНПФС в модели его результатов фигурируют лишь динамические ресур-
сы, расходуемые в ходе операции. Ресурсы, расходуемые на разработку и
создание ЦУТС, а также на организацию ЦНПФС, учитываются косвенно
через параметры их моделей и расходуются в ходе операции опосредован-
но вместе с техническим ресурсом, надёжностью и живучестью ЦУТС, а
также с устойчивостью и эффективностью ЦНПФС, которые на протяже-
нии жизненного цикла ЦУТС снижаются. В моделях, описывающих эти
свойства, "агрегаты" должны фигурировать как убывающие функции вре-
мени. Если скорости снижения свойств (качеств) ЦУТС и ЦНПФС невели-
ки, то на протяжении одной операции они могут считаться постоянными
(что обычно и делается). ▲
5.5.7} При решении многих (большинства) задач ТЭЦНП (см. гл. 6 и 7)
для большей наглядности и лучшей интерпретируемости результатов ис-
следования предпочтительнее целевой эффект представлять в относитель-
ных (нормированных) единицах, выраженных в долях максимально воз-
можных (в конкретных условиях) результатов и характеризующих, таким
образом, "степень" приближения к ним, например, доля (процент) выпу-
щенной продукции относительно плановой; доля поражённой части цели
относительно всей её площади; доля вскрытых объектов от всех наблю-
даемых и т.п. При этом, как будет показано на примерах конкретных ОС и
ОК, наряду с наглядностью модели ЦНПФС приобретают универсальную
форму, позволяющую описывать в единых символах целевой эффект как
количественного, так и качественного характера (см. гл.7). А
5.5.8} Заметим, что поскольку при наличии функциональной зависимо-
сти между компонентами показателя L виртуального качества резуль-
татов операции для определения закона его распределения используется
аппарат функций случайных аргументов, то играющая роль такого аргу-
мента ГК может быть названа генеральным аргументом (ГА). ▲
5.5.9} В литературе [40, 84 и др.] критериальные функции называются
моделями ЦУТС и ЦНПФС, а их максимизация (минимизация) целью опе-
рации. Однако, как было показано в данной главе, по существу: КФР - это
ОФЛ, а КФП - это ФСВ. Что касается цели операции, то ни в КФР, ни в
КФП она не отражается (см. (2.4.1) - (2.4.14)). А

Раздел III
МОДЕЛИ
Глава 6
КОМПЛЕКСНЫЕ ФУНКЦИОНАЛЬНЫЕ МОДЕЛИ
ЦЕЛЕНАПРАВЛЕННЫХ ПРОЦЕССОВ
В предыдущих разделах были изложены концептуальные и методоло-
гические основы комплексного (системного) исследования качества ЦУТС
и эффективности её целевого применения, а также общие методы решения
этих задач. При этом процедуры их решения были проиллюстрированы
фрагментарно на ряде упрощённых примеров. Цель данного раздела - про-
демонстрировать методики решения задач исследования эффективности
ЦНПФС в возможно полном объёме изложенной выше методологии.
Этой цели в первую очередь служит настоящая глава, посвященная
рассмотрению агрегированных математических моделей абстрактных
ЦНПФС, которые носят достаточно общий характер и пригодны для опи-
сания широкого класса операций. Следует подчеркнуть, что в каждом из
параграфов главы речь идёт именно о классах операций, а следовательно, и
о классах их моделей, конкретизируемых при исследовании ЦУТС и
ЦНПФС, значения параметров и ЭТХ которых определяют значения агре-
гированных параметров моделей. Принципиальной особенностью таких
моделей (определяемой их названием) является учёт качества выполнения
ЦУТС своих функций через качество целевого эффекта операции, показа-
тель которого входит в явном виде в показатель виртуального качества ре-
зультатов операции.

332
Глава 6. Комплексные функциональные модели ЦНП
6.1. ЛИНЕЙНАЯ ФУНКЦИОНАЛЬНО-
СТОХАСТИЧЕСКАЯ МОДЕЛЬ НЕПРЕРЫВНОГО
ЦЕЛЕНАПРАВЛЕННОГО ПРОЦЕССА
Как известно, линейные модели занимают важнейшее место в задачах
исследования объектов самой различной природы. Это модели систем и
процессов регулирования и управления [25, ПО, 151, 152, 161], модели
сложных производственно-экономических систем и процессов [16, 53, 59,
62, 76, 80, 85, 179], математические модели систем и процессов в задачах
их оптимизации [65, 70, 74, 84, 100, 117, 155, 181], модели объектов в зада-
чах их статистического исследования [63, 100, 136, 148, 157, 170, 171, 173]
и т.д. Столь широкое использование линейных моделей обусловлено це-
лым рядом причин.
Во-первых (и это главное), во многих случаях как реальные объекты,
так и их поведение (ПФ) достаточно адекватно описываются соотноше-
ниями (уравнениями, функциями, функционалами и т.п.) линейного типа.
Во-вторых, (и это весьма важно), математическая теория линейных
моделей наиболее разработана и доведена до конструктивных и эффектив-
ных методик решения практических задач [25, 59, 65, 68, 76,148, 152,157].
В-третьих (и это заманчиво), линейные модели обладают целым рядом
ценных свойств, упрощающих их исследование и придающих результатам
большую наглядность и интерпретируемость.
Следует заметить, что последние два обстоятельства носят субъектив-
ный характер и, естественно (изученность и простота), не могут служить
обоснованием для применения линейных моделей, однако существуют и
объективные факторы, расширяющие область применения линейных мо-
делей и на нелинейные объекты (системы и процессы). Это так назы-
ваемый принцип малых отклонений и основанный на нём метод линеари-
зации нелинейных моделей [25, 30, 152, 170, 173]. В основе этого метода
лежит предположение о малости отклонений управляемых параметров мо-
дели от номинальных (базовых, исходных, расчётных) значений и близо-
сти в пределах этих отклонений нелинейных соотношений, описывающих
модель объекта, к линейным (см. п. 4.3.2). Если эти предположения право-
мерны, то линеаризованные модели оказываются достаточно адекватными
описываемым ими объектам.
6.1.1. СОДЕРЖАТЕЛЬНАЯ (ВЕРБАЛЬНАЯ) ПОСТАНОВКА ЗАДАЧИ
Некоторая ЦУТС, параметры и ЭТХ которой описываются вектором
A,k,y проводит операцию (ЦНПФС), параметры и ЭТХ которой описыва-
ются вектором А?к*, в условиях, описываемых векторами В'^л (условия

6.1. Линейная функционально-стохастическая модель непрерывного ЦНП 333
функционирования ЦУТС) и BfL. (условия применения ЦУТС).
Качество результатов операции описывается в симплексной канони-
ческой форме и характеризуется вектором
*<Э> = (Л»Л,Л>. (6.1.1)
где ух - целевой эффект;
у2 - суммарный расход операционных ресурсов различных видов
(см. п. 5.3.2);
у3 - операционное время.
Для достижения цели операции должен быть получен целевой эффект
не менее ъх за время, не превосходящее z3; запас операционных ресурсов
равен £2.
При нормальном течении ЦНПФС производительность ЦУТС, обуслов-
ленная её качеством (Д'Лл), организацией (Л*-О ЦНПФС и условиями
функционирования ЦУТС (BLx), постоянна.
В ходе операции возможны временные задержки, обусловленные раз-
личными факторами, основными из которых являются: недостаточная ква-
лификация и ошибки операторов; сбои и отказы аппаратуры; задержки
введения операционных ресурсов; задержки поступления требуемой ин-
формации; поступление приоритетных заявок и т.п., а также связанные с
такими задержками дополнительные расходы [перерасходы (см. (5.3.19))]
ресурсов гпр.
6.1.1) Способность ЦУТС и ЦНПФС парировать подобные задержки
целесообразно называть их функционально-технологической надёжно-
стью. А
Требуется построить математическую модель операционного ком-
плекса (его элементов), позволяющую решать задачи анализа качества
ЦУТС и ЦНПФС и их синтеза по критериям требуемой или максимальной
эффективности операции, и провести исследование качества ЦУТС и эф-
фективности ЦНПФС.
6.1.2. ПОСТРОЕНИЕ АГРЕГИРОВАННОЙ МАТЕМАТИЧЕСКОЙ
МОДЕЛИ ОПЕРАЦИОННОЙ СИСТЕМЫ
Сформулированная в п. 6.1.1 операционная ситуация носит весьма об-
щий характер и может служить вербальной моделью широкого класса опе-
раций, реализуемых ЦУТС различного назначения.
Следующий шаг моделирования ОС состоит в формализации и кванти-
фицировании её вербальной модели, т.е. в аналитическом её описании с

334
Глава 6. Комплексные функциональные модели ЦНП
учётом качественных и количественных характеристик, взаимосвязей её
элементов. Именно на этом этапе с целью построения наиболее адекватной
математической модели показателя L качества результатов ЦНПФС ус-
танавливаются (возможно более точно и достоверно) физические и опера-
ционные свойства элементов ОС.
Итак, в соответствии со схемой алгоритма, изображённой на рис. 5.2.1,
определяется спецификация операционных эффектов - атрибутов ЦНПФС.
Для большей наглядности введём следующие обозначения:
yx = v - целевой эффект, выраженный в относительных единицах , т.е.
0<t><l;
d
j2=A3v- расход операционных ресурсов, включающих в рамках модели
ресурс-сырье (г,), ресурс-энергию (г2), ресурс-технологию (г3);
d
у3=т - операционное время, отсчитываемое от момента *0=0 модель-
ного начала операции до момента tK её окончания (не зависяще-
го от исхода операции).
6.1.2) Как будет показано на примерах конкретных ЦНПФС, в их моде-
лях момент t0 может не совпадать с моментом tH начала функционирова-
ния ЦУТС из-за не мгновенной её реакции на инициирующее операцию
событие (приказ, операционная ситуация, действия противника и т.п.). А
Согласно схеме рис. 5.2.1 определяются спецификации (перечни) пара-
метров ЦУТС и ЦНПФС [компонент векторов А',к*, А?к* (блок 2)] и харак-
теристик условий функционирования ЦУТС [компонент вектора J5L
(блок 3)]. Мы это сделаем при описании агрегированных параметров моде-
ли ЦНПФС. Тогда же будет сказано о блоке 4.
В рамках данного параграфа будем строить модель операционного
функционала (блок 5) в классе аддитивных линейных моделей в следую-
щей форме:
г=г0(и,г10,г20,г3в;4.))+71(г2',Гз';М(41)). (6.1.1)
Здесь т0 - "технологическое операционное время" (ТОВ), потребное для
получения целевого эффекта объёма v ;
г, - "временная операционная задержка" (ВОЗ) ЦНПФС по отме-
ченным выше причинам;
Относительно полного или планового объёма работ, максимально возможного це-
левого эффекта (наносимого или предотвращаемого ущербов, добываемой информации
и т.п.).

6.1. Линейная функционально-стохастическая модель непрерывного ЦНП 335
А, к- агрегированные параметры модели ТОВ, где
4 = 404,2?'), [i = l{l)S.];
М,х - агрегированные параметры модели ВОЗ, где
Mj=JUj{A,B',B"), [/ = 1(1)5,].
Как видно из (6.1.1), в общем случае технологическое время ?0 и время
задержки г, зависят от операционных расходов i?,3v, а также от парамет-
ров (ЭТХ) ЦУТС и ЦНПФС и условий проведения операции. При этом, с
одной стороны, с ростом расходов сырьевых ресурсов г, растёт целевой
эффект V, растёт расход энергетических ресурсов г2 и вместе с ними рас-
тёт и ТОВ, а с другой - с ростом расхода г3, технологических ресурсов
(идущих на совершенствование технологии ЦНПФС, повышение произво-
дительности и живучести ЦУТС и т.п.) ТОВ уменьшается.
Что касается времени задержки тх, то естественно полагать, что расхо-
ды ресурсов г2 и гъ направлены на его уменьшение. Легко заметить, что
соотношение (6.1.1) описывает ЭР-функцию [см. (5.3.2), (5.3.7)] в услож-
нённой из-за слагаемого тх{г'29г'ъ) форме.
6.1.3) В общем случае задержки г, могут зависеть и от величины v це-
левого эффекта,т.е. г, = ^(r^r^v).
Для выявления характера зависимостей т0\р;г*,г2,г") и т,(г2',г3';1>)
нужны специальные исследования конкретных ЦУТС и ЦНПФС. Однако
общие их свойства достаточно очевидны и могут быть учтены на уровне
"правдоподобных рассуждений". ▲
Будем рассматривать ЦУТС, облик которой (структура и основные
ЭТХ), а также технология ЦНПФС известны. В этом случае в соответствии
с технологией в ходе операции расходуются все имеющиеся в системе ре-
сурсы и, следовательно, у2 = z2, т.е. имеет место "эффект поглощения" (см.
п. 3.3.4). При этом расходуемый сырьевой ресурс равен предельному, т.е.
r10 = r1<w,, так что фигурирующий в (6.1.1) целевой эффект v = v{r°n). Что
касается энергетического и технологического ресурсов, то они будут опре-
делять поведение (значения) агрегированных параметров модели, т.е.
4 = 4fevr), ['=i(i)£.] (6-1.2)
или в векторной форме
Mj=Mjlr?>'rl [/=i(i)^,] (6-1.3)
или в векторной форме

336
Глава 6. Комплексные функциональные модели ЦНП
6.1.4) В общем случае как As \, так и M,s\ могут с течением времени
изменяться, т.е.
^feVrb \з.)(г?>гГ Л M(Si)(r±",r±»)= М{В1)(г1\г±"Л
что должно учитываться в модели. А
В общем случае зависимости
^ = ^кгЛг20,г3°;Л(5в)ЦА>,^))]; (6.1.4)
*i =T1lr^r3S-i;,Jlfrt^4*>^o^oll (6Л'5)
могут иметь самый различный характер. Однако очевидно, что с ростом
целевого эффекта v технологическое время т0 растёт, т.е. dr0/dv>0. При
этом поскольку производительность ЦУТС постоянна, т.е.
dr0/dv = a = const, то в рамках линейной модели будет иметь место сле-
дующее соотношение:
f = av + rl9 (6.1.6)
где а = а[г*,г3°;А^,В^) - агрегат.
6.1.5) Как видно из (6.1.4), при отсутствии задержек "агрегат" a = T0/v
характеризует ресурсоёмкость ЦНПФС по операционному времени, а если
учесть, что при постоянной производительности ЦУТС расход г, сырье-
вых ресурсов пропорционален технологическому времени т0, т.е. г, =г,т0,
то агрегат аг =rxlv = rla характеризует ресурсоёмкость ЦНПФС по сырь-
евым операционным ресурсам. А
Итак, пусть законы распределения <рд{р) и <pf (r) виртуального целево-
го эффекта v и временной задержки fx известны. Требуется определить
закон распределения
Фу{2) (л,л) = *<«»М = *Ь * v)f\(f < т)]
показателя К- = (yl,y3) = (v,f) качества результатов ЦНПФС, т.е. реали-
зовать блок 7 схемы алгоритма, приведённой на рис. 5.2.1.
Достаточно универсальной вероятностной моделью относительного це-
левого эффекта v может служить четырехпараметрическое бета-
распределение [65], позволяющее описывать весьма широкий класс рас-
пределений ограниченных случайных величин. Плотность бета-
распределения имеет выражение [65, 169]

6.1. Линейная функционально-стохастическая модель непрерывного ЦНП 337
l\ |«|< / • \ (v-vy(v'-vYn(v;v',v") .....
ям-fi w.» -"^)'«(,Д^1)(;. _>)'•"•■; ,(6' '7)
где v',v" - параметры положения [границы носителя (v'9v") бета-
распределения] случайной величины v;
71>-\>р>"-\ - параметры формы бета-распределения случайной вели-
чины v;
В(т] +1,/7 +1) - бета-функция (интеграл Эйлера I рода),
W ^ ' Г{г] + р + 2) 0J
/"(^ +1) - гамма-функция (интеграл Эйлера II рода),
r(i7 + l)=f/VA,
о
при п целом положительном Г(п +1) = n!.
В общем случае параметры (6.1.7) определяются соотношениями:
t/=t/(r2V3°M,i?');
v" = vir?,r?;A,B');
rj = Tj(r!,r!;A>B');
p = p(rlr!;A,B'); J
(6.1.7)
т.е. параметры распределения (6.1.5) являются агрегированными ЭТХ
ЦУТС и ЦНПФС (см.{2.3.14}, {3.6.2}).
Семейство кривых бета-распределения (6.1.7) для различных значений
параметров 7], р приведено на рис. 6.1.1.
При r/ = m и p = n (iff, n - целые неотрицательные) выражение (6.1.7)
принимает вид
/\ [б]< > » \ {v-v')~{v"-v)m(m + n + l)l „, , »\,гЛО,
(pAv)=n\v;v>v ,"*,") = - Д *mL\ , ,—-n{v;v,v ).(6.1.8)
[V -V) mini
Моделью времени f, задержки может служить трёхпараметрическое
(смещённое) гамма-распределение, позволяющее путём варьирования па-
раметров описывать широкий диапазон вероятностного поведения случай-
ной величины f j. Плотность смещённого гамма-распределения определя-
ется выражением
4=*,ferUr.-r „ R\jF-rf* '
^Л^)^^^^^^^^^^ Ж-Л (6.1.9)

338
Глава 6. Комплексные функциональные модели ЦНП
\(plf]{v;v',v",7j,p)
7] = р<0
Рис. 6.1.1
где к = К, Р - параметры гамма-распределения [носитель которого - луч
(0,°°)]. При этом
P = p(rl,rl;A,B'); (6.1.9')
r = r,(r2Srз1;^J?,), J
т.е. параметры распределения (6.1.8) - это агрегированные ЭТХ ЦУТС и
ЦНПФС (см. {2.3.14}, {3.6.2}).
Семейство кривых смещённого гамма-распределения (6.1.8) для раз-
личных значений параметров К, J3 приведено на рис. 6.1.2.
При К +1 = к - целом положительном, J3 = —, // > О и т = О "смещён-
№
ное" гамма-распределение называется распределением Эрланга k-го поряд-
ка и имеет плотность
Л, М = ff^iM -1,1) = <p[?}{t; k,ju) = 0^e-"TA(r). (6.1.10)
Итак, согласно (6.1.4) с учётом эффекта поглощения операционных ре-
сурсов "агрегатами модели" симплексная каноническая форма показателя
KKv качества результатов операции свелась к двухкомпонентной, т.е.
Y{K)=t2)=(yl,y3) = (v,f).
(6.1.11)

6.1. Линейная функционально-стохастическая модель непрерывного ЦНП 339
\-1<К,<0
0<К,<1
Х4>1
Рис. 6.1.2.
Для завершения построения модели ОС (см. рис. 1.2.1 и 5.2.1) необхо-
димо найти закон распределения Ф^ (Г/2\) случайного вектора Е2*.
Хотя, как отмечалось в (6.1.2), в общем случае между величинами v и
ft может существовать зависимость, однако в рамках рассматриваемой
линейной модели целесообразно под ix понимать лишь временную за-
держку, не связанную с получением целевого эффекта v, а обусловленную
лишь организационно-технологическими факторами. В этом случае f0 и f,
будут взаимно независимыми и, следовательно,
ftW^J^ft.W.
(6.1.12)
где * - символ композиции (свертки) законов распределения случайных
величин.
Будем искать плотность распределения вектора (6.1.11) по формуле
Поскольку при фиксированном значении v целевого эффекта v
r0=av = const и, следовательно,
f = r0+fl=av + tl , (6.1.14)
то согласно (6.1.12)
^/Д^;^)=^о/Дг;г;)*^|(г)=^(г-аг;)*^1(г)=

340
Глава 6, Комплексные функциональные модели ЦНП
(т-ССУ-т\)
(т-av-r'.Ye р а( ч //-ilex
= л т— ч „»+, Air-av). (6.1.15)
Г(к + 1)/Г+1 v '
Подставив (6.1.7) и (6.1.15) в (6.1.13), будем иметь
ф (v T)-(v-vy(v"-vY(*-<xv-T;ye~ ' , , v«Mr-ao\-
Ww'r>- jB(7+i,p+i)(u*-u'r+1r(«+i)^- /7^w'v Wr отЬ
(т-ау-т[)
= G-(v-v'Y{v"-vY(T-av-il)*e~ p П{ь;ь\ь*)А{т-ао).(6Л.Щ
Для реализации блока 7 схемы алгоритма, изображенной на рис. 5.2.1,
достаточно проинтегрировать (6.1.16), т.е. имеем
<р^{1^(р{ф,г)=])(р{ф\г')иь'йг'. (6.1.17)
Пример 6.1.1. Для большей наглядности дальнейших построений кон-
кретизируем модель ОС, положив: v' = v, г/ = 1, // = /? = 0, а = 1,
fi = l/ju. Тогда выражения (6.1.8), (6.1.10), (6.1.15), (6.1.16) и (6.1.17) соот-
ветственно примут вид:
1—v
*t, (*)=?*, (r;l,//) = //e-"r4r);
И />~//(T_aU)
Фт(У^) = ^\е^П{ьЫ,\)
\це ^A{^x-av^)dxx
(6.1.18)
(6.1.19)
(6.1.20)
(6.1.21)
dvx. (6.1.22)
На рис. 6.1.3 изображён носитель распределения [заштрихованная об-
ласть (t/,l]x(ari>,oo)] случайного вектора iL =(v,i), из которого видно,
что область интегрирования имеет неоднородности, обусловленные взаим-
ной зависимостью и ограниченностью случайных величин v и £ (их носи-
телей распределения), которые при реализации формулы (6.1.21) должны
учитываться путём соответствующих изменений пределов интегрирования.

6.1. Линейная функционально-стохастическая модель непрерывного ЦНП 341
*"♦
1и<^>в}
(XV
Рис. 6.1.3
С учётом рис. 6.1.3 формула (6.1.22) примет вид
1-v'
П{у;у',1)А{т-а) l,Mav>
1-v'
JMe'^dT'
Lav
\dv'+
\це-»ит'
\_av
\dv'. (6.1.22')
За пределами носителя распределения \(t),f) }=(l/,l]x(ari>,<») случай-
ного вектора (#,f) функция 0,6tAv,t) доопределяется естественным об-
разом [29]:
4>{6,f)(v,T)=Q[A{v-i)+A{av-T)]+Ru{v)A(T-°<>)+
+ Ft(r)A(v'-v)+ A{v'-v)a{t-oo). (6.1.22")
Интегрирование согласно (6.1.22') с учётом (6.1.22") даёт
ф<в.А»>*)=
"<«.♦>
т-av
[a(l-v') /ia{l-v')
1 [\ - р-мк-<">))
+
\-v
IT(v;v',i)l7(t;av, a)+
7 т Tvv^ -e i\IT(v;v',i)A{T-a)+
1-v' /ia{l-v')K '\ v ' v '
A(v>-v)\\lZ^ l^(1_e-/'(-«0)|/7(r.OT,',a)+
v y\[a(l-v') //cr(l-t/)v 'J v '
Lu>-a)L (6.1.23)
1 J—л (e""("4r) - e""(r-m''))
//a(l-v') _

342
Глава б. Комплексные функциональные модели ЦНП
где а = а(Х') ; v' = v'(X') ; ju = ju(x) - агрегаты вектора U = (Ay,ByS)
управляемых параметров ОС.
При этом очевидно
A{Sn) = лм(х)=л{3)(х)=(л1(х'),лг(х%л3{х))=
= {а{х'\ь'{х'Ых)).
На рис. 6.1.4 изображена поверхность функции распределения (6.1.23),
построенная при а = 1; t/ = 0.2; ju = 1. А
Рис. 6.1.4
Отыскание зависимостей
Y(n)\X'(m')J => Y(nl)=K(nl)VM>¥M) =>
и составляет задачу построения математической модели ОС, решение ко-
торой завершается выделением из состава вектора Х',т« ^(А^9ЩЛ
управляемых компонент £/,'л = (AL уВ?гА.
6.1.6) Заметим, что если в рамках модели (6.1.4) задержки отсутствуют,
то f, = 0, и, следовательно,

6.1. Линейная функционально-стохастическая модель непрерывного ЦНП 343
т.е. целевой эффект v и операционное время f связаны функционально. В
этом случае определение функции распределения Ф,ьЛь,т) может быть
основано на применении теоремы 5.4.1.
Поскольку в условиях рассматриваемой модели известным предполагается
закон распределения <p0{v) виртуального целевого эффекта V, то он являет-
ся генеральным аргументом и согласно (5.4.11) будет иметь место равенство
*W>M=р*Ш]- Ъ (v)=F*fy - fM=
_r/a-v
\-v
n(v; v', 1)П(т; av, a)+
1-v
1-v
-I7(v;v',l)+A(v' -v)
\A(r-a)+
т-av
a-av
7П(т;аь',а)+А(т-а)
A(if-v)+A(v'-v)A{*-<*)- (6.1.23')
Поверхность функции (6.1.23) при а = 1, t/ = 0.2, ju = °° изображена на
рис. 6.1.5. A
Рис. 6.1.5
Как отмечалось (см. п. 5.4.3), определение закона распределения
Fi(2>lZ(2))nOKa3aTeJM
Z(2)=(£1,£3> = <^^3), (6Л.24)
где vT - требуемое (минимально допустимое) значение целевого эффек-
та t), fd - директивное (максимально допустимое) значение операционно-

344
Глава 6. Комплексные функциональные модели ЦНП
го времени f. Отметим, что определение требуемых значений качества
результатов ЦНПФС является прерогативой суперсистемы. Для иллюстра-
ции методики исследования эффективности ЦНПФС рассмотрим конкрет-
ный пример.
Пример 6.1.2. Будем предполагать, что функция распределения
F- (^(2\) вектора Z,2, известна и что распределения предельно допусти-
мых (директивных) величин vT и тд принадлежат тем же классам (6.1.5) и
(6.1.8), что и распределения виртуальных величин v и f показателей опе-
рационных свойств (аспектов) результатов ЦНПФС. Тогда F- \2,гА будет
иметь следующее выражение:
^-n(v;v'T,v;)
VT-VT
x(i-^<^))4t-<), (6.1.25)
где vT, vT, тэ, v - агрегаты,
^ v'T = v'T(X"); v'T = v'T(X"); т'д = т'д(Х"); v = v(x"),
причём X" = В". А
Определив функцию распределения F% \Z,2A случайного вектора Z,2y
мы согласно схеме рис. 5.2.1 как бы забежали вперед, миновав блоки 9-11
алгоритма. Однако в рамках рассматриваемого примера это естественно
(см. (5.2.1».
Так, блок 9 реализуется "автоматически" совместно с блоком 1, по-
скольку компоненты у. и zg9 [i = l(l)#i] соответственно векторов Км и
Z, v семантически идентичны и их перечни (спецификации) совпадают.
Для реализации блока 10 необходимо предварительное изучение усло-
вий применения ЦУТС для выявления характеризующих их параметров
В?* = Х?«, обусловливающих директивные (предельно допустимые) зна-
чения Z,2v показателей K2v качества результатов операции (РО).
Блок 11 устанавливает зависимости директивных показателей качества
РО от условий применения ЦУТС, описываемые в агрегативной форме
функционалом, выражаемым зависимостями:
N{Si) =N{Si)(X') = N{4)(xn = {v;(X%v;(X%f'd(X%v(X')),
гЛеХ" = (А,В',В").
Отыскание зависимостей Z,Ax")=>N,sAx")=^Fi [z,,;N,s\) и со-
ставляет задачу построения МОСТ, решение которой завершается выделе-

6.1. Линейная функционально-стохастическая модель непрерывного ЦНП 345
нием из состава вектора ЛТ^ =(А,куВ^Л управляемых компонент
IJ" — I Ay R"y
Поскольку из содержательной постановки задачи (п. 6.1.1) следует, что
цель операции равносильна выполнению условий
G/,:(t)>t5r)n(^<f/7)n(f<Ta)=(t5(r„)>vr)n(f(rJ7)<T3), (6.1.26)
то модель операционного комплекса можно считать построенной и пере-
ходить непосредственно к решению задачи исследования эффективности
ЦНПФС и качества ЦУТС, включающей в себя подзадачи:
- оценивания эффективности ЦНПФС;
- анализа ЦНПФС и ЦУТС;
- синтеза ЦНПФС и ЦУТС.
6.1.3. ОЦЕНИВАНИЕ ЭФФЕКТИВНОСТИ ЦНПФС
6.1.3.1. Детерминированные требования к результатам ЦНПФС
Как было показано в (3.2.7), при детерминированном (предельно допус-
тимом, заданном) директивном значении Zj\ показателя качества резуль-
татов операции вероятность достижения её цели определяется равенством
[см. (3.2.19)]
^=^(^«)=Фк(я)Ц«>)^ (6.L27)
которое в условиях примера 6.1.1 при а=1; & = 0,2; ju = 1 и
(г?7, тэ)е (&, 1 ]х (ягг?, °°) примет следующее выражение:
Pau=r(Y{i)^1))=p[(#>0T)n(i<Ts)]=0{,{)(#T,T;)) =
тз -а#т 1 (1 £-м(ъ-<**г)\
а(\-&) //a(l-t?')v '
х Я( г?Г; &, 1) П ( тэ; а &т, а ) +
1-Л.
( g-f («■»-«) _ е-м(ъ-**т ) \
1-гГ ца(\-&)
хЯ(г?г;^,1)^(гэ-ог) =
= 1.25 [тд-0т-(1-е-м{т>-*') )]я(г?г; 0.2,1) Я(гэ; t?r,l) +
+ 1.25 [1-0г-(е~',(,'»~,)-е~/,(т'"*))]л(0г; 0.2,1)Л (тэ-1), (6.1.29)

346
Глава б. Комплексные функциональные модели ЦНП
где(г?г,гэ)€(г^,<]х[гэ,оо).
Пример 6.1.3. Пусть:
а) г?г = 0,8; тд = 2; тогда формула (6.1.28) даёт (см. рис. 6.1.7,
кривая 4.1)
Рда=Ф(^}(0.8,2) = 0.17;
(6.1.29)
б) тЗт = 0,5; тэ = 4; тогда из (6.1.28) следует (см. рис. 6.1.7, кривая 4.2)
^да=Ф(^,,)(0.5,4) = 0.60. (6.1.30)
6.1.3.2. Стохастические требования к результатам ЦНПФС
В общем случае, когда показатель Z, v требуемого качества результатов
операции случаен, вероятность достижения её цели определяется соотно-
шением [см. (3.2.10)]
^=i>(F(„)^„>)=].W.]a>,(>)(z(„>)rfFi()(z<(l>), (6.1.31)
которое в условиях примеров 6.1.1 и 6.1.2 при (tfT, €%.~\%^{& Л) примет
вид:
т-агг?
1 (1„р-м(т-а*)\
"(*-*э)
]dT\d& +
т-ад
1 (\-e~t1 (*-<** A
ve-v(T-T>)dT\d& +
= л({д, е- (а"г') + С, [<Г (e*",i} - ev (e*"«i) ] } J («4 - <)+
+(/)1-51e-'(e-,;)-C1e-"(e,?-,i,-C2e-''(,i-'",;)}ff(i/a;atrna<)+

6.1. Линейная функционально-стохастическая модель непрерывного ЦНП 347
+{D2 -В,еМа-^+Сг [е-'М-*)_е-мЫ-«*) ] }я(г;.aifT>a)+
+{D3-B2e-M{T>-a) + C2[e-M{T'>-a*)-e-',{r'-a*n\}A(T'a-a)), (6.1.32)
где
А = -±-; Вх=—/!—. Bi= "
1-&' ! av(ju + v)' 2 aju(ju + v)'
Vv2 (/* + *)«-<)' 2 а2//2 (/* + *)«-«)'
_//у2<2+(2//у-у2-2ог//у2^)тэ
2а2//у2«-#)
от2 //у2 г^2 +(огу2 -2a{iv)ti'T + 2ju-v
+ 2a2//v2(#-#) '
= 2(//-у)+2//у<-а//у(^-г?;), <-г?;
2 2a//v ' 3 2
6.1.7) В рамках примеров 6.1.1 и 6.1.2 компоненты векторов Г,2* и Z/2>
представляют собой ограниченные случайные величины. При этом носите-
ли их распределений
(«,#], («,#]С(0М); (Л^],(т$,<]с(0,оо].
Поскольку границы носителей распределения случайных величин г? и
г?г, а также f и fэ могут располагаться относительно друг друга по-
разному, то существует 12 вариантов представления соотношения (6.1.32).
Здесь же рассмотрен лишь один вариант, соответствующий случаю
#<%<€£<€? и т'<т'ъ при т"=Тэ = °о.
Рекомендуем читателю в качестве упражнения проанализировать ос-
тальные варианты. А
На рис. 6.1.3 границы области интегрирования по формуле (6.1.32) вы-
делены жирной линией. Поскольку нижняя часть этой линии ломаная, а
интегрируемая функция Ф/# ^{д*?) в различных частях носителя рас-
пределения {(*?>£/ J имеет различные выражения [см. (6.1.23)], то область
интегрирования распадается на три подобласти, в каждой из которых
подынтегральное выражение остаётся неизменным [см. (6.1.32)].
Пример 6.1.4. Пусть а=1; г?' = 0,2; /1 = 1; г^=0,3; г?* = 0,3; v = l;
т'ь = 0,5, тогда формула (6.1.32) даёт

348
Глава 6. Комплексные функциональные модели ЦНП
РДЦ=р[(#>0т)п(т<тэ)]=О.2ОЯ.
Если при тех же прочих условиях т'д = 1, то
РДЦ=р[(ё>дт)п(т<тд)]=0.300. А
6.1.8) Оценка РДЦ вероятности Рдц может быть получена и без вычис-
ления интеграла (6.1.32) методом статистических испытаний (см.
п. 3.4.1.3). Для этого:
- одним из известных методов моделируется последовательность
( ( &т\ > Tai )> (&тг 9 *Э2 )'•••>( &tn 9zdN )} значений случайного вектора
Z/2x = ( Ьт, fэ ) в соответствии с законом его распределения (6.1.25);
- затем для каждой точки (г?Гу., fdJ ) [j = l(l)N ] вычисляется зна-
чение Ф,^ f\[&Tj>*dj) Функции распределения Ф/# ^{д*?) случайного
вектора F(2> = (4 ,fa);
- находится оценка Рд^ вероятности Рд// достижения цели опера-
ции по формуле
^=^i^,f)(^j9Tdj). (6.1.34)
▲
6.1.9) Как известно, априорная вероятность Рдц достижения цели опе-
рации удовлетворительно оценивает эффективность массовых операций.
Для оценивания эффективности уникальных операций служит гарантируе-
мая вероятность а)гдц (у) достижения цели, для вычисления которой необ-
ходимо знать закон распределения F {a) (^) супериндикатора
Из соотношения (3.1.56) и рис. 6.1.3, 6.1.6 видно, что в условиях при-
меров 6.1.1 и 6.1.2 значение функции F {1) {со ) равно интегралу Стилтьеса
(3.1.56) по области {(г?, г)}а, ограниченной кривой Ф,^ fAtf,r) = a) и
границами пересечения носителей распределений \( &т, тъ) JП ](г?,г ) J.
Значение а)г определяется соотношением
, Я *%,<№>*)=г- с6-1-35)
В общем случае эта задача может быть решена численным методом на
ЭВМ.

6.1. Линейная функционально-стохастическая модель непрерывного ЦНП 349
Рис. 6.1.6
6.1.3.3. Метод ведущих компонент
Для исследования эффективности ЦНПФС может быть использовано
непосредственно соотношение (6.1.32), представляющее собой зависи-
мость средней вероятности РДЦ достижения цели операции от агрегиро-
ванных параметров математической модели операционного комплекса.
Однако, как видно из (6.1.32), даже в рамках сравнительно простого при-
мера эта зависимость достаточно громоздка и труднообозрима. Поэтому,
как отмечалось в п. 3.3.3, для упрощения задачи целесообразно произвести
"свёртывание модели" методом ведущих компонент. Поскольку при свёр-
тывании часть параметров исходной модели "исчезает" и фигурирует в
свёрнутой модели опосредованно (через оставшиеся параметры), то это
должно учитываться при определении ведущих компонент так, чтобы ис-
следуемые характеристики (параметры и ЭТХ) ЦУТС и ЦНПФС присутст-
вовали в свёрнутой модели в явном виде.
А. Средняя вероятность
Для конкретности предположим, что задачей последующего исследова-
ния является анализ влияния на эффективность операции параметров
ЦУТС и ЦНПФС, обусловливающих оперативность последнего. В этом

350
Глава 6. Комплексные функциональные модели ЦНП
случае в качестве ведущей компоненты показателя K2v = (г?г, тд) качества
результатов операции должно фигурировать операционное время f (см.
<6.1.8».
Как следует из (3.3.12), функция распределения ведущей компоненты
t, условная (апостериорная) относительно события Н~\р>$т) , в усло-
виях примеров 6.1.1 и 6.1.2 имеет вид
Здесь
Ън(т)= JFfJt;^)dF^). (6.1.36)
=[а{0)+Ь{&)т+с{&)е-,'т]п{т;а0,а)п{0;гГ,1)+
+[l-d{&)e-Mt \л{т-а) П{&; 0',!), (6.1.36')
где
л(г?)=_л±да> c{v)=
е»а°
ца{1-0)' v ' /m(l-t?)'
//яг(1-г?)#
Пример 6.1.5. На рис. 6.1.7 приведены графики функции (6.1.36') в ус-
ловиях примера 6.1.1 при а=1; г?, =0,8; // = 1 (кривая (3.1)), г?, =0,5
(кривая (3.2)). Пунктиром обозначены аппроксимирующие кривые, урав-
нение которых
Ff±e{T;^Ff±6(t;^[l-e-^-^))\A(T-T'(&)), (6.1.37)
где
T,{^)=-[ln(ef"x-ема* )-lnjua{l-&)].
Из сравнения выражений (6.1.36') и (6.1.37) видно, что при т>а они
полностью совпадают.
Пусть, как и в примере 6.1.3:
а)г?г=0,8;гэ=2;
б)г?Г=0,5;тэ=4.

6. 1. Линейная функционально-стохастическая модель непрерывного ЦНП 351
i
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
"
^t(t)^f,e(r)%jT;^)^{^t); / = 1.2,г?, =0.8,tf2 =0.5
^0^====Z
///^
Qjf/f
III ^^_^@
lll^s^0
1 ®lff/
\ i IV
I s^~ °
\JJjl/
i агаз as o.76/o.9j 2 3 4 T
aei
Рис. 6.1.7
Тогда
а) т'(г?г ) = т'(0.8 )=/и2.45 = 0.90 и согласно (6.1.37)
Ffl^r;0.8)=[l-e-(*-ft9)]j(r-0.9), (6.1.38)
что при тэ = 2 даёт
*Рда =P(f<2/ v>0,S) = Ff^{2; 0,8 ) = 0,67; (6.1.38')
б) т'(г?г ) = т'(0,5 ) = /и2.14 = 0.76 и согласно (6.1.37)
#;1Дт;0,5)=[1-в-(т-в-76)]^(т-0,7б), (6.1.39)
что при тэ = 4 даёт
"-Рад =p(f<4/*?>0,5)=FfliJ(4; 0,5) = 0,96. (6.1.39')
На рис. 6.1.7 приведён график функции Ft (r) безусловного (априорно-
го, маргинального) распределения виртуального операционного времени

352
Глава 6. Комплексные функциональные модели ЦНП
£ кривая 1. Как видно из рис. 6.1.4 и 6.1.7, в условиях примеров 6.1.1 -
6.1.5 имеет место тождественное равенство
FM = FfjT;0') = 0{.f)(ti',T), (6.1.40)
где г?'= 0,2. ▲
6.1.10) Из сравнения (6.1.29) с (6.1.38) и (6.1.30) с (6.1.39) видно, что
метод ведущих компонент даёт завышенные значения РДЦ. Однако это не
следствие ошибки, а закономерный факт, поскольку в рамках этого метода
определяются условные (относительно качества результатов ЦНПФС по
ведомым компонентам) вероятности достижения цели операции (см.
(3.3.18». А
Как нетрудно было заметить, выражение (6.1.36) определяет функцию
распределения ведущей компоненты £ вектора iL = (г?, £) относительно
события Н -\&>&т), т.е. при детерминированных требованиях к ведомой
компоненте *? вектора iL = / г?, f ).
Подставив (6.1.36') в (6.1.36) и произведя интегрирование, получим
Ftl„{t) = a
b+ju(a-r)ln-
а-т
+ (с + е"а Ех{ц{а-т)))е-мг\п{т ; а#т ;а#т)+
+[l + d+fid(a-T)+ge~ftT\n(t;a^;a)+
+ [l-he-Mr\A{t-a),
(6.1.41)
где
а =
/1а(1%-#т)
; b = -jua&T ;
c = -El{/ia{l-4))e"a ; d = aln\^;
g = a[Et{Ml-#r ))-ЕЛма(1-^т))]е"а ;
h = a\
Е,{ца{\-#т))-Ех{ца{\-%))-?-
,м<* .
eo -I
E\[z)= J dt - интегральная показательная функция [168].
7 *

6.1. Линейная функционально-стохастическая модель непрерывного ЦНП 353
FtM
О 0.3 0.8}
Пример 6.1.6. На рис. 6.1.7 (кривая 2) и 6.1.8 приведены на графике
функции (6.1.41), построенные в условиях примеров 6.1.1 и 6.1.2 при
а = 1, ju = 1, dj - 0,3, д" = 0,9. Пунктиром отмечена аппроксимирующая
кривая, уравнение которой
^W«^W = [l-^"(T"M,2)]^-0,812), (6.1.42)
где Tf = Tf(a,ju,i¥T,i%) = —lnh.
При г > а равенство (6.1.42) становится точным.
Пусть, как и в примере 6.1.3, т\ = 2, тогда
*>г
Если тэ =4, то
^=p(f<^)=Ff///fe)=Ff/7/(2) = 0,69.
P^=p(f<^)=Ff///fe)=Ff/f/(4) = 0,96.
(6.1.42')
(6.1.42м)
▲
6.1.11) Как видно из сравнения (6.1.38') с (6.1.42') и (6.1.39') с (6.1.42") в
условиях рассматриваемых примеров рандомизации функции распределе-
ния (6.1.36) по виртуальному целевому эффекту лишь незначительно уточ-
няет значение показателя эффективности РДЦ. Причём с ростом директив-
ного операционного времени тэ значения *ТРДЦ и *ТРДЦ сближаются. А
Итак, были получены оценки Рдц вероятности Рдц достижения цели
операции методом ведущих компонент при детерминированных требова-
ниях к результатам операции (по одному и по двум аспектам).
12 Зак. 3303

354
Глава 6. Комплексные функциональные модели ЦНП
Пусть теперь директивное операционное время тд случайно. Тогда
средняя (априорная) вероятность достижения цели
РДЦ=Р(т<тд)= \FtlH{r]dFtt{r).
(6.1.43)
Пример 6.1.7. В условиях примеров 6.1.2 и 6.1.4 формула (6.1.43) даёт
Рдц = ]Ч»(*КМ= Ъ-е-^Ч*-Ле-у('-М*-г'М* =
= Л(т>-г'д)-Н-ема<)
tia{i%-i%)
Ex{va{\-tfT))-Ex{ii(x{\-tf))-ln
1-tT
+ Л{т;-т)
JU + V
l-tfT
1-ft
Ма№-#т)
(6.1.44)
При а = 1, ju = l, #=0.3, tfr=0.9, v = l и < = 0.5 формула (6.1.44)
даёт
РДЦ =0.365, (6.1.44')
при тех же прочих условиях и^=1 формула (6.1.44) даёт
РДЦ =0.586. (6.1.44")
Из равенств (6.1.44') и (6.1.44") следует, что с ростом параметра т'л (т.е.
при снижении требований к оперативности ЦНПФС) вероятность Рдц дос-
тижения цели операции растёт. ▲
6.1.12) Заметим, что в отличие от (6.1.32) формула (6.1.44) охватывает
два случая: т'> т'д я г' < т'д. ▲
из-за
Б. Гарантируемая вероятность
В рассмотренном выше общем случае (% = 2, т.е. У,2. =(&,т})
громоздкости процедуры определения гарантируемой вероятности
й)ДЦ (у) = F~*t) (l - у) достижения цели операции по её поводу было выска-

6.1. Линейная функционально-стохастическая модель непрерывного ЦНП 355
зано лишь замечание (6.1.5). Теперь на основе метода ведущей компонен-
ты имеется возможность продемонстрировать методику её определения в
полном объёме. Схема применения методики подробно освещена в п. 3.3.3,
поэтому здесь для наглядности вновь будем исходить из условий примеров
6.1.1,6.1.2,6.1.5.
Пример 6.1.8. Пусть функции распределения виртуального (f) и ди-
рективного (fd) операционного времени определяются выражениями
(6.1.42) и (6.1.25) соответственно, т.е.
Ъ{т)~Р,1и{т)=Ь-е-м™]А{*-Л, (6-1.45)
Fjr)=[l-e-"(^)j4r-<). (6.1.46)
Тогда, положив со = &х = Ff (fd), согласно (3.1.48) получим
f»=fJf,-V)]=
-v('<)
{1-0))м
1-е
Теперь, подставив (6.1.47) в (3.1.82), будем иметь
П(а>;0 vFt{т'д),l)+A{a-l). (6.1.47)
+Р„ = й> = \a>dF&{a>)=^-e^A{T>-T'u)+\ \-^-
V e-M«-r-)
а согласно (3.1.68) получим
\4<-А
(6.1.48)
^M=F,[F,:'(l-r)]=
\-yve
v-/&-<)
[4<-/)+4/-<)4^И-г)1-
(6.1.49)
Пусть по-прежнему а = \, ju = l, $=0.1, $ = 0.3, $ = 0.9, v = l,
т'д =0.5, у = 0.9. Согласно (6.1.41), (6.1.42)
/=*-'(а,//,$,$)=-/ий = 0.812.
№
Тогда формулы (6.1.48) и (6.1.49) дают:
*Рдц=Ш = 0.366;
*^(r)=^^(r>=ar^l,(0.9)=0.0.
Если при тех же прочих условиях х\ = 1, то формулы (6.1.48) и (6.1.49)
дают:
*Р^=Й> = 0.586;
'rs;„w=^s;„(o.9)=o.254. а
6.1.13) Легко заметить, что соотношения (6.1.44) и (6.1.48) эквивалент-
ны, если учесть, что

356
Глава 6. Комплексные функциональные модели ЦНП
т.е. параметры (6.1.48) более агрегированы. А
6.1.4. АНАЛИЗ ЭФФЕКТИВНОСТИ ЦНПФС И КАЧЕСТВА ЦУТС
Как было показано в гл. 2, 3, 4, исследование эффективности ЦНПФС и
качества ЦУТС представляет собой триединую задачу (оценивания, анали-
за и синтеза).
В п. 6.1.3 были рассмотрены методики оценивания эффективности
ЦНПФС [а следовательно, и качества ЦУТС (см. п. 2.5)]. Что касается их
анализа, то, как отмечалось в п. 4.1, он включает в себя ряд аспектов, пре-
допределяющих методику его проведения в зависимости от объекта иссле-
дования (ЦУТС, ЦНПФС), задач исследования объекта (анализ, синтез) и
характера математической модели объекта [моделей элементов ОК (см.
гл. 5)]. Так, если объект исследования ЦУТС, то в качестве управляемых
(анализируемых) параметров модели фигурируют параметры и ЭТХ
ЦУТС, т.е. вектор U',n = A'J,^; если объект исследования ЦНПФС, то
фигурирует вектор U?r« = А?^; если исследуется влияние на качество
ЦУТС и эффективность ЦНПФС условий функционирования и примене-
ния ЦУТС, то фигурируют соответственно векторы U',f^-B',L и
UVL = ву!к. Однако поскольку в математической модели ЦНПФС (его ре-
зультатов) фигурируют параметры моделей всех элементов ОК, т.е. ком-
поненты всех перечисленных выше (четырёх) векторов, то соответствую-
щие им исследования могут осуществляться одновременно (совместно),
тем более что некоторые агрегированные параметры модели зависят от ха-
рактеристик нескольких (или даже всех) из отмеченных объектов исследо-
вания. Поэтому в дальнейшем объект исследования конкретизируется не
на этапе постановки задачи его анализа, а в ходе самого анализа при обсу-
ждении влияния его параметров и ЭТХ на эффективность ЦНПФС.
6.1.4.1. Анализ влияния условий применения ЦУТС
на эффективность ЦНПФС
Сразу заметим, что следует различать параметрический и аспектный
(обобщённый) анализы (см. (4.1.14)). В первом случае анализируется влия-
ние характеристик (параметров) В71к условий применения ЦУТС на пока-

6.1. Линейная функционально-стохастическая модель непрерывного ЦНП 357
затели РДЦ и соГдц (у) эффективности ЦНПФС, а во втором - влияние на
РдЦ и о)дЦ(у), определяемых условиями В^ директивных (потребных -
предельно допустимых) требований Z,, = Z,AB?rA [см. (2.3.9)] к резуль-
татам К» =F/ АА,куВ^л) операции. При этом в случае, когда вектор Z/.
случаен, анализируется влияние параметров его распределения и числовых
характеристик.
Для большей наглядности дальнейших рассуждений рассмотрим мето-
дику аспектного анализа ЦНПФС в условиях п. 6.1.3.1, т.е. при детермини-
рованных требованиях к результатам ЦНПФС (к их качеству) по двум ас-
пектам: результативности и оперативности, определяемых вектором
ZL = \z3X9zl) = (vT9td) в условиях примеров п. 6.1.3.
Пример 6.1.9. Пусть в условиях примеров 6.1.1, 6.1.2
где \v,t) ] и \vT,td) ] - носители распределений случайных векторов
K2v={(v,f)} и Z,2}={(vT,fd)\ соответственно, и пусть при этом а = 19
v = 0.2, jjl -1. Тогда средняя вероятность Рдц достижения цели операции
будет определяться равенством (6.1.28).
Для последовательности рг = Ргдц(vT,Td)= 0.3(0.1)0.9 значений веро-
ятности Рдц построим кривые, уравнения которых
тд=гд(ут;рг\ (6.1.50)
Графики этих кривых приведены на рис. 6.1.9.
Как видно из рис. 6.1.9, для каждого фиксированного значения рг веро-
ятности достижения цели операции кривая Т^ =тд\у^;рг) «изоэффа»
представляет собой компромиссное множество Парето уровня рг, элемен-
ты которого (ут>Р/ суть показатели гарантированного с гарантийной ве-
роятностью рг качества результатов операции.
Используя дополнительную информацию о директивных значениях
(vT,Td), можно по номограмме рис. 6.1.9 уточнять требования, предъяв-
ляемые к качеству операции, и прогнозировать ожидаемую её эффектив-
ность. А
На данном этапе анализа весьма полезно знать о степени влияния каж-
дого из аспектов (результативности, ресурсоёмкое™) на эффективность
операции и о возможностях управления ею через параметры vT и тд. Для

358
Глава 6. Комплексные функциональные модели ЦНП
этого определяются коэффициенты влияния и потенциалы управления по
формулам (4.1.19) и (4.1.21).
Рис. 6.1.9
Пример 6.1.10. В условиях примера 6.1.3 для v^=fll5, т"=4 будем
иметь:
дРЙ
ЭР
U;t=fa\fvt | = 0.727;1
>
U' = \h' |Lrd = 0.049.
Для И=0.8,т? = 2
И/ = h' v! = -0.874 * 0.8 = -0.595; I
vT vT i |
F£ = Л* т* = 0.0835 * 2 = 0.167;
(6.1.51)
(6.1.5Г)
(6.1.52)

6.1. Линейная функционально-стохастическая модель непрерывного ЦНП 359
и; = \h" LfvJ = 0.874 * 0.6 = 0.524;]
, ! (6Л.52')
U;t = |*£ \\Att\ = 0.0.835 * 4 = 0.334. J
Из равенств (6.1.51) и (6.1.5 Г) видно, что, с одной стороны, эффектив-
ность операции в большей степени зависит от требуемой результативно-
сти. А с другой - возможности управления эффективностью через эту ха-
рактеристику также высоки. А
6.1.14) Следует заметить, что результаты (6.1.51), (6.1.5 Г), а следова-
тельно, и выводы по ним зависят от номинальных значений М-,1%) пара-
метров (vT,Td), при которых вычисляются рассмотренные характеристики.
Наконец, весьма полезными могут оказаться характеристики замещения
операционных аспектов показателя \УгТ9^1) гарантированного качества ре-
зультатов операции.
Пример 6.1.11. В условиях примера 6.1.3 показатель предельной нормы
замещения определяется по формуле (4.1.26) при V* =(Х5, т° = 4 примет
значение
I>t =|L = _K = M^ = 0.081, (6.1.53)
VtT' дтд hpVr 1.212
а при v' =018, т' = 2 - примет значение
3>, = А = -^ = М835 = а096. (6.1.53')
Л Эгд н;т 0.874
Как видно из соотношений (6.1.53) и (6.1.53'), для компенсации потери
эффективности операции за счёт недостаточной результативности необхо-
димо в среднем десятикратное увеличение оперативности ЦНПФС. А
6.1.15) Характеристики (4.1.25) - (4.1.28) позволяют проводить ещё бо-
лее тонкий анализ эффективности ЦНПФС. С примерами такого анализа
можно ознакомиться в монографии [59]. Однако следует иметь в виду, что
применительно к задаче исследования эффективности ЦНПФС в отличие
от [59] в формулах (4.1.23) - (4.1.28) фигурируют «параметрические ре-
сурсы», а роль продукта играет эффективность (Рдц) операции. Рекомен-
дуем читателю в качестве упражнения провести такой анализ в условиях
приведённых примеров. А
6.1.16) Следует напомнить, что согласно постулату (5.3.4) ЭР-функции
рис. 6.1.5 выпуклы и, следовательно, выпукло множество {(vj.,r^)} дирек-

360
Глава 6. Комплексные функциональные модели ЦНП
тивных результатов операции гарантированного качества. Другими слова-
ми, допустимые значения (удт,тдд) показателя (угт,тгд), обеспечивающие
вероятность достижения цели операции не ниже рг, лежат выше и левее
компромиссного множества Парето уровня рг. В условиях примера 6.1.8
это множество представляет собой компромиссную кривую [162]. А
6.1.17) Иногда [84, 177] аспекты называются критериями1, а простран-
ство аспектов - пространством критериев [84]. В рассматриваемом приме-
ре 6.1.8 пространством аспектов является плоскость vT0td. A
6.1.4.2. Анализ влияния на эффективность операции
параметров и ЭТХ ЦУТС и ЦНПФС
В общем случае данная задача может решаться и в условиях примера
6.1.8, т.е. при детерминированных требованиях (у1,г3д\ к результатам опе-
рации. Решение, наиболее адекватное реальной операционной ситуации,
может быть получено путём анализа соотношения (6.1.32). Однако из-за
его громоздкости пострадает наглядность рассматриваемой методики. По-
этому последующее изложение основано на методе ведущих компонент,
т.е. на определении вероятности РДЦ достижения цели операции с помо-
щью соотношения типа (6.1.44) или более агрегированного выражения
(6.1.48). Для наглядности по-прежнему будем проводить анализ в рамках
примеров 6.1.1, 6.1.2, 6.1.7, 6.1.8.
Пример 6.1.12 Пусть эффективность ЦНПФС оценивается в условиях
примера 6.1.8 по формуле (6.1.48), т.е.
дц ju + v K д)
JU + V
А(т'д-т'). (6.1.54)
Требуется провести анализ влияния параметров ОК на эффективность
ЦНПФС. Для решения этой задачи прежде всего следует выявить, через
какие агрегированные параметры ЦНПФС влияют на его эффективность
параметры элементов ОК.
В условиях рассматриваемой модели (см. примеры 6.1.1 и 6.1.2) для её
агрегатов имеют место следующие соотношения:
Подобное словоупотребление нельзя считать корректным (см. (2.2.5)).

6.1. Линейная функционально-стохастическая модель непрерывного ЦНП 361
а - а [А^ у A(k.j, В^);
v' = АА(иуА(куВ(г)>В(0) *
V =V \A(k')>A{kyB(l')>B(l'))i [
Т = Т [А^ у А^ у В^ у В^);
// = // \Ащ у А^ у В^ у В^); J
vT = vT [Ащ у A(k.j у В^);
vT = vT [A^ у А^ у В^);
v = v(B{r)). J
Прокомментируем соотношения (6.1.55) в рамках одной из возможных
их интерпретаций. Легко заметить, что равенства (6.1.55) описывают зави-
симости от параметров ЦУТС и ЦНПФС и условий проведения операции
агрегированных параметров модели операционной системы (МОС), а ра-
венства (6.1.55') - зависимости агрегированных параметров модели опера-
ционной ситуации (МОСТ) (см. рис. 5.2.1, 5.2.2).
Так, поскольку а характеризует ресурсоёмкость лежащей в основе
ЦНПФС технологии, а а'1 - его производительность, то этот агрегат зави-
сит от параметров и ЭТХ ЦУТС \А',к*), от организации ЦНПФС [А7к^)9 а
также от условий [В^) функционирования ЦУТС, влияющих на её ЭТХ и
параметры ЦНПФС.
Функциональные возможности ЦУТС характеризуются её способно-
стью давать целевой эффект v. Поэтому параметры v , v" распределения
целевого эффекта v являются агрегатами его модели и, естественно, зави-
сят от параметров и ЭТХ ЦУТС, т.е. от А^*, которые, в свою очередь, за-
висят от условий Вц* функционирования ЦУТС, а также от организации
ЦНПФС, т.е. от А?к*, которая зависит от условий проведения операций,
т.е. как от BLk , так и от В^.
Что касается агрегатов - параметров модели временных задержек f,
возникающих в ходе операции, то из анализа порождающих их причин (см.
п. 6.1.1) следует, что в общем случае они зависят как от параметров ЦУТС
и ЦНПФС, так и от характеристик условий проведения операции.
(6.1.55)
(6.1.55')

362
Глава 6. Комплексные функциональные модели ЦНП
Теперь о соотношениях (6.1.53). Хотя в них в качестве аргументов ос-
новную роль играют характеристики BZ* условий применения ЦУТС, тем
не менее агрегаты - параметры МОСТ в общем случае зависят и от ЭТХ
ЦУТС, и от организации ЦНПФС.
Так, например, требования vT и тд, предъявляемые к целевому эффекту
v и операционному времени f, могут задаваться с учётом операционной
ситуации (см. (5.2.7)). Другими словами, параметры v'T, Vj и т'д, v распре-
делений требуемого целевого эффекта vT и директивного операционного
времени тд в общем случае могут зависеть от всех характеристик
(А' 9А" ,В' 9В") = X, у Аналитические выражения таких зависимостей мо-
гут быть получены лишь при исследовании конкретных ЦУТС и ЦНПФС
путём проведения их статистических испытаний или имитационного моде-
лирования. Поэтому соотношения (6.1.52) и (6.1.53) носят концептуально-
иллюстративный характер и более детально рассматриваться не будут, т.е.
в дальнейшем будут по-прежнему рассматриваться агрегированные пара-
метры модели элементов ОК. А
Для иллюстрации методики анализа ЭТХ ЦУТС и ЦНПФС будем пред-
полагать, что управляемыми являются лишь параметры а и ju = 1/т, , ха-
рактеризующие соответственно ресурсоёмкость (производительность)
ЦНПФС и функциональную надёжность (ЦУТС) (см.(6.1.1)), т.е.
V (г) =(<*>/*)•
Начнём параметрический анализ ЦУТС и ЦНПФС с определения харак-
теристик чувствительности и влияния в условиях п. 6.1.3.3 и примера 6.1.7.
Пример 6.1.13. Полагая в выражении (6.1.44) тд>т', по формулам
(4.1.4), (4.1.19), (4.1.21),(4.1.26) при |^о| = 0.5, |^//| = 0.5 получим:
а да
= -0.3403;
й'=^- = 0.2805;
м Ъц
Vpa = К = -0.3403;
VMP =Л;= 0.2805;
Upa =\K\Ac\ = 0.1701;
#;=|й;|л7/| = 0.1402; J
(6.1.56)
(6.1.57)
(6.1.58)

6.1. Линейная функционально-стохастическая модель непрерывного ЦНП 363
Д=0Л805 = а824
«* hpa 0.3403
Из приведённых равенств следует, что на эффективность операции
сильнее влияет ресурсоёмкость ЦНПФС, чем функциональная надёжность
ЦУТС. В связи с этим выше потенциал управления по параметру а, чем
по параметру ju, а также предельная норма замещения ресурса параметра
а ресурсом параметра /л меньше единицы, т.е. из (6.1.59) следует, что
для компенсации изменения ju на единицу, а достаточно изменить на
0.824.
Следует иметь в виду, что сформулированные выводы носят частный
характер и справедливы лишь в рамках рассмотренного примера. А
Продолжим параметрический анализ ЦУТС и ЦНПФС, построив в про-
странстве aOju компромиссные множества (кривые) Парето, определяе-
мые изоквантами - изоэффами (см. п. 4.1.3) в условиях п. 6.1.3.3 и приме-
ра 6.1.7.
Пример 6.1.14. На рис. 6.1.10 приведены построенные в условиях
предшествующих примеров «изокванты» и «изокосты» показателя РДЦ
эффективности операции, уравнения которых соответственно
Рдц = (а>м)=Рг = 0.1(0.1)... (6.1.60)
hZ(aE-a)+h£(juB--ju)=p3= 0.l(0.l)... (6.1.61)
Кривая, соединяющая точки касания изоквант и изокост, представляет
собой траекторию «наиболее экономичного» управления эффективно-
стью ЦНПФС через параметры а и ju (см. п. 4.1.3). ▲
Как видно из рис. 6.1.10, вероятность Рдц достижения цели операции
растёт по мере роста параметра ju и убывания параметра а. Если парамет-
ры а и ju можно считать взаимно независимыми1, то область их допусти-
мых значений (ОДЗ) будет представлять собой прямоугольник, т.е.
{(аэ,//э)}=[а>1х[У,/Г],
нижняя и правая границы которого соответствуют "наилучшим" значениям
параметров а и ju соответственно, а верхняя и левая - их "наихудшим"
значениям. Поскольку при решении задачи синтеза ЦУТС и ЦНПФС эф-
фективность операции оптимизируется (максимизируется), а функция
Рдц{ос,]и) монотонна по обоим аргументам, то в качестве ОДЗ вектора
1 Поскольку как ОС, так и JU зависят от параметров ЦУТС и ЦНПФС [см. (6.1.55)],
то в общем случае они зависимы.

364 Глава 6. Комплексные функциональные модели ЦНП
а
а"
7
6
5
4
3
2
Рис. 6.1.10
(от,//) может рассматриваться расширенная область
{a\MS)}=[<x',~)x[0,M"l
На этом закончим рассмотрение методики анализа качества ЦУТС и
эффективности ЦНПФС. Понятно, что задача не исчерпывается рассмот-
ренными примерами и при необходимости её решение может быть про-
должено как вширь, так и вглубь. Однако рамки монографии этого не по-
зволяют. Заинтересованный читатель может легко это сделать самостоя-
тельно.
6.1.5. СИНТЕЗ ЭФФЕКТИВНОГО ЦНПФС
И КАЧЕСТВЕННОЙ ЦУТС
Перейдём к рассмотрению методики решения обратной задачи исследо-
вания ЦУТС и ЦНПФС, целью которого является определение значений их
параметров и ЭТХ, обеспечивающих максимальную или "требуемую" эф-
фективность операции.
Рх=0Л

6.1. Линейная функционально-стохастическая модель непрерывного ЦНП 365
Как отмечалось в п. 4.2, методика решения обратной задачи зависит как
от характера функции РДЦ\и,Л показателя Рдц эффективности операции
от управляемых параметров U,, так и от формулировки задачи синтеза.
Рассмотрим различные её варианты, по-прежнему опираясь на операцион-
ную ситуацию, сформулированную в п. 6.1.1 и примерах 6.1.1, 6.1.2, 6.1.7.
6.1.5.1. Синтез по критерию пригодности
Синтез ЦНПФС и ЦУТС по критерию пригодности производится путём
неформального анализа пространства \U?A "эффективных по Парето"
значений I/Л вектора управляемых параметров. Как было показано, "эф-
фективные" точки U?к лежат на изоэффах и, следовательно, задача синтеза
сводится к отысканию на них в каком-то смысле наилучшей точки, отве-
чающей дополнительным условиям, не вошедшим в формулировку задачи.
Проиллюстрируем сказанное на примере.
Пример 6.1.15. Пусть выполняются условия примеров 6.1.7, 6.1.12 и
построено семейство кривых (рис. 6.1.10). Требуется определить значения
a", ju" параметров a, ju, обеспечивающие вероятность /^достижения
цели не ниже РТДЦ.
Решение. Любая точка принадлежащая ОДЗ
W(i)}- \\°^*Мд)\ и удовлетворяющая неравенству
РДЦ{апфп)>РТР, (6.1.62)
будет отвечать критерию пригодности ЦНПФС и ЦУТС, однако меньшим
затратам на управление параметрами an, jun отвечают точки кривой
pw{(x,m)=pZ. (6.1.63)
метров а"', цп , удовлетворяющие системе уравнений
При этом наиболее "экономичными" являются значения аэ, //эпара>
шетворяющие си
Рдц{аф) = РТдц->
h
h>a(a°-a)+h№-n)=P", | (6,L64)

366
Глава 6. Комплексные функциональные модели ЦНП
6.1.5.2. Синтез по критерию оптимальности
Для наглядности вновь обратимся к примеру.
Пример 6.1.16. Пусть выполняются условия примеров 6.1.7, 6.1.12 и
построено семейство кривых (рис. 6.1.10).
Требуется определить значения а0, //° параметров а9 ju, обеспечи-
вающие максимальное (наибольшее) значение PJ}™ вероятности РДЦ дос-
тижения цели операции.
Решение. Поскольку функция Рдц(ос,]и) монотонна по обоим аргу-
ментам, то наибольшее её значение достигается на границе области
{(аэ,//э)|. Поэтому, как следует из рис. 6.1.10, искомые значения парамет-
ров а и ju определяются равенством
(а\//°) = (*>"). (6.1.65)
А
6.1.5.3. О приближённом синтезе
Как отмечалось в п. 4.2.3, приближённый синтез основан на аппрокси-
мации функции Рдц \fj,r)) линейной или полиномиальной функцией и при-
менении известного метода математического программирования (см.
п. 4.2.3).
Пример 6.1.17. Пусть вероятность Рдц достижения цели операции оп-
ределяется равенством (6,L44) и пусть т'д>т'. Будем считать, что в преде-
лах области [a/,al?Jx[//i?,////J функция (6.1.44) мало отличается от линей-
ной. Проведём её линеаризацию, для чего разложим её в ряд Тейлора в ок-
рестности точки (аБ,// у [где аБ, juB - базовые (расчётные, номиналь-
ные) значения параметров a ,fi] и сохраним в разложении лишь линейные
члены [см. (4.2.26)].
В результате получим следующее линейное представление показателя
эффективности операции как функции параметров a ,ju :
Рдц{а,м)~Рдц(аБ,мБ)+К(аБ
(6.1.66)
Как видно из уравнения (6.1.66), описываемые им прямые представляют
собой изокосты [ср. с (6.1.61)], т.е. линии уровня затрат параметрических
ресурсов.

6.1. Линейная функционально-стохастическая модель непрерывного ЦНП 367
Поскольку градиент функции РДЦ{ос,/1) направлен вправо-вниз, то ре-
шение задачи линейного программирования (ЗЛП) при
|(a<,,//d)j=[cir/,oo)x[0,//>5f] даёт в качестве оптимального то же значение
(a0 ,ju°) = (#',//") вектора (a,ju). A
6.1.18) Если параметры а и ju взаимно зависимы, то их ОДЗ \UL\
будет иметь более сложные, чем на рис. 6.1.10, очертания и задача отыска-
ния оптимального значения U?2\ усложнится. В этом случае границы об-
ласти \Ut\\ (в общем случае области {#£)]) аппроксимируются линейны-
ми функциями, после чего задача вновь может быть сведена к ЗЛП. А
6.2. НЕЛИНЕЙНЫЕ ФУНКЦИОНАЛЬНО-
СТОХАСТИЧЕСКИЕ МОДЕЛИ НЕПРЕРЫВНЫХ
ЦЕЛЕНАПРАВЛЕННЫХ ПРОЦЕССОВ
Прежде всего заметим, что рассматриваемые в данном параграфе моде-
ли принадлежат, как и предыдущая линейная модель, классу функцио-
нально-стохастических моделей целенаправленных процессов непрерыв-
ного типа. Поэтому основные системные свойства всех этих моделей ана-
логичны. Особенностью моделей, рассматриваемых в данном параграфе,
является нелинейная зависимость виртуального целевого эффекта опера-
ции от технологического времени, обусловленная свойствами ЭР- и
РЭ-функций (см. п. 5.3.1) и являющаяся принципиальной для широкого
класса ЦНПФС.
Поскольку линейная функционально-стохастическая модель (ЛФСМ)
была достаточно подробно рассмотрена в п. 6.1, то применительно к нели-
нейным моделям (НФСМ) будут реализованы лишь этапы построения ма-
тематической модели показателя виртуального качества результатов
ЦНПФС. Поэтому знакомству с НФСМ должно предшествовать внима-
тельное и подробное изучение ЛФСМ.
6.2.1. ФУНКЦИОНАЛЬНО-СТОХАСТИЧЕСКАЯ МОДЕЛЬ
НЕПРЕРЫВНОГО НОРМАТИВНОГО ЦНП
Определение 6.2.1. Модель операции, достижению цели которой со-
путствует увеличение целевого эффекта, называется нормативной (НМ).
А

368
Глава 6. Комплексные функциональные модели ЦНП
Соответствующий этой модели ЦНП также называется нормативным
(МНЦНП). Физический смысл данного определения будет ясен из содер-
жательного описания рассматриваемого ЦНПФС и его модели.
6.2.1.1. Содержательная (вербальная) постановка задачи
Некоторая ЦУТС функционирует в условиях п. 6.1.1 с тем отличием, что
при нормальном течении ЦНПФС по мере накопления целевого эффекта
производительность ЦУТС (темп освоения ресурсов) падает (см. п. 5.3.1).
Это весьма распространённая на практике ситуация, называемая иногда
"эффектом насыщения ресурсами", проявляющаяся в том, что по мере
приближения относительного целевого эффекта v к единице (т.е. к макси-
мально возможному абсолютному эффекту) производительность (удельная
отдача [59]) ресурсов падает.
6.2.1) Напомним, что в рамках рассматриваемых в данной главе моде-
лей целевой эффект ve [ОД]. Это свойство целевого эффекта v не обяза-
тельно, но придаёт модели показателя F,3v качества результатов операции
кроме большой наглядности целый ряд других положительных свойств
(см. п. 6.1.2). А
Требуется построить математическую модель показателя }L качества
результатов операции.
6.2.1.2. Построение агрегированной математической
модели ЦНПФС
Пусть, как и в п. 6.1.2, операционное время г представимо в виде суммы
г = г0(у;Л(5о))+гДм(,1)), (6.2.1)
где сохранены обозначения (6.1.1). При этом в отличие от (6.1.6)
ЭР-функция т0 =T0(v) нелинейна.
Как можно было заметить, в модели п. 6.1.2 в качестве генеральной ком-
поненты показателя K2v = (yt,у3) = (v,f) фигурировал целевой эффект v.
6.2.2) Как отмечалось (см. п. 5.4.1), роль "генерального аргумента"
(ГА) - "генеральной компоненты" (ГК) призвана играть компонента векто-
ра F/v или её составляющая), вероятностные характеристики которой из-
вестны (или могут быть определены), что, в свою очередь, обусловлено

6.2. Нелинейные функционально-стохастические модели непрерывных ЦНП 369
физической сущностью рассматриваемого ЦНПФС. Так, для ПФ системы
наблюдения некоторого разведывательного признака - это, скорее, техно-
логическое время f 0; для ПФ информационно-вычислительной системы -
это относительная полнота v ответа на запрос и т.п. А
Пусть для разнообразия в рассматриваемом случае роль "генерального
аргумента" выполняет технологическое время f0. Это означает, что из-
вестны законы распределения <pf (т) и <pf (т) технологического времени f0
и временной задержки f,. Требуется определить закон распределения
Фут{Уг>У*) = %,)М= P[(v > v)n(f < т)]
показателя iL = (ух, уъ) = (v, f) виртуального качества результатов
ЦНПФС.
Весьма распространённой и достаточно адекватной моделью операци-
онной функции "нормативного ЦНП" является показательная РЭ-функция
вида
iJ = »(f)=v(f)=ll-€-A(*b|f)]^(f-<), (6.2.2)
где т\ =TZ\f£,r£;Aikx,Btft) - технологическое время, расходуемое на опе-
рации обеспечения ЦНП (подготовки, кон-
троля, управления и т.п.) - "агрегат";
Л = Л(г2%г3%#Л,^,2?'(/')) - агрегированный параметр (ЭТХ) модели
ЦНПФС- "агрегат".
6.2.3) Функция
и(г-<)=Л.(г-<)= )z(t)dt (6.2.3)
или при X{t) = Я = const
и(т-<)=Л.(г-<) (6.2.3»)
часто называется "целевым потенциалом" или "потенциалом целевого
действия" (ПЦД) ЦНПФС (ЦУТС). Так, если ЦНПФС - процесс наблюде-
ния (например, некоторого разведывательного признака) и Z(t) - его ин-
тенсивность, то uyv-rl) называется "потенциалом наблюдения" (см.
гл. 7, п. 6.3 и [3]). Если ЦНПФС - обстрел объекта (цели) противника; v -
наносимый объекту относительный ущерб, X{t) - интенсивность потока
поражающих объект выстрелов, то и[т — т%) называется "потенциалом по-
ражения" (см. [48, 130]). А
Пусть технологическое время f 0 подчинено равномерному закону рас-
пределения на интервале (г^,Гд], т.е.

370
Глава 6. Комплексные функциональные модели ЦНП
nW-ft'M.O-^?2. (6-2-4)
П-П
где т'„ и г, - "агрегаты" [см. (6.2.2)],
и пусть по-прежнему
^,W=^OTl(f;y",<)=>"^(r-<)4t-<), (6.2.5)
где JU и т[ - "агрегаты"
ц = //Цл), Я('г)); < = т[{А{к)9В[п).
Будем искать плотность распределения случайного вектора (v,f) по
формуле
<PtwU^3) = ^,,)(v^) = ^(v)^(r;v) . (6.2.6)
С учётом соотношения (6.2.2)
(\ г / Mi ^/ м n(v;v',v") я(у;0,1-*"А(<~о) ,, „ч
Поскольку при фиксированном значении v целевого эффекта v
и, следовательно,
^o=<-jtn{l-v)
f = T0+f1=<-|/«(l-v)+f1,
(6.2.8)
то согласно (6.1.12), (6.2.5) и (6.2.8)
<РФ {г; v) = <Ptjt (*; v) * <ph (т) = ^fr - < + j /и(1 - v)J * pt> (т)=
-^[r-<-li+i/n(l-v)
*■-<-<+-/n(l-v)
(6.2.9)
где * - символ композиции законов распределения.
Подставив (6.2.7) и (6.2.9) в (6.2.6), будем иметь
хА\ r-T'l-T'0+—ln(l-v)
L ™
Наконец, проинтегрировав (6.2.10), окончательно получим
0{i,f)(v,r)=P[{v > v)D (f < т)]= J )<p{.i{)(v,r)dvdT =
. (6.2.10)

6.2. Нелинейные функционально-стохастические модели непрерывных ЦНП 371
= \ч>*Щ \ч>цАъ*)*т
dv =
1_
1-е { х >
о "о
V
T-<-< + -/n(l-v)-
/J
П{т;т'9 +<,< + <)+
+
/ 1 / \ 1 ( ,,(Г г' г-\ -м(г-<-<*\и^-»))
<-<+т/и(1_у)--К е
j(r-<-<)
X
*•"*.
х
хЯ(т;< + <,< + <)+
Л(т-т;-т') х
То'_т; _1(в-/.<~:-«> _е-/.(~{-<>)1
- № J J
x^(-v). (6.2.11)
Соотношение (6.2.11) [аналог соотношения (6.1.23)], представляющее
собой вероятностную модель показателя Y,^ =(v9i) виртуального качест-
ва результатов операции, в то же время является агрегированной моделью
ОС и реализуемого ею ЦНПФС. Дальнейшее его использование осуществ-
ляется по методике, изложенной в п. 6.1.
6.2.4) Если временные задержки отсутствуют, т.е. f, = 0, то f = f0 и,
следовательно,
^Н = ^Д^) = ^^Я(г;<,<)+4^-<) • (6.2.12)
Поскольку целевой эффект tf и технологическое время f0 связаны
функционально, т.е.
v = l-e
-Л(**-т'о)
ТО
f0=r;;-i//»(i-v)
и согласно теореме 5.4.1
0m{v^Fit(r)-FjT(v)] = Ffu{T)-FfU-^ln{l-v)
T + -ln(l-v)-t'e
- -Ь Я (r;<,<)tf(v;0,l -<Г^>)+
т"-т'
т-т,
LT0-70
^Я(т;<,<)+47-<)
4-v)+

372
Глава 6. Комплексные функциональные модели ЦНП
А{т-т;). (6.2.13)
6.2.2. ФУНКЦИОНАЛЬНО-СТОХАСТИЧЕСКАЯ МОДЕЛЬ
НЕПРЕРЫВНОГО ДИРЕКТИВНОГО ЦНП
Определение 6.2.2. Модель операции, достижению цели которой со-
путствует уменьшение целевого эффекта, называется директивной (ДМ).
▲
Соответствующий этой модели ЦНП также называется директивным
(ДЦНП). Физический смысл данного определения будет ясен из содержа-
тельного описания рассматриваемого ЦНПФС и его модели.
6.2.2.1. Содержательная (вербальная) постановка задачи
Некоторая ЦУТС функционирует в условиях п. 6.1.1 с тем отличием,
что собственно целевой эффект v количественно заведомо удовлетворяет
предъявляемым к нему требованиям, т.е.
{v>vT)=U => P{v>vT)=l ,
но его соответствие по качеству является случайным. При этом с ростом
технологического времени качество целевого эффекта растёт, однако ин-
тенсивность его повышения ("производительность" ЦУТС - темп освоения
ресурсов) с течением времени падает. Подобная ситуация имеет место, ко-
гда качество целевого эффекта характеризуется его "точностью". Такой
характеристикой чаще всего является величина ё абсолютной погрешно-
сти (оценивания, измерения, вычисления и т.п.), которая является убы-
вающей функцией затрат ресурсов г2°, г3° и технологического времени f 0.
Требуется построить математическую модель показателя виртуального
качества результатов операции.
6.2.2.2. Построение агрегированной математической
модели ЦНПФС
Пусть, как и в п. 6.1.2, операционное время т представимо в виде суммы
* = *o\?;A(s,)kb{M{Si)), (6.2.14)

6.2. Нелинейные функционально-стохастические модели непрерывных ЦНП 373
где сохранены обозначения (6.1.1). При этом в отличие от (6.1.6)
ЭР-функция т0 = т0(е) - нелинейна.
Поскольку с ростом длительности г0 измерений точность оценивания
наблюдаемого признака растёт, то при минимальных временных затратах
т'0 ошибка е" = ем - максимальна и с увеличением технологического вре-
мени т0 до максимального т^ она монотонно убывает до минимальной е'.
Систему оценивания можно интерпретировать как систему автомати-
ческого управления (САУ) [132], в которой ошибка е измерения является
аналогом сигнала рассогласования устойчивой линейной системы, описы-
ваемого дифференциальным уравнением вида
e(t) = -Ae(t),
решение которого
e{t) = eMe-*A(t), (6.2.15)
где ем =£(0).
Положив в (6.2.15) t = г - т[ , будем иметь
е = e{t)=R{t)=eMe-l{-{<)A{i-<) , (6.2.16)
где Tq - минимальное значение технологического времени, необходимого
для получения целевого эффекта (с максимальной погрешностью
ем) - "агрегат", характеризующий трудоёмкость измерений,
Я - агрегированный параметр (ЭТХ) модели, характеризующий ин-
тенсивность измерений в данном ЦНПФС - "агрегат",
А = Л(г2\г?;А{к),В'{П).
6.2.5) По аналогии с примерами из (6.2.3) функция u(t-t[) = A,(t-t[)
может быть названа "потенциалом оценивания (измерения, вычисления и
т.п.)". А
6.2.6) В принципе качество целевого эффекта может быть охарактери-
зовано также величиной v = 1/ё, обратной к относительной погрешности,
или относительной величиной V = \ё - sM\jeM отклонения абсолютной по-
грешности от максимальной, и, таким образом, "директивная" модель
ЦНПФС может быть сведена к "нормативной". Однако в результате такой
замены может пострадать физическая сущность задачи и, как следствие,
формулировка цели операции (так как к величинам v , v" трудно предъя-
вить обоснованные требования) и интерпретация результатов исследова-
ния её эффективности, поскольку величины v и ё, хотя и связанные меж-

374
Глава 6. Комплексные функциональные модели ЦНП
ду собой (через операционный функционал), но независимые (самостоя-
тельные) компоненты показателя ГДу результативности ЦНПФС. А
Пусть генеральным аргументом является технологическое время f0 ,
подчинённое равномерному закону распределения с параметрами т'0, т^,
т.е.
^Jr)=^Hr;<,<) = ^%^5 (6.2.17)
*•-*•
где г0 и г0 - "агрегаты",
Временная задержка может быть обусловлена целым рядом случайных
факторов, таких, как пропуски измерений из-за флуктуации полезного сиг-
нала, сбои в работе аппаратуры и операторов, циклический режим переда-
чи результатов измерений (см. п. 6.3 и гл. 7) и т.п. Поэтому в зависимости
от характера факторов, обусловливающих задержку, она включает в себя
две составляющие: технологическую (детерминированную) т\ и чисто
случайную f,', т.е. f х = г[ + f[ .
Хорошей моделью случайной составляющей т[ временной задержки f,,
соответствующей постулату 5.3.4, является показательный закон распреде-
ления^ при котором суммарная временная задержка имеет смещённое пока-
зательное распределение с плотностью
^r) = pfW,<) = /^(~;)4r-<), (6-2.18)
где ju и г[ - "агрегаты",
М = м[А{к),В'{г)); t[ = r[{A{k)9B[v)).
Требуется определить закон распределения
Ffm(yt,y3)=Fm{e,T) = P[{e<e)n{f<T)}
показателя K2v = (j>,, j>3) = (ё, t) виртуального качества результатов
ЦНПФС.
Будем искать плотность распределения случайного вектора (ё9т) по
формуле
^(1)(УпЛ) = ^>^) = л(^)Л/*^)- (62Л9)
С учётом соотношения (6.2.14)
Поскольку при фиксированном значении е ошибки ё оценки

6.2. Нелинейные функционально-стохастические модели непрерывных ЦНП 375
и, следовательно,
1 €
(6.2.21)
то, согласно (6.1.12), (6.2.18) и (6.2.21)
(
-"■'^
^
-А(г-<-т',)/
/ _' .1 , ^
т-т1-т0+-/и— .
Л £„ )
(6.2.22)
Подставив (6.2.20) и (6.2.22) в (6.2.19), будем иметь
хА\т-т1-тй + —1п—
* ем J
(6.2.23)
Наконец, проинтегрировав (6.2.23) в соответствии с физическим смыс-
лом "целевого эффекта" ё, окончательно получим
Fm{e,r)=P[{e<e)^{f<t))= ))<р{ф,т)йейт =
1 / , , 1. е 1
1-е { х £м)
П\
7;r0 + т, - -/и—,т0 + т, - -/«—
л е^ я ем)
**-<Л*тА
хЛ\
х<
Я ем)1 7о~то
«■-*;-<--(l-e~*(M{_,;))
+
к7-<-<)№"^)- (6-2.24)

376
Глава 6. Комплексные функциональные модели ЦНП
Соотношение (6.2.24) [аналог (6.1.23)] представляет собой вероятност-
ную модель показателя К2ч=(£,г) виртуального качества результатов
операции и в то же время является агрегированной моделью ОС и реали-
зуемого ею ЦНПФС. Дальнейшее её использование осуществляется по ме-
тодике, изложенной в п. 6.1.
6.2.7) Если временные задержки отсутствуют, т.е. f, = 0, то f = f0 и,
следовательно,
Ft{r) = Fu{r)= T^tf(r;<,<)+4r-<) • (6-2.25)
7о-*"о
Поскольку "целевой эффект" £ и технологическое время t0 связаны
функционально, т.е.
ТО
и согласно теореме 5.4.1
F{lJe,T)=F{>{t)-F{}rM=PfM)-Fit
(
1
Ч Л £м
1, е
% П(т;т;,т;)п(е;еме-*«-<Кем)+
тЛ-тЛ
?-£м)
\л(т-т:)+
т-т,
.*•-*■.
\п{т;т[,т:)+А{т-т;)
А(е-ем)
(6.2.26)
▲
6.2.3. ФУНКЦИОНАЛЬНО-СТОХАСТИЧЕСКАЯ МОДЕЛЬ
НЕПРЕРЫВНОГО НОРМАТИВНО-ДИРЕКТИВНОГО ЦНП
Определение 6.2.3. Модель операции, достижению цели которой со-
путствует увеличение одних и уменьшение других компонент показателя
YP\ целевого эффекта, называется нормативно-директивной (НДМ). ▲

6.2. Нелинейные функционально-стохастические модели непрерывных ЦНП 377
Соответствующий этой модели ЦНП также называется нормативно-
директивным (НДЦНП). Физический смысл данного определения будет
ясен из содержательного описания ЦНПФС и его модели.
6.2.3.1. Содержательная (вербальная) постановка задачи
Некоторая ЦУТС, параметры и ЭТХ которой описываются вектором
Л!к*9 проводит операцию (ЦНПФС), параметры и ЭТХ которой описыва-
ются вектором А^к.у в условиях, описываемых векторами В',* (условия
функционирования ЦУТС) и В"^ (условия применения ЦУТС).
Виртуальное качество результатов операции описывается в комплекс-
ной канонической форме и характеризуется вектором
Y -Y -F -Y -lf(x) F(2) F(3)\-/v(,) v(l) v(2) v(3)\ -/v £ Я f\
где v - величина целевого эффекта (в относительных величинах);
€ - отклонение качества целевого эффекта от номинального;
г - суммарный расход операционных ресурсов различных видов;
f - операционное время;
= - знак символического равенства.
Особенностью рассматриваемого ЦНПФС является то, что технологи-
ческий процесс состоит из двух последовательных стадий (фаз). На первой
стадии создаётся "валовой" целевой эффект v (подвозится сырьё, делаются
заготовки, собирается информация, фиксируются данные об объектах на-
блюдения и т.п.), а на второй стадии, путём обработки исходного материа-
ла (сырья, заготовок, информации, данных и т.п.) целевому эффекту при-
даётся необходимое качество, характеризуемое погрешностью е целевого
эффекта. При этом длительности f 0 и f, стадий процесса взаимно незави-
симы, а следовательно, независимы и величины v и ё. Кроме того, как и в
предшествующих моделях, материально-технические ресурсы (г) под-
вергнуты воздействию "эффекта поглощения" (см. пп. 3.3.4 и 6.1.2).
Для достижения цели операции необходим целевой эффект не менее vT,
с отклонением по качеству, не превосходящим ед; за время, не превосхо-
дящее тэ ; запас операционных ресурсов равен г.
В ходе операции возможны временные задержки, обусловленные раз-
личными факторами (см. п. 6.1.1 и (6.1.1)).
Требуется построить математическую модель операционной системы
(её элементов), позволяющую решать задачи анализа ЦУТС и ЦНПФС и
их синтеза по критериям требуемой или максимальной эффективности
операции.

378
Глава 6. Комплексные функциональные модели ЦНП
6.2.3.2. Построение агрегированной математической
модели ЦНПФС
Сформулированная в п. 6.2.3.1 операционная ситуация носит весьма
общий характер и может служить вербальной моделью широкого класса
операций, реализуемых ЦУТС различного назначения.
Как следует из содержательной постановки задачи, в рассматриваемом
случае операционное время представляет собой сумму трёх взаимно неза-
висимых (независимых в совокупности) слагаемых, т.е.
f = f0+f,+f2 , (6.2.27)
где f 0 - "технологическое операционное время" (ТОВ), расходуемое на
получение целевого эффекта объема f? ;
f j - "технологическое операционное время" (ТОВ), расходуемое на
обработку данных "с точностью" ё ;
f 2 - "временная операционная задержка" (ВОЗ) по отмеченным в
п. 6.1.1 причинам.
С учётом физической сущности слагаемых суммы (6.2.27) и отражаю-
щих её моделей (см. пп. 6.2.1 и 6.2.2) соотношение (6.2.27) может быть
представлено в виде
f = r0(v)+r1(^)+f2, (6.2.28)
где согласно (6.2.8) и (6.2.21)
*o(v) = <-^/"(l-v); (6.2.281)
Л
тх{е) = т'х-\-1п—, (6.2.28")
где t'Q9 т[9 Д0, Я, - агрегированные параметры и ЭТХ модели - "агрегаты",
причём
С целью охвата наиболее широкого круга возможных организаций
ЦНПФС в рассматриваемом случае в качестве генеральных аргументов
выделяются целевой эффект f? и технологическое операционное время f l ,
подчинённые (как и в моделях, рассмотренных в пп. 6.1.2, 6.2.2.2) равно-
мерным законам распределения с параметрами v , 1 и т[ , т" соответст-
венно, т.е.
^(v) = ^(v;v',l) = ^fe^ . (6-2.29)
1-v
где v = v\A{k),В'{г)) - "агрегат";

6.2. Нелинейные функционально-стохастические модели непрерывных ЦНП 379
Л1(г) = ^1(г;<,0 = ^Я. (6-2.30)
1 1
где г,' , х"х - "агрегаты",
<=<{\ув'(1-))-,т;=т;[А{к),в[п).
Временная задержка f 2 по-прежнему подчинена смещенному показа-
тельному закону распределения с параметрами //иг|, т.е.
<Pii{r)=<ptn]{r;ti,<)=^e-''^A{r-r'1), (6.2.31)
где ju и т\ - "агрегаты";
Требуется определить закон распределения
^^W,),^,)^1(3))=^M,f>(''^^)=*^v)n(^^f)n(f<r)]
показателя
F(3)=(F(^F(if) = (j)j'),^),^) = (v^,f)
виртуального качества результатов ЦНПФС.
Будем искать функцию распределения случайного вектора (у,ё,т) по
формуле
ф<^>(^0 = ^^ (6.2.32)
где
Ф{Щ{г,е)=Р[(у>г)Г1(ё<е)] ; (6.2.32»)
*WT;v^)=ptf * rA* ^ v)fl(^ < *)] . (6.2.32")
6.2.8) Отличие методики определения функции распределения (6.2.32)
от (6.1.17), (6.2.11) и (6.2.24) обусловлено, с одной стороны, спецификой
показателя K^l^jj, ], в частности, взаимной независимостью его
компонент v и ё, а с другой - целесообразностью демонстрации приме-
нимости различных подходов к решению аналогичных задач и выявления
их преимуществ в конкретных случаях. А
Поскольку случайные величины v и ё взаимно независимы, то функ-
ция их совместного распределения определяется следующим соотношени-
ем:
ф(*,е)М = Ф* *)П{ё<е)]= P(v>v)p{e<e)=*,(v)F,(*). (6.2.33)
Поскольку v - генеральный аргумент и плотность его распределения
имеет вид (6.2.29), то

380
Глава 6. Комплексные функциональные модели ЦНП
1-v
*»00= k(vVv = 4v'-v)+- ;tf(v;v',l). (6.2.34)
1 — v
Поскольку функция (6.2.28 ) - монотонно убывающая, то [29]
Я £
му «т*£
/л £м - Ins
4«-<)J
И^е^-Ч** )+(*-**)
Согласно (6.2.28)
где
(6.2.35)
(6.2.36)
(6.2.36')
(6.2.36")
*.+*,=УГ,(*)+/Г'(*).
v=/.(fo)=[i-^(Vr')k(^o-<);
^=/,(^)=^^(f'"<)^./<,0-
Поэтому, когда v>v и ё<е , f0 > r0 = /0"! (v) и f, > г, = /j"1 (f).
Следовательно,
f>T0+TI=/e-'(v)+/r,(f)- (6-2.37)
В пространстве т,то0т2 соотношение (6.2.37) иллюстрируется рис. 6.2.1.
С учётом сказанного условная функция распределения (6.2.32) будет
определяться следующим соотношением:
Ffl{^(t;v,e)=P[f<T/{v>v)r\{e<e)] =
= p[f,f+f1'+f2<r/(f0>/0-,(v))n(f1>/r,(f))]=
= F{r{t)=Ffl{t)*Ff{{t)*Ff2(t), (6.2.38)
где Ff, (т) и Ffy (r) - "усечённые слева" распределения случайных величин
f0 и f, соответственно [29,167],
Согласно (6.2.38) и рис. 6.2.1
рщ»4)(ъ*>е)= КМ
"I "0
rfTft
drx =

6.2. Нелинейные функционально-стохастические модели непрерывных ЦНП 381
.Т = Т0 + Т, + Тг
Рис. 6.2.1
7,. =/.»+/•,-'(*)
где
=л КМ
К (О
"1 'О
</т0
rfr,, (6.2.39)
А-
^.[/."'wKl/r'^J *,№(*)"
Как видно из (6.2.39), для определения условной функции распределе-
ния РфЛ^;у9е) необходимо найти плотность распределения <pfo{t) тех-
нологического операционного времени f0 и произвести интегрирование.
С учётом (6.2.28'), (6.2.36'), согласно которым
v(r0) = l-^(^);
r0(v)=<-^/#i(i-v),

382
Глава 6. Комплексные функциональные модели ЦНП
будем иметь
^.W=^[v(r)]|v'(T)| = 4^-T-7 iT-tJ+-Lfa(i_F')j. (6.2.40)
Подставив (6.2.30), (6.2.31) и (6.2.40) в (6.2.39) и произведя интегриро-
вание, получим
^(M)(^v,f)=^{[r-r;-5.(l-,-^>)+C.(l-^-^)]x
х л(т;^,<)+[< -г; -я-И^ -,-*<«")+
+ с (е-"(м5) - *-"(Mi) )Jzl (т - т*)}, (6.2.41)
где t' = tJ +т'х+т'г+—1пеи; В= ^
т;=т'-^-/»(1-у)-^-/»е; -t;=t*-^-/«(1-v).
Перемножив (6.2.34), (6.2.35) и (6.2.41), окончательно получим
{[г_г;_д(1-^(*-^
1-v
(i-•)(<-<)'
х^(г-т;)}я(у;у,,1)я(£;£^-А'(гГ-г;ил/), (6.2.42)
где за пределами носителя распределения случайного вектора (у,ё,т)
функция (6.2.42) доопределяется в соответствии с общими вероятностны-
ми свойствами функции совместного распределения системы трёх случай-
ных величин.
Соотношение (6.2.42) представляет собой вероятностную модель пока-
зателя К3х = (y,€,t) виртуального качества результатов операции и в то же
время является агрегированной моделью ОС, т.е. ЦУТС и реализуемого ею
ЦНПФС. Подчеркнём, что в отличие от моделей, рассмотренных в п. 6.1 и
пп. 6.2.1 и 6.2.2, в данной модели целевой эффект описывается как количе-
ственно, так и качественно (комплексно).
6.2.9) Если временные задержки отсутствуют, т.е. f2 = 0, то f = f0 + f,,
и поскольку случайные величины f0 и f, взаимно независимы, v и f, -

6.2. Нелинейные функционально-стохастические модели непрерывных ЦНП 383
генеральные аргументы, а функция v(r0) - монотонно возрастающая, то
функция безусловного распределения операционного времени будет иметь
следующее выражение:
Ff (r)=F{> (r)*Ffi (т)=F,[v(r)]*Ffi (r), (6.2.43)
а функция условного ("усечённого слева") распределения операционного
времени будет определяться соотношением вида
где F., (v) и Ff, (г) - функции "усечённых слева" распределений генераль-
ных аргументов v и f, соответственно. А
Поскольку компоненты f0, f, операционного времени f связаны функ-
ционально соответственно с генеральными аргументами vffl9 т.е.
v=v(f0)=[i-,-^-)j4f.-<);
*i=*i(A)=*i.
то
*.=*.(*) =
<-i-/„(l-v)
J(v-v');
*i=*i(*i)"A.
и согласно теореме 5.4.1 или непосредственно по схеме алгебры событий
будем иметь
^j,tMe,r) = P[(v > v)n {s < e)f] (t < т)]=
= p[(v>v)(]{fAf^e)n(/;l(v)+i1<T)]=
= p[(v<v</e[r-/r,(f)])n(/r'(f)^^<^-/.-,(v))]-
= k[/.(r-/r,(^))]-^(v)}{Fjr-/e-(v)]-FfiU-,(^)]}=
{[т_^_1г.(1_^(^))+С.(1-^^))]я(т;^,т;)+
1-v
(l-vO«-<)'
+ [т*_^_д.(е-л(^)_еч(^))+с.(е-А(^)_е-м^))]4т_^)}х
+c.(i-«^>]M*;«^)+k^
+C- (е-"™ -е-'^Ц A(t-TZ)}n{v;v',l)A{e -eT)+

384
Глава 6. Комплексные функциональные модели ЦНП
+пЛ^{[^-^-^-(1-^(г-4))+С-(1-^(^))Ыт;г;,^)+
г,-г,
+ С • (*-^> - *ГЛ™^)] А(* ~ т* )V(V' ~ V)A(€ ~ e")> (6-245)
где т' = т'ъ+т\+т'1 + —-1пем\ В= ^
т" = т',+т;+т'2; С = ^ •
T'£=T'-—ln{l-v)-—lne;
6.2.10) В заключение параграфа заметим, что рассмотренные в (6.2.4),
(6.2.7) и (6.2.9) модели сохраняют основные свойства не только при пол-
ном отсутствии временных задержек, но и в случае, когда эти задержки
носят детерминированный (неслучайный) характер и соответственно рав-
ны: т[ - в моделях НЦНП, ДЦНП htJ-b модели НДЦНП.
Поскольку детерминированная временная задержка технологического
процесса проявляется в равном величине задержки увеличении виртуаль-
ного операционного времени, то в модели показателя виртуального каче-
ства результатов операции она учитывается соответствующим смещением
("вправо") носителя распределения операционного времени f. Формально
это равносильно замене аргумента т на Т-тх в формулах (6.2.13), (6.2.26)
и на г - т\ в формуле (6.2.45). А

6.3. Функционально-стохастическая модель циклического ЦНП 385
6.3, ФУНКЦИОНАЛЬНО-СТОХАСТИЧЕСКАЯ МОДЕЛЬ
ЦИКЛИЧЕСКОГО ЦЕЛЕНАПРАВЛЕННОГО ПРОЦЕССА
В п. 6.1 была подробно рассмотрена модель ЦНПФС, обладающая це-
лым рядом свойств, которые обеспечивают наибольшую наглядность и
простоту анализа исследуемого объекта. При практическом использовании
подобной модели с самого начала постулируется её линейность, т.е. пред-
полагается, что ЦНПФС может быть достаточно адекватно описан линей-
ной моделью [68].
Как отмечалось, при построении модели любого объекта главным усло-
вием её пригодности является адекватность моделируемому объекту (а не
наглядность и простота), и поскольку многообразие ЦНПФС практически
неограниченно, то их модели, естественно, не могут быть исчерпаны клас-
сом линейных моделей. Поэтому необходимы модели, отличные от линей-
ных, но также пригодные для описания широкого класса реальных
ЦНПФС. Для демонстрации общности рассматриваемой здесь методики
представляется целесообразным рассмотреть класс существенно нелиней-
ных и к тому же дискретно-непрерывных моделей, так называемых цикли-
ческих ЦНП, реализуемых многими ЦУТС самого различного назначения
(вычислительные комплексы, навигационные системы, системы связи,
системы наблюдения и т.п.).
6.3.1. СОДЕРЖАТЕЛЬНАЯ (ВЕРБАЛЬНАЯ)
ПОСТАНОВКА ЗАДАЧИ
Некоторая ЦУТС, параметры и ЭТХ которой описываются вектором
А,к,у ведет наблюдение (ЦНПФС) признака я M(i) некоторого процесса
n(i). Признак лM(t) доступен для наблюдения периодически в течение
интервалов времени (f',,*",] длительности rn [i = l(l)...], разделённых
паузами (**м**'/] длительности вп [i = l(l)...]. Совокупность (объедине-
ние) паузы (/*м**'/] иинтервала (/',,/*,] наблюдения,т.е.
имеет длительность 7) =в.+тп [i = l(l)...] и называется циклом наблюде-
ния.
Параметры и ЭТХ процесса наблюдения - ЦНПФС описываются векто-
ром AL*, характеристики условий проведения операции описываются век-
торами В?,* (условия функционирования) и В?^ (условия применения
13 Зак. 3303

386
Глава 6. Комплексные функциональные модели ЦНП
ЦУТС). Качество результатов операции описывается в симплексной кано-
нической форме и характеризуется вектором
где ух - целевой эффект;
у2 - суммарный расход операционных ресурсов различных видов (см.
п. 5.3.2);
уъ - операционное время.
Для достижения цели операции должен быть получен целевой эффект
не менее zx за время, не превосходящее £3; запас операционных ресурсов
равен £2.
За счёт повторных наблюдений признака nM(t) и изменений интенсив-
ности его проявления темп y2(t) освоения вводимых в операцию ресурсов
изменяется во времени.
Наблюдённый признак км (t) идентифицируется с некоторой вероятно-
стью Рид- Требуется построить математическую модель операционной
системы (её элементов), позволяющую решать задачи анализа качества
ЦУТС и ЦНПФС и их синтеза по критериям требуемой или максимальной
эффективности операции.
6.3.2. ПОСТРОЕНИЕ АГРЕГИРОВАННОЙ МАТЕМАТИЧЕСКОЙ
МОДЕЛИ ОПЕРАЦИОННОЙ СИСТЕМЫ
Начнём формализацию описанной в п. 6.3.1 операционной ситуации с
построения временных диаграмм процессов, протекающих в ОС, с помо-
щью индикаторов - селекторов временных интервалов [130, 169], на кото-
рых соответствующие процессы протекают.
На рис. 6.3.1 изображены реализации индикаторов процессов nn(t)9
IIH{t), np{t):
Пп({) - индикатор процесса проявления признака nM(t)\
IIH(t) - индикатор процесса наблюдения признака nM(t)\
IIp(t) -индикатор процесса результативного функционирования
ЦУТС;
tn - момент начала проявления признака nM (t);
7С -длительность проявления признака км (/);
т, - длительность i-го сеанса наблюдения признака км{$)\
в1 - длительность #-й паузы в наблюдениях;
vt - реализованная длительность 1-го сеанса наблюдения.

6.3. Функционально-стохастическая модель циклического ЦНП 387
1
71
О '/7
1
-^
-ft
-*з
^""Ч-
«•w
К?
4
О U-
Рис. 6.3.1
В дальнейшем для большей наглядности рассуждений предполагает-
ся1, что процесс nH{t) наблюдений регулярный, т.е. сеансы наблюдений
проводятся через равные интервалы в<=вп, [# = l(l)...] времени и имеют
одинаковые длительности T/=rc [i = l(l)...]. На рис. 6.3.1 это допущение
учтено.
В соответствии с алгоритмом рис. 5.2.1 определяется спецификация
операционных эффектов - атрибутов ЦНПФС. Введём обозначения:
d
yx=v - целевой эффект, выраженный в относительных единицах
(0<i><l), смысл которого раскрывается в ходе построения
модели;
d
у2= z2=r - расход операционных ресурсов всех видов (равенство y2=z2
следует из вербальной постановки задачи);
d
у3=т - операционное время, отсчитываемое от момента tn начала
проявления признака nM(t) (модельного начала операции) до
момента её окончания (см. (6.1.2)).
Допущение не принципиальное, модель может быть обобщена на произвольный
процесс /7Я(/).

388
Глава 6. Комплексные функциональные модели ЦНП
В терминах рассматриваемой задачи темп у2{*) освоения ресурсов оп-
ределяет интенсивность X{t) наблюдения1, т.е.
y2(t) = cA(t)9 (6.3.1)
где а - коэффициент, имеющий размерность расходуемых ресурсов (объ-
ёма памяти средств наблюдения, объёмов носителей информации и т.п.).
Пусть ф§(в) - плотность распределения интервала времени в между
последовательными наблюдениями признака ftM{t), а К§{в) - дополни-
тельная функция его распределения, тогда [129]
^)=^^=%(0;*). (6.3.2)
Как видно из (6.3.2), интенсивность A(t) наблюдения имеет смысл ус-
ловной плотности вероятности наблюдения признака в момент / + 0, т.е. это
значение условной плотности распределения момента в наблюдения при-
знака 7CM(t) при условии, что он не наблюдался уже в течение времени t2.
Из (6.3.2) следует
<рё(в)=Я{в)е° , (6.3.3)
а также
Интеграл
Кё(в)=е ° (6.3.4)
\X{i)dt = A{t) (6.3.5)
называется ведущей функцией потока наблюдений [129] или потенциа-
лом наблюдения [3] и в случае ординарного потока наблюдений численно
равен математическому ожиданию числа наблюдений признака 7CM(t) за
время х.
6.3.1) Поскольку в общем случае при нестационарном потоке наблюде-
ний потенциал наблюдения зависит от момента /0 начала отсчёта интерва-
ла (О, г], более удобной является ведущая функция вида [129]
1 Обратим внимание на то, что эта характеристика носит индивидуальный характер
[129].
Эта функция аналогична интенсивности (опасности) отказа [137]. Если поток со-
бытий ординарный, то A\t) численно равна интенсивности (плотности) потока собы-
тий (наблюдений) [129].

6.3. Функционально-стохастическая модель циклического ЦНП 389
t0+r
Л(т) = A(r,t0)= $A{t)dt= \A(t0+t)dt=:A{t0+T)-A(t0). (6.3.6)
'о О
В дальнейшем будет использоваться форма (6.3.5) потенциала наблю-
дения. А
Как легко понять, соотношение (6.3.4) определяет вероятность
R$(v)=P[6>v) того, что за время v признак AM{t) наблюдаться не бу-
дет. Поэтому вероятность того, что за время v он будет наблюден, равна
PH(v)=p(e<v)=Fe(v) = l-Re{v) = l-e • 'Л=1-е-я{у). (6.3.7)
Поскольку результаты наблюдения идентифицируются лишь с вероят-
ностью РИд, то вероятность вскрытия (определения) признака яM(t) будет
определяться соотношением
v = P„PHa=Pm(^-e-A(v)). (6.3.8)
В дальнейшем для простоты1 будем считать идентификацию идеальной,
т.е. РИд-\, а поток наблюдений - стационарным, т.е. A(t) = A = const. То-
гда потенциал наблюдения
A{v)=)x(t)dt = Av (6.3.9)
о
и формула (6.3.8) примет вид
v = v(v) = l-e-Av. (6.3.10)
Вероятность v представляет собой целевой эффект ЦНПФ ЦУТС на-
блюдения и имеет смысл доли вскрытых и идентифицированных объектов
наблюдения, обладающих признаком nM{t).
Как видно из рис. 6.3.1, полное время наблюдения признака 7iM{i) оп-
ределяется равенством
v = ^v„ (6.3.11)
/=1
где vi - реализованная длительность 1-го сеанса наблюдения;
т(т) - число сеансов наблюдения, реализованных за операционное
время t = t(v), т.е. за время набора целевого эффекта не ме-
нее V.
Согласно (6.3.1) и (6.3.9)
Допущение не принципиальное
а

390
Глава 6. Комплексные функциональные модели ЦНП
r(v)=y2H= ly2{t]dt = a\A{t)dt = cdv , (6.3.12)
о о
т.е. количество расходуемых в ходе наблюдения ресурсов пропорциональ-
но времени v наблюдения. При этом РЭ-функция имеет выражение типа
(6.3.10), т.е.
г_{у)
v = v(r) = l-e-*v=l-e a. (6.3.13)
Таким образом, время v наблюдения представляет собой обобщённый
показатель расходуемых ресурсов, а суммарная длительность
т = °)Tn(t)dt (6.3.14)
сеансов наблюдения на периоде (*0,*0+tJ проведения операции (ЦНПФС)
характеризует их запас в ЦУТС. При этом согласно равенству y2=z2 время
тП9 [i = l(l)nf] всех сеансов наблюдения, проведённых на интервале
(/0,/0+т], используется результативно, т.е. у^тЦ9 [i = l(l)iw-l] , где m -
номер сеанса, в котором наблюдение заканчивается (не обязательно в кон-
це iw-ro сеанса). На рис. 6.3.1 результативные части сеансов (на которых
велось наблюдение) заштрихованы.
Итак, из вербальной постановки задачи следует, что в ходе наблюдения
расходуются все имеющиеся в ЦУТС ресурсы (j>2<£2), т.е. имеет место
"эффект поглощения" (см. п. 3.3.4). Поскольку при этом {y2^z2) = U, то
РДЦ=р[(ь<щ)п{т<тд)] (6.3.15)
и, следовательно, для оценивания эффективности процесса наблюдения
модель показателя качества его результатов будет описываться функцией
распределения 0^fAv9r) случайного вектора (v,t).
Поскольку, как было показано [см. (6.3.10), (6.3.13)], в рамках рассмат-
риваемой задачи все аспекты показателя качества результатов ЦНПФС вы-
ражаются через его временные характеристики, то с методической точки
зрения вначале целесообразно найти закон распределения случайного век-
тора (Vff), т.е.
0^f){v,T)=P[{v>v)n{f <т)], (6.3.16)
а затем с помощью соотношения (6.3.10) перейти к функции распределе-
ния
<f><w)(w,r)= ф > v)n(f < т)]. (6.3.17)
Закон распределения (6.3.16) будем искать в виде
0m{v,r)=P[{v>v)n{i<t)]=P{v>v)P{i<tlv>v)=
=J^(v)F^(t;v), (6.3.18)

6.3. Функционально-стохастическая модель циклического ЦНП 391
где Rp{v) - дополнительная функция распределения времени v наблюде-
ния;
FfLf{i;v) - условная функция распределения операционного времени f
относительно (при условии) события (v > v).
Как видно из рис. 6.3.1, вероятность P(y>v)=R^(v) обусловлена вза-
имным расположением на временной оси момента in начала проявления
наблюдаемого признака и моментов i. начала сеансов его наблюдения, а
также длительностями V. сеансов наблюдения и длительностью ж прояв-
ления наблюдаемого признака.
Рассмотрим плоскость nOtn и определим на ней область возможных
значений случайных величин к и in (рис. 6.3.2), где [a,b] - носитель рас-
пределения длительности к, а (О,0л1+тс1] - носитель распределения мо-
мента in. Таким образом, прямоугольник (л,й]х(О,0л1+тс1] представляет
собой носитель распределения случайного вектора (ж, if ).
Из равносильности случайных событий
(у>у)=[(л,!П)е(нЦ, (6.3.19)
где (н\ - область плоскости ftOtn, при попадании в которую вектора
(#,*я) выполняется неравенство (v>v), следует
Д»= P{t > v) = p[{/t,tH)e{H)v\. (6.3.20)
Представляется достаточно очевидным, что параметрами искомой зави-
симости (6.3.20) будут являться длительности fci - сеансов наблюдения
[1 = 1(1)т]и0„. - пауз в наблюдении [# = 1 (l)ira ], где т - наибольшее чис-
ло сеансов наблюдения, которые могут быть проведены за время проявле-
ния признака.
6.3.2) Случайный характер величин f ы и §ы существенно усложняет
математические модули процесса Пн (t) наблюдения и процесса Пр (t) ре-
зультативного функционирования ЦУТС, а следовательно, и решение за-
дачи. Эффективным методом решения таких задач является метод функ-
ции Грина [130, 169] (метод рандомизации), в рамках которого вначале на-
ходится частное решение задачи при детерминированных значениях
tci и 6ni параметров fci и впП а затем это решение рандомизируется
по формуле полной вероятности. Наряду с этим во многих случаях само-
стоятельный интерес могут представлять и сами частные решения, най-
денные при характеристических значениях случайных параметров f ci и
вп.. В качестве таких значений могут фигурировать их математические

392
Глава 6. Комплексные функциональные модели ЦНП
а) в"
0
к
(Н)б
а
A J
/ /
v,0)
У//
Л6(4Л
о„
V
в„+*с
У///////////}
^х^(яР><УХ/(я)зО<
Лн\
\ь .
1вп + тс 2вп + 1хс Ъвп + 2гс Зв„+Угс л
оп+ъ
а в А
%+тсММ
2вп + 2тс Звп + 1х}6п + Ътс n
Ъвп+Ъгс л;
Рис. 6.3.2
ожидания, моды распределений, наибольшие или наименьшие значения, а
также квантили распределений любого уровня. При этом должно учи-
тываться различное (прямо противоположное) влияние на вероятность

6.3. Функционально-стохастическая модель циклического ЦНП 393
P(v > v) величин rci и Oni, т.е. при увеличении - rci эта вероятность рас-
тёт, а при увеличении 6ni - падает. Понятно, что при крайних значениях -
т«> ^ш- и г1> &"i параметров fd, 6ni будут соответственно получены "оп-
тимистические" и "пессимистические" оценки вероятности Р(у > у).
Если рассеяние случайных величин f ci и 0ni невелико, а также при ана-
лизе ЦНПФС на длительном промежутке времени, рандомизированное
решение задачи будет мало отличаться от частного полученного при наи-
более вероятных или средних значениях параметров tci и впГ При этом
влияние различий распределений длительностей fci, fcj сеансов наблюде-
ний и длительностей вni, вп. пауз также будет несущественным (закон
больших чисел). А
С учётом (6.3.2) для большей наглядности последующих построений
будем решать задачу в предположении, что fci =TC = const; 0ni=0„ - const,
[i = l(l)...]. В этом случае единственными источниками случайности рас-
сматриваемых математических моделей nH{t), I7P(t) и ЦНПФС будут
величины ?яи1
Поскольку наблюдение осуществляется циклически и необходимый по
объему v целевой эффект может быть набран в момент времени, распо-
ложенный в любом из приходящихся на период [*#,*#] проявления на-
блюдаемого признака сеансов (циклов) наблюдения, то конкретный вид
области (н\ зависит от значения величины V, для которого вычисляет-
ся вероятность P(v > v).
Иллюстрацией процедуры построения модели показателя (v,t) каче-
ства результатов ЦНПФС служит рис. 6.3.2, построенный в условиях
тс< а <в„< Ъ. При других соотношениях параметров a, ft, тс, вп он будет,
естественно, отличным от приведённого, однако сущность сопутствующих
ему рассуждений сохранится. При этом рис. 6.3.2,а соответствует случаю
ve[0,rc], рис. 6.3.2,6 - случаю V€[rc,2rc], рис. 6.3.2,в - случаю
ve[2rc,3rc]. Через {н)к, [Л = 0(1)з] на рис. 6.3.2 обозначены области
пространства {(я",^)} возможных значений параметров (я*,^), при попа-
дании в которые вектора (ft,in) длительность у наблюдения признака
равна ровно ктс, т.е. v = ктс.
Таким образом, искомая вероятность P(v > v) равна значению двойного
интеграла по области (н\ от плотности распределения случайного векто-
ра (я, in), т.е.

394
Глава 6. Комплексные функциональные модели ЦНП
R^hP(v>vhP[(^tn)e{H)v\=
(#)„ (H)v
Как видно из рис. 6.3.2, двойной интеграл (6.3.21) может быть сведён к
двукратному, и притом двумя способами. Поскольку правомерно считать
случайные величины я и in взаимно независимыми, то выражение
(6.3.21) может быть приведено к следующему виду:
*>)=
о
\<pt{x)to
./(t;v,i)
dt;
J 9*Щ
ev(W,+v)
КО*
|_*i(>w)
Лг,
(ve[/rc,(/ + l)rj ;/ = e(l)[ft/fe+Tc)])f
(6.3.22)
где вид функций /, gx, g2 зависит от текущего значения v, играющего в
их выражениях наряду с номером к = / +1 цикла наблюдения роль пара-
метра. Понятно, что первое из приведённых выражений (6.3.22) проще, по-
этому оно и реализуется во всех последующих выкладках.
Чтобы получить явное выражение для функции распределения ДДу),
необходимо знать явные выражения для плотностей распределения фА\я)
и (p~t \t). В принципе эти выражения могут носить различный характер, за-
висящий от целого ряда факторов, таких, как этап жизненного цикла СТС
(отработка, испытания, целевое применение и т.п.), характер наблюдаемо-
го признака, тип объекта, характеризуемого наблюдаемым признаком, и
т.п. Однако в любом случае решение задачи определяется соотношением
(6.3.22) и для его реализации необходима конкретизация выражений ф^уЯ)
и (p~t (t). Для наглядности дальнейшие построения проводятся примени-
тельно к конкретному примеру и опираются на "правдоподобные рассуж-
дения" [135].
Представляется достаточно правомерным предположение (на нём осно-
ван целый ряд исследований [130]) о том, что поскольку в общем случае
момент i п начала проявления наблюдаемого признака неизвестен, закон
его распределения целесообразно считать равномерным на интервале
{0,От+те]\т.е.
77(*;О,0Л+О
*.(') = ■
в -т
(6.3.23)
1 После момента в^гТс начинается новый аналогичный цикл и отсчёт времени ti

6.3. Функционально-стохастическая модель циклического ЦНП 395
Что касается длительности it проявления признака, то класс возмож-
ных его распределений значительно шире. При этом конкретный вид зако-
на распределения <рл(я) зависит от характера объекта наблюдения. Поэто-
му в условиях максимальной неопределённости информации об объекте
наблюдения целесообразно считать закон распределения длительности л
также равномерным2 на интервале (a,b\, т.е.
Ъ-а
(6.3.24)
Тогда интеграл (6.3.21) или, что то же самое, (6.3.22) будет равен отноше-
нию мер (площадей) областей (н\ и носителя распределения
случайного вектора (ж,£я). В результате интегрирования (6.3.22) будем
иметь
2{Ь-а){в„+тс)
^гь{еп+тс)-{гк+\)ег-г{ге„+те)у , (к+1)т)+
{Ь-твп)2 + 2{Ь-тв„){т + 1)тс-2[2(Ь-тв11) + {т + 1)тс]у + 3v2
х
2{Ь-а)(в„+тс)
хП(у;штс,{т + 1)тс), (6.3.241)
где к =
= е\
целая часть — с отставанием
л
V VI V ( V
(т.е. при — = к, €\ — = А -1, а при — = к + 0,е\ — \ = к);
т =
ь
в +Т
L л с_
= Е
' ь )
- целая часть
е.+т„
Теперь с учётом соотношения (6.3.10) может быть получена функция
распределения /?Дг?) целевого эффекта г?. Поскольку функция г? = г?(у)
монотонно возрастающая, то
rM=r,[v(0)]=4-*)+
1 Подчеркнём, что сделанные предположения непринципиальны и служат лишь для
простоты и наглядности.
Принцип неопределённости Лапласа.

396
Глава 6. Комплексные функциональные модели ЦНП
2{Ь-а1еи + тУ{вп-а)г + -(ея-а)1Г{\-^--\bt{\-*)
,—% г * Щ№Л-' +
2(b-aM-rc) K '
iM2ft(^+Te)-(2*+l>?+^(2^+Te)fa(l-v)
+ £ т ^Ц ф;1-е-*г;1-е^к)+
2{Ь-а\е„+тс)
{Ь - тв„У + 2{Ь - mejm + l)re + -[2(* - тв„)+ (т + l)rj/«(l - г?)
fMl-*?)
2(A-a)(<9.-rJ
2(A-aX^„-Tc)
77(г?;1-е-^,1-е-д(,я+,к)
(6.3.25)
или
где
R&) = A{- €)+ [С, + Д0 /«(1 - t>)+ Л /«2(1 - г?)]^(г?/г?0,1?|)+
+ Z[Ct+BM*-*)WWk,0M)+
k=\
+ \Ст + Вт /и(1 - г?)+ Л /и2(1" ф7{0;#т,#т+1)> (6-3.26)
_ 2(б-аХ0„ + О-(0,,-а)2, _ 2{2в„+тс) .
4> =
-3
2Л2(А-аХ*„+0'
_2ф„+гс)-(2^ + /К2, _ 2(20,+Q ,
С*" 2(*-Х'„ + 0 '^"ЖЛ-.Х^ + О*
= (г>-т<9„)+2(г>-ш^Хт + 1)тс ^ 2(&-«*.)+(ж + l)rf .
2(A-aXtf.+Te) ' "* Л(Ь-а\вЙ+тс) '
Л=-Л = 2Д2(*-«)(0„ + гс);
tf0=0; #t=l-<?-^r<; [ft = l(l)»t + l].
Вероятности Pk = P(v = ktc), [A = 0(l)/w + l] определяются следующи-
ми соотношениями:
P__AzfO!_. »_ 202-(0я-а)2 .
П-2(*-«Х^„+гсГ ^"2(A-«X0„+rJ'

6.3. Функционально-стохастическая модель циклического ЦНП 397
Р= й
* (*-«)(*.+тс)
, [Л = 2(1)|я-1]
_2в?,-((т + 1)е„+ттс-Ь)\ _ (твп + {^ + ^с-Ь)2
Г~ _ / - \ / - \ ? гт+1 —
2{Ь-а)(0„+тс)
2{Ь-а){еи + Тс)
Графики функций распределения R^{v) и R#{i9) приведены соответст-
венно на рис. 6.3.3, а, б.
0,25 0,50 0,75 о,88 0>9 #
Рис. 6.3.3
Перейдём к отысканию условной функции распределения Ffl^(r,t?)
операционного времени f относительно события
Как и прежде, для большей наглядности хода решения задачи вначале
найдём функцию распределения Ft±^(r,i9)9 а затем, используя соотноше-
ние (6.3.10), перейдём к искомой.
Поскольку операционное время f зависит от того, в каком цикле на-
блюдения был набран требуемый целевой эффект г? (соответствующее ему
время наблюдения v = v(#) = — ln\ ), то номер к этого цикла служит
параметром закона распределения, т.е. Ffl^(r,t?) = Ffip (r;V,k).
При определении функции распределения Ff±^(r,^) необходимо
иметь в виду следующее:
- операционное время f не может быть меньше времени v наблюде-
ния, т.е. f > v;
- если время v наблюдения, обеспечивающее требуемый целевой эф-
фект г? (т.е. потребное время наблюдения), не было набрано в преде-
лах Л-го цикла наблюдения, то к затраченному времени v наблюдения
добавляются длительности вп всех {кЛ) пауз, предшествующих за-

398
Глава 6. Комплексные функциональные модели ЦНП
вершающему А-му циклу наблюдения (циклу, в котором был завершён
набор требуемого целевого эффекта г?);
существуют отличные от нуля вероятности равенства операционного
времени f конкретным значениям k0n + v и (k + i)0n+v, соответст-
венно равные
P(t=ken+v)=p(en<in<aMk+i)rc-yh{j^t^;
[Л = 1(1)ш-1];
- на интервалах (квя+у,(к + 1)вИ+у] операционное время f распреде-
лено равномерно.
Графики функций Ff # (т ,г?) приведены на рис. 6.3.4.
6.3.3) Как видно из рис. 6.3.4, в, результативное операционное время f
не может превзойти длительность к проявления наблюдаемого признака,
максимальное значение которой равно Ъ. По определению (см. п. 2.3.2),
операционным временем называется время, необходимое и достаточное
для достижения целевого эффекта г? не менее требуемого г?г (т.е. г?> г?г).
Поэтому если полученный (набранный) за время f целевой эффект г?(тр)
недостаточен (меньше требуемого целевого эффекта г?г), то операционное
время может интерпретироваться (формально) как бесконечно большое.
Другими словами, безусловное распределение операционного времени f
удовлетворяет условию Ff(°o)<l и, следовательно, является несобствен-
ным {дефектным) [183]. При этом
гДе $тах = 1 -е'ЫГс (в условиях рис. 6.3.2, 6.3.4 т = 3 => t?mflJC = 1 - *ГЗЯГс).
Обратим внимание, что в выражении (6.3.26) параметр а не фигурирует
(см. также рис. 6.3.4), так как длительность к проявления признака равна
ему с нулевой вероятностью (т.е. Р(я = а) = 0) и, следовательно, значение
f операционного времени обусловлено лишь временем у наблюдения и
длительностями вп пауз. ▲
С учётом замечания (6.3.3) и рис. 6.3.4, имеет место следующее выра-
жение:
т-\
^M)=I
r-2v + (k + l)rr -кв„ „/ ,Л ,, <Чл ч
у ' с а-П(г;кв„ +у,(к + 1)вп +v) +

6.3. Функционально-стохастическая модель циклического ЦНП 399
Ff±f{r;v,i)
б)
О v тс
\FtL9{r;v,k + l)
#n 0»+v е„ + тс
о„
+(*
е„
+ l)rc-v
ktc<v<{k + l)rc
МЗ, +Ф*\{к+ф„ +тс)+%
kO„+'v к(в„+тс)+тс {k + l)0.+v
в) 1
1
Ъ-т6„ +{m+l)tc
в +Т
р/ {m+i)re-v
' Ff±p(r;v,«)
-2v /
/lb —
/ m-\
\-S/ /
b\.. Vh/
\
\
\
b + 2v\(m-l)en-m rc
A+Tc
/\m-\)Tc <v<mrc
b
' v ►
Te)me„+vm(e„+Tc)+Tc r
Рис. 6.3.4

400
Глава 6. Комплексные функциональные модели ЦНП
+A{T-{k+i)e„-v)
xn{v;krc,{k + l)rc)+
T-2v+(m+l) тс -m 6n
в +т
п с
X
хП (т;т вп + У,Ь)+А{т-Ь)
П{у;тгс9{т + \)гс). (6.3.27)
Перейдя в (6.3.27) от у к г?, будем иметь
FfJw)=£
*=0
т- =-1п (1 - г?)+ (Л + \)гс - кв„
Я П{т;тМтк+М))+
в„+т.
ПС
+А{т-тк+М))
П{у;ттс,{т+1)тс),
(6.3.28)
где Tk{#) = ke„-\ln{l-0), [Л = 0(l)iii + l];
Я
#к=\-еш', [* = 0(l)m + l]
ИЛИ
+ А (т - tk+t (tf ))}я((г?;г?, ,г?,+1)) , (6.3.29)
где tfe = 0; 0k=l-e-Ut',[k = l(l)m + l];
Tk{0) = ke„-jln(l-0),[k = O{l)m];Tk+l(0)=b;
0„ + r/ Я{в„+тс)
в +т
n "с
Перемножив выражения (6.3.26) и (6.3.29) согласно (6.3.18), оконча-
тельно получим
^t)M=R^)FtJt^)=A{-ii)x
ЦРЦ^П{т;*,еп+тс)+А{г-вп-гс)
. (0„ + О

6.3. Функционально-стохастическая модель циклического ЦНП 401
+ t{[c*+Bkln{l-t>)+AJn2{l-#)][DT + Eln{l-#) + Gk]+A{T-Tll+t)}x
хп{т;тМ>*М)п{ЪАЛ«)+
+|^(-г?)+1[с,+^/и(1-г?)+^/й2(1-^)]я(г?;^,^+1)|^(г-А)+
+ А{-€)А(т-Ь) (6.3.30)
или
+£{[c*+4/"(1-^)+4^(i-^)][^'+£/"(i-^)+G*]+47-^+iH)}x
хп(т;тк(0),тм(0))п{0;0к,0м)+
+ {^(-^)+Ёк/»2(1-г?)+^/«(1-г?)+С,]я(г?;г?4,г?Л+1)|х
хА(т-Ь)+А(-0)А(т-Ь), (6.3.31)
где 4=0; 4=1-<ГЛ*\ [* = i(l)m + i];
Гд (г?) = кв„ - jln(l - г?), [к = о(1)т]; г.»-А;
Л = -Л; Л=о» [* = /(/)»!-/];
Нк=АкЕ, Lk=AkGk+BkE;
Mk=BkGk+CkE; Nk=CkGk;
Qk=AkD> Rk=BkD,
Sk = CkD [см.(6.3.26) и (6.3.29)].
Поверхность, описываемая соотношением (6.3.31), изображена на рис.
6.3.5.
6.3.4) Выражение (6.3.31) наиболее компактно, однако в нём в явном
виде не фигурируют агрегаты а = а(Х), b = b(x), в„ = 6„(х), Тс = ТС\Х),
Я = Я(х) модели ЦНПФС. Поэтому для анализа зависимости его эффек-
тивности от параметров и ЭТХ ЦУТС и ЦНПФС необходимо фигурирую-
щие в (6.3.31) коэффициенты представить в развёрнутом виде, т.е. опреде-
лить функцию распределения Ф^Лд,?) путём перемножения функций
(6.3.25) и (6.3.28). Получаемое при этом выражение достаточно громоздко
и здесь не приводится. Рекомендуем читателю в качестве упражнения вы-
вести его самостоятельно. ▲

402 Глава 6. Комплексные функциональные модели ЦНП
Рис. 6.3.5
Функция распределения Ф^ЛдуТ) показателя \&>?) качества резуль-
татов процесса наблюдения I7H(t) является исчерпывающей его вероят-
ностной характеристикой и может быть использована для решения целого
ряда задач анализа качества ЦУТС и эффективности ЦНПФС, а также оп-
тимального синтеза ЦУТС и ЦНПФС.
Поскольку методики решения таких задач весьма подробно были рас-
смотрены в п. 6.1, то здесь они не приводятся. Советуем читателю реали-
зовать их применительно к модели циклического ЦНПФС.

6.4. Комментарии
403
6.4. КОММЕНТАРИИ
В заключение главы кратко прокомментируем основное её содержание
применительно к реальным практическим задачам.
6.4.1} При описании методик исследования различных объектов возни-
кают две в значительной мере противоречивые методические проблемы. С
одной стороны, рассматриваемая методика должна носить как можно бо-
лее общий и универсальный характер, что может быть достигнуто лишь на
достаточно высоком уровне абстрагирования и формализации. С другой
стороны, требуемая для понимания методики наглядность её изложения
приводит к необходимости конкретизировать рассматриваемый в её рам-
ках пример (как правило, иллюстративный), естественно, сужающий пред-
ставление о степени универсальности методики.
В связи с этим ещё раз обратим внимание на необходимость вдумчивой
проработки материала данной главы, сопровождающейся осмыслением
весьма большой общности содержательных постановок задач, и на отсут-
ствие принципиальных ограничений на применимость рассмотренных ме-
тодик, кроме характеристик класса исследуемого ЦНПФС. Так, в п. 6.1,
п. 6.2 были рассмотрены ЦНПФС, в ходе которых ресурсы превращаются в
целевой эффект непрерывно, а в п. 6.3 - ЦНПФС, в котором ресурсы пре-
вращаются в целевой эффект циклически из-за периодичности дееспособ-
ного состояния операционной системы. А
6.4.2} Как можно было заметить, при построении математической моде-
ли показателя виртуального качества результатов операции возможна одна
из трёх существенно различных ситуаций.
1. Компоненты показателя Y,, виртуального качества результатов опе-
рации связаны функционально. В этом случае для построения модели по-
казателя К v достаточно знать закон распределения подвектора Г/\ его
взаимно независимых компонент (называемых генеральными). Тогда закон
распределения Ф$ (К v) определяется в соответствии с теоремой 5.4.1.
Методика решения задачи в этом случае рассмотрена в п. 5.4.2 и проил-
люстрирована примером 5.4.1 (см. также (6.1.5)).
2. Компоненты показателя К* виртуального качества результатов опе-
рации связаны стохастически. В этом случае, как отмечено б (5.4.6), роль
функции связи играют уравнения регрессии. Однако, с одной стороны, эти
уравнения учитывают лишь связи средних значений (математических ожи-
даний) компонент вектора L, а с другой стороны, относительно линий
регрессии происходит рассеяние (остаточное) значений компонент вектора

404
Глава 6. Комплексные фунщиональные модели ЦНП
Ум, связанных этим уравнением с доминирующей компонентой. Для учёта
такого рассеяния или должны проводиться специальные исследования, или
должен учитываться опыт анализа аналогичных ситуаций.
Методики решения задач в подобных случаях подробно рассмотрены и
проиллюстрированы на множестве примеров в п. 6.1, п. 6.2. При этом в ос-
нову описания дополнительного рассеяния операционного времени f бы-
ли положены "правдоподобные рассуждения" (ПР) и постулаты теории
ОФЛ (см. п. 5.3.4).
Обратим внимание, что "правдоподобные рассуждения11 - это научный
метод ("экспертный"), опирающийся на опыт и компетенцию исследовате-
ля и лежащий в основе первой стадии любых исследований. По мере нако-
пления информации об исследуемом объекте модель может уточняться,
однако на первом этапе исследования метод ПР представляет собой един-
ственное реальное его орудие.
3. Наконец, возможна ситуация, когда функции связей между компо-
нентами показателя L виртуального качества результатов операции не
известны и не могут быть выражены в явном виде. В этом случае вероят-
ностная модель показателя L строится непосредственно путём модели-
рования элементов (этапов, стадий, циклов) ЦНПФС на основе анализа ре-
альной стохастической ситуации и динамики её развития во времени. Что
касается моделей элементов ЦНПФС, то они или определяются экспери-
ментально, или обосновываются методом ПР (МПР).
Методика построения математической (вероятностной) модели показа-
теля F/v виртуального качества результатов операции в этом случае рас-
смотрена в п. 6.3. Исследование эффективности и качества ЦУТС здесь,
как и во всех рассмотренных случаях, проводится по методикам, подробно
описанным в главах 4, 5 и п. 6.1. А

Глава 7
СПЕЦИАЛИЗИРОВАННЫЕ МОДЕЛИ
ЦЕЛЕНАПРАВЛЕННЫХ ПРОЦЕССОВ
В предыдущей главе были рассмотрены два класса комплексных моделей
ЦНПФС непрерывного и циклического типа. Как отмечалось, комплекс-
ность рассмотренных моделей обеспечивалась учётом всех компонент пока-
зателя iL качества виртуальных результатов операции. Хотя для нагляд-
ности была реализована его симплексная каноническая форма, тем не менее
рассмотренные методики применимы и в более общем случае. Как было по-
казано в п. 6.1, модель позволяет проводить исследования с различной сте-
пенью детализации и наглядности, т.е. в развёрнутой и свёрнутой (методом
ведущих компонент) формах. При этом ведущая компонента показателя К3\
выделялась уже после построения его вероятностной модели. Понятно, что
в качестве такой компоненты мог быть выбран любой аспект, т.е. любое
операционное свойство ЦНПФС. Если в соответствии со специализацией и
спецификой ЦНПК ведущая компонента показателя iL виртуального каче-
ства результатов операции определена заранее, то процедура построения
модели ОС и ОК в ряде случаев может быть упрощена.
В данной главе рассматривается класс специализированных моделей так
называемых циклических оперативных ЦНПФС, т.е. циклических процес-
сов, ведущей компонентой показателя качества результатов которых явля-
ется операционное время. Выделение таких моделей в самостоятельный
класс обусловлено методическими особенностями как процедур их по-
строения, так и их вероятностной интерпретации.
Одной из наиболее широких и весьма содержательных является интер-
претация циклического ЦНПФС как процесса массового обслуживания
(ПМО). Класс таких процессов весьма широк, и поэтому их модели носят
достаточно универсальный характер.
Заметим, что в соответствии с назначением ЦНПФС - ПМО в рамках
его моделей используется специфическая терминология (получившая ши-
рокое распространение в литературе). Так, операционный комплекс (ОК)
называется комплексом массового обслуживания (КМО), сложная техниче-
ская система (СТС - ЦУТС), проводящая операцию, - системой массового
обслуживания (СМО), процесс функционирования СТС (ПФС) - процес-
сом массового обслуживания (ПМО). Поскольку эти модели подробно
освещены в монографиях [129], [130], то здесь рассматриваются лишь их
основные свойства и методики их построения.

406
Глава 7. Специализированные модели ЦНП
7.1. ОПРЕДЕЛЕНИЕ И КЛАССИФИКАЦИЯ Г-ПРОЦЕССОВ
7.1.1. Г-ПРОЦЕСС И ЕГО ХАРАКТЕРИСТИКИ
Пусть операция - это процесс функционирования некоторой ЦУТС (т.е.
ЦНПФС), результат которого оценивается по времени, расходуемому сис-
темой на полное выполнение задачи (с гарантированным качеством).
Определение 7.1.1. Целенаправленный процесс, ведущей компонентой
показателя качества результатов которого является длительность г перио-
да полного выполнения задачи ЦУТС (операционное время), называется
Г-процессом. А
В общем случае длительность периода выполнения задачи ЦУТС (опе-
рационное время) зависит от целого ряда факторов, основными из которых
являются:
- трудоёмкость задачи;
- производительность системы;
- эксплуатационно-техническая надёжность системы (см. {2.7.9});
- организация процесса функционирования системы;
- условия функционирования системы и т.д.
Большинство (а в ряде случаев все) из перечисленных факторов содер-
жат элемент неопределённости, т.е. являются случайными. Следовательно,
длительность f периода выполнения задачи есть величина случайная, не-
посредственно для оценивания качества и эффективности Г-процесса ис-
пользована быть не может: для этих целей должны применяться её вероят-
ностные характеристики (закон распределения, квантили распределения,
моменты распределения, числовые характеристики и т.п.).
Наиболее полной характеристикой степени приспособленности
Г-процесса к выполнению поставленной перед системой задачи (к дости-
жению цели операции) по "критерию пригодности", являющейся показате-
лем его пригодности, может служить вероятность
PB3 = P{rH<f<b)=Ff{Td)-Ff{T„), (7.1.1)
где тн - нижняя граница периода выполнения задачи, называемая норма-
тивным операционным временем;
Тд - верхняя граница периода выполнения задачи, называемая ди-
рективным операционным временем.
В общем случае как минимально допустимое - нормативное операци-
онное время гн, так и максимально допустимое - директивное операцион-
ное время тд являются случайными, поскольку обусловливающие их фак-

7.1. Определение и классификация Т-процессов
407
торы - состояние системы, внешние условия (обстановка), ресурс времени
на операцию и т.п. - всегда содержат элемент неопределённости. В связи с
этим вероятность Рвз выполнения задачи ЦУТС будет определяться выра-
жением
Рвз = /»(f„<f <fj= mfc{tm*t<tt)dFt{T)- ]Ff4(r)dFf{r)=
= ]fo>)-F,#(T)]rfF,(T) (7.1.2)
ИЛИ
Рю = Р{тд >t>f> ]^(т)^(г)- ]^(r)rfF,(r)=
— oo —ее
= )[Rit{r)-Rt{T)]dFf{T). (7.1.3)
Нетрудно видеть, что соотношения (7.1.2) и (7.1.3) имеют соответствен-
но следующий смысл:
Рвз=Ш?-со'х=Ш?\
где &[, &"х , $2> ^Г -индексные супериндикаторы [128] первого ранга
первого порядка:
6>\=Ft($); a>;=Fttf);
<&;=J?Jf); d,'2=Rft(t);
G)\, &\ - обобщённые супериндикаторы {гипериндикаторы [128]):
a>*t=Ff<(t)-Ffi(t);
d>l=Rft(t)-R{i(i).
Соотношения (7.1.2) и (7.1.3) исследуются методами теории стохасти-
ческой индикации [128].
7.1.2. КЛАССИФИКАЦИЯ Г-ПРОЦЕССОВ
В п. 7.1.1 был рассмотрен самый общий случай, когда операционное
время f ограничено как снизу, так и сверху. Однако на практике чаще
встречаются Г-процессы, качество (пригодность) которых определяется
лишь одним из неравенств: f>fH или Т<хд.

408
Глава 7. Специализированные модели ЦНП
Определение 7.1.2. Г-процесс, пригодность которого равносильна вы-
полнению условия
*>*., (7.1.4)
называется нормативным. А
Если, например, для выполнения задачи системы достаточно лишь её
безотказности в течение нормативного времени fw, то процесс её функ-
ционирования - нормативный Г-процесс.
Определение 7.1.3. Г-процесс, пригодность которого равносильна вы-
полнению условия
f<td, (7.1.5)
называется директивным или оперативным. ▲
Так, если на выполнение задачи системе отводится директивное время
Тд, то процесс её функционирования - директивный Г-процесс.
7.1.1) Обратим внимание на различие смысла переменной f в критери-
ях (7.1.4) и (7.1.5). Так, в (7.1.4) f - это время безотказного функциониро-
вания ЦУТС, т.е. характеристика её "эксплуатационно-технической на-
дёжности" ("живучести", см. {2.7.9}, {2.7.10}), а в (7.1.5) f - это собствен-
но операционное время, т.е. время, потребное для достижения цели опера-
ции, и, следовательно, характеристика как ЦУТС, так и ЦНПФС. А
7.2. ПОСТАНОВКА ЗАДАЧИ ИССЛЕДОВАНИЯ
ЭФФЕКТИВНОСТИ Г-ПРОЦЕССОВ
МАССОВОГО ОБСЛУЖИВАНИЯ
7.2.1. ОПЕРАТИВНЫЙ Г-ПРОЦЕСС КАК МОДЕЛЬ ПМО
Как уже отмечалось, в зависимости от задач исследования для описания
реальных процессов могут использоваться различные математические мо-
дели и методы. Применительно к процессам массового обслуживания наи-
более распространёнными являются дифференциальный и интегральный
методы, основанные на составлении и последующем решении соответст-
венно дифференциальных или интегральных уравнений для вероятностей
состояний СМО, описывающих процесс её функционирования [129]. Соот-
ветствующие этим методам модели ПМО не эквивалентны и отвечают раз-
личным степеням детализации процесса, диктуемой совокупностью опре-
деляемых показателей его качества. В задачи данной главы не входит

7.2. Постановка задачи исследования эффективности Т-процессов МО 409
сравнительный анализ указанных методов , поэтому здесь лишь отметим,
что её целям в большей степени отвечает интегральный метод. Для его
реализации был разработан метод, основанный на бинарной модели ПМО
и дающий решение задачи минуя этапы составления и решения интеграль-
ных уравнений [130].
Пусть КМО - сплочённый (см. п.2.6.2). Тогда результат операции будет
отражаться на всех элементах комплекса и для оценивания эффективности
ПМО целесообразно выбрать (определить) индивидуальный показатель
(см. п. 2.6.1.3), поскольку он в полной мере учитывает "интересы" как
СМО, так и "клиентуры", что абсолютно необходимо в случаях, когда ис-
точники требований входят в суперсистему в качестве её составных эле-
ментов2.
В зависимости от назначения ЦУТС существенной может оказаться та
или иная характеристика результата (тот или иной аспект) процесса её
функционирования. Поэтому на первый взгляд ЦУТС различного назначе-
ния по эффективности процессов их функционирования несравнимы, хотя
представляется очевидным, что такое сравнение может оказаться весьма
полезным, поскольку позволяет получить абсолютную оценку качества ор-
ганизации ЦНПФС.
В работе [130] отмечалось, что понятию эффективности ЦНПФС дают-
ся различные определения, однако везде существенной деталью (аспектом)
является время результативного функционирования ЦУТС, т.е. операци-
онное время. В связи с этим время f, потребное для выполнения стоящей
перед ЦУТС задачи, т.е. минимально возможное {виртуальное) время, рас-
ходуемое на достижение требуемых значений z/V характеристик качества
целевого эффекта операции, может служить "идеальной" ведущей компо-
нентой показателя Y,. качества её результатов. Напомним, что при реали-
зации метода ведущей компоненты все варианты (реализации) ЦНПФС,
результаты которых не удовлетворяют условию ^/„\el*/„)j (и™
Y.^Z,.) хотя бы по одной компоненте, считаются неконкурентоспособ-
ными, т.е. имеющими нулевую эффективность, и из рассмотрения исклю-
чаются. При таком подходе все операции, ведущей компонентой пока-
зателя результатов которых является операционное время т (т.е. все опе-
ративные Г-процессы), становятся сравнимыми по эффективности.
В дальнейшем под операцией будем понимать процесс "массового" об-
служивания одного произвольного требования и показателем качества это-
го процесса считать длительность f периода [0,f ] полного обслуживания
такого требования, поступившего в СМО, т.е. операционное время f.
1 Такой анализ дан в работах [129,130].
2 Именно такие КМО рассматриваются в [130].

410
Глава 7. Специализированные модели ЦНП
7.2.1) Приведённый тезис требует пояснения. "Массовость" обслужива-
ния "одного" требования проявляется, во-первых, в том, что это произ-
вольное требование, т.е. "полномочный представитель" всей массы (всего
потока) требований, а во-вторых, в том, что характеристикой "качества"
процесса обслуживания произвольного требования является его продолжи-
тельность (длительность), зависящая от характеристик всего потока требо-
ваний. ▲
Удобной аналитической математической моделью такого ПМО является
индикатор процесса обслуживания (ПО) произвольного требования, опре-
деляемый соотношением
d «в
d
/0=0
, (7.2.1)
где /, - момент начала i-го цикла обслуживания;
i\ - момент окончания i-го цикла обслуживания;
ft - длительность i-го цикла обслуживания.
На рис. 7.2.1 изображена временная диаграмма возможной реализации
циклического процесса n(t) \ где t0 = 0 - момент поступления требования
в СМО; г- операционное время; остальные обозначения те же, что и в вы-
ражении (7.2.1).
J
1
пц
Ю
*-*,-
X
Г*"2'1
- *«-
►
*о=0 'i
< h t\
Рис. 7.2.1
В идеальном случае, когда обслуживание требования начинается в мо-
мент его поступления в СМО и не прерывается до полного завершения,
выражение (7.2.1) принимает вид
ЯиДг) = я(/;£1,/;)=я(^/0,£1,)=Я(/;0,г), (7.2.2)
иллюстрацией которому может служить рис. 7.2.2, где тобс- время обслу-
живания требования.
В дальнейшем процесс и его математическая модель терминологически отождест-
вляются.

7.2. Постановка задачи исследования эффективности Т-процессов МО 411
'#„,(')
1
Легко заметить, что
Рис. 7.2.2
IAJt)A = t,,
(7.2.3)
где tp - время работы СМО по обслуживанию требования ("наработка"
СМО на одно произвольное требование). Как будет показано, в общем
случае f,*^.
В "идеальном" случае из формулы (7.2.2) следует, что
)njt)dt = )n{t;0,f)dt =jdt = f, (7.2.4)
0 0 0
Из выражений (7.2.1), (7.2.2) и рис. 7.2.1, 7.2.2 видно, что математиче-
ской моделью ПМО является оперативный Г-процесс. В дальнейшем он
будет кратко обозначаться ОПМО (см. (7.2.1».
7.2.2. ПОКАЗАТЕЛИ ЭФФЕКТИВНОСТИ ОПМО И
МАТЕМАТИЧЕСКАЯ ФОРМУЛИРОВКА ЗАДАЧИ
ЕГО АНАЛИЗА
Оценивание качества результатов ОПМО будем проводить по "крите-
рию пригодности" (см. (2.2.2), (2.2.3)). Это значит, что ОПМО считается
качественным (успешно завершённым), если длительность f периода [0,f ]
полного обслуживания требования, поступившего в СМО (операционное
время f), не превзойдёт максимально допустимое (директивное) время тд,
т.е. если выполняется условие (7.1.5). При этом предполагается, что по ря-
ду ведомых компонент1 вектора - показателя К» качества результатов
ОПМО задача выполняется "автоматически", т.е. обслуживание заявок
("клиентов") отвечает предъявленным требованиям (по качеству) и расхо-
ды на "качественное" обслуживание и организацию ОПМО) не превосхо-
дят предельно допустимых (см. (2.3.1)).
По второстепенным компонентам аспектов.

412
Глава 7. Специализированные модели ЦНП
В сформулированных условиях показатель эффективности ОПМО - ве-
роятность Рвз выполнения задачи СМО равна вероятности полного об-
служивания требования, которая при принятом критерии оценивания его
качества будет определяться одним из следующих выражений:
Рвз = P(t <fj = jF,(r)dF,# (*■)=©, (7.2.5)
ИЛИ
Рвз = Р{тд >т)= ]^(т)^(г) = йТ2. (7.2.6)
Здесь <ЬХ и со2 - супериндикаторы первого класса (а>х ,сд2) [128],
Ъ(*) = Ft„ (*); Rti (*) = Rfi/n (*),
где H = (Y;^Ztt{n_^ (см. п. 3.3.3).
Формулы (7.2.5) и (7.2.6) определяют среднее значение (математиче-
ское ожидание) вероятности выполнения задачи ЦУТС, хорошо оцени-
вающее эффективность массовой (многократно повторяющейся) опера-
ции (см. п. 3.2).
Если же требуется оценить эффективность уникальной (одиночной)
операции, то более надёжными её характеристиками являются гаранти-
руемые вероятности
о>Гвз(г)=а>[(г)=Р»!(1-гУ, (7-2.7)
<(Г) = <(У)=^'(1-У). (7-2-8)
позволяющие учитывать неопределенности как возможностей СМО, так и
предъявляемых к ним требований.
Для получения ответов на подобные вопросы необходимо знать закон
распределения Ff(t) виртуальной длительности f периода полного об-
служивания произвольного поступившего в СМО требования (виртуально-
го операционного времени f), называемый "законом обслуживания", и
закон распределения Ff (r) предельно допустимой длительности тд пе-
риода обслуживания этого требования (директивного операционного вре-
мени тд ), называемый "законом обслуженности". Методики их опреде-
ления будут рассмотрены ниже. Здесь же предположим, что эти законы
уже известны.
В общем случае каждое из распределений Ff (t) и Ff(t) будет характе-
ризоваться соответственно совокупностью параметров /7f=/7?l и
/7f =/7М, которые, в свою очередь, являются функциями параметров

7.2. Постановка задачи исследования эффективности Т-процессов МО 413
A'ik*, A'Lk КМО, а также характеристик jBL и В^ условий его функцио-
нирования и применения, т.е.
Ff(r) = Ff(r;^f) = Ff[r,^g(^,^,50j; (7.2.9)
Ffo{T)=Ffd(r;nf)=Ff\T;n^)\. (7.2.10)
Поэтому показатели Рвз, 0)гвз{у) эффективности ОПМО будут также зави-
сеть от этих параметров:
Рвз = Рвз{А{к),В{1)); (7.2.11)
«ш=<м=<м*л); (7-2Л2>
0>гМ = 0)гг{г)=0)гг{г;А{к),В{1)). (7.2.13)
Эффективным средством исследования влияния характеристик КМО и
условий его функционирования и применения на эффективность ПМО яв-
ляется аппарат теории чувствительности [151], на базе которого определя-
ются характеристики влияния (см. п. 4.1), являющиеся в руках исследова-
теля мощным орудием анализа ОПМО и его оптимального синтеза.
7.2.3. МЕТОДЫ ОПРЕДЕЛЕНИЯ ЗАКОНА ОБСЛУЖИВАНИЯ
Определение 7.2.1. Закон обслуживания - это закон распределения
Ff (r) виртуальной длительности f периода полного обслуживания про-
извольного требования, поступившего в СМО. А
Закон обслуживания является весьма содержательной характеристикой
качества ОПМО, реализующей его многофакторное (многоаспектное, мно-
гокомпонентное) исследование. Покажем это.
Как отмечалось ранее (см. п. 2.3.1), операционное время является пря-
мым показателем качества операции и явно или неявно фигурирует в лю-
бом показателе её эффективности. Более того, для большинства характери-
стик результатов (компонент вектора Y, 0 значения, достигаемые к концу
операции, существенно зависят от её длительности.
Известно, что многие требуемые качества результатов ЦНПФС, не
обеспечиваемые ЦУТС непосредственно в ходе операции, могут быть дос-
тигнуты за счет временного резерва (^временной избыточности"). Так, для
повышения качества продукции (за счёт её тщательной обработки), для
повышения точности расчётов и достоверности их результатов (путём
двойного - тройного просчёта и т.п.), для повышения достоверности пере-
даваемых сообщений (путём повторных посылок, помехоустойчивого ко-

414
Глава 7. Специализированные модели ЦНП
дирования и т.п.), для увеличения ущерба, наносимого противнику в ходе
боевой операции, и повышения вероятности его поражения (за счёт по-
вторных ударов) и т.д. требуется дополнительное время. При наличии ре-
зерва времени он часто может быть "перекачан" в другие качества резуль-
татов операции ("обменен" на них). В принципе указанный "обмен" обра-
тим. Так, точность удара по цели может быть "обменена" (в определенных
пределах) на его мощность, и наоборот [133]. Обе эти характеристики уда-
ра могут быть "обменены" на число ударов и, как следствие, на время про-
ведения операции (на операционное время).
Итак, в общем случае одна из компонент показателя Y. % качества ре-
зультатов операции - ОПМО - это операционное время f, т.е. длитель-
ность периода полного обслуживания произвольного требования, посту-
пившего в СМО.
Как отмечалось выше, при объявлении операционного времени f ве-
дущей компонентой вектора К» на остальные его компоненты налага-
ются ограничения и они переводятся в разряд параметров IIf. Что это
означает физически?
Пусть f = j>. Тогда ведомые компоненты образуют вектор
YZ-i) = (У\уУг9*"9Уп-\) 9 a накладываемые на них ограничения определяются
предикатом
($.,>е tol)=(*£-.> ц:-.>). с7-2-14)
означающим, что вектор ГЛ_^ имеет "усечённое" вектором Zf ,v распреде-
ление [29]. Поскольку многие (возможно, все) компоненты вектора Y^_X)
зависят от операционного времени f, то параметры
IIf = /7г\ = UFj 9щ ,...,лг,|') распределения Ff (т) будут зависеть от пара-
метров Пр распределения Ff. vF(*-i>) , а так как распределение векто-
ра Г, ^ усечённое и зависит от характеристик А,к^ СМО и характери-
стик В,л условий проведения операции, то от них и от параметров П^
распределения вектора Z/*_i\ будут зависеть и параметры пР\ распре-
деления операционного времени f, т.е.
Ff(т)= F{(т,П{)= Ff М^Л^>UzU>AW>B0 )J= Ф>п1.,) )• <7-2Л5)
где П^ =(я^),Я^1),^),Д(/)) = (^,<,..,< >•
До сих пор говорилось о характеристиках операции (её результатов),
влияющих на её продолжительность f косвенно (через параметры и ЭТХ

7.2. Постановка задачи исследования эффективности Т-процессов МО 415
СМО и ПМО, через "обмен" качеств на время и т.п.). Однако существует
характеристика требования, влияющая на операционное время f непо-
средственно. Это "объём" v или, другими словами, трудоёмкость требо-
вания^ время, необходимое для полного (и качественного) обслуживания
(без прерываний) требования в СМО с данной производительностью //. В
идеальном случае, когда обслуживание требования начинается в момент t0
его поступления в СМО и не прекращается до полного завершения, f = v
(рис. 7.2.2). Если задержка в обслуживании требования обусловлена лишь
наличием очереди на обслуживание, то
где f ож - время ожидания требованием начала обслуживания;
f np - время пребывания требования в СМО (в простейшем случае).
Представляется, что сделанных замечаний достаточно для уяснения от-
личий понятия "период обслуживания" от понятий "время обслуживания"
и "время пребывания в СМО". В ходе изложения последующего материала
производится дальнейшее раскрытие сущности этих понятий1.
Из всего сказанного следует, что при исследовании ОПМО среди ис-
ходных данных кроме параметров П? * должен быть и закон распределе-
ния F-(v) объема v требования.
При наличии всех этих данных закон распределения Ff (r) операцион-
ного времени f будет представлять собой их отображение на интервал
[ОД] некоторым оператором Qx, т.е.
Ft{r)=£2\F}{v);nl%)\. (7.2.16)
Перейдем к описанию методики определения функции Ff (r) [130].
Как видно из выражения (7.2.16), все исходные данные, кроме объема v
требования, детерминированы и при отыскании закона распределения вре-
мени f должны быть заданы. Тогда закон обслуживания Ff(r) будет
представлять собой преобразование закона распределения F-(v) объема v
требования {произвольного) оператором Qx процесса функционирования
конкретной субсистемы КМО - СМО, т.е.
Ff(r)=^{F,(v)}, (7.2.17)
где Д - оператор, определяемый принятой моделью ОПМО.
Итак, задача отыскания закона обслуживания сводится к реализации
преобразования (7.2.17) и может быть решена либо аналитически, либо ме-
тодом статистического моделирования.
Все временные характеристики ОПМО подробно рассмотрены в [130].

416
Глава 7. Специализированные модели ЦНП
Раскроем сущность аналитического решения задачи методом функции
Грина. Введём в рассмотрение систему случайных величин (v,f), и пусть
v - фиксированное значение (из множества возможных) объема v требо-
вания. Тогда функция
Ff(r;v)=Ff/-(r,v)=P(f<r/v = v) = G{zl(r-v)} (7.2.18)
представляет собой функцию Грина G рассматриваемой задачи [130,
169]- частное решение задачи, соответствующее данному значению v
"параметра" v, общее решение которой находится путём рандомизации
[130,183] частного решения, т.е.
Ff(r-v)= ]Ffv{r;v)dF,{v). (7.2.19)
Таким образом, метод функции Грина позволяет существенно упро-
стить задачу и свести её к отысканию функции распределения Ff (t;v)
длительности fv периода полного обслуживания произвольного требова-
ния фиксированного объёма v. Методики определения функции Грина
Ff (t;v) рассмотрены ниже.
7.2.2) При внимательном обобщающем взгляде можно заметить, что ме-
тод функции Грина (как и любой метод рандомизации), в сущности, реали-
зует "формулу полной вероятности" в интегральной форме. А
7.2.3) Представляется целесообразным дать содержательную интерпре-
тацию рассматриваемой модели показателя Y. * качества результатов опе-
рации (ОПМО) в терминах сформулированной в главах 2-5 методологии.
А
Пусть показатель К * определяется в симплексной канонической фор-
ме, т.е.
f{a)=(&,fi,f)9 (7.2.20)
где 6) - показатель целевого эффекта от обслуживания произвольного
требования;
р - показатель количества ресурсов, расходуемых на обслуживание
произвольного требования;
f - время, затрачиваемое на полное обслуживание произвольного
требования (операционное время).
Поскольку, как отмечалось, в рамках теории массового обслуживания
вообще и применительно к оперативным Г-процессам в частности харак-

7.2. Постановка задачи исследования эффективности Т-процессов МО 417
теристикой "качества массового обслуживания"1 является его своевремен-
ность, то все компоненты вектора К3* выражаются во временных едини-
цах.
В общем случае согласно (5.3.11) целевой эффект & и расходуемые на
его получение ресурсы р связаны соотношением
Ты*
a)=a\p{t)dt = ap{To6c\ (7.2.21)
о
где p{t) - темп (скорость) освоения ресурсов при обслуживании требова-
ния;
тобс - время обслуживания требования;
р(тобс) - количество ресурсов, освоенных за время тобс обслуживания
требования;
а - размерный коэффициент.
Поскольку при исследовании ПМО понятие частичного (не полного)
обслуживания требования не рассматривается, т.е. требование может пре-
бывать (оказаться) лишь в одном из двух состояний: "обслужено" или "не
обслужено", то целевой эффект & может принимать лишь одно из двух
значений: 1 или 0.
Положим в (7.2.21) со = 1 и разрешим полученное уравнение относи-
тельно времени обслуживания тобс. В результате получим
v = arg{ap{To6c) = l}=p-i
1 ' (7.2.22)
ос;
Легко понять, что время v, потребное для полного обслуживания тре-
бования (т.е. чтобы было со = 1), представляет собой его временную ресур-
соёмкость. Если теперь предположить2, что при обслуживании требования
ресурсы всегда есть и темп их освоения постоянный3, т.е. p{t)= p = const,
то равенство (7.2.22) примет вид
v = (ap)~l (7.2.23)
и, таким образом, трудоемкость v требования характеризует и ресурсоём-
кость операции (ПМО) по его обслуживанию.
Итак, из сказанного следует, что в процессе обслуживания требования
расходуются все имеющиеся ресурсы, потребные для получения целевого
эффекта &, т.е. имеет место "эффект поглощения" (см. п. 3.3.4) ресурсов
1 Качество собственно обслуживания требования постулируется как заведомо при-
годное.
2 В теории массового обслуживания это предполагается всегда.
3 Это предположение не принципиально.
14 Зак. 3303

418
Глава 7. Специализированные модели ЦНП
р целевым эффектом & , а поскольку приемлемым (пригодным) считается
лишь целевой эффект со = 1, то он, в свою очередь, "поглощается" трудо-
ёмкостью v требования, описывающей требуемую результативность опе-
рации (ОМПО) исчерпывающим образом. Другими словами, с учётом вве-
денной ранее абстрактной символики трудоёмкость требования имеет сле-
дующую интерпретацию:
z,~cbT~ v, (7.2.24)
где знак эквивалентности. А
7.2.4) С учётом введенной выше временной интерпретации трудоёмко-
сти (объёма) требования (см. (7.2.3)) для его полного обслуживания долж-
но выполняться условие f > v, т.е. операционное время, при котором тре-
бование может быть обслужено, должно быть не менее его объема. Следо-
вательно, временная трудоёмкость требования представляет собой норма-
тивное время ОПМО, т.е. v = fH. Другими словами, достижение его цели
(выполнение задачи СМО) равносильно условию
(v<t<id)=(iu<f<td), (7.2.25)
которое при фиксированных (неслучайных) значениях объёма требования
и директивного времени (срока) тд его обслуживания принимает вид
(v<f<rj=(r„<f<rj. (7.2.26)
С учётом сказанного ОПМО может быть назван нормативно-
оперативным Г-процессом, а показатель его эффективности определён в
случае (7.2.25) выражением
PB3=P(v<i<td) (7.2.27)
или в случае (7.2.26) выражением
PB3=P(v<f<rd). (7.2.28)
Поскольку в рамках рассматриваемого подхода, реализующего метод
функции Грина, основу решения задачи оценивания эффективности
ОПМО составляет определение условной функции распределения Ff {t;v)
операционного времени f v относительно фиксированного объёма v требо-
вания, то величина v играет роль параметра этого распределения, с помо-
щью которого нормативное требование f > v к операционному времени
fv выполняется "автоматически". В этом можно убедиться на примере,
рассматриваемом в п. 7.4.

7.2. Постановка задачи исследования эффективности Т-процессов МО 419
7.2.4. МЕТОДЫ ОПРЕДЕЛЕНИЯ ЗАКОНА ОБСЛУЖЕННОСТИ
Определение 7.2.2. Закон обслуженности - это закон распределения
Ff (т) директивной длительности f д периода полного обслуживания про-
извольного требования, поступившего в СМО. А
Как отмечалось, время f д зависит от целого ряда факторов (в общем
случае случайных - неопределённых) и может принимать различные зна-
чения, предопределяющие в каждом конкретном случае качество опера-
тивного Г-процесса.
Пусть, например, обслуживание требования состоит в сборе информа-
ции о состоянии управляемого объекта, её обработке с целью определения
необходимого управляющего воздействия и передаче команды управления
на объект. Тогда для того, чтобы управляемый процесс имел требуемые
характеристики, все указанные операции должны быть выполнены во
вполне определённые сроки тд, превышение которых приводит к срыву
процесса управления.
В отличие от обычных технических систем автоматического управле-
ния, в которых максимально допустимое запаздывание управляющего воз-
действия определяется лишь параметрами объекта и системы управления и
для каждого режима работы последней известно, в больших системах
(КМО) дело обстоит гораздо сложнее и величина fд, как правило, точно
не известна.
В общем случае для рассматриваемых ОПМО директивное время тд
может зависеть не только от состояния управляемого объекта, но и от ус-
ловий, в которых он находится, и которые в управляющем звене точно не
известны (тем более априори), от требуемой в этих условиях оперативно-
сти выполнения задачи управления, диктуемой общей текущей ("опера-
тивной") обстановкой, которая, в свою очередь, зависит от состояния су-
персистемы (супер-КМО) и т.д.
При реализации метода ведущей компоненты, очевидно, аналогичную
компоненту имеет и показатель Z,x требуемого качества результатов опе-
рации (ОПМО) (см. п. 3.3.3). Пусть это компонента z„=fd. Тогда ведомые
компоненты образуют вектор Zf^ =(£r,£*,...,C-i)> определяющий в вы-
ражении (7.2.14) границы усечения распределения случайного вектора
Y"
В отличие от вектора L компоненты вектора Z v слабо связаны ме-
жду собой, так как каждое из требований £,, [/= l(l)#i] выдвигается супер-
системой (точнее, ситуацией) и на уровне субсистемы, в сущности, не-

420
Глава 7. Специализированные модели ЦНП
управляемо (см. п. 5.4.3.). Поэтому возможности для "перекачки" требова-
ний Z"in_x\-> к результатам ГЛ_^ операции в требование тд к её длительно-
сти f здесь невелики. Тем не менее параметры nfa = Ш*\ закона рас-
пределения Ff (т) директивного операционного времени тд косвенно за-
висят от параметров П*. распределения вектора Z?tS, а так как распре-
деление F%. \?и-\)) зависит от условий В^г. применения КМО, то от
них будут зависеть и параметры пР\ распределения директивного опера-
ционного времени f д, т.е.
Ff»= Ff>;tfJ= Г<\т;П®\рьч),^0)]= фп^}), (7.2.29)
где Я{1> = (Я^,^0) = (^,^,>.,<>.
До сих пор говорилось о требовании f д, которое должно быть предъяв-
лено к длительности f ОПМО, но которое априорно неизвестно, в то вре-
мя как на этапе проектирования и создания КМО и организации ОПМО к
качеству его результатов уже должны быть предъявлены требования. Для
решения таких задач, как известно, определяются некоторые гипотетиче-
ские (расчётные) условия проведения ПМО, применительно к которым и
производятся все расчёты.
Если наряду с вектором параметров ПР \ известен закон распределе-
ния Ff (т) расчётного (гарантируемого на уровне ФОК, см. (5.4.10)) ди-
рективного операционного времени f д, то закон распределения Ff (т)
времени тд будет представлять собой их отображение на интервал (0,l]
некоторым оператором 122 , т.е.
FfJr)=i22K(T);fffJ. (7.2.30)
Поскольку на этапе проектирования суперсистемы в общем случае
трудно предвидеть все возможные условия её функционирования (все си-
туации, в которых она может оказаться), то распределение Ff (r) , как
правило, либо вовсе неизвестно, либо определяется как вырожденное, т.е.
FfJr)=j(r-rJ, (7.2.31)
где т^- расчётное директивное операционное время, назначаемое экспер-
тами априорно [130] (см.{1.4.7}).
В зависимости от этапа жизненного цикла суперсистемы и обусловлен-
ного этим опыта её эксплуатации и применения для определения функции

7.2. Постановка задачи исследования эффективности Т-процессов МО 421
распределения Ff (г), а также и Ff (т) могут быть использованы различ-
ные приёмы и методы. Наиболее приемлемыми в практическом отношении
являются следующие три метода1:
- метод экспертного оценивания;
- экспериментальный метод;
- метод имитационного статистического моделирования.
7.2.5. О МЕТОДАХ РЕШЕНИЯ ЗАДАЧ ОПТИМАЛЬНОГО
СИНТЕЗА КМО И ОПМО
Общие вопросы синтеза ЦУТС и ЦНПФС были подробно рассмотрены
в п. 4.2. Всё сказанное там в полной мере относится к синтезу КМО и
ОПМО. Поэтому здесь будут рассмотрены лишь специфические особенно-
сти их синтеза. При решении задачи синтеза КМО и ПФК кроме "функ-
циональной эффективности" ОПМО должен учитываться целый ряд до-
полнительных факторов, и в первую очередь его стоимостные характери-
стики (показатели "экономической эффективности")2 (см. {2.7.12}). Пока-
затели "функциональной и экономической эффективности", как правило,
находятся в противоречии, так как для достижения большего целевого эф-
фекта (v) требуются большие затраты (f). Для разрешения этих противо-
речий обычно применяется один из вариантов бифакторной схемы, т.е. оп-
тимизация показателя "функциональной (экономической) эффективности"
при ограничениях на показатель "экономической (функциональной) эф-
фективности" (см. <2.4.6), (2.4.12), п. 4.3.1).
Сразу отметим, что анализ "экономической эффективности" ОПМО
представляет собой весьма сложную задачу из-за отсутствия данных о
стоимостных характеристиках элементов КМО и ПФК и о зависимости
этих характеристик от времени. Чаще всего эта зависимость принимается
линейной. Тогда для стационарного режима ПФК один из вариантов пока-
зателя "экономической эффективности"3 может быть представлен в сле-
дующем виде:
Щт)=э(т,х{т))=^,х{я))^^
= [UPB3-CM^Ps3hC3p3N-Cn{l-p3)N]T9 (7.2.32)
В более общей постановке эти методы освещены в п. 5.4.3, поэтому здесь они
лишь перечисляются.
2 Напомним, что эффективность одна (см.{2.7.12}) и здесь речь идёт об аспектах
операционных свойств ОПМО.
Точнее, "экономического эффекта ".
14* Зак. 3301

422
Глава 7. Специализированные модели ЦНП
D(x) и Oft,X) - средний доход, приносимый КМО в единицу времени
и за время Т;
С(х) и С(Т,Х) - средние суммарные затраты в единицу времени и за
время Т;
d =d(x) - средний доход в единицу времени от обслуживания
одного требования;
Ск=Ск(х) - средние потери (штраф) в единицу времени от не об-
служивания одного требования;
Сп = Сп(х) - средние потери (штраф) в единицу времени из-за про-
стоя одного обслуживающего аппарата;
Сэ=Сэ(х) - средние затраты в единицу времени на эксплуатацию
одного обслуживающего аппарата;
N - число обслуживающих аппаратов в СМО;
Я - интенсивность (плотность) входящего потока требо-
ваний;
Рвз - вероятность полного обслуживания требования, по-
ступившего в СМО;
р3 - вероятность того, что в произвольный момент времени
произвольный обслуживающий аппарат СМО занят
требованием.
Легко заметить, что все перечисленные параметры соотношения (7.2.32)
представляют собой "агрегаты".
Выражение (7.2.32) учитывает лишь динамические затраты, т.е. затраты,
производимые в процессе эксплуатации и целевого применения КМО. Од-
нако в него может быть введено отрицательное слагаемое, учитывающее
средние затраты Ср на разработку и создание КМО, не зависящие от вре-
мени его функционирования, т.е.
Э{Т) = 2>( Г) -С(Т)-Ср = {D-С)Т-Ср . (7.2.33)
В результате может быть определён момент tn начала режима прибыль-
ного функционирования КМО (если он существует), т.е.
Св
t ==-£=. (7.2.34)
Из равенства (7.2.34) видно, что для существования такого режима
должно выполняться условие D >С.
Поскольку оба показателя Рвз и Э(т) зависят от одних и тех же пара-
метров X(w) КМО, то задача их оптимизации в бифакторной схеме реша-
ется как было сказано выше. Однако часто при поиске приемлемого реше-
ния задачи синтеза ОПМО либо нет возможности варьировать значения
всех указанных параметров, либо если такая возможность и есть, то при

7.2. Постановка задачи исследования эффективности Т-процессов МО 423
большом значении параметров и значительных диапазонах их допустимых
значений эта задача оказывается весьма неопределённой и трудоёмкой. В
таких случаях могут оказаться весьма полезными коэффициенты и функ-
ции чувствительности критериальных функций к этим параметрам
(7.2.35)
позволяющие решать целый ряд важных для практики задач, таких, как:
- выделение параметров, к изменению которых показатели эффектив-
ности наиболее чувствительны, и определение необходимых их из-
менений, обеспечивающих требуемое повышение эффективности
ОПМО;
- определение точки X*,, пространства параметров, в которой эта
чувствительность минимальна;
- сравнительный анализ влияния различных параметров на "функцио-
нальную и экономическую эффективность" ОПМО и т.д.
В заключение подчеркнём (и напомним), что ещё большими возможно-
стями анализа качества КМО и эффективности ПМО обладает аппарат ха-
рактеристик влияния, рассмотренный в п. 4.1.
7.2.6. О ХАРАКТЕРИСТИКАХ ОПЕРАТИВНОСТИ ОПМО
Введём в рассмотрение случайную величину
f„=f,-f, (7.2.36)
которую будем называть показателем оперативности ОПМО по времени
(ПОВ). При этом положительные возможности значения величины f0 на-
зываются показателем резерва оперативности, а отрицательные - пока-
зателем дефицита оперативности.
Представляется очевидным, что характеристики показателя оператив-
ности ОПМО могут иметь практический интерес. Поскольку величина f 0
случайная, то эти характеристики должны быть вероятностными. В прин-
ципе может быть найдена исчерпывающая вероятностная характеристика
случайной величины f 0 - закон её распределения, однако здесь мы огра-
ничимся рассмотрением лишь числовых характеристик ПОВ f 0, называе-
мых также показателями оперативности, но различающихся физическим
смыслом. Целесообразно различать три типа показателей оперативности:

424
Глава 7. Специализированные модели ЦНП
- показатель средней оперативности (ПОС);
- показатель среднего резерва оперативности (ПРОС);
- показатель вероятностного резерва оперативности (ПРОВ).
Определение 7.2.3. Математическое ожидание т0 ПОВ f 0 называется
показателем средней оперативности по времени (или "оперативностью
в среднем"). А
Из определения 7.2.3 следует:
*.=r*-r=]fc>)-**(*)k*-
(7.2.37)
Средняя оперативность т0 численно равна алгебраической сумме пло-
щадей, заштрихованных на рис. 7.2.3 и взятых с указанными там знаками.
Определение 7.2.4. Математическое ожидание f0+ положительного зна-
чения f * ПОВ f 0 называется показателем среднего резерва оперативно-
сти (или «резервом оперативности в среднем»). ▲
F{(t)\Fft(t)
Рис. 7.2.3
Из определения 7.2.4 и рис. 7.2.3 видно, что
(7.2.38)
Средний резерв оперативности т0+ численно равен заштрихованной на
рис. 7.2.3 площади со знаком плюс.
Определение 7.2.5. Вероятность Р+ того, что ПОВ f0 примет положи-
тельное значение, называется показателем вероятностного резерва опе-
ративности (или «резервом оперативности по вероятности»). ▲

7.2. Постановка задачи исследования эффективности Т-процессов МО 425
По определению 7.2.5 вероятность Р+ - есть вероятность ненулевого ре-
зерва или нулевого дефицита оперативности. Из равносильности нера-
венств
следует:
(fe>0)=fo>f)
P+=P(f0>0)=P(f-fJ=g71=Pi
вз
(7.2.39)
Пример 7.2.1. Пусть случайные величины f и fд имеют смещённые
(двухпараметрические) показательные распределения с параметрами
// = 1, а = 1иу = 1,с = 2 соответственно, т.е.
Ff (т) = [l - е-м{т~а)]А {т - а) = [l - e^]А (г -1); (7.2.40)
^W=[l-^(T"c)k(^-^)=[l-^(T"2)k(^-2). (7.2.41)
Графики функций Ff (т) и Ft(t) изображены на рис. 7.2.4.
Ж) <
1
<
*7
► F*»
*W.
^^^^^^^_
п>
г
•)
\
/4W
►
0 ** = т,
Тогда
Рис. 7.2.4.
г.+ =г;-Г+=3-2 = 1;
р+ =й) =1 L_e-/«<~) = 1-Ie-' =0.82
//+v 2
(7.2.42)

426
Глава 7. Специализированные модели ЦНП
Пример 7.2.2. Пусть случайные величины распределены одинаково, т.е.
Ff(r)sFf§(r). Тогда
г0+=г;-г=о;
/>+ = й>1=1 —*-*<*-*> = 1-1 = 0.50
// + v 2
(7.2.43)
Пример 7.2.3. Пусть в условиях примера 7.2.1 // = 0.5; а = 1 и v = l;
с = 2. Тогда
^о = ^ - ^ = 3 - 3 = °;
f0+ = г; - Г = 2.63 - 2.26 = 0.37;
_У_е-м(с-ш) = j _ ±е-г = 060
// + v 3
(7.2.44)
Из сравнения результатов примеров 7.2.1 - 7.2.3 следует, что в общем слу-
чае средний и вероятностный резервы оперативности существенно различ-
ные, мало связанные между собой характеристики, и когда ПОС и ПРОС
ракны нулю, ПРОВ, т.е. вероятностный резерв оперативности, может ока-
заться значительным. Таким образом, анализ ОПМО и их синтез по одним
средним показателям их качества практически неприемлемы.
7.2.7. ОБ ЭКСПЕРТНОМ ОЦЕНИВАНИИ ОПЕРАТИВНОСТИ ОПМО
Как было показано в п. 5.4.3, одним из основных методов построения ма-
тематической модели показателя требуемого качества результатов операции
является экспертный метод, вариант которого - задание экспертами детерми-
нированных значений его компонент, включающих в свой состав и дирек-
тивное время тэд. Такая методика реализуется прежде всего на этапе проекти-
рования КМО, когда назначается директивное время тдр, в которое должна
укладываться длительность f полного обслуживания «произвольного требо-
вания» (операционное время). Если это время задано (назначено), то при на-
личии закона обслуживания Ff(r) вероятность выполнения задачи ЦУТС
(СМО) определяется равенством
Рвз = р(? ^rJ=Ff(rJ=g>, = <. (7.2.45)
Нетрудно заметить, что выражение (7.2.45) реализует КС-схему (см.
п. 3.4.3) оценивания качества результатов операции и может использоваться

7.2. Постановка задачи исследования эффективности Т-процессов МО 427
для оценивания её качества «снизу» или «сверху» путём назначения и под-
становки в (7.2.45) соответственно значений т'д = min тд или т"д = max тд.
Причём такое оценивание может производиться на любом этапе жизненного
цикла КМО.
Раскроем физический смысл равенства (7.2.45). В принципе, как было ука-
зано, директивное время f д случайно и имеет некоторое (часто неизвестное
экспертам) распределение Ff (r). Назначение неслучайного расчётного ди-
рективного времени тдр равносильно замене истинного распределения Ff (r)
вырожденным ступенчатым распределением
Fft{t)=A{T-Tdp), (7.2.46)
"скачок" которого происходит в точке, соответствующей
100 /7-процентному квантилю тп распределения Ff{t). Описанная схема
реализует "критерий пригодности", уровень значимости которого равен rj
(рис. 7.2.4). При этом апостериорная вероятность щ выполнения задачи
СМО [128] будет не менее со[(у) с вероятностью y = l-Tj. Таким образом,
оценивание эффективности ОПМО по формуле (7.2.45) сопряжено с риском,
определяемым вероятностью 7]. Естественно, что при определении тдр экс-
перты стремятся уменьшить этот риск и инстинктивно (интуитивно, эвристи-
чески) занижают значение тдр (поскольку распределение Ff(r), а следова-
тельно, и его квантиль т^, соответствующий вероятности 7], неизвестны).
Это, разумеется, повышает уровень у гарантии получаемой оценки эффек-
тивности ОПМО, но в то же время существенно снижает само значение
(Q* [у) этой оценки. Покажем это на примере.
Пример 7.2.4. Пусть случайные величины f и f д имеют смещённые
(двухпараметрические) показательные распределения с параметрами ju = 1,
0 = 1hv = 1,c = 2 соответственно,т.е.
Ff(T)=Ff(c;//,a) = [/-e-"(^]j(T.a) = [/.e-(r-,)]j(T-7); (7.2.47)
F{ (r) = Ff{r;v,c) = [/-e-v{T-c)]A{T-c)=[l-е(т-2)]л{г-2). (7.2.48)
Графики функций Ff (r) и Ff (т) изображены на рис. 7.2.5.
Пусть уровень значимости г/ = 0.05 [130]. Тогда
тдр =rv = F{-l{Tj)=Ff:l{l-r) = 2.05 (7.2.49)
и согласно выражениям (7.2.45) и (7.2.47)
<(у)= F,(r,_r)= F,(rJ= F{ (2,05) = 0,65, (7.2.50)

428
Глава 7. Специализированные модели ЦНП
Ff(rY
1
(О?
0.05
(
чм
Ft(r
> а
)-
С
чГ~
*■*>
\
)
►
т
Рис. 7.2.5
т.е. с вероятностью у = 1 - Г] = 0,95 апостериорная вероятность й, выпол-
нения задачи СМО не меньше й^(0,95) = 0,65. Но при этом средняя (ап-
риорная) вероятность выполнения задачи СМО (см. {3.2.7}, {3.2.13})
К = Щ" = Ft(*J= Ff (2,05)= 0,65.
(7.2.51)
Теперь найдём точное значение Рвз априорной вероятности выполне-
ния задачи. Использовав формулу (1.4.83) из [128], получим
РВЗ = Щ=1-
Л_е-М(с~а) = j _ Q5e-1 = 082
/U + V
(7.2.52)
Пример 7.2.5. Пусть случайные величины f и fa распределены одина-
ково, т.е. Ft(t) = Ff (т). Тогда согласно (3.1.50) при любом Т}, в частности
при J] = 0,05,
Рвэ = <(r)=F{(tJ= tj = 0,05. (7.2.53)
Но согласно теореме 3.1.3
Рвз=со1=0,5.
(7.2.54)
▲
Из сравнения равенств (7.2.51) и (7.2.52), а также равенств (7.2.53) и
(7.2.54) видно, что первые из них при приемлемом уровне у гарантии за-
метно занижают оценку эффективности ОПМО, и при решении задач его
синтеза будут существенно завышать требования к его организации и ха-
рактеристикам КМО (к агрегатам их моделей), что, в свою очередь, приве-
дёт к большим материально-техническим, экономическим и другим затра-
там.

7.3. Определение и классификация моделей циклических ОПМО 429
7.3. ОПРЕДЕЛЕНИЕ И КЛАССИФИКАЦИЯ МОДЕЛЕЙ
ЦИКЛИЧЕСКИХ ОПМО
Перейдём к описанию методов построения и исследования математиче-
ских моделей ОПМО с целью оценивания их эффективности. Как было по-
казано в п. 7.2, для оценивания эффективности ОПМО необходимо знать
законы обслуживания и обслуженности. Поскольку закон обслуженности
определяет требования, предъявляемые суперсистемой к оперативности
ОПМО, то, как было отмечено (см. п. 5.4.3), его задание является прерога-
тивой высшего звена управления суперсистемы, определяющей цели
ОПМО и задачи КМО.
В данном параграфе излагаются методы анализа и синтеза эффективных
ОПМО в КМО при сформулированных целях операции, организуемой су-
персистемой, и задачах, стоящих перед КМО. Поэтому в его рамках реша-
ется задача отыскания закона обслуживания, являющегося исчерпываю-
щей характеристикой качества результатов ОПМО, позволяющей решать
как задачу его анализа, так и ряд задач его синтеза.
Как отмечалось в {2.7.9}, в целях упрощения математической модели
операции (ОПМО) возможна декомпозиция (разбиение) показателей её ка-
чества на целевые и обеспечивающие, позволяющая представить показа-
тель её эффективности - вероятность выполнения задачи ЦУТС (КМО) в
виде трёх или двух независимых сомножителей, каждый из которых может
вычисляться самостоятельно. Это соответствует представлению модели
ЦНПФС (ОПМО) с помощью двух независимых моделей, одна из которых
описывает процесс функционирования обеспечивающей подсистемы
ЦУТС (НМО), а другая - процесс функционирования её целевой подсис-
темы.
Модели циклических ОПМО позволяют описывать ЦНПФС в целом без
его декомпозиции. Это свойство циклических моделей в ряде случаев ока-
зывается весьма полезным, так как позволяет выявить непосредственное
влияние характеристик обеспечивающих подсистем на эффективность
ОПМО в целом.
В заключение отметим, что в основу п. 7.3 положены концепции моно-
графии [130], в связи с чем все сколько-нибудь подробные комментарии и
математические выкладки здесь опущены.
73.1. ЦИКЛИЧЕСКИЙ ОПМО И ЕГО МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
Начнём с содержательного определения циклического процесса обслу-
живания (ЦНПО).

430
Глава 7. Специализированные модели ЦНП
Определение 7.3Л. Обращение требования к СМО за обслуживанием
называется попыткой на обслуживание. А
Определение 7.3.2. Процесс обслуживания требования, реализуемый в
одной попытке, называется циклом или сеансом обслуживания. А
Определение 7.3.3. Процесс обслуживания требования, реализуемый в
результате ряда попыток, называется циклическим. А
Если процесс обслуживания массовый и каждое требование обслужива-
ется циклически, то процесс называется "циклическим процессом массово-
го обслуживания" (ЦНПМО). Если этот процесс к тому же и оперативный,
то он называется "циклическим оперативным процессом массового обслу-
живания" (ЦОПМО).
Теперь построим математическую модель ЦОПМО. Для этого необхо-
димо уточнить упоминавшееся ранее (см.{2.7.9}) понятие дееспособности.
Определение 7.3.4. Состояние КМО, в котором он реально может вы-
полнять возложенную на него задачу, называется состоянием дееспособ-
ности (или "дееспособным состоянием" - ДС). А
Определение 7.3.5. Состояние КМО, в котором он выполняет постав-
ленную перед ним задачу, называется состоянием результативного
функционирования (или "результативным состоянием" - PC). A
Определение 7.3.6. Состояние КМО, в котором стоящая перед ним за-
дача выполняется, называется состоянием эффективного функциониро-
вания (или "эффективным состоянием" - ЭС). А
Различие между PC и ЭС станет ясным из дальнейших рассуждений.
Пусть (ТРБС) - период работоспособного состояния (РБС) СМО;
(ТГТС) - период готовного состояния (ГТС) СМО; (ТДС) - период дееспо-
собного состояния КМО; (Трс) - период результативного состояния КМО;
(Гэс) - период эффективного состояния КМО1. Тогда согласно определе-
ниям 7.3.4 - 7.3.6 и сопровождающим их комментариям
(Гэс)с(Г^)с(гдс)с(Гггс)с(7'тес). (7.3.1)
Из (7.3.1) следует
(Тх)~ (Трвс)Г1 (Tm)C\ (ГДС)П (ТК)Г\ (Гэс)- (7-3-2)
Для каждого из пяти рассмотренных состояний СМО и КМО - работо-
способного, готовного, дееспособного, результативного, эффективного -
существует противоположное, т.е. соответственно неработоспособное
(НРБС), неготовное (НГТС), недееспособное (НДС), нерезультативное
(НРС), неэффективное (НЭС); следовательно, каждому из понятий "рабо-
Каждый из этих периодов может складываться из ряда непересекающихся между
собой подпериодов.

7.3. Определение и классификация моделей циклических ОПМО 431
тоспособность", "готовность", "дееспособность", "результативность", "эф-
фективность" может быть поставлена в соответствие бинарная модель
процесса функционирования СМО и КМО.
В связи со стремлением к наиболее полному исследованию операций,
проводимых КМО, в дальнейшем будут использоваться лишь относящиеся
к нему понятия "дееспособность", "результативность" и "эффективность".
Определение 7.3.7. Индикатор (см. определение 3.1.1) периода (ТДС)
дееспособного состояния КМО называется Д-процессом и имеет следую-
щее аналитическое выражение:
I(t ,(<)= W{t)= ±n(t;ik>i'k)= ±n(t;ik,tk + wk), (7.3.3)
где ik - момент начала Л-го подпериода ДС КМО;
i[ - момент окончания Л-го подпериода ДС КМО;
wk - длительность Л-го подпериода ДС КМО. А
Из определения 7.3.7 следует:
'7^(*)А = Гдс(гя), (7.3.4)
'о
где t0- момент начала наблюдения ПФ КМО;
тн- время наблюдения ПФ КМО;
Тдс(тн) - длительность периода ДС КМО за время тн его наблюдения. А
Определение 7.3.8. Индикатор периода (Тндс) недееспособного состоя-
ния КМО называется ЯД-процессом и им^ет следующее аналитическое
выражение
7(f,J') = ^')= tn(t;t'JkJ= ±n(t;i'J'k+vk), (7.3.5)
где i[- момент начала Л-го подпериода НДС КМО см. (7. 3.1),(7.3.2);
ik+l - момент окончания Л-го подпериода НДС КМО;
vk - длительность Л-го подпериода НДС КМО. А
Из определения 7.3.8 следует:
''*1уШ< = Тндс(тн), (7.3.6)
где Тндс(тн) - длительность периода НДС КМО за время тн его наблюде-
ния.
Из определений 7.3.7 и 7.3.8 непосредственно следуют соотношения:
Тдс{Тн)+ТНдсМ = *н'> (7.3.7)

432
Глава 7. Специализированные модели ЦНП
W(t)+V{t) = l. (7.3.8)
Определение 7.3.9. Индикатор периода (ТРС) результативного состоя-
ния КМО называется РГ-процессом и имеет следующее аналитическое
выражение:
I(Tte)(t)LAK{t) = A(f-t)±n^;SltS^ =
= *{* -t)$,n(t;S„S, +f,), (7.3.9)
1=1
где 5, = t0 = 0 - момент поступления требования в СМО;
f - длительность периода полного обслуживания произвольного тре-
бования (операционное время);
5,.- момент начала i-го цикла (сеанса) обслуживания требования;
S. - момент окончания i-го цикла обслуживания требования;
т.- длительность i-го результативного цикла обслуживания требова-
ния. А
Определение 7.3.10. Индикатор периода (Тэс) эффективного состоя-
ния КМО называется ЭГ-процессом или циклическим оперативным
процессом обслуживания (ЦОПО) и имеет следующее аналитическое
выражение:
/(^) = 77и(*) = 4*-01^('ДД+)=
/=1
= (f-t)t,Jl(t;S„S, +f?), (7.3.10)
1=1
где Sf— момент окончания i-го эффективного цикла обслуживания произ-
вольного требования;
ft - длительность i-го эффективного цикла обслуживания произволь-
ного требования. А
Фрагменты временных диаграмм возможных реализаций всех четырех
определённых выше процессов - W(t), V(t), J7K{t), I7KL(t) - изображены
на рис. 7.3.1, где обозначено: в§ - длительность #-й паузы в обслуживании
требования [*==1(1)#ю-1], Т. = т, + в§ - длительность интервала времени ме-
жду 1-й и (/+1)-й попытками на обслуживание требования [i=l(l)#if-l], ос-
тальные обозначения те же, что и в формулах (7.3.3) - (7.3.10). При этом
импульсы РГ-процесса заштрихованы горизонтально, импульсы ЭТ-

7.3. Определение и классификация моделей циклических ОПМО 433
процесса - вертикально, а импульс завершающего цикла, в котором закан-
чивается обслуживание требования {произвольного), - наклонно.
В дальнейшем попытка, в которой т§ > 0, называется успешной или ре-
зультативной; результативная попытка, в которой ft, называется эффек-
тивной; эффективная попытка, в которой 5* =т, называется завершаю-
щей. Аналогично называются и соответствующие им циклы обслужива-
ния.
Как видно из рис. 7.3.1, в изображённых на нём реализациях 1, 3 и т-й
циклы результативны; 1, 3 и т-й циклы эффективны; т-й цикл завершаю-
щий; 2-я и 4-я попытки безуспешны.
Представляется очевидным, что после т-й попытки (если их продол-
жать) могут быть как успешные, так и безуспешные попытки, однако про-
цессы TIK(t) и J7KL{t) обрываются в момент1 времени S^=T9 т.е. когда
обслуживание требования завершено. Таким образом, в отличие от про-
цессов W{t) и V(t), периоды которых (ТДС) и (Тндс) распределены по всей
временной оси, периоды (Трс) и (Тэс) процессов IJK{i) и I7KL{t) сосредо-
точены на отрезке времени [0,т], что нашло отражение в соответствующих
аналитических моделях.
7.3.2. МОДЕЛЬ АБСТРАКТНОГО КМО
В п. 7.3.1 была определена математическая модель ЦОПО произвольно-
го одиночного требования, поступившего в СМО. Однако в данной главе
речь идёт о массовом обслуживании, которое существенно зависит от
структуры и характеристик КМО в целом. Их определение и составляет
цель данного пункта.
Из выражений (7.3.3), (7.3.5), (7.3.9) и (7.3.10) видно, что определяемые
ими модели протекающих в КМО процессов стохастические, т.е. характе-
ристики этих процессов подвержены воздействию случайных факторов и
должны исследоваться вероятностными методами. Исходными данными
при реализации этих методов являются вероятностные характеристики (за-
коны распределения, числовые характеристики) параметров исследуемых
процессов, которые, в свою очередь, определяются структурой КМО и ор-
ганизацией взаимодействия его элементов.
Численно длительность f периода полного обслуживания требования (операци-
онное время) и момент Sm его окончания равны.

434
Глава 7. Специализированные модели ЦНП
А *»
X

7.3. Определение и классификация моделей циклических ОПМО 435
Все исследуемые в данной главе модели ЦОПМО полностью определя-
ются моделями процессов W(i), J7K(t), ITKL(t), находящихся в последова-
тельном "соподчинении":
W(t)ynK(t)>nKL{t), (7.3.11)
где >— знак доминирования (отношения порядка).
Доминирование процессов ряда (7.3.11) проявляется в том, что характе-
ристики его предшествующего члена влияют на характеристики после-
дующего при отсутствии обратного влияния. Таким образом, их математи-
ческое моделирование должно начинаться с процесса W{t), характеристи-
ки которого определяются динамикой ПФК1.
В данной главе рассматривается класс моделей КМО, в которых исход-
ным является процесс V(t), а процесс W(i) определяется из соотношения
(7.3.8). Для наглядного их представления на рис. 7.3.2 изображена струк-
турная схема абстрактного КМО, где обозначено:
КМО - комплекс массового обслуживания;
И- источник требований;
Ип - источник помех обслуживанию требований;
/(/) - входящий поток требований;
In(t) - входящий поток помех;
СМО - система массового обслуживания;
УО - узел обслуживания;
Н- накопитель требований;
Нп - накопитель помех;
r(t) - поток попыток на обслуживание требований;
l'n(t)- поток помех, поступающих в УО для устранения;
БО - блок организации процесса обслуживания требований;
Д- диспетчер, управляющий потоком /'(*) попыток на обслуживание
требований;
С*2, Сз - сигналы управления потоком /'(*);
I"(t) - выходящий поток обслуженных требований;
Гп (t) - выходящий поток устранённых помех;
I"(t) - поток отказов на обслуживание требований, полученных на входе
вУО;
I"(t) - поток отказов на обслуживание требований, полученных во время
их обслуживания в УО.
1 Именно такая схема моделирования реализуется в п. 7.4 при исследовании процес-
са функционирования конкретного КМО.

436
Глава 7. Специализированные модели ЦНП
К М D
ГГГТТП
пш
Рис. 7.3.2
Раскроем смысл понятия "помеха".
Определение 73.11. Все события, происходящие в КМО и препятст-
вующие обслуживанию поступившего в него требования, называются по-
мехами. А
Как физическая природа помех, так и сложность создаваемых ими пре-
пятствий обслуживанию требований могут быть самыми различными. Это
могут быть неисправности и отказы в работе СМО; требования более вы-
сокого ранга, обладающие приоритетом на обслуживание; помехи, созда-
ваемые противником, и т.п. [130]. Общим для помех всех типов является
свойство делать невозможным обслуживание требования до их устране-
ния. В принципе эта "невозможность" может быть как абсолютной, так и
относительной, т.е. возникающей сразу с появлением помехи или спустя
некоторое время и в соответствии с некоторыми дополнительными усло-
виями. Другими словами, приоритет помех на их устранение перед обслу-
живанием требований может быть как абсолютным, так и относительным
[129,130].
Здесь рассматривается случай абсолютного приоритета помех, когда
обслуживание требования возможно лишь при их полном отсутствии. При

7.3. Определение и классификация моделей циклических ОПМО 437
первом появлении помех обслуживание требования прерывается и возоб-
новляется лишь в следующем цикле. При этом различают два случая:
а) во время устранения помех они продолжают возникать с прежней
интенсивностью;
б) во время устранения помех новые помехи не возникают.
Поскольку в рассматриваемой постановке помехи - суть требования,
обладающие абсолютным приоритетом, и устранение помех равносильно
обслуживанию этих требований в некоторой СМО, то по отношению к по-
мехам случаи "а" и "б" соответствуют ПМО с "чистым" ожиданием и ПМО
с "чистыми" отказами.
Следует заметить, что в зависимости от характера помех "обслуживаю-
щая" их СМО может быть как отличной от СМО, обслуживающей требо-
вания, так и той же самой. Однако реализуемый в данной главе метод
функции Грина позволяет не делать этого различия и рассматривать обе
СМО как одну.
Обратимся вновь к структурной схеме КМО (рис. 7.3.2) и перечислим
допущения относительно его элементов, при которых будет исследоваться
ЦОПМО:
1) СМО - одноканальная система массового обслуживания произволь-
ного типа;
2) входящий поток l(t) требований - квазирекуррентный поток одно-
родных событий [129, 130];
3) входящий поток In(t) помех - рекуррентный поток однородных со-
бытий [129, 130];
4) поток I'(i) попыток на обслуживание требований - рекуррентный
поток однородных событий;
5) закон распределения F^v) объема v требования - произвольный;
6) закон распределения Fu(u) времени и устранения одной помехи -
произвольный;
7) режим работы СМО по устранению помех - установившийся (стацио-
нарный).
Поскольку помехи обладают абсолютным приоритетом, то они "обслу-
живаются" (устраняются) совершенно независимо от процессов поступле-
ния и обслуживания требований (как будто их не существует). Это позво-
ляет раскрыть структуру процесса V{t), которая в каждом из отмеченных
выше случаев "а" и "б" имеет свои особенности. Фрагменты временных
диаграмм реализаций процесса V(t) для каждого из этих случаев изобра-
жены на рис. 7.3.3, а, б, где обозначено:
gj - момент возникновения (обнаружения)у-й помехи;
£j - момент окончания устранения у-й помехи;

438
Глава 7. Специализированные модели ЦНП
в • - интервал времени между моментами возникновения (/-1)-й иу-й
помех, вj = gj - gM;
иj - момент начала/-го периода недееспособности КМО (периода заня-
тости СМО устранением помех);
t\ - момент начала /-го периода недееспособности КМО (периода заня-
тости СМО устранением помех);
tk - момент начала А-го периода дееспособности КМО (периода незаня-
тости СМО);
V, - длительность /-го периода недееспособности КМО;
wk - длительность А>го периода дееспособности КМО.
МО
а)
1\
»>t*\
V,
и>,
1>,
иА
W,
1>,
«5 \*~»6
£
б)
М')
0,
£, G
М,
&
1£
i +
r+W,
г—v.
А
И\
Р*
t'
% £ t
-е.
в*
-V,
и>,
f, U-wt
6
в\
А
%
А-
Рис. 7.3.3
В связи с перечисленными выше допущениями все протекающие в
КМО процессы W(t), V{t), J7K(t), J7KL(t) на интервалах их определения

7.3. Определение и классификация моделей циклических ОПМО 439
стационарны, поэтому их одномерные плотности распределения имеют
следующие выражения:
*м==^ад+=^*(*--1);
w v+w v+w
0V(*>*')=:r^=<?(z)+^-=£(z-l);
v+w v+w
в
9йш (za)=\ rM т^*Ь)+fT¥*b -1)
^Jz;<) = {rA^S(z)+^S(z-1
(7.3.12)
(7.3.13)
+ Ft(t)S(z)U(t); (7.3.14)
+ Ff(t)S(z)\A(t). (7.3.15)
Сделаем ряд замечаний о потоках /(/) и /'(/), так как рассматриваемый
здесь случай требует пояснения. На рис. 7.3.4 показаны фрагменты вре-
менных диаграмм их возможных реализаций, где обозначено:
ц' - момент поступления в СМО Л-го требования;
б\ - интервал времени между моментами поступления Л-го и (Л+1)-го
требований, вк = t(k+x) - t(k);
Г3 - директивное время обслуживания Л-го требования;
S)k' - момент совершения i-й попытки на обслуживание к-то требова-
ния;
0; - интервал времени между i-й и (/+1)-й попытками на обслужива-
ние Л-го требования, в\к) = S$ - Sf°.
t(M\..t
t^ + rt* &Ф ^/.w + t?>
Рис. 7.З.4.

440
Глава 7. Специализированные модели ЦНП
С помощью 8 -функции потоки l(t) и /'(/) могут быть заданы анали-
тически:
/(')= is(t-t^); (7.3.16)
к=-оо
I'{t)=A(fM-t)Zs(t-Slk)), (sP = tP), (7.3.17)
где тк' - длительность периода полного обслуживания Л-го требования.
Так как в дальнейшем рассматривается процесс обслуживания произ-
вольного требования, то в обозначениях соответствующих ему элементов
математической модели его номер к будет опускаться. При этом для крат-
кости процесс будет называться ЦОПО (см. определение 7.3.10).
В заключение сделаем замечание относительно характеристик процес-
сов ПK(t) и JJKL(t). Как видно из рис. 7.3.1, длительности т,. и т? (соот-
ветственно результативного и эффективного циклов обслуживания) всегда
удовлетворяют соотношению
Ti>T:,[i = l(l)'nl (7.3.18)
причём поскольку процессы П К (t) и ПKL (t) начинают обрываться в мо-
мент времени iQ и i0 + г, не связанные с процессом W(t)9 то в общем слу-
чае распределения длительностей (f, , f,+ ) и (fm , £*) их первых и послед-
них (завершающих) циклов, соответственно, будут отличными от распре-
делений длительностей f,, f,+, [i = 2(l)m -1] остальных циклов.
7.3.3. МАТЕМАТИЧЕСКАЯ ФОРМУЛИРОВКА ЗАДАЧ
ИССЛЕДОВАНИЯ ЦОПО
В п. 7.4 будут рассматриваться методики решения прямой и обратной
задач исследования ЦОПО. Раскроем их содержание (см. п. 2.3.5, гл. 3,4).
А. Прямая задача (задача анализа ЦОПО):
- определение вероятности РВз выполнения задачи КМО при произ-
вольном директивном времени тд;
- анализ чувствительности показателя Рвз к параметрам и ЭТХ СМО и
ЦОПО и влияния управляемых параметров на эффективность ЦОПО.
Б. Обратная задача (задача синтеза ЦОПО и СМО): определение "опти-
мальных" (в некотором смысле) значений управляемых параметров и ЭТХ
СМО и ЦОПО.
Дадим математическую формулировку этих задач.

7.3. Определение и классификация моделей циклических ОПМО 441
А. Как было отмечено (см. п. 7.2.7), в рамках данной главы "закон об-
служенное™" принимается ступенчатым (вырожденным)1. Это означает,
что директивное время тд - не случайно и задача определения вероятности
Рвз сводится к отысканию функции распределения Ff (т) периода f, при
наличии которой
PB3 = P(i<td)=F{{rd). (7.3.19)
На этапе анализа ЦОПО все его параметры считаются заданными и за-
дача определения "закона обслуживания" Ff(r) сводится к отысканию
преобразования (7.2.17), т.е.
Ff(T) = i2,{F»}, (7.3.20)
где Qx - оператор, определяемый моделью ЦОПО;
v - объём требования.
При реализации метода функции Грина преобразование (7.3.20) имеет
вид
Ff(r)=]Ffv(r^VF,(^). (7.3.21)
Здесь Ff(r;v) = Ff/d(T;v)= P(t <t/v = v) = A{a(t-v)} - функция Грина
рассматриваемой задачи [130,169], которая при циклическом ОПО опреде-
ляется одним из следующих выражений:
FtM;v)= iPm(v)Ft{m)(r), (7.3.22)
m=\
где Pm (v) - вероятность того, что обслуживание требования объема v за-
кончится в т-м цикле;
fm - длительность периода [0,fv] обслуживания требования v при
условии, что оно заканчивается на w-м цикле;
F{St;v)=±p;(t)Rum{v), (7.3.23)
где Ря'(т) - вероятность того, что за время т будет совершено п эффек-
тивных циклов обслуживания требования;
н>(я) - суммарная длительность п эффективных циклов обслуживания
требования.
Б. Как уже указывалось (см. гл. 4), множество постановок обратной за-
дачи практически неисчерпаемо, в связи с чем общая их математическая
формулировка отсутствует2. В рамках данной главы она заключается в
Это допущение не принципиально и принято лишь для наглядности изложения.
2 Формулировка обратной задачи, приведённая в п. 4.2.1, не исчерпывает всего её
многообразия с учётом неформальных методов её решения.
15 Зак. 3303

442
Глава 7. Специализированные модели ЦНП
отыскании значений параметров и ЭТХ процесса ПKL{t), обеспечивающих
гарантируемую (требуемую) его эффективность (см. п. 4.1.4), т.е. в основу
решения обратной задачи положен " критерий пригодности "
Сэ:Рвз>Ртвр3=Рг. (7.3.24)
Из определения процессов W(t), V{t), nK(t)9 ПKL(t) и абстрактной
модели КМО (см. рис. 7.3.1 - 7.3.4) следует, что их стохастические свойст-
ва определяются в первую очередь свойствами таких элементов КМО, как
входящие потоки l(t) и In (t) требований и помех, поток r(t) попыток на
обслуживание требований, время и устранения помехи, длительности f. и
f/" результативных и эффективных циклов обслуживания требований и т.д.
В принцице все перечисленные объекты могут быть "управляемыми"
(регулируемыми), и тогда задача синтеза ЦОПО будет заключаться в оты-
скании оптимальных значений характеристик всех их. Однако здесь рас-
сматривается решение задачи в предположении (весьма естественном), что
помехи неуправляемы, следовательно, неуправляемы процессы V(t) и
W(t), и синтез ЦОПО заключается в выборе типа потока I'(t) попыток на
обслуживание требований, способа (механизма) воспроизведения обслу-
живания требований в циклах, следующих за прерванным, и ряда других
характеристик, перечень которых приводится в следующем пункте.
7.3.4. КЛАССИФИКАЦИЯ МОДЕЛЕЙ ЦОПО
И ЗАДАЧ ЕГО СИНТЕЗА
Основными элементами организации ЦОПО, предопределяющими его
стохастические свойства, являются поток I'(t) попыток на обслуживание
требования и способ воспроизведения обслуживания после его прерыва-
ния.
Рассматриваются три модификации потока /'(')> определяющие классы
(К) моделей процесса nK(t)9 и три модификации способа воспроизведения
обслуживания, определяющие типы (L) моделей процесса nKL(i).
1. Модель I[(t) потока I'(t), в которой в моменты Si9 [i = l(l)ni] сто-
хастически независимы от процесса W(t). Одним из видов такого потока,
допускающих обобщения результатов, является детерминированный по-
ток. Здесь рассматривается его простейшая модификация - регулярный по-
ток, в котором события происходят через равные по длительности (в)
промежутки времени, т.е.

7.3. Определение и классификация моделей циклических ОПМО 443
i[(t)=A{t0-t)is(t-ie). (7.3.25)
2. Модель I2(t) потока Г(t), в которой моменты Si9 [j = l(l)nt] сов-
падают с моментами ?., [i = l(l)ni] "освобождения" СМО от всех помех,
накопившихся за время их устранения, т.е.
l'2(t)=A(fv-t)i S(t-it), [i0Uy (7.3.26)
3. Модель l'3(t) потока l'(t), в которой моменты Sn [i = l(l)nf], сов-
падают с моментами g'n [i = l(l)w] окончания устранения отдельных оди-
ночных помех, т.е.
r3{t)=A{t.-t)± S(t-i;), [?,иу (7.3.27)
Нетрудно видеть, что модели I[(t) и r2(t) реализуют крайние случаи
стохастической зависимости потока r(t) попыток от процесса fV(t) дее-
способности КМО (от полной независимости до жёсткой связи). Другие
возможные модели потока I'{t), очевидно, могут рассматриваться в этом
смысле как промежуточные. В терминах теории массового обслуживания
модели i2(t) и r3(t) потока r(t) соответствуют ПМО помех "с чистым
ожиданием" и "с чистыми отказами". При этом модель r3(t) даёт более
простое аналитическое решение задачи, в ряде случаев удовлетворительно
аппроксимирующее решение, соответствующее модели I'2{t).
Итак, модели I[(t), I2{t), r3(t) потока r(t) определяют модели /7,(*)>
n2(t), n3(t) результативного процесса nK(t) и классы niL(t), n2L(t),
n3L(t) моделей эффективного процесса nKL(t).
Опишем механизмы обслуживания требования при различных спосо-
бах его воспроизведения после прерывания в предыдущем цикле.
1. Без накопления результатов. При этом способе в каждом цикле об-
служивание воспроизводится с "начала", т.е. так, как будто этот цикл пер-
вый и обслуживание требования еще не производилось. При этом резуль-
таты обслуживания в предыдущих циклах (если они были) пропадают. Это
самый неэффективный режим обслуживания.
2. С полным накоплением результатов. При этом способе в каждом
цикле обслуживание возобновляется с того места (фазы, стадии), на кото-
ром было прервано в предыдущем цикле. При этом результаты обслужи-
вания в предыдущих циклах полностью сохраняются и накапливаются. Это

444
Глава 7. Специализированные модели ЦНП
самый эффективный режим обслуживания, однако организация такого ре-
жима не всегда возможна [130].
3. С частичным накоплением результатов. Такой способ воспроизве-
дения обслуживания возникает в случаях, когда процесс обслуживания
распадается на ряд этапов (фаз, стадий), каждый из которых должен реали-
зоваться без прерываний, и обслуживание требования в каждом цикле во-
зобновляется с начала этапа, прерванного в предыдущем цикле. При этом
результаты завершённых этапов обслуживания сохраняются и накаплива-
ются, а результаты прерванных этапов теряются. Эффективность такого
режима обслуживания принимает промежуточное значение между эффек-
тивностями режимов 1 и 2.
7.3.1) Первые два способа воспроизведения обслуживания являются част-
ными случаями последнего, поскольку обслуживание без накопления ре-
зультатов - суть обслуживание их с частичным накоплением при одном
этапе обслуживания, длительность которого равна объёму требования, а
обслуживание с полным накоплением результатов - суть обслуживание с
их частичным накоплением при бесконечно большом числе этапов беско-
нечно малой длительности. А
Итак, каждый из способов воспроизведения обслуживания определяет
тип L эффективного процесса nKL(t) класса К. Таким образом, сово-
купность класса if модели IK (t) потока / (/) и типа L способа воспроиз-
ведения обслуживания требования определяет конкретную модель nKL{t)
циклического оперативного ЭГ-процесса обслуживания. Нетрудно видеть,
что таким образом синтезируются девять моделей ЦОПО (табл. 7.3.1).
Таблица 7.3.1
Класс К
1
2
3
Тип L
1
Kit)
Kit)
Kit)
2
Kit)
Kit)
Kit)
3
Kit)
Kit)
Kit)
В заключение приведём перечень основных характеристик ЦОПО и
СМО, определение которых составляет содержание обратной задачи их ис-
следования.
Класс К и тип L модели nKL(t) ЦОПО определяют набор его управ-
ляемых параметров, а также параметров, оказывающих основное влияние

7.3. Определение и классификация моделей циклических ОПМО 445
на его качество и эффективность. Набор параметров - "агрегатов" ЦОПО,
которые могут оптимизироваться, приведён в табл. 7.3.2.
Таблица 7.3.2
Класс К
1
2
3
Тип L
1
&М >6мФт
д>М„
д>Мт
2
&М> в\1>Рт
д>Мт
ti'Vn,
3
&М> ОмФт'Лт
0>M.**J.
0>мт,пт
В табл. 7.3.2.обозначено1:
дм = дтах - максимальный объём требования, допускающий его обслужи-
вание за период Тъ с требуемой вероятностью РЦ;
7]m = 7jmjn - минимальное число этапов (фаз, стадий), обеспечивающее об-
служивание требования за период т# с требуемой вероятно-
стью Pgj;
вм = 9тах - максимальная периодичность попыток, обеспечивающая об-
служивание требования за период тд с требуемой вероятно-
стью Рвз ;
Mm - Mmin ~ минимальное быстродействие (производительность) СМО,
обеспечивающее обслуживание требования за период т^ с тре-
буемой вероятностью РЦ.
Приведённый в табл. 7.3.2 набор параметров ЦОПО, естественно, не ис-
черпывает всего их многообразия, тем не менее он охватывает наиболее
важные его характеристики. Кроме того, в дальнейшем определяется ряд
параметров, не вошедших в табл. 7.3.2.
Методики решения задач анализа и синтеза всех девяти (а с учётом мо-
дификаций - восемнадцати) моделей ЦОПО подробно рассмотрены в мо-
нографии [130], к которой мы отсылаем заинтересованного читателя. Од-
нако для иллюстрации сущности перечисленных моделей ЦОПО и области
их применения в следующем параграфе рассматривается типичный пример
его исследования.
Аналогичные сокращения используются и в дальнейшем.

446
Глава 7. Специализированные модели ЦНП
7.4. МОДЕЛЬ ПРОЦЕССА ФУНКЦИОНИРОВАНИЯ
ВОССТАНАВЛИВАЕМОЙ ЦУТС
Рассматриваемая в данном параграфе математическая модель ЦНПФС
пригодна для описания процесса функционирования ЦУТС различного на-
значения, поэтому её наименование здесь не приводится.
7.4.1. СОДЕРЖАТЕЛЬНАЯ (ВЕРБАЛЬНАЯ) ПОСТАНОВКА ЗАДАЧИ
На ЦУТС возложена задача, для выполнения которой при заданных
ЭТХ ЦУТС требуется время г?. Система имеет ограниченную надёжность.
В случайные моменты времени д. в системе возникают неисправности,
каждая из которых приводит к отказу в работе системы.
Первая из возникших неисправностей начинает немедленно устраняться
ремонтным органом (РЕО) ЦУТС. При этом неисправности продолжают
возникать с прежней интенсивностью. Попытки продолжить выполнение
задачи совершаются после устранения каждой из неисправностей в поряд-
ке их возникновения, однако система возобновляет результативное функ-
ционирование лишь по устранении всех неисправностей, причём выполне-
ние задачи возобновляется с "начала".
Задача считается выполненной, если для этого потребовалось время ftf,
не превышающее некоторого предельно допустимого (директивного) зна-
чения тд. Режим работы системы установившийся (стационарный).
Требуется определить (оценить) эффективность процесса функциони-
рования ЦУТС и исследовать её зависимость от ЭТХ системы и объёма
(трудоёмкости) задачи, характеризуемого временем г?.
7.4.2. ПОСТРОЕНИЕ АГРЕГИРОВАННОЙ МАТЕМАТИЧЕСКОЙ
МОДЕЛИ ЦОПО
Как следует из постановки задачи, ЦНПФС представляет собой цикли-
ческий оперативный Г-процесс массового обслуживания (ЦОПМО), инди-
катор эффективной компоненты которого имеет следующее аналитическое
выражение:
77э(/) = ^(г,-г)|:77[^5/,5/+г?4^-^)], (7.4.1)
/=i
где 5. = £.'_,, [/ = 1 (l)iw ] - момент совершения j-й попытки на выполнение
задачи;

7.4. Модель ПФ восстанавливаемой ЦУТС
447
bj у [/ = 0 (l)°°] - момент окончания устранения у-й неисправности
P,d
(помехи), где £0=0.
Пусть в результате статистического (или экспертного) анализа было
установлено:
- поток неисправностей - простейший и имеет интенсивность Я;
- время v устранения одной (произвольной) неисправности подчинено
показательному закону распределения с параметром ju;
- неисправности устраняются в порядке их возникновения.
Тогда в терминах теории массового обслуживания поставленная задача
имеет следующую формулировку.
На вход одноканальной СМО (РЕО ЦУТС) "с чистым ожиданием" по-
ступает простейший поток требований (неисправностей) на обслуживание.
ЦУТС справляется с возложенной на неё задачей, если на периоде времени
[0,тэ] найдётся хотя бы один интервал времени, не меньший г?, в течение
которого её РЕО будет свободным (что равносильно отсутствию неисправ-
ностей - помех).
w{t)
пМп31(*)
-0-
£
*—гА
5,=0
$г $г {$4-3»
V{t)
г?п
d
W.-+
г?,
И-И.-Н
и>,
[—г92—|
и>,
6
£
£
Рис. 7.4.1.
Легко увидеть, что в сформулированных условиях 77э(*) = 7731(/). Та-
ким образом, моделью рассматриваемого ЦОПО (ЦОПМО) может служить

448
Глава 7. Специализированные модели ЦНП
процесс 7731 (/) (см. [130] п. 2.4.1), временная диаграмма реализации ко-
торого приведена на рис. 7.4.1.
7.4.3. ОЦЕНИВАНИЕ ЭФФЕКТИВНОСТИ ЦНПФС
Поскольку модель V731 (t) подробно исследована в работе [130], то здесь
выкладки опускаются и приводятся лишь основные соотношения.
Итак, показатель эффективности ЦНПФС (ЦОПО) - вероятность РВз
выполнения задачи ЦУТС (СМО) - определяется следующим выражением:
Pw=P(f,<fa) = ]Fjr;*?)</Fjr), (7.4.2)
где -%ф(т;0)= [l-(l-Р^У'""™]^-*);
А
Р% - — коэффициент готовности ЦУТС в момент /0 = 0.
№
График функции F^ (г;г?) при г? = 1 изображён на рис. 7.4.2 (кривая al).
8 9 10 11 12 г
Рис. 7.4.2.
В результате интегрирования согласно (7.4.2) получим
^=/>(ft?<ra) = Ffrf(ra;t?)=Fftf(ra;tf,A,//) =

7.4. Модель ПФ восстанавливаемой ЦУТС
449
= [l - А, {&УА{»)Т> ]4тэ - #). (7.4.3)
Л{д)=рЯе-х».
Числовые характеристики длительности i6 периода выполнения задачи
ЦУТС (операционного времени) определяются равенствами
е™ - В
т* = »+-уГ; (7А4)
Dit = Л(г?)Л-'г?2 + 2Д (г?)Л"2(г?)- [г?+ Ах{&)Л-х{&УА(а)°\. (7.4.5)
Пример 7.4.1. Пусть *? = 1,Л = 1,// = 2. Тогда формулы (7.4.4) и
(7.4.5) дают
т,=5,44; Df= 28,38; а = 5,32 . (7.4.6)
А
В частном случае, когда в момент начала функционирования ЦУТС го-
това с вероятностью Д, = 1, формулы (7.4.3) - (7.4.5) соответственно при-
мут вид (рис. 7.4.2, кривая а.2):
P^F^^^-AMV^Mb -*Ь (7А7)
где AM={l-e-MVM''1' \
Л{&)=рХе-м,
ем-1
f°-*+-er! (7А8>
Dfa ^A^V^ + lA^A-^d)-^ ]\ (7.4.9)
Пример 7.4.2. Пусть, как и в примере 7.4.1, г? = 1,Л = 1,// = 2.Тогда
формулы (7.4.8) и (7.4.9) дают:
Тх « 4,44; Df « 25,83; afi « 5,02 . (7.4.10)
▲
Из сравнения решений примеров 7.4.1 и 7.4.2 следует, что с повышени-
ем готовности ЦУТС средняя продолжительность ftf периода полного об-
служивания требования уменьшается и, следовательно, оперативность (а
поскольку имеет место эффект поглощения, то и эффективность) ЦНПФС
растёт.
Пример 7.4.3. Предположим теперь, что объём и требования случаен и
распределён равномерно на интервале [ а, А), т.е.

450
Глава 7. Специализированные модели ЦНП
ф)=Е^Л, (0<а, 6<~). (7.4.11)
Тогда в общем случае
Ъ-а
'0
V
М
безусловное математическое ожи-
дание операционного времени f *
0
При [a,b)= [l,2) ju = 3, Л = 2 формула(7.4.12) даёт
f «36,4. (7.4.13)
Равенство (7.4.13) означает, что если, например, на обслуживание тре-
бования необходимо в среднем г? = (а + ft)/2 = 1,5 [ч], в ЦУТС в среднем
возникают две неисправности в час и на устранение одной неисправности
в среднем расходуется Л = l/ju = 1/3 [ч], то на полное обслуживание тре-
бования в среднем необходимо (расходуется) 36,4 ч. А
7.4.1) Напомним, что поскольку директивное время тэ детерминирова-
но, то условная [относительно директивной длительности fa операции
(ЦНПФС - ЦОПО)] вероятность *У,=^(£Э) выполнения задачи ЦУТС
имеет вырожденное распределение FA (со)=Л[со-0)г) (см. (3.2.13)),
вследствие чего средняя и гарантируемая вероятности выполнения задачи
ЦУТС численно равны, т.е.
Рвз = ^=^-Г)=<з(г)=0)г, ре [ОД]. (7.4.14)
А
7.4.4. АНАЛИЗ ЭФФЕКТИВНОСТИ ЦНПФС И КАЧЕСТВА ЦУТС
Из выражения (7.4.3) видно, что вероятность РВз выполнения задачи
ЦУТС зависит от трёх параметров - "агрегатов" г?, Я, ju, соответственно
определяющих основные ЭТХ ЦУТС: производительность, надёжность,
ремонтопригодность. Выявление их влияния на эффективность ЦНПФС
представляет собой одну из важнейших задач при организации эксплуата-
ции и технического обслуживания ЦУТС.
В условиях рассматриваемой задачи весьма информативными характе-
ристиками эффективности ЦНПФС и качества ЦУТС являются вероят-
ность РВз выполнения задачи и средняя длительность периода её выполне-
ния, т.е. математическое ожидание т# операционного времени £^.
Введём обозначения (см. (4.1.1)):

7.4. Модель ПФ восстанавливаемой ЦУТС
451
Г{1)(и{3);тд)=(рвз(и{3);тд), Та(и{3))) , (7.4.15)
где и,ък =(г?Д,//) - вектор управляемых ЭТХ ЦУТС и ЦНПФС. Тогда
матрица чувствительности показателей качества ЦНПФС будет иметь сле-
дующий вид:
dU,
^Ы h'Kyb) %Къ)\
Ф{») од,)) кЮ
(7.4.16)
,/•_<
ЭР,
дРв
где Л, ^ , А, ЭА , Л, ^ ,
*~Э* ' А"ЭД ' *'"Э/1 '
Произведя дифференцирование согласно (7.4.16), получим:
*;(1?Л/1;га) = -Д1^^^И[2-^^ + Я(1-^е-^)(тв--1?)];(7.4.17)
А;(г?,Д,//;тэ) =
~-е
- + у0Лг?+ГуЗАг?+ — - ll(l - у0<Гя* \хъ - 0)
; (7.4.18)
/,;(г?Д,//;гэ) = Ае-я[^-(^.М][1 + 4-^Х*э "*)] ; (7-4-19)
(//-А)
К(#,я,м)=
м
(м-яу
(7.4.20)
(7.4.21)
(7.4.22)
Пример 7.4.4. Пусть |?0 = 1,Я0 = 1,//0=2. Тогда формулы (7.4.17) -
(7.4.22) дают:
Л;(1,1,2/тэ)=-0.5е-(аШТз+а816)(0.816гд+1) ; (7.4.23)
Л/(1,1,2;гэ )=-е_(,и84Г8+а8|б)(0.408тэ + 0.592) ; (7.4.24)

452
Глава 7. Специализированные модели ЦНП
Л£(1Д,2;гэ) = 0.25<Г(а184Тз+,Ш6)(0.816тэ +0.184); (7.4.25)
hi (1,1,2) = 6,44; (7.4.26)
h\ (1,1,2) = 6,44; (7.4.27)
А; (1,1,2) = -2,72. (7.4.28)
На рис. 7.4.3 изображены графики функций чувствительности (7.4.23) -
(7.4.25) вероятности Рвз выполнения задачи ЦУТС к её ЭТХ D, Л , ju .Из
этих графиков, в частности, видно, что Рвз более чувствительна к Я (т.е. к
надежности ЦУТС), чем к 1) (т.е. к производительности ЦУТС), и что её
чувствительность зависит от тэ, т.е. от требований к оперативности
ЦНПФС. Коэффициенты чувствительности (7.4.26) - (7.4.28) показателя
f e этого выявить не позволяют. ▲
0,2
0,1
0
-0,1
-0,2
-0,3
-0,4
-0,5
Рис. 7.4.3
Домножив функции (7.4.23) - (7.4.25) и коэффициенты (7.4.26) -
(7.4.28) чувствительности на значения соответствующих управляемых па-
раметров, можно получить функции и коэффициенты влияния этих пара-
метров на эффективность и оперативность ЦНПФС. Рекомендуем читате-
лю проделать это в качестве упражнения.
Пример 7.4.5. В условиях примера 7.4.4 коэффициенты влияния управ-
ляемых параметров на оперативность ЦНПФС соответственно равны:
VI =|й*|-# = 6.44-1 = 6.44 ; (7.4.29)
\п^пх>К
7 Та

7.4. Модель ПФ восстанавливаемой ЦУТС
453
Ух = |*1| • Л = &44 • 1 = 6.44 ; (7.4.30)
К;=|а;|.// = 2,72-2 = 5.44 . (7.4.31)
А
Из сравнения равенств (7.4.26) - (7.4.28) и (7.4.29) - (7.4.31) видно, что
оперативность ЦНПФС (ее показатель) более чувствительна к изменениям
производительности (г?) и надежности (Л) ЦУТС, чем к её ремонтопри-
годности (//), однако при заданных значениях г?0 , Л0 ,//0 этих ЭТХ их
влияние на оперативность (f^) ЦНПФС практически одинаково.
Как было отмечено (см. 7.2.4), в рамках рассматриваемой модели иссле-
дуемой ЦНПФС может интерпретироваться как нормативно-директивный.
Поэтому несомненный интерес представляет анализ влияния на эффектив-
ность ЦНПФС нормативной и директивной характеристик его оперативно-
сти, которыми являются трудоёмкость (объём) д требования и директив-
ное операционное время тд завершения операции.
На рис. 7.4.4 изображено семейство "компромиссных кривых" Парето
уровней рг = Ргвз = 0,04{ЛРВЗ) 0,99 в системе координат г^Ог^ построен-
ные при Л = 1 и ju = 8, точки которых определяют гарантируемые с веро-
ятностями рг значения & ,тгь нормативного и директивного времён вы-
полнения задачи.
7.4.2) Рис. 7.4.4 представляет собой "сетчатую номограмму" уравнения
г = У^2)(г?;/1г), связывающего три переменные: $£, Тгь, рг. В принципе
число операндов номограммы может быть увеличено до любого требуемо-
го числа [186]. В частности, в рамках рассматриваемой задачи могут быть
учтены все агрегаты модели, включая Л и /и путём номографирования
уравнения т = /щ\&;А,р9р*). Понятно, что аналитические возможности
номограммы при этом повышаются, однако значительно усложняется про-
цедура её построения и падает наглядность получаемых на её основе вы-
водов. Тем не менее при решении практических расчётных задач номогра-
фический метод весьма эффективен. А
Как отмечалось (см. п. 4.1), подобные кривые (множества) позволяют
решать целый ряд задач неформального (качественного, содержательного)
анализа и синтеза ЦУТС и ЦНПФС. В частности, рис. 7.4.4 даёт наглядное
представление о соотношении трудоёмкости (объёма) г?г задачи и мини-
мально возможного времени тг, потребного для её выполнения, гаранти-
руемых с вероятностью рг, определяемой пометкой соответствующей

454
Глава 7. Специализированные модели ЦНП
О 1 2 3 4 г?/
Рис. 7.4.4.
кривой Парето. При наличии дополнительной информации на этой кривой
может быть выделена соответствующая ей подобласть |(г?г,тЛ } или точка
Изображённые на рис. 7.4.4 прямые определяют точки постоянного
суммарного влияния на эффективность ЦНПФС "аспектов" г?г и тд. При
этом точки касания этих прямых с кривыми Рвз{&т>тъ)- Р* соответствуют
максимальным значениям показателя РВз эффективности ЦНПФС при
фиксированном суммарном влиянии "аспектов".
Этот факт может служить одним из руководящих принципов (кри-
териев) при выборе предпочтительной точки на компромиссной кривой
Парето.
7.4.3) Обратим внимание, что рабочая область номограммы рис. 7.4.4
расположена выше прямой тд = г?, что обусловлено физическим смыслом
операционных характеристик г? и тэ. А
На этом заканчивается рассмотрение комплексных аналитических мо-
делей ЦНПФС, применяемых в задачах исследования эффективности опе-
раций.
В заключение заметим, что рамки монографии не позволили осветить
целый ряд вопросов как методологического, так и прикладного характера,

7.4. Модель ПФ восстанавливаемой ЦУТС
455
однако они нашли достаточное отражение в уже упоминавшихся источни-
ках [112, 129, 130]. Особенно рекомендуем читателю внимательно ознако-
миться с комментариями в монографии [130].
7.5. КОММЕНТАРИИ
В дополнение к замечаниям, носящим локальный характер и сделанным
в контексте по ходу изложения материала, кратко прокомментируем про-
блематику данной главы в целом.
7.5,1} В настоящее время известен целый ряд исследований, посвящен-
ных проблемам анализа и синтеза ЦНПФС - ПМО, в которых использу-
ются показатели эффективности, отличные от рассмотренных здесь.
Следует сказать, что применение детерминированных (не ве-
роятностных) показателей для оценивания эффективности ЦНПФС (что
часто имеет место) в принципе некорректно, так как не соответствует фи-
зической сущности рассматриваемого явления и не может дать исследова-
телю его объективную характеристику.
Из вероятностных характеристик ЦНПФС - ПМО, как правило, исполь-
зуются различного рода средние, например: математическое ожидание
числа обслуженных требований за определённый период времени, среднее
число отказов в обслуживании за тот же период и т.п.
Следует обратить внимание, что при определении этих показателей не
всегда правильно формулируется условие обслуживания требования.
В классических работах по теории массового обслуживания наиболее
полно изучены ПМО при простейших их организациях, когда полное об-
служивание требования интерпретируется как его принятие на обслужива-
ние. Однако совершенно очевидно, что в случае циклических Г-процессов
(а именно с ними мы сталкиваемся при исследовании сложных КМО) эта
классическая схема неприемлема, так как, во-первых, в таких КМО требо-
вания пребывают в СМО ограниченное время, которого часто недостаточ-
но для полного их обслуживания, а, во-вторых, в общем случае объёмы г?
требований могут не совпадать со временем тобс их "полного" обслужива-
ния. Так, например, если обслуживание требования состоит в приёме неко-
торой информации, объём которой измеряется необходимым для её приёма
временем г? [причём сеанс связи (приёма) считается успешным, если при-
нята некоторая часть г/ < г? информации, достаточная для её осмыслива-
ния и принятия соответствующего решения1], то описанный механизм
Весьма распространённая на практике ситуация.

456
Глава 7. Специализированные модели ЦНП
(стратегия) обслуживания требования не укладывается в рамки классиче-
ских задач ТМО и для его описания должны разрабатываться специальные
методы.
Этим требованиям в полной мере отвечает рассмотренная в данной гла-
ве методика, основанная на самом общем определении понятия "полное
обслуживание требования". Действительно, вероятность Рвз выполнения
задачи (полного обслуживания произвольного требования) может быть оп-
ределена совершенно независимо от того, что понимается под "полным об-
служиванием".
Пусть рассматривается ЦНПФС - ОПМО в стационарном режиме и
пусть за исследуемый промежуток времени [0,тэ] в СМО поступает в
среднем Л(тд) требований. Тогда, если вероятность РВз известна, то ма-
тематическое ожидание К(тд) числа К{ть) требований, обслуженных за
время тэ, будет определяться равенством
к(т9) = Л(тд)Рю.
Таким образом, вероятность Рвз позволяет находить и ряд дополни-
тельных показателей качества ОПМО. Однако несмотря на то, что показа-
тели Рвз и К(тд) функционально связаны и по оцениванию результатив-
ности ОПМО практически равносильны (см. п.2.6.1), вероятность Рвз вы-
полнения задачи СМО в семантическом отношении богаче, так как прямо
отвечает на вопрос о степени приспособленности ОПМО к решению стоя-
щей перед ним задачи, тогда как показатель К(тд) отвечает на этот вопрос
косвенно.
В заключение сделаем следующее замечание. Рассмотренные выше по-
казатели Рвз и Э(т) для СМО являются несобственными (внешними),
если поступающие в СМО требования входят в суперсистему. Но именно
по ней следует судить о качестве ЦНПФС - ПМО.
В принципе возможно определение и собственных показателей качества
и эффективности ПМО, однако и в этом случае требования к их уровням
должны назначаться по иерархическому принципу на основе требований к
показателям Р$3 и Э(т). Так, например, последовательность сеансов ра-
боты элементов КМО (СМО) и их готовность зависят как от плана их ра-
боты, так и от принятой стратегии и дисциплины их обслуживания, опре-
деляющих, какие сеансы каждого цикла обслуживания должны использо-
ваться, как результаты циклов обслуживания учитываются при назначении
приоритетов требований на обслуживание и т.п.
Все эти вопросы составляют проблему синтеза ЦНПФС (ЦУТС), исход-
ные данные которой должны вытекать из соотношений (7.2.5) или (7.2.6),
где fd - характеристика требований, предъявляемых к ОПМО суперсисте-
мой, а также из (7.2.7) или (7.2.8). ▲

7.5. Комментарии
457
7.5.2} В принципе в рассмотренную в данной главе схему вписывается и
процесс "массового" обслуживания одиночного требования, образующего
входящий "поток", состоящий из одного события, происходящего в мо-
мент поступления требования в СМО. В сущности, произвольность требо-
вания, фигурирующего в рассмотренной модели ЦОПО, позволяет интер-
претировать его как одиночное. А
7.5.3} Если в момент поступления требования в СМО в ней уже имеют-
ся требования [в узле ожидания (кроме помех)], то при обслуживании их в
порядке поступления длительность f периода полного обслуживания
вновь поступившего требования увеличится на суммарное время обслужи-
вания всех предшествующих требований. При учёте такой возможности
модель ЦОПО превращается в модель ЦОПМО. Сказанное относится ко
всем упомянутым в п. 7.3.4 моделям ЦОПО. Однако для рассматриваемо-
го произвольного требования требования, находящиеся в УО, являются
помехами и, таким образом, рассматриваемые модели их учитывают. А
7.5.4} На первый взгляд понятие "дееспособность" является синонимом
понятия "работоспособность", а также перекликается с понятием "готов-
ность". Поэтому необходимо уточнить его семантическую самостоятель-
ность.
Понятие "работоспособность" в основном применяется по отношению
к техническим устройствам и системам и означает их техническую ис-
правность, т.е. "потенциальную" готовность производить работу. Таким
образом, это понятие техническое.
Понятие "готовность" - эксплуатационно-техническое и означает не
только исправность технических устройств или систем, а и их реальную
готовность к выполнению возложенных на них задач. Оно применимо как
к чисто техническим, так и к человеко-машинным ("эргатическим") систе-
мам.
Оба эти понятия по отношению к характеризуемой ими системе явля-
ются внутренними (собственными) и никак не связаны с объектами, на ко-
торые система должна воздействовать (или с которыми она должна взаи-
модействовать), если эти объекты не входят в её состав. Нетрудно предста-
вить ситуацию, когда СМО находится в работоспособном состоянии, гото-
ва к действию, но недееспособна (НДС) из-за противодействия противника
или по причинам кинематического характера, так как требования для неё
недосягаемы.
Таким образом, понятие готовности достаточно для характеристики со-
стояния СМО и недостаточно для характеристики состояния КМО, в со-
став которого кроме СМО входят также требования и их источники [129].
Применительно к КМО готовность - это "потенциальная дееспособность".

458
Глава 7. Специализированные модели ЦНП
В принципе возможна ситуация, когда, будучи в дееспособном состоянии,
КМО функционирует, но не выполняет поставленной перед ним задачи из-за
неправильной организации взаимодействия его элементов (СМО и требова-
ний), из-за противодействия требований или их источников в разобщённых
КМО (см. п. 2.6.2) и т.п. В связи с этим целесообразно ввести ещё два поня-
тия: "результативного" и "эффективного" состояний КМО. А
7.5.5} Необходимо отметить, что часто (точнее, как правило) эффектив-
ность ЦНПФС отождествляется с его результативностью. Однако при такой
её трактовке теряется сама суть понятия эффективности, абсолютно необхо-
димого при комплексном системном подходе к анализу и оптимальному син-
тезу ЦНПФС, в рамках которого наряду с результативностью ЦНПФС учи-
тываются также его ресурсоёмкость и оперативность.
Вообще говоря, любой результат ЦНПФС даёт тот или иной эффект. Оче-
видно, этим и обусловлено отмеченное смешение понятий. Тем не менее по-
нятия "результативный", т.е. дающий некоторый (всё равно какой) результат,
и "эффективный" (а не эффектный), т.е. "действенный" [159], дающий нуж-
ный результат, принципиально различны.
Совершенно очевидно, что необходимым условием эффективности
ЦНПФС является его результативность, и притом позитивная. Однако ни
один из результатов ЦНПФС в отдельности не может хоть сколько-нибудь
полно охарактеризовать его эффективность. Для этого должны учитываться
все его результаты в целом и во взаимосвязи. Более того, даже совокупное
рассмотрение всех результатов (эффектов) ЦНПФС еще не даёт ответа на во-
прос, эффективен он или нет, поскольку показатель качества его результатов
сам по себе не отражает цели реализуемой ЦУТС операции. Поэтому кор-
ректная постановка задачи исследования эффективности ЦНПФС требует её
формулировки в замкнутой схеме через критерий пригодности, являющийся,
таким образом, математическим выражением цели операции и требуемого
уровня её достижения (см. п. 2.3).
В связи с этим следует отметить, что распространённое в настоящее время
оценивание эффективности операций с помощью функций от показателей их
результатов в принципе является некорректным и допустимо лишь в отдель-
ных частных случаях, в каждом из которых должно обосновываться (см.
п. 2.4). А
7.5.6} В дополнение к сказанному в п. 7.2.7 отметим следующее. Если ко
всем статическим характеристикам Y, _,ч качества результатов ЦНПФС-
ОПМО в принципе могут быть предъявлены конкретные требования Z?^,
то предельно допустимое время f э обслуживания требования (директивное
операционное время) фактически непредсказуемо, так как характеризует да-

7.5. Комментарии
459
намику операции и существенно зависит от оперативной обстановки (усло-
вий применения ЦУТС - СМО), в которой она протекает и которая априори
неизвестна. Поэтому получаемые при детерминированном директивном опе-
рационном времени тд решения задач анализа и синтеза ОПМО и КМО не-
обходимо рандомизировать по распределению случайной величины тэ по
формуле (7.4.2). А

Обычно новые научные истины побеж-
дают не так, что их противников убежда-
ют и они признают свою неправоту, а боль-
шей частью так, что противники эти по-
степенно вымирают, а подрастающее поко-
ление усваивает истину сразу.
М. Планк. "Единство физической картины мира"
То, что имеет основанием истину, следу-
ет напоминать, не боясь показаться надоед-
ливым.
Н.И. Пирогов
ЗАКЛЮЧЕНИЕ
Теперь, когда стал известен язык ТЭЦНП, целесообразно дать краткий
обзор изложенного материала и сделать ряд критических замечаний отно-
сительно основных проблем ТЭЦНП, её настоящего состояния и перспек-
тив развития. Многие из таких замечаний были уже высказаны по ходу из-
ложения материала, а также в комментариях. Поэтому здесь, возможно,
будут повторены наиболее принципиальные в концептуально-методо-
логическом плане положения.
Несмотря на сравнительную "древность" проблемы повышения эффек-
тивности целенаправленной деятельности людей, до настоящего времени
теория эффективности такой деятельности недостаточно разработана. В
известной литературе, посвященной вопросам исследования эффективно-
сти ЦНПФС (часто ошибочно называемой эффективностью систем -
ЦУТС), рассмотрены многочисленные методы её анализа, направленные
на решение большого круга частных задач, но лишенные основополагаю-
щих концепций, дающих с единых методологических позиций общий под-
ход к проблеме и позволяющих разрабатывать методики исследования эф-
фективности процессов целевого функционирования любых сложных тех-
нических систем (ЦУТС). Вообще до настоящего времени методологиче-
ские аспекты теории эффективности в литературе освещались недоста-
точно. Там же, где им уделено внимание, постановка проблемы, как пра-
вило, не обладает необходимой общностью.
Понятно, что объём монографии не позволил исчерпывающе рассмот-
реть все проблемы ТЭЦНП и вряд ли это возможно сделать в рамках одной
конкретной научной дисциплины, поскольку инженерная практика непре-
рывно развивается, порождая новые проблемы в самых различных науч-
ных областях. Тем не менее в настоящей монографии нашли отражение

Заключение
461
главные из концептуальных, методологических и методических аспектов
ТЭЦНП.
В результате проработки материала книги должны быть уяснены
основополагающие принципы практического применения ТЭЦНП.
Прокомментируем их.
ТЭЦНП является математическим инструментом исследования опе-
раций на этапе внешнего проектирования сложных больших систем и
перспективного планирования процессов их целевого функционирова-
ния (применения).
Так как проект - это замысел - план [159], то на этапе ВНЕПР ЦУТС
и ЦНПФС рассматриваются их модели, прогнозное качество которых и
составляет предмет анализа и синтеза. Таким образом, модель - это
предвосхищенное представление проектировщика (в широком смысле)
об объекте исследования. Поскольку на этом этапе исследования про-
блемы научной разработки народнохозяйственной или технической про-
граммы (проекта) проводятся в условиях максимальной неопределённо-
сти, то используемые исходные данные, основанные как на информации
о прототипах и прецедентах, так и на прогнозах о состоянии и развитии
производительных сил, техники, производства, сырьевой базы и т.п., но-
сят в значительной степени случайный (неопределённый) характер.
Из всего сказанного следует, что модели проектируемых объектов
(ЦУТС и ЦНПФС) являются принципиально стохастическими и, следо-
вательно, методы их исследования должны быть вероятностными. При
этом следует иметь в виду, что получаемые на вероятностных моделях
оценки качества исследуемых объектов (ЦУТС и ЦНПФС) в принципе
являются прогнозными, т.е. реализуемыми с соответствующими вероят-
ностями, распределение которых обусловлено распределением влияю-
щих на них случайных факторов, таких, как параметры и ЭТХ проекти-
руемых ЦУТС к ЦНПФС, а также условий проведения операции (см.
п. 2.3.3).
Необходимо ещё раз особо подчеркнуть, что поскольку как ЭТХ, так
и условия функционирования и применения реализуемой впоследствии
ЦУТС априори (на этапе её ВНЕПР) не известны, то и параметры и ЭТХ
моделей ЦУТС и ЦНПФС описываются в вероятностных терминах. Это
означает, что на этапе ВНЕПР речь идёт о проектировании целых клас-
сов ЦУТС и стратегий их целевого применения, конкретные реализации
которых обладают различной степенью приспособленности к выполне-
нию ЦУТС её функций. Для стохастических моделей ОС и ОК это
учитывается в рамках вероятностных показателей качества синтезируе-
мых объектов (ЦУТС и ЦНПФС), имеющих весьма чёткую и содержа-
тельную частотную интерпретацию: чем выше качество ЦУТС, а следо-
вательно, и эффективность ЦНПФС, тем чаще будет выполняться задача
ЦУТС, т.е. достигаться цель операции.

462
Заключение
Следует обратить внимание, что при детерминированном подходе к
проблеме ВНЕПР случайные факторы либо не учитываются, либо учиты-
ваются характеристическими значениями (средними, граничными - песси-
мистическими и т.п.). Однако следует иметь в виду, что в будущих опера-
циях эти расчётные значения параметров моделей ЦУТС и ЦНПФС могут
реализоваться лишь с нулевой вероятностью (о чем обычно забывают или
не знают). Поэтому если рассеяние реализации параметров ЦУТС в реаль-
ных ситуациях относительно расчётных (модельных) значений существен-
но (а такая возможность всегда существует), то детерминированная модель
оказывается неадекватной исследуемому объекту, получаемые на ней ре-
шения не обладают требуемой репрезентативностью [160] и, следователь-
но, непригодны для практического использования.
Иногда приходится слышать утверждение о том, что вероятностные ме-
тоды имеют узкую сферу применения. По этому поводу следует сказать,
что детерминированные модели представляют собой частные случаи веро-
ятностных (стохастических) моделей и всегда могут быть получены из по-
следних при вырожденных распределениях их параметров. Другими сло-
вами, детерминированная модель - это вырожденная стохастическая мо-
дель, но не наоборот (см. п. 3.5.1).
В дополнение к высказанным ранее замечаниям и комментариям на ос-
нове всего материала монографии можно сделать ряд важных для практики
выводов.
Рассмотренная в книге общая постановка задач исследования эффек-
тивности операции (ЦНПФС) должна служить базой для их комплексного
многокомпонентного анализа в условиях воздействия случайных факторов,
всегда сопутствующих ВНЕПР ЦУТС и ЦНПФС. Другие известные поста-
новки этой задачи, по существу, являются её частными случаями и имеют
более узкие сферы применения.
Методы теории стохастической индикации могут служить инструмен-
том для исследования качества объектов самой различной природы при
произвольной размерности векторов их характеристик.
Построенные на базе теории стохастической индикации показатели и
критерии позволяют исследовать эффективность уникальных (единичных)
операций и качество уникальных (единичных) ЦУТС, что является их не-
сомненным преимуществом по сравнению с показателями средних и га-
рантируемых результатов (целевых эффектов).
Методы исследования эффективности ЦНПФС должны опираться на
концепции теории стохастической индикации. При этом проблема сводит-
ся либо к определению законов распределения показателей виртуального и
требуемого качества результатов операции и последующему аналитиче-
скому решению задачи, либо к построению имитационной статистической
модели ЦНПФС и последующему исследованию на ней эффективности
процесса целевого применения ЦУТС.

Заключение
463
Рассмотренные в главе 6 функционально-стохастические модели
ЦНПФС специального назначения (СН) позволяют решать широкий круг
задач анализа и оптимального синтеза специальных ЦУТС и процессов их
функционирования.
Основанные на понятии Г-процесса и рассмотренные в главе 7 специа-
лизированные модели ЦНПФС могут служить базой для построения мате-
матических моделей широкого класса так называемых оперативных про-
цессов массового обслуживания.
Совокупность рассмотренных в монографии методов позволяет иссле-
довать эффективность ЦНПФС как на этапах проектирования и создания
ЦУТС, так и в процессе их целевого применения при весьма общих пред-
положениях о характеристиках их элементов и подсистем.
Итак, задачи исследования качества ЦУТС и эффективности ЦНПФС на
этапе их ВНЕПР должны решаться на базе изложенной выше теории эф-
фективности целенаправленных процессов. Однако за рамками ТЭЦНП
остаются две важные проблемы, окончательное решение которых невоз-
можно в принципе, поскольку они возникают совместно с возникновением
идеи новой программы (проекта). Это прежде всего проблема определения
операционных функционалов, обусловливающих свойства операционных
систем и комплексов, а также проблема определения (теоретически, экспе-
риментально или методом экспертных оценок) законов распределения ко-
личественных характеристик требуемого качества результатов ЦНПФС. В
сущности, решение этих проблем и составляет основу (ядро) задачи иссле-
дования качества ЦУТС и эффективности ЦНПФС на этапе их ВНЕПР.
В заключение коротко о роли ТЭЦНП как научной дисциплины в ста-
новлении учёного и инженера.
ТЭЦНП принадлежит к числу дисциплин так называемого системотех-
нического цикла. К таким дисциплинам относятся: "Общая теория систем",
"Анализ систем", "Системотехника", "Прикладная кибернетика", "Иссле-
дование операций", "Теория массового обслуживания", "Теория надёжно-
сти", "Теория принятия решений" и т.п. Более того, ТЭЦНП, с одной сто-
роны, определяет их методологическую основу, а с другой - служит инст-
рументом количественного анализа и синтеза исследуемых объектов в рам-
ках этих дисциплин. Она развивает у будущих инженеров системное
мышление, прививает навыки комплексного подхода к исследованию про-
цессов целевого функционирования ЦУТС на всех этапах их жизненных
циклов — от проектирования и разработки до эксплуатации (целевого
применения) — на основе рассмотрения комплексного операционного
свойства ЦНПФС - эффективности, а не только частных свойств ЦУТС -
надёжности, живучести и т.п. (хотя и достаточно важных).
Дело в том, что давно замечена склонность людей несколько преувели-
чивать значение той области деятельности, в которой они считают себя
специалистами. При проектировании технических систем, при планирова-

464
Заключение
нии каких-либо мероприятий это зачастую проявляется в том, что разра-
ботчик отдельного элемента технической системы или составитель плана
мероприятий стремится улучшать соответственно характеристики проек-
тируемого элемента или планируемого мероприятия, не принимая во вни-
мание другие элементы системы, другие мероприятия. Каждый специалист
преследует свою цель, и примирить их можно, только оценив каждое ре-
шение исходя из общих интересов, т.е. с учётом интересов всех элементов,
подсистем и проектируемой системы в целом.
Для успешного решения таких задач важно не только в совершенстве
владеть техникой и грамотно эксплуатировать её, но и уметь оценивать
эффективность применения техники, выявлять факторы, влияющие на эф-
фективность, и намечать пути повышения эффективности её целевого при-
менения.

ПРИЛОЖЕНИЯ
Приложение 1
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
= - знак равенства;
= - знак тождественного равенства;
d
= - знак равенства по определению;
= - знак условного (символического) равенства;
>]
знаки отношения порядка;
знаки отношения доминирования (превосходства);
знак отношения эквивалентности;
= - знак равносильности высказываний (событий);
=> - знак импликации высказываний. Так, если АиВ- высказы-
вания, то (А => 2?)=(из А следует В)=(А влечёт 2?)=(если
А, то В);
<=> - знак эквиваленции высказываний. Так, если АиВ- выска-
зывания, то (А <=> В) = (А тогда и только тогда, когда
2?)=(для того чтобы А, необходимо и достаточно В);
п - знак булева пересечения (пересечения множеств, конъюнк-
ция высказываний, "произведения" событий);
и - знак булева объединения (объединения множеств, дизъюнк-
ция высказываний, "суммы" событий);
<z,cz - знаки строгого и нестрогого включения одного множества в
другое соответственно. Так, если АиВ- множества, то
{АаВ) = (А есть собственное подмножество множества В);
е,ё - знаки принадлежности и непринадлежности элемента мно-
жеству соответственно. Так (aczA) = (a есть элемент мно-
жества А);
х - знак прямого (декартового) произведения;
л - знак операции взятия минимума. Так (а л Ь) = min{a, b};
v - знак операции взятия максимума. Так (a v b) = max{a,b};

466
Приложения
V - квантор общности. Так (\/л;) = (для всех х);
3 - квантор существования. Так (Зд:)«(существует
*);
( ) - скобки в нижнем индексе, обозначающие век-
тор;
[ ] - скобки в нижнем индексе, обозначающие мат-
рицу;
{ } - скобки в нижнем индексе, обозначающие ко-
нечное множество;
X v =[jc1,jc2,...,jc/i] - л-мерныйвектор-столбец1;
Х?к=(х1,х2,...,хп) - я-мерный вектор-строка1;
О/ s = (0,0,...,0) - нулевой я-мерный вектор;
1/v = (l,l,...,l) - единичный я-мерный вектор;
В[тп] = |ft J" - матрица размерности тхп;
В[т,п]= № ~ транспонированная матрица для матрицы В[тп];
Ъ9 - квадратная матрица порядка т;
В'1 =В^] - матрица, обратная для матрицы В[ту,
|j?| = |l?[m]| - определитель матрицы В[ту9
®[«,я] = II0,у|Г - нулевая матрица размерности тхп;
\т,п]= 1 lyf ~ единичная матрица размерности тхп;
2?[да] = ||^у|Г - единичная диагональная матрица порядка т;
Ия)ГИя)^и».))] ~ область (множество) значений вектора Xv,
удовлетворяющих условию (описанию) U\X, , );
^М = fa i» ={ai > аг >•"•> ап} ~ конечное множество п элементов ах, а2,..., ап;
d
{а-}= {а^ ={а,,а2,...} - счётное множество элементов а,-;
При необходимости основные обозначения Х,\ и Х,\ векторов могут быть ин-
версированы.

Приложение 1. Основные обозначения
467
[# = Л(/)л]=(| = Л,Л + /Д + 2/,...,л) - последовательность значений це-
лочисленной переменной г { I -
шаг последовательности);
d
(а.) =(а,, а2 ,..., ап), [ л = 2 (l)... ] - упорядоченная последовательность
(кортеж) элементов а19 а2,..., а„;
А « (л! с А) - подмножество множества А;
а - приближённое значение (оценка)
величины я;
У = /(*) = у{х) - функция;
У = #[/(*)] = ф[Я*)] - функционал;
^(jc) = /2{/(л;)}= /2{j;(jc)} - оператор;
х = f~l(y) = x(y) - функция, обратная для функции
У = Ах) = у(х);
y = i//[x, Л=у/\Х,п\;А,кА - функция от п переменных
[ii = l(l)..J (A{k)=(al9a29...9ak) -
параметры);
Y(m\ =V/(m)[X/„\;Ak)) ~ вектор-функция от п переменных
[л=i(i)~];
dX{n){t)^
dt
dxx{t) dx2(t) dx„(t)'
dt ' dt '"" dt
вектор-столбец;
Фи)<1Фм) Фу) ФЛ
-*-={ 5-L-, L-!->—» } - вектор-строка;
dX{n) \ dx, dx2 dxn /
drJxjAdy^xJ
'(»)V>)/1
ax,
матрица размерности тхп;
, _ /J 0, при х<а,
\x a)-< _ селект0р (индикатор) луча1
\a,oo) = [x: a < x < «> j (еди-
ничная функция Хевисайда);
x( \ л>( \d\ °°> nPu X = a + Q> . tt l
o{x - a) = Л [х- а)=< - дельта-функция Дирака ;
[ 0, при хФа + 0
Определение функции в точке разрыва соответствует её вероятностным приложе-
ниям.

468
Приложения
а
I7(x;a,b)=A(x-a)-A(x-b) =
0, при х<а,
1, при а<х<Ь,
О, при х>Ь
е(х;а)={1> "PUX = a>
[О, прихФа
d Г1, яри I = О,
[ О, #*/Ш I * у
p(a/b)=p(a/b=v)
{^}или{х(;}
/?-(*)=P(.£>*).
селектор (индикатор) интервала,
единичный прямоугольный им-
пульс;
- селектор (индикатор) точки {а};
- дельта (символ) Кронекера;
символ случайного объекта [события
А, величины jc, w-мерного вектора
Х,у функции x(t)9 вектор-функции
- вероятность случайного события А;
- условная вероятность случайного
события А относительно события
В (где U - достоверное событие);
- носитель распределения [множе-
ство (область)] возможных значе-
ний случайных величины х или
вектора Х{п);
- функция распределения случайной
величины х;
плотность распределения случай-
ной величины х;
х =F71(tj) = -R^1(x) - ЮО/7-процентный квантиль рас-
пределения случайной величины
Pt(z,)=P(z = z§)
ряд распределения дискретной
случайной величины z;
Определение функции в точке разрыва соответствует её вероятностным приложе-
ниям

Приложение 1. Основные обозначения
469
а
F*/y(x;y)=P(x<x/y = y);
Rm(x;y)=P(x>x/y = y);
d
F*ry(x;y) =P(x < x/y < y);
Fi±y{x;y)=P{x<x/y>y)
d
<Pi/y(x;y) =Fi/y(x;y)=-R'i/y{x;y);
d
<Р*гу(х;у) =Р*ту(х;у)=-Кту{х;у);
d
<РхЛх>у) =Fw(x;y)=-и'ш(х; у)
Fi/H(x)=P(x<x/H = U);
Ri/H{x)=P(x>x/HBU);
d
<Pi/H (x) = Kih (x) = -R'i/н (x);
FX,.) \X(n))= F{x„i„..,i.)(Xl>X2,...,Xn) =
f)(x, < x,)
П(*,.>*(.)
=/fn(*,^,)l;
L/=i J
OXx OX2 •••uXn
условные функции распреде-
ления случайной величины х
относительно случайной вели-
чины у;
условные плотности распреде-
ления случайной величины х
относительно случайной вели-
чины у;
условные функции и плотность
распределения случайной ве-
личины х относительно собы-
тия Н (здесь U - достоверное
событие)
d
= Р\
d
= Р\
функции и плотность распре-
деления случайного вектора
AT/* (отношения >,<,>,<
определяются существом за-
дачи);

470
Приложения
Fm.(X';X")=p(x' < Х'/Х" = X");
Fx,Tx.{X';X")=p(x' < Х'/Х" < X");
Fx'±Ax'>'x")=p(x' < x'/x" * x")>
Фх.1х.{Х';Х")=р(х'1Х'/х"±Х")
<pm.{X';X')=F'm.{X';X');
<Pz,Tx.(X';X")'=F'z,Tz.{X';X');
9jt.±i.(X';X*)LF't.jJl.(X';X')
условные функции распределе-
ния случайного вектора Х',«
относительно случайного век-
тора Х*^;
- условные плотности распреде-
ления случайного вектора X',\
относительно случайного век-
тора Х{п.};
F,/h{x)LP(x<x/Hbu);
RXIH{X)=P(X>XIH = U);
Фш{х)=р{х*х1н = и);
<P*Ih(x) = F*I„{x)
Ft{x;t)=Fm{x)=P(x(t)<x)
d d
9*{x}*)=4>«t){x)=K{xit) \
d
=Ф(0<^.)пИО<^)];
9*Лх1>хг>'*1>'г) =
д2РХ{){х19х2;^2)
дх1 дх2
*(2>
- условные функции и плотность рас-
пределения случайного вектора X,,
относительно события Н (здесь U -
достоверное событие);
- одномерные (1-порядка) функция и
плотность распределения случайной
функции x(t);
двухмерные (2-го порядка) функция и
плотность распределения случайной
функции x(t);
Gz\Z)-lLPz\m)Xm - производящая функция дискретной
т целочисленной случайной величины
z;
d °°
g-(u)= \eiuxdF-(x) - характеристическая функция произ-
вольной случайной величины х;

Приложение 1. Основные обозначения
471
ср{(т) = L{<pf (r)}= fe~*(<pf {v))dr - преобразование Лапласа неотрица-
о тельной случайной величины f
(плотности <рх{х) её распределения);
Мок - мода распределения случайной величи-
ны х;
Мек - медиана распределения случайной ве-
личины jc;
хк =М[хл]=1'л[.х] - Л-й начальный момент распределения
случайной величины к;
d
х = M-=M[x] = v1[x] -математическое ожидание случайной
величины х;
~d ~ _
х=х - х - центрированная случайная величина х;
хк = М[хк\= juk [x] - Л-й центральный момент распределения
случайной величины х;
х2 = D- = D[x] = /i2 [x] - дисперсия случайной величины х;
ак = <?[x\=^Dk - среднее квадратическое отклонение
случайной величины х;
Ек = p4lak - вероятное отклонение случайной вели-
чины х\
о _х-х _НОрМИр0ванная По ок центрированная
сх случайная величина х;
ic = - нормированная по Ек центрированная
* случайная величина х;
vk = -^ - коэффициент вариации случайной ве-
х личины х;
ах = з ~ коэффициент асимметрии распределе-
*** ния случайной величины х;
е£ = 4 -3 - коэффициент эксцесса распределения
о* случайной величины х;
Fa{x) = FlH](x;0,l) = -jL )/* dz
- функция и плотность нормирован-
ного по ок нормального распре-
деления случайной величины х;

472
Приложения
FE{*) = Fi
[и]
<рЕ{х) = <рГ\х;Н,
[н]
--Р- je-^dz;
Р-е-^
p4i) 4n
функция и плотность нормиро-
ванного по Е. нормального рас-
пределения случайной величины
х;
а
Х(„) = Mfi = \Xt, Хг ,..., Хп )
ка = кх,х, = к[Х1,^]=м[^ Xj]= х, Xj
*["] = **,., = К L
КхЬ,фм[хк) x(t2) ]=i(/,)i(/2) -
К^>*г)=м[хЬЖфЩШд ~
Фх=-г=\е~ггйг;
ЫЯ о
02=lP)e-^dz
ЫП о
В{а+ 1,0 + 1)=
I v ; r{a+fi + 2)
r{a+l)=\tae-'dt
о
Ex{z)=]—dt
it
математическое ожидание п -мер-
ного случайного вектора Х.к;
корреляционный момент случай-
ных величин х., Xj;
корреляционная матрица я-мер-
ного случайного вектора Х^;
автокорреляционная функция
случайной функции x{t)\
взаимная корреляционная функция
случайных функций x(t), y(t);
функции Лапласа;
- бета-функция (интеграл Эйлера
1-го рода);
- гамма-функция (интеграл Эйлера
2-го рода);
интегральная показательная функ-
ция;

Приложение 1. Основные обозначения
А1Ъ
Р*(а)=—^—^ - частота появления события А в
п серии п независимых однород-
ных испытаний;
х? - г-я порядковая (ранговая) стати-
стика (#• - ранг (порядок) вариан-
та х¥)\
d Л п
F*k(х;п) = F* (х)=— ]£А(х-xf) - статистическая (выборочная)
функция распределения случай-
ной величины х;
F^(x) - кумулята распределения случай-
ной величины х;
* - символ статистики (статистиче-
ской, выборочной характери-
стики случайной величины).
П г=1
16 Зак. 3303

474
Приложения
Приложение 2
АББРЕВИАТУРЫ
АНС -
АС -
БК -
ВНЕПР -
ВНУПР -
ВОЗ -
ВОУ -
ВТК -
ВТС -
ВЭА -
ГА -
ГК -
ГОУ -
ГТС -
ГУЕМР -
ГУЩП -
ДК -
ДМ -
дсс -
дцнп -
жцс -
злп -
ЗУР -
исо -
КБ -
KB -
квм -
к-к -
ККФ
кмо -
КМУ -
к-с -
КФП -
КФР -
ЛПР -
ЛФСМ -
мвк -
мгк -
мок -
анализ систем;
атрибутивное свойство;
базисная компонента;
внешнее проектирование;
внутреннее проектирование;
временная операционная задержка;
виртуальный относительный ущерб;
военно-технический комплекс;
военно-техническая система;
военно-экономический анализ;
генеральный аргумент;
генеральная компонента;
гарантируемый относительный ущерб;
готовное состояние;
гарантируемое значение показателя результата операции;
гарантирующее значение параметра;
доминирующая компонента;
директивная модель;
дееспособное состояние;
директивный целенаправленный процесс;
жизненный цикл системы;
задача линейного программирования;
зенитная управляемая ракета;
исследование операций;
конструкторское бюро;
комплекс вооружения;
квалиметрия;
комплексно-комплексная;
комплексная каноническая форма;
комплекс массового обслуживания;
компромиссное множество уровня;
комплексно-симплексная;
критериальная функция параметров системы;
критериальная функция результатов операции;
лицо, принимающее решение;
линейная функционально-стохастическая модель;
метод ведущих компонент;
метод главной компоненты;
модель операционного комплекса;

Приложение 2. Аббревиатуры
475
мое -
мост -
МПВКРО -
МПР -
МПТКРО -
мпэцнп -
нгте -
ндм -
НДС -
ндцнп -
НИИ -
нм -
НРБС -
НРС -
НФСМ -
нцп -
нэс -
одз -
ок -
оке -
оов -
опмо -
опо -
ОС -
ост -
отс -
ОУ -
ОФ -
ОФЛ -
ПВО -
пд -
ПК -
пмо -
по -
пов -
помц -
ПОР -
пос -
ПРК -
ПРОВ -
ПРОС -
модель операционной системы;
модель операционной ситуации;
модель показателя виртуального качества результатов
операции;
метод правдоподобных рассуждений;
модель показателя требуемого качества результатов
операции;
модель показателя эффективности ЦНП;
неготовное состояние;
нормативно-директивная модель;
недееспособное состояние;
нормативно-директивный целенаправленный процесс;
научно-исследовательский институт;
нормативная модель;
неработоспособное состояние;
нерезультативное состояние;
нелинейная функционально-стохастическая модель;
нормативный целенаправленный процесс;
неэффективное состояние;
область допустимых значений;
операционный комплекс;
окружающая среда;
область операционных возможностей;
оперативный процесс массового обслуживания;
оперативный процесс обслуживания;
операционная система;
операционная ситуация;
общая теория систем;
относительный ущерб;
операционная функция;
операционный функционал;
противовоздушная оборона;
показатель действительности;
показатель качества;
процесс массового обслуживания;
процесс обслуживания;
показатель оперативности по времени;
приведённая область малой цели;
потребитель решения;
показатель оперативности в среднем;
прикладная кибернетика;
показатель резерва оперативности по вероятности;
показатель резерва оперативности в среднем;

476 Приложения
ПС -
ПСР -
ПФ -
ПФК -
ПФС -
под -
РБС -
РЕО -
РЗС -
РЛС -
РОК -
РФ -
РЭ -
РЭФ -
СИ -
СИМ -
СИТ -
с-к -
СКФ -
смо -
сок -
СОУ -
ее -
с-с -
есс -
стк -
стс -
ТБЭ -
тмо -
тов -
тпо -
ТПР -
тси -
тэ -
ТЭА -
тэцнп -
УО -
УПО -
УПП -
УПС -
УФС -
ФОК -
ФС -
процесс стрельбы;
показатель существенных результатов;
процесс функционирования;
процесс функционирования комплекса;
процесс функционирования системы;
потенциал целевого действия;
работоспособное состояние;
ремонтный орган;
результативное состояние;
радиолокационная станция;
разобщённый операционный комплекс;
развернутая форма;
ресурс-эффект;
РЭ-функция;
статистические испытания;
статистическое имитационное моделирование;
системотехника;
симплексно-комплексная;
симплексная каноническая форма;
система массового обслуживания;
сплоченный операционный комплекс;
система организационного управления;
сложная система;
симплексно-симлексная;
суперсистема;
сложный технический комплекс;
сложная техническая система;
теория боевой эффективности;
теория массового обслуживания;
технологическое операционное время;
теория полезности;
теория принятия решений;
теория стохастической индикации;
теория эффективности;
технико-экономический анализ;
теория эффективности целенаправленных процессов;
узел обслуживания;
условия проведения операции;
упреждающее противодействие противнику;
условия применения системы;
условия функционирования системы;
функция организационного компромисса;
функция стоимости;

Приложение 2. Аббревиатуры
All
ФСВ - функция связи;
ФЭА - функционально-экономический анализ;
ФЭК - функция экспертного компромисса;
ФЭКО - функция экспертного компромисса по оперативности;
ФЭКР - функция экспертного компромисса по ресурсоёмкое™;
ЦНП - целенаправленный процесс;
ЦНПНФ - целенаправленный процесс функционирования;
ЦНПФК - целенаправленный процесс функционирования
комплекса;
ЦНПФС - целенаправленный процесс функционирования системы;
ЦОПМО - циклический оперативный процесс массового
обслуживания;
ЦОПО - циклический оперативный процесс обслуживания;
ЦПМО - циклический процесс массового обслуживания;
ЦПО - циклический процесс обслуживания;
ЦР - центр рассеяния;
ЦУС - целеустремлённая система;
ЦУТС - целеустремлённая техническая система;
ЭА - экономический анализ;
ЭВМ - электронно-вычислительная машина;
ЭКВ - элемент комплекса вооружения;
ЭР - эффект - ресурс;
ЭРФ - ЭР-функция;
ЭТХ - эксплуатационно-технические характеристики;
ЭФС - эффективное состояние.

Приложение 3
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Агрегат 299,303,369,373
Агрегативная модель 24,25,26,
219
Агрегированная модель 24,219,
331
Агрегированный параметр 292,
331
Адекватность модели 11
Анализ 222
- аспектно-параметричес-
кий 247
-аспектный 247,356
- военно-экономический 274
-качества 42,50
- параметрический 247,356
- систем 22
-системный 23
-стоимостный 274
- технико-экономический 274
- функционально-экономи-
ческий .....274
- экономический 270
- эффективности 69
— неформальный 235
Аргумент генеральный.... 301,330,
368
Аспект 58
Атрибут 41
Базисная компонента 316
Балансные соотношения 296
Вероятность 65
- апостериорная (условная)... 144
- априорная (безусловная) 146
- выполнения задачи
системы 66,89
- гарантийная 148,237,238
-гарантированная 219
- гарантируемая 147,173,354
- достижения цели операции... 66,
89,143
гарантированное
значение 151
гарантируемая 148
условная 144
- объективная 109
- средняя 140,144,173
- субъективная 109
ВЕРОЯТНОСТНЫЙ РЕЗЕРВ
ОПЕРАТИВНОСТИ 424
ВНЕШНЕЕ
ПРОЕКТИРОВАНИЕ 11,24
ВНУТРЕННЕЕ
ПРОЕКТИРОВАНИЕ 11,25
Время виртуальное 409
-директивное 408
- нормативное 408
- операционное 31,334,408
— директивное 406
— нормативное 406
— технологическое 334
временная избыточность 413
временная операционная
задержка 334

Приложение 3. Предметный указатель
479
временной резерв 413
временной ресурс 37,302
Гарантируемое значение
показателя результата
операции 238,357
Гарантирующее требуемую
эффективность значение па-
раметра 238
Генеральная компонента 368
Генеральная совокупность 137
Генеральный аргумент 368
Гипериндикатор 407
Главная компонента 157
Готовное состояние 430
Готовность 91,457
-техническая 91
- функциональная 93
- эксплуатационно-техничес-
кая 91
Дееспособное состояние.... 93,430
Дееспособность 93,457
Действенность 41
Действительность , 58
Действительный 58
Дефицит оперативности 423
Директивная модель ЦНП 372
- критериальная функция 238
Доминирующая компонента... 316
Д-ПРОЦЕСС 431
Достоверность события 108
Живучесть 91,95
ЖИЗНЕННЫЙ ЦИКЛ
СИСТЕМЫ 274
ЗАДАЧА анализа качества
объекта 50
- - эффективности операции ...69,
222
--эффективности ЦНП 222
-исследования 50
— вырожденная 205
— многокомпонентная 152
— многокритериальная 151
— обратная 50,69
— прямая 50,69
— эффективности 69
обратная 69
прямая 69
— оценивания качества
объекта 50
— эффективности операции.. 69,
205
вырожденная 205
— принятия решения
многокритериальная... 151
с векторным показателем
качества 152
с многокомпонентным
показателем качества 152
— синтеза объекта 50
— эффективной операции 69
-СИСТЕМЫ 32
ЗАКОН
ОБСЛУЖЕННОСТИ...412,419
— ОБСЛУЖИВАНИЯ .412,413
- распределения
— апостериорный 160
— Бернулли 136
— бета 336
— вырожденный 135,147
— гамма 337
--логарифмический 126,398
— нормальный 119
— показательный 374
— равномерный 369,374
— смещённый гамма 337
— смещённый показатель-
ный 202,374
— условный 160
— Эрланга А-го порядка 338
Затраты времени
— виртуальные 142
- - директивные 142

480
Приложение 3. Предметный указатель
- динамические 274
-косвенные 277
- непосредственные 276
- опосредованные 276
-прямые 276
-ресурсов 141
— виртуальные 141
— предельные 141
-сопряжённые 277
-сопутствующие 277
- статические 274
Значение гарантированное 259
- показателя качества
результатов
гарантируемое 238
- управляемого параметра
гарантирующее 238
Изокванта 231,363
Изокоста 231
Изоэффа 231,238,357,363
ИНДИКАТОР
константный 111
-МНОЖЕСТВА 104
— стохастический 110
- процесса обслуживания 410
-распределения 118
— собственный 118,126
- случайного события 111
-стохастический 106
--константный 111
— функциональный 112
ИССЛЕДОВАНИЕ
ОПЕРАЦИЙ 27
основные принципы ИО 29
КАЧЕСТВО 32,42,43
- виртуальное 67,367
-гарантированное 357
- гарантируемое 238
- объекта 42,66
— доминирующее 236
— требуемое 67
- операции 56
-процесса 56
- результатов операции 56
виртуальное 67,367
гарантированное 357
требуемое 67
-системы 80
— виртуальное 81
— требуемое 81
- требуемое 67,367
КВАЛИМЕТРИЯ 42
постулат квалиметрии
— второй 43
— первый 43
--третий 44
КВАНТИЛЬ
РАСПРЕДЕЛЕНИЯ 131
- стохастического
супериндикатора
графический метод
определения 129
Класс критериев оценивания
качества 44
-объектов 55
Классификация операций 34
-результатов операции 36
-ресурсов 36
КОМПЛЕКС 31,299
- военно-технический 31
- массового обслуживания ....405
сплочённый 409
- ОПЕРАЦИОННЫЙ 33
— разобщённый 85
— сплочённый 85
Комплексная каноническая
форма ПК РО 59
Комплексность 39
КОМПОНЕНТА 157
- базисная 316
-генеральная 316,368
- главная 157
-доминирующая 316

Приложение 3. Предметный указатель
481
- показателя качества
результатов
операции 59
ВЕДОМАЯ 160
ВЕДУЩАЯ... 160
Компромисс экспертный 258
- - средний 258
Коэффициент важности 155
-влияния 229
- действенности управле-
ния 229
-нестабильности 229
- чувствительности 226
-эластичности 230
- - замещения 230
- - показателя 231
Кривая компромиссная 240
- логистическая 264
Критериальные ограничения 236
КРИТЕРИЙ 44
- ОПТИМАЛЬНОСТИ 45
- ОЦЕНИВАНИЯ 44,54
- - векторный 45
- КАЧЕСТВА 44,52
результатов операции... 67
- - многокомпонентный 152
- скалярный 45
- эффективности опера-
ции 89
схема классификации
критериев
оценивания эффектив-
ности 78
- ПРЕВОСХОДСТВА 46
- ПРИГОДНОСТИ 45
Лицо, принимающее решение... 66
Метод анализа 222
- - эффективности 222
-аналитический 175
-аналогий 181
- базисной статьи калькуля-
ции 281
- базисных коэффициентов ...281
- ведущих компонент 159
-вкладов 325
- главной компоненты 152,157
- графический 119,129
- - определения квантиля
распределения
стохастического суперинди-
катора 129
— построения ЗР суперинди-
катора 119
-графоаналитический 235
-имитационный 222,245
- интегральный 409
-калькуляционный 281
- каскадный 157
- компромисса 152,235
-лексикографический 152
- обратной функции 118
- определения затрат 279
калькуляционный 281
статистический 282
метод производственных
функций 282
- последовательных уступок. 152
- правдоподобных рассужде-
ний 285,404
- производственных функций281
-прототипов 281
-рандомизации 220,391
-статистический 282
- статистических испыта-
ний 324
- статистического имитацион-
ного моделирования 183
- функции Грина 391,416
- циклический 157
эффект поглощения 165
Методология научного
исследования
схема 285

482
Приложение 3. Предметный указатель
Механизм обслуживания
требования 443
без накопления результатов443
с полным накоплением
результатов 443
с частичным накоплением
результатов 444
МНОЖЕСТВО
детерминированное 115
- допустимых точек 236
-истинности 107
- КОМПРОМИССНОЕ 235
— - гарантированное 237
— УРОВНЯ/ 237
- логических возможностей... 105,
107
- неопределённое 115
-Парето 235
-переменное 115
- случайное 115
-универсальное 105
-управлений 236
индикатор множества 104
селектор множества 105
МОДЕЛЬ 461
- агрегативная 24,25,26,219
- агрегированная 24,219,331
— математическая 331,333
- аналитическая 182,222,321
-бинарная 409
-вербальная 333
- вероятностная 293
- виртуальной оперативно-
сти 293
- виртуальной результатив-
ности 293
- виртуальной ресурсоём-
кое™ 293
- виртуальных результатов
операции 293
- детерминированная 261,462
- директивная 372
-имитационная 182,183,222
--математическая 182
— смешанная 182
--физическая 182
- качества результатов
операции 293
виртуального 293
требуемого 293
-квазирегулярная 74,261
- комплекса массового
обслуживания 408,433
- комплексного качества
(эффективности)
операции 293
-концептуальная 11,25
-линейная 332
- МАТЕМАТИЧЕСКАЯ. 182,290
--агрегированная 331
— квазирегулярная 74
-нелинейная 367
-ОПЕРАЦИИ 287
-ДИРЕКТИВНАЯ 372
— - дискретно-непрерывная 385
— НОРМАТИВНАЯ 367,
369
— НОРМАТИВНО-
ДИРЕКТИВНАЯ 376
- операционного комплекса.. 261,
289
- операционного функционала
схема построения 309
- операционной системы 261,
289
- операционной ситуации 289
- операционной функции 293
- показателя качества
результатов операции 293
виртуального 293
требуемого 293
-ПОКАЗАТЕЛЯ
ЭФФЕКТИВНОСТИ 293
- предельной ресурсоёмкости293
- процесса

Приложение 3. Предметный указатель
483
— функционирования
системы 286
— массового обслужива-
ния 408
бинарная 409
оперативного 408
— - обслуживания 432
циклического.. 429,432
оперативного 432
- системы 286
- сложного объекта 285
-смешанная 182
-статистическая 321,324
- стохастическая 332,367,385
- требуемой оперативности ...293
- требуемой результатив-
ности 293
- требуемых результатов
операции 293
-физическая 182
- функции связи 293
- функциональная 290
- функционально-стохасти-
ческая 332
директивного ЦНП 372
линейная 332
нелинейная 367
нормативного ЦЫП.... 367
нормативно-
директивного ЦНП 376
циклического ЦНП 385
специализи-
рованная 405
- целенаправленного про-
цесса 331
непрерывного 367
специализированная... 405
циклического 429
- эффективности операции ....293
агрегированность модели 286
адекватность модели 11
комплексность модели 286
Надоперационный ресурс 271
НАДЕЖНОСТЬ 94
-техническая 94
-функциональная 95
— функционально-техническая 93
— функционально-
технологическая 333
— эксплуатационно-техни-
ческая 91,94
НАДСИСТЕМА 31
ЯД-ПРОЦЕСС 431
НЕОПРЕДЕЛЁННОСТЬ 109
Номограмма 238
-сетчатая 238,453
Носитель распределения.... 134,322,
328,340,391
Область операционных
возможностей 312
ОБЛИК 25
Объём требования 415
Обслуживание требования 443
— без накопления результа-
тов 443
— с полным накоплением
результатов 443
— с частичным накоплением
результатов 444
Ограничения 236
-критериальные 236
-параметрические 236
-функциональные 236
Объект оптимальный
по Парето 236
ОКРУЖАЮЩАЯ СРЕДА 33
Оперативность 58
Оперативный процесс 408
— массового обслужива-
ния 408,430
— обслуживания 432
— циклический 432

484
Приложение 3. Предметный указатель
- функционирования
системы 408
ОПЕРАЦИОННАЯ модель
системы 287
-СИСТЕМА 33
-СИТУАЦИЯ 33
-ФУНКЦИЯ 296
Операционное время 31,334,408
- виртуальное 409
- директивное 408
- нормативное 406
- технологическое. 334
Операционные ресурсы 58,271,
334
- временные задержки 334
-свойства 34,58,61
ОПЕРАЦИОННЫЙ
КОМПЛЕКС 33
- разобщённый 85
-сплочённый 85
свойства элементов ОК 35
структурная схема ОК 34
ОПЕРАЦИОННЫЙ
ФУНКЦИОНАЛ 165,296
схема построения модели
ОФЛ 309
ОПЕРАЦИЯ 30,40
- массовая 36
- уникальная 36
классификация операций ...34-36
результаты операции 32
Оптимальность по Парето 236
Оптимальный синтез 23
Организация 23
-операции 23
- системы 23
-ЦНП 23
- ЦНПФС 366
Отдача ресурса 311
Отношение Парето 235
Оценивание 50
- абсолютное 55
-качества 50
— объекта (ЦУТС,
ЦНПФС) 44,78
--операции 56
уровни оценивания
качества операции 56
— результатов операции.... 148
-косвенное 54
- относительное 54
-прямое 54
- эффективности операции 69
этапы оценивания 54
ОЦЕНКА 52
- гарантированная 251,284
- качества 50
-модальная 259
-оптимистическая 259
-пессимистическая 259
— вероятности 220
- прогнозная 147
Параметр 64
-агрегированный 299
-неуправляемый 287
— системы 287
— ЦНПФС 287
-системы 64,81
-управляемый 287
— системы 287
— ЦНПФС 287
-ЦНПФС 64
Параметрические ограничения 236
Параметровооруженность 231
Параметроёмкость 231
Период готовного состояния
ЦУТС 430
- дееспособного состояния
ОК 430
- полного обслуживания
требования 409
- работоспособного состояния
ЦУТС 430
- результативного состояния
ОК 430

Приложение 3. Предметный указатель
485
- эффективного состояния
ОК 430
ПОДСИСТЕМА 31
ПОКАЗАТЕЛЬ 54
- абсолютный 54
- боеготовности 93
- боеспособности 93
- векторный 44
- ВЕРОЯТНОСТНОГО
РЕЗЕРВА ОПЕРАТИВ-
НОСТИ 424
- готовности 91
— - боевой 93
--оперативной 93
— технической 93
--функциональной 93
— функционально-
технической 93
— - эксплуатационно-
технической 93
- действенности управления...229
- дефицита оперативности 423
- затрат операционных
ресурсов 59
- КАЧЕСТВА 44
— - векторный 44
— виртуального 67,321
— ОБЪЕКТА 44
векторный 44
скалярный 43
частный 43
— операции 65
косвенный 54
прямой 54
схема классификации
показателей 78
— результатов операции 59,
67,140,320
виртуальных 67,320
допустимых 59,140
комплексная
каноническая форма 59
предельно допусти-
мых 141
симплексная канони-
ческая форма 60
требуемых 141,323
— скалярный 43,141
--системы 78,80
— требуемого 67,323
— частный 43
косвенный 54
многокомпонентный 45-46
оперативности ЦНП 423
по вероятности 424
по времени 423
в среднем 424
операционного времени 59
— целевого эффекта 58
относительный 54
предельной нормы замеще-
ния 230
— производительности
параметра 230
ресурса 230
- производительности 230
- - параметрических ресур-
сов 230
предельной 230
средней 230
-ресурсов 230
предельной 230
средней 230
-системы 336
- прямой 54,56
- резерва оперативности 423
- результативности операции... 82
— групповой 84
— динамический 84
— индивидуальный 84
— интегральный 84
— косвенный 82
— локальный 84
— прямой 82
--статический 84

486
Приложение 3. Предметный указатель
— функциональный 82
— - экономический 82
-свойства 43
- СРЕДНЕГО РЕЗЕРВА
ОПЕРАТИВНОСТИ 424
- СРЕДНЕЙ ОПЕРАТИВНО-
СТИ ПО ВРЕМЕНИ 424
- - производительности
параметра 230
- существенных результатов ...58
- свойств 43
- функциональной способ-
ности 93
- целевого эффекта 58
- экономического эффекта...97,98
-эластичности 230
— замещения 230
— показателя 231
по параметру 230
- эффекта операции 77
- ЭФФЕКТИВНОСТИ 77,89
схема классификации
показателей
эффективности 78
требования к показателю
эффективности 62
ПОМЕХА 436
ПОПЫТКА НА
ОБСЛУЖИВАНИЕ 430
завершающая 433
результативная 433
эффективная 433
Порядок закона распреде-
ления 126,338
логарифмического 126
Эрланга 338
- стохастического
супериндикатора 116
Постулат квалиметрии
— второй 43
— первый 43
— третий 44
- теории операционных
функционалов
второй 310
первый 309
третий 311
четвёртый 312
Потенциал наблюдения 369,388
-оптимизации 229
- оценивания (измерения) 373
-поражения 369
- целевого действия 369
-целевой 369
-управления 229
Предикат 115
Прикладная кибернетика 22
Принцип аналогий 181
- максимизации целевого
эффекта 261
- неопределённости Лапласа. 395
- правдоподобности
рассуждений 181,404
- экономии ресурсов 263
Принципы исследования
операций 29
- системного подхода 21
ПРОБЛЕМА 24
- "эффективность-стоимость". 98
ПРОБЛЕМНАЯ СИТУАЦИЯ ....24
Прогресс научно-технический... 14
ПРОЕКТ 11
ПРОЕКТИРОВАНИЕ И
- ВНЕШНЕЕ 11,24
-ВНУТРЕННЕЕ 11,25
- параметрическое 24
-системное 24
- системно-агрегативное 24
- структурно-параметрическое 25
Производительность 336
- ресурса 265
--предельная 265
— средняя 265

Приложение 3. Предметный указатель
487
ПРОИЗВОДСТВЕННАЯ
ФУНКЦИЯ 297
- аддитивная 304
--Кобба-Дугласа 303
- - линейная 304
- - мультипликативная 304
Пространство аспектов 236
- критериев 235,236
-параметров 236
- элементарных событий 115,
137
ПРОЦЕСС
детерминированный 108
-директивный 372
- массового обслуживания 405
оперативный 430
произвольного
требования 409,456
циклический 430
-наблюдения 369
- нормативный 368
-случайный 108
-циклический 385
ЦИКЛИЧЕСКИЙ ОПЕРА-
ТИВНЫЙ ПРОЦЕСС
ОБСЛУЖИВАНИЯ 432
- целенаправленный функциони-
рования системы 30
Д-ПРОЦЕСС 431
ЯД-ПРОЦЕСС 431
РГ-ПРОЦЕСС 432
Г-ПРОЦЕСС 406
- ДИРЕКТИВНЫЙ 408
- - нормативно-оператив-
ный 418
-НОРМАТИВНЫЙ 408
- - ОПЕРАТИВНЫЙ 408
нормативно-
оперативный 418
ЭГ-ПРОЦЕСС 432
Работоспособность 457
Ранг стохастического супер-
индикатора 116
Распределение безусловное
(априорное) 146
-Бернулли 136
-бета 336
-вырожденное 135,147
-гамма 337
-дефектное 398
- логарифмическое 126
-несобственное 398
- нормальное 119
-показательное 374
- равномерное 369,374
- смещённое показатель-
ное 202,374
- собственного индикатора.... 122
-трансформируемое 116
- трасформирующее 116
- условное (апостериорное)... 144,
160
- факторизованное 122
- Эрланга Анго порядка 338
бета-распределение 336
гамма-распределение 337
носитель распределения 134,
322,328,340
смещённое гамма-распре-
деление 337
собственный индикатор
распределения 126
Резерв оперативности 423
- вероятностный 424
- средний 424
Результативность 58
РЕЗУЛЬТАТЫ ОПЕРАЦИИ ...32,
80,81
- виртуальные 66
- гарантированные 357
- допустимые 67
- неоднородные 36
- - однородные 36

488
Приложение 3. Предметный указатель
- предельно допустимые .... 141
- предельные 141
- - требуемые 96,141
классификация результатов
операции 36
РЕСУРС 32
-активный 37,61,300
- временной 37,302
-динамический 37,300
-информационный 302
- надоперационный 271
-операционный 271,334
- параметра 363
- параметрический....230,302,359
- пассивный 37,61,300
-статический 37,61,300
- структурно-параметри-
ческий 301
-сырьевой 300
- технический 301
- технологический 301
-трудовой 301
- финансовый 302
-энергетический 301
классификация ресурсов 36
отдача ресурса 311
Ресурсоёмкое^ 58,336
- целевого эффекта 265
предельная 265
средняя 265
Решение аналитическое 175
- неформальное 235
-приближённое 256
-формальное 222
-численное 176
РГ-ПРОЦЕСС 432
РЭ-ФУНКЦИЯ 297
Свёртывание векторных
показателей 151-174
аддитивное 154,155
вероятностное 43
линейное 156
логическое 154
обобщённое 156
мультипликативное 154
СВОЙСТВО 32
- агрегативное 58
-атрибутивное 43
- обеспечивающее 57
- операционное 34,58,61
- системно-агрегативное 25
- функциональное 57
-целевое 57
- эксплуатационно-техни-
ческое 57
системное свойство 31
СЕАНС наблюдения 386
- ОБСЛУЖИВАНИЯ 430
СЕЛЕКТОР интервала 105
-луча 105
- множества 105
-точки . 105
Симплексная каноническая форма
ПКРО 60
Синтез объекта 248
- по критерию
оптимальности 254
пригодности 248
- приближённый 256
- системно-агрегативный 24,
248
- структурно-
параметрический 24,248
- операционной системы 248
-эффективной операции 69
СИСТЕМА 30
- автоматического управ-
ления 373
- военно-техническая 30
- массового обслуживания ....405
- операционная 33
-СЛОЖНАЯ 30
- ЦЕЛЕУСТРЕМЛЁННАЯ
ТЕХНИЧЕСКАЯ 30

Приложение 3. Предметный указатель
489
производительность
системы 336
ресурсоёмкое^ системы 336
ЭЛЕМЕНТ СИСТЕМЫ 31
Системные исследования 21
- направления в науке 21
-свойства 31
СИСТЕМНЫЙ
- анализ 23
-ПОДХОД 21,22,39
принципы системного
подхода 21
Системотехника 22
СИТУАЦИЯ
- ОПЕРАЦИОННАЯ 33
-ПРОБЛЕМНАЯ 24
Случайность 109
Событие 105
- достоверное 105
-невозможное 108
-случайное 108
СОСТОЯНИЕ
-готовное 430
-дееспособности 430
- операционного комплекса...291
- операционной системы 291
- процесса функционирования
системы 291
-работоспособности 430
- результативного
функционирования 430
- системы 291
- эффективного
функционирования 430
СРЕДА
- ОКРУЖАЮЩАЯ 33
Статистические испытания 176
Статистическое имитационное
моделирование 181
Стохастический индикатор 106
СТРАТЕГИЯ 32
СУБСИСТЕМА 31
СУПЕРИНДИКАТОР 114,116
- индексный 114
- собственный 118
- стохастический 114
— - второго порядка 116
— первого порядка 116
ранг стохастического
супериндикатора 116
СУПЕРСИСТЕМА 31
Схема имитационных испыта-
ний 194
— комплексно-комплекс-
ная 196
— - комплексно-симплекс-
ная 196
— симплексно-комплекс-
ная 196
— симплексно-симплекс-
ная 195
- классификации факторов,
обуславливающих эффек-
тивность 98
- методологии научного
исследования 285
- оценивания 50
- качества 50
замкнутая 51,54
разомкнутая 51,54
- эффективности 66
- построения модели опера-
ционного функционала 309
- статистического
имитационного
моделирования
комплексно-
симплексная 184
симплексно-
комплексная 184
Г-ПРОЦЕСС 406
—ДИРЕКТИВНЫЙ 408
— нормативно-оператив-
ный 418
— НОРМАТИВНЫЙ 408

490
Приложение 3. Предметный указатель
— ОПЕРАТИВНЬШ 408
Темп освоения ресурсов 388
ТЕОРИЯ
-вероятностей 38
- живучести 95
- массового обслуживания 87,
455
- надёжности 94
- операционных функцио-
налов 309
- полезности 22
- принятия решений 22
- стохастической индикации.. 102,
462
- ЭФФЕКТИВНОСТИ
ЦЕЛЕНАПРАВЛЕННЫХ
ПРОЦЕССОВ 16,25,29
предмет изучения ТЭЦНП... 16
Технико-экономический
анализ 274
Траектория
- оптимального управления ...231
- экономичного управления
эффективностью 363
Трансформация законов
распределения 115
Трудоёмкость требования 415
Уровень гарантии качества
объекта 238
УСЛОВИЯ
- ПРИМЕНЕНИЯ СИСТЕ-
МЫ 33,100
- ПРОВЕДЕНИЯ ОПЕРА-
ЦИИ 33,100
- ФУНКЦИОНИРОВАНИЯ
СИСТЕМЫ 33,100
Устойчивость 95
ФУНКЦИОНАЛ
- ОПЕРАЦИОННЫЙ... 165,296
схема построения модели
ОФЛ 309
ФУНКЦИЯ
-выпуска 297
-затрат 297
- интегральная показатель-
ная 352
-критериальная 71
— аддитивная 72,155
дизъюнкция 154
квазирегулярная 74
сепарабельная 156
— директивная 238
--мультипликативная 73
квазирегулярная 74
конъюнкция 154
результатов 153
параметров 153
— от целевых функций 73
квазирегулярная. .74
— параметров системы 72
сепарабельная 72
— - результатов операции 71
сепарабельная 72
- линейно однородная 311
- множества характеристи-
ческая 104
-надёжности 94
- однородная степени у 311
- операционная 296
- организационного
компромисса 326
-параметров 75
-производственная 297
— аддитивная 304
— Кобба-Дугласа 303
— линейная 304
— мультипликативная 304
-результатов 75
- СВЯЗИ 296
-стоимости 281
- характеристическая 104
-целевая 71,78
- ЧУВСТВИТЕЛЬНОСТИ ...225

Приложение 3. Предметный указатель
491
— - показателя эффектив-
ности 225
- экспертного компромисса ...326
бета-функция 337
гамма-функция 337
РЭ-функция 297
-вогнутая 310
ЭР-функция 297
-выпуклая 310
ФУНКЦИЯ СВЯЗИ 296
ХАРАКТЕРИСТИКА
- влияния параметра 229
- замещения параметрического
ресурса 230
- качества операции 65
- производительности
параметрического
ресурса 230
- чувствительности 224
Характеристическая функция. 104
- - множества 104
ЦЕЛЕВОЙ ЭФФЕКТ 32
ЦЕЛЕНАПРАВЛЕННЫЙ
ПРОЦЕСС
- - функционирования
системы 30
ЦЕЛЕУСТРЕМЛЁННАЯ
ТЕХНИЧЕСКАЯ
СИСТЕМА 30
ЦЕЛЬ 31,40
-ОПЕРАЦИИ 31,40
— математическая
формулировка 59
— формальное выражение.. 64
ЦИКЛ
-наблюдения 385
-обслуживания 430
Экономический анализ 270
Экспертное оценивание 324
Экспертный компромисс 258
- средний 258
Эксплуатационно-технические
характеристики 25
ЭЛАСТИЧНОСТЬ
ПРОИЗВОДСТВА 305
ЭЛЕМЕНТ СИСТЕМЫ 31
ЭР-ФУНКЦИЯ 297
ЭГ-ПРОЦЕСС 432
ЭФФЕКТ 41
- насыщения ресурсами 368
- ПОГЛОЩЕНИЯ 165
-ЦЕЛЕВОЙ 32,334
— виртуальный 141,367
--требуемый 141
Эффективная точка 235
Эффективное состояние 430
ЭФФЕКТИВНОСТЬ 42,56,58,
89,458
- боевая 97
- техническая 97
- функциональная 82,97,421
-целевая 97
- экономическая 82,97,421
схема классификации факторов,
обуславливающих эффектив-
ность 98
Эффективность - стоимость 270
Эффективный 41

БИБЛИОГРАФИЯ
1. Актуальные проблемы теории эффективности /А.Я. Иоффе, Л.М.
Морозов, Г.Б. Петухов, P.M. Юсупов. - МО СССР, 1977. - 37 с.
2. Абраменко Б.С., Маслов А.Я., Немудрук Л.Н. Эксплуатация автома-
тизированных систем управления. - МО СССР, 1984. - 485 с.
3. Абчук В.А., Суздаль В.Г. Поиск объектов. - М.: Сов. радио, 1977. -
334 с.
4. Азгальдов Г.Г., Райхман Э.П. О квалиметрии. - М.: Изд-во стандар-
тов, 1973.-172 с.
5. Айвозян С.А., Енюков И.С., Мешалкин Л.Д. Исследование зависи-
мостей. - М.: Финансы и статистика, 1986. - 487 с.
6. Акоф Р., Эмери Ф. О целеустремленных системах. - М.: Сов. радио,
1974.-272 с.
7*. Акоф Р., Саниени М. Основы исследования операций. - М.: Мир,
1971.-534 с.
8. Алтарев В.П., Шакун Г.И., Трофимов П.И. Процессы отказов и
восстановлений в системах ПД. - М.: Связь, 1977. - 113 с.
9*. Андриевский В.В., Горощенко Л.Б. Управление полетом и эффек-
тивность авиационного комплекса. - М.: Машиностроение, 1974. - 176 с.
10*. Ануреев И., Татарченко А. Применение математических методов
в военном деле. - М.: Воениздат, 1967. - 243 с.
11. Бакланов Г.И. Как статистика изучает эффективность и качество
в промышленности. - М.: Статистика, 1978. - 119 с.
12. Бакут П.А., Жулина Ю.В., Иванчук Н.А. Обнаружение движущих-
ся объектов. - М.: Сов. радио, 1980. - 288 с.
13. Блюмберг В.А., Глущенко В.Ф. Какое решение лучше? Метод рас-
становки приоритетов. -Л.: Лениздат, 1982. - 160 с.
14. Берзин Е.А. Оптимальное распределение ресурсов и элементы
синтеза систем. - М.: Сов. радио, 1974. - 304 с.
15. Бешелев С.Д., Гурвич Ф.Г. Математико-статистические методы
экспертных оценок. - М.: Статистика, 1974. - 159 с.
16. Биргер И.А. Техническая диагностика. - М.: Машиностроение,
1978.-239 с.
17. Браверман Э.М. Математические модели планирования и
управления в экономических системах. - М.: Наука, 1976. - 366 с.
18. Бронштейн И.Н., Семендяев К.А. Справочник по математике. -
М.: Наука, 1986.-544 с.
19. Бурков В.Н., Кондратьев В.В. Механизмы функционирования ор-
ганизационных систем. - М.: Наука, 1981. - 383 с.

Библиография
493
20. Бусленко В.Н. Автоматизация имитационного моделирования
сложных систем. - М.: Наука, 1977. - 239 с.
21*. Бусленко Н.П. Моделирование сложных систем. - М: Наука,
1968.-355 с.
22*. Бусленко Н.П., Калашников В.В., Коваленко И.Н. Лекции по тео-
рии сложных систем. - М: Сов. радио, 1973. - 439 с.
23. Вагнер Г. Основы исследования операций. - М.: Мир, т. I, 1972,
239 с; т. II, 1973,488 с; т. III, 1973, 501 с.
24. Васильев Б.В. Прогнозирование надежности и эффективности
радиоэлектронных устройств. - М.: Сов. радио, 1970. - 335 с.
25. Васильев Д.В., Филиппов Г.С. Основы теории и расчета следящих
систем. - М. - Л.: Госэнергоиздат, 1959. - 428 с.
26*. Вентцель Е.С. Введение в исследование операций. - М.: Сов. ра-
дио, 1964.-388 с.
27*. Вентцель Е.С. Исследование операций. - М.: Сов. радио, 1972. -
551с.
28. Вентцель Е.С. Теория вероятностей- М.: Физматгиз, 1962. - 564 с.
29*. Вероятностные методы в прикладной кибернетике / Под ред.
Р.М. Юсупова. - МО СССР, 1976. - 426 с.
30. Вероятностные методы оценки эффективности вооружения / Под
ред. А.А. Червоного. - М.: Воениздат, 1979. - 95 с.
31. Военный энциклопедический словарь. - М.: Воениздат, 1983. -
863 с.
32*. Волгин И.О., Махров Н.В., Юровский В.А. Исследование опера-
ций. - Л.: ВМА им. А.А. Гречко, 1982. - 293 с.
33. Волков Л.И., Топчий В.Д. Основы планирования эксплуатации
вооружения. - МО СССР, 1982. - 178 с.
34. Гаврилов В.М. Оптимальные процессы в конфликтных ситуаци-
ях. - М.: Сов. радио, 1969. - 160 с.
35. Гаспарский В. Праксеологический анализ проектно-конструктор-
ских разработок. - М.: Мир, 1978. - 172 с.
36. Гафт М.Г. Принятие решений при многих критериях. - М.: Зна-
ние, 1979.-64 с.
37*. Гермейер Ю.Б. Введение в теорию исследования операций. - М.:
Наука, 1971.-383 с.
38*. Гличев А.В. Экономическая эффективность технических сис-
тем. - М.: Экономика, 1971. - 270 с.
39. Горбунов В.А. Эффективность обнаружения целей. - М.: Воениз-
дат, 1980.-160с.
40. Горелик В.А., Ушаков И.А. Исследование операций. - М.: Маши-
ностроение, 1986. - 286 с.

494
Библиография
41. Горичев Ю.В., Лебедев А.Н., Миронов В.И. Обеспечение качества
и надежности сложных технических систем на этапе проектирования
(элементы системного проектирования). - МО СССР, 1984. - 141 с.
42*. Гуд Г.Х., Макол Р.Э. Системотехника (введение в проектирование
больших систем). - М.: Сов. радио, 1962. - 383 с.
43*. Гурин Л.С, Дымарский Я.С., Меркулов А.Д. Задачи и методы
оптимального распределения ресурсов. - М.: Сов. радио, 1968. - 463 с.
44. Гухман А.А. Введение в теорию подобия. - М.: Высш. шк., 1973. -
295 с.
45*. Де Гроот М. Оптимальные статистические решения. - М.: Мир,
1974.-491 с.
46. Дегтярев Ю.И. Исследование операций. - М.: Высш. шк., 1986. -
320 с.
47. Дедков В.К., Северцев Н.А. Основные вопросы эксплуатации
сложных систем. - М.: Высш. шк., 1976. - 406 с.
48*. Динер И.Я. Методы исследования операций. Основы теории
эффективности. - Л.: ВМОЛА, 1965. - 235 с.
49*. Директор С, Рорер Р. Введение в теорию систем. - М.: Мир,
1974.-464 с.
50*. Дружинин В.В., Конторов Д.С. Идея, алгоритм, решение. - М.:
Воениздат, 1972. - 326 с.
51*. Дружинин В.В., Конторов Д.С. Системотехника. - М.: Радио и
связь, 1985.-200 с.
52*. Дубов Ю.А., Травкин СИ., Якимец В.Н. Многокритериальные
модели формирования и выбора вариантов систем. - М.: Наука, 1986. -
295 с.
53*. Дубров A.M. Математико-статистическая оценка эффективно-
сти в экономических задачах. - М.: Финансы и статистика, 1982. - 176 с.
54*. Евланов Л.Г., Кутузов В.А. Экспертные оценки в управлении. -
М.: Экономика, 1978. - 134 с.
55*. Емельянов СВ., Ларичев О.И. Многокритериальные методы
принятия решений. - М.: Знание, 1985. - 32 с.
56. Ермаков СМ., Михайлов Г.А. Курс статистического моделирова-
ния. - М.: Наука, 1976. - 319 с.
57. Ефимов А.Н. Информация: ценность, старение, рассеяние. - М.:
Знание, 1978.-64 с.
58. Заде Л. Понятие лингвистической переменной и его применение
к принятию приближенных решений. - М.: Мир, 1976. - 165 с.
59*. Иванилов Ю.П., Лотов А.В. Математические модели в экономи-
ке. - М.: Наука, 1979. - 303 с.
60. Ивахненко А.Г. Долгосрочное прогнозирование и управление
сложными системами. - Киев: Техника, 1975. - 311 с.

Библиография
495
61. Инженерный справочник по космической технике / Под ред. А.В.
Солодова. - М.: Воениздат, 1969. - 693 с.
62*. Интрилигатор М. Математические методы оптимизации и эко-
номическая теория. - М.: Прогресс, 1975. - 606 с.
63*. Иоффе А.Я. Статистическое моделирование. - Л., 1964. - 146 с.
64*. Иоффе А.Я., Петухов Г.Б. Методы теории стохастической инди-
кации в задачах оценки эффективности и планирования испытаний
технических систем. - М: Изв. АН СССР, Техническая кибернетика, 1976,
№3, с. 198-204.
65. Иоффе А.Я., Петухов Г.Б., Миров Ю.Н. Лекции по математиче-
ской статистике. - Л., 1970. - 176 с.
66. Иоффе А.Я., Юсупов P.M. Методы линейного и нелинейного про-
граммирования. - Л., 1973. - 149 с.
67*. Исследование операций / Под ред. Дж. Моудера, С. Элмаграби. -
М.: Мир, 1981, т. 1,712 с; т. II, 677 с.
68. Каазик Ю.Я. Математический словарь. - Таллин: Валгус, 1985. -
293 с.
69. Кади Дж. Количественные методы в экономике. - М.: Прогресс,
1977.-247 с.
70. Калашников В.В. Организация моделирования сложных систем. -
М.: Знание, 1982.-64 с.
71*. Калашников В.В. Сложные системы и методы их анализа. - М.:
Знание, 1980.-63 с.
72. Калинин В.Н., Резников Б.А. Теория систем и оптимального
управления. - МО СССР, 1978. - 417 с.
73*. Кемени Дж., Снелл Дж., Томпсон Дж. Введение в конечную ма-
тематику. - М.: Изд-во иностр. лит., 1963. - 486 с.
74*. Кемени Дж., Снелл Дж. Кибернетическое моделирование. - М.:
Сов. радио, 1972.-192 с.
75*. Клиланд Д., Кинг В. Системный анализ и целевое управление. -
М.: Сов. радио, 1974. - 179 с.
76. Кобринский Н.Е., Майминас Е.З., Смирнов А.Д. Введение в эконо-
мическую кибернетику. - М.: Экономика, 1975. - 34 с.
77. Коваленко И.Н. Анализ редких событий при оценке эффективно-
сти и надежности систем. - М.: Сов. радио, 1980. - 209 с.
78. Колмогоров А.Н. Основные понятия теории вероятностей. - М.:
Наука, 1974.-119 с.
79. Колмогоров А.Н., Фомин СВ. Элементы теории функции и функ-
ционального анализа. - М.: Наука, 1961. - 496 с.
80*. Комплексный анализ эффективности технических решений в
энергетике / Под ред. В.Р. Окорокова, Д.С. Щавелева. - Л.: Энергоатомиздат,
1985.-175 с.

496
Библиография
81. Кофман А. Введение в теорию нечетких множеств. - М.: Радио и
связь, 1982.-432 с.
82. Кофман А. Методы и модели исследования операций. - М.: Мир,
1966.-523 с.
83*. Крапивин В.Ф. О теории живучести сложных систем. - М: Нау-
ка, 1978.-247 с.
84*. Краснощекое П.С. Математические модели в исследовании
операций. - М.: Знание, 1984. - 63 с.
85*. Красе И.А. Математические модели экономической динамики. -
М.: Сов. радао, 1976. - 279 с.
86. Крон Г. Исследование сложных систем по частям - диакоптика. -
М.: Наука, 1972.-542 с.
87. Лазарев И.А. Композиционное проектирование сложных агрега-
тивных систем. - М.: Радио и связь, 1986. - 312 с.
88*. Лебедев В.В., Кругов В.А. Техническая эффективность
пилотируемых космических аппаратов. - М.: Машиностроение, 1985. -
253 (89. Ли Т.Г., Адаме Г.Э., Гейнв У.М. Управление процессами с помо-
щью ЭВМ. Моделирование и оптимизация. - М.: Сов. радио, 1972. - 312 с.
90. Липаев В.В. Распределение ресурсов в вычислительных систе-
мах. - М.: Статистика, 1979. - 242 с.
91. Липаев В.В., Яшков С.Ф. Эффективность методов организации
вычислительного процесса в АСУ. - М.: Статистика, 1975. - 255 с.
92. Липочкин В.А., Голынкер Е.И. Принятие решений на основе про-
гнозирования в условиях АСУ. - М.: Финансы и статистика, 1981. - 111 с.
93. Лопатников Л.И. Экономико-математический словарь. - М.: Нау-
ка, 1987.-509 с.
94. Мартин Ф. Моделирование на вычислительных машинах. - М.:.
Сов. радио, 1972.-288 с.
95. Мартыщенко Л.А., Панов В.В. Методы военно-научных исследо-
ваний в задачах разработки и испытания вооружения. Ч. 1. - МО СССР,
1981.-279 с.
96. Мартыщенко Л.А., Панов В.В., Филютин А.Е. Методы военно-
научных исследований в задачах разработки и испытания вооружения.
4.2. - МО СССР, 1985. - 232 с.
97*. Матвеевский С.Ф. Основы системного проектирования ком-
плексов летательных аппаратов. - М.: Машиностроение, 1987. - 239 с.
98. Математика и кибернетика в экономике (словарь-справочник). -
М.: Экономика, 1971.-223 с.
99*. Мачулин В.В., Пятибратов А.П. Эффективность систем обработ-
ки информации. - М.: Сов. радио, 1972. - 280 с.
100. Медич Дж. Статистически оптимальные линейные оценки и
управление. - М.: Энергия, 1973. - 440 с.

Библиография
497
101. Меламедов И.М. Физические основы надежности. - Л.: Энергия,
1970.-152 с.
102*. Мельников Ю.Н. Достоверность информации в сложных сис-
темах. - М.: Сов. радио, 1973. - 192 с.
103*. Месарович М., Такахара Я. Общая теория систем. - М.: Мир,
1978.-311 с.
104. Миркин Б.Г. Анализ качественных признаков и структур. - М.:
Статистика, 1980. - 319 с.
105. Миркин Б.Г. Проблема группового выбора. - М.: Наука, 1974. -
256 с.
106. Миронов В.И. Эффективность, надежность и испытания систем
управления. - МО СССР, 1981.-200 с.
107. Митряев Е.В., Ростовцев Ю.Г., Рышков Ю.П. Контроль верности
информации в морской радиосвязи. Л.: Судостроение, 1979. - 101 с.
108*. Мищенко В. А. Метод селектирующих функций в нелинейных
задачах контроля и управления. - М.: Сов. радио, 1973. - 184 с.
109*. Модели и методы анализа экономических целенаправленных
систем / Под ред. К.А. Банриновского и Е.Л. Берлянда. - Новосибирск: Нау-
ка, 1977.-238 с.
ПО. Морозов В.В., Сухарев А.Г., Федоров В.В. Исследование опера-
ций в задачах и упражнениях. - М.: Высш. шк., 1986. -187 с.
111*. Морозов В.П., Дымарский Я.С. Элементы теории управления
ГАП. - Л.: Машиностроение, 1984. - 333 с.
112*. Морозов Л.М., Петухов Г.Б., Сидоров В.Н. Методологические
основы теории эффективности. - МО СССР, 1982. - 236 с.
113*. Надежность и эффективность в АСУ /Под ред. Ю.Г. Заренина. -
Киев: Техника, 1975. - 368 с.
114*. Надежность и эффективность в технике. Справочник, Т.1 /Под
ред. А.И. Рембезы. - М.: Машиностроение, 1986. - 223 с.
115*. Надежность и эффективность в технике. Справочник, Т.З/Под
ред. В.Ф. Уткина, Ю.В. Крючкова. - М.: Машиностроение, 1988. - 328 с.
116*. Нарусбаев А.А. Введение в теорию обоснования проектных
решений. -Л.: Судостроение, 1976.-223 с.
117. Нечеткие множества в моделях управления и искусственного
интеллекта / Под ред. Д.А. Поспелова. - М.: Наука, 1986. - 311 с.
118. Нечеткие множества и теория возможностей /Под ред. P.P. Яге-
ра. - М.: Радио и связь, 1986. - 406 с.
119*. Никитин СВ., Петухов Г.Б. Методы теории чувствительности в
задачах исследования эффективности целенаправленных процессов. В
сб. ВК-74: Теория чувствительности и её применение / Под ред. P.M. Юсупо-
ва и Ю.Н. Кафанова. - М.: АН СССР НСКПК, 1981, с. 6-21.
120*. Окунев Ю.Б., Плотников В.Г. Принципы системного подхода к
проектированию в технике связи. - М.: Связь, 1976. - 183 с.

498
Библиография
121*. Орлов А.И. Задачи оптимизации и нечеткие переменные. - М:
Знание, 1980.-53 с.
122. Орловский С.А. Проблемы принятия решений при нечеткой ис-
ходной информации. - М.: Наука, 1981. - 206 с.
123*. Основы исследования операций в военной технике / Под ред.
Ю.В. Чуева. - М.: Сов. радио, 1965. - 591 с.
124*. Основы синтеза систем летательных аппаратов / Под ред. А.А.
Лебедева. - М.: Машиностроение, 1987. - 224 с.
125*. Петров В.А., Медведев Г.И. Системная оценка эффективности
новой техники. - Л.: Машиностроение, 1978. - 256 с.
126*. Петухов Г.Б. Прикладная математика. Вып. 1. Основы комби-
наторного анализа. - Л.: ВИКА, 1973. - 132 с.
127*. Петухов Г.Б. Методическое пособие по математической
символике. - Л.: ВИКА, 1973. - 38 с.
128*. Петухов Г.Б., Белоконь Н.К. Методы теории стохастической ин-
дикации в исследовании операций и прикладной кибернетике. - МО
СССР, 1988.-191 с.
129. Петухов Г.Б. Основы теории массового обслуживания. - МО
СССР, 1974.-248 с.
130*. Петухов Г.Б. Теоретические основы и методы исследования
эффективности оперативных целенаправленных процессов. - МО СССР,
1979.-176 с.
131. Петухов Г.Б., Девяткин А.М., Якунин В.И. Идентифицирование
законов распределений ограниченных случайных величин. Уч.-метод,
пособ. - СПб.: ВКА, 2004. - 30 с.
132. Петухов Г.Б., Якунин В.И., Шумилов К.А. Математическая мо-
дель процесса измерений в задачах оценивания его качества. Изв. ВУЗ-ов
СССР. - Приборостроение. - 1988, т. XXXI, №1, с. 3 - 6.
133*. Петухов Г.Б. Основы теории эффективности целенаправлен-
ных процессов. Часть 1. Методология, методы, модели. Учебник. - МО
СССР, 1989.-660 с.
134. Петухов Г.Б. Методологические основы научного и делового
общения: к проблеме коммуникации в деловых и конфликтных ситуа-
циях. Мегодич. пособ. - МО СССР, 1996. - 106 с.
135. Подиновский В.В. Математическая теория выработки решений
в сложных ситуациях. - МО СССР, 1981. - 211 с.
136*. Пойа Д. Математика и правдоподобные рассуждения. - М.:
Наука, 1975.-413 с.
137. Половко А.М. Основы теории надежности. - М.: Наука, 1964. -
446 с.
138. Поспелов Г.С., Ириков В.А. Программно-целевое планирование
и управление. - М.: Сов. радио, 1976. - 400 с.

Библиография
499
139. Поспелов Д.А. Ситуационное управление. - М.: Наука, 1986. -
284 с.
140. Потапов В.В. Модификации теории "полезности". - М.: Мысль,
1984.-134 с.
141. Проблемы программно-целевого планирования и управления /
Под ред. Г.С. Поспелова. - М.: Наука, 1981. - 460 с.
142. Прохоров Ю.В., Розанов Ю.А. Теория вероятностей. - М: Наука,
1973.-494 с.
143. Пшеничный Б.Н. Метод линеаризации.- М.: Наука, 1983.- 136 с.
144*. Радвик Б. Военное планирование и анализ систем. - М.: Воениз-
дат, 1972.-477 с.
145*. Райветт П., Акоф Р.Л. Исследование операций. - М.: Мир, 1966. -
143 с.
146*. Райфа Г. Анализ решений. - М.: Наука, 1977. - 407 с.
147. Раков В.И. Эффективность судовых радиоэлектронных сис-
тем. - Л.: Судостроение, 1974. - 328 с.
148. Рао СР. Линейные статистические методы и их применения. -
М.: Наука, 1968.-548 с.
149. Раяцкас Р.Л., Плакунов М.К. Количественный анализ в экономи-
ке. - М.: Наука, 1987. - 391 с.
150. Реклейтис Г., Рейвиндран А., Рэгсдел К. Оптимизация в техни-
ке. - М.: Мир, 1986, т. I, 349 с; т. II, 320 с.
151*. Розенвассер Е.Н., Юсупов P.M. Чувствительность систем
управления. - М.: Наука, 1981. - 464 с.
152. Ройтенберг Я.Н. Автоматическое управление. - М.: Наука,
1971.-395 с.
153. Романов В.И. Оптимизационные задачи управления качеством
продукции. - М.: Статистика, 1979. - 70 с.
154. Романов O.K. Оптимальные решения. - М.: Статистика, 1975. -
96 с.
155*. Саркисян С.А., Ахундов В.М., Минаев Э.С. Большие техниче-
ские системы. - М.: Наука, 1977. - 350 с.
156*. Сборник задач по прикладной кибернетике: Вып. 1. Вероятно-
стные методы в прикладной кибернетике / Под ред. Г.Б. Петухова. - МО
СССР, 1982.-277 с.
157. Себер Дж. Линейный регрессионный анализ. - М.: Мир, 1980. -
456 с.
158. Седякин Н.М. Об одном физическом принципе теории надежно-
сти и некоторых его приложениях. - МО СССР, 1965. - 41 с.
159. Словарь русского языка / Под ред. СИ. Ожегова. - М.: ГИИНС,
1953.-848 с.
160. Словарь иностранных слов /Под ред. И.В. Лехина и Ф.Н. Петро-
ва. - М.: ГИИНС, 1955. - 856 с.

500
Библиография
161. Снапелев Ю.М., Старосельский В.А. Моделирование и управле-
ние в сложных системах. - М.: Сов. радио; 1974. - 264 с.
162*. Соболь И.М., Статников Р.Б. Наилучшие решения - где их ис-
кать. - М.: Знание, 1982. - 64 с.
163. Соболь И.М. Численные методы Монте-Карло. - М.: Наука,
1973.-311 с.
164. Солнышков Ю.С. Оптимизация выбора вооружения. - М:
Воениздат, 1968. - 103 с.
165*. Справочник офицера противовоздушной обороны / Г.В. Зимин,
С.К. Бурмистров, Б.М. Букин и др. - М.: Воениздат, 1987. - 512 с.
166*. Справочник по исследованию операций / В.А. Абчук, Ф.А.
Матвейчук, Л.П. Томашевский. - М.: Воениздат, 1979. - 368 с.
167*. Справочник по вероятностным расчетам / Г.Г. Абезгауз, А.П.
Тронь, Ю.Н. Копейкин, И.А. Коровина. - М.: Воениздат, 1970. - 536 с.
168. Справочник по специальным функциям / Под ред. М. Абрамо-
вича и И. Стиган. - М.: Наука, 1979. - 830 с.
169*. Справочное пособие по прикладной математике / А.Я. Иоффе,
Г.Б. Петухов, Л.М. Морозов. - МО СССР, 1975. - 253 с.
170. Статистические методы в прикладной кибернетике / Под ред.
P.M. Юсупова. - МО СССР, 1980. - 377 с.
171. Статистические методы обработки результатов наблюдений /
Под ред. P.M. Юсупова. - МО СССР, 1984. - 563 с.
172*. Статистические модели и многокритериальные задачи приня-
тия решений / Под ред. И.Ф. Шахнова. - М.: Статистика, 1979. -184 с.
173. Субетто А.И. Эффективность как мера качества систем и
процессов. - МО СССР, 1985. - 46 с.
174. Табак Д., Куо Б. Оптимальное управление и математическое
программирование. - М.: Наука, 1975. - 279 с.
175. Таха X. Введение в исследование операций. - М.: Мир, 1985, т.1,
479 с; т. II, 496 с.
176. Теоретические основы эксплуатации вооружения / Под ред.
В.М. Эйбшица. - МО СССР, 1979. - 333 с.
177*. Теория выбора и принятия решений /И.М. Макаров, Т.М. Ви-
ноградская, А.А. Рубчинский, В.Б. Соколов. - М.: Наука, 1982. - 327 с.
178*. Теория прогнозирования и принятия решений / Под ред. С.А.
Саркисяна. - М.: Высш. шк., 1977. - 351 с.
179*. Терехов Л.Л. Производственные функции. - М.: Статистика,
1974.-128 с.
180. Тихомирова А.В. Оценка эффективности управления
производством. - М.: Экономика, 1964. - 103 с.
181. Утеуш Э.В., Утеуш З.В. Введение в кибернетическое моделиро-
вание. - М.: Энергия, 1971. - 209 с.

Библиография
501
182. Федулов А.А., Федулов Ю.Г., Цыгичко В.Н. Введение в теорию
статистически ненадежных решений. - М.: Статистика, 1979. - 279 с.
183. Феллер В. Введение в теорию вероятностей и ее приложения. -
М.: Мир, 1964, т. 1,498 с; 1967, т. П, 752 с.
184. Флеминг У., Ришел Р. Оптимальное управление детерминиро-
ванными и стохастическими системами. - М.: Мир, 1978. - 207 с.
185. Флейшман Б.С. Элементы теории потенциальной эффективно-
сти сложных систем. - М.: Сов. радио, 1971. - 225 с.
186. Хованский Г.С. Основы номографии. -М.: Наука, 1976. - 351 с.
187. Червоный А.А., Лукьященко В.И., Котин Л.В. Надежность слож-
ных систем. - М.: Машиностроение, 1976. - 287 с.
188. Черноруцкий И.Г. Оптимальный параметрический синтез. - Л.:
Энергоатомиздат, 1987. - 128 с.
189. Черчмен У., Акоф Р., Арноф Л. Введение в исследование опера-
ций. - М.: Наука, 1968. - 486 с.
190*. Чуев Ю.В. Исследование операций в военном деле. - М.: Воен-
издат, 1970.-256 с.
191. Чумаков Н.М., Серебряный Е.И. Оценка эффективности сложных
технических устройств. - М.: Сов. радио, 1980. - 191 с.
192. Шаракшане А.С., Железное И.Г., Иваницкий З.А. Сложные систе-
мы. - М.: Высш. шк., 1977. - 247 с.
193. Шилейко А.В., Кочнев В.Ф., Химушин Ф.Ф. Введение в информа-
ционную теорию систем. - М.: Радио и связь, 1965. - 278 с.
194*. Шиханович Ю.А. Введение в современную математику. - М.:
Наука, 1965.-376 с.
195. Шульгин В.А. Контроль и управление в больших системах. - Л.:
Изд-воЛГУ, 1981.-170 с.
196. Элементы теории испытаний и контроля технических систем /
Под ред. P.M. Юсупова. -Л.: Энергия, 1978. - 191 с.
197*. Эффективность и надежность сложных систем / И.Л. Плетнев,
А.И. Рембеза, Ю.А. Соколов, В.А. Чалый-Прилуцкий. - М.: Машинострое-
ние, 1977.-216 с.
198. Якунин В.И. Анализ эффективности процесса функционирова-
ния информационно-справочной системы. Научн.-техн. сб. (труды). Вып.
2(51). Методы получения и обработки информации. - Б.м., МО СССР, 1986,
с. 72-75.
199. Якунин В.И. Оценивание эффективности процесса поиска ава-
рийных объектов. Научн.-техн. сб. (труды). Вып. 1(53). Актуальные вопро-
сы обработки информации. - Б.м., МО СССР, 1988, с. 35-38.

ИЗДАТЕЛЬСКАЯ ГРУППА
КАЖДАЯ ПЯТАЯ КНИГА РОССИИ
ПРИОБРЕТАЙТЕ КНИГИ ПО ИЗДАТЕЛЬСКИМ UEHAM
В СЕТИ КНИЖНЫХ МАГАЗИНОВ(Цква)
МОСКВА:
• м. «Алексеевская», Звездный б-р, 21, стр. 1, т. 232-19-05
• м. «Алексеевская», пр. Мира, 176, стр. 2 (Му-Му), т. 687-45-86
• м. «Бибирево», ул. Пришвина, 22, TU «Александр Ленд», этаж 0.
• м. «Варшавская», Чонгарский б-р, 18а, т. 110-89-55
• м. «ВДНХ», проспект Мира, владение 11 7
• м. «Домодедовская», ТК «Твой Дом», 23-й км МКАД, т. 727-16-15
• м. «Крылатское», Осенний б-р, 18, корп. 1, т. 413-24-34, доб. 31
• м. «Кузьминки», Волгоградский пр., 132, т. 172-18-97
• м. «Медведково», XL TU Мытищи, Мытищи,
ул. Коммунистическая, 1
• м. «Новослободская», 26, т. 973-38-02
• м. «Новые Черемушки», ТК «Черемушки», ул. Профсоюзная, 56,
4-й этаж, пав. 4а-09, т. 739-63-52
• м. «Павелецкая», ул. Татарская, 14, т. 959-20-95
• м. «Парк культуры», Зубовский б-р, 17, стр. 1, т. 246-99-76
• м. «Перово», ул. 2-я Владимирская, 52/2, т. 306-18-91
• м. «Петровско-Разумовская», ТК «XL», Дмитровское ш., 89,
т. 783-97-08
• м. «Сокол», ТК «Метромаркет», Ленинградский пр., 76, корп. 1,
3-й этаж, т. 781-40-76
• м. «Сокольники», ул. Стромынка, 14/1, т. 268-14-55
• м. «Сходненская», Химкинский б-р, 16/1, т. 497-32-49
• м. «Таганская», Б. Факельный пер., 3, стр. 2, т. 911-21-07
• м. «Тимирязевская», Дмитровское ш., 15, корп. 1, т. 977-74-44
• м. «иарииыно», ул. Луганская, 7, корп. 1, т. 322-28-22
• м. «Бауманская», ул. Спартаковская, 10/12, стр. 1
• м. «Преображенская плошадь», Большая Черкизовская, 2, корп. 1,
т. 161-43-11
Заказывайте книги почтой в любом уголке России
107140, Москва, а/я 140, тел. (095) 744-29-1 7
ВЫСЫЛАЕТСЯ БЕСПЛАТНЫЙ КАТАЛОГ
Приобретайте в Интернете на сайте www.ozon.ru
Издательская группа ACT
129085, Москва, Звездный бульвар, д. 21, 7-й этаж
Книги ACT на территории Европейского союза у нашего
представителя: «Express Kurier GmbH» Tel. 00499233-4000
Справки по телефону:
(095) 615-01-01, факс 615-51-10
E-mail: astpab@aha.ru http://www.ast.ru
МЫ ИЗЛАЕМ
КНИГИ

РЕГИОНЫ:
Архангельск, 103-й квартал, ул. Садовая, 18, т. (8182) 65-44-26
Белгород, пр. Хмельницкого, 132а, т. (0722) 31-48-39
Волгоград, ул. Мира, 11, т. (8442) 33-1 3-19
Екатеринбург, ул. Малышева, 42, т. (3433) 76-68-39
Калининград, пл. Калинина, 17/21, т. (0112) 65-60-95
Киев, ул. Льва Толстого, 11/61, т. (8-10-38-044) 230-25-74
Красноярск, «ТК», ул. Телевизорная, 1, стр. 4, т. (3912) 45-87-22
Курган, ул. Гоголя, 55, т. (3522) 43-39-29
Курск, ул. Ленина, 11, т. (07122) 2-42-34
Курск, ул. Радищева, 86, т. (07122) 56-70-74
Липецк, ул. Первомайская, 57, т. (0742) 22-27-16
Н. Новгород, TU «Шоколад», ул. Белинского, 124, т. (8312) 78-77-93
Ростов-на-Дону, пр. Космонавтов, 15, т. (8632) 35-95-99
Рязань, ул. Почтовая, 62, т. (0912) 20-55-81
Самара, пр. Ленина, 2, т. (8462) 37-06-79
Санкт-Петербург, Невский пр., 140
Санкт-Петербург, ул. Савушкина, 141, TU «Меркурий»,
т.(812)333-32-64
Тверь, ул. Советская, 7, т. (0822) 34-53-11
Тула, пр. Ленина, 18, т. (0872) 36-29-22
Тула, ул. Первомайская, 12, т. (0872) 31-09-55
Челябинск, пр. Ленина, 52, т. (3512) 63-46-43, 63-00-82
Челябинск, ул. Кирова, 7, т. (3512) 91-84-86
Череповец, Советский пр., 88а, т. (8202) 53-61-22
Новороссийск, сквер им. Чайковского, т. (8617) 67-61-52
Краснодар, ул. Красная, 29, т. (8612) 62-75-38
Пенза, ул. Б. Московская, 64
Ярославль, ул. Свободы, 12, т. (0862) 72-86-61
Заказывайте книги почтой в любом уголке России
107140, Москва, а/я 140, тел. (095) 744-29-17
ВЫСЫЛАЕТСЯ БЕСПЛАТНЫЙ КАТАЛОГ
Приобретайте в Интернете на сайте www.ozon.ru
Издательская группа ACT
129085, Москва, Звездный бульвар, д. 21, 7-й этаж
Справки по телефону:
(095) 615-01-01, факс 615-51-10
E-mail: astpab@aha.ru http://www.ast.ru
МЫ ИЗДАЕМ
КНИГИ

ISBN 5-17-03ЧЬ52-2
ртищ
9ll785170ll346523»
Любое использование материала данной книги,
полностью или частично, без разрешения
правообладателя запрещается.
Научное издание
Петухов Георгий Борисович
Якунин Владимир Иванович
Методологические основы внешнего проектирования
целенаправленных процессов и целеустремленных систем
Подписано в печать с готовых диапозитивов заказчика 05.10.05.
Формат 70x1001 /16. Бумага офсетная. Печать офсетная.
Усл. печ. л. 41. Тираж 2000 экз. Заказ 3303.
Общероссийский классификатор продукции ОК-005-93, том 2;
953004 — научная и производственная литература
Санитарно-эпидемиологическое заключение
№ 77.99.02.953.Д.001056.03.05 от 10.03.05 г.
ООО «Издательство ACT»
170000, Россия, г. Тверь, пр-т Чайковского, д. 19 а, оф. 214
Наши электронные адреса: WWW.ACT.RU
E-mail: astpub@aha.ru
Издано при участии ООО «Харвест».
Лицензия № 02330/0056935 от 30.04.04.
РБ, 220013, Минск, ул. Кульман, д. 1, корп. 3, эт. 4, к. 42.
Республиканское унитарное предприятие
«Издательство «Белорусский Дом печати».
220013, Минск, пр. Независимости, 79.