А. Н. БОРИСОВ,
О. А. КРУМБЕРГ,
И. П. ФЕДОРОВ
ПРИНЯТИЕ
РЕШЕНИИ
НА ОСНОВЕ
НЕЧЕТКИХ
МОДЕЛЕЙ
ПРИМЕРЫ ИСПОЛЬЗОВАНИЯ

РИЖСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
А. Н. БОРИСОВ, О. А. КРУМБЕРГ,
И. П. ФЕДОРОВ
ПРИНЯТИЕ
РЕШЕНИЙ
НА ОСНОВЕ
НЕЧЕТКИХ
МОДЕЛЕЙ
Примеры использования
РИГА «ЗИНАТНЕ» 1S90

ййлй
Б825
УДК 519.816
Борисов А. Н., Крумберг О. А., Федоров И. П. Принятие
решений на основе нечетких моделей : Примеры использования. — Рига : Зи-
натне, 1990. — 184 с. — ISBN 5-7966-0459-7.
Рассматриваются вопросы построения моделей принятия решений при
неточной исходной информации. Для описания элементов задач в процессе
построения моделей используются понятия нечеткого множества,
лингвистической переменной, распределения возможностей, нечеткого свидетельства.
Систематически излагаются методы обработки нечеткой информации:
построение функций принадлежности нечетких множеств, выполнение операций
над нечеткими числами, сравнение и упорядочение нечетких множеств и
чисел, действия с распределениями возможностей и нечеткими
свидетельствами. Описываются способы построения моделей принятия решений,
использующие различную структуру нечеткой исходной информации.
Описанные методы и пути их реализации поясняются на примерах.
Табл. 33, ил. 82, библиогр. 48 назв.
Ответственный редактор проф., д-р техн. наук Я. Я. Осис
Рецензенты:
проф., д-р техн. наук А. Н. Мелихов
канд. техн. наук А. В. Язенин
.1602110000-078 31 д0
БМ811A1)-90
ISBN 5-7966-0459-7 © А. Н. Борисов, О. А. КрУмберг, И. П. Федоров,

Взрослые очень любят цифры ... Когда
говоришь взрослым: «Я видел красивый
дом из розового кирпича, в окнах у
него герань, а на крыше голуби», —
они никак не могут представить себе
этот дом. Им надо сказать: «Я видел
дом за сто тысяч франков», — и тогда
они восклицают: «Какая красота!»
Антуан де Сент-Экзюпери
ПРЕДИСЛОВИЕ
Под принятием решений понимается выбор одной альтернативы из
полученного или заданного множества альтернатив. Реализация
любой альтернативы предполагает наступление некоторых последствий,
анализ и оценка которых по векторному критерию эффективности
полностью характеризуют альтернативу. Решение задач сводится к
выявлению и исследованию предпочтений лица, принимающего решения
(ЛПР), а также к построению на этой основе адекватной модели
выбора наилучшей в некотором «конкретном смысле альтернативы.
Важной особенностью задач принятия решений является необходимость
учета субъективных суждений ЛПР при формализации предпочтений
и выборе наилучшей альтернативы. Эта особенность означает, что
различные ЛПР в одной и той же ситуации принятия решений, на основе
одной и той же модели могут получить различный результат.
Сложность связей ситуации принятия решений, отсутствие точного
прогноза последствий приводят к тому, что при оценке и выборе
альтернатив возможно, а зачастую и необходимо использовать и
обрабатывать качественные нечеткие оценки.
Будем полагать, что в ситуациях принятия решений, когда хотя бы
один из элементов (исходы, критерии, предпочтения и т.д.)
описывается качественно, нечетко, имеют место задачи многокритериального
принятия решений при нечеткой исходной информации.
Перспективным направлением разработки методов принятия
решений при нечеткой исходной информации является лингвистический
подход на базе теории нечетких множеств и лингвистической переменной.
К настоящему времени в этом направлении получены конкретные
практические и теоретические результаты. Их анализ позволяет
сформулировать основные вопросы, возникающие при разработке и релизации
методов и моделей принятия решений при нечеткой исходной
информации. К ним можно отнести следующие:
— построение функций принадлежности нечетких множеств;
— выполнение операций над нечеткими числами;
— сравнение и упорядочение нечетких множеств и чисел;
— разработка моделей принятия решений.
Концептуальные и вычислительные особенности реализации
перечисленных методов настолько отличаются от традиционных, что часто
являются тормозом для широкого их использования. Перечисленные

6 Предисловие
задачи решены с разной степенью глубины, а иногда только найдены
пути их решения. Эти результаты публикуются в виде статей,
отражающих лишь основные идеи, что не может служить руководством для
использования. Как правило, они требуют глубокой методической
доработки — создания алгоритмов и программных средств и т.д.
Подобные разработки ведутся в научных коллективах и отражаются в
полном объеме только в малодоступных научных отчетах. В то же время
литературы или руководств по численным методам реализации
моделей принятия решений на базе теории нечетких множеств не
существует. Настоящая монография подготовлена с целью восполнить этот
пробел и построена в соответствии с перечисленными вопросами. При
рассмотрении конкретного метода наряду с кратким его описанием
приводятся примеры реализации, доведенные до численного результата.
В целом соотношение между объемами теоретического и практического
материала выбрано в пользу последнего.
Авторы стремились показать, что аппарат теории нечетких множеств
является полезным инструментом при создании моделей принятия
решений, и надеются, что их усилия будут способствовать дальнейшему
развитию прикладных работ в этом направлении. При подготовке
рукописи авторы постоянно пользовались доброжелательными и
конструктивными консультациями А. В. Алексеева, Г. В. Меркурьевой,
В. А. Попова, В. И. Глушкова, Н. Н. Слядзя. Монография была бы
невозможна без тех результатов, которые получены в рассматриваемой
области сотрудниками группы прикладных методов теории нечетких
множеств кафедры автоматизированных «систем управления Рижского
технического университета.
Все замечания и предложения просим направлять по адресу: 226010
ГСП, Рига, ул. Аусекля, 7. Рижский технический университет.
Авторы

Глава 1
МЕТОДЫ ПОСТРОЕНИЯ
ФУНКЦИЙ ПРИНАДЛЕЖНОСТИ
НЕЧЕТКИХ МНОЖЕСТВ
1.1. ПОСТРОЕНИЕ
ФУНКЦИЙ ПРИНАДЛЕЖНОСТИ
НА ОСНОВЕ ПАРНЫХ СРАВНЕНИЙ
Рассматривается метод построения функций принадлежности,
основанный на обработке матрицы оценок, отражающих мнение эксперта
об относительной принадлежности элементов множеству или степени
выраженности у них свойства, формализуемого множеством [3, 8].
Краткие сведения о методе. Пусть Х={х} .— множество из п
элементов. Нечеткое подмножество S множества X есть совокупность пар
вида
где \is(x) — степень принадлежности элемента х множеству S. Если
функция принадлежности \i(x) принимает значения только 0 или 1,
то множество S становится обычным. Потребуем, чтобы для всех
элементов множества S выполнялось равенство
Степень принадлежности элементов множеству будем определять
посредством парных сравнений. При этом используются оценки,
приведенные в табл. 1.1. Оценку элемента х\ по сравнению с элементом
Xj с точки зрения свойства S обозначим через ац. Для обеспечения
согласованности примем а^==1/а^. Оценки ац составляют матрицу
A = ||aij||. Найдем w= (w\,..., wn) — собственный вектор матрицы А,
решая уравнение Aw=^w, где К — собственное значение матрицы А.
Вычисленные значения, составляющие собственный вектор w,
принимаются в качестве степени принадлежности элементов х множеству S:
Так как всегда выполняется равенство Aw=rtw, то найденные
значения тем точнее, чем ближе Яшах к я. Отклонение А,тах от п может
служить мерой согласованности суждений экспертов.
Примеры использования метода. Рассмотрим задачу оценки
освещенности предметов. Освещенность поверхности определяется как
количество светового потока на единицу площади. Для нахождения
различий в освещенности четырех идентичных объектов в зависимости от

Глава 1. Методы построения функций принадлежности
Таблица 1.1
Шкала для определения матрицы суждений
Оценка
важности
Качественная оценка
Примечание
2, 4,6,8
Одинаковая значимость
Слабое превосходство
Сильное (или существенное)
превосходство
Очевидное превосходство
Абсолютное превосходство
Промежуточные значения
соседними оценками
между
По данному критерию
альтернативы имеют одинаковый ранг
Соображения о предпочтении
одной альтернативы перед другой
малоубедительны
Имеются надежные доказательства
существенного превосходства одной
альтернативы
Существуют убедительные
свидетельства в пользу одной
альтернативы
Свидетельство в пользу
предпочтения одной альтернативы перед
другой в высшей степени убедительно
Используются, когда необходим
компромисс
их расстояния до источника был проведен следующий эксперимент.
Визуальное сравнение интенсивности освещенности проводили
независимо друг от друга две группы людей. Предметы находились на
следующих расстояниях от источника света: 9, 15, 21 и 28 единиц длины.
В примерах 1.1 и 1.2 представлены две матрицы парных сравнений
освещенности предметов, пронумерованных в возрастающем порядке
в зависимости от их близости к источнику света.
Пример 1.1. Матрица парных сравнений в первом эксперименте
имеет вид
1
1/5
1/6
1/7
5
1
1/4
1/6
6
4
1
1/4
7
6
4
1
Необходимо найти собственный вектор w, для которого выполняется
условие Aw=^w, где К — собственное значение матрицы.
Обратимся к решению задачи нахождения собственных значений
(A—A,E)w=0. Эта неоднородная система имеет нетривиальное решение
тогда и только тогда, когда определитель матрицы А—ЯЕ равен нулю.
Найдем его:
1-Я
1/5
1/6
1/7
5
1-Я
1/4
1/6
6
4
1-Я,
1/4
7
6
4
1-Я
и приравняем к нулю. Уравнение имеет решение
h = -0,362; Я2=-0,140+1,305 /; Я3= —0,140—1,305 I; Я4=4,390.

1.1. Построение функций на основе парных сравнений
Следовательно, Ятах=4,390. Найдем собственный вектор:
1-4,390 5 6
1/5 1-4,390 4
1/6 1/4 1 -4,390
1/7
1/6
1/4
7
6
4
1-4,390
•
XS)o
= 0.
Вводится условие нормировки:
тему
=l. Рассмотрим
сис0,2^1 - 3,390иу2+4йУ3 + 6^4=0;
0,166о> 1 + 0,25ш2—3,390ш3+4я>4=0;
—3,390ш4=0.
A.1)
Система A.1) имеет только нулевое решение. Для нахождения
собственного вектора w используется замена одного из уравнений (\Л\
условием нормировки. В результате решения системы получаем
собственный вектор:
= 0,619; ^2 = 0,235; ш3 =
(при
При поочередной подстановке условия нормировки вместо
уравнений системы результат решения не изменяется.
Пример 1.2. Матрица парных сравнений во втором эксперименте
имеет вид
1
1/4
1/6
1/7
4
1
1/3
1/4
6
3
1
1/2
7
4
2
1
=Я4-4Я3-1,687 Я-0,133.
Аналогично приведенному выше описанию находим определитель:
1-Я 4 6 7
1/4 1-Я 3 4
1/6 1/3 1-Я 2
1/7 1/4 1/2 1-Я
Приравняем найденный определитель к нулю. Уравнение имеет
решение
Я, = -0,782; Я2 = 0,120-0,645i; Я3= -0,120+0,645 i; Я4=4Д02.
Следовательно, Яшах=4,102. Найдем собственный вектор:
-3,102 4 6 7
1/4 -3,102 3 4
1/6 1/3 -3,102 2
1/7 1/4 1/2 —3,102
Ws
= 0.

10 Глава 1. Методы построения функций принадлежности
Решим систему
—3,102^
0,25^1 -
1 0,166^1-
0,142wt + 0,25w2 + 0,5w3 - 3,102ш4=0
О;
0,166ш 1 + 0,ЗЗЗш2 - 3,102w3 + 2я>4 = 0; ' '
ПрИ
Система A.2) имеет только нулевое решение, для нахождения
собственного вектора w используется замена одного из уравнений A.2)
условием нормировки. В результате решения системы получаем
собственный вектор:
Ш! = 0,617; о;2 = 0,224; ш3 = 0,097; ау4 = 0,062 (при Ятах = 4,102).
При поочередной подстановке условия нормировки вместо
уравнений системы результат решения остается без изменения.
Матрица, в которой используются обратные величины (ац = 1/ац),
отражает согласованные суждения тогда и только тогда, когда Атах=я.
Кроме того, всегда Хтах^п, поэтому Яшах —я дает меру
несогласованности и указывает, когда суждения экспертов следует проверить. Так,
в первом эксперименте при п = 4 Ктах = 4,390; мера несогласованности
равна 0,390. Во втором эксперименте Яшах = 4,102, мера
несогласованности равна 0,102. Следовательно, во втором эксперименте
согласованность суждений экспертов выше, чем в первом.
1.2. ПОСТРОЕНИЕ
ФУНКЦИИ ПРИНАДЛЕЖНОСТИ
ЛИНГВИСТИЧЕСКИХ ТЕРМОВ
С ИСПОЛЬЗОВАНИЕМ
СТАТИСТИЧЕСКИХ ДАННЫХ
Описываемый метод основан на обработке статистических данных.
В качестве степени принадлежности элемента множеству принимается
оценка частоты использования понятия, задаваемого нечетким
множеством, для характеристики элемента. Благодаря использованию
специальных матриц подсказок получаются гладкие функции
принадлежности [4].
Краткие сведения о методе. При построении автоматизированных
систем управления возникает задача моделирования деятельности
человека-оператора. Один из путей ее решения — использование теории
нечетких множеств на основе понятия функции принадлежности.
Функция принадлежности \ia(u) ставит в соответствие каждому
элементу u^U число из интервала [0, 1], характеризующее степень
принадлежности элемента и множеству Л. Человек, воспринимая
информацию, не пользуется конкретными числами, а переводит их в свои
понятия — значения лингвистической переменной. Каждое значение
лингвистической переменной описывается функцией принадлежности,
которая индивидуальна для каждого человека.
Предположим, что, наблюдая за объектом в течение некоторого
времени, человек п раз фиксирует свое внимание на том, имеет место
факт А или нет. Событие, заключающееся в п проверках наличия

1.2. Метод, использующий статистические данные It
Таблица 1.2
Оценка отклонения параметра технологического процесса
в терминах лингвистической переменной «Относительная величина»
Интервал
Значение
8 9 I 10 | Л I 12 I 13 I 14 I 15 I 16 I 17 I 18 I 19 I 20
ОЧЕНЬ МАЛО 3730 100000000000 1000
МАЛО 00104164100000000000
СРЕДНЕ 00000002257000000000
МНОГО 00000000003807523000
ОЧЕНЬ 00000000000000 1 25752
МНОГО
факта А, будем называть оценочным. Пусть в k проверках имел место
факт А. Тогда оператор регистрирует частоту p = k/n появления факта
А и оценивает ее с помощью слов типа «часто», «редко» и т. п.
Оценивая частоту р, человек опирается на свой опыт, который
отражает частоту появления факта А в событиях прошлого,
представляющихся человеку аналогичными оцениваемому событию. К нему
поступает также информация, основанная на наблюдении других людей
появления факта А, т. е. информация, отражающая общественный опыт.
В зависимости от степени доверия к источнику такого рода информации
она запоминается с различными весами.
На универсальной шкале [0, 1] необходимо разместить значения
лингвистической переменной: ВЕСЬМА РЕДКО, БОЛЕЕ-МЕНЕЕ
РЕДКО, БОЛЕЕ-МЕНЕЕ ЧАСТО, ВЕСЬМА ЧАСТО. Тогда степень
принадлежности некоторого значения вычисляется как отношение числа
экспериментов, в которых оно встречалось в определенном интервале
шкалы, к максимальному для этого значения числу экспериментов по
всем интервалам. Метод основывается на условии, что в каждый
интервал шкалы попадает одинаковое число экспериментов. Это условие
часто не соблюдается. В реальных случаях составляется эмпирическая
таблица (табл. 1.2), в которой эксперименты могут быть распределены
неравномерно по интервалам, а в некоторые интервалы могут вообще
не попасть.
Предположим, что оператору в процессе управления предлагают
оценить в значениях лингвистической переменной «Относительная
величина» отклонения AS параметра технологического процесса, где В—
максимально возможное отклонение, а АВ лежит в интервале [0, В].
Значения лингвистической переменной следующие: ОЧЕНЬ МАЛО,
МАЛО, СРЕДНЕ, МНОГО, ОЧЕНЬ МНОГО. Возьмем АВ/В —
оцениваемое отношение. Как интервал [0, В], так и АВ/В разделены на 20
отрезков, по которым собирается статистика, характеризующая,
насколько часто человек употреблял данные слова для выражения своего
представления. Аналогичная таблица может быть составлена для
оценки частоты появления какого-либо факта. Значения
лингвистической переменной при этом следующие: ВЕСЬМА РЕДКО,
БОЛЕЕ-МЕНЕЕ РЕДКО, НИ ЧАСТО, НИ РЕДКО, БОЛЕЕ-МЕНЕЕ ЧАСТО,
ВЕСЬМА ЧАСТО.
Используя свойства функций принадлежности, необходимо
предварительно обработать данные табл. 1.2 таким образом, чтобы умень-

12
Ц< 0i05 1 0,1 1 0И5
Глава
1
1.
0,2
Методы
построения
Значения
АВ/В
| 0»S5
1 °'3 1
функций
функций
0,35 1
принадлежности
принадлежности
0,4 | 0.45 |
М-2
1,0
0
0
0
0
1,0
0
0
0
0
0,75
0,25
0
0
0
0,47
0,52
0
0
0
0,2
0.8
0
0
0
0
1,0
0
0
0
0
1,0
0
0
0
0
0,67
0,33
0
0
0
0,33
0,67
0
0
шить искажения, вносимые экспериментом. Естественными свойствами
функций принадлежности являются наличие одного максимума и
гладкие, затухающие до нуля фронты. Для обработки статистических
данных можно воспользоваться так называемой матрицей подсказок.
Предварительно из табл. 1.2 удаляются явно ошибочные элементы
(например, элемент ОЧЕНЬ МАЛО — 17). Критерием удаления служит
наличие нескольких нулей в строке вокруг этого элемента.
Элементы матрицы подсказок вычисляются по формуле kj= 2j Ъц9
/=1, 20. Матрица подсказок представляет собой строку ||3 7 4 0 5 1
6635 1080764975 2Ц. В строке табл. 1.2 выбирается
максимальный элемент: kmdLX=maxkj и далее все ее элементы
преобразуются по формуле
Для столбцов, где kj = Ot применяется линейная аппроксимация:
Для построения функций принадлежности находятся максимальные
элементы по строкам табл. 1.2: C;max=niaxctj, *"=1> 5, /=1, 20.
Функция принадлежности вычисляется по формуле \щ = сц/ътех-
На рис. 1.1 сплошной линией показаны функции принадлежности
значений лингвистической переменной «Относительная величина» после
обработки эмпирической таблицы. Как видно, функции принадлежности
удовлетворяют свойствам, описанным выше. Для сравнения пунктирной
линией показана функция принадлежности значения МАЛО без
обработки таблицы.
В качестве примера приведем численный расчет значений функции
принадлежности терма ОЧЕНЬ МАЛО. Выберем &^10
Преобразуем элементы матрицы:
* = 1> /=1,

1.1 Метод, использующий статистические
лингвистической переменной
1 0,5 | 0,55 1 0,6 1 0,65 1 0,7 |
Данные
0,75 1
0,8 1
0.85
Та
0v9.
а
блица 1.3
0^5 1.0
0
0
1,0
0
0
0
0
0,7
0,3
0
0
0
0
1,0
0
0
0
0
1,0
0
0
0
0
1,0
0
0
0
0
0,83
0,16
0
0
0
0,5
0,5
0
0
0
0,33
0,55
0
0
0
0
1,0
Та
0
0
0
0
1,0
блица
0
0
0
0
1,0
1.4
Оценка времени
Значение
работы
1 | 2 3
программ
4 5
В
6
пакетном
7 8 1 9
режиме
Интервал
10 | 11 | 12
13
14
,5
.6
а,
ОЧЕНЬ МАЛО 234 100 000000000
МАЛО
СРЕДНЕ
МНОГО
ОЧЕНЬ
МНОГО
001257 300000000
000 002 463751000
000 000 0000032586
000 000 000000000
0
0
0
6
1
0
0
0
3
2
0
0
0
i
1
0
0
0
0
8
0
0
0
0
9
Матрица
1
С
• 1
3
«1
5
•1
7
6 1
9 | 10
/
и
1»
A3 | 1
16
Табл
17 | 18
ица
1 «• 1
1.5
20
1
2
3
4
5
9
0
0
0
0
9
0
0
0
0
7,2
1,8
0
0
0
3
6
0
0
0
0
9
0
0
0
0
7
2
0
0
0
з,(
5,
0
0
00000 00000 0 00
7 3,9 000 00 00000 0 00
999 9 2,3 0 0000 0 00
0 0 0 0 6,8 9 9 9 7,7 5,4 4,5 0 0
0 0 0 0 0 0 0 0 1,3 3,6 4,5 9 9
ДВ/В=~—0,1;
; ДВ/В JL_=o,15;
1_
±

Глава i. Методы построения функций принадлежности
Значения функций принадлежности термов лингвистической
*
0,05 I
№ 1
Ц2 0
Цз 0
|х4 0
Цб 0
«л |
1
0
0
0
0
0,15
0,8
0,2
0
0
0
0,2
0,333
0,666
0
0
0
АВ/В
0,25
0
1
0
0
0
0,3 |
0
0,777
0,22
0
0
0,35 |
0
0,43
0,57
0
0
0,4
0
0
1
0
0
| 0,45 |
0
0
1
0
0
Результаты вычислений сведены в табл. 1.3.
Пример использования метода. Пример 1.3. Необходимо оценить
в термах лингвистической переменной «Относительная величина»
время работы машинных программ при пакетном режиме обработки в
студенческой системе STAR. Собранная статистика приведена в
табл. 1.4. В данном случае значения В (время работы программ, мин)
изменяются в интервале [0, 20]. Необходимо аппроксимировать
функцию принадлежности. На основе табл. 1.3 определяем матрицу
подсказок ||2 353597637542587528 9||. Ее элементы нахо-
5
дятся по формуле &j= 2j b%h /=1,20. Вычисляем элемент новой
матрицы (табл. 1.5)
Сц =
i =1,5, / = 1,20.
Значения функций принадлежности определяем по формуле |л^ =
= Cij/CimaLXy 1=1, 5, /=1, 20; Cimax = 9; C2max = 9; C3max = 9; C4max = 9;
Сь max == 9.
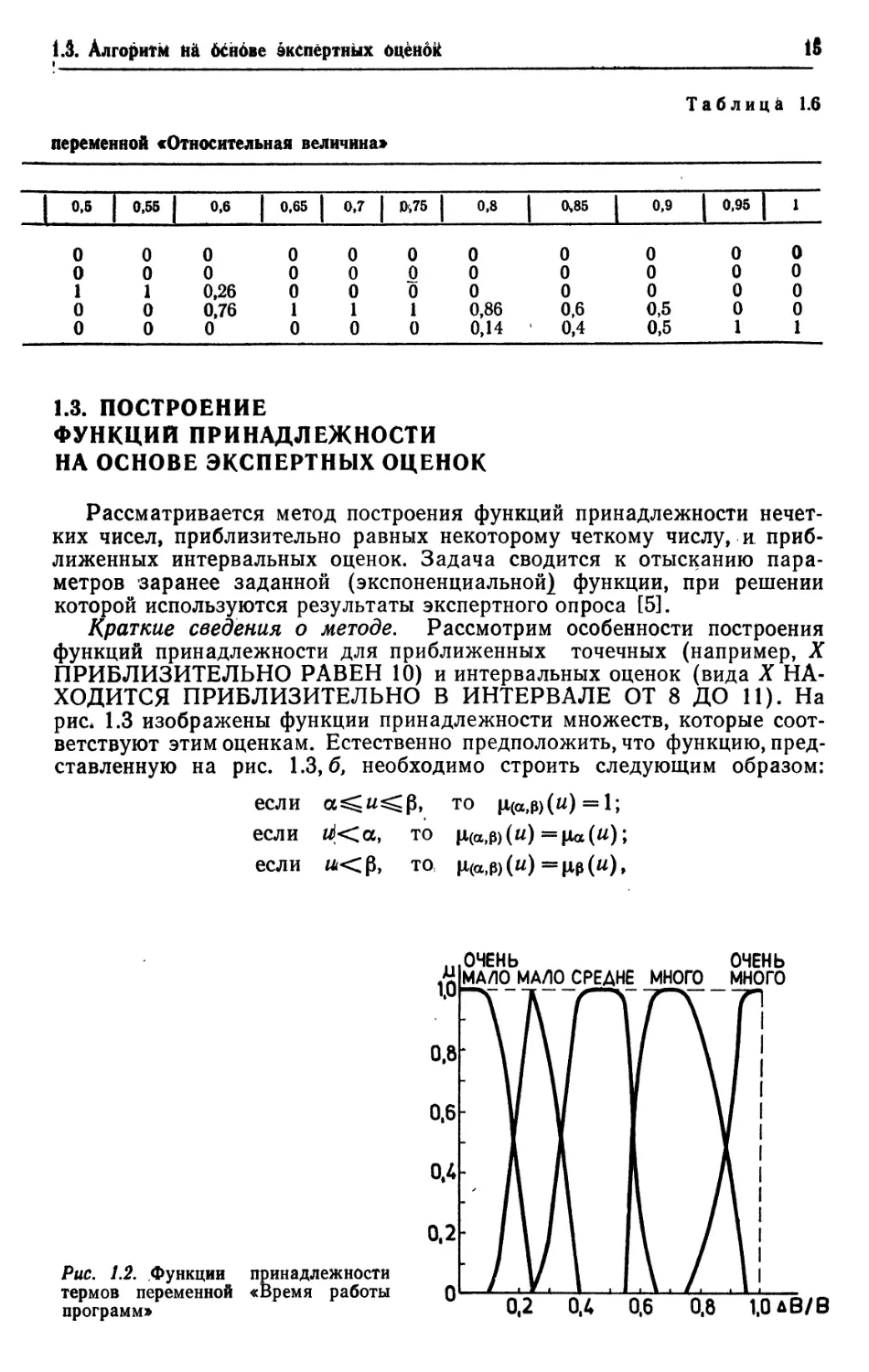
Результаты приведены в табл. 1.6. Функции принадлежности для
каждого терма лингвистической переменной представлены на рис. 1.2.
1.0
0.8
0,6
0Л
0,2
0
ОЧЕНЬ ОЧЕНЬ
МАЛО МАЛО СРЕДНЕ МНОГО МНОГО
0,2 0Л 0,6 0,8 1.0АВ/В
Рис. 1.1. Функции принадлежности
значений лингвистической переменной
«Относительная величина»

1.1 Алгоритм ни бснбве экспертных оцёйбк
18
переменной «Относительная величина»
1 0,5 1 0,55 0,6 0,65 1 0,7 0,
75 0,8
«я |
0,9
Таблица
| 0.95 |
1.6
1
о
о
1
о
о
о
о
1
о
о
о
о
0,26
0,76
О
О
О
О
1
О
о
о
о
1
о
о
о
о
1
о
о
о
о
0,86
0,14
О
О
О
0,6
0,4
О
О
О
0,5
0,5
О
О
О
О
1
О
О
о
о
1
1.3. ПОСТРОЕНИЕ
ФУНКЦИЯ ПРИНАДЛЕЖНОСТИ
НА ОСНОВЕ ЭКСПЕРТНЫХ ОЦЕНОК
Рассматривается метод построения функций принадлежности
нечетких чисел, приблизительно равных некоторому четкому числу, и
приближенных интервальных оценок. Задача сводится к отысканию
параметров заранее заданной (экспоненциальной) функции, при решении
которой используются результаты экспертного опроса [5].
Краткие сведения о методе. Рассмотрим особенности построения
функций принадлежности для приближенных точечных (например, X
ПРИБЛИЗИТЕЛЬНО РАВЕН 10) и интервальных оценок (вида X
НАХОДИТСЯ ПРИБЛИЗИТЕЛЬНО В ИНТЕРВАЛЕ ОТ 8 ДО И). На
рис* 1.3 изображены функции принадлежности множеств, которые
соответствуют этим оценкам. Естественно предположить, что функцию,
представленную на рис. 1.3,6, необходимо строить следующим образом:
если
то (г(а,э)(и) = 1;
если «!<а, то
если
то
1.0
0.8
0,6
0.2
Рис. 1.2. Функции принадлежности
термов переменной «Время работы О
программ»
ОЧЕНЬ ОЧЕНЬ
МАЛО МАЛО СРЕДНЕ МНОГО МНОГО
0,2 0Л 0,6 0,8 1,0 А В/В

?*лава i. Методы построений функций принадлежности
Рис. 1.3. Функции принадлежности нечетких множеств, соответствующих
приближенной точечной оценке
где (Х(а,э)(«) — функция принадлежности нечеткому интервалу (а, р);
jia(tt) и (хр (и) — функции принадлежности нечетким множествам
чисел, приближенно равных соответственно аир. Они строятся
аналогично функции, график которой приведен на рис. 1.3, а.
При построении функции принадлежности чисел, приблизительно
равных некоторому числу К, можно использовать функцию
[1к(и)=е-<*(к-и)\ A.3)
где а зависит от требуемой степени нечеткости \хк(и) и определяется
из выражения
4 In 0,5
Р — расстояние между точками перехода для |ля(и), т.е. точками, в
которых функция вида A.3) принимает значение 0,5. На рис. 1.3, а эти
точки обозначены а и Ь.
Таким образом, задача построения \хк(и) для некоторого числа
сводится к отысканию параметров а и Ь, чтобы затем можно было
определить Р(х), с помощью р (л:) — а и, используя а, построить \хк(и).
Для определения множества вида ЧИСЛО, ПРИБЛИЗИТЕЛЬНО
РАВНОЕ К, следует выяснить, как эксперты представляют себе гра-
Та блица 1.7
Расстояния между точками перехода
1, 2, 3, 4, 6, 7, 8, 9
10, 20, 30, 40, 60, 80, 90
35, 45, 55, 65, 75, 85, 95
5
15
25
50
Прочие двузначные числа
0,46-*
@,357-0,00163*)*
@,213-0,00067*)*
2,8
6,48
6,75
24

i.3. Алгоритм на основе экспертных оценок 17
ницы классов таких чисел. Для этого проводились статистические
исследования. Опрашиваемым предлагали назвать такие а (К) и Ь(К),
которые, по их мнению, отделяют числа, приблизительно равные
заданному К, от чисел, таковыми не являющихся. Полученные
результаты после некоторой обработки сведены в табл. 1.7. Рассмотрим
натуральное число К. Пусть его младшая значащая цифра имеет
порядок q. Разобьем возможные значения q на классы вычетов по модулю
3 и введем переменную d, значения которой будут являться
представителями данных классов {0, 1, 2}. Получим классы эквивалентности:
Md{d=0, 1, 2}, rf=?modC).
Введем целочисленную переменную X, изменяющуюся в пределах
от 1 до 99, и будем считать, что для каждого ее значения известны
параметры а(х) и Ь(х), а следовательно, и Р(#). На основании
результатов опроса выяснилось, что значения $(х) в зависимости от X
можно находить так, как показано в табл. 1.7 ([...] — целая часть
числа). Значение $(х) зависит также от того, к какому классу Md
принадлежит число К.
Обозначим через rq цифру, стоящую в q-u разряде числа К. Тогда:
1. При К(=М0 (например, 300, 300 000, 5-108 и т.д.) р(/С) зависит
только от младшей значащей цифры числа К> т.е. от rq: Х = гяЛй\
Р(/() =$(х) -Ю^2, где р(х) находится из табл. 1.7.
2. При /feMi (например, 101, 202 000, 5-Ю9 и т.д.) возможны два
варианта:
а) rq+i = 0, тогда р(/С) зависит только от rq: x=rq; $(K)=fi(x)X
X109-*;
б) rq+i^0, тогда р(/С) зависит от двух последних значащих цифр
числа К: x = rq+i-l0+rq; р(/С) = Р(*) • Ю*-1.
3. При /С^М2 (например, 2140, 20 и т.д.) также возможны два
варианта:
а) rq+i = 0t тогда x = rq-10; p(K) =р(х) -Ю^2;
б) гд+1ф0у тогда * = />н-10 + гд; р(Я) =Р(*)-Ю*-1.
После того как для числа К найдено значение Р(/С), строим
функцию принадлежности \лк(и) для u^U, используя формулу A.3).
С помощью указанного алгоритма могут быть также построены
функции принадлежности в случае, когда К выражается десятичной
дробью. При этом алгоритм применяется к мантиссе дроби, а затем
учитывается ее порядок.
Примеры использования метода. Пример 1.4. Имеем
приближенную точечную экспертную оценку X ПРИБЛИЗИТЕЛЬНО РАВЕН 235.
Согласно вышеописанному алгоритму, /(=235. Далее определяем
значение переменных q, rq> rq+i и d. Младшая значащая цифра числа К
стоит в разряде единиц, т.е. имеем <7=1; г{ = 5 — младшая значащая
цифра числа К; г2 = 3 — цифра, имеющая порядок на единицу выше
порядка младшей значащей цифры.
При делении числа q на 3 в остатке получаем 1, т.е. число К
принадлежит к классу эквивалентности М\ и переменная d получает значение
единицу. Следуя описанному методу, переходим к п. 2.6, так как rq+i =
= г2ф0. Тогда выражение для переменной X: X = rq+i- 10 + 10
5 5
П +
Определим интересующую нас величину р(/С) =р(х)-Ю*-1, где p
находится из табл. 1.7. Так, для рC5) р(*) = @,213-0,0006*)*; рC5) -
2-23^

18 Глава i. Методы построения функций принадлежности
= @,213-0,0006.35) -35=6,634. Окончательно рB35)=рC5) -Ю1-1»
= 6,634.
Теперь, зная расстояние между точками перехода, можно построить
функцию принадлежности нечеткого множества, соответствующую
экспертной оценке X ПРИБЛИЗИТЕЛЬНО РАВЕН 235, по формуле
Полученная функция принадлежности приведена на рис. 1.4, где а и
b — точки перехода:
а-*_-Ш--235 --^-==231,682;
4 =238,317.
Пример 1.5. Имеем оценку X НАХОДИТСЯ ПРИБЛИЗИТЕЛЬНО
В ИНТЕРВАЛЕ ОТ 8 ДО 11. На этом интервале функция
принадлежности равна единице, а за его пределами будет повторять функции
принадлежности, соответствующие точечным оценкам X
ПРИБЛИЗИТЕЛЬНО РАВЕН 8 и X ПРИБЛИЗИТЕЛЬНО РАВЕН 11 слева и
справа от интервала. Для построения функции принадлежности
нечеткого множества, соответствующего интервальной оценке, необходимо
дважды воспользоваться описанным выше методом.
Имеем К=8. Находим q, rq, rq+i и d\ q=\, так как единственная
значащая цифра стоит в разряде единиц; r{ = 8, гд+1=г2 = 0, поскольку
в разряде десятков значащих цифр нет. При делении q на 3 в остатке
получаем 1, следовательно, d=l. В соответствии с методом переходим
к п. 2.а. Выражение для нахождения переменной X: Х=гя = Г\ = 8. Для
величины р(/() имеем р(/() = р(х) -lOe-i; р(8) .10^=р(8), где р(8)
находится по табл. 1.7: р(8) =0,46-8 = 3,68.
Теперь определим расстояние между точками перехода р(К) для
/(=11. Находим значения переменных q, rq, rq+i и d: младшая
значащая цифра числа К стоит в разряде единиц, т.е. имеем q=l, r^=ri = 1;
rq+i = r2=l — цифра, порядок которой на единицу выше порядка
младшей значащей цифры К. При делении числа q на 3 в остатке
получаем 1, следовательно, число К принадлежит к классу эквивалентности
Мь переменная d получает значение единицу.
Так как /v+-i?=0, переходим к п. 2.6, где X=rg+i-10+rg=r2-10+r1 =
= 10+1 = 11. Интересующая нас величина р(/() определяется в соот-
Рис. 1.4. Функция принадлежности не-
.,, ^ четкого множества, соответствующего
235 238 32— ]К точечной оценке ПРИБЛИЗИТЕЛЬНО
235

1.4. Параметрический метод
Рис. 1.5. Функция
принадлежности нечеткого множества,
соответствующего интервальной оценке
ПРИБЛИЗИТЕЛЬНО В
ИНТЕРВАЛЕ ОТ 8 ДО 11
в 9 10 11 12 13
ветствии с выражением р(/С) =($(*) -10*-1, где р(*)=рA1) находится
из табл. 1.7, т.е.
Здесь 0A5) =6,45; рA) =0,46 найдены по табл. 1.7. Таким образом,
рA1)=^- F,45+0,46) =3,455.
Для построения функции принадлежности нечеткого множества,
соответствующего интервальной оценке, построим функции
принадлежности нечетких множеств, соответствующих точечным оценкам с
вершинами 8 и 11.
Функция принадлежности будет иметь вид, приведенный на рис. 1.5,
где
— точки перехода.
1.4. ПАРАМЕТРИЧЕСКИЙ ПОДХОД
К ПОСТРОЕНИЮ
ФУНКЦИЙ ПРИНАДЛЕЖНОСТИ
Рассматривается метод построения модифицированных нечетких
термов на основе имеющихся. При этом определяются параметры
дробно-линейного преобразования, соответствующего нечеткому
модификатору, и с его помощью преобразуется исходный терм [2, 7].
Краткие сведения о методе. Описываемый метод получения функций
принадлежности основан на предположении, что эксперт, характеризуя
лингвистическое значение какого-либо признака, с минимальным
напряжением может указать три точки универсальной шкалы: А, В, С,
из которых В и С — точки, по его мнению, еще (или уже) не принад-
2*

Глава 1. Методы построения функций принадлежности
1.0
0,3
0,6
0,4
0,2
МОЛОДОЙ
ОЧЕНЬ СТАРЫЙ
10 20 30 40 50 60 70 80 90 100 X
Рис. 1.6. Функции
принадлежности нечетких термов переменной
«Возраст»
лежащие описываемому лингвистическому значению, А — точка,
определенно принадлежащая ему.
Описание значений лингвистической переменной «Возраст» строится,
как показано на рис. 1.6.
1. На прямой у=1 отмечается точка напротив того значения
носителя хи которая определенно принадлежит данному терму (точки А
и D).
2. На носителе (оси X) слева и справа от хх отмечаются точки,
ближайшие к х\, которые определенно не принадлежат данному терму
(точки В и С).
3. Отмеченные на оси X и прямой у=\ точки соединяются
отрезками прямой.
4. Штриховкой помечается часть носителя, относящаяся к
построенному описанию.
Пусть имеется параметрическое описание термов t и f двух
значений некоторой лингвистической переменной. Один из термов может
представлять собой модификацию (ограничение) другого: t' = h(t)y где
h — ограничение на t типа ДОВОЛЬНО, БОЛЕЕ-МЕНЕЕ, НЕ ОЧЕНЬ
и т. п. Задача состоит в том, чтобы, используя параметры термов t:
(zi, z2, 2з) и t': (Wi, w2, иуз), описать переход от t к ? (параметры
считаются упорядоченными отношением «меньше»).
а)
м
1.0
б)
и
1.0
U Z, Z2 Z3 Z
Рис. 1.7. Параметрическое задание термов
Ь)
ijo

1.4. Параметрический метод 21
Основные виды функции принадлежности приведены на рис. 1.7.
Очевидно, что S-образную функцию (см. рис. 1.7, б, в) можно
рассматривать как вырожденный случай треугольной функции (см. рис. 1.7,а),
в которой один из параметров zx или гъ стремится к бесконечности.
Таким образом, задача состоит в том, чтобы описать переход между
любыми двумя формами, представленными на рис. 1.7.
Для решения этой задачи используется аппарат автоморфных
функций. Рассмотрим дробно-линейное отображение прямой на себя вида
Эти преобразования удобно расширить, включив в действительную
прямую R точку оо. Если условиться, что Т( — 8/у) = оо и Г(оо) =а/у,
то окажется, что дробно-линейное преобразование взаимно однозначно
отображает расширенную прямую IR U{°°} на себя. Бесконечное
множество преобразований A.4), где а, р, у, б — действительные числа,
представляет собой так называемую модулярную группу: обратные
преобразования и произведения дробно-линейных отображений также
являются дробно-линейными.
Преобразование jM, обратное Г, получается, если уравнение z=
разрешить относительно w:
yw+Ъ
yz-a
Таким образом, при параметрическом представлении функций
принадлежности задача описания перехода от одного терма /: (zit z2, z3) к
другому t'\ (wu w2, w3) решается непосредственным подсчетом
четырех параметров-коэффициентов дробно-линейного преобразования по
формулам
-Z2) +WiW3Z2(Z3-Zi) +W2W3Z1(ZZ-Z3);
A.6)
Эти же коэффициенты при подстановке в A.5) определяют обратный
переход от f к t.
Рассмотрим теперь переход от терма t треугольной формы к терму
V с S-образной функцией принадлежности. Для дробно-линейных
преобразований этому случаю соответствует переход одной из крайних
заданных точек в положение бесконечно удаленной точки. Если 2i = oo
(переход от рис. 1.7, а к рис. 1.7, в), то параметры дробно-линейного
преобразования
A.7)
у = W2 ~ Wz\ б = Wi (W9— W2) .

22
Глава 1. Методы построения функций принадлежности
1,0
0,8
0,6-
0.4
0,2
^ЛЕДЯНАЯ
ПРОХЛАДНАЯ.
2 Д 6 8 10 12 U 16 18 20 22 t,eC
1,0
0,8"
0,6
• 0,4
0,2
0
ОЧЕНЬ НЕ
ТЕПЛАЯ.
ОЧЕНЬ
ттг
ИГ
ПРОХЛАДНАЯ, i , '
\\ I
ii I
НЕ ТЕПЛАЯ
/ПРОХЛАДНАЯ
6 в 10 12 U 16 18 t,°C
1.0
0,8
0,6
0,4
0.2
0
Рис. 1.8. Термы
лингвистической переменной
«Температура воды в
море»:
а — переход от S-образной
к треугольной функции
принадлежности; б — переход
между двумя 5-образными
функциями принадлежности;
в — переход между двумя
треугольными функциями
принадлежности
ХОЛОДНАЯ
ОЧЕНЬ
ХОЛОДНАЯ
ОЧЕНЬ-
ОЧЕНЬ
.ХОЛОДНАЯ
2 4 6 8 10 12 14 t,°C
Если 23=oo (переход от рис. 1.7, а к рис. 1.7,6), то
A.8)
Рассмотрим теперь случай, когда оба терма описываются только
двумя параметрами, т. е. когда функции принадлежности
представляются S-образной или просто наклонной кривой. В этом случае имеет
место линейное отображение прямой
A.9)
A.10)
A.11)
Параметры преобразования A.9)
a=-
Х2-Хг
Обратный переход (у->-х) осуществляется по формуле
a
Примеры использования метода. Пример 1.6. Пусть экспертом
составлены следующие описания исходного терма ПРОХЛАДНАЯ и

1.4. Параметрический метод 23
модифицированного терма НЕ ПРОХЛАДНАЯ, полученного с помощью
модификатора «не» для переменной «Температура воды для купания
в Черном море» (рис. 1.8,а).
В данном случае необходимо осуществить переход от терма с S-об-
разной функцией принадлежности ПРОХЛАДНАЯ (?i = °o, 22=14, 23 =
= 16) к терму треугольной формы НЕ ПРОХЛАДНАЯ (t^± = 17, to2=18,
Доз=20). Переход от исходного терма к модифицированному
производится в соответствии с формулой w= ( — 8z+$)/(yz—а), где z — точки,
принадлежащие исходному терму, а обратный переход — по формуле
2= (aw + $)/(yw + 8). Для вычисления коэффициентов дробно-линейного
преобразования используем выражения
14- A8—17) +16- A7-20) = -34;
-Wi) + w3z2(Wi-w2) = 18-16- B0-17) +
+ 20-14-A7-18) =584;
Y = oy2—ш3== 18»—20= —2;
8 = wl(w3-w2) = 17- B0-18) =34.
Пусть теперь имеется терм ЛЕДЯНАЯ (z\ = ooy г2 = 4, 2з = 6).
Использовав найденное преобразование, определим модифицированное
значение терма НЕ ЛЕДЯНАЯ:
б 34 „
Zi = oo; wt=—==—-=17;
У 2
-6z2+p -34-4 + 584 __
z=4; ш=—== 17,2;
yz2--a —2-4 + 34
, fi. И1 -34,6 + 584
 = 6j Шз==' -2.6 + 34 =17Д
Полученный терм приведен на рис. 1.8, а.
Пример 1.7. Рассмотрим переход между двумя термами,
имеющими S-образную функцию принадлежности: исходный терм 'НЕ
ТЕПЛАЯ B?i = oo, ^2=16, 2з=17) и модифицированный терм ОЧЕНЬ НЕ
ТЕПЛАЯ (о>1 = оо, ш2=13, tc3=14). Переход от исходного терма к
модифицированному осуществляется по формуле ш = аг+р, где z, w —
точки, принадлежащие исходному и модифицированному термам
соответственно. Коэффициенты для описания перехода:
__ W3—w2__ 14—13
а== z3_z2 ~ 17 — 16 ~~ '
w2z3-w3z2 13-17-16-14 221-224
6=' =' '— :; ~= —о.
р Z3—Z2 1 1
1 в
Обратный переход осуществляется по формуле z=—до——.
Использовав найденное преобразование, перейдем от терма ПРОХЛАДНАЯ
Bi = oo, 22=14, z3=16) к терму ОЧЕНЬ ПРОХЛАДНАЯ:
Zt = oo; шА = оо; z2= 14; t02=az2+P= 1-14 — 3= 11;
г3=16; ш3=Ы6-3=13.
Полученный терм (^i = oo, w2=ll, ш3=13) представлен на рис. 1Д6.

24 Глава 1. Методы построения функций принадлежности
Пример 1.8. Рассмотрим переход между двумя термами,
имеющими треугольную форму: исходный терм ХОЛОДНАЯ Bi = 4, 22=10,
23=14) и модифицированный терм ОЧЕНЬ ХОЛОДНАЯ (wt = 4, w2=9,
w3=ll) для той же переменной «Температура воды для купания в
Черном море».
Переход от исходного терма к модифицированному осуществляется
в соответствии с выражением w= ( — 8z+$)/(yz—a), a обратный
переход — по формуле 2 = (aw + $)/(yw + 8)9 где z, w — точки,
принадлежащие исходному и модифицированному терму соответственно.
Коэффициенты для описания перехода:
3 — wx) +z2z3(w2--w3) =
= 4-10- D —9) +4-14- (И—4) + 10-14- (9—11) = —88;
p = a;1akz3Bi-z2) + wlw3z2(z3-zi) +w2w3Zi(z2—z3) =
= 4-9-14- D-10) +4-1Ы0- A4-9) +9-11 -4- A0-14) = -208;
= 10-D-11)+4-A1-9)+14-(9-4) =8;
6 = ^1^2B1-22) +^1^3B3-21) + w2w3(z2-z3) =
>=4.9. D-10)+4.11.A4-4)+9-11.A0-14) = -172.
Найдем теперь параметры терма ОЧЕНЬ-ОЧЕНЬ ХОЛОДНАЯ,
применив преобразование к терму ОЧЕНЬ ХОЛОДНАЯ Bi = 4, 22 = 9,
2з=И):
-б2! + р 172-4-208 А
2i=4; Wi = — = л А , gR ^=4;
yZi — а о • 4 + оо
172-9-208 о
=9; W*= 8-9+88 =8;
172-11-208
И 1°
2з==И;^= 8-11+88 1°-
Полученный терм изображен на рис. 1.8, в.
1.5. ПОСТРОЕНИЕ
ФУНКЦИЙ ПРИНАДЛЕЖНОСТИ
НА ОСНОВЕ
ИНТЕРВАЛЬНЫХ ОЦЕНОК
Описывается метод построения функции принадлежности для
решения задач выбора, в которых отсутствует четкая грань между
допустимым и недопустимым (в пространстве неуправляемых
параметров) и между идеальным и неудовлетворительным состояниями (в
пространстве критериев) [1, 6].
Краткие сведения о методе. Рассмотрим ситуацию, когда известна
связь между некоторым параметром Z и критерием выбора h. Напри-

1.5. Метод, использующий интервальные оценки
25
идеальная область; 1Г@)«1,0
Нечеткая область; Возможность
признания объекта а идеальным.*
0<7T(Q)<1,0
Недопустимая область,- 7T(Q)=0
Рис. 1.9. Расположение областей критериальных
значений
мер, при конкурсном отборе образцов новой техники одним из
критериев (h) является точность работы. ЛПР известно, что критерий h
зависит от освещенности (параметр Z) среды функционирования
анализируемых изделий. При этом группа экспертов, подготавливающая
решение, ставит перед собой некоторую цель, например выбрать
«хорошую» альтернативу или выбрать «объект на уровне мировых
стандартов» (цель может быть сообщена и заказчиком — организатором
экспертизы). Начальная цель экспертизы, представленная в лингвистичес-
ской форме, вносит элемент нечеткости в последующий анализ,
который в результате этого должен содержать формализацию
использованных понятий.
Теория возможностей [8] основывается на предположении, что
эксперт может указать интервал [/i*, h°] значений критерия h, который
соответствует высказанному пожеланию выбрать, например, «хороший»
объект. При этом граничные значения интервала имеют следующую
интерпретацию. Пусть ha — результат измерения значения
характеристики h для объекта а. Тогда /i* является границей «идеальной»
области, т.е., если /ta^/i*, объект следует признать идеально
соответствующим понятию «хороший». Возможность такого утверждения Jt(Q) =
= 1,0 (Q — субъективное событие, заключающееся в том, что объект,
с точки зрения эксперта, находится в состоянии «хороший»).
Если ha^.h°f ситуация интерпретируется так: возможность того, что
объект d — «хороший», n(Q)=0. Очевидно, что при h°<ha<h*
соответствующие возможности имеют значения 0<n(Q)<l,0.
AJ2(h)
Рис. 1.10. Способы определения оценок возможностей:
а — линейный случай; б — нелинейный случай

26 Глава 1. Методы построения функций принадлежности
Рассмотрим способы нахождения оценки n(Q). Пусть А* = 80, Л°=
= 50, Ла=70. Тогда объект а находится ближе к идеальной границе
(рис. 1.9), если для измерения пользоваться линейной мерой.
Ощущения эксперта позволяют использовать рабочую гипотезу,
заключающуюся в том, что с приближением значения ha к границе h*
возможность признания а «хорошим» объектом линейно возрастает.
Если эксперт подтверждает указанную логику размышлений,
воспользуемся формулой
О, если h
———, если Л°<Ла<Л*; A12)
1, если /
В данном примере я(<3)=-^г—ртг = v^7=0,67. Результатом является
ои — OU jt5U
утверждение, что возможность признания объекта а «хорошим» я((?) =
= 0,67. Графическая интерпретация изложенного приведена на
рис. 1.10, а.
До настоящего момента предполагалось, что h представляет собой
критерий типа «выигрыш», т.е. /i*>ft° при всех значениях z. Если
h°>h* (критерий типа «штраф»), для расчета возможностей в
линейном случае в формулу A.12) вносятся соответствующие изменения.
Кроме того, представления эксперта могут не позволить применить
формулу A.12). Например, если испытуемым на конкурсе-экзамене на
замещение вакантных должностей операторов предлагают решить
задачи, упорядоченные по сложности, то эксперт может считать, что
решение шести-семи задач за фиксированное время еще не
представляет собой «ничего особенного» (см. рис. 1.10,6), а решение восьми
задач позволяет признать претендента «хорошим» оператором. (Такое
мнение может быть связано с субъективными наблюдениями общего
уровня претендентов при повторных экспертизах.) Может иметь место
и противоположное мнение (выпуклая вниз функция |х(Л)).
Обратимся к основной задаче настоящего параграфа: построению
функции принадлежности на множестве значений параметра z при
наличии интервальных оценок [h°, Л*].
Задачу выбора модели можно решить приближенно, предлагая
эксперту в единичном интервале [0, 1] указать место некоторой средней
альтернативы. Например, испытуемый решил 6,5 задачи, или точность
работы анализируемого изделия 65 единиц (см. рис. 1.10,а). Эксперту
задается вопрос «Где на шкале [0, 1] находится такой объект?» Ответ
«Около точки 0,5» дает гипотезу о линейной модели, другие ответы —
о выпуклой вверх или вниз функции \x(h). Наличие трех значений
функции \i(h) (указанное экспертом, а также 0 и 1) позволяет полностью
восстановить ее в интервале [Л°, Л*]. При этом необходимо выяснить и
сопоставить мнение эксперта о точности своего ответа с точностью
измерений или оценки характеристики ha, а также с требуемой
точностью экспертизы.
В примере выбора изделий эксперты могут считать, что границы Л°
и Л* при фиксированном освещении 2=50 лк имеют значения,
приведенные на рис. 1.11.

1.5. Метод, использующий интервальные оценки
2?
Рис. 1.11. Экспертные данные:
а — дискретные оценки; б — уровневые ограничения
С понижением освещенности изделия рассматриваемого типа
работают хуже в смысле критерия А, поэтому экспертам можно предложить
оценить А° и А* еще в нескольких точках г. Аппроксимируя данные,
получаем аналитические выражения двух функций А* = /*(г) и А° =
= /°(г), которые называются уровневыми ограничениями. Эти функции
путем экспертного опроса можно построить таким образом, чтобы
охватить весь диапазон реального изменения параметра Z.
Для получения полного представления об альтернативе а
необходимо провести ряд экспериментов по определению оценки Аа при
различных значениях z. В результате аппроксимации имеем функцию У =
= fa(z)9 представленную на рис. 1.12, а. Для ряда значений z по одному
из указанных принципов (в данном случае по формуле A.12))
рассчитываются значения nz(Q)> аппроксимируя которые получаем (рис.
1.12,6) степень соответствия альтернативы понятию эксперта
«хорошая альтернатива» на множестве значений параметра Z.
Полученная функция называется распределением возможностей и
представляет собой нечеткое ограничение на значениях параметра Z:
возможность применения изделия плавно меняется от идеальной
пригодности до недопустимости его использования.
На практике возможны различные мнения экспертов о характере
уровневых ограничений (рис. 1.13). Можно назвать основные типы и
вероятные ситуации, приводящие к определенному виду функций А° =
= f(z) иА* = Г(г):
а) согласованные функции могут возникать в случаях достаточно
ясных представлений экспертов о предметной среде, при отсутствии
глобального влияния значения параметра на сам способ решения
задачи выбора;
б) расходящиеся функции могут свидетельствовать о том, что
эксперту недостаточно известно поведение объекта при больших значениях
параметра Z и/или большие значения z маловероятны;
в) сходящиеся функции могут возникнуть в задачах оценки
объектов, имеющих экстремальный характер функционирования при
больших значениях z\
г) функции с конечными разрывами отражают либо качественные
скачки в процессах физического мира, либо влияние законов,
нормативных актов на мнение экспертов;

28
Глава 1. Методы построения функций принадлежности
h°=f°(z)
h*=f*(z)
hrt=f°(z)
30
50 Z./Ж
50 Ztf\K
Рис. 1.12. Результаты оценки:
а — сопоставление альтернативы и уровневых ограничений; б — распределение
возможностей альтернативы
д) соединяющиеся и разъединяющиеся функции могут возникнуть
в случаях, когда в некоторых областях значений параметра Z эксперты
имеют четкое мнение (требования заказчиков, ГОСТ и т.п.);
е) несогласованные функции представляют собой случай, когдЪ
предварительно трудно найти мотивацию такому мнению эксперта
(подобная модель «безразличия», вероятно, является следствием ошибки
эксперта);
а).
б).
ч,
9\
г).
е),
S
Рис» L13. Виды уровневых ограничений

l.S. Метод, использующий интервальные оценки
Рис. 1.14. Распределение возможностей:
1, 6 — амодальные; 3 — унимодальное; 2, 4 — субнормальные; 5
локолообразное
ж) унимодальные функции должны быть использованы экспертом,
если ему известно, что все объекты имеют унимодальную
характеристику ha=fa(z);
з) пересекающиеся функции соответствуют «реверсивной» задаче
выбора, когда при определенных значениях параметра Z меняется
характер использования критерия (от критерия типа «выигрыш» к типу
«штраф» или наоборот).
На рис. 1.13, а—г, е приведены уровневые ограничения, отражающие
ситуацию, когда функция ha = fa(z) является монотонно возрастающей
либо многоэкстремальной функцией с тенденцией общего увеличения.
В противном случае естественно использовать монотонно убывающие
функции типа а—д. Использование монотонно убывающих уровневых
ограничений при возрастающих характеристиках объектов ha=fa(z)
(и наоборот) свидетельствует либо о неосведомленности эксперта, либо
о наличии альтернатив, существенно не соответствующих
предъявляемым им требованиям. Наиболее типичные распределения возможностей
представляют собой амодальные или унимодальные функции (рис. 1.14).
Таблица 1.8
Описание объекта и ограничений
Значения

параметра Z
Объект ha
Варианты
I
h*
h°
II
h* 1 h°
III
h*
h°
3
6
9
12
15
15
35
70
90
105
65
81
92
95
100
20
32
40
50
55
25
30
70
115
150
10
20
30
75
120
25
40
80
100
110
15
20
30
60
75
Распределения
п(г)
я, B)
Л2B)
возможностей
» 1
0
0,330
0
6.
0,061
U000
0,750
г
9
0,577
1,000
0,800
12?
0,889
0,375
0,750
Таблица 1.9
15
1,000
0
0,889

36 Глава 1. Методы построения функций принадлежнбстй
Если объект а во всем рассматриваемом диапазоне значений
параметра Z не имеет ha^h*, распределение возможностей будет
субнормальным, т.е. не достигает значения 1,0 (см. рис. 1.14,2, 4).
Пример использования метода. Пример 1.9. Необходимо найти
распределения возможностей для приведенной в табл. L8
характеристики объекта па и трех вариантов пар уровневых ограничений.
На основе формулы A.12) в первом варианте получаем (табл. 1.9)
амодальную, монотонно возрастающую, во втором — колоколообраз-
ную, в третьем — субнормальную немонотонную функцию n(z).
Использование распределений возможностей для анализа решений
рассмотрено в параграфе 2.5 и главе 7.

Глава 2
ВЫПОЛНЕНИЕ ОПЕРАЦИЙ
НАД НЕЧЕТКИМИ ЧИСЛАМИ
2.1. ОПЕРАЦИИ
НАД НЕЧЕТКИМИ ЧИСЛАМИ
НА ОСНОВЕ
ПРИНЦИПА ОБОБЩЕНИЯ
Рассматривается выполнение операций над нечеткими числами с
треугольным представлением. Вследствие того что исходные числа и
результат операции задаются только тремя числами, операции
существенно упрощаются [3, 10].
Краткие сведения о методе. Приведем основные определения,
касающиеся нечетких чисел и операций над ними.
Определение 2.1. Нечеткое число А на действительной
прямой — это нечеткий набор, характеризуемый функцией
принадлежности \i~ : R ->[0, 1]. Нечеткое число А может быть выражено как
А
А
где \i~ (x)^[Q, 1] — степень принадлежности jcg R множеству А,
А
/ — объединение по всем jcg |RL ; \х ~ (х)/х означает, что степень
принадлежности х множеству А равна |л„ (х).
А
Определение 2.2. Нечеткое число А на действительной прямой
выпукло, если для каких-либо реальных чисел х, yf ze R с
()(\ () H())
А А А
Определение 2.3. Нечеткое число А на действительной прямой
называется нормальным, если тах|л~ (*) = 1.
Рис. 2.1. Примеры нечетких чисел

52 Глава 2. Выполнение операций над нечеткими чИсЛаМи
На рис. 2.1 показаны различные виды нечетких чисел: А\ —
выпуклое, А2 — нормальное, Аъ — нормальное выпуклое.
Сформулируем принцип обобщения. Пусть А и В — нечеткие числа
на действительной прямой R . Тогда * можно выполнить над
нечеткими числами А и В, используя соотношение
А*В=$тЩ\л„ (x)ii „ (у))/(х*у).
А В
Заменив гипотетическую операцию * арифметическими операциями +,
—, X, :, получим определение этих действий над двумя нечеткими
числами:
в
~ (у)I(х—у)\
в
~ (У))/(хХу);
B.1)
B.2)
B.3)
1~(х)р„ (у))/(х:у).
Эти операции пригодны для любых нечетких чисел и, в частности,
для дискретных, однако они громоздки. Для непрерывных нечетких
чисел, отличающихся тем, что их функцию принадлежности можно
определить, зная ее границы, применим другой принцип.
Определение 2.4. Число а называется границей функции
принадлежности, если выполняются следующие соотношения:
=0; |i(a-6)=0; ji(
Функция принадлежности имеет две границы: верхнюю и нижнюю.
Таким образом, непрерывное нормальное выпуклое нечеткое число
можно записать в виде
А Ъ
А= \{х-аIх+ 1(Ь-хIх, B.5)
а А
где а, Ь — нижняя и верхняя границы функции принадлежности.
Например, нечеткое число 2 (ПРИБЛИЗИТЕЛЬНО 2) можно представить
в виде
2 3
C-x)/x
2
Рис. 2.2. Нечеткое число ПРИБЛИЗИТЕЛЬНО 2

2.1. Операции на основе принципа обобщений
(рис. 2.2). Пусть * — двухместная операция; Л и Б — непрерывные
нормальные выпуклые нечеткие числа:
А Ъ В Ъ'
а' В
= J fix (х)/х+ I „ (х)/х,
а"
а" и Ь" получают из а, Ь, а', Ь' в зависимости от конкретной операции.
Функция \i ~ ^ определяется в зависимости от конкретной операции
И НОрМИрОВКИ (I.
Рассмотрим четыре арифметические операции:
А Ь Л 6'
а А А А
Ь'
,~(х)!х = С, B.7)
с с
i + a'9 b" = b + b'. B.8)
Функцию jLX — будем искать в виде u~ =^k\X-\-k<2. Исходя из нормировки
с с
имеем для а"^х^.С
х-а"
для
\ U Uff U \kl=
Таким образом,
fe/fe
а" С
Аналогично для остальных арифметических операций получаем
С Ь"
а '
где а" = а-Ь', Ь" = Ь-а\ С=А-В.
Для операции умножения имеем
1ГУ А-С. B.U)
«" уС-Уа" с уь"-ус
3 - 2307

где а" =
Глава 2. Выполнение операций над нечеткими числами
', b// = bXb/y C=AxB, для операции деления:
с ь"
где а" = а\Ь\ b" = b:a\ C=A:B.
Замечание. Для операции умножения функцию 4и~ ищем в виде
с
\к~ =к\Ух + к2, для операции деления — в виде \i~ =—+Л2. Например,
2хГ
= (J (x-l)/x+ jC-x)/x)x (J {x-2)/x-j D-x)/x) =
2
в „
2 У6-У2
6 У12-У6
8 10 4 6
8:4= (J (x-6)/x+ J A0—x)/x ) : (J (x-2)/*+ JF-x)/* ) =
-;•
1J
Г 2х
¦j
Отметим еще одну особенность непрерывных нормальных выпуклых
нечетких чисел: найти нечеткое число, полученное в результате
арифметической операции, можно, не проводя лингвистического анализа,
поскольку точно известно, при каком х функция принадлежности равна
единице.
--.-8 . 14
11 12 13 U 15 16 Т7Х
Рис. 2.3. Нечеткие числа ПРИБЛИЗИТЕЛЬНО 2,
ПРИБЛИЗИТЕЛЬНО 6, ПРИБЛИЗИТЕЛЬНО 8, ПРИБЛИЗИТЕЛЬНО 14

2.1. Операции на Основе принципа обобщения 35
Пример использования метода. Пример 2.1. Возьмем два
нечетких числа ПРИБЛИЗИТЕЛЬНО 6 = 6 и ПРИБЛИЗИТЕЛЬНО 8 = 8,
графически изображенных на рис. 2.3:
в 7
6= J(*-5)/*+JG-x)/x.
5 6
Пусть
х = 6 (значение подставляется только в одно из слагаемых): 6|^=6
= 6-5=1;
7
Итак, имеем
6= {0/5; 0,5/5,5; 1/6; 0,5/6,5; 0/7}.
Аналогично
8 10
8-6 / * 10-8
6
Пусть
8
= 6:~8|х=в = J—^§-;ж-в = 6-6 = 0; х=-7: 8|ж=т =
о о
10
= 1; х = 9: 8|x=9 = J - J*=9= ^~ = 0,5;
Итак, 8= {0/6; 0,5/7; 1/8; 0,5/9; 0/10}. Графики функций
принадлежности приведены на рис. 2.3.
В соответствии с принятыми ранее обозначениями найдем верхние
и нижние границы и вершины чисел: для 6 а = 5, & = 7, /1 = 6; для 8
^ = 6, ^=10, В = 8.
Рассмотрим выполнение арифметических операций над числами 6
и 8.

36 Глава 2. Выполнение операций над нечеткими числами
Сложение. Согласно B.8) определим границы и вершину
результата (суммы нечетких чисел 6 и 8): а" = а + а' = 5 + 6 = И; b" = b-\-
+ // = 7+10=17; С = Л+В = 6 + 8=14.
Тогда в соответствии с B.9) имеем
14 17
Г л:— 11 / f 17—л: / ~-
6 + 8= J —— I х+ J —— J х= И.
Вычислим значения функции принадлежности результата с нескольких
точках:
14
12,5-11
*=12,5; lW J-^1^^- 12>5П -0,5;
.= 15,5; 14|^ =
14 6 *
Итак, получили 14= {0/11; 0,5/12,5; 1/14; 0,5/15,5; 0/17}. Графическое
изображение приведено на рис. 2.3.
Вычитание. Значения границ и вершины результата (разности
нечетких чисел 8 и 6): а" = а'-а = 6-5= 1; b" = b'-b= 10-7 = 3; С =
= В — Л = 8 — 6 = 2. В соответствии с B.9) получим
Определим значения функции принадлежности в нескольких точках:
2
*=1,5; 2|x=i,5= J(^-l)|x=if5= 1,5-1 =0,5;
1
з
х=2,5; 2|«в2.5= J C-х) 1^2,5 = 3-2,5 = 0,5.
Получен результат 8-6=2= {0/1; 0,5/1,5; 1/2; 0,5/2,5; 0/3}. График
приведен на рис. 2.3.
Умножение. Найдем границы и вершину результата умножения
6 на 8: а" = аа' = 5.6 = 30; fc// = &6/ = 7-10 = 70; С=Л? = 6-8 = 48.
Выражение для функции принадлежности имеет вид
30
A
V48—УЗО *8 У70-У48

2.1. Операции на основе принципа обобщения
37
Рис. 2.4. Нечеткое число
ПРИБЛИЗИТЕЛЬНО 48
30 40 50 60 70 X
Вычислим значения функции принадлежности в промежуточных
точках. Пусть
Х = «
-5,48
У34-5,48
30
*-39:
^ т/44 5 48 ~
х=44: 48|Ж=44=Г—г-^ 0,8; х=53:48|*=5
1 O
70
f 8,37-
= J 1,44
4о
8,37-У53
1,44
=°'76'
1,44
1,44
Итак, получили 6X8=48= {0/30; 0,24/34; 0,53/39; 0,8/44; 1/48; 0,76/53;
0,52/58; 0,26/64; 0/70}. График приведен на рис. 2.4.
Деление. Найдем границы и вершину результата деления 8 на 6:
а" = а':а = 6:5=1,2; &" = 6':& = 10:7= 1,43; С=В :А = 8 : 6=1,33.
Выражение для функции принадлежности имеет вид
1,33
• (Л OQ 1 С\
1,33
1,43
A,43-х). 1,33
A,43-ьзз).х
f
1.33
f (х-1,2) -1,33 / f (l,43-x)-l,33
' ^ OILл: / х+J JTTT
1,2 У,П х 1Л 0,1-х

38 Глава 2. Выполнение операций над нечеткими числами
0,8
0,6
0,4
0.2
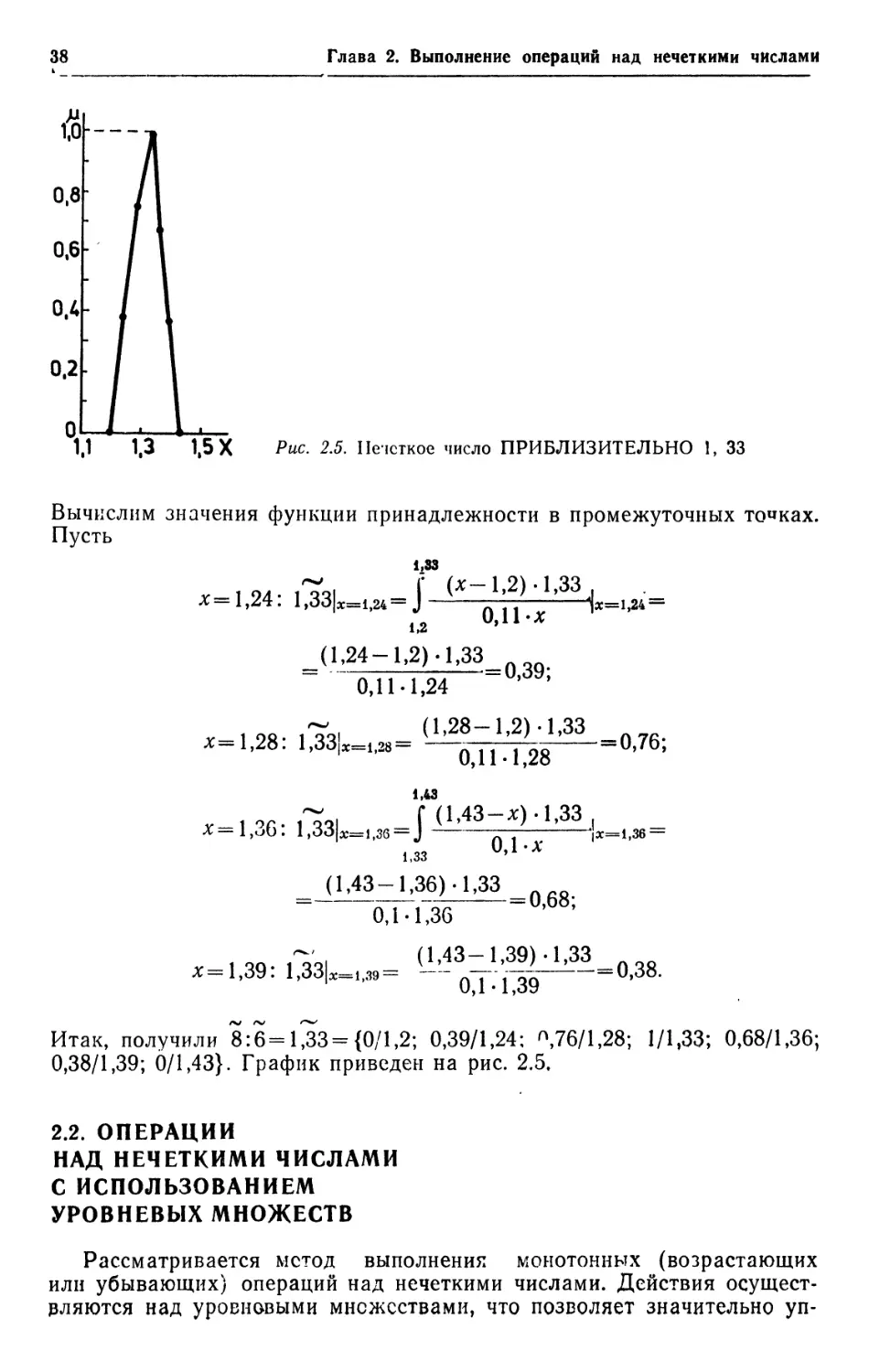
1,1 1,3 1,5 X Рис. 2.5. Нечеткое число ПРИБЛИЗИТЕЛЬНО !, 33
Вычислим значения функции принадлежности в промежуточных точках.
Пусть
1,83
f1J
1,2 V,ll-X
A,24-1,2)-1,33 поп
" 0ДЫ.24 "U>l3y;
A,28-1,2).1,33
-1,28. 1,33,^,28=
1,43
=1,36: 1,33|3c=i,3e = J
1,33
Итак, получили 8:6= U3= {0/1,2; 0,39/1,24; ^,76/1,28; 1/1,33; 0,68/1,36;
0,38/1,39; 6/1,43}. График приведен на рис. 2.5.
2.2. ОПЕРАЦИИ
НАД НЕЧЕТКИМИ ЧИСЛАМИ
С ИСПОЛЬЗОВАНИЕМ
УРОВНЕВЫХ МНОЖЕСТВ
Рассматривается метод выполнения монотонных (возрастающих
или убывающих) операций над нечеткими числами. Действия
осуществляются над уровновыми множествами, что позволяет значительно уп-

2.2. Операции, использующие уровневые множества
V
39
ростить вычисления по сравнению с операциями на основе принципа
обобщения [4, 8].
Краткие сведения о методе. Кроме характеристик нечетких чисел
(определения 2.1—2.4) в этом параграфе потребуется следующее
определение.
Определение 2.5. Бинарная операция * на |R называется
возрастающей, если (xi>#b Х2>у2)=>хх*х2>у\*у2' Аналогично операция
Н< называется убывающей, если (xi>*/i, #2>y2)=^*i>l<#2<*/i>l<f/2-
Арифметические операции над нечеткими числами можно выполнить
с использованием принципа обобщения. В соответствии с ним
бинарная арифметическая операция * может быть обобщена на случай
нечетких чисел, и результат обобщенной операции >К над нечеткими
числами М и N с функциями принадлежности \хм и \iN соответственно есть
нечеткое число L = M^N, задаваемое функцией принадлежности
[Xl (z) = sup min (tiM (x), [iN (y)).
z=x*y
Конкретно операции определяются следующим образом:
сложение |ы M^N (z) = sup min(jiM (*)»
вычитание И M_N (*) = sup min(ixM{x)t \iN{y));
умножение p, MXJV(z) = sup min(\im(x), \iN(y));
z=xX у
деление [x M. N (z) = sup min (^M (x), [iN (y)) .
z=x: у
Эти операции применимы для любых нечетких чисел, но
соответствующие вычисления достаточно громоздки.
Может быть использован следующий способ, являющийся
дальнейшим развитием принципа обобщения. Любое непрерывное нечеткое
число может быть разложено на выпуклые, возможно
ненормализованные, нечеткие подмножества с функциями принадлежности,
являющимися либо строго возрастающими, либо строго убывающими, либо
постоянными (рис. 2.6). Кроме того, непрерывное нечеткое число может
быть дискретизировано по конечному числу уровней со*, t'=l,& (<oi =
— О, (ofe=l). С каждым i-м уровнем связано множество
Xi={xtl , хг-2,..., Хи}, хц<= R ,
Рис. 2.6. Участки одинаковой монотонности
множества М:
Ми Мз — возрастающие; М2, Ma — постоянные;
Мь — убывающий
M
- Y

40 Глава 2. Выполнение операций над нечеткими числами
Рис. 2.7. Дискретизация множества по уров-
ням
Таким образом, нечеткое число может быть представлено в виде
n; 0J/^21;...; юл/Xfci;.-.; @2/^22;
(рис. 2.7).
Вследствие дистрибутивности обобщенной операции * и операции
объединения нахождение результата обобщенной операции над
нечеткими числами сводится к выполнению операции над участками
одинаковой монотонности отдельно. Операции выполняются над
абсциссами точек, расположенных на одном уровне и участках одинаковой
монотонности соответствующих функций принадлежности. Конечный
результат будет объединением соответствующих частей. Например,
результатом обобщенной операции * над нечеткими числами М и N,
представленными в виде
будет нечеткое число
L=M*N= {coi/(*h*j/ii); aJ/(*2i*#2i); ©1/(^12*^12)}. B.13)
Сказанное относится к случаю, когда операция * является
возрастающей либо убывающей. Операции вычитания и деления не
являются такими, однако их можно представить следующим образом:
B.14)
B.15)
Примеры использования метода. Пример 2.2. Определив
B.16)
B.17)
рассмотрим два нечетких числа: ПРИБЛИЗИТЕЛЬНО 2 (обозначим 2)
и ПРИБЛИЗИТЕЛЬНО 3 (обозначим 3). Выполним над ними четыре
обобщенные арифметические операции ( + , —, X, :) (рис. 2.8). В дис-
кретизированном виде их можно представить следующим образом:
?={0/1; 0,5/1,5; 1/2; 0,5/2,5; 0,3};
3={0/2; 0,5/2,5; 1/3; 0,5/3,5; 0/4}.

2.2. Операции, использующие уровневые множества
41
f—\-~\
-] 0 1 *> 3 А 5 6 7 8 9 10—12
Х.У
Рис. 2.8. Результаты выполнения обобщенных арифметических
операций
В этом случае в соответствии с B.13) найдем сумму:
3 + 2= {0/B+1); 0,5/B,5+1,5); 1/C + 2); 0,5/C,5 + 2,5);
0/D + 3)} = {0/3; 0,5/4; 1/5; 0,5/6; 0/7}.
Аналогично вычислим произведение:
3X2!= {0/2; 0,5/3,75; 1/6; 0,5/8,75; 0/12}.
В соответствии с B.14) и B.16) определим разность:
-2={0/(-3); 0,5/(-2,5); 1/(-2); 0,5/(-1,5); 0/(-1)};
?-2 = 3+(-2) = {0/B-3); 0,5/B,5-2,5); 1/C-2);
0,5/C,5-1,5); 0/D-1)} = {0/(-1); 0,5/0; 1/1; 0,5/2; 0/3}.
По B.15) и B.17) найдем частное:
2-*= {01A:1); 0,5A:1,5); 1/A:2); 0,5/A:2,5); 0/A:3)} =
-{0/1; 0,5/0,66; 1/0,5; 0,5/0,4; 0/0,33} ={0/0,33; 0,5/0,4;
1/0,5; 0,5/0,66; 0/1};
^^ ={0/0,66; 0,5/1; 1/1,5; 0,5/2,33; 0/4}.

42 Глава 2. Выполнение операций над нечеткими числами
ь
2.3. АНАЛИТИЧЕСКОЕ ВЫПОЛНЕНИЕ
АРИФМЕТИЧЕСКИХ ОПЕРАЦИЙ
Рассматривается метод аналитического выполнения арифметических
операций над нечеткими числами, в основе которого лежит принцип
обобщения [6].
Краткие сведения о методе. Пусть заданы два нечетких числа X
и У, их область определения Vx={x} и VY={y}, Vx, VYa (R , а также
функции принадлежности в аналитическом виде.
Использование минимаксных операций пересечения и принципа
обобщения позволяет представить выполнение арифметической операции
над нечеткими числами X и У в виде
Z=X*Y=U min(j^(x), iiY(y))[(x*y)=(}
где символ *, обозначает некоторую из четырех операций.
Областью определения нечеткого числа Z будет являться
Vz=[min (x°*y°, х°*у\ х**у°, х**г/*),
max (Jt°**/°, x°*y*, x°*y*y x**y*)] = [z°,z*], B.18)
x°=minx, х*=тахл:, y°=miny, у* = max у, z°=minz, <г*=тахг.
Если z^Vz, то для любого
V'X= [ max ( min (zot/°, Zoy*),x°),
min (max B<>y0, гоу*), х*)]
можно найти y^V'Y
V'y = [max (min (zojt°, гох*), y°), B.20)
min (max (zox°y z<>x*), y*)]y
такой, что z = x^y, x = z°yy y = Zox, где ° — обратная операция по
отношению к *. При этом значение функции принадлежности \xz{z)
определяется следующим образом:
max (\ix(x)\[ix(x)-=\xY(zoX))i если Зх: \ix(x)= \iY(z>x)\
^ Х, / ч /u w й ч , B.21)
min ( max \ix(x), max^iy(y)), если^х: \хх (х) ^\iY (z°x).
Примеры использования метода. Пример 2.3. Пусть даны два
нечетких числа: Х={0/1; 0,3/2; 1/7; 0/9}, У-{0/14; 1/17; 0/19}.
Необходимо определить их сумму.
1. Найдем область определения возможного решения: Vz =
= [min((l + 14), A + 19), (9+14), (9+19)), max((l + 14), A + 19), (9 +
+ 14), (9+19))] = [15; 28] (см. формулу B.18)).
2. Выберем из данной области такое z, для которого необходимо
определить значение функции принадлежности, например г=16 (где
z — сумма х и у);

2.3. Аналитическое выполнение операций
43
Н
1.0
0.8
0,6
0Л
0,2
1 2 79 1415 ft 19
Рис. 2.9. Исходные нечеткие числа
1
28 X, У
3. Найдем области определения V'x и V'y, в которых находятся
такие х и у, что их сумма равна данному z\ V'x= [max(min(A6—14),
A6-19)), 1); min(max(A6-14), A6-19)), 9)] = [max(-3,l), min
B,9)] = [1; 2] (см. формулу B.19)); 1^= [max(min (A6-1), A6-9)),
14; min(max(A6-l), A6-9)), 19)] = [maxA4,7), minA5,19)] = [14; 15]
(см. формулу B.20)).
4. Определим функцию принадлежности для ?/=15, так как в
данной точке она не задана. Используем уравнение прямой, проходящей
через две точки:
02-01
02-01
v2-v{
Так как
I, 02=17, щ
.~ 1-0
2=1, 0 = у=15, найдем
-|W-W .- 17__и - 17_ 1
5. Построим функцию принадлежности \xy{z — х). Для этого
отобразим область V'y на V'x, причем x=z—y. Пусть ?/=14; таким образом,
л:= 16—14 = 2. При ?/=15 я=16 —15=1. Значения функции
принадлежности сохраняются при соответствующих у.
6. Как видно из рис. 2.9, функции |ял- и (лу на области определения
V'x пересеклись. Найдем точку пересечения. Запишем уравнения
данных прямых в виде u = av + b, где
02-01
Для первой прямой 0i = I; Wi = 0; 02 = 2; i
02-01
^1- '
2-1
2-1
= 0,30-0,3; для второй 0i = l; «i = 0,3; 02 = 2; «2=0; u = v-—— IX
2» — 1
X °2"^°j3 +0,3=-0,30 + 0,6. Найдем v: 0,30-0,3= -0,30 + 0,6; 0=1,5.
При а:= 1,5 |х*(л:)=0,15.
Таким образом, в соответствии с B.21) значение функции
принадлежности \iz при г=16 равно 0,15.

44 Глава 2. Выполнение операций над нечеткими числами
2.4. ОПЕРАЦИИ НАД
НЕЧЕТКИМИ ЧИСЛАМИ
С УЧЕТОМ ИХ ВЗАИМОДЕЙСТВИЯ
Рассматриваются вопросы применения аппарата теории одномерной
полезности для случая, когда значения вероятностей заданы в
словесной форме. Описывается алгоритм вычисления ожидаемой
полезности, дающий более точные результаты по сравнению с аналогичными
методами вследствие учета ограничения, накладываемого на значения
вероятностей.
Краткие сведения о методе. Рассмотрим классическую постановку
задачи одномерной теории полезности. Необходимо выбрать
альтернативу а из множества А. Каждая из альтернатив имеет исходы Х\>
*2,..., хп, задаваемые распределением вероятностей их наступления.
Исходы имеют различную важность для ЛПР, и в соответствии со
своими предпочтениями оно может упорядочить их следующим образом:
*i^S*2^ • • • ^хп. Здесь Х\ и хп — соответственно наименее и наиболее
предпочтительные исходы.
Значения полезностей исходов Uj> /=1, п, определяются в ходе
диалога с ЛПР, в котором исследуется его поведение в условиях риска.
Обозначим полезность наихудшего исхода через ии полезность наилуч-
чего — ип. Для каждого х$> /=1, п, ЛПР должно назвать вероятность
Pj такую, что ему будут безразличны следующие ситуации:
1) ПОЛУЧИТЬ ИСХОД Xj\
2) получить хп с вероятностью pj или исход х\ с вероятностью 1 —
-Pi-
Тройка (хп, pj, x\) называется лотереей. Ожидаемая полезность
лотереи
Uj = unpj + Ui(l-pj) . B.22)
или в случае, если Wi = 0, un=l, Uj = pj. Исход Xj называется
эквивалентным лотерее (хп, Pj, x\).
Ситуации, в которых ЛПР может указать точные значения pj, / =
— 1,п, и, следовательно, полезности Wj, очень редки. Практически оно
в состоянии различить лишь такие значения, как ОЧЕНЬ ВЕРОЯТНО,
ВЕРОЯТНО, НЕОПРЕДЕЛЕННО, МАЛОВЕРОЯТНО, ОЧЕНЬ
МАЛОВЕРОЯТНО, которые обычно переводятся в числа из интервала [0, 1]
некоторым образом. Гораздо лучше представлять pj, являющиеся
лингвистическими термами, в виде нечетких чисел (рис. 2.10).
Лингвистической лотереей называется ситуация, в* которой исходы альтернативы
,vb *2, ...,*n наступают с вероятностями (лингвистическими) Ри Р2,...
..., Рп, представляемыми нечеткими числами на интервале [0, 1].
Особенностью выпуклых нормализованных нечетких множеств
является существование значения pj такого, что Vj l*~ (Pj) = 1, гДе М-~ —
функция принадлежности Pj. В четком случае для вероятностей дол-
п
жно выполняться условие 2j pj~ 1. Для нечетких вероятностей qhq
преобразуется в

2.4. Выполнение операций с учетом взаимодействия
45
1.6
ОЧЕНЬ НЕ- МАЛО- ОЧЕНЬ
ВЕРОЯТНО ВЕРОЯТНО НЕОПРЕДЕЛЕННО ВЕРОЯТНО ВЕРОЯТНО
10 Pj
Рис. 2.10. Тер м-множество лингвистической вероятности
Нечеткая функция полезности строится следующим образом. Пусть,
как и ранее, х\ и хп — наихудший и наилучший из возможных
исходов, а п\ и ип — соответствующие им полезности (имеющие точное
значение, так как не существует исхода лучшего, чем хп, и худшего,
чем х\). Полезность исхода хр обозначаемая U(xj), определяется
следующим образом:
U{x.)
(и) = sup
B.23)
где Pj — лингвистическая вероятность; Xj — исход, эквивалентный
лингвистической лотерее (х\, Pj и хп).
Рассмотрим вычисление ожидаемой полезности альтернативы а,-,
/=1, /п, исходы которой Xj, /=1, п, наступают с лингвистическими
вероятностями Pij и имеют нечеткие полезности м?. Обозначим p=(pi,
2, • • •, pn), и— (U[9' п2, ..., tin) и pu— 7, pjUj. Тогда нечеткая ожидае-
мая полезность альтернативы щ есть нечеткое множество
v „•
(и) = supminmin(|A
B.24)
p,u j=i
при ограничениях
В дальнейших расчетах будет использоваться а-сечение нечеткого
подмножества А универсального множества U — четкое множество
, ac=[0,l].
B.25)
Рассмотрим возможные варианты вычисления нечеткой ожидаемой
полезности [7, 9].

46 Глава 2. Выполнение операций над нечеткими Числами
Точные вероятности, нечеткие полезности. В этом
случае для каждой альтернативы
где + — операция обобщенного сложения [8]. Если Uj— выпуклое и
непрерывное, а-сечение есть замкнутый интервал: Uja = [#j(a)bj(a)] и
X 11
п п
B.26)
Таким образом, дискретизацией Uj можно получить сколько угодно
точек Vi.
Нечеткие вероятности, точные полезности. В этом
случае вычисляется сумма со взаимодействующими переменными Pi/
Vi= ext (p-i
где cxt означает обобщенное умножение.
Обозначим Рца =[тц(а)> Af<j(a)l и предположим, что щ
упорядочены по возрастанию. Тогда a-сечение Vi есть замкнутый интервал
с границами
k-i /i-i
inf Via= max ( ^jAf<j(a)M,+ A- 2j Af,-j(a) -
B.27)
sup V{ = min
ft-i
2.J m^i (a
« (a) tti) • B-28)
В работе [9] доказано, что существует единственный индекс Аг\ при
котором достигается max в B.27) такой, что
и единственный индекс ?+, при котором достигается min в B.28)
такой, что
1-

2.4. Выполнение операций с учетом взаимодействия 47
Алгоритм вычисления ожидаемой полезности состоит в следующем:
Шаг 1. Упорядочить Uj по возрастанию.
Шаг 2. Выбрать а<=[0, 1].
Ш а г 3. Найти kr и fe+ из условия
1— 2jAfij(a)-^j/Vfij(a)etm,-/,-(a), Afl7r(a)];
j==1 i=ft++i
Шаг 4. Вычислить inf V\a , используя B.27). с k = k~y вычислить
sup V,a , используя B.28) с k = k+.
Нечеткие вероятности, нечеткие полезности. Пусть
Dja~ laj(a), bj(a)]\ Рца=1ти(а), Mij(a)]. Алгоритм вычисления
полезности состоит в следующем:
Шаг 1. Упорядочить п) (соответственно и bj):
... bn.
Шаг 2. Найти kr и Л+, как в предыдущем алгоритме.
Шаг 3. Вычислить inf V; , используя B.27) с k = k~ и Uj = а
^вычислить sup Via , используя B.28) с k = k+ и Uj = bj.
Примеры использования метода. Пример 2.4. Определим нечеткую
ожидаемую поле:ность альтернативы, имеющей четыре возможных
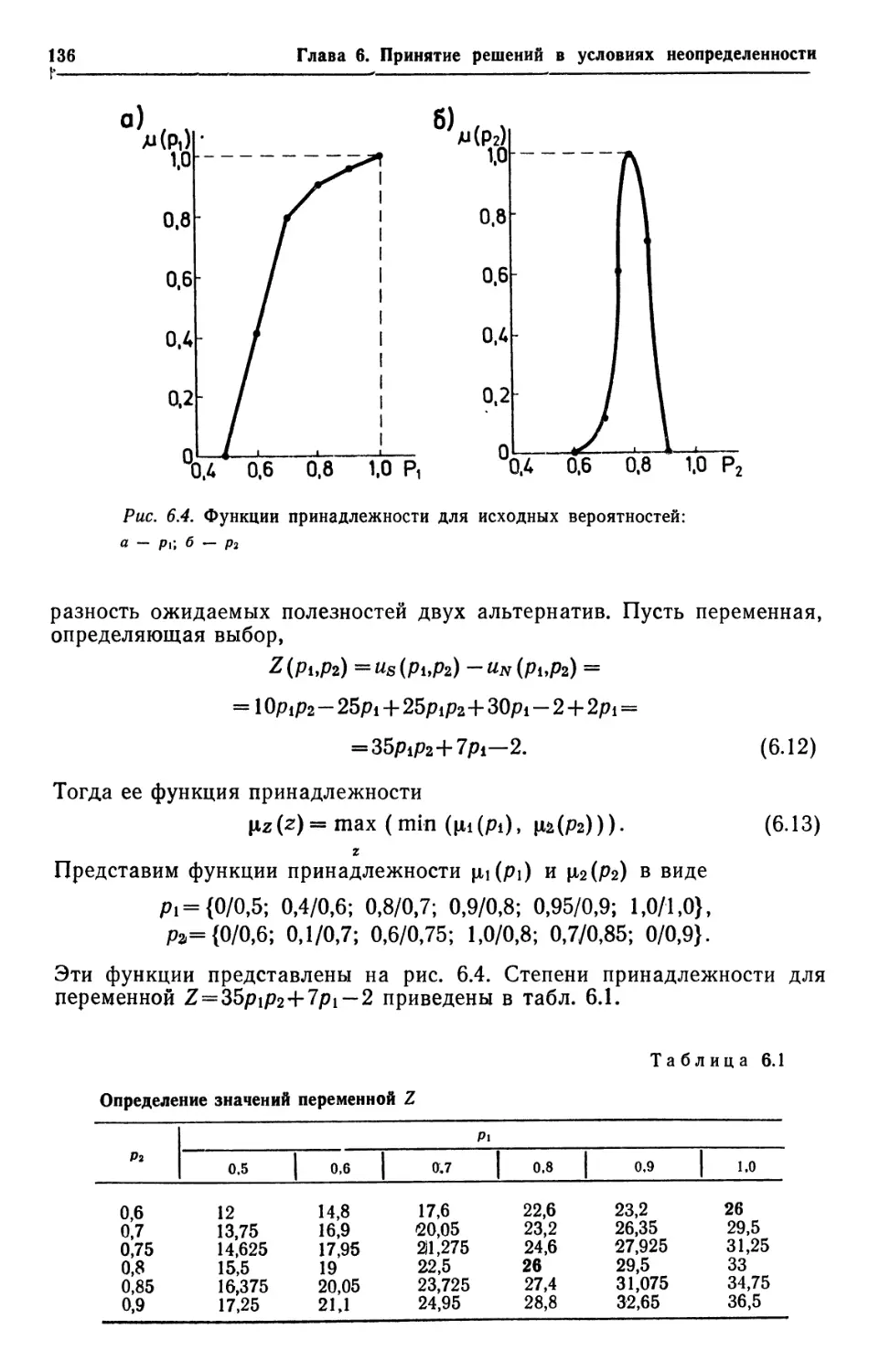
исхода с нечёткими вероятностями Ри ?2, -Рз, Ра (см. рис. 2.11 и 2.12):
л-,; G, = ОКОЛО 0,2;
хо; ГГо = ОКОЛО 0,3;
л'з; Г73 = ОКОЛО 0,4, НО ВОЗМОЖНО, МНОГО МЕНЬШЕ;
х<\ ^4 = ОКОЛО 0,5 ИЛИ НЕМНОГО МЕНЬШЕ;
р.-ОКОЛО 0,3 С БОЛЬШОЙ НЕОПРЕДЕЛЕННОСТЬЮ;
Ро = ОЧЕНЬ БЛИЗКО К 0,1;
Рз = ОКОЛО 0,4;
Р4 = БЛИЗКО К 0,2.
Проведем поэтапно вычисления для различных уровневых множеств.
Этап 1. а = 0,75. Уровневые множества приведены в табл. 2.1.
Шаг 1. а? и Ь, уже упорядочены по возрастанию.
Шаг 2. Найдем kr путем перебора конечного числа значений.
& = 4. Проверим l-(Mi+Af2 + Af3)e[m4, М41:
1- @,375 + 0,112 + 0,45) = 1-0,937 = 0,062; 0,062^[0,175; 0,225].
fe = 3. Проверим I — (М{+М2) —гп^Ыз, Af3l:
1-@,375 + 0,112)-0,175= 1-0,662 = 0,337; 0,3375^[0,35; 0,45].
fe = 2. Проверим 1 — М{— (тз + т4) е[т2М2]:
1 —0,375— @,35 + 0,175) = 1 —0,9 = 0,1; 0,1ge[0,087; 0,112].
Условие выполняется, следовательно, k~ = 2. Найдем &+ путем подбора.
k = 4. Проверим 1 — (mi —т2 + тз)^[т4; MJ:
1-@,225 + 0,087 + 0,35)-1-0,662 = 0,337; 0,337^[0,175; 0,225].

48
Глава 2. Выполнение операций над нечеткими числами
1.0
0,75
0.50
0.25
R__J5
0.1 0.2 0.3 0.4 0.5 0.6
Рис. 2.11. Нечеткие вероятности исходов X\t #2, хъ и х4
k = 3. Проверим 1 — (тх + т2) — Af4^[m3; Мг]:
1-@,2254-0,0875)-0,225= 1-0,537 = 0,462; 0,462^[0,35; 0,45].
k = 2. Проверим 1 — mi—(iW3+Af4)e[/n2; M2]:
1-0,225+@,45 + 0,225) = 1-0,9 = 0,1; 0,l€=[0,087; 0,112].
Условие выполняется, следовательно, ?+ = 2.
Шаг 3. В соответствии с B.27)
= 0,375 • 0,175 + A - 0,375 - @,35 + 0,175)) • 0,275+0,35 • 0,325 +
+ 0,175 • 0,425 = 0,375 • 0,175 + 0,1 • 0,275 + 0,35 • 0,375 +
+ 0,175-0,475 = 0,29.
Таблица 2.1
Множества а-уровня

Характеристика
1
2
Исходы
1
а = 0,75
[0,175; 0,2251 [0,275; 0,3251 [0,325; 0,425] [0,425; 0,51
[0,225; 0,3751 [0,087; 0,1121 [0,35; 0,451 [0,175; 0,2251
[0,15; 0,251 [0,25; 0,351 [0,25; 0,451 [0,45; 0,51
[0,15; 0,451 [0,075; 0,1251 [0,3; 0,51 [0,15; 0,251
а = 0,25
[0,125; 0.2751 [0,225; 0,3751 [0,175; 0,4751 [0,425; 0,51
[0,075; 0,5251 [0,062; 0,0821 [0,25; 0,551 [0,125; 0,2751
[0,1;
[0;
0,3]
0,61
[0,2;
[0,05;
0,41
0,151
[0,1;
[0,2;
0,51
0,61
[0,4;
[0,1;
0,5]
0,31

2.4. Выполнение операций с учетом взаимодействия
49
MS;
1.0
0,75
0.50
0,25
0,1 - 0,2 0,3 0,4 0.5 Uj
Рис. 2.12. Нечеткие полезности исходов х1у хо, х3 и х4
В соответствии с B.28)
sup Votl5 = mlbl + [l-mi-(
= 0,225.0,225 + A - 0,225 - @,45 + 0,225)). 0,325 +
+ 0,45 • 0,425 + 0,225 - 0,5 = 0,386.
Этап 2. а = 0,5. Уровневые множества приведены в табл. 2.1.
Шаг 1. Значения а$, Ь, упорядочены по возрастанию.
Ш а г 2. Найдем кг путем перебора.
k = 4. Проверим условие
1- @,45 + 0,125 + 0,5) -1-1,025; 0,025^[0,15; 0,25].
k = 3. Проверим условие
1-@,45 + 0,125) -0,15-0,275; 0,275^[0,3; 0,5].
& = 2. Проверим условие
1-0,45- @,3 + 0,15) =0,1; 0,1<=[0,075; 0,125].
Следовательно, /г~=2.
Найдем &+.
k = 4. Проверим условие
1-@,15 + 0,075 + 0,3)-0,475; 0,475^[0,15; 0,25].
^ — 3. Проверим условие
1-@,15 + 0,075)-0,25-0,525; 0,525^[0,3; 0,5].
к — 2. Проверим условие
1-0,15-@,5 + 0,25)-0,1; 0,1<=[0,075; 0,125].
Следовательно, Л+=2.
ШагЗ.
intV0,5 = 0,45.0,15+A-0,45-@,3 + 0,15)).0,25 + 0,3-0,25 +
+ 0,15.0,45-0,45.0,15 + 0,Ь0,25 + 0,3.0,25 + 0,15.0,45-0,235;
sup 1/0,5 = 0,15.0,25+ A -0,15- @,5 + 0,25)) .0,35 + 0,5-0,45 +
+ 0,25.0,5 = 0,15.0,25 + 0,1.0,35 + 0,5.0,45 + 0,25.0,5 = 0,422.
Этап 3. а = 0,25. Уровневые множества приведены в табл. 2.1.
Шаг 1. Расположим а, в порядке возрастания: 0,125^0,175^
^0,225^0,425. Значения bj уже упорядочены.
4 — 2307

50 Глава 2. Выполнение операций над нечеткими числами
|,О
Рис. 2.13. Функция принадлежности вы-
п. - » jt= 7Г-; г-=— численной нечеткой ожидаемой полез-
0,1 0.2 0,3 О.й 05U „ости
Ш а г 2. Найдем k~.
k=4; 1- @,525 + 0,082 + 0,55) =-0,1575^ [0,125; 0,2751;
k = 3; 1 -@,525 + 0,082) -0,125 = 0,267е= [0,25; 0,55].
Следовательно, k~=3.
Найдем k+.
6=4; I- @,075+0,062 + 0,25) = 0,672?[0,125; 0,275];
k = 3; 1-@,075 + 0,062)-0,275 = 0,587^ [0,25; 0,55];
6 = 2; 1-@,075-@,55+0,275) =0,1^[0,062; 0,082];
k = l; 1-@,082 + 0,55 + 0,275) =0,092е [0,075; 0,525].
Следовательно, &+=1.
Шаг 3. int 1/0,25 = 0,525-0,125+ 0,082-0,175+ A- @,525 + 0,082)-
- 0,125) • 0,225 + 0,125 • 0,425 = 0,525 • 0,125+0,082 • 0,175 +
+ 0,267-0,225 + 0,125-0,425 = 0,193; sup Ко,25= A - @,082 + 0,55 +
+ 0,275)) • 0,275 + 0,082 • 0,375+0,55 • 0,425 + 0,275 • 0,5=
= 0,092 • 0,275 + 0,082 • 0,375 + 0,55 • 0,425 + 0,275 • 0,5=0,455.
Этап 4. а = 0. Уровневые множества приведены в табл. 2.1.
Значения bt упорядочены по возрастанию: 0,3^0,4^0,5^0,5,
упорядочим а*: 0,1 <0,1 ^0,2^0,4.
Шаг 2. ?- = ?
k = A; 1- @,6+0,15 + 0,6) = -0,35?[0,1; 0,3].
k = 3; 1- @,6+0,25) -0,1=0,15*[0,2; 0,6].
k = 2; 1-0,6- @,2 + 0,1) =0,1 «=[0,05; 0,15].
Итак, k~=2.
6+=?
k = 4; I-@+0,05 + 0,2) =0,75*10,1; 0,3].
k = 3; 1-@+0,05)-0,3 = 0,65^[0,2; 0,6].
k = 2; 1-0- @,6+0,3) =0,le=[0,05; 0,15].

2.5. Вариационный подход к использованию операций 51
Итак, &+=2.
Шаг 3. int V0 = 0,6-0,l + A—0,6— @,2 + 0,1)) -0,1+0,2-0,2 + 0,1-0,4 =
= 0,6.0,1+0,1-0,1+0,2.0,2 + 0,1-0,4 = 0,15,
sup V0 = 0.0,3+ A-0- @,6 + 0,3)).0,4 + 0,6-0,5 + 0,3.0,5 = 0,49.
Этап 5. a=l. Vx = 0,3-0,2 + 0,2 + 0,1.0,3 + 0,4-0,4 + 0,2.0,5 = 0,35.
Полученная функция принадлежности нечеткой ожидаемой
полезности альтернативы изображена на рис. 2.13.
2.5. ВАРИАЦИОННЫЙ ПОДХОД
К ИСПОЛЬЗОВАНИЮ ОПЕРАЦИЙ
НАД НЕЧЕТКИМИ МНОЖЕСТВАМИ
Рассматривается метод построения комплексной (результирующей)
функции принадлежности на основе распределений возможностей
альтернатив, которые заданы на значениях параметра (см. параграф 1.5).
Выполнение некоторых операций над отдельными распределениями
позволяет получить комплексную оценку соответствия альтернативы
лингвистически сформулированной предварительной установке
экспертизы.
Краткие сведения о методе. Пусть имеется два распределения
возможностей одной альтернативы — nl(z) и я2(г). Необходимо на
основе операндов я1 и я2 для ряда значений параметра Z найти
комплексные значения nk с целью восстановления функции nk(z), которая
может быть далее использована для сравнения альтернатив. В
практических приложениях теории нечетких множеств для объединения и
пересечения используются различные операции. Рассмотрим наиболее
часто используемые формулы. Пусть А и В — два нечетких множества.
Тогда
= тах (Va (х), [хв (х))/х; B.29)
) > тах ^А W > №(х))/*; B.30)
\iAUB (х) = (\ia(x) +iib(x) -vla(x)vlb(x))/x. B.31)
Операция пересечения множеств А и В определяется следующим
образом:
А ПВ W
min (Va (x), \хв (х))/х; B.33)
)-^a(x)ixb(x))/x. B.34)
Вопрос о применении тех или иных формул в конкретных задачах
остается открытым. Так как распределения возможностей я* (г) по сути
дела представляют собой нечеткие подмножества, формально операции
B.29) — B.34) применимы. Однако в задаче получения комплексной
оценки nk(z)y в отличие от традиционных задач обработки нечетких
чисел, априори не определен даже тип операции (А[}В или А[\В).
Психометрические опыты могут выявить различные способы обработки
операндов я1 и я2, которыми пользуются ЛПР.
Приведем следующий пример. Параметр Z представляет собой
время, яаг.1(г) — распределение возможностей, индуцируемое крите-

52
Глава 2. Выполнение операций над нечеткими числами
Zo Zt Z2 Z3
Рис. 2.14. Ограничения на значения параметра
рием К\ «доступность запасных частей», ла. 2(z) индуцируется
критерием /С2 «престижность» (рис. 2.14). Необходимо дать комплексную
оценку возможностей будущего использования в конкретной
организации а-го устройства i-й модели. На рис. 2.14 обозначены следующие
ключевые моменты: z0 — начало производства i-й модели; гх —
появление новой, i+1-й модели; z2 — конец выпуска t-й модели;' г3 —
существенное сокращение выпуска запасных частей для i-й модели; г4 —
прекращение выпуска запасных частей для устройств i-й модели.
Основные типы поведения отражены на рис. 2.15. Позицию ЛПР-
супероптимиста можно сформулировать следующим образом. Конечно,
плохо, что один операнд имеет низкое значение (в данном случае
nQi2{z), см. рис. 2.14), однако значение второго операнда л;а.(г)
гораздо лучше. Поэтому будем руководствоваться тем, что с фактором
К\ долгое время не будет особых проблем, и считаем, что
комплексная оценка находится на уровне nl(z) (см. B.29)) или даже выше
(см. B.30) и B.31)). Такой «контрастный» способ работы «по
максимуму» может найти применение при решении задач поиска
альтернатив, имеющих резко выделяющиеся характеристики в некоторой части
пространства критериев (поиск «звезд» и «талантов»).
Формула B.30) в силу высокой степени неопределенности
результата, вероятно, не имеет практического значения. Выражение B.31)
позволяет учитывать второй операнд я2 (г) и дает результирующую
функцию nh(z), значения которой в каждой точке z на величину япл
(добавочную возможность) выше, чем max (я1, я2) в той же точке.
Индекс п зависит от пары значений (я1, я2) в точке z.
Применение формулы B.31) подразумевает следующие особенности
мыслительного комбинирования возможностей. Пары высоких, а также
низких значений операндов должны иметь минимальные добавочные
возможности япА (в первом случае «нет проблем», во втором — «все
потеряно»). Как видно из табл. 2.2, функция яА(я') имеет максимум
для пары я1 = я2=0,5, что соответствует стремлению ЛПР выбрать
сбалансированные по всем критериям объекты.

2.5. Вариационный подход к использованию операций
53
Таблица 2.2
Добавочная возможность
я1
0,1
0,3
0,5
0,7
0,9
1,0
я2
0,1
0,3
0,5
0,7
0,9
1,0
я'л;2
0,01
0,09
0,25
0,49
031
1,0
0,19
0,51 '
0,75
0,91
0,99
1,0
л*
0,09
0,21
0,25
0,21
0,09
0
Формула B.31) соответствует также определенному отношению
ЛПР к парам с различающимися значениями я1 и я2. Составленные на
основе табл. 2.3 графики (рис. 2.16) показывают, что добавочная
возможность увеличивается для пар операндов с небольшим значением
А=|я1 —я2|, причем ял выше, если арифметическая сумма операндов
стремится к единице. В интервале сумм операндов A; 2) имеет место
обратная зависимость.
Выражения B.32) — B.34) отражают мнение ЛПР, что следует
руководствоваться «жесткими» соображениями: комплексное значение
кк равно минимальному из операндов или даже ниже его. В случае^
B.32) предполагается, что отрицательные моменты, связанные с соот-*
ветствующими ограничениями (я4<1,0 и/или я2<1,0), не
взаимодействуют (не складываются). Выражение B.33) характерно для ситуации
«сильного» взаимодействия, когда тот факт, что я4<1,0 и/или я2<1,0,
приводит к весьма неопределенной интервальной оценке, которую можно
трактовать как «глубокое сожаление» (о том, что ограничения частично
не соответствуют требованиям). Формула B.34) позволяет учесть мне-
Способы расчета
комплексных значении
Возможностей
Рис. 2.15. Схема выбора операций для расчета комплексных значений воз-
i можностей

54
Глава 2. Выполнение операций над нечеткими числами
Таблица 2.3
Влияние суммы операндов на добавочную возможность
я'+я2
0,4
0,5
0,7
1,0
я1
0,4
0,3
0,2
0,5
0,4
0,3
0,7
0,6
0,5
0,4
1,0
0,9
0,7
0,6
0,5
я2
0
0,1
0,2
0
0,1
0,2
0
0,1
0,2
0,3
0
0,1
0,3
-0,4
0,5
0,4
0,37
0,36
0,5
0,46
0,44
0,7
0,64
0,6
0,58
1,0
0,84
0,79
0,24
0,75
я*
0
0,07
0,16
0
0,04
0,14
0
0,04
0,10
0,18
0
0,04
0,09
0,16
0,25
ние ЛПР, что при формировании пессимистической оценки кк следует
принимать во внимание оба операнда. Возможность яь, вычисленную
по данному принципу, можно трактовать как отражение некоторого
«сожаления» о том, что ни один операнд не оказался равным единице.
(Оба ограничения в точке z не лучшим образом соответствуют
требованиям.) Например, если я1==0,8, я2=1,0, то согласно выражению B.34)
дЬ = 0,8, т.е. результат соответствует B.32), однако при ^ = 0,8, я2 = 0,9
l2
по B.34) получаем Kft =
следовательно, лк<
и nfe меньше
даже минимального из операндов.
До сих пор предполагалось, что в области значений параметра Z
(по крайней мере в области определения функций я1 (г) и я2(г)) для
расчета значений nk(z) используется один из упомянутых принципов.
Однако может иметь место и другой подход. На рис. 2.15
представлена классификация методов расчета комплексных значений
возможностей, в которой введен промежуточный случай — способ действий
«объективиста».
Основная идея заключается в том, что операнды я1, я2 при я*<я2
должны дать значение nk такое, что я1<я/г<я2. Это соответствует
мнению ЛПР о субъективной зависимости операндов: низкую степень
соответствия требованиям по одному критерию можно компенсировать
высокой степенью удовлетворения требований по другому критерию.
Введением коэффициентов относительной важности (ai + a2=l,0),
критериев К\ и К2, индуцирующих распределения возможностей я1 (г) и
я2(г), можно реализовать расчет значений функции я*(г) для
необходимого количества точек z:
nh{z)=a^{z)+ain*(z). B.35)
Существуют разнообразные способы (в том числе итеративные)
установления в диалоге с ЛПР системы коэффициентов важности, однако
в основной процедуре оценки альтернатив ранее найденные коэффи-

2.5. Вариационный подход к использованию операций
55
Рис. 2.16. Характеристика добавочной возможности:
/ _ я1 + л2=0,4; 2 — я' + Я2=0,5; 3 — я' + Я2=0,7; 4 — Я' + Я2=1,О
циенты aj остаются неизменными (будем считать, что при несогласии
ЛПР с результатом ранжирования начинается новый анализ).
При необходимости выполнения операций с распределениями
возможностей такой подход представляется недостаточным. Основным
принципом вариационного подхода к выполнению операций над
нечеткими множествами является (в широком смысле) применение
различных выражений (см. B.32) — B.35)) для определенных областей
значений параметра Z. «Переключение» с одного правила на другое
обусловливается физической природой сравниваемых объектов (или среды
их функционирования), а также субъективными факторами.
Рассмотрим вариационный подход в узкой интерпретации. Пусть
заданы распределения возможностей ni(z) и я2 (г) с областями
определения PczZ и Z2cnZ, Zl(]Z2?=0-
Применение выражения B.35) основывается на предположении, что
существующая в сознании ЛПР субъективная зависимость операндов
имеет одну и ту же «силу» для всех рассматриваемых z^lZK Однако
практические задачи не ограничиваются упомянутым случаем. Легко
представить ситуацию, когда, степень силы связи операндов я1 и я2
изменяется с увеличением значений г.
Внутри данного класса задач можно сформулировать различные
способы расчета значений я*, соответствующие определенной точке
зрения ЛПР. Так, можно выделить индивидуумов типа «оптимист» в
оценке nk вариационным способом: тск больше значения т1п(я1, я2),
но не превышает max (я1, я2). Кроме того, при я* = 0, я2>0 все-таки
имеет место nh>Q (аналогично из я2=0, я*>0 также следует я*>0).
Если я1==0 и в процессе изменения значений z я2->0, то оптимист,
верный своим принципам, заявит, что ял-^я2. Если я1 (z) и я2 (г) —
монотонно убывающие функции, то сила связи операндов я1 и я2 меняется
с возрастанием z от относительно слабой при больших значениях
операндов до более сильной при я1->0 и я2-**), т.е. в последней ситуации
при расчете nh в большей степени низкие значения одного операнда
можно компенсировать высокими значениями другого. Из сказанного
следует, что для формируемого образа оптимиста характерно более
«строгое» отношение к проблеме при высоких значениях я1 и я2:
чение я* близко к min (я1, я2).

56
Глава 2. Выполнение операций над нечеткими числами
Рис. 2.17. Характерная точка системы нечетких ограничений
Для создания методики расчета значений пк сформулируем
основной мотив субъективного комбинирования возможностей, определяющий
рациональное поведение ЛПР типа «оптимист». Принцип «поощрения
возможности»: в процессе приближения гшгЦя1, я2) к нулю возрастает
ctj для max (я1, я2). Особое значение имеет точка, в которой в процессе
возрастания z впервые гп1п(я1, я2)=0 (например, на рис. 2.17: в ней
я2B0) =0,45). Данное значение указано на рис. 2.18 как характерная
точка с координатами я1==0, я2=0,45 (далее обозначается я202).
Поощрение возможности происходит по некоторым психическим
законам, и для их моделирования можно использовать линейные или
степенные функции (по аналогии с экспериментально установленными
степенными функциями психофизических законов [2]). На рис. 2.18
показаны некоторые примеры изменения «поощрения» в зависимости от
уровня возможности я1. Вид функций т определяется конкретной
ситуацией.
о г~ Рис: 2.18. Варианты законов поощрения
0 л 2 возможностей

2.5. Вариационный подход к использованию операций
57
0,2 0,4 0,6 0,8 1,01Г2
0,2 0,4 0,6 0,8 1,0 ПГ2
~>ис. 2.19. Нахождение весовых коэффициентов:
а — общий принцип; б — примеры с разными характерными точками и парами
операндов
Рассмотрим методику нахождения коэффициентов Г\ и г2 для
любого значения zeZ, что позволяет построить соответствующую
представлениям оптимиста функцию распределения возможностей по
выражению
1г. B.36)
Проекция характерной точки с координатами я* = 0, я2=0,45 на линию
равных возможностей (рис. 2.19, а) делит ее на две части: wi и w2
(Wi + w2=w). Отношения r\ = w{/w и r2 = w2fw будем интерпретировать
как веса возможностей пг^ и я2о2 в точке z0. Как видно из рис. 2.19, а,
при фиксированном я2(г0) =0,45 /*2>0,5 для любой пары (я1 = 0, я2=#0),
а в общем случае г2^0,5 при всех характерных точках я2о2 (О<я2о 2^
^1,0), что соответствует образу оптимиста (см. рис. 2.19,6). На этом
рисунке изображены интервалы wi и w2 только для ситуации я1 = 0,60
при характерной точке яго2 = О,45, однако, как видно из других при-
Рис. 2.20. Зависимость весовых
коэффициентов от характерных точек
1,0 X

58
Глава 2. Выполнение операций над нечеткими числами
меров (я1 = 0,60 и лго2 = 0,70), пары (wu w2) различаются. Например,
для всех точек (я1 = 0,6, я2) расчет весовых коэффициентов при я2о2=
= 0,45 заключается в следующем (предполагается, что (V) Ы* (z) <
* ()))
w
°'96
——
1,41
=0,68; г2= =
а;
а;
1,41
=0,32.
Для ситуации я2о2=0,7 соответственно r'i = 0,73; г'2 = 0,37. При я1 = 0,4
имеем г! = 0,53; г/1 = 0,61 и г2 = 0,47; /2 = 0,39. Таким образом, на
коэффициенты Г\ и г2 влияют характерная точка nZo и текущее значение
гтп(я\ я2).
Кроме данного свойства рассмотренный способ расчета
возможностей nh обладает «разумностью» в том смысле, что при большой разнице
в значениях я1 (-г) и я2 (г) поощрение возможностей в рамках
представлений оптимиста происходит более сдержанно. В этом нетрудно
убедиться (см. рис. 2.19, б), если рассчитать пары коэффициентов Г\ и г2для
ряда точек с координатами (я* = 0, я2=И=0). Результаты приведены на
рис. 2.20, где х представляет собой характерное значение я Zo 2. Как
видно из рисунка, в ситуации, когда я2(г) = 1,0, но уже имеет место
я1 (z)= 0, коэффициент г2 принимает значение 0,5. Когда оба
ограничения столь резко не различаются (например, л: = Я202=0,4), г2 = 0,8 в
характерной точке.
Необходимо отметить, что данный метод применим для амодальных
функций я (г) ив случаях, когда более сложные функции можно
заменить несколькими амодальными. Полезной для практических задач
является более широкая трактовка характерной точки: может
рассматриваться достижение одним операндом не нулевого, а яе-уровня [3, 5],
т.е. некоторого порога пренебрежимо малой возможности. Это важно,
так как на практике могут быть ситуации, когда ни одна функция я* (г)
не имеет нулевого значения в области анализа параметра Z.
Рассмотрение случаев, когда />2, и других возможных мотиваций
индивидуумов и методик объединений нечетких ограничений выходит
за рамки книги.
Пример использования метода. Пример 2.5. На рис. 2.21,6
приведены два распределения возможностей профессионального баскет-
0,2 0,4 0,6 0,8 1,01i2 30 31 32 33 34 35 36 37 Z
Рис. 2.21. Определение комплексного распределения возможностей:
а ~- расчет весовых коэффициентов; б — полученное распределение возможностей

2.6. Операции дополнительного вычитания и деления 59
Результаты анализа
я1
я2
Г\
г?,
л*
0,9
1,0
0,92
0,08
0,92
0,7
0,98
0,77
0,23
0,73
возможностей
0,5
0,96
0,62
0,38
0,68
0,3
0,9
0,45
0,55
0,64
баскетболистов
0,2
0,82
0,37
0,63
0,59
0,1
0,68
0,30
0,70
0,51
0,05
0,57
0,26
0,74
0,43
0
0,45
0,22
0,78
0,35
0
0,3
0,22
0,78
0.23
Таблица 2.4
0
0,2
0,22
0,78
0,16
0
0,1
0,22
0,78
0,078
болиста. Ценность игроков определяется скоростью реакции ji2(z) и
физическими способностями nl(z)y которые с течением времени
ухудшаются (Z — возраст), причем с последними это происходит быстрее.
Необходимо проанализировать комплексные игровые возможности на
основе двух операндов. Баскетбол — игра, где многое определяется
интеллектом, поэтому применение формулы B.32) неадекватно.
Результаты расчетов при узкой интерпретации вариационного (рис. 2.21, а)
подхода приведены в табл. 2.4 и на рис. 2.21,6.
В данном примере (см. рис. 2.21,6) характерная точка го = 34 года,
Лго2=О,45. Для z>z0 коэффициенты г{ и г2 не меняются, так как nl(z) =
= 0. После возраста 37 лет nk(z)=Q, вследствие чего профессиональный
баскетболист, по мнению экспертов, должен завершить выступления.
Ограничение nk(z) дает представление о возможностях конкретного
баскетболиста в разном возрасте.
2.6. ОПЕРАЦИИ ДОПОЛНИТЕЛЬНОГО
ВЫЧИТАНИЯ И ДЕЛЕНИЯ
Рассматриваются операции дополнительного вычитания и деления
[1], позволяющие определить противоположные и обратные нечеткие
числа и, таким образом, находить точные решения нечетких уравнений.
Краткие сведения о методе. В ряде задач, связанных с
использованием нечетких чисел, возникает необходимость решения нечетких
уравнений вида
D, B.37)
где А, В, D — нечеткие числа; X — неизвестное.
Арифметические операции, основанные на принципе обобщения [4],
не позволяют отыскать противоположное число А' (такое, что А+А' =
«О) и обратное число А" (такое, что АхА"=1). Кроме того, имеют
место неравенства (А-В)+ВФА; (А:В)хВфА.
Для точного решения нечетких уравнений B.37) вводятся
операции дополнительного вычитания (— —) и дополнительного деления
)
Дополнительное вычитание. Рассмотрим частный случай
B.37), уравнение вида
X+B=D. B.38)
Его решением является множество X=D В.
Пусть носителем множества В является Sb=[&i, b2], носителем
множества D — интервал Sd~ Ы\, *У, Тогда носитель множества X, най-

60 Глава 2. Выполнение операций над нечеткими числами
денного с помощью операции дополнительного вычитания, определяется
следующим образом:
Sx=[dudb] [bub2] = [di-bi,d2-b2]. B.39)
Функция принадлежности множества X задается выражением
= inf sup (ae=[0,l]|min (\ib(z—x),a)
B.40)
—'nf i *' если
|Xd, если
Операция дополнительного вычитания определена только для
нечетких чисел D и В, у которых
г—Ь2 или d2 — di^b2 — bu B.41)
т.е. у уменьшаемого длина интервала носителя должна быть больше,
чем у вычитаемого.
Дополнительное деление. Рассмотрим уравнение вида
AX=D,
решением которого является множество X = D//A.
Пусть носителем множеств А и D являются соответственно
интервалы SA=[a\t a2] и Sd=Wi, d2]. Носитель множества X, найденного
с помощью операции дополнительного деления, определяется
следующим образом:
di:aud2:a2> если SA>0; Sd>0;
Sx=[did2]//[aua2i] =
di:a2jd2:ai* если 5а>0; Sd<0;
d2:audi:a2, если 5А<0; SD>0;
d2:a2ydr.au если 5А<0; SD<0.
Функция принадлежности множества X задается выражением
[Хх(х) = inf sup (йе[0,1]| min (juIa(^) , а)
B.43)
t
=inf Jb если ^(^)<^@; B44)
t \ll(t) еСЛИ |i(^)>|i(/)
Операция дополнительного деления определена не для любых
нечетких чисел А и D. Их интервалы-носители должны удовлетворять
следующим условиям:
d2:di>a2:ai, если 5а>0; Sd>0\
d2:di>ai:a2, если 5А>0; 5D<0; B 45)
dl:dz>a2:au если &л<0; SD>0;
di:da>at:a2, если Sa<0; Sd<0.
Примеры использования метода. Пример 2.6. Решить уравнение
B D, если ^ПРИБЛИЗИТЕЛЬНО 8= {0/6; 0,5/7; 1/8; 0,5/9;
0/10}:
?> = ПРИБЛИЗИТЕЛЬНО 14={0/Ю; 0,5/12; 1/14; 0,5/16; 0/18}.

2.6. Операции дополнительного вычитания и деления
61
7 « 9 10 11 12 13 U 15 16 17 18 X
Ямс. 2.22. Функции принадлежности множеств для
операции дополнительного вычитания
Функции принадлежности приведены на рис. 2.22. Определим
интервалы-носители множеств 5в=[6; 10]; Sd=[10; 18]. Условие B.41)
выполняется, так как 18—10> 10 — 6, следовательно, можно
использовать операцию дополнительного вычитания. Найдем носитель
множества X в соответствии с B.39): Sx=[10-6; 18— 10] = [4; 8].
Определим значения функции принадлежности множества для
элементов Sx согласно формуле B.40). Используемые данные приведены
в табл. 2.5. В ней прочерк означает, что функция принадлежности не
определена, курсивом выделены значения \id(z), для которых ри>B)^
^\ib(z — x), жирным шрифтом — наименьшее из таких \iD(z),
которое и дает значение функции принадлежности \хх(х) (см. рис. 2.22).
Таким образом, получили Х={0/4; 0,5/5; 1,0/6; 0,5/7; 0/8}.
Для иллюстрации свойств дополнительного вычитания найдем
сумму множеств X и В. Воспользуемся принципом обобщения и
соответствующей операцией сложения (см. параграф 2.1). Функция
принадлежности множества D\ являющегося суммой множеств X и В,
определяется следующим образом:
\iD(z)=sup min(|ijr(*), \ib (у) ) = sup mm (iix(x)9 \xB(z-x)).
x,y: z*=x+y x
Используемые для ее нахождения данные приведены в табл. 2.6.
Таким образом, получили Z)'={0/10; 0,5/17; 1,0/14; 0,5/16; 0/18}.
Таблица 2.5
Данные для расчета
функции принадлежности
X
U
множества X-
=D—
в
Z
10
11 | 12
13
14 | 15
16
17
18
Vx С*)
4
5
G
7
8
\ib{z-x)
VLb(z-x)
\ib(z-x)
\id(z)
IIb(z-x)
\xb(z-x)
0
0
0
0
0
0
0,5
0,25
0
0,25
0,25
0,25
0,25
1,0
0,5
0,5
0,5
0
0,5
0,5
0,5
0,5
0,75
0,1
0,75
0,5
0,75
0
0,75
0,75
0
1,0
0,5
L0
1,0
1,0
0,5
1,0
0
1,0
0,75
0
0,75
0,5
0,75
1,0
0,75
0,5
0,75
0,5
0,5
0
0,5
0,5
0,5
1,0
0,5
0,25
0,25
0,25
0
0,25
0,5
0,25
0
0
0
0
0
0
0
0,5
1,0
0,5
0

62
Глава 2. Выполнение операций над нечеткими числами
Данные
функции
z
10
12
14
16
18
для расчета
принадлежности
\1х(х)
[Xb(z-x)
\ib(z-x)
Tslzlx)
IIX(X)
\ib(z-x)
VLb(z-x)
множества D'=X+B
4
0
0
0
1,0
0
0
0
0
5
0,5
0,5
0,5
0,5
0,5
0,5
0,5
X
6
1,0
1.0
0
1,0
1,0
1,0
0
1,0
7
0,5
0,5
0,5
0,5
0,5
0,5
0,5
Ta6j
1 8
0
0
0
0
0
1,0
0
0
i ица 2.6
0
0,5
1,0
0,5
0
Видно, что множества D и D' равны, т. е. операция дополнительного
вычитания дает точное решение уравнения X + B = D.
Найдем теперь решение уравнения, пользуясь обобщенной
операцией вычитания — над уровневыми множествами Г8] (см. параграф
2.2). Как было показано ранее,
где ( — В) — множество, противоположное В.
По определению (-В) = {0/-10; 0,5/-9; 1,0/ —8; 0,5/-7; 0/-6}.
Тогда обобщенная сумма
X = D+(-B) =.{0/10; 0,5/12; 1,0/14; 0,5/16; 0/18} +
+ {0/-10; 0,5/-9; 1,0/-8; 0,5/-7; 0/-6} =
= {0/0; 0,5/3; 1,0/6; 0,5/9; 0/12}.
Таблица 2.7
Данные для расчета
множества X=D//B
X
u
функции
принадлежности
6
14
t
« 1
36
50
1
2
3
4
5
0
0
0
0
0
0
0,5
0,5
0,5
0,5
0,5
0,5
1,0
1,0
1,0
1,0
0
1,0
1,0
0,5
0,5
0,5
0,5
0,5
0,6
0,5
0
0
0
0
0
0
0
0,5
1,0
0,5
0

2.6. Операции дополнительного вычитания и деления
63
-10 -8-6-4-2 24 68 10 12 U 16 18 20 22Х
Рис. 2.23. Функции принадлежности множеств для операции
вычитания на основе уровневых множеств
Найдем, как это делали ранее, множество D" — сумму множества
X и множества В:
= {0/0; 0,5/3; 1,0/6; 0,5/9; 0/12} +
+ {0/6; 0,5/7; 1,0/8; 0,5/9; 0/10} = {0/6; 0,5/10; 1,0/14; 0,5/18; 0/22}.
Полученные множества представлены на рис. 2.23. Как видим,
множества D и D" не равны, DczD". В этом и состоит различие операций
дополнительного и обобщенного вычитания.
Пример 2.7. Решить уравнение AX = Dy если А =
ПРИБЛИЗИТЕЛЬНО 8= {0/6; 0,5/7; 1,0/8; 0,5/9; 0/10}, D = ПРИБЛИЗИТЕЛЬНО
24= {0/6; 0,5/14; 1,0/24; 0,5/36; 0/50}.
Функции принадлежности приведены на рис. 2.24. Определим
интервалы-носители множеств: Sa=[6; 10]; Sd=[6; 50]. Так как 50:6>
>10:6, то условие B.45) выполняется и можно использовать операцию
дополнительного вычитания. Найдем носитель множества X согласно
B.43): Sx=[6:6; 50:10] = [1, 5].
Определим значения функции принадлежности множества в
соответствии с B.44). Используемые данные приведены в табл. 2.7. В ней
прочерк означает, что функция принадлежности не определена,
курсивом выделены значения jid(/)> для которых \iD(t)^\iA(t/x), жирным
шрифтом — наименьшее из таких jid(O> которое дает значение \ix(x).
Полученная функция принадлежности приведена на рис. 2.24.
Решением уравнения является множество X={0/l; 0,5/2; 1,0/3; 0,5/4; 0/5}.
50 х
Рис. 2.24. Функции принадлежности множеств для операции
дополнительного деления

Глава 3
МЕТОДЫ СРАВНЕНИЯ
НЕЧЕТКИХ МНОЖЕСТВ
И ЧИСЕЛ
3.1. СРАВНЕНИЕ НЕЧЕТКИХ ЧИСЕЛ
С ПОМОЩЬЮ
ОБОБЩЕННЫХ ОПЕРАЦИЙ
«БОЛЬШЕ ИЛИ РАВНО»
Рассматривается метод сравнения нечетких чисел [5], заданных в
виде /?1-представления. Дается определение возможности того, что
одно нечеткое число больше другого. Ответ нечеткий и представляется
как нечеткое множество на базовых переменных {да, нет}.
Краткие сведения о методе. Пусть Я и N — два нечетких числа,
и и v — две действительные переменные, имеющие соответственно
распределения возможностей \i~ и и~. Возможность получения и = х и
М N
v = y равна гшп(и~(л;), |i~ (у)).
м n
Возможность того, что М больше или равно N, обозначается
N)= supmin (ji~ (*), ц~ (*/))> C.1)
т.е. это наименьшая верхняя грань возможности того, что и = х и v = yy
и х^у, где \i~ и u ~ — соответственно распределение
возможности м
тей действительных переменных и и v.
Рассмотрим случай представления нечетких чисел в виде Я= (т,
а, р) и N=(n, у, б), где тип — средние значения нечетких чисел
М и N\ а и у — левые границы, а р и б — правые границы
соответственно Ш и N.
Пусть [а, р] и [у, б] пересекаются, т.е. а<у<Р и v<P<6» a
среднее значение числа Я меньше среднего значения числа N.
Из рис. 3.1 видно, что V(N^M) = 1. Так как u~(m) = l, u~ (лг) = 1
М N
и n>m, то из определения следует, что
V(N^M) = supmin (\х~ (т),\х „ (л)) = 1. C.2)
п>т М »
Значение V(N^M) равно высоте мнол<ества (M(]N), т.е. ординате
D — точке, являющейся общей для нечетких чисел Я и N со средними
значениями п^т:
V(#>Я) = высота (Л?П#)= ордината (D). C.3)
Проверим данное утверждение для различных пар х^у. Для этого
разобьем интервал [а, б] на отрезки [а, у], [у> rf], [а, р] и [р, в]. Для

3.1. Сравнение с помощью операций «больше или равно»
65
Рис. 3.1. Пример сравнения
нечетких чисел
ос
и Х,У
участка [а, у] проверка не проводится, так как условие х^у
невыполнимо. Для участка [7, d] возьмем пару х' и у', для которой
выполняется условие х'^у'.
Как видно из рис. 3.1, ц~ (x')>\i~(y'), и так для любой пары х^у
М N
на данном отрезке, т.е. min (\i~ (x), jx~ (у)) принадлежит числу N на
[V; d]x^y M N
данном отрезке. Для W, р] возьмем пару х" и */", для которых
выполняется условие xf'^y". Из рис. 3.1 видно, что ^jl — (х/7)^ц^ (у"), т. е.
для любой пары значений, удовлетворяющих условию х^уу данное
неравенство выполняется. Следовательно, min (\x~ (я), ц^ (у)) принадле-
жит числу М на данном отрезке.Если y'^iy, d], a /e[d, p] и х">у'\
то 11,4, (x//)<ji /ч, (у77). Отсюда следует, что минимум принадлежит нечет-
М N
кому числу М на {у, р]. Отрезок [р, б] не рассматривается.
Из вышесказанного следует, что min (р,~ (л:), \i~(y)) принадлежит
х^у М N
участку, отмеченному на рис. 3.1 пунктиром.
Из способа задания чисел М и N следует, что
м
/т—х \
если
а
если
L ( ) ,
\ у /
^ / П-у \
\ fi / '
если
где L и R — функции (рис. 3.2), имеющие следующие свойства:
1) L@)=i?@) = l; 2) L{-x)=L{x)\ R(-x)=R(x); 3) L и R — не
увеличивающиеся на [0, оо]; 4) L( + oo) = #( + оо) =0.
(d) =[i ~ (d), т.е.
Ордината точки D находится из выражения
т — d
Следовательно,
Y
i-d
d—m nfi + my
V+P
б — 2307

66 Глава 3. Методы сравнений нечетких Множеств
1,0
X Рис. 3.2. Вид функций L и R
Подставив d в ц— 1 э получим:
\ У I
C.4,
Ответ на вопрос «Может ли Ж быть больше Ю» нечеткий и
представляется как нечеткое подмножество множества {да, нет}:
A = {V(M^N)/w; V(N^M)/neT}. C.5)
Замечание. Неопределенность ответа максимальна, когда
Если М и N не выпуклые и не нормализованные, используется
формула C.1). При этом берутся только те значения х и у, которые
соответствуют максимуму функций \i~ и |х ~ .
М V
Пусть элементы множества m\...nik (соответственно rt\... щ)
являются локальными максимумами непрерывного числа М на IR
(соответственно N на L). Тогда может использоваться формула
(hgt (itffW), maxmin ([л^ (тг), ц ^ (>Ъ))), C.6)
где hgt — высота нечеткого множества.
Возможность для нечеткого числа М быть больше k нечетких
множеств Mi на R
...,|x~ D)). C.7)
М
(| ()>V
t M Ml
Выражение C.7) — это обобщение C.1), предложенное в работе [3].
Оно справедливо, когда нечеткие множества являются нечеткими
числами, где
= min V(JBt>JBti).
Примеры использования метода. Пример 3.1. Пусть М= C, 0, 7) RL,
а N=(8,4, 9)lr (рис. 3.3, а). Проверим, что для точки D V(№N)
=ордината (D).

3.1. Сравнение С пбмоЩью операции «больше или равно*
7 8 9Х
1 2 3 А 5 6 7 8 Х,У
1 2 3 4 5 6 7 8 9 10Х.У
Рис. 3.3. Границы нечетких чисел: а — а
Согласно определению, V(M^N)=sup min(jui^ (л:), \i~ (у)).
х^у М N
Рассмотрим пары значений х и у, удовлетворяющих условию
в интервале [4, 7].
*=6,5; у=4,5; min (\i - (x),\i „ (у)) = min @,12, 0,25) =0,12;
л:=6; у=5: min @,26; 0,35) =0,26;
*=5,6; у = 5,3: min @,38; 0,48) =0,38;
*=*5,3; у = 5,3: min @,48; 0,48) =0,48.

6& Глава 3. Методы сфавйейий нечетки* йнбжеств
Тогда согласно определению для заданных х и у
@,12; 0,26; 0,38;
= ордината (Z)).
(y))p@,12; 0,26; 0,38; 0,48) =0,48=n~(d) =
N M
ЛГ
Итак, (>),
Найдем V(N^M\=sup min(fi^ (х), jx~ (у)). Рассмотрим пары зна-
*<!/ М N
чений х и у:
х=5,3; i/=8: min (ц,„ E,3), \i ~ (8)) =0,48;
м n
х=3\ у=8: min (jx^ C), jut^ (8)) = 1.
М N
Следовательно, V(N^M) =sup@; 0,48; 1) = 1. Ответ на вопрос
«Больше ли М, чем N?» представляется нечетким множеством Л =
= {0,48/да; 1/нет}.
Пример 3.2 (см. рис. 3.3,6). Пусть М= D, 3,6)дь,а #=G,1, 8)ья;
Убедимся в том, что V(ffi^N) = ордината (D). Пусть
jc = 5,6, y = 5,3: ji- (jc) =0,15; \i „ (у) =0,8; min(u~ (л:), |i^ (r/)) =0,15;
М N М N
х = 5; у=4,6: min@,45; 0,7) =0,45;
jc=4,6; y = 4,6: min @,7; 0,7) =0,7;
jc = 4,6; y = 4,5: min@,7; 0,69) =0,69;
jc = 4,3; у = 3,5: min@,79; 0,51) =0,51;
jc = 3,5; y = 3,2: min@,95; 0,45) =0,45.
Тогда согласно C.1) V(M^N) =sup min(fx^ (#), |i^ (y))=sup
@,15; 0,45; 0,7; 0,69; 0,51; 0,45) =0,7=ц~ (d)=\i~ (^)=ордината (D).
M N
Определим V(N^M). Для этого рассмотрим следующие пары
значений х и у:
х=6; у = 7: min (ц~ F)» ^^ G)) =0;
М N
^=4,6; r/=7: min(fi~ D,6), \х~ G)) =0,7;
*=4; у = 7: тгп((х^ D), jx^
В соответствии с C.1) V(N^M) =sup@; 0,7; 1) = 1. Нечеткое
множество, являющееся ответом на вопрос «Больше ли М, чем i^?», имеет
вид Л ={0,7 / да; 1 / нет}.
Пример 3.3 (рис. 3.3,б). Пусть М= B, 0, 5)RLy а #= G, 3,10)ья-
Покажем, что для точки D V(M^N) =ордината (D). Рассмотрим пары
значений х и у:
х=4,5; у=3,5: min (ц„ (х), р„ {у))= min @,2; 0,18) =0,18;
М N
л: = 4,5; #=3,6: mim((i^ (х)у ц^ (у)) = min@,2; 0,22) =0,2;
ч М N

3.2. Сравнение подмножеств единичного интервала 69
*=4,3; #=3,8: min @,22; 0,29) =0,22;
х=4; #=4: min @,32; 0,32) =0,32.
Согласно C.1) для заданных х и у
supmin(n~ (х), [л„ (у)) = sup @,18; 0,2; 0,22; 0,32) =0,32=^1^ (d) =
Л* W М
= u~ (d) = ордината (/)).
Итак, V(M^N) =0,32.
Найдем ^(Л^Л?) =sup min (ix~ (х), jx ~ (у)).
Возьмем пары значений х и у:
х=5; у = 7: min(jx^ E), \i~ G)) =0;
х = 4;у = 7: min(ц^ D), [i~ G)) =0,32;
х = 2; х = 7: min(|i^ B), ц- G)) = 1.
М N
Следовательно, V(N^M) =sup @; 0,32; 1)=1. Ответ на вопрос
«Больше ли М, чем ^?» представляется нечетким множеством: А =
= {0,32/да; 1/нет}.
3.2. СРАВНЕНИЕ
НЕЧЕТКИХ ПОДМНОЖЕСТВ
ЕДИНИЧНОГО ИНТЕРВАЛА
Вводится функция, облегчающая сравнение нечетких подмножеств
единичного интервала. Эта функция представляет собой интеграл
объединения уровневых множеств и является точечной оценкой нечеткого
множества [6].
Краткие сведения о методе. Определим функцию /% отображающую
подмножества единичного интервала / на него же. Эта функция
упорядочивает нечеткие подмножества /, что позволяет сравнивать
любые (дискретные, непрерывные) нечеткие подмножества единичного
интервала.
Предположим, что А — нечеткое подмножество /. Уровневое
множество определяется как [1]
C.8)
и является обыкновенным подмножеством /.
Предположим, что V — подмножество /: V= {х\, х% ..., хп}.
Определим M(V) как среднюю величину элементов V> т.е.
г=1
Если V={a^jc^b}, то
^±L (зло)

70
Глава 3. Методы сравнения нечетких множеств
1.0
0.8
0.6
0.2
0.8
0,6
0Л
0,1
1,0
0,1 0,3 0,5 0,7 1,0 X ^мс< Я-4- Нечеткое множество А
Если
среднее значение
ш
и V= (J
г), ТО
C.11)
Предположим, что А — нечеткое подмножество / с максимальной
степенью принадлежности членов, равной ctmax. Определим функцию
упорядоченности F(A) следующим образом:
C.12)
!?тах
F(A)=) M(V)da.
Примеры использования метода. Пример 3.4. Рассмотрим
нечеткое подмножество А, представленное на рис. 3.4. Найдем а-уровневые
множества:
А»={0,1; 0,3; 0; 5; 0,7; 1}; 0<а^0,1;
Ах={0,3; 0,5; 0,7; 1}; 0,1<а<0,4;
Ла={0,5; 0,7; 1}; 0,4<а^0,6; Л«={0,7; 1}; 0,6<а<0,8;
1.0
0,8
0.6
0.4
0.2
У)
0,64
0,36
• 0,1
т
0,16
0,1 0,3 0,5 0,7 1,0 X Рис. 3.5. Нечеткое подмножество А2

3.2. Сравнение подмножеств единичного интервала 71
Отсюда определим М:
М (Л„)=2,6/5=0,52, 0< а г=? 0,1; М (Ла) = 2,5/4=0,625,
0,1,<а<0,4; М(Аа) =2,2/3=0,733, 0,4<а<0,6;
М(Аа) = 1,7/2 = 0,85, 0,6<а<0,8; М(Аа) = 1/1 = 1,
Найдем значение функции упорядочения:
1 0,1 0,4 0,6
F(A) = $M(Aa)da= Jo,52doc + Jo,625da + Jo
0 0 0,1 0,4
0,8 1
+ Jo,85cfa+Jlrfa =
0,6 0,8
= 0,52 • 0,1 + 0,3 • 0,625 + 0,2 • 0,733 + 0,2 • 0,85 + 0,2 • 1 = 0,756.
Рассмотрим множество ОЧЕНЬ А (А2, рис. 3.5). В этом случае
Лх2.= {0,1; 0,3; 0,5; 0,7; 1}; 0<а^0,01, М(А^) =0,52;
Ла* = {0,3; 0,5; 0,7; 1}; 0,0Г<а<0,16, М{Аа2) =0,625;
Ла2={0,5; 0,7; 1}; 0,16<а<0,36, М(Аа2) =0,733;
Ла2={0,7; 1}; 0,36<а^0,64, M(AJ) =o,85;
Аа2={1}; 0,64<а<1,
Значение функции упорядочения
1
\)da =0,843.
о
Рассмотрим множество ОЧЕНЬ-ОЧЕНЬ А, определяемое
следующим образом: Л*@,1) =0,0001; Л4@,3) =0,002; Л4@,5) =0,129; Л4@,7) =
= 0,409; Л4A) = 1. Найдем для него
^) =0,052; a<a^0,0001; M(AJ) =0,625;
0,0001<a<0,002; M(AJ) =0,733; 0,002<a<0,129;
Л1(Ла4)=0,85; 0,129<a<0,409; М(Ла4) = 1; 0,409<а<1.
l
Тогда ^(Л4)== / 'M(Aai)da=0,9231. Можно заметить, что так как А —
о
некоторая форма множества ОКОЛО 1, то ОЧЕНЬ Л означает ОЧЕНЬ
БЛИЗКО К 1 и Л4 — ОЧЕНЬ-ОЧЕНЬ БЛИЗКО К 1 и F(A)<F(A2)<
<F(A*).
Рассмотрим множество ПРИМЕРНО А, обозначенное А'!*. Тогда
А1''@,1) =0,32; Л'/.@,3) =0,63; Л%@,5) =0,775;
Л'/»@,7)=0,89; Л'/*A) = 1; М(Щ =0,52; 0<а<0,32;

72
Глава 3. Методы сравнения нечетких множеств
1,0 X
0.6 0.8 1,0 X
Рис. 3.6. Непрерывное нечеткое множество А
Рис. 3.7. Нечеткое множество ПРИБЛИЗИТЕЛЬНО 0,8
М(АЦ-0,625; 0,33<а<0,63;
А1 (Л1/.) =0,85;
=0,733; 0,63 < а sS 0,775;
= \\ 0,89<а<1.
Следовательно, F(A^) = fM(Aa1/*)da= 0,674.
Пример 3.5. Рассмотрим А — непрерывное нечеткое
подмножество / (рис. 3.6): \ха(х)==х, яе[0,1]. Оно используется во многих
случаях как лингвистический эквивалент ИСТИННО. Тогда
поэтому Ла={а, 1}, средняя величина Л1а=A+а)/2 и атах=1.
Следовательно,
Эта ситуация сходна с дискретным случаем. Если мы рассмотрим
А2, ОЧЕНЬ ИСТИННО (цл»(х)=^), то
Л2а= {*|*е=/. л:2^а} = {4*%<x< 1}.
Поэтому
= D-а+4-«3/2 ) Г =0,833.
\ 2 3 /In
0,2 0,4 0,6 0,8 1,0 X
Рис. 3.8. Нечеткие множества
ПРИБЛИЗИТЕЛЬНО 0,4 и
ПРИБЛИЗИТЕЛЬНО 0,7

3.2. Сравнение подмножеств единичного интервала 73
В общем случае для п>\
^l l^L C.13)
Эта функция монотонно возрастает пол и стремится к единице.
Подобным образом можно показать, что
л11п i « и л/ 1+ссП ev/Лч f 1+a» 1,1 1 /О1„,
Аа = {в», 1}; Afa=_^_, /^(Л ) = J —^—=_+_ __ C.14)
В этом случае F — функция, монотонно убывающая по п, которая
асимптотически приближается к 1/2- С возрастанием п А1/п стремится
к единице, что является лингвистическим эквивалентом для НЕ ЗНАЮ
и НЕИЗВЕСТНО.
Пример 3.6. Рассмотрим нечеткое подмножество А (рис. 3.7):
10, если
5х-3, если 0,6<х<0,8;
-5а:+ 5, если 0,8<л;^1,
которое формализует понятие ПРИБЛИЗИТЕЛЬНО 0,8. Тогда
п л лл ч д„ 1 -0,2а + 0,2а+ 0,6 ло
,6, 1-0,2а); Ма= ^0,8
Таким образом, для нечеткого подмножества ПРИБЛИЗИТЕЛЬНО 0,8
функция F имеет значение 0,8.
В более общем случае пусть А — нечеткое подмножество
единичного интервала с ae[0, 1], такое, что \xa((i) = 1, А симметрично а, т.е.
\ха(п + у) =\ia(ci — у). Тогда F(A)=a. Следствием этого свойства
является то, что все нечеткие числа: БЛИЗКО К а, ОЧЕНЬ БЛИЗКО К а,
ПРИБЛИЗИТЕЛЬНО а, ОКОЛО а и т.д., которые определены
симметрично относительно а, имеют одинаковое значение F.
Пример 3.7. Требуется сравнить два нечетких множества —
ПРИБЛИЗИТЕЛЬНО 0,4 и ПРИБЛИЗИТЕЛЬНО 0,7 (рис. 3.8).
А = ПРИБЛИЗИТЕЛЬНО 0,4= {0/0,2; 0,25/0,25; 0,5/0,3; 0,75/0,35; 1/0,4;
0,75/0,45; 0,5/0,5; 0,25/0,55; 0/0,6}.
Разбиваем А на уровневые множества:
Ах={0,25; 0,3; 0,35; 0,4; 0,45; 0,5; 0,55; 0,6}, 0<а<0,25;
Ла={0,3; 0,35; 0,4; 0,45; 0,5; 0,55; 0,6}, 0,25<а^0,5;
Ла={0,35; 0,4; 0,45; 0,5; 0,55; 0,6}, 0,5<а^0,75;
Ла={0,4; 0,45; 0,5; 0,55; 0,6}, 0,75<а<1.

74 Глава 3. Методы сравнения нечетких множеств
Находим средние значения на каждом уровне:
,. 0,25+0,3+-0,35+0,4+0,45+ 0,5'+0,55+0,6 з,4 лпс
Af.» _ >=—=0,425;
.. 0,3+0,35+0,4+0,45+0,5+0,55 + 0,6 3,15
Мщ= =—=—=0,45;
., 0,35+0,4 + 0,45+0,5+0,55+0,6 2.85
М3= =——=0,475;
.. 0,4+0,45 + 0,5+0,55 + 0,6 2,5 пс
Л10,5.
Л14===
о о
Значение функции упорядочения
1 0,25 0,5 0,75 1
F(A)l= jM(Aa)da= $0,425da+ Jo,45da+ J 0,475cfa+ Jo,5da=
0 0 0,25 0,5 0,75
=0,25 (;0,425 + 0,45+0,475 + 0,5) = 1,85 • 0,25 = 0,462.
Те же действия производим и для множества В:
В = ПРИБЛИЗИТЕЛЬНО 0,7= {0/0,5; 0,25/0,55; 0,5/0,6; 0,75/0,65;
1/0,7; 0,75/0,75; 0,5/0,8; 0,25/0,85; 0/0,9}.
5а={0,55; 0,6; 0,65; 0,7; 0,75; 0,8; 0,85; 0,9}, 0<а<0,25;
Ва={0,6; 0,65; 0,7; 0,75; 0,8; 0,85; 0,9}, 0,25<а<0,5;
Ва={0,65; 0,7; 0,75; 0,8; 0,85; 0,9}, 0,5<а<0,75;
?«={0,7; 0,75; 0,8; 0,85; 0,9}, 0,75<а<1;
о
4 ПЧ
М4=-~^-=
о
= J AI(Дв)Лс=0,25@,725+0,75+0,78+0,806) -
о
=3,116-0,25=0,779.
Теперь можно сравнить F(A) и F(B): 0,462<0,779. Следовательно,
А<В.
Пример 3.8. Сравнить А = ПРИБЛИЗИТЕЛЬНО 0,41 и В =
ПРИБЛИЗИТЕЛЬНО 0,43 (рис. 3.9).
А = ПРИБЛИЗИТЕЛЬНО 0,41 = {0/0,2; 0,25/0,25; 0,5/0,32; 0,75/0,37;
1/0,41; ,0,75/0,48; 0,5/0,55; 0,25/0,83; 0/0,7};
Ла={0,25; 0,32; 0,37; 0,41; 0,48; 0,55; 0,83; 0,7}, 0<а^0,25;

3.3. Упорядочение, характеризующее неприятие риска
75
0,1 0,2 0,3 0Л 0,5 0,6 0,7 0,8 0,9 X
Рис. 3.9. Нечеткие множества ПРИБЛИЗИТЕЛЬНО
0,41 и ПРИБЛИЗИТЕЛЬНО 0,43
Ла={0,32; 0,37; 0,41; 0,48; 0,55; 0,63; 0,7}, 0,25<а^0,5;
Ах ={0,37; 0,41; 0,48; 0,55; 0,63; 0,7}, 0,5«а<0,75;
Ла={0,41; 0,48; 0,55; 0,63; 0,7}, 0,75<а^1;
Afi = 0,464; M2'=0,494; M3 = 0,523; М4=0,554; F(A) =0,509.
Далее, для множества В:
^ПРИБЛИЗИТЕЛЬНО 0,43= {0/0,1; 0,25/0,18; 0,5/0,26;
0,75/0,354; 1/0,43; 0,75/0,54; 0,5/0,65; 0,25/0,78; 0/0,9};
Яа={0,18; 0,26; 0,35; 0,43; 0,54; 0,65; 0,78; 0,9}, 0<а<0,25;
5а={0,26; 0,35; 0,43; 0,54; 0,65; 0,78; 0,09}, 0,25<а<0,5;
Б№={0,35; 0,43; 0,54; 0,65; 0,78; 0,9}, 0,5<а==?0,75;
Ва={0,43; 0,54; \0,65; 0,78; 0,9}, 0,75<а<1;
Afi=0,511; М2=0,559; Мг=0,608; М4=0,66; F(B) =0,584.
Сравниваем F(A) и F(B): 0,509<0,584. Отсюда видно, что А<В.
3.3. УПОРЯДОЧЕНИЕ
НЕЧЕТКИХ ЧИСЕЛ,
ХАРАКТЕРИЗУЮЩЕЕ
НЕПРИЯТИЕ РИСКА
Рассматриваемый в данном параграфе метод позволяет учесть
возможный «пессимизм» ЛПР при установлении порядка на нечетких
числах. Для решения этой проблемы используется отношение «больше
или равно» для двух четких чисел [2].

76 Глава 3. Методы сравнения нечетких множеств
Краткие сведения о методе. Пусть v и w — два четких
положительных числа. Тогда
v>w -<==>- >е[0,5; П; v = w<==>- = =0,5;
v + w L J v + w w + v
[0; 0,5].
J
v + w
Рассмотрим указанные условия для случая установления порядка
между двумя нечеткими числами V и W, такими, что V— \j \i~ (v)fv
ve=V V
и W= IJ \i~(w)/w, где V и W — области определения нечетких чи-
w
сел V и W; \i~ ии^, — функции принадлежности соответственно.
V W
Определим нечеткие отношения
v+w
C.15)
w w
г= v . t)?V, weW
v+w
где \1р„ и \хр „ — функции принадлежности нечетких отношений Р~
V W V
и Р~ соответственно;
w
VICID^ («) = mm (ц ^ (о), ц^ (ш)).
Следуя C.15), определим отношение «больше»:
Р, где Р={@;
; 0,5]; z'fe[0,5; 1]; (ЗЛ6)
v w
Нечеткое отношение Р в C.16) соответствует понятию СТРОГО
(ВСЕГДА) БОЛЬШЕ. При этом возможны ситуации:
1) Р„*()Р=Р~- Тогда W(]V=0 и Р. ПР~ =0, а следовательно,
И V V W
Р„ аР и V>W. Это наиболее тривиальный случай, так как устано-
v
вить отношение «больше» между V и W в этой ситуации можно
однозначно.

11 Упорядочение, Характеризующее неприятие риски 11
2) Р~ (\РФР~. Тогда 7[\№ф0 и Р~ {\Р ~ Ф,0. Именно данный
V V V W
случай заслуживает внимания, так как в соответствии с C.16) не
удается установить искомое отношение БОЛЬШЕ между V и W> т.е.
нечеткое отношение Р~ &Р. Для решения проблемы предлагается
интегральная оценка близости двух нечетких множеств Р~н Р— величина
d~~, определяемая выражением
V W
— для непрерывных нечетких чисел V и W
0,5 1
-l** - (z))dz+ JV~ (z)dz'> C17)
V V
0 V 0,5
— для дискретных нечетких чисел V и W
п' т'
C.18)
где n'+n"9 m'+m" — количество точек области определения,
представляющих нечеткие числа V и W соответственно; г^Е[0; 0,5] и г"ц^
€=[0,5; 1].
Аналогично выражениям C.17) и C.18) можно рассчитать
интегральную оценку близости d— нечетких отношений Р~ и Р. Учиты-
V W W
вая равенство \1р„ I——J =\лр„ I——— I, легко показать, что а„ „ +
+d~~ =1, а следовательно, для установления отношения БОЛЬШЕ
v w
между V и W необходимо и достаточно, чтобы d~~>0,5, т.е. формально
V W
F>TF^==^d_€=[0,5; 1]. C.19)
V W
Для равенства двух нечетких чисел V и W должно выполняться
V=W<==>d~~=d~»=0,5. C.20)
V W WV
Отметим, что в соответствии с условием C.20) два числа, одно из
которых четкое — W> а другое нечеткое — F, могут находиться в
отношении РАВНО. При этом, если носителем W является единственное
число w, а носителем V — интервал [v°t w*], легко показать, что для
выполнения равенства V—W должно иметь место w = yv°v* при
симметричной линейной функции принадлежности \i~ (и). Указанные
свойства упорядочения нечетких чисел на основе предложенной процедуры
C.15) — C.20) характеризуют «осторожное» поведение Л ПР.
Примеры использования метода. Пример 3.9. Пусть V — нечеткое
число ПРИБЛИЗИТЕЛЬНО 0,4= {0/0,2; 0,25/0,25; 0,5/0,3; 0,75/0,35;
1/0,4; 0,75/0,45; 0,5/0,5; 0,25/0,55; 0/0,6}, W — четкое число 0,4.

Глава 3. Методы сравнения нечетких множеств
М
1.0
0.8
0.6
0Л
0.2
0.2 0,4 0.6 0.8 1.0V.W.Z
Рис. 3.10. Нечеткое число
ПРИБЛИЗИТЕЛЬНО 0,4 и четкое число 0,4
Построим отношение Р~ согласно C.15). В расчетах z= —
И*,
0,2
0,6
0
0,25
0,65
0,25
! вычислений:
0,33
0
0,38
0,25
V
0,3
0,7
0,5
0,43
0,5
0,35
0,75
0,75
0,47
0,75
0,4
0,8
1
0,5
1,0
0,45
0,85
0,75
0,53
0,75
0,5
0,9
0,5
0,56
0,5
v + w
0,55
0,25
0,25
0,58
0,25
0,6
0
0
0,6
0
Функции принадлежности jx~ и \ip „ нечеткого числа F, нечеткого от-
V v
ношения Р„ и четкое число W изображены на рис. ЗЛО. Интегральная
v
оценка близости Р~ и Р,— d ~ характеризует отношение между V nW:
v v w
0,5 1
dv w =
Так как определенный интеграл геометрически представляет собой
площадь криволинейной трапеции, то на рис. 3.12 d~ равно площади
V W
заштрихованной части. Для дискретного представления функции
принадлежности
ъ п
г=1
Тогда C.21) примет вид
0,5
0,5
W
= U-dz-
0,5
•~ (г)йг--
v

3.3. Упорядбченнё, Характеризующее неприятие риека
Рис. 3.11. Нечеткие числа
ПРИБЛИЗИТЕЛЬНО 0,4 и
ПРИБЛИЗИТЕЛЬНО 0,7
1
0.2 0,4 0.6 0.8 1.0V.W.Z
<z )
B »¦
где а*, 6,- — соответственно нижний и верхний пределы изменения
функции принадлежности отношения цр ^ (z); «i — количество точек,
V
для которых цр„ (г)ф0; г'е[0; 0,5]; z"e[0,5; I]. Тогда
v
v w 2
1 0,5-0,33
0,6-0,5
(z ) =
= 1 /2 - 0,042 @,25 + 0,5 + 0,75 +1,0) + 0,025 A, - 0,75+0,5+0,25) =
= 1/2 + 0,042.2,5+0,025.2,5=1/2-0,106 + 0,0625=0,456;
d~ <0,5, следовательно, P < W, т. е. для «осторожного» ЛПР 0,4
больше^ чем ПРИБЛИЗИТЕЛЬНО 0,4.
Пример ЗЛО (рис. 3.11).
Г= ПРИБЛИЗИТЕЛЬНО 0,4= {0/0,2; 0,25/0,25; 0,5/0,3;
0,75/0,35; 1/0,4; 0,75/0,45; 0,5/0,5; 0,25/0,55; 0/0,6};
W=ПРИБЛИЗИТЕЛЬНО 0,7= {0/0,5; 0,25/0,55; 0,5/0,6;
0,75/0,65; 1/0,7; 0,75/0,75; 0,5/0,8; 0,25/0,85; 0/0,9}.
Находим значения базового множества отношения:
П' °'2-=0,29;
Zl=-
0,2+0,5 0,7
0,25
0,25
-=-—-=0,31;
0,3
-=0,33;
" 0,25 + 0,55 0,8 ' ' - 0,3 + 0,6
24=0,35; 25 = 0,364; z6 = 0,374; г7=0,383; г8=0,393; 29=0,4.

86 Глава 3. Методы сра&нения нечетких
Функция принадлежности отношения имеет вид
(Хр^ (z) = {0/0,29; 0,25/0,31; 0,5/0,33; 0,75/0,35; 1/0,364;
v
0,75/0,374; 0,5/0,383; 0,25/0,393; 0/4}.
Воспользуемся определением криволинейного интеграла:
П1 П2
Ь\ — С1\ \ ^ ь^2"Н~^2 \ ^
d ^ /ч/==: "»*5"-" ————— j^^j jjip /ч/ \Z f -f-~~^ .^^j H'JP/ч/ '^ /»
где аг- и Ьг- — пределы изменения функции принадлежности; т —
точки, в которых \1р„(г)ф0; z'^[0; 0,5]; z"^[0,5; 1]. Так как в дан-
v
ном случае таких значений z" нет, то второе слагаемое исчезает.
Получаем
„_.-w-iizS Д ^. w-0,5- "•4-°-29 х
v w Wi *^ v 7
X @,25+0,5+0,75 +1+0,75 +0,5 +0,25) =0,5- 0>11'4 =
= 0,5-0,062 = 0,448.
Значение d <0,5, т.е. попадает в интервал [0; 0,5]. Следовательно,
vw
V<W.
3.4. УПОРЯДОЧЕНИЕ
НЕЧЕТКИХ МНОЖЕСТВ
С ИСПОЛЬЗОВАНИЕМ ОТНОШЕНИЙ
Рассматривается метод упорядочения альтернатив путем
нахождения их принадлежности оптимальному множеству. Последнее
определяется как пересечение критериальных оценок альтернатив и
нечеткого отношения предпочтения.
Краткие сведения о методе. Рассмотрим задачу принятия решений.
Имеется множество п альтернатив: {аь ...,ап}. Каждая из них
характеризуется нечетким множеством Ai={\iA (x)/x}, x^ R (в
рассматриваемых примерах д:е[0, 1]). Требуется определить множество
оптимальных альтернатив 0= {\io(i)/i}, te N , где |Ао@ может
рассматриваться как степень соответствия альтернативы щ понятию
«наилучшая альтернатива». Для этой цели вводится нечеткое отношение Рц =
^'W (*u Xj)/(xu *j)}, Xj(=E R , гдецг^ (xif Xj) выражает степень
превосходства х\ над Xj или насколько Хг лучше Xj. Пусть функция
f(Xi, Xj) задает различие в полезностях значений хг и ху, f(xu Xj) =
= u(xi) —u(Xj), т.е. \ip =f(Xi, Xj). В простейшем случае это может
быть линейная функция: [ip =Xi — Xj (рис. 3.12 и 3.13).

5.4. Упорядочение с использованием отношений
Рис. 3.12. Функция принадлежности отношения
Р12 при и(х)=х
Множество оптимальных альтернатив определяется как пересечение
декартова произведения нечетких оценок, задающих альтернативы и
отношения предпочтения Рц: O = Pij(](AiXAj). Степень принадлежности
альтернативы а* множеству О находится как максимальное значение
соответствующих функций принадлежности:
ио@ = supmin ([iA .(хг)> Iia.(Xj); \iP . (*<, Xj)), 1ф\, ie{l, 2}. C.22)
г г lj
Примеры использования метода. Пример 3.11. Пусть
Л4= {0,2/0,5; 0,8/0,6; 1/0,7; 0,8/0,8; 0,1/0,9};
Л21= {0,1/0,1; 0,8/0,2; 1/0,3; 0,8/0,4; 0,1/0,5}.
Рис. 3.13. Функция принадлежности отношения
Р2\ при и(х)=х
6 — 2307

82
Глава 3. Методы сравнений нечетких множеств
Рис. 3.14. Функция принадлежности отношения
при У
Тогда
0,5
0,6
0,7
0,8
0,9
0,1 0,2 0,3 0,4 0,5
0,1 0,2 0,2 0,2 0,1
0,1 0,8 0,8 0,8 0,1
0,1 0,8 1,0 0,8 0,1
0,1 0,8 0,8 0,8 0,1
0,1 0,1 0,1 0,1 0,1
В операции А\ХА2 значения базового множества получаются из
значений базовых множеств нечетких множеств А\ и Лг, причем на
первом месте находится значение базового множества А\. Значение \х
выбирается наименьшим из значений слагаемых нечетких множеств А\
и Л2.
Рис. 3.15. Функция принадлежности отношения
Р2\ при и(*)=У*

3.4. Упорядочение t использованием отношений
Теперь построим функции принадлежности Р\2 и Р21. Так как
12 (ATI, X2)i=X\— X2, ТО ЭТО ИМееТ СМЫСЛ ДЛЯ Х^Х^
О 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9
0,1
0,2
0,3
0,4
Р\2(хи%ъ)== 0,5
0,6
0,7
0,8
0,9
1,0
Отношение P2i
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
0,1
0,2 0,1
0,3 0,2 0,1
0,4 0,3 0,2
0,5 0,4 0,3
0,6 0,5 0,4
0,7 0,6 0,5
0,8 0,'
7 0,6
0,9 0,8 0,7
записывается
0,1
0,2
0,3
0,4
0,5
0,6
0,1
0,2
0,3
0,4
0,5
аналогично Р
х2 на Х\. Находим пересечение полученных
Р12ПИ1/
<А%) --
0.5
0,6
= 07
0,8
0,9
0,1
0,1
0 1
01
0,1
0,1
0,2
0,2
04
0 5
0,6
0,1
0,1
0,2
0,3
0,4
12 С
0,1
0,2 0,1
0,3 0,2
заменой х\
множеств:
0,3
0,2
0,3
0,4
0,5
0,1
0,4
0,1
0?
03
0,4
0,1
0,5
—
01
0,1
од
0,1
0,1
на
Чтобы выполнить операцию Р\г\\{А\УуАг), необходимо сравнить
базовые значения множеств РJ и АхХА2. Выбираем слагаемое, у
которого значение [i меньше, и в соответствии с выражением C.22) имеем
для первой альтернативы цо A) =0,6. Найдем пересечение для второй
альтернативы: Р21П(-^iХЛ2) =0, следовательно, цоB)=0. Итак,
множество оптимальных альтернатив O={0,6/ai, 0/a2}.
Пример 3.12. Пусть теперь функция полезности имеет вид и(х) =
— Ух. Таким образом, ця..(*,-, Xj)=yx, — У*,-. Функции принадлежности
|хр,2 и цр24 представлены на рис. 3.14 и 3.15. Определим отношение
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
0,3
0,4
0,5
0,6
0,7
0,8
0,8
0,9
0,9
1,0
0,1
0,2
0,3
0,4
0,5
0,5
0,6
0,6
0,7
0,1
0,2
0,3
0,3
0,4
0,5
0,5
0,6
0,1
0,2
0,2
0,3
0,3
0,4
0,5
0,1
0,1
0,2
0,3
0,3
0,4
0,1
0,1
0,2
0,2
0,3
0,1
0,1
0,2
0,2
0,1
0,1 0,1
0,2 0,1
0,1

84
(Глава h. Методы сравнения нечетких Множеств
Рис. 3.16. Функция принадлежности отношения Р\2
при и(х)=х2
Нечеткое отношение Р2\ записывается аналогично Р\2 с заменой хх
на х2.
Тогда пересечение полученных множеств
0,1 0,2 0,3 0,4 0,5
0,5
0,6
0,7
0,8
0,9
0,1
0,1
0,1
0,1
0,1
0,2
0,3
0,4
0,5
0,1
0,2
0,2
0,3
0,3
0,1
0,1
0,1
0,2
0,3
0,1
0,1
0,1
0,1
од
В соответствии с C.22) определим принадлежность первой
альтернативы множеству оптимальных альтернатив: до A) =0,5.
Рис. 3.17. Функция принадлежности отношения
P2i при и(х) =х2

3.4. Упорядочение с использованием отношений
85
Аналогично для второй альтернативы P2if\(A\XA2)=0, т. е. [юB) =
= 0. Тогда множество оптимальных альтернатив О={0,5/аь 0/а2}.
Пример 3.13. Рассмотрим случай и (х) =х2, т. е. \i p (хи Xj) = xf —
— Xj2. Пусть
Ai= {0,7/0,5; 0,9/0,6; 0,1/0,7; 0,4/0,8; 0,2/0,9};
А*= {0,7/0,1; 0,3/0,2; 0,2/0,3; 0,9/0,4; 1/0,5}.
Тогда
0,5
0,6
0,7
0,8
0,9
0,1 0,2 0,3 0,4 0,5
0,7 0,3 0,2 0,7 0,7
0,7 0,3 0,2 0,9 0,9
0,1 0,1 0,1 0,1 0,1
0,4 0,3 0,2 0,4 0,4
0,2 0,2 0,2 0,2 0,2
(см. пояснение к примеру 3.11).
Построим функцию принадлежности Рп и Р2\ (рис. 3.16 и 3.17). Так
как функция принадлежности \i,pi2(xi, хг)=х\2—Х22, то это имеет смысл
для х\~^х2. Таким образом, отношение
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9
0,1
0,2
0,3
0.4
0,5
0,6
0,7
0,8
0,9
1,0
о
о о
0,1 0 0
0,2 0,2 0,2 0,1
0,3 0,2 0,3 0,1 0,1
0,4 0,4 0,4 0,3 0,2 0,1
0,5 0,5 0,5 0,4 0,3 0,2 0,1
0,6 0,6 0,6 0,5 0,4 0,3 0,2 0,1
0,8 0,8 0,8 0,7 0,6 0,5 0,4 0,3 0,2
1,0 1,0 1,0 0,9 0,8 0,7 0,6 0,5 0,4 0,1
Отношение Р2\ записывается аналогично Р\2 с заменой х\ на х2,
а Х2 на х\. Находим
0,1 0,2 0,3 0,4 0,5
0,5
0,6
0,7
0,8
0,9
0,2 0,3 0,1 0,1 —
0,4 0,3 0,2 0,2 0,1
0,1 0,1 0,1 0,1 0,1
0,4 0,3 0,2 0,4 0,3
0,2 0,2 0,2 0,2 0,2
Итак, для первой альтернативы цоA)=0,4. Для второй
альтернативы P2i(](AiXA2)=0 и, следовательно, цоB)=0.
Таким образом, множество оптимальных альтернатив O={0,4/oi,
0/с2}.

Глава 4
МНОГОКРИТЕРИАЛЬНАЯ ОЦЕНКА
И ВЫБОР АЛЬТЕРНАТИВ
НА ОСНОВЕ
НЕЧЕТКИХ МНОЖЕСТВ
4.1. ПРИНЯТИЕ РЕШЕНИЙ
В УСЛОВИЯХ ОПРЕДЕЛЕННОСТИ
Рассматривается метод анализа альтернатив в случае, когда
критериальные оценки задаются как степени соответствия альтернатив
понятиям, определяемым критериями. Используется свертка на основе
операции пересечения нечетких множеств [1].
Краткие сведения о методе. Пусть имеется множество из m
альтернатив
Тогда для критерия С может быть рассмотрено нечеткое множество
2,... ,\ic(am)/am},
где \xc(ai)^[Of 1] — оценка альтернативы щ по критерию С,
характеризует степень соответствия альтернативы понятию, определяемому
критерием С.
Если имеется п критериев: С\, Сг,... ,СП, то лучшей считается
альтернатива, удовлетворяющая и критерию Ci, и Сг, и ..., и Сп. Тогда
правило для выбора1 наилучшей альтернативы может быть записано
в виде пересечения соответствующих нечетких множеств:
?>=С,ПС2Л...ПС„. D.1)
Таблица 4.1
Шкала оценок важности
Относительная важность
критериев С{ и Ci
Элемент
Равная важность
Немного важнее
Важнее
Заметно важнее
Намного важнее
Промежуточные значения
1
3
5
7
9
2, 4, 6, 8

4.1. Принятие решений в условиях определенности 87
Операции пересечения нечетких множеств соответствует операция min,
выполняемая над их функциями принадлежности:
(а,), /=1,т. D.2)
г=1,п
В качестве лучшей выбирается альтернатива а*, имеющая наибольшее
значение функции принадлежности
\id (a*) = maxjiD (а,}). D.3)
В случае, если критерии Сг- имеют различную важность, каждому
из них приписывается число сц^О (чем важнее критерий, тем больше
си), и правило выбора принимает вид
^-сГ^^П.-.ПС^; D.4)
п
l
^.i—1. D.5)
п Г?
Коэффициенты относительной важности определяются на основе
процедуры парного сравнения критериев. Вначале формируется матрица В,
элементы которой находятся из табл. 4.1 и удовлетворяют следующим
условиям: 6«=1; Ьц=1/Ьц.
Затем согласно процедуре, описанной в параграфе 1.1, находится
w — собственный вектор матрицы В, соответствующий максимальному
собственному значению imax:
Bw = A,maxW. D.6)
Искомые значения коэффициентов щ получаются умножением
элементов w на п для выполнения условия D.5):
ai = nWi. D.7)
Примеры использования метода. Пример 4.1. Критерии равной
важности. Рассмотрим задачу выбора директором производственного
объединения руководителя подчиненного ему предприятия из пяти
претендентов: а\ — главный инженер вышеуказанного предприятия; а2 —
директор более мелкого подчиненного предприятия; аз — сотрудник
НИИ; «4 — третий заместитель директора; а$ — молодой талантливый
инженер.
Претенденты оцениваются по следующим критериям: С\ —
профессиональные навыки; Сг — организаторские способности; Съ — опыт
работы такого рода; d — авторитет; С$ — умение работать с людьми;
Се — возраст.
Выявив, насколько каждый из кандидатов соответствует
рассматриваемым критериям, получим следующие множества:
2; 0,6/а3; 0,8/а4; 0,5/а5};
C2={0,8/ai; 0,9/а2; 0,5/а3; 0,7/а4; 0,6/а5};
Cs={0,7/ai; 0,9Д%; 0,8/а3; 0,5/а4; 0,3/а5};

88
Глава 4. Многокритериальная оценка и выбор
С4={0,9/аь 0,8/а2; 0,5/а3; 0,6/а4; 0,5/а5};
С5={0,9/а1; 0,9/а2; 0,4/а3; 0,7/а4; 0,6/а5};
C6={0,9/ai; 0,4/а2; 0,8/а3; 0,7/а4; 0,5/а5}.
Тогда правило выбора имеет вид
?>={mirK @,9; 0,8; 0,7; 0,9; 0,9; 0,9)/a*;
min @,9; 0,9; 0,9; 0,8; 0,9; 0,4)/a2;
min @,6; 0,5; 0,8; 0,5; 0,4; 0,8)/a3;
mini @,8; 0,7; 0,5; 0,6; 0,7; 0,7)/a4;
min @,5; 0,6; 0,3; 0,5; 0,6; 0,5)/a5} =
= {0,7/ai; 0,4/a2; 0,4/a3; 0,5/a4; 0,3/a5}.
Видно, что лучшей является альтернатива а\.
Пример 4.2. Критерии различной важности. Рассмотрим задачу
выбора места для строительства химического комбината исходя из
следующих критериев: С\ — близость к потребителю; С2 — близость
к источникам сырья; Сз — наличие в городе свободной рабочей силы.
Предполагаемые места строительства: аь а2, а3, #4-
Нечеткие множества, характеризующие альтернативные варианты с
точки зрения различных критериев:
Ci={0,5/ai; 0,7/a2; 0,3/a3; 0,6/a4};
C2 = {0,5/ai; 0,4/a2; 0,8/a3; 0,4/a4};
C3={0,2/ai; 0,l/a2; 0,6/a3; 0,9/a4}.
Критерии имеют различную важность, результаты их попарного
сравнения представлены матрицей
Ci С2 С3
s= c2
Собственный вектор матрицы В: te>i = 0,06; до2=0,27; а>з = 0,67. Тогда
коэффициенты относительной важности критериев а\ = 3-0,06=0,18,
02=3-0,27=0,81, ссз=3-0,67=2,01.
Модифицируем множества Сс
C,°.I8= {0,5°-18/ai; 0,7°.18/a2; 0,3°.18/a3; 0,6°.18/a4} =
= {0,88/a,; 0,94/a2; 0,81/a3; 0,91/a4};
i; 0,48/a2; 0,83/a3; 0,48/a4};
i; 0,01/c2; 0,36/a3; 0,81/a4}.
1
1/5
3
5
1
9
1/3
1/9
1

4,2. Выбор альтернатив при аддитивности критериев
89
Получим множество
Z)={0,04/ai; 0,01/a2; 0,36/a3; 0,48/a4}.
Максимальное значение принадлежности имеет альтернатива а4 —
ее и следует выбрать в качестве возможного места строительства.
4.2. ОЦЕНКА
И УПОРЯДОЧЕНИЕ АЛЬТЕРНАТИВ
ПРИ АДДИТИВНОСТИ КРИТЕРИЕВ
Рассматривается метод ранжирования альтернатив на основе
аддитивной свертки [2], обобщенной на случай нечеткой исходной
информации. Используется треугольное представление нечетких оценок
альтернатив и коэффициентов важности критериев.
Краткие сведения о методе. Пусть необходимо упорядочить m
альтернатив, оцениваемых по п критериям: ab a2,..., ат.
Соответствующую оценку обозначим Rijy i=l,m. Относительная важность каждого
критерия задается коэффициентом Wj, /=l,n. В этом случае
взвешенная оценка i-ik альтернативы вычисляется по формуле
D.8)
D.9)
или, если оценки нормированы,
3=t
Рассмотрим расчет Rif когда оценки альтернатив по критериям и
коэффициенты относительной важности задаются функциями
принадлежности соответственно \iR (r2j) и \i w (Wj), где rijf Wj<= R .
Так как в данном случае R{j и Wj являются нечеткими числами, R{
определяется в соответствии с формулой D.8) или D.9) на основе
принципа обобщения [3]. Бинарную операцию * (в данном случае это
М
1.0
Рис. 4.1.
числа
Границы и вершина нечеткого
х" X

Глава 4. Многокритериальная оценка и выбор
1,0
0,8
0,6
0.4
0.2
0
УДОВЛЕТВОРИТЕЛЬНАЯ ХОРОШАЯ
/\
\
\
0,2 0,4 0,6 0,8 1,0 Rtj
Рас. 4.2. Функции
принадлежности критериальных оценок
для случая двух альтернатив
операция сложения или умножения) можно обобщить на случай
нечетких чисел (например, X и У), задаваемых функциями принадлежности
([ix(х) и \ir(y) соответственно). Результат обобщенной операции * —
нечеткое число Z, определяемое функцией принадлежности
(\xx(x), \iY{y)). D.10)
Другой способ вычисления Ri может быть использован в случае,
когда Rij и Wj заданы функциями принадлежности треугольного вида
(рис. 4.1).
Определив левую X' и правую X" границы нечеткого числа Хх а
также его вершину X*:
Y6:
=0;
довольно
НЕВАЖНЫЙ
ОЧЕНЬ
ВАЖНЫЙ
Рис. 4.3. Функции принадлежности коэффициентов
важности Wu W2

4.2. Выбор альтернатив при аддитивности критериев
1,0
0,82
0,2 0,4 0,6 0,8 1,0 1,2 UR,-
Рис. 4.4. Функции принадлежности взвешенных оценок
Ль #2
можно доказать, что нечеткое число Z = X^Y также определяется
функцией принадлежности треугольного вида, а границы и вершина
находятся следующим образом:
Z'=X'*Y', Z"=X"*Y", Z* = X**Y*. D.11)
После того как взвешенные оценки R\ получены, необходимо
сравнить альтернативы на их основе. Для этого вводится нечеткое
множество /, заданное на множестве индексов альтернатив {1, 2,..., т},
и значение соответствующей функции принадлежности
интерпретируется как характеристика степени того, насколько альтернатива й\
является лучшей. Значение \xi(i) вычисляется по формуле
@ mini [Ад ,.(г,), D.12)
Л*
1,0
HE ОЧЕНЬ
_ ВАЖНЫЙ
//
ДОВОЛЬНО
ВАЖНЫЙ ВАЖНЫЙ
"Л"Л~
/ у V
W
ОЧЕНЬ
ВАЖНЫЙ
д
' \
\
\
\ \
0.2
0.4
0,6 0,8
LOW)
Рис. 4.5. Функции принадлежности коэффициентов
важности Wu Wb №з, WA

92 Глава 4. Многокритериальная оценка и выбор
Таблица 4.2
Критериальные


терий
оценки
ДЛЯ
1
случая
двух альтернатив
Альтернатива
1
1 ХОРОШАЯ УДОВЛЕТВОРИТЕЛЬНАЯ
2 УДОВЛЕТВОРИТЕЛЬНАЯ ХОРОШАЯ
и, как нетрудно видеть, равно ординате точки пересечения
взвешенной оценки альтернативы и оценки наилучшей альтернативы.
Примеры использования метода. Пример 4.3. Рассмотрим задачу
ранжирования двух альтернатив, имеющих оценки, приведенные в
табл. 4.2.
Первый критерий определен как ОЧЕНЬ ВАЖНЫЙ, второй —
ДОВОЛЬНО НЕВАЖНЫЙ. Термы заданы функциями принадлежности,
представленными на рис. 4.2 и 4.3. В этом случае на основании D.11)
^//i2= 1,0-1,0+ 0,8-0,4 =1,32;
2H7*2 = 0,8 -1,0 + 0,6- 0,2 = 0,92.
Аналогично /?'2 = 0,32, /?'2=1,2, /?*2 = 0,76. Полученные функции
принадлежности изображены на рис. 4.4. Тогда в соответствии с формулой
D.12) (ш/A) = 1; \иB) =0,76. Следовательно, наилучшей является
первая альтернатива, а степень того, что вторая альтернатива лучшая,
равна 0,76.
Пример 4.4. Рассмотрим задачу ранжирования четырех
альтернатив, оценки которых приведены в табл. 4.3.
Первый критерий определен как ВАЖНЫЙ, второй — ДОВОЛЬНО
ВАЖНЫЙ, третий — ОЧЕНЬ ВАЖНЫЙ, четвертый — НЕ ОЧЕНЬ
ВАЖНЫЙ. Термы заданы функциями принадлежности,
представленными на рис. 4.5 и 4.6.
Построим функции принадлежности взвешенных оценок для
альтернатив:
= 0,2 • 0,4 + 0,6 • 0,2 + 0,6 • 0,6 + 0,2 • 0 = 0,56;
Таблица 4.3
Критериальные
Критерий
оценки
1
ДЛЯ
1
случая
2
четырех
альтернатив
Альтернатива
1 *
1 ПЛОХАЯ ХОРОШАЯ УДОВЛЕТВОРИТЕЛЬНАЯ ПЛОХАЯ
2 ХОРОШАЯ
3 „ „ ПЛОХАЯ
4 ПЛОХАЯ „ ХОРОШАЯ

4.2. Выбор альтернатов При аддитивности критериев
1.0
УДОВЛЕТВО-
ПЛОХАЯ РИТЕЛЬНАЯ ХОРОШАЯ
0.2 0./, 0.5
1.0 Ry
Рмс. 4.6. Функции принадлежности критериальных оценок
для случая четырех альтернатив
0,6-0,8+1-0,6+1-1+0,6-0,4=2,32;
=0,4 • 0,6+0,8 • 0,4 + 0,8 • 0,81-4- 0,4 • 0,2 = 1,28.
Аналогично
#'2=0,72; Я'з^О.Зб; /?/4 = 0,2
#=2,8; /?"з = 2,12; R'\=l,6
#*2=1,6;
#*з=1,08;
Полученные функции изображены на рис. 4.7. Тогда в соответствии
с формулой D.12) ц/A)=0,83, ц7B) = 1; ^C) =0,73; ^D) =0,55. Слв-
0.5 1.0 1,5 2.0 2.5 R,
Рис. 4.7. Функции принадлежности взвешенных оценок

94 Глава 4. Многокритериальная оценка и выбор
довательно, наилучшей является вторая альтернатива, а степень того,
что первая альтернатива лучшая, равна 0,83, третья — 0,73,
четвертая — 0,55.
Итак, получено следующее упорядочение альтернатив: 2, 1,3, 4.
4.3. ВЫБОР АЛЬТЕРНАТИВ
С ИСПОЛЬЗОВАНИЕМ
ПРАВИЛА НЕЧЕТКОГО ВЫВОДА
Рассматривается метод многокритериального выбора альтернатив
на основе композиционного правила агрегирования описаний
альтернатив с информацией о предпочтениях ЛПР, заданных в виде
нечетких суждений [5, 6].
Краткие сведения о методе. Пусть U — множество элементов, А —
его нечеткое подмножество, степень принадлежности элементов
которого есть число из единичного интервала [0,1]. Подмножества А
являются значениями лингвистической переменной X.
Пусть множество решений характеризуется набором критериев
Хи Х2,...уХр, т.е. лингвистических переменных на базовых
множествах U\9 U2y..., Up соответственно. Например, переменная Ху
«Квартирная плата» может иметь значение НИЗКАЯ, а переменная Х2
«Расположение квартиры» — значение ХОРОШЕЕ и т. п. Набор из
нескольких критериев с соответствующими значениями характеризует
представления ЛПР об удовлетворительности (приемлемости)
решения. Переменная S «Удовлетворительность» также является
лингвистической. Пример высказывания:
d{: «Если Х^НИЗКАЯ и Х2 = ХОРОШЕЕ, то Я^
В общем случае высказывание di имеет вид
dr. «Если Х{=Ац и X2=A2i и ... Xp = Apiy то S = Bi». D 13)
Обозначим пересечение (Xi=Auf\X2=A2i[]. ..Xp=Api) черезX=Ai.
Операции пересечения нечетких множеств соответствует нахождение
минимума их функций принадлежности:
.(V) = ПИП (|ХАЙ(«1),|1АЙ(«2), • • • ,\lAip (Up)), D.14)
где V=U\XU2X ... XUP; v=(U\, u2,...,up); [iAij (uj) — значение
принадлежности элемента Uj нечеткому множеству Aij. Тогда D.12)
можно записать в виде
dr. «Если Х=Аи то 5 = Вг». D.15)
Для придания общности рассуждениям обозначим базовое
множество U или V через W. Тогда Лг- — нечеткое подмножество W, в то
время как Вг — нечеткое подмножество единичного интервала /.
Импликация нечетких множеств D.15) выражается следующим
образом:
0)Ь D16)

4.3. Bbidop с использованием нечеткого вывода Й§
где Н — нечеткое подмножество на Wxl, w^W, te/. Аналогичным
образом высказывания d\, d% . •.>dq преобразуются в множества #ь
Я2,..., Ня. Их объединением является множество D:
D.17)
и для каждого (w, i)
|1л^ {w,i))9 j=T7q. D.18)
Далее опишем способ выбора альтернатив, каждая из которых
описывается нечетким подмножеством С из W.
Удовлетворительность альтернативы находится на основе
композиционного правила вывода:
G = CoZ), D.19)
где G — нечеткое подмножество интервала /. Тогда
jag @ = max (min (\ic (w), |1d (<M))) • D.20)
Сопоставление альтернатив происходит на основе точечных оценок.
Для нечеткого множества Aczl определим а-уровневое множество
(ае[0, 1]):
D.21)
Для каждого Аа можно вычислить среднее число элементов — М(Аа):
1) для множества из п элементов М (Аа)
2) для Ла=
3) для
71
2=1
Тогда точечное значение для множества А
«max
J M (Aa) da, D.22)
CXmax
где аШах — значение, при котором А имеет максимум.
При выборе альтернатив для каждой из них находится
удовлетворительность и вычисляется соответствующая точечная оценка. Лучшей
считается альтернатива с наибольшим ее значением.
Пример использования метода. Пример 4.5. Руководство
института рассматривает кандидатов на замещение вакантной должности на
факультете. Задача заключается в том, чтобы, используя описанный

4. Многокритериальная оценка и выбор
выше метод, выявить наилучшего из них. Обсуждение среди членов
факультета дало следующий результат:
d\\ «Если кандидат — опытный исследователь, имеет некоторый
производственный стаж и опыт преподавания технических дисциплин, то
он — удовлетворяющий (отвечающий требованиям)»;
d2: «Если он вдобавок к вышеописанным требованиям может
преподавать теорию информационных систем, то он — более чем
удовлетворяющий»;
d3: «Если он вдобавок к условиям d2 имеет способность найти
заказчика наукоемкой продукции, то он — безупречный»;
d4: «Если он имеет все, оговоренное в d$t кроме способности
преподавать теорию информационных систем, то он — очень
удовлетворяющий»;
d$: «Если кандидат — очень опытный исследователь, имеет
способность найти заказчика и хороший преподаватель, но не имеет
производственного стажа, он все же будет удовлетворяющим»;
rf6: «Если он не имеет квалификации исследователя или не имеет
проверенной способности к преподаванию, он — неудовлетворяющий».
Анализ шести информационных фрагментов дает пять критериев,
используемых в принятии решения: Х\ — исследовательские
способности; Х2 — производственный стаж; Х3 — опыт преподавания
технических дисциплин; Х4 — опыт преподавания теории информационных
систем; Х$ — способность найти заказчика.
Будем измерять эти переменные на базовом множестве U
кандидатов. Обращаясь к шести фрагментам, получаем:
dx\ «Если Хх = ОБРАЗОВАННЫЙ и Х2 = НЕКОТОРЫЙ ОПЫТ и
Х3=ХОРОШИЙ, то У=УДОВЛЕТВОРЯЮЩИЙ»;
d2: «Если Хх = ОБРАЗОВАННЫЙ и Х2 = НЕКОТОРЫЙ ОПЫТ и
Х3 = ХОРОШИЙ и Х4 = СПОСОБНЫЙ, то У=БОЛЕЕ ЧЕМ
УДОВЛЕТВОРЯЮЩИЙ»;
d3: «Если ^ОБРАЗОВАННЫЙ и Х2 = НЕКОТОРЫЙ ОПЫТ и
Х3 = ХОРОШИЙ и Х4 = СПОСОБНЫЙ и Х5 = СПОСОБНЫЙ, то У=
= БЕЗУПРЕЧНЫЙ»;
d4: «Если ^ОБРАЗОВАННЫЙ и Х2=НЕКОТОРЫЙ ОПЫТ и
*3 = ХОРОШИЙ и Х5 = СПОСОБНЫЙ, то У==ОЧЕНЬ
УДОВЛЕТВОРЯЮЩИЙ»;
d5: «Если Xi = O4EHb ОБРАЗОВАННЫЙ и Х2=НЕ ИМЕЕТ
ОПЫТА и Х3 = ХОРОШИЙ и Х5 = СПОСОБНЫЙ, то У = УДОВЛЕТВО-
РЯЮЩИЙ»;
d6: «Если *! = HE ОБРАЗОВАННЫЙ или Х3 = НЕ СПОСОБНЫЙ К
ПРЕПОДАВАНИЮ, то У=НЕ УДОВЛЕТВОРЯЮЩИЙ».
Переменная У задана на множестве /= {0; 0,1; 0,2;...; 1}.
УДОВЛЕТВОРЯЮЩИЙ определено как \xs(x)=x, xe=J, БОЛЕЕ
ЧЕМ УДОВЛЕТВОРЯЮЩИЙ — как \ims(x) =уД'*<=/,
БЕЗУПРЕЧНЫЙ — как
1, если х=1;
ОЧЕНЬ УДОВЛЕТВОРЯЮЩИЙ - как ц^(*)-х2, *«=/, НЕ
УДОВЛЕТВОРЯЮЩИЙ — как ^s(x) = l-x, **=/.

4.3. Выбор с использованием нечеткого вывода 97
Выбор производится из пяти кандидатов U={u\, u% из, и^, иь}.
Имеются следующие оценки каждого кандидата:
А = ОБРАЗОВАННЫЙ ИССЛЕДОВАТЕЛЬ = {0,8/и4; 0,6/и2;
0,5/из; 0,1/ад 0,ЗЫ;
5 = НЕК0Т0РЫЙ ПРОИЗВОДСТВЕННЫЙ ОПЫТ= {0,5/at;
С = ХОРОШАЯ СПОСОБНОСТЬ ПРЕПОДАВАНИЯ = {0,6/ад
0,9/а2; 1/м3; 0,7/м4; 1/м5};
D = СПОСОБНОСТЬ ПРЕПОДАВАНИЯ ТЕОРИИ
ИНФОРМАЦИОННЫХ СИСТЕМ={1/и4; 0,ЗМ2; 1/и3; 0/м4; 0/и5};
/Г = СПОСОБНОСТЬ ПОЛУЧЕНИЯ ВНЕШНЕГО ФОНДА =
= {0/uu 0,5/w2; 1/и3; 0,8/w4; 0,1/и5}.
После этого фрагменты знаний принимают вид
dx\ Если Х=А, и В, и С, то Y = S;
d2: Если Х = Л, и В, и С, и D, то Y=MS;
d3: Если Х = А, и В, и С и Д и ?, то Y=P;
dk\ Если Х = Л, и В, и С, и Е, то У- VS;
db\ Если Х^очень Л, и не В, и С, и Е, то y = S;
d6: Если Х = не А или не С, то Y=US.
Используя правило D.14) для перевода этих операций, получаем
для di\ yiM[(u) = min (\ia(и)^iB(и)^с(и))\
i; .0,6/^2; 0/и3\ 0,1/м4;
для d2: |хлг2(«) = min
для d3: |ым3(^) = min {\ia(u),\лв{и)y\ic{u),\jld{u),
М3={0/иц 0,3/u2\ 0/tts; O/w4; 0/«5};
для d4: |im4(w)= min {\ia{u),\iB(u),\ic(u) ,\ie(u));
Af4={0/M4; 0,5/и2; 0/w3;
^5: |хм5(м) = mi(n (^А2{и)Л
Af5={0/tt1; 0/w2; 0/a3; 0,01/«4;
для d6: [гм6(«;) = min A-\ia(u),1-[ic(u));
M6={0A/uu 0,4/«2; 0,5/w3; 0,9/a4; 0,
7 - 2307

Глава 4. Многокритериальная оценка и выбор
Таким образом,
dii Если
d2: Если
ds: Если
dc Если
d5: Если
rf6: Если
Х = Ми то Y = S;
= M2f то Y=MS;
Х = М* то Y=P;
= М4у то Y=VS;
Х = МЬ, то У=5;
= М6, то 7=(/S.
Используя правило D.18) преобразования импликации «Если Х = МУ
то Y=Q» в выражении jxi>(t/, i) = min(l,l — \км{и) + M-q(^)), для каждой
пары (и, i)^UxJ получаем следующие нечеткие подмножества из
UXJ:
"l
«2
Из
Ы4
M5
Ml
М2

М4
Ы5
«1

Из
М4
«5
И1
и2
«3
И4
«5
0
0,5
0,4
1
0,9
0,7
0
0,5
0,7
1
1
1
0
1
0,7
1
1
1
0
1
0,5
1
0,9
0,9
0,1
0,6
0,5
1
1
0,8
0,1
0,53
0,73
1
1
1
0,1
1
0,7
1
1
1
0,1
1
0,51
1
0,91
0,91
0,2
0,7
0,6
1
1
0,9
0,2
0,59
0,79
1
1
1
0,2
1
0,7
1
1
1
0,2
1
0,54
1
0,94
0,94
0,3
0,8
0,7
1
1
1
0,3
0,66
0,86
1
1
1
0,3
1
0,7
1
1
1
0,3
1
0,59
1
0,99
0,99
0,4
0,9
0,8
1
1
1
0,4
0,75
0,95
1
1
1
0,4
1
0,7
1
1
1
0,4
1
0,66
1
1
1
0,5
1
0,9
1
1
1
0,5
0,85
1
1
1
1
0,5
1
0,7
1
1
1
0,5
1
0,75
1
1
1
0,6
1
1
1
1
1
0,6
0,96
1
1
1
1
0,6
1
0,7
1
1
1
0,6
1
0,86
1
1
1
0,7
0,7
1
1
1
1
1
0,7
1
0,7
1
1
1
0,7
1
0,99
1
1
1
0,8
1
1
1
1
1
0,8
1
1
1
1
1
0,8
1
0,7
1
1
1
0,8
1
1
1
1
1
0,9
1
1
1
1
1
0,9
1
1
1
1
1
0,9
1
0,7
1
1
1
0,9
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1 ||
1
1
1
1 1

4.3. Выбор с использованием нечеткого вывода
«1
«2
%= Us
Щ
M5
«1
«2
D6= us
«4
«5
0
1
1
1
0,99
1
0
1
1
1
1
1
0,1
1
1
1
1
1
0,1
1
1
1
1
1
0,2
1
1
1
1
1
0,2
1
1
1
0,9
1
В результате получаем
«1
ы2
?>= ыз
«4
«5
D = D
0
0,5
0.4
1
0,9
0,7
0,1
0,53
0.5
1
0,91
0,8
0,2
0,59
0,54
1
0,9
0,9
0,3
1
1
1
1
1
0,3
1
1
1
0,8
1
0,4
1
1
1
1
1
0,4
1
1
1
0,7
0,9
0,5
1
1
1
1
1
0,5
1
1
1
0.6
0,8
0,6
1
1
1
1
1
0,6
1
1
0,9
0,5
0,7
0,7
1
1
1
1
1
0,7
0,9
0,9
0,8
0,4
0,6
0,8
1
1
1
1
1
0,8
0,8
0,8
0,7
0,3
0,5
общее функциональное решение:
0,3
0,66
0,59
1
0,8
0,99
в, т
0,4
0,75
0,66
1
0,7
0,9
е. hd(u,l) =
0,5
0,85
0,7
1
0,6
0,8
0,6
0,96
0,7
0,9
0.5
0,7
0,9
1
1
1
1
1
0,9
0,7
0,7
0,6
0,2
0,4
min ((.id.(«,/)):
3=1,6
0,7
0,9
0,7
0,8
0,4
0,6
0,8
0,8
0,7
0,7
0,3
0,5
0,9
0,7
0,7
0,6
0,2
0,4
1
1
1
1
1
1
1
0,6
0,6
0,5
од
0,3
1
0,6
0,6
0,5
0,1
0,3
Для вычисления удовлетворительности каждой из альтернатив
применим правило композиционного вывода D.19) в нечеткой среде: Ей —
= Gb°Dy где Ей — степень удовлетворения альтернативы k\ Gk —
изображение альтернативы k в виде нечеткого подмножества О; D —
функциональное решение. Тогда |i?fc(/) =max(min((io (м), (х^. (и, 0))-
Кроме того, в этом случае \юк (м)=0, ифиъ\ \юк (u) = l1 u = Uk. Отсюда
IXEh (i) =[iD(uk, i). Другими словами, Eh есть k-я строка в матрице D.
Теперь применим процедуру для сравнения нечетких подмножеств
Eif Еъ Е3, Еь, Еь в единичном интервале для получения наилучшего
решения.
Для первой альтернативы
?1= {0,5/0; 0,53/0,1; 0,59/0,2; 0,66/0,3; 0,75/0,4; 0,85/0,5; 0,96/0,6;
0,9/0,7; 0,8/0,8; 0,7/0,9; 0,6/1}.
Вычисляем уровневые множества Eja- Их мощность M(Eja) находится
по формуле
7*

100 Глава 4. Многокритериальная оценка и выбор
где
?la={0; 0,1; 0,2; 0,3; 0,4; 0,5; 0,6; 0,7; 0,8; 0,9; 1}; M(?la)=0,5;
0,5<a<0,53; da = 0,03;
?la={0,l; 0,2; 0,3; 0,4; 0,5; 0,6; 0,7; 0,8; 0,9; 1}; M(Ela) =0,55;
0,53<a^0,59; da = 0,06;
?la={0,2; 0,3; 0,4; 0,5; 0,6; 0,7; 0,8; 0,9; 1}; Af(?la)=0,6;
0,59<a^0,6; da = 0,01;
?ia={0,3; 0,4; 0,5; 0,6; 0,7; 0,8; 0,9; 1}; M(EXa) =0,65;
0,6<a^0,66; da = 0,06;
?la={0,3; 0>4; 0,5; 0,6; 0,7; 0,8; 0,9}; Af(?ta)=0,6;
0,66<a^0,7; da = 0,04;
?la,= {0,4; 0,5; 0,6; 0,7; 0,8; 0,9}; M(Ela) =0,65;
={0,4; .0,5; 0,6; 0,7; 0,8}; Af(?la)=0,6;
a={0,5; 0,6; 0,7; 0,8}; M(Eia) =0,65;
0,8<a^0,85; da = 0,05;
?la={0,5; 0,6; 0,7}; Af(?la)=0,6;
0,85<a^0,9; da = 0,05;
^ia={0,6; 0,7}; M(Eia) =0,65;
?ia={0,6}; Af(?la)=0,6.
Найдем точечную оценку Ei:
DC ov 0,96
1 f 1 f
F(Ei)'= J M(Ela)da=-— J M(Eia)da =
Otmax 0 U>yD0
= 1 /0,96 @,5 • 0,5 + 0,55 • 0,03 + 0,6 • 0,06+0,65 • 0,01 + 0,6 • 0,06 +
+ 0,65 • 0,04 + 0,6 • 0,05+0,6 • 0,05 + 0,65 • 0,05 + 0,65 • 0,05 + 0,6 • 0,06) =
= 0,554.

4.3. Выбор с использованием нечеткого вывода 101
Для второй альтернативы
?2 = {0,4/0; 0,5/0,1; 0,54/0,2; 0,59/0,3; 0,66/0,4; 0,7/0,5;
0,7/0,6; 0,7/0,7; 0,7/0,8; 0,7/0,9; 0,6/1}.
Уровневые множества:
Еш={0; 0,1; 0,2; 0,3; 0,4; 0,5; 0,6; 0,7; 0,8; 0,9; 1}; А1(?») =0,5;
0,4<а^0,5; fi?a=0,l;
Я* ={0,1; 0,2; 0,3; 0,4; 0,5; 0,6; 0,7; 0,8; 0,9; 1}; М(?*,) = 0,55;
0,5<а^0,54; da=0,04;
?•^={0,2; 0,3; 0,4; 0,5; 0,6; 0,7; 0,8; 0,9; 1}; М{Еш)=0$;
0,54<asS0,59; da = 0,05;
?sa={0,3; 0,4; 0,5; 0,6; 0,7; 0,8; 0,9; 1}; ЛЦЕ^) =0,65;
0,59<а<0,6; da=0,01;
?»={0,4; 0,5; 0,6; 0,7; 0,8; 0,9; 1}; Л1(?2а)=0,7;
?аа={0,4; 0,5; 0,7; 0,8; 0,9}; Af(?to) =0,65;
0,66<а<0,7; da = 0,04;
?ях={0,5; 0,6; 0,7; 0,8; 0,9; 1}; Af (?»*)= 0,75.
Точечная оценка
F(E2) = 1/0,7 @,5-0,4+0,55-0,1+0,6-0,04 + 0,65-0,05+0,7-0,01
+ 0,65-0,06+0,75-0,04) =0,554.
Для третьей альтернативы
?з={1/0; 1/0,1; 1/0,2; 1/0,3; 1/0,4; 1/0,5; 0,9/0,6; 0,8/0,7;
0,7/0,8; 0,6/0,9; 0,5/1};
F(E3) = 1/1 @,5 -0,5+0,45 -0,1 +0,4-0,1 +0,35-0,1 +
+ 0,3-0,1+0,25.0,1) =0,425.
Для четвертой альтернативы
?4= {0,9/0; 0,91/0,1; 0,9/0,2; 0,8/0,3; 0,7/0,4; 0,6/0,5;
0,5/0,6; 0,4/0,7; 0,3/0,8; 0,2/0,9; 0,1/1};
F (?4) = 1/0,91 • @,5 + 0,45+0,4+0,35 + 0,3 + 0,25 + 0,2 +
+0,15+0,1).0,1+0,1-0,01 =0,298.

102 Глава 4. Многокритериальная оценка и выбор
Для пятой альтернативы
Е5= {0,7/0; 0,8/0,1; 0,9/0,2; 0,99/0,3; 0,9/0,4; 0,8/0,5;
0,7/0,6; 0,6/0,7; 0,5/0,8; 0,4/0,9; 0,3/1};
F(E5) = 1/0,99@,5-0,3+ @,45 + 0,4 + 0,35 + 0,3-3) -0,1 +
+ 0,3-0,09) =0,391.
Таким образом, точечная оценка удовлетворительности для
альтернативы щ равна 0,554, и2 — 0,554, и3 — 0,425, и4 — 0,298, иъ — 0,391.
В качестве наилучшей выбираем альтернативу и2, так как в расчетах
ее оценка до округления была больше.
4.4. РАНЖИРОВАНИЕ АЛЬТЕРНАТИВ
НА ОСНОВЕ
ЭВРИСТИЧЕСКОГО ПОДХОДА
Данный метод [4] позволяет упорядочивать альтернативы на основе
композиции нечетких критериальных оценок и эвристических
соображений ЛПР в виде лингвистических оценок полезности.
Краткие сведения о методе. Модель процесса принятия решения
включает: оценки альтернатив, представления ЛПР, описание процесса
принятия решения.
Каждую альтернативу можно описать с помощью критериев
качества Dit i=l,n. Область определения представляется как декартово
произведение п множеств Du D = DiXD2X ... XDn. Точка задается
соответствующим набором из п значений (rfj, d2i... ,4)еД где di^
еД-, и обозначается d<4
Если значения критериев неточно определены (подразумеваются
нечеткими), то альтернатива А есть нечеткое подпространство D и
представляется как декартово произведение нечетких множеств на Df.
A = F(Dt)xF(D2)x... XF(Dn),
где F(Di) — нечеткое подмножество D{.
Функция принадлежности |ju(d(n)) находится в соответствии с
обычным определением нечеткой композиции:
где [iA(di) — функция принадлежности оценки альтернативы по
критерию Di.
Множество всех возможных альтернатив обозначается через А и
является множеством нечетких подмножеств.
Элементы и универсального множества U выбираются ЛПР в
соответствии с некоторыми простыми правилами, например
U= {ВЫСОКАЯ, ДОСТАТОЧНО ВЫСОКАЯ, СРЕДНЯЯ,
ДОСТАТОЧНО НИЗКАЯ, НИЗКАЯ}.
Словарь может быть расширен введением модификаторов, таких, как
ОЧЕНЬ, ВПОЛНЕ, БОЛЕЕ-МЕНЕЕ, Полезность может быть интерпре-

4.4. Ранжирование на основе эвристического подхода
103
низкая средняя
/достаточно
<АЯ ВЫСОКАЯ
Рис. 4.8. Функции принадлежности
лингвистических лолезностей
V> и*
тирована как лингвистическая переменная, значения которой есть
термы нечеткого множества, определенного в интервале [0, 1]. Знание
о полезности задается нечетким отношением Ф из D={d^} в U={u},
являющимся нечетким множеством на декартовом произведении DxU.
Ф характеризуется с помощью функции \1ф(&п\ и), посредством
которой каждой паре присваивается значение из интервала [0, 1].
Отношение Ф обычно представляется в виде таблицы, дающей полезность
различных точек из D.
Знание о полезности как нечетком отношении Ф дает возможность
характеризовать альтернативу ЛеА нечетким подмножеством VaU,
где У=Аоф, с помощью формулы
\iv(и) = max ( min (^ф(dSn\u),\la(u))).
В соответствии с определением множества V каждая альтернатива
А имеет более одного значения полезности, которые характеризуются
разными степенями принадлежности. Ранжируя альтернативы,
необходимо установить их упорядочение, используя оценки ЛУЧШЕ,
РАВНОЗНАЧНО, ХУЖЕ, а также выяснить, насколько одно нечеткое
множество лучше другого.
Иногда полезность с наибольшей степенью принадлежности может
быть принята в качестве характерного представителя для сравнения
альтернатив. Путем ранжирования альтернатив устанавливается
полезность в виде предложения, составленного из элементов U. Оно
выражает V лингвистически. Кроме того, V может быть выражено
графически, что позволяет визуально сравнить альтернативы.
Примеры использования метода. Пример 4.6. Есть возможность
часть фонда факультета распределить в виде надбавки к стипендии
студентам, В выборе кандидата на надбавку принимают участие две
заинтересованные стороны: деканат и «треугольник» группы (староста,
комсорг, профорг), которые высказывают свои предпочтения
относительно кандидата. Их высказывания определяют совокупность
критериев эффективности и цели, в частности:
— успеваемость студента Di = {отличная, хорошая,
удовлетворительная};
— активность студента в общественных делах D2= {очень высокая,
эысокая, приемлемая, низкая};

104
Глава 4. Многокритериальная оценка и выбор
— дисциплина (посещаемость) студента D3= {хорошая,
приемлемая, низкая};
— материальное положение студента D4= {плохое,
приемлемое, хорошее}.
Универсальное множество для полезности задается следующим
образом:
U= {ВЫСОКАЯ, ДОСТАТОЧНО ВЫСОКАЯ, СРЕДНЯЯ,
ДОСТАТОЧНО НИЗКАЯ, НИЗКАЯ}.
Здесь же можно использосать модификаторы и, или, очень. На основе
опроса представителей деканата и треугольника группы определены
лингвистические величины полезности (рис. 4.8). Базовая переменная
полезности изменяется в интервале [0, 1].
Эвристики деканата:
1) успеваемость отличная предпочтительнее хорошей;
2) активность может быть приемлемой, если успеваемость отличная,
но должна быть очень высокой, если успеваемость хорошая;
3) дисциплина должна быть хорошей;
4) материальное положение не учитывается.
Эвристики треугольника группы:
1) успеваемость не должна быть удовлетворительной;
2) полезность высокая при приемлемой активности, отличной
успеваемости и плохом материальном положении; полезность достаточно
высокая при очень высокой или просто высокой активности, хорошей
успеваемости, хорошем материальном положении;
3) оценка дисциплины не учитывается;
Таблица 4.4
Отношение полезности

Успеваемость

ОТЛИЧНАЯ
ХОРОШАЯ
»»

ОТЛИЧНАЯ
ХОРОШАЯ
»>

ОТЛИЧНАЯ
ХОРОШАЯ
»
Активность
ОЧЕНЬ
ВЫСОКАЯ
То же
ВЫСОКАЯ
t»

УДОВЛЕТВОРИТЕЛЬНАЯ
То же
., »
Дисциплина

Материальное
положение
ХОРОШАЯ ПЛОХОЕ
ХОРОШЕЕ
ПЛОХОЕ
ХОРОШЕЕ
ПЛОХОЕ
ХОРОШЕЕ
ПЛОХОЕ
ХОРОШЕЕ
ПЛОХОЕ
ХОРОШЕЕ
ПЛОХОЕ
ХОРОШЕЕ
Полезность
для деканата
ОЧЕНЬ-
ОЧЕНЬ
ВЫСОКАЯ
То же
ВЫСОКАЯ
ОЧЕНЬ
ВЫСОКАЯ
То же
ВЫСОКАЯ
»*
ДОСТАТОЧНО
ВЫСОКАЯ
То же
СРЕДНЯЯ
»
Полезность
для
треугольника группы
ОЧЕНЬ-
ОЧЕНЬ-
ОЧЕНЬ
ВЫСОКАЯ
То же
ОЧЕНЬ-
ОЧЕНЬ
ВЫСОКАЯ
ВЫСОКАЯ
ОЧЕНЬ*
ОЧЕНЬ
ВЫСОКАЯ
ВЫСОКАЯ
ОЧЕНЬ
ВЫСОКАЯ
ДОСТАТОЧНО
ВЫСОКАЯ
То же
СРЕДНЯЯ
ДОСТАТОЧНО
ВЫСОКАЯ
СРЕДНЯЯ

4.4. Ранжирование на основе эвристического подхода
105
Таблица 4.5
Значения полезности


тернатива
в виде нечетких
деканат
множеств
Группы
ЛПР
треугольник
Л, {ВЫСОКАЯ}
Л2 {0,6/ОЧЕНЬ ВЫСОКАЯ;
0,4/ДОСТАТОЧНО ВЫСОКАЯ}
Лг {0,2/ОЧЕНЬ ВЫСОКАЯ;
0,6/ДОСТАТОЧНО ВЫСОКАЯ;
0,2/ОЧЕНЬ ВЫСОКАЯ;
0,4/ДОСТАТОЧНО ВЫСОКАЯ;
0,2/ВЫСОКАЯ;
0,3/СРЕДНЯЯ; 0,2/ВЫСОКАЯ;
0,3/СРЕДНЯЯ}
(ОЧЕНЬ-ОЧЕНЬ ВЫСОКАЯ}
{0,6/ОЧЕНЬ-ОЧЕНЬ ВЫСОКАЯ;
0,4/ДОСТАТОЧНО ВЫСОКАЯ}
{0,2/ВЫСОКАЯ; 0,6/СРЕДНЯЯ;
0,2/ОЧЕНЬ-ОЧЕНЬ ВЫСОКАЯ;
0.4/ДОСТАТОЧНО ВЫСОКАЯ;
0,2/ОЧЕНЬ ВЫСОКАЯ;
0,3/СРЕДНЯЯ;
0,2/ДОСТАТОЧНО ВЫСОКАЯ;
0,3/ДОСТАТОЧНО ВЫСОКАЯ}
4) при хорошем материальном положении кандидат рассматривается
только при условии отличной успеваемости и очень высокой активности.
Идеальный кандидат с точки зрения деканата: отличная
успеваемость, очень высокая активность, хорошая дисциплина. Идеальный
кандидат с точки зрения треугольника: отличная успеваемость, очень
высокая активность, плохое материальное положение.
Конструирование отношения полезности.
Пространство эффективности D содержит 3X4X3X3 = 108 я-наборов.
Отбрасывая на основании рассмотренных эвристик несущественные для обеих
групп критериальные оценки эффективности, получаем сокращенные
наборы значений критериев: Z)i= {отличная, хорошая}; D2= {очень
высокая, высокая, удовлетворительная}; D3= {хорошая}; D4= {плохое,
хорошее}.
Таким образом, число я-наборов, покрывающих область полезности,
уменьшается до 2X3X1X2=12 точек (я-наборов). После этого группы
договариваются об оценках полезности /г-наборов. Отношение
полезности Ф для оценки альтернатив сведено в табл. 4.4.
Пусть имеется три кандидата на надбавку к стипендии, которых
можно охарактеризовать следующим образом:
1. Студент с хорошей успеваемостью, очень высокой активностью,
хорошей дисциплиной и плохим материальным положением: А\ =
{хорошая, очень высокая, хорошая, плохое}.
2. Для второго студента активность оценивается скорее как
высокая, чем удовлетворительная. Это может быть выражено нечетким
множеством F(D2) = {0,6/высокая; 0,4/удовлетворительная}. Величины
остальных критериев являются четкими. Альтернатива описывается
следующим образом:
М- {0,6/(отличная, высокая, хорошая, плохое); 0,4/(отличная,
удовлетворительная, хорошая, плохое)}.
3. Оценки третьего кандидата могут быть записаны следующим
образом: F{D\) == {0,6/отличная; 0,3/хорошая}; F(D2) = {0,2/высокая; 0,8/
удовлетворительная}; F(Dz) = {1/хорошая}; F(DA) = {0,6/хорошее; 0,4/
плохое},

106
Глава 4. Многокритериальная оценка и выбор
Чо
0,8
0,6
0.2
f\2 0,4 0,6 0,е 1,0 U*
Рис. 4.9. Окончательные оценки
полезности для деканата
Третья альтернатива задается как прямое произведение множеств,
при этом берется min по функциям принадлежности:
Л3= {0,2/(отличная, высокая, хорошая, хорошее);
0,6/(отличная, удовлетворительная, хорошая, хорошее);
0,2/(отличная, высокая, хорошая, плохое);
0,4/(отличная, удовлетворительная, хорошая, плохое);
0,2/(хорошая, высокая, хорошая, хорошее);
0,3/(хорошая, удовлетворительная, хорошая, хорошее);
0,2/(хорошая, высокая, хорошая, плохое);
0,3/(хорошая, удовлетворительная, хорошая, плохое)}.
Вычисление полезности альтернатив. На основании
описания альтернатив и таблиц оценок полезности наборов значений
для каждой из групп находим величины полезности V(Ai) (табл. 4.5).
Упорядочение альтернатив. Полезности альтернатив
представлены как нечеткие множества V. Следующий шаг состоит в
ранжировании нечетких множеств и тем самым в установлении лучшей
альтернативы. Каждый терм полезности может быть представлен как
нечеткое множество на базовой переменной ?/*=[0,1] (рис. 4.9). Эле-
Таблица 4.6
Значения полезностей альтернатив в упрощенном виде

Альтернатива
Группы ЛПР
деканат
треугольник
Л, ВЫСОКАЯ
А2 ОЧЕНЬ ВЫСОКАЯ или
ДОСТАТОЧНО ВЫСОКАЯ
Л3 ДОСТАТОЧНО ВЫСОКАЯ
ОЧЕНЬ-ОЧЕНЬ ВЫСОКАЯ
ОЧЕНЬ-ОЧЕНЬ ВЫСОКАЯ или
ДОСТАТОЧНО ВЫСОКАЯ
СРЕДНЯЯ или ДОСТАТОЧНО
ВЫСОКАЯ, но НЕ ОЧЕНЬ-ОЧЕНЬ
ВЫСОКАЯ

4.4. Ранжирование на основе эвристического подхода
107
«¦
0,8
0,6
0.4
0,2
Рис. 4.10. Окончательные оценки
полезности для треугольника группы
0,2 0Л 0,6 0,8 1,0, U"
мент нечеткого множества V можно представить как нечеткое
подмножество U* вместо U, т.е. если ВЫСОКАЯ= {1/1; 0,7/0,9; 0,3/0,8}, то
0,5/ВЫСОКАЯ= {0,5/1; 0,5/0,9; 0,3/0,8}. При этом применяется
«правило минимума», которое сохраняет коммутативность, т.е. порядок
выполнения вычислений несуществен. Это означает, что если V
вычислено на U и затем переведено на [/*, то такое же значение будет
получено, если вычислять V сразу на ?/*. После перевода с U на U*
элементы V могут быть скомбинированы с помощью «правила максимума».
Полученные результаты выражают каждую альтернативу
лингвистически (табл. 4.6). Нечеткие множества V (полезность альтернатив)
приведены на рис. 4.10, позволяющем визуально сравнить полезности
альтернатив для групп, принимающих решение.
На основании полученных функций (см. рис. 4.9 и 4.10) можно
сделать вывод, что наилучшей является альтернатива А\\ {хорошая
успеваемость, очень высокая активность, хорошая дисциплина, плохое
материальное положение}.
Этот результат был получен по формуле
полезность
рассматгде А — деканат; В — треугольник группы; и
риваемой альтернативы.

Глава 5
МНОГОКРИТЕРИАЛЬНЫЙ
ВЫБОР
АЛЬТЕРНАТИВ
НА ОСНОВЕ
НЕЧЕТКОГО ОТНОШЕНИЯ
ПРЕДПОЧТЕНИЯ
5.1. ВЫБОР НА ОСНОВЕ
ОТНОШЕНИЯ ПРЕДПОЧТЕНИЯ
НА МНОЖЕСТВЕ АЛЬТЕРНАТИВ
Рассматривается метод принятия решений, предполагающий
построение множества недоминируемых альтернатив на основе нечеткого
отношения предпочтения. Находится свертка отношений предпочтения
по критериям, имеющим различные веса [6, 7].
Краткие сведения о методе. Пусть задано множество альтернатив X
и каждая альтернатива характеризуется несколькими признаками с
номерами /=1,т. Информация о попарном сравнении альтернатив по
каждому из признаков / представлена в форме отношения
предпочтения Rj. Таким образом, имеется m отношений предпочтения Rj на
множестве X. Требуется по данной информации выбрать альтернативу из
множества {X, /?ь ..., Rm}.
Дадим некоторые определения [4, 5].
Определение 5.1. Нечетким отношением R на множестве X
называется нечеткое подмножество декартова произведения ХхХ,
характеризующееся функцией принадлежности \xr: ХхХ-*[0, 1]. Значение
jxh(jc, у) этой функции понимается как степень выполнения отношения
xRy.
Определение 5.2. Нечетким отношением нестрогого
предпочтения на X называется любое заданное на этом множестве
рефлексивное нечеткое отношение.
Определение 5.3. Функция принадлежности отношения строгого
предпочтения
8 ( \ = f
** ( >У) \ 0, если vlr (x,y) ^ jxh (yfx).
Определение 5.4. Пусть X — множество альтернатив и [Ir —
заданное на нем нечеткое отношение предпочтения. Нечеткое
подмножество недоминируемых альтернатив множества (X, \iR) описывается
функцией принадлежности
\mm (х) = 1 - sup \iR8 (у, х), хеX.
Пользуясь определениями 5.3 и 5.4, можно показать, что
цянд (х) = 1 - sup (\kR (у,х)- iiR (х, у)),

5.1. Выбор на основе отношения предпочтения 109
Определение 5.5. Четко недоминируемыми называются
альтернативы, для которых [хйнд(х) = 1, а множество таких альтернатив
Определение 5.6. Носителем нечеткого множества А с функцией
принадлежности \ха(х) является множество {х\х^Х, \ia(x)>0}.
Рассмотрим простейшую ситуацию, когда отношения Rj
описываются заданными функциями полезности ff. Jf-*R, . Значение функ-
ции fj можно понимать как числовую оценку альтернативы X по
признаку /. Альтернатива с большей оценкой fj(x) полагается более
предпочтительной по признаку /. Задача заключается в том, чтобы выбрать
альтернативу, имеющую наибольшие оценки по всем признакам.
Рациональным в этом случае естественно считать выбор альтернативы
хо^Х, обладающей свойством
fi(y)>fj(*o), 1=1,т=>!з(У)Чз(хо)> 1 = 1>т- E.1)
Такие альтернативы называют эффективными; решением данной
задачи выбора является множество всех эффективных альтернатив.
Каждая из функций fj описывает обычное отношение предпочтения на X
следующего вида:
Ъ={(х, у)\х, у^Ху Ш^Ш). E.2)
Пусть Qi=j| Rj- Тогда множество всех эффективных альтернатив в
множестве (Ху Qi) совпадает с множеством эффективных альтернатив
для набора функций fjy /=1, т.
Таким образом, для нахождения множества эффективных
альтернатив можно вместо набора отношений Rj, j=lym, использовать
пересечение этих отношений Qi и найти множество недоминируемых
альтернатив в множестве (Ху Q{).
Представим теперь пересечение отношений Rj в несколько иной
форме. Пусть
1, если (х, •,,*_.,;,, E3)
О, если (л',
1
— функция принадлежности Rj. Тогда пересечению этих множеств
соответствует функция принадлежности
№ i (Х>У) = min (jit (x,y),... ,|im (x,y)), E.4)
аналогичная свертке критериев fj вида
F(x) =
применяемой в многокритериальных задачах принятия решений. Числа
Wj в свертке представляют собой коэффициенты относительной
важности рассматриваемых критериев. В свертке отношений E.4) Wj=l,

110 Глава 5. Выбор альтернатив на основе отношения предпочтения
До сих пор предполагалось, что все заданные отношения одинаково
важно учитывать при выборе альтернатив. Если же отношения Rj
различаются по важности, т. е. различаются по важности
соответствующие признаки, по которым нужно сравнивать альтернативы, то в
свертке E.4) можно, вообще говоря, использовать различные по значению
коэффициенты Wj. Однако при этом необходимо рассмотреть более
широкий класс нечетких отношений. Иными словами, в определении
функций принадлежности E.3) числа 0 и 1 следует понимать не как
значения булевой переменной, свидетельствующей о принадлежности
элемента множеству Rj, а как крайние точки единичного интервала
возможных значений степени принадлежности.
В результате свертки исходных отношений Rj с коэффициентами Wj
т
такими, что 2j Wj=l, ш?^0, /=l,m, получаем функцию
принадлежности вида
\^Qi (Х>У) = min (О>1|Ы1 (*>#)>• • • >Wm\lm{Xyy))y E.5)
т. е. функцию принадлежности нечеткого отношения предпочтения.
Нетрудно видеть, что это отношение предпочтения, вообще говоря, не
рефлексивно и не позволяет учесть различия в относительной важности
заданных отношений.
Введем свертку исходных отношений другого вида:
И<?2(х, У) = Xj WW(*> У) E.6)
и рассмотрим ее использование в сформулированной задаче
рационального выбора альтернатив. Заметим, что результирующее нечеткое
отношение \iq2, полученное в результате свертки исходных обычных
отношений Rj, рефлексивно, так как рефлексивны исходные отношения
Пусть, как и прежде, все исходные отношения предпочтения
одинаковы по важности. В E.6) это соответствует тому, что Wj=lfm, / =
= 1, т. Построим нечеткое подмножество недоминирующих
альтернатив множества {X, (л^}, пользуясь определениями, приведенными
далее:
pX, E.7)
у<=Х j==l
Обозначим через Xi4UJS< подмножество четко недоминируемых
альтернатив множества {Ху \iQl) (АУШД — множество эффективных
альтернатив для набора функций fj(x)t /=l,mj и через Х2ЧНД —
соответствующее множество {X, ixQ2}. Покажем, что
Xjw^Xi1**. E.8)
Рассмотрим свойства альтернатив из множества — носителя ^р2вд.
Функция \iQ2m(x) принимает лишь значения вида k/m, где k — нату-

5.1. Выбор на основе отношения предпочтения 111
ральное число, и k^m. Пусть для некоторой альтернативы X' \iQ2im=
= k/m. Согласно E.7) это означает, что
sup 2j (v>s(y>x')—\ij(x'>y))=m-~k> E-9)
или
т
Ij (wW-w(^)Kw-* E.10)
j=i
при любом i/el.
Поскольку члены суммы в E.10) принимают лишь значения 0 и ±1,
из E.10) следует, что разность между числом членов этой суммы,
равных +1, и числом членов, равных —1, не превышает 1— k при
любом у^Х. Этот факт можно пояснить следующим образом. Пусть
Р(У> х) — число функций fj из заданного набора, по каждой из
которых альтернатива у строго лучше х, и q(yy x) — число функций, по
которым х строго лучше у. Если \iQ2m(x') =к/т, то р(у> xf)—q(y, x')^
^m — k при любом у^Х.
Таким образом, функция \iQ2m упорядочивает альтернативы по
степени их недоминируемости. Например, если \xq2hu(x0) =3А, т.е. т — А=1,
и некоторая альтернатива j/eX строго лучше альтернативы хо по
каким-либо двум критериям, то не менее чем по одному из остальных
Хо строго лучше у. Если взять пересечение множеств Xx4*** и |iQ2HK» to
получим соответствующее упорядочение на множестве эффективных
альтернатив, пользуясь которым можно осуществить выбор среди них.
Если же в свертке E.6) коэффициенты w, неодинаковы, то каждая из
введенных выше характеристик р(у, х') и q(y, x) будет представлять
собой не число соответствующих критериев, а их суммарную важность.
Применение свертки E.6) исходных обычных отношений
предпочтения в задаче принятия решений по набору функций позволяет
получить дополнительную информацию об относительной степени
недоминируемости эффективных альтернатив и тем самым сузить класс
рациональных выборов до множества
Хчт = {х\х^Ху ^ (х) = sup
h4m
В общей задаче, когда на множестве альтернатив заданы нечеткие
отношения предпочтения /?j, j=l,m, и коэффициенты Wj относительной
важности этих отношений, можно поступать аналогичным образом.
Процедура решения задачи выбора.
1. Строим нечеткое отношение Qi (пересечение исходных
отношений):
Ш?4 (Х>У) = min (^1 (Х>У) » ... .[Am (Х>У) )
и определяем нечеткое подмножество недоминируемых альтернатив в
множестве (Ху |iQl):
J (х) =! - SUP (W! (У*х) —\iQi (Х>У)) •

112 Глава 5. Выбор альтернатив на основе отношения предпочтения
2. Строим нечеткое отношение Q2 (свертка отношений типа E.6)):
и определяем нечеткое подмножество недоминируемых альтернатив в
множестве (X, |iQ2):
^Д2(^) = 1- sup 22
Данная функция упорядочивает альтернативы по степени их не-
доминируемости.
3. Находим пересечение множеств \iQtm и \iQ2m:
4. Рациональным считаем выбор альтернатив из множества
ц*Д (х) = sup [г«Д (х')}.
Наиболее рациональным следует считать выбор альтернативы из
множества X11*, имеющей максимальную степень недоминируемости.
Примеры использования метода. Пример 5.1. В процессе
разработки САПР по машинной разводке печатных плат возникла
необходимость выполнить задания, не связанные с основной тематикой.
Сроки разработки проекта требуют как можно скорее выполнить этот
этап.
У руководителя есть три возможности: 1) обучить своего
сотрудника; 2) принять на работу сотрудника, умеющего выполнять
требуемые функции; 3) заключить договор с другой организацией о
выполнении задания.
Руководитель принимает решение по следующим критериям: 1)
быстрота выполнения работы; 2) материальные затраты на ее
выполнение; 3) качество выполнения.
Будем считать, что все критерии одинаковы по важности. Каждый
критерий порождает отношение предпочтения на множестве
альтернатив, (возможностей).
Обозначим альтернативы хи х2, х$. Тогда отношения предпочтения
будут:
Ri — Xi одинаковы по предпочтению с х2у а хз предпочтительнее, чем
х2у по критерию 1;
R2 — xx предпочтительнее, чем х2 и х3, а х2 предпочтительнее, чем х3,
по критерию 2;
Rz — X\, х2 равны по предпочтению, а х$ лучше х\ по критерию 3.
По этим данным составляются матрицы отношений /?i, R2, Rz:
1, если /-я альтернатива лучше /-й по критерию k\
), если альтернативы одинаковы по предпочтению
или t-я альтернатива хуже /-й по критерию k.

5.1. Выбор на основе отношений предпочтений
113
В результате
Xi
Xl
fil= Хг
Хз
1
1
0
получаем
Хг
1
1
1
Решаем задачу
1. Строим
\
Хз
0
0
1
г выбора в
Xi
Xi
= х2
Хз
1
0
0
хг
1
1
0
Хз
1
1
1
Xl
}Аз= хг
Хз
соответствии с описанной
нечеткое отношение Q
i<?,(*
i,Xj) = min
=
(lil(XUX
Xl
Xi
х2
Xt
1
0
0
= R\V\
j).H2
Хг
1
1
0
/?2Паз:
(Л,*,-), |A3(*.-.*i)
Хз
0
0
1
Xl
1
1
1
Хг
1
1
0
Хз
0
0
1
процедурой.
) =
Находим подмножество недоминируемых альтернатив в множестве
\IQ 1 (Xi) = 1 - SUp
(XjyXi)
x.el
по всем i и / Aф)):
нд.
1 = 1- sup { x
M*Q4 (-^3, X\)-\kQi{xuXz)) = l- sup @-1,0-0) = 1;
= 1 - SUp (\lQi(XuX2)~\iQl (X2, Xi),
= 1 - sup A -0,0-0) =0;
НД
= 1 - sup (|iQ t (хихз) —\iQ {{ХзМ),
\iQl(X21x3)-[iQi(X3>x2)) = l- sup @-0, 0-0) = 1.
Xi X2 Х
Итак, (iQlHfl=||l 0
2. Строим отношение Q2:
J-l
В данном случае Ш1 =
Получаем
2=вуз, следовательно, о»,-='/з — по определению.
= 1/3@+1+0) = 1/3;
8 - 2307

114
Глава 5. Выбор альтернатив на основе отношения предпочтения
|AQ2(*2,*i) = 1/3A+0+1) =2/3;
{X,
fi<? 2 (X2M) = 1/3 @+1 +0) = 1/3;
Ш?2(*зЛ) = 1/3@ + 0+1) = 1/3;
|Xq 2 (*3,*s) = 1/3 A + 0 + 0) = 1/3;
Ц«,(*зЛ) = 1/3A + 1 + 1) = 1.
X\ X2 Хз
xi 1 1 1/3
Иа2{хих,) = х2 2/3 1 1/3
x3 1/3 1/3 1
Находим подмножество недоминируемых альтернатив множества
) = !- SUP
по всем i и /, 1Ф]\
= 1 - SUp
(X2,Xi) ~
=1- sup
B1 1 \ 2
1-T "з"~У/ ="з";
- sup
—, —
=1.'
X\ X2 XZ
Итак, jxQ2H«(x0 = IU 0 l||.
3. Результирующее множество недоминируемых альтернатив есть
пересечение множеств р,с?1НД и |ыр2нд:
4. Следовательно, рациональным необходимо считать выбор
альтернативы х\ либо хз, имеющих максимальную степень недоминируемости.

5.2. Использование отношений порядка 115
5.2. ИСПОЛЬЗОВАНИЕ
ОТНОШЕНИЯ ПОРЯДКА
НА МНОЖЕСТВЕ
ЛИНГВИСТИЧЕСКИХ
ВЕКТОРНЫХ ОЦЕНОК
Рассматривается метод выбора решений, основанный на
установлении отношения порядка на нечетких оценках, которое определяется
через вероятностные оценки для их четких эквивалентов [1].
Краткие сведения о методе. Рассмотрим задачу принятия решений
при лингвистических оценках альтернатив. Пусть А={аи а2,...
...,ап} — множество альтернатив, S={si, s2,..., sn} — множество
исходов, причем исход s2- обусловлен альтернативой щ, K(si) = (K\(Si),
K2(Si)y..., Km(Si)) — лингвистическая векторная оценка исхода siy
Kq(Si) — лингвистическая оценка (нечеткое число) исхода по q-му
критерию.
Введем нечеткое отношение порядка ^ на множестве
лингвистических векторных оценок К= {/((si),..., K(sn)}, для чего определим
функцию принадлежности нечеткого отношения следующим образом:
/С/СГ, 1].
Обозначим [х^ (Kq(Si), Kq(Sj)) через \i^*Q(Si, Sj). Значение функции
\i^q(si> sj) для нечетких чисел Kq(Si) и Kq(Sj) может быть вычислено
по формуле
VL^(A,B) = l-ii<(A9B)=li> (Л,В)+^=(Л,В), E.11)
где А и В — нечеткие числа; |л> — нечеткое отношение порядка типа
«больше» на множестве нечетких чисел.
Степень истинности \х<(А, В) нечеткого высказывания А<В
определим как вероятность того, что точное значение нечеткого числа А
будет меньше точного значения нечеткого числа В: \i<(A, В) =P(pv(A)<
<pv(B))y где pv(A) — четкое значение нечеткого числа А. Таким
образом,
п-1
1=1
Естественно считать, что случайные величины, построенные на
нечетких числах А и В, независимы. Тогда
P(pv(A) =Xi&pv(B) >Xi) =P(pv(A) =хг) xP(pv(B)'>Xi) =
= vA(Xi)(l-P(pv(B)^:xi))=VA(Xi)(l-P(pv(B)<xi+i)), i(=Nn-i
и, значит,
n-l
|X< (Л, Д) =Xj (vA(^)(l-©B(xi+1))), E.12)
где ve(X) — вероятность того, что в качестве точного значения
нечеткого числа Е ЛПР использует величину х; ые(х) — вероятность

116 Глава 5. Выбор альтернатив на основе отношения предпочтения
того, что в качестве точного значения нечеткого числа Е ЛПР
выбирает величину у<х:
FU3)
У<х
, E.14)
где \iE(x) — функция принадлежности.
Функцию ц-s определим следующим образом:
где * — знак обобщенной операции. Тогда, поскольку между
множеством альтернатив и исходов имеет место взаимно однозначное
соответствие, 'нечеткое отношение преддочтения на множестве альтернатив
определится функцией принадлежности \i^F: ЛхА->[0, 1], которая
может быть вычислена по формуле \i> F(ai, a,j) =\i^ (K(s;), K(Sj)).
Заметим, что для случая четкого векторного критерия
и выражения для ^^ позволяют получить матрицу парных сравнений
альтернатив по предпочтению O=ll(Xij||nxn » гДе № = ]*.-&F(<*i, aj)-
Решим задачу ранжирования альтернатив на основе матрицы Ф.
1. Пусть /j — множество индексов такое, что Ij = Nn\{j}, j^Nn.
Определим нечеткое отношение предпочтения между альтернативой aj и
всеми остальными альтернативами с помощью функции
принадлежности
Тогда решение задачи ранжирования альтернатив будет описываться
соотношениями
где r$ — ранг альтернативы. Наинизший ранг имеет наиболее
предпочтительная альтернатива.
В случае, когда матрица Ф не позволяет провести ранжирование
альтернатив (матрица Ф такова, что значительная часть степеней
принадлежности или все они равны нулю), можно воспользоваться
следующей процедурой. Найдем ранги альтернатив, для которых величины
ji^f оказались не равными нулю. Пусть индексы этих альтернатив
принадлежат множеству /*. Сформируем матрицу Ф размерностью 1x1,
где 1= \Nn\U\, учитывая лишь те альтернативы, индексы которых при-

5.2. Использование отношения порядка
117
надлежат множеству Nn\I*. Затем вновь применим соотношение E.15),
учитывая номера рангов, уже использованные на предыдущем шаге.
2. Во второй процедуре решения задачи используется
ранжирование альтернатив на основе матрицы парных сравнений. Данная
процедура состоит в отыскании собственного вектора \i = (jxi, цг,..., |яп)
матрицы Ф, соответствующего положительному собственному числу X
этой матрицы, путем решения уравнения Ф\1 = Х\1. Если решение
уравнения существует, то вектор \х положителен. Решение задачи
ранжирования в данном случае описывается соотношениями rj<rk<==>\ij>\ik\
rj = rfe4==^p;7 = ^fe. Наилучшей признается альтернатива, получившая
наинизший ранг.
Для реализации описанного метода необходимо выполнить
следующие этапы:
1. Вычислить функцию принадлежности \х<.
2. Вычислить нечеткое отношение \\^.
3. Минимизировать это отношение.
4. Вычислить отношение предпочтения на множестве альтернатив.
5. Сравнить отношения предпочтительности альтернативы с
остальными.
Примеры использования метода. Пример 5.2. Пусть А = {п\, а^
аз} — множество альтернатив. Векторный критерий К={К\, Къ Кз},
где Кг — лингвистический критерий. Определим задачу вида
К (а) = (/Ci(ai), Kt(a2), Ki{a3))-+- max.
Тогда векторный лингвистический критерий Кг для альтернативы а^
представим в виде матрицы
К\ Кг Кз
к=
«3
ОВ
в
с
с
он
ОВ
в
н
н
где
ОЧЕНЬ НИЗКИЙ: ОН ={1,0/1; 0,8/2; 0,2/3};
НИЗКИЙ: Н= {0,8/1; 0,9/2; 0,5/3; 0,2/4};
СРЕДНИЙ: С= {0,3/3; 0,7/4; 1,0/5; 0,8/6; 0,2/7};
ВЫСОКИЙ: В= {0,2/7; 0,5/8; 0,9/9; 0,8/10};
ОЧЕНЬ ВЫСОКИЙ: ОВ= {0,2/8; 0,8/9; 1,0/10}.
Базовая переменная Х={1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.
Проведем расчеты в соответствии с ранее описанными этапами.
Этап 1. Вычисление функции принадлежности. Используя
формулы E.12) и E.13,), находим
A- :

118 Глава 5. Выбор альтернатив на основе отношения предпочтения
В соответствии с E.14) для различных альтернатив имеем
[1К{ (а4 ) (Хт)
VK .(аг)(Хт) =-
V*.<a2)(*m)=—
VK
где i=l, 3.
Каждому лингвистическому критерию Кг для альтернативы а,
соответствует оценка (ОН, Н, С, В, ОВ). Например, для К\(п\) — ОВ;
К\(а2) — В; К\(аг) — С и т.д. Для каждой оценки имеются свои
функции принадлежности. Например, \iKi{ai){x\) =0,2; \ккх{а^(х2) =0,8 и т.д.
Следовательно,
li*^)^) =0,2 + 0,8+1,0 = 2,0;
Ця4(а2)(у) -0,2 + 0,5 + 0,9+0,8 = 2,4;
t (a3) (У) = 0,3 + 0,7 +1,0 + 0,8+0,2 = 3,0.
Аналогично находятся 2^(ej)> t = 2,3, / = 2,3.
Таким образом, имеем
0,8/. 0,2 + 0,5 \( , 0,3 + 0,7 \ , 1,0 /, 0,2+0,5 + 0,9 \
2^ 11 2А~) \ 1 ЗХ~/ + 2^ \ U /
0,3 + 0,7+1,0 \ _0,2/ O^W W) 0,8/ 0,7\
3^ / ~2fi V~2a)\1 3,0/ +2^\ ! 2Д/
Х

5.2. Использование отношения порядка 119
0,7/ 1,8 W 1,0 \ 1,0/ 2,0 W 2,0 \
l)l-2j5) +3^i1~2^/l1-2^/ =0>057;
,0,5/ 1,7 \/ 1,7 \ 0,9/ 2,2 W 2,2
Этап 2. Вычисление нечеткого отношения
, Л (a*), /C< (as));
(a3)) =0,673;
(a3)) =0,943;
^ ), /Cs(a3)) =0,943.
Этап З. Минимизация отношения ц^:
= min @,673; 0,943; 0,943) =0,673.
*
Этап 4. Вычисление отношения предпочтения на множестве
альтернатив:
^ (ai,a2,a3)=^ (/C(fli), /C(fli), K(a3)) =0,673.
+
Этап 5. Таким образом, степень предпочтения \л^ (ai) =0,673.
Теперь вычислим степень предпочтения альтернативы а2.
Этап 1. к №(а2),К1(а1),К,(а3))= Щ (l- Ц-) (l- Щ
0,5/. 1,0 \ Л 1,0 \, 0,9/ 2,0 \/ 2,0 \
0,8
°'8/i °'2\/i 0,8 \ 0,9/ 0.7
Этап 2. |i>(*i(a2), /С,(а,), К,(а3)) =0,863; ц>(/С2(а2),
К2(аз)) =0,462; ц> (Кз(а2), К3(а{), Кг(а3))= 0,709.
Этап 4. ц> (/С(оа), /((а,), К{аг)) = min@,863; 0,462; 0,709) =0,462.
Этап 5. ц^ (а2) =0,462.
Этап 3. H>()(

120
Глава 5. Выбор альтернатив на основе отношения предпочтения
Альтернатива а\ предпочтительнее а2.
Вычислим степень предпочтения альтернативы аз.
, К3(а2)) =
Этап 2. ^ (Ki(a3), Ki(ax)9 Ki(a2)) =0,835; ^ (tf2(a3), *2(a,),
/C2(a2)) =0,928; |х>(/Сз(а3), /Сз (аО, /Сз(а2)) =0,709.
Этап 3. |jb,(/((a3), tf(fli), /C(a2)) =min@,835; 0,928; 0,709) =0,709.
Этап 4. \x^ (a3) =0,709.
Этап 5. Так как \i^ {ах)<\к^ (a3), получаем ответ: a3
предпочтительнее.
Пример 5.3. Пусть А = {а\\ а2} — множество альтернатив.
Векторный критерий R={K\, /С2, /Сз, Дч}, где Кг — лингвистический критерий.
Определим задачу вида К{а) = (/(j(ai), /C2(a2))->max. Тогда
векторный лингвистический критерий /Сг- для альтернативы а, представим в
виде матрицы
/Ci /C2 /Сз Кь
В В Н С
он с ов н
к=
где термы и базовая переменная задаются так же, как в примере 5.2.
Этап 1. Вычисление функции принадлежности
МЛ_М\ °'5/ 1,0+0,8
2,4
Ь
1,0 + 0,8 + 0,2
2,0
—) +0=0,34;

5.2. Использование отношения порядка 121
(,) -0.47;
Этап 2. Вычисление нечеткого отношения ц^:
11^(^@,), /С1(ое)) = 1-ц< (/С*(а4),
li^^iTai). /Ci (%)) =0,66; ц^ (/C»(fli), ^2@2)) =0,358;
4^(^(ai), А:з(а2))=0,53; >-" (/D(a,), /C4(as)) =0,831.
Этап З. Минимизация отношения ц:
= min@,66; 0,358; 0,53; 0,831) =0,358.
Этап 4. Вычисление отношения предпочтения на множестве
альтернатив
^ <аьО2)=|1^ (/C(aOf К(a2)) =0,358.
Этап 5. Сравнение отношения предпочтительности альтернативы
с остальными
fx>k(ai) = min ixt> (aua2) =0,358.
Степень предпочтения \л^ (п\) =0,358.
Вычислим степень предпочтения альтернативы аг.
Этап Г. ,.<(*,(«,). ±(M)L8

122 Глава 5. Выбор альтернатив на основе отношения предпочтения
Этап2. ^ (/Ci(a2), Ki(ax)) = l -0,77 = 0,23; »> (K2(a2),
= 0,678; ^(/Сз(а2), Яз(аО) =0,36; ^ (/C4(a2), K4(ai))=0,3.
Этап 3. Vl> (/C(a2), 7((ai)) =min@,23; 0,678; 0,36; 0,3) =0,23.
Этап 4. |л^ (аг, #i) =0,23; ^-> (a2)=0,23. Степень предпочтения a2
равна 0,23.
Этап 5. Альтернатива п\ предпочтительнее, так как
5.3. ВЫБОР ПРИ НАЛИЧИИ
НЕЧЕТКОГО ОТНОШЕНИЯ
ДОМИНИРОВАНИЯ
Рассматривается метод принятия решений с использованием
критерия эффективности на множестве альтернатив. На его основе строятся
отношение предпочтения и нечеткое множество недоминируемых
альтернатив [2, 3].
Краткие сведения о методе. Пусть X — множество альтернатив, из
которых делается выбор. Аналогично параграфу 5.1 примем, что Хчнд
есть множество х^Х, которые не доминируются ни одним у^Х в
четком смысле, \1ия(х) — функция принадлежности нечеткого множества
решений, строго не доминируемых ни одним у^Х. Дадим некоторые
определения.
Определение 5.7. Бинарным нечетким отношением
предпочтения называется нечеткое множество R= (Ey \xr(x, у)), где Е —
область определения, х^Х, у^Х и 0^jih(x, y)^l.
Определение 5.8. Критерием эффективности называется
функция K(Xi), определенная на X. Критерий эффективности порождает
некоторое отношение порядка на X: если из K(xi) >K(xs) следует, что
Xi^xs, то K(Xi) является критерием типа «выигрыш».
Рассмотрим взаимосвязь критерия эффективности и функции
принадлежности. Пусть на X задан критерий эффективности
где Wi — коэффициенты относительной важности критериев, причем
7=1
Отношение предпочтения на парах решений с использованием
критерия эффективности введем следующим образом:
R: /С(*)-*(У)>0; R~l:K(x)-K(y)^Q, х, уеХ.
Далее можно ввести следующую функцию принадлежности:
|i(^)-a(/CW-#C(y))+p. E.16)
Потребуем \х(х, у) = 1/2, тогда C=1/2 и одновременно выполняется
)=1 ' E.17)

5.3. Выбор при наличии отношения доминирования 123
Коэффициент а зададим исходя из следующего условия:
^=l, E.18)
где d = max(K(x) — К(у)), ху у^Х, является диапазоном шкалы
критерия эффективности.
Получим a=l/2d, и E.16) примет вид
Функция ц(х, у), определенная по E.19), удовлетворяет условию
1 K(x)-K(z) I K(z)-K(y)
1 1 К(х)-К(у) , 1
для всех я, у,
Наилучшие решения, в соответствии с критерием эффективности
К(х), находятся следующим образом:
Хк* = {х\х<=Х, max /((л:)}. E.20)
хеХ
Рассмотрим взаимосвязь этих решений с четкими
недоминируемыми решениями в соответствии с заданной функцией
принадлежности. Введем обозначение 2jW(z)K(z) —К. Тогда \х(х)= —^ ?
а также
{x\xseX, max | K^"K |} E.21)
и, следовательно, А'*к = ^чнд. В случае принятия решений при наличии
нечеткого отношения предпочтения, если \i(x, у) удовлетворяет
условию
)
обоснованным становится подход к принятию решений при четком
отношении предпочтения на основе функции \х(х)> которая с точностью до
линейного преобразования (шкала интервалов) совпадает с критерием
эффективности К(х).
Рассмотрим случаи принятия наилучших решений при
противоречивых нечетких признаках. Пусть имеется набор нечетких отношений
предпочтения на X:
М = {|Xi (x,y), ц2 {х,у),... ,jim (х9у)}, E.22)

124 Глава 5. Выбор альтернатив на основе отношения предпочтения
где х, i/eX При наличии набора нечетких признаков нечеткое
отношение строгого доминирования с учетом всех нечетких признаков
формулируется следующим образом:
(*,</) =
тт\1)(х,у)- т\пщ(у,х)=а(х,у), если а(лг,*/)>0;
j=l,
О, если a(xfy)<0,
после чего можно записать
E.23)
E.24)
где [хнд — функция принадлежности нечеткого множества' решений,
строго не доминируемых ни одним у^Х. При этом имеет место
Х™*= {х\^(хуу) =0, t/€E*}, E.25)
откуда получаем, что jce^411^ если для него выполняется неравенство
min \ij (y,x) ^ mini \ij (x,y). E.26)
Если \ij{x, у)t /=1, m, не удовлетворяет условию
[i (х,у) =- ^ (x,z) + ц (z,y) —j E.27)
для всех х, у, z^X, то формулу E.25) можно переписать в более
общем виде:
max
где
а (^,У) = {/Vi (^У) ^ W (УД)} > P (^) = {/IW (^>У) ^ ^i (У^)} • E.29)
Примеры использования метода. Пример 5.4. Построим множество
^чнд с помощью критерия эффективности.
Пусть имеем критерий эффективности
К(х) = {(К(Хг), шг)} = {D; 0,1); C; 0,3); E; 0,1); A; 0,1);
F; 0,2); B; 0,2)}.
Тогда
^(z) K(z) =4- 0,1 +3-0,3 + 5.0,1 + 1-0,1 +6-0,2 + 2-02^
= 0,4 + 0,9+0,5+0,1 + 1,2+0,4 = 3,5;

5.3. Выбор при наличии отношения доминирований
125
max
0,5 0,5
_; —;
1,5 2,5 2,5
—; —; —;
1,5
Пример 5.5. Построим множество ^'шд с помощью нечетких
отношений предпочтения. Пусть имеем набор нечетких отношений
предпочтения на X:
(ХиУ)
(Х2,У)
\i(x,y)= (х3,У)
{ХьУ)
(Хь,У)
(УМ)
(ум)
И (#.*) = (УМ)
(УМ)
(УМ)
Определим множество
<*(х,у) = {1'\ы(х,У)>\
Найдем,
fii
0,1
0,5
0,8
0,2
0,5
Hi
0,3
0
0,7
0,2
0,6
*Лу,х)}
Р (х,у) = {/К (х,у) < ^ (у,х)}
0,4
0,6
0,3
0,1
0,7
Ц2
0,1
0,2
0,5
0
0,3
=
=
Mi
i
0,2
0,1
0,7
0,4
0,2
A3
0
0,4
0,6
0,3
0,5
(ХиУ)
(Хг,У)
(Хз,У)
(Xi,y)
(Хъ,У)
2,
1,
1,
1,
2,
(ХиУ)
(ХьУ)
(хз,У)
(Xi,y)
(хъ,У)
1,
3,
2,
1,
1,
0,7
0,4
0,5
0,8
0,4
Ц4
0,6
0,8
0,3
0,9
0,7
3,
2,
3,
2,
5
5
4
5
4
3,
0,3
0,2
0,1
0,6
0,8
0,5
0,1
0,4
0,4
0,8
4
5
4
3,
4,
Используя а{х, у) и $(х, у), вычисляем
max (ц,(*> У)~1Ч(У, *))=тах @,3; 0,2; 0,1; 0,5; 0,4; 0,1; 0,1;
0,1; 0,2; 0; 0,1; 0,1; 0,2; 0,4; 0)=0,5;
max (ц,(у, x)-\kj{x, y))=max @,2; 0,2; 0,3; 0,4; 0,2; 0,3; 0;
0,1; 0,1; 0,3; 0,3; 0) =0,4.
Окончательно получаем Хчнд== {д;| 0,5^=0,4}

Глава 6
ПРИНЯТИЕ РЕШЕНИИ
ПРИ КАЧЕСТВЕННОЙ
И ВЕРОЯТНОСТНОЙ
НЕОПРЕДЕЛЕННОСТИ
6.1. ПРИНЯТИЕ РЕШЕНИЙ
НА ОСНОВЕ
НЕЧЕТКОГО ОПИСАНИЯ
СОСТОЯНИЯ СИСТЕМЫ
И ИСХОДОВ
Рассматриваются ситуации принятия решений, в которых состояния
системы известны неточно и, кроме того, неточно определены
полезности альтернатив в различных ее состояниях. Описываются процедуры
нахождения оптимальной альтернативы для следующих случаев: четкие
полезности альтернатив и нечеткие состояния системы; нечеткие
полезности и четкие состояния; нечеткие полезности и нечеткие
состояния. Указанные случаи иллюстрируются примерами [2].
Краткие сведения о методе. Рассмотрим пример задачи принятия
решений. Пусть необходимо выбрать одежду, соответствующую погоде,
выходя на улицу. Возможные варианты: одеться тепло, одеться легко,
взять зонт и т.д. Решение зависит от состояния внешней среды —
погоды (солнечно, пасмурно, идет дождь и т.д.), точно оценить
которое часто не представляется возможным. Выбор альтернативы при
различных состояниях среды характеризуется различной полезностью,
анализ которой и позволяет принять решение.
Итак, имеется множество альтернатив А = {аь а2,..., ат}, выбор
одной из которых зависит от состояний среды: Х= {хь х2у..., хп).
Известно, что если система находилась в состоянии Xj и выбрана
альтернатива aif то ее полезность будет иц. Для различных альтернатив
и возможных состояний имеем матрицу тХп:
11 ... Uin
Umn
При известном состоянии системы
натива, имеющая наибольшую полезность:
лучшей является
альтерq= max
Однако если состояние системы или полезности альтернатив известны
нечетко, то оптимальная альтернатива может быть представлена только
в виде нечеткого множества: Ао = U |х~ (а,-)/аь где |л~ (а*) — степень
Ао Aq
г
принадлежности ai нечеткому множеству Aq.

6.1. Нечеткое описание состояния системы и исходов 127
Нечеткое состояние системы. Пусть состояние системы
описывается нечетким множеством
Х= \J\l~{xk)/Xk, Xh(=X.
W X
X
k
В этом случае полезность альтернативы не может быть определена
точно. Однако, воспользовавшись информацией о состоянии системы,
ее можно выразить в виде
ff< = \Jul~ (uh)/uh, F.1)
где uh = uik и pi~ (uh)=\i ~ (**)•
и{ х
Отметим, что здесь и далее, если некоторый элемент области
определения в ходе вычислений появляется k раз с различными
значениями принадлежности: \хи \i2,..., цл, то степень его
принадлежности \1=\1\ + [12+ ... + \lh, ГДе \ll + \X2= М.1 -Ь |Jt2 — \l\\l2.
Выбор оптимальной альтернативы основан на рассмотрении
максимальной полезности альтернативы и степени принадлежности ему
различных значений полезности. При этом используется понятие
максимизирующего множества.
Максимизирующим множеством функции f на множестве У
называется нечеткое множество M(f)y такое, что степень принадлежности
ему некоторого у характеризует близость f(y) к sup f. Аналогично
максимизирующим множеством M(Y) множества У называется
нечеткое подмножество, степень принадлежности к которому для y^Y
выражает в некотором смысле близость у к sup У.
Рассмотрим множество У, содержащее все возможные значения
полезности для данного нечеткого состояния:
У =
г=1
Затем определим максимизирующее множество для альтернативы
Uim =
h im
где u~ (ии) = (Uki umSLX)n; «max = sup У; n — целое число, выбираемое
"irn
в зависимости от задачи.
Далее определяется множество Uw на основе пересечения нечетких
множеств Uim и Uс
Множество, представляющее оптимальную альтернативу, находится
следующим образом: \х~ (аг)=тах|л^ (ии). Очевидно, лучшей будет
Ло k UiQ
альтернатива а0, имеющая наибольшее значение принадлежности
множеству Л о: \х~ (ao)=max\i~ (аг).

128
Глава 6. Принятие решений в условиях неопределенности
Нечеткие полезности. Пусть теперь полезность
ная с альтернативой at при состоянии Xj, является нечеткой:
(J

связанF.2)
Тогда матрица полезностей имеет вид
Он ... Оы
/mi
...On
Если известно состояние системы х^Х, определение оптимальной^
альтернативы аналогично рассмотренному ранее. Из информации о
нечетком состоянии находится нечеткая полезность альтернативы а^А,
задаваемая множеством Ui, которое затем используется для
определения степени принадлежности этой альтернативы множеству Ло.
В рассматриваемом случае, если Xj четкое, множество Пг определяется
следующим образом: и{={Уц.
Нечеткие полезности и состояние. Нечеткая
полезность альтернативы аг при некотором нечетком состоянии системы,
обозначаемая V*i, задается в виде
где Ok =
', \i
F.3)
. Нечеткое множество?/** состоит, в свою
@к)=р„
ui* X
очередь, из нечетких множеств. Оно может быть сведено к нечеткому
множеству на четких значениях полезностей. Если элемент множества
O*i есть
\i~ (Uk)/Uk = ii~ (\i\~ fai)lui)f(ayh (u\)/Ui),
US ut* uih 'h
то значение степени принадлежности четкого значения щ множеству
O*i определяется из принадлежности его Uik и принадлежности
последнего U* с
\х~ (и\) = min ([\~ (Xh), [i\ /ч, (и\)). F.4)
Ui* ^ "ik
Данная процедура повторяется для всех k, после чего множество Ui*
будет содержать полезности щ и их степени принадлежности, т.е.
будет сведено к множеству [/*г>:
Uir* = \k~ (u\)/ut. F.5)
U*ir
Затем для Ui = U*ir повторяется уже описанная процедура нахождения
нечеткого множества Ло лучшей альтернативы.
Примеры использования метода. Пример 6.1. Нечеткое состояние,
четкие полезности. Пусть имеется множество альтернатив А = {а\, a<i,
аз} и система может находиться в одном из состояний Х={х\, х2> х&,
Х4, х$, хе, Х7, Х8, Xq, X\o}. Матрица полезностей имеет вид
и=
аа
9
2
6
7
1
4
Хз
2
7
3
Xi
2
8
4
Хь
3
1
5
•*6
1
7
6
Xi
7
6
8
*8
8
4
5
8
3
2
Хю
4
8
3

6.j. Нечёткое описание состояния Системы й исходов 129
» _._,...„ ^...
Состояние системы задано:
2={О,4/лг3, 0,8/*4, 1,0/х», 0,7/** 0,3/*7}.
Определим нечеткие полезности альтернатив при данном состоянии
системы:
*7г = {ц~ (Uik)/uik}, причем ц~ (uh) =и~ (**)» Xk = uih;
ffi= {0,4/2; 0,8/2; 1,0/3; 0,7/1; 0,3/7} =
= {@,4+0,8-0,4-0,8)/2; 2,0/3; 0,7/1; 0,3/7} =
= {0,88/2; 1,0/3; 0,7/1; 0,3/7};
?72= {0,4/7; 0,8/8; 1,0/1; 0,7/7; 0,3/6} =
= {@,82/7; 0,8/8; 1,0/1; 0,3/6};
т= {0,4/3; 0,8/4; 1,0/5; 0,7/6; 0,3/8}.
Найдем множество У:
= {2, 3, 1, 7} U {7, 8, 1, 6} U {3, 4, 5, 6, 8} =
= {1, 2, 3, 4, 5, 6, 7, 8}.
Определим максимизирующие множества
Uim={\l~ («ft) /«ft}>
где
М<~ («ft) = \ ) ; «max= SUp Y.
Vim "max
В данном случае «max = 8, а я выберем равным единице. Тогда
8 8 8
= {0,25/2; 0,375/3; 0,125/1; 0,875/7};
г72т= {0,875/7; 1/8; 0,125/1; 0,75/6};
Ош= {0,375/3; 0,5/4; 0,625/5; 0,75/6; 1,8/8}.
Найдем оптимизирующие множества Сг0:
ц„ (uh) = min (ц,~ («ft); ц,~ («ft)):
Cf10={min@,25; 0,88)/2; min @,375; =1,0)/3;
min @,125; 0,7)/1; min @,875; 0,3)/7} =
= {0,25/2; 0,375/3; 0,125/1; 0,3/7};
?720= {0,82/7; 0,8/8; 0,125/1; 0,3/6};
Uao= {0,375/3; 0,5/4; 0,625/5; 0,7/6; 0,3/8}.
9 - 2307

OB
H
В
Xi
В
ОН
с
Хз
н
в
н
Xi
н
ов
с
Хь
С
он
с
Хв
ОН
в
в
х1
В
в
ов
Xs
ОВ
с
с
х9
ОВ
с
н
Хю
С
ов
н
130 Рлава 6. Йринятгие решений в усЛойййХ небЙредёЛенндстй
Отсюда получим нечеткое множество, характеризующее оптимальную
альтернативу Ло:
\х~ (аг) = maxp,~ (uk);
ц„ (а4) = тах @,25; 0,375; 0,125; 0,3) =0,375;
Ao
|i~ (а2)=0,82; и~ (аз) =0,7, т.е.
Ло Aq
^o={0,375/ai; 0,82/a2; 0,7/a3}.
Таким образом, лучшей является альтернатива аг, имеющая
наибольшее значение принадлежности Aq.
Пример 6.2. Четкое состояние, нечеткие полезности. Пусть
множество альтернатив А и множество состояний X — те же, что и в
примере 6.1, а матрица полезностей имеет вид
= а2
где полезности заданы лингвистически нечеткими множествами:
НИЗКИЙ: Н = {0,4/1; 1,0/2; 0,5/3};
ОЧЕНЬ НИЗКИЙ: ОН,= {1,0/1; 0,4/2};
СРЕДНИЙ: С= {0,4/3; 0,7/4; 1,0/5; 0,7/6; 0,4/7};
ВЫСОКИЙ: В= {0,5/7; 1,0/8; 0,5/9};
ОЧЕНЬ ВЫСОКИЙ: ОВ= {0,5/9; 1,0/10}.
Состояние системы известно: х9. Найдем нечеткие полезности для
различных альтернатив при этом состоянии системы:
ffj = OB= {0,5/9; 1,0/10};
Cf2 = C={0,4/3; 0,7/4; 1,0/5; 0,7/6; 0,4/7};
ff3=H= {0,4/1; 1,0/2; 0,5/3}.
Найдем множество
У={9, 10} U {3, 4, 5, 6, 7} U 0, 2, 3} =
= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.
Следовательно, нтах=Ю. Положив л=1, найдем максимизирующие
множества:
Uim= Ц/9; j^/io} ={0,9/9; 1/10};
ff2m= {0,3/3; 0,4/4; 0,5/5; 0,6/6; 0,7/7};
Я»,-{0,1/1; 0,2/2; 0,3/3}.

6.1. Нечёткие бписание состояний Системы и исходов 131
Соответствующие оптимизирующие множества:
ff,o= fain @,5; 0,9)/9; min A,0; 1,0)/10} = {0,5/9; 1,0/10};
«7»= {0,3/3; 0,4/4; 0,5/5; 0,6/6; 0,4/7};
?7зо= {0,1/1; 0,2/2; 0,3/3}.
В этом случае нечеткое множество, характеризующее лучшую
альтернативу, определяется следующим образом: ц~ (щ) =тах@,5; 1,0) = 1,0;
ц~ (а2)=0,6; ц~ (а3)=0,3, т.е. J?o={l,0/ai; 0,6/а2; 0,3/а3}. Отсюда еле-
е, Ао До
дует, что лучшей является альтернатива а\, имеющая наибольшее
значение принадлежности.
Пример 6.3. Нечеткое состояние, нечеткие полезности. Пусть
состояние системы является нечетким и задано, как в примере 6.1, а
матрица полезностей аналогична матрице из примера 6.2. Тогда для
нечетких полезностей альтернатив имеем
Ui*={lt~ (Он)/Он),
где Uh=tfih\ ц~ iPh) =р~
ut* х
; 0,8/Н; 1,0/С; 0,7/ОН; 0,3/В} =
= {0,4+ 0,8-0,4-0,8)/Н; 1,0/С; 0,7/ОН; 0,3/В} =
= {0,88/Н; 1,0/С; 0,7/ОН; 0,3/В};
?72*={0,4/В; 0,8/ОВ; 1,0/ОН; 0,7/В; 0,3/В} =
= {@,4 + 0,7-0,4-0,7)/В; 0,8/ОВ; 0,7/В; 1,0/ОН} =
=\{0,82/В; 0,8/ОВ; 0,7/В; 1,0/ОН} =
= {0,864/В; 0,8/ОВ; 1,0/ОН};
?73* = {0,4/Н; 0,8/С; 1,0/С; 0,7/В; 0,3/ОВ} =
= {0,4/Н; 1,0/С; 0,7/В; 0,3/ОВ}.
Рассмотрим U*\ и подставим вместо Н, С, ОН, В их значения:
^•, = {0,88^0,4/1; 1,0/2; 0,5/3};
1,0Д{0,4/3; 0,7/4; 1,0/5; 0,7/6; 0,4/7};
0,7/{1,0/1; 0,4/2};
0,3/{0,5/7; 1,0/8; 0,5/0}}.
Упрощаем на основании ц~ («i) =min((j,^, (Xk), и, „ («i)):
?7,* = {min @,88; 0,4)/l; min @,88; l,0)/2; min @,88; 0,5)/3;
min A,0; 0,4)/3; min A,0; 0,7/4; min A,0; 1,0)/5;
min A,0; 0,7)/6; min A,0; 0,4)/7; min@,7; l,0)/l;

132 Глава 6. Принятие решений в условия* Неопределенности
min@,7; 0,4)/2; min @,3; 0,5)/7; min @,3; 1,0)/8;
min @,3; 0,5)/9^= {0,4/1; 0,88/2; 0,5/3; 0,4/3; 0,7/4;
1,0/5{ 0,7/6; 0,4/7; 0,7/1; 0,4/2; 0,3/7; 0,3/8; 0,3/9} =
= {0,82/1; 0,928/2; 0,7/3; 0,7/4; 1,0/5; 0,7/6; 0,58/7; 0,3/8; 0,3/9}.
Аналогично
ffi*-{1,0/1; 0,4/2; 0,5/7; 0,864/8; 0,75/9; 0,8/10};
0з* = {0,4/1; 0,4/2; 0,64/3; 0,7/4; 1,0/5; 0,7/6; 0,7/7;
0,7/8; 0,65/9; 0,3/10}.
Найдем множество
У={1, 2, 3, 4, 5, 6, 7, 8, 9}U{1. 2, 7, 8, 9, 10}U
U{1, 2, 3, '4, 5, 6, 7, 8, 9, 10}-{1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.
Следовательно, Mmax=10.
Соответствующие максимизирующие множества:
0im= {0,1/1; 0,2/2; 0,3/3; 0,4/4; 0,5/5; 0,6/6;
0,7/7; 0,8/8; 0,9/9};
0*п= {0,1/1; 0,2/2; 0,7/7; 0,8/8; 0,9/9; 1,0/10};
0зт= {0,1/1; 0,2/2; 0,3/3; 0,4/4; 0,5/5; 0,6/6;
0,7/7; '0,8/8; 0,9/9; 1,0/10}.
Найдем оптимизирующие множества
0ю= {min@,1; 0,82)/1; mm @,2; 0,928)/2; min @,3; 0,7)/3;
min @,4; 0,7)/4; mm @,5; 1,0) /5; min @,6; 0,7)/6;
min @,7; 0,58)/7; min @,8; 0,3)/8; min @,9; 0,3)/9} =
= {0,1/1; 0,2/2; 0,3/3; 0,4/4; 0,5/5; 0,6/6; 0,58/7; 0,3/8; 0,3/9};
CTao= {0,1/1; 0,2/2; 0,5/7; 0,8/8; 0,75/9; 0,8/10};
03o= {0,1/1; 0,2/2; 0,3/3; 0,4/4; 0,5/5; 0,6/6;
0,7/7; 0,7/8; 0,65/9; 0,3/10}.
Тогда множество Ло определим через ц~ (а,):
ц„ (ai) = max @,1; 0,2; 0,3; 0,4; 0,5; 0,6; 0,58; 0,3; 0,3) =0,6;
ц~ (а2)=0,8; ц~ (а3)=0,7,
т.е. Ло={Оу6/а{; 0,8/02*, 0,7/аз}. Из этого следует, что лучшей является
альтернатива а2.

6.2. Неточность и неопределенность описания исходов 133
! ,
6.2. ВЫБОР РЕШЕНИЙ
ПРИ НЕТОЧНОСТИ
И НЕОПРЕДЕЛЕННОСТИ
ОПИСАНИЯ ИСХОДОВ
Рассматривается метод анализа решений в случае, когда исходы
альтернатив известны неточно и вероятности их наступления
оцениваются с помощью функции принадлежности [3]. Используются
результаты теории ожидаемой полезности, обобщенные на нечеткий случай.
Рассмотрим простое дерево решений (рис. 6.1).
Краткие сведения о методе. Необходимо выбрать одно из двух
решений, описываемых лотереями А и В, которые зависят от различных
случайных событий [1]. В лотерее А имеется вероятность р выиграть
приз, полезность которого равна щ, и вероятность A— р) выиграть
приз, полезность которого U2. Используя правила теории ожидаемой
полезности, выбирают эту лотерею тогда и только тогда, когда рщ +
+ A —p)u>2*>qv\+ (I — q)v2. Здесь величины и, следовательно, степень
предпочтения одной альтернативы другой точно неизвестны.
Пусть |ха(я), \ьв(Ь) — степени принадлежности а, Ь множествам
ожидаемых полезностей лотерей Л и В, тогда согласно принципу
обобщения
(гл(а)= max (min (\iP(p),\iAi («i),m2 («2))); F.6)
put+(l-p)u2
\1в(Ь)= max (min (\jlq (q) ,\jlb г (»i).|ab2(%))), F.7)
где \ip(p) — степень принадлежности р множеству возможных
значений для этой вероятности. Распределения ожидаемой полезности для
каждой лотереи, вычисленные с помощью этих выражений, приведены
на рис. 6.2. Наблюдается значительное перекрытие между двумя
распределениями, и, хотя пик функции \ха(х) имеет место при большем
значении, чем пик функции \хв(х), этого недостаточно для
утверждения, что А лучше В.
Чтобы оценить степень, с которой А предпочтительнее В,
воспользуемся следующим методом:
F.8)
Как видно из выражения, степень, с которой из некоторого нечеткого
предложения X следует какое-то другое нечеткое предложение У, есть
степень истинности высказывания «Или не X, или У». Последняя, в
Рис, 6.L Простое Дерево решений

134 Глава 6. Принятие решений в условиях неопределенности
Рис. 6.2. Вычисленные нечеткие распределения
полезности
свою очередь, равна большему из значений степени истинности «не X»
и степени истинности «У». В более общей постановке, если X и У
есть нечеткие отношения между двумя переменными а и 6,
представляемые функциями принадлежности \лх{а, 6) и juiy(a, 6),
|i(^y)=min (max (l-|ix(a,6), pY(aJb))). F.9)
a,b
Это определение смысла нечеткого высказывания не является
единственно возможным, но оно достаточно эффективно для
рассматриваемых целей.
Пусть У — утверждение о предпочтении:
Yx: «А строго предпочтительнее В»,
1, если а>Ь\
0, если
У2: «А в некоторой степени предпочтительнее В»,
II, если а> F + 0,2);
0,5+2,5(a-fc), если F + 0,2)
0, если а< F-0,2),
где \хх(а, 6) — степень, с которой а принадлежит множеству
ожидаемых полезностей для лотереи Л и 6 — множеству для лотереи В. Из
этого следует, что
При таких определениях можно использовать F.9) для вычисления
степени предпочтения:
lx(X-^Yi) = min [max A-fx*(a,6), (x^ (
а,Ь
= min [max A— min (jaa(a), Mb))> ^
a,b
Для a>b \1п(а, 6) = 1. Если существует пара (а, 6), для которой
аргумент min меньше единицы, то а^б. Таким образом,
а, Ь
= l~max (min
a<b

6.2. Неточность и неопределенность описания исходов 185
о|Чо<Ь°ч% Побмать1
Рис. 6.3. Дерево решений капитана рыболовного сейнера
Можно показать, что максимум имеет место в граничной точке при
а = Ь. Следовательно,
1х(Х-^У!) = 1- max (min (\iA(a), jib (a))),
и из рис. 6.2 можно получить значения min(\iA(a)y iiB(a)). Его
максимальное значение 0,96, a \i(X-+Y\) =0,04. Аналогичные вычисления
дают |ш(Х-^У2)=0,12.
Степень истинности высказывания «А строго предпочтительнее В»
меньше, чем высказывания «Л в некоторой степени предпочтительнее
В». Соответствующие степени истинности суждений о предпочтении В
относительно А равны нулю, как и предполагалось.
Пример использования метода. Пример 6.4. Пусть цель капитана
рыболовного сейнера — вернуться на базу с уловом промысловой
рыбы. На глубине замечен косяк рыбы. Необходимо решить,
сбрасывать трал (сеть) для ловли рыбы или нет. Точно неизвестно, является
ли рыба в данном косяке промысловой. Если при подъеме сети
окажется, что рыба не промысловая, то будет потеряно время для ловли
и, кроме того, будет нанесен урон подводному миру в этом районе.
Помимо этого, существует вероятность, что рыба может быть не
поймана при сбросе сети. Вероятность того, что рыба будет поймана,
одинакова для любого ее вида.
Задача, которая возникает перед капитаном рыболовного сейнера,
представлена на рис. 6.3. Полезности в данной задаче известны и четко
структурированы. Ожидаемые полезности для двух альтернатив
(ловить или не ловить):
us(PuP2)= Pi • A0р2—25A—р2)); F.10)
pi), F.11)
где р\ — вероятность того, что косяк — промысловая рыба; рч —
вероятность того, что рыба будет поймана.
Основной является вероятность р\, но она интуитивно менее
надежна, поскольку вероятность успешного улова рг может быть
уточнена в результате конкретных исследований, тогда как р\ основывается
на неопределенной информации, которая не может быть уточнена.
Так как одна из вероятностей (р\) в данной задаче появляется у
двух различных исходов дерева решений, то удобнее рассматривать

136
Y
Глава 6. Принятие решений в условиях неопределенности
1,4 0,6 0,8 1.0 Р,
0Л 0,6 0,8 1,0 Р2
Рис. 6А. Функции принадлежности для исходных вероятностей:
а — рх\ б — р2
разность ожидаемых полезностей двух альтернатив. Пусть переменная,
определяющая выбор,
Z(PuP2) =Ws(pi,p2) — Un(Pi,P2) =
= 1ОР1Р2 — 25pi + 25pip2+30pt —• 2 + 2pi =
F.12)
))• F.13)
—2.
Тогда ее функция принадлежности
(min
z
Представим функции принадлежности in(pi) и \х2(р2) в виде
Р!= {0/0,5; 0,4/0,6; 0,8/0,7; 0,9/0,8; 0,95/0,9; 1,0/1,0},
ра= {0/0,6; 0,1/0,7; 0,6/0,75; 1,0/0,8; 0,7/0,85; 0/0,9}.
Эти функции представлены на рис. 6.4. Степени принадлежности для
переменной Z=35pip2+7p1-~2 приведены в табл. 6.1.
Определение
0,6
0,7
0,75
0,8
0,85
0,9
значений
0.5
12
13,75
14,625
15,5
16,375
17,25
переменной
0,6 |
14,8
16,9
17,95
19
20,05
21,1
Z
р\
ат |
17,6
20,05
21,275
22,5
23,725
24,95
0,8
22,6
23,2
24,6
26
27,4
28,8
Та
0,9
23,2
26,35
27,925
29,5
31,075
32,65
блица 6.1
| ..0
26
29,5
31,25
33
34,75
36,5

6.2. Неточность и неопределенность описания исходов 137
f .
Степень принадлежности
fizB)= max (min(fAi(pi), |да(Л))Ь F.14)
Для определения значения р,2 при Z = 26 необходимо поступить
следующим образом:
1. В табл. 6.1 значению 26 (выделено жирным шрифтом)
соответствуют вероятности pi = 0,8; рг=0,8 и pi = 1,0; р2 = 0,6.
2. Из определения pi и р2 видно, что
Hi (Pi = 0,8) =0,9;
М/>2 = 0,8) = 1,0; jx2(P2=0,6)<=0.
3. Используя F.14), определим
liz B6) = max (i min (jlh (Pi) , \i2 (p2))) =
z=26
= max (min @,9, 1,0), min A,0, 0))=max @,9, 0)=0,9.
z=26
Аналогично находятся остальные значения функции
принадлежности нечеткого множества, задающего переменную
Z={0/12; 0/13,75; 0/14,625; 0/14,8; 0/15,5; 0/16,375;
0,1/16,9; 0/17,25; 0/17,6; 0,4/17,95; 0,4/19; 0,4/20,05;
0,4/21,1; 0,6/21,275; 0,8/22,5; 0/22,6; 0,1/23,2;
0,7/23,725; 0,6/24,6; 0/24,85; 0,9/26; 0,1/26,35;
0,7/27,4; 0,6/27,925; 0/28,8; 0,95/29,5; 0,7/31,075;
0,6/31,25; 0/32,65; 1,0/33; 0,7/34,75; 0/36,5}.
Значение функции принадлежности может быть вычислено путем
определения степени подтверждения для различных нечетких значений.
Рассмотрим следующие модификации утверждений:
/?ь «Ясно, что ловить рыбу лучше, чем не ловить».
Данное высказывание является четким и, учитывая, что Z — разница
между решениями «ловить» или «не ловить» (т.е. если г>0, то
решение должно быть «ловить»), функция принадлежности будет выглядеть
так:
I, если
3, если г<0;
R2: «Ясно, что не ловить рыбу лучше, чем ловить».
[, если z,<0;
3, если

138
Результаты |
расчета
« 1
431,75
Глава
44,625
6. Принятие решений
г
J4.8 15,5| 16,375 16t,9
в условиях
17,25 | 17,6
неопределенности
Таблица 6.2
17,95 | 19 |
\-\iz(z)
()
111 111
111 1 J 1
0 0 0 0 0 0
0,8 0,84 0,865 0,87 0,89 0,9
0,9 1 1 0,6 0,6
11111
0 0 0 0 0
0,92 0,93 0,94 0,95 0,98
20,05
l-\iz(z) 0,6
\lRt(z) I
\xr2(z) о
VR3(Z) 1
27,,925
\ — \iz(z) 0,4
\lRt(z) I
\XR2(z) 0
[IRS(Z) I
21,1 |
0,6
1
0
1
28,8
1
1
0
1
21,275 |
0,4
1
0
1
| 29,5
0,05
1
0
1
г
22,5 |22,6
0,2
1
0
1
| 31,075
0,3
1
0
1
23.2Г
1 0,9
1 1
0 0
1 1
z
3,1,25
0,4
1
0
1
231,725
0,3
1
0
1
$2,65 1
1
1
0
1
| 24,6
0,4
1
0
1
33
0
1
0
1
| 24,96
34,75
0,3
1
0
1
1
1
0
1
1
26
0,1
1
0
1
36,5
1
1
0
1
2Г6.35
0,9
1
0
1
|27,4
0,3
1
0
1
/?з: «Ловить, кажется, несколько лучше, чем не ловить».
10, если 2s?-20;
0,5 + 0,025, если-20<г<20;
1, если гГ>20.
Последнее высказывание является нечетким.
Определим степень истинности высказываний R\, R2, Rs'
= mm (max ((l-
где Y=Rif t=l, 2, 3.
Если X — утверждение о разности ожидаемых полезностей, то
степень, с которой X подразумевает любое из приведенных выше
утверждений, задается формулой
, |1я<(*))). F.15)
В табл. 6.2 сведены значения 1—^B), \iri(z), !Ля2(г)>
танные по формуле F.15).
Окончательно получаем

рассчиF.16)
Таким образом, окончательное решение капитана; «Ловить лучше,
чем не ловить».

Глава 7
МОДЕЛИ ПРИНЯТИЯ РЕШЕНИИ
С НЕЧЕТКИМИ
ОГРАНИЧЕНИЯМИ ВЫБОРА
7.1. ДЕТЕРМИНИРОВАННАЯ ЗАДАЧА
Рассматривается задача принятия решений в ситуации
неопределенности, когда ЛПР или эксперты могут указать лишь желаемые
границы изменения критериев, зависящих от параметров [2, 3].
Краткие сведения о методе. Пусть на основе уровневых
ограничений (см. параграф 1.5) найдены распределения возможностей naix(z)
и na2l(z) ДВУХ альтернатив а\ и аг, индуцируемые одним (в данной
задаче) критерием h{ (далее верхний индекс опускается). Если в
области рассуждений [г'щщ, zmax] оба распределения представляют собой
амодальные функции, возможны следующие варианты:
— одно из распределений абсолютно доминирует (рис. 7.1, а);
— ни одно из распределений абсолютно не доминирует (рис. 7.1,6).
Из рис. 7.1, а видно, что а{^а2 для всех гЕ[2тщ, гтах], так как
возможности признания альтернативы, например технического
устройства, п\ «хорошим» или «на мировом уровне» (соответствующим той
лингвистической установке, которая являлась основой для построения
уровневых ограничений), везде выше, чем у пч, кроме начала
интервала, где эти возможности одинаковы: nai(z) = na2(z) =1,0.
На рис* 7.1,6 в интервале Bmim Z\) доминирует альтернатива а\,
в интервале (гь <г3) — а% Для определения наилучшей альтернативы
нужна дополнительная информация от ЛПР:
а) имеется ли гипотеза о том, какие значения z чаще
наблюдаются?
б) важно ли то, что при больших значениях параметра устройство
работает лучше, чем при малых (или наоборот)?
в) важно ли то, что устройство имеет широкую область
ненулевых возможностей [2т1ш гп1?
В случае утвердительного ответа на последний вопрос в силу 2з>22
имеет место а2)>аь хотя в значительной части области [zmin, z{\ ах
доминирует над а,2. Данное решающее правило назовем доминированием
по параметру.
Ответ «Да» на второй вопрос свидетельствует о ситуации, когда
ЛПР имеет определенную структуру предпочтений, связанную с
параметрами, т. е. важны высокие значения возможности не вообще в
области рассуждений, а в определенных ее частях. Данная ситуация
анализируется й параграфе 7.4.
Если ответ на первый вопрос свидетельствует о том, что известно

140
Глава 7. Принятие решений с нечеткими ограничениями
о)
б).
1,0
Zmin Zy 7.1 Ъ
Рис. 7.1. Варианты распределений возможностей:
а — абсолютно доминирующие; б — недоминирующие
распределение вероятностей (может быть, субъективное) значений
параметра, то имеет место постановка, рассматриваемая в параграфе 7.2.
В остальных случаях в качестве решающего правила можно
использовать интегральную возможность:
G.1)
V=J na.(z)dz.
Если naiz^na2Zh то СJ
Пример использования метода. Пример 7.1. Необходимо выбрать
лучшее из устройств а\ и а2 на основе критериев качества работы
устройств К\ и /С2. Критерий К\ зависит от освещенности помещения
(параметр Zi), /C2 — от уровня вибраций, которым подвергается объект
(Z2). На основе знаний экспертов путем построения уровневых
ограничений (см. параграф 1.5) получены распределения возможностей (рис.
7.2) для каждой альтернативы а\ и а2. Условия работы устройств
ухудшаются при малых значениях Z\ (измеряется в люксах) и больших г2
(измеряется амплитудой колебаний).

?Л. Детерминирбваннйй
141
(Z2)
Z2mJn Z2 Z2 2
Рис. 7.2. Распределения возможностей устройств:
a — по критерию Кг, б — по критерию Кг
Пусть ЛПР заранее зафиксировало крайние значения параметров
областей рассуждений гцщп и 22min, т.е. наихудшие возможные значения
параметров Z\ и Z2. С целью последующей нормировки и сравнения
распределений возможностей необходимо определить область
рассуждений, т.е. указать и те значения параметров, начиная с которых
устройству следовало бы работать идеально. Если ЛПР этого не знает,
интервал [zmin, 2maxl можно назначить автоматически, как показано на
рис. 7.2: второй его конец находится в той точке шкалы параметра,
где появляется различие между альтернативами Bimax и ^mm
соответственно). Рассмотрим выбор решения согласно правилу доминирования
по параметру.
Как видно из рис. 7.2, а, для критерия К\ распределения
возможностей альтернатив таковы, что принцип доминирования по параметру
дает а^^пх. Тот факт, что в большей части области рассуждений п\
доминирует над а2, во внимание не принимается. По распределениям
яд. 2(?2) (см. рис. 7.2,6) можно сделать вывод: ai>a2, так как z'2>z.
Объединения оценок по критериям реализуем по выражениям
-; G.2)

142 Глава 7. Принятие решений с нечёткими Ограничениями
=|Vz?^l_ . G.3)
* ?2 ?2i
G.4)
где <х; — коэффициент относительной важности критериев kj.
ПуСТЬ 2imin = 2, 21тах=Н, z'i = 3, z"i=4,5, Z2min = 2, г2тах=13, z'2=12,
2//2=10, <xi = (X2 = 0,5 (ЛПР признает критерии К\ и /B равноважными).
Тогда согласно G.2) га11 = 0,79, za21 = 0,92, выражение G.3) дает
2ai2=0,91, гО22 = 0,73, вследствие чего по G.4) получаем zai2=0,85, za2s =
= 0,825. Рекомендация для выбора: ai^>a2.
Заметим, что данный подход может применяться, если
распределения возможностей не субнормальны, а сами функции лаг(г) амодальны.
В этих случаях следует использовать выражение G.1).
Рассмотрим выбор на основе интегральной оценки возможности
альтернатив G.1). Применяя численные методы интегрирования согласно
рис. 7.2, можно рассчитать, например, naizi = 44,2, Jta2zi = 31,l, Па** =
= 57,5, jifl2Z2=38,4. Для сопоставления результатов по разным критериям
необходимо рассчитать «полную возможность», т. е. идеальный случай
n, гтах])(я(г) = 1,0) согласно G.1):
zimax
i
= J
Отношения
~i Л< 44,2 ~, 31,1
позволяют на основе выражения G.4), заменяя za.j на nutz* при ai =
= a2 = 0,5, получить результат ai>a2: zai2 = 0,5 -0,53 + 0,5 -0,75 = 0,64;za2s =
= 0,5-0,37 + 0,5.0,5 = 0,435.
Применение аддитивной свертки G.4) в настоящем примере
является условным, так как возможны и другие свертки [1]. ЛПР должно
отдавать себе отчет в том, что G.4) предполагает интуитивную
допустимость компенсации не особенно хорошего значения по одному
критерию улучшением по другому.
7.2. ЗАДАЧА ВЫБОРА
СО СЛУЧАЙНЫМИ ПАРАМЕТРАМИ
Рассматривается задача принятия решений, когда либо известна
статистика наблюдений параметров среды, либо имеются экспертные
субъективные распределения вероятностей значений параметров.
Используется модель расчета ожидаемой возможности [4].

?j>. Задача выбора сб случайными параметрами
а)
F(z)
. 7.3. Задача выбора со случайным параметром:
а — функция плотности Р(г) и распределения возможностей; б — функция
распределения вероятностей F(z)
Краткие сведения о методе. Аналогично задаче параграфа 7.1
предполагается, что ЛПР не заинтересовано, чтобы возможности
альтернатив были выше для больших значений (в окрестности гтах (рис. 7.3))
параметра Z.
Как и прежде, ЛПР заинтересовано в том, чтобы точки г' и г"
находились как можно правее на шкале Z.
На рис. 7.3,а приведены два распределения возможностей nai(z) и
вероятностная оценка ожидаемых значений параметра Z: функция
плотности вероятности p(z). Тогда ожидаемая возможность
альтернативы п\ определяется по формуле
"max
min
G.5)
Необходимо отметить, что применение формулы G.5) корректно,
если процедуры определения уровневых ограничений и восстановления
распределения субъективных вероятностей независимы, т. е. знания
эксперта о вероятностях не влияют на выбор функций h°—h°(z) и А* =
= /i*(z). При опросе экспертов и расчете интеграла G.5) функцию

144 Глава 7. Принятие решении с нечёткими ограничениями
плотности вероятности p(z) удобно заменить функцией распределения
вероятностей (другой математической формой записи мнения эксперта
или статистических данных).
Функция распределения вероятностей F(z) (рис. 7.3,6)
показывает, что значения ?<zmin и 2>zmax не наблюдаются (или, согласно
мнению эксперта, не ожидаются), а вероятность, например р = 0,5, —
это вероятность того, что значение z будет находиться в интервале
temin, 20,5]. Значения 2о,25, 2o,s, zo,75 называются квантилями
распределения, и их относительно легко [1] найти в диалоге с экспертом.
Одним из простейших вариантов приближенного расчета значения
ожидаемой возможности является аппроксимация квантилями (см.
рис. 7.3, б):
Я*Ц~0,50 Па .B0,50) + 0,25(яа .
Для примера, изображенного на рис. 7.3, б:
яРа4 «0,50-0,90 + 0,25- @,95 + 0,65) =0,85;
я*>а2 «0,50-0,80 + 0,25- @,75 + 0,85) =0,80.
Следовательно, ^
Для более точных расчетов можно вместо трех квантилей
использовать 10 значений 2пдля точек, где р(гп)>0, или при наличии
компьютера — достаточное количество точек для достижения требуемой
точности.
Пример использования метода. Пример 7.2. Для интерпретации
рис. 7.3 можно было использовать предыдущий пример, где Z2 —
уровень вибраций, однако с целью демонстрации разнообразия
параметрических задач выбора рассмотрим следующую ситуацию.
Пусть z — сумма капиталовложений предприятия, измеряемая в
рублях на одного работающего. Предприятия конкретного
министерства, переходя на полный хозрасчет и самофинансирование, должны
планировать свой доход d, связанный с параметром г. Критерий d
измеряется в рублях на одного работающего в год. Плановыми
работниками министерства накоплена статистика о взаимосвязи d и z на
разных предприятиях данной отрасли. При этом экспертным путем
выделены разные классы (рис. 7.4) предприятий с точки зрения
фондовооруженности (низкая: 2—4 тыс. руб. на одного работающего и
т.д.). Как видно из рис. 7.4, при одинаковой фондовооруженности
могут быть разные уровни доходов в зависимости от конкретных условий
предприятий: rf* — «лучше не бывает», d° — «хуже не бывает». Таким
образом, множества точек типа d* и d° могут быть интерпретированы
как уровневые ограничения (см. параграф 1.5). Путем аппроксимации
получаем функции d* = d*(z) и d° = d°(z), а функция dai = fi(z)
характеризует мнение экспертов предприятия аг о возможном доходе при
различных значениях z (многовариантный план).
Сравнивая мнения экспертов министерства d* — d*{z) и d° = d°(z)
и предприятий а\ (dai = fi(z)), находим распределения возможностей
На B), которые показывают, насколько i-e предприятие планирует
использовать потенциальные возможности получения дохода. Например,
два предприятия (а\ и а^) в течение года имеют значение z—2 (см. рис.
7.4). На фиксированный период определены плспы развития
материальной базы и соответствующие функции дохода d\(z) и d2(z). Из-
эестно мнение экспертов из министерства о материальных возможное-

7.2. Задача выбора со случайными параметрами
145
12
u
Рис. 7.4. Взаимосвязь фондовооруженности и доходов
предприятий
тях развития предприятий данного класса, которое сформулировано в
виде функции плотности субъективных вероятностей p(z). Из рис. 7.4
видно, что в плановый период параметр z не может превышать 14 тыс.
руб., а наиболее вероятно, что 2 = 7 тыс. руб. на одного работающего.
Задача принятия решений заключается в том, чтобы определить,
какое из предприятий: ах или а2 составило лучший план развития.
Исходные данные для расчета ожидаемой возможности (возможности
признания плана «хорошим» с точки зрения министерства) приведены
в табл. 7.1. Аппроксимация интеграла G.5) реализована на основе
десяти точек.
Замечание. Функции плотности p(z) на рис. 7.4 полностью
соответствует функция распределения F(z) на рис. 7.3. Для расчета
Kai(z) и яО2B) на основе данных рис. 7.4 использована формула A.12).
Для приближенного расчета ожидаемых возможностей
воспользуемся следующей формулой аппроксимации:
ю
G.6)
71=1
Распределение возможностей и вероятностей
Таблица 7.1

Распределение
F(z)
nui(z)
3
0,05
0,9
1,0
1 4
0,1
0,75
1,0
5
0,18
0,50
0,87
1 «
0,25
0.36
0,72
z
7
0.5
0,49
0,55
8
0,65
0,48
0,48
9
0,82
0,41
0,28
1
1
0,88
0,25
0
1 и
0,92
0,11
0
12
0,95
0
0
10 - 2307

i 46 Глава ?. Принятие решений с нечеткими ограничениями
В результате имеем
я**. «0,1 -@,9-0,05 + 0,75.0,1 +0,50-0,18+ 0,56-0,25 +
+ 0,49 • 0,5 + 0,48 - 0,65 + 0,41 - 0,82 + 0,25 - 0,88 +
+ 0,11-0,92 + 0-0,95) =0,156;
яра, «0,1 -A,0-0,05+1,0-0,1 +0,87-0,18 + 0,72-0,25 +
+ 0,56 • 0,5 + 0,48 - 0,65 + 0,28 • 0,82 + 0 - 0,88 +
+ 0-0,92 + 0-0,95) =0,13.
Так как Ла1р>яа2р, то
В рассматриваемой задаче интерпретация уровиевых ограничений
могла быть и иной. Например, d* = d*(z) и d° = d°(z) могут
представлять собой пожелания сотрудников министерства, которые базируются
только на статистике. В этом случае уровневые ограничения, вероятно,
были бы более гладкими функциями и распределения возможностей,
в отличие от табл. 7.1, получились бы монотонно возрастающими.
Распределения вероятностей значений параметра в некоторых ситуациях
также могут иметь другой смысл, например на каждом предприятии
может быть собственное представление (и реальные возможности) о
приобретении основных фондов. Впоследствии для каждого
предприятия будет найдена своя функция Pi(z), так что па% v необходимо
рассчитывать согласно выражению
"
fnaax
=1 паг HPiWdz. G.7)
7.3. ЗАДАЧА ВЫБОРА
ПРИ СТОХАСТИЧЕСКОЙ
ЗАВИСИМОСТИ КРИТЕРИЕВ
И ПАРАМЕТРОВ
В параграфах 7.1 и 7.2 рассматривались ситуации, когда
альтернатива at в модели представлена в виде аналитической зависимости
(например, доход предприятия ас. dai = fi(z)) или по крайней мере
таблицы значений критерия в различных точках г. Однако на практике
точные значения dai иногда неизвестны эксперту ввиду ограниченности
ресурсов (в том числе временных), выделяемых на исследование
проблемы, или учитываемая связь по своей природе является
стохастической.
Краткие сведения о методе. На рис. 7.5, а приведены функции
плотности вероятности значений критерия h для альтернатив а\ и аг в
точке Zi. Заметим, что в других точках пространства параметра z вид
функций может быть другим и расположены они могут быть иначе (см.
рис. 7.5,6). Ситуацию (см. рис. 7.5, а) можно рассматривать по
упрощенной схеме путем использования наиболее вероятных значений hai
и ha2 для расчета возможностей согласно подходу, изложенному в па-

7.3. Стохастическая забйсИмость критериев и параметров
Ш
О)
fV г—,
б)
Рис. 7.5. Стохастическая связь между параметром и критерием:
а — допустимые альтернативы; б — частично допустимая альтернатива
раграфе 1.5. При этом информация о виде распределения вероятностей
никак не используется. Для ситуации рис. 7.5, а Па1>па2=^^\^>^2'
Так как обе функции плотности вероятности pai(h) и pa2(h)
определены внутри интервала разрешенных значений, выполняется аксиома
непрерывности предпочтений [1] и методом гипотетических лотерей
может быть построена условная функция полезности u(h) для точки
Z[. Расчет ожидаемой полезности
G.8)
h°
для каждой альтернативы а* в нескольких точках гп позволяет
восстановить функции и а. (?)• Они могут быть использованы для
ранжирования альтернатив аналогично G.1) или G.5), если заменить функции
возможности функциями иа. (z).
В ситуации, представленной на рис. 7.5, б, часть распределения
значений критерия h альтернативы а,\ находится в недопустимой зоне,
вследствие чего модель ожидаемой полезности неприменима. Это
объясняется тем, что нарушается аксиома непрерывности предпочтений.
Для построения функции полезности нельзя использовать
гипотетическую лотерею L, например, типа
В данной лотерее h\ (см. рис. 7.5, б) представляет собой
запрещенную с точки зрения ЛПР величину, вследствие чего лотерея L не имеет
детерминированного эквивалента и построение функции полезности
u(h) невозможно, если h<h°.
В случае, когда распределения критериальных значений
захватывают область [Д°, — оо), возможны другие решающие правила:
1. Строгое соблюдение границы недопустимости
G.9)
где X — признак «отсева» альтернативы.
ю*

148
Глава 7. Принятие решений с нечеткими ограничениями
13
Ah
h*=i3
11
9
7
5
h°=3<
1
V,^ P0,(h) ^""^ h*=f(z)
V *
- \^(h) j ho_f(z) ^
4 \ '''''
¦\Po,(W I *'
: т
23 Z
Puc. 7.6. Оценка возможностей альтернатив при
фиксированном значении параметра
2. Слабое соблюдение границы недопустимости:
(Э2)(йв,<А°)(Ха<).
G.10)
Оставшиеся после операции X альтернативы (множество ЛДОп)
могут быть ранжированы аналогично случаям, отраженным рис. 7.5, а.
Однако на практике могут встречаться ситуации, когда мощность
множества Лдоп слишком мала или ЛДОп = 0. Тогда следует проверить
разумность столь жестких требований h° = f°(z). Если ЛПР не
отказывается от своего мнения, следует ввести некоторую штрафную
функцию g(h), применение которой рассмотрено ниже.
Пример использования метода. Пример 7.3. В трех районах аь а2,
аз союзной республики действует значительное количество
промышленных предприятий конкретной отрасли. Критерий h — интегральная
оценка освоения капиталовложений предприятиями данной отрасли в
текущем году (параметр Z — время). Руководством министерств
сформулированы уровневые ограничения — точка зрения о требуемой
скорости освоения выделенных в данном году капиталовложений.
На рис. 7.6 приведены значения уровневых ограничений Л* и h°
только в точках Z\, z2, гъ. Интервал [z0, 2il соответствует январю, [zu
z2] — февралю и т. д. В конце января руководство министерства имеет
статистические данные об успехах предприятий всех районов в виде
трех функций распределения вероятностей ра.(Л). Распределение ра2(Л),
например, показывает, что предприятия района освоили
капиталовложения в пределах от 6 до 13%, а3 — от 1,5 до 7%. Таким
образом, район аз частично попал в «запретную зону», в свою очередь,
многие предприятия района ах работали идеально. Ситуация в точке
Z\ очевидна: аС^а^аъ. Однако данный простой пример позволяет
продемонстрировать способ определения степени превосходства
альтернатив.
Пусть шкала критерия h разделена на элементарные интервалы Ah.

7.3. Стохастическая зависимость критериев и параметров 149
Тогда область определения каждой функции pai(h) содержит /i=l,m
меток hn. Возможность признания альтернативы а*, соответствующей
уровневым ограничениям (ХОРОШО, НОРМАЛЬНО и т. п.), в точке
zi приближенно находим согласно выражению
mi ha -h°
значение функции распределения вероятностей в точке
hn. Для примера, отраженного на рис. 7.6, имеем
13-3
л*>а= 1/8@-1,0 + 0,1 -0 9 + 0,15-0,8+0,3-0,7+0,5-0,6 +
+ 0,8.0,5 + 0,9 -0,4 + 1,0- 0,3) = 0,22.
Объединение оценок лп1р для всех Z/, /=1, 12, дает дискретное
представление распределения возможностей paip(z)y которое отражает
процесс освоения капиталовложений в районе а,\ в течение года. Задача
принятия решений заключается в определении наилучшего района на
основе критерия h по текущим итогам всего года. Хотя все районы аи
а2 и аз в конце года, может быть, и достигли 100%-ного результата,
важно, как это было сделано: неритмичность работы явно видна из
графиков функций paxv{z) и учитывается при использовании
решающего правила G.1).
Рис. 7.6 имеет и другие интерпретации. Например, может быть
рассмотрена задача планирования, где функции рп{ (h) отражают мнение
руководителей предприятий или региональных объединений о
возможностях освоения капиталовложений, функции h*(z) и h°(z), как и
прежде, — мнение министерства.
Далее рассмотрим проблему, заключающуюся в том, что
альтернатива пъ частично недопустима (см. рис. 7.6), так как некоторые
предприятия данного района имеют результат ha3<h°, где Л°=3°/о.
Допустим, ЛПР считает, что сформулированные в настоящем параграфе
принципы выбора G.9) и G.10) слишком строгие (отставание в одном
месяце сводило бы к нулю итоги всего года). С другой стороны,
применение результата расчета возможности по формуле G.11)
яра, =1/5@-0,4 + 0,15.0 3 + 0,3.0,2 + 0,5-0,1+0,7-0) =0,031
о
также нелогично, поскольку имеются (или при другой постановке —
могут появиться) недопустимые результаты. Указанное отрицательное
влияние на оценку всего состояния дел может быть учтено с помощью
некоторой штрафной функции
Воспользовавшись формулой
Я*>'а. = Яраг?я, G.13)

150 Глава 7. Принятие решений с нечеткими ограничениями
получим итоговое значение na.p/<Jia.p, что соответствует логике (см. рис.
7.6): g* = y/o,9- gZy + bO-g^rj-OJ и, следовательно, ля.р' =
Х0,7 = 0,217.
Полученное таким образом, распределение возможностей na.p'(z)
далее может использоваться в решающих правилах G.1) и G.5). В
последнем случае предполагается, что задано распределение вероятностей
значений параметра p{z), которое зависит от одних факторов, а
распределения pGi (h) для всех z^Z — от других. Например, в задаче
выбора автомобиля предполагаемая скорость езды p(z) на автомобиле а*
будет зависеть от случайных факторов дорожной ситуации и
имеющегося у водителя времени, а расход топлива рui{h) — кроме скорости
и от степени износа автомобиля, направления ветра и навыков
вождения.
7.4. ОЦЕНКА
УСЛОВНОЙ ПОЛЕЗНОСТИ
ЗНАЧЕНИЙ КРИТЕРИЕВ
Рассмотрим ситуацию, когда ЛПР считает, что выполнение его
требований (отражены в уровневых ограничениях) при определенных
значениях параметров более важно, чем при других. Например,
экстремальные условия функционирования объектов, конец планового
периода, приближение ревизии, т.е. ряд не управляемых ЛПР
параметров, могут быть связаны со специфической структурой предпочтений.
В результате одна и та же степень возможности яа. при различных
значениях Z\, гъ ... параметра z будет иметь различную полезность для
ЛПР, вследствие чего решающие правила G.1) и G.5) неприменимы.
Краткие сведения о методе. Согласно используемой аксиоматике [4]
каждое значение параметра z обладает некоторой полезностью U7>
которая трактуется как полезность того, что в этой точке выполняются
требования ЛПР, заложенные в уровневые ограничения. Однако данное
выполнение может быть разным: 0^я2^1,0. Согласно аксиоме
монотонности предпочтений для всех z имеет место закономерность: если
Zj>Zi+i, то Uz. >U2{+1, либо если Zi>Zi+h то U 2. <Uzi+i. Для
дальнейших рассуждений будем считать, что имеет место первый случай:
полезности Uz монотонно растут с увеличением z. Следовательно, если
jizn=P и nZm =Р@<р^1,0) при zm>zn, то по втором случае значение
полезности выше.
Определение 7.1. Функцией распределения полезностей Uz
называется функция Un вещественного аргумента z, задаваемая
равенством U*(z) =u(Z={zn}f zn<z).
Функция Un(z) характеризует распределение полезностей по
значениям параметра z. Из определения 7.1 видно, что функция un(z) не
относится к одному значению z, а дает представление полезности
интервала значений, меньших текущего z.
Для пояснения понятия распределения полезностей приведем
физическую аналогию. Пусть имеется балка (рис. 7.7), состоящая из т
элементарных пластинок гп, каждая из которых имеет свою плотность рп,
причем pi< ... <рп< ... <рт. Тогда ги гт можно отождествлять с ко-

7.4. Оценка условной полезности значений критериев
161
1.0
Zmax Z
ШШЖШШШ
Рис. 7.7. Иллюстрация аналогии плотности
элементарных тел и полезностей
нечными значениями zmm, zmax некоторой области рассуждений [гт\п,
^таХ] на значениях параметра г, а рп — с полезностью uz. Если все
пластинки имеют одинаковый «единичный» объем, суммарную массу
пластинок /*!,,..,гп (левее r = rn+i) можно отождествить со значением
функции распределения полезностей un(z)> по которой можно судить,
с какой скоростью возрастает полезность (плотность) элементов.
В результате легко понять, что ип(гт\п)=0, un(zmax) = 1,0, т.е. по
аналогии вся масса балки находится левее ее правого конца, un(z)
является строго возрастающей функцией и может не совпадать для
разных экспертов (см. кривые /—3 на рис. 7.7). Построение функции
un(z) в режиме диалога ЛПР—ЭВМ основывается на системе аксиом
комбинирования возможностей [4], которые на практике не
предъявляют слишком жестких требований к ЛПР.
Процедура диалога построения функции un(z) имеет некоторую
аналогию с построением функции полезности для сравнения альтернатив,
заданных распределениями вероятностей исходов [1]. ЛПР также
предлагается оценить, какой из гипотетических объектов с определенными
свойствами более предпочтителен. Таким образом, накапливается
информация о структуре предпочтений ЛПР, используемой затем для
сравнения реальных объектов — альтернатив, которые ему следует
оценить и выбрать.
Основным математическим понятием при практическом построении
функции un(z) является специальное распределение возможностей: воз-
можностная смесь а-уровня (далее а-смесь).
Определение 7.2. а-Смесью называется множество пар {nz, z}t
где для всех z^[zm, zj я2=а, 0<а^1,0.
Определение 7.3. Полной а-смесью называется а-смесь, которая
определена на всей области рассуждений [zmin, zmAXl-
Последовательность определения функции un(z):
1. Формируется полная 0,5-смесь. Легко видеть, что, имея ее (рис.
7.8), ЛПР получает 0,5 от максимальной (единичной) полезности.
Такой полезностью обладала бы смесь (распределение возможностей),

152
Глава 7. Принятие решений с нечеткими ограничениями
а)
1.0
0.5
б)
1i
1,0
0±
-гп!п
», 1 „
п' ~п
Рмс. 7.5. Восстановление функции
a — полная 0,5-смесь; б — 1.0-смесь
(варьируемая)
которая в интервале [zmm, zmax\ имеет только значения яг=1,0, т.е.
полная 1,'0-смесь: идеальный объект.
2. Формируется некоторая 1,0-смесь, которая не является полной.
Полезность такой смеси меньше 1,0, и она априори неизвестна.
3. ЛПР предлагается сравнить предпочтительность полной 0,5-смеси
и 1,0-смеси. Если ЛПР признает, что одна из них предпочтительнее,
генерируется новая 1,0-смесь с более широким базисом, или наоборот
(в зависимости от ответа ЛПР).
4. Полная 0,5-смесь и вновь созданная 1,0-смесь предъявляются
ЛПР для сравнения.
Процедура продолжается до тех пор, пока ЛПР считает, что обе
смеси одинаково предпочтительны. Формальное следствие: 1,0-смесь с
текущим носителем [zm[n, zn] имеет полезность 0,5 (поскольку такова
полезность полной 0,5-смеси). Иными словами, полезность всех точек
левее гп равна 0,5: итого ил(гп) =0,5.
Таким образом, найдена третья точка функции распределения полез-
ностей (un(zm{n) =0, un(zmSiX) = l — по определению).
Для более точного восстановления функции un(z) можно найти еще
два ее значений: 0,25 и 0,75. ЛПР предлагается сравнить полную 0,25-
смесь с 1,0-смесью и полную 0,75-смесь с 1,0-смесью по изложенному
алгоритму.
До этого ЛПР имело дело с гипотетическими «прямоугольными»
распределениями возможностей — a-смесями. Восстановленную
функцию un(z) можно использовать для расчета полезности альтернатив,
имеющих произвольные распределения па.{г).
Разделим носитель [г0, zn] распределения дс<(г) на N интервалов Az.
Пусть для обоих концов интервалов (zn и zn+i) рассчитаны значения

7.4. Сценка условной полезности значений критериев
153
а)
яг
1,0
0.5
1,0-смесь (оператор /J2)
0,5-смесь (оператор/JO
А000
10000 Z
бIГ
1,0
0,5
1000
9000 10 000 Z
1,0
0,5(-
0
1000
8000 10000 Z
Рис. 7.9. Итеративный поиск значения ия(г) =0,5:
а — первая итерация: б — вторая итерация; в — третья итерация
un(zn), м"(г„+1), na((zn), na((zn+i)- Тогда получаемая полезность
альтернативы а{ приближенно определяется по формуле [4]
N
GЛ4)
п=1
Пример использования метода. Пример 7.4. Пусть необходимо
выбрать оператора сложного объекта из множества Претендентов ах
и а2-иРабота оператора характеризуется точностью выполняемых
операций (критерий Л), которая зависит от скорости (параметр г)
процессов, протекающих в не управляемой оператором внешней среде.
Для ЛПР в целом лучше, если оператор работает качественнее при
относительно больших скоростях процессов внешней среды.
Процедура по восстановлению функции распределения полезностей
un(z) заключается в следующем:
1. Устанавливается область рассуждений [2mm, zmax] таким
образом, чтобы данный интервал включал носители распределений
возможностей обоих претендентов. Пусть zmin=1000, zraax= 10 000.
2. На экране дисплея появляется текст: «Вообразите гипотетическую
ситуацию — оператор р, демонстрирует возможности на уровне 0,5 во
эсем интервале скоростей [1000, 10 000]».

154
Глава 7. Принятие решений с нечеткими ограничениями
1000
8000 10 000 Z
1000
10000 Z
Рис. 7.10. Исходные данные для расчета получаемой
полезности:
а — функция распределения полезностей;. б — распределение
возможностей альтернатив
3. Новое сообщение: «Вообразите оператора р2, возможности
которого на интервале [zi = 1000, г2=4000] равны Вашему идеалу A,0), а
на интервале 1>2 = 4000, 23= 10000] полностью не соответствуют @).
Укажите предпочтительность операторов в отношении предъявляемых
требований».
Возможные ответы ЛПР: a) Pi>p2; б) p2>Pi; в) pi — Р2; г) не
знаю,
Ответ ЛПР: а).
Замечание. Значение 22=4000 сгенерировала ЭВМ случайным
образом (рис. 7.9).
4. Генерируется новый интервал l>i = 1000, г'2 = 9000] для текста
шага 3.
Значение z'2 ЭВМ генерирует так, чтобы г'2>г2.
Ответ ЛПР: б).
5. Генерируется интервал [zi = 1000, г'2 = 8000].
Ответ ЛПР: в).
Таким образом, ип (8000) =0,5.
6. Процедура повторяется путем сравнения гипотетического опера-
тора 7ь имеющего распределение возможностей в виде 0,25-смеси, с
гипотетическими операторами ^2 с различными 1,0-смесями.
После получения ответа в) эксперт аналогично сравнивает 0,75- и
1,0-смеси.
На рис. 7.10, а приведена найденная функция un(z), на рис. 7.10, б —
экспериментально полученные распределения возможностей
претендентов п\ и а2, из которых видно, что при низких скоростях z оператор а{
работает лучше, при больших — а2 превосходит а\. (Такая ситуация

7.4. Оценка условной полезности значений критериев
155
Исходные данные
Распределение
2
з
5
Z, ТЫС.
6
ед.
7
Таблица
8 9 |
7.2
10
-у (nai(Zn)+na2{Zn+l))
— (Па2 (Zn) +Яа2
U*(Zn+l)-U*(Zn)
1,0 0,95 0,82 0,6 0,33 0,18 0,08 0,02 0
0,9 0,8 0,6 0,5 0,4 0,3 0,2 0,18 0.1
0.08 0,09 0,07 0,070 0,7 0,06 0,06 0,11 0,39
может быть объяснена психологическими особенностями претендентов:
у п2 снижается внимание при простой работе.) Распределения, nai(z)
и na2(z) могут быть найдены на основе методов, приведенных в
параграфах 1.5, 2.5 и 7.3.
Исходные данные (рис. 7.10 и 7.11) для расчета по G.14)
получаемой полезности при выборе альтернатив а{ и а2 приведены в табл. 7.2.
Определяем полезность альтернатив:
й*а^ =0,08.1,0 + 0,09-0,095+ 0,07-0,82 + 0,07.0,6 +
+ 0,07 • 0,33+0,06 • 0,18+0,06 • 0,08+0,11.0,02 +
+0,39-0=0,306;
и*а2 =0,08.0,9+0,09.0,8+0,07-0 6 + 0,07-0,5 +
0,06.0,5+0,07.0,4 + 0,06.0,3+0,06.0,2+0,11-0,18+
+ 0,39-0,1=0,378.
Следовательно,
1000
10 000 Z
5)
1000
Рис. 7.11. Исходные данные для приближенного расчета
получаемой полезности:
а — альтернатива ац б — альтернатива а.

Глава 8
ПРИНЯТИЕ РЕШЕНИЙ
НА ОСНОВЕ ИНФОРМАЦИИ
В ВИДЕ
НЕЧЕТКИХ СВИДЕТЕЛЬСТВ
8.1. ИСПОЛЬЗОВАНИЕ ПОНЯТИЯ
БЕЗУСЛОВНОГО СВИДЕТЕЛЬСТВА
Рассматривается метод, позволяющий на основе использования
нечетких безусловных свидетельств [9] вычислять лингвистические
вероятности событий при формировании лингвистических лотерей [3, 7].
Краткие сведения о методе. Определим формально лотерею Q как
случайную величину с заданным распределением вероятностей.
Представление лотереи Q имеет вид
Q=(pu xu...,pi, xi), /e= iM >
где N — множество натуральных чисел. Лотерея Q может быть
интерпретирована как действительный или гипотетический вариант
решений, приводящих к исходу Xi с вероятностью ри причем / { р\; = 1.
Рассмотрим случайную величину Ху принимающую значения из
множества {Хи ... ,Хг). Каждое Xit leNi, — нечеткая переменная,
представляемая нечетким множеством С*. = \J \i x{ (и)/и.
u<=Ux
Обозначим через Рг- нечеткое число, характеризующее вероятность
того, что случайная величина X примет значение Х{, или
лингвистическую вероятность значения Xi. Она представляется нечетким
множеством
с*\= U pP
Определение 8.1. Распределением лингвистических
вероятностей случайной величины X называется список значений
лингвистических вероятностей (Рь ..., Р/), /е N , соответствующий множеству
возможных значений (Хь ..., Xt).
Определение 8.2. Лингвистической лотереей называется набор
L=(PU X\\...\Pu Xi) с заданным распределением лингвистических
вероятностей.

8.1 Использование безусловного свидетельства 157
Заметим, что, вообще говоря, ^j Р%ф\ для любой совокупности ис-
ходов и соответствующего распределения лингвистических вероятностей.
Для формирования лингвистической лотереи необходимо задать
вектор (Ри ••• •, Pi)- Основная проблема при этом состоит в следующем:
в лотерее с / исходами определить вероятность исхода Xt при
заданных вероятностях исходов Х\,..., Xi-i. Приведем пример
лингвистической лотереи: L3= (вероятность ОЧЕНЬ БОЛЬШАЯ,
производительность НИЗКАЯ; вероятность НЕ ОЧЕНЬ БОЛЬШАЯ,
производительность ВЫСОКАЯ; вероятность МАЛАЯ, производительность ОЧЕНЬ
ВЫСОКАЯ).
Пусть задана двухисходная лингвистическая лотерея L2=(PU Х\\
Р2, Х2). Функции принадлежности соответственно имеют вид |mpi(p),
V>xi(u)f \ix2(u), p^[0, 1], где р — значения вероятности нечеткого
события, обусловленного исходом
где fx(u) — плотность вероятности, связанная с X.
Распределение вероятностей на оценках исходов неизвестно. Однако
степень возможности К некоторой fx(u) =fx°(u) на (R /n(fx°(u))
ограничивается известной функцией принадлежности |xplf (p). Иначе говоря,
Величина n(fx°(u)) определяет также степень возможности вероятности
р2 исхода Х2у т. е.
Итак,
\1х2(Р2/!х(и)=Гх(и))=^ (Sf°x(u)[lxi (U)du).
Поскольку h: fx(u)-+p2 — сюрьективное отображение и, то
|1р2 (р2) = max \xp l (Jfx (и) (utx1 (и) du)
Пи)
при условии, что,
Jfx(u)\ix2<(u)du=p2\ Jfx(u)du=l.
Эту вариационную проблему необходимо решать в случае непрерывных
нечетких чисел (u^D, где D — область в R ).
Если рассматривать задачу с дискретными нечеткими числами,
описывающими Хи Хъ то нахождение ^(Рг) сводится к задаче
нелинейного программирования вида
= max
р(и.)

158 Глава 8. Принятие решений на основе нечетких свидетельств
где ле 1\1 — число точек дискретизации.
Решение задачи нелинейного программирования декомпозируем на
этапы.
Этап 1. Пусть /?2 фиксировано. Определяем множество значений
я
функции 2j P(ut)\iXi(ui) на области определения, удовлетворяющей
условиям
P(Ui)\iX2(Ui)=p2\ (8.1)
1=1
= 1. (8.2)
П
Найденные значения образуют множество Р. Функция 2j р(щ)Х
X\iXi(Ui) принимает значения из [р'ь р"\\, причем
p'i= min 2jP(w»)^i(m<) при условиях (8.1) и (8.2);
п
\jp(Ui)\ixx{Ui) при условиях (8.1) и (8.2).
р(и.) г=1
Этап 2. Находим максимальное значение Цр2(р) на [р7ь р'М.
Приведем алгоритм определения неизвестной вероятности двухисход-
ной L-лотереи.
Шаг 1. Разбиваем [0,11 на интервалы равной длины точками р\
/еЛ/л, т.е. осуществляем отображение [0, l]->-{pj}in.
Шаг 2. Фиксируем р2 = Р*2, где /?*2^{pj}in, и исследуем Р —
допустимое множество распределений р(щ) с учетом (8.1), (8.2). Если
Р = 0, то перейти к шагу 3, если т(Р) = 1, где т — мощность
множества, то перейти к шагу 4, иначе — к шагу 5 (т(Р) — мощность
континуума).
Шаг 3. Положим [Хр2(Р2)=0. Переходим к шагу 8.
п
Шаг 4. Вычисляем pi = 2] р(щ)\\хЛт) и определяем *ip2(P*2) =
(P)
Переходим к шагу 8.
Ш а г 5. Определяем р'\.
Шаг 6. Определяем p'V
Шаг 7. Находим \iP2(p2) =max np,(Pi).
Pl'u Р"\\

8.1 Использование безусловного свидетельства 199
Ш а г 8. Если не все множество {рь ..., рп) просмотрено, переходим
к шагу 9, иначе — к шагу 2.
Шаг 9. Со = U М«Р2((Р2)/Р2 — искомая величина (вернее, ее ап-
проксимация).
Рассмотрим процедуру формирования гипотетических лотерей [5].
Итак, имеется совокупность некоторых утверждений в= {0ь ..., 6П},
/2GM Каждое 0ь teNn, несет вполне определенную информацию о
некоторой величине. Эта совокупность утверждений рассматривается в
контексте некоторых «условий внешней среды». Например, на завод
поступила новая техника. Тогда утверждения будут отражать влияние
техники на производительность, экономичность и т.п.
Совокупность в представляется как л-исходная L-лотерея: в={Рь
0i ;... ; Рп, 0п}, причем известны \хР. (р), i^Nn-U \\$. (и),/еЛ/п,т.е.
налицо уже рассмотренная задача определения вероятности /г-исходной
лингвистической лотереи. Каждое 9г = Х обладает свойством Кг с
лингвистической вероятностью pi, i^Nn, причем Рп неизвестна и
требуется ее определить.
Отметим, что X^U= К — нечеткие подмножества универсального
множества. Рассматривается случай дискретного распределения.
Величина Рп является ответом на вопрос «Если известно в= {0ь ... ,0w-i},
чему равно Рп в утверждении: Qn = X обладает свойством Кп с
лингвистической вероятностью Рп»?
На основании опроса имеем оценки величин, входящих в
утверждения Ki= \J iiKi (и)fu, i'eAfn-1, P — базовое множество. Это общий
случай. На самом деле эксперт дает оценки К= М \хк(и)/и для не-
ыеР
которого базового /С. Например, пусть в 0г- входят следующие К: НЕ
ОЧЕНЬ ВЫСОКИЙ, ОЧЕНЬ НЕВЫСОКИЙ, НЕВЫСОКИЙ и т.д.
Пусть К= ВЫСОКИЙ, и эксперта просят дать оценки только этому
понятию. Далее, Pj= \J \iPt {p)lp> /е^п_ь 5 — базовое множество.
p€=S
Обозначим К=\1к(и)/щ Р] = \1Р;(р)/р, /e#n-i. Преобразуем
утверждения 0?- в
я(р)=|1р ( J Px(u)iiK(u)du J.
V
Тогда nj(p)=\iPj (J Рх(и)\хк. (u)du).
V
Рассматриваются дискретные распределения, поэтому
1 =№) \ 2-i pWkj (и) J, /eJV».,, (8.3)
где Px — плотность вероятности, связанная с X.

160 Глава 8. Принятие решений на основе нечетких свидетельств
В рассматриваемых ниже примерах плотности вероятности
задаются в виде
Pmx/U= U \LPmX(u)Itl9 ?\1РтХ(и) = 1, (8.4)
Из (8.3), используя (8.4) и заданные распределения, получаем
j(Pix). (8.5)
Найдем
P(Pi)=f(Px, ^)
Затем определим неизвестное распределение вероятностей
Рп= jn(P)/P(p).
[0,1]
Примеры использования метода. Пример 8.1. Был проведен опрос
хоккейного эксперта и получена совокупность утверждений, связанная
с количеством шайб, пропущенных хоккейной командой за матч: в =
= {01. 9г.' 9з, 04}-
0i: «То, что число пропущенных шайб БОЛЬШОЕ, НЕ ОЧЕНЬ
ВЕРОЯТНО»;
02: «То, что число пропущенных шайб ОЧЕНЬ БОЛЬШОЕ, ОЧЕНЬ
НЕВЕРОЯТНО»;
8з: «То, что число пропущенных шайб НЕ ОЧЕНЬ БОЛЬШОЕ,
ВЕРОЯТНО»;
04: «То, что число пропущенных шайб НЕБОЛЬШОЕ,
НЕВЕРОЯТНО».
Здесь случайная величина X — число пропущенных шайб, К\ =
= БОЛЬШОЕ, /С2 = ОЧЕНЬ БОЛЬШОЕ, Кз= НЕ ОЧЕНЬ БОЛЬШОЕ,
Я4= НЕБОЛЬШОЕ; Р, = НЕ ОЧЕНЬ ВЕРОЯТНО, Р2 = ОЧЕНЬ
НЕВЕРОЯТНО, Р3 = ВЕРОЯТНО, Р4 = НЕВЕРОЯТНО.
Рассмотрим утверждение вида: 6б: «То, что число пропущенных шайб
ОЧЕНЬ НЕБОЛЬШОЕ, Р5». Необходимо определить лингвистическую
вероятность Р5 утверждения 05.
Имеем следующие распределения:
Кх = БОЛЬШОЕ ={0/0; 0/1; 0/2; 0,1/3; 0,2/4; 0,5/5; 0,7/6;
1,0/7; 0,9/8; 0,6/9; 0,2/10; 0,1/11; 0/12};
/B = ОЧЕНЬ БОЛЬШОЕ={0/0; 0/1; 0/2; 0/3; 0/4; 0,1/5; 0,3/6;
0,5/7; 0,6/8; 0,6/9; 0,3/10; 0,9/11; 1,0/12};
/C = НЕ ОЧЕНЬ БОЛЫПОЕ={1/0; 1/1; 1/2; 0,9/3; 0,7/4; 0,6/5;
0,4/6; 0,3/7; 0,2/8; 0,2/9; 0,1/10; 0,1/11; 0/12};
/С4 = НЕБОЛЬШОЕ ={1,0/0; 1,0/1; 0,9/2; 0,7/3; 0,6/4; 0,4/5;
0,3/6; 0,2/7; 0,1/8; 0,0/9; 0/10; 0/11; 0/12};

8.1. Использование безусловного свидетельства 161
Р, = НЕ ОЧЕНЬ ВЕРОЯТНО= {1,0/0; 1,0/1; 0,9/0,2; 0,9/0,3;
0,8/0,4; 0,75/0,5; 0,6/0,6; 0,3/0,7; 0,1/0,8; 0/0,9; 0/1,0};
Р;> = ОЧЕНЬ НЕВЕРОЯТНО= {1,0/0; 1/0,1; 0,8/0,2; 0,8/0,3;
0,6/0,4; 0,4/0,5; 0,2/0,6; 0,1/0,7; 0/0,8; 0/0,9; 0/1,0};
Рз=ВЕРОЯТНО={0/0; 0/0,1; 0,1/0,2; 0,1/0,3; 0,25/0,4;
0,45/0,5; 0,6/0,6; 0,7/0,7; 0,8/0,8; 0,95/0,9; 1,0/1,0};
Р«= НЕВЕРОЯТНО ={1,0/0; 1,0/0,1; 0,9/0,2; 0,85/0,3; 0,6/0,4;
0,5/0,5; 0,4/0,6; 0,15/0,7; 0,1/0,8; 0,1/0,9; 0/1,0}.
Приведем утверждения согласно выражению (8.3) к следующему
виду:
Получим
Как уже отмечалось, Рх — плотность вероятности, связанная в
нашем случае с числом пропущенных командой шайб за матч. Зададим
Рх:
Pix= {0,4/0; 0,1/1; 0,03/2; 0,05/3; 0,1/4; 0,15/5; 0,06/6;
0,03/7; 0,02/8; 0,02/9; 0,02/10; 0,02/11; 0/12};
Р2Х= {0,14/0; 0,1/1; 0,06/2; 0,1/3; 0,1/4; 0,1/5; 0,05/6;
0,05/7; 0,04/8; 0,07/9; 0,19/10; 0/11; 0/12};
Ргх= {0,3/0; 0,1/1; 0,04/2; 0,11/3; 0,05/4; 0,2/5; 0/6;
0,05/7; 0,01/8; 0,1/9; 0,02/10; 0,02/11; 0/12};
Я4*={0/0; 0,05/1; 0,1/2; 0,15/3; 0,5/4; 0/5; 0/6; 0,05/7;
0/8; 0/9; 0,15/10; 0/11; 0/12}.
Рассмотрим формулу
3=1 Л
где
l)V'K.(Uq)
11 - 2307

162
Глава 8. Принятие решений на основе нечетких свидетельств
Найдем величины щ(Р{х), *, /^N4. Предварительно определим
значения
12
Rij= 2*jpixMvKj (ия)> *. h
q=0
12
= 0,4-0+0,1-0 + 0,03.0+0,05.0,1+0,1-0,2 + 0,15-0,5 +
+ 0,06.0,7 + 0,03.1,0+0,02.0,9 + 0,02.0,6 + 0,02-0,2 + 0,02.0,1 +
+ 0 - 0 = 0,005 + 0,2 + 0,075 + 0,042 + 0,03 + 0,018 +
+ 0,012 + 0,004 + 0,002 = 0,208.
Остальные значения Rij вычисляются аналогично и образуют
матрицу
p
0,208
0,281
0,146
0,195
Вернемся к выражению
Щ(Ргх)
0,106
0,268
0,145
0,145
= Цр.(Я
0,339
0,586
0,735
0,665
«), »",/еЛ
0,708
0,493
0,634
0,555
Возникает задача: Р,- — дискретные распределения, причем точки
дискретизации детерминированы, а аргументы Ru по величине в общем
случае не совпадают с точками дискретизации распределений;
необходимо вычислить цр. (Ru).
Одним из способов решения этой задачи может быть
линеаризация, при которой точки дискретизации соединяются отрезками, которые
будут представлять недостающую функцию принадлежности. Используя
данный метод, построим таблицу значений щ(Р\х) (табл. 8.1).
Далее определим
12
Значения лингвистических вероятностей
для задачи о числе пропущенных шайб
Рх
PiX
Ргх
Рзх
Рьх
Ях{Рх)
0,936
0,343
0,657
0,877
п2(Рх)
1,0
0,692
0,580
0,580
0,202
0,586
0,735
0,665
Таблица 8.1
пЛРх)
mini nt{Px)
/—1,4
0,151 0,152
0,493 0,493
0,418 0,418
0,370 0,370

8.1. Использование безусловного свидетельства 163
P(pi) =0,81 -0,05 + 0,64-0,1 +0,25-0,15+ 0,09-0,06+
+ 0,01 -0>02+ 0,16-0,02 + 0,64.0,02+0,81 -0,02«0,18;
P(fh) =0,81 -0,1+0,64-0,1 +0,25-0,1 +0,09-0,05+
+0,01 • 0,04 + 0,16- 0,07+0,64 • 0,19 = 0,307;
Р(Рг) =0,81-0,11+0,64-0,05+ 0,25-0,2+0,09-0+
+ 0,01 -0,01 +0,16-0,1 +0,64-0,02 + 0,81 -0,02+0=0,216;
P(pi) =0,81 -0,15+0,64-0,5 + 0,64-0,15 =
=0,1215+0,32+0,096 = 0,538.
Итак, искомая вероятность
Р5= {0,16/0,18; 0,5/0,31; 0,32/0,22; 0,45/0,54}.
Пример 8.2. Рассматривается множество утверждений
2= Ци |г, |з, |4, 1ъ}-
Данное множество утверждений связано с процессом производства:
на некотором заводе происходит реконструкция, предприятие
оснащается новой техникой. Утверждения выглядят следующим образом:
li: «To, что объем производства продукции БОЛЬШОЙ,
ВЕРОЯТНО»;
|г: «То, что объем производства продукции ОЧЕНЬ БОЛЬШОЙ, НЕ
ОЧЕНЬ ВЕРОЯТНО»;
|з: «То, что объем производства продукции НЕ ОЧЕНЬ БОЛЬШОЙ,
НЕВЕРОЯТНО»;
til «To, что объем производства продукции НЕБОЛЬШОЙ, ОЧЕНЬ
НЕВЕРОЯТНО»;
15: «То, что объем производства продукции ОЧЕНЬ НЕБОЛЬШОЙ,
НЕВОЗМОЖНО».
В качестве X в данном примере выступает объем производства
продукции. Используются следующие оценки: К\ = БОЛЬШОЙ; /Сг=
= ОЧЕНЬ БОЛЬШОЙ; К3 = НЕ ОЧЕНЬ БОЛЬШОЙ; Я4 =
НЕБОЛЬШОЙ; /E = ОЧЕНЬ НЕБОЛЬШОЙ; Pt = ВЕРОЯТНО; Р2=НЕ ОЧЕНЬ
ВЕРОЯТНО; Р3= НЕВЕРОЯТНО; Р4 = ОЧЕНЬ НЕВЕРОЯТНО; Ръ=
= НЕВОЗМОЖНО.
Требуется определить лингвистическую вероятность утверждения ?в:
|в: «То, что объем производства продукции ДОСТАТОЧНО
БОЛЬШОЙ, Р6».
Специалист по вопросам производства, которого попросили ответить
на некоторые вопросы, дал следующие оценки:
/(^БОЛЬШОЕ ={0/200; 0/210; 0/220; 0/230; 0,2/240;
0,5/250; 0,9/260; 1,0/270};
К2=ОЧЕНЬ БОЛЬШОЕ = цк,2 (и)/«;
Яз=НЕ ОЧЕНЬ БОЛЬШОЕ = A - цк,2 («))/и;
/С4=НЕБОЛЬШОЕ=A-|гк,(и))/ы;
А:5=ОЧЕНЬ НЕБОЛЬШОЕ» A-цк,(«)J/м;

164 Глава 8. Принятие решений на основе нечетких свидетельств
Pi = BEPOHTHO={0/0; 0/0,1; 0,1/0,2; 0,1/0,3; 0,25/0,4;
0,45/0,5; 0,6/0,6; 0,7/0,7; 0,8/0,8; 0,95/0,9; 1,0/1,0};
Р2=НЕ ОЧЕНЬ ВЕРОЯТНО=A-|лР,2(р))/р;
Рз= НЕВЕРОЯТНО = A - |*Р1 (р)) /р-
Р4 = ОЧЕНЬ НЕВЕРОЯТНО=A-цР1(р)J/р;
Р5=НЕВОЗМОЖНО=A-цР1(/?)K/р.
Проделаем операцию, аналогичную вышеприведенной, а именно1
Итак:
ueV
ueV
где Px — плотность вероятности, связанная с рассматриваемой
величиной,
Р1Х= {0/200; 0,1/210; 0,05/220; 0,2/230; 0,4/240; 0,02/250;
0,16:260; 0,07/270};
Р2Х= {0,3/200; 0,1/210; 0,01/220; 0,05/230; 0,15/240;
0,3/250; 0/260; 0,09/270};
Pzx= {0/200; 0,25/210; 0,13/220; 0,08/230; 0,4/240; 0,1/250;
0,04/260; 0/270};
Pix= {0,5/200; 0/200; 0,1/220; 0,05/230; 0,2/240;
0,1/250; 0/260; 0,05/270};
Рьх= {0,12/200; 0,01/210; 0,2/220; 0,3/230; 0,2/240;
0,05/250; 0,01/260; 0,11/270}.
Для определения величины п,(Ргх) предварительно найдем
&)= 2ml Pix(u)\tK .(и), i, /<=ЛГ5;
,l-0 + 0,05.0+0,2-0 + 0,4-0,2 + 0,02-0,5 +
+0,16-0,9+0,07-1,0=0,08+0,01+0,155+0,07=0,304.

8.2. Использование условных нечетких свидетельств
165
Значения
?х
PiX
Pzx
Рзх
Рьх
Рьх
лингвистических вероятностей
0,101
0,89
0,743
1,4
0,65
0 999
0,804
1,000
1,000
1,000
ЛИЯ,,
0,221
0,29
0.052
0,003
0.008
пая,,
0,093
0.51
0,210
0,01
0,008
Та
л-ЛРх)
0,059
0,64
0,321
0,04
0,029
блица 8.2
min nt(Px)
?—1,5
0,059
0,51
0,052
0,003
0,008
Остальные значения Rij вычисляются аналогично и образуют
матрицу
0,304 0,221 0,779
0,270 0,171 0,829
R = 0,166 0,073 0,927
0,140 0,083 0,917
0,184 0,139 0,861
Далее применяем описанный выше метод линеаризации для
построения таблицы значений nt(Pix), i, j^N5 (табл. 8.2).
Таким образом, имеем
0,696
0,731
0,834
0,860
0,825
0,613
0,631
0,749
0,803
0,771
P(pi) =0,4-2%+0,02-0,5%+0,16-0,9% +
+ 0,07-1=0,249;
Р (р2) = о, 15 • 0,2%+0,3 • 0,5'/*+0,09 • 1 = 0,209;
Я(рз)=0,4.0,2э/-+0,Ь0,5%+0,04-0,9%+0=0,105;
Р(р4)= 0,2-0,2^ + 0,1-0,5%+0,05-1=0,102;
Р (рь) = 0,2 • 0,2%+0,05 - 0,5%+0,01 • 0,9%+
+ 0,11-1=0,154.
Значение искомой вероятности
Я6= {0,06/0,25; 0,05/0,21; 0,02/0,11; 0,005/0,10; 0,01/0,15}.
8.2. УПОРЯДОЧЕНИЕ АЛЬТЕРНАТИВ
НА ОСНОВЕ
УСЛОВНЫХ НЕЧЕТКИХ
СВИДЕТЕЛЬСТВ
Рассматривается метод выбора альтернатив на основе условных
нечетких свидетельств, связывающих значения некоторой величины и
влияющих параметров. Сравнение альтернатив происходит на основе

1j66 Глава 8. Принятие решений на основе нечетких свидетельств
интервалов, задаваемых оценками ожидаемой необходимости и
достаточности [1, 5, 6].
Краткие сведения о методе. Определим свидетельство Е как набор
утверждений gi,...,giv вида gi=Y есть Gt.
Пусть заданы: распределение вероятностей Рх = {Р\, ¦ ¦ •, Pn}, где
Pi — нечеткая вероятность того, что случайная величина X = i> и
условное распределение возможностей я(У|Х), где n(Y/x=i) = Gu i=l,
2,..., N.
Запишем свидетельство в символической форме: Е={РХу n(Y\X)}.
Пусть U — универсальное множество, GidU, F — нечеткое значение
переменной X.
Тогда из утверждения «Если X есть F, то Y есть G» будет
следовать n(Y\X) =F'\]G, где я(У|Х) — условное распределение
возможностей, задаваемое значением X; F и Ь — цилиндрические расширения
F и G в UXV.
Условное распределение возможностей, задаваемое значением X,
n(Y\X) (vyu)= max (l-\iF{u); \iG(v))y
где \xF и \xG •— функции принадлежности F и G.
Условная возможность F с учетом распределения возможностей
Poss {X есть F\Y есть G}= sup max (\if{u); \ig(u)).
и
Определим условную возмолшость достижения критериального
значения Q:
Poss {У есть Q\X}= Poss {У есть Q\Y есть Gx}~
- sup
Так как X — случайная величина, то можно определить
ожидаемую возможность достижения величины
ЕП (Q) = Ex Poss {У есть Q\X} = 2j рг sup (Q(]Gt).
г
Ожидаемая необходимость будет иметь вид
ЕС (Q) = Ex Cert {Уесть Q\X} = 1 - ЕП (<?') =
Множества функций En(Q) и EC(Q) могут быть интерпретированы
как нечеткие меры. Однако в общем случае они не являются ни
нормированными, ни аддитивными. Вместо этого для любых нечетких
подмножеств Qi и <?2
ЕС (QiUQa) > EC (Qi) + EC (Q2) ~ EC (Qif^);
ЕП (dUQa) < ЕП (Q0 + ЕП (Q2) - ЕП (Q4nQ2).
Основной вопрос связан со способом комбинирования двух или
более свидетельств. Пусть заданы два свидетельства: E={Ei, E2}, где
Е1 = {Р*И n(Y\X{)}; E2={Px2, ЩУ\Х2)}. Пусть Хх и Х2 заданы на
множествах индексов щ = {1,.,, ,N\), ^=={1,... ,Л^2} и связаны с сов-

8.2. Использование условных нечетких свидетельств
167
En(Q)=0i75; EC(Q)=O
ЕП@)=0,8; EC(Q)=O
10 1.0
0,8
1.0
ЕЛ(О)=1; EC(Q)=0,375
1.0
En(Q)=0,375; EC(Q)=0,16
1,0
0,375
0
1.0 1.0
0.375
0.16
0
1.C
1.0
ЕП(О)=О,33; EC(Q)=0
En(Q)r0,«1;EC(Q)=0.16
0,33
0
1.0 1.0
1.0
0,16
01
Рис. 8.1. Ожидаемая возможность и ожидаемая
необходимость нечеткого события для различных
видов функций G и Q
местным распределением вероятностей Р(х\, х2), где Рц — вероятность
того, что X\ = i, X2 — j. Тогда ожидаемая возможность нечеткого события
q = «Y есть Q»
ЕП (Q)=E(xux2) Poss {Y есть Q\(xux2)} =
Ожидаемая необходимость будет иметь вид
ЕС (Q) =?(*ь х2) Cert {Y есть Q|(jc,, л:2)}
Определение ожидаемой возможности и необходимости
проиллюстрировано на рис. 8.1 для случая одного свидетельства с одним
интервалом значений условия [6].

168 Глава 8. Принятие решений на основе нечетких свидетельств
Приведем алгоритм решения задачи.
Шаг 1. Выявить события, которые будем оценивать (открытие
месторождения, наличие какой-либо болезни у больного, выполнение
работы и т.д.).
Шаг 2. Определить критерии, по которым будем оценивать
события (производительность, продолжительность и т.д.).
Ш а г 3. Определить признаки, от которых зависят критериальные
оценки выбранных событий (наличие поискового признака
месторождения, количество человек в бригаде, наличие каких-либо симптомов
болезни и т.д.).
Шаг 4. Разбить множества значений признаков на такие
интервалы значений, чтобы по каждому интервалу можно было оценить
событие по выбранному критерию.
Ш а г 5. Для первого события определить первый интервал значений
первого условия, от которого зависит оценка первого события по
выбранному критерию.
Ш а г 6. Оценить по выбранному критерию событие при условии, что
значение признака находится в определенном интервале.
Ш а г 7. Если оценены события для всех интервалов признака, то
перейти к шагу 8, в противном случае — к шагу 6.
Шаг 8. Если событие оценено по всем признакам, то перейти к
шагу 9, в противном случае — к шагу 6.
Шаг 9. Если оценка проведена для всех событий, то перейти к
шагу 10, если нет — перейти к первому интервалу первого признака
для следующего события в шаге 6.
Шаг 10. Определить первый интервал значений для первого
признака.
Шаг 11. Оценить вероятность того, что значение признака будет
находиться в определенном интервале.
Шаг 12. Если все интервалы признака оценены по вероятности,
то перейти к шагу 13, иначе — к шагу 11.
Шаг 13. Если все признаки оценены по вероятности, то перейти к
шагу 14, если нет — выбрать первый интервал следующего признака
и перейти к шагу 11.
Шаг 14. Определить ожидаемую возможность и ожидаемую
необходимость для каждого события.
Шаг 15. Определить лучшее событие из оцененных по данному
критерию.
Примеры использования метода. Пример 8.3. Рассмотрим задачу
выбора географического района для строительства промышленного
объекта [2]. Имеется три района. Необходимо выбрать тот, где
экономический эффект от строительства объекта будет наибольший.
Экономический эффект зависит от численности незанятого населения и
наличия сырьевых ресурсов в рассматриваемых районах.
Формализуем задачу. Пусть У — экономический эффект от
строительства объекта; Х\ — численность незанятого населения; Х2 —
наличие сырьевых ресурсов. Будем оценивать экономический эффект в
терминах лингвистической переменной:
ОЧЕНЬ МАЛЫЙ={1/0; 0,56/0,2; 0,17/0,5; 0,03/0,8; 0/1};
СРЕДНИЙ={0/0; 0,3/0,2; 1/0,5; 0,3/0,8; 0/1};
БОЛЬШОЙ ={0/0; 0,07/0,2; 0,44/0,5; 1/0,8; 0,7/1};
ОЧЕНЬ БОЛЬШОЙ ={0/0; 0,03/0,2; 0,17/0,5; 0,56/0,8; 1/1}.

8.2. Использование условных нечетких свидетельств 169
Проведем опрос эксперта:
Аналитик: Назовите такое число интервалов значений для
численности незанятого населения, чтобы по каждому интервалу можно
было высказать суждение об экономическом эффекте, отличное от
суждений по соседним интервалам.
Эксперт: Три интервала: 0—100; 100—300; 300—10 000.
Аналогично выясняем, что для наличия сырьевых ресурсов также
необходимы три интервала: 0—100; 100—1000; 1000—10 000.
Теперь перейдем к непосредственному нахождению экономического
эффекта от строительства объекта при наличии определенного условия,
проводя диалог следующего типа:
Аналитик: Каков экономический эффект, если фактор наличия
сырьевых ресурсов имеет значение 1000—10 000?
Эксперт: Средний.
Аналитик: Каков экономический эффект, если фактор наличия
сырьевых ресурсов имеет значение 100—1000?
Эксперт: Большой.
Аналитик: Каков экономический эффект, если фактор наличия
сырьевых ресурсов имеет значение 1000—10 000?
Эксперт: Очень большой.
Аналитик: Каков экономический эффект, если численность
незанятого населения имеет значение 0—100?
Эксперт: Очень малый.
Аналитик: Каков экономический эффект, если численность
незанятого населения имеет значение 100—300?
Эксперт: Средний.
Аналитик: Каков экономический эффект, если численность
незанятого населения имеет значение 300—10 000?
Эксперт: Очень большой.
В результате этого диалога получили свидетельство Е с суждениями
об экономическом эффекте от строительства объекта при наличии
определенного условия:
Е=(Еи ?а);
где Нц — лингвистические переменные.
Рассмотрим конкретный район и оценим вероятностное
распределение факторов по интервалам значений. Будет проведен диалог
следующего типа:
Аналитик: Какова вероятность того, что к моменту ввода
объекта численность незанятого населения будет иметь значение 0—100
в первом районе?
Эксперт: Вероятность 0,15.
Аналитик: Какова вероятность того, что к моменту ввода
объекта численность незанятого населения будет иметь значение 100—300
в первом районе?
Эксперт: Вероятность 0,5.
Аналитик: Какова вероятность того, что к моменту ввода
объекта численность незанятого населения будет иметь значение 300—
10 000?
Эксперт: Вероятность 0,35.

170
Глава 8. Принятие решении на основе нечетких свидетельств
Результаты опроса
1
1
2
3
0—100
100—300
300—10 000
о численности населения
Таблица 8.3
Номер района
I
ОЧЕНЬ МАЛЫЙ Я|, = 0,15
СРЕДНИЙ Р12в0,5
ОЧЕНЬ Pis = 0,35
БОЛЬШОЙ
II
Р\1 = 0А
in
Результаты опроса о наличии ресурсов
Таблица 8.4
Номер района
»
ш
1 0—100 СРЕДНИЙ
2 100—Л 000 БОЛЬШОЙ
3 1000—10 000 ОЧЕНЬ
БОЛЬШОЙ
Таким образом, мы получили распределение вероятностей Р\хх =
= @,15; 0,5; 0,35) для фактора «Численность незанятого населения» в
первом районе.
Аналогично получим распределение вероятностей Pia-2=@,2; 0,65;
0,15) для фактора «Наличие сырьевых ресурсов» в первом районе.
Таким же образом определим распределения вероятностей для
факторов во втором и третьем районах: ЯПХ1=@,5; 0,4; 0,1); PibY2=@,8;
0,15; 0,05); PnUl= @,6; 0,3; 0,1); PmXi = @,2; 0,3; 0,5).
В конечном виде вся полученная информация будет выглядеть так,
как показано в табл. 8.3 и 8.4.
Определим ожидаемую возможность того, что экономический
эффект от строительства будет очень большим, т.е. Q = ОЧЕНЬ
БОЛЬШОЙ:
;
ЕП(<2)= ?jFii ^^maxmm (щ>; цн
Для первого района:
En,(Q)=0,15-@Jmax(min@; 1; 0); min@,03; 0,56; 0,3); min@,17;
0,17; 1); min@,56; 0,03; 0,3); min(l; 0; 0)) +
+ 0,65max(min@; 1; 0); min@,03; 0,56; 0,07); min@,17; 0,17; 0,44);
min@,56; 0,03; 1); min(l; 0; 0,7)) +
+ 0,15max(min@; 1; 0); min@,03; 0,56; 0,03); min@,17; 0,17; 0,17);
min@,56; 0,03; 0,56); min(l; 0; 1))) +
+ 0,5-@,2max(min@; 0; 0); min@,03; 0,3; 0,3); min@,17; 1; 1);

8.2. Использование условных нечетких свидетельств 171
min@,56; 0,3; 0,3); min(l; 0; 0)) +
+ 0,65 max (min @; 0; 0); min @,03; 0,3; 0,07); min @,17; 1; 0,44);
min @,56; 0,3; 1); min A,0; 0; 0,7)) +
+ 0,15 max (min @; 0; 0); min@,03; 0,3; 0,03); min@,17; 1; 0,17);
min @,56; 0,3; 0,56); min A; 0; 1))) +
+ 0,35- @,2 max (min @; 0; 0); min@,03; 0,03; 0,3); min@,17; 0,17; 1);
min@,56; 0,56; 0,3); min(l; 1; 0))) +
+ 0,65 max (min @; 0; 0); min @,03; 0,03; 0,07); min @,17; 0,17; 0,44);
min@,56; 0,56; 1); min(l; 1; 0,7)) +
+ 0,15max(min@; 0; 0); min@,03; 0,03; 0,03); min@,17; 0,17; 0,17);
min@,56; 0,56; 0,56); min(l; 1; 1)) =
= 0,15-@,2max@; 0,03; 0,17; 0,03; 0)+0,65max@; 0,3; 0,17; 0,03; 0) +
+ 0,15 max @; 0,3; 0,17; 0,03; 0)) +
+ 0,5-@,2max@; 0,03; 0,17; 0,3; 0)+0,65max@; 0,03; 0,17; 0,3; 0) +
+ 0,15max@; 0,3; 0,17; 0,3; 0,17; 0,3; 0)) +
+ 0,35-@,2max@; 0,03; 0,17; 0,3; 0)+0,65max@; 0,03; 0,17; 0,56; 0,7) +
+ 0,15max@; 0,03; 0,17; 0,56; 1)) =0,15@,2-0,17 +
+ 0,65.0,17 + 0,15-0,17) +0,5@,2-0,3 + 0,65-0,3 + 0,15-0,3) +
+ 0,35 @,2 • 0,3 + 0,65 • 0,56+0,15-1) = 0,376.
Теперь определим ожидаемую необходимость для Q:
з з
V V
ЕС (Q) = Zj Pa ZjP2jminmax(|iQmax (\1ни\\1н2.)).
Для первого района
=0,15@,2min(max@; max(l,0)); max(O,3; max@,56^ 0,3));
max@,17; max@,17; 1)); max@,56; max@,03; 0,3)); maxA,0;
max@; 0))) +
+ 0,65min(max@; max(l,0; 0)); max@,03; max@,56; 0,07));
max0,17; max@,17; 0,44)); max@,56; max@,03; 1,0));
max(l,0; max@; 0,7))) +
+ 0,15min(max@; max(l,0; 0)); max@,03; max@,56; 0,03));
max@,17; max@,17; 0,17)); max@,56; max@,56; 0,03));
max(l,0; max@; I, 0))) +
+ 0,35 @,2 min (max @; max@; 0)); max @,03; max @,3; 0,3));
max@,17; max(l,0; 1,0)); max@,56; max@,3; 0,3));
maxA,0; max@; 0))) +
+ 0,65 min (max @; max@; 0)); max @,03; max @,3; 0,07); max @,17;

172 Глава 8. Принятие решений на основе нечетких свидетельств
maxA,0; 0,44)); max@,56; max@,3; 1,0)); maxA,0; max@; 0,7))) +
+ 0,15 min (max @; max@; 0)); max@,03; max@,3; 0,07)); max@,17;
maxA,0; 0,17)); max@,56; max@,3; 0,56)); maxA,0; max@; 1,0))) +
+ 0,35@,2min(max@; max@; 0)); max@,03; max@,03; 0,3)); max@,17;
max@,17; 1,0)); max@,56; max@,56; 0,3)); maxA,0; maxA,0; 0))) +
+ 0,65 min (max @; max@; 0)); max@,03; max@,03; 0,007)); max@,17;
max@,17; 0,44)); max@,56; max@,56; 1,0)); maxA,0; maxA,0; 0,7))) +
+ 0,15 min (max @; max@; 0)); max@,03; max@,03; 0,03)); max@,17;
max@,17; 0,44)); max@,56; max@,56; 0,56)); maxA,0; maxA,0; 1,0))) =
= 0,15@,2min@; 0,44; 0,17; 0,7; 1)+0,65min@; 0,44; 0,56; 0,56; 1) +
+ 0,15 min @; 0,44; 0,83; 0,56; 1)) +
+ 0,5@,2 minA; 0,7; 0,17; 0,7; 1)+0,65 min A; 0,7; 0,56; 1) +
+ 0,15 min A; 0,7; 0,17; 0,56; 1)) +
+ 0,35@,2minA; 0,7; 0,17; 0,56; 1)+0,65min(l; 0,93; 0,56; 0,56; 1) +
+ 0,15min(l; 0,97; 0,83; 0,56; 1)) =0,5-@,2-0,17 + 0,650,17 +
+ 0,15-0,17) +0,35- @,2-0,17 + 0,65-0,56 + 0,15-0,56) =0,253.
Итак, для первого района имеем EFIi(Q) =0,3764; ECi(Q) =0,2537.
Аналогичные расчеты проведем для второго и третьего районов:
ЕПц(ф) =0,5- @,8-0,17 + 0,15-0,17 + 0,05-0,17) +
+ 0,4- @,8-0,3 + 0,15-0,3 + 0,05-0,3) +
+0,1-@,8-0,3 + 0,15-0,56+0,05-1) =0,2424;
ECii(Q) =0,4- @,8-0,17+0,15-0,17 + 0,05-0,17) +
+ 0,1 - @,8-0,17 + 0,15-0,56+0,05-0,56) =0,092;
ЕПШ(<Э) =0,6- @,2-0,17 + 0,3-0,17 + 0,5-0,17) +
+ 0,3 • @,2 • 0,3 + 0,3 • 0,3 + 0,5 • 0,3) +
+ 0,1 • @,2-0,3 + 0,3-0,56 + 0,5-1) =0,2648;
ЕСш(<2) =0,3- @,2-0,17 + 0,3-0,17+0,5-0,17) +
+ 0,1 • @,2 • 0,17+0,3 • 0,56 + 0,5 • 0,56) = 0,099.
Отложим на числовой оси значения ожидаемой возможности и
ожидаемой необходимости для трех районов (рис. 8.2,а). Как видно, для
строительства промышленного объекта предпочтение следует отдать
первому району.
Пример 8.4. Рассмотрим задачу из предыдущего примера, но при
решении будем использовать два критерия оценки исхода при
неизменных остальных исходных данных [4]. Экономический эффект Yt от
строительства объекта и объем неиспользованных ресурсов района Y%
зависят от численности незанятого населения А', и наличия сырьевых
ресурсов Х2 в рассматриваемых районах. Будем оценивать выбор
географического района в терминах лингвистической возможности:
ОЧЕНЬ МАЛЫЙ = {1/0; 0^56/0,2; 0,17/0,5; 0,03/0,8; 0/1};
СРЕДНИЙ ={0/0; 0,3/0,2; 1/0,5; 0,3/0,8; 0/1};
БОЛЬШОЙ = {0/0; 0,07/0,2; 0,44/0,5; 1/^0,8; 0,7/1};

8.2. Использование условных нечетких свидетельств 173
а)
1ш . i
ECD(Q) 0.2 БПй(О)БПш(О) ЕГДО 0,4
БСШ(О)
Рис. 8.2. Ожидаемые воз- < »
можности и необходимо- W
сти нечетких событий в
случае одного (а) и двух .. . ECi ЕП\ ЕП
(б) критериев оценки 7Z it Г? *Т± 7~* ' 71
исходов °'2 ЕС3 0,3 ЕП3 0,4 0,5
ОЧЕНЬ БОЛЬШОЙ = {0/0; 0,03/0,2; 0,17/0,5; 0,56/0,8; 1/1};
ПОЧТИ НЕТ = {1/0; 0,22/0,2; 0/05; 0/0,8; 0/1};
МАЛЫЕ = {0,6/0; 1/0,2; 0,33/0,5; 0,03/0,8; 0/1};
БОЛЬШИЕ- {0/0; 0,03/0,2; 0,33/0,5; 1/0,8; 0,6/1};
ОЧЕНЬ БОЛЬШИЕ- {0/0; 0,02/0,2; 0,14/0,5; 0,46/0,8; 1/1}.
Далее проведем опрос эксперта:
Аналитик: Назовите такое число интервалов значений для
сырьевых ресурсов, чтобы по каждому интервалу можно было высказать
суждение о выборе района для строительства промышленного объекта,
отличное от суждений по соседним интервалам.
Эксперт: Три интервала: 0—100; 100—1000; 1000—10000.
Аналогично выясняем, что для признака «Незанятое население»
необходимо пять интервалов значений: 0—100; 100—300; 300—1000;
1000—5000; 5000—10 000.
Теперь перейдем непосредственно к выбору района, учитывая
экономический эффект от строительства предприятия и объем
неиспользованных ресурсов района при наличии определенного условия.
Проведем диалог следующего типа:
Аналитик: Каков экономический эффект, если наличие сырьевых
ресурсов имеет значение 0—100?
Эксперт: Средний. в
Аналитик: Каков экономический эффект, если наличие сырьевых
ресурсов имеет значение 100—1000?
Эксперт: Большой.
Аналитик: Каков экономический эффект, если наличие сырьевых
ресурсов имеет значение 1000—10 000?
Эксперт: Очень большой.
Аналитик: Каков объем неиспользованных ресурсов района, если
наличие сырьевых ресурсов имеет значение 0—100?
Эксперт: Нет информации.
Аналитик: Каков объем неиспользованных ресурсов района, если
наличие сырьевых ресурсов имеет значение 100—1000?
Эксперт: Малый.
Аналитик: Каков объем неиспользованных ресурсов района, если
наличие сырьевых ресурсов имеет значение 1000—10000?
Эксперт: Большой.
Аналогичный диалог проведем, чтобы выяснить связь
экономического эффекта и объема неиспользованных ресурсов с численностью
^занятого населения,

174
Глава 8. Принятие решений на основе нечетких свидетельств
Зависимость Yu Y2
от Х2 и вероятности значений факторов
Таблица 8.5
H22j
Номер альтернативы
1 0—100
2 100-1000
3 1000—10 000
СРЕДНИЙ
БОЛЬШОЙ
ОЧЕНЬ
БОЛЬШОЙ
ПОЧТИ НЕТ
МАЛЫЕ
БОЛЬШИЕ
0,2
0,65
0,15
0.8
0,15
0,05
0,2
0,3
0,5
Таблица 8.6
Зависимость Yu Y2
от Х\ и вероятности значений
i
х„
факторов
нш
Н2\г
1
Номер
альтернативы
2
P2ig
3
1
2
3
4
5
0—100
100-300
300—1000
1000—5000
5000—40 000
ОЧЕНЬ МАЛЫЙ
СРЕДНИЙ
ОЧЕНЬ
БОЛЬШОЙ
То же
ПОЧТИ НЕТ
»
МАЛЫЕ
БОЛЬШИЕ
ОЧЕНЬ
БОЛЬШИЕ
0,15
0,35
0,3
0,1
0,1
0,25
0,25
0,2
0.15
0,05
0,5
0,2
0,15
0,1
0,05
Теперь рассмотрим три района и оценим распределение вероятностей
признаков Х\ и Х2 по интервалам значений.
Аналитик: Какова вероятность того, что численность незанятого
населения будет иметь значение 0—100 в первом районе?
Эксперт: Вероятность 0,15.
Аналитик: Какова вероятность того, что численность незанятого
населения будет иметь значение 100—300 в первом районе?
Эксперт: Вероятность 0,35.
Аналитик: Какова вероятность того, что численность незанятого
населения будет иметь значение 300—1000 в первом районе?
Эксперт: Вероятность 0,3, и т. д.
Таким образом, получаем распределение вероятностей Р^=@,15;
0,35; 0,3; 0,1; 0,1) для численности незанятого населения в первом
районе и аналогично — для сырьевых ресурсов. Для второго и третьего
районов проводим подобный опрос. Окончательно полученная
информация о зависимости Y\ и У2 от Х\ и Х2 будет выглядеть следующим
образом (табл. 8.5 и 8.6):
«Если
\ = Х\, то У1 =
«Если Х\ = Хи то У2 =
«Если Xi=X^ то 1^1 = Я12»;
«ЕСЛИ ^2 = ^2, ТО У2 =

8.2. Использование условных нечетких свидетельств 175
Приступим к непосредственным вычислениям. По каждому Ут, т =
= 1, 2, для всех рассматриваемых районов оценим степень возможности
и определенности достижения целей Y{ = Ti = БОЛЬШОЙ ДОХОД,
У2=Г2 = МАЛЫЕ НЕИСПОЛЬЗОВАННЫЕ РЕСУРСЫ, вычислим
и выберем такой район, для которого эти оценки имеют наилучшие
значения. Для этого найдем
EUt(Tm) = 2jZjp^HP^maxmin ^Tm ; ^нш1.; \»>нт2.);
ECt(Tm) =
г 3
Пусть Г, = БОЛЬШОЙ ДОХОД. Тогда
5 3
= 0,15- @,2 max @; 0,07; 0,17; 0,03; 0)+0,65 max @; 0,07; 0,17; 0,03; 0) +
+ 0,15max@; 0,03; 0,17; 0,03; 0))+0,35-@,2max@; 0,07; 0,44; 0,3; 0) +
+ 0,65max@; 0,07; 0,44; 0,3; 0)+0,15max@; 0,07; 0,17; 0,3; 0)) +
+ 0,5-@,2max@; 0,03; 0,17; 0,3; 0)+0,65 max@; 0,03; 0,17; 0,56; 0,7) +
+ 0,15max@; 0,03; 0,17; 0,56; 0,7)) =0,15-@,2-0,17+0,65-0,17 +
+ 0,15-0,17) +0,35- @,2-0,44 + 0,65-0,44 + 0,15-0,3) +
+ 0,5- @,2-0,3 + 0,65-0,7 + 0,15-0,7) =0,482;
5 3
ЕП2G\) = 2j2-1 PzmPzigmaxmin (цг/, Цнш ; Цн,2.) =
= 0,35- @,8-0,17 + 0,15.0,17 + 0,05-0,17) =0,25- @,8-0,44 +
+ 0,15-0,44 + 0,05-0,3) +0,4- @,8-0,3 + 0,15-0,7+0,05-0,7) =0,319;
5 3
En3G'i) = 2^ 2^ PsmPsig max min ((iTl; цнш ; hh12j ) =
= 0,5- @,2-0,17 + 0,3-0,17 + 0,5-0,17) +0,2- @,2-0,44 +
+ 0,3 • 0,44 + 0,5 • 0,3) + 0,3 • @,2 - 0,3 + 0,3 • 0,7 + 0,5 • 0,7) = 0,345.
Далее
5 3
ECi(rt) = ZjXjPijHPiig minmax (цГ,; max (цн ш ; hh12j )) =
i=i j=i
= 0,15- @,2 min@; 0,44; 0,44; 1; 1) +0,65min@; 0,44; 0,56; 1; 0,7) +
+0,15min@; 0,44; 0,83; 1; 0,7))+0,15min(l; 0,7; 0,44; 1; 0,7) +

176 Глава 8. Принятие решений на основе нечетких свидетельств
+ 0,5@,2min(l; 0,7; 0,44; 1; 0,7) +0,65min(l; 0,93; 0,56; 1; 0,7) +
+ 0,15min(l; 0,97; 0,83; 1; 0,7))-0,35-@,2.0,44 + 0,65-0,44 +
+ 0,15-0,44) +0,5- @,2.0,44 + 0,65-0,56 + 0,15.0,7) =0,432;
5 3
2jiiP2ig minmax (ixT^ max (\хнш ; [1н^ )
= 0,35- @,8-0,44 + 0,15-0,44 + 0,05-0,44) +0,4- @,8-0,44 +
+ 0,15-0,56 + 0,05-0,7) =0,298;
5 3
minmax
{; max (\xH ш ; \ih{2. )) =
-0,2-@,2-0,44 + 0,3-0,44 + 0,5.0,44)+0,3-@,2-0,44 +
+ 0,3-0,56 + 0,5-0,7) =0,2698.
Пусть Г2 = МАЛЫЕ НЕИСПОЛЬЗОВАННЫЕ РЕСУРСЫ. Тогда
5 3
= 0,5-@,2-0,6 + 0,65-0,6 + 0,15-0,03)+0,3-@,2-0,6 + 0,65-1 +
+ 0,15-0,33) +0,1 - @,2-0,03 + 0,65-0,33 + 0,15-0,33) +
+ 0,b @,2-0,02 + 0,65.0,14 + 0,15.0,14) =0,541;
5 3
ЕП2(Г2) = 2j2j ^2j/fP2^ max min (\xr2; цн21. ; |Xh22j ) =
= 0,6-@,8-0,6 + 0,15-0,6+0,05-0,03)+0,2-@,8-0,6 + 0,15-1 +
+ 0,05-0,33) +0,15- @,8-0,03 + 0,15-0,33 + 0,05.0,33) +
+ 0,05- @,8-0,02 + 0,15-0,14 + 0,05-0,14) =0,487;
5 3
ЕП3(Г2) = 2^.2-i PsjnPsigmax min (|Хг2; М^я2И ; IAh^. ) =
2=1 j=l
= 0,7- @,2-0,6 + 0,3-0,6 + 0,5-0,03) +0,15- @,2-0,6 + 0,3-1 +
+ 0,5-0,33) +0,1 • @,2-0,03 + 0,3-0,33 + 0,5-0,33) +
+ 0,05- @,2-0,02 + 0,3-0,14 + 0,5-0,14) «0,341,
Далее
5 3
ECiG2)= Zjt-iPwPiig minmax (цг2; max (цн21. ; цн^. ))
= 0,5 • @,2 • 0,6+0,65 • 0,6+0,15 • 0,03) + 0,3 • @,2 • 0,6+0,65 • 0,6 +
+0,15-0,03) +0,1 • @,2-0,03+0,65-0,03+0,15-0,03) ^0,414;

8.2. Использование
условных
Оценки альтернатив
t
1
2
3
0,482
0,319
0,345
Еп,(Г„
0,541
0,487
0,341
нечетких свидетельств
0,432
0,298
0,269
ECf<r2)
0,414
0,461
0,270
ЕП,(Г) =
0,482
0,319
0,341
177
Таблица 8.7
0,414
0„298
0.269
ЕС2(Г2) =
min max
2'
max
= 0,6- @,8-0,6+0,15-0,6+0,05.0,03) +0,2- @,8-0,6+0,15.0,6 +
+ 0,05-0,03)+0,15-@,8-0,03 + 0,15-0,03 + 0,05-0,03) =0,461;
5 3
ЕС3(Г2)==
max
= 0,7- @,2-0,6+0,3-0,6+0,5-0,03) +0,15- @,2-0,6 + 0,3-0,6+
+ 0,5-0,03) +0,1 • @,2-0,03 + 0,3-0,03 + 0,5-0,03) =0,270.
Полученные результаты сведены в табл. 8.7.
Отложим на числовой оси значения ожидаемой возможности и
ожидаемой необходимости для трех районов (рис. 8.2,6). Как видно, для
строительства промышленного объекта предпочтение следует отдать
первому району.
\2 - 2307

ЗАКЛЮЧЕНИЕ
Теория нечетких множеств переживает период становления,
которое естественным образом сопровождается и блестящими примерами ее
применения, и неудачными рекламными работами. Развернулись
бурные дискуссии о ее фундаментальном и прикладном значении. Спектр
мнений — от приписываний теории мифических возможностей до
заявлений о ее логической несостоятельности. По математическим аспектам
данного направления опубликованы десятки монографий за рубежом,
начинают издаваться книги такого рода и в нашей стране. В
теоретическом плане достигнуты существенные успехи: пройден большой путь
от понятий нечеткого множества и функции принадлежности к
созданию теории возможностей, обоснованию понятия гранулярности
информации, нечеткой логики, нечеткого моделирования и управления.
Однако прикладным аспектам теории нечетких множеств посвящены лишь
отдельные статьи или ведомственные издания.
Рассмотренный в книге материал имеет своей целью частично
компенсировать недостаток в методической литературе и ориентирован на
решение прикладных задач, примеры которых приведены ниже:
— в автоматизированном проектировании при выборе
окончательного варианта сложного технического объекта необходимо осуществить
синтез разнородных требований;
— в задаче размещения энергетических объектов, промышленных
предприятий и т. п. необходимо найти компромисс между множеством
противоречивых требований;
— при определении энергетической политики возникает задача
анализа и сравнения альтернативных способов производства
электроэнергии (гидро- и тепловых электростанций, атомных электростанций
и т. д.);
— при выборе направлений научных исследований необходимо
проанализировать одновременно такие важные элементы проблемы, как
квалификация предполагаемых исполнителей, имеющийся научный
задел, техническая база и ее уровень, оценка перспективности
исследований и т.д.;
— при освоении новых газоносных месторождений, строительстве
комплексов по транспортировке, хранению и переработке газа
требуется принимать во внимание экономические, политические, социальные,
геологические и другие факторы, учитывать вопросы безопасности на-

Заключение 179
селения, охраны окружающей среды, надежности газотранспортных
средств и т.д.
Характерными особенностями перечисленных задач наряду с много-
критериальностью, большим числом альтернатив, внутренней
сложностью является необходимость обработки качественной информации
(описания компонентов векторного критерия, оценок вероятностей
последствий принимаемых решений и др.). Существует несколько путей
ее формализации и создания соответствующих моделей.
Рассмотренные в книге методы принятия решений ориентированы на
использование теории нечетких множеств.
Применение описанного подхода связано с решением ряда проблем
прикладного характера. Прежде всего это вопросы программной
реализации обработки нечеткой информации и создания диалоговых
систем поддержки принятия решений, реализующих предложенные
модели.
Построение моделей принятия решений на основе понятий
нечеткого множества и лингвистической переменной предполагает
алгоритмическое описание всех процессов в этих моделях. В связи с этим
возникает задача создания математического обеспечения выполнения
нечетких алгоритмов на ЭВМ. Для этой цели необходима разработка
алгоритмического языка для формального их представления,
соответствующего транслятора и библиотеки стандартных программ. В
данном направлении уже достигнуты некоторые успехи, однако основные
работы впереди. Начаты исследования и получены обнадеживающие
результаты по аппаратной реализации нечетких алгоритмов. Кроме
того, для принятия решений на основе нечетких моделей необходимо
располагать соответствующими программными средствами. В
настоящее время созданы и продолжают развиваться системы поддержки
принятия решений. Это интерактивные автоматизированные системы,
которые помогают ЛПР использовать нечеткие данные и модели для
решения плохо формализуемых задач.
12*

СПИСОК ЛИТЕРАТУРЫ
К ГЛАВЕ 1
1. Крумберг О. А. Теория психологической возможности для моделирования выбора
в условиях неопределенности // Методы принятия решений в условиях
неопределенности. — Рига: Риж. политехи, ин-т, 1980. — С. 47—52.
2. Кузьмин В. Б. Параметрическое описание лингвистических значений переменных
и ограничений // Модели выбора альтернатив в нечеткой среде: Тез. докл. Все-
союз. семинара. — Рига: Риж. политехи, ин-т, 1980. — С. 75—76.
3. Саати Т. Л. Взаимодействие в иерархических системах // Техн. кибернетика. —
1979. — № 1. — С. 68—84.
4. Сваровский С. Т. Аппроксимация функций принадлежности значений
лингвистической переменной // Математические вопросы анализа данных. — Новосибирск:
ВЦ СО АН СССР, 1980. — С. 127—131.
5. Скофенко А. В. О построении функций принадлежности нечетких множеств,
соответствующих количественным экспертным оценкам // Науковедение и
информатика. — Киев: Наук, думка, 1981. — Выго. 22. — С. 70—79.
6. Borisov A., Krumberg О. Possibility theory for decision- making // Fuzzy Sets
Systems. — 1983. — Vol. 9, N 1. — P. 13—24.
7. Kuzmin V. B. A parametric approach to description of linguistic values of variables
and hedges // Fuzzy Sets Systems. — 1981. — Vol. 6, N 1. — P. 27—41.
8. Saaty T. L Measuring the fuzziness of sets // J. Cybernetics. — 1974. — Vol. 4,
N 4. — P. 53—61.
К ГЛАВЕ 2
1. Алексеев А. В. Применение нечеткой математики в задачах принятия решений //
Методы и системы принятия решений: Прикладные задачи анализа решений в
организационно-технических системах. — Рига: Риж. политехи, ин-т, 1983. —
С. 38—42.
2. Борисов А. И., Крумберг О. А. Интерактивные методы анализа альтернатив в
слабо определенных задачах принятия решений // Модели и методы
формирования и многокритериального выбора предпочтительных вариантов систем. — М.:
ВНИИ сист. исслед., 1981. — Вып. 1. — С. 104—114.
3. Модели принятия решений на основе лингвистической переменной / А. Н.
Борисов, А. В. Алексеев, О. А. Крумберг и др. — Рига: Зинатне, 1982. — 256 с.
4. Заде Л. А. Понятие лингвистической переменной и его применение к принятию
приближенных решений: Пер. с англ. — М.: Мир, J976. — 165 с.
5. Крумберг О. А. Теория психологической возможности для моделирования выбора
в условиях неопределенности // Методы принятия решений в условиях
неопределенности. — Рига: Риж. политехи, ин-т, 1980. — С. 47—52.
6. Попов В. А. Аналитическое выполнение арифметических операций над
нечеткими числами // Модели выбора альтернатив в нечеткой среде: Тез. докл. Всесоюз.
семинара. — Рига: Риж. политехи, ин-т, 1980. — С. 14—15.
7. Dubois D., Prade H. Various kinds of interactive addition of fuzzy numbers.
Application to decision analysis in presence of linguistic probabilities // 13th IEEE
conf. decision control. — New York, 1979, — P, 783—787.

Список литературы
8. Dubois D., Prade H. Fuzzy sets and systems: Theory and applications. — New
York: Acad. Press, 1980. — 394 p.
9 Dubois D., Prade H. Additions of interactive fuzzy numbers // IEEE Trans.
Automatic Control. — 1982. — Vol. 26, N 4. — P. 926—936.
10. Mizumoto M., Tanaka K. Some properties of fuzzy numbers // Advances in fuzzy
set theory and applications. — Amsterdam: North-Holland Publ. Corp., 1979. —
P. 153—164.
К ГЛАВЕ З
1. Заде Л. Понятие лингвистической переменной и его применение к принятию
приближенных решений: Пер. с англ. — М.: Мир, 1976. — 165 с.
2. Попов В. А. Выбор оптимального варианта развития электрической сети при
нечеткой исходной информации // Методы и системы принятия решений:
Прикладные задачи анализа решений в организационно-технических системах. — Рига: Риж.
политехи, ин-т, 1983. — С. 43—49.
3. Baas S. M.. Kwakernaak H. Rating and ranking of multiple-aspect alternatives using
fuzzy sets // Automatica. — 1977. — Vol. 3, N 1. — P. 47—58.
4. Baldwin J. F., Guild N. C. F. Comparison of fuzzy sets on the same decision space //
Fuzzy Sets Systems. — 1979. — N 2. — P. 213—231.
5. Dubois D., Prade H. Decision-making under fuzziness // Advances in fuzzy set
theory and applications / Ed. by M. M. Gupta, R. K. Ragade, R. R. Yager. —
Amsterdam: North-Holland Publ. Corp., 1979. — P. 279—302.
G. Yager R. R. A procedure for ordering fuzzy subsets of the unit interval // Inform.
Sci. — 1981. — Vol. 24, N 2. — P. 143—161.
К ГЛАВЕ 4
1. Беллман Р., Заде Л. Принятие решений в расплывчатых условиях // Вопросы
анализа и процедуры принятия решений: Пер. с англ. — М.: Мир, 1976. —
С. 172—215.
2. Baas S. M., Kwakernaak H. Rating and ranking of multiple-aspect alternatives using
fuzzy sets // Automatica. — 1977. — Vol. 3, N 1. — P. 47—58.
3. Dubois D., Prade H. Fuzzy sets and systems: Theory and applications. — New
York: Acad. Press, 1980. — 394 p.
4. Efstalhiou /., Rajkcvich V. Multi-attribute decision-making using a fuzzy heuristic
approach // Intern. J. Man-Machine Studies. — 1980. — Vol. 12, N 2. — P. 141—156.
5. Yager R. R. Multiple-objective decision-making using fuzzy sets // Intern. J. Man-
Machine Studies. — 1977. — Vol. 9, N 4. — P. 375—382.
6. Yager R. R. Multicriteria decisions with soft information: an application of fuzzy
set and possibility theory // Fuzzy Mathematics. — 1982. — Pt 1. — Vol. 2, N 2. —
P. 21—28; Pt 2. — Vol. 2, N 3. — P. 7—16.
К ГЛАВЕ 5
1. Алексеев А. В. Лингвистические модели векторной оптимизации // Модели выбора
альтернатив в нечеткой среде. — Рига: Риж. политехи, ин-т, 1980. — С. 33—35.
2. Жуковин В. Е. Модели и процедуры принятия решений. — Тбилиси: Мецниереба,
1981. - 118 с. '
3. Жуковин В. Е. Нечеткие многокритериальные модели принятия решений. —
Тбилиси : Мецниереба, 1988. — 70 ,с.
4. Заде Л. А. Основы нового подхода к анализу сложных систем и процессов
принятия решений // Математика сегодня: Пер. с англ. — М.: Знание, 1974. —
С. 5-49.
5. Кофман А. Введение в теорию нечетких множеств : Пер. с англ. — М.: Радио
и связь, 1982. — 432 с.
6. Орловский С. А. Нечеткие отношения предпочтения в задачах принятия решения //
Математические методы оптимизации и структурирования систем. — Калинин:
Калинин, гос. ун-т, 1980. — С. 120—131.
7. Орловский С. А. Проблемы принятия решений при нечеткой исходной
информации. — М.: Наука, 1981. — 208 с.

182 Список литературы
К ГЛАВЕ 6
1. Кини Р. Размещение энергетических объектов: Выбор решений: Пер. с англ. —
М.: Энергоатомиздат, 1983. — 320 с.
2. Jain R. Decision-making in the presence of fuzzy variables // IEEE Trans. Systems,
Man Cybernetics. — 1976. — Vol. 6, N 1. — P. 698—703.
3. Watson S. R., Weiss J. /., Donnell M. L Fuzzy decision analysis. — IEEE Trans,
Systems, Man Cybernetics. — 1979. — Vol. 9, N 1. — P. 1—9.
К ГЛАВЕ 7
1. Кини Р. А., Райфа Х. Принятие решений при многих критериях : Предпочтения
и замещения: Пер. с англ. — М. : Радио и связь, 1981. — 560 с.
2. Крумберг О. А. Теория психологической возможности для моделирования выбора
в условиях неопределенности // Методы принятия решений в условиях
неопределенности. — Рига : Риж. политехи, ин-т, 1980. — С. 47—52.
3 Крумберг О. А. Анализ возможностей исходов в дереве решений // Модели
выбора альтернатив в нечеткой среде : Тез. докл. межресп. науч. конф. — Рига :
Риж. политехи, ин-т, 1984. — С. 30—31.
4. Модели принятия решений на основе лингвистической переменной / А. Н.
Борисов, А. В. Алексеев, О. А. Крумберг и др. — Рига : Зинатне, 1982. — 256 с.
К ГЛАВЕ 8
1. Борисов А. Н. Оценка альтернатив на основе величин ожидаемой возможности
и определенности // Управление при наличии расплывчатых категорий : Тез. докл.
6-го науч.-техн. семинара. — Пермь: НИИ упр. машин и систем, 1983. — С.14—17.
2. Борисов А. Н., Глушков В. И. Использование понятия гранулярности информации
при решении задач с неоднозначно определенными исходными данными //
Методы и системы принятия решений : Прикладные задачи анализа решений в
организационно-технических системах. — Рига: Риж. политехи, ин-т, 1983. — С. 4—9.
3. Борисов А. #., Меркурьева Г. В. Формирование и свойства лингвистических
лотерей в моделях анализа решений // Принятие решений в условиях нестатисти-
че:кой неопределенности. — Рига: Риж. политехи, ин-т, 1982. — С. 19—26.
4. Глушков В. И., Деркач О. И. Выбор альтернатив с учетом нечеткого описания
последствий // Методы и системы принятия решений: Автоматизированные
системы поддержки принятия решений в управлении и проектировании. — Рига: Риж.
политехи, ин-т, 1985. — С. 29—41.
5. Меркурьева Г. В. Диалоговая система построения и анализа лингвистических
лотерей // Методы и системы принятия решений: Прикладные задачи анализа
решений в организационно-технических системах. — Рига: Риж. политехи, ин-т,
1983. — С. 27—32.
Ч). Обработка нечеткой информации в системах принятия решений / А. Н.
Борисов, А. В. Алексеев, Г. В. Меркурьева и др. — М.: Радио и связь, 1989. — 305 с.
7. Borisov A. N.t Merkuryeva G. V. Linguistic lotteries-construction and properties //
BUSEFAL. Ete. — 1982. — N 11. — P. 39—46.
8. Yager R. R. Application of information granularity to political and other decisions //
Policy Inform. — 1981. — Vol. 5, N 1. — P. 135—139.
9. Zadeh L. A. Fuzzy sets as a basis for a theory of possibility // Fuzzy Sets
Systems. — 1978. — Vol. 1, N 1. — P. 3—28.
10. Zadeh L. A. Fuzzy sets and information granularity // Advances in fuzzy sets
theory and applications / Ed. by M. M. Gupta, R. K. Ragade, R. R. Yager. —
Amsterdam: North-Holland Publ. Corp., 1979. — P. 3—18.

ОГЛАВЛЕНИЕ
Предисловие 5
Глава 1. Методы построения функций принадлежности нечетких множеств . . 7
1.1. Построение функций принадлежности на основе парных сравнений . . 7
1.2. Построение функций принадлежности лингвистических термов с
использованием статистических данных 10
1.3. Построение функций принадлежности на основе экспертных оценок . 15
1.4. Параметрический подход к построению функций принадлежности . . 19
1.5. Построение функций принадлежности на основе интервальных оценок 24
Глава 2. Выполнение операций над нечеткими числами 31
2.1. Операции над нечеткими числами на основе принципа обобщения . . 31
2.2. Операции над нечеткими числами с использованием уровневых множеств 38
2.3. Аналитическое выполнение арифметических операций 42
2.4. Операции над нечеткими числами с учетом их взаимодействия ... 44
2.5. Вариационный подход к использованию операций над нечеткими
множествами 51
2.6. Операции дополнительного вычитания и деления 59
Глава 3. Методы сравнения нечетких множеств и чисел 64
3.1. Сравнение нечетких чисел с помощью обобщенных операций «больше или
равно» 64
3.2. Сравнение нечетких подмножеств единичного интервала 69
3.3. Упорядочение нечетких чисел, характеризующее неприятие риска ... 75
3.4. Упорядочение нечетких множеств с использованием отношений ... 80
Глава 4. Многокритериальная оценка и выбор альтернатив на основе нечетких
множеств 86
4.1. Принятие решений в условиях определенности 86
4.2. Оценка и упорядочение альтернатив при аддитивности критериев . . 89
4.3. Выбор альтернатив с использованием правила нечеткого вывода ... 94
4.4. Ранжирование альтернатив на основе эвристического подхода . . . 102
Глава 5. Многокритериальный выбор альтернатив на основе нечеткого
отношения предпочтения 108
5.1. Выбор на основе отношения предпочтения на множестве альтернатив 108
5.2. Использование отношения порядка на множестве лингвистических
векторных оценок . 115
5.3. Выбор при наличии нечеткого отношения доминирования .... 122
Глава 6. Принятие решений при качественной и вероятностной неопределенности 126
6.1. Принятие решений на основе нечеткого описания состояния системы и
исходов 126
6.2. Выбор решений при неточности и неопределенности описания исходов 133
Глава 7. Модели принятия решений с нечеткими ограничениями выбора . . 139
7.1. Детерминированная задача 139
7.2. Задача выбора со случайными параметрами 142
7.3. Задача выбора при стохастической зависимости критериев и параметров 146
7.4. Оценка условной полезности значений критериев 150

184 Оглавление
Глава 8. Принятие решений на основе информации в виде нечетких свидетельств 156
8.1. Использование понятия безусловного свидетельства 156
8.2. Упорядочение альтернатив на основе условных нечетких свидетельств 165
Заключение 173
Список литературы 180
АРКАДИЙ НИКОЛАЕВИЧ БОРИСОВ
ОЯР АРНОЛЬДОВИЧ КРУМБЕРГ
ИГОРЬ ПЕТРОВИЧ ФЕДОРОВ
ПРИНЯТИЕ РЕШЕНИИ
НА ОСНОВЕ
НЕЧЕТНЫХ МОДЕЛЕЙ
ПРИМЕРЫ ИСПОЛЬЗОВАНИЯ
Редактор Н. Дундина. Художественный редактор И. Егере. Технический редактор
И. Дорофеева. Корректор А. Тихомирова
ИБ № 3128
Сдано в набор 24.11.89. Подписано в печать 26.06.90. ЯТ 07317. Формат 70x100/16. Бумага
типогр. № 1. Гарнитура литературная. Высокая печать. 11,5 физ. печ. л.; 14,95 усл. печ. л.; 15,44
усл. кр.-отт.; 10,64 уч.-изд. л. Тираж 1850 экз. Заказ № 2307. Цена 1 р. 60 к. Заказное.
Издательство «Зинатне», 226530 ГСП Рига, ул. Тургенева, 19. Отпечатано в производственном
объединении «Полиграфисте», 226050 Рига, ул. Кр. Валдемара, в.