See discussions, stats, and author profiles for this publication at: https://www.researchgate.net/publication/332863667

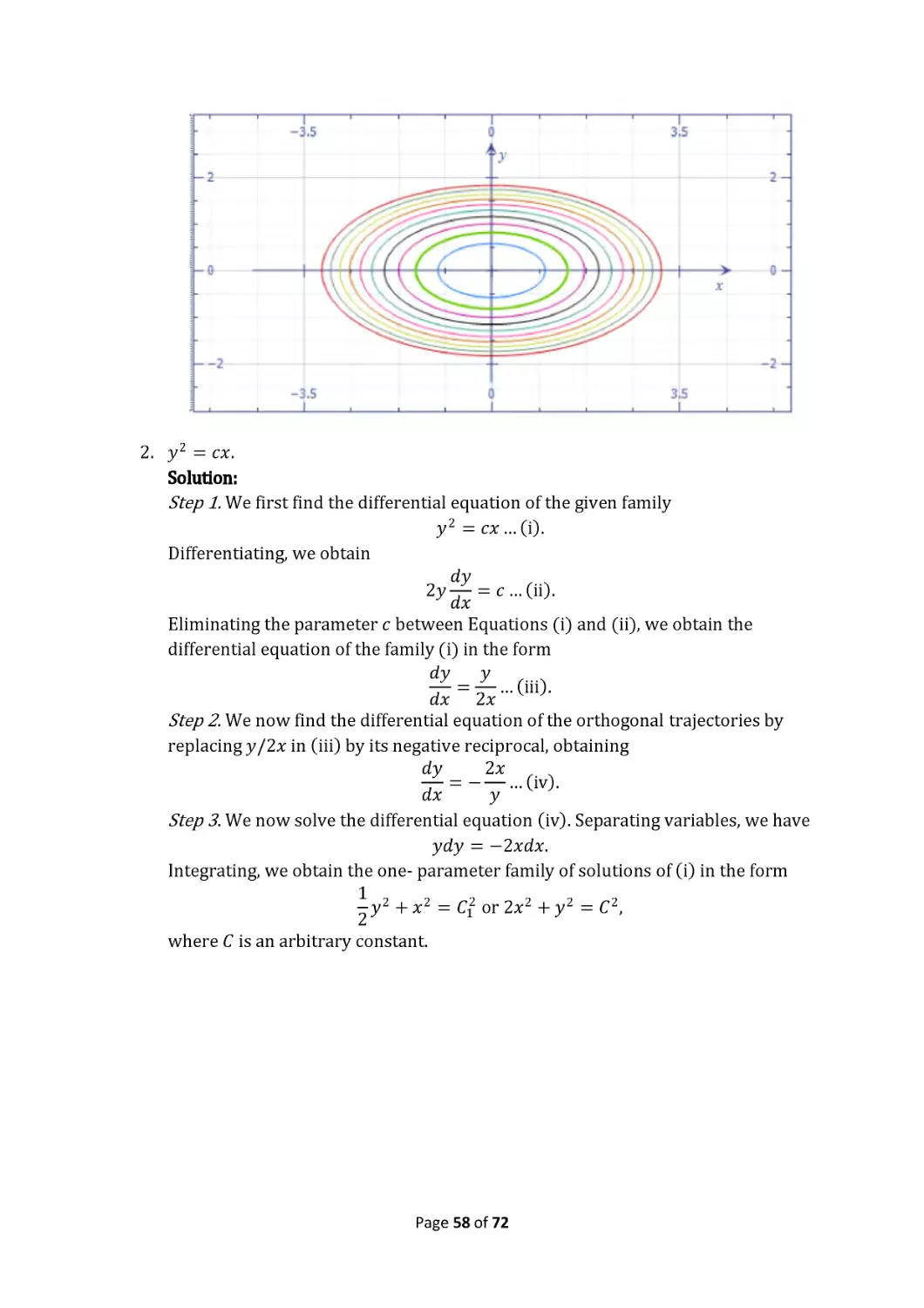
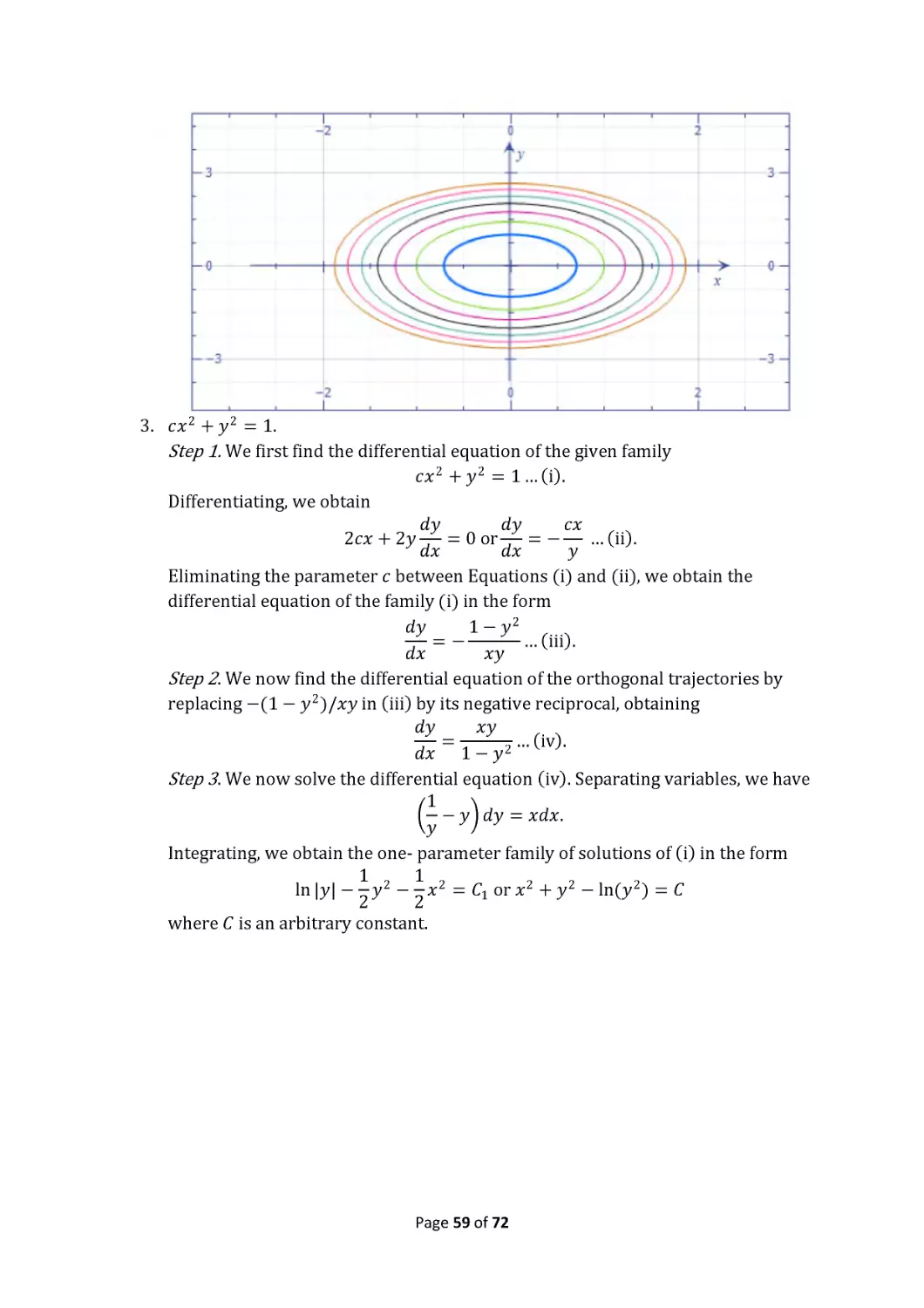
PROBLEM SET & SOLUTIONS: DIFFERENTIAL EQUATION
Chapter · May 2016

CITATIONS

READS

0

246,010

1 author:
Ibnu Rafi
Universitas Negeri Yogyakarta
16 PUBLICATIONS 46 CITATIONS
SEE PROFILE

Some of the authors of this publication are also working on these related projects:

Post-examination analysis View project

Developing open approach-based lesson plan and worksheet View project

All content following this page was uploaded by Ibnu Rafi on 30 March 2021.
The user has requested enhancement of the downloaded file.

PROBLEM SET & SOLUTIONS
DIFFERENTIAL EQUATION
By: Ibnu Rafi
e-mail: ibnu257fmipa@student.uny.ac.id

Table of Contents
Table of Contents ...................................................................................................................................................2
Solution of Exercise 1 (Linear and Nonlinear D.E)................................................................................3
Solution of Exercise 2 (Ordinary and Partial D.E) .................................................................................4
Solution of Exercise 3 (Solution of D.E) ......................................................................................................6
Solution of Exercise 4 (Initial Value Problem) ..................................................................................... 11
Solution of Exercise 5 (Separable D.E) ..................................................................................................... 13
Solution of Exercise 6 (General Solution of Separable D.E) ........................................................... 15
Solution of Quiz.................................................................................................................................................... 21
Solution of Exercise 7 (Homogeneous D.E) ........................................................................................... 22
Solution of Exercise 8 (Solution of Homogeneous D.E) ................................................................... 23
Solution of Exercise 9 (Non Homogeneous D.E) ................................................................................. 28
Solution of Exercise 10 (Solution of Non Homogeneous D.E) ...................................................... 29
Solution of Exercise 11 (Exact and Non Exact D.E) ............................................................................ 35
Solution of Exercise 12 (Integrating Factor) ......................................................................................... 42
Solution of Exercise 13 (Grouping Method) .......................................................................................... 44
Solution of Quiz.................................................................................................................................................... 45
Solution of Exercise 14 (Linear D.E) ......................................................................................................... 48
Solution of Exercise 15 (Solution of Linear D.E) ................................................................................. 50
Solution of Exercise 16 (Properties of Linear D.E) ............................................................................ 51
Solution of Exercise 17 (Integrating Factor of Linear D.E) ............................................................ 53
Solution of Exercise 18 (Orthogonal and Oblique Trajectories).................................................. 57
Solution of Exercise 19 (Problem in Mechanics (Frictional Forces)) ....................................... 64
Solution of Exercise 20 (Rate Problems (Rate of Growth and Decay and Population)
Growth) ................................................................................................................................................................... 66
Solution of Exercise 21 (Mixture Problem) ........................................................................................... 68
Solution of Exercise 22 (Reduction of Order) ....................................................................................... 70

Page 2 of 72

Solution of Exercise 1 (Linear and Nonlinear D.E)
We will determine whether the equations under consideration is linear or nonlinear. To
determine whether the equations under consideration is linear or nonlinear we should
know that differential equation are said to be nonlinear if any product exist between the
dependent variable and its derivatives, between the derivatives themselves, or the
dependent variable is trancedental function.
1.

𝑑2 𝑦
𝑑𝑥

𝑑𝑦

+ 5 𝑑𝑥 + 6𝑦 = 0 (Linear differential equation)

Since we see that the dependent variable of the differential equation above is 𝑦
and its various derivatives occur to the first degree only.
2.

𝑑4 𝑦
𝑑𝑥4

𝑑3𝑦

𝑑𝑦

+ 𝑥 2 𝑑 𝑥 3 + 𝑥 3 𝑑𝑥 = 𝑥𝑒 𝑥 ( Linear differential equation)

Since we see that the dependent variable of the differential equation above is 𝑦
and its various derivatives occur to the first degree only.
3.

𝑑2 𝑦
𝑑𝑥2

𝑑𝑦

+ 5 𝑑𝑥 + 6𝑦 2 = 0(Nonlinear differential equation)

Since we see that the dependent variable of the differential equation above is 𝑦
and its various derivatives occur to the first degree only, but then, the differential
equation above contains the product between the dependent variable
themselves, that is in the term 6𝑦 2 . Therefore, the differential equation
𝑑2 𝑦
𝑑𝑥2

4.

𝑑𝑦

+ 5 𝑑𝑥 + 6𝑦 2 = 0 is nonlinear differential equation.

𝑑2 𝑦

𝑑𝑦 3

𝑑𝑥

𝑑𝑥

2 +5

+ 6𝑦 = 0 (Nonlinear differential equation)

Since we see that the dependent variable of the differential equation above is 𝑦,
but in the term 5

𝑑𝑦 3
𝑑𝑥

involves the third degree of the first derivative or in the

othere word there is product between three derivatives. Therefore, the
𝑑2 𝑦

differential equation 𝑑 𝑥 2 + 5
5.

𝑑2 𝑦
𝑑𝑥2

𝑑𝑦 3
𝑑𝑥

+ 6𝑦 = 0 is nonlinear differential equation.

𝑑𝑦

+ 5𝑦 𝑑𝑥 + 6𝑦 = 0 (Nonlinear differential equation)

Since we see that the dependent variable of the differential equation above is 𝑦,
but there is product between the dependent variable and its derivative in the
𝑑𝑦

term 5𝑦 𝑑𝑥 . Therefore, the differential equation
nonlinear differential equation.

Page 3 of 72

𝑑2 𝑦
𝑑𝑥2

+5

𝑑𝑦 3
𝑑𝑥

+ 6𝑦 = 0 is

Solution of Exercise 2 (Ordinary and Partial D.E)
We will classify of the following differential equations as ordinary or partial differential
equations, state the order of each equation, and determine whether the equation under
consideration is linear or nonlinear.
Ordinary differential equation is the differential equation involving ordinary
derivatives of one or more dependent variables with respect to a single
independent variable.
Partial differential equation is the differential equation involving ordinary
derivatives of one or more dependent variables with respect to more than one
independent variable.
The order of a differential equation is equal to the order of the highest
differential coefficient that it contains.
The degree of a differential equation is the highest power of the highest order
differential coefficient that the equation contains after it has been rationalized.
1.

𝑑𝑦
𝑑𝑥

+ 𝑥 2 𝑦 = 𝑥𝑒 𝑥 .

The differential equation

𝑑𝑦
𝑑𝑥

+ 𝑥 2 𝑦 = 𝑥𝑒 𝑥 is ordinary differential equation (since

it has only one independent variable, that is 𝑥), first order ordinary differential
equation,

𝑑𝑦
𝑑𝑥

, first degree ordinary differential equation, and linear differential

equation (since no product between dependent variable (𝑦) themselves, no
product between 𝑦 and/or any of its derivatives, and its various derivatives
occur to the first degree only).
2.

𝑑3 𝑦

𝑑2 𝑦

𝑑𝑦

+ 4 𝑑 𝑥 2 − 5 𝑑𝑥 + 3𝑦 = sin 𝑥.
𝑑𝑥3
The differential equation

𝑑3𝑦
𝑑𝑥3

𝑑2 𝑦

𝑑𝑦

+ 4 𝑑 𝑥 2 − 5 𝑑𝑥 + 3𝑦 = sin 𝑥 is ordinary differential

equation (since it has only one independent variable, that is 𝑥), third order
ordinary differential equation,

𝑑3𝑦
𝑑𝑥3

, first degree ordinary differential equation,

and linear differential equation (since no product between dependent variable
(𝑦) themselves, no product between 𝑦 and/or any of its derivatives, its various
derivatives occur to the first degree only, and no trancendental function of 𝑦
and/ or its derivatives occur).
3.

𝜕2𝑢
𝜕𝑥2

𝜕2𝑢

+ 𝜕 𝑦 2 = 0.

The differential equation

𝜕 2𝑢
𝜕𝑥2

𝜕 2𝑢

+ 𝜕𝑦 2 = 0 is partial differential equation (since it

has more that one independent variable involved, that is 𝑥 and 𝑦), second order
Page 4 of 72

partial differential equation, first degree partial differential equation, linear
differential equation (since no product between dependent variable (𝑢)
themselves, no product between 𝑦 and/or any of its derivatives, and no
trancendental function of 𝑢 and/ or its derivatives occur).
4. 𝑥 2 𝑑𝑦 + 𝑦 2 𝑑𝑥 = 0.
𝑦2

𝑑𝑦

The differential equation is 𝑥 2 𝑑𝑦 + 𝑦 2 𝑑𝑥 = 0 ⇔ 𝑑𝑥 = − 𝑥 2 ordinary differential
equation (since it has only one independent variable involved, that is either 𝑥 or
𝑦), first order ordinary differential equation, first degree ordinary differential
equation, nonlinear differential equation (since there is a product either between
dependent variable 𝑦 themselves ( if 𝑦 is dependent variable) or between
dependent variable 𝑥 themselves ( if 𝑥 is dependent variable) ).
5.

𝑑4 𝑦

𝑑2 𝑦

𝑑𝑥

𝑑𝑥2

4 +3

5

+ 5𝑦 = 0.

The differential equation

𝑑4𝑦

+3
𝑑𝑥4

𝑑2𝑦
𝑑𝑥2

5

+ 5𝑦 = 0 is ordinary differential

equation (since it has only one independent variable involved, that is 𝑥), fourth
order ordinary differential equation, first degree ordinary differential equation,
nonlinear differential equation (since in term 3

𝑑2𝑦
𝑑𝑥2

5

involves the fifth power of

the second derivatives ).
6.

𝜕4𝑢
𝜕𝑥2

𝜕𝑦2

𝜕2𝑢

𝜕 2𝑢

+ 𝜕 𝑥 2 + 𝜕 𝑦 2 + 𝑢 = 0.

The differential equation

𝜕 4𝑢
𝜕𝑥2

𝜕𝑦 2

𝜕 2𝑢

𝜕𝑢

+ 𝜕 𝑥 2 + 𝜕 𝑦 2 + 𝑢 = 0 is partial differential

equation (since it has more than one independent variable involved, that is 𝑥 and
𝜕4

𝑦), fourth order partial differential equation (𝜕 𝑥 2 𝜕 𝑦 2 is the fourth derivatives of
𝑢 𝑥, 𝑦 ), first degree partial differential equation, linear differential equation
(since since no product between dependent variable (𝑢) themselves, no product
between 𝑢 and/or any of its derivatives, and no trancendental function of 𝑦 and/
or its derivatives occur).
7.

𝑑2 𝑦
𝑑𝑥2

+ 𝑦 sin 𝑥 = 0.

The differential equation

𝑑2𝑦
𝑑𝑥2

+ 𝑦 sin 𝑥 = 0 is ordinary differential equation

(since it has only one independent variable, that is 𝑥), second order ordinary
differential equation,

𝑑2𝑦
𝑑𝑥2

, first degree ordinary differential equation, and linear

differential equation (since no product between dependent variable (𝑦)
themselves, no product between 𝑦 and/or any of its derivatives, and no
trancendental function of 𝑦 and/ or its derivatives occur).
Page 5 of 72

𝑑2 𝑦

8.

𝑑𝑥2

+ 𝑥 sin 𝑦 = 0.

The differential equation

𝑑2𝑦
𝑑𝑥2

+ 𝑥 sin 𝑦 = 0 is ordinary differential equation

(since it has only one independent variable, that is 𝑥), second order ordinary
differential equation,

𝑑2𝑦
𝑑𝑥2

, first degree ordinary differential equation, and

nonlinear differential equation (since its dependent variable is 𝑦, but then, there
is trancendental function of 𝑦 occur in term 𝑥 sin 𝑦).
𝑑6 𝑥

9.

𝑑𝑡6

+

𝑑4𝑥

𝑑3𝑥

𝑑𝑡 4

𝑑𝑡 3

+ 𝑥 = 𝑡.

The differential equation

𝑑6𝑥
𝑑𝑡6

+

𝑑4𝑥

𝑑3𝑥

𝑑𝑡 4

𝑑𝑡 3

+ 𝑥 = 𝑡 is ordinary differential

equation (since it has only one independent variable, that is 𝑡), sixth order
ordinary differential equation,

𝑑6𝑥
𝑑𝑡6

, first degree ordinary differential equation,

and nonlinear differential equation (since there is a product between the various
derivatives of 𝑥 with respect to 𝑡 in the term
10.

𝑑𝑟 3
𝑑𝑠

=

𝑑2𝑟
𝑑 𝑠2

𝑑4𝑥

𝑑3 𝑥

𝑑𝑡 4

𝑑𝑡3

).

+1

The differential equation

𝑑𝑟 3
𝑑𝑠

=

𝑑2𝑟
𝑑 𝑠2

+ 1 is ordinary differential equation

(since it has only one independent variable, that is 𝑠), second order ordinary
differential equation, , first degree ordinary differential equation, and nonlinear
differential equation (since in term

𝑑𝑟 3
𝑑𝑠

involves the third power of the first

derivatives).

Solution of Exercise 3 (Solution of D.E)
1. a) We will show that 𝑓 𝑥 = 𝑥 + 3𝑒 −𝑥 is a solution of the differential equation that be
𝑑𝑦

defined as 𝑑𝑥 + 𝑦 = 𝑥 + 1 on every interval 𝑎 < 𝑥 < 𝑏 of the 𝑥 axis. To show this, we
must show that 𝑓 𝑥 = 𝑥 + 3𝑒 −𝑥 satisfies the differential equation

𝑑𝑦
𝑑𝑥

+𝑦=𝑥+1

( ordinary linear nonhomogen differential equation). By differentiating 𝑓 𝑥 , we
obtain 𝑓 ′ 𝑥 = 1 − 3𝑒 −𝑥 , ∀𝑥 ∈ 𝑎, 𝑏 . Afterwards, subtituting 𝑓(𝑥) for 𝑦, 𝑓 ′ 𝑥 for

𝑑𝑦
𝑑𝑥

in the mentioned differential equation. We obtain
𝑑𝑦
𝑑𝑥

+ 𝑦 = 1 − 3𝑒 −𝑥 + 𝑥 + 3𝑒 −𝑥 = 1 − 3𝑒 −𝑥 + 𝑥 + 3𝑒 −𝑥 = 𝑥 + 1,

that is, 𝑥 + 1 = 𝑥 + 1. Therefore, the given differential equation is satisfied by
𝑓 𝑥 = 𝑥 + 3𝑒 −𝑥 . In the other word, 𝑓 𝑥 = 𝑥 + 3𝑒 −𝑥 is a solution of the differential
𝑑𝑦

equation that be defined as 𝑑𝑥 + 𝑦 = 𝑥 + 1 on every interval 𝑎 < 𝑥 < 𝑏 of the 𝑥 axis■
Page 6 of 72

b) We will show that 𝑓 𝑥 = 2𝑒 3𝑥 − 5𝑒 4𝑥 is a solution of the differential equation
that be defined as

𝑑2𝑦
𝑑𝑥2

𝑑𝑦

− 7 𝑑𝑥 + 12𝑦 = 0 on every interval 𝑎 < 𝑥 < 𝑏 of the 𝑥 axis. To

show this, we must show that 𝑓 𝑥 = 2𝑒 3𝑥 − 5𝑒 4𝑥 , ∀𝑥 ∈ 𝑎, 𝑏
differential equation

𝑑2 𝑦
𝑑𝑥2

satisfies the

𝑑𝑦

− 7 𝑑𝑥 + 12𝑦 = 0. By differentiating 𝑓(𝑥), we obtain

𝑓 ′ 𝑥 = 6𝑒 3𝑥 − 20𝑒 4𝑥 and 𝑓 ′′ 𝑥 = 18𝑒 3𝑥 − 80𝑒 4𝑥 . Afterwards, subtituting 𝑓(𝑥) for
𝑦, 𝑓 ′ (𝑥) for

𝑑𝑦

, and 𝑓 ′′ (𝑥) for
𝑑𝑥

𝑑2𝑦
𝑑𝑥2

in the mentioned differential equation. We obtain

𝑑2 𝑦
𝑑𝑦
−
7
+ 12𝑦 = 0
𝑑𝑥 2
𝑑𝑥
⇔ 18𝑒 3𝑥 − 80𝑒 4𝑥 − 7 6𝑒 3𝑥 − 20𝑒 4𝑥 + 12 2𝑒 3𝑥 − 5𝑒 4𝑥 = 0
⇔ 18𝑒 3𝑥 − 80𝑒 4𝑥 − 42𝑒 3𝑥 + 140𝑒 4 + 24𝑒 3𝑥 − 60𝑒 4𝑥 = 0
⇔ 18 − 42 + 24 𝑒 3𝑥 + −80 + 140 − 60 𝑒 4𝑥 = 0
⇔ 0. 𝑒 3𝑥 + 0. 𝑒 4𝑥 = 0
⇔ 0 𝑒 3𝑥 + 𝑒 4𝑥 = 0
⇔ 0 = 0.
Therefore, the given differential equation is satisfied by 𝑓 𝑥 = 2𝑒 3𝑥 − 5𝑒 4𝑥 . In the
other word, 𝑥 = 2𝑒 3𝑥 − 5𝑒 4𝑥 is a solution of the differential equation that be
𝑑2 𝑦

𝑑𝑦

defined as 𝑑 𝑥 2 − 7 𝑑𝑥 + 12𝑦 = 0 on every interval 𝑎 < 𝑥 < 𝑏 of the 𝑥 axis■
c) We will show that 𝑓 𝑥 = 𝑒 𝑥 + 2𝑥 2 + 6𝑥 + 7 is a solution of the differential
equation that be defined as

𝑑2𝑦
𝑑𝑥2

𝑑𝑦

− 3 𝑑𝑥 + 2𝑦 = 4𝑥 2 on every interval 𝑎 < 𝑥 < 𝑏 of the

𝑥 axis. To show this, we must show that 𝑓 𝑥 = 𝑒 𝑥 + 2𝑥 2 + 6𝑥 + 7, ∀𝑥 ∈ 𝑎, 𝑏
satisfies the differential equation

𝑑2 𝑦
𝑑𝑥2

𝑑𝑦

− 3 𝑑𝑥 + 2𝑦 = 4𝑥 2 . By differentiating 𝑓(𝑥), we

obtain 𝑓 ′ 𝑥 = 𝑒 𝑥 + 4𝑥 + 6 and 𝑓 ′′ 𝑥 = 𝑒 𝑥 + 4. Afterwards, subtituting 𝑓(𝑥) for 𝑦,
𝑑𝑦

𝑑2𝑦

𝑓 ′ (𝑥) for 𝑑𝑥 , and 𝑓 ′′ (𝑥) for 𝑑 𝑥 2 in the mentioned differential equation. We obtain
𝑑2 𝑦
𝑑𝑦
−3
+ 2𝑦 = 4𝑥 2
2
𝑑𝑥
𝑑𝑥
⇔ 𝑒 𝑥 + 4 − 3 𝑒 𝑥 + 4𝑥 + 6 + 2 𝑒 𝑥 + 2𝑥 2 + 6𝑥 + 7 = 4𝑥 2
⇔ 𝑒 𝑥 + 4 − 3𝑒 𝑥 − 12𝑥 − 18 + 2𝑒 𝑥 + 4𝑥 2 + 12𝑥 + 14 = 4𝑥 2
⇔ 1 − 3 + 2 𝑒 𝑥 + 4𝑥 2 + −12 + 12 𝑥 + 4 − 18 + 14 = 4𝑥 2
⇔ 0. 𝑒 𝑥 + 4𝑥 2 + 0. 𝑥 + 0 = 4𝑥 2
⇔ 0 + 4𝑥 2 + 0 + 0 = 4𝑥 2
Page 7 of 72

⇔ 4𝑥 2 = 4𝑥 2 .
Therefore, the given differential equation is satisfied by 𝑓 𝑥 = 𝑒 𝑥 + 2𝑥 2 + 6𝑥 + 7. In
the other word, 𝑓 𝑥 = 𝑒 𝑥 + 2𝑥 2 + 6𝑥 + 7 is a solution of the differential equation
𝑑2𝑦

𝑑𝑦

that be defined as 𝑑 𝑥 2 − 3 𝑑𝑥 + 2𝑦 = 4𝑥 2 on every interval 𝑎 < 𝑥 < 𝑏 of the 𝑥 axis■
1

d) We will show that 𝑓 𝑥 = 1+𝑥 2 is a solution of the differential equation that be
𝑑2 𝑦

defined as 1 + 𝑥 2

𝑑𝑥2

𝑑𝑦

+ 4𝑥 𝑑𝑥 + 2𝑦 = 0 on every interval 𝑎 < 𝑥 < 𝑏 of the 𝑥 axis. To
1

show this, we must show that 𝑓 𝑥 = 1+𝑥 2 satisfies the differential equation
(1 + 𝑥 2 )𝑦 ′′ + 4𝑥𝑦′ + 2𝑦 = 0. By differentiating 𝑓(𝑥), we obtain 𝑓 ′ 𝑥 = −
𝑓 ′′ 𝑥 = −

2 1+𝑥 2

2

−2𝑥 2 1+𝑥 2 2𝑥
1+𝑥 2 4

1+𝑥 2

=

8𝑥 2 −2 1+𝑥 2
1+𝑥 2 4

=

6𝑥 2 −2

.
1+𝑥 2 3

2𝑥
1+𝑥 2 2

and

Afterwards subtitut-

𝑑2 𝑦

𝑑𝑦

ing 𝑓(𝑥) for 𝑦, 𝑓 ′ (𝑥) for 𝑑𝑥 , and 𝑓 ′′ (𝑥) for 𝑑 𝑥 2 in the mentioned differential equation.
We obtain
1 + 𝑥 2 𝑦 ′′ + 4𝑥𝑦 ′ + 2𝑦 = 0
6𝑥 2 − 2
2𝑥
+ 4𝑥 −
2
3
1+𝑥
1 + 𝑥2

⇔ 1 + 𝑥2

6𝑥 2 − 2
8𝑥 2
⇔
−
1 + 𝑥2 2
1 + 𝑥2

1
=0
1 + 𝑥2

+2

2 + 2𝑥 2
+
=0
2
1 + 𝑥2 2

⇔

6 − 8 + 2 𝑥 2 + −2 + 2
=0
1 + 𝑥2 2

⇔

0. 𝑥 2 + 0
=0
1 + 𝑥2 2

⇔

0
1 + 𝑥2

2

2

=0

⇔ 0 = 0.
1

Therefore, the given differential equation is satisfied by 𝑓 𝑥 = 1+𝑥 2 . In the other
1

word, 𝑓 𝑥 = 1+𝑥 2 is a solution of the differential equation that be defined as
1 + 𝑥2

𝑑2 𝑦

𝑑𝑥2

+ 4𝑥

𝑑𝑦
𝑑𝑥

+ 2𝑦 = 0 on every interval 𝑎 < 𝑥 < 𝑏 of the 𝑥 axis■

2. a) We will show that 𝑥 3 + 3𝑥𝑦 2 = 1 ⇔ 𝑦 =
of the differential equation 2𝑥𝑦

𝑑𝑦
𝑑𝑥

1−𝑥 3
3𝑥

⇔ 𝑦2 =

1−𝑥 3
3𝑥

is an implicit solution

+ 𝑥 2 + 𝑦 2 = 0 on the interval 0 < 𝑥 < 1. To

show this, firstly, we differentiating 𝑥 3 + 3𝑥𝑦 2 = 1 implicitly with respect to 𝑥. We
obtain
Page 8 of 72

𝑑 𝑥 3 + 3𝑥𝑦 2
𝑑 1
=
𝑑𝑥
𝑑𝑥
𝑑 𝑥3
𝑑 3𝑥𝑦 2
𝑑 1
⇔
+
=
𝑑𝑥
𝑑𝑥
𝑑𝑥
⇔ 3𝑥 2 + 3

𝑑 𝑥𝑦 2
=0
𝑑𝑥

⇔ 3𝑥 2 + 3 1. 𝑦 2 + 𝑥 2𝑦

⇔ 3𝑥 2 + 3𝑦 2 + 6𝑥𝑦
⇔

=0

𝑑𝑦
=0
𝑑𝑥

𝑑𝑦
3(𝑥 2 + 𝑦 2 )
=−
∀𝑥 ∈ (0,1) … ∗ .
𝑑𝑥
6𝑥𝑦

By subtituting (*) to 2𝑥𝑦
2𝑥𝑦

𝑑𝑦
𝑑𝑥

𝑑𝑦
𝑑𝑥

+ 𝑥 2 + 𝑦 2 = 0 we obtain

𝑑𝑦
+ 𝑥2 + 𝑦2 = 0
𝑑𝑥

3(𝑥 2 + 𝑦 2 )
⇔ 2𝑥𝑦 −
+ 𝑥2 + 𝑦2 = 0
6𝑥𝑦
⇔ − 𝑥2 + 𝑦2 + 𝑥2 + 𝑦2 = 0
⇔ − 𝑥2 +

1 − 𝑥3
1 − 𝑥3
+ 𝑥2 +
= 0, ∀𝑥 ∈ (0,1)
3𝑥
3𝑥

⇔ 0 = 0.
Thus, we can conclude that 𝑥 3 + 3𝑥𝑦 2 = 1 is an implicit solution of the differential
equation 2𝑥𝑦

𝑑𝑦

+ 𝑥 2 + 𝑦 2 = 0 on the interval 0 < 𝑥 < 1 ■

𝑑𝑥

b) We will show that 5𝑥 2 𝑦 2 − 2𝑥 3 𝑦 2 = 1 is an implicit solution of the differential
equation 𝑥

𝑑𝑦
𝑑𝑥

5

+ 𝑦 = 𝑥 3 𝑦 3 on the interval 0 < 𝑥 < 2. To show this, firstly, we

differentiating 5𝑥 2 𝑦 2 − 2𝑥 3 𝑦 2 = 1 implicitly with respect to 𝑥. We obtain
𝑑 5𝑥 2 𝑦 2 − 2𝑥 3 𝑦 2
𝑑 1
=
𝑑𝑥
𝑑𝑥
⇔ 10𝑥 2 𝑦

𝑑𝑦
𝑑𝑦
+ 10𝑥𝑦 2 − 4𝑥 3 𝑦
− 6𝑥 2 𝑦 2 = 0
𝑑𝑥
𝑑𝑥

⇔ 10𝑥 2 𝑦 − 4𝑥 3 𝑦

𝑑𝑦
= 6𝑥 2 𝑦 2 − 10𝑥𝑦 2
𝑑𝑥
Page 9 of 72

𝑑𝑦 6𝑥 2 𝑦 2 − 10𝑥𝑦 2
5
⇔
=
,
∀𝑥
∈
0,
… ∗
𝑑𝑥
10𝑥 2 𝑦 − 4𝑥 3 𝑦
2
and
5𝑥 2 𝑦 2 − 2𝑥 3 𝑦 2 = 1
⇔ 5𝑥 2 − 2𝑥 3 𝑦 2 = 1
⇔𝑦=

1

=

5𝑥 2 − 2𝑥 3

1
𝑥 5 − 2𝑥

By subtituting (*) and (**) to 𝑥
𝑥

, ∀𝑥 ∈ 0,
𝑑𝑦
𝑑𝑥

5
… ∗∗
2

+ 𝑦 − 𝑥 3 𝑦 3 = 0 we obtain

6𝑥 2 𝑦 2 − 10𝑥𝑦 2
1
+
= 𝑥 3𝑦3
2
3
2
3
10𝑥 𝑦 − 4𝑥 𝑦
5𝑥 − 2𝑥

⇔𝑥

𝑥𝑦 2 3𝑥 − 5
1
+
= 𝑥 3𝑦3
2
𝑥 𝑦 5 − 2𝑥
𝑥 5 − 2𝑥

⇔𝑦

3𝑥 − 5
1
+
= 𝑥 3𝑦3
5 − 2𝑥 𝑥 5 − 2𝑥

⇔
⇔
⇔
⇔

3𝑥 − 5
𝑥 5 − 2𝑥

5 − 2𝑥

3𝑥 − 5 + 5 − 2𝑥
𝑥 5 − 2𝑥

5 − 2𝑥

𝑥
𝑥 5 − 2𝑥

5 − 2𝑥

1
5 − 2𝑥

⇔ 𝑥3

⇔𝑥

5 − 2𝑥

+

1
𝑥 5 − 2𝑥

= 𝑥3𝑦3
= 𝑥3𝑦3

= 𝑥 3𝑦3

1
𝑥 3 5 − 2𝑥
1

3

𝑥 5 − 2𝑥

= 𝑥3𝑦3

5 − 2𝑥

= 𝑥 3𝑦3

3

= 𝑥 3 𝑦 3 , ∀𝑥 ∈ 0,

5
2

5

⇔ 𝑥 3 𝑦 3 = 𝑥 3 𝑦 3 , ∀𝑥 ∈ 0, 2 .
Thus, we can conclude that 5𝑥 2 𝑦 2 − 2𝑥 3 𝑦 2 = 1 is an implicit solution of the
differential equation 𝑥
5

𝑑𝑦
𝑑𝑥

+ 𝑦 = 𝑥3𝑦3 ⇔ 𝑥

0<𝑥<2■
Page 10 of 72

𝑑𝑦
𝑑𝑥

+ 𝑦 − 𝑥 3 𝑦 3 = 0 on the interval

Solution of Exercise 4 (Initial Value Problem)
1. Show that 𝑦 = 4𝑒 2𝑥 + 2𝑒 −3𝑥 is a solution of initial- value problem
𝑑 2 𝑦 𝑑𝑦
+
− 6𝑦 = 0,
𝑑𝑥 2 𝑑𝑥
𝑦 0 = 6,
𝑦 ′ 0 = 2.
Is 𝑦 = 2𝑒 2𝑥 + 4𝑒 −3𝑥 also a solution of this problem? Explain why and why not.
Proof
Assume that 𝑦 = 4𝑒 2𝑥 + 2𝑒 −3𝑥 is a solution of given initial- value problem. Since
𝑦 = 4𝑒 2𝑥 + 2𝑒 −3𝑥 , we obtain 𝑦 ′ = 8𝑒 2𝑥 − 6𝑒 −3𝑥 , 𝑦 ′′ = 16𝑒 2𝑥 + 18𝑒 −3𝑥 , and
𝑦 ′′ + 𝑦 − 6 = 16𝑒 2𝑥 + 18𝑒 −3𝑥 + 8𝑒 2𝑥 − 6𝑒 −3𝑥 − 24𝑒 2𝑥 − 12𝑒 −3𝑥 = 0 (satisfied).
Moreover, by subtituting 𝑥 = 0 to 𝑦 = 4𝑒 2𝑥 + 2𝑒 −3𝑥 and 𝑦′ = 8𝑒 2𝑥 − 6𝑒 3𝑥 we
obtain 𝑦(0) = 4𝑒 0 + 2𝑒 0 = 𝑒 0 4 + 2 = 1.6 = 6 (the initial condition is satisfied)
and 𝑦 ′ 0 = 8𝑒 0 − 6𝑒 0 = 𝑒 0 8 − 6 = 1.2 = 2 (the second condition is satisfied).
From this result we can say that our assumption is accepted. Therefore, we can
conclude that 𝑦 = 4𝑒 2𝑥 + 2𝑒 −3𝑥 is the solution of given initial- value problem. ■
Afterward, we will observe whether 𝑦 = 2𝑒 2𝑥 + 4𝑒 −3𝑥 is also a solution of the
given problem or not. We know that 𝑦 ′ = 4𝑒 2𝑥 − 12𝑒 −3𝑥 , 𝑦 ′′ = 8𝑒 2𝑥 + 36𝑒 −3𝑥
and
𝑦 ′′ + 𝑦′ − 6𝑦 = 8𝑒 2𝑥 + 36𝑒 −3𝑥 + 4𝑒 2𝑥 − 12𝑒 −3𝑥 + 12𝑒 2𝑥 + 24𝑒 −3𝑥 = 0
(satisfied). Moreover, by subtituting 𝑥 = 0 to 𝑦 = 2𝑒 2𝑥 + 4𝑒 −3𝑥 and 𝑦 ′ = 4𝑒 2𝑥 −
12𝑒 −3𝑥 , we obtain
𝑦 0 = 2𝑒 0 + 4𝑒 0 = 𝑒 0 2 + 4 = 1.6 = 6 (satisfied)
and
𝑦 ′ 0 = 4𝑒 0 − 12𝑒 0 = 𝑒 0 4 − 12 = 1 −8 = 8 ≠ 2 (unsatisfied).
From this result, we can conclude that 𝑦 = 2𝑒 2𝑥 + 4𝑒 −3𝑥 is not the solution of
given problem since one of the initial conditions in initial- value problem, that is
𝑦 ′ 0 = 2 not be satisfied when we subtituting 𝑥 = 0 to 𝑦 ′ = 4𝑒 2𝑥 − 12𝑒 −3𝑥 .
2. Every solution of the differential equation

𝑑2 𝑦
𝑑𝑥2

+ 𝑦 = 0 may be written in the

form 𝑦 = 𝑐1 sin 𝑥 + 𝑐2 cos 𝑥, for some choice of the arbitrary constants 𝑐1 and 𝑐2 .
Using this information, show that boundary problem (a) and (b) possess
solution but that (c) does not.
𝑎

𝑑2 𝑦
𝜋
+
𝑦
=
0,
𝑦
0
=
0,
𝑦
= 1.
𝑑𝑥 2
2

Page 11 of 72

𝑑2 𝑦
𝜋
′
𝑏
+
𝑦
=
0,
𝑦
0
=
1,
𝑦
= −1.
𝑑𝑥 2
2
𝑑2 𝑦
𝑐
+ 𝑦 = 0, 𝑦 0 = 0, 𝑦 𝜋 = 1.
𝑑𝑥 2
Solution
𝑑2 𝑦

(a) Since every solution of differential equation 𝑑 𝑥 2 + 𝑦 = 0 may be written in
𝜋

form 𝑦 = 𝑐1 sin 𝑥 + 𝑐2 cos 𝑥, by subtituting 𝑥 = 0 and 𝑥 = 2 to 𝑦 = 𝑐1 sin 𝑥 +
𝑐2 cos 𝑥, we obtain
𝑦 0 = 𝑐1 sin 0 + 𝑐2 cos 0 = 𝑐2 = 0
and
𝑦

𝜋
𝜋
𝜋
= 𝑐1 sin
+ 𝑐2 cos
= 𝑐1 . 1 + 𝑐2 . 0 = 𝑐1 = 1.
2
2
2

Therefore, the given boundary problem possess solution and it particular
solution is 𝑦 = sin 𝑥.
𝑑2 𝑦

(b) Since every solution of differential equation 𝑑 𝑥 2 + 𝑦 = 0 may be written in
form 𝑦 = 𝑐1 sin 𝑥 + 𝑐2 cos 𝑥, by subtituting 𝑥 = 0 to 𝑦 = 𝑐1 sin 𝑥 + 𝑐2 cos 𝑥 we
obtain that
𝑦 0 = 𝑐1 sin 0 + 𝑐2 cos 0 = 𝑐1 . 0 + 𝑐2 . 1 = 𝑐2 = 1.
Since 𝑦 = 𝑐1 sin 𝑥 + 𝑐2 cos 𝑥, we obtain that 𝑦 ′ = 𝑐1 cos 𝑥 − 𝑐2 sin 𝑥. By
𝜋
subtituting 𝑥 = to 𝑦 ′ = 𝑐1 cos 𝑥 − 𝑐2 sin 𝑥, we obtain
2

𝑦′

𝜋
𝜋
𝜋
= 𝑐1 cos
− 𝑐2 sin
= 𝑐1 . 0 − 𝑐2 . 1 = −𝑐2 = −1 ⇔ 𝑐2 = 1.
2
2
2

Since, the value of 𝑐2 consistent, that is 𝑐2 = 1, we can conclude that the given
boundary problem possess solution. Moreover, the general solution for such
boundary problem is 𝑦 = 𝑐1 sin(𝑥) + cos(𝑥).
𝑑2 𝑦

(c) Since every solution of differential equation 𝑑 𝑥 2 + 𝑦 = 0 may be written in
form 𝑦 = 𝑐1 sin 𝑥 + 𝑐2 cos 𝑥, by subtituting 𝑥 = 0 and 𝑥 = 𝜋 to 𝑦 = 𝑐1 sin 𝑥 +
𝑐2 cos 𝑥, we obtain
𝑦 0 = 𝑐1 sin(0) + 𝑐2 cos(0) = 𝑐1 . 0 + 𝑐2 . 1 = 𝑐2 = 0
and
𝑦 𝜋 = 𝑐1 sin 𝜋 + 𝑐2 cos 𝜋 = 𝑐1 . 0 + 𝑐2 . −1 = −𝑐2 = 1 ⇔ 𝑐2 = 1.
Since the value of 𝑐2 inconsistent, we can say that the given boundary
problem has no solution.
Page 12 of 72

***

Solution of Exercise 5 (Separable D.E)
Determine whether each of the following differential equations is or is not separable.
Note: An equation of the form 𝐹 𝑥 𝐺 𝑦 𝑑𝑥 + 𝑓 𝑥 𝑔 𝑦 𝑑𝑦 = 0 … (∗) is called an
equation with variables searable or simply a separable equation. Equation (*) can be
𝐹 𝑥

restated 𝑓
1.

𝑑𝑦
𝑑𝑥

𝑥

𝑔 𝑦

𝑑𝑥 + 𝐺

𝑦

𝑑𝑦 = 0.

= 3𝑦 2 − 𝑦 2 𝑝

Solution:
Since
𝑑𝑦
= 3𝑦 2 − 𝑦 2 sin 𝑥
𝑑𝑥
𝑑𝑦
⇔
= 𝑦 2 3 − sin 𝑥
𝑑𝑥
1
⇔ 2 𝑑𝑦 = 3 − sin 𝑥 𝑑𝑥
𝑦
1
⇔ 3 − sin 𝑥 𝑑𝑥 − 2 𝑑𝑦 = 0,
𝑦
we can conclude that the differential equation
2.

𝑑𝑦
𝑑𝑥

𝑑𝑦
𝑑𝑥

= 3𝑦 2 − 𝑦 2 sin 𝑥 is separable.

= 3𝑥 − 𝑦 sin 𝑥

Solution:
Since
𝑑𝑦
= 3𝑥 − 𝑦 sin 𝑥
𝑑𝑥
⇔ 𝑑𝑦 = 3𝑥 − 𝑦 sin 𝑥 𝑑𝑥
⇔ 𝑦 sin 𝑥 − 3𝑥 𝑑𝑥 − 𝑑𝑦 = 0,
𝑑𝑦

we can conclude that the differential equation 𝑑𝑥 = 3𝑥 − 𝑦 sin(𝑥) is not
separable.
3. 𝑥

𝑑𝑦
𝑑𝑥

= 𝑥−𝑦

2

Solution:
Since
𝑑𝑦
𝑥
= 𝑥−𝑦 2
𝑑𝑥
⇔ 𝑥 𝑑𝑦 = 𝑥 − 𝑦 2 𝑑𝑥
1
1
⇔
𝑑𝑦 = 𝑑𝑥
2
𝑥−𝑦
𝑥
1
1
⇔
𝑑𝑦 − 𝑑𝑥 = 0,
2
𝑥−𝑦
𝑥
we can say that the differential equation 𝑥
4.

𝑑𝑦
𝑑𝑥

𝑑𝑦
𝑑𝑥

= 1 + 𝑥2
Page 13 of 72

= 𝑥−𝑦

2

is not separable.

Solution:
Since
𝑑𝑦
= 1 + 𝑥2
𝑑𝑥
⇔ 𝑑𝑦 − 1 + 𝑥 2 𝑑𝑥 = 0,
𝑑𝑦

we can conclude that the differential equation 𝑑𝑥 = 1 + 𝑥 2 is separable.
5.

𝑑𝑦
𝑑𝑥

+ 4𝑦 = 8

Solution:
Since
𝑑𝑦
+ 4𝑦 = 8
𝑑𝑥
𝑑𝑦
⇔
= 8 − 4𝑦
𝑑𝑥
⇔ 𝑑𝑦 = (8 − 4𝑦)𝑑𝑥
1
⇔
𝑑𝑦 − 𝑑𝑥 = 0
8 − 4𝑦
we can conclude that the differential equation
6.

𝑑𝑦
𝑑𝑥

𝑑𝑦
𝑑𝑥

+ 4𝑦 = 8 is separable.

+ 𝑥𝑦 = 4𝑥

Solution:
𝑑𝑦
+ 𝑥𝑦 = 4𝑥
𝑑𝑥
𝑑𝑦
⇔
= 4𝑥 − 𝑥𝑦
𝑑𝑥
𝑑𝑦
⇔
= 𝑥 4−𝑦
𝑑𝑥
1
⇔
𝑑𝑦 = 𝑥 𝑑𝑥
4−𝑦
1
⇔
𝑑𝑦 − 𝑥𝑑𝑥 = 0,
4−𝑦
we can conclude that the differential equation
7.

𝑑𝑦
𝑑𝑥

𝑑𝑦
𝑑𝑥

+ 𝑥𝑦 = 4𝑥 is separable.

+ 4𝑦 = 𝑥 2

Solution:
Since
𝑑𝑦
+ 4𝑦 = 𝑥 2
𝑑𝑥
𝑑𝑦
⇔
= 𝑥 2 − 4𝑦
𝑑𝑥
⇔ 𝑑𝑦 = 𝑥 2 − 4𝑦 𝑑𝑥
⇔ 𝑑𝑦 − 𝑥 2 − 4𝑦 𝑑𝑥 = 0,
𝑑𝑦

we can say that the differential equation 𝑑𝑥 + 4𝑦 = 𝑥 2 is not separable.
8.

𝑑𝑦
𝑑𝑥

= 𝑥𝑦 − 3𝑥 − 2𝑦 + 6
Page 14 of 72

Solution:
Since
𝑑𝑦
= 𝑥𝑦 − 3𝑥 − 2𝑦 + 6
𝑑𝑥
𝑑𝑦
⇔
= 𝑥−2 𝑦−3
𝑑𝑥
1
⇔
𝑑𝑦 − 𝑥 − 2 𝑑𝑥 = 0,
𝑦−3
𝑑𝑦

we can say that the differential equation 𝑑𝑥 = 𝑥𝑦 − 3𝑥 − 2𝑦 + 6 is separable.
9.

𝑑𝑦
𝑑𝑥

= sin 𝑥 + 𝑦

Solution:
Since
𝑑𝑦
= sin 𝑥 + 𝑦
𝑑𝑥
⇔ 𝑑𝑦 − sin 𝑥 + 𝑦 𝑑𝑥 = 0,
𝑑𝑦

we can say that the differential equation 𝑑𝑥 = sin(𝑥 + 𝑦) is not separable.
𝑑𝑦

10. 𝑦 𝑑𝑥 = 𝑒 𝑥−3𝑦

2

Solution:
Since
𝑑𝑦
2
𝑦
= 𝑒 𝑥−3𝑦
𝑑𝑥
𝑑𝑦
𝑒𝑥
⇔𝑦
=
𝑑𝑥 𝑒 3𝑦 2
2
⇔ 𝑦𝑒 3𝑦 𝑑𝑦 − 𝑒 𝑥 𝑑𝑥 = 0,
we can conclude that the differential equation 𝑦

𝑑𝑦
𝑑𝑥

2

= 𝑒 𝑥−3𝑦 is separable.

***

Solution of Exercise 6 (General Solution of Separable D.E)
Find the general solution for each of the following. Where possible, write your answer
as an explicit solution.
1.

𝑑𝑦
𝑑𝑥

= 𝑥𝑦 − 4𝑥

Solution:
𝑑𝑦

𝑑𝑦

1

Since 𝑑𝑥 = 𝑥𝑦 − 4𝑥 ⇔ 𝑑𝑥 = 𝑥 𝑦 − 4 ⇔ 𝑦−4 𝑑𝑦 − 𝑥 𝑑𝑥 = 0, assume 𝑦 ≠ 4, we
obtain that
1
𝑑𝑦 −
𝑦−4

𝑥 𝑑𝑥 = 𝐶1

1
⇔ ln 𝑦 − 4 − 𝑥 2 = 𝐶1
2
1
⇔ ln 𝑦 − 4 = 𝑥 2 + 𝐶1
2
Page 15 of 72

1 2
+𝐶

⇔ 𝑦 − 4 = 𝑒 2𝑥

1

, 𝑙𝑒𝑡 𝐶 = 𝑒 𝐶1

1 2

⇔ 𝑦 − 4 = 𝐶𝑒 2𝑥

as the general solution for the differential equation

𝑑𝑦
𝑑𝑥

= 𝑥𝑦 − 4𝑥.

Note:
1 2

Since 𝑦 − 4 = 𝐶𝑒 2𝑥 ,
1 2

𝑦−4 =

2.

𝑑𝑦
𝑑𝑥

1 2

𝐶𝑒 2𝑥 𝑖𝑓 𝑦 ≥ 4
1 2

−𝐶𝑒 2𝑥

𝐶𝑒 2𝑥 + 4
⇔
𝑦
=
1 2
1 2
= 𝐾𝑒 2𝑥 𝑖𝑓 𝑦 < 4
𝐾𝑒 2𝑥 + 4

= 3𝑦 2 − 𝑦 2 sin 𝑥

Solution:
𝑑𝑦

1

Since 𝑑𝑥 = 𝑦 2 3 − sin 𝑥

⇔ 𝑦 2 𝑑𝑦 − 3 − sin 𝑥 𝑑𝑥 = 0, we obtain that

1
𝑑𝑦 − 3 − sin 𝑥 𝑑𝑥 = 𝐶1
𝑦2
1
⇔ − − 3𝑥 + cos 𝑥 = 𝐶1
𝑦
1
⇔ − = 3𝑥 + cos 𝑥 + 𝐶1
𝑦
1
⇔𝑦=−
, 𝑙𝑒𝑡 𝐶 = −𝐶1
3𝑥 + cos 𝑥 + 𝐶1
1
⇔𝑦=
𝐶 − 3𝑥 − cos 𝑥
𝑑𝑦

as the general solution for the differential equation 𝑑𝑥 = 3𝑦 2 − 𝑦 2 sin 𝑥 .
3.

𝑑𝑦
𝑑𝑥

= 𝑥𝑦 − 3𝑥 − 2𝑦 + 6

Solution:
𝑑𝑦

𝑑𝑦

1

Since 𝑑𝑥 = 𝑥𝑦 − 3𝑥 − 2𝑦 + 6 ⇔ 𝑑𝑥 = 𝑥 − 2 𝑦 − 3 ⇔ 𝑦−3 𝑑𝑦 − 𝑥 − 2 𝑑𝑥 = 0,
we obtain
1
𝑑𝑦 −
𝑦−3

(𝑥 − 2) 𝑑𝑥 = 𝐶1

1
⇔ ln 𝑦 − 3 − 𝑥 2 + 2𝑥 = 𝐶1
2
1
⇔ ln 𝑦 − 3 = 𝑥 2 − 2𝑥 + 𝐶1
2
1 2
−2𝑥+𝐶1

⇔ 𝑦 − 3 = 𝑒 2𝑥

, 𝑙𝑒𝑡 𝐶 = 𝑒 𝐶1

1 2
−2𝑥

⇔ 𝑦 − 3 = 𝐶𝑒 2𝑥

as the general solution for differential equation
Note:
1 2
−2𝑥

Since 𝑦 − 3 = 𝐶𝑒 2𝑥

,
Page 16 of 72

𝑑𝑦
𝑑𝑥

= 𝑥𝑦 − 3𝑥 − 2𝑦 + 6.

1 2
−2𝑥

𝑦−3 =
4.

𝑑𝑦
𝑑𝑥

𝐶𝑒 2𝑥
1 2
−2𝑥

−𝐶𝑒 2𝑥

1 2

𝐶𝑒 2𝑥 −2𝑥 + 3
⇔
𝑦
=
1 2
1 2
= 𝐾𝑒 2𝑥 −2𝑥 𝑖𝑓 𝑦 < 3
𝐾𝑒 2𝑥 −2𝑥 + 3
𝑖𝑓 𝑦 ≥ 3

= tan 𝑦

Solution:
𝑑𝑦

1

Since 𝑑𝑥 = tan(𝑦) ⇔ tan

𝑦

𝑑𝑦 − 𝑑𝑥 = 0, assume tan(𝑦) ≠ 0, we obtain

1
𝑑𝑦 − 𝑑𝑥 = 𝐶1
tan 𝑦
cos 𝑦
⇔
𝑑𝑦 − 𝑑𝑥 = 𝐶1
sin 𝑦
1
⇔
𝑑 sin(𝑦) − 𝑑𝑥 = 𝐶1
sin(𝑦)
⇔ ln | sin 𝑦 | − 𝑥 = 𝐶1
⇔ ln | sin 𝑦 | = 𝑥 + 𝐶1
⇔ sin 𝑦 = 𝑒 𝑥+𝐶1 , 𝑙𝑒𝑡 𝐶 = 𝑒 𝐶1
⇔ sin 𝑦 = 𝐶𝑒 𝑥
𝑑𝑦

as the general solution for 𝑑𝑥 = tan(𝑦).
Note:
Since sin 𝑦

= 𝐶𝑒 𝑥 ,
𝐶𝑒 𝑥 𝑖𝑓0 ≤ sin(𝑦) ≤ 1
arcsin(𝐶𝑒 𝑥 )
sin(𝑦) =
⇔
𝑦
=
−𝐶𝑒 𝑥 = 𝐾𝑒 𝑥 𝑖𝑓 −1 ≤ sin(𝑦) < 0
arcsin(𝐾𝑒 𝑥 )
5.

𝑑𝑦
𝑑𝑥

𝑦

=𝑥

Solution:
𝑑𝑦

𝑦

1

1

Since 𝑑𝑥 = 𝑥 ⇔ 𝑦 𝑑𝑦 − 𝑥 𝑑𝑥 = 0, we obtain
1
1
𝑑𝑦 −
𝑑𝑥 = 𝐶1
𝑦
𝑥
⇔ ln 𝑦 − ln 𝑥 = 𝐶1
⇔ ln 𝑦 = ln 𝑥 + ln 𝑒 𝐶1
⇔ ln 𝑦 = ln(𝑒 𝐶1 |𝑥|) , 𝑙𝑒𝑡 𝐶 = 𝑒 𝐶1
⇔ 𝑦 = 𝐶|𝑥|
𝑑𝑦

𝑦

as the general solution for the differential equation 𝑑𝑥 = 𝑥 .
6.

𝑑𝑦
𝑑𝑥

6𝑥 2 +4

= 3𝑦 2 −4𝑦

Solution:
𝑑𝑦

6𝑥 2 +4

Since 𝑑𝑥 = 3𝑦 2 −4𝑦 ⇔ 3𝑦 2 − 4𝑦 𝑑𝑦 − 6𝑥 2 + 4 𝑑𝑥 = 0, assume 3𝑦 2 − 4𝑦 ≠ 0 we
obtain
3𝑦 2 − 4𝑦 𝑑𝑦 −

6𝑥 2 + 4 𝑑𝑥 = 𝐶

⇔ 𝑦 3 − 2𝑦 2 − 2𝑥 3 − 4𝑥 = 𝐶

Page 17 of 72

2𝑥 3 + 4𝑥 + 𝐶
⇔𝑦=
𝑦 2 − 2𝑦
𝑑𝑦

6𝑥 2 +4

as the general solution for the diffeential equation 𝑑𝑥 = 3𝑦 2 −4𝑦 .
7.

𝑥2 + 1

𝑑𝑦
𝑑𝑥

= 𝑦2 + 1

Solution:
Since 𝑥 2 + 1

𝑑𝑦
𝑑𝑥

1

1

= 𝑦 2 + 1 ⇔ 1+𝑦 2 𝑑𝑦 − 1+𝑥 2 𝑑𝑥 = 0, we obtain

1
1
𝑑𝑦
−
𝑑𝑥 = 𝐶
1 + 𝑦2
1 + 𝑥2
⇔ 𝑎𝑟𝑐 tan 𝑦 − arctan 𝑥 = 𝐶
⇔ arctan 𝑦 = arctan 𝑥 + 𝐶
⇔ 𝑦 = tan(arctan 𝑥 + 𝐶)
as the general solution for differential equation 𝑥 2 + 1
8.

𝑦2 − 1

𝑑𝑦
𝑑𝑥

𝑑𝑦
𝑑𝑥

= 𝑦 2 + 1.

= 4𝑥𝑦 2

Solution:
Since 𝑦 2 − 1

𝑑𝑦
𝑑𝑥

= 4𝑥𝑦 2 ⇔

𝑦 2 −1
𝑦2

𝑑𝑦 − 4𝑥𝑑𝑥 = 0, assume 𝑦 ≠ 0, we obtain

𝑦2 − 1
𝑑𝑦 − 4𝑥 𝑑𝑥 = 𝐶
𝑦2
1
⇔
1 − 2 𝑑𝑦 − 4𝑥𝑑𝑥 = 𝐶
𝑦
1
⇔ 𝑦 + − 2𝑥 2 = 𝐶
𝑦
2
𝑦 +1
⇔
= 2𝑥 2 + 𝐶
𝑦
as the general solution for the differential equation 𝑦 2 − 1
9.

𝑑𝑦
𝑑𝑥

𝑑𝑦
𝑑𝑥

= 4𝑥𝑦 2 .

= 𝑒 −𝑦

Solution:
𝑑𝑦

1

Since 𝑑𝑥 = 𝑒 −𝑦 ⇔ 𝑒 −𝑦 𝑑𝑦 − 𝑑𝑥 = 0 ⇔ 𝑒 𝑦 𝑑𝑦 − 𝑑𝑥 = 0, we obtain
𝑒 𝑦 𝑑𝑦 −

𝑑𝑥 = 𝐶

⇔ 𝑒𝑦 − 𝑥 = 𝐶
⇔ 𝑒𝑦 = 𝑥 + 𝐶
⇔ 𝑦 = ln 𝑥 + 𝐶
𝑑𝑦

as the general solution for differential equation 𝑑𝑥 = 𝑒 −𝑦 .
𝑑𝑦

10. 𝑑𝑥 = 𝑒 −𝑦 + 1
Solution:
𝑑𝑦

1

Since 𝑑𝑥 = 𝑒 −𝑦 + 1 ⇔ 𝑒 −𝑦 +1 𝑑𝑦 − 𝑑𝑥 = 0, we obtain
1
𝑑𝑦 −
+1

𝑒 −𝑦

𝑑𝑥 = 𝐶1
Page 18 of 72

𝑒𝑦
𝑑𝑦 − 𝑑𝑥 = 𝐶1
𝑒𝑦 + 1
1
⇔
𝑑 𝑒 𝑦 − 𝑑𝑥 = 𝐶1
𝑦
𝑒 +1
⇔ ln 𝑒 𝑦 + 1 − 𝑥 = 𝐶1
⇔ ln 𝑒 𝑦 + 1 = 𝑥 + 𝐶1
⇔ 𝑒 𝑦 = 𝑒 𝑥+𝐶1 − 1 , 𝑙𝑒𝑡 𝐶 = 𝑒 𝐶1
⇔ 𝑦 = ln |𝐶𝑒 𝑥 − 1|
⇔

𝑑𝑦

as the general solution for differential equation 𝑑𝑥 = 𝑒 −𝑦 + 1.
𝑑𝑦

11. 𝑑𝑥 = 3𝑥𝑦 3
Solution:
𝑑𝑦

1

Since 𝑑𝑥 = 3𝑥𝑦 3 ⇔ 𝑦 3 𝑑𝑦 − 3𝑥𝑑𝑥 = 0, assume 𝑦 ≠ 0, we obtain
1
𝑑𝑦 − 3𝑥𝑑𝑥 = 𝐶1
𝑦3
1
3
⇔
− 𝑥 2 = 𝐶1
2
−2𝑦
2
1
⇔ 2 = −3𝑥 2 − 2𝐶1 , 𝑙𝑒𝑡 𝐶 = −2𝐶1
𝑦
1
⇔ 𝑦2 =
𝐶 − 3𝑥 2
As the general solution for differential equation
𝑑𝑦

𝑑𝑦
𝑑𝑥

= 3𝑥𝑦 3 .

2+ 𝑥

12. 𝑑𝑥 = 2+

𝑦

Solution:
Since

𝑑𝑦
𝑑𝑥

=

2+ 𝑥
2+ 𝑦

⇔ 2 + 𝑦 𝑑𝑦 − 2 + 𝑥 𝑑𝑥 = 0, we obtain

2 + 𝑦 𝑑𝑦 −

2 + 𝑥 𝑑𝑥 = 𝐶2

2
2
⇔ 2𝑦 + 𝑦 𝑦 − 2𝑥 − 𝑥 𝑥 = 𝐶2
3
3
1
1
⇔ 2𝑦 1 +
𝑦 = 2𝑥 1 +
𝑥 + 𝐶2
3
3
3+ 𝑦
3+ 𝑥
𝐶2
𝐶2
⇔𝑦
=𝑥
+ , 𝑙𝑒𝑡 𝐶1 =
3
3
2
2
𝑥
⇔𝑦=

⇔𝑦=

3+ 𝑥
+ 𝐶1
3

3+ 𝑦
3
𝑥 3+ 𝑥 +𝐶

, 𝑙𝑒𝑡 𝐶 = 3𝐶1

3+ 𝑦
𝑑𝑦

2+ 𝑥

as the general solution for the differential equation 𝑑𝑥 = 2+ 𝑦 .
Page 19 of 72

𝑑𝑦

13. 𝑑𝑥 − 3𝑥 2 𝑦 2 = −3𝑥 2
Solution:
𝑑𝑦

𝑑𝑦

1

Since 𝑑𝑥 − 3𝑥 2 𝑦 2 = −3𝑥 2 ⇔ 𝑑𝑥 − 3𝑥 2 𝑦 2 − 1 = 0 ⇔ 𝑦 2 −1 𝑑𝑦 − 3𝑥 2 𝑑𝑥 = 0, we
obtain
1
𝑑𝑦 − 3𝑥 2 𝑑𝑥 = 𝐶
2
𝑦 −1
1
1
2
⇔
− 2
𝑑𝑦 −
𝑦−1 𝑦+1

3𝑥 2 𝑑𝑥 = 𝐶1

1
1
ln 𝑦 − 1 − ln 𝑦 + 1 − 𝑥 3 = 𝐶1
2
2
𝑦−1
⇔ ln
= 2(𝑥 3 + 𝐶1 )
𝑦+1
𝑦−1
3
⇔
= 𝑒 2𝑥 +𝐶 , 𝑙𝑒𝑡 𝐶 = 2𝐶1
𝑦+1
⇔

⇔ 𝑦 − 1 = 𝑦 + 1 𝑒 2𝑥

3 +𝐶

as the general solution from the differential equation
𝑑𝑦

𝑑𝑦
𝑑𝑥

− 3𝑥 2 𝑦 2 = −3𝑥 2 .

14. 𝑑𝑥 − 3𝑥 2 𝑦 2 = 3𝑥 2
Solution:
𝑑𝑦

𝑑𝑦

1

Since 𝑑𝑥 − 3𝑥 2 𝑦 2 = 3𝑥 2 ⇔ 𝑑𝑥 = 3𝑥 2 1 + 𝑦 2 ⇔ 1+𝑦 2 𝑑𝑦 − 3𝑥 2 𝑑𝑥 = 0, we obtain
1
𝑑𝑦 − 3𝑥 2 𝑑𝑥 = 𝐶
1 + 𝑦2
⇔ arctan 𝑦 − 𝑥 3 = 𝐶
⇔ 𝑦 = tan(𝑥 3 + 𝐶)
𝑑𝑦

as the general solution of differential equation 𝑑𝑥 − 3𝑥 2 𝑦 2 = 3𝑥 2 .
𝑑𝑦

15. 𝑑𝑥 = 200𝑦 − 2𝑦 2
Solution:
𝑑𝑦

1

1

Since 𝑑𝑥 = 200𝑦 − 2𝑦 2 ⇔ 200𝑦 −2𝑦 2 𝑑𝑦 = 𝑑𝑥 ⇔ 200 𝑦 −2𝑦 2 𝑑𝑦 − 𝑑𝑥 = 0, assume
𝑦 ≠ 100, we obtain
1
𝑑𝑦 − 𝑑𝑥 = 𝐶2
200𝑦 − 2𝑦 2
1
⇔
𝑑𝑦 − 𝑑𝑥 = 𝐶2
2𝑦 100 − 𝑦
1
1
100 +
200
⇔
𝑑𝑦 − 𝑑𝑥 = 𝐶2
2𝑦
100 − 𝑦
1
1
ln 𝑦 −
ln 100 − 𝑦 − 𝑥 = 𝐶2
200
200
1
𝑦
⇔
ln
= 𝑥 + 𝐶2
200 100 − 𝑦
⇔

Page 20 of 72

𝑦
= 200 𝑥 + 𝐶2 , 𝑙𝑒𝑡 𝐶1 = 200𝐶2
100 − 𝑦
𝑦
⇔
= 𝑒 200𝑥+𝐶1 , 𝑙𝑒𝑡 𝐶 = 𝑒 𝐶1
100 − 𝑦
⇔ 𝑦 = 100 − 𝑦 𝐶𝑒 200𝑥
⇔ ln

as the general solution for the differential equation

𝑑𝑦
𝑑𝑥

= 200𝑦 − 2𝑦 2 .

Solution of Quiz
1. Solve
𝑒 𝑣 + 1 cos 𝑢 𝑑𝑢 + 𝑒 𝑣 sin 𝑢 + 1 𝑑𝑣 = 0.
Solution:
From the differential equation
𝑒 𝑣 + 1 cos 𝑢 𝑑𝑢 + 𝑒 𝑣 sin 𝑢 + 1 𝑑𝑣 = 0,
dividing both side by 𝑒 𝑣 + 1 (sin 𝑢 + 1), with the assumption that
sin(𝑢) ≠ −1 and we obviously 𝑒 𝑣 ≠ −1, we obtain
cos 𝑢
𝑒𝑣
𝑑𝑢 + 𝑣
𝑑𝑣 = 0.
sin 𝑢 + 1
𝑒 +1
cos 𝑢
𝑒𝑣
𝑑𝑢 +
𝑑𝑣 = 𝐶1
sin 𝑢 + 1
𝑒𝑣 + 1
1
1
⇔
𝑑 sin 𝑢 +
𝑑 𝑒 𝑣 = 𝐶1
𝑣
sin 𝑢 + 1
𝑒 +1
⇔ ln sin 𝑢 + 1 + ln 𝑒 𝑣 + 1 = 𝐶1 … (∗)
⇔ ln sin 𝑢 + 1 = − ln 𝑒 𝑣 + 1 + 𝐶1
𝑣
⇔ sin 𝑢 = 𝑒 − ln 𝑒 +1 +𝐶1 − 1, 𝑙𝑒𝑡 𝐶 = 𝑒 𝐶1
𝑣
−1
⇔ 𝑢 = arcsin 𝐶𝑒 ln 𝑒 +1 − 1
⇔ 𝑢 = arcsin(𝐶 𝑒 𝑣 + 1 −1 − 1)
as the general solution of the separable differential equation 𝑒 𝑣 + 1 cos 𝑢 𝑑𝑢 +
𝑒 𝑣 sin 𝑢 + 1 𝑑𝑣 = 0. It is enough for us if we say that (*) is the general solution
of given separable differential equation.
2. Solve
𝑦 + 2 𝑑𝑥 + 𝑦 𝑥 + 4 𝑑𝑦 = 0, 𝑦 −3 = −1.
Solution:
From 𝑦 + 2 𝑑𝑥 + 𝑦 𝑥 + 4 𝑑𝑦 = 0, dividing both side by 𝑦 + 2 (𝑥 + 4), with the
assumption that 𝑦 ≠ −2 and 𝑥 ≠ −4, we obtain
1
𝑦
𝑑𝑥 +
𝑑𝑦 = 0
𝑥+4
𝑦+2
1
𝑦
𝑑𝑥 +
𝑑𝑦 = 𝐶
𝑥+4
𝑦+2
1
𝑦+2 −2
⇔
𝑑𝑥 +
𝑑𝑦 = 𝐶
𝑥+4
𝑦+2
1
2
⇔
𝑑𝑥 +
1−
𝑑𝑦 = 𝐶
𝑥+4
𝑦+2
Page 21 of 72

⇔ ln 𝑥 + 4 + 𝑦 − 2 ln 𝑦 + 2 = 𝐶
⇔ 𝑦 − 2 ln 𝑦 + 2 = − ln 𝑥 + 4 + 𝐶
⇔ ln(𝑒 𝑦 ) − ln 𝑦 + 2 2 = − ln 𝑥 + 4 + 𝐶
𝑒𝑦
⇔ ln
= − ln 𝑥 + 4 + ln 𝑒 𝐶
𝑦+2 2
𝑒𝑦
𝑒𝐶
⇔ ln
= ln
𝑦+2 2
𝑥+4
𝑦
𝐶
𝑒
𝑒
⇔
=
… (∗)
𝑦+2 2
𝑥+4
Afterwards, we apply the initial condition to (*) and we obtain
𝑒 −1
𝑒𝐶
=
⇔ 𝐶 = −1.
−1 + 2 2
−3 + 4
Therefore, we can conclude that the solution of the initial- value problem under
consideration is
𝑒𝑦
𝑒 −1
=
𝑦+2 2
𝑥+4
or it can be written as
𝑥+4 𝑦
𝑒 = 𝑒 −1 .
𝑦+2 2

Solution of Exercise 7 (Homogeneous D.E)
Definition
An equation in differential form 𝑀 𝑥, 𝑦 𝑑𝑥 + 𝑁 𝑥, 𝑦 𝑑𝑦 = 0 is said to be homogeneous,
𝑑𝑦

if when written in derivative form 𝑑𝑥 = 𝑓 𝑥, 𝑦 = 𝑔
𝑓 𝑥, 𝑦 = 𝑔

𝑦
𝑥

𝑦
𝑥

there exist a function 𝑔 such that

.

Identify whether the following differential equations is homogeneous or not.
1. 𝑥 − 𝑦 𝑑𝑥 + 𝑥𝑑𝑦 = 0
Solution:
Since 𝑥 − 𝑦 𝑑𝑥 + 𝑥𝑑𝑦 = 0 can be written as
𝑦
𝑑𝑦
𝑥−𝑦
𝑦
𝑦
=−
= −1 + = − 𝑥
+
𝑦 𝑥
𝑑𝑥
𝑥
𝑥
𝑥
𝑦
we obtain that there exist a function 𝑔 such that 𝑓 𝑥, 𝑦 = 𝑔 𝑥 . Therefore, we
can conclude that the differential equation 𝑥 − 𝑦 𝑑𝑥 + 𝑥𝑑𝑦 = 0 is
homogeneous.
2. 𝑥 2 + 𝑥𝑦 𝑑𝑥 − 𝑦 2 𝑑𝑦 = 0
Page 22 of 72

Solution:
Since 𝑥 2 + 𝑥𝑦 𝑑𝑥 − 𝑦 2 𝑑𝑦 = 0 can be written as
𝑑𝑦 𝑥 2 + 𝑥𝑦
𝑥 2 𝑥
1
1
=
=
+
=
+
,
𝑦 2 𝑦
𝑑𝑥
𝑦2
𝑦
𝑦
𝑥
𝑥
we obtain that there exist a function 𝑔 such that 𝑓 𝑥, 𝑦 = 𝑔

𝑦
𝑥

. Thus, we can

conclude that the differential equation 𝑥 2 + 𝑥𝑦 𝑑𝑥 − 𝑦 2 𝑑𝑦 = 0 is homogeneous.
3. 𝑥 2 + 𝑥𝑦 + 𝑦 2 𝑑𝑥 − 𝑦 2 + 𝑥 𝑑𝑦 = 0
Solution:
Since 𝑥 2 + 𝑥𝑦 + 𝑦 2 𝑑𝑥 − 𝑦 2 + 𝑥 𝑑𝑦 = 0 can not be written as a function 𝑔

𝑦
𝑥

,

that is

𝑦
𝑦
𝑥
𝑥
𝑑𝑦 𝑥 2 + 𝑥𝑦 + 𝑦 2 𝑥𝑦 𝑦 + 1 + 𝑥
𝑦+1+𝑥
=
=
=
𝑦 1
𝑦 1
𝑑𝑥
𝑦2 + 𝑥
𝑥𝑦 𝑥 + 𝑦
𝑥+𝑦
can not be written as a function 𝑔

𝑦
𝑥

, we say that the differential equation

𝑥 2 + 𝑥𝑦 + 𝑦 2 𝑑𝑥 − 𝑦 2 + 𝑥 𝑑𝑦 = 0 is not homogeneous.
4.

𝑥 2 + 𝑥𝑦 + 𝑦 2 𝑑𝑥 − 𝑦 3 + 𝑥 2 𝑦 𝑑𝑦 = 0
Solution:
Since 𝑥 2 + 𝑥𝑦 + 𝑦 2 𝑑𝑥 − 𝑦 3 + 𝑥 2 𝑦 𝑑𝑦 = 0 can not be written as a function
𝑔

𝑦
𝑥

, that is,

𝑦
𝑥
𝑑𝑦 𝑥 2 + 𝑥𝑦 + 𝑦 2 𝑥𝑦(𝑦 + 1 + 𝑥 ) 1
=
=
=
𝑦2
𝑑𝑥
𝑦3 + 𝑥 2𝑦
𝑥
𝑥 2𝑦 2 + 1
𝑥
can not be written as a function 𝑔
2

2

3

𝑦
𝑥

𝑦
1
𝑦 +1+𝑥
𝑥
𝑦 2
𝑥 +1

, we can conclude that the differential

equation 𝑥 + 𝑥𝑦 + 𝑦 𝑑𝑥 − 𝑦 + 𝑥 2 𝑦 𝑑𝑦 = 0 is not homogeneous.
***

Solution of Exercise 8 (Solution of Homogeneous D.E)
Theorem
If 𝑀 𝑥, 𝑦 𝑑𝑥 + 𝑁 𝑥, 𝑦 𝑑𝑦 = 0 is a homogeneous differential equation, then the change of
variables 𝑦 = 𝑣𝑥 transform 𝑀 𝑥, 𝑦 𝑑𝑥 + 𝑁 𝑥, 𝑦 𝑑𝑦 = 0 into a separable equation in the
variables 𝑣 and 𝑥.

Page 23 of 72

1. Find the general solution of

𝑑𝑦
𝑑𝑥

=

𝑥𝑦 +𝑦 2
𝑥2

.

Solution:
The given differential equation in derivative form is homogeneous since
𝑑𝑦 𝑥𝑦 + 𝑦 2 𝑦
𝑦 2
𝑦
=
=
+
=
𝑔
.
𝑑𝑥
𝑥2
𝑥
𝑥
𝑥
𝑑𝑦
𝑑𝑣
Now, let 𝑦 = 𝑣𝑥. We obtain 𝑑𝑦 = 𝑣𝑑𝑥 + 𝑥𝑑𝑣 ⇔ 𝑑𝑥 = 𝑣 + 𝑥 𝑑𝑥 and
⇔𝑣+𝑥

𝑑𝑣
= 𝑣 + 𝑣2
𝑑𝑥

𝑑𝑣
= 𝑣2
𝑑𝑥
1
1
⇔ 2 𝑑𝑣 − 𝑑𝑥 = 0
𝑣
𝑥
integrating
1
1
𝑑𝑣 −
𝑑𝑥 = 𝐶
2
𝑣
𝑥
1
⇔ − − ln 𝑥 = 𝐶
𝑣
𝑦
substituting 𝑣 = 𝑥 , we obtain
𝑥
𝑥
− − ln 𝑥 = 𝐶 ⇔ 𝑦 = −
,
𝑦
ln 𝑥 + 𝐶
⇔𝑥

as the general solution of of
𝑑𝑦

𝑑𝑦
𝑑𝑥

=

𝑥𝑦 +𝑦 2
𝑥2

.

2. Solve 2𝑥𝑦 𝑑𝑥 = 𝑥 2 + 𝑦 2 given that 𝑦 = 0 at 𝑥 = 1.
Solution:
The given equation in derivative form is
𝑑𝑦 𝑥 2 + 𝑦 2
𝑥
𝑦
1
1 𝑦
=
=
+
=
+
𝑑𝑥
2𝑥𝑦
2𝑦 2𝑥 2 𝑦
2 𝑥
𝑥
and from this form we obtain that the given differential equation is
𝑑𝑦

𝑑𝑣

homogeneous. Now, let 𝑦 = 𝑣𝑥. We obtain 𝑑𝑦 = 𝑣𝑑𝑥 + 𝑥𝑑𝑣 ⇔ 𝑑𝑥 = 𝑣 + 𝑥 𝑑𝑥 and
𝑑𝑣
1 1
=
+ 𝑣
𝑑𝑥 2𝑣 2
𝑑𝑣
1 1
⇔𝑥
=
− 𝑣
𝑑𝑥 2𝑣 2
𝑑𝑣 1 − 𝑣 2
⇔𝑥
=
𝑑𝑥
2𝑣
2𝑣
1
⇔
𝑑𝑣
−
𝑑𝑥 = 0
1 − 𝑣2
𝑥
integrating
2𝑣
1
𝑑𝑣 −
𝑑𝑥 = 𝐶1
2
1−𝑣
𝑥
1
1
2
⇔−
𝑑
−𝑣
−
𝑑𝑥 = 𝐶1
1 − 𝑣2
𝑥
⇔ − ln 1 − 𝑣 2 − ln 𝑥 = 𝐶1
𝑣+𝑥

Page 24 of 72

⇔ − ln 1 − 𝑣 2 𝑥 = 𝐶1
⇔ ln 1 − 𝑣 2 𝑥 = 𝐶 (let 𝐶 = −𝐶1 )
⇔ 1 − 𝑣2 𝑥 = 𝑒𝐶 .
𝑦
Substituting 𝑣 = 𝑥 we obtain

𝑦2
𝑦2
𝐶
𝑥
=
𝑒
⇔
𝑥
−
= 𝑒𝐶.
𝑥2
𝑥
Using the initial condition 𝑦 = 0 at 𝑥 = 1, we obtain
1 − 0 = 𝑒 𝐶 ⇔ 1 = 𝑒 𝐶 . It means that
1 − 𝑣2 𝑥 = 𝑒 𝐶 ⇔

𝑥−

𝑦2

1−

= 1. From this result, we obtain

𝑥
2

𝑦
𝑦2
= −1 ⇔ 𝑦 2 = 𝑥 2 + 𝑥 or 𝑥 −
= 1 ⇔ 𝑦 2 = 𝑥 2 − 𝑥.
𝑥
𝑥
as the solution for the given initial value problem.
𝑥−

𝑑𝑦

3. Solve 𝑑𝑥 =

𝑥+𝑦
𝑥

and find the particular solution when 𝑦 1 = 1.

Solution:
𝑑𝑦

Since 𝑑𝑥 =

𝑥+𝑦
𝑥

𝑦

=1+

𝑥

=𝑔

𝑦
𝑥

, 𝑥 + 𝑦 𝑑𝑥 − 𝑥𝑑𝑦 = 0 is homogeneous.
𝑑𝑦

𝑑𝑣

Moreover, let 𝑦 = 𝑣𝑥 and we will obtain that 𝑑𝑦 = 𝑣𝑑𝑥 + 𝑥𝑑𝑣 ⇔ 𝑑𝑥 = 𝑣 + 𝑥 𝑑𝑥
and
𝑑𝑣
𝑑𝑣
1
=1+𝑣 ⇔𝑥
= 1 ⇔ 𝑑𝑣 − 𝑑𝑥 = 0 … (∗).
𝑑𝑥
𝑑𝑥
𝑥
Integrating (*), we obtain
1
𝑑𝑣 −
𝑑𝑥 = 𝐶 ⇔ 𝑣 − ln |𝑥| = 𝐶 … ∗∗
𝑥
𝑦
Substituting 𝑣 = 𝑥 to (**) we obtain 𝑦 = 𝑥 ln 𝑥 + 𝐶𝑥.
𝑣+𝑥

Using initial condition, we obtain 1 = 1 ln 1 + 𝐶 ⇔ 𝐶 = 1.
Therefore, we can conclude that 𝑦 = 𝑥 ln |𝑥| + 𝑥 is the particular solution for the
given initial value problem.
𝑑𝑦

1

4. Solve 𝑥 𝑑𝑥 = 𝑥 − 𝑦 and find the particular solution when 𝑦 2 = 2.
𝑑𝑦

Since 𝑑𝑥 =

𝑥−𝑦
𝑥

𝑦

=1−𝑥 =𝑔

𝑦
𝑥

, 𝑥 − 𝑦 𝑑𝑥 − 𝑥𝑑𝑦 = 0 is homogeneous.
𝑑𝑦

𝑑𝑣

Moreover, let 𝑦 = 𝑣𝑥 and we will obtain that 𝑑𝑦 = 𝑣𝑑𝑥 + 𝑥𝑑𝑣 ⇔ 𝑑𝑥 = 𝑣 + 𝑥 𝑑𝑥
and
𝑑𝑣
𝑑𝑣
1
1
=1−𝑣 ⇔𝑥
= 1 − 2𝑣 ⇔
𝑑𝑣 − 𝑑𝑥 = 0 … (∗).
𝑑𝑥
𝑑𝑥
1 − 2𝑣
𝑥
Integrating (*), we obtain
1
1
𝑑𝑣 −
𝑑𝑥 = 𝐶1
1 − 2𝑣
𝑥
1
⇔ − ln 1 − 2𝑣 − ln 𝑥 = 𝐶1
2
⇔ ln 1 − 2𝑣 + ln 𝑥 2 = 𝐶 (let 𝐶 = −2𝐶1 )
⇔ ln 1 − 2𝑣 𝑥 2 = 𝐶
⇔ 1 − 2𝑣 𝑥 2 = 𝑒 𝐶
𝑣+𝑥

Page 25 of 72

⇔ 𝑥 2 − 2𝑣𝑥 2 = 𝑒 𝐶 … ∗∗
𝑦
Substituting 𝑣 = 𝑥 to (**) we obtain 𝑥 2 − 2𝑥𝑦 = 𝑒 𝐶 .

Using initial condition, we obtain 4 − 2 = 2 = 𝑒 𝐶 .
Therefore, we can conclude that 𝑥 2 − 2𝑥𝑦 = 2 is the particular solution for the
given initial value problem.
𝑑𝑦

5. Solve 𝑑𝑥 =

𝑥−2𝑦
𝑥

and find the particular solution when 𝑦 1 = −1.

Solution:
𝑑𝑦

Since 𝑑𝑥 =

𝑥−2𝑦
𝑥

= 1−2

𝑦
𝑥

=𝑔

𝑦
𝑥

, 𝑥 − 2𝑦 𝑑𝑥 − 𝑥𝑑𝑦 = 0 is homogeneous.
𝑑𝑦

𝑑𝑣

Moreover, let 𝑦 = 𝑣𝑥 and we will obtain that 𝑑𝑦 = 𝑣𝑑𝑥 + 𝑥𝑑𝑣 ⇔ 𝑑𝑥 = 𝑣 + 𝑥 𝑑𝑥
and
𝑑𝑣
𝑑𝑣
1
1
= 1 − 2𝑣 ⇔ 𝑥
= 1 − 3𝑣 ⇔
𝑑𝑣 − 𝑑𝑥 = 0 … (∗).
𝑑𝑥
𝑑𝑥
1 − 3𝑣
𝑥
Integrating (*), we obtain
1
1
𝑑𝑣 −
𝑑𝑥 = 𝐶1
1 − 3𝑣
𝑥
1
⇔ − ln 1 − 3𝑣 − ln 𝑥 = 𝐶1
3
⇔ ln 1 − 3𝑣 + ln(𝑥 2 𝑥 ) = 𝐶
(let 𝐶 = −3𝐶1 )
2
⇔ ln 1 − 3𝑣 𝑥 𝑥 = 𝐶
⇔ 1 − 3𝑣 |𝑥|𝑥 2 = 𝑒 𝐶
⇔ 𝑥 3 − 3𝑣𝑥 3 = 𝑒 𝐶 … ∗∗
𝑦
Substituting 𝑣 = 𝑥 to (**) we obtain
𝑣+𝑥

𝑒𝐶
𝑥 − 3𝑥 𝑦 = 𝑥 𝑥 − 3𝑦 = 𝑒 ⇔ 𝑥 − 3𝑦 = 2 .
𝑥
3

2

2

𝐶

Using initial condition, we obtain 1 + 3 =

𝑒𝐶
1

4

⇔ 𝑒 𝐶 = 4.

Therefore, we can conclude that 𝑥 − 3𝑦 = 𝑥 2 =

2 2
𝑥

is the particular solution

for the given initial value problem.
𝑑𝑦

𝑥+𝑦

6. Given that 𝑑𝑥 = 𝑥−𝑦 , prove that arctan

𝑦
𝑥

1

= 2 ln(𝑥 2 + 𝑦 2 ) + 𝐴 where 𝐴 is an

arbitrary constant.
Proof:
Since
1
𝑦 +1
𝑦
𝑥
=𝑔
, 𝑥 + 𝑦 𝑑𝑥 − (𝑥 − 𝑦)𝑑𝑦 = 0
1
𝑥
−
1
𝑦
𝑥
is homogeneous. Moreover, let 𝑦 = 𝑣𝑥 and we will obtain that
𝑥
𝑑𝑦 𝑥 + 𝑦 𝑦 + 1
=
=
=
𝑑𝑥 𝑥 − 𝑦 𝑥 − 1
𝑦
𝑑𝑦

𝑑𝑣

𝑑𝑦 = 𝑣𝑑𝑥 + 𝑥𝑑𝑣 ⇔ 𝑑𝑥 = 𝑣 + 𝑥 𝑑𝑥 and

Page 26 of 72

1
𝑑𝑣 𝑣 + 1
𝑑𝑣 1 + 𝑣 − 𝑣 + 𝑣 2
1−𝑣
1
𝑣+𝑥
=
⇔𝑥
=
⇔
𝑑𝑣
−
𝑑𝑥 = 0 … (∗).
𝑑𝑥 1 − 1
𝑑𝑥
1−𝑣
1 + 𝑣2
𝑥
𝑣
Integrating (*), we obtain
1−𝑣
1
𝑑𝑣 −
𝑑𝑥 = 𝐴
2
1+𝑣
𝑥
1
1
2𝑣
1
⇔
𝑑𝑣
−
𝑑𝑣
−
𝑑𝑥 = 𝐴
1 + 𝑣2
2 1 + 𝑣2
𝑥
1
1
⇔ arctan 𝑣 − ln 1 + 𝑣 2 − ln(𝑥 2 ) = 𝐴
2
2
1
⇔ arctan 𝑣 = ln 1 + 𝑣 2 𝑥 2 + 𝐴 … (∗)
2
𝑦
Substituting 𝑣 = 𝑥 to (*), we obtain
𝑦2

1

1

arctan(𝑣) = 2 ln 1 + 𝑥 2 𝑥 2 + 𝐴 = 2 ln(𝑥 2 + 𝑦 2 ) + 𝐴.■
𝑑𝑦

7. Find the general solution of 2𝑥 2 𝑑𝑥 = 𝑥 2 + 𝑦 2 .
Solution:
𝑑𝑦

Since 𝑑𝑥 =

𝑥 2 +𝑦 2
2𝑥 2

1 𝑦 2

1

=2+2

𝑥

=𝑔

𝑦
𝑥

, 𝑥 2 + 𝑦 2 𝑑𝑥 − 2𝑥 2 𝑑𝑦 = 0 is

homogeneous. Moreover, let 𝑦 = 𝑣𝑥 and we will obtain that
𝑑𝑦 = 𝑣𝑑𝑥 + 𝑥𝑑𝑣 ⇔

𝑑𝑦
𝑑𝑥

=𝑣+𝑥

𝑑𝑣
𝑑𝑥

and

𝑑𝑣 1 + 𝑣 2
𝑑𝑣
𝑣−1 2
2
1
=
⇔𝑥
=
⇔
𝑑𝑣
−
𝑑𝑥 = 0 … (∗).
𝑑𝑥
2
𝑑𝑥
2
𝑣−1 2
𝑥
Integrating (*), we obtain
2
1
2
2
𝑑𝑣 −
𝑑𝑥 = 𝐶 ⇔ −
− ln |𝑥| = 𝐶 ⇔
= ln |𝑥| + 𝐶 … ∗∗
2
𝑣−1
𝑥
𝑣−1
1−𝑣
𝑦
Substituting 𝑣 = 𝑥 to (**) we obtain
2𝑥
2𝑥
= ln 𝑥 + 𝐶 ⇔ 𝑦 = 𝑥 −
𝑥−𝑦
ln 𝑥 + 𝐶
𝑣+𝑥

𝑑𝑦

as the general solution of 2𝑥 2 𝑑𝑥 = 𝑥 2 + 𝑦 2 .
8. Find the general solution of 2𝑥 − 𝑦

𝑑𝑦
𝑑𝑥

= 2𝑦 − 𝑥 .

Solution:
Since
1
2− 𝑦
𝑑𝑦 2𝑦 − 𝑥
𝑥 = 𝑔 𝑦 , (2𝑦 − 𝑥)𝑑𝑥 − (2𝑥 − 𝑦)𝑑𝑦 = 0
=
= 𝑥
=
2
𝑑𝑥 2𝑥 − 𝑦 2
𝑥
𝑦 −1 𝑦 −1
𝑥
is homogeneous. Moreover, let 𝑦 = 𝑣𝑥 and we will obtain that
𝑥
2−𝑦

𝑑𝑦

𝑑𝑣

𝑑𝑦 = 𝑣𝑑𝑥 + 𝑥𝑑𝑣 ⇔ 𝑑𝑥 = 𝑣 + 𝑥 𝑑𝑥 and

Page 27 of 72

1
𝑑𝑣 2 − 𝑣
𝑑𝑣 2𝑣 − 1 − 𝑣(2 − 𝑣)
𝑣−2
1
𝑣+𝑥
=
⇔𝑥
=
⇔− 2
𝑑𝑣 − 𝑑𝑥 = 0 … (∗).
𝑑𝑥 2 − 1
𝑑𝑥
2−𝑣
𝑣 −1
𝑥
𝑣
Integrating (*), we obtain
𝑣−2
1
− 2
𝑑𝑣 −
𝑑𝑥 = 𝐶1
𝑣 −1
𝑥
1
2𝑣
2
1
⇔−
𝑑𝑣
+
𝑑𝑣
−
𝑑𝑥 = 𝐶1
2 𝑣2 − 1
𝑣2 − 1
𝑥
1
1
1
1
1
⇔−
𝑑 𝑣2 +
−
𝑑𝑣 −
𝑑𝑥 = 𝐶1
2
2 𝑣 −1
𝑣−1 𝑣+1
𝑥
1
⇔ − ln 𝑣 2 − 1 + ln 𝑣 − 1 − ln 𝑣 + 1 − ln 𝑥 = 𝐶1
2
⇔ ln 𝑣 2 − 1 − ln 𝑣 − 1 2 + ln 𝑣 + 1 2 + ln(𝑥 2 ) = 𝐶2
(let 𝐶2 = −2𝐶1 )
2
2 2
𝑣 −1 𝑣+1 𝑥
⇔ ln
= 𝐶2
𝑣−1 2
𝑣2 − 1 𝑣 + 1 2 𝑥 2
⇔
= 𝑒 𝐶2 = 𝐶 … (∗∗) let 𝐶 = 𝑒 𝐶2 .
𝑣−1 2
𝑦
Substituting 𝑣 = 𝑥 to (**), we obtain
2
2
𝑦2
𝑦
2
2
2 𝑦
−
1
+
1
𝑥
𝑦
−
𝑥
+
1
2
𝑦+𝑥
𝑥
𝑥
𝑥
=
=
𝑦+𝑥
2
2
𝑦
𝑦−𝑥
𝑦−𝑥
−
1
𝑥
𝑥2
𝑑𝑦
as the general solution of 2𝑥 − 𝑦 𝑑𝑥 = 2𝑦 − 𝑥 .

2

=𝐶

***

Solution of Exercise 9 (Non Homogeneous D.E)
Note: If

𝑝
𝑎

𝑞

𝑟

= 𝑏 ≠ 𝑐 , suppose

𝑝
𝑎

𝑞

= 𝑏 = 𝑚, then the differential equation

𝑎𝑥 + 𝑏𝑦 + 𝑐 𝑑𝑥 + 𝑝𝑥 + 𝑞𝑦 + 𝑟 𝑑𝑦 = 0 can be written as
𝑎𝑥 + 𝑏𝑦 + 𝑐 𝑑𝑥 + 𝑚 𝑎𝑥 + 𝑏𝑦 + 𝑟 𝑑𝑦 = 0. To solve this, let 𝑢 = 𝑎𝑥 + 𝑏𝑦.
Find the solution of 𝑥 + 𝑦 + 1 𝑑𝑥 + 2𝑥 + 2𝑦 + 1 𝑑𝑦 = 0.
Solution:
Since 𝑥 + 𝑦 + 1 𝑑𝑥 + 2𝑥 + 2𝑦 + 1 𝑑𝑦 = 0 ⇔ 𝑥 + 𝑦 + 1 𝑑𝑥 + 2 𝑥 + 𝑦 + 1 𝑑𝑦 = 0,
let 𝑢 = 𝑥 + 𝑦. We obtain 𝑑𝑢 = 𝑑𝑥 + 𝑑𝑦 ⇔ 𝑑𝑥 = 𝑑𝑢 − 𝑑𝑦 and
𝑢 + 1 𝑑𝑥 + 2𝑢 + 1 𝑑𝑦 = 0
⇔ 𝑢 + 1 𝑑𝑢 − 𝑑𝑦 + 2𝑢 + 1 𝑑𝑦 = 0
⇔ 𝑢 + 1 𝑑𝑢 − 𝑢 + 1 𝑑𝑦 + 2𝑢 + 1 𝑑𝑦 = 0
⇔ 𝑢 + 1 𝑑𝑢 + −𝑢 − 1 + 2𝑢 + 1 𝑑𝑦 = 0
⇔ 𝑢 + 1 𝑑𝑢 + 𝑢𝑑𝑦 = 0.
Dividing both sides of 𝑢 + 1 𝑑𝑢 + 𝑢𝑑𝑦 = 0 by 𝑢, we obtain

Page 28 of 72

𝑢+1
𝑑𝑢 + 𝑑𝑦 = 0.
𝑢
Furthermore, we obtain
𝑢+1
𝑑𝑢 + 𝑑𝑦 = 𝐶
𝑢
1
⇔
1 + 𝑑𝑢 + 𝑑𝑦 = 𝐶
𝑢
⇔ 𝑢 + ln 𝑢 + 𝑦 = 𝐶 … (∗)
Substituting 𝑢 = 𝑥 + 𝑦 to (*), we obtain
⇔ 𝑥 + 𝑦 + ln 𝑥 + 𝑦 + 𝑦 = 𝐶
⇔ 𝑥 + 2𝑦 + ln |𝑥 + 𝑦| = 𝐶
as the general solution of 𝑥 + 𝑦 + 1 𝑑𝑥 + 2𝑥 + 2𝑦 + 1 𝑑𝑦 = 0.
***

Solution of Exercise 10 (Solution of Non Homogeneous D.E)
1. Solve 3𝑥 − 𝑦 + 1 𝑑𝑥 − 6𝑥 − 2𝑦 − 3 𝑑𝑦 = 0.
Solution:
Since
3𝑥 − 𝑦 + 1 𝑑𝑥 − 6𝑥 − 2𝑦 − 3 𝑑𝑦 = 0 ⇔ 3𝑥 − 𝑦 + 1 𝑑𝑥 − 2 3𝑥 − 𝑦 − 3 𝑑𝑦 = 0,
1

1

3

3

let 𝑢 = 3𝑥 − 𝑦. We obtain 𝑑𝑢 = 3𝑑𝑥 − 𝑑𝑦 ⇔ 𝑑𝑥 = 𝑑𝑢 + 𝑑𝑦 and
𝑢 + 1 𝑑𝑥 − 2𝑢 − 3 𝑑𝑦 = 0
1
1
⇔ 𝑢+1
𝑑𝑢 + 𝑑𝑦 − 2𝑢 − 3 𝑑𝑦 = 0
3
3
1
1
⇔ 𝑢 + 1 𝑑𝑢 + 𝑢 + 1 𝑑𝑦 − 2𝑢 − 3 𝑑𝑦 = 0
3
3
1
1
5
10
⇔
𝑢 + 𝑑𝑢 + − 𝑢 +
𝑑𝑦 = 0.
3
3
3
3
1
1
5
10
5
10
Dividing both sides of 3 𝑢 + 3 𝑑𝑢 + − 3 𝑢 + 3 𝑑𝑦 = 0 by − 3 𝑢 + 3 , we obtain
𝑢+1
𝑑𝑢 + 𝑑𝑦 = 0.
−5𝑢 + 10
Furthermore, we obtain
𝑢+1
𝑑𝑢 + 𝑑𝑦 = 𝐶2
−5𝑢 + 10
−5 𝑢 + 1
⇔
𝑑𝑢 + 𝑑𝑦 = 𝐶2
−5 −5𝑢 + 10
1 −5𝑢 + 10
−15
⇔ −
+
𝑑𝑢 + 𝑑𝑦 = 𝐶2
5 −5𝑢 + 10 −5𝑢 + 10
1
3
−5
⇔−
𝑑𝑢 −
𝑑𝑢 + 𝑑𝑦 = 𝐶2
5
5 −5𝑢 + 10
1
3
1
⇔−
𝑑𝑢 −
𝑑 −5𝑢 + 10 + 𝑑𝑦 = 𝐶2
5
5 −5𝑢 + 10
1
3
⇔ − 𝑢 − ln −5𝑢 + 10 + 𝑦 = 𝐶2 … (∗)
5
5
Page 29 of 72

Substituting 𝑢 = 3𝑥 − 𝑦 to (*), we obtain
1
3
− 3𝑥 − 𝑦 − ln −5 3𝑥 − 𝑦 + 10 + 𝑦 = 𝐶2
5
5
⇔ 3𝑥 − 𝑦 + 3 ln −15𝑥 + 5𝑦 + 10 − 5𝑦 = −5𝐶2
⇔ 3𝑥 − 6𝑦 + 3 ln 5 −3𝑥 + 𝑦 + 2 = 𝐶1
𝐶1
⇔ 𝑥 − 2𝑦 + ln 5 + ln −3𝑥 + 𝑦 + 2 =
3
𝐶1
⇔ 𝑥 − 2𝑦 + ln −3𝑥 + 𝑦 + 2 = − ln 5
3
⇔ 𝑥 − 2𝑦 + ln | − 3𝑥 + 𝑦 + 2| = 𝐶
as the general solution of 3𝑥 − 𝑦 + 1 𝑑𝑥 − 6𝑥 − 2𝑦 − 3 𝑑𝑦 = 0.
2. Solve the initial value problem of 2𝑥 + 3𝑦 + 1 𝑑𝑥 + 4𝑥 + 6𝑦 + 1 𝑑𝑦 = 0;
𝑦 −2 = 2.
Solution:
Since
2𝑥 + 3𝑦 + 1 𝑑𝑥 + 4𝑥 + 6𝑦 + 1 𝑑𝑦 = 0
⇔ 2𝑥 + 3𝑦 + 1 𝑑𝑥 + 2 2𝑥 + 3𝑦 + 1 𝑑𝑦 = 0,
1

3

let 𝑢 = 2𝑥 + 3𝑦. We obtain 𝑑𝑢 = 2𝑑𝑥 + 3𝑑𝑦 ⇔ 𝑑𝑥 = 2 𝑑𝑢 − 2 𝑑𝑦 and
𝑢 + 1 𝑑𝑥 + 2𝑢 + 1 𝑑𝑦 = 0
1
3
⇔ 𝑢+1
𝑑𝑢 − 𝑑𝑦 + 2𝑢 + 1 𝑑𝑦 = 0
2
2
𝑢+1
3𝑢
3
⇔
𝑑𝑢 −
𝑑𝑦 − 𝑑𝑦 + 2𝑢𝑑𝑦 + 𝑑𝑦 = 0
2
2
2
𝑢+1
𝑢−1
⇔
𝑑𝑢 +
𝑑𝑦 = 0
2
2
𝑢+1
𝑢 −1
Dividing both sides of 2 𝑑𝑢 + 2 𝑑𝑦 = 0 by

𝑢−1
2

, we obtain

𝑢+1
𝑑𝑢 + 𝑑𝑦 = 0
𝑢−1
𝑢−1 +2
⇔
𝑑𝑢 + 𝑑𝑦 = 0
𝑢−1
2
⇔ 1+
𝑑𝑢 + 𝑑𝑦 = 0.
𝑢−1
Furthermore, we obtain
2
1+
𝑑𝑢 + 𝑑𝑦 = 𝐶1
𝑢−1
⇔ 𝑢 + 2 ln |𝑢 − 1| + 𝑦 = 𝐶1 … (∗)
Substituting 𝑢 = 2𝑥 + 3𝑦 to (*), we obtain
2𝑥 + 3𝑦 + 2 ln 2𝑥 + 3𝑦 − 1 + 𝑦 = 𝐶1
⇔ 2𝑥 + 4𝑦 + 2 ln 2𝑥 + 3𝑦 − 1 = 𝐶1
𝐶1
⇔ 𝑥 + 2𝑦 + ln 2𝑥 + 3𝑦 − 1 =
2
⇔ 𝑥 + 2𝑦 + ln |2𝑥 + 3𝑦 − 1| = 𝐶 … (∗∗)
Afterwards, we substituting 𝑥 = −2 and 𝑦 = 2 (initial condition) to (**), we obtain
−2 + 4 + ln | − 4 + 6 − 1| = 𝐶 ⇔ 2 + ln(1) = 𝐶 ⇔ 2 = 𝐶.
Page 30 of 72

Therefore, 𝑥 + 2𝑦 + ln |2𝑥 + 3𝑦 − 1| = 2 is the solution for the given initial value
problem.
***
Part 3
Solve the following differential equations.
1.

𝑑𝑦
𝑑𝑥

2𝑥 −7𝑦

= 3𝑦 −8𝑥

Solution:
𝑦
𝑥 2−7
𝑑𝑦 2𝑥 − 7𝑦
𝑥
=
=
𝑑𝑥 3𝑦 − 8𝑥
1
𝑦 3−8 𝑦
𝑥

1
= 𝑦
𝑥

𝑦
𝑥
8
3− 𝑦
𝑥

2−7

𝑦

Let 𝑦 = 𝑣𝑥 ⇔ 𝑣 = 𝑥 . We obtain, 𝑑𝑦 = 𝑥𝑑𝑣 + 𝑣𝑑𝑥 ⇔
consequence, we obtain
𝑑𝑣 1 2 − 7𝑣
=
𝑑𝑥 𝑣 3 − 8
𝑣
𝑑𝑣 2 − 7𝑣
⇔ 𝑣+𝑥
=
𝑑𝑥 3𝑣 − 8
𝑑𝑣 −3𝑣 2 + 𝑣 + 2
⇔𝑥
=
𝑑𝑥
3𝑣 − 8
3𝑣 − 8
1
⇔− 2
𝑑𝑣 − 𝑑𝑥 = 0
3𝑣 − 𝑣 − 2
𝑥
6
1
1
⇔−
−
𝑑𝑣 − 𝑑𝑥 = 0
3𝑣 + 2 𝑣 − 1
𝑥
2.3
1
1
⇔
−
𝑑𝑣 + 𝑑𝑥 = 0.
3𝑣 + 2 𝑣 − 1
𝑥
Furthermore, we obtain
2.3
1
1
−
𝑑𝑣 +
𝑑𝑥 = 𝐶
3𝑣 + 2 𝑣 − 1
𝑥
⇔ 2 ln 3𝑣 + 2 − ln 𝑣 − 1 + ln 𝑥 = 𝐶
3𝑦
𝑦
⇔ 2 ln
+ 2 − ln − 1 + ln |𝑥| = 𝐶
𝑥
𝑥
𝑑𝑦
2𝑥−7𝑦
as the general solusion of 𝑑𝑥 = 3𝑦 −8𝑥 .
⇔ 𝑣+𝑥

2. 𝑥 3 + 1

𝑑𝑦
𝑑𝑥

+ 6𝑥 2 𝑦 = 6𝑥 2

Solution:
𝑑𝑦
+ 6𝑥 2 𝑦 = 6𝑥 2
𝑑𝑥
𝑑𝑦
⇔ 𝑥3 + 1
= 6𝑥 2 1 − 𝑦
𝑑𝑥
1
6𝑥 2
⇔
𝑑𝑦 − 3
𝑑𝑥 = 0.
1−𝑦
𝑥 +1
𝑥3 + 1

Page 31 of 72

𝑑𝑦
𝑑𝑥

𝑑𝑣

= 𝑣 + 𝑥 𝑑𝑥 and as a

Afterwards, we obtain
1
3𝑥 2
𝑑𝑦 − 2
𝑑𝑥 = 𝐶1
1−𝑦
𝑥3 + 1
1
1
⇔−
𝑑𝑦 − 2
𝑑 𝑥 3 = 𝐶1
𝑦−1
𝑥3 + 1
⇔ − ln 𝑦 − 1 − 2 ln 𝑥 3 + 1 = 𝐶1
⇔ ln 𝑦 − 1 + ln 𝑥 3 + 1 2 = −𝐶1 = 𝐶
as the general solution of 𝑥 3 + 1
3.

𝑑𝑦
𝑑𝑥

2𝑥 2 +𝑦 2

𝑑𝑦
𝑑𝑥

+ 6𝑥 2 𝑦 = 6𝑥 2 .

= 2𝑥𝑦 −𝑥 2

Solution:
𝑦 2
2
𝑥
2
+
𝑑𝑦 2𝑥 + 𝑦
𝑥
=
=
2
𝑥
𝑥
𝑑𝑥 2𝑥𝑦 − 𝑥
𝑦2 2 𝑦 − 𝑦

𝑦 2
2
+
1
𝑥
.
2 = 𝑦 2
2
1
−
𝑦
𝑦 2
𝑥
𝑥
𝑥
𝑦
𝑑𝑦
𝑑𝑣
Let 𝑦 = 𝑣𝑥 ⇔ 𝑣 = 𝑥 . We obtain, 𝑑𝑦 = 𝑥𝑑𝑣 + 𝑣𝑑𝑥 ⇔ 𝑑𝑥 = 𝑣 + 𝑥 𝑑𝑥 and as a
2

2

consequence, we obtain
𝑑𝑣
1 2 + 𝑣2
𝑣+𝑥
=
𝑑𝑥 𝑣 2 2 − 1
𝑣 𝑣2
𝑑𝑣 2 + 𝑣 2
⇔ 𝑣+𝑥
=
𝑑𝑥 2𝑣 − 1
𝑑𝑣 −(𝑣 2 − 𝑣 − 2)
⇔𝑥
=
𝑑𝑥
2𝑣 − 1
1 − 2𝑣
1
⇔ 2
𝑑𝑣 − 𝑑𝑥 = 0
𝑣 −𝑣−2
𝑥
−1
1
1
⇔
−
𝑑𝑣 − 𝑑𝑥 = 0
𝑣−2 𝑣+1
𝑥
Moreover,
−1
1
1
−
𝑑𝑣 −
𝑑𝑥 = 𝐶1
𝑣−2 𝑣+1
𝑥
⇔ − ln |𝑣 − 2| − ln |𝑣 + 1| − ln |𝑥| = 𝐶1
⇔ ln |𝑣 − 2| + ln |𝑣 + 1| + ln |𝑥| = −𝐶1
⇔ ln 𝑣 − 2 𝑣 + 1 𝑥 = 𝐶
𝑦
𝑦
⇔ ln
−2
+1 𝑥 =𝐶
𝑥
𝑥
𝑦2 𝑦
⇔ ln
− −2 𝑥 =𝐶
𝑥2 𝑥
𝑦2
⇔ ln
− 𝑦 − 2𝑥 = 𝐶
𝑥
𝑑𝑦

2𝑥 2 +𝑦 2

as the general solution of 𝑑𝑥 = 2𝑥𝑦 −𝑥 2 .
4. 3𝑥 − 5𝑦 𝑑𝑥 + 𝑥 + 𝑦 𝑑𝑦 = 0
Page 32 of 72

Solution:
3𝑥 − 5𝑦 𝑑𝑥 + 𝑥 + 𝑦 𝑑𝑦 = 0
𝑑𝑦 − 3𝑥 − 5𝑦
⇔
=
𝑑𝑥
𝑥+𝑦

⇔

𝑑𝑦
𝑦
=−
𝑑𝑥
𝑥

1
3 𝑦 −5
𝑥
.
𝑦
1+𝑥
𝑦

𝑑𝑦

𝑑𝑣

Let 𝑦 = 𝑣𝑥 ⇔ 𝑣 = 𝑥 . We obtain, 𝑑𝑦 = 𝑥𝑑𝑣 + 𝑣𝑑𝑥 ⇔ 𝑑𝑥 = 𝑣 + 𝑥 𝑑𝑥 and as a
consequence, we obtain
3
−5
𝑑𝑣
𝑣+𝑥
= −𝑣 𝑣
𝑑𝑥
1+𝑣
𝑑𝑣 −3 + 5𝑣
=
𝑑𝑥
1+𝑣
𝑑𝑣 −𝑣 2 + 4𝑣 − 3
⇔𝑥
=
𝑑𝑥
1+𝑣
1+𝑣
1
⇔− 2
𝑑𝑣 − 𝑑𝑥 = 0
𝑣 − 4𝑣 + 3
𝑥
2
1
1
⇔−
−
𝑑𝑣 − 𝑑𝑥 = 0
𝑣−3 𝑣−1
𝑥
1
2
1
⇔
−
𝑑𝑣 − 𝑑𝑥 = 0.
𝑣−1 𝑣−3
𝑥
Furthermore, we obtain
1
2
1
−
𝑑𝑣 −
𝑑𝑥 = 𝐶
𝑣−1 𝑣−3
𝑥
⇔ ln 𝑣 − 1 − 2 ln 𝑣 − 3 − ln 𝑥 = 𝐶
𝑦
𝑦
⇔ ln − 1 − 2 ln − 3 − ln 𝑥 = 𝐶
𝑥
𝑥
as the general solution of 3𝑥 − 5𝑦 𝑑𝑥 + 𝑥 + 𝑦 𝑑𝑦 = 0.
5. 𝑥 2 + 𝑦 2 𝑑𝑥 − 2𝑥𝑦𝑑𝑦 = 0; 𝑦 1 = 0
Solution:
𝑑𝑦 𝑥 2 + 𝑦 2 1 1 1 𝑦
𝑥 2 + 𝑦 2 𝑑𝑥 − 2𝑥𝑦𝑑𝑦 = 0 ⇔
=
= .𝑦 + . .
𝑑𝑥
2𝑥𝑦
2
2 𝑥
𝑥
𝑦
𝑑𝑦
𝑑𝑣
Let 𝑦 = 𝑣𝑥 ⇔ 𝑣 = 𝑥 . We obtain, 𝑑𝑦 = 𝑥𝑑𝑣 + 𝑣𝑑𝑥 ⇔ 𝑑𝑥 = 𝑣 + 𝑥 𝑑𝑥 and as a
⇔ 𝑣+𝑥

consequence, we obtain
𝑑𝑣
1 𝑣
𝑣+𝑥
=
+
𝑑𝑥 2𝑣 2
𝑑𝑣 1 + 𝑣 2
⇔ 𝑣+𝑥
=
𝑑𝑥
2𝑣
2
𝑑𝑣 1 − 𝑣
⇔𝑥
=
𝑑𝑥
2𝑣
Page 33 of 72

2𝑣
1
𝑑𝑣 − 𝑑𝑥 = 0.
2
1−𝑣
𝑥
Furthermore, we obtain
−2𝑣
1
−
𝑑𝑣
−
𝑑𝑥 = 𝐶1
1 − 𝑣2
𝑥
1
1
⇔−
𝑑 −𝑣 2 −
𝑑𝑥 = 𝐶1
2
1−𝑣
𝑥
⇔ − ln 1 − 𝑣 2 − ln 𝑥 = 𝐶1
⇔ ln 1 − 𝑣 2 + ln 𝑥 = 𝐶
𝑦2
⇔ ln 1 − 2 + ln |𝑥| = 𝐶 … (∗)
𝑥
Substituting 𝑥 = 1 and 𝑦 = 0 (initial condition), we obtain
ln 1 − 0 + ln 1 = 𝐶 ⇔ 0 = 𝐶.
⇔

𝑦2

Therefore, ln 1 − 𝑥 2 + ln |𝑥| = 0 is the solution of the given inital value problem.
6. 5𝑥 + 2𝑦 + 1 𝑑𝑥 + 2𝑥 + 𝑦 + 1 𝑑𝑦 = 0
Solution:
Let 𝑢 = 5𝑥 + 2𝑦 + 1 and 𝑣 = 2𝑥 + 𝑦 + 1. We obtain 𝑑𝑢 = 5𝑑𝑥 + 2𝑑𝑦 and
𝑑𝑣 = 2𝑑𝑥 + 𝑑𝑦. Using elimination, we obtain 𝑑𝑥 = 𝑑𝑢 − 2𝑑𝑣 and 𝑑𝑦 = 5𝑑𝑣 − 2𝑑𝑢.
Afterwards, we obtain
𝑢𝑑𝑥 + 𝑣𝑑𝑦 = 0
⇔ 𝑢 𝑑𝑢 − 2𝑑𝑣 + 𝑣 5𝑑𝑣 − 2𝑑𝑢 = 0
⇔ 𝑢𝑑𝑢 − 2𝑢𝑑𝑣 + 5𝑣𝑑𝑣 − 2𝑣𝑑𝑢 = 0
⇔ 𝑢 − 2𝑣 𝑑𝑢 + −2𝑢 + 5𝑣 𝑑𝑣 = 0
𝑣
𝑣
⇔ 1 − 2 𝑑𝑢 + −2 + 5 𝑑𝑣 = 0.
𝑢
𝑢
𝑣
Let 𝑤 = ⇔ 𝑣 = 𝑢𝑤. As a consequence, we obtain 𝑑𝑣 = 𝑤𝑑𝑢 + 𝑢𝑑𝑤 and
𝑢

1 − 2𝑤 𝑑𝑢 + −2 + 5𝑤 𝑤𝑑𝑢 + 𝑢𝑑𝑤 = 0
⇔ 𝑑𝑢 − 2𝑤𝑑𝑢 − 2𝑤𝑑𝑢 − 2𝑢𝑑𝑤 + 5𝑤 2 𝑑𝑢 + 5𝑤𝑢𝑑𝑤 = 0
⇔ 1 − 4𝑤 + 5𝑤 2 𝑑𝑢 + −2 + 5𝑤 𝑢𝑑𝑤 = 0
1
−2 + 5𝑤
⇔ 𝑑𝑢 +
𝑑𝑤 = 0.
𝑢
1 − 4𝑤 + 5𝑤 2
Moreover, we obtain
1
−2 + 5𝑤
𝑑𝑢 +
𝑑𝑤 = 𝐶
𝑢
1 − 4𝑤 + 5𝑤 2
1
1
−4 + 10𝑤
⇔
𝑑𝑢 +
𝑑𝑤 = 𝐶
𝑢
2 1 − 4𝑤 + 5𝑤 2
1
1
1
⇔
𝑑𝑢 +
𝑑 1 − 4𝑤 + 5𝑤 2 = 𝐶
𝑢
2 1 − 4𝑤 + 5𝑤 2
1
⇔ ln 𝑢 + ln 1 − 4𝑤 + 5𝑤 2 = 𝐶
2
1
4 2𝑥 + 𝑦 + 1
2𝑥 + 𝑦 + 1 2
⇔ ln |5𝑥 + 2𝑦 + 1| + ln 1 −
+5
=𝐶
2
5𝑥 + 2𝑦 + 1
5𝑥 + 2𝑦 + 1
as the general solution of 5𝑥 + 2𝑦 + 1 𝑑𝑥 + 2𝑥 + 𝑦 + 1 𝑑𝑦 = 0.
Page 34 of 72

Solution of Exercise 11 (Exact and Non Exact D.E)
( In exercises 1-10 determine whether or not each of the given equation is exact; solve
those that are exact).
1. 3𝑥 + 2𝑦 𝑑𝑥 + 2𝑥 + 𝑦 𝑑𝑦 = 0.
Solution:
Our first duty is to determine whether or not the equation is exact or not. Here
𝑀 𝑥, 𝑦 = 3𝑥 + 2𝑦, 𝑁 𝑥, 𝑦 = 2𝑥 + 𝑦,
𝜕𝑀 𝑥, 𝑦
𝜕𝑁 𝑥, 𝑦
= 2,
= 2.
𝜕𝑦
𝜕𝑥
Since
𝜕𝑀 𝑥, 𝑦
𝜕𝑁 𝑥, 𝑦
=
=2
𝜕𝑦
𝜕𝑥
we can conclude that the differential equation 3𝑥 + 2𝑦 𝑑𝑥 + 2𝑥 + 𝑦 𝑑𝑦 = 0 is
exact differential equation. Furthermore, we must find 𝐹 such that
𝜕𝐹 𝑥, 𝑦
𝜕𝐹 𝑥, 𝑦
= 𝑀 𝑥, 𝑦 = 3𝑥 + 2𝑦 and
= 𝑁 𝑥, 𝑦 = 2𝑥 + 𝑦.
𝜕𝑥
𝜕𝑦
From the first of these,
3
𝐹 𝑥, 𝑦 = 𝑀 𝑥, 𝑦 𝜕𝑥 + 𝑕 𝑦 =
3𝑥 + 2𝑦 𝜕𝑥 + 𝑕 𝑦 = 𝑥 2 + 2𝑥𝑦 + 𝑕 𝑦 .
2
Then
𝜕𝐹 𝑥, 𝑦
𝑑𝑕 𝑦
= 2𝑥 +
𝜕𝑦
𝑑𝑦
But we must have
𝜕𝐹 𝑥, 𝑦
= 𝑁 𝑥, 𝑦 = 2𝑥 + 𝑦.
𝜕𝑦
Thus
𝑑𝑕 𝑦
𝑑𝑕 𝑦
2𝑥 + 𝑦 = 2𝑥 +
⇔𝑦=
.
𝑑𝑦
𝑑𝑦
1

Thus 𝑕 𝑦 = 2 𝑦 2 + 𝐶0 , where 𝐶0 is an arbitrary constant, and so
3
1
𝐹 𝑥, 𝑦 = 𝑥 2 + 2𝑥𝑦 + 𝑦 2 + 𝐶0 .
2
2
Hence a one- parameter family of solution is 𝐹 𝑥, 𝑦 = 𝐶1 , or
3 2
1
𝑥 + 2𝑥𝑦 + 𝑦 2 + 𝐶0 = 𝐶1
2
2
Combining the constsnts 𝐶0 and 𝐶1 we may write this solution as
3 2
1
𝑥 + 2𝑥𝑦 + 𝑦 2 = 𝐶
2
2
where 𝐶 = 𝐶1 − 𝐶0 is an arbitrary constant.
So, we conclude that the general solution of the exact differential equation
3

1

3𝑥 + 2𝑦 𝑑𝑥 + 2𝑥 + 𝑦 𝑑𝑦 = 0 is 2 𝑥 2 + 2𝑥𝑦 + 2 𝑦 2 = 𝐶.

2. (𝑦 2 + 3)𝑑𝑥 + 2𝑥𝑦 − 4 𝑑𝑦 = 0.
Solution:
Our first duty is to determine whether or not the equation is exact or not. Here
𝑀 𝑥, 𝑦 = 𝑦 2 + 3, 𝑁 𝑥, 𝑦 = 2𝑥𝑦 − 4,
Page 35 of 72

𝜕𝑀 𝑥, 𝑦
𝜕𝑁 𝑥, 𝑦
= 2𝑦,
= 2𝑦.
𝜕𝑦
𝜕𝑥
Since

𝜕𝑀 𝑥, 𝑦
𝜕𝑁 𝑥, 𝑦
=
= 2𝑦
𝜕𝑦
𝜕𝑥
we can conclude that the differential equation (𝑦 2 + 3)𝑑𝑥 + 2𝑥𝑦 − 4 𝑑𝑦 = 0 is
exact differential equation. Afterwards, we must find 𝐹 such that
𝜕𝐹 𝑥, 𝑦
𝜕𝐹 𝑥, 𝑦
= 𝑀 𝑥, 𝑦 = 𝑦 2 + 3 and
= 𝑁 𝑥, 𝑦 = 2𝑥𝑦 − 4.
𝜕𝑥
𝜕𝑦
From the first of these,
𝐹 𝑥, 𝑦 =

𝑀 𝑥, 𝑦 𝜕𝑥 + 𝑕 𝑦 =

𝑦 2 + 3 𝜕𝑥 + 𝑕 𝑦 = 𝑥𝑦 2 + 3𝑥 + 𝑕 𝑦 .

Then
𝜕𝐹 𝑥, 𝑦
𝑑𝑕 𝑦
= 2𝑥𝑦 +
𝜕𝑦
𝑑𝑦
But we must have
𝜕𝐹 𝑥, 𝑦
= 𝑁 𝑥, 𝑦 = 2𝑥𝑦 − 4.
𝜕𝑦
Thus
𝑑𝑕 𝑦
𝑑𝑕 𝑦
⇔ −4 =
.
𝑑𝑦
𝑑𝑦
Thus 𝑕 𝑦 = −4𝑦 + 𝐶0 , where 𝐶0 is an arbitrary constant, and so
𝐹 𝑥, 𝑦 = 𝑥𝑦 2 + 3𝑥 + −4𝑦 + 𝐶0 .
Hence a one- parameter family of solution is 𝐹 𝑥, 𝑦 = 𝐶1 , or
𝑥𝑦 2 + 3𝑥 + −4𝑦 + 𝐶0 = 𝐶1
Combining the constsnts 𝐶0 and 𝐶1 we may write this solution as
𝑥𝑦 2 + 3𝑥 + −4𝑦 = 𝐶
where 𝐶 = 𝐶1 − 𝐶0 is an arbitrary constant.
So, we conclude that the general solution of the exact differential equation
(𝑦 2 + 3)𝑑𝑥 + 2𝑥𝑦 − 4 𝑑𝑦 = 0 is 𝑥𝑦 2 + 3𝑥 + −4𝑦 = 𝐶.
3. 2𝑥𝑦 + 1 𝑑𝑥 + 𝑥 2 + 4𝑦 𝑑𝑦 = 0.
Solution:
Our first duty is to determine whether or not the equation is exact or not. Here
𝑀 𝑥, 𝑦 = 2𝑥𝑦 + 1, 𝑁 𝑥, 𝑦 = 𝑥 2 + 4𝑦,
𝜕𝑀 𝑥, 𝑦
𝜕𝑁 𝑥, 𝑦
= 2𝑥,
= 2𝑥.
𝜕𝑦
𝜕𝑥
Since
𝜕𝑀 𝑥, 𝑦
𝜕𝑁 𝑥, 𝑦
=
= 2𝑥
𝜕𝑦
𝜕𝑥
we can conclude that the differential equation 2𝑥𝑦 + 1 𝑑𝑥 + 𝑥 2 + 4𝑦 𝑑𝑦 = 0 is
exact differential equation. Afterwards, we must find 𝐹 such that
𝜕𝐹 𝑥, 𝑦
𝜕𝐹 𝑥, 𝑦
= 𝑀 𝑥, 𝑦 = 2𝑥𝑦 + 1 and
= 𝑁 𝑥, 𝑦 = 𝑥 2 + 4𝑦.
𝜕𝑥
𝜕𝑦
From the first of these,
2𝑥𝑦 − 4 = 2𝑥𝑦 +

Page 36 of 72

𝐹 𝑥, 𝑦 =

𝑀 𝑥, 𝑦 𝜕𝑥 + 𝑕 𝑦 =

2𝑥𝑦 + 1 𝜕𝑥 + 𝑕 𝑦 = 𝑥 2 𝑦 + 𝑥 + 𝑕 𝑦 .

Then
𝜕𝐹 𝑥, 𝑦
𝑑𝑕 𝑦
= 𝑥2 +
𝜕𝑦
𝑑𝑦
But we must have
𝜕𝐹 𝑥, 𝑦
= 𝑁 𝑥, 𝑦 = 𝑥 2 + 4𝑦.
𝜕𝑦
Thus
𝑑𝑕 𝑦
𝑑𝑕 𝑦
⇔ 4𝑦 =
.
𝑑𝑦
𝑑𝑦
Thus 𝑕 𝑦 = 2𝑦 2 + 𝐶0 , where 𝐶0 is an arbitrary constant, and so
𝐹 𝑥, 𝑦 = 𝑥 2 𝑦 + 𝑥 + 2𝑦 2 + 𝐶0 .
Hence a one- parameter family of solution is 𝐹 𝑥, 𝑦 = 𝐶1 , or
𝑥 2 𝑦 + 𝑥 + 2𝑦 2 + 𝐶0 = 𝐶1
Combining the constsnts 𝐶0 and 𝐶1 we may write this solution as
𝑥 2 𝑦 + 𝑥 + 2𝑦 2 = 𝐶
where 𝐶 = 𝐶1 − 𝐶0 is an arbitrary constant.
So, we conclude that the general solution of the exact differential equation
2𝑥𝑦 + 1 𝑑𝑥 + 𝑥 2 + 4𝑦 𝑑𝑦 = 0 is 𝑥 2 𝑦 + 𝑥 + 2𝑦 2 = 𝐶.
4. 3𝑥 2 𝑦 + 2 𝑑𝑥 − 𝑥 3 + 𝑦 𝑑𝑦 = 0.
Solution:
Our first duty is to determine whether or not the equation is exact or not. Here
𝑀 𝑥, 𝑦 = 3𝑥 2 𝑦, 𝑁 𝑥, 𝑦 = −𝑥 3 − 𝑦,
𝜕𝑀 𝑥, 𝑦
𝜕𝑁 𝑥, 𝑦
= 3𝑥 2 ,
= −3𝑥 2 .
𝜕𝑦
𝜕𝑥
Since
𝜕𝑀 𝑥, 𝑦
𝜕𝑁 𝑥, 𝑦
= 3𝑥 2 ≠
= −3𝑥 2
𝜕𝑦
𝜕𝑥
we can conclude that the differential equation 3𝑥 2 𝑦 + 2 𝑑𝑥 − 𝑥 3 + 𝑦 𝑑𝑦 = 0 is
not exact (non- exact) differential equation.
5. 6𝑥𝑦 + 2𝑦 2 − 5 𝑑𝑥 + 3𝑥 2 + 4𝑥𝑦 − 6 𝑑𝑦 = 0.
Solution:
Our first duty is to determine whether or not the equation is exact or not. Here
𝑀 𝑥, 𝑦 = 6𝑥𝑦 + 2𝑦 2 − 5, 𝑁 𝑥, 𝑦 = 3𝑥 2 + 4𝑥𝑦 − 6,
𝜕𝑀 𝑥, 𝑦
𝜕𝑁 𝑥, 𝑦
= 6𝑥 + 4𝑦,
= 6𝑥 + 4𝑦.
𝜕𝑦
𝜕𝑥
Since
𝜕𝑀 𝑥, 𝑦
𝜕𝑁 𝑥, 𝑦
=
= 6𝑥 + 4𝑦
𝜕𝑦
𝜕𝑥
we can conclude that the differential equation
6𝑥𝑦 + 2𝑦 2 − 5 𝑑𝑥 + 3𝑥 2 + 4𝑥𝑦 − 6 𝑑𝑦 = 0 is exact differential equation.
Moreover, we must find 𝐹 such that
𝜕𝐹 𝑥, 𝑦
𝜕𝐹 𝑥, 𝑦
= 𝑀 𝑥, 𝑦 = 6𝑥𝑦 + 2𝑦 2 − 5 and
= 𝑁 𝑥, 𝑦 = 3𝑥 2 + 4𝑥𝑦 − 6.
𝜕𝑥
𝜕𝑦
𝑥 2 + 4𝑦 = 𝑥 2 +

Page 37 of 72

From the first of these,
𝐹 𝑥, 𝑦 =
=

𝑀 𝑥, 𝑦 𝜕𝑥 + 𝑕 𝑦
6𝑥𝑦 + 2𝑦 2 − 5 𝜕𝑥 + 𝑕 𝑦

= 3𝑥 2 𝑦 + 2𝑥𝑦 2 − 5𝑥 + 𝑕 𝑦
Then
𝜕𝐹 𝑥, 𝑦
𝑑𝑕 𝑦
= 3𝑥 2 + 4𝑥𝑦 +
𝜕𝑦
𝑑𝑦
But we must have
𝜕𝐹 𝑥, 𝑦
= 𝑁 𝑥, 𝑦 = 3𝑥 2 + 4𝑥𝑦 − 6.
𝜕𝑦
Thus
𝑑𝑕 𝑦
𝑑𝑕 𝑦
⇔ −6 =
.
𝑑𝑦
𝑑𝑦
Thus 𝑕 𝑦 = −6𝑦 + 𝐶0 , where 𝐶0 is an arbitrary constant, and so
𝐹 𝑥, 𝑦 = 3𝑥 2 𝑦 + 2𝑥𝑦 2 − 5𝑥 − 6𝑦 + 𝐶0 .
Hence a one- parameter family of solution is 𝐹 𝑥, 𝑦 = 𝐶1 , or
3𝑥 2 𝑦 + 2𝑥𝑦 2 − 5𝑥 − 6𝑦 + 𝐶0 = 𝐶1
Combining the constsnts 𝐶0 and 𝐶1 we may write this solution as
3𝑥 2 𝑦 + 2𝑥𝑦 2 − 5𝑥 − 6𝑦 = 𝐶
where 𝐶 = 𝐶1 − 𝐶0 is an arbitrary constant.
So, we conclude that the general solution of the exact differential equation
6𝑥𝑦 + 2𝑦 2 − 5 𝑑𝑥 + 3𝑥 2 + 4𝑥𝑦 − 6 𝑑𝑦 = 0 is 3𝑥 2 𝑦 + 2𝑥𝑦 2 − 5𝑥 − 6𝑦 = 𝐶.
6. 𝜃 2 + 1 cos 𝑟 𝑑𝑟 + 2𝜃 sin 𝑟 𝑑𝜃 = 0.
Solution:
Our first duty is to determine whether or not the equation is exact or not. Here
𝑀 𝑟, 𝜃 = 𝜃 2 + 1 cos 𝑟 , 𝑁 𝑟, 𝜃 = 2𝜃 sin 𝑟,
𝜕𝑀 𝑟, 𝜃
𝜕𝑁 𝑟, 𝜃
= 2𝜃 cos 𝑟 ,
= 2𝜃 cos 𝑟.
𝜕𝜃
𝜕𝑟
Since
𝜕𝑀 𝑟, 𝜃
𝜕𝑁 𝑟, 𝜃
=
= 2𝜃 cos 𝑟
𝜕𝜃
𝜕𝑟
we can conclude that the differential equation 𝜃 2 + 1 cos 𝑟 𝑑𝑟 + 2𝜃 sin 𝑟 𝑑𝜃 = 0
is exact differential equation. Moreover, we must find 𝐹 such that
𝜕𝐹 𝑟, 𝜃
𝜕𝐹 𝑟, 𝜃
= 𝑀 𝑟, 𝜃 = 𝜃 2 + 1 cos 𝑟 and
= 𝑁 𝑟, 𝜃 = 2𝜃 sin 𝑟
𝜕𝑟
𝜕𝜃
From the first of these,
3𝑥 2 + 4𝑥𝑦 − 6 = 3𝑥 2 + 4𝑥𝑦 +

𝐹 𝑟, 𝜃 =
=

𝑀 𝑟, 𝜃 𝜕𝑟 + 𝑕 𝜃
𝜃 2 + 1 cos 𝑟 𝜕𝑟 + 𝑕 𝜃

= 𝜃 2 + 1 sin 𝑟 + 𝑕 𝜃
Then

Page 38 of 72

But we must have

𝜕𝐹 𝑟, 𝜃
𝑑𝑕 𝜃
= 2𝜃 sin 𝑟 +
𝜕𝜃
𝑑𝜃
𝜕𝐹 𝑟, 𝜃
= 𝑁 𝑟, 𝜃 = 2𝜃 sin 𝑟.
𝜕𝜃

Thus

𝑑𝑕 𝜃
𝑑𝑕 𝜃
⇔0=
.
𝑑𝜃
𝑑𝜃
Thus 𝑕 𝜃 = 𝐶0 , where 𝐶0 is an arbitrary constant, and so
𝐹 𝑟, 𝜃 = 𝜃 2 + 1 sin 𝑟 + 𝐶0 .
Hence a one- parameter family of solution is 𝐹 𝑟, 𝜃 = 𝐶1 , or
𝜃 2 + 1 sin 𝑟 + 𝐶0 = 𝐶1
Combining the constsnts 𝐶0 and 𝐶1 we may write this solution as
𝜃 2 + 1 sin 𝑟 = 𝐶
where 𝐶 = 𝐶1 − 𝐶0 is an arbitrary constant.
So, we conclude that the general solution of the exact differential equation
𝜃 2 + 1 cos 𝑟 𝑑𝑟 + 2𝜃 sin 𝑟 𝑑𝜃 = 0 is 𝜃 2 + 1 sin 𝑟 = 𝐶.
7. 𝑦 sec 2 𝑥 + sec 𝑥 tan 𝑥 𝑑𝑥 + tan 𝑥 + 2𝑦 𝑑𝑦 = 0.
Solution:
Our first duty is to determine whether or not the equation is exact or not. Here
𝑀 𝑥, 𝑦 = 𝑦 sec 2 𝑥 + sec 𝑥 tan 𝑥 , 𝑁 𝑥, 𝑦 = tan 𝑥 + 2𝑦,
𝜕𝑀 𝑥, 𝑦
𝜕𝑁 𝑥, 𝑦
= sec 2 𝑥 ,
= sec 2 𝑥.
𝜕𝑦
𝜕𝑥
Since
𝜕𝑀 𝑥, 𝑦
𝜕𝑁 𝑥, 𝑦
=
= sec 2 𝑥
𝜕𝑦
𝜕𝑥
we can conclude that the equation 𝑦 sec 2 𝑥 + sec 𝑥 tan 𝑥 𝑑𝑥 + tan 𝑥 + 2𝑦 𝑑𝑦 =
0 is exact differential equation. Furthermore, we must find 𝐹 such that
𝜕𝐹 𝑥, 𝑦
𝜕𝐹 𝑥, 𝑦
= 𝑀 𝑥, 𝑦 = 𝑦 sec 2 𝑥 + sec 𝑥 tan 𝑥 and
= 𝑁 𝑥, 𝑦 = tan 𝑥 + 2𝑦.
𝜕𝑥
𝜕𝑦
From the first of these,
2𝜃 sin 𝑟 = 2𝜃 sin 𝑟 +

𝐹 𝑥, 𝑦 =
=

𝑀 𝑥, 𝑦 𝜕𝑥 + 𝑕 𝑦
𝑦 sec 2 𝑥 + sec 𝑥 tan 𝑥 𝜕𝑥 + 𝑕 𝑦

= 𝑦 tan 𝑥 + sec 𝑥 + 𝑕 𝑦 .
Then
𝜕𝐹 𝑥, 𝑦
𝑑𝑕 𝑦
= tan 𝑥 +
𝜕𝑦
𝑑𝑦
But we must have
𝜕𝐹 𝑥, 𝑦
= 𝑁 𝑥, 𝑦 = tan 𝑥 + 2𝑦.
𝜕𝑦
Thus

Page 39 of 72

𝑑𝑕 𝑦
𝑑𝑕 𝑦
⇔ 2𝑦 =
.
𝑑𝑦
𝑑𝑦
Thus 𝑕 𝑦 = 𝑦 2 + 𝐶0 , where 𝐶0 is an arbitrary constant, and so
𝐹 𝑥, 𝑦 = 𝑦 tan 𝑥 + sec 𝑥 + 𝑦 2 + 𝐶0 .
Hence a one- parameter family of solution is 𝐹 𝑥, 𝑦 = 𝐶1 , or
𝑦 tan 𝑥 + sec 𝑥 + 𝑦 2 + 𝐶0 = 𝐶1
Combining the constsnts 𝐶0 and 𝐶1 we may write this solution as
𝑦 tan 𝑥 + sec 𝑥 + 𝑦 2 = 𝐶
where 𝐶 = 𝐶1 − 𝐶0 is an arbitrary constant.
So, we conclude that the general solution of the exact differential equation
𝑦 sec 2 𝑥 + sec 𝑥 tan 𝑥 𝑑𝑥 + tan 𝑥 + 2𝑦 𝑑𝑦 = 0 is 𝑦 tan 𝑥 + sec 𝑥 + 𝑦 2 = 𝐶.
tan 𝑥 + 2𝑦 = tan 𝑥 +

8.

𝑥
𝑦2

+ 𝑥 𝑑𝑥 +

𝑥2
𝑦3

+ 𝑦 𝑑𝑦 = 0.

Solution:
Our first duty is to determine whether or not the equation is exact or not. Here
𝑥
𝑥2
𝑀 𝑥, 𝑦 = 2 + 𝑥, 𝑁 𝑥, 𝑦 = 3 + 𝑦,
𝑦
𝑦
𝜕𝑀 𝑥, 𝑦
2𝑥 𝜕𝑁 𝑥, 𝑦
2𝑥
=− 3,
= 3.
𝜕𝑦
𝑦
𝜕𝑥
𝑦
Since
𝜕𝑀 𝑥, 𝑦
2𝑥 𝜕𝑁 𝑥, 𝑦
2𝑥
=− 3≠
= 3
𝜕𝑦
𝑦
𝜕𝑥
𝑦
we can conclude that the differential equation

𝑥
𝑦2

+ 𝑥 𝑑𝑥 +

𝑥2

𝑦3

+ 𝑦 𝑑𝑦 = 0 is

not exact (non- exact) differential equation.
9.

2𝑠−1
𝑡

𝑑𝑠 +

𝑠−𝑠 2
𝑡2

𝑑𝑡 = 0.

Solution:
Our first duty is to determine whether or not the equation is exact or not. Here
2𝑠 − 1
𝑠 − 𝑠2
𝑀 𝑠, 𝑡 =
, 𝑁 𝑠, 𝑡 =
,
𝑡
𝑡2
𝜕𝑀 𝑠, 𝑡
1 − 2𝑠 𝜕𝑁 𝑠, 𝑡
1 − 2𝑠
=
,
=
.
2
𝜕𝑡
𝑡
𝜕𝑠
𝑡2
Since
𝜕𝑀 𝑠, 𝑡
𝜕𝑁 𝑠, 𝑡
1 − 2𝑠
=
=
𝜕𝑡
𝜕𝑠
𝑡2
2𝑠−1
𝑠−𝑠 2
we can conclude that the differential equation 𝑡 𝑑𝑠 + 𝑡 2 𝑑𝑡 = 0 is exact
differential equation. Furthermore, we must find 𝐹 such that
𝜕𝐹 𝑠, 𝑡
2𝑠 − 1
𝜕𝐹 𝑠, 𝑡
𝑠 − 𝑠2
= 𝑀 𝑠, 𝑡 =
and
= 𝑁 𝑠, 𝑡 =
.
𝜕𝑠
𝑡
𝜕𝑡
𝑡2
From the first of these,
𝐹 𝑠, 𝑡 =
=

𝑀 𝑠, 𝑡 𝜕𝑥 + 𝑕 𝑡
2𝑠 − 1
𝜕𝑠 + 𝑕 𝑡
𝑡
Page 40 of 72

Then

𝑠2 − 𝑠
=
+𝑕 𝑡 .
𝑡

𝜕𝐹 𝑠, 𝑡
𝑠 2 𝑠 𝑑𝑕 𝑡
𝑠 − 𝑠 2 𝑑𝑕 𝑡
=− 2+ 2+
=
+
𝜕𝑡
𝑡
𝑡
𝑑𝑡
𝑡2
𝑑𝑡
But we must have
𝜕𝐹 𝑠, 𝑡
𝑠 − 𝑠2
= 𝑁 𝑠, 𝑡 =
.
𝜕𝑡
𝑡2
Thus
𝑠 − 𝑠 2 𝑠 − 𝑠 2 𝑑𝑕 𝑡
𝑑𝑕 𝑡
=
+
⇔0=
.
2
2
𝑡
𝑡
𝑑𝑡
𝑑𝑡
Thus 𝑕 𝑡 = 𝐶0 , where 𝐶0 is an arbitrary constant, and so
𝑠2 − 𝑠
𝐹 𝑠, 𝑡 =
+ 𝐶0 .
𝑡
Hence a one- parameter family of solution is 𝐹 𝑥, 𝑦 = 𝐶1 , or
𝑠2 − 𝑠
+ 𝐶0 = 𝐶1
𝑡
Combining the constsnts 𝐶0 and 𝐶1 we may write this solution as
𝑠2 − 𝑠
=𝐶
𝑡
or we can write this as 𝑠 2 − 𝑠 = 𝐶𝑡, where 𝐶 = 𝐶1 − 𝐶0 is an arbitrary constant.
So, we conclude that the general solution of the exact differential equation
2𝑠−1
𝑡

10.

3

2𝑦 2 +1
1
𝑥2

𝑑𝑠 +

𝑠−𝑠 2

𝑑𝑡 = 0 is 𝑠 2 − 𝑠 = 𝐶𝑡.

𝑡2
1

1

𝑑𝑥 + 3𝑥 2 𝑦 2 − 1 𝑑𝑦 = 0.

Solution:
Our first duty is to determine whether or not the equation is exact or not. Here
3

𝑀 𝑥, 𝑦 =

Since

2𝑦 2 + 1
1

1 1

, 𝑁 𝑥, 𝑦 = 3𝑥 2 𝑦 2 − 1,

𝑥2
1
1
𝜕𝑀 𝑥, 𝑦
𝑦 2 𝜕𝑁 𝑥, 𝑦
3 −1 1 3 𝑦 2
=3 1,
= 𝑥 2𝑦2 =
.
𝜕𝑦
𝜕𝑥
2
2 12
2
𝑥
𝑥
1

1

𝜕𝑀 𝑥, 𝑦
𝑦 2 𝜕𝑁 𝑥, 𝑦
3 𝑦2
=3 1≠
=
𝜕𝑦
𝜕𝑥
2 12
𝑥2
𝑥
3
we can conclude that the differential equation
is not exact (non- exact) differential equation.

Page 41 of 72

2𝑦 2 +1
1
𝑥2

1

1

𝑑𝑥 + 3𝑥 2 𝑦 2 − 1 𝑑𝑦 = 0

Solution of Exercise 12 (Integrating Factor)
( In each of the following equations determine the constant 𝐴 such that the equation is
exact, and solve the resulting exact equation).
a. 𝑥 2 + 3𝑥𝑦 𝑑𝑥 + 𝐴𝑥 2 + 4𝑦 𝑑𝑦 = 0.
Solution:
Suppose
𝑀 𝑥, 𝑦 = 𝑥 2 + 3𝑥𝑦 and 𝑁 𝑥, 𝑦 = 𝐴𝑥 2 + 4𝑦.
Then, we obtain
𝜕𝑀 𝑥, 𝑦
𝜕𝑁 𝑥, 𝑦
= 3𝑥 and
= 2𝐴𝑥.
𝜕𝑦
𝜕𝑥
In order to make the differential equation become exact differential equation, it
must be
𝜕𝑀 𝑥, 𝑦
𝜕𝑁 𝑥, 𝑦
=
= 3𝑥.
𝜕𝑦
𝜕𝑥
Thus
3
2𝐴𝑥 = 3𝑥 ⇔ 𝐴 = .
2
Therefore, we obtain that the differential equation
3

𝑥 2 + 3𝑥𝑦 𝑑𝑥 + 2 𝑥 2 + 4𝑦 𝑑𝑦 = 0 is exact differential equation. Furthermore,
we must find 𝐹 such that
𝜕𝐹 𝑥, 𝑦
𝜕𝐹 𝑥, 𝑦
3
= 𝑀 𝑥, 𝑦 = 𝑥 2 + 3𝑥𝑦 and
= 𝑁 𝑥, 𝑦 = 𝑥 2 + 4𝑦.
𝜕𝑥
𝜕𝑦
2
From the first of these,
1
3
𝐹 𝑥, 𝑦 = 𝑀 𝑥, 𝑦 𝜕𝑥 + 𝑕 𝑦 =
𝑥 2 + 3𝑥𝑦 𝜕𝑥 + 𝑕 𝑦 = 𝑥 3 + 𝑥 2 𝑦 + 𝑕 𝑦 .
3
2
Then
𝜕𝐹 𝑥, 𝑦
3
𝑑𝑕 𝑦
= 𝑥2 +
.
𝜕𝑦
2
𝑑𝑦
But we must have
𝜕𝐹 𝑥, 𝑦
3
= 𝑁 𝑥, 𝑦 = 𝑥 2 + 4𝑦.
𝜕𝑦
2
Thus
3 2
3
𝑑𝑕 𝑦
𝑑𝑕 𝑦
𝑥 + 4𝑦 = 𝑥 2 +
⇔ 4𝑦 =
.
2
2
𝑑𝑦
𝑑𝑦
Thus 𝑕 𝑦 = 2𝑦 2 + 𝐶0 , where 𝐶0 is an arbitrary constant, and so
1
3
𝐹 𝑥, 𝑦 = 𝑥 3 + 𝑥 2 𝑦 + 𝐶0 .
3
2
Hence a one- parameter family of solution is 𝐹 𝑥, 𝑦 = 𝐶1 , or
1 3 3 2
𝑥 + 𝑥 𝑦 + 2𝑦 2 + 𝐶0 = 𝐶1
3
2
Combining the constsnts 𝐶0 and 𝐶1 we may write this solution as
1 3 3 2
𝑥 + 𝑥 𝑦 + 2𝑦 2 = 𝐶
3
2
where 𝐶 = 𝐶1 − 𝐶0 is an arbitrary constant.
Page 42 of 72

So, we conclude that the general solution of the exact differential equation
𝑥 2 + 3𝑥𝑦 𝑑𝑥 +
b.

1
𝑥2

1

+ 𝑦 2 𝑑𝑥 +

3

𝑥 2 + 4𝑦 𝑑𝑦 = 0 is

2
𝐴𝑥 +1
𝑦3

1
3

3

𝑥 3 + 2 𝑥 2 𝑦 + 2𝑦 2 = 𝐶.

𝑑𝑦 = 0.

Solution:
Suppose
𝑀 𝑥, 𝑦 =

1
1
𝐴𝑥 + 1
+ 2 and 𝑁 𝑥, 𝑦 =
.
2
𝑥
𝑦
𝑦3

Then, we obtain

𝜕𝑀 𝑥, 𝑦
2
𝜕𝑁 𝑥, 𝑦
𝐴
= − 3 and
= 3.
𝜕𝑦
𝑦
𝜕𝑥
𝑦
In order to make the differential equation become exact differential equation, it
must be
𝜕𝑀 𝑥, 𝑦
𝜕𝑁 𝑥, 𝑦
2
=
= − 3.
𝜕𝑦
𝜕𝑥
𝑦
Thus
𝐴
2
= − 3 ⇔ 𝐴 = −2.
3
𝑦
𝑦
Therefore, we obtain that the differential equation
1
𝑥2

1

+ 𝑦 2 𝑑𝑥 +

−2𝑥+1
𝑦3

𝑑𝑦 = 0 is exact differential equation. Furthermore, we

must find 𝐹 such that
𝜕𝐹 𝑥, 𝑦
1
1
𝜕𝐹 𝑥, 𝑦
−2𝑥 + 1
= 𝑀 𝑥, 𝑦 = 2 + 2 and
= 𝑁 𝑥, 𝑦 =
.
𝜕𝑥
𝑥
𝑦
𝜕𝑦
𝑦3
From the first of these,
1
1
1 𝑥
𝐹 𝑥, 𝑦 = 𝑀 𝑥, 𝑦 𝜕𝑥 + 𝑕 𝑦 =
+ 2 𝜕𝑥 + 𝑕 𝑦 = − + 2 + 𝑕 𝑦 .
2
𝑥
𝑦
𝑥 𝑦
Then
𝜕𝐹 𝑥, 𝑦
2𝑥 𝑑𝑕 𝑦
=− 3+
.
𝜕𝑦
𝑦
𝑑𝑦
But we must have
𝜕𝐹 𝑥, 𝑦
−2𝑥 + 1
= 𝑁 𝑥, 𝑦 =
.
𝜕𝑦
𝑦3
Thus
−2𝑥 + 1
2𝑥 𝑑𝑕 𝑦
1
𝑑𝑕 𝑦
=− 3+
⇔ 3=
.
3
𝑦
𝑦
𝑑𝑦
𝑦
𝑑𝑦
1

Thus 𝑕 𝑦 = − 2𝑦 2 + 𝐶0 , where 𝐶0 is an arbitrary constant, and so
1 𝑥
1
𝐹 𝑥, 𝑦 = − + 2 − 2 + 𝐶0 .
𝑥 𝑦
2𝑦
Hence a one- parameter family of solution is 𝐹 𝑥, 𝑦 = 𝐶1 , or
1 𝑥
1
− + 2 − 2 + 𝐶0 = 𝐶1
𝑥 𝑦
2𝑦
Combining the constsnts 𝐶0 and 𝐶1 we may write this solution as

Page 43 of 72

1 𝑥
1
− + 2− 2=𝐶
𝑥 𝑦
2𝑦
where 𝐶 = 𝐶1 − 𝐶0 is an arbitrary constant.
So, we conclude that the general solution of the exact differential equation
1
𝑥2

1

+ 𝑦 2 𝑑𝑥 +

−2𝑥+1
𝑦3

1

𝑥

1

𝑑𝑦 = 0 is − 𝑥 + 𝑦 2 − 2𝑦 2 = 𝐶.

Solution of Exercise 13 (Grouping Method)
( Solve using grouping method)
1.

1
𝑥

𝑦

𝑑𝑦 − 𝑥 2 𝑑𝑥 = 0.

Solution:
1

𝑦

From 𝑥 𝑑𝑦 − 𝑥 2 𝑑𝑥 = 0 we obtain
𝑑
So

𝑦
=𝑑 𝐶 .
𝑥

𝑦
=𝐶
𝑥
1
𝑦
is the general solution of the differential equation 𝑥 𝑑𝑦 − 𝑥 2 𝑑𝑥 = 0.
𝑑𝑦

2. 2𝑥𝑦 𝑑𝑥 + 𝑦 2 − 2𝑥 = 0.
Solution:
𝑑𝑦
2𝑥𝑦
+ 𝑦 2 − 2𝑥 = 0
𝑑𝑥
𝑑𝑦
⇔ 2𝑥𝑦
= 2𝑥 − 𝑦 2
𝑑𝑥
⇔ 2𝑥 − 𝑦 2 𝑑𝑥 − 2𝑥𝑦𝑑𝑦 = 0
From 2𝑥 − 𝑦 2 𝑑𝑥 − 2𝑥𝑦𝑑𝑦 = 0, we group the term as follows
2𝑥𝑑𝑥 − (𝑦 2 𝑑𝑥 + 2𝑥𝑦𝑑𝑦) = 0.
Thus
𝑑 𝑥 2 − 𝑑 𝑥𝑦 2 = 𝑑 𝐶 .
So,
𝑥 2 − 𝑥𝑦 = 𝐶
𝑑𝑦

is the general solution of the differential equation 2𝑥𝑦 𝑑𝑥 + 𝑦 2 − 2𝑥 = 0.

3. 2 𝑦 + 1 𝑒 𝑥 𝑑𝑥 + 2 𝑒 𝑥 − 2𝑦 𝑑𝑦 = 0.
Solution:
From 2 𝑦 + 1 𝑒 𝑥 𝑑𝑥 + 2 𝑒 𝑥 − 2𝑦 𝑑𝑦 = 0, we group the term as follows
2𝑦𝑒 𝑥 𝑑𝑥 + 2𝑒 𝑥 𝑑𝑦 + 2𝑒 𝑥 𝑑𝑥 − 4𝑦𝑑𝑦 = 0.
Thus
𝑑 2𝑦𝑒 𝑥 + 𝑑 2𝑒 𝑥 − 𝑑 2𝑦 2 = 𝑑 𝐶 .
Page 44 of 72

Therefore,
2𝑦𝑒 𝑥 + 2𝑒 𝑥 − 2𝑦 2 = 𝐶
is the general solution of the differential equation
2 𝑦 + 1 𝑒 𝑥 𝑑𝑥 + 2 𝑒 𝑥 − 2𝑦 𝑑𝑦 = 0.
4. 2𝑥𝑦 + 6𝑥 𝑑𝑥 + 𝑥 2 + 4𝑦 3 𝑑𝑦 = 0.
Solution:
From 2𝑥𝑦 + 6𝑥 𝑑𝑥 + 𝑥 2 + 4𝑦 3 𝑑𝑦 = 0, we group the term as follows
2𝑥𝑦𝑑𝑥 + 𝑥 2 𝑑𝑦 + 6𝑥𝑑𝑥 + 4𝑦 3 𝑑𝑦 = 0.
Thus
𝑑 𝑥 2 𝑦 + 𝑑 3𝑥 2 + 𝑑 𝑦 4 = 𝑑 𝐶 .
So,
𝑥 2 𝑦 + 3𝑥 2 + 𝑦 4 = 𝐶
is the general solution of the differential equation
2𝑥𝑦 + 6𝑥 𝑑𝑥 + 𝑥 2 + 4𝑦 3 𝑑𝑦 = 0.

Solution of Quiz
1. Which of the following differential equations can be made exact by multiplying
by 𝑥 2 ?
𝑑𝑦

2

(a) 𝑑𝑥 + 𝑥 𝑦 = 4.
Solution:
𝑑𝑦 2
𝑑𝑦
2
2
+ 𝑦=4⇔
= 4 − 𝑦 ⇔ 4 − 𝑦 𝑑𝑥 − 𝑑𝑦 = 0
𝑑𝑥 𝑥
𝑑𝑥
𝑥
𝑥
By multiplying both sides by 𝑥 2 , we obtain
4𝑥 2 − 2𝑥𝑦 𝑑𝑥 + −𝑥 2 𝑑𝑦 = 0.
Here
𝑀 𝑥, 𝑦 = 4𝑥 2 − 2𝑥𝑦, 𝑁 𝑥, 𝑦 = −𝑥 2 ,
𝜕𝑀 𝑥, 𝑦
𝜕𝑁 𝑥, 𝑦
= −2𝑥,
= −2𝑥
𝜕𝑦
𝜕𝑥
Since
𝜕𝑀 𝑥, 𝑦
𝜕𝑁 𝑥, 𝑦
=
= −2𝑥
𝜕𝑦
𝜕𝑥
we can conclude that the differential equation 3𝑥 + 2𝑦 𝑑𝑥 + 2𝑥 + 𝑦 𝑑𝑦 = 0
is exact differential equation. In the other word, the differential equation
𝑑𝑦

2

+ 𝑦 = 4 can be made exact by multiplying by 𝑥 2 .

𝑑𝑥
𝑥
𝑑𝑦

(b) 𝑥 𝑑𝑥 + 3𝑦 = 𝑥 2 .
Solution:
𝑑𝑦
𝑑𝑦
𝑥
+ 3𝑦 = 𝑥 2 ⇔ 𝑥
= 𝑥 2 − 3𝑦 ⇔ 𝑥 2 − 3𝑦 𝑑𝑥 + −𝑥 𝑑𝑦 = 0.
𝑑𝑥
𝑑𝑥
By multiplying both sides by 𝑥 2 , we obtain
𝑥 4 − 3𝑥 2 𝑦 𝑑𝑥 + −𝑥 3 𝑑𝑦 = 0.
Page 45 of 72

Here
𝑀 𝑥, 𝑦 = 𝑥 4 − 3𝑥 2 𝑦, 𝑁 𝑥, 𝑦 = −𝑥 3 ,
𝜕𝑀 𝑥, 𝑦
𝜕𝑁 𝑥, 𝑦
= −3𝑥 2 ,
= −3𝑥 2 .
𝜕𝑦
𝜕𝑥
Since

𝜕𝑀 𝑥, 𝑦
𝜕𝑁 𝑥, 𝑦
=
= −3𝑥 2
𝜕𝑦
𝜕𝑥
we can conclude that the differential equation
𝑥 4 − 3𝑥 2 𝑦 𝑑𝑥 + −𝑥 3 𝑑𝑦 = 0 is exact differential equation. In the other
𝑑𝑦

word, the differential equation 𝑥 𝑑𝑥 + 3𝑦 = 𝑥 2 can be made exact by
multiplying by 𝑥 2 .
1 𝑑𝑦

1

(c) 𝑥 𝑑𝑥 − 𝑥 2 𝑦 = 𝑥.
Solution:
1 𝑑𝑦 1
1 𝑑𝑦
1
1
1
− 2𝑦 =𝑥 ⇔
= 𝑥 + 2 𝑦 ⇔ 𝑥 + 2 𝑦 𝑑𝑥 + − 𝑑𝑦 = 0.
𝑥 𝑑𝑥 𝑥
𝑥 𝑑𝑥
𝑥
𝑥
𝑥
2
By multiplying both sides by 𝑥 , we obtain
𝑥 3 + 𝑦 𝑑𝑥 + −𝑥 𝑑𝑦 = 0.
Here
𝑀 𝑥, 𝑦 = 𝑥 3 + 𝑦, 𝑁 𝑥, 𝑦 = −𝑥,
𝜕𝑀 𝑥, 𝑦
𝜕𝑁 𝑥, 𝑦
= 1,
= −1.
𝜕𝑦
𝜕𝑥
Since
𝜕𝑀 𝑥, 𝑦
𝜕𝑁 𝑥, 𝑦
=1≠
= −1
𝜕𝑦
𝜕𝑥
we can conclude that the differential equation
𝑥 3 + 𝑦 𝑑𝑥 + −𝑥 𝑑𝑦 = 0 is not exact differential equation. In the other
1 𝑑𝑦

1

word, the differential equation 𝑥 𝑑𝑥 − 𝑥 2 𝑦 = 𝑥 can not be made exact by
multiplying by 𝑥 2 .
1 𝑑𝑦

1

(d) 𝑥 𝑑𝑥 + 𝑥 2 𝑦 = 3.
Solution:
1 𝑑𝑦 1
1 𝑑𝑦
1
1
1
+ 2𝑦 =3⇔
= 3 − 2 𝑦 ⇔ 3 − 2 𝑦 𝑑𝑥 + − 𝑑𝑦 = 0.
𝑥 𝑑𝑥 𝑥
𝑥 𝑑𝑥
𝑥
𝑥
𝑥
By multiplying both sides by 𝑥 2 , we obtain
3𝑥 2 − 𝑦 𝑑𝑥 + −𝑥 𝑑𝑦 = 0.
Here
𝑀 𝑥, 𝑦 = 3𝑥 2 − 𝑦, 𝑁 𝑥, 𝑦 = −𝑥,
𝜕𝑀 𝑥, 𝑦
𝜕𝑁 𝑥, 𝑦
= −1,
= −1.
𝜕𝑦
𝜕𝑥
Since
𝜕𝑀 𝑥, 𝑦
𝜕𝑁 𝑥, 𝑦
=
= −1
𝜕𝑦
𝜕𝑥
we can conclude that the differential equation

Page 46 of 72

3𝑥 2 − 𝑦 𝑑𝑥 + −𝑥 𝑑𝑦 = 0 is exact differential equation. In the other word,
1 𝑑𝑦

1

the differential equation 𝑥 𝑑𝑥 + 𝑥 2 𝑦 = 3 can be made exact by multiplying by

𝑥 2.
2. Consider the differential equation
4𝑥 + 3𝑦 2 𝑑𝑥 + 2𝑥𝑦𝑑𝑦 = 0.
(a) Show that this equation is not exact.
Proof. Here
𝑀 𝑥, 𝑦 = 4𝑥 + 3𝑦 2 , 𝑁 𝑥, 𝑦 = 2𝑥𝑦,
𝜕𝑀 𝑥, 𝑦
𝜕𝑁 𝑥, 𝑦
= 6𝑦,
= 2𝑦.
𝜕𝑦
𝜕𝑥
Since
𝜕𝑀 𝑥, 𝑦
𝜕𝑁 𝑥, 𝑦
= 6𝑦 ≠
= 2𝑦
𝜕𝑦
𝜕𝑥
we can conclude that the differential equation 4𝑥 + 3𝑦 2 𝑑𝑥 + 2𝑥𝑦𝑑𝑦 = 0 is
is not exact differential equation. ■
(b) Find an integrating factor of the form 𝑥 𝑛 , where n is a positive integer.
Solution:
From (a) we know that the differential equation 4𝑥 + 3𝑦 2 𝑑𝑥 + 2𝑥𝑦𝑑𝑦 = 0
is not exact. But then, we can find an integrating factor 𝑢 𝑥, 𝑦 = 𝑥 𝑛 , where 𝑛
is a positive integer such that the differential equation 𝑥 𝑛 4𝑥 + 3𝑦 2 𝑑𝑥 +
𝑥 𝑛 2𝑥𝑦 𝑑𝑦 = 0 is exact.
Assume that 4𝑥 + 3𝑦 2 𝑑𝑥 + 𝑥 𝑛 2𝑥𝑦 𝑑𝑦 = 0 is exact differential equation.
Here
𝑥 𝑛 4𝑥 + 3𝑦 2 𝑑𝑥 + 𝑥 𝑛 2𝑥𝑦 𝑑𝑦 = 0
⇔ 4𝑥 𝑛+1 + 3𝑥 𝑛 𝑦 2 𝑑𝑥 + 2𝑥 𝑛+1 𝑦 𝑑𝑦 = 0.
Let
𝑀 𝑥, 𝑦 = 4𝑥 𝑛+1 + 3𝑥 𝑛 𝑦 2 and 𝑁 𝑥, 𝑦 = 2𝑥 𝑛+1 𝑦.
Then, we obtain
𝜕𝑀(𝑥, 𝑦)
𝜕𝑁 𝑥, 𝑦
= 6𝑥 𝑛 𝑦 and
= 2𝑛 + 2 𝑥 𝑛 𝑦
𝜕𝑦
𝜕𝑥
Since 4𝑥 + 3𝑦 2 𝑑𝑥 + 𝑥 𝑛 2𝑥𝑦 𝑑𝑦 = 0 is exact differential equation, we must
obtain
𝜕𝑀(𝑥, 𝑦) 𝜕𝑁 𝑥, 𝑦
6𝑥 𝑛 𝑦 =
=
= 2𝑛 + 2 𝑥 𝑛 𝑦,
𝜕𝑦
𝜕𝑥
that is
6𝑥 𝑛 𝑦 = 2𝑛 + 2 𝑥 𝑛 𝑦.
Hence 𝑛 = 2.
Thus, the integrating factor of the form 𝑥 𝑛 , where 𝑛 is a positive integer such
that the differential equation 𝑥 𝑛 4𝑥 + 3𝑦 2 𝑑𝑥 + 𝑥 𝑛 2𝑥𝑦 𝑑𝑦 = 0 is exact is 𝑥 2 .
(c) Multiplying the given equation through by the integrating factor found in (b)
and solve the resulting exact equation.
Solution:

Page 47 of 72

From (b) we know that the differential equation 4𝑥 3 + 3𝑥 2 𝑦 2 𝑑𝑥 +
2𝑥 3 𝑦 𝑑𝑦 = 0 is exact. Now, we will find the solution of this exact differential
equation or in the other word we must find 𝐹 such that
𝜕𝐹 𝑥, 𝑦
𝜕𝐹 𝑥, 𝑦
= 𝑀 𝑥, 𝑦 = 4𝑥 3 + 3𝑥 2 𝑦 2 and
= 𝑁 𝑥, 𝑦 = 2𝑥 3 𝑦.
𝜕𝑥
𝜕𝑦
From the first of these,
𝐹 𝑥, 𝑦 =
=

𝑀 𝑥, 𝑦 𝜕𝑥 + 𝑕 𝑦
4𝑥 3 + 3𝑥 2 𝑦 2 𝜕𝑥 + 𝑕 𝑦

= 𝑥4 + 𝑥3𝑦2 + 𝑕 𝑦 .
Then
𝜕𝐹 𝑥, 𝑦
𝑑𝑕 𝑦
= 2𝑥 3 𝑦 +
𝜕𝑦
𝑑𝑦
But we must have
𝜕𝐹 𝑥, 𝑦
= 𝑁 𝑥, 𝑦 = 2𝑥 3 𝑦.
𝜕𝑦
Thus
𝑑𝑕 𝑦
𝑑𝑕 𝑦
⇔0=
.
𝑑𝑦
𝑑𝑦
Thus 𝑕 𝑦 = 𝐶0 , where 𝐶0 is an arbitrary constant, and so
𝐹 𝑥, 𝑦 = 𝑥 4 + 𝑥 3 𝑦 2 + 𝐶0 .
Hence a one- parameter family of solution is 𝐹 𝑥, 𝑦 = 𝐶1 , or
𝑥 4 + 𝑥 3 𝑦 2 + 𝐶0 = 𝐶1
Combining the constsnts 𝐶0 and 𝐶1 we may write this solution as
𝑥 4 + 𝑥 3𝑦2 = 𝐶
where 𝐶 = 𝐶1 − 𝐶0 is an arbitrary constant.
So, we conclude that the general solution of the exact differential equation
4𝑥 3 + 3𝑥 2 𝑦 2 𝑑𝑥 + 2𝑥 3 𝑦 𝑑𝑦 = 0 is 𝑥 4 + 𝑥 3 𝑦 2 = 𝐶.
2𝑥 3 𝑦 = 2𝑥 3 𝑦 +

Solution of Exercise 14 (Linear D.E)
Solve the given differential equations.
𝑑𝑦
3𝑦
1. 𝑑𝑥 + 𝑥 = 6𝑥 2 .
Solution:
Here
𝑃 𝑥 =
and hence
Therefore, we obtain
𝑒

𝑃 𝑥 𝑑𝑥

𝑦=

𝑒

𝑒

𝑃 𝑥 𝑑𝑥

𝑃 𝑥 𝑑𝑥

=𝑒

3
𝑑𝑥
𝑥

3
, 𝑄 𝑥 = 6𝑥 2
𝑥
3

= 𝑒 3 ln 𝑥 = 𝑒 ln 𝑥 = 𝑥 3 .

𝑄 𝑥 𝑑𝑥
Page 48 of 72

⇔ 𝑥 3𝑦 =

2.

𝑥 3 6𝑥 2 𝑑𝑥

⇔ 𝑥 3𝑦 = 𝑥 6 + 𝐶
1
⇔ 𝑦 = 𝑥3 + 3 𝐶
𝑥
as the genaral solution of the given differential equation, where 𝐶 is an arbitrary
constant.
𝑑𝑦
𝑥 4 𝑑𝑥 + 2𝑥 3 𝑦 = 1.
Solution:
𝑑𝑦
𝑑𝑦 2𝑥 3
1
𝑑𝑦 2
1
𝑥4
+ 2𝑥 3 𝑦 = 1 ⇔
+ 4 𝑦= 4⇔
+ 𝑦 = 4.
𝑑𝑥
𝑑𝑥
𝑥
𝑥
𝑑𝑥 𝑥
𝑥
Here
2
1
𝑃 𝑥 = ,𝑄 𝑥 = 4
𝑥
𝑥
and hence
Therefore, we obtain
𝑒

𝑃 𝑥 𝑑𝑥

𝑦=

⇔ 𝑥 2𝑦 =

𝑒
𝑥2

𝑃 𝑥 𝑑𝑥

𝑒

𝑃 𝑥 𝑑𝑥

=𝑒

2
𝑑𝑥
𝑥

2

= 𝑒 2 ln 𝑥 = 𝑒 ln 𝑥 = 𝑥 2 .

𝑄 𝑥 𝑑𝑥

1
𝑑𝑥
𝑥4

1
⇔ 𝑥 2𝑦 = − + 𝐶
𝑥
1
1
⇔𝑦 =− 3+ 2𝐶
𝑥
𝑥
as the genaral solution of the given differential equation, where 𝐶 is an arbitrary
constant.

3.

𝑑𝑦

+ 3𝑦 = 3𝑥 2 𝑒 −3𝑥 .
Solution:
Here
𝑑𝑥

and hence
Therefore, we obtain
𝑒

𝑃 𝑥 𝑑𝑥

𝑦=

⇔ 𝑒 3𝑥 𝑦 =

4.

𝑒

𝑃 𝑥 𝑑𝑥

𝑃 𝑥 = 3, 𝑄 𝑥 = 3𝑥 2 𝑒 −3𝑥
𝑒

𝑃 𝑥 𝑑𝑥

=𝑒

3𝑑𝑥

= 𝑒 3𝑥 .

𝑄 𝑥 𝑑𝑥

𝑒 3𝑥 (3𝑥 2 𝑒 −3𝑥 )𝑑𝑥

⇔ 𝑒 3𝑥 𝑦 = 𝑥 3 + 𝐶
𝑥3
1
⇔ 𝑦 = 3𝑥 + 3𝑥 𝐶
𝑒
𝑒
as the genaral solution of the given differential equation, where 𝐶 is an arbitrary
constant.
𝑑𝑦
+ 4𝑥𝑦 = 8𝑥.
𝑑𝑥
Solution:
Page 49 of 72

Here
𝑃 𝑥 = 4𝑥, 𝑄 𝑥 = 8𝑥

and hence
𝑒

Therefore, we obtain
𝑒

𝑃 𝑥 𝑑𝑥

𝑦=

2

⇔ 𝑒 2𝑥 𝑦 =
2

⇔ 𝑒 2𝑥 𝑦 = 2
2

⇔ 𝑒 2𝑥 𝑦 = 2
2

𝑃 𝑥 𝑑𝑥

𝑒

𝑃 𝑥 𝑑𝑥

=𝑒

4𝑥𝑑𝑥

2

= 𝑒 2𝑥 .

𝑄 𝑥 𝑑𝑥

2

𝑒 2𝑥 (8𝑥)𝑑𝑥
𝑒 2𝑥

2

(4𝑥)𝑑𝑥

2

𝑒 2𝑥 𝑑 2𝑥 2
2

⇔ 𝑒 2𝑥 𝑦 = 2𝑒 2𝑥 + 𝐶
1
⇔ 𝑦 = 2 + 2𝑥 2 𝐶
𝑒
as the genaral solution of the given differential equation, where 𝐶 is an arbitrary
constant.

Solution of Exercise 15 (Solution of Linear D.E)
Consider the differential equation

𝑑𝑦
+ 𝑃 𝑥 𝑦 = 0.
𝑑𝑥
(a) Show that if 𝑓 and 𝑔 are two solutions of this equation and 𝑐1 and 𝑐2 are arbitrary
constants, then 𝑐1 𝑓 + 𝑐2 𝑔 is also a solution of this equation.
Proof:
Here
𝑑𝑦
𝑑𝑦
𝑑𝑦
+𝑃 𝑥 𝑦=0⇔
= −𝑃 𝑥 𝑦 ⇔
+ 𝑃 𝑥 𝑑𝑥 = 0 … ∗ .
𝑑𝑥
𝑑𝑥
𝑦
By integrating both sides of (*), we obtain
𝑑𝑦
+ 𝑃 𝑥 𝑑𝑥 = 𝐶0
𝑦
⇔ ln 𝑦 = −

𝑃 𝑥 𝑑𝑥 + 𝐶0

⇔ |𝑦| = 𝑒 − 𝑃 𝑥 𝑑𝑥 𝑒 𝐶0
⇔ 𝑦 = 𝐶𝑒 − 𝑃 𝑥 𝑑𝑥 ,
where 𝐶0 and 𝐶 are constants, as the general solution of the differential equati on
𝑑𝑦
+ 𝑃 𝑥 𝑦 = 0. Now, let 𝑓 and 𝑔 are two solutions of that equation, 𝑓 and 𝑔 are
𝑑𝑥
given as follow
𝑓 = 𝐶𝑓 𝑒 − 𝑃 𝑥 𝑑𝑥 and 𝑔 = 𝐶𝑔 𝑒 − 𝑃 𝑥 𝑑𝑥 ,
where 𝐶𝑓 and 𝐶𝑔 are constants.
For 𝑐1 and 𝑐2 are arbitrary constants, we have
𝑐1 𝑓 + 𝑐2 𝑔 = 𝑐1 𝐶𝑓 𝑒 − 𝑃 𝑥 𝑑𝑥 + 𝑐2 𝐶𝑔 𝑒 − 𝑃 𝑥 𝑑𝑥
= 𝑐1 𝐶𝑓 + 𝑐2 𝐶𝑔 𝑒 − 𝑃 𝑥 𝑑𝑥
Page 50 of 72

= 𝐶𝑕 𝑒 − 𝑃 𝑥 𝑑𝑥 … (∗),
where 𝐶𝑕 is constant. From (*) we can conclude that 𝑐1 𝑓 + 𝑐2 𝑔 also a solution of the
𝑑𝑦
differential equation 𝑑𝑥 + 𝑃 𝑥 𝑦 = 0 ■.
(b) Extending the result of (a), show that if 𝑓1 , 𝑓2 , … , 𝑓𝑛 are 𝑛 solutions of this equation
and 𝑐1 , 𝑐2 , … , 𝑐𝑛 are 𝑛 arbitrary constants, then
𝑛

𝑐𝑘 𝑓𝑘
𝑘=1

is also a solution of this equation.
Proof:
By extending the result of (a), let 𝑓1 , 𝑓2 , … , 𝑓𝑛 are 𝑛 solutions of the differential
𝑑𝑦
equation 𝑑𝑥 + 𝑃 𝑥 𝑦 = 0. Then
𝑓1 = 𝐶𝑓1 𝑒 − 𝑃 𝑥 𝑑𝑥 , 𝑓2 = 𝐶𝑓2 𝑒 − 𝑃 𝑥 𝑑𝑥 , … , 𝑓𝑛 = 𝐶𝑓𝑛 𝑒 −
where 𝐶𝑓1 , 𝐶𝑓2 , … , and 𝐶𝑓𝑛 are constants.
For 𝑐1 , 𝑐2 , … , 𝑐𝑛 are 𝑛 arbitrary constants, we obtain

𝑃 𝑥 𝑑𝑥

,

𝑛

𝑐𝑘 𝑓𝑘 = 𝑐1 𝐶𝑓1 𝑒 −

𝑃 𝑥 𝑑𝑥

+ 𝑐2 𝐶𝑓2 𝑒 −

𝑃 𝑥 𝑑𝑥

+ ⋯ + 𝑐𝑛 𝐶𝑓𝑛 𝑒 −

𝑃 𝑥 𝑑𝑥

𝑘=1

= 𝑐1 𝐶𝑓1 + 𝑐2 𝐶𝑓2 + ⋯ + 𝑐𝑛 𝐶𝑓𝑛 𝑒 − 𝑃 𝑥 𝑑𝑥
= 𝐶𝑝 𝑒 − 𝑃 𝑥 𝑑𝑥 … (∗),
where 𝐶𝑝 is constant. From (*) we can conclude that
the differential equation
𝑑𝑦
+ 𝑃 𝑥 𝑦 = 0 ■.
𝑑𝑥

𝑛
𝑘 =1 𝑐𝑘 𝑓𝑘

is also a solution of

Solution of Exercise 16 (Properties of Linear D.E)
(a) Let 𝑓1 be a solution of
and 𝑓2 be a solution of

𝑑𝑦
+ 𝑃 𝑥 𝑦 = 𝑄1 𝑥
𝑑𝑥

𝑑𝑦
+ 𝑃 𝑥 𝑦 = 𝑄2 𝑥 ,
𝑑𝑥
Where 𝑃, 𝑄1 , and 𝑄2 are all defined on the same real interval 𝐼. Prove that 𝑓1 + 𝑓2 is
a solution of
𝑑𝑦
+ 𝑃 𝑥 𝑦 = 𝑄1 𝑥 + 𝑄2 𝑥
𝑑𝑥
On 𝐼.
Proof:
Since 𝑓1 is a solution of
𝑑𝑦
+ 𝑃 𝑥 𝑦 = 𝑄1 𝑥
𝑑𝑥
and 𝑓2 is a solution of
𝑑𝑦
+ 𝑃 𝑥 𝑦 = 𝑄2 𝑥 ,
𝑑𝑥
we have
Page 51 of 72

𝑓1 = 𝑦1 =

𝑒

𝑃 𝑥 𝑑𝑥

𝑄1 𝑥 𝑑𝑥

𝑒

𝑃 𝑥 𝑑𝑥

𝑄2 𝑥
𝑃 𝑥 𝑑𝑥

𝑑𝑥

.
𝑒
𝑒
Since 𝑃, 𝑄1 , and 𝑄2 are all defined on the same real interval 𝐼, we know that the
solution of
𝑑𝑦
+ 𝑃 𝑥 𝑦 = 𝑄1 𝑥 + 𝑄2 𝑥 ,
𝑑𝑥
is
𝑒 𝑃 𝑥 𝑑𝑥 𝑄1 𝑥 + 𝑄2 𝑥 𝑑𝑥
𝑦=
𝑒 𝑃 𝑥 𝑑𝑥
𝑃 𝑥 𝑑𝑥
𝑒
𝑄1 (𝑥) + 𝑒 𝑃 𝑥 𝑑𝑥 𝑄2 (𝑥)𝑑𝑥
=
𝑒 𝑃 𝑥 𝑑𝑥
𝑒 𝑃 𝑥 𝑑𝑥 𝑄1 𝑥 𝑑𝑥
𝑒 𝑃 𝑥 𝑑𝑥 𝑄1 𝑥 𝑑𝑥
=
+
𝑒 𝑃 𝑥 𝑑𝑥
𝑒 𝑃 𝑥 𝑑𝑥
= 𝑓1 + 𝑓2 . ■
(b) Use the result of (a) to solve the equation
𝑑𝑦
+ 𝑦 = 2 sin 𝑥 + 5 sin 2𝑥.
𝑑𝑥
Solution:
Let 𝑃 𝑥 = 1, 𝑄1 𝑥 = 2 sin 𝑥, and 𝑄2 𝑥 = 5 sin 2𝑥.
Since
𝑒 𝑃 𝑥 𝑑𝑥 𝑄1 𝑥 𝑑𝑥
𝑦1 =
𝑒 𝑃 𝑥 𝑑𝑥
𝑥
2𝑒 sin 𝑥 𝑑𝑥
=
𝑒𝑥
𝑒 𝑥 sin 𝑥 − 𝑒 𝑥 cos 𝑥 + 𝐶1
=
𝑒𝑥
𝐶1
= sin 𝑥 − cos 𝑥 + 𝑥
𝑒
𝑑𝑦
is the solution of 𝑑𝑥 + 𝑦 = 2 sin 𝑥,
and
𝑒 𝑃 𝑥 𝑑𝑥 𝑄2 𝑥 𝑑𝑥
𝑦2 =
𝑒 𝑃 𝑥 𝑑𝑥
𝑥
5𝑒 sin 2𝑥 𝑑𝑥
=
𝑒𝑥
𝑥
𝑒 sin 2𝑥 − 2𝑒 𝑥 cos 2𝑥 + 𝐶2
=
𝑒𝑥
𝐶2
= sin 2𝑥 − 2 cos 2𝑥 + 𝑥
𝑒
𝑑𝑦
is the solution of 𝑑𝑥 + 𝑦 = 2 sin 𝑥,
using the result (a), we obtain
𝑦 = 𝑦1 + 𝑦2
𝐶
𝐶
= sin 𝑥 − cos 𝑥 + 𝑒 1𝑥 + sin 2𝑥 − 2 cos 2𝑥 + 𝑒 2𝑥
𝐶1 + 𝐶2
= sin 𝑥 − cos 𝑥 + sin 2𝑥 − 2 cos 2𝑥 +
𝑒𝑥
= sin 𝑥 − cos 𝑥 + sin 2𝑥 − 2 cos 2𝑥 + 𝐶𝑒 −𝑥 ; 𝐶 = 𝐶1 + 𝐶2
as the solution of
𝑃 𝑥 𝑑𝑥

and 𝑓2 = 𝑦2 =

Page 52 of 72

𝑑𝑦
+ 𝑦 = 2 sin 𝑥 + 5 sin 2𝑥.
𝑑𝑥

Notes:

2𝑒 𝑥 sin 𝑥 𝑑𝑥 = 2𝑒 𝑥 sin 𝑥 −

2𝑒 𝑥 cos 𝑥 𝑑𝑥

= 2𝑒 𝑥 sin 𝑥 − 2𝑒 𝑥 cos 𝑥 +

2𝑒 𝑥 sin 𝑥 𝑑𝑥

2𝑒 𝑥 sin 𝑥 − 2𝑒 𝑥 cos 𝑥 + 𝐶0
2
= 𝑒 𝑥 sin 𝑥 − 𝑒 𝑥 cos 𝑥 + 𝐶1 .
=

5𝑒 𝑥 sin 2𝑥 𝑑𝑥 = 5𝑒 𝑥 sin 2𝑥 − 2

5𝑒 𝑥 cos 2𝑥 𝑑𝑥

= 5𝑒 𝑥 sin 2𝑥 − 10𝑒 𝑥 cos 2𝑥 + 4

5𝑒 𝑥 sin 2𝑥 𝑑𝑥

5𝑒 𝑥 sin 2𝑥 − 10𝑒 𝑥 cos 2𝑥 + 𝐶0
=
5
= 𝑒 𝑥 sin 2𝑥 − 2𝑒 𝑥 cos 2𝑥 + 𝐶2 .

Solution of Exercise 17 (Integrating Factor of Linear D.E)
Solve each differential equation by first finding an integrating factor.
1. 5𝑥𝑦 + 4𝑦 2 + 1 𝑑𝑥 + 𝑥 2 + 2𝑥𝑦 𝑑𝑦 = 0.
Solution:
Here
𝑀 𝑥, 𝑦 = 5𝑥𝑦 + 4𝑦 2 + 1 and 𝑁 𝑥, 𝑦 = 𝑥 2 + 2𝑥𝑦
Since
𝜕𝑀 𝑥, 𝑦
𝜕 5𝑥𝑦 + 4𝑦 2 + 1
𝜕𝑁 𝑥, 𝑦
𝜕 𝑥 2 + 2𝑥𝑦
=
= 5𝑥 + 8𝑦 ≠
=
= 2𝑥 + 2𝑦,
𝜕𝑦
𝜕𝑦
𝜕𝑥
𝜕𝑥
we can say that the differential equation 5𝑥𝑦 + 4𝑦 2 + 1 𝑑𝑥 + 𝑥 2 + 2𝑥𝑦 𝑑𝑦 = 0
is not exact (non- exact) differential equation. Furthermore, we will find an
integrating factor 𝑢(𝑥, 𝑦) such that the differential equation
𝑢 𝑥, 𝑦 5𝑥𝑦 + 4𝑦 2 + 1 𝑑𝑥 + 𝑢(𝑥, 𝑦) 𝑥 2 + 2𝑥𝑦 𝑑𝑦 = 0 is exact differential
equation. Let 𝑢(𝑥) is the integrating factor depends only upon 𝑥. Then we have

Since

we obtain

𝑢 𝑥 =𝑒

𝜕𝑀 𝑥,𝑦
𝜕𝑁 𝑥,𝑦
−
𝜕𝑦
𝜕𝑥
𝑑𝑥
𝑁 𝑥,𝑦
.

𝜕𝑀 𝑥, 𝑦
𝜕𝑁 𝑥, 𝑦
− 𝜕𝑥
5𝑥 + 8𝑦 − 2𝑥 − 2𝑦 3(𝑥 + 2𝑦) 3
𝜕𝑦
=
=
= ,
𝑁 𝑥, 𝑦
𝑥 2 + 2𝑥𝑦
𝑥(𝑥 + 2𝑦) 𝑥
3

3

𝑢 𝑥 = 𝑒 𝑥 𝑑𝑥 = 𝑒 ln 𝑥 = 𝑥 3 .
Multiplying the differential equation by this integrating factor, we obtain exact
differential equation
5𝑥 4 𝑦 + 4𝑥 3 𝑦 2 + 𝑥 3 𝑑𝑥 + 𝑥 5 + 2𝑥 4 𝑦 𝑑𝑦 = 0.

Page 53 of 72

Moreover, we will find a solution of this exact differential equation by using
grouping method. From 5𝑥 4 𝑦 + 4𝑥 3 𝑦 2 + 𝑥 3 𝑑𝑥 + 𝑥 5 + 2𝑥 4 𝑦 𝑑𝑦 = 0, we group
the terms as follows
5𝑥 4 𝑦𝑑𝑥 + 𝑥 5 𝑑𝑦 + 4𝑥 3 𝑦 2 𝑑𝑥 + 2𝑥 4 𝑦𝑑𝑦 + 𝑥 3 𝑑𝑥 = 0.
Thus
1
𝑑 𝑥 5𝑦 + 𝑑 𝑥 4𝑦2 + 𝑑 𝑥 4 = 𝑑 𝐶 .
4
So,
1
𝑥 5𝑦 + 𝑥 4𝑦2 + 𝑥 4 = 𝐶
4
is the general solution of exact differential equation 5𝑥 4 𝑦 + 4𝑥 3 𝑦 2 + 𝑥 3 𝑑𝑥 +
𝑥 5 + 2𝑥 4 𝑦 𝑑𝑦 = 0.
2. 2𝑥 + tan 𝑦 𝑑𝑥 + 𝑥 − 𝑥 2 tan 𝑦 𝑑𝑦 = 0.
Solution:
Here
𝑀 𝑥, 𝑦 = 2𝑥 + tan 𝑦 and 𝑁 𝑥, 𝑦 = 𝑥 − 𝑥 2 tan 𝑦.
Since
𝜕𝑀 𝑥, 𝑦
𝜕 2𝑥 + tan 𝑦
𝜕𝑁 𝑥, 𝑦
𝜕 𝑥 − 𝑥 2 tan 𝑦
=
= sec 2 𝑦 ≠
=
= 1 − 2𝑥 tan 𝑦,
𝜕𝑦
𝜕𝑦
𝜕𝑥
𝜕𝑥
we can say that the differential equation 2𝑥 + tan 𝑦 𝑑𝑥 + 𝑥 − 𝑥 2 tan 𝑦 𝑑𝑦 = 0
is not exact (non- exact) differential equation. Furthermore, we will find an
integrating factor 𝑢(𝑥, 𝑦) such that the differential equation
𝑢 𝑥, 𝑦 2𝑥 + tan 𝑦 𝑑𝑥 + 𝑢(𝑥, 𝑦) 𝑥 − 𝑥 2 tan 𝑦 𝑑𝑦 = 0 is exact differential
equation. Let 𝑢(𝑦) is the integrating factor depends only upon 𝑦. Then we have
𝑢 𝑦 =𝑒

−

𝜕𝑀 𝑥,𝑦
𝜕𝑁 𝑥,𝑦
−
𝜕𝑦
𝜕𝑥
𝑑𝑦
𝑀 𝑥,𝑦
.

Since
𝜕𝑀 𝑥, 𝑦
𝜕𝑁 𝑥, 𝑦
− 𝜕𝑥
sec 2 𝑦 − 1 + 2𝑥 tan 𝑦 tan 𝑦 tan 𝑦 + 2𝑥
𝜕𝑦
=
=
= tan 𝑦,
𝑀 𝑥, 𝑦
2𝑥 + tan 𝑦
2𝑥 + tan 𝑦
we obtain
− tan 𝑦 𝑑𝑦

−sin 𝑦
𝑑𝑦
cos 𝑦

1
𝑑 cos 𝑦
cos 𝑦

𝑢 𝑦 =𝑒
=𝑒
=𝑒
= 𝑒 ln |cos 𝑦| = cos 𝑦.
Multiplying the differential equation by this integrating factor, we obtain exact
differential equation
2𝑥 cos 𝑦 + sin 𝑦 𝑑𝑥 + 𝑥 cos 𝑦 − 𝑥 2 sin 𝑦 𝑑𝑦 = 0.
Moreover, we will find a solution of this exact differential equation by using
grouping method. From 2𝑥 cos 𝑦 + sin 𝑦 𝑑𝑥 + 𝑥 cos 𝑦 − 𝑥 2 sin 𝑦 𝑑𝑦 = 0, we
group the terms as follows
2𝑥 cos 𝑦 𝑑𝑥 − 𝑥 2 sin 𝑦 𝑑𝑦 + sin 𝑦 𝑑𝑥 + 𝑥 cos 𝑦 𝑑𝑦 = 0.
Thus
𝑑 𝑥 2 cos 𝑦 + 𝑑 𝑥 sin 𝑦 = 𝑑 𝐶 .
So,
𝑥 2 cos 𝑦 + 𝑥 sin 𝑦 = 𝐶
is the general solution of the exact differential equation 2𝑥 cos 𝑦 + sin 𝑦 𝑑𝑥 +
𝑥 cos 𝑦 − 𝑥 2 sin 𝑦 𝑑𝑦 = 0.
3. 𝑦 2 𝑥 + 1 + 𝑦 𝑑𝑥 + 2𝑥𝑦 + 1 𝑑𝑦 = 0.
Solution:
Here
Page 54 of 72

𝑀 𝑥, 𝑦 = 𝑦 2 𝑥 + 1 + 𝑦 = 𝑥𝑦 2 + 𝑦 2 + 𝑦 and 𝑁 𝑥, 𝑦 = 2𝑥𝑦 + 1.

Since
𝜕𝑀 𝑥, 𝑦
𝜕(𝑥𝑦 2 + 𝑦 2 + 𝑦)
𝜕𝑁 𝑥, 𝑦
𝜕(2𝑥𝑦 + 1)
=
= 2𝑥𝑦 + 2𝑦 + 1 ≠
=
= 2𝑦,
𝜕𝑦
𝜕𝑦
𝜕𝑥
𝜕𝑥
we can say that the differential equation 𝑦 2 𝑥 + 1 + 𝑦 𝑑𝑥 + 2𝑥𝑦 + 1 𝑑𝑦 = 0 is
not exact (non- exact) differential equation. Furthermore, we will find an
integrating factor 𝑢(𝑥, 𝑦) such that the differential equation
𝑢 𝑥, 𝑦 𝑦 2 𝑥 + 1 + 𝑦 𝑑𝑥 + 𝑢(𝑥, 𝑦) 2𝑥𝑦 + 1 𝑑𝑦 = 0 is exact differential
equation. Let 𝑢(𝑥) is the integrating factor depends only upon 𝑥. Then we have

Since

𝑢 𝑥 =𝑒

𝜕𝑀 𝑥,𝑦
𝜕𝑁 𝑥,𝑦
−
𝜕𝑦
𝜕𝑥
𝑑𝑥
𝑁 𝑥,𝑦
.

𝜕𝑀 𝑥, 𝑦
𝜕𝑁 𝑥, 𝑦
−
2𝑥𝑦 + 2𝑦 + 1 − 2𝑦
𝜕𝑦
𝜕𝑥
=
= 1,
𝑁 𝑥, 𝑦
2𝑥𝑦 + 1

we obtain
𝑢 𝑥 = 𝑒 𝑑𝑥 = 𝑒 𝑥 .
Multiplying the differential equation by this integrating factor, we obtain exact
differential equation
[𝑦 2 𝑒 𝑥 (𝑥 + 1) + 𝑦𝑒 𝑥 ]𝑑𝑥 + 2𝑥𝑦𝑒 𝑥 + 𝑒 𝑥 𝑑𝑦 = 0.
Moreover, we will find a solution of this exact differential equation by using
grouping method. From [𝑦 2 𝑒 𝑥 (𝑥 + 1) + 𝑦𝑒 𝑥 ]𝑑𝑥 + 2𝑥𝑦𝑒 𝑥 + 𝑒 𝑥 𝑑𝑦 = 0, we
group the terms as follows
[𝑦 2 𝑒 𝑥 𝑥 + 1 𝑑𝑥 + 2𝑥𝑦𝑒 𝑥 𝑑𝑦] + (𝑦𝑒 𝑥 𝑑𝑥 + 𝑒 𝑥 𝑑𝑦) = 0.
Thus
𝑑 𝑥𝑦 2 𝑒 𝑥 + 𝑑 𝑦𝑒 𝑥 = 𝑑 𝐶 .
So,
𝑥𝑦 2 𝑒 𝑥 + 𝑦𝑒 𝑥 = 𝐶
is the general solution of exact differential equation [𝑦 2 𝑒 𝑥 (𝑥 + 1) + 𝑦𝑒 𝑥 ]𝑑𝑥 +
2𝑥𝑦𝑒 𝑥 + 𝑒 𝑥 𝑑𝑦 = 0.
4. 2𝑥𝑦 2 + 𝑦 𝑑𝑥 + 2𝑦 3 − 𝑥 𝑑𝑦 = 0.
Solution:
Here
𝑀 𝑥, 𝑦 = 2𝑥𝑦 2 + 𝑦 dan 𝑁 𝑥, 𝑦 = 2𝑦 3 − 𝑥.
Since
𝜕𝑀 𝑥, 𝑦
𝜕(2𝑥𝑦 2 + 𝑦)
𝜕𝑁 𝑥, 𝑦
𝜕(2𝑦 3 − 𝑥)
=
= 4𝑥𝑦 + 1 ≠
=
= −1,
𝜕𝑦
𝜕𝑦
𝜕𝑥
𝜕𝑥
we can say that the differential equation 2𝑥𝑦 2 + 𝑦 𝑑𝑥 + 2𝑦 3 − 𝑥 𝑑𝑦 = 0 is not
exact (non- exact) differential equation. Furthermore, we will find an integrating
factor 𝑢(𝑥, 𝑦) such that the differential equation
𝑢 𝑥, 𝑦 2𝑥𝑦 2 + 𝑦 𝑑𝑥 + 𝑢(𝑥, 𝑦) 2𝑦 3 − 𝑥 𝑑𝑦 = 0 is exact differential equation. Let
𝑢(𝑦) is the integrating factor depends only upon 𝑦. Then we have
𝑢 𝑦 =
Since

𝜕𝑀 𝑥,𝑦
𝜕𝑁 𝑥,𝑦
−
𝜕𝑦
𝜕𝑥
−
𝑑𝑦
𝑀 𝑥,𝑦
𝑒
.

𝜕𝑀 𝑥, 𝑦
𝜕𝑁 𝑥, 𝑦
−
4𝑥𝑦 + 2
2 2𝑥𝑦 + 1
2
𝜕𝑦
𝜕𝑥
=
=
=
,
𝑀 𝑥, 𝑦
2𝑥𝑦 2 + 𝑦 𝑦 2𝑥𝑦 + 1
𝑦
Page 55 of 72

we obtain

1
𝑦2

1
.
𝑦2
Multiplying the differential equation by this integrating factor, we obtain exact
differential equation
1
𝑥
2𝑥 + 𝑑𝑥 + 2𝑦 − 2 𝑑𝑦 = 0.
𝑦
𝑦
Moreover, we will find a solution of this exact differential equation by using
1
𝑥
grouping method. From 2𝑥 + 𝑦 𝑑𝑥 + 2𝑦 − 𝑦 2 𝑑𝑦 = 0, we group the terms as
𝑢 𝑦 =𝑒

−

follows

2𝑥𝑑𝑥 +

2
𝑑𝑦
𝑦

= 𝑒 −2 ln |𝑦| = 𝑒

ln

=

1
𝑥
𝑑𝑥 − 2 𝑑𝑦 + 2𝑦𝑑𝑦 = 0.
𝑦
𝑦

Thus
𝑑 𝑥2 + 𝑑

𝑥
+ 𝑑 𝑦2 = 𝑑 𝐶 .
𝑦

So,

𝑥
+ 𝑦2 = 𝐶
𝑦
is the general solution of the exact differential equation
1
𝑥
2𝑥 + 𝑑𝑥 + 2𝑦 − 2 𝑑𝑦 = 0.
𝑦
𝑦
𝑥2 +

Find an integrating factor of the form 𝑥 𝑝 𝑦 𝑞 and solve.
4𝑥𝑦 2 + 6𝑦 𝑑𝑥 + 5𝑥 2 𝑦 + 8𝑥 𝑑𝑦 = 0.
Solution:
Here
𝑀 𝑥, 𝑦 = 4𝑥𝑦 2 + 6𝑦 and 𝑁 𝑥, 𝑦 = 5𝑥 2 𝑦 + 8𝑥.
Since
𝜕𝑀 𝑥, 𝑦
𝜕(4𝑥𝑦 2 + 6𝑦)
𝜕𝑁 𝑥, 𝑦
𝜕 5𝑥 2 𝑦 + 8𝑥
=
= 8𝑥𝑦 + 6 ≠
=
= 10𝑥𝑦 + 8,
𝜕𝑦
𝜕𝑦
𝜕𝑥
𝜕𝑥
we can say that the differential equation 4𝑥𝑦 2 + 6𝑦 𝑑𝑥 + 5𝑥 2 𝑦 + 8𝑥 𝑑𝑦 = 0 is not
exact (non- exact) differential equation. Furthermore, we will find an integrating factor
of the form 𝑥 𝑝 𝑦 𝑞 such that the differential equation
4𝑥 𝑝+1 𝑦 𝑞+2 + 6𝑥 𝑝 𝑦 𝑞+1 𝑑𝑥 + 5𝑥 𝑝+2 𝑦 𝑞+1 + 8𝑥 𝑝+1 𝑦 𝑞 𝑑𝑦 = 0
is exact differential equation.
Since
4𝑥 𝑝+1 𝑦 𝑞+2 + 6𝑥 𝑝 𝑦 𝑞+1 𝑑𝑥 + 5𝑥 𝑝+2 𝑦 𝑞+1 + 8𝑥 𝑝+1 𝑦 𝑞 𝑑𝑦 = 0
is exact differential equation,
𝜕 4𝑥 𝑝+1 𝑦 𝑞+2 + 6𝑥 𝑝 𝑦 𝑞+1
𝜕 5𝑥 𝑝+2 𝑦 𝑞+1 + 8𝑥 𝑝+1 𝑦 𝑞
=
𝜕𝑦
𝜕𝑥
𝑝+1 𝑞+1
𝑝 𝑞
⇔ 4 𝑞+2 𝑥 𝑦
+ 6 𝑞 + 1 𝑥 𝑦 = 5 𝑝 + 2 𝑥 𝑝+1 𝑦 𝑞+1 + 8 𝑝 + 1 𝑥 𝑝 𝑦 𝑞 … ∗ .
From (*) we have
4 𝑞 + 2 = 5 𝑝 + 2 ⇔ 5𝑝 − 4𝑞 = −2 … ∗∗
and
6 𝑞 + 1 = 8 𝑝 + 1 ⇔ 8𝑝 − 6𝑞 = −2 ⇔ 4𝑝 − 3𝑞 = −1 … ∗∗∗ .

Page 56 of 72

From (**) and (***) we obtain 𝑝 = 2 and 𝑞 = 3. Hence, 𝑥 2 𝑦 3 is the integrating factor as
desired. Moreover, we will find the solution of the exact differential equation
4𝑥 3 𝑦 5 + 6𝑥 2 𝑦 4 𝑑𝑥 + 5𝑥 4 𝑦 4 + 8𝑥 3 𝑦 3 𝑑𝑦 = 0
by using grouping method. From 4𝑥 3 𝑦 5 + 6𝑥 2 𝑦 4 𝑑𝑥 + 5𝑥 4 𝑦 4 + 8𝑥 3 𝑦 3 𝑑𝑦 = 0, we
group the terms as follows
4𝑥 3 𝑦 5 𝑑𝑥 + 5𝑥 4 𝑦 4 𝑑𝑦 + 6𝑥 2 𝑦 4 𝑑𝑥 + 8𝑥 3 𝑦 3 𝑑𝑦 = 0.
Thus
𝑑 𝑥 4 𝑦 5 + 𝑑 2𝑥 3 𝑦 4 = 𝑑 𝐶 .
So,
𝑥 4 𝑦 5 + 2𝑥 3 𝑦 4 = 𝐶
is the general solution of the exact differential equation
4𝑥 3 𝑦 5 + 6𝑥 2 𝑦 4 𝑑𝑥 + 5𝑥 4 𝑦 4 + 8𝑥 3 𝑦 3 𝑑𝑦 = 0.

Solution of Exercise 18 (Orthogonal and Oblique Trajectories)
In exercises 1 − 4 find the orthogonal trajectories of each give family of curves. In each
case sketch several numbers of the family and several of the orthogonal trajectories on
the same set of axes.
1. 𝑦 = 𝑐𝑥 3 .
Solution:
Step 1. We first find the differential equation of the given family
𝑦 = 𝑐𝑥 3 … i .
Differentiating, we obtain
𝑑𝑦
= 3𝑐𝑥 2 … ii .
𝑑𝑥
Eliminating the parameter 𝑐 between Equations (i) and (ii), we obtain the
differential equation of the family (i) in the form
𝑑𝑦 3𝑦
=
… iii .
𝑑𝑥
𝑥
Step 2. We now find the differential equation of the orthogonal trajectories by
replacing 3𝑦/𝑥 in iii by its negative reciprocal, obtaining
𝑑𝑦
𝑥
= − … iv .
𝑑𝑥
3𝑦
Step 3. We now solve the differential equation iv . Separating variables, we have
3𝑦𝑑𝑦 = −𝑥𝑑𝑥.
Integrating, we obtain the one- parameter family of solutions of i in the form
3 2 1 2
𝑦 + 𝑥 = 𝐶12 or 𝑥 2 + 3𝑦 2 = 𝐶 2 ,
2
2
where 𝐶 is an arbitrary constant.

Page 57 of 72

2. 𝑦 2 = 𝑐𝑥.
Solution:
Step 1. We first find the differential equation of the given family
𝑦 2 = 𝑐𝑥 … i .
Differentiating, we obtain
𝑑𝑦
2𝑦
= 𝑐 … ii .
𝑑𝑥
Eliminating the parameter 𝑐 between Equations (i) and (ii), we obtain the
differential equation of the family (i) in the form
𝑑𝑦
𝑦
=
… iii .
𝑑𝑥 2𝑥
Step 2. We now find the differential equation of the orthogonal trajectories by
replacing 𝑦/2𝑥 in iii by its negative reciprocal, obtaining
𝑑𝑦
2𝑥
= − … iv .
𝑑𝑥
𝑦
Step 3. We now solve the differential equation iv . Separating variables, we have
𝑦𝑑𝑦 = −2𝑥𝑑𝑥.
Integrating, we obtain the one- parameter family of solutions of i in the form
1 2
𝑦 + 𝑥 2 = 𝐶12 or 2𝑥 2 + 𝑦 2 = 𝐶 2 ,
2
where 𝐶 is an arbitrary constant.

Page 58 of 72

3. 𝑐𝑥 2 + 𝑦 2 = 1.
Step 1. We first find the differential equation of the given family
𝑐𝑥 2 + 𝑦 2 = 1 … i .
Differentiating, we obtain
𝑑𝑦
𝑑𝑦
𝑐𝑥
2𝑐𝑥 + 2𝑦
= 0 or
=−
… ii .
𝑑𝑥
𝑑𝑥
𝑦
Eliminating the parameter 𝑐 between Equations (i) and (ii), we obtain the
differential equation of the family (i) in the form
𝑑𝑦
1 − 𝑦2
=−
… iii .
𝑑𝑥
𝑥𝑦
Step 2. We now find the differential equation of the orthogonal trajectories by
replacing −(1 − 𝑦 2 )/𝑥𝑦 in iii by its negative reciprocal, obtaining
𝑑𝑦
𝑥𝑦
=
… iv .
𝑑𝑥 1 − 𝑦 2
Step 3. We now solve the differential equation iv . Separating variables, we have
1
− 𝑦 𝑑𝑦 = 𝑥𝑑𝑥.
𝑦
Integrating, we obtain the one- parameter family of solutions of i in the form
1
1
ln |𝑦| − 𝑦 2 − 𝑥 2 = 𝐶1 or 𝑥 2 + 𝑦 2 − ln(𝑦 2 ) = 𝐶
2
2
where 𝐶 is an arbitrary constant.

Page 59 of 72

4. 𝑦 = 𝑒 𝑐𝑥 .
Step 1. We first find the differential equation of the given family
𝑦 = 𝑒 𝑐𝑥 … i .
Differentiating, we obtain
𝑑𝑦
= 𝑐𝑒 𝑐𝑥 … ii .
𝑑𝑥
Eliminating the parameter 𝑐 between Equations (i) and (ii), we obtain the
differential equation of the family (i) in the form
𝑑𝑦 ln 𝑦 ln 𝑦
𝑑𝑦
𝑦 ln 𝑦
=
𝑒
or
=
… iii .
𝑑𝑥
𝑥
𝑑𝑥
𝑥
Step 2. We now find the differential equation of the orthogonal trajectories by
replacing 𝑦 ln |𝑦| /𝑥 in iii by its negative reciprocal, obtaining
𝑑𝑦
𝑥
=−
… iv .
𝑑𝑥
𝑦 ln 𝑦
Step 3. We now solve the differential equation iv . Separating variables, we have
𝑦 ln |𝑦| 𝑑𝑦 = −𝑥𝑑𝑥.
Integrating, we obtain the one- parameter family of solutions of i in the form
1 2
1
1
𝑦 ln |𝑦| − 𝑦 2 + 𝑥 2 = 𝐶1 or 2𝑦 2 ln |𝑦| − 𝑦 2 + 2𝑥 2 = 𝐶,
2
4
2
where 𝐶 is an arbitrary constant.

Page 60 of 72

***
12.
Find the value of 𝐾 such that the parabolas 𝑦 = 𝑐1 𝑥 2 + 𝐾 are the orthogonal trajectories
of the family of ellipses 𝑥 2 + 2𝑦 2 − 𝑦 = 𝑐2 .
Solution:
Step 1. We first find the differential equation of the given family
𝑥 2 + 2𝑦 2 − 𝑦 = 𝑐2 … i .
Differentiating, we obtain
𝑑𝑦 𝑑𝑦
𝑑𝑦
2𝑥
2𝑥 + 4𝑦
−
= 0 or
=−
… ii .
𝑑𝑥 𝑑𝑥
𝑑𝑥
4𝑦 − 1
Step 2. We now find the differential equation of the orthogonal trajectories by replacing
−2𝑥/(4𝑦 − 1) in ii by its negative reciprocal, obtaining
𝑑𝑦 4𝑦 − 1
=
… iv .
𝑑𝑥
2𝑥
Step 3. We now solve the differential equation iv . Separating variables, we have
1
1
𝑑𝑦 =
𝑑𝑥.
4𝑦 − 1
2𝑥
Integrating, we obtain the one- parameter family of solutions of i in the form
1
1
1
ln |4𝑦 − 1| − ln |𝑥| = 𝑐2 or 𝑦 = 𝑐1 𝑥 2 + ,
4
2
4
where 𝑐2 and 𝑐1 are arbitrary constants.
Hence, the value of 𝐾 that we want is 1/4, 𝐾 = 1/4.
***
13.
Find the value of 𝑛 such that the curves 𝑥 𝑛 + 𝑦 𝑛 = 𝑐1 are orthogonal trajectories of the
family
𝑥
𝑦=
.
1 − 𝑐2 𝑥
Solution:
Page 61 of 72

Step 1. We first find the differential equation of the given family
𝑦=

𝑥
… i .
1 − 𝑐2 𝑥

Differentiating, we obtain
𝑑𝑦
1
=
… ii .
𝑑𝑥
1 − 𝑐2 𝑥 2
Eliminating the parameter 𝑐2 between Equations (i) and (ii), we obtain the differential
equation of the family (i) in the form
𝑑𝑦
1
𝑑𝑦 𝑦 2
=
or
=
… iii .
𝑑𝑥
𝑑𝑥 𝑥 2
𝑥 2
1− 1−𝑦
Step 2. We now find the differential equation of the orthogonal trajectories by replacing
𝑦 2 /𝑥 2 in iii by its negative reciprocal, obtaining
𝑑𝑦
𝑥2
= − 2 … iv .
𝑑𝑥
𝑦
Step 3. We now solve the differential equation iv . Separating variables, we have
𝑦 2 𝑑𝑦 = −𝑥 2 𝑑𝑥.
Integrating, we obtain the one- parameter family of solutions of i in the form
1 3 1 3
𝑦 + 𝑥 = 𝑐2 or 𝑥 3 + 𝑦 3 = 𝑐1 ,
3
3
where 𝑐2 and 𝑐1 are arbitrary constant.
Therefore, the value of 𝑛 that we want is 3, 𝑛 = 3.
***
15.
Find a family of oblique trajectories that intersect the family of circles 𝑥 2 + 𝑦 2 = 𝑐 2 at
angle 45o .
Solution:
Step 1. We first find the differential equation of the given family
𝑥 2 + 𝑦2 = 𝑐2.
Differentiating, we obtain
𝑑𝑦
𝑑𝑦
𝑥
2𝑥 + 2𝑦
= 0 or
=− … i .
𝑑𝑥
𝑑𝑥
𝑦
Step 2. We replace 𝑓 𝑥, 𝑦 = −𝑥/𝑦 in Equation (i) by
𝑥
−𝑦 +1 𝑦 − 𝑥
𝑓 𝑥, 𝑦 + tan 𝛼
=
𝑥 = 𝑦 + 𝑥.
1 − 𝑓 𝑥, 𝑦 tan 𝛼
1+𝑦
Thus the differential equation of the desired oblique trajectories is
𝑑𝑦 𝑦 − 𝑥
=
… ii .
𝑑𝑥 𝑦 + 𝑥
Step 3. We now solve the differential equation (ii). Observing that it is a homogeneous
differential equation, we let 𝑦 = 𝑣𝑥 to obtain
𝑑𝑣 𝑣 − 1
𝑣+𝑥
=
.
𝑑𝑥 𝑣 + 1
Page 62 of 72

After simplifications this becomes
𝑣+1
𝑑𝑥
𝑑𝑣 = − .
2
𝑣 +1
𝑥
Integrating we obtain

or

1
ln 𝑣 2 + 1 + arctan(𝑣) = − ln 𝑥 + 𝐶1
2

ln 𝑥 2 𝑣 2 + 1 + 2 arctan 𝑣 = 𝐶.
Replacing 𝑣 by 𝑦/𝑥, we obtain the family of oblique trajectories in the form
𝑦
ln 𝑦 2 + 𝑥 2 + 2 arctan
= 𝐶,
𝑥
where 𝐶 is an arbitrary constant.
***
16.
Find a family of oblique trajectories that intersect the family of parabolas 𝑦 2 = 𝑐𝑥 at
angle 60o .
Solution:
Step 1. We first find the differential equation of the given family
𝑦 2 = 𝑐𝑥 … i .
Differentiating, we obtain
𝑑𝑦
𝑑𝑦
1
2𝑦
= 𝑐 or
=
𝑐 … ii .
𝑑𝑥
𝑑𝑥 2𝑦
Eliminating the parameter 𝑐 between Equation (i) and (ii), we obtain the differential
equation
𝑑𝑦
𝑦
=
… iii .
𝑑𝑥 2𝑥
of the given family of parabolas.
Step 2. We replace 𝑓 𝑥, 𝑦 = 𝑦/2𝑥 in Equation (iii) by
𝑦
+ 3
𝑓 𝑥, 𝑦 + tan 𝛼
2𝑥
=
.
1 − 𝑓 𝑥, 𝑦 tan 𝛼
𝑦 3
1 − 2𝑥
Thus the differential equation of the desired oblique trajectories is
𝑦
𝑑𝑦 2𝑥 + 3
=
… iv .
𝑑𝑥
𝑦 3
1 − 2𝑥
Step 3. We now solve the differential equation (iv). Observing that it is a homogeneous
differential equation, we let 𝑦 = 𝑣𝑥 to obtain
1
𝑣+ 3
𝑑𝑣
𝑣+2 3
𝑣+𝑥
= 2
=
.
𝑑𝑥 1 − 1 𝑣 3 2 − 𝑣 3
2
After simplifications this becomes

Page 63 of 72

1
3
2 2𝑣 3 − 1 − 2 𝑑𝑣 = − 𝑑𝑥 .
𝑥
𝑣2 3 − 𝑣 + 2 3
Integrating
1
1
3
𝑑𝑣
=
−
𝑑𝑥
𝑣
𝑥
𝑣2
𝑣2 − 3 3 + 2
1
2𝑣 3 − 1
3
1
⇔
𝑑𝑣
−
𝑑𝑣 = −
2 𝑣2 3 − 𝑣 + 2 3
2
3
3
69
𝑣 2 − 2 6 𝑣 + 36 + 36
1
2

⇔

⇔

2𝑣 3 − 1

3
𝑑𝑣 −
2
3−𝑣+2 3

1
2

1
2

2𝑣 3 − 1
𝑣2 3 − 𝑣 + 2 3

2𝑣 3 − 1
𝑣2 3 − 𝑣 + 2 3

𝑑𝑣 −

𝑑𝑣 −

3
2

1
3
𝑣− 6

3 36 69
2 69 6

2

+

2 𝑑𝑣

69
6
6
69

6𝑣 − 3
69

=−

1
𝑑𝑥
𝑥

𝑑𝑣 = −

2

1
𝑑𝑥
𝑥

+1

1
𝑑𝑥
𝑥

1
3
6𝑣 − 3
ln 𝑣 2 − 𝑣 + 2 3 −
3 arctan
+ ln 𝑥 = 𝐶1
2
23
69
6
6𝑣 − 3
⇔ ln |𝑣 2 − 𝑣 + 2 3| −
3 arctan
+ ln 𝑥 2 = 𝐶.
23
69
Substituting 𝑣 = 𝑦/𝑥, we obtain
𝑦
6𝑥 − 3
6
2
2
ln 𝑦 − 𝑥𝑦 − 2𝑥 3 −
3 arctan
= 𝐶.
23
69
⇔

Therefore, the family of oblique trajectories in the form
ln 𝑦 2 − 𝑥𝑦 − 2𝑥 2

𝑦
6𝑥 − 3
6
3 −
3 arctan
= 𝐶.
23
69
***

Solution of Exercise 19 (Problem in Mechanics (Frictional Forces))
A man is pushing a loaded sled across a level field of ice at the constant speed of 10
ft/sec. When the man in halfway across the ice field, he stops pushing and lets the
loaded sled continue on. The combined weight of the sheld and its load is 80 lb
3

(𝑤 = 80 lb); the air resistence (in pounds) is numerically equal to 4 𝑣, where 𝑣 is the
velocity of the sheld (in feet per second); and the coefficient of fraction of the runners
on the ice is 0.04 (𝜇 = 0.04). How far will the sheld continue to move after the man
stops pushing?
Solution:
Page 64 of 72

3
5 𝑑𝑣
0.04 80 − 𝑣 =
4
2 𝑑𝑡
16 3
5 𝑑𝑣
⇔
− 𝑣=
5 4
2 𝑑𝑡
1
1
⇔ 𝑑𝑡 =
𝑑𝑣
32 3
5
−
𝑣
5 2
1
1
⇔ − 𝑑𝑡 =
𝑑𝑣
3
32
5
2𝑣 − 5
Integrating
1
1
− 𝑑𝑡 =
𝑑𝑣
3
32
5
2𝑣 − 5
1
2
1
3
⇔−
𝑑𝑡 =
𝑑 𝑑𝑣
5
3 3 𝑣 − 32 2
2
5
1
2 3
32
⇔ − 𝑡 = ln 𝑣 −
+ 𝐶1
5
3 2
5
3
3
32
⇔ − 𝑡 + 𝐶2 = ln 𝑣 −
10
2
5
3
64
⇔ 𝐶𝑒 −10 𝑡 +
= 𝑣(𝑡)
15
We know that 𝑣 0 = 10 feet/sec. Thus
64 150
86
𝐶+
=
⇔𝐶= .
15
15
15
Therefore
86 − 3 𝑡 64
𝑒 10 +
=𝑣 𝑡 .
15
15
The shled will stop when 𝑣 𝑡 = 0.
3
32
10
32
𝑒 −10 𝑡 = −
⇔ − ln −
=𝑡
43
3
43
Integrating this we obtain
172 − 3 𝑡 64
𝑥 𝑡 =−
𝑒 10 + 𝑡 + 𝐶4
9
15
We know that 𝑥 0 = 0. Thus
172
= 𝐶4 .
9
Therefore
172 − 3 𝑡 64
172
𝑥 𝑡 =−
𝑒 10 + 𝑡 +
9
15
9
and
10
32
𝑥 𝑡 = − ln −
≈ 9.09 feet.
3
43
Therefore, in 9.09 feet the sheld will continue to move after the man stops pushing.
***

Page 65 of 72

Solution of Exercise 20 (Rate Problems (Rate of Growth and Decay and
Population) Growth)
5. Assume that the population of a certain city increases at a rate proportional to
the number of its inhabitants at any time. If the population doubles in 40 years,
in how many years will it triple?
Solution:
Let 𝑥 be the number of individuals in at time 𝑡. We know that the population of a
certain city increases at a rate proportional to the number of its inhabitants at
any time. Hence, we are led to the differential equation
𝑑𝑥
= 𝑘𝑥 … i ,
𝑑𝑡
where 𝑘 is a constant of proportionality. The population 𝑥 is positive and is
increasing and hence 𝑑𝑥/𝑑𝑡 > 0. Therefore, from (i), we must have 𝑘 > 0. Now,
suppose that at time𝑡0 = 0 the population is 𝑥0 . Then, in addition to the
differential equation (i), we have the initial condition
𝑥 𝑡0 = 𝑥(0) = 𝑥0 … ii .
The differential equation (i) is separable. Separating variables, integrating, and
simplifying, we obtain
𝑥 = 𝐶𝑒 𝑘𝑡 .
Applying the initial condition, 𝑥 = 𝑥0 at 𝑡 = 𝑡0 = 0, to this, we have
𝑥0 = 𝐶𝑒 𝑘𝑡0 = 𝐶
From this we at once find 𝐶 = 𝑥0 𝑒 −𝑘𝑡0 and hence we obtain the unique solution
𝑥 = 𝑥0 𝑒 𝑘 𝑡−𝑡0
of the differential equation (i), which satisfies the initial condition (ii). Now,
when 𝑡 = 40, we have 𝑥 = 2𝑥0 . Hence, we obtain
ln 2
2𝑥0 = 𝑥0 𝑒 40𝑘 ⇔ 2 = 𝑒 40𝑘 ⇔
= 𝑘.
40
If we let 𝑥 = 3𝑥0 , then we obtain
ln 2
ln 2
ln 2
ln 3
3𝑥0 = 𝑥0 𝑒 40 𝑡 ⇔ 3 = 𝑒 40 𝑡 ⇔ ln 3 =
𝑡 ⇔ 𝑡 = 40
≈ 63.40
40
ln 2
Therefore, the population will triple in about 63.40 years.
6. The population of the city of Bingville increases at a rate proportional to the
numbers of its inhabitants present ant any time 𝑡. If the population of Bingville
was 30,000 in 1970 and 35,000 in 1980, what will be the population of Bingville
in 1990?
Solution:
According to the formula in the exercise 5, we have
𝑥 = 𝑥0 𝑒 𝑘 𝑡−𝑡0 .
Hence we obtain
35,000
1
7
𝑥 1980 = 30,000𝑒 𝑘 1980 −1970 ⇔
= 𝑒 10𝑘 ⇔
ln
= 𝑘.
30,000
10
6
Therefore, the population of Bingville in 1990 is

Page 66 of 72

𝑥 1990 = 30,000𝑒 2 ln
***

7
6

≈ 40,833.

9.
The human population 𝑥 of a certain island satisfies the logistic law
𝑑𝑥
= 𝑘𝑥 − 𝜆𝑥 2 … (i)
𝑑𝑡
with 𝑘 = 0.03 = 3 10 −2 , 𝜆 = 3 10 −8 , and time 𝑡 measured in years.
(a) If the population in 1980 is 200,000, find a formula for the population in future
years.
Solution:
We must solve the separable differential equation (i) subject to the initial
solution
𝑥 1980 = 200,000 … ii .
Separating variable in (ii), we obtain
𝑑𝑥
𝑑𝑥
= 0.03𝑥 − 3 10 −8 𝑥 2 ⇔
= 𝑑𝑡
−2
𝑑𝑡
3 10 𝑥 − 3 10 −8 𝑥 2
and hence
𝑑𝑥
= 𝑑𝑡.
3 10 −2 𝑥 1 − (10 −6 𝑥]
Using partial fractions, this becomes
100 1
10 −6
+
= 𝑑𝑡.
3 𝑥 1 − 10 −6 𝑥
Integrating, assuming 0 < 𝑥 < 106 , we obtain
100
ln 𝑥 − ln 1 − 10 −6 = 𝑡 + 𝐶1
3
and hence
𝑥
3
ln
=
𝑡 + 𝐶2 .
1 − 10 −6
100
Thus we find
3𝑡
𝑥
= 𝐶𝑒 100 .
−6
1 − 10
Solving this for 𝑥, we finally obtain
3𝑡

𝑥=

𝐶𝑒 100
3𝑡
−6 𝐶𝑒 100

… iii .

1 + 10
Now, applying the initial conditions (ii) to this, we have
𝐶𝑒 59.4
2 10 5 =
,
1 + 10 −6 𝐶𝑒 59.4
from which we obtain
2 10 5
10 6
𝐶 = 59.4
=
.
𝑒
1 − 2 10 5 10 −6
4𝑒 59.4
Substituting this value for 𝑐 back into (iii) and simplifying, we obtain the solution
in the form
Page 67 of 72

10

𝑥=

6

3𝑡 … iv .
1 + 4𝑒 59.4−100
This gives the population 𝑥 as a function of time for 𝑡 > 1980.
Therefore, we can conclude that the formula for the population in future years is
given by
10 6
𝑥=
3𝑡 .
59.4−
100
1 + 4𝑒
(b) According to the formula of part (a), what will be the population in the year
2000?
Solution:
Let 𝑡 = 2000 in (iv) and we obtain
10 6
𝑥=
≈ 312,965.
1 + 4𝑒 −0.6
Therefore, the population in the year 2000 is 312,965 people.
(c) What is the limiting value of the population as 𝑡 → ∞?
Solution:

10

lim 𝑥 = lim

𝑡→∞

𝑡→∞?

1+

6

3𝑡
4𝑒 59.4−100

= 10

6

= 1,000,000.

***

Solution of Exercise 21 (Mixture Problem)
18.
A large tank initially contains 200 gal of brine in which 15lb of salt is dissolved. Starting
at 𝑡 = 0, brine containing 4lb of salt per gallon flows into the tank at the rate of 3.5
gal/min. The mixture is kept uniform by stirring and the well- stirred mixture leaves the
tank at the rate of 4 gal/min.
(a) How much salt is in the tank at the end of one hour?
Solution:
Let 𝑥 denotes the amount of salt in the tank at time 𝑡. We apply the basic
equation
𝑑𝑥
= 𝐼𝑁 − 𝑂𝑈𝑇.
𝑑𝑡
The brine flows in at the rate of 3.5 gal/min, and each gallon contains 4 lb of salt.
Thus
𝐼𝑁 =(4 lb/gal)(3.5 gal/min)=14 lb/min,
and
𝑂𝑈𝑇 = (𝐶lb/gal)(4 gal/min)=4𝐶 lb/min,
where 𝐶 lb/gal denotes the concentration. But here, since the rate of outflow is
different from that of inflow, the concentration is not quite so simple. At time
𝑡 = 0, the tank contains 200 gal of brine. Since brine flows in at the rate of 3.5
gal/min but flows out at the faster rate of 4 gal/min, there is a gross gain of
Page 68 of 72

3.5 − 4 = −0.5 gal/min of brine in the tank. Thus at the end of 𝑡 minutes the
amount of brine in the tank is
200 − 0.5𝑡 gal.
Hence the concentration at time 𝑡 minutes is
𝑥
lb/gal,
200 − 0.5𝑡
and so
4𝑥
𝑂𝑈𝑇 =
lb/min.
200 − 0.5𝑡
Thus the differential equation becomes
𝑑𝑥
4𝑥
8𝑥
= 14 −
= 14 −
… i .
𝑑𝑡
200 − 0.5𝑡
400 − 𝑡
Since there was initially 15 lb of salt in the tank, we have the initial condition
𝑥 0 = 15 … ii .
The differential equation (i) is not separable but it is linear. Putting it in standard
form, we obtain
𝑑𝑥
8
+
𝑥 = 14,
𝑑𝑡 400 − 𝑡
we find the integrating factor
8
1
exp
𝑑𝑡 = 400 − 𝑡 −8 =
.
400 − 𝑡
400 − 𝑡 8
Multiplying through by this we have
1
𝑑𝑥
8
14
+
𝑥=
8
9
400 − 𝑡 𝑑𝑡
400 − 𝑡
400 − 𝑡 8
or
𝑑
1
14
𝑥 =
.
8
𝑑𝑡 400 − 𝑡
400 − 𝑡 8
Thus
1
2
𝑥=
+𝐶
8
400 − 𝑡
400 − 𝑡 7
or
𝑥 = 400 − 𝑡 + 400 − 𝑡 8 𝐶.
Applying condition (ii), 𝑥 = 15 at 𝑡 = 0, we obtain
15 = 400 + 4008 𝐶
or
375
𝐶=−
.
4008
Thus the amount of salt at any time 𝑡 > 0 is given by
400 − 𝑡 8
𝑥 = 400 − 𝑡 − 375
400
Therefore, the amount of salt in the tank at the end of one hour (𝑡 = 60) is
340 8
𝑥 60 = 340 − 375
= 340 − 375 ≈ 238 lb.
400
(b) How much salt is in the tank when the tank contains only 50 gal of brine?
Page 69 of 72

Solution:
According to part (a), we know that at the end of 𝑡 minutes the amount of brine
in the tank is
200 − 0.5𝑡 gal.
Thus we obtain
200 − 0.5𝑡 = 50
and hence
𝑡 = 300.
Therefore, the amount of salt in the tank when the tank contains only 50 gal of
brine is
100 8
𝑥 300 = 100 − 375
≈ 100 lb.
400

Solution of Exercise 22 (Reduction of Order)
1. Prove that the differential equation
𝑑 2 𝑦 𝑑𝑦
−
− 2𝑦 = 0
𝑑𝑥 2 𝑑𝑥
has two solutions of the form 𝑦 = 𝑒 𝑎𝑥 , with 𝑎 is a constant.
Proof:
Let 𝑦 = 𝑒 𝑎𝑥 be the solution of the given differential equation. Then we obtain
𝑑 2 𝑒 𝑎𝑥
𝑑 𝑒 𝑎𝑥
−
− 2𝑒 𝑎𝑥 = 0
𝑑𝑥 2
𝑑𝑥
𝑑 𝑎𝑒 𝑎𝑥
⇔
− 𝑎𝑒 𝑎𝑥 − 2𝑒 𝑎𝑥 = 0
𝑑𝑥
⇔ 𝑎2 𝑒 𝑎𝑥 − 𝑎𝑒 𝑎𝑥 − 2𝑒 𝑎𝑥 = 0
⇔ 𝑒 𝑎𝑥 𝑎2 − 𝑎 − 2 = 0
⇔ 𝑒 𝑎𝑥 𝑎 + 1 𝑎 − 2 = 0
⇔ 𝑒 𝑎𝑥 = 0 ⋁𝑎 + 1 = 0⋁𝑎 − 2 = 0.
Hence there are two values for 𝑎, i.e., 𝑎 = −1 or 𝑎 = 2. Therefore, we can conclude
that the given differential equation has two solutions of the form 𝑦 = 𝑒 𝑎𝑥 , i.e.,
𝑦 = 𝑒 −𝑥 or 𝑦 = 𝑒 2𝑥 . ■
2. If a differential equation has general solution of the form
𝑦 = 𝑐1 𝑒 2𝑥 + 𝑐2 𝑒 −3𝑥 ,
then determine that differential equation.
Solution:
Consider the second order homogeneous differential equation with constant
coefficient
𝑑2 𝑦
𝑑𝑦
+
𝑎
+ 𝑏𝑦 = 0.
𝑑𝑥 2
𝑑𝑥
𝑟𝑥
Suppose that 𝑦 = 𝑒 , 𝑟 ∈ ℝ is the solution of that differential equation (where 𝑟 will
be determined). Then we will have the characteristic equation
𝑟 2 + 𝑎𝑟 + 𝑏 = 0.
Page 70 of 72

Thus, in order to 𝑦 = 𝑒 𝑟𝑥 becomes the solution for that differential equation, 𝑟 has to
satisfies that characteristic equation. One of the possibilities for the roots of the
characteristic equation above is if the characteristic equation has two different roots,
say 𝑟1 , 𝑟2 ∈ ℝ, then the general solution for the differential equation above is
𝑦 𝑥 = 𝑐1 𝑒 𝑟1 𝑥 + 𝑐2 𝑒 𝑟2 𝑥 .
Since we have that the general solution of a differential equation is
𝑦 = 𝑐1 𝑒 2𝑥 + 𝑐2 𝑒 −3𝑥
we obtai that the roots of a characteristic equation are 𝑟1 = 2 or 𝑟2 = −3. Moreover,
the characteristic equation that we want is
𝑟 − 2 𝑟 + 3 = 0 ⇔ 𝑟 2 + 𝑟 − 6 = 0.
Hence we obtain 𝑎 = 1 and 𝑏 = −6.
Therefore, the diferential equation that has the general solution
𝑦 = 𝑐1 𝑒 2𝑥 + 𝑐2 𝑒 −3𝑥
is
𝑑 2 𝑦 𝑑𝑦
+
− 6𝑦 = 0.
𝑑𝑥 2 𝑑𝑥
3. Given that 𝑦1 𝑥 = 𝑥 2 is one of the solutions of the differential equation
𝑑 2 𝑦 1 𝑑𝑦 4
+
−
𝑦 = 0 … (i)
𝑑𝑥 2 𝑥 𝑑𝑥 𝑥 2
Determine a general solution of that differential equation.
Solution:
Observe that 𝑦1 𝑥 = 𝑥 2 does satisfy the given differential equation, i.e.,
𝑑2 𝑥 2
1 𝑑 𝑥2
4
1
+
− 2 𝑥 2 = 2 + 2𝑥 − 4 = 0.
2
𝑑𝑥
𝑥 𝑑𝑥
𝑥
𝑥
Let 𝑦2 (𝑥) = 𝑥 2 𝑣(𝑥). We have
𝑑 𝑦2 𝑥
𝑑 𝑣 𝑥
= 𝑥2
+ 2𝑥𝑣 𝑥
𝑑𝑥
𝑑𝑥
and
𝑑 2 𝑦2 𝑥
𝑑2 𝑣 𝑥
𝑑 𝑣 𝑥
2
=𝑥
+ 4𝑥
+ 2𝑣 𝑥 .
2
2
𝑑𝑥
𝑑𝑥
𝑑𝑥
Substituting the expression for 𝑦, 𝑑𝑦/𝑑𝑥, and 𝑑 2 𝑦/𝑑𝑥 2 into Equation (i), we obtain
𝑑2 𝑣 𝑥
𝑑 𝑣 𝑥
1 2𝑑 𝑣 𝑥
4
2
𝑥
+ 4𝑥
+ 2𝑣 𝑥 +
𝑥
+ 2𝑥𝑣 𝑥 − 2 𝑥 2 𝑣 𝑥 = 0
2
𝑑𝑥
𝑑𝑥
𝑥
𝑑𝑥
𝑥
or
𝑑2 𝑣 𝑥
𝑑 𝑣 𝑥
2
𝑥
+
5𝑥
= 0.
𝑑𝑥 2
𝑑𝑥
Letting 𝑤 = 𝑑𝑣/𝑑𝑥 we obtain the first- order homogeneous linear equation
𝑑𝑤
𝑥2
+ 5𝑥𝑤 = 0.
𝑑𝑥
Treating this as a separable equation, we obtain
1
5
1
1
𝑑𝑤 = − 𝑑𝑥 ⇔
𝑑𝑤 + 𝑑𝑥 = 0.
𝑤
𝑥
5𝑤
𝑥
Integrating this, we obtain the general solution
1
1
𝑐55 𝑐4
ln |𝑤| + ln |𝑥| = 𝑐6 ⇔ ln 𝑤 5 𝑥 = ln 𝑐5 ⇔ 𝑤 = 5 = 5
5
𝑥
𝑥
where 𝑐6 , 𝑐5 , and 𝑐4 are constants.
Page 71 of 72

Afterwards, we choose 𝑐4 = 1, we recall that 𝑑𝑣/𝑑𝑥 = 𝑤 and integrate to obtain the
function 𝑣 given by
1
𝑣 𝑥 = − 4.
4𝑥
Now forming 𝑦2 𝑥 = 𝑦1 𝑥 𝑣(𝑥), where 𝑦1 (𝑥) denotes the known solution, we obtain
the function 𝑦2 defined by
1
1
1
𝑦2 𝑥 = 𝑥 2 − 4 = − 2 = − 𝑥 −2 .
4𝑥
4𝑥
4
Therefore, the general solution of Equation (i) is
1
𝑦(𝑥) = 𝑐1 𝑥 2 + 𝑐3 − 𝑥 −2 = 𝑐1 𝑥 2 + 𝑐2 𝑥 −2
4
where 𝑐1 , 𝑐2 , and 𝑐3 are constants.

Page 72 of 72

View publication stats