Автор: Джейкобсон Н.
Теги: математика алгебра высшая математика переводная литература издательство мир теория колец
Год: 1964
Текст
• i ЛЖ(к1>МГ0«1
• i ЛЖ(к1>МГ0«1
Interscience Tracts in Pure
and
Applied Mathematics
number 10
NATHAN JACOBSON
LIE ALGEBRAS
Interscience Publishers
A Division of John Wiley and Sons
New York—London
V
Н. ДЖЕКОБСОН
АЛГЕБРЫ ЛИ
Перевод с английского
А. Б. ЖИЖЧЕНКО
Под редакцией
А. И, КОСТРИКИНА
ИЗДАТЕЛЬСТВО cM
Москва 1964
Автор книги — один из виднейших специалистов в этой
области, его труды — «Теория колец" (ИЛ, 1947) и .Строение
колец" (ИЛ, 1961)—получили заслуженное признание советских
математиков Джекобсон четко и подробно излагает теорию
алгебр Ли. Он приводит классификацию простых расщепляемых
алгебр Ли, излагает основные результаты теории представлений
алгебр и описывает автоморфизмы полупростых алгебр Ли над
алгебраически замкнутым полем характеристики нуль. К до-
достоинствам книги относятся весьма удачно подобранные упраж1-
нения, часто снабженные указаниями и схемами доказательств.
Книга будет служить учебным пособием и основой для
специальных курсов по теории алгебр Ли. Кроме того, она
представит безусловную ценность для аспирантов и студентов
старших курсов математических факультетов университетов
и пединститутов, а также для научных работников — математи-
математиков, физиков и механиков, занимающихся теорией алгебр Ли
или использующих ее в своих исследованиях.
Редакция литературы по математическим наукам
ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
Алгебры Ли прочно вошли в математику в конце прошлого зека.
Их теория благодаря вниманию многих выдающихся математиков
обогатилась целым рядом тонких и красивых результатов, влияние
которых простирается далеко за пределы алгебры. Поэтому отсут-
отсутствие книги учебного характера по теории алгебр Ли давно воспри-
воспринималось как досадный пробел в математической литературе. Отчасти
это объяснялось тем фактом — благоприятным во всех других отноше-
отношениях, — что теории групп Ли и алгебр Ли продолжительное время
развивались параллельно, а преобладание методов анализа и топо-
топологии лишь способствовало укоренившейся привычке смотреть на
аппарат алгебр Ли прежде всего как на полезное и мощное средство
линеаризации теоретико-групповых задач. Алгебраические же осно-
основания теории оставались до некоторых пор в тени, созревая на
страницах журнальных статей, особенно многочисленных за послед-
последние два десятилетия.
Между тем потребность в книге, специально посвященной алгеб-
алгебрам Ли, ощущалась как со стороны начинающих математиков,
так и со стороны тех, кто хотел бы освежить или пополнить свои
знания в этой важной области алгебры, ,не прибегая к посредни-
посредничеству групп Ли и не ограничивая себя классическими полями комп-
комплексных или вещественных чисел. Изданные у нас III том замеча-
замечательной монографии К. Шевалле (Шевалле [3]) и труды семинара
„Софус Ли) (Семинар „Софус Ли" [1]) отличайщиеся высоким науч-
научным уровнем, по целому ряду причин нельзя отнести к категории
руководств для первоначального ознакомления с предметом.
Указанный пробел заполняет книга, перевод которой предлагается
вниманию советского читателя. Нет ничего удивительного в том, что
ее написал Н. Джекобсон, автор хорошо известных у нас двух мо-
монографий по теории ассоциативных колец [1], [3]. Ему принадлежат
также глубокие работы по алгебрам Ли, оставившие заметный след
в теории, особенно в той ее части, которая связана с переходом
к произвольному основному полю. Нет нужды подчеркивать методи-
методические достоинства новой книги проф. Джекобсона, сумевшего
избежать слишком большой абстрактности изложения, но в то
же время достичь той степени общности, которая позволяет по-но-
по-новому взглянуть на вещи даже квалифицированному читателю.
Для чтения книги требуется сравнительно небольшая алгебра-
алгебраическая подготовка, и ее вполне можно рекомендовать студентам,
аспирантам и математикам-неалгебраистам. Это особенно относится
') По поводу всей литературы, упомянутой в предисловии, см. список
в конце книги.
Предисловие редактора перевода
к первым шести главам, содержащим наиболее традиционный мате-
материал. Разумеется, цели, стоящие перед автором, исключали мысль об
энциклопедичности изложения. В книге совершенно не затронута
теория алгебраических алгебр Ли — предмет упомянутой выше мо-
монографии К. Шевалле. Лишь два параграфа уделены теории кого-
мологий алгебр Ли, чуть в большем объеме содержащейся в трудах
семинара „Софус Ли". Интересующийся более глубокими результатами
теории когомологий должен обращаться к специальной литературе.
В целом упомянутые три книги по теории алгебр Ли, совпадая
в некоторых своих частях, удачно дополняют друг друга и, надо думать,
удовлетворят вкусы и потребности значительного круга читателей.
В книге, в форме упражнений и вставок в основной текст, выде-
выделяется своеобразие теории в случае поля характеристики р > 0.
Хотя затрагиваются далеко не все вопросы, даже эпизодические све-
сведения наводят на мысль, что в этом направлении открывается боль-
большой простор для дальнейших исследований. Так именно и обстоит
дело. В частности, теория полупростых алгебр, давно принявшая
стройную и законченную форму в случае алгебраически замкнутого
поля характеристики р = 0, при р > 0 представляет собой набор
разрозненных фактов. Некоторые идеи о путях описания простых
алгебр, наметившиеся за последнее время, еще далеки от своей реа-
реализации. Интересно отметить, что алгебры Ли характеристики р
нашли применение в теории абстрактных групп, о чем вскользь упо-
упоминается в книге. Как раз в этом прикладном аспекте предста-
представляется весьма желательным развернутое изложение всех относящихся
сюда фактов, не только из-за их собственной ценности, но и ввиду
того, что многие нерешенные вопросы об алгебрах Ли конечной ха-
характеристики получили бы более плодотворную и естественную по-
постановку. Краткое добавление к книге, очевидно, не решало бы этой
задачи, а введение большого количества теоретико-группового ма-
материала вовсе не входило в замысел автора, поэтому вышесказанное
имеет своей целью лишь придать более определенный смысл тем
страницам книги, где характеристика р играет роль отрицательного
героя. Той же цели отчасти служит указатель литературы, несколько
расширенный при переводе, но отнюдь не претендующий на исчерпы-
исчерпывающую полноту.
Опечатки и мелкие неточности, часть которых была любезно
сообщена нам автором книги, исправлены без каких-либо примеча-
примечаний. Ссылки на американские источники частично заменены, а там,
где это не сделано (например, ссылка на лекции автора [2]), чита-
читатель без труда подберет русский эквивалент. В данном случае лю-
любые вводные курсы абстрактной алгебры и линейной алгебры (на-
(например, А. Г. Курош [1] и Д. И. Мальцев [4]) содержат все
необходимые сведения.
А. Кострикин
ПРЕДИСЛОВИЕ
Настоящая книга основана на курсах лекций, которые автор чи-
читал в Иельском университете в течение последних десяти лет, осо-
особенно на курсе лекций, читанном в 1959/1960 учебном году. Это
в первую очередь учебник для самостоятельного изучения предмета
студентами, или пособие при изучении курса лекций по алгебрам/Ли.
Кроме обычного знакомства с общими алгебраическими понятиями,
у читателя предполагается хорошее знание линейной алгебры (ли-
(линейных преобразований, билинейных форм, тензорных произведений).
Перечисленного достаточно для понимания первых девяти глав. Для
понимания десятой главы требуется также знание теории Галуа и не-
некоторых результатов из структурной теории Веддербёрна ассоци-
ассоциативных алгебр.
Теорию алгебр Ли весьма полезно изучать сразу вслед за курсами
общей абстрактной алгебры и линейной алгебры, имея в виду как
красоту результатов этой теории, так и широкие контакты ее с дру-
другими областями математики (теорией групп, дифференциальной гео-
геометрией, дифференциальными уравнениями, топологией). В предла-
предлагаемом изложении мы стремились избежать излишней абстрактности
исследования и последовательно проводили взгляд на теорию алгебр
Ли как на ветвь линейной алгебры. .
Общие абстрактные понятия сконцентрированы в две группы:
первая, необходимая для структурной теории, в гл. I; вторая, необ-
необходимая для теории представлений, в гл. V. Главы с I по IV по-
посвящены структурной теории, центральным результатом которой
является классификация так называемых „расщепляемых простых
алгебр Ли". Основные результаты теории представлений излагаются
в гл. с VI по VIII. В гл. IX определяются автоморфизмы полупро-
полупростых алгебр Лц над алгебраически замкнутым полем характеристики 0.
Эти результаты в гл. X применяются для изучения проблемы клас-
классификации простых алгебр Ли над произвольным полем.
В книге не было сделано никаких попыток дать картину исто-
исторического развития теории алгебр Ли или оценить индивидуальный
вклад отдельных математиков. В этом отношении мы ограничились
краткими указаниями, разбросанными в разных местах, на лиц, ко-
которым принадлежат основные идеи. Автор пользуется случаем отме-
отметить большое влияние, оказанное на него одним из великих созда-
создателей этой теории, профессором Германом Вейлем, чьи вдохно-
8 Предисловие
вляющие лекции в Институте Высших научных исследований в 1933—
1934 годах привели к исследованиям автора в этой области. Необхо-
Необходимо отметить также, что в этих лекциях профессор Вейль, перво-
первоначально интересовавшийся теорией Ли непрерывных групп, поставил
предмет этой книги на особенную основу, введя ъ первый раз термин
„алгебра Ли" вместо „инфинитезимальной группы", которая изучалась
до тех пор.
В конце книги приводится обширная библиография; тем не менее
она ни в коей мере не полна. Главной целью при составлении биб-
библиографии было указать направление дальнейшего изучения вопро-
вопросов, затронутых в книге, и вопросов, связанных с ними.
Я очень признателен моему коллеге Г. Селигману, тщательно
просмотревшему рукопись и внесшему много предложений по улуч-
улучшению изложения. Доктор Р. Кон и доктор А. Мьюбори сделали
много существенных замечаний, и все трое помогали читать кор-
корректуру. Пользуюсь случаем принести всем троим искреннюю благо-
благодарность.
Натан Джекобсон
28 мая 1961 г.
Нью-Хэйвен, Коннектикут
Глава I
ОСНОВНЫЕ ПОНЯТИЯ
Теория алгебр Ли выросла из теории Ли непрерывных групп.
Основным результатом последней является сведение „локальных" за-
задач, относящихся к группам Ли, к соответствующим задачам теории
алгебр Ли, т. е. к задачам линейной алгебры. Каждой группе Ли
сопоставляется алгебра Ли над полем вещественных или комплексных
чисел, и устанавливается соответствие между аналитическими под-
подгруппами группы Ли и подалгебрами ее алгебры Ли, при котором
инвариантным подгруппам соответствуют идеалы, абелевым подгруп-
подгруппам — абелевы подалгебры и т. д. Изоморфизм алгебр Ли эквива-
эквивалентен локальному изоморфизму соответствующих групп Ли. Мы
не будем подробно разбирать эти вопросы, поскольку имеются пре-
превосходные современные изложения теории Ли. Читатель может обра-
обратиться к одной из следующих книг: Шевалле „Теория групп Ли",
Понтрягин „Непрерывные группы*.
В последнее время введение соответствующих алгебр Ли ока-
оказалось полезным при изучении двух других разделов теории групп.
Первым из этих разделов является теория свободных групп, кото-
которую можно изучать при помощи свободных алгебр Ли, пользуясь
методом, впервые предложенным Магнусом. Хотя эта связь не та-
такая тесная, как в теории Ли, применение алгебр Ли привело к важ-
важным результатам относительно свободных групп и других классов
абстрактных групп. В частности, необходимо отметить результаты
по так называемой ослабленной проблеме Бернсайда: ограничены ли
порядки конечных групп, имеющих фиксированное число г обра-
образующих и удовлетворяющих соотношению хт = 1, где т — фикси-
фиксированное положительное целое число? Стоит указать, что важную
роль в этих приложениях к теории абстрактных групп играют ал-
алгебры Ли простой характеристики. Мы опять-таки не будем входить
в детали и отошлем интересующегося этим вопросом читателя
к статьям Лазара [2] и Хигмана [1], где дается хорошее изложение
этого метода в теории групп.
Тип соответствия между подгруппами группы Ли и подалгебрами
ее алгебры Ли, который возник в теории Ли, имеет точный аналог
в теории Шевалле линейных алгебраических групп. Линейная алгеб-
алгебраическая группа является, коротко говоря, подгруппой группы
10 Гл. I. Основные понятия
невырожденных квадратных матриц порядка п, определенной системой
полиномиальных уравнений, которым удовлетворяют элементы этих
матриц. Примером является ортогональная группа, определяемая си-
системой уравнений 2а?; = 1, 2a//a«ft = 0. ./=?*. У. А = 1 п
i I
относительно элементов аг;. матрицы (а.ф. Шавалле определил для
каждой алгебраической группы соответствующую алгебру Ли (см.
Шевалле [2]), дающую полезную информацию о группе. Эта инфор-
информация является исчерпывающей в теории линейных алгебраических
групп над полем характеристики нуль.
Поскольку теория алгебр Ли имеет теоретико-групповой фунда-
фундамент, не удивительно, что основные понятия теории алгебр Ли носят
теоретико-групповой оттенок. Это нужно все время иметь в виду
при изучении алгебр Ли и, в частности, при чтении настоящей главы,
содержащей основные понятия, необходимые для той части струк-
структурной теории, которая будет развита в II—IV главах.
К вопросам, касающимся основных понятий, необходимых для
теории представлений (гл*. VI, VII), мы еще вернемся в гл. V.
§ 1. Определение и построение алгебр Ли
и ассоциативных алгебр
Напомним определение • алгебры (не обязательно ассоциативной)
% над полем Ф. Это просто векторное пространство % над Ф,
в котором определен билинейный закон умножения. Таким образом,
каждой паре (л:, у), х, у ? ЭД, мы можем сопоставить произведение
ху ? ЭД, удовлетворяющее условиям билинейности
A)
B)
Аналогично определяется алгебра над коммутативным кольцом Ф,
имеющим единичный элемент (единицу) 1. Это левый Ф-модуль
с произведением ху?%, удовлетворяющим условиям A) и B). Нас
будут интересовать главным образом алгебры, определенные над по-
полями, и, более того, алгебры, имеющие конечные размерности как
векторные пространства. У таких алгебр существует базис (ev е2, ...
.... еп), и мы можем написать
где Тг/*?Ф- i,J, A = l, ..., п. Эти п3 элементов fy* называются
структурными константами алгебры (относительно выбранного
базиса). Они дают значение каждого произведения e^j, i,j =
=?=}, 2, ..,, п. Более того, эти константы определяют каждое про-
$ /. Определение алгебр Ли и ассоциативных алгебр 11
изведение в %. Пусть, действительно, х и у — два любых элемента
из ЭД; запишем их в форме х = 2 4ei< У = 2 7i//- Ч< I; € *• Тогда,
согласно условиям A) и B),
ху = B ^Д B 71;е/Д — 2
\Т А/ ;;; t,j
21- / Ч Ч V1
Ч (ei С7!//))== 2л
I, i «. j
что определяется произведениями егву.
Это рассуждение дает общий способ построения конечномерных
алгебр. Мы исходим из произвольного векторного пространства Ж
и базиса (е;) в ЭД. Для каждой пары индексов (г, J) произвольным
п
образом определяем е,в: как элемент из ЭД. Тогда при jc = 2 4ei>
i
п
У — 2 71;е; произведение ху определяется формулой
ХУ — 2 ^irt; (*/*/)• C)
Непосредственно проверяется, что это произведение билинейно,
т. е. что выполняются соотношения A) и B). Выбор e-fij эквивален-
эквивалентен выбору элементов fi;ft в Ф, таких, что е^у = 2 Tijkek-
Рассмотренное понятие алгебры (которую мы до сих пор не пред-
предполагали ассоциативной) слишком общо, чтобы оно могло привести
к интересным структурным результатам. Для получения таких ре-
результатов нужно наложить некоторые дополнительные условия на
операцию умножения. В дальнейшем преимущественно будут исполь-
использоваться условие ассоциативности и условия Ли.
Определение 1. Алгебра ЭД называется ассоциативной,
если ее операция умножения удовлетворяет условию ассоциативности
(xy)z = x(yz). D)
Алгебра ЭД называется алгеброй Ли, если ее операция умножения
удовлетворяет условиям
х2 = 0, {xy)z-\-{yz) x-\-{zx)y = 0. E)
Второе из этих условий называется тождеством Якоби.
Поскольку эти типы алгебр определяются тождествами, очевидно,
что подалгебры и гомоморфные образы этих алгебр имеют тот же
тип, т. е. являются ассоциативными или лиевыми. Если % — алгебра
Ли и х, у?%, то 0 = (лг + уJ = х2-\- ху-\-ух-\-у2 = лгу + ух,
так что условие
ху = — ух F)
12 Гл. /. Основные
выполняется в любой алгебре Ли. Обратно, если это условие вы-
выполнено, то 2jc2 = 0, так что jc2 = O, если характеристика отлична
от двух. Поэтому для алгебр с характеристикой, не равной 2,
первое из условий E) в определении алгебры Ли может быть заме-
заменено условием F).
Предложение 1. Для ассоциативности алгебры % с ба-
базисом (ег еп) над Ф необходимо и достаточно, чтобы вы-
выполнялись условия (eleJ)ek = el(eJek), t,j,k — l, 2, ...,я, или,
что то же самое,
2 Т//гТг*. = 2 Itrsijkr- t.J,k,S= 1.2 П. G)
Г Т
где туг(€Ф)—структурные константы базиса (ev ..., е„)
алгебры $: е(е, = 21ijrer Алгебра % является алгеброй Ли
Т
в том а только том случае, когда е2—0, eleJ = — е}е.,
(eie,) ** + (е/*) ei + (ekei) ej = °
ei + (ekei) ej
для i,j,k=l,2 п. В терминах структурных констант
эти условия выражаются следующим образом:
nk — 0. Ti/ft —
Агкз+^jкr^rts+ чшъ^—°- (8)
Доказательство. Если алгебра % ассоциативна, то (е{е^) ek =
= el(ejek). Обратно, предположим, что эти условия выполнены для et.
Если х = 2 het' У = 2 Vjej' z ~ 2 ^kek> т0
(ху) 2 = 2 \(nf.h (etej) ek и x (yz) = 2 ^^1 (ejek)-
Поэтому (ху) z — x (yz) и 91 ассоциативна. Если ^г,- —2 tij^r T0
(*^)«* —STyrTrtA и^(«у**) = 21т/гЛлкЛ- Из линейной незави-
Г, S Г, S
симости et следует, что условия (etej) ek = et (ejek) эквивалентны усло-
условиям G). Доказательство в лиевом случае аналогично вышеприве-
вышеприведенному и поэтому опускается.
На самом деле для построения примеров ассоциативных алгебр и
алгебр Ли редко используется гот общий способ, который был ука-
указан выше. Исключение в этом смысле составляют лишь алгебры ма-
малых размерностей. Для определения алгебр Ли размерностей один,
два и три мы применим в § 4 изложенный выше метод. В лиевом
случае можно сделать два замечания, которые упрощают дело. Во-
§ 2. Алгебры линейных преобразований. Дифференцирования 13
первых, если в некоторой алгебре ^ = 0 и etej = — е^е{, то из
равенства (eieJ)ell-\-(ejelt)ei-\-(ekel)ej = O для какой-нибудь тройки
чисел /, j, k следует равенство (eJei)ek-\-(e[ell) eJ-\-(ekeJ)el = 0.
Так как в нем, очевидно, допустимы циклические перестановки ин-
индексов, тождество Якоби выполняется для (?,¦?;-)?*' при любых
I', j', k', получаемых перестановкой индексов /, j, k. Пусть, далее,
I = j. Тогда e\ek + (*Л) ef + (Vl) et = 0 + (*/*) е, - (*,**) ',=<>.
Поэтому из соотношений ^ = 0, ^г = — е е{ или, что то же
самое, из условия Jt2 = 0 в $ следует, что тождества Якоби выпол-
выполняются для et, et, ej. В частности, тождества Якоби являются след-
следствием условия х2*=0, если dim 91^ 2.
Если же dim 91 = 3, то необходимо проверить лишь, что
(ехе2) ег -f (еге3) е1 -f (e3ej e2 — 0.
§ 2. Алгебры линейных преобразований. Дифференцирования
В действительности нет необходимости специально строить при-
примеры ассоциативных и лиевых алгебр с помощью базисов и таблиц
умножения, поскольку эти алгебры возникают естественным путем.
Простые примеры ассоциативных алгебр получаются следующим об-
образом.
Пусть ЯЯ — векторное пространство над полем Фи® — множе-
множество линейных преобразований пространства Зй в себя. Напомним,
что если А а В принадлежат (Е и а?Ф, то А-\- В, а.А и АВ опре-
определяются равенствами х (А -(- В) = хA -J- хВ, х (аЛ) = а (хА),
х (АВ) = (хА) В для любого х в 9И. Тогда, как хорошо известно,
Ш, является векторным пространством относительно сложения (-(-) и
умножения на скаляр, и умножение (А, В)—> АВ ассоциативно и
удовлетворяет условиям A) и B).
Поэтому (§. является ассоциативной алгеброй. Известно также, что
если пространство Ш m-мерно, т < оо, то d имеет размерность т2
над Ф. Если (ev е2, ..., е„^ — базис Ш над Ф, то линейные преоб-
преобразования Etj, такие, что elEij = eJ; егЕ^==0, если г Ф i, t,j =
= 1 т, образуют базис алгебры 6 над полем Ф. Если Л?E:,
то мы можем написать et А = 2 aijej< ' = 1 т, ц (а) = (аг,) будет
матрицей преобразования А в базисе (et). Соответствие Л—>(а) является
изоморфным отображением алгебры Ф. на алгебру Фт jn X т-матриц
с элементами а.1}- из Ф.
Такая алгебра (§. называется (ассоциативной) алгеброй линей-
линейных преобразований пространства 9И на Ф. Любая подалгебра Ш
алгебры (Е, т. е. подпространство пространства 6, замкнутое отно-
относительно умножения, называется алгеброй линейных преобразований.
14 Гл. I. Основные пднЯТиЯ
Если §( — произвольная (неассоциативная) алгебра ') и а ? %, то
отображение aR, которое переводит х в ха, является линейным пре-
преобразованием. Легко проверить, что (а-\- b)R = aR-\-bR, (a.a)R = aaR
и если Ж ассоциативна, то (ab)R = aRbR. Отсюда следует, что если
$ -4 ассоциативная алгебра, то отображение a->aR является гомо-
гомоморфизмом алгебры % в алгебру Щ линейных преобразований век-
векторного пространства 9L Если 91 имеет единичный элемент (единицу)
1, то a->aR является изоморфизмом 91 в 6. Поэтому 31 изоморфна
некоторой алгебре линейных преобразований. Если 31 не имеет еди-
единичного элемента, то мы можем присоединить к этой алгебре извест-
известным способом единицу и получить алгебру W, обладающую единич-
единичным элементом и такую, что dim 91* = dim 9t-f- 1 (см. Джекобсон [2],
т. I, стр. 84). Поскольку алгебра 9Г изоморфна алгебре линейных
преобразований, то же самое верно и для §(.
Если алгебра 3t имеет конечную размерность, это рассуждение
показывает, что 91 изоморфна алгебре линейных преобразований
конечномерного векторного пространства.
Алгебры Ли получаются из ассоциативных алгебр очень простым
способом. Пусть 91 — ассоциативная алгебра. Определим произведение
Ли или (аддитивный) коммутатор элементов х, у ? 91 следующим
образом:
= JO> — ух. (9)
Легко проверяется непосредственными вычислениями, что
а.[ху] —
Кроме того,
[хх] = х2 — х2 = 0,
Uxy]z] + [[yz]x]+[[zx]y] =
= (ху ~yx)z — z (ху ~ ух) -f {yz — zy)x —
— x(yz — zy) -f- (zx — xz)y — y (zx — xz) = 0.
Таким образом, коммутатор [ху] удовлетворяет всем условиям,
налагаемым на произведение в алгебре Ли. Алгебра Ли, получаемая
таким способом, называется алгеброй Ли ассоциативной алгебры 9С.
Мы будем обозначать ее через %L. В частности, из алгебры Ш. по-
получается алгебра QlL. Любая подалгебра 2 алгебры 6Х называется
') Здесь и ниже заключенное в круглые скобки слово „неассоциативиая",
стоящее перед словом .алгебра", подчеркивает лишь тот факт, что рассмат-
рассматриваемая алгебра не обязательно ассоциативна. — Прим. ред.
§ 2. Алгебры линейных преобразований. Дифференцирования 15
алгеброй Ли линейных преобразований. Мы увидим дальше, что
каждая алгебра Ли изоморфна подалгебре алгебры Ли %L, где %—неко-
%—некоторая ассоциативная алгебра. Ввиду только что доказанного свойства
ассоциативных алгебр, это эквивалентно утверждению, что каждая
алгебра Ли изоморфна лиевой алгебре линейных преобразований.
Рассмотрим теперь некоторые важные примеры подалгебр лиевых
алгебр @?, где 6 — ассоциативная алгебра линейных преобразований
векторного пространства ffi над полем Ф.
Ортогональная алгебра Ли. Пусть в ЯЯ задана невырожденная
симметрическая билинейная форма (х, у), и предположим, что 9Й
имеет конечную размерность. Тогда каждому линейному преобразо-
преобразованию Л пространства 9И соответствует сопряженное к Л относи-
относительно (х, у) линейное преобразование Л*, удовлетворяющее условию
(хА, у) — (х, у А*). Отображение А -> А* является антиавтоморфизмом
алгебры (S: (А-\- В)* = А* + В*, (аЛ)* = аЛ*. (АВ)* = В*А*. Обозна-
Обозначим через © множество таких линейных преобразований Л?($, что
Л* = — Л. Тогда © является подпространством пространства Ш, и
если А* = — А, В* = — В, то [АВ]* = (АВ — ВА)* = В*А*— А*В*=
— ВА — АВ = [ВА] = — [АВ\. Поэтому [Л?]?© и 6—подалгебра
алгебры (?L.
Если Ф — поле вещественных чисел, то лиева алгебра © является
алгеброй Ли ортогональной группы пространства ЯЯ относительно
формы (х, у). Это группа линейных преобразований О простран-
пространства Ж, ортогональных в том смысле, что (хО, уО) = (х, у),
х, у ? ЯЯ. Поэтому мы называем © ортогональной алгеброй Ли
относительно (jc, у).
Симплектическая алгебра Ли. Предположим теперь, что (л:, у)—
невырожденная кососимметрическая форма: (х, х) = 0и dim 3R < оо.
Напомним, что из этих условий следует, что d\mffl. — 2l, т. е. раз-
размерность Ш четная. Пусть опять Л* — линейное преобразование,
сопряженное к Л(?й) относительно (х, у). Тогда множество ©
кососимметрических линейных преобразований (Л* = — Л) образует
подалгебру в (§,L. Эта подалгебра связана с симплектической группой,
и мы поэтому будем называть ее симплектической алгеброй Ли ©
относительно кососимметрической формы (jc, у).
Треугольные линейные преобразования. Пусть Ос: Шг с Ш^ с
с ... с: Шт = Ш — цепочка подпространств пространства ffi с усло-
условием dim 9Иг = /, и пусть % — множество таких линейных преобразо-
преобразований Т, что Ш{Г с 9Иг. Очевидно, что % — подалгебра ассоциатив-
ассоциативной алгебры 6; поэтому %L — подалгебра алгебры QlL. Можно выбрать
базис (хг, х2, . ¦ ., хт) в пространстве 9И так, что (xv jc2, .... Jt;)
будет базисом подпространства 3№(. Тогда из условия Т^Т ? 5Ш».
16 Г л I Основные понятии
где Г??, следует, что матрица преобразования Т в базисе (xt, х2, • ¦ •
х1) имеет вид
хп 0 .... О
T2i т22 0
A0)
Такая матрица называется треугольной, и соответственно мы
будем называть каждое Т ? ? треугольным линейным преобразованием.
Алгебры дифференцирований. Пусть % — произвольная (неассо-
(неассоциативная) алгебра. Дифференцированием D алгебры % назы-
называется линейное отображение алгебры % в себя, удовлетворяющее
условию
(xy)D = (xD)y + x(yD). A1)
Пусть ?)(§() — множество всех дифференцирований алгебры §t. Если
Dv ?>2 ?©(«), то
(ху) (D, + D2) = (*у) D, + (*у) D2 = (*D,) y + x (yDj +
-Ь (*Da) у + * (yD2) = (* (D, + Dj)) у + x (у (D, + O2)).
Поэтому Dj -f- D2 ? 3) (9t); легко проверить также, что aDx ^ 3) (9l)t
если а^Ф. Далее,
(*у) DA = ((xD^ у + х (yDj) D2 =
= (xD.D,) у + (* D,) (yDj) + (xDj) (yDx) + x (yDA)-
Перестановка Dt и D2 в предшествующей формуле и вычитание по-
полученного таким образом равенства из предыдущего приводит к со-
соотношению
(ху) iDfid = (* [D
Поэтому [DjD^ ^ 5) (S(), так что ?)(ЭД) является подалгеброй в ®х.
где Ш — алгебра линейных преобразований векторного пространства St.
Мы назовем ее алгеброй Ли дифференцирований алкебры ft.
Лиева алгебра 5) (Щ является алгеброй Ли группы автоморфизмов
алгебры 5Я, если % — конечномерная алгебра над полем вещественных
чисел. Мы не будем доказывать никаких утверждений о связях между
группами Ли и алгебрами Ли. По этому вопросу мы отошлем чита-
читателя к литературе по группам Ли. Тем не менее мы укажем сейчас
на внутреннее сходство между группой автоморфизмов и алгеброй
дифференцирований. Пусть D — дифференцирование. Тогда индукцией
по п получаем формулу Лейбница
)l). A2)
§ 2 Алгебры линейных, преобразований Дифференцирования 17
Если характеристика поля Ф равна нулю, то можно разделить
обе части равенства на ге! и получить равенство
г-о
Если §( имеет конечную размерность над полем вещественных чисел,
то, как легко проверить (см. Джекобсон [2], т. II, стр. 197), ряд
сходится для каждого линейного отображения D алгебры 91 и- линей-
линейное отображение expD, определенное рядом A3), взаимно одно-
однозначно. Пользуясь равенством A2'). легко установить также, что
если D — дифференцирование, то O = expD удовлетворяет условию
(ху)О =(xG)(yG). Поэтому О — автоморфизм алгебры 9L
Связь между автоморфизмами и дифференцированиями может
быть установлена и чисто алгебраическим способом, что важно для
приложений. Предположим, что основное поле алгебры Я — произ-
произвольное поле характеристики 0. Пусть D — нильпотентное диффе-
дифференцирование, скажем DN = 0.
Рассмотрим отображение
пг Dff-i
^r+ ...+^_туг. A4)
Запишем это отображение в виде O = l-f-Z, Z = D-\-(D2/2l)-\-
-f- ... -\-(DN-y(N — l)\) и заметим, что Z" = 0. Поэтому 0 = 1-+-Z
имеет обратное отображение 1—Z-\-Z2—... ± ZN~X, так что О
|вляется взаимно однозначным отображением %. на 91.
Далее,
1=0 / \ /
1N1
п=0 л
г 2W-2 In . \ 2N-2
Переход от 2d\2d \~7Г) \(я —Л1/1 K 2j (jpy) ИГ
по формуле A2')- I Поэтому О является автоморфизмом алгебры
D
ИГ осУЩествЛяется
18 Гл I Основные понятия
§ 3. Внутренние дифференцирования ассоциативных алгебр
и алгебр Ли
Пу^ть а — произвольный элемент (неассоциативной) алгебры %.
Тогда а определяет два отображения aL:x~>ax и ад:х—>ха
алгебры §( в себя. Эти отображения называются левым и правым
умножениями, определяемыми элементом а. Определяющие алгебру
условия A) и B) показывают, что aL и aR — линейные отображения
и отображения a—>aL и a->aR*—линейные отображения % в про-
пространство Ш линейных преобразований алгебры 9L Пусть теперь
Ш — ассоциативная алгебра. Положим Da = aR — aL; тогда Da — ли-
линейное отображение х—>ха — ах. Из равенства
хуа— аху — (ха— ах)у-\- х(уа— ау) A5)
следует, что Da— дифференцирование ассоциативной алгебры %.
Назовем такое дифференцирование внутренним дифференцирова-
дифференцированием, определяемым элементом а.
Пусть теперь й — алгебра Ли. Учитывая способ, при помощи
которого алгебры Ли получаются из ассоциативных алгебр, произ-
произведение в 8 обычно обозначают через [ху\; этим обозначением мы
и будем пользоваться дальше. Правое умножение aR(==— aL, по-
ско1ьку [ха] = — [ах]) обычно обозначают через ad а и называют
присоединенным отображением (эндоморфизмом), определенным эле-
элементом .а.
Из равенств
[ [ху] «] + [ [уа] х] + [ [ах] у] = О,
[ [ху] а] = -[ [уа] х] — [ [ах] у] = [х [уа] ] + [ [ха] у]
следует, что отображение ad a : х->[ха] является дифференцирова-
дифференцированием. Мы будем называть это отображение также внутренним диф-
дифференцированием, определенным элементом а ?2.
Подмножество 58 (неассоциативной) алгебры §( называется идеа-
идеалом, если AJ} — подпространство векторного пространства $ и B)
ab, Ьа?%$ для любых а ? % b ? 23. Рассмотрим множество элементов
вида 2йРь где ai и bi?%. Обозначим это множество через %2,
легко проверить, что это идеал в 91. Если 91 = 2 — алгебра Ли, то
82 принято обозначать через 8' и называть производной алгеброй
(или производным идеалом) алгебры 2. Если 2 — алгебра Ли, то из
кососимметричности умножения следует, что подпространство 33 из 2
является идеалом тогда и только тогда, когда [ab] (или [Ьа]) при-
принадлежит 33 для каждых а ? 2, b ? 33. Отсюда следует, что подмно-
подмножество 6 таких элементов с, что [ас] —0 для всех а?2 образует
идеал. Этот идеал называется центром алгебры 2. Алгебра 2 назы-
рается абелевой, если 8 = 6, что эквивалентно условию 8' = 0.
§ 3 Дифференцирования ассоциативных алгебр и алгебр Ли i9
Предложение 2. Если % — ассоциативная или лиева ал-
алгебра, то внутренние дифференцирования образуют идеал 3ЭД
в алгебре дифференцирований ?$
Доказательство. В каждой (неассоциативной) алгебре спра-
справедливы соотношения (a-\-b)L = aL-\-bL, (a.a)L = aaL, (a-\-b)R —
= aR~\-bR, (a.a)R = a.aR. Поэтому если Da = aR — aL, то Da+b =
— Da-\-Db, Daa — a.Da и внутренние дифференцирования ассоциатив-
ассоциативной или лиевой алгебры образуют подпространство пространства ?)(?{).
Пусть D — дифференцирование алгебры %. Тогда (ад;) D = (aD) х-\-
-\-a(xD) или {ax)D — a(xD) = (aD)x. В операторной форме это
записывается в виде (xaL)D — (xD) aL = x(aD)L или [aLD] =
— aLD — DaL = (aD)L. Аналогично [aRD] = (aD)R и, следовательно,
[DaD] — DaD. Эти формулы показывают, что если ЭД — ассоциатив-
ассоциативная или лиева алгебра, /—внутреннее дифференцирование, а D—лю-
D—любое дифференцирование, то [ID] — внутреннее дифференцирование.
Поэтому 3(90— идеал в 3)(ЭД).
Пример. Пусть 8— алгебра с базисом (е, /), таким, что [е/] =
— е —— 1/е], а все остальные произведения базисных элементов
равны 0. Тогда [aa] = 0 в 2 и, поскольку dim 8 = 2, 8 является
алгеброй Ли. Производная алгебра 8' = Фг. Если D — дифференци-
дифференцирование любой алгебры ЭД, то WD с $2. Поэтому если D — диф-
дифференцирование алгебры 8, то eD = be. Далее, ad 8/ обладает
тем свойством, что e(adbf) = [e, bf] = be. Поэтому если E — D —
— ad 8/, то ? — дифференцирование и еЕ — 0. Тогда из условия
e = [ef] следует, что 0 — [е, /Е], откуда fE = ^e. Кроме того,
ad(—7г) удовлетворяет условиям ?ad(—^) = 0» /ad(—f?) =
= [/, — y^I === Т [?/1 — Тг- Поэтому Е = ad (— ~[е) — внутреннее диф-
дифференцирование и D — E-\-adbf — также внутреннее дифференци-
дифференцирование. Таким образом, каждое дифференцирование алгебры
% = Фе-\-Ф/ является внутренним.
В теории групп принято называть совершенной всякую группу,
все автоморфизмы которой являются внутренними и центр которой
состоит из единичного элемента. Если подгруппа Н совершенна и
инвариантна в G, то Н является прямым множителем группы G. По
аналогии мы будем называть алгебру Ли совершенной, если все ее
дифференцирования внутренние, а центр нулевой.
Предложение 3. Если &—совершенная алгебра, являю-
являющаяся идеалом в 8, то 8 = $®23, где 23 — идеал в 8.
Доказательство. Заметим прежде всего, что если $—идеал
в 8, то и его централизатор 23, т. е. множество элементов ft?g,
таких, что [kb] = 0 для всех k ? R, также является идеалом. Оче-
Очевидно, что 23 — подпространство, и если 6?23, а?8, то [k[ba]] =
c=—[a[kb]]—[b[ak]]=zQ—[b, k'\, k' = [ak]?$t, откуда [k [ba] ]=. 0
20 Г л / Основные понятия
для всех k?R и [?aj?23. Таким образом, 23 является идеалом.
Пусть теперь R — совершенная алгебра. Если c?$f|23, то с при-
принадлежит центру $ и, следовательно, с = 0. Поэтому $Г|23 = О.
Пусть, далее, а ?8. Поскольку $ — идеал в 2, ad а переводит $
в себя и поэтому Индуцирует дифференцирование D идеала $. Это
дифференцирование внутреннее, и, значит, мы можем найти такой
элемент &?$, что xD = [xa\ = [xk\ для каждого х?$. Тогда
Ь = а — к?Ъ и a = b-\-k, 6?23, k?R. Таким образом, 8 = $ +
-(- 23 = $ф23, а это и требовалось доказать.
Пример. Алгебра Фг+Ф/ из предыдущего примера является
совершенной.
§ 4. Описание алгебр Ли малых размерностей
Мы опишем теперь все алгебры Ли, размерность которых меньше
четырех. Пусть (ev е2 г„)—базис алгебры Ли 8; тогда [г,г(] = 0,
[ete Л = — [*ув(]. и поэтому для задания таблицы умножения в этом
базисе достаточно определить произведения [etej] для / < j. Мы
будем использовать в наших рассуждениях эти сокращенные таблицы
умножения:
I. dimg=l. Тогда 8 = Фг, [е'е] = 0.
II. dimg = 2
(а) 8' = О, й —абелева.
(б)й'^О. Поскольку 8 = Ф*-|-Ф/, й' = Ф[г/] имеет раз-
размерность единицу. "Мы можем выбрать элемент е так, что 2' = Фе.
Тогда [ef] = ae ф 0, и замена / на а-1/ позволяет положить \ef]=e.
Следовательно, 8 совпадает с алгеброй, рассмотренной в примере § 3.
Эта алгебра — единственная неабелева алгебра Ли размерности 2.
III. dim 2 = 3.
(а) 8' = 0, 8 абелева.
(б) dim 8' = 1, 8' с 6, где 6 — центр. Если 8' = Фе, то мы
запишем 8 = Фе -f- Ф/ ~Ь Ф^. Тогда 8' = Ф [fg]. Поэтому можно
положить [fg\ — е. Таким образом, алгебра 8 имеет базис (е, /, g)
с таблицей умножения
[/*] = *. [*/] = 0. [eg) = 0. A6)
Имеется лишь одна алгебра Ли, удовлетворяющая нашему условию
(если выполнены равенства A6), то условие Якоби удовлетворяется),
(в) dim8'=l, 8'$ 6, где 6 — центр. Если 8' = Фг, то суще-
существует элемент /, такой, что [ef] Ф 0. Тогда [е/] = фе Ф0 и можно
положить [ef] = e. Поэтому Фг-|-Ф/ — неабелева алгебра $t раз-
размерности 2. Так как $ 3 2', St — идеал, а так как $ — совершен-
совершенная алгебра, то 2 = ft®23, где 23 = Ф#. Поэтому 8 имеет базис
(е' /• S) с таблицей умножения
0. [fg] = 0. A7)
$ 4 Описание алгебр Ли малых размерностей 21
(г) dim 8' = 2. Алгебра 8' не может быть неабелевой двумерной
алгеброй Ли $, так как тогда имели бы место равенства 8 = $©23
и 8'= $' = $. Но St'czR. Поэтому 8' абелева. Пусть 8' = Фг +
+ Ф/ и 8 = Фе + Ф/ +Ф?. Тогда 8' = Ф [eg] -f Ф [fg] и, следова-
следовательно, adg индуцирует взаимно однозначное линейное отображение
в 8'. Поэтому алгебра 8 имеет базис (е, /, g) с таблицей умножения
fa. p\
где А = ( * ) — невырожденная матрица. Обратно, в каждом про-
\Т V
странстве 8 с базисом (е, /, g) мы можем определить произведе-
произведение [ab] так, что выполнены условия A8) и условие [аа] = 0. Тогда
llef]g]-{-l[fg]e]-{-llge]f] = O, и поэтому 8 является алгеброй Ли.
Какие изменения можно внести в таблицу умножения A8)? Наш вы-
выбор базиса равносилен следующему: мы выбираем базис (е, /)
алгебры 8' и дополняем его элементом g так, чтобы получить базис
алгебры 8 При изменении базиса 8' матрица А переходит в подоб-
подобную матрицу М~1АМ. Допустимым изменением элемента g является
-Замена этого элемента на элемент pg-{-x, рфО, р?Ф, х?8'. Тогда
[е, pg~^-x] — p[eg], lf,pg-\-x] = p[fg], вследствие чего матрица Л
переходит в матрицу рА. Поэтому матрицу А в таблице умножения
A8) мы можем заменить любой матрицей вида рВ, где В — матрица,
подобная А. Это означает, что мы имеем взаимно однозначное соот-
соответствие между алгебрами 8, удовлетворяющими условиям dim 8 — 3,
dim 8'"=2, и классами сопряженных элементов в двумерной группе
коллинеаций.
Если основное поле алгебраически замкнуто, мы можем выбрать А
в одной из следующих форм:
о
Это приводит к таким таблицам умножения:
= 0, [eg\ = e + $f, [fg]=f.
Различным элементам а соответствуют различные алгебры'), по-
поэтому мы получаем бесконечно много неизоморфных алгебр.
') Следует исключить случай, когда элементы а ф 0, а' ф 0 связаны
соотношением аа'= 1. Тогда они определяют одну и ту же алгебру, так как
1 /0 1\/1 0\,0 1\ /1 0\ „
_!_
Гл. I. Основные пон&тиЬ
(д) dim?' = 3. Пусть (ev ev е3)— базис, и положим [e2e3]~fv
[ezeA = f2, [e, е2\ = /ъ. Тогда (/р /2, Д)— тоже базис. Запишем
з
fi = 2^i/./' где А — (<хи) — невырожденная матрица. Единственное
условие Якоби, которое нужно наложить, следующее: [/i
-f- [/Зе3] = 0- Отсюда получаем соотношение
О = а12 [е2ех\ + а13 [e^il + <*2i ^1*2] + а2з \.еъеч\ + a3i
+ а32 1*2*з1 — —а12/з + а1з
Поэтому а;у = ау,> так что Л — симметрическая матрица. Пусть
(«р е2, е3) — другой базис, где 0, = 2lV/*yi >М==(^у)—невырожден-
>М==(^у)—невырожденная матрица. Положим 7j = [e2e3], /2 = fe3eib /з=[*1*2]> Для тройки
(i. У» Л), полученной циклической перестановкой индексов A, 2, 3),
имеем формулы
T, S
Матрица N = (vt]) = аи] M'— (M')~x dzi M'l). Матрица А свя-
свях
~х
зывает элементы / с элементами е, а матрица М~х связывает эле-
элементы е с элементами е. Поэтому, если А — матрица (al7-), такая,
что /, = 2 «г/у то
1 1 • A9)
Матрицы А и В называются мультипликативно коградиентными,
если В = pN'AN, где Af — невырожденная матрица и р — отличный
от нуля элемент поля Ф. В этом случае можно записать В =
=pa2(a~W)' A(a~1N), 0 = pdetAf, и если матрицы имеют три столбца
и три строки, то мы положим M = qN~x и В = \у.{М~1у АМ~1,
jj, =^ро2 = det Ж. Таким образом, мы получаем соотношение A9).
Вследствие этого матрицы Л и Л (симметрические) должны быть
мультипликативно коградиентны. Поэтому каждой алгебре й, удо-
удовлетворяющей нашим условиям, однозначно сопоставляется единствен-
единственный класс невырожденных мультипликативно коградиентных симме-
симметрических матриц. Имеется столько алгебр, сколько существует
классов таких матриц. Далее в этом параграфе мы будем предпола-
предполагать, что характеристика основного поля отлична от 2. Тогда каждый
коградиентный класс содержит диагональную матрицу вида diag {a, {3,1},
') Здесь М' — матрица, получающаяся из М транспоиировавием,
jM' — присоединенная матрица матрицы М', det Ш — определитель ма-
матрицы М'.—Прим. ред.
§ 4. Описание алгебр Ли малых размерностей 23
оф ф 0. Отсюда следует, что базис может быть выбран так, что
выполняются равенства
[eie2] = e3, [е2 e3]~aev [еъех\ — ^е2. B0)
Если основное поле — поле вещественных чисел, то имеются две
различные алгебры, соответствующие выбору а = C=1 и а = —1,
р = 1. Если поле алгебраически замкнуто, то можно положить
а == р = 1. Мы опишем сейчас некоторую частную алгебру в семей-
семействе алгебр, удовлетворяющих условию dim й = 3 = dim й . Наложим
на алгебру й следующее условие: существует элемент Л ?2, такой,
что ad А имеет характеристический корень а ф 0, а?Ф. Тогда най-
найдется вектор е Ф 0, такой, что [eh] — ead h = ae Ф 0, и так как
[М] = 0, то е и h — линейно независимы и являются частью базиса
(ev е2, e3)=z(e, h, /). Если (/р /2, Д) определены как раньше, то
симметрическая матрица (a(j) имеет вид
«12
a
«22 0 . B1)
О О/
Из формул [eh]=ae, [h, h] = 0, [fh] =— a/— ane — o.l2h сле-
следует, что характеристические корни эндоморфизма ad h равны 0, а,
— а.
Мы можем заменить / характеристическим вектором, соответ-
соответствующим корню — а!), так как этот вектор линейно независим
относительно пары (е, h). Поэтому мы можем предположить, что
[eh] = ae, [fh] = — а/. Если заменить h на 2a.~lh, то получится
[eh] = 2e, [fh] = — 2/. Из формулы B1) следует, что [ef]~$hфQ.
Заменив / на (З/, мы получим базис (е, /, К) с законом умно-
умножения
[eh] = 2e, [fh] = — 2/, [ef] = h. B2)
Мы видим, таким образом, что существует единственная алгебра,
удовлетворяющая нашим условиям.
Вскоре мы покажем, что каждая алгебра й, удовлетворяющая
условию dimfi = dimfi' = 3, проста, т. е. не имеет идеалов, отлич-
отличных от себя самой и от 0, и й' Ф 0. Если эта алгебра обладает
также тем свойством, что присоединенный эндоморфизм ad h неко-
некоторого ее элемента h имеет ненулевой характеристический корень
а в Ф, то она называется расщепляемой трехмерной простой
алгеброй Ли. В дальнейшем эта алгебра будет играть важную роль.
1) Вряд ли должно вызывать смущение употребление в этой книге еди-
единого прилагательного „характеристический" перед существительными „век-
„вектор", .корень", „многочлен" вместо более распространенных у нас терми-
терминов „собственный вектор", „собственное значение" и т. д.—Прим. ред,
24 Гл. I Основные понятия
§ 5. Представления и модули
Если ЭД — ассоциативная алгебра над полем Ф, то представлением
алгебры 31/называется гомоморфизм 31 в алгебру (S линейных пре-
преобразований векторного пространства Ш над Ф. Если в этом пред-
представлении а->А, Ь->В, то, по определению, a -{-b-> A -j- В,
<ха—>аЛ, <х?Ф, и ab->AB. Правым модулем над ассоциативной
алгеброй % (или правым ЭД-модулем) называется векторное простран-
пространство Ш над Ф вместе с отображением произведения Ш X 31 в 2К,
при котором элемент (х, а), х?Ш, а?ЭД, переходит в элемент
ха ? Ш. Это отображение должно удовлетворять условиям:
1. (xl-\-x2)a = xla-\-x2a, х(а1-\-а2) = ха1-{-ха2.
2. а(ха) = (ах)а = х(аа), а?Ф.
3. x(ab) = (xa)b.
Если а -> А — представление алгебры ЭД, то пространство пред-
представления 9Й мы можем превратить в правый ЭД-модуль, определив
ха==хА, х?Ш. Таким образом, мы получаем следующие равенства:
(jCj-(- х2) а = (jCj -f- х2) А = х1А-\-х2А— хха-\- х\а,
х (ах + о2) = х(А1Г-\- А2) = хА1 + хА2 = хах-\- ха2,
а (ха) = а (хА) = (ах) А — (ах) а,
а (хА) = л; (аА) = х (аа),
х (ab) = л; (АВ) = (хА)В = (ха) Ь.
Обратно, если 9Й—правый ЭД-модуль, то для каждого а?ЭД обозна-
обозначим через Л отображение л; -> ха. Тогда первая часть вышеприве-
вышеприведенного условия 1 и первая часть условия 2 показывают, что А—ли-
А—линейное преобразование пространства 9Й над Ф. Из условий 1—3
следует также, что а-*А является представлением.
В теории представлений, а также -в других разделах теории
ассоциативных алгебр изучаются преимущественно алгебры с единицей.
Действительно, часто бывает удобно ограничиться рассмотрением
таких алгебр и изучать лишь гомоморфизмы, отображающие единич-
единичный элемент в единичный.
В дальнейшем, однако, иногда будет полезно рассматривать ассо-
ассоциативные алгебры без единицы. Поэтому мы примем следующее
соглашение о терминологии: под алгеброй без каких-либо допол~
нательных оговорок мы будем всегда понимать ассоциативную
алгебру с единичным элементом, „подалгеброй" такой алгебры
мы будем называть подалгебру в обычном смысле, содержащую еди-
единичный элемент, и „гомоморфизмом" — обычный гомоморфизм, ото-
отображающий единицу в единицу'). В частности, это будет относиться
1) Разумеется, и алгебра Ли часто называется просто алгеброй, но из
контекста всегда ясно, что именно имеется в виду. — Прим. ред.
S Представления и модули
и к представлениям. Соответствующее понятие модуля определяется
условиями 1 — 3, а также условием
4. xl —х, х?Т1.
'Если мы захотим рассматривать алгебры, которые, возможно, не
имеют единицы, то мы будем говорить об „ассоциативной алгебре" St.
В случае же, если мы будем опускать условие 4, то мы будем
говорить о „модуле над ассоциативной алгеброй", а не о модуле
над „алгеброй". Алгебра 9t может рассматриваться как правый
; SC-модуль, если определить произведение ха, как оно определено
в ЭД. Тогда выполнение условий 1—3 следует из аксиом алгебры,
> а выполнение условия 4 следует из определения единицы. Предста-
Представление а-+А, где А является линейным преобразованием х-+ха,
. называется регулярным представлением. Мы видели (§ 2), что ре-
;;гулярное представление является точным или, иными словами, изо-
|§морфизмом.
Пусть теперь 8 — алгебра Ли. Назовем представлением алгебры 8
iгомоморфизм /—>/. алгебры й в алгебру Ли ®?, где (S — алгебра
^линейных преобразований векторного пространства Ш над Ф. Усло-
Условия, которым должен удовлетворять этот гомоморфизм, следующие:
lx->Lv 12->L2, то
И -+LL ~LL—LL B3)
^Определим теперь произведение xl, где д: ^ 9Й, / ^ й, формулой
" Kl — xL. Тогда равенства B3) и линейность преобразования L дают
?<5ледуюшие условия:
1 • l^i """у Ло) ' — -' Ait I Ant» A l'| I *oJ "'""* Afrj ""j" Afrn»
3. jc I/j/2] = (jc/,) /a — (де/д) /j.
Мы используем теперь эти условия для определения понятия
|?-модуля, где й—алгебра Ли. Назовем 8-модулем векторное про-
пространство Ш над Ф, для которого существует такое отображение
: X й в SR, что образ xl удовлетворяет вышеприведенным усло-
Гвиям 1—3.
Как и в ассоциативном случае, понятия модуля и представления
9КВивалентны. Так, мы уже указывали, что если отображение 1-+L
Является представлением, то пространство представления 9Й можно
рассматривать как модуль. С другой стороны, если Ш—~модуль
над й, то для / ? й мы обозначим через L отображение л; -> xl.
Тогда L линейно относительно WI над Ф и 1-+L — представление
алгебры й линейными преобразованиями в 9Й над Ф.
Заметим далее, что алгебра й сама может быть рассмотрена как
S-модуль, если определить xl как произведение [xl] в й. 1огда
условия 1 и 2 являются следствиями аксиом алгебры, а условие 3
26 Гл I Основные понятия
следует из тождества Якоби и кососимметричности. Мы обозначали
преобразование, соответствующее I: х—> [xl], через ad/.
Представление / —> ad /, определенное этим модулем, называется
присоединенным представлением алгебры й. Напомним, что ото-
отображения ad/ являются дифференцированиями алгебры й.
Если Ш — модуль над алгеброй Ли 8, то мы можем рассматри-
рассматривать WI как абелеву алгебру Ли с произведением [лгу] = 0 Тогда
отображения x->xl являются линейными преобразованиями в Ш и,
вследствие тривиальности операции умножения в Ш,—также дифферен-
дифференцированиями. Обобщая эту ситуацию, предположим, что простран-
пространство Ш является й-модулем и в то же время алгеброй Ли, и до-
допустим, что операции х —>¦ xl суть дифференцирования алгебры Зй.
Таким образом, в дополнение к аксиомам алгебры Ли в й и 2К и
к условиям 1—3, приведенным выше, получаем также условие
4. [xlx2]l = lxll, x2]+[xv jc2/].
Пусть теперь Л — прямая сумма векторных пространств й и ffl.
Определим в Л закон умножения по формуле
[*, -+- lv х2 -Ь у = [ххх2] -(- xxl2 — x2lx 4- 1Щ- B4)
Очевидно, что так определенное умножение будет билинейным, и,
таким образом, в пространстве Л вводится структура (неассоциативной)
алгебры.
Более того, верны следующие соотношения:
[х + 1, x + l\ = Q-\-xl — xl + 0 = 0;
хг-\- 1ъ\ = [[х1х2\хъ]-\-[[х112\хд\ +
\к\ хъ\ + [[*i*2l 'з! +
+ [\хх12\ /3] -Ь [[/,*21 у + \\Ш У =
— [[х1х2\хъ\-{-[х112, хь\ — [x2lv х3] — х3[Щ-f-
+ \ххх2] /3 + (*А) ^з — (*А) 'з + [ВД 'з! =
= [[х1х2]х3]-\-[х112, х3]
Если мы переставим циклически индексы 1, 2, 3 и сложим полу-
полученные равенства, то члены, в которых л; или / встречаются три
раза, при сложении дадут нуль (это следует из выполнения тожде-
тождества Якоби в алгебрах й и Ш); члены, в которых встречаются два jc
и одно /, при сложении дадут равенство
[xxl2, x3]~ [x2lv *3]-И*А. x2] + [xv х2У4-
-\-[х21г, хх] — [хъ12, хх]-\-[Х21у *314 [*2. *А1 +
Ч- [^i> х2] — [хх13, х2] -f [лг3/2, хх] 4- [лг3, хх12] == 0.
§ 5. Представления и модули 27
Члены, в которых встречаются два / и один х, при сложении дают
равенство
(Л) h + (') h -+¦ (* A) k
A) 'з
Это показывает, что пространство 5t = 8 © 2К является алгеброй
Ли. Из определяющего соотношения B4) и того факта, что [л:/] ? Зй
для л:?2К, /?й, немедленно следует, что й— подалгебра алгебры 5t,
а 2К — идеал в Л. Назовем 5t расщепляемым расширением ал-
алгебры й посредством алгебры 9Й1).
Мы получим важный частный случай описанной ситуации, если
предположим, что 2К = Й — алгебра Ли и й = 35, где 35 — алгебра
дифференцирований. Так как 35 есть по определению алгебра Ли
линейных преобразований, то тождественное отображение является
представлением алгебры 3) в й Алгебра й наделяется строением
©-модуля, если мы определим произведение ID = ID, где/^й, D?3).
Расщепляемое расширение алгебры 3) посредством алгебры й,
ф = 3) фй, называется голоморфом алгебры й. Это аналогично
понятию голоморфа группы, который является расширением самой
этой группы при помощи гррты ее автоморфизмов.
Мы можем применить подобную конструкцию 5t = 3)j © й в том
случае, когда й— алгебра Ли и Ъх — некоторая подалгебра ее алгебры
дифференцирований. В частности, это бывает полезным, когда
<SI = <i>D — подалгебра кратных некоторого определенного дифферен-
дифференцирования D алгебры 8.
Другой важный случай расщепляемого расширения получается,
если взять две произвольные алгебры Ли й и Ш и рассмотреть 9Й
как тривиальный модуль над 8, положив ml = 0, m^SK, /?й.
Алгебра Ли & = Й©ЗЙ называется прямой суммой алгебр й и SK.
Вообще, если й^ й2. •••. йг — алгебры Ли, прямой суммой этих
алгебр й = fij © Й2 © ¦.. © йг является прямая сумма векторных
пространств алгебр ?,, в которой определено произведение Ли
[Г Г I Г
2^> 2OTi =2['t/7*J- Как и в теории групп, если й — алгебра Ли,
содержащая такие идеалы й?, что ? = ?1фй2ф ... фйг как вектор-
векторное пространство, то [ltlj] ?йг ПЙ; = О, где ^?й;, f/€?/ и/^у.
Тогда й изоморфна прямой сумме алгебр Ли й^, и мы будем
говорить, что алгебра й является прямой суммой своих идеалов ?,.
1) Этот термин употребляется в книге семинар „Софус Ли" [1]. Прихо-
Приходится считаться с тем, что в терминологии, принятой в теории расширений
алгебр Ли и в теории расширений абстрактных групп, имеются расхожде-
расхождения, обусловленные разными причинами. Впрочем, в настоящей книге воп-
вопросам теории расширений отведено скромное место —Прим. ред.
28 Гл I. Основные понятия
Ядро R гомоморфизма tj алгебры Ли 8 в алгебру Ли WI есть
идеал в 8, а образ 2у\ — подалгебра, алгебры 2Й. Основная теорема
о гомоморфизмах утверждает, что йт)~ й/$ (при соответствии
/-|-S?->h)): Напомним, что фактор й/$ является векторным простран-
пространством й/$, в котором структура алгебры вводится заданием умноже-
умножения [^-j-Л. ^2 + ЭД = [^2]Н~^- Таким образом, Й/& есть алгебра Ли.
Ядром присоединенного представления является множество таких
элементов с, что [хс] = 0 для всех х. Следовательно, ядро совпадает
с центром (§. алгебры й. Образом 2 = ad й является алгебра внутрен-
внутренних дифференцирований, и мы получаем изоморфизм 8/6^2. Если
E = 0, Toadfi — алгебра Ли линейных преобразований, изоморфная й.
В этом случае мы очень просто получаем точное представление
алгебры Ли 8. В дальнейшем будет показано, что каждая алгебра
Ли 8 имеет точное представление и что каждая конечномерная
алгебра Ли имеет точное конечномерное представление, т. е. точное
представление, действующее в конечномерном пространстве.
Примеры. Определим теперь матрицы присоединенных предста-
представлений для двух наших примеров:
а) Пусть 8—алгебра Ли с базисом (е, /), [ef] = е. Тогда е ad е = 0,
/ade = — е, eadf — e, /ad/ = 0. Поэтому в базисе (е, /) матрич-
матричное представление имеет вид
/ 0 0\ /1 ON
е~*\—1 о)' f~*\0 0,
б) Пусть й — алгебра Ли с базисом (ev e2, е^ и таблицей умно-
умножения \е1е2\ = еь, [e2e3\ = ev [е3ех\ = е2. В этом случае elade1=O,
ejade3 = — e2, e2ade3 = ev e3ade3 = 0. Поэтому матричное предста-
представление имеет вид
'0 0 0\ / 0 0 1\ /0 -1 0^
0 0 —1 J. <?2-И 0 0 0J, ег-Л 1 0 0
vo 1 о/ V—1 оо/ \о о о;
Заметим, что эти матрицы кососимметричны, и они образуют базис
в пространстве кососимметрических матриц. Поэтому алгебра й изо-
изоморфна алгебре Ли кососимметрических матриц в матричной алгебре Ф3.
§ 6. Некоторые основные операции над модулями
Понятие подмодуля W модуля Ш над ассоциативной алгеброй или
над алгеброй Ли очевидно: 9f есть подпространство в Ш, замкнутое
относительно умножения на элементы алгебры. Если 0? — подмодуль,
то можно получить фактормодуль Ш/Ш, который является простран-
пространством классов смежности SK/51? с операцией умножения (х-\-Ща =
§ 6 Некоторые основные операции над модулями
29
= jca-|-9^> где а принадлежит алгебре. Если fflx и 9Й2 — два модуля
над ассоциативной алгеброй или алгеброй Ли, то пространство
2^1 © Ш2 является модулем относительно умножения (лгх -f- x2) a =
= хха-\-х2а, xt?Tlt. Этот модуль называется прямой суммой
Ш1@Ш2 двух заданных модулей. Аналогичная конструкция может
быть применена для любого числа модулей.
Понятия из теории модулей, которые мы только что ввели, при-
ложимы как к ассоциативным алгебрам, так и к алгебрам Ли. Рас-
Рассмотрим теперь понятия, применимые только в случае алгебр Ли.
К ним относятся понятие тензорного произведения модулей и понятие
контрагредиентного модуля, аналогичные хорошо известным понятиям
в теории представлений групп.
Предположим сначала, что 1->LX и 1—>L2 — два представления
алгебры Ли ? линейными преобразованиями, действующими в одном
и том же векторном пространстве WI над Ф. Допустим, кроме того,
что если Lx — любое преобразование из первого представления и
М2 — из второго, то [LXM2] = LXM2— M2LX — O. Определим теперь
некоторое новое отображение алгебры й в алгебру 6? линейных
преобразований пространства 9Й следующим образом:
1->LX + L2. B5)
Так как это отображение является суммой линейных отображений
1—>LX и 1—>L2, то оно тоже линейно. Пусть теперь т-+Мх, т—>М2,
так что в новом отображении т —> Мх -j- M2. Тогда
М2] =
B6)
и поскольку [tm] -> [ЬХМХ] ~\~ [L2M2], новое отображение будет пред-
представлением. (Замечание: ничего подобного не имеет места в ассо-
ассоциативном случае.)
Предположим далее, что Tlt, Tl2 — любые два модуля над алге-
алгеброй Ли й. Пусть 2К = 2К1®2Я2(=з2Я1®ф2К2) — тензорное (или
кронекеровское, или прямое) произведение модулей SKj и 9Й2.
Напомним, что если At — линейное преобразование в 9Й(, то отобра-
отображение 2 х) ® i>j -> S XjAx (g) yjA2, где Xj ^ fflv y} ? 3ft2, является
.линейным преобразованием Л1 ® Л2 в Шх ® 9Я2. Тензорное произведе-
произведение удовлетворяет следующим условиям:
ш
(Ах -f Bj) ® А2 = А! ® А2
Ах ®(Л2 -f В2) = Ах ® А2 4-
® Л2,
®В2,
B7)
30 Г л I. Основные понятия
Из этих соотношений легко следует, что отображение Al->A1 ® 12,
где 12 — единица в 9Й2, будет гомоморфизмом алгебры ©(SKj) линей-
ных преобразований пространства 2R, в алгебру ® (SKj ® 2Й2). Ана-
Аналогично отображение Л2->11®Л2 является гомоморфизмом алгебры
(S ЗК в 6 BЙ! ® 2К2). Пусть теперь Rt — представление, определен-
определенр
ное модулем 3Rt. Линейное преобразование / ', соответствующее
определяется как xt
Композиция гомоморфизма Ли /—>/*' с ассоциативным (а сле-
следовательно, и лиевым) гомоморфизмом алгебры Щ, (Wtt) в (S (ЗС?! ® 2К2)
есть представление алгебры й, действующее в SKj ® 9Й2. Таким
образом, мы получаем два представления алгебры 8:
l-+lRl®\3 и /-^Ц®^. B8)
Если I, m ? 2, то
(/*«® la)(l,®»'?') = ''?1®»'?l = 0i®«ft)(''?1® lj)- B^)
Поэтому упомянутое выше условие коммутативности выполняется.
Отсюда следует, что отображение
1->1^®\2+\х®1*г C0)
является представлением алгебры 2, действующим в SWj®^. Поэтому
2Ki® 2К2 есть 2-модуль с законом композиции, определенным ра-
равенством
Модуль Шх ® Ш2, определенный таким образом, называется тен-
тензорным произведением двух модулей 2К2. Та же самая терминология
применяется и в случае представлений; тензорное произведение двух
представлений мы будем обозначать .через RX®R2-
Рассмотрим теперь модуль Ли Ш и дуальное пространство 9Й*
линейных функций на 9Й (со значениями в основном поле). Обозна-
Обозначим через {х, у*) значение линейной функции у* на векторе л; ? ffi..
Тогда {х, у*) ? Ф, и это произведение билинейно:
(х, у\ + yl) = (х, у$ +<*.*;>. C2)
(ах, у*) = а(х, у*)=(х, ауГ).
Это произведение также невырождено. Каждое линейное преобра-
преобразование А пространства Ш определяет сопряженное (или транспони-
транспонированное) преобразование А* пространства Ш*, такое, что
(хА, у*) = (х, у*А*). C3)
§ 6 Некоторые ot новные операции нао моду гями 31
Отображение А—уА* является ассоциативным антигомоморфизмом
6 BЯ) в 6 (Щ*). Рассмотрим теперь отображение А -> — А*. Оно
линейно, и для него выполняются условия
[ — А*, — В*] = [А*, В*]~А*В* — В*А* =
C4)
Поэтому А -> — А* есть гомоморфизм & (Tt)L в (S (Ш\. Если взято
композицию представления l—>lR, определенного модулем ffl, и
отображения А —>— Л*, то получится новое представление 1—>
алгебры g. Для соответствующего модуля ffl* это дает
Поэтому характеристическим свойством, связывающим два модуля,
является соотношение
{х, y'l) + {xl, у*> = 0. C5)
Мы называем модуль Ш*, определенный таким способом, конгпра-
гредиентным модулем модуля Ш и обозначаем соответствующее
представление через R*.
Напомним, что если 9Й — конечномерное пространство, то суще-
существует естественный изоморфизм пространства Ш <2> 2К* на векторное
пространство й(Ш). Если 2 х,® У*?2Я ® Ш*, то соответствующим
линейным преобразованием пространства Ш является преобразова-
преобразование х->2(*> У^)хг Если 2К —модуль над й, то 2Й* и 2Я <g> ЗИ* —
также модули. По определению,
Если мы обозначим отображение лг-^-л;/ через lR, то отображе-
отображением — {lR)* будет л;* -> л;*Л Тогда в пространстве представления
2Я®2К* отображение, соответствующее /, переводит 2*/® У/
в 2*^*®У1 — 2 Лi ® Уг (^)*- Элементы алгебры 6BЙ), соответ-
соответствующие этим двум преобразованиям, следующие:
- 2<
Из этих формул следует, что В = [А, lR]. Мы можем интерпре-
интерпретировать этот результат следующим образом Рассмотрим произ-
произвольный й-модуль WI и алгебру ®BК). Если lR — преобразование,
Соответствующее I, то отображение X—>[Х, lR] является предста-
32 Г л I Основные понятия
влением алгебры 8, действующим в (§.. Факт, который мы только
что доказали, заключается в том, что это представление эквивалентно
представлению в Ш <g> 9И*. т. е. модули ® и *ДО ® Ш* изоморфны.
Только что указанный результат может быть обобщен на пару
векторных пространств SDlj, SDtj. Напомним, что множество линей-
линейных преобразований E(9й2, SWj) пространства 2^ в пространство Шг
является векторным пространством при обычном определении ?ло-
жения и скалярного умножения. Если пространства конечномерны,
то существует естественный изоморфизм тензорного произведения
а^фЭДг на ®(9R2. Щ\ при котором элементу 2 *; ® У*- х1?Ш1,
У*?9Я2, соответствует линейное отображение у->2 {У> y*i)xi
пространства 9Й2 в Щг. Если Шг и 9Й2 есть й-модули, то и
6 (ЗИг, Tii) является й-модулем относительно ^закона композиции АТ-ёэ
isX/*' — lR*X, Как и в случае одного пространства, этот модуль
изоморфен SWj®^ при изоморфизме пространств, определенном
ранее.
§ 7. Идеалы, разрешимость, нильпотентность
Пусть Sj и 332 — подпространства алгебры Ли 8. Обозначим
через З^ПЗЗг пересечение этих подпространств, а через З^ + ЭЗг —
подпространство, натянутое на 58: и 582. Подпространство З^-ЪЗЗг
является совокупностью элементов вида Ьх + Ьг, где ^ ? 93,. Опреде-
Определим теперь [QSjSSal Как подпространство, натянутое на все произве-
произведения [ЬгЬ2], */€®е Отсюда сразу следует, что элементами про-
пространства [SSj^y являются суммы 2l*iA;l' ^/€®г- ^ы предпола-
предполагаем, что читатель знаком со (структурными) свойствами множества
подпространств с введенными в нем законами композиции П и +•
а сейчас хотим сформулировать основные свойства закона компози-
композиции [SBjSy- Ниже мы перечислим эти свойства, оставив проверку
их читателю.
1.
2. [93, + 562, »а1 = [5ВД + [ВД
з. i [»,зз2] з
4. [33,П»2.
Подпространство 93 является идеалом тогда и только тогда,
когда [-ЙЙ] ? &• Пересечение и сумма идеалов вновь образует идеал,
а свойство 3, если положить 233 = й, показывает, что это же верно
для (лиева) произведения идеалов. В частности, очевидно, что члены
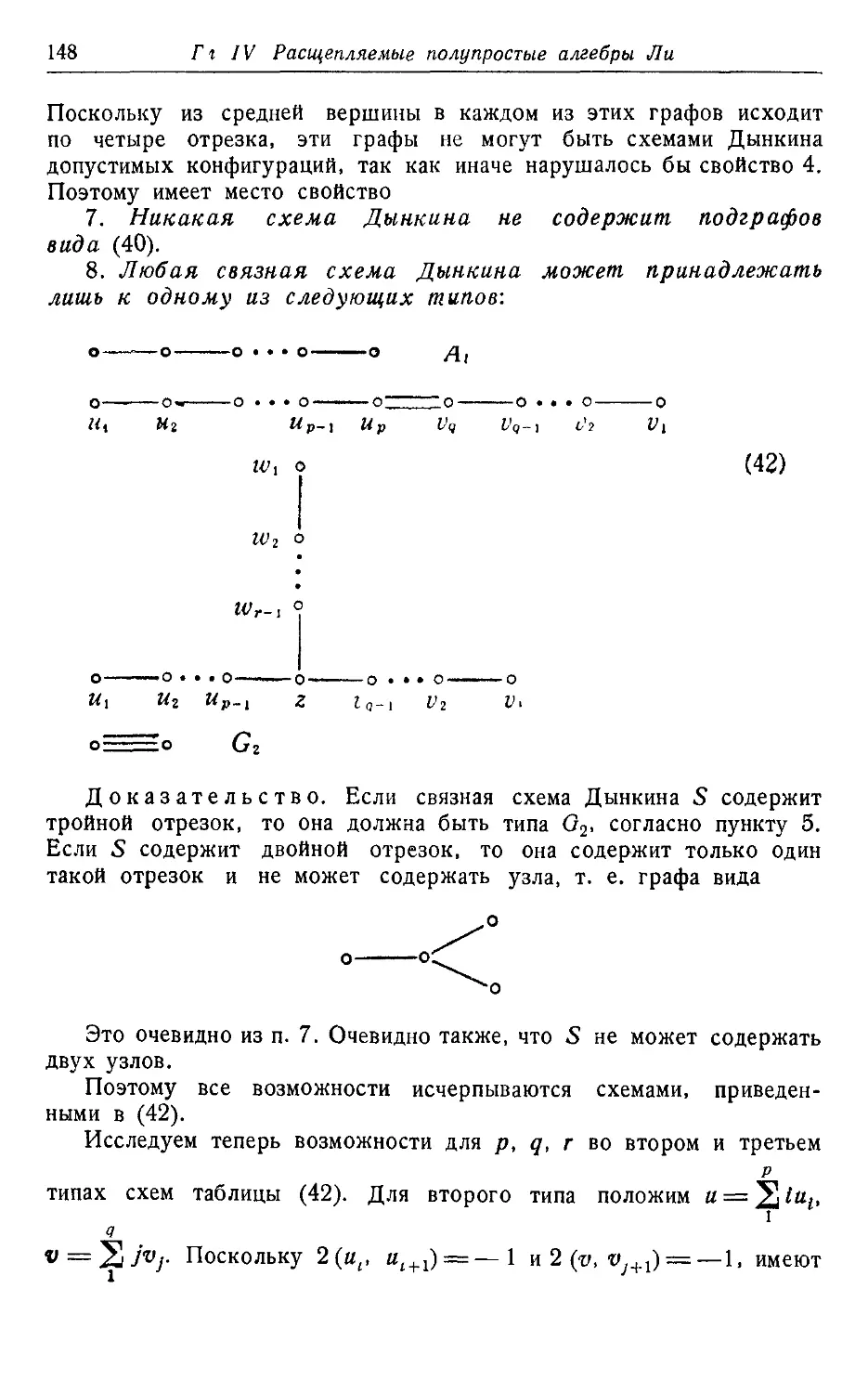
§ 7 Идеалы разрешимость, нильпотентность 33
производного ряда
2э8' = [22] э
Э8" = [2'2']Э ... C6)
являются идеалами'). То же самое верно для членов нижнего цен-
центрального ряда
2 = 22=2'3
... C7)
Эти ряды аналогичны производному ряду и нижнему центральному
ряду группы. Вообще если 23 есть идеал в 2, то производные
алгебры 23 и степени 23 являются идеалами. Заметим также, что
если т; — гомоморфизм алгебры 8 в другую алгебру Ли, то (81))т; =
= Bт;)(<) и B*) т; = Bт))г. Эти тождества легко доказываются индук-
индукцией по /.
Алгебра Ли называется разрешимой, если 2<Л) = 0 для некото-
некоторого положительного числа Л. Каждая абелева алгебра разрешима,
и из описания алгебр Ли размерностей, не превосходящих 3, сле-
следует, что все эти алгебры разрешимы, за исключением тех, для
которых dim 2 = 3 = dim 8'. Другим примером разрешимых алгебр
Ли является алгебра треугольных матриц (см. упражнение 12 в конце
главы).
Лемма. Любая подалгебра и любой гомоморфный образ
разрешимой алгебры Ли разрешимы. Если 8 содержит разре-
¦ шамый идеал 23, такой, что факторалгебра 8/23 разрешима,
то и сама алгебра 2 разрешима.
Доказательство. Первые два утверждения очевидны. Если,
далее, 23 — такой идеал в 2, что 2/23 разрешима, то 2<Л) ? 23 для
некоторого положительного числа п. Действительно, пусть у\ — ка-
канонический гомоморфизм / —>- / —(— 23 алгебры 8 на 2/23. Тогда
(8(Л)) т) = Bт))(Л) = B/23)(Л) = 0, если h достаточно велико. Поэтому
8(Л) Яв 23. Если идеал 23 разрешим, то 23(А) = 0 для некоторого k.
Поэтому чз 2(Л)?23 следует, что 2(Л+6) с ©<*> == 0, и 8 — раз-
разрешима.
') Иногда (например, в книге семинара „Софус Ли" [1]) вводят не-
несколько иную нумерацию для членов производного ряда, а именно
э _ _ -Прим. ред
3 Н Джекобсон
34 Гл 1 Основные понятия
Предложение 4. Сумма любых двух разрешимых идеа-
идеалов есть снова разрешимый идеал.
Доказательство. Пусть 23: и 232 — разрешимые идеалы.
По одной из известных теорем об изоморфизмах пересечение 93г П 232
есть идеал в 33j и B^ -f- 232)/232 ^ ®i/(®i П 232). Последняя фактор-
алгебра разрешима, поскольку она является гомоморфным образом
разрешимой алгебры 23j. Так как идеал 232 разрешим, то по пред-
предшествующей лемме идеал 93г -+- 232 также разрешим.
Предположим теперь, что алгебра 8 имеет конечную размерность,
и пусть ® — разрешимый идеал максимальной размерности в й.
Тогда из предложения 4 следует, что если 23 — любой разрешимый
идеал в й, то © + 23 — также разрешимый идеал. Но ®-|-23 = ®,
поскольку размерность идеала ® максимальна по предположению.
Следовательно, ® Ш 23. Этим доказано существование разрешимого
идеала S, содержащего любой другой разрешимый идеал. Мы на-
назовем ® радикалом алгебры й. Если ® —О, т. е. если алгебра 8
не имеет разрешимых идеалов, отличных от 0, то алгебра й назы-
называется полупростой. Если 8 не имеет вообще идеалов, отличных
от 0 и й, и если й' Ф О, то, как мы уже упоминали в конце § 4,
алгебра й называется простой. Если й проста, а ®— ее радикал,
то либо 8 = ®, либо ® = 0. Но если 8 = ®, то S' с: ® и ®'—
идеал, так что в'= 8' = 0, что противоречит определению. Поэтому
® = 0, т. е. из условия простоты следует полупростота*. Если
® — радикал, то любой разрешимый идеал в 8/© имеет вид 23/®,
где 23 — идеал в й. Но идеал 23 разрешим по лемме; поэтому 23 С ®
и 23/® = 0. Таким образом, алгебра 8/® полупроста. Если 23 — не-
ненулевой разрешимый идеал в й и %ф~1) Ф 0, 23(Л) = 0, то 230' —
абелев идеал в 8, отличный от нуля. Поэтому алгебра 8 полупроста,
если в ней нет ненулевых абелевых идеалов.
Трехмерные алгебры Ли, для которых dim8/ = 3 (или 8' = 8),
просты. Действительно, если 23 — идеал в й, такой, что 0 =? 23 =? 8,
то 23 и й/23 имеют размерность один или два, т. е. разрешимы.
Но тогда и 8 разрешима, что противоречит условию 8' = 8.
Алгебра Ли й называется нильпотентной, если 8й = 0 для не-
некоторого положительного числа k.
Предложение 5. [S'S-'l с 8'Ч
Доказательство. По определению [S'S] = 8'+1. Допустим,
что уже доказано включение [S'S-'] S %l+l для всех /. Тогда
[«V+11 = [8* [8;8] ] с [ [8'Й18'] +
-1- [ ViW] 8] S [8/+1Й;1 -f [S'+'S] с 8'+/+1.
Из этого результата следует, что произведение k сомножителей 8
при любой расстановке скобок содержится в 8*. Поскольку 8(*'
§ 7 Идеалы, разрешимость, нильпотентность 35
является произведением 2й таких сомножителей, то 8<ft) ? 82 . По-
этому, если алгебра 8 нильпотентна, например 8 =0, то 8 =0
и 8 разрешима. Обратное утверждение неверно, поскольку двумер-
двумерная неабелева алгебра Ли разрешима, но не нильпотентна. Множество
нильтреугольных матриц, т. е. множество треугольных матриц
с нулями на диагонали, является нильпотентной подалгеброй ал-
алгебры Ф„?, где Ф„ — алгебра всех я X я-матриц.
Предложение 6. Сумма нильпотентных идеалов ниль-
нильпотентна.
Доказательство. Заметим сперва, что если 23— идеал, то
любое произведение [. .. [ [^Д21 $з1 •¦¦ ^fel- B котором h сомножи-
сомножителей $( = 23, а остальные ^,==2, содержится в 23ЛB3° = 8). Этот
результат получается простой индукцией по к. Рассмотрим далее
два идеала 23: и 232 и идеал 251 + S82. Тогда B3:-f-232)m содержится
в сумме членов [...[[%%]%]¦¦¦ %т\. где % = % или 232.
Каждый такой член содержит или [/я/2] раз сомножителем 23^ или
[/я/2] раз 232, где [от/2] — целая часть числа от/2; поэтому этот
член содержится в SB1/"'21 либо в 232т/21. Следовательно,
? 23[im/2]
Отсюда, если 23: и 232 нильпотентны, то и сумма 33^ —1— 332 нильпо-
нильпотентна.
Теперь, так же как и в случае разрешимых идеалов, можно
сделать заключение, что в конечномерной алгебре Ли 2 существует
нильпотентный идеал У1, содержащий каждый нильпотентный идеал
из 8. Мы назовем 31 ниль-радикалом алгебры 8. Он содержится
в радикале ©. В случае двумерной неабелевой алгебры Фе-(~Ф/,
\ef] = e, <S = 8 и У\ = Фе. Факторалгебра 8/ЭТ абелева и поэтому
нильпотентна. Таким образом, возможно строгое включение бэ?!,
а 8/!ЭТ может иметь ненулевой ниль-радикал.
Теория нильпотентных идеалов и радикалов имеет аналог в слу-
случае ассоциативных алгебр. Если 2^ и 232 — подпространства ассо-
ассоциативной алгебры %, то через ЗЭ^ обозначается подпространство,
натянутое на все произведения Ьф2, bt ? 23f. Алгебра Щ называется
нильпотентной, если существует такое положительное число k,
что %k = 0 (Ж1 — 21, Жк =Жк~1Ж). Это эквивалентно тому, что
каждое произведение k элементов из % равно 0. Если 3^ и 512 —
нильпотентные идеалы в %, то, как легко доказать, 9^1 +^г — тоже
нильпотентный идеал. Поэтому, если алгебра Щ конечномерна, то
в % существует максимальный нильпотентный идеал SR, содержащий
каждый нильпотентный идеал. Идеал SR называется радикалом
алгебры %. Алгебра St/SR полупроста в том смысле, что она
36 Г л I Основные понятия
не имеет нильпотентных идеалов, отличных от нуля. Доказательства
этих утверждений аналогичны соответствующим доказательствам для
алгебр Ли и предлагаются в качестве упражнений,
§ 8. Расширение основного поля
Мы будем предполагать, что читатель знаком с основными опре-
определениями и результатами относительно тензорных произведений и
расширений поля операторов векторных пространств и (неассоциа-
(неассоциативных) алгебр. Приведем без доказательств основные свойства,
которые понадобятся нам в дальнейшем.
Пусть Ж, 58 — произвольные (неассоциативные) алгебры над Ф.
Тогда в векторном пространстве Ж <g> 23 (% ® ф 23) можно ввести
структуру (неассоциативной) алгебры, определив закон умножения
равенством (^ at ®bt\ (^ a'}®b'\ — 2 a^'^bfi'^ где а(, а'}?Ж,
br Ь'.^Ъ Если Ж, 23 ассоциативны, то алгебра Ж®23 также ассо-
ассоциативна. Если Р—расширение поля Ф и Щ — произвольная алгебра,
то Ф-алгебру Р ®Ж можно рассматривать как (неассоциативную)
алгебру над Р, определив закон умножения равенством рBр<® я/) =
= 2 РР< ® ai> Р> Р( <Е Р> ai 6 $• Обозначим это „расширение" алгебры %
через Ур. Такие расширения алгебр Ли будут играть иногда в даль-
дальнейшем важную роль.
Напомним некоторые основные свойства расширений ЖР и Шр,
где ЭД? —векторное пространство над Ф, а Шр — тензорное произ-
произведение Р®Ш, рассматриваемое как векторное пространство над Р
относительно умножения на скаляры р B Р< <8>-*0 = 2 РР<® хг ?•
р(?Я, х^Ш. Если {е(| /?/} —базис пространства Ш? над Ф, то
A<2)ег) — базис пространства Ш1Р над Р. Множество Ф-линейных
комбинаций этих элементов совпадает с подмножеством {1 ®х\х? W\
пространства Ш1Р. Это множество является Ф-подпространством про-
пространства Шр, изоморфным с Ш. Мы можем отождествить 1 ® х
с х, а множество {1®jc} — с Ш. Таким образом, Зй можно рас-
рассматривать как Ф-подпространство в 9ЛР, удовлетворяющее следую-
следующим двум условиям: A) Р-пространство, натянутое на Ш, есть $IР,
B) любое подмножество в Ш, линейно независимое над Ф, является
линейно независимым над Р. Отсюда следует, что любой базис про-
пространства Ш над Ф является базисом пространства Ш над Р. Если
Ж — (неассоциативная) алгебра, то только что описанное отожде-
отождествление позволяет рассматривать Ж как Ф-подалгебру алгебры ЖР.
Свойства A) и B) являются характеристическими. Действительно,
пусть Ш — векторное пространство над Р, Ф — подполе поля Р,
так что Ш можно рассматривать и как пространство над Ф. Допу-
Допустим, что Ш — подпространство пространства Ш над Ф, удовлетво-
§ 8 Расширение основного поля 37
*• ряющее условиям A) и B). Тогда отображение
Pi?P, хс?Ш, — изоморфизм Шр и Ш. Аналогично если % — (не-
f ассоциативная) алгебра над Р и % — Ф-подалгебра, удовлетворяющая
условиям A) и B), то имеет место указанный изоморфизм алгебр
; - 9СР и С
Если Ж — ассоциативная алгебра, то из выполнения условия
, (аа1) а" — а (а'а") в % следует, что алгебра $р также ассоциативна.
ш* Аналогично если 31 — алгебра Ли, то из условий [аа] = 0, [аа'\~
Г = — [а'а], {[аа'\а"\-\- [[а'а"\а\-\-{[а"а\а'\ = 0 следует, что
ф. 4 ШР — алгебра Ли.
sJ Если Ш — подпространство в 9Й, то Р-подпространство P9f,
-*1* * порожденное 91, можно отождествить с Шр. Если S — подалгебра
j, (идеал) в %, то 8Р(=Я$8) является подалгеброй (идеалом) в %р.
i* Идеал (ЭДРJ алгебры %р будет множеством Р-линейных комбинаций
элементов аа', а,а'^%. Поэтому (йрJ = (%2)Р. Если 8 — алгебра
Ли, то йг есть множество линейных комбинаций произведений вида
^ [...[а1а2] ... аг], а^8. Отсюда следует, что (йОр = (ЙР)Г. Анало-
т'~ гично второй член производного ряда 2" есть множество линейных
J. комбинаций произведений вида [ [аго2] [а3а41 Ь 2'" — множество ли-
' нейных комбинаций произведений вида
и т. д. Поэтому (йр)(г) = (8(г))р. Из этих рассмотрений следует, что
алгебра Ли 2 коммутативна, нильпотентна или разрешима тогда и
" только тогда, когда алгебра 2Р соответственно коммутативна, ниль-
нильпотентна или разрешима
Если Е — расширение поля Р, то мы можем образовать Ttt
и (9Йр)г Первое из этих пространств есть тензорное произведение
*' 2®Ф5Ш, в то время как второе есть S ® р (Р ® ф Ш\, Хорошо из-
' вестно, что существует естественный изоморфизм пространств (ШР\
Щ %, переводящий а®(р®х) в ар®л:, а^Е, р^Я, х?Ш. Поэтому
• можно отождествить (Шр\ с 2US.
Если А—линейное отображение пространства Ш в другое век-
^ торное пространство Ш над Ф, то А может быть единственным
'Образом продолжено до линейного отображения (которое мы также
" ' будем обозначать через Л) пространства Шр в ШР. При этом
- Й р,д?,) А = 2 р, (*И). р.6^. ле*€ЗИ- ОбРаз 9ИРЛ = («ШЛ)р> а ядро
йродолжения Л есть $р> где й — ядро отображения Л в Si. По-
<!< „ этому Л эпиморфно (т. е. является отображением ка) в том и только
' 'том случае, когда его продолжение эпиморфно, и взаимно однозначно
' 18 том и только том случае, если его продолжение взаимно одно-
„ '|шачно. Если % — (неассоциативная) алгебра и Л — гомоморфизм
к! (антигомоморфизм, дифференцирование), тр егс продолжение Л на ЭДР
38 Гл. I. Основные понятия
тоже будет гомоморфизмом (антигомоморфизмом, дифференциро-
дифференцированием).
Пусть теперь й — алгебра Ли, Ш есть 2-модуль, a R— соот-
соответствующее представление. Если а ?2, то aR имеет единственное
продолжение aR, являющееся линейным преобразованием в 9ЙР. Для
этих продолжений выполняются равенства (a-\-b)R = aR-{-bR,
(aa)R = aaR, [ab]R = [aR, bR], <х?Ф. Отсюда следует, что если
Pi^P, а,?2, то отображение ^tpial->'^piaf есть гомоморфизм R
алгебры 2Р в алгебру Ли 6BUp)i линейных преобразований про-
пространства ШР. Поэтому имеется продолжение R гомоморфизма R,
которое является представлением алгебры йр, действующим в ШР.
Для модуля ШР, определенного таким образом, справедливо равен-
равенство Jc(Spi«;) = 2Pi(«i). ?i^P' а/62> х?Шр, и если х =
— "j&p'Xj, х.?Ш, p'j^P. то лга = 2р/(-*^а)' а?%. Аналогичным
образом представление R ассоциативной алгебры ЭД определяет пред-
представление R алгебры ЭДР и правый модуль ffl над $ определяет
правый модуль ШР над ШР.
Упражнения
1. Пусть 91, 33 — ассоциативные алгебры. Показать, что если 6 — гомо-
гомоморфизм алгебры % в SB, то 6 является гомоморфизмом алгебры %L в 33^,
а если 6 — антигомоморфизм Ж в 8, то —9 — гомоморфизм %L в S8L. По-
Показать, что если 8 — антигомоморфизм алгебры % в 21, то подмножество <& Ct, 6)
6-антиинвариантных элементов (а9 = — а) является подалгеброй в %L. Пока-
Показать, что если D — дифференцирование алгебры 21, то D — дифференциро-
дифференцирование алгебры %L. Привести примеры алгебр 31 н S3, которые не изоморфны
и не антиизоморфиы, ио для которых %L ^ 33^. {Указание: в качестве %, 33
взять коммутативные алгебры.) Привести пример дифференцирования ал-
алгебры %v не являющегося дифференцированием алгебры St.
2. Если S — подмножество в лиевой алгебре й, то централизатором
(? E) является подмножество таких элементов с, что [sc] = 0 для всех s € 5.
Показать, что й (S) — подалгебра. Если 23 — подпространство в й, то его
нормализатором является множество таких элементов I ? й, что [Ы\ ? 33
для каждого * ? 33. Показать, что нормализатор S3 является подалгеброй.
3. Пусть D — дифференцирование (неассоциативной) алгебры 31. Пока-
Показать, что множество элементов г ? 31, удовлетворяющих условию zD = О,
образует подалгебру (такие элементы называются D-константами). Показать,
что множество элементов г, удовлетворяющих условию zD' = 0 для неко-
некоторого i, образует подалгебру.
4. Показать, что если О — дифференцирование алгебры Ли, коммути-
коммутирующее с каждым внутренним дифференцированием, то образ Й?>С6, где
& — центр. (Если (J = 0, то отсюда следует, что центр алгебры дифферен-
дифференцирований 6 B)) = 0. Поэтому также <? B B) (8)) = 0 и т. д.).
5. Показать» что каждая трехмерная простая алгебра Ли характеристики
рф2 совершенна.
6. Доказать, что каждая четырехмерная нильпотентная алгебра Ли имеет
трехмерный идеал. Использовать этот факт для классификации четырехмер-
четырехмерных нильпотеитных алгебр Ли.
Упражнения 39
7. Проверить, что если 2 имеет базис (еи е2 еа) с таблицей умно-
умножения
[е,е2] = е5, [е{ег] = е6, [е{е4] = е7, [е{е5] = — ей,
[е2ез] = е8, [е2е^ = е6, [^2гб] — — ет \.егеЛ == — е5>
= —1?8; все остальные [etej] — О
для < < j, [etet] = 0, [г/*/] = — [ejet], то 8 — нильпотентная алгебра Ли.
8. Подалгебра Шей называется субинвариантной в 8, если существует
цепочка подалгебр 8 = 8( Ш 82 Э • • ¦ 3 8, = 33, где 8; — идеал подалгебры
8/_i. Показать, что если имеется такая цепочка, то [... [ЙЗЗ] 58 ... 33] с 83,
как только в левой части подалгебра S3 встречается не менее s раз.
9. (Шенкман.) Показать, что если 91 и S3 — подпространства алгебры Ли,
то [2tS3n] с [... [2123] 33 ... 33], где 3S встречается в правой частил раз.
Использовать это для доказательства следующего факта: если подалгебра 33
оо
субинвариантна в й, то ЭЗШ = |**|33' есть идеал в 8.
< = 1
10. Пусть й — нильпотентная алгебра Ли. Показать, что подмножество S
алгебры 8 порождает й в том и только в том случае, когда классы смежно-
смежности s + й2, s ?S, порождают Й/С2. Вывести отсюда, что минимальное число
образующих конечномерной нильпотентной алгебры Ли в 8 равно dim й/82.
11. Показать, что в нильпотентной алгебре Ли 8 каждая подалгебра
субинвариантна. Показать также, что если 93 — ненулевой идеал в й, то
33 П <? ф 0, где <? — центр алгебры й.
12. Пусть % — алгебра Ли треугольных лХл-матриц. Определить про-
производный ряд и нижний центральный ряд алгебры %.
13. Доказать, что конечномерная алгебра Ли разрешима лишь в том слу-
случае, когда существует цепочка 8 = й0 з Й1 гз 82 :э ... :э 8Я = 0, где dim 2; =
= л — i и 8j есть идеал в йг_,.
14. Если 2 — алгебра Ли, то верхний центральный ряд 0 С (S, с S2 С ...
определяется следующим образом: Gt, — центр алгебры й, a G^ — идеал в й,
такой, что (?,-/(?,•_, — центр алгебры й/6г_,.
Показать, что верхний центральный ряд заканчивается самой алгеброй 8
(т. е. существует такое s, для которого fes = й) тогда и только тогда, когда
алгебра й нильпотентна. Показать, что наименьшее число s, удовлетворяю-
удовлетворяющее этому условию, равно минимальному числу t, для которого й<+1 = 0.
15. Доказать, что каждая нильпотентная алгебра Ли имеет внешнее
(т. е. не являющееся внутренним) дифференцирование. (Указание: запишем
8 = Ш © Фе, где 9К — идеал. Если г ? Q = <? (9К), то линейное отображение,
при котором 9й->0, е->г, является дифференцированием. Если г выбран
в 3, но г i 8"+1, где п удовлетворяет условиям Q С 8", ,83=йл+1, то диф-
дифференцирование, определенное элементом z, будет внешним.)
16. Пусть А — линейное преобразование в л-мерном пространстве. Пред-
Предположим, что А имеет п различных характеристических корней $,, S2, ..., ?„.
Доказать, что ad А, действующее в Gf, имеет п2 характеристических корней
%~6у/./=1, 2 п.
17. Пусть 9К — конечномерный модуль, а Ш* — контрагредиентный мо-
ДУль. Показать, что если 41 — подмодуль модуля 9К, то 9fl-L = {?*| (у, г*) = 0,
У 6 Щ будет подмодулем модуля Ш*. Вывести отсюда, что модуль 9Й непри-
неприводим тогда и только тогда, когда неприводим модуль 9К*.
18. Пусть 5Ш и Ш* определены, как в упражнении 17. Показать, что
8К09К* содержит такой элемент и j= 0, что ul = 0 для всех /. Допустим,
что модуль 5Щ неприводим, а Ш — произвольный модуль, обладающий тем
40 Гл I. Основные понятия
свойством, что ЭК (g) 9t содержит элемент и Ф 0, ul = 0 для всех / ? й. По-
Показать, что 9t содержит подмодуль, изоморфный Эй*.
19. Пусть 91 — (неассоциативная) алгебра, разложимая в прямую сумму
91 = 8С, ф Ж2 ф ... ф 8СП где 9Г,—идеалы, удовлетворяющие условию 9l| = 9t;.
Показать, что алгебра дифференцирований 33 разложима в прямую сумму
2) = ?>1©2>2© •¦ ¦ ©?>/-. гДе ®/ — идеал в 33, изоморфный алгебре диффе-
дифференцирований идеала 9fy.
20. Показать, что производная алгебра Ф'п1 алгебры Ли $nL состоит из
матриц со следом 0. Показать, что центр алгебры Фд1 совпадает С множе-
множеством Ф1 кратных 1 (единичная матрица) и что- единственными идеалами
в Фп1 являются &nL и Ф1, кроме случая, когда п = 2 и характеристика поля Ф
равна 2.
21. Привести пример алгебры Ли над полем С комплексных чисел, не
имеющей вид ЙС] где й — алгебра Ли над полем R вещественных чисел.
(Указание: рассмотреть алгебры Ли, удовлетворяющие условиям dim 8 = 3,
dim 8'= 2.)
22. Пусть й — идеал (неассоциативной) алгебры 2t, D — ее дифференци-
дифференцирование. Показать, что сумма 23 + 23D является идеалом. Показать, что если
91 — конечномерная ассоциативная алгебра характеристики 0 с радикалом Ш,
то 9Ш С 31 для каждого дифференцирования D алгебры %. (Это неверно
в случае характеристики рфО, см. стр. 88.)
Доказать этот же результат для алгебр Ли.
23. Показать, что если (?—коммутативная ассоциативная алгебра (с еди-
единицей 1) и 8 — алгебра Ли, то E® 8 — алгебра Ли.
Привести пример, когда тензорное произведение ассоциативной алгебры
и алгебры Ли не будет алгеброй Ли, и пример, когда тензорное произведе-
произведение двух алгебр Ли не будет алгеброй Ли. (Указание: для построения пер-
первого примера в качестве ассоциативной алгебры взять Ф2 и заметить, что
Ф„®53э;8л, где 8 — любая неассоциативная алгебра и 8„ — алгебра Х
матриц с элементами из S3.)
Глава II
РАЗРЕШИМЫЕ И НИЛЬПОТЕНТНЫЕ
АЛГЕБРЫ ЛИ
Главной темой предшествующей главы была аналогия между алге-
алгебрами Ли и группами Ли. Основная идея, которой мы руководствуемся
в этой главе, — параллелизм и взаимные связи между алгебрами Ли
и ассоциативными алгебрами. Рассматривается ассоциативная алгебра Щ.
(обычно алгебра линейных преобразований конечномерного векторного
пространства) и подалгебра 2 алгебры 3ti. Нас интересует изучение
связей между строением алгебры 2 и строением подалгебры 2*сЭД,
порожденной алгеброй 8. Особое внимание обращается на тот случай,
когда 2 — разрешимая или нильпотентная алгебра. Результаты, полу-
получаемые на этом пути, включают классические теоремы Ли и Энгеля
о разрешимых алгебрах Ли линейных преобразований и критерий
полной приводимости алгебры Ли линейных преобразований. Мы
л'\ »введем понятие весовых подпространств и установим свойства раз-
, ложения на весовые подпространства векторного пространства, на
\s котором действует расщепляемая нильпотентная алгебра Ли линейных
•( " преобразований. Эти результаты будут играть важную роль в струк-
? турной теории, излагаемой в следующей главе.
) § 1. Слабо замкнутые подмножества ассоциативной алгебры
?f&i Наши первые результаты могут быть установлены для более
Широкого класса подмножеств ассоциативной алгебры, чем алгебры
•Пи. Исследование этих более общих систем не вносит больших ос-
осложнений, в то же время они оказываются полезными для изучения
¦самих алгебр Ли.
Определение 1. Подмножество 98 ассоциативной алгебры $
над полем Ф называется слабо замкнутым, если каждой упорядо-
Ч паре (а, Ь), где а, ??2В, сопоставляется элемент ~\{а, Ь)?Ф,
что ab-\-~{{a, Ь)Ьа?Ш. Предположим, что отображение
*)~>Tf(a> *) фиксировано, и обозначим а X b~ ab-{-f (a, b)ba.
одмножество Uc9B называется подсистемой, если cy.d?U для
каждых с, d?U; если же ау,с?\\ (соответственно aXc(U,
?U) для каждых а ? 2В, c?U, то Ц — левый идеал (соответ-
(соответственно идеал) системы 2В.
42 Гл II. Разрешимые и нильпотентные алгебры Ли
Примеры
1) Каждая подалгебра Й алгебры %L слабо замкнута в % отно-
относительно отображения i(a> ?) = —1.
2) Если 2(S$) — алгебра Ли с базисом (е, /, п), таким, что
\ef\ = h, \eh\ — 2e, \fh\ — — 2f, то 28 = Ф<? U Ф/U ФЛ является ее
подсистемой 8.
3) Множество симметрических матриц слабо замкнуто в алгебре Фл
матриц типа п X п, если положить ~((а, b) = l.
4) Пусть 2В = § U S, где <§> — множество симметрических матриц,
а 3 — множество кососимметрических матриц. Положим f (a, ft)=l,
если а м b симметричны, и f (а, 6) ——1 в противном случае.
Тогда 28 слабо замкнуто и ?> — идеал в 2В.
5) Положив 1 (а, 6) = 0, мы получим мультипликативную полу-
полугруппу в 31.
Определение 2. Если © -^ подмножество ассоциативной ал-
алгебры Й (или просто алгебры — ассоциативной алгебры с единицей),
то через в*E+) обозначим подалгебру алгебры 31 (подалгебру, со-
содержащую единицу), порожденную подмножеством 5. Назовем 3* (Sf)
обертывающей ассоциативной алгеброй (обертывающей алге-
алгеброй) подмножества © (в Ж).
При доказательстве основной теоремы о слабо замкнутых систе-
системах нам понадобятся некоторые их свойства, которые мы сейчас и
отметим.
I. Если W — элемент слабо замкнутой системы 2В, то
3 = {W}*f|2B является подсистемой в 2В, причем 3* = {W}*.
Доказательство. Обертывающая ассоциативная алгебра {W}*
есть не что иное, как алгебра многочленов относительно W с рав-
равными нулю постоянными членами. Если Wx и W2 — два таких много-
многочлена, то и произведение Wx X W2 — такой же многочлен. Поэтому
3 = {W}* П 2В — подсистема. Так как 3 Э w- то 3* 3 [Щ*. Поскольку
3= [W]* и [WY является подалгеброй, л>о 3 ?{№}*. откуда %*=[W\*.
II. Если 58 — подсистема системы Ш и W — такой элемент
из 2В, что BXW^* для каждого 6^58, то
W сГ23* + 58*. A)
Доказательство. Элементы из 58* являются линейными ком-
комбинациями одночленов ВХВ2 . .. Вг, Вг?58. Если В?Ъ, то BW =
= — f(B, W)WB-\-BX W?W%*-\-<&*. Индукцией по г получаем,
что если В(? 58, то В, ... BrW ? №58* -f- 58*. Это доказывает вклю-
включение A).
III. Пусть 58 — подсистема системы 2В, обладающая тем
свойством, что 58* нильпотентна и 58*=?2В*. Тогда существует
такой элемент W^ 2В, что tt^58*, «о fiX^^S* для кащдого
длемента В из 58,
§ 2. Сгабо замкнутые ниЛь-шожесТвс1 43
Доказательство. Из предположения 23* Ф 28* следует, что
существует элемент №,?2В, W,^23*. Если BXW, €23* ,пя всех
В ?23, то положим W = WV В противном случае для некоторою Я,
элемент W2= ВгХ ^г^Ш, (?23*. Повторим тогда рассуждение, за-
заменив Wx на W2. Если W2 вновь не является искомым элементом, то
найдется элемент Wz = В2 X W2 == В2 X (^ X W\) € 28- ? 35*- Либ<>
этот процесс приводит через конечное число шагов к требуемому
элементу W, либо получается бесконечная последовательность эле-
элементов Wv W2, .... W, = Bt_l X Wt-V где Г,?2В, но W^®*. По-
Покажем, что это невозможно, и тем самым завершим наше доказатель-
доказательство. Заметим, что Wk является линейной комбинацией произведений
из k—1 элементов В?*8> и Wv Поскольку 23* нильпотентна, суще-
существует такое целое положительное число п, что любое произведение п
элементов из 23 является нулем. Но Wln есть линейная комбинация
членов вида С, ... CjWxDx ... Dk, где Сг и Ds принадлежат Ъ и
j-\- k — 2n — 1. Либо j > п, либо k^-n, так что С, ... CJW1D1. ..
... Dk = 0. Поэтому W2n = 0 и W2n ? 23*, что противоречит пред-
предположению.
§ 2. Слабо замкнутые ниль-множества
Основной результат о слабо замкнутых системах состоит в сле-
следующем:
Теорема 1. Пусть 28 — слабо замкнутое подмножество
ассоциативной алгебры 6 линейных преобразований конечно-
конечномерного векторного пространства ffi над Ф. Предположим,
что каждый элемент W^?2B ассоциативно нильпотентен, т. е.
Wk = Q для некоторого целого положительного числа k. Тогда
обертывающая ассоциативная алгебра 2В* системы 2В ниль-
нильпотентна.
Доказательство. Докажем этот результат индукцией по раз-
размерности пространства Ш. Утверждение теоремы очевидно, если
dimSK —0 или если 2В = {0). Поэтому допустим, что dim2)t>0,
ШфЩ. Пусть 2 — семейство подсистем 23 множества 2В, таких,
что 23* нильпотентны, и пусть 23 — элемент из Q, для которого раз-
размерность ассоциативной алгебры 23* максимальна (среди элементов
множества 2).
Покажем, что 23* = 2В*, откуда и будет следовать утверждение
теоремы. Заметим сначала, что 23* Ф 0. В самом деле, пусть W — не-
ненулевой элемент из 2В. Тогда из свойства I предыдущего параграфа
следует, чтоЗ = 2ВП {Щ*—подсистема и 3*={W}*. Поскольку {W}*
является множеством многочленов относительно W со свободными
44 tn. II Разрешимые и нильШёМные алгебры Ли
членами, равными нулю, {W}* нильпотентна. Поэтому 3 6 2, а так
как 3 Ф °> то и 33* =/= 0. Отсюда следует, что подпространство 9t,
натянутое на все векторы вида хВ*, х ? Ш, В* ? 58*. — ненулевое.
Далее, VI Ф Ш. Действительно, в против'ном случае каждый элемент х
может быть записан в виде х = ^ixlBi, Xi ? ffi, В(?58.
Если записать в таком же виде каждое хг. то мы получим х =
= ^lyjB*!C], В] и С) принадлежат 23*. Повторение этого процесса
приводит к равенству х = 22ft^fti^ft2 • • • Bkr, где Bk] ? 58 . По-
Поскольку 58* нильпотентно, отсюда следует, что х — 0 и Ш = 0 вопреки
предположению. Итак, мы получили, что 2№з!Пз0. Пусть E,— под-
подмножество элементов С?2В, таких, что ШС с; !R. Очевидно, что
E,— подсистема, содержащая 58. Более того, б индуцирует слабо
замкнутые системы нильпотентных линейных преобразований в 9f и
в факторпространстве WI/91. Поскольку dim ffi, dim Ш/Ш < dim 9К,
можно предположить, что индуцированные системы имеют нильпо-
тентные обертывающие ассоциативные алгебры. Из нильпотентности
алгебры в ffi/Ш следует, что существует целое положительное число р,
такое, что хСхС2 ... Ср?Ш для любого элемента х из Ш и произ-
произвольного набора элементов Cv C2, .... Ср из 6. Существует также
число q, такое, что уЦг ... Dq = 0, если D,, D2, .... Dq ? 6 и у ? ?R.
Отсюда следует, что если Сх Ср+д?&< т0 ^1^2 ••• Cp+q~®-
Поэтому 6* нильпотентна и 6^2. Покажем теперь, что ЖВ* = 58*.
В противном случае, как это следует из свойства III предыдущего
параграфа, существует элемент W?2В, (?Ъ*, такой, что B\W?%$*
для всех В ?58. Согласно свойству II из предыдущего параграфа,
для любых jc ? Ш, В* ? $8* справедливо равенство хВ W=x (WBi-\-B*2),
где В* ?58*. Отсюда 3W ? ЭТ, так что Г ?6. Поскольку W?58*.
dim 6* > dim 58*. и так как 6 ? 2, это противоречит выбору 58. По-
Поэтому ассоциативная алгебра 58*== SB* нильпотентна.
Если 2В — множество нильтреугольных матриц, т. е. треугольных
матриц с нулями на диагонали, то 2В* содержится в ассоциативной
алгебре нильтреугольных матриц. Так как эта алгебра нильпотентна,
то и Ш* нильпотентна. Поэтому следующий результат является в сущ-
сущности несколько иной формулировкой теоремы 1.
Теорема 1'. Пусть Ш имеет, тот же смысл, что и в тео-
теореме 1. Тогда существует такой базис в Ш, что матрицы
всех элементов W ? 2В в этом базисе нильтреугольны.
Доказательство. Можно предполагать, что Ж Ф 0. Тогда
из доказательства теоремы 1 следует, что ЗКгэШШ*. где Tlffi* — про-
пространство, натянутое на векторы xW*, x?Tl, №*?2В*. Вообще если
У1 — подпространство и <5 — множество линейных преобразований.
2 Слабо замкнутые ниль-множёства
45
то подпространство, натянутое на все векторы вида yS, где у?ЭД,
S?<S, мы будем обозначать через 9?©. Легко получить равенство
ЗЙ(ЗВ*J = BШ*)ЗВ*. Если ШШ*фО, то рассуждения, аналогичные
вышеприведенным, показывают также, что 9ЯЗВ*з!№BВ*J. Следо-
, вательно, цепь включений Ш з ЗЙЗВ* з 2R BВ*J з Ш BВ*K з ...
... => ЗК CВ*)" з 2R (ЗВ*)" = 0, если CB*f = 0 и CВ*)" -? о.
Выберем теперь базис (ev ..., е„) в пространстве Эй, такой, что
... (е\ еп)—базис в подпространстве Т1 (ЗВ*) , {е\ еПх, ...
. ¦ ¦ ?я,+я2)—базис в подпространстве ^(ЗВ*)^, .... (е^ еП1, ...
еп+п+ +nj — базис в подпространстве ^{(ЗВ*)^""*. Из соотношений
i 2 .,' ^ * v-ft+i
следует, что матрица любого W ^ ЗВ
имеет вид
0
0
*
"TV
Теорема 1 может быть обобщена на идеалы в слабо замкнутых
системах. Для этой цели мы установим следующее общее важное
свойство обертывающих ассоциативных алгебр слабо замкнутых систем.
IV. Пусть 2В— слабо замкнутое подмножество ассоциатив-
ассоциативной алгебры, и пусть 23 — идеал в SB, а 23*. 2В* — обертывающие
ассоциативные алгебры систем 23 и SB соответственно. Тогда
ЗВ*B3*)*еB3*)*2В* + B3*)*,
B3*)* 2В* S 2В* B3*)* + B3*)*, B)
(ЗВ*23*)* ? ЗВ*B3*)*, B3*2В*)* Е B3*)* ЗВ*. C)
Доказательство. Согласно свойству II параграфа 1, из усло-
условия BXW?23' где В?23, Г?ЗВ, следует, что 23*Г с'Г23*4-23*.
Отсюда если Wx, W2 ГГ?ЭВ, то ^*WXW2.. ,Wr S 3B*23*-f 23*.
Поэтому 23*2В* S 2В*ЯЗ* + 23*. Легко доказывается по индукции, что
B3*)ft2B*c2B*B3*)ft-l-B3*)ft. Аналогично, из условия, Что 23 является
левым идеалом, легко следует первое из включений B). Утвержде-
' ние C) очевидно для случая k = 1; если оно выполняется для неко-
.торого k, то
<ЗВ*23*)* +1 = (ЗВ*23*)*ЗВ*23* с SB* B3*)* ЭВ*23* ?
? SB* BB*23*ft -f- 23**) 23* ? SB* B3*)ft+'.
46 Гл II Разрешимые и ни гьпотентные алгебры Ли
Аналогично доказывается и вторая часть утверждения C). Мы
теперь в состоянии доказать следующее утверждение.
Теорема 2. Пусть 2В—слабо замкнутая система линей-
линейных преобразований, действующих в конечномерном вектор-
векторном пространстве, и пусть 23— идеал в 28, такой, что каждый
элемент из 23 нильпотентен. Тогда 23* {а поэтому и 23) со-
содержится в радикале 91 алгебры Ш".
Доказательство. ЯВ*23*-|-23* является идеалом, поскольку
2В* B3*23* + 23*) s 2В*23* и BВ*23* + 23*) 2В* с 2В* BВ*23* ¦+- 23*) -+-
-f-2B*23*-f 23* = 2В*23*+23*. Кроме того, (9B*23*+23*)*c2B*23*-f B3Т-
По теореме 1 ассоциативная алгебра 23* нильпотентна. Поэтому k
может быть выбрано так, что BВ*23* + 23*)ft ? 2В*23*. С другой сто-
стороны, BВ*23*)г С 2В* B3*)г и I может быть выбрано так, что
BВ*23*)' = 0. Поэтому 2В*23*-|-23* является нильпотентным идеалом
и, следовательно, содержится в 31. Отсюда следует, что 23* и 23
также содержатся в SR.
§ 3. Теорема Эигеля
Теорема 1 применима, в частности, к алгебрам Ли. Соответ-
Соответствующее утверждение известно как теорема Энгеля об алгебрах Ли
линейных преобразований: если 8—алгебра Ли линейных пре-
преобразований конечномерного векторного пространства и если
каждый элемент L ? g нильпотентен, то и алгебра 8* ниль-
нильпотентна. То же самое утверждение может быть высказано в сле-
следующей форме: существует такой базис исходного векторного про-
пространства, в котором матрицы всех элементов из 2 нильтреугольны.
С помощью присоединенных представлений этот результат пере-
переносится на произвольные конечномерные алгебры Ли спедующим
образом.
Теорема Энгеля для абстрактных алгебр Ли.
Конечномерная алгебра Ли 8 нильпотентна тогда и только
тогда, когда присоединенный эндоморфизм ad а нильпотентен
для каждого элемента а ? 2.
Доказательство, Для того чтобы алгебра Ли 2 была ниль-
нильпотентна, необходимо и достаточно, чтобы существовало такое
число N, что [... [[а1а2]а3] ... aN\ = Q для любых а;?2. Отсюда
следует, что [.,. [ [ха] а] ... а] = 0, если произведение содержит
сомножитель а N—1 раз. Таким образом, (ad а)" = 0. Обратно,
пусть 2 — конечномерная алгебра и преобразование ad а нильпо-
тентно для каждого элемента а ? 2. Множество ad 8 линейных пре-
преобразований ad а (действующих в 2) является алгеброй Ли нильпо-
тентных линейных преобразований. Поэтому ассоциативная алгебра
§ 4 Прииарные компоненты Весовые подпространства 47
(ad 8)* иильпотентна. Другими словами, существует такое число N,
что ad агadа2. . . adaN~Q для любых а1 ?8. Поэтому [... [ааг]а2...
.. . aN]—0 и, следовательно, 8W+1 —0.
Теорема 2 предыдущего параграфа может быть использована для
получения двух характеризаций ниль-радикала алгебры Ли.
Теорема 3. Пусть 8 — алгебра Ли конечной размерности.
Тогда ниль-радикал Ш алгебры 8 может быть охарактери-
охарактеризован двумя следующими способами:
1) для каждого а?Щ преобразование ad а (действующее в 8)
нильпотентно, и если 58— такой идеал в 8, что adb нильпо-
тентно (в 2) для каждого 6 ? 33, то 23 с 9f.
2) !R — множество таких элементов 6 ?8, что ad# прм-
надлежит радикалу ffi. ассоциативной алгебры (ad 8)*.
Доказательство. 1) Если Ь?Ш и а?Й, то {ab] ? !R и
[. .. [ [а?>]?] . . . Ь] = 0, если 6 повторяется как сомножитель доста-
достаточно большое число раз. Поэтому ad b нильпотентно. Пусть
теперь 23 — такой идеал, что ad b нильпотентно для каждого #?58.
Тогда ограничение ads6 преобразования ad b на 23 нильпотентно,
и идеал 23 нильпотентен по теореме Энгеля. Поэтому 23 ? !R.
2) Образ ad?R ниль-радикала ?R при присоединенном отображении
является идеалом в ad 8, состоящим из нильпотентных преобразований.
Поэтому по теореме 2 ad !R с *ft. Очевидно, что iftfladS — идеал
в ad 8. Поэтому его прообраз ЭТ1 относительно присоединенного
представления является идеалом в 8. Но Шх—'Множество таких эле-
элементов Ь, что adb ?9t. Каждое ad%tb, Ь?Щг — нильпотентно. Поэтому
идеал Щг нильпотентен и 31, с Я. Раньше мы получили, что ad !R ? Ш,
так что W с 9^, откуда ЭТ=^Г
§ 4. Примарные компоненты. Весовые подпространства
Хорошо известная лемма Фиттинга утверждает, что если линей-
линейное преобразование А действует в конечномерном векторном про-
пространстве 2t, то пространство Ш можно представить в виде прямой
суммы tyl0A ф Т11А двух подпространств %RiA, инвариантных относи-
относительно преобразования А, причем индуцированное преобразование
в подпространстве Ш0А нильпотентно, а в подпространстве 2>{]Л
является автоморфизмом. Мы назовем Т10А и ЗЙ1Л соответственно
фиттинговой О-компонентой (или нуль-компонентой) и фиттинговой
1-компонентой пространства Ш относительно преобразования А.
со
Пространство Tl1A = f\fflA\ а 9Я0Л= [z\zAl = 0 для некоторого i].
Доказательство существования такого разложения проводится сле-
следующим образом. Очевидно, что Ш з 2КЛ Э $1А2 Э . • ¦'< поэтому
48 Гл. /I. Разрешимые и нильпотентные алгебры Ли
существует такое число г, что ШАГ — TlAr+i — ... = Ш1А. Пусть
3;== {zl\ziAi = Q}. Тогда 3i ? З2 S • • •. так что найдется такое
число s, что 3S —3s+i— ••• — $W Пусть t — max(r, s). Тогда
$R0A = 3t и ^u = 2Яч4'- Если jc ? 2R, то Jt Л' = уЛ2' для некоторого у,
поскольку ША* = ЗИЛ2'. Отсюда х = (х — уЛ') + уЛ' и уЛ'? 2RM,
атак как(х—уЛ/)Л/ = 0, tojc —уЛ^ЗИол- Поэтому 2R:=3MM-f ЗЙ1Л.
Пусть 2 ? Ш?ол П Шы; тогда z = wAf и 0 —.гЛ^^Л2'. Поскольку
¦ш Л2/ = 0, то w ? ЗИ0Д — 3< и даЛ' = 0. Значит г = 0и Зйол П Ш1А = 0;
Отсюда 2R = Ш0А ф ЗИ1Л. Поскольку ЭД„л —3<- Л' = 0 в 2»гол> а так
как 9И1Л = 9ЛЛ'' = 2'М''+1 = 9?{1ЛЛ, то линейное преобразование под-
подпространства 9й1Л есть гомоморфизм на. Поэтому Л является авто-
автоморфизмом в 9И1Л.
Мы напомним также другой тип разложения пространства Ш
относительно преобразования Л, а именно разложение на примар-
ные компоненты. Это разложение записывается в виде Ш = Шща ©
© ШъА ® ¦ ¦ ¦ 9 ШЦд. где ie, = ie,(X), {«, (X) ier(X)} — непри-
неприводимые множители минимального (или характеристического) много-
многочлена преобразования А с коэффициентами при старших членах,
равными единице. Если ja(A) — некоторый многочлен, то
WlpA— [z\z\>.(A)r — Q для некоторого г] D)
(см. Джекобсон [2], т. II, стр. 130).
Если [л (X) = тс(X) — неприводимый многочлен с 1 в качестве
старшего коэффициента, то 2)^ = 0, если только тс не равно тсг
для некоторого I. Пространство Ш?^, очевидно, инвариантно относи-
относительно Л. Характеристический многочлен преобразования простран-
пространства Шп л. индуцированного преобразованием А, имеет вид тс((А)%
a dim 9JL д = «//•/, где rL = deg тсг (X). Если тсг(Х) = Х, то характе-
характеристический многочлен преобразования Л в Ш\А имеет вид Xе, так
что Лг-0 в Ш^А и 9ЯХЛ ? Ш0А. Если тсг(А)=?А, то характеристи-
характеристический многочлен ограничения Л на $1%.а не делится на X, сле-
следовательно, это ограничение является автоморфизмом. Поэтому Stf* д =
= 2КК(дЛ = .... так что ШгЯ(д е Шы- Таким образом, Sl,A
так как ЗИ = Ш0А ф ЗЯМ = Ж1А ф 2 ^.д, то Ш0А = ШХА,
В частности, фиттингова нуль-компонента является характеристи-
характеристическим подпространством, соответствующим характеристическому
корню 0 преобразования Л, а размерность dim Ш0А есть кратность
этого корня в характеристическом многочлене преобразования Л.
§ 4 Примарные компоненты Весовые подпространства
49
Мы распространим сейчас эти результаты на нильпотентные
алгебры Ли линейных преобразований. Для этой цели было бы до-
достаточно рассмотреть разложение на примарные компоненты, так
как результат разложения Фиттинга может быть отсюда легко получен.
Однако разложение Фиттинга применимо в других ситуациях (на-
(например, для векторных пространств, определенных над кольцами
с делением), так что интересно исследовать это разложение и неза-
независимо. Нам понадобятся две важные формулы коммутирования.
Пусть 2t — ассоциативная алгебра, а?ЭД; рассмотрим внутреннее
дифференцирование Da : х—>лг'н=[ха] алгебры Щ. Если обозначить
x<ft> = (jc(*~1))'. x(-0) = x, то легко вывести по индукции следующие
формулы:
(^ {^ E)
¦=xan —
x aR
F)
Используем их для доказательства следующего утверждения:
Лемма 1. Пусть А и В—линейные*преобразования конечно-
конечномерного векторного пространства. Предположим, что суще-
ствует такое число N, что [. . . [ [ВА] А\ ... А] = 0. Тогда компо-
компоненты Фиттинга М0А, ЯЯ1А пространства Ш относительно А
инвариантны относительно преобразования В.
Доказательство. Предположим, что хАт — 0. Тогда
k N
для
Поэтому xB?Wl0A. Пусть, далее, x?2R1A. Если t — число, встре-
встречающееся в доказательстве леммы Фиттинга, то мы можем написать
\ Тогда
— «ы-
, Таким образом, ШХАВ ? Ж
мл-
р»
Теорема 4. Пусть Й — нильпотентная алгебра Ли линей-
'•,,ны.х преобразований конечномерного векторного простран-
оо
Ш, и пусть 5W0 = f|5W0^, Эг1 = р|ЗК(8*У. Тогда подпро-
ъ:'Шранства $10 и Шх инвариантны относительно 2 (т. е.
50 Гл //. Разрешимые и нильпотентные алгебры Ли
инвариантны относительно каждого преобразования В ?2) и
SW = SHo®SW,. Более того> 2Ri = 2 Зам-
Замлев
Доказательство. Предположим вначале, что Ш = Т10А для
каждого А ?8. Тогда 9Им = 0 для всех А и 2^1л = °-
Далее, по теореме Энгеля (8)^ = 0 для некоторого N. Поэтому
оо
2){, = О 9Я (8*)' = 0. Таким образом, в этом случае утверждение
теоремы справедливо. Применим теперь индукцию по dim ЗК и
допустим, что Т10А Ф 9Л для некоторого А. По лемме 1 каждое
преобразование В?8 отображает подпространство ffi.0A в себя и
поэтому 8 индуцирует нильпотентную алгебру Ли линейных преобра-
преобразований в Ш — ffiOA<zTl. Мы можем записать !R = !R0©?J], где
5l' = 2jW1B и ЭТои 5lj инвариантны относи-
тельно й. Тогда Ш = Шо ф !Rt ф ЗИ1Д. Как легко следует из опре-
определений, !R0 = Шо П Жов ё % + 2»ы S 2 5W1B S П Шг (8*)'- С ДРУ"
гой стороны, по теореме Энгеля алгебра, индуцированная 8* в Шо,
нильпотентна, так ч/го 5Ш0 (Й*) =0 для некоторого N. Поэтому
f=т0 (S*f+ш, (Z*f -+- аи, д (8*f s
с 51, + 2»M.
Отсюда SIj + SIKij = 2^1В1=-П^B*)'. что и доказывает утвер-
¦868 г1
ждение теоремы.
Теория разложения на примарные компоненты будет основана на
критерии существования кратных множителей многочленов. Обозначим
через Ф [X] кольцо многочленов относительно переменного X с коэф-
коэффициентами в поле Ф. Построим последовательность линейных ото-
отображений D0=l, ?),, D2 .. ¦ кольца Ф[Х] следующим образом:
Dt — линейное отображение, действие которого на элемент Х-' базиса
A, X, X2, ...) кольца Ф[Х] над Ф определяется по формуле
. G)
1де к| = 0 при I > у. Таким образом, \iD1 = jkJ~l, так что Dx —
обычное дифференцирование кольца Ф[Х]. Далее, \'D[=j(j— 1) ...
. . . U — i + 1)Х;= n^'jX^^ilX^D,. Поэтому, если характе-
характеристика поля равна нулю, то Dl = ^-D[. Если ср(Х)^Ф[Х], то будем
§ 4 Ирииарные Компоненты Весовые подпространства 51
писать cp( = cpDr Тогда получаем правило Лейбница
к
(?<№* = Sjivh-i- (8)
Действительно, достаточно проверить это соотношение для <p = \J,
ф = Х^' в базисе A, X, X2, ...). В таком случае
ft
Поскольку 2j [ ¦) [ ь^. •) — \ ь J )' предшествующее равенство сво-
'=0
дится к равенству ( J )X;+-' =(X;+;)ft. Поэтому соотноше-
соотношение (8) справедливо.
Докажем теперь следующее предложение.
Лемма 2. Если т)(Х)*+1 |(л(Х), то ^(Х)|[лг(Х), / = 0, 1, 2 &.
Доказательство. Это утверждение справедливо при & —0,
поскольку ^0 (X) == [л (X). Запишем [* (X) = ср (X) ф (X), где 7jfe|<p и т]|ф.
Тогда можно предположить, что т] j [j.;-, 7j| еру для У = 0, 1, 2 А—1
и т)|ф0. Поэтому ¦») | (<рф)й = (А* ввиду формулы (8).
г
Пусть ф (X) = 2а^*- Умножив равенство E) на aft и просум-
к = 0
мировав по &, получим равенство
*ф(а)=*<1»(а).к + '|>1(в)*/ + Ф2(в)*- ... Ч-л<г>. (9)
которое понадобится нам при доказательстве следующего утверждения.
ЛеммаЗ. Пусть А, В — линейные преобразования конечно-
конечномерного векторного пространства, удовлетворяющие условию
N
Вт = [,..[[ВА] А] ... Л] = 0
при некотором N. Пусть ^(Х)—многочлен и WI„д= {у | у[л(Л)т=0
д некоторого т). Тогда Ш^А инвариантно относительно В.
Доказательство Пусть у ? 9ИцЛ, и предположим, что
= 0. Положим 7j (X) — (л (X)m, ф (X) = т; (X)^v = jj. (Х)^. Тогда
ввиду равенства (9)
4*
Ш /*л. //. Разрешимые U ниЛькотектные алгебры Ли
По лемме 2 г, (X) |ф;. (X), J < Л/ — 1, откуда уф; (А) ~ О, у<Л/ — 1,
0. Поэтому
Теор-ема 5. Пусть % — нильпотентная алгебра Ли линей-
линейных преобразований конечномерного векторного простран-
пространства Ш. Тогдаг Ш можно представить в виде 2)J = 2)ij©
ф Ш2 ф . .. ф Шг где fflt— инвариантные относительно 8 под-
подпространства, и минимальный многочлен преобразования,
индуцированного любым элементом А?8 на подпростран-
подпространстве ЗЯ(, является степенью неприводимого многочлена.
Доказательство. Если характеристический многочлен каждого
преобразования Л?8 является степенью неприводимого многочлена,
то все доказано. В противном случае существует некоторое пре-
преобразование А ? 8, такое, что Ш = ЗЯ* а ф • ¦ • Ф 2М* д, где тс(. = т^ (X)
неприводим, и ШжАф0, 5>1. По лемме 3 Шж.аВ^ШпА для
каждого Л ? 8. Доказательство теоремы легко получается отсюда
индукцией по dim 2ft.
Если основное поле алгебраически замкнуто, то минимальные
многочлены в подпространствах 2^ имеют вид (X — а(Л)) iA, где Л?й.
Полагая Zt(A)= А — а.(А) для пространства Ш[, мы видим, что
Z;(i4) будет нильпотентным преобразованием в Wlt. Следовательно,
каждое преобразование А ?8, ограниченное на Ш[, есть скаляр плюс
нильпотентное преобразование. Мы получаем, таким образом,
Следствие (Цассенхауз). Если 8 — нильпотентная ал-
алгебра Ли линейных преобразований конечномерного вектор-
векторного пространства над алгебраически замкнутым полем, то
пространство Tt может быть представлено в виде прямой
суммы 3fti ф аИ2 ф . . . ф Шг, где Tlt — инвариантные подпро-
подпространства, такие, что ограничение любого преобразования
А ^ 8 на Ttt есть скаляр плюс нильпотентное линейное пре-
преобразование.
Рассмотрим разложение пространства Ш, указанное в теореме 5.
Любой паре I и А можно сопоставить такой неприводимый много-
многочлен тс/л(Х), что тсг.д(Х)*м будет минимальным многочленом ограни-
ограничения А на 2Иг. Поэтому отображение ¦к1: А ->¦ тсм(X) является при-
марной функцией относительно 8 в смысле следующего определения.
Определение 3. Пусть 8 — алгебра Ли линейных лреобразо-
ваний пространства Tt. Тогда отображение тс : А -> кА (X), где А ?8,
а чсд(Х) — неприводимый многочлен со старшим коэффициентом 1,
называется примарной функцией пространства Ш относительно 8,
если существует отличный от 0 вектор х, такой, что xwA{A)mjc'A = 0
для каждого А ? 8. Множество векторов (включая нулевой вектор),
§ 4. Примарные Компоненты. Весовые подпространства S3
удовлетворяющих этому условию, образует подпространство, назы-
называемое примарной компонентой fflv, соответствующей п.
Пользуясь этой терминологией, мы можем сказать, что подпро-
подпространство fflt из теоремы 5 содержится в примарной компоненте 2JL .
Объединив некоторые подпространства ЗЯг, если необходимо, можно
предположить, что отображения к{ : А —> тс/л (X) и тс^: А —> тс;-л (X),
определенные соответственно подпространствами ffit и 2Юу, ? =jfc у,
различны. Покажем теперь, что в этом случае 2йг совпадает с 2JL
и иг—единственные существующие примарные функции. Действительно,
пусть тс: Л-> тсл (X)—примарная функция, х?Шж. Пусть, кроме того,
¦тс =5^= тг/, т. е. существуют такие элементы А^Ч, что тсл (Х)=? тсгл (X).
Запишем х = х1 + ... + хг, xt? 9Иг. Поскольку л; ? 9ИЛ, найдется
такое положительное целое число т, что
Так как разложение Ш = Шг © ... © 2Rr прямое, то Х;тсл. (Л,)т = О
а так как т:л (X) Ф п[А (X), то х( = 0. Отсюда вытекает, что если
¦к Ф ¦к1 для всех /=1, 2 г, то х — 0, что противоречит
определению примарной функции. Поэтому единственными примар-
ными функциями являются функции тсг. Тот же довод показывает,
что если х ? 50Ц, то х ? Ttt, откуда ЗМг = Шж..
Только что приведенные рассуждения основывались на следую-
следующих двух свойствах разложения:
1) ЭД?( с 2JL, где тсг — примарная функция, и
2) тс, ф Tij, если i Ф j.
Существование такого разложения вытекает из теоремы 5. Таким
образом, доказана следующая
Теорема 6. Если й—нильпотентная алгебра Ли линей-
линейных преобразований конечномерного векторного простран-
пространства Ш, то й имеет лишь конечное число примарных функ-
функций. Соответствующие примарные компоненты являются
подмодулями, и пространство Ш разлагается в прямую сумму
этих подмодулей. Пусть, далее, 2К = 3^ ф Ш2 ф ... ф Шг — не-
некоторое разложение пространства Ш в прямую сумму под-
подпространств Ttt ф 0, инвариантных относительно 8, которое
удовлетворяет условиям:
1) для каждого I минимальный многочлен ограничения
любого преобразования А ?й на 2№г, есть степень неприводи-
неприводимого многочлена %д(^)тм;
2) если I Ф j, то существует такое линейное преобразова-
преобразование А, что тсм(X) ф 1г;-л(X). Тогда отображения
54 Гл II Разрешимые и нильпотентные алгебры Ли
/ = 1, 2 г, являются примарными функциями, а подпро-
подпространства 2Я, — соответствующими примарными компонен-
компонентами.
Нетрудно установить связь между примарным разложением и
разложением Фиттинга: Шо есть примарная компонента Ш^, если
отображение Л->Х—примарная функция, и 0 в противном случае;
ЗЯ1 есть не что иное, как сумма примарных компонент Ш%, и Ф X.
Проверку этого утверждения мы оставляем читателю.
Допустим теперь, что характеристические корни каждого эле-
элемента А ?2, где 2— нильпотентная алгебра Ли линейных преобразо-
преобразований, лежат в основном поле. Алгебра Ли, обладающая таким свой-
свойством, будет называться расщепляемой Очевидно, что если основное
поле Ф алгебраически замкнуто, то любая алгебра Ли линейных пре-
преобразований конечномерного векторного пространства над Ф будет
расщепляемой.
Итак, пусть алгебра Ли 2 нильпотентна и расщепляема. Ясно,
что характеристический многочлен ограничения А на примарную
компоненту, соответствующую отображению А—>пА(\), имегт вид
пА(Ъ)г. Поскольку этот многочлен является множителем характери-
характеристического многочлена преобразования А, а ттл (X) — неприводимый
многочлен, то из нашего предположения следует, что tza(\) = X — а (А),
а(Л)? Ф. В этих условиях естественно заменить отображение А—.>кД(К)
отображением Л~>а(А) алгебры 2 в поле Ф и сформулировать
следующее
Определение 4. Пусть 2 — алгебра Ли линейных преобра-
преобразований пространства Ш. Тогда отображение а: Л~>а(Л) алгебры 2
в основное поле Ф называется весом пространства (точнее, модуля) Ш
относительно 2, если существует ненулевой вектор х, такой, что
х(А — са(А) I)*- л = 0 для всех А?2. Множество векторов, удо-
удовлетворяющих этому условию, образует вместе с 0 подпростран-
подпространство Шл, которое мы будем называть весовым подпространством
пространства Ш, соответствующим весу а.
В терминах весов и весовых подпространств теорема 6 может
быть переформулирована следующим образом.
Теорема 7. Пусть 2 — расщепляемая нильпотентная ал-
алгебра Ли линейных преобразований конечномерного векторного
пространства Ш. Тогда 2 имеет лишь конечное число различ-
различных весов, весовые подпространства являются подмодулями
и Ш разлагается в прямую сумму этих подмодулей. Более
того, пусть Tt = Tt1@Tt2@ ... © Шг — произвольное разложе-
разложение ЭД? на подпространства 2№г Ф 0, инвариантные относи-
относительно 2, такое, что A) для каждого i ограничение преобра-
преобразования Л ?2 на подпространство ЗЯг имеет лишь один харак-
характеристический корень cti(A) {некоторой кратности); B) если
§ 5 Алгебры Ли с полупростыми обертывающими алгебрами 55
i Ф j, mo существует такое преобразование Л?й, что
а((Л) Ф а;(Л). Тогда отображения Л->аДЛ) являются весами
и подпространства Ш{ — весовыми подпространствами.
§ 5. Алгебры Ли с полупростыми ассоциативными
обертывающими алгебрами
Основным результатом этого параграфа будет описание строения
алгебры Ли й линейных преобразований, обертывающая ассоциатив-
ассоциативная алгебра й* которой полупроста. Доказательства теорем Ли, при-
приводимые в следующем параграфе, будут основываться на этом же
результате. В ближайших двух параграфах характеристика основного
поля предполагается равной нулю. Напомним, что след линейного
преобразования Л конечномерного векторного пространства, опреде-
п
ляемый выражением 2 а« Для любой матрицы (а ) преобразования Л,
равен сумме корней р(, i = 1 п, характеристического многочлена
п
преобразования Л. Далее, tr Ak = 2 pf (tr В есть след В). Если Л ниль-
« = i
потентно, то все корни р, равны нулю, так что tr Ak = 0, k = 1, 2
В том случае, кО1да характеристика поля Ф равна 0, верно и обрат-
обратное: если ^Л* = 0, k=l, 2, ..., то Л нильпотентно. Действи-
Действительно, пусть 2pf = O> k = l, 2 Формулы (тождества Нью-
Ньютона; см. Джекобсон [2], т. I, стр. ПО), выражающие 2 Р* через
элементарные симметрические функции от р(, показывают, что если
характеристика основного поля равна 0, то из нашего условия сле-
следует равенство нулю всех элементарных симметрических функций
от р(, так что все р( равны 0. Поэтому преобразование Л нильпо-
нильпотентно. Мы используем этот результат при доказательстве следую-
следующего утверждения.
Лемма 4 Пусть С — элемент алгебры й линейных преобра-
преобразований конечномерного векторного пространства над полем
Т
характеристики 0, представляемый в виде C = 2lA^(l- г^е
Л(, В,(ё и [СЛ(] —0, / = 1, 2, ..., г. Тогда преобразование С
нильпотентно.
Доказательство. Выполняются условия [C*~M,] = 0, k=l,
г
2, ... (С° = 1). Следовательно, С* = 2 С ИД — BtAt) =
Ck~1BJ— (c*~1fi,)A)=2lA- C*"ISJ Так как след
56 Гл. II. Разрешимые и нильпотентные алгебры Ли
любого коммутатора равен 0, то trС* = 0 для k = l, 2 Поэтому
С нильпотентно.
Основным результатом является следующий.
Теорема 8. Пусть 8— алгебра Ли линейных преобразова-
преобразований конечномерного векторного пространства над полем харак-
характеристики 0. Предположим, что обертывающая ассоциатив-
ассоциативная алгебра 8* полупроста. Тогда 8^=8i©6, где 6 — центр
алгебры 8, a 8j— ее полупростой {как алгебра Ли) идеал.
Доказательство. Пусть ® — радикал алгебры 8. Покажем
сначала, что он совпадает с центром 6 алгебры 8. Действительно,
в противном случае <Sj = [8<3] — ненулевой разрешимый идеал. Пред-
Предположим, что 6(/° = 0, <3(ift~ 1} ф 0, и положим <S2 = ®(iA~1), вз=[©2Й].
Если С?в3- то c = SlA5/l> Ai€®2< Bi?%' и \CAi\ = 0, так как
S3 S ®2 и ®2 абелев. Поэтому по лемме 4 С — нильпотентное пре-
преобразование. Таким образом, каждый элемент идеала <S3 алгебры 8
нильпотентен, вследствие чего по теореме 2 ®3 содержится в ради-
радикале алгебры й*. Так как 8* — полупростая алгебра, то <?3 —0. Но
©3=[©22]. поэтому 62?®. Поскольку <В2 S [8®] S й', каждый
элемент С?®2 имеет вид 2tA- ^Ь Л- ^«62 и [СЛг] = 0, так как
©2 S €.. Как следует из только что проведенного рассуждения,
32 = 0, что противоречит нашему первоначальному предположению
о том, что ®j = [8<3] Ф 0. Поэтому [й®] = 0 и © = 6. Рассуждения,
которые мы уже дважды проводили, могут быть применены для до-
доказательства того, что 6 П S' = 0. Поэтому можно найти такое под-
подпространство 8j э 8', что 8 = 81ф6. Так как ^ содержит 8', то
8j — идеал. Кроме того, алгебра 8, = 8/6 = 8/(S полупроста. Это
завершает доказательство.
Замечание. В следующей главе мы покажем, что 8j = 8', так
что на самом деле имеет место равенство 8 = 8'® 6, где 8' полу-
полупроста.
Следствие 1. Алгебра Ли 8, удовлетворяющая условиям
предыдущей теоремы, разрешима тогда и только тогда, когда
8 абелева. Более общо, если 8 — разрешимая алгебра Ли и
Ш — радикал ассоциативной алгебры 8*. то 8*/SR — коммута-
коммутативная алгебра.
Доказательство. Если алгебра Ли 8 абелева, то она разре-
разрешима, а если 8 разрешима и Й* полупроста, то 8 = 6ф8Р где
8j — полупростая алгебра. Так как алгебра Ли может быть полу-
полупроста и разрешима одновременно только в том случае, если она
нулевая, то 8j = 0 и 8 = 6, т. е. алгебра 8 абелева.
Для доказательства второго утверждения удобно несколько изменить
точку зрения и рассмотреть 8 как подалгебру алгебры %^, где % —
§ 5. Алгебры Ли с полупростыми обертывающими алгебрами 57
конечномерная ассоциативная алгебра над полем характеристики 0.
К алгебрам 8 и 31 применима теорема 8, так как алгебру ЭД можно
рассматривать как подалгебру ассоциативной алгебры Щ линейных
преобразований конечномерного векторного пространства.
Допустим теперь, что алгебра 8 разрешима, так что алгебра
(8-|-9t)/9t, являющаяся гомоморфным образом алгебры 8, также раз-
разрешима. Более того, обертывающей ассоциативной алгеброй этой
алгебры Ли является полупростая ассоциативная алгебра 8*/91. По-
Поэтому алгебра (8-f-9t)/9t абелева, откуда вытекает выполнение соот-
соотношения (а + Щ(Ь-\-$) — (Ь-+-№)№-+-№) Для любых а, &?8. Так
как классы смежности а+ 91 порождают 8*/91, то алгебра 8*/91 является
коммутативной.
Следствие 2. Пусть 8—алгебра Ли линейных преобразо-
преобразований конечномерного векторного пространства над полем
характеристики 0, <& — радикал алгебры 8 и Ш — радикал
ассоциативной алгебры 8*. Тогда 8f|9t состоит из всех ниль-
нильпотентных элементов радикала <5 и [S8] ? 91.
Доказательство. Так как 91 — ассоциативная нильпотентная
алгебра, то она нильпотентна и как алгебра Ли. Поэтому 8 0 915®-
Более того, элементы 91 нильпотентны, так что 8 П 91S в0, где
<30 — множество нильпотентных элементов радикала©. Если обозна-
обозначить через 910 радикал- обертывающей ассоциативной алгебры <?*, то
ввиду следствия 1 факторалгебра в*/^ коммутативна. Каждый
нильпотентный элемент алгебры порождает нильпотентный идеал и,
таким образом, принадлежит радикалу. Поскольку алгебра ®*/^о
полупроста, она не имеет нильпотентных элементов, отличных от 0.
Отсюда следует, что 910— множество нильпотентных элементов ал-
алгебры <S* и, таким образом, <50 = 910П@ будет.подпространством в 8.
Рассмотрим теперь (8-f-9t)/9t. Обертывающей ассоциативной ал-
алгеброй этой алгебры Ли будет полупростая алгебра 8*/9t. Поэтому
радикал алгебры (8 + 91) содержится в ее центре. Так как (<S + 9t)/9i —
разрешимый идеал алгебры (8 + 9t)/9t, то [(S-f 91/91, (8 + 9t)/91] = 0,
откуда следует, что [®8] ? 91. Таким образом, [©8] ? 8 П 91 ? <В0.
Тогда, в частности, [<S08] ? <S0 и <S0—идеал алгебры 8. Так как
элементы из <S0 нильпотентны, то по теореме 2 <S0 S 91. Отсюда
®о S 8 П 91 и <В0 = 8 П 91, чем и завершается наше доказательство.
Существует более употребительная формулировка теоремы 8,
в которой предположение о строении алгебры 8* заменено некоторым
предположением о действии алгебры 8 на Ш.' Прежде чем сформу-
сформулировать это предположение, напомним некоторые стандартные поня-
понятия из теории линейных преобразований.
Пусть Е — некоторое множество линейных преобразований конечно-
конечномерного векторного пространства Ш над полем Ф. Напомним, что
совокупность L(L) подпространств, инвариантных относительно
58 Гл. I!. Разрешимые и нильпотентные алгебры Ли
? (VIA ? У1, Л??), является подструктурой структуры всех подпро-
подпространств в Ш.
Назовем элементы из L(Ii) ^-подпространствами простран-
пространства Ш. Если tH — некоторое подпространство, то совокупность
элементов А ? (?, таких, что ША ? Ш, образует подалгебру в (?.
Отсюда следует, что если 9???(Е), то Ш инвариантно относительно
каждого элемента обертывающей ассоциативной алгебры Е* множе-
множества Е и относительно каждого элемента обертывающей алгебры Е+,
Мы получаем, таким образом, что L (Е) = L (Е ) = L (Ef).
Множество Е называется неприводимым множеством линейных
преобразований, а пространство Ш — L-неприводимым, если
А(Е)={ЗЙ, 0} и Ш ф 0. Множество Е называется неразложимым
множеством, а Ш — L-неразложимым пространством, если не
существует разложения 9D? = SJ?! ф 9ЭТ2• гДе ЭЙ/ — ненулевые элементы
из ?(Е). Из неприводимости, конечно, сразу следует неразложимость.
Множество ? (и 9Jt относительно Е) называется вполне приводимым,
если 2)t=?2№a, 9J2a ??(?), где Ша неприводимы. Напомним следую-
следующий, хорошо известный результат.
Теорема 9. Множество Е вполне приводимо тогда и
только тогда, когда подструктура L(L) дополняема, т. е. если
для каждого 9???(Е) существует ^'^/.(Е), такое, что
m W. Если это условие выполнено, то W = Ш1 ф ЭД2 © . ..
йг, где Tli ? ? (Е) неприводимы.
Доказательство. Предположим, что 2Я = 2^Щ*> гДе ^а не"
приводимы в L(E), и пусть ffi?Z.(E). Если dim 9? = dim Зй, то 9? = ЗМ
и 9й = ЭТ©0. Предположим теперь, что dim %l < dim 9JJ, и допустим,
что теорема доказана для подпространств З^, таких, что dim tflx >
> dim Щ. Так как S^czSBJ = E2)Ja, то существует такое Ша, что Шл ф ЭТ.
Рассмотрим подпространство Ша П 91?. Это Е-подпространство непри-
неприводимого Е-пространства 2Я„. Поэтому либо 2)Ja fl 9^ = Tta, либо
9Jta П 91? = 0. В первом случае 9f ^ 35Ja, что противоречит нашему
предположению. Поэтому Tlaf]!R = O и Щг — 9^+ ЭИЯ = 9?фШ{а. Мы
можем применить теперь индуктивное предположение и вывести, что
5Й = Я,©Яь Wl6^(S). Тогда TO = 9^©OWC[©9^1' = 9A©9^', где
Ш =2)fa©9(ii ^L(E). Обратно, предположим, что Z.(E) дополняемо.
Пусть 2Jij — минимальный отличный от 0 элемент в ?(Е). (Такие
элементы существуют, поскольку dim Tt конечна.) Тогда 27? = 2Я1® 9?,
где 9^^Z-(E). Заметим теперь, что условие, которое мы предполо-
предположили выполненным для Ш, выполняется также и для til. Пусть ^
будет Е-подпространством в 9?. Тогда 2К = ^©^', где. 5JJ' ^ L (Е).
Далее, согласно модулярному закону Дедекинда, 9f —3Wn9fi =
= 5Р + EР'П9^), поскольку т^<$. Если мы обозначим ?j3" = ^'n9^,
то 5р"П^ = ?П^'П9^ = О. Поэтому ^ = ^ф5р", гд; ^^(?) и
§ 5. Алгебры Ли с полупростыми обертывающими алгебрами 59
Ч$" с: Ш. Мы можем повторить теперь для Щ рассуждения, относя-
относящиеся к Ш. Иными словами, можно написать 9? = 2){2ф5р, где Ш2,
^p^Z-(E) и Ш2 неприводимо. Продолжая эти рассуждения, мы полу-
получим вследствие конечности размерности пространства разложение
а^Ш^фЗЯг® ...®2КГ, где Шс неприводимы и ЭЙ,?/.(?). Этим
и завершается наше доказательство.
Предположив далее, что ? = ЭД есть подалгебра ассоциативной
алгебры 6 (быть может, не содержащая единицы), получим следую-
следующее необходимое условие полной приводимости.
Теорема 10. Из полной приводимости ассоциативной ал-
алгебры Ж линейных преобразований конечномерного векторного
пространства следует, что ЭД — полупростая алгебра.
Доказательство. Пусть Ш—радикал алгебры ЭД. Предполо-
Предположим, что Ш = 2 2^- где $Ш„ ?/.($) и Шл неприводимы. Рассмотрим
подпространство %RJR, натянутое на векторы вида yN, где у ? 2№я,
N?Ш. Это ЭД-подпространство, содержащееся в Ша. Так как Шк = 0
для некоторого k, то должно иметь место строгое включение
SOJjiRcSOij, (см. доказательство теоремы 1). Поскольку 2Ма неприво-
неприводимо, можно заключить, что 2fta9t = 0 для каждого Шл. Так как
2I = 23)^. то 2Ж=0, т. е. SR—0. Следовательно, % — полупростая
алгебра.
Поскольку множество ? вполне приводимо тогда и только тогда,
когда ?* и 2+ вполне приводимы, мы получаем
Следствие. Если множество Б вполне приводимо, то S*
и Ef полупросты.
Будем говорить, что линейное преобразование А полупросто, если
минимальный многочлен (i(X) преобразования А является произведе-
произведением различных неприводимых многочленов. Это условие эквивалентно
тому, что {i4jf не имеет нильпотентных элементов, отличных от 0.
В самом деле, пусть [j. (X) = Uj (X)ei тс2(Х)е2 . . . тсг(Х)е'1. Тогда Z =
= тсДЛ)^^) ... тсг(Л) — нильпотентный элемент и Z Ф 0, если не-
некоторое ег> 1. Напротив, предположим, что ¦к1 — различные непри-
неприводимые многочлены и все el = l. Пусть преобразование Z = cp(i4)
нильпотентно. Если Zr = 0, то <р(-<4)г —0 и ?(^)г Делится на [*(Х).
Поэтому «р(^) делится на [j.(X) и Z = <p(^) —0-
Мы можем теперь доказать следующее утверждение.
Теорема 11. Пусть 2 — вполне приводимая алгебра Ли
линейных преобразований конечномерного векторного простран-
пространства над полем характеристики 0. Тогда %^=^,@iv где (Б —
центр, a gj — полупрдбтой идеал. 'Кроме того, ёАеМеНты из E
полупросты.
60 Гл. II. Разрешимые и нильпотентные алгебры Ли
Доказательство. Если 2 вполне приводима, то й*— полу-
полупростая алгебра. Поэтому существует разложение S = 608j, как
следует из теоремы 8. Предположим теперь, что 6 содержит неко-
некоторый неполупростой элемент С. Тогда {С}+ содержит отличный от
нуля нильпотентный элемент N. Далее, {С}+ — множество многочле-
многочленов относительно С, так что элемент N тоже есть многочлен отно-
относительно С. Значит N принадлежит центру алгебры 8f. Поэтому
коль скоро это так, N%f = %fN — идеал в й+. Кроме того,
(W^fg/V^^O для достаточно большого k. Так как N? Л/?+,
то iVS+ — ненулевой нильпотентный идеал алгебры gf, что противо-
противоречит полупростоте 8f.
Позже будет показано (теорема 3.10), что верно и обратное
утверждение, так что приведенные выше условия необходимы и до-
достаточны для полной приводимости алгебры Ли линейных преобра-
преобразований в случае характеристики 0. Ничего подобного не может
иметь места в случае характеристики р Ф 0 (см. § 6.3). Заметим также,
что верно обратное утверждение по отношению к теореме 10. В ассо-
ассоциативном случае имеется, таким образом, простое необходимое и
достаточное условие полной приводимости, верное при любой харак-
характеристике основного поля. Обращение теоремы 10 значительно глубже,
чем сама .теорема. Это утверждение, впрочем, не будет играть зна-
значительной роли в последующем.
§ 6. Теоремы Ли
Напомним определение- композиционного ряда относительно множе-
множества Е линейных преобразований и смысл этого ряда на языке матриц.
Цепочка Е-подпространств Ш = З^зЗЯг3 • • • ^^s^^s+i = 0 назы-
называется композиционным рядом для ЗЯ относительно Е, если ни для
какого i не существует такого подпространства Ж' ? L (Е), что
9Игз2Тз9Иг+1. Если fR есть Е-подпространство в ЗЯ, то Е индуци-
индуцирует множество Е линейных преобразований пространства ЗЯ/Э?. Как
хорошо известно (и легко проверяется) для групп с операторами,
Е-подпространства пространства Ш/!Я имеют вид ^/Э'?, где ^
есть Е-подпространство в ЗЯ, содержащее ЭТ.
Отсюда следует, что пространство Ш/IR Е-неприводимо в том и
только в том случае, когда не существует такого ^p^L(E), что
ЭДз^эЭ?. Поэтому 2№ = аК1'эЗЙ2э ..'. 32Rs+1 = 0 является компо-
композиционным рядом в том и только в том случае, когда каждый фак-
фактор ЗЯ//ЗЯг+1 Ег-неприводим, где Ег — множество индуцированных
преобразований в Ш^/9Иг+1, порожденных элементами Л^Е.
Конечность размерности пространства Tt гарантирует существо-
существование композиционного ряда. Пусть теперь 9И2 — максимальное Е-под-
§ 6. Теоремы Ли 61
пространство, строго содержащееся в ШХ = Ш. Тогда Ш1'^>Ш2 и
TljWli неприводимо. Пусть, далее, 9И3 — максимальное инвариантное
подпространство в Ш2, не равное Tt2 и т. д. Получаем, таким образом,
композиционный ряд Ш^зЗйг^З^з3 • • • зЗ)!р5КН1 = 0 для Ш.
Пусть Ш = ШгзШ2з2В3э ... з35?5+1 — убывающая цепочка Е-под-
пространств и {ех, .... еп) — такой базис пространства Tt, что
(е1 ещ) будет базисом в Ш$, (ev .... еП{+„2) — базисом в 2W5_j
и т. д. Очевидно, что если Л??, то матрица преобразования А
в базисе (ег) имеет вид
Мг О
* Ж2
A0)
Итак,
е .А = 2 \>h!)e ,,-4- х, A1)
л,+ ... +П/_,+* Y " «1+ •••+";¦ -И '
ft, /=1 tlj,
где л; — вектор из Tts_j+2. Таким образом, в равенстве A0) матрица
М . = (vfJ)\ Классы смежности еп h +n. +k s= еп.л. ...+„, , + * +
-f-2Jii-/+2. ft= 1. ••¦- «;- образуют базис факторпространства
Tts_j+1jTis_!+2- Из соотношения A1) следует равенство
ё"л+. +„. +И ~ 2 РЙЧ, + +„ +г> A2)
показывающее, что матрица линейного преобразования, индуцирован-
индуцированного преобразованием А в факторпространстве 9Иу_;+1/ЗНу_у+2 есть
матрица Mj.
Посмотрим теперь, что можно сказать о разрешимых алгебрах Ли
линейных преобразований конечномерного векторного пространства
над алгебраически замкнутым полем характеристики 0. Нам потре-
потребуется следующая
Лемма 5. Пусть й — абелева алгебра Ли линейных пре-
преобразований конечномерного векторного пространства Ш над Ф,
где Ф — алгебраически замкнуто. Предположим, что Ш непри-
неприводимо. Тогда пространство Ш одномерно.
. Доказательство. Если А ? 8, то А имеет отличный от нуля
характеристический вектор х, т. е. хА = ах, где <х?Ф. Пусть
теперь Tta — множество векторов у, удовлетворяющих этому уравне-
уравнению. Тогда, если S?g и у?Ша, то {уВ) А = уАВ — ауВ. Поэтому
уВ?Ша. Это показывает, что Tta инвариантно относительно каждого
преобразования Л??. Так как 9R неприводимо, 2№ = 2Яа, т. е. Л = а1
62 Гл. II. Разрешимые и нилыготентные алгебры Ли
в Ш. То же самое справедливо для каждого элемента Л ?8. Отсюда
следует, что любое подпространство в SM является 8-подпростран-
ством. Так как 2)? 2-неприводимо, то 9И не имеет подпространств, от-
отличных от 0 и от самого себя. Поэтому SM одномерно.
Мы можем теперь доказать следующее утверждение.
Теорема Ли. Если 8— разрешимая алгебра Ли линейных
преобразований конечномерного векторного пространства 3)?
над алгебраически замкнутым полем характеристики О, то
матрицы из 2 могут быть приведены одновременно к треуголь-
треугольному виду.
Доказательство. Пусть Ш = 2)^=3 2К2=э . . . :z>2ft:S+1 = 0 —
композиционный ряд для Ш относительно 8. Обозначим через 2г мно-
множество индуцированных линейных преобразований в неприводимом
пространстве Шг/Ш1+1. Тогда 8г является разрешимой алгеброй Ли
линейных преобразований, поскольку она есть гомоморфный образ ал-
алгебры 2. Кроме того, 2г неприводима и поэтому вполне приводима
в ЗЙ4/9№<+1. Вследствие этого 2; абелева по теореме 11. Из леммы
следует, что dim2K//9Wi+1= 1. Это означает, что если мы используем
базис, соответствующий композиционному ряду, то все матрицы Mt
в равенстве A0) однострочные. Поэтому каждая матрица М, соот-
соответствующая элементу Л ?2, треугольна.
Если алгебра 2 нильпотентна, то она разрешима, и в этом слу-
случае применима теорема Ли. Заметим также, что лемма 5 и, следова-
следовательно, теорема Ли, справедливы для любого поля характеристики 0
при условии, что характеристические корни линейных преобразова-
преобразований принадлежат этому полю. Мы назвали такие алгебры Ли линей-
линейных преобразований расщепляемыми. Если соединить теперь это обоб-
обобщение теоремы Ли с теоремой 7, то получится
Теорема 12. Пусть 2 — расщепляемая нильпотентная ал-
алгебра Ли линейных преобразований конечномерного векторного
пространства Ш над полем характеристики 0. Тогда Ш есть
прямая сумма своих весовых подпространств 2Ка, и матрицы
в весовом подпространстве SMa могут быть одновременно при-
приведены к виду
а (Л) 0
a (A)
а (Л)
A3)
Доказательство. Ранее было доказано, что 9R является прямой
суммой весовых подпространств 3№а. Из равенства хл(А — а (Л) 1)т=0
§ 7 Приложения к абстрактным алгебрам Ли. Некоторые примеры 63
для каждого ха в $Ra следует, что единственным характеристическим
корнем преобразования Л в SMa будет а (Л). Так как диагональные
элементы в матрице A0) являются характеристическими корнями,
то матрицы Mt для преобразования Л в формуле A0) равны а (Л).
Поэтому матрица преобразования А в пространстве Ш^ имеет вид A3).
Из доказательства этого результата следует, что в SMa суще-
существует такой ненулевой вектор х, что хА = а(А)х, Л?8. Если
Л, 5?Й, то х(Л+В) = (а(Л) + а(В))х=а(Л+Й)х,
= ра(А)х = я(р(А))х. р?Ф, и х[АВ] = (а(Л)а(В) — а(В)
= а([ЛВ])л\ Первые два из этих соотношений показывают,
что а — линейная функция на 2. Так как каждый элемент производ-
производной алгебры 8' есть линейная комбинация элементов [АВ\ то из
линейности и из последнего условия вытекает, что а(С) —0, С ?8'.
Мы получаем, таким образом, важное для дальнейшего следствие
теоремы 12.
Следствие. В предположениях теоремы 12 веса а: Л—>а(Л)
суть линейные функции на 8, обращающиеся в 0 на 8'.
§ 7. Приложения к абстрактным алгебрам Ли.
Некоторые противоречащие примеры
Рассмотрение множества линейных преобразований ad 2, где 8 —
абстрактная алгебра Ли, дает возможность применить полученные
результаты об алгебрах Ли линейных преобразований к абстрактным
алгебрам Ли. Мы приведем два результата, которые могут быть по-
получены таким путем.
Теорема 13. Пусть 8 — конечномерная алгебра Ли над
полем характеристики 0, <В — радикал и Щ — ниль-радикал.
Тогда [й®] С Ш.
Доказательство. Согласно следствию 2 теоремы 8, [ad8,
ad<S] содержится в радикале алгебры (ad 8)*. Отсюда следует, что
существует такое целое число N, что для любых N преобразо-
преобразований вида [ad at, adsj, a,-^8, Sj^®. имеет место равенство
[ad aj, adSj] ... [ad aN, ad 5^1 = 0. Поэтому ad[a1s1]ad[a2s2] • • •
... ad [0^^1 = 0, т. e. [...[ [x [a^J ] [a2s2] ] ..., [a^H^O для
любого х ? 8. Следовательно, [&%]N+l = 0, так что [<58] нильпо-
тентна. Поскольку это идеал, [<S8] ? ffi-
"Следствие 1. Производная алгебра л ~i6ou конечномерной
разрешимой алгебры Ли характеристики 0 нильпотентна.
Доказательство. Достаточно положить ? = ® в предыдущей
теореме.
64 Гл II Разрешимые и нильпотентные алгебры Ли
Следствие 2. Пусть <5 — разрешимая конечномерная
алгебра Ли характеристики О, У1 — ее ниль-радикал. Тогда
<&D с Щ для любого дифференцирования D алгебры <В.
Доказательство. Пусть 8 = ®фФ?)— расщепляемое рас-
расширение подалгебры Фй посредством <?> (см. гл. I, § 5). Здесь <?> —
идеал в 8 и [s, D] — sD для любого $?в. Так как фактор-
алгебра 8/<S одномерна, то алгебра 8 разрешима. Поэтому Й' —
нильпотентный идеал в 8. С другой стороны, 8' = <S' + <S?>, так что
<5'-|-<SD — нильпотентный идеал в <В и <5'-\-&D с Щ. Следова-
Следовательно, <BD С %1.
Теорема 14 (Ли). Пусть 8 — конечномерная разрешимая
алгебра Ли над алгебраически замкнутым полем характе-
характеристики 0. Тогда существует цепочка идеалов 8 = 8я:э8я_1:э ...
. ..г^гэО, такая, что сНт8г = ;.
Доказательство. Поскольку алгебра Й разрешима, ad8 —
разрешимая алгебра Ли линейных преобразований, действующих
в векторном пространстве 8. Пусть 8 = 8!=382=5 ••• =z>8s+1 == 0 —
композиционный ряд алгебры 8 относительно ad 8. Тогда условие
йг ad 8 Е Й,- эквивалентно утверждению, что 8г есть идеал. Из дока-
доказательства теоремы Ли следует, что. имеет место равенство
dim8,/8i+1 = 1. Поэтому композиционный ряд и дает цепочку идеалов
требуемого типа.
Мы покажем теперь, что предположение о равенстве нулю ха-
характеристики поля существенно для получения результатов § 5 и 6.
При построении противоречащих примеров в случае характеристики
р Ф 0 будем исходить из р-мерного векторного пространства SM
над полем Ф характеристики р'). Пусть Е и F — линейные преоб-
преобразования пространства SM, действие которых на базис (ev e2, .... ер)
задается формулами
etE — el+l, f<p— I,
ерЕ = е1, A4)
«/¦ = (*— 1)«,.
, uv </?— 1, epEF = 0, и elFE = (l — l)
epFE = — ev Поэтому
Тогда e,EF — teuv г</?— 1, epEF = 0, и
eM. ep[EF) = ev
так что имеет место равенство [EF] = Е. Вследствие этого S =
= ФЕ-\-ФР будет двумерной разрешимой алгеброй Ли. Мы утвер-
утверждаем, что Ш 8-неприводимо. В самом деле, пусть ЭТ — 8-подпро-
') Для простоты предполагается, что р Ф 2. В случае р = й приводимые
ниже примеры, как легко убедиться, нуждаются в небольшой модифика-
модификации. — Прим. ред.
§ 7. Приложения к абстрактным алгебрам Ли. Некоторые примеры 65
странство. отличное от нуля, и x^=^<te^0 — элемент из
Тогда
A5)
Определитель Вандермонда
11 ... 1
v=
О 1 ... p~\
0 I"-1 ... (p-1
A6)
отличен от нуля.
Если мы умножим xF на алгебраическое дополнение элемента
с индексом (j, i) определителя V и просуммируем по J, то полу-
получим, что V^e^iR и, таким образом, ?гег?ЭТ. Отсюда следует, что ЭТ
содержит один из векторов et. Если подействовать теперь на et
с помощью степеней преобразования Е, то получится любой вектор е,-.
Таким образом, 9^ = SDt, что доказывает неприводимость и показы-
показывает, что теорема 11 не верна в случае характеристики р. Более
того, поскольку из полной приводимости следует полупростота
(в действительности алгебра 2* = 6 проста), теорема 8 также не
верна в случае характеристики р.
Пусть, далее, <В — двумерная неабелева алгебра Ли Фе-}-Ф/'
[ef] = e, над полем Ф характеристики р. Тогда отображение е->Е,
f->F, задаваемое равенствами A4), определяет представление
алгебры ©, действующее в SM, и Ш есть ©-модуль с базисом
(ev е2, ..., ер). Пусть $—расщепляемое расширение, $ = <S®2R.
Тогда SM — абелев идеал алгебры $ и факторалгебра $/2Я = ® раз-
рйпима. Поэтому и 5? разрешима. Производная алгебра $' = Фе-]~
-\-[ШВ] =Фе~\-ЗЯ. Далее, ($'J = ($'K = ... =S№, поскольку
[Tie] = SME = 9R. Поэтому алгебра Я' не нильпотентна. Это пока-
показывает, что теорема 13 также не верна в случае характеристики р.
Казалось бы, возможно, что теорема Ли остается верной и для
характеристики р, если заменить слово „разрешимая" словом „ниль-
потентная". Тогда из теоремы Ли следовало бы, что существует
удобная ' каноническая форма A3) для нильпотентных алгебр Ли.
Однако это также не имеет места. Пусть Е и F определены, как
раньше. Тогда из равенства EF — FE — E следует, что E{FE~x) —
)Е=1. Положим G = FE~ , Н—\. Тогда мы получим
[EG]=:H, [?Я] = 0 = [ОЯ]. A7)
5 Н. Джекобсон
66 Гл. II'. Разрешимые и нильпотентные алгебры Ли
Отсюда вытекает, что Щ = ФЕ -f- ФО -\- ФН—нильпотентная ал-
алгебра Ли. С другой стороны, ассоциативная алгебра !R* = 8*(# =
— Ф?-|" Ф/) непривоцима даже если основное поле алгебраически
замкнуто. Поэтому матрицы не могут быть приведены одновременно
к треугольному виду. Если X— \E-\-r\G-\-{\, то, как нетрудно
проверить, {X— (S-f-Q 1)р = 0. Поэтому отображение Л"->?-)-С=
~a(io является единственным весом для 1R. Заметим, что это ото-
отображение линейно. (О линейности весов в случае более общих ниль-
потентных алгебр см. упр. 24 гл. V).
Упражнения
В этих упражнениях все алгебры и векторные пространства конечно-
конечномерны.
1. Пусть Ф — алгебраически замкнутое поле характеристики 0, и пусть
33 — разрешимая подалгебра размерности т алгебры Ли 8, строго содержа-
содержащаяся в 8. Показать, что 33 содержится в подалгебре размерности /и —|— 1.
2. Пусть поле Ф такое же, как в упражнении 1, а 8 разрешима; по-
показать, что в алгебре 8 существует базис (elt e2, ..., еп) с таблицей умно-
i
жения [etej\ = 2 Vijkek< l < J-
3. Пусть Ф такое же, как в упражнении 1. Пусть 8 — разрешимая под-
подалгебра в Фп[. Доказать, что dira8<!n(/i-r-l)/2 и 8 может быть вложена
в разрешимую подалгебру размерности n(n-\-\)j2. Показать, что если 8j
и 82 — разрешимые подалгебры размерности n(n-\-\)j2, то существует такая
невырожденная матрица А, что 22= A~l2iA.
4. Показать, что если 8 не нильпотентна над алгебраически замкнутым
полем, то 8 содержит двумерную неабелеву подалгебру.
5. Пусть Ф — алгебраически замкнутое поле произвольной характе-
характеристики. Если а — характеристический корень линейного преобразования А,
то соответствующее подпространство Ша = {ха \ х^(А — al)* = 0 для некото-
некоторого k}. Имеет место разложение 2Jt = 2 © 2Jta. Пусть А — автоморфизм
(неассоциативной) алгебры 9?, и пусть % — 2 (g 9Га — разложение алгебры Ж
как векторного пространства на характеристические подпространства отно-
относительно А. Показать, что
О, если ар не является характеристическим корнем,
~ 91ая, если ар — характеристический корень.
Пусть 5 — такое линейное преобразование в Ж, что 5 = а1 в 9Га для
каждого а. Показать, что 5 — автоморфизм, перестановочный с А, и что
U=S~1A — автоморфизм, имеющий вид \-\-Z, где Z — нильпотентное
преобразование.
6. Пусть Ф такое же, как в упражнении 5, 8 — алгебра Ли над ф,
А — автоморфизм алгебры 8. Пусть 8 = 2ф8а — разложение 8 на характе-
характеристические подпространства относительно преобразования А. Пусть 2В =
= U ad 8а, где ad8a= {ad;ca | Jca?8a}- Показать что 9В слабо замкнуто от-
относительно А X В = [АВ].
7. Пусть Ф, 8, А, 9В такие же, как в упражнении 6. Допустим, что А
имеет простой порядок. Показать, что если х = 0 — единственный элемент
Упражнения 67
алгебры 8, такой, то хА — х, то каждый элемент из Щ нильпотентен. От-
Отсюда вывести, что если алгебра Ли над любым полем имеет автоморфизм
простого порядка без неподвижных точек (за исключением 0), то 8 ниль-
потентна.
8. Пусть D — дифференцирование (неассоциативной) алгебры 2Г, и пусть
ЗС = 2ф91а — ее разложение на характеристические подпространства отно-
относительно D. Показать, что
10, если а-}-Р не является характеристическим корнем
преобразования D,
[ S= Sfa+p> еслиа-j-f) — характеристический корень.
Пусть S — такое линейное преобразование алгебры Ж, что S = al в Ч1а для
каждого а. Показать, что S — дифференцирование, перестановочное с D,
и D — S = Z — нильпотентное дифференцирование.
9. Доказать, что алгебра Ли 8 над полем характеристики 0 ннльпо-
тентна, если на ней определено дифференцирование без ненулевых констант.
10. (Диксмье — Листер.) Показать, что если 8 — нильпотентная алгебра
Ли, как в упражнении 1.7, то каждое дифференцирование D удовлетворяет
условию QD С 8' и поэтому нильпотентно. Показать, что эта алгебра Ли
не может быть производной алгеброй никакой другой алгебры Ли.
11. Пусть 8 — такая алгебра Ли линейных преобразований, что каждый
элемент А ? 8 имеет вид а (А) 1 -f- Z, где а (А) ? Ф, а Z нильпотентен. Дока-
Доказать, что 8 нильпотентна.
Следующая группа упражнений посвящена доказательству конечности
башни дифференцирований любой алгебры Лн с нулевым центром. Соот-
Соответствующий результат для конечных групп принадлежит Виланду, а дока-
доказательство его в случае алгебр Ли — Шенкману. Оно в точности следует
доказательству Виланда для группового случая, но использует некоторые
результаты, справедливые именно для алгебр Ли. Благодаря этому дости-
достигается существенное упрощение, а конечный результат оказывается более
сильным, чем в теоретико-групповом случае.
Пусть 8 — алгебра Ли с нулевым центром. Тогда 8 изоморфна идеалу 8!
внутренних дифференцирований алгебры дифференцирований 82 = 35 (8). Мы
можем отожцествить 8 с 8] и таким образом рассмотреть 8 как идеал в С2-
Мы видели (упражнение 1.4), что 82 имеет нулевой центр. Значит этот про-
процесс может быть повторен, и мы получим 8! с ?2 с 8з, где 8з = X) (X) (8)) —
алгебра дифференцирований алгебры 3) (8), а 82 отождествляется с идеалом
своих внутренних дифференцирований. Этот процесс приводит к цепочке
8 = 8|C82c5jC ,.., где каждый член 8г- инвариантен в 81+i. Поэтому
алгебра 8i = S субинвариантна в 8; (упражнение 1.8) и каждая алгебра 8;
имеет нулевой центр. Теорема о башне утверждает, что, начиная с некоторого
шага, будет 8r = 8r+i= .... Это означает, что если алгебра 8 имеет нулевой
К
I 1
центр, то для некоторого К алгебра 35 (Ж (... 3) (С)...) — совершенная ал-
алгебра Ли.
Для дальнейшего нам понадобятся упражнения 1.4, 1.8 н 1.9. Кроме
этого потребуются лишь элементарные результаты и теорема Энгеля о том,
что если присоединенный эндоморфизм ad a любого элемента а из 8 ниль-
нильпотентен, то алгебра 8 ннльпотентна.
12. Доказать, что каждая алгебра Ли 8 обладает разложением 8 =
со
= 8м -f- у> где 8Ш — | 181 и ф — нильпотентная подалгебра •
68 Гл II. Разрешимые и нильпотентные алгебры Ли
13. Пусть 8 — алгебра Ли и 3 — централизатор идеала 8™. Показать,
что если 8 имеет нулевой центр, то Q сг Sm- Набросок доказательства: Q—
идеал; запишем 8 = 8ш-4-4>, где ф — нильпотентная подалгебра, положим
8, = 3 + 4)> причем 8i является подалгеброй, так как 3 — идеал. Запишем
8j = |)j -\- 8™, где |)j — нильпотентная подалгебра. Тогда Cj*cg и 8 =
!- Если Si —центр подалгебры $и то 8D®i содержится в центре 8>
8П© ° О ©iПЗ = °> ?fl8
+ 4! i р р $и 8D р
так что 8П©1 = °- Отсюда следует, что ©iПЗ = °> поскольку
идеал в ?j. Поэтому Q = 8J' с 8т.
14. Пусть 31 субинвариантна в 8, и допустим, что централизатор под-
подалгебры SI в 8 равен 0. Доказать, что централизатор 3 подалгебры Э1Ш
в 8 содержится в ЭГ".
Набросок доказательства. Допустим, что З?^ Тогда, со-
согласно упражнению 8, Зс?2Г, 3 — идеал и R — Q-{-9t — подалгебра, причем
Яп>2Г. Нормализатор % в Ш строго содержит ЗГ и содержит элемент
г 6 8. № Далее, 33 = Фг -\- Ж — подалгебра, такая, что ЯЗШ = 5ГШ. Центра-
Централизатор подалгебры 33'° в 93 содержит ¦г?5В<"> поэтому, как следует из
упражнения 13, ЭЗ имеет ненулевой центр и, таким образом, централизатор 3t
в У отличен от нуля, что противоречит предположению.
15. Пусть 8 — алгебра Ли, 33 — субинвариантная подалгебра, Ж—идеал
в ©. Показать, что если централизатор идеала 91 в 33 и централизатор под-
подалгебры 33 в 8 равны 0, то и централизатор подалгебры ЗГ в 8 равен 0.
16. Пусть 8 = 8iC0scfi,c ..., 8* = ?>(8г_1) — башня алгебр диф-
дифференцирований алгебры Ли 8Ф с нулевым центром. Показать, что
централизатор алгебры 8i в 8, равен 0, а централизатор подалгебры 8™
в 8, содержится в 8™. Пусть S (8™) — центр 8™ и © (8™) — ее алгебра диф-
дифференцирований. Доказать, что
dim 8, < dim S (8f) + dim Ъ (8?).
Отсюда вывести, что существует такое число т, что 8т = 8т+,= .... Это
и есть теорема Шенкмана о башне дифференцирований.
17. Пусть 8 — алгебра Ли линейных преобразований векторного про-
пространства над полем характеристики 0, й — такая ее субинвариантная под-
подалгебра, что каждый элемент К^й нильпотентен. Доказать, что $ содер-
содержится в радикале алгебры 8*. (Указание. Воспользоваться упражне-
упражнением 1.22.)
18. Пусть 8 — нильпотентная алгебра Ли линейных преобразований
векторного пространства Ж, такая, что Ш есть сумма конечномерных под-
подпространств, инвариантных относительно ?. Показать, что 2Л = 2 ф Ш^, где
fflK — примерные компоненты, соответствующие примерным функциям %
А~>к (А). Показать, что Шк инвариантны. Показать, что если 94 — любое
инвариантное подпространство, то 9? = Еф9?„, где 91Л =
Глава III
КРИТЕРИЙ КАРТАНА И ЕГО СЛЕДСТВИЯ
В этой главе будут рассмотрены фундаментальные вопросы струк-
структурной теории конечномерных алгебр Ли характеристики 0.
Мы изучим строение полупростых алгебр этого типа, докажем
теорему о полной приводимости конечномерных представлений и
теорему Леви об отщеплении радикала. Все эти результаты полу-
получаются при помощи некоторых критериев разрешимости и полупро-
полупростоты, формулируемых в терминах следов. Одним- из них является
критерий Картана: конечномерная алгебра Ли характеристики 0 раз-
разрешима тогдг и только тогда, когда tr (ad af = 0 для любого а ? 8'.
Очевидно, это условие есть ослабленное условие Энгеля, заклю-
заключающееся в том, что эндоморфизм ad а нильпотентен для любого
а ?8'. Метод, применяемый для доказательства этого результата и
других аналогичных результатов, является классическим и основы-
основывается на изучении некоторых нильпотентных подалгебр, называемых
подалгебрами Картана. Этот же метод будет использован и в сле-
следующей главе для получения классификации простых алгебр Ли над
алгебраически замкнутым полем характеристики 0.
§ 1. Подалгебры Картана
Пусть 58— подалгебра алгебры Ли 8. Нормализатором !У? под-
подалгебры 58 называется множество всех элементов х ? 8, таких, что
[jcSB] S 33, т. е. [xb] ? 58 для каждого b ? 23. Из определения немед-
немедленно следует, что нормализатор ЭТ есть подалгебра, содержащая 33,
и 58 является идеалом в ЭТ. Так же как и в теории групп, $1 — наи-
наибольшая подалгебра, в которой 58 содержится в качестве идеала.
Дадим теперь следующее
Определение 1. Подалгебра ф алгебры Ли й называется
подалгеброй Картана, если 1) ф нильпотентна и 2) § совпадает
со своим нормализатором в 8.
Пусть ф — нильпотентная подалгебра конечномерной длгебры Ли 8,
и пусть 8 = 80 ф 8j — разложение Фиттинга алгебры g относительно
dg?>. Напомним, что Йо= {х | л: (ad A)* = 0, Л?ф, дл» некоторого
целого k). Установим теперь следующий критерий.
70 Гл III Критерий Картана и его следствия
Предложение 1. Нильпотеншная подалгебра ф конечно-
конечномерной алгебры Ли 8 является подалгеброй Картана тогда
и только тогда, когда ?> совпадает с компонентой 80 в раз-
разложении Фиттинга алгебры 8 относительно ad ?>.
Доказательство. Заметим сначала, что 80 =? W, где %1 — нор-
нормализатор подалгебры ?>. Действительно, если х ? У1, то [х/г] ? ф
для любого А?ф. Так как подалгебра •§> нильпотентна, то выпол-
выполняется условие
[... [ [xh] А] .. . А] = х (ad А)* = 0
для некоторого k. Поэтому х?80. Таким образом, если Э^гэф, то
80:э?>. Допустим теперь, что 80зф. Подалгебра 80 инвариантна
относительно ad ¦?>, и каждое ограничение ad«0 А, где A ? ф, нильпо-
тентно. Кроме того, ?> есть инвариантное относительно ad ?> под-
подпространство пространства Йо. Таким образом, мы получаем инду-
индуцированную алгебру Ли •§> линейных преобразований, действующих
в ненулевом пространстве Й0/ф. Так как эти преобразования ниль-
потентны, то один из вариантов теоремы Энгеля утверждает, что
(x-f-?>)ф = 0, где х + ф — некоторый отличный от нуля вектор.
Это означает, что выполняется условие [xh] ? ф для каждого h\
поэтому х?Ш и х(?$>, так что ЭТзф. Итак, !Я:э?> тогда и только
тогда, когда 80:эф, а это как раз то, что и требовалось доказать.
Предложение 2. Пусть ?> — нильпотентная подалгебра
конечномерной алгебры Ли 8, и пусть 8 = 80ф 8j — разложение
фиттинга алгебры 8 относительно ad?>. Тогда йд — подалгебра
и [?,8о1 = 8i-
Доказательство. Пусть А^§, а^80. Тогда выражение
I
[. .. [ [ah] A] ... A] = 0 для некоторого k. Отсюда
[. . . [ [ad a ad A] ad A] ... ad A] — 0.
Из этого соотношения и леммы 1 § 4 гл. 2 следует, что фиттин-
говы подпространства Йо ad л и 8i ad л алгебры 8, соответствующие
эндоморфизму ad А, инвариантны относительно ad а. Так как 80 =
= |) 8о ad л и 8i = 2 8j ad л. то 8о ad а ? 8о и 8i ad а с gb Так
как а —произвольный элемент в 80, то [Й080] S 80 и [SjSq] с 8j.
Определение 2. Элемент А?8 называется регулярным,
если размерность фиттинговой нуль-компоненты алгебры 8 относи-
относительно ad А минимальна. Если эта размерность равна /, то число /
называется рангом алгебры 8').
') Автор называет рангом число dim 8 — I. Возможно, для этого и есть
некоторые основания, но мы сочли более удобным придерживаться тради-
традиционной терминологии. — Прим. ред.
§ 1. Подалгебры Картана 71
Мы видели, что размерность фиттинговой нуль-компоненты ли-
линейного преобразования А равна кратности корня 0 характеристи-
характеристического многочлена /(X) = det(Xl—А) преобразования А. Следова-
Следовательно, элемент /г регулярен тогда и только тогда, когда кратность
характеристического корня 0 для ad h минимальна. Так как [h/г] = О
для любого Л, то линейное преобразование ad /г, очевидно, вырождено
для любого /г. Поэтому число / в предыдущем определении больше 0.
Заметим также, что алгебра 8 имеет ранг, равный размерности над
основным полем, в том и только в том случае, когда каждый эндо-
эндоморфизм ad А нильпотентен. По теореме Энгеля это условие выпол-
выполняется тогда и только тогда, когда 8 — нильпотентная алгебра Ли.
Регулярные элементы могут быть использованы для конструирования
подалгебр Картана в силу следующего утверждения.
Теорема 1. Если 8 — конечномерная алгебра Ли над
бесконечным полем Ф и если а — регулярный элемент алгебры 8,
то фиттингова нуль-компонента ф алгебры Й относительно ad a
является подалгеброй Картана.
Доказательство. Пусть 2 = ф©$—разложение Фиттинга
алгебры 8 относительно ad а. Тогда, согласно предложению 2, ф есть
подалгебра и [?>$] с $. Мы утверждаем, что любое преобразова-
преобразование adjpi», &??>, нильпотентно. В противном случае пусть b — эле-
элемент подалгебры ?>, которому соответствует ненильпотентный эндо-
эндоморфизм ad§ft. Выберем базис в алгебре 8, состоящий из базисов
подпространств ^) и R. Матрица любого преобразования ad h, §
в этом базисе записывается в виде
о
где (pj)—матрица преобразования ad^/z, а (р2) — матрица преобразо-
преобразования ads h. Пусть
— матрицы преобразований ad a и ad b соответственно. Тогда из не-
невырожденности (а2) следует, что det(a2)^fc0. Кроме того, по пред-
предположению матрица (Bj) не нильпотентна. Поэтому если / — ранг
алгебры 8, то dim§ = /, и характеристический многочлен матрицы (Bj)
не делится на X'. Пусть теперь X, р, v — алгебраически независимые
переменные, и пусть F(X, \x, v)—характеристический многочлен,
F (X, (a, v) = det(Xl—ц.А — vB) Выполняется равенство FQ., p., v) =
^^(Х, р,, v)F2(X, (j., v), где
72 Г л III. Критерий Картана и его следствия
Мы видели, что многочлен F2(X, I, O) = det(Xl—(<х2)) не делится
на X и что многочлен Fj(X, 0, l) = det(Xl—(8j)) не делится на \1.
Поэтому наибольшая степень X, на которую делится многочлен F (X, p. v\
есть Хг , где /' < /. Так как поле Ф содержит бесконечное множество
элементов, можно выбрать |а0 и v0 в поле Ф так, что многочлен
F (X, (а0, v0) не будет делиться на X +\ Положим с = роа -J- vQ?.
Тогда характеристический многочлен
det(Xl— adc) = det(Xl — НА — vo5) = F(X, н, v0)
не делится на Хг +1. Поэтому кратность характеристического корня О
преобразования ad с равна /' < /. Это противоречит регулярности
элемента а. Мы доказали, таким образом, что для каждого *?ф
преобразование ad$b нильпотентно. Следовательно, по теореме
Энгеля, ф—нильпотентная алгебра Ли. Пусть Йо—фиттингова нуль-
компонента алгебры ? относительно ad ?>. Тогда ii0 с ?>, так как
ф—фиттингова нуль-компонента преобразования ad а и а?ф.
С другой стороны, ?0 з ф для любой нильпотентной подалгебры ф.
Поэтому йо = ф и, согласно предложению 1, ф — подалгебра Картана.
Другим полезным замечанием о регулярных элементах и подал-
подалгебрах Картана является следующее: если подалгебра Картана со-
содержит регулярный элемент а, то ф однозначно определяется эле-
элементом а как фиттингова нуль-компонента алгебры ? относительно ad a.
Действительно, если Щ есть эта компонента, то, очевидно, 5t 3 ф,
так как ф нильпотентна. С другой стороны, мы только что видели,
что Э? нильпотентна Если, следовательно, !Rn§, то Ш содержит
такой элемент ?(;§, что [zfy] ? § (см упражнение 1). Это проти-
противоречит тому предположению, что ф подалгебра Картана. В качестве
непосредственного следствия из этого результата мы получаем, что
две подалгебры Картана, имеющие один и тот же регулярный эле-
элемент, совпадают. Дальше мы увидим (см. гл. IX), что если Ф — алге-
алгебраически замкнутое поле характеристики 0, то каждая подалгебра
Картана содержит регулярный элемент. Укажем сейчас совершенно
эффективный способ нахождения регулярных элементов (предполагая,
что поле Ф бесконечно). Для этой цели нам потребуется ввести
понятие общего элемента и характеристического многочлена алгебры Ли.
Пусть 2—алгебра Ли с базисом (е, е2, . ., еп) нал полем Ф.
Пусть $j, S2. ' ¦ -Лп — независимые переменные иР — Ф($j, $2 ?л)—
иоле рациональных функций от ^. Построим расширение &р = Ре1-\-
п
-\~Ре2-\- ... ~\-Реп. Элемент * = 2^вг алгебры ?р называется
общим элементом алгебры 2, а характеристический многочлен /Ж(Х)
преобразования ad л; (в 2Р) называется характеристическим мно-
§ 1, Подалгебры Картана 73
гочленом алгебры Ли ?. Если за базис алгебры ?р принять
(«1. е2 еп), то
K*]=SpiA. «=1. 2 «. C)
где ptj—однородные функции степени 1 относительно ?j. Отсюда
следует, что
1-(р)) =
-1)Ч-гШ^ D)
где xt — однородные многочлены степени i относительно перемен-
переменных \ и tn_;($) Ф 0, но tn_J+ft = 0, если k > 0. Так как х ad х = 0
и х =jfc 0, то det (р) = 0 и / > 0. Характеристический многочлен любого
элемента а=2 <х(/( ? g получается специализацией ?г=<хг, 2=1, 2 я,
в равенстве D). Поэтому очевидно, что кратность корня 0 характе-
характеристического многочлена преобразования ad а не меньше /. С дру-
другой стороны, если Ф — бесконечное поле, то поскольку много-
многочлен т„_гE) отличен от 0 в полиномиальной алгебре Ф[^, ?2, .... ?„],
можно выбрать ?, = <хг так, что "с„_г(а) Ф 0. Тогда преобразование ad a
для элемента а — 2 «Л имеет в точности / характеристических кор-
корней, равных 0, и, следовательно, элемент а регулярен. Таким обра-
образом, в случае бесконечного основного поля элемент а регулярен
тогда и только тогда, когда выполняется условие
W«)=?0. E)
В этом смысле „почти все" элементы алгебры 2 регулярны. (Регу-
(Регулярные элементы образуют открытое множество в смысле алгебраи-
алгебраической геометрии.) Очевидно также, что ранг алгебры й равен /.
Изложенная выше конструкция зависит от выбора базиса (е).
Однако легко выяснить, что происходит при переходе к другому
базису (Д, /2 /„), где /, = 2ад. Если •»},, щ ч\п —
независимые переменные, то у = 2 f\Ji = 2 W;//1 Поэтому харак-
характеристический многочлен fy(k) получается из многочлена fxfl) под-
подстановкой ?; —> 2 tfiV-ij в ег0 коэффициентах (при степенях X)-
Если 2 — некоторое расширение поля Ф, то (е) есть базис алгебры 2а
над 2. Поэтому элемент х = 2 ^fit также будет общим элементом
алгебры й2. а характеристический многочлен fx(k) не изменяется
при расширении основного поля Ф до поля Q. Отсюда с очевид-
очевидностью следует, что если Ф — бесконечное поле, то элемент а ? i
регулярен в ? тогда и только тогда, когда а регулярен как элемент
алгебры йа- (В обоих случаях условие E) есть условие регуляр-
регулярности.) Мы видели, что фггтингова нуль-компонента ф относи-
относительно ad а, где а — регулярный элемент, совпадает с подалгебро!
74 Гл. Iff. Критерий Картана и его следствия
Картана. Размерность подалгебры ф равна /, где / — кратность ха-
характеристического корня 0. Отсюда следует, что подалгебра Кар-
Картана, определенная элементом а в Й2. совпадает с подалгеброй ф2.
§ 2. Произведения весовых пространств
Понятия весов и весовых подпространств, введенные нами для
алгебры Ли линейных преобразований, целесообразно перенести
на абстрактную алгебру Ли ? и представление R алгебры ?. Пусть
WI — модуль над й (соответствующий представлению R). Отображе-
Отображение а—>а(а) алгебры ? в поле Ф называется весом модуля Ш (или
представления R), если существует ненулевой вектор х ? Ш, такой,
что
a(a)l)k — 0 F)
для некоторого k. Множество векторов, удовлетворяющих этому
условию, образует вместе с 0 подпространство Sdla, называемое весо-
весовым подпространством, соответствующим весу а (относительно
веса а или просто с весом а). Если алгебра ? нильпотентна, то
из леммы I гл. 2 следует, что Ша — подмодуль. Если 9№ = 9№в, то
мы будем называть 9№ весовым модулем над алгеброй ?, соответ-
соответствующим весу а.
Пусть й — алгебра Ли и ffi — конечномерный весовой модуль
над алгеброй ? относительно веса а. Тогда для каждого элемента
л;?9И выполняется условие x{aR — <х(аI)* = 0, если k достаточно
велико. Более того, если 6\тШ = п, то многочлен (к — <х(а))л
является характеристическим многочленом эндоморфизма aR. Поэтому
выполняется условие x(aR — <x(a)l)" = 0 для всех х?9№. Рассмо-
Рассмотрим контрагредиентный модуль 3№\ который соответствует предста-
представлению R*, удовлетворяющему условию
{xaR, f) + {x, /a«*) = 0. G)
где х ? Ж, у* ? W. Справедливо равенство
— <a(a)*, /)+<*. a(a)y*) = 0. (8)
Если мы сложим равенства G) и (8), то получим равенство
<*(a«-a(a)l), />+<*• /(<*«• +а (о) 1)> = 0. (9)
Повторение этого процесса приводит к равенству
{x(aR — a(a)l)ft. /) + (*, y*(a«* + a(a) l*) = 0. A0)
Если k = n, то x(aR — a(a)l)" = 0 для всех х и, следовательно,
выполняется условие {х, у* (aR*-\-а (а) 1)л)=г0, как вытекает из ра-
равенства A0). Поэтому y*(aR*-\-a.(a)l)a = 0 для всех y*?W. Это
показывает, что Ш* есть весовой модуль с весом —а.
§ 2. Произведения весовых пространств 75
Предложение 3. Если Ш — конечномерный весовой модуль
над алгеброй Й с весом а, то контрагредиентиый модуль ЗЛ*
является весовым модулем с весом —а.
Рассмотрим теперь, что происходит, когда мы берем тензорное
произведение двух весовых пространств. Пусть Ш и 91 — весовые
модули над алгеброй ? относительно весов аир. Пусть R и 5 —
представления в Ш и 5t соответственно. Тогда любой элемент х ? Ш
удовлетворяет условию
x(aR — <х(аIN = 0 A1)
при некотором k > О, а каждый элемент у с Л удовлетворяет
условию
у (а* — р(аI)*' = О A2)
для некоторого k' > 0. Пусть ф = 2Н®9B; обозначим представление
алгебры ? в ф через Г. Тогда
(х® у) аТ = ха1 ® у -f-x®yas A3)
или ат — aR ® I -j- I ® as. Поэтому
= (a« ® 1 — о (о) 1 ® 1)-|- A ® о* — 1 ® р (о) 1). A4)
Так как два преобразования в скобках перестановочны между
собой, то можно применить теорему о биноме и получить следую-
следующее равенство:
'. A5)
Если применить это равенство к элементу х ® у, то получится
равенство
(х ® у) (аг — (a (a) -f- р (а)) 1 )т =
10
1=0
Если, далее, положить m = k-\-k'—1, то для каждого числа I
либо х(а* — a(a)iy = 0, либо у (as — 0(a) l)m"' = 0. Поэтому
(x®y)(ar—(a (a)-f-p (a)) l)m=:0, и мы получаем следующее
Предложение 4. Если %I и Щ — весовые модули над ?
относительно весов и к р соответственно, то
весовой модуль с весом a-f- p. 4
76 Гл. III. Критерий Картана и его следствия
Предположим теперь, что ?—конечномерная алгебра Ли, $ —
нильпотентная подалгебра, а Ш—конечномерный модуль над 2,
а следовательно, и над ф. Пусть R — представление в Ш, a ads —
присоединенное представление в ?. Предположим, что ф# и adg§
являются расщепляемыми алгебрами Ли линейных преобразований,
т. е. характеристические корни линейных преобразований hR и adg h,
где h ? ф, принадлежат основному полю Ф. Это условие автомати-
автоматически выполняется, если основное поле алгебраически замкнуто.
Если hR —><x{hR)— вес на !qr, то отображение h —> а (А) == а \hR)
является весом на ф модуля 9№. Из теоремы 2.7 о весовых про-
пространствах расщепляемых алгебр Ли линейных преобразований сле-
следует, что 9Й есть прямая сумма весовых модулей Шр Аналогично
мы получаем разложение алгебры ? на весовые модули ёа. Запишем
эти разложения:
2К = ЗИр©ЗЯ.©...©3I« A7)
и
A8)
где р, о, ... — отображения подалгебры § в Ф, такие, что если
х ? Т1 , то xp(hR — р(/гI)т = О для некоторого m и т. д. Веса
а, р соответствующие adg§, будут называться корнями алгебры 8
относительно подалгебры ф. Так как отображения h-*hR и h—>adg/j
линейны, то очевидно, что в случае характеристики 0 веса р, ..., t
и корни а 8 являются линейными функциями на ф, обращаю-
обращающимися в 0 на ф'.
Следующий важный результат связывает разложения A7) и A8)
относительно ф.
Предложение 5. 3№рйа с ЗИр+а, если р-)-а есть вес .мо-
.модуля Ж относительно ф; в противном случае 9№р2а = О.
Доказательство. Элементы ЗИрй,, записываются в виде
2 J8a. Из характеристического свойства тен-
тензорного произведения двух пространств следует, что существует ли-
линейное отображение п: SK ® 8а —>¦ 9№ 8„, такое, что
Мы покажем, что « является в действительности гомоморфизмом
ф-модулей. Пусть h ? ф. Тогда
(*„® а.)Л = xji®aa-trxp® \aji\ -^ (x?h) аЛ-+- xp(о„А) = (xfajh.
С другой стороны, образом х ®аа при гомоморфизме « является
xfaa. Если же умножить это на h, то мы опять получим (х aa)h.
Мы доказали, таким образом, что Ш^.а есть гомоморфный образ
§ 3 Пример 77
модуля 9Яр ® 8а. Более того, 9Мр ® 8„ — весовой модуль с весом р + а.
Но из определения ясно, что гомоморфный образ весового модуля
с весом р есть либо 0, либо снова весовой модуль с весом р. Отсюда
немедленно следует требуемое утверждение.
Применяя этот результат в случае, когда 931 = 8 и когда пред-
представление является присоединенным представлением алгебры 8, мы
получаем такое
Следствие. [8а8р] с 8а+р, если <х-|-р является корнем,
и [8а8р] = 0 в противном случае.
§ 3. Пример
Прежде чем приступить к структурной теории, будет полезно рас-
рассмотреть один пример.
Пусть 9J?—«-мерное векторное пространство над алгебраически
замкнутым полем Ф, и пусть (S — ассоциативная алгебра линейных
преобразований пространства Ш, а 8 = 6? — соответствующая алгебра
Ли. Определим регулярные элементы в 8 и соответствующие под-
подалгебры Картана.
Пусть Л?8 и 9# = 2>Ц ф Зй^ ф ... ©ЭД^— разложение про-
пространства 9)? на весовые подпространства относительно ФЛ. Эле-
Элементы <хг, отличные друг от друга, принадлежат полю Ф и являются
характеристическими корнями линейного преобразования Л; 33^ —
соответствующие характеристические подпространства. Хорошо из-
известно, что разложение пространства в прямую сумму подпространств
приводит к разложению дуального пространства в прямую сумму под-
Пространств, которые можно рассматривать как пространства, сопря-
сопряженные к компонентам исходного разложения. Таким образом, мы
получаем разложение
где ffii можно отождествить с сопряженным пространством к Ша.
ЗЯг инвариантно относительно преобразования—А и, как следует
из предложения 3, 9I/ является весовым модулем над алгеброй Ли ФЛ
с весом — <хг. Соответственно этому мы обозначаем Ш] через TVLa,
и получаем следующее разложение:
Рассмотрим теперь модуль 9Ji (gi 5Ш* относительно ФЛ. Хорошо известно,
г
что имеет место следующее равенство: Ш ® Ш* = 2 2Jk ® 9№la..
78 Гл. III. Критерий Картана и его следствия
Согласно предложению 4, слагаемое Tla. ® 3W_a. является весовым
модулем над ФА с весом a.L — а;. Если обозначить через А1} ли-
линейное преобразование в ШЛ. ® 9J?_a., соответствующее А, то
(Aij — (аг — а^I)*У = 0 для некоторого ktj. Поэтому АГ] невыро-
невырождено, если аг — а;-=? О, и Ац нильпотеитно, если аг = а;-. Отсюда
следует, что фиттингова нуль-компонента пространства Ш ® Ш* от-
относительно линейного преобразования А, соответствующего линей-
линейному преобразованию А (отображение А—>А является представле-
т
нием алгебры 2 в Ш®Ш*), есть 2^ ®2Я1«. Если dim ШЛ =nit
т
то размерность этого пространства Фиттинга равна 2 п\- Так как
2 nt =«, то 2лг минимальна в том и только в том случае, когда
каждое число пь — 1, что эквивалентно существованию п разных
характеристических корней преобразования А. Напомним теперь, что
модуль Ш ® Ш* изоморфен модулю Й = d,L относительно присоеди-
присоединенного отображения Х-*-\ХА].
Поэтому мы убеждаемся, что размерность фиттинговой нуль-
компоненты алгебры E относительно ad Л минимальна в том
и только том случае, когда преобразование А имеет п раз-
различных характеристических корней. Таким образом, А регу-
регулярно в g = Ц^ тогда и только тогда, когда А имеет п различных
характеристических корней. Соответствующая подалгебра Картана ф
есть фиттингова нуль-компонента алгебры ? относительно ad А, и
dim § — п.
Так как А имеет п различных характеристических корней, то мы
можем выбрать такой базис в Т1, что матрица преобразования А
будет диагональна в этом базисе. Пусть фх — множество линейных
преобразований, матрицы которых в этом базисе записываются в диа-
диагональной форме. Тогда dim^l^=n и [ЯЛ] —0 для каждого #?фг
Поэтому §j с. $. С другой стороны, dim ф = п. Поэтому ^ = ф и
подалгебра Картана, определенная Л, есть централизатор линейного
преобразования А.
.Пусть (вр е2, ..., еп) — базис в Т1, такой, что егЛ = агег. Тогда,
как мы видели, подалгебра Картана ф совпадает с множеством ли-
линейных преобразований, имеющих диагональные матрицы в этом ба-
базисе. Поэтому, если Я?ф, то eiH — L(H)ei, \(Н)?Ф, и можно
предположить, что в наших обозначениях Xi(A) — a.i. Пространства
Фег(=2Чаг) являются весовыми подпространствами, причем Фег соот-
соответствует весу ^t(H). Поэтому мы будем обозначать пространство Фег
через Ш\.. Как и в случае единственного линейного преобразования Л,
можно написать Ш* — 2КЦ ф Ш\ ф . . . ф «Ш*-лд и Ш® Ш* =
§ 4. Критерии Картана 79
2(® 5Ш1х.) (сумма прямая). Слагаемое 93i>7 ® 9Wl\. является
весовым подпространством относительно подалгебры Картана ф, соот-
соответствующим весу Хг — Xj. Мы можем суммировать наши результаты
в виде следующего утверждения.
Теорема 2. Пусть !8 = (?i — алгебра Ли линейных пре-
преобразовании п-мерного векторного пространства Ш над алге-
алгебраически замкнутым полем Ф. Тогда Л ?8 регулярен в том
и только в том случае, когда характеристический, многочлен
det (XI — А) имеет п различных корней. Подалгебра Картана ф,
определенная преобразованием А, совпадает с множеством
таких линейных преобразований Н, что [НА] = 0. Если \(Н), ...
..., ХЛ(Я) — значения весов на линейном преобразовании Н, дей-
действующем в Ш, то Xj(H) — \(Н), I, У=1,..., п,—значения
соответствующих корней (весов присоединенного представле-
представления в 8).
Если Ф — бесконечное, но алгебраически незамкнутое поле, то
обычное рассуждение с расширением поля, как в § 1, показывает
опять, что элемент А регулярен в (Е^ тогда и только тогда, когда А
имеет п различных характеристических корней (в алгебраическом за-
замыкании Q поля Ф). Хорошо известно, что централизатор такого
преобразования А есть алгебра Ф [А] многочленов относительно А и
dim Ф [Л] —я. Так как размерность подалгебры Картана, определен-
определенной А, равна п, то эта подалгебра совпадает с Ф[А].
Если 8 — ортогональная или симплектическая алгебра Ли в 2/-мер-
ном пространстве над бесконечным полем, то можно показать, что
ранг этой алгебры равен / (см. упражнения 4 и 5). Не трудно опре-
определить также подалгебры Картана для других важных примеров
алгебр Ли, с которыми мы сталкивались (см. упражнение 3).
§ 4. Критерии Картана
Рассмотрим теперь конечномерную алгебру Ли над алгебраически
замкнутым полем Ф, нильпотентную подалгебру ф алгебры ? и мо-
модуль Ш над 8, конечномерный над Ф. Пусть
— разложения модулей Si и 8 на весовые подмодули относительно ф.
Мы видели, что
@, если р + а не есть вес модуля 9Й,
р « | с W если p-f а — вес,
' , d B0)
О, если а + р не есть корень,
если a -f- P — корень.
80 Гл. III. Критерий Картана и его следствия
Предположим теперь, что ф — подалгебра Картана. Тогда ф = 80,
где 80 — корневой модуль, соответствующий корню 0. Мы имеем
также равенство 8' = [??] = 2 [2я2р]> где сумма берется по всем
корням а, р. Из формулы для [йа8р] следует равенство
«П 8'= 2 [8.8..]. . ' B1)
а
где суммирование берется по всем а, таким, что —а — также корень
(в частности, <х = 0).
Докажем теперь следующее утверждение.
Лемма 1. Пусть Ф — алгебраически замкнутое поле харак-
характеристики 0, ф — подалгебра Картана алгебры ? над Ф и
3)? — модуль над 8. Предположим, что, наряду с а, —а также
является корнем. Пусть еа?8а, е_а?2_11, ha = [eae_a]. Тогда
p(ha) — рациональное кратное а(/га) для каждого веса р мо-
модуля 9№ относительно подалгебры ф.
Доказательство. Рассмотрим функции вида р(Л)-(- tcn(h),
1 = 0, ±1, ±2, .... являющиеся весами, и построим подпростран-
подпространство Щ = 2 ^o+te' гДе суммирование распространено на соответ-
ствующие весовые подпространства. Это пространство инвариантно
относительно ф и, вследствие условий B0), инвариантно также отно-
относительно линейных преобразований е#, е^а, где R — представление
алгебры 8, определенное модулем 3)f. Поэтому, если обозначить
через tr^ след индуцированного отображения в Щ, то tr?JA^ =
= trMre^, eRa] = 0. С другой стороны, ограничение эндоморфизма hRa
на 9М0 имеет единственный характеристический корень е(/га). Поэтому
где в общем случае я„ = dim Tta. Таким образом, мы получаем ра-
венство
B «Р+|.) Р (А.) + B я, W) * (А.) = 0.
Так как сумма 2 n9+ia является положительным целым числом, то
p(ha) является рациональным кратным ca(hx).
Мы можем теперь доказать критерий разрешимости алгебр Ли,
принадлежащий Картану.
Пусть 8 — конечномерная алгебра Ли над полем характе-
характеристики 0. Предположим, что алгебра 8 обладает таким
конечномерным модулем Ш, что A) ядро $ ассоциированного
с ним представления R разрешимо и B) tr(a#J = 0 для
каждого а ?8'. Тогда алгебра 8 разрешима.
§ 4. Критерии Картам 81
Доказательство. Допустим сначала, что основное поле Ф
алгебраически замкнуто. Достаточно доказать, что 8'с8, ибо усло-
условия A) и B) были бы тогда справедливы для 8' и Ш как 8'-модуля.
Поэтому мы имели бы следующую цепочку
8=>8'=>8"=> ..
Итак, предположим, что ?' = 2. Пусть ф — подалгебра Картана
и пусть Ш и 8 имеют разложения относительно ф, как в равен-
равенствах A9). Тогда из формулы B1) следует, что Ф = 2[2«2-оЬ где
суммирование проводится по таким корням а, что —а — также корень.
Выберем такой корень а, положим еа?8а, е_а?8_я и рассмотрим
элемент ha = \еае_а\. Из формулы Ф=2[2«8_а] слеДУет> что каждый
элемент из ф есть сумма членов вида [еае_а]. Ограничение эндомор-
эндоморфизма /г# на ЗИ имеет единственный характеристический корень р(АЛ
Поэтому ограничение (ftfJ имеет единственный характеристический
корень p(AJ2. и если dim$R =п , то
По предшествующей лемме р (hj = rp<x (hj, где гр — рациональное
число. Поэтому а(йаJBл г2) = 0. Так как числа я положительны,
то <х(/га) = О и, значит, р(/гг) = О. Так как функции р являются ли-
линейными функциями и каждый элемент h ? ф представим в виде суммы
элементов /га, Л?, ... и т. д., то р(/г) = О. Таким образом, 0 является
единственным весом модуля Ш, т. е. Ж = 2f0. Если а — некоторый
корень, то из условий B0) следует равенство 9№8а = 0 для всякого
а ф 0. Это значит, что ядро 51 представления /? содержит все ?а, <х=?0.
Поэтому ?л^?/$ есть гомоморфный образ подалгебры Картана ф.
Таким образом, йл нильпотентна и алгебра 8 разрешима, что проти-
противоречит нашему предположению ?' = ?.
Если основное поле Ф алгебраически незамкнуто, то пусть 2—его
алгебраическое замыкание. Тогда ffls есть модуль над ga и $а — ядро
соответствующего представления. Так как идеал $ разрешим, то $s раз-
разрешим. Заметим далее, что из условий tr(a#J = 0 и ixaRbR = txbRali
следует, что
to a*b* = j
i [tr (а^ -|- *лJ — tr (алJ — tr(**Jj == 0.
Поэтому если а. ^2 и <о. ^2, то trBw^fJ = S40;01/ trafa^ = 0.
Вследствие этого условие B) выполняется также и в 8а. Из первой
части доказательства следует, таким образом, что 82 разрешима.
Поэтому и алгебра 8 разрешима, что и требовалось доказать.
6 Н Джекобсон
82 Гл III. Критерий Картана и его следствия
Следствие. Если характеристика поля Ф равна О, то
алгебра 8 разрешима в том и только том случае, когда
tr(adflJ = 0 для каждого а ?8'.
Доказательство. Достаточность этого условия сразу сле-
следует из критерия Картана, поскольку ядро присоединенного пред-
представления совпадает с центром. Обратно, пусть алгебра 8 разрешима.
Тогда из следствия 2 теоремы 2.8, примененного к ad Й> вытекает, что
элементы ad^a, a ?8', принадлежат радикалу (ad 8)*. Поэтому эндо-
эндоморфизм adg а нильпотентен и tr (adg aJ = 0.
Пусть R — представление алгебры Ли в конечномерном простран-
пространстве Ш. Тогда функция
f(a, b)==ixaRbR B2)
является, очевидно, симметрической билинейной формой на Ж*
со значениями в Ф. Такую форму мы назовем формой следа ал-
алгебры 8. В частности, если 8 конечномерна, то мы получаем форму
следа tr (ad a) (ad b), которую будем называть формой Киллинга
алгебры 8. Если / — форма следа, определенная представлением R, то
/([ас], 6) +/(a, [bc]) = tr([ac]RbR + aR [bc]R)
= tr ([aRcR] bR -j- aR [bRcR\)
=ti[aRbR, cR] = 0.
Билинейная форма f(a, b) на 8, удовлетворяющая условию
/Нас]. b) + f(a, [bc]) = Q, B3)
называется инвариантной формой на 8. Мы проверили, таким об-
образом, что формы следа инвариантны. Заметим теперь, что если
f(a, b) — произвольная симметрическая инвариантная форма на 8,
то радикал 8 этой формы, т. е. множество элементов г, таких, что
f(a, z) = 0 для всех а ?8, есть идеал. Это очевидно, поскольку
/(с, [zb)) = — f({ab], z) = Q.
Мы можем теперь вывести критерий Картана полупростоты.
Если й — конечномерная полупростая алгебра Ли над полем
характеристики 0, то форма следа, ассоциированного с любым
взаимно однозначным представлением алгебры 8, невырождена.
Если форма Киллинга невырождена, то алгебра 8 полупроста.
Доказательство. Пусть R — взаимно однозначное предста-
представление алгебры 8 в конечномерном векторном пространстве Ш, и
пусть f(a, b) — соответствующая форма следа. Тогда 8^ — идеал
алгебры 8 и f(a, a) = tr {aRf = 0 для каждого о ?8-4 Поэтому
идеал 8 разрешим, согласно первому критерию Картана. Так как 8
полупроста, то й-1-= 0 и f(a, b) невырождена. Предположим теперь,
что 8 не полупроста. Тогда в Й содержится абелев идеал 23 Ф 0.
§ 5 Структура полупростых алгебр 83
Если мы выберем базис в й так, что первые векторы его образуют
базис в 23, то матрицы преобразований ad а, я?й, na.db, &?23,
записываются в этом базисе соответственно в виде
'* 0\ /О О
*; и U о
Отсюда следует, что tr(ad&)(ad а) — 0. Поэтому 23 S 2"L и форма
Киллинга вырождена.
Если f(a, b) — симметрическая билинейная форма в конечномер-
конечномерном пространстве и (е,, е2 еп) — базис в этом пространстве, то,
как хорошо известно, форма / невырождена в том и только том
случае, когда det(/(e(-, efi) Ф 0. Пусть й — конечномерная алгебра Ли
характеристики 0 с базисом (е,, е2, ..., еп) и pS(jF = tradeiade/,
тогда й полупроста в том и только том случае, когда det(p,^)=?O.
Это другая форма только что доказанного критерия Картана. Если
2 — расширение основного поля алгебры й, то (ev е2, ..., еп) —
базис алгебры йч над 2. Поэтому имеет место
Следствие. Конечномерная алгебра Ли й над полем Ф
характеристики О полупроста тогда и только тогда, когда
алгебра йа полупроста для каждого расширения Q поля Ф.
§ б. Структура полупростых алгебр
Мы в состоянии теперь доказать основную структурную теорему
для полупростых алгебр Ли. Доказательство, которое мы приводим
ниже, является принадлежащим Дьедонне упрощением первоначаль-
первоначального доказательства Картана. Метод рассуждений применим на самом
деле к произвольным (неассоциативным) алгебрам, и мы приводим
здесь утверждения в этой общей форме.
Пусть % — (неассоциативная) алгебра над полем Ф. Билинейная
форма f(a, b) на ЭД (со значениями в Ф) называется ассоциатив-
ассоциативной, если
f(ac, b) = f(a, cb). B4)
Если /—инвариантная форма на алгебре Ли, то /([ас], Ь)-\-
+ /(а, [Ьс]) = О. Поэтому /([ас], b) — f(a, [cb]) — Q и / ассо-
ассоциативна. Пусть теперь f (а, Ь) — симметрическая ассоциативная форма
на %, а 23 — идеал в §(. Пусть а?23Ч так что f(a, b) = 0 для
всех 6 ?23. Тогда / (ac, b) — f(a, cb) — Q для каждого с?ЭД, так
как с&?23. Кроме того, f(ca, b)~f(b, ca) = f(bc, а) = 0, по-
поскольку #с?23. Поэтому 23-1- — идеал.
Важность ассоциативных форм явствует из следующего результата.
- Теорема 3. Пусть ЭД — конечномерная (неассоциативная)
алгебра над полем Ф, такая, что A) на % существует сам-
84 Гл. 111. Критерий Картана и его следствия
метрическая невырожденная ассоциативная форма f м B) 31 не
имеет идеалов 23, удовлетворяющих условию 232 = О. Тогда Ж
есть прямая сумма идеалов, являющихся простыми алгебрами.
(Напомним, что 31 проста, если 31 не имеет идеалов кроме 0 и 31
и 3t2 Ф 0.)
Доказательство. Пусть 93 — минимальный отличный от 0
идеал в 31. Тогда 93 П 23-1- является иделом, содержащимся в 23.
Поэтому либо 23 П 23^ = 93, либо 23n93J- = O. Предположим, что
имеет место первый случай, и пусть bv #2?23, а?ЭД. Тогда
f (ЬгЬ2, a) = f(bv b2a) = 0. Поскольку / невырождена, то bxb2 — Q и
232 = 0, что противоречит предположению. Следовательно, 23 П 23 = 0.
Как хорошо известно, из этого условия вытекает, что 3t = 93©93-1"
и 23^ есть идеал. Из этого разложения следует, что 9323J- = 0 = 93^93,
и поэтому каждый 93-идеал является идеалом. . Значит, алгебра 23
проста. Более того, алгебра 93^ удовлетворяет тем же условиям,
что и 31, поскольку ограничение формы / на 23^ невырождено и
каждый 23~'~-идеал является идеалом. Индукцией по dim 31 полу-
получаем разложение 93-L = 3l2© ••¦ ф 3tr. где 3t; являются идеалами и
в то же время простыми алгебрами. Тогда для 5СХ == 33 мы получаем
разложение • 31 = %х © 312 © • • • ф %> где 31г — идеалы и простые
алгебры.
Из этого результата и невырожденности формы Киллинга для
полупростых алгебр Ли характеристики 0 следует наиболее слож-
сложная часть основного утверждения.
Структурная теорема. Конечномерная алгебра Ли над
полем характеристики 0 полупроста тогда и только тогда,
когда существует разложение 8 = 8t ф 82ф ... ф gr, где 8j —
идеалы, являющиеся простыми алгебрами.
Доказательство. Если алгебра 8 полупроста, то 8 имеет
указанную структуру. Обратно, предположим, что существует раз-
разложение 8 = 8\ ф 82 ф ... ф 8Г, где 8; — идеалы и простые алгебры.
Рассмотрим множество линейных преобразований ad 8 = {ad a | a ?8),
действующих в 8. Инвариантные относительно этого множества под-
подпространства являются идеалами в 8. Так как 8 = 8t ф 82 ф ... ф 8Г,
где 8г неприводимы, то множество ad 8 вполне приводимо. Поэтому
если 23 — отличный от 0 идеал алгебры 8, то 8 = 93ф2). где Ъ —
также идеал (теорема 2.10).
Более того, из доказательства этой теоремы следует, что мы можем
считать © взятым в форме 2) = 8<1ф8/2Ф ... ® 8/ft для некоторого
подмножества {8<а} идеалов 8^. Тогда 93 = 8/(8^ ф ... ф 8/ ) =
= 2/,ф2;2© ••• ©?/,¦ где %jv — оставшиеся 8f. Так как 8f просты.
§ 5. Структура полупростых алгебр 85
ft = 2,. Следовательно, (8/, ©«,2 ©... © S/,J = 8/, ©8/2 © . .. © 8/г
и, значит, 232 = 23. Таким образом, 23 не является разрешимым идеа-
идеалом. Тем самым мы показали, что 8 не имеет ненулевых разреши-
разрешимых идеалов. Поэтому 8 полупроста.
Только что проведенное рассуждение о разложении
58 = 8; ©й/ © ... © 8у имеет следующее приложение.
Следствие 1. Каждый идеал полупростой алгебры Ли
характеристики О является полупростой алгеброй.
Если 8г — простая алгебра, то производная алгебра йг = йг. По-
Поэтому из структурной теоремы вытекает
Следствие 2. Если 8 — полупростая алгебра характери-
характеристики О, то й' = 8.
Замечание. Мы показали в гл. 2, что если й — вполне приво-
приводимая алгебра Ли линейных преобразований конечномерного вектор-
векторного пространства над полем характеристики 0, то 8 = 0!.©!^, где
E.— центр, а 8] — полупростой идеал. В таком случае 8 =81 = 8!.
Поэтому 8 = 6© 8', где 8' полупроста.
Мы докажем теперь следующую общую теорему единственности.
Теорема 4. Если Ж — (неассоциативная) алгебра и
Я = Й! © $2 © ... © % = 8, © 232 ф ... © »,.
где Ш.1 u?8j— идеалы, являющиеся простыми алгебрами, то г -=s
и 23/ совпадают с %t с точностью до перестановки.
Доказательство. Рассмотрим ^ П 23у, /' = 1. 2, .... s. Это
идеал, содержащийся в 3A и 23,-. Поэтому если Щ Л 23/ ?= 0, то
2tj = 5tj f| 23/ = 23/, так как ^ и 23/ просты. Отсюда следует, что
% П 23у ф 0 не более чем для одного 23/. С другой стороны,
если \ П 23/ = 0 для всех ;, то 9^23/ S 1] П 23/ = 0 для всех у.
Поскольку 51 = 23! © 232 © ... © 23^, отсюда следует, что %х% = 0;
это противоречит предположению Sti Ф 0. Поэтому существует
такое J, что ^ = 23/. Аналогично мы получаем, что каждый идеал §tj
совпадает с одним из 23/ и каждый 23^ совпадает с одним из %t.
Отсюда легко следует требуемый результат.
Нетрудно проверить также, что если алгебра ЭД удовлетворяет
условиям теоремы 4, то эта алгебра имеет в точности 2Г идеалов,
а именно идеалы 9Ц © ... ©3l«ft. где (^ ik} есть подмно-
подмножество в A, 2 г]. Доказательство мы опускаем.
Основная структурная теорема неверна, если характеристика рфО.
Для того чтобы получить противоречащий пример, рассмотрим
алгебру (Ei линейных преобразований векторного пространства Ш,
размерность которой п делится на р. Легко проверить (см. упражне-
упражнение 1.20), что единственными идеалами в 6А являются (Si и Ф1 —
86 Га III Критерий Картана и его следствия
множество кратных 1. Так как ($? есть множество линейных преобразо-
преобразований со следом 0, a trl=w = O, то «Ид:©/.. Поэтому алгебра
8 = (§Л/Ф1 имеет единственный идеал, а именно 6^/Ф1, который
является простой алгеброй. Отсюда следует, что С*^/Ф1 полупроста,
но, поскольку 6^,/Ф1 есть единственный идеал в (§?/Ф1, (?Л/Ф1 не
представляется в виде прямой суммы простых идеалов. Из этого
утверждения и из теоремы 3 следует, что на 6^/Ф1 не существует
невырожденной симметрической ассоциативной билинейной формы.
Закончим этот параграф следующей характеризацией радикала
в случае характеристики 0.
Теорема 5. Если 8— конечномерная алгебра Ли над
полем характеристики О, то радикал © алгебры 8 есть орто-
ортогональное дополнение S'-'" производной алгебры 8' относи-
относительно формы Киллинга f(a, b).
Доказательство. Алгебра 58 = 8 является идеалом, и если
ft ?23', то tr(ada bf = fib, ft) = 0. Ядро представления a—>adg a,
а ? 23, абелево. Поэтому 23 разрешима по критерию Картана, и 2? с ©.
Пусть, далее, s?6, a, ft ?2. Тогда /(s, [aft]) = /([sa], b). Мы видели
(следствие 2 теоремы 2.8), что ad [sa] содержится в радикале
обертывающей ассоциативной алгебры (ad 8)*. Следовательно, эндомор-
эндоморфизм ad [sa] ad b нильпотентен для каждого b и поэтому / ([sa], b) = 0.
Таким образом, f(s, [ab]) = 0 и s^S'-1-. Отсюда ® с: 2'-1- и, следо-
следовательно, © = 8 .
§ 6. Дифференцирования
Напомним, что присоединенный эндоморфизм ad а является диф-
дифференцированием, называемым внутренним, и множество ad 2 таких
дифференцирований образует идеал в алгебре дифференцирований 3) (8).
Действительно, справедлива формула [ad a, D] = adaD, где D — диф-
дифференцирование. Поэтому имеет место равенство
[ad a ad Ь, D] = ad a ad (bD) -j- ad (aD) ad b,
откуда следует, что
О — tr [ad a ad b, D] — tr ad a ad (bD) -\- tr ad (aD) ad b.
Таким образом, форма Киллинга f (a, b) = tradaaub удовлетво-
удовлетворяет условию
/(с, bD) + f(aD, b) = 0, B5)
т. е. каждое дифференцирование является кососимметрическим пре-
преобразованием относительно формы Киллинга.
Докажем теперь следующую теорему, прчнадлежащую Цассенхаузу.
§ 6 Дифференцирования 87
Теорема 6. Если 8— конечномерная алгебра Ли, обла-
обладающая невырожденной формой Киллинга, то каждое диф-
дифференцирование D алгебры 8 внутреннее.
Доказательство. Отображение д: —> tr (ad x)D есть линейное
отображение алгебры 8 в поле Ф, т. е. это элемент пространства 8*,
сопряженного к 8. Так как форма f(a, b) невырождена, то суще-
существует такой элемент d?8, что f(d, х) — tr (ad х) D для всех х?й.
Обозначим через Е дифференцирование D — add. Тогда
tr (ad х) Е = tr (ad x) D — tr (ad x) (ad d) = tr (ad x)D — f (d, x) = 0.
Итак
tr (ad x) E = Q. B6)
Далее,
f(xE, y) = tr (ad xE) ad у —
— tr [ad x, E] ad у =
¦= tr ((ad x) E ad у — E ad x ad y) =
= tr (E ad у ad x — E ad x ad y) =
= tr?[ady, adx] =
Последнее равенство этой цепочки следует из соотношения B6). Так
как / невырождена, то Е = 0. Поэтому дифференцирование D = ad d
внутреннее.
Из этого результата вытекает, что все дифференцирования конечно-
конечномерной полупростой алебры Ли над полем характеристики 0 являются
внутренними. Напомним также, что если алгебра <3 конечномерна,
разрешима и характеристики 0, то ® отображается в ниль-радикал 4R
каждым дифференцированием алгебры <3. (См. следствие 2 тео-
теоремы 2.13.) Мы можем доказать теперь следующее утверждение.
Теорема 7. (I) Пусть 8 — конечномерная алгебра Ли над
полем характеристики 0, <& — ее радикал, Щ. — ниль-радикал.
Тогда каждое дифференцирование D алгебры 8 отображает <&
в W. B) Пусть 8 — идеал некоторой конечномерной алгебры 8Р <St
a 9f j — ее радикал а ниль-радикал. Тогда © = 8 П <3]. ЭД = 2 П %¦
Доказательство. Докажем сначала утверждение B) для
радикала. Очевидно, что Sfl®! — разрешимый идеал в й, поэтому
2 П <S] S <S- Далее @/(Й П ©t) — разрешимый идеал алгебры 8/(8 П ®i)-
С другой стороны, 8/(8fl®i) = (8-|-©i)/@i. причем последний является
идеалом в S^©,. Поэтому (i-\-<Bl)l<B1 и 8/(8 0®!) полупросты.
Отсюда <S/(8fl<S1) = 0 и 6 = 8fl®i- Пусть теперь 8t — голоморф
алгебры 8, a ©J и 5fi1—радикал и ниль-радикал алгебры 8,. Тогда,
как известно, [S'l, Sj ? ^ (теорема 2.13). Так как <& S ©! согласно
первой части рассуждения, то [8\<S] С C^ П 8) с !Я. Отсюда следует,
88 Гл. III. Критерий Картана и его следствия
что каждое дифференцирование в 8 переводит б в 3?, что и дока-
доказывает утверждение A). Пусть теперь 8j — произвольная конечно-
конечномерная алгебра Ли, содержащая алгебру й в качестве идеала.
Если fli^Sp то преобриование ad ax индуцирует дифференцирова-
дифференцирование идеала )?. Поэтому ИНайпу S ЭТ ввиду утверждения A). Это озна-
означает, что 71 — идеал в йг так что %t ? 3f] f| S. где S^ — ниль-радикал
в Zv Поскольку обратное включение очевидно, ?ft = Э^ П й.
Этот результат неверен в случае характеристики р Ф 0. Для по-
построения противоречащего примера рассмотрим сначала коммутативную
ассоциативную алгебру 3 с базисом A, z, z2 zp~l) и усло-
условием 2р = 0. Радикал SR алгебры 3 имеет базис (z, z2, ..., zp~l)
и 3/3^ ^ Ф1 • Легко проверить, что если w — произвольный элемент
из 3- то существует дифференцирование алгебры 3- отображающее z
в w. В частности, существует дифференцирование D, такое, что
zD — l. Пусть теперь 23 — произвольная простая алгебра Ли и
8 — алгебра Ли 23 ®3- Элементы последней записываются в виде
S*i®*<. *«€23. *i€3- и [{b®z){b'®z')\ = [bb'\®zz'. 8 дей-
действительно является алгеброй Ли (упражнение 1.23), a 23®SR—ниль-
потентным идеалом. Более того, факторалгебра 8/B3 ® Щ = 23 ® Ф1 ^23
проста. Поэтому 23®SR есть радикал и ниль-радикал алгебры 8.
Если D — некоторое дифференцирование ассоциативной алгебры 3>
то отображение ^ibi®zi->^ibi®ztD является дифференцирова-
дифференцированием алгебры 8. Если выбрать D [так, что zD—l, а О=?&?23,
то b® z->b® \ ^^8®3t. Поэтому мы получаем дифференцирова-
дифференцирование, которое не отображает радикал в себя.
§ 7. Полная приводимость представлений полупростых алгебр
В этом параграфе мы докажем основную структурную теорему
для модулей над полупростыми алгебрами Ли характеристики 0 и
получим наиболее существенные следствия этой теоремы. Основная
теорема принадлежит Вейлю и была доказана им с помощью транс-
трансцендентных методов, основанных на связи между алгебрами Ли и
компактными группами. Первое алгебраическое доказательство было
дано Казимиром и Ван-дер-Варденом. Доказательство, которое мы
приводим здесь, принадлежит в основном Уайтхеду. Следует отме-
отметить, что доказательство Уайтхеда было одним из основополагаю-
основополагающих камней в теории когомологий алгебр Ли, которую мы рассмо
трим в § 10. Заметим также, что в случае характеристики р суще
ствует, по-видимому, очень слаба* связь между строением алгебры Ли
и строением ее модулей, поскольку, как будет показано дальше,
каждая конечномерная алгебра Ли характеристики р Ф 0 имеет точ-
§ 7. Полная приводимость представлений полупростых алгебр 89
ные представления, которые не являются вполне приводимыми,
а также вполне приводимые точные представления.
Докажем сперва критерий того, что множество Е линейных
преобразований конечномерного векторного пространства 2JJ вполне
приводимо. Мы видели (теорема 2.9), что Е вполне приводимо тогда
и только тогда, когда каждое инвариантное подпространство VI в 9Я
имеет дополнение ^J, инвариантное относительно Е. Пусть теперь
W — любое дополнительное подпространство к3f, %R — ?R@ W. Такое
разложение ассоциируется с проекцией Е пространства Ш на ?ft.
Любой элемент х ? 2К можно представить единственным образом
в виде суммы х — у-\-у', у?У1, y'?W, и Е— линейное отобра-
отображение х->у. Обратно, если Е — произвольное идемпотентное линей-
линейное отображение, такое, что 101 = ШЕ, то Щ' = ШA —Е) есть допол-
дополнение к 51 в 1. Рассмотрим теперь линейное преобразование
[АЕ]==АЕ — ЕА, Л?Е. Если х ? 9И, то xAE??R и хЕА^Ш; сле-
следовательно, [АЕ] — отображение пространства Ш в 91. Если y?3f,
то уАЕ = уА. Поэтому [АЕ] переводит W в 0. Если обозначить
через X множество линейных преобразований пространства Ш, ото-
отображающих 9К в !R и 9f в 0, то [/Ш]?Ж. Ясно, что Ж — подпро-
подпространство пространства 6 линейных преобразований в 2JL Докажем
теперь следующее утверждение.
Лемма 2. Подпространство 3f имеет инвариантное допол-
дополнение ^5 тогда и только тогда, когда существует преобра-
преобразование D?X, такое, что [AE] = [AD] для всех А?Ё. Здесь
Е — произвольная проекция на Hi.
Доказательство. Пусть ^$ — дополнение к Ш, инвариантное
относительно Е, и F — проекция пространства Ш на !R, определенная
разложением Ш = ЭТ © ty. Поскольку ty инвариантно, F коммутирует
с каждым преобразованием Л^Е, т. е. \AF] = 0. Поэтому [.<4О] =
= [АЕ] для D — E — F. Кроме того, поскольку Е и F — проекции
на ЭД, Е — F отображает Ш в 3f и Ш в 0. Следовательно, D^X, как
и требовалось. Предположим, обратно, что существует преобразова-
преобразование ?>?Х, такое, что [AE] = [AD]. Тогда F = E — D коммутирует
с каждым A?L. Если х?Ш, то xF = x(E — D)? !R, а если у^!К,
то yF = yE = у. Поэтому F2 = F и 9? = ЭД/7. Тогда ^5 = Ш A — /=")
есть дополнение к 3f в SDJ, и ^$ инвариантно относительно Е, по-
поскольку F коммутирует с каждым Л^Е.
Предположим теперь, что S — алгебра Ли, Ш — 8-модуль, a -ft —
некоторый его подмодуль. Мы можем применить наши рассмотрения
к множеству й# преобразований aR, где R — представление алгебры 2.
определенное модулем Ш. Пусть Е — проекция пространства 9Я на St.
Если а?й, положим /(а) = [а#, Е\. Тогда a—>f(a) есть линейное
отображение алгебры. 2 в пространство X линейных преобразований
пространства Ш, переводящих Ш в Ш и !R в 0. Если <Y ? $ и о ^ 2,
90 Г л. III. Критерий Картана и его следствия
то [Ха^]^Ж. В самом деле, если х?Ш, то х [Ха^\^Щ., а если
у ? ЭД, то yXaR = 0 и yaRX = 0. Обозначим отображение X -> [Za#]
через aR. Совершенно очевидно, что отображение а -> aR является
представлением алгебры 8, а пространство X—ассоциированным
с этим представлением модулем. Справедливо соотношение
= I [aRE\ bR\-\-[aR [bRE\ ] =
Мы должны теперь рассмотреть следующую ситуацию: имеется
модуль X над 8 и линейное отображение a->f(a) алгебры 8 в X,
такое, что выполняется равенство
f{[ab\) = f{a)b — f(b)a. B7)
„Тривиальный" пример такого отображения получается, если поло-
положить f{a) = da, где d?X. Действительно, в этом случае мы имеем
равенство
f ([ab\) = d[ab\ = {da)b — (db)a=f(a)b — f (b) a.
Ключевым результатом при доказательстве полной приводимости мо-
модулей над полупростой алгеброй Ли характеристики 0 является
следующая
Лемма 3 (Уайтхед). Пусть 8 — конечномерная полу-
полупростая алгебра Ли характеристика 0, и пусть X — конечно-
конечномерный модуль над 8, a a->f(a) — линейное отображение
алгебры 8 в Ж, удовлетворяющее условию B7). Тогда существует
элемент d?X, такой, что f{a) = da.
Доказательство. Доказательство основывается на важном
понятии оператора Казимира. Предположим сперва, что й — ал-
алгебра Ли, а %х и ЗЭ2 — такие идеалы в 8, что представления алгебры й
в 93] и ЗЭ2 контрагредиенты. Мы предполагаем, таким образом, что
пространства Ъу и ЗЭ2 связаны невырожденной билинейной формой
(by, b2), b[?%${, (by, #2)G Ф. такой, что для любого a?2 выполняется
условие
(М- Ь2) + (Ьу, [Ь2а]) = 0. B8)
Если (Uy ит) — базис в ЗЭр то мы можем выбрать сопряженный
или дуальный базис (и1, и2, ..., ит) в 332, удовлетворяющий условиям
(ult uJ) = b{j. Пусть [иго] = 2;а/Л и ["^^^Pw"'- Тогда
([up], и*)=B «у«у. «*)=2 *ifijk=aik и («г. [«*«])=(«<. 2 Рм«0=
= pfti. Поэтому из условия B8) следует, что a/ft = — $ki, т. е. ма-
§ 7. Полная приводимость представлений полупростых алгебр 91
трицы (а) и ф), определенные дуальными базисами, удовлетворяют
условию ф) = — (а)', где (а)' — матрица, транспонированная к (а).
Пусть теперь R — некоторое представление алгебры 8. Назовем эле-
элемент
m
г= 2 «?««
оператором Казимира представления R. Имеем следующие ра-
равенства
[Г, а*] = 3[и?в*]и'*Н-2 «?[«'*«*] =
i
= 2 «//«?«'*+2 fc>«f«'* =
i, i i, i
= 2 «.,«?«'*-2 «;*«?«'*=
2.;/2
Таким образом, Г коммутирует с образами aR всех элементов а ? 8
при представлении R.
Пусть теперь алгебра 8 удовлетворяет условиям леммы. Обозначим
через $ ядро представления R, определенного модулем Ж. Мы можем
тогда написать 8 = ft©8i. где Sj— идеал. Ограничение R на 8t
взаимно однозначно, и алгебра 8j полупроста. Поэтому форма следа
{b\,b-i)z=iibyb2, где й/ ? йь не вырождена на 8Г Мы знаем также,
что форма следа, соответствующая представлению, инвариантна. По-
Поэтому условие B8) выполняется для bt ? 8t и а ? 8. Таким образом,
представление алгебры 8 в 8: совпадает с контрагредиентным к нему
представлением, и если {их ат), (и1, ..., ат) — базисы в 8lt
т
удовлетворяющие условиям (мг, и*) — Ьу, то элемент Г=2М?М
есть оператор Казимира, коммутирующий с каждым aR. Заметим
также, что tiT = 2 tf и?и'Л = 2 (а/. а') = m = dim 8t.
Разложим теперь X на его компоненты Фиттинга Хо и 3f1 относи-
тельйо Г, так что Г индуцирует нильпотентное линейное преобразова-
преобразование на Жо и невырожденное преобразование на Э^. Так как TaR =
= а^Г, то $jGR С Х;- и Ху- являются подмодулями. Мы можем написать
f(a) = fo(a)-{-fl(a), где f](a)?Sj, откуда немедленно следует,
что a—>fj(a) есть линейное отображение алгебры 8 в $у, удовле-
удовлетворяющее условию B7). Если теперь оба пространства Ху- ненулевые,
то dim X,- < dim X для j — 0, 1 .... Поэтому можно использовать
92 Гл. III. Критерий Картана и его следствия
индукцию по dimX и вывести, нто существует элемент d;?X;-, такой,
что fj(a) = dja. Тогда элемент d = do-\-d1 удовлетворяет условию
f (с) = da, что и требовалось доказать. Поэтому остается рассмотреть
следующие два случая: Ж = Ж0 и $ = $!.
X = $0. В этом случае оператор Г нильпотентен. Поэтому m =
= tr Г = 0. Это означает, что ядром представления R является вся
алгебра Й, т. е. aR = 0 для всех а. Тогда условие B7) записывается
в виде /([ab]) = 0, a, ??Й. Таким образом, f(a') — 0 для всех
а'?2'. Так как й/ = й, то /(с) = 0, так что элемент d = 0 удовле-
удовлетворяет требованиям леммы.
m
$ = $1. Положим у = 2 /(«()"'¦ где> как и раньше, (и;) и (мг) —
дуальные базисы в 8j. Тогда
2 (/ («,) а) и'+ 2
S (/ («?) в) «г + S Pi
2 (/ (в,) в) и1 - 2 «;i/ («г) и' =
S (/ («г) в) «' — 2
2 (/ (»i) а) и1 - 2 (/ (в,) в) и' + S (/ (о) «*)«'
? г <
Так как'оператор Г невырожден, той = уГ~ удовлетворяет условию
леммы f(a) — da. Этим и завершается доказательство леммы Уайтхеда.
Мы можем доказать теперь следующую фундаментальную теорему.
Теорема 8. Если Й — конечномерная полупростая алгебра
характеристики 0, то каждый конечномерный модуль над Й
вполне приводим.
Доказательство. Пусть 9W—конечномерный Й-модуль и Щ —
некоторый его подмодуль. Пусть, далее, Ж — пространство таких ли-
линейных преобразований в Ш, которые отображают Ш в tft, а tft в 0.
Рассмотрим X как Й-модуль относительно композиции Ха =э [X, aR],
где R — представление, определенное модулем Ш. Пусть Е — произ-
произвольная проекция модуля Ш на Щ. Положим /(с) = [с/?, Е]. Тогда
/ (с) удовлетворяет условиям леммы Уайтхеда. Поэтому существует
элемент D?X, такой, что f (a) = Da = [D, aR\. Как мы видели
§ 7. Полная приводимость представлений полупростых алгебр 93
раньше, отсюда следует, что существует дополнительное к У1 под-
подпространство, инвариантное относительно Й. Так как это рассужде-
рассуждение применимо к любому подмодулю Vt, то модуль Ш вполне при-
приводим.
Если Й—подалгебра алгебры Ли В, то дифференцированием D ал-
алгебры 2 в S3 называется линейное отображение алгебры Й в 23, удо-
удовлетворяющее условию
B9)
для каждых /j и /2?Й. Как легко видеть, множество 35 (Й, В) дифферен-
дифференцирований алгебры Й в В образует подпространство пространства
всех линейных отображений алгебры Й в алгебру В. Из доказанной
выше леммы Уайтхеда (лемма 3) вытекает следующее важное утвер-
утверждение о дифференцированиях.
Теорема 9. Пусть В — конечномерная алгебра Ли харак-
характеристики 0, с 2 — ее полупростая подалгебра. Тогда каждое
дифференцирование Й в В может быть продолжено до внут-
внутреннего дифференцирования алгебры 33.
Доказательство. Рассмотрим В как Й-модуль относительно
умножения [Ы], где /?Й, b ?23. Тогда дифференцирование D алгебры Й
в В определяет отображение f(l) = lD, удовлетворяющее условию
леммы Уайтхеда. Поэтому существует такой элемент d ? Ъ, что ID =
= f(J.) = [d, I]. В этом случае D может быть продолжено до внут-
внутреннего дифференцирования, определенного элементом —d.
Напомним, что, как мы показали в гл. 2 (теореме 2.11), вполне
приводимая алгебра Ли Й линейных преобразований конечномерного
векторного пространства Ш над полем характеристики 0 обладает
прямым разложением fi = 2j® (S, где fij — полупростой идеал, аи —
центр. Более того, элементы С?(§ полупросты в том смысле, что
их минимальные многочлены являются произведениями различных не-
неприводимых многочленов. Мы можем установить теперь обратное
утверждение. Наше доказательство будет основываться на соображе-
соображениях следующего типа о расширении поля. Предположим, что мы
имеем множество ? линейных преобразований пространства Ш над Ф.
Если 2 — расширение поля Ф, то каждое преобразование Л?? может
быть продолжено единственным образом до линейного преобразования,
обозначаемого также через А, пространства 9J?g. Мы получаем, таким
образом, множество ?={Л} линейных преобразований 9Ws над 2.
Лемма 4. Пусть ? — множество линейных преобразований
конечномерного векторного пространства ffl над Ф. Пусть
24 Гл. III. Критерий Картана и его следствия
множество продолжений этих преобразований до преобразова-
преобразований пространства SWs над 2, где 2 — расширение поля Ф,
вновь обозначается через Е. Предположим, что множество ?
в Шя вполне приводимо. Тогда и исходное множество ? вполне
приводимо в Ш.
Доказательство. Пусть ЭТ— подпространство в Ш, инва-
инвариантное относительно ?, и пусть Е— проекция WI на ЭТ. Тогда,
согласно критерию для дополнений (лемма 2), дополнительное к ЭТ под-
подпространство, инвариантное относительно ?, существует тогда и
только тогда, когда можно найти линейное преобразование D про-
пространства Ш, переводящее 2I в Я, а Я в 0 и удовлетворяющее
условию [AE]^=[AD] для всех Л??. Если Аг, А2 Ak — макси-
максимальное множество линейно независимых элементов из ? н 5г = [Лг?],
то достаточно найти преобразование D, такое, что [ЛгО]=5г,
г=1, 2 k. Мы получаем, таким образом, систему из k линей-
линейных уравнений относительно D в конечномерном векторном про-
пространстве Ж линейных преобразований пространства Ш, отображаю-
отображающих 2R в ЭТ и ЭТ в 0. Если (Uv U2 Ur) — базис пространства X,
г г
то можно записать Bt = 2 $iSUs< 1Л^л1 — 2 Т»ь^. О —2?>/^/>
и наши уравнения эквивалентны обычной системе 2 7«А ~ Р-ч»
h
i=\, 2, ..., k, s=l, 2 г, относительно элементов bj из Ф.
Поэтому подпространство 91 имеет ?-инвариантное дополнение в том
и только том случае, когда эта система имеет решение. Перейдем
теперь к Tts и к инвариантному подпространству ЭТ2 относительно
множества ? продолжений преобразований Л??. Тогда, по нашему
предположению, ЭТг имеет ?-инвариантное дополнение в Ша- Про-
Продолжение Е отображения Е есть проекция Шз на ЭТд. Поэтому суще-
существует линейное отображение D пространства SMs. переводящее Tig
в ЭТа, а ЭТ2 в 0 и такое, что [AtD] — Bt = [Лг?], 1=1, 2 k.
Продолжения , преобразований Uv U2 Ur образуют базис про-
пространства линейных преобразований в 9И2, отображающих Т1я в Ш3>
г
а ЭТз в 0. Поэтому, если D = 2 ^/^/> то элементы И удовлетворяют
~ 1
системе 2 ТглА ^ Ри- Так как элементы ^ihs и р^ принадлежат
h
полю Ф, то эта система имеет решение (8lt . . ., §г), где §^ ^ Ф. По-
Поэтому существует преобразование D?3k\ такое, что [AD] = [АЕ],
Л?Е, и, следовательно, подпространство ЭТ обладает ?-инвариант-
ным дополнением в 97t.
Мы можем теперь доказать следующее утверждение.
Теорема 10. Пусть & — алгебра Ли линейных преобразова-
преобразований конечномерного векторного пространства Ш над полем
§ 7. Полная приводимость представлений полупростых алгебр 95
характеристики 0. Тогда 2 вполне приводима в Ш тогда и
только тогда, когда выполняются следующие условия: A) й =
= 8i©(?, где 2t— полупростой идеал, а & — центр, и B) эле-
элементы из (S полупросты.
Доказательство. Необходимость была доказана раньше.
Допустим теперь, что выполняются условия A) и B), и обозначим
через Q алгебраическое замыкание основного поля. Тогда, как сле-
следует из предшествующей леммы, достаточно доказать, что множество 8
продолжений элементов алгебры 2 вполне приводимо в 9Иа- Мно-
Множество Q-линейных комбинаций элементов из 2 может быть ото-
отождествлено с 2а1 аналогичные утверждения верны для 2j и (S. Пусть
теперь С ? &. Так как минимальный многочлен преобразования С имеет
различные неприводимые множители и так как основное поле имеет
характеристику 0, то минимальный многочлен преобразования С в Шз
имеет различные линейные множители в Q. Следовательно, Шз можно
разложить в прямую сумму Ttai ® ... ®2№«ft, где
и a.v <х2 <хг— различные характеристические корни преобразова-
преобразования С. Так как АС = СА для А ?8, то ЖцА <= ШХ{. Мы можем
применить то же самое рассуждение к Ша1 относительно любого
другого преобразования D ? (S. Это приводит к разложению про-
пространства Ша = Шг © 2К2 © • • • © Шг на 2-инвариантные подпро-
подпространства, такие, что преобразования, индуцированные в Tlt каждым
элементом С?&, являются умножениями на скаляр. Для доказа-
доказательства того, что 8 вполне приводимо в Ша, достаточно показать,
что множества индуцированных в fflt преобразований вполне при-
приводимы, а так как элементы из & являются скалярными в Tit, доста-
достаточно показать, что 8t вполне приводима в каждом Ш^. Инвариант-
Инвариантные относительно 2j подпространства в Tii инвариантны и относительно
Q%v множества 2-линейных комбинаций элементов из 8j. Но 28Х
есть гомоморфный (в действительности изоморфный) образ расширения
алгебры 8is, которая полупроста. Поэтому и 28t — полупростая ал-
алгебра Ли линейных преобразований, вполне приводимая по теореме 8.
Мы доказали, таким образом, что 8 вполне приводима в 9Ws и, сле-
следовательно, в Ш.
Встанем теперь на несколько иную точку зрения и рассмотрим
конечномерную алгебру Ли 8 характеристики 0 и два конечномерных
вполне приводимых модуля Ш и Ш над 8. Покажем, что модуль
Ш ® 91? вполне приводим. Пространство ^ = 2R © Ш есть модуль
относительно композиции (х -f- у) I = xl -\- yl, х ? Ш, у ? У1. Очевидно,
что ф вполне приводим и Т1 ® Ш есть подмодуль модуля ^ ® ^р.
Поэтому достаточно доказать, что модуль У$ ® $ вполне приводим.
Если заменить 2 на 8/51, где 51—ядро представления в Щ, то можно
96 Гл. III. Критерий Картана и его следствия
предполагать, что представление R, соответствующее модулю ty,
взаимно однозначно. Тогда, как мы знаем, Й = Й1фй. где 21 — полу-
полупростой идеал, a (S — центр. Более того, элементы CR, где С?&,
полупросты. Имеет место общий факт: если R— точное представле-
представление алгебры Ли Й, то представление R®R в ^5®*$ также точно.
Таким образом, если а?Й и преобразование aR не есть умножение
на сиаляр, то, поскольку алгебра линейных преобразований в ^5®?Р
есть тензорное произведение алгебр линейных преобразований в Щ.
элементы aR®aR, aR®\, l®aR и 1®1 линейно независимы, и
в частности aR ® I -f-1 ® aR ф 0. Поэтому если aR®R = 0, то пре-
преобразование aR должно быть скаляром, aR = a.. Тогда aR®R = 2a
(в ф®^) и а = 0. Так как представление R взаимно однозначно,
то и а = 0. Мы можем сделать заключение, что Йл® =2i® +6
где алгебра 2f ®л ^8i полупроста, а &к®л есть центр. Требуемый
результат следует теперь из критерия теоремы 10 при условии, что
мы можем доказать полупростоту каждого элемента
где ?
Пусть 2 — алгебраическое замыкание основного поля, и пусть
aj, <х2 <xft — различные характеристические корни преобразова-
преобразований CR. Тогда из доказательства теоремы 10 следует, что
где xaCR=a.xa_ для лц?^. Поэтому
и yCR&R = (а.-{-а^у для каждого элемента у?9^ ®^Л.. Отсюда
следует, что минимальный многочлен преобразования CK®R в Eр®9|$)8
имеет различные корни. Так как этот многочлен есть также мини-
минимальный многочлен преобразования CR®R в $®^, то он является
произведением различных неприводимых множителей. Поэтому эле-
элемент CR®R полупрост, и нами доказана
Теорема 11. Пусть Й — конечномерная алгебра Ли над
полем характеристики 0, и пусть Ш и !ft — конечномерные
вполне приводите модули над Й. Тогда модуль Ш®Ш вполне
приводим.
§ 8 Представления расщепляемой трехмерной простой алгебры Ли 97
§ 8. Представления расщепляемой трехмерной
простой алгебры Ли
В § 1.4 трехмерная простая алгебра Ли R была названа расще-
расщепляемой, если она содержит такой элемент А, что присоединенный
эндоморфизм ad h имеет ненулевой характеристический корень р,
принадлежащий основному полю. Мы показали, что в любой такой
алгебре можно выбрать базис (е, /, А) так, что таблица умножения
будет иметь следующий вид:
[eh] = 2e. [//*] = —2/, [ef] = h. C0)
Теория представлений этой алгебры играет важную роль в деле глу-
глубокого изучения структуры полупростых алгебр Ли и их предста-
представлений (гл. IV, VII, VIII). Рассмотрим сейчас случай, когда харак-
характеристика поля Ф равна 0. Предположим сперва, что поле Ф алге-
алгебраически замкнуто и что Ш — конечномерный модуль над $.
Представление в *В1 определяется образами Е, F, Н базисных эле-
элементов е, f, h, и мы имеем следующие соотношения:
[Е, Н] = 2Е, [F, Н] — — 2F, [E,F] = H. C1)
Обратно, любые три линейных преобразования Е, F, Н, удовлетво-
удовлетворяющие соотношениям C1), определяют представление алгебры 5?
и, следовательно, 51-модуль. Пусть а — характеристический корень
преобразования Н, а х — соответствующий характеристический век-
вектор: х Ф 0, xH — oix. Тогда
{хЕ)Н = х{НЕ-\-2Е) = (хЕ)(а. + 2). C2)
Если хЕ Ф 0, то из равенства C2) следует, что a -f- 2 есть харак-
характеристический корень преобразования Я, а хЕ — соответствующий
характеристический вектор. Мы можем заменить х вектором хЕ и
повторить процесс. Это приводит к последовательности отличных
от нуля векторов х, хЕ, хЕ?, ..., соответствующих характеристи-
характеристическим корням a, a-f-2, a-f 4, ... преобразования Н. Но Н имеет
лишь конечное число различных характеристических корней, поэтому
последовательность обрывается на некотором шаге, т. е. существует
такое число k, что хЕк Ф 0, а хЕк+1 = 0,
Если заменить х на \Ek, то можно предположить с самого
начала, что х Ф 0 и что
хН = ах, хЕ = 0. .. C3)
Положим хо = х и xL-= x^^F. Тогда аналогично равенству C2) мы
получаем соотношение
xtH = {a—2l)xlt C4)
7 Н. Джекобсон
Гл. III. Критерий Картана и его следствия
и рассуждение, применявшееся к векторам хЕ1, показывает что суще-
существует такое неотрицательное число ш, что х0, хх хт все
отличны от нуля, а хт+1 = 0. Таким образом, xFm+1 = 0, xF"'Ф0.
В этом случае x-v 0<^t^m, есть характеристический вектор
преобразования Я, соответствующий характеристическому корню
а — 21. Поскольку элементы поля а, а — 2, а — 4, ..., а — 2т все
отличны друг от друга, векторы xt линейно независимы. Пусть
m
5? = 2 Ф*;, так что Щ. будет (/и-f- 1)-мерное подпространство про-
странства 5№. Покажем, что ?Я инвариантно и неприводимо относи-
относительно $. Выведем сначала формулу
*,? = (—Ах+ /(*— 1) )*,_!. C5)
Для случая i = 0 формула C5) верна (л:0? = 0). Предположим,
что формула C5) справедлива и для I—1. Тогда
xfi = xt_xFE = xt_x (EF — Я) =
что и требовалось доказать.
Из равенств C4), C5) и равенства xtF = л:;+1 следует, что Щ.
есть ^-подпространство в Ш. Так как Я=[?^], то ^гэгЯ = 0.
Отсюда, используя равенство C4), получаем, что (т-\-1)а —
— m(m-|-l) = 0. Таким образом, а = т. Наши формулы записы-
записываются теперь в следующем виде:
х1Н — (т — 21)х1, 1 = 0 т,
XiF = xi+v i — 0 от —1, xmF = 0, C6)
лго? = О, xtE=^{—mi-{-i(i — \))xt_v i = l т.
Заметим, что в последнем равенстве
Пусть теперь Шг — ненулевое инвариантное подпространство в Щ, и
пусть вектор
§ 8 Представления расщепляемой трехмерной простой алгебры Ли 99
где рг Ф О, принадлежит Щ.у Тогда xm = §~lyFm~l ? У1у Поэтому
в соответствии с последним равенством в C6) каждый вектор xt ? У1г
и Э^^ЭД. Таким образом, если исходное пространство 2R было
й-неприводимо, то Ш = ?Я. Теорема о полной приводимости пока-
показывает, что пространство Ш есть прямая сумма неприводимых инва-
инвариантных подпространств, аналогичных пространству 9?.
Мы можем теперь опустить предположение, что поле Ф алгебраи-
алгебраически замкнуто, предполагая только, что характеристика поля Ф
равна 0. Заметим, что имеет место следующая
Лемма 5. Пусть $— расщепляемая трехмерная простая
алгебра Ли над полем Ф характеристики 0, и пусть отобра-
отображение е—>Е, f—>F, h->H определяет ее конечномерное пред-
представление. Тогда характеристические корни преобразования Н
являются целыми числами.
Доказательство. Если Ш — модуль этого представления и
2 — алгебраическое замыкание поля Ф, то 2№д является модулем
над алгеброй из, удовлетворяющей тем же условиям над Q. что и $
над Ф; ЭКа есть прямая сумма неприводимых подпространств ?Я,
базисы которых (л:0, х^ хт) удовлетворяют условиям C6).
При надлежащем выборе базиса в Шз матрица преобразования И
в этом базисе будет диагональной матрицей с целочисленными эле-
элементами. Диагональные элементы будут также характеристическими
корнями преобразования Н в Ш.
Мы можем доказать теперь следующее утверждение.
Теорема 12. Пусть $—расщепляемая трехмерная алгебра
Ли над полем Ф характеристики 0. Тогда каждому целому
числу т = 0, 1, 2, ... соответствует один и только один,
с точностью до изоморфизма, неприводимый ^.-модуль Т1 раз-
размерности т-\- 1. Пространство Ш обладает таким базисом
(х0, хх л:т), что преобразования (Е, F, Н) модуля Ш, соот-
соответствующие каноническому базису (е, /, п) алгебры R, опреде-
определяются формулами C6).
Доказательство. Пусть Ш — конечномерный неприводимый
модуль над й- Тогда характеристические корни преобразования Н
являются целыми числами. Поэтому можно найти целое число а и
вектор х Ф 0 в Ш, такие, что хН = ах. Мы можем предположить,
как и раньше, что хЕ = 0. Тогда <x = m, и в пространстве Ш суще-
существует базис (х0, xv .... хт), для которого выполняются условия C6).
Эти формулы полностью определяются размерностью т-\- 1 про-
пространства Щ. Поэтому любые два (m-f-1)-мерных неприводимых
модуля на J? изоморфны. Остается показать, что для каждого
/я —0, 1, ... существует неприводимый (т-\-1)-мерный модуль
100 Гл. III. Критерий Картана и его следствия
над $. Пусть Ш — пространство с базизом (х0, хх хт); опре-
определим линейные преобразования Е, F, Н формулами C6). Тогда
= — 2xtF,
= (-mi + i(t—
= {m — 2i) xt =
Поэтому Е, F и Н удовлетворяют требуемым условиям коммутиро-
коммутирования и, следовательно, определяют представление алгебры J?. Как
и раньше, пространство Ш будет $-неприводимо.
Теорема о полной приводимости здесь также применима, и вместе
с предшествующим результатом она описывает строение любого
конечномерного ^-модуля.
§ 9. Теоремы Леви и Мальцева — Хариш-Чандра
Теорема Леви об „отщеплении радикала" утверждает, что всякая
конечномерная алгебра Ли 23 характеристики 0, обладающая разре-
разрешимым радикалом <3, содержит полупростую подалгебру 2, такую,
что 23 = 2-f-<3. Отсюда следует, что 2П© = 0, так что 23 = 2ф<5
и 2 = 23/®. Таким образом, подалгебра 2 изоморфна факторалгебре
алгебры 23 по ее радикалу. Обратно, если 23 содержит подалгебру 2,
изоморфную 23/©, то алгебра 2 полупроста. Поэтому 2 П *2 — 0, и
так как dim23 = dim(S-|-dim23/<3 = dim<3-|-dim2, то 23 = 2-f-<5.
Заметим далее, что теорему достаточно доказать в случае & = 0,
т. е. когда радикал <2? абелев. Действительно, предположим, что
©2=?0. Тогда если 23-=23/<52, то dim23<dim23. Поэтому, используя
индукцию по размерности алгебры, мы можем предположить, что
утверждение верно для алгебры 23. Далее, (Э —<5/<52 есть радикал
алгебры 23, и 23/<5^23/<5. Поэтому алгебра 23 содержит поцалгебру
2^23/©. Как подалгебра алгебры 23, 2 имеет вид Ъ^2, где 23t есть
подалгебра алгебры 23, содержащая <52. Но ©2 — радикал алгебры 23!
и 231/©2^23/<3, так что dim 23t < dim 23. Применяя индуктивное
предположение, мы получаем, что алгебра 23] содержит подалгебру
2-=23/<3, чем и завершается доказательство утверждения для алгебры 23.
§ 9 Теоремы Леей и Мальцева—Хариш-Чандра 101
Предположим теперь, что <52 = 0, и на некоторое время опустим
предположение о том, что алгебра 23 = 23/© полупроста. Так, E
будет подмодулем модуля 23 относительно 23 (присоединенное пред-
представление). Поскольку <52 = 0, то <& лежит в ядре представления
алгебры 23, определяемого модулем <3. Поэтому мы получаем инду-
индуцированное представление алгебры 23 = 23/®. Для соответствующего
модуля выполняется равенство sb = [s, b], s?@, й?23.
Мы можем найти взаимно однозначное линейное отображение
а-.Ь-^-Ь" алгебры 23 в 23, такое, что Ъ°==Ь. Это отображение легко
построить, исходя из разложения 23 = © © ©, где ® — подпростран-
подпространство. Имеется- проекция алгебры 23 на ®, определенная этим разло-
разложением. Так как © есть ядро, то мы получаем индуцированный
линейный изоморфизм а алгебры 23 на ®, а следовательно, и в 23.
Если b = s-\-g, s?<2>, g?®, то по определению b"' = g и b=g,
так что Ъ" ~g =Ъ, как и требовалось. Пусть, обратно, b->b°
является взаимно однозначным линейным отображением 23 в 23, таким
что о = Ъ. Тогда (& = 23" есть дополнение к © в 23. Если s ? © и
b ? 23, то закон композиции в модуле © удовлетворяет соотношениям
Пусть bv ?2?23; рассмотрим элемент
[К ь°2]—[*,*„]• €»• C7)
Если мы применим гомоморфизм b—>b алгебры 23 на 23 и исполь-
используем свойство Ъ" = Ь, то получим равенства
[Щ = \р\, Щ = [ЪфД, ЩгГ = 1Ш = СШ-
Поэтому выполняется условие
g(bJ2) = \b\, bl\ — [W€®.
Нетрудно проверить, что {bv b2)->g(b1, b2) есть билинейное отобра-
отображение произведения 23 X 23 в в.
Предположим теперь, что ® = 23" — подалгебра алгебры 23.
Тогда [bi, *г]б®> и поэтому g(bu ft2) ? ® Г) <5 = 0, так что
g(bv Ь2) = 0 для всех bx, b2. Обратное утверждение также очевидно,
поскольку из условия g(bv Ь2) — 0 следует, что \Ь\, ^г] = [^1*2] 6®-
Поэтому ® является подалгеброй в том и только в том случае, когда
билинейное отображение g нулевое.
Если 23° не есть подалгебра, то мы постараемся изменить а так,
чтобы получить другое отображение х алгебры 23 с образом 23,
102 Гл 111. Критерий Картана и его следствия
являющимся подалгеброй. Предположим, что это возможно. Тогда *
будет взаимно однозначным линейным отображением алгебры 23 в 23,
таким, что tf = Ъ vl [^l&a]—[^АГ —^ для всех ^v ^2- Пусть теперь
р = а — т. Тогда р есть линейное отображение алгебры 23 в 2?, удо-
удовлетворяющее условию
Поэтому 6P?S, и мы можем рассматривать р как линейное отобра-
отображение 23 в S. Имеют место следующие равенства:
Если элемент s& определен так же, как и ранее, то s6 = [s&T]. Таким
образом, если мы сможем выбрать каким-либо способом дополнение
к ©, являющееся подалгеброй, то билинейное отображение g(bz, &2)
произведения 23 X 23 в © может быть выражено через линейное
отображение р алгебры 23 в © с помощью формулы
g (blt b2) = b\h — Wbi — [Ш?. C8)
Предположим, обратно, что существует линейное отображение р
алгебры 33 в ©, удовлетворяющее этому условию. Тогда х = а — р
является другим взаимно однозначным линейным отображением
алгебры 23 в 23, таким, что 6х = Ь, и, повторяя рассуждения в обрат-
обратном порядке, можно показать, что \р\, bl] = [bib2\c', поэтому
23х — подалгебра.
Наши результаты могут быть сформулированы следующим образом.
Критерий, Пусть 23—алгебра Ли, C — такой идеал в 23,
что ©2 = 0, и пусть 23 = 23/©. Тогда © есть Ъ-модуль с зако-
законом умножения sb — [sb]. Существуют также взаимно одно-
однозначные линейные отображения о алгебры 23 в 23, такие, что
Ь°~Ь, 6 ?23. Если а — одно из таких отображений, то
Кроме того, © имеет дополнительное подпространство, являю-
являющееся подалгеброй в том и только в том случае, когда суще-
существует линейное отображение р алгебры 23 в ©, такое, что
g Фъ b2) = b\h — b% — [ЬгЬ2]9.
§ 9 Теоремы Леей и Мальцева—Хариш-Чандра 103
Определенное выше на 8 X 8 билинейное отображение g задает в <2>
множество элементов g{bt, bj), обычно называемое системой фак-
факторов. Заметим далее, что система факторов удовлетворяет неко-
некоторым условиям, являющимся следствиями специальных свойств
умножения в алгебре Ли. Ясно, например, что
g(b, ft) = 0, C9)
а поэтому g(b1, Ь2) = — g(b2, Ьг). Запишем, далее,
и вычислим
1 [Ь\, U2\ #3
Если поменять
| = |^ [^1^2]" Ь%
== [ [^1^2! Ь$]
местами bv
;]+
•+
к
¦к-
г(
*3
№. &2)Й] =
[ft,ft2l. *з) + 1
циклически,
сложить полученные
равенства и использовать тождества Якоби в 23 и Ж, то мы получим
равенство
[v ь2), bl]-\-g([b2b3], *,) +
h). b\\+g{{bzh\, b2) + [g(h, bx), Й] = 0. D0)
Наше доказательство теоремы Леви завершается доказательством
следующей леммы, принадлежащей Уайтхеду.
Лемма 6. Пусть 8 — конечномерная полупростая алгебра
Ли характеристики 0, 5ft — конечномерный ^-модуль и (lv /2)->
-^¦gih' h) — билинейное отображение произведения 8 X « в Ш,
удовлетворяющее условиям
г (/.О = о (D
+ g (/2. h) h+g( [?ib k) 4- g (/3. /1) '2 = 0. (II)
Тогда существует линейное отображение l—>lf алгебры 8 в Ш,
такое, что
g(h, l2) = l\l2 — lUl — \hl2\9- (Ш)
Доказательство. Пусть §t, 8j, и,, «', Г такие же, как и
в доказательстве первой леммы Уайтхеда; й—ядро представления,
8! — такой идеал, что 8 = $©8!, (ut) и (и1), i=l, .... т, — дуаль-
дуальные базисы пространства 8j, сопряженные относительно формы следа
данного представления, и, наконец, Г—оператор Казимира, опре-
определенный элементами и, и и1. Напомним, что Г является отображе-
104 Гл. Ш. Критерий Картана и его следствия
m
нием х -> 2 (хади' в ^* Положим /3 —и* в соотношении (II) и
умножим последнее (в модуле Ш) на и ; взяв сумму по I, находим:
0
2 * (U2«il. *i) "' -+¦ S (г ft. «i) '0 «' 4-
2 2
+ S в ([Л У+ 2
=? (/,. щ г -ь S в' (i ад. «о«' -ь
4
Если мы теперь используем выражения 1иг/] = 2аг/и/- 1И'Л =
= 2 Рг7«'' и вспомним, что $ц — — а}1 [см. равенство B8)], то получим:
2*(*а. я,) [/,«'] =S в'ft. 1яА1)я'. D1)
S в' (я*. У \hA == 2 в'([яА1. /,)«' • D2)
Из этих равенств и из кососимметричности g следует обращение в 0
четырех членов в предшествующих равенствах. Мы получаем, таким
образом, что
4- 2 (g ft. «/)«') *! 4- 2 (^ (я,. У и') /2. D3)
Если оператор Г невырожденный, то определим
ui)alV-\ D4)
2i
Тогда из формулы D3) следует требуемое соотношение (III). Если
оператор Г нильпотентен, то, как и в доказательстве первой леммы
Уайтхеда, m = 0, $ — й, так что представление является нулевым.
Соотношение (II) в этом случае редуцируется к следующему:
• g ([ад. Q+g(. ш. /,) 4- g ([Щ. у == о. (но
Обозначим теперь через X векторное пространство линейных Отобра-
Отображений алгебры 8 в Ш. Это пространство можно снабдить структурой
Й-модуля, если определить для элементов Л?$, х, /?2 умножение
§ 9. Теоремы Леви и Мальцева—Хариш-Чандра 105
= —[xl] А, т. е. Л/ = — (ad/) А Легко видеть, что при этом
удовлетворяются условия, определяющие модуль (см. § 1.6). Для
каждого I ? 8 можно определить элемент Ах ? X как отображение
x->g(x, /)?9K. Тогда 1->А1 есть линейное отображение алгебры 8
в X, удовлетворяющее следующим условиям:
= — g([xl2], у,
{[xll], Z2).
Поэтому из кососимметричности g и из (IF) следует
А1г1,. D5)
Таким образом, выполняется условие первой леммы Уайтхеда. След-
Следствием этого является существование такого элемента р ? Ж, что
А- = р/. Иначе говоря, имеется линейное отображение р алгебры 2
в Ш, удовлетворяющее условию
g(x, /) = — [*. /]р. D6)
Из определения $ как модуля и из условия D6) следует соотноше-
соотношение (III). Этим доказывается утверждение в случае, когда оператор Г
нильпотентен. Если же Г вырожден, но не нильпотентен, то имеет
место разложение *Ш = 2Jt0 ф ЯЭТг, где Ш1 — компоненты Фиттинга
пространства 9К относительно Г, и обе эти компоненты отличны от 0.
Эти пространства являются подмодулями, и мы можем записать
g(h h) — go(lv y-f-?i(*i. У- SiO-v У€2Кг- Отображения g, удо-
удовлетворяют условиям, наложенным на g, так что мы можем пред-
представить их в форме (III) в силу индуктивного предположения о раз-
размерности модуля 9К. Складывая линейные преобразования для Tlt,
мы получаем утверждение для 9Й.
Как уже отмечалось раньше, эта лемма завершает доказательство
следующей теоремы.
Теорема Лев и. Если 95 — конечномерная алгебра Ли ха-
характеристики 0 с радикалом <&, то существует полупростая
подалгебра 8 алгебры 93, такая, что 93 = 8®©.
Подалгебра 8, удовлетворяющая этим условиям, называется фак-
фактором Леей алгебры 93. Первым следствием теоремы Леви является
такой результат.
Следствие 1. Пусть 93, © и 8 такие же, как в теореме
Леви. Тогда [236] = 93/П©.
Доказательство. Из разложения 93 = 8 © © вытекает, что
8' = [88] + [936]. Так как [93©] ? ©, то 33' П © = ([88] П ©) + [93©] =
= [93©].
106 Гл III. Критерий Картана и его следствия
Мы видели, что [©23] с. Щ, где У1 — ниль-радикал в 2? (тео-
(теорема 2.13); можно утверждать поэтому, что ЗУ Г)© ? Ш. Мы знаем
также, что радикал идеала совпадает с пересечением идеала и ради-
радикала объемлющей алгебры. Поэтому пересечение ЗУ П ® есть радикал
производной алгебры ЗУ. Таким образом, имеет место
Следствие 2. Радикал производной алгебры конечномер-
конечномерной алгебры Ли характеристики 0 нильпотентен.
Рассмотрим теперь вопрос об однозначности факторов Леви.
Оказывается, что эти факторы, как правило, определены не одно-
однозначно. Они, однако, сопряжены в некотором сильном смысле, ко-
который мы сейчас определим. Напомним, что если z принадлежит Щ,
ниль-радикалу алгебры 23, то эндоморфизм ad z нильпотентен. Так
как ad z — дифференцирование, то, как мы уже знаем, Л —exp(ad z)
является автоморфизмом. Обозначим через 2t группу автоморфизмов,
порожденную операторами exp (ad z), z (j Щ. Тогда имеет место сле-
следующая теорема о сопряженности.
Теорема (Мальцев — Хари ш-Чандра). ПустьЪ—конечно-
ПустьЪ—конечномерная алгебра Ли над полем характеристики 0, допускаю-
допускающая разложение вида 23 = ©® 2, где ©— разрешимый идеал,
а 2— полупростая подалгебра. Тогда, какова бы ни была
полупростая подалгебра 2г алгебры 33, найдется автоморфизм
Л?21, такой, что 2? с 2.
Доказательство. Каждый элемент /j^gj может быть запи-
записан (единственным образом) в виде 11==1\-\-1'1. где Z>'?g и /??<?,
так что существуют линейные отображения X и а подалгебры 21 в i
и в © соответственно. Так как 2j полупроста, то gj f) © = 0; по-
поэтому отображение X взаимно однозначно. Если /2 G -^1» то
Ш = \hkt + Ш' = [№ I + [№] + [#2] + Ш]. D7)
Поэтому
[/,//=[&?]. Ы=[гА]-№]+Ш]. D8)
Второе из этих соотношений показывает, что [/^Г 6 №&] S 9^> где
Ш — ниль-радикал алгебры 8. Так как 2[^=21, то отсюда следует,
что 1°?Ж для каждого Zj^gj и, таким образом, gjEg©^. Мы до-
докажем по индукции, что существует автоморфизм Л^31(Л1 = 1),
такой, что g^Sg+5?@, где %1{1) есть г-й член производного ряда
алгебры Щ. Так как Э? разрешима, то отсюда будет следовать требуе-
требуемое утверждение. Поскольку уже доказано, что gj S g ф -ft, то до-
достаточно провести один шаг индукции. Мы можем упростить обо-
обозначение и считать, что g,S 2 + ^ • Покажем теперь, что суще-
существует элемент Л ?21, такой, что gf E 2-\-$1(к+1). Используя
§ 9. Теоремы Леей и Мальцева—Харшы-Чандра ТОГ
обозначения, введенные ранее, мы ви-дим, что из включения 8j g:
SES-f-^*' следует, что /<г?ЭД(А!), /i?8i. Как показывает первое из
соотношений D8) Ш можно наделить структурой ^-модуля, положив
zh — [z, l\], z?%{k), !v?%v Тогда !ft(*+!) является подмодулем, так
что ЭД(А!)/9^*+1) есть ^-модуль с законом1 композиции z/j = [z/i], где
z?ffi(k) и z — z-\-^k+l\ Рассмотрим теперь классы вычетов относи-
относительно 3f(*+1) членов второго соотношения D8). Так как [llll] ^ Я**:),
то
[Щ=[Щ - [Щ = 4 - i&.
Положим далее / (Zj) = ([; тогда 1Х —> / (/j) является линейным ото-
отображением подалгебры 8j в ^-модуль wk'ffi +1) и предшествующее
уравнение может быть переписано в виде
l2-f(k)li- D9)
Поэтому, по первой лемме Уайтхеда, существует элемент
(*1). такой, что/(/1) = 2/1, т. е.
l\ = [z, l\] или Zl = [z, /i](mod!R(*+1)). E0)
Пусть Л = exp (ad z). Тогда
E1)
Очевидно, g?^8i, и из E1) следует, что 81* S8-f !R(*+1). Мы мо-
можем доказать теперь утверждение индукцией по k.
Следствие 1. Любая полупростая подалгебра конечно-
конечномерной алгебры Ли характеристики 0 может быть вложена
в фактор Леей.
Доказательство. Если А — такой же автоморфизм, как
в теореме, то 21 содержится в факторе Леви 8
Следствие 2. Если 23 = 8j © © = &, © ®. где 8j « 82 — яолу-
простые подалгебры, то существует автоморфизм А^'й, та-
кой, что 8^ = 8г-
108 Тл III Критерий Картана и его следствия
§ 10. Группы когомологий алгебр Ли
Две леммы Уайтхеда могут быть переформулированы как теоремы
теории когомологий алгебр Ли. Исторически эти утверждения были
путеводными нитями, приведшими к возникновению теории когомоло-
когомологий. Другим импульсом к развитию этой теории послужило изучение
топологии групп Ли, начало чему было положено Картаном. В этом
параграфе мы дадим конкретное определение групп когомологий и
укажем обобщение „Г-невырожденного" случая леммы Уайтхеда до
общей теоремы о когомологиях. Позднее (гл. V), пользуясь общим
методом производных функторов Картана — Эйленберга, мы дадим
другое определение групп когомологий.
Пусть Й— алгебра Ли, а 9К — некоторый й-модуль. Если /^1,
то /-мерной ЗЭТ-коцепью в й мы назовем /-линейное кососимметриче-
ское отображение / прямого произведения 8 X 8 X • • • X 8 * экзем-
экземпляров алгебры Й в Ш. Другими словами, f(lv ..., /г)?9К для лю-
любого набора (/,, /2, .... /г), где /?(:й; для фиксированных значений
lv .., I v lg+l lt отображение /?->/(/j Ij) алгебры S
в Ш является линейным. Кососимметричность означает, что / изменяет
знак на обратный, если поменять местами любые два аргумента I.
(а остальные оставить без изменения). Если / = 0, то можно опре-
определить 0-мерную ЗЧ-коцепь в 8 как „постоянную" функцию на Й со
значениями в 9К, т. е. как отображение 1->и, где и — фиксирован-
фиксированный элемент в Ш. Если / есть /-мерная коцепь (или просто „/-коцепь"),
i^>0. то с ней сопоставляется (t-\- 1)-мерная коцепь /8, называемая
ее кограницей и определяемая по формуле
/»('i. *i+i) = 2(-i)l+1~7(/, V ¦••• li+i)i9 +
i+i
+ 2 (- i)r+7(/, \ I h+v tv,i)• E2)
g<r-l
Здесь крышечка ~ над аргументом обозначает, что этот аргумент
должен быть опущен (например, f(lv Г2, I3) = f(lv /3)). В случае
/ = 0 это нужно интерпретировать следующим образом: (/8) (/) = и/,
если / — отображение х —> и ? ffi.
Множество С1 (й, Ш) /-мерных 9К-коцепей образует векторное про-
пространство относительно обычных операций сложения функций и умно-
умножения их на скаляры, а /->/8 является линейным отображением,
пограничным оператором, пространства С(8. ffl) в С'+1(й, ffl), i^-0.
Кроме уже рассмотренного случая
/8 (/) = и/, если / : х -> и, E3)
§ 10 Группы когомологий алгебр Ли 109
можно легко вычислить оператор кограницы для /, равного 1 и 2
/5 (/,, у = — / (у /, + / (у /2 — / ([Щ), E4)
(/5) (/,, /2. у = / (Z2, у /, - / (/,. у l2+ / (/,. у /3 -
— /(/3. UAD4-/C2. UA1) — f(lv Ш)- E5)
Некоторая /-коцепь / называется коциклом, если /8 = 0, и когра-
кограницей, если f — gb, где g — некоторая ({—1)-коцепь. Множество
Z'(8, 9К) /-коциклов образует ядро гомоморфизма 8: C->C/+1, так
что Z( есть подпространство в С1. Аналогично, множество /-кограниц
В1 (8, 9К) является подпространством в С1, так как В' — образ про-
пространства С' при гомоморфизме Ь. Можно доказать прямыми вы-
вычислениями, что В1 ? Z1, т. е. кограницы являются коциклами. Это
сводится к основному свойству 82 == 0 кограничного оператора. Мы
не будем проверять это в общем случае, поскольку такое утвержде-
утверждение будет следовать далее из общих соображений. Сейчас же про-
проверим только, что /82 = О, когда / есть 0 или 1-коцепь. Пусть
f = u, т. е. / есть отображение х->«. Тогда /8(/) = и/ и
/82(/j, у = —ul2lx-\-ul-J.2—b[/j/2] = 0 по определению модуля
Если / есть 1-коцепь, то /8 (/р /2) задается равенством E4) Поэтому
из E5) следует
/82(/,, /2, у = — /(у у, + /(у у, — ИШ)к +
+ / (У V2 - / (*i) V2 + / (Ш )h—f Ca) 'i'3 +
+ /(У /А- /WAD*84- /(UA1) 'з- / (У I*A1 +
+ / (fe ['А11) - / (I'A1) h+/ (У I* A1 -
Нетрудно проверить, что эта сумма равна 0. Поэтому /82 = Q для
всякой 1-коцепи /.
После того как выяснено, что 82 = 0, можно определить 1-мер-
1-мерную группу (пространство) когомологий алгебры 8 относи-
относительно модуля Ш как факторпространство
8, sot).
Если / = 0, то условимся считать В1 = 0, поскольку нет (^—1)-
коцепей. В этом случае Я0 (8, 2R) = Z°(g, 2R). Это пространство
можно отождествить с подпространством /(9К) элементов и?9К, та-
таких, что и/ = 0 для всех / Такие элементы называются инвариан-
инвариантами модуля 2>{. Равенство Я((й, 2H = 0 означает, что Z'(8, u)f) =
= 5' (8, 2){)> т- е- чт0 каждый i-коцикл есть кограница В случае
*=1 это сводится к утверждению, что если линейное отображение
/->/(/) алгебры И в Ш удовлетворяет соотношению —/
110 Гл. III. Критерий Картана и его следствия
М2 /A]) = 0> то существует такой элемент и ? Ш, что
f(l) = ul. Это не что иное, как утверждение первой леммы Уайтхеда.
Аналогично вторая лемма Уайтхеда является утверждением о 2-й
группе когомологий. Эти два результата могут быть объединены те-
теперь следующей теоремой.
Теорема 13. Если % — конечномерная полупростая алгебра
характеристики 0, то Я1 (8, 2U) = 0 и Я2 B, 5Ш) = 0 для каж-
каждого конечномерного модуля Ш над 8.
Легко видеть, что если Ш = SDij © ЗЙ2> где ^i — подмодули мо-
модуля W, то Я'(8. ЭД) = Яг(8. З^) ©#'(?• 2К2)- Отсюда и из тео-
теоремы о полной приводимости следует редукция групп Я' (8, Ш) для
конечномерного модуля 3J? к случаю, когда 9)f неприводим. Здесь можно
различать два случая: A) 5Ш8 ф 0 и B) 9К8 = 0. Во втором случае
из неприводимости следует, что dim Ш = 1, так что Ш можно отожде-
отождествить с полем Ф. Тогда f-коцепь есть г-линейная кососимметрическая
функция от (/; lj) со значениями в Ф, и, поскольку представле-
представление является тривиальным, формула кограницы имеет вид
/&(/i h+i)= S (-i)r+7d 7,, .... fr..... /г+1[уг1)-
E6)
Оказывается, что для полупростых алгебр Ли группы когомологий
со значениями в 2>? = Ф очень интересны, поскольку они соответ-
соответствуют группам когомологий групп Ли. С другой стороны, случай
9№8 ф 0 не очень интересен (для полупростых алгебр 8 и конечно-
конечномерных неприводимых модулей Ш), за исключением применений к тео-
теореме о полной приводимости и к теореме Леви, поскольку имеет
место следующий общий результат.
Теорема 14 (Уайтхед). Пусть 8 — конечномерная полу-
полупростая алгебра Ли над полем характеристики 0, и пусть Ш —
конечномерный неприводимый модуль, такой, что 2N8 ф 0.
Тогда Я'(8, Ш) — 0 для всех *>0.
Если / = 0, то из неприводимости и условия Ш& ф 0 следует,
что равенство «8 = 0 выполняется только в случае и = 0. Это озна-
означает, что Я0 (8, 9Я) —0. Доказательство утверждения для i > 0 ана-
аналогично доказательству двух лемм Уайтхеда в случае невырожденного
оператора Г. Детали доказательства мы оставляем читателю.
§ 11. Еще о полной приводимости
Для дальнейшего исследования этого вопроса нам понадобятся
некоторое понятие замыкания для алгебр Ли линейных преобразова-
преобразований и теорема о вложении нильпотентных элементов в трехмерные
§ It Еще о полной приводимости 111
расщепляемые простые алгебры. Первое понятие основано на одном
свойстве ассоциативных алгебр. Имеется в виду следующий частный
случай теоремы Веддербёрна, аналогичной теореме Леви для алгебр Ли.
Теорема 15. Пусть % = Ф[х]— конечномерная алгебра
{ассоциативная с единицей), порожденная единственным эле-
элементом х над полем Ф характеристики 0, и пусть 9t — ра-
радикал алгебры'й. Тогда % содержит полупростую подалгебру %v
такую, что ЭД^^фЭТ.
Доказательство. Пусть /(X)— минимальный многочлен эле-
элемента х, и пусть
e ... icr(X)e' E7)
— разложение /(X) на неприводимые многочлены с единичными стар-
старшими коэффициентами, причем nt (X) ф тг;- (X), если 1ф], и degit;(X) ]> 0.
Заметим сперва, что если все et = 1, то Ж не имеет ненулевых
нильпотентных элементов (см. стр. 59), так что ЭД полупроста и
доказывать нечего. В произвольном случае положим
/1(Х) = 7г1(Х)тг2(Х) ... тгДХ) E8)
1
и г = /г(х). Тогда, взяв е = тах(ег), получаем ze = (f1 (х))е =
= 'к1(х)е . . . itr(x)e = 0, так что г нильпотентен. Поскольку % ком-
коммутативна, идеал (г), порожденный элементом г, нильпотентен,
поэтому (?)?$№. С другой стороны, /j (х) =& 0 (mod (z)). Поэтому
минимальный многочлен класса смежности х = x-\-(z) в %j{z) есть
произведение различных неприводимых множителей. Так как х поро-
порождает %l(z), это означает, что алгебра 31/B) полупроста. Следова-
Следовательно, Br) = 9t. Нетрудно показать также, что fx (X) является мини-
минимальным многочленом элемента х — х-\-Ш. Поэтому достаточно
доказать, что в % найдется элемент у, минимальным многочленом кото-
которого будет /j (X). Мы получим такой элемент методом „последова-
„последовательных приближений", начав с хг — х. На первом шагу имеем
/j (jc^ss 0(mod9t) и х зз Xj (mod 94). Предположим, что мы уже
определили xk так, что fx (xft)^0(mod9t*) и x^xft(mod9t).
Положим xk+l = xk-\-w, где и1 должен быть определен в ffik так,
чтобы f1(xk+1)=^0(mod$lk+1). Из разложения многочлена по фор-
формуле Тейлора следует, что
Поскольку основное поле—поле характеристики 0, многочлен fx (X)
имеет различные корни в алгебраическом замыкании поля Ф. Поэтому
/j (X) взаимно прост со своей производной /J(X). Отсюда следует,
112 Гл. III. Критерий Картана и его следствия
что элемент и = f'x (хЛ = f'x (хЛ ~\-Ш имеет обратный v в
Положим w = — f\(xk)v- Тогда w з= 0 (mod 9t*), так что
- л ()
= Л (**) - /1 (**) (mod 3l*+1) s
Определен, следовательно, такой элемент xk+v что jft+1
^0(mod9(ift+1) и л;^ xft+1 (mod ffi). Так как идеал SR нильпотентен,
в результате этого процесса мы получаем элемент у, удовлетворяю-
удовлетворяющий условиям /,(}/)=: 0 и у —х (mod Ж). Поэтому подалгебра
$tj = Ф-ty] удовлетворяет условию 31 = Sti © 9t. Поскольку /j (X)—ми-
(X)—минимальный многочлен элемента х, минимальным многочленом эле-
элемента у будет также /\ (X).
Мы можем доказать теперь следующее утверждение.
Теорема 16. Пусть X — линейное преобразование конечно-
конечномерного векторного пространства над полем характери-
характеристики 0. Тогда имеется разложение X = Y~\-Z, где Y и
Z — многочлены относительно X, такие, что Y — полупростое
преобразование, а Z—нильпотентное. Если, далее, X = Yl~\-Z1,
где Yx — полупростое преобразование, a Zj — нильпотентное,
причем Y1 и Z, коммутируют с X, то Y1 = Y, Zx—Z.
Доказательство. Существование разложения X =
получается, если применить теорему 15 к алгебре Ф [X]. Предположим
теперь, что X = Y-[-\-Zv где Kj и Zx обладают свойствами,.указан-
свойствами,.указанными в теореме. Так как Y и Z — многочлены относительно X,
то они коммутируют с К! и Zj. Линейное преобразование в правой
части равенства Y — Yl — Z-l — Z нильпотентно, поскольку Z и Zx
нильпотентны и коммутируют. Так как Y и Yx полупросты, а основ-
основное поле имеет характеристику 0, то из доказательства теоремы 11
следует, что преобразование Y — К, полупросто. Так как единствен-
единственным преобразованием, одновременно полупростым и нильпотентным,
является нулевое преобразование, то
К —K1 = 0 = Z —Zj.
Поэтому Y = YV Z = ZV
Однозначно определенные линейные преобразования Y и Z из
теоремы 16 назовем полупростой и нильпотентной компонен-
компонентами преобразования X.
Определение 3. Алгебра Ли 2 линейных преобразований
конечномерного векторного пространства над полем характеристики 0
§ 11 Еще о полной приводимости
называется почти алгебраической !), если она содержит нильпотент-
ную и полупростую компоненты любого элемента <Y?2.
Для доказательства упомянутой выше теоремы вложения потре-
потребуются две следующие леммы.
Лемма 7. (Морозов). Пусть Й— конечномерная алгебра
Ли характеристики 0; предположим, что Й содержит эле-
элементы fun, связанные соотношением [fh] = — 2/, причем
Тогда найдется элемент е? if, такой, что
2е. [<?/] = А. ([/А] = — 2/). E9)
Доказательство. По условию h — [zf] для некоторого эле-
элемента z?2. Положим F = ad /, W=ad/z, Z= ad г, так что имеют
место соотношения
[FH] = — 2F. H = [ZF\. F0)
Из первого равенства следует, что эндоморфизм F нильпотентен
(лемма 2.3). Выполняется также соотношение
[[гА] —2г. /] = [ [zf] /*] + [* [A/]] —2 [г/] =
Поэтому [г/г] = 2z~\- xv где Xj принадлежит $? — подалгебре, состоя-
состоящей из элементов х, таких, что 1х/] = 0. Так как [FH\ = — 2F,
то bHF — b(FH-{-2F) — 0 для любого элемента Ь?$. Поэтому
ЬН?$ и, таким образом, R#c&. Имеют место также равенства
[ZFi] = [ZF]Fi~1-\-F[ZF]Fi~2-\- ... ~\-Fi~1[ZF] =
^hf'^ + fhf1'2-^ ... +f'-1w
и, поскольку HFk~FkH~{-2kFk,
F1)
Пусть ftgSnSF'"'1. Тогда b~aFl~x и bF = aFlz=0. Поэтому
• taF1'1 (Я+(? — 1)) = e(ZF' — F'Z) = (eZ) Fl 6 Й/7'.
Следовательно, b(H-\-(t—l))?$n2F'. Из этих соотношений и
из нильпотентности F следует, что, если b ? Л, то
б ) = 0 F2)
') Это понятие принадлежит А. И. Мальцеву который назвал его
расщепляемостью алгебры. Терминологическая замена этого понятия .почти
алгебраичностью" оправдана тем, что оно несколько слабее, чем понятие
Шевалле алгебраической алгебры Ли линейных преобразований. Кроме того,
мы предпочли использовать термин „расщепляемой алгебры Ли" в контексте»
ке имеющем никакого отношения к понятию Мальцева.
8 Н Джекобсон
114 Г л III. Критерий Картана и его следствия
для некоторого целого положительного числа т. Характеристические
корни ограничения преобразования Я на $ являются поэтому не-
неположительными целыми числами. Отсюда, в частности, Я—2 инду-
индуцирует невырожденное линейное преобразование в R, и, следовательно,
существует элемент ух ? R, такой, что ух (Я—2) — xv где хх—эле-
хх—элемент, определенный равенством \zh\-2z-\- хх. Тогда [y^h] = 2yl-\-xl.
Поэтому, положив е = z — yv мы получим равенство \eh\ = 2e.
Точно так же [ef] = [zf\ —/z. Таким образом, доказано выполнение
соотношений E9).
Лемма 8. Пусть 2— алгебра Ли линейных преобразований
конечномерного векторного пространства над полем характе-
характеристики 0. Предположим, что каждый нильпотентный эле-
элемент F Ф0 из 2 может быть вложен в подалгебру с базисом
(Е, F, Н), таким, что [ЕН] = 2Е, [FH\=—2F\ [EF]=H.
Пусть В.— любая подалгебра алгебры 2 с дополнительным
пространством Щ., инвариантным относительно умножения
на R: ? = К©9<?, [ЭД с 31. Тогда Л обладает свойствами,
указанными для 2.
Доказательство. Пусть F — отличный от нуля нильпотент-
нильпотентный элемент из $. Тогда можно выбрать ? и Я в 2 таким образом,
что выполняются указанные соотношения. Запишем Н = Н-1-{- Н2,
Я^й, Н2^т,Е=Ех-{-Е2, ?,?& Е2?Ш. Очевидно, —2F=[FH] =
= [/7Я1] + [/7Я2] и [FHJZ&, [FH2]?9l. Поэтому—2F = [FH1]. Далее
Я = [?'/7] = [?'1/7]-)-[?2/7]- Отсюда следует, что Hl = [E1F\^[^F].
Таким образом, выполняются условия леммы 7, если заменить в ней 2,
/, h на R, F и H-i соответственно. Поэтому существуют Е', Н' в St,
такие, что [FH'\=— 2F, [E'H'] = 2Ef, \E'F] = H'. Подалгебра,
порожденная элементами F, Е', Я', является гомоморфным образом
расщепляемой трехмерной простой алгебры. Поскольку F фО,
это изоморфизм, так что F, Е', Н' линейно независимы и удовле-
удовлетворяют требуемым условиям. Установим теперь второй критерий
полной приводимости.
Теорема 17. Пусть 2 — алгебра Ли линейных преобразо-
преобразований конечномерного векторного пространства Ш над полем
характеристики 0. A) Предположим, что 2 вполне приводима.
Тогда каждый отличный от нуля нильпотентный элемент
из 2 может быть вложен в трехмерную расщепляемую про-
простую подалгебру алгебры 2 и алгебра 2 почти алгебраична.
B) Предположим, что каждый отличный от нуля нильпотент-
нильпотентный элемент из 2 может быть вложен в трехмерную простую
подалгебру алгебры 2 и что центр 6 алгебры 2 почти алге-
браичен. Тогда 2 вполне приводима.
§ 11. Еще о полной приводимости 115
Доказательство. A) Предположим, что 8 вполне приводима.
Обозначим через 6 полную алгебру линейных преобразований про-
пространства 94. Пусть F — нильпотентное линейное преобразование
и Ш — Ш} © Ш2 © . . . 0 ЗЯГ — разложение пространства Ш на цикли-
циклические инвариантные относительно F подпространства. В 2Хг суще-
существует базис (л;0, xv ..., xm), такой, что x}F — Xj+1, xm</7 = 0.
Определим НкЕкак линейные преобразования, оставляющие каждое Wlt
на месте и удовлетворяющие соотношениям xJH=(ml — 2j)x},
хо?=О, х}Е = (— mJ-\- у (у— \))x}_v у > 0 (см. C6)). Тогда, как
и в § 8, [?#] = 2?\ [F#] = — 2F, [EF] = H. Это показывает, что
преобразование/7 может быть вложено в подалгебру ФЕ-\-ФР-\-ФН
требуемого типа. Покажем, далее, что имеет место разложение
б? = Й0 9Ч, где ЭТ — подпространство, удовлетворяющее условию
[3^8] cz sft. Тогда из леммы 8 будет следовать, что каждый отличный
от нуля нильпотентный элемент из 8 может быть вложен в рас-
расщепляемую трехмерную простую подалгебру алгебры 8. Напомним,
что алгебра (?"t эквивалентна как модуль над 8 (закон композиции —
присоединенное представление) модулю 2W®2KX, где Ш* — контра-
греднентный модуль. Легко видеть, что 2I* вполне приводим. Поэтому,
по теореме 11, 9К®2I* и, следовательно, ©^ вполне приводимы
относительно 8. Так как 8 есть подмодуль модуля ($'L относительно 8,
то существует такое дополнение У1, что (SL = 8©?{, [!R2l с 91. Это
завершает доказательство первой части утверждения A). Пусть теперь
X — произвольный элемент из 8, а К и Z — его полупростая и
нильпотентная компоненты. Тогда
ade A' = ad<jK-f- adeZ,
[adg Y adfeZ] = 0, и преобразование ad^Z нильпотентно (из условия
Zm = Q следует, что (adeZJ"^1 = 0). Отождествляя E с Т1®Ш*
и применяя доказательство теоремы 11, получаем, что adg,K полу-
полупросто. Поэтому adg,K и adgZ — полупростая и нильпотентная ком-
компоненты преобразования &d(s,X и, следовательно, являются много-
многочленами от ай<$Х. Так как SadfeA'cS, a adgK, ad^Z — многочлены
от ай^Х, то 8adgK?8, 8adcs.Zc8. Таким образом, отображения
L-±[LY], L-±[LZ\ являются дифференцированиями алгебры 8. Мы
можем записать 8 = 8' 0 6, где 8' — полупростая подалгебра,
а 6—центр. Так как все дифференцирования 8' являются внутрен-
внутренними, то любое дифференцирование в 8, которое отображает E в 0,
есть внутреннее дифференцирование, определенное элементом из 8'.
Так как Z есть многочлен от X, то из условия [ХС\ = 0 следует,
что [ZC] = 0, а поэтому дифференцирование L -> [LZ] отображает 6
в 0. Следовательно, существует элемент Zj^S', такой, что [LZ] =
— \LZ^, L ? 8. Поскольку Z нильпотентно, ad«'Zj = adn'Z также
нильпотентно. Так как 8' — полупростая подалгебра, то из только
116 Г л III. Критерий Картана и его следствия
что доказанного результат (примененного к ad Й') следует, что суще-
существует такой элемент ?У ? й', что [ad^Zi, ad^ U] = 2 adg-Zi. Тогда
[Z1?/j = 2Z1, а отсюда следует, что Zx нильпотентно. Далее, [ZZ,] = 0,
поскольку [XZ] = 0, [<YZ,] = 0 и поскольку Z—многочлен от X.
Отсюда следует, что Z — Zx нильпотентно. Так как [L, Z — Zj] = 0,
/-?8, и Z — Zx — преобразование из обертывающей ассоциативной
алгебры 2*. то Z — Zx лежит в центре алгебры Й*. Так как Й* вполне
приводима, a Z — Z, нильпотентно, то Z — Zx = 0, так что Z = Zx ? й.
Поэтому также К = А' — Z??. Этим завершается доказательство
того факта, что Й почти алгебраична. B) Предположим, что ал-
алгебра Й имеет почти алгебраический центр и ее нильпотентные эле-
элементы удовлетворяют условию теоремы. Пусть C — радикал алгебры й.
и пусть F ? [Й®]. Тогда, как мы знаем, элемент F нильпотентен
(следствие 2 теоремы 2.8). Если F—ненулевой элемент, то он может
быть вложен в трехмерную простую подалгебру R. Так как R П <S ф О
и $ простая, то йсб, что невозможно ввиду разрешимости ради-
радикала <5. Поэтому F — Q и [йв] = О. Отсюда следует, что <S = S
есть центр. По теореме Леви Й = 6фЙ1, где Й1 — полупростая под-
подалгебра. Поскольку (?, есть центр, отсюда следует, что Йх является
идеалом. Теперь можно применить теорему 10 для доказательства
полной приводимости алгебры й, если только мы сумеем доказать,
что каждый элемент С ? 6 полупрост. Допустим теперь, что C—D-\-E,
где D — полупростое преобразование, Е — нильпотентное, a D и Е ^ E.
Если Е Ф0, то можно вложить его в трехмерную простую подалгебру.
Очевидно, что это невозможно, поскольку Е принадлежит центру.
Этим завершается доказательство утверждения B).
Отсюда немедленно следует, что если Й — почти алгебраическая
алгебра, то ее центр E также почти алгебраический. Поэтому
в утверждении 2 предположение о почти алгебраичности центра
можно заменить предположением, что Й — почти алгебраическая
алгебра. Напомним, что централизатор Eg E) подмножества 5 состоит
из множества элементов у^Й, таких, что [sy] = 0 для всех s?S.
Централизатор является подалгеброй алгебры Й. Мы используем
предшествующий критерий для доказательства следующего утвер-
утверждения.
Теорема 18. Пусть Й — вполне приводимая алгебра Ли
линейных преобразований конечномерного векторного про-
пространства Ш надлолем характеристики 0, и пусть %х — вполне
приводимая подалгебра алгебры й. Тогда централизатор
йг = Sg (Й1) вполне приводим.
Доказательство. Пусть X?й2. Тогда, поскольку й вполне
алгебраична, полупростая и нильпотентная компоненты У, Z пре-
преобразования X принадлежат й. Поскольку К и Z являются много-
многочленами от X, из равенства [СХ] = 0 для С ? Sj следует, что
Упражнения
117
[ = O = [CZ]. Поэтому Y, Z?82 и централизатор Й2 почти
алгебраичен. Покажем, далее, что 2 = 22©23, где Й3—подпростран-
Й3—подпространство в 2, такое, что [2322] ? 23. Тогда из теоремы 17 и леммы 8
будет следовать, что каждый нильпотентный элемент централиза-
централизатора Й2 может быть вложен в трехмерную расщепляемую простую
алгебру, а сам централизатор 22 будет вполне приводим по теореме 17.
Но мы знаем, что алгебра ad<j2i вполне приводима (доказательство
теоремы 17). Поскольку 2 есть подмодуль модуля (S над 2j, алгебра 2
вполне приводима относительно ads 2ь Поэтому мы можем записать
= 3»!© 2^0 ...
k,
где [SERfSjI с Ш,, / = 1 k, и 9)t, — неприводимый подмодуль
относительно adg2i. Допустим, что Ш( перенумерованы так, что
[ШР^ — О, t=\ h, и [Ш^фО, если j > h. Поскольку мно-
множество Зг элементов zt, таких, что [гД] = 0, есть подмодуль в Wlt,
то очевидно, что имеет место разложение
Положим 23 = 2Kft+1 + ... + 2ЙЙ. Тогда 2 = 22©23. Если />VA,
то [2КД]=?0 и l^S^-f-ll^AlSiH- ••• есть отличный от нуля
2гподмодуль в Шг Поэтому 5Шг = [2й,21] -|- [ l^SJ 2J+ ....Отсюда
следует, что
8з = [8з81И-[[83811811+ ••• SISS,].
С другой стороны, 2 = й2 ф 23; поэтому [28j] = [i^] S 83. Отсюда
8з = [88,] и
[2322] = [ [88J 8а] с [2 [8,82] ] +1 [222] 2J S [88J = 23.
Итак, для дополнения 23 к централизатору 22 в алгебре 2 имеет
место включение [%i2] ? 23, что и требовалось доказать.
Упражнения
Во всех упражнениях характеристика основного поля равна 0. Размер-
Размерность всех пространств предполагается конечной, если только номер упраж-
упражнения не помечен звездочкой.
1. Показать, что подалгебра Картана § алгебры 8 является максималь-
максимальной нильпотентной подалгеброй в 8. Показать на примере алгебры
*л? (п ¦**¦ ^' чт0 °бРатное утверждение неверно.
2. Пусть |> — нильпотентная алгебра Ли линейных преобразований про-
пространства 90t, и пусть 501 = Шо © 2Ki — разложение Фиттинга относительно |>.
Показать, что если поле Ф бесконечно, то существует преобразование А € |>,
такое, что 5010 = Ш0А, 9Jlj = SOtj., где Ш[А — фиттинговы компоненты отно-
относительно А.
3. Показать, что диагональные матрицы со следом 0 образуют подалгебру
Картана алгебры Ли 8 треугольных матриц со следом 0. Показать, что Й
совершенна.
118 Гл. III. Критерий Картана и его следствия
4. Пусть Й — подалгебра алгебры Ф2г/ матриц А, удовлетворяющих усло-
условию S~~lA'S = — А, где
н: й- -
(Эта алгебра изоморфна ортогональной алгебре Ли). Показать, что диаго-
диагональные матрицы
diag {X,, ..., Хг, —X, —Хг}
образуют подалгебру Картана алгебры й.
5. Все то же, что в упражнении 4, но матрица S заменена на матрицу
«-и о-:
6. Обобщить упражнение 2.9 следующим образом. Пусть 8 алгебра Ли,
$>— нильпотентная подалгебра алгебры дифференцирований алгебры 8.
Предположим, что единственным элементом / ? Й, таким, что ID = 0 для всех
?>?$>, является элемент 1 — 0. Доказать тогда, что 8 — нильпотентная алгебра.
7. Показать, что если 8, — полупростой идеал в 8, то 8 = 8i©82, где
Й2 — другой идеал.
8. Пусть й — идеал алгебры Й, факторалгебра 8/й по которому полу-
полупроста. Доказать существование такой подалгебры 8i в 8, что 8 = Я©Й1.
9. Пусть 8 — простая алгебра над алгебраически замкнутым полем Ф и
пусть f (а, Ь) — инвариантная снмметрическая билинейная форма на й. Пока-
Показать, что / пропорциональна форме Киллинга. Обобщить это утверждение
на полупростую алгебру Й.
10. Пусть Шп — я-мерный неприводимый модуль над расщепляемой
трехмерной простой алгеброй Ли. Получить разложение модуля 501л (g) ffir
на неприводимые подмодули.
11*. Пусть е н А — элементы ассоциативной алгебры, связанные соотно-
соотношением [ [eh] А] = 0. Показать, что если А алгебраичен, т. е. если существует
такой отличный от нуля многочлен у (X), что у (А) = 0, то элемент [eh] ниль-
потентен.
12*. Пусть St — ассоциативная алгебра с единичным элементом 1. Пред-
Предположим, что 21 содержит элементы е, /, А, удовлетворяющие соотношениям
[eh]—2e, [/А] = — 2/, [ef] = А. Показать, что если 9 (А) € 21—многочлен
от А, то е'у (А) = у (h-\- 2i) e', i = 0, I, 2, ..., f (A)/'=/'9 (A-f-2i)- Дока-
Доказать также, что если run — положительные целые числа, г ^п, то
tr/2| r-2j
13*. Пусть ЗГ, А, е, f такие же, как в упражнении 12*. Показать, что
если em ~ 0, то
2т-1
П (А + т-о = а
i-\
14. Доказать, что если е — элемент полупростой алгебры Ли й, которому
соответствует нильпотентный присоединенный эндоморфизм ad e, то для
любого представления R алгебры Й эндоморфизм ек также иильпотентен.
15. Доказать, что если й — полупростая алгебра над алгебраически
замкнутым полем, то й содержит элемент е Ф 0, такой, что ad e нильпотентен.
Упражнения 119
16. Доказать, что каждая отличная от нуля конечномерная алгебра Ли
над алгебраически замкнутым полем имеет неразложимые модули произ-
произвольно большой конечной размерности. (Указание: показать, что существуют
элемент е ? 8 и представление R, такие, что эндоморфизм eR нильпотентен
и отличен от нуля. Если Ш — соответствующий модуль, то размерности не-
неприводимых компонент модулей Ш, Ш®Ш, Ш®Ш®Ш, ... неограничены.)
17. Доказать, что каждая полупростая алгебра имеет неприводимые мо-
модули произвольно высокой размернссти.
18. Показать, что алгебра дифференцирований любой алгебры Ли алге-
браична. (Указание: использовать упражнение 2.8.)
19. Алгебра Ли 8 называется редуктивной, если ad 8 вполне приводима.
Показать, что 8 редуктивна тогда и только тогда, когда 8 обладает взаимно
однозначным вполне приводимым представлением.
20. Подалгебра $ алгебры 8 называется редуктивной в 8, если ad? $
вполне приводима. Доказать, что если С — вполне приводимая алгебра Ли
линейных преобразований и Я редуктивна в 8, то Я вполне приводима.
21. Показать, что любая редуктивная коммутативная подалгебра полу-
полупростой алгебры Ли может быть вложена в подалгебру Картана.
22. Показать, что каждая полупростая алгебра Ли содержит коммута-
коммутативные подалгебры Картана.
23. Пусть А — автоморфизм полупростой алгебры Ли 8. Показать, чго
подалгебра, состоящая из элементов у, для которых у (А — 1)т — 0 при не-
некотором от, является редуктивной подалгеброй. (Указание: использовать
упражнение 2.5.)
24. (Мостов — Тафт.) Пусть G — конечная группа автоморфизмов алге-
алгебры Ли 8. Показать, что 8 имеет фактор Леви, инвариантный относительно G.
25. Пусть fa (?i) = det QA — ad a) — характеристический многочлен пре-
преобразования ad a в алгебре Ли 8, и пусть D — дифференцирование в $.
Показать, что если t — независимая переменная, то
Указан ие: использовать тот факт, что / д (I.) = fa (к), если А — автомор-
автоморфизм, н то, что exp tD = 1 -f- tD -f- (t2D2/2\) -f- . •. есть вполне определенный
автоморфизм в 8„, где Р—поле степенных рядов относительно t с коэф-
коэффициентами из Ф.)
п* 2 "{
и пусть Tj (a,, ..., а;) — линеаризованная форма относительно тг, определен-
определенная формулой
(«1. ..., а*) = 77 К (fli + • • ¦ + аг)'
+ 2
Показать, что tj (ax at) есть симметрическая г'-линейная функция и что
т(.(а,Д а2, ...,ai) + -H(au a2D, a3, ..., at)-\- ... +Ti(«i. ¦••> Ч-ъ «;?>) = 0
для любого дифференцирования D.
Глава IV
РАСЩЕПЛЯЕМЫЕ ПОЛУПРОСТЫЕ
АЛГЕБРЫ ЛИ
Настоящая глава посвящена классификации простых алгебр Ли
над алгебраически замкнутым полем характеристики 0. Эта задача
впервые была решена Киллингом; его доказательство содержало не-
некоторые неточности, исправленные Картаном. Дальнейшие упрощения
принадлежат Вейлю, Ван-дер-Вардену, Коксетеру, Витту и Дынкину.
В нашем изложении мы придерживаемся метода Дынкина, весьма
близкого к первоначальному методу Картана. Однако формулировки
всех утверждений даны в терминах расщепляемых полупростых
алгебр Ли над произвольным основным полем характеристики 0.
Легко видеть, что предположение об алгебраической замкнутости
основного поля используется в классических исследованиях только
для того, чтобы гарантировать существование разложения алгебры
2 = ? ф 2а © Йр ф ... ф 28, где ф — подалгебра Картана, а 2в —
корневые подпространства относительно -?>. Но такое же разложение
существует, если допустить существование „расщепляющей подал-
подалгебры Картана" (см. § 1). Кажется более естественным и ясным
использовать это последнее предположение вместо более сильного
предположения об алгебраической замкнутости основного поля.
Для сведения читателя, который имеет некоторое знакомство
с теорией ассоциативных алгебр, можно заметить, что расщепляемые
простые алгебры Ли, изучаемые в классической теории, аналогичны
простым матричным алгебрам Ф„ в ассоциативной теории.
Часть результатов этой главы (теорема об изоморфизме и теорема
существования) будет получена снова более изощренным способом
в гл. VII.
Проблема классификации, разрешаемая в этой главе для случая
алгебраически замкнутого основного поля (или для расщепляемых
алгебр Ли), будет изучаться в гл. X для случая простых алгебр Ли
над произвольным полем характеристики 0. Следует отметить, что
классификация, которую мы дадим дальше, имеет место также в слу-
случае характеристики р Ф 0 при довольно мягких предположениях,
более сильных однако, чем предположение о простоте. Это впер-
впервые было показано Селигманом и в более усовершенствованной форме
Миллсом и Седигманом.
§ 1 Свойства корней и корневых подпространств 121
§ 1. Свойства корней и корневых подпространств
Назовем подалгебру Картана ф конечномерной алгебры Ли рас-
расщепляющей подалгеброй Картана (кратко"р. п. к.), если характери-
характеристические корни каждого преобразования adg/z, А^ф, принадлежат
основному полю. Мы скажем, что алгебра Й расщепляема, если она
обладает расщепляющей подалгеброй Картана. Если основное поле Ф
алгебраически замкнуто, то любая конечномерная алгебра 2 расще
пляема и всякая подалгебра Картана является р. п. к.
Пример. Пусть й = Ф„?, и пусть ф — подалгебра диагональных
матриц. Мы видели (§ 3.3), что ¦?> является р. п. к. алгебры Ф„?,
так что Ф„? расщепляема. Пусть теперь Ф — поле вещественных
чисел, a A — матрица, характеристические корки которой %t (в ком-
комплексном поле) отличны друг от друга, но не все %1 ? Ф. Тогда полино-
полиномиальная алгебра Ф [А] является подалгеброй Картана алгебры й.
Характеристический многочлен преобразования .ad А имеет вид
п
JJ (X — (^ — ?)), и некоторые корни его не принадлежат полю Ф.
Поэтому Ф [А] не есть р. п. к.
До конца этой главы Й будет обозначать расщепляемую конечно-
конечномерную полупростую алгебру Ли над полем Ф характеристики
О, <?>—расщепляющую подалгебру Картана, а (а, Ь)— форму Кил-
линга f(a, b) — trad a ad b алгебры Й. Изье^тно, что форма (а, Ь)
невырождена. Наши предположения относительно -?> заключаются
в том, что adg$ — расщепляемая алгебра линейных преобразований.
Поэтому, как нам уже известно, Й можно разложить в прямую сумму:
2 = #®8.®8„® ...®Й„. A)
где а, f 8 — ненулевые корни. Эти корни являются линейными
функциями на <?>, и подпространство Й„ состоит из множества таких
элементов л:а?2, что xs(adA — а(й))г = 0 для некоторою r = r(h),
А?ф (см. § 2.4 и § 3.2). Аналогично -?> = Й0. где й0 — фиттингова
нуль-компонента алгебры Й относительно ф. Имеет место включение
[йдЙ^ЕЙц+р, если а + р есть корень, в то время как [ЙаЙ?]=О, если
а—^- р не является корнем.
Нашей первой задачей будет получение дополнительной инфор-
информации об ф, о корнях а и о соответствующих корневых подпро-
подпространствах Sa. Мы будем нумеровать эти результаты римскими цифрами.
I. Если а и р—любые (включая и 0) два корня и фф—а,
то Йа и Йр ортогональны относительно формы Киллинга.
Доказательство. Покажем сперва, что ф = Й0 _j_ йв, еслисс=?О.
Пусть А?ф, ея(;Йа, и выберем h' так, что cc(/z')?-O. Тогда ограни-
ограничение преобразования ad h' на Й„ есть ненулевой скаляр плюс ниль-
потентное преобразование, так что оно невырождено. Отсюда еле-
122
Г л IV Расщепляемые полупростые алгебры Ли
дует, что для любого k=l, 2, ... мы можем найти такой элемет
е<*> ? 8 , что еа = [...[ [в^й'] h'\ . .. h'\. Поскольку форма Киллинга
инвариантна, имеет место равенство
он не равен 0 и [e
не есть корень, то
тельно, (еа, е?) = 0 и
(ea, A) = ([... [<«A'J ... A'], A) = (e<*\ [A' [A' . . . [ A'A] ...]]).
Поскольку ¦?> нильпотентна, число А может быть выбрано так, что
[А' ... [А'А] . . .]=0. Тогда из соотношения, указанного выше, сле-
следует, что (еа, А) = 0. Таким образом, ф JL 8И для а Ф 0. Пусть теперь
р^=—а, и пусть вр^8р. Как и раньше, запишем *„ = Г^'А']. Тогда
и , е ) —(FefWl, «g) =— (A', [е^о])- Если a-f-p есть корень, то
fp. Поэтому (/г', [в^вр]) = 0. Если a-fp
= 0 и снова Пг', \е^еЛ \ = 0. Следова-
J_8p-
II. Подалгебра %>—неизотропное подпространство в 8 (отно-
(относительно (а, Ь)). Если а есть корень, то —а также корень
и 8а и 8-а являются дуальными подпространствами относи-
относительно формы (а, Ь).
Доказательство. Если г?§ и 2 J_ <?>, то 2 _]_ 8, поскольку,
ввиду свойства I, z JL 2a для всех ос=?О. Так как форма (а, 6) невы-
невырождена, то 2 = 0. Если a — корень, а —а не есть корень, то
8a J_ 8р для каждого корня р. Тогда 8aJ_8, что противоречит невы-
невырожденности формы Киллинга. Тот же самый довод, примененный
ка = 0, показывает, что если 2^=0 лежит в 8я, то существует эле-
элемент ¦да?8_а, такой, что B, 11>)ф0. Аналогично, если 1?>Ф0 — эле-
элемент из 8_я, то существует 2^8а, такой, что B, 1ш)Ф0. Отсюда
следует, что 8а и 8_я являются дуальными подпространствами отно-
относительно (а, Ь).
Напомним, что матрицы ограничений преобразований ad A,
на 8а могут быть приведены одновременно к виду
а (А) 0
а (А)
B)
(§ 2.6). Если
*
= raa и h,
(h,
а (Л)
, то отсюда получается формула
где а — корень. "C)
§ 1. Свойства корней и корневых подпространств 123
Напомним также, что ос(/г') = О для всех /г' ? ?>'. Отсюда выте-
вытекают два следующих результата.
III. Существует I линейно независимых корней, где 1 =
Доказательство. Корни являются линейными функциями и,
таким образом, принадлежат сопряженному к <§> пространству .?>*,
dim?)*.—г. Поэтому, если наше утверждение неверно, то подпро-
подпространство в ¦?)*, порожденное корнями, имеет размерность V < /. Отсюда
следует существование ненулевого вектора h(z$?< такого, что ос(/г) = О
для любого корня а. Тогда из формулы C) следует, что (/г, k) = О
для любого k ? ¦?>, что противоречит утверждению II.
IV. ¦?>— абелева подалгебра.
Доказательство. Если ft' ? ф' = [?>§], то ос(/г') = О для
всех а. Тогда (/г', &) —0 для всех &, и Л' —0. Поэтому §'=0,
т. е. <р абелева.
Если р — любой элемент из ¦?)¦*, т. е. некоторая линейная функ-
функция, то, поскольку ограничение формы Киллинга на ¦?> невырождено,
существует однозначно определенный вектор h ? ¦§», такой, что
(h, Ap) = p(A). D)
Отображение р->/гр пространства §* в ф есть отображение на,
и оно взаимно однозначно. Если р, о ? ф*, то определим
(р, о) = (А А„). E)
Тогда
(р, о) = р(А„) = о(Ар), F)
откуда непосредственно следует, что (р, а) есть невырожденная сим-
симметрическая билинейная форма над ф* X -§>*• •
V. Пусть еа—элемент подпространства йа, такой, что \eji\ —
= a(h)ea, /г^ф, м пусть е_а — произвольный элемент подпро-
подпространства 2_а. Тогда
[е_аеа] = (е_а, еа)Аи. G)
Доказательство. Имеют место равенства
([в_вв„], А) = («.„, [«„А]) = («_„. а(А)О = <»(А)(е_в. О-
((*_„. О*.- А) = («_„, ee)(A«. A)=(e_a, e,)a(h).
Соотношение G) следует из невырожденности скалярного произ-
произведения (ft, ft) в -р.
VI. Каждый ненулевой корень а неизотропен относительно
билинейной формы (р, о) в ф*.
124 Гл. IV. Расщепляемые полупростые алгебры Ли
Доказательство. Заметим сперва, что преобразование айеа
нильпотентно, если а — ненулевой корень и еа ? 2а. Для этого до-
достаточно показать, что если хв ? й8. то существует такое целое по-
р р к
I I
ложительное число k, что [ ... [[x^ejej ... еа] = 0. Рассмотрим
последовательность
Г V 0 1 \\ Y 0 Л Р Л \\\ Y Р \ Р \ Р \
Векторы этой последовательности либо равны 0, либо соответствуют
корням C -f- a, C -f- 2a, C -f- 3a Поскольку существует лишь ко-
l i
нечное число различных корней подалгебры ?>, то [. . -[х?еа]. . .еа] =0
для некоторого А. Выберем вектор ?я=?0 в 2а так, что {eaft] = a (ft) ea
[см. B)], и вектор е_а?2_а, удовлетворяющий условию (еа, е_а)=1.
Последний выбор может быть осуществлен, поскольку 2а и 2_а —
дуальные подпространства относительно формы Киллинга.
Для любого элемента р из §* положим 2р = 0, если р не есть ко-
корень, и будем считать 8 корневым подпространством, соответ-
соответствующим р, если р — корень. Положим
оо
Из свойства произведения корневых подпространств вытекает, что
оо
2S_?a является нильпотентной подалгеброй алгебры 8. Далее,
со оо
Ф^а+ 2 S_ftaecTb подалгебра, содержащая 2 8_fta B качестве идеала.
оо
Поэтому подалгебра Фка~\- 2й_йя разрешима. Если х_а?8_а, то
[eax_J является кратным ha, как следует из равенства G). Если же
k>l, то K8_fejs8-(ft-1)a; наконец, [eafia] = a (fta) в„ = (а, a) ea.
со
Это показывает, что К есть подалгебра алгебры 8, а Ф/га+ 2S-fetl
в случае, когда (а, а) = 0, является идеалом в К.
Поскольку этот идеал разрешим и ему соответствует одномерная
факторалгебра, из равенства (а, а) = 0 следует, что подалгебра $
разрешима. Тогда adg$ является разрешимой алгеброй линейных
преобразований, действующих в 2. Так как преобразование ad ea
нильпотентно, то оно принадлежит радикалу обертывающей ассоци-
ассоциативной алгебры для adg$ (следствие 2 теоремы 2.8). Поэтому то же
самое справедливо для (ad ea)(ad е_я), откуда следует равенство
§ 1 Свойства корней и корневых подпространств 125
(еа, ?_a) = tr ad еа ad е_а = 0, противоречащее условию (еа, е_а)=1
Таким образом, (а, а)=?0.
VII. Если а — ненулевой корень, то ла = dim йа = 1. Кроме
того, целые кратные ka корня а являются корнями только
в том случае, когда k = 0, 1, —1.
Доказательство. Пусть еЛ, е_а, $ определены, как в до-
доказательстве утверждения VI [см. равенство (8)]. Тогда $ будет
инвариантным относительно ad Л, /г?ф, подпространством в 2, по-
поскольку [eak]=a(h)ea, [hah] — 0 и [8_ftaA] ? S_fea. Ограничение
преобразования ad h на й_йя имеет единственный характеристический
корень — ka. {h). Поэтому
и, в частности,
trftad(Aa) = (a,a)(l— п_л — 2«_2а— ...). (9)
Так как К есть подалгебра, содержащая еа и е_а, то она инва-
инвариантна относительно преобразований ad ел u ad е_л и, поскольку
[«-«*.]=*..• [айЯе-«- adSea] = ad«\- Поэтому tr(adeAe) = O. Так
как (а, а) Ф 0, то из предыдущего условия и из равенства (9) сле-
следует, что 1 —п_а — 2я_2а— ... = 0. Это может произойти только
в том случае, когда л_а=1, л_2а = «_3а= ••• =0. Поэтому —2а,
— За, ... не являются корнями и л_а= 1. Так как мы можем заменить
в предшествующем рассуждении а на — а, то мы получаем также,
что па = 1 и 2а, За, ... не могут быть корнями.
Если а — ненулевой корень, то йя = Феа и [e^h] = a.(h)ea.
Кроме того, как следует из равенства G), [eae_J = ha, если вы-
выбрать еа и е_а так, что (еа, е_а) = — 1. Тогда [eaha] = (а, а)еа,
\e_Jia] = — (а, ос)е_а. Если положить
е'^е> е' =&=:-, h' = ^-, A0)
а а' -а (а, а) ' а (а, а) *¦ ;
ТО
Таким образом, базис (е^, e'_a, h'\ является нормализованным ба-
базисом того типа, какой мы рассматривали ранее для расщепляемой
трехмерной простой алгебры. Этим доказано следующее утверждение.
VIII. Если а — ненулевой корень, то ФАв + 2а + й_я есть рас-
расщепляемая трехмерная простая подалгебра алгебры й.
Теперь мы располагаем всей необходимой информацией об умно-
умножении в ф, о произведениях элементов из ^> на элементы из йя и о
произведениях вида [еае_а], еа?йа, е_а^й_я. Остается исследовать
произведения вида [еае?], где аир являются ненулевыми корнями
126 Гл. IV. Расщепляемые полу простые алгебры Ли
и р Ф — ос. Мы сделаем это после того, как установим в следующем
параграфе один из основных результатов о представлениях полупро-
полупростых алгебр Ли.
§ 2. Основная теорема о представлениях
и ее приложения к структурной теории
В настоящее время нам понадобится только часть следующей тео-
теоремы. Результат в полном виде будет играть важную роль в теории
представлений.
Теорема 1. Пусть й— конечномерная расщепляемая полу-
полупростая алгебра Ли над полем характеристики О, ?> — рас-
расщепляющая подалгебра Картана, ? = ?> + ^Феа — разложение
алгебры й на корневые подпространства относительно $.
Пусть па и (р, о) для р и а из сопряженного пространства |>*
определены, как раньше [см. D), E)], и пусть еа и е_а выбраны
так, что [еае_а} = па. Если Ш — конечномерный модуль над й,
a R — соответствующее представление, то Ш является расще-
расщепляемым модулем над ?>, и если Ш&. — весовой модуль над ?>,
соответствующий весу А, то линейное преобразование, инду-
индуцированное преобразованием hR в Ш&, является скаляром A(h)l.
Пусть ?(а) = ?)-|- Феа~\-Фе_а. Тогда й(а) есть подалгебра,
а Ш — вполне приводимый ^-модуль. Любой неприводимый
^-подмодуль !Я модуля Ш имеет базис (у0, ух, ..., ут), та-
такой, что
Ж / = 0, 1 т
0' i = 0 т~1 A2)
) \
т.
где М — вес и 2(Ж, а)/(а, а.) = т. Кроме того, если у— некото-
некоторый ненулевой вектор, такой, что yh = M(h)y и уеа = 0, то у
порождает неприводимый ^-подмодуль модуля Т1. Пусть
А—вес модуля Ш над $ и пусть Е — совокупность весов вида
Л-j-ioc, где i—целое число, а а—фиксированный ненулевой
корень. Тогда Е является арифметической прогрессией с пер-
первым членом Л — га, разностью а и последним членом A-\-qa,
причем
^Нг = (г-*I. A3)
(а, а) ч ^' v '
Если х — ненулевой вектор, такой, что xh — (A-\-qo.)(h) x,
то х порождает неприводимый ^-под моду ль и каждый вес.
§ 2 Основная теорема о представлениях 127
принадлежащий Е, оказывается весом этого подмооуля отно-
относительно ф. Если Л—некоторый вес, то
2(Ао)
л = л_а
(а, а)
— также вес и
dim2KA = dimaKA-. A5)
Доказательство. Из утверждения III следует, что мы можем
найти базис в §*, состоящий из I корней а,, а2, ..., а;. Соответ-
Соответствующие элементы ha^ ка^, ..., /г^ образуют базис в ф. Алгебра
<?t = ф/га -)- Феа -f- Фе_а. является расщепляемой трехмерной простой
алгеброй Ли, и, согласно A0), векторы е'а, е'_а = 2е_ /(а, а.\,
h'a. = 2ha Кщ, щ) образуют канонический базис в йг. Если мы вспом-
вспомним вид неприводимых модулей над такой алгеброй (см. § 3.8) и
используем тот факт, что конечномерные модули вполне приводимы, то
увидим, что существует базис модуля Ш, в котором матрица преобра-
преобразования h'f.a поэтому и преобразования hR =A/г)(а1. ai)K^' имеет
диагональный вид. Это эквивалентно двум следующим утвер-
утверждениям относительно А#: характеристические корни h% лежат
в поле Ф, и № есть полупростое линейное преобразование. Поскольку
№ коммутируют между собой, стандартные рассуждения показывают,
что существует базис (ар и2 uN) модуля Ш, такой, что каждое
преобразование h# имеет диагональную матрицу в этом базисе (см.
доказательство теоремы 3.10). Так как ha образуют базис в ф, то
преобразование hR имеет диагональную матрицу в базисе (м;-), иными
словами Ujh~kj{h)ur /г?ф, У=1, 2 N. Поэтому очевидно,
что §й является расщепляемой абелевой алгеброй Ли линейных пре-
преобразований и что Aj — Aj(h) являются весами относительно ф.
Кроме того, hR есть скаляр А (/г) 1 в весовом пространстве ЗИА (базис
которого состоит из Uj, таких, что Ау = А). Это доказывает первое
утверждение теоремы. Пусть теперь а — ненулевой корень. Рассмот-
Рассмотрим подпространство 2(а' = ф-|- Феа-\- Фе_а. Так как § — абелева
подалгебра и [eji] = a (h) еа, [е_яА] = — а (А) е_а, то ?(а) — подалгебра.
Пусть §0—подпространство, натянутое на элементы h из ?>, опре-
определенные условием а(А) = 0. Тогда Ф = Фо + ФАа и S(a) = ф0 ф 51,
где R есть трехмерная расщепляемая простая алгебра Ли с базисом
(««. е-«' ла)-
Из условия [ф0Ж] = 0 следует, что ф0 является центром под-
подалгебры й(а). Мы видели, что преобразование hR полупросто для
каждою А?ф. Поэтому из основного критерия полной приводимости
128 Гл. IV. Расщепляемые полу простые алгебры Ли
(теорема 3.10) следует, что Ш вполне приводим как й(<х)-модуль.
Пусть !ЭТ — неприводимый fc(a)-подмодуль модуля Ш. Тогда ЭТ содер-
содержит такой вектор у Ф 0, что yh = M(h) у, где М — вес. Если за-
заменить у одним из векторов последовательности у, уе?, у(е%J
то можно предполагать также, что уеа = 0. Пусть Е = e'aR, F = e'fa,
H=h'^, где (е'а, е'_а, h'\ — базис подалгебры $, определенный фор-
формулами A0). Тогда
yH — yh = , v "' у = ; ¦¦'.' у
* * а (а, а) * (а а) *
и уЕ = 0. Рассуждения § 3.8 показывают, что 2 (Ж, «)/(а, а) есть
неотрицательное целое число m (строго говоря, m ¦ 1) и что
(у, yF yFm) является базисом неприводимого ^-модуля. Имеет
место также равенство yFm+1 = 0; индукцией по I нетрудно пока-
показать, что (yFl)h — (M — io.)(Ji)yFl. Поэтому 2 ФУ^' есть й(а)-под-
модуль модуля !Я, и, поскольку Ш является неприводимым й(а)-моду-
лем, ?Я = ^ФуР1. Перейдем теперь к новому базису в Щ, заменив
yF1 на t
Тогда мы получаем соотношения: yth = (M — ia)(h)yt, yte_a = l+v
где / = 0, 1, .... m—1 и Ут«_а = 0. Последняя формула из C.36)
E = (— mt-\-t(t— l))yFt~1, i=l m,
принимает вид
ytea = (- mi + / (/ - 1)) -^ yt_v
что совпадает с последним из уравнений A2). Таким образом, ра-
равенства A2) доказаны. Это рассуждение показывает также, что любой
ненулевой вектор у из Ti, удовлетворяющий условиям yh = M(h)y,
уеа = 0, порождает неприводимый S(a)-подмодуль модуля Ш. Тем
самым доказано наше утверждение относительно 8(а). Пусть теперь
А — некоторый вес, и пусть Е — множество весов вида А.-\-1а, где
а — фиксированный ненулевой корень, а I — целое число.
Вес Л является весом относительно ф в одном из неприводимых
8(а)-подмодулей Ш, на которые может быть разложен модуль Ш, и
можно предположить, что подмодуль !Я порожден таким элементом у,
что yh = М (й) у, уеа = 0. Тогда Л = М — ka, где 2 (Л1, «)/(а, а) = m
и 0 ^ k -<^ т. Пусть q — наибольшее целое число, для которого
Л -f 9а есть вес- Тогда, если элемент х Ф 0 выбран так, что
xft = (A-j- qa)(h)x, то хеа = 0, поскольку Л + (q -f 1)а не является
§ 2. Основная теорема о представлениях 129
весом. Поэтому х порождает неприводимый 8 -подмодуль размер-
размерности s-f- 1, где
2(Л + <7«, а)__2(А, а) , р
(а, а) (а, а) ' н'
С другой стороны, М=К~\-Ы есть вес, так что k^Cq, и
мы получаем, что m = 2 (Ж, ос)/(ос, а) = 2 (Л -f- ken, а)/(а, а) =
= 2 (Л, а)/(а, a)-\-2k. Тогда
, 2 (Л, а) ,
k — m = / ' k,
(а, а)
2 (Л, а) A6>
так что fe — m^-q— s. Далее, веса в модуле 91, порожденном век-
вектором у, и в модуле, порожденном вектором х, записываются соот-
соответственно в виде
Л-f/fea, A + (fc—-l)a, .... A + (fc —w)a
— l)a A-\-(q — s)a.
Поскольку k^q и Q' — s^.k — m, все члены первой прогрессии
содержатся во второй, и, поскольку Л — произвольный вес из S,
совокупность S совпадает со второй последовательностью. Так как
Л содержится в этой последовательности, то q — s<C0. Если мы
положим г = — (q — s), то последний член будет иметь вид Л — га,
где г^>0. Кроме того, 2 (Л, а)/(а, a) = s — 2q = r — q, что доказы-
доказывает соотношение A3). Очевидно, А' = А — [2 (Л, a)/(a, a)]a =
= A~\-Bq — s)oc, где —г ^ 2q — s^G, как следует из наших
неравенств. Поэтому Л' ? Б, так что Л' — вес. Остается доказать
формулу A5).
Заметим, что проведенное выше рассуждение показывает,
что Л' встречается также в первой последовательности A7), т. е.
Л' является весом в каждом неприводимом й'"'-подмодуле Щ, в кото-
котором Л — вес. Мы имеем dim 5ЯД = 1 = dim ЭДл' • Поэтому, если
Ш = Б © fflj—прямое разложение модуля Ш на неприводимые
й -подмодули, то размерность dim 2>JA равна числу !ЭТ;-, для которых
Л является весом относительно ф. Поэтому
dim 9JiA = dim 2>гА'.
Этот результат можно применить, в частности, к присоединенному
представлению алгебры й. Наш результат утверждает, что если
Р и a—любые два корня, афО, то корни вида 8-j~^a> где i — целое
число, образуют арифметическую прогрессию с разностью а. Мы
назовем ее а-серией корней, содержащей 8. Если эта серия состоит
9 Н Джекобсон
130 Гл. IV. Расщепляемые полупростые алгебры Ли
из элементов C—га, C — (г—1)а, .... §-\-qa., то
??-(,-«1. • (.8)
Из теоремы 1 можно вывести ряд следствий. Мы продолжим
нумерацию § 1.
IX. Если а, р « а -f- р — корни, не равные нулю, то [еае?] Ф 0
для любого еа Ф 0 в йа и любого е^ФО в йр.
Доказательство, а-серией, содержащей C, является после-
последовательность C — га. C-f #а, где q^-l. Ни один из этих
корней не равен 0, поскольку никакое целое кратное а не является
корнем, за исключением 0, +<х. Так как корневые подпространства,
соответствующие ненулевым корням, одномерны, то это верно и для
рассматриваемой серии. Пусть х — ненулевой элемент из 2р+в« . Тогда
[xh] = ($-\-qa.)(fi) x. Если выбрать е_а так, что [еае_а] = ha, то, как
показывает теорема, элементы х, хайе_л, x(ade_aJ x(ade_ay+g
ОТЛИЧНЫ ОТ 0 И ПОрОЖДаЮТ ПОДПрОСТраНСТВа йэ+9а. 8p+(9_l)a йр-л*-
В частности, е^ является ненулевым кратным элемента x(ade_0)'1.
Из формулы A2) следует, что
х (ad O? ad ea = =i^±l> (а, а) х (ad e_J-\ A9)
и выражение в правой части отлично от нуля, поскольку г ^- 0
и ?>0. Поэтому
I V«l * °-
Мы видим также, что [ [e^ej e_a] = — (q(r-\- 1)/2) (а, а)ер. Эта
формула верна даже в том случае, когда C + а не является корнем,
так как тогда [е^еа] = 0 и q = 0. Далее, если (J = — а, то а-серией,
содержащей [3, является последовательность а, 0, —а, так что
г = 0, q = 2. Правая часть формулы равна в этом случае —(а, а)в_а,
а левая есть [ [е_аеа] e_J = — [*„«_„] = [е_Л] = — (<*• а) е-а> так что
формула остается верной. Мы доказали, таким образом, следующее
утверждение.
X. Пусть аир — ненулевые корни, и пусть элементы
ep€V е«€К< е-*€%-* удовлетворяют условию [еае_J == Аа.
Предположим, что а-серией, содержащей C, является последо-
последовательность C — га, .... C, .... f5-f~9a- Тогда
Заметим также, что если аи —а поменять местами, то г и q
меняются местами, и мы получаем соотношения [е_аеа] = — па = й_а,
§ 2. Основная теорема о представлениях 131
(—а, —а) = (а, а). Поэтому другой формой равенства B0) является
равенство
[ [врв-«1 «Л = ~{9fl)r (а, а) «„. B0')
XI. Никакое кратное ненулевого корня а «е может быть
корнем, за исключением 0, а, —а.
Доказательство. Пусть р = &<х является корнем. Тогда
2 (а, Р)/(а, а) = 2й есть целое число, и можно предположить, что оно
нечетно и положительно. Тогда, как легко видеть, а-серия, содер-
содержащая р, содержит также f = -j а. Это противоречит тому факту,
что а = 2f не может быть корнем (см. VII).
XII. а-серия, содержащая р (а, р =? 0), содержит не более
четырех корней. Поэтому 2 (а, Р)/(а, а) = 0, ±1, ±2, ±3.
Доказательство. Можно считать, что р=/=а, —а, поскольку
а-серия, содержащая а, состоит из трех корней а, 0, —а. Пред-
Предположим, что мы имеем по крайней мере пять корней. Изменяя
обозначения, мы можем считать, что этими корнями являются р — 2а,
Р_а, р, р + а, р + 2а. Тогда 2а = (Р + 2а) — р и 2(p-fa) =
= (Р -f- 2a) -j- p не могут быть корнями.
Поэтому р-серия, содержащая р —(— 2а, состоит всего из одного
элемента р + 2а и, следовательно, (р -j—2a. Р) = 0. Аналогично
Р—2а—р и р—2а-|-Р не могут быть корнями, так что (р — 2а, Р) = 0.
Складывая, мы получаем (р, Р) = 0, что противоречит факту неизо-
неизотропности ненулевых корней. Вследствие этого 2 (a, P)/(a, a) = (r—q),
в то время как r-\~q-\- 1 <!4. Отсюда г ^3, q ^ 3 и
2(а, р)/(а, а) = 0, ±1, ±2, ±3.
Всюду дальше мы будем отождествлять простое подполе поля Ф
с полем Q рациональных чисел. Пусть, как и раньше, ф* — про-
пространство, сопряженное к §, и пусть ф* обозначает Q-пространство,
натянутое на корни.
Мы видели, что корни порождают ф*. Докажем теперь
XIII. dim ?>o = / = dim?.
Доказательство. Достаточно показать, что если (а,, а2, ...
.... а2) есть базис пространства ф*. состоящий из корней, то каждый
корень Р является линейной комбинацией корней a.t с рациональными
коэффициентами. Известно, что Р=2^аг- ^гб®- Следовательно,
(Р, ау) = 2^(«4. а;), 7 = 1, 2 I, и
Л 2 (аг, аЛ
132 Гл. IV. Расщепляемые полупростые алгебры Ли
Это система уравнений с целыми коэффициентами
[2 (а,, ау)/(а;, а,)], [2 (р. ау)/(ау. а/>]
и с определителем
(о- «Л\ 21
У^0' B2)
поскольку форма (р, о) невырождена, а <хг образуют базис в .§>*.'
Поэтому система B1) имеет единственное рациональное решение.
Таким образом, Хг — рациональные числа.
Если Л есть вес относительно ф представления алгебры 2, то,
как мы видели, число 2 (Л, а)/(а, а) является целым для каждого
ненулевого вектора а. Только что проведенное рассуждение показы-
показывает, что Л является рациональной линейной комбинацией корней оь,
/=1, 2, ..., /. Поэтому любой вес Л?фо-
XIV. Значение формы Киллинга (р, о) является рациональ-
рациональным числом для р, <з?ф(ь и форма (р, о) суть положительно
определенная симметрическая билинейная форма на ф0-
Доказательство. Напомним формулу C) для (Л, k), h, &?.§>.
Принимая во внимание тот факт, что йя одномерно, мы можем пере-
переписать ее в виде
(А, *)= 2 а (А) а (А). B3)
а—корень
Пусть р, о ? ф*. Тогда
(р, о)=(А Ав) = 2«(Ар)а(Ав) = 2(Ар. А.)(А,. А„).
а а
Поэтому
(р. о) =2 (Р. <*)(«. <>)¦ B4)
Пусть теперь C — ненулевой корень. Тогда (C, ^) = 2ф' aJJ
a
пусть ^-серией, содержащей а, будет следующая последовательность:
Из формулы A8) следует, что 2(а, §Щ, §) = r~~q~ и (а, р> =
)/2р р). Поэтому
Так как (р, р) ^= 0, то 2 «(^р — Яа?J ^0»
(P. P)=V7-i гг B5)
§ 3. Простые системы корней 133
есть рациональное число. Следовательно, (а, E) = [(гар — <7ар)/2]ф, р)
i
рационально для любых корней а, р. Если р, о?ф0. то р = 2 РЛ-
1
i
<з = 2 vjaj- r^e Рг» v; € Ф> а аг — корни. Тогда (р, о) = 2 РЛ/О^* a/) € Q-
Далее, (р, р) = 2(р> аJ^0. и из условия (р, р) = 0 следует, что
каждое (р, а) = 0. Тогда р = 0, поскольку корни а порождают ф*.
Напомним, что в пространстве, снабженном невырожденной би-
билинейной формой (р, о), отображение Sa:
где a — неизотропный вектор, является линейным преобразованием,
оставляющим на месте каждый вектор в гиперплоскости, ортогональ-
ортогональной к а, и переводящим а в —а. Назовем это преобразование сим-
симметрией 1), определенной корнем а. Она принадлежит к ортогональ-
ортогональной группе формы (р, о). Мы видели (теорема 1), что если Л—вес
относительно •§> представления алгебры 2, то A' = ASa =
= А — [2 (Л, a)/(a, a)] (a) также есть вес. Симметрии Sa, где a — корень,
порождают группу линейных преобразований в фо. называемую
группой Вейля W алгебры g (относительно •§>). Эта группа играет
существенную роль в теории представлений алгебры 2. Результат,
о котором мы только что упоминали, состоит в том, что веса дан-
данного представления образуют множество векторов, инвариантных
относительно группы Вейля. В частности, это верно и для корней.
Если два элемента группы W индуцируют одну и ту же перестановку
корней, то они совпадают, поскольку корни порождают все про-
пространство фо- Так как существует только конечное число корней,
то W — конечная группа.
§ 3. Простые системы корней
Введем отношение порядка в рациональном векторном простран-
пространстве фо- Для этой цели выберем базис из корней аг, а2, . . ., аг и
назовем вектор р = 2^аг ^€Ф> положительным, если первый
отличный от нуля коэффициент \ положителен. Множество положи-
положительных векторов замкнуто относительно сложения и относительно
умножения на положительные рациональные числа. Будем говорить,
что о > р (о, р ? фо)> если о— о > 0. Благодаря этому §о становится
В оригинале употреблен термин „reflection". — Прим. ред.
134 Гл. IV. Расщепляемые полу простые алгебры Ли
линейно упорядоченным, и если о > р, то о-f- х > р-|-х и Х<з>Хр
или Хо < \р в зависимости от того, взято ли X > 0 или \ < 0. На-
Назовем введенное таким образом отношение порядка в фо лексико-
лексикографическим упорядочением, определенным упорядоченным мно-
множеством корней (otj, <х2 <хг) (которые образуют базис простран-
пространства фо).
Лемма 1. Пусть pv р2 pk ? фо- Предположим, что
р(>0 в (рг, ру)^О, если f т*=у. Тогда pv ..., pft линейно незави-
независимы над Q.
Доказательство. Предположим, что Р* — 2 ^гР*—
eS^,+ 2^- где 1<?, s<ft—I. V>0, Г<0. Поло-
Положим 2^дРо —°> 2^"р$~х' Поскольку pft > 0, o=ftO. В таком
случае (о, т) = 2^^'(р,. Р4)>°- Поэтому
(Pjk, о) = (о. о)+(о. т)>0.
С другой стороны, (pft> <з) = 24(Рй' Р?)^^, что приводит к противо-
противоречию. Следовательно, pv р2, ••¦, р^ являются Q-независимыми.
Определение 1. Назовем корень а простым относительно
упорядочения, введенного в фо. если а > 0 и а не может быть
записан в виде fJ + f» где р и f— положительные корни.
XV. Пусть « — совокупность простых корней относительно
заданного лексикографического упорядочения в фо- Тогда:
A) Если a, fJ?it, а Ф $, то а. — р «е является корнем.
B) Если а и р ^ it, а ф р, ./ио (а, р) < 0.
C) Множество it образует базис пространства фо «Д^ Q.
р — любой положительный корень, то р = 2^аа- г^е
&„—неотрицательные целые числа.
D) Если р — положительный корень и р ^ it, ш> существует
такой корень а^тс, ч/ио разность р — а является положитель-
положительным корнем.
Доказательство. A) Если а, Р?тс и разность а — р является
положительным корнем, то а = р-(-(а — р), что противоречит опре-
определению it. Если а—р — отрицательный корень, то, записав р
в виде р = (Р — а)-(-«, мы опять получаем противоречие. B) Пусть
последовательность р — га, р — (г—1)а Р + 9« есть а-серия,
содержащая р. Тогда 2 (а, р)/(а, а) = г — q. Так как (а, а)>0,
а г = 0 ввиду утверждения A), то (а, Р)^0. C) Линейная незави-
независимость корней, содержащихся в множестве it, следует непосред-
§ 3. Простые системы корней 135
ственно из B) и из леммы. Пусть 8 — положительный корень, и
предположим, что мы уже знаем, что каждый корень у, удовле-
удовлетворяющий условию В > 7 > 0, может быть записан в виде 2 ?ца>
где ka — неотрицательные целые числа. Можно предположить также,
что в?тс, так что 8 = B,-j-B2, h > °- Тогда-8>В, и 8, = 2^.
82 = 2 &аа> где ka, ka — неотрицательные целые числа. Поэтому
$ = '2i(k'a-\-k"a)о., т. е. В записывается в требуемом виде. Если В —
отрицательный корень, то —8 положителен. Отсюда 8 = 2 &«,<*• гДе
ka — целые числа, не превосходящие 0. Отсюда, а также из линей-
линейной независимости элементов множества тс, следует первое утвержде-
утверждение из C). D) Пусть В — положительный корень, не принадлежа-
принадлежащий «. Из леммы и утверждения C) следует существование такого
корня <x?ir, что (8, а)>0. Тогда 2(8, а)/(а, а) = г— q>0 (г, q
имеют тот же смысл, что и раньше). Поэтому г>0 и В — а есть
корень. Если 8 — а<0, то а — 8>0 и а = 6-{-(а— 8), что про-
противоречит простоте а?тс. Поэтому В — а>0 и 8 = (В — a)-f-a, где
Запишем теперь ir = (a1( a2, .... <хг) и назовем совокупность тс
простой системой корней алгебры 2 относительно ф и данного
упорядочения в фо1)- ^ы видели, что каждый корень Р = 2^Л'
где kt — целые числа, причем либо все kl'^-0, либо все kl-^.0.
Это свойство вполне характеризует простые системы. Действительно,
пусть п = (otj, a2, .... otj), где / = dim ф и аг — такие корни, что
каждый корень 8 может быть записан в виде 8 = 2 ^Л> гДе &{ — 4е*
лые числа одного знака (рациональные числа также могли бы
использоваться). Очевидно, из нашего предположения следует, что ти
есть базис в ф*. Введем лексикографическое упорядочение в ф*,
основанное на корнях <хг:
2Vi>°> если ^i= ••• =*vj = O. ^a+i>0> h<l-
Тогда положительными корнями В = 2 &А будут такие, для которых
все 4|^.О и некоторые kt > 0. Очевидно, что ни один из корней a.t
не может быть суммой положительных корней. Поэтому все a.t
просты. Поскольку любая простая система состоит из / корней,
множество ir = (aj, o^ а.^ является простой системой, опре-
определенной этим упорядочением.
Если Tc = (aj, a2, ..., аг)—простая система корней, то матрица
(Atj), Atj = 2 (<хг, ау)/(агаг) называется матрицей Картана алгебры 2
(относительно ф). Диагональные элементы этой матрицы Аи = 2,
') Простая система называется также фундаментальной'системой корней
алгебры У (см. также упр. 4 в гл. VIII). —Прим. ред.
136 Гл. IV. Расщепляемые полупростые алгебры Ли
а элементы вне диагонали Ai} равны 0, —1, —2 или —3 (XII и XV B)).
Если i Ф j, то корни at и oty линейно независимы, так что, если 8;;-
есть угол между а.1 и a.j, то 0^cos2Q^<l. Это приводит к нера-
неравенству 0<4(аг, ауJ/(а;, а,)(а;-, о^) < 4; поэтому 0<!Л;;.Лл<4
Отсюда следует, что либо числа Ац и А}1 равны 0 одновременно-
либо одно из них равно —1, в то время как другое равно —1,
—2 или —3. Определитель матрицы Картана {Ац) есть ненулевое
кратное определителя матрицы ((аг, а^)). Следовательно, det (Atj) Ф 0.
Выберем теперь элементы еа ? 8а., е_а ? 8_<*. так, что \еа,#-<*.] = Аа ,
и обозначим
ei = ea., /г = 2е_аг/(аг> щ), А4 = 2Ав//(о?. а/). B7)
Эти элементы имеют каноническую таблицу умножения для расщепляе-
расщепляемой трехмерной простой алгебры Ли: {eji-^ = 2e;, [/;/zJ =
= — 2/(, [ег/(] = А,. Кроме того, [ej}\ = 0, если I Ф j, так как
а._а;. не будет корнем, [е^] = 2(а,, а;)/(а;., a.j)ei = A]lel и [/г^] =
= — ^4«Л- Последние соотношения включают также равенства
[ethi] = 2ei, [/гА,] = — 2/г. Таким образом, элементы ег> /г, Аг удо-
удовлетворяют следующим 'соотношениям:
[А,Ау] - 0,
[e//;] = 8yAi (8,у=1. если *==./. 8/у = 0. если t ^= j),
[eth}] == V/. B8)
Iffi^-Ajtf,, U 7 = 1, 2 /.
Мы хотим показать, что 3/ элементов е;, /г, Аг (или 11 элемен-
элементов в[, f[, поскольку А; = [eJi]) порождают алгебру 8. Более того,
мы покажем, что в алгебре Й существует базис, таблица умножения
которого полностью определяется числами Ац. Тем самым будет
доказано, что алгебра 8 определяется своей матрицей Картана,
Назовем высотой корня Р = 2 *Л число | Р | = 2 I *г I- Высота —
положительное целое число, и положительными корнями высоты
один являются в точности корни аг?«.
XVI. Множество корней определяется простой системой к
и матрицей Картана. Другими словами, последовательности
(kv ft2 kt), соответствующие корням 2^Л- могут быть
восстановлены по матрице (Atj).
Доказательство. Достаточно найти все положительные
корни. Положительные корни высоты один исчерпываются корнями
a.l ^ it. Предположим теперь, что мы уже знаем положительные корни
высоты, не превосходящей п, где я — положительное целое число.
Укажем метод отыскания положительных корней высоты ra-f-1.
Согласно утверждению (XV), эти корни имеют вид p = a-)-ai, где
§ 3. Простые системы корней 137
а > 0 и высоты п, О/?тс. Поэтому задача заключается в том, чтобы
определить для данного а>0 с |а|=га, какие из сумм а-)-а;'
где <х-^ти, являются корнями. Если а = о^, то а-|-а;- не будет кор-
корнем. Следовательно, можно предположить, что а = 2 kfa и неко-
некоторое kt > 0 для i Ф j. Тогда линейные формы а — а;-, а—2а;.,
соответствующие корням, положительны и имеют высоту меньше п.
Поэтому известно, какие из них являются корнями. В частности,
известно число г, такое, что а;-серия, содержащая а, имеет вид
а — raj, ..., а а-|-<7ау. В таком случае
i
q = r — 2(z, aj)l(aj, oy) = r — 2 My*.
и поэтому число q может быть вычислено при помощи матрицы
Картана. Тем самым задача фактически решена, поскольку условие
q >_0 необходимо и достаточно для того, чтобы сумма a-J-a, была
корнем.
Пример. Пусть матрица Картана имеет вид
2 -1
-Ъ 2
т. е. 2(at> a2)/(aj, aj) = —1, 2(at, a2)/(a2, a2) = — 3. Поскольку
otj — a2 не корень, из этих соотношений следует, что агсерией,
содержащей а2, и а2-серией, содержащей at, являются соответственно
a2, a2+«i.
, aj~f-3a2.
Единственным положительным корнем высоты два является aj-f-a2.
Так как a2-f-2a1 не есть корень, то aj-)-2a2 — единственный поло-
положительный корень высоты три. Так как 2aj-j-2a2 не корень, то
единственным положительным корнем высоты четыре будет aj-f-3a2.
Кроме того, 2(aj-f-3a2, aj)/(alt aj) = 2 — 3 = —1, откуда следует,
что (otj -f- 3a2)-|- a: = 2aj-f- 3a2 — корень. Так как aj-j-4a2 не является
корнем, то 2aj--j-3a2 будет единственным положительным корнем
высоты пять. Поскольку Bocj -j- 3a2)-f- aj = 3 (o^ ~f <*2) и Bai ~f" 3a2) -f-
-\- a2 = 2 (otj -f- 2a2) не являются корнями, корней высоты шесть или
выше нет вообще. Поэтому множество
± аг ± a2, ± (а, -|- а2)> — (
±(а1 + 3а2), ±B^ + 3^) C1)
исчерпывает совокупность корней.
138 Гл. IV. Расщепляемые полупростые алгебры Ли
Простая индукция по высоте показывает, что любой положитель-
положительный корень р может быть записан в виде
Р = <**, + <**,+ ••• +%. C2)
где а1 ?тс, таким образом, что каждая частичная сумма
, V C3)
будет корнем. Число k в формуле C2) есть не что иное, как высота
корня р. Мы будем теперь сокращенно писать [х{х2 . .. хг] вместо
[... [х^^] ... хг], где xt?%. Тогда из утверждения IX следует
что элемент
и поэтому порождает йр. Отсюда следует также, что
[ft А • ¦ • ft J * °-
и этот элемент порождает й_^. Так как корни а(-?тс образуют базис
пространства ф*, то К. и, следовательно, Лг образуют базис про-
пространства ф. Поскольку 2 = Ф + 2BрН~2_р). где суммирование
распространено по всем положительным корням, это доказывает сле-
следующее утверждение.
XVII. Пусть ir = (aj, a2, .... а{) — простая система корней
алгебры 2 относительно ф, и пусть et, ft, ht определены фор-
формулами B7). Тогда 3/ элементов et, ft, ht порождают алгебру 8.
Любой положительный корень р можно представить в виде
Р = аг +аг + ••• +% /как, что каждая частичная сумма
% + • • • + аг . и •< k, является корнем. Далее, элементы
определенные положительными корнями р, образуют базис
алгебры й.
Нас, естественно, интересует закон умножения в этом базисе.
Для этого нам потребуется следующее утверждение.
XVIII. Пусть В — положительный корень, и пусть последо-
последовательность iv t2 lk определена корнем р, как это описано
в утверждении (XVII). Пусть 1', 2', .... k' будет перестанов-
перестановкой индексов 1, 2, .... k. Тогда [eiv, ei2, ... et ,1 отличается
от элемента \et , et ... et 1 рациональным множителем, при-
причем последний определяется числами Ац. Аналогичные утвер-
утверждения справедливы для элементов /.
§ 3. Простые системы корней 139
Доказательство. Утверждение очевидно в случае k=l,
так что мы используем индукцию. Предположим, что утверждение
справедливо для положительных корней высоты k— 1. Ecnnlk = 1^' = /•
то можно предположить, что для корня р — a.j выбирается последо-
последовательность tv l2, . .., /ft_!. Тогда из индуктивного предположения
следует, что \et t ... ei 1 = ^ Г^? ... et 1, где t — рациональ-
ное число, определенное числами Atj. Поэтому \et f .. . et l =
= \е, .. . е, e,] = t\e, ...e, eA = t\e, . . . е, Л. Предполо-
L lv '(*-i)r >i у i '*-i }i I i *J
жим, далее, что ik= j ф lkr> и используем запись
\e, ... e, 1 = \e, ... e, e, ... e, 1,
L lv lk'\ У lr Vr > lk'\
где выделенный элемент ej является последним, встречающимся в этом
выражении. Если ни одна из частичных сумм 0Liv-{- ... +a,m,
не будет корнем, то \et ... et ,1 = 0- Поскольку этот факт может
быть выведен из свойств матрицы Картана, результат в этом случае
верен. Предположим теперь, что каждая частичная сумма а. -|- . .. аг ,
является корнем. Тогда fet r ... e-t 1 =^= 0. Так как [/у.] = 0, для
i Ф j, то [ad /;, ad et] = 0 и
[ely, .. . V е} . . . %,/у]» [% . . . V ejfj . . . %,].
Из формулы B0) следует, что
^поскольку ^ , + ... +аг , — корень, отличный от 0V где q и г —
целые числа, g > 0, г^.0, определенные а,-серией, содержащей
Эта серия известна, так как нам задана матрица Картана (АЛ.
Аналогичные рассуждения показывают, что
L lr lk' J1 >\ у lv lk'\
где s—отличное от нуля целое число, определяемое числами Ац.
Отсюда следует, что
S[% ¦¦%•} = [%¦¦¦ %¦///] =
Таким образом, [«*,, ¦ ¦ • «v] = / [^, ... е*г,\42), •••%• «у], где
t — рациональное число, определяемое числами Aiv Итак, мы при-
140 Гл. IV. Расщепляемые полу простые алгебры Ли
ходим опять к первому случаю. Элементы / могут быть исследованы
аналогично.
Мы можем доказать теперь следующую основную теорему.
Теорема 2. Пусть тс = (а1, а2, .... аг)—простая система
корней расщепляемой полупростой алгебры Ли 2 относи-
относительно расщепляющей подалгебры Картана ?>. Пусть et, ft, hv
lz=\, 2 I,—образующие алгебры 8, заданные формулами B7),
и пусть базис ht, Ге; ... е- ], Г/г ... /; 1 алгебры 2 определен,
как в утверждении XVII. Тогда таблица умножения в этом
базисе имеет рациональные коэффициенты, определяемые
матрицей Картана (Л,;-).
Доказательство. Из формул B8) следует, что [ЛгЛ;] = О
k
и [eh ¦ ¦ ¦ eikh;] = 2i Alim [eh . . . elk]. Аналогично [fh . .. f^hj] =
— — 2 Aji \fi{ • • • fib]- Остается рассмотреть произведения эле-
элементов е и /.
Поскольку
[V ¦¦%} = [¦¦¦ [ен%\ ¦¦• eik\ то adK •••%] =
= [...[ad.(iad^2]... ad%] и [х, [е1{ •••%]] =
= *[... [ade^ade^] ... ad et J.
Правые части этих равенств могут быть получены действием
на х некоторых (некоммутативных) многочленов относительно
ade^ &^е1ь' ОТС1°Да и из аналогичных рассуждений относительно
элементов / следует, что достаточно показать, что Г \et ... etA еЛ,
Wh ¦¦¦ hk\ej\' [[eh •¦¦ %]Л]' [[fh ¦•• ftk]fj\ являются Рад-
Радиальными комбинациями базисных элементов с коэффициентами,
определяемыми числами Л;;-.
Рассуждения для двух первых и для последних двух произведе-
произведений совершенно одинаковы, так что мы рассмотрим только первые
два. Для вычисления [ [ег ... ег 1 еЛ выясним сначала, является ли
корнем $-\-a.j, где Р = аг -f- ... -{-ol,. Если нет, то произведение
равно 0. С другой стороны, если f = ^ + ay есть корень, то,
согласно утверждению XVIII, \\et . .. е1 1 еЛ есть рациональное
кратное некоторого е-базисного элемента, соответствующего f-
с коэффициентом, определенным матрицей Картана. Рассмотрим
далее [[fit .. . /ift] е;]. Если й = 1, то произведение равно 0,
за исключением того случая, когда tl=j и [/jie^] = — hy Если
k^.2, то мы докажем по индукции, что это произведение есть
рациональная линейная комбинация /-базисных элементов. Действи-
§ 3. Простые системы корней 141
тельно, если k = 2, то это произведение равно 0, за исключением
случаев j — ll или j — t2. Для [[/(,//] еу] выполняется соотношение
[ Wj] еА=[A W)+[ [ fhej] fi] = - [Wj] = A^ A • поскольку
li=h J и [/*,«/] = 0. Из только что выведенного соотношения сле-
следует также, что [ [///г 1 е,1=—Ад /г,- Предположим теперь, что
Д; > 2. Если ни одно из 1Т не равно j, то произведение равно 0.
В противном случае, пусть tr+1 есть последний индекс в Г/г ... ft 1,
равный у. Тогда
• • • /(f/y • • • Л,] •;] = [[ [/,, • ¦ • ft/j\ e,\ ftr+t . • ¦ fh\ =
= -[•¦¦ [[Л, ••¦ К\Ч ¦¦¦ /
Первый член пропорционален /-базисному элементу, причем коэф-
коэффициент рационально выражается через А1}. По индуктивному пред-
предположению то же верно и для второго члена. Этим завершается
доказательство.
Сводка результатов. Прежде чем продолжать анализ,
будет полезно собрать воедино полученные нами результаты. Для
любой расщепляемой полупростой алгебры Ли й с расщепляющей
картановской подалгеброй ф мы нашли каноническую систему обра-
образующих et, ft, ht, /=1, 2, ..., I, удовлетворяющих определяющим
соотношениям B8). Исходным пунктом для получения этих образую-
образующих был выбор простой системы корней it. Характеристическим
свойством системы ти является то, что каждый корень записывается
в виде а = 2 &Л> аг € «• где все kt одновременно либо неотрица-
1
тельные, либо неположительные целые числа. Такие системы мы
получаем, вводя лексикографическое упорядочение в пространстве фд
рациональных линейных комбинаций корней и выбирая положитель-
положительные корни, не представимые в виде суммы a—f- p, где a, p > 0 в этом
упорядочении. Канонической системой образующих, соответствую-
соответствующих it, является система элементов Лг = 2йа/(аг, а,), ei = ea
fi = 2е_я /(аг, аг), где еа — любой отличный от нуля элемент из Йа ,
а е_а так выбирается в 2_а , что [?„ е_а 1 = йа.. Заметим, что
элемент ht однозначно определен корнем a.t, в то время как et может
быть заменен любым |лгег, где 0 Ф Pi(z Ф. Тогда ft заменяется на pj1fr
Элементы et, ft, ht образуют канонический базис расщепляемой трех-
трехмерной простой алгебры Ли 8г. Кроме того, как легко проверить,
Л'г = Л(, e'l=\i.lel, f'l = p-lft для любого другого канонического
базиса eti f\, h'^ алгебры й(., такого, что А^2гПФ-
Если et, ft, hi — канонические образующие, то канонический
базис алгебры й строится следующим образом: образующие h(
142 Г л IV Расщепляемые полупростые алгебры Ли
составляют базис подалгебры ф, а для каждого ненулевого корня р
базисным элементом е9 подпространства 8р будет [etj ... et 1, если
Р > 0, и \ft ... ft], если р < 0, где последовательность (^ .. . /ft)
такова, что аг,+ ¦ • • +<**. = ± р. и каждая частичная сумма
является корнем.
Таблица умножения в каноническом базисе рациональна и опре-
определяется матрицей Картана (А1}), где Л(; = 2(<х,, а;)/(а,, аг). Эле-
Элементы Л,; — целые числа, Аи = 2, и если i =? j, то либо Л<; = 0 = A}i,
либо одно из чисел А1г Ац есть —1, в то время как другое
равно —1, —2 или —3. Заметим также, что группа ортогональных
линейных преобразований, порожденная симметриями
и являющаяся подгруппой группы Вейля W, конечна. (Позднее мы
выясним, что эта подгруппа совпадает со всей группой W.) Симмет-
Симметрии S, определяются матрицей Картана. Так, если мы выберем базис
(av <x2, .... <хг), то преобразование S; полностью описывается
формулой
с 2(а„а;)
аД = а, ^-^ а, = а; - Atjat.
Отмеченные условия, которым удовлетворяют элементы Ai},
весьма многочисленны. Иногда мы будем использовать одну часть
этих условий, в других случаях — другую.
§ 4. Теорема об изоморфизме. Простота
Теорема 2 предыдущего параграфа делает почти очевидной сле-
следующую теорему об изоморфизме.
Теорема 3. Пусть й, 8' — расщепляемые полупростые
алгебры Ли над полем Ф характеристики 0 с расщепляющими
подалгебрами Картана ф, ф' одной и той же размерности I.
Пусть (av <х2 а\ (a'v а'2, . . ., а'Л—простые системы корней
алгебр 8 и 8' соответственно. Предположим, что мат-
матрицы Картана B (<хг, <х;)/(<хг, <хг)), B(aJ. ay)/(<V «;)) совпа-
совпадают. Пусть et< ft, hr e'r f'{, h't,t=l,2 I,—канонические
образующие алгебр 8 и 8', заданные соотношениями B7).
Тогда существует однозначно определенный изоморфизм ал-
алгебр 8 и 8', отображающий et в е[, f\ в f'v a ht в й'(.
Доказательство. Как мы знаем из утверждения XVI, сумма
2 kla!l является корнем относительно ф тогда и только тогда,
§ 4. Теорема об изоморфизме. Простота 143
когда ^ ^ia'i — корень относительно ф'. Если р — положительный
корень относительно ф, то пишем ?) = а/ -\- ... -\- сц , так что ча-
частичная сумма at -)-... -|-щ есть корень для всех m^.k. Тогда
Р' = a't + ... -}- ь\ и каждая частичная сумма а'{ -}-••• + »',
1 k \ m
является корнем. Мы можем принять за базисные элементы в кано-
каноническом базисе C6) алгебр й и 8' элементы [е/ •¦•%]> I/' "••/'*]>
\е\ • • • е\ 1 • \f\ • • • /'г ]• Тогда теорема 2 показывает, что коэффи-
коэффициенты таблицы умножения в этих базисах для алгебр й и й' совпа-
совпадают. Поэтому линейное отображение, устанавливающее попарное соот-
соответствие между этими базисными элементами, и есть искомый изо-
изоморфизм. Так как et, ft, ht являются образующими, то изоморфизм
определен однозначно.
Только что доказанное утверждение является основным в проблеме
описания простых алгебр Ли. Этот результат оказывается также
полезным при изучении автоморфизмов некоторой фиксированной
алгебры Ли, что будет рассмотрено позднее. Отметим сразу, что из
утверждения теоремы 3 следует существование автоморфизма алгебры й,
при котором et —>/,, ft —>et, ht-> — /z(. Это следует из того, что
система корней <х^ = — <xt, i = \ I, является простой, а элементы
e'l = fl, f'i = e[, h't = — ht составляют соответствующее множество
образующих. Это понадобится нам в § 7.
Определение 2. Простая система корней •к = (а1, <х2, ..., <хг)
называется неразложимой, если невозможно разбить и на непустые
неперекрывающиеся подмножества и', и", такие, что А1} = 0 для
любых at ? к', а.] ? и".
Теорема 4. Алгебра Й является простой тогда и только
тогда, когда соответствующая ей простая система корней и
неразложима.
Доказательство. Предположим сначала, что и = (ар ...,ай)и
U(a*+p ....аг). 1 <!&</, так что AtJ = 0, t^Ck, />А. Выберем
канонические образующие е{, ft, ht и обозначим через %х подалгебру,
порожденную элементами ej, fj, hj, j <; k. Очевидно, что йх = ФН-
+ 2' 2Т. где §j есть подпространство пространства ф, натянутое
на hr а суммирование распространено на корни f, линейно завися-
зависящие от a.j. Поэтому Ос^сй. Если г > k, j -^k, то Л;г = 0 и,
поскольку a.j — аг не корень, а;-|-аг также не будет корнем. По-
Поэтому [е;ег] = 0 и [fj, er] = 0. Точно так же [/гд] = 0, и следова-
следовательно, ег принадлежит нормализатору подалгебры йх. Аналогично fr
принадлежит нормализатору подалгебры gj. Поскольку Й! содержится
б своем нормализаторе, то Й является нормализатором подалгебры ?,
144 Гл. IV. Расщепляемые полупростые алгебры Ли
Поэтому 2j является идеалом, и алгебра 2 не проста. Предположим,
обратно, что алгебра 2 не проста. Тогда 2 = 21ф22. где 2г — соб-
собственные ненулевые идеалы. Пусть а будет ненулевым корнем и еа?2а.
Тогда еа = е^ + 42). «?'} 6 Й( и [еяй] = a (h) ea для h ? ф, откуда
следует, что \e^h} = a(h)e^K Так как 2а одномерна, то либо 2Я?21,
либо 2as22. Поскольку [81Й2] = 0 и [2a2_J^0, то либо 2я + 2_яс21>
либо 2а + 2_ас22. В частности, мы можем перенумеровать канони-
канонические образующие ev ft так, что ev fv .... ek, /ь?%1- ek+i<
/ft+1 ev /г?22. Поскольку 2г являются ненулевыми идеалами,
1<А<; и O = lejlerfr]] = lejhr] = Arjej, если у<* и г > *.
Поэтому AJr = Arj = O, и простая система корней разложима.
§ 5. Отыскание матриц Картана
Результаты последнего параграфа позволяют свести проблему
классификации простых алгебр Ли к следующим двум задачам: A) отыс-
отыскание матриц Картана (Ai}), соответствующих неразложимым простым
системам корней; B) построение простых алгебр, соответствующих
матрицам Картана. Мы рассмотрим сейчас задачу A), а задача B)
будет изучена в следующем параграфе. Заметим сперва, что условие
неразложимости равносильно тому, что невозможно расположить
индексы (или корни <хг) так, чтобы матрица имела „ящичный" вид
В О
О С
где В, С не пусты.
Мы сопоставим теперь матрице Картана (Ац) некоторую схему,
называемую схемой Дынкина. Выберем на плоскости I точек otj,
<х2 <хг и соединим <хг с <х;-, 1ф], АцА^ отрезками. Отнесем
также каждой точке <хг вес" (аг <хг). Если Ац = 0 = Ад, то at и а;
не соединяются, а если Ац Ф 0, Ajt Ф 0, то Л;7/Лг;=(аг, аг)/(а;., а;).
Поэтому AjtjAtj и AtjAji могут быть определены из этой схемы.
Поскольку Atj неположительны, этой информации достаточно для
определения Ац и Ajt. Таким образом, матрица может быть восста-
восстановлена по схеме точек, отрезков и весов. Рассмотрим два примера:
3
о
«1
1
0—
1
1
— 0
I
1
а,
1
1
а
C7)
§ 5. Отыскание матриц Картана
145
Для 02 A2JAv = {av aj)/(<x2, <х2) = 3, Л12Л21 — 3, откуда следует,
что Л12 = —1, Л21 = —3. Поэтому матрица Картана в данном
случае есть матрица из B9). Для А1 мы имеем соотношения Аи = 2,
Л12 = Л21 = Л23 = А32¦=...— At_ur = Аи г_х = — 1, все остальные
Ац = 0. Следовательно, матрица имеет вид
2—1 0"
— 1
2 —1
¦1 2
О
— 1
C8)
При описании схем Дынкина мы вначале опускаем веса (at, at)
точек и рассматриваем только набор точек и соединяющих их отрез-
отрезков. Имеем I точек alf a2, ... a^; a? и a;-, i=?/, не соединяются,
если AijAji = O, и соединяются At]A]t = \, 2, 3 отрезками, если
АцА^фО. Элементы <хг являются линейно независимыми векторами
в евклидовом пространстве Ео над полем рациональных чисел. Это
пространство может быть погружено в евклидово пространство
E = E0R над полем R вещественных чисел. Если обозначить через 0(;-
угол между at и <х;-, то А^А}1 = 4 cos2 9,;- и cos 0tJ- ^ 0.
Каждое конечное множество ap a2 аг линейно независимых
векторов в евклидовом пространстве (над полем вещественных
чисел) называется допустимой конфигурацией, если 4cos26iy- =
= 4 (a,, a-J/(a,, a,) (a,, a,) = 0, 1,2 или З и cos 9,, ^0 для любых
¦" J J 11 1
i, j, i ф j. Таким образом cos6^ = 0, — -у, —T r ^ или—o"Y^ и
соответственно Ъ1} = 90°, 120°, 135° или 150°. Мы можем заменить at
единичным вектором ut, являющимся положительным кратным век-
вектора at. Тогда указанное выше условие принимает следующий вид:
{щ, щ) = \, 4(u[u]f^0, 1, 2 или 3, (иг> и;)<0,
1ф}, I, у=1, 2, ... I. C9)
Схема Дынкина (без весов) допустимой конфигурации и является
совокупностью точек иг, / = 1, ...,/, и отрезков, соединяющих
эти точки в соответствии с правилом, данным ранее: ut и Uj не
соединяются, если (и(, «у) = 0иигс и;- соединяются 4 (иг, иJ=1, 2
или 3 отрезками в противном случае. Допустимая конфигурация
называется неразложимой, если невозможно разбить и на непересе-
непересекающиеся непустые подмножества и', тс", такие, что (иг, и;) = 0
для иг?и', и;.?и". Соответствующим понятием для схем Дынкина
146 Гл. IV. Расщепляемые полупростые алгебры Ли
является связность: если и, v?iz, то существует последовательность
ui ==й, tit , ... , ui=v, такая, что и/, и «ь+1 соединены в схеме
отрезком. Если известна схема Дынкина, то известны все (иг, и}).
Мы определим схемы Дынкина для всех неразложимых допустимых
конфигураций после нескольких простых предварительных рас-
рассуждений.
1. Если S есть схема Дынкина, то схема, получаемая аз
нее выбрасыванием некоторого количества точек и инцидент-
инцидентных им отрезков, является схемой Дынкина допустимой
конфигурации, получаемой из исходной допустимой конфигу-
конфигурации выбрасыванием векторов, соответствующих этим
точкам.
2. Если I—число вершин {точек) в схеме Дынкина, то
число пар точек (и, v, (и, v) Ф 0), соединенных отрезками,
меньше I.
t
Доказательство. Пусть и = 2 ui- Тогда 0<(и, «) = (-)-
+ 2 2(«г. «;)• Если ("<¦ "у)^0' то 2 ("*М;Х—'• Поэтому нера-
кУ
венство показывает, что число пар и(, Uj, таких, что (и(и;) ф 0,
меньше I.
3. Схема Дынкина допустимой конфигурации не содержит
циклов (под циклом понимается последовательность точек иг uk,
таких, что ut соединена с иг+1, i^.k—1, a uk — с иг).
Доказательство. Подмножество, образующее цикл, было бы
схемой допустимой конфигурации, нарушающей свойство 2.
4. Число отрезков (с учетом их кратности), исходящих
из одной вершины, не превышает трех.
Доказательство. Пусть и — вершина, vv v2, . . ., vk — вер-
вершины, соединенные с и. Никакие две вершины vt не соединены,
поскольку в схеме нет циклов. Поэтому (vt, г/;) = 0, i+j. В про-
пространстве, натянутом на векторы и и vt, соответствующей допустимой
конфигурации, можно выбрать вектор v0, такой, что (г/0, г/0)=1,
а векторы v0, vx vk будут взаимно ортогональны. Поскольку
и и ?,, /^1, линейно независимы, и не может быть ортогонально
к v0, так что (и, v0) Ф 0. Далее, и = 2(«. vj) v]t следовательно,
(и, «) = («, г/0J+(и, г^Н-•••+(«. ек? = 1,
k k
Поэтому 2(м> **?)<* и S^(M- Vif < 4- А это и есть наше
утверждение, так как 4 (и, г/(J равно числу отрезков, соединяю-
соединяющих и и v(.
§ 5 Отыскание матриц Картана 147
5. Единственной связной схемой Дынкина допустимой кон-
конфигурации, содержащей тройной отрезок, является
Это очевидным образом вытекает из свойства 4.
6. Пусть те допустимая конфигурация, и пусть vx, v2, ... > vk—
такие ее векторы, что соответствующие точки схемы обра-
образуют простую цепь, т. е. каждая точка соединяется со сле-
следующей единственным отрезком. Пусть те' состоит из векторов
конфигурации тс, не принадлежащих простой цепи vx vk,
k
а также из вектора г/=2г'г Тогда те' является допустимой
конфигурацией.
Доказательство. По условию 2(г/,, vl+x) = — 1, i = 1, . . .
. .., k—l. Поэтому (v, v)=k-\- 2 2(^1- vi)- Поскольку в схеме не
может быть циклов, (vt, г»;) = 0, если i < j, за исключением случая
j = t-\-l. Поэтому (v, v) = k — {k—1)=1, и v является единич-
единичным вектором. Пусть теперь и?тс, и Ф vr Тогда и соединяется не
более чем с одним из v,, скажем с v., поскольку циклы отсутствуют.
В таком случае (и, v) = (u, 2^ }== (Mi vj) и 4(и, vJ = 4(и, v J=
= 0, 1,2 или 3, что и требовалось доказать.
Схема конфигурации те' получается из схемы конфигурации те
стягиванием простой цепи в точку. Мы заменяем, таким образом,
все вершины vl единственной вершиной v и соединяем ее с каждой
вершиной и, соответствующей вектору и?те, ифю^ столькими
отрезками, сколькими соединялась вершина и со всеми Vj в исход-
исходной схеме. Рассмотрим для примера следующие графы:
-О • •
D0)
о
которые редуцируются соответственно к графам
148 Г г IV Расщепляемые полупростые алгебры Ли
Поскольку из средней вершины в каждом из этих графов исходит
по четыре отрезка, эти графы не могут быть схемами Дынкина
допустимых конфигураций, так как иначе нарушалось бы свойство 4.
Поэтому имеет место свойство
7. Никакая схема Дынкина не содержит подграфов
вида D0).
8. Любая связная схема Дынкина может принадлежать
лишь к одному из следующих типов:
О • • • О
«2 «P-1 Up Vq У,-1 Oi Vi
iv, о D2)
W2 О
о ¦ »о • • • о — о-* о • • • о о
и, иг Ир-, г г„-| Vi v.
Доказательство. Если связная схема Дынкина S содержит
тройной отрезок, то она должна быть типа О2> согласно пункту 5.
Если S содержит двойной отрезок, то она содержит только один
такой отрезок и не может содержать узла, т. е. графа вида
Это очевидно из п. 7. Очевидно также, что S не может содержать
двух узлов.
Поэтому все возможности исчерпываются схемами, приведен-
приведенными в D2).
Исследуем теперь возможности для р, q, г во втором и третьем
р
типах схем таблицы D2). Для второго типа положим и = 2 tai>
ч
v — ^jvj. Поскольку 2 (и,, «t+1) = — 1 и 2 (v, г>;+1) = — 1, имеют
§ 5 Отыскание матриц Картана 149
место равенства
р р-1
1 1
= р(р+1)/2.
(г;, г>) = ?(?+1)/:
Кроме того,
(и, v)=pq(up, vq) = (pq
и
(и, г/J = /?2^2/2
В силу неравенства Шварца
:-р(/>-1)/2-
2,
г/2J(ир, *,)
<« + !>
D3)
D4)
D5)
C4R4
2 2
Так как pq^>0, то (р-(- 1) (?+ 1) > 2р#. что эквивалентно нера-
неравенству (^—l)(q—1)< 2. Поэтому единственными возможностями
для положительных целых чисел р, q являются следующие:
р—1, q произвольно; ^ = 1, р произвольно; р = 2 = ^. D7)
Первые два случая отличаются только обозначением. Поэтому
9. Связными схемами Дынкина второго типа в таблице D2)
могут быть только
' D8)
о о " 'о о /•"
Рассмотрим, наконец, третий тип из D2). Положим и = 2 iut,
1
G-1 г-1
f = 2 Jvj> >w~'2ikwk- Векторы и, г/, w взаимно ортогональны,
и z не лежит в пространстве, порожденном этими векторами. По-
Поэтому, если обозначить через 81Р 62, 63 соответственно углы между
z и и, г/, w, tocos261 + cos262-[-cos263 < 1 (см. доказательство
пункта 4 выше).
Тогда
cos261==(m, 2J/(и, и) = ввиду D3) =
Аналогично
2I cos283=I(l — l/r),
150
Гл. IV. Расщепляемые полупростые алгебры Ли
так что
или
— < 1
D9)
Мы можем предположить, что р ^q^>rQ>2). Тогда p~l-^.q~1-^.r~1,
и из условия D9) следует, что Ъг~1 > 1. Поскольку г ~^2, это дает
г = 2. Тогда из формулы D9) вытекает неравенство p~x-\-q~x > 7г-
Поэтому 2*? > -j. и ^ < 4. Следовательно, 2 ^ # < 4. Если # = 2,
то мы получаем условие /г > 0, выполняемое при всех р. Если
q — Z, то получаем условие р > 1/6 или /? < 6. Значит, в этом
случае р = 3, 4, 5. Таким образом, решения для р, q, г следую-
следующие:
r = q = 2, p произвольно,
г = 2, 9 =
= 3, 4, 5.
E0)
Этим доказано
10. Единственными связными схемами Дынкина третьего
типа в таблице D2) являются
-о-
о
А
E1)
E2)
?..
Итак, мы завершили доказательство такой теоремы.
Теорема 5. Все связные схемы Дынкина исчерпываются
схемами Av J>1, Bl = Cl, /!>2, Dv />4, и пятью „исключи-
§ 5. Отыскание матриц Картана
151
тельными" схемами G2, F4, Е6, Е7, ?8, указанными в таблицах
D2), D8), E1) и E2).
Введем теперь вновь веса в схемах. Это даст нам все возможные
матрицы Картана. Напомним, что в схеме Дынкина, получаемой из
простой системы 7r = (aj, a2, .... <хг), А^Ад (i ф j) есть число
отрезков, соединяющих at и <х;.. Если AtJ Ф О, AJi Ф 0, то Л;г/Лг;=
= (аг, аг)/(<Ху, aj) и Atj или Ajt равно —1, в то время как другое
из этих чисел равно —1, —2 или —3.
Поскольку ничто не изменится, если умножить все <хг на некото-
некоторое фиксированное вещественной число, отличное от нуля, можно
допустить, что один из at есть единичный вектор. Если в схеме
встречаются только одинарные отрезки, то все (at, at) = 1, так как
схема связна. Поэтому схемы типов At, Dt, E6, E7, ?8> снабженные
весами, имеют вид
Аг.
о-
1
1
1
о
а,
аг
1
-о
?,:
1
о
1
— 0-
аг
1
-о-
1
о-
Для G2 обозначения уже были выбраны так, что
1
—о •
152 Г л IV Расщепляемые полупростые алгебры Ли
Для FA можно выбрать веса следующим образом:
112 2
F,; о о о—-—о
а, аг а3 ««
В качестве В1 и Ct можно принять схемы
„22221
Вь • о о о • • • о ' о , / 2j 2
«! аг а3 «;-i oil
Cl '. О О • • • О о О , / ^ З1 ,
Эти схемы дают все возможные матрицы Картана.
§ 6. Построение алгебр
Настало время вывести на сцену основных персонажей нашей
истории — расщепляемые простые алгебры Ли. Каждой связной схеме
Дынкина допустимой конфигурации, которые описаны нами в § 5,
соответствует матрица Картана (At]), а для этой матрицы существует
расщепляемая простая алгебра Ли с каноническими образующими е(,
/г> ht, 1 = 1, 2, ., /, такими, что [elh]] = A]lel. Мы укажем про-
простейшее (линейное) представление алгебр, соответствующих схемам
Av BL, Сi, DL, G2, Fi и Е6. Позднее (в гл. VII) будет использсвлн
другой метод для доказательства существования расщепляемых про-
простых алгебр Ли, соответствующих схемам Е7 и Es.
Напомним, что если 2 — неприводимая алгебра Ли линейных
преобразований конечномерного векторного пространства над полем
характеристики 0, то g = gi©(E, где gj — полупростая алгебра,
а © — центр. Поэтому такая алгебра полупроста в том и только
том случае, когда 6 = 0. Заметим также, что если полупргста?
алгебра 8 содержит абелеву подалгебру ф, такую, что 2 = $>©Фекф
© Фе ф • •. гДе а> В .. . — ненулевые отображения подалгебры
ф в Ф, удовлетворяющие условиям [eah] =a[h]ea, h?$>, то § есть
расщепляющая подалгебра Картана для 2, и алгебра 2 расщепляема
Мы используем эти факты в наших построениях.
Пусть 6—алгебра всех линейных преобразований (/-)- 1)-мерного
векторного пространства 2Ю над полем Ф, /^>1. Как хорошо изве-
известно (и легко доказывается), (? неприводима на STO. Имеет место раз-
разложение 6л = ®?фФ1, где 8s2®/. — производная алгебра, являю-
являющаяся множеством линейных преобразований со следом 0. Очевидно,
чго каждое ©/.-инвариантное подпространство вместе с тем 6^-инва-
§ 6 Построение алгебр 153
риантно. Поэтому алгебра ? = (?/, неприводима. Разложение ®, =
= (»?©Ф1 показывает также, что центром алгебры (*? является 0.
Следовательно, алгебра ®? полупроста.
Отождествим теперь 6 с алгеброй Фг+1 A-\- 1) X ('+ 1)-матриц,
элементы которых принадлежат полю Ф, а 8—с подалгеброй Фг'+1—
множеством матриц со следом 0. Рассмотрим обычный матричный
базис (е1}), tj=\, ..., 1-\-\, алгебры Фг+1, элементы которого
связаны соотношениями
р п __ § а ^ о == 1 /KЧ^
?^ к/к jk itn* ^J it ' \ *-^/
Базис алгебры 2 имеет следующий вид:
"¦k==ekk ei+i, i+i' ^-^-'1 eij< L Ф J — ^ /~f~l. E4)
i
Положим h='^imkhk. Тогда множество элементов h образует
абелеву подалгебру ф размерности /, причем
2S«>.. E5)
Р~\-1 линейных функций h->w, — шг, h->4-4-wr, h—> — (т-4-ш>
различны между собой и являются ненулевыми весами относительно
adg§. Имеет место разложение 8 = ф_|_ 28Я> где а пробегает мно-
множество этих весов. Отсюда следует, что ф есть расщепляющая под-
подалгебра Картана, а а—ненулевые корни. Положим
а1 = Ш1 — Ш2- а2 = Ш2 — шз
Тогда
-ш,)= E7)
ft=l, 2 /-1;
—«о, + 1) +
(+2) + • • • + (ш; — ш;+1) = E8)
Это показывает, что каждый корень имеет вид 2&га(> гДе kt—це-
kt—целые числа и либо kt ^ 0 для всех I, либо kt -^ 0 для всех I. По-
Поэтому а( образуют простую систему корней алгебры 2 относи-
относительно ф. Соотношения E7) и E8) показывают, что a,-)-a(+1 — ко-
корень, если 1<^г<^/—1, а a(-|-2a(+1 не является корнем, так же
154 Гл. IV. Расщепляемые полупростые алгебры Ли
как и a(-j-ay, если />2-|-1. Это означает, что элементы Atj ма-
матрицы Картана принимают следующие значения:
Al+ltl = -l = ALl+v 1</<Z
Аи = 0, если />/ + ! или j<t— I. ( ;
Поэтому схема Дынкина есть связная простая цепь
Аг.
Отсюда следует, что 2— простая алгебра типа At (т. е. со схемой
Дынкина Лг). Итак, мы получили следующее утверждение.
Теорема 6. Пусть 2— алгебра Ли всех линейных преоб-
преобразований со следом О в A-\-1)-мерном векторном простран-
стве над Ф. Тогда 2 является расщепляемой простой алгеб-
алгеброй Ли типа Av
Допустим теперь, что 2Ю есть л-мерное векторное пространство
над Ф, снабженное невырожденной билинейной формой (х, у), сим-
симметрической или кососимметрической. Пусть 2 — алгебра Ли всех
линейных преобразований А, кососимметричных относительно формы
(х, у), т. е. удовлетворяющих условию (хА, у) = — (лг, у А) (см.
§ 1.2). Нам потребуется следующая
Лемма 2. Алгебра 2 неприводима, если п~^Ъ.
Доказательство. Пусть -ЭТ — ненулевое подпространство,
инвариантное относительно 2, и пусть z— ненулевой вектор в W.
Пусть, далее, и — любой вектор в ортогональном дополнении Фгх.
Выберем г>(?Фг и рассмотрим линейное преобразование А : х —»
->(лг, u)v — (г/, л:) и. Нетрудно установить, что А ? 8. Кроме того,
вектор zA = — (v, z) и Ф 0 лежит в W. Поэтому W содержит Фг-1
для каждого z?W. Отсюда следует, что dim tft^- п — 1 и dim tft = nt
кроме того случая, когда If? = Фг^- для каждого z ? If?. Тогда ffi
вполне изотропно и dim 9?<;[я/2] (см. Джекобсон [2], т. II, стр. 170).
Отсюда следует, что л = 2, а это противоречит условию леммы.
Мы будем различать следующие три случая: В. Форма (х, у)
симметрическая и л = 21 -f- 1, / ^- 1; С. Форма (х, у) коеосимметри-
ческая, так что л четно, например л = 21, /> 1; D. Форма (д:, у)
симметрическая и л = 2/, /> 1. Кроме того, мы будем предполагать,
что билинейная симметрическая форма в случаях (В) и (D) имеет
максимальный индекс Витта. Это означает, что Ш содержит вполне
изотропное подпространство 9? размерности /.
В. Пусть (uv u2, .... ип) — бачис пространства 9W, и пусть
(и(, Uj) = o(y, s = (о/;). Линейное преобразование А принадлежит
§ 6. Построение алгебр 155
алгебре g тогда и только тогда, когда (и(Л, uj) = — (и,, UjA) для
г, /=1 и. Если uiA — ^ia.lkuk, то эти условия записываются
в виде 2а(Л; — — S0(ftayft' или в матричной форме
as — — sa', a = (ay). F0)
Поскольку наша форма имеет максимальный индекс Витта, базис
может быть выбран так, что
/о 0 0
5= 0 0 о-1,
\0 о-1г О
где 1г обозначает единичную матрицу с / строками и столбцами
а о — ненулевой элемент поля Ф (см. Джекобсон [2], т. II, стр. 168).
Так как ничто не изменится, если перейти к пропорциональной
форме с отличным от нуля коэффициентом, то можно допустить, что
О 0\
0 0 1,1. F1)
V0 1, О/
Если мы разобьем матрицу а тем же способом, что и s,
2 21 22
где Су^Ф^, Ир и2 являются (/X 1)-матрицами, а Wj, г;2 — A XI)-
матрицами, то путем несложных вычислений можно установить, что
соотношения F0) выполняются в том и только в том случае, когда
П il
Из этих условий вытекает, что следующее множество элементов обра-
образует базис алгебры й, отождествленной с алгеброй матриц, удовле-
удовлетворяющих условиям F0):
ф j,
< j. F3)
i. i'
' el, i+l+V
156 Гл. IV. Расщепляемые полупростые алгебры Ли
где I, У=1, ..., I- Множество Ф—{2ША} образует абелеву под-
подалгебру алгебры 8. Линейные формы, используемые в качестве ниж-
нижних индексов, могут быть отождествлены с линейными отображе-
отображениями h->a(h), где h=='^iwihi. Таким образом, [ea,h] = aea,
а = шг — ш-, шг-)-шу и т. д. Отсюда следует, что ф есть расщеп-
расщепляющая подалгебра Картана, а а — ненулевые корни. Алгебра 8 дей-
действует неприводимым образом на Ш, и если элемент z = h0-f- 2 PA
принадлежит центру, то из соотношения [z/z] — 0 следует равенство
Sp.«(A)e. = 0.
Поскольку ек линейно независимы, pa<x(/z) = O для всех h.
Так как а =? О, то ра = 0. Поэтому z = h0. Но тогда из [2eJ —О
следует, что a (/z0) = 0 для всех а. Так как существует / линейно
независимых корней а (например, шг, /=1 /), то йо = О. Сле-
Следовательно, центр равен 0, и 8 является полупростой расщепляемой
алгеброй.
Будем предполагать теперь, что / ^- 2, и пусть
а, = ш, — ш9, а, = ш, — ш,, .. .,
112 2 2 3
<* = ш ш а = ш
Легко установить, что это есть простая система корней со схе-
схемой Дынкина BL:
2 2 2 2 1
О- •—*- О " * • О' о ~ о
а, а2 а(-2 а;-! а(-
Поэтому й — простая алгебра типа BL. Мы установили, таким обра-
образом, следующее утверждение.
Теорема 7. Пусть 8 — алгебра Ли линейных преобразо-
преобразований 21-{-1-мерного пространства, /]>2, кососимметричных
относительно невырожденной симметрической билинейной
формы максимального индекса Витта. Тогда 8 — расщепляе-
расщепляемая простая алгебра Ли типа В{.
С. Пусть Ш имеет размерность 21, /^1, (х, у) — невырожден-
невырожденная кососимметрическая билинейная форма над Tt X 9№- Пусть, далее,
й — алгебра Ли линейных преобразований, кососимметричных отно-
относительно формы (х, у). Мы можем выбрать базис (иг, и2 к2г)
так, что матрица ^ = ((иг, uj)) будет иметь вид
§ 6 Построение алгебр 157
Как и в случае В, алгебра 8 может быть отождествлена с алгеброй
Ли матриц а?Ф2;> таких, что aq = — qa'. Это означает, что
1 «1
a = [ I, а,,?Ф,, F6)
21 2/
*12
«
где
«22 = -flll' ^2= «12' «21 ^«2Г F7)
Поэтому 8 имеет базис
"¦i= eu ei+i, i+v
ew}-o)l==eij ej+l,i + l' l Ф J,
e-ai-aj = eli}+l + e]tl+t. 1<J. F8)
где /, У=1, 2 l. Как и в случае В, можно показать, что
ф—{2<пА} есть подалгебра Картана, а линейные формы ±ш1 ± ш,,
используемые в качестве нижних индексов в соотношениях F8),
определяют корни относительно •§>. Далее, алгебра 8 имеет нулевой
центр и, следовательно, по лемме 2 алгебра 8 полупроста. Корни
образуют простую систему со схемой Дынкина СР если l^-Ъ. Этим
доказана
Теорема 8. Пусть 8 — алгебра Ли линейных преобразова-
преобразований 21-мерного пространства, I ^ 3, кососимметричных относи-
относительно невырожденной кососимметрической билинейной формы
{симплектическая алгебра Ли). Тогда 8 есть расщепляемая
простая алгебра Ли типа Ct.
D. Пусть Ш — 2/-мерное пространство, 1^-2, (х, у) — симметри-
симметрическая форма максимального индекса Витта. В данном случае базис (и()
можно выбрать таким образом, что матрица t = ((ur и)) примет вид
и алгебра 8 ото'ждествляется с алгеброй Ли матриц, удовлетворяющих
условию at = — ta'. Очевидно,
/«11 «12\
а = [ , аи?Ф,, G1)
где
г21 «22
«12 = -«12' «21 =-«2Г
158 Гл. IV. Расщепляемые полупростые алгебры Ли
Элементы
hi — eu — ei+i> i+f
earaj = eji — el+t:j+l, 1ф], G3)
—ej+i, f KJ.
где I, J~ 1,2,...,/, образуют базис алгебры 8. Тогда ф = {2 ШЛ)
есть ее расщепляющая подалгебра Картана, а нижние индексы
± шг ± шу в соотношениях G3) определяют корни.
Центр алгебры 2 равен 0. Поэтому 8 полупроста. Положим
Тогда эти аг 'образуют простую систему корней, схема Дынкина
которой есть Dv если 1^-4. Этим доказана
Теорема 9. Пусть 2 — алгебра Ли линейных преобразова-
преобразований 21-мерного пространства, /^>2, кососимметричных отно-
относительно невырожденной симметрической билинейной формы
максимального индекса Витта. Тогда алгебра 8 при 1^>4
является расщепляемой простой алгеброй Ли типа DL.
Четыре класса алгебр Ли А, В, С и D называются „большими"
классами простых алгебр Ли. Эти классы (или серии) соответствуют
линейным группам, которые Вейль назвал классическими группами
в своей книге под аналогичным названием. Нетрудно убедиться непо-
непосредственно или рассмотрев базисы, что имеет место следующая
таблица размерностей
Тип Размерность
At /( 1 + 2)
с, !?+!) ™
Dl 1B1-1)
Из определения простых систем и общей теоремы об изоморфиз-
изоморфизмах (теорема 3), а также из критерия простоты (теорема 4) вытекает
ряд изоморфизмов для ортогональных и симплектических алгебр Ли
небольших размерностей. Проверка нижеследующих утверждений
оставляется читателю.
1. Ортогональная алгебра Ли в 3-мерном пространстве Ш,
определенная формой максимального индекса Витта, а также сим-
плектическая алгебра Ли в 2-мерном пространстве являются рас-
расщепляемыми трехмерными простыми алгебрами и, следовательно,
изоморфны алгебре матриц со следом 0 в 2-мерном пространстве.
§ 6. Построение алгебр 159
2. Ортогональная алгебра Ли, определенная формой максималь-
максимального индекса Витта в 4-мерном пространстве, является прямой
суммой двух идеалов, изоморфных расщепляемой трехмерной простой
алгебре Ли.
3. Симплектическая алгебра Ли в 4-мерном пространстве изо-
изоморфна ортогональной алгебре Ли в 5-мерном пространстве, опре-
определенной симметрической формой максимального индекса Витта.
4. Ортогональная алгебра Ли в 6-мерном пространстве, опреде-
определенная формой максимального индекса Витта, изоморфна алгебре Ли
линейных преобразований со следом 0 в 4-мерном пространстве.
Остальные расщепляемые простые алгебры Ли типов О2, Fit ?6,
Е7 и Es называются исключительными. Мы укажем неприводимые
представления для алгебр G2, Ft, ?6, удовольствовавшись формули-
формулировкой рез\'льтатов без доказательств, несмотря на то, что некоторые
из этих доказательств нетривиальны. Полное изложение этих вопро-
вопросов читатель может найти в статье автора (Джекобсон [11]).
Алгебры G2 и F^ будут реализованы в виде алгебр дифференци-
дифференцирований некоторых неассоциативных алгебр, а именно алгебры чисел
Кэли 6 и исключительной простой йордановой алгебры Мз-
Следуя Цорну, мы определим расщепляемую алгебру Кэли или
векторно-матричную алгебру 6 следующим образом. Пусть
V — трехмерная векторная алгебра над полем Ф. Таким образом,
V — пространство с базисом I, j, k над Ф, в котором определены
билинейное скалярное произведение (х, у) и кососимметрическое век-
векторное произведение Х- Если I, j, к — ортогональные единичные
векторы, то
lXJ=='i> yX» = ii «X'5^./' ('")
Пусть E,— множество 2 X 2-матриц вида
а4
a, b?V. G7)
Сложение матриц и умножение их на элементы поля Ф определены
обычным образом, так что 6 — 8-мерное пространство над Ф. Снаб-
Снабдим 6 строением алгебры, определив операцию умножения формулой
( oq — (a, d) + + ХЛ
^ ) G8)
Заданная таким образом алгебра 6 называется расщепляемой алгеб-
алгеброй Кэли.
Алгебра 6 не является ни коммутативной, ни ассоциативной, но
удовлетворяет некоторому ослабленному условию ассоциативности,
160 Г л IV Расщепляемые полупростые алгебры Ли
так называемому альтернативному закону:
х2у = х(ху), ух'1 — {ух)х. G9)
Пусть 8 — алгебра Ли дифференцирований алгебры 6. Единичная
матрица 1 является единицей в E,, и, поскольку 12=1, Ш = 0 для
каждого дифференцирования D. Пространство 60 элементов со сле-
следом 0 (а -\-$ — 0) совпадает с пространством, натянутым на ком-
коммутаторы [ху] = ху — ух, х, у ? (L
Следовательно, S0Z) с 60 для всякого дифференцирования D.
Поэтому 60 есть 7-мерное подпространство в 6, инвариантное отно-
относительно 8. Представление в ©0 точно и неприводимо.
Если Т — линейное преобразование в V со следом 0, а Т*—со-
Т*—сопряженное относительно скалярного произведения преобразование,
то, как нетрудно проверить, отображение
0
есть дифференцирование алгебры 6. Множество этих дифференциро-
дифференцирований образует подалгебру 80, изоморфную алгебре Фз^. В любой
альтернативной алгебре всякое отображение вида Da< b = [aLbL] -)-
~h[ai^/?]~T" [а#Ьд\ является дифференцированием; здесь a, b — эле-
элементы алгебры, a aL, aR обозначают левое и правое умножения
(х —>ах, х—>ха), определенные элементом а. Всякое дифференци-
дифференцирование алгебры 6 имеет вид Д,„ а,2 -(- De2t bn -f- Do, где
1 0\ /О О
о о)' е2==\о ,
О а\ /0 ^ (81)
fll2~~\o о/' *21~V* о
и Do ^ 80. Если ф — подалгебра Картана алгебры 80, то •?> является
подалгеброй Картана и в 8. Если отождествить 80 с Фз?, то за !q
можно принять множество матриц вида ш1Л1-|-ш2Л2, hx = en — е^,
h2 = е22 — е3з- Тогда ф будет расщепляющей подалгеброй Картана
алгебры 8, а корнями алгебры 8 относительно ф будут:
± u)j, ± uJ, ±(u)j — ш2), ±(ш1 + ш2), ±Bш1 + ш2), ± (u)!-f-2uJ).
Центр алгебры 8 равен 0, и, поскольку 8 действует неприводимым
образом в 60, алгебра 8 полупроста. Корни а1 = ш1 — ш2, а2 = ш2
образуют простую систему со схемой Дынкина G2. Следовательно.
8 — расщепляемая простая алгебра типа О2.
§ 6 Построение аггебр 161
Алгебра Кэли E, обладает антиавтоморфизмом х—>х периода 2,
таким, что 1=1, х ——х, если х?60. Обозначим через М%
пространство эрмитовых 3 У. 3-матриц Кэли, определенных этим
антиавтоморфизмом. Таким образом, М\ является множеством матриц
вида
(82)
Если X, Y?Ml to
Х- Y = ~(XY+YX)^Ml (83)
1де А!"К есть обычное матричное произведение Операция умножения,
определенная соотношением (83), наделяет пространство Жз строе-
строением неассоциативной алгебры. Кроме того, операция умножения
в Жз удовлетворяет условиям
X ¦ Y = Y • X, (X2 ¦ Y) ¦ X = X2 ¦ (Y ¦ X). (84)
Этими тождествами характеризуется класс так называемых йор-
дановых алгебр. Следствием тождеств (84) является тот факт, что
если RA обозначает отображение А*->X ¦ А— А ¦ X, то
Da, в = [RaRb) (85)
есть дифференцирование алгебры.
Пусть 8 — алгебра Ли дифференцирований алгебры Жз, и пусть 8о
обозначает подалгебру тех дифференцирований, которые отображают
элементы
e1 = diag{l, 0, 0}, e2 = diag {0, 1, 0}, (86)
e3=diag{0, 0, 1}
в 0. Тогда 80 изоморфна ортогональной алгебре Ли, соответствую-
соответствующей симметрической форме максимального индекса Витта в 8-мерном
пространстве. Пусть ?> — подалгебра Картана алгебры 80, соответ-
соответствующая подалгебре Картана, определенной выше для ортогональ-
ортогональной алгебры Ли (типа ZL). Тогда •?> является расщепляющей под-
подалгеброй Картана алгебры 8.
Алгебра дифференцирований отображает 26-мерное пространство Уо
матриц из Жз со следом 0 в себя. Представление в Уо точно и
неприводимо. Центр алгебры 8 равен 0, так что 8 полупроста.
11 Н Джекобеон
162 Г л IV Расщепляемые полупростые алгебры Ли
Корнями алгебры 8 относительно ф являются:
±шг±ш; I <у = 1, 2, 3, 4
где А( = -д-
(87>
Ш
'2 Ш3 ~Г Ш4^
Корни 1111
ai — ~2 Ш1 2<°2 2 Шз 2 Ш4' а2 ~ Ш4'
ССо - (On ' '¦ * СО*. ОС* -" "~ СОо -—— Шо
образуют простую систему со схемой
112 2
О О . о О
типа F4. Поэтому 8 — расщепляемая простая алгебра типа F4.
Обозначим теперь через 3) алгебру дифференцирований алгебры М\,
а через 8 — множество линейных преобразований в М\, имеющих
Очевидно, что эти преобразования образуют подпространство в про-
пространстве линейных преобразований алгебры М\. Кроме того, если
tr? = O и Е?Ъ, то
IRaRb] € $>. IRaE] = Rae- (89)
Поскольку [3), Щ ? 5), из этих соотношений следует, что 2 есть
алгебра Ли линейных преобразований. Далее, 2 действует в УИз
неприводимым образом и имеет нулевой центр. Поэтому 8 — полу-
полупростая алгебра. Обозначим через $ подалгебру Картана алгебры 3),
определенной выше, и положим $> = <&Rei-.ei-\-<&Rei-e3-^-R. Тогда ф
будет подалгеброй Картана алгебры 8 с корнями
±о>г ±о>;, *<У=1. 2, 3, 4,
± (А, ± ?(«,-«,)). (90)
§ 7 Компактные форчы 163
где S-i и М1 определены соотношениями (87). Корни
I 1 < Ч
а,= — а>! -f- -g- («>б — •"?.)• a2==«i — ">2, а3 = со2 —со3.
а4 = шЗ-Г-Ш4- а5 = —^1 -Г-уК —Шб)' а6 = шЗ — Ш4
образуют простую систему типа Е6. Следовательно, 8 — простая
алгебра типа ?6
Перечисление корней дает следующую таблицу размерностей-
Тип Размерность
О2 14
F4 52 (91)
Ь6 78.
Мы утверждаем также (не приводя доказательства), что алгебры Е7
и Е& существуют и имеют размерности 133 и 248 соответственно.
Заключение. Каждая расщепляемая простая алгебра Ли над
произвольным полем характеристики 0 изоморфна одной из алгебр Av
/>1, Bv />2, С,, />3, D,, />4, построенных выше, или одной
из исключительных алгебр Ли О2, F4, E6, Е7 или ?8. Дальше мы
увидим (гл IX), что перечисленные здесь алгебры неизоморфны
Следовательно, эти результаты дают полную классификацию расщепляе-
расщепляемых простых алгебр Ли над произвольным полем характеристики 0.
В частности, мы получили полную классификацию простых алгебр
Ли над алгебраически замкнутым полем характеристики 0.
§ 7. Компактные формы
Одна из наиболее плодотворных и глубоких идей в теории
групп Ли нашла свое выражение в методе Вейля, с помощью ко-
которого проблемы представлений групп Ли и алгебр Ли сводятся
к случаю компактных групп Ли. Вейль дал этому методу замечатель-
замечательное название „унитарный трюк"') и впервые доказал при помощи
него полную приводимость представлений полупростых алгебр Ли
над алгебраически замкнутым полем характеристики 0. Он исполь-
использовал этот метод также для изучения неприводимых представлений,
для вычисления соответствующих характеров и размерностей этих
представлений. Мы рассмотрим эти вопросы позже. Метод Вейля
делает также возможным применение анализа — через теорию ком-
компактных групп — к алгебрам Ли. Сущность этого метода была фор-
формализована Шевалле и Эйленбергом в следующем виде.
') В оригинале «unitary trick», что, впрочем, более прозаически назы-
называют и унитарным приемом (Вейль [1]). — Прим. ред.
11"
164 Гл. IV. Расщепляемые полупростые алгебры Ли
Свойство Р алгебр Ли называется линейным свойством, если
A) выполнение Р для 8 влечет за собой выполнение Р для 22, где
2 — любое расширение основного поля, и B) если Р выполняется
для Из, где 2 — некоторое расширение основного поля, то оно
выполняется для 8. Тривиальным примером является утверждение,
что dim 8 = п. Из критерия Картана следует, что свойство полу-
полупростоты есть линейное свойство алгебр Ли характеристики 0. Можно
доказать также, что свойство конечномерных представлений таких
алгебр быть вполне приводимыми есть линейное свойство.
Мы введем теперь некоторый класс полупростых алгебр Ли над
полем R вещественных чисел и увидим, что из выполнения линей-
линейного свойства Р для всех этих алгебр следует выполнение свойства Р
для всех полупростых алгебр характеристики 0. Класс, который нам
потребуется, задается следующим определением.
Определение 3. Алгебра Ли 8 над полем R вещественных
чисел называется компактной, если ее форма Киллинга является
отрицательно определенной (отсюда следует полупростота).
Важность компактных алгебр Ли заключается в том, что соот-
соответствующие им группы Ли являются компактными группами. Сле-
Следующий результат есть непосредственное следствие классификации,
принадлежащей Картану, простых алгебр Ли над полем веществен-
вещественных чисел. Доказательство, которое мы приводим ниже и в котором
не используется структурная теория Картана, принадлежит Вейлю.
Теорема 10. Пусть 8— полупростая алгебра Ли над по-
полем С комплексных чисел. Тогда существует компактная
алгебра Ли 8а над полем вещественных чисел, такая, что
„комплексификация" (8а)с^8.
Доказательство. Наша структурная теория применима, так
как поле С алгебраически замкнуто. Пусть et, ft, ht — канонические
образующие алгебры 8, и пусть канонический базис выбран, как
в § 4. Мы видели, что существует такой автоморфизм о алгебры 8,
что e"l=fl, /° = ег Тогда ef = er f"l=:fi и, поскольку ev fi
порождают 8, о2 = 1. Если мы вспомним вид канонического базиса,
определяемого образующими eL, ft, ht, то сразу же станет очевид-
очевидным, что И» = 8-е для любого ненулевого корня а. Поэтому при
любом еа Ф 0 из 8а элемент е'а Ф 0 лежит в 8_а, причем (ел, е"а) =
= ft Ф 0. Если заменить е на е' = Х е , то, очевидно, {е , е'г^ = Х2у)
и, поскольку мы имеем дело с алгебраически замкнутым полем, можно
выбрать \а так, чтобы Х^ = —1. Поэтому мы можем предполагать,
что (еа, е°) = —1 для каждого а. Если выбрать е_а = е'л для по-
положительных корней а (относительно некоторого упорядочения в фоI
§ 7. Компактные формы 165
то это соотношение будет выполняться для всех ненулевых корней,
так как о2 = 1.
Примем теперь за базис алгебры 8 множество элементов
(hv hv ..., hv еа, е_а, ..Л где е_а = е"л, причем эти элементы
удовлетворяют условию
(«.. в.в) = -1 (92)
для каждого ненулевого корня а. Если и и р — ненулевые корни и
3 ф ± а, то
Ke?]=N^n^0, (93)
если а—(-р есть корень, и [еаер] = О в противном случае.
Применив автоморфизм о к этому соотношению, мы получим
соотношение
[e-ae_p] = Na9e_(a+fi или же [е_ае_р]=0. (94)
Нам известно также, что из равенства (еа, е_0[)=— 1 следует [еае_а] = ha,
и ha является рациональной линейной комбинацией элементов ht.
Если теперь ot-f-B также будет корнем, то
(95)
С другой стороны,
e-J e-?\ —
что следует ьз соотношения B0).
Предшествующая цепь равенств может быть продолжена до
Так как а и 8 линейно независимы, то ha и йр также линейно не
зависимы. Сравнивая последнее соотношение и соотношение (95)
находим, что N\$ = [q{r-\- l)/2](a, а) есть положительное рациональ-
рациональное число. Поэтому все числа Na*, где а и В — корни, являются
вещественными.
Поскольку [eahl\=a(hi) еа и а(Л;) рационально, очевидно, что
таблица умножения в базисе, который мы выбрали, имеет вещест-
вещественные коэффициенты. Следовательно, множество линейных комби-
комбинаций элементов базиса с вещественными коэффициентами является
алгеброй 8Х над полем вещественных чисел R, такой, что 81С = Й.
i66 Г л IV Расщепляемые полупростые алгебры Ли
Поскольку еаа = е_а, Л* = — hv а индуцирует в 8Х автоморфизм
периода два. Несколько изменим этот автоморфизм, скомбинировав
его со стандартным автоморфизмом р —> р поля комплексных чисел
А именно, обозначив выбранный базис через (Mt), мы рассмотрим
отображение х ¦ 2рЛ->2р*к°- являющееся полуавтоморфизмом
алгебры 8 в том смысле, что х есть полулинейное преобразование
и [jcy]T = [jcTyT]. Действительно, как нетрудно проверить, (jc-f-y)T =
= *'С+УТ> (pjc)T = pjcT, р^С. Выполнение соотношения [лгу]т = [лгтут]
для отображения т следует прямо из того, что таблица умножения
в базисе ut имеет вещественные коэффициенты Очевидно также,
что х есть автоморфизм алгебры 8, рассмотренной как алгебра над
полем R. Поэтому множество 8а неподвижных относительно т точек
есть /^-подалгебра алгебры 8 Покажем, что 8а и есть требуемая
компактная форма алгебры 2 Очевидно, что х2=1. Поэтому
8B={jc-f-Jc |jc?8}. Отсюда следует, что каждый элемент алгебры 8а
является вещественной линейной комбинацией элементов ut-\-и^,
Y—1 («, — их\ Использовав вид базы {«,} и соотношения hj =
= h'i = — ht, el = el = e_a, мы убедимся в том, что каждый эле-
элемент алгебры 8„ представим в виде вещественной линейной комби-
комбинации элементов
V ' (96)
где а пробегает положительные корни. Эти элементы образуют базис
алгебры 8 над С, откуда следует, что (8а)с = Й. Мы видим также,
что каждый элемент из й„ имеет вид
2 5; У, + 2 (ра+р>-Л
1 и>0
где \} — вещественные числа, ра — комплексные, ра—сопряженные
к ним. Поскольку 8 = (8а)с. форма Киллинга алгебры 8„ является
ограничением на Йв формы Киллинга алгебры 8. Поэтому мы можем
использовать свойства ортогональности и соотношения (еа, е_а)~ — 1
для вычисления
(х, *) = — (*, Щ — 2SpJ.. (97)
а
где А = 2 \lhl Так как (Л, К) > 0, кроме случая h = 0, то очевидно,
что (х, х) < 0 всякий раз, когда х Ф 0. Следовательно, форма
Киллинга яелштся отрицательно определенной.
Пусть теперь Р — линейное свойство алгебр Ли, которым обла-
обладают все компактные алгебры Ли над полем R вещественных чисел
Упражнения 167
f
Пусть, далее, Й— полупростая алгебра Ли над полем Ф характери-
характеристики О, Q — алгебраическое замыкание поля Ф. Тогда алгебра 8а
расщепляема и, следовательно, имеет вид 8оа. где 80—алгебра Ли
над полем Q рациональных чисел.
Но в таком случае 80С есть простая алгебра Ли над комплексным
полем С, поэтому по теореме 10 существует компактная алгебра
Ли 8а над полем вещественных чисел, такая, что ЙаС = 80С. По-
Поскольку свойство Р выполняется для ?а, оно выполняется также
для 8аС = 80С. а поэтому для 80 и для 8og = 2a. Следовательно,
свойством Р обладает алгебра 2.
* Упражнения
Ниже предполагается, что основное поле имеет характеристику 0, а все
v алгебры и модули конечномерны Необъясненные обозначения те же, что
4, ив тексте
1. Показать, что f) является подалгеброй Картана полупростой алгебры
Ли 8 тогда и только тогда, когда A) ?>— максимальная коммутативная
подалгебра и B) ф редуктивна в 8, т. е. adg$> вполне приводима.
2 Пусть ф — подалгебра Картана полупростой алгебры Ли 8. Показать,
что если R — любое конечномерное представление алгебры 8, то hR полу-
полупросто для каждого Л € ф.
3. Пусть 8, — полупростая подалгебра полупростой алгебры Ли С, и
пусть ?i -«¦ подалгебра Картана в 8^ Показать, что ф, может быть вложена
в подалгебру Картана алгебры 8.
.'*& s 4. Использовать метод § 3 для получения канонического базиса и таб-
^» лицы умножения алгебр А2 и О2.
? 5 Использовать метод § 3 для получения корней расщепляемой алгебры Ли
*" типа Е7 (предполагая, что такая алгебра существует) и показать таким спо-
*"i собом, что размерность этой алгебры равна 133
6. Не использ}я описания связных схем Дынкина, показать, что схема
3 _ 1 1
не может быть схемой Дынкина никакой матрицы Картана. (Указание по-
показать, что множество корней, определенных этой схемой, содержит такой
корень р, что 2р также является корнем)
7 Показать, что структурные константы канонического базиса (§ 3)
' расщепляемой полупростои алгебры Ли являются рациональными числами,
Знаменатели которых имеют вид 2*3', где k и 1-^ целые числа
8. Доказать, что любая расщепляемая полупростая алгебра Ли может
быть порождена двумя элементами.
** 9. Пусть 8 = ©?, где (? — алгебра линейных преобразований A-\- 1)-мер-
ного векторного пространства, и пусть (Л В) — форма Киллинга ал1е-
бры 8. Показать, что
(А В) =!
(Указание использовать упражнение 3 9.)
10. Выразить формы Киллинга алгебр типов Вь Ci и D; через формы
следа tr AB, используя представление этих алгебр, указанное в § 6.
168 Г л IV. Расщепляемые полупростые алгебры Ли
11. Показать, что если 8 — расщепляемая алгебра, а ф — расщепляю-
расщепляющая подалгебра Картана, то f)-)-2^« есть максимальная разрешимая под-
а>0
алгебра, а 2 8<* — максимальная нильпотентная подалгебра алгебры 8.
а>0
12. Определить группу Вейля расщепляемой алгебры Ли типа С?2 и
расщепляемой алгебры Ли типа Ai.
13. Пусть а, — простой корень и а—положительный корень, отличный
от Oj. Показать, что каждый корень вида a-\-ka.i, где k — целое число, по-
положителен. Показать, что 2' (a -f- fe*(, а,) = 0, где суммирование распро-
ft
странено по всем таким k, что a-f- kal есть корень (а — любой положитель-
положительный корень). Доказать, исходя из этого, что 2 (а> ai) = (ак ai) или
tt>0
а>0
Глава V
УНИВЕРСАЛЬНЫЕ ОБЕРТЫВАЮЩИЕ
АЛГЕБРЫ
В этой главе вводится понятие универсальной обертывающей
(ассоциативной) алгебры U алгебры Ли й. Основное значение ал-
алгебры U заключается в возможности сведения теории представлений
алгебры 8 к теории представлений ассоциативной алгебры U. Важное
свойство ал1ебры U состоит в том, что алгебра 8 изоморфна под-
подалгебре алгебры U^. Это дает возможность получить точное пред-
представление каждой алгебры Ли. Для конечномерных алгебр Ли в сле-
следующей главе будет получено усиление этого результата, а именно
будет показано, что каждая такая алгебра имеет точное конечно-
конечномерное представление. В этой главе мы рассмотрим основные свой-
свойства алгебры U. Некоторые из них будут использованы для дока-
доказательства важной формулы Кэмпбелла — Хаусдорфа, выражающей
произведение экспоненциалов в ассоциативной алгебре. Мы дадим
также принадлежащее Картану и Эйленбергу определение групп
когомологий алгебр Ли.
Исследование в этой главе не будет ограничиваться ни случаем
конечномерных алгебр, ни случаем алгебр характеристики 0. В дей-
действительности часть этой главы будет посвящена некоторым понятиям,
характерным для случая характеристики р Ф 0. Основным здесь
является понятие ограниченной алгебры Ли характеристики р, 'воз-
'возникающее при рассмотрении подпространств ассоциативной алгебры,
замкнутых относительно отображения а->ар, а также относительно
произведения [ab\ = ab— ba. Ограниченные алгебры Ли имеют
ограниченные представления, ограниченные дифференцирования и т. д.
Кроме того, можно определить „ограниченную" универсальную оберты-
обертывающую алгебру, называемую «-алгеброй. После краткого обсуждения
этих понятий мы рассмотрим теорию абелевых ограниченных алгебр Ли.
§ 1. Определение и основные свойства
Центральное понятие этой главы — понятие универсальной обер-
обертывающей алгебры алгебры Ли — является основным инструментом при
изучении представлений и, более общо, при изучении гомоморфизмов
алгебры Ли Й в алгебру Ли ty.L, где % — ассоциативная алгебоа
с единичным элементом. Любой такой гомоморфизм может быть
170 Гл. V. Универсальные обертывающие алгебры
„продолжен" до гомоморфизма (ассоциативной) универсальной обер-
обертывающей алгебры U в И. Всюду в этой главе мы будем иметь дело
с алгебрами Ли и ассоциативными алгебрами, содержащими единич-
единичный элемент. Напомним, что мы условились (гл. I) о следующей
терминологии: под „алгеброй" мы будем понимать ассоциативную
алгебру, содержащую единичный элемент 1, под „подалгеброй" —
подалгебру в обычном смысле, содержащую 1, и под гомоморфизмом
алгебр—гомоморфизм в обычном смысле, переводящий 1 в 1.
Определение 1. Пусть 8 алгебра Ли (произвольной раз-
размерности и характеристики). Пара (U, I), где U — алгебра, а I — гомо-
гомоморфизм алгебры 2 в \Xlt называется универсальной обертываю-
обертывающей алгеброй алгебры 8, когда выполняется следующее условие:
если ЭД — любая алгебра и б — гомоморфизм алгебры Й в %L, то
существует однозначно определенный гомоморфизм 9' алгебры И в 5(,
такой, что % = 1%'. Другими словами, диаграмма
11 = U/.
,1
2 в 21 = ЗЦ
где I и 9 — гомоморфизмы алгебры 8, может быть дополнена до
коммутативной диаграммы
где 9'— гомоморфизм алгебры U.
Ряд важных свойств алгебры (U, V) заключен в этом определении
или является простым следствием основных фактов из теории пред-
представлений. Мы сформулируем эти свойства в виде следующей
теоремы.
Теорема 1.
1. Пусть (U, I), B3, j) — универсальные обертывающие ал-
алгебры для 8. Тогда существует однозначно определенный изо-
изоморфизм j' алгебры U на 23, такой, что j = ij'.
2. Алгебра U порождается образом 8i.
3. Пусть 8а и 82—алгебры Ли, a (U,, /j), (U2, i2)—соответ-
i2)—соответствующие универсальные обертывающие алгебры, и пусть
§ 1. Определение и основные свойства 171
а — гомоморфизм алгебры 8j в 82. Тогда существует одно-
однозначно определенный гомоморфизм а' алгебры U[ в Ц2, такой,
что otf2 —fi*', т. е. диаграмма
коммутативна.
4. Пусть 23— идеал в 8, и пусть $—идеал в Ц, порожден-
порожденный образом 23/. Если /?8, то J: / + 23-»•/i-f-$ есть гомо-
гомоморфизм факторалгебры 8/23 в ЗЗ^ где 23 = Ц/$, и C3, У) есть
универсальная обертывающая алгебра для 8/23.
5. Алгебра U обладает однозначно определенным анти-
антиавтоморфизмом к, таким, что /тс = — /. Кроме того, те2=1.
6. Существует один и только один гомоморфизм Ь', назы-
называемый диагональным отображением алгебры U eU®U, такой,
что ай'= а/® 1 + 1 ®. а/, а ?8.
7. Ясли D — дифференцирование алгебры Ли 8, то суще-
существует такое однозначно определенное дифференцирование D'
алгебры U, что Di = Ш'.
Доказательство.
1. Если мы используем определяющее свойство универсальной
обертывающей алгебры (U, /) и гомоморфизм 8 = у алгебры 8 в 23^,
то получим однозначно определенный гомоморфизм j' алгебры Ц
в 33, такой, что j = ij'. Подобным же образом получаем гомомор-
гомоморфизм /' алгебры 33 в U, такой, что i~ji'. Поэтому j — ji'j' и
i = ij'i'. С другой стороны, j = j\v, где \v есть тождественное
отображение в 33. Из свойства единственности гомоморфизма 6'
в определении алгебры C3, j), примененного к тому случаю, когда
6= j, следует, что i'j'=\v. Аналогично j't' = \a — тождественное
отображение в U. Поэтому / является изоморфизмом алгебры U
на 23.
2. Пусть 33 — подалгебра, порожденная образом 8/. Отображе-
Отображение i может быть рассмотрено как отображение алгебры Ли 8 в 23?.
Поэтому существует однозначно определенный гомоморфизм I' ал-
алгебры U в 23, такой, что i = ii'. Поскольку t = t\u и гомоморфизм /'
можно рассматривать как отображение Ц в U, из условия однознач-
однозначной определенности гомоморфизма следует, что i' = lu. Поэтому
и = Шв = Ш'Е», откуда 33 = U.
172 Гл. V. Универсальные обертывающие алгебры
3. Если а — гомоморфизм Й1 в Й2. то а?2 — гомоморфизм 2г в \X2L.
Поэтому существует однозначно определенный гомоморфизм а'
алгебры Uj в U2, такой, что /ja' = a/2.
4. Заметим сначала, что отображение /—>// +ft алгебры Й
в 23 = U/ft есть гомоморфизм алгебры й в 23А. Поскольку 23/Е ft,
23 отображается в 0 при этом гомоморфизме. Мы получаем, таким
образом, индуцированный гомоморфизм /-f- 23-> II-\~ ft алгебры Й/23
в 35?. Это и есть отображение у. Пусть теперь 6 — гомоморфизм
алгебры Ли Й/23 в %L, где % — алгебра. Тогда отображение
yj: I —> (I -\- 23) 6 будет гомоморфизмом Й в %L. Поэтому существует
гомоморфизм if алгебры U в 31, такой, что irf = г\. Если 6 ?23,
то 6^ = 0, так что Ы лежит в ядре гомоморфизма rf. Но тогда
и ft принадлежит ядру гомоморфизма if, и, следовательно, мы по-
получаем индуцированный гомоморфизм 0': и -\- ft —> urf алгебры
23=U/ft в$. Далее, (Z-f 23) 6 = l-q = Urf и (/+23O6' = (//•+ ft) 6' =
= Urf. Поэтому 6=у6', что и требовалось установить.
Остается доказать, что гомоморфизм 6' определен однозначно.
Для этого достаточно показать, что (Й/23) у порождает 23. Согласно
п. 2, алгебра U порождена образом й/, откуда следует, что 23 по-
порождена классами смежности li -\- ft. Поскольку (/ -f- 23) у = // -f- ft,
алгебра 23 порождается множеством элементов вида (/-f~23)y, т. е.
множеством (Й/23) у. Этим завершается доказательство 4.
5. Если имеется антигомоморфизм \х' алгебры 51 в алгебру 23,
то нетрудно проверить непосредственно, что — [л/ будет гомомор-
гомоморфизмом 3Ii в 93^. Пусть U — алгебра, антиизоморфная алгебре U
при отображении и—>И[л/ алгебры U. (Очевидно, что такая алгебра
существует.) Отображение 6 = — /ц/ является гомоморфизмом ал-
алгебры Й в ML. Поэтому существует гомоморфизм 6' алгебры U в U,
такой, что 6 = — i\x' = /6'. Пусть тс = 6'([л/) :- Тогда тс—антигомо-
тс—антигомоморфизм алгебры U в себя, причем /тс = — /. Поэтому /тс2 = /, и
так как 8/ порождает U, а тс2 есть гомоморфизм, то тс2=1. Следо-
Следовательно, тс—антиавтоморфизм алгебры U. Тот факт, что тс опре-
определен однозначно, также немедленно следует из того, что Й/ поро-
порождает U.
6. Соображения, использованные при определении произведения
представлений и модулей (§ 1.6), показывают, что отображение
а —> ai ® 1 -\- 1 ® ai, а ? Й, является гомоморфизмом алгебры Й
в (U & U)t. Поэтому существует однозначно определенный гомомор-
гомоморфизм 8' алгебры U в И (g U, такой, что а/8' = а/ ® 1 -f- I ® at.
7. Пусть D — дифференцирование алгебры Ли Й. Построим
алгебру 112 B X 2)-матриц с элементами в универсальной оберты-
обертывающей алгебре U и рассмотрим отображение
at aDC
0 а
§ 1. Определение и основные свойства 173
алгебры 2 в V^. Это отображение линейно, причем
at aDt\/bi bDt\ / bt bDi\/ai апГ
О at До Ы )~\0 Ы До at
[at, Ы] [at, bDi]^- [aDi, bi]\ /{ab]i [a, b\Di\
О [at, bt] / \- О [ab]i )' B)
Поэтому 6 является гомоморфизмом 2 в U2?- Отсюда следует, что
существует гомоморфизм 8' алгебры U в U2. такой, что 6 = /6'.
Поскольку
at aDi \
Ш'6' = ^0 at ) C)
и элементы ai порождают U, мы получаем, что для любого х ? Ц
где у однозначно определен элементом л;. Выразим этот факт, запи-
записав у = xD'. Вычисление, подобное доказательству формулы B),
показывает, что D' — дифференцирование алгебры й. Тогда фор-
формула C) дает равенство aiD' = aDi. Поэтому tD'= Di, что и тре-
требовалось установить. Единственность D' следует из того, что Ш
порождает U, а дифференцирование полностью определяется своим
действием на образующие.
Займемся теперь построением универсальной обертывающей ал-
алгебры. Обозначим через 2! тензорную алгебру над векторным про-
пространством 2. По определению
2 = 01981882® ••• Ф2,ф .... E)
где 2j = g и 2; = 2®2® ... ®2 (t раз). В %, кроме обычных
операций векторного пространства, определено умножение, обозна-
обозначаемое через ® и характеризуемое свойством
= хг® ... ®xl®yl® ... ® у}. F)
Пусть 5? — идеал з X, порожденный всеми элементами вида
[ab] — a®b + b®a, а, Ь?й, G)
и пусть 11 = 27$. Обозначим через i ограничение на 2 ==2, канониче-
канонического гомоморфизма алгебры % на алгебру U. Тогда
[ab] I — ai ®Ы-\- Ы ® ai —
= $ = 0 (в U).
t
174 Гл V. Универсальные обертывающие алгебры
Поэтому i является гомоморфизмом g в UL. Докажем теперь сле-
следующее утверждение.
Теорема 2. Алгебра (U, i) является универсальной обер-
обертывающей алгеброй алгебры 8.
Доказательство. Напомним сначала основное свойство тен-
тензорной алгебры, заключающееся в том, что любое линейное отобра-
отображение 6 алгебры 8 в алгебру % можно продолжить (единственным
образом) до гомоморфизма алгебры % в %. Действительно, если
{Uj\j?J} есть базис в 8, то хорошо известно (и легко доказы-
доказывается), что различные тензорные одночлены и. ®и ® ... ®и
h H 'п
степени п образуют базис в 8Я. При этом а. ®а. ® ... ®м. =
— uk ® ик ® .. . <g) ик в том и только том случае, когда j'r — kT,
г=1, 2, ..., п. Элемент 1 и различные тензорные одночлены сте-
степеней 1, 2, ... образуют базис в U. Легко проверить, что линей-
линейное отображение 6" алгебры J в 51, такое, что 16" = 1,
(и. ®uj.®...®uJ\B" = fUj 6)(и. 6\ . .. (Uj 6), является гомо-
гомоморфизмом X в $, причем аб" = аб для a?8(==gjC!J). Пусть
теперь 6 — гомоморфизм алгебры Ли Й в 3Ii и 6" — продолжение
этого гомоморфизма до гомоморфизма алгебры J в 21. Если
а, Ь?й, то
[ab] 6" — (ев*) F8") + F6") (об") =
= [ab] 6 — (ад) F6)+(Ьд) (ад) =
= [аЬ, Ьд] — (аЪ)фд)-{-фд)(ад) —
= 0.
Следовательно, образующие G) идеала К принадлежат ядру гомо-
гомоморфизма 6". Мы получаем, таким образом, индуцированный гомо-
гомоморфизм 6' алгебры И в 21, такой, что aZ6' = (a-f-SSN' = ab" = ад.
Поэтому 6 = ;6', и существование требуемого гомоморфизма дока-
доказано. Тензорная алгебра 2! порождается алгеброй g, откуда следует,
что алгебра U порождается Ш. Поскольку два гомоморфизма, сов-
совпадающие на образующих, тождественны, существует лишь один
гомоморфизм 6', такой, что id' = 6.
§ 2. Теорема Пуанкаре — Биркгофа — Витта
Как мы уже отмечали, если {«/|/?./}, где J—некоторое
множество, является базисом в g, то тензорные одночлены
tt] ®Uj (g) .. ®Uj степени п образуют базис в 8Я, ге>1. Пред-
Предположим теперь, что множество индексов упорядочено; мы исполь-
используем это -упорядочение для введения частичной упорядоченности
§ 2. Теорема Пуанкаре—Биркгофа—Витта 175
в множестве одночленов любой заданной степени п ^ 1. Определим
индекс одночлена и. ®и. ® . . . ® и . , полагая
Jl }2 >п
ind(M ®и ® ... ®и )= 2 4k> (8)
где
\ 1. если /,>/,
для всех /, ?, t <C k. Заметим, что индекс равен 0 в том и только
в том случае, когда j\ <^ у2 ^ ... <! jn. Одночлены, обладающие
этим свойством, будут называться стандартными. Предположим
теперь, что jk > jk+v и сравним
indfa. ®u ® ... ®и, )
и
ind/м. ® ... ®и ®и. ® . . . ®и ),
где второй одночлен получается из первого перестановкой и . , и.
Обозначим через r\lk числа t\ для второго одночлена. Тогда
^ч=\г если 1' -!фк> ^Н-1''
i, у
еСЛИ
если
Следовательно,
indfM, (gi ... ®и \ =
— l-\-\nd(u. ® ... ®и, ®и. ® ... ®и. V
V ;l ¦'ft+l •'ft ¦'n/
Мы используем эти замечания для изучения алгебры U = XjR, отно-
относительно которой докажем сначала следующее утверждение.
Лемма 1. Каждый элемент из X сравним по mod ^
с Ф-линейной комбинацией единицы и стандартных одно-
одночленов.
Доказательство. Достаточно доказать это утверждение для
одночленов. Упорядочим одночлены по степеням, а для данной сте-
степени— по 1 ндексам. Чтобы доказать наше утверждение для одно-
одночлена и, ®м. ® ... ®и, , достаточно предположить, что оно
•Ч }2 >п
выполнено для одночленов меньшей степени, а также для одночле-
одночленов той же степени п, но меньшего индекса, чем данный одночлен.
176 Гл. V. Универсальные обертывающие алгебры
Допустим, что наш одночлен нестандартный, и предположим, что
h > Jk+v Тогда
и, ® ... ®и. = и ® ... ®и, ®а, ® ...®а, +
>\ 'п h 'к+\ 'к 'п
-\-и. ® ... ®(и ®и — и ®а. )® ... ®и .
Поскольку а, ®и. —и. ®и.~=\и.и. 1 (modК),
а. ® ... ®и ==и, ® ... ®и. ®и, ® ... ®и. +
>\ 'п h >k+i >k 'п.
+ и, ® ... ®\и. а. ]® ... ®а. (mod К).
Первый член правой части равенства имеет меньший индекс, чем
данный одночлен, а второй член является линейной комбинацией
одночленов меньшей степени. Требуемый результат получается отсюда
по индукции.
Мы покажем теперь, что классы смежности 1 и стандартных
одночленов линейно независимы и, следовательно, образуют базис
в алгебре U. Для этого рассмотрим векторное пространство *$„
с базисом и1и1 . . . аь , ;, ^ ;2 <С .. . <^я, lj?J> и векторное про-
пространство ^ = Ф1 ©^©^2© • • •• Требуемая линейная независи-
независимость будет легко вытекать из следующего утверждения.
Лемма 2. Существует линейное отображение о алгебры 2
в ?р, такое, чтр
1о = 1. (ati ®uh® ... ® uln) a = utuh ... и^,
если 1Х <^2^ • • • ^С1п< (9
(и. ® ... ® и — и. ® ... ®а. ®ut ® ... ® и. \ а =
= {и.{® ... ®[ujkujkj® ...®u.y. A0)
Доказательство. Положим 1о= 1. Пусть gBiy—подпростран-
gBiy—подпространство в Йя, натянутое на одночлены степени п и индекса, не превос-
превосходящего у. Предположим, что линейное отображение а уже опре-
определено на Ф1©Й,© ... ©2„_1, причем для одночленов из этого
пространства выполняются условия (9) и A0). Распространим о по
линейности на 01©^© ... ©Й„_,©ЙЛ|0, положив
для стандартных одночленов степени п. Допустим, далее, что о уже
определено на Ф1 ©Sj© ... ©8n_j©8ni/_j, причем выполняются
условия (9) и A0) для одночленов, принадлежащих этому простран-
пространству. Пусть теперь одночлен и, ® ... ®и. имеет индекс i^-l,
§ 2. Теорема Пуанкаре—Биркгофа—Витта 177
1 пусть jk > Jk+v Тогда положим
(и ® ... ®и )а = (и ® ... ®и ®и
-Н(«Л® ... ®[«;Л + 1]® ... ®«Уя)а. A1)
Это определение корректно, поскольку оба члена в правой части
равенства принадлежат пространству «Pl©^© ... ©2„_1©2„, t_v
Покажем сперва, что определение A1) не зависит от выбора пары
C/ftA+i)- Jk>Jk+v пУсть (yWi+i) —Другая пара, где jt> jt+v
Возможны два существенно различных случая: I. / > k -\- 1,
И. l = k-\-l.
I. Положим и ~и, и. =v, и. =w, и =х. Тогда по
'k >k+\ 'i ]i+i
тредположению индукции мы можем записать правую часть равен-
равенства A1) следующим образом:
(. . . v®a® ... ® x®w® .. .)а-\-
... ®v®u® ... ®[wx]® ...)a +
. . . [uv]® ... ®x®w® . . .
Если же мы начнем с пары (у'г, /;+i). то получим
... ®x®w® .. .)а-\-
u®v® ... ®[wx]® ...
= (... ®v®u® ... ®x®w® ..
••• ®x®w® ...
Мы видим, что результат получился тот же, что и в первом
случае.
II. Положим и, —и, и —v — u., и. =w. Используя
предположение индукции, можно придать правой части равен-
равенства A1) вид
(... w®v®u .. . ) о -f- (. .. [vw] ®u . . .) a -j-
-f-( . .. v®[uw] ... )<j-f-(... [mi;]® w .. . )a. A2)
Аналогично, если мы начнем с выражения
(... u®w®v ... )о + (... и® [vw] . . . )о,
то придем к выражению
(.. .tw®v®u ., . )о + (. . . w®[uv] ... )a-f
... [uw]®v ...)a + (... и®[щда] ... )a. A3)
178 Г л V Универсальные обертывающие алгебры
Таким образом, нам нужно показать, что о аннулирует следующий
элемент пространства Ф1ФЙ!© ... ®%
. • ¦ u®[uw] . . .) — (. . . [uw]®v . . .)+ A4)
(. . . [uv] ® w . . .)— (.. . w ®[uv] . . .).
Из свойств отображения а на пространстве Ф1ф ... ф2л-1 легко
следует, что если (. . . а ® Ъ . . .)? 2„_г где а, Ь?%х, то
(... a®b ...)o—(... b®a ...)e — (... [ab] . . .)а —0. A5)
Поэтому применение а к элементу A4),дает
(. . . [[vw]u] . . .)a-f(. . . [v[uw]] . . .)а +(. . . \\uv\w\ . . .)а. A6)
Так как
[ [vw] u]-\-[v [uw] ]-\-[ [uv] w] = [ [vw] u]-\-[ [wu\v]-\-[ [uv] w] = 0,
то выражение A6) равно 0. Следовательно, и в этом случае правая
часть равенства A1) однозначно определена. Мы применим теперь
равенство A1), чтобы определить отображение а для одночленов
степени п и индекса L Линейное продолжение этого отображения на
пространство Й„_, дает отображение пространства Ф1 ф .. . фЙ„_1ф
фЙл>(, удовлетворяющее нашему условию. Этим завершается доказа-
доказательство леммы. Мы можем доказать теперь следующую теорему.
Теорема 3. (Пуанкаре — Биркгоф — Витт). Классы
смежности единицы и стандартных одночленов образуют ба-
базис алгебры U —?/$.
Доказательство. Лемма 1 показывает, что каждый класс
смежности является линейной комбинацией 1 —)— S? и классов смежно-
смежности стандартных одночленов. Лемма 2 позволяет построить линейное
отображение о алгебры J b^J, удовлетворяющее условиям (9) и A0).
Легко видеть, что каждый элемент идеала 5? есть линейная комбина-
комбинация элементов вида
uji ® ... ®Ujn — uJi® ... ®ujk^®ujk® ... ®и,п —
~ujx® ... ®[ujkujk+i]® ... ®ujn.
Поскольку а переводит эти элементы в 0, $а = 0 и, следовательно, a
индуцирует линейное отображение алгебры и = ?/$ в ^Р- Из усло-
условия (9) следует, что индуцированное отображение переводит классы
смежности единицы и стандартного одночлена ut ® ... ® щ соот-
1 tl
ветственно в 1 и at Ui ... Ui . Из линейной независимости образов
в 9(J мы получаем линейную независимость в U классов смежности
единицы и стандартных одночленов. Этим завершается доказательство.
§ 2. Теорема Пуанкаре—Биркгофа—Витта 179
Следствие 1. Отображение I алгебры 2 в U взаимно одно-
однозначно и Ф1П& = 0.
Доказательство. Если (uj) — базис алгебры 2 над Ф, то
l = l-f-$ и классы смежности up — a;-f- $ линейно независимы.
Отсюда следуют оба утверждения.
Введем теперь следующее упрощение в наши обозначения. Будем
обозначать произведение в U обычным для ассоциативных алгебр спо-
способом через ху, а единичный элемент в U—через 1 и будем ото-
отождествлять 2 с ее образом 2/ в U. Это подалгебра алгебры Ли \\L,
поскольку тождественное отображение является изоморфизмом 2 в Ui.
8 также порождает U, и теорема Пуанкаре—Биркгофа-—Витта
утверждает, что если {Uj\jczJ}, где J—упорядоченное множество,
является базисом в 2, то элементы
1, uiui2... tt.r, /1<i2<..., A7)
образуют базис в U. В частности, если алгебра 8 имеет конечный
базис ttj, м2> ..., ип, то элементы
м*1м*2 ... и*», k. = 0, 1, 2, ... A8)
(и0.— Is), образуют базис в U. Определяющее свойство алгебры Ц
может быть переформулировано следующим образом: если 6 есть
гомоморфизм алгебры 2 в %L, где % — некоторая алгебра, то 6 может
быть однозначно продолжен до гомоморфизма 6 (ранее обозначавше-
обозначавшегося через 6') алгебры И в 51 В частности, представлению R алге-
алгебры Ли 2 соответствует однозначно определенное представление R
алгебры Ц.
Отсюда следует, что любой модуль Ш над алгеброй 2 может
быть рассмотрен одним и только одним способом как правый U-мо-
дуль, в котором xl, х ?Ш, /?2 определено для Ш как для 2-модуля.
Обратно, ограничение на 2 представления алгебры U является пред-
представлением алгебры 2, и любой правый U-модуль определяет правый
2-модуль, если ограничиться умножением на 2- В дальнейшем мы
будем свободно переходить от S-модулей к Ц-модулям и обратно
без каких-либо оговорок.
Теорема Пуанкаре — Биркгофа — Витта (далее при ссылках на
нее мы будем обозначать эту теорему П — Б — В) дает характериза-
цию универсальной обертывающей алгебры в следующем смысле.
Пусть 2 — подалгебра алгебры Ли %L, где 21 — алгебра, обладающая
тем свойством,f что если {Uj\j?J} есть некоторый упорядоченный
базис в 2, то элементы 1 и стандартные одночлены М/ ut .. . ut ,
^i -^2^ • • • ~^h< образуют базис в %. Тогда % (рассматриваемая
вместе с тождественным отображением) является универсальной оберты-
обертывающей алгеброй для 2. В самом деле, существует гомоморфизм
универсальной обертывающей алгебры Ц в %, совпадающий на 2
12*
180 Г л V. Универсальные обертывающие алгебры
с тождественным отображением. Наше условие показывает, что этот
гомоморфизм взаимно однозначен и является отображением на. По-
Поэтому 31 может рассматриваться как универсальная обертывающая
алгебра.
Предположим теперь, что 93 — подалгебра алгебры Й, и пусть
U — универсальная обертывающая алгебра для 2. Мы можем выбрать
упорядоченный базис {uj\j?J} в Й таким образом, что J — K[) L,
К [\L= 0, &</, если k?K, l^L, и {uk\k?K} будет упорядо-
упорядоченным базисом в 23. Пусть 93 — подалгебра алгебры U, порожден-
порожденная 23 (или элементами uk). Тогда, очевидно, 1 и стандартные одно-
одночлены «*,«*, ... «й > kx ^ &2 ^ • • • ^ ks, образуют базис в 93. Поэтому
можно принять 93 за универсальную обертывающую алгебру для 23.
Допустим теперь, что 23 есть идеал в Й и что обозначения со-
сохранены прежние. Пусть $—идеал в U, порожденный идеалом 23.
По теореме 1 (часть 4) 93=U/5t и отображение а-)-23—>а-|-$
определяют универсальную обертывающую алгебру для Й/23. Согласно
следствию 1, отображение а -\- 23 —>• а -\- R взаимно однозначно, так
что мы можем отождествить Й/23 с подалгеброй (й-)- &)/Я алгебры 93г.
Эта подалгебра является множеством классов смежности а-\-$ и
имеет базис {at-\- $|Z?L}. Поэтому, по теореме П — Б — В, классы
смежности 1 -\-R и щ щ ... ut -\-R, lx <CZ2 ^С • • • ^С<> образуют
базис в 93. Если, в частности, 55 есть подпространство, порожден-
порожденное 1 и стандартными одночленами и^и^ ... щ то ?)П$ = 0. За-
Заметим далее, что любой стандартный одночлен вида
«ft,«ft2 ••¦ ик$щх ... U[t, A9)
где s^-1 и f^-О, лежит в К, и эти одночлены вместе с 1 и М/ ... щ ,
h ^ h ^ • • • ^С h' исчерпывают все элементы стандартного базиса
алгебры U. Отсюда следует, что элементы A9) образуют базис в 5?.
Основные результаты о подалгебрах и идеалах, полученные нами,
могут быть суммированы в виде такого утверждения.
Следствие 2. Пусть Й—алгебра Ли, Ц — ее универсаль-
универсальная обертывающая алгебра. Тогда подалгебра в U, порожден-
порожденная подалгеброй 23 алгебры Ли Й, может быть принята за
универсальную обертывающую алгебру для 23. Если 23 есть
идеал в Й, то факторалгебра Й/23 может быть отождествлена
с (Й + Я)/Я, где К—идеал в U, порожденный 23, и 23 = U/$ есть
универсальная обертывающая алгебра для й/23. Кроме того,
множество стандартных одночленов A9) образует базис в К,
если (Uj) — такой упорядоченный базис в Й, что (uk) является
базисом в 23.
Положив в этом следствии 23 = й, мы увидим, что идеал Uo,
порожденный алгеброй Й в U, имеет базис, состоящий из стандарт-
§ 2. Теорема Пуанкаре—Виркгофа—Витта 181
ных одночленов и* и* ... U[ , t^^i^^. ,.. ^.ir. Поскольку эти эле-
элементы вместе с 1 образуют базис в U, мы получаем
Следствие 3. Пусть U^—идеал в U, порожденный алгеб-
алгеброй Ли 8. Тогда Ц = Ф1фио.
Поскольку вложение 8 в U взаимно однозначно и поскольку каж-
каждая алгебра (ассоциативная алгебра с единицей) имеет точное пред-
представление, мы получаем
Следствие 4. Каждая алгебра Ли имеет точное пред-
представление линейными преобразованиями.
Остается переформулировать следующие основные свойства алге-
алгебры Ц, установленные в теореме 1.
2'. Алгебра 8 порождает Ц.
3'. Всякий гомоморфизм алгебры Ли gj в алгебру Ли 82 может
быть продолжен до однозначно определенного гомоморфизма универ-
универсальной обертывающей алгебры Uj алгебры Ях в универсальную
обертывающую алгебру U2 алгебры Й2.
5'. Существует единственный антиавтоморфизм тс алгебры U, удо-
удовлетворяющий условию атг =—а для а ?2.
6'. Существует такой гомоморфизм Ь (диагональное отображение)
алгебры U в U®U, что а8 = а®1-|-1®а, a?g.
Т'. Любое дифференцирование D алгебры Ли 2 может быть про-
продолжено единственным образом до дифференцирования D алгебры U.
Докажем далее
Следствие 5. Диагональное отображение 8 алгебры U
в U®U взаимно однозначно.
Доказательство. Разложение U —Ф1 0UO индуцирует разло-
разложение и®и = ФA®1)еA®ио)е(ио®1)©(ио®ио), где 1®UO —
подпространство элементов вида 1®6, ??U0, UO®1—подпростран-
UO®1—подпространство элементов вида b®\, b?U0, и U0®U0 — подпространство эле-
элементов вида 2^®^'> Ь< ^'6^0- Справедливы равенства 18=1® It
ab = a®l-\-l®a, а?%. Поскольку U0®U0 есть идеал в U®U,
легко доказать индукцией по г, что
[щи^... и1т)Ъ==щх ... uit®\ + \%u1x ... «ir(modU0®U0),
где (и() — базис в 8. Отсюда следует, что образы элементов стан-
стандартного базиса 1, Ui ... ui , t1 -<j2 ^ ... <ir, при отображении Ь
линейно независимы. Поэтому 8 взаимно однозначно.
Примеры. A). Пусть 8 — алгебра Ли с базисом и, v и табли-
таблицей умножения [uv] = и. Тогда Ц имеет базис v^uk, причем выпол-
выполняется условие коммутирования
uv — vu = и. B0)
182 Гл. V. Универсальные обертывающие алгебры
Следовательно,
)u. B1)
Элементами алгебры U являются многочлены
vo~\-v1a-\-v2u2+ ... +vmam,
где vi ? Ф [v]. При умножении этих многочленов, кроме обычных
правил, нужно учитывать также соотношения
u"f(v) — f(V-^k)uk, k = 0, I, 2, .... B2)
являющиеся следствием условия B1). Это тип кольца разно-
разностных многочленов.
B) Пусть й — абелева алгебра с базисом (uj). Тогда U — коммута-
коммутативная алгебра с базисом, состоящим из 1 и одночленов и,- «; . .. н,- ,
г1^г'2^ •¦• -С^л- Это означает, что элементы и;- алгебраически не-
независимы и что U есть алгебра многочленов относительно Uy
§ 3. Фильтрация и градуированная алгебра
со
Алгебра 91 называется градуированной, если %=^%, (сумма
прямая), tде 2^ — такие подпространства, что %%j С %1+1- Примером
градуированной алгебры является тензорная алгебра 2 = ®1®2j®
ф22ф ..., где мы полагаем ?0 = Ф1, %1 = Ч1, если i > 0. Другим
примером является алгебра многочленов от алгебраически независимых
элементов; в этой алгебре % будет пространством однородных эле-
элементов степени L Если ?! — произвольная градуированная алгебра, то
элементы из %i называются однородными элементами степени i,
и каждый элемент а ? 3( может быть представлен единственным спо-
оо
собом в виде а = 2 ai< аг€^г> гДе «; = 0 для всех I, кроме конеч-
о
ного числа. Элементы at называются однородными компонентами
элемента а. Левый (правый) идеал 23 в % называется однородным,
00
если 23 = 2 (® П $;)• Это эквивалентно тому, что #?23 тогда и
2=0
только тогда, когда его однородные компоненты #г?23.
Говорят, что семейство подпространств 91A> (/ — неотрицательное
целое число) определяет на алгебре ЭД фильтрацию, если выпол-
выполнены следующие условия:
A) ti]^t}\ если *</;
B) U ^"==31;
§ 3. Фильтрация и градуированная алгебра 183
C) ЧИи)Жи) е 9t(i+;). Если % — градуированная алгебра, и мы поло-
положим %{1) = 2 $/> т0 тем самым на алгебре Щ. будет определена фильт-
i
рация. Другим стандартным приемом получения алгебры с фильт-
фильтрацией является следующий. Пусть % — произвольная алгебра, и пусть
Ш — подпространство в %, порождающее % как алгебру. Отсюда
следует, что ЭД = Ф1 -\-Ш-\-Ш2-\- ..., где Ш' — подпространство,
порожденное всеми произведениями из I элементов, взятых из Ш.
Положим 5СA) = Ф1 —(— Ш2 —Ь~ ¦•• +ЗИ'. Тогда очевидно, что подпро-
подпространства ЭД(() определяют фильтрацию на %. Эта конструкция при-
применима, в частности, к универсальной обертывающей алгебре U
алгебры Ли 8 и к пространству 2I = 2 образующих алгебры 91.
Важным понятием, относящимся к алгебре ЭД с фильтрацией,
является понятие ассоциированной градуированной алгебры
9t = G(9t). Эту алгебру можно получить из векторного пространства
2, Я/ = Я1')/^'). B3)
2=0
где мы полагаем ?t(~I) = 0. Умножение в ЭД определяется покомпо-
покомпонентно формулой
(al + ^l-1))(aJ-\-^-1))=salaJ-t^l'1~l\ B4)
если at€%ll), а}?%и\ Если в, s ft, (mod S^') и eysas^^od^),
то a^j — bfoj(mod$( + ¦^~1)). Поэтому формула B4) дает однозначно
определенное произведение элемента из 91; на элемент из ЭД;-, причем
результат лежит в %i+j. Это можно распространить по аддитивности
на все пространство %. Легко видеть, что мы получаем, таким обра-
образом, градуированную алгебру %, где ЭД; является пространством одно-
однородных элементов степени /.
Пусть Ъ ? % и, более того, Ь ? 21(п>, Ъ ? %{п~1). Элемент"* = b + %\(п'1)
является однородным элементом степени п в % и называется стар-
старшим членом элемента Ь. Если b — 0, то мы полагаем старший член
равным 0. Если b и с имеют один и тот же старший член степени п,
то b — с^ЭД*"*. Любой однородный элемент из 91 является старшим
членом какого-либо элемента из %. Если b — старший член эле-
элемента Ь, а с — старший член для с, то либо Ьс = О, либо be является
старшим членом элемента be. Из этих замечаний следует, что если 23 —
левый идеал в %, то множество сумм старших членов элементов из 23
является однородным левым идеалом 23 в %. Мы можем доказать
теперь следующую теорему.
184 Гл. V. Универсальные обертывающие алгебры
Те©рема 4. Пусть ЭД-— алгебра с фильтрацией, Щ.— ассо-
ассоциированная с ней градуированная алгебра. Если Ж не имеет
делителей нуля, отличных от нуля, то % тоже не имеет
делителей нуля, не равных нулю. Если кольцо $ нётерово
слева (справа), то и% нётерово слева (соответственно справа)
(определение см. ниже).
Доказательство. Пусть Ь, с ?%, ЬфО, с ФО. Предположим,
что Ъ и с — их старшие члены. Тогда по определению ЬфО, сфО
и, следовательно, ЬсФО. Поэтому be есть старший член элемента be,
и он отличен от 0. Следовательно, ЬсфО. Утверждение о том, что
некоторое кольцо является нётеровым слева, означает, что в этом
кольце выполняется условие обрыва возрастающих цепей для левых
идеалов. Как хорошо известно, это эквивалентно условию конечности
базисов для каждого левого идеала. Предположим, что $ обладает
этим свойством. Пусть 23 — левый идеал в 31, и пусть 23— соответ-
соответствующий однородный левый идеал в %, состоящий из сумм старших
членов элементов b ? 23. По предположению 23 имеет образующие
(bv b2, ¦ • ¦, br). Пусть Ь1—старший член элемента bt ? 23 (/ = 1, . . ., г).
Мы утверждаем, что элементы bt порождают 23, т. е. каждый эле-
элемент 6 ?23 имеет вид 2 cfii< ^?91-
Допустим, что старший член b элемента b имеет степень п. Можно
предположить, что утверждение верно для элементов со старшими
членами степени меньше п. Очевидно, b = ^icibl, ct<^%. Опуская
некоторые из членов cibi (при сравнении однородных компонент), мы
получаем Ь = 2 сД/> гДе элемент с;- однороден и Cjbj однороден
степени п. Тогда Cj есть старший член элемента Cj, а старший член
элемента 2 cfij есть Ь. Следовательно, d = b—2 СА/6 ^" • так
что d принадлежит левому идеалу, порожденному элементами bj. По-
Поэтому b принадлежит левому идеалу, порожденному bj. Для правых
идеалов доказательство аналогично.
Докажем теперь следующий результат из теории колец, который
мы применим к универсальной обертывающей алгебре конечномерной
алгебры Ли.
Теорема 5. (Голди — Орэ). Пусть % — кольцо (ассоциа-
(ассоциативное с 1) без ненулевых делителей нуля, удовлетворяющее
условию обрыва возрастающих цепей для левых идеалов. Тогда
кольцо Щ. обладает левым телом частных (определение см.
ниже).
Доказательство. Голди принадлежит следующая часть этого
утверждения; для любых двух ненулевых элементов а, Ь^Ш суще-
§ 3. Фильтрация и градуированная алгебра 18d
ствует ненулевое общее левое кратное m = Ь'а = а'Ь. Это утвержде-
утверждение эквивалентно тому, что пересечение главных левых идеалов
%а П Ш> Ф 0. Для доказательства этого рассмотрим [следуя Лезье
(Lesieur) и Круазо (Croisot)] последовательность идеалов Жа,
%a-\-%ab, %а^ГЖаЬ-\-%аЬ2, .... Из условия обрыва возрастаю-
возрастающих цепей следует, что найдется число k, для которого abk+l ?$La-\-
.. + %abk. Тогда abk+1 = хоа-\- хгаЬ-\- . .. -\-хkabk,
t^ Поскольку в % нет делителей нуля, abk+l Ф 0, так что не
все Х; = 0. Если обозначить через xh первый отличный от нуля коэф-
коэффициент, то abk+1 = x/labfl-\-xh+1abh+l-{- ... -\-xkabk, х1гФ0. Со-
Сокращая на bh, получаем
Поэтому в % выполняется свойство общего (левого) кратного. Орэ
показал, что любое кольцо без ненулевых делителей нуля имеет левое
тело частных тогда и только тогда, когда для каждой пары ненуле-
ненулевых элементов a, b существует ненулевое общее левое кратное
т= а'Ь — Ь'а. Напомним, что 3) называется левым телом частных
для кольца $, если A) 5D есть кольцо с делением (тело); B) %—под-
кольцо кольца 5D; C) каждый элемент кольца 2) имеет вид а~1Ь,
а, Ь?% (см. Джекобсон [1], стр. 223).
Применим теперь наши результаты к универсальной обертываю-
обертывающей алгебре Ц алгебры Ли 2. Как и раньше, используем фильтра-
фильтрацию алгебры U, определенную подпространствами
и@) = Ф1, и(г) = Ф1 + 2 + Й2+ ... +Йг, />1. B5)
Пусть U = G(U) — ассоциированная градуированная алгебра. Из опре-
определения G(U) легко следует, что ? —иA)/и@) = (Ф1 —|— Й)/Ф 1 поро-
порождает U, поскольку U порождается алгеброй 8. Отсюда если {iij\j?J},
где J—упорядоченное множество, есть базис в 2, то классы смеж-
смежности Uj— и.;-\-Ф\ в \ХХ порождают всю алгебру U. Из равенств
вуа, = и//И-и^),_й4а";=:вйву4-иA) и ujull — uku]=^[ujuH]^U{1)сле-
uku]=^[ujuH]^U{1)следует, что uktij= u]uk. Таким образом, образующие алгебры U коммути-
коммутируют и, следовательно, U является коммутативной алгеброй. Каждый
элемент из U представляется в виде линейной комбинации элементов
1 (= 1), «г,"^ ... Uin, ii <^2< ... -Оя- Из определения и из тео-
теоремы П — Б — В легко следует, что различные стандартные одно-
одночлены, указанные здесь, образуют базис в U. Это означает, что му
алгебраически независимы и U есть обычная алгебра многочленов от
этих элементов. Из полученных нами общих результатов и свойств
колец многочленов вытекает следующая теорема относительно U.
186 Г л V Универсальные обертывающие алгебры
Теорема 6.
1. Универсальная обертывающая алгебра U любой алгебры
Ли 2 не имеет ненулевых делителей нуля.
2. Если алгебра 2 конечномерна, то U удовлетворяет усло-
условию обрыва возрастающих цепей для левых и правых идеалов
и у алгебры U существует левое (и правое) тело частных.
Доказательство.
1. Поскольку U является кольцом многочленов от алгебраически
независимых элементов над некоторым полем, в U не существует не-
ненулевых делителей нуля. Следовательно, по теореме 4 в самой
алгебре U нет делителей нуля, отличных от нуля.
2. Если в 2 имеется конечный базис uv и2, ..., ип, то Й является
алгеброй многочленов от uv u2 ип. Эта алгебра удовлетворяет
условию обрыва возрастающих цепей идеалов по теореме Гильберта
о базисе. Следовательно, по теореме 4 кольцо U нётерово слева и
справа и, согласно теореме Голди — Орэ, обладает левым и правым
телом частных.
§ 4. Свободные алгебры Ли
Понятие свободной алгебры (свободной алгебры Ли), порожден-
порожденной множеством X = [Xj\j?J}, может быть введено таким же спо-
способом, что и понятие универсальной обертывающей алгебры ал-
алгебры Ли.
По определению свободная алгебра (свободная алгебра Ли) есть
пара (g. О ((?$• 0)> гДе 3 — алгебра (соответственно алгебра Ли g2)
и / — отображение множества X в § (Зй)« такое, что если 0 — любое
отображение множества X в алгебру % (алгебру Ли 23), то суще-
существует единственный гомоморфизм б' алгебры g (§2) в % B3), лая
которого б = <9'.
Легко построить свободную алгебру, порожденную любым мно-
множеством X. Для этой цели возьмем векторное пространство Ш с ба-
базисом X и образуем тензорную алгебру g (= ?) =г ф 1 ф 2)? ф
0BИ®2И)ф ... над Ш.
За отображение I можно принять вложение множества X в §.
Пусть теперь 9 — отображение множества X в алгебру %. По-
Поскольку X есть базис в Ш, 9 может быть продолжено единственным
образом до линейного отображения пространства Ш в алгебру 91,
последнее в свою очередь может быть продолжено до однозначно
определенного отображения 8 алгебры g в 9t. Поэтому § и отобра-
отображение вложения X в g есть свободная алгебра, порожденная мно-
множеством X.
Прямая конструкция свободной алгебры Ли, порожденной мно-
множеством X, несколько громоздка. Удобнее получить эту алгебру
§ 4 Свободные алгебры Ли 187
с помощью свободной алгебры g, порожденной X. Обозначим через %%
подалгебру алгебры Ли %L, порожденную подмножеством X. Пусть
9 — отображение X в алгебру Ли 23, и пусть U — универсальная
обертывающая алгебра для 23, содержащая эту алгебру Ли (по тео-
теореме Пуанкаре — Биркгофа — Витта последнее предположение оправ-
оправдано). Тогда мы имеем право рассматривать 9 как отображение X
в U, которое может быть продолжено до гомоморфизма б алгебры §
в U. Кроме того, 9 является гомоморфизмом алгебры Ли gz, B Йл и,
поскольку б отображает X в подмножество алгебры 23 (<S U), огра-
ограничение 9 на подалгебру gg алгебры ^L, порожденную X, есть гомо-
гомоморфизм §g в 23. Мы показали, таким образом, что 6 можно про-
продолжить до гомоморфного отображения §g в 23. Так как X поро-
порождает §g, б единственно. Поэтому пара §g и отображение вложения X
в gg является свободной алгеброй Ли, порожденной множеством X.
Заметим, далее, что % (и отображение вложения) есть универ-
универсальная обертывающая алгебра алгебры gg. Действительно, пусть
6—гомоморфизм gg в алгебру Ли %L, где ЭД — некоторая алгебра.
Тогда существует гомоморфизм 9' алгебры g в 21, совпадающий
с ограничением б на X. Очевидно, 9' является также гомоморфизмом
алгебры Ли %L в Щ.ь, и, следовательно, ограничение 9" гомомор-
гомоморфизма б' на gg будет гомоморфизмом gg в %L.
Поскольку хб" = х9 для всех х?Х и X порождает gg, оче-
очевидно, что б" совпадает с заданным гомоморфизмом б алгебры gg
в %L. Таким образом, мы продолжили б до гомоморфизма 6' ал-
алгебры gel. Так как gg порождает §> то ясно, что это продолже-
продолжение единственно. Поэтому § является универсальной обертывающей
алгеброй алгебры Ли gg.
Только что полученные результаты могут быть сформулированы
в виде следующей теоремы.
Теорема 7 (Витт). Пусть X—произвольное множество,
и пусть §—свободная алгебра, (свободно) порожденная мно-
множеством X. Обозначим через $g подалгебру алгебры Ли ^L,
порожденную элементами из X. Тогда gg является свободной
алгеброй Ли, порожденной X, а § — ее универсальной оберты-
обертывающей алгеброй.
Для простоты мы ограничимся теперь случаем, когда множество X
конечно: Х = [хх, х2, ..., хг}. Тогда
и мы будем писать g=^{x, хг). Алгебра % градуирована,
причем Шт = 2В ® Ш ® ... (g 2Я (т раз) будет пространством одно-
однородных элементов степени т. Базисом этого пространства является
188 Г л V Универсальные обертывающие алгебры
множество одночленов вида XiXi ... X; , Ь«=1, 2, ..., г; по-
12 m J
этому dim Ttm = г .
Элемент а ? g называется элементом Ли, если а ? g8. Мы полу-
получим два важных критерия того, что некоторый элемент алгебры g
является элементом Ли. Заметим сначала, что достаточно исследовать
тот случай, когда данный элемент а является однородным. Действи-
Действительно, рассмотрим совокупность линейных комбинаций элементов Ли
вида
где ij = \, 2 г, т=1, 2 Из тождества Якоби следует,
что это подпространство есть подалгебра в ^L. Поскольку эта под-
подалгебра содержит xt, она совпадает с %%. Мы видим, таким образом,
что каждый элемент из §8 является суммой однородных элементов
Ли. Поэтому некоторый элемент будет элементом Ли тогда и только
тогда, когда его однородные компоненты будут элементами Ли. Мы
видим также, что если а — однородный элемент Ли степени т, то а
есть линейная комбинация элементов вида B6).
Пусть g'—идеал 2){ф (Ш ® Ш) Q .. . в %. Элемент из g лежит в 3'
в том и только том случае, когда он является линейной комбина-
комбинацией одночленов xi ... X; , т^>\. Поскольку различные одно-
одночлены этого типа образуют базис в ^', мы получаем линейное ото-
отображение о идеала %' в %%, определяемое соотношениями
Рассмотрим также присоединенное представление алгебры §8. Так
как % есть универсальная обертывающая алгебра для §8, то это
представление может быть продолжено до гомоморфизма 0 алгебры §
в алгебру <Е(^8) линейных преобразований пространства %^. При
этом
К • • • XimXh ¦ ¦ ¦ XJt)a = l •¦[[¦ ¦•[XhXl>\ • • • XUX'l] • • • */,]=»
Отсюда следует равенство
(uv) a = (ио) (-У0), и ? 8'- v?%. B8)
Если а, #?§2. то
[ab]a = (ab) о — фа) о = (аа) F6) — фа) (аб) =
= (аа) adb — (ba) ad a —
= [аа, b} + [a, ba]. B9)
Таким образом, ограничение отображения о на §8 SS §' является
дифференцированием алгебры gg. Мы можем использовать этот ре-
результат для получения следующего критерия.
§ 4. Свободные алгебры Ли 189
Теорема 8 (Шпехт — В е в е р). Если Ф— поле характе-
характеристики О, то однородный элемент а степени т > 0 является
элементом Ли тогда и только тогда, когда ао — та, где а —
линейное отображение §' в §й> определенное соотношениями B7).
Доказательство. Это условие, очевидно, является достаточ-
достаточным (даже для случая характеристики р при условии, что p-fm).
Пусть теперь а — однородный элемент Ли степени т. Используем
индукцию по т. Мы видели, что а есть линейная комбинация чле-
членов вида B6). Поэтому достаточно доказать равенство аа = та для
элемента а вида B6). В этом случае
[... [х, х,-2] ... */J° = [[. • ¦ [*,,*«,] ¦ • • *«„_,]о. **
„ „
откуда и следует требуемое утверждение.
Другой наш критерий для элементов Ли, уже не требующий ре-
редукции к однородным элементам, заключается в следующем.
Теорема 9 (Фридрихе). Пусть ^ = Ф[х1, ..., хг} — сво-
свободная алгебра, порожденная элементами xt над полем харак-
характеристики^), и пусть 8— диагональное отображение алгебры g.
т. е. гомоморфизм алгебры § в S®S- такой, что х,Ъ =
= *i ® 1 + 1 ® xt. Тогда a^g будет элементом Ли в том и
только в том случае, когда a8==a®l-f-l®a.
Доказательство. Из равенства [а®1-\- I ® а, Ь®1-\~
-\- 1 ®b] = [ab] ® I -f-1 ®[ab] следует, что множество элементов а,
удовлетворяющих условию a8 = a®l-f-l®a, образует подалгебру
алгебры Ли §?• Эта подалгебра включает в себя xt. Поэтому она
содержит gg. Пусть ylt у2, ... будет базис в §й. Тогда, поскольку g
есть универсальная обертывающая алгебра для §8, элементы
у\ху\г ... у„т, где т — произвольное число, kt ^ 0 (у0. —IV обра-
образуют базис в §. Поэтому произведения
образуют базис в §®S- Справедливо равенство
C0)
190 Гл. V. Универсальные обертывающие алгебры
где * обозначает линейную комбинацию базисных элементов вида
у1'У>12 ¦ ¦ ¦ yis® У1\У1<2~ • • • У* с 2^ > 1- Слагаемые от второго до
(от+1)-го включительно не входят в аналогичные выражения ни для
какого другого базисного элемента у[^у2г • ¦ ¦ yls- Таким образом,
для того чтобы аа было линейной комбинацией базисных элементов
вида у^1 ... yl/®\ и \®у[х ... yJ/, необходимо и достаточно,
чтобы в выражении а через выбранный базис входили с отличными от
нуля коэффициентами только базисные элементы у^ ... у^1, где все
k. — O, кроме одного &( = 1. Это означает, что а есть линейная
комбинация у{. Поэтому а?§й. Итак, условие ab = a® l-^-l ® a
необходимо и достаточно, чтобы а ? §Й
§ б. Формула Кэмпбелла — Хаусдорфа
С помощью нашего критерия для элементов Ли выведем теперь
формулу Кэмпбелла — Хаусдорфа для произведения экспоненциалов
в алгебре. С этой целью нам потребуется расширить свободную ал-
алгебру § = Ф {xv ¦ ¦ ., хг] до алгебры g формальных степенных рядов
от переменных xt. Вообще, пусть % — градуированная алгебра, %i —
подпространство ее однородных элементов степени I, / = О,*4!, 2
Пусть % — полная прямая сумма пространств %t. Таким образом, эле-
оо
ментами % являются выражения вида 2 аг = аоН~ ai H~ •••• причем
о
2ai = 2*i тогда и только тогда, когда ai = bi, i = 0, I, 2, ....
Сложение и умножение на скаляры определены покомпонентно. Мы
введем умножение в % при помощи формулы
где
Легко проверить, что % будет алгеброй. Кроме того, подмножество
в "Ж тех элементов 2 ai- У которых компоненты at — 0 для всех
i > m, m —0, 1, 2, .... есть подалгебра, которую можно отожде-
отождествить с 91. Подмножество 91(г> элементов вида al-\- at+l-\- ... обра-
образует идеал в %, причем П $((> = 0. Определим норму в %, полагая
|0| = 0, |а| = 2^, если афО и a?$(i), a?S(i+1). При этом вы-
выполняются следующие свойства:
(I) [ а | ^> 0 и |а| = 0 лишь в том случае, когда а = 0.
§ 5. Формула Кэмпбелла—Хаусдорфа 191
(II) |eft|<|e||ft|.
(Ill) |e + ft|<max(|e|, |*|).
Введенное нормирование наделяет 2( структурой топологической ал-
алгебры. Сходимость рядов Xj + x2+ ..., X; ? 9t, определяется обыч-
обычным способом. Из неархимедовости нормы (свойство (HI)) вытекает
очень простой критерий сходимости: ряд Xj + x2+ ... сходится
тогда и только тогда, когда |х, |—>0. Очевидно, что подалгебра 91
всюду плотна в %.
Если характеристика основного поля равна 0 и z?2t(I), то
?г + ?г+... C1)
--J— ... C2)
являются однозначно определенными элементами в Ж (т. е. указан-
указанные ряды сходятся). Прямое вычисление показывает, что
exp(log(l + z))=l + 2, log (exp z) = z. C3)
Далее, если zv Z2?%{]) и [2j22] = 0, то
exp 2, exp 22 = exp Bj + z2) C4)
log(l + ^)A + 22) = log(l + zt)+ log(l + z2). C5)
Рассмотрим все эти построения применительно к алгебре 9l = g=
= Ф{х1 хг}. В результате мы получим алгебру 3> называемую
алгеброй формальных степенных рядов от переменных xt. При-
меним также эту конструкцию к алгебре §®§. Поскольку § = 2
1=0
(сумма прямая), где $, есть подпространство однородных элементов
степени I, то 3 ® 3 = 2 (§г ® 3/) (сУмма прямая). Далее, (Зг®3;)Х
XC«'®3/')S3«"+«' ®3/+/'- Поэтому, если мы положим C®3)*=
3®3 + 3®3+ +33 gg(gg
o о* ft,
S C ® 3)*+г и 3 ® 3 = 2 C ® 3)*- Отсюда следует, что 3 ® 3 есть
градуированная алгебра, а C®3)* — подпространство однородных
элементов степени k. Мы можем поэтому построить алгебру 3 ® 3-
оо
Если a = 2ai- аг€3г> то элементы 2(а/®0 и 2A ®ai) ПРИ-
о
надлежат алгебре 3 ® 3l будем обозначать их через а ® 1 и 1 ® а
соответственно. Отображения а—>а®1 и а->1®а являются изо-
изоморфизмами и гомеоморфизмами алгебры 3 в 3®3- При этом
192 Г л V Универсальные обертывающие алгебры
[а ® 1, 1 ® Ь] = 0 для любых а, ? ? $. В случае характеристики О имеют
место также формулы ехр (а ® 1) = ехр а ® 1, ехр A ® а) == 1 ® ехр а
и аналогичные формулы для функции логарифм.
Обозначим через §Й подмножество элементов ^ вида Ь1~\- Ь2-{- • ¦ •.
где ^г — элемент Ли из подпространства §;. Очевидно, что §Й — под-
подалгебра алгебры Ли %L. Диагональный изоморфизм S алгебры § в
может быть продолжен до изоморфизма алгебры *g в *g®S- Заметим
сначала, что если а;?^г, то #;§ ? (S ® §)г- Это утверждение полу-
т
чается индукцией по I с помощью формул S;= 2 x$i-\> xft —
} = i
CO
= xJ®l-\-l®x]. Поэтому если a = 2a<> аг63г> T0 S a^ будет
вполне определенным элементом алгебры *g® *g. Обозначим эту сумму
через аЬ. Ясно, что отображение 8: a—>a8 является изоморфизмом
и гомеоморфизмом алгебры^ ⧮^. Если применить теорему Фрид-
рихса к а(, то нетрудно вывести, что в случае характеристики О
элемент a=2a;> ai6S,-> принадлежит алгебре Ли $8 в том и только
том случае, когда аЪ — а®1-\-1®а.
Допустим теперь, что г = 2, обозначим образующие через х, у
и запишем ^ = ф{х, у). Допустим также, что характеристика равна 0.
Рассмотрим элемент ехр х ехр у алгебры §. Можно записать этот
элемент в виде 1 -f- z, где z = zl-\- z2-\- ..., zt^^t, так что
ехр х ехр у = 1 -\- z — ехр w, C6)
где w = \og(l -\-z). Мы докажем
Предложение 1. Элемент w = log (ехр х ехр у) является
элементом Ли, т. е. да^^й.
Доказательство. Рассмотрим (ехр х ехр у) 8. Очевидно,
(ехр х ехр у) 8 = (ехр хЬ) (ехр уЬ) =
= ехр (х ® 1 -f 1 ® х) ехр (у ® 1 + 1 ® У) =
= ехр(х® 1)ехрA ® х)ехр(у® 1)ехрA ® у) =
— (ехр х ® 1) A ® ехр х) (ехр у ® 1) A ® ехр у) =_
= (ехрх ® 1)(ехру ® 1)A ® ехр х)A ® ехр у) =
— (ехр х ехр у ® 1) A ® ехр х ехр у).
1 >этому A -г 2)8 = (A -f г)® 1)A ®A + z)) и, следовательно,
= log(l + z) ® 1 -|- 1 ® log A + z).
§ 6. Когомологии алгебр Ли. Стандартный комплекс 193
Это показывает, что элемент log (I -f- z) удовлетворяет условию тео-
теоремы Фридрихса об элементах Ли. Поэтому Iog(l-)- 2)?^#.
Теперь, когда нам известно, что w — \og(\ -f г) есть элемент Ли,
мы можем получить, используя теорему Шпехта — Вевера, явную фор-
формулу для этого элемента. Действительно,
V х" у"
г = ехр х ехр у— x=2u~pTq\l />4<7>0,
р. я
и
i > 0. C7)
V V
и 2л
m
i
Pi+4i>
x"< /i
0.
=ss
Поэтому
SV1 (— \\ml x v?1 xPm \ч™
Так как это элемент Ли, то, применив оператор о к членам степени k,
мы получим k раз взятую однородную компоненту степени k этого
элемента. Отсюда мы находим следующее выражение Iog(l-f-2) как
элемента Ли:
log(l -j-z) =
Р\ «i "m
(-I)-1 f... [...[¦¦¦ \...\[xx\...x]y}... у] '...у] ...у] ^
2(^ + 9/) P^Q^ ... PjqJ
C9)
Легко вычислить первые несколько членов этого ряда. Получается
следующая формула:
logA + z) = х -f- у + j [ху] + ~ [ [ху] у] + ~ [ [ух]х]-\- D0)
§ в. Когомологии алгебр Ли. Стандартный комплекс
В этом параграфе мы дадим принадлежащее Картану и Эйленбергу
определение групп когомологии алгебр Ли и покажем, что оно экви-
эквивалентно определению, данному ранее в § 3.10. Для получения опре-
определения Картана — Эйленберга будем исходить из поля Ф, рассма-
рассматривая его как тривиальный модуль над У, т. е. положим '/ = 0,
?? Ф, /?8. Как этот, так и все другие ^-модули могут рассматри-
рассматриваться как правые модули над универсальной обертывающей алгеброй U
алгебры fc, поскольку каждое представление алгебры Ли й единствен-
13 Н. Джекобсон
194 Гл. -V. Универсальные обертывающие алгебры
ным образом продолжается до представления алгебры U. Всюду в даль-
дальнейшем под U-модулем мы будем понимать правый U-модуль. Напом-
Напомним, что модуль называется свободным, если он является прямой
суммой подмодулей, изоморфных модулю U. Предположим, что имеется
последовательность свободных U-модулей Хо, Хх, Х2, ... с U-гомо-
морфизмом е модуля Хо в Ф и U-гомоморфизмами di_l модулей Xt
в Xi_l, такими, что последовательность
Оч— ф^—^^-^^-^ч— ... D1)
точна, т. е. е является гомоморфизмом на, ядро Кеге равно образу
Imd0 и KerdJ_i = lmd/ для каждого i~^>\. Последовательность D1)
называется свободной резольвентой модуля Ф. Пусть теперь Ш будет
произвольным модулем над 8, а следовательно, и над U. Обозначим
через Hom(Xi, Ш), t^-О, множество U-гомоморфизмов модуля Xi
в 2Я. Обычные операции сложения и умножения на скаляры наде-
наделяют Нот (Xt, ffi) структурой векторного пространства над Ф. Если
т); ? Нот (Xt, ffi), то dpii ? Нот (^/+i, Ш). Мы получаем, таким образом,
отображение 8,: т;(—>й(т)г пространства Y\om{Xlt Ш) в Нот(А'<+1, Ш),
I > 0. Это отображение линейно; более того, из точности последо-
последовательности D1) следует, что dl+ldi = Q, /^-0, откуда 8(8i+1 = O.
Поэтому ImS; s Кег8г+1. Теперь можно определить i-ю группу кого-
мологий алгебры 8 относительно модуля Ш как факторпространство
KerS^ImS^p />>1, и Кег80 для / = 0. Теория Картана — Эйленберга
показывает, что эти группы не зависят от выбора резольвенты D1)
для Ф.
Не вдаваясь здесь в детали этой теории, мы удовлетворимся тем,
что дадим конструкцию резольвенты D1), которая, как нам кажется,
со
наиболее полезна. Пространство Xss^X^ которое мы получим,
о
называется стандарным комплексом алгебры 8. Оказывается, что
стандартный комплекс имеет, помимо структуры векторного простран-
пространства, еще и структуру алгебры. Вследствие этого при надлежащих
условиях можно определить алгебру когомологий вместо групп кого-
мологий.
Предположим теперь, что нам дано представление R алгебры Ли 8
дифференцированиями алгебры 21. Пусть U будет универсальной
обертывающей алгеброй для 8. Определим тогда новую алгебру
B1, U, R) — алгебру дифференциальных операторов представле-
представления R алгебры й. Пространством алгебры (&, U, R) будет 31 <g U.
Поскольку отображение, ставящее в соответствие элементам v?VL их
левые умножения vL(u—>vu), является антигомоморфизмом, отобра-
отображение /-> —lL является представлением алгебры 8, действующим в U.
Мы образуем теперь тензорное произведение этого представления и
заданного представления R в Ж. Полученное представление отобра-
§ 6. Когомологии алгебр Ли. Стандартный комплекс 195
жает / в линейное преобразование, переводящее а ® а в alR ®а —
— а® 1а. Можно продолжить это представление до представления
алгебры U, которое мы будем записывать теперь как ttL, где к — анти-
антигомоморфизм алгебры U, такой, что /тг =— /, /?й, и L — антигомо-
антигомоморфизм алгебры U в алгебру линейных преобразований простран-
пространства 91®II. Образ элемента v?VL при отображении L обозначим
через Lv. Тогда (а ® и) {I (irZ.)) = alR ® а — а® la; поэтому
(а ® ujLt = a®lu — alR®u. D2)
Если Ъ ?21, то мы определим Lb как линейное преобразование в 21® U,
такое, что
(a®u)Lb = ba®u. D3)
Отображение b-+Lb будет антигомоморфизмом алгебры Щ. в алгебру
линейных преобразований пространства it®U. Из формул D2) и D3)
следует, что
(а ® и) Z.UZ., — ba®lu — фа) lR®u =
— ba®lu — blRa®u — b(alR)® a,
(a ® u) LtLb = ba®lu — b(alR) ® a,
{a®u)LblR—{blR)a®a.
Поэтому мы получаем формулу
{LbL^ = -LblR, D4)
которая показывает, что множество линейных преобразований Lb
образует идеал в алгебре Ли линейных преобразований вида Lb -\- Lv
Отсюда следует, что обертывающая алгебра X этого множества пре-
преобразований является множеством отображений вида 2 Lu La (см. § 2.2).
Мы имеем каноническое отображнние пространства $®U в X,
переводящее 2а/®мг в 2 Lu La. Если /^8, то \lR---Q, так как
lR — дифференцирование. Поэтому A ® v) Lt === 1 ®lv и, следовательно,
A ®v)La= I ®uv, и, v^\X. Отсюда A ® \)LuLa = а®и, так что
^tai®ui = 0, если ^LuLa=Q. Таким образом, отображение
2jflj®"j->2^ La является изоморфизмом векторных пространств.
Поскольку множество отображений вида ^LuLa есть алгебра, мы
можем наделить пространство 21 ®U структурой алгебры, условив-
условившись считать наше отображение антиизоморфизмом алгебр. Получен-
Полученная алгебра, пространством которой является 21 ®U, и будет той
алгеброй (U, U, R), которую мы хотели определить.
Из наших определений непосредственно вытекает, что подмноже-
подмножество в B1, U, R) элементов вида а ® 1 образует подалгебру, изо-
изоморфную %. Мы отождествим ее с Ж и будем писать элемент а вместо
196 Гл. V. Универсальные обертывающие алгебры
а® 1. Аналогично, множество элементов вида 1 ®и, где и?Ц, обра-
образует подалгебру, изоморфную U. Мы отождествим ее с U и будем
писать и вместо l<g,M. Отображение алгебры B1, U, /?) = 2t®U в X
переводит а = а® 1 в LlLa = Lawu=l®UB LULX = Lu. Формула
D4) дает следующую основную формулу коммутирования в B1, U, R):
. D5)
Поскольку каждый элемент из Ж имеет вид 2 ^« ^-а,. каждый элемент
из Bt, U, R) имеет вид 2 aiui< #/6$.
тогда и только тогда, когда 2а(®м; = 0 в
Установим теперь следующее свойство „универсальности" алгебры
(I, U, Я).
Предложение 2. Пусть 2)—некоторая алгебра, и пусть
0j — гомоморфизм алгебры Щ. в 2), а 62— гомоморфизм алгебры U
в 3), связанные соотношением
[Ьв1,Щ = {Ьв1){1в2) — Aв2)(Ьв1) = (Ь1«)в1, Ь?П, /?2. D6)
Тогда существует единственный гомоморфизм б алгебры Ct, U, У?)
в D, такой, что Ьд = ЬЬг, мб = и02.
Доказательство. Образуем прямую сумму B1, U, /?)©2),
которую будем рассматривать как алгебру пар (х, d), x?Bt, U, У?),
d?2); сложение и умножение определяются покомпонентно. Суще-
Существуют гомоморфизмы itj, ir2 этой алгебры соответственно на C1, U, R)
и на D, определенные равенствами <х, d)uj = x, (x, d)t:7 — d. Пусть
g) - подалгебра этой прямой суммы, порожденная элементами (a, a9j)
и (м, иб2), а ?21, M^U. Отображение Uj индуцирует гомоморфизм
подалгебры *}) на C1, U, Я), а отображение те2 индуцирует гомомор-
гомоморфизм S)J на подалгебру алгебры I), порожденную элементами аЬх и
йй2, ag2t, «^U.
Из формул D5) и D6) мы получаем следующее соотношение в ty:
(а, аЬ{)A, /62) — (/, /92)(а, 06^ = (а/*, (а/*) в^. D7)
Это позволяет нам осуществить собирательный процесс, подобный
тому, который мы осуществляли при обсуждении конструкции алгебры
B1, U, R), для записи элементов подалгебры ^) в виДе
2 (с,. а,в,) («,, иг62). «*€«• «i€«-
Из свойств тензорного произведения 2t(gU(=BL U, R)) следует,
что существует гомоморфизм векторного пространства (ЭД, U, У?) на ^),
переводящий 2 а(мг в 2 (ar c/^i)(Mi' м(бг)- Из существования этого
отображения вытекает, что пх является изоморфным отображением
подалгебры §) на B1, U, R). Тогда e = uf!u2 будет гомоморфизмом
§ 6. Когомологии алгебр Ли. Стандартный комплекс 197
алгебры C1, U, R) в D, таким, что аО = ащ 'к2 = (а, а61)тг2 = а01
и мб = ищ \г2 = (и, и62)тс2 = и02. Единственность гомоморфизма 0
следует из того, что 31 и U порождают C1, U, R).
Замечание. Если Ш — множество образующих алгебры 31, то,
для того чтобы имело место утверждение предложения 2, достаточно,
чтобы соотношения D6) выполнялись для всех b ? Ш. Это следует
из того непосредственно проверяемого факта, что множество элемен-
элементов Ь, удовлетворяющих условию D6) для всех /?8. образует под-
подалгебру алгебры 31.
Мы рассмотрим теперь некоторое обобщение понятия дифферен-
дифференцирования.
Определение 2. Пусть 3t и 23 — алгебры, sx и s2 — гомо-
гомоморфизмы алгебры 31 в 23. Тогда линейное отображение d алгебры 31
в 23 называется (sv s^-дифференцированием, если выполняется ра-
равенство
(ab)d = (asx)(bd)-\-(ad)(bs2). D8)
Как легко проверить, условия, которым удовлетворяет отображе-
отображение d, в точности таковы, чтобы Гарантировать, что отображение
'as, ad\
О asj <49)
будет гомоморфизмом алгебры 31 в алгебру 232 2 X 2-матриц. (Частный
случай этого замечания был использован в доказательстве пункта 7
теоремы 1.) Если 3t — подалгебра алгебры 23 и sx— соответствующее
вложение, то отображение d мы назовем 82-дифференцированием,
а если s2 — также вложение, то мы получаем дифференцирование
алгебры 31 в алгебру 23. Нетрудно проверить либо непосредственно,
либо с помощью гомоморфизма D9), что если d есть {sx, s2)-диффе-
s2)-дифференцирование, то его ядро является подалгеброй. Отсюда следует,
что d — Q, если 9JJd = O, где Ш — множество образующих алгебры 31.
Далее, если dx и d2 являются (sx, 52)-дифференцированиями, то и
dx—d2 будет (Sj, $2)-диффереицированием. Поэтому очевидно, что
dx — d2, если xdx = xd2 для каждого х ? Ш.
Рассмотрим теперь снова алгебру Ct, U, R) и докажем следующий
результат о ее дифференцированиях.
Предложение 3. Пусть D—некоторая алгебра, a sv s2—го-
s2—гомоморфизмы алгебры C1, U, R) в D. Пусть, далее, dx—(sx, s2)-
дифференцирование алгебры 31 в D, a d2 — (sx, 52)-дифференци-
рование алгебры 11 в J). {Отображения sx, s2 являются огра-
ограничениями на 31, U соответственно отображений sx, s2 алгебры
C1, U, R).) Предположим, что
(bsx) (ld2) -f- {bdx) (ls2) — (lsx) (bdx) — (ld2) (bs2) — {blR) dx E0)
198 Гл V. Универсальные обертывающие алгебры
для всех элементов ?>?ЭД, /?8. Тогда существует единственное
(Sj, s^-дифференцирование d алгебры (&, U, R) в 2), такое, что
bd = bdv ud—ud2.
Доказательство. Рассмотрим отображения 0t и 02 алгебр %
и U соответственно, такие, что
bs, bd.\ fusx ud
0 bS2 ) V° US1
Поскольку dt есть {sv s2)-дифференцирование, 9, и 02 являются гомо-
гомоморфизмами в матричную алгебру 3J. Прямое вычисление показывает,
что условие D6) является следствием условия E0). Поэтому из пред-
предложения 2 следует существование гомоморфизма 0 алгебры (ЭД, U, R)
в $J, такого, что bQ = bQv м0 = м02, а ?ЭД, m?U. Ясно, что 0
имеет вид
0 : х+ Л
\ 0 xs2
Положим y = xd. Тогда, поскольку 6 является гомоморфизмом,
d будет (sP 52)-дифференцированием алгебры Bt, U, R) в S). Оче-
Очевидно, bd = bdx, ud = ud2, что и требовалось доказать. Единствен-
Единственность, как нетрудно видеть, также имеет место.
Доказательство предложения 3 и замечания, следующие за пред-
предложением 2, показывают, что достаточно предположить выполнение
условия E0) для всех элементов Ь?Ш, где 9Й—множество обра-
образующих алгебры ЭД. Нам потребуется в дальнейшем эта усиленная
форма предложения 3.
Пусть Ш — векторное пространство над Ф и пусть ? BЯ) — внеш-
внешняя алгебра (или алгебра Грассмана) над Ш. Напомним, что Е есть
факторалгебра тензорной алгебры Z = Ф1 ф2Кф (Ш &2Я)ф ... по
идеалу, порожденному элементами вида х® х. Отсюда немедленно сле-
следует, что если s—линейное отображение пространства 9Я в алгебру $$ и
(xs)t = 0 для каждого х ? Ш, то s может быть продолжено до един-
единственного гомоморфизма алгебры ? в 8. Естественное отображение
алгебры 2 на Е является изоморфизмом на пространстве Ф1ф2И.
Можно отождествить Ф1ф2И с его образом. Очевидно, что Ш по-
порождает Е. Мы будем обозначать умножение в Е просто через ab
(не придерживаясь более сложного обозначения а/\Ь, принятого
в дифференциальной геометрии). Если а;, у ? Ш, то ху -f- ух =
= (л: —|- уJ—х2—у2 = 0. Алгебра Е градуирована, и W" является
пространством Ет однородных элементов степени т. Если \ttj\j?J} —
упорядоченный базис в Ш, то множество одночленов вида tij ttj ...
... Uj , j\ < j2 < ... < Jm, образует базис в Ет. В частности,
если dim 3Ji = п, то Ет = 0, для т > п и dim Ет = ( п j, для /»¦<«.
§ 6 Когомологии алгебр Ли Стандартный комплекс 199
Поэтому dim E = 2". Существует такой автоморфизм v\ внешней ал-
алгебры, что хг\ = — а; для всех х ? Ш. Если хт ? Ет, то хтч\ =(—1)тхт.
Нас интересуют дифференцирования и ^-дифференцирования внеш-
внешней алгебры Е(Ш) в алгебры 23, содержащие Е в качестве подал-
подалгебры. Такие "^-дифференцирования будут называться антидиффе-
антидифференцированиями алгебры ? в 23. Нам понадобится следующий
критерий.
Предложение 4. Пусть 23 — алгебра, содержащая внеш-
внешнюю алгебру E = E(ffl) в качестве подалгебры. Пусть d — ли-
линейное отображение пространства 2Я в 23. Тогда d может быть
продолжено до дифференцирования (антидифференцирования)
алгебры Е в 23 тогда и только тогда, когда x(xd)-\-(xd)x = 0,
(х (xd) — (xd) x — 0) для всех х ? Ш.
Доказательство. Условия необходимы, поскольку из равен-
равенства х2 = 0 в Е следует, что a: (xd) -f- (xd) x = 0 или x(xd) —
— (xd)x = 0, в зависимости от того, будет d дифференцированием
или антидифференцированием. Предположим, обратно, что условия
выполняются. В первом случае рассмотрим отображение
'х xd\
чо ху
а во втором — отображение
/' х xd
\0 — х
пространства Ш в матричную алгебру 232. В обоих случаях легко
проверить, что (хвJ — 0. Поэтому 6 можно продолжить до гомо-
гомоморфизма алгебры Е. Завершающие рассуждения те же, что и в до-
доказательстве предложения 3.
Ясно, что условия предложения 4 обеспечивают единственность
продолжения.
Мы применим это утверждение в следующей ситуации. Пусть
8— алгебра Ли, Ш — модуль над 8 и Е = Е(Ш) — внешняя алгебра,
определенная модулем 2Я. Если х ? Ш, I ? 8, то xl ? 5Ш, так что
a: (xl) -\- (xl) х = 0 в Е. Поэтому существует единственное дифферен-
дифференцирование dt алгебры Е, такое, что xd[ = xl, x^ffl. Далее, xdi1+ll =
I, /j, Z2?8, так как Ш является 8-модулем Поскольку все отобра-
отображения, рассмотренные здесь, являются дифференцированиями и по-
поскольку Ш порождает Е, имеют место равенства dt^h = dit -\- div
dtIi=adi, d\iui} =[ditdi,]. Следовательно, отображение l—>dl есть
представление алгебры Ли 8 дифференцированиями внешней алге-
алгебры Е(Ш).
200 Гл. V. Универсальные обертывающие алгебры
Рассмотрим следующий частный случай этой ситуации: пусть
2}J = 8 и представление присоединенное. Образуем алгебру X —
= (?(8), U, А), где через А обозначено продолжение присоединен-
присоединенного представления до представления дифференцированиями внешней
алгебры ?(8). В наших обозначениях есть небольшая трудность,
поскольку мы имеем дело с двумя экземплярами алгебры 8 — одним,
содержащимся в U, другим — из Е. Мы будем обозначать поэтому
элементы экземпляра в U через /, /?8, и будем писать 8={7}.
Соответствующие элементы в Е обозначим через /, а сам экземпляр
алгебры — через 8. Для того чтобы избежать путаницы, обозначим
композицию Ли в 8 (не совпадающую с произведением Ли в EL)
через [/j о /jb Тогда мы получим изоморфизм алгебр Ли 8 и 8: /—>/;
поэтому [1Х о l2] = [/j/2] = /j/2 — /,/j. Поскольку 8 и 8 порождают U
и Е соответственно, 8 U 8 порождает X. Основную роль играют
следующие соотношения, связывающие эти образующие:
[/„ /2]=J/,oy, P=0;
[/„ /2] = [/,<>/,],
где lt ? 8. Последнее из них является следствием соотношения D5).
Из последнего соотношения E1) вытекает, что если х^Е^ то
[xt, I] ? Et. Отсюда легко следует, что &^'>Е1 = ?;8<;) для 8<;) =
= Ф1 -j- 2 -f- ... -|-8<;) в U. Поэтому \XEt = Ej\\. Если мы положим
Л"; —?(U, то получим соотношения XlXj = ElWEJ\X ? Ei+j\X = Xi+j.
Далее, поскольку X = Е\Х^Е®]Х, из свойств тензорного произве-
произведения следует, что X = ~^jXt = 2 Et\X (с.уммы прямые). Это показывает,
что X— градуированная алгебра, z Xt = Et\X — пространство ее одно-
однородных элементов степени /.
Предложение 5. Существуют однозначно определенные
автоморфизм -ц алгебры Х = {Е($), U, А) и г\-дифференцирова-
ние d алгебры X в X, такие, что
ld=l, ld = Q, Z?8.
Кроме того, -r\d-\~ dr\ — Q a d2 = 0.
Доказательство. Очевидно существование такого гомомор-
гомоморфизма Tjj алгебры Е в X, что lt\x = — l, l?ii, и такого гомомор-
гомоморфизма У}2 алгебры U в X, что I~q = J. Условие D6) в случае b = lv
I =12, 61=7]], 92 = т]2 записывается в виде [/jY|j, J2y|2] = [lx о /2] tjj,
что эквивалентно условию [—lv 1-}]=—['i0^!- Это легко следует
из соотношения E1). Поэтому можно применить предложение 2 для
§ 6. Когомологии алгебр Ли. Стандартный комплекс 201
доказательства существования и единственности автоморфизма т\.
Очевидно, что отображение d2 = 0 является ^-дифференцированием
алгебры U в X. Условия предложения 4 выполнены, поскольку
//"—II = [Ц] = [1 о 1] = 0, и, таким образом, существует антидиффе-
антидифференцирование dx алгебры ?(Й) в X, такое, что ldx=l, /?8. Про-
Проверим теперь выполнение условия E0) в случае b = lv l = l2, Si = l,
s2 = ~q, dx = dx, d2 — d2. Левая часть соотношения равна
ifl + Vl -Ui - о (- h) = ui T2].
Правая часть равна [/г/2] rfj = [1г °l2] dx — [^ ° l2] = [1г12\. Поэтому
условие E0) выполняется для этих элементов, и, согласно замечанию,
следующему за предложением 3, существует единственное У|-диффе-
ренцирование d алгебры X, удовлетворяющее условиям E2). Оче-
Очевидно, X0d — 0, и, пользуясь равенством Xl = Xi_lXl, получаем по
индукции, что ^rf С Х(.[, где Xl=ElVL, 1^-1. Легко проверить
непосредственно, что xir\ = (—II xt, если х^Х^ Поэтому х^й —
= (—\I хгй и х;^т] = (—\)l~lXid. Отсюда r[d-{-dr\ = 0. Если
*. у?Х, то (ху)& = {х{уа) + (xd){yrl))d^=x(yd^^r{xd){ydti)-^
+ (jcd)(y7|dL (xd2)(yr?) = x(yd2)-\-(xd2)(yrf). Поскольку Y|2=:l,
это показывает, что d2 является дифференцированием. С другой сто-
стороны, из условий E2) следует, что ld2 = 0=Jd2. Поэтому d2 = 0,
что и завершает наше доказательство.
Обозначим через dt_x, /=1, 2 ограничение d на Xt. Тогда
dt_x отображает Xi в Xt_x и didi_1 = 0. Поскольку \Хй == 0, ото-
отображения d и dt коммутируют с правыми умножениями на элементы
из U. Поэтому, если мы рассмотрим Xt как U-модуль, то dt будет
U-гомоморфизмом. Напомним также, что Xt = Et\X S Et ® U и Х =
= '2iXt (сумма прямая). Поэтому любой Ф-базис в Et есть множество
свободных образующих модуля X\ относительно U. Таким образом,
каждое однородное пространство Xi является свободным U-модулем.
По определению Хо = U. Если обозначить через U' идеал в U, по-
порожденный элементами /, /?2, то U/и'^Ф. Пусть {uj\j?J} —
упорядоченный базис в 8. Тогда, как мы знаем, элементы 1,
и г,, ui ... и/ • ^i -^ h -^ • • • ^ if образуют базис в U. Определим ото-
отображение е алгебры U в Ф, полагая as = а для любого элемента
а = <*1-|-2а/1 ... i Ui Ui ... ui . Это отображение будет U-гомо-
U-гомоморфизмом пространства X0 — VL в Ф, если рассматривать Ф ка*
U-модуль: <xU' = 0, al =a, а^Ф. Очевидно, что е—отображение н~
Пусть Ь?ХУ Тогда b = ^iupj, где {и;} — базис в Й, Vj^U.
Отсюда bd0 = bd = 2 ujVj6 U' и bdoe=O. Обратно, пусть а?Х0,
202 Гл. V Универсальные обертывающие алгебры
и допустим, что се = 0. Тогда а = 2a/,...f Ui ..."i ?U' и e =
= bd0 для b = ^Ui Bаг ...i ui ••• ui )• Мы показали, таким
образом, что последовательность 0 <- Ф <-— Хо <-j- .Y, точная. Остается
показать, что Ker d,_j = Im dt, /^-1. Для этой цели рассмотрим
сначала случай, когда 2 абелева; тогда 11 будет полиномиальной ал-
алгеброй от алгебраически независимых и коммутирующих перемен-
переменных Uj. В абелевом случае также [ml] = [т о /] = 0, т, /?2. По-
Поэтому элементы алгебры 11 коммутируют с элементами из Е(й).
Следовательно, X есть тензорное произведение пространств Е и U,
рассматриваемых как алгебры.
Пусть теперь 2 = 5№ф?Я, где Ш, %1 — подпространства, а по-
поэтому и подалгебры абелевой алгебры Ли 2.
Пусть, далее, F = E(W), 33 = U(9K), У = Х(Ж), G = E(W),
2В = U (Ш), Z = X (Щ). Легко видеть, что F можно отождествить
с подалгеброй, порожденной подпространством Ш во внешней ал-
алгебре Е, S3 — с подалгеброй в U, порожденной Ш=[т?Ш} и
Y — с подалгеброй в X, порожденной 5Ш+5Ш. Аналогичные утвер-
утверждения верны для G, 2B, Z. Эти результаты легко получить, по-
посмотрев на базисы этих алгебр. Аналогично мы предоставляем чита-
читателю убедиться в том, что X = YZ, где Y и Z — указанные выше
подалгебры, и что имеет место изоморфизм Y®Z и X как вектор-
векторных пространств, причем у ® z переводится в yz, у ? Y, z?Z. Из
этих результатов следует, что если (л — линейное отображение в Y,
a v — линейное отображение в Z, то найдется единственное линейное
отображение X в X, такое, что (yz)\ = (y\i)(zv).
Рассмотрим теперь пополняющее отображение е модуля Хо в Ф
как отображение Хо в подалгебру Ф1 а X и продолжим его до
линейного отображения всего пространства X, полагая ЛГге = 0, / ^-1.
После этого можно считать, что е — (пополняющий) гомоморфизм
алгебры X на подалгебру Ф. Докажем теперь
Предложение 6. В X = X B), где 2 — абелева алгебра Ли,
существует такое линейное отображение D, что Dd-\-dD =
Доказательство. Предположим сначала, что dim 2 = 1 и
(и) — базис в 2. Тогда в X существует базис 1, и, и2, и3, .. . ;
и, ии, ии2, ... , причем a'd== 0, ииЧ = и1+1, />-0; 1е = 1,й'+1е =
= 0, ии'е = 0. Поэтому, если определить D как линейное отобра-
отображение, такое, что Ш = 0, ul*lD = uul, uulD = 0, /^>0, то, как
нетрудно проверить, dD -f- Dd =1 — е, т. е. в этом случае доказа-
доказательство закончено. Заметим также, что y\D-\-Dr\ = Q, если т) —
автоморфизм, ранее определенный в X (и\ = и1, uult\ = —ии1).
§ 6. Когомологии алгебр Ли. Стандартный комплекс 203
Кроме того, имеют место соотношения ed = 0 = de и ?т) = е = т;е.
Предположим теперь, что 8 = 2Яф!Я, где W — одномерная подал-
подалгебра. Тогда X = YZ, Y = X(Wl), Z = X0l), где У и Z — алгебры,
определенные выше. Очевидно, что Y и Z инвариантны относительно
отображений d, e и ¦/), ограничения которых являются просто соот-
соответствующими отображениями в X (Ж) и X (Щ). Пусть D2— только
что определенное отображение в Z, и пусть D,— любое отображение
в К, удовлетворяющее условию <Юг + Dxd = 1 — е в Y. Существует
единственное линейное отображение D в X, такое, что
(yz)D = y(zD2) + (yDl)(ze), y?Y, z?Z. E3)
Тогда
(yz) Dd = у (zD2d) + (yd) (zD2ri) + (yD,)
= у (zD2d) + (yd) (zD2ri) +
(yz) dD = (y (zd) + (yd) (zri)) D =
= y(z dD2) + (yD,) B
= у (z dD2) + (yd) B7jD2) + (y dD,) (ze).
Поэтому
(yz) (Dd+ dD) = y(z(\—€)) + (y(\—€)) (ze) =
(ze) — (ye) (ze) = yz A — e).
Из приведенного рассуждения следует по индукции требуемое утвер-
утверждение в конечномерном случае; в бесконечномерном случае необ-
необходимо применить трансфинитную индукцию или лемму Цорна.
Из доказанного предложения вытекает точность последователь-
последовательности Хо«--j- Х1 <—j- Х2 < ... . Действительно, пусть элемент
xf 2 X, удовлетворяет условию xd = Q. Тогда х = хA—е) =
= х (dD + Dd) = (xD) d ? Im d. Отсюда следует, что Ker d,_, = Im d,,
Рассмотрим теперь общий случай произвольной алгебры Ли 8 и
введем фильтрацию в X, используя пространство образующих Щ. =
Мы полагаем, таким образом, Хи) = Ф1-\-Щ-\-Щ2-\- ...
является
подкомплексом. Очевидно также, что ЛГ(-" есть сумма однородных
подпространств относительно градуировки, имеющейся в X. Можно
образовать факторкомплекс X^'/X^J~ , градуировка которого инду-
индуцирована градуировкой в X. Если [Uj\j?J]—упорядоченный базис
в 8, то классы смежности базисных элементов uj ... aj tti ¦ ¦ •
• • • uik, ji<h< ¦¦¦ <jh< ti <i2 < ... < /ft, h-{-k = j, относи-
относительно X^~l) образуют базис в Х^^/Х^'^. Мы отождествим эти
... + W — S Eh%k. Поскольку (Ehik) й Е fft-^*4, АГ(У)
204 Гл. V. Универсальные обертывающие алгебры
классы смежности с элементами базиса. Тогда мы можем сказать,
что оператор d в X(l)\X(i~l) определяется по формуле
К ••• <VV ••%)<* =
= 2(-1)Л~Ч ...%•.. «;дв|, ... Sv .. Ъ, . E4)
где символ *¦ означает, что ttj опущен; индексы в произведении
элементов и расположены в неубывающем порядке. В определении
этого дифференцирования не используется строение алгебры 2.
Поэтому оно совпадает с тем дифференцированием, которое было
получено в случае абелевой алгебры Ли. В последнем случае про-
пространство, натянутое на одночлены, стоящие в левой части равен-
равенства E4) и подчиненные условию, что число A-f- k = j фиксировано,
образует подкомплекс комплекса X, а X есть прямая сумма-таких
подкомплексов для / = 0, 1 Отсюда следует, что если л; при-
принадлежит одному из*этих подкомплексов, а также однородной ком-
компоненте Xt_v /^-1, и xd = 0, то x = yd, y^Xt ну принадлежит
комплексу, содержащему х. Результат о точности последовательно-
последовательности D1), которой мы хотели доказать, будет теперь следовать ин-
индукцией по индексу у (в Лг(;)) из леммы.
Лемма 3. Пусть Y — подкомплекс градуированного /сом-
плексаХ = 2^ДсУммапРямая)> такой, что Y = 2(^ П Xj). Пусть
г=о (=о
со
Z = XJY = 2 Zt. Zt =s XJiY П Xt).
0
2
(=0
Предположим, что условие Ker dt_x = Im dt, i^l, выполнено
для Y и для Z. Тогда это условие выполнено и для X.
Доказательство. Пусть х ? 2 X, удовлетворяет условию
xd = 0. Тогда (x-\-Y)d = 0. Поэтому существует такой элемент
x'-\-Y, что (л;'+ Y)d = x-\- Y. Таким образом, x'd = x-\-y,
y?Y. Далее, yd = x'd2 — xd = 0, и, следовательно, существует
элемент у' ? Y, такой, что y = y'd. Поэтому x = x'd — y = x'd —
— y'd = (x' — y')d.
Тем самым завершено доказательство следующей теоремы.
Теорема 10. Пусть Х = (Е(&), U, А)—алгебра дифферен-
дифференциальных операторов, ассоциированная с внешней алгеброй
Е(%) и продолжением присоединенного представления алгебры
Ли У в Е. Пусть d— антидифференцирование алгебры X, опре-
определенное в предложении E), и пусть Xi = El(U). Тогда после-
последовательность Ф<—— Хо <-— Х1 * ... является свободной
резольвентой модуля Ф.
§ 6. Когомологии алгебр Ли. Стандартный комплекс 205
Остается показать, что группы когомологии. (пределенные этой
резольвентой, совпадают с группами, определенными в § 3.10. Пусть
ср—U-гомоморфизм модуля X, в (правый) U-модуль Ш, а (/,. /2, ...
..., /,) — упорядоченное множество из / элементов ал)ебры 8. Опре-
Определим отображение / декарт- ва произведения 8 X . - X il (/ раз) в Т1
фJpмyлoй / (/, /,) = Aх1г .../;) ср, где /,/2 ... /г ? Et ? Xt.
Очевидно, что / является полилинейным и знакопеременным, и
легко видеть, что если /—любое полилинейное знакопеременное
отображение произведения 8 X • • • X 2 в 5Ш, то существует линей-
линейное отображение ср пространства Et (Й) в WI, такое, что (/j/2 ... lt) cp =
—/(Jj, ..., /;). Это отображение ср имеет единственное продолжение
в U-гомоморфизм пространства Xi в Ш. Мы получаем, таким обра-
образом, взаимно однозначный линейный изоморфизм пространства U-
гомоморфизмов X, в Ш и пространства полилинейных знакопере-
знакопеременных отображений /-кратного произведения Й X ... Ч Й в Ш.
Если /—отображение последнего типа, то мы определим /8 фор-
формулой
E5)
Нам известно, что
и, согласно D5),
r>q
r>q
Поэтому
l + l
a,... //+I)d= 2 (-i)'+1-4 ... f
1
,
Отсюда следует, что
*+iJ()/A, .*+,),
= 2 (-i)r+9/(/, /„ I /i+1. iyri)- E6)
Но это как раз и есть определение кограничного оператора, дан-
данное в § 3.10.
206 Гл. V. Универсальные обертывающие алгебры
§ 7. Ограниченные алгебры Ли характеристики р
Часто в случае характеристики р Ф 0 приходится сталкиваться
с естественно возникающими структурами, которые несколько богаче
обычных алгебр Ли. Пусть, например, 31—произвольная (неассоциа-
(неассоциативная) алгебра, и пусть ©B1) — множество дифференцирований
алгебры 2L Тогда, как известно, ?)C1) будет подалгеброй алгебры Ли
линейных преобразований в %. Заметим также, что имеет место
формула Лейбница
k
2(*) E7)
для любого дифференцирования D. Она легко доказывается индукцией
по k. Допустим теперь, что основное поле алгебры 51, а следова-
следовательно, и алгебры DCI) имеет характеристику р, и положим в фор-
формуле E7) k — p. Тогда биномиальные коэффициенты I . I ===== 0, если
1 <! i <! р — 1. Поэтому формула E7) сводится к равенству
E8)
откуда следует, что Dp также является дифференцированием. Таким
образом, множество 3) C1) замкнуто относительно отображения D —> Dp,
так же как и относительно обычных операций алгебры Ли. Анало-
Аналогично пусть 31—ассоциативная алгебра и с-» с — антиавтоморфизм
в Ж. Как мы знаем, подмножество 2= (а | а ?31, а — — с} является
подалгеброй алгебры Ли %L. Кроме того, в случае, когда харак-
характеристика равна р, из условия с = — а следует, что ар = ар =
— (—а)р = — ар. Поэтому ар?2, так что опять мы получаем
алгебру Ли, замкнутую относительно ^-отображения. Только что
рассмотренные системы D C1) и 2 являются примерами ограниченных
алгебр Ли, которые будут определены нами абстрактно.
Для этой цели нам понадобятся некоторые соотношения, связы-
связывающие ар с операциями в алгебре Ли %L, где % — ассоциативная
алгебра характеристики р. Напомним сперва о следующих двух
тождествах в Ф [X, \х\, где X и fi — алгебраически независимые пере-
переменные, а Ф — поле характеристики р:
(х-^'-^^У7-1-'. E9)
Первое из этих тождеств хорошо известно, а второе является след-
ствием первого и тождества Хр — м,р = (Х — u.) I ^^V ') Ясно,
\«-о /
§ 7. Ограниченные алгебры Ли характеристики р 207
что соответствующие тождества имеют место и для коммутирующих
элементов a, b в любой ассоциативной алгеоре. В частности, мы можем
положить a — bR, b — bL, где bR и bL — правое и левое умножения
определенные элементом Ь^'й. Отсюда получаем,-что
i=0
ИЛИ
F0)
1 l P-\
[...[ \ab\ й] ... ft] = 2 bp~x~labl. F1)
Очевидно также, что
(аа)р = арар. * F2)
Используем соотношение [61] для доказательства формулы
р-\
(а + *)" = ар + *" + 2 *, (о. »). F3)
где ^(а, *) есть коэффициент при X' в
. F4)
X — независимая переменная. Для доказательства введем кольцо
многочленов 31 [X] и запишем
p-i
(Хо-г-*)р = Х"о''-|-*р+ 2 st(a. b)\l, F5)
1 = 1
где st(a, b) — многочлен от с, Ь общей степени р. Продифферен-
Продифференцировав тождество F5) по X, мы получим равенство
р-\ Р-\
2 (ka + bI a(ka + b)p-l-x= 2 **,(*. Ь)\1~\
1=0 «=1
Из него и из соотношения F1) получаем, что
Р-\
a (ad (Xа -+-Ь))Р~!= 2 ***(в. *)Х'"!. F6)
Таким образом, мы видим, что Is^a, b) есть коэффициент при X'
в a (ad (Хс -|- Ь) )р . С другой стороны, подстановка Х = 1 в F5)
дает соотношение F3). Очевидно, что «До, Ь) получается примене-
208 Гл V Универсальные обертывающие алгебры
нием операций сложения и коммутирования к а, ft и, следова-
следовательно, принадлежит подалгебре Ли, порожденной элементами а, Ь
алгебры %L. Например,
5, (a, b) = [ab], если р — 2\
s,(a, b) = [[ab]b], 2s2(a, b) — [ [ab] а], если р — Ъ;
Sl(a, b) = [[[[ab]b]b]b],
2s2 (a. b) = [[[ [ab} a] ft] ft] + [[[!«»] »] «1 *] 4- Ш [oft] ft] ft] a].
3s3(a, ft) = [ [ [ [oft] a] a] ft] + [ [ [ [ab} a] ft] a] + [ [ [ [aft] ft] c] a],
4s4(c, ft] = [ [ [ [aft] с] с] а], если p — 5.
Эти предварительные соображения приводят к следующему опре-
определению.
Определение 4. Алгебра Ли 2 характеристики рфО назы-
называется ограниченной, если в X. задано отображение о->о1^1, удовле-
удовлетворяющее условиям
(I) * [ac]tpl = aV",
Р-\
(II) (с + ft)tpl = c!pl -+- ft[pl + 2 s, (a, ft),
где tst(a, ft) есть коэффициент при X' в a (ad(Xc + ft))p~1 и
(III) [aftlpl] = y
Если 31 — ассоциативная алгебра характеристики р, то предше-
предшествующие рассуждения показывают, что 51 определяет ограниченную
алгебру Ли, в которой заданы операции векторного пространства 21,
[oft] = aft — ftc и clpl = ар. Мы обозначим эту ограниченную алгебру Ли
через %L (так же, как и обычную алгебру Ли). Гомоморфизм S
ограниченной алгебры Ли в другую ограниченную алгебру Ли есть
по определению отображение, удовлетворяющее условиям (а-\- ftM =
— as-\-bs, (aa)s = <xas, [abf = [asbs], (a"'i)s = (as)"'1. Идеалы и
подалгебры определяются очевидным образом. Представлением огра-
ограниченной алгебры Ли 2 называется гомоморфизм алгебры 2 в огра-
ограниченную алгебру Ли 6?, где 6—алгебра линейных преобразова-
преобразований векторного пространства Ш над Ф. Если R — представление,
действующее в пространстве Ш, то WI является 2-модулем относи-
относительно операции xa==xaR, х ? Ш, а ?8. Закон композиции
(х, а)->ха удовлетворяет обычным условиям в модуле над алгеб-
алгеброй Ли и дополнительному условию: ха\р\ = (... (ха) с) ... с, где а
взято р раз.
Рассмотрим теперь следующие два основных вопроса.
A). Каждая ли ограниченная алгебра Ли имеет взаимно однознач-
однозначное представление?
§ 7 Ограниченные алгебры Ли характеристики р 209
B). Каким условиям должна удовлетворять обычная алгебра Ли,
чтобы она была ограниченной алгеброй Ли при подходящем опре-
определении aW?
Что касается B), то ясно, что необходимое условие заключается
в том, чтобы для каждого а ? й дифференцирование (ad af было
внутренним, ибо в ограниченной алгебре Ли (ad а)р = ad a'^l. Вскоре
будет показано, что это условие является и достаточным. Мы уви-
увидим, что можно даже ограничиться требованием, чтобы (ad ut)p было
внутренним для каждого ut в базисе {ut} алгебры Й. Заметим также,
что если Й является ограниченной алгеброй Ли относительно р-ото-
бражений а—>с'р1' и а—>а1р'21 то /(с)=а'р'1 — а'^2 принадлежит
центру алгебры й, поскольку [b, f (а)] = [Ь аМ>)— [Ьо1рЩ =
= b(ada)p— b(ada)p = 0. Из условий (II) и (I) видно, что
/ (a-I-ft) = /(«) + /(*). /(аа) = а'/(в). F7)
Отображение одного векторного пространства характеристики р ф 0
в другое, обладающее такими свойствами, называется полулинейным
р-отображением. Обратно, если Й — ограниченная алгебра относи-
относительно отображения а—» a'Ph и а—>/(с) есть полулинейное /?-ото-
бражение алгебры Й в центр 6 алгебры Й, то й будет также огра-
ограниченной алгеброй относительно а -» о'рЬ == дИ. _|_ f (а). Ядро полу-
полулинейного ^-отображения является подпространством. Поэтому, если
/(и() = 0, где ut принадлежат базису, то / = 0. Отсюда вытекает,
что если два ^-отображения с—>с'р1' и с—> а'рЬ наделяют Й струк-
структурой ограниченной алгебры и совпадают на базисе, то они тожде-
тождественны.
Предположим теперь, что й — алгебра Ли с базисом {и,|*?/},
где /—упорядоченное множество, и пусть U — универсальная оберты-
обертывающая алгебра алгебры й. Теорема Пуанкаре — Биркгофа — Витта
утверждает, что „стандартные одночлены" вида «f'« 2 ... и г,
/, < /2 < ... < lr, k} > 0, образуют базис в U. Подпространства
U(ft)==(J>l 4-2-г-Й + ••• +2* определяют на алгебре U фильтра-
фильтрацию. Легко показать (индукцией по k и обычным рассуждением
об „упорядочении"), что одночлены a*'«*2 ... a*r, такие, что
^i + &2+ ... -{-&,.<;&, образуют базис в U(ft). Допустим теперь,
что для каждого базисного элемента at найдутся положительное
целое число п1 и элемент zt, принадлежащий центру 6 алгебры U,
такие, что
vi = a1i-zi F8>
лежит в Ц(я'~ ). Тогда имеет место следующая
Лемма 4. Элементы вида
и г
'* ... и г, F9)
210 Гл. V. Универсальные обертывающие алгебры
где il<i2< ... <tr йу>0, 0 <Ху < ntj, г = 1, 2, 3 обра-
образуют базис в U.
Доказательство. Покажем сперва, что каждый элемент
и*1 ... и*'", &.^>0, является линейной комбинацией элементов
1 Г '
вида F9). Будем рассуждать по индукции относительно k = kx-\~
-\-k2-\- ... -+¦ &,¦• Если каждое kj < «г , то результат очевиден.
Поэтому мы можем предположить, что kj ^- щ для некоторого у.
Тогда можно заменить и^ на г», -\~zl и получить
*1 *r ftl kj~nli "r , *i kj~nlj "r
и/, • • • «гг = **,«*, • • • «^ ' ... Utr-\-uli ... utj }vtj ... Uir .
Элементы «f1 ... ик.1~"Ч ... и?' и второй член правой части лежат
'l j Г
в U^ ~ . Следовательно, эти элементы являются линейными комбина-
комбинациями элементов вида F9). Поскольку множество элементов вида F9)
замкнуто относительно умножения на любой центральный элемент zt,
это утверждение очевидно. Покажем, далее, что элементы вида F9)
линейно независимы. Заменив в z,1 ... z-TuA ... us элемент z.
м 'г м V Ч
на г, =u.J— v. , получим соотношение
Ч Ч li
гнЛ ... zhrui ... и г = М*г№» ... zhrU)r ==
'l V 'l lr l\ 1 2 l2 lT lT
t 2 r ;), G0)
r
если k= 2 (hjni -\-bj). Поэтому элемент zh^ ... z^uI ... u\r —
= Ui ' ... Ui r -J- *, где * есть линейная комбинация стан-
стандартных одночленов, принадлежащих пространству U**'. Отсюда
следует, что если существует нетривиальное линейное соотношение,
связывающее элементы вида F9), то мы получаем также соотношение
г
для членов с фиксированной „степенью* k = ^i(hjtii, + \/)* А это
приводит к соотношению с теми же коэффициентами, связывающему
соответствующие стандартные одночлены ui ' ... «г Т . По-
Поскольку стандартные одночлены линейно независимы, должны выпол-
выполняться равенства hjtii -j-X;- = kj, j=l, .... г, для элементов
вида F9), которые входят в исходное соотношение с ненулевыми
§ 7. Ограниченные алгебры Ли характеристики р 211
коэффициентами. Так как \j < nt , то hj, Xj однозначно опреде-
определяются уравнением h]tii.-\-\j = k]. Поэтому в соотношение входит
только один член. Это невозможно ввиду равенства G0). Следова-
Следовательно, элементы вида F9) линейно независимы и, значит, образуют
базис в U.
Мы можем доказать теперь следующую теорему.
Теорема 11. Пусть 2 — алгебра Ли характеристики р фО
с упорядоченным базисом {«;}, таким, что для каждого ut
дифференцирование (ad и,)р является внутренним, т. е.
каждому ut соответствует такой элемент и'/7' ? 2, что
(ad uty = ad u\pl Тогда существует единственное отображе-
отображение а —>- а'-Р' алгебры 2 8 2, совпадающее с заданным выше
соответствием на множестве базисных элементов и опреде-
определяющее в 2 структуру ограниченной алгебры Ли.
Доказательство. Пусть U — универсальная обертывающая
алгебра алгебры 2. Поскольку (ad и\р = ad «М, элемент zt — ир — «И
коммутирует с каждым / ? 2. Поэтому zt принадлежит центру
алгебры U и и? = zt + иИ, где и'/7' ? 2. На основании леммы 4,
следовательно, можно сделать заключение, что элементы
*ЭД ¦ • ¦ *ЭД ¦¦¦иЬ <71>
где /, < 12 < ... < /г, hj^O, 0 <;Ху^ /? — 1, образуют базис в U.
Обозначим через 23 идеал в U, порожденный элементами zt. Тогда
очевидно, что подмножество нашего базиса, состоящее из элементов
вида G1), у которых некоторый показатель йу>0, является бази-
базисом в 23. Поэтому классы смежности элементов ui ... и/,
0 ^ Ху -<; р — 1, образуют базис в алгебре U = U/23. Поскольку кано-
канонический гомоморфизм х—> х = х-\-Ъ является гомоморфизмом
алгебры \XL в )\L, ограничение его на 2 будет гомоморфизмом
алгебры Ли 2 на 2 = B + 23)/23. Так как классы смежности
и, = и, + 23 линейно независимы, отображение 1—> I =1-\- 23 будет
изоморфизмом алгебр 2 и 2. Заметим, далее, что 2 есть подалгебра
в \XL, рассматриваемой как ограниченная алгебра Ли. В самом деле, так
как и? = (и, + 23)р = «f + 23 = и\Р^ -f 23 ? 2, то из соотношений F3)
и F2) следует, что B а,я;)р ? 2, а это как раз и доказывает наше
утверждение. Изоморфизм между алгебрами 2 и 2 позволяет нам
рассматривать 2 как ограниченную алгебру Ли, р-отображение /->/'р|'
в которой определяется формулой /'pll = /p. При этом имеет место
14*
212 Гл V Универсальные обертывающие алгебры
равенство и^Ь = uf -\- 23 = и^1 -(- 23 или u^ = u\p\ так что /?-ото-
бражение действительно продолжает заданное соответствие. Полагая
теперь /"'= /'"', мы завершаем доказательство.
Напомним результат из § 3 6 о том, что каждое дифференциро-
дифференцирование конечномерной алгебры Ли 8 с невырожденной формой Кил-
линга является внутренним. Очевидно также, что центр такой
алгебры 8 равен 0. Поэтому если характеристика равна р, то для
каждого элемента а ? 8 найдется единственный элемент- flfl, такой,
что дифференцирование (ad а)р = ad a^K Отсюда вытекает, что мы
можем определить в 8 одним и только одним способом /^-оператор,
благодаря которому 8 превращается в ограниченную алгебру Ли.
Мы получаем, таким образом,
Следствие. В конечномерной алгебре Ли 8 характери-
характеристики рфО с невырожденной формой Киллинга существует
одно и только одно р-отображение, наделяющее 8 структурой
ограниченной алгебры Ли.
Предположим теперь, что 8 есть произвольная ограниченная ал-
алгебра Ли и докажем следующую теорему.
Теорема 12. Пусть 2 — ограниченная алгебра Ли харак-
характеристики рфО, U — ее универсальная обертывающая алгебра,
23— идеал в U, порожденный элементами вида аР — а№, а ? 8,
U = 11/23. Тогда отображение а->а = а-\-Ъ является изомор-
изоморфизмом алгебры 8 в ограниченную алгебру Ли \XL. ЕслиБ— гомо-
гомоморфизм алгебры 8 в ограниченную алгебру Ли %L, где
%—некоторая алгебра {ассоциативная и с 1), то существует
единственный гомоморфизм алгебры U в 21, такой, что a—>as.
Если 8 имеет конечную размерность п, то dim U = рп.
Доказательство. Поскольку fllp' = ар — ар-\- 23, отобра-
отображение а-* а есть гомоморфизм ограниченной алгебры Ли 8 в огра-
ограниченную алгебру Ли Vll. Если {ut} — базис в 8 над Ф, то из свойств
/7-степеней и операции а —> a^l следует, что разность ар—а\Р является
линейной комбинацией элементов вида uf— иИ. Поэтому идеал 23
порождается также элементами up— и^'. Доказательство пред-
предшествующей теоремы показывает, что классы смежности ui = ui -f- 23
линейно независимы, поэтому отображение а—*а является изомор-
изоморфизмом алгебры 8 в Vll. Пусть теперь 5 — гомоморфизм алгебры 8
в ограниченную алгебру Ли %L, где 21 — некоторая алгебра Тогда
существует однозначно определенный гомоморфизм алгебры U в 21,
переводящий а?8 в as. При этом отображении ар —>(as)p = (alP*)s.
Поэтому разность аР—а^ принадлежит ядру и, таким образом,
§ 8 Абелевы ограниченные алгебры Ли 213
23 принадлежит ядру. Следовательно, мы имеем индуцированный гомо-
гомоморфизм U = 11/33 в Ш, такой, что a—>as. Если алгебра й имеет
конечный базис uv u2 ип, то, как мы видели, классы смежности
элементов и^и? ... ипп, 0^Xf^/?—1, образуют базис в U. Этим
доказано последнее утверждение нашей теоремы.
Алгебра U = 11/23, определенная в формулировке последней тео-
теоремы, будет называться и-алгеброй ограниченной алгебры Ли Й.
Она играет для алгебры Ли й как ограниченной алгебры ту же самую
роль, что и алгебра U для й, рассматриваемой как обычная алгебра Ли.
В частности, представление алгебры й как ограниченной алгебры
определяет представление алгебры U и обратно. Поскольку U обла-
обладает точным представлением, каждая ограниченная алгебра Ли имеет
точное представление. Более того, если й — конечномерная алгебра,
то U также конечномерна и поэтому имеет точное представление,
действующее в конечномерном пространстве. Следовательно, это
верно также и для алгебры й.
§ 8. Абелевы ограниченные алгебры Ли
Абелева ограниченная алгебра Ли есть векторное пространство й
с отображением а->ар (отныне мы будем так обозначать /^-операцию)
в й, таким, что v
Теория таких алгебр является частным случаем теории полулинейных
отображений. Она эквивалентна теории модулей над определенными
типами некоммутативных полиномиальных областей целостности
(см. Джекобсон, [1] гл. 3). В данном случае полиномиальное
кольцо является множеством многочленов вида а0 ~\- ta.x -f- ... -\- tmam,
где а( ? Ф, a t—независимое переменное, такое, что at = tap. Если
поле Ф совершенно, то можно показать, что это кольцо не имеет
делителей нуля, и каждый левый и правый идеал в кольце — главный.
Изучение указанного кольца и модулей над ним является естествен-
естественным инструментом для изучения абелевых ограниченных алгебр Ли.
Тем не менее мы не пойдем по этому пути. Не используя полино-
полиномиальных колец, мы получим два основных результата об алгебрах Ли.
Теорема 13. Пусть 2 — конечномерная абелева ограни-
ограниченная алгебра Ли над алгебраически замкнутым полем харак-
характеристики р. Допустим, что р-отображение в 2 взаимно
однозначно. Тогда в й существует базис {av a2 а„), такой,
что af = аг
214 Гл. V. Универсальные обертывающие алгебры
Доказательство. Пусть а?8, афО, и пусть m — такое наи-
наименьшее положительное число, что ар = oc1a-f-a2a/' + • • • + атарП •
Тогда элементы а, ар, .... ар линейно независимы и каждая
степень ар есть их линейная комбинация. Если аг = О, то положим
$t = a\lP,l = 2 т. Toraa(apm-l — $2a-...-$m_lapm-y = Q,
пГП — 1 n , in п/П-2
откуда следует, что а* =р2а-(- ... +рт_]Я , а это противо-
противоречит выбору т. Поэтому ctj Ф 0. Отсюда вытекает, что а есть
линейная комбинация элементов ар, ар* Мы покажем теперь,
что существует такой элемент Ь= (^а+Рг^Ч" ... -f- §тарШ~х Ф 0,
что Ьр = Ь. Это будет иметь место в случае, когда коэффициенты (Зг
не все равны нулю и удовлетворяют следущей системе уравнений
Путем последовательных подстановок получаем уравнение
„fit tlt—l -til — 1 -Jtl — 2 _
?< +p^ «? ++?:«
Поскольку <*! =^= 0 и Ф алгебраически замкнуто, уравнение G4) имеет
ненулевое решение для (Зт. Тогда остальные (^ для i<^m—1
могут быть определены из уравнений G3), а при i = tn соотношение
будет выполнено ввиду G4). Предположим теперь, что мы уже нашли
линейно независимые элементы ах, а2, ..., аг, удовлетворяющие
условиям ае = а.. Тогда 8j = 2®at будет подалгеброй алгебры Й.
Предположим, что а — такой элемент алгебры й, что ар?Й,. Так
как а есть линейная комбинация элементов ар, ар то отсюда
следует, что а ? 81# Мы показали тем самым, что 8/8t есть ограни-
ограниченная алгебра Ли, удовлетворяющая условиям теоремы. Поэтому
если й отлично от 8,, то можно найти элемент 6(?8,, такой, что
г
Ьр =з b (mod fij). Таким образом, Ьр—^ = 2т*й/' ^ы можем опре-
определить'8^ так, что Ьр — 5г —f— Yf=== *-*• *=1. 2 г. Тогда элемент
Йг+1 = Н2;Ц удовлетворяет условиям a^+i^Sj, af+1=ar+1.
Поэтому результат следует по индукции. »
Теорема 14. Пусть 8 — абслева ограниченная алгебра Ли
конечной размерности над алгебраически замкнутым полем.
Предположим, что р-отображение а->ар взаимно однозначно.
Тогда любой конечномерный модуль ffl над 8 вполне приводим
и разлагается на одномерные подмодули. Если (av а2 ап)—
Упражнения 215
такой базис в 2, что af=at и а = ^Х/аг, то каждый вес
модуля Т1 имеет вид А (а) = 2 тЛ> г^е все mi принадлежат про-
простому полю.
Доказательство. Пусть базис (а,, а2, ..., ап) выбран
в соответствии с условиями теоремы, и пусть ai-*Ai — данное
конечномерное представление. Тогда А^ = At, так что минимальный
многочлен преобразования А1 является делителем многочлена Хр — X =
= Д (X — т). Таким образом, минимальный многочлен преобразова-
преобразования At имеет различные корни, принадлежащие простому полю.
Отсюда вытекает, что существует такой базис (xv x2 хп) в ffi,
что XjAt = mi}Xj, где т{) принадлежат простому полю. Поскольку
At коммутируют, мы можем найти базис, который обладает этим
свойством для всех At одновременно A = 1, 2 л). Тогда
xj B^/-'4«)==B/и//в<) ¦*;¦ так чт0 ^ является прямой суммой не-
неприводимых инвариантных подпространств Фхр и веса имеют вид
Замечание. Первую часть теоремы 14 легко распространить
на случай произвольного основного поля характеристики р, т. е.
полная приводимость имеет место, если р-отображение взаимно
однозначно. С другой стороны, Хохшильдом [4] было показано, что
если все модули над ограниченной алгеброй Ли (всё конечномерно)
вполне приводимы, то й — абелева алгебра с невырожденным р-ото-
бражением.
Упражнения
1. Пусть 8 — алгебра Ли над полем характеристики нуль, U — ее уни-
вереальная обертывающая алгебра. Показать, что каждый элемент алгебры U
является линейной комбинацией степеней элементов из 2.
2. (Витт). Пусть g2 — свободная алгебра Ли с г (свободными) обра-
образующими хи хг, ..., хг над полем характеристики 0, g — ее универсальная
обертывающая алгебра. Пусть ©2)л = 32 П Зл. где Зл — пространство одно-
однородных элементов из 3 степени п. Показать, что
dira(gS)n = i
djn
где [J. — функция Мёбиуса.
3. Пусть 2 — конечномерная алгебра характеристики О, 9J — ее ниль-
нильрадикал. Показать, что совокупность линейных преобразований exp (ad г),
г € 9J, образует группу относительно умножения.
4. Показать, что если Z — иильпотентиое линейное преобразование
в конечномерном векторном пространстве над полем характеристики 0, то
преобразование exp Z унимодулярно (det exp Z = 1). Показать, что если
Z кососимметричио относительно невырожденной симметрической или
Г л V. Универсальные обертывающие алгебры
кососимметрической билинейной формы, то exp Z ортогонально относительно
этой формы.
5. Если 8[ — алгебра, то в 91 ® 91 существует единственный автомор-
автоморфизм 1 периода два, такой, что {a (g) 6) х = b (g) а. Показать, что если
й — универсальная обертывающая алгебра алгебры Ли, то U5 содержится в
подалгебре г-неподвижных элементов алгебры U®tt.
6. Пусть U. — универсальная обертывающая алгебра алгебры Ли, и пусть
Ц*—пространство, сопряженное к U. Если <р, 4* €11*, то существует един-
единственная линейная функция <f®<\> на UB)tt, такая, что (<у ® 40 B ui ® vi) —
= 2 У (и^ ^ (v^~ Определим произведение <р\/ ? II* формулой (^ф) (и) =
= (? ® Ф) ()> гДе 5 ~~ диагональное отображение алгебры Ц в U (g) U. Тем
самым U* наделяется структурой алгебры. Показать, что эта алгебра комму-
коммутативна и ассоциативна.
7. Доказать следующий аналог теоремы Фридрихса в случае характе-
характеристики р фО. элемент а 6 § удовлетворяет условию a5 = a(g>l-|-l(g)a
тогда и только тогда, когда а принадлежит ограниченной алгебре Ли,
порожденной элементами x-t.
8. Пусть 8 — конечномерная алгебра Ли, 2i и 82 — идеалы в 8, являю-
являющиеся контрагредиентными модулями над 2 относительно присоединенного
представления. Пусть («i ип), (и1 и") — дуальные базисы в 8i и 82,
как в определении оператора Казимира некоторого представления (§ 3.7).
Показать, что элемент 7=2Ц'М' принадлежит центру универсальной обер-
обертывающей алгебры U алгебры 2.
9. Обозначения те же, что и в упражнении 8. Пусть R — конечномер-
конечномерное представление алгебры Ли 2 (а следовательно, н алгебры U), и пусть
f{u) = iru^, и ? U. Показать, что элемент
2 /(«(iv4)*'lM'2 •••*''
принадлежит центру алгебры IX. Более общо, показать, что если б — пере-
перестановка индексов 1, 2, ..., г, то элемент
У f(u{ и, ...и{ ) и1и*...иг
I, ...<r-i V I9 29 г9)
принадлежит центру алгебры U.
10. Найти центр универсальной обертывающей алгебры трехмерной
расщепляемой простой алгебры над полем характеристики нуль.
11. Пусть Ф — поле, Ф[/,-] = Ф[/,, t2, ..., tr] — алгебра многочленов от
переменных tt, Ф {t{) = Ф (tu t2 /г) = Ф [^] — замыкание алгебры Ф [//],
рассматриваемой как градуированная алгебра с обычной градуировкой
(однородным элементом степени k является однородный многочлен степени k
в обычном смысле). Алгебра Ф (//) называется алгеброй формальных сте-
степенных рядов от переменных tt, а ее поле отношений Р — полем фор-
формальных степенных рядов от rj. В Ф (/;) существует нормирование, опре-
определенное по образцу § 5. Таким образом, если a = ak-\-ak+l-\-ak+2-\- ...»
где aj — однородный элемент степени j и акф0, то |a| = 2~*. Это норми-
нормирование имеет единственное продолжение до нормирования поля Р, удовле-
удовлетворяющего условию |ой| = |а|[й|. Пусть Р„—алгебра иХи-матРиц
с элементами из Р. Положим | (ay) \ = max | ац |. Показать, что этим опре-
определяется нормирование в Рп, и показать, что если Du D2 Dr —
Упражнения 217
матрицы с элементами из Ф, то существует единственный непрерывный
гомоморфизм алгебры $ =*Ф {xt хт) (см. § 5) в Рп, при котором
х,->01. /=1, 2, .... г.
12. Пусть 2— конечномерная алгебра Ли над полем Ф характеристики О,
Р—поле, определенное в упражнении 11. Пусть ?>,, D2, ..., Dr — диффе-
дифференцирования алгебры 8 над Ф; их продолжения на алгебру Up над Р обозначим
также через ?>,, D2 Dr. Показать, что G = ехр <,?>, exp t2D2 ... exp trDr
есть корректно определенный автоморфизм алгебры 8р и что G = exp D,
где D — элемент подалгебры, порожденной ?>/ в алгебре Ли дифференци-
дифференцирований алгебры 8р.
13. Пусть 2 — конечномерная ограниченная алгебра Ли, в которой
каждый элемент нильпотентен: ар = 0 для некоторого k > 0. Показать, что
и-алгебра алгебры 8 имеет вид Ф1 -f- 9J, где ffi — радикал.
14. Многочлен вида кр -j-о,А.р -)-...-j-omX называется р-многочле-
ном {регулярным, если атф0). Пусть 8 — ограниченная алгебра Ли (воз-
(возможно, бесконечной размерности), обладающая тем свойством, что для
каждого а ? 8 существует такой регулярный />-многочлен \>.а (к), что
[Аа (а) = 0. Показать, что если с — элемент алгебры 8, для которого все
корни многочлена ;л.г (X) лежат в основном поле Ф, то с принадлежит
центру S алгебры 8. Вывести отсюда, что 8 абелева, если Ф алгебраически
замкнуто. Показать, что каждая конечномерная неабелева ограниченная
алгебра Ли над алгебраически замкнутым полем содержит элемент z =j= 0,
такой', что zp — 0.
15. Пусть 8 — ограниченная алгебра Ли, каждый элемент а которой
удовлетворяет условию ар = аа, где <х — фиксированный элемент поля Ф,
отличный от 0. Доказать, что 8 — абелева.
16. Использовать упражнения 14 и 15 для доказательства того факта,
что если ар = а в ограниченной алгебре Ли 8, то 8 абелева. Гипотеза:
алгебра Ли 8 абелева, если арП{а)=а, п (а) > 0.
17. Доказать, что если 8 — ограниченная алгебра Ли характеристики 3
и а3 = 0 для всех а, то каждая конечнопорожденная подалгебра алгебры 8
конечномерна. Гипотеза (возможно, верная лишь при каких-то дополнитель-
дополнительных условиях): если 8 — конечнопорождеиная ограниченная алгебра Ли
характеристики р и каждый элемент из 8 алгебраичен в том смысле, что
существует ненулевой />-многочлен ;л.а (X), такой, что ;л.а (а) = 0, то
2 конечномерна.
18. Назовем дифференцирование D ограниченной алгебры Ли ограни-
ограниченным, если apD = (aD) (ad о)'. Заметим, что каждое внутреннее Диф-
Дифференцирование ограничено. Показать, что дифференцирование ограничено
тогда и только тогда, когда оно может быть продолжено до дифференци-
дифференцирования и-алгебры. Показать, что если центр алгебры 8 равен 0, то каждое
дифференцирование ограниченное.
19. Пусть 8 — абелева конечномерная ограниченная алгебра Ли над
совершенным полем. Показать, что S3 = 8о © 8i, где 80 — пространство ниль-
потентных элементов (ар = 0) и 8] = П8Р-
20. Пусть 8 — как в упражнении 19, причем основное поле бесконечно
и совершенно. Предположим, что 80 = 0. Показать что 8 — циклична в том
смысле, что существует такой элемент Ъ. что i' = 2 Ф^Р
21. Пусть 91 — групповая алгебра над полем характеристики р цикли-
циклической группы порядка р Тогда й обладает базисом A, х, х2, ..., хр '),
хр = 1. Показать, что алгебра дифференцирований Ъ алгебры Ж имеет
218 Гл. V. Универсальные обертывающие алгебры
базис Di, i = 0, I, .... р—1, где xDi = xl+l. Проверить, что
(/-у) D/+/,
Доказать, что © — простая алгебра Ли. © называется алгеброй Bumma.
22. Обобщить упражнение 21, рассмотрев алгебру дифференцирований
групповой алгебры 91 прямого произведения г циклических групп по-
порядка р (поле Ф имеет характеристику р). Эти алгебры дифференцирований
также являются простыми.
23. Доказать следующее тождество для а-лгебр Ли характеристики
Рф0:
р-1
Ь 2 (ad a)P~2-l (ad с) (ad аI =
= с У, (ad a)"'2'1 (ad b) (ad a)'.
/to
24. ') Пусть Й нильпотентная алгебра Ли линейных преобразований
конечномерного векторного пространства 501 над полем характеристики
1
р Ф 0, такая, что [... [ [АВ] В] ... В] = 0 для всех А, В б 2. Показать, что
(Л -|- В)р = Ар -f- Bp. В случае алгебраической замкнутости основного поля
использовать этот факт для доказательства линейности весов пространства Ш
относительно 2.
25. Пусть ?0 — алгебра Ли треугольных п X и-матриц со следом 0 над
полем характеристики р Ф 0, р^'п. Показать, что алгебра S?o'совершенна.
[Указание: показать, что каждое дифференцирование ограничено, если
рассматривать ?0 как ограниченную алгебру Ли, и изучить действие диф-
дифференцирования на диагональную матрицу с различными диагональными
элементами (поле Ф можно предполагать бесконечным).]
') У автора это упражнение сформулировано не совсем верно. Здесь
дана исправленная формулировка.—Прим. ред.
Глава VI
ТЕОРЕМА АДО —ИВАСАВЫ
В этой главе мы докажем, что каждая конечномерная алгебра Ли
имеет точное конечномерное представление. Будут рассмотрены от-
отдельно два случая: характеристики 0 и характеристики р. Результат
в первом случае известен как теорема Адо. Для этого случая мы
даем доказательство, которое по существу является упрощением до-
доказательства, принадлежащего ХЯриш-Чандре. В случае характе-
характеристики р результат принадлежит Ивасаве. Предлагаемое нами до-
доказательство проще его доказательства и приводит к некоторым
другим результатам о представлениях над полем характеристики р.
§ 1. Предварительные результаты
Если R— гомоморфизм алгебры Ли й в %L, где %—конечно-
%—конечномерная алгебра (ассоциативная с единицей 1), то, как мы знаем,
R имеет единственное продолжение до гомоморфизма R алгебры U
в 31. Если $ — ядро, то U/X = U^ ? 31, так что факторалгебра U/X
конечномерна. Вообще, если Ш — подпространство векторного про-
пространства Ш, то размерность пространства 9К/ЭТ будет называться
коразмерностью пространства Ш в 9М. Таким образом, R опреде-
определяет идеал I в И конечной коразмерности. Гомоморфизм R является
изоморфизмом алгебры й тогда и только тогда, когда $ПЙ = О.
Обратно, пусть Ж — идеал в U, для которого ХПЙ = О и Ж имеет
конечную коразмерность в U. Тогда ограничение на 8 канонического
гомоморфизма алгебры U в U = U/$ является изоморфизмом алгебры Й
в конечномерную алгебру WL. Так как любая конечномерная алгебра
имеет точное конечномерное представление, то ясно, что алгебра Ли й
будет иметь точное конечномерное представление тогда и только
тогда, когда универсальная обертывающая алгебра U алгебры Й
содержит идеал $ конечной коразмерности, удовлетворяющий усло-
условию $ПЙ = О.
Напомним, что элемент а алгебры "& называется алгебраическим,
если существует такой ненулевой многочлен ср(Х), что ср(а) —0. Это
эквивалентно предположению, что подалгебра в 31, порожденная эле-
элементом а, конечномерна. Следовательно, каждый элемент конечно-
конечномерной алгебры алгебраичен. Если $—идеал в 51. то мы скажем,
220 Гл. VI Теорема Адо — Ивасавы
что элемент а из % алгебраичен по модулю Ж, если существует
такой ненулевой многочлен ср (X), что ср(а)?$. Это эквивалентно
тому, что класс смежности а = а-\-Ж алгебраичен в Ш — Ж/Ж. От-
Отсюда следует, что если Ж имеет конечную коразмерность, то каждый
элемент алгебры ЭД алгебраичен по модулю Ж. Сформулируем теперь
следующий критерий для универсальной обертывающей алгебры U
алгебры Ли.
Лемма 1. Пусть й— конечномерная алгебра Ли, (и,, и2, ...
..., ип) — базис в й, U — универсальная обертывающая алгебра
для Й, Ж — некоторый идеал в U. Тогда Ж имеет конечную
коразмерность site том и только том случае, когда каждый
элемент и, алгебраичен по модулю Ж.
Доказательство. Необходимость условия леммы была полу-
получена выше. Пусть теперь ср, (X) — ненулевой многочлен, для которого
?<("/)€•?• и пУсть я, = deg срг (X). Тогда каждый элемент и* сравним
по модулю Ж с линейной комбинацией элементов 1, и(, и^, ...
.... к"'. Множество стандартных одночленов а\хи\г ... и*л,
kt ^> 0, является базисом алгебры U, а из только что сделанного
замечания следует, что эти одночлены сравнимы по модулю $ с ли-
линейной комбинацией одночленов их' и1^ . .. и*", где 0 ^ Х( < nt Так
как эти одночлены образуют конечное множество, то факторалгебра
U/X конечномерна.
Лемма 2. При тех же предположениях, что и в лемме 1,
пусть Ж и g)—идеалы в U. Если Ж и ?J конечной коразмер-
коразмерности, то идеал Ж^) тоже имеет конечную коразмерность в U.
Доказательство. Пусть ср^(X), ^(X) — ненулевые многочлены,
для которых <Р/(«,)?$, ф,(И;)^2). Тогда <pt (X) ^ (X) обладают тем
свойством, что у1 (и() (^ (ut) ? $2), и результат следует из леммы 1.
Лемма 3. Пусть $—алгебра, В — множество ее обра-
образующих и D — дифференцирование алгебры Ж. Предположим,
что для каждого и ?В существует такое целое положитель-
положительное число п(и), что и?>л(и) = 0. Тогда для каждого а?Щ.
существует такое целое положительное число п(а), что
aDn(a) = 0. Если алгебра % конечномерна, то дифференциро-
дифференцирование D нильпотентно.
Доказательство. Пусть 23 обозначает подмножество элемен-
элементов Ь, таких, что 6/У(г>) —0 для некоторого целого числа п(Ь)^>0.
Если bv 62?23 и t>iDn> — 0 = b2D'h, то ф^ b2)D" = 0 для п —
§ 2 Случай характеристики нуль 221
= тах(л1> л2), (a61)D"'==0 для а
при N = «,+ «2—1- Следовательно, 23 является подалгеброй и,
так как 23 3 В, то 23 — 31. Это доказывает первое утверждение. Вто-
Второе утверждение непосредственно отсюда следует.
§ 2. Случай характеристики нуль
Для нашего доказательства теоремы Адо необходима следующая
Лемма 4. Пусть <S — конечномерная разрешимая алгебра
Ли над полем характеристики нуль, Щ — ниль-радикал ал-
алгебры ©, U — универсальная обертывающая алгебра для <&.
Предположим, что Ж—идеал в U конечной коразмерности,
такой, что каждый элемент из Щ. нильпотентен по модулю Ж-
Тогда существует такой идеал 3 в U, что: A) 3 ^ Ж, B) 3 имеет
конечную коразмерность, C) QD ?= 3 &ля каждого дифферен-
дифференцирования D алгебры <? (продолженного на U), D) каждый
элемент из 9? нильпотентен по модулю 3-
Доказательство. Пусть ^) идеал в U, порожденный Ж и Ш.
Тогда 5K$ и 2)/Х будет идеалом в U/X, порожденным (У1-\-ЖIЖ.
Так как (У1-\-ЖIЖ является идеалом в алгебре Ли (<S-j-X)/3? и эле-
элементы этого идеала нильпотентны в конечномерной обертывающей
ассоциативной алгебре ]\/Ж алгебры (<&-\-ЖIЖ, то из теоремы 2.2
следует, что (Щ -f- Ж)/Ж содержится в радикале алгебры Ц/Ж Следо-
Следовательно, 2)/Х содержится в этом радикале. Это означает, что суще-
существует такое целое число г, что 3==?Г 9= Ж. Если 1?<& и D —
дифференцирование алгебры <?, то мы знаем, что Ю^У1 (теорема 3.7).
Отсюда вытекает, что UDc^J), В частности, g)D с ЭД и поэтому
QD = s))rD с 2)г = 3- Следовательно, утверждение C) выполняется
для 3 и. как мы уже отмечали, утверждение A) тоже выполняется.
Так как J!) содержит Ж, то ^) — идеал конечной коразмерности, но
тогда и 3 = W имеет конечную коразмерность в U. Это доказывает
утверждение B) Если г?У1, то г"?Ж для некоторого положитель-
положительного целого числа п. Следовательно, z" ? g) и гя/1 ? g)r = 3- Это
доказывает утверждение D).
Теорема 1. Пусть ? = <?фй1, где © — разрешимый идеал
и SJj — подалгебра конечномерной алгебры Ли Й характе
ристики 0. Предположим, что мы имеем такое конечномер
ное представление S алгебры <S, ч/ио элемент zs нильпотен
тен для каждого элемента z из ниль-радикала Ш алгебры S-
Тогда существует конечномерное представление R алгебры 1'
удовлетворяющее условиям: A) если л:^ = 0 для л; мз ®, то
222 Гл. VI. Теорема Ado — Ивасавы
Xs = 0, B) yR нильпотентен для каждого у вида y = z-\-u,
где г?Щ, а элемент a?2j таков, что преобразование ad®-и
нильпотентно.
Доказательство. Представление 5 определяет гомоморфизм
универсальной обертывающей алгебры U для ©, ядро Ж которого
имеет конечную коразмерность. Кроме того, если z?ffl, то (zs)" = 0,
так что z" ? Ж и Ж удовлетворяет условиям леммы 4. Пусть 3 обоз-
обозначает идеал из утверждения этой леммы. Мы определим требуемое
представление R в U/3- Определим сначала представление R' алгебры
8 = ©фйР действующее в пространстве U. Положим sRI = sR (пра-
(правое умножение в U, определенное элементом s) для s?©. При /?8;
определим lR как дифференцирование алгебры U, продолжающее
дифференцирование 5—>[sl] алгебры <&. Отображения R', заданные
на 6 и на й], приводят к единственному линейному отображению R'
на й, которое является представлением подалгебр б и S, в отдель-
отдельности. Чтобы доказать, что R' является представлением для й, до-
достаточно показать, что [sl]R = \sR , lR\, s?©, 1?%V Ho [si] ?©,
так что [si]'* = [sl]R.
С другой стороны, если D — дифференцирование алгебры U и
а ?11, то условие для дифференцирования дает [aRD]-=(aD)R. Сле-
Следовательно, мы имеем [slf ^=[sl]R = (slR')R = [sR, /*'] = [ss\ lR'\,
что и требовалось. Так как 3 — такой идеал в U, что 3^ ?ё 3 ПРИ
любом дифференцировании D алгебры ©, то 3 является подпро-
подпространством в U, инвариантным относительно представления R' ал-
алгебры й, действующего в U. Следовательно, мы имеем индуцирован-
индуцированное представление R в конечномерном факторпространстве U/3-
Пусть х ? © удовлетворяет условию xR = 0. Это означает, что xR
отображает U в 3- Следовательно, д;?3> х^Ж и поэтому xs = Q.
Пусть z?ffl. Тогда, согласно лемме 4, элемент z нильпотентен по
модулю 3- Следовательно, преобразование zR нильпотентно. Так
как $1 ¦ является идеалом в й (теорема 3.7), то отсюда вытекает,
что zR принадлежит радикалу 01 алгебры линейных преобразований,
порожденной образом 2й. Пусть теперь y = z-\-u, где г?Ш, и?8j
и преобразование ad® и нильпотентно.
Поскольку zR ? 8fc, для доказательства нильпотентности преобра-
преобразования yR достаточно установить, что uR нильпотентно. Согласно
определению, uR' является дифференцированием алгебры U, которое
совпадает с ad© и на © и ad® и нильпотентно. Так как © поро-
порождает U, то из леммы 3 следует, что для каждого а ? U существует
такое целое число п(а), что a(uR')nW = 0. Следовательно, для каж-
каждого а ? U/3 мы имеем такое п(а), что а(ий)"(а) =0. Поскольку
факторалгебра U/3 конечномерна, это означает, что uR нильпотентно.
Таким образом, R удовлетворяет условиям A) и B).
§ 2 Случай характеристики нуль 223
Теорема Ад о. Каждая конечномерная алгебра Ли 2 ха-
характеристика нуль имеет точное конечномерное представ-
представление.
Доказательство. Напомним, что ядро присоединеннбго пред-
представления А совпадает с центром 6 алгебры й. Поэтому достаточно
будет доказать существование конечномерного представления R
алгебры й, которое точно на центре (L Действительно, в таком
случае мы можем образовать прямую сумму представлений R и А.
Ядро этого представления является пересечением ядер из R и А.
Следовательно, это представление и точно, и конечномерно. Мы
приступаем к построению R. Пусть © — радикал, а Ш — ниль-
нильрадикал. Пусть Ш1 = &<=.Щ2с: ... cz%lh = %l, где каждое 3^ является
идеалом в ffli+x и dim^/+1 = dim %lt-\- 1. Такая последовательность
существует, поскольку идеал Ш разрешим и содержит 6. Если
dim(? = c, то в (c-f-1)-мерном векторном пространстве! существует
такое нильпотентное линейное преобразование z, что z° ф 0. В таком
случае центр 6 изоморфен алгебре Ли с базисом (z, z2, ..., zc) и
поэтому имеет точное представление нильпотентными линейными пре-
преобразованиями в конечномерном пространстве. Поскольку каждая
подалгебра 9^ нильпотентна и 9f(+i = 9?;фФИ(+1, где Фи(+1 — не-
некоторая подалгебра, можно последовательно применять предыдущую
теорему. В результате мы получаем конечномерное представление Т
идеала VI нильпотентными линейными преебразованиями, причем Т
точно на (L
Рассмотрим теперь последовательность подпространств ©, =
= ^с®2с; ... c®ft=®, где ©, — идеал в ©i+1 и dim©i+1 =
= dim ©г ~|-1 • В таком случае ©i+1 = (S;-f- <I> . Кроме того,
Щ является ниль-радикалом каждого ©( (теорема 3.7). Следовательно,
опять можно применить предыдущую теорему, начав с Г, и получить
представление 5 радикала <5, которое конечномерно, точно на 6
и представляет элементы из $1 нильпотентными линейными преобра-
преобразованиями. Запишем, наконец, й в виде 2 = ©-г-21, где %г—под-
%г—подалгебра (теорема Леви). Тогда опять можно применить теорему 1
и получить требуемое представление R алгебры 8.
Замечание. Построенное представление R обладает тем свой-
свойством, что zR нильпотентен для каждого z ? Ш. То же самое имеет
место для присоединенного представления. Поэтому прямая сумма
также обладает этим свойством. Таким образом, доказано существо-
существование точного конечномерного представления, такого, что преобра-
преобразования, соответствующие элементам из 91, нильпотентны, а сле-
следовательно, принадлежат радикалу обертывающей ассоциативной ал-
алгебры.
224 Г л VI Теорема Адо — Ивасавы
§ 3. Случай характеристики р
Напомним, что если Ф имеет характеристику р, то многочлен
вида <х0Хр -\- otjXp -\- ... -\- остХ, ос( ? Ф, называется р-многочле-
ном. Если [а(Х) — многочлен степени т, то
t = 0, 1, 2 m, A)
где степень rt (X) меньше т. Так как пространство многочленов
степени меньше т w-мерно, то существует <х(, / = 0, .... т, не все
равные нулю и такие, что '^ialrl(\) = 0. Тогда из равенств A) сле-
следует, что 2аЛР — Р(^)BаЛ(^))- Мы доказали таким образом,
что каждый многочлен является делителем некоторого ненулевого
р-многочлена.
Пусть теперь й — конечномерная алгебра Ли над Ф, U — ее уни-
универсальная обертывающая алгебра. Пусть а?2 и р(Х) — ненулевой
многочлен, для которого jj. (ad а) = 0. Такой многочлен существует,
поскольку алгебра линейных преобразований пространства й конечно-
мерна. Пусть от(Х) = Хр -\- ахкр -)-...-(- атХ — /(-многочлен, де-
делящийся на (х(Х). Тогда
(ad а)рШ + «1 (ad af'1 + • • • -f am (ad о) = 0. B)
Другими словами, для каждого b ? й мы имеем
pm p"i-l
1 i i i
1 = 0. B')
С другой стороны, мы знаем, что [... [Ьа] ... а] = [Ьар]. Итерируя
это равенство, получаем
.. i] = [*a"*]. C)
Поэтому B') означает, что
[*, а"т^а1а"т-1+ ... +ата] = 0. D)
b ^ 2, откуда следует, что элемент
гэа^ + ^Ч ...+а„о E)
принадлежит центру 6 алгебры U. Нами доказана таким образом
следующая
Лемма 5. Пусть 2 конечномерная алгебра Ли над полем
характеристики /?=?0 и W — ее универсальная обертывающая
§ 3 Случай характеристики р 225
алгебра Тогда для каждого а?й существует такой много,
член таA), что та{а) принадлежат центру 6 алгебры U.
Только что доказанный результат и лемма 5.4 являются основ-
основными пунктами в нашем доказательстве теоремы Ивасавы.
Теорема Ивасавы. Каждая конечномерная алгебра Ли
характеристики р Ф 0 имеет точное конечномерное предста-
представление.
Доказательство. Пусть (и{, и2 ип) — базис алгебры й
и т,(Ц— р-многочлен, для которого ml(ul) = zi принадлежит 6,
центру универсальной обертывающей алгебры. Если degml(l) = pmK
то zi = up '-\-vt, где v^Up '~г. Следовательно, в силу леммы 5.4
элементы z^z1^ ¦ • • fy u\l ... tfy, ht > 0, 0 <X( < pmi, образуют,
базис алгебры Ц. Пусть 23 — идеал в U, порожденный элементами zt.
Как уже отмечалось в доказательстве теоремы 5.11, классы смеж-
смежности элементов и^ ... ип, 0<^Х(</?т<, образуют базис в U/23.
Следовательно, эта алгебра конечномерна и каноническое отображе-
отображение а—> a — a-f-23, а??, является изоморфизмом алгебры й в U^,
Ц = Ц/23. Отсюда следует, что существует точное конечномерное
представление алгебры Ли й.
Мы покажем теперь, что в случае характеристики р Ф 0 не су-
существует никакой связи между строением алгебр Ли и полной при-
приводимостью модулей. В следующей теореме нам потребуется дока-
доказанный в главе II (теорема 2.10) результат о том, что алгебра %
линейных преобразований конечномерного векторного пространства,
имеющая ненулевой радикал, не может быть вполне приводимой.
Нам потребуется также результат,' который несколько труднее
доказать, а именно, что если z — элемент конечномерной алгебры, не
принадлежащий ее радикалу, то существует такое неприводимое пред-
представление R алгебры, при котором zR ф 0. (См., например, Дже-
кобсон [3], теорема 3.1 и определение 1.1.)
Теорема 2. Каждая конечномерная алгебра Ли над полем
характеристики р Ф 0 имеет взаимно однозначное конечно-
конечномерное представление, не являющееся вполне приводимым,
а также взаимно однозначное конечномерное вполне приводи-
приводимое представление.
Доказательство. Пусть ut и zl = ml{ut) — такие же, как
в доказательстве теоремы Ивасавы. Пусть Ъх — идеал в U, порожден-
порожденный элементами (z\, zy .. , z\. Тогда, очевидно, Zj-f-Sj Ф 0 в U/Sj,
но {zx -f-SjJ = 0. Следовательно, z,-f-23j является ненулевым цен-
центральным нильпотентным элементом конечномерной алгебры ll/S^
Идеал, порожденный таким элементом, нильпотентен. Поэтому алгебра
15 Н 'Д'кекобсон
226 Гл. VI Теорема Адо — Ивасавы
/2?! не полупроста, и, следовательно, любое взаимно однозначное
представление этой алгебры не является вполне приводимым. По-
Поскольку (8-f-SBj)/©! порождает U/Sj, это представление индуцирует
представление алгебры Ли 2, которое тоже не вполне приводимо.
Использованное ранее рассуждение показывает, что каноническое
отображение алгебры 2 в U/S, является изоморфизмом. Следова-
Следовательно, отмеченное выше представление будет взаимно однозначным
на 2, что и доказывает наше первое утверждение.
Пусть теперь а — любой ненулевой элемент алгебры 2; возьмем
и, = а в базисе (uv и2, ..., ип) алгебры 2. Пусть а Ф 0 принад-
принадлежит Ф. Тогда т1 (к) — а не делится на X и является минимальным
многочленом элемента а —(— 032 в U/252, где 232— идеал, порожденный
множеством m1(u1)—a., m2(u2j mn(un). Таким образом, элемент
а-)-232 не нильпотентен и поэтому не принадлежит радикалу. Отсюда
следует, что существует такое конечномерное неприводимое предста-
представление алгебры U/232, что a-f-232 не представляется нулем. Это пред-
представление приводит к конечномерному неприводимому представле-
представлению Ra алгебры 2, для которого aRa ф 0. Пусть $а — ядро пред-
представления Ra (в 2). Тогда Г\ $а = 0. Поскольку алгебра 2
конечномерна, можно найти конечное число ах, а2 ат элемен-
элементов а в 2, для которых ("^а. = 0. Образуем теперь модуль Ш,
являющийся прямой суммой т. неприводимых модулей Ш}-, соответ-
соответствующих представлениям Ra.. Тогда очевидно, что модуль Ш вполне
приводим, и ядро ассоциированного с ним представления равно
П$а- = 0. Это и есть точное конечномерное вполне приводимое
представление алгебры Ли 2.
Упражнения
1. Показать, что любая конечномерная алгебра Ли характеристики р
имеет неразложимые модули произвольно большой конечной размерности.
Упражнения 2—4 предназначены для доказательства следующей теоремы.
Пусть 81 — некоторая алгебра над алгебраически замкнутым полем характе-
характеристики 0, 8 — конечномерная простая подалгебра в %L, содержащая нену-
ненулевой алгебраический элемент. Тогда подалгебра в St, порожденная алгеб-
алгеброй Ли 8, конечномерна. Можно предположить, кроме того, что эта под-
подалгебра совпадает с Si, и поэтому достаточно показать, что 8 имеет базис,
состоящий из алгебраических элементов.
2. Показать, что 8 содержит отличный от нуля нильпотентныи элемент е.
{Указание: использовать упражнение 3.11.)
3. Показать, что в 2 существует отличный от нуля алгебраический эле-
элемент /г, содержащийся в некоторой подалгебре Картана $> алгебры 2. (Ука-
(Указание: использовать теорему 3.17 и упражнение 3.13.)
4. Пусть элементы е«, ha определены разложением алгебры 8 относи-
относительно подалгебры ?> (см. гл. IV). Показ'ать, что ha, ea, е_„ алгебраичны
для некоторого корня а=/=0. Показать затем, что это выполняется для каждого
Упражнения 227
корня а и что, следовательно, 8 имеет базис из алгебраических элементов.
Использовать это для доказательства сформулированной теоремы.
5. Обобщить сформулированную выше теорему на полупростую алгебру 2
при более сильном предположении: 8 содержит такое множество алгебраи-
алгебраических элементов, что идеал в 8, порожденный этим множеством, совпадает
со всей алгеброй й.
6. Обобщить результат из упражнения 5 на случай, когда основное поле
является произвольным полем характеристики 0.
7. (Хариш-Чандра). Пусть й — конечномерная алгебра Ли над полем
характеристики 0, R — ее точное конечномерное представление линейными
преобразованиями со следом 0 в 501. Пусть Rlt i— I, 2 обозначает пред-
представление в Ш (g) ffl (g) ... 0 Ш (i раз) и Jj — ядро в U представления R[.
оо
Доказать, что П Ж,- = 0.
8. Показать, что любая конечномерная алгебра Ли имеет точное конеч-
конечномерное представление линейными преобразованиями со следом 0.
Глава -VII
КЛАССИФИКАЦИЯ НЕПРИВОДИМЫХ
МОДУЛЕЙ
Основная цель этой главы заключается в том, чтобы получить
классификацию конечномерных неприводимых й-модулей, где й—рас-
й—расщепляемая полупростая алгебра Ли над некоторым полем характе-
характеристики 0. Основополагающий результат (принадлежащий Картану)
устанавливает взаимно однозначное соответствие между модулями
указанного типа и „доминантными целыми" линейными функциями на
расщепляющей подалгебре Картана ф алгебры й. Существование ко-
конечномерного неприводимого модуля, соответствующего любой доми-
доминантной целой функции, было получено Картаном путем исследова-
исследования отдельных классов простых алгебр Ли и, таким образом, зави-
зависело от классификации этих алгебр. Более изящный метод для
изучения этого вопроса был найден Шевалле и Хариш-Чандра (неза-
(независимо друг от друга). Этот метод не требует рассмотрения отдель-
отдельных случаев. Более того, он дает единообразное доказательство
существования расщепляемой полупростой алгебры Ли, соответствую-
соответствующей каждой матрице Картана или схеме Дынкина, и другое доказа-
доказательство единственности (в смысле изоморфизма) эгой алгебры.
Доказательство этих результатов у Хариш-Чандра очень сложно !).
Изложение, даваемое нами, является сравнительно простым. Оно
основано на явном определении некоторой алгебры Ли 2 бесконеч-
бесконечной размерности и на изучении некоторых циклических модулей,
„экстремальных модулей", над 2. Алгебра 2 задается целочисленной
матрицей (Ац), которая удовлетворяет некоторым условиям, выпол-
выполняющимся и для матриц Картана. Основные средства, нужные при
нашем рассмотрении, — это теорема Пуанкаре — Биркгофа — Витта и
теория представлений для расщепляемых трехмерных простых ал-
алгебр Ли.
§ 1. Определение некоторых алгебр Ли
Пусть (Аи), i, j — 1, 2, ...,/, —матрица целых чисел AtJ-, обла-
обладающая следующими свойствами (выполняющимися, как известно, для
') Доказательство Шевалле не было опубликовано.
§ 1. Определение некоторых алгебр Ли 229
матрицы Картана любой конечномерной расщепляемой полупростой
алгебры Ли над полем характеристики 0):
(а) Аи = 2, A,j < 0, если I Ф J; из А^ — О следует AJi = 0;
(б) йеНАи)ф0;
(в) если (aj, a2 осг)— базис некоторого /-мерного векторного
пространства -?>о над полем рациональных чисел, то группа W, поро-
порожденная / линейными преобразованиями Sa
конечна.
Пусть Ф — произвольное поле характеристики 0. Мы определим
алгебру Ли 2 над Ф, задаваемую матрицей (Ац). Начнем со сво-
свободной алгебры Ли $8 (§ 5.4), порожденной свободными образую-
образующими et, /,, й(, /=1, 2, ..., I. Пусть ^—идеал Ли в §й, поро-
порожденный элементами
\ethj[ - Ajte,,
Положим 2 = 58/^- Пусть ф — подпространство алгебры $й, натя-
натянутое на элементы йг, и at — линейная функция на §, заданная соот-
соотношениями
al(hJ) = AJi, /=1, ...,/. C)
Условие (б) означает, что / функций at образуют базис простран
ства •§)*, сопряженного к ф.
Так как §8 свободным образом порождается образующими et,
/., hi, i=l, 2, ..., /, то любое сопоставление им линейных пре-
преобразований некоторого векторного пространства определяет (одно-
(однозначно) представление алгебры §8. Другими словами, произволь-
произвольное векторное пространство $ с базисом {uj} может быть снабжено
структурой §2-модуля посредством задания произведений и^е^ Ujft,
tijhi как совершенно произвольных элементов из $. Пусть теперь
$ — свободная (ассоциативная) алгебра, порожденная / свободными
образующими jCj, х2 xv В этом случае $ имеет базис 1,
Xi ... Xi , /у = 1. 2 /, г = 1, 2 Пусть Л = Л (й) будет
некоторой линейной функцией на §>. Тогда из только что сделан-
сделанного замечания следует, что мы можем превратить $ в §8-модуль,
230 Гл. VII Классификация неприводимых модулей
полагая
(х,, ... х,г)А = (А —а,,- ... -л,г)хч ... xi;,
1/, == xt. xti ... Xi/, = x,{ ... xirxt;
1 0
_8у(А-Я|1- ... -«/,_,) (A,) *,,... */r_,.
В этих соотношениях и в тех, которые будут появляться впослед-
впоследствии, мы сокращаем Л(й) до Л и т. д., но пишем полностью Л(/гг)
и т. д.1). Пусть $' — ядро представления алгебры gg в Ж. Мы при-
приступаем к доказательству того, что §.' з 5? (идеал, определяющий й).
Последнее будет означать, что $ можно рассматривать как простран-
пространство представления алгебры g, т. е. что оно является модулем
над й. Линейное преобразование в Ж, соответствующее й, имеет
относительно выбранного базиса диагональную матрицу. Следова-
Следовательно, любые два из этих преобразований коммутируют и, таким
образом, [fifij] ? $'• Отметим, далее, что линейное преобразование,
соответствующее ft, является правым умножением xiR в Ж, опреде-
определенным xt. Из последнего и четвертого уравнений в D) получаем,
что
Это означает, что [etf}] — 8^й( лежит в ядре $?'• Далее,
1 \fih\ = 1 (/,А — А/,) = х,А — Ал, = (А — а,) *, — Ах, =
Xi, ... x^j^A — (А — аг,— ... —a.i^Xix
(Л—а^— ... —air — ai)xti ¦¦¦ XifXt —
— (A — Bii— ... — air)x(i ... X/rx,=
Следовательно, [/гА]-|-а,/г^ Jt'. Отсюда получаем, что если х—эле-
х—элемент из Ж, для которого хА = М (А) х = Жх, то (л;//)й = (УИ—аг)Х
') Это соглашение, имеющее своим досадным следствием смешение
функции с одним из ее значений, действует на многих последующих стра-
страницах, и о нем нужно постоянно помнить. — Прим. ред.
§ 1. Определение некоторых алгебр Ли 231
X (xfi), или (хх,) h~(M — a^xxi). Мы утверждаем теперь, что
[х, ... л,е,)Л = (А — а4[ — ... —a^-j-oc,).*;^ ... лг^е^. Это ясно
для г = 0, если условиться, что соответствующий базисный элемент
равен 1. Предположим теперь, что утверждение верно для г—1.
Тогда
(хч ... *,ге,) А = ((*,, ... *,г1в|)*,г)А-
= (Л — a([— . .. -«i,.,^»!-»!,)^, • • • *;re().
Это доказывает наше утверждение, из которого следует, что
*<, •¦• xlf[elh] = xii ... xlr{elh — hel) =
= (Л — alf— ... — a,-r-f-a,)x(i .. . xtei —
— (Л — afi— ... —%)*», ••• xlel =
Поэтому [eth] — aiei ^ ^'. Мы, таким образом, доказали, что все
образующие идеала $ содержатся в $'. Следовательно, $ с $' и $
можно рассматривать как модуль над ST=§g/$t Докажем теперь
следующую теорему.
Теорема 1. Пусть %Ч — свободная алгебра Ли, порожден-
порожденная 3/ элементами et, ft, ht, 1=1, 2, ..., /, $—идеал в gg,
порожденный элементами вида B), и ?=^2/$. Тогда: 1) кано-
t
нический гомоморфизм алгебры gg «a g отображает 2 Фе<4~
i
-f- 2 Ф/i ¦+ 2 ФА,- в й изоморфно, так что можно отожде-
1 о 1
ствить соответствующие подпространства; 2) подпростран-
подпространство g,- = Фег -f- Ф/(- -f- Фй,- алгебры g является расщепляемой
трехмерной простой подалгеброй; 3) подалгебра g~_ в g, поро-
порожденная элементами ft, является свободной алгеброй Ли
с системой свободных образующих {/,}, и подобное же утвер-
ждение верно для подалгебры g+, порожденной элементами
г;, § = 2 Фй( — абелева подалгебра и имеет место разложение
1
в сумму векторных пространств
g = &®g_®g+; E)
232 Гл. VII. Классификация неприводимых модулей
4) если U — универсальная обертывающая алгебра для й, то
U = 33U+U_, где Ъ — подалгебра, порожденная ф, U+ — подал-
подалгебра, порожденная й+, и U_— подалгебра, порожденная й_.
Доказательство. Временно обозначим # + $, #(;?52>
через х. Рассмотрим представление R алгебры 2, определенное в Ж
линейной функцией Л = 0 на ?>. Если h ? §> и h = О, то %R = ft# = О,
откуда следует, что (аг -|- ... -|- а(- ) (ft) = 0 при любом выборе
элементов а1 . Так как <xlt a2, ..., аг образуют базис сопряженного
пространства, то это означает, что h = 0. Следовательно, отобра-
отображение h->h взаимно однозначно. Очевидно, [efti] — 2el, \fi}ii]=^
= — 2ft, [eJjS—li^ поэтому Фег + Ф// + Фйг—подалгебра алгебры
Ли й, являющаяся гомоморфным образом расщепляемой трехмерной
простой алгебры Ли. В силу простоты последней образ этот будет
либо 0, либо изоморфен трехмерной расщепляемой простой алгебре.
Так как ht Ф 0 по нашему первоначальному результату, то мы имеем
изоморфизм. Этим доказано 2).
Далее, [hh'] = O для любых h, h' б2Фй/ и [ёД] = аг (Л) ??,
[ffy = — al (h) 7(. Поскольку линейные функции 0, ± at все раз-
различны, обычные весовые соображения показывают, что из соотноше-
соотношения вида
следует, что ?( —0, ^); = 0 для всех I и ft' = 0. Тогда ft' = O,
по нашему первоначальному результату. Таким образом, отобра-
отображение х->х является изоморфизмом на 2Фег + 2 ^/i + S^*r
Мы отождествим это пространство с его образом и в дальнейшем
будем писать et, ft, ht и т. д. вместо eL, ft, ht и т. д. Положим
2( видели, что ф является /-мерной абеяевой подал-
подалгеброй в 2. Как уже отмечалось ранее, fR = xiR (правое умножение
в X, определенное элементом xt), где R — представление алгебры Й,
действующее в Ж. Пусть U_ — универсальная обертывающая алгебра
для Й_, подалгебры в 2, порожденной элементами ft. Тогда мы
имеем гомоморфизм алгебры U_ в алгебру линейных преобразова-
преобразований в Ж, отображающий /( в xlR. Если мы скомбинируем его
с обращением изоморфизма a->aR алгебры Ж (регулярное предста-
представление), то получим гомоморфизм алгебры U_ в Ж, переводящий fl
в ж,.
§ I. Определение некоторых алгебр Ли 233
С другой стороны, поскольку Ж свободно порождается элемен-
элементами xt, мы имеем гомоморфизм алгебры I в Й, отображающий xt
в ft. Отсюда следует, что оба указанных гомоморфизма являются
эпиморфными изоморфизмами. Так как свободная алгебра Ли реали-
реализуется в виде алгебры Ли, порожденной образующими свободной
ассоциативной алгебры, то ясно, что й_ будет свободной алгеброй Ли,
порожденной элементами /г, и U_ будет свободной ассоциативной
алгеброй, порожденной элементами /;. Теорема Пуанкаре — Бирк-
гофа — Витта позволяет также отождествить алгебру U_ с подалге-
подалгеброй в U, порожденной й_, т. е. элементами /,-. Из основного свой-
свойства свободных образующих следует существование автоморфизма
алгебры §Й, переводящего ei->fi, fi~>er ht-> — ht. Этот авто-
автоморфизм отображает образующие B) идеала S в й к, таким обра-
образом, индуцирует автоморфизм алгебры Ли 2 = gg/$, отображающий
fi в ev Поскольку подалгебра, порожденная элементами /г, свободна,
отсюда следует, что подалгебра й + , порожденная элементами е,,
тоже свободна и что ее универсальная обертывающая алгебра U+
является свободной ассоциативной алгеброй, порожденной элемен-
элементами ег Эту алгебру-можно отождествить с подалгеброй в U, поро-
порожденной элементами et. Остается доказать E).
Действительно, коль скоро это сделано, то соотношение U =
= 93U+U_ следует из теоремы Пуанкаре—Биркгофа—Витта, стоит
только выбрать упорядоченный базис в й так, чтобы за упорядочен-
упорядоченным базисом в ф следовал упорядоченный базис в й+, а затем упо-
упорядоченный базис в Й_. Чтобы доказать E), мы покажем сначала,
что 2~! == ф -\~ %+ -\- й_ есть подалгебра алгебры Й. Рассуждения по-
подобны тем, которые использовались ранее (§ 4.3). Отметим прежде
всего, что каждый элемент из Й+ является линейной комбинацией
элементов Ге/ е(- .. . ei 1 —[• • • [^/ ?i ] • • • в/1 и каждый элемент
из й_ является линейной комбинацией элементов Г/г ... /A. Тож-
Тождество Якоби и индукция по г дают, что
IIе'. ••• 4]ft]=K+a<-2+ ••
[[/',¦•¦/',]*]=-(«'.+«'.+
Следовательно, [й1ф] S ЙГ Очевидно, \ejj\ ^ ф, и индукцией по г ^> 2
можно показать, что ГГег( ... е( 1/Л ? Й+. Отсюда следует, что
fijad/;cg,. Итерируя это включение и используя тождество Якоби,
получаем, что [SjfiL] ? йг Подобным же образом получаем, что
234 Гл. VII. Классификация неприводимых модулей
[§!§+] с: gj. Эти включения и соотношение [2,$] S ^ означают,
что ?! является подалгеброй. Поскольку et, /г, ht0iv отсюда сле-
следует, что 2, = 2, т. е. 2 = 2+-f-§> -|-2_. Из уравнений F) следует,
что 2 является прямой суммой корневых подпространств относи-
относительно ф и что ненулевыми корнями будут функции ±(а; -|- • • • +аг )•
Ясно, что 2+ есть сумма корневых подпространств, соответствующих
корням аг -j— . .. -f a/f, a 2_— сумма корневых подпространств,
соответствующих корням —(a2i~b ••• ~г"аг )• Отсюда следует, что
2 = 2+®§)®2_. Это завершает доказательство теоремы.
§ 2. О некоторых циклических модулях над 2
Модуль Ли Ш является циклическим с образующей х, если
Ш — наименьший подмодуль в Ш, содержащий х. Если U — уни-
универсальная обертывающая алгебра алгебры Ли, то x(VL)— (хм | a ?11}
есть наименьший подмодуль, содержащий х. Следовательно, Ш
цикличен с л: в качестве образующей тогда и только тогда, когда
2Н = xVL. Модуль Ж над алгеброй Ли 2 = ^2/$, который был по-
построен в § 1, является циклическим с 1 в качестве образующей,
поскольку 1/г ... /; — Х[ ... xt , а эти элементы вместе с 1
образуют базис в Ж.
Будем называть модуль Ш над 2 е-экстремальным, если он
цикличен и образующая х может быть выбрана так, что xh = A(h)x,
xet = 0, i=l, 2, ..., I. Из соотношений D) явно следует,
что Ж — е-экстремальный модуль с 1 в качестве образующей требуе-
требуемого типа. Таким образом, мы видим, что для каждой линейной
функции Л (ft) на ф существует е-экстремальный модуль, для кото-
которого образующая х удовлетворяет условиям xh = A(fi)x, xei = Q.
Рассмотрим теперь теорию е-экстремальных модулей над 2. Подоб-
Подобную же теорию можно развить и для /-экстремальных модулей,
которые определяются как циклические модули с образующей у,
такой, что yh = A(h)y, yfl = Q, 1=1, 2 /. Мы ограничимся
рассмотрением е-экстремальных модулей, но будем пользоваться и
соответствующими результатами для /-экстремальных модулей, когда
это потребуется.
Пусть Ж — е-экстремальный модуль с образующей х, удовле-
удовлетворяющей условиям xh = A(h)x, xet = 0. Мы знаем, что универ-
универсальная обертывающая алгебра Й для 2 может быть представлена
в виде U = 2iU+U_, где SB, U+ и U_ — подалгебры, порожден-
порожденные §>, 2+ и 2_ соответственно. Значит, Ш— хй = x23U+U_.
Так как xh = A (ft) х, то хЗЗ = Фх, и так как xei = 0, то хй+ = Фх,
§ 2. О некоторых циклических модулях над 8 235
Следовательно, Ш = x23U+U_ = xll_. Кроме того, U_ порождается
элементами /;. Следовательно, каждый элемент модуля Ш будет
линейной комбинацией элементов
*/,;•¦¦/,,. G)
где мы уславливаемся, что ft ... fir—\, если г —0. Очевидно,
[/i.---/.r.*] = -K4-...+«,,)/,,.../,,
(индукция по г) и х/г = Лх. Из этих соотношений следует, что
(xflt . . . flr)h = x\fh ... fir, h]+{xh)fh .../,,=
= (А-аг,- ... -%)xftl ... f,r.
Поэтому
(*/,, .. . /,r) h = (Л - в|| - ... - a(f) (х/(- ... /,,). (8)
Таким образом, 3R является прямой суммой весовых подпространств
относительно § и веса имеют вид
i
Л - (ah + ah + . . . + «О = Л - 2 ЛЛ. (9)
где &г—неотрицательные целые числа. Ясно также, что ограничение
на весовое подпространство линейного преобразования, соответст-
соответствующее любому ft, сводится к умножению на элемент поля. Ясно
также, что весовое подпространство ?№д, соответствующее Л, имеет х
в качестве базиса и потому одномерно. Весовое подпространство Шм,
соответствующее весу М — Л — 2 ^гаг> натягивается на векторы
вида G), для которых <хг + ... +аг =^iklai. Очевидно, что
существует лишь конечное число таких последовательностей (iv i2 iT),
для которых a-i -\~ ... +аг = 2 ^гаг> гДе *, — некоторые фикси-
фиксированные неотрицательные целые числа. Следовательно, Шм конеч-
конечномерно.
Вес Л можно охарактеризовать как единственный вес модуля Ш
относительно ф, такой, что каждый вес имеет вид Л—2*/а/>
kl — неотрицательные целые числа. Мы будем называть Л старшим
весом модуля Ш относительно ф (или просто модуля ?№). Если
модуль VI изоморфен 9I, то VI тоже будет е-экстремальным и стар-
старший вес его будет Л. Отсюда следует, что два е-экстремальных
й-модуля, имеющие различные старшие веса, не могут быть изо-
изоморфными.
Пусть Ш — некоторый подмодуль модуля Ш = 2 УЯ-м (сУмма
прямая), где ffl.M — весовой подмодуль, соответствующий М. Если
у ?9^, то у?Шм + ... +ШМ, где {Ml Mk] —некоторое
236 Гл. VII. Классификация неприводимых модулей
конечное подмножество множества весов. Следовательно, у^Э^П
П (SK^ij + • • • + ^лгь) и последний является подмодулем конечно-
k
мерного ^-модуля 2 ^-м- Такой ^-модуль расщепляем и является
прямой суммой весовых подмодулей, веса которых принадлежат
множеству {Mj) (ср. § 2.4). Это означает, что 1Я П B ^м ) —
= 2 ffi П %ЯМ ). Поскольку у — любой элемент модуля 9ч\ мы имеем
также 9f—2^ж (сумма прямая), где 91М = 91()ШМ. Если 91мф0,
то М — вес модуля 9ч относительно ф. Во всяком случае, ясно,
что У1 является прямой суммой весовых подмодулей и что веса
модуля Щ находятся среди весов модуля Ш относительно ф.
Пусть теперь Ш' будет подпространством модуля ?№, натянутым
на $IМ, где М Ф Л, и предположим, что подмодуль 9ч" ф Ш. В этом
случае мы должны иметь Ша = 0, так как в противном случае Щ&. = 9Лд,
а подмодуль ЭЛд одномерен. Тогда х^Щ. и 9f = xU = 9}J вопреки
предположению. Таким образом, мы видим, что любой собственный
подмодуль 9t= 2 %lM с $Iг<г.Ш. Отсюда следует, что сумма ^5
всех собственных подмодулей модуля Ш содержится в 9)J'cr9)J и
поэтому является собственным подмодулем. Это доказывает существо-
существование максимального (собственного) подмодуля ^5 модуля Ш. Более
того, $ однозначно определен.
Рассмотрим опять модуль X, построенный в § 1, который, как
мы сейчас покажем, является „универсальным" е-экстремальным моду-
модулем со старшим весом Л в том смысле, что каждый модуль Ш этого
типа есть гомоморфный образ модуля Ж. Для этой цели определим
линейное отображение 6 модуля Ж на Т1, такое, что (xt ... xt ) 6 =
= xfti ... fir(xti ... xir=\, если r = 0). Тогда
[xh . . . x,rft) 6 =(xti . . . xlrxt) 6 =
= */*, .../«,/, = ((*,, ••• xt^)flt A0)
x
trN =
§ 3 Конечномерные неприводимые модули 237
Мы можем использовать последнее соотношение, чтобы по индукции
относительно г получить формулу
(*,, ... xiret)B = (xti ... xird)et. A2)
Так как элементы et, ft, ht порождают Й, то уравнения A0), A1)
и A2) означают, что отображение 6 является гомоморфизмом мо-
модуля Ж на Ш.
Только что полученный результат показывает, что любой е-экстре-
мальный й-модуль со старшим весом Л изоморфен некоторому модулю
вида X/9J, где Щ — подмодуль модуля Ж. Если 9И неприводим, то
9К = Х/^3, где ^3-—максимальный подмодуль модуля Ж- Мы видели,
что такой подмодуль существует лишь один. Ясно, следовательно,
что любые два е-экстремальных модуля с одинаковым старшим весом
изоморфны. Существование неприводимого е-экстремального модуля
со старшим весом Л также очевидно, так как модуль Ш == Ж/^3 удо-
удовлетворяет этим требованиям.
Наши основные результаты суммирует следующая
Теорема 2. Пусть обозначения будут те же, что и
в теореме 1, и пусть Л(й)—некоторая линейная функция
на §». Тогда существует неприводимый е-экстремальный %-мо-
%-модуль со старшим весом Л. Веса такого модуля имеют вид
Л — 2 *Л- ?« — некоторые неотрицательные целые числа. Весо-
Весовое подпространство, соответствующее Л, одномерно, и все
весовые подпространства конечномерны. Каждый элемент ft?-§>
действует как скалярный оператор в каждом весовом под-
подпространстве. Два неприводимых е-экстремальных 2-модуля
изоморфны тогда и только тогда, когда они имеют одинако-
одинаковый старший вес.
§ 3. Конечномерные неприводимые модули
Линейную функцию А на § мы будем называть целой, если
Л (ft;)—целое число для каждого /=1, 2, ..., /; целую линейную
функцию будем называть доминантной, если Л(/г;)^>0 для всех i.
В этом параграфе устанавливается взаимно однозначное соответствие
между этими функциями и классами изоморфных конечномерных
неприводимых модулей над й. Ввиду соответствия между классами
изоморфных неприводимых е-экстремальных й-модулей и старшими
весами, которое было установлено в теореме 2, достаточно доказать
две вещи: A) каждый конечномерный неприводимый модуль е-экстре-
мален со старшим весом, который является доминантной целой функ-
функцией; B) любой неприводимый е-экстремальный модуль со старшим
весом, являющимся доминантной целой линейной функцией, конечно-
конечномерен. Докажем сначала следующую теорему.
238 Гл. VII. Классификация неприводимых"модулей
Теорема 3. Пусть й — определенная ранее алгебра Ли,
Ш — конечномерный неприводимый ^.-модуль. Тогда Ш е-экстре-
мален и его старший вес является доминантной целой линей-
линейной функцией на ф.
Доказательство. ?№ — конечномерный модуль над подалгеб-
подалгеброй 2; — Фе1-\-Ф/1-\-Фп1, которая является расщепляемой трехмер-
трехмерной простой алгеброй Ли. Следовательно, Ш—вполне приводим как
йгмодуль. Вид неприводимых модулей над 8г (§ 3.8) показывает,
что существует такой базис (х[1\ х^ х$\ в Ш, что x^h( =
~tnlkx^, где mik — целые числа. Так как [АгАу] = О, то линейные
преобразования, соответствующие разным ht, коммутируют; следова-
следовательно, можно найти базис (хг, х2 xN), для которого xkhl =
= mikxk, i—I, .... I, k = \ N. Если Ak обозначает такую
линейную функцию на <?>, что Ak (ht) = mik, то Ak целая и
xkh = Akxk, k=l, 2 Л^. A3)
Функции Ak будут весами модуля Ш относительно §. Пусть
§о—рациональное векторное пространство, натянутое на линейные
функции а.{. Легко видеть, что линейная функция а?фо тогда и
только тогда, когда значения a(ht) рациональны для /—1, 2, .... I
(ср. доказательство предложения XIII в § 4.2). Следовательно, веса
Л&?фо и> таким образом, можно выбрать среди них наибольший
вес Л в смысле отношения порядка в ?>0. характеризующегося тем,
i
что 2 ^iai > 0. если первый коэффициент Xi Ф 0 положителен. Ясно
при этом, что А-|- at не будет весом ни для какого at. Пусть х — такой
ненулевой вектор, что хп = Ах. Тогда {xet)h ==(А + аг)(хег), так
что xet = 0 в силу максимальности Л. Так как Ш неприводим и
xU — подмодуль модуля ?№, то ясно, что Ш = хй. Следовательно, Ш
е-экстремален и имеет Л в качестве своего наибольшего веса, являю-
являющегося также и старшим в смысле предыдущего параграфа. Резуль-
Результаты § 2 показывают, что каждый вес имеет вид Л — 2 ^iai<
ki — целые неотрицательные числа. С другой стороны, доказательство
теоремы о представлениях, а именно теоремы 4.1 (примененное
к ф-|-Фег-)- Ф/i), показывает, что если М—вес модуля ?№ отно-
относительно ф, то М — M(hi)at тоже будет весом. Следовательно, для
каждого / функция Л — Л(йг)а(- является весом и, таким образом,
имеет вид Л—2 kp-i- Отсюда следует, что A(hl) = ki ^>0. Итак,
мы видим, что Л — доминантная целая функция. Это завершает
доказательство.
Пусть теперь Л—любая доминантная целая линейная функция
на § и Ш — неприводимый модуль, задаваемый теоремой 2, с макси-
§ 3. Конечномерные неприводимые модули 239
мальным весом Л. Веса модуля Ш относительно ф имеют вид
Л — 2 kiai> kt — целые и неотрицательные. Следовательно, эти веса
целые и, таким образом, их можно упорядочить в соответствии
с отношением порядка, введенного в <?>о- Мы докажем, что Ш — ко-
конечномерный модуль. Доказательство будет основываться на несколь-
нескольких леммах.
Лемма 1. Пусть Qij = fj(adJfi)~AlJ+1, 1ф]=\, 2 /.
Тогда [в^ек] = О, k = 1, 2 I, и 9Й8(.;. = 0 для любого е-экстре-
мально неприводимого ^-модуля 9К.
Доказательство. Если k ф i, то [ftek] = O; следовательно,
[ad fi ad ek] = 0. В таком случае
[Виек] = fj (ad ftyAiJ+l ad ek = f} ad ek (ad ffA4"' =
При &=??=у это равно 0. При k = j получаем [6?;efc] — — Ajift (ad fi)~A'J.
Если Л,7 = 0, то Л;г = 0, согласно условию (а) из § 1, так что
результат равен 0 в этом случае. В противном случае — А1 - > 0 и
fi(adfi)~AiJ = O. Пусть, наконец, k — i. Тогда
j j
Напомним формулу коммутирования: akx = xak — ( J x'ak~l -\-
+ {l)x"ak~2~ ¦¦¦' где х'=[ха], x"z=[x'a\, ... (уравнение 2.6).
Используя эту формулу и таблицу: [eifi\ = hi, [ [eJJ ft] = 2ft,
[ i [/l/j]/i]^0' получаем соотношение:
/у (ad /;ГЛг;+1 ad et = f} ad et (ad /г)'л^+1 —
— (— AlJ-\-l)fJudhl(udfl)-AU, если Л,у = 0,
/;(ad /()-л^+1 ade. = ;
- (- Au+ \)fj ad ft; (ad fi)
-^;.+ l)(-Ay)/;(ad2/?)(ad/?)-^-1, если - Al} > 0.
Первые члены в обоих случаях можно опустить, так как fj ad et =
/ 0 Л
— [//*] = 0- Если Atj = O, то fjad hi = [fjhi] = O. Если—AtJ > О,
то, используя вторую формулу и / • ad ht = [f,ht\ — — Atjf j, получаем
- (- A,j + 1) (- Au) fj (ad ft)~A4 +
-j- (- Ai}-Y 1)(- AtJ)fj(tidfd-A4 =0.
240 Гл. VII. Классификация неприводимых модулей
Это завершает доказательство равенства [6(-;efc] = 0. Пусть, далее,
Ш — неприводимый е-экстремальный Й-модуль и, как и прежде,
SR' — подпространство, натянутое на весовые подпространства, соот-
соответствующие весам, отличным от старшего веса А. Рассмотрим под-
подмодуль ?№9;yU = 9W6(/8U+U_, гДе 53 > Й+ и U_ такие же, как в тео-
теореме 1. Используя тот факт, что отображение ad ft является диф-
дифференцированием и что [fih] = — a;/j. мы получаем, что
9уА = АВу + [ВуА] = АВу + (- «у + (AtJ - 1) a,) 6tJ,
откуда следует,' что ЗКВуЭЗ = 9И6у. Кроме того, Ь^еь = eft8y, поэтому
дКВуй+ = аКВу. Следовательно, 2RByU = 2K6yU_. Если х —канони-
—каноническая образующая модуля Ш, т. е. xft = Ax, xev — 0, i = 1, 2 /,
то каждый элемент модуля 9И будет линейной комбинацией элемен-
элементов вида xft ¦. ¦ fi и каждый элемент подпространства W будет
линейной комбинацией этих элементов с г^>1. Из определения эле-
элементов By вытекает, что ?№8г;- с ЗИ'. Ясно также, что 2JJ'U_ S 9)?'.
Следовательно, SKByU E W и, таким образом, ЗЯВуЦ является соб-
собственным подмодулем модуля Ш. Так как 97J неприводим, то должно
быть ЗК8у = О и доказательство закончено.
Лемма 2. Пусть Ш—неприводимый е-экстремальный модуль
над й, старший вес А которого является доминантной целой
линейной функцией. Тогда для любого у?ЭД? существуют такие
положительные целые числа rt, st, что
yii = Q = yf*li, i = \, 2 /.
Доказательство. Пусть х — образующая модуля Ш, для
которой xh — Ах, хег = 0, /=1, 2, ..., /. Тогда каждый элемент
модуля Ш является линейной комбинацией элементов вида xfi .. .fi .
Достаточно доказать утверждение для каждого у = xfi ... fi .
Имеем yh = My, M = A — 2 *гаг> ^г^-0 — целые числа. В таком
случае (yekJ+1) h = (Ж + (А.+ 1)а() уе**+1. Так как M+(kl + 1)а,
не является весом, то ye^l+1 = 0, что доказывает утверждение для е(..
(Это рассуждение справедливо для произвольных е-экстремальных
й-модулей.) Пусть A(ft() = mt ^> 0. Мы покажем теперь, что
xf™i+1 — 0. Имеем xhi = mix, xei = 0. Следовательно, применяя
теорию е-экстремальных модулей к алгебре %.1 = Фе1-\-Ф/1-\-Фп1
(вместо й), мы видим, что й(-подмодуль 2йг, порожденный элементом х,
будет пространством, натянутым на х, х/г, хрь Предполо-
Предположим, что он имеет собственный подмодуль efll Ф 0. Так как
(xfj)h( — (mi — 2k\xfk., то пространства Фх/* будут весовыми под-
§ 3 Конечномерные неприводимые модули 241
пространствами относительно Фйг. Следовательно, 311 натягивается
на некоторые из подпространств Фх/* и k^-l, так как 9?(.<г9К(.
Более того, если х/^5^(.,Чо х/*? 3ii для всех q^-k. Поэтому
¦ЭТ.= 2 Фх/Ч, где & — наименьшее положительное целое число,
для которого xf\ ? 9i;. Очевидно, что 9?г с ЗИ'. Отметим теперь,
что %1Л с ?Jf., поскольку (х/«) ft = (Л — qa^(х/<?), и !1,е4 с !Л., так
как это ясно при k = i и выполняется при k ФI ввиду равенства
xf4.ek = xekf<l = 0. Поэтому 31123 = Щ. и 3^U+ = !Rr В таком случае
W,U = !R/«U+U_ = SR?U_S9K'. т. е. Э1,Й является собственным
й-подмодулем модуля Ш ф 0. Это противоречит неприводимости
модуля Ш и, таким образом, доказывает, что 2Й( на самом деле
йгнеприводим. Далее, в § 3.8 мы построили конечномерный непри-
неприводимый Й;-модуль с образующей х', для которой x'hl = mlx'',
x'ei = 0 и х'/'."'+1^=О. Из результата об изоморфизме неприводи-
неприводимых е-экстремальных модулей (теорема 2) следует, что этот модуль
изоморфен модулю ^..Следовательно, х/™'+1 = 0. Предположим те-
теперь, что существует целое число /и^-О, для которого (xfi ... ft \f™=
= 0. При ir = i отсюда вытекает, что (xfi .../г)/™ = 0. При
lT = J Ф i мы используем соотношение
'"fi (ad fd'AtJ (mod 4'
где §ij такие же, как в лемме 1, и сравнение пишется по модулю
идеала в U, порожденного 6^. Из леммы 1 следует, что
• • • 4-
Применяя индукцию по г, получаем утверждение относительно ft.
Лемма 3. Пусть 9JJ обозначает то же, что и в лемме 2.
Тогда, если М является весом модуля Ш относительно ф,
то М — M(hi)al будет весом для i = l, 2 /.
Доказательство. Пусть у — ненулевой вектор, для которого
yh — M(h)y. При M{h^)%Q выберем q так, чтобы г = уе\фО>,
уе?+1=0, а т — так, чтобы г/™ =? 0, г/?1+1 = 0. Это можно сде-
сделать, согласно лемме 2. Тогда описание конечномерных неприводимых
16 Н. Джекобсон
242 Г г. VJ1. Классификация непривооимих модулей
т
модулей над 2г = Ф^ + ФЛ + ФА/ (§ 3.8) показывает, что 2
k = 0
будет таким модулем и что zht = mz. С другой стороны, равенство
yh = M(h)y дает zh = (уе|) А = (Ж + ?а.) (h) z и (/*)й
= (М + ^ — /га() (Л) zff. Следовательно, (Ж -f ?<*,) (А,-) =
-f- 2q — m и
M-\-qo.i, M-\-(q—1)аг, ..., Ж + (<7— m)at
являются весами (соответствующими z, zft zff)- Мы имеем
Ж — Ж (А;) а; = Ж -\- Bq — т) аг и q — m^2q — т < q, так как
M(ht) = m — 2q^-0 и g^-0. Следовательно, Ж — M(hi)al содер-
содержится в написанной выше последовательности. При Ж(Аг)^0 мы
меняем ролями элементы et и ft и рассуждаем аналогичным образом.
Мы можем доказать теперь следующую теорему.
Теорема 4. Пусть Ш—неприводимый е-экстремальный
модуль над И со старшим весом Л, являющимся доминантной
целой линейной функцией. Тогда Ш конечномерен.
Доказательство. Пусть 5а обозначает линейное отобра-
отображение ?—>-? — l(hi)ai в пространстве §о рациональных линейных
комбинаций линейных функций at, для которых a.t (hj) = Ajt. Мы
имеем a.jSa. =a.j= Aijat, так что Sa есть одно из линейных преоб-
преобразований, определяемых аксиомой (в) из § 1. Эта аксиома утвер-
утверждает, что группа W, порожденная преобразованиями Sa., конечна.
С другой стороны, лемма 3 показывает, что множество весов модуля ffi.
относительно ф инвариантно относительно W. Рассмотрим теперь
множество S образов максимального веса Л при действии W. Это
множество конечно, так что оно имеет наименьший элемент Ж отно-
относительно лексикографического упорядочения, которое было введено
в ?>о (в начале этого параграфаI). Пусть у — ненулевой вектор,
такой, что yh = My. Так как Ж — Ж(Аг)а(^Е, то Ж^Ж —
— Ж(Аг)аг, а поэтому мы имеем Ж(Аг)<^0, г' = 1, 2, .... /. Одна
из линейных функций Ж — аг, M-\-at не будет весом. Действительно,
Ж=Л5, S?W, и если Ж — аг, Ж-)-аг являются весами, то Л —
— aiS~1 = (M — <х;) S и Л + ^5 будут весами. Однако одна из
последних функций больше Л относительно упорядочения в фо> что
противоречит максимальности веса Л. Если M-\-ai не является
весом, то yet = Q, а также уАг=Ж(А,)у. Как и в доказательстве
леммы 3, у порождает неприводимый 1',-модуль размерности
') Единственное место в нашем изложении, где используется аксиома (в).
§ 4. Теоремы существования и изоморфизма для полупростых алгебр Ли 243
M{hj)-\-\. Следовательно, М(/гг)>0. Так как Л(А()<0, то
Ж(йг) = 0. Если бы М — аг было весом, то мы имели бы также,
что
M — ai — {M — at) (ht) a, == М — at + 2а; = М + а,
было бы весом вопреки предположению. Таким образом, М — ai не
будет весом, если M-\-ai не является весом. Следовательно, в любом
случае М — а.1 не является весом. Поэтому yft == 0, / =: 1, 2, ...,/. По-
Поскольку Ж неприводим, WI — уЙ. Таким образом, мы видим, что ЯJ
является /-экстремальным модулем. Отсюда следует, что веса мо-
модуля Ш относительно ¦§> имеют вид Л1-|-2Ла/1 Л^О— целые
числа. Если М—Л—S^a;> то ясно, что веса имеют вид Л —
— 2^гаг>чгде O^C^j^'i- Таким образом, существует лишь конеч-
конечное число различных весов, и так как каждое весовое подпростран-
подпространство конечномерно, то мы видим, что и модуль WI имеет конечную
размерность.
§ 4. Теоремы о существовании и изоморфизме
для полупростых алгебр Ли
Пусть F обозначает совокупность конечномерных неприводимых
представлений алгебры Ли 2 и Ко—ядро совокупности F, т. е.
множество элементов b ? й, таких, что bR — 0 для каждого R(^F.
Тогда $0 будет идеалом в й. Если R?F, то можно определить
представление R алгебры Ли S==S/S?0, полагая A-^-^)^ = 1^. Так
как множество преобразований lR соответствующего модуля то же
самое, что и при представлении алгебры й, то ясно, что R будет
конечномерным неприводимым представлением алгебры Ли Й. Мы
покажем теперь, что й — расщепляемая полупростая алгебра Ли,
а положенная в основу определения алгебры й матрица (AjA является
матрицей Картана для й. Именно, имеет место следующая
Теорема 5. Пусть Й~—^й/$, где $Й — свободная алгебра
Ли, порожденная элементами ео /;, ht, i=\, 2 I, и $ —
идеал в §й, порожденный элементами B). Пусть $0 будет
ядром всех конечномерных неприводимых представлений
алгебры Й и Й —й/$0. Тогда: A) Й является конечномерной
расщепляемой полупростой алгеброй Ли; B) каноническое
i i
отображение пространства §+2^i+S*/i s 8 является
1 1
изоморфизмом, так что это подпространство можно отожде-
отождествить с его образом; C) '•§) — расщепляющая подалгебра
Картана, функции ai образуют простую систему корней, и эле-
16*
244 Гл. VII. Классификация неприводимых модулей
менты hr et, ft составляют множество канонических обра-
образующих; ассоциированная с ними матрица Картана совпадает
с заданной матрицей (Atj); D) пусть Ч — любая конечномер-
конечномерная расщепляемая полупростая алгебра Ли с 1-мерной рас-
расщепляющей подалгеброй Картана <§> и каноническими обра-
образующими hit et, ft, которым соответствует матрица (AlJ).
Тогда существует изоморфизм алгебры 2 на Si, такой, что
й,-+й,, в/->7(, /,->/,. /=1, 2 I.
Доказательство. Пусть Хг обозначает линейную функцию
на ¦§>, для которой Х/(Л/-) = 8/у. В таком случае Хг есть доминантная
целая линейная функция, и поэтому она соответствует некоторому
конечномерному неприводимому представлению Rt в модуле 5Мг
над й (и над 2). Функции Хг образуют базис в §*, и каждая доми-
доминантная целая линейная функция имеет вид Л = 2/ИЛ> mi <^ О—
целые числа. Покажем сначала, что ядро $0 можно охарактеризовать
как ядро конечного множества представлений Rt. Итак, пусть 5Й —
любой конечномерный неприводимый модуль и Л=2/иЛг —его
старший вес. Пусть ^} — модуль, являющийся тензорным произведе-
произведением т1 экземпляров модуля 2)^, т2 экземпляров модуля Ш2, .. ., mt
экземпляров модуля Шг. Пусть xf — образующая модуля Ttj, для
которой Xjh — 'kjXj, /z??>, Xjet = 0, 1=1, 2, .... I. Положим
I I I
® ... ®x2® ®хг® ••• ®xv A4)
В этом определении и формуле мы условимся, что если все
/гег = 0, а это имеет место тогда и только тогда, когда Л = 0, то Ш
будет одномерным модулем с базисом х и xl — 0, 1?%. Тогда в любом
случае xh==Ax, хе( = 0, так что xU является е-экстремальным
модулем со старшим весом Л. Следовательно, неприводимый модуль Ш,
соответствующий весу Л, является гомоморфным образом модуля дгп.
Предположим, что 1?К и lRi =0 для 1=1, 2 I. Тогда Щ1=
= 0; следовательно ^1 = 0 и лгШ = 0. Это означает, что 9Ю —0,
т. е. /я = 0. Этим доказано утверждение о том, что S?o — ядро ко-
конечного множества представлений Rit или, что равносильно, ядро
единственного представления 5, а именно прямой суммы представле-
представлений Rt. Очевидно, что 5—конечномерное вполне приводимое пред-
представление, a S = У/^о = 25 — конечномерная вполне приводимая ал-
алгебра Ли линейных преобразований. Так как хг/г = Хг(й) xt, /г?ф,
то из равенства /г5—0 следует, что Х,(й) = О для всех I. Так' как
функции Х^ образуют базис для §*, то это означает, что h = 0.
§ 4. Теоремы существования и изоморфизма для полупростых алгебр Ли 245
Поэтому $ представляется точно при помощи 5, а следовательно,
и при каноническом отображении алгебры 2 на 2. Отсюда вытекает,
что простые алгебры 2г представляются точно. В таком случае
доводы, использованные при доказательстве соответствующего утвер-
утверждения в теореме 1, показывают, что имеет место утверждение B).
Поскольку 2 является прямой суммой ¦§> и подпространств 2дг> соответ-
соответствующих корням М = + B kp-i)' k^O — целые числа, то же самое
утверждение выполняется для й. Отсюда следует, что ¦§> есть рас-
расщепляющая подалгебра Картана алгебры 2. Следовательно, центр (Е
алгебры 2 содержится в ф.
Если /zo?E,, то мы должны иметь [егй0] = аг(/г0)е; = 0. В таком
случае a/(/zo) = O для всех i, и /г0 —0. Таким образом, E, = 0. Так
как 2 изоморфна конечномерной вполне приводимой алгебре Ли
линейных преобразований и имеет нулевой центр, то й — полупростая
алгебра. Следовательно, установлена справедливость утверждения A).
Так как [eji] = агег и каждый корень алгебры й относительно §
имеет вид ± B kp.^), kt ¦— целые и неотрицательные, то корни аг
образуют простую систему. Мы имеем [etf]\=bljhi, [ethj\ — A^e^
\fi^j\== — A jiff Это означает, что ег?2а., /г?8_а,. образующие
ev ff hi — канонические, а ассоциированная с ними матрица Картана
есть (Atj) (ср. § 4.3). Это завершает доказательство утверждения C).
Пусть теперь алгебра Ли 2 такова, как это требуется в D). Ясно, что
существует гомоморфизм алгебры 2 на 2, при котором ei-^-el,
ft-*-fi, hi-^-ht. Так как 2 полупроста, то она может быть ото-
отождествлена с вполне приводимой алгеброй Ли линейных преобразо-
преобразований конечномерного векторного пространства, и гомоморфизм
алгебры 2 на 2 можно рассматривать как представление. Поскольку
$о отображается в 0 при любом конечномерном неприводимом пред-
представлении, гомоморфизм алгебры 2 отображает So в 0 и, таким
образом, мы имеем индуцированный гомоморфизм алгебры 8 на 2>
при котором ei-^-ei, fi-+ft, hi~^-~hi. Так как подпространство ф
Z-мерно, то этот гомоморфизм отображает •§) изоморфно. Если $: —
ядро гомоморфизма алгебры 2 на 2, то, поскольку $2 — идеал, он
будет инвариантен относительно adg?>. Отсюда следует, что если
5?! Ф 0, то он содержит либо отличный от нуля элемент из ¦§>, либо
одно из (одномерных) корневых подпространств 2а, афО. Первое
исключается, так как ^A^ = 0. Если S, Э 8„, то 5^ Э [8e2_J=?0.
Так как [2ай_а] ? §, то это тоже исключено. Следовательно, Ki = 0
и гомоморфизм алгебры 2 является изоморфизмом. Это доказывает
утверждение D).
Теоремы 3 и 4 устанавливают взаимно однозначное соответствие
между классами изоморфных конечномерных неприводимых модулей
246 Гл VII Классификация неприводимых модулей.
над (бесконечномерной) алгеброй Ли 8 и совокупностью доминантных
целых линейных функций на ¦?>. Из определения алгебры 8 ясно
также, что любой конечномерный неприводимый 8-модуль будет
2-модулем. Обратное очевидно, поскольку 8 является гомоморфным
образом алгебры 8. Следовательно, мы видим, что теоремы 3 и 4
устанавливают взаимно однозначное соответствие между классами
изоморфных конечномерных неприводимых модулей над конечномер-
конечномерной расщепляемой полупростой алгеброй Ли и совокупностью доми-
доминантных целых линейных функций на расщепляющей подалгебре
Картана ф алгебры 8.
Напомним, что множество ? линейных преобразований векторного
пространства Ш над Ф называется абсолютно неприводимым, если
соответствующее множество (множество продолжений) линейных пре-
преобразований неприводимо в Шр для любого расширения Р основного
поля. Из этого условия следует неприводимость, так как можно
взять Я —Ф. Термин „абсолютно неприводимый" имеет столь же
очевидный смысл и в применении к модулям и представлениям. Из
определения ясно, что некоторый модуль Ш над алгеброй Ли 8 будет
абсолютно неприводимым тогда и только тогда, когда Шр непри-
неприводим над ?р для любого расширения Р поля Ф.
Далее, пусть 8 — расщепляемая полупростая .алгебра Ли над Ф,
как в теореме 5, и Ш—конечномерный неприводимый 8-модуль.
Мы утверждаем, что Ш абсолютно неприводим. Действительно, мы
знаем, что Ш является е-экстремальным модулем с образующей х,
для которой xel = 0, 1=1, 2, ..., I, и xh = A.(ti)x, Л ? ф, где
Л —доминантная целая линейная функция на ¦§>. Мы знаем также,
что весовое подпространство ЗИд, соответствующее Л, совпадает
с Фх. Рассмотрим Tip как модуль над 8р. Так как этот модуль
конечномерен и алгебра 8р полупроста, то он вполне приводим.
Каждый неприводимый подмодуль ЭД модуля Шр разлагается на весо-
весовые подмодули относительно ?>р. Следовательно, каждый весовой
подмодуль относительно §р в Tip можно разложить на сумму под-
подмодулей, содержащихся в неприводимых компонентах разложения
модуля Tip на неприводимые 8р-модули. В частности, это верно для
(Шь)р~Рх. Поскольку этот модуль одномерен, х содержится в не-
некотором неприводимом подмодуле Ш модуля Шр. Так как х поро-
порождает Шр, то У1 — Шр и Шр, неприводим. Это доказывает абсолют-
абсолютную неприводимость модуля Ш.
§ 5. Существование алгебр Е7 и Еь
В § 4.6 мы установили существование расщепляемых простых
алгебр Ли типов, соответствующих каждой схеме Дынкина, за исклю-
исключением E-j и Ей. (Наш способ доказательства—явная конструкция
§ 5. Существование алгебр Е7 и Еа
247
для каждого типа — был, правда, отчасти эскизным для исключи-
исключительных типов О2, ^4 и ^6-) ^ нас имеется теперь в распоряжении
другой метод, основанный на теореме 5. Он требует проверки того,
что матрицы Картана (Ai}), получаемые из схем Дынкина, удовле-
удовлетворяют условиям (а), (б), (в) из § 1. Мы проведем сейчас такую
проверку для схем Е7 и Es и тем самым установим существование
алгебр Ли этих типов. Отметим с самого начала, что условие (а)
проверяется непосредственно, коль скоро выписана матрица, а (б)
вообще легко проверяется. Для доказательства (в) нужно найти
некоторое конечное множество векторов в §о. которые порождают
¦§>о и инвариантны относительно симметрии Вейля 5а. Этим будет
доказана конечность группы W, порожденной преобразованиями Sa
?8. Матрица Картана в этом случае есть
(А,-) =
2
1
0
0
0
0
0
0
— 1
2
j
0
0
0
0
0
0
1
2
— 1
0
0
0
0
0
0
1
2
— 1
0
0
0
0
0
0
\
2
j
0
1
0
0
0
0
J
2
— 1
0
0
0
0
0
0
—1
2
0
0
0
0
0
—1
0
0
2
A5)
Отсюда видно, что det(Ai])=l, так что (б) очевидно. Усло-
Условие (а) тоже очевидно. Введем векторы
Х3 = 3 (а3
Х4 = 3 (а4
2а6
Х7 = — а6 -f- а7
где (а,, а2, ..., а8) — базис 8-мерного векторного пространства над
полем рациональных чисел. Сразу же видно, что (Хг) образуют базис.
Симметрию Вейля 5а , определенную равенством A), мы обозначим
через Sj. Можно проверить, что St, 1 <О<*^, переставляет Х^ и X
i+1
248 Гл. VII. Классификация неприводимых модулей
и оставляет другие ~kj на месте, в то время как
Пусть ? есть следующее множество векторов:
где индексы все различны и берутся из множества A, 2, ..., 8).
Легко видеть, что эти векторы порождают все пространство. Так
как 5;, 1-^.7, являются перестановками символов X, то ясно, что
эти St отображают ? в себя. Непосредственно проверяется также,
что 58 оставляет ? инвариантным. Это означает, что группа W,
порожденная преобразованием St, конечна.
Е7. Пусть aj, а2, ..., а8 — простая система корней типа Es рас-
расщепляемой алгебры Ли Е&. Матрица (Ajk) = B (а;., aft)/(a;, а^)),
у, k — 2, ..., 8, есть матрица Картана типа Ег Она удовлетворяет
условиям (а) и (б). Более того, выполняется и условие (в), так как
группа, порожденная преобразованиями 5Я2, ..., S4, конечна; сле-
следовательно, группа, порожденная ограничениями этих отображений
на подпространство из ?>*, натянутое на векторы а2 а8, тоже
конечна. Это доказывает существование алгебры Е7.
Аналогичный метод применим и к Е6. Легко убедиться также
в том, что если ег, /г, ht G=1, ..., 8) есть множество канониче-
канонических образующих алгебры ?8, то подалгебра, порожденная элемен-
элементами еу, f j, hj (j — 2 8), совпадает с алгеброй Е7 (см. упра-
упражнение 1 в конце главы).
§ в. Базисные неприводимые модули
Пусть й — расщепляемая конечномерная полупростая алгебра Ли
над полем характеристики 0 и, так же как в доказательстве теоремы 5,
Ttt — конечномерный неприводимый модуль, соответствующий доми-
доминантной целой линейной функции Хг, для которой Xi(hj) = blj,
t, J=l, 2, ..., I. Если векторы xt определены так же, как в до-
доказательстве теоремы 5, а х — равенством A4), то рассуждение,
использованное в § 4 для доказательства абсолютной неприводи-
§ 6. Базисные неприводимые модули 249
мости, показывает, что подмодуль модуля
I 1
. .. ®Tit® ... ® Wlt, порожденный элементом x, является непри-
неприводимым модулем, соответствующим весу Л=2тЛ- Задача явного
нахождения неприводимых й-модулей конечной размерности сводится
поэтому к задаче отождествления модулей 9К;, которые мы будем
называть базисными неприводимыми модулями над 8. Мы про-
проведем сейчас,это для некоторых простых алгебр Ли. Другие случаи
рассматриваются в упражнениях.
Av Как мы видели в § 4.6, Лг есть алгебра Ли {1-\- 1)Х(Ч~ 1)-
матриц со следом 0 над Ф. Если (е^) — обычный матричный базис
алгебры Фг+1, а подалгебра Картана и простая система корней
выбраны так же, как в § 4.6, то множество соответствующих им
канонических образующих будет иметь вид
1— eI2> У 2— е23' •¦¦> /l— el, l4\' UDJ
h\ = e\\ — e22. h2 = ^22 — e33 hl = ell — el + \, l + V
Матрица Картана (Atj) приведена в гл. IV [см. C8)]: Аи = 2,
Ai+hi = —1=Л(-г+1, At] = 0 в других случаях. Это может быть
проверено вычислением [eih]]= A}ieit если использовать равенства A6).
Простой корень аь определяется равенством аг(hj) = А-;1. Симметрией
Вейля 5а будет преобразование ?—>-? — |(йг)аг.
Рассмотрим сначала представление алгебры At алгеброй Ли ли-
линейных преобразований со следом 0 в A-\- 1)-мерном векторном
пространстве 9Я. Базис (uv и2 ui+i) можно выбрать так, что
uihl = ui, uH1ht = — ui+i< Ujhi — Q, j Ф i, l-\-\. В таком случае
и;/г = Аг(/г) u-v где веса А; задаются таблицей:
А,(А1)=1, Л,(/г,) = 0, 1ф\,
_ _ _ A7)
]ф1—\, i, 1 = 2 I.
Аг + 1(Аг) = —1, А,+1(Ау) = 0.
Отсюда и из таблицы для аг следует, что
Таким образом, 5». переставляет А; и Аг+1 и оставляет на месте
остальные веса А;. Группа преобразований весов А,, порожденная
этими отображениями, будет симметрической группой степени / —J— 1.
250 Гл. VII. Классификация неприводимых модулей
Для некоторого целого числа г, 1 <><;/, образуем тензорное
произведение Ш ® Ш ® ... ® Ш (г раз). Пусть Шг обозначает
подпространство кососимметрических тензоров, или г-векторов,
в ЗЯ ® ... ® Tt. По определению, это есть пространство, натянутое
на все вектора вида
(Уг У2 JVl^Siy
где суммирование берется по всем перестановкам P = (i1, l2, ..., 1Г)
множества A, 2 г) и знаки -j- или — ставятся соответственно
тому, будет ли Р четной или нечетной. Нетрудно убедиться в том,
что если {uv и2, . . ., и1+1) — базис пространства 2К = 2Я1, то
векторов
образуют базис в Шг. Если а^2 = Л;, то
(У1. У2 УЛа = \У\а' У2 У Л +
Ч- [У1> Уга> Уз УГ1 + • • • + [Ур У2. • • • • Уга1- B°)
откуда следует, что Шг является подмодулем модуля WI ® ... ® ЭК.
Можно предположить, что Ujh — Л;(/г) My. В таком случае равен-
равенство B0) дает
[V4 4]* =
Следовательно, определяемый равенством A9) базис состоит из весо-
весовых векторов. Мы имеем tr/z = O, откуда следует, что Лг+1 =
= — (Aj -f ... -)-Лг). С другой стороны, из формулы A7) вытекает,
что Aj-j- ... + Ak=Xk, где \k(ht) = blk, если l^ft^Z. Поэтому
множество Aj Аг будет базисом в ?>*. Если /г = /-|-1, то
А/,4- ••• +А/, = —(А*,+ ••• +А*,_(Г_„). где Aj fti_(r-i,
есть дополнение множества (y"j, . . ., jT_-^ в A, 2, ..., I). Отсюда следует,
что если Л + ... +Л =Л -+ ... +Л -, где j\ < . . . < J
Jl >r Jl >r
И j[ < ... <j'r, TO j\=j"v J2 = j Jr==j"r- MbI BH^HM- ЧТО
весовое подпространство, соответствующее весу Ay —J— Ay -f-...-f-Лу
натягивается на Ги. , и.,..., и. 1 и поэтому одномерно. Пусть
Щ — ненулевой неприводимый подмодуль в 2IJr Тогда ЭТ содержит
одно из весовых подпространств, соответствующее, например, весу
Л = Л/ + ... +А/ . С другой стороны, если Л'= Л.'-)- ... -4-Л.-
r h h
есть любой другой вес, то существует такой элемент 5 группы,
§ 6. Базисные неприводимые модули 251
порожденной симметриями 5а., что A' = AS. Но в таком случае,
согласно теореме 4.1, Л' тоже будет весом подмодуля 31 относи-
относительно •§>, и \и -,..., и >1 ? Ш. Таким образом, 9^ = 2)^, и поэтому
модуль Шг неприводим. Мы видели, что Лх —J— ... -\-Аг=\г, а это
есть доминантная целая линейная функция. Из определения г-вектора
[yj, у2 уг] очевидно, что [yv у2 Уг] = 0, если какие-нибудь
два из элементов yt равны. Это можно использовать для проверки
того, что [uv и2 иг] et — 0, i=l, 2 I. Так как [uv ..., иг] h—
— (Aj-|-A2-f- ••• +АГ)[И!, .... иг], то Шг является е-экстремаль-
ным модулем с максимальным весом Xf. Нами доказана, таким образом,
Теорема 6. Пусть А1— алгебра Ли A-\- 1) X (/+ \)-матриц
над Ф со следом 0 и $ — подалгебра Картана диагональных
матриц в Ар ht = eu—ei+lii+l, i=l, 2, .... I. Пусть Tir
(\^.r^l) — пространство г-векторов. Тогда Tir будет непри-
неприводимым модулем над Ар соответствующим доминантной
целой линейной функции Хг на .?>, для которой \r(hr)=\,
\r(hj) — Q при }фг.
Вр 1~^2. Используя простую систему корней для В1 из § 4.6,
мы получаем канонические образующие
i + l,l+2 >
ft = 2 (e e
ni == ei + l, i + 1 el + l+\, l + i + 1 ei+2, /
kt — 2 (бг + ьг + 1
Элементы матрицы Картана (Aij) = (aj(hi)) имеют значения Аи = 2,
AjiJ+1=—l=A]+1J, j=l, ...Л —2, Al_ul = —l,Atil_1 = -2,
все другие Л;;- = 0. В представлении алгебры Вг алгеброй Ли косо-
симметрических линейных преобразований пространства Ш размер-
размерности /г = 2/—(— 1 мы имеем базис (ир м2 ап)> такой, что игп = 0,
u2h—Al (h) u2 иг+1А=Л, (/г) ul+1; ul+2h=—Al (h) ul+2 u2l+1h=
— — Л, (/г) u2t+l, где линейные функции Лу(/г) удовлетворяют условиям
Л; (/*,)= 1,
А/(Ау_1) = -1, Ау(Ау)=1.
ЬФУ—I, J, у = 2, .... /—1. B3)
А,(А,_1)=—1, Лг(/гг)=2, А,(Л»)=0,
252 Гл VII. Классификация неприводимых модулей
Очевидно, Aj-j- ... + Л,. = \, г ^1—l.Aj-f- ••• + Лг = 2Хг, где
kl(hJ) = blj, i, У=1 /. Следовательно, функции At образуют
базис в ф*. Симметрия Вейля 5а., у = 1, ..., /—1, переставляет Л;-
и Л^+1 и оставляет остальные Ak на месте. Симметрия 5а оставляет
на месте каждую функцию Л;-, у = 1, ..., /—1. и отображает А1
в —Av Следовательно, порожденная ими группа содержит все пере-
перестановки функций А[ и все отображения, которые заменяют любое
подмножество функций А1 их противоположными, оставляя все другие
функции на месте. Нетрудно убедиться в том, что группа, порожден-
порожденная преобразованиями Sa., имеет порядок 211\. В следующей главе
мы покажем, что эта группа является полной группой Вейля.
Пусть г — целое число, 1-^г-^/—1, а Шг — пространство
r-векторов. Как легко видеть, [и2 и,.+1] А —Х,.(й)[и2 иг+\]
и [и2 ur+l]ei = 0, /=1, 2, ..., I. Мы утверждаем, что поро-
порожденный элементом [и,, ..., иг+1] циклический модуль неприводим.
Следовательно, это будет требуемый неприводимый модуль, соответ-
соответствующий доминантной целой линейной функции Хг Вообще заметим,
что если Ш — конечномерный е-экстремальный модуль над конечно-
конечномерной расщепляемой полупростой алгеброй Ли 2, то W неприводим.
Действительно, Ш вполне приводим и образующая х, соответствую-
соответствующая старшему весу Л, порождает весовое подпространство относи-
относительно ф, соответствующее Л. Значит, х содержится в некотором
неприводимом подмодуле Ш' модуля W. Поскольку х порождает Ш,
мы видим, что Ш = 31' неприводим.
Только что указанный результат об описании неприводимых
модулей, соответствующих X,., г=\ I—1, можно улучшить.
На самом деле этот модуль есть полный модуль r-векторов ffir—утвер-
ffir—утверждение, для доказательства которого следовало бы установить, что
Шг неприводим. Мы не будем давать здесь прямого доказательства
этого результата, а получим его позднее (в гл. VIII) как следствие
формулы Вейля для размерности неприводимого модуля со старшим
весом Л. Для представления с весом Л = ХГ мы получим размер-
B14-1\ п ™
ность I I. Поскольку это есть размерность модуля wtr, отсюда
будет следовать, что Шг неприводим.
Если рассмотреть пространство /-векторов, то подобные же рас-
рассуждения покажут, что это будет неприводимый модуль над Bv
соответствующий старшему весу Лх —(— ... -(- Лг = 2Хг. Следовательно,
это не обеспечивает существования недостающего модуля, соответ-
соответствующего линейной функции Хг Чтобы найти этот модуль, следует
рассмотреть так называемое спинорное представление алгебры Bt.
Входить в подробности было бы слишком длинно. Мы удовлетво-
удовлетворимся поэтому здесь сводкой результатов, не давая полных дока-
зательств.
§ 6. Базисные неприводимые модули 253
Напомним сначала определение алгебры Клиффорда C(Tt, (х, у))
конечномерного векторного пространства Ш над полем Ф характери-
характеристики, не равной двум, относительно симметрической билинейной
формы (х, у) в Ш. Для этого образуется тензорная алгебра
г = Ф1©аиф2й2© ... ®щ® .... Ttt = w® ... ®т ц раз).
Пусть R—идеал в X, порожденный всеми элементами вида
х®х — (х, хI. ' B4)
Тогда C(Tt, (x, у)) = %1&. (Подробнее об алгебрах Клиффорда
читателю рекомендуется смотреть книги Шевалле [1], стр. 93—104,
или Артина [1], стр. 186—193.) Ясно, что $ содержит все элементы
х®у-]-у®х~ 2(х, у) I =(х + у)®(х ¦+ у) —
— (х + у, х~{-уI — х®х~{-(х, хI— у®>> + (>>, уI. B5)
Известно, что каноническое отображение пространства Tt в С.=
= С(Ш, (х, у)) является изоморфизмом, так что можно отожде-
отождествить ffi с его образом в С. Мы сделаем это и запишем ассоциатив-
ассоциативное произведение в С в виде ab. Если (uv и2 ип) — базис
пространства ffi, то известно, что dim С = 2" и что множество эле-
элементов
«'•и** .. . ип, г.=0, 1, B6)
будет базисом в С. Так как элементы B5) принадлежат идеалу $-
то имеет место фундаментальное „йорданово соотношение"
(х, уI B7)
для любых х, у ? Tt.
На С как на алгебре градуировка не определена. Однако она,
как мы сейчас покажем, является естественно градуированным век-
векторным пространством. Пусть xv х2 xr ? ffi. Определим тогда
индуктивно r-произведенче [х,, х2 хг] ? С по следующим фор-
формулам:
B8)
2k] x
где [ab\~ab — ba и a ¦ b = -^(ab-\-ba) для a,
Лемма 4. Произведение [хР ..., x,.] = 0, если какие-нибудь
два элемента xi равны. Следовательно, для любой переста-
перестановки P = (lv l2 if) индексов A, 2, ..., г) имеет место
равенство [х^ ,хг \= + [х1 хг], где ставится знак -\-
254 Гл VII. Классификация неприводимых модулей
или — в зависимости от того, будет ли Р четной или
нечетной.
Доказательство. Так как [хх хг] определяет поли-
полилинейную функцию своих аргументов, то второе утверждение следует
из первого. Первое утверждение мы докажем индукцией по г. Оче-
Очевидно, [хх] = 0. Пусть г > 2, и предположим, что xk = x = xv где
1<^&</<>. Если I < г, то [хг, .... xt] = 0 по предположению
индукции, и равенство [х1 хг] —0 вытекает из B8). Следова-
Следовательно, можно предположить, что / = г. Опять из индуктивного
предположения вытекает, что [хг хг_г]~ + [. . . х], поэтому
мы должны показать, что [х1 ... xr_2xx] = 0. Имеется два случая:
четное г и нечетное г; они сводятся к доказательству следующих
соотношений: [а ¦ х, х] — 0 и [ах] • х = 0 для а?С, х?Ш. Для
первого из них мы имеем
Г-к (ах + ха), х 1 = у (ах2 -{-хах — хах — х2а) —
— (ах2 x2a)
= — (ах2 — x2a) = -j(x, x)a —
— ^ (х, х)а = 0,
а второе следует из
[ах] ¦ х = y (ах — ха) х + у х (ах — ха) = у ах2 — у х2а = 0.
Это завершает доказательство.
Лемма 5. Пусть Шг обозначает подпространство алгебрыС,
натянутое на все элементы [х1 хТ], где 0 <; г -^ п = dim ffi,
и 2К0 = Ф1. [Тогда dimTtr = (nf) и 0 = 0102^0^0 ... ®Шп.
Доказательство. Если (и,, и2 ип) — базис в Т1, то
из кососимметричности и полилинейности произведения [х1 хг]
следует, что каждый элемент из Шг, г^-1, будет линейной комби-
комбинацией элементов Ги^, и^, ,,,,«,], где г\ < г2 < ... -< /г = 1 п.
Предположим теперь, что базис ортогональный: (ut, Uj) = O при i=hj.
(Хорошо известно, что такие базисы существуют.) Из условия
(ut, и) = 0 и соотношения B7) следует, что utu, = —м;иг. Поэтому
К • ¦ • **,_,)**,= ±aJ,(a*i • ' • "'г-.) при /j < г2 < ... < /г; знак +
или — ставится в зависимости от того, будет ли г — 1 четным или
нечетным. Из только что отмеченного соотношения и определения
произведения [д:1 хг] получаем, что \и1 , . . ., иь 1 = 2kuli ... и1 ,
где (иг)— ортогональный базис. Так как 2" элементов вида иь ... иь ,
h < h < • • ¦ < V- образуют базис в С, то ясно, что для фиксиро-
§ 6 Базисные неприводимые модули 255
ванного г элементы [и,( и,], 1Х < ... < 1Г, образуют базис
в Шт. Следовательно, dim2Kr = (^), и ясно, что С = Ф
20 ©в
Пусть х, у, z ? Ш. Тогда
(х • у) • z — х ¦ (у ¦ г) = (х, y)z — (у, z) х.
С другой стороны,
(х ¦ у) ¦ z — х ¦ (у ¦ z) = ^\^
-г- (xyz -\ - yxz -\- zxy -\- zyx — xyz — xzy — yzx — zyx) —
Следовательно, имеет место соотношение
\[y[xz]] = (x, y)z-(y, z)x. B9)
Мы можем доказать теперь следующее утверждение.
Теорема 7. Пространство Ш2 является подалгеброй ал-
алгебры Ли СL. Если форма (х, у) не вырождена, то эта алгебра
Ли изоморфна ортогональной алгебре Ли, определенной при
помощи (х, у) в ffi.
Доказательство. Пространство Tt2 есть множество сумм
лиевых произведений [ху], х, у ^ Ш. В силу формулы B9) мы имеем
равенство
[ [У*] [xz] \ = [[y [xz] ], /] + [У- [/ [xz] ] ] =
= 4(х, y)[zt]-4(y, «)[*/]+4(*, t)[yz] —
— 4(t,z)[yx]. C0)
Следовательно, Tt2 — подалгебра алгебры СL. Соотношения C0)
и B9) означают также, что Т1-\-Ш2 является подалгеброй алгебры CL
и что ограничение присоединенного представления подалгебры 2R-j-9J?2
на подалгебру 2JJ2 имеет Ш в качестве подмодуля. Если R обозначает это
представление, то B9) показывает, что \xz]R есть отображение
у->4(х, y)z — 4(у, z)x. C1)
Если форма (х, у) не вырождена, то отображение C1) будет лежать
в ортогональной алгебре Ли. Более того, каждый элемент орто-
ортогональной алгебры Ли представляется в виде суммы отображений C1).
Следовательно, образ алгебры ffi2 относительно R совпадает
256 Гл. VII. Классификация неприводимых модулей
с ортогональной алгеброй Ли. Так как обе эти алгебры имеют
одну и ту же размерность I"), то R является изоморфизмом.
Обертывающая алгебра алгебры 3I2 в СТ1, ((х, у)) будет обо-
обозначаться через С+ = С+(Ш, (х, у)). Если (и,, .... и„)— ортого-
ортогональный базис в Ш, то элементы utUj, i < у, составляют базис
алгебры Tt2. Так как ц2 = (и(, «г)=1 и uluj —— u.ut при i ф у, то
легко убедиться в том, что пространство, натянутое на элементы
щ и, . . . Ui , /j < t2 < . . . < %• r = °- 1 • 2, • • •, [я/212,' является
подалгеброй алгебры С. Поскольку и^и; ... и^ —(и^и^ . ..
. .. (U( ut \ эта подалгебра содержится в С , и так как она
содержит 2^2- то она совпадает с С+. Теперь очевидно, что С есть
подалгебра четных элементов алгебры С, или так называемая
вторая алгебра Клиффорда, соответствующая форме (х, у). Ее
размерность равна 2я. Строение' алгебр С и С известно. Мы
сформулируем лишь то, что требуется для теории представлений
алгебр В1 и Dt. Для них симметрическая билинейная форма (х, у)
не вырождена и имеет максимальный индекс Витта. Если п = 21-{-1,
то С изоморфна полной алгебре ® линейных преобразований 2^-мер-
ного векторного пространства Tt над Ф. Изоморфизм можно явно
определить следующим образом.
Пусть (ир и2, .... ип) — базис в Ш того типа, который был
использован, чтобы получить матрицы для В1 (§ 4.6). Таким образом,
(Mj, Mj)— I, (ult at+l)= 1 =(ul+l, uj), если 1 = 2 l-\-1, а все
другие произведения равны 0. Положим vl=alui+l, wl = uluH l+v
/ = 2, ..., l. Тогда легко убедиться в том, что элементы vL и wl
порождают С+, что vtVj= — VjVt, ^ = 0, w.Wj = — •w.wv wt = 0
при l ф j, и что подалгебры, порожденные отдельно элементами v
и w, изоморфны внешней алгебре над Z-мерным пространством.
Базис алгебры С+ есть множество элементов vi ... vi Wj .. . -wj ,
где i\ < ii < ... < lr, j\ < j2 < ... < js- Мы имеем соотношения
v(wi -f" wlvi == — 2, г/гда; = — WjVi при ^ -/- y. C2)
Подпространство !R, натянутое на векторы
. . wJs< у, < у2 < ... < у,, C3)
будет 2'-мерным правым идеалом в С+. Правые умножения на а?С+
в ^ дают все линейные преобразования подпространства Щ, и соот-
соответствие между а и ограничением на W преобразования aR является
изоморфизмом алгебры С+ на алгебру й линейных преобразований в Ш.
§ 6. Базисные неприводимые модули 257
Представление a->a'R, a'R—ограничение на Щ преобразования aR,
индуцирует представление подалгебры ffi2 алгебры С?. Поскольку ffi2
изоморфна Bv это дает представление алгебры Bv действующее в Ш.
Вг-модуль Ш неприводим, и этот неприводимый модуль имеет старший
вес Хг, который и требовался. Мы наметим рассуждения, которые
можно использовать для получения этого утверждения.
Заметим сначала, что матрицу et, г = 1, 2, ..., I—1 (см.г B2)),
можно отождествить с линейным преобразованием х—>(х, иг+г+2)и/+1—
— (х, ui+l)ui+l+2 относительно выбранного нами базиса (и,, и2 ип).
Аналогично, et можно отождествить с линейным преобразованием
х—* (х, и1)и[+1— (х, ul+l)uv h{ (г =1,2, ...,1—1) —с х->
ni — с x->2 (x, u2l+1)uM — 2(x, ul+1) u2l+1.
При этом изоморфизме с ffi2 (ср. B9)) мы имеем
ir I— l ¦—-]
et->\\uv «/+1]=1«/+1, C4)
1 1
1
Пусть 2 = ^ . . . vt€?R. Тогда zej = 0, j—l /, zht = Q,
i=\ I— 1, и zht = z. Отсюда следует, что циклический
В^модуль, порожденный элементом z, является неприводимым модулем,
соответствующим весу Хг. Можно показать, что этот модуль сов-
совпадает с Щ. Мы будем называть fft спинорным модулем над Bt.
Результаты о Bt резюмирует следующая
Теорема 8. Пусть BL(l^2) — ортогональная алгебра Ли
в B1~\-1)-мерном пространстве, определенная невырожденной
симметрической билинейной формой максимального индекса
Витта. Пусть базис подалгебры Картана ф алгебры В1
состоит из элементов hv 1=1, 2 I, определенных равен-
равенствами B2), и пусть Х^ — линейная функция на ф, для кото-
которой \j(hl) = bij. Тогда неприводимый модуль над Вг со старшим
весом Ху, у=1, ..., /—1, является пространством j-векто-
ров ffij. Неприводимый модуль со старшим весом Xz является
спинорным модулем %1, определенным выше.
17 Н. Джекобсон
258 Гл. VII Классификация неприводимых модулей
02. Если (а,, а2) — простая система корней алгебры G2, то матри-
матрицей Картана будет
/ 2 —1\
(-3 2> <35>
так что
а, (А,) = 2, а,(А2) = —3, а,(А,) = —1, а2(Л2) = 2. C6)
Мы видели в § 4.3, что положительными корнями будут а,, а2,
а, -)- а2, а, + 2а2, а, -f- За2, 2а, -\- За2. Наибольшим из них является
2а, + За2. Очевидно, Bа, -f- За2) (Л,) = 1, Bа, -+- За2) (Л2) = 0, так что
2а, 4- За2 есть линейная функция X,, для которой X, (Л,) = 1, X, (h2) = 0.
Поскольку алгебра G2 простая, присоединенное представление непри-
водимо. Таким образом, алгебра Й(=О2) сама является неприво-
неприводимым модулем, старший вес которого есть X,. Покажем теперь, что
если G2 представлена алгеброй Ли дифференцирований расщепляемой
алгебры Кэли S, то представление, индуцированное в семимерном
пространстве So элементов со следом 0, будет неприводимым пред-
представлением, соответствующим линейной функции Х2, для которой
X2(Aj) = O, Хз (Аз) = 1. Мы покажем это, доказав, что размерность
любого модуля Ш над О2, удовлетворяющего условию ТЮ2Ф0,
будет ^- 7, а если размерность равна 7, то модуль неприводим и
соответствует Х^
Выразим сначала корни через базис X,, Х2. Согласно формуле C6),
а, = 2Х, — ЗХ2, а2 = — X, -\- 2Х2. Положительными корнями будут
О1 О} \ ] О\ \ \ \ } 1 О1 Л а7\
Если Л = m,Xj -\- т^ ^ фц и 5, = Sa , 52 = Sa — симметрии Вейля,
определенные корнями а, и а2 соответственно, то
AS, == А — А (А,) а, = А — m, BX, — ЗХ^ =
Если Л — старший вес модуля ЗИ относительно ф, то т2 неотрица-
неотрицательны и не равны 0 одновременно, и следующие линейные функции
рудут весами модуля 2№ относительно ф:
Л = ffijXj -j- ttiifa, A
Л52 = (mj+m2)Xj—m^ 12(,
AS^i = — (тг -\- m2) X! -\- (Ът1 -f- 2m2) X2,
AS1S2Sl = — Bm, -f- m2) X, + Cm1 + 2/Из) Х2,
Л525,52 = Bm, + m2) X, — Cm, + 2m2) l^,
A E,5aJ *= (m, + m2) X, — Cm, + 2^^ L,,
A E,52J =t — Bm, + uij) X, + Cm,
A (S,^J 5, = — (m, -)- m2) X, -j- Щ^.
Л (S^J S = m,X, — Cm, -f- m2) Xjj,
X i A
Упражнения 259
При тх > о> Щ > 0 этот список дает двенадцать различных весов,
а это означает, что dim2R^>12. При от2 = 0 этот список дает
шесть различных весов:
2/njXj — 3ffijX2,
Если mj = l, то 9№ содержит подмодуль, изоморфный g, и
поэтому dim2Ji^>14. Если ml>\, то, поскольку Xj— корень и
Xj-серия, содержащая OTjXj, содержит также и —OTjXj, в этой серии
имеется по крайней мере 2тх -\-1 ^> 5 весов. Это добавляет три
новых веса к списку и показывает, что dim ffi ^- 9. Пусть теперь тх = 0.
Тогда различны следующие шесть весов:
— "^2^1 "*f" 2/Я2Х2,
Если от2=1, то Хз-серия, содержащая т^, содержит 0 в качестве
веса, а поэтому dimSW^-7. Если т2> 1, то Х^серия, содержащая
^ содержит по крайней мере пять весов, а это означает, что
t^-9. Таким образом, показано, что dimTt^-7 и dim3I = 7
может иметь место лишь тогда, когда старший вес Л = Х2. Так как
существует модуль So над О2, для которого dimS0 = 7, то отсюда
следует, что модуль (?0 неприводим и его старший вес есть Xj.
Теорема 9. Неприводимым модулем над g = G2 со стар-
старшим весом X; является сама алгебра 2. Неприводимым моду-
модулем над О2 со старшим весом Х2 будет семимерный модуль 6q
элементов со следом 0 в расщепляемой алгебре Кэли E.
Упражнения
Ниже мы придерживаемся обозначений этой главы: 2 — конечномерная
расщепляемая полупростая алгебра Ли иад полем характеристики 0, § — рас-
расщепляющая подалгебра Картана, et, flt ht — канонические образующие
алгебры 2, U — универсальная обертывающая алгебра и т. д.
1. Пусть et, /„ ht (/ = 1, 2 О—канонические образующие алгебры 8.
Показать, что подалгебра 8(, порожденная элементамие]у fj, п., j = 1, ..., k,
k^l, будет расщепляемой полупростой алгеброй Ли. Показать, что Et
является подалгеброй алгебры Е7, а Е7 — подалгеброй алгебры ?8.
2. Показать, что 2 имеет лишь конечное число неэквивалентных не-
неприводимых модулей размерности <; N для любого положительного целого
числа N.
3. Пусть ? — ядро в Ц представления, определенного модулем Зй, и
пусть ?И обозначает ядро модуля 9Й ® ... ® 9К (s раз). Показать, чтс
конечномерный модуль 9К можно выбрать так, что если $ — любой идеал
в U конечной коразмерности, то существует такое s, для которого X(J)c Щ.
4. Пусть $ — ортогональная алгебра Ли, определенная некоторой невы-
невырожденной симметрической билинейной формой в пространстве ш размер-
размеряй.
260 Гл. VII Классификация неприводимых модулей
ностн л!>3. Доказать, что пространство Шт r-векторов й-непрнводимо для
1<г</ при п = 2/-(-1 н для 1 <г</— 1 при я = 2/.
5. Показать, что пространства г-векторов, 1 <: г <: I, являются базис-
базисными неприводимыми модулями над Ci, J>4.
6. Показать, что минимальная размерность неприводимого модуля Ш над Et
такого, что Ш?6 ф 0, есть 27. Вывести отсюда, что Ев и Вв, а также Et,
н Се не изоморфны.
7. Доказать, что модуль, соответствующий спинорному представлению
алгебры Di во второй алгебре Клиффорда (четных элементов), разлагается
в прямую сумму двух неприводимых модулей Показать, что эти два модуля
вместе с пространствами r-векторов, 1<г</~-2, будут базисными не-
неприводимыми модулями над Dt, />4.
8. Показать, что базис (gb g2, .... р) А можно выбрать так, что
fagj] = V<- [f'Sj] = - \]fi- ПУСТЬ Л = 2 J2 ft = 2 !^«Л«- ™e 'Л< € Ф. Пусть
2ъ«„ гДе каждое ?< =? 0, и пусть / = 2"^~1!\Л- Доказать, что
> /» Л) — канонический базис расщепляемой трехмерной простой алгебры
и Ё. Доказать, что ada Ё будет прямой суммой / нечетномерных неприво-
неприводимых модулей над Ё. (Подалгебра ft называется .главной трехмерной
подалгеброй" алгебры 2. Такие подалгебры играют важную роль в изучении
когомологий алгебры 2. См. Костант [3].)
9. Описать алгебру Ё (см .8) для А^ Найти характеристические корнн при-
присоединенного эндоморфизма ada h и использовать это для получения раз-
размерностей неприводимых компонент модуля ada $.
10. Пусть Ш — конечномерный модуль над 2, 2+— (нильпотентная)
подалгебра алгебры 2, порожденная элементами ее и Q — подпространство
в 5Ш элементов г, для которых zt = O, /?2+. Показать, что dim Q есть
число неприводимых подмодулей в прямом разложении модуля 5Ш на не-
неприводимые подмодули. (Это число, согласно теореме Крулля — Шмидта,
не зависит от способа разложения; см. также § 8.5.)
11. Пусть Ж и -й — два неприводимых конечномерных модуля над 2 и
2R* — модуль, контрагредиентныи к Ш. Пусть R к S — представления соот-
соответственно в 9К н 91, R* — представление в Ш*. Показать, что число под-
подмодулей в разложении модуля Ш* ® 9t в прямую сумму неприводимых под-
подмодулей равно dim Q, где Q — подпространство пространства (S EШ, 9?)
(гг ш* ® 9t, согласно гл. 1) линейных отображений модуля Ш в % опреде-
определенное равенством
{ R
Й
12. (Дынкин). Если Ш\ и ЭК2 — конечномерные неприводимые 2-модули
со старшими весами А, и А, и каноническими образующими соответ-
соответственно Xi и х2, то про 5Щ2 говорят, что он подчинен Ши когда из х{и = 0
следует х2и = 0 для каждого и из универсальной обертывающей алгебры Ц_
подалгебры 8_ в 2, порожденной элементами /,. Показать, что модуль 5Ш2
подчинен модулю Ш\ тогда и только тогда, когда А] = А2 + М, где М — доми-
доминантная целая линейная функция на ф. (Указание: заметим, что если
9J — конечномерный неприводимый модуль со старшим весом М и у — кано-
каноническая образующая, то Ш\ можно считать подмодулем модуля 5Ш2 ® %
порожденным элементом х2 ® у.)
13. Заметим, что определение подчиненности в упражнении 12 экви-
эквивалентно следующему существует U-гомоморфизм модуля ЭД^ на 5Ш2,
отображающий хх в х2 Использовать это для доказательства того, что если
конечномерный неприводимый модуль 5Ш со свойством 5Ш2 Ф 0 имеет мини-
минимальную размерность (среди всех таких модулей), то 2R — базисный модуль.
Глава VIII
ХАРАКТЕРЫ НЕПРИВОДИМЫХ
МОДУЛЕЙ
Основным результатом настоящей главы является формула, при-
принадлежащая Вейлю, для характера любого конечномерного неприво-
неприводимого модуля над расщепляемой полупростой алгеброй Ли 2 характе-
характеристики 0. Если основное поле есть поле комплексных чисел и
R — конечномерное неприводимое представление, то характером пред-
представления R называется функция на подалгебре Картана ф, опреде-
определенная соотношением
X(A)=trexpA*. A)
где, как обычно, ехр а = 1 -f- a -f а2/2! -\- .... Если © — связная
полупростая компактная группа Ли, то соотношение A) задает
характер в обычном смысле неприводимого представления группы ©.
Действительно, в этом случае ф соответствует максимальному тору,
а, как известно, любой элемент группы © сопряжен какому-нибудь
элементу из данного тора. Соотношение A) тогда задает значения
характеров для элементов тора. Мы знаем, что h действует диаго-
диагонально, т. е. базис можно выбрать так, что матрицей для h будет
d!ag{A(A), M(h). ...}, B)
где А (Л), М (h), ... — веса представления R относительно ф. Тогда
матрица ехр hR равна diag {ехр A(/z), expM(fi), ...}; следовательно,
Ц C)
где пм—кратность веса M(h), т. е. размерность весового подпро-
подпространства Шм.
Если заменить экспоненциалы ехр М (h) в равенстве C) формаль-
формальными экспоненциалами, которые являются элементами некоторой
групповой алгебры, то получится чисто алгебраическая форма опре-
определения характера х(^)- Формула Вейля дает выражение для харак-
характера хА конечномерного неприводимого модуля со старшим весом А
в виде отношения двух весьма простых альтернированных выражений
от этих экспоненциалов.
262 Гл. VIII. Характеры неприводимых модулей
Первоначально Вейль получил свою формулу, используя интегри-
интегрирование на компактных группах. Фрейденталю принадлежит элемен-
элементарный чисто алгебраический метод, которому мы и следуем в нашем
изложении. В качестве предварительного шага будет доказано рекур-
рекуррентное соотношение Фрейденталя для кратностей пм. При помощи
формулы Вейля можно найти выражение для размерности неприводи-
неприводимого модуля со старшим весом Л. Она может быть также исполь-
использована для получения неприводимых компонент тензорного произведе-
произведения двух неприводимых модулей.
§ 1. Некоторые свойства группы Вейля
В этом параграфе будут рассмотрены некоторые свойства группы
Вейля, которые потребуются для доказательства формулы Вейля и
для описания автоморфизмов полупростых алгебр Ли над алгебраи-
алгебраически замкнутым полем характеристики 0 (гл. IX). Как обычно, 8
обозначает конечномерную расщепляемую полупростую алгебру Ли
над полем Ф характеристики 0, et, f{, hi A = 1, 2 Г) — кано-
канонические образующие алгебры, такие же, как в гл. IV и VII, и ф —
расщепляющую подалгебру Картана, натянутую на элементы ht. Пусть
ф* — сопряженное к ф пространство, ф* — рациональное векторное
пространство, натянутое на корни алгебры 8 относительно ф. Если а —
ненулевой корень, то симметрия Вейля есть отображение
~« * * (a, a) v '
в фд. Здесь (?, т]) — положительно определенное скалярное произ-
произведение в ф*, рассматривавшееся в § 4.1. Отображение 5а как ли-
линейное преобразование в ф* характеризуется тем, что оно переводит a
9 —аи оставляет инвариантным каждый вектор, ортогональный к а.
Симметрия Sa — ортогональное преобразование относительно ($, ?)),
осуществляющее перестановку весов относительно ф любого конечно-
конечномерного модуля над 8. Симметрии Sa порождают группу Вейля W,
которая является конечной группой. Если Г — ортогональное пре-
преобразование, такое, что <хТ будет корнем при некотором корне а;=?0,
то прямое вычисление показывает, что
T~XS T = S E)
В частности, это выполняется для каждого T?W. Отметим также,
что если a — корень, то —a — тоже корень, и из формулы D) ясно,
Корни af, /=1, 2, .... I, такие, что a2 (hj) = Л;7, (Л^) — матрица
Картана, образуют простую систему. Понятие простой системы кор-
корней, введенное в § 4.3, зависит от лексикографического упорядочения
§ 1. Некоторые свойства группы Вейля 263
рационального векторного пространства Щ. Напомним, что / корней
образуют простую систему лишь в том случае, когда каждый корень
а = ± (V kfii), где k{ — неотрицательные целые числа. Этот крите-
критерий означает, что если ¦к=[а1, а2> ..., а{] — простая система и Г —
линейное преобразование в ф*, оставляющее множество корней инва-
инвариантным, то ъТ— [ахТ oijT} есть снова некоторая простая
система корней. Множество Р положительных корней в смысле того
лексикографического упорядочения, которое приводит к простой си-
системе к, есть множество ненулевых корней вида ЕА^а,, &г^0.
С другой стороны, если упорядочение задано, так что Р известно,
то к будет множеством элементов из Р, которые не могут быть
записаны в виде р + ?, Р- Тб^3- Таким образом, Рки определяют
друг друга. С любой простой системой корней ассоциируется мно-
множество канонических образующих et, ft, Л( (ср. § 4.3).
Лемма 1. Пусть u={aj, a2, .... at]— простая система
корней и a — положительный (отрицательный) корень. Тогда
aSai>0«0) при афа.; (чф — а,) и aSa. < 0 (> 0) при а =
= а,(а = — а,).
Доказательство. Если a — отрицательный корень, то — a
будет положительным корнем, и утверждение относительно а вытекает
из утверждения относительно —а. Следовательно, достаточно пред-
предположить a > 0. Имеем, равенство a = 2^Л> kj ^- 0. и
Если a=jfcai( то, поскольку никакое кратное корня, за исключением 0,
±сс, не является корнем, афИр.^ и, следовательно, k^Q для не-
некоторого }ф1. В таком случае выражение для ctSai имеет положи-
положительный коэффициент при некотором'а;-, и следовательно, aS > 0.
Если a = a(, то aSa(-= — a,- < 0. Это завершает доказательство.
Результаты относительно W будут сформулированы в двух тео-
теоремах.
Теорема 1. Если ic={aj, a2, ..., a;}—простая система
корней, то группа Вейля W (относительно ф) порождается
симметриями SH, ol^tz. Если a — любой ненулевой корень, то
существуют такие «у^« и S?W, что ayS = a.
Доказательство. Пусть W — подгруппа группы W, поро-
порожденная элементами Sai. Покажем сначала, что любой положительный
корень а имеет вид a^5, cty? и, 5^ W. Напомним, что если ix = ^iklai,
то 2*г есть высота корня а. Мы докажем результат по индукции
264 Гл. VIII. Характеры неприводимых модулей
относительно высоты. Утверждение очевидно, если высота равна еди-
единице, так как это условие эквивалентно включению а ? те. Если
2&г>1. то a^it и существует такой корень at, что (a, 0Lt) > 0.
В противном случае (а, аг)<;0 для всех I, и поскольку а = 2&гаг.
Aij^-O, то (а, а)^0 вопреки тому, что (а, а) > 0. Выберем OLt так,
что (а, а^) > 0. Тогда 8 = aSai > 0 по лемме 1 и мы имеем
В== 2 */а/ + (&?—[2(а, а2)/(аг, аг)])аг Таккак(а, аг) > 0, товысота
корня В меньше высоты корня а. Следовательно, предположение
индукции дает, что 8=а^>', а^? и, 5' ? W. В таком случае a=ajS'Sat,
как и требовалось. Так как а = а;5, где 5 ? W', то 5а = S~lSa,S ? №'.
Поскольку Sa = 5_a, это показывает, что каждая симметрия <Sa?W,
поэтому U^' = W. Остается показать, что если a — любой ненулевой
корень, то a —a^S, а^тс, S?W. Это было показано для a > 0.
Так как aSa = — а, то утверждение очевидно также и для a < 0.
Теорема 2. Пусть и н ic' — любые две простые системы
корней. Тогда существует, и притом только один, элемент
S?W, такой, что uS = tc'.
Доказательство. Пусть Р и Р' обозначают множества поло-
положительных корней, определенных соответственно системами it и и'.
Ясно, что Р и Р' содержат одно и то же число q элементов, по-
поскольку оно равно половине числа ненулевых корней. Ясно также,
что Р = Р' тогда и только тогда, когда ic = it', и если РфР', то
it с? Р' и тс'фР. Пусть г — число элементов в пересечении Р f| P'.
Если r = q, то Р = РГ и 5=1 удовлетворяет равенству u5 = u',
так что в этом случае утверждение выполняется. Применим теперь
индукцию по q — г. Можно предположить, что r<Cq< или Рфр'.
В этом случае существует такой корень а,- ? и, что аг (? Р', и, следо-
следовательно, — ixi==:aiSai^P'. Если ф?Р(\Р', то по лемме 1 В5а/^Р.
Поэтому $SH?PnP'Sar Кроме того, а, = (— аг)Sai 6ЯП^'Sa,.
Значит, Pf\P'Sat содержит по крайней мере г-\- 1 элементов. Простой
системой, соответствующей P'SH, будет u'S^, поэтому предположе-
предположение индукции позволяет нам утверждать, что существует такой эле-
элемент T?W, что ¦KT = K'Sa[. Тогда S = TSa[ удовлетворяет равенству
i:S = u'. Это доказывает существование 5. Для доказательства един-
единственности достаточно показать, что если S? W удовлетворяет ра-
равенству и5 = те, или, что эквивалентно, равенству PS = P, то 5=1.
Мы дадим здесь элементарное, хотя и немного длинное доказательство
этого факта, а в одном из упражнений (упражнение 2, см. ниже)
укажем на короткое доказательство, основанное на теореме суще-
существования для неприводимых модулей. Будем писать Si=Sar По
§ 2. Формула Фрейденталя 265
теореме 1 5 = 5^5^ ... Sim, tj = l, 2, ..., I. Значение /я = 1
исключается, так как a2lS2j= — a(l (?ic, а если m — 2, то a^S^ = — a^
и так как (— ацЛ Si2 = a^S^S^ > 0, то по лемме 1 12 = iv Таким
образом, 5 = 5? = 1 • Будем считать теперь тп > 2, предполагая, что
если T = SJlSj2 ... 5Уг, r<m, и иГ = и, то 7=1. Пусть 5' =
= 5^5*2 ... 5im_j, так что S = S'Sim. Так как S?=Sim> S'?= 1 и
5' является произведением /и — 1 элементов Sjt то PS' Ф Р в силу
предположения индукции. В таком случае существует о,-?я, для
которого a;S' < 0. Поскольку a S'Sim > 0, из леммы 1 вытекает,
что а.5' = — а*т. Аналогично если В — любой положительный корень,
для которого BS' < 0, то неравенство $S'Sim > 0 означает, что
8S' = — агт = а.5'; следовательно, Br=a^. Таким образом, S' имеет
следующие два свойства: a S'= — alm и В5'> 0 для каждого поло-
положительного В Ф aj. Положим Sia = 1. Тогда a Si0 > 0 и
Значит, существует такое k, I ^k ^m—1, что oljSiqSi1 ... Sikl > 0
и a.fSi0Stl ... Sik < 0. Так кака;5г0 . .. 5Ift_j > 0 и (ajSio ... Si^) X
X Stk < 0, то ajS^S^ ... Sik_x = aik- Следовательно, если поло-
положить r==S2o5ij ... SlkV то T~1SjT = Sik, или SjT = TSik. В таком
случае S' = Г5;/' = SjTT', где Г' = Sik+1 ... Sim_1 лля k <m—I
кТ' = 1 для k = m — 1. Отсюда вытекает, что ТТ' = SjS'. Если
a — положительный корень, не равный oij, то В = aSj тоже будет
положительным корнем, отличным от a.j. Поэтому аТТ' = aSjS' =
= BS' > 0. Кроме того, a;7T' = a;S;5' = (— aj) S' = aim > 0. Следо-
Следовательно, tzTT' = v: и так как ТТ' является произведением m — 1
элементов 5^, то предположение индукции дает равенство 7Т' = 1.
Тогда SjS'—l, так что S' = Sj и S = SilSj. Поэтому 5 = 1, со-
согласно случаю m = 2, который был рассмотрен выше.
§ 2. Формула Фрейденталя
Пусть SM — конечномерный неприводимый модуль над 8 со стар-
старшим весом Л, являющимся доминантной целой линейной функцией
на ф. Мы знаем, что 3JJ есть прямая сумма весовых подпространств
относительно ф и что весами являются целые линейные функции на §
вида Л—Hkp-L, kt — неотрицательные целые числа. Если М — любая
целая линейная функция на •§>, то мы полагаем, по определению,
266 Гл. VIII. Характеры неприводимых модулей
кратность пм функции М в Ш равной 0, когда М не является
весом, и равной пм = dim Шм, когда М — вес, а Шм — соответ-
соответствующее весовое подпространство модуля SM относительно <§>. На-
Напомним, что лд = 1 для старшего веса Л. Мы хотим теперь по-
получить принадлежащую Фрейденталю рекуррентную формулу, которая
выражает пм через пм<, где М' > М при лексикографическом
упорядочении пространства Фд. определенном простой системой кор-
корней 1г= \ov Oj, .... аД.
Пусть а — некоторый ненулевой корень относительно §. Выберем
ва?8а, е_а?8_а так, что (еа, е_а) = — 1, где (х, у) = tr ad x ad у —
форма Киллинга алгебры 2. Как нам известно (§ 4.1), [eae_J = ha,
где Ар для произвольного р ? ф* есть такой элемент из §, что (Л, Лр) =
= р(А). Как и в § 4.2, Й(а) будет обозначать подалгебру ф+Фва-|-
+ Фв_„. Тогда мы знаем, что 9Я как 8<а)-модуль вполне при-
приводим (теорема 4.1). Рассмотрим какое-нибудь разложение модуля 2R
в прямую сумму неприводимых 8(а)-подмодулей, которые мы будем
называть неприводимыми ^-компонентами модуля Ш. Пусть Ш —
одна из них. Тогда мы знаем, что 3? имеет базис (у0, уг ут),
такой что
yfi = (М — ia) yt, i = 0, 1 т,
У(*-« = 3'*-ц. Уте-* = 0' / = 0. 1. .... /Я—1. G)
Уо*. = О. J>tg«= '"^-^-^ (a, a)yt_v
i—l, 2, .... m.
Мы знаем также, что
т = 2(М, аI(а., а), (8)
где (р, о) = р (Л„) = о (Лр), как и в § 4.1. Из уравнений G) следует,
что
г = 0, 1, .... т.
Отметим также, что Jft является прямой суммой весовых подпро-
подпространств, что веса равны М, М — а, М — 2а М — то, а ве-
весовые подпространства %1м-ра = ШМ-рап31 одномерны.
Пусть М — такой вес модуля SM относительно ф, что М~\-о не
является весом. Тогда а-серией весов модуля Ш, содержащей М,
будет М, М — о Ж —та, где т = 2(Ж, а)/(а, а). Пусть
0<Ср<Ст. Тогда М — ра является весом, и Шм-Ра будет прямой
суммой весовых подпространств тех неприводимых 8^'-компонент,
которые имеют М—ро в качестве своего веса. При 0-^/?-^
, а)/(а, а) таковыми являются неприводимые 8*а)-компоненты.
§ 2 Формула ФрейденталА 26?
имеющие максимальные веса М, М — а, ..., М — ра. Пусть /и;.,
O^.j^C(M, а)/(а, а), обозначает число неприводимых й(а)-компонент
старшего веса М—/а. Тогда ясно, что
и+ ... +/»/, A0)
так что
mj—n-M-ja «Ж-(/-1)а. A1)
Если 0-^.j-^.p-^.(M, а)/(а, а), то весовое подпространство,
соответствующее М — р а в неприводимой 8 -компоненте, имеющей
старший вес М — ja, натягивается на вектор yp_j в обозначениях
формул G). Размерность этого модуля равна 2 (Ж — ja, a)/(a, а)-(-
~\- 1 =(/и — 2у) —j— 1. Следовательно, можно заменить в (9) i на р—j
и тп на /м — 2/ и получить соотношение
Это можно использовать для вычисления tr.js^_ ae^ae^, следа огра-
ограничения е^ае^ на SM^. a. Заметим, что
так что 9Яж-ра инвариантно относительно е^ае$. Согласно равен-
равенству A2), вкладом m,j неприводимых 8(а)-компонент со старшим весом
Ж —у а в Ь,Жм_р/1ае% будет
следовательно,
p
у-О
/-о
Поскольку /м/2 = (Ж, а)/(а, а), мы получаем формулу
*Ч,-„«-.'? = - Д «л- J.{М - ja, а) A3)
при 0</><(Ж, а)/(а, а).
268 Гл. VIII Характеры неприводимых модулей
Пусть теперь (Ж, а)/(а, а)</?-^т. Применяя симметрию Вейля
5а к Ж— ра, получаем, что Ж— ра—2 ((Ж— ра, а)/(а, а))а =
= Ж— {т — р)а, поскольку т = 2 (Ж, а)/(а, а). Итак, 0^/м — р -^
<С(Ж, а)/(а, а), и мы видим, что Ж— ра является весом неприво-
неприводимых 8 -компонент, имеющих старшие веса Ж, Ж— а, ...
..., Ж— {т — р)а и только эти. Рассуждение, использованное для
получения формулы A3), дает теперь соотношение
т~ р—1
при (Ж, а)/(а, а)</?-^т. Напомним, что если М — вес, то MSa
тоже будет весом и nM = nMSa (теорема 4.1). Следовательно, пм-ja —
= iM-(m-j)a- С другой стороны, (Ж — ja, а)-\-(М — (т. — j)a,a) =
= BЖ — та, а) = 0. Поэтому
*nM-ja(M — ja, а.)-\-пм_(т_1)л(М — (да — У)а. а) = 0. A5)
Отсюда и из A4) вытекает, что формула A3) выполняется также при
р > (Ж, а)/(а, а). Напомним, что Ж было произвольным весом
модуля Ш относительно ?>, таким, что Ж-f-a не являлось весом.
Следовательно, М — ра может представлять любой вес модуля Ш
относительно <§>. Мы изменим теперь обозначение и будем писать Ж
вместо Ж — ра. Если учесть, что пм- = 0, когда Ж' не является
весом, то можно формулу A3) переписать в виде
со
**»«*?.*? = - S nM+ja(M-\-ja, a) A6)
для любого веса Ж и любого корня
Рассмотрим, далее, элемент Казимира, определенный формой Кил-
линга. Это есть элемент T — ^ufu11*, где (и Л, (и1) — дуальные
базисы алгебры 8 относительно (х, у). Мы знаем, что [аЛГ] = 0
для всех а ? 8. Так как представление R абсолютно неприводимо,
то из леммы Шура следует, что Г = f 1, т?Ф (ср. Джекобсон
[2], II, р. 276). Дуальные базисы мы выбираем следующим образом:
(/Zj, ..., Лг), (Л1 Л') — дуальные базисы в § относительно (х, у);
тогда, поскольку (ея, е_а) = — 1 и вектор еа ортогонален к ф и
к каждому ер, р Ф — а, следующие базисы будут дуальными:
(*i hv e-«. е-р. •••)•
(Л1 Ч1, -еа, — *р, ...).
В этом случае
2
§ 2. Формула, ФрейденТаЛА 26У
Беря след индуцированных отображений в Шм, где Ж— вес, по-
получаем, что
Так как оператор Л# сводится в Шм к умножению на Ж (Л), то
так что первый член в правой части равенства A8) равен
пм 2 M (hd м (А')- Покажем теперь, что 2М(/г,)Ж(Л'")=(Ж, Ж).
В самом деле, пусть ЛЛ1 = 2^г- Тогда (Ж, Ж) = 2(А*. Ay)[j.([j.y и
M(hi) = (hM, /гг) = Е^(Лг А,), М(А') = (АЛ. А') = Ц|*ДАу, Лг) = [лг.
Следовательно, 2 Ж(Л()Ж(Аг) = 2№. ^/Эм^ — О^, М). Отсюда
следует, что 2 *гда hffiiR = nM(M, Ж). Используя этот результат и
формулу A6), из A8) получаем
2 «)• A9)
Члены пм(М, а) и «^(Ж, —а) в этой формуле сокращаются, так
сю оо
что можно заменить 2 на 2 • Получающаяся формула справед-
лива даже в случае, когда Ж не является весом. В этом случае
пм = 0. Если для некоторого фиксированного а ни одно ^
оо
не будет весом, то для этого элемента a nM+jll = O и сумма 2 л
Х(Ж-|-Уа> а) = 0. Если М-\-ja является весом для некоторого
j ^ 1, то ни одно Ж — Ы не будет весом для k ^ 1, поскольку
а-серия, содержащая Ж-j-y'a, не содержит Ж. Следовательно, мно-
множеством {M-\-ka \k^> 1} исчерпывается вся a-серия, содержащая
оо
M-\-ja. В таком случае 2 nM+ja(M-\- jo., a) = 0, поскольку nM+ja X
X (Ж -f- ya, a) = — Я(м+^а) s ((^ + jo) Sa, a). Таким образом, во всех
оо
случаях 2 nM+ja(M-{- ja, a) = 0, и равенство A9) выполняется.
Это рассуждение показывает также, что равенство
оо
2 nM+ka(M + ?a, a) = 0 B0)
k=— оо
выполняется для любой целой линейной функции Ж на ?>. Это означает,
оо оо
что ^пм_ка(М — ка, —а) = пм(М, а)-^^пм+ка(М-^ка, а),
к = I ft = 1
270 Гл. Vlll. Характеры Неприводимых модулей
00
так что, беря в равенстве A9) сумму 2> получаем соотношение
/1
2 пм(М, a) + 2S%J,(M + k, a).
а>0 ft=l
а>0
Полагая В = ('/г) ( 2 а) • выводим отсюда следующую формулу:
\«>о /
= (Л1. Л1 + 28) ял + 242ял+».(Л! +*«.«)• B1)
Если Ж = Л—старший вес модуля SM относительно ф, то пм—\
и лЛ+4в = 0 при а > 0, &^>1. Следовательно, из B1) получается
выражение
7 = (Л, Л+28) = (Л+8, Л+8) — (8, 8),
подстановка которого снова в B1) приводит к рекуррентной фор-
формуле Фрейденталя
((Л + 8, Л+8) — (М + 8. М + Ь))пм = 2 ^пм+ы{М + Ы, а).
">° B2)
Мы покажем теперь, что эта формула дает эффективный способ для
вычисления пм, начиная с гад = 1. Для этого нам понадобятся две
леммы.
Лемма 2. Пусть 8 = A/2) 2а- Тогда 8(Ае) = 1, / = 1, 2 I,
а>0
если et, ft, ht есть множество канонических образующих алге-
алгебры 8. Кроме того, если S Ф 1 — элемент группы W, то 8 — 85
будет ненулевой суммой различных положительных корней.
Доказательство. Если а — положительный корень, то мы
знаем (лемма 1), что а5г^а5„ =а — а(Л2)а2>0 для всех 1^ан
aiSl = — а{. Следовательно,
а>0
Кроме того, (bSt, at) = (8, atSt) = (8, — at). Следовательно, (8—at, a2) =
= (8, —a2) и 2 (8, а2)={аг, а2). Таким образом, 8 (Аг)=2 (8, <х?)/(а?, а2)==1,
/ = 1, 2, .... /. Так как любое S?W отображает корни в корни,
то, очевидно, 85 = 8—2 р. где суммирование берется по р = — <х5>0.
Если таких р нет, то а5 > 0 для всех а > 0. Отсюда по теореме 2
следовало бы, что 5=1, а это противоречит предположению.
§ 2. Формула Фрейденталя 271
Лемма 3. Пусть А—старший вес модуля Ш относительно §.
Тогда
(Ж+ 8, Ж + 8)<(Л+8. Л + 8) B3)
для .любого веса Ж *j= Л модуля Ш относительно §.
Доказательство. Докажем, что существует вес Ж' > Ж,
для которого (Ж'+ 8, /М'-f-8) >(М + 8, Ж+8). Отсюда будет
вытекать нужный результат; следует лишь воспользоваться очевид-
очевидным рассуждением о возрастающих цепочках. Предположим сначала,
что существует такое /, что Ж(/^)<0, Лг принадлежит множеству
канонических образующих. В этом случае, положив M'
= М — M(hl)<zl > Ж, мы получаем
(АГ + 8, М' + Ъ) — (Ж+ 8,
. а,).
поскольку M(ht) = 2 (Ж, аг)/(аг, а2). Ввиду того что (8, а^)>0,
это показывает, что (М'-|~8, Ж'-f-S) >(Ж + 8, Ж+ 8). Предпо-
Предположим теперь, что M{hj)~^-Q, i = \, 2 /. Если ни одно Ж + а{
не является корнем и х Ф 0 удовлетворяет равенству xh = Mx, то
д;^ = 0 для всех I VI х будет канонической образующей некоторого
^-экстремального 8-модуля. Этот модуль должен совпадать с SM,
так что М является старшим весом вопреки предположению. Далее,
пусть а.1 — один из простых корней, для которого М' = M-\-ai
является корнем. Тогда М' > М и
(Ж' + 8, М' + 8) — (Ж + 5. Ж + 8) = 2(Ж + 8, аг) + (а?. а2).
Так как Ж(Л2)>0, то (Ж, аг)>0. Кроме того, (В, а2) > 0 и
(а^, а2) > 0, так что опять
(Ж' + 8, Ж' + 8)>(Ж + 8, Ж + 8).
Теперь ясно, что формула B2) может быть использована для
нахождения весов и их кратностей. В самом деле, начинаем с яд = 1.
Предположим, что для данного М = А — 2 kpi ify — неотрицатель-
неотрицательные целые числа и по крайней мере одно kt > 0) мы уже знаем
пМ' для каждого М' = Л. — 2*гаг> ki — целые числа, 0 ^.ki-^k^
М' Ф М. Тогда каждый член в правой части формулы B2) известен.
Кроме того, если (Л-f 8, Л + 8) = (Ж + 8, Ж + 8), то, согласно
лемме 3, Ж не является весом и «^ = 0. В противном случае
коэффициент при пм в B2) отличен от нуля, так что п^ можно
найти из этой формулы,
272 Гл. VIII. Характеры неприводимых модулей
§ 3. Формула Вейля для характеров
Чтобы получить общее выражение для формулы Вейля, верное
для любого поля, необходимо заменить экспоненциалы, входящие
в эту формулу, на „формальные" экспоненциалы. Этому понятию
можно придать точный смысл путем введения групповой алгебры
над основным полем группы целых линейных функций на <?>. На-
Напомним, что элемент М ? §* называется целым, если /И (ft,)—-целое
число для / = 1, 2 /, где ev ft, hl — канонические образующие
алгебры 2. Множество 3 целых линейных функций образует группу
относительно сложения; ясно, что 3 является прямой суммой цикли-
циклических групп, порожденных элементами \ из 3> Для которых
\t (fij) = Ьц. Введем теперь алгебру Ж над Ф с базисом [е (Л1) | М ? 3} •
находящимся во взаимно однозначном соответствии с элементами
из 3- Таблица умножения в этом базисе задается формулой
е(М)е(М') = е(М + М'). B4)
Тогда % есть групповая алгебра над Ф группы 3> а е @) = 1 — еди-
единичный элемент в St. Элементы алгебры ЭД и являются теми формаль-
формальными экспоненциалами, которые только что упоминались. Мы опре-
определяем характер х конечномерного модуля Ш как формальный
экспоненциал
X = 2»Af«(Al). B5)
м
где пм — кратность линейной функции М?% определенная ранее:
пм — 0, если М не является весом, и пм = д\тШм (размерность весо-
весового подпространства Шм), если М — вес. Суммирование в фор-
формуле B5) происходит по всем М ? 3- Это конечная сумма, так как
пм ф 0 лишь для конечного числа М.
Пусть xt = е (Хг), Хг (Л.) = btj. Так как любая целая линейная
функция одним и только одним способом может быть записана в виде
уИ—2ОТА- где т1 — целые числа, то базисный элемент е(М) =
= е (S «Л) = е (т,Х,) • • • <mi\) = е (М™1 ¦¦¦ е ^Р = х ... х™К
Мы назвали М доминантной, если Ж(Л()^.О для г=1, 2 /.
Это эквивалентно неравенству mi^>0. Множество линейных ком-
комбинаций элементов е(М), Ж—доминантная функция, является подалгеб-
подалгеброй алгебры 3t, которая совпадает с множеством линейных комбинаций
одночленов х ... х , mi^.O. Множество этих одночленов, по-
полученное с помощью последовательностей целых чисел (mv . . ., tnj),
т^О, линейно независимо. Следовательно, отмеченная выше под-
подалгебра может быть отождествлена с коммутативной алгеброй мно-
многочленов Ф[х1, х2 Xj\ от алгебраически независимых переменных
¦*} Ху Каждый элемент алгебры % имеет вид fj/' ... x^j f,
§ 3. Формула Вейля для характеров 273
где rt ^- 0 и / ? Ф [лгр .. ., xt]. Хорошо известно, что Ф [х1 xt\
является областью целостности. Отсюда следует, что 9t — коммута-
коммутативная область целостности.
Каждому элементу 5 группы Вейля W поставим в соответствие
линейное отображение в 2t, такое, что e(M)S = e (MS). Поскольку
— е (Ж5+ M'S) = e (MS) e (M'S) = е (М) Se (M1) S,
ясно, что 5 является автоморфизмом в St. Множество элементов S
образует группу автоморфизмов в %, изоморфную группе W. Эле-
Элемент a?2t называется симметрическим, если aS = a, S?W, и
кососимметрическим, если aS = (detS)a, S?W, где det5 — опре-
определитель ортогонального преобразования 5 в ф0. Таким образом,
det5= ± 1, иесли5 = 5а — симметрия Вейля относительно корня а,
то detSa = — 1. В частности, detS/ = — 1 для Si = S(l . Поскольку
симметрии Si порождают W, а симметричен в том и только том
случае, когда aSi = a, /=1, 2 I, u а кососимметричен в том
и только том случае, когда а5г = — а для всех i. Множество
симметрических элементов образует подалгебру; множество кососиммет-
рических элементов образует подпространство. Произведение двух косо-
симметрических элементов симметрично, а произведение кососимметри-
ческого элемента и симметрического элемента кососимметрично. Так как
nMS = nM для S?W, то характер у_ = 2 пме (^) является симмет-
симметрическим элементом. Отметим, далее, что
<? = *(-8)П (*(«)-1) = е(Ь) ПA -«(-<*)) ¦ B6)
где 8 ==A/2) | 2 а| — целая линейная функция, введенная в § 2,
\»>о /
является кососимметрическим элементом алгебры St. В самом деле, мы ви-
видели (доказательство леммы 2), что bSt = 8 — at, поэтому (— 8) S( =
= — 8 + «i и е(—b)Si = e(—b)e(at). Мы знаем также, что St
переставляет положительные корни, не равные at, и переводит
ai в —аг. Следовательно,
П («(«)-1M, = /П («(«)-0\ («(-«()-!)
а>0 I а>0 )
J
а > О
Ф
274 Гл. VIII. Характеры неприводимых модулей
Положим
. / = <&. - B7)
Этот элемент кососимметричен. Оказывается, что можно получить
формулу для /, что в свою очередь даст формулу для х-
Рассмотрим о=2 (det S) S как линейный оператор в 31. Для
любого TCW имеем аТ = 2 (det S)ST = (det Г)2 (det 5ГMГ =
s s
= (det Г) о и аналогично Та = (det Г) о. Если а — любой элемент
из 31, то (ао) Т = (det Г) (ао). Следовательно, аа является кососим-
Метрическим элементом. Если а кососимметричен с самого начала,
то aS = (uetS)a и, таким образом, aa = wa, где w — порядок
группы Вейля. Отсюда следует, что (\jw)<s является оператором
проектирования алгебры 3t на пространство кососимметрических
элементов. Поэтому любой кососимметрический элемент имеет вид
аа, а ?91, и, следовательно, такой элемент будет линейной комби-
комбинацией элементов е (М) а, М — целая линейная функция. Поскольку
Sa= + а, ясно, что е (М) а можно заменить на е (MS) а, а поэтому
любой кососимметрический элемент можно выразить в виде линейной
комбинации элементов е (М) а, где М будет наибольшей среди своих
сопряженных MS относительно группы Вейля. В частности, мы можем
предположить, что М^> МSt = M — M(h^at, т. е. можно считать
M(ht)^.O для г =1,2, . ..,/. Предположим, что M(hj) — O для
некоторого i, или, что эквивалентно, MSt=:M. Тогда е(М)а =
=—e(M)Sia = — e(MS()o = — е(М)а и е(М)а = 0. Можно поэтому
сделать заключение, что каждый кососимметрический элемент будет
линейной комбинацией элементов е(М)а, где M(ht) > 0, /--=1,2 I.
Применим теперь эти рассуждения к элементу Q, определенному
равенством B6). Раскрывая произведение в B6), мы видим, что Q
является линейной комбинацией элементов е (Ж), где М = Ь — р и
р — сумма некоторого подмножества положительных корней. Таким
образом, М = G2) 2 еаа> гДе еа == — ^ • и любая функция MS, со-
а>0
пряженная к М относительно группы Вейля, опять имеет вид 8 — р' =
— ('/г) 2 ela- ГДе р' — сумма положительных корней и е^= ± 1.
а> О
Применяя оператор проектирования (\/w)o к указанному выражению
для Q, мы можем представить Q в виде линейной комбинации элемен-
элементов е (М) о, где М имеет вид 8 — р (р — сумма положительных корней).
Мы видели, кроме того, что можно предполагать М удовлетворяю-
удовлетворяющим неравенствам M(hL) > 0, г= 1, 2 /. Эти условия означают,
что М = 8. В самом деле, если М = Ь — р, р = 2 *А> где ^1 —
неотрицательные целые числа, то 0 < M(hi)=b(hl) — р(йг)— 1 —р(йД
Так как р?3> то р(й^) — целое число. Следовательно, должно вы-
выполняться неравенство р(/гг)<^0. С другой стороны, 0^(р, р) =
§ 3 Формула Вейля Оля характеров 275
= 2*г(а(' Р) = С1/2J ki(ai< ад р(Л()<^°- Следовательно, (р, р) = 0
и р = 0. Таким образом, показано, что Q = 7je(8)o, т;(;Ф. Далее,
е (§) а = 2 (det 5)е (85)- По лемме 2 85 Ф 8 при 5 =? 1. Следовательно,
s
е(8)о = «E) + 2±«(Л), где Ж = 8 — р, р ф О, и является суммой
положительных корней. Кроме того, из формулы B6) очевидным
образом вытекает, что Q = ?(8)-|~2 ± е(М). Поскольку Q = tj?(8)o,
отсюда следует, что т\ = 1. Тем самым нами доказана
Лемма 4. Пусть Q = e(—8) Ц(?(а)—1). Тогда
Q = e(8)o= 2 (det5)е(85). B8)
Введем теперь векторное пространство §*®ФЭД и определим не-
некоторые линейные отображения этого пространства и алгебры %.
Элементы из §*<g>2t имеют вид 2 Р; ® fli> ?/(:§*• #*(:$• Закон
умножения в алгебре % приводит к линейному отображению произ-
произведения 9(<2)ф9( в 3t, при котором а%Ь-+аЬ. Это в свою очередь
дает линейное отображение пространства (ф* ® Ж) <g> 3t = ф* ® Ct ® Ж)
в §*®3t, при котором (р <g> а) ® Ь -> р ® аЬ. Отсюда следует, что если
положить B Рг % o.j) b = 2 Pi ® а/*> т0 эт0 произведение определено
однозначно и совпадает с образом элемента 2Pi®a<®* в &*®$-
Ясно, что умножение B Рг® а/)* = 2р/ ® afi вводит в ф*®ЭД
структуру правого St-модуля. Напомним, что в ф* имеется билиней-
билинейная форма (p. o) = (ftp, й„), которая определяет линейное отображе-
отображение пространства §*®фф* в Ф, при котором p®t—>(p, x). Если
взять композицию этого отображения и линейного отображения про-
пространства %®% в 3t, то получится линейное отображение про-
пространства ($* <gi Ж) ® (§* ® Щ в Ф ® %1 = ЭД, при котором (р ® а) ®
® (х ® b) -^ (p, t) а&. Тем самым определено Ф-билинейное отобра-
отображение пространства ф*® 31, такое, что значение (р® a, %®b)=(p, x)ab.
"Так как форма (р, о) симметрична и алгебра 3t коммутативна, то мы
имеем симметрическую билинейную форму. Если, далее, с ? %, то
((р®а)с, х®#) = (р®ас, х®*) = (р, х) асЬ и. (р®а, х®й)с =
= (р, \)аЬс и аналогично (р$а, (t® b) c) = (p® a, x®b)c. Это
означает, что форма (л:, у), х, у?|>*®3(, является 31-билинейной.
Определим теперь линейное отображение G, называемое градиен-
градиентом, алгебры ЧЦ в §*®ЭД : e(M)G — М ® е(М) и линейный опера-
оператор Д (лапласиан) в алгебре 3t: е(Ж)Д = (уИ, М)е(М). Очевидно,
(е (М) е (М1)) G = е (М -f М') О =
)t)
t=zM®e(M)e(M')-\-M'®e{M')e(M)
¦= (е (М) О) е(Мг) -1- (е (М') G) е (Ж).
2?6 Рл. VIII. Характеры неприводимых модулей
Из линейности градиента следует тогда, что
а, Ь^ЧЦ. B9)
Аналогично
(е (М) е (ЛГ)) Д = е (М + ЛГ) Д ==
= (Л1+ЛГ, М-{-М') е (М) е (М') =
= (Л1, /И)е(Л1)е(ЛГ) + 2(Л1, ЛГ) е (Л!) е (ЛГ) +
+ (Л1', Л1') е (Л1) е (Л10 =
= (г (Л1) Д) е (ЛГ) + 2 (М ® в (Л1), Л1' ® е {М')) +
-f- (е (Л1') Д) е (Л1) =
=• (е (Л1) Д) е (/И') + 2 (е (Л1) О, в (ЛГ) О) +
') Д) е (Л1).
Это означает, что
(а*)Д = (аД)* + 2(аО, й<3) + (М)а. C0)
Мы возвращаемся теперь к формулам, которые были получены
для кратности пм целой линейной функции М в конечномерном
неприводимом модуле со старшим весом Л. Напомним, что f — эле-
элемент из Ф (рациональное число), определенный оператором Кази-
Казимира. Рассмотрим опять равенство A9):
со
Умножим обе части на е(М) и просуммируем по М. Это дает
равенство
со
ТХ = УА + 2 S S «ж+;а (Л + У«. «)«(М)•
7И а^=0 / = 0
члены которого мы умножаем на выражение
П (*(«)-1)= П («(«о -1) П («(-«)- 0=± Q2.
а^О а>0 а>0
получающееся из формулы B6). Это дает
2 2 2 П(«(Р)-1)»Л+У.(А1 + /«. «)(«(Af + «)-e(Af)). C1)
7И а^О ;=0 Р^=и У
§ 3. Формула Вейля для характеров 277
Коэффициент при е(М-\-а) в правой части соотношения C1) равен
/ со
П (« (Р) - 1) ( 2 *М+1* (М + /а, а) ^~
- 2 nM+{J+l).
7-0
= П
Следовательно, соотношение C1) может быть записано в виде
±та<2
= 2
^0
2
7И
= (± Q2Q, Х0) = ± 2 ((QG) Q, ХО). C2)
Поэтому
UQ2 — (ХД) Q2 = 2 ((QO) Q, хО) =
= 2(QO, ZG)Q.
Сокращая это равенство на Q^=0 в области целостности 5t, получаем
в силу C0). Полагая, как и прежде, / = xQ> находим, что
T/ = /A-(QA)x- C3)
Так как Q= 2 detS(*(85)) и (85, 85) = (8, 8), то ОД = (8, 8)Q.
Кроме того, -у == (А—|- S, Л + 8)—(8, 8) (см. выражение после B1)). Под-
Подставляя все это в C3), получаем следующее фундаментальное урав-
уравнение для /:
8 8 C4)
Элемент f = y<Q кососимметричен и, следовательно, является
линейной комбинацией элементов вида е(М)о. Более того, можно
ограничить множество необходимых здесь линейных функций М,
посмотрев на выражения для х и 0- Действительно, Х==2Л7ие(^)>
где суммирование теперь берется в точности по весам представления.
Мы видели также, что Q-— 2 (det5)?(85). Перемножая эти равен-
S? W
ства, получаем представление ^0 в виде линейной комбинации членов
Гл. VIII. Характеры неприводимых модулей '
e(M~\-bS), где М — вес: / =
получим
так что е (М + 55) лежит в характеристическом подпространстве,
соответствующем характеристическому корню [MS + 8, MS ! + 8)
оператора Д. Так как / принадлежит характеристическому корню
(Л-|-8, Л+ 8) оператора Д и характеристические подпространства,
соответствующие разным характеристическим корням, линейно неза-
независимы, то / будет линейной комбинацией элементов е (М + 85),
таких, что (.MS+ 8, уИ5~1 + 8) = (Л+8, Л + 8). Согласно лемме 3,
равенство (Л15"' + 8, MS+ 8) = (Л+8, Л + 8) для веса MS'1
означает, что MS 1=Л. Следовательно, мы видим, что / является
линейной комбинацией членов е(Л+8M. Применяя оператор проек-
проектирования {\jw)<s к /, видим, что
' / = т;е (Л + 8) а = т) 2 (det S) <? (Л + 8) S.
Так как 85 < 8 при 5=^=1, то (Л + 8M<Л+8, если 5^1. Сле-
Следовательно, коэффициентом при е (Л + 8) в выражении для / будет т;.
С другой стороны, коэффициент при этом члене в %Q есть пА = 1.
Поэтому т) = 1, и нами доказана
Теорема Вейля. Пусть ЗК — неприводимый модуль над 8
со старшим весом Л. Тогда характер /А = 2 п
алгебры 2 в Ш задается формулой
Хл 2 (det5)<?(85)= 2 det5(e(A+8M), C5)
S?W S?W
где 8 = G2Ja> a—корень.
a>0
Эта теорема свидетельствует о том, что выражение справа делится
на Q = 2 (det 5) е (85) в 31, и частное есть в точности характер х
s
представления.
Нетрудно убедиться в том, что этот результат дает в комплекс-
комплексном случае первоначальную формулу Вейля
2 detSe*p((A + &)S)(A)
v (ft) = liZ_^ . C6)
АЛ ' 2 detexp(8S)(A)
§ 3. Формула Вейля для характеров 279
Вейль использовал свой результат для получения при помощи
предельного перехода размерности модуля Ш, которая равна
2лД[ = Хд@)- Мы получим тот же самый результат, используя
отчасти аналогичный прием.
Рассмотрим алгебру Ф {() формальных степенных рядов от пере-
переменной t с коэффициентами из Ф. Напомним, что отображение,
сопоставляющее степенным рядам их свободные члены, является
гомоморфизмом С алгебры Ф (t) на Ф. При помощи экспоненциалов
ехрг= 1 ~\- z-{-(z2/2!)-(- ..., которые определены для любого
г?Ф(^) с нулевым свободным членом, можно определить также
гомоморфизм алгебры 31 в Ф (t). Имеет место соотношение
exp (Zj -f- 22) = (exp 2j) (exp z2); следовательно, если X, p, р?ф*. то
ехр(Х, p)fexp((A, p)^ = exp(X-f-(i, p)t. В частности, это выполняется
для целых линейных функций X. = Ж, (л = Ж' на ф, что означает ввиду
равенства B4) существование гомоморфизма алгебры ЭД в Ф (?), для
которого в(Ж)Ср = ехр(Ж, р)Л Рассмотрим теперь Хд.^- Поскольку
ХА = 2 пмемз т0 Za^p = 2 ге7иехР(^> Р)^ и> так как свободный
член экспоненциала равен 1, то Хд.^р'*== 2 пм == ^im ^- Ф°РМУЛУ для
dim Tt мы получим, применяя С.С к C5) и полагая р = 8 = A/2) 2 а-
а>0
Пусть, как и прежде, о= 2 (det 5) 5 и Ж, Ж' — целые линей-
ные функции. Тогда
е (М) оСлг = 2 det 5 exp (MS, M') t =
s
Следовательно,
е (М) оС8 = е (8) оСЛ = (лемма 4) = е (- 8) Сж Д
а>0
= ехр(—8, М) t JJ (exp (а, Л1)*—1) =
= Д (exp i (а, Ж) t — exp 1 (— a, Ж) f), C7)
a >0
поскольку 8 = (!/2) 2 a> Применяя это к C5), получаем
СУаСЛ I I (exp-fr (a, 8)^—exp-jr(—a, 8)n =
= JJiexp-K-(a, Л-(-8) ^ — ехр-н-(—a, Л-|-8)п. C8)
«> о
280 Гл VIII Характеры неприводимых модулей
Далее,
JJ(expi-(a, M)f-exp-g-(— a, A!)f)== JJ(a, M)**(mod*ft+I). C9)
а>(Л J a>0
где k — число положительных корней. Если разделить обе части
выражения C8) на tk и применить затем гомоморфизм С, который
выделяет свободный член, то мы получим формулу
(dimSW) П (<*• 8)= П (<*• 8 + Л)-
a>0 a>0
ИЛИ
П(а,8 + Л)
0 D0)
= ¦
J1 («. 8)
а>0
§ 4. Некоторые примеры
Покажем теперь, как вычислить размерность
dim Tt = П (А+ 5- а)/П (§. а)>
а>0 / а>0
исходя из схемы Дынкина для Й. Пусть wt = 1, 2 или 3 будет вес
вершины at в схеме и аг — один из корней в простой системе,
такой, что wr = \. Заменим скалярное произведение (а, р) на
(а, [3)' = 2 (a, fJ)/(ar> ar). Тогда, очевидно,
dim ЭЙ = П (А-+ 8, «)'/П (8- аУ-
а>0 /а>0
Пусть Л=2тЛ> »»;>0, a = 2fyay *;>0. Тогда, поскольку
(Ёх«)(йу) = 1 и 8(fty) = l, У=1 /, 8 = 2Х«- Следовательно,
нам нужны B («/+ !)^> 2 *;а;)' = 2
2kj(Kt. а/. Но
2(Х>
Следовательно, (Л + 8, a)'= J?(tni-\-l)wlkl и (8, а)' = 2и^.
а поэтому
dim SW = 11-^—1 • D1)
§ 4. Некоторые примеры 281
где произведение берется по всем последовательностям (Jtv k2, .'.., kt),
k^O, для которых 2 *;ау является корнем. Мы видели, что это
множество, так же как и веса wit может быть определено из схемы
Дынкина.
О2. Здесь ¦ш1 = 3, w2—l и корнями будут av а2, aj-f-a2,
aj-j-2a2, aj-(-3a2, 2aj-f-3a2. Формула D1) дает в таком случае
соотношение
dim Ш = ~ [(да, + 1) (щ + 1) C/»! + т2 + 4) X
X (Зщ + 2т2 + 5) (да, + т2 + 2) Bт, + т2 + 3)], D2)
если старшим весом модуля Ж является m1X1-f-«2X2. Для Л = ХХ и
Л = Х2 мы находим соответственно 14 и 7, что и было получено
ранее.
Bv 1^-2. В данном случае ¦до1 = 1до2= ... ==Wj_1 = 2, -н^ = 1
и весами будут
D3)
Они дают следующие множители в формуле для размерности:
ml + mt+1+ ...+mj + J-l+l 1</<;</ ,
«z-i)+"z+2(*-0 +1
1^f</. D4)
Пусть Л = ХЙ, 1<;&<^/—1, так что mk — \, ml = (
Произведение, взятое по первому множеству сомножителей в D4),
равно
k 1-1
J-L±l — (r
Второе множество сомножителей дает
21 — 21 + 3 _
21 — 2х + 1 ~ 21 — 2&-Н
Ту 21 — 21 + 3 _ 21+1
282 Гл. Vlll. Характеры неприводимых модулей
и последнее —
к I
(V) A)
U)
Общее их произведение равно
dim2R = ( ). D5)
\ k J
Напомним, что как раз этот результат требовался для завершения
доказательства (§ 7.6) неприводимости модуля А-векторов относи-
относительно Bt.
§ 5. Применения и дальнейшие результаты
Будем называть теперь характер конечномерного неприводимого
представления алгебры 2 примитивным характером. Такой характер
имеет вид Хд ~ е №) ~Ь S пме (¦/^)> где суммирование берется по
М < Л в смысле лексикографического упорядочения в ф* или в 3«
Так как в (Л) составляют базис групповой алгебры 31 группы 3i To
ясно, что из равенства хА| = Ха следует, что Л, = Ag, а это озна-
означает, что ассоциированные с ними представления эквивалентны.
Обратно, эквивалентность конечномерных неприводимых представле-
представлений влечет равенство характеров. Из выражения, указанного для
примитивного характера, ясно также, что различные примитивные
характеры линейно независимы. Если ЗК — любой конечномерный
модуль над й, то он будет прямой суммой, скажем, /я, неприводимых
модулей с характером Хд • Щ —с характером Хд Ф Хд и т- д>
В таком случае характер х модуля Ш имеет вид
. D6)
Поскольку эта запись единственна, мы видим, что если х и прими-
примитивные характеры известны, то числа т1 можно найти. В итоге опре-
определяются классы (с точностью до изоморфизма) и кратности непри-
неприводимых компонент модуля Ш. Как следствие получаем, что эти
классы и кратности не зависят от вида разложения модуля ЗК на
неприводимые компоненты.
Характеры можно использовать для отыскания классов (с точностью
до изоморфизма) и кратносте^ тензорного произведения двух непри-
§ 5. Применения и дальнейшие результаты 283
водимых модулей. Предположим, что (xv ..., xm) — такой базис
модуля 2№, что xih = Al(h)xi, и (у, уп)—такой базис модуля Ш,
что yjh = Mj(h)yj. Тогда шп произведений xt®yj образуют базис
в Ш®Ш, и
(xt ® у} h = (Л,- + Mj) (А) (х, ® у,).
Поэтому получаются следующие выражения для характеров модулей
Таким образом, мы видим, что характер модуля 2)?®^ является
произведением в 31 характеров модулей Ш и Щ. Записав произве-
произведение двух характеров в виде суммы примитивных характеров,
находим строение модуля Т1 ® Ш. В случае алгебры Ли Ах имеется
классическая формула для этого, называемая формулой Клебша —
Гордана. Мы приведем обобщение этого результата, принадлежащее
Р. Штейнбергу. В его основе лежит явная формула для кратности пм
веса М в неприводимом модуле со старшим весом Л. Эта формула
получена Костантом; простое доказательство, приводимое здесь,
принадлежит Картье и Штейнбергу (независимо).
Введем .сначала функцию разбиения Р(М) для М?3>. которая
аналогична функции (неупорядоченных) разбиений в теории чисел.
Если М?5> т0 Р(Щ есть число способов записи М в виде суммы
положительных корней, т. е. число решений (ka, к$, .... /гр) урав-
уравнения 2 кла. = М, где ka — неотрицательные целые числа и
о>0
{а, р р}—множество положительных корней. Очевидно, Р@) = 1
и Р(М) = 0, кроме того случая, когда M = 2W(^' гДе> как и
прежде, mt — неотрицательные целые числа, Хг(й;) = 8^. В послед-
последнем случае е(М) = х™1 ... х™1, х. = е{Х,\. Удобно расширить груп-
групповую алгебру 31 до поля 31 степенных рядов вида (л;™1 ... xfty f,
где / — бесконечный ряд с коэффициентами из Ф от элементов
л; ... x"i, п. — целые неотрицательные. В 31 можно рассмотреть
„производящую функцию" 2 Р(М)е(М), которая определена, по-
поскольку Р(М) = 0, если М =?2/яЛ> т^О. Ясно, что мы имеем
тождество
2
а>
Поскольку A — е(а))~1 = 1 -\-е(а.)-\-еBа)-\- .... имеет место
равенство
2 Р (М) е Щ)\ Д A — е(а) )= 1. D7;
284 Гл. VIIJ. Характеры неприводимых модулей
Перепишем формулу Вейля C5) в виде
С?пме(М)) 2 (det 5) е (85) = 2 (det S) е (Л + 8) 5.
sew sew
Заменяя здесь М на — М и умножая результат на е (8), получаем
B «л*е (— м)) 2 (det 5) е (8 — 85) = 2 (det 5) в (8-(А + 8) S). D8)
S?W S?W
По лемме 4
Q = 2(det5)в(85) = в(8) П О-*(-«)).
Следовательно,
2 (det5)e(8-8S)= ДО-*(*))•
S6W а>0
Поэтому, умножая обе части равенства D8) на 2 ^ (Щ е (М), полу-
чаем ввиду D7), что
%пме(-М) =
= B (det5)e(8 —(А+8M))B
\sew /улез
= 2 (detS)P(M)e(M + h~(A+8M). D9)
sw
Сравнение коэффициентов при е (— М) дает формулу Костанта для
кратности пм в неприводимом модуле со старшим весом Л, а именно
пм= 2 (detS)P((A + 8)S-(M-f-8)). E0)
sw
Рассмотрим теперь формулу для хА хА . где хА = 2
характер неприводимого модуля 9Кг со старшим весом Аг. Мы видели,
что Хд Хд = 2 тдХА> гле ягА — кратность в Шх ® 9К2 неприводимого
модуля со старшим весом Л. Суммирование берется по всем доми-
доминантам (т. е. доминантным целым линейным функциям) А. Умножая
обе части этого равенства на 2 (det 5) е (85) и применяя формулу
sew
Вейля, получаем, что
B «$e(M)V2 (det Г)в((А,+ 8) Г)) =
= 2"»д 2 (det 5) в ((А+ 8) 5).
Л AS?W
Суммирование в правой части можно брать по всем А?3> если
положить /яА = 0 для Л, не являющихся доминантами. Применяя
Упражнения 285
формулу E0) к «$, находим соотношение
i 2 B (det5)P((A, + 8)S-(Al + 8))e(Al))ix
= S »A S2^(det S) e ((A + 8) S).
Следовательно,
2), 2 (det5r)P((A1 + 5M —(Ж + 8))Х
Л*?3 S, T?W
(detS)e((A+8)S).
Полагая (Л2+8)Г+Ж = Л-(-о в левой части, получаем равенство
2 2 (detSr)P((A1
( S,T?W
2
Следовательно,
2
2
5PW
Легко видеть, что если функция А доминантна, то (A-f-8M и, сле-
следовательно, (A-f-8M — 8 не доминантны при Бф1. Поэтому
/Я(А+аM-5 = 0 при ?>ф1 для всех доминантных А, так что мы полу-
получаем формулу
()( + ) + B ) (A+ 28)) E1)
S, T? W
для кратности модуля со старшим весом А в 2)^ ® ЗИ2.
Упражнения
Обозначения и соглашения те же, что и в гл. VII.
1. Пусть р ё ©о- Дэть прямое доказательство того факта, что р !> pS для
каждого S$W тогда и только тогда, когда р (ht) ;> 0, / = 1, 2,..., /.
2. (Селигман). Доказать утверждение о единственности в теореме 2, ис-
используя тот факт, .что существует конечномерный неприводимый модуль Ш
со старшим весом Л, удовлетворяющий условию: Л (Л,) различны и положи-
286 Гл. VIII. Характеры неприводимых модулей
тельиы. Заметим, что AS = Л, если xS = S, так что 2 (Л, <^)/(аг, at) =
= 2 (AS, ojS)/(a;S, aft) = 2 (A, a;S)/(a;S, a,S). Это приводит к равенству
A (ht) = A (hj) при atS — а/.
3. Назовем вес А в ЭК крайним весом, если для каждого корня афО
либо А-(-а, либо А — а не является весом. Показать, что если Ш конечно-
конечномерен и иеприводим, то любые два крайних веса сопряжены относительно
группы Вейля.
4. Основное поле — поле вещественных чисел. Пусть а — корень,
а Ра — гиперплоскость в ф, определенная равенством а (К) = 0. Камера
определяется как связная компонента (связное максимальное подмножество)
дополнения множества (J Ра в ф. Показать, что каждая камера С является
выпуклым множеством. Множество корней ? есть определяющая система
для С, если С — множество элементов h, удовлетворяющих неравенству
о (й) > 0 для всех а ? 2. Минимальные определяющие системы называются
фундаментальными системами. Показать, что последние в точности совпа-
совпадают с простыми системами корней, определенными лексикографическими
упорядочениями в ф*.
5. Показать, что групповая алгебра 21 (группы Q целых функций на ф)
является областью с однозначным разложением на множители.
6. Доказать, что если Р € 91 кососимметричен, то Р делится на Q —
= 2(detS)e(»S).
s
7. Пусть ¦>) — автоморфизм алгебры 9Г, для которого е (А) = е (—А).
Показать, что если х—характер конечномерного модуля 9К, то у7) — харак-
характер контрагредиентного модуля 501*.
8. Пусть 501—конечномерный неприводимый модуль, характер которого
удовлетворяет равенству уч = -^. Предположим, что основное поле алгебраи-
алгебраически замкнуто. Показать, что образ 2й при представлении R в 501 является
подалгеброй ортогональной или симплектической алгебры Ли линейных
преобразований в Ш.
9. Пусть $ — расщепляемая трехмерная простая алгебра Ли с канони-
каноническим базисом е, /, h. Показать, что характер (т -\- 1)-мерного неприводи-
неприводимого модуля fflm+i над й равен хт-\-хт-х-\-... -\-х~т, где х = е(К),
\ (h) = 1. Использовать это для получения неприводимых компонент модуля
S»mti ® Шп+1.
10. (Дынкин). Пусть ЗК и ^ — конечномерные неприводимые модули
иад S. Доказать, что 501 ® 9f неприводим тогда и только тогда, когда для
каждого элемента / из произвольного простого идеала алгебры S либо
$91/ = 0, либо 91/ = 0.
11. Используя формулу Вейля, показать, что размерности четырех базисных
неприводимых модулей над F4 равны соответственно 26, 52, 273, 1274. Ис-
Используя формулу Фрейденталя, получить характер 26-мерного базисного
модуля.
12. Используя формулу Вейля, доказать, что dim ЭК = 21, если модуль ЯК
над Bi имеет старший вес \.
13. (Штейнберг). Пусть Ш — конечномерный неприводимый модуль со
старшим весом А. Показать, что М — вес модуля ffl, если А — MS является
суммой положительных корней для каждого S$W.
14. (Костаит). Доказать следующую рекуррентную формулу для функ-
функции разбиений Р(М):
— 2 (detS)P(M —(S —6S)).
56 W
5*1
Глава IX
АВТОМОРФИЗМЫ
Эта глава посвящена изучению групп автоморфизмов полупростых
алгебр Ли над алгебраически замкнутым полем характеристики нуль.
Если элементу z алгебры Ли й характеристики 0 соответствует ниль-
потентный присоединенный эндоморфизм ad z, то, как мы уже знаем,
exp(adz) является автоморфизмом. Всевозможные произведения авто-
автоморфизмов этого типа будут называться инвариантными автоморфиз-
автоморфизмами. Они образуют подгруппу О0 (й) группы автоморфизмов О (й)
алгебры й. Если х — некоторый автоморфизм, то x^^expad^t^^
= exp ad zz и эндоморфизм ad zx нильпотентен. Отсюда следует, что
О0 есть инвариантная подгруппа группы О.
Основной задачей, которую мы рассмотрим в этой главе, является
вычисление индекса подгруппы О0 в О для простой алгебры й ко-
конечной размерности над алгебраически замкнутым полем Ф характе-
характеристики 0. Мы покажем сначала, что если алгебра й (не обязательно
простая) имеет конечную размерность над Ф, то О0 действует тран-
зитивно на множестве подалгебр Картана, т. е. для любых двух под-
подалгебр Картана $i и $2 найдется элемент о?О0, для которого
.g>J = ?>2- Теорема о сопряженности такого типа была впервые дока-
доказана Картаном в случае, когда й — полупростая алгебра, определен-
определенная над полем комплексных чисел, и была применена им для изучения
автоморфизмов этих алгебр. Обобщение и строгое доказательство
теоремы о сопряженности принадлежит Шевалле. Этот результат сво-
сводит изучение вложения подгруппы О0 в О к изучению автоморфиз-
автоморфизмов, которые отображают подалгебру Картана в себя.
В случае, когда Й — полупростая алгебра, важную роль в рассмот-
рассмотрениях играет группа Вейля. Нам потребуются также некоторые
прямые -вычисления инвариантных автоморфизмов, принадлежащие
Селигману. Конечным результатом будет описание групп автоморфиз-
автоморфизмов алгебр Ли Av Bv Ct, Dt, I > 4, O2 и F4. Следует отметить,
что аналогичные результаты могут быть получены также в случае
характеристики р (см. Джекобсон [8] и Селигман [4]). Как обычно,
мы ограничимся для простоты случаем характеристики 0. В следую-
следующей главе результаты, полученные для неисключительных простых
288 Гл IX Автоморфизмы
алгебр Ли, определенных над алгебраически замкнутыми полями,
будут распространены на алгебры этого типа над произвольным
основным полем (характеристики 0).
§ 1. Леммы из алгебраической геометрии
Пусть Ж — конечномерное векторное пространство с базисом
(«j, и2> •••> мт)> определенное над бесконечным полем Ф. Любой
элемент х однозначно представляется в виде •^ = 2^гмг> гДе ^ —
координаты х в базисе (мг). Пусть /(X,, .... Xm)— элемент полино-
полиномиального кольца Ф [\v . . ., Хто] относительно m переменных Х;
с коэффициентами из Ф. Тогда /(Xj, .... Хт) и базис (ut) определяют
отображение / пространства WI в поле Ф, заданное уравнением
/ (jc) = /(?) = / ($j Sm) (в этой главе мы будем чаще пользо-
пользоваться обозначением f (х), а не xf или xf). Назовем / полино-
полиномиальной функцией на Ж. Если (и'х, ..., и'\ — другой базис в 2U,
то, как легко заметить, функция / может быть определена другим
элементом кольца Ф [Xj Хст] относительно базиса (и/). В этом
смысле понятие полиномиальной функции не зависит от выбора базиса
в ЗК ')• Множество полиномиальных функций является алгеброй Ф [Ш\
относительно обычных операций сложения и умножения функций.
Напомним, что если / и g — функции на 3№ со значениями в Ф, то
(/ + *)(*) = /(*)+*(*). (*/)(¦*) = */(*). а?ф- и (/?)(*)=*
T=f(x)g(x). Отображение f(\ lm) ->/ ? Ф [9К] будет гомомор-
гомоморфизмом кольца Ф [Xj \т] в алгебру Ф (Ш). Поскольку поле Ф бес-
бесконечно, из равенства f{ix, . . ., ?m) = 0 для всех ?г?Ф следует, что
/(Xj, ..., Xm) = 0. Следовательно, этот гомоморфизм является изо-
изоморфизмом, переводящим Х( в функцию проектирования 1^, такую,
что ^E) = ^. Поэтому очевидно, что тгг порождают алгебру Ф[9К].
Пусть ЭД —другое конечномерное пространство над Ф с базисом
(vv v2, .. .-, vn). Полиномиальным отображением Р простран-
т
ства Ш в пространство 9t называется отображение вида X = 2 ^iui ~*
п
% где nj = pj#v .... у, pj(\ Хт)^Ф[Х! XJ.
Это понятие не зависит от выбора базиса. Множество полино-
полиномиальных отображений пространства Ш ъ Щ есть векторное про-
пространство относительно обычного сложения отображений и умножения
их на скаляры.
!) Читатель, предпочитающий иметь дело с инвариантным определением
полиномиальных функций и полиномиальных отображений, может обратиться
ко второму тому монографии Шевалле [2]. — Прим. ред.
§ 1. Леммы из алгебраической геометрии 289
Композиция полиномиального отображения Р пространства Ш в У1
и полиномиального отображения Q пространства Ш в 4$ есть поли-
полиномиальное отображение PQ пространства 2№ в ?р.
Понятие полиномиальной функции является частным случаем по-
полиномиального отображения, когда образ — одномерное простран-
пространство Ф. Поэтому если Р — полиномиальное отображение простран-
пространства ЗМ в ЭД и / — полиномиальная функция на 3t, то Р/ будет
полиномиальной функцией на ЗК. Отображение f~>Pf есть отобра-
отображение алгебры Ф[Ш] полиномиальных функций на Ш в Ф[9Л]. По-
Посмотрим, как записывается это отображение.
Пусть Р(х) = у, где *- = 2^я/> У —
4 = Р}&,..., U (!)
Pj(\ O€$Pv •••• U-
Далее, /(y) = /(ij, ?)„), /(ц, 1^ПNФ^1 ft,], где
fiz — независимые переменные. Поэтому Р/ переводит х в
/(PiE). />2tf) Р„E)). B)
где pjft^pji^, % Sm). Если /.
*/(Pi(«) P« ©) = «(/(Pi«) P»
Это показывает, что отображение f->Pf является гомоморфизмом <зр
алгебры Ф[Щ в Ф[ЗЛ].
Обратно, пусть о — гомоморфизм алгебры Ф \Щ в алгебру Ф [9И].
Рассмотрим проекцию ру : 21 '"I*"* "*¦ ^у Предположим, что р} —
отображение S^M<~*"//(^i' ^2- •••• ^m)> и пусть Р — полиномиаль-
полиномиальное отображение пространства 9Л в пространство У1: 2 ^и; "*¦ 2 ^у.
где i]j = fj(i.). Тогда Рру отображает 2^*i в /ДО' так что ^>Р/=г
= f,. Поскольку р, порождают алгебру Ф[9?], гомоморфизм о со>
впадает с гомоморфизмом ор, определенным при помощи Р. Таким
образом, каждый гомоморфизм алгебры Ф[5!] в Ф[9Л] (отображаю-
(отображающий 1 в 1) реализуется полиномиальным отображением пространства
9Л в Щ. Легко видеть, что если Р и Q — два таких полиномиальных
отображения, то равенство P — Q является необходимым и достаточ-
достаточным условием эквивалентности гомоморфизмов up = aQ. Итак, мы
получаем взаимно однозначное соответствие между полиномиальными
отображениями пространства Ш в Ш и гомоморфизмами алгебры Ф[!ЭТ]
в Ф [9Л]. Особенно важным для нас является множество гомоморфизмов
алгебры Ф [Щ в основное поле Ф. Его можно получить окольным пу-
путем, отождествляя Ф с алгеброй Ф [ЗА] полиномиальных функций на
19 Н Дж«кобюн
290 Гл IX Автоморфизмы
пространстве % = 0 и применяя предшествующие результаты. Однако
можно это сделлть и непосредственно. Заметим, прежде всего, что
если y?9f, то отображение о :/->/(у), специализация / в точке у,
является гомоморфизмом алгебры Ф [Щ в Ф. Обратно, если о — про-
произвольный гомоморфизм алгебры Ф [№] в Ф, то положим ч\. ~f,
как раньше. Тогда непосредственно видно, что о = <зу, где у = 2 j°i-
Очевидно также, что если ухфу2 в ^> т0 "у^^г-
Пусть / ? Ф [Ш] и пусть а — 2 аг«» 6 ^- Тогда мы можем опре-
определить линейную функцию daf на Ш равенством
Легко видеть, что dj не зависит от выбора базиса. Линейное ото-
отображение daf называется дифференциалом функции f в точке а.
Это отображение обладает следующими свойствами:
da(<Lf) = a(dJ)t D)
da (fg) = / (a) (dag) + g (a) (dj).
Если t — независимая переменная и функция / продолжена в функ-
функцию на пространстве Шфц) обычным способом, то в алгебре Ф [t]
мы имеем следующее соотношение, являющееся следствием формулы
Тейлора:
f(a+tx) = f (a) +1 (dj) (x) (mod t3). E)
т
Более общо, пусть Р — полиномиальное отображение х = 2 ?««/-*¦
2i)) пространства ЗК в пространство Ш. Определим тогда
дифференциал daP отображения Р в точке а как линейное ото-
отображение, задаваемое формулой
Можно проверить, что это определение также не зависит от выбора
базиса в пространствах Ш и У? Нетрудно также получить следующее
полезное обобщение формулы E):
G)
§ 1. Леммы из алгебраической геомртрии 291
Система образующих пространства образа Tt(daP) есть множество
векторов
Поэтому отображение йаР эпиморфно тогда и только тогда, когда
ранг матрицы Якоби
V
и. 7=1. 2 я. (9)
равен «.
Лемма 1. Предположим, что поле Ф совершенно, и пусть
отображение йаР эпиморфно для некоторого а. Тогда гомо-
гомоморфизм <зр является изоморфизмом алгебры Ф \Щ в Ф [Ш].
Доказательство. Из нашего предположения следует, что
некоторый минор «-го порядка матрицы (dp;/dXt) отличен от нуля.
Если <3р не есть изоморфизм, то существует такой многочлен
/Oh IV)^O, что/(/>,(?), р2(?) ря(?)) = 0 для всех 6,6 Ф-
Отсюда следует, что / (/^ (X) р„ (X)) = О, т. е. многочлены
px(kv .... Xm) Рп(\ ^m) алгебраически зависимы. В этом
случае мы можем предположить, что многочлен /^=0, осуществляю-
осуществляющий эту зависимость, имеет наименьшую степень. Из равенства
/ (Pi (х). • • • • Рп (х)) = ° следует, что
n- df ~\( df\ дР) /-1
~ат—i t = i т.
Это противоречит нашему предположению о матрице Якоби, если
только не выполняются равенства (df/d^j) (рг (X) рп (X)) = 0.
Поскольку из всех многочленов, обращающихся в 0 после подста-
подстановки в них /?i(X) Pm(X), многочлен / имеет наименьшую сте-
степень, (д//д\>.}) = 0, j=\ п. Отсюда следует, что / является
отличным от нуля элементом поля Ф, если характеристика поля Ф
отлична от 0. Это невозможно. Если же характеристика поля Ф равна
рфО, то мы получаем, что / является многочленом от ц?, ц? ^
Так как поле Ф совершенно, то f — gp, где g — многочлен от пере-
переменных (J-. Тогда giPxft), ..., J3m(X)) = 0. что опять противоречит
предположению о минимальности степени многочлена /.
Для доказательства теоремы о сопряженности подалгебр Картана
нам потребуется следующий основной результат.
Теорема 1. Пусть поле Ф алгебраически замкнуто, и
пусть Р — полиномиальное отображение пространства Ш
19*
292 Гл IX Автоморфизмы
в пространство Щ, такое, что йаР эпиморфно для некоторого
а?Ш. Если f — ненулевая полиномиальная функция на про-
пространстве Ш, то существует ненулевая полиномиальная функ-
функция g на ЭД, обладающая следующим свойством: для произ-
произвольного элемента ,у?У{, удовлетворяющего условию g{y)=h4,
найдется элемент х?Ш, такой, что /(х)ФО и Р(х)~у
Этот результат имеет следующий геометрический смысл: если
в пространстве Ш задано „открытое" множество, состоящее из эле-
элементов х, удовлетворяющих условию /(х)фО для некоторого нену-
ненулевого многочлена /, то существует открытое множество в простран-
пространстве Щ, определяемое условием g(y)фO, g — ненулевой многочлен,
которое содержится в образе при отображении Р заданного откры-
открытого множества пространства Ш. Мы увидим, что теорема 1 является
простым следствием такой теоремы о продолжении гомоморфизмов
Теорема 2. Пусть Ф — алгебраически замкнутое поле, и
пусть Г — расширение поля Ф, 21— подалгебра в Г и 21' — рас-
расширение алгебры 21, имеющее вид W = %[uv и2, ..., иг], где
м,^Г. Пусть / — ненулевой элемент алгебры W. Тогда суще-
существует ненулевой элемент g ?21, такой, что всякий гомомор-
гомоморфизм в алгебры 21 в поле Ф, удовлетворяющий условию ga ФО,
можно продолжить до гомоморфизма х алгебры. W в Ф, для
которого /т=?0.
Доказательство. Предположим сначала, что г—\, так что
2t' = 2l[M]. Случай I: и — трансцендентный элемент над полем 2с:Г,
порожденным алгеброй 21. Запишем / = f'0-(-f\u-\- ... -\-fmum,
fi € 5t> fm ^ 0- Положим g — fm, и пусть о — гомоморфизм алгебры %[
в Ф, для которого g''фO. Рассмотрим многочлен /o+/i^+ ...
"к в Ф[^], где А—независимое переменное. Поскольку
, этот многочлен имеет не более т корней в Ф, так что мы
можем выбрать такой элемент с ? Ф, что 2 /°с' Ф 0 Пусть х:
о
2 я, и'-> 2 0°с/ — гомоморфизм алгебры 2С —$ [и] в Ф. Очевидно,
этот гомоморфизм является продолжением гомоморфизма а, причем
/ТФ0, как и требовалось. Случай II: и — алгебраический элемент
над S. Канонический гомоморфизм алгебры 2t[A], где л — независимая
переменная, на алгебру W— U[u] (тождественный на 21 и переводя-
переводящий л в и) имеет ненулевое ядро 5JJ. Поскольку /?2t [и], / также
алгебраичен над Е. Пусть р (A), q (X) — ненулевые многочлены наи-
наименьшей степени в 2([л], такие, что р(и) — 0 и q(f) = Q. Тогда они
ив Е [л] являются многочленами наименьшей степени, для которых
/?(и) —0, q(f) = Q. Поэтому эти многочлены неприводимы в S [А].
Пусть gl — коэффициент при старшем члене многочлена р(А),
§ I Леммы из алгебраической геометрии 293
g2~q@)- Покажем, что элемент g — gig^ обладает требуемыми
свойствами относительно /. Предположим, что о— гомоморфизм
алгебры 21 в поле Ф, удовлетворяющий условию g" = g\g°2 Ф О, и
предположим, что х есть некоторое продоложение гомоморфизма а
до гомоморфизма алгебры W = %\и\ в поле Ф. Так как g(f) = 0,
то и g°{fz) — 0, откуда следует, что f ФО, поскольку g°(Q)^Q.
Таким образом, нам остается только показать, что гомоморфизм о
может быть продолжен до гомоморфизма алгебры W. Для этого
рассмотрим гомоморфизм х' алгебры ЭД[Х], который совпадает с о
на 2t и переводит X в с, где с —корень уравнения /?J(X) = 0. Пусть
h(k)—-некоторый элемент идеала SJJ. Тогда из минимальности степени
многочлена р(Х) следует, что существует неотрицательное целое
число k, такое, что g\h(k) делится на/?(Х) в 21 [К]. Из соотношения
р<(с) = 0 вытекает равенство (?*)* й*(с) = 0, а так как g\фQ, то
/г"(с) = О. Поэтому h(Kf =0, и, таким образом, Ц отображается
в нуль при гомоморфизме х' Отсюда следует, что х' индуцирует
гомоморфизм х алгебры %' =St[M] = 2t[X]/5p, который является про-
продолжением гомоморфизма о.
Допустим теперь, что утверждение верно для г — 1. Пусть
23 = 2t[ar], чак что 2Г —23[Hj, ..., иг_х]. Тогда существует такой
элемент Л ^ 23, что любой гомоморфизм р алгебры 23, удовлетворяю-
удовлетворяющий условию И.?ф0, может быть продолжен до гомоморфизма х
алгебры 2Г, для которого /хф0. Из рассмотренного случая г —1
следует существование такого элемента ^^21, что любой гомомор-
гомоморфизм а алгебры % в Ф, удовлетворяющий условию g''фO, может
быть продолжен до гомоморфизма р алгебры 23 = Щиг], для кото-
которою h? фО. Поэтому х есть продолжение гомоморфизма о, такое,
что f Ф 0, как и требовалось.
Приведем теперь
Доказательство теоремы 1. Из предположения относи-
относительно daP следует, что ар является изоморфизмом алгебры Ф[Щ]
в Ф[Ш]. Пусть Я = Ф[Я]'реЯ' = Ф[ЭК]. Если щ
бражения проектирования пространства Ш в Ф, то Ж' = Ф [ttj т
= 21[тс,, ..., irm]. Поскольку %' — область целостности, мы можем
считать ее вложенной в свое поле частных Г. Поэтому можно при-
применить теорему 2 к алгебрам 21 и W. Пусть /—ненулевой элемент
алгебры ЭД' = Ф[ЗЙ]- Тогда существует ненулевой элемент ^^Ф[3^],
такой, что если g (у) Ф 0, у ? Ш, то гомоморфизм a: h p -> h (у) алгебры
21=:ф[^] р в Ф, удовлетворяющий условию g p —g (у)фО, может
быть продолжен до гомоморфизма х алгебры Ф [Ш] в пойе Ф, для
294 Г л IX Автоморфизмы
которого /т=?0. Мы видели, что х имеет вид k~>k(x), где х
Тогда /(х)Ф0 и А*я = А*я" для каждого Л?ЭТ. Это означает, что
Л(Р(л;)) = Л(у). Поэтому Р(х) = у, и теорема доказана.
§ 2. Сопряженность подалгебр Картана
Пусть й — конечномерная алгебра Ли над алгебраически замкну-
замкнутым полем характеристики 0 и, пусть ф—подалгебра Картана алгебры й.
Пусть, далее,
Й-Ф+22. (И)
— разложение алгебры й на корневые подпространства, соответ-
соответствующие корням 0, а, §, ... относительно подалгебры ф, действую-
действующей в й. Если А ? ф и еЛ ? Йа, то найдется такое число г, что
ea(adA— а(АI)г = 0 Это эквивалентно условию, что а (Л) — един-
единственный характеристический корень ограничения эндоморфизма ad Л
на й„. Корни а—линейные функции на ф. Если л;?Й. (р = 0 или
Рт^О), то или [хеа] = 0, или р + а есть корень и [хеа] ? Йр+а. В по-
последнем случае либо [ [JceJ ej — 0, либо р —j- 2a есть корень н
[[хеа] е J ? йр4 2а' Продолжая эют процесс и принимая во внимание,
что существует лишь конечное число различных корней, мы прихо-
приходим к заключению, что Jc(adea)ft = O для достаточно большого k.
Отсюда следует, что присоединенный эндоморфизм ad еЛ нильпотентен
для каждого еЛ?2Л, а=?0. Поэтому если ^?1'^ е<1й€2ай.где
ар а2, ..., ak — ненулевые корни, то
Tj = exp(ade(Xl)exp(ade[t2) ... exp(adeaft) A2)
будет инвариантным автоморфизмом алгебры Й.
Пусть теперь (А,, А2 hv el+1 еп) — базис алгебры й,
такой, что (Aj, A2, ..., hj) — базис подалгебры ф, а элементы
е1+1 еп лежгт в корневых подпространствах Й„, а=^0.
Пусть Xj Хл — независимые переменные, Р=ф(Х1, ..., Хд);
образуем элемент
ехР (ad хг+1ег+1) ¦ • • exp (ad Xn еп) ==
I п
= IiPi(\ K)ht+ Ъ+хР}{\ К)е,, A3)
где pt и pj — многочлены относительно X, определяющие полино-
полиномиальное отображение
Р: ^ihi+'gtjej -* 2lPiQi)hl + 2iPJ®ej A4)
алгебры ? в себя.
§ 2. Сопряженность подалгебр Картанй 295
Произведение оф ... р ненулевых корней является ненулевой
полиномиальной функцией. Поэтому a(A°){J(A°) ... р(Л°)=?О для неко-
i
торого элемента Л° =2 ??А,, ???Ф; это означает, что характеристи-
1
1
ческие корни ограничения эндоморфизма ad Л° на 8„ + 8э-)- ... -f-8p
все отличны от нуля и, таким образом, это ограничение эндомор-
эндоморфизма ad Л° не вырождено.
Вычислим теперь дифференциал d^P отображения Р в точке Л°.
< I п
Для этой цели положим x — h-±-e, Л = 2$,Л,, ?=2S;e/; f —не-
1 i+i
зависимая переменная. Рассмотрим
== (А° -f Щ ехр (ad ^г+1ег+1) exp (ad tll+2el+i) ...
). A5)
Сравнив формулы A5) и G), мы увидим, что d^P будет отобра-
отображением
A6)
Отсюда следует, поскольку отображения h—>h и е—>-[А°е] не
вырождены, что d^P является эпиморфизмом. Мы можем поэтому
применить теорему 1. В результате получаем следующее утвержде-
утверждение. Пусть / Ф 0 — полиномиальная функция на Й. Тогда существует
полиномиальная функция g Ф 0 на Й, обладающая тем свойством, что
если у?Й и ^гООт^О, то найдется элемент л;?й, удовлетворяющий
условиям Р(х) = у и /{х)фО.
Напомним, что регулярным элементом алгебры g мы называем
такой элемент а, для которого ad а имеет наименьшее число /' нулевых
характеристических корней. Напомним также, что если а — регулярен,
то множество векторов А, принадлежащих нулевому характеристиче-
характеристическому корню эндоморфизма ad а, образует подалгебру Картана. Дру-
Другими словами, подалгебра Картана §, содержащая регулярный эле-
элемент а, состоит в точности из множества элементов Л?й, таких, что
A(ada)r = 0 для некоторого г. Нам потребуется также критерий
регулярности элементов, данный в § 3.1. Для этого возьмем элемент
I
2Vy Р .\ Ля)> и рассмотрим харак-
296 Гл. IX. Автоморфизмы
теристический многочлен
/ц (X) == det (XI — adM) =
= Xя — хж(X,)X—1 Н- ... + (-1)"-'' *«-«- ihn1'. A7)
Тогда in-i'Q-i> ¦••> ^л) — ненулевой однородный многочлен степени
п— /' относительно X, и если л = 2^( + 2^у> то отображение
x->tn-i' (¦*) = *«-*' («1. •••¦ ?я) является полиномиальной функцией
на Й. Элемент х регулярен в й тогда и только тогда, когда т„_г< (л;) =? О
(из теоремы, которую мы собираемся доказать, будет следовать, что
/' = /).
Рассмотрим снова подалгебру Картана § и базис (kl h.vel+v ...
.. ., еа) в 8. Применим теорему 1 к полиномиальной функции /=т°?г, ко-
которая отлична от нуля, поскольку хя_г- ^Оизр— изоморфизм. В соот-
соответствии с этим существует ненулевая полиномиальная функция g
на Й, такая, что каждый элемент у ? й, удовлетворяющий условию
g(i>) Ф 0. может быть записан в виде Р(х), где /(лс) = *я-г (Р(х)) =
= ^я-г (У) =? 0- Поэтому каждый элемент у, для которого ^
регулярен, и если дс = 2^А/-+-S ^/в/> т0 У = ^* 0*0 — CS 5«А<) X
1 i+i
X (exp ad^+1ei+1) ... (exp ad ?„е„) = ft11, где A = 2^Aj и tj — инва-
инвариантный автоморфизм. Таким образом, у является образом некото-
некоторого Элемента /г?ф при инвариантном автоморфизме. Отсюда сле-
следует, что элемент h = уТ1 регулярен. Теперь уже нетрудно дока-
доказать теорему о сопряженности подалгебр Картана.
Теорема 3. Если §j и §2 — подалгебры Картана конечно-
конечномерной алгебры Ли над алгебраически замкнутым полем
характеристики 0, то существует такой инвариантный авто-
автоморфизм 7], ЧТО §? = §2-
Доказательство. Существует ненулевая полиномиальная
функция gt, обладающая тем свойством, что всякий элемент у, удо-
удовлетворяющий условию gi(y)-?0, представим в виде у = /гД где
ht — регулярный элемент в фг и т^—инвариантный автоморфизм.
Поскольку ^,#2 Ф 0, мы можем выбрать у таким образом, что
?i (У) Ф 0 и g2 (у) Ф 0. Тогда у = fCt = А?2, где hi — регулярный
элемент в |>г, a t\t — инвариантный автоморфизм. Поэтому
А2 = А?. где Tj==irji'i»j2~1. Так как элемент hx регулярен и содер-
содержится в фь то ф2 = Ф?-
Замечание. Из этой теоремы следует, что каждая подалгебра
Картана содержит регулярные элементы и что все подалгебры Кар-
Картана имеют одну и ту же размерность /, совпадающую с числом /',
указанным выше. Пользуясь введенными ранее обозначениями, можно
§ 3. Неизоморфность расщепляемых простых алгебр Ли 297
также утверждать, что регулярные элементы алгебры 8, принадле-
принадлежащие ф, являются как раз теми элементами А0, для которых
°Р°ОО
§ 3. Неизоморфность расщепляемых простых алгебр Ли
Мы применим теорему о сопряженности подалгебр Картана для
разрешения вопроса, который оставался до сих пор открытым,
а именно вопроса о том, все ли расщепляемые простые алгебры Ли,
перечисленные в § 4.5—4.6, попарно неизоморфны. Напомним, что
к ним относились Av Z>1, ?,, />2, Сг, Z>3, Dv Z>4, G2, F4,
Е6, Е7 и Вь. Размерности этих алгебр приведены в следующей таб-
таблице:
Тип Размерность
А
Bi
%
°2
F4
Eg
Е7
Ео
1A+2)
К21+У)
1B1—1)
14
52
78
133
248
Размерности классических алгебр и алгебр G2, F4 и Е6 были
найдены в § 4,6. Существование алгебр Е7 и Е8 доказано в § 7.5.
Размерности этих алгебр Ли могут быть получены путем перечисле-
перечисления положительных корней, исходя непосредственно из матриц Кар-
Картана. Мы не будем останавливаться на этом, предоставив проверку
читателю.
Для доказательства неизоморфности любых двух приведенных
выше алгебр Ли достаточно предположить, что основное поле ал-
алгебраически замкнуто. Это ясно, поскольку из изоморфизма Й! = й2
следует, что ^1Р = Я2р Для любого расширения Р основного поля.
Мы считаем поэтому поле Ф алгебраически замкнутым. Пусть Xt —
одна из наших алгебр Ли (например, At, E6), где индекс I указывает
на размерность подалгебры Картана. Из теоремы о сопряженности
следует, что это число является инвариантом алгебры. Поэтому для
изоморфизма алгебры Xt и Кг- необходимы следующие условия:
1 = 1' и dimArj = dimKj-.
Взгляд на таблицу размерностей убеждает нас, что единственно воз-
возможными являются изоморфизмы между В1 и Сг, I ^> 3, между В6 и Е6
298 Гл. IX. Автоморфизмы
и между С6 и Б6. Но последние две возможности были исключены
в одном из упражнений (упражнение 7.6). Остается только показать,
что Bt $CV 1^>Ъ.
Поскольку С1 имеет неприводимый модуль размерности 21, доста-
достаточно показать, что если Ш — неприводимый модуль над Bt, такой,
что ШВЬ Ф О, то dim Ш^- 2/ —{— 1. Можно было бы установить это
так же, как и в аналогичном рассуждении относительно G2 (§ 7.6),
используя инвариантность множества весов относительно группы Вейля.
Однако мы можем получить сейчас утверждение гораздо проще, ис-
используя формулу Вейля для размерности. Заметим сначала, что, как
показывает формула (8.41), неприводимый модуль Т1 наименьшей
размерности, удовлетворяющий условию ЗМВг ф 0, является базисным
(см. также упражнение 7.13). Размерности таких модулей равны
/2/+! \, k = \, 2 I— 1, и 21 [ср. (8.45) и упражнение 8.12].
Поскольку I ;> 3, эти числа больше 21. Это доказывает наше утвер-
утверждение и завершает доказательство неизоморфности алгебр В1 и Ct
для I > 3.
§ 4. Автоморфизмы полупростых алгебр Ли
над алгебраически замкнутым полем
Пусть й — конечномерная полупростая алгебра Ли над алгебраи-
алгебраически замкнутым полем характеристики 0, <§> — подалгебра Картана,
тс= [а1 аг}—простая система корней относительно ?>, a ev ft, ht,
1 = 1, 2 /, — система канонических образующих алгебры 8,
определенная системой тс. Таким образом, hl образуют базис подал-
подалгебры ф, ег?й„, /j^2_af, и имеют место следующие соотношения:
[А,*,! = О,
где (Ац) — матрица Картана, соответствующая системе и.
Пусть т — некоторый автоморфизм. Тогда фт — вторая подалгебра
Картана. Поэтому существует инвариантный автоморфизм о, такой,
что $° = ty. Автоморфизм х =хо переводит § в себя. Рассмотрим
теперь автоморфизм х (— х'), который сохраняет подалгебру Картана.
Если е«^8а, то [еЛИ\ == a (ft) еа. Поэтому \elhz\ == а (Л) el. Отсюда сле-
следует, что 2а = Йр, где |3 — корень. Этим способом мы получаем ото-
отображение а —>- C множества корней в себя. Так как el ? йэ, то [elhz] =
= ^{fii)elL. Следовательно, имеет место равенство
§ 4 Автоморфизмы алгебр Ли над алгебраически замкнутым полем 299
Пусть 1* обозначает автоморфизм Пространства ф\ сопряженный
к ограничению автоморфизма t на ф. По определению если ??•§>*,
то Г* (Л) = ? (йт). Тогда из равенства A9) следует, что (Г =а или
р^га''1*'. Таким образом, мы получаем следующее
Предложение 1. Пусть х— автоморфизм алгебра 8, со-
сохраняющий подалгебру Картана'. §? = •§. Тогда для любого
корня а алгебры 2 относительно ф
К = 2.(^-1. B0)
где х*—автоморфизм пространства ф*, сопряженный к огра-
ограничению автоморфизма х «а ф.
Заметим, далее, что если it=={ar ..., аЛ и C?=а(тТ\ то
ir'={p,, ..., рг} — простая система корней. В самом деле, каждый
корень имеет вид ± 2 &,ai> гДе kt — неотрицательные целые числа.
Применяя преобразование (х*)~ , мы получим, что каждый корень
может быть записан также в виде ±^]&$г. Это гарантирует, что
¦к' — простая система. Докажем далее
Предложение 2. Пусть тс и к' — простые системы кор-
корней. Тогда существует инвариантный автоморфизм о, такой,
что ?>' = ?> и тс('п =я'.
Доказательство. Пусть тс= {оц, а2, ..., аг}, тс'= {р,, .. ., рг}.
Тогда как мы знаем (теоремы 8.1, 8.2), тс' = тс5„ Sa. ... 5a. при
М '2 'г
подходящем выборе симметрии Вейля 5„. Поэтому очевидно, что
достаточно доказать наше утверждение для тс' = tcS,, . С этой целью
введем инвариантные автоморфизмы expacU/, и expad$ef, где ??Ф.
В наших вычислениях будут использованы формулы C6) из § 3.8
для неприводимых представлений трехмерных расщепляемых простых
алгебр Ли. Заметим, что матрицы ограничений преобразований ad fl
auet на 1&1 — Фе1-\-Фп1-{-Ф/1 в базисе {et, ht, [hj,]) имеют вид
/0 1 0\ /0 00\
ad/,-*! 0 0 1 ). ade,->( —2 0 0 ). B1)
\ 0 0 0 / \ 0 — 2 0 У
Поэтому преобразованиям exp ad \fit exp ad %et в Йг соответствуют
матрицы
/ 1 \ $2/2 \ /10 0
0 15 , Б,E)=»( -2$ 1 0 |. B2)
0 0 1 / ( V 2? —1\
300 Гл. IX. Автоморфизмы
Отсюда следует, что матрица инвариантного автоморфизма
o^ — expad^expadr'^expadS/;, B3)
ограниченного на 2,-, имеет вид
/0 0 Щ2 \
А^)В.\\~Х)А({\)~\ 0 _1 0 ]. B4)
\ 2Г2 0 0/
В частности, hi " = — Af. Пусть, далее, элемент Л?ф удовле-
удовлетворяет условию аДЛ) —0. Тогда [Лег] = 0 = [Л/г] и, следовательно,
й*'(?>1=й. Так как ф является прямой суммой Фhl и подпростран-
подпространства таких векторов Л, что аДЛ) —О, то очевидно включение
ф'»й?§. Кроме того, ограничение автоморфизма в4(?) на ф яв-
является симметрией, определенной элементом Лг:
А-*Л-[2(А. Лг)/(Л(, h,)]ht =
= А — [2 (А, Л«/)/(Л«.- Ав/) ] Ла. = Л — [2а,- (А)/в/ (Ав/) ] К..
Если р^ф*, то
p A —
Это показывает, что преобразование, являющееся обратным к
сопряженному ограничения автоморфизма вД?) на ф, есть симметрия
Вейля 5а в ф*. Поэтому инвариантный автоморфизм ^вг ($) удовле-
удовлетворяет условию iz('i®*) —izSz— тс', что и требовалось доказать.
Предложение 2 и рассуждения, предшествовавшие ему, пока-
показывают, что если т — некоторый автоморфизм, сохраняющий подал-
подалгебру Картана ф (фт = ф), то существует инвариантный автоморфизм о,
обладающий тем же свойством, и если t' — xa'1, то тс((т')*)~' ==те
для простой системы тс. Упростим снова наши обозначения и будем
писать х вместо х'. Тогда мы имеем подстановку г->/' множества
г —1, 2, ..., I, для которой а^*' =аг'. Кроме того, [e1h}] = 2e'l,
f//A|] = —2/J, [eJ/2] =-= Al. Так как е^Ц-. Л€2-.г. то e] = liier.
f} = 4ifr. Поэтому Aj = |AiV;A/'. Из соотношений [в/'А,->] = 2ег
= 2e] вытекает равенство (Ajv/[г,'А;'] = 2(А,-е/', так что v^ =
= |а^ и h) = hi'. Так как [е/А}] = Лу-,е], то [е/-Ау] = Аце^. Сле-
Следовательно, мы получаем систему равенств
Л,.у, = Л/у, *, У=1. 2 /. B5)
§ 4. Автоморфизмы алгебр Ли над алгебраически замкнутым полем 301
Подгруппу симметрической группы подстановок i->i' степени I,
удовлетворяющую условиям B5), мы назовем группой автоморфизмов
матрицы Картана (Aij). Вспомним определение схемы Дынкина,
ассоциированной с матрицей Картана. Ясно, что если а,, а2 аг
будут вершинами схемы, то каждый элемент 1->1' группы автомор-
автоморфизмов матрицы (Afj) определяет автоморфизм схемы Дынкина, т. е.
взаимно однозначное соответствие а/ —>• а/', такое, что (аг, а/) = (аг, аг),
и для любой пары индексов I, J число отрезков, соединяющих а1
с ау и ау с a.j', одно и то же (см. § 4.5).
Рассуждения, использованные нами для доказательства того, что
матрица Картана восстанавливается по схеме Дынкина, показывают
также, что верно и следующее утверждение. Если a*—xxj-— авто-
автоморфизм схемы Дынкина, то l—>i' — автоморфизм матрицы Картана.
Предположим теперь, что т — автоморфизм, удовлетворяющий
условиям 8а. = 8а, где i = l, 2, .... I. Тогда в предшествующем
рассуждении мы получаем тождественное отображение l—>i' = i.
Это показывает, что ej = |A/e,-, fl — v-71fi< h\ = hl. Поэтому х дей-
действует как тождественное отображение в §. Обратно, предложение 1
показывает, что если ограничение автоморфизма х на ф является
тождественным отображением, то йа==2а для каждого а, т. е.
*г = {*<«/> //=|АГ//- Для этих автоморфизмов имеет место сле-
следующее
Предложение 3. Если t — автоморфизм, такой, что
ff — п для каждого h из подалгебры Картана § алгебры Й,
то т—инвариантный автоморфизм.
Доказательство. Мы видели, что е/ = (д,,ег и fl~y,Jlfi.
Пусть оДЕ) — инвариантный автоморфизм, определенный равенством
B3), и пусть
"»iF) = o(E)ej(l). B6)
Известно также, что /#(c) — — hv А"«(Е) = А, если а,(й) —0. Отсюда
следует, что bf№=;h для всех Л. В базисе (e-v ht, [hj^) матрица
ограничения автоморфизма a>t(l) на йг является произведением мат-
матрицы из равенства B4) и матрицы, полученной из нее подстановкой
$ = 1. В результате мы получаем
diag{lj2, 1, Г2}. B7)
Следовательно,
e;/«W^ = ^ B8)
Мы хотим теперь вычислить еш.'^ для }Ф1. Из равенства Г/.еЛ-=О
и Iffii] = — Aiff j следует, что /;- порождает неприводимый модуль
302
Гл. IX. Автоморфизмы
над Йг. Имеется четыре возможности: —А^ = 0, 1, 2 или 3. Если
Ац = —2, то модуль эквивалентен Йг, и только что приведенное рас-
рассуждение показывает, что f№ = \-Aijf, откуда следует, что е™<ю =
==(— \)АИеу Если Аи — 0, то [/.g;] = 0 и поэтому ej^ — e^
А
)А
= (—%)АЧв]. Пусть теперь Аи =—1. Тогда матрицы эндоморфиз-
эндоморфизмов ad/;, ade; модуля, порожденного элементом /у, записываются
соответственно в виде
0 0
-1 о
B9)
имеет
Отсюда следует, что матрица ограничения автоморфизма
вид
0 \ \
-Г1 о)' <3°>
а матрица ограничения автоморфизма соДЕ) — diag {—?, —?"'}. Таким
образом, /™;(Е) = — \ff и emJ& = — ^ej=:(—k)Aijer Наконец,
пусть Ац — —3. Тогда матрицы эндоморфизмов ad/;, ad et имеют
в соответствии с формулой C6) из § 3.8 вид
0 1 0 0 \ / 0 0
0 0 1 0 | / —3 0
0 1 Г I 0—4
0 0/ \ О О
Отсюда следует, что матрицей ограничения автоморфизма
определенного равенством B3), будет
О 53/6
О
О
О
О
C1)
О
О
О
-6Г3
О
о
О
— -kl о
-1
О
о
C2)
Следовательно, матрица ограничения автоморфизма ш; («) на мо-
модуль, порожденный элементом /;-, имеет вид diag}—?3> —?, —5. —S~3}.
у р /; g}
Отсюда ft<у = -\zf. и «J*(i) = (— \yz ej = (—
зом, во всех случаях
(у = / или
Положим теперь
= »! (- ?х) «>2 (— У • • • ^ С
Таким обра-
C3)
- C4)
§ 4. Автоморфизмы алгебр Ли над алгебраически замкнутым полем 303
Тогда из C3) следует, что
е) == l?i/tyi . .. %Uer j = 1, 2 I. C5)
Напомним, что матрица (Л,;) невырождена и ее определитель есть,
очевидно, целое число d. Поэтому найдется целочисленная мат-
матрица (Btj), такая, что (Лгу)(/?^) = й1. При фиксированном J положим
lt = (y,y*fj*. k=sl I. Тогда
е)
) («. Ч) {$*)В*АЧ+ ¦ - +B»AU e = W)" e W C6)
^,., если
- Очевидно, что некоторое, надлежащим образом выбранное про-
произведение инвариантных автоморфизмов, определенных здесь для
у = 1, 2, ..../, совпадает с заданным автоморфизмом х на et, ft, ht.
Поскольку эти элементы являются образующими алгебры Й, т — ин-
инвариантный автоморфизм. Теперь нетрудно показать, что индекс инва-
инвариантной подгруппы Go группы G не превосходит порядка группы
автоморфизмов матрицы Картана. Более того, мы можем указать
такую подгруппу KcG, изоморфную группе автоморфизмов матрицы
Картана, что каждый элемент т?О сравним по модулю О0 с элемен-
элементом tP(zK. В самом деле, пусть Р:1->1' — автоморфизм матрицы
Картана. Тогда имеют место соотношения
[frhr\ = — Ап/Г.
Поэтому из теоремы об изоморфизме для расщепляемых полупростых
алгебр Ли (теорема 4.3) следует, что существует (единственный)
автоморфизм хр алгебры Й, для которого e^ = ev, flp=.fi,. Мно-
Множество таких автоморфизмов образует, очевидно, подгруппу KcG,
изоморфную группе автоморфизмов матрицы Картана. Пусть теперь
х — произвольный автоморфизм алгебры Й. Мы видели, что х сравним
по модулю Go с автоморфизмом tlt сохраняющим подалгебру Кар-
Картана: фт' = ф. Мы знаем также, что хг сравним по модулю О0 с не-
которым автоморфизмом т2, таким, что ф*2 = ф и ir-^ = ic для
простой системы корней л = {<*!, а2, ..., а,} относительно ?>. Итак,
8а'=ЙаГ. /=1, 2 /, и t->t' — автоморфизм Р матрицы Кар-
Картана. Пусть хр — соответствующий элемент подгруппы К. Тогда авто-
автоморфизм о = х2Хр* удовлетворяет условиям 8« =»й«, й1а, = 8-а,.
/=1, 2 /. Поэтому, согласно предложению 3, о является ин-
инвариантным автоморфизмом. Таким образом, автоморфизм х сравни^
по модулю Gp с автоморфизмом t». .
304 Гл. IX. Автоморфизмы
Можно показать, что К и О0 пересекаются лишь по единичной
подгруппе, так что G — полупрямое произведение подгрупп К и О0.
Это утверждение эквивалентно тому факту, что индекс подгруппы
Go в G равен порядку группы автоморфизмов матрицы Картана.
Доказательство этого утверждения намечено в упражнениях. Огра-
Ограничим теперь нашу задачу рассмотрением простой алгебры Ли 8.
Сформулированный результат для алгебр Ли Av Bv Cv Dv 1ф4,
G2 и F4 будет следовать из явного описания групп автоморфизмов
этих алгебр, которое будет дано в следующем параграфе. Результат
будет также очевиден для алгебр F7 и F%.
Изучим теперь группы автоморфизмов связных схем Дынкина. На-
Напомним, -что такие схемы соответствуют простым алгебрам Ли Й.
Их типы следующие: Л,, />1, Bt, />2, С,, />3, Dt, />4,
G2, F4, E6, Ev fg1)- Сам вид схем, приведенных в § 4.5, показы-
показывает, что группы автоморфизмов схем Av Bv Cv G2, Ft, E7 и ?8
единичны. Для Av />2:
1.1 1 ' 1,
о о» • • о—'—о
а', осг ari-, а»
существует, кроме единичного, еще автоморфизм
Схема
txi-г
обладает единственным нетождественным автоморфизмом <хг -> а(
1-^.1 — 2, а(_,->аг, aj-^-aj.j, если /^-5. В случае / = 4 схема
имеет автоморфизмы, которые переставляют a.v 6c3, a4. оставляя а2
на месте. Группа этих автоморфизмов изоморфна симметрической
группе третьей степени. Группа автоморфизмов схемы
1 1
1 1 1
?«: о о о о о
') Как и ранее, простые алгебры Ли и соответствующие им схемы обо-
обозначаются одними и теми же символами. — Прим. ред,
§ 5. Явное описание автоморфизмов простых алгебр Ли 305
состоит из тождественного отображения и отображений <х6
Из этих результатов следует
Теорема 4. Пусть 2— конечномерная простая алгебра
Ли над алгебраически замкнутым полем характеристики 0,
G— группа автоморфизмов алгебры Й, Go— подгруппа инва-
инвариантных автоморфизмов. Тогда G = G0, кроме тех случаев,
когда Й — алгебра одного из следующих типов: Av />1, Dt
или F6. В этих случаях, кроме g = D4> индекс [G:G0]<^2,
а для алгебры Д, индекс [О:О0]<^6.
3 амечание. Группа G — алгебраическая линейная группа (см.
Шевалле [2]). Легко видеть, что Go—является алгебраической ком-
компонентой единичного элемента группы G. Если Ф — поле комплекс-
комплексных чисел, то G — топологическая группа и О0 — ее связная компо-
компонента единичного элемента.
§ 5. Явное описание автоморфизмов простых алгебр Ли
Пусть Й — полупростая подалгебра алгебры Ли (HL, где @ — ал-
алгебра линейных преобразований конечномерного векторного про-
пространства над Ф. Пусть Z— элемент алгебры Й, которому соответ-
соответствует нильпотентный эндоморфизм ad Z. Так как алгебра линейных
преобразований ad«2 полупроста, то из теоремы 3.17 следует, что
существует элемент #?Й, такой, что [ZH] = Z. Отсюда следует
(лемма 4 § 2.5), что преобразование Z нильпотентно. По определе-
определению adZ = Z/? — ZL{ZR: X-^-XZ, ZL: X—>ZX). Поэтому
exp ad Z = exp (ZR — ZL) — exp ZR exp (—¦ ZL),
поскольку [ZRZL] — 0. Тогда
exp ad Z = (exp Z)R (exp (— Z) )L =
)-1. C7)
Если мы положим А — exp Z, то отображение
X-±A~lXA C8)
будет автоморфизмом exp ad Z алгебры Й.
Рассмотрим теперь простые алгебры Ли типов At, BL, Cv Dv
G2 и F4.
At. В этом случае g есть алгебра Ли линейных преобразований
с нулевым следом (/-)- 1)-мерного векторного пространства. Мы
можем отождествить 2 с алгеброй Ли матриц со следом 0 из Ф1+г
Если А — невырожденная матрица, то преобразование X—>А~1ХА
будет автоморфизмом алгебры Й. Поскольку единственными матри-
306 Гл. IX. Автоморфизмы
цами, перестановочными со всеми матрицами с нулевым следом,
являются скалярные матрицы, то очевидно, что автоморфизмы
X->А~1ХА, X~>В ХХВ совпадают тогда и только тогда, когда
В==рЛ, р?Ф. Кроме автоморфизмов X —> А 1ХА, имеются также
автоморфизмы X -> — X' алгебры 8 и, более общо, имеются авто-
автоморфизмы вида X —> — А X А. Предположим, что автоморфизм
X -*¦ — X' совпадает с одним из автоморфизмов X -> А ХХА. Тогда
для всех матриц X со следом 0 выполняется соотношение
А'1ХА — — X'. C9)
Отсюда вытекает, что
- х = а'х' «Г1 = - а'а-'ха (а')'\
так что матрица А (А') ' перестановочна со всеми X. Поэтому
Л' = рЛ, т. е. А' = ± А. Условие C9) может быть переписано
в виде равенства А }Х'А = — X. Множество матриц X, удовле-
удовлетворяющих этому условию, является либо симплектической алгеброй
Ли, либо ортогональной алгеброй Ли. В зависимости от этого раз-
размерность равна либо A-\- 1) (/ -f- 2)/2 (только для нечетных I}, либо
1A-\-1)/2 (для четных и нечетных /). Поскольку размерность про-
пространства (/-{- 1) X ('Ч~ 1)-матриц со следом 0 равна /2 —(— 2/. должно
быть либо /24-2/ = (/+1)(/-}-2)/2. либо Р+21 — 1Ц+1)/2.
Единственным решением является / = 1; в этом случае Р-\-21 =
==(/-f-1)(/-}-2)/2. Таким образом, мы видим, что автоморфизм вида
X -> — X' совпадает с автоморфизмом вида Х-+А 1ХА только
-1 / ° 1\
при 1=1. Если 1=1, то —X =А ХА для А = у J а
всех матриц X со следом 0.
Из результата, полученного в начале этого параграфа, следует,
что каждый инвариантный автоморфизм алгебры 8 имеет вид
X -> А ХА, где А — произведение экспоненциалов нильпотентных
матриц. Для" алгебры Ли Ах это будет полная группа автоморфиз-
автоморфизмов. Для At, />1, существует неинвариантный автоморфизм
ЛТ-> — X'. Поэтому [G :О0] = 2, и автоморфизмами являются ото-
отображения Х->А~1ХА и Х->— А^Х'А.
Теорема 5. Группа автоморфизмов алгебры Ли 2X2-
матриц со следом 0 состоит из отображений Х->А~ХХА.
Группа автоморфизмов алгебры Ли » X п-матриц со следом 0,
п > 2, состоит из отображений X-> А~ХХА и Х-±— А~1Х>А.
(Основное поле Ф алгебраически замкнутое характери-
характеристики 0.)
§ 5. Явное Описание автоморфизмов простых алгебр Ли 307
Bv Cv Dv Элементами этих алгебр являются матрицы X, удовле-
удовлетворяющие условию S~*XS = — X, где 5=1 для В, и D, и
5' = — 5 для С,. Порядок матриц из Ct и Dt равен 21, из Bt — 2/—j— 1.
Мы считаем />• 2 для Bv l^-Ъ для С{ и /> 4 для D,. Пусть О —
такая матрица, что
O'SO = pS, D0)
где р Ф 0 — элемент поля Ф. Тогда О не вырождена, и если
то матрица К = О '.АГО удовлетворяет условию
= - s~lo'sxs~' {o')~ls =—per1*
1 = — К.
Поэтому К ?8 и, следовательно, отображение X->Y = O~lXO
является автоморфизмом алгебры Й. Поскольку основное поле алге-
алгебраически замкнуто, мы можем заменить матрицу О на p-^O = Ov
получив в результате O\^XO\ = Y, O\SO\ — S. Если снова писать О
вместо Ov то будет видно, что для а-лгебр fi, и D, матрица О
является ортогональной матрицей (S —1), а для С1 — симплекти-
ческой матрицей. Легко проверить, что обертывающей ассоциативной
алгеброй алгебры Й является полная матричная алгебра. Проверку
этого утверждения мы оставляем читателю. Отсюда следует, что един-
единственными матрицами, перестановочными со всеми элементами ал-
алгебры 8, являются скалярные матрицы. Поэтому если О\ХХО\~
= О^ХО2 для всех ЛГ?8, то 02 = р0,, р?Ф.
Пусть Z — элемент алгебры 8, которому соответствует нильпо-
тентный эндоморфизм adZ. Тогда, как мы видели, сам Z нильпотен-
тен, и автоморфизм expadZ имеет вид X-> А~}ХА, где A = txpZ.
Из нильпотентности элемента Z следует, что expZ — унимодуляр-
ная матрица (упражнение 5.4). Кроме того,
5 (exp Z)S = S'1 (exp Z') 5 =
= exp5"az'5 = ехр(— Z) = (exp Zf\
Поэтому матрица ^4 = expZ ортогональная в случае В{ и Dt и сим-
плектическая в случае Cz. Каждый автоморфизм алгебр В, и Ct
является инвариантным и, значит, в этих случаях автоморфизмы ал-
алгебры 8 имеют вид Х->О~1ХО, где О — унимодулярная матрица,
удовлетворяющая условию О'5О = 5. Для В1 это означает, что
О — собственно ортогональная матрица (соответствующая вращению).
В случае Ct известно, что симплектическая матрица О (O'SO = S)
обязательно унимодулярна (см. Артин [1], стр. 139, или упражне-
упражнение 12 ниже). Следовательно, это условие может быть опущено. Рассмо-
308 Гл IX. Автоморфизмы
трим теперь D,. В этом случае существуют ортогональные матрицы О
с определителем — 1, и не может быть равенства О = рОР где
О, — собственно ортогональная матрица. Действительно, если O = pOj,
то р = ± 1, и в любом случае det О = det pOj = det O} = 1. Из этого
противоречия вытекает, что автоморфизм X —*¦ О~1ХО, где О — не-
несобственно ортогональная матрица, не инвариантен и, следовательно,
Gr>G0. Если I > 4, то индекс [G:G0]<;2; поэтому индекс в точ-
точности равен 2, и каждый автоморфизм алгебры D{ имеет вид
X—>О~ХХО, где О — ортогональная матрица. Мы получаем, таким
образом, следующее утверждение.
Теорема 6. Пусть Ф — алгебраически замкнутое поле
характеристики 0, и пусть 2— алгебра Ли кососимметри-
ческих матриц или .„симплектическая* алгебра Ли матриц X,
таких, что S X S~ — X, где S — — 5. Допустим, что по-
порядок матриц «^>5 в нечетно мерном кососимметрическом
случае-, »^6 в симплектическом случае и /г^>10 в четно мер-
мерном кососимметрическом случае. Тогда группа автоморфиз-
автоморфизмов алгебры 2 кососимметрических матриц (четномерных и
нечетно мерных) состоит из отображений X ->О~ЛХО, где
О — ортогональная матрица. В нечетномерном случае можно
добавить условие, что О собственно ортогональна. В сим-
симплектическом случае группа автоморфизмов состоит из мно-
множества отображений X —>О~гХО, где OSO = S.
Случай алгебры DA не покрывается этой теоремой. Можно по-
показать, что для нее группа GjO0 изоморфна симметрической группе
третьей степени, и группа О может быть описана. Об этом говорится
в некоторых упражнениях, приводимых ниже.
Рассмотрим теперь алгебру Ли Ч = О2. Используем представление
алгебры Й как алгебры дифференцирований алгебры Кэли 6 (§ 4.6).
Вообще, если 6 — (неассоциативная) алгебра, D — ее дифференциро-
дифференцирование и А — автоморфизм, то A *DA также будет дифференцирова-
дифференцированием. Отсюда следует, что отображение X—>А~ХХА, определенное
автоморфизмом алгебры 6, является автоморфизмом алгебры диффе-
дифференцирований Й —$)(б). Как мы знаем, в случае когда алгебра E
является алгеброй Кэли над алгебраически замкнутым полем харак-
характеристики 0, каждый автоморфизм алгебры Й инвариантен и, таким об-
образом, представляется в виде произведения отображений X—>• А~ХХА,
где /l = expZ, Z?8, Z —нильпотентное линейное преобразование
в E. Так как Z?8, то Z — дифференцирование алгебры 6. Отсюда
следует, что A = expZ — автоморфизм алгебры 6. Мы видим, таким
образом, что каждый автоморфизм алгебры 2 имеет вид X -> А }ХА,
где А — автоморфизм алгебры E.
Упражнения 309
Аналогичное рассуждение применимо и к алгебре Ли FA. В этом
случае мы представляем 2 как алгебру дифференцирований исключи-
исключительной йордановой алгебры ж| и приходим к выводу, что группа
автоморфизмов алгебры 2 состоит из отображений X —> А ХА, где
А — автоморфизм алгебры М%.
Теорема 7. Пусть 2 — алгебра Ли дифференцирований
алгебры Кэли G или йордановой алгебры М\ над алгебраически
замкнутая полем характеристики 0. Тогда автоморфизмы
алгебры Й имеют вид X -> А ХА, где А — автоморфизм ал-
алгебры 6 или М\.
Упражнения
Во всех упражнениях основное поле имеет характеристику 0, а все про-
пространства предполагаются конечномерными.
1. Показать, что любое невырожденное линейное преобразование А может
быть представлено в виде AaAs, где Аа — унипотентное преобразование,
т. е. Аа = 1 -f- N,' N нильпотентно, a As полупросто, причем As и Аи — много-
многочлены от А. Доказать, что если А = BsBa, где Ва и Bs перестановочны и
Ва унипотентно, a Bs полупросто, то Аа — Ва и AS = BS. (Указание: при-
применить теорему 3.16.)
2. Пусть т — автоморфизм (неассоциативной) алгебры ЭГ, и пусть
1 — ТцТ^—его представление, как в упражнении 1.
Доказать, что ts и ти — автоморфизмы. (Указание: в предположении, что
основное поле алгебраически замкнуто, применить упражнение 2.5. Расши-
Расширить основное поле для получения результата в общем случае.)
3. Пусть Й —- конечномерная простая алгебра Ли над алгебраически зам-
замкнутым полем, Go — группа ее инвариантных автоморфизмов. Доказать, что
алгебра Й неприводима относительно Go. '
4. Пусть Ё—расщепляемая алгебра Кэли над алгебраически замкнутым
полем, (Jo — подпространство ее элементов со следом 0: а-\-а — 0. Мы ви-
видели, что алгебра дифференцирований 3) (= G2) действует неприводимо в (Уо
(§ 7.6). Использовать этот результат для доказательства того, что (?0 непри-
неприводимо относительно группы автоморфизмов G алгебры 6.
5. Доказать то же самое, что и в упражнении 4, заменив алгебру 6
на Ml (см. § 4.6).
В упражнениях 6—9 доказывается, что если Й — полупростая алгебра
над алгебраически замкнутым полем, то факторгруппа G/Go изоморфна
группе автоморфизмов матрицы Картана или схемы Дынкина, определенной
подалгеброй Картана ф алгебры Й. Во всех этих упражнениях 8, ф, G, Ga
и пр. имеют смысл, указанный в тексте.
6. Если а?Й и Sa= {z | [za\ = 0}, TodimSa!>/, где / — размерность
подалгебры Картана алгебры Й. Набросок доказательства: ясно, что dim &a=
= dim Й— ранг (ad а). Показать, что если а — регулярный элемент, то &а = ф,
так что dim Qa — I. Если (u,, ..., ип) — базис алгебры 8 над Ф и ($, ?„) —
независимые переменные, то х = 2 %iut — регулярный элемент алгебры 2Р,
где Р = Ф (?/), так что ранг (ad х) = п — /. Если а = 2 aiui> T0 специализа-
специализация S; = ац показывает, что ранг (ad а) ¦< п — I. Поэтому dim Sa > /.
7. Пусть t — автоморфизм в Й и /. — множество неподвижных точек
автоморфизма -: Ьх — Ь. Доказать, что если т — инвариантный автоморфизм,
3lO Гл. tX. Автоморфизмы
то dim/->/. Набросок доказательства: по условию, T = expZ, expZ2...
... exp Zr, где Zi = ad zt — нильпотентный эндоморфизм, и нам нужно дока-
доказать, что rank (т — 1)< п—/. Пусть ^ 1Г—независимые переменные,
и пусть Р — поле формальных степенных рйдОв от ?/, т.е. поле частных алге-
алгебры Ф (^i, ..., ir) формальных степенных рядов От ^ с коэффициентами
в поле Ф. Тогда х (?) з= exp ?,Z, exp ?2Z2 ... exp \rZr — инвариантный автомор-
автоморфизм алгебры 8р. Матрица автоморфизма х (?) в базисе (а,, ..., ип) алгебры 8
имеет элементы, являющиеся многочленами от ?,-, и при специализации 5j = 1
мы получаем матрицу автоморфизма т в этом базисе. Поэтому если dim /t (у >Л
то из соображений о специализации следует, что dim /т !> / (полупростота
и ранг не изменяются при переходе от 8 к 8р). Применяя формулу для
экспоненциалов, можно показать, что т (S) = expiiZ, ... expirZr = exp Z,
Z = ad z, z € 8p (упражнение 5.12). Поэтому /т (?) з &г, так что dim Ix ,Е) > /,
согласно упражнению 6.
8. Пусть т — инвариантный автоморфизм, такой, что фт = ф и тс<т*> = к,
где я — простая система корней. Тогда /гт = Л для каждого элемента /г € ф.
Набросок доказательства: автоморфизм (х*) индуцирует на множестве
корней подстановку, которую мы можем записать в виде произведения циклов
(Р, Рг)(Ъ> ¦••> Ъ) ••¦ • Поскольку тс<т*> ==1с, (т*) оставляет инвариант-
инвариантным множество положительных корней. Поэтому р( в цикле ($t,...,$r)
либо все положительны, либо все отрицательны. Подпространство
8т + ... + Йр инвариантно относительно t. Если вр базисный элемент
подпространства 8р, то «J = ч{е^, ej = ч2е$ • • • •> е\ = \*р . так чт0 харак-
характеристический многочлен автоморфизма т, ограниченного на Йр + • • • + 8р ,
равен А. —v, ... чг. Если ч, ... vr Ф 1, то X—1 не является делителем
этого многочлена и, следовательно, /йр •+ ... + Йр ^П/т = 0. Если это
условие выполняется для каждого цикла, то /,. с ф, поскольку
ЙФ^Ш ©8ф(Йф @\)+ ¦¦¦¦ Так как dim/T>/,
согласно упражнению 7, то отсюда следует, что /.,¦=?> и Лт = А для
всех Л € §• Пусть теперь а — автоморфизм в 8, такой, что h" = h, h € ф,
к е\ = y-lei Ф 0, /J = [if V( (?(, /(, Лг — канонические образующие). Мы пока-
показали ранее, что а—инвариантный автоморфизм. Если а—положительный корень,
S a ft ft, ft. a -ft -ft, -ft.
А(»г И ee = Ii1V22 •• •(*('««> a й-а = ^1 1*2 •••!*/ 'й-а- Авт0"
морфизм t' = st удовлетворяет тем же условиям, что ит,«р = ч'ге^ , ..., е^ =
= vV , где a) v' ... v' = v ... v u.1*! ... (а*/, если 8 положительны и
Г Pi \ I \ I \ I I
Р, -f- ... + Р/- — 2 s'a' ^ ^' s* — неотрицательные целые числа, б) Nj ... ч\ =
1
= v ... ¦'.("¦Г*1 ... I*"*', если 8 все отрицательны и р, •+•... +РГ = —2 5'а'"
Так как s( =;fc 0 для - некоторого г, то мы можем выбрать элементы ^ так,
что vj ... v( Ф 1 для каждого цикла. Тогда рассуждение, применявшееся
ранее, показывает, что Лт' = Л, Л С ф. Поэтому Ат == Л, Л € ф.
9. Доказать, что факторгруппа G/Go изоморфна группе автоморфизмов
матрицы Картана.
Упражнения 311
10. Пусть 8 = Ф/'+1. /+1 = 2л, и пусть т — автоморфизм вида
— А~1Х'А алгебры 2. Показать, что dira/T>r и что существует
автоморфизм т, для которого dim /т == Л
11. Пусть 8 — полупростая алгебра над алгебраически замкнутым полем,
и пусть п (соответственно К)—подгруппа группы Go, состоящая из авто-
автоморфизмов Tj (соответственно ?), для которых §1с§ (соответственно ffi = h
для всех /г€ф). Показать, что К — инвариантная подгруппа в Я и H/K^^W
(концептуальное описание группы Вейля).
12. Используя доказательство теоремы 6, показать, что если О — сим-
плектическая матрица с элементами в поле характеристики 0, то det 0=1.
13. Пусть S — расщепляемая алгебра Кэли, и пусть a — al—а0, если
a = al-\-aa, ao?<Sa- Положим N(a) = aa=~aa и (а, Ь) — -g" W (а + *) ~~
— N (а)— N {Ь)\. Проверить, что (а, Ь)—невырожденная симметрическая
билинейная форма максимального индекса Витта. Доказать, что N (ас, Ь) =
— N (a, be) и что N (са, b) = N (a, cb). Вывести отсюда, что если с € ®0,
то cR (х -> хс), cL (х -> сх) н R = -=- (cL -f- сд) принадлежа-т ортогональной
алгебре Ли (D4) пространства S относительно формы (а, Ь). Показать, что
каждый элемент этой алгебры Ли имеет вид #<, + 2 [#<, #d 1 > гДе
с, ch dt 6 е0.
14. Используя альтернативный закон (равенство 4.79), доказать следую-
следующее тождество в (S:
с (ab) + {ab) с = {са) b + a (be),
или 2 (ab) R? = (acL) b-\-a (bcRy Использовать это для доказательства прин-
принципа локальной тройственности: для каждого линейного преобразования А
в 6, кососимметричного относительно (а, Ь), существует единственная
пара (В, С) кососимметричных линейных преобразований, таких, что
(ab)A = (aB)b + а(ЬС),
15. Показать, что отображения А -> В и А -> С, определенные в упражне-
упражнении 14, являются автоморфизмами ортогональной алгебры Ли. Доказать, что
каждый автоморфизм этой алгебры Ли имеет вид X ->О~1ХО, где О — орто-
ортогонально или же является произведеиием одного из автоморфизмов, опреде-
определенных в упражнении 14, на автоморфизм X ->О~*ХО.
16. Пусть 8, и йг — две подалгебры алгебры D4, изоморфные алгебре D3.
Доказать, что существует автоморфизм алгебры ?>4, отображающий 8i на йа.
17. Показать, что автоморфизм в А[, I > 1, такой, что «(->/(, /(->е/
(см. стр. 143), не инвариантен. Показать, что для Dt, />4, этот автомор-
автоморфизм инвариантен тогда и только тогда, когда / четно.
18. (Штейнберг). Пусть § — подалгебра Картана, и пусть Go (ф) — группа
автоморфизмов, порожденная элементами вида exp ad e, где е принадлежит
корневому подпространству алгебры Й относительно ?> (см. Шевалле [7]). Пусть
$i—Другая подалгебра Картана, Go (?>,) — соответствующая группа авто-
автоморфизмов. Показать, что существуют элементы ¦>) 6 Go (?>) и ^ С С?о (§,),
такие, что ^1) = |)Jl1. Тогда § = §J1'1'~- Отсюда следует, что Ge (§) =
= пг'^о №0 V). так чт0
Go (©) = ТЧ ($) ч = ^lG0 ($,) 1J, = О0 (?,).
19. Доказать, что О0 (§) = Go, где Gq — группа инвариантных авто-
автоморфизмов.
Глава X
ПРОСТЫЕ АЛГЕБРЫ ЛИ
НАД ПРОИЗВОЛЬНЫМ ПОЛЕМ
В этой главе рассматривается проблема классификации конечно-
конечномерных простых алгебр Ли над произвольным полем характеристики 0.
Известные методы, связанные с этой задачей, включают в себя ре-
редукцию к проблеме классификации простых алгебр Ли над алгебраи-
алгебраически замкнутым полем характеристики 0, которая рассматривалась
в гл. IV. Сначала определяют некоторое расширение Г основного
поля, называемое центроидом простой алгебры Ли и обладающее тем
свойством, что й может быть рассмотрена как алгебра над Г, причем
(й над ГJ = 2 ® гй является простой для каждого расширения 2
поля Г. Естественно заменить данное основное поле Ф полем Г.
Таким образом, проблема классификации сводится к частному случаю
классификации простых алгебр Ли й, для которых из— простая ал-
алгебра при любом расширении 2 основного поля. Если й — именно
такая алгебра Ли и 2 — алгебраическое замыкание основного поля,
то возможности для Йе известны (At, Bt, Ct и т. д.) и мы приходим
к задаче описания всех алгебр й, для которых й2 — одна из извест-
известных простых алгебр Ли над алгебраически замкнутым полем 2.
Эта задача допускает аналогичную формулировку, когда алгебраи-
алгебраически замкнутое поле 2 заменяется на конечное нормальное расши-
расширение Р поля Г и йр — одна из расщепляемых простых алгебр Ли
над Р. Это эквивалентно задаче описания конечных групп таких
автоморфизмов алгебры йр, рассматриваемой как алгебра над Ф,
которые являются полулинейными преобразованиями в 8Р над Р.
Подробно мы рассмотрим последнюю задачу для йр одного из
классических типов At — D,, за исключением D4. Наши результаты
не будут давать полкой классификации даже в этих случаях, хотя
в целом задача сводится к довольно стандартным вопросам об ассо-
ассоциативных алгебрах. Для некоторых основных полей (например, поля
вещественных чисел) известны полные решения возникающих здесь
задач, так что в этих случаях проблема классификации допускает
решение.
Проблема классификации для поля вещественных чисел очень
старая. Полное ее решение было дано Картаном в 1914 г. Упроще-
Упрощения в трактовке принадлежат Ларди и Гантмахеру. В случае произ-
произвольного основного поля характеристики 0 результаты для классиче-
§ 1. Алгебра умножений и центроид неассоциативной алгебры 313
ских типов принадлежат Ландхеру и автору, для О2—автору и для
F4 — Томберу. Не составляет трудности большинство результатов
перенести также на случай характеристики р Ф 0. • Это было пока-
показано автором. Ссылки на литературу можно найти в библиографии.
§ 1. Алгебра умножений и центроид неассоциативной алгебры
Пусть % — произвольная (неассоциативная) алгебра над полем Ф.
Для любого элемента а ? % правое (левое) умножение aR (aL) есть
линейное отображение х -&¦ ха (х -> ах). Мы определяем -алгебру
умножений Х(Ж) как обертывающую алгебру всех aR и aL, a?%.
Таким образом, Ж(Ж) будет алгеброй (ассоциативной и с 1), поро-
порожденной элементами aL и aR. Если % — алгебра Ли, то ?(ЭД) будет
обертывающей алгеброй алгебры Ли ad St. Назовем центроидом Г(ЭД)
алгебры Щ. централизатор алгебры %.(&) в алгебре О,(Ж) всех линей-
линейных преобразований в St. Таким образом, элементы из Г = Г(?Г)
являются линейными преобразованиями f, для которых [f, A] — Q
при всех А? %.(Щ. Очевидно, что if ?Г тогда и только тогда, когда
[faR] = 0 = [ffl/,] для всех а?ЭД, и эти условия можно записать
в виде
(в*) т = (ат) * = о (*i). а, &?Я. A)
Лемма 1. Если 9t2 = St, то центроид Г коммутативен.
Доказательство. Пусть -у, 8?Г, а, &?$. Тогда (a&)fS =
== ((а-у)Ь)Ъ — (flf)(ЬЬ) и (ab) 76 = (а(Ь^))8 = (аЬ)ф-[). Меняя местами
f и 8, получаем, что (ab) 8f = (ab) (bf) = (af) (ЬЬ). Следовательно,
(ab) (-(Ь — 8f) = 0. Так как W = % то любой элемент с алгебры St
имеет вид c = ^ialbl. Отсюда следует, что с(-\Ь — 8-у) = 0 для всех с,
т. е. Г коммутативен.
Как обычно, (неассоциативная) алгебра % называется простой,
если она не имеет (двусторонних) идеалов, отличных от 0 и 31, и
ЭД2 Ф 0. Так как W является идеалом, то отсюда следует, что ЭД2 = ЭД
для простой алгебры % . Следовательно, согласно лемме, центроид Г
простой алгебры коммутативен.
Идеалами алгебры являются в точности подпространства, которые
инвариантны относительно правых и левых умножений, или, другими
словами, подпространства, инвариантные относительно алгебры умно-
умножений ? = ?(ЭД). Отсюда следует, что алгебра % будет простой
тогда и только тогда, когда % — неприводимая алгебра линейных
преобразований. При х ?91 наименьшим ^-инвариантным подпростран-
подпространством, содержащим х, является jcJ. Следовательно, если х Ф 0 и St
проста, то х% = %. В обратном тоже легко убедиться: если W Ф 0
и х% = St для каждого х Ф 0, то St проста. Напомним хорошо
известную лемму Шура: если 2 — неприводимая алгебра линейных
314 Гл. X. Простые алгебры Ли над произвольным полем
преобразований, то централизатор алгебры Z будет алгеброй с деле-
делением (см., например, Джекобсон [2], т. И, стр. 271). Для частного
случая 2 = 2C1), где % — простая алгебра, из этой леммы и леммы 1
вытекает следующая
Теорема 1. Центроид Г простой (неассоциативной) алгебры
является полем.
Поскольку центроид Г является полем, можно рассматривать 31
как (левое) векторное пространство над Г, полагая уа = af, a ? ЭД,
7?Г. Тогда условие A) можно переписать в виде
отражающем тот факт, что 31 как векторное пространство над Г
является (неассоциативной) алгеброй над Г относительно произведе-
произведения ab, определенного в %. над Ф.
Алгебра 31 будет называться центральной, если ее центроид Г
совпадает с основным полем. Если 31 — простая алгебра с центрои-
центроидом Г, то 31 будет центральной простой алгеброй над Г, ибо имеет
место
Теорема 2. Пусть % — простая (неассоциативная) алгебра
над полем Ф и Г(эФ) — ее центроид. Рассмотрим 31 как ал-
алгебру над Г, определяя fa = af, а ?31, f?r. Тогда 31 проста
и центральна над Г, и алгебра умножений алгебры 31 над Г
является тем же самым множеством преобразований, что и
алгебра умножений алгебры 31 над Ф.
Доказательство. Поскольку Гэф, ясно, что Г-идеал ал-
алгебры % является Ф-идеалом, так что 31 будет Г-простой. Анало-
Аналогично этому центроид Г алгебры 31 над Г содержится в Г; следова-
следовательно, Г = Г и 31 центральна. Пусть % обозначает алгебру умно-
умножений алгебры ЗС над Г. Ясно тогда, что 2 равно Г?, т. е. мно-
множеству Г-линейных комбинаций элементов из ?. Далее, пусть ?0 —
подмножество таких элементов А из ?, что fA?Z для всех f из Г.
Ясно, что ?0 является Ф-подалгеброй алгебры X. Если а, х ? %, то
•у(ах) — а(^х) = (^а)х\ это означает, что -[aL — aLl — ("ia)L- ^°"
этому aL?%й и аналогично aR^%Q. Таким образом, ?0 содержит
все левые и правые умножения и, следовательно, ?0 = ?. Значит,
г=га=г. ^
Рассмотрим теперь вопрос о расширении основного поля (неассо-
(неассоциативной) простой алгебры. Основным результатом в этой связи
является следующая
Теорема 3. Если % — (неассоциативная) центральная про-
простая алгебра над Ф и Р—любое расширение поля Ф, то ЭДР
будет центральной простой алгеброй над Р. Пусть, далее,
§ 1. Алгебра умножений и центроид 'неассоциативной алгебры 315
21— произвольная {неассоциативная) алгебра над Ф и Д — под-
подполе {над Ф) центроида. Предположим, что ^-алгебра Г®д21
является простой. Тогда 21 проста над Ф и Д = Г.
Доказательство. Для доказательства первого утверждения
нам потребуется известная теорема о плотности неприводимых алгебр
линейных преобразований (см., например, Джекобсон [2], т. II,
стр. 272). Частный случай этого результата утверждает, что если
% — ненулевая неприводимая алгебра линейных преобразований век-
векторного пространства 21 над Ф и централизатор алгебры % в 6B1)
является множеством Ф скалярных умножений, то X будет плотной
алгеброй линейных преобразований в 21 над Ф. Это означает, что
если {х,, х2, ..., хп)— упорядоченное конечное множество линейно
независимых элементов пространства 21 и yv у2 Уп — произ-
произвольные п элементов из 21, то существует такое Т(^Х, что xiT = yi,
/—1, 2 п. Теорема о плотности применима к алгебре умно-
умножений X центральной простой (неассоциативной) алгебры.
Пусть теперь Р—некоторое расширение поля Ф. Рассмотрим
расширенную алгебру 21р, для которой мы выбираем базис {иа : а?/},
состоящий из элементов иЛ ? 21. Пусть х и у — любые элементы ал-
я л
гебры 21Р и х Ф 0. Тогда х= 21 ^-"ч- У= 2 ixi> гДе {х\> хч> •••> хп\ —
подходящее подмножество базиса {иа\ и элементы S и -ц лежат в Р.
Можно предположить также, что ^ Ф 0. Продолжение на 2СР любого
элемента из Ж принадлежит алгебре умножений ? алгебры 2СР над Р.
Следовательно, существуют такие Л(??, что xlAl = xi и XjAl = 0
при }ф\, 1—1, 2 п. В такем случае xAl==ilxl и
п
А = 21 ^A^^^ и удовлетворяет равенству хА = у. Таким обра-
образом, х% 3 у и, поскольку у произвольно, х% — %р. Это означает,
что алгебра 21Р проста, согласно критерию, отмеченному вьине. Пусть
С такое линейное преобразование в 2СР, что [СА] = 0 для всех А ? 2,
и пусть иа — один из базисных элементов. Применим предыдущие
рассуждения к'х = иа~х1, у = иаС. Пусть Аг?%. удовлетворяет
равенствам х1А1 = х1, xiA1 = 0, 1ф\. Тогда иЛС — x-fi — х1А1С —
= х1СА1 = уАх = tjjATj = щиа. Поскольку ^ зависит от иа, мы пишем
7ii = Pa" так чт0 U*C = P*U*> Pt?P- Отметим теперь, что если иа и
Мр — любые два базисных элемента, то существует такое В^?Х, что
иАр== Urp• Это ясно ввиду плотности алгебры X. В таком случае
Рз«3 = ufi — «АрС = иасв^ = PASa3 = PaMp- Следовательно, pa =
= рэ = р и С является скалярным умножением на элемент р. Это
показывает, что центроидом будет Р, так что алгебра ЭДР центральна
над Р. Тем самым завершено доказательство первого утверждения.
316 Гл. X Простые алгебры Ли над произвольным полем
Предположим теперь, 'что 31— такая (неассоциативная) алгебра
над Ф, что алгебра Г®д31 проста над Д, где Д — подполе центроида Г
алгебры 31, содержащее Ф. Мы можем рассматривать 31 как алгебру
над Д (Ьа — аЪ, а ?31, 8?Д). Покажем сначала, что алгебра 31 проста
над Д. Итак, пусть 23— Д-идеал в 31. Тогда подмножество элементов
вида 217» ® bi> I» G Г. bt ? 23, будет Д-идеалом в Г % Д3(. Свойства тен-
тензорных произведений над полями показывают, что если Ъ Ф 0, 23 Ф 3(,
то отмеченный идеал является собственным ненулевым Д-идеалом
в Г®дЗ(. Следовательно, 8 = 0 или 23 = 31. Кроме того, W Ф О,
поскольку (Г® ьЩ2 ФО. Значит, алгебра 31 проста над Д. Из дока-
доказательства теоремы 2 вытекает, что алгебра умножений % алгебры 31
над Ф есть то же самое множество, что и алгебра умножений ал-
алгебры % над Д. Поскольку мы имеем х%. = % для всех х Ф 0, ясно
теперь, что алгебра 31 проста также над Ф и Г является полем. Рас-
Рассмотрим опять 31 как алгебру над Д. Тогда без труда проверяется,
что отображение
21ъ®«г->21тл(=2«гЪ) B)
Т(?Г. a(?9L будет Д-гомоморфизмом алгебры Г®Д3( на 2{. Пред-
Предположим, что Г zd Д, и пусть f ? Г, (? \, так что 1, f будут Д-не-
зависимы. Тогда соотношение j (g) a1-\~ 1 ® а2 = 0, аг?31, означает,
что элементы 'аг = 0. Возьмем а1 = аФ0, п2 = — f#. Тогда
-\® ах-\-\ ®а2ф0, а образом этого элемента при отображении B)
будет -\а — -[а = §. Следовательно, при Г =? Д отображение B) имеет
ненулевое ядро, а также и ненулевой образ. Это противоречит
предположению о том, что алгебра Г®Д31 проста над Д. Следова-
Следовательно, Г = Д, и доказательство теоремы завершено.
Непосредственно проверяется, что плотная алгебра % линейных
преобразований конечномерного векторного пространства будет всей
алгеброй 6C1). В самом деле, если (jtj хп) — базис и А —
любое линейное преобразование, то Ж содержит такое 7', что
xjT = xiA. Следовательно, А — Т?%. Если 31 — (неассоциативная)
простая алгебра с центроидом Г, то, как мы видели, алгебра умно-
умножений X является плотной алгеброй линейных преобразований в 31,
рассматриваемой как векторное пространство над Г. Следовательно,
если алгебра 31 конечномерна над Ф, а значит, и над Г, то X будет
алгеброй всех линейных преобразований в 31 над Г. Поэтому имеет
место следующая
Теорема 4. Пусть 31—конечномерная простая алгебра
с центроидом Г и алгеброй умножений %. Тогда % является
множеством всех линейных преобразований алгебры 31, рас-
рассматриваемой как векторное пространство над Г.
§ 1. Алгебра умножений и центроид неассоциативной алгебры 317
Пусть размерность [9(: Ф) алгебры 91 над Ф равна га, [Г:Ф]=г
и [91: Г] —т. Тогда хорошо известно, что n — mr, И мы видим
теперь, что [% : V[ — /и2 и [2 : Ф] = fft2r.
Пусть опять алгебра 91 произвольна и а -> а9 — изоморфное
отображение алгебры 91 на другую (неассоциативную) алгебру 91.
Тогда 8 взаимно однозначно, линейно и (а&)е = аДО, откуда сле-
следует, что
aLQ = Ha% bRb = W%- C)
Таким образом,
Это означает, что отображение Л"->6 'А'б является изоморфным
отображением алгебры умножений ?(91) на Ж(Ш). Ясно также, что
Y —> т ^= 9 79 будет изоморфным отображением центроида Г (91)
на Г (Щ. Если a^?t, то (a^f— (am *-f)e = ae7e- В частности, если
алгебра 51 простая и рассматривается как векторное пространство
над Г, то
Далее, пусть D — дифференцирование алгебры ЭД. Тогда D линейно
и {ab)D — (aD)b-\-a(bD), откуда следует, что
[aL, D] = (aD)L, [bR, D] = (bD)R. E)
Это означает, что внутреннее дифференцирование Х->[Х, D]
алгебры 6(ЭД) отображает ?(ЭД) в себя. Следовательно, оно инду-
индуцирует дифференцирование f -> -f ^ \~[D\ центроида Г(Щ). По опре-
определению ~\d мы имеем равенство {а-() D — {aD) i-\-а^*, так что для
простой алгебры %
= ffl + T(«D)- F)
Только что отмеченные результаты удобно сформулировать в сле-
следующем виде.
Теорема 5. Пусть Ж и %¦—центральные простые (не-
(неассоциативные) алгебры над полем Г и Ф — подполе поля Г.
Тогда любое изоморфное отображение 9 алгебры 91 над Ф
на Щ. над Ф устанавливает полулинейное соответствие между 91
и 91 как алгебрами над Г. Любое дифференцирование D алгебры 9t
над Ф удовлетворяет соотношению {-\a)l =ida~\-'[(aD), -f ? Г,
а ?91, где d — дифференцирование Г как поля над Ф.
К этому мы добавим одно замечание. Предположим, что
(uv ..., ип) — базис в 91 над Г и мги;= 2 Ty*u*> T;;* 6 Г. —таб-
—таблица умножения в этом базисе. Взаимно однозначное полулинейное
318 Гл. X. Простые алгебры Ли над произвольным, полем.
отображение 8 алгебры % на % переводит элементы ut в базисные
элементы м^, /==1 га, алгебры %. над Г. Если 6 есть Ф-изо-
морфизм, то и\иь =21f^/fcMft> гДе 6 действует на ¦\ijk как автомор-
автоморфизм поля Г, ассоциированный с полулинейным отображением б
алгебры %. Во многих интересных случаях базис можно выбрать
так, что -Щи € Ф> т- е- ЭД = ЭДор- где ^о — (неассоциативная) алгебра
над Ф. Тогда uW. = 21 ~ii]ku\' откУДа следует, что ЭД и ЭД изо-
изоморфны как алгебры над Г.
§ 2. Изоморфизм алгебр, получающихся расширением
основного поля
Пусть 31 — (неассоциативная) алгебра над Ф, Р — конечное нор-
нормальное расширение поля Ф и G = {1, s и]—группа Галуа
поля Р над Ф. В этом параграфе мы получим обозрение классов,
с точностью до изоморфизма, таких алгебр 33, что 23Р^ЭДР. На-
Напомним, что если % — векторное пространство над Ф, то ЭД можно
отождествить с подмножеством алгебры %р. Это подмножество
является Ф-подпространством алгебры ЭДР, которое порождает Щ.р
как векторное пространство над Р и обладает тем свойством, что
любое Ф-независимое множество элементов из % будет также Р-не-
зависимым. Более того, эти свойства являются характеристическими.
Если (рр р2, ..., р„) — базис поля Р над Ф, то любой элемент
алгебры ЭДР имеет однозначное представление в виде 21 Pixf xt € ЭД-
Любой элемент s группы G определяет полулинейное преобразова-
преобразование Us в %Р по правилу
Легко проверяется, что Us не зависит от выбора базиса в Р над Ф,
что автоморфизмом поля Р, ассоциированным с Us, будет s (т. е.
UsUt = Ust, U, = \. (8)
Следовательно, элементы Us образуют группу, изоморфную О. Если
взять pi = l. то элементы алгебры % будут иметь вид ргх1г х^^Ж,
и из G) ясно, что эти элементы остаются на месте при каждом Us,
s?G. Нетрудно непосредственно показать, что % является в точ-
точности множеством элементов, неподвижных относительно всех Us.
Это следует также из такой основной леммы.
Лемма 2. Пусть ft — векторное пространство над конеч-
конечным нормальным расширением Р поля Ф. Предположим, что
каждому элементу s группы Галуа О поля Р над Ф поста-
§ 2. Изоморфизм алгебр над расширенным полем 319
влено в соответствие некоторое полулинейное преобразова-
преобразование Us в St, причем автоморфизмом, ассоциированным с Us, будет s
и U1 = l, UsUt = Ust. Пусть % = {х\х?%, xUs = x при всех
s?G). Тогда St является Ф-подпространством алгебры St,
таким, что St = St|>.
Доказательство. Непосредственно проверяется, что St яв-
является Ф-подпространством в St. Если х ? St и р ? Р, то 2 Р*
поскольку B р* (xUs)) Ut = 2 р* (*ОД) = 2 P**^ = 2
Пусть (pj, p2 pn) — базис поля Р над Ф. Тогда, как известно,
(п X и)-матрица, строками которой являются (р|, р*, ..., ps\, s?Q,
не вырождена. Отсюда следует, что х будет Р-линейной комбина-
комбинацией п элементов 21р*(*^)' которые принадлежат St. Таким обра-
зом, Р-пространство РЖ, натянутое на 3t, совпадает с St. Пусть,
далее, *,, лг2, .... д:г — Ф-независимые элементы из С Предполо-
г
жим, что существуют такие ?/?Я, не все равные нулю, что 21?/*у —0.
Можно взять тогда г минимальным для таких соотношений и пред-
предположить, что ?[ = 1. Очевидно, что г> 1, и можно предположить,
что ?2*?Ф- Тогда 0 = ('2lljXj\Us=-']PiiSjXj и s в О можно выбрать
так, что И =? Ь- Мы можем поэтому получить нетривиальное соот-
Т Т
ношение 0 = 2 ?/¦*/ — 21 t'jxj — 20* — ^*) ¦**• более короткое,
1 1 к ^2
Г
чем соотношение '2ibjXj = Q. Это противоречие показывает, что эле-
элементы Xj будут Я-независимы. Следовательно, 31 = 3(я.
Если x = ^ijXj, lj?P, Xj?% то xUs = '2jtSjXj. Таким обра-
образом, Us являются преобразованиями, построенными нами ранее для %р.
Мы возвращаемся к ситуации, которая была уже рассмотрена, когда
нам было дано 3t = Stp и Us определялись правилом G). Как мы
видели, St содержится в Ф-подпространстве 23 элементов, остающихся
неподвижными при всех Us. С другой стороны, $ = ЭДР = 23Р.
Пусть К} — базис в St над Ф и ft?23. Тогда ft =
{e*)- 23
xi(z{e*)- Так как элементы х{ и Ь лежат в 23, то это соотношение
означает их Ф-зависимость, и поскольку элементы xt Ф-независимы,
b = 2ia.lxl, <хг?Ф. Следовательно, ftgSt и 23 = 21, так что St есть
в точности множество элементов, остающихся неподвижными при
всех Us. Наши результаты означают, что имеет место
320 Гл X. Простые алгебры Ли над произвольным полем
Теорема 6. Пусть % — векторное пространство над
конечным нормальным расширением Р поля Ф, и пусть
{Us:s?Q}—такое {конечное) множество полулинейных пре-
преобразований в % над Р, что: A) U1==l, UsUt = Ust, B) авто-
автоморфизмом поля Р, ассоциированным с преобразованием Us,
будет s. Пусть также % — Ф'-пространство неподвижных
относительно всех Us элементов. Тогда ЭД = ЭДР, и соответ-
соответствие {Us}->'& между конечными множествами полулинейных
преобразований, удовлетворяющих условиям A) и B), и Ф-под-
пространствами %. в §t для которых 3t = 5lp, будет биек-
биективным 1).
Предположим теперь, что $ — (неассоциативная) алгебра над Ф.
Тогда легко проверяется, что преобразования Us, определенные
равенством G), являются автоморфизмами пространства ЭД = 91Р, рас-
рассматриваемого как алгебра над Ф. Обратно, если задана группа {Us\
полулинейных преобразований в ЭД и каждый элемент Us является
автоморфизмом в ЭД над Ф, то подпространство ЭД неподвижных
элементов будет алгеброй над Ф. Следовательно, соответствие, опре-
определенное в теореме 6, приводит к взаимно однозначному соответ-
соответствию между множеством групп {Us\ автоморфизмов в ЭД над Ф и
множеством Ф-подалгебр ЭД, таких, что ЭДр = йХ Пусть ЭД и 23 — две
Ф-подалгебры, причем ЭДР = 23Р, и предположим, что А — изоморф-
изоморфное отображение алгебры ЭД на 23. Пусть {Vs} — группа полулиней-
полулинейных преобразований, соответствующая 23, и [Us] — группа, соот-
соответствующая % Изоморфизм А имеет единственное продолжение
в автоморфизм А алгебры % над Р. Отображение A~1USA является
полулинейным преобразованием в ЭД с соответствующим ему авто-
автоморфизмом s поля Р. Кроме того, A~1UlA = 1 и (A~1UsA)(A~1UtA) —
= A~xUstA. Множеством элементов, неподвижных относительно всех
A~XUSA, будет пространство 23. Следовательно, A~1USA = VS, s?G.
Обратно, пусть {Us}, [Vs\—группы полулинейных преобразований,
как в теореме 6, таких, что Us, Vs являются автоморфизмами
(неассоциативной) алгебры С над Ф. Пусть также существует такой
Р- автоморфизм А алгебры ft, что
Vt = A-1UtA. s?Q. (9)
Тогда ША = 23 для соответствующих (неассоциативных) алгебр ЭД и 23.
Следовательно, 51 и 23 изоморфны как алгебры над Ф.
Поэтому имеет место следующая теорема.
') Отображение / множества А в множество В называется биективным,
если оно взаимно однозначно и / (А) = В. В дальнейшем взаимно однознач-
однозначное соответствие будет пониматься именно в этом смысле. — Прим. ред.
§ 3. Простые алгебры Ли типов А—D 321
Теорема 7. Пусть Щ. — (неассоциативная) алгебра над
конечным нормальным расширением Р поля Ф. Тогда соот-
соответствие, определенное в теореме 6 между множествами полу-
полулинейных преобразований {Us\ в 91, удовлетворяющих усло-
условиям A)м B), и Ф-подпространствами %., для которых ЭДР = ЭД
сохраняется и в том случае, если каждое преобразование Us
будет автоморфизмом Ф-алгебры, а каждое подпространство
Щ. — Ф-подалгеброй. Соответствующие Ф-подалгебры изоморфны
тогда и только тогда, когда существует такой автоморфизм А
алгебры $ над Р, что для соответствующих групп выпол-
выполняется равенство (9):
Если 33— такая (неассоциативная) алгебра над Ф, что 23Р = ЭДР.
то алгебру 23 можно отождествить с ее образом в ЭД = ЭДР. Таким
образом, мы убеждаемся в том, что теорема 7 дает обозрение клас-
классов, с точностью до изоморфизма, таких алгебр 23, что 23Р = ЭДР>
при помощи некоторых классов подобия групп автоморфизмов
алгебры ?{ над Ф. Это и есть результат, который мы хотели получить.
В дальнейшем мы будем иметь дело с конечномерными (неассо-
(неассоциативными) алгебрами над полем Ф характеристики 0, и нас будет
интересовать условие равенства 9ts = 232 для двух таких алгебр,
где 2—алгебраическое замыкание основного поля Ф. Пусть (ej em),
(fv •••• /m) — базисы алгебр 'й над Ф и 23 над Ф соответственно.
Тогда равенство ЭД2 = 23а означает, что /(=рг/;> Р*;?^>
I, /=1 т. Пусть S — подполе над Ф, порожденное элемен-
элементами рч. Поскольку каждый элемент рг/- алгебраичен над Ф и всего
их лишь конечное число, Е будет конечным расширением поля Ф.
Так как 2 алгебраично и имеет характеристику 0, то поле ?
содержится в некотором подполе Р поля 2, которое является конеч-
конечным нормальным расширением поля Ф. Поскольку ра^Р, ясно, что
т т
^iPfi^^Pe,. Выполняется и обратное включение, так как е,—
1 1 '
= 2Р/;/у (Р//)==(Рг/)~1* Ясн0 также, что элементы fl и ei образуют
линейно независимые множества над Р. Следовательно, 2 Pei = $р
и 2^/* —23р- так что равенство ЭД2 = 23а для алгебраического
замыкания 2 основного поля Ф означает, что ЭДР = 23Р, где Р — не-
некоторое конечное нормальное расширение поля Ф.
§ 3. Простые алгебры Ли типов А — D
Мы займемся теперь основной задачей этой главы: классификацией
конечномерных простых алгебр Ли над любым полем Ф характери-
характеристики 0. Если 2 — такая алгебра и Г — ее центроид, то Г будет
21 Н Джекобсон
322 Гл X. Простые алгебры Ли над произвольным полем
конечным расширением поля Ф, а 2— конечномерной центральной
простой алгеброй Ли над Г. Обратно, если 2 конечномерна, цен-
центральна и проста над каким-либо конечным расширением Г поля Ф,
то 2 конечномерна и проста над Ф. Если gj и 22 — две изоморфные
простые алгебры Ли над Ф, то соответствующие центроиды Г1 и Г2
изоморфны, так что обе алгебры можно рассматривать как централь-
центральные и простые над одним и тем же полем Г^Г!^Г2. Более того,
теорема 5 показывает, что существует некоторое полулинейное ото-
отображение 8 алгебры 2j над Г на 22 над Г, являющееся Ф-изомор-
физмом Sj на 22 как алгебр над Ф. Эти результаты сводят проблему
классификации простых алгебр Ли над Ф к следующим задачам:
A) классификация конечных расширений Г поля Ф; B) классификация
конечномерных центральных простых алгебр Ли над фиксированным
полем Г из задачи A); C) отыскание условий для существования
полулинейного соответствия 8 между двумя центральными простыми
алгебрами Ли над Г, являющегося их изоморфизмом как Ф-алгебр.
Для конкретности рассмотрим важный частный случай, когда
Ф — поле вещественных чисел. В этом случае любое алгебраическое
расширение Г поля Ф либо совпадает с Ф, либо изоморфно полю
комплексных чисел. Если Г — поле комплексных чисел, то оно алге-
алгебраически замкнуто, и нам известна классификация конечномерных
простых алгебр Ли над Г. Напомним, что все алгебры в этой клас-
классификации {Av Bt и т. д.) имеют вид 2ог. 20 — алгебра над Ф
(теорема 4.2). Из замечания после теоремы 5 следует, что алгебры
из этого списка (не являющиеся Г-изоморфными) не изоморфны над Ф.
Таким образом, для завершения классификации над полем веществен-
вещественных чисел остается описать центральные простые алгебры над этим
полем.
Предположим теперь, что 2 — конечномерная центральная простая
алгебра Ли над Г, произвольным полем характеристики 0. Если
Q — алгебраическое замыкание поля Г, то 2s — простая алгебра.
Обратно, если 2 имеет конечную размерность над Г и алгебра 2а
простая, что 2, очевидно, есть простая алгебра Ли, так что ее
центроид Г' является конечным расширением поля Г. Его можно
считать подполем поля Q. Тогда алгебра 2г простая, поскольку
простой является алгебра Bг'J==122. Следовательно, 2 — центральная
алгебра согласно теореме 3. Таким образом, для того чтобы алгебра
Ли 2 была центральной и простой над Г, необходимо и достаточно,
чтобы алгебра 2а была простой над Q.
Поскольку Q алгебраически замкнуто и характеристики 0, то нам
известно, каковы будут алгебры 2а- Они являются алгебрами Ли А{,
/>1, Bv />2, Cv l^-Ъ, Dv />4, G2, F4, E6, Ev E8 в списке
Киллинга — Картана. Если 2а — алгебра Ли из этого списка, то мы
будем говорить, что 2 типа X. Обычно индекс I будет опускаться,
и мы будем говорить просто об алгебрах 2 типа А, типа В и т. д.
§ 3. Простые алгебры Ли типов А—D 323
Для каждого типа X мы выбираем фиксированную алгебру 20 этого
типа. Например, можно взять в качестве 20 расщепляемую алгебру
Ли над Г типа X. Тогда наша задача сводится к классификации
простых алгебр Ли Й, для которых 8а = 2оа- Для фиксированной
алгебры 2 существует такое конечное нормальное расширение Р,
что 8р — йор, и мы видели, что для описания алгебр 8. которые
удовлетворяют этому условию при фиксированном Р, нужно рас-
рассматривать автоморфизмы алгебры йОр над Г. Мы изучим ситуацию
для алгебр й0 типов At, Bt, Cv Dt, I > 4. В этом параграфе при-
приводятся некоторые конструкции алгебр Ли типов от А до D. В сле-
следующем параграфе даются условия для изоморфизма этих алгебр Ли
и в § 5 доказывается, что каждая алгебра Ли типа Av Bv Cv Dt,
I > 4, может быть получена указанным здесь способом.
Исходным пунктом для наших рассмотрений является фундамен-
фундаментальная структурная теорема Веддербёрна о простых ассоциативных
алгебрах: любая конечномерная простая ассоциативная алгебра %
изоморфна алгебре (S всех линейных преобразований конечномерного
векторного пространства 5Ш над конечномерной алгеброй с делением
(телом) Д. Эквивалентной формулировкой является изоморфизм Й — Дп.
где Дя — алгебра всех га X га-матриц над конечномерной алгеброй
с делением Д (доказательства см. Джекобсон [3] или Ван-дер-Вар-
ден [1] т. II). Если основное поле Г алгебраически замкнуто, то
единственной конечномерной алгеброй с делением над Г будет само Г,
так что в этом случае ЭД — Гя для некоторого п. Если основное
поле есть поле вещественных чисел, то известно, что для Д имеется
точно три возможности: Д = Г, Д = Г (i) — поле комплексных чисел
или Д — алгебра кватернионов (теорема Фробениуса, см. Курош [1],
стр. 277, или Понтрягин [1], стр. 175). Центр Gt конечномерной
простой ассоциативной алгебры является полем, а центроид состоит
из отображений cL = cR, с ? (L Его можно отождествить с центром.
Если % — центральная алгебра ((?. = Г) и Q — алгебраическое замыка-
замыкание поля Г, то алгебра Sta конечномерна и проста над Q. Следова-
Следовательно, $а ^ё 2„ для некоторого п. Поскольку [Й : Г] = [ЭД2 : Q] =
= [Qn : Q] = га2, это показывает, что размерность любой конечно-
конечномерной центральной простой ассоциативной алгебры является
квадратом.
Пусть ЭД — конечномерная центральная простая ассоциативная
алгебра над Г. Рассмотрим производную алгебру S = ^tz. алгебры
Ли $?. Если Q — алгебраическое замыкание поля Г, то Й2 = (^/.J =
= (ЭДа)^ = 2лЬ поскольку $2 = 2„. С другой стороны, мы знаем,
что если n = l-\-\, Z^-l, то 2^, — алгебра Ли (Z-f- 1) X ('+ 1)-
матриц со следом 0, т. е. простая алгебра Ли Л, над Q. Так как
8s = 2Я/.. то отсюда следует, что 2 = Ul — центральная простая
алгебра Ли типа AL.
21*
324 Гл. X. Простые алгебры Ли над произвольным полем
Пусть теперь ЭД — конечномерная простая ассоциативная алгебра
с инволюцией J. По определению J есть антиавтоморфизм периода
два алгебры ЭД. Следовательно, —J будет автоморфизмом алгебры ?li.
Множество © (ЭД, J) У-кососимметричных элементов (aJ= — а) есть
подмножество неподвижных элементов относительно автоморфизма—J.
Следовательно, это множество будет подалгеброй алгебры $.L. Анти-
Антиавтоморфизм J индуцирует автоморфизм в центре E алгебры %, который
либо тождествен, либо периода два. В первом случае J—инволюция
первого рода, а во втором — второго рода.
Предположим сначала, что J второго рода. Более точно, мы
предположим, что E, = Р = Г(<7)— квадратичное расширение основ-
основного, поля Г и что qJ = — q. Пусть ф (%, J) — пространство ./-симме-
./-симметричных элементов (а-' = а). Любой элемент а ? ЭД имеет вид а = b -f- с.
и с = ^(а— aJ)?<2>. Если Ь?$, то qb?<B и
q?$ при с?<&. Следовательно, отображение x->qx является
взаимно однозначным отображением подалгебры S на ф, так что имеет
место равенство размерностей: [<S : Г] = [$>: Г]. Поскольку <Sn4? = 0
и Й = ®Н-ф, то $ = <S®& и [9(:Г] = 2[6:Г]. Таким образом,
[ЭД : Р] =-к [ЭД : Г] = [@ : Г]. Напомним также, что [ЭД : Р] есть неко-
некоторый квадрат п2, так что [<3:Г] = ге2. Пусть (а^ апг) — базис
подалгебры C над Г. Тогда каждый элемент алгебры ЭД имеет вид
2 <V*,--r- 2М?а*)=2р«в«- Р/ = аг + Р^. аг. Р/6Г- Отсюда сле-
следует, что элементы о,- образуют базис в ЭД (или ?ti) над Р. Это
означает, что <SP = Йд над Р. Пусть Q — алгебраическое замыкание
поля Г, которое можно считать расширением поля Р. Тогда
<3а = (врJ = (&L над PJ^Qni, поскольку (Й над Р)д^2„. Пусть
Й — производная алгебра <S'=<SBt, У)'. Тогда Sg^Q^z., так что
1Й2:2] = «2—1 и [®(ЭД, У)':Г]=л2_1. Если « = /-(- 1, />1, то
Йа — простая алгебра Ли At. Следовательно, й — центральная про-
простая алгебра типа Av
Мы привели две конструкции алгебр Ли типа А. Наши резуль-
результаты суммирует
Теорема 8. Пусть ЭД — конечномерная центральная про-
простая ассоциативная алгебра над Г, %фТ. Тогда производная
алгебра %l является центральной простой алгеброй Ли типа
Av /]>1. Пусть, далее, % — конечномерная простая ассоциа-
ассоциативная алгебра с центром Р, являющимся квадратичным рас-
расширением основного поля Г. Предположим, что Ж обладает
инволюцией J второго рода, а также что ЧИфР. Если <5(й, У) —
алгебра Ли кососимметричных элементов из %, то производ-
§ 3. Простые алгебры Ли типов А—D 325
ная алгебра <S (% S)' является центральной простой алгеброй Ли
типа Av /> 1.
Прежде чем переходить к рассмотрению алгебр Ли <3(ЭД, У), где
J—инволюция первого рода, мы сформулируем некоторые хорошо
известные результаты относительно инволюций в алгебрах линейных
преобразований (Джекобсон [3], гл. IV, § 12). Пусть Ti— конечно-
конечномерное векторное пространство над алгеброй с делением Д и (S— алге-
алгебра линейных преобразований в Tt над Д. Тогда известно, что
алгебра (§ имеет некоторую инволюцию А —> AJ лишь в том случае,
когда Д обладает антиавтоморфизмом d—>d периода один или два.
Если период равен единице, то d^d и из равенства d1d2 = d2d1
следует, что Д коммутативно. Обратно, если Д коммутативно, то
можно взять d = d. Если отображение d—>d задано, то можно опре-
определить невырожденную эрмитову или косоэрмитову форму (х, у) в Ti
над Д относительно d->d. Такая форма определяется условиями
(dx, y) = d(x, у), (х, dy) = (x, y)d
для х, xv х2, У. ух, У2€2Я
(x, y) = (y, x) или (л:, y) = — (у. х), A1)
в зависимости от того, эрмитова форма или косоэрмитова. Невыро-
Невырожденность означает, что из равенства (х, z) = 0 для всех х следует
z = 0. Если d s= d, то получаем симметрическую или кососимметри-
ческую билинейную форму. Если (йх, и2 ип) — базис в Ti над Д,
то равенство (л:, у) = 2 ^г7!/ Для * ==: 2 ^а/> У — 2 '"I;"/ определяет
невырожденную эрмитову форму, а (л:, у) = 2 ^Р7!/ будет невыро-
невырожденной косоэрмитовой формой при р = — рфО. При d s= d невы-
невырожденные кососимметрические билинейные формы в Ti существуют
лишь в том случае, когда Ti имеет четную размерность над Г. Пусть
(х, у) — любая невырожденная эрмитова или косоэрмитова форма,
соответствующая антиавтоморфизму d—>d в Д. При А?Ш пусть А1
обозначает сопряженное к А относительно (х, у) преобразование, т. е.
А1 — такое лиьейное преобразование в Ti, что (хА, у) — (х, yAJ)
для х, у ? Ti. тогда, как легко видеть, A->AJ является инволюцией
в S. Более того, имеется фундаментальная теорема о том, что каж-
каждая инволюция J в (S получается таким способом.
В частности, предположим, что Д = Г—алгебраически замкнутое
поле. Поскольку Д = Г, единственным антиавтоморфизмом Д как
алгебры над Г является тождественное отображение. Следовательно,
(дг, у) будет либо невырожденной симметрической билинейной формой,
22 н- Джекобсон
326 Гл X Простые алгебры Ли над произвольным полем
либо невырожденной кососимметрической билинейной формой. По-
Последнее может встретиться лишь в случае четной размерности. Алге-
Алгебра Ли ©((S, J), определенная этой формой, будет алгеброй Ли Bv
если форма симметрична и dim Ш = 21 -\- 1. Алгебра Ли ©((?,./)
совпадает с Cv если форма кососимметрична и сИт9Я = 2/, и с Dv
если форма симметрична и difti Ti = 21.
Пусть теперь Ж — конечномерная центральная простая ассоциа-
ассоциативная алгебра над Г, обладающая инволюцией J первого рода. Если
2 — алгебраическое замыкание поля Г, то ЭДа = 2„. Продолжение J
инволюции J до линейного преобразования алгебры ЭДа является инво-
инволюцией в St2 и E(ЭД2> 7) = <3 (St, J)Q. Поскольку ЭДа = 2„ и J—инво-
J—инволюция в 2„, предшествующий результат показывает, что © (St2, J)
совпадает с одной из алгебр Ли Bv Ct или Dt. Предположим теперь,
что /^>2, /^-3 или /^-4 в зависимости от того, будет ли©(ЭД2. J)
совпадать с Bv Ct или Dv Тогда алгебра (S($a. J) проста, и мы
видим, что © (&, J)— центральная простая алгебра над Ф одного из
типов Bv Cv или Dv Напомним, что п есть размерность рассматри-
рассматривавшегося ранее пространства Ш и п2 = [2„ : 2] == [9t: Г]. Для Bt
имеем я = 2/+1 и [©(Я, У):Г] = [6(^2, У): 2] = /B/-j- 1). Для
Сг п = 21 и [©:Г] = /B/Ч-1)идляДг п==21 и [© :Г] = /B/—1).
Мы можем сформулировать теперь следующую теорему.
Теорема 9. Пусть ЭД — конечномерная центральная про-
простая ассоциативная алгебра над Г размерности л2; предполо-
предположим, что ?t обладает инволюцией J первого рода. Пусть
<S (&, J)—алгебра Ли J-кососимметричных элементов алгебры %
Если « = 2/-f 1, то [©($, У):Г] = /B/Н- 1) и 6 — центральная
простая алгебра типа Bt при I ;> 2. Если п — 21, то [<& : Г] =
= Ц21-\- 1) или 1B1—1). В первом случае предположим, что
t ;> 3 Тогда © — центральная простая алгебра типа Ct. При
га = 2/ и [©:Г] = /B/—1) предположим, что /^-4. Тогда
© — центральная простая алгебра типа Dt.
§ 4. Условия изоморфностн
Пусть 8j и g2 — конечномерные центральные простые алгебры Ли
над полем Г характеристики 0. Предположим, что Ф — подполе
поля Г и что &1 и Й2 изоморфны как алгебры над Ф:Й1 = фЙ2. Тогда
мы знаем, что Ф-изоморфизм в алгебры gj на Й2 является полулиней-
полулинейным отображением алгебры %г над Г на 82 над Г. Обозначим соот-
соответствующий автоморфизм в Г также через в, так что (f а)в = f9ав
при f ?Г. a?iij. Пусть (flj, .... ат) — базис в 5^ над Г с таблицей
умножения [a^j] — 2 Tijka»- Тогда (a? a^,) — базис в Ч2 над Г
и [ягвя'] = 27</ййА- Пусть 2 — алгебраическое замыкание поля Г.
Тогда, как известно из теории Галуа, автоморфизм 9 поля Г может
§ 4 Условия изоморфности 327
быть продолжен до автоморфизма 0 поля 2. Элементы at образуют
базис алгебры 8i2 над 2, а элементы ai образуют базис в Йга над 2.
Отсюда следует, что отображение 2шгаг~> 2 ш?йг шг € ®< является
Фгизоморфизмом алгебры 8i2 на Йга. Таким образом, Йга^фЙга-
С другой стороны, 8ia простая алгебра над алгебраически замкнутым
полем 2. Следовательно, она имеет базис над 2, структурные кон-
константы которого принадлежат простому полю и, таким образом,
полю Ф. Это означает (см. замечание после теоремы 5), что 8i2 = 2822-
Мы доказали поэтому следующее утверждение.
Лемма 3. Пусть ^ и Й2'—конечномерные центральные про-
простые алгебры Ли над полем Г характеристики нуль. Пусть
Ф — некоторое подполе поля Г и 2 — алгебраическое замыка-
замыкание поля Г. Тогда из Й1 = фЙг следует Й12=фЙ22-
Этот результат означает, что в классе алгебр, описываемых тео-
теоремами 8 и 9, единственно возможными являются Ф-изоморфизмы
между алгебрами, определенными в теореме 8, и Ф-изоморфизмы
между алгебрами одного и того же тииа (Bv Cv Dj) из теоремы 9.
Будем называть алгебры Ли вида 31^ из теоремы 8 алгебрами Ли
типа А{, а алгебры вида <SBt, J)', J—второго рода, — алгебрами
Ли типа Ац. В последнем случае предполагается, что /> 1, если
тип алгебры есть Аг. Это равнозначно предположению [ЭД : Р] — п2 > 4.
Будем предполагать также с этих пор, что / > 4 для алгебр типа Dt.
Рассмотрим Теперь обертывающие ассоциативные алгебры алгебр Ли
из теорем 8 и 9.
Лемма 4. Пусть Ф, Г, 2 обозначают то же, что в лемме 3.
A). Пусть % — конечномерная центральная простая ассоци-
ассоциативная алгебра над Г размерности л2 > 1. Тогда оберты-
обертывающей ассоциативной алгеброй алгебры Й = 31? над Ф будет St.
B). Пусть 31 — конечномерная простая ассоциативная алгебра
с центром Р, который является квадратичным расширением
поля Г, и с инволюцией J второго рода. Предположим, что
[Ж : Р] = п2 > 4. Тогда обертывающей ассоциативной алгеброй
алгебры Ли ? = ©($, J)' над Ф будет 21. C). Пусть % —ко-
—конечномерная центральная простая алгебра над Г с инволю-
инволюцией J первого рода и [% : Г[ = п2 > 1. Тогда обертывающей
ассоциативной алгеброй алгебры Ли % = <®(Ж, J) над Ф будет %
Доказательство. Отметим сначала, что во всех случаях
обертывающая ассоциативная алгебра алгебры Ли й над Ф совпадает
с обертывающей ассоциативной алгеброй алгебры S над ее центро-
центроидом Г. Действительно, так как Й — векторное пространство над Г,
то fl ? 8 при 1 ? Г и / ? Й. Следовательно, обе отмеченные оберты-
обертывающие ассоциативные алгебры совпадают с множеством сумм всевоз-
всевозможных произведений /х/2 ... /*./<62. Это замечание показывает,
328 Гл. X. Простые алгебры Ли над произвольным, полем
что можно предположить основное поле Ф равным Г, что мы и сде-
сделаем. В случаях 1 и 3 мы вводим алгебру $2 = 2,,, я> 1, и рас-
рассматриваем алгебру Ли йа, которая является подалгеброй алгебры 2„д.
Мы знаем, что йа—алгебра Ли матриц Av Bv Ct или Dt, как это
определено в § 4.6. Во всех случаях прямое элементарное вычисле-
вычисление с базисами из § 4.6 показывает, что 2-подалгебра, порожден-
порожденная алгеброй Ли 8а. совпадает с 2„, т. е. (&>)* = 2„, где * обозначает
переход к обертывающей ассоциативной алгебре. Если 2* —оберты-
—обертывающая ассоциативная алгебра для й над Ф (в Ж), то ясно, что
2-подпространство в 2„, натянутое на й*, совпадает с B2)* = 2„. Сле-
Следовательно, й* содержит базис алгебры 2„ над 2. Поскольку эле-
элементы этого базиса содержатся в ЭД, отсюда вытекает, что они соста-
составляют базис алгебры %. Таким образом, мы имеем 2* = ЭД.
Только что использованные рассуждения нельзя непосредственно
применить к случаю 2 (к алгебрам Ли типа Аи), так как в этом
случае ЭД2 —2„02„. Мы продолжаем поэтому доказательство не-
несколько другим способом. Пусть Р = Ф(д), где, как и прежде,
qJ = — q. Тогда q?<?>(%,J) и % = <&($, /) + ?©($. /) = <3 (Я, ¦/)'.
Следовательно, достаточно показать, что й* 3 © (&, J). Так как
ф = Г и g = ©', то [©: Ф\ = п2 и [й:Ф]=ге2— 1. Поэтому до-
достаточно показать, что й* содержит некоторый элемент а?©, а(?©'.
Предположим, что это не так: Й'П©^©'- Пусть bi(i=\, 2, 3) —
кососимметричные элементы. Тогда очевидно, что {6162Z>3} ^=^i6263~r~
-\-Ьф2^\ будет кососимметричным элементом. Если 6г(;©', то
{b^b^} ?©' = ?* П©- Рассмотрим теперь алгебру (& над РJ = 2„.
Мы видели, что эта алгебра имеет базис, состоящий из элементов
алгебры в, и что алгебра 2„? имеет базис из элементов алгебры
Ли 2 = ©'. Полилинейный характер элементов {616263} означает, что
{*1*2*з}?^я? для всех *€^яА' ^сли взять bi=:b, то это будет
означать, что b3?Q'nL при 6?2^. Таким образом, мы должны иметь
tr 63 = 0 для всех Ь, удовлетворяющих условию tr 6 == 0. Но это
невозможно при п > 3. Например, можно взять Ь — 2еп — е22 — еш,
так что tr6 == 0, tr?3 = 6=^=0. Полученное противоречие показывает,
что й* = © и 2* = Й.
Мы готовы теперь доказать основные теоремы об изоморфизме.
Во всех этих теоремах Ф, Г и 2 обозначают то же, что и в пред-
предшествующих рассуждениях.
Теорема 10. Пусть % а 23 — конечномерные центральные
простые ассоциативные алгебры над Г и б — некоторый изо-
изоморфизм алгебры Ли %'L над Ф на Ъ[ над Ф. Предположим,
что [% : Т] = п2 > 1 и [й : Г] > 1. Тогда прип = 2 изоморфизм б
можно продолжить одним и только одним способом до изо-
изоморфизма алгебры % над Ф на 2} над Ф, а если п > 2, то его
§ 4. Условия изоморфности 329
можно продолжить одним и только одним способом либо до
изоморфизма, либо до антиизоморфизма со знаком минус
алгебры $ над Ф на 23 над Ф.
Доказательство. Мы имеем $2 = 2„ и SB2S2И> Согласно
лемме 3, ЭДда —2^?2; следовательно, Q'nL=Q'mL и т = п. Таким
образом, можно предположить, что $2 = 2,, = -82, так что 2„ имеет
такой базис (а\ а„0> что элементы ai образуют базис алгебры %
над Г. Можно предположить также, что (ai #„2-1) является
базисом в ЭДд над Г. Далее, 8 есть полулинейное отображение ал-
алгебры %'L над Г на 23^ над Г. Ассоциированный с ним автоморфизм
поля Г мы также обозначаем через б. В таком случае (а\, ...
• • • > ая2-0 — базис алгебры Ли 23^ над Г. Если 8 продолжен до
я'-!
автоморфизма 9 поля Q, то 2 °\й» ""*¦ 2 w]a\ является автомор-
автоморфизмом 8' алгебры Ли Q'nL над Ф, который будет полулинейным
преобразованием с соответствующим автоморфизмом 8 поля 2.
Пусть {еф (i, j=\ п) — обычные матричные единицы в 2Я.
Тогда отображение 2 wijeij~> 2 iOiieij' ш«./6^> является автомор-
автоморфизмом 8" ассоциативной алгебры 2Я над Ф, которому в 2 соот-
соответствует автоморфизм 8 индуцирует автоморфизм 8" алгебры Ли
Q'nL и, так как с 8' и 8" ассоциирован один и тот же автоморфизм
поля 2, то у] = (8") 8' является автоморфизмом алгебры Ли Q'nL
над 2. По теореме 9.5 этот автоморфизм имеет вид X -> М~1ХМ при
ге = 2, а при п > 2 либо имеет такой же вид, либо вид X —>— М~1Х'М.
Так как отображение Х->М~1ХМ является автоморфизмом алгебры 2Я
и X—> — М~1Х'М является ее антиавтоморфизмом, то -г\ можно ре-
реализовать автоморфизмом алгебры 2Я над Q при п = 2 и либо авто-
автоморфизмом, либо антиавтоморфизмом со знаком минус алгебры 2Л
над 2 при п > 2. Тогда 8' = 8" можно продолжить до автомор-
автоморфизма С алгебры 2Я над Ф, если п = 2, и автоморфизма С или до
автоморфизма С со знаком минус алгебры 2П над Ф, если п > 2.
Поскольку 8' есть отображение 2 шга» —*¦ 2 шга»> ясно, что оно
совпадает с данным отображением 8 на $?. Так как обертывающая
ассоциативная алгебра над Ф алгебры Ли %' совпадает с 2L а соот-
соответствующая алгебра для Ъ'ь совпадает с 23, то отсюда следует, что С
отображает ЭД на 23, и, следовательно, 8 можно продолжить до изо-
изоморфизма или до антиизоморфизма со знаком минус алгебры % над Ф
на алгебру 23 над Ф. Поскольку %'L порождает ЭД над Ф, ясно, что
это продолжение единственно.
Этот результат показывает, что если %'L и 23^ изоморфны как
алгебры над Ф, то Ш и 23 либо изоморфны, либо антиизоморфны
330 Гл X. Простые алгебры Ли над произвольным полем.
как Ф-алгебры. Обратное тоже ясно, поскольку любой изоморфизм
алгебры % на 23 индуцирует изоморфизм алгебры Ли ЭД^наЗЗ^, и если
8 — антиизоморфизм алгебры Ж на 39, то —8 индуцирует изомор-
изоморфизм алгебры WL на ?&'L. Из нашего результата вытекает также опи-
описание группы автоморфизмов алгебры Ли %'L. Если п = 2 или же St
не имеет антиавтоморфизма, то группу автоморфизмов алгебры Ли WL
над Ф можно отождествить с группой автоморфизмов алгебры St
над Ф. Если п > 2 и % обладает некоторым антиавтоморфизмом J,
то при помощи расширения полей легко доказать, что автоморфизм
а—>—aJ в WL не может иметь вид а—>а®, где б — автоморфизм
алгебры ЭД. Отсюда следует, что группа автоморфизмов алгебры %
над Ф изоморфна некоторой подгруппе индекса два группы авто-
автоморфизмов алгебры Ли WL над Ф.
Если взять Ф = Г, то известный результат ассоциативной теории
утверждает, что каждый автоморфизм алгебры ЭД над Ф является
внутренним. Это также можно получить из вида автоморфизмов
алгебры Ли Q'nL, .используя расширения полей. Поэтому получаем,
что автоморфизмы алгебры Ли ЭД^. над Ф имеют вид x—>m~1xm
или х—>—m~ixJm, где J—некоторый фиксированный антиавто-
антиавтоморфизм в 31.
Теорема 11. Пусть %t (/=1, 2) — конечномерная простая
ассоциативная алгебра над Г с центром Pl = T(q1) явля-
являющимся квадратичным расширением поля Г, и с такой инво-
инволюцией Jt второго рода, что qJ^ =— q.. Предположим, что
Ш{ : Р^\ = п\ > 4, и пусть Ф — подполе поля Г. Тогда любой
Ф-изоморфизм 9 алгебры Ли <&($iv J{)' на ®Ct2> J$ может
быть продолжен одним и только одним способом до Ф-изо-
Ф-изоморфизма алгебры % на §12- Алгебра Ли 6 (St^)' не изоморфна
никакой алгебре Ли 23^. типа А{.
Доказательство. Можно так выбрать базис (аь ..., ani)
в Sti над Pi, что (fli я„2_1) будет базисом в © (%, J{)' над Г
и в $i? над Pj. Если 2 — алгебраическое замыкание поля Г (содер-
(содержащее Pi и Р2), то (Sfi над Р1J = 2„1, так что ©($ь ЛJ = 2я,г
и ©(йь J\)' = Q'niL- Аналогично имеем <&(%, ./2)а = 2я2?. Предполо-
Предположим, что существует Ф-изоморфизм алгебры Ли &(%, J{)' на
<5(f!t2, J$. Тогда, как мы знаем, 2я,д = а2я^. поэтому п\ = п2 = п,
и можно предпЪдожить, что Щ и Щ являются такими Ф-подалгеб-
рами алгебры 2Л, что любой Ргбазис в 31г будет базисом в 2Я.
Пусть 6 — Ф-изоморфизм алгебры Ли ^ = © (%, JJ' на Й2 = © (%, J2)'.
Тогда в полулинейно отображает 8j над Г на 82 над Г, и ему со-
ответ'ствУет автоморфизм 6 поля Г. Если (av ..., ап*-{) — базис
4. Условия изоморфности . 331
в gj над Г, то (а\ an2_i) будет базисом в ?2 над Г, и оба они
являются базисами алгебры Ли 2ni над 2. Если автоморфизм в
поля Г продолжен до автоморфизма 9 поля 2, то отображение
л»-1
2 «^tfj-^S ®\а\ будет автоморфизмом в 2^ над Ф, которому
в 2 соответствует 9. Доказательство теоремы 10 показывает, что
этот автоморфизм может быть продолжен до автоморфизма или до
антиавтоморфизма со знаком минус ассоциативной алгебры 2„ над Ф.
Так как обертывающая ассоциативная алгебра алгебры <S (%t, Jt)'
над Ф совпадает с St;, то отсюда следует, что изоморфизм 9 на 2\
над Ф можно продолжить до изоморфизма или антиизоморфизма со
знаком минус алгебры 5fj над Ф на ЭД2 над Ф. Если имеет место
вторая возможность, то пусть С обозначает соответствующий анти-
антиизоморфизм. Тогда J^. является изоморфизмом алгебры 9^ на 312
и при a ?©($!, 7j)' имеем соотношение а = — а^а^, поскольку
а^== — а для a?<5Dlv J{)'. Следовательно, Jj. будет изоморфиз-
изоморфизмом алгебры 9tj, совпадающим с 9 на ©(§!,, У^'. Таким образом,
в любом случае можно продолжить 9 до изоморфизма алгебры %г
на ЭД2. Это продолжение единственно, так как 21Х — обертывающая
ассоциативная алгебра алгебры Ли ©B^, J{)'. Тем самым доказано
первое утверждение теоремы.
Пусть теперь 81 = ©(Щ1, JJ'. Предположим, что имеется Ф-изо-
морфизм _9 алгебры Si на Й2 = ^г, где S — центральная простая
ассоциативная алгебра над Г. Только что использованное рассужде-
рассуждение для $tj и 9t2 показывает, что 9 может быть продолжен до изо-
изоморфизма 9 алгебры ^ на 23. Так как центроиды алгебр Ли
©($1. -А) и 2?? состоят из умножений (x—>ix) на элементы Tf?P
в этих алгебрах Ли, то 9 отображает Г в себя. Следовательно, />1 =
= T(ql) отображается в некоторое подполе алгебры 23, которое
строго содержит Г. С другой стороны, Рг — центр алгебры ЭДР так
что оно отображается в центр Г алгебры 58. Это противоречие дока-
доказывает, что 21 = ©(§A) ./j)' не может быть изоморфна алгебре З)^.
Рассмотрим, далее, алгебры Ли типов В, С и D, определенные
в теореме 9. Основным результатом об изоморфизме этих алгебр
является следующая
Теорема 12. Пусть ЭД; (/ = 1. 2) — конечномерная цен-
центральная простая ассоциативная алгебра над Г, имеющая
инволюцию Jx первого рода. Если [% :Г] = я1 то [©($;, Л):Г] =
= /гB/,-|-1) при щ = 21г-\-\ и [©($/, 4):Г] = /,B/,+ 1) или
liQh—1) при ni = 2ll. В указанных случаях ми предполагаем
соответственно, что lt ^-2, lt ]> 3, /; > 4. Если Ф — подполе
поля Г, то любой Ф-изоморфизм б алгебры Ли ©(ЭД^ J{) на
332 Гл. X. Простые алгебры Ли над произвольным полем
2 Л) может быть продолжен одним и только одним спо-
способом до Ф-изоморфизма алгебры %г на Щ.
Доказательство. Если 2 — алгебраическое замыкание поля Ф,
то %iu = 2Л/, и <В (%, Ji)a является алгеброй Ли В1г Сц или D[(
в зависимости от того, будет ли nt = 2и -\-1, nt = 2lt и [<S ($г, У,): Г] =
= /,B/,+ 1) или nl = 1ll и [<5(%, У,): Г] = /,B/,— 1). Отсюда сле-
следует, что если ©(З^, Л)=ф®(^2> Л)> то п1 = п2 = п, и мы можем
предположить, что $1а = 2„ = %а и © ($ь У02 = 6 (%, У2J есть
либо алгебра Ли кососимметрических матриц в 2„ (типа В или D),
либо алгебра Ли матриц, удовлетворяющих условию Q~lAQ — — А,
где Q — кососимметрическая матрица с элементами из простого поля
(тип С). Пусть (ах а„)(т — 1B1-\- 1) или 1B1— 1)) — базис
алгебры Ли <&(&v J{) над Г и, следовательно, алгебры Ли <Ss над Q.
Если б — Ф-изоморфизм алгебры Ли ©(Stj, Ух) на <5(ЭД2- Л)> то ^ —
полулинейное отображение с ассоциированным автоморфизмом 9
поля Г и (дц, .... а„) будет базисом в ©(ЭДг. Л) над Г и в <5а
над 2. Если 6 продолжен до автоморфизма 6 поля Q, то отобра-
отображение 2 ш;Я/->2 ш*а?> «0(^2, является автоморфизмом 6' алгебры
<5а над Ф, которому соответствует автоморфизм 6 поля 2. Если
(etj) — обычный матричный базис алгебры 2Л над 2, то 2 шг/г./-*¦
-> 2 mijeii является автоморфизмом б" алгебры 2Л над 2, которому
соответствует автоморфизм 6 поля 2. Кроме того, поскольку эле-
элементы матрицы Q принадлежат полю Ф, б" отображает <5а в себя
и, таким образом, индуцирует некоторый автоморфизм 6" в <3а над Ф.
Отсюда следует, что 6' (б") будет автоморфизмом алгебры Ли <5а
над Й. Во всех случаях этот автоморфизм имеет вид Х-+М~1ХМ
и поэтому может быть продолжен до внутреннего автоморфизма
алгебры 2„ над 2. Отсюда следует, что б' может быть продолжен
до некоторого автоморфизма С алгебры 2П над 2. Так как ограни-
ограничение автоморфизма С на <5 ($LV Ух) совпадает с данным б, а обер-
обертывающей ассоциативной алгеброй для <В(й(, Jt) служит 31^, то С
отображает Щх изоморфно на ЭД2 и совпадает с 6 на.<В(%, J{). Таким
образом, б может быть продолжен до Ф-изоморфизма алгебры ЭДХ
на ЭД2. Поскольку <5($iv Jx) порождает Щх, это продолжение един-
единственно.
§ 5. Теоремы полноты
Пусть Й — конечномерная центральная простая алгебра Ли типа А
над Г. Тогда существует конечное нормальное расширение Р поля Г,
для которого 2р = РЛ?. «!>2. Таким образом, можно предполагать,
§ 5. Теоремы полноты 333
что 2 есть такая Г-подалгебра алгебры Ли Pni, что Р-пространство,
натянутое на 2, совпадает с Pni и Г-независимые элементы алгебры
Ли 2 являются Р-независимыми. Мы видели также, что каждому
элементу s группы Галуа О поля Р над Г соответствует такой авто-
автоморфизм Us алгебры P'nL над Г, что (рх) U s = ps (xU s). Если
(av ..., an2_i) — базис в 2 над Г, а поэтому и в PnL над Р, то
П2-1
Us есть отображение 2 Р/а*->" 2 Р/аг Кроме того, 1^ = 1,
Upt = Ust и 2, которое является множеством элементов вида
2чЛ- Т/6*1, будет множеством элементов неподвижных при
всех Us, s?G. Как мы видели в последнем параграфе, Us имеет
такое продолжение Us на обертывающую ассоциативную алгебру Рп
алгебры Ли PnL, что Us будет автоморфизмом алгебры Рп над Г
при я = 2 и Us будет либо автоморфизмом, либо антиавтоморфиз-
антиавтоморфизмом со знаком минус алгебры Р„ над Г при п > 2. Каждый элемент
у ? Р„ есть сумма произведений Xi jc2 ... д:г, лг( ? Р^?, и если р ? Р
иУ5 — автоморфизм алгебры Р„, то (pJCj ... хг) Us = (pXjl^) (x2Us) • • •
... (*rl/,) = Ps (ж,1/,) ... (xrUs) = p» ((^ ... жг) f/s). Если t/, —
антиавтоморфизм со знаком минус, то (рх1... xr)Us = (—1)г(лгг^) ...
... v(x2Us) (9XlUs) = (-l)rp^ (xrUs) ... (XlUs) = p» ((*! ... лг) t/,).
Следовательно, в любом случае Us есть полулинейное отображение
с ассоциированным автоморфизмом s поля Р. Так как UsUt и L/s<
одинаково действуют на множестве образующих PnL алгебры Р„, то
UsUt = Usl. По тем же причинам Л/х == 1 в Р„. Если Us a Ut —
антиавтоморфизмы со знаком минус, то Ust-i = UsU^1 является авто-
автоморфизмом. Отсюда непосредственно следует, что подмножество Н
таких элементов s?G, что Us — автоморфизм алгебры Р„ над Г,
является подгруппой индекса один или два в G.
Случай I. Н = О. Подмножество элеменов из Р„ неподвижных
относительно всех Us, есть Г-подалгебра Щ. алгебры Рп, для которой
<&р = Рп (теорема 7). Следовательно, 31 — конечномерная централь-
центральная простая алгебра над Г. Очевидно, что 2 ? 91, и поэтому 2' =
= Й?$л. С другой стороны, [2:Г] = я2—1 и [щ2:Г] = л2—1.
Следовательно, 2 = 9li является алгеброй Ли типа Ах в соответствии
с определением на стр. 327.
Случай II. Н ФО. Тогда Н имеет индекс два в О. Мы знаем
также, что в этом случае п > 2. Подмножество тех элементов ?
из Р, для которых \s = 5, s?H, является квадратичным подполем
л'-1
Г(^) над Г. По виду элементов Us заключаем, что х= 2 Piat Уд0"
влетворяет равенству xUs = x, s^H, тогда и только тогда, когда
334 Гл X Простые алгебры Ли над произвольным полем
все элементы Р/?Г(#). Таким образом, 2г(?). множество Г (^-линей-
(^-линейных комбинаций элементов at, есть множество элементов алгебры Ли
Р'„1, которые остаются на месте при всех Us,s?H, Н—группа Галуа
поля Р над T(q). Из разобранного случая I следует, что 2г(?) = $л,
где 91— центральная простая алгебра над Г(^), являющаяся оберты-
обертывающей ассоциативной алгеброй алгебры Ли 2г (?)• Пусть теперь
л»-1
t?G, t(fcH. Так как Н имеет индекс два в G, то элемент 2 РА-
из 2г(?) принадлежит 2 тогда и только тогда, когда BРга/)^< =
= 2рЛ- Далее, Ut = — У, где У—антиавтоморфизм алгебры Рп
над Г. Так как B?iai)Ut = 2Piaf рДе Pi?T(q) и р — элемент, со-
сопряженный с р относительно нетождественного автоморфизма поля
Г(q) над Г, то У=—Ut отображает 2г(?) в себя. Следовательно,
У индуцирует антиавтоморфизм в обертывающей алгебре 31 алгебры
Ли 8г(?). Если p?T(q), y^%, то (py)J = pyJ. Поэтому У индуцирует
автоморфизм р->р в Г(<7), так что У второго рода. Так как aUt — a
для а?|2, то aJ = —a и а?<5(й. У). Таким образом, 2?<5($, У)
и g' = 2 ? <В (U, У)'. Сравнение размерностей над Г показывает, что
2 = ©(ЭД, У)'. Следовательно, 2 — простая алгебра Ли типа Ап.
Нами доказана поэтому
Теорема 13. Любая центральная простая алгебра Ли
типа А, изоморфна либо алгебре Ли %L, где % — конечномер-
конечномерная центральная простая ассоциативная алгебра, либо
алгебре <5 (%, У)', где %. — конечномерная простая ассоциа-
ассоциативная алгебра с инволюцией J второго рода.
В следующей теореме мы рассмотрим алгебры Ли типов
В, С и D.
Теорема 14. Пусть 2 — центральная простая алгебра Ли
типа Bv />2, Cv l^>3, или ?>,, 1^-5. Тогда 2 изоморфна
алгебре Ли <5(ЭД, У), где Ш. — конечномерная центральная про-
простая ассоциативная алгебра, а У—инволюция первого рода
в %
Доказательство. Существует такое конечное нормальное
расширение Р поля Г, что 2р является алгеброй Ли <3(РП, У) У-косо-
симметрических матриц из Р„, где У—инволюция Х->Х' (X' —
транспонированная матрица) или инволюция X-+Q~1XQ, где Q' =
= — Q и элементы матрицы Q лежат в простом поле. Кроме того,
по условию п ^-5, если n = 2l-{- \, n ^> 6, если п = 21 и инволю-
инволюцией является X—>Q~lXQ, и /t^lO в оставшемся случае. Для
каждого s из группы Галуа О поля Р над Г мы имеем автоморфизм
§ 6 Еще об условиях изоморфности 335
Us алгебры Ли ЧР над Г: 2р(а(-*2р^г гДе
зис в 2 над Г и в 2р над Р. 2 — подмножество элементов из Яр, кото-
которые неподвижны относительно всех Us. Условия на п служат гаран-
гарантией того, что Us может быть продолжен до автоморфизма Us
обертывающей ассоциативной алгебры Р„ алгебры Ли 8Р (теорема 12).
Продолжение Us полулинейно в Р„, и ему соответствует автомор-
автоморфизм s, причем в Рп выполняются равенства Ux = 1 и UsUt — Ust.
Следовательно, подмножество элементов из Рп, которые неподвижны
относительно всех Us, s?G, является подалгеброй 31 в Рп, для
которой 31р = Р„. Поэтому 31— конечномерная центральная простая
алгебра над Г. Если X ? ©р, то XJ — — X и XUS ? <ВР. Следова-
Следовательно, XJUS — — XUS — {XUS)J. Таким образом, в <ВР выпол-
выполняется равенство JUS = USJ. Поскольку Рп — обертывающая ассоциа-
ассоциативная алгебра для <Sp = ®(Pn, J), JUS~UJ также и в Рп. Это
означает, что J отображает 91 в себя и поэтому индуцирует в §1
над Г инволюцию, которая будет первого рода, поскольку Г — центр
алгебры St. Если а ?2, то aJ = — а, так что a?o(9t, У) н ? ?
?6B1, У). С другой стороны, 6A, У)Р?б(Р„, У) = 2Р. Следова-
Следовательно, 2 —©(Й, У). Это завершает доказательство.
§ 6. Еще об условиях изоморфности
Как мы видели в § 4, если Уг(/ = 1, 2) — инволюция (любого рода)
в конечномерной простой ассоциативной алгебре %.t над Ф, то из
условия <&{%, Jx)' ^ф<5 (%, J2)' следует, что % и % изоморфны.
Достаточно поэтому ограничиться одной алгеброй 31 = Щ = ЭД2 и
рассмотреть вопрос об изоморфности алгебр <5($, У)' и <5($, К)',
где J и К инволюции в ЭД. Мы видели, что любой изоморфизм б
алгебры Ли <5(ЭД, У)' на <5(ЭД, К)' может быть реализован автомор-
автоморфизмом алгебры % Если a?<SBt, У)', то аЛ = — аь = аьк. Таким
образом, в <3(ЭД, У)' выполняется равенство У6 = б/С. Поскольку
обертывающие Ф-алгебры алгебр Ли <SBt, У)' и 6C1, К)' совпадают
с 3t, то Ув = б/<" в 31, или /С = 6~1У8. Будем называть инволю-
инволюции У и К алгебры 31 коградиентными, если существует такой
автоморфизм 8 алгебры Ш, что /С = 6~гУ6. Как мы видели, когредиент-
ность является необходимым условием для изоморфизма алгебр
6C1, У)' и 6C(, К)'. Обратно, если У и К коградиентны и К =
= Q~1JQ, где б — автоморфизм, то б отображает <5(ЗС, У) на
5 (Я, К) и 6C1, У)' на ©C1, /С)'. Следовательно, б индуцирует
изоморфизм алгебры Ли 6 C1, У)' на 6C1, АС)'. Таким образом,
3 Ct, У)' GS ф © 0Й, /С)' тогда и только тогда, когда J и К когра-
коградиентны. Мы видим также, что группа автоморфизмов алгебры Ли
336 Гл. X. Простые алгебры Ли над произвольным полем
<В (ЭД, J)' может быть отождествлена с подгруппой группы автомор-
автоморфизмов б алгебры %, для которых QJ—JQ.
Пусть теперь % = @ — алгебра линейных преобразований конеч-
конечномерного векторного пространства WI над конечномерной алгеброй
с делением Д. Пусть а->а — инволюция в Д и (х, у)— эрмитова или
косоэрмитова форма, соответствующая этой инволюции. Тогда ото-
отображение Л->Л*, А?6, А* — сопряженное к А преобразование,
будет инволюцией в б. Напомним, что А* — однозначно определен-
определенное линейное преобразование, при котором (хА, у) = (х, у А*), и мы
имеем соотношение (у, х) = г(х, у), где е=1 или—1 в зависи-
зависимости от того, будет ли форма эрмитова или косоэрмитова. Пред-
Предположим, что а->а' — вторая инволюция в Д и (х, у\ — вторая
эрмитова или косоэрмитова форма, соответствующая этой инволюции,
так что (у, хI = г1(х, у)ь где е} = ± 1. Предположим, что инво-
инволюция в й, определенная этой формой, совпадает с инволюцией,
заданной формой (л:, у). Таким образом, если (л:, уА*) — (хА, у),
то (х, уА*I = (хА, у\. Пусть и и v — произвольные векторы из Т1.
Тогда х->{х, и)v есть линейное преобразование в Ш и, как легко
проверить, сопряженным к нему преобразованием относительно (х, у)
будет х-*г(х, v) и. Следовательно,
((*, и) v, y\=(x, e(y, v)u\,
(х, u)(v, у\ = г(х, и\(у, v)'.
Поскольку х, у, и, v произвольны, это показывает, что (л:, у\ —
= (х, у) р, р Ф 0 — элемент из Д. При а ? Д равенство (х, ау\ —
= {х, у\а.' дает (х, у)ар = (х, у)ра'; следовательно, a'ssp^ap.
Кроме того, (у, х)р — е1 ((*, у) р)' = е/ (х, у)' = г1?~^р (х, у) р =
= е1ер~1р(у, х)р. Следовательно, р == SjSp. Обратно, пусть р — лю-
любой элемент из Д, удовлетворяющий условию р = + р Ф 0. Тогда
прямая проверка показывает, что a->a' = p~1ap является инволюцией
в Д и (х, у\^(х, у)р будет эрмитовой или косоэрмитовой относи-
относительно этой инволюции формой. Если (х, у) косоэрмитова и р =
= — р, то (л:, у)р эрмитова. Следовательно, если Д содержит косо-
симметричный элемент, отличный от 0, то косоэрмитову форму
можно заменить на эрмитову, которая дает ту же самую инволюцию
А—*-А* в @. Если Д не содержит таких элементов, то р = р для
всех р ? Д, а это означает, что Д — поле. Следовательно, мы можем
ограничиться рассмотрением эрмитовых и кососимметрических форм
(Д—поле). Две такие формы (д:, у\ и (х, у) дают одинаковые ин-
инволюции в @ тогда и только тогда, когда (д:, у\ = (л:, у) р, р = р.
если а—>а—инволюция, соответствующая форме (л:, у).
§ 7. Центральные простые вещественные алгебры Ли 33?
Известно, что любой автоморфизм алгебры @ имеет вид Л-*-5-1Л5,
где 5 — полулинейное преобразование в Т1 над Д (Джекобсон [3],
стр. 72). Если б — автоморфизм в Д, ассоциированный с S, то без
труда проверяется, что форма (л:, у\ = (xS, yS) - эрмитова или ко-
сосимметрическая с инволюцией а->(ае)е .Кроме того, если
т0 (xAS, у5)« -1 = (xSS~l AS,
= {xS,
Таким образом, (хА, y^ —(x, y{S{S~lAS) S'1^ и инволюция в (§,
определенная формой (х, у\, совпадает с А-> S(S~l ASj S'1. По-
Поэтому если обозначить Л->Л* через J и Л-^S/iS через б, то
новая инволюция /С = 6У6~Х будет коградиентна У. Учитывая эту
связь, естественно расширить обычное понятие эквивалентности форм
следующим образом. Две эрмитовы формы (х, у) и (х, уI называются
5-эквивалентными, если существует взаимно однозначное полулиней-
полулинейное преобразование S с ассоциированным изоморфизмом 6, такое,
что (х, yI = (xS,ySf~\
Хорошо известно, что любые две невырожденные кососимметри-
ческие формы эквивалентны в обычном смысле. Следовательно, ин-
инволюции в @, определенные двумя такими формами, коградиентны.
Кроме того, они не коградиентны никакой инволюции, определенной
эрмитовой формой. Полученные результаты означают также, что не-
невырожденные эрмитовы формы (х, у) и (л:, у\ определяют когра-
коградиентные инволюции в d тогда и только тогда, когда (л:, y)i =
= (xS, yS) р, где S — полулинейное преобразование с автоморфиз-
автоморфизмом б и р — элемент, симметричный относительно а->а'=(а6)9 .
§ 7. Центральные простые вещественные алгебры Ли
Применим теперь полученные нами результаты и известные резуль-
результаты об ассоциативных алгебрах к классификации центральных про-
простых алгебр Ли типов А — D (за исключением D4) над полем Ф
вещественных чисел. По теореме Фробениуса конечномерными алге-
алгебрами с делением над Ф являются: Ф; поле комплексных чисел Р =
= Ф @, 42 = —1; алгебра кватернионов с делением Д с базисом 1,
I, j, k и таблицей умножения
fi = p = k2 = — \, ij = — jl = k,
A2)
338 Гл. X. Простые алгебры Ли над произвольным полем
Д имеет стандартную инволюцию a =a-(-^-f- ij'-{-bk-+a =a —
— $t — if — bk. Так как автоморфизмы алгебры Д все внутренние,
то каждая инволюция в Д либо совпадает со стандартной, либо имеет
вид a->q~1aq, где q — — q. Размерность пространства элементов,
кососимметричных относительно стандартной инволюции, равна трем,
а относительно инволюции a—>q~1aq — единице. Мы обозначаем
нетождественный автоморфизм поля Р над Ф через р —> р.
По теореме Веддербёрна конечномерные простые ассоциативные
алгебры над Ф исчерпываются полными матричными алгебрами Фп,
Рп и Дя. Их можно отождествить с алгебрами й(Ф,я), (feP, n) и
Й(Д, л) линейных преобразований в Ш соответственно над Ф, Р и Д.
Алгебры Ф„ = © (Ф, п) и Д„ S © (Д. п) — центральные и имеют лишь
внутренние автоморфизмы. Центр алгебры @(Р, я) = Р„ совпадает
с Р. Дополнительно к внутренним автоморфизмам @(Я, п) имеет
внешние автоморфизмы X->S~!XS, где S — полулинейное преобра-
преобразование с ассоциированным автоморфизмом р —*¦ р поля Р.
Все рассматриваемые алгебры обладают инволюциями, причем
б(Р, я) имеет инволюции второго рода. Инволюции алгебры (§(Ф, л)
имеют вид Х-+Х*, где X* преобразование, сопряженное к X от-
относительно невырожденной симметрической или косос,имметрической
билинейной формы в Ш над Ф. Инволадии, определенные кососимме-
трическими формами, не коградиентны никаким инволюциям, опреде-
определенным симметрическими формами. Любые две невырожденные
кососимметрические билинейные формы эквивалентны, так что они
дают единственный класс коградиентных инволюций. Если (х, у) и
(х, y)i не вырождены, то критерий последнего параграфа показывает,
что инволюции, определенные формами (л:, у) и (х, у),, коградиентны
тогда и только тогда, когда (л:, у) эквивалентна некоторой форме,
кратной (л:, у\. Так как (л:, у) эквивалентна любой форме, положи-
положительно кратной (х, у), то отсюда следует, что эквивалентность форм
(х, у) и ± (л:, у)х является необходимым и достаточным условием ко-
градиентности инволюций, определенных формами (х, у) и (л:, у)х.
Если (л:, у) — невырожденная симметрическая форма, то, как хорошо
известно, в WL существует такой базис (и^ и2 м„), что
(и,, и,)=1, 1<г<р,
(uj,a}) = — 1, /»<7<я. A3)
(в,, и;) = 0, 1ф/.
Число р является инвариантом в силу теоремы Сильвестра. Поэтому
мы получаем [/г/2] —j— 1 классов коградиентных инволюций, которые
соответствуют значениям р==0, 1 [л/2]. Простое вычисление
с использованием канонического базиса A3) показывает, что размер-
размерность над Ф пространства кососимметричных элементов, определен-
§ 7. Центральные простые вещественные алгебры Ли 339
ных формой (х, у), равна п(п —1)/2. Это означает, что алгебра Ли
<5(®, J) этих элементов имеет тип В или D в зависимости от того,
будет ли п нечетным или четным. Алгебра Ли, определенная косо-
симметрической билинейной формой (х, у), имеет тип С.
Рассмотрим теперь в алгебре (§(Р, п) инволюции второго рода.
Такая инволюция является сопряженным отображением относительно
невырожденной эрмитовой формы {х, у) в WI над Р. Базис
(«j, и2 ип) можно выбрать так, что выполняются соотношения
A3). Пусть (х, у) будет S-эквивалентна форме (х, у\ в том смысле,
что существует полулинейное преобразование S с ассоциированным
автоморфизмом р->р поля Р, такое, что (х, y) = (xS, yS\. Тогда
(e,S. UiS\ = 1, 1 < t < p, (UfS, UjS\ = — 1, p < J < n, (e,S. u}S\ =
= 0, t Ф j. В этом случае (л:, у) и (л:, у\ эквивалентны в обычном
смысле. Поскольку (л:, у) эквивалентна форме f (x, у), где f — веще-
вещественное положительное число, то (л:, у) и (х, у\ определяют когре-
диентные инволюции тогда и только тогда, когда (л:, у) эквивалентна
форме + (л:, у\. Этот результат и теорема Сильвестра для эрмитовых
форм опять означают, что число некогредиентных инволюций второго
рода в @(Р, п) равно [ft/2]-f-l.
Только что проведенное рассуждение дословно переносится на
эрмитовы формы в Т1 над Д, для которых инволюция в Д является
стандартной. Можно выбрать базис, удовлетворяющий соотноше-
соотношениям A3) (ср. Джекобсон [2], т. II, стр. 159). Число классов когре-
диентных инволюций, задаваемых каноническими эрмитовыми фор-
формами, равно [»/2]-f-l. Используя канонический базис, для которого
выполняются соотношения A3), легко вычислить, что размерность
алгебры <5(@(Д, n)J), определенной ассоциированной инволюцией У,
равна пBп-\-1). Так как Др^Я2« т0 ®(Д> t)p^P2n- Поскольку
<5(@(Д, п), J)p имеет над Р размерность пBп-\- 1\ <S — центральная
простая алгебра типа Сп.
Остается рассмотреть эрмитовы формы (х, у) в WI над Д, которым
соответствуют инволюции в Д, имеющие вид a-+q~laq, q = — q.
Заменяя (х, у) на (х, y)q-1, получаем косоэрмитову форму относи-
относительно стандартной инволюции. Мы предпочитаем рассматривать
последние.
Лемма 5. Если q1 и q%—ненулевые элементы из Д, косо-
симметричные относительно стандартной инволюции, то
в Д существует такой элемент а Ф 0, что q2 = aq^a.
Доказательство. Отметим сначала, что если Ь1 и Ь2 — эле-
элементы из Д, не принадлежащие Ф и имеющие равные следы и нормы,
то существует изоморфизм поля Фф^ на Ф(?>2)> отображающий bt
в Ь2. Этот изоморфизм можно продолжить до внутреннег > автомор-
автоморфизма алгебры Д (Джекобсон, Строение колец, стр. 238). Отсюда
340 Гл. X. Простые алгебры Ли над произвольным полем
следует, что ^ и Ь2 подобны, т. е. b2 = cblc~1 для некоторого с
из Д. В частности, если N(q2) = N (q^), то, поскольку следы T(ql) =
— 0=T(qo), существует такой элемент с, что q2 = cqlc~l=-
= N (с) cq^. Отметим также, что норма любого ненулевого эле-
элемента положительна, поэтому q1 обязательно подобен некоторому
подходящему положительному кратному элемента q2. Мы видим теперь,
что достаточно доказать лемму для q2 = ~[qv -[ > 0. Рассмотрим
тогда квадратичное поле Ф (q{) = Ф (q2). Очевидно, f = N (с) для
некоторого с в этом поле. Следовательно, q2 = N {c)ql = cqlc. что
и требовалось доказать.
Обычный метод получения диагональной матрицы для эрмитовой
или косоэрмитовой формы приводит теперь к следующему результату.
Лемма 6. Если (х, у)— невырожденная косоэрмитова
билинейная форма относительно стандартной инволюции
в Д, то в ffl существует такой базис (иР и2, .... и„), что
матрица ((ut, uj)) имеет вид
diagf?, q, ..., q), A4)
где q — любой фиксированный ненулевой кососимметричный
элемент из Д.
Этот результат означает, что в @(Д, п) существует в точности
один класс когредиентных инволюций, задаваемый косоэрмитовыми
формами в Т1 над Д. Используя A4), можно вычислить размерность
алгебры Ли, определенной этой инволюцией. Она равна пBп—1);
следовательно, это центральная простая алгебра Ли типа Dn.
Мы можем теперь указать представителей классов изоморфных
центральных простых алгебр Ли типов А — D над Ф.
Тип А{. Ф'пи л> 1; Д^л. я>1.
Тип Ап. Предполагая я > 1, положим
р ( "Р
1, —1 —1}. A5)
Пусть <В(Р, п, р) обозначает алгебру Ли матриц Х?Рп, для кото-
которых 5p1XS/, = — X. Тогда наш список состоит из алгебр Ли
®(Р, п, р) для р = 0, 1 1«/2].
Тип В. Пусть <5(Ф, «, р) — алгебра Ли матриц Х?Фп, цля
которых S^XSp — — X. Тогда наш список исчерпывается множе-
множеством алгебр Ли <5(Ф, п, р) с нечетным п, п ^-5.
Тип С. Пусть <2>(Д, п, р) — алгебра Ли матриц Х^Ь.п, удовлетво-
удовлетворяющих условию Sp1x'Sp = — X, и пусть <5(Ф, In, Q) — алгебра Ли
матриц в Ф2п, для которых Q~1XQ = — X, где Q — любая кососим-
метрическая матрица. Тогда в список входят <3(Д, п, р), ^Ъ
р - 0 [«/2] и 6 (Ф, 2«, Q), п > 3,
Упражнения 341
Тип D. Пусть <Э(Д, п, Q) — алгебра Ли матриц в Дя, удовлетво-
удовлетворяющих условию Q~1XQ = — X, где Q — некоторая косоэрмитова
матрица. В список входят ®(Д, ft, Q), п > 5, и ®(Ф, 2п, Sp), ft>5,
р = 0, 1 п.
Упражнения
1. Описать группы автоморфизмов простых вещественных алгебр Ли
типов А — D, за исключением D4.
2. Найти инвариантную невырожденную симметрическую билинейную
форму для каждой центральной простой вещественной алгебры Ли типа
А — D. Использовать это для перечисления компактных алгебр Ли в при-
приведенном выше списке (ср. § 4.7).
3. Показать, что алгебры Ли @ (Д, 4, Q) и @ (Ф, 8, Si) в обозначениях § 7
изоморфны. (Это показывает, что теорема 12 не верна для алгебр Ли типа Dt,
поскольку Д4 и Ф8 не изоморфны.)
4. Обобщенная алгебра кватернионов над произвольным полем Ф
определяется как алгебра с базисом 1, i, j, k, и таблицей умножения
B=а1, У2 = Р1, ?2 = — сф1=^О,
ij = — )i~ k, jk = — kj = — p/, */ = — ik = — a),
где 1 — единица. Показать, что некоторая алгебра Д будет обобщенной
алгеброй кватернионов над Ф тогда и только тогда, когда Д2 s й2 Для
алгебраического замыкания Q поля Ф.
5. Неассоциативиая алгебра S над произвольным полем Ф называется
алгеброй Кэли, если E имеет единицу 1, G содержит некоторую подалгебру
кватернионов Д с единицей 1, и каждый элемент алгебры E может быть
записан одним и только одним способом в виде а-\-Ьи, а, 6€Д, и—элемент
алгебры (? для которого
а (Ьи) = (Ьа) и, (Ьи) а = (Ьа) и, (аи) (Ьи) = ц&а,
где (х — некоторый ненулевой элемент поля Ф. Показать, что алгебра (S
альтернативна (ср. § 4.6) и что отображение х = а-\-Ьи->а — Ьи является
инволюцией в (S. Доказать, что хх = 7V (х) 1 = хх, где TV (x) б Ф и удовлетво-
удовлетворяет соотношению N (xy) = N (х) N (у). Пусть (х, у) = -^ [N(*+.y)—JV (дг) —
— N (У)]' Показать, что (х, у)—невырожденная симметрическая билинейная
форма и что две алгебры Кэли изоморфны тогда и только тогда, когда их
формы (х, у) эквивалентны. Доказать, что неассоциативная алгебра E
является алгеброй Кэли лишь в том случае, когда @а — расщепляемая
алгебра Кэли из § 4.6.
6. Используя теорему 9.7 и упражнение 5, доказать, что две алгебры
Кэли над полем характеристики 0 изоморфны лишь в том случае, когда
изоморфны их алгебры дифференцирований.
7. Доказать, что центральная простая алгебра Ли над полем характери-
характеристики 0 будет иметь тип G тогда и только тогда, когда она изоморфна
алгебре дифференцирований некоторой алгебры Кэли.
ЛИТЕРАТУРА»)
А до И. Д.
[1] Представление алгебр Ли матрицами, Успехи матем. наук, сер. 2. № б
B2), A947), 159—173.
А л б е р т, Франк (Albert A. A., Frank M. S.)
. [1] Simple Lie algebras of characteristic p, Univ. e Politecnico Torino, Rend.
Sem. Mat. Fis., 14 A954—1955), 117—139.
Артин (Artin E.)
[1] Geometric algebra, Interscience, 1967.
Блок (Block R.)
[1] New simple Lie algebras of prime characteristic, Trans. Am. Math. Soc,
89 A958), 421—449.
[2] On Lie algebras of classical type, Proc. Am. Math. Soc, 11 A960),
377—379.
[3*] Trace forms on Lie algebras, Canad. I. of Math., 14 A962),№4, 553—564.
Б op ел ь (В or el A.)
[1] Topology of Lie groups and characteristic classes, Bull. Am. Math. Soc,
61 A955), 3,97—432.
[2] Groupes lineaires algebriques, Ann. Math., 64 A956), 20—82.
Борель, Мостов (Borel A., Mostow G. D.)
[1] On semi-simple automorphisms of Lie algebras, Ann. Math., 61 A955),
3891—504.
Борель, С e p p (Borel A., S e r r e J. P.)
[1] Sur certains sous-groupes des groupes de Lie compacts, Comment math.
Helv.,27 A953), 128—1392).
Борель, Шевалле (Borel A., Chevalley C.)
[1] The Betti numbers of the exceptional groups, Mem. Am. Math. Soc, № 14
(J955), 1-9.
Бурбаки (Bourbaki N.)
[1*] Elements de mathematique, XXVI, Groupes et algebres de Lie, Ch. I, Al-
gebres de Lie, Paris, 1960.
В ей ль (Weyl H.)
[1] Классические группы, их инварианты и представления, ИЛ, М., 1949.
[2] Theorie der Darstellung kontinuierlicher halb-einfacher Gruppen durch
lineare Transformationen. I, II and III; I: Math. Z., 23 A925), 271—509.
II: Math. Z., 24 A926), 328—376. Ill: Math. Z., 24 A926), 377—395.
Витт (Witt E.)
[1] Treue Darstellung Liescher Ringe, /. reine und angew. Math., 177 A937),
152-160.
[2] Spiegelungsgruppen und Aufzahlung halbeinfacher Liescher Ringe, Ab-
handl. Math. Sem. Univ. Hamburg, 14 A941), 289—337.
') Звездочкой отмечена литература, добавленная при переводе. — Прим.
ред.
2) Изложение результатов статьи содержится в гл. 20 книги семинара
«Софус Ли» [1]. — Прим. ред.
Литература 343
[3] Treue Darstellungen beliebiger Liescher Ringe, Collect. Math, 6 A953),
107—114.
[4] Die Unterringe der freien Lieschen Ringe, Math. Z., 64 A956), 195—216.
Гантмахер Ф. P.
[1] Canonical representation of automorphisms of a complex semi-simple Lie
group, Мат. сборник, 5 A939), 101—146.
[2] On the classification of real simple Lie groups, Мат. сборник, 5 A939),
217—249.
r p ев и ч Г. Б.
[1] Стандартные алгебры Лн, Мат. сборник, 35 A954), 437-460,
Г у 1
[1]
Джекобсон (Jacobson N.)
[1] Теория колец, ИЛ, М., 1943.
[2] Lectures in Abstract Algebra, Vols. I and II. I: Van Nostrand, 1951.
II: Van Nostrand, 1953.
[3] Строение колец, ИЛ, М., 1961.
[4] Abstract derivation and Lie algebras, Trans. Am. Math. Soc. 42 A937),
206—224.
[5] Simple Lie algebras over a fieLd of characteristic zero, Duke Math. J., 4
A938), 534—551.
[6] Cayley numbers and simple Lie algebras of type Q., Duke Math. J., 5
A939), 775—783.
[7] Restricted Lie algebras of characteristic p. Trans. Am. Math. Soc, 50
A941), 15—25.
[8] Glasses of restricted Lie algebras of characteristic p, I and II. I: Am. J.
Math., 63 A941), 481—515. II: Duke Math. J., 10 A943), 107—121.
[9] Commutative restricted Lie algebras, Proc. Am. Math. Soc, 6 A955),
476—481.
[10] Composition algebras and their automorphisms, Rend. Circolo Mat. Pa-
Palermo B) 7 A958), 55—80.
[11] Exceptional Lie Algebras, Jale mimeographed notes, 1957.
[12] Some Groups of transformations defined by Jordan algebras, I, II and
III. I: /. reine und angew. Math., 201 A959), 178—195, II: J. reine und
angew. Math., 204 A960), 74—98, HI: /. Reine Angew math., 207A961),
61—85.
[13] A note on automorphisms of Lie algebras Pacific J. Math., 12 A962),
303—315.
Дженингс, Рн (Jennings S. H., Ree R.)
[1] On a family of Lie algebras of characteristic p, Trans, Am. Math. Soc,
84 A957), 192—207.
Диксон (Dickson L. E.)
[1] Algebras and their Arithmetics, Chicago Univ. Press, 1923.
Диксмье (Dixmier J.)
[1] Sur un theoreme d'Harish-Chandra, Ada Set. Math. Szeged, 14 A952),
145—156.
[2] Sur ies algebres derivees d'une algebre de Lie, Proc. Cambridge Phil.
Soc, 51 A955), 541—544.
[3] Sous-algebres de Cartan et decompositions de Levi dans Ies algebres de Lie,
Trans. Roy. Soc. Canada, Sec III C) 50 A956), 17—21.
[4] Certaines factorizations canoniques dans l'homologie et la Cohomologie
des algebres de Lie, /. math, pures et appl. (9) 35 A956), 77—86.
[5*] Cohomologue des algebres des Lie nilpotents, Acta. scient Math., 16
A955), 246-250.
Д н к с м ь е, Л н с т е р (Dixmier J., Lister W. G.)
[1] Derivations of nilpotent Lie algebras, Proc. Am. Math. Soc.{ 8 A957),
155—158.
344 Литература
Д ы н к и н Е. Б.
[1] Структура полупростых алгебр Ли, Успехи матем. наук (н. сер.), 2
A947), 59—127.
[2] О представлении ряда log(e*e") для некоммутирующих х и у через ком-
коммутаторы, Мат. сборник, 25 A949), 155—162.
[3] Полупростые подалгебры полупростых алгебр Ли, Мат. сборник, 30
A952), 349—466.
[4] Максимальные подгруппы классических групп. Труды моек, матем.
об ва, 1 A952), 39—166.
Д ь е д о и н е (D i e u d о п п ё, J.)
[1] La Geometrie des Oroupes Classiques, Ergeb. Math. Berlin, 1955.
[2] Sur les groupes de Lie algebriques sur un corps de caracteristique p > 0,
Rend. Circ, Mat. Palermo B) 1 A952), 380—402.
[3] Sur quelques groupes de Lie abeliens sur un corps de caracteristique
p > 0, Arch. Math, 5 A954), 274—281.
[4] Lie groups and Lie hyperalgebras over a field of characteristic p >0,1—VI;
I: Comment. Math. Helv. 28 A954), 87—118; II: Am. J. Math. 77A955),
218—244; III: Math. Z., 62 A955), 53—75; IV: Am. J. Math, 77 A955),
429—452; V: Bull. Soc. Math. France, 84 A956), 207—239; VI Am. J.
Math, 79 A957), 331—388.
[5] Witt groups and hyperexponential groups. Mathematika, 2 A955), 21—23.
[6] On simple groups of tipe Bn, Am. J. Math. 79 A957), 922—923.
[7] Les algebres de Lie simples associees aux groupes simple algebriques sur
un corps de caracteristique p > 0. Rend. Circ. Mat. Palermo B), 6
A957), 198-204.
Ивасава (Iwasawa K)
[1] On the representations of Lie algebras, Japan J. Math., 19 A948),
405—426.
Ивахори (Iwahori N.)
[1] On some matrix operators, /. Math. Soc. Japan, 6 A954), 76—105.
[2] On real irreducible representations of Lie algebras, Nagoya Math. J., 14
A959), 59—83.
Капланский (Kaplansky J.)
[1] Lie algebras of characteristic p, Trans. Am. Math. Sog., 89 A958),
149—183.
Картан (Cartan E.)
[1] These, Paris, 1894, 2nd ed., Vuibert, Paris, 1933.
[2] Les groupes reels simples, finis et continue, Ann. Set. Ecole Norm.
Super., 31 A914), 263—355.
[3] Les groupes projectifs qui ne laissent invariante aucune multiplicite plane.
Bull. Soc. Math. France, 41 A913), 53—96.
[4] Les groupes projectifs continus reels qui ne laissent invariante aucune
multiplicite plane, /. Math, pures et appl., 10 A914), 149—186.
[5] La geometrie des groupes de transformations, /. Math. Pures et Appl., 6,
Ser. 9 A927), 1—119.
Картан, Эйленберг (Cartan Н„ Eilenberg S.)
[1] Гомологическая алгебра, ИЛ, М., 1958.
Картье (С artier P.)
[1] Seminaire Sophus Lie, Vol. II (Hyperalgebres et groupes de Lie formels)
A957) Ecole Norm. Sup.
[2] Dualite de Tannaka des groupes et des algebres de Lie, Comptes Rendus,
242 A956) 322 325
[3*] On H. We'yl s character formula, Bull. Amer. Math. Soc, 67 A961), 2.
Литература 345
Кертис (Curtis С. W.)
[1] Modular Lie algebras, I and II. 1: Trans. Am. Math. Soc, 82 A956),
160—179, II. Trans. Am. Math. Soc, 86 A957), 91—108.
[2] On the dimensions of the irreducible modules of Lie algebras of classical
type, Trans. Am. Math. Soc, 96 (I960), 135—142.
[3*! Representations of Lie algebras of classical type with applications to li-
linear groups, /. Math. Mech., 9 A960), 307—326.
[4*] An isomorphism theorem for certain finite groups, Illinois ]. Math., 7
A963), № 2, 279—304.
Кил л инг В. (Killing W.)
[1] Die Zusammensetzung der stetigen endlichen Transformationsgruppen, I,
II, III and IV, I: Math. Ann., 31 A888), 252—290. II: Math. Ann., 33
A889), 1—48. Ill: Math. Ann. 34 A889), 57—122. IV: Math. Ann., 36
A890), 161—189.
Кокстер (Coxeter H. S. M.)
[1] The product of the generators of a finite group generated by reflections
Duke Math. L, 18 A951), 765—782.
Кон (Cohn P. M.)
[1] Lie Groups, Cambridge Tracts in Math, and Math. Phys., 46, Cambridge,
1957.
Костант (Kostant B.)
[1] On the conjugacy of real Cartan subalgebras, 1, Proc Nat. Acad. Sci.
U. S., 41 A955), 967—970.
[2] A theorem of Frobenius, a theorem of Amitsur-Levitski and cohomology
theory. J. Math. Mech., 7 A958), 237—264.
[3] The principal three-dimensional subgroups and the Betti numbers of a
complex simple Lie group, Am. J. Math., 81 A959), 973—1032.
[4] A formula for the multiplicity of a weight, Trans. Am. Math. Soc, 93
A959), 53—73.
Кострикин А. И.
[1] О кольцах Ли, удовлетворяющих условию Энгеля, Докл. АН СССР
(н. с), 108 A956), 580—582.
[2]'О связи между периодическими группами и кольцами Ли, Изв. АН СССР,
сер. мат., 21 A957), 29—310.
[3] Кольца Ли, удовлетворяющие условию Энгеля, Изв. АН СССР. сер. мат.,
21 A957), 515—540.
[4] О локальной нильпотентности колец Ли, удовлетворяющих условию Эн-
Энгеля, Докл. АН СССР (н. с), 118 A958), 1074—1077.
[5] О проблеме Бернсайда, Изв. АН СССР, сер. мат., 23 A959), 3—34.
[6*] О простых р-алгебрах Ли, Труды МИАН СССР, 64 A961), 79—89.
[7*] О сильной вырожденности простых р-алгебр Ли, Докл. АН СССР, 150
A963), № 2, 248—250.
[8*] Алгебры Ли и конечные группы. Proc. of the Internat. Congress of
Math., Stockholm, 1962, 264—269.
Кошу ль (KoszulJ. L.)
[1] Homologie et cohomologie des algebres de Lie, Bull. Soc. Math. France,
78 A950), 65—127.
Крекнин В. А.
[1*] О разрешимости алгебры Ли с регулярным автоморфизмом конечного
периода. Докл. АН СССР, 150 A963), № 3, 467—469.
Крекнин В. А., Кострикин А. Н.
[1*] Об алгебрах Ли с регулярным автоморфизмом. Докл. АН СССР, 149
A963), № 2, 249-251.
Курош А. Г.
[1*] Лекции по общей алгебре, Физматгиз, М., 1962,
346 Литература
Лазар (Lazard M.)
[1] Sur les algebres enveloppantes universelles de certaines algebres de Lie,
Comptes Rendus, 234 A952), 788—791.
[2] Sur les groupes nilpotents et les anneaux de Lie, Ann. sclent Bcole norm.
sup., ser. 3, 71 A954), 101—190.
[3] Sur les algebres enveloppantes unverselles de certain algebres de Lie,
Publ. Sci. Univ. Algerie, Ser A, 1 A954), 281—294 A955).
[4] Lois de groupes et analyseurs, Ann. Sci. Ecole Norm. Sup. C) 72 A955),
299—400.
Ландхер (L an dh er r W.)
[1] Ober einfache Liesche Ringe, Abhandl. Math. Sem. Univ. Hamburg, 11
A935), 41—64.
[2] Liesche Ringe vom Typus A, Abhandl. Math. Sem. Univ. Hamburg, 12
A938), 200—241.
Ларди (Lardy P.)
[1] Sur la determination des structures reelles de groupes simples, finis et
continus, au moyen des isomorphies involutives, Comment, math, helv.,
8 A935), 189—234.
Леджер (Leger Q. F.)
[1] A note on the derivations of Lie algebras, Proc. Am. Math. Soc.A A953),
511—514.
Леджер, Того (Leger Q., Togo S.)
[1*] Characteristically nilpotent Lie algebras, Duke Math. L, 26 A959.), № 4,
623—628.
Мальцев А. И.
[1] О полупростых подгруппах групп Ли, Изв. АН СССР, сер. мат., 8 A944)\
143—174.
[2] О разрешимых алгебрах Ли, Изв. АН СССР, сер. мат.,9 A945), 329—356.
[3] Коммутативные подалгебры полупростых .алгебр Ли, Изв. АН СССР,
сер. мат., 9 A946), 291—300.
[4*] Основы линейной алгебры, Физматгиз, М., 1956.
Манин Ю. И.
[1*] Замечание о р-алгебрах Ли, Сиб. матем. журнал, III, 1962, № 3,
479—480.
Миллс (Mills W. Н.)
[1] Classical type Lie algebras of characteristic 5 and 7, /. Math. Mech., 6
A957), 559—566.
Монтгомери, Цнппин (Montgomery D., Zippin L.)
[1] Topological Transformation. Groups, Interscier.ee, 1955.
Мостов (Most ow G. D.)
[1] Fully reducible subgroups of algebraic groups, Am. I. Math., 68 A956),
200—221.
[2] Extension of representations of Lie groups, II Am. I. Math, 80 A958).
331—347.
Oho (On о Т.)
[1] Sur les groupes de Chevailey, /. Math. Soc. Japan, 10 A958), 307—313.
Понтрягин Л. С.
[1] Топологические группы, М., 1954.
Ри (Ree R.)
[1] On generalized Witt algebras, Trans. Am. Math. Soc, 83 A956),
510—546.
Литература 347
[2] On some simple groups defined by С Chevalley, Trans. Am. Math. Soc,
84 A957), 392—400.
[3] Lie elements and an algebra associated with shuffles, Ann. Math., 68
A958), 210—220.
[4] Generalized Lie elements, Can. 1 Math., 12 A960), 439—502.
[5] A family of simple groups associated with the simple Lie algebra of type
(u2), Am. I. Math., 83 A961), 432—462.
[6] A family of simple groups associated with the simple Lie algebra of type
(F4), Am. I. Math., 83 A961), 401—420.
Самельсон (Samelson H.)
[1] Topology of Lie groups, Bull. Am. Math. Soc, 58 A952), 2—37.
Селигман (SeligmanQ. В.)
[1] On Lie algebras of prime characteristic Mem. Am. Math. Soc, № 19, 1956.
[2] Some remarks on classical Lie algebras, /. Math. Mech., 6 A957),
549—558.
[3] Characteristic ideals and the structure of Lie algebras, Proc Am. Math.
Soc, 8 A957), 159—164.
[4] On automorphisms of Lie algebras of classical type, I, II and III. I:
Trans. Am. Math. Soc, 92 A959), 430—448. II: Trans. Am. Math. Soc,
94 A960), 452—482. III. Trans. Am. Math. Soc, 97 A960), 286—316.
Селигман, Миллс (Seligman G. В., Mills W. H.)
[1] Lie algebras of classical type, J. Math. Mech., 6 A957), 519—548.
Семинар «Софус Ли» [1] Теория алгебр Ли, топология групп Ли, ИЛ,
М, 1962.
Срндхаран (SridharanR.)
[1] Filtered algebras and representations of Lie algebras, Trans. Amer. Math.
Soc, 100 A961), № 3, 530—550.
Тите (Tits J.)
[1] Sur les analogues algebriques des groupes semi-simples complexes, collo-
que d'Algebre, Brussels (Dec. 1956).
[2] Les groupes de Lie exeptionnels e't leur interpretation geometrique, Bull.
Soc. Math. Belg., 8 A956), 48—8 IT"
[3] Sur la geometrie des #-espaces, /. Math, pures et appl., 36 A957), 17—38.
[4] Les «formes reelles» des groupes de type ?s, Seminaire Bourbaki A958),
Paris.
[5] Sur la trialite et certains groupes qui s'en deduisent, Publs. Math. Inst.
des Hautes-Etudes, № 2 A959), 14—60.
[6] Sur la classification des groupes algebriques semi-simples, Comptes Ren-
dus, 249 A959), 1438—1440.
[7*] Les groupes simples de Suzuki et de Ree, Seminaire Bourbaki, December
A961), 210/1—210/18.
[8*] Groups simples et geometries associees, Proc. of the Internat. Congress
of Math., Stockholm, 1962, 197—221.
Томбер (Tomber M. L.)
[1] Lie algebras of type F, Proc. Am. Math. Soc, 4 A953), 759—768.
Франк (Frank M. S.)
fl] A new class of simple Lie algebras, Proc. Nat. Acad. Set. U. S., 40 A954)
713—719.
Фрейденталь (Freudenthal H.)
[1] Oktaven, Ausnahmegruppen und Oktavengeometrie, Mimeographed, Ut-
Utrecht, 1951.
[2] Sur le groupe exceptionnel E7, Indag. Math., 15 A953), 81—89.
348 Литература
[3] Sur les invariants caracteristiques des groupes semi-simples, Indag. Math.,
15 A953), 90—94.
[4] Sur le groupe exceptional Et, Indag. Math., 15 A953), 95—98.
[5] Zur ebenen Oktavengeometrie, Indag Math., 15 A953), 195—200.
[6] Zur Berechnung der Charakter der halbeinfachen Lieschen Qruppen, I, II
and III; I: Indag. Math., 16 A954), 369—376. II: ibid. 487—492, III;
ibid. 18 A956), 511—514.
[7] Beziehungen der ?7 und ?g zur Oktavenebene, I—IX 1: Indag. Math., 16
A954), 218—230. II: Indag. Math., 16 A954), 363-368. III. Indag.
Math., 17 A955), 151—157. IV: Indag. Math., 17 A955), 277—285. V:
Indag. Math., 21 A959), 165—179. VI: Indag. Math., 21 A959), 180—191.
VII: Indag. Math., 21 A959), 192—201. VIII: Indag. Math., 21 A959),
447—465. IX: Indag. Math., 21 A959), 466—474. •
Хариш-Чандра (Harish-Chandra)
[1] On representations of Lie algebras, Ann. Math., 50 A949), 900—915.
[2] Lie algebras and the Tannaka duality theorem, Ann. Math., 51 A950),
299—330.
[3] Some applications of the universal enveloping algebra of a semi-simple
Lie algebra, Trans. Am. Math. Soc, 70 A951), 28—99.
Хигман (Higman Q.)
[1] Lie ring methods in the theory of finite nilpotent groups, Proc.
of the International Congress of Mathematicians, Edinburgh., 1958,
307—312.
Хохшильд (Hochschild Q.)
[1] Representation Theory of Lie algebras, Technical Report of the Office of
Naval Research. University of Chicago Press, 1950.
[2] Cohomology of restricted Lie algebras, Am. J. Math., 76 A954), 555—580.
[3] Lie algebra kernels and cohomology, Am. J. Math., 76 A954), 698—716.
[4] Representations of restricted Lie algebras of characteristic p, Proc. Am.
Math. Soc, 5 A954), 603—605.
[5] On the algebraic hull of a Lie algebra, Proc. Am. Math. Soc, 11 A960),
195—199.
Хохшнльд, Мостов (Hochschild Q., Mostow Q. D.)
[1] Extensions of representations of Lie groups and Lie algebras, I, Am. J.
Math., 79 A957), 924—942.
[2] Representations and representative functions of Lie groups I and II. I:
Ann. Math., 66 A957), 495—542, II: Ann. Math., 68 A958), 295—313.
Хохшильд, Cepp (Hochschild Q., Serre J. P.)
[1] Cohomology of Lie algebras, Ann. Math., 57 A953), 591—603.
к (Hooke R.)
1] Linear p-adic groups and their Lie algebras, Ann. Math., 43 A942),
641—655.
Ц а с с е н x а у з (Z a s s e n h a u s H.)
[1] Ober Liesche Ringe mit Primzahlcharakteristik, Abhandl. Math. Sem.
Univ. Hamburg, 13 A939), 1—100.
[2] Ein Verfahren jeder endlichen p-Gruppe einen Lie-Ring mit der Cha-
Charakteristik p zuzuordnen, Abhandl. Math. Sem. Univ. Hamburg, 13
A939), 200—207.
[3] Darstellungstheorie nilpotenter Lie-Ringe bei charakteristik p > 0, J.,reine
und angew. Math., 182 A940), 150—155.
[4] Uber die Darstellungen der Lie-Algebren bei Charakteristik 0, Comment
math, helv., 26 A952), 252—274.
[5] The representations of Lie algebras of prime characteristic, Proc. Glasgow
Math, Assoc, 2 A954)г 1—36.
Литература 349
[6*] On trace bilinear forms on Lie algebras, Proc. Glasgow Math, associa-
association, IV, ч. 2 A959), 67—72.
ЧангХо-чжу (ChangHo-Jui)
[1] Ober Wittsche Lie-Ringe, Hamburg Abhandl., 14 A941), 151—184.
Шевалле (ChevalleyC.)
Теория групп Ли, т. 1, ИЛ, М., 1946.
Теория групп Ли, т. 2, ИЛ, М., 1958.
Теория групп Ли, т. 3, ИЛ, М., 1958.
The algebraic theory of spinors, Columbia Univ. Press., 1954.
An algebraic proof of a property of Lie groups, Am. J. Math., 63 A941),
785—793.
[6] A new kind of relationship between matrices, Am. J. Math., 65 A943),
521—531.
[7] Sur certains groupes simples, Tdhoku Math. J., 7—8, Ser. 2 A955—1956),
14—66.
[8] Seminaire Chevalley, Vols. I and II (Classification des groupes de Lie
algebriques) A956—1958), Ecole Norm. Sup.
Шевалле, Шафер (Chevalley С, Schaffer R. D.)
[1] The exceptional simple Lie algebras Ft and Et, Proc. Nat. Acad.Sci. U.S,
36 A950), 137—141.
Шевалле, Эйленберг (Chevalley С, Eilenberg S.)
[1] Cohomology theory of Lie groups and Lie algebras, Trans. Am. Math.
Soc, 63 A948), 85—124.
Шенкман (Schenkman E. V.)
[1] A theory of subinvariant Lie algebras, Am. J. Math., 73 A951), 453—474.
Ширшов А. И.
[1] Подалгебры свободных алгебр Ли, Мат. сборник B), 33 A953), 441—452.
Штейнберг (Steinberg R.)
[1] Prime power representations of finite linear groups, I and II. I: Can.
J. Math., 8 A956), 580—591. II: Can. J. Math., 9 A957), 347—351.
[2] Variations on a theme of Chevalley, Pacific J. Math., 9 A959), 875—891.
[3] The simplicity of certain groups, Pacific J. Math., 10 A960), 1039—1041.
[4] Automorphisms of classical Lie algebras, Pacific. J. Math., 11 A961),
Штифель (Stiffel E.)
[1] Ober eine Beziehung zwischen geschlossenen Lieschen Qruppen und di-
skontinuierlichen Bewegungsgruppen Euklidischer Raume und ihre An-
wendung auf die Aufzahlung der einfachen Lieschen Qruppen, Comment,
math. Helv., 14 A941—1942), 350—380.
[2] Kristallographiesche Bestimmung der charaktere der geschlossenen Lie-
Lieschen Gruppen, Comment Math. Helv., 17 A944—1945), 165—200,
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абелева алгебра Ли 18
ограниченная 213—
215
Абсолютно неприводимое множество
линейных преобразований 246
Автоморфизмы алгебр типа At, Bi,
Си Dh G2, Ft 305—309
Алгебра альтернативная 160
— ассоциативная 11
линейных преобразований
13
ннльпотентная 35
полупростая 35
свободная 186
— векторно-матричная 159
— Внтта 218
— внешняя 198
— градуированная 182
— Грассмана 198
— дифференциальных операто-
операторов 194
— йорданова 161
— кватернионов обобщенная 341
— Клиффорда вторая 256
— Кэли 159
— Ли 11
ассоциативной алгебры 14
— — дифференцирований 16
• исключительная 159
компактная 164
линейных преобразований
15
. расщепляемая 54, 62
ннльпотентная 34
ограниченная характери-
характеристики рфО 208
ортогональная 15
полупростая 34
— расщепляемая 121
' простая 34
разрешимая 33
редуктивная 119
свободная 186
¦ снмплектнческая 15
совершенная 19
— неассоцнатнвная 10
— — центральная 314
—¦ обертывающая 42
Алгебра производная 18
— умножений 313
— универсальная обертывающая
170
— формальных 'степенных рядов
191,216
Антндифференцнрование 199
At, Bi, б(-модули неприводимые
249—259
а-серня корней, содержащая E 129
Базисные неприводимые модули
249
Вектор положительный 133
Вес 54, 74
— крайний 286
— старший 236
Весовое подпространство 54, 74
Высота корня 136
Голоморф 27
Гомоморфизм ограниченной алгебры
Лн 208
Группа автоморфизмов матрицы Кар-
тана 301
— Вей ля 133, 262—265
— когомологнй алгебры Лн 109,
194
Дифференциал отображения в точке
290
— функции в точке 290
Дифференцирование 16
— алгебры Ли 93
— внутреннее 18
— ограниченное ограниченной
алгебры Лн 217
Допустимая конфигурация 145
неразложимая 145
D-константа 38
Идеал 18, 48
— однородный 182
Инволюции коградиентные 335
Инволюция 324
— второго рода 324
«гг первого рода 324
Предметный указатель
351
Кограница 108, 109
Коммутатор 14
Компонента линейного преобразова-
преобразования ннльпотентная 112
однородная 112
— примерная 48, 53
Коразмерность 219
Корень алгебры Ли 76
— простой 134
Коцикл 109
Лемма Морозова 113
— Уайтхеда 90, ПО
— Фиттннга 47
Линейное свойство 164
8°-компонента неприводимая 266
Матрица Картана 136
— нильтреугольная 35
— треугольная 16
Матрицы, мультипликативно когра-
коградиентные 22
Многочлен характеристический 72
Модуль 24
— кон.трагредиентный 31
— свободный 194
— спинорный 257
— циклический 234
— е-экстремальный 234
Неприводимость для множества лн-
нейных преобразований 58
Неразложимость для множества ли-
иейных преобразований 58
Ниль-радикал 35
Нормализатор 38, 69
Оператор Казимира 91
Отображение полиномиальное 288
Подалгебра Картана 69
расщепляющая 121
Подсистема 41
Поле формальных степенных рядов
216
Полная приводимость 58, 88—96,
110—117
Почти алгебраическая алгебра Ли
113
Представление алгебры Ли 25
присоединенное 26
— ассоциативной алгебры 24
— ограниченной алгебры Лн
; 208
— регулярное 25
— спинЪрное 252
— точное 25
Представление трехмерной простой
алгебры Ли 97—100
Принцип локальной тройственности
311
Присоединенное отображение 18
Произведение Ли 14
Пространство весовое 74
— 2-неприводимое 58
— 2-неразложимое 58
Прямая сумма 27, 29
Радикал алгебры Лн 34
— ассоциативной алгебры 35
Разложение Фнттннга 47—49, 69
Расширение алгебры Ли 70
— основного поля 27
Расщепляемая алгебра Ли 54, 62,121
— трехмерная простая алгебра
Лн 23
Расщепляемое расширение (алгебры
Ли) 27
Расщепляемые простые алгебры Ли
А,, Ви d, D,, G2, Ft, Fs 152—163,
246—248
Fr,F,
Редуктнвкая подалгебра алгебры Ли
119
Ряд верхний центральный 39
— композиционный 60
— нижний центральный 33
— производный 33
Симметрия, определенная корнем 133
Система корней простая 135
неразложимая 143
— определяющая 286
— факторов 103
— фундаментальная 286
Слабо замкнутое подмножество гх.-
соцнатнвной алгебры 41
Сопряженность подалгебры Картана
296
Стандартный комплекс 194
— одночлен 175
Старший член элемента 123
Структурная теорема для полупро-
полупростых алгебр Ли 84
Структурные константы 10
СубннВариантная подалгебра 39
Сх*ем"з ДШКЙНа 144
(si, вг)-Дйфференц*йрование 197
Х-подгфостранства 58
Тело частных (левое) 185
Тензорное произведение 30
ТеоремЬ Адо 223
— Вейля 278
352 Предметный указатель
Теорема Витта 187 Форма Киллинга 82
— Голди-Оре 184 — следа 82
— Ивасавы 225 Формула Вейля для размерности 279
— изоморфизма для пол> простых характеров 278
алгебр Ли 142, 243 — Витта 215
— Леви 105 — Константа 284
¦—¦ Ли 62, 64 — Кэмпбелла — Хаусдорфа
— Мальцева — Хариш — Чан- 190—193
дры 106 — Фрейденталя 270
— Мостова — Тафта 119 — Штейнберга 286
— Пуанкаре — Биркгофа — Функция доминантная 237
Витта 178 — примарная 52
¦— существования для полупро- — полиномиальная 288
стых алгебр Ли 243 —¦ целая 237
— Фридрихса 189
— Цассенхауза 52 Характер 272
— Шенкмана о башне диффереи- — примитивный 283
цирований 68 Характеристический многочлен 72
— Шнехта— Вевера 189
— Энгеля 46 Центр 18
Тождества Якобн 11 Централизатор 38
Центроид 313
Унипотентное преобразование 309
u-алгебра ограниченной алгебры Ли Элемент алгебраический 118, 219
213 — кососимметрический 273
— Ли 188
Фактор Леви 105 — общий (алгебры Ли) 72
Фильтрация 182 — однородный степени 182
Форма ассоциативная 83 — регулярный 70
— инвариантная 82 — симметрический 273
ОГЛАВЛЕНИЕ
Предисловие редактора перевода .... 5
Предисловие ; 7
Глава I. Основные понития 9
§ 1. Определение и построение алгебр Ли и ассоциативных алгебр 10
§ 2. Алгебры линейных преобразований. Дифференцирования ... 13
§ 3. Внутренние дифференцирования ассоциативных алгебр и ал-
алгебр Ли 18
§ 4. Описание алгебр Ли малых размерностей 20
§ 5. Представления и модули 24
§ 6. Некоторые основные операции над модулями 28
§ 7. Идеалы, разрешимость, нильпотентность 32
§ '8. Расширение основного поля ¦ 36
Упражнения 38
Глава II. Разрешимые и иильпотентные алгебры Ли 41
§ 1. Слабо замкнутые подмножества ассоциативной алгебры .... 41
§ 2. Слабо замкнутые ииль-множества 43
§ 3. Теорема Энгеля 46
§ 4. Примарные компоненты. Весовые подпространства 47
§ 5. Алгебры Ли с полупростыми ассоциативными обертывающими
алгебрами 55
§ 6. Теоремы Ли 60
§ 7. Приложения к абстрактным алгебрам Ли. Некоторые противо-
противоречащие примеры 63
Упражнения 66
Глава III. Критерий Картана и его следствия 69
§ 1. Подалгебры Картана 69
§ 2. Произведения весовых пространств 74
§ 3. Пример 77
§ 4. Критерии Картана 79
§ 5. Структура полупростых алгебр 83
§ 6. Дифференцирования 86
§ 7. Полная приводимость представлений полупростых алгебр ... 88
§ 8. Представления расщепляемой трехмерной простой алгебры Ли 97
§ 9. Теоремы Леви и Мальцева — Хариш-Чандра 100
§ 10. Группы когомологий алгебр Ли 108
§ 11. Еще о полной приводимости ПО
Упражнения 117
Глава IV. Расщепляемые полупростые алгебры Ли 120
§ 1. Свойства корней и корневых подпространств 121
§ 2. Основная теорема о представлениях и ее приложения к стру-
структурной теории 126
354 Оглавление
§ 3. Простые системы корней 133
§ 4. Теорема об изоморфизме. Простота 142
§ 5. Отыскание матриц Картана 144
§ 6. Построение алгебр ¦ 152
§ 7. Компактные формы 163
Упражнения 167
Глава V. Универсальные обертывающие алгебры 169
§ 1. Определение и основные свойства 169
§ 2. Теорема Пуанкаре — Биркгофа — Витта 174
§ 3. Фильтрация н градуированная алгебра 182
§ 4. Свободные алгебры Ли 186
§ 5. Формула Кэмпбелла — Хаусдорфа 190
§ 6. Когомологии алгебр Ли. Стандартный комплекс 193
§ 7. Ограниченные алгебры Лн характеристики р 206
§ 8. Абелевы ограниченные алгебры Ли 213
Упражнения 215
Глава VI. Теорема Адо — Ивасавы 219
§ 1. Предварительные результаты 219
§ 2. Случай характеристики нуль 221
§ 3. Случай характеристики р 224
Упражнения 226
Глава VII. Классификация неприводимых модулей 228
§ 1. Определение некоторых алгебр Ли 228
§ 2. О некоторых циклических модулях над Й 234
§ 3. Конечномерные неприводимые модули 237
§ 4. Теоремы о существовании и изоморфизме для полупростых
алгебр Ли 243
§ 5. Существование алгебр Е7 и ?8 246
§ 6. Базисные неприводимые модули 248
Упражнения 259
Глава VIII. Характеры неприводимых модулей 261
§ 1. Некоторые свойства группы Вейля 262
§ 2. Формула Фрейденталя 265
§ 3. Формула Вейля для характеров 272
§ 4. Некоторые примеры 280
§ 5. Применения и дальнейшие результаты 282
Упражнения 285
Глава IX. Автоморфизмы 287
§ 1. Леммы из алгебраической геометрии 288
§ 2. Сопряженность подалгебр Картаиа 294
§ 3. Неизоморфность расщепляемых простых алгебр Ли 297
§ 4. Автоморфизмы полупростых алгебр Ли над алгебраически
замкнутым полем ..--.. * , 298
§ 5. Явное описание автоморфизмов простых алгебр Ли 305
УпраЯйгеиий • 309
Глава X. Простые алгебры Ля над произвольным полем 312
§ 1. Алгебра умножений и центроид неассоциативной алгебры . . 313
§ 2. Изоморфизм алгебр, получающихся расширением основного
пбля 318
Оглавление 355
§ 3. Простые алгебры Ли типов А — D 321
§ 4. Условия нзоморфности 326
§ 5. Теоремы полноты 332
§ 6. Еще об условиях изоморфности .... - 335
§ 7. Центральные простые вещественные алгебры Лл 337
Упражнения 341
Литература 342
Предметный указатель 350
354
Упраж
Глава
Глава
§
Упра
Глав
§
§
Н. Джекобсон
АЛГЕБРЫ ЛИ
Редактор Г. М. Цукерман
Художник В. П. Зашеин
Художественный редактор В. И. Шаповалов
Технический редактор Л. П. Кондюкова
Сдано в производство 27/IX 1963 г.
Подписано к печати 6/Ш 1964 г.
Бумага 60x90/16 11,1 бум. л. 22,3 печ. л.
Уч. изд. л. 21,1. Изд. № 1/1606
Цеяа 1 р. 68 к. Зак. 1Ь99
(Темплан 1964 г., изд-ва ИЛ, пор Ms 3.)
' ИЗДАТЕЛЬСТВО « МИР »
Москва, 1-й Рижский пер., 2
Ленинградская типография № 2
имени Евгении Соколовой
«Главполиграфпрома» Государственно! о
комитета Совета Министров СССР
по печати. Измайловский проспект, 29.
Упра
Глав
Упр
Гла]
УП1
Гла
ЗАМЕЧЕННЫЕ ОПЕЧАТКИ
Стр.
119
152
223
223
236
329
Строка
10 СН.
10, 11 сн.
16 сн.
11 сн.
3 сн.
16 сн.
Напечатано
(-1)'^)
\0Ф,
Х-^-М-'Х'М
Следует читать
<5©8,
'г-1 'г/ г'
Зак. 1699