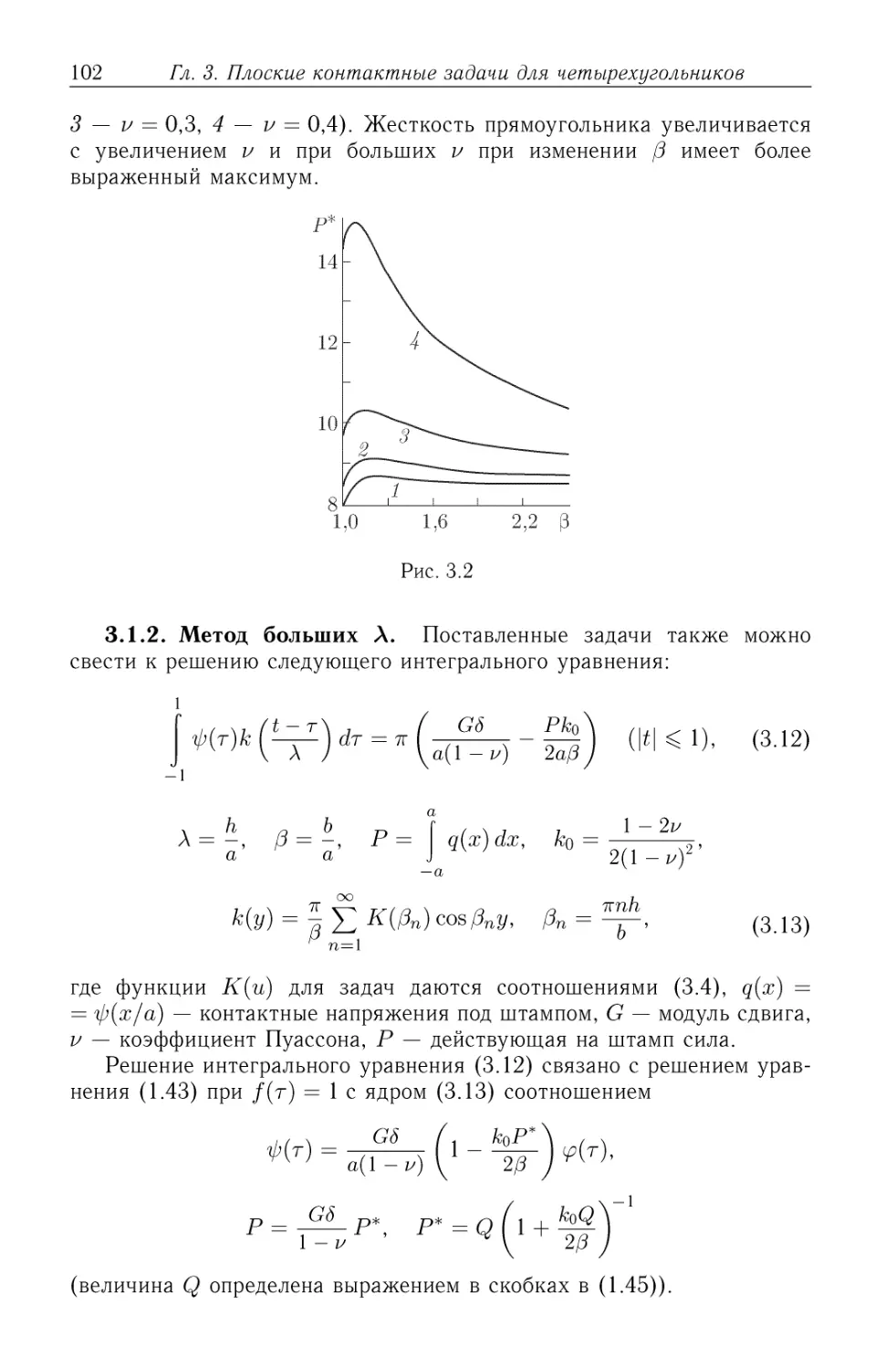
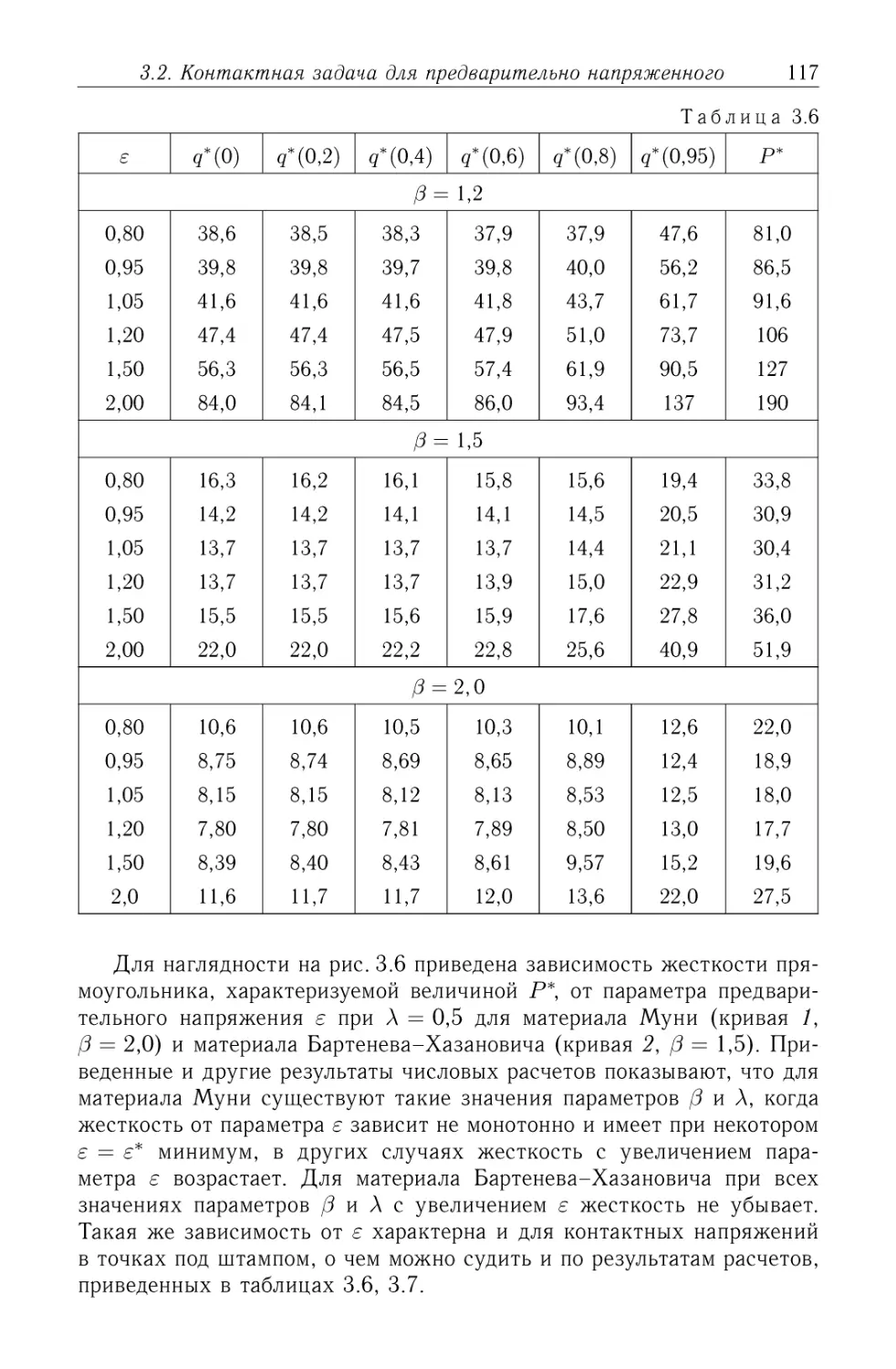
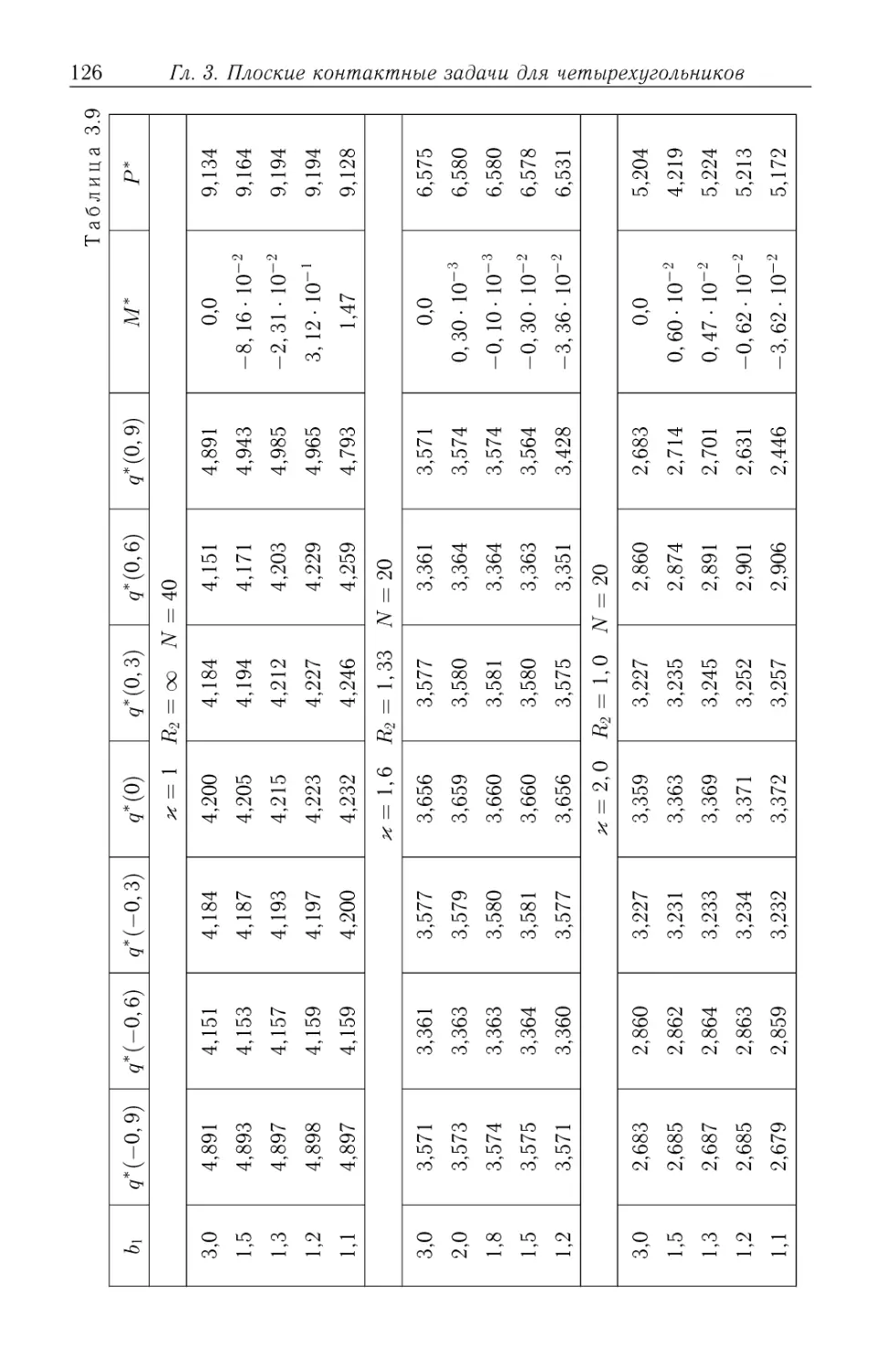
Автор: Александров В.М. Чебаков М.И.
Теги: механика деформируемых тел упругость деформация механика математическая физика
ISBN: 5-9221-0519-1
Год: 2004
Текст
УДК ооУ.о рр Издание осуществлено при поддержке
ББК 22.251 ь» срри Российского фонда фундаментальных
Д46 ~~ ** ~~ исследований по проекту 04-01-14059д
Александров В. М., Чебаков М. И. Аналитические методы
в контактных задачах теории упругости. — М.: ФИЗМАТЛИТ, 2004. —
304 с. - ISBN 5-9221-0519-1.
Излагаются аналитические методы и результаты решения большого кру-
круга неклассических задач механики контактных взаимодействий упругих
тел. Рассмотрены статические и динамические контактные задачи теории
упругости для тел сложной конфигурации, неоднородных тел и контактные
задачи с усложненными условиями в зоне контакта. Для решения указанных
задач разработаны эффективные аналитические методы решения парных
рядов-уравнений, интегральных уравнений и бесконечных систем линей-
линейных алгебраических уравнений. Получен ряд качественно новых и важных
результатов, касающихся зависимости контактных напряжений, жесткости
системы штамп-упругое тело, размеров области контакта и деформации
свободной поверхности от параметров задач.
Практическая значимость результатов связана с возможностью исполь-
использования их для создания методик расчетов контакта элементов конструкций
и деталей в машиностроении, строительстве и электронной промышленности
с учетом различных факторов, а также для тестирования пакетов программ,
реализующих прямые численные методы.
Приведенные методы найдут применение также в механике разрушения,
гидроаэромеханике, электростатике, термодинамике и теории диффузии,
радиофизике и акустике.
Для специалистов в области механики контактных взаимодействий, ме-
механики сплошных сред и математической физики, инженеров, а также ас-
аспирантов и студентов механико-математических и физических факультетов
университетов.
© ФИЗМАТЛИТ, 2004
© В. М. Александров, М. И. Чебаков,
ISBN 5-9221-0519-1 2004
ОГЛАВЛЕНИЕ
Предисловие 5
Введение 6
Глава 1. Постановка контактных задач, некоторые общие методы
решения уравнений и другие вспомогательные результаты .... 22
1.1. Постановка контактных задач 22
1.2. Методы решения парных рядов-уравнений 28
1.3. Асимптотический метод больших Л решения интегральных уравне-
уравнений 36
1.4. Точное решение некоторых интегральных уравнений 43
1.5. Некоторые соотношения обобщенной ортогональности однородных
решений 45
Глава 2. Контактные задачи для цилиндрических тел конечных
размеров 51
2.1. Кручение штампом кругового цилиндра 51
2.2. Контактная задача о вдавливании штампа в торец кругового ци-
цилиндра 67
2.3. Контактная задача для предварительно напряженного конечного
цилиндра 79
2.4. Взаимодействие бандажа с цилиндром конечных размеров 87
2.5. Взаимодействие бандажа с предварительно напряженным цилин-
цилиндром конечных размеров 92
Глава 3. Плоские контактные задачи для четырехугольников. ... 97
3.1. Контактные задачи для прямоугольника 97
3.2. Контактная задача для предварительно напряженного прямоуголь-
прямоугольника ПО
3.3. Контактные задачи для кольцевого сектора, кольца и усеченного
клина 118
3.4. Контактная задача для усеченного клина 148
3.5. Точное решение некоторых антиплоских контактных задач для ко-
конечных канонических областей 153
Оглавление
Глава 4. Контактные задачи для сектора сферического слоя, сфе-
сферического слоя, усеченных шара и конуса 158
4.1. Контактные задачи для сектора сферического слоя 158
4.2. Контактная задача для тонкого сферического слоя (сферический
подшипник скольжения) 165
4.3. Контактная задача для усеченного конуса 172
4.4. Контактная задача для усеченного шара 180
Глава 5. Контактные задачи для тел конечных размеров некано-
неканонической формы 183
5.1. Метод однородных решений в контактных задачах для тел некано-
неканонической формы 183
5.2. Контактные задачи для криволинейной трапеции 191
5.3. Вдавливание штампа в плоскую грань криволинейной трапеции . . 198
5.4. Контактная задача для тела вращения с криволинейной образующей 212
5.5. Некоторые выводы 221
Глава 6. Контактные задачи для тел периодической структуры . . 223
6.1. Колебания струны периодической структуры 224
6.2. Динамическая контактная задача для полосы периодической струк-
структуры 225
6.3. Динамическая контактная задача для цилиндра периодической
структуры 237
Глава 7. Контактные задачи для двухслойного полупространства
с учетом сил трения в неизвестной области контакта 245
7.1. Постановка контактных задач 246
7.2. Решение интегральных уравнений 249
7.3. Числовые расчеты 252
Заключение 263
Список литературы 265
Дополнение 287
Предисловие
Монография посвящена обобщению исследований авторов в обла-
области статических и динамических задач контактного взаимодействия
тел сложной конфигурации, неоднородных тел и задач с усложненны-
усложненными условиями в зоне контакта на основе разработанных аналитиче-
аналитических методов. Актуальность темы монографии обусловлена важностью
технических приложений теории контактных взаимодействий, кото-
которая находит широкое применение в машиностроении, строительстве,
электронике и других отраслях человеческой деятельности. Несмотря
на значительный прогресс в этой фундаментальной области знаний,
на практике изучение реальной картины напряженно-деформируемого
состояния в зоне контакта взаимодействующих тел потребовало иссле-
исследования новых контактных задач и разработки новых методов расчета.
Это прежде всего относится к контактным задачам для тел конеч-
конечных размеров канонической и неканонической формы, периодически
неоднородных тел, пространственным контактным задачам и к зада-
задачам с учетом сил трения в области контакта, в том числе с заранее
неизвестной областью контакта. Численные методы в чистом виде во
многих случаях не решают возникающих здесь проблем.
Монография написана при финансовой поддержке Федеральной це-
целевой программы «Интеграция» и Российского фонда фундаменталь-
фундаментальных исследований.
Введение
Исследование проблем контактного взаимодействия в механике
сплошных сред представляет важную задачу науки и техники, от
решения которой во многом зависят успехи в машиностроении, стро-
строительстве, электронике, сейсморазведке, неразрушающем контроле из-
изделий и материалов и в других областях человеческой деятельности.
Кроме того, широкий интерес к задачам контактного взаимодействия
обусловлен не только важностью их технических приложений, но
и внутренней логикой развития этого современного раздела механики
сплошной среды, что в свою очередь является сильнейшим стимулом
развития соответствующих фундаментальных разделов математики.
В математическом плане характерной особенностью задач контакт-
контактного взаимодействия (контактных задач) является то, что они сводятся
к исследованию краевых задач для систем дифференциальных уравне-
уравнений механики сплошной среды со смешанными граничными условиями.
При этом для контактных задач характерно то, что, если рассмат-
рассматриваемая область, занятая какой-либо сплошной средой, ограничена
конечным числом гладких поверхностей (граней), то хотя бы на одной
из этих граней на различных ее участках должны быть сформули-
сформулированы различные граничные условия. Такие задачи также называют
собственно смешанными [253]. А те задачи, когда ни на одной из
граней области условия не являются смешанными, но различны на
разных гранях, называют несобственно смешанными. В дальнейшем
речь будет идти о собственно смешанных задачах.
Исследования по классическим контактным задачам методами ма-
математического моделирования берут свое начало, по всей видимости,
от работ Г. Герца A881 г.), Я. Буссинеска A885 г.), С. А. Чаплыгина
A890), М. А. Садовского A928) и др. Эти исследования получили даль-
дальнейшее развитие в основополагающих трудах В.М. Абрамова, Н.М. Бе-
Беляева, Л.А. Галина, А.Н. Динника, А.Ю. Ишлинского, Н.А. Кильчев-
ского, М.Я. Леонова, А. И. Лурье, В. И. Моссаковского, Н.И. Мусхели-
швили, Д. И. Шермана, И.Я. Штаермана и других. Существенного про-
продвижения в области исследования контактных задач удалось достичь
начиная примерно с 40-х годов XX в. Такая задержка в математическом
развитии теории контактного взаимодействия объясняется недостаточ-
недостаточностью математических средств, применявшихся в прошлом для ее
исследования. В то время как Г. Герц в конце XIX в. располагал лишь
формулами теории потенциала для однородного эллипсоида, начиная
примерно с 30-х годов XX в. в распоряжении ученых оказались эффек-
эффективные методы теории функций комплексного переменного, развитые
Введение
Н.И. Мусхелишвили, его учениками и соратниками, и были получе-
получены фундаментальные результаты в области интегральных уравнений,
теории потенциала и, что особенно важно, в методах интегральных
преобразований.
После бурного старта в середине XX в. теория контактного взаимо-
взаимодействия механики сплошной среды продолжает и в настоящее время
интенсивно развиваться. Показателем этого являются тысячи опуб-
опубликованных работ, десятки защищенных докторских и кандидатских
диссертаций и опубликованных монографий, в том числе и в последние
годы. Так в 2001 г. была опубликована коллективная монография под
редакцией И. И. Воровича и В.М. Александрова [217], содержащая
обзор основных достижений российских исследователей по методам
и результатам решения задач механики контактных взаимодействий за
последние годы.
Ряд монографий и обзорных статей содержат подробное изложение
опубликованных работ по ряду многочисленных направлений теории
контактных взаимодействий. Среди монографий отметим обзорную мо-
монографию под редакцией Л.А. Галина[260], монографии В.М. Алек-
Александрова, Е.В. Коваленко [27], В.М. Александрова, СМ. Мхитаря-
на [35], В.М. Александрова, Д.А. Пожарского [36, 349], В.М. Алек-
Александрова, Б.Л. Ромалиса [37], В.М. Александрова, Б.Н. Сметанина,
Б. В. Соболя [38], Н.Х. Арутюняна, А. В. Манжирова [47], Н.Х. Ар-
утюняна, А. В. Манжирова, В.Э. Наумова [48], В. А. Бабешко [51],
В.А. Бабешко, Е.В. Глушкова, Ж.Ф. Зинченко [57], И.И. Воровича,
В.М. Александрова, В. А. Бабешко [88], И.И. Воровича, В. А. Бабешко
[89], И. И. Воровича, В.А. Бабешко, О. Д. Пряхиной [90], Л.А. Гали-
Галина [106], А. Г. Горшкова, Д. В. Тарлаковского [128], И. Г. Горячевой
[360], И. Г. Горячевой, М.Н. Добычина [123], В.Т. Гринченко [133],
В.Т. Гринченко, А.Ф. Улитко [137], К. Джонсона [142], В. И. Довно-
ровича [144], Н.А. Кильчевского [162], А.И.Лурье [206], В.И. Мос-
саковского, Н.Е. Качаловской, С.С. Голикова [227], B.C. Никишина,
Г. С. Шапиро [232], В. В. Панасюка, М.И. Теплого [240], В.З. Партона,
П. И. Перлина [244], А.Н. Подгорного, П. П. Гонтаровского и др. [246],
Г.Я. Попова [251, 252], В.Б. Поручикова [254], В. Л. Рвачева, B.C. Про-
ценко [265], В.С.Саркисяна [271], В.М. Сеймова[272], М.И. Теплого
[280], Я. С. Уфлянда [288], И. Я. Штаермана [307] и др.
Широко известны обзорные статьи Б.Л. Абрамяна [1], Б. Л. Абра-
Абрамяна, А.Я. Александрова [4], В.М. Александрова [13], B.C. Губенко,
А.Ф. Улитко [138], А.И. Каландия, А.И. Лурье, Г.Ф. Манджавидзе,
В.К. Прокопова, Я.С. Уфлянда [155], Г.Я. Попова, Н.А. Ростовцева
[253], В. Л. Рвачева [264] и др.
Наряду с вышеупомянутыми авторами монографий и обзорных ста-
статей теория контактных взаимодействий развивалась многими другими
исследователями.
Настоящая монография посвящена обобщению исследований авто-
авторов в области статических и динамических задач контактного взаимо-
Введение
действия для тел сложной конфигурации, неоднородных тел и задач
с усложненными условиями в зоне контакта на основе разработанных
аналитических методов.
Не останавливаясь подробно на всех направлениях развития теории
контактных взаимодействий, приведем краткий обзор тех работ, кото-
которые в той или иной мере связаны с тематикой книги.
Контактные задачи условно можно разделить на две большие груп-
группы: контактные задачи для бесконечных и полубесконечных тел (обла-
(областей) и контактные задачи для тел конечных размеров.
Остановимся более подробно на контактных задачах для тел конеч-
конечных размеров и методах их решения. Исследованию смешанных задач
для тел конечных размеров посвящено большое количество работ,
предложено значительное количество методов их решения.
Если оставить в стороне прямые численные методы [45, 222, 225,
226, 245, 350, 353], методы функций комплексной переменной и син-
сингулярных интегральных уравнений [216, 223], то одним из наиболее
распространенных методов решения задач теории упругости для конеч-
конечных и полубесконечных тел со смешанными граничными условиями
является метод однородных решений, получивший свое название в ра-
работах П.А. Шиффа[373] и В.А. Стеклова [277].
Дальнейшее развитие метод получил в работах Л. Файлона [358,
359], П.Ф. Папковича [241-243], Д. Фадле [357], в которых рассмат-
рассматривалась задача о полуполосе и прямоугольнике.
В работе П.Ф. Папковича [242] ставится проблема базиса для
однородных решений, т. е. возможность представления двух граничных
функций в виде рядов по однородным решениям. В работе Г. А. Грин-
Гринберга [130] дано решение для случая, когда на границе пластинки
задан прогиб и изгибающий момент. В общем случае эта проблема
оказалась тесно связана с проблемой двукратной полноты собственных
и присоединенных векторов некоторого дифференциального пучка опе-
операторов.
Впервые исследовал поведение собственных чисел и функций,
а также сходимость разложений по ним для некоторых пучков, по-
порожденных обыкновенными дифференциальными операторами, по-ви-
по-видимому, Я.Д. Тамаркин [279]. Постановка основных задач и первые
важные результаты содержатся в работах М.В. Келдыша [160, 161].
Здесь были введены понятия присоединенных векторов, кратность соб-
собственного числа, кратной полноты собственных и присоединенных век-
векторов. Для некоторого класса пучков, порожденных обыкновенными
дифференциальными операторами были доказаны теоремы о полно-
полноте, асимптотике собственных значений и сходимости кратных разло-
разложений.
Используя свойства исходной эллиптической краевой задачи [193]
и оценку функции Грина [279], важные результаты о полноте и схо-
сходимости кратных разложений были получены М.Г. Джавадовым [139],
И. И. Воровичем, В.Е. Ковальчуком [91].
Введение
Новый этап в развитии спектральной теории пучков связан с рабо-
работами М.Г. Крейна и Г. Лангера [183, 184]. Основываясь на полученных
ими обобщениях известной теоремы Л.С. Понтрягина [250] по теории
индефинитно сопряженных операторов [6, 84], была доказана важная
теорема о полноте кратных разложений. Используя этот результат,
Ю.А. Устинов и В. И. Юдович [287] доказали полноту элементарных
решений в пространстве бигармонических функций с конечной энер-
энергией. Фактически развита более общая теория, включающая, напри-
например, неоднородные по толщине плиты. Среди более поздних работ
отметим М.Г. Гасымова, А.Н. Златина, А.Г. Костюченко, В.В. Лид-
ского, К. С. Мамедова, Г. Мюллера, М.Б. Оразова, Г. В. Разневского,
А.А. Шкаликова, Ю.А. Устинова, С.Я. Якубова и др. [8, 12, 112, 149,
174-176, 192, 212, 239, 261, 262, 285, 286, 306, 346, 368], а также
монографию А. С. Маркуса [207], имеющую обзорный характер.
Кроме работ [160, 161, 183, 184] применительно к задачам меха-
механики поведение собственных чисел исследовалось в работах [88, 150,
192]. Удобные для вычислений асимптотические формулы приводятся
в работе [150].
В дальнейшем идеи П.Ф. Папковича по однородным решени-
решениям получили развитие в работах А. И. Лурье [202, 203, 205, 206],
В.К. Прокопова [256, 257], И.И. Воровича и O.K. Аксентян [10, 11]
и др. Подробную библиографию можно найти в обзорных статьях
[87, 88, 140, 141, 255, 256, 260]
Метод однородных решений применительно к контактным задачам
развивался в работах В.М. Александрова [15], В.М. Александрова и
М.И. Чебакова [39, 42], А.Н. Цветкова и М.И. Чебакова [299-302,
304], М.И. Чебакова [158, 313, 316-318, 321, 326-328, 331].
Другой подход к исследованию граничных задач для тел конечных
размеров, метод суперпозиции, берет свое начало от идеи, высказанной
Ламе [362]. Ламе рассмотрел задачу для параллелепипеда, находяще-
находящегося под действием нормальных нагрузок. Общее решение Ламе строит
в виде суперпозиции трех последовательных частных решений для пе-
периодически нагруженного слоя, обладающей необходимым произволом
для удовлетворения любых граничных условий. Развитие теории беско-
бесконечных систем и появление ЭВМ позволило существенно продвинуться
в этом направлении (Б. Л. Абрамян [2, 3, 5] и X. Сайто [372]).
Теория бесконечных систем линейных алгебраических уравнений
успешно применялась к решению задач теории упругости в работах
Б.М. Кояловича [177], Л. В. Канторовича, Н.Х. Арутюняна и др.
В настоящее время с помощью метода суперпозиции получены
значительные результаты при изучении равновесия и установившихся
колебаний тел конечных размеров [79, 86, 115, 116, 133, 135-137].
Отметим также работу А. В. Белоконя [68], в которой предлагается
новый подход к решению такого рода задач: строя общее решение
аналогично методу суперпозиции, автор вводит в рассмотрение некото-
10 Введение
рую вспомогательную задачу, позволяющую свести решение к системе
интегральных уравнений.
Авторами работ [131, 132, 163, 296] был разработан ряд мето-
методов, основанных на специально сконструированных системах функ-
функций. Подробную библиографию по методу суперпозиции можно найти
в [133, 137].
Метод i^-функций изложен в [265], где продемонстрированы его
широкие возможности в применении к контактным задачам.
В работах [230, 231] развит приближенный аналитический метод —
метод возмущения формы границы, идейная основа которого заложена
в работах А.Н. Гузя. Этот метод применялся к решению краевых задач
для кусочно однородных неканонических областей с поверхностями
раздела, близкими к каноническим.
К настоящему времени существует довольно большой набор ана-
аналитических методов решения собственно смешанных задач для тел
конечных размеров канонической формы. Подробный обзор таких
методов можно найти в [13, 312]. Назовем только некоторые из
них: метод сечения [111], метод парных рядов [17, 19, 40, 58, 59,
187-189, 291-294, 310, 311, 315, 337], метод интегральных урав-
уравнений первого рода с периодическими ядрами [13, 54, 201], метод
кусочно-однородных решений [190, 235-238] и метод однородных ре-
решений [15, 42, 158, 159, 317, 318, 321, 322, 324]. Все указанные
методы сводят задачу к линейной бесконечной алгебраической системе.
В большинстве случаев эти системы оказываются квазивполне или
вполне регулярными, за исключением двух последних методов, которые
сводят задачу к нормальной системе Пуанкаре-Коха.
Многие работы посвящены исследованию контактных задач для об-
областей, ограниченных прямыми линиями. Первая граничная задача для
прямоугольника в общей постановке рассмотрена Б. Л. Абрамяном [2].
Результаты этой работы были использованы В.Н. Акопяном [9] в кон-
контактной задаче о сжатии круглого диска двумя прямоугольниками.
К.С. Чобанян, И.О. Галфаян [ПО, 111, 344] рассмотрели контакт-
контактную задачу для составного упругого прямоугольника и свели задачу
к квазивполне регулярной бесконечной системе. Некоторые контакт-
контактные задачи исследовались в работах Г.М. Валова [82], А. А. Бабло-
яна, И.О. Гулканяна [60], А.А. Баблояна, A.M. Мкртычана [64, 65],
М.Г. Мелконяна, A.M. Мкртычана [215].
Разработке асимптотических методов и их применению к контакт-
контактным задачам для цилиндрических тел посвящена работа В.М. Алек-
Александрова и А. В. Белоконя [23].
Контактные задачи для конечных цилиндров рассматривались в ра-
работах А.А. Баблояна, А. П. Мелконяна [62, 63], А. П. Мелконяна
[213, 214], З.А.Мартиросяна, B.C. Тонояна [209], А.В. Белоконя [68],
А. В. Белоконя, Т. И. Ватульян [69-71], А. В. Белоконя, Е.П. Маликова
[72-74], М.И. Чебакова [311, 317, 327] и других авторов.
Введение 11
В настоящей монографии предлагается развитие схемы, предложен-
предложенной ранее одним из авторов [15], на тела, часть границы которых отли-
отличается от координатной. В этом случае известные методы не позволяют
получить бесконечную систему приемлемого качества, кроме того воз-
возникают проблемы с суммируемостью полученных разложений, поэтому
краевые условия на криволинейной части границы удовлетворяются
приближенно при помощи конечной линейной комбинации однородных
решений, используя такие методы, как метод коллокации, метод наи-
наименьших квадратов или методы наилучшего приближения (методы Ре-
Ремеза). Такая полуаналитическая схема позволяет использовать хорошо
известные результаты для полубесконечных тел и гибкость численных
методов [298-300, 303, 304].
Существует несколько подходов в использовании однородных ре-
решений для удовлетворения краевых условий. Один из них, берущий
начало в работе П.Ф. Папковича [242], использует соотношение обоб-
обобщенной ортогональности [147, 173, 258, 274, 321], при этом для неко-
некоторых краевых условий можно получить явное разложение, в общем
случае задача сводится к решению бесконечной системы [258, 260].
К бесконечной системе сводится задача и при использовании соответ-
соответствующих вариационных принципов [222, 226].
Если ограничиться конечным числом однородных решений, то кра-
краевым условиям можно удовлетворить приближенно, используя вариа-
вариационные принципы [222] или прямые численные методы: коллокации,
наименьших квадратов [196, 224, 299, 300, 302-304], метод Галеркина
и т. п.
Идея использования минимизации квадратичной погрешности в
краевых условиях встречается в работах Ф. Тольке [374], И. Фадле
[357] и В. Кепке [361].
Используя метод коллокации, Д.Ю. Айзенберг и Г. С. Шапиро [7]
решили задачу о передаче давления через слой со свободным круговым
отверстием. Основное достоинство метода коллокации — простота. Он
достаточно хорошо работает на координатных поверхностях. Вместе
с тем, он весьма неустойчив по выбору точек. На этот факт обращали
внимание многие авторы [7, 134].
Область применимости метода наименьших квадратов шире, однако
он требует дополнительных затрат на вычисление интегралов по бо-
боковой поверхности, кроме того, возникающие при его использовании
острые всплески невязок, имеющие порядок решения, физически труд-
трудно интерпретировать.
Использование однородных решений для удовлетворения краевым
условиям на поверхностях, достаточно сильно отличных от коорди-
координатных, требует привлечения более сложных методов аппроксима-
аппроксимации [49, 170, 194, 268, 355, 356, 370].
Краевую задачу мы будем сводить к переопределенной системе Че-
бышева или к задаче о наилучшем приближении на компакте, которую
будем решать методом Ремеза [267-270].
12 Введение
Основа теории приближения была заложена в трудах П. Д. Чебыше-
ва, дальнейшее развитие связано с именем С.Н. Берштейна, Д. Джек-
Джексона, А.Н. Колмогорова, П. С. Урысона [49, 356, 363, 370].
Алгоритмические основы теории впервые были рассмотрены
Е.Я. Ремезом [267-270], более поздние результаты содержатся
в работах [49, 148, 152, 153, 170, 233, 234, 281, 351, 355, 363, 365-367,
369-371, 375, 376].
Контактные задачи для тел периодической структуры с неперио-
непериодическим нагружением имеют значительно меньшую библиографию.
Здесь следует отметить работы М.Л. Бурышкина и его композици-
композиционный метод [80, 81]. Задачам механики сплошной среды для об-
областей периодической структуры, в том числе и о распростране-
распространении волн в телах и волноводах периодической структуры, посвяще-
посвящены работы Л. Бриллюэна, М. Пароди [78], Л.А. Вайнштейна [83],
В. В. Владимирского [85], И. И. Воровича, Л. В. Кучерова, М.И. Чеба-
кова [92, 94-96], М.И. Чебакова [320, 334, 341], И.М. Гельфанда
[114], М.В.Дьякова, Ю.А.Устинова [146], В. И. Короза, Е.С. Сухов-
ского [171], П.Е. Краснушкина [181], П.Е. Краснушкина, С.П.Ломне-
ва [182], М.Г. Крейна, Г.Я. Любарского [185], Р. Кристенсена [186],
Л.И. Слепяна [273], Е.С. Суховского [278], Ю.А. Устинова [284],
В. А. Якубовича, В.М. Старжинского [347, 348], и др.
Большое внимание исследователей привлекали контактные задачи
для тел, имеющих угловые точки или линии (клин, конус, линза
и т.п.). Подробный обзор работ этого направления опубликован в ра-
работе Д. А. Пожарского [248].
В последние годы значительное развитие получили исследования
по контактным задачам с учетом сил трения, износа и тепловыделе-
тепловыделения от трения. По этому направлению следует отметить исследования
В.М. Александрова, Л.А. Галина, И.Г. Горячевой, Д.В. Грилицкого,
М.Н. Добычина, Ю.Н.Дроздова, Е.В.Коваленко, М.В. Коровчинского,
A. С. Кравчука, Н.В. Крагельского, Р. И. Мазинга, Д.А. Пожарского,
А.А.Спектора и др., опубликованные в работах [21, 25, 28-32, 34, 102,
103, 106-109, 117-124, 126, 127, 143, 145, 154, 166, 167, 169, 180, 220,
221, 283] и др. Детальный обзор работ этого направления содержится
в статьях И. Г. Горячевой, И. А. Солдатенкова [125], Е.В. Коваленко
[165], А.С.Кравчука [178].
Исследованию контактных задач для предварительно напряженных
тел также посвящено большое количество исследований, подробный
обзор которых в статическом случае можно найти в работе Т. И. Бе-
лянковой и Л.М. Филипповой [75], а в случае динамики — в работе
B. В. Калинчука [156]
Настоящая монография посвящена разработке и развитию аналити-
аналитических и численно-аналитических методов исследования статических
и динамических контактных задач для тел сложной конфигурации,
неоднородных тел и контактных задач с усложненными условиями
в зоне контакта. На основе этих методов исследован широкий класс
Введение 13
задач для тел ограниченных размеров классической формы, гранич-
граничные поверхности которых совпадают с координатными поверхностями
распространенных ортогональных систем координат: декартовых, ци-
цилиндрических, полярных, сферических, биполярных и бисферических.
Исследован также ряд контактных задач для ограниченных тел нека-
неканонической формы, когда часть граничных поверхностей не совпадает
с координатными поверхностями. Исследованы некоторые квази-перио-
дические задачи, когда геометрия упругого тела или его механические
свойства имеют периодическую структуру, а нагружения таковыми не
являются. Исследован ряд пространственных задач о взаимодействии
штампа со слоистым полупространством с учетом сил трения в области
контакта.
Большое внимание в монографии уделено разработке новых и раз-
развитию известных аналитических и численно-аналитических методов
перечисленных выше задач. Основными из них являются: 1) метод
сведения парных интегральных уравнений (ИУ) и парных рядов-урав-
рядов-уравнений к бесконечным системам линейных алгебраических уравнений
(БСЛАУ) первого рода с сингулярной матрицей; специальный способ
решения этих систем; 2) метод однородных решений применительно
к телам конечных размеров канонической и неканонической формы;
3) метод сведения парных интегральных уравнений к ИУ 1-го и 2-го
рода с разностным ядром; 4) метод больших Л, построение всех членов
разложения с помощью алгебраических рекуррентных соотношений;
5) метод малых Л построения решения парных уравнений; 6) ме-
метод переходных операторов построения решения задач о возбуждении
и распространении колебаний в волноводах периодической структуры.
Изложим кратко содержание книги.
Книга состоит из семи глав, заключения и списка цитированной
литературы.
Глава 1 посвящена постановке контактных задач, некоторым общим
методам решения уравнений и выводу некоторых соотношений обоб-
обобщенной ортогональности однородных решений теории упругости.
В § 1.1 этой главы дается краткая постановка контактных задач
для тел конечных размеров канонической формы для цилиндра, пря-
прямоугольника, кольцевого сектора, кольца, усеченного клина, сектора
сферического слоя, сферического слоя и усеченного конуса (п. 1.1.1),
контактных задач для тел конечных размеров неканонической формы
в виде криволинейной трапеции и тела вращения с криволинейной
образующей (п. 1.1.2), динамических контактных задач для слоя и ци-
цилиндра периодической структуры (п. 1.1.3), пространственных контакт-
контактных задач для слоя, лежащего на жестком основании или на упругом
полупространстве с учетом сил трения в зоне контакта (п. 1.1.4).
В § 1.2 излагается метод решения парных рядов-уравнений, к ко-
которым сводятся некоторые рассмотренные в монографии задачи, путем
сведения их к БСЛАУ первого рода с сингулярной матрицей коэффици-
коэффициентов. Излагается также два подхода получения приближенного реше-
14 Введение
ния бесконечных систем: первый подход основан на сведении к системе
второго рода путем выделения и обращения главной сингулярной со-
составляющей матрицы коэффициентов (п. 1.2.1), второй подход основан
на сведении их к конечной системе с учетом знания асимптотического
поведения решения систем (п. 1.2.2).
В § 1.3 дается решение ИУ первого и второго рода, к которым сво-
сводятся некоторые рассматриваемые контактные задачи, методом боль-
больших Л с построением всех членов их решения разложением в ряд
по отрицательным степеням безразмерного параметра Л с помощью
простейших рекуррентных соотношений.
В § 1.4 приводится точное решение ИУ, соответствующих сдвиго-
сдвиговым контактным задачам для тел конечных размеров канонической
формы, в форме, содержащей эллиптические функции Якоби.
В § 1.5 получены значения некоторых интегралов от решений ос-
основных задач об установившихся колебаниях слоя, сферического слоя
и кольцевого слоя в форме, содержащей граничные значения перемеще-
перемещений и напряжений. Эти интегралы используются при решении контакт-
контактных задач методом однородных решений. В случае, когда граничные
условия являются однородными, эти интегралы дают соответствующие
соотношения обобщенной ортогональности однородных решений.
Глава 2 посвящена решению осесимметричных контактных задач
для цилиндрических тел конечных размеров канонической формы, ко-
когда штамп воздействует на плоскую или цилиндрическую части их гра-
границы. Для решения задач применяется метод сведения парных рядов-
уравнений к БСЛАУ первого рода с сингулярной матрицей с последу-
последующей регуляризацией (п. 1.2.1) и метод однородных решений. Метод
однородных решений позволяет свести задачи к решению БСЛАУ
второго рода типа Пуанкаре-Коха с экспоненциально убывающими
элементами матрицы и правой части и хорошо изученным ИУ для слоя
с различными правыми частями. Как известно, решение таких беско-
бесконечных систем может быть получено при любых значениях параметров
методом редукции.
В §2.1 рассмотрены указанными выше методами две задачи (С\
и С2) о кручении цилиндра штампом, закрепленным на плоской поверх-
поверхности, противоположная поверхность которого закреплена, а боковая
поверхность свободна или закреплена. Произведен расчет при различ-
различных значениях параметров задач, обнаружено согласование результа-
результатов, полученных обоими методами. В совокупности методы дополняют
друг друга и позволяют полностью исследовать задачи. Эти задачи
можно рассматривать как модельные, так и имеющие самостоятельный
практический и теоретический интерес.
В § 2.2 этими же методами рассмотрена задача Сз о вдавливании
штампа в плоскую грань цилиндра. Произведен расчет контактных на-
напряжений под штампом и так называемой жесткости системы штамп-
цилиндр, т. е. зависимости вертикального перемещения штампа от ве-
величины действующей на него силы. Показано, что боковая поверхность
Введение 15
оказывает преимущественное влияние на распределение контактных
напряжений на краю штампа (для задач С\ и С^ это также характерно).
Обнаружена немонотонная зависимость жесткости от относительного
удаления боковой поверхности от края штампа, которая вначале рас-
растет, а затем убывает, приближаясь к решению для слоя. При этом,
естественно, другие параметры задачи остаются неизменными.
В § 2.3 исследована методом сведения парных рядов-уравнений к
БСЛАУ первого рода задача С\ о внедрении штампа в плоскую грань
предварительно напряженного в радиальном направлении цилиндра.
Здесь также произведен расчет контактных напряжений и жесткости
системы штамп-цилиндр при различных значениях параметров задачи,
в т.ч. и параметра предварительного напряжения.
В § 2.4 рассмотрена этим же методом симметричная задача С§
о взаимодействии бандажа с цилиндрической поверхностью полого ци-
цилиндра, в § 2.5 рассмотрена задача С$ для предварительно напряжен-
напряженного в осевом направлении сплошного цилиндра. Произведен расчет
контактных напряжений и жесткости системы штамп-бандаж.
Глава 3 посвящена исследованию контактных задач для упругих тел
канонической формы, имеющих в сечении форму четырехугольников
в декартовой или полярной системах координат. Для решения этих
задач будут использованы метод сведения парных рядов-уравнений к
БСЛАУ первого рода с сингулярной матрицей коэффициентов, метод
однородных решений и асимптотический метод больших Л.
В §3.1 в декартовой системе координат рассмотрены контактные
задачи Q\, Q^ и Q% для прямоугольника о вертикальном воздействии
штампа без трения на одну из его граней, смежные грани находятся
в условиях скользящей заделки. В задачах Q\ и Q^ противополож-
противоположная грань соответственно лежит без трения на жестком основании
или жестко защемлена, а штамп расположен симметрично. Эти зада-
задачи исследуются с помощью методов сведения парных рядов-уравне-
рядов-уравнений к БСЛАУ первого рода с сингулярной матрицей коэффициентов
и асимптотическим методом больших Л. В задаче Q% штамп располо-
расположен несимметрично и для исследования использован метод однород-
однородных решений. Произведен расчет контактных напряжений и жесткости
системы штамп-прямоугольник. Здесь также как и для задачи С% об-
обнаружена аналогичная немонотонная зависимость жесткости системы
штамп-прямоугольник относительного расстояния боковой грани от
края штампа, при этом немонотонность более ярко выражена при боль-
больших значениях коэффициента Пуассона. Также показано, что влияние
боковой грани затухает обратно пропорционально величине этого рас-
расстояния для задачи Q\ и по экспоненциальному закону для задачи Q^.
В § 3.2 рассмотрена задача Q\ для предварительно напряженного
прямоугольника методом сведения парных рядов-уравнений к БСЛАУ
первого рода с сингулярной матрицей коэффициентов. Граничные усло-
условия для добавочного напряженно-деформированного состояния такие
же, как и в задаче Q\. Для решения БСЛАУ использовался метод ре-
16 Введение
гуляризации. Здесь также произведен расчет контактных напряжений
и жесткости системы штамп-прямоугольник.
В § 3.3 в полярных координатах рассмотрены контактные задачи
для таких областей как кольцевой сектор, усеченный клин и кольцо.
Использовались метод сведения парных рядов-уравнений к БСЛАУ и
метод однородных решений.
Методом сведения парных рядов-уравнений к БСЛАУ первого рода
с сингулярной матрицей коэффициентов рассмотрена задача Q$ для
кольцевого сектора, когда штамп несимметрично вдавливается в ци-
цилиндрическую поверхность. По постановке задача аналогична зада-
задаче Eз для прямоугольника. Методом однородных решений исследована
аналогичная симметричная задача Qq для кольцевого сектора. Произ-
Произведен расчет контактных напряжений и жесткости системы штамп-
кольцевой сектор. Здесь также, как и для задач Сз, Q\ и Q2, об-
обнаружена аналогичная немонотонная зависимость жесткости системы
штамп-прямоугольник от относительного расстояния боковой грани
от края штампа. Кроме того для задачи Q$ показано, что возможно
такое несимметричное расположение штампа, когда момент контактных
напряжений под штампом будет равен нулю.
Рассмотрена также обобщенно-периодическая контактная задача Qj
для кольца, когда на ее внешней поверхности периодически располо-
расположено несколько штампов и при этом один из штампов перемещается
в направлении радиуса к центру кольца, а другие неподвижны. Для
решения такой задачи используется подход М. Л. Бурышкина. Согласно
этому подходу задача сводится к ряду периодических задач типа Qq,
которые решаются методом сведения парного ряда-уравнения к БСЛАУ
первого рода с сингулярной матрицей коэффициентов. Подробно ис-
исследован случай четырех штампов. Произведен под каждым штампом
расчет контактных напряжений, вектора и момента контактных напря-
напряжений.
Проведено исследование двух контактных задач Qs и Qg для тон-
тонкого кольцевого слоя о взаимодействии с его внутренней поверхно-
поверхностью штампа в форме цилиндра близкого радиуса. Рассматриваются
случаи, когда внешняя поверхность закреплена или взаимодействует
с гладкой жесткой обоймой. Такие задачи хорошо моделируют работу
цилиндрического подшипника. Для решения задач используется метод
сведения парных рядов к БСЛАУ с сингулярной матрицей с после-
последующим получением их асимптотического решения при относительно
малых толщинах кольцевого слоя.
В § 3.4 методом однородных решений исследована контактная зада-
задача Qiq о сдвиге штампом усеченного плоского клина. Задача сведена
к решению бесконечной системы второго рода высокого качества ти-
типа систем Пуанкаре-Коха с экспоненциально убывающими элемента-
элементами матрицы и правой части. Задача имеет самостоятельный интерес
и в тоже время может служить моделью для значительно более слож-
сложных задач.
Введение 17
В § 3.5 на основе точных решений ИУ первого рода, содержащих
в качестве ядер эллиптические функции Якоби (см. § 1.4), получено
точное решение контактных задач теории упругости о чистом сдвиге
штампом (в общем случае деформируемым) цилиндрического тела,
представляющего собой в сечении область, ограниченную координат-
координатными линиями ортогональной линейной системы координат на плоско-
плоскости, коэффициенты Ламе которой удовлетворяют некоторым условиям.
Сюда относятся декартовы, полярные, биполярные, параболические,
гиперболические и др. координаты. Подробнее в биполярных координа-
координатах рассмотрены контактные задачи Qn, Qu для усеченной луночки.
Решения задач этого пункта представляют не только самостоятельный
интерес, но служат основой для решения контактных задач о внедре-
внедрении штампов в поверхности таких же тел путем выделения и обраще-
обращения главных частей ядер соответствующих ИУ.
Глава 4 посвящена решению контактных задач в сферических коор-
координатах для сектора сферического слоя, сферического слоя и усечен-
усеченного конуса и в бисферических координатах для усеченного шара.
В §4.1 рассматриваются две контактные задачи для сектора сфе-
сферического слоя: задача S\ о кручении сектора сферического слоя
штампом, симметрично расположенным на сферической поверхности,
и задача S^ о симметричном вдавливании штампа в сферическую
поверхность. Для решения задач используется метод однородных ре-
решений, который здесь также позволил свести задачи к бесконечным
системам линейных алгебраических уравнений типа Пуанкаре-Коха
и соответствующим ИУ для сферического слоя.
В § 4.2 рассматривается задача теории упругости S% о взаимодей-
взаимодействии шара с внутренней поверхностью сферического упругого слоя,
внешняя поверхность которого жестко закреплена. Такая задача до-
достаточно хорошо моделирует работу сферического самосмазывающего
подшипника, особенно при нагрузках, когда размер площадки контакта
соизмерим с шириной подшипника. Для решения используется метод
сведения парного ряда-уравнения к БСЛАУ первого рода с сингуляр-
сингулярной матрицей коэффициентов. Предполагая, что толщина слоя мала,
а радиусы шара и внутренней сферы слоя близки, получено асимптоти-
асимптотическое решение БСЛАУ. В результате получены простые удобные для
инженерных расчетов формулы для контактных напряжений, размера
области контакта и жесткости системы штамп-сферический слой.
В § 4.3 в отличии от 4.1 рассмотрена в сферической системе коорди-
координат контактная осесимметричная задача S± о кручении штампом тела
конечных размеров, ограниченного конической и двумя сферическими
поверхностями. Здесь предполагается, что сферические поверхности
неподвижны, а на конической поверхности осесимметрично жестко
закреплен штамп (бандаж) постоянной ширины, находящийся под дей-
действием крутящегося момента. Для исследования задачи используется
метод однородных решений, что позволяет свести ее к решаемой при
любых значениях параметров бесконечной системе линейных алгебра-
18 Введение
ических уравнений типа нормальных систем Пуанкаре-Коха. Произ-
Произведен расчет контактных напряжений и жесткости системы бандаж-
усеченный конус при некоторых значениях параметров, произведено
сравнение в частных случаях с результатами, полученными другими
способами, в том числе и авторами монографии.
В § 4.4 рассмотрена осесимметричная контактная задача теории
упругости ^5 о кручении усеченного шара жестко прикрепленным
к его плоской границе круговым цилиндрическим штампом. При этом
сферическая часть поверхности шара неподвижна. Построено решение
задачи методом больших Л, изложенным в § 1.3, для случая, когда
радиус штампа в достаточной мере меньше радиуса среза шара. Произ-
Произведен расчет контактных напряжений, результаты хорошо согласуются
в частных случаях с известными результатами, полученными другими
способами, в том числе и авторами монографии.
Глава 5 посвящена развитию метода однородных решений в кон-
контактных задачах для тел конечных размеров сложной неканонической
формы. Показывается, что использование однородных решений на кри-
кривых, отличных от координатных, требует привлечения существенно
более сложных численных методов, в частности, алгоритмов Ремеза
нахождения наилучшего приближения. Исследованы в декартовых ко-
координатах контактные задачи для конечного тела в форме криволиней-
криволинейной трапеции (задачи N\, ЛГ2, ЛГ3) и в цилиндрических координатах для
конечного тела вращения с криволинейной образующей (задача 7V4).
Параграф 5.1 посвящен развитию метода однородных решений
в контактных задачах для тел конечных размеров сложной неканони-
неканонической формы. Дается общая постановка задач, приводится описание
схемы метода. Показывается, что метод однородных решений может
быть с успехом применен к широкому классу существенно смешанных
задач для тел, часть границы которых совпадает с парой координатных
поверхностей канонической системы координат, на которой задаются
смешанные граничные условия, а другая часть границы задается доста-
достаточно произвольно, и на ней ставятся несмешанные граничные условия.
Дается сравнительная характеристика эффективности и границ приме-
применимости различных численных методов для удовлетворения краевым
условиям при помощи однородных решений, отмечаются трудности,
возникающие при использовании методов коллокации и наименьших
квадратов, показываются преимущества использования методов Ремеза
первого и второго рода.
Параграф 5.2 посвящен решению контактной задачи о чистом сдви-
сдвиге бесконечного цилиндрического тела, имеющего сечением симмет-
симметричную криволинейную трапецию, одно из оснований которой сдвига-
сдвигается полосовым штампом, другое защемлено. Задача рассматривается
в двух вариантах, когда криволинейная часть границы свободна (зада-
(задача N\) и защемлена (задача N2). Обсуждаются численные результаты,
показывается высокая эффективность метода в широком диапазоне
параметров. Прослеживаются переходы полученного решения к вырож-
Введение 19
денному и к решению для слоя. Здесь под вырожденным понимается
решение несмешанной задачи о чистом сдвиге прямоугольника. Ис-
Исследуется напряженное состояние внутри области, занимаемой телом,
строятся диаграммы линий постоянных смещений.
В § 5.3 рассматривается плоская контактная задача Щ для криволи-
криволинейной трапеции, в верхнее основание которой вдавливается плоский
штамп, нижнее лежит без трения на гладкой плоской поверхности.
Криволинейная часть границы свободна от напряжений. Обсуждают-
Обсуждаются вычислительные аспекты получения неоднородного решения, для
которого получены выражения, эффективные во всей области, занима-
занимаемой телом. Следы вертикальных смещений однородных решений под
штампом имеют осцилляции, количество которых растет с увеличением
номера однородных решений. Поэтому существующие методы реше-
решения интегрального уравнения недостаточно эффективны. Предлагает-
Предлагается эффективная численная схема решения интегрального уравнения
контактной задачи с осциллирующей правой частью, основанная на
известных спектральных соотношениях для многочленов Чебышева
и алгоритме Ремеза. Обсуждаются численные результаты, показывает-
показывается эффективность предложенного метода. Прослеживаются переходы
полученного решения к вырожденному, соответствующему однородной
деформации прямоугольника, и к решению для слоя.
В § 5.4 рассматривается осесимметричная контактная задача 7V4 для
тела вращения с плоскими основаниями, в одно из которых вдавлива-
вдавливается плоский штамп, а другое без трения лежит на гладкой плоскости.
На боковой поверхности, задаваемой достаточно произвольной образу-
образующей, отсутствуют напряжения. Обсуждаются вопросы эффективной
численной реализации всей схемы в целом. Приводятся выражения
для неоднородного решения эффективные во всей области, занимаемой
телом. Для решения ИУ используется схема, предложенная в § 5.3.
Дается анализ полученных численных результатов.
Параграф 5.5 содержит некоторые выводы, связанные с использова-
использованием различных численных методов удовлетворения краевым условиям
на кривых, отличных от координатных, при помощи конечной линейной
комбинации однородных решений.
В гл. 6 приводятся результаты, полученные при исследовании стаци-
стационарных задач о возбуждении штампом колебаний в полуограниченных
телах (волноводах) типа цилиндра и полосы с периодически изменяю-
изменяющимися механическими свойствами вдоль продольной координаты. От-
Отрезок рассматриваемых волноводов, соответствующий минимальному
периоду изменения механических свойств, может состоять из любого
количества однородных областей (конечные цилиндры или прямоуголь-
прямоугольники) различной длины с различными упругими постоянными. Для
исследования этих задач был разработан эффективный метод, основан-
основанный на построении специального оператора перехода, который позволя-
позволяет по значениям вектора перемещений и тензора напряжений на одном
поперечном сечении волновода находить их значения на другом попе-
20 Введение
речном сечении, отстоящем от первого на расстоянии, равном величине
минимального периода изменения свойств волновода. С помощью этого
метода удалось получить ряд результатов, связанных с особенностью
распространения колебаний в таких волноводах. Показано, например,
что для таких волноводов на всем бесконечном интервале изменения
частот существуют чередующиеся конечные интервалы, когда колеба-
колебания в волноводе при удалении от источника затухают (волновод за-
заперт) или распространяются (волновод открыт) соответственно. На ос-
основе анализа уравнения движения массивного штампа показано, что
на промежутках запирания волновода существуют В-резонансы, т. е.
амплитуда колебаний массивного штампа, закрепленного на полосе,
при конечных нагрузках становится бесконечной.
В §6.1 в качестве модельной рассмотрена задача о колебаниях
струны с периодическим изменением плотности, лежащей на винкле-
ровском основании. На примере этой простейшей задачи изложен пред-
предлагаемый подход к решению задач для упругих тел, имеющих периоди-
периодическую структуру своих механических и геометрических свойств при
условии, что геометрия приложения внешнего воздействия не носит
периодического характера.
В § 6.2 рассмотрена задача теории упругости Р\ об установившихся
антиплоских колебаниях штампа на поверхности полосы с продольной
кусочно-однородной периодической структурой механических характе-
характеристик. Отрезок волновода, соответствующий минимальному периоду
изменения свойств, может состоять из любого количества однородных
областей (прямоугольников) с различными механическими параметра-
параметрами. Построено интегральное уравнение задачи и построено его ре-
решение методом больших Л. Показано, что на интервалах запирания
волновода ядро интегрального уравнения действительнозначно.
В § 6.3 аналогично рассмотрена стационарная контактная задача
теории упругости Р% о возбуждении жестким бандажом крутильных
колебаний в круговом бесконечном цилиндре. В цилиндре задано пе-
периодическое изменение механических свойств вдоль оси, в попереч-
поперечном направлении эти свойства не изменяются. Отрезок волновода,
соответствующий минимальному периоду изменения свойств, также
может состоять из любого количества однородных областей (конечных
цилиндров) с различными механическими параметрами. Здесь также
построено интегральное уравнение задачи и показано, что на интерва-
интервалах запирания волновода ядро интегрального уравнения действитель-
действительнозначно.
В гл. 7 рассматриваются трехмерные контактные задачи теории
упругости о действии штампа произвольной формы на поверхность
слоя конечной толщины, лежащего на упругом полупространстве с дру-
другими упругими постоянными. Зона контакта предполагается заранее
неизвестной и зависящей от величины действующих на штамп нор-
нормальной и тангенциальной сил. Предполагается также, что между
штампом и слоем имеют место силы кулоновского трения, которые
Введение 21
коллинеарны направлению действия тангенциальной силы. Штамп не
поворачивается в процессе взаимодействия. Вне штампа поверхность
слоя свободна от напряжений, а на другой поверхности слоя заданы
условия жесткого соединения слоя с упругим полупространством (зада-
(задача Li) или условия равенства нормальных напряжений и перемещений
в слое и полупространстве и равенства нулю касательных напряже-
напряжений в слое и полупространстве (задача L^). Рассматривается случай
предельного равновесия, случай квазистатического движения штампа
по поверхности слоя в подвижной системе координат может быть рас-
рассмотрен аналогично. Получены ИУ, для решения которых использован
метод нелинейных граничных ИУ. Исследовано влияние коэффициента
трения Кулона, формы штампа, упругих констант и толщины слоя
на величину контактных напряжений, на зависимость вертикального
перемещения штампа от вдавливающей силы, на величину и форму об-
области контакта и на перемещение точек поверхности слоя вне области
контакта. Получен важный результат о влиянии коэффициента Пуассо-
Пуассона слоя на перемещение точек поверхности слоя вне области контакта
и положение области контакта. При малых значениях коэффициента
Пуассона зона контакта, как показывают расчеты, смещается в проти-
противоположном направлении действия касательной силы, а при больших —
в направлении действия этой силы. При больших значениях коэффи-
коэффициента Пуассона поверхность слоя вне области контакта в некоторой
ее окрестности в направлении действия касательной силы выше, чем
в симметричных точках относительно точки первоначального касания.
При малых значениях коэффициента Пуассона картина деформации по-
поверхности меняется на противоположную. Такая асимметрия в переме-
перемещении точек поверхности увеличивается с увеличением коэффициента
трения и увеличением жесткости полупространства. Более детально
рассмотрен случай, когда слой взаимодействует с абсолютно жестким
основанием (соответственно задачи Ь% и L4).
Глава 1
ПОСТАНОВКА КОНТАКТНЫХ ЗАДАЧ,
НЕКОТОРЫЕ ОБЩИЕ МЕТОДЫ РЕШЕНИЯ
УРАВНЕНИЙ И ДРУГИЕ ВСПОМОГАТЕЛЬНЫЕ
РЕЗУЛЬТАТЫ
В этой главе дается краткая постановка рассматриваемых в книге
контактных задач теории упругости и излагаются некоторые общие
методы решения интегральных уравнений, парных рядов-уравнений
и бесконечных систем, к которым сводятся поставленные контактные
задачи, а также некоторые другие результаты, имеющие общий харак-
характер.
1.1. Постановка контактных задач
Рассматриваемые в монографии контактные задачи можно условно
разделить на четыре группы в соответствии с геометрией взаимодей-
взаимодействующих со штампом упругих тел.
К первой группе относятся контактные задачи для тел конечных
размеров канонической формы, граничные поверхности которых сов-
совпадают с координатными поверхностями цилиндрических, декартовых,
полярных, биполярных и сферических координат. Ко второй группе от-
относятся контактные задачи для тел конечных размеров неканонической
формы, когда часть граничных поверхностей не является координатной
поверхностью (декартовы и цилиндрические координаты). К третьей
группе относятся контактные задачи для полубесконечных тел (полоса,
цилиндр) периодической структуры. И к четвертой группе относятся
плоская и пространственные контактные задачи для слоя.
Отметим, что в рассматриваемых задачах обычно задан характер
и величина перемещения штампа и требуется, как правило, определить
распределение контактных напряжений в области контакта, область
контакта (если она не задана), связь между перемещением штампа
и приложенными к нему нагрузками в зависимости от параметров
задач. Для отдельных задач проводилось исследование и других зави-
зависимостей механического и геометрического характера, например, таких
/./. Постановка контактных задач 23
как деформация поверхности упругих тел вне штампа, В-резонансы
и других.
1.1.1. Контактные задачи для тел конечных размеров канони-
канонической формы. В цилиндрических координатах (г, ср, z) рассмотрены
осесимметричные контактные задачи для цилиндра, когда штампы
взаимодействуют, либо с плоской либо с цилиндрической его поверх-
поверхностью.
Задачи С\, С% Пусть абсолютно жесткий штамп закреплен в об-
области г ^ а поверхности z = h упругого цилиндра г ^ R, О ^ z ^
^ h (a < R) и поворачивается на некоторый угол 5 приложенным
к штампу моментом. При этом поверхность цилиндра z = 0 закреплена,
вне штампа поверхность z = h свободна от напряжений, а поверхность
г = R либо закреплена (задача С\), либо свободна от напряжений
(задача С^) (см. рис. 2.1 на стр. 51).
Задача С%. Рассматривается тот же цилиндр и в его поверхность
z = h в области г ^ а вдавливается штамп, трение между штампом
и цилиндром отсутствует, поверхность цилиндра z = 0 лежит без
трения на жестком основании, а на боковой поверхности г = R заданы
условия отсутствия нормальных перемещений и касательных напряже-
напряжений (см. рис. 2.4 на стр. 68).
Задача С\. Пусть круговой цилиндр г ^ R, \z\ ^ h из нелинейно-
упругого изотропного несжимаемого материала равномерно сжат или
растянут силами, приложенными к боковой поверхности г = R. Торцы
цилиндра свободны от нагрузки. На описанную однородную конечную
деформацию накладывается малая деформация, обусловленная внед-
внедрением в торцы цилиндра при г ^ а двух симметрично расположен-
расположенных круговых штампов. Трение между штампами и упругим телом
отсутствует, а на боковой поверхности цилиндра г = R заданы усло-
условия отсутствия касательных напряжений и нормальных перемещений
(см. рис. 2.6 на стр. 79). В силу предположений о малости добавочной
деформации контактная задача рассматривается в линеаризованной
постановке.
Задача С$. На внешнюю поверхность полого цилиндра \z\ ^b, R\ ^
^ г ^ i?2 симметрично насажен жесткий бандаж длины 2а в области
\z\ ^ а < Ъ с внутренним радиусом R^ — 5(z), а торцы цилиндра взаимо-
взаимодействуют с жесткой плоской опорой. Будем считать, что трение между
бандажом и цилиндром, торцевой опорой и цилиндром отсутствует
(см. рис. 2.8 на стр. 87).
Задача С§. Рассматривается сплошной круговой цилиндр г ^ R,
\z\ ^ Ъ из нелинейного упругого изотропного несжимаемого материала.
Цилиндр предварительно подвергнут однородному осевому растяже-
растяжению или сжатию и закреплен торцами между гладкими жесткими по-
поверхностями таким образом, что отсутствуют нормальные перемещения
и трение. На описанную деформацию, которая считается конечной,
накладывается малая осесимметричная деформация, вызванная внедре-
24 Гл. 1. Постановка контактных задач, некоторые общие методы
нием в поверхность цилиндра при \z\ < а жесткого бандажа, при этом
трение между цилиндром и бандажом отсутствует, а бандаж имеет
радиус R-6, E > 0) (см. рис. 2.10 на стр. 92).
В декартовой системе координат (х, у, z) рассмотрены некоторые
плоские контактные задачи для прямоугольника.
Задачи Q\, Q^. Рассмотрены две симметричные контактные задачи
о действии штампа без трения на поверхность у = h прямоугольника
\х\ < Ь, 0 < у < h на отрезке \х\ < а < Ъ. На поверхностях \х\ = Ъ
заданы условия отсутствия нормальных перемещений и касательных
напряжений, а поверхность у = 0 либо закреплена (задача Q\), либо
лежит без трения на жестком основании (задача Q2) (см. рис. 3.1 на
стр. 97).
Задача Q%. Отдельно другим методом рассмотрена аналогичная за-
задаче Q2 несимметричная контактная задача для прямоугольника —Ъ ^
^ж^с, О^уОо действии штампа на отрезке \х\ ^ а < min (a, b)
(см. рис. 3.4 на стр. 104).
Задача Q4. Рассматривается плоская задача теории упругости
о взаимодействии штампа с гранью у = h прямоугольника \х\ ^ Ь, 0 ^
^ у ^ h, в котором создано однородное поле начальных напряжений.
На смежных гранях х = ±6 прямоугольника заданы условия отсут-
отсутствия нормальных перемещений и касательных напряжений, проти-
противоположная грань у = 0 лежит без трения на жестком основании
(см. рис. 3.5 на стр. 111). Для описания свойств упругого тела исполь-
используется модель нелинейного несжимаемого изотропного материала.
В полярных координатах г, (р рассмотрены контактные задачи для
сектора кольцевого слоя, кольцевого слоя и усеченного клина.
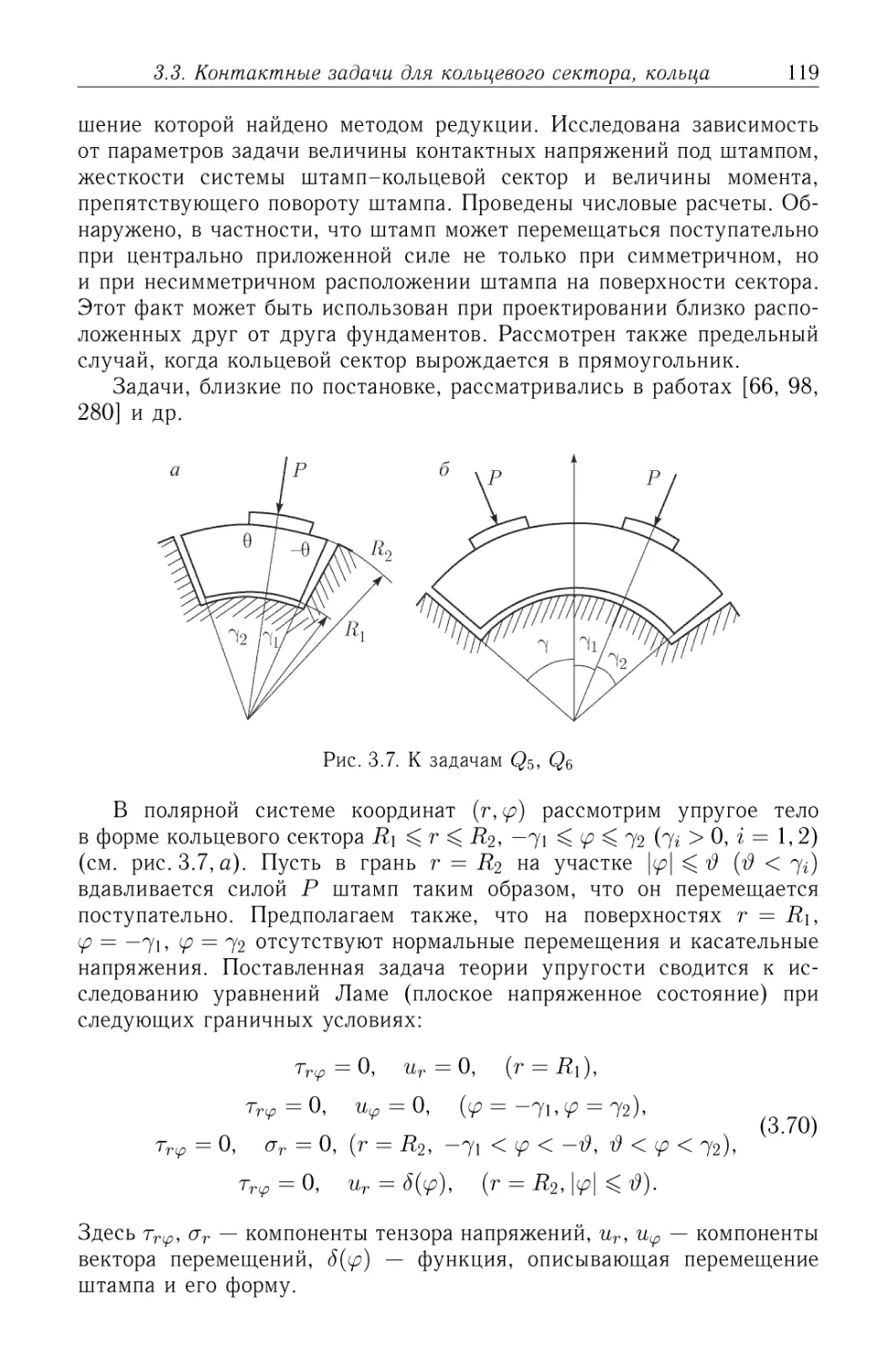
Задача Q$. Рассматривается упругое тело в форме кольцевого сек-
сектора R\ ^ г ^ R2, —7i ^ ^ ^ 72 Gг > 0, г = 1, 2). Пусть в грань г =
= i?2 на участке \(р\ ^ $ ($ < 7г) вдавливается силой Р штамп таким
образом, что он перемещается поступательно. Предполагаем также,
что на поверхностях г = R\, ср = —71, <р = 72 отсутствуют нормальные
перемещения и касательные напряжения (см. рис. 3.7, а на стр. 119).
Задача Qq. Рассматривается другим методом частный случай зада-
задачи Q$, когда 7i — 72 — 7 (см- Рис- 3.7, б на стр. 119).
Задача Qj. Рассматривается упругое тело в форме кольца R\ <
< г < R2 с центром в начале полярных координат. На грань г = R^
действуют п штампов, расположенных так, что ось ср = 0 проходит
через центр первого из них, а остальные нумеруются в положительном
направлении отсчета ср и центры их расположены друг от друга на
угловом расстоянии 27 = 2тг/п. На грани г = R\ заданы нулевые
нормальные перемещения и либо нулевые касательные напряжения
(скользящая заделка), либо нулевые касательные перемещения (жест-
(жесткая заделка). Первый штамп движется поступательно в радиальном
направлении, тогда как остальные неподвижны. Трение под штампами
отсутствует. Угловые размеры штампов совпадают и равны 2д (д < 7)
(см. рис. 3.8 на стр. 132).
/./. Постановка контактных задач 25
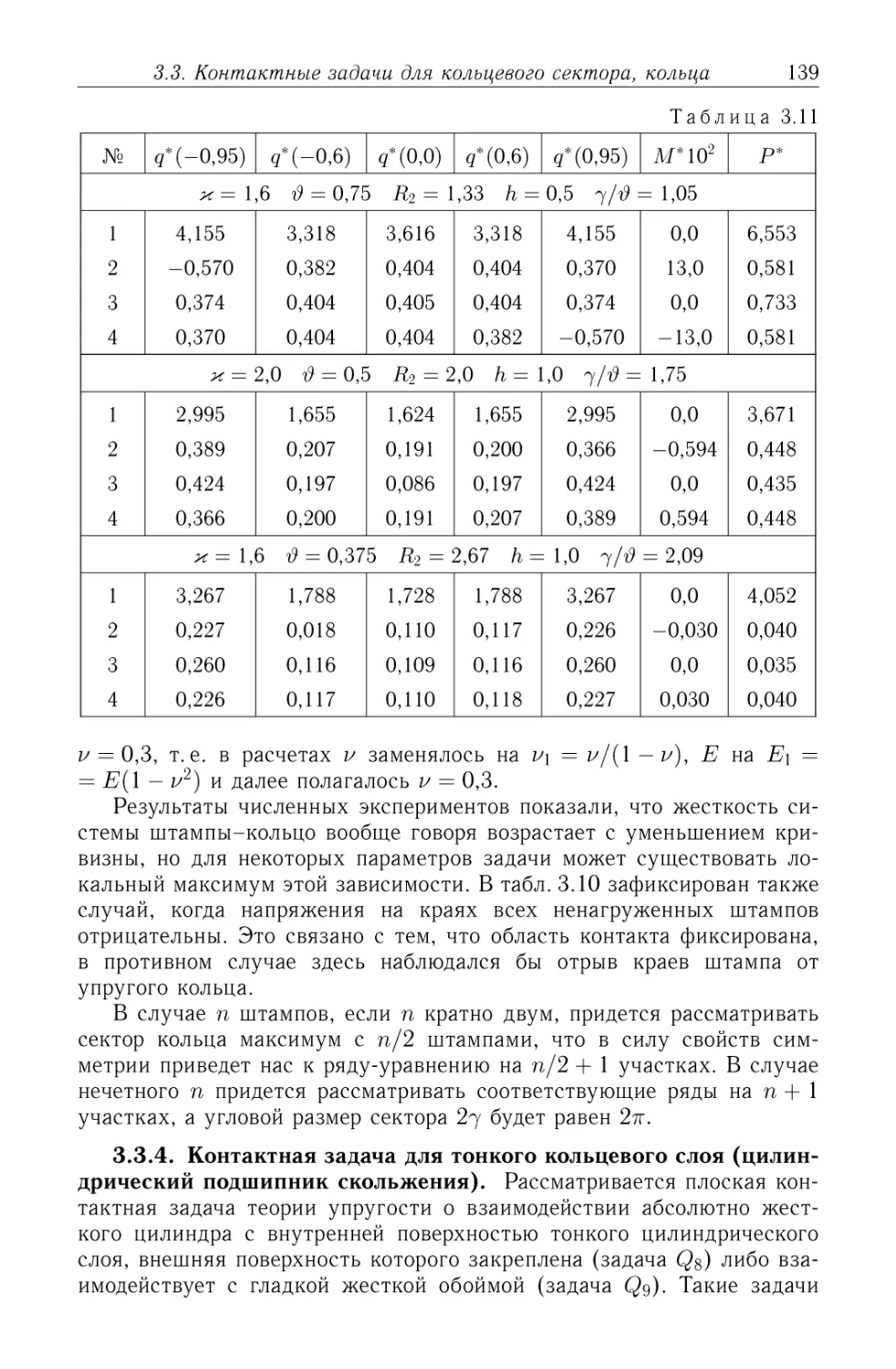
Задачи Q$, Qg. В цилиндрической системе координат (r,(p,z) рас-
рассматривается цилиндрический слой R\ ^ г ^ R2, у которого поверх-
поверхность г = Щ неподвижна (задача Q$) либо взаимодействует без трения
с жесткой поверхностью (задача Qg), а в поверхность г = R\ силой Р
вдавливается штамп в форме цилиндра радиуса Ro = R\ — А с точкой
первоначального касания ср = 0, г = R\ (см. рис. 3.9 на стр. 140).
Предполагается, что трение между штампом и цилиндрическим слоем
отсутствует, сила Р направлена вдоль луча ср = 0, а величина А мала.
Задача Qio- Рассматривается контактная задача о чистом сдвиге
полосовым штампом вдоль образующей цилиндрического упругого тела
R\ < г < R2, 0 < (р < 7' поперечное сечение которого занимает область,
ограниченную сторонами клина и двумя концентрическими окруж-
окружностями с центром в вершине клина. Штамп закреплен на плоской
грани тела (р = 7> ПРИ этом другая плоская грань (р = 0 закреплена,
а цилиндрические поверхности г = R\ и г = R2 либо закреплены, либо
свободны от напряжений (см. рис. 3.10 на стр. 149).
Задачи Q\\ и Qi2- Рассматривается цилиндрическое тело, описыва-
описываемое в координатах а, C, z (а и C — криволинейные ортогональные
координаты на плоскости) соотношениями \а\ < R, В\ < /3 < В<2, —оо <
< z < оо. Пусть штамп жестко закреплен на грани C = В^ в области
\а\ ^ А < R и сдвигается вдоль положительного направления оси z
усилием Т, приложенным к каждой единице его длины; грань C = В\
защемлена, а грани \а\ = R защемлены (задача Q\\) или свободны от
напряжений (задача Qi2)- На рисунках 3.11, а и 3.11,6 на стр. 154
изображены схемы соответственно задач Qn и Qi2 в случае биполяр-
биполярных координат для усеченной луночки.
Ниже в сферических координатах г, $, (р @ ^ г < оо, 0 ^ $ ^ 2тг,
О ^ (р ^ тг) дается краткая постановка некоторых контактных задач для
сектора сферического слоя, сферического слоя и усеченного конуса.
Задача S\. Рассматривается осесимметричная задача о кручении
упругого тела, ограниченного сферическими поверхностями г = R\, r =
= i?2 и конической поверхностью (р = (р2, круговым штампом, сцеп-
сцепленным с упругим телом по сферической поверхности г = R2, ip ^ ip\.
Считаем, что сферическая поверхность г = R2 вне штампа ((р\ < (р <
< Lp2) свободна от напряжений, а остальная часть границы упругого
тела жестко закреплена. Нагружение производится поворотом штампа
относительно оси симметрии ср = 0 на некоторый угол г (см. рис. 4.1
на стр. 159).
Задача S2. Рассматривается осесимметричная контактная задача о
вдавливании штампа в сферическую поверхность г = R2 в области (р ^
^ (р\ сектора шарового слоя, описанного в предыдущей задаче S\. Вне
штампа поверхность г = R2 свободна от напряжений, грань г = R\
закреплена, а на конической поверхности заданы условия отсутствия
нормальных перемещений и касательных напряжений (см. рис. 4.2 на
стр. 164).
26 Гл. 1. Постановка контактных задач, некоторые общие методы
Задача S%. В сферических координатах (г, #, ф) рассматривается
шаровой слой R\ ^ r ^ i?2, 0 ^ $ ^ 2тг, 0 ^ ср ^ тг, у которого по-
поверхность г = R2 неподвижна, а в поверхность г = R\ вдавливается
силой Р штамп в форме шара радиуса Ro с точкой первоначального
касания (р = 0, г = R\. Предполагаем, что трение между штампом
и шаровым слоем отсутствует, сила Р направлена вдоль прямой ср = О,
а величина А = R\ — Rq мала (см. рис.4.3 на стр. 166).
Задача S±. Рассматривается тело (усеченный конус), ограниченное
координатными поверхностями (р = ^ < и, г = R\ и г = R2 (R\ < i^)-
На конической поверхности ц> = j при R\ < а ^ г ^ b < R2 закреплен
штамп, который закручивается моментом М на угол г вокруг оси сим-
симметрии. Сферические поверхности г = Ri {г = 1,2) неподвижны, вне
штампа коническая поверхность свободна от напряжений (см. рис.4.4
на стр. 172).
1.1.2. Контактные задачи для тел конечных размеров некано-
неканонической формы. В миографии рассмотрен ряд контактных задач
для тел конечных размеров, когда часть их граничной поверхности не
является координатной поверхностью какой-либо системы координат.
Проведено исследование некоторых плоских контактных задач для
криволинейной трапеции и осесимметричных задач для тел вращения
с криволинейной образующей.
Задачи N\, N2. Рассматривается в декартовых координатах (х, у)
контактная задача теории упругости о чистом сдвиге штампом беско-
бесконечного цилиндра @ ^ у ^ h, \x\ ^ R(y)) (см. рис. 5.4, а на стр. 191).
Эта задача служит модельной для более сложных задач, однако может
представлять и самостоятельный интерес. Пусть к поверхности у = h
цилиндрического тела, имеющего сечение в виде симметричной криво-
криволинейной трапеции, жестко присоединена бесконечно длинная полоса
(штамп) шириной 2а, ось которой параллельна оси z. Поверхность
вне штампа будем считать свободной от напряжений за исключением
основания, которое жестко защемлено. На боковой поверхности тела
х = ±R(y) будем рассматривать два типа условий: жесткое защемление
(задача N\) и отсутствие напряжений (задача N2).
Задача Щ. Рассматривается плоская контактная задача о вдав-
вдавливании штампа в плоскую грань упругого тела \х\ < R(y), 0 < у <
^ h, имеющего форму симметричной упругой трапеции (см. рис. 5.10
на стр. 198). Предполагается, что под штампом отсутствует трение,
другая плоская грань упругого тела лежит без трения на плоском
основании, боковая поверхность свободна от напряжений. Соответ-
Соответствующую краевую задачу для уравнения Ламе можно симметрично
продолжить в область у < 0. В этом случае получаем эквивалентную
задачу (см. рис. 5.11, а на стр. 208 и 5.11,6 на стр. 208) о внедрении
двух штампов в грани у = ±h упругого тела, занимающего область
\х
R(y), У ^ h, считаем R(y) четной функцией.
/./. Постановка контактных задач 27
Задача 7V4. В цилиндрической системе координат (г, (р, z) рассмат-
рассматривается тело вращения (см. рис. 5.15 на стр. 212), ограниченное
поверхностями z = О, z = h и г = R(z), R(z) — гладкая функция.
В области контакта (z = h,r < а) задано вертикальное смещение штам-
штампа, вне штампа отсутствуют напряжения. Тело вращения опирается на
гладкое жесткое основание, боковая поверхность г = R(z) свободна от
напряжений.
1.1.3. Контактные задачи для тел периодической структуры.
Задача Р\. В прямоугольной системе координат рассматривается по-
полоса 0 < у < h, —оо < х < оо. Пусть область полосы \х\ < хо имеет
модуль сдвига G, плотность р, а области хп + kL < х < хп+\ + kL
(п = О, 1, 2,..., т — 1; к = О, 1, 2,..., оо) имеют соответственно модули
сдвига Gn и плотности рп. Обозначим хп+\ — хп = 1п, хш — хо = L,
где L период изменения свойств полосы вдоль продольной координа-
координаты х влево и вправо соответственно от точек х = — хо и х = — х§. Далее
пусть на поверхности полосы у = h в области \х\ < а закреплен штамп,
совершающий вдоль оси z гармонические колебания с частотой и под
действием сдвигающей силы Pq = Р exp (—iuit), поверхность полосы
вне штампа свободна от напряжений, а поверхность у = 0 неподвижна
(см. рис. 6.1 на стр. 226).
Задача Р% Рассматривается бесконечный цилиндр радиуса R в ци-
цилиндрической системе координат (r,(p,z). Пусть область цилиндра
\z\ ^ zq имеет модуль сдвига G, плотность р, области zn + kL < \z\ <
< zn+\ + kL, (n = 0, 1,..., m — 1, к = 0, 1,..., оо) имеют соответственно
модули сдвига Gn и плотности рп, a zn+\ — zn = ln. При этом L =
= zm — zq — период изменения механических свойств цилиндра вдоль
продольной координаты z влево и вправо соответственно от точек z =
= —zq и z = zq. Далее пусть на поверхности \z\ ^ а < zo, r = R
закреплен бандаж, который совершает крутильные колебания вокруг
оси z под действием момента Mq = Me~luJt (см. рис. 6.5 на стр. 237).
1.1.4. Пространственные контактные задачи для слоя с учетом
сил трения в области контакта. Задачи L\, L2. Пусть жесткий
штамп в форме эллиптического параболоида, лежащий на поверхности
z = h слоя 0 ^ z ^ h с модулем сдвига G\ и коэффициентом Пуассо-
Пуассона и\, находится под действием нормальной силы Р и тангенциальной
силы Т, направленной вдоль оси Ох. Здесь (х, у, z) — прямоугольная
система координат, начало которой находится на нижней поверхности.
Предполагается, что силы трения под штампом параллельны силе Т
и штамп находится в условиях предельного равновесия и не поворачи-
поворачивается, а поверхность слоя z = 0 жестко соединена с упругим полупро-
полупространством с другими упругими постоянными G<i и z/2 (задача L\) или
взаимодействует с ним без трения при условии равенства нормальных
напряжений и перемещений (задача L^). Схема взаимодействия штампа
со слоем, лежащим на полупространстве, изображена на рис. 7.1 на
стр. 246.
28 Гл. 1. Постановка контактных задач, некоторые общие методы
Задачи L3, L4. Более подробно рассматриваются задачи, которые
соответственно будут частными случаями задач L\, L2, когда модуль
сдвига полупространства стремится к бесконечности, т. е. слой взаимо-
взаимодействует с недеформируемым основанием.
Для исследования выше поставленных контактных задач исполь-
использованы различные подходы, более детальная постановка этих задач
и методы их решения изложены ниже в соответствующих разделах.
1.2. Методы решения парных рядов-уравнений
Многие смешанные задачи теории упругости для областей конеч-
конечных размеров (прямоугольник, цилиндр, усеченный клин, усеченный
конус, кольцевой сектор, сектор шарового слоя и др.) сводятся к ис-
исследованию парных рядов-уравнений по какой-либо полной системе
ортонормированных с весом функций, порожденных соответствующей
задачей Штурма-Лиувилля на конечном интервале.
1.2.1. Сведение парного ряда-уравнения общего вида к бес-
бесконечной системе первого рода с сингулярной матрицей. Ниже
будет приведен метод сведения широкого класса таких парных рядов-
уравнений к бесконечным системам линейных алгебраических урав-
уравнений первого рода с сингулярной матрицей и некоторые подходы
к исследованию таких систем [40, 310, 311, 336]. Аналогично могут
быть рассмотрены и тройные ряды-уравнения.
Рассмотрим парный ряд-уравнение вида
Y^ akK(uk)y(uk, x) = f(x) @ < х < а),
A.1)
к, х) = 0 (а < х < Ъ).
к=0
Здесь ак — искомые постоянные, у(ик,х) и ик соответственно система
собственных функций и собственных чисел осесимметричной задачи
Штурма-Лиувилля для дифференциального уравнения второго поряд-
порядка на конечном интервале
(L - и2)у = 0, Ly = r(x)[s(x)y']' + t(x)y @ < х < b)),
\y(u,0)\ < oo, y'(u,b) +ay(u,b) = 0.
Будем предполагать, что s(x) > 0 при х е (О, Ь), г(х) — знакоопреде-
ленная функция при х G (О, Ь), К (и) — четная мероморфная функция,
представимая в виде
f[( ^)( iY\ A = const, A.3)
1.2. Методы решения парных рядов-уравнений 29
где ±i5n и ±г7п — счетное множество простых нулей и полюсов
функции К (и). Рассматривая уравнение A.1) в общем виде, будем
предполагать, что 5п и 7п монотонно возрастают по модулю с ростом
номера, обеспечивая сходимость бесконечного произведения A.3), а на
любой правильной системе контуров Сп в плоскости комплексного
переменного и имеет место оценка
К (и) = О(\и\р), р<1, п^оо.
Не нарушая общности будем считать, что f(x) = y(ie,x), имея в виду,
что в общем виде функция f(x) может быть представлена рядом по
функциям у(щ,х).
Как известно [191, 210], функции y(uk,x) составляют при х G
G [0,Ь] полную ортогональную с весом г~ (х) систему функций. Будем
считать, что эти функции нормированы с тем же весом так, что \\y\\ =
= 1.
Практический интерес представляет функция
q(x) = ? аку(ик,х) @ < х < а), A.4)
k=Q
которая обычно в контактных задачах выражает распределение напря-
напряжений в зоне контакта. Используя тот факт, что Ly(u,x) = и2у(и,х),
парный ряд может быть представлен в виде
APx(L)q(x) = P2(L)y(ie,x) @ < х < а),
q(x)=0 (а^х^Ъ),
где P\(L) и P2(L) — дифференциальные операторы бесконечного по-
порядка. Последние соотношения могут быть преобразованы после реше-
решения дифференциального уравнения бесконечного порядка и записаны
в следующем виде:
q(x) = K-l(ie)y(ie9x) ^f^xJ-^Щ @ < х < а),
q(x)=0 (а^х^Ъ).
Определение входящих в A.5) коэффициентов хп после ряда гро-
громоздких преобразований сводится к решению следующей бесконечной
системы линейных алгебраических уравнений:
-B2)X(e) = Dl(e)+D2(e). A.6)
ат
m
следующих соотношений:
(В! + В2)Х(е) = Di(e) + D2(e). A.6)
Здесь Вг = {Ь^п} - матрицы, Х(е) = {хп(г)}, Вг(г) = {d$(e)} -
вектор-столбцы бесконечного порядка (г = 1,2), представимые в виде
следующих соотношений:
30 Гл. 1. Постановка контактных задач, некоторые общие методы
il _ у(г6п, a)r}f(ijm, a) - y(iSn, a)r}(ijm, a)
пт
, a) - y'jiSn, a)y(i^rn, a)
г, а)
ч _ y(is,a)r]'(i^frn,a) — y/(is,a)rj(i^rn,a)
Z) = ? g >
K(is)(s — Jrn)r](ijrn,a)
у (is, a)y'(i^m, a) - у (is, a)y(ijm, a)
K(is)(s -J
A-8)
b)
Здесь rj(u,x) — является решением уравнения A.2), линейно незави-
независимым с у(и,х).
В частных случаях при рассмотрении конкретных задач, связанных
с определенной системой координат, функциями y(uk,x) и г](и,х) явля-
являются либо тригонометрические функции, либо функции Бесселя, либо
функции Лежандра, либо другие известные специальные функции.
Конкретный вид систем A.6) можно найти в работах [17, 19, 40,
41, 43, 51, 54, 310, 311, 336] и др. Характерной особенностью системы
A.6) является то, что матрица Bi может быть представлена в виде
B,=E + Bt, E = {((*„-7тГ'}. A-9)
В реальных случаях при и —> оо
5n = c-n + g{ ± ici In n + O(n~l In n), A-Ю)
7n = с - n + g2 ± ic2 In n + O(n-1 In n),
где с, ci, C2, §*!, §2 ~~ известные константы. Поэтому матрица Е со-
содержит неубывающие по диагонали элементы, в то же время элементы
матриц В\ = {Ь?}п} и Въ убывают с ростом ш, п, по крайней мере
обратно пропорционально номеру.
Таким образом решение парных рядов-уравнений A.1) сводится
к решению систем бесконечных линейных алгебраических уравне-
уравнений A.6)-A.8) с сингулярной матрицей коэффициентов. Заметим, что
в работах [50-53] и др. использован другой подход сведения от-
отдельных интегральных уравнений, эквивалентных парным уравнениям
типа A.1), к системам линейных алгебраических уравнений такого же
вида.
Имеется несколько подходов решения бесконечных систем первого
рода A.6). Здесь будет использовано два подхода. Один из них заклю-
заключается в регуляризации бесконечной системы A.6) путем выделения
и точного обращения ее сингулярной составляющей. В результате этого
система сводится к бесконечной системе второго рода, допускающей
1.2. Методы решения парных рядов-уравнений 31
получение решения методом редукции. Такой подход использовался
во многих работах, например, [40, 52, 53, 88, 311] и других. Метод
дает приемлемое решение при малых значениях некоторого геомет-
геометрического параметра Л. Здесь также возможно получение асимптоти-
асимптотического решения при Л —> 0. Заметим, что, например, в контактной
задаче для слоя Л = h/a, где h — толщина слоя, а — полуширина
области контакта. Другой подход [133, 177, 305] основан на знании
характера поведения решения системы A.6) при больших номерах,
что может быть определено, например, из анализа поведения решения
исходных задач в особых точках. Это позволяет свести бесконечную
систему к эффективно решаемой конечной системе. Метод не требует
факторизации функции К (и), что характерно для первого подхода,
позволяет найти главный член решения бесконечных систем и вместе
с этим найти в явном виде особенности решений задач в точках смены
граничных условий. Предлагаемый подход практически не накладыва-
накладывает ограничений на параметры задач, а численная его реализация не
требует больших затрат времени ПК.
1.2.2. Метод решения бесконечной системы путем сведения
ее к бесконечной системе второго рода. Используя матрицу Е~\
обратную к Е, с элементами [52]
т„т = [{Kz\iim))'K'+{-i5n){lm - 5п)]-\ Е~х = {тпт},
—1 /1 1 1 \
ПО
п=\
где К (и) = К+(и)К-(и) — результат факторизации функции К {и)
относительно действительной оси, можно показать, что система A.6)
будет равносильна бесконечной системе второго рода
, A.12)
решение которой при определенных значениях входящих в нее пара-
параметров может быть получено методом последовательных приближе-
приближений [52]. Если в бесконечной системе A.6) перейти к пределу при Ъ —>
—> оо, то матрица В2 и вектор-столбец D2 обратятся в нуль и получим
бесконечную систему
B,X(e) = D1(e)>
соответствующую задачам для полубесконечной области.
Точная факторизация функции К (и) иногда связана с большими
трудностями, в этом случае можно воспользоваться приближенной
факторизацией [56], для чего функцию К (и) аппроксимируем функ-
функцией
32 Гл. 1. Постановка контактных задач, некоторые общие методы
г=\
при условии
S
KmQL(u)=A, т.е. ЦЫ/<иJ =
где В — известная постоянная, pi и qi — определяются в процессе
аппроксимации.
Функция L(u) легко факторизуется, что позволяет получить про-
простые приближенные соотношения для элементов матрицы Е~х\
АпFп-1т)}-\ A.14)
Рп - qn x A
Рп - qn x A qk - Рп
к=\
кфп
2B^/BBn-2S-2)\\yrPk-an
*{2n-2S-l)\\ \}
R+{-iqm){Pm -
s
ТТ
I I
/c/m
gfc-/3m
^^A; ( > }'
(-iu) = Д Г f 1/2 - *i
у7Г\ 7Г
Здесь Г(ж) — гамма-функция, г5п и г7т — соответственно нули и
полюса функции L(u), а именно
Рп (п < 5),
7m 1т=тгВ~1(т-S - 1/2) (m>S).
Решение системы A.12) в дальнейшем будем получать методом
редукции, урезанную систему представляем в виде [40]
оо N / оо \
%п — / J TjiYYiUfYi -\- у ^ I у ^ 7~птРтп \ %к \^ — А, Z, ... , iv J, (^ 1. 1Ь)
771=1 к=\ V т=1 /
Ьтп = ь1тп + ь2тп, dm = dlm(o) + <4(о),
1.2. Методы решения парных рядов-уравнений 33
и находим ее решение на ПК. Значение N выбираем в зависимости от
заданной точности. Если в аппроксимирующей функции A.13) число
В <С 1, то 5п и 7т ПРИ п > S будут большими числами, так как,
согласно A.15), при п > S они обратно пропорциональны В. Тогда
можно показать, что при номерах больших S свободные члены и эле-
элементы матрицы системы A.16) будут малы, и, следовательно, в си-
системе A.16) N можно считать равным S. Но при этом, к сожалению,
при фиксированном значении S с уменьшением В ухудшается точность
аппроксимации A.13).
1.2.3. Метод решения бесконечной системы первого рода пу-
путем сведения к конечной системе первого рода. В этом разделе
излагается другой подход (см., например, [133, 177, 305, 319] и др.)
к решению бесконечных систем линейных алгебраических уравнений
первого рода с сингулярной матрицей коэффициентов A.6). Метод
основан на знании характера поведения решения систем при больших
номерах, что может быть определено из анализа поведения решения
исходных задач в особых точках. Это позволяет свести бесконечную
систему к эффективно решаемой конечной системе. Метод не требует
факторизации функций, позволяет найти главный член решения бес-
бесконечных систем и, вместе с этим, найти в явном виде особенности
решений задач в точках смены граничных условий. Предлагаемый
подход практически не накладывает ограничений на параметры задач,
а численная его реализация не требует больших затрат времени ПК.
Если предположить, что зона контакта фиксирована, а трение меж-
между штампом и упругим телом отсутствует, то
Q(x) ~ х(х — а)~1^2 (х —> a, x = const)- A-17)
Учитывая, что в реальных смешанных задачах, связанных с распро-
распространенными системами координат, при п —> оо
y(i6n,x) = О(е5-Х) @<с^х^а), A.18)
то соотношение A.17) позволяет определить характер поведения коэф-
коэффициентов хп при п —> оо, исходя из известной суммы ряда
к=о
Сопоставляя соотношения A.5), A.17)-A.19), получим, что
Отмеченный выше факт позволяет бесконечную систему A.6) све-
свести к конечной системе уравнений, если предположить, что
2 В.М. Александров, М.И. Чебаков
34 Гл. 1. Постановка контактных задач, некоторые общие методы
Хп = Xn Г9 mi " (n ^ N> Xn = constO- A.21)
[Zn)..
Тогда бесконечная система A.6) будет с некоторой погрешностью
эквивалентна системе из N уравнений:
N
Е bmnxn + BmxN = dm (m = 1,2,..., N), A.22)
n=\
где
_ ^ Bn-l)!!
°m ~ 2^ Bn)\\ mn'
n=N V J
Как показывает опыт, погрешность решения соответствующих задач
после замены системы A.6) системой A.22) будет тем меньше, чем
больше значение N.
Получение теоретических оценок сходимости метода связано с
большими трудностями, поэтому эффективность его продемонстрируем
на задаче теории упругости со смешанными граничными условиями,
имеющей точное решение.
Рассмотрим задачу теории упругости о чистом сдвиге вдоль обра-
образующей штампом упругого бруса бесконечной длины с прямоугольным
сечением [336]. Предполагается, что между штампом, симметрично
расположенным на одной из граней бруса, и брусом осуществляется
полное сцепление, при этом противоположная грань бруса неподвижна,
а боковые грани свободны от напряжений.
Такая задача отражает все особенности других более сложных
задач, если для их решения использовать метод сведения парных рядов
к бесконечным системам с сингулярной матрицей.
Поставленная задача сводится [336] к исследованию парного ряда
A.1), в котором
y(uk,x) = cosukX, f(x) = 1, A-23)
К (и) = г^ thuh, Uk = тгк/b.
Здесь h — высота прямоугольника, 2Ь — его ширина, 2а — ширина
штампа. Элементы матриц и правой части бесконечной системы A.6)
описаны в работе [10].
Распределение касательных напряжений под штампом в соответ-
соответствии с соотношением A.5) определяется по формуле
h^hZ^Xn~^~\ (ж <а)> О-24)
n=l J
с- ттп тгBт — 1)
где G — модуль сдвига, 5 — смещение штампа.
1.2. Методы решения парных рядов-уравнений
35
Связь между смещением штампа и приложенной к нему силой Т
дается соотношением
A.25)
п=\
Матрица и правая часть бесконечной системы A.6) поставленной
задачи обладает всеми необходимыми свойствами. Поэтому в соответ-
соответствии с предложенной схемой контактные напряжения и величину Т
найдем по формулам
Т =
2GS
n=\
N-\
E<
n=l
ch5n
n=N
thdna
n=N
[2n- 1)!! ch5nx
Bra)!! ch^na
2n- 1)!! th^na
72^)П ^Г
A.26)
A.27)
где коэффициенты хп(п = 1,2,... ,7V) находятся из системы линейных
алгебраических уравнений A.22). Основная проблема для численной
реализации полученных соотношений заключается здесь в вычислении
суммы плохо сходящихся бесконечных рядов в A.26) и A.27). Члены
этих рядов ведут себя при больших номерах как п~3/2. Эту трудность
здесь легко преодолеть при помощи известного приема улучшения
сходимости рядов, что позволяет их вычислять с высокой точностью
и быстро с помощью конечных сумм.
Ряд в A.26) при 0 ^ х < а сходится как бесконечная убывающая
геометрическая прогрессия, при х = а он расходится, но главную часть
ряда в окрестности х = а легко просуммировать и тем самым выделить
особенность в поведении напряжений при х —> а.
Используя сумму ряда A.19), получим соотношение для контакт-
контактных напряжений с явно выделенной особенностью
в(х) = T
N-\
n=l
Xn
-Ждг
ch 5a
Bn- 1)!!
-Хдг +
— e
-25na
n=\
1+e
-28na
. A.28)
Из последнего выражения найдем коэффициенты при особенности
Ко = Ит л/а2 - х2 q{x) = G5xNJ2a/(nh). A.29)
Поставленная здесь задача имеет точное решение [42, 168].
С целью проверки эффективности предложенной схемы решения
бесконечной системы A.6) для поставленной задачи был произве-
36 Гл. 1. Постановка контактных задач, некоторые общие методы
ден расчет безразмерных контактных напряжений q*(x) = q(x) a/(G5),
сдвигающей силы Т* = T/(G5) и коэффициента при особенности Щ =
= Ko/(V2G5) по формулам A.26)—A.29) в зависимости от параметров
Л = h/a, C = b/a и числа уравнений N системы A.22). Расчеты показа-
показали хорошую сходимость предложенной схемы решения рассмотренной
модельной задачи. Для достижения заданной точности при уменьше-
уменьшении параметра Л или увеличении параметра C число уравнений N
уменьшается. Характер сходимости метода мало зависит от парамет-
параметров и таков, что позволяет контролировать точность путем сравнения
результатов счета при различных значениях числа уравнений N.
Таблица 1.1
N
2
6
10
[305]
т**
(А = 5)
1280
1231
1231
1231
Т**
(А = 10)
1266
979
970
970
q**
(А = 5)
942
895
895
894
(А = 10)
973
718
708
707
(А = 5)
300
273
274
275
К*о*
(А = 10)
334
222
216
218
и Kq* =
В табл. 1.1 приведены величины Т** = Т*103, д** = д*@,9I03
q qIO3 при C = оо, значениях Л = 5, Л = 10 и некоторых
значениях N. В последней строке таблицы представлены значения этих
же величин, вычисленные по точным соотношениям работ [42, 168].
Видно, что решение задачи по предложенной схеме может быть эф-
эффективно получено с небольшими затратами при Л ^ 10. Увеличивая
число уравнений в системе A.22), решение задачи можно получить
практически при любых значениях параметров.
1.3. Асимптотический метод больших Л решения
интегральных уравнений
Среди асимптотических методов исследования интегральных урав-
уравнений теории смешанных задач широкое распространение получил
метод больших Л ([14, 24, 88, 99, 101, 201, 308, 309, 325] и др.), когда
решение интегральных уравнений представлено в форме асимптотиче-
асимптотического разложения по отрицательным степеням некоторого безразмер-
безразмерного параметра Л. Как правило, удавалось построить лишь несколько
членов такого асимптотического разложения.
Ниже методом больших Л исследуются некоторые типы интеграль-
интегральных уравнений первого и второго рода, для которых предлагается
методика построения всех членов асимптотического разложения. Ко-
Коэффициенты в разложении искомого решения по отрицательным сте-
степеням Л представлены в виде многочленов основного аргумента и для
1.3. Асимптотический метод больших А решения интегральных ур-ий 37
коэффициентов этих многочленов получены простейшие рекуррентные
формулы.
1.3.1. Решение методом больших Л интегрального уравнения
второго рода, главная часть ядра которого дельта-функция. Рас-
Рассмотрим уравнение
(|?| < 1), A.30)
-1
М(у)= \ [I-L(u)} cos uydu=J2bk\y\k (\y\<B<oo), A.31)
k0
k=0
где 0 < Л < оо — безразмерный параметр, g(t) — известная функция.
Пусть ряд A.31) сходится равномерно при \у\ < В < оо (В — сколько
угодно большое число).
Возможна и другая форма записи A.30)—A.31):
J ф) (^) dr =
-1
ОО
г
К(у) = L(u)cosuydu.
о
Будем разыскивать решение интегрального уравнения A.30) с яд-
ядром A.31) в виде [43, 323, 325, 335]
_ \ A.32)
n=0
Подставляя A.32) и ряд A.31) в A.30) и приравнивая коэффи-
коэффициенты при одинаковых ступенях Л, получим для определения (pn(t)
рекуррентные соотношения
п-\ 1
П г=0 -1
A.33)
Предположим, что g(t) = 1. Тогда, разыскивая ipn(t) в виде (квад-
(квадратные скобки в пределах суммирования здесь и далее означают целую
часть числа)
[п/2]
Vn(t) = ^2 rjn,it2i (n=l,2,...), A.34)
г=0
38 Гл. 1. Постановка контактных задач, некоторые общие методы
подставляя A.34) в A.33) и приравнивая в полученном соотношении
коэффициенты при одинаковых степенях ?2, найдем рекуррентные фор-
формулы для определения г\п^
2\Чо/ n,L _ .. /^(-1)РB^-2/+1+р)-
тгB/с)! ^ (/-2/с)! ^
v у l=2k к ' Р=0
)/2]
Bр + /-2/с+ 1)~V-/-i,p> A.35)
'- — У^Ь/ У^ ??n-z-i,pBp +Z + 1) *, A.36)
[П/2] 2/-1 чр/ ч-1
7^п \п/2] = — / B/ — 1)'^2/ — \Т]п—21 \п/2] — 1 / 77^7 \~i—i •
7Г ^ ^ ^ J B1 — 1 — р)\р\
1=0 р=0
A.37)
В A.35) к = 1,2,..., [п/2], если п нечетное, и /с = 1,2,..., [(п —
— 1)/2], если п четное; в A.37) п четное.
Аналогичным образом для больших Л может быть построено ре-
решение уравнения A.30), A.31) в случае, когда g(t) = tm (m — любое
натуральное число), а также в случае когда g(t) представимо в виде
ряда по положительным степеням аргумента t.
Можно доказать следующее утверждение. Если g(t) G Пх' (—1,1)
и справедливо неравенство
A.38)
u) | du,
%= \\1-L(u)\du,
J
о
тогда решение интегрального уравнения A.30) с ядром A.31) в классе
Нх' (—1,1) существует, единственно и может быть получено методом
больших Л.
Здесь Нх' (—1,1) — пространство функций, первая производная
которых удовлетворяет условию Гельдера с показателем 1/2 на отрез-
отрезке (-1,1).
1.3. Асимптотический метод больших А решения интегральных ур-ий 39
Если в интегральном уравнении A.30)
оо
М(у)=^Ъпу2п (|2/| < г/о), A-39)
п=0
оо
g(t) = ]Г an\-2nt2n (\t\ < t0), A.40)
n=0
тогда, аналогично предыдущему, решение уравнения A.30) с ядром
A.39) и правой частью A.40) для больших значений Л может быть
построено в виде
оо j оо j
tp(t) = у \~2i у ajit% + у А"(у+1) У (Зпг2\ A.41)
j=0 г=0 j=0 г=0
где aji и /3j^ определяются из следующих рекуррентных соотношений:
V у foi 7
!Z^Bfc-2i)! 2^ 2m + 2k-2i+l ^-U'1'-'J
/c=i m=0
i-* A
2 у 6fcBfc)! V "j-fc."» (i = 0\ i)
Bi)!^Bk2i)\^2m+2k2i+l У ' J;>
1.3.2. Решение методом больших Л интегрального уравнения
первого рода с логарифмической главной частью ядра. Многие
плоские смешанные задачи механики сплошной среды сводятся к ре-
решению интегрального уравнения [88]
^(t)A; (^J dt = тг/(т), |r| < 1, A.43)
-i
где Л — безразмерный геометрический параметр, /(г) — известная
функция, к (у) — ядро, представимое в виде
= -]n\y\-F(y), F(y) = ^diyz\ A.44)
г=0
Последний ряд абсолютно сходится при \у\ < у$, следовательно, ана-
аналогичный ряд для функции F((t — т)/Х) при \t\ < 1, \т\ < 1 будет
сходиться, если Л > 2/уо.
40 Гл. 1. Постановка контактных задач, некоторые общие методы
Было показано [88], что если f'(r) e Z/p[_1?1], р > 3/4, то любое
решение интегрального уравнения A.43) из класса Lp[_1?1], p > 1, будет
также решением интегрального уравнения
ttVI -i
J
^) 4
ln2A
f(t)dt
-1
-1 -1
1
Q = \ v(t) dt
x-t
dx
Решение интегрального уравнения A.45) будем искать в виде [88, 201]
сю
<p(t) = ? A>n(t).
n=0
Тогда для определения (pn(t) получим рекуррентные соотношения
Try 1 — t2
™ 1
T-t
-1
'\ -г2 dr f , w
т — t J
(m ^ 1).
Если в последнем соотношении представить бином (х — тJг~х в виде
многочлена и изменить порядок интегрирования, то получим
m 2г-1
A.46)
г=1 /с=0
Здесь
Rk(t) =
A.47)
-1
-1
1.3. Асимптотический метод больших А решения интегральных ур-ий 41
Сингулярный
n+1
i=o
1
си
интеграл
1 ч,
-м
Rk(t)
ъ>0),
з 2,
Bг- 1)
' /с!Bг-/с-
I
¦1)!
представляется
R2n+2(t)
_{2к-
^к Bк -
= 7Г
-1)!
\-2)\
в виде
п+1
i=o
!
! ^
многочлена [88]
A.48)
Подставляя A.48) в A.46) и изменяя порядок суммирования, полу-
получим представление
в котором коэффициенты amj и /3mj- определяются из простых рекур-
рекуррентных соотношений
?п—1 г—1 ?тг —г—1
B + 2i-2n- 1)!!
2р + 2г- 2гг)!!
j+l n=j p=0
m-1
5]c2nfm5n-j-i*omП"l (m^l,0^j^m-l), A.50)
7П—1 г—1 ?тг—г
о\^л V^ Y^/Q Bр + 2г-2гг-3)!!^
2^ C2n+i,i5n_j 2^ ^m-1'PBp + 2i-2n-2)!!
i=j n=j-l ^=°
i/0 j/-l
m— 1
c2n+i,m5n-j^omn (m ^ !> 0 < j < m).
n=j-l
n/-l
При переходе от A.46) к A.49), A.50) постоянные Ф^ (т ^ 1) были
вычислены подстановкой A.49) во второе соотношение A.47).
Постоянные Ф§, участвующие в соотношениях A.50), выражаются
через правую часть интегрального уравнения A.43) по формуле
Bfc)!! -' ^* "'
1 A.51)
f+1 = - | /'(т)л/1--г2Т*(т)<*т (fc > 0),
-1
42 Гл. 1. Постановка контактных задач, некоторые общие методы
1
2/+2 = - J ff(r)Vl-r4Tk(r)dr (к > 0),
-1
JkKJ) 2
J-kKJ) 2_^ Bп)\\
n=0 V }
Учитывая линейную зависимость Ф^ от Q, даваемую первым соот-
соотношением A.51), представим решение исходного интегрального урав-
уравнения A.43) в форме
[Q(X){t)B){t)\ A.52)
j=0
Коэффициенты /3^ находятся по рекуррентным соотношени-
соотношениям A.50), в которых /3mj надо заменить на /3^-,
A.53)
Bfc)H '
а коэффициенты а2т^ и /3^ находятся по рекуррентным соотноше-
соотношениям A.50), в которых amj и f3mj надо соответственно заменить на
a^j и ffinj причем Ф^ = Ф^, где Ф^ определяется вторым, третьим
и четвертым соотношениями A.51).
Для нахождения интегральной характеристики Р решения инте-
интегрального уравнения A.43) воспользуемся вторым равенством A.45),
тогда
оо "I -1 Г оо "I
-J2 x~2kPk\ \Qo-J2x~2kPk L С1-54)
к=0 J L k=0 J
1
-1
Bk-2m- 1)!!
m=0 V У
m=0
1.4. Точное решение некоторых интегральных уравнений 43
г=0 m=0 p=0
Bm-
q
чтг Bm)!!Bm)!Bi-2m)!*
В ряде случаев полезно знать и такую интегральную характеристику:
1
М = t(p(t) dt. A.55)
-i
Подставляя первое соотношение A.52) в A.55), получим
ОО 771—1
т=\ j=0
Видно, что все искомые величины, связанные с решением инте-
интегрального уравнения A.43), выражены через элементарные функции.
В решении фигурируют постоянные Ф^ и Qo, представимые в виде
интегралов от /(?). В случае, когда /(?) — многочлен, эти интегралы
берутся в явном виде.
Из условия сходимости ряда A.44) получаем, что решение инте-
интегрального уравнения A.43) изложенным методом может быть получено
при Л > 2/уо, где уо — радиус сходимости ряда в A.44).
1.4. Точное решение некоторых интегральных
уравнений
Рассмотрим интегральное уравнение [168]
1
\[1(х + ?) + 1(х — ?)]ip(x) dx = 5(?) @ ^ ? ^ 1), A-57)
о
ядро 1(у) которого представимо в виде
^^г A-58)
где $ G @, оо) — некоторый параметр,
0 = 0, Хк = -^— - (случаи А),
^0=2^, Afc = — (случаи Б).
К рассматриваемым интегральным уравнениям в декартовых, по-
полярных и биполярных координатах могут быть сведены в главном
многие контактные задачи для тел конечных размеров и периодические
44 Гл. 1. Постановка контактных задач, некоторые общие методы
смешанные задачи [13, 276]. В работе [13] указано, что интегральные
операторы получаемых здесь уравнений могут быть точно обращены
путем решения некоторых краевых задач Римана для автоморфных
функций [113].
Ряды A.58) можно просуммировать [168], используя разложения
для эллиптических функций Якоби по параметру
q = exp[-7iK'(k)/K(k)}
(см. [275]), где к — модуль эллиптических функций, К (к) — полный
эллиптический интеграл первого рода, а К'(к) = К(<\/(\ — к2)).
Будем иметь
( ()х) A.59а)
1 п 1+ ( л
1 + dn ну
Здесь sny, en у, day — эллиптические функции Якоби модуля к,
который определяется из трансцендентного уравнения
К\к) _ 7
К (к) #'
В дальнейшем будет рассматриваться случай А, выражения для
случая Б получаются заменой спу, dny соответственно на dny, cny.
Путем дифференцирования уравнения A.57) по ? получим A'(у) =
1
[к(х + ?) + к(х — ?)](р(х) dx = 5'(?) @ ^ ? ^ 1),
о A.60)
к(у) =
Используя четность функции </?(?) и соотношения [129] между
функциями Якоби, при помощи замены переменных г = sn x^/ sn x, ( =
= sn xx/ sn х преобразуем интегральное уравнение A.60) к уравнению
с ядром Коши
: 1), A.61)
-1
1.5. Некоторые соотношения обобщенной ортогональности 45
решение которого известно [228] и имеет вид
1
1 /
7rVl-?2 .
Учитывая A.62), получим
dn>r?sn>r ЛГ
к sn к J sn кг —
-1
2 К — SI12 Х?7 .
A.64)
Величина 7V0 определяется подстановкой решения A.64) в уравне-
уравнение A.57).
Если считать 5(а) = 5 = const, то формула A.64) упрощается, а
значения постоянной 7V0 можно выписать в явном виде:
A-65)
При |^| -^ 1 найденное решение A.65) имеет корневую особенность
с коэффициентом
о; = hm (O 1 С А^
В случае, когда параметр i? стремится к бесконечности, то к —> 1, а эл-
эллиптические функции переходят в гиперболические функции: sny ^
—> thy; en у, dny -^ sechy, а н -^ тгB7)~1. Отсюда получим извест-
известное решение интегрального уравнения контактной задачи о сдвиге
слоя [27].
1.5. Некоторые соотношения обобщенной
ортогональности однородных решений
В этом разделе приводятся соотношения обобщенной ортогонально-
ортогональности (СОО) однородных решений об установившихся колебаниях слоя,
кольца и сферического слоя [321, 327]. Соотношения обобщенной
ортогональности приводятся в виде, который позволяет одновременно
вычислять необходимые интегралы и от функций, не являющихся
однородными решениями соответствующих уравнений.
1.5.1. Соотношения обобщенной ортогональности в задаче об
установившихся колебаниях слоя. Рассмотрим упругий слой \z\ < h,
г ^ 0 (г, z, (р — цилиндрические координаты), пусть его грани z = ±/1
а) неподвижны, б) свободны от напряжений или в) грань z = h непо-
46 Гл. 1. Постановка контактных задач, некоторые общие методы
движна, а грань z = —h свободна от напряжений. Разыскивая решение
уравнений Ламе в виде
uk(r,z)=Ak(z)Ji(pkr), wk(r,z)=Bk(z)J0{pkr), A.66)
где uk(r,z)etuJt и wk(r,z)etuJt — соответственно проекции вектора пе-
перемещений на оси г и z, ио — частота колебаний, t — время, получим
систему дифференциальных уравнений
К + D - <*Л)Ак - A - 2и)-*ркВ'к = О,
A.67)
аВ'1 + (Щ - р1)Вк + A - 2iy)-lpkA'k = О,
1 1л ' l-2i/
при условиях
a)Ak(±h)=Bk(±h)=0,
6)a*zk(±h)=T*k(±h)=0, A.68)
в) Ak(h) = Bk(h) = a*zk(-h) = т*к{-К) = 0,
где р — плотность, \i, v — упругие постоянные материала, компоненты
тензора напряжений без учета временного множителя имеют вид
°~zk(r,z) — /icr*/c(^)^o(P/cr)» Trzk{r,z) — fiTk(z)J\(pkr),
A.69)
ark = /i[cr*fc(^)Jo(p/cr) - 2Ak(z)r J\(pkr)},
<k(z) = PPkAk(z) + aB'k(z), t%(z) = Afk(z)-pkBk(z),
a;k(z) = apkAk(z) + /3B'k(z), /3 = ^-.
Пусть задача A.67), A.68) имеет только простые собственные
значения и р^ ф р\, тогда ее собственные функции удовлетворяют
следующим соотношениям обобщенной ортогональности (Л — упругая
постоянная материала):
h
Ujn = J [pjpnBjBn + 4AjAn - AfjAfn] dz = 0, A.70)
-h
h
Vjn = J [pjPnAjAn + $\BjBn - B'jB'n\ dz = 0,
-h
h 2
-h
1.5. Некоторые соотношения обобщенной ортогональности 47
Первые два соотношения A.70) получены аналогично тому, как
это было сделано в работе [147] для плоской задачи. Также можно
показать, что
Wjn = 2(p2 -p2)-i lpna*zn(z)Bj(z) -PnBn(z)a*zj(z) -
-pjr*{z)An{z)+PjAj{z)r*n{z)}\h_h. A.71)
Отсюда следует последнее соотношение A.70) с учетом любых гранич-
граничных условий A.68).
1.5.2. Соотношения обобщенной ортогональности в задачах об
установившихся колебаниях сферического слоя. В сферической
системе координат г, $, (р рассмотрим однородные решения уравнений
Ламе в осесимметрических задачах об установившихся колебаниях
шарового слоя R\ ^ r ^ R2, поверхности г = R\ и г = R2 которого:
а) неподвижны, б) свободны от напряжений либо в) поверхность г =
= R\ неподвижна, а поверхность г = R% свободна от напряжений (или
наоборот). Собственные функции этих задач будем искать в виде
d ¦ A72)
u^kir.Lp) = V?(r)— Pak_i/2(cos(p)elu;t,
где Upk, urk — проекции вектора перемещений соответственно на оси (р
и r,PaA;_i/2(cos(^) — функции Лежандра, и — частота колебаний,
t — время, ak (к = 1,2,3,...) — собственные числа. Для определения
W?(r) и VJ?(r) получим систему обыкновенных дифференциальных
уравнений
- [(А + 2ц)D - 1/4)г"' - pcu2r]V{! +
+ (А + n)W%' + 2(А + 2/j,)r-]W% = 0, A.73)
Vk°) = (А + 2/i)rHf' + 2(А + 2M)Wfc0' - [2(А
+ (а2к - 1/4)М - pcA-ViW°k - (А + М)(а1
|1yfc° = 0) A.74)
где A, /i — коэффициенты Ламе, р — плотность, L\ и L^ соответству-
соответствующие дифференциальные операторы. Граничные условия примут вид
= дао = да2)=о,
a*rk{Rx) = a*rk(R2) = Tfc*(i?0 = ^№) = 0-
= <к№ = ^№) = о.
48 Гл. 1. Постановка контактных задач, некоторые общие методы
При этом компоненты тензора напряжений
iM, A.76)
a*k = 2Xr-lW°k(r) + (A + 2»)W% - X(a2k -
°
a;k = 2(A + /i)r_,^ + XW°k - (A
Теорема. Если задача A.73)—A.75) имеет только простые собствен-
собственные значения и а\ ф а2п, то справедливы следующие СОО:
A.77)
Доказательство. Используя уравнения A.73), A.74), рассмотрим
очевидные равенства
J [V*L2{Wl Vk°) - Vk°L2(Wl V*)]r dr = 0,
\ [W%(W°k, Vk°) - W*Lx(Wl V°)]rdr = 0,
из которых соответственно найдем
-(T/fcVn°)(A + 2M)(al - al) = ^V«V« -
+ (A + MrV%W%) - (rV°W°k)] + 2(A
1-а2п) = (Х-
rmfg)= \rmf(r)g(r)dr
1.5. Некоторые соотношения обобщенной ортогональности 49
Далее рассмотрим выражение
(al-a2n)W°kn, A.79)
где W%n дается соотношением A.77). В A.79) а^п и т? заменим выра-
выражениями по формулам из A.76) и раскроем скобки, после чего во вновь
полученном соотношении соответствующие слагаемые заменим выра-
выражениями в правых частях равенств A.78). Выполнив интегрирование
по частям, вычислим интеграл A.79) и к полученному соотношению
прибавим и вычтем выражение
Перегруппировав соответствующим образом слагаемые, окончательно
получим
+ r2Vu(a2 - l/4)r* -r2V°(a2 - 1/4Ы] A 80)
Из A.80) следует, что Wkn = 0 при любых граничных условиях
A.75), если а2п ф а\. Вывод формул A.80) не связан с видом граничных
условий для уравнений Ламе, следовательно, они будут справедливы
для любых неоднородных граничных условий. В этом случае в частных
неоднородных решениях вида A.72) и формулах A.80) следует считать
ак = к. Случай, когда одно из решений в A.80) неоднородное, а другое
однородное, понадобится для вычисления интеграла C.105).
Как видно из доказательства, СОО A.77) справедливы и при uj = 0.
В этом случае они совпадают с известными [263].
1.5.3. Соотношения обобщенной ортогональности в задачах об
установившихся колебаниях кольцевого слоя. В цилиндрической
системе координат г, ср, z рассмотрим однородные решения уравнений
Ламе в плоских задачах об установившихся колебаниях кольца R\ ^
< г < i?2 на поверхностях которого г = R\ и г = R% заданы любые
однородные условия, аналогичные условиям для задач п. 1.5.2 предыду-
предыдущего раздела. Если собственные функции таких задач записать в виде
игк = W%(r)cosak(peiujt, иф = W%(r) smak(peiujt, A.81)
где ак (к = 1,2,...) — собственные числа, то соответствующие компо-
компоненты тензора напряжений примут вид
aqk = E*o~qk(r) cosak(pelu; , q = r,(p, A.82)
771
rr(fk = Е*тк(г) sinak(pelu;t; E* = ^.
50 Гл. 1. Постановка контактных задач, некоторые общие методы
Аналогично п. 1.5.1, используя систему уравнений для W% и V^,
можно вычислить интеграл
W°kn = J Kk{r)V%{r) - T°n(r)W°k(r)] dr =
«I
= rD - a*) [akVX - akvyn + anWonaork - anWokaorn]RR\ A.83)
Из последнего соотношения следует, что при любых однородных
граничных условиях типа A.75) получим СОО
W°kn=0, A.84)
если а\ ^ а2п и все oik — простые собственные значения.
Отметим, что, как и в формуле A.80), значение интеграла A.83) не
зависит от вида граничных условий, и случай, когда одно из частных
решений неоднородное, будет также использован в дальнейшем (гл. 4).
Соотношения A.84) справедливы также и при w=0 и совпадают
с известными [172, 274].
СОО A.77) и A.84) дают возможность эффективно исследовать
с использованием однородных решений широкий класс осесимметрич-
ных задач для сектора шарового слоя и плоских задач для кольце-
кольцевого сектора. Для решения таких контактных задач, когда смешан-
смешанные граничные условия заданы на сферических и цилиндрических
поверхностях, может быть использован, например, метод, изложенный
в работах [15, 321].
Глава 2
КОНТАКТНЫЕ ЗАДАЧИ
ДЛЯ ЦИЛИНДРИЧЕСКИХ ТЕЛ КОНЕЧНЫХ
РАЗМЕРОВ
В этой главе рассматриваются собственно смешанные осесиммет-
ричные задачи теории упругости для кругового цилиндра конечного
радиуса и конечной толщины. Смешанные граничные условия задаются
на торцах цилиндра или на боковой поверхности. На смежных поверх-
поверхностях ставятся такие граничные условия, которые могут быть удо-
удовлетворены с помощью условий ортогональности либо условий обоб-
обобщенной ортогональности. Для решения задач этой главы и некоторых
других глав используются метод сведения парных рядов к бесконечной
алгебраической системе первого рода с сингулярной матрицей коэффи-
коэффициентов [17, 40] и метод однородных решений [15, 317].
М
2.1. Кручение штампом кругового цилиндра
Остановимся предварительно на решении двух смешанных
теории упругости о кручении штампом кругового цилиндра при
вии жесткого защемления боковой поверх-
поверхности (задача С\) и отсутствия на ней на-
напряжений (задача С^) (см. рис. 2.1). Эти
задачи можно рассматривать как модель-
модельные для демонстрации эффективности пред-
предложенных методов исследования, в то же
время они представляют и самостоятельный
интерес.
Поставленные задачи будут эквивалент-
эквивалентны следующим двум краевым задачам от-
относительно функции перемещений г;(г, z)
вдоль оси (р:
задач
усло-
услодг г дг
dz
Рис. 2.1. К задачам С\, С^
О, B.1)
52 Гл. 2. Контактные задачи для цилиндрических тел конечных размеров
v = 5г при 0 ^ г ^ a, z = h,
rZ(p = G-^- = О при a <r < R, z = h, B.2)
v = О при О ^ г ^ R, z = О,
v = О при г = R, O^z^h (задача Ci), B.3)
- — - ) =0 при г = R, 0 < z < h (задача G^). B.4)
r
Здесь 5 — угол поворота штампа, a — радиус штампа, i? — радиус
цилиндра, h — высота цилиндра, G — модуль сдвига.
Для решения поставленных задач используем метод сведения пар-
парных рядов к бесконечным системам первого рода с сингулярной матри-
матрицей коэффициентов и метод однородных решений.
2.1.1. Метод сведения парных рядов к бесконечным системам
первого рода. Разыскивая г;(г, z) в виде
оо
v(r,z) = 5 Y^ anshunz(unchunh)~lJ\(unr) B.5)
п=\
для определения коэффициентов ап получаем парное уравнение-ряд
A.1), где у(щ,х) = Jv(ukx) — собственные функции задачи Штурма-
Лиувилля A.2) при r(x) = —x~\ s(x) = x, t(x) = u2x~2 и в котором
следует положить
z/ = 1, f(x)=x, К{и) = и tYiuh. B.6)
Выпишем этот парный ряд в несколько общем виде:
JT akK(uk)Jv(ukx) = f(x) (O^x ^ a),
/с=1
B.7)
Здесь ^(ж) — функции Бесселя (у ^ —1/2), свойства функции К (и)
такие же как и в A.1).
В общем случае ик — нули уравнения
-Jv(ukx)+aJv(ukx)\ =0. B.8)
Для задач С\ и С% дифференциальное уравнение B.1) и крае-
краевые условия B.2) будут удовлетворены. Удовлетворяя условиям B.3)
и B.4), для определения постоянных ик получим соответственно урав-
уравнения
Ji(ukR)=0, J2(ukR)=0, B.9)
2.1. Кручение штампом кругового цилиндра 53
которые являются частным случаем уравнения B.8) соответственно
при а = оо и а = 1.
Пусть в B.7) f(x) = Jv(iex). При этом будем иметь в виду, что
в общем случае функция j{x) может быть разложена в ряд по функ-
функциям Ju(iskx). Тогда парный ряд-уравнение B.7) будет равносилен
бесконечной системе вида A.6)-A.8), которую здесь можно переписать
в следующем виде:
пт /г-2 2\ту/ \г /г \
[оп — ryrn)Ku[/yrna)lu[ona)
К ( I ( ) + I ( Ж ( ) B.Ю)
dm{e) = ————^—^ ~—: "—~—'
72 / \ ]ТП J-U — 1 \JTYl @j 11 у \?п I ?1 у — 1 ( ей ) 1 у \JTTl п I т~ъ ( • Т~)\
dm(?) = ~ \ 2 \J, , ,rl.\ LB(lJm,R),
i'jm, R) = 7m u '^m —Y~—'
Связь между коэффициентами a^ (к = 1,2,...) уравнения B.7) и
решением бесконечной системы B.10) выражается следующими соот-
соотношениями:
сю
K-l(ie)Jv(iex) + ? xn{s)Jn{i5nx)I-\5na) @ < ж < a),
0 (a < х < Д),
?A) = ^оаМ. B.12)
Решение бесконечной системы B.10) может быть получено по ана-
аналогии с решением системы A.6).
Контактные напряжения под штампом определятся из соотношения
сю
ТпДг,0) = G5 ]Г anJx(unr) @ < г < a). B.13)
п=\
Учитывая соотношение
г = lira — J\(er
s^O ds v '
и B.11), B.12), получим
54 Гл. 2. Контактные задачи для цилиндрических тел конечных размеров
d fr°°-i _i
?^ V n=l
уп = lim — хп(е),
где хп{е) — решение бесконечной системы B.10) при v = 1, а = оо
(задача Ci) и а = 0 (задача С^). Дифференцируя по г систему B.10)
и полагая после этого г = 0, для определения коэффициентов уп (п =
= 1,2,...) получим бесконечную систему
B-Y = D, B = B1+B2 = {6mn}, Y = {yn}, T> = {dn}, B.15)
yma)] с. _ Tin _ тгBш — 1)
—^—г^ (задача C\),
2;^m , (задача С2).
^2GтГ)
Матрицы Bi и В2 описаны в B.10) при v = 1.
Используя соотношение B.14), получим связь между моментом М,
приложенным к штампу, и углом поворота 5
Tllf)\ BЛ6)
j дп1\(дпа)
n=l
Для задачи С^ при Д = а из B.15) получим dm = 0, Ьшп ф 0,
и, следовательно, решение бесконечной системы B.15) уп =0. Таким
образом при R = a формулы B.14) и B.16) дадут известное точное
решение задачи о кручении стержня штампом, радиус которого равен
радиусу стержня.
Найдем главный член асимптотики решения бесконечной системы
B.15) при малых h/a и (R — a)/h > 0. Используя зависимость 5п =
= im/h, ут = тгBт — \)/2h и асимптотику функций 1п(х) и Кп(х)
при больших значениях аргумента х, для малых значений h/a будем
иметь [40, 311, 339]
В! = Е + В3, В3 - {3[8а21т5пEп - 7т)]},
^ / D°
/ D°' B.17)
|±ехрИт(йа)I
где элементы матрицы Е приведены в A.9). Здесь и далее знак плюс
соответствует задаче С\, минус — задаче С^.
2.1. Кручение штампом кругового цилиндра 55
Воспользовавшись малостью элементов матриц В2 и В3, по срав-
сравнению с элементами матрицы Е при h/a —> 0 и (R — a)/h > Ro > О,
получим бесконечную систему
EY0 = D0, Y0 = {y°n}, B.18)
решение которой будет главным членом асимптотики решения беско-
бесконечной системы B.15) при малых h/a и (R — d)jh > Ro > 0. Матрица
Е имеет обратную матрицу Е с элементами A.11), которые для
рассматриваемых задач принимают вид
/iBra-2)!!Bm-2)!!Bra-2m+l)' v' '
Кроме того, известно [52] решение бесконечной системы B.18) с пра-
правой частью {а/B/г7ш)}- Используя этот факт и обратную матри-
матрицу B.19), получим решение системы B.18) в виде
[ОО -\
J_ \_ уу Bт - 3)!! ехр (-тг(Д - a)Bm - \)/h) I
4^ ^ Z-/ Bm-2)!!Bn-2m+l)Bm+l) \
B.20)
При малых h/a формулу B.16) асимптотически можно преобразо-
преобразовать к виду
M = 7rG5a3(?- + — |>Лп\ B-21)
а формулу B.14), если О<го<г^а, — к виду
rrip(r, 0) = G5 \г- + 2АД ? ^?п(гI, B.22)
-Б(г) = ехр — — ((
Если г ^ 0, то
/2а
O(r3)j. B.23)
Ряд в B.22) сходится равномерно при всех г ^ а — е\, ?\ > 0. При
г ^ а ряд расходится, что свидетельствует о наличии особенности
у функции тГ(Дг,0). Выделим эту особенность, для чего B.20) преоб-
преобразуем к виду
)\ B-24)
Bm-2)!!Bn-2m+l)
771=1
56 Гл. 2. Контактные задачи для цилиндрических тел конечных размеров
Подставляя B.14) в B.22) и суммируя один из рядов, получим
(O<eo<r^a). B.25)
Здесь ряд при г = а сходится и особенность явно выделена. При
больших значениях параметра (R — a)/h
B.26)
и тогда при фиксированном малом значении параметра h/a и больших
значениях параметра (R — a)/h
B.27)
,, ^езГа , 2In4 .
2/г тг tt2E(R)_
Заметим, что при малых /г/а и (R — a)/h -^ оо формулы B.27)
будут совпадать с соответствующими результатами работы [20], где
рассматривалась задача о кручении штампом слоя.
Формула B.27) позволяет сделать вывод о том, что при фиксиро-
фиксированном малом значении h/a влияние боковой поверхности плиты на
распределение контактных напряжений под штампом экспоненциально
затухает с увеличением параметра (R — a)/h и практически уже при
(R — a)/h ^ 1 этим влиянием можно пренебречь.
Как показывают числовые расчеты, формулу B.27) можно использо-
использовать с относительной погрешностью, не превышающей 10% при h/a <
<0,5 и (R-a)/h ^0,3.
Для получения решения рассматриваемых задач для тех обла-
областей изменения параметров, где асимптотические формулы, выведен-
выведенные выше, теряют свою эффективность, исследуем бесконечную си-
систему B.15) методом урезания, предварительно регуляризовав ее по
схеме A.12). Урезанную систему представляем в виде A.16) и находим
ее решение на ЭВМ. Значение N выбираем в зависимости от заданной
точности. Как показывают числовые расчеты, сходимость метода уре-
2.1. Кручение штампом кругового цилиндра
57
зания улучшается при увеличении параметра (R — a)/h. Одновременно
с решением системы A.16) вычислялось значение величины
= max
N
rnmbmk
что позволяло приближенно судить о том, при каких значениях пара-
параметров R/a и h/a решаемая бесконечная система будет вполне регу-
регулярной.
Так, например, при N = 43, \± < 1, если R/a = 1,05, h/a ^ 4,10
@,28); R/a = 1,1, h/a < 4,05 @,39); R/a = 2, h/a < 4,28 B,09); R/a =
= 4, h/a ^ 4,3 D,07). Здесь число в скобках соответствует задаче Сг,
рядом стоящее без скобок — задаче С\. При этом, если в неравенствах
последнюю цифру увеличить на единицу, то при таком и большем
значении параметра h/a будет ц ^ 1.
о
0,5
h/a =2,0
'0,1 0,3 0,5 0,7 r/a 0,1 0,3 0,5 0,7 r/a
Рис. 2.2
На рис. 2.2 приведены зависимости величины г = rrip(r,0)(G5)~l от
r/a для некоторых значений параметров h/a и (R — а)/а для задачи С\,
вычисленные методом урезания бесконечной системы по схеме A.16)
и по формуле B.14) при N = 43.
Кривые 1-7 на рис. 2.2, а, построе-
построены соответственно при следующих
значениях параметров h/a и (R —
-а)/а\ 1, оо; 1, 0,5; 1, 0,1; 0,3, оо;
0,3, 0,1; 0,3, 0,05; 0,3, 0,01. Кривые
1-6 на рис. 2.2, б — при следую-
следующих: 2, оо; 2, 0,5; 0,5, оо; 0,5, 0,1;
0,5, 0,05; 0,5, 0,01.
На рис. 2.3 даны зависимости
2,0
0,0.
4
од
0,3
0,5
Рис. 2.3
0,7 h/a
величины т = 3M(\6G5a ) от h/a для значений параметра
(R — а)/а = оо, 0,1, 0,05, 0,01 (соответственно кривые 1-4).
При (R — а)/а = оо кривые построены по асимптотическим фор-
формулам работы [20], где рассматривалась задача о кручении штампом
слоя. С этими кривыми на рис. 2.2 практически сливаются кривые
распределения напряжений под штампом, если {R — a)/h ^ 1.
58 Гл. 2. Контактные задачи для цилиндрических тел конечных размеров
Графики показывают, что боковая поверхность плиты оказывает
преимущественное влияние на распределение напряжений под штам-
штампом вблизи его границы.
2.1.2. Метод однородных решений. Здесь на примере смешан-
смешанной осесимметричной задачи С\ теории упругости о кручении штам-
штампом кругового цилиндра конечных размеров, поставленной в этом
параграфе, излагается метод однородных решений для исследования
контактных задач для тел конечных размеров, границы которых сов-
совпадают с координатными поверхностями ортогональных систем коор-
координат [317]. Этот метод позволяет получить решения подобных задач
практически для любых значений параметров. Такая эффективность
метода определяется тем, что решение задачи сводится к решению бес-
бесконечной алгебраической системы второго рода высокого качества типа
нормальных систем Пуанкаре-Коха. Решение рассматриваемой здесь
задачи для случая большого значения отношения (R — a)/h и малых
значениях отношения Л = h/a получено в этом пункте выше.
Сведение задачи С\ к бесконечной системе Пуанкаре-Коха.
Предлагаемый здесь метод однородных решений заключается в сле-
следующем. На первом этапе найдем предварительно решение уравне-
уравнения B.1), когда
r(r) (<Kr<a, z = h), A)_
О (r>a, z = h), V U [Z V)-
С помощью интегрального преобразования Ханкеля получим (J\(x) —
функция Бесселя первого рода)
\r(p)pdp —-—- J\(ur)J\(up)uduy
J ] uchuh
0
B.28)
a oo
r^ ;(r,^) = r(p)pdp -^—^J\{ur)J\{up)udu.
о о
Далее на втором этапе найдем частные однородные решения урав-
уравнения B.1), когда
Суммируя однородные решения, получим
сю
v^2\r,z) = ^2 Bk8hukzJ\(ukr), B.29)
к=\
^^ / 1 \
rz2J(r>z) = Yl BkukchukzJ\(ukr), uk = г- [к - -) .
к=\ h V lJ
2.1. Кручение штампом кругового цилиндра 59
Используя ортогональность функций sh ukz на отрезке [0,/г], най-
найдем Вк из условия
v(r, z) = vA)(r, z) - vB)(r, z)=0 (r = Д), B.30)
lk = -iuk. B.31)
0
Теперь нетрудно убедиться в том, что функция v(r,z) = y(l\r,z) —
— yB\r,z) удовлетворяет уравнению B.1) и граничным условиям B.2).
На третьем этапе, удовлетворяя граничному условию B.3), получим
интегральное уравнение относительно функции распределения кон-
контактных напряжений:
сю
С^Вк(-\)к+х1\Ы) (г^а), B.32)
к=\
сю
Кг = r(p)pdp t\iuhJ\(ur)J\(up) du.
о о
Представим решение этого уравнения в виде
сю
т(г) = Gro(r) -GY, Вк(-\)к+1тк(г), B.33)
к=\
где функции тк(г) удовлетворяют уравнениям
Тогда, подставляя B.33) в B.31), для определения постоянных
Вк = Xk[hI\(R/jk)]~\ получим бесконечную систему линейных алгеб-
алгебраических уравнений
сю
хк = gk - 52 акпхп (к =1,2,...), B.35)
п=\
Т b n 2(-
l0,k, akn =
ar B-36)
Тп,к = J rn(p)Ii(pjk)pdp.
о
Исследуем бесконечную систему B.35). Можно показать, что
а
Тп,к < {2na)-lIl{a-fk)Mn, Mn = 2тг|г„(г)г2dr.
60 Гл. 2. Контактные задачи для цилиндрических тел конечных размеров
Оценим Мп(п > 1), для этого обе части уравнения B.34) при к > 1
умножим на гто(г) и проинтегрируем от 0 до а. Изменив порядок
интегрирования, получим
Отсюда следуют оценки
\gk\ < ^
Принимая во внимание асимптотическое поведение модифицирован-
модифицированных функций Бесселя К\(х) и 1\(х) при больших значениях аргумента,
получим
i i 1
Г tt(R — а) п 1Ч1 n ч
ехР h— (fc + ^ - 1) (fc, n ^ оо).
Видим, что при R > а свободные члены системы B.35) и коэф-
коэффициенты ее матрицы экспоненциально убывают с ростом номеров.
Таким образом, система B.35) относится к типу нормальных систем
Пуанкаре-Коха.
Такие системы возникают также при исследовании некоторых типов
смешанных задач методом кусочно-однородных решений [235].
Для вычисления элементов системы B.35) необходимо знать ре-
решения интегральных уравнений B.34), которые соответствуют хорошо
изученной контактной задаче о кручении штампом упругого слоя, и по-
поэтому для их решения с успехом могут быть использованы эффектив-
эффективные асимптотические методы [88].
Решение интегрального уравнения B.34) методом больших Л.
Уравнение B.34) эквивалентно парному интегральному уравнению
Фк(т) tht\Jx(tx) dr = fk(x) (О < х < 1),
B-37)
)Ji(rx)rdr = 0 (х > 1),
1
Фк(и) = ^r]k(y)Ji(uy)ydy, rjk(y) =rk(ya) (k = 1,2,...),
о
fk(x) = [5x, если к = 0; a~xI\(a^kx), если к > 1], Л = -.
Ob
2.1. Кручение штампом кругового цилиндра 61
В свою очередь, парное уравнение B.37) эквивалентно интеграль-
интегральному уравнению Фредгольма второго рода [43]
(^) (|*| ^ 1), B.38)
-1
°° оо
М(у) = Ъ\[1 -thu]cosuydu= ]T bky2k, B.39)
к0
о к=0
оо
dk(t) = B5k, если к = 0; а~х sh(a7fc?), если к ^ 1).
При этом
1 1
k(
2 d Г cpk(r)dr
2
/ у /Д) = -
r 0
B.40)
В соответствии со схемой метода больших Л (см. § 1.3 и [325])
решение уравнения B.38) будем разыскивать в виде
оо
Vm{t) = ? <(t)A-n. B.41)
n=0
Можно убедиться, если следовать схеме § 1.3, что
^(t) = dm(t), 4>?a(t) = $>;3*2''+1 (s > 3), B.42)
где a^- и /З^ находятся с помощью следующих рекуррентных соотно-
соотношений:
s — 2 s — k — 2 ш
2 ^
kj k 2s 2к - 2j + 2р+ 1 I 0 < j < 5 - 3 ) '
B.43)
m _ _^ l от _
sj - ^ ZSjOS-Dsj
s — о s — к — о
2 ^Ofc 2
2fc - 2j + 2p+ 1 I 0 < j < s - 1 ) '
62 Гл. 2. Контактные задачи для цилиндрических тел конечных размеров
sj
25Bs-2j+l)-1 (m =
Bfc)!
1-1
""
7ra
B.44)
Таким образом, формулы B.40), B.41), B.42), B.43) позволяют
получить решение интегрального уравнения B.34) с любой степенью
точности в области сходимости предложенного здесь метода больших Л
в виде элементарных и удобных для расчетов выражений
2 B.45)
B-46)
Воспользовавшись формулами B.36) и B.40), найдем
сю
s=\
x-2s-l
)=dm(t) +
s-1
Wm(t
СЮ
s=3
A-2S
s-3
EO
Подставив сюда (рп(т) в виде B.45), B.46), получим
9 2
Гр z,U/ [Q г 7-i/c | тт/ / трк \1 /'О Л7^
^0,/с = [^^-^1 "Ь ^0(-^j+l/J' \^Л1)
7Г
т1 — ?5L Г J_ /^shaGfc +7n) _ {lк - In)
П'к тг [2а2 V 7fc+7n 7fc - 7n
A^п(^+1) описывается по аналогии с B.46)). Теперь элементы беско-
бесконечной системы B.35) вычислим с использованием B.47), а прибли-
приближенное решение этой системы найдем методом редукции.
Контактные напряжения под штампом rZ(p(r, h) = г (г) вычисляются
по формуле B.33), в которой, если использовать B.40), B.45), B.46),
тк{га) = -
mr)dr „T (Q , ХЛ
+Щ{БЩ' B-48)
2)fc[Bj+l)r2-2(j-fc)]
(Wk(Sj(r)) описывается по аналогии с B.46)).
2.1. Кручение штампом кругового цилиндра 63
Связь между моментом М, приложенным к штампу, и углом пово-
поворота штампа 5 найдем из условия
М = 2тг \r(r)r2dr. B.49)
о
Используя B.33), B.40), B.45), B.46), получим
Мк = 8а3 \npk(r)dr, Мк = 8а3 \a~xF^ + Wk
Mo = 8a3
3) описывается по аналогии с B.46), F^ см. B.44)).
Таким образом, используя метод больших Л для решения уравне-
уравнения B.34), удалось получить решение задачи для больших значений
параметра Л через решение бесконечной системы B.35) в элементарных
выражениях с любой степенью точности, при этом в формулах для
контактных напряжений особенность явно выделена. Коэффициенты
бесконечной системы также получены в элементарных выражениях.
Об области применимости такого подхода к решению задачи будет
сказано ниже.
Решение интегрального уравнения B.34) методом малых Л.
Рассмотрим парное уравнение B.37), эквивалентное уравнению B.34),
и получим его решение методом сведения к бесконечной системе
линейных алгебраических уравнений с сингулярной матрицей [41].
В качестве решения последней возьмем главный член его асимптотики
при малых Л [56].
Согласно [40]
то(г) = ^ + 5 ? ylh{5nr)I^\5na), 5n = ^,
B.51)
ОО
п=\
Yk = {i/n} (fc ^ 0) — вектор, являющийся решением бесконечной си-
системы линейных алгебраических уравнений
64 Гл. 2. Контактные задачи для цилиндрических тел конечных размеров
тзлл/с т\к -о \ ^шКъ{^шаI\{5па) + 5nh{5na)K\{^rna)\
о Y = D , г$ = < —z ^\ : :—: : ( »
B.52)
аК2(/Уто)
Здесь В, Dfc — символы матрицы и вектора соответственно, 5^ —
символ Кронекера. При малых Л главный член асимптотики решения
бесконечной системы является решением вырожденной бесконечной
системы [56]
Система B.53) формально получена из системы B.52) в результате
предельного перехода при Л —> 0 Eп, 7т ^ оо (п,т^ 1)). Для матри-
матрицы Е известна обратная матрица Е B.19) и, следовательно, решение
системы B.53), а соответственно и главный член асимптотики решения
системы B.52) примут вид
0_
Уп-
B.54)
Bn-l)!!Bfe-3)!! , fc = 2 ,
2fe+l) l ' А^---;-
Вывод второй формулы B.54) очевиден, а первая формула B.54)
в таком виде получена, например, в работе [40].
Величина контактных напряжений под штампом и величина момен-
момента, приложенного к штампу, с использованием B.33), B.51), B.49),
B.50), B.54) при малых Л примут вид
м _ 27ra3G6 I 1 Л у> Bп- 1)!!/2(^па
~ ' 1т + -> ^ nBn)!!/iEno)" |'
Bk- 1)!!
a5h\l а ^ к Bк - 2)!!Bга - 2/с + 1)
2.1. Кручение штампом кругового цилиндра 65
где Xk (к = 1,2,...) — решение бесконечной системы B.35), в которой
с учетом малости параметра Л и формул B.51) и B.54)
_ )\ 1 у. Bт-1)!!
2/_1\fc+n+le-Gfc+7rx)(^-a)/2ri _ ПИ
пкп =
тгBк- 1)Bп-2)!!
^ Bm - 1)!!
^ Bт - 2)\\Bт - 2п + 1)Bш + 2к - 1)'
га=1
При получении формул B.55), B.56) использовалась малость пара-
параметра Л = h/a, если же, кроме этого, потребовать малости параметра
к = h/(R — а), то выражения B.55), B.56) для величин контактных
напряжений и момента можно значительно упростить. Учитывая соот-
соотношение 7/с — 7гB& — l)Bh)~\ можно показать, что
е-тг/Bж)^ + О(е~7Г/^)),
aSh\l a Bn-
Подставив сюда вместо х\ значение gx из B.56), получим
Bm)!!Bm+
B.57)
Формулы B.55), B.57) дают простое асимптотическое решение
задачи при малых значениях параметров Лих.
Учитывая, что l2Ena)I^\Sna) ~ 1 при малых Л, и взяв zn в виде
B.57), вторую формулу B.55) можно упростить, просуммировав в ней
ряд. Получим
М = nGSa3 \JL + 2-М + 1 e-AR-a)/h{l + о(Ае-1/ж)) + О(АI
L2A % П B.58)
Аналогично при малых Лих упрощается первая формула B.55),
если 0<г^а
т(г) = G6\^ + L Д [A -
l/г Л V г
О(\)]\. B.59)
Здесь явно выделена особенность при г ^ а.
Таким образом, при малых значениях параметра Л для искомых
величин задачи получено два набора формул: B.55), B.56), B.35)
3 В.М. Александров, М.И. Чебаков
66 Гл. 2. Контактные задачи для цилиндрических тел конечных размеров
и B.58), B.59). Первый набор связан с решением бесконечной си-
системы B.35), B.56), второй набор с этим не связан, но учитывает
малость параметра к. Об области применимости этих результатов
сказано ниже.
Числовые примеры и анализ результатов. Исследуем численно
безразмерные величины
М* = 3/\6(G5a3)-lM, т*(р) = (G5)-lr(pa) (О < р < 1), B.60)
характеризующие соответственно связь между приложенным к штампу
моментом и углом поворота штампа и контактные напряжения под
штампом, при разных значениях параметров Л = h/a и R* = R/a.
При этом для вычисления величин М и г* (г) будем использовать
алгоритмы и формулы, полученные выше.
Метод больших Л позволяет с использованием ПК находить с лю-
любой степенью точности величины М* и т(р) при А ) 1 и любых
практически возможных Д*. Ограничение по А связано со сходимостью
рядов типа B.46).
Бесконечную систему B.35)-B.36) будем решать методом уреза-
урезания. Обозначим через щ число уравнений системы. Коэффициенты
этой системы и величины B.60) будем вычислять с точностью до чле-
членов порядка О(\~п<2) При этом щ и щ будем выбирать такими, чтобы
погрешность окончательных результатов не превышала заданного зна-
значения. Заметим, что выбор значения п^ зависит только от параметра А,
а выбор значения щ зависит от значения величины (R — a)/h. При
этом чем меньше А, тем большим должно быть щ, и чем меньше
(R — a)/h, тем большим должно быть щ.
Например, погрешность в 0,01 % при А = 1 достигается при щ = 60,
при А = 1,5 — П2 = 10, а погрешность в 1 % при А = 1 достигается при
щ = 20. Для того, чтобы при (R — a)/h > 0,1 погрешность не превы-
превышала 0,1%, необходимо брать щ ^ 5, хотя уже при (R — a)/h > 0,2
и п\ = 5 погрешность не будет превышать 0,0003%. Погрешность в 1 %
при (R — a)/h = 0,0007 достигается, если щ =30, при (R — a)/h =
= 0,07 - щ = 5.
Использование метода малых А (см. § 3) позволяет находить при-
приближенное значение величин М* и т*(р) по формулам B.55), B.56),
B.35) с использованием ПК с погрешностью, не превышающей 3%
при А ^ 0,5. Если 0,5 < А < 1, то для вычислений коэффициентов
бесконечной системы B.35) необходимо методом урезания находить
решение системы B.52), асимптотически не упрощая ее, как это было
сделано в работе [40]. Относительно выбора щ здесь справедливо
сказанное выше.
Формулы B.58), B.59) позволяют вычислять М* и т*(р) с погреш-
погрешностью, не превышающей 3% при А < 0,5 и (R — a)/h > 0,5.
В табл. 2.1 приведены значения величин М* и т*(р) при разных
значениях параметров р, А и R.
2.2. Контактная задача о вдавливании штампа в торец кругового 67
Таблица 2.1
R*
А
т*@,1)
т*@,3)
т*@,5)
т*@,7)
г* @,9)
т*@,95)
М*
Д*
Л
т*@,1)
т*@,3)
т*@,5)
т*@,7)
г* @,9)
т*@,95)
М*
1,3; 1,5
0,1
1,000
3,000
5,000
7,000
9,235
10,77
3,448
1,01
0,1
1,000
3,000
5,000
7,001
9,606
12,79
4,131
1,3
1,5
0,1492
0,4689
0,8697
1,503
3,266
4,864
1,244
1,01
1,0
0,1782
0,5689
1,097
2,082
6,068
11,09
2,940
1,5
0,3
0,3336
1,002
1,679
2,422
3,853
5,117
1,464
1,05
0,1
1,000
3,000
5,000
7,001
9,336
11,29
3,606
1,5
1,0
0,1469
0,4572
0,8380
1,422
3,007
4,441
1,145
1,05
1,5
0,1709
0,5437
1,038
1,911
4,896
7,966
1,973
1,5
1,0
0,1457
0,8336
2,983
1,021
1Д
0,1
1,000
3,000
5,000
7,001
9,255
10,87
3,478
1,5
1,5
0,1417
0,4442
0,8188
1,400
2,983
4,412
1,135
1,1
1,5
0,1646
0,5258
0,9913
1,778
4,220
6,524
1,627
При Л ^ 1 использованы результаты пункта, когда решение инте-
интегрального уравнения B.34) находилось методом больших Л, в этом
случае значения М* и т* приведены с точностью до четырех цифр. При
Л < 1 использованы результаты пункта, когда решение интегрального
уравнения B.34) находилось методом малых Л. В этом случае чем
меньше Л, тем точнее результат.
Числовые результаты хорошо согласуются с результатами, получен-
полученными выше методом сведения парных рядов к бесконечным системам
первого рода с сингулярной матрицей.
2.2. Контактная задача о вдавливании штампа в торец
кругового цилиндра
Рассмотрим осесимметричную контактную задачу теории упруго-
упругости, которую назовем задачей Сз, о вдавливании силой Р штампа ради-
радиуса а в плоскую границу цилиндра радиуса R и высоты h (см. рис. 2.4).
Предполагается, что противоположная плоская граница цилиндра
покоится без трения на жестком основании, а боковая его поверхность
68 Гл. 2. Контактные задачи для цилиндрических тел конечных размеров
Рис. 2.4. К задаче С3
находится в условиях скользящей заделки,
т. е. отсутствуют нормальные перемещения
и касательные напряжения. Для решения
задачи используются метод, основанный на
сведении возникающих парных рядов-урав-
рядов-уравнений к бесконечной алгебраической систе-
системе первого рода с сингулярной матрицей
коэффициентов, и метод однородных реше-
решений [310, 311, 316, 318, 321].
В цилиндрической системе координат г,
(р, z рассмотрим упругий цилиндр 0 ^ z ^
^h, r < R. Поставленная контактная задача
теории упругости для этого цилиндра сводится к краевой задаче для
уравнений Ламе в цилиндрических координатах [266] при следующих
граничных условиях E(г) — функция, описывающая форму и переме-
перемещение штампа):
uz = 5 (г) (z = h, 0 < г < a), az = 0 (z = h, a<r < Д),
uz=0, rrz=0 (z = 0, 0 < r < Д),
ur = 0, rrz = 0 @ < z < h, r = R).
2.2.1. Метод сведения парных рядов к бесконечным системам.
Как и в случае задач С\ и С^, задача С% может быть сведена к иссле-
исследованию парного ряда-уравнения B.7), где
К(и) =
ch2u-
B.61)
v = 0, f(x) = 5(x) — функция, описывающая перемещение штампа и
его форму, Uk — нули уравнения J^UkR) = 0.
Пусть 5(х) = 5 = const, тогда ряд-уравнение B.7) будет равно-
равносильно бесконечной системе B.10), которая в этом случае примет
следующий вид:
ВХ = D, B.62)
-{
6nIiFn/\)Ko(<ym/\)
E2п-72ш)К0Gш/ХI0Eп/Х)
- 6nIiFn/\)Ii(>ym/X)
где
Ьпт
EZn-7Zm)Kob
dm = [ iftGm/A) - ВAшЪ/ХIхAш/Х) \ B, , = Kx(x)
m \ 7mi^oGm/A) J ' IX(x)
Здесь A = h/a, b = R/a, ±i5n и ±i/ym — счетное множество простых
нулей и полюсов функции B.61), В = {Ьтп} — матрица, D = {dm},
X = {хп} — векторы-столбцы бесконечного порядка.
2.2. Контактная задача о вдавливании штампа в торец кругового 69
Контактные напряжения под штампом через решение системы
B.62) выразятся по формуле
az(pa,h) = q(p) =
G5
-i/)Aa\
О). B.63)
Связь между силой Р, приложенной к штампу, и перемещением
штампа 5 определяется соотношением
р _ 2тгав6 Г J_ ^ Xn /i(<WA)l /9 R
АA - I/) |_2А + ^ 5n IoFn/\)\' { °
В B.63)-B.64) А = НтК(м) = 0,5 (и -> оо), G - модуль сдвига, */ -
коэффициент Пуассона.
Известно, что |7т|> \$т\ ~ ш Gт 7^ йт) ПРИ m "^ °°> тогда, учи-
учитывая асимптотическое представление Кп(х) и 1п(х) при ж -^ оо,
систему B.62) можно регуляризовать путем выделения и обращения
бесконечной сингулярной матрицы Е с элементами A.9).
Получим бесконечную систему второго рода вида A.12)
X = E-'D - Е-^В - Е)Х. B.65)
Точная факторизация функции К (и) связана с большими трудно-
трудностями, поэтому воспользуемся приближенной факторизацией [56], для
чего функцию К (и) аппроксимируем функцией L(u) A.13). Функция
L(u) легко факторизуется, что позволяет получить простые прибли-
приближенные соотношения для элементов матрицы Е в виде A.14).
Таким образом, контактные напряжения и связь между силой Р
и перемещением штампа 5 определяются соответственно по формулам
B.63) и B.64), где хп — решение бесконечной системы B.65), 5п и 7т
определяются соотношениями A.15).
Числовые результаты. Решение системы B.65) получим методом
урезания, урезанную систему представляем в виде A.16) и находим
ее решение на ПК. Значение N выбираем в зависимости от заданной
точности. Числовые расчеты показывают, что сходимость метода улуч-
улучшается при увеличении параметра (R — a)/h.
Если в аппроксимирующей функции A.13) число В <С 0,5, то 5п
и 7т ПРИ п> S будут большими числами, так как, согласно A.15),
при п > S они обратно пропорциональны В. Тогда можно показать, что
при номерах больших S свободные члены и элементы матрицы системы
A.16) будут малы, и, следовательно, в системе A.16) N можно считать
равным S. Но при этом, к сожалению, при фиксированном значении S
с уменьшением В ухудшается точность аппроксимации A.13).
Если В = 0,5 и 5 = 2, то при р{ = 1,174, р2 = 2,208, qx = 1,496,
<22 = 1,732 относительная погрешность аппроксимации A.13) не превы-
превышает 2%.
70 Гл. 2. Контактные задачи для цилиндрических тел конечных размеров
Для вычисления безразмерных величин
а(р) = q(p)a(l - v){G5)~\ Q =
-1 B.66)
использовались формулы B.63), B.64) и решение системы A.16).
В табл. 2.2 приведены значения величин а(р) и Р для различных
значений параметров р, X,b = R/a.
Таблица 2.2
Л
ъ
<т@,0)
<т@,5)
сг@,95)
Q
Л
сг(О,О)
ст@,5)
сг@,95)
Q
0,3
1,1
6,643
6,620
8,058
23,08
0,5
2,0
3,835
3,800
5,838
14,54
0,3
1,2
6,615
6,563
8,261
23,22
1,0
1,3
1,960
2,010
3,737
8,438
0,3
1,5
6,593
6,514
8,092
22,91
1,0
1,5
1,919
1,982
4,049
8,741
0,5
1,1
3,976
3,976
5,227
14,26
1,0
1,7
1,888
1,954
4,105
8,747
0,5
1,3
3,897
3,882
5,966
14,92
1,0
2,0
1,860
1,926
4,080
8,659
0,5
1,5
3,857
3,829
5,927
14,76
1,0
2,5
1,843
1,906
4,034
8,566
1,0
3,0
1,838
1,901
4,018
8,536
Анализ приведенных выше числовых значений величины Q при
фиксированном значении Л позволяет сделать следующий вывод: при
увеличении параметра Ь от 1 до некоторого значения сопротивление
цилиндра внедрению штампа растет, а при дальнейшем увеличении
параметра это сопротивление уменьшается и стремится к некоторому
постоянному значению. Этот факт может быть использован на практи-
практике при выборе максимальной жесткости упругого конечного кругового
цилиндра, помещенного без зазора в жесткий «стакан» с гладкими
стенками.
2.2.2. Метод однородных решений. Здесь поставленная выше
контактная задача Сз решается методом однородных решений. Рас-
Рассмотрен числовой пример, который показывает, что при фиксированных
значениях высоты цилиндра и радиуса штампа сопротивление ци-
цилиндра внедрению штампа является немонотонной функцией радиуса
цилиндра.
На этапе получения бесконечной системы Пуанкаре-Коха несколь-
несколько обобщим постановку задачи и рассмотрим осесимметричную кон-
контактную задачу См о вертикальных нерезонансных колебаниях штам-
штампа радиуса а, лежащего без трения на плоской границе кругового
цилиндра радиуса R и высоты h, под действием вертикальной силы
pe-%ujt ПрИ следующих граничных условиях:
2.2. Контактная задача о вдавливании штампа в торец кругового 71
az(r, z) = О (z = h, а < г < R), w(r, z) = 5(г) (z = h, r < a),
rrz{r, z) = О (z = h, z = 0, r < R), w(r, z) = 0 (z = 0, r < Д),
rrz(r, z) = u(r, z)=0 (r = R, 0 < z < Л). B-67)
Здесь ue~luJt, we~luJt — проекции вектора перемещения соответственно
на оси г и z, aze~tu;t, rrze~tu;t — компоненты тензора напряжений.
Задача C^d Другим методом изучалась в работе [69], ряд близких
по постановке осесимметричных контактных задач для цилиндра рас-
рассматривался в работах [62, 63, 76, 151, 208, 213] и др.
Для решения задачи C^d применим метод однородных реше-
решений [321]. В соответствии с изложенной выше схемой этого метода на
первом этапе найдем решение задачи для слоя, когда
az(r,z)=q(r) (z = h,r^a), az(r,z)=0 (z = h,r>a),
rrz(r,z)=0 (z = h), rrz(r,z)=w(r,z)=0, (z = O).
Используя принцип предельного поглощения [282], нагрузим пра-
правые части уравнений Ламе соответственно членами
dt '
(г — коэффициент фиктивного поглощения) и будем разыскивать ре-
решение таких уравнений в виде ue~luJt, we~luJt. Разделяя переменные
и применяя к полученным уравнениям для и и w преобразование
Ханкеля, получим
а оо
w^(r,z) = — q(p)pdp L?(z,u)Jo(ur)Jo(up)udu, B.69)
/Jj J J
о о
a oo
1 г г
v,(l\r,z) = - q(p)pdp L\?(z,u)J\(ur)Jo(up)udu,
Uj J J
о о
a oo
r^ir.z) = \q(p)pdp L2?(z,u)J\(ur)Jo(up)udu,
J J
о о
L?(z, u) = B(z, u)j(u), L\?(z, u) = A(z, u) = A(z, u)j(u),
L2?(z, u) = [Af(z, u) - uB(z, и)]-у(и), -y(u) = [f3uA(h, u) + aB'(h, u)]~\
A(z, u) = ux~x[(rf? + v?) sh ?7е/г ch k?z — 2я?г]? ch rj?z sh xe/i],
5(^, u) = — [{rf? + г^2) sh 7/g/i sh x?^ — 2u2 sh ry?^ sh хе/г],
где штрих означает производную по первому аргументу.
72 Гл. 2. Контактные задачи для цилиндрических тел конечных размеров
На втором этапе решения построим систему однородных решений
видоизмененных указанным выше образом уравнений Ламе для слоя,
когда
az(r, z) = rrz(r, z) = 0 (z = h), w(r, z) = rrz(r, z) = 0 (z = 0).
Эти граничные условия будут равносильны условиям б) в A.68),
если краевую задачу симметрично продолжить в область — h < z < 0.
Проекции вектора перемещений и компоненты тензора напряжений
будут иметь вид A.66), A.69), где
Ak(z) = A(z,pk), Bk(z) = B(z,pk), B.70)
и при этом к\ и гЦ необходимо заменить соответственно на
2 _ 2 pcJ2(l-\-is) 2 _ 2 pcJ2(l+is)
ks Pk A + 2/i ' 'hs k /л
(f3PkAk(h)+aBfk(h)=0),
где pk — корни уравнения, приведенного в скобках. На третьем этапе
введем в рассмотрение функции
сю сю
uW(r,z) = J2 DkAk{z)J{{pkr), w^(r,z) = Y, DkBk(z)J0(pkr),
B.7.,
T\ ) (rp y\ \ 7~O n-T' ( у\ ~[ л (ТЛ1 У*)
„ « I / , /6 1 — 7 J-sk I h, I/O I U \ \jJ k ' I 9
k=\
где rk(z) обозначено в A.69). Здесь суммирование ведется по всем рк,
для которых Im(pfc) > 0, Dk — неизвестные коэффициенты.
Тогда решение задачи, поставленной в этом пункте, запишем в виде
u(r, z) = ^xA)(r, z) - uW(r, z), w(r, z) = w{l\r, z) - wW(r, z). B.72)
При этом коэффициенты Dk разложения B.71) найдем из условия
lt(r 7\ — о Т (г 7\ — T0)/V 7) — т^ — 0 (г — R)
которое перепишем в виде
J2 DkAk(z)Jx(pkR) =UW(R,z), J2 DkTt(r)Ji(pkR) = ц-1т$A1>г)-
В последних соотношениях умножим первое равенство на a*j из A.69),
второе — на Bj(z), из первого вычтем второе и проинтегрируем в пре-
пределах от —h до к. Учитывая последнее соотношение A.70), которое
справедливо и при г ф 0, получим
2.2. Контактная задача о вдавливании штампа в торец кругового 73
Dk = J
~h
= (^WkkJx(pkR))-x \q(p)Qk(p)pdp, B.73)
0
oo
flk(p) = Mk(u)J\(uR)Jo(up)udu,
о
h
Mk(u) = 7(U) j [A(z, u)a*rk(z) - (A'(z, u) - uB(z, u))Bk{z)} dz.
-h
Сравнивая последние соотношения B.73) и A.70), получим Mk(pj) =
— l(Pj)Wkj, где функция j(u) описана в B.69). Учитывая граничные
условия для однородных решений и соотношение A.71) для Wkj, по-
получим
M() = 2uBk(h)(u2-p2k)-\
сю
пк(р) = 2Bk(h) \ ^-^ J{(uR)J0(up) du =
J и -рк
° = -2Bk(h)ipkh(-ippk)Kx(-iRpk).
Последний интеграл взят из [129] с учетом того, что \т(рк) ф 0
для всех рк, 1о(х) и К\(х) — модифицированные функции Бесселя.
Теперь все граничные условия B.67) выполнены, кроме условия
w(r, z) = w^\r, z) — w^\r, z) = 5{r) (z = h, r ^ a).
Введем оператор K^hq = w^l\r, h), где w^l\r, К) описывается одной
из формул B.69). Тогда, удовлетворяя последнему условию, для кон-
контактного давления q(p) под штампом получим интегральное уравнение
сю
lTxK%hq = 5(г) + ? DkBk(h)J0(Pkr) (г < а).
/с=1
Если q(p) представить в виде
[сю
qo(p) + j: DkBk(hqk)(p) , B.74)
k=\
где qk{p) — решение интегральных уравнений
Kerh% = (\-vM(r) (r<a), Ksrhqk = (l-v)J0(Pkr),
\Z,. to)
(k^\, r^a),
и подставить B.74) в B.73), получим бесконечную систему линейных
алгебраических уравнений для определения постоянных Dk разложе-
разложения B.74):
74 Гл. 2. Контактные задачи для цилиндрических тел конечных размеров
Xk = gk + ? акпхп {хк = DkBk{h)Ix (^) , к > 1), B.76)
акп = -2ilkW^Bi(h)K, (^*) /j (^) Тп,ь
0,ь 7fc =
о
До сих пор считалось, что коэффициент фиктивного поглощения
среды е > 0. Устремляя г к нулю, получим решение исходной задачи 1.
При этом следует учесть [55], что некоторые нули и полюсы функции
L?(h,u) B.69) при г —> 0 перейдут на действительную ось, что вызовет
деформацию контура интегрирования в выражении ядра интегральных
уравнений B.75). О том, как будет выглядеть этот контур Г, подробно
сказано в работе [55].
Таким образом, контактное давление определяется формулой
[оо
Qo(p) + J2 XkIi~l \JiTj qk(ti ' B.77)
где Хк — решение системы B.76) при г = 0, qk(p) — решение из-
известных [55] интегральных уравнений (qk{ctp) = ^fc(p))» записанных
в безразмерных переменных
1
[L(uX)J0(ur)J0(up)du = fk(r) (г < 1), B.78)
г
Л--,
Цт) = 2 2К } 2 22
4т к г]chrjsh>zr — (rj +т) sh?7ch>zr B.79)
, (А; = 0); h{^f) , (Л < 1)}. B.80)
В формулах B.78) далее будем считать, что 7/с — полюсы функции
L(t) B.79). Контур Г совпадает с положительной частью веществен-
вещественной оси всюду, за исключением отрезков, содержащих вещественные
полюсы функции L(t) [55]. В случае чередования нулей и полюсов
этой функции указанные отрезки обходятся контуром снизу [55].
Исследуем бесконечную систему B.76). Известно [55], что функция
Ь(т) имеет конечное число действительных нулей и полюсов и число
их возрастает с ростом приведенной частоты Щ. Комплексные полюсы
функции Ь(т) при больших номерах имеют следующее асимптотиче-
2.2. Контактная задача о вдавливании штампа в торец кругового 75
ское представление [211] (а^ (г = 1,2,3,4) — действительные посто-
постоянные):
zn = ihjn ~ гпа\ + а^ In (а^п + а±). B.81)
Учитывая B.81), можно показать, как это было сделано в работах
[15, 317], что с ростом номеров коэффициенты бесконечной системы
B.76) имеют следующую асимптотику (к,п —> оо):
BJ2)
Следовательно, система B.76) принадлежит к типу нормальных систем
Пуанкаре-Коха и ее решение может быть получено методом редукции
при любых значениях параметра (R — a)/h > 0.
В случае uj = 0 получаем поставленную ранее статическую осесим-
метричную контактную задачу С% о вдавливании силой Р штампа ра-
радиуса а в плоскую границу кругового цилиндра радиуса R и высоты h.
Граничные условия имеют вид B.67), где u,w — проекции вектора
перемещения, az,rrz — компоненты тензора напряжений.
Здесь, как и при uj ^ 0, найдем контактное давление по формуле
B.77), в которой Xk — решение системы вида B.76) с коэффициентами
-7—
, 2Л/ т^ [^Ук\ T-lfR/yk
tg 7fcAi —r— lx —r—
L{u) = (ch2u- l)Bu + sh2u)-\ B.84)
Функция Tn>fc описана в B.76), qk(ap) — решение интегрального
уравнения B.78), где /&(г) имеет вид B.80), г7/с — комплексные полю-
полюсы функции 1/(т), лежащие в верхней полуплоскости. Так как функция
не имеет действительных полюсов, то контур Г в уравнении B.78)
будет полностью совпадать с положительной частью вещественной оси.
Бесконечная система B.76), B.83) здесь также будет принадлежать
к типу нормальных систем Пуанкаре-Коха.
Решение интегральных уравнений B.78). К интегральным урав-
уравнениям типа B.78) сводятся аналогичные контактные задачи для упру-
упругого слоя. Такие уравнения хорошо изучены и для нахождения их
решения можно воспользоваться, например, асимптотическими мето-
методами [88]. Известно (см., например, [43]), что уравнение B.78) при
условии limL(r) = 1 + О(т~2) (т —> 0) равносильно интегральному
уравнению второго рода
dr + dk(t) (|tKl), B.85)
-1
М(у) = [1 - L(u)] cosuydu, B.86)
г
76 Гл. 2. Контактные задачи для цилиндрических тел конечных размеров
где L(u) есть B.79) (и ф 0), либо B.84) (и = 0). Для динамической
задачи контур Г расположен как было описано выше; для статической
задачи он совпадает с положительной частью действительной оси.
Кроме того
1 t
^l^L j I rJ0±. B.87)
0
Для решения интегрального уравнения B.85), B.86) используем
метод больших Л (см. § 1.3 и [325]), для него необходимо представить
ядро B.86) в виде ряда по положительным степеням \у\. В случае и =
= 0 это нетрудно сделать:
7Г dr
dk(t) = j-
dt
оо (_
М(у) = ? Ъку2к, Ьк =
[1 - L(u)]
u2k du,
B.88)
и в этом случае решение уравнения B.85), B.88) для больших Л можно
записать в виде [317, 325]
м м
3=0 s=j
где М — сколь угодно большое число, коэффициенты
деляются из простых рекуррентных соотношений
s— I s — к— 1 rn
2 Ps-k-\,v
B.89)
и а™- опре-
опреp=0
2k-2j+l
s-1
s-fc-1
№j = -\°- bsZsjF^
TO_
m
as-k,P
k=j
p=0
2p+2k- 2j + 1
B.91)
> 1).
Таким образом, в случае больших значений параметра Л (Ао < А <
< оо) решение B.89) может быть получено с любой степенью точности.
Для ядра B.86) в случае и ф 0 можно показать, что справедливо
разложение [321]
B.92)
к=0
и в этом случае решение также можно получить методом больших А.
2.2. Контактная задача о вдавливании штампа в торец кругового 11
Числовой пример. Рассмотрим статическую задачу С% о внедрении
штампа с плоской подошвой E(г) = 5 = const) в упругий цилиндр. Для
этой задачи контактные напряжения
9 Г M 1
qk(pa) = '- W H){\)Sj{p) + Gk{p) (p < 1, M -* сю),
Lj=o J
G0(p)=a-lS0(p),
Связь между силой Р, действующей на штамп, и перемещением штам-
штампа 5 определяется формулой
р = 4^ Гро + \_ g ^/riGfcjR//l)PJ f B.94)
м
До = fo-1, Дд. = ha~2%1 sh te) (jfc > 1),
где Xfc — решение бесконечной системы B.76) с коэффициента-
коэффициентами B.83), в которых
9 2 Г М
9
м = — ? Щ(Щ + *га (М ^ оо), B.95)
71 L J
aik f - hsh ta^7n + ^fc)/^ i hsh ta(^n ~
^ 2 ( + )
27 \ ¦ 27 \
2a Gn + 7fc) 2a Gn - 7fc)
Величины F^ определяются формулой B.91), Hj(X) — формула-
формулами B.89), B.90), 7m — нули функции 2^ + sin2^x, лежащие в правой
полуплоскости Gт ф 0)» ПРИ больших номерах т известно их асимп-
асимптотическое поведение [88]
7т ~ тг I т - - j ± - In Dтгш - тг) (ш -^ оо).
Для численного исследования задачи была составлена программа
для ПК. Исследовались безразмерные величины
Р* = РA-и)(ц6а)-\ q%p)=q(pa)(l-u)a(fi5)-1 (p < 1) B.96)
при разных значениях параметров Л и R* = i?/a.
78 Гл. 2. Контактные задачи для цилиндрических тел конечных размеров
Значения Р и q(r) определялись соответственно формулами B.94)
и B.93). Предложенный алгоритм позволяет находить величины р*
и q*(p) при Л > 1 практически с любой степенью точности, при этом
решение бесконечной системы линейных алгебраических уравнений
находится методом редукции. В формулах B.93)-B.95), B.89) М счи-
считалось конечным числом, что позволяло находить Р* и q*(p) с точно-
точностью до членов порядка Х~2М~\ Отметим, что чем больше параметр
(R — a)/h, тем меньше требовалось брать уравнений в редуцированной
бесконечной системе (более подробно о сходимости предложенного
алгоритма см. [317]). Ниже при-
приведены значения величин Р* и
q*(p) в зависимости от параметров
А, Я* и р.
Анализ числовых значений вели-
величины Р* при фиксированном значе-
значении параметра Л позволяет сделать
следующий вывод: при увеличении
параметра R* от единицы до некото-
некоторого значения, которое зависит от Л,
сопротивление цилиндра внедрению
штампа растет, а при дальнейшем
увеличении параметра R* это со-
сопротивление уменьшается и стре-
стремится к некоторому постоянному значению. Наглядно это можно про-
проследить на рис. 2.5, где изображена зависимость Р* от R* при Л = 2.
Таблица 2.3
р*
6,2
6,0
5,8
5,6
5.4
Х = 2
1,4 1,8 2,2 2,6 3,0 3,4 3,8
Рис. 2.5
Л = 2
R*
Р*
д*@,20)
q*@,95)
1,5
5,426
0,971
2,509
6
1
2
2,0
,096
,022
,995
2,2
6,142
1,029
3,053
2,4
6,143
1,032
3,053
2,6
6,126
1,034
3,051
6
1
3
2,8
,103
,035
,043
3,0
6,082
1,036
3,033
оо
6,024
1,039
3,002
Л = 4
R*
Р*
д*@,20)
<f @,95)
1,5
2,948
0,460
1,351
2,0
4,075
0,612
2,001
2,5
4,616
0,702
2,311
3,0
4,844
0,750
2,444
3,8
4,940
—
—
оо
4,882
0,801
2,480
Отметим, что алгоритм позволяет находить решение динамической
задачи См также с любой степенью точности при Л > А*(о;), при этом
А* (о;) увеличивается с увеличением частоты и.
2.3. Контактная задача для предварительно напряженного
79
2.3. Контактная задача для предварительно
напряженного конечного цилиндра
Ниже рассмотрена задача С\ о внедрении симметрично располо-
расположенных штампов в торцы кругового цилиндра при наличии в цилин-
цилиндре однородного поля начальных напряжений [294, 295]. Использует-
Используется модель нелинейно-упругого изотропного несжимаемого материала
(см. рис. 2.6 на стр. 79).
Задача приведена к парному ряду-уравнению, решение которого
сводится к бесконечной системе линейных алгебраических уравнений
с сингулярной матрицей. Излагается метод решения этой системы. Для
некоторых распространенных мо-
моделей резиноподобных материалов
вычислены контактные напряжения
и жесткость цилиндра в зависи-
зависимости от степени предварительного
бокового сжатия или растяжения,
а также геометрических параметров
цилиндра.
Постановка задачи. Рассмот-
Рассмотрим круговой цилиндр из нелиней-
нелинейно-упругого изотропного несжима-
несжимаемого материала, равномерно сжа-
сжатый или растянутый силами, при-
приложенными к боковой поверхности.
Торцы цилиндра свободны от на-
нагрузки. На описанную однородную
конечную деформацию накладыва-
накладывается малая деформация, обусловленная внедрением в торцы цилиндра
двух симметрично расположенных круговых штампов. Будем считать,
что трение между штампами и упругим телом отсутствует, а на бо-
боковой поверхности цилиндра заданы условия отсутствия касательных
напряжений и нормальных перемещений. В силу предположений о ма-
малости добавочной деформации контактную задачу будем рассматривать
в линеаризованной постановке. Линеаризованные уравнения равнове-
равновесия для осесимметричной добавочной деформации несжимаемого тела
имеют вид [289]
д2и 1 ди и\ (д2и d2w \ dq _ ~
дгг г дг rl I \ Qzz drdz I dr
Р
Рис. 2.6. К задаче С\
d и . d w . v du . я dw . dq ~
drdz Or r dr r dr dz
ди
дг
dw
= 0,
B.97)
ц =
80 Гл. 2. Контактные задачи для цилиндрических тел конечных размеров
Ж (*•«= 1.2.3). B-98)
Здесь г, z — цилиндрические координаты в предварительно дефор-
деформированной среде, и, w — компоненты вектора перемещений соответ-
соответственно в радиальном и вертикальном направлениях, q — добавочное
нормальное напряжение в горизонтальных сечениях цилиндра, П =
= П(?ь?2>?з) ~~ функция удельной потенциальной энергии деформа-
деформации, определяющая упругие свойства материала. В рассматриваемом
случае е\ = е^ = ?, ?з — ?~2> гДе (? — 1) — относительное удлинение
горизонтальных волокон в начальном деформированном состоянии.
Для упругого материала, свойства которого задаются трехпарамет-
рическим потенциалом [343], имеем (G, п, C — постоянные)
П = Gn-\\ + /?)(е? + ?? + ?? - 3) + A - /3)(^п + е2~п + е~п - 3)],
(л = Gn-le-2n[(l - C)е-п + 1 + /3][п + 1 + (п - 1)е3п],
v = Gn-{?-2n(l - г3п)(\ - г6)-{[\ + /3 + A - C)гп\,
к = Gn-xe-2n(\ - е3п)(е~6 - \)~1[\ + /3 + A - C)еп\.
Частными случаями трехпараметрического потенциала является потен-
потенциал Муни [204] (Ci,C2 — постоянные)
п = сх(е\ + 4 + е23 - з) + с2D4 + 44 + 44 - з),
/х = 2г2(\ + 3?-6(Ci + С2?2), v = 2е~\Сх + С2г2),
1(
к = 2е1(Сх + С2?2), 2(Ci + С2) = G B.99)
и потенциал Бартенева-Хазановича [204]
П = 2G(ex + г2 + е3 - 3), /х = 4fe-2 B.100)
2С 2Gs4
V=^ о", К = о-
е\\+е3) 1+?3
Здесь и далее G означает модуль сдвига материала при малых де-
деформациях из ненапряженного состояния. При С% = 0 материал Муни
называется неогуковским [204].
Поставленная контактная задача имеет следующие граничные
условия:
^ ^ = 0 (r = R), B.101)
при z = dz/г
q = 0 (a<r<R), B.102)
+ ^=0 @<:r<R).
dr
2.3. Контактная задача для предварительно напряженного 81
В B.101), B.102) 2h — толщина цилиндра, R — радиус цилиндра, а —
радиус штампа, 5 — смещение штампа, (р(г) — функция, задающая
форму штампа.
Решение краевой задачи B.97), B.101), B.102) будем искать в виде
разложений
сю сю
u(r,z) = ? Un(z)Jx(knr), w(r,z) = ? Wn(z)J0(knr),
n=o n=o B.103)
oo
q(r,z) = YQn(z)Jo(knr),
n=0
где Jo(r), Ji(r) — функции Бесселя. Если набор постоянных kn под-
подчинить условию J\(knR) =0, то граничные условия B.101) на боко-
боковой поверхности цилиндра будут выполнены. Удовлетворяя при помо-
помощи B.103) уравнениям B.97) и краевым условиям B.102), приходим
к парному ряду-уравнению вида A.1) или B.7) с неизвестными Вп\
l,Lyu - у\г)) \г ^ а;,
B.104)
]Г BnK(knh)J0(knr) = 2Gh~lU(S - <p(r)) (r < a),
n=0
СЮ
J2 BnJ0(knr) + Бо = 0 (a < r < Д),
n=0
^ ^ ~~ mA(m)
Д(гх) =a(l+/32)[/i-z/(l+a2)]sh^/3ch^a-
' BЛ05)
- C( 1 + а2) [{1 - и( 1 + /З2)] sh ^ ch uC, B.106)
а2)(\ + f32) - fi(\ - af3) R
где ui\, и>2 — положительные корни уравнения
vuja - (/i - 2v)uj2 + х = 0. B.107)
Функции в B.103), образующие решение задачи, выражаются через
постоянные Вп следующим образом:
Wn(z) = Bn[Ansh(knaz) + Cnsh(knf3z)}, B.108)
Un{z) = -Bn[aAn ch (knaz) + CCn ch (knCz)],
Qn(z) = Bnkn{aAn[ii - u(l +a2)}ch(knaz) +
An = (l+C2)sh(knCh)k-[A-\knh),
Cn = -A +a2)sh(knah)k-lA~l(knh).
82 Гл. 2. Контактные задачи для цилиндрических тел конечных размеров
Решение парного ряда-уравнения и числовые примеры.
В B.104) функция К (и) является четной, мероморфной и может быть
представлена в виде A.3), где
А= limK(u) = G-\a + f3)-l[v(l +a2)(l +/32)-/i(l - аC)}. B.109)
Здесь для решения парного ряда B.104)—B.105) использован метод
(см. § 1.2) сведения его к исследованию бесконечной системы линей-
линейных алгебраических уравнений первого рода с сингулярной матрицей
коэффициентов вида B.62).
Предположим, что ср(г) = 0 (случай ср(г) ф 0 рассматривается ана-
аналогично [40]), тогда неизвестные контактные напряжения под штампом
найдем по формуле [311]
аАХ
B.110)
((Kp^l),
а связь между силой Р, приложенной к штампу, и перемещением
штампа 5 найдем из соотношения
i Р*Ап2~1
= 2G5uaQ*, Q* = Р* 1 - ^-^
| 7ri?
2тг| 1 , v-?n . /М ,_i /О
/ г -^ 1 I л / -^П I л
^-^ оп V А у и V А
п=1
где А = h/a, xn — решение упомянутой выше бесконечной системы.
Решение бесконечной системы здесь получено приближенно по схе-
схеме A.16) с использованием аппроксимации A.13) при В = А.
Приведем результаты некоторых числовых расчетов. Рассмотрим
материал Муни B.99). В этом случае функция К (и) и постоянная п
парного ряда B.104) будут иметь вид
К(и) = shushus3[e-3(e&+lJ-4}
B.113)
Для проведения расчетов потребуется величина
А = lim К (и) = (g66+ 1) ~ 4g3 B.114)
«-0 (г6+ IJ -4
2.3. Контактная задача для предварительно напряженного
83
и значения параметров pit qi аппроксимирующей функции L(u), за-
заданной выражением A.13). В случае неогуковского материала фор-
формулы B.112)-B.114) сохраняют свой вид, если в B.113) положить
С<2 = 0. Аналогичными будут и параметры pi, q^. Для материала Бар-
тенева-Хазановича на основании B.100) получим
К(и) =
(Зг6- \)shz(u?6/z)
u[Cs3 - 1) sh (us3/2) ch (ue3/2) + us3/2(\ + s3)}'
B.115)
Зг3 - 1
Ос.7/2 '
A =
3s3 - 1
В табл. 2.4 приведены значения параметров pi, qi (i = 1,2) аппрок-
аппроксимации A.13) при S = 2, В = А для материала Муни (колонки 2-5)
и Бартенева-Хазановича (колонки 7-10) в зависимости от параметра
предварительного напряжения г. Там же в шестой и одиннадцатой ко-
колонках приведено значение максимальной относительной погрешности
аппроксимации в процентах.
Таблица 2.4
г
0,8
0,9
1,1
1,2
1,3
1,4
1,5
Р\
5,038
2,754
1,392
1,177
1,124
1,100
1,061
Р2
1,667
1,304
0,8786
0,7763
0,7820
0,8321
0,7354
2,927
2,082
1,135
0,9133
0,8695
0,9118
0,7626
Q2
2,870
1,724
1,077
1,000
1,011
1,004
1,024
%
5,1
4,4
2,3
1,2
0,78
0,48
0,34
Pi
5,093
2,733
1,468
1,136
1,116
0,8718
0,8352
Р2
1,603
1,312
0,9168
0,7344
0,7592
0,5913
0,5297
2,864
1,935
1,199
0,8952
0,8343
0,6350
0,5601
2,850
1,852
1,122
0,9320
1,016
0,8118
0,7898
%
6,0
4,5
2,0
1,5
1,7
1,6
1,2
Для нахождения числовых значений контактных напряже-
напряжений B.110) и действующей на штамп силы Р B.111) была составлена
программа для ПК. Вычислялись безразмерные величины
<т(р) =
2GS
B.116)
при этом в рядах B.110), B.111) удерживалось N членов. При умень-
уменьшении параметра (R — a)/h для достижения заданной точности N
увеличивалось. В приводимых расчетах в наиболее неблагоприятных
случаях N = 40. Числовые результаты контролировались путем срав-
сравнения их при различных значениях N. Погрешность для контактных
напряжений наибольшая при приближении к краю штампа при фик-
фиксированном N, но с увеличением N может быть достигнута любая
84 Гл. 2. Контактные задачи для цилиндрических тел конечных размеров
Таблица 2.5
Л = 0,3 /3=1,3
г
*@)
сг@,5)
сг@,95)
Q
0,9
22,59
22,28
24,85
74,90
1,0
18,69
18,54
23,60
65,39
1Д
16,97
16,91
23,37
61,46
1,2
16,52
16,49
24,14
61,36
1,3
7,09
17,09
25,85
64,44
1,4
18,40
18,43
28,41
70,03
Л = 0,3 /3=1,5
г
а@)
сг@,5)
сг@,95)
Q
0,9
16,00
5,76
7,43
52,80
1,0
12,83
12,68
15,75
44,59
1Д
11,11
11,05
15,25
40,16
1,2
10,52
10,49
15,43
39,09
1,3
10,70
10,69
16,34
40,48
1,4
11,40
11,41
17,86
43,64
Л = 0,5 /3=1,3
<г@)
<т@,5)
<т@,95)
Q
0,9
14,44
14,29
19,35
51,59
1,0
12,86
12,87
19,81
48,91
1,1
12,25
12,32
20,39
48,29
1,2
12,30
12,44
21,49
49,67
1,3
12,93
13,13
23,17
52,89
1,4
14,09
14,34
25,59
58,08
Л = 0,5 /3=1,5
?
<г@)
сг@,5)
сг@,95)
Q
0,9
9,620
9,485
12,71
34,07
1,0
8,070
8,011
12,40
30,88
1,1
7,287
7,330
12,53
29,16
1,2
7,101
7,192
13,05
29,39
1,3
7,361
7,493
14,05
31,10
1,4
7,930
8,108
15,48
13,94
заданная наперед точность. Исключение составляет точка г = а, где
напряжения обращаются в бесконечность.
В табл. 2.5 для материала Муни приведены значения величин а(р)
и Q, вычисленные по формулам B.116) при различных значениях
параметров р, А, /3 = R/a, г. При этом полагалось С^/Сх = 1/5.
Как показали многочисленные расчеты, результаты которых частич-
частично приведены в табл. 2.5, жесткость системы штамп-цилиндр с уве-
увеличением е убывает до некоторого минимального значения, а затем
возрастает. При этом с увеличением высоты цилиндра при неизменном
его радиусе значение г, при котором система имеет минимальную
жесткость, смещается в сторону меньших значений. Например, для ма-
материала Муни (С2/С1 = 1/5) при г = 0,1, /3 = 1,3 минимум достигается
при Л « 1,3, а при г = 0,3, /3 = 1,3 — при Л « 1,15.
2.3. Контактная задача для предварительно напряженного
85
Таблица 2.6
Л = 0,3 /3=1,3
г
*@)
сг@,5)
сг@,95)
Q
0,9
23,33
23,01
25,66
77,37
1Д
16,40
16,33
22,57
59,37
1,2
15,36
15,35
22,49
57,11
1,3
15,33
15,33
23,18
57,77
1,4
15,84
15,87
24,50
60,34
1,5
16,79
16,83
26,29
64,29
Л = 0,3 /3=1,5
г
а@)
сг@,5)
сг@,95)
Q
0,9
16,53
16,28
18,00
54,54
1Д
10,73
10,67
14,73
38,77
1,2
9,781
9,758
14,38
36,39
1,3
9,610
9,602
14,67
36,36
1,4
9,797
9,810
15,38
37,54
1,5
10,32
10,35
16,46
39,87
Л = 0,5 /3=1,5
г
<г@)
о-@, 5)
<т@,95)
Q
0,9
14,92
14,76
19,98
53,28
1,1
11,83
11,90
19,69
46,63
1,2
11,45
11,58
20,00
46,22
1,3
11,62
11,79
20,81
47,54
1,4
12,12
12,34
22,03
49,97
1,5
12,95
13,22
23,74
53,68
Л = 0,5 /3=1,5
<г@)
сг@,5)
сг@,95)
Q
0,9
9,933
9,790
13,12
35,15
1,1
7,040
7,080
12,10
28,16
1,2
6,619
6,706
12,17
27,43
1,3
6,409
6,505
11,48
26,22
1,4
6,841
6,992
13,35
29,28
1,5
7,252
7,434
14,34
31,25
В табл. 2.6 приведены значения величин а(р) и Q для неогуковского
материала. Здесь поведение жесткости системы в зависимости от г
такое же, что и в предыдущем случае.
Значение величин а(р) и Q для материала Бартенева-Хазановича
при различных значениях /3, Л, р, г приведено в табл. 2.7. Здесь
наблюдается совершенно иная по сравнению с материалом Муни зави-
зависимость жесткости системы от параметра г, а именно: с увеличением Л
жесткость системы монотонно убывает.
На рис. 2.7, а, б для наглядности приведены зависимости жестко-
жесткости системы штамп-цилиндр, выражаемой величиной Q, от параметра
предварительного напряжения г соответственно для материала Муни
(С2/С1 = 1/5) и материала Бартенева-Хазановича при Л = 0,5, /3 = 1,3
(кривая /) и Л = 0,3, /3=1, (кривая 2). Отметим также, что для рас-
86 Гл. 2. Контактные задачи для цилиндрических тел конечных размеров
Таблица 2.7
Л = 0,3 /3=1,3
?
<г@)
сг@,5)
сг@,95)
Q
0,9
21,39
21,09
23,55
70,93
1Д
16,70
16,62
23,05
60,52
1,2
14,99
14,98
22,39
56,19
1,3
13,84
13,86
21,80
53,10
1,4
12,76
12,83
21,15
50,18
1,5
11,81
11,93
20,39
47,38
Л = 0,3 /3=1,5
?
<г@)
сг@,5)
сг@,95)
Q
0,9
15,15
14,92
16,51
50,00
1,1
10,92
10,85
15,01
39,46
1,2
9,458
9,435
14,21
35,51
1,3
8,498
8,502
13,61
32,84
1,4
7,612
7,655
13,02
30,37
1,5
6,887
6,962
12,45
28,27
Л = 0,5 /3=1,3
<г@)
сг@,5)
сг@,95)
Q
0,9
13,67
13,52
18,37
48,84
1,1
12,05
12,11
20,14
47,56
1,2
11,29
11,45
20,08
46,04
1,3
10,69
10,91
19,74
44,43
1,4
10,11
10,39
19,23
42,72
1,5
9,557
9,893
18,61
40,90
Л = 0,5 /3=1,5
<г@)
ет@, 5)
сг@,95)
Q
0,9
9,059
8,921
12,01
32,09
1,1
7,157
7,195
12,362
28,70
1,2
6,448
6,551
12,15
27,07
1,3
5,966
6,116
11,92
25,87
1,4
5,525
5,728
11,62
24,66
1,5
5,148
5,392
11,27
23,53
смотренных материалов при стремлении радиуса цилиндра к радиусу
штампа жесткость неограниченно возрастает.
Рис. 2.7
2.4. Взаимодействие бандажа с цилиндром конечных размеров 87
2.4. Взаимодействие бандажа с цилиндром
конечных размеров
Рассмотрим в цилиндрической системе координат (г, (р, z) контакт-
контактную задачу С$ (см. рис. 2.8) для полого кругового цилиндра \z\ ^ Ь,
R\ ^ r ^ R2 длины 2Ь с внутренним и внеш-
внешним радиусами R\ и R% соответственно.
Пусть на внешнюю поверхность цилин-
цилиндра симметрично насажен жесткий бандаж
длины 2а в области \z\ ^ а < Ъ с внутренним
радиусом i?2 — 5(z), а торцы цилиндра взаи-
взаимодействуют с жесткими плоскими опорами.
Будем считать, что трение между бандажем
и цилиндром, торцевыми опорами и цилин-
цилиндром отсутствует.
Рассмотрим поставленную выше задачу
в рамках линейной теории упругости. То- рис 2.8. К задаче С$
гда получим краевую задачу для уравнений
Ламе в случае осевой симметрии [266] со следующими граничными
условиями:
ar=rrz=0
rrz=0 (г = Д2),
ar = 0 (г = R2, a < \z\ <b), u = 5(z) (\z\ < a, r = Д2),
rrz=0
z\=b),
B.117)
где и и w — перемещения соответственно вдоль осей г и z\ ar,
rrz — компоненты тензора напряжений; 5(z) — функция, описывающая
форму контактирующей поверхности бандажа.
Разыскивая решение полученной краевой задачи в форме Папко-
вича-Нейбера, с помощью преобразования Фурье сведем поставлен-
поставленную задачу к парному ряду-уравнению вида A.1), в котором функ-
функции y(uk,x) =
QkK(uk) cosukx + Qoko =
G
k=\
_,
S(xR)
1 ^ a
QkCO8UkX =
< \x\ < -
B.118)
Здесь uk = nkR/b, R = Д2, G — модуль сдвига. Если обозначить
неизвестные контактные давления под штампом через q(z), то q(z)
через решение парного ряда-уравнения B.118) представимо в виде
B.119)
к=0
88 Гл. 2. Контактные задачи для цилиндрических тел конечных размеров
В B.118) функция К(ик) и постоянная ко известны:
К{ик) = Ak[4(l -v)- wfciofc(l)] -Bk +
где х = R\/R2-
Постоянные Ак, Вк, Ск, Dk определяются из системы
Ak[xukiOk(x) - 2A - v)iXk(x)\ + Bkiik(x) -
- Ск[хиккОк{х) - 2A - v)kik(x)] - Dkkxk{x) = О,
Ak[ukiOk(l) - 2A - v)\ + Bk - Ck[ukkOk(l) + 2A - v)\ - Dk = 0,
Лк[C - 2v)xukivk(x) - DA - v) + н2и\)чк{н)\ +
+ Bk[iik(x) - xukiOk(x) - Cfc[C - 2v)xukk0k(x) +
+ DA - v) + x2u\)k{k(x)} - Dk[klk(x) + xukkOk(x)} = 0,
Afc[C - 2v)uki0k(\) - DA - v) + u\)\ + Bk[\ - ukiOk(l)] -
- Cfc[C - 2v)ukkok(l) + DA - v) + u\)\ -Dk[l+ ukkOk(l)} = 1
2A -I/)"
B.121)
В B.120) и B.121) введены обозначения
{
В дальнейшем при вычислениях потребуется величина
К@) = 1~г/ + ^A + г/) . B.123)
2[1 + v - к\1 + is)](l - V)
В том случае, если цилиндр сплошной (R[ = 0), соотношения
B.120)-B.121), B.123) преобразуются к виду
- [2A - V) + ui]lf(uk)
2.4. Взаимодействие бандажа с цилиндром конечных размеров 89
Решение парного ряда-уравнения B.118) построим по аналогии
с решением парного ряда A.1) § 1.1. Учитывая, что
q{z)dz = ^P, B.125)
О
парный ряд B.118) преобразуем к виду
оо
^2 Qk cos ukx —
к=0
B.126)
а* = —, Ъ* = —. B.127)
Решение парного ряда-уравнения B.118) так же, как и парного
ряда-уравнения A.1), может быть получено методом сведения его к ис-
исследованию бесконечной системы линейных алгебраических уравнений
первого рода с сингулярной матрицей коэффициентов A.6).
Рассмотрим парный ряд-уравнение в более общем виде, считая, что
f(x) = cosiex, К (и) обладает теми же свойствами, что и аналогичная
функция парного ряда-уравнения A.1), и коэффициенты Uk являются
корнями уравнения
a cos икЪ* + sin икЪ* = 0. B.128)
При сделанных предположениях парный ряд-уравнение может быть
сведен к следующей бесконечной системе линейных алгебраических
уравнений первого рода A.6), в которой элементы матриц В^ = {Ьгтп}
и правых частей T>i(e) = {dlm(e)} даются следующими соотношениями:
т 1 _ 7m ch 5па* + 5п sh 5na*
{оп -Jm)chdna
* B.129)
72 л /7*47mchdna sh7m« -onshdna -
От г, = —Am[O —S
°mn
,\ / ч _ 7m Ch ?CL* + S Sh ?CL*
* . . . * B-130)
-eshea chfa
(e2-'
Am(b*) = Vm "f .—r^. B.131)
7sh7& +ach7& v y
90 Гл. 2. Контактные задачи для цилиндрических тел конечных размеров
Здесь также, полагая, что |7Ш|, \5т\ ~ т при т —> оо, систе-
систему B.126) можно регуляризовать путем выделения и обращения мат-
матрицы Е A.9), представив матрицу Bi в виде
0 6пехр(-6па) BЛ32)
и получить ее решение методом редукции, представив в виде A.16).
Положив г = 0 и хп = xn@)f, где / есть B.127), выразим через жп
неизвестные контактные давления и интегральную характеристику Р
соотношениями
26 , , „vv/ w=l
жг
B.133)
^ 8ь5„а/Л <2Л34)
n=\
Из последних двух соотношений найдем
P=^-vP\ P-Q^ + ^-^eI. B.135)
Подставляя B.135) в B.133), получим
G<5
q,(z) _[.+^
К@)
4=
B.136)
Напомним, что в формулах B.134), B.136) хп@) (п = 1,2,...)
являются решением бесконечной системы A.6) с элементами B.129)
при г = 0, при этом в этой системе, а также в B.134), B.136) при
числовых расчетах в качестве i5n и г^ш берутся нули и полюсы ап-
аппроксимирующей функции L(u) A.13). В табл. 2.8 приводятся значения
коэффициентов pit qi аппроксимации функции К (и) из B.120) при
некоторых значениях к и v. В последней колонке табл. 2.8 приведены
значения относительной погрешности такой аппроксимации в %.
Отметим, что при к > щ у функции К (и) из B.120) появляются
действительные нули, что свидетельствует о появлении под бандажом
знакопеременных контактных напряжений.
2.4. Взаимодействие бандажа с цилиндром конечных размеров
91
Таблица 2.?
0,0
0,0
од
V
0,3
0,5
0,3
2
1
1
Р\
,1586
,0124
,3415
Р2
1,2245
1,2999
1,8556
2
1
1
ох
0540
1046
6836
42
1,2868
1,1815
1,4785
с
1
2
1
,1
,9
,2
R/a =03
v = 0,3
На основе изложенного здесь алгоритма решения поставленной
задачи была составлена программа для компьютерного вычисления
контактных напряжений и интегральной характеристики Р.
В табл. 2.9 приведены безразмерные значения контактных на-
напряжений q*(z) и величины Р*, вычисляемые соответственно по
формулам B.136), B.135). При рас-
расчетах полагалось а = 1, v = 0,3, 0,5.
При расчетах в редуцированной
бесконечной системе A.20) оставля-
оставлялось 40 уравнений.
Для наглядности на рис. 2.9
изображена зависимость жесткости
системы цилиндр-бандаж, характе-
характеризуемой величиной Р* в зависимо-
зависимости от параметра C = Ъ/а при фик-
фиксированных значениях других пара-
параметров. Как видно из рис. 2.9, при
определенных значениях /3 = /3* си-
система обладает максимальной жест-
жесткостью. Величина /3* зависит от зна-
значения других параметров.
Р*
14,4
14,0
13,6
13,2
12,8
1,0
1,2 1,4 1,6
Рис. 2.9
1,8
Таблица 2.9
Ь/а
2,0
1,5
1,2
1,1
1,05
2,0
1,5
1,2
1,1
1,05
д*@)
5,494
6,335
6,726
6,899
6,972
12,58
20,08
49,53
123,9
338,7
<f@,2)
5,991
6,333
6,725
6,898
6,972
12,58
20,08
49,53
123,9
338,7
<f @,4)
и =
5,984
6,326
6,721
6,897
6,972
ж =
12,58
20,08
49,53
124,0
338,7
<f@,5)
0,0; г/ =
5,979
6,321
6,720
6,897
6,972
0,0; iy =
12,58
20,08
49,54
124,0
338,7
<f@,6)
<f@,8)
0,3; R/a = 0,5
5,976
6,320
6,722
6,900
6,974
6,081
6,436
6,847
7,00
7,033
0,5; R/a = 0,5
12,58
20,09
49,57
124,0
338,8
12,74
20,35
50,18
125,2
340,8
<f@,9)
6,660
7,053
7,475
7,504
7,339
13,69
21,88
53,83
132,7
353,7
g*@,95)
8,022
8,500
8,947
8,715
8,123
16,17
25,85
63,31
152,5
389,7
p*
12,85
13,59
14,41
14,61
14,50
26,80
42,79
105,4
261,3
703,1
92 Гл. 2. Контактные задачи для цилиндрических тел конечных размеров
2.5. Взаимодействие бандажа с предварительно
напряженным цилиндром конечных размеров
В этом параграфе изучено влияние предварительного осевого рас-
растяжения или сжатия кругового упругого цилиндра конечной длины на
его контактную жесткость и распределение контактных напряжений
при взаимодействии с жестким бандажом меньшего радиуса (зада-
(задача Сб). Предполагается, что бандаж расположен на боковой поверхно-
поверхности цилиндра симметрично и без трения, а торцы цилиндра взаимо-
взаимодействуют с жесткими гладкими поверхностями [291]. Используется
модель нелинейного упругого изотропного несжимаемого материала
общего вида [204, 289, 352].
В цилиндрической системе координат (г, z) рассмотрим сплошной
\\
круговой цилиндр г ^ R,
Ь из нелинейного упругого изотропного
несжимаемого материала. Цилиндр
предварительно подвергнут однород-
ному осевому растяжению или сжа-
тию и закреплен торцами между глад-
кими жесткими поверхностями таким
образом, что отсутствуют нормальные
перемещения и трение. На описан-
ную деформацию, которая считается
конечной, накладывается малая осе-
симметричная деформация, вызванная
внедрением в поверхность цилиндра
при \z\ <a жесткого бандажа, при
этом трение между цилиндром и бан-
бандажом отсутствует, а бандаж имеет радиус R — 5, 5 > 0 (см. рис. 2.10).
Используя [204, 289, 352], для добавочной деформации получим
линеаризованные уравнения
Рис. 2.10. К задаче С6
fl
д2и I ди и
дг2 г дг г
д2
д2
~Т~ 7 ?>™?>~ * ^ ^ 2 ~^ Л^,
fara
и
2
dz2
drdz
г dz
+ 7
^ гу 1 ^w;
ди
дг
и
г
аг2
dw
д5_
dz
= 0,
= 0,
B.137)
B.138)
7 =
е3-!
П -^
к =
д2и
s3-\
(к, s= 1,2,3).
Здесь (и, w) — радиальная и осевая составляющие вектора добавочных
перемещений, а — добавочное нормальное напряжение в сечениях
2.5. Взаимодействие бандажа с предварительно напряженным 93
цилиндра z = const, П = П^ь^^з) — упругий потенциал материала,
заданный как функция главных растяжений ?*.. В рассматриваемом
случае е\ = е2 = г3^2, е% = г, причем (г — 1) — относительное осевое
удлинение в начальном деформируемом состоянии. В B.137) учтено,
что начальное напряженное состояние является одноосным и, следова-
следовательно, отлично от нуля только нормальное напряжение tzz.
Граничные условия поставленной контактной задачи при z = ±6
имеют вид
ф + ф = 0, w = 0, B.139)
or oz
а при г = R
ди . dw А ди . , и
дг г vii
ди . dw А г /
B.140)
Краевые условия B.139) на торцах цилиндра будут удовлетворены,
если решение уравнений B.137) разыскивать в виде
сю
U = Yl Un{r) COSpnZ, pn = ^,
П=° B.141)
СЮ
w = 5Z Wn(r) sinpnz, a =J2 Bn(r) cospnz.
n=0 n=0
Из уравнений B.137) вытекает, что Щ = 0, Во = const.
Более подробно исследуем случай материала Муни, для которого
п = сх(е\ + 4 + 4 -з) + с2(Ф! + 44 + 44 -з), B.Н2)
где Сь G2 — известные постоянные. Из B.138), B.140) для материала
Муни получим
2\Ъ
v = 2г{(С{ + Сз^1), к = 2е\Сх + Сз^1),
ф = 2С{е-\\ + ?3) + 2С2е~2C - е3).
Подставляя B.141) в уравнения B.137), с учетом B.142) получим
систему уравнений для определения Un,Wn, и Вп из которых найдем
Un = AnXIx(pnr) + An2Ii(s^2pnr),
Wn = -Amlolpnr) + An2s^2I0(s^2Pnr), B.143)
Bn = -1урп[2Ап110(Рпг) +?3/2An2(l +е3I0(е3/2рпг)},
где Ап\, Ап2 — постоянные, 1п(х) — модифицированные функции Бес-
Бесселя.
94 Гл. 2. Контактные задачи для цилиндрических тел конечных размеров
Из первого граничного условия B.140) получим
Ап2 = —Ап\- ц—т^Тз 7* B.144)
Удовлетворяя оставшимся граничным условиям из B.140), получим
парный ряд-уравнение B.126), в котором f(x) = 5, а* = a/R, b* = b/R,
1 3 2
K(U)= АЫ[A+?) '
о* = к
B.145)
В B.145) /i — модуль сдвига материала в недеформированном состо-
состоянии.
Неизвестные коэффициенты Q^ уравнения B.126) связаны с посто-
постоянными Ak\ из B.143) соотношением
(Ol). Qo = Bo. B.146)
)
Тогда с учетом B.141), B.143), B.144) и B.146) искомые контакт-
контактные давления под штампом через решение уравнения B.126) найдем
по формуле
(|) а), B.147)
x\ < -|
Yl Qk COS CkX,
fc=0
Для решения парного ряда-уравнения воспользуемся также методом
сведения его к бесконечной системе линейных алгебраических уравне-
уравнений первого рода с сингулярной матрицей. Функция К (и) из парного
ряда обладает необходимыми для этого свойствами. Для преодоления
в дальнейшем трудностей, связанных с факторизацией функции К (и),
аппроксимируем ее на действительной оси функцией A.13) при В = А.
Числа S, р/с, и ^ A0О) выбираются из условия наилучшего
приближения. Здесь, как и в предыдущем параграфе, парный ряд-
уравнение для поставленной задачи сводится к решению бесконечной
2.5. Взаимодействие бандажа с предварительно напряженным
95
системы первого рода с сингулярной матрицей A.6), B.129)—B.131).
Реализуя схему предыдущего параграфа для поставленной задачи, по-
получаем выражение для контактных напряжений:
/ ч 2а6
q(x) = -^
Оь
К
аК@)Р*
где
qo(x) =
ch6nx
K@)
2b
n-\
-1
/Л / ч /о i/io\
qo(x) )qo(x), B.148)
B.149)
2a
RK(O)
n-l
B.150)
Используя B.148), найдем интегральную величину, характеризую-
характеризующую жесткость системы цилиндр-бандаж:
Р=
B.151)
Для дальнейших числовых расчетов были найдены коэффициенты
аппроксимирующей функции A.13) при S = 2, которые приводятся в
табл. 2.10 для некоторых значений параметра г, С = 0,2.
Таблица 2.10
г
0,8
0,95
1,05
1,2
1,5
Р\
1,8124
1,2551
0,8786
10,556
5,4246
Р2
3,7757
2,2358
1,4460
10,663
5,4323
q\
2,7130
1,6610
1,1503
8,6250
4,2741
2,5324
1,7056
1,1166
12,898
6,8659
%
2,0
1,9
2,2
1,8
0,8
В последней колонке приведены значения относительной погрешно-
погрешности такой аппроксимации.
Был произведен расчет контактных напряжений и жесткости систе-
системы штамп-цилиндр, вычислялись безразмерные величины qo(ra/R) =
— q*(T) (lrl < 1) и Р* соответственно по формулам B.148), B.150),
при этом в соответствующих рядах B.149) и B.150) удерживалось N
членов, а бесконечная система A.6), B.129)—B.131) урезалась до N
уравнений; N выбиралось в зависимости от заданной точности. С уве-
увеличением параметра (b — a)/R для достижения выбранной точности
96 Гл. 2. Контактные задачи для цилиндрических тел конечных размеров
Таблица 2.11
г
0,8
0,8
0,8
0,95
0,95
0,95
1,2
1,2
1,2
1,5
1,5
1,5
&
1,2
1,5
2,0
1,2
1,5
2,0
1,2
1,5
2,0
1,2
1,5
2,0
q*@)
45,9
20,3
13,2
48,0
19,3
12,3
58,3
21,5
13,1
171
25,0
14,9
g*@,5)
45,4
20,0
13,0
47,8
19,2
12,2
58,3
21,6
13,1
171
25,0
14,9
9* @,9)
46,5
20,1
13,1
51,7
20,6
13,0
65,5
24,3
14,8
216
29,7
17,7
Р*
95,1
41,7
27,2
101
40,8
25,9
125
46,5
28,3
393
54,8
32,7
требуется брать меньшее число уравнений
бесконечной системы.
В табл. 2.11 для некоторых значений па-
параметров г, г и C = Ъ/а при R/a = 0,5
приведены значения величин q*(r) и Р*.
При выбранных коэффициентах аппрокси-
аппроксимации A.13), приведенных в табл. 2.10,
дальнейшие расчеты проводились с немень-
неменьшей точностью.
Для наглядности на рис. 2.11 приведе-
приведена зависимость жесткости Р* системы бан-
бандаж-цилиндр от параметра предваритель-
предварительного напряжения е при R/a = 0,5 и неко-
некоторых значениях C (/: C = 1,2; 2: C = 1,5;
3: C = 2,0).
Анализ приведенных результатов число-
числовых расчетов показывает, что с увеличени-
увеличением параметра предварительного напряже-
напряжения в сторону растяжения жесткость систе-
системы бандаж-цилиндр увеличивается. Суще-
Существуют также такие сочетания геометрических параметров системы,
при которых ее жесткость возрастает и с увеличением предваритель-
предварительного сжатия (с уменьшением г при г < 1).
420
90
56
40
33
25
0,8
X 1,5
Рис. 2.11
Глава 3
ПЛОСКИЕ КОНТАКТНЫЕ ЗАДАЧИ
ДЛЯ ЧЕТЫРЕХУГОЛЬНИКОВ
В этой главе будут рассмотрены смешанные задачи для упругих
тел, имеющих в сечении форму четырехугольника в декартовой или
полярной системе координат. Для решения этих задач будут использо-
использованы методы, изложенные в гл. 1, а также метод однородных решений,
схема которого изложена подробно на примере задачи С\ в гл. 2.
3.1. Контактные задачи для прямоугольника
В декартовых координатах (х, у) рассмотрим изображенный на
рис. 3.1 прямоугольник 0 < у < h, —b^x^b. Пусть нижняя часть
прямоугольника лежит без трения на
жестком основании (задача Q\), либо
закреплена (задача Q2). Далее для обе-
обеих задач будем предполагать, что на бо-
боковых гранях \х\ = b отсутствует трение
и нормальное перемещение, а в грань
х = h внедряется на величину 5 штамп,
форма подошвы которого описывается
функцией f(x).
Эти задачи и аналогичные им по
постановке рассматривались, например,
в работах [2, 33, 60, 61, 65, 82, 201, 219, Рис. 3.1. К Задачам Qu Q2
229] и др.
Математически поставленная задача сводится к исследованию урав-
уравнений Ламе [266] (плоская деформация) со следующими граничными
условиями:
4 В.М. Александров, М.И. Чебаков
-Ь -а
Ь
98 Гл. 3. Плоские контактные задачи для четырехугольников
тху = 0, v = 0 (у = 0) (задача Qi),
и = 0, v = 0 (y = 0) (задача Q2),
(о. 1)
и = 0, тху = 0 (\х\ = Ь), тху = 0 (y = h),
а (у) = О (у = h, a <\x\ <b), v = 5 — f(x) (у = h, \х\ < а).
Здесь и, v — компоненты вектора перемещения соответственно вдоль
осей х, у, тху, Оу — компоненты тензора напряжений.
3.1.1. Метод сведения парных рядов к бесконечным системам.
Поставленная задача сводится к исследованию парного ряда-уравнения
вида A.1), где у(щ,х) = cosukX, или вида B.126):
k=0
сю
^2 Qk cos ukx — 0 (a* ^ \x\ <b*),
k=0
где
V ; C.3)
7 , \ — 2v irhk * a , * 6
г^/ ч 2>zrsh2i/ — 4гг / ^ ч V • /
К (и) = s 9~ (заДача Q2),
гхB^сЬ2гх+ I + к2 + Аи2)
где х = 3 — 4/у, ту — коэффициент Пуассона.
Из C.3)-C.4) получаем, что
2
п0 = — « (задача Qi), n0 = 0 (задача Q2). C.5)
2A -zy)
Через решение парного уравнения C.2), C.3) контактные напряже-
напряжения под штампом выражаются соотношением
ay(x,h) = -q(x), C.6)
сю
q(x) = ^2 Qk cos Ukxh~l (\x\^a). C.7)
fc=o
Парный ряд может быть сведен к исследованию бесконечной си-
системы A.6), в которой элементы матриц В^ = {Ьгтп} и правых частей
T>i(e) = {d^e)} даются формулами B.129)-B.131), где а = 0, г = 0, а
и Ъ следует заменить соответственно на ah~x и bh~K Тогда контактные
3.1. Контактные задачи для прямоугольника 99
давления определятся через решение этой бесконечной системы из
следующих соотношений:
1~ hnoP*\ / ч
\ qo{x)>
b — а . koa Нщ ^,
1 Ь
Ъ К@)Ь Ъ
где qo(x), Q и Е определяются выражениями
C.9)
Связь между силой Р, действующей на штамп, и перемещением
штампа 5 найдем из соотношения
Р= \q(x)dx=^P*. C.10)
— a
Полученные формулы для контактных напряжений q(x) и жестко-
жесткости Р5~х позволяют провести качественный анализ их зависимости
от безразмерного параметра /3* = bh~l. Из вида элементов матрицы
и правой части бесконечной системы и формул C.9) можно заключить,
что при /3* —> оо
i(^-a)/i-1)), C.11)
Q = Qo + O(exp (-2 Re 7i(b - a)h~1)),
E = Eo + O(exp (-2 Re 71F - a)/T*)),
где ijm — полюсы функции К (и), причем Re 7m > 0, а величины
Qoo(x), Qo, Eo от параметра /3* = bh~l не зависят.
Анализируя теперь соотношения C.8) и учитывая, что соглас-
согласно C.5) для задачи Q\ щ ф 0, а для задачи Q2 ^о = 0» получим
важный качественный вывод о влиянии параметра /3* на распределение
контактных напряжений и жесткость прямоугольника [332], а именно:
при увеличении параметра /3* его влияние затухает как 1//3* для
задачи Q\ и по экспоненциальному закону для задачи Q2.
Проведен численный анализ влияния геометрических параметров и
коэффициента Пуассона на q(x) и Р* для задачи Q\. При вычислениях
принималось р\ = 1,174, _р2 = 2,208, gi = 1,496, #2 = 1,732 и при этом
погрешность аппроксимации A.13) для задачи Q\ не превышает 2%.
100
Гл. 3. Плоские контактные задачи для четырехугольников
В табл. 3.1 приведены значения безразмерных контактных напряже-
напряжений и жесткости
_ а(\-и)
fW =
q(x),
GS чу J' G6 '
где q(x) и Р вычисляются по формулам C.8), C.10) при Л = 0,5,
некоторых значениях коэффициента Пуассона v и /3. При вычислениях
число уравнений системы A.16) равнялось 40.
&
1,1
1,1
1,1
1,1
1,1
1,2
1,2
1,2
1,2
1,2
1,3
1,3
1,3
1,3
1,3
1,4
1,4
1,4
1,4
1,4
1,6
1,6
1,6
1,6
1,6
V
од
0,2
0,3
0,4
0,5
0,1
0,2
0,3
0,4
0,5
0,1
0,2
0,3
0,4
0,5
0,1
0,2
0,3
0,4
0,5
0,1
0,2
0,3
0,4
0,5
q*@)
4,035
4,243
4,849
7,002
4,010
4,202
4,751
6,610
39,76
3,991
4,166
4,661
6,263
23,36
3,978
4,139
4,589
5,987
17,07
3,964
4,102
4,482
5,596
11,90
g*(.2)
4,034
4,242
4,848
7,001
4,007
4,199
4,748
7,605
39,73
3,987
4,162
4,687
6,256
23,33
3,973
4,134
4,583
5,980
17,05
3,958
4,096
4,475
5,888
11,88
q*(A)
4,032
4,240
4,846
6,997
4,000
4,191
4,739
6,594
39,66
3,976
4,151
4,644
6,239
23,27
3,960
4,120
4,567
5,958
16,99
3,940
4,078
4,456
5,863
11,83
g*(.5)
4,032
4,241
4,847
6,998
3,997
4,189
4,736
6,589
39,63
3,970
4,145
4,637
6,230
23,23
3,951
4,111
4,557
5,946
16,95
3,930
4,067
4,444
5,548
11,80
<f(.6)
4,037
4,246
4,853
7,007
4,009
4,192
4,740
6,595
39,67
3,971
4,145
4,638
6,230
23,24
3,949
4,109
4,555
5,943
16,95
3,924
4,062
4,437
5,541
11,78
g*(.8)
4,147
4,362
4,985
7,198
4,149
4,348
4,916
6,840
41,14
4,123
4,305
4,816
6,471
24,13
4,097
4,263
4,726
6,166
17,58
4,062
4,204
4,593
5,735
12,19
q*(.9)
4,542
4,777
5,640
7,883
4,696
4,921
5,564
7,741
46,56
4,709
4,916
5,500
7,390
27,56
4,687
4,887
5,406
7,054
20,11
4,642
4,805
5,249
6,554
13,93
Табли
g*(.95)
5,370
5,648
6,454
9,320
5,803
6,080
6,875
9,565
57,53
5,891
6,150
6,881
9,244
34,48
5,881
6,120
6,784
8,851
25,24
5,824
6,028
6,586
8,223
17,48
ца 3.1
p*
8,631
9,078
10,38
14,98
276,0
8,740
9,158
10,36
14,41
86,66
8,731
9,114
10,20
13,70
51,09
8,697
9,050
10,03
13,09
37,32
8,642
6,945
9,773
12,20
25,94
Продолжение на следующей странице
3.1. Контактные задачи для прямоугольника
101
1,8
1,8
1,8
1,8
1,8
2,0
2,0
2,0
2,0
2,0
3,0
3,0
3,0
3,0
3,0
5,0
5,0
5,0
5,0
5,0
10
10
10
10
10
20
20
20
20
20
V
0,1
0,2
0,3
0,4
0,5
0,1
0,2
0,3
0,4
0,5
0,1
0,2
0,3
0,4
0,5
0,1
0,2
0,3
0,4
0,5
0,1
0,2
0,3
0,4
0,5
0,1
0,2
0,3
0,4
0,5
д*@)
3,956
4,079
4,408
5,335
9,668
3,952
4,062
4,453
5,148
8,423
3,943
4,015
4,200
4,663
6,093
3,936
3,979
4,086
4,337
4,991
3,931
3,952
4,004
4,121
4,395
3,928
3,939
3,964
4,021
4,147
д*(.2)
3,950
4,072
4,401
5,327
9,652
3,946
4,055
4,346
5,139
8,409
3,936
4,008
4,193
4,655
6,083
3,929
3,972
4,079
4,300
4,983
3,924
3,945
3,997
4,114
4,387
3,927
3,932
3,958
4,014
4,140
д*(.4)
3,931
4,053
4,380
5,302
9,607
3,927
4,036
4,325
5,114
8,369
3,917
3,989
4,173
4,632
6,054
3,910
3,953
4,059
4,309
4,958
3,905
3,926
3,968
4,094
4,366
3,903
3,913
3,939
3,995
4,120
д*(.5)
3,920
4,041
4,367
5,268
9,579
3,915
4,023
4,312
5,099
8,344
3,905
3,976
4,160
4,618
6,035
3,898
3,940
4,047
4,295
4,943
3,893
3,914
3,966
4,081
4,352
3,890
3,901
3,926
3,982
4,107
д*(.6)
3,913
4,034
4,360
5,227
9,562
3,907
4,016
4,304
5,089
8,328
3,897
3,968
4,151
4,609
6,023
3,890
3,933
4,039
4,287
4,933
3,885
3,906
3,958
4,073
4,344
3,883
3,893
3,919
3,974
4,099
д*(.8)
4,045
4,171
4,507
5,455
9,885
4,038
4,150
4,447
5,259
8,606
4,026
4,100
4,289
4,761
6,222
4,019
4,063
4,172
4,429
5,096
4,014
4,035
4,089
4,208
4,487
4,011
4,022
4,048
4,106
4,235
д*(.9)
4,618
4,761
5,145
6,228
11,29
4,607
4,734
5,074
6,000
9,819
4,592
4,676
4,882
5,431
7,097
4,584
4,634
4,759
5,052
5,813
4,578
4,603
4,664
4,800
5,119
4,575
4,588
4,618
4,683
4,830
д*(.95)
5,789
5,368
6,450
7,807
14,15
5,773
5,933
6,358
7,519
12,30
5,753
5,868
6,129
6,804
8,891
5,743
5,806
5,962
6,329
7,283
5,736
5,767
5,843
6,013
6,413
5,732
5,747
5,785
5,867
6,051
8,613
8,880
9,597
11,62
21,05
8,599
8,837
9,471
11,20
18,33
8,576
8,733
9,135
10,14
13,25
8,561
8,654
8,887
9,433
10,86
8,550
8,596
8,709
8,964
9,558
8,544
8,567
8,623
8,746
9,020
На рис. 3.2 для задачи Q\ изображена зависимость жесткости
прямоугольника от коэффициента Пуассона при некоторых значениях
параметров /3 = Ъ/а и Л = h/a = 0,5 (кривая 1 — и = 0,1, 2 — и = 0,2,
102
Гл. 3. Плоские контактные задачи для четырехугольников
3 — v = 0,3, 4 — v = 0,4). Жесткость прямоугольника увеличивается
с увеличением v и при больших v при изменении /3 имеет более
выраженный максимум.
Р*
14
12
10
1,0 1,6 2,2 C
Рис. 3.2
3.1.2. Метод больших Л. Поставленные задачи также можно
свести к решению следующего интегрального уравнения:
1
-1
GS
Pk0
1), C.12)
A = -,
/3=-, -P = q(x)dx,
M a' J УМ
п=\
Cn =
1 -
2A-
irnh
C.13)
где функции К (и) для задач даются соотношениями C.4), q(x) =
= ф(х/а) — контактные напряжения под штампом, G — модуль сдвига,
v — коэффициент Пуассона, Р — действующая на штамп сила.
Решение интегрального уравнения C.12) связано с решением урав-
уравнения A.43) при /(г) = 1 с ядром C.13) соотношением
/ / \ GS
-i
1 - v" ' - Т ' 2/3
(величина Q определена выражением в скобках в A.45)).
3.1. Контактные задачи для прямоугольника
103
Ядро C.13) может быть представлено в виде A.44), где В^г — числа
Бернулли):
2гBг)!
; оо
о2г — 1
(г =1,2,...).
п=\
Используя результаты § 1.3, для поставленных задач получим
N т 1
+ 2 ]Г Л~2ш ]Г /3^?2^ + О(Л~2ЛГ-2) , C.14)
m=l j=0 J
g = ^[ln2A-^A-24 + O(A-27V-2)j ',
L fc=o -I
где f3xmj вычисляются по рекуррентным соотношениям из A.50), в кото-
которых /3mj надо заменить на /3^-, а Ф^ взять из A.53), pk вычисляются
по формулам из A.54).
Формулы C.14) выписаны с точностью до членов О(А~2ЛГ~2) и зна-
значение N выбирается в зависимости от заданной точности.
Как показали числовые эксперименты, сходимость метода (выбор
значения N) не зависит от параметра /3 и улучшается с увеличением А.
При этом решение можно получить с любой степенью точности при
А > 1. Важно отметить, что коэффициенты при степенях А в суммах
из C.14) знакопеременны.
Для получения заданной погрешности, например в 1 %, в C.14)
следует взять N = 3 при А = 2, N = 8 при А = 1,3, N = 17 при А = 1,2,
N = 26 при А= 1,15.
Таблица 3.2
Л
1,2
1,2
1,2
1,5
1,5
1,5
2,0
2,0
2,0
N
19
20
21
8
9
10
2
3
4
Q*
4,803
4,833
4,808
4,012
4,010
4,011
3,159
3,143
3,147
д*@)
1,905
1,910
1,906
1,560
1,559
1,559
1,210
1,213
1,213
д*@,4)
1,948
1,953
1,949
1,607
1,606
1,607
1,250
1,254
1,254
д*@,8)
2,381
2,388
2,382
2,003
2,002
2,002
1,582
1,574
1,577
<f @,95)
3,919
3,975
3,927
3,346
3,340
3,343
2,687
2,637
2,645
В табл. 3.2 для демонстрации сходимости метода больших Л для
задачи Q\ приведены значения величины Р*, характеризующей жест-
104
Гл. 3. Плоские контактные задачи для четырехугольников
кость прямоугольника, и величины безразмерных контактных напря-
напряжений /1 \ /1 \
*( \ — а\^ ~ v) ( \ — а\^ ~ v) I ( \ (\ >п
1,0
3,0
5,0
при некоторых значениях параметров Л, N, т и C = Ъ/а = 1,5.
В результате проведенных исследо-
исследований этим методом также обнаруже-
обнаружена немонотонная зависимость жесткости
прямоугольника (величины Р*) от пара-
параметра C при фиксированном значении Л.
На рис. 3.3 для задач Q\ (сплошная ли-
линия) и Q2 (штриховая линия) приведе-
приведены зависимости Р* от C при разных Л.
Видно, что при определенных значени-
значениях C в обеих задачах прямоугольник име-
имеет максимальную жесткость, при даль-
дальнейшем увеличении C жесткость умень-
уменьшается и стремится к предельному зна-
значению, соответствующему задачам для
слоя. Следует подчеркнуть, что в зада-
задаче Q2 при C —> оо Р* гораздо быстрее
приближается к своему значению для слоя (C = оо), чем в задаче Q\.
3.1.3. Метод однородных решений в несимметричной контакт-
контактной задаче для прямоугольника. В декартовой системе коорди-
координат рассмотрим упругий прямоугольник, описываемый неравенствами
—Ъ ^ х ^ с, 0 ^ у ^ h. Предполо-
Предположим, что на гранях у = 0, х = —Ь,
х = с отсутствуют касательные на-
напряжения и нормальные перемеще-
перемещения, а в грань у = h на участке \х\ ^
^ а вдавливается силой Р штамп
на величину 5. Схема такой задачи
изображена на рис. 3.4.
Поставленная задача Q^ сводит-
сводится к краевой задаче для уравне-
уравнений Ламе [13] (плоская деформа-
деформация) с граничными условиями
У "
Рис. 3.4. К задаче
= 0 (у = 0) 1
/ = h), о» = О
>ху
= 0 (х = —Ь, х = с),
(у = h, —Ъ < х < —а, а < х < с),
C.15)
v = 5 (у = h, \x\ ^ а).
C.16)
Для исследования задачи используем метод однородных решений.
Заменим граничное условие C.16) условием
а (у) = q(x) (у = h,
C.17)
3.1. Контактные задачи для прямоугольника 105
где q(x) — неизвестные контактные напряжения.
Решение уравнений Ламе с граничными условиями C.15), C.17)
разыскиваем в виде
и(х,у) =u{l\x,y) -u{2\x,y), v(x,y) =v(l\x,y) -уB\х,у), C.18)
где u(l\ v^ — решение уравнений Ламе для полосы 0 < у < h с гра-
граничными условиями
rxy = v = 0 (у = 0) тху = 0 (y = h), C.19)
(У h
a u^\ v^ — суперпозиция однородных решений уравнений Ламе для
полосы 0 ^ у ^ h с граничными условиями
rxy = v = 0 B/ = 0), тху = ау = 0 (y = h). C.20)
Опуская выкладки, приведем выражения для компонентов вектора
перемещений и тензора напряжений:
da,
— сю
сю
— сю
сю
оХу
— СЮ
da, C.21)
x л
где
— a
сю
Г Q(a) т*(у a)
А(а)
[ q(x)e~iax dx, Д(а) = 2aft + sh 2aft, C.22)
J
?/*, г;*, g%, a*, r* — известные функции, из которых нам в дальнейшем
понадобится лишь
v*(h,a) = A -u)(ch2ah- 1). C.23)
106 Гл. 3. Плоские контактные задачи для четырехугольников
Для суперпозиции однородных решений аналогично получим
v{2\x,y) = J2 vk(y)(AkeiakX + Bke~iakX) + v0,
k=\
<г?Чх>У) = 2GJ2 ахк(у)(АкегакХ + Вке~гакХ) + ax0, /3^4)
fc=i
сю
, У) = Ж Е
a*x) + тхф.
к=\
Здесь суммирование ведется по всем нулям ак функции А(а),
удовлетворяющих условию Re (год) > 0, при этом а2к = — ce2fc+i-
В C.24) функции Ufc, v/c, сгж/с, сгу/с, r^, (fc ^ 1) являются известными,
а в дальнейшем нам понадобится только
vk(h)=2(l-v)aksh2akh. C.25)
Отдельно выписанные слагаемые в C.24) являются элементарными
однородными решениями и соответствуют равномерному растяжению
и перемещению слоя вдоль оси х
щ = Ао(\ - v)x + Во, ^о = -Aovy, ax0 = 2G. C.26)
Удовлетворяя граничному условию C.16), получим относительно
q(x) интегральное уравнение
^DDeWfcX + Вке~гакХ), C.27)
C.28)
Представим д(ж) в виде
г Г °°
)\ ( '
к=\
C.29)
где Akvk(h) = хкегакС, Bkvk(h) = укегакЬ, a qo(x) и ^(ж) являются
решением интегральных уравнений
Kq0 = тг, Kq{ = тге(-{)Чак. C.30)
3.1. Контактные задачи для прямоугольника 107
Удовлетворим теперь оставшемуся граничному условию C.15) при
х = — Ь и х = с, воспользовавшись условием обобщенной ортогональ-
ортогональности однородных решений
{ 0, k^j, k,j > 1,
{
Wkk = 4A -
и значением интегралов
h h
axk dx = 0, (сгжо^/с - ЩП) dx = 0 (k > 1).
В результате найдем постоянные Ао, Во и хк, ук:
В полученные формулы для ж^., ^ подставим C.29), в результате
прийдем к бесконечной системе линейных алгебраических уравнений
для нахождения хк, ук:
Ь\ + yke-ia*^ + Е (аЦхп + аЦуп), C.33)
П=1
Ук = Ь{ + xke-ia*^ + ? (аЦхп + а2п1кУп),
Ь{ = Рке~гакЬТ' Я =
аЦк =
afk =
R _ A - u)shA akh
Pk — з~~з >
akn
a
Цк = \ »We(-1)iMiIic, ТЦ = | Чгп{х)е^хУгакХйх. C.34)
Можно показать, что элементы матрицы и правой части бесконеч-
бесконечной системы C.33) убывают с ростом номеров по экспоненциальному
закону при Ъ > а, с > а, что говорит о том, что эта система относится
к типу нормальных систем Пуанкаре-Коха и ее решение может быть
получено методом редукции.
108 Гл. 3. Плоские контактные задачи для четырехугольников
Подставляя C.32) в C.29) и интегрируя C.29) в пределах от —а
до а, найдем
!_„. * "- 1-.,. "\7„ . J"', C.35)
k=\
Ро=
-l
k= q{(
-l
Г
, PJk= q{(x)dx.
Контактные напряжения под штампом примут вид
q(x) = = 1 +
Qo(x)
k=\
. C.36)
Таким образом, контактные напряжения под штампом даются соот-
соотношениями C.36), а связь между силой Р и перемещением штампа —
соотношением C.35), в которых Xk, Ук — решения бесконечной систе-
системы C.33), a qk(x) — решения интегральных уравнений C.30).
Для замыкания поставленной задачи найдем решения интеграль-
интегральных уравнений C.30), для чего воспользуемся методом, изложенным
в §1.3.
Вместо уравнений C.30), рассмотрим уравнение
ip(t, а)к
dt =
C.37)
где к (у) дается соотношением C.28).
Решения уравнений C.30) и C.37) связаны соотношением
\x\ < 1).
C.38)
Опуская выкладки, выпишем результат с точностью до членов по-
порядка О(Л"8):
(х,0) =
-^(l -2x2)- А G_8х2-
3.1. Контактные задачи для прямоугольника
109
где
Ро =тг I In 2Л — do -.
2 - -L (9d2 + d2) - -ig B5d3 + did2)l
4Л 4Л J
-1
C.40)
ф, а) = l { ^ ф, 0) - aG(x, a) + Щ-Jl (a)x +
Try 1 — x2 I ^o Л
ол2
Ц FA - 2x2) J2(a) - 4жA - Зж2) J^a) + 4xJ3(a)) + =% ^(а)ж -
Л Л
АН
-6(J5(a)-lj3(a)-^
где
2{а) + J\a)) + 15(J2(a) - 2j\a))x - 60J2(a)x4 +
15DJ3(a) +J'(a))x3 +
о
+ 30J1 (a)x5] + ^ DJ3(a) + 5J1 (a))x + ^ J1 (a)x +
-I Л Л
C.41)
7 Л—2 т2/ \ , 7 Л —4 /т4/ \ , ' т2/ \\
¦diA ^(а) + й2А (^-Г(а) + - J2{a)J
3 ,_f
d3X-\jQ(a)+8J\a) + ljHa)) + ^
при этом
Р1=Р{{-\)Чап/а).
Выше введены обозначения
1 1
Jp(a) = a I* xv-xeax\]\ - х2 dx, G(x, a) =
Используя C.39)-C.44) найдем
гуд —T((—]Viui/\) TtJ' — Т((— ])triij i
, d\ 7d2
2dx
5do)d2J2(a)
t-x
C.42)
-dx. C.43)
C.44)
3did2
Л2 Л4 Ab 2\ь
ПО
Гл. 3. Плоские контактные задачи для четырехугольников
(J2(a) + J4(a))
- 2J4(a))
J (a) ¦
Выше обозначено /i& = аь/h, А = h/a,
i i i
Sp(f3)= \^==dx, G* («,/?) = I I eat+PX^LJLdtdx. C.45)
-l -l-i
Заметим, что при численных расчетах интегралы C.43), C.45) вы-
вычислялись путем почленного интегрирования разложений в ряд подын-
подынтегральных функций.
В табл. 3.3 приведены значения величин Р* и q*(x) = а(\ — v) x
х q(x/a)/{G5) при Л = h/a = 2,0 и некоторых значениях параметров
/3\ = b/а, /32 = с/а.
3.2. Контактная задача для предварительно
напряженного прямоугольника
В этом разделе рассматривается плоская задача теории упруго-
упругости Q4 о взаимодействии штампа с гранью прямоугольника, в котором
создано однородное поле начальных напряжений. На смежных гранях
прямоугольника заданы условия отсутствия нормальных перемещений
3.2. Контактная задача для предварительно напряженного
111
Таблица 3.3
1Д
1,3
1,5
1,7
1,9
2,0
4,0
1,9
1,7
1,1
1,1
1,3
1,5
1,7
1,9
2,0
4,0
1,1
1,3
1,9
д*(-.95)
1,537
1,796
2,029
2,169
2,252
2,280
2,366
1,375
1,648
2,421
q*(-.9)
1,229
1,448
1,578
1,658
1,706
1,721
1,765
1,119
1,342
1,823
g*(-.6)
1,003
1,163
1,158
1,158
1,155
1,153
1,133
0,963
1,108
1,204
q*(-.3)
1,004
1,134
1,103
1,085
1,070
1,063
1,027
0,994
1,093
1,090
g*(.3)
1,004
1,134
1,103
1,085
1,070
1,063
1,027
1,090
1,129
0,994
g*(.6)
1,003
1,163
1,158
1,158
1,155
1,153
1,133
1,204
1,216
0,963
q*(.9)
1,229
1,448
1,578
1,658
1,706
1,721
1,765
1,823
1,766
1,119
g*(.95)
1,537
1,796
2,029
2,169
2,252
2,280
2,366
2,421
2,318
1,375
p*
3,098
3,474
3,419
3,366
3,304
3,272
2,953
3,170
3,407
3,170
и касательных напряжений, противоположная грань лежит без трения
на жестком основании [292, 293](см. рис. 3.5).
Для описания свойств упругого тела используется модель нели-
нелинейного несжимаемого изотропного материала [343]. Задача приве-
приведена к парному ряду-уравнению по тригонометрическим функциям,
для решения которого используется метод
сведения его к бесконечной системе алгеб-
алгебраических уравнений с сингулярной матри-
матрицей. После регуляризации найдено реше-
решение системы и проведен числовой анализ
поставленной задачи в зависимости от раз-
различных параметров задачи [292].
Рассмотрим плоское упругое тело, за-
занимающее в декартовых координатах пря-
прямоугольную область \х\ ^ b, \y\ ^ h. В теле
имеется однородное поле начальных на-
напряжений, создаваемое силами, приложен-
приложенными к вертикальным кромкам х = ±6
и действующими в горизонтальном направ-
направлении. Грани прямоугольника х = ±6 находятся в условиях скользящей
заделки. Это означает, что точки вертикальных граней могут скользить
без трения вдоль прямых \х\ = Ь, не отрываясь от них. В горизонталь-
горизонтальные грани прямоугольника внедряются симметрично расположенные
штампы ширины 2а, контактирующие с упругим телом без трения. Эта
задача равносильна исходной задаче Q^.
Уравнения равновесия изотропного несжимаемого упругого тела,
линеаризованные в окрестности состояния с однородной деформацией,
Рис. 3.5. К задаче Q\
112 Гл. 3. Плоские контактные задачи для четырехугольников
имеют вид
д2и .
11 -\— 7
дх2
[290]
д2и !
dv
d2v
" дхду
= 0, /
п
+ 8q _
дх
i = 2в2П
0 г 9'w
" дхду
I —ZTT |
2 ~г <ь 1J-J-11 —г
"дх2
С-2ТТ
- ?21122 — .
2 2
= 0,
C.46)
C.47)
Здесь и, v — перемещения в горизонтальном и вертикальном направле-
направлениях, q — добавочное нормальное напряжение в горизонтальных сече-
сечениях бруса, е\, ?2, ?з — главные растяжения в начальном деформиро-
деформированном состоянии; П = Т1(е\,е2,?з) — удельная потенциальная энергия
деформации, определяющая упругие свойства материала. В дальней-
дальнейшем предполагается, что в начальном напряженном состоянии тело
испытывает плоскую деформацию, при этом г\ = г, ?2 = г~\ е% = 1.
Граничные условия поставленной контактной задачи имеют вид
| + ?=0 (NO, |»|=Л), C.48)
q = 0 (а < \х\ < b, \y\ = h), v = ±[S - у>(х)] (\x\ < а, \у\ = h),
^^udu=0 U = Q nx\=b). C.49)
дх ду vi i /
Здесь 5 — смещение штампа, (р(х) — функция, задающая форму осно-
основания штампа. Условия C.49) будут выполнены, если искать решение
в виде
оо оо
и = Y^ Un(y) sin anx, v = Yl Vn(y)cosanx,
п=\ п=0
C.50)
Qn(y) cosanx, an = —.
п=0
Удовлетворяя уравнениям C.46) и граничным условиям C.48), по-
получим парный ряд-уравнение
сю
^2 QnK*(an) cosanx = 5 - tp(x) (\x\ < а),
п=\
C.51)
сю
^2 Qn cos апх + Qo =0 (а < \х\ < Ь),
п=\
3.2. Контактная задача для предварительно напряженного 113
weQn = Qn(h) (n= 1,2,3,...).
К*(ап) = а2п(и2П2 - и2Пх) sYiunxhsYiun2hC~\
Сп = [ца2п - v(a2n + и2Пх)]иПх chu;nihshu;n2h(a2n + u;22) -
- [/ia2 - 1/(а^+^2)Ц2 chu;n2/i • shu;n2/i • (a2 + u2nx). C.52)
Здесь a;ni, u;n2 — корни характеристического уравнения
vu*n + Bi/ - fi)a2nuj2n + xc? = 0. C.53)
В частности, для материала Муни имеем
П = Сх(е\ + 4 + 4 ~ 3) + С2{е\е\ + 44 + 44 ~ 3)>
K = Ge2, u = Qe~2, /i = G(e2+ 3e~2), C.54)
G = 2(d + C2), uni = an, uni = e2an,
jr*, ч_ s2(s4 - \)shs2anh • shanh
Gan[(l-\-s ) chanh • she anh — As chs anh • shanh]
где G — модуль сдвига материала при малых деформациях из ненапря-
ненапряженного состояния.
Из C.54) следует, что
lim К* (%) = h?^?~l) , и = anh, C.55)
u-0 V/гУ G[(l+?4J-4]
г^* ^'u^ /l?2(?4 - 1) / ч
К - « ч , 0 у—5- (и —> оо).
V/гУ ^[A+4J42] V 7
Выражение C.52) непригодно для случая кратных корней урав-
уравнения C.53). Чтобы исследовать этот случай, положим ищ = anui,
ujn2 = ап(и -\- е) и перейдем в C.52) к пределу при г —> 0.
Получим
A(an) = {2(/х - г/ + 8u;2)(l + uo2)uoanh +
+ [/i(u;2 - 1) + (u;2 + lJz/] sh2u;an/i}. C.56)
Для материала Бартенева-Хазановича справедливы формулы
)
х = 2G(e2 + l)"^3, /i = AGe~\ v = 2Ge~\e2 + I), w = i
Из C.56), C.57) получаем для материала Бартенева-Хазановича
? Sll EOLnh
G?an[(l + ? )ап/г- + (be — e ) sh sanh ch sanh]
114 Гл. 3. Плоские контактные задачи для четырехугольников
Из C.58) следует, что
НтГ^) = DG)-leh, C.59)
К - « ъ (и -^ оо).
Для получения решения парного ряда-уравнения C.51) воспользу-
воспользуемся методом, изложенным в [19, 336]. Приведем C.51) к виду A.1)
при у(ип,х) = cosunx или к виду B.126):
сю
J2 QnK(un) cosunx = f(x) (\x\ < а*),
п=° C.60)
^2Qncosunx = 0 (а* < \х\ < Ь*).
п=0
Здесь введены обозначения
% ±(fy C.61)
f(x) = f^-[5- ф)] + Q0K@), un = anh, a* = a/h, 6* = Ъ/h.
C.62)
Из соотношений C.54)-C.55) для материала Муни получим с уче-
учетом C.61)
jst \ t(?)sh^?shi/ /о ^о\
К (и) = тг-^—о—о \ о > C.63)
u[t(s) chи-shus2 + As2(s2 - I) sh(it(e2 - 1))]
*(e) = (г3 + ?2 + ? - 1)(?3 - e2 + ? + 1),
О = ^^ , A = lim ВД = , t(?L .
22B \) v y Bl)D 3)
Из соотношений C.58), C.59) для материала Бартенева-Хазанови-
ча с учетом C.61) получим
ts( \ (Зе — l)sh us /о сл\
К(и) = 2^ 1 , C.64)
и[е{\ + е )и + Cs — l)shussh.us]
^ 3s2 - \ A r „, v 3s2 - 1
2 K J
2e J As
Контактные давления под штампом с решением парного ряда C.60)
связаны соотношением
Y.f (N<o). C.65)
k=0 П
3.2. Контактная задача для предварительно напряженного
115
Для определенности считаем штамп плоским (<р(х) = 0), тогда,
следуя, например, [19, 336], получим для определения контактных
напряжений следующее соотношение:
q(x) =
2GSU
h
1 +
AhPx
26
qo(x),
Qo(x) = j
хп$^Ш, C.66)
n=\
nchEna/h)'
Q = ^h+2T,
C.67)
T = Y^ xnshEna/h)[5nchEna/h)}
n=\
-l
Здесь хп — решение бесконечной системы A.6), в которой элементы
матрицы В^ = {Ьгтп} и правой части D = {dn(e)} даются соотношени-
соотношениями B.129)-B.131) при г = О и а = 0.
Решение полученной бесконечной системы получим путем регуля-
регуляризации по схеме A.12) и A.16), используя аппроксимацию функции
К (и) функцией L{u) вида A.13).
Связь между действующей на штамп силой Р и перемещением
штампа 5 найдем из соотношения
P = 2G5QPU C.68)
где Р\ — дается формулой C.67). При выводе формул C.66), C.67),
C.68) использовано равенство
Для численной реализации алгоритма необходимо аппроксимиро-
аппроксимировать функции C.63), C.64) функцией A.13). В табл. 3.4 для неко-
Таблица 3.4
г
0,80
0,90
0,95
1,05
1,10
1,20
1,40
1,60
1,80
2,00
Pi
3,3590
2,4177
2,0578
1,7303
1,5508
1,3474
1,1547
1,0872
1,0120
0,91782
Р2
1,4471
1,2366
1,0713
0,99283
0,93390
0,86384
0,80738
0,78309
0,67426
0,66374
qi
2,2607
1,7563
1,6389
1,4064
1,2518
1,1001
0,93045
0,84537
0,69841
0,68410
2,1501
1,7023
1,3451
1,2214
1,1569
1,0580
1,0020
1,0071
0,97696
0,89051
А
4,4
3,5
3,3
2,4
2,2
1,8
1Д
0,7
0,4
0,2
116
Гл. 3. Плоские контактные задачи для четырехугольников
Таблица 3.5
г
0,70
0,80
0,90
0,95
1,05
1,10
1,20
1,40
1,60
1,80
2,00
Р\
5,7092
3,2979
2,4185
2,1222
1,7316
1,5751
1,3426
1,1254
1,0005
1,0961
0,65854
Р2
1,6699
1,3926
1,2374
1,1312
0,98527
0,95339
0,85231
0,71225
0,61491
0,83955
0,44397
3,1470
2,2354
1,7468
1,5816
1,4208
1,2759
1,0831
0,79012
0,65588
0,90902
0,48126
3,0295
2,0545
1,7133
1,5179
1,2008
1,1770
1,0565
1,0145
0,93805
1,0124
0,60752
А
6,6
5,0
3,7
2,9
2,4
2,3
1,9
1,5
1,4
1,7
0,9
торых е приведены значения коэффициентов аппроксимации A.13)
для материала Муни, в табл. 3.5 — для материала Бартенева-Хаза-
новича.
В последних колонках таблиц 3.4, 3.5 указаны значения относи-
относительной погрешности такой аппроксимации (в %).
Был проведен расчет контактных давлений и жесткости системы
«штамп-прямоугольник», характеризуемой величиной Р/5. Функции
q(z) и Р вычислялись по форму-
формулам C.66), C.67), C.68), в кото-
которых хп — решение системы линей-
линейных алгебраических уравнений ви-
вида A.16), в которой значение N вы-
выбиралось в зависимости от заданной
точности. С увеличением парамет-
параметра (Ъ — a)/h для достижения задан-
заданной точности значение N уменьша-
уменьшается. Например, при (Ъ — a)/h = 0,2
погрешность в 3% достигается при
N = 40, а при (Ь - a)/h = 2, ко-
когда N = 10.
В таблицах 3.6, 3.7 для некото-
некоторых значений параметров /3 = Ь/а,
Л = h/a, г приведены значения ве-
величин
C.69)
28
26
24
22
20
18
0,8 1,0 1,2 1,4 1,6 1,8
Рис. 3.6
2GSq\a
2GS
для материала Муни (Л = 0,5) и материала Бартенева-Хазановича
(Л = 1,0) соответственно.
3.2. Контактная задача для предварительно напряженного
117
Таблица 3.6
г
0,80
0,95
1,05
1,20
1,50
2,00
0,80
0,95
1,05
1,20
1,50
2,00
0,80
0,95
1,05
1,20
1,50
2,0
q*@)
38,6
39,8
41,6
47,4
56,3
84,0
16,3
14,2
13,7
13,7
15,5
22,0
10,6
8,75
8,15
7,80
8,39
11,6
g*@,2)
38,5
39,8
41,6
47,4
56,3
84,1
16,2
14,2
13,7
13,7
15,5
22,0
10,6
8,74
8,15
7,80
8,40
11,7
<f@,4)
Р =
38,3
39,7
41,6
47,5
56,5
84,5
Р =
16,1
14,1
13,7
13,7
15,6
22,2
10,5
8,69
8,12
7,81
8,43
11,7
q*@fi)
1,2
37,9
39,8
41,8
47,9
57,4
86,0
1,5
15,8
14,1
13,7
13,9
15,9
22,8
2,0
10,3
8,65
8,13
7,89
8,61
12,0
g*@,8)
37,9
40,0
43,7
51,0
61,9
93,4
15,6
14,5
14,4
15,0
17,6
25,6
10,1
8,89
8,53
8,50
9,57
13,6
g*@,95)
47,6
56,2
61,7
73,7
90,5
137
19,4
20,5
21,1
22,9
27,8
40,9
12,6
12,4
12,5
13,0
15,2
22,0
p*
81,0
86,5
91,6
106
127
190
33,8
30,9
30,4
31,2
36,0
51,9
22,0
18,9
18,0
17,7
19,6
27,5
Для наглядности на рис. 3.6 приведена зависимость жесткости пря-
прямоугольника, характеризуемой величиной Р* от параметра предвари-
предварительного напряжения г при Л = 0,5 для материала Муни (кривая /,
/3 = 2,0) и материала Бартенева-Хазановича (кривая 2, /3 = 1,5). При-
Приведенные и другие результаты числовых расчетов показывают, что для
материала Муни существуют такие значения параметров /ЗиЛ, когда
жесткость от параметра г зависит не монотонно и имеет при некотором
г = ?* минимум, в других случаях жесткость с увеличением пара-
параметра г возрастает. Для материала Бартенева-Хазановича при всех
значениях параметров /ЗиЛе увеличением г жесткость не убывает.
Такая же зависимость от г характерна и для контактных напряжений
в точках под штампом, о чем можно судить и по результатам расчетов,
приведенных в таблицах 3.6, 3.7.
118
Гл. 3. Плоские контактные задачи для четырехугольников
Таблица 3.7
г
0,80
1,05
1,50
1,80
2,00
0,80
1,05
1,50
1,80
2,00
0,80
1,05
1,50
1,80
2,00
q*@)
29,1
38,2
53,5
82,5
125
8,25
9,01
9,70
10,6
10,9
4,85
4,54
4,19
4,19
4,10
g*@,2)
29,1
38,3
53,7
82,8
125
8,24
9,07
9,76
10,7
11,0
4,84
4,54
4,23
4,24
4,15
g*@,4)
P =
29,1
38,5
52,0
83,9
127
P =
8,24
9,17
10,0
11,0
11,3
4,82
4,60
4,37
4,41
4,33
q*@fi)
1,2
29,4
43,3
56,2
87,0
132
1,5
8,29
9,52
10,7
11,8
12,1
2,0
4,83
4,79
4,72
4,81
4,75
g*@,8)
31,2
39,4
62,5
96,9
147
8,87
10,9
12,7
14,1
14,6
5,15
5,56
5,79
5,99
5,95
g*@,95)
45,5
64,5
93,6
145
221
13,5
18,0
21,5
23,9
24,8
7,80
9,45
10,3
10,8
0,7
p*
65,0
87,5
124
191
289
18,6
21,9
24,5
26,9
27,7
10,9
11,1
11,0
11,2
11,1
3.3. Контактные задачи для кольцевого сектора,
кольца и усеченного клина
В этом параграфе в полярной системе координат методом сведения
парных рядов-уравнений к бесконечным системам линейных алгебра-
алгебраических уравнений с сингулярной матрицей и методом однородных
решений исследован ряд контактных задач для кольцевого сектора,
кольца и усеченного клина.
3.3.1. Несимметричная контактная задача для кольцевого сек-
сектора. Метод сведения парных рядов к бесконечным системам.
Рассмотрим плоскую статическую задачу теории упругости Q$ о вдав-
вдавливании без трения штампа в цилиндрическую поверхность кольце-
кольцевого сектора. Предполагается, что штамп расположен несимметрично,
остальные границы сектора взаимодействуют с гладкими неподвижны-
неподвижными поверхностями [189]. Задача исследуется путем сведения получен-
полученных тройных рядов-уравнений к бесконечной системе линейных алгеб-
алгебраических уравнений первого рода с сингулярной матрицей (см. § 1.2).
После обращения главной части получена система второго рода, ре-
3.3. Контактные задачи для кольцевого сектора, кольца
119
шение которой найдено методом редукции. Исследована зависимость
от параметров задачи величины контактных напряжений под штампом,
жесткости системы штамп-кольцевой сектор и величины момента,
препятствующего повороту штампа. Проведены числовые расчеты. Об-
Обнаружено, в частности, что штамп может перемещаться поступательно
при центрально приложенной силе не только при симметричном, но
и при несимметричном расположении штампа на поверхности сектора.
Этот факт может быть использован при проектировании близко распо-
расположенных друг от друга фундаментов. Рассмотрен также предельный
случай, когда кольцевой сектор вырождается в прямоугольник.
Задачи, близкие по постановке, рассматривались в работах [66, 98,
280] и др.
Рис. 3.7. К задачам Qs, <2б
В полярной системе координат (г, ф) рассмотрим упругое тело
в форме кольцевого сектора R\ ^r ^ R2, —71 ^ ^ ^ 72 (ъ > 0, * — 1» 2)
(см. рис. 3.7, а). Пусть в грань г = R^ на участке \tp\ ^ # (# < 7г)
вдавливается силой Р штамп таким образом, что он перемещается
поступательно. Предполагаем также, что на поверхностях г = R\,
(р = —7ь ^ = 72 отсутствуют нормальные перемещения и касательные
напряжения. Поставленная задача теории упругости сводится к ис-
исследованию уравнений Ламе (плоское напряженное состояние) при
следующих граничных условиях:
тГ(р =0, ur = 0,
TrLp =0, u^ = 0, ((/?
= 72),
тГ(р
=0, аг = 0, (г = Д2, -71 < <Р < -#> # < <Р < 72),
C.70)
Здесь тГ(р, аг — компоненты тензора напряжений, иг, и^ — компоненты
вектора перемещений, 5{ф) — функция, описывающая перемещение
штампа и его форму.
120 Гл. 3. Плоские контактные задачи для четырехугольников
Поставленная задача Q$ равносильна симметричной задаче QI
о вдавливании двух штампов в сектор \ф\\ ^ 7 = 7i + 72> R\ ^ r ^ ^2
(см. рис. 3.7, б). Здесь (г,(р\) — новая полярная система координат
с началом отсчета угловой координаты от луча (р = —71 (ip\ = <р +
+ 7i)- При этом штампы вдавливаются на одну и ту же величину
в радиальном направлении в поверхность г = Щ на участках
7i - fi < щ < 71 + #, -G1 + ^) ^ Ч>\ ^ -G1 - ^)»
а на поверхностях |(^i| = 7 и г = i?i отсутствуют нормальные переме-
перемещения и касательные напряжения.
Для задачи Q\, разыскивая решение уравнений Ламе в виде со-
соответствующих рядов Фурье, придем к исследованию тройного ряда-
уравнения:
J2 QkK(a) cosаку>1 =
к=0
C.71)
сю
=0, @ < щ < #i, #2 < <Pi < 7)'
где а/с = тгк/'у, $\ = 71 — $, ^2 = 7i + ^> Qfc — коэффициенты, подле-
подлежащие определению, через которые неизвестные контактные давления
под штампом находятся из соотношения
crr(i?2> Ф) — я(ц>) — E ^ cosa/c((^ + 71), (|(?>| ^ i?). C.72)
Правая часть тройного уравнения C.71) имеет вид
п0 = К@) -A -г/2)(х2-
где х = Щ/Ях, Е — модуль Юнга.
Ядро тройного уравнения C.71) является четной мероморфной
функцией и дается соотношением
К(а) = |& C.74)
А,(а) = 2A -г/J[сЬBа1пх)- 1] +
+ а2[2A - vf + A + i/)C - ;у)(х2 + х~2) - 8 ch Ba In ж)],
3.3. Контактные задачи для кольцевого сектора, кольца 121
Д(а) = 2A -а2){2A - v) [ch Bа In к) - 1] +
+ 4а sh Bа In ж) + а2[A + v)k2 + 2A - v) + {у - 3)я~2}}.
Переходя в C.74) к пределу при а —» 0, найдем величину
А = К@) =
= [4A -г/J1п2^ + 2A - vf + {\ + v){Z - v){k2 + ж~2) - 8\ х
х {2[4( 1 - v) In2 х + 8 In я + A + i/)*2 + 2( 1 - I/) + (^ - 3)я~2}}-'.
C.75)
Для решения уравнения C.71) используем метод, основанный на
сведении его к бесконечным системам линейных алгебраических урав-
уравнений первого рода с сингулярной матрицей (см. § 1.2). Предположим,
что перемещение штампа и его форма задаются соотношением 5((р) =
= Scostp, E = const). Тогда, решив уравнение C.71) с правой частью
f(ipi) =cose(ip{ -71), C.76)
получим его решение и с правой частью C.73), считая г = 0 и г = 1.
Обозначим через Q?k решение уравнения C.71) с правой частью
C.76), а соответствующее ему значение функции C.72) через q?((f)-
Тогда, применяя известную методику [19, 41], найдем
i ОО
+ н Е Ы + Ук) ^ Skip ch"' 6кд + D + у%) ch 6кср ch"' 6к0], C.77)
к=\
где ж| и у| являются решениями бесконечных систем
ВПХ?+В12У?=Б1?,
В# = Е - В^, C.78)
Здесь В^ = (СЬ К = {ЪЦП}, Е = {Eп - /3fc)-'} - матрицы, Y? =
= {^|}, Х? = {х?к}, Т>г? = {d\(e)} — векторы с элементами
х [1 + ехр (-/Зк(ъ - tf)) сЬ/З^зЬ 7i/3fc] (г ^ ]),
^ ехр (-2*„#) + ехр (-/3fcGi - t?)) sh"' /
x sir1 25nti[5nch/3k'dch25n'd - /3ksh/3ktish25n'd]],
Ккп = -№- /3fc)"' [^ ехр (-2*„#) + ехр (-/3fcGi - t?)) sh"' /3fc7i x
122 Гл. 3. Плоские контактные задачи для четырехугольников
d{(e) = {г2 + f32k)-[K-[(?)[f3kchi?tf + iesbietf +
+ exp {-Pkiij ~ ¦&)) sh -fj/3k[ieshie^ch/3ki9 - /3kchiei9shpki9]}.
C.79)
В C.77) и C.79) i5n, i/3k являются соответственно нулями и полюсами
функции К (а), определяемой соотношениями C.74). В работе [327]
приведена асимптотика полюсов при больших номерах, она имеет вид
/Зк ~ак + Ъх +i\n(d{k + d2). C.80)
Можно показать, что и асимптотика нулей будет иметь аналогич-
аналогичный вид:
5п ~ an + 62 + 2 In {d^n + di), C.81)
где a, bi, di — известные постоянные.
Асимптотики C.80)—C.81) позволяют показать, что диагональные
элементы матриц В11 и В22 не убывают, а все элементы матриц BqJ
убывают с ростом номеров. Согласно A.11) матрица Е имеет извест-
известную обратную Е = {rnk}.
Используя обратную матрицу Е, бесконечную систему первого рода
C.78) преобразуем к бесконечной системе второго рода:
Х? = Т~1В1е + Е~1В101Х? - E-'B^Y8,
C.82)
Y? = E~lB2e + Е-^Х6 - E~lBl2Y?.
Система C.82) может быть исследована методом редукции [88].
Наибольшие трудности реализация изложенной методики встречает
при вычислении обратной матрицы Е, где необходима факторизация
функции К (а). Для преодоления этой трудности воспользуемся при-
приближенной факторизацией, для чего аппроксимируем на действитель-
действительной оси функцию К (и) функцией A.13).
При такой замене погрешность решения не превосходит погрешно-
погрешности аппроксимации [88], и элементы rnk матрицы Е легко вычисля-
вычисляются по формулам A.14).
Напомним, что при выполнении числовых расчетов в качестве г5п
и i/3k следует брать соответственно нули и полюсы функции L(a).
Если предположить, что к близко к единице (х —> 1), то в этом слу-
случае можно показать, что 5п и /3k будут велики (<5П —> oo,Ck —> 00). Это
приведет к тому, что принебрежимо малыми будут элементы матриц
В12, В21, Bq1, Bq2 по сравнению с элементами матрицы Е. Асимп-
Асимптотически упростив далее элементы векторов Т)г?, получим из C.82)
при 7г > # (i = 1,2)
X - Y - Е-^^), В(е) = Ше)}, C.83)
3.3. Контактные задачи для кольцевого сектора, кольца 123
Тогда соотношение C.77) примет вид
оо
q?(ip) =K~\e) cosеср + ]Г 4 ch^ch 5k&, C.84)
k=\
где x?k необходимо взять из C.83), причем выражения для них можно
выписать в явном виде [52].
Отметим, что при я^ 1 аппроксимация A.13) уже при
L(a)=a~lthAa C.85)
дает достаточно хорошее приближение, и в этом случае
4 = [(тг^2Bк- l)!!)/BABfc)!!)] [Re (Г) + Re(iT/Ek - г))] C.86)
х°к = Bк - l)!!)/(ABfc)!!), Г = е^ГA + гЛ/тг)/ГA/2 + гЛ/тг),
где Г (и) — гамма-функция.
Это позволяет суммировать главную часть ряда из C.84). Решение
задачи, полученное с помощью изложенного в этом пункте асимп-
асимптотического подхода, не учитывает влияния боковых граней сектора
и справедливо при близких значениях радиусов сектора Щ и R\.
Принимая во внимание соотношения C.73) правой части уравне-
уравнения C.71) для поставленной задачи Q$, можем найти функцию распре-
распределения контактных давлений под штампом:
q{<p) = {E5/BR2d))q%<p) = {E5/{2R2))qx{v) + QQnm{^), C.87)
ается соотношением C.77). Константа Qo с ис-
иссоотношения из C.73) находится по формуле
= (E5/BR2))[j - п0Р0Т1Р?, C.88)
где q?{ip) (в = 0, 1) дается соотношением C.77). Константа Qo с ис-
использованием второго соотношения из C.73) находится по формуле
Связь между приложенной к штампу силой Р и его перемещением 5
найдем из соотношения
P = R2 [ q((p) cos (p dip. C.89)
Исходя из представления C.87)-C.88), это соотношение можно
преобразовать к виду
Р = (Е6/2)Р*, Ql = BR2/(E5))Q0n0, C.90)
Р* = K~\0JQl sin# + К~\\)[$ + sin Bi?)] +
сю
5\Г\х{ +yl + Q*0(x°k + j/2)](sini? + Sk costf thM).
k=\
124 Гл. 3. Плоские контактные задачи для четырехугольников
Для того, чтобы штамп перемещался поступательно, к нему необ-
необходимо приложить момент
М = -Щ \ q(ip) cos ip sin ip dip. C.91)
-•в
Подставляя C.87), C.77) в C.91), получим
М = (E5R2ti/2)M*,
k=\
х [Sk sin 2$ ctg 5kti - 2 cos 2Щ. C.92)
Соотношения C.87), C.90), C.92) и другие, связанные соответ-
соответственно с вычислениями контактных напряжений под штампом, силы Р
и момента М, содержат неизвестные коэффициенты ж|, у?к (г = 0, 1).
Их будем находить из редуцированных бесконечных систем C.82).
Число уравнений N в редуцированной системе выбираем в зави-
зависимости от заданной точности, а при вычислении величин по форму-
формулам C.77), C.88), C.90), C.92) ряды заменяем конечными суммами
из N слагаемых.
В случае к —> 0 можно воспользоваться соотношениями C.86), и
тогда искомая величина q*(ip) может быть найдена из явных соотно-
соотношений
f + ^ВД) [A - expXfo, - ^А4)Г1/2 - 1] +
2yf
П=1
C.93)
Величина Р* вычисляется по формуле C.90), где х\, х^ следует
брать из соотношений C.86).
Вычислялись величины q*(<p), P* и М* характеризующие соот-
соответственно безразмерные контактные напряжения под штампом, жест-
жесткость системы штамп-сектор и величину безразмерного момента, пре-
препятствующего повороту штампа.
Вычисления производились для случая плоской деформации при
v = 0,3, т.е. в расчетах v заменялось на v\ = vj{\ — и), Е на Е\ =
= Е/{\ — и2), и далее полагалось v = 0,3.
Число уравнений N редуцированной бесконечной системы выбира-
выбиралось в зависимости от заданной точности. При увеличении N может
3.3. Контактные задачи для кольцевого сектора, кольца
125
быть достигнута любая наперед заданная точность. Так, например,
если h = R2- R\ = 0,5, v = 0,3, к = 1,1, Ь\ = b2 = 3 (bi = 71/1?, b2 =
= 7/1?), то при переходе от значения N = 5 к TV = 10 относительная
разность для Р* составляет 1,1 %, при переходе от N = 10 к N = 20 —
0,8% и при переходе от 7V = 20 к N = 30 - 0,36%.
В табл. 3.8 для сравнения приводятся значения величин q*((p) и
Р* вычисленные методом редукции и асимптотическим методом для
некоторых значений х, bi =62, /1 = 0,5 и и = 0,3.
В столбцах 2-6 приводятся значения величин q*(<p), Р*, получен-
полученные с использованием формул C.87), C.90), а в следующих пяти —
с использованием формул C.86). Следует отметить, что при х—> 1,
т. е. с уменьшением кривизны, жесткость сектора увеличивается, а зна-
значения вычисляемых величин приближаются к соответствующим зна-
значениям задачи для прямоугольника. Во всех расчетах здесь и ниже
принималось R2d = 1.
Таблица 3.8
bi
3,0
1,6
1,2
3,0
1,6
1,2
<f@,0)
4,143
4,479
4,745
3,358
3,920
4,492
<f@,6)
4,137
4,475
4,739
2,860
3,425
4,016
<f@,9)
4,890
5,291
5,501
2,682
3,416
3,996
<f@,95)
6,073
6,572
6,719
x =
3,135
4,091
4,658
P*
<f@,0)
1,1 #2 = 5,5
8,950
9,680
10,169
2,0 h
5,203
6,232
7,214
4,146
4,486
4,766
l2 = 1,0
3,381
3,969
4,566
<f@,6)
4,141
4,482
4,762
2,895
3,491
4,097
g*@,9)
4,897
5,303
5,637
2,821
3,582
4,356
<f@,95)
6,085
6,591
7,007
3,400
4,373
5,362
P*
8,930
9,666
10,271
5,278
6,351
7,439
Из таблицы 3.8 видно, что при увеличении кривизны происходит
распределение контактного давления с относительным увеличением
в точке (р = 0. Кроме того, хорошо видна область применимости асимп-
асимптотического решения.
В табл. 3.9 приведены значения величин q*(<p), P*, М*, вычислен-
вычисленных методом редукции, при различных значениях параметров х, Ь\,
Ь2 = 6 — b\, v = 0,3 и h = 0,5. Значение х, равное единице, означает,
что в данном случае мы имеем дело с прямоугольником, причем вели-
величина $ — это уже линейная полуширина штампа, Ь\, Ъ2 — отношения
соответствующих величин расстояний от центра штампа до боковых
граней сектора к величине #, равной единице.
Из таблицы 3.9 видно, что существуют такие величины Ъ\ ^ Ь2,
при которых величина момента М* будет равна нулю. Это означа-
означает, что существует такое несимметричное расположение штампа на
126
Гл. 3. Плоские контактные задачи для четырехугольников
СО
К
VO
ей
н
*
*
о
%
о
*
СО"
о
*
о
^ч
СО"
о"
1
S*
О
1
оГ
о
1
*
о
8
11
^Ч
СО
of
о
о
о^
00
LO
00
о
о
CS|
4f
00
1—1
^
LO
^
00
4f
о
СО
CD
of
CM
1
о
CD
00
1
СО
О)
1П
о
CS|
00
^
СО
LO
СО
00
LO
^Ч
О)
о$
см
I
О
СО
CS|
1П
ОО
^
СО
О
CS|
^
CS|
,-н
CS|
1П
CS|
^
СО
LO
^
00
СО
^ч
О)
о$
о
CS|
«
1П
CD
О)
^
СП
CS1
CS|
^
CS|
CS|
^
со
CS|
CS|
^
О)
О)
LO
'—I
ОО
00
^
CS|
ОО
CS|
о$
-Г
со
|>~
1П
CS|
CD
CS|
CSI
со
CS|
4f
8
CSI
o>
LO
'—I
o>
00
CM
CO
CO
'I
CD
LO
cd"
о
о
[^^
LO
CO
CD
CO
CO
[~^«
LO
CO
CD
LO
CD
CO
^
LO
CO
CD
CO
CO
[~^.
LO
CO
О
CO
О
00
CD~
со
1
О
О
CO
[~^.
LO
CO
со
CO
CO
О
OO
LO
CO
C75
LO
CD
CO
O>
IN-
LO
CO
CO
CD
CO
CO
CO
LO
CO
О
CS|
о
00
CD~
со
|
О
О
о
1
[~^.
LO
CO
со
CO
CO
00
LO
CO
О
CD
CD
CO
О
00
LO
CO
CO
CD
CO
CO
[~^.
LO
CO
00
OO
CD~
CM
|
О
О
CO
о
CD
LO
CO
CO
со
CO
CO
О
00
LO
CO
О
CD
CD
CO
00
LO
CO
CD
CO
CO
in
LO
CO
LO
CO
CD~
CM
1
о
CD
CO
CO
OO
CM
CO
in
CO
CO
Ю
LO
CO
со
LO
CD
CO
^
LO
CO
О
CD
CO
CO
[~^.
LO
CO
CM
о
CS|
о
о
II
*
s
LO~
о
о
со
OO
CD
CM
CD
00
CS|
CS|
CS|
CO
C75
LO
CO
CO
CM
CSI
CO
О
CD
00
CS|
CO
oo
CD
CS|
о
CO
O)
CM
1
о
о
l>~
CS|
[~^.
00
CS|
LO
CO
CS|
CO
CO
CD
CO
CO
CO
CSI
CO
CS|
CD
00
CS|
in
oo
CD
CS|
LO
CS|
LO~
CM
I
О
1^
о
CS|
C75
00
CM
LO
CM
CO
C75
CD
CO
CO
CO
CO
CSI
CO
CD
00
CS|
OO
CD
CS|
CO
CO
LO~
CM
1
О
CM
CD
О
1
CO
CD
CM
о
О)
CS|
CS|
LO
CS|
CO
[~^.
CO
CO
CO
CSI
CO
CO
CD
00
CS|
in
OO
CD
CS|
CS|
CS|
l>~
LO~
CM
|
О
CS|
CD
CO
CD
CM
CD
О
О)
CM
LO
CM
CO
CM
CO
CO
CM
CO
CM
CO
LO
00
CS|
[~^.
CD
CS|
rt
3.3. Контактные задачи для кольцевого сектора, кольца 127
поверхности сектора, когда он перемещается поступательно в случае
только симметрично приложенной к штампу силы. Этот факт может
быть практически использован при проектировании фундаментов близ-
близко расположенных сооружений.
3.3.2. Контактная задача для кольцевого сектора. Метод од-
однородных решений. Рассмотрим статическую контактную задачу Q§
для кольцевого сектора R\ ^ r ^ R2, \ф\ ^ 7 ° вдавливании штампа
в поверхность г = R2, при этом поверхность г = R\ лежит без тре-
трения на жестком основании, а на гранях (р = ±7 отсутствуют каса-
касательные напряжения и нормальные перемещения (см. рис. 3.7, а при
71 =72 =7)-
Граничные условия такой задачи E — перемещение штампа)
ur = 5cos(p (г = Д2, M^tf), C-94)
аг = О (г = Д2, # < М < 7), тГ(р = О (г = йьг = Д2),
ur=0 (r = Ri), rr^ = 0, u^=0 (М<т).
Решение уравнений Ламе при условиях C.94) будем искать в виде
ur(r,ip)=uW-42\ и(р(г,1Р)=иМ-и$\ C.95)
где щ , щ>* — решение уравнений Ламе для кольца, когда заданы
граничные условия
ar(R2^) = {q(r), (И<1?); 0 (И > #)},
Trip(R2,(p) =0, rry,(i?i, у?) = гхг(Дь у?) =0,
B) B) о тт
auf ,и5з; - суперпозиция однородных решении уравнении Ламе для
кольца, когда заданы граничные условия
оу(Д2,<р) = Tr(p(R2,y>) = 0, Tr(p(Ri,ip) = ur(R2,(p) = 0.
В этом случае решения уравнений Ламе с граничными условиями
C.96) имеют вид
k=\ У ' k=\
C.97)
а соответствующие компоненты тензора напряжений
сю
«^EsM^Mcos^ (9 = *-,?>), C-98)
k=\ ^ '
оо «3
# Е ^) fc () ^' ^ {«() C0S kt dt-
k=\
128 Гл. 3. Плоские контактные задачи для четырехугольников
В формулах C.97), C.98) функции Wk(r), Vk(r), ark, rk(r) и ^)
известны (в дальнейшем понадобится только Wk(r) и A(fc)), q(t) —
функция распределения контактных давлений, которую необходимо
определить.
Имеем
= ? AfeWfcW coaakip, u<?> = ? DkV%(r) sinafc?>, C.99)
а«2) =Е*Ц Dk°qk{r) cos akcp (q = r,ip),
Здесь суммирование ведется по всем нулям ак функции А(ак), распо-
расположенным в правой полуплоскости. Заметим, что A(fc) = A (fc) (к ^ 2)
(см. C.108)).
Таким образом, функции C.95), C.97), C.99) удовлетворяют урав-
уравнениям Ламе и граничным условиям C.94), кроме первого и последне-
последнего, которые теперь примут вид
(\ip\ < 0), C.100)
4,°(г, 7) - <>(г,т) = 0, тгф(г,7) - rrB)(r,7) =0, № < г < Д2).
Представим неизвестные контактные напряжения в виде
сю
q(t) = E*[6qo(t) + E DkW%(R2)qk(t)]. C.101)
Удовлетворяя первому граничному условию C.100), для определе-
определения qk(t) (к = 0, 1, 2,...) получим ряд интегральных уравнений
К^о = собц>; K^qk = cosakp, fc^l (|y?| > 0), C.102)
где интегральный оператор К^ при учете четности функции q(t) может
быть приведен к виду
K^q = [ M(t- <p)q(t) dt, M(y) = ^ ^Щ1 cos кУ- C-103)
Два последних условия C.100) перепишем в виде
Е Dkr%(r) sinак-у= ^
Умножим первое соотношение на а^ и вычтем из полученного
равенства второе соотношение, умноженное на W®, после чего полу-
3.3. Контактные задачи для кольцевого сектора, кольца 129
ченное выражение проинтегрируем в пределах от R\ до Щ. Используя
СОО A.84), получим
DkWkk sin akj = — S^ anSin^ [Vna°k - rnWk] dr. C.104)
Учитывая, что пары функций V^, Wn и V®, W® удовлетворяют одной
и той же системе уравнений, интеграл из C.104) может быть вычислен
с использованием интеграла A.83) и граничных условий C.96), C.97):
Д2 0
||~ТТ" (I Т Т Т\ I ~\ 7 I U -Ж. Xs/ т v Is* \ -М- 1уу / Су Т1 'Yl \ J. Xj/ I / /~\ -4 /^v ^ \
J [Ki^fe - ТПИ^] dr = 2 _ 2 ' (ЗЛ05)
Так как
00 4.-4. ' f \
(-п \ _ \( \ V^ n cos n^ sm nt _ 7т sin (тг — 7)<2fc cos tak
^—J n - a\ 2 sin ттак
то выражение C.104) преобразуется к виду
fc№) sinGr — 7)afc Г /хч , ,, /o 1ЛСЧ
q(t) cos afct dt C.106)
0
Подставляя C.101) в C.106), получим бесконечную систему для опре-
определения коэффициентов Dk:
сю
Ук=Ък + У?акпУп (к =1,2,...), Dk= у*ш , C.107)
к=0 Wk
h г гр СкТкп
"к = ОСк1ко, пкп = -г-
sin an
sin (тг -7)<Xk rr Г /,ч
]±Л-, Tfcn = qn(t) cosafc
J
Можно показать, что Ткп =
Таким образом, для отыскания функции распределения контактных
напряжений под штампом получена формула C.101), где qk(t) находят-
находятся из интегральных уравнений C.102), C.103), а Dk — из бесконечной
системы C.107). Отметим, что к уравнениям C.102), C.103) сводятся
аналогичные контактные задачи для кругового кольца. Таким образом,
здесь проблема решения контактной задачи для кольцевого сектора
сведена к уже хорошо изученной контактной задаче для кольца. Кроме
того, бесконечная система C.107) относится к типу нормальных систем
Пуанкаре-Коха, т. е. ее коэффициенты Ьк и акп убывают с ростом
номеров по экспоненте, что будет показано ниже. Следовательно, ее
5 В.М. Александров, М.И. Чебаков
130 Гл. 3. Плоские контактные задачи для четырехугольников
решение может быть получено методом редукции при любых значениях
параметров.
Как видно из формул C.101)—C.103) и C.107), для исследования
решения задачи понадобятся лишь выражения Wfc(i?2)A~1(fc), W?(i?2),
Wkk и собственные числа од. Указанные выражения получить нетрудно
(см., например, [163]), и они здесь не приводятся, найдем только
асимптотику чисел од ПРИ больших к. Как было отмечено, од — корни
уравнения
А0 (од) = 2A -г/)с
+ /х0а|-2A -у) =0, C.108)
Можно установить, что при больших номерах корни этого уравне-
уравнения имеют следующую асимптотику:
од - [1п(|тг/хоB1пх)-1|(/с- 1/4))+г2тг(й- 1/4)]B]пх)~\ C.109)
что, в свою очередь, позволяет оценить элементы матрицы в правой
части бесконечной системы C.107) при больших номерах к, п
\Ък\ < Рк exp [-&G - 1?)], \акп\ < Pfcn exp [-(& + /Зп)G - #)],
C.110)
_7T(fe-l/4)
Л" In х '
где Pfc и Pkn — ограниченные величины. Это означает, что бесконечная
система C.107) относится к типу нормальных систем Пуанкаре-Коха
и ее решение может быть получено методом редукции при любых
значениях параметров.
Замечания. 1°. Для элементов dk = DkWk(R2)qk(t) ряда C.101)
выполняется соотношение dk = о[ехр (—/3&G — $))] ПРИ любых |?| < #
и при больших /с, а следовательно, ряд C.101) при \t\ < $ сходится не
медленнее, чем сумма членов геометрической прогрессии со знамена-
знаменателем, меньшим единицы.
2°. Ядро интегральных уравнений C.102), C.103) можно предста-
представить, учитывая асимптотику функции ^№)/А(&) при больших к,
в виДе 9о
9
М(у) = - *"* In 2sin|
|
C.111)
ИЛИ
2i^2 V^ Cth B/cln >гг)
, , , /о 1 1 o\
cos ky + F2(y), C.112)
где Fi(y) и F2(y) — непрерывные при всех \у\ < M < oo функции.
Представление ядра в виде C.111) позволяет получить эффективное
3.3. Контактные задачи для кольцевого сектора, кольца 131
решение интегральных уравнений C.102), C.103) методом ортогональ-
ортогональных многочленов [33], а представление C.112) позволяет [13] точно
обратить главную часть интегрального оператора уравнений C.102),
C.103) и свести их к интегральным уравнениям второго рода.
3.3.3. Контактная обобщенно-периодическая задача теории
упругости для кольца. Предлагается схема решения плоской
статической контактной задачи теории упругости для кольца, взаи-
взаимодействующего с системой периодически расположенных жестких
штампов, когда их радиальные перемещения, вообще говоря, не равны
друг другу [188].
Предлагаемая схема опирается на работы [80, 81]. Решение ис-
исходной задачи представляется в виде суперпозиции решений более
простых задач для кольца, которые эквивалентны соответствующим
задачам для сектора кольца с одним или несколькими штампами
с известными условиями на торцах и могут быть сведены к парным
(тройным и т. д.) рядам-уравнениям и далее к бесконечным систе-
системам линейных алгебраических уравнений первого рода с сингуляр-
сингулярной матрицей. Последние урезаются специальным образом с учетом
асимптотического поведения их решения [305, 319] и решаются лю-
любым прямым методом. Приводятся результаты численной реализации
решения задачи с четырьмя штампами, когда три штампа неподвижны,
а перемещение четвертого задано. Исследована зависимость величин
контактных напряжении, сил и моментов для каждого штампа в зави-
зависимости от параметров задачи. Периодические контактные задачи для
кольца рассматривались в работах [66, 98, 187, 280] и др.
Рассмотрим упругое тело в форме кольца R\ < г < R% с центром
в начале полярных координат (г,ф). На поверхность г = R% действу-
действуют п штампов, расположенных так, что ось ф = 0 проходит через центр
первого из них, а остальные нумеруются в положительном направлении
отсчета ф и расположены друг от друга на угловом расстоянии 2^ =
= 2тг/п. На поверхности г = R\ заданы нулевые нормальные переме-
перемещения и либо нулевые касательные напряжения (скользящая заделка),
либо нулевые касательные перемещения (жесткая заделка). Переме-
Перемещения под штампом с номером к + 1 описываются функцией 5к(ф),
к = 0, 1,..., п — 1, причем 5к(ф) = 0 для к ^ 1, а 5о(ф) = 5 соБф, где
5 = const, т. е. первый штамп внедряется поступательно в радиальном
направлении, тогда как остальные неподвижны. Трение под штампами
отсутствует. Угловые размеры штампов совпадают и равны 2$. Иссле-
Исследуется плоское напряженное состояние.
Схема решения состоит в том, что решение исходной задачи пред-
представляется в виде суперпозиции решений задач, которые отличаются от
поставленной выше функциями 5к(ф), а именно, для любого к 5к(ф) =
= ±5cos(p ((р = ф — 2&7). Такие задачи в силу свойств симметрии
эквивалентны соответствующим задачам для сектора кольца с одним
или несколькими штампами и известными условиями на торцах.
132
Гл. 3. Плоские контактные задачи для четырехугольников
Рассмотрим случай, когда число штампов равно четырем (задача
7, см. рис. 3.8). Для этого, в соответствии с предложенной схемой
введем в рассмотрение три задачи (верх-
(верхний индекс соответствует номеру за-
задачи):
1) 5[1\ф) = 50(ф), к = О, 1, 2,
3, \ср\ < $ — соответствуют симмет-
симметричной задаче для сектора кольца со
скользящими боковыми заделками (см.
п.п. 3.3.1, 3.3.2);
2) 5^ (Ф) = 5о((р) cos7rk, к = 0,1,
2, 3 — соответствуют условиям на боко-
боковых гранях ар = 0, иг = 0 (|(/?| =7M
к = 0, 1,2, 3 — соответствуют задаче для
сектора с двумя симметрично располо-
расположенными штампами на участках ^ — д <
< М < 7 + $> а на боковых гранях условия соответствуют условиям
задачи 2).
Нетрудно убедиться в том, что в силу симметрии, контактные
напряжения под штампом для каждой задачи можно представить в сле-
следующем виде:
ттк . ттк
>s т ~sm т
Рис. 3.8. К задаче
. м
% (
где функции q(l\(p) = % (ф) (i = 1,2,3) — контактные напряжения
под первыми штампами соответствующих задач.
Также нетрудно убедиться и в том, что если взять суперпозицию
решений этих трех задач и задачи, которая получается поворотом
задачи 3) на угол равный тг/2, что соответствует замене к на к + 1, то
для получения искомых величин исходной задачи нам остается взять
среднее арифметическое соответствующих величин решений, входящих
в эту суперпозицию. Таким образом искомое контактное давление q(ijj)
будет вычисляться по следующей формуле:
3.3. Контактные задачи для кольцевого сектора, кольца 133
или, с учетом симметрии в задаче 3):
кк\ 1 *i/ ч *2/ \ / *з/ \ *3/ \\ ^^
4 2
C.113)
Q [<Р
Соответствующие интегральные характеристики контактных напря-
напряжений под штампом выражаются следующим образом:
Р* = I [р* + р* cos тгк + 2Р3* cos ттк/2}, M*h = X- M3* sin ттк/2,
C.114)
где сила Р&, действующая на штамп с номером к-\- 1, связана с вели-
величиной Р^ соотношением Р^ = 1/2Е^Р^Р, а момент М^ от напряжений
связан с величиной М? формулой М& = 1/2М?Е5к2$. Величины q*l((p)
найдем из решения соответствующих задач.
Найдем решение задачи 3). Граничные условия соответствующей
краевой задачи для уравнений Ламе имеют вид
G^=0, ur = 0 (|V>|=27), тГ(р = 0 (г = Д2), C.115)
ur = 6cos(\i/;\ -7), (г = Д2, 7 - ^ < \Ф\ < 7 + ^)»
TrLp = 0, г^г = 0 (г = R\) (скользящая заделка),
иг = 0, г^ = 0 (г = R\) (жесткая заделка),
где ф = (р + 7, 7Vc? = rr-0, cr^ — компоненты тензора напряжений, г^г,
Up = иф — перемещения.
Решение уравнений Ламе представляем в виде рядов
оо оо
иг = J2 wk cos акф, Up = J2vk sin акф, ак = <к<у~l (k + 1 /2).
Тогда, после удовлетворения граничным условиям C.115), искомые
контактные напряжения под штампами выражаются следующим об-
образом:
q(i/>) = аг(к2ф) = JTQk cosfc ф, \ф\ < 1?,
/с=0
где Qk — решение тройного ряда-уравнения:
сю
^ЯкК{ак)оо*акф = !{ф) G-^<^<7 + ^), C.116)
к=0
сю
J2 Qk cos акф = 0 (O<'0<7-^'7 + ^<V;< 27),
134 Гл. 3. Плоские контактные задачи для четырехугольников
Здесь Е — модуль Юнга, К {а) для случая скользящей заделки на
нижней грани приведено в C.74) (п. 3.3.1), а для случая ее жесткого
защемления имеет вид
К (а) = 1/2 A + v) (а2 - \)~1 [(у - 3) (н2а Bа - 1 + у) -
- к~2а Bа + 1 - у) - к2а2 A + у)) - к~2(а2(\ + уJ + 8A - у)) -
- 2A - У2)(а2 - 1)}/[(х2а + х~2а)(у - 3)A + у) - к2а2(\ + уJ -
- к~2(а2(\ + уJ + 8A - у)) + 2(а2 - 1)A + иJ].
Решение ряда-уравнения C.116) будем разыскивать методом сведе-
сведения его к бесконечной системе линейных алгебраических уравнений
с сингулярной матрицей, изложенным в § 1.2. Система в этом случае
имеет вид
сю сю
^ > / 11 12 \ j\ ^ Л / 21 i^ 22 \ л 2 /о 1 1 г7\
п=\ п=\
ij _ 7m + 5п + (-l)jEn - 7m) exp (-25п$)
™т.п. . _о о s , . ', . s а ', ГТ Г7Т ~Г
тг = 7m cos fl - sin fl exp (-
m A+7 +
Здесь ? = 2, г5п и г7т — соответственно нули и полюсы функции if (а),
лежащие в правой полуплоскости. Функция q*3((p) находится из фор-
формулы
rC— 1
Для решения бесконечной системы применим метод, изложенный
в п. 1.2.3. Исходя из того, что при ср, близком к $, ряды выраже-
выражения C.118) должны содержать особенности вида (# — (р)~1/2, можно
показать, что при больших п
= O(g(n)), g(n)=B^~[,)!!. C.119)
3.3. Контактные задачи для кольцевого сектора, кольца 135
Положим поэтому для всех п, больших некоторого числа N,
хп = XNg(n), yn = yNg(n). В этом случае система примет вид
(ш= 1,...,ЛГ):
N— 1 оо оо
TV—1 oo oo
n=l n=7V n=7V
Для удобства численной реализации аппроксимируем функцию
К(г^) функцией A.13) и используем в качестве 5п и 7т нули и полюсы
функции L(u), хотя метод позволяет использовать непосредственно
нули и полюсы функции К (и). Для ускорения сходимости рядов си-
системы C.120) представим коэффициенты a^n для п > N в виде
aJL^n'+^iC + bJL. ^ = ![^^- C.121)
Тогда систему C.120) можно записать следующим образом:
N N
Е (^ncmn - УпС^п) = dim, E (^ncmn - ync^n) = d2m, C.122)
n=l n=l
umn amn \IL ^ iV /'
Коэффициенты, входящие в правую часть формулы C.121) имеют
вид (? = 2)
7))-', C.123)
exp(-2C7m7)).
(-l)j2SneX.p(-2Sn'&)
(l)expB$7mG^)) 2^nexpB(?n^(l(l)expB^7m^))
1 B^) (^ ^)( ()^B*?))
7mGm - <5n) + (~1L^« + 7m) exp (-2g
<5n(<5n ~7m)
136
Гл. 3. Плоские контактные задачи для четырехугольников
В соотношение C.118) для контактных напряжений входят мед-
медленно сходящиеся ряды. Совершив подстановку хп, уп для п > N
аналогичную той, которую мы произвели в бесконечной системе, и вы-
выделив ряды, суммирующиеся в явном виде, выпишем соотношение для
д*3((/?), где останутся только ряды, быстросходящиеся для значений ср,
близких к #:
*3(
x (xN
п=1
n=i
™'A-^^
'UN
Ждг
exp (-(УП(
1 + exp (-25ni?)
^)) ~ exp (SnC& - \<p\))
1 - exp (-26nfi)
C.124)
Проделав аналогичные операции по ускорению сходимости, полу-
получим соотношения для величин Р3*> Щ:
гз -
ЛГ-1
^ 4
f ^
cos4-
M3* =
N-\
-У
n=\
ь sin 2i? cth 5nti-2 cos 2tf] + улг - sin 2i?Ei
сю
п-(п-5)т
— exp (—5п$
i^lg(n). C.125)
Опуская выкладки, выпишем парный ряд-уравнение задачи 2):
), 0< |<р| < i?, ()
k=Q
3.3. Контактные задачи для кольцевого сектора, кольца 137
°° W 1
Бесконечная система линейных алгебраических уравнений будет
иметь вид оо
п=\
а соответствующая редуцированная система —
N
ЕТ r21 _ J1 ( _ 1 дт-Ч /О 1О?\
n=l
где коэффициенты с^п вычисляются по формуле C.122) с исполь-
использованием соотношений C.123). Величину q*2((f) можно получить из
соотношений C.124), где коэффициенты уп следует положить равными
нулю, а хп являются решением системы C.126).
Задача 1) была подробно рассмотрена в пп. 3.3.1, 3.3.2, поэтому
здесь мы приведем формулу для д*1 ((/?), выраженную через решения
редуцированных систем
N
У^ х^сшп = dP (j = 0,l; m=l,...,7V), C.127)
п=\
где cmn совпадает с с^п, если в формулах C.123) принять ? = 1.
Выражение для q*l((f) имеет вид
К@) ' К{\)
N-\
П=1
exP(-Sn(M+t?))-exp(-SnCt?-M))
A f
^
Выражение для Pj* можно получить, подставив в форму-
iy C.125) для Р3* вместо переменной х\ выражение (xln + Q*°n°x^)
п = 1,2, ...,ЛГ), где величину Q*0 следует вычислять по формуле
i - по Иг
138
Гл. 3. Плоские контактные задачи для четырехугольников
п=1
7Г
n=N
Величина n°, равная разности между пределом функции К (и) при и —>
—> О и значением if @), отлична от нуля в случае скользящей заделки
на нижней грани и равна нулю в случае ее жесткого защемления.
Теперь с помощью формул C.113), C.114) можно определить зна-
значение основных характеристик задачи.
В таблицах 3.10, 3.11 приводятся значения функции q*((p) и вели-
величин М*г, Р*г для каждого штампа исходной задачи. Вычисления про-
проводились для различных значений параметров h = R\ — R2, к = R2/R1
и ядер интегральных уравнений, соответствующих скользящей и жест-
жесткой заделкам по внутренней окружности кольца.
Таблица 3.10
№
1
2
3
4
1
2
3
4
1
2
3
4
д*(-0,95)
к= 1
4,586
0,172
0,099
0,090
к =
3,412
0,271
0,079
0,104
х= 1,
3,727
0,049
0,038
0,038
д*(-0,6)
g*@,0)
g*@,6)
6 ^ = 0,75 #2=1,33 h =
4,031
0,325
0,016
0,050
4,518
0,128
0,012
0,128
4,031
0,050
0,016
0,325
2,0 & = 0,5 R2 = 2,0 h=]
1,988
1,116
0,049
0,071
2,001
0,083
0,046
0,083
1,988
0,071
0,049
0,116
6 tf = 0,375 R2 = 2,67 h =
2,108
0,018
0,014
0,015
2,100
0,013
0,011
0,013
2,108
0,015
0,014
0,018
g*@,95)
0,5 7/1? =
4,586
-0,090
-0,099
-0,172
,0 7/1? =
3,412
0,104
0,079
0,271
: 1,0 7/1?
3,727
0,038
0,038
0,049
M*102
= 1,05
0,0
-5,61
0,0
5,61
1,75
0,0
-0,388
0,0
0,388
= 2,09
0,0
-0,245
0,0
0,245
p*
7,913
0,207
-0,010
0,107
4,376
0,208
0,104
0,208
4,773
0,040
0,035
0,040
Во всех случаях число уравнений редуцированных систем C.122),
C.126), C.127) было равно 15. Числовые результаты, приведенные
в таблицах 3.10, 3.11 соответственно при жестком защемлении и от-
отсутствии трения, получены для случая плоской деформации при
3.3. Контактные задачи для кольцевого сектора, кольца
139
Таблица 3.11
№
1
2
3
4
1
2
3
4
1
2
3
4
g*(-0,95)
q
>^= 1,6
4,155
-0,570
0,374
0,370
>. = 2,0
2,995
0,389
0,424
0,366
>c= 1,6
3,267
0,227
0,260
0,226
*(-0,6)
•& = 0,75
3,318
0,382
0,404
0,404
tf = 0,5
1,655
0,207
0,197
0,200
•& = 0,375
1,788
0,018
0,116
0,117
f @,0)
3,616
0,404
0,405
0,404
1,624
0,191
0,086
0,191
R2 =
1,728
0,110
0,109
0,110
q*@fi)
1,33 h =
3,318
0,404
0,404
0,382
2,0 h=\
1,655
0,200
0,197
0,207
-- 2,67 h =
1,788
0,117
0,116
0,118
g*@,95)
0,5 7/0 -
4,155
0,370
0,374
-0,570
,0 7/0 =
2,995
0,366
0,424
0,389
: 1,0 7/0
3,267
0,226
0,260
0,227
M*102
= 1,05
0,0
13,0
0,0
-13,0
1,75
0,0
-0,594
0,0
0,594
= 2,09
0,0
-0,030
0,0
0,030
p*
6,553
0,581
0,733
0,581
3,671
0,448
0,435
0,448
4,052
0,040
0,035
0,040
v = 0,3, т.е. в расчетах v заменялось на v\ = z//(l — v), E на E\ =
= E(\ — v2) и далее полагалось v = 0,3.
Результаты численных экспериментов показали, что жесткость си-
системы штампы-кольцо вообще говоря возрастает с уменьшением кри-
кривизны, но для некоторых параметров задачи может существовать ло-
локальный максимум этой зависимости. В табл. 3.10 зафиксирован также
случай, когда напряжения на краях всех ненагруженных штампов
отрицательны. Это связано с тем, что область контакта фиксирована,
в противном случае здесь наблюдался бы отрыв краев штампа от
упругого кольца.
В случае п штампов, если п кратно двум, придется рассматривать
сектор кольца максимум с п/2 штампами, что в силу свойств сим-
симметрии приведет нас к ряду-уравнению на п/2 + 1 участках. В случае
нечетного п придется рассматривать соответствующие ряды на п + 1
участках, а угловой размер сектора 27 будет равен 2тг.
3.3.4. Контактная задача для тонкого кольцевого слоя (цилин-
(цилиндрический подшипник скольжения). Рассматривается плоская кон-
контактная задача теории упругости о взаимодействии абсолютно жест-
жесткого цилиндра с внутренней поверхностью тонкого цилиндрического
слоя, внешняя поверхность которого закреплена (задача Q$) либо вза-
взаимодействует с гладкой жесткой обоймой (задача Qg)- Такие задачи
140
Гл. 3. Плоские контактные задачи для четырехугольников
достаточно хорошо моделируют работу цилиндрического подшипника
скольжения особенно при нагрузках, когда угловой размер поверхно-
поверхности контакта соизмерим с шириной подшипника, а модуль упругости
вкладыша значительно ниже модуля упругости других деталей под-
подшипника.
Для поставленных задач теории упругости построены асимптотиче-
асимптотически точные решения для случая относительно малых толщин упруго-
упругого цилиндрического слоя, произведен
расчет контактных напряжений, обла-
области контакта и перемещения шипа.
В отличие от ранее рассмотрен-
рассмотренных подобных задач (см., например,
[22, 280]), здесь обращено внимание
на построение простых асимптотиче-
асимптотически точных расчетных формул для от-
относительно тонкого цилиндрического
слоя.
В цилиндрической системе коорди-
координат (г, (р, z) рассмотрим цилиндриче-
цилиндрический слой R\ ^ r ^ R2, у которого
поверхность г = Щ неподвижна (за-
(задача Qs) либо взаимодействует без
трения с жесткой поверхностью (зада-
(задача Q$), а в поверхность г = R\ силой Р вдавливается штамп в форме
цилиндра радиуса Rq = R\ — А с точкой первоначального касания
(р = 0, г = R\ (рис. 3.9). Предполагается, что трение между штампом
и цилиндрическим слоем отсутствует, сила Р направлена вдоль луча
(р = 0, а величина А мала. В этом случае приходим к решению плоской
краевой задачи для уравнений Ламе (плоская деформация) со следую-
следующими граничными условиями:
C.128)
C.129)
C.130)
Рис. 3.9. К задачам
ur = 5cosLp — АA — cos(?>) (r = R\, \
аг = 0 (г = ДьИ>#), тг^=0
иг = и^ = 0 (г = Д2) (задача
иг = 0, тг^ = 0 (г = Д2) (задача Qg),
где 5 — смещение штампа, иг — перемещение в слое вдоль оси г,
о~г, тГ(р — компоненты тензора напряжений, \ср\ ^ # — область кон-
1 пр
такта.
Разыскивая решение уравнений Ламе в виде
иг = Yl akwk(r) cos k(p,
k=0
— Л akVk(r) cos k(p,
k=\
C.131)
где и^р — перемещение в упругом слое вдоль оси ip, и удовлетворяя гра-
граничными условиям C.128-3.130), найдем неизвестные функции Wk(r)
3.3. Контактные задачи для кольцевого сектора, кольца 141
и Vk(r), а для нахождения неизвестных коэффициентов а& получим
парный ряд-уравнение
сю
^2 акК(к) cos kip = f(ip) @ ^ ip ^ $),
к=0 сю (ЗЛ32)
^2 ак cos kip = 0 ($ < ip > и),
к=0
где G — модуль сдвига, v — коэффициент Пуассона,
'-A]-aofco, C.133)
2A
2A -« )A -
^0
2A -
Здесь для задачи Q$
Lx(u) = -A - 2z/)C -
+ 2A - z/)C - 4z/)^(
+ 8A -z/)(l -2j/)x-2A -2z/), C.134)
L2(^x) = C - \v\k2u + к~2и) + u2(x2 + к~2 - 2) +
+ 8(l-z/)(l-2z/)x-2 + 2,
а для задачи Qg
Li(ix) = [A - 2uJ - Au2(\ - v)\k2u + к~2и) +
+ u\k2 + x-2)C - \v) + 2A - 2z/J] - 2A - 2z/J, C.135)
L2(u) = -A - 2v)(k2u + к~2и) -2u{\- v)(k2u - к~2и) +
+ г^2[-2A - 2v) + C - 4z/)x~2 - я2} + 2A - 2z/).
Отметим, что для задачи Qs &o = 0, задачи Qg &o ^ 0, что делает
алгоритм получения решения задачи Qg несколько более сложным, чем
задачи Q8.
Контактные напряжения ar(R\,(p) = —q(<p) через неизвестные ко-
коэффициенты парного ряда C.132) выражаются соотношением
сю
H ak cos k(p.
к=0
142 Гл. 3. Плоские контактные задачи для четырехугольников
Для получения решения парного ряда (C.132) используем ме-
метод сведения его к бесконечной системе линейных алгебраических
уравнений (БСЛАУ) с сингулярной матрицей коэффициентов [19],
который в сочетании со специальным методом решения получаемой
БСЛАУ [305] позволяет исследовать задачи при любых значениях
их параметров. Вместе с тем метод позволяет получить достаточно
простое асимптотическое решение при относительно малых толщинах
кольцевого слоя.
Решение парного ряда. Представим неизвестную функцию q(tp)
в виде
Г Ы, C.136)
Y, C.137)
/с=0
где коэффициенты аг? подлежат определению из парного ряда A.5),
когда
f(cp) = cosiecp (ie = 0;l). C.138)
В соответствии с упомянутым выше методом парный ряд C.132),
C.138) может быть сведен к решению следующей БСЛАУ:
Y,<bmn = -d*K-l(ie) (m=l,2,...,oo), C.139)
где
, 6п), С
о/ г \ _ Irn ch 5п$ + 5п sh 5п$
Eп -7m)ch5n^
_ ехр (-7т(тг -
(Sn - 7m) sh7m^ ch 5n$
где i5n, i~fm — соответственно нули и полюсы функции К (и).
Функция qi?, даваемая формулой C.137), через решение БСЛАУ
C.139) будет выражаться следующим соотношением:
cosie<p у. is chSni
n=\
Отметим, что функция К {и) для обеих задач обладает следующими
свойствами:
lim К (и) = А = const, lim К (и) = 1. C.142)
3.3. Контактные задачи для кольцевого сектора, кольца 143
Это позволяет ее аппроксимировать на интервале @, оо) функцией
К* (и) =u~lthAu. C.143)
Предельные значения функций К (и) и К* (и) при больших и ма-
малых и совпадают, а максимальная относительная погрешность в наи-
наихудшем случае (малые к) не превышает 11 %. Числовые расчеты пока-
показывают, что с уменьшением относительной толщины слоя (х —> 1) наи-
наибольшая погрешность аппроксимации C.142) уменьшается и достига-
достигается при больших значениях аргумента и. Учитывая этот факт, можно
утверждать [88], что при использовании аппроксимации с уменьшени-
уменьшением относительной толщины слоя точность получаемого решения будет
увеличиваться.
В дальнейшем, когда речь будет идти о функции К (и), ее нулях
и полюсах, будем иметь в виду функцию К*(и), ее нули и полюсы, не
меняя обозначения. Используя аппроксимацию C.143), найдем
™ *(/2). C.144)
«п, 7го.
Отметим важный для дальнейшего факт, что при к —> 1 (R\ —>
—> R2) величина А —> 0. Поэтому рост абсолютных значений нулей
и полюсов с уменьшением относительной толщины упругого слоя поз-
позволяет асимптотически упростить систему C.140)—C.141) и другие
соотношения.
При малых значениях А система C.140)—C.141) асимптотически
будет эквивалентна системе
оо
Y.<{^-lm)-X = -^K-\ie) (m=l,2,...,oo), C.145)
C.146)
? -7m
Бесконечная система C.145)—C.146) имеет точное решение [88]
_ тг Bn-l)!! ^ f, ДгA/2-шА/тг)
Ay/A 2Bn-2)!!f +W"V^ ГA-шА/тг) '
где Г(ж) — гамма-функция.
Исследование контактных задач. Соотношение C.136) совместно
с C.141) и C.147) даст достаточно простую зависимость распреде-
распределения контактных напряжений в поставленных контактных задачах,
если будут известны постоянная а^ (для задачи Qg) и величина #,
характеризующая величину области контакта.
144 Гл. 3. Плоские контактные задачи для четырехугольников
Уравнение для отыскания величины а^ может быть получено из
условия
C.148)
7Г J ^' ' '
О
Получим
GQ
- (ЗЛ49)
о
С учетом соотношений C.147) можно показать, что ряды в C.139)
расходятся. Можно также показать, что
ql?{v) = О{{д - V)-) (<Р^#). C.150)
Предполагая, что контактные напряжения ограничены во всей об-
области контакта, приравняем нулю коэффициент при корневой особен-
особенности в формуле C.136). С учетом C.139), C.147) получим уравнение
F + A) Re (™%{-ff ) ~ -j= (A + k*0Q) = 0, C.151)
которое позволит найти величины # и 5, если к нему добавить условие
статики
Р = 2i?i [ <?((/?) cos ^ dip. C.152)
о
Последнее соотношение можно преобразовать к виду
E + Д)Л + (А + ^о*д)Ро = РA2~^, C.153)
^. C.154)
о
Таким образом мы имеем два уравнения C.151) и C.153) для
определения # и 5, при этом сила Р, действующая на штамп, предпо-
предполагается заданной.
С учетом соотношений C.148), C.151) формулы C.136) для расчета
контактных напряжений можно преобразовать к виду
- (Д + ЩО)%(ф)], C.155)
г> Ы<Р) = \> C.156)
п=\
C.157)
3.3. Контактные задачи для кольцевого сектора, кольца 145
Отметим, что ряд в C.156) при (р = $ сходится.
В расчетных формулах C.151), C.153), C.155) участвуют вели-
величины, вычисляемые по формулам C.149) и C.154). Теперь с уче-
учетом C.155)—C.157), их можно переписать в виде
D sin?? D 2tf
C.158)
В C.11) Fm(i?) (m = 1,2) содержит сходящиеся ряды, члены ко-
которых при больших номерах п ведут себя как О(п~5/2). После улуч-
улучшения их сходимости и с учетом того, что при сделанных предполо-
предположениях относительно геометрических параметров задач th.5nd = 1 +
+ О(ехр (—25п'д)) при 5п —> оо (п ^ 1), функции -Fm(#) запишем в виде
(ЗЛ59)
s_n R
C.160)
V^Bn— 1)!! пголплг
77 => ^ v^0'684016.
^ Bn)!!n2
n=l v y
В формулах C.159)-C.160) члены рядов при больших номерах
ведут себя как О(п~7/2) и для их вычисления с относительной погреш-
погрешностью не больше 0,1 % достаточно 10 членов. Одновременно отметим,
что члены, содержащие ряды в формулах C.159)—C.160) при малых А
эквивалентны О(А2) и поэтому в случаях, когда значения величины А
достаточны малы, такими членами можно пренебречь.
Числовые расчеты. Проведены числовые расчеты области кон-
контакта (величина #), перемещения штампа 5 и контактных напряже-
напряжений в зависимости от величины Р* = P/G при различных значения
параметров R\, h = R^ — R\, А и v. Величины # и 5 находились
с использованием формул C.151), C.153), C.157)—C.160). В рядах
формул C.159), C.160) удерживалось 10 членов, что позволяло их
считать с относительной погрешностью не больше 0,1%. Контактные
напряжения вычислялись по формулам C.8)—C.10) в точках ср = щ =
= Ы/5 (к = 0, 1,2,3,4,5). Члены рядов C.156) затухают экспоненци-
экспоненциально при ср < $, при ср = $ напряжения должны обращаться в ноль.
Далее размерные величины указаны в системе СИ.
146 Гл. 3. Плоские контактные задачи для четырехугольников
Таблица 3.12. Задача Q$
р*
1
5
10
20
1
5
10
20
1
5
10
20
•д
40,2
61,5
70,4
77,7
61,5
79,6
83,9
86,5
69,9
83,4
86,0
87,4
S
Ч\
I/ = 0,3 А = 0,05 ft = 0,5 .
0,0159
0,0565
0,103
0,194
0,112
0,397
0,725
1,37
0,107
0,380
0,692
1,30
0,0939
0,329
0,597
1,12
i/ = 0,3 А = 0,01 ft = 0,5 .
0,0113
0,0480
0,0933
0,184
0,0795
0,337
0,656
1,29
0,0760
0,321
0,625
1,23
0,0659
0,276
0,535
1,05
i/ = 0,3 А = 0,01 ft =1,0 .
0,0205
0,0928
0,183
0,363
0,0725
0,328
0,646
1,28
0,0693
0,313
0,616
1,22
0,0599
0,268
0,527
1,04
<7з
А = 0,0203
0,0716
0,247
0,445
0,829
0,0410
0,138
0,245
0,451
А = 0,0203
0,0495
0,204
0,393
0,770
0,0276
0,111
0,212
0,413
А = 0,0404
0,0449
0,198
0,388
0,768
0,0251
0,108
0,211
0,417
<&
0,00115
0,00098
0,000 894
0,000 827
0,000980
0,000 203
0,000 772
0,000 750
0,00160
0,00149
0,00146
0,00145
В табл. 3.12 приведены результаты расчетов величин # (в граду-
градуl
для задачи
сах), 5, qk = G-lq(ipk) (k = 0, 1,2,3,4), q* =
а в табл. 3.13 — для задачи Qg для некоторых значений параметров Р*,
ft, A, v и A (R\ = 10,0). Относительная величина q^, как видно из
таблиц, достаточна мала, но не обращается в нуль и ее значения могут
служить показателем относительной погрешности используемых рас-
расчетных формул. Видим, что погрешность уменьшается с увеличением
параметра к и является приемлемой при к > 0,5. Величина А, приве-
приведенная в таблицах, значительно меньше единицы, что в соответствии
с C.144) дает дополнительное подтверждение правомерности исполь-
используемых выше предельных переходов при получении асимптотического
решения БСЛАУ при используемых в расчетах значениях параметров
задач.
Из таблиц также видно, что при одних и тех же значениях пара-
параметров в задаче Qg значение перемещения штампа 5 и угол контакта $
больше, чем в задаче Qs- При расчетах также наблюдается увеличе-
увеличение 5 при уменьшении коэффициента Пуассона v в обеих задачах, но #
в задаче Q$ также уменьшается, а в задаче Qg увеличивается. В табли-
таблицах 3.14 и 3.15 приведены соответственно для задач Qs и Qg некоторые
результаты числовых расчетов величины #, 5 и А в зависимости от v
при ft = 0,5 и ft = 1,0, Д = 0,005, Rx = 10,0, Р* = 5,0.
3.3. Контактные задачи для кольцевого сектора, кольца
147
р*
•д
5
Ч\
Таблица 3.13
<7з
Задача Qg
<&
I/ = 0,3 А = 0,05 h = 0,5 А = 0,0244
1
5
10
20
42,4
64,55
73,7
81,0
0,0177
0,0629
0,115
0,217
0,107
0,384
0,703
1,33
0,102
0,367
0,672
1,27
0,0894
0,318
0,579
1,09
0,0682
0,238
0,431
0,805
0,0391
0,133
0,237
0,437
0,00165
0,00122
0,00107
0,000974
I/ = 0,3 А = 0,01 h = 0,5 А = 0,0244
1
5
10
20
64,6
82,9
87,2
89,8
0,0126
0,0535
0,104
0,205
0,0767
0,330
0,643
1,27
0,0734
0,314
0,612
1,21
0,0635
0,269
0,523
1,03
0,0476
0,198
0,383
0,753
0,0265
0,107
0,206
0,402
0,00122
0,000951
0,000897
0,000867
I/ = 0,3 А = 0,01 /г =1,0 А = 0,0476
1
5
10
20
72,7
86,3
88,9
90,3
0,0226
0,102
0,202
0,401
0,0706
0,322
0,636
1,26
0,0675
0,307
0,606
1,20
0,0583
0,263
0,518
1,03
0,0437
0,194
0,380
0,754
0,0245
0,106
0,207
0,408
0,00194
0,00173
0,00169
0,00167
Таблица 3.14. Задача Q$
V
h
&
5
А
0,1
0,5
85,6
0,0707
0,0242
0,2
0,5
85,0
0,0602
0,0231
0,3
0,5
83,9
0,0466
0,0203
0,4
0,5
81,0
0,0281
0,0140
0,1
1,0
86,8
0,137
0,0474
0,2
1,0
86,5
0,118
0,0456
0,3
1,0
86,0
0,0914
0,0404
0,4
1,0
84,5
0,0555
0,0281
Таблица 3.15. Задача
V
h
•&
5
А
0,1
0,5
85,7
0,0710
0,0244
0,2
0,5
86,0
0,0622
0,0244
0,3
0,5
87,2
0,0,521
0,0244
0,4
0,5
91,1
0,0398
0,244
0,1
1,0
86,9
0,138
0,0476
0,2
1,0
87,2
0,121
0,0476
0,3
1,0
88,9
0,101
0,0476
0,4
1,0
93,8
0,0769
0,0476
Отдельно было проведено численное исследование величины обла-
области контакта # в зависимости от толщины слоя h при фиксированных
значениях других параметров.
148
Гл. 3. Плоские контактные задачи для четырехугольников
Здесь при некоторых значениях параметров была обнаружена немо-
немонотонная зависимость величины # от h. А именно, при увеличении h от
значения, близкого к нулю, вначале область контакта растет, а начиная
с некоторого значения h = h* область контакта начинает уменьшаться.
Большее уменьшение области контакта при h > h* наблюдается при
больших значениях коэффициента Пуассона, а также в задаче Qg по
сравнению с задачей Qs- Разумеется, значение величины h* зависит
также и от других параметров задач. При малых значениях величи-
величины А и некоторых значениях других параметров расчеты показывают,
что возможны ситуации, когда область контакта (величина 2$) больше
180°. В таблицах 3.16 и 3.17 приведены соответственно для задач Qs
и Qg некоторые результаты числовых расчетов величины #, 5 и А
в зависимости от h при v = 0,1 и v = 0,4, А = 0,005, R\ = 10,0,
Р* = 5,0.
Таблица 3.16. Задача Qs
h
v
•д
5
А
0,1
0,1
75,7
0,0154
0,00492
0,5
0,1
85,6
0,0707
0,0242
1,5
0,1
86,9
0,201
0,0696
4,0
0,1
85,2
0,480
0,166
0,1
0,4
64,1
0,00647
0,00278
0,5
0,4
81,0
0,0281
0,0140
2,5
0,4
86,2
0,140
0,0714
5,0
0,4
85,4
0,284
0,143
Таблица 3.17. Задача
h
V
$
5
А
0,1
0,1
75,9
0,0155
0,00498
0,5
од
85,7
0,0710
0,0244
1,5
од
86,9
0,201
0,0698
4,0
0,1
85,3
0,480
0,167
0,1
0,4
74,6
0,00924
0,00498
0,5
0,4
91,1
0,0398
0,0244
1,5
0,4
94,1
0,113
0,0699
4,0
0,4
91,4
0,280
0,167
3.4. Контактная задача для усеченного клина
В этом параграфе рассмотрим контактную задачу Qio о чистом
сдвиге полосовым штампом вдоль образующей цилиндрического упру-
упругого тела, поперечное сечение которого занимает область, ограничен-
ограниченную сторонами клина и двумя концентрическими окружностями с цен-
центром в вершине клина. Штамп закреплен на плоской грани тела, при
этом другая плоская грань закреплена, а цилиндрические поверхности
либо закреплены, либо свободны от напряжений [42] (рис. 3.10).
Поставленная задача имеет самостоятельный практический и тео-
теоретический интерес и в тоже время ее можно рассматривать как мо-
модельную для более сложных контактных задач для усеченного клина.
3.4. Контактная задача для усеченного клина
149
Для решения задачи используется метод однородных решений, который
позволяет свести рассматриваемые задачи к исследованию бесконечных
систем линейных алгебраических
уравнений второго рода высокого
качества типа Пуанкаре-Коха с экс-
экспоненциально убывающими элемен-
элементами матриц и правых частей. Их
решение может быть получено мето-
методом редукции при любых значениях
параметров задач.
Рассмотрим упругое тело, зани-
занимающее область R\ ^ r ^ R2, 0 ^
< (р < 7' —°° < z < оо (г, ср, z — ци-
цилиндрические координаты). Такую
область здесь будем называть усе-
усеченным клином, так как исследование рассматриваемой задачи будет
опираться на решение некоторых задач для бесконечного клина.
Задача о сдвиге штампом усеченного клина будет эквивалентна
следующей краевой задаче относительно функции перемещения w(r, z)
вдоль оси z\
*1 |- + ^, C-161)
дг 2 д2
Рис. 3.10. К задаче
w = 5 ((p = 7, a\
G
дг2 г дг г2 дер2
CL2), w = О (ср = О, R\ < г < R2),
pz = — -^ = 0 (<р = 7,
w = 0 (r = Дь г = Д2, 0 < ср
C.162)
где 5 — перемещение штампа, G — модуль сдвига, t^z — касательные
напряжения. Последнее условие означает закрепление цилиндрических
поверхностей, аналогично может быть рассмотрена задача, когда ци-
цилиндрические поверхности свободны от напряжений.
В соответствии со схемой метода однородных решений [15] найдем
на первом этапе решение уравнения C.161) для бесконечного клина,
когда
| т(г) (а\ ^ г ^ с&2, (р = 7)'
^ | 0 @ < г < а\, а,2 < г < оо, (р = j),
В этом случае
w =
а2
1
2Gtti
r(p)dp
sin scp ( p
C.163)
150 Гл. 3. Плоские контактные задачи для четырехугольников
где контур интегрирования L в плоскости комплексного переменного
s = г + г5 — прямая, параллельная мнимой оси при условии —тг/27 <
< г < тг/27-
Далее построим систему однородных решений уравнения C.161)
для бесконечного клина, когда
и введем в рассмотрение их линейную комбинацию
w^\r,v) = E sm<xMCkr-ak+Dkra*], ak = 7rBk~l\ C.164)
k=\ 7
Тогда решение исходной задачи C.161), C.162) представим в виде
w(r, ф) = ww(r, у) - гуB)(г, у). C.165)
В этом случае граничные условия C.162), кроме первого и по-
последнего будут удовлетворены. Последнее условие C.162) представим
в виде
Е f) (j = 1,2),
k=\
откуда, используя ортогональность sina^ на [0,7], найдем
[CkRj"* + DkRf] I = Sj^RJ{-iyak Jr(p)p(-1)iafc dp (j = 1,2).
C.166)
Первое граничное условие C.162) с учетом C.163)—C.165) поз-
позволяет получить интегральное уравнение относительно неизвестной
функции распределения контактных напряжений
сю
Yl sinак-у(Скг-ак + Dkrak)] (ai < г < a2), C.167)
к=\
где оператор Кг имеет вид
Кгт(р) = ^r(p)k(p/r)dp, k(y) = ^L j *I?Vds. C.168)
(L)
Представим r(r) в виде
/
т(т) = G(Sro(r)
\ к=\
= Ck sin ak<y, x2kR~ak = Dk sin ak<y, C.169)
3.4. Контактная задача для усеченного клина
151
где го (г), rJk(r) — соответственно решения интегральных уравнений
Кгт0(р) = 1, Kr<rl(p)=r(-Vdak, (ai<r<a2, j=l,2). C.170)
Подставляя C.169) в C.166), получим бесконечную систему линей-
линейных алгебраических уравнений для определения неизвестных коэффи-
коэффициентов х\, и х\\
0-2
п=\
dp,
= 1,2,...), C.171)
-(-i)^.Tp^ (ЗЛ72)
l)Pakdp. C.173)
Исследуем бесконечную систему C.171), для этого оценим ее ко-
коэффициенты. Так как
а2
\Ч\ < а{Р~])РакП, То = j то(р) dp < оо,
Т°
(зл74)
Для оценки коэффициентов Т^ второе интегральное уравне-
уравнение C.161) умножим на то (г) и проинтегрируем в пределах от а\
до а,2. Учитывая, что для ядра C.168) этого уравнения справедливо
соотношение к (у) = к(\/у), изменив порядок интегрирования, получим
Тогда
и, следовательно
и, 2
rJk(p)dp= f T0(r)r(-
a>2
VPak\ I rj(n)r1n < а
\jTn\P)aP ^ a
f
<3175)
Учитывая, что R\ < a\ < a^ < Щ, otn ~ n (n —> оо), из оценок C.174),
C.175) заключаем, что коэффициенты бесконечной системы C.171)
и ^к экспоненциально убывают с ростом номеров к, п. Следо-
а
152
Гл. 3. Плоские контактные задачи для четырехугольников
вательно, система C.171) принадлежит к типу нормальных систем
Пуанкаре-Коха и ее решение может быть получено методом редукции
для любых значений параметров задачи.
Таким образом, контактные напряжения под штампом определя-
определяются формулой C.169), в которой xJk — решение бесконечной си-
системы C.171), а функции тк(г) — решения интегральных уравне-
уравнений C.170). При этом следует особо отметить, что для интегральных
уравнений C.170) может быть получено точное решение [16], не со-
содержащее квадратур.
Опуская выкладки, выпишем решение уравнений C.170):
rrJk(r) =
Т(х) =
к
ж = А1п—-1,
CL\
тгBк- IJ
=
Vchb-chbx
_/ ч 2k- 1 d / ч
(pk{x) = — —r]q{x)
2V2 dx I4K J
2V2 dx
= t— , A = 2 In -
Л7 \ a\
(x) =b\ch-
I)
К [J1 - th2 u- д/2(сЬЬ-сЬЬж)
~l
-1
— ch bx x
[fe-I/2] fc-2™-
2 № 2
m=0 p=0
7rch(b/2)Pfc-i(chb)
2(fc-2m-l-p)
- P_1/2(chb)P/_,(chb)]
P-i/2(ch&)
Здесь К (к) — полный эллиптический интеграл, Р?(х) — присоединен-
присоединенные функции Лежандра.
Используя C.176), найдем выражения для коэффициентов C.172),
C.173) бесконечной системы C.171)
], Т{ =
3.5. Точное решение некоторых антиплоских контактных задач 153
^_ _ тгBп- l)Bfc- 1) р ^ _ 7rAch(fr/2)Pfc_i(chfr)
1kn~ Б ^fc.n, ifcO-
_ shb[Pn_i(chb)Pfc-i(chb) - Pfc-i
x Bk- I)
Выражения для контактных напряжений и коэффициентов бесконеч-
бесконечной системы не содержат квадратур и могут быть легко подсчитаны.
Отметим также, что для получения практически приемлемого решения
задачи для широкого диапазона изменения параметров бесконечную
систему достаточно урезать до двух-четырех уравнений.
3.5. Точное решение некоторых антиплоских
контактных задач для конечных канонических
областей
На основе точных решений интегральных уравнений первого рода,
содержащих в качестве ядер эллиптические функции Якоби (см. § 1.4),
получено точное решение контактных задач теории упругости о чистом
сдвиге штампом (в общем случае деформируемым) цилиндрическо-
цилиндрического тела, представляющего собой в сечении область, ограниченную
координатными линиями ортогональной линейной системы координат
на плоскости, коэффициенты Ламе которой удовлетворяют некоторым
условиям [168]. Сюда относятся декартовы, полярные, биполярные,
параболические, гиперболические и другие координаты. Аналогичные
задачи в случае полосы изучались в работе [44], здесь же предложена
схема построения точного решения рассматриваемых задач путем кон-
конформного отображения полосы на конечную область.
Рассмотрим цилиндрическое тело, описываемое в координатах а,
C, z (а и C — криволинейные ортогональные координаты на плос-
плоскости) соотношениями \а\ ^ R, В\ ^ /3 ^ В^, —оо < z < oo. Пусть
штамп жестко закреплен на поверхности /3 = В% в области \а\ ^ А <
< R и сдвигается вдоль положительного направления оси z усилием Т,
приложенным к каждой единице его длины; грань /3 = В\ защемле-
защемлена, а поверхности \а\ = R защемлены (задача Q\\) или свободны от
напряжений (задача Qn)- На рис. 3.11, а, б изображены схемы соответ-
соответственно задач Q\\ и Qi2 в случае биполярных координат для усеченной
луночки.
Математически поставленная задача сводится к интегрированию
уравнения Ламе в координатах а, C для перемещения w вдоль оси z:
154
Гл. 3. Плоские контактные задачи для четырехугольников
= 0,
Рис. 3.11. К задачам Qn,
1 Г д ( д \ д ( д
*>Р = и и I — I "Вое— ) Н ' h-a
C.177)
где На = На(а,/3), Нр = Нр(а,/3), — коэффициенты Ламе криволи-
криволинейных координат (а,C), с краевыми условиями
= 0
= Д) (задача <2п),
|а
= R) (задача Qi2), C.178)
Taz = H~ldw/da = <
w = D(a) (/3 = B2, \a
(P = B2, A < \a\ < Д).
Здесь D(a) — заданное перемещение штампа как функция от а.
Следуя методу разделения переменных и полагая w(a, C) =
= X(a)Y(C), получим
X
X да
KPY" Y'
Y Y
Отсюда вытекает, что переменные в C.177) разделяются, если вы-
выполняется одно из условий
да
^=0.
C.179)
C.180)
Тогда целесообразно сделать замену (а, C, z) на (?, rj, z), следующую
при условии C.179) из выполнения соотношения
д
C.181)
3.5. Точное решение некоторых антиплоских контактных задач 155
а при условии C.180) — из равенства
д _ aha/зд
д^ да
При учете соотношений C.179), C.181) найдем
C.182)
BlB C.183)
DO
D 1 p
а = Д &=—, 7=- hpa(a,f3)df3,
CL CL J
Si
и принимая во внимание соотношение C.180), C.182), запишем
а.
hap(a,[3)da, r?(/3) = - (C - В,), C.184)
a
0
а= \hai3(a,C)da, $=- \ hap{a, C) da, 7=1(/3-Б1).
J Оь J ft
О О
В результате этих замен краевая задача C.177), C.178) сводится
к граничной задаче в координатах ?, rj, z относительно новой функции
u(?,ri)=0 G7 = 0),
u(^r])=0 (|^|=i?) (задача Qn), C.185)
du(?,ri)/dZ = O (|^|=i?) (задача Q12),
= O (г] = 7, 1<|^|<1?).
Используя представления решений в виде рядов Фурье, сведем
поставленные задачи Q\\ и Qi2 к нахождению из интегрального урав-
уравнения A.57) (соответственно случаи А и Б) функции </?(?), которая
в случае C.179), C.181) связана с контактными напряжениями под
штампом соотношением
TPz(a,B2) = G(aHa)-[v@, C.186)
а в случае C.180), C.182) выражением
трх(а,В2) = G{aHp)-xV(i). C.187)
156 Гл. 3. Плоские контактные задачи для четырехугольников
Контактные напряжения под штампом rpz определяются по фор-
формулам C.186) или C.187) при учете замен переменных C.183) или
C.184) соответственно. При этом связь между сдвигающей силой Т,
действующей на штамп, и его смещением 5(?) дается выражением
Т= J rf3z(a,B2)da = G J <р(?)Н-1(а(?),В2)<%, C.188)
-А -1
где а(?) = at; в соответствии с C.183), а в случае C.184) функция
а(?) находится как решение дифференциального уравнения da/dt; =
= ahpa(a,C).
В случаях прямоугольных, а также биполярных, эллиптических,
параболических и гиперболических координат коэффициенты Ламе
совпадают между собой и, следовательно, замены переменных C.183),
C.184) линейны.
В частности, для прямоугольных координат (а = х, C = у)
, В2) = Gp Q , Т = GNOS-^ K'(cnя),
где величина к определена на стр. 44.
Для биполярных координат (q — половина расстояния между по-
полюсами)
а величина Т определяется по формуле C.188).
Для полярных координат (а = (р, C = г) запишем
= ? In-? а = А,
Усилие Т имеет вид C.188).
Найдем связь между постоянной 7V0, входящей в соотношение
A.65), и
Р= [ (p(x)dx. C.189)
-1
Подставляя вторую формулу A.65) в C.189), получим
C.190)
В случае, когда правая часть исходного интегрального уравне-
уравнения A.57) отлична от постоянной, для определения постоянной Nq,
3.5. Точное решение некоторых антиплоских контактных задач 157
входящей в решение A.64), целесообразно пользоваться теоремой 3.7
[27]. При учете соотношений A.65), C.188), C.190) будем иметь
^T. C.19D
J v(t)
-1
Используя метод, приведенный выше, можно исследовать нечетный
вариант интегрального уравнения A.57) (при замене Z(#±?) на 1{х =f
Т?))- Не останавливаясь на подробностях, запишем
^@ J sn^r-sn^
-l
Последний результат не имеет физического смысла, но в совокуп-
совокупности с формулами A.64), A.65), C.188)—C.191) часто оказывается
полезным для регуляризации интегральных уравнений первого рода
двумерных контактных задач для областей, ограниченных координат-
координатными линиями некоторых систем криволинейных координат на плоско-
плоскости [276].
Глава 4
КОНТАКТНЫЕ ЗАДАЧИ ДЛЯ СЕКТОРА
СФЕРИЧЕСКОГО СЛОЯ, СФЕРИЧЕСКОГО СЛОЯ,
УСЕЧЕННЫХ ШАРА И КОНУСА
В этой главе рассмотрены некоторые контактные задачи для тел,
границы которых могут быть описаны координатными поверхностями
сферической или бисферической систем координат. Для решения задач
используется метод однородных решений, метод сведения парных рядов
к бесконечным системам линейных алгебраических уравнений первого
рода с сингулярной матрицей и метод больших Л.
4.1. Контактные задачи для сектора
сферического слоя
Рассматриваются две контактные задачи для сектора сферического
слоя: задача S\ о кручении сферического слоя штампом, симметрично
расположенным на сферической поверхности и задача ^ о симметрич-
симметричном вдавливании штампа в сферическую поверхность. Для решения
задач используется метод однородных решений, который здесь также
позволил свести задачи к бесконечным системам типа Пуанкаре-Ко-
Пуанкаре-Коха и соответствующим интегральным уравнениям для сферического
слоя [158, 159, 327].
4.1.1. Кручение штампом сектора сферического слоя. Рассмот-
Рассмотрим осесимметричную задачу S\ о кручении круговым штампом упру-
упругого тела с упругими постоянными и, G, ограниченного сферическими
поверхностями г = R\, г = Щ и конической поверхностью (р = (р2-
Пусть штамп соединен с упругим телом по сферической поверхности
г = R2, ip ^ ip\. Считаем, что сферическая поверхность г = R^ вне
штампа (ср\ < (р < Lp2) свободна от напряжений, а остальная часть
границы упругого тела жестко закреплена. Нагружение производится
поворотом штампа относительно оси симметрии ср = 0 на некоторый
угол г (рис. 4.1).
4.1. Контактные задачи для сектора сферического слоя
159
В сферических координатах г, (р, $
граничные условия имеют вид
u#(Ri,ip)=0 ((К (^(^2), D.1)
щ(В,2,(р) =
щ(Я,<р2)=0
В специальных координатах t, х,
[46], связанных со сферическими г, у?,
соотношениями
V
t = In —-, ж =
(О < ср < ср\),
D.2) R2
v<?2), D.3)
D.4)
задача сводится к решению дифференци-
дифференциального уравнения [46]
Рис. 4.1. К задаче S\
-д- - 4ж^- = О
с граничными условиями
Ф(а,ж) =0
ot t=o
Ф(*,Ь) =0
Здесь введены обозначения
<ж< 1),
= 0 (Ь < х < с),
D.5)
D.6)
D.7)
D.8)
D.9)
1 -^1 7
a = ln—-, о = cos (f2, c =
R2
4f(t,x) =
D.10)
Для решения поставленной задачи используется метод однородных
решений.
Приведем решение задачи о кручении сферического слоя, одна из
поверхностей которого (г = R\) жестко закреплена, заданной поверх-
поверхностной нагрузкой Tf&@,x) = т(х), приложенной к другой поверхности
Задача сводится [26] к решению дифференциального уравнения
D.5) с граничными условиями
Ф(а,ж)=0 — 1 < ж < 1,
т(х), c^
0, -1
_
t=0~
D.11)
D.12)
160 Гл. 4. Контактные задачи для сектора сферического слоя, и пр.
Решение уравнения D.5) запишем в виде ряда (п — натуральное
число):
Ф*(*, х) = е-3*/2 f] [Ап sh (unt) + Вп ch (unt)] ^^, D.13)
n=\
где An, Bn — произвольные постоянные, Рп(х) — полиномы Лежандра,
un = n + 1/2.
Граничное условие D.11) будет удовлетворено, если
Вп = -Anih(una). D.14)
Граничное условие D.12), с учетом D.14), примет вид
7 ::";' D.is>
_ 0 — 1 < x < с,
где Рп(х) — присоединенные функции Лежандра первого порядка.
Разложим заданную поверхностную нагрузку в ряд
оо
п=\
1
D.16)
Приравнивая коэффициент при Рп(х) в левой и правой части ра-
равенства D.15), получаем
1
Ап = ап \r(^)Pnd^ D.17)
с
где _1
ап — ип < I ип — I ип -\- — tn \VjnQj) (_т >
Функция перемещения Ф*(?, х) D.13), удовлетворяющая граничным
условиям D.11) и D.12), принимает вид
-U/2
\§j*U х\ — е х
п=1
4.1. Контактные задачи для сектора сферического слоя 161
Построим однородные решения осесимметричной задачи о кручении
сферического слоя, т.е. найдем функцию Ф°(?,#), удовлетворяющую
дифференциальному уравнению D.5) и граничным условиям
Ф°(а,ж)=0 (-1 < х < 1), D.19)
d4f°(tjж) (-1 < х < 1). D.20)
dt t=o K J v ;
Решением дифференциального уравнения D.5) являются [46] функ-
функции
;), D.21)
где С&, Dk — произвольные постоянные, /i& — действительные числа.
Граничные условия D.19) и D.20) будут удовлетворены, если реше-
решение дифференциального уравнения D.5) записать в виде ряда
sin (№^ + cos Ш)} ? х/2+щъ
k J ах
D.22)
где /ifc — корни трансцендентного уравнения
3
-— sin (/Xfca) + cos (/Zfca) = 0. D.23)
Составим конструкцию из функций Ф*(?,ж) D.18), Ф°(^, ж) D.22):
Ф(*, х) = Ф*(?, ж) - Ф°(*, ж). D.24)
Функция Ф(^, ж) D.24) удовлетворяет дифференциальному уравне-
уравнению D.5) и (при заданной нагрузке т^@,х)) граничным услови-
условиям D.6), D.8). Потребуем, чтобы Ф(?, ж) D.24) удовлетворяла и гра-
граничному условию D.3), т.е.
Ф°(*,Ь) = Ф*(*,Ь) (O^t^a). D.25)
Из соотношения D.25) определим постоянные Dk, используя свой-
свойство ортогональности на отрезке [0, а] функций
Легко получить, выполнив элементарные выкладки [129], следую-
следующий результат
\ а , 3B
k ^ - + -
о К
б В.М. Александров, М.И. Чебаков
162 Гл. 4. Контактные задачи для сектора сферического слоя, и пр.
Умножая левую и правую часть равенства D.25) на функцию
e3t/2T/c(t) (fc = 1,2,...) и интегрируя полученные равенства в пределах
от 0 до а, получим
а 1
\Tk{t)dt [
1 J J
VI -b2
о с
оо
х ^2 ^n[sh (unt) — th (una) ch (un?)] Р^(Ь)Р^(^)б?^. D.26)
Учитывая, что [67, 129]
3
ar. un +-th (una)
Tk(t)[sh (unt) - th (una) ch (unt)] dt = f -2 ,
EUnPn(b)P
hi - 1/4)(m!
n=1 hi
получаем
D-27)
Удовлетворив с помощью функции Ф(?,ж) D.24) граничному усло-
условию D.7), получим интегральное уравнение для определения контакт-
контактных напряжений на поверхности г = R^ сектора сферического слоя
J n=i k=\ D.28)
(с<х< 1).
Интегральное уравнение D.28) отличается от интегрального урав-
уравнения задачи о кручении шарового слоя круговым штампом [26] лишь
видом правой части.
Решение уравнения D.28) будем искать в виде ряда
J2. D.29)
к=\
Здесь го(х) определяется решением задачи [26] о кручении шарового
слоя круговым штампом. Функции тк(х) определяются решением еле-
4.1. Контактные задачи для сектора сферического слоя 163
дующих интегральных уравнений (к = 1,2,...):
1
г °° 1
^Щ (с < ж < 1).
n=\
D.30)
Решения интегральных уравнений D.30) можно получить способом,
изложенным в [26]. Не повторяя всех выкладок, отметим, что решения
тк (х) получаются заменой в выражении то(х) [26] функции ePl(x) на
функцию Р_1/2_^(ж).
Для определения коэффициентов Dk получаем, согласно D.27),
D.29), бесконечную систему линейных алгебраических уравнений:
оо
Dk= J2 akmDm + ak0, D.31)
т=\
1
f D-32)
+ 1/4) c c
Исследуем бесконечную систему D.31), D.32), сделав замену пере-
переменных
DkchfjLkip2 =xk. D.33)
Тогда она примет вид
сю
Хк = Y1 ЬктХт + dk, D.34)
771=1
Можно показать, что
IT/ < Pf (т*)Р' (т*)Мк (A 4fi^
П ТХ) *"^^ Г\ 1/0 I Aii \ W J -L 1/0 I Aim \ Ш } -^ '-*- ( ) 1 \ ^ • ^ ^ /
где с ^ х* < 1,
0<
Учитывая, что при больших номерах fik пропорционально номе-
номеру к, и принимая во внимание асимптотическое поведение функций
х*) при больших значениях цк [67] и оценку D.36), можно
164 Гл. 4. Контактные задачи для сектора сферического слоя, и пр.
показать, что при больших кит для элементов матрицы и правой
части бесконечной системы D.34) справедливы соотношения
\Ькт
D.37)
где 0 < ip* ^ (р\, В, D, b, d — известные положительные постоянные.
Из оценок D.37) следует, что бесконечная система D.34) принад-
принадлежит к типу нормальных систем Пуанкаре-Коха и ее решение может
быть получено методом редукции. Свойства решений таких систем
позволяют показать, что ряд D.29), выражающий распределение на-
напряжений под штампом, сходится не хуже геометрической прогрессии
со знаменателем, меньшим единицы.
4.1.2. Вдавливание штампа в сектор сферического слоя.
В этом разделе рассмотрим осесимметричную контактную задачу S2
о вдавливании штампа в сферическую поверхность сектора шарового
слоя, описанного в предыдущем разделе. Методом однородных
решений эта задача может быть сведена к решению бесконечной
системы линейных алгебраических уравнений типа нормальных
систем Пуанкаре-Коха, если следовать схеме предыдущего пункта
и использовать соотношения A.80) обобщенной ортогональности
однородных решений. Эти соотношения используются также и для
вычисления некоторых интегралов ти-
Р па A.77) от неоднородных решений со-
соответствующих уравнений Ламе.
Граничные условия такой задачи бу-
будут иметь следующий вид (см. рис. 4.2):
иг = 5 cos (р (г = R2, (р ^ (р 1),
о~г = 0 (г = R2, (р\ < (р < ^2)»
Тг<р = 0 (r = Ri,r = Д2), D.38)
' пр
ur = U [г =
= 0, и<р = 0
Рис. 4.2. К задаче #2
q(t) = Sqo(t)
где 5 — вертикальное перемещение
штампа.
В этой задаче контактные напряже-
напряжения под штампом
D.39)
п=\
Здесь qn(t) (п = 0, 1, 2,...) определяются из интегральных уравнений
(\(p\ < <pi), D.40)
4.2. Контактная задача для тонкого сферического слоя 165
о fc=°
a Dn находятся из бесконечной системы
п=0
, Ьк = -5скТОк,
0 f
Wk(R2) co
скТпк с = ttR22W^(R2) cos ак<р2
cos an
Tkn =Тпк.
В D.39)-D.41) приняты обозначения по аналогии с контактной за-
задачей для кольцевого сектора, изложенной в п. 3.3.2, W^(i?2) соответ-
соответствует однородной задаче, W(R2)/A(k) — неоднородной, ак — корни
уравнения А(ак) = 0, лежащие в правой полуплоскости. Не останав-
останавливаясь на исследовании ряда D.39), интегральных уравнений D.40)
и бесконечной системы D.41), отметим, что здесь, как и в предыдущей
задаче и в задаче для кольцевого сектора (см. п. 3.3.2), можно показать,
что элементы Ък и акп системы D.41) убывают с ростом номеров по
экспоненте, ряд в D.39) сходится не медленнее, чем сумма членов
бесконечно убывающей геометрической прогрессии, а решение инте-
интегральных уравнений D.40) может быть получено при помощи большого
набора эффективных методов, в том числе и асимптотических, разра-
разработанных для подобного класса уравнений (например, [88, 260]).
4.2. Контактная задача для тонкого сферического
слоя (сферический подшипник скольжения)
Для оценки ресурса работы самосмазывающегося сферического
подшипника важно знать распределение напряжений в месте контакта
шипа с антифрикационным покрытием, перемещение шипа от воздей-
воздействия на него радиальной нагрузки, а также размер области контак-
контакта [145]. Ниже производится расчет этих величин с помощью задачи
теории упругости о взаимодействии шара со сферическим упругим
слоем, внешняя граница которого жестко закреплена [315] (задача S3,
см. рис. 4.3). Такая задача достаточно хорошо моделирует работу сфе-
сферического самосмазывающего подшипника, особенно при нагрузках,
когда размер поверхности контакта соизмерим с шириной подшипника.
Здесь также принимается во внимание, что модуль упругости анти-
166 Гл. 4. Контактные задачи для сектора сферического слоя, и пр.
Р
фрикационного покрытия значительно ниже модуля упругости других
деталей подшипника.
Для рассмотренной задачи теории упругости построено асимпто-
асимптотически точное решение для случая малых толщин упругого слоя,
произведен расчет необходимых вели-
величин для разных значений исходных па-
параметров.
В сферических координатах (г, #, ср)
рассмотрим шаровой слой R\ ^ г ^ R2,
О < $ < 2тг, 0 < (р < тг, у которого по-
поверхность г = R2 неподвижна, а в по-
поверхность г = R\ вдавливается силой Р
штамп в форме шара радиуса Ro с точ-
точкой первоначального касания ср = О,
г = R\. Предполагаем, что трение меж-
между штампом и шаровым слоем отсут-
отсутствует, сила Р направлена вдоль пря-
^ , о тY о мой ld = 0, а величина А = R\ — Rn
Рис. 4.3. К задаче S3 ™
мала. В этом случаем приходим к ре-
решению осесимметричной краевой зада-
задачи для уравнений Ляме в сферических координатах со следующими
граничными условиями:
ur =
аг =0
=0 (г = i?
(r = R\, \(p\ ^ 7)'
Ru \<p\ >7)»
Ur = Uy = 0 (г = i?2),
D.42)
где 5 — смещение штампа, иг — перемещение вдоль оси г, аг и тГ(р
компоненты тензора напряжений, \ср\ ^ 7 ~~ область контакта.
Разыскивая решение уравнений Ляме в виде разложений
k=o
k=o
1/2,
где Up — перемещение вдоль оси cp, Pu(cos(p) — функции Лежандра,
и удовлетворяя граничным условиям, найдем неизвестные функции
Wfc(r) и 14(г), а для нахождения неизвестных коэффициентов ак
получим парный ряд-уравнение
akK(ak)Pak_i/2(cos(p) =
)
((К
r-i
7)
¦ [5 cos (p — A( 1 — cos (p)],
D.43)
4.2. Контактная задача для тонкого сферического слоя 167
сю
Y, akP(ak)Pak_l/2(cos(p) = О G < <р < тг).
к=0
Здесь G — модуль сдвига, v — коэффициент Пуассона,
w \ Ai(a) R\ /a a a\
ВД=д^. х=-, D.44)
Ai =2(l-2z/)[Bi(a)chBalnx)-
А = A -
Bi = 2[a2(-48z/ + 64z/ - 20) + 2z/ - 1],
B2 = 2[a3(-32u2 + 56z/ - 24) + а(\6и2 - 26z/ + 10)],
Б3 = a4A6z/ - 12) + a2C2u2 - 52z/ + 19),
B4 = 4a4 + a2F4v2 - 96z/ + 31), B5 = A - 2z/)(8a4 - 10a2 + 2),
Ai =2[a4A28z/2- 160z/ + 48) +
+ a2(-384z/3 + 544z/2 - 224z/ + 24) + A8z/ - 9)],
A2 = 2[a3(-256z/3 + 512z/2 - 320z/ + 64) + a(96u2 - \\\v + 48)],
A3 = 16A - 2z/)a6 - 40A - 2v)aA + a2A28z/3 - 64z/2 - 146z/ + 73),
AA = 16A - 2u)a6 + a4(-512z/3 - 1024z/2 - 560z/ + 88) +
+ a2(l 152z/3 - 2304z/2 + 1422z/ - 279),
A5 = A - 2z/)(-32a6 + 112a4 - 98a2 - 18).
Из последних соотношений нетрудно найти величину А = limK(a)
при а —> 0, которая потребуется в дальнейшем:
А = -2Ki/K2(l -^), D.45)
Кх = -4я2(\ - 2v) In2 к - 8я2 Ink(%v2 + 13z/ - 5) +
+ x4C2z/2 - 52z/ + 19) + x2(-96z/2 + 148z/ - 50) + 32Bz/ - 3)z/ + 31,
K2 =
22 + 352z/ + 50) + 576z/2 - 864z/ + 279.
168 Гл. 4. Контактные задачи для сектора сферического слоя, и пр.
Неизвестные контактные давления под штампом определяются че-
через решение парного уравнения D.43) из соотношения
оо
Q(v) = J2 akPak_l/2(cos(p). D.46)
k=0
Для решения парного уравнения D.43) воспользуемся методом све-
сведения его к бесконечной системе линейных алгебраических уравнений
с сингулярной матрицей коэффициентов (см. § 1.2).
Если ввести в рассмотрение парное уравнение
сю
Y, al?K(ak)Pak_l/2(cosp) = Pt?_l/2(cosp) (О < р < 7)> D-47)
к=0
ею
J^ al?Pak_l/2(cos(p) = О G < ip < тг),
к=0
то контактные напряжения под штампом через его решение будут
найдены по формуле
СЮ
4 D.49)
fc=0
Парное уравнение D.47) может быть сведено к бесконечной системе
где Х.г? = {х™} — неизвестный вектор, В = {Ьтп}, Т>г? = {d1^} —
соответственно матрица и вектор бесконечного порядка с элементами
-7т)^-1/2+г5п(с)Р-1/2+г7п(-с)
am — I T^i-_\, 2 Jin i л ~"~
-С) + Р-1/2+«(с)Р11/2+<7т(-с)
K(i?)G^-?2)P-l/2+i7n(-c)
Р11/2+,6(с)Р_1/2+г7т(с) - Р_1/2+ге
4.2. Контактная задача для тонкого сферического слоя 169
Через решение бесконечной системы D.50) функция qi?((p) нахо-
находится из соотношения
^^^ D.51)
где г5п — нули функции К (а).
В реальных самосмазывающихся подшипниках скольжения толщи-
толщина антифрикционного покрытия обычно значительно меньше размера
области контакта. Поэтому в рассматриваемой задаче теории упругости
естественным является предположение об относительной малости тол-
толщины упругого слоя (h = R^ — R\ <С R\ sin 7)- В этом случае функция
К (а) может быть аппроксимирована функцией [88]:
K*(a) = (thAa)/a, D.52)
где А дается соотношением D.45). Предельные значения функций
К* (а) и К (а) при больших и малых а совпадают. Числовые расчеты
показывают, что с уменьшением толщины слоя наибольшая погреш-
погрешность аппроксимации функцией D.52) достигается при больших а.
Поэтому можно утверждать, что с уменьшением толщины упругого
слоя точность решения после использования аппроксимации будет уве-
увеличиваться.
В дальнейшем, когда речь будет идти о функции К (а), а также ее
нулях и полюсах, будем иметь ввиду функцию К* (а) и естественно,
ее нули и полюсы, не меняя обозначения.
Отметим важный для дальнейшего факт, что при к —> 1 {R\ —> R2)
величина А —> 0, а следовательно при к —> 1, 5п —> оо и jm —> 00. Здесь
^7ш — полюсы функции К (а). Используя аппроксимацию D.52), имеем
<5n = ^, 7m = j(m-l/2). D.53)
Рост полюсов и нулей функции К (а) с уменьшением относительной
толщины упругого слоя позволяет асимптотически значительно упро-
упростить систему D.50) и другие соотношения. Используя асимптотику
функций Лежандра при больших индексах, можно показать, что си-
система D.50) асимптотически эквивалентна системе
где матрица Е имеет вид A.9), а векторы Сг? = {с^} имеют вид
7m+ 1/4 т 12т +
Решения систем D.54), D.55) известны [3]:
170 Гл. 4. Контактные задачи для сектора сферического слоя, и пр.
XJ =
_
Ay/A 2Bn-2)!!f П-[и)~У 7Г ГA+шА/тг) '
Sn - 3i/2j '
A
где Г(х) — гамма-функция.
Асимптотически также упрощаются формулы для контактных на-
напряжений:
@ < <p <7).
n=l
Отметим, что последние соотношения справедливы при (р > 0.
В случае (р = 0 имеем
Л— Gч/9 @) = —-— D 58)
\ / / \ / /
В полученных асимптотических соотношениях D.48), D.57), D.58)
неопределенными еще являются размер области контакта (величина 7)
и перемещение штампа 5 в зависимости от приложенной силы Р. Для
нахождения этих величин воспользуемся соотношением
7
Р = 2nR\ q(<p) cos ip sin Lp dip D.59)
0
и тем фактом, что ряды в D.57) при ср —> 7 расходятся и после
суммирования при у? ф 7 дают корневую особенность, если у? —> 7-
Предполагая контактные напряжения ограниченными, приравняем ну-
нулю коэффициент при особенности в формуле D.48) с учетом D.57),
D.58). Получим уравнение
- cos7 — ^ sin7j К-C/2) — , , . Re a(K-(\/2)) = 0.
D.60)
Соотношение D.59) позволяет получить другое уравнение:
5 + А = A^- Р + АР1/2) р-,1 D.61)
sin2 7 .
РШ= 27Г
1/2 7^A/2)
D.62)
2тг [ 1 - cos3 7 , v I ц?
4.2. Контактная задача для тонкого сферического слоя 171
2 D.64)
Таким образом, система двух уравнений D.60), D.61) позволяет
найти в зависимости от заданной силы Р перемещение штампа 5 и
размер области контакта 7-
Соотношение D.60) позволяет также исключить из формул для
контактных напряжений D.57) расходящиеся части рядов, что дает
возможность представить контактные напряжения через экспоненци-
экспоненциально сходящиеся ряды. Формально они совпадают с D.57), в которых
х1^ необходимо заменить на х^\
D.65)
,з/2 = 3snTr
Ряд D.64) является плохо сходящимся. Улучшив сходимость, заме-
заменим его конечными суммами
D.66)
N
„1/2
Уп '
S3/2 = sin^
N 3/2
V^ X
F2 = Щ- ln4Re [A cos7 - | sin7
Здесь TV = E(E/2eJ/5), где Е(...) означает целую часть от числа, г —
заданная точность вычисления рядов.
Были проведены числовые расчеты. Исходными данными являются:
Р (кг), и, G (кг/мм2), Rq (мм), h = Щ — R\ (мм), А (мм). Далее из
системы трансцендентных уравнений D.60), D.61) находились переме-
перемещение штампа 5 и размер области контакта 7- При этом использова-
использовались соотношения D.62), D.63), в которых Е^? считались по форму-
формулам D.66), D.67). После этого рассчитывались контактные напряжения
172 Гл. 4. Контактные задачи для сектора сферического слоя, и пр.
под штампом с использованием формул D.48), D.57), D.58). Здесь при
использовании формул D.57) необходимо хг? заменить на х^ из D.65).
Таблица 4.1
р- ю-3
1
2
3
4
5
6
7
59,6
67,7
72,1
75,0
77,1
78,6
4,696
8,973
13,261
17,573
21,905
26,252
4,379
8,351
12,327
16,321
20,332
24,357
3,448
6,538
9,616
12,701
15,793
18,891
1,968
3,692
5,396
7,095
8,794
10,493
(МО2
0,4947
0,8319
1,154
1,470
1,783
2,095
В табл. 4.1 для некоторых значений исходных параметров (Rq = 13;
h = 0,5; v = 0,4; G = 71; А = 0,005) приведены расчетные значения
внедрения штампа 5 в мм, размера площадки контакта 7 B градусах
и контактных давлений в кг/мм (q((pk)) B четырех точках (рь =
(fc = 0, 1, 2, 3). При (р = 7 контактные давления обращаются в нуль.
4.3. Контактная задача для усеченного конуса
В этом параграфе в отличие от §4.1 рассмотрим в сферической
системе координат другую смешанную осесимметричную задачу 54
теории упругости о кручении штам-
штампом тела конечных размеров, ограни-
ограниченного конической и двумя сфериче-
сферическими поверхностями. Здесь предпола-
предполагается, что сферические поверхности
неподвижны, а на конической поверх-
поверхности осесимметрично жестко закреп-
закреплен штамп (бандаж) постоянной шири-
ширины, находящийся под действием крутя-
крутящегося момента [326] (см. рис. 4.4).
Для исследования задачи использу-
используется метод однородных решений, что
позволяет свести ее к решаемой при
любых значениях параметров беско-
бесконечной системе линейных алгебраиче-
алгебраических уравнений типа нормальных си-
систем Пуанкаре-Коха. Задача о круче-
кручении штампом бесконечного конуса изу-
изучалась в работах [236, 364].
В сферической системе координат г, (р, # рассмотрим тело (усе-
(усеченный конус), ограниченное координатными поверхностями ср = 7 <
< тг, г = R\ и г = i?2 (R\ < Ri)- На конической поверхности ср = 7
Рис. 4.4. К задаче
4.3. Контактная задача для усеченного конуса 173
при R\<a^r^b<R2 закреплен штамп, который закручивается
моментом М на угол г вокруг оси симметрии. Сферические поверх-
поверхности г = Ri (i = 1,2) неподвижны, требуется найти распределение
напряжений под штампом и связь между моментом М и углом поворота
штампа г.
В этом случае описанная выше задача будет эквивалентна следую-
следующей краевой задаче относительно функции перемещения и вдоль оси $:
л и к л ^и , 2 ди . ctgcp ди . 1 д2и /а го\
Аи--2—о—= 0, Аи = —? + -л" + —т^ тт" + -г—г' D-68)
г sin <^j ^r ^ дг г2 д^р г2 д(р2
и = rssiwy (cp = 7, a ^r ^b),
и = 0 (г = Ri (г = 1,2), 0< ^ <7)»
V V 'У' ^ У ^ /У' ^ ^
G I ди
кuctgip] , {(р = 7, R\ < г < а, Ъ < г < Д2),
где т^^ — касательные напряжения, G — модуль сдвига. Для решения
задачи D.68), D.69) используем метод однородных решений [15]. В со-
соответствии со схемой этого метода найдем решение вспомогательной
задачи для уравнения D.68), когда
Г т(г) (a^r^b, 4> = i),
r^tf = I D.70)
I 0 @ < г < а, Ъ < г < оо, ср = 7).
Воспользовавшись преобразованием Меллина по переменной г, найдем
и(г,<р) =«<»(,•,„) = f. \r{p)dp \ §Ц^ (?)' ds, D.71)
a (L)
где контур интегрирования L есть прямая, параллельная мнимой оси
плоскости комплексной переменной s = а + ir при условии 0 < а < 1
[236], Psn_i(cos(^) — функция Лежандра.
Далее найдем однородные решения уравнения D.68) при условии
т<р0=О ((/? = 7, 0 < г < оо). D.72)
Они будут иметь следующий вид:
u(r,<p) = u±k{r,ip) =P/'fe_1/2(cos^)r±^-1/2, D.73)
где /3k — корни уравнения
^0. D.74)
Все /3k — вещественные числа, так как являются собственными
значениями задачи Штурма-Лиувилля для уравнения Лежандра с гра-
граничным условием D.74) при этом /3k = —/З-k- Далее считаем /3k > О
174 Гл. 4. Контактные задачи для сектора сферического слоя, и пр.
и поэтому однородные решения для задачи D.68), D.72) записываем
в виде D.73).
Учитывая асимптотику функций Р™(х) при больших значениях v
[67], получим
7ГD1)Ш (fc=1'2,...)- D-75)
Решение задачи D.68), D.69) представим в виде
и(г, ф) = uw(r, ф) - uW(r, ф), D.76)
где для u(l\r,(p) справедливо D.71), а
Последнее выражение представляет сумму однородных решений
D.73) с неопределенными коэффициентами Xk, Ук- Соотношение D.76),
удовлетворяющее уравнению D.68) и третьему граничному усло-
условию D.69), содержит неизвестную функцию распределения контактных
напряжений г (г) и неизвестные коэффициенты Xk, Ук, которые найдем
из условия удовлетворения первым двум граничным условиям D.69).
Согласно второму условию D.69)
u(Ri, ф) = uw(Ri, ф) - v,W(Ri, Ч>) = 0 (г = 1,2). D.78)
Для определения Хк и у^ воспользуемся условием ортогональности
функций Р}_Х12+рк{о,оъф) на отрезке [0,7] [67]:
Р-1/2+/3* (C0S Ф)Р-\/2+Eк (C0S Ф) sin VdV
0
J' n'_k D.79)
Получим
^ ( it" ) +Ук = л/^2 ^-1/2+/зЛСО87)^2/с^г, *, D.80)
= 1,2), D.81)
4.3. Контактная задача для усеченного конуса 175
* ^=1.2), D.82)
Последний интеграл вычислен по формуле D.79) при условии
D.74). С учетом D.83) и правил контурного интегрирования
)dp, k(y)= \ PJ-
Ujk(p) = -sin7^-Pi1/2+A(cos7)Wi?i)(-1^A + 1/2 (j = 1,2).
Подставляя последнее соотношение в D.81), получим
Sjk =sin7Pl1/2+A(cos7) ^G^-'^. + V^-1 jr(/3)/9(-.)^fc + ./2
D.84)
О" =1.2).
Удовлетворяя теперь первому условию D.69)
u^\r,j) — uB\r,j) = resiwy (a < г < 6),
получим интегральное уравнение для определения т(р)
где оператор
^ \ PJ^°S^ D.86)
i(cos7)
Представим решение уравнения D.85) в виде
т(г) = G<ssmjT()(r) + У^\хкЩкт1(г) + укЩ^кт1{г)] >, D.87)
I fc=i J
где го (г), т^(г) являются решениями интегральных уравнений
X Т3(п\ - {-\)jCk-\/2 / • _ 1 о 7i < < 74
Кгт0(р)=г (а^г^Ъ). D.88)
176 Гл. 4. Контактные задачи для сектора сферического слоя, и пр.
Подставляя D.87) в D.80), D.84), для определения Хк, Ук получим
систему двух бесконечных систем линейных алгебраических уравнений
Хк + Ук (V) = gi + Е [акпхп + аЦУп],
z п=\
Хк{т) +^=gfc + ?[4Un + 42n2/n] (Л =1,2,...), D.89)
П=1
где обозначено
акп -
akn - bk-ti Щ lkn, akn - ЬкЩ 1кп,
bk = sm7[Pl1/2+/3fc(cos7)]2B/3fc^)-1, D.90)
(p=l,2). D.91)
Таким образом, поставленная задача для усеченного конуса сведена
к исследованию бесконечной системы D.89) и интегральных уравне-
уравнений D.88), отличающихся друг от друга правыми частями. Ниже будет
показано, что система D.89) относится к системам типа нормальных
систем Пуанкаре-Коха, и ее решение поэтому может быть получено
методом редукции для любых значений параметров. Интегральные
уравнения D.88) соответствуют смешанным задачам об осесимметрич-
ном кручении бесконечного конуса, когда на его поверхности при а ^
^ г ^ b заданы перемещения и = Г(-{УPk-W2 (j? /- — \2) или и = г.
Отметим, что аналогичным образом может быть исследована задача
о кручении усеченного конуса, когда граница г = R\ закреплена, а
граница г = R^ свободна от напряжений, и наоборот.
Оценим величины D.91). Можно показать, что
dp <оо. D.92)
Умножим первое соотношение D.88) на гто(г) и проинтегрируем
в пределах от а до Ь. Далее в левой части полученного соотношения
изменим порядок интегрирования и, учитывая, что ядро D.86) удовле-
удовлетворяет условию
к(у) = ук(\/у),
4.3. Контактная задача для усеченного конуса 177
получим
ъ
' lp = TJk0 (J = 1,2). D.93)
Тогда, используя D.92), D.93), получим
\Ты\ < а
\ < 6А+/3"-3МО. D.94)
Подставляя D.92), D.94) в D.90), найдем поведение коэффициентов
системы D.89) при больших номерах к, п:
^ (b/R2)P^ (fe.n^oo).
D.95)
Учитывая асимптотику D.75) и R\ < а < Ь < R2, заключаем, что
система D.89) принадлежит к типу нормальных систем Пуанкаре-
Коха.
Рассмотрим числовой пример. Для вычислений коэффициентов бес-
бесконечной системы D.89) и контактных напряжений D.87) необходимо
знать решение интегральных уравнений D.88). Для некоторых частных
случаев параметров различными авторами получены решения второ-
второго уравнения D.88) для то (г), которые можно обобщить на уравне-
уравнения D.88) для т^(г). Сюда можно отнести работы [236, 364], когда
а = 0, работу [77], когда 7 = тг/2, и др.
Рассмотрим задачу S4, когда 7 — тг/2, R\ = а = 0, R\ = Ъ. В этом
случае имеем задачу о кручении круговым штампом полушара, ин-
интегральные уравнения D.88) имеют точные решения, так как они
соответствуют задаче о кручении упругого полупространства, а систе-
система D.89) примет вид
хк=0,
сю
Ук = d + E afnVn, (Л= 1,2,...)- D.96)
п=\
178 Гл. 4. Контактные задачи для сектора сферического слоя, и пр.
Числа Ck (к = 1,2,...) определяются из соотношения P2Ll/2+Rk@) =
= 0, отсюда следует, что Ck = 2к — 1/2. Можно показать, что инте-
интегральные уравнения D.88) будут равносильны уравнениям
Ъ оо
\rk(p)pdp [ Ji(ur)Ji(up)du = r2k~l (O^r^b) (к = 1,2,...),
о о
D.97)
где тк(р) = т| (р) (к = 1,2,...), то(р) = т\(р), J\(u) — функция Бесселя.
Если воспользоваться результатами работы [43], то точное решение
уравнений D.97) можно выписать в виде
1 г
2Ъ2к~2 d Г $k(r)dT Q , v d [ t2h~ldt
7Г dr ] y^T^ С?Г J ^/T2_t2
Вычисляя последние интегралы, получим
тк(гЬ) = Ъ2к-\к{г),
\ 2 Bfc)!!
Воспользовавшись формулами D.79), D.91) найдем
Т22 _ 2 6Bfe)!!Bn)!! _ 2feBfe - 1) ,
кп~ it BAJ-l)!!Bn-l)!!Bife + 2n+l)> fc " 4fc - 1 ' l
Подставляя D.100) в D.90) получим простые выражения для коэф-
коэффициентов бесконечной системы D.96):
7 Bfe-2)!!Bfe+ 1)'
D.101)
22 _ 2 /_6_\2(n+/c)-i Bfc-3)!!Bn)!!
k ttKRJ Bfc-2)!!Bfc-l)Bfc + 2ra-1)'
Итак, контактные напряжения и связь между моментом М, при-
приложенным к штампу, и углом поворота штампа г выразятся, соответ-
соответственно, формулами
((Kr^l), D.102)
4.3. Контактная задача для усеченного конуса
179
Если при вычислении величин D.102) и D.103) достаточно огра-
ограничиться членами порядка О(А7), то урезая систему D.96) до двух
уравнений и асимптотически упрощая ее решение, получим
AGsr
т(гЪ) =
М =
Для численного исследования величин
М* = Тб
= (Ge)-lr(rb)
D.104)
D.105)
D.106)
с использованием формул D.101)—D.103) и D.96) для ПК была со-
составлена программа, которая позволяла находить их с любой степенью
точности. Бесконечная система решалась методом редукции.
Задача о кручении штампом полушара, как частный случай иссле-
исследовалась в работах [43, 325].
В табл. 4.2 с точностью до четырех значащих цифр приведены
значения величин М* и г* (г) для некоторых значений параметров Л
и г. Эти числовые результаты хорошо согласуются с числовыми ре-
результатами работы [325], которые изложены в следующем параграфе.
Например, при Л = 0,5 все четыре цифры совпадают.
Отметим, что для получения решения с погрешностью до 0,1 % при
Л ^ 0,9 достаточно в редуцированной системе взять 6 уравнений, а при
Л ^ 0,95 — 12 уравнений.
В последних четырех строках табл. 4.2 приведены результаты, по-
полученные по асимптотическим формулам D.104), D.105). Сравнение
показывает, что эти формулы можно использовать с погрешностью
до 8 % при Л < 0,9.
Таблица 4.2
Л
0,5
0,7
0,8
0,9
0,95
0,99
0,5
0,7
0,8
0,9
М*
1,057
1,184
1,323
1,625
1,992
3,006
1,057
1,181
1,305
1,514
т*@,1)
0,1350
0,1478
0,1483
0,1717
0,1800
0,1904
0,1350
0,1478
0,1583
0,1722
т*@,3)
0,4224
0,4635
0,4687
0,5432
0,5715
0,6005
0,4224
0,4637
0,4981
0,5456
т*@,5)
0,7758
0,8546
0,8772
1,022
1,088
1,153
0,7758
0,8550
0,9246
1,027
г* @,7)
1,318
1,461
1,532
1,821
1,990
2,174
1,318
1,461
1,596
1,807
т*@,9)
2,779
3,111
3,347
4,219
4,993
6,229
2,779
3,105
3,434
3,985
т*@,95)
4,095
4,600
4,983
6,465
8,023
11,32
4,095
5,586
5,091
5,948
180 Гл. 4. Контактные задачи для сектора сферического слоя, и пр.
М
4.4. Контактная задача для усеченного шара
Рассмотрим осесимметричную задачу теории упругости S^ о кру-
кручении усеченного шара жестко прикрепленным к его плоской границе
круговым цилиндрическим штампом. При этом
будем считать, что сферическая часть поверхно-
поверхности шара неподвижна (см. рис. 4.5). Эта задача
рассматривалась в работах [41, 43, 58, 288, 314,
325, 330]. В работах [58, 288] она была сведена
к интегральному уравнению второго рода. Реше-
Решение последнего в них не строилось. В работе [43]
построено приближенное (замкнутое) решение
задачи на основе специальной аппроксимации
ядра интегрального уравнения, а в работе [41]
построено ее асимптотическое решение в случае,
когда радиус штампа близок к радиусу среза.
Ниже будет построено решение задачи мето-
методом больших Л [325], изложенным в § 1.3, для случая, когда радиус
штампа в достаточной мере меньше радиуса среза шара.
Как известно [43], поставленная задача может быть сведена к инте-
интегральному уравнению A.30) с ядром и правой частью (со — постоянная,
определяемая из условия ср(\) =0)
Рис. 4.5. К задаче 05
М(у) = [1 — thTra tb.'yu] cos uydu,
D.107)
D.108)
Здесь 7 ? [0, тг] — параметр, характеризующий степень усечения шара,
а — радиус штампа, Ъ — радиус среза, R — радиус шара.
Ядро D.107) и правую часть D.108) можно разложить соответ-
соответственно в ряды A.39) и A.40), где
Bп)\
ап = соа*п -а*п
2{2п)Г
а0 =
к—U
- у/2 ,
D.109)
Таким образом, в случае больших значений Л решение интеграль-
интегрального уравнения A.30) с ядром D.107) и правой частью D.108) пред-
ставимо в виде A.41), A.42) при условии A.32).
4.4. Контактная задача для усеченного шара
181
Введем обозначение
естественным образом связанное с представлением правой части
D.108) интегрального уравнения в виде разности двух величин. Тогда
из условия (р(\) =0
Для удобства численного определения величины касательных на-
напряжений под штампом [43] методом больших Л представим их в виде
, 0) = -^ Ge\(\ + chaK/2
v'O)
sh ao v ch ao — ch a
_d_
dr
<p'(r\)
shr
r=a0
d \d {<p'(t\)\ 1 1 r-r r— , 1
dr I ат у shr I shrl J
D.110)
г=0
г=0
Здесь а = Arth(r/b) (r — расстояние точек усеченного шара от оси
симметрии), G — модуль сдвига, г — угол поворота штампа.
Таблица 4.3
7
7Г
7Г
7Г
2
2
2
тг/2
тг/2
тг/2
1
1
0,5
0,5
a
6
од
0,5
0,7
0,1
0,5
0,7
0,1
0,5
0,7
0,1
0,5
0,1
0,3
0,1280
0,1308
0,1356
0,1280
0,1326
0,1411
0,1280
0,1350
0,1447
0,1281
0,1456
0,1287
0,1509
1=0,3
0,4005
0,4094
0,4252
0,4005
0,4152
0,4425
0,4006
0,4224
0,4529
0,4009
0,4545
0,4028
0,4692
0,7352
0,7521
0,7840
0,7353
0,7628
0,8163
0,7354
0,7758
0,8329
0,7359
0,8303
0,7394
0,8507
1,248
1,279
1,341
1,248
1,297
1,397
1,249
1,318
1,426
1,249
1,401
1,255
1,418
2,629
2,698
2,864
2,630
2,737
2,985
2,630
2,779
3,191
2,632
2,949
2,644
2,921
182 Гл. 4. Контактные задачи для сектора сферического слоя, и пр.
Связь между моментом М, действующим на штамп, и углом пово-
поворота г штампа при больших Л определится соотношением
U J ch3(t/2)
В табл. 4.3 для различных j и X приведены значения безразмерной
величины
T*=Tvz(r,0)(Ge)-\
подсчитанной по формулам D.110), A.41), A.42) с погрешностью не
более 0,01%.
Если через р обозначить кратчайшее расстояние точек штампа при
г = а до неподвижной сферической границы шара, то, как показывают
расчеты, метод больших Л дает решение задачи, когда отношение р/а
достаточно велико.
Данные табл. 4.3 достаточно хорошо согласуются с соответству-
соответствующими данными, приведенными для этой задачи в таблицах ра-
работ [41, 43].
Глава 5
КОНТАКТНЫЕ ЗАДАЧИ ДЛЯ ТЕЛ КОНЕЧНЫХ
РАЗМЕРОВ НЕКАНОНИЧЕСКОЙ ФОРМЫ
В этой главе рассмотрены контактные задачи теории упругости
для тел конечных размеров, когда часть их граничной поверхности не
является координатной поверхностью какой-либо системы координат.
Дано решение некоторых плоских задач для криволинейной трапеции
и осесимметричных задач для тел вращения с криволинейной обра-
образующей. Для решения задач предложен метод однородных решений,
который в сочетании с известными методами решения интегральных
уравнений для полубесконечных областей позволяет их эффективно
исследовать [298-304].
5.1. Метод однородных решений в контактных
задачах для тел неканонической формы
Рассмотрим некоторую каноническую систему координат (г, (р)
(рис. 5.1), в которой переменные в уравнении Ламе разделяются. То-
Тогда существует счетный набор однородных решений для областей,
ограниченных парами координатных кривых одного семейства. Извест-
Известно [218], что таких систем координат конечное число и они связаны
с группой симметрии уравнений Ламе.
Далее мы будем рассматривать задачи теории упругости только для
двухмерных областей, хотя аналогичный подход может применяться
и для существенно трехмерных задач.
Рассмотрим следующую задачу теории упругости. Пусть область,
занимаемая телом, ограничена парой координатных кривых L\, L^ и
двумя достаточно гладкими произвольными кривыми G\, G2, которые
назовем боковыми поверхностями (рис. 5.1). На кривых L\, L2 зададим
смешанные граничные условия, а на кривых G\, G2 несмешанные.
Группа симметрии уравнений Ламе не очень велика, но тем не
менее в предлагаемую схему вписывается достаточное количество ин-
184
Гл. 5. Контактные задачи для тел конечных размеров
Рис. 5.1
тересных задач. В этой главе рассмотрены только три вида задач:
антиплоские и плоские задачи для криволинейной трапеции и осе-
симметричные задачи для тела вращения с плоскими основаниями
и криволинейными образующими. Аналогично могут быть рассмотрены
смешанные задачи для частей полосы,
кольца, шарового слоя, клина и конуса,
полученных вырезанием при помощи до-
достаточно произвольной образующей.
Решение поставленной задачи строим
в виде суперпозиции однородных решений
для полубесконечной области, ограничен-
ограниченной кривыми Li, 1/2, и некоторого неодно-
неоднородного решения для этой области. Неод-
Неоднородное решение выбирается так, чтобы
выполнялись смешанные граничные усло-
условия на Li, 1/2. Используя произвол в вы-
выборе коэффициентов линейной комбинации однородных решений, удо-
удовлетворим краевым условиям на боковой поверхности.
Такой подход позволяет использовать хорошо разработанную тео-
теорию для полубесконечных тел [88, 260]. Из граничных условий на
поверхностях L\, L2 получаем известное интегральное уравнение, для
которого есть достаточное количество эффективных методов реше-
решения [260].
Если краевым условиям на боковой поверхности удовлетворять
точно, то мы столкнемся с рядом проблем. Следы однородных реше-
решений на кривых отличных от координатных из-за экспоненциальных
членов обладают гораздо худшими аппроксимационными свойствами,
чем на координатных кривых. Поэтому невозможно известными спо-
способами [260] получить бесконечную систему приемлемого качества.
Если же мы получим решение такой бесконечной системы, то остается
открытым вопрос о сходимости полученных разложений. Ряд вопросов,
связанных с суммируемостью разложений такого рода, обсуждается
в работах [49, 192, 345].
В силу вышеназванных трудностей краевые условия на боковой
поверхности мы будем выполнять приближенно при помощи численных
методов коллокаций, наименьших квадратов и вариационных, исполь-
используя первые N однородных решений.
Аппроксимационные свойства следов однородных решений на кри-
кривых, отличных от координатных, ухудшаются с ростом N, кроме того
растут издержки на вычисление неоднородного решения. Известно
также [49], что скорость сходимости наилучших приближений су-
существенно выше скорости сходимости частных сумм рядов, поэто-
поэтому целесообразно свести задачу удовлетворения условиям на боковой
поверхности к задаче Чебышева о наилучшем приближении краевых
условий линейной комбинацией однородных решений. Для численного
5.1. Метод однородных решений в контактных задачах
185
решения задачи о наилучшем приближе-
приближении мы будем использовать методы Ре-
Ремеза [267-270] первого и второго рода.
Изложим некоторые особенности
применения численных методов при удо-
удовлетворении краевым условиям на кри-
криволинейной части границы при помощи
однородных решений.
Предположим для определенности,
что задана декартова система координат
(х, у) (рис. 5.2). На поверхности L2 за-
заданы краевые условия, соответствующие
вдавливанию гладкого штампа:
Рис. 5.2
Ь),
Vy(x, К) = —5, тху(х, К) = 0, (а ^
ay(x,h)=0, rxy(x,h) = 0, (x<aUx>b).
Поверхность L\ жестко защемлена
V(x,y)
= 0.
E.1)
E.2)
E.3)
Боковые поверхности, заданные кривыми G\\ x = Щ(у), G^'. x = R\(y),
свободны от напряжений:
тп=0, (х,у) е G\
E.4)
Здесь V(x,y) = (Vx(x,y),Vy(x,y)) — вектор перемещения, ах(х,у),
ау(х,у), тху(х,у) — компоненты тензора напряжений.
Приближенное решение поставленной задачи ищем в виде следую-
следующей конечной линейной комбинации:
N
п=\
E.5)
где VH(x,y) — решение неоднородной задачи для полосы, ограни-
ограниченной координатными кривыми L\, L2 с несмешанными краевыми
условиями
ау(х, К) = —q(x) (а < х < Ь), E.6)
ay(x,h)=0 (x <aUx>b), E.7)
тху(х,К)=0 ((x,y)eL2), E.8)
V(x,y)=0 ((x,y) GLi), E.9)
— однородные решения для той же области с краевыми усло-
условиями
<гу(х,у)\ь2 =0, тху(х,у)\ь2 =0, V(x,y)\Ll =0.
E.10)
186 Гл. 5. Контактные задачи для тел конечных размеров
Подставляя E.5) в первое краевое условие E.1), получим интегральное
уравнение
Kq(x) = 5+J2DnVn(x>h), E.11)
п=\
где
о
г
Kq(x) = q(a)k(a,x)da,
а
k(a,x) — ядро интегрального уравнения контактной задачи для слоя
[88]. Решение уравнения E.11) удобно искать в виде
N
q{x) = qo(x) + Yl DnQn{x),
n=\
тогда qn(x) — решения следующих интегральных уравнений, не зави-
зависящих от Dn,
E, п = О,
%(x,h), n>0.
Обозначим через V^(x,y) решение задачи E.6)-E.9), где вместо q(x)
берется qn(x), тогда E.5) примет вид
V(x,y) = V»(x,y) + f Dn(y°n(x,y) + VZ(x,y))
ИЛИ _ _ N _
V(x,y) = V0(x,y) + Y, DnVn{x,y), E.12)
71=1
где _ _ _ _ _
V0(x, y) = V${x, y), Vn(x, y) = V°n(x, y) + V»(x, y).
Vo(x,y) будем далее называть неоднородным решением, a Vn(x,y) —
кусочно-однородными решениями (им соответствуют нулевые смеще-
смещения под штампом и нулевые напряжения вне его).
Краевым условиям на боковой поверхности мы будем удовлетворять
приближенно, используя оставшийся произвол в выборе коэффици-
коэффициентов Dn. Заметим, что E.12) точно удовлетворяет краевым услови-
условиям E.1), E.2) при любых Dn.
Используя представление E.12), из краевых условий E.4) получим
TOl(y) = ax(Ri(y),y)-R'i(y)Txy(Ri(y),y)=O (г = 0,1), E.13)
Ти(у) = Щу)GуA1г(у),у)-тхуAи(у),у) = 0 (г = 0,1), E.14)
где ах(х,у), ау(х,у), тху(х,у) — напряжения, соответствующие полю
перемещений E.12). Здесь введены функции невязок краевых условий
5.1. Метод однородных решений в контактных задачах 187
Tji(y). Первый индекс соответствует номеру краевого условия, вто-
второй — боковой поверхности. Собрав члены с одинаковыми Dn, получим
Тц(у) = Т${у) + ? DnTfjn(y), E.15)
п=\
где
У),У) ~ T*(Ri(y),y),
а^(х,у), а^(х,у), т^у(х,у) — компоненты тензора напряжений, соот-
соответствующие неоднородному решению, а а™(х,у), о~у(х,у), г^у(х,у) —
кусочно-однородным решениям.
Далее мы рассмотрим несколько подходов приближенного удовле-
удовлетворения краевым условиям, использующих представление E.12).
Метод коллокаций. Потребуем, чтобы краевые условия E.4) вы-
выполнялись точно в 2М точках ml (s = 1,..., М; г = 0, 1) с координа-
координатами (Ri(ylm), угт), для этого возьмем N = AM однородных решений.
Из E.15) получим N линейных уравнений для N неизвестных:
2т
T*(yJJ + J2DnT?jn(ym)=0 (m=l,...,M, г = 0,1, j = 0, 1).
п=\
E.16)
Решая линейную систему, находим неизвестные коэффициенты Dn.
Преимущество такого подхода заключается в его простоте и малых
вычислительных издержках. Вместе с тем остается открытым вопрос
о рациональном выборе положения точек коллокаций.
На неустойчивость по выбору точек обращали внимание авторы
работ [7, 134] и др. Самый простой подход, заключающийся в рав-
равномерном расположении точек вдоль по кривой, в некотором смыс-
смысле один из худших. Более рационально выбрать узлы коллокаций
в нулях полиномов Чебышева первого рода. Некоторые теоретические
и эмпирические соображения в пользу такого выбора можно найти
в [49, 355, 356]. В нашем случае метод приемлемо работает только для
границ очень близких к координатным кривым и малом количестве то-
точек коллокаций. С другой стороны, если необходимо быстро получить
приближенное решение, преимущества его несомненны.
188 Гл. 5. Контактные задачи для тел конечных размеров
Метод наименьших квадратов. Неизвестные Dn можно найти из
условия минимальности нормы L^{G\ U G2) невязки краевых условий
E.13), E.14), т.е. из условия минимума функционала
J(Dn) =
J г=0 V n=\
G.
Тогда получаем линейную систему
dj N
+ \ ? (тЯ(у) + ? DnTiik(y)) dy. E.17)
J, i=0\ n=\ /
n=l,...,7V) или J2Dnanm = dm (га = 1,..., N),
n=\
E.18)
где
= \
G
J, i=0 J, i=0
G\ G2
Основное достоинство метода — высокая устойчивость, вместе
с тем он требует существенных затрат на вычисление интегралов вдоль
боковых поверхностей. Кроме того, для боковых поверхностей, силь-
сильно отличающихся от координатных, невязка краевых условий E.13),
E.14) имеет высокие пики, которые имеют порядок решения, хотя
малы по среднеквадратичной норме (см. рис. 5.3, крив. 2, стр. 191).
Такие всплески не влияют на интегральные параметры задачи, однако
нарушают физическую картину вблизи боковой границы.
Вариационные методы. Если решение в виде E.12) подставить
в вариационные интегралы, то мы также получим замкнутую систе-
систему линейных уравнений. Этот метод дает несколько более сложные
соотношения для коэффициентов линейной системы, чем E.19), но
в целом очень похож на метод наименьших квадратов. Такой подход
имеет смысл применять, если краевые условия на боковой поверхности
содержат одновременно напряжения и смещения.
Дискретный вариант метода наименьших квадратов. Зададим
на боковой поверхности G\ U G^ М точек (см. рис. 5.2). Если в функ-
функционале E.17) интегралы заменить конечными суммами по выбранным
точкам {rrii}^, причем М не меньше числа однородных решений N, то
5.1. Метод однородных решений в контактных задачах 189
для определения коэффициентов Dn мы получим следующую линей-
линейную систему:
N
Y,Dnanm = dm (m= l,...,i\0, E.20)
п=\
где
1 1 М
EEE Tijm(ya)Tijk(ya), E.21)
г=0 j=Os=l
1 1 М
i=0j=0s=\
Такой подход занимает промежуточное положение между методом кол-
локаций и наименьших квадратов, требует достаточно малых вычис-
вычислительных затрат и не так чувствителен к выбору точек. Однако для
границ, достаточно отличающихся от координатных, острые всплески
невязки еще более ярко выражены, чем в методе наименьших квад-
квадратов. Этот метод достаточно эффективно работает в более широкой
области, чем метод коллокаций.
Метод наилучших приближений. Для выполнения краевых усло-
условий поставим задачу Чебышева о наилучшем приближении [49]:
min max max max Тц(у)\ n=l,...,N, г = 0,1, 7=0,1; E.22)
{D}? i j уес гзУУП J
т. е. Dn выберем так, чтобы погрешность удовлетворения краевых
условий была минимальна. Эту нелинейную задачу можно решать
численно, используя методы Ремеза [268, 270] или методы уравнивания
максимумов [234, 355]. Подробное изложение метода Ремеза можно
найти в [194]. Несмотря на нелинейность, такой подход более эффекти-
эффективен, чем метод наименьших квадратов, так как не требует вычисления
интегралов на границе и не возникают всплески невязки. Попутно
получается величина погрешности удовлетворения краевым условиям,
что важно знать при выборе количества однородных решений в E.5).
Из-за экспоненциальных членов аппроксимационные свойства однород-
однородных решений ухудшаются с ростом номера, а такой подход позволяет
наиболее эффективно использовать первые по порядку однородные ре-
решения, что позволяет для получения решения с той же точностью брать
меньшее количество однородных решений, чем в методе наименьших
квадратов.
Для неодносвязных областей реализация метода Ремеза достаточно
сложна, поэтому имеет смысл вместо условия E.22) рассмотреть его
дискретный вариант.
Метод переопределенных систем Чебышева. Пусть на боковой
поверхности задано 2М точек, причем 2М строго больше числа одно-
190 Гл. 5. Контактные задачи для тел конечных размеров
родных решений N. Потребуем чтобы максимальная невязка краевых
условий в этих точках была минимальной, т. е. Dn найдем из условия
min max max Д VCD) s=l,...,M, i,j = 0,l, E.23)
где AlJ(D) — невязка в точке ms краевого условия г на поверхности j,
она линейно зависит otDh имеет вид
Д*'(Я) = ТЦ(у\) + ? DnTfjn(yi). E.24)
п=\
Таким образом, задача свелась к решению переопределенной системы
Чебышева [268]
N
h-Y^ainDn = Si (г= 1,...,4М), min max |^|, E.25)
n=1 {Dn}? i=l,-AM
где
=Т$(у8), E.26)
= T°jn(yl8), 5=1,...,M, n=l,...,N, i,j=0, 1.
Существует достаточное количество численных методов решения таких
задач [153, 268, 351, 355, 363]. Заметим только, что E.23) легко сво-
сводится к задаче линейного программирования. Далее будет в основном
использован альфа-алгоритм Ремеза [268] («альфа-процесс последова-
последовательных взвешенных квадратических приближений» по терминалогии
автора) как самый простой в реализации.
Как показала практика, этот подход наиболее адекватно подходит
к решению поставленной задачи. Он требует существенно меньших за-
затрат, чем метод наилучшего приближения и не дает всплесков невязки.
Полученное решение близко к оптимальному.
Для практических расчетов использовался также несколько моди-
модифицированный алгоритм. По ходу итераций альфа-алгоритма Ремеза
в переопределенную систему E.23), E.25) добавлялись уравнения по
стратегии, близкой к стратегии в методе Ремеза первого рода.
Завершая изложение подходов решения контактных задач для
тел неканонической формы, проиллюстрируем сказанное на приме-
примере контактной задачи о сдвиге штампом криволинейной трапеции
(рис. 5.4, а), рассмотренной подробно ниже.
Пусть полуширина штампа а = 1,0 (рис. 5.4, б), высота трапеции
h = 2,0, угол наклона боковой поверхности, образованной отрезком
прямой, (р = 120, полуширина верхнего основания R = 2,0.
На рис. 5.3, а приведены графики невязок краевого условия, по-
полученные при использовании пяти однородных решений. График /
соответствует использованию метода Ремеза, 2 — методу наименьших
квадратов, 3 — методу коллокаций. Узлы коллокаций расположены
через равные промежутки. Величина вертикального деления 0,01.
5.2. Контактные задачи для криволинейной трапеции
191
2\
Рис. 5.3
На рис. 5.3, б приведены те же величины при использовании 11 од-
однородных решений. Цена деления 0,005. График для метода колло-
каций не приведен из-за слишком большой величины отклонения.
Отметим только, что при увеличении числа однородных решений с 5
до 11 невязки, получаемые методом коллокаций увеличились.
Из сравнения двух рисунков видно, что наиболее устойчивые ре-
результаты получаются по методу наилучших приближений.
5.2. Контактные задачи для криволинейной трапеции
Рассмотрим контактную задачу теории упругости о чистом сдви-
сдвиге бесконечного цилиндра штампом (рис. 5.4, а). Эта задача служит
модельной для более сложных задач, описанных в следующих разде-
разделах, однако может представлять и самостоятельный интерес, особенно
в гидродинамической трактовке.
Рис. 5.4. К задачам N\, N2
Пусть к поверхности у = h цилиндрического тела, имеющего се-
сечение в виде симметричной криволинейной трапеции, жестко присо-
присоединена бесконечно длинная полоса (штамп) шириной 2а, ось которой
параллельна оси z. Поверхность вне штампа будем считать свободной
от напряжений за исключением основания, которое жестко защемле-
защемлено. Под штампом возникнут касательные напряжения q(x) = rzy(x,h)
(\х\ < а), подлежащие определению.
192 Гл. 5. Контактные задачи для тел конечных размеров
На боковой поверхности тела будем рассматривать два типа усло-
условий: жесткое защемление (задача N\) и отсутствие напряжений (зада-
(задача Щ).
Уравнение Ламе и закон Гука для поставленных задач имеет вид
AV(x,y) = 0,
д д E-27)
rzx(x, у) = G— V(x, у), ryz(x, у) = G— V(x, у),
где G — модуль сдвига; V(x,y) — смещение вдоль оси z; rzx, ryz —
компоненты тензора напряжений.
При сделанных предположениях граничные условия имеют вид для
задачи N\
V(x,h) = -5 (|ж| < a), Tyz(x,h)=0 (\x\ > а),
E.28)
V(x,y)=0 (x = R(y), O^y^h), V(x,0) = 0,
где х = R(y) — форма боковой поверхности.
Соответственно для задачи 7V2
V(x,h) = -5 (\х\ < a), ryz(x,h)=0 (\x\ > а),
тп(х,у)=0 (х = R(y), O^y^h), E.29)
V(x,0) =0,
где rn — касательное напряжение на боковой поверхности.
Предположим, что контактные напряжения q(x) известны, тогда,
следуя изложенной выше схеме, решение такой несмешанной задачи
будем искать в виде суперпозиции однородных решений для слоя и
некоторого неоднородного решения
V(x, у) = VH(x, y) + jr DnV*(x, у), E.30)
п=\
где VH(x,y) — неоднородное решение, V®(x,y) — однородные ре-
решения.
Полная система однородных решений для слоя со свободной верх-
верхней и защемленной нижней поверхностью имеет вид
V®(х, h) = sinany chапх, ап = —- Bп — 1) (п=1,2,...). E.31)
В качестве неоднородного решения возьмем решение несмешанной
задачи для слоя с граничными условиями:
ryz(x,h) = -q(x) (\x\ < a), ryz(x,h)=0 (\x\ > а),
E.32)
V(x,0)=0.
5.2. Контактные задачи для криволинейной трапеции
193
За счет выбора q(x) и Dn можно удовлетворить всем граничным усло-
условиям исходной смешанной задачи.
Контактные напряжения q(x) для исходной задачи будем искать
в виде
сю
q{x)=qo(x) + Y,Dnqn{x), E.33)
п=\
тогда E.30) примет вид
V(x,y) = V0H(x,y)
V*(x,y)],
n=\
где V^{x,y) есть решение несмешанной задачи с граничными услови-
условиями E.32), когда вместо q(x) берется qn(x) из формулы E.33).
Из граничных условий на поверхности у = h для qn(x) получим
интегральные уравнения
а (Я
[ qn(t)k(t-x)dt=\ * '
J I 7гс
-а к
7гсп.апх, п > 0,
E.34)
где
7 / \ 1
k{u) = -In
th
Л — безразмерный параметр, равный отношению высоты трапеции
к полуширине штампа.
При помощи преобразования Фурье неоднородное решение получа-
получаем в виде
— x)shay
LJh
Внутренний интеграл берется явно, окончательно имеем
V (х, у) = —
7ГЖ
У7Т
У7Т
5.2.1. Особенности реализации метода однородных решений.
В случае антиплоской задачи вычисление неоднородных решений не
представляет трудностей, поэтому остановимся на решении интеграль-
интегрального уравнения. Интегральное уравнение E.34) допускает точное ре-
решение, но в целях эффективной численной реализации всей схемы
решения в целом воспользуемся асимптотическим методом больших Л,
изложенном в § 1.3. Выбор этого метода связан также с тем, что прак-
практический интерес представляет область значений параметров задачи,
7 В.М. Александров, М.И. Чебаков
194 Гл. 5. Контактные задачи для тел конечных размеров
когда отношение высоты трапеции к полуширине штампа достаточно
велико. Тогда решение E.34) примет вид
n=0
где коэффициенты а^(А) вычисляются с помощью следующих реку-
рентных соотношений вида A.50):
где Р имеет смысл удельной контактной жесткости:
— а
г
i=j k=j p=°
i/0 /c/0
n—1 г n=i
/Я** /-р+г-к
k=j i=j k=j p=0
/c/0
p=
In 2Л - E3 - E4'
oo oo г
EScE
/=0 n=/ г=0 j=0 p=0
oo
^2M
~ Z Z^ Z^ Z^ Л2п+2г S /^
г=0 j=0 n=/ г=0 j=0 p=0
Здесь введены обозначения
-1, m = 0,
C^1 — биномиальные коэффициенты, ^ — коэффициенты разложения
ядра интегрального уравнения
г=0
5.2. Контактные задачи для криволинейной трапеции
195
еп — коэффициенты разложения правой части E.34) в ряд Тейлора.
Для расчета в этом асимптотическом разложении удерживалось 10 чле-
членов по Л.
5.2.2. Численные примеры. Таблицы 5.1 и 5.2 содержат резуль-
результаты численных расчетов для задач N\ и 7V2 соответственно, когда
боковая поверхность — отрезок прямой (см. рис. 5.4,6). Полуширина
штампа а = 1, полуширина верхнего основания R, h — высота трапе-
трапеции, (р — угол наклона образующей к оси х.
Таблица 5.1
R
7,0
2,0
2,0
2,0
1,5
1,5
1,5
1,5
1,5
1,3
1,2
h
2,0
2,0
2,0
2,0
2,0
2,0
2,0
2,0
2,0
2,0
2,0
Ч>
90°
60°
90°
120°
70°
80°
90°
100°
110°
90°
90°
д*@)
0,615
1,10
0,765
0,710
1,64
1,18
1,02
0,970
0,889
1,23
1,38
д*@,25)
0,634
1,15
0,791
0,733
1,71
1,22
1,05
0,970
0,918
1,27
1,42
д*@,5)
0,707
1,33
0,881
0,818
1,97
1,38
1,17
1,08
1,02
1,41
1,57
д*@,75)
0,921
1,83
1,16
1,06
2,72
1,83
1,54
1,41
1,33
1,85
2,03
д*@,9)
1,93
4,11
2,46
2,25
6,12
3,95
3,27
2,97
2,80
3,89
4,21
Р
1,87
2,84
2,19
2,08
3,98
3,07
2,74
2,58
2,47
3,24
3,58
А
1 • Ю-7
з- ю-3
1 • Ю-5
з- ю-3
2-Ю-2
2.10-2
1 • Ю-3
3-ю-2
3-ю-2
7- Ю-3
2.10-2
Таблица 5.2
R
2,0
2,0
2,0
1,5
1,5
1,5
1,5
1,5
1,05
1,2
1,1
h
2,0
2,0
2,0
2,0
2,0
2,0
2,0
2,0
2,0
2,0
2,0
Ч>
60°
90°
120°
70°
80°
90°
100°
110°
90°
90°
90°
д*@)
0,331
0,508
0,575
0,293
0,356
0,417
0,465
0,501
0,278
0,341
0,303
д*@,25)
0,339
0,523
0,593
0,292
0,364
0,429
0,479
0,516
0,233
0,351
0,312
д*@,5)
0,353
0,581
0,660
0,290
0,394
0,476
0,535
0,576
0,301
0,392
0,346
д@*,75)
0,402
0,751
0,859
0,294
0,486
0,614
0,696
0,752
0,358
0,510
0,448
<f@,9)
0,704
0,566
1,80
0,404
0,954
1,27
1,46
1,58
0,667
1,07
0,941
Р
1,32
1,64
1,78
1,24
1,33
1,45
1,54
1,62
1,15
1,27
1,19
А
1- Ю-2
1- Ю-4
1- 10-2
ь ю-2
5- Ю-3
з- ю-3
5- Ю-3
ь ю-2
0,20
0,04
0,14
196
Гл. 5. Контактные задачи для тел конечных размеров
В таблицах приведены значения безразмерной жесткости упругого
тела
Р= J q(x)dx-(G5)-\
величины безразмерных контактных давлений
q*(x) = q(ax)-^
и абсолютная погрешность удовлетворения краевым условиям на боко-
боковой поверхности А.
На рис. 5.5, а, б приведены следы однородных решений на обра-
образующей боковой поверхности, когда ср = 135° и 90° соответственно.
На горизонтальной оси откладывается у, на вертикальной — функ-
функция fk(y) = Vk(R(y),y).
Рис. 5.5
Из рисунков видно, что чем больше угол (р отличается от 90°
и чем больше номер однородного решения, тем больше однородное
решение сосредотачивается в даль-
дальнем от оси у угле трапеции, что при-
приводит к ухудшению аппроксимаци-
онных свойств однородных решений.
В этом случае необходимо привле-
привлекать большее количество однород-
однородных решений, что приводит к росту
вычислительных затрат. Тем не ме-
менее, из таблиц 5.1, 5.2 видна прием-
приемлемость метода для достаточно боль-
больших углов ср.
На рис. 5.6 приведены коорди-
координаты точек альтернанса Чебышева
[194] в зависимости от ctgcp, где (р — угол наклона образующей, когда
а = 1, R = 1,2, h = 1, число однородных решений М = 5. Штриховой
6
----^
У
¦^
1
3
Рис. 5.6
5.2. Контактные задачи для криволинейной трапеции
197
линией показана относительная погрешность удовлетворения краевому
условию. Из рисунка видно, что для метода коллокаций целесообразно
брать узлы, сгущающиеся к дальнему от оси у краю.
Рис. 5.7
О 9
0,7
0,5
0,3
0.1
Рис. 5.8
Рис. 5.9
В случае антиплоской задачи без значительных затрат можно вы-
вычислить поле перемещений внутри области. На рис. 5.7, а приведены
линии одинаковых смещений для прямоугольника, три грани которого
защемлены (задача N\), а с четвертой стороны прикладывается штамп
и смещается на 1. На рис. 5.7, б приведены изолинии для задачи N^.
198
Гл. 5. Контактные задачи для тел конечных размеров
На рис. 5.8, а, б приведены изолинии для трапеции с прямолинейными
образующими для задачи N\ и N% соответственно. На рис. 5.9, а (за-
(задача N\), б (задача N2) приведены результаты расчетов для боковой
поверхности, образованной волной косинуса.
5.3. Вдавливание штампа в плоскую грань
криволинейной трапеции
Рассмотрим плоскую задачу о вдавливании штампа в плоскую
грань упругого тела, имеющего форму симметричной упругой трапеции
(задача 7V3, рис. 5.10). Предполагается, что под штампом отсутствует
трение, другая плоская грань упругого тела
лежит без трения на плоском основании, бо-
боковая поверхность свободна от напряжений.
Выше подобные задачи рассматривались для
канонических областей, причем на боковой по-
поверхности обычно задаются так называемые
парные граничные условия, которые позволя-
позволяют применять свойство обобщенной ортого-
ортогональности. Здесь предлагается решение зада-
задачи для тела, часть границы которого отлична
от канонической, где заданы непарные гранич-
граничные условия, т. е. такие, что условия обобщен-
обобщенной ортогональности не позволяют получить коэффициенты разложе-
разложения по однородным решениям явно.
5.3.1. Постановка задачи и реализация метода однородных ре-
решений. Пусть в прямоугольной системе координат (х,у) (рис.5.10)
упругое тело занимает область \х\ ^ R(y), 0 ^ у ^ h. Предполагаем, что
на грани у = 0 заданы условия отсутствия нормальных перемещений
и касательных напряжений, а штамп с плоской подошвой внедряется
симметрично относительно оси в грань у = h на величину 5. Соответ-
Соответствующую краевую задачу для уравнения Ламе можно симметрично
продолжить в область у < 0. В этом случае получаем эквивалентную
задачу (см. рис. 5.11 на стр. 208) о внедрении двух штампов в грани
Рис. 5.10. К задаче
R(y),
h, счи-
счиу = ±h упругого тела, занимающего область \х
таем R{y) четной функцией. Таким образом, приходим к исследованию
краевой задачи для уравнения Ламе при следующих граничных усло-
условиях:
vyx, п) — о, тху — и у\х\ ^ а;, ^о.оо;
v(x,—h) = 5, rxy(x,—h)=0 (\x\ < а),
(ту(х,у)=0, тху(х,у)=О (у = ±h, \x\ > а), E.36)
о~п = 0, тп = 0 (x = ±R(y))t E.37)
5.3. Вдавливание штампа в плоскую грань криволинейной трапеции 199
где ау(х,у), тху(х,у) — компоненты тензора напряжений, ап, тп — нор-
нормальное и касательное напряжение на боковой поверхности, v(x, у) —
перемещение вдоль оси у, \х\ ^ а — область контакта.
Далее мы будем использовать представление решения уравнения
Ламе, компонент тензора напряжений и вектора перемещений через
функцию Эри Ф(х,у). Согласно общей схеме, решение будем искать
в виде суперпозиции
сю
Ф(х, у) =52 Dn^°n(x, у) + Фн(х, у), E.38)
п=\
где Ф^(х,у) соответствует однородным решениям для полосы \у\ < h
при отсутствии напряжений на границах \у\ = h, а Фн(х,у) является
решением бигармонического уравнения при следующих условиях на
границах:
ay(x,±h) = —q(x) (\х\ ^ а),
E.39)
ay(x,±h) =0 (\х\ > а), тху(х, ±h) = 0.
В этом случае граничное условие E.36) исходной краевой задачи будет
удовлетворено. Из условия E.35) получим интегральное уравнение
относительно неизвестной функции контактных напряжений
Kg = \$ + V Dnv°n(x, /1I j^—, E.40)
где К — интегральный оператор контактной задачи для слоя [88];
Vn(x,y) — следы вертикального смещения соответствующих однород-
однородных решений под штампом. Введем следующие безразмерные вели-
величины:
х = ах, у = ау, и = ап, v = av,
q(ax) = — (p(x), A = -, 5 = -.
Далее мы будем иметь дело только с безразмерными величинами,
поэтому надчеркивание будем опускать. В новых обозначениях инте-
интегральный оператор К будет иметь вид
1 сю
ts 1 Г / \л Г Liu) (t — т) -, tt лл\
К(р= - (p(r)dr —^ cos уv } du, E.41)
7Г \ U Л
j J
-1 0
где символ ядра имеет вид [39]
ци) = fi*". E.42)
200
Гл. 5. Контактные задачи для тел конечных размеров
В правой части интегральное уравнение E.40)-E.42) содержит
счетное число неизвестных коэффициентов Dn. Для их нахождения
используем условие E.37), предварительно преобразовав E.40). Пред-
Представим ip(x) в виде ряда
ф) = qo(x) + ? DnQn(x),
п=\
E.43)
в котором qn(x) (n = 0, 1,2,...) является решением интегральных урав-
уравнений _ ^
\ о, \ч UZn №<1)- E-44)
Эти уравнения, соответствующие контактным задачам для полосы,
хорошо изучены, и для их решения может быть использован большой
арсенал эффективных методов.
Если через Ф^(х,у) обозначить функцию Эри, найденную при
граничных условиях E.39), в которых q(x) следует заменить на qn(x),
соотношение E.38) преобразуется к виду
оо
Ф(х, у) = Фоя(х, у) + Y1 ?>п[Ф°п(х, у) + Ф^(ж, у)]. E.45)
п=\
Функция Эри, представленная таким образом, при произвольных Dn
позволяет удовлетворить граничным условиям E.35), E.36) исходной
краевой задачи. Заметим, что Ф^(х,у) соответствует задаче о внед-
внедрении штампа в слой, а Ф^(х,у) + Ф^(х,у) есть кусочно-однородные
решения, имеющие нулевые вертикальные смещения под штампом
и нулевые напряжения вне его.
Краевые условия E.37) для функции Эри преобразуются к виду
~дх
= С2,
E.46)
где С\, С2 — известные константы [297], Г — боковая граница х =
= R(y).
Введем линейные относительно Dn функции невязки краевых
условий
Э) = |^ С2. E.47)
Тогда проблема удовлетворения граничных условий E.37) сводится
к нахождению Dn таких, чтобы невязки Т\ и Т2 обратились в ноль.
Краевым условиям на боковой границе мы будем удовлетворять при-
приближенно, т. е. в бесконечной сумме E.45) оставим конечное число
членов. Для чего мы будем использовать альфа-алгоритм Ремеза.
Следующие два пункта посвящены вопросам эффективной числен-
численной реализации предлагаемого метода. Здесь мы сталкиваемся с двумя
5.3. Вдавливание штампа в плоскую грань криволинейной трапеции 201
трудностями. Правые части интегральных уравнений E.44) содержат
осциллирующие функции. Выражения для неоднородных решений, по-
полученные двукратным применением преобразования Фурье, содержат
интегралы, которые трудно определить численно. Как показывается
далее, эти трудности легко преодолеваются, если qn(x) искать в виде
представления, используемого в методе ортогональных многочленов.
5.3.2. Однородные и неоднородные решения для полосы. Бу-
Будем искать решение однородной задачи.
ay(x,h)=0, rxy(x,h)=0, ay(x,-h)=O, Txy(x,-h)=0, E.48)
в виде
Ф(х, у) = F(y) cospx,
тогда в бигармоническом уравнении переменные разделяются и, ис-
используя краевые условия E.48), мы получаем счетный набор однород-
однородных решений
о с±Щ8±Ш E.49)
Щ
chpkX
где Pk — корни хорошо изученного [88, 150] спектрального соотно-
соотношения
+2pfc = 0, E.50)
которые расположены на четырех симметричных относительно осей
координат ветвях. Нас будут интересовать только корни, лежащие
в правой полуплоскости. Занумеруем их в порядке возрастания модуля,
так что
Р2п =Р2п+\-
Выражения для компонент тензора напряжений и вектора смеще-
смещений, соответствующие однородным решениям для рк ф 0, имеют вид
ако(х, у) = G°3(y,pk) cosркх, ако(х,у) = -G°{(y,pk) cosркх, E.51)
тху(х'У) =G°2(y,pk)smpkx,
Vok&У) = \ [A - v)GUy,pk) - B - v)G°2(y,pk^
E.52)
- г, shpky(pkXshpk\ -
G°(v v ) = bll^fe^fe/4pll^fcA~ 2chpfcA) -pkyshpkychpkX
^yo/ \ _ shpky(pkXshpkX- 3chpfcA) - pkychpkychpkX
4 ' pkshpkXchpkX
Однородные решения, соответствующие кратному корню рк = 0, есть
ах = А + 2Ву, о-у = 0, тху = 0, E.53)
202 Гл. 5. Контактные задачи для тел конечных размеров
и(х, у) = —— (Ах + 2Вху) + щ-
v(x9y) = -%(Ay + 2Bi?)+vo-
где А, В, щ, vq, uoq — произвольные константы. Далее нам понадобятся
выражения для вертикальных смещений под штампом, соответствую-
соответствующие однородным решениям
V (х) = (у — 1) . E.54)
Рк
Неоднородные решения, т.е. решения задачи E.39) при q(x) =
= qk(x), ищем в виде следующего интеграла Фурье:
сю
г
Фк(х,у)= Fk(y,p) cos px dp. E.55)
о
Тогда образ функции Эри
т? ( \ — oQkip) pyshpXshpy — (shpX -\-pXchpX) chpy .- -^^
p2 sh 2pX + 2pX
где
2 Г
Qk(p) = - qk(x)cospxdx E.57)
7Г J
0
— преобразование Фурье контактных давлений. Для компонент тензо-
тензора напряжений и вектора смещений имеем следующие выражения:
сю
акх(х,у) = J F%(y,p) cos px dp, E.58)
0
сю
o-y(x,y) = - p2Fk(y,p) cos px dp, E.59)
о
oo
"» У) = \ pFk(y,p) sin px dp, E.60)
E.61)
E.62)
E.63)
E.64)
E.65)
тху(х
5.3. Вдавливание штампа в плоскую грань криволинейной трапеции 203
G (р у) = 2ру shрХ shру ~ ^shрХ + рХ chpX^chp^ E 66)
г / .ч _ op?/shpAshp?/-pAchpAchp?/ ,- R ,
G2(P'У) ~ Z sh2pA + 2pA ' E-Ь7)
G (p у) = 2РУ ShpX ShИ/ + (shpA - pA chpA) chpg/
sh 2рл ~г ?рл
„ , л _ ^pyshpAchpt/ + BshpA -
Gi{P'V) ~ 2 Sh2pX + 2p
Анализ показывает, что численно напряжения и смещения на боко-
боковой поверхности Г непосредственно по формулам E.58), E.69) не могут
быть получены, так как приходится считать несобственный интеграл
от осциллирующей, слабо убывающей функции. Для эффективной чис-
численной реализации проведем некоторые преобразования. Представим
qk(x) в виде
E.70)
'" л / 1 _ ^2
n=0
где Тп(х) полиномы Чебышева первого рода. Тогда его преобразование
Фурье имеет простой вид
сю
Qk(p) = Е xn(-l)nj2n{p). E.71)
п=0
Далее мы проинтегрируем плохо сходящуюся часть в интегралах
E.58)—E.61), для этого введем следующие функции:
^ч (Р' У) = G\(Р' У) ~ (р(у — А) — \)ер(уУ~х),
Gl(p,y) = G2(p,y) -p(y - \)ер<уУ~х\ E.72)
G%{p,y) = G3(p,y) - A +р(у- \))ер(у~х\
которые экспоненциально убывают по р.
Используя интегралы
: + z)dp= ^- «, E.73)
0 (x + zJ + (\-yJ
О Ф = ,; у/о :.—^. E-74)
сю
0
сю
ое-р(^-у) sinp(
204
Гл. 5. Контактные задачи для тел конечных размеров
и соотношение E.71), получим следующие удобные для вычисления
формулы:
п=0
(-l)n J2n{p)G*3{p, у) cospxdp -
0
1
dz\, E.76)
n=0
(-l)n J2n(p)G\(p,y) cospxdp-
(A - yf
2 T2n(z)
-1
dz\, E.77)
n=0
2
-i
-dz
E.78)
В соотношениях E.76), E.77) в первых интегралах подынтеграль-
подынтегральная функция экспоненциально убывает равномерно по всем парамет-
параметрам, второй интеграл тригонометрической заменой сводится к соб-
собственному интегралу по конечному отрезку. Такое представление оди-
одинаково хорошо работает как под штампом, так и вне его, что позволяет
рассматривать образующие боковой поверхности х = R(y), пересекаю-
пересекающие прямую х = а.
Дополнительно вычислим вертикальные смещения под штампом
для неоднородного решения задачи E.39), когда
q{x)=T2n{x){\-x2)-x'2.
Из E.61) имеем
1
= \ \ Qk{p)[(l - v)G^p, A) - B - v)G2{p, A)] cospxdp.
0
5.3. Вдавливание штампа в плоскую грань криволинейной трапеции 205
Используя спектральное соотношение [252]
J \/1-С2
и интеграл [88]
тг/пТп(х), п >
оо
f cosut - е~и i,l /r oa\
аи = In - E.80)
J u t
о
аналогично тому как это делается в методе ортогональных многочленов
[88, 252], получаем
оо
+ \ {ф{р)Мр) cosрх + е~р) dp, E.81)
о
оо
'dp (fc>0), E.82)
где
Заметим, что, взяв N однородных решений E.49)-E.53) и М неод-
неоднородных решений задачи E.39), когда q(x) = Т2П(х)/\/\ — х2 (п =
= 1,...,М) (см. E.76)-E.78) и E.81), E.82)) и использовав метод
Галеркина или вариационные принципы, получим простую и доста-
достаточно эффективную численную схему решения поставленной задачи.
С другой стороны, решая интегральное уравнение E.40), а затем вы-
выполняя условия E.46) на боковой поверхности, можно без больших
дополнительных затрат решать несколько задач для разных форм бо-
боковой поверхности при заданной постоянной Л одновременно. В данной
работе нас в большей степени будет интересовать задача удовлетворе-
удовлетворения краевых условий на боковой поверхности Г, а последний подход
позволяет применять численные методы нахождения наилучшего при-
приближения, эффективность применения которых, в такого рода задачах,
будет далее показана.
5.3.3. Решения интегрального уравнения с осциллирующей
правой частью. Здесь предложен новый метод решения интеграль-
интегрального уравнения E.44), хотя для его решения существует большое
количество методов. Однако в нашем случае применение их затруднено
наличием в правой части интегрального уравнения E.44) осциллирую-
осциллирующих функций. Далее предлагается эффективный метод решения таких
уравнений, основанный на использовании метода Ремеза и спектраль-
спектральных соотношений E.79). Для эффективного вычисления неоднородных
206 Гл. 5. Контактные задачи для тел конечных размеров
решений E.76)-E.78) нам необходимо получить qk(x) в виде отрезка
разложения по полиномам Чебышева
Чк(х) = ^Х*^Щ. E.84)
п=0
Наиболее удобен в этом случае метод ортогональных многочленов, но
как показывает опыт, применение этого метода ограничено наличием
в правой части интегрального уравнения осциллирующих функций.
Скорость изменения этих функций увеличивается с ростом номеров од-
однородных решений и уменьшением А, что приводит к неоправданному
увеличению линейной системы для достижения необходимой точности
и увеличению М в E.84). При увеличении же М растут затраты
на вычисление сумм E.76)-E.78). Для преодоления этой трудности,
а также с целью унификации подходов в удовлетворении граничных
условий на боковой поверхности и под штампом, сведем задачу на-
нахождения решения уравнений E.44) к задаче Чебышева о наилучшем
равномерном приближении на компакте.
Воспользовавшись тождеством E.79) и проведя известные преобра-
преобразования [252, 260], получим следующую задачу
min max\Rk(t)\ (к = 0, 1, 2,...), E.85)
м
Rk\t) = / XnQ,n(tj — §"/Д^)> E.8о)
п=0
оо
ao(t) = 1п2А + [ \u~l U(u) cos ^ Jo (^] - е~и)] du, E.87)
JL V А \ А/ ) \
о
оо
и (п>0), E.88)
ffcV.A) (*>0). E.89)
Корректность поставленной задачи следует из свойств полиномов Че-
Чебышева и оператора интегрального уравнения [88]. Так как область
определения компактна и система функций an(t) есть система Чебыше-
Чебышева при достаточно больших А, то к задаче можно применить алгоритм
Ремеза как I, так и II рода. Численный эксперимент показывает эф-
эффективность применения обоих методов, и трудно отдать предпочтение
одному из них. Отметим только, что алгоритм II рода требует несколько
больших затрат времени, но значительно проще в реализации.
Полученное таким образом решение при к = 0 сравнивалось с из-
известным решением [88]. Сравнение показало высокую эффективность
в достаточно широком диапазоне изменения А. Для А > 0,1 достаточно
5.3. Вдавливание штампа в плоскую грань криволинейной трапеции 207
10 членов в разложении E.84) для получения решения с погрешностью
не больше чем 0,001. При Л > 0,5 точно при таком М погрешность не
больше 10~5.
При использовании такого подхода попутно определяется абсолют-
абсолютная погрешность, с которой полученное решение удовлетворяет уравне-
уравнению. Во всех рассмотренных в § 5.3 случаях она не превышала 0,01 %.
5.3.4. Численные примеры. С целью определения степени вли-
влияния боковой поверхности криволинейной трапеции на распределение
контактных напряжений и интегральной жесткости системы штамп-
упругое тело в зависимости от ее формы и степени удаленности от
штампа был проведен ряд численных расчетов. Одновременно иссле-
исследовались границы применимости метода, а также проблема выбора
наилучших параметров численной схемы.
Как уже отмечалось, наша задача сводится к следующей задаче
Чебышева:
min max max{Ti(x, у), Т^{х, у)}, E.90)
lDk}" ye[o,\]
x=R(y)
которая решается численно с помощью альфа-алгоритма Ремеза.
Исходными параметрами являются: N — количество однородных
решений, Л — безразмерная величина, равная отношению высоты приз-
призмы к полуширине штампа (рис. 5.10), R(y) — функция, задающая
форму боковой поверхности.
По этим исходным данным вычисляются: контактные давления
q(x), жесткость системы штамп-упругое тело
1
р=±. Г q(x)dx E.91)
-1
и функция при особенности для контактного давления
Приводится также величина А, равная максимальной абсолютной по-
погрешности удовлетворения краевым условиям на боковой поверхности.
Ниже в виде графиков и таблиц приводятся результаты числен-
численных расчетов для трех серий численных экспериментов. В первой
серии форма боковой поверхности задается отрезком прямой парал-
параллельной оси у (R(y) = b), меняется расстояние (Ь — а) до края штампа
(рис. 5.11, a (if = 0)). Во второй — форма боковой поверхности задается
наклонной прямой, пересекающей прямую у = Л в точке Ъ = const,
меняется угол (р ее наклона к оси у (рис. 5.11, а). В третьей серии
форма боковой поверхности есть волна синусоиды R(y) = В -\- А{\ —
— cos (ти//2А)) с переменной амплитудой А (рис. 5.11, б). Такая форма
боковой поверхности выбрана для того, чтобы избежать особенностей
в углах криволинейной трапеции.
208
Гл. 5. Контактные задачи для тел конечных размеров
Для первой серии экспериментов исходными параметрами являются
Л = 2, N = 10, (р = 0. Расстояние Ъ между осью у и образующей меня-
меняется от 1,0 до 4,0. На рис. 5.12, а приведены Р/2 (кривая /), давление
в центре штампа q@) (кривая 2), коэффициент при особенности хA)
(кривая 3).
р-
Рис. 5.11
1,5
1,0
0,5
0,0.
а
2
S
i i
1
4
Р
Рис. 5.12
0,6 0,9 1,0
't
Видно как решение при Ъ —> оо переходит в решение для слоя, а при
Ъ —> 1 — к вырожденному решению, т. е. решению соответствующему
несмешанной задачи о сжатии прямоугольника, причем в этом заведо-
заведомо худшем случае x(t) отличается от точного не более чем на 3,5%.
На рис. 5.12,6 приведены функции x(t) при Ъ = 1 (кривая 4), Ъ =
= 1,1 (кривая 3), Ъ = 1,5 (кривая 2) и Ъ = 2,0 (кривая /). Видно
как происходит перераспределение давления под штампом от краев
к центру при приближении края боковой поверхности к штампу.
В табл. 5.3 приведены значения контактных напряжений q(x), жест-
жесткость Р, погрешность А, а в табл. 5.4 значения x(t) в тех же точках
и под краем штампа.
Во второй серии изменяется угол наклона боковой поверхности
(рис. 5.11, а). На рис. 5.13, а приведены те же величины, что и на
рис. 5.12, а для Л = 2, N = 10, Ь = 2. Угол ip меняется от -15° до +30°
(положительное направление против часовой стрелки). На рис. 5.13,6
5.3. Вдавливание штампа в плоскую грань криволинейной трапеции 209
оГ
о
0,7)
0,4)
СО^
о"
см
о"
^ N
о
см
о
о
S
см
со
о
,938
о
951
о
,967
о
,979
о
00
00
О)
о
оЗ
о"
О)
о
ё
о
о
о
см
,04
,01
,998
о
,994
о
993
о
о!
о"
8?
о
О)
О)
о
8
о"
см
СО
см
СО
см
,05
,02
,01
999
о
о"
О)
о
(Т>
ОО
О)
о
см
00
о"
LO
см
О-
СО^
,29
,07
,03
,01
00
о"
СО
с?
о
со
О)
о
LO
СО
о"
00
СО
см
СО
со
,37
61'
,09
,03
995
о
о
о"
ю
LO
О)
о
СО
О)
о
о
см
006
0,0
о
см
ю
со
,39
см
о
,04
,00
о
00
о"
&
о
см
ю
О)
о
о
СО
003
0,0
СО
см
СО
°ч
,41
см
см
см
,05
016
53
о"
ю
О)
о
СО
со
О)
о
о
006
0,0
см
°ч
,41
см
см
см
,06
,02
СО
О)
о"
О)
о
LO
со
О)
о
о
СО
LO
ей
лиц
н
о
*
00
о
о
СтГ
о
о"
*
о
СО
см
о
*
о
см
LO
СО
о
°
СО
ю
см
°
О)
СО
°
О)
LO
°
СО
°
809
°
см
00
00
°
LO
СО
о"
о
О)
°
1,0
О)
см
8
см
°
00
СО
°
LO
см
LO
°
ОО
СО
°
00
°
828
°
о
О)
00
°
СО
о"
О)
CD
О5
О)
°
СО
СО
см
СО
°
о
ОО
°
СО
О)
LO
°
О)
СО
°
СО
°
844
°
ОО
О)
00
°
00
СО
о"
°
СП
ОО
О)
°
см
LO
CN
СО
°
LO
СО
°
СО
СО
|>~
°
ОО
°
со
00
°
875
°
О)
о
О)
°
LO
СО
о"
LO
О)
о
СП
со
О)
°
LO
00
СО
см
о
О-
°
°
СО
о
00
°
см
СО
00
°
о
00
°
00
00
°
ю
о
О)
°
см
о"
СО
СО
О)
о
СО
О)
°
о
см
СО
О-
°
LO
°
00
о
00
°
о
00
°
00
со
00
°
893
°
О)
°
о
СО
о"
см
О)
о
см
ю
О)
°
СО
|>~
CN
СО
о
ОО
о
СО
00
о
ОО
00
о
00
00
о
903
о
см
О)
о
О)
о"
со
LO
О)
о
СО
со
О)
о
|>~
см
СО
о
ОО
о
О)
00
о
см
LO
00
о
00
о
906
о
см
О)
о
СО
О)
о"
LO
LO
О)
о
LO
со
О)
о
210
Гл. 5. Контактные задачи для тел конечных размеров
приведена зависимость функции к{Ь) от (р при (р = —15° (кривая /),
(р = 0° (кривая 2), (р = 15° (кривая 3), (р = 30° (кривая 4). Здесь
с изменением угла (р наблюдается перераспределение напряжений от
краев к центру. В табл. 5.5 приведены контактные напряжения q(x),
жесткость Р, погрешность А для тех же параметров что и для
рис. 5.13, а, б.
1,4
1,2
0,9
-
^^^ 1
^_^_ 2
i
а
8
i i
+15
+30
Ф
K{t)
0,925'
0,8
0,675
0
0,4
0,8 1,0
t
Рис. 5.13
В табл. 5.6 приведены те же величины, что и в табл. 5.5 но для
Л = 4. Видно как изменяется поведение системы штамп-упругое тело
при увеличении толщины слоя. Отметим, что эффективность метода
при различных значениях параметра целиком зависит от способа ре-
решения интегрального уравнения E.40). В нашем случае при Л > 0,1
погрешность решения не более 0,01 %.
Третьей серии соответствует рис. 5.14, а. Приведены Р/2, (р@), хA)
(соответственно кривые /, 2, 3), когда боковая поверхность трапеции
описывается соотношением R(y) = В + А(\ — cos(iry/2\)) при В = 1,5,
Л = 2,0, N = 10 в зависимости от параметра А, меняющегося от —0,5
до +0,5.
1,4
1,1
0,6
0,1
-0,5 -0,25 0,0
0,25 0,5
А
K[t)
0,9
0,5
0,0 0,25 0,5 0,75 1,0
t
Рис. 5.14
На рис. 5.14, б приведена зависимость x(t) при А= —0,5, —0,25,
0,0, 0,5 (соответственно кривые /, 2, 3, 4).
5.3. Вдавливание штампа в плоскую грань криволинейной трапеции 211
LO
LO
к
VO
H
о
осГ
сгГ
Lq
^ N
CO"
о
CO
8
о
со
CM
CO
1,32
CO
1,07
1,024
CO
0,9
CD
CM
$
о
LO
°l
о
LO
|
CO
8
О
00
CO
"
CO
CXD
1,37
1,09
1,03
LO
LO
0,9
о
CD
LO
LO
о
CO
°l
о
О
8
О
О)
со
1,38
О)
-^
1,09
1,03
0,9
О)
СО
О)
°
СО
LO
О)
°
о
LO
+
СО
g
°
О)
со
см
°°
1,38
о
см
1,10
1,04
0,9
см
CD
СО
LO
О)
о
LO
°1
о
О
СО
СО
LO
S
VO
н
<
0,9)
о
со"
О
LO"
О
о
СО"
о
о
о
,05
о
О)
см
758
о
00
8
О
см
ю
LO
о
СО
см
ю
о
о
LO
о
CD
о
о
СО
00
о
00
о
о
LO
1
005
о
О)
LO
,09
СО
см
00
о
см
о
LO
СО
о
^
СО
о
О)
00
LO
о
СО
ю
о
СО
СО
LO
о
СО
ю
ю
о
о
°
004
о
см
,22
СО
8
о
о
о
СО
СО
о
СО
о
О)
СО
о
00
(У)
ю
о
ю
00
LO
о
LO
ю
о
о
ю
+
004
о
LO
256
см
см
о
00
о
СО
о
о
LO
СО
о
см
СО
о
ю
о
LO
00
LO
о
LO
LO
о
о
о
СО
212
Гл. 5. Контактные задачи для тел конечных размеров
В табл. 5.7 приведены контактные давления, жесткость и погреш-
погрешность для этой серии. Видно как ухудшаются аппроксимационные
свойства однородных решений при искривлении боковой границы.
В табл. 5.8 приведены результаты для той же серии, но при увели-
увеличенном N = 15. Видно, что при увеличении количества однородных
решений точность удовлетворения краевых условий существенно воз-
возрастает для слабо искривленной поверхности и незначительно для
сильно искривленной.
Из вышеизложенного видно, что для достаточно искривленной об-
образующей получаются во всех отношениях приемлемые результаты.
Все расчеты требовали минимального расчетного времени на ПК, что
также говорит о высокой эффективности метода.
5.4. Контактная задача для тела вращения
с криволинейной образующей
В цилиндрической системе координат (г, ср, z) рассмотрим тело вра-
вращения (задача 7V4, рис. 5.15, а), ограниченное поверхностями z = О,
z = h и г = R(z), R(z) — гладкая функция. В области контакта (z =
= h,r ^ а) задано вертикальное смещение штампа, вне штампа при
z = h напряжения отсутствуют. Тело вращения опирается на гладкое
жесткое основание, боковая поверхность свободна от напряжений.
Р
Рис. 5.15. К задаче Щ
Поставленная задача сводится к решению краевой задачи для
осесимметричных уравнений Ламе в цилиндрических координатах
[164, 266]
л* , д2и , 1 /л* , dw
д w д и
]_ди
где Л^ — дифференциальный оператор
Л* - д* + 1 д к1
5.4. Контактная задача для тела вращения
213
l6
с*
К
VO
H
A
oo"
t^"
LO"
0,4)
0,3)
cm"
o"
о
05
о
LO
CO
CM
CM
LO
1,09
C?>
,03
,02
LO
1
о
о
о
LO
CM
LO
Ю
LO
1,13
,02
,00
<y>
CD
00
о
-0,25
я
LO
CM
CD
1,15
00
CO
,00
987
о
C?>
CJ>
О
О)
C?>
О)
О
0,0
CM
о
о
, ,
С?>
СМ
см
см
1,16
00
СО
998
о
980
о
00
СУ)
CD
2
СУ)
CD
0,25
06
о
см
С?>
СМ
С?>
-н~
СО
1,16
СМ
987
о
967
о
ю
СУ)
CD
*
СУ)
CD
LO
00
лица 5
VO
н
<
оГ
оо"
LO"
0,4)
0,3)
0,2)
0,0)
0,05
LO
СО
СМ
о
00
С?>
,03
,02
,01
,01
1
0,007
о
LO
СМ
см
,02
,00
994
о
987
о
,25
о
1
0,0003
LO
см
С?>
00
00
СО
,00
987
о
976
о
969
о
о
о
0,009
^н
С?>
СМ
С?>
00
-
СО
998
о
980
о
968
о
960
о
LO
СМ
0,06
см
С?>
СМ
С?>
СО
С?>
СМ
987
о
967
о
954
о
944
о
LO
S a),
z = ft, a < r),
= 0),
Л, r = R(z)),
h, r = R(z)),
E.92)
E.93)
E.94)
E.95)
E.96)
214 Гл. 5. Контактные задачи для тел конечных размеров
при следующих граничных условиях:
w = -S (z = h,
rrz=0 (z = h), az=0
rrz = 0, w = 0
ar - R'{z)rrz = 0 (O^z
azR'(z) -rrz=0 @ < z
где rrz, ar, az — компоненты тензора напряжений, w — перемещения
вдоль оси z, и — вдоль оси г, 5 — перемещение штампа, а — радиус
штампа, h — высота тела вращения.
5.4.1. Однородные и неоднородные решения для слоя. Реше-
Решение поставленной краевой задачи для уравнений Ламе будем разыски-
разыскивать в виде
u(r, z) = uH(r, z) + u°(r, z), w(r, z) = wH(r, z) + w°(r, z), E.97)
где uH(r,z), wH(r,z) — решение уравнений Ламе для слоя в цилин-
цилиндрических координатах при следующих граничных условиях
rrz = 0, w = 0 (z = 0), E.98)
rrz = 0 (z = ft); az = -q(r) (r^a), az = 0 (r > a).
u°(r,z), w°(r,z) — суперпозиция осесимметричных однородных реше-
решений для слоя, когда на границе заданы условия
rrz=0, w = 0 B = 0), rrz=0, az=0 (z = h). E.99)
Решение неоднородной краевой задачи для уравнений Ламе при
условиях E.98) построим с помощью преобразования Ханкеля. Выра-
Выражения для перемещений и компонент тензора напряжений выпишем
в виде (G — модуль сдвига материала, Jn(x) (п = 0, 1) — функции
Бесселя)
7 оо
uH(r,z) = 1 J QG)ii(^7)JiG07d7, E-100)
о
оо
wH(r,z) = I J QG)i2(^7)JbGrOd7, E-101)
о
сю
rH(r,z) = J Q(-y)L3(z*y)Ji(>yr)>yd>y, E.102)
о
сю
J Qb) \L4(z7)Jobr) + ^f± J,Gr)| 1d1, E.103)
5.4. Контактная задача для тела вращения 215
*(r,z) = J Q(j)L6(zj)J0(jr)jdjt E.104)
Li G, z) = 7~ЧС^7^[A ~ 2^) sh7^ — jhchjh]
?2G, z) = ^~x{sh.^z[^hc}i^h + 2A — v)
L±(i,z) = 2G2: sh 72:0117/1 + chjz[shjh — 7/1 ch7/1])A \/yh),
^5G» 2) — —2{ch7^[(l — 2v) sh7/i — 7/1 ch7/1] + ^)
где
A(^) =
— преобразование Ханкеля контактных давлений
E.106)
о
Однородные решения уравнений Ламе при условии E.99) могут
быть получены аналогично неоднородной задаче. Выпишем их супер-
суперпозицию для компонент вектора перемещений и компонент тензора
напряжений:
u\r,z) = ? DnL°in{*)Ji(pnr/h), w\r,z) = ? DnL°2n(z)J0(Pnr/h),
П П
T°rz(r,z) = 0^ DnLln{z)Jx{pnr/h), E.107)
П
a°r(r,z) = GJ2 Dn[L\n{z)J0(pnr/h) + (Pkr/h)-lL°5n(z)Jl(pnr/h)]y
П
a°z(r,z) = Gj: DnLl(z)MPnr/h),
П
где функции L9 (z) через функции Ln(^(,z) выражаются с помощью
соотношения L\n(z) = Lk(pn/h, z)A(pn)pn/h.
В E.107) суммирование проводится по всем лежащим в правой
полуплоскости корням уравнения
А(р„) = 0 (P2n = P2n-i)- E.108)
Если решение исходной контактной задачи искать в виде E.97), то
граничные условия E.93), E.94) будут удовлетворены. Удовлетворяя
граничному условию E.92), получим интегральное уравнение
E.109)
216 Гл. 5. Контактные задачи для тел конечных размеров
оо
Цр,г) = J
Решение интегрального уравнения E.109) удобно представить в виде
q(r) = у^ ко(г) + ? DnL2n(h)qn(r)\, E.110)
In J
где qk(r) — решения интегральных уравнений
btalr/Ч itVulZ <5И1)
Здесь К(...) — интегральный оператор, стоящий в левой части соотно-
соотношения E.109).
5.4.2. Решение интегральных уравнений. Ранее уже отмеча-
отмечалось, что прямой счет по формулам E.100)—E.106) практически неосу-
неосуществим, так как приходится считать плохо сходящиеся осциллирую-
осциллирующие интегралы. Далее мы проинтегрируем плохо сходящуюся часть.
Предварительно получим решение интегрального уравнения E.109)
в удобной форме, аналогичной представлению используемому в методе
ортогональных многочленов [252, 260],
m=0
где Pm(x) — полином Лежандра. Заметим, что при применении метода
ортогональных многочленов для получения решения с достаточной
точностью необходимо выбирать М неоправданно большим. Это свя-
связано с особенностями предлагаемого метода. В нашем случае правые
части интегрального уравнения E.111) содержат при больших п до-
достаточно сильно осциллирующие функции, что приводит к увеличению
порядка линейной системы. Для преодоления этой трудности, а также
с целью унификации подходов в удовлетворении граничных условий
на боковой поверхности и под штампом, сведем задачу нахождения
решения интегрального уравнения к задаче Чебышева о наилучшем
приближении. Для этого воспользуемся известными спектральными
соотношениями [252, 260]
1
E.113)
л/1 - v'z
о
где
2 ""^ * = j J0(tx)J0(ty)dt,
о
5.4. Контактная задача для тела вращения 217
Проведя преобразования, аналогичные методу ортогональных мно-
многочленов, получим следующую задачу о наилучшем приближении:
min max \Rk(t)\ (k = 1,..., N), E.114)
M
Rk(t) = J2xknan(t)-gk(t), E.115)
n=0
где gk(t) — есть правые части интегральных уравнений E.111), a an(t)
имеет вид
сю
an(t) = vnP<in{\J\ -t2) +cn \ip(s\)Jo(st)J2n(s)ds,
о EП6)
Сп = (-1)пР2п@),
где jn(s) — сферические функции Бесселя 1-го рода. Поставленную
задачу Чебышева мы будем решать численно, используя метод Ремеза
I рода.
Далее нам понадобятся преобразования Ханкеля от контактного
давления. Используя [259], получим
м
QG) = ?xmi^^j2mG) E.117)
m=0 V У"
или в форме удобной для вычислений
м
QG)= ? Xm(-l)"lP2ro@)j2mG).
m=0
Для эффективной численной реализация выделим из соотноше-
соотношений E.100)—E.104) медленно убывающую часть, для чего введем сле-
следующие функции:
L*2G,z) = L2G,z) -7"'G(Л- z) +2A -
ЩЪ z) = L3G, z) - 27(z - h)e«*-h\
i
которые убывают при 7 —> oo не медленнее чем e~lh.
Подставим решение E.112) интегрального уравнения в соотноше-
соотношение E.100)—E.104). В получившихся двухкратных интегралах для
218
Гл. 5. Контактные задачи для тел конечных размеров
быстро убывающих частей E.118), используя E.117), свернем внут-
внутренний интеграл, а для медленно убывающих — внешний, используя
следующие известные интегральные соотношения [259]:
E.119)
Нам понадобятся следующие значения этого интеграла:
2к(ЬлсУ
4тгA - k2)(bc
ш
/2
Е{к),
b < с
b > с
x E(k) - k\l - k2)(b2 - c2 - p2)K(k)
где
(-1)" д
7 .
к = smcp =
2-к
- к2 ) - K(k)F(ipiy/l - к2
if(fc) — полный эллиптический интеграл 1-го рода, Е(к) — полный
эллиптический интеграл 2-го рода, F{k) — эллиптический интеграл
1-го рода, Qv(h) — функции Лежандра 2-го рода.
5.4. Контактная задача для тела вращения
219
Получим следующие удобные для вычислений соотношения для
неоднородных решений:
1
г
Q(/y)L\(z,/y)J\(/yr)/yd/y —
L о
a -i
- [ q(s)s (A - 2iy)A°0l (h - z, s, r) + (z - h)Al0l (h - z, s, r)\ ds ,
n -I
E.120)
wH(r,z) = q
- I q(s)s B( 1 - v) A°0l (h - z, s, r) - (z - h)A[m (h - z, s, r)) ds ,
0 ^
E.121)
oo
0
a
-2^q(s)s
0
:Alm(h-z,s,r) -
- z, s, r)(h -z)
¦ Al0l (h - z, s, r) + (z- h)A20l (h - z, s, r)) ds, E.122)
a
- J q(s)s Uz - h)A20l (h-z,s,r) + (l- 2iy)~lA20l (h - z, s, rj\ ds,
0
E.123)
oo a
Tr,z(r, z) = j Q(l)L3(z, 7) J!(jr)^ - 2(z - h) j q(s)sA20l(h - z, s, r) ds.
j
о о
E.124)
5.4.3. Числовые примеры. В качестве примера было взято те-
тело вращения, осевое сечение которого есть равнобедренная трапеция
220
Гл. 5. Контактные задачи для тел конечных размеров
(см. рис. 5.15, б). Далее в виде таблиц приведены значения безразмер-
безразмерных давлений под штампом
q*(r) = -l-
G6
(г, Л)
и безразмерной жесткости системы штамп-упругое тело
а
Р* = A -*/)^|, Р = 2тг \q(r)rdr
О
для некоторых значений угла наклона (р образующей к оси у и полу-
полуширины верхнего основания R. Для удовлетворения краевых условий
на боковой поверхности использовались метод коллокаций и дискрет-
дискретный вариант метода наименьших квадратов. В табл. 5.9 приведены
некоторые результаты, полученные при помощи метода наименьших
квадратов, когда боковая поверхность совпадает с канонической. Точки
выбирались равномерно вдоль по образующей. N — число однород-
однородных решений, М — количество точек на боковой поверхности. Далее
в табл. 5.10 приведены результаты аналогичных расчетов, полученных
методом коллокаций. Точки выбирались в нулях полиномов Чебышева.
Звездочкой помечены результаты, когда точки располагались равномер-
равномерно. N — число точек коллокаций.
Таблица 5.9
R
1,2
1,3
1,3
1,3
1,5
1,5
1,5
1,5
1,6
2,0
2,5
3,0
ч>
0
0
0
0
0
0
0
0
0
0
0
0
<f@)
1,01
1,06
1,03
1,02
1,07
1,06
1,10
1,10
1,12
1,14
1,15
0,15
q*(a/2)
1,15
1,29
1,21
1,20
1,24
1,25
1,33
1,33
1,35
1,38
1,40
1,40
<fEa/6)
1,68
2,26
2,12
2,10
2,05
2,10
2,32
2,33
2,34
2,39
2,41
2,43
р*
3,68
5,64
5,41
5,39
5,13
5,26
5,72
5,74
5,84
5,94
6,00
6,03
М
24
10
16
16
8
10
10
24
10
10
10
10
N
8
6
6
8
4
4
8
8
6
6
6
6
Наклонной образующей соответствуют таблицы 5.11 и 5.12, где
приводятся результаты для метода наименьших квадратов и метода
коллокаций соответственно.
Из таблиц видно, что метод коллокаций работает устойчиво только
на поверхностях, слабо отличающихся от канонических и при достаточ-
5.5. Некоторые выводы
221
Таблица 5.10
R
1,5
1,5
1,5
1,5
Ч>
0
0
0
0
q*@)
1,13
1,13
1,09
1,34*
q*(a/2)
1,37
1,36
1,32
1,82*
g*Ea/6)
2,31
2,29
2,33
3,76*
Р*
5,66
5,64
5,70
7,12*
N
4
6
8
8
Таблица 5.11
R
1,5
1,5
1,5
1,5
1,5
1,5
Ч>
0
10
20
0
10
20
q*@)
1,10
1,10
1,10
1,10
1,10
1,10
q*(a/2)
1,33
1,33
1,34
1,33
1,33
1,33
g*Ea/6)
2,32
2,36
2,41
2,33
2,37
2,41
Р*
5,72
5,80
5,86
5,74
5,81
5,85
М
10
10
10
24
24
24
N
6
6
5
8
8
8
Таблица 5.12
R
1,5
1,5
1,5
1,5
1,5
1,5
Ч>
0°
10°
20°
0°
10°
20°
д*@)
1,13
1,13
1,13
1,09
1,10
1,12
q*(a/2)
1,36
1,36
1,37
1,32
1,33
1,38
g*Ea/6)
2,29
2,31
2,36
2,33
2,39
2,45
Р*
5,64
5,76
5,88
5,70
5,75
5,91
N
6
6
6
8
8
8
но малом количестве точек коллокаций. Область применения метода
наименьших квадратов несколько шире. Эти подходы могут с успехом
применяться для быстрого получения приближенного решения.
5.5. Некоторые выводы
Как показано в этой главе, следы однородных решений на кривых,
отличных от координатных, обладают худшими аппроксимационными
свойствами, чем на координатных кривых, что не позволяет эффек-
эффективно использовать метод коллокаций, который в этом случае весьма
неустойчив. Метод наименьших квадратов и вариационные методы
требуют существенных затрат на вычисление интегралов по боковой
поверхности. Кроме того, при их использовании возникают острые
всплески невязки, имеющие тот же порядок, что и решения, но малы
по среднеквадратичной норме и не влияют на интегральные параметры
222 Гл. 5. Контактные задачи для тел конечных размеров
задачи, однако нарушают физическую картину вблизи границы. В этой
ситуации наиболее эффективно работают методы Ремеза наилучшего
равномерного приближения. Достоинство метода Ремеза в том, что для
получения приемлемого приближения требуется одна-две итерации.
В случае задачи наилучшего приближения на нескольких отрезках
можно использовать модифицированный метод Ремеза первого рода,
однако, здесь для этой цели использовался альфа-алгоритм Ремеза как
более простой в реализации. Такой подход позволяет контролировать
погрешность удовлетворения краевым условиям, требует привлечения
малого количества однородных решений для получения численного
решения задачи с приемлемой точностью, что обуславливает высокую
численную эффективность и надежность всей схемы в целом.
Другая трудность, возникающая при решении контактных задач ме-
методом однородных решений, — получение эффективных выражений для
неоднородных решений, используемых при удовлетворении смешанным
краевым условиям. Для этой цели использована хорошо разработанная
теория для полубесконечных тел. В отличии от классического случая,
получаемые интегральные уравнения в правой части содержат осцил-
осциллирующие функции. Для их решения предложен эффективный метод,
основанный на известных спектральных соотношениях и методе Ре-
Ремеза. Основываясь на специальном представлении решения интеграль-
интегрального уравнения, в соотношениях для неоднородного решения плохо
сходящаяся часть интегрируется, что позволяет получить соотношения
удобные для численной реализации. Результаты исследований, приве-
приведенные в этой главе, показали, что метод однородных решений являет-
является удобным и эффективным средством решения контактных задач для
тел, достаточно сильно отличающихся от канонических.
Глава 6
КОНТАКТНЫЕ ЗАДАЧИ ДЛЯ ТЕЛ
ПЕРИОДИЧЕСКОЙ СТРУКТУРЫ
В этой главе приводятся результаты, полученные при исследовании
стационарных задач о возбуждении штампом колебаний в полуогра-
полуограниченных телах (волноводах) в форме кругового цилиндра и полосы
с периодически изменяющимися механическими свойствами вдоль про-
продольной координаты. Отрезок рассматриваемых волноводов, соответ-
соответствующий минимальному периоду изменения механических свойств,
может состоять из любого количества однородных областей (конечные
цилиндры или прямоугольники) различной длины с различными упру-
упругими постоянными [92-96, 100, 320, 334, 341].
Для исследования этих задач был разработан эффективный метод,
основанный на теории Флоке-Ляпунова [185] и связанный с построе-
построением специального «оператора перехода», который позволяет по значе-
значениям вектора перемещений и тензора напряжений на одном попереч-
поперечном сечении волновода находить их значения на другом поперечном
сечении, отстоящем от первого на расстоянии, равном величине ми-
минимального периода изменения свойств волновода. С помощью этого
метода удалось получить ряд результатов, связанных с особенностью
распространения колебаний в таких волноводах. Показано, например,
что для таких волноводов на всем бесконечном интервале изменения
частот существуют чередующиеся конечные интервалы, когда колеба-
колебания в волноводе при удалении от источника затухают (волновод за-
заперт) или распространяются (волновод открыт) соответственно. Кроме
того, на интервалах затухания амплитуда колебаний тяжелого штампа
может неограниченно возрастать, т. е. могут существовать В-резонан-
сы [90]. Отметим, что открытие резонансов в полуограниченных телах
было сделано И. И. Воровичем, и поэтому они получили название В-ре-
зонансов.
224 Гл. 6. Контактные задачи для тел периодической структуры
6.1. Колебания струны периодической структуры
На простейшем модельном примере изложим подход к решению
задач для тел, имеющих периодическую структуру своих механических
и геометрических свойств, когда характер приложения внешних воз-
воздействий не носит периодического характера, и приведем некоторые
типичные результаты исследования таких задач. Статическая задача
такого типа для кольца уже рассматривалась в п. 3.3.3. Здесь предла-
предлагается другой подход.
Рассмотрим задачу Pq о колебаниях бесконечной периодической
струны, лежащей на винклеровском основании. Пусть в каждом пери-
периоде струны содержатся два участка длины / разной плотности, соот-
соответственно р\ и р2- Пусть а и Ь — координаты левого и правого концов
отрезка струны длиною в один период, а с (а < с < Ъ) — точка смены
плотностей (с — а = b — с = I).
Дифференциальное уравнение колебаний струны с постоянной
плотностью pi (г = 1 или 2) можно представить в виде
Тихх = piUU -ku, F.1)
где Т — натяжение струны, и — ее смещение в перпендикулярном
направлении, к — коэффициент постели винклеровского основания.
Рассматривая установившиеся колебания, обозначим
и(х, t) = v(x) exp (Iut),
здесь и далее / — мнимая единица. Предположим, что при х = а
известны смещение и производная от него
v(a) = (ра, v'(a) = фа. F.2)
Найдем величины v(b) и vf(b), для чего последовательно решим задачу
Коши F.1), F.2) при г = 1 и аналогичную задачу при г = 2, когда
начальные условия типа F.2) заданы при х = с.
В результате получим, что
где \х — вектор с двумя компонентами v(x) и v'(x), а Ф = {а^/} —
матрица второго порядка с компонентами
аи = cos 77i cos 772 — — sin 771 sin 772,
a\2 = ^2 cosr?i sin772 + xj sin771 cos772,
G&21 = —>t\ sin 771 cos 772 — щ sin 772 cos 771,
a22 = sin 771 sin 772 — cos 771 cos 772,
где r]i = щ1, щ = \/(uo2pi - k)/T.
6.2. Динамическая контактная задача для полосы периодической 225
Найдем собственные числа матричного оператора Ф:
XU2=P±Vp2- 1, А1Л2 = 1, F.3)
р = cos 771 cos r]2 — - ( — + 772^71 ) sin 771 sin 772 •
Если ввести безразмерные параметры
то собственные числа А^ (г = 1, 2) будут функциями от этих параметров
в соответствии с F.3), где rj\ и щ примут вид
Нетрудно заметить, что при фиксированных значениях параметров pif
ко с увеличением приведенной частоты г] выражение р2 — 1 будет
бесконечное число раз менять знак, а собственные числа при этом
будут переходить из комплексной области на действительную прямую
и наоборот.
Произведение собственных чисел, как следует из F.3), равно еди-
единице. Пусть действительные |А!| ^ 1, |А2| ^ 1. Из физических сообра-
соображений рассматриваем только собственное число А1. Комплексные же
собственные числа будут находиться на единичной окружности. Таким
образом, действительным числам будет соответствовать уменьшение
амплитуды колебаний при переходе от точки а к точке Ь, а комплекс-
комплексным — ее неизменность.
Из проведенного анализа следует вывод: волновод в виде беско-
бесконечной периодической струны, лежащей на винклеровском основании,
имеет счетное число чередующихся непересекающихся интервалов ча-
частот Одп и Осп, уходящих в бесконечность, когда он соответственно
заперт и открыт.
В случае, когда р = 1 (однородный волновод), rj\ =772,
Следовательно при rf < ко имеем р2 > 1, а при rf2 ^ ко имеем р2 ^ 1.
Получаем известный результат: при г]2 < ко волновод закрыт, а при
г]2 ^ ко волновод открыт.
6.2. Динамическая контактная задача для полосы
периодической структуры
В этом параграфе рассмотрена задача Р\ теории упругости об уста-
установившихся антиплоских колебаниях штампа на поверхности полосы
с продольной кусочно-однородной периодической структурой механи-
8 В.М. Александров, М.И. Чебаков
226 Гл. 6. Контактные задачи для тел периодической структуры
ческих характеристик. Метод решения задачи как и в предыдущем
параграфе основан на построении оператора переноса значений функ-
функций напряжения и перемещения с одной грани периода на другую
и изучении его собственных чисел и функций. Здесь также показано,
что для рассматриваемого волновода существуют чередующиеся про-
промежутки на интервале изменения частоты вынужденных колебаний,
когда волновод соответственно открыт или заперт, т. е. когда амплитуда
колебаний вдоль продольной координаты соответственно остается по-
постоянной или уменьшается. Кроме того, показано также, что на проме-
промежутках запирания волновода существуют В-резонансы, т. е. амплитуда
колебаний массивного штампа, закрепленного на полосе при конечных
нагрузках становится бесконечной.
Рис. 6.1. К задаче Р\
6.2.1. Постановка задачи. В прямоугольной системе координат
рассмотрим полосу 0 ^ у ^ h, —оо < х < оо. Пусть область полосы
\х\ ^ xq имеет модуль сдвига G, плотность р, а области хп + kL < х <
< хп+\ + kL (п = 0, 1, 2,..., т — 1; к = 0, 1, 2,..., оо) имеют соответ-
соответственно модули сдвига Gn и плотность рп. Обозначим хп+\ — хп = 1п,
хш — xq = L, L — период изменения свойств полосы вдоль продольной
координаты х влево и вправо соответственно от точек х = — xq и х =
= — xq. Далее пусть на поверхности полосы у = h в области \х\ ^ а
закреплен штамп, совершающий вдоль оси z гармонические колебания
с частотой и под действием сдвигающей силы Pq = Pexp (—loot). Пусть
поверхность полосы вне штампа свободна от напряжений, а поверх-
поверхность у = 0 неподвижна (рис. 6.1).
Следует отметить, что с точки зрения применяемого здесь метода
исследования период может состоять из произвольного числа областей,
имеющих различные константы.
Поставленная задача теории упругости может быть сведена к иссле-
исследованию уравнения Гельмгольца с периодическими коэффициентами G
и р
GAw + puo2w = 0
со следующими граничными условиями
w = 0 (y = 0),
w!y = 0 (у = h, \х\ > a), w = 5 (у = h, \x
F.4)
6.2. Динамическая контактная задача для полосы периодической 227
где wexp(—loot) — упругие перемещения вдоль оси z, 5ехр(—loot) —
перемещение штампа. Чтобы избежать рассмотрения уравнений Ламе
с переменными коэффициентами [348], используем изложенный выше
метод, который можно назвать методом переходных операторов, и ко-
который основан на построении специального оператора, позволяющего
по известным перемещениям и напряжениям при х = xq находить их
при х = х\, а, следовательно, и при х = хп, (п = 2,4,...), учитывая
периодическое строение полуполосы х ^ xq. В дальнейшем проблема
заключается в удовлетворении условиям на бесконечности и сопряже-
сопряжении решений, обладающих некоторым произволом, для областей \х\ ^
^ xq и \х\ ^ xq на границах х = ±#о-
6.2.2. Построение оператора перехода. Рассмотрим для одно-
однородной области 0 ^ у ^ h, х > xq задачу Коши для уравнения Гельм-
гольца:
GiAw + piuo2w = 0,
w = 0 (y = 0), wfy=0 (y = h), F.5)
w = Wi(y), г = GiWrx = n(y) (x = Xi),
где i = 0, Wi(y)exp(—Iu;t), Ti(y)exp(—Icdt) — соответственно переме-
перемещения и касательные напряжения в сечении х = Х{. Требуется опре-
определить значения напряжений и перемещений при х > xq. Используя
соответствующие однородные решения для полосы, получим
А
F.7)
Соотношение F.6) позволяет по заданным значениям напряжений
и перемещений при х = Xi находить их при любом х > Xi, в том числе
и при х = #г+1- Перепишем соотношения F.6) при х = Жг+ь получим
jt)dt, F.8)
fc=0 о
iG«*)-'*"V<). F9,
\-Gia\sina\li cosa\h )
Если теперь рассмотреть задачу F.5) при г = 1 для области 0 ^
у ^ h, х ^ х\, то Wi(?/) и т\(у), найденные на основе F.6), F.7)
228 Гл. 6. Контактные задачи для тел периодической структуры
или F.8), F.9) при г = 0, будут известны и аналогично будет построен
оператор F.6), F.7) и F.8), F.9) при г = 1, позволяющий также по
заданным напряжениям и перемещениям при х = х\ находить их при
х > х\. Дальнейшее многократное применение оператора F.8), F.9) со-
соответственно при г = 0, 1,..., (га — 1) дает возможность «перебросить»
граничные условия с х = xq на х > хш. После ряда преобразований
искомый оператор перехода Ф можно записать в виде
2 °° 7 ~m. . F10)
fc=O
где Ф^ — матрица второго порядка
С= П А?. F.11)
п=т— 1
В случае га = 2 элементы а^- матрицы Ф^ определяются из соотно-
соотношений
k 9 1 G\QLb. . о . 1
af! = cos т^ cos ry^ 1 sin щ sin ry^,
С2а/е
/с 1 2-1,1.2 1
a 12 = Г cos Vk sin % + 2~ sin % C0S ^k'
C2afc F12)
a = ^2<^I sinr?i cosrlk — G\a\, cost?): sinry^,
a2i = ~
Вид оператора Фт при га = 2 не изменяется при перестановке па-
параметров G\, p\, 1\ и G2, P2, h, точно так же он не изменится при
любом значении га при циклической перестановке параметров Gi, pi,
U (г = 0, 1,...,(га-1)).
Таким образом, если известны значения перемещений и напряже-
напряжений при х = xq, они могут быть найдены в любой точке области х > xq
с помощью операторов F.6), F.7) и F.10), F.11).
Чтобы в дальнейшем использовать представление напряжений и пе-
перемещений на границах х = хт+пь (п = 0, 1, 2,...) в виде разложений
по собственным функциям оператора F.10), найдем его собственные
числа.
6.2. Динамическая контактная задача для полосы периодической 229
6.2.3. Исследование собственных чисел. Используя представле-
представление единичного оператора в виде
Т, , 2^ . f . /10
1(. ..) = — 2_^ sin х/е?/ sm х^т 1(...) ат, 1 = I ^ ,
к=о о ^
из соотношения Ф а = Аа, где а — произвольный вектор, получим
оо h
г = 0. F.13)
к=0 о
И тогда условие для нахождения собственных чисел примет вид
Ф^ - А1| =0 (fc = 0, 1,2,...)
или
Отсюда
= 0 (А; = 0,1,2,...), 2рк=акп
А = Рк ± \/р1 - 1 •
При m = 2 получим
2pfc = 2 cos T]l cos т]°к -
F.14)
F.15)
F.16)
что по форме совпадает с аналогичными соотношениями F.3) для
струны на винклеровском основании. _
При получении F.14) учтено, что определители матриц AJJ, а соот-
соответственно и матриц Ф^ , равны единице.
Нетрудно показать, что рк — действительные числа. На рис. 6.2
в зависимости от приведенной частоты О = у7'puj2h2/G приведен
график изменения ро ПРИ следую-
следующих значениях параметров: h/a = 10,
Gi/Go = 4, pi/po = 2, lo = h = 1,5a.
Другие числа рк ведут себя сходным
образом, при этом первый участок
монотонности (убывания) с ростом к
увеличивается.
Обозначим через Aj. и А| пары кор-
корней возвратного уравнения F.14) для
каждого к, при этом Aj.A| = 1. Соб-
Собственные числа условно можно раз-
разделить на две группы: 1) |А^| ф 1
и 2) |А^| = 1, в зависимости от частоты и номера к. При этом все
комплексные собственные числа находятся на единичной окружности.
Будем считать, что в первой группе |А|.| < 1, а |А|| > 1.
1
-1
Рис. 6.2
230 Гл. 6. Контактные задачи для тел периодической структуры
Рис. 6.3
На рис. 6.3 схематически на комплексной плоскости изображены
линии перемещения собственных чисел в зависимости от изменения
частоты. Сплошная линия соответствует случаю, когда в F.15) взят
плюс, а пунктирная — минус.
Проведен детальный аналитический и численный анализ чисел AJJ
в зависимости от частоты ш, номера к и числа т однородных областей
с различными свойствами в периоде. Уста-
Установлено существование интервалов Одп
изменения частоты и, где все \Х%\ ^ 1,
и существование интервалов Qcn, где есть
хоть одно |А^| = 1. Если предположить,
что волновое поле может быть представле-
представлено в виде ряда по собственным функциям
оператора перехода Фт, то тогда на про-
промежутках uRn колебания в волноводе при
удалении на бесконечность будут затухать
(волновод заперт), а на промежутках псп
будут присутствовать незатухающие моды (волновод открыт). Так как
flRn и flcn чередуются, то и полосы запирания и пропускания волно-
волновода будут чередоваться. Таким образом, имеем «полосатость» полосы
пропускания, которая была отмечена ранее для слоистых областей типа
полуплоскости в [157, 185] и др. Непересекающихся промежутков Одп
не менее двух, если весь волновод не является однородным.
Введем в рассмотрение удобную для интерпретации результатов
функцию
f(u) = {1, если oj е Одп; — 1, если и; е &сп}-
Когда /(О) = 1, волновод заперт, а когда /(О) = — 1, волновод от-
открыт.
Были проведены расчеты собственных чисел операторов типа Фт
для некоторых значений безразмерных параметров волноводов G*j =
= Gj/Go, р* = Pj/po, lj = lj/h U — 0> l,...,m — 1). На рисунках
6.6-6.14 приведены графики функции /(О) (О < 5) для аналогичной
задачи о крутильных колебаниях кругового цилиндра, рассмотренной
в § 6.3. Здесь они будут выглядеть схожим образом, с той лишь разни-
разницей, что график функции /(О) в окрестности п = 0 равен единице.
Если Go = G\ = ... = Gm_i и ро = Р\ = ••• = Рт-и то существует
такое ио = Ukp, когда при и < иокр все А^ — действительны, а при
ио > uokp — комплексны (ukp — частота «отпирания» однородного вол-
волновода).
Анализ результатов расчета показал: 1) для кусочно-однородных
волноводов в виде полосы всегда существуют чередующиеся интервалы
Uru (волновод заперт) и псп (волновод открыт), п > 2 (однород-
(однородный волновод открыт при и ^ uJkp т^ 0); 2) характер распространения
колебаний в волноводе качественно сходен, если один из парамет-
параметров G или р не изменяется, а другой изменяется по тому же закону;
6.2. Динамическая контактная задача для полосы периодической 231
3) чем больше скачок изменения G или р в соседних однородных
участках волновода, тем большей длины появляются интервалы flRn;
4) с увеличением длины более жесткого или более плотного однород-
однородного участка волновода интервалы Одп появляются при более низкой
частоте; 5) с увеличением частоты число интервалов uRn и их длина
уменьшается.
Таким образом, на основе проведенных числовых экспериментов и с
учетом сделанных выше выводов можно выбрать волновод с заданными
заранее свойствами.
6.2.4. Условие на бесконечности. Собственные функции опе-
оператора перехода, как уже было отмечено и для собственных чисел,
можно разделить на две группы: соответствующие действительным
собственным числам и комплексным. Ко второй группе отнесем и те,
когда собственные числа кратны и равны ±1. Используя представление
перемещений и напряжений через собственные функции оператора пе-
перехода, для выполнения условия на бесконечности (\х\ —> оо) в первой
группе собственных функций следует естественно исключить те, ко-
которые дают растущую амплитуду, т. е. соответствующие собственным
числам \\ (|А|| > 1).
Для отбора собственных функций из второй группы используем
принцип фиктивного поглощения. Если ввести в среду малое внутрен-
внутреннее трение, пропорциональное е > О, то в дифференциальном уравне-
уравнении F.5) uJ1 необходимо заменить на uj\ = uJ1 + Ieuj [89]. Соответствен-
Соответственно в результате этого собственные числа оператора перехода получат
малое возмущение. Обозначим их через \^{е).
Заменяя в F.14)—F.15) и2 на uj\ при малых г и \р^\ < 1, когда
собственные числа невозмущенного оператора перехода комплексны,
получим
F.17)
Отметим, что знаки ± в F.17) соответствуют аналогичным знакам
в F.15).
Из F.17) видно, что при введении малого трения модуль одного
собственного числа уменьшается (|А|.(?)| < 1), а другого увеличивается
(|А|(?)| > 1) в соответствии со знаком числа q^. Таким образом, одно
собственное число смещается во внутрь единичного круга, другое (ком-
(комплексно сопряженное) — во внешность. Схематически это изображено
на рис. 6.3.
Таким образом, при удовлетворении условию на бесконечности сле-
следует исключить из рассмотрения те собственные функции оператора
перехода, которые при введении трения соответствуют |А|(г)| > 1.
В соответствии с этим для комплексных собственных чисел обозна-
обозначим AJJ = ИтХ^(г) (п= 1,2) при г —> оо.
232 Гл. 6. Контактные задачи для тел периодической структуры
В случае, когда \к = 1,
А*(е)«1±>/^A-/) (qk> 0,е^0),
)
F.18)
Afe(e) « 1 ± >/=i<fc A + /) fe < 0, г -+ 0).
Здесь также одно собственное число смещается во внутрь единич-
единичного круга, другое — во внешность (см. рис. 6.3). Поэтому при отборе
в этом случае следует взять одну собственную функцию, соответству-
соответствующую А/с = Aj. = 1. Аналогично следует поступить и при Хк = — 1.
Представление решения в области \х\ > х$. Соотношение F.13)
при х = хо перепишем в виде
($fc-AI)bfc=O (A; = 0,1,...)» F-19)
1
о
Так как определитель системы F.19) равен нулю, найдем
4s
«22
F.21)
гДе Чш = hm при А = А^ (п = 1,2).
Последнее позволяет с учетом свойств собственных функций опе-
оператора перехода найти представление функций и(х,у) и т(х,у) в обла-
областях хо + sL ^ х < х\ + sL (s = 0, 1,...). Получим
n=\k=0
n=lfe=0
F.22)
Ъпы (х) = Dfcn(exp (IalO + PI exp (-Ia
bnk2{x) = IoPkGxDkn{^V (HO ~ К exp (-
= x — xq — sL.
В соответствии с принципом предельного поглощения в F.22) сле-
следует оставить слагаемые, соответствующие Aj., для чего необходи-
необходимо Dk2 = 0.
Тогда из F.22) при х = xq получим
6.2. Динамическая контактная задача для полосы периодической 233
w(xo,y) =
r(xo,y) =
оо
сю
sin xky,
F.23)
k=0
oxoJIaoGo/(Ia°Go + al
Ek = exp (IaokxoJIaokGo/(Ia°kGo + alk),
где постоянные
\х
определятся из условия сопряжения областей
xq и х ^ xq. Операторы F.10)—F.12) позволят, используя F.22),
F.23), легко найти перемещения и напряжения в любой точке обла-
области X ^ Xq.
6.2.5. Построение интегрального уравнения. Рассмотрим об-
область \х\ ^ xq. Решение в ней представим в виде суперпозиции со-
соответствующих однородных решений для полосы и решения задачи
для полосы, когда в области \х\ ^ а на грани у = h заданы касатель-
касательные напряжения rxz подлежащие затем определению из интегрального
уравнения. Получим
w = wq(x, y) = wH\x, y) + ^2 Ak sin кку cos oPkx,
k=0
н
Здесь rxz(x,h,t) = q(x)exp(—Iut), (\x\ ^ a), Ak — неизвестные по-
постоянные, подлежащие определению из условия сопряжения областей
\х\ ^ xq и х ^ xq, контур интегрирования а в комплексной плоско-
плоскости совпадает с положительной действительной полуосью всюду за
исключением конечного числа действительных полюсов функции L(u)
(см. F.27)), которые он обходит снизу [89].
Используя соотношения F.23) и F.24), удовлетворим условию
непрерывности перемещений и напряжений при х = xq.
, у) = wo(y),
Go-^wo(x,y)
= то(у).
F.25)
Из последнего соотношения, учитывая ортогональность sin>cky на
отрезке @, h), найдем постоянные Dk и Ак. Подставляя найденное
значение Ак в F.24) и удовлетворяя последнему граничному усло-
условию F.4), получим интегральное уравнение основной поставленной
234 Гл. 6. Контактные задачи для тел периодической структуры
задачи
^ j ф)к (l^*) dt = S (|г|<1), F.26)
-1
if(t)=q(at),
Г th V/v? — О2
к\(у) = L(u)cosuydu, L(u) = — , F.27)
= Y,bkcosaky, ак = ^/П2-(тт(к+1/2)У, F.28)
^9 pto h л h
/ — /iaj. sin akl,
Bk2 = Gctfc sin akl + /iaj. cos од/.
Ядро интегрального уравнения F.26) состоит из двух слагаемых
к\(у) и к2(у), при этом к\(у) является ядром уравнения хорошо изу-
изученной аналогичной задачи для однородной полосы, к2(у) является
гладкой функцией и содержит информацию о периодической структуре
слоя,
Ьк = О((\/к) ехр (-2тгЫ)) (к -^ оо). F.30)
Решение интегрального уравнения F.26) может быть получено с
использованием широкого спектра методов, в том числе изложенных
в работах [23, 88] и др. Здесь используем метод больших Л [23]. Ядро
уравнения F.26) представим в виде
к(у) = - In \y\ + a20 + In \y\Fi (у) + F2(y),
оо С6 ЗП
ВД = ? од/2* (г =1,2).
к=\
Для получения разложения F.31) достаточно к\(у) представить в виде
fei (у) = \ (ПоЩ - Щ(Пу)) + J th ^?~^2~ ~ cos ty dt, F.32)
где Jo (ж), Щ(х) — функции Бесселя, а степенные ряды для cos оду
и cost?/ подставить соответственно в F.28) и F.32) и изменить порядок
суммирования в F.28), а в F.32) — суммирования и интегрирования.
Получим
6.2. Динамическая контактная задача для полосы периодической 235
а20 = io + So + irI/2 - С - In
a{k = {-\)k+\k\)-\u/2Jk, F.33)
a2fc = -oifc(Sfc + ttJ/2 - С - In (fi/2)) + (-l)fc(ife + Sk)/Bk)\,
OO
#fc= E bn(<*kJk, С = 0,577 215 66.
n=0
Следуя методу больших Л [23], решение интегрального уравнения
F.26)-F.28) может быть представлено в виде
u;(t) = Е Е ^fcn WA-fc lnn A, F.34)
k=0 n=0
где [k/2] — целая часть от числа к/2, Ukn(t) ~ функции, определяемые
из рекуррентных соотношений [23]. Считая параметр Л достаточно
большим, ограничимся в разложении F.34) членами порядка не выше
О(А~41п Л). В этом случае будем иметь
^оо = /о~1(Л)' ^ю = 0, и;зо=О, a;3i = 0,
^20 = Г1(\)(апA,5 - In2) + a3i)(l - 2t2),
^21 = -/0-1(А)а11A -2i2),
/о(А) = а30 + (азг + an)A + lnBA)(l - ацЛ
F.35)
Соотношения F.34), F.35) позволяют проанализировать решение
поставленной задачи для относительно больших толщин рассматрива-
рассматриваемой полосы (Л > 2) [23, 88].
6.2.6. Исследование 1?-резонансов. Если рассматривать колеба-
колебания массивного штампа, то, как отмечено в работе [97], для одно-
однородного волновода в интервале @,0^), где О^ частота отпирания
волновода, может наступить неограниченное возрастание амплитуды
колебаний штампа, т. е. возникнет Б-резонанс. Ниже будет показано,
что в рассматриваемой задаче для периодической кусочно-однородной
полосы эти резонансы возникают на тех интервалах частот, где вол-
волновод заперт, причем такие интервалы чередуются с интервалами, где
волновод открыт и нет Б-резонансов. Размеры и расположение этих
интервалов зависят от механических свойств и геометрии волновода.
Из уравнения колебаний штампа массы то под действием гармо-
гармонически меняющихся усилий с равнодействующей Pexp(-Iu)t), имею-
имеющего вид [97]
236
Гл. 6. Контактные задачи для тел периодической структуры
-т*П25 = R-5T,
га* =
T = ip(t)dt,
F.36)
-i
следует, что Б-резонансы будут иметь место, если
га* = ТО
и Т действительно.
Покажем, что на интервалах запирания волновода величина Т яв-
является действительной и, таким образом, если Т > О, найдется такая
масса то, что возникает Б-резонанс.
Рассмотрим представление ядра интегрального уравнения F.26)
в виде F.27), F.28). Пусть р2п < п2 < р2п+х (п = 1,2,...), Рп =
= тг(п — 1/2). Тогда подынтегральная функция в F.27) имеет на поло-
положительной части действительной оси полюса qk = a& и, следовательно,
мнимую часть функции к\(у) дадут полувычеты этой функции.
Найдем
где lm(x) — мнимая часть х.
Если предположить, что значение О лежит в интервале запирания
волновода, то ряд F.28), F.29) будет содержать га комплекснозначи-
мых членов, тогда как остальные его члены будут иметь действитель-
действительные значения. Вычисляя мнимую часть функции к2(у), получим
1т(к2(у)) = —Im(fci (?/)).
При О < тг/2 функции кг(у) (г = 1,2) действительнозначны.
Таким образом, если О принадлежит интервалу запирания, то ядро
к (у) интегрального уравнения F.26) действительнозначно и, следо-
следовательно, действительнозначной бу-
будет и величина Т, если решение
уравнения F.26) единственно. На
других частотах величина Т имеет
комплексные значения.
Используя решение F.34), F.35),
найдем
1,8
О
\
ч
1
V
= тг/0-1(А). F.37)
0.8
3,2
Рис. 6.4
Численный анализ выражения
F.37) подтверждает изложенные вы-
выше выводы. В предельном переходе
к однородному волноводу численные результаты совпадают с соответ-
соответствующими результатами работы [97]. На рис. 6.4 дана зависимость
безразмерной массы от безразмерной резонансной частоты О при следу-
6.3. Динамическая контактная задача для цилиндра
237
ющих значениях параметров: т = 2, Л = 5, Gq/G = 4, G\ = G, pi = p,
po/p = 8, lo = l\ = 2a, xo = 1,5a.
Расчет показывает, что путем соответствующего подбора парамет-
параметров периодического волновода можно управлять его волнопроводящими
и резонансными свойствами.
6.3. Динамическая контактная задача для цилиндра
периодической структуры
Рассмотрим осесимметричную стационарную контактную задачу
теории упругости Р% о возбуждении жестким бандажом крутильных
колебаний в круговом бесконечном цилиндре (см. рис. 6.5). В цилин-
цилиндре задано периодическое изменение механических свойств вдоль оси,
в поперечном направлении эти свойства не изменяются. Отрезок вол-
волновода, соответствующий минимальному периоду изменения свойств,
может состоять из любого количества однородных областей (конечных
цилиндров) с различными механическими параметрами.
6.3.1. Постановка задачи. Пусть область \z\ < zq цилиндра г <
< R (r, (p, z — цилиндрические координаты) имеет модуль сдвига G,
плотность р, области zn + kL < \z\ < zn+\ + kL, (n = 0, 1,..., m —
— 1; k = 0, 1,..., oo) имеют соответственно модули сдвига Gn и плот-
плотность рп, а zn+\ — zn = ln, при этом L = zm — zq — период изменения
механических свойств цилиндра вдоль продольной координаты z влево
и вправо соответственно от точек z = — zq и z = zq. Далее пусть на
поверхности \z\ ^ а < zo, r = R закреплен бандаж, который совершает
крутильные колебания вокруг оси z под действием момента Mq =
= Me~iu;t.
Рис. 6.5. К задаче Р^
Схема решения поставленной задачи та же, что и в задаче для
периодической полосы, рассмотренной в предыдущем разделе.
Построение оператора перехода. Рассмотрим часть цилиндра при
z ^ zq. Угловые перемещения v(r,z,t) удовлетворяют уравнению
1 ,г , ~2т,
v(r, z, t) = V(r,
а2 =
F.38)
238 Гл. 6. Контактные задачи для тел периодической структуры
где G — модуль сдвига, р — плотность, ио — частота колебаний,
А — оператор Лапласа. Пусть на поверхности цилиндра отсутствуют
напряжения, а на плоской поверхности z = zq будем считать извест-
известными касательные напряжения rzip и перемещения v. Требуется найти
напряжения и перемещения на поверхности z = zm. Иными словами,
требуется построить соответствующий оператор переноса и изучить
некоторые его свойства. Приходим к задаче типа Коши для уравне-
уравнения F.38) при следующих граничных условиях:
V = V0(r), G0V^ = r0(r) {z = z0), F.39)
V'--V = O (r = R). F.40)
r
Отметим, что в F.38) a — кусочно постоянная функция координа-
координаты z
a(z) = an (zn^z < zn+\, 0 < п < га), а2п = pnuj2G~x. F.41)
Используя однородные решения задачи F.38), F.40) и условие их
ортогональности, нетрудно найти напряжения и перемещения в цилин-
цилиндре при zq ^ z ^ z\. По аналогии с предыдущим разделом, это можно
записать в операторной форме. Теперь, зная напряжения и перемеще-
перемещения на поверхности z = z\, получим задачу, аналогичную F.38)-F.40),
в которой условие F.39) следует заменить на условие
V = Vi(r), GiVZ = n(r) (z = z{), F.42)
где
Vn(r) = V(r, z^, тп(г) = rZip(r, zn). F.43)
Задачу F.38), F.40), F.42) решаем аналогично задаче F.38)-F.40).
И так далее, находя каждый раз значения напряжений и перемещений
на поверхностях z = zn, находим решение задачи в области zn ^ z ^
< zn+\ @ < п < га- 1).
Опуская выкладки, выпишем в операторной форме значения
Vn+\(r), rn_|_i(r) через значения Vn(r), тп(г) @ ^ п ^ га — 1)
Ъп+1(г) = 2^^ А*\ Mt)bn(t)tdt F.44)
fc=o k о
Здесь Ъп(г) и А^ — соответственно вектор и матрица
Уп{г)\ ln=( coso#*n (Спапк)-[зшарЛ
тп(г))' к \-Gna%8iaapn cosa%ln )'
F.45)
() () () () ?
^к = V 4 - "к '
6.3. Динамическая контактная задача для цилиндра 239
где щ = О, а при к > 1 х& — положительные корни уравнения
J^^kR) = О, Л (г) — функция Бесселя.
Если необходимо знать значения напряжений и перемещений при
zn < z < zn+\, достаточно в формулах F.44)-F.48) 1п заменить
на (z-zn).
Используя F.44), F.45), нетрудно теперь выразить b (r) че-
через b (r):
Ь>) = Фт(ь\т)),
оо R
*m(-) = 2E^*nifc(r)(-)rdr' F-46)
k=0 о
*fc = П Ak- F-47)
n — jYl— I
— матрица второго порядка
Таким образом, построен искомый оператор переноса значений
напряжений и перемещений с одной границы периода на другую.
Свойства рассматриваемого волновода будут определяться свойствами
построенного оператора Фт, в том числе и его собственными числами.
Следуя схеме предыдущего раздела, можно показать, что собствен-
собственные числа Л оператора Фт есть собственные числа матриц Ф^ , т. е.
являются корнями квадратных уравнений
\\ - 2ХкРк +1=0, F.48)
где 2pk = (а\х + а|2), a a\x и а\2 — элементы матриц Ф& = {а^}.
При получении формулы F.48) учтено, что определители матриц
AJJ, а соответственно и матриц Ф^ равны единице.
В случае, когда т = 2, Ф& = А\ • А°к и
= cosa{h cosa% - \ (^ + ^4) smalkh ыпа%. F.49)
Выше ^было отмечено, что если собственные числа Л^, (г = 0, 1)
матрицы А^ действительны и не равны единице, то соответствующие
им однородные колебания в волноводе затухают вдоль продольной
координаты, а если собственные числа равны единице или комплексны,
то соответствующие им однородные колебания будут распространять-
распространяться не затухая. Заметим, что А^Л^ = 1. Для случая т = 2 в рабо-
работах [92, 329] также показано, что существуют интервалы изменения
частоты и;, когда все Л^ (к ^ 0) действительны и не равны единице.
Следовательно на этих интервалах в целом колебания будут затухать.
Такие интервалы могут чередоваться с интервалами, где хотя бы при
одном значении к соответствующие собственные числа Л^ комплексны
или равны единице и, следовательно, на этих интервалах соответ-
240 Гл. 6. Контактные задачи для тел периодической структуры
ствующие однородные колебания будут распространяться с постоянной
амплитудой в точках продольной оси, отстоящих друг от друга на
расстоянии, равном значению периода.
Рассмотрим случай, когда т произвольное число, что представляет
самостоятельный интерес, и в тоже время это может быть предложено
в качестве аппроксимации непрерывного изменения упругих постоян-
постоянных волновода вдоль продольной координаты.
Введем безразмерный параметр п (п2 = R2co2poGq1), связанный
с частотой и;, и, как это было сделано в § 6.2, удобную для графи-
графической интерпретации результатов функцию /(О), характеризующую
некоторые свойства рассматриваемых волноводов с параметрами га, pj,
Gj, lj, R (j = 0, 1,..., (га — 1)) и определяемую следующим образом:
/(О) = 1, если собственные числа определителя матрицы F.47) все
действительны и не равны единице, и /(О) = — 1, если последнее усло-
условие не выполняется. Построенная таким образом функция характери-
характеризует проводимость волновода. На тех безразмерных частотах О, когда
= 1, колебания в волноводе затухают (волновод «заперт»), а когда
= — 1, колебания в волноводе распространяются с незатухающей
амплитудой (волновод «открыт»).
Были проведены расчеты собственных чисел определителей мат-
матриц F.47) и построены графики функций /(О) (О2 = R2uo2pqGqX) для
большого числа вариантов рассматриваемых волноводов с различными
безразмерными параметрами G!- = Gj/Gq, p*j = Pj/po, Ц = Ij/Iq, (j =
= 0, 1,..., га — 1). Некоторые результаты построения функций /(О)
в зависимости от О приведены на рисунках 6.6-6.14. Отметим, что
если в подрисуночных подписях не приведены значения некоторых
параметров, это означает, что они равны единице.
Из анализа результатов расчетов можно сделать следующие ос-
основные выводы: 1) если однородный цилиндрический волновод всегда
«открыт», то как только параметры волновода становятся кусочно-
однородными, сразу начинают появляться частоты, при которых вол-
волновод «закрывается»; 2) качественный вид функции /(О) сходен, если
один из параметров G или р не изменяется, а другой изменяется по
одному и тому же закону; 3) чем больше скачок изменения G или р
в соседних однородных участках, тем большей длины появляются
интервалы, где волновод «закрыт» (сравни рис. 6.6-6.7,6.9-6.10 и др.);
4) с увеличением более жесткого или плотного участка интервалы
частоты, где волновод «закрыт», появляются при более низкой частоте
(сравни рис. 6.7-6.8); 5) с увеличением частоты число интервалов и их
длина, где волновод «закрыт», уменьшается.
Таким образом на основе проведенных числовых экспериментов
в том числе и с учетом сделанных выше выводов можно выбрать
волновод с заданными заранее свойствами на определенных частотах
или определенных интервалах частот путем подбора его параметров.
6.3. Динамическая контактная задача для цилиндра 241
О 1
2 3
Рис. 6.6. т = 2, G* = 1, G2 = 32
h
О 12 3
Рис. 6.7. m = 2,Gt = l, G\ = 1,1
О 1
Рис. 6.8. т = 2, G? = 1, Go = 1,1, /* = 1, Г2 = 2
О 1 2 3
Рис. 6.9. т = 6, G* = 1, G| = 1,1, G3 = 1,2, GJ = 1,3, G*b = 1,4, Gg = 1,5
О
1
2
3
4
5
Рис. 6.10. т = 6, G* = 1, G2 = 2, Gl = 3, GJ = 4, G? = 5, Gl = 6
0
1
2
3
4
Рис. 6.11. m = 6, G\ = 1, G2* = 2, GJ = 4, GJ = 8, G^ = 16, GJ = 32
0
1
2
3
Л
5
Рис. 6.12. m = 6, G? = 1, Gl = 2,Gl = 8, Gl = 32, G? = 8, Gl = 2
0
1
2
3
4
5
Рис. 6.13. m = 4, G? = 1, G2* = 2, G? = 4, GJ =
rft
Рис. 6.14. m = 4, G* = 1, G2 = 2, G3 = 8, G4 = 2
242 Гл. 6. Контактные задачи для тел периодической структуры
6.3.2. Построение интегрального уравнения. Считая временно
известными контактные напряжения rr^ = tq{z) = r(z) exp(—loot) при
\z\ ^ а и г = R, получим краевую задачу для рассматриваемого цилин-
цилиндра, когда на его поверхности г = R при \z\ ^ а заданы касательные
напряжения to(z), а при \z\ > а поверхность свободна от напряжений.
Решение такой задачи сконструируем из двух частей, содержащих
неизвестные константы, которые будут определены из условия равен-
равенства напряжений и перемещений слева и справа от сечения z = zq.
Первую часть при \z\ < zq построим из суммы решения для беско-
бесконечного цилиндра с параметрами G и р, когда на его поверхности при
\z\ ^ а заданы касательные напряжения tq(z), а остальная поверхность
свободна от напряжений, и суперпозиции однородных решений для
этого цилиндра, когда его поверхность свободна от напряжений. В ито-
итоге для перемещения v(r,z,t) = V(r, z)exp(-Iujt) получим следующие
соотношения:
V(r,z) = VH(r,z) + V0(r,z),
V0(r,z) = J2 ckjk(r) cos akz.
k=0
Здесь введены следующие обозначения:
= 0,
х& (fc ^ 1) являются корнями уравнения J^in^K) = 0, Jn(x) — функции
Бесселя, а — контур интегрирования, который совпадает почти везде
с вещественной полуосью, обходя действительные положительные по-
полюсы подынтегральной функции снизу, а отрицательные — сверху.
Вторую часть решения при z ^ zq с периодически изменяющими-
изменяющимися свойствами построим, воспользовавшись выше приведенными ре-
результатами для кусочно-однородного цилиндра z ^ Zq с однородными
граничными условиями. Удовлетворяя условию на бесконечности, как
это было сделано для полосы в § 6.2, получим при z = zq + 0 для
перемещений и напряжений соответственно следующие соотношения:
оо оо л _ к
V(r, го) = Y, Dkjk(r)f3k, т{г, z0) = ? Dkjk(r), fa = ^^,
к=0 к=0 в21
F.51)
где Л/с являются собственными числами оператора перехода F.47).
6.3. Динамическая контактная задача для цилиндра 243
Теперь из условий равенства напряжений и перемещений слева
и справа при z = zq найдем постоянные Ск и Dk. Для построения
интегрального уравнения нам потребуются только Ск
о Г
/3kakG)
>
+ CkakG sin akzo,
(fc^l) Wb ^
Подставляя С& в F.50) и удовлетворяя условию в области контакта,
получим интегральное уравнение для определения неизвестных кон-
контактных напряжений (^-амплитуда угла поворота бандажа)
a
\ r(x)k(y-x)dx = nG5 (\у\ < а), F.53)
F.54)
( )
ki(t) = J K(a)cosatdt, К (a) = V—#, У ^ , F.55)
^2@ = Yl bk cos akt, F.56)
fc=0
где а+ — контур интегрирования, совпадающий с положительной дей-
действительной полуосью, обходя действительные полюсы подынтеграль-
подынтегральной функции снизу, 1п(х) — функции Бесселя мнимого аргумента, bk
содержит информацию о периодических свойствах волновода:
= 7Г—— [K ^ 1), On =
RaA V / У' и
[K ^ 1), On = Z7T,
RakAk V / У' и Ra0A0
A*k = sin akz0 - CkakG cos akZQ.
Можно показать, что
bk = O((l/fc) exp (-2тгЬ0)) (fc -^ 00). F.57)
Как видно из F.54)-F.56), ядро интегрального уравнения F.53)
состоит условно из двух слагаемых. Первое слагаемое соответствует
ядру интегрального уравнения аналогичной контактной задачи для од-
однородного цилиндра с параметрами G, р, а второе слагаемое содержит
информацию о периодических свойствах волновода и является гладкой
функцией.
Учитывая оценку F.57), решение интегрального уравнения F.53)
можно получить с использованием широкого спектра известных ана-
аналитических методов.
244 Гл. 6. Контактные задачи для тел периодической структуры
6.3.3. Исследование В-резонансов. На интервалах запирания
периодических волноводов \z\ > zq, когда все А& действительны и не
равны единице, найдем мнимые части функций k\(t) и k2(t). Получим
т /7 UW т /7 U\\ f % г , Х^
где fcg — число действительных полюсов функции К (а).
Таким образом, на интервалах запирания волновода ядро инте-
интегрального уравнения F.53) принимает действительные значения, сле-
следовательно действительнозначным будет и его решение. Это дает ос-
основание полагать, что на интервалах запирания волновода могут суще-
существовать В-резонансы.
Глава 7
КОНТАКТНЫЕ ЗАДАЧИ ДЛЯ ДВУХСЛОЙНОГО
ПОЛУПРОСТРАНСТВА С УЧЕТОМ СИЛ ТРЕНИЯ
В НЕИЗВЕСТНОЙ ОБЛАСТИ КОНТАКТА
В этой главе рассматриваются трехмерные контактные задачи тео-
теории упругости о действии штампа произвольной формы на поверхность
слоя толщины h, жестко соединенного с упругим полупространством
с другими упругими постоянными (задача L\) или лежащего на нем
без трения (задача L2) [198, 333, 338, 340, 342, 354]. Зона контакта
предполагается заранее неизвестной и зависящей от величины дей-
действующих на штамп нормальной силы Р и тангенциальной силы Т.
Предполагается также, что между штампом и слоем имеют место си-
силы кулоновского трения, которые коллинеарны направлению действия
тангенциальной силы Т. Штамп не поворачивается в процессе взаи-
взаимодействия. Вне штампа поверхность слоя свободна от напряжений.
Рассматривается случай предельного равновесия, случай квазистати-
квазистатического движения штампа по поверхности слоя в подвижной системе
координат может быть рассмотрен аналогично.
Получены интегральные уравнения поставленных контактных за-
задач, для решения которых в случае неизвестной области контак-
контакта использован метод нелинейных граничных интегральных уравне-
уравнений [104, 105]. Исследовано влияние коэффициента трения Куло-
Кулона, формы штампа, упругих констант и толщины слоя на величину
контактных напряжений, на зависимость вертикального перемещения
штампа от вдавливающей силы, на величину и форму области кон-
контакта и на перемещение точек поверхности слоя вне области кон-
контакта.
С учетом сил трения плоские контактные задачи рассматривались
в работах [18, 106, 195], пространственные для полупространства —
в работах [109, 179] и для клина — в работах [247, 249].
246 Гл. 7. Контактные задачи для двухслойного полупространства
7.1. Постановка контактных задач
Пусть жесткий штамп, лежащий на поверхности слоя z = h, нахо-
находится под действием нормальной силы Р и тангенциальной силы Т,
направленной вдоль оси Ох. Здесь (х, у, z) — прямоугольная система
Рис. 7.1. К задачам L\, L^
координат, начало которой находится на нижней поверхности. Предпо-
Предполагается, что силы трения под штампом параллельны силе Т и штамп
находится в условиях предельного равновесия и не поворачивается.
Будем считать, что слой имеет модуль сдвига G\ и коэффициент
Пуассона щ, а упругое полупространство — соответственно G2 и щ
(рис. 7.1).
Граничные условия для уравнений Ламе будут иметь вид
=s-f(x,y),
ryz=0
= h, (х,у)еп),
= тМ =0
' yz w
,0) =„B)
„A) =„B)
нA) = ,„B)
G.1)
ri1]=a{2\
(задача
= af\
A) _ ^-B) _ _A) _ _B) _ А / _ А\ /ооттоцо ГОА
rz "" гж/ — гу/ — ryz — v [z — и) (^задача ь2).
Кроме того, выполняются условия статики:
Р= \\<тг(х,у,0)<К1, Т =
компоненты вектора перемещений соот-
(i) U) (г)
T TyZ
В G.1) и(г\ у(г\ ttfW
(i) U) (г)
ветственно вдоль осей х, у, z, gz , Txz , TyZ — компоненты тензора
напряжений в слое (г = 1) и полупространстве (г = 2), /л — коэффи-
коэффициент трения, 5 — перемещение штампа, f(x, у) — форма основания
штампа, О — область контакта.
7.1. Постановка контактных задач 247
Перемещения в слое и полупространстве можно представить как
суперпозицию перемещений точек основания, вызванного приложением
в области контакта некоторого нормального давления q(x,y), и пере-
перемещений, обусловленных действием тангенциальной нагрузки fiqix, у)
в направлении оси х. Принимая это во внимание и представляя ком-
компоненты вектора перемещения в слое в виде двойного преобразования
Фурье по координатам х, у, получим интегральные уравнения постав-
поставленных контактных задач для определения неизвестного контактного
давления q(x, у) под штампом
^F-f(x,y)), (х,у)еп. G.2)
п
Ядра k(t, т) можно представить в виде двух слагаемых
k(t, г) = h (t, r) + ek2(t, г), г = M(o1l/l), G.3)
оо оо
kn(t,T) = ^l \ Kn{a,p)e-i{-at+^dadC (n=l,2), G.4)
— сю —сю
Ki(a,/3) =7"'
где
Для задачи L\
Nx = 2x2(sh2u + 2u)G2 + A6/xi/x2 ch2u + Ащщ sh2?x - 8urj2)G
N2 =
4^x2 + к\ + 1), G.5)
а для задачи L2
- 1 +2^2ryf1), G.6)
- 1 -2u).
248 Гл. 7. Контактные задачи для двухслойного полупространства
Здесь приняты следующие обозначения:
G=Q-, r/i = l-2i/i, щ=\-2щ,
Щ = 3 — 4щ, K2 = 3 — 4Z/2, /1\ = \ — Щ, /i2 = 1 — ^2-
В случае, когда G = 1, z/i = щ задача L\ переходит в задачу
для упругого полупространства и ядра интегральных уравнений G.2)
примут вид
^ Ц G.7)
Г + т
Это совпадает с ядрами интегрального уравнения аналогичной за-
задачи для полупространства, рассмотренной в работе [109].
Когда G = 0 F?2 = об), получаем задачи для слоя, соединенного с
жестким основанием (задача L^) или лежащего без трения на жестком
основании (задача L4).
Соответственно получим для задачи Ь%
т. / ч 2щ sh 2u — Аи
К\{и) = ^ к,
2к\ ch 2и + Аи + 1 + щ
G-8)
2н\ ch 2и + 4гг + I + щ
а для задачи L4
^ / ч 2sh2^
G.9)
sh2«- 2мA - 2v)
=
Отметим, что интегральные уравнения G.2) только с ядрами k\(t,r)
соответствуют контактным задачам о вдавливании штампа в слой без
трения [88].
Ядра интегральных уравнений могут быть упрощены и представле-
представлены в виде однократных интегралов
V^T^ G.10)
G.11)
где Jn(x) (п = 0, 1) — функции Бесселя.
К интегральным уравнениям G.2) с ядрами G.10)—G.11) кроме
условий статики необходимо добавить также условие для нахождения
области контакта, которое будет сформулировано и реализовано ниже.
7.2. Решение интегральных уравнений 249
При выводе соотношений G.10)—G.11) использовалась замена пере-
переменных а = 7cosф, C = 7sin?/; и значения интегралов [88]
тг/2
cos (a cos ф) cos (b sin ф)Aф = — Jo f v а2
о
тг/2
cos ^ sin (а cos ф) cos F sin ф)Aф =
о
7.2. Решение интегральных уравнений
Для решения интегральных уравнений G.2) с ядрами G.3), G.10),
G.11) применим метод нелинейных граничных уравнений, развитый
в работах [104, 105]. Этот метод позволяет одновременно находить
не только функцию распределения контактных напряжений, но и об-
область контакта, а также и перемещения точек поверхности слоя вне
штампа в некоторой области, содержащей область контакта. Инте-
Интегральные уравнения с такими же свойствами исследовались в рабо-
работах [197, 199, 200].
Не нарушая общности результатов, предположим, что штамп имеет
форму эллиптического параболоида, вытянутого вдоль оси у. Тогда
функция f(x,y), стоящая в правой части уравнения G.2), примет вид
где R\, R2 — радиусы кривизны штампа соответственно в плоскостях
у = 0 и х = 0.
В соответствии с методом нелинейных граничных уравнений [104,
105] предположим, что область контакта О заключена в прямоуголь-
прямоугольнике S = {\х\ < а, \у\ ^b}, b^ а.
Введем следующие безразмерные переменные и величины:
*¦ = !¦ *¦ = !• s' = i-
а Л h Л Ъ
?о = ъ, \0 = v A=—,
G.13)
R = — Р' = ~V P
2Д2' 2СЬ2 '
250 Гл. 7. Контактные задачи для двухслойного полупространства
В этом случае область контакта п перейдет в область п', а прямо-
прямоугольник S в прямоугольник S' = {\xf\ ^ so, \yf\ ^ 1}, го ^ 1.
Здесь параметр Ло характеризует относительную толщину слоя, а
параметр so — эксцентриситет области контакта.
Заметим, что размеры а и Ъ прямоугольника S могут быть выбраны
исходя из точного решения задачи о вдавливании без трения штампа в
форме эллиптического параболоида в упругое полупространство [206],
но в большинстве случаев они могут быть взяты в виде а = y/25R\ ,
Щ
Окончательно поставленные задачи будут сведены в безразмерном
виде к следующей системе, состоящей из интегрального уравнения и
неравенств
Kq'>f'(x',y'),q'(x',y')=O, (x',yf) € (S' \ П'), G.15)
где
f(xf,yf)=5f-Axf2-Byf2,
а оператор К(...) имеет вид
С 1 /J й nJ ^\
?> G.16)
T{t,T)= [Ki{u)~ l]Jl(uy/t2+T2)du
R = V ix' ~ 02 + (y' - vJ ¦
Система G.14), G.15) содержит условие для определения области
контакта и может быть сведена к нелинейному граничному интеграль-
интегральному уравнению типа Гаммерштейна [104, 105]. Это нелинейное урав-
уравнение имеет вид (см. A.4) в работе [104])
> У') + (Е- /i0iOQ+^ @^ У') е S1). G.17)
Здесь параметр /io может принимать произвольные значения, Е —
тождественны
ем [104, 105]
тождественный оператор, а оператор Q+ определяется соотношени-
Q+(ip)=sup{<p(x',y'),O},
(x',y')GSf.
7.2. Решение интегральных уравнений 251
Связь между решениями системы G.14), G.15) и нелинейного урав-
уравнения G.17) имеет вид
Решение нелинейного уравнения G.17) будет найдено численно
методом последовательных приближений с использованием модифици-
модифицированного метода Ньютона [104]. Алгоритм этого метода позволяет
одновременно находить контактные напряжения и область контакта,
когда известно перемещение штампа 5. Дискретизация уравнения осу-
осуществлялась с учетом симметрии области контакта, а узлы дискрети-
дискретизации в области Sf выбирались равномерно по осям координат.
Схема решения уравнения G.17) предполагает [104, 105], что из-
известно перемещение штампа 5, а сила Р находится как интеграл от
функции распределения контактных напряжений.
Здесь будем считать, что задана сила Р, а перемещение штампа 5
необходимо найти. Положим qr = 5'q*, a = y/25R\ , b = л/25Щ, тогда
Sq = л/Щ /i?2 и после ряда преобразований контактные напряжения
представим в виде
q(x,y) = q(x',y'), G.18)
а связь между силой, действующей на штамп, и его перемещением
будет определяться равенством
Р = 2ttG5(\ - vx)-x^25R2P\ G.19)
где
^ G.20)
a q*(x',y') есть решение системы G.14), G.15) или уравнения G.17),
где
Как показывают числовые расчеты, итерационный процесс числен-
численного решения нелинейного граничного интегрального уравнения G.17)
с правой частью G.21) хорошо сходится.
Перепишем соотношение G.19) в виде
5 = (РA - z/i)J/3BttGP*\/Щ)~2/3 = D(S) G.22)
и будем рассматривать G.22) как уравнение для определения переме-
перемещения штампа 5. Это уравнение является нелинейным, так как, исходя
из соотношения G.16), величина Р* зависит от Ло = h/b = h/\/25R<2
нелинейно, а следовательно и от 5 зависит нелинейно.
252 Гл. 7. Контактные задачи для двухслойного полупространства
Функция DE) в соответствии с соотношениями G.20), G.22) вы-
вычисляется через решение системы G.14), G.15), G.21). Уравнение G.22)
будем решать методом последовательных приближений по схеме
6n = DEn.i) (n=l,2,...). G.23)
В случае, когда h = оо, а Р* и соответственно DE) от 5 не зависят,
естественно за нулевое приближение 5о в G.22) взять величину 5
внедрения штампа в полупространство (Ао = оо) при неизменности
других параметров задач.
Как показывают числовые расчеты, итерационный процесс G.23)
сходится достаточно быстро, скорость его сходимости в основном за-
зависит от глубины слоя: чем больше относительная глубина слоя, тем
быстрее сходимость.
7.3. Числовые расчеты
Окончательно алгоритм решения поставленных контактных задач
в случае, когда заданы механические свойства слоя и его толщина,
форма штампа, коэффициент трения и действующая на штамп нормаль-
нормальная сила Р, состоит из следующих этапов. На первом этапе решается
задача для полупространства. Для этого надо решить уравнение G.17),
G.21), положив в G.16) T(t,r) = 0, найти перемещение штампа 5 =
= 5о и величину Ао = h/л/25оЩ. На следующем этапе необходимо
реализовать итерационный процесс G.23), на каждом шаге которого ре-
решается уравнение G.17), G.21) при Ао = h/^/25n-\R2 (n = 0, 1,2,...),
где п — номер итерации. После того, как заданная точность вычис-
вычисления величины перемещения штампа будет достигнута, на заключи-
заключительном этапе могут быть вычислены контактные напряжения, форма
поверхности слоя вне штампа, форма области контакта и величина
момента, удерживающего штамп в вертикальном положении.
В таблицах и на графиках приведены некоторые результаты чис-
числовых расчетов. Контроль точности результатов производился путем
их сравнения при разных значениях числа узлов дискретизации нели-
нелинейного интегрального уравнения G.17) и также путем сравнения их
с известными частными случаями при \± = 0 [88, 206].
В результате проведенных числовых расчетов было установлено, что
при заданной силе Р перемещение штампа 5 практически не зависит
от коэффициента трения /i, но существенно зависит от коэффициента
Пуассона щ и других параметров.
В таблицах 7.1 и 7.2 соответственно для задач L\ и Ь% приведены
значения перемещения штампа 5 при Р = 107, G\ = 7,0 • 1010, fi = 0,9,
V2 = 0,3, R\ = i?2 — 1,0 при некоторых значениях коэффициента Пуас-
Пуассона и\, параметра G и толщины слоя h. Заметим, что при любых Р
и G\ результаты не меняются, если P/G\ = const, a G и другие неза-
независимые параметры фиксированы. Здесь и далее размерные величины
указаны в системе СИ.
7.3. Числовые расчеты
253
Таблица 7.1. Задача L\
№
п/п
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
0,4
0,35
0,1
0,4
0,1
0,4
0,1
0,4
0,1
0,4
0,1
0,4
0,1
0,4
0,1
0,4
0,1
0,4
0,1
0,4
0,1
0,4
0,1
0,4
0,1
0,4
0,1
0,4
0,1
h
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,05
0,05
0,05
0,05
0,05
0,05
0,05
0,05
0,1
0,1
0,1
0,1
0,1
0,1
0,1
0,1
G
0,0
0,0
0,0
0,1
0,1
0,25
0,25
0,5
0,5
1,5
1,5
2,0
2,0
0,25
0,25
0,5
0,5
1,5
1,5
2,0
2,0
0,25
0,25
0,5
0,5
1,5
1,5
2,0
2,0
5- 103
0,428
0,468
0,618
0,498
0,689
0,599
0,791
0,758
0,950
1,32
1,50
1,57
1,75
0,760
1,01
0,854
1,11
1,19
1,45
1,34
1,61
0,869
1,16
0,922
1,21
1,11
1,41
1,19
1,49
Ь
0,0293
0,0306
0,0352
0,0316
0,0371
0,0346
0,0398
0,0389
0,0436
0,0514
0,0548
0,0560
0,0591
0,0390
0,0450
0,0413
0,0471
0,0488
0,0539
0,0517
0,0567
0,0417
0,0481
0,0429
0,0492
0,0471
0,0530
0,0487
0,0546
Стах
0,660
0,638
0,597
0,581
0,543
0,495
0,479
0,395
0,402
0,214
0,242
0,173
0,201
0,350
0,344
0,324
0,322
0,259
0,267
0,239
0,248
0,314
0,308
0,303
0,300
0,275
0,276
0,264
0,267
Ж*
-од
0
0,15
-0,05
0,15
0
0,2
0
0,2
0,15
0,25
0,2
0,3
0,1
0,2
0,1
0,25
0,1
0,2
0,1
0,2
0,1
0,25
0,1
0,25
0,1
0,25
0,1
0,25
М*
-0,0427
-0,000683
0,0905
-0,0145
0,0831
0,00394
0,0724
0,0139
0,0582
0,0137
0,0301
0,0115
0,0237
0,0157
0,564
0,0157
0,0502
0,0135
0,0337
0,0122
0,0289
0,0172
0,0489
0,0166
0,0453
0,0134
0,0354
0,0124
0,0322
254 Гл. 7. Контактные задачи для двухслойного полупространства
Таблица 7.2. Задача L2
№
п/п
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
0,4
0,285
0,28
0,1
0,4
0,1
0,4
0,1
0,4
0,1
0,4
0,1
0,4
0,1
0,4
0,1
0,4
0,1
0,4
0,1
0,4
0,1
0,4
0,1
0,4
0,1
0,4
0,1
0,4
0,1
0,4
0,1
h
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,02
0,05
0,05
0,05
0,05
0,05
0,05
0,05
0,05
0,05
0,05
0,1
0,1
0,1
0,1
0,1
0,1
0,1
0,1
0,1
0,1
G
0,0
0,0
0,0
0,0
0,25
0,25
0,5
0,5
1,5
1,5
2,0
2,0
0,0
0,0
0,25
0,25
0,5
0,5
1,5
1,5
2,0
2,0
0,0
0,0
0,25
0,25
0,5
0,5
1,5
1,5
2,0
2,0
S- 103
0,509
0,554
0,556
0,626
0,728
0,829
0,966
1,04
3,01
2,15
4,39
3,19
0,725
0,920
0,857
1,05
0,992
1,18
1,97
1,79
2,70
2,31
0,854
1,11
0,924
1,18
1,00
1,25
1,51
1,58
1,88
1,85
Ъ
0,0319
0,0333
0,0334
0,0354
0,0382
0,0407
0,0440
0,0456
0,0776
0,0655
0,0937
0,0798
0,0381
0,0429
0,0414
0,458
0,0445
0,0485
0,0628
0,0599
0,0735
0,0679
0,0413
0,0470
0,0430
0,0486
0,0447
0,500
0,0549
0,563
0,0613
0,0609
Стах
0,537
0,557
0,558
0,581
0,387
0,447
0,295
0,358
0,105
0,170
0,588
0,116
0,355
0,364
0,319
0,333
0,291
0,308
0,195
0,235
0,162
0,203
0,316
0,315
0,302
0,304
0,290
0,294
0,235
0,260
0,209
0,240
ж*
-од
0,0
0,0
од
0,0
од
0,0
од
0,2
0,2
0,3
0,3
0,1
0,2
0,1
0,2
0,1
0,2
0,1
0,2
0,1
0,2
0,1
0,25
0,1
0,25
0,1
0,25
0,1
0,2
0,1
0,2
М*
-0,0556
-0,000416
0,00175
0,0683
-0,0101
0,0484
0,00102
0,0354
0,00161
0,0112
0,000742
0,00545
0,0112
0,0612
0,0131
0,0508
0,0132
0,0432
0,00538
0,0216
0,00316
0,0140
0,0169
0,0516
0,0161
0,0467
0,0149
0,0422
0,00758
0,0280
0,00522
0,0208
Продолжение на следующей странице
7.3. Числовые расчеты
255
№
и/и
33
34
35
36
37
38
39
40
41
42
0,4
0,1
0,4
0,1
0,4
0,1
0,4
0,1
0,4
0,1
h
0,5
0,5
0,5
0,5
0,5
0,5
0,5
0,5
0,5
0,5
G
0,0
0,0
0,25
0,25
0,5
0,5
1,5
1,5
2,0
2,0
(МО3
0,977
1,29
0,992
1,31
1,01
1,32
1,11
1,39
1,18
1,44
Ъ
0,0442
0,0508
0,0445
0,0511
0,0449
0,0514
0,0471
0,0527
0,0487
0,0537
Стах
0,293
0,289
0,291
0,288
0,289
0,286
0,275
0,279
0,267
0,274
Ж*
0,1
0,25
0,1
0,2
0,1
0,25
0,1
0,2
0,1
0,2
М*
0,0161
0,0411
0,0157
0,0401
0,0152
0,0393
0,0123
0,0357
0,0110
0,0332
В этих же таблицах приведены значения безразмерного момента М*
контактных напряжений под штампом, определяемого формулой
М* =M(AitGx52R2)-\ М = I" lq(x,y)xdx,
п
и максимальных безразмерных контактных напряжений <ттах =
= q*(x*,0), определяемых формулой
q \ъ'ъ) =ЧУХ>У)УЬ
Отметим, что величина х* (\х*\ < 1) вычислена с абсолютной погреш-
погрешностью не больше 0,05, при этом остальные величины вычисляются
с относительной погрешностью не больше 0,1 %. Как видно из таблиц,
перемещение штампа в задаче L2 больше, чем в задаче L\ при одних
и тех же геометрических и механических параметрах. Кроме того, при
постоянной силе Р перемещение штампа 5 в одних случаях уменьша-
уменьшается с увеличением коэффициента Пуассона щ (у2 = 0,3), а в других
случаях увеличивается. Последнее может происходить при больших
значениях параметра G (G\ = const), в табл. 7.2 это можно наблюдать
в строках 9-12, 31-32.
Из таблиц также видно, что при малых значениях параметра G
(G2 > G\) при изменении коэффициента Пуассона слоя щ от 0 до 0,5
происходит уменьшение момента контактных напряжений, в некото-
некоторых случаях может происходить изменение знака момента контактных
напряжений. В табл. 7.2 это можно наблюдать в строках 2-3, 5-6,
а в табл. 7.1 — в строках 2-5.
Следует также отметить, что координаты точки области контакта,
в которой контактные напряжения принимают максимальные значения,
существенно зависят от коэффициента Пуассона: при изменении ко-
коэффициента Пуассона слоя щ от 0 до 0,5 происходит перемещение
256 Гл. 7. Контактные задачи для двухслойного полупространства
этой точки в отрицательном направлении оси х, в некоторых слу-
случаях значение может быть отрицательным (см. в табл. 7.2 строку 1,
в табл. 7.1 строки 1,4). Было проведено также численное исследование
вертикальных перемещений точек поверхности слоя z = h и формы
области контакта. Здесь также наблюдается существенная зависимость
этих характеристик от коэффициента Пуассона и\, толщины слоя h
и от коэффициента трения /i.
Более подробно остановимся на задачах Ь% и L\ (G = 0).
В табл. 7.3 приведены значения перемещения 5 • 103 при Р = 107,
\i = 0,9, R\ = R2 = 1,0 при некоторых значениях коэффициента Пуассо-
Пуассона и\, модуля сдвига G\ и толщины слоя h. Для задачи Ь% результаты
приведены в строках 1-7, для задачи L\ — в строках 8-11. Заметим,
что при любых Р и G\ результаты не меняются, если P/G\ = const.
Таблица 7.3
Gi • Ю-10
7,0
1,0
7,0
0,1
0,2
0,3
0,4
0,1
0,3
0,4
0,1
0,2
0,3
0,4
h = 0,5
1,29
1,19
1,08
0,967
4,52
3,79
3,39
1,29
1,19
1,09
0,977
h = 0,2
1,21
1,12
1,01
0,906
4,04
3,37
2,99
1,22
1,13
1,03
0,930
/i = 0,l
1,09
1,01
0,912
0,811
3,36
2,79
2,45
1,11
1,03
0,942
0,854
h = 0,05
0,907
0,833
0,750
0,657
2,55
2,10
1,80
0,919
0,858
0,793
0,725
h = 0,02
0,617
0,566
0,504
0,430
1,65
1,34
1,10
0,626
0,583
0,548
0,508
Как видно из таблицы 7.3, при постоянной силе Р перемещение
штампа 5 уменьшается с увеличением коэффициента Пуассона ^ ис
уменьшением толщины слоя h.
В табл. 7.4 приведены значения величины 5 • 103 при некоторых
значениях Р, h, щ = 0,3, G\ = 7 • 10ю, /х = 0,9, Rx = R2 = 1,0, h = 0,1
и h = 0,02. При других значениях \± < 1 они будут подобными.
Проведено детальное численное исследование вертикальных пере-
перемещений точек поверхности слоя z = h и формы области контакта.
Здесь также наблюдается существенная зависимость этих характери-
характеристик от коэффициента Пуассона щ, толщины слоя h и от коэффициента
трения II.
На рис. 7.2,6-7.9, б (задача Ь%) и рис. 7.10, 6-7.13, б (задача L4)
приведены графики величины w*(x,y) = —w(x,y,0)/5 (у = 0), соответ-
7.3. Числовые расчеты
257
Р 1 С\~7
г • 1U
1,0
2,0
3,0
4,0
5,0
6,0
7,0
8,0
9,0
10,0
Задача
h = 0,1
0,910
1,37
1,73
2,03
2,31
2,55
2,78
2,99
3,19
3,37
и
h = 0,02
0,500
0,708
0,864
1,00
1,12
1,22
1,32
1,41
1,49
1,58
h = 0,
0,940
1,42
1,81
2,13
2,43
2,70
2,93
3,17
3,38
3,58
Таблица 7.4
Задача L\
1
h = 0,02
0,544
0,774
0,954
1,10
1,23
1,36
1,47
1,57
1,66
1,76
ствующей вертикальным перемещениям точек поверхности слоя z = h
в плоскости у = 0, при значениях параметров из таблицы 7.5.
На этих рисунках \х\ ^ 5а, a w*(x,0) > —0,02. Последнее условие
соответствует тому, что на этих рисунках не изображены перемещения
точек на некоторой части области контакта, которые равны переме-
перемещениям соответствующих точек штампа. Значения величины а • 102
приведены в табл. 7.6 при тех же значениях параметров, что и табл. 7.3.
Таблица 7.5
№ рис.
7.2, 7.10
7.3, 7.11
7.4, 7.12
7.5, 7.13
7.6
7.7
7.8
7.9
р- ю-7
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
d • Ю-10
7,0
7,0
7,0
7,0
7,0
7,0
1,0
1,0
0,9
0,9
0,9
0,9
0,5
0,5
0,9
0,9
h
0,02
0,02
0,1
0,1
0,02
0,02
0,1
0,1
v\
0,1
0,4
0,1
0,4
0,1
0,4
0,1
0,4
Rx
1,0
L,0
L,0
1,0
L,0
L,0
1,0
L,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
На рис. 7.2, a-7.9, а (задача L^) и рис. 7.10, a-7.13, а (задача L^)
приведена граница области контакта (кривая 0) при у ^ 0 при значе-
значениях параметров, указанных в табл. 7.5.
На этих же рисунках приведены также линии равных значений
функции q*(x/h, у/Ъ) = q(x,y)^/R2/(/nG\f25) (кривые 1-6), соответ-
соответствующие безразмерным значениям контактных напряжений q(x, у)
G.18). На этих рисунках кривые с номером п соответствуют значениям
д* = 0,1 • п. В табл. 7.7 приведены наибольшие значения величины
9 В.М. Александров, М.И. Чебаков
258 Гл. 7. Контактные задачи для двухслойного полупространства
0
а
Г10
0.02
-0.02
Ъа
Рис. 7.2. (Gi • 10~ш = 7,0, /х = 0,9, h = 0,02, щ = 0,1, 5 • Ю6 = 0,617,
а- 102 = 3,51)
й
ш
и
7т
11
/
/1 ¦*
( 1/
а
——-.
——~.
"¦—-«^
——^
\
\
\
Y
\\
\\
\\
X
Рис. 7.3.
О
а
-10
0,02
0.02
I I I I I I |\ I I I I
-5а О
• 10"ш = 7,0, /х = 0,9, h = 0,02, щ = 0,4, 5 • Ю6 = 0,430,
а • 102 = 2,93)
77
Ж
О
а
л-10
0.02
-0,02
5 а
Ъа
Рис. 7.4. (Gi • 1O~1U = 7,0, /х = 0,9, h = 0,1, и = 0,1, 5 • Ю6 = 1,08,
а • 102 = 4,68)
7/
%
/
I
1
х-
а
\
\
\V
\
\
X
Рис. 7.5.
О
а
л-10
0.02
-0,02
10-10 = 7,0, /х = 0,9, h = 0,1, щ = 0,4, 5 - 103 = 8,811,
а • 102 = 4,03)
7.3. Числовые расчеты
259
0,02
х
* -0,02
-5 а
Л 67
Рис. 7.6. (G, • 1(Г10 = 7,0, /х = 0,5, h = 0,02, г/, = 0,1, 8 ¦ 103 = 0,614,
а- Ю2 = 3,51)
о Г
0,02
-0,02
Рис. 7.7. (Gi • Ю-10 = 7,0, /х = 0,5, h = 0,02, щ = 0,4, 5 • 103 = 0,427,
а- 102 = 2,92)
0,02
-^ -0,02
-5 а
i—i—i—гуг
5а
Рис. 7.8. (Gi • Ю-10 = 1,0, /х = 0,9, h = 0,1, i/i = 0,1, 5 • 103 = 3,36,
а- 102 = 8,20)
о
а
л-10
0,02
¦ -0,02
Рис. 7.9. (Gi • Ю-10 = 1,0, /х = 0,9, h = 0,1, щ = 0,4, 5 • 103 = 2,45,
а- 102 = 7,00)
260 Гл. 7. Контактные задачи для двухслойного полупространства
0<Z>
0.02
X
a
¦+- -0.02
а б
Рис. 7.10. (Gi • 10-10 = 7,0, /x = 0,9, h = 0,02, щ = 0,1, 5 • 103 = 0,626,
a • 102 = 3,54
0,02
43.02
Рис. 7.11. (G\ • 100 = 7,0, \i = 0,9, h = 0,02, щ = 0,4, S • 103 = 0,508,
a- 102 = 3,19)
7
1
(V
LA
\
К
f'2
\У
a
/
S
V
\
\
\\
X
0,02
-0,02
Рис. 7.12. (Gi • 100 = 7,0, /x = 0,9, /г = 0,1, щ = 0,1, S • 103 = 1,11,
a • 102 = 4,70)
(
a
nN
N
\
\\
\
X
0,02
^ -0,02
-5 a
Рис. 7.13. (Gi • 10-10 = 7,0, ii = 0,9, /г = 0,1, щ = 0,4, 6 • 103 = 0,854,
a- 102 = 4,13)
7.3. Числовые расчеты
261
Таблица 7.6
Gx • Ю-10
7,0
1,0
7,0
v\
од
0,2
0,3
0,4
0,1
0,3
0,4
0,1
0,2
0,3
0,4
h = 0,5
5,07
4,87
4,64
4,40
9,51
8,71
8,24
5,08
4,88
4,66
4,42
h = 0,2
4,92
4,72
4,50
4,26
8,99
8,21
7,73
4,94
4,75
4,54
4,31
h = 0,1
4,68
4,49
4,27
4,03
8,20
7,47
7,00
4,70
4,53
4,34
4,13
h = 0,05
4,26
4,08
3,87
3,62
7,15
6,48
6,00
4,29
4,14
3,98
3,81
h = 0,02
3,51
3,36
3,17
2,93
5,74
5,16
4,70
3,54
3,42
3,31
3,19
q*(x',y') в области контакта при значениях параметров задач, соответ-
соответствующих указанным рисункам. Очевидно, что в этих точках у' = 0,
а значения х' указаны в табл. 7.7.
Таблица 7.7
№
рис.
3,а
6, а
9, а
12,а
х'
0,15
0,1
0,25
-од
gV,0)
0,597
0,326
0,365
0,537
№
рис.
4, а
7, а
10, а
13,а
х1
-од
0,1
0,05
0,25
q*(xf,0)
0,661
0,605
0,378
0,315
№
рис.
5, а
8, а
11,а
14,а
х1
0,25
-0,05
0,1
0,1
gV,0)
0,318
0,659
0,582
0,316
Координаты точек в табл. 7.7 указаны с абсолютной погрешностью,
равной не более 0,05а.
При Р = 107, Gi = 7 • 10ю, fi = 0,9, h = 0,02, Rx = R2 = 1, на
рис. 7.14, а (щ =0,1, 5 = 0,000617, a = 0,0351) и 7.14,6 (щ =0,4,
-2 а
2а
~~2 а
Рис. 7.14.
262 Гл. 7. Контактные задачи для двухслойного полупространства
5 = 0,000430, а = 0,0293) для задачи L2 приведена для наглядности
функция перемещения точек поверхности, отнесенная к перемещению
штампа 5, в окрестности штампа и под штампом, что соответствует
значениям функции w*(x,y) при \х\ ^ 2а, 0 < у < 2а. На рис. 7.14
z' = z-h.
Анализ результатов числовых расчетов, позволяет сделать следу-
следующие важные выводы, часть из которых приведена выше: 1) при
заданной силе Р перемещение штампа 5 практически не зависит от
коэффициента трения /i, но существенно зависит от коэффициента
Пуассона щ; 2) при /i/Ои при малых значениях коэффициента Пуас-
Пуассона v\ при х > 0 поверхность слоя z = h вне области контакта в неко-
некоторой ее окрестности выше, чем в симметричных точках при х < 0,
при этом с уменьшением h перемещение поверхности в отрицательном
направлении оси z при х > 0 уменьшается и, начиная с некоторого
значения h, происходит подъем поверхности выше плоскости z = h;
3) при \i т^ 0 и больших значениях v\ картина деформации поверхности
меняется на противоположную, а именно, при х < 0 поверхность вне
штампа выше, чем при х > 0, при этом с уменьшением h перемещение
в отрицательном направлении оси z уменьшается и также происхо-
происходит подъем поверхности, начиная с некоторого /i*. Такая асимметрия
в перемещении точек поверхности увеличивается с увеличением ко-
коэффициента трения /х; 4) при \± ф 0 и малых щ зона контакта, как
показывают расчеты, смещается в противоположном направлении дей-
действия касательной силы Т, а при больших щ зона контакта смещается
в направлении действия силы Т.
Заключение
В монографии обобщены исследования авторов в области стати-
статических и динамических задач контактного взаимодействия для тел
сложной конфигурации, неоднородных тел и задач с усложненными
условиями в зоне контакта на основе разработанных аналитических
и численно-аналитических методов.
Основные результаты заключаются в следующем.
1. Разработаны и развиты аналитические методы решения парных
рядов-уравнений, связанных с разложениями, порождаемыми соответ-
соответствующими задачами Штурма-Лиувилля, путем сведения их к ИУ
с разностным ядром или к БСЛАУ с сингулярной матрицей. Развиты
некоторые методы решения полученных ИУ и бесконечных систем
первого и второго рода. Получено точное решения одного важного
класса ИУ, к которым сводятся некоторые плоские контактные задачи
для канонических тел конечных размеров.
2. На основе однородных решений разработан эффективный метод
исследования контактных задач для тел конечных размеров канониче-
канонической формы, позволяющий свести их к решению БСЛАУ второго рода
типа нормальных систем Пуанкаре-Коха с экспоненциально убываю-
убывающими элементами и ряду хорошо изученных ИУ для соответствующих
полубесконечных тел.
3. На основе этих методов исследован широкий класс контактных
задач для конечного цилиндра, прямоугольника, кольцевого сектора,
кольца, сектора шарового слоя, тонкого сферического слоя, усеченного
конуса и усеченного шара, в том числе исследованы контактные задачи
для предварительно напряженных цилиндра и прямоугольника.
4. Для ряда задач выявлены практически важные зависимости
контактных напряжений и жесткости системы штамп-упругое тело от
параметров задач для канонических тел, в том числе:
— обнаружен немонотонный характер зависимости жесткости си-
системы штамп-упругое тело от величины расстояния штампа до боковой
границы тела;
— показано, что влияние боковой границы тела на контактные
напряжения экспоненциально затухает, если основание упругого тела
закреплено, и затухает обратно пропорционально расстоянию, если
основание упругого тела лежит без трения на жестком основании;
— показано, что возможно такое несимметричное расположение
штампа на поверхности упругого тела, когда момент контактных на-
напряжений равен нулю при поступательном перемещении штампа.
264 Заключение
5. Разработан на основе использования однородных решений и ме-
метода Ремеза нахождения наилучшего приближения и применен к ис-
исследованию ряда плоских и осесимметричных задач эффективный по-
полуаналитический метод решения контактных задач для тел конечных
размеров неканонической формы. Изучено влияние формы боковой
границы на распределение контактных напряжений.
6. На основе использования однородных решений развит аналити-
аналитический метод решения стационарных динамических контактных задач
для полубесконечных тел, имеющих периодическую структуру меха-
механических свойств вдоль продольной координаты. На примере слоя
и цилиндра изучены особенности возбуждения и распространения ко-
колебаний в таких волноводах. Показано, что существуют чередующиеся
промежутки на всем бесконечном интервале изменения частот, когда
такой волновод соответственно открыт или заперт. Также показано
существование В-резонансов (неограниченного возрастания амплитуды
колебаний тяжелого штампа) на тех частотах (в том числе и на высо-
высоких), когда волновод закрыт.
7. Исследован ряд пространственных контактных задач для двух-
двухслойного полупространства с учетом сил трения в зоне контакта. По-
Получены результаты, демонстрирующие качественно новую зависимость
формы области контакта, деформации свободной поверхности и распре-
распределения контактных напряжений от коэффициента Пуассона.
8. Созданы на основе разработанных методов и алгоритмов эф-
эффективные компьютерные модели для быстрого анализа влияния па-
параметров задач на особенности контактного взаимодействия штампов
с упругими телами.
Список литературы
1. Абрамян Б. Л. Контактные (смешанные) задачи теории упругости // Изв.
АН СССР. МТТ. 1969. №4. С. 181-197.
2. Абрамян Б. Л. К плоской задаче теории упругости для прямоугольника //
ПММ. 1957. Т. 21, вып. 1. С. 89-101.
3. Абрамян Б. Л. Об одном случае плоской задачи теории упругости для
прямоугольника // Докл. АН Арм. ССР. 1955. Т. 21, № 5. С. 65-72.
4. Абрамян Б.Л., Александров А.Я. Осесимметричные задачи теории упру-
упругости // Труды 2-го Всесоюзного съезда по теоретической и прикладной
механике. Вып. 3. — М.: Наука, 1966. С. 7-37.
5. Абрамян Б.Л., Маклукян М.М. Решение плоской задачи в перемещени-
перемещениях // Докл. АН Арм. ССР. 1957. Т. 25, №4. С. 177-184.
6. Азизов Т.Я., Иохвидов И. С. Основы теории линейных операторов в про-
пространствах с индефинитной метрикой. — М.: Наука, 1986. — 352 с.
7. Айзенберг Д. Л., Шапиро Г. С. О передаче давления через слой, имеющий
цилиндрическое отверстие // Инженерный сборник. 1950. Т. 7. С. 65-68.
8. Акимов Г.П., Рубинов A.M. Метод последовательных приближений для
разыскания полноты полученного приближения // Докл. АН СССР. 1964.
С. 503-505.
9. Акопян В. И. О контакте кругового диска с двумя прямоугольниками при
температурных воздействиях // Изв. АН Арм. ССР. Механика. 1980.
Т. 33, №4. С. 3-18.
10. Аксентян O.K. Особенности напряженно-деформированного состояния
плиты в окрестности ребра // ПММ. 1967. Т. 31, вып. 1. С. 178-186.
11. Аксентян O.K., Ворович И.И. Напряженное состояние плиты малой тол-
толщины // ПММ. Т. 27. 1963. С. 1057-1074.
12. Алахвердиев Дж.Э., Гасанов Э.Э. Теоремы полноты систем собственных
и присоединенных элементов операторных пучков в банаховом простран-
пространстве // Изв. АН Аз. ССР. Сер. физ. прикл. и мат. наук. 1974. №5.
С. 54-66.
13. Александров В.М. Аналитические методы решения задач теории упруго-
упругости для тел конечных размеров с собственно смешанными граничными
условиями // Актуальные проблемы механики деформируемых сред. Дне-
Днепропетровск. 1979. С. 21-27.
14. Александров В.М. Асимптотические методы в контактных задачах тео-
теории упругости // ПММ. 1968. Т. 32, вып. 4. С. 672-683.
15. Александров В.М. Метод однородных решений в контактных задачах для
тел конечных размеров // Изв. Сев.-Кавказ, научн. центра высш. шк. Сер.
Естеств. н. 1974. №4. С. 12-16.
266 Список литературы
16. Александров В.М. Об одной контактной задаче для упругого клина //
Изв. АН АрмССР. Механика. 1967. Т. 20, №4. С. 620-631.
17. Александров В.М. Об одном методе сведения парных рядов уравнений
к бесконечным алгебраическим системам // ПММ. 1975. Т. 39, вып. 2.
С.324-332.
18. Александров В.М. О плоских контактных задачах теории упругости при
наличии сцепления или трения // ПММ. 1970. Т. 34, вып. 2. С. 246-257.
19. Александров В.М. О решении одного класса парных уравнений // Докл.
АН СССР. 1973. Т. 210, № 1. С. 55-61.
20. Александров В.М., Александрова Г. П. Кручение круглым штампом жест-
жестко защемленного по основанию слоя // Пластинки и оболочки. Ростов-на-
Дону, Тр. Ростовск. инж.-строит, ин-та. 1971.
21. Александров В.М., Аннакулова Г. К. Контактная задача термоупругости
с учетом износа и тепловыделения от трения // Трение и износ. 1990.
Т. 11, №1. С. 24-28.
22. Александров В.М., Бабешко В.А., Белоконъ А.В. и др. Контактная за-
задача для кольцего слоя малой толщины // Инж. ж. МТТ. 1966. № 1. С.
23. Александров В.М., Белоконъ А. В. Асимптотическое решение одного
класса интегральных уравнений и его применения к контактным за-
задачам для цилиндрических упругих тел // ПММ. 1967. Т. 31, вып. 4.
С. 704-710.
24. Александров В.М., Ворович И. И. О действии штампа на упругий слой
конечной толщины // ПММ. 1960. Т. 24, вып. 2. С. 323-333.
25. Александров В.М., Галин Л.А., Пириев Н.П. Плоская контактная задача
при наличии износа для упругого слоя большой толщины // МТТ. 1978.
№4. С. 60-67.
26. Александров В.М., Карпенко В. А. Кручение шарового слоя сферическим
кольцевым штампом // ПММ. 1980. Т. 44, вып. 1. С. 143-150.
27. Александров В.М., Коваленко Е.В. Задачи механики сплошных сред со
смешанными граничными условиями. — М.: Наука, 1986. — 336 с.
28. Александров В.М., Коваленко Е.В. К вопросу об изнашивании сопряже-
сопряжения вал-втулка // Трение и износ. 1982. Т. 3, №6. С. 1016-1025.
29. Александров В.М., Коваленко Е.В. Контактные задачи теории упругости
при наличии нелинейного износа // Контактная жесткость в приборо-
приборостроении и машиностроении: Докл. конф. Рига: Рижский политехи, ин-т,
1979. С. 62-63.
30. Александров В.М., Коваленко Е.В. К теории контактных задач при на-
наличии нелинейного износа // МТТ. 1982. №4. С. 98-108.
31. Александров В.М., Коваленко Е.В. Методы решения контактных задач
термоупругости с учетом износа взаимодействующих поверхностей //
ПМТФ. 1985. №6. С. 129-131.
32. Александров В.М., Коваленко Е.В. Осесимметричная контактная задача
для линейно-деформируемого основания общего типа при наличии изно-
износа // МТТ. 1978. № 5. С. 58-66.
Список литературы 267
33. Александров В.М., Коваленко Е. В. Периодические контактные задачи
для упругой полосы // Изв. АН Арм. ССР. Сер. механика. 1977. Т. 30,
№4. С. 18-33.
ЗА. Александров В.М., Коваленко Е.В. Плоские контактные задачи теории
упругости для неклассических областей при наличии износа // ПМТФ.
1980. №3. С. 163-171.
35. Александров В.М., Мхитарян СМ. Контактные задачи для тел с тонки-
тонкими покрытиями и прослойками. — М.: Наука, 1983. — 488 с.
36. Александров В.М., Пожарский Д. А. Неклассические пространственные
задачи механики контактных взаимодействий упругих тел. — М.: Факто-
Факториал, 1998. - 288 с.
37. Александров В. М., Ромалис Б.Л. Контактные задачи в машинострое-
машиностроении. — М.: Машиностроение, 1986. — 176 с.
38. Александров В.М., Сметанин Б.И., Соболь Б.В. Тонкие концентраторы
напряжений в упругих телах. — М.: Наука, 1993. — 223 с.
39. Александров В.М., Чебаков М.И. Метод однородных решений в смешан-
смешанных задачах теории упругости // Тезисы докладов 3-го республиканского
симпозиума по дифференциальным уравнениям. Одесса. 1982. С. 134-135.
АО. Александров В.М., Чебаков М.И. Метод парных рядов по функциям
Бесселя в смешанных задачах теории упругости для круглой плиты //
ПММ. 1977. Т. 41, вып. 3. С. 486-492.
41. Александров В.М., Чебаков М.И. Об одном методе решения парных
интегральных уравнений // ПММ. 1973. Т. 37, вып. 6. С. 1087-1097.
42. Александров В.М., Чебаков М.И. О методе однородных решений в сме-
смешанных задачах теории упругости для усеченного клина и кольцевого
сектора // ПММ. 1983. Т. 47, вып. 5. С. 790-798.
A3. Александров В.М., Чебаков М.И. Смешанные задачи механики сплош-
сплошных сред, связанные с интегральными преобразованиями Ханкеля и Ме-
лера - Фока // ПММ. 1972. Т. 36, вып. 3. С. 494-504.
44. Александрова Г. П. Об одной, решаемой в замкнутом виде, контактной
задаче теории упругости для цилиндрического тела // Инж. журн. МТТ.
1968. №2. С. 149-153.
45. Алексидзе М.А. Решение граничных задач методом разложения по неор-
неортогональным функциям. — М.: Наука, 1978. — 230 с.
46. Арутюнян Н.Х., Абрамян Б.Л. Кручение упругих тел. — М., 1963. —
688 с.
47. Арутюнян Н.Х., Манжиров А. В. Контактные задачи теории ползучести.
Ереван, АН АрмССР. 1990. - 320 с.
48. Арутюнян Н.Х., Манжиров А.В., Наумов В.Э. Контактные задачи меха-
механики растущих тел. — М.: Наука, 1991. — 176 с.
49. Ахиезер Н.И. Лекции по теории аппроксимации. — М.: Наука, 1965. —
421 с.
50. Бабешко В. А. К теории и приложениям некоторых интегральных уравне-
уравнений первого рода // Докл. АН СССР. 1972. Т. 204, № 2. С. 309-312.
268 Список литературы
51. Бабешко В. А. Обобщенный метод факторизации в пространственных ди-
динамических смешанных задачах теории упругости. — М.: Наука, 1984. —
256 с.
52. Бабешко В.Л. Об одном асимптотическом методе при решении интеграль-
интегральных уравнений теории упругости и математической физики // ПММ.
1966. Т. 30, вып. 4. С. 732-741.
53. Бабешко В.Л. Об одном эффективном методе решения некоторых ин-
интегральных уравнений теории упругости и математической физики //
ПММ. 1967. Т. 31, вып. 1. С. 80-89.
54. Бабешко В.Л. Периодические уравнения свертки и свойства их реше-
решения // Докл. АН СССР. 1970. Т. 192, № 1. С. 52-58.
55. Бабешко В.Л., Векслер В.Е. Возбуждение вибрирующим штампом волн
в слое // ПММ. 1975. Т. 39, вып. 5. С. 884-888.
56. Бабешко В.А., Гарагуля В.А. Асимптотическое решение задачи о дей-
действии штампа, круглого в плане, на упругий слой // Изв. АН СССР.
МТТ. 1971. №1. С. 76-79.
57. Бабешко В.А., Глушков Е.В., Зинченко Ж.Ф. Динамика неоднородных
линейно-упругих сред. — М.: Наука, 1989. — 343 с.
58. Баблоян А. А. Решение некоторых парных рядов // Докл. Арм. ССР. 1964.
Т. 39, №3. С. 43-48.
59. Баблоян А. А. Решение некоторых парных уравнений, встречавшихся в
задачах теории упругости // ПММ. Т. 31, вып. 4. 1967. С. 678-689.
60. Баблоян А.А., Гулканян И.О. Об одной смешанной задаче для прямо-
прямоугольника // Изв. АН Арм. ССР. мех. 1969. Т. 22, № 1. С. 3-16.
61. Баблоян А.А., Енгибарян А.А. Контактная задача для прямоугольника
при наличии сцепления // Изв. АН Арм. ССР. Механика. 1977. Т. 30,
№3. С. 3-14.
62. Баблоян А.А., Мелконян А.П. Об одной осесимметричной контактной
задаче для цилиндра конечной длины // Изв. АН Арм. ССР. Механика.
1973. Т. 26, №5. С. 3-19.
63. Баблоян А.А., Мелконян А.П. О двух смешанных осесимметричных за-
задачах теории упругости // Изв. АН Арм. ССР. Механика. 1969. Т. 22,
№5. С. 3-15.
64. Баблоян А.А., Мкртчан A.M. Об одной смешанной задаче для прямо-
прямоугольника // Изв. АН Арм. ССР. Механика. 1971. Т. 24, №9. С. 3-15.
65. Баблоян А.А., Мкртчан A.M. Решение плоской смешанной задачи для
прямоугольника // Изв. АН Арм. ССР. Механика. 1972. Т. 25, №2.
С. 3-14.
66. Баблоян А. А., Саакян В.Г. Решение смешанной задачи теории упругости
для кольцевого сектора // Изв. АН Арм. ССР. Механика. 1967. Т. 20,
№5. С. 3-20.
67. Бейтмен Г., Эрдейн Ф. Высшие трансцендентные функции. — М., 1973.
Т. 1. - 296 с.
68. Белоконъ А. В. Об одном методе решения задач теории упругости для тел
конечных размеров // Докл. АН СССР. 1977. Т. 233, № 1. С. 56-59.
Список литературы 269
69. Белоконь А.В., Ватульян Т.П. Динамическая контактная задача для
конечного цилиндра // Жесткость машиностроительных конструкций: Тр.
всесоюзн. научно-технич. конф. Брянск. 1976. С. 99-104.
70. Белоконь А.В., Ватульян Т.П. Динамическая контактная задача о взаи-
взаимодействии двух штампов с анизотропным конечным цилиндром // Сме-
Смешанные задачи механики деформируемого тела: Тезисы докл. Всесоюз.
науч. конф. 4.2. Ростов-на-Дону: РГУ, 1977. С. 125.
71. Белоконь А.В., Ватульян Т.П. Контактные задачи теории упругости для
полуплоскости и конечного цилиндра // Тезисы докл. XV научного со-
совещания по тепловым напряжениям в элементах конструкций. — Киев:
Наукова думка, 1980. С. 8.
72. Белоконь А.В., Маликов Е.П. Динамическая смешанная задача для ко-
конечного трансверсально-изотропного цилиндра // Смешанные задачи ме-
механики деформируемого тела: Тезисы докл. Всесоюз. науч. конф. 4.2.
Ростов-на-Дону: РГУ, 1977. С. 126-127.
73. Белоконь А.В., Маликов Е.П. Смешанная задача теории упругости для
конечного трансверсально-изотропного цилиндра // Тезисы докл. Всесо-
Всесоюз. конф. по теории упругости. Ереван. 1979. С. 54-56.
74. Белоконь А.В., Маликов Е.П. Установившиеся вынужденные колебания
конечного трансверсально-изотропного цилиндра // Деп. в ВИНИТИ
18.06.79. №2174. — Ростов-на-Дону, 1979. — 31 с.
75. Белянкова Т.П., Филиппова Л.М. Статические контактные задачи для
тел с начальными напряжениями // Механика контактных взаимодей-
взаимодействий. — М.: Физматлит, 2001. С. 233-241.
76. Бородачев Н.М. О вдавливании штампа в торец полубесконечного упру-
упругого цилиндра // Прикл. механ. 1967. Т. 3, вып. 9. С. 83-89.
77. Борадачев П.М., Борадачева Ф.Н. Кручение упругого полупространства,
вызванное поворотом кольцевого штампа // Инж. журн. МТТ. 1966. № 1.
С. 94-99.
78. Бриллюэн Л., Пароди М. Распространение волн в периодических струк-
структурах. — М., 1959. — 457 с.
79. Буланов Г.С, Шалдырван В.А. К улучшению сходимости метода одно-
однородных решений // ПММ. 1980. Т. 44, вып. 5. С. 957-960.
80. Бурышкин М. Л. Обобщенная периодическая задача теории упругости //
ПММ. 1978. Т. 42, вып. 3. С. 521-531.
81. Бурышкин М.Л. О построении приближенных аналитических решений
несимметричных плоских задач для симметричных сред с полостями,
ядрами, прямолинейными трещинами и жесткими включениями // Ме-
Механика деформируемых тел и конструкций. — Ереван: Изд-во АН Арм.
ССР, 1985. С. 103-108.
82. Валов Г.М. Об одной смешанной задаче для прямоугольника // Изв. АН
СССР. Мех. и машин. 1961. №3. С. 133-142.
83. Вайнштейн Л. А. Электронные волны в периодических структурах //
Журнал технической физики. 1957. Т. 27, № 10. С. 2340-2352.
84. Виленкин П.Я., Горин Е.А., Костюченко А.Г. и др. Функциональный
анализ. — М.: Наука, 1964. — 321 с.
270 Список литературы
85. Владимирский В. В. Распространение разноволн вдоль цепочки симмет-
симметричных эндовибраторов // Докл. АН СССР. 1946. Т. 52, №3.
86. Власов А. Г. Метод переопределенных рядов в некоторых краевых задачах
математической физики // Вопр. динам, теории распространения сейсм.
волн. 1959. Вып. 3. С. 403-463.
87. Ворович И. И. Некоторые математические вопросы теории пластин и обо-
оболочек // Тр. II Всесоюз. съезда по теорет. и прикл. механике. Механика
твердого тела. — М.: Наука, 1966. С. 116-136.
88. Ворович И.И., Александров В.М., Бабешко В.А. Неклассические сме-
смешанные задачи теории упругости. — М.: Наука, 1974. — 456 с.
89. Ворович И.И., Бабешко В.А. Динамические смешанные задачи теории
упругости для неклассических областей. — М.: Наука, 1979. — 320 с.
90. Ворович И.И., Бабешко В.А., Пряхина О. Д. Динамика массивных тел
и резонансные явления в деформируемых средах. — М.: Наука, 1999. —
246 с.
91. Ворович И.И., Ковальчук В.Е. О базисных свойствах одной системы
однородных решений // ПММ. 1967. Т. 21, № 5. С. 861-863.
92. Ворович И.И., Кучеров Л.В., Чебаков М.И. В-резонансы в задаче об
установившихся колебаниях штампа на поверхности полосы периодиче-
периодической структуры // Изв. РАН. МТТ. 1992. №3. С. 95-100.
93. Ворович И.И., Кучеров Л.В., Чебаков М.И. Динамические свойства вол-
волновода периодической структуры // Динамич. задачи механики сплошной
среды. Теор. и прикл. вопросы вибрационного просвечивания Земли:
Тезисы докл. 3-й Региональной конф. Краснодар. 1990. — С. 54.
94. Ворович И.И., Кучеров Л.В., Чебаков М.И. Динамические свойства слоя
периодической структуры // Изв. вузов. Сев.-Кавк. регион. Спецвыпуск.
1994. С. 87-89.
95. Ворович И.И., Кучеров Л.В., Чебаков М.И. Интегральные уравнения
задачи о колебаниях штампа на поверхности полосы периодической струк-
структуры // Современные проблемы механики контактных взаимодействий:
Тезисы докл. научн. симпозиума. Ереван. 1992.
96. Ворович И.И., Кучеров Л.В., Чебаков М.И. К теории периодических вол-
волноводов // Ростовский государственный университет. Ежегодник. Ростов-
на-Дону, 1991. С. 4-9.
97. Ворович И.И., Пряхина О.Д. Аналитический метод определения резонан-
сов // Изв. АН СССР. МТТ. 1987. №3. С. 101-106.
98. Ворович И.И., Сафронов Ю.В., Устинов Ю.А. Прочность колес сложной
конструкции. М., 1967. 1983. — 194 с.
99. Ворович И.И., Устинов Ю.А. О давлении штампа на слой конечной
толщины // ПММ. 1959. Т. 23, вып. 3. С. 445-455.
100. Ворович И.И., Чебаков М.И. Об одном подходе к исследованию рас-
распространения колебаний в полуограниченных волноводах периодической
структуры // Современные проблемы механики сплошной среды: Тр.
3-й междунар. научн. конф. Т. 1. 7-9.10.1997. — Ростов-на-Дону: МП
«Книга», 1997. С. 83-87.
101. Ворович И.И., Юдович В.И. Удар круглого диска о жидкость конечной
глубины // ПММ. 1957. Т. 21, вып. 4. С. 525-532.
Список литературы 271
102. Гавриков М.В., Мазинг Р. И. Наследственно-стареющая модель изнаши-
изнашивания и ее применение к задачам с монотонно растущей зоной контакта //
Трение и износ. 1988. Т. 9, № 2. С. 274-279.
103. Гавриков М.В., Мазинг Р. И. Применение наследственно-стареющей мо-
модели изнашивания к осесимметричной контактной задаче // Трение и из-
износ. 1989. Т. 10, №6. С. 981-986.
104. Галанов Б. А. Метод граничных уравнений типа Гаммерштейна для кон-
контактных задач теории упругости в случае неизвестных областей контак-
контакта // ПММ. 1985. Т. 49, вып. 5. С. 627-835.
105. Галанов Б. А. Нелинейные граничные уравнения контактных задач теории
упругости // Докл. АН СССР. 1987. Т. 296, №4. С. 812-815.
106. Галин Л.А. Контактные задачи теории упругости и вязко упругости. —
М.: Наука, 1980. - 303 с.
107. Галин Л.А. Контактные задачи теории упругости при наличии износа //
ПММ. 1976. Т. 40, вып. 6. С. 981-986.
108. Галин Л.Л., Горячева И.Г. Осесимметричная контактная задача теории
упругости при наличии износа // ПММ. 1977. Т. 41, вып. 5. С. 807-812.
109. Галин Л.Л., Горячева И.Г. Пространственная контактная задача о дви-
движении штампа с трением // ПММ. 1982. Т. 46, вып. 6. С. 1016-1022.
ПО. Галфаян П. О. Решение одной смешанной задачи теории упругости для
прямоугольника // Изв. АН Арм. ССР. Серия физ-мат. наук. 1964. Т. 17,
№1. С. 33-61.
111. Галфаян П. О., Чобанян К. С. Решение одной контактной задачи для
упругого прямоугольника // ПММ. 1966. Т. 30, вып. 3. С. 569-575.
112. Гасымов М.Г., Джавадов М.Г. Кратная полнота части собственных
и присоединенных функций дифференциальных операторных пучков //
Докл. АН СССР. 1972. Т. 203, №6. С. 1235-1237.
113. Гахов Ф.Д. Краевые задачи. — М.: Наука, 1977. — 640 с.
114. Гельфанд И.М. Разложение по собственным функциям уравнений с пе-
периодическими коэффициентами // Докл. АН СССР. 1950. Т. 73, №6.
С. 1117-1121.
115. Гомилко A.M., Гринченко В. Т., Мелешко В.В. О возможностях метода
однородных решений в смешанной задаче теории упругости для полосы //
Теоретическая и прикладная механика. 1987. Вып. 18. С. 3-8.
116. Гомилко A.M., Гринченко В. Т., Мелешко В.В. О методах однородных
решений и суперпозиции в статических граничных задачах для упругой
полуполосы // Прикладная механика. 1986. Т. 22, № 8. С. 84-93.
117. Горячева И. Г. Контактная задача при наличии износа для кольца, вло-
вложенного в цилиндр // ПММ. 1980. Т. 44, вып. 2. С. 363-367.
118. Горячева И. Г. Контактные задачи теории упругости для системы изнаши-
изнашиваемых штампов // МТТ. 1987. №6. С. 62-68.
119. Горячева И. Г. Плоские и осесимметричные контактные задачи для шеро-
шероховатых упругих тел // ПММ. 1979. Т. 43, вып. 1. С. 99-105.
120. Горячева И.Г., Добычин И.М. Влияние покрытия на контактные характе-
характеристики радиальных подшипников скольжения // Трение и износ. 1984.
Т. 5, № 3. С. 442-450.
272 Список литературы
121. Горячева И.Г., Добычин Н.М. Изнашивание неоднородно-упрочненных
поверхностей // Трение и износ. 1986. Т. 7, №6. С. 985-992.
122. Горячева И.Г., Добычин Н.М. Кинетика изнашивания твердого смазоч-
смазочного покрытия цапфы подшипника скольжения // Трение и износ. 1984.
Т. 5, №4. С. 581-588.
123. Горячева И.Г., Добычин М.Н. Контактные задачи в трибологии. — М.:
Машиностроение, 1988. — 254 с.
124. Горячева И.Г., Добычин Н.М. Механизм формирования шероховатости
в процессе приработки // Трение и износ. 1982. Т. 3, №4. С. 632-642.
125. Горячева И.Г., Солдатенков И.А. Контактные задачи с учетом изно-
износа // Механика контактных взаимодействий. — М.: Физматлит, 2001.
С. 289-302.
126. Горячева И.Г., Солдатенков И. А. Теоретическое исследование приработ-
приработки и установившегося режима изнашивания твердых смазочных покры-
покрытий // Трение и износ. 1983. Т. 4, № 3. С. 420-431.
127. Горячева И.Г., Чекина О.Г. Управление формоизменением поверхностей
при изнашивании // Трение и износ. 1989. Т. 10, № 1. С. 5-12.
128. Горшков А.Г., Тарлаковский Д.В. Динамические контактные задачи с
подвижными границами. — М.: Наука, 1995. — 352 с.
129. Градштейн И. С, Рыжик И.М. Таблицы интегралов, сумм, рядов и про-
произведений. — М.: Наука, 1971. — 1108 с.
130. Гринберг Г. А. О методе предложенном Папковичем П.Ф. для решения
плоской задачи теории упругости для прямоугольной области и задачи
изгиба прямоугольной тонкой плиты с двумя закрепленными кромками
и о некоторых его обобщениях // ПММ. 1953. Т. 17, вып. 2. С. 212-218.
131. Гринберг Г. А. О решении плоской задачи теории упругости и задаче об
изгибе тонкой плиты с закрепленным контуром // Докл. АН СССР. 1951.
Т. 76, №5. С. 661-664.
132. Гринберг Г. А., Лебедев Н.Н., Уфлянд Я. С. Метод решения общей бигар-
монической задачи для прямоугольной области при задании на контуре
значений функции и ее нормальной производной // ПММ. 1953. Т. 17,
вып. 5. С. 73-84.
133. Гринченко В. Т. Равновесие и установившиеся колебания упругих тел
конечных размеров. — Киев: Наукова думка, 1978. — 264 с.
134. Гринченко В. Т., Городецкая Н.С. Отражение волн Лэмба от границ раз-
раздела в составном волноводе // Прикладная механика. 1985. Т. 21, №5.
С.121-125.
135. Гринченко В. Т., Коваленко А.Д., Улитко А.Ф. Анализ напряженного
состояния жестко защемленной пластины на основе решения простран-
пространственной задачи теории упругости // Труды VII Всесоюзной конференции
по теории оболочек и пластин. — М., 1970. — 910 с.
136. Гринченко В. Т., Мелешко В.В. Гармонические колебания и волны в упру-
упругих телах. — Киев: Наукова Думка, 1981. — 283 с.
137. Гринченко В.Т., Улитко А.Ф. Пространственные задачи теории упруго-
упругости. Т. 3. Равновесие упругих тел канонической формы. — Киев: Наукова
думка, 1985. - 280 с.
Список литературы 273
138. Губенко B.C., Улитко А.Ф. Смешанные задачи теории упругости для
полупространства и слоя с несколькими круговыми линиями раздела
краевых условий // Контактные задачи и их инженерные приложения. —
М.: НИИмаш, 1969. С. 31-40.
139. Джавадов М. Г. Об m-кратной полноте половины собственных и при-
присоединенных функций обыкновенного дифференциального оператора //
Докл. АН СССР. 1965. Т. 160, №4. С. 754-757.
140. Джанелидзе Г.Ю. Обзор работ по теории изгиба толстых и тонких плит,
опубликованных в СССР // ПММ. 1948. 12. Вып. 1. С. 109-128.
141. Джанелидзе Г.Ю., Прокопов В.К. Методы однородных решений в ма-
математической теории упругости // Труды VI Всесоюз. матем. съезда.
Секционные обзорные доклады. Т. 1. — Л.: Наука, 1964. С. 551-557.
142. Джонсон К. Механика контактного взаимодействия. — М.: Мир, 1989. —
509 с.
143. Добычин П.М. Кинетика изнашивания дискового сопряжения // Трение
и износ. 1990. Т. 11, №2. С. 206-212.
144. Довнорович В. И. Пространственные контактные задачи теории упруго-
упругости. - Минск: Изд-во БГУ, 1959. - 107 с.
145. Дроздов Ю.Н., Павлов Ю.Г., Пучков В. П. Трение и износ в экстремаль-
экстремальных условиях. — М.: Машиностроение, 1986. — 224 с.
146. Дьяков М.В., Устинов Ю.А. Дифракция сдвиговых волн на бесконечной
и конечной периодической системах разрезов в упругом слое // Акусти-
Акустический журнал. 1997. Т. 43, №2. С. 176-181.
147. Зилъберглейт А. С, Нуллер Б.М. Обобщенная ортогональность однород-
однородных решений в динамических задачах теории упругости // Докл. АН
СССР. Т. 234. 1977. Вып. 2. С. 333-335.
148. Зингер М.Я. Элементы дифференциальной теории чебышевских прибли-
приближений. — М.: Наука, 1975. — 255 с.
149. Златин А.П. Некоторые теоремы разложения по однородным решени-
решениям для цилиндра // Изв. АН Арм. ССР. Механика. 1979. Т. 32, №5.
С.16-24.
150. Златин А. П. О корнях некоторых трансцендентных уравнений, встречав-
встречавшихся в теории упругости // Прикладная механика. 1980. 12. С. 69-74.
151. Златин А. П. Растяжение цилиндра, содержащего периодически располо-
расположенные дискообразные трещины // Докл. АН СССР. 1978. Т. 241, №6.
С. 1300-1302.
152. Зуховицкий СП. Алгоритм для построения Чебышевского приближения
непрерывной функции полиномом // Докл. АН СССР. Т. 120. 1958.
С.693-699.
153. Зуховицкий СП. Алгоритмы для решения чебышевской задачи прибли-
приближения в случае конечной несовместной системы линейных уравнений //
Докл. АН СССР. 73. 4. 1951. С. 561-564.
154. Ишлинский А.Ю., Крагелъский П.В., Алексеев Н.М. и др. Проблемы
изнашивания твердых тел в аспекте механики // Трение и износ. 1986.
Т. 7, №4. С. 581-592.
274 Список литературы
155. Каландия А.И., Лурье А.И., Манджавидзе Г. Ф. и др. Линейная теория
упругости // Механика в СССР за 50 лет. Т. 3. — М.: Наука, 1972.
С. 5-70.
156. Калинчук В. В. Динамические контактные задачи для тел с начальными
напряжениями // Механика контактных взаимодействий. — М.: Физмат-
лит, 2001. С. 289-302.
157. Карасева Г.М., Любарский Г. Я. Полосы пропускания периодических вол-
волноводов // Учен. зап. Харьков, ун-та. (Тр. физич. отделения). Харьков.
1952. №3.
158. Карпенко В.А., Чебаков М.И. Кручение сектора сферического слоя кру-
круговым штампом // Механика сплошной среды. Ростов-на-Дону. 1985.
С. 83-90.
159. Карпенко В. А., Чебаков М.И. Некоторые смешанные задачи теории упру-
упругости для сектора шарового слоя // Тезисы докладов 2-й Всесоюзной
конференций по теории упругости. Тбилиси. 1984. С. 128.
160. Келдыш М.В. О полноте собственных функций некоторых классов неса-
несамосопряженных уравнений // Успехи математических наук. 1971. Т. 26,
№4. С. 15-42.
161. Келдыш М.В. О собственных значениях и собственных функциях неко-
некоторых классов несамосопряженных уравнений // Докл. АН СССР. 1951.
77. № 1. С. 11-14.
162. Кильчевский И. А. Динамическое контактное сжатие твердых тел. Удар. —
Киев: Наукова думка, 1976. — 320 с.
163. Китовер К. Л. Об использовании специальных систем бигармонических
функций для решения некоторых задач теории упругости // ПММ. 1952.
XVI. Вып. 6. С. 739-748.
164. Коваленко А.Д. Основы термоупругости. — Киев: Наукова думка,
1970. - 239 с.
165. Коваленко Е.В. Контактные задачи с учетом тепловыделения от тре-
трения // Механика контактных взаимодействий. — М.: Физматлит, 2001.
С. 476-490.
166. Коваленко Е.В. К расчету изнашивания сопряжения вал-втулка // МТТ.
1982. №6. С. 66-72.
167. Коваленко Е.В. Исследование осесимметричной контактной задачи об
изнашивании пары кольцевой штамп-упругое шероховатое полупростран-
полупространство // ПММ. 1985. Т. 49, вып. 5. С. 836-843.
168. Коваленко Е.В., Тарасов Д.Г., Чебаков М.И. Точное решение контактной
задачи для конечных канонических областей // ПММ. 1990. Т. 54, вып. 5.
С. 837-941.
169. Коваленко Е.В., Теплый М.И. Контактные задачи при нелинейном законе
изнашивания для тел с покрытиями. 4.1 // Трение и износ. 1983. Т. 4,
№3. С. 440-448. Коваленко Е.В., Теплый М.И. Контактные задачи при
нелинейном законе изнашивания для тел с покрытиями. 4.2 // Трение
и износ. 1983. Т. 4, №4. С. 676-682.
170. Коллатц Л., Крабе В. Теория приближения. Чебышевские приближения
и их приложения. — М.: Наука, 1978. — 215 с.
Список литературы 275
171. Короза В.И., Суховский Е.С. К вопросу о дисперсии волн в периоди-
периодических волноводах // Радиотехника и электроника. 1976. Т. 21, №12.
С.2466-2472.
172. Костарев А. В. О соотношениях ортогональности однородных решений
двумерных задач теории упругости // Тепловые напряжения в элементах
конструкций: Сб. статей. — Киев: Наукова думка, 1978. Вып. 18. С. 83-87.
173. Костарев Л. В. Применение соотношений расширенной ортогональности
к решению краевых задач теории упругости // Изв. АН Арм. ССР. Сер.
Механика. 1973. Т. 26, № 1. С. 15-22.
174. Костюченко Л.Г., Оразов М.Б. Задача о колебаниях упругого полу-
полуцилиндра и связанные с ней самосопряженные квадратичные пучки //
Труды сем. им. И. Г. Петровского. — М.: Изв. Московского ун-та, 1981.
Вып. 6. С. 97-146.
175. Костюченко Л.Г., Шкаликов А. А. К теории самосопряженных квадра-
квадратичных пучков операторов // Вестник МГУ. Сер. Математика, механика.
1983. №6. С. 40-51.
176. Костюченко Л.Г., Шкаликов А. А. Самосопряженные квадратичные пуч-
пучки операторов и эллиптические задачи // Функциональный анализ и его
приложения. 1983. Т. 17, вып. 2. С. 38-61.
177. Коялович Б.М. Исследования о бесконечных системах линейных уравне-
уравнений // Тр. физ.-матем. ин-та им. В. А. Стеклова 1930. Т. 3. С. 41-167.
178. Кравчук А. С. Контактные задачи с односторонними связями и учетом
сил трения // Механика контактных взаимодействий. — М.: Физматлит,
2001. С. 491-498.
179. Кравчук А. С. Решение некоторых пространственных контактных задач
с учетом трения на поверхности соприкосновения // Трение и износ. 1981.
Т. 2, №4. С. 589-595.
180. Крагелъский И.В., Добычин М.Н., Комбалов B.C. Основы расчетов на
трение и износ. — М.: Машиностроение, 1977. — 526 с.
181. Краснушкин П.Е. Преобразование нормальных волн в периодических и
гладких волноводах без потерь // Радиотехника и электроника. 1974.
Т. 19, №7. С. 1345-1358.
182. Краснушкин П.Е., Ложнее СП. Метод точного расчета однородных яче-
ячеистых волноводов // Радиотехника и электроника. 1966. Т. 11, №6.
С. 1051-1065.
183. Крейн М., Лангер Г. К. К теории квадратических пучков самосопряжен-
самосопряженных операторов // Докл. АН СССР. 1964. 154. №6. С. 1258-1261.
184. Крейн М.Г., Лангер Г. К. О некоторых математических принципах ли-
линейной теории демпфированных колебаний континуумов // Приложение
теории функций в механике сплошной среды. Т. 2. — М.: Наука, 1965.
С.283-322.
185. Крейн М.Г., Любарский Г. Я. К теории полос пропускания периодических
волноводов // ПММ. 1961. Т. 25, вып. 1. С. 24-37.
186. Кристенсен Р. Введение в механику композитов. — М.: Мир, 1982. —
334 с.
187. Кучеров Л.В., Цветков А.Н., Чебаков М.И. Контактная задача для коль-
кольцевого сектора // Деп. ВИНИТИ. 26.01.88. №681-В88. - 18 с.
276 Список литературы
188. Кучеров Л.В., Чебаков М.И. Контактная обобщенно периодическая за-
задача теории упругости для кольца // Изв. АН СССР. МТТ. 1991. №4.
С. 111-118.
189. Кучеров Л.В., Чебаков М.И. Несимметричная контактная задача для
кольцевого сектора. Изв. СКНЦ ВШ. Сер. естеств наук. 1989. №4.
С. 58-64.
190. Лащеков В.К., Нуллер Б.М. Об одном обобщенном методе кусочно-одно-
кусочно-однородных напряжений // Изв. ВНИИ Гидротехники. 1983. 169. С. 9-15.
191. Левитан В.М., Саргсян И.С. Введение в спектральную теорию. — М.:
Наука, 1970. - 671 с.
192. Лидский В. В. О суммируемости рядов по главным векторам несамосо-
несамосопряженных операторов // Тр. Моск. матем. об-ва. Т. 11. — М.: ЕИОМЛ,
1962. С. 3-35.
193. Лионе Я.Л., Мадженес Э. Неоднородные граничные задачи и их прило-
приложения. — М.: Мир, 1971. — 320 с.
194. Лоран П.Ж. Аппроксимация и оптимизация. — М.: Мир, 1975. — 496 с.
195. Лоренц X., Чебаков М.И. Теретические и экспериментальные исследова-
исследования контактного взаимодействия штампа с нагретой полосой // Современ-
Современные проблемы механики сплошной среды: Труды 2-й Междунар. научн.
конф. 19-20.09.1996. - Ростов-на-Дону: МП «Книга», 1997. С. 89-92.
196. Лоусон Ч., Хенсен Р. Численное решение задач методом наименьших
квадратов. - М.: Мир, 1989. - 210 с.
197. Лубягин И. А., Пожарский Д. А., Чебаков М.И. Внедрение штампа в фор-
форме эллиптического параболоида в упругий пространственный клин //
ПММ. 1992. Т. 56, вып. 2. С. 286-295.
198. Лубягин И. А., Пожарский Д. А., Чебаков М.И. Действие эллиптического
в плане штампа на упругий пространственный клин // Проблемы контакт-
контактного взаимодействия и износа. Тезисы докладов выездной сессии Межве-
Межведомственного совета по трибологии. — Ростов-на-Дону, 1990. С. 68.
199. Лубягин И. А., Пожарский Д. А., Чебаков М.И. Обобщение задач Бусси-
неска и Черрути для случая пространственного клина // Докл. АН СССР.
1991. Т. 321, №1. С. 58-62.
200. Лубягин И.А., Пожарский Д.А., Чебаков М.И. Пространственная кон-
контактная задачадля упругого клина // В кн. 7-й Всес. съезд по теоретич.
и прикл. механике. Аннотации докладов. — Москва, 1991. С. 232-233.
201. Лубягин И.А., Чебаков М.И. К асимптотическому методу больших Л //
ПММ. 1989. Т. 53, № 1. С. 121-126.
202. Лурье А. И. К теории толстых плит // ПММ. 1942. Т. 6, №2-3.
С.151-168.
203. Лурье А.И. Напряженное состояние в упругом цилиндре, нагруженном
на боковой поверхности // Инженерный сборник. 1953. Т. 17. С. 43-58.
204. Лурье А.И. Нелинейная теория упругости. — М.: Наука, 1980. — 512 с.
205. Лурье А.И. Пространственные задачи теории упругости. — М.: ГИТТЛ.
1955. - 322 с.
206. Лурье А.И. Теория упругости. — М.: Наука, 1970. — 939 с.
Список литературы 277
207. Маркус А. С. Введение в спектральную теорию полиномиальных опера-
операторных пучков. Кишинев. 1986. — 260 с.
208. Мартиросян З.А. О двух контактных задачах для круглых упругих ци-
цилиндров конечной длины // Изв. АН Арм. ССР. Механика. 1978. Т. 31,
№ 5. С. 36-47.
209. Мартиросян З.А., Тоноян B.C. О контактном взаимодействии соосных
цилиндров конечных длин // Изв. АН СССР. МП. 1981. №6. С. 94-102.
210. Марченко В. А. Спектральная теория операторов Штурма-Лиувилля. —
Киев: Наукова думка, 1972. — 218 с.
211. Масхма В. К. Трехмерные динамические задачи установившихся колеба-
колебаний плит. Автореф. канд. дис. Ростов-на-Дону: Изд-во РГУ, 1979. — 16 с.
212. Мациев В.И., Могульский Е.З. Некоторые признаки кратной полноты си-
системы собственных и присоединенных векторов полиномиальных пучков
операторов // Теория функций, функциональный анализ и их приложе-
приложения. 1971. Вып. 13. С. 2-45.
213. Мелконян А. П. Об одной смешанной осесимметричной задаче теории
упругости для цилиндра конечной длины // Изв. АН Арм. ССР. Механи-
Механика. 1971. Т. ХХШ. № 2. С. 3-13.
214. Мелконян А. П. Осесимметричная контактная задача для сплошного ци-
цилиндра // Докл. АН Арм. ССР. 1978. 66. № 1. С. 27-36.
215. Мелконян М.Г., Мкртчан И.М. Об одной контактной задаче для двух
прямоугольников // Изв. АН Арм. ССР. Механика. 1975. Т. 28, №3.
С. 13-28.
216. Метод граничных интегральных уравнений. — М.: Мир. Механика, новое
в зарубежной науке. 1978. Вып. 15. — 215 с.
217. Механика контактных взаимодействий / Под ред. И. И. Воровича,
В.М. Александрова. — М.: Физматлит, 2001. — 672 с.
218. Миллер У. Симметрия и разделение переменных. — М.: Мир, 1981. —
342 с.
219. Минасян Р. С. О смешанной граничной задаче уравнения Лапласа для
прямоугольника // ПММ. 1952. Т. 16, вып. 3. С. 293-304.
220. Михин А. И. Зависимость сближения между шероховатыми поверхностя-
поверхностями контактирующих тел от нагрузки при упругом контакте // Трение
и износ. 1990. Т. 11, №2. С. 328-331.
221. Михин Н.М., Горячева И.Г., Сляднев М.А., Муравьева Т.И. Теоретиче-
Теоретическое и экспериментальное исследование напряженно-деформированного
состояния в контакте индектор — твердое смазочное покрытие // Трение
и износ. 1982. Т. 3, № 3. С. 490-494.
222. Михлин С. Г. Вариационные методы в математической физике. — М.:
Наука, 1970. - 512 с.
223. Михлин С. Г. Многомерные сингулярные интегралы и интегральные урав-
уравнения. — М.: Физматгиз, 1962. — 265 с.
224. Михлин С.Г. Проблема минимума квадратичного функционала. — М.; Л.:
ГИТТЛ, 1952. - 233 с.
225. Михлин С. Г. Прямые методы в математической физике. — ЧГТТИ,
1950. - 323 с.
278 Список литературы
226. Михлин С. Г. Численная реализация вариационных методов. — М.: Наука,
1966. - 324 с.
227. Моссаковский В.И., Качаловская Н.Е., Голикова С. С. Контактные зада-
задачи математической теории упругости. — Киев: Наукова думка, 1985. —
176 с.
228. Мусхелишвили Н.И. Некоторые основные задачи математической теории
упругости. — М.: Наука, 1966. — 707 с.
229. Нахмейн Е.Л., Нуллер Б.М. Об одном методе решения контактных пери-
периодических задач для упругой полосы и кольца // Изв. АН СССР. МТТ.
1976. №3. С. 53-61.
230. Немиш Ю.Н. Трехмерные граничные задачи теории упругости для нека-
неканонических областей // Прикл. мех. 1980. Т. 16, №2. С. 3-39.
231. Немиш Ю.Н., Чернопиский Д.И. Осесимметричное состояние деформи-
деформируемых цилиндров переменной толщины // Прикладная механика. 1975.
Т. 11, №10. С. 3-18.
232. Никишин В. С, Шапиро Г. С. Задачи теории упругости для многослойных
сред. - М.: Наука, 1973. - 132 с.
233. Никольский СМ. Приближение функций многих переменных и теоремы
вложения. — М.: Наука, 1969. — 380 с.
234. Новодворский Е.П., Пискер И.Ш. Процесс уравнивания максимумов //
УМН. 1951. 6D2). С. 174-181.
235. Нуллер Б.М. Контактные задачи для упругого полубесконечного цилин-
цилиндра // ПММ. 1970. Т. 34, вып. 4. С. 620-631.
236. Нуллер Б.М. К смешанной задаче о кручении упругого конуса // Инж.
журн. МТТ. 1966. №4. С. 146-151.
237. Нуллер Б.М. Об одном методе решения смешанных задач теории упруго-
упругости конечных областей // Изв. АН СССР. МТТ. 1970. № 3. С. 36-42.
238. Нуллер Б.М. О новых обобщениях метода кусочно-однородных реше-
решений // Изв. ВНИИГ. 1978. Т. 124. С. 20-30. Т. 120. С. 36-42.
239. Оразов М.Б., Шкаликов А. А. Об n-кратной базисности собственных
функций некоторых регулярных краевых задач // Сибирский математиче-
математический журнал. 1976. Т. 17, №3. С. 627-639.
240. Панасюк В.В., Теплий М.Й. Деяю контакта задач! теорп пружность
Кшв: Наукова думка, 1975. — 196 с.
241. Папкович П. Ф. Два вопроса теории изгиба упругих плит // ПММ. 1941.
Т. 5, вып. 3. С. 359-374.
242. Папкович П. Ф. Об одной форме решений плоской задачи теории упру-
упругости для прямоугольной полосы // Докл. СССР. 1940. Т. 27, №4.
С. 627-639.
243. Папкович П.Ф. Строительная механика корабля. Т. 2. — М.: Госстройиз-
дат, 1941. - 953 с.
244. Партон В.З., Перлин П. И. Интегральные уравнения теории упругости. —
М.: Наука, 1977. - 312 с.
245. Пацальт И. Применение квадратичного программирования в контактных
задачах теории упругости // Publ.Techn. Univ Heavy. 3. 1979. D. 33. №4.
P. 171-174. (С. 220-221).
Список литературы 279
246. Подгорный Л.И., Гонтаровский П. П. и др. Задачи контактного взаимо-
взаимодействия элементов конструкций. — Киев: Наукова думка, 1989. — 232 с.
247. Пожарский Д. А. О трехмерной контактной задаче для упругого клина
при учете сил трения // ПММ. 2000. Т. 64, вып. 1. С. 151-159.
248. Пожарский Д. А. Пространственные контактные задачи для упругих тел
сложной геометрии // Механика контактных взаимодействий. — М.:
Физматлит, 2001. С. 181-198.
249. Пожарский Д. А. Трехмерная контактная задача для упругого клина при
учете трения в неизвестной области контакта // Докл. РАН. Т. 372, № 3.
С.333-336.
250. Понтрягин JI. С. Эрмитовы операторы в пространстве с индефинитной
метрикой // Изв. АН СССР. 1944. Сер. мат. №6. С. 243-280.
251. Попов Г. Я. Контактные задачи для линейно-деформируемого основа-
основания. — Киев-Одесса: Вища школа, 1982. — 168 с.
252. Попов Г. Я. Концентрация упругих напряжений возле штампов, разрезов,
тонких включений и подкреплений. — М.: Наука, 1982. — 344 с.
253. Попов Г.Я., Ростовцев П.А. Контактные (смешанные) задачи теории
упругости // Труды 2-го Всесоюзного съезда по теоретической и приклад-
прикладной механике. Вып. 3. - М.: Наука, 1966. С. 235-252.
254. Поручиков В. Б. Методы динамической теории упругости. — М.: Наука,
1986. - 328 с.
255. Прокопов В. К. Обзор работ по однородным решениям теории упругости
и их приложениям // Труды ЛГИ. 1967. № 279. С. 31-46.
256. Прокопов В. К. Об одной плоской задаче теории упругости для прямо-
прямоугольной области // ПММ. 1952. Т. 16, вып. 1. С. 45-47.
257. Прокопов В. К. Однородные решения теории упругости и их приложения
к теории тонких пластинок. Тр. II Всесоиз. съезда по теорет. и прикл.
механике. Механика твердого тела. — М.: Наука, 1966. С. 253-259.
258. Прокопов В. К. О соотношениях обобщенной ортогональности, имевших
приложения к теории упругости // Труды симп. по механике и родствен-
родственным проблемам анализа. Т. 1. Тбилиси. 1973. С. 206-213.
259. Прудников А.П., Брычков Ю.А., Маричев О.П. Интегралы и ряды. Спе-
Специальные функции. — М.: Физматлит, 2003. — 664 с.
260. Развитие теории контактных задач в СССР / Под ред. Л. А. Галина. —
М.: Наука, 1976. - 493 с.
261. Разневский Г. В. О базисах, состоящих из производных цепочек, отвечав-
отвечавших краевым задачам // Докл. АН СССР 1980. Т. 251, № 2. С. 283-284.
262. Разневский Г. В. Об одном способе доказательства минимальности и ба-
зисности части корневых векторов // Функциональный анализ и его
приложения. 1983. Т. 17, вып. 1. С. 24-30.
263. Раппопорт P.M. Некоторые вопросы расчета толстых сферических обо-
оболочек при несимметричной деформации // Изв. Всесоюв. н.-и. ин-та
гидротехники. 1971. Т. 9. С. 49-58.
264. Рвачев В. Л. Исследования ученых Украины в области контактных задач
теории упругости // Прикл. механика. 1967. Т. 3, вып. 10. С. 109-116.
280 Список литературы
265. Рвачев В.Л., Проценко B.C. Контактные задачи теории упругости для
неклассических областей. — Киев: Наукова думка, 1977. — 235 с.
266. Рекач В. Г. Руководство к решению задач по теории упругости. — М.:
Высшая школа. 1977. — 215 с.
267. Ремез Е.Я. Вопросы единственности или множественности решений Че-
бышевской задачи для системы несовместных линейных уравнений и по-
понятие Чебышевского решения // Укр. математический журнал. 1956. Т. 8.
С. 34-53.
268. Ремез Е.Я. Общие вычислительные методы Чебышевского приближе-
приближения. - Киев: изд. АН УССР. 1957. - 454 с.
269. Ремез Е.Я. О графо-аналитическом решении некоторых задач Чебышев-
Чебышевского приближения // Укр. математический журнал. 1955. 7. 1. С. 71-90.
270. Ремез Е.Я. Основы численных методов Чебышевского приближения. —
Киев: Наукова думка, 1969. — 350 с.
271. Саркисян B.C. Контактные задачи для полуплоскостей и полос. Ереван:
Ереван, ун-т, 1983. — 260 с.
272. Сеймов В.М. Динамические контактные задачи. — Киев: Наукова думка,
1976. - 284 с.
273. Слепян Л. И. Возбуждение волн и динамика разрушения в упругих си-
системах периодической структуры // Новожиловский сборник. С-Пб. 1992.
С. 87-97.
274. Слепян Л. И. Теорема Бетти и соотношения ортогональности для соб-
собственных функций // Изв. АН СССР. 1979. МТТ. С. 83-87.
275. Справочник по специальным функциям с формулами, графиками и ма-
математическими таблицами / Под ред. М. Абрамовича, И. Стиган. — М.:
Наука, 1979. - 830 с.
276. Статические и динамические смешанные задачи теории упругости / Под
ред. И. И. Воровича. — Ростов-на-Дону: Изд-во Ростов, ун-та, 1983. —
263 с.
277. Стеклов В. А. О равновесии упругих тел вращения // Сообщения Харьк.
мат. об-ва. Сер. 2. 1982. Т. 3, №4-5. С. 172-251.
278. Суховский Е. С. Приближенный расчет электромагнитных волн в пери-
периодическом волноводе // Радиотехника и электроника. 1972. Т. 17, №2.
С. 232-239.
279. Тамаркин Я. Д. О некоторых общих задачах теории обыкновенных ли-
линейных дифференциальных уравнений и о разложении произвольных
функций в ряды. — Петроград, 1917. — 889 с.
280. Теплый М. И. Контактные задачи для областей с круговыми границами. —
Львов: Вища школа, 1983. — 176 с.
281. Тихомиров В. И. Наилучшие методы приближения и интерполирования
дифференцируемых функций в пространстве С[— 1,— 1] // Математиче-
Математический сборник. 80A0). 1969. С. 290-304.
282. Тихонов А. Н., Самарский А. А. Уравнения математической физики. — М.:
Наука, 1966. - 724 с.
Список литературы 281
283. Усов П.П., Дроздов Ю.Н., Николашев Ю.Н. Теоретическое исследование
напряженного состояния пары вал-втулка с учетом износа. Машиноведе-
Машиноведение. 1979. №2. С. 80-87.
284. Устинов Ю.А. К теории твердых волноводов периодической структу-
структуры // Ростовский гос. университет. Ежегодник-95. Ростов-на-Дону. 1996.
С. 136-141.
285. Устинов Ю.А. Некоторые свойства однородных решений неоднородных
плит // Докл. АН СССР. 1974. Т. 216, №4. С. 323-328.
286. Устинов Ю.А. О полноте системы однородных решений теории плит //
ПММ. 1976. Т. 40, вып. 3. С. 536-543.
287. Устинов Ю., Юдович В. И. О полноте системы элементарных решений
бигармонического уравнения в полуполосе // ПММ. 1973. Т. 37, вып. 4.
С. 706-714.
288. Уфлянд Я. С. Интегральные преобразования в задачах теории упруго-
упругости. — Л.: Наука, 1967. — 402 с.
289. Филиппова Л.М. О влиянии начальных напряжений на раскрытие круго-
круговой трещины // ПММ. 1983. Т. 47, вып. 2. С. 286-290.
290. Филиппова Л.М. Распределение напряжений вблизи кромки трещины
в предварительно напряженном упругом теле // Прикл. математика и ме-
механика. 1986. 50. Вып. 2. С. 320-327.
291. Филиппова Л.М., Цветков А.Н., Чебаков М.И. Взаимодействие жест-
жесткого бандажа с предварительно напряженным упругим конечным цилин-
цилиндром // Изв. АН СССР МТТ. 1991. № 5. С. 51-56.
292. Филиппова Л.М., Цветков А.Н., Чебаков М.И. Плоская контактная за-
задача для предварительно напряженного состояния тела прямоугольного
сечения // Прикладная механика. 1990. Т. 26, № 12. С. 81-89.
293. Филиппова Л.М., Чебаков М.И. Взаимодействие жесткого штампа с вы-
сокоэлластичным прямоугольным амортизатором // Методы расчета изде-
изделий из высокоэлластичных материалов: Тезисы докл. Всес. конференции.
Рига. 1989. С. 173.
294. Филиппова Л.М., Чебаков М.И. Контактная задача для предварительно
напряженного цилиндра // Изв. АН СССР. МТТ. 1988. № 2. С. 62-69.
295. Филиппова Л.М., Чебаков М.И. Некоторые контактные задачи для пред-
предварительно напряженного цилиндра конечных размеров // Аннотации
докладов IV Всесоюзного съезда по теоретической и прикладной механи-
механике. — Ташкент, 1986. С. 615.
296. Филоненко-Бородич М.М. Об одной системе функций и ее приложения
в теории упругости // ПММ. 1946. Т. 10, вып. 1. С. 193-208.
297. Хан X. Теория упругости. — М.: Мир, 1988. — 343 с.
298. Цветков А.И. Метод однородных решений в контактных задачах
для неканонической формы. Автореферат дисс. канд. физ.-мат. наук.
Ростов-на-Дону. 1991. — 22 с.
299. Цветков А.Н., Чебаков М.И. Контактные задачи для конечного тела
вращения со свободной боковой поверхностью // Изв. АН СССР. МТТ.
1989. №2. С. 77-82.
282 Список литературы
300. Цветков Л.Н., Чебаков М.И. Об использовании однородных решений
в контактных задачах для тел с криволинейной границей // Гидроаэро-
Гидроаэромеханика и теория упругости. Математическое моделир. в гидроаэроди-
гидроаэродинамике и теории упругости. — Днепропетровск: ДГУ, 1989. С. 114-119.
301. Цветков Л.Н., Чебаков М.И. Об одном методе решения контактных
задач для тел неканонической формы // Смешанные задачи механики
деформируемого тела: Тезисы докл. 4-й Всес. конфер. Ч. 2. — Одесса.
1989. С. 127-128.
302. Цветков Л.И., Чебаков М.И. О некоторых контактных задачах теории
упругости для тел конечных размеров неканонической формы // Совре-
Современные проблемы теории контактных взаимодействий: Материалы выезд-
выездного заседания научного совета АН СССР по трению и смазкам. — Луцк,
1987. С. 76-78.
303. Цветков Л.Н., Чебаков М.И. Осесимметричная контактная задача для
тела вращения конечных размеров со свободной боковой поверхностью /
Ростов-на-Дону. 1985. деп. ВИНИТИ №8481-885. - 18 с.
304. Цветков Л.Н., Чебаков М.И. Плоская контактная задача для криволи-
криволинейной трапеции // Изв. АН СССР. МТТ. 1990. №6. С. 43-48.
305. Цветков А.Н., Чебаков М.И. Эффективный способ решения одного клас-
класса бесконечных систем в контактных задачах теории упругости // ПММ.
1991. Т. 55, вып. 2. С. 344-348.
306. Шкаликов Л.Л. Некоторые вопросы теории полиномиальных операторных
пучков // УМН. 1983. Т. 38, вып. 3. С. 189-190.
307. Штаерман И.Я. Контактная задача теории упругости. — М.; Л.: Гостех-
издат, 1949. — 272 с.
308. Чебаков М.И. Задача о крутильных колебаниях упругого полупростран-
полупространства // Статические и динамические смешанные задачи теории упруго-
упругости. — Ростов-на-Дону, 1983. С. 142-146.
309. Чебаков М.И. К задаче Рейсснера-Сагочи // Прикл. механ. 1973. Т. 9,
вып. 12. С. 58-63.
310. Чебаков М.И. Контактная задача для круглой плиты, лежащей на вин-
клеровском основании // Смешанные задачи механики деформируемого
тела: Тезисы докладов Всесоюзной научной конференции Ростов-на-Дону.
1977. Т. 1. С. 99.
311. Чебаков М.И. Контактная задача теории упругости для кругового цилин-
цилиндра конечных размеров // Механика сплошной среды. — Ростов-на-Дону:
РГУ, 1981. С. 134-139.
312. Чебаков М.И. Контактные задачи для тел конечных размеров // Меха-
Механика контактных взаимодействий. — М.: Физматлит, 2001. С. 157-180.
313. Чебаков М.И. Кручение штампом усеченного конуса конечных разме-
размеров // Механика сплошной среды. — Ростов-на-Дону, 1982. С. 91-102.
314. Чебаков М.И. Кручение штампом усеченного шара // Статические и ди-
динамические смешанные задачи теории упругости. — Ростов-на-Дону,
1983. С. 27-32.
315. Чебаков М.И. К теории расчета сферического подшипника // Изв. РАН.
МТТ. 1992. №5. С. 58-63.
Список литературы 283
316. Чебаков М.И. Метод однородных решений в контактной задаче теории
упругости для кругового цилиндра конечных размеров // Тезисы докладов
Всес. конференции по теории упругости — Ереван. 1979. С. 365-368.
317. Чебаков М.И. Метод однородных решений в смешанной задаче для круго-
кругового цилиндра конечных размеров // ПММ. 1979. Вып. 6. С. 1073-1075.
318. Чебаков М.И. Метод однородных решений в смешанных задачах теории
упругости для кругового цилиндра конечных размеров // Статические
и динамические смешанные задачи теории упругости. Ростов-на-Дону.
1983. С. 35-41.
319. Чебаков М.И. Метод решения одного класса бесконечных систем в кон-
контактных задачах теории упругости // Современные проблемы теории
контактных взаимодействий: Тез. докл. выездного заседания Межвед.
науч. совета по трибологии. Ереван: 1988. С. 143-145.
320. Чебаков М.И. Некоторые динамические контактные задачи для полубес-
полубесконечных тел периодической структуры // Изв. Вузов. Сев.-Кав. регион.
Естеств. Науки. 2000. №3. С. 177-180.
321. Чебаков М.И. Некоторые динамические и статическая контактные задачи
теории упругости для кругового цилиндра конечных размеров // ПММ.
1980. Т. 44, вып. 5. С. 923-933.
322. Чебаков М.И. Некоторые методы решения контактных задач теории упру-
упругости для тел конечных размеров // Тезисы докладов V Всесоюзного
съезда по теоретической и прикладной механике. — Алма-Ата. 1981.
С. 353.
323. Чебаков М.И. Об одном методе решения некоторого интегрального урав-
уравнения с разностным ядром // Изв. СКНЦВШ. Серия естественные науки.
1974. №4. С. 130.
324. Чебаков М.И. Об одном методе решения смешанных задач теории упру-
упругости для тел конечных размеров, основанном на использовании одно-
однородных решений // Смешанные задачи механики деформируемого тела:
Тезисы докл. 3-й Всесоюзной конференции. — Харьков, 1985. С. 44-45.
325. Чебаков М.И. О дальнейшем развитии метода больших Л в теории сме-
смешанных задач // ПММ. 1976. Т. 40, вып. 3. С. 561-565.
326. Чебаков М.И. О двух смешанных задачах теории упругости для усечен-
усеченных конуса и клина конечных размеров // Смешанные задачи механики
деформируемого тела: Тезисы 2-й Всесоюзной конференции. — Днепро-
Днепропетровск. 1981. С. 41-42.
327. Чебаков М.И. О некоторых контактных задачах теории упругости для
кольцевого сектора и сектора шарового слоя // ПММ. 1987. Т. 51, вып. 1.
С. 101-109.
328. Чебаков М.И. О некоторых контактных задачах теории упругости для
кольцевого сектора и сектора шарового слоя / Ростовский ун-т. Ростов-
на-Дону. 1984. Рук. депонирована в ВИНИТИ 30.01.84. №1140-84. -
22 с.
329. Чебаков М.И. О некоторых особенностях распространения колебаний
в цилиндрическом волноводе периодической структуры // Современные
проблемы механики сплошной среды: Труды 2-й междунар. научн. конф.
Т. 1. 19-20.09.1996. Ростов-на-Дону, 1997. С. 142-145.
284 Список литературы
330. Чебаков М.И. О парных интегральных уравнениях, связанных с преоб-
преобразованием Мелера-Фока // Изв. АН СССР. МТТ. 1974. №6. С. 66-71.
331. Чебаков М.И. О применении однородных решений к исследованию сме-
смешанных задач теории упругости для тел конечных размеров // Тезисы
докладов школы-семинара по теории упругости и вязкоупругости. — Ере-
Ереван, 1982.
332. Чебаков М.И. О характере влияния границ на контактную жесткость тел
конечных размеров // Дифференциальные уравнения и их приложения:
Тезисы докладов Республиканской конференции. Ч. 2. — Одесса. 1987.
С. 126-127.
333. Чебаков М.И. Пространственная контактная задача для слоя с учетом
трения в неизвестной области контакта // Докл. РАН. 2002. Т. 383, № 1.
С. 67-70.
334. Чебаков М.И. Расчет периодического волновода с произвольным числом
различных однородных областей в периоде // Современные проблемы
механики сплошной среды: Труды 4-й междунар. научн. конф. Т. 2.
27-28.10.1998. - Ростов-на-Дону: Из-во СКНЦ ВШ, 1998. С. 204-208.
335. Чебаков М.И. Решение интегральных уравнений методом больших Л //
Статические и динамические смешанные задачи теории упругости. —
Ростов-на-Дону, 1983. С. 26-27.
336. Чебаков М.И. Сдвиг штампом бруса прямоугольного сечения // Жест-
Жесткость машиностроит. конструкций: Тезисы докл. научн.-техн. конф.
Брянск, 1976. - М., 1976. С. 88-92.
337. Чебаков М.И. Смешанные задачи для кругового цилиндра конечных
размеров // Статические и динамические смешанные задачи теории упру-
упругости. - Ростов-на-Дону. 1983. С. 32-35.
338. Чебаков М.И. Трехмерная контактная задача для слоя с учетом трения
в неизвестной области контакта // Изв. РАН. МТТ. 2002. №6. С. 59-68.
339. Чебаков М.И. Удар круглого диска о жидкость малой глубины // ПММ.
1974. Т. 38, вып. 4. С. 675-681.
340. Чебаков М.И. Учет сил трения в пространственной контактной задаче для
закрепленного слоя // Современные проблемы механики сплошной среды:
Труды 7-й междунар. научн. конф. памяти академика РАН И. И. Воровича.
22-25.10.2001. - Ростов-на-Дону: Из-во СКНЦ ВШ, 2001. С. 205-209.
341. Чебаков М.И., Лоренц X. Динамическая контактная задача для цилиндра
периодической структуры // Современные проблемы механики сплош-
сплошной среды: Труды 5-й междунар. научн. конф. Т. 2. 27-28.10.1999. —
Ростов-на-Дону: Из-во СКНЦ ВШ, 1999. С. 194-197.
342. Чебаков М.И., Лоренц X. Пространственные контактные задачи для слоя
с учетом сил трения в зоне контакта // Современные проблемы механики
сплошной среды: Труды 6-й междунар. научн. конф. 19-23.10.2000. —
Ростов-на-Дону: Из-во СКНЦ ВШ, 2000. С. 232-235.
343. Черных К. Ф. Нелинейная теория упругости в машиностроительных рас-
расчетах. — Л.: Машиностроение, 1986. — 336 с.
344. Чобанян К. С, Галфаян И.О. Об одной задаче теории упругости для
составного прямоугольника // Изв. АН Арм. ССР. Сер. физ.-мат. наук.
1963. Т. 14, №2. С. 43-54.
Список литературы 285
345. Эдварде Р. Ряды Фурье в современном изложении. — М.: Мир, 1985. —
421 с.
346. Якубов С.Я., Мамедов К. С. О кратной полноте системы собствен-
собственных и присоединенных элементов полиномиального операторного пучка
и кратных разложений по этой системе // Функциональный анализ и его
приложения. 1975. Т. 9, вып. 1. С. 91-93.
347. Якубович В.А., Старжинский В.М. Параметрический резонанс в линей-
линейных системах. — М.: Наука, 1987. — 328 с.
348. Якубович В.Л., Старжинский В.М. Линейные дифференциальные урав-
уравнения с периодическими коэффициентами и их приложения. — М.: Наука,
1972. - 718 с.
349. Alexandrov V.M., Pozharsky D.A. Three-dimensional contact problems.
Kluwer Academic Pablishers, 2001. - 406 p.
350. Anderson T. Alan-Persson. Finite element method for plane contact prob-
problems // Progr. Boindary Elem. Meth. Uol. 2. London. Plymuth. 1983.
P. 136-137.
351. Bartelse R.N., Golub G.N. Stable numerical methods for obtaining the
Chebysheu solution to an overdeternened system of equations // Commun
ACM. 11F) 1968. P. 401-406. P. 428-430.
352. Biot M.A. Mechanics of Incremental Deformation. — New Jork: Willey,
1965. - 504 p.
353. Chand В., Hang E.J., Rim K. Analysis if ubonded contact problems by means
of quadratic programming // J. Optimiz. Theory and Appl. 1976. 20. №2.
P. 171-189.
354. Chebakov M.I. The three-dimensional contact problems for the two-layer
half-space in presence of friction forces in unknown contact area // Contact
mechanics of coated bodies. Abstracts of Euromech colloquium 434. —
Moscow, 2002. P. 21.
355. Cheney E. W. Five lectures on the algorithmig aspects of approximation
theory // Lest. Notes. Math. 1985. № 1129. P. 1-20.
356. Davis P. Interpolation and approximation // Blaisdell Publ. Somp. 1963.
357. Fadle J Die Selbstspannungs — Eigenwertfunktionem der quadratiscnen
Soheibe // IngrArch. 1941. B. 11. №2. P. 125-149.
358. Filon L.N. G. On the expansion of polynomials in series of functions // Proc.
London Math. Soc. Ser. 3. 1907. V. 4. P. 396-430.
359. Filon L.N. G. On the approximate solutions for bending of a beam of rect-
rectangular cross-section under ang system of load, nith special reference too
points of concentrated of discontinuons loading // Philos Trang. Roy. Soc. —
London, 1903. Ser. A. №201. P. 28-130.
360. Goryacheva I. G. Contact Mechanics in Tribology. — Dordrecht-Boston-Lon-
Dordrecht-Boston-London.: Kluver Academic Publishers, 1998. — 360 p.
361. Koepcke W. Uber das Randwertproblem an rechteckigen Platten // Dr. Diss.
Techn. Hochschu'e. — Berlin, 1970.
362. Lame G. Lecons sur les coordonners survilignes et leurs diverses appleca-
tion // Paris, 1859. — 368 p.
286 Список литературы
363. Laurson C.L. Bibliography of recent publications in approximation theory
with emphasis on computer applications. Tet Propulsion, sec. 314. Tech.
Rep., 201. Salif Inst. of Fechn. August. 1968.
364. Low R.D. On the Torsion of an Elastic Cone as a Mixed Boundary Value
Problem // Quart. J. Mech. and Appl. Math. 1966. V. 19, № 1. P. 57.
365. Mairhuber J. On Haars theorem concerning Chebysheff approximation prob-
problems having unique solutions // Proc. Amer. Math. Soc. F. 1956. P. 609-615.
366. Marinov P.G., Andreev A.S. A modified Remes algorithm for approximate
determination of the rational function of the best approxifmation in Hausdorff
metric // Докл. Болг. АН. 1987. 40. №3. P. 13-16.
367. Moursund D.G., Stroud A.H. The best Chebyshev approximation to a func-
function and its derivative on n + 2 points // SIAM J. Nim. Anal. Ser. B. 2.
1965. P. 15-23.
368. Muller P.N. Eigenwerbs schatzungen fur glaichungen vom Тур
(I -A- B)x = 0 // Arsh. Math., 1961. 12. № 4. P. 307-310.
369. Murnaghan F.D., Wrench J.W. The determination of the Chebyshev app-
approximation polynomial for a differentiable functions // Math. Jables. 1959.
V. 13. P. 185-193.
370. Rice J.R. Best approximations and interpolating functins // Tpans. Amer.
Math. Soc. 1961. V. 101. №3. P. 477-498.
371. Rice J.R. On the convergence of an algorithm for best Tshebycheff approxi-
approximations // SIAM. J. 1959. V. 7. P. 133-142.
372. Saito N. Axisymmetric strain of a finite cercular cylinder and disk // Trans.
Jah. Soc Mech. Eng. 1952. V. 18, №68. P. 58-63.
373. Schiff P. A. Sur l'equilibre d'un cylindre d'elastique // J. math, pures et appl.
Ser. 3. 1883. V.9. P. 407-421.
374. Tolcke F. Wasserkraftanlagen. Handbibliotek fur Bauingenier. Berlin. 1938.
Ill Teil. W. 9. P. 358-408.
375. Veidingev L. On the numelerical determination of the best approximation in
the Shebyshev sense // Numer. Math. V. 2. 1960. P. 99-105.
376. Walsh Harro. A stochastic Remes algorithm // J. Approxim. Theory. 1987.
V.49. №1. P. 79-92.
Дополнение
О некоторых особенностях контактного
взаимодействия штампа и упругого слоя при наличии
сил трения в области контакта
Рассматриваются плоские контактные задачи теории упругости
о взаимодействии штампа, имеющего основание в форме параболоида
или плоское основание, со слоем при наличии сил кулоновского трения
в области контакта. Предполагается, что нижняя грань слоя либо
закреплена, либо на ней отсутствуют нормальные перемещения и каса-
касательные напряжения, а на штамп действуют нормальные и касательные
усилия. При этом система штамп-слой находится в условиях предель-
предельного равновесия и штамп в процессе деформации слоя не поворачива-
поворачивается. Случай квазистатики, когда штамп перемещается по поверхности
слоя равномерно, может быть рассмотрен аналогично в подвижной
системе координат. Задачи исследуются методом больших Л (см. § 1.3).
ИУ, к которым сводятся поставленные в дополнении задачи, обладают
иными свойствами по сравнению с ИУ § 1.3. Здесь для них также
получены простые рекуррентные соотношения для построения любого
количества членов разложения решения ИУ в ряд по отрицательным
степеням безразмерного параметра Л, связанного с толщиной слоя.
Целью исследования поставленных задач является получение и ана-
анализ чисто аналитическими методами результатов, связанных с вли-
влиянием геометрических и механических параметров задач (особенно
коэффициента Пуассона и толщины слоя) на положение области кон-
контакта, форму деформированной поверхности слоя вне области контакта
и эпюру контактных напряжений при учете сил трения в области кон-
контакта. Ранее эти зависимости были исследованы численными методами
решения ИУ для пространственных контактных задач о взаимодей-
взаимодействии штампа в форме эллиптического параболоида с упругим слоем,
лежащим на полупространстве (гл. 7).
Плоские контактные задачи для слоя с учетом сил трения в зоне
контакта ставились и исследовались во многих работах (см. например
[1,2, 5] и др.).
Постановка задач. В декартовых координатах (х, у) рассмотрим
слой 0 ^ у ^ h (рис. 1). Пусть штамп с формой подошвы в виде пара-
параболы с радиусом кривизны R в вершине взаимодействует с границей
слоя у = h, на штамп действуют нормальная сила Р и касательная
сила Т = fiP, в зоне контакта действуют силы кулоновского трения
288
Дополнение
с коэффициентом трения /i, при этом нижняя граница слоя у = О
либо закреплена (задача 1), либо на ней отсутствуют нормальные
перемещения и касательные напряжения (задача 2). Рассматривается
случай предельного равновесия, штамп не поворачивается в процессе
деформации слоя.
Задачи, когда штамп имеет плоскую подошву, назовем соответ-
соответственно задачами 3 и 4 (рис. 2).
Рис. 1.
Рис. 2.
Поставленные контактные задачи с помощью преобразования Фу-
Фурье сводятся относительно неизвестных нормальных контактных на-
напряжений под штампом q(x) [2] к следующему ИУ:
«КО*
ядро которого представимо в виде двух слагаемых:
(t) = kl(t)-ek2(t),
i
и [smut
i= 1
A)
B)
Здесь для задач 1, 3
— Аи
L2(u) =
\
2(l 2v)~x
2>c(ch2u- 1)-4гГA -2v)
а для задачи 2, 4
сЬ2гх-1
sh2it-2(l -2v\
=
C)
D)
Дополнение 289
В формулах A)-C) введены следующие обозначения:
^=у^, 5(х)=5-/3х2 (/3=^), я = 3-4и, E)
1 — V lit
где [—а, Ъ] — область контакта, G — модуль сдвига, v — коэффициент
Пуассона, fi — коэффициент трения, 5 — перемещение штампа в вер-
вертикальном направлении.
В задачах 1 и 2 область контакта —а ^ х ^ Ъ заранее не известна,
зависит от величины силы Р и будет определяться в процессе их
решения. В задачах 3 и 4 область контакта фиксирована, основание
штампа прямолинейно, поэтому для них в E) следует положить /3 = 0
и будем предполагать, что а = Ъ.
В дальнейшем все общие аналитические преобразования проведем
для задач 1 и 2. Они будут справедливы и для задач 3 и 4 при /3 = 0
и а = Ъ.
Сделаем в уравнении A) замену переменных
а + Ь а — Ь /гч
тогда оно преобразуется к виду
1
v(T)k(^)dT = <irf(t)\x\^l, G)
-1
где обозначено
Для задач 1 и 3 в силу закрепления нижней грани у = 0 условия
статического равновесия полосы очевидны. Проверим эти условия для
задачи 2 и 4, для чего по аналогии с работой [3] найдем величину R
вектора нормальных напряжений ах(х,у) в любом сечении слоя х = xq
(xq < —a, xq > b):
h
г
R= ax(x0,y)dy.
0
Используя представление нормальных напряжений ах(х,у) в слое
в виде интеграла Фурье [2], после несложных преобразований найдем
а
г
— а
Из последнего соотношения получим
10 В.М. Александров, М.И. Чебаков
290 Дополнение
что говорит о закреплении слоя при х —> ±оо и, соответственно, о его
равновесии.
Решение ИУ. Для решения ИУ G)-(8) с ядрами B)-D) использу-
используем метод больших Л. Предварительно преобразуем ядра B)-D) к ви-
виду [1]
kx(t) = -ln|*| +Fj(*), k2(t) = |sgn(t) +F2(t), (9)
где функции Fi(t) представимы в виде рядов
оо оо
2 -?bit2i-1 A0)
г=0 г=1
с коэффициентами
оо _ оо
do= J l-Ll^-e~Udu, dt = ^ Ul - L^u)}^-1 du (i>l),
0 ° A1)
оо v ;
- L2(u)]u2i-2 du (г>1).
0
В работе [1] показано, что уравнение G), (9) эквивалентно урав-
уравнению
1 1
тгЛ
-1
при условии
1 1 1
р* =
-1 -1 -1 -1
A3)
Здесь приняты следующие обозначения:
F(f) = —F^(f) 4- rFo(f) Х(т) = П 4- т){/2+^(] — г"»1/2
A4)
7 = - arctg?, е\ = е0 = ^,
где С — постоянная Эйлера, ф(х) — пси-функция Эйлера [4].
Дополнение 291
Представим решение уравнения A2) в виде разложения
сю
ф) = Y, А">„(х) A5)
п=0
и подставим его в левую и правую части A2). После ряда преобразова-
преобразований в правой части приравняем слева и справа в A2) выражения при
одинаковых степенях Л. В результате получим следующие рекуррент-
рекуррентные соотношения для нахождения функций (рп(х):
Vo{x) = ^щ [Р* - ?,/„(*)] + eQf'(x), A6)
1 I
dt ~
1
5 z>* Un-.wft-xr1^ (i7)
где Ci — коэффициенты представления функции F(t) в виде ряда
Y^ с4\ c2i = di, c2i-\ = ebi, A8)
г=0
l
//(ТТ)_ХЖ(Т) dr- A9)
-l
В дальнейшем потребуются значения следующих интегралов [4, 6]:
1
Ql= \ rkX(r)dr= |(-l)fc(l -47)л/1 +?2F(J+7,-^3;2y B0)
-i
i
Q4= f ^y = 7r(-i)Vi+e2i?(^-7,-fc;i;2), B1)
-1
1
K,{t)= [ ^^=^tmX(t)-^^TT^tmB7 + t)+rm(t), B2)
-1
r^(t) = E Q^_fc_itfc (m > 1), ro(t) = 0. B3)
k=Q
В B0), B1) F(a,—k;n;2) — гипергеометрическая функция [4], в
более общем случае она представима гипергеометрическим рядом, но
ю*
292 Дополнение
так как здесь второй аргумент — отрицательное целое число, то ряд
обрывается и превращается в конечную сумму [4]
k-\ , ч ,,ч
F(a, -к; п; 2) = V [а)'} *H 2\
to г]М* B4)
(a)i = а(а + 1)... (а + г — 1), (а)о = 1
и, следовательно, величины Q& и Q^ также являются конечными эле-
элементарными суммами.
Учитывая, что
f(t) = ао + а^ + a2t2, /o(t) = а\Щ(г) + 2a2i?]\ B5)
где
найдем
(a - 6 - 27(a + 6)), B6)
/Зоо = ^ И 2^]
Покажем, что функция Х(ж)<^п(ж) представима в виде многочлена
степени n: n
Х(ж)</?п(ж) = V /Зп/сЖ^ (п > 1), B7)
для этого в соотношениях A7) разложим бином (t — т)г~х на слагае-
слагаемые, изменим порядок суммирования и интегрирования и после ряда
громоздких преобразований получим
v. (ein~2 к n~l (-1Г
yvy^vj^/fiy^vj — s у Ju f . '/^"п,тКсотп к 1
I k=0 т=к+\
n—\ /_|\m m ^
_ ?x (Ory _i_ тЛ \^ ^ ^ ж ^ L ^9Я^
— Vz 7 ^ x/ / j i жп,т ( > Vzo/
7Г ^—' ?Tl!
m=0 ^
где
n -| /c
г< — V г'С^ p* p* _ V^ /3. /~) /OQ\
>%,ra — /^ Л- «то 1М n—г,г—Ш—1' ^/с,т ~~ Z^ НкрЧр+т- \A^)
л \i III 1 ) !
i=m+\ v ' p=0
Из B8) видно, что функция Х(х)фп(х) действительно есть мно-
многочлен степени п. Также легко увидеть, что в правой части B8)
фигурируют коэффициенты Ck,р только при к ^ и — 1.
Дополнение 293
Если теперь в левую часть B8) подставить вместо Х(х)(рп(х) вы-
выражение B7), то для определения коэффициентов (Зп^ после довольно
громоздких преобразований получим следующие рекуррентные соотно-
соотношения:
/3„,„ = -(-1)пР* 0О1)
7Г
C0)
9 и
Рп,/с — ~2
7Г
= k-\-\
Здесь введено обозначение
п~х i\c- n~i
Гп,т = 2^ U_m_ \\\ /-^ Pn-i,pQp+i-m-\
C1)
)!
Таким образом, окончательно решение ИУ G) представляется в ви-
виде A5), B6), B7) с учетом рекуррентных соотношений C0).
Отметим, что рекуррентные соотношения C0) содержат только
арифметические операции, что позволяет их легко программировать
и с помощью программ, выполняющих аналитические преобразования
(типа Maple), получать в аналитическом виде любое конечное число
членов в разложениях A5), B7). Это позволяет находить решение ИУ
с любой степенью точности в области сходимости ряда A5).
Ниже выпишем коэффициенты (Зп^ только для случаев п = 1 и
п = 2, хотя в нижеприведенных результатах числовых расчетов будем
использовать коэффициенты (Зп^ и при различных п > 2 в зависимости
от величины параметра Л и заданной точности,
27Р* P*
7Г 7Г
— 1272) + #/3?1б?17A — 472) тт 7(« + b) — 2(а — b) ,
Lo J
- 472) Г| (а + b) - 2(a - b)] , C3)
/Ъ = -.
294 Дополнение
Вывод основных соотношений. Зная решение ИУ G), контактные
напряжения под подошвой штампа при —а^х^Ь найдем по формуле
C4)
предварительно определив для задач 1 и 2 границы области контакта из
условия равенства нулю контактных напряжений при х = —а и х = Ь.
В результате получим следующую систему двух нелинейных уравнений
с двумя неизвестными а и Ь\
V?(-l) =0, у>A) =0. C5)
Система C5) достаточно громоздка даже в случае, если находить
решение ИУ с точностью до членов порядка О(А~3). Поэтому в каждом
конкретном случае ее решение будем находить численно с достаточно
высокой точностью, что не вызывает больших затруднений в силу
представления уравнений системы в виде равенства нулю многочленов
относительно искомых величин.
Отметим, что с учетом C5) функция (p(t) представима в виде
ip(t) =X(-t)cp*(t), C6)
где ip*(t) — непрерывная и ограниченная при \t\ ^ 1 функция.
Если же решение ИУ G) находить с точностью до членов порядка
О(А~2), то формулы для определения зоны контакта в задачах 1 и 2
асимптотически при больших значениях h (h^> max (a, b)) примут вид
C7)
0 <
7rG/?(l-27) ' bs~y 7rG/3(l+27) ' U^7<2-
В случае задачи 2 соотношение из C7) для величины d после
вычисления интеграла в Ъ\ по формуле A1) упростится и примет вид
)' bi =-2^уbi «0.7685745. C8)
Отметим, что в задаче 2 величина Ь* в соответствии с A1) не
зависит от коэффициента Пуассона и, а в задаче 1 зависит.
В формулах C7), C8) величина d > 0, интервал (—as,bs) — зо-
зона контакта при взаимодействии штампа с полупространством, при
этом всегда as > bs, за исключением случая v = 0,5 G = 0), когда
as = bs. На основании формул C7), C8) можно сделать некоторые
предварительные выводы о характере зависимости области контакта
от некоторых параметров: например, при уменьшении толщины слоя
величина а уменьшается, а величина b увеличивается. Кроме того при
увеличении силы Р величина d растет быстрее величин as и bs. Таким
образом, при уменьшении толщины слоя и увеличении силы Р и коэф-
Дополнение 295
фициента Пуассона v происходит смещение зоны контакта в положи-
положительном направлении оси х, что оказывает существенное влияние на
характер распределения контактных напряжений, величину их момента
и деформацию свободной поверхности. Об этом более подробно речь
пойдет ниже.
Для числовых расчетов необходимо также найти зависимость вер-
вертикального перемещения штампа 5 от приложенной нормальной си-
силы Р и форму деформированной свободной поверхности вне области
контакта.
Для нахождения 5 воспользуемся соотношением A2), которое с уче-
учетом B5) преобразуется к виду
5 = ^—=- < (In Л + D) у——гт Ь
-ф|, C9)
-1 -1
В D0) подставим значения функции (p(t) в виде A5), B7), получим
1 °° ш О
тг z—' z—' г)! ^
7Г ^^ ^^ р\
771=0 р=0
т—р / w n I 2
^ (Ш — n)!cm-n V^ /3 ^ _|_ т-ст sr^
f- (m-n-p)! ;f- n/c ^-^-^+fc (m-p)! 7?^.
D1)
Найдем момент контактных напряжений. В соответствии с фор-
формулой
М = I* xq(x) dx D2)
— а
после замены переменных F) получим
1 1
М = {-^? | Mt) dt - °^- | ф) dt. D3)
-1 -1
Окончательно в соответствии с представлением ip(t) в виде рядов
B6), B7) найдем
Л А П JZ ftnkQk+\ + JZ ftokQk+\ n— Р' (^)
п=\ к=0 к=0 J
296 Дополнение
Перемещение свободной поверхности вне штампа представляется
соотношением
w(x) = W Bx + a~b\ (ж < -а, ж > Ь),
а + о )
1 D5)
-1
С учетом (9) запишем W(t) в виде
W(t) = -°^{Wi(t) + 7^W2(t) + W3(t)\, D6)
где
1
г
Wi(t) = ip(r)ln\r-t\dr-F
-i
i
(р(т) sgn(r — t) dr, D7)
-l
l
(f(r)F I —-— J dr.
-l
Используя A5), B7), с точностью до членов порядка
найдем
N к 2
W\(t) = У^ Л~^ У^ 0kmtm(t) + У^ 00 tm(t) ~
к=0 тп=0 тп=\ " ' "
D8)
tm= [ -fr^ \n\r-t\dr, D9)
W2(t) = {Р*, если t < -1; -Р*, если t > 1}, E0)
N к ,гп
?зЩ = > Л > ( —1) —г Qkm -
РЧкm
2^ (h_n_ m\\ Z^ РпрЧк+p-n-m t ,, _ ч( 2^
n=0 V ;' p=0 V ;' p=l
E2)
Дополнение 297
Числовые расчеты для задач 1 и 2. Были проведены расчеты
границ зоны контакта а и Ь, контактных напряжений q(x) (—а ^ х ^
^ Ь), момента контактных напряжений М, вертикальных перемещений
штампа 5 и вертикальных перемещений поверхности вне зоны контак-
контакта w(x).
Введем обозначения
«!® М' = ?, 6* = f. E3)
<f{x) = , М = ?, 6 = f.
В табл. 1 и 2 соответственно для задач 1 и 2 приведены значения
величин а, Ь, х*, #*(#*), М* и 5*, где х = х* — точка зоны контакта
с максимальными контактными напряжениями, при некоторых значе-
значениях параметров Pq = P/G, h, и, /i и R = 1. Исходные параметры
задавались в системе СИ. Все результаты приведены с точностью до
членов порядка О(Л~7), кроме результатов первой строки в табл. 1 (они
помечены звездочкой), которые вычислялись с точностью до членов по-
порядка О(Л~П) и приведены с целью демонстрации точности расчетов.
Отметим, что если вычислять зону контакта исходя из простейших
асимптотических формул C7), то при Pq = 1, h = 3 для задачи 2
получим, что а = 0,834, Ъ = 0,695, если v = 0,1, и а = 0,587, Ъ = 0,597,
если v = 0,45. Эти результаты близки к соответствующим результатам,
приведенным в табл. 2.
На рис. 3 приведен график распределения контактных напряжений
в зоне контакта для задачи 2 при h = 1,0, fi = 0,5, v = 0,1 и v = 0,45.
Результаты расчетов, приведенные в табл. 1, 2 и на рис. 3, а также
простейшие асимптотические формулы C7), позволяют сделать ряд
принципиально важных выводов: при уменьшении толщины слоя h,
либо при увеличении силы Р, либо при увеличении коэффициента
Пуассона v зона контакта смещается в положительном направлении
оси х; при изменении коэффициента Пуассона v в пределах от 0 до
0,5 момент контактных напряжений может менять свой знак, при этом
точка зоны контакта х = х*, где контактные напряжения максимальны,
также может менять свой знак. В соответствии с величинами а и Ъ
меняется и характер деформации свободной поверхности в окрестно-
окрестности штампа: если а > Ь (у — мало), то в окрестности точки х =
= Ъ деформация больше, чем в окрестности точки х = —а, если а <
< Ъ {у — близко к 0,5), то наоборот. Всегда найдется такое значение
коэффициента Пуассона z/, когда картина распределения контактных
напряжений и деформация свободной поверхности будут почти симмет-
симметричными, а момент контактных напряжений будет равен нулю. Кроме
того, перемещение штампа 5 практически не зависит от коэффициента
трения /i.
Числовые расчеты для задач 3 и 4. Для этих задач область
контакта заранее известна и а = Ъ.
Были проведены расчеты контактных напряжений q(x) {—а ^ х ^
^ а), момента контактных напряжений М, вертикальных перемещений
298
Дополнение
Ро
h
V
а
Ъ
Ж*
Таблица 1.
М*
Задача 1
6*
д = 0,5
1
1
1
1
1
1
1
1
1
1
1
2
2
2
0,1
0,1
0,3
0,45
0,1
0,3
0,45
0,775*
0,768
0,638
0,513
0,820
0,687
0,567
0,578*
0,574
0,552
0,540
0,653
0,607
0,575
-0,186*
-0,188
-0,0897
0,00916
-0,182
-0,0955
-0,00934
0,956*
0,962
1,077
1,214
0,873
0,988
1,116
-0,130*
-0,129
-0,0603
0,0105
-0,117
-0,0592
-0,000579
0,362*
0,364
0,278
0,191
0,527
0,406
0,290
Ро
h
V
а
Ъ
Ж*
Таблица 2.
д*(ж*)
М*
Задача 2
8*
д = 0,5
1
1
1
1
1
1
1
1
1
1/2
1/2
1/2
1
1
1
2
2
2
3
3
3
1
1
1
0,1
0,3
0,45
0,1
0,3
0,45
0,1
0,3
0,45
од
0,3
0,45
0,764
0,632
0,517
0,816
0,683
0,567
0,834
0,699
0,582
0,597
0,501
0,418
0,599
0,591
0,584
0,663
0,623
0,592
0,672
0,625
0,590
0,475
0,441
0,415
-0,169
-0,0648
0,0273
-0,176
-0,0860
-0,00203
-0,184
-0,0961
-0,00125
-0,135
-0,0727
-0,0133
0,947
1,046
1,159
0,869
0,976
1,099
0,852
0,964
1,086
0,597
0,677
0,764
-0,114
-0,0364
0,0302
-0,110
-0,0489
0,00766
-0,116
-0,0570
-0,00169
-0,0429
-0,0222
-0,00268
0,369
0,307
0,259
0,537
0,441
0,366
0,647
0,528
0,434
0,372
0,302
0,247
11 = 0,9
1
1
1
1
1
1
1
1
1
3
3
3
0,1
0,3
0,45
0,1
0,3
0,45
0,826
0,646
0,489
0,912
0,734
0,580
0,544
0,577
0,609
0,625
0,602
0,594
-0,291
-0,113
0,0492
-0,327
-0,172
-0,0225
0,955
1,050
1,160
0,846
0,961
1,086
-0,196
-0,0631
0,0544
-0,206
-0,102
-0,00301
0,366
0,304
0,260
0,657
0,530
0,434
Дополнение
299
штампа 5 и вертикальных перемещений поверхности вне зоны контак-
контакта w(x).
Введем обозначения
v = 0,45
у = ОД
wyvj~ P ' ±v± - Pa' u " P' ш yvj~ Ga '
где гу(ж) — вертикальные перемещения точек поверхности слоя у = h.
В табл. 3 и 4 соответственно для задач 3 и 4 приведены значения
величин 5*, М* ?*, a(U), а(-0,9), а@,9), w*(-l,l) и w*(l,l), где
х* = at* — точка зоны контакта с мини-
минимальными контактными напряжениями,
при некоторых значениях параметров h,
v и II = 0,9.
На рис. 4 приведен график функции
o~{t) распределения безразмерных кон-
контактных напряжений в зоне контакта
для задачи 1 при Л = 2,0, \± = 0,9,
v = ОД (сплошная линия) и v = 0,45
(пунктирная линия).
На рис. 5 приведен график функции
w*(t), соответствующей безразмерным
перемещениям поверхности слоя у = h,
при Л = 2,0, /i = 0,9, v = ОД (сплошная
линия) и v = 0,45 (пунктирная линия).
Результаты расчетов, приведенные в табл. 3, 4 и на рисунках 4, 5
позволяют также и для задач 3, 4 сделать ряд принципиально важных
выводов: при изменении коэффициента Пуассона v от минимального
значения до максимального момент контактных напряжений может
менять свой знак, при этом точка х* минимальных контактных напря-
О"
1,0
0,8
0,6
0,4
0,1
о
0,6 0,4 0,2 0 0,2 0,4 t
Рис. 3.
1,0|l\ v = ОД у = 0,45 '
-1,0 -0,5 0
Рис. 4.
0.5 1.0 t
-0,3-
1,5 1,0
Рис. 5.
жений перемещается справа налево и может менять свой знак. В со-
соответствии с характером распределения напряжений при изменении
коэффициента Пуассона меняется и характер деформации свободной
поверхности в окрестности штампа: если v мало, то в окрестности
300
Дополнение
точки х = а деформация больше, чем в окрестности точки х = —а,
если v близко к 0,5, то наоборот. Всегда найдется такое значение
коэффициента Пуассона z/, когда картина распределения контактных
напряжений и деформация свободной поверхности будут почти симмет-
симметричными, а момент контактных напряжений будет равен нулю. Кроме
того, перемещение штампа 5 практически не зависит от коэффициента
трения /i.
Л
2
2
2
3
3
4
4
2
2
V
0,1
0,45
0,423
од
0,45
0,1
0,45
0,1
0,45
5*
0,326
0,136
0,152
0,432
0,189
0,511
0,232
0,322
0,135
М*
-0,210
0,0401
0,0008
-0,197
0,0208
-0,198
0,00691
-0,123
0,0222
и
1
0,417
-0,304
-0,175
0,228
-0,141
0,193
-0,0819
I
0,244
-0,188
a(U)
u = 0,c
0,332
0,369
0,373
0,320
0,346
0,311
0,335
и = 0?
0,349
0,373
сг(-0,9)
0,883
0,583
0,630
0,889
0,650
0,899
0,684
0,804
0,615
Таблица 3.
сг@,9)
0,455
0,704
0,659
0,504
0,725
0,513
0,725
0,545
0,682
гу*(-1,1)
0,175
0,0863
0,0962
0,246
0,124
0,310
0,161
0,194
0,0797
Задача 3
гу*A,1)
0,229
0,0610
0,0767
0,342
0,113
0,427
0,158
0,221
0,0656
Л
V
S*
М*
и
<t(U)
^(-0,9)
Таблица 4.
*@,9)
гу*(-1,1)
Задача 4
гу*A,1)
/х = 0,9
2
2
2
3
3
4
4
0,1
0,45
0,37
0,1
0,45
0,1
0,45
0,332
0,204
0,229
0,440
0,263
0,522
0,308
-0,183
0,0952
0,0007
-0,181
0,0518
-0,188
0,0280
0,308
-0,361
-0,178
0,179
-0,192
0,164
-0,121
0,340
0,339
0,355
0,322
0,332
0,312
0,328
0,850
0,543
0,646
0,870
0,624
0,887
0,665
0,491
0,811
0,695
0,523
0,782
0,526
0,762
0,182
0,154
0,160
0,257
0,199
0,321
0,238
0,233
0,118
0,143
0,350
0,181
0,435
0,229
д = 0,5
2
2
0,1
0,45
0,330
0,202
-0,107
0,0530
0,169
-0,217
0,348
0,348
0,788
0,608
0,570
0,755
0,201
0,143
0,227
0,124
Дополнение 301
Список литературы к дополнению
1. Александров В.М. О плоских контактных задачах теории упругости при
наличии сцепления и трения // ПММ. 1970. Т. 34, вып. 2. С. 246-257.
2. Александров В.М., Коваленко Е.В. Задачи механики сплошных сред со
смешанными граничными условиями. — М.: Наука, 1986. — 336 с.
3. Александров В.М., Сметанин Б.И. О симметричных и несимметричных
контактных задачах теории упругости // ПММ. 1985. Т. 49, вып. 2.
С. 136-141.
4. Градштейн И. С, Рыжик И.М. Таблицы интегралов, сумм, рядов и произ-
произведений. - М.: Наука, 1971. - 1108 с.
5. Попов Г. Я. К решению плоской контактной задачи теории упругости при
наличии сил сцепления или трения // Изв. АН Арм. ССР. Сер. физ.-мат. н.
1963. Т. 16, №2. С. 15-32.
6. Прудников А.П., Брычков Ю.А., Маричев О.И. Интегралы и ряды. Элемен-
Элементарные функции. — М.: Физматлит, 2003. — 632 с.
Научное издание
АЛЕКСАНДРОВ Виктор Михайлович
ЧЕБАКОВ Михаил Иванович
АНАЛИТИЧЕСКИЕ МЕТОДЫ В КОНТАКТНЫХ
ЗАДАЧАХ ТЕОРИИ УПРУГОСТИ
Редактор О. В. Салецкая
Оригинал-макет: В.В. Худяков
ЛР №071930 от 06.07.99. Подписано в печать 05.07.04.
Формат 60x90/16. Бумага офсетная. Печать офсетная.
Усл. печ. л. 19. Уч.-изд. л. 20,5. Тираж: 300 экз. Заказ №
Издательская фирма «Физико-математическая литература»
МАИК «Наука/Интерпериодика»
117997, Москва, ул. Профсоюзная, 90
E-mail: fizmat@maik.ru, fmlsale@maik.ru
http://www.fml.ru
Отпечатано с готовых диапозитивов
в ППП «Типография «Наука»
121099, Москва, Шубинский пер., 6