Автор: Галанин А.Д.
Теги: общее машиностроение технология машиностроения ядерная физика ядерная энергетика ядерные реакторы
ISBN: 5-283-03858-0
Год: 1990
Текст
А. Д. Галанин
ЭНЕРГОАТОМИЗДАТ
УДК 621.039.524
Галанин А. Д. Введение в теорию ядерных ре-
акторов на тепловых нейтронах. — 2-е изд., пере-
раб. и доп. — М.: Энергоатомиздат, 1990. — 536 с.
ISBN 5-283-03858-0
Изложены основы теории ядерных реакторов на тепловых
нейтронах. Основное внимание уделено физическим явлениям,
происходящим в реакторе. В приложении и в первой главе
собран значительный справочный материал. 2-е издание (1-е
изд. — 1984 г.) дополнено материалами по динамике реактора,
теории возмущений. Числовые значения постоянных уточнены
в соответствии с последними экспериментальными данными.
Для научных и инженерно-технических работников, спе-
циализирующихся в ядерной энергетике.
Табл. 70. Ил. 112. Библиогр.: 278 иазв.
збогогоооо—365
Г 051(01)-90
232-90
© Энергоатомиздат, 1984
ISBN 5-283-03858-0
© Автор, 1990, с изменениями
ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
Прошло уже более 40 лет со времени осуществления цепной
реакции деления ядер урана. За это время теория ядерных
реакторов оформилась в самостоятельную научную дисципли-
ну, имеющую свою историю развития.
В первые годы основное внимание уделялось физике яв-
лений, происходящих в ядерном реакторе. Количественное
описание было приближенным и опиралось на наиболее про-
стые методы. На следующем этапе основное внимание уделя-
лось созданию более сложных и более точных аналитических
методов. Иногда эти методы непосредственно приводили к
определению интересующих пас параметров, но в большинстве
случаев требовались еще и численные расчеты. При этом роль
аналитических методов сводилась к упрощению исходных урав-
нений, поскольку непосредственное их численное решение
было слишком трудоемким.
В связи с развитием вычислительной техники наступил тре-
тий этап, когда центр тяжести переместился на численное ре-
шение исходных уравнений, возможно, с некоторыми (мини-
мальными) упрощениями, описывающих распределение ней-
тронных полей в реакторе по пространству, энергии, а иногда
и по времени. В связи с появлением такой возможности мно-
гие методы, разработанные на втором этапе, потеряли свое
значение. Однако общие физические основы теории и простые
приближенные методы, позволяющие провести качественный
анализ явлений, никогда не следует забывать. Четкое понима-
ние физических основ теории необходимо как для анализа ре-
зультатов, получаемых с помощью сложных программ на ЭВМ,
так и для качественного анализа, либо получения приближен-
ного ответа с точностью, достаточной для принятия того или
иного решения при проектировании или эксплуатации ядер-
ного реактора.
Эти соображения побудили автора написать книгу, в кото-
рой не применяются сложные аналитические методы и не из-
лагается методика численных расчетов. Вместе с тем ограни-
читься только изложением приближенных методов, без сравне-
ния их с результатами численных расчетов, было бы непра-
вильно. Овладевая приближенными методами, надо всегда
3
представлять себе их погрешность. Поэтому во всех основных
разделах книги приводятся также и результаты численных
расчетов.
Теория ядерных реакторов является прикладной дисципли-
ной. Поэтому очень важно представлять себе численное зна-
чение тех величин, которые входят в уравнения теории и, как
правило, берутся из опыта. Первая глава, где сконцентриро-
ваны основные экспериментальные данные, носит характер
справочника с небольшими пояснениями. Часть эксперимен-
тальных данных вынесена в приложение. Некоторые данные
приведены непосредственно в тексте. Из огромного количества
экспериментальных данных приводятся только те, которые су-
щественны для реакторов на тепловых нейтронах. При этом
автор не ставил перед собой задачу оценки экспериментальных
данных и отдавал предпочтение тому или иному справочнику
или оригинальной работе, стараясь приводить только наиболее
точные данные.
Хотя автор стремился написать «простую» книгу, он не сни-
жал обычных для физика требований к владению математи-
ческим аппаратом, и, например, преобразования Фурье или
Лапласа используются без объяснений, что это такое. Чисто
математические вопросы теории нигде не излагаются.
В некоторых местах, возможно, разбираются слишком мел-
кие детали, однако именно это позволяет читателю совершен-
ствовать свое владение материалом. Во многих параграфах
имеются задачи с подробными решениями. Одни задачи явля-
ются простыми упражнениями, а другие требуют более слож-
ных вычислений. Результаты, полученные в ряде задач, ис-
пользуются в основном тексте.
Некоторые весьма важные вопросы теории, как, например,
динамика и устойчивость, а также методы расчета защиты
реактора не получили в книге достаточного развития. Этим во-
просам должны быть посвящены специальные работы.
Литературные ссылки не претендуют на полноту.
Автор признателен своим коллегам П. П. Благоволину,
Б. И. Ильичеву, Б. Л. Иоффе, Б. П. Кочурову, В. М. Михай-
лову, А. П. Рудику, Б. 3. Торлину, совместная работа с кото-
рыми способствовала выяснению тех или иных вопросов тео-
рии.
Автор благодарит рецензентов за полезные замечания.
ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
Во втором издании общий план книги и характер изложения
остались прежними. Наиболее крупные изменения следующие:
1) в гл. 5 введен в § 5.3, в котором изложена новая форма
теории возмущений для уравнения с одной группой нейтронов;
2) в гл. 12 добавлен § 12.4 об энерговыделении продуктов де-
ления после длительной выдержки; 3) в гл. 13 введен § 13.6,
посвященный получению радиоактивных нуклидов в реакторе
и выгоранию поглотителей; 4) в гл. 14 добавлен § 14 3 о ки-
нетике реактора с отражателем; 5) образована новая гл. 15,
куда перенесен параграф из гл. 12 о ксенонных колебаниях,
параграф из гл. 14 о температурном коэффициенте и написан
новый §15.3, где рассмотрено влияние взаимного расположе-
ния датчика и регулятора на устойчивость; 6) увеличен объем
дополнений: приближение Р2, вывод формулы для числа столк-
новений при замедлении, вывод формулы для резонансного
поглощения в гомогенной среде с тяжелым поглотителем
(Ахиезер и Померанчук, 1947 г.); 7) изъят §9 3, так как из-
лагавшийся в нем материал не используется на практике.
Несмотря на некоторое увеличение разделов по динамике
и устойчивости, по-прежнему они рассмотрены недостаточно
полно, и читатель здесь отсылается к специальной литературе.
В остальном тексте проведены многочисленные уточнения
редакционного характера, незначительные сокращения, ис-
правлены замеченные опечатки и ошибки. В наибольшей сте-
пени это коснулось гл. 1, 8, 13. Экспериментальные данные
о сечениях, по возможности, заменены более новыми. Частично
обновлен список литературы.
Автор признателен Б. П. Кочурову и Б. 3. Торлину за об-
суждение некоторых вопросов, вошедших во второе издание.
Часть I
ГОМОГЕННЫЙ РЕАКТОР
Г л а в а 1
Некоторые сведения из нейтронной физики
1j' ЧИСЛО ВТОРИЧНЫХ НЕЙТРОНОВ ПРИ ДЕЛЕНИИ ЯДЕР
важной характеристикой процесса деления является
сРеднее число вторичных нейтронов, возникающих в акте де-
^еНия. Если ядро поглощает медленный нейтрон (энергия ней-
Ч3 Она много меньше 1 МэВ), то среднее число вторичных
Нейтронов v не зависит от энергии поглощенного нейтрона. Ве-
личина v есть сумма двух слагаемых: среднего числа мгновен-
ных vP и запаздывающих Vd нейтронов, вылетающих из оскол-
деления (-vd<gCvP, см. § 1.3):
V = Vt — Vp-\-Xd. (1.1.1)
В табл. 1.1 приведены значения v для деления тепловыми
Нейтронами основных делящихся нуклидов, полученные в ре-
зультате анализа всех экспериментальных данных, известных
И Определенному году. Из этой таблицы видно, какой сущест-
^блица 1.1. Значения v для основных делящихся нуклидов*
Год 283U 23S(J 23ари 24ipU 2 5 2Qf Лите- ратура
й-52 R 9б5 969 973 974 97 g 983 ]984 2,55(6) 2,51(3) 2,504(8) 2,494(9) 2,487(7) 2,492(8) 2,482(10) 2,479(6) 2,488(6) 2,4933(39) 2,5(1)* ** 2,47(5) 2,47(3) 2,442(6) 2,130(8) 2,423(7) 2,418(8) 2,419(8) 2,416(5) 2,427(5) 2,4251(34) 3,0(1) 2,91(6) 2,90(4) 2,898(11) 2,871(14) 2,880(9) 2,871(6) 2,873(16) 2,862(8) 2,876(7) 2,8768(57) 3,06(4) 3,016(11) 2,969(23) 2,934(12) 2,927(14) 2,934(17) 2,924(10) 2,937(7) 2,9369(73) 3,772(15) 3,765(12) 3,74(1) 3,757(15) 3,746(9) 3,766(5) 3,7675(40) [2] [2 [3 (4 [5 [6 [7 [81 [9] [Ю] [11]
* По рекомендации Международного союза чистой и прикладной физики [1] слово
^л^ид. а ие изотоп должно употребляться для обозначения разновидности атомов, идеи-
по своему атомному номеру н массовому числу. Различные нуклиды, имеющие один
щ же атомный номер, следует определять как изотопы, или изотопные нуклиды. Раз-
^и^ые нуклиды, обладающие одним и тем ж? массовым числом, следует определять как
Зо5ары, или изобарные нуклиды-
** В скобках указаны погрешности в последних цифрах, например 2,934(17)=2,934±:
х"и»017. Такой способ записи принят далее во всех таблицах.
3
Рис. 1.1. Среднее значение числа вторичных нейтронов при делении 235U
(сплошные липни) и 239Ри (штриховые линии) тепловыми нейтронами по дан-
ным разных лет
венный прогресс достигнут в точности измерений в 50-х и на-
чале 60-х годов. Однако начиная с 1965 г. точность измерений
v практически не изменяется и только в 1983 г. несколько воз-
росла. Долгое время не удавалось устранить расхождения
при измерении v 2S2Cf различными методами. Поскольку v
252Cf служит стандартом при измерении v, погрешность v 252Cf
сказывалась на значениях у всех других нуклидов. Устране-
ние этой систематической погрешности к 1984 г. привело к
увеличению v всех нуклидов на 0,4—0,6 % по сравнению со
значением v, измеренным в 1977 г. Ниже везде будут исполь-
зоваться данные [И].
На рис. 1.1 данные табл. 1.1 для 235U и 239Ри изображены
графически.
Число вторичных нейтронов vp растет с ростом энергии ней-
трона, вызвавшего деление. В [12] приведена полуэмпириче-
ская формула, позволяющая вычислить ур как функцию атом-
ного номера Z, массового числа А и энергии нейтрона Еп:
yp(Z, А, Еп) — 2,33+0,06 [2—(—1)A+1-Z—
- (—1)z]+0,15 (Z-92) +0,02 (А—235) +
+ [0,13+0,006(4—235)] (Еп—Епор), (1.1.2)
где значения Епор приведены в табл. 1.2.
7
Таблица 1.2. Значения параметра £11ор
Нуклид SS2Th 23 3(J «’»U 235Ц язву 238Ц 239ри S40pu 24ipU
Епор» МэВ 1,7 —1,38 0,56 —0,41 1,37 1,45 —0,89 0,31 —0,91
Для ядер, делящихся тепловыми нейтронами, формулу
(1-1.2) можно записать и так:
Vp = V/,°+ [0,13+0,006 (А—235) ] Еп, (1.1.3)
где ур° — значение v для теплового нейтрона. Погрешность
формулы (1.1.2) около 0,01—0,02, если £п<6 МэВ.
В [13] рекомендуется следующая аналитическая аппрокси-
мация для 235U (Е, МэВ):
vp(£')=2,398 + 0,05656£+0,03954£2— 0,0057 33F0<£<2,25; 1 j
vp(£>2,334+0,142^+0,001577£2—0,0001086Д’2,25<£<15.}( ’ ‘
Более подробные данные можно найти в [13—16].
Средние значения v для 232Th и 238U по спектру нейтронов
деления, т. е.
- р(Е) Of (E)%(E)dE
v= +---------------, (1.1.5)
j Of (E) X (E) dE
где Of(E) — сечение деления (см. § 1.4, 1.5); % (Б) — спектр
нейтронов деления (см. § 1.2), равен 2,4 для 232Th и 2,8 для
238U.
В каждом данном акте деления число вторичных нейтро-
нов может сильно отличаться от среднего значения у. Вероят-
ность возникновения х нейтронов приблизительно равна
р(л) = -Д-exp I - f^Yl, (1.1.6)
|/л д [ \ д J J
где v — среднее значение х, а дисперсия А составляет 1,6.
Поэтому, если в равные промежутки времени происходит рав-
ное число делений, то это еще не означает, что в реакторе по-
является равное число вторичных нейтронов. Однако если
число делений п велико, то среднее отклонение от пу убывает
как (nv)“1/2. Например, если реактор имеет мощность 1 МВт,
то число делений в 1 с равно n=3-1016 и величина (пт)~|/2=
= 10-8, т. е. весьма мала *.
* По данным [280], величина т,, для 239Рц при энергиях, соответствую-
щих нейтронным резонансам ниже, чем при тепловой энергии на (0,5н-5) %;
среднее значение ур в интервале 0,3 эВ<Е„<4 кэВ ниже, чем в тепловой
области, на ~0,5 %.
8
1.2. СПЕКТР МГНОВЕННЫХ НЕЙТРОНОВ ДЕЛЕНИЯ
Спектр мгновенных нейтронов деления хорошо описывается
максвелловским распределением (рис. 1.2)
Х(Е) = 2|/ехр(-4-)- (1-2.1)
содержащим только один параметр — эффективную темпера-
туру 0. Спектр (1.2.1) нормирован на единицу:
[X(E)dE=l. (1.2.2)
6
Средняя энергия нейтронов Е связана с 0 так:
£=-|-0. (1.2.3)
Максимум функции %(Е) расположен при £=0/2 и равен
(£=2 МэВ)
Г 9 1
= 1/—-S-= 0,36. (1.2.4)
т у те 9 ’ ’
Число нейтронов, энергия которых меньше Е, равно
jx(£)d£ = erf]/4~pT’/4exp(_Jr)- (к2-5>
о
При E<^Q имеем (£—2 МэВ; Е измеряется в МэВ):
_ Е
Х(Е) = 0,73/Е; j X (Е) dE = 0,5 Е3'2, (1.2.6)
о
т. е. спектр медленно спадает при малых энергиях. Например,
при Е=0,1 МэВ %(Е)=0,2, что только незначительно ниже,
чем максимум (1.2.4). Однако интеграл (1.2.5) до 0,1 МэВ
равен 0,015, т. е. только 1,5 % всех нейтронов имеют энергию
меньше 0,1 МэВ.
Рис. 1.2. Спектр нейтро-
нов деления %(£), %(w),
где и=1п£о/£ (при Е=
=6 МэВ и £=10 МэВ
масштаб по оси ординат
увеличен, а по оси абс-
цисс уменьшен)
9
Таблица 1.3.Средняя энергия нейтронов деления
Нуклид 233Ц 235Ц 2 39pu 24ipU 2 5 2Q
Е, МэВ 2,01 1 ,97 2,06 2,04 2,13
При E^>Q из (1.2.5) следует Е 0 (1 + — k 2Е ] хр(-т) . (1.2.7)
Спектр нейтронов простирается до 10—18 МэВ, но число
нейтронов столь больших энергий мало. Из (1.2.7) получаем,
что число нейтронов с энергией больше 6 МэВ равно ~3%,
больше 12 МэВ ~ 0,04 %'.
В табл. 1.3 приведены значения Е для основных нуклидов
(см. [9, 17, 18]; погрешность составляет около 0,04).
На рис. 1.2 представлен также спектр нейтронов деления
в логарифмической шкале (u=ln£0/E, £’0=2-106 эВ). При
переходе к логарифмической шкале надо учесть, что
Z(£)d£ = X(м) | du | ; | du [ = —,
Е
и поэтому ('0 в МэВ)
-X (и) = |т=[2ехр (- н)]3/2 ехр [- (1.2.8)
Между средней энергией Е и средним числом нейтронов v
имеется полуэмпирическая зависимость (см., например, [19];
погрешность этой формулы ~5%; формула относится также
и к спонтанному делению):
Ё = 0,750,65 ]/ТдД. (1.2.9)
Для описания спедтра нейтронов деления кроме (1.2.1) ис-
йользуются и другие аппроксимации. Наиболее употребитель-
на формула Уатта [20]
Х(Ё) = Сехр(—£)sh]/2Z?, (1.2.10)
где С = ~ = 0,4839 и определяется из условия нормировки.
В 21 проведен анализ экспериментальных данных и получен
поправочный множитель f(E) к формуле (1.2.10):
Z(£) = Cexp(— E)shV2Ef(E), (1.2.11)
ю
где
/(£) =
0,913 +0,75£
0,944 + 0,0644£~0'608
L2,94exp(— 11,3/£)
0,01 <£<0,25;
0,25 <£< 10;
10 <£< 18.
Множитель f(E) отличается от единицы на .5—10%,. за ис-
ключением области больших энергий, где отклонения более
значительны (40—50 %) (см. также [22]).
1.3. ЗАПАЗДЫВАЮЩИЕ НЕЙТРОНЫ
Число запаздывающих нейтронов мало по сравнению с чис-
лом мгновенных. Тем не менее их роль в работе весьма велика
(см. гл. 14). Долгое время не удавалось надежно идентифи-
цировать все осколки, испускающие запаздывающие нейтро-
ны. Поэтому преобладал макроскопический подход к их опи-
санию: изучалось запаздывающее нейтронное излучение всей
совокупности осколков деления. Оно аппроксимировалось не-
которым количеством эффективных излучателей (групп).Обыч-
но использовалось шесть групп.
В последние 10—15 лет накоплен большой эксперименталь-
ный материал по нуклидам, испускающим запаздывающие ней-
троны, и появилась возможность микроскопического описания
(списки нейтронных излучателей см., например, в [23, 24]).
При делении 235U тепловыми нейтронами главную роль (около
70 % в -vd) играют следующие нуклиды (в скобках периоды
полураспада, с): 87Вг (55,67), 1371 (24,5), 88Вг (15,88), 1381
(6,63), 89Вг (4,55), 94Rb (2,83), 1391 (2,47), "Вг (1,63).
Суммарное число запаздывающих нейтронов
I
где у, — выход осколка при делении (см. § 1.6); Pi — вероят-
ность излучения нейтрона. В [24] приведено 66 нуклидов, для
которых известны Pi, и 50, для которых Р, получены путем
теоретической оценки (вклад последних в vd не более 10%).
В [24] указывается, что результаты, полученные из микроско-
пических данных, не противоречат макроскопическим, но все
же уступают им по точности. О механизме испускания запа-
здывающих нейтронов см. [25].
Общее количество запаздывающих нейтронов на один акт
деления различных нуклидов приведено в табл. 1.4 (по дан-
ным обзора [26]; для 232Th и 238U данные относятся к делению
быстрыми нейтронами, для остальных нуклидов — тепловыми;
зависимость vd от энергии нейтрона, вызвавшего деление, весь-
11
аблица 1.4. Абсолютное и относительное р число запаздывающих
нейтронов
Нуклид 233Ц 255U 239ри 24ipU 232Th 2 3
vd-103 Р-ЮЗ 6,64(18) 2,66 16,54(42) 6,82 6,24(24) 2,17 15,6(16) 5,32 54,7(12) 22,8 45,1(6) 16,1
ма слабая). В большинстве случаев в расчеты входит отно-
шение
P = vd/v (1.3.1)
которое также приведено в табл. 1.4 [для 232Th, 238U, Vd отне-
сено к среднему значению (1.1.5)].
Обратим внимание на тот факт, что количество запазды-
вающих нейтронов, возникающих при делении 233U и 239Ри,
существенно меньше, чем при делении 235U, а при делении
232Th и 238U, наоборот, больше. Это обстоятельство надо учи-
тывать при рассмотрении реактора, топливо которого изме-
няется по своему составу со временем.
В табл. 1.5 приведены относительные выходы р(/р различ-
ных групп запаздывающих нейтронов, а в табл. 1.6 — соот-
ветствующие постоянные распада X (см. обзор [26]). Посто-
Т аблица 1.5. Относительные выходы запаздывающих нейтронов р;/р, %
Номер группы аЭЗЦ assy азэри 24,pu 232Th 2S8[J
1 8,6(4) 3,8(4) 3,8(4) 1,0(3) 3,4(3) 1,3(1)
2 27,4(7) 21,3(7) 28,0(6) 22,9(6) 15,0(7) 13,7(3)
3 22,7(52) 18,8(24) 21,6(27) 17,3(25) 15,5(31) 16,2(30)
4 31,7(16) 40,7(10) 32,8(15) 39,0(50) 44,6(22) 38,8(18)
5 7,3(21)1 12,8(12) 10,3(13) 18,2(19) 17,2(19) 22,5(19)
6 2,3(10) 2,6(4) 3,5(7) 1,6(5) 4,3(9) 7,5(7)
Таблица 1.6. Постоянные распада запаздывающих нейтронов, с-1
Номер группы азау 2 3 5Ц 23»ри 241рц 232Th гзац
1 0,0126(6) 0,0127(3) 0,0129(3) 0,0128(2) 0,0124(3) 0,0132(4)
2 0,0334(21) 0,0317(12) 0,0311(7) 0,0299(6) 0,0334(16) 0,0321(9)
3 0,131(7) 0,115(4) 0,134(4) 0,124(13) 0,121(7) 0,139(7)
4 0,302(36) 0,311(12) 0,331(18) 0,352(18) 0,321(16) 0,358(21)
5 1,27(39) 1,40(12) 1,26(17) 1,61(15) 1,21(13) 1,41(10)
6 3,1(Ю) 3,87(55) 3,21(38) 3,5(17) 3,29(44) 4,02(32)
12
Таблица 1.7. Периоды и выходы фотонейтронов дейтерия и бериллия
D Be
X, с-1 т1/2 3-105 X, с-1 г 1/2 р-105
6,27.10-7 12,8 сут 0,05 6,27.10—7 12,8 сут 0,057
3.63-10—6 53 ч 0,103 2,48-10-6 77,7 ч 0,038
4,38-10—5 4,4 ч 0,323 1,59-10—° 12,1 ч 0,26
1,17.10—4 1,65 ч 2,34 6,19-10-» 3,И ч 3,2
4,28-10—4 27 мин 2,07 2,67-10—4 43,2 мин 0,36
1,5-Ю-з 7,7 мин 3,36 7,45-10-4 15,5 мии 3,68
4,81-Ю-з 2,4 мин 7,0 3,6-10-з 3,2 мин 1,85
1,69-10-2 41 с 20,4 8,89-10-з 1,3 мин 3,66
2,77-10—1 2,5 с 65,1 2,26-10-2 31 с 2,07
Сумма вы- — 1,01-10-з — 1,52-10—4
ХОДОВ
янная распада А, время жизни Т и период полураспада Т1/2
связаны соотношениями
А=1/7’; Т1/2=Т In 2.
(1.3.2)
Средняя энергия запаздывающих нейтронов 490± 100 кэВ
(см. [27]), что заметно меньше, чем средняя энергия мгновен-
ных (и определена она с меньшей точностью). Спектр имеет
сложный характер с большим числом максимумов. На рис. 1.3
приведен усредненный спектр запаздывающих нейтронов для
деления 235U тепловыми нейтронами (по данным [28]; в этой
же работе приведены спектры для каждой группы запазды-
вающих нейтронов) *.
Если в реакторе присутствует тяжелая вода или бериллий,
то возникает дополнительный источник запаздывающих нейтро-
нов в результате действия у-квантов продуктов деления. Пе-
риоды и относительные выходы нейтронов для фоторасщепле-
ния дейтерия и бериллия у-квантами осколков деления приве-
дены в табл. 1.7 (поданным [25] хл--------------------------
для у-излучения продуктов де-
ления 235U). Порог (уп) -реакции
для D равен 2,226(3) МэВ, для
9Ве — 1,666(2) МэВ .
При использовании данных
табл. 1.7 надо учитывать что
продукты деления не выходят из
блока урана. Поэтому у-кван-
ты прежде чем попасть в замед-
Рис. 1.3. Спектр запаздывающих не!
тронов при делении 23SU тепловьге
нейтронами
* Обзор по запаздывающим нейтро-
нам см. в [29].
13
литель (D20, Be), должны пройти некоторый путь в плотном ве-
ществе тепловыделяющего элемента. Вероятность поглощения
при этом не мала, и соответствующая поправка должна вно-
ситься в данные о выходах нейтронов.
1.4. ВЗАИМОДЕЙСТВИЕ НЕЙТРОНА С ЯДРАМИ
Взаимодействие нейтрона с ядрами характеризуется «эф-
фективным сечением» или просто «сечением» о. Число взаи-
модействий, происходящих в единице объема в единицу вре-
мени, равно *
A = vNtw, (1.4.1.)
где N — число нейтронов; п — число ядер в единице объема;
v — средняя относительная скорость нейтрона и ядер. Во мно-
гих случаях ядра можно считать неподвижными, и тогда v —
средняя скорость нейтронов. Сечение имеет размерность см2 и
измеряется обычно в барнах**:
1 б=10~24 см2 =10~28 м2.
Произведение па называется макроскопическим сечением
(размерность см-1):
2 = по. (1.4.2)
Если А в (1.4.1) — число всех взаимодействий, то о на-
зывают полным сечением: сц=о, 2t=S. Все взаимодействия
можно разделить на две группы: упругие и неупругие. При
упругом взаимодействии сумма кинетических энергий и сумма
импульсов нейтрона и ядра не изменяются при столкновении.
Упругое взаимодействие называют упругим рассеянием и обо-
значают cn,n = Oei — css. Ниже будет использоваться обозначе-
ние crs, S8.
При неупругом взаимодействии появляются новые частицы
и изменяется- состояние ядра. К неупругим взаимодействиям
относятся:
1) деление ядер; соответствующие сечения обозначают anf,
"Snf или of, 2/;
* Фактически в каждом опыте при полностью идентичных условиях чис-
ло взаимодействий будет различным. Под А (1.4.1) понимается среднее зна-
чение по большому числу опытов. Чем больше А, тем меньше роль случай-
ных флуктуаций.
** В Международной системе единиц (СИ) единица площади «барн» исклю-
чена (см., например, [30]). Ближайшая дольная единица — квадратный фем-
тометр (1 фм=10~15 м): 1 6=100 фм2. Однако все справочники, даже издан-
ные в последнее время, например [16, 33], приводят сечения в барнах.
В этих же единицах записаны библиотеки констант в памяти ЭВМ. Поэто-
му, чтобы избежать нежелательных недоразумений, здесь сечения будут вы-
ражаться в барнах (б),
14
2) захват нейтрона ядром с последующим испусканием у-
кванта (радиационный захват); используются обозначения
оПу=Оу=ос, ниже будет использоваться обозначение
ат или ос;
3) реакции с вылетом двух, трех нейтронов и т. д.: ап,2г<;
(Уп,3п • •
4) реакции с вылетом заряженной частицы: протона, а-
частицы и др.: оп,р', оп,а . .;
5) сумма сечений
••• ••• (1.4.3)
называется сечением поглощения (абсорбции);
6) неупругое рассеяние, когда часть кинетической энергии
нейтрона уходит на возбуждение ядра, которое затем испускает
у-квант и переходит в основное состояние; обозначения: <зпп, ~
ain-
Ниже используется обозначение otn- Неупругое рассеяние,
приводящее к испусканию у-кванта, возможно только при
больших энергиях нейтрона — сотни килоэлектрон-вольт и вы-
ше. При малых энергиях, сравнимых с энергией теплового дви-
жения молекул, возможны неупругие столкновения, при кото-
рых часть энергии уходит на возбуждение молекул или пере-
дается кристаллической решетке.
Сумма сечений всех неупругих процессов обозначается ох:
а., - о , -4- а„ = — а . /1 4
х п,п' 1 а * nt п9
а сумма ап> п, 4- ап_ п есть полное сечение рассеяния as. Поскольку
неупругие рассеяния играют малую роль в реакторах на теп-
ловых нейтронах, мы сохраним обозначение сц для упругого
рассеяния.
Все сечения взаимодействий нейтрона с ядрами являются
функциями энергии нейтрона. Некоторые данные по числен-
ным значениям сечений приводятся в последующих парагра-
фах настоящей главы, гл. 3, 8, приложении. Более подробные
данные можно найти в справочниках [4, 7, 13, 31—37].
Упругое рассеяние при энергиях меньше 100 кэВ происхо-
дит изотропно в системе центра инерции (см. § 2.2), т. е. все
углы рассеяния в этой системе равновероятны. При больших
энергиях рассеяние становится анизотропным. В этом случае
надо знать дифференциальное сечение рассеяния
-^-= аД£, cos 9); dQ = 2it sin 9d9, (1.4.5)
где 0 — угол между направлением движения нейтрона до и
после столкновения. Величину анизотропии можно характери-
15
Рис. 1.4. Зависимость среднего коси- Рис. 1.5. Зависимость сечения упру-
ауса угла рассеяния для 238U от энер- того а„, „ и неупругого ап. п- рассея-
гии (погрешность дана ориентнровоч- иия нейтронов для 238U от энергии
но) (погрешность дана ориентировочно)
зовать средним значением косинуса угла рассеяния
+1
J as(E, И) Мн
cos9 = КД) = =1--------------. (1 -4-6)
f as(£, р)ЙЦ
—1
Для примера на рис. 1.4 приведена зависимость \к(Е) для
рассеяния на ядре 238U. Видно, что при Е<0,1 МэВ средний
косинус равен нулю, а при 1 МэВ анизотропия существенна.
С помощью ц определяется транспортное сечение
cstr=cst—'pels, 0-4.7)
которое играет большую роль в процессах переноса нейтронов.
Подробные данные об анизотропии упруго рассеянных ней-
тронов можно найти в [38]. Для реакторов на тепловых ней-
тронах роль анизотропии рассеяния невелика.
При неупругом рассеянии возникают нейтроны разных энер-
гий. Если Е — энергия падающих нейтронов, Е' — рассеян-
ных, то распределение по энергии Е' можно записать так:
(Д) = СД [Т (Д)]~®ехр ,
где Т (Е) сравнительно слабо зависит от энергии и от массо-
вого числа ядра, на котором произошло рассеяние, причем
(Т(Е) в МэВ) [13]:
0,3<Т(Е) <0,8.
На рис. 1.5 представлена зависимость и для 238U
[13] (погрешность дана ориентировочно, для ап,п' она значи-
тельна; данные разных авторов иногда различаются в 2 раза).
16
1.5. СЕЧЕНИЯ ОСНОВНЫХ НУКЛИДОВ
Сечения взаимодействия с медленными нейтронами приня-
то приводить для моноэнергетических нейтронов, имеющих
скорость 2200 м/с. Эта скорость соответствует средней квад-
ратичной скорости максвелловского распределения с темпера-
турой 20,4 °C (см. подробнее § 2.4). Среднее сечение для макс-
велловского спектра нейтронов с этой температурой получает-
ся с помощью множителя g (см. подробнее § 2.4). В табл. 1.8
приведены сечения поглощения оа=сг/+о? деления о/, рассея-
ния crs, множители g, а также величины
г]=у<Т//сга=у/(1+а); a = crv/oy, (1.5.1)
Таблица 1.8 составлена по данным обзоров [И, 32] (кро-
ме ga ДЛЯ 238U).
Таблица 1.8. Характеристики основных нуклидов при взаимодействии
с тепловыми нейтронами
Параметр 233[_J 2 3 5(7 230pu 24ipL1 »’«U
’а 574,7(10) 680,9(11) 1017,3(29) 1369,4(77) 2,68(2)
529,1(12) 582,6(11) 748,1(20) 1011,1(62) 4-10-e
12,6(3) 14,0(5) 7,3(4) 9,1(10) 9,38(9)
Sa 0,9996(11) 0,9788(8) 1,0784(24) 1,0442(20) 1,002
St 0,9955(15) 0,9761(12) 1,0558(23) 1,0440(49)
•n 2,2957(40) 2,0751(33) 2,1153(52) 2,1686(80)
а 0,0861(15) 0,1687(15) 0,3600(32) 0,3543(57)
Массовая концентрация 235U в естественной смеси изотопов
урана равна [39] 0,7106 %, отношение чисел ядер 235U и 238U
равно 0,7249 % *, атомная концентрация 235U равна 0,7196.
Кроме 235U и 238U в естественной смеси присутствует 0,0055 %'
234U **. Величина г| для естественной смеси определяется так:
'Г>е~ ea5nS + oaana+'Saini — 7,5 ( + > ( • • )
где
__ °аапа . „ ___ aaini
> Чь >
(1.5.3)
* Только в одном месторождении урана наблюдалось сильное отклонение
отношения па/иа от среднего значения — Окло в Западной Африке, где при-
мерно 2 млрд, лет тому назад происходила в природных условиях цепная
ядериая реакция деления [39, 40]. Поиски следов природных ядерных реак-
торов в других месторождениях пока не привели к положительным резуль-
татам. Незначительные (±5-10-6) изменения п6/па в различных месторож-
дениях не связаны с цепной реакцией [39].
** 234U является продуктом распада 238U->234Th->234Pa->234U. В усло-
виях равновесия 233U с продуктами распада должно быть Пь1па = Т\/Та =
= 5,5-10~5, где 7’4,8 — периоды полураспада (см. (У)___
2—6053 ‘ Г '-17
Рис. 1.6. Зависимость сечений деле-
ния а/ и поглощения ао для 233U и
235U от энергии Е
Рис. 1.7. Зависимость сечений деления
Of и поглощения <уа для 239Ри и 24,Ри
от энергии Е
Подставляя в (1.5.2) значения сечений из табл. 1.8 и отно-
шение чисел ядер, получаем для нейтронов со скоростью
2200 м/с (сечение 234U приведено в приложении, q^—O,001):
т)е=1,344(5). (1.5.4)
Введя в (1.5.2) g-факторы, получим значение т]е Для максвел-
ловского распределения нейтронов с температурой 20,4 °C:
т)е=1,329(5). (1.5.5)
Значение qs [см. (1.5.3)] равно (с учетом g-факторов)
<78 = 0,5559(43). (1.5.6)
Непосредственное измерение qs [41] дает
</8=0,5655(25), (1.5.7)
что удовлетворительно согласуется с (1.5.6) [из (1.5.7) полу-
чим ос8=2,726(13) ].
Зависимость о;- и оа от энергии нейтрона при £<0,5 эВ
представлена на рис. 1.6, 1.7. По оси ординат на этих рисун-
ках отложена величина о ]/£. Поэтому если справедлив закон
\/v (см. гл. 2):
= о(£) = /^-о(£н), (1.5.8)
где Пн=2200 м/с, £н=0,0253 эВ, то на графике должна по-
лучиться прямая линия, параллельная оси абсцисс. Из рис. 1.6,
1.7 видно, что для 233U и 235U отклонения от закона \/v не
очень сильные, а для 239Ри и 241Ри весьма значительные.
На рис. 1.8 представлена зависимость
п(£)=у(£)ф(£)/сга(£) (1.5.9)
18
Рис. 1.8. Зависимость эффек-
тивного числа вторичных ней-
тронов т] от энергии для изото-
пов урана и плутония
при £<0,5 эВ, а на рис. 1.9—
та же величина как функция
логарифма энергии от 0,001 до
107 эВ [42]. Изрис. 1.9 видно,
какие сильные колебания ис-
пытывает величина г] (особен-
но для 235U и 239Ри). Только
при Е>0,1 МэВ для всех нук-
лидов значение т](£) монотон-
но возрастает и достигает 3—
4 при энергии 10 МэВ.
Сечение поглощения 238U
при малых энергиях почти
точно следует закону 1/и (получено из данных по резонанс-
ным уровням, см. гл. 8):
Оа(£) = Оя(£н)^/^[1+0,167 (£-£„)]; £<0,5 эВ. (1.5.10)
Формуле (1.5.10) соответствует ^-фактор, приведенный в
табл. 1.8.
Сечение деления 238U при малых энергиях нейтрона ничтож-
но мало (см. табл. 1.8). При больших энергиях (£>1 МэВ)
Рис. 1.9. Зависимость Г| (£) для 233U, 235U, 229Pu во всем энергетическом ин-
тервале
2*
19
Таблица 1.9- Средние сечения радиационного захвата и деления
в спектре нейтронов деления, б
Нуклид °! У Нуклид °f
232Th о, 1 0,07 239Рц 0,04 1,824(20)
233Ц 0,1 1,85 240рц 0,09 1,33
23BJJ 0,1 1,245(18) 237fJp 1,442(23)
238Ц 0,08 0,313(3)
На рис. 1.10 дана зависимость пД£)_для 2з2ТЬ и 238U. Пред-
ставляют интерес средние значения оу и 07 по спектру ней-
тронов деления. Эти данные для ряда нуклидов приведены в
табл. 1.9 [43, 44].
1.6. ПРОДУКТЫ ДЕЛЕНИЯ*
В подавляющем большинстве случаев ядро делится на два
осколка (вероятность тройного деления порядка Ю-4—10-3).
Распределение продуктов деления по относительным атомным
массам имеет два максимума (рис. 1.11; данные [45] для де-
ления тепловыми нейтронами): с 4 = 904-100 и с 4=1354-145.
Максимальная вероятность появления осколка с данным 4
составляет около 6—7%. При увеличении массы делящегося
ядра .максимума незначительно смещаются в сторону боль-
ших значений 4. При увеличении энергии нейтрона, вызываю-
щего деление, до нескольких мегаэлектрон-вольт значение
функции у (4) в минимуме возрастает.
Так как относительное число нейтронов (4—Z)/4 в деля-
щихся ядрах больше, чем в стабильных ядрах со средней атом-
ной массой, то осколки испытывают р--распады с превраще-
нием нейтрона в протон или, в незначительном числе случаев,
испускается запаздывающий нейтрон. Типичная цепочка пре-
вращений имеет такой вид [46]:
з/Rb 0Л7бГ'385г ^sgY^-’oZr^-^Nbi^-
I 87,7% ; 43тТс6,01ч
“Мо1
66ч | 12,3%
Каждый нуклид этой цепочки, кроме
как непосредственно при делении, так и в
крайних, возникает
результате р-распа-
* Термин «продукты деления» применяется для осколков на последних
стадиях их радиоактивных превращений [23].
20
Рис. 1.10. Зависимость сечений деле-
ния 232Th и 238U от энергии; штрихо-
вой линией показано произведение
о>(£)Х(£)-10 для 238U, где х(£) —
нормированный спектр деления
(1-2.1)
Рис. 1.11. Распределение продуктов
деления по массам для деления 235U
и 239Ри тепловыми нейтронами
да нуклида с меньшим Z. Вероятность непосредственного вы-
хода осколка с данным Z в цепочке А определяется выраже-
нием
Z+1/2
Уа= j P(A,Z)dZ, (1.6.1)
Z—1/2
где Р(А, Z) дается гауссовой функцией:
D/J 7^ 1 Г 1 lZ-ZP^\2].
P(AZ) = -—^ехр -------------- ,
а 2л L ' J
(1.6.2)
ег—si
ZP(A); о — параметры, характеризующие распределение. На
рис. 1.12 для примера приведены экспериментальные значения
Улг [47] и вычисленные при Zp (Л) =39,68 и о=0,72 [45].
Обычно используют следующую терминологию.
Независимый выход — вероятность образования нуклида
при делении после испускания мгновенного нейтрона, но до
радиоактивного распада его самого и его предшественника.
Кумулятивный выход — вероятность образования нуклида
при делении после испускания мгновенных и запаздывающих
21
Рис. 1.12. Зависимость неза-
висимого выхода от Z для
цепочки /4=99:
X — вычисленные значения;
Л — экспериментальные
нейтронов до его радиоактивного рас-
пада, но после распадов всех его пред-
шественников (очевидно, что такое со-
стояние физически реализуется, толь-
ко если период полураспада данного
нуклида много больше, чем его пред-
шественников; тем не менее этим тер-
мином удобно пользоваться и в дру-
гих случаях). Кумулятивный выход
есть сумма независимого выхода дан-
ного нуклида и всех независимых вы-
ходов его предшественников в цепочке
распада.
Выход цепочки — вероятность об-
разования стабильного нуклида при
делении после испускания мгновенных
и запаздывающих нейтронов и после
распада всех его предшественников.
Выход цепочки — сумма всех незави-
симых выходов или кумулятивный выход последнего члена це-
почки (иногда данному массовому числу принадлежат две це-
почки, не связанные между собой распадом; в этом случае по-
следнее определение неверно).
Поглощение нейтронов продуктами деления рассмотрено в
гл. 12. Данные о 0- и у-излучении продуктов деления можно
найти в справочниках [46, 48].
Отметим, что выходы у удовлетворяют двум законам сохра-
нения
St/И) = 2; 2/1у(Л)== + l-v,
А А
где у (А) — выход цепочки с массовым числом А; Аа — мас-
совое число делящегося ядра; v — среднее число нейтронов в
одном акте деления. Наличие этих условий учитывается при
обработке экспериментальных данных, что увеличивает досто-
верность результата.
Таблица 1.10. Выход 3Н, 4Не на 101 делений
Делящийся нуклид 3Н ‘Не
235Ц 1,08(4) 17,0(3)
239рц 1,42(7) 22,2(7)
241рЦ 1,41 (6) 18,6(5)
22
Истинное тройное деление, когда возникает три осколка с
массами одного порядка, происходит крайне редко (~10-7).
Чаще наряду с двумя осколками возникает легкая частица 'Н,
2Н, 3Н, 4Не и др. [13]. Для реактора наибольший интерес
представляет 3Н, поскольку тритий радиоактивен. В табл. 1.10
приведены выходы 3Н и 4Не (длиннопробежные а-частицы)
при делении тепловыми нейтронами (по данным [49]).
1.7. ЭНЕРГОВЫДЕЛЕНИЕ ПРИ ДЕЛЕНИИ
Энергия, выделяющаяся в акте деления ядра, складывает-
ся из следующих составляющих: кинетической энергии оскол-
ков деления Ек, кинетической энергии нейтронов, рожденных
при делении, fin; энергии у-квантов, испускаемых при делении,
Ev («мгновенные» у-кванты, условная граница запаздывания
Ю-3 с); энергии у-квантов, испускаемых продуктами деления,
fib (время запаздывания >10~3 с); энергии р-частиц, испус-
каемых продуктами деления, Е$; энергии, уносимой антиней-
трино, Еу. Таким образом,
Wo = Ек + Еп + Еи + + fig + fiv. (и. i)
В реакторе не выделяются энергия, уносимая антинейтрино
fiv, и энергия Afi, выделяющаяся при распаде продуктов де-
ления с очень большим периодом распада (>108 с=3 года),
поскольку она, как правило, выделяется уже вне реактора,
в выгруженном топливе (Afi=0,14-0,2 МэВ). Таким образом,
в реакторе выделяется энергия
W' = Wq-Ev—ЛЕ. (1.7.2)
Кроме того, v—1 нейтрон поглощается в реакторе или за-
щите. Пусть средняя энергия, выделяющаяся после захвата
нейтронов, равна Wn (эта велечина зависит от конструкции
реактора, однако практически такая зависимость очень сла-
бая). Тогда полная энергия, выделяющаяся в реакторе на одно
деление, равна
№=lF+(v-l) Wn=Ef. (1.7.3)
Детальный анализ энерговыделения в реакторе проведен в
[50]. Полное энерговыделение 1FO может быть выражено через
дефекты масс разделившегося ядра и осколков деления:
WG = m(A, Z)—Zyitn(Ai, Zi) — (v—l)mn, (1-7.4)
i
где m(X, Z)=M(A, Z) — Am0 — дефект массы делящегося
ядра с масовым числом А и зарядом Z; yi — выход i-ro ста-
бильного нуклида I 1иуг=2). тп—Мп—то=8,О7 МэВ — из-
23
быток массы нейтрона (т0 — атомная единица массы, см. при-
ложение).
Поскольку дефект массы слабо зависит от А и Z в той
области относительных атомных масс, для которых tji макси-
мальны, погрешность в выходах сильно компенсируется усло-
вием нормировки 2^4 =2- Благодаря этому обстоятельству
i
вычисление Wo по равенству (1.7.4) с использованием экспе-
риментальных данных о выходах продуктов деления оказы-
вается точнее, чем определение по (1.7.1), поскольку экспери-
ментальные погрешности отдельных слагаемых в (1.7.1) до-
вольно значительны. Таким образом, оказывается, что сумма
Wo известна точнее, чем слагаемые в (1.7.1). В [50] вся сово-
купность данных обработана по методу наименьших квадра-
тов. Результаты приведены в табл. 1.11 (для 238U учитывалась
энергия нейтрона, вызвавшего деление).
В [50] приведены значения энергии, выделяющейся при
захвате нейтрона в различных веществах (табл. 1.12). Для ши-
Таблица 1.11. Различные составляющие эиерговыделения, МэВ
Составляющие энерго выде- ления S15U »»»и »8»Ри »41Ри
Ek ' 166,2(13) 166,9(13) 172,8(19) 172,2(22)
Еп 4,8(1) 5,5(1) 5,9(1) 5,9(1)
^71 8,0(8) 7,5(13) 7,7(14) 7,6(14)
Е-, 7,2(11) 8,4(16) 6,1(13) 7,4(15)
7,0(3) 8,9(6) 6,1(6) 7,4(6)
Е, 9,6(5) И,9(7) 8,6(7) 10,2(7)
г0 202,7(1) 205,9(3) 207,2(3) 210,6(3)
W. 192,9(5) 193,9(8) 198,5(8) 200,3(8)
Таблица 1.12. Энерговыделение при захвате нейтрона
Нуклид |Г, МэВ Нуклид W, МэВ Нуклид МэВ
н 2,22 Сг 9,29 236JJ 6,54
D 6,26 Fe 7,8 23вЦ 5,46
юв 2,79 Ni 8,53 238JJ 5,69
С О 4,95 3,38 Нержавеющая сталь 8,37 239ри 240Рц 6,53 5,24
А1 10,74 Zr 8,07 241рц 6,31
Si 8,56 issxe Другие про- дукты деления 7,31 8,1 242Ри 5,24
24
Таблица 1.13. Суммарная энергия на один акт деления, выделяющаяся
в реакторе, МэВ
Нуклид 2330 2850 238(J asspu 24ipU
Ef 198,6 (6) 201,6 (7) 204,9 (10) 210(1) 212,1 (10)
рокого класса реакторов на тепловых нейтронах среднее значе-
ние Wn оценено в [50] так:
^ = ^^> = 6,1(3), (1.7.5)
i
где Wi — значения из табл. 1.12; qt — вероятность захвата
ядром i в расчете на одно деление.
В табл. 1.13 приведено полное энерговыделение в реакторе
на одно деление, полученное из (1.7.3). Максимальная раз-
ница энерговыделений при делении различных нуклидов со-
ставляет примерно 6 %.
Близкие результаты получены также в [51, 52]; данные
для 233U в табл. 1.13 взяты из [51].
Попытка определить энерговыделение путем излучения
энергетического баланса на работающем реакторе была сде-
лана в [53] [реактор с водой под давлением, мощность
150 МВт (эл.), глубина выгорания 11,5 МВт-сут/кг]. При этом
учитывалось, что заметная доля общей энергии в реакторе
обусловлена делением 239Ри. Поэтому проводилось соответст-
вующее усреднение данных [50], причем получилось, что в тот
момент, когда происходили измерения, энерговыделение на
одно деление было равно Ef = 203,6 (11). Измерения на реак-
торе (среднее значение из трех независимых способов опреде-
ления энергетического баланса, подробнее см. [53]) привели
к следующему результату: Ef=204,2 (60) МэВ, что находится
в согласии с [50], но имеет меньшую точность.
Учитывая, что 1 МэВ = 1,602-10-13 Дж, легко определить,
сколько граммов вещества должно разделиться, чтобы выдели-
лась энергия 1 МВт-сут (табл. 1.14).
Таблица 1.14. Масса вещества, выделяющая при делении
энергию 1 МВт-сут
Нуклид 2330 235 0 2SS|J = 39Ри 24ipu
mf, г 1,051 1,044 1,04 1,019 1,018
g0, МВт - сут 0,951 0,958 0,962 0,981 0,982
25
Погрешность данных табл. 1.14 около 0,5%. Величина gv =
= mf-i равна энергии, МВт-сут, которая выделяется при де-
лении 1 г. С погрешностью 2—4 % справедливо простое пра-
вило:
1 г разделившегося вещества = энергии 1 МВт-сут.
Под «уничтоженными» ядрами будем понимать сумму раз-
делившихся и перешедших в более тяжелые изотопы элемен-
та, которые не делятся тепловыми нейтронами: 235U+n->-236U
(см. гл. 13). Тогда количество уничтоженного 2з5П при энер-
говыделении 1 МВт-сут равно
(1.7.6)
где mf —- см. в табл. 1.13, а а — отношение сечений радиа-
ционного захвата и деления, усредненное по спектру нейтронов
в данном реакторе (см. § 2.4). Заменив приближенно а на
а (1.5.1), получим:
1,22 г уничтоженного 235и=энергии 1 МВт-сут.
Для 239Рц такая оценка мало что дает, так как 240Ри после
захвата нейтрона превращается в 214Ри, который делится теп-
ловыми нейтронами, и подсчет уничтоженных ядер плутония
более сложен.
Энергия £'/=200 МэВ соответствует примерно 0,1 %' пол-
ной энергии покоя Мс2 ядра урана. Энергия, выработанная,
например, за один год электростанцией электрической мощ-
ностью 1 ГВт, при КПД 30 % эквивалентна массе 1 кг. Сле-
довательно, общая масса выгруженного на АЭС топлива (вклю-
чая продукты деления) должна быть меньше, чем масса за-
груженного топлива, на 1 кг, что составляет 0,1 % массы про-
дуктов деления *.
После остановки реактора в топливе продолжается выде-
ление энергии по следующим причинам: 1) продолжается де-
ление, вызываемое запаздывающими нейтронами (см. § 14.2);
2) выделяется энергия при распаде трансурановых элементов
[для реакторов на естественном или слабообогащенном уране,
главным образом 239Np (см. § 13.1)]; 3) выделяется энергия
при распаде продуктов деления.
Пусть в момент 1=0 произошло деление. Мощность р- и
у-излучения продуктов деления можно аппроксимировать сум-
мой экспонент:
ffi/o(0= 2а;ехР('-М, О-7-7)
* В этом рассуждении не учитывается, что некоторая часть нейтронов,
возникающих прн делении, захватывается замедлителем и конструкционны-
ми материалами; масса этих нейтронов для рассматриваемого примера также
близка к 1 кг.
26
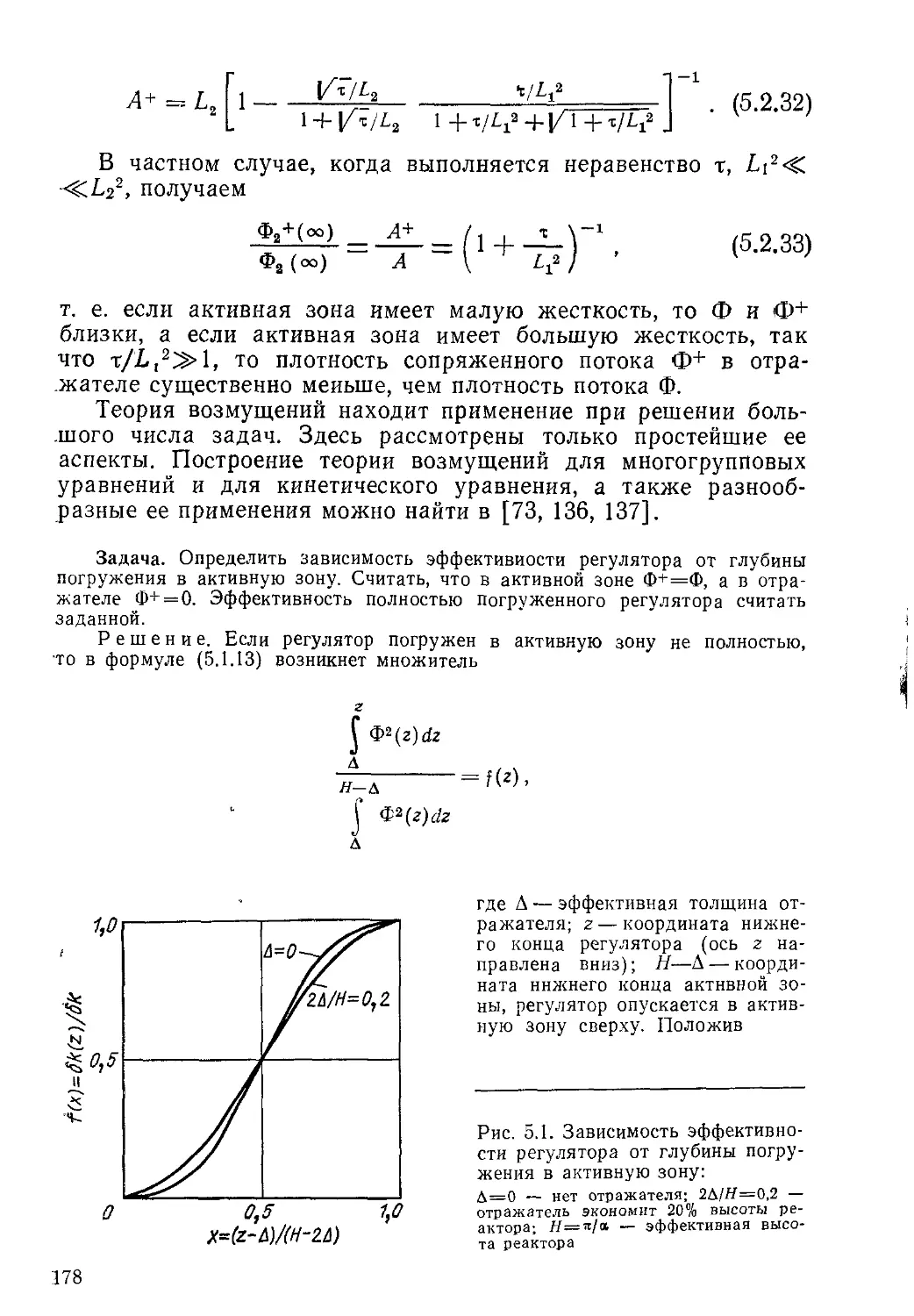
Рис. 1.13. Относительное энсрговыдс-
ление продуктов деления при беско-
нечно длительной работе реактора до
остановки: сплошная линия — 23SU;
штриховая — 239Ри; штрихпунктир-
ная — энерговыделение за счет рас-
пада 239Np
где значения постоянных at и
для деления 235U и 239Ри теп-
ловыми нейтронами приведены
в [54] (см. также [55]; аппрок-
симация, предложенная в [56],
дает несколько меньшее значе-
ние Wo). Если реактор работал
на мощности W в течение вре-
мени Т, а после остановки
прошло время t, то мощность
излучения продуктов деления р
Wo = ^~ f w0 (t) dt = W [F (t) — F (tТ)], (1.7.8)
Ef t
где
Е(0 = Ег’2«Л_,ехр(-М (1-7-9)
и Ef — энергия деления, МэВ. График функции F(f) для 235U и
239Ри показан на рис. 1.13. В приложении VIII приведена таб-
лица значений функции F(t) для ряда нуклидов (по [57]). По-
дробные данные об излучении продуктов деления можно найти
в справочниках [13, 46, 48]. Если после выгрузки топлива из ре-
актора прошло около 3 лет, то основной вклад в энерговыделе-
ние и активность вносит сравнительно малое число нуклидов.
Их перечень приведен в § 12.4.
Энерговыделение за счет распада 239Np после остановки ре-
актора можно определить по формуле
«Ч = (V - 1 ~ «- q) ехр(— < (1.7.10)
где W—мощность реактора; Evp/E,-=2-10-3 — отношение энер-
гии, выделяющейся при распаде 239Np, к энергии деления; а
имеет тот же смысл, что в (1.7.6); q — отношение числа нейтро-
нов, поглощенных всеми нуклидами, кроме 235U и 238U, к числу
делений, Х=0,294 сут~‘. Для реакторов на слабообогащеином
27
или естественном уране значение v—1—а—q близко к единице
(см. § 13.1). Тогда
№NP/r=2-10-3 exp (—0,294f), (1.7.11)
где t — время, сут. На рис. 1.13 величина (1.7.11) дана штрих-
пунктиром. Видно, что энерговыделение за счет 239Np много
меньше, чем энерговыделение продуктов деления. При очень
большом времени выдержки выгруженного топлива (сотни и
более лет) необходимо учитывать энерговыделение за счет рас-
пада долгоживущих трансактинидов (см. § 13.2).
1.8. РЕАКЦИЯ (я, 2п)
Размножение нейтронов, кроме реакции деления, происходит
также и по реакции (и, 2и). Эта реакция имеет порог около
6 МэВ, и ее среднее сечение в спектре нейтронов, который имеет
место в ракторе на тепловых нейтронах, мало. Поэтому она ока-
зывает малое влияние на реактивность. Исключение составляет
9Ве, у которого порог реакции (и, 2и) равен 1,85 МэВ и среднее
сечение на порядок больше, чем у тяжелых ядер (табл. 1.15).
На рис. 1.14 приведены сечения реакций (и, 2и) и (и, Зп) для
238U [4, 13, 37].
Иногда, однако, в результате реакции (и, 2и) возникает та-
кой нуклид, который другим путем в реакторе образоваться не
может. Для правильного определения концентрация такого нук-
лида надо знать сечение реакции (/г, 2я). Если считать, что
спектр нейтронов в реакторе при Е>6 МэВ совпадает со спек-
тром деления 235U, то достаточно знать среднее значение
0= Jo„,M(E)X(E)d£, (1.8.1)
Таблица 1.15. Среднее сечение реакций (я, 2я) и (я, Зя), мб
Нуклид Реакция c Литература
D (и, 2я) 5,1 Вычислено по (1.8.1),
сечение [37]
9Ве (n, 2n) 144(6) 37]
азати (n, 2») 15,7(7) 37]
234Ц (n, 2n) 7 59]
234Ц (n, 3») 0,042 59]
236(J (n, 2n) 10 Вычислено по (1.8-1),
сечение [16]
236JJ (n, 3n) 0,02 То же
23SJJ (n, 2n) 15,7(8) [37]
238JJ (n, 3») 0,2 Вычислено по (1.8.1),
сечение [4]
23?Np (n, 2n) 4,66(47) [58], ДЛЯ 262Cf
2,5(10) [58], для 23BU
28
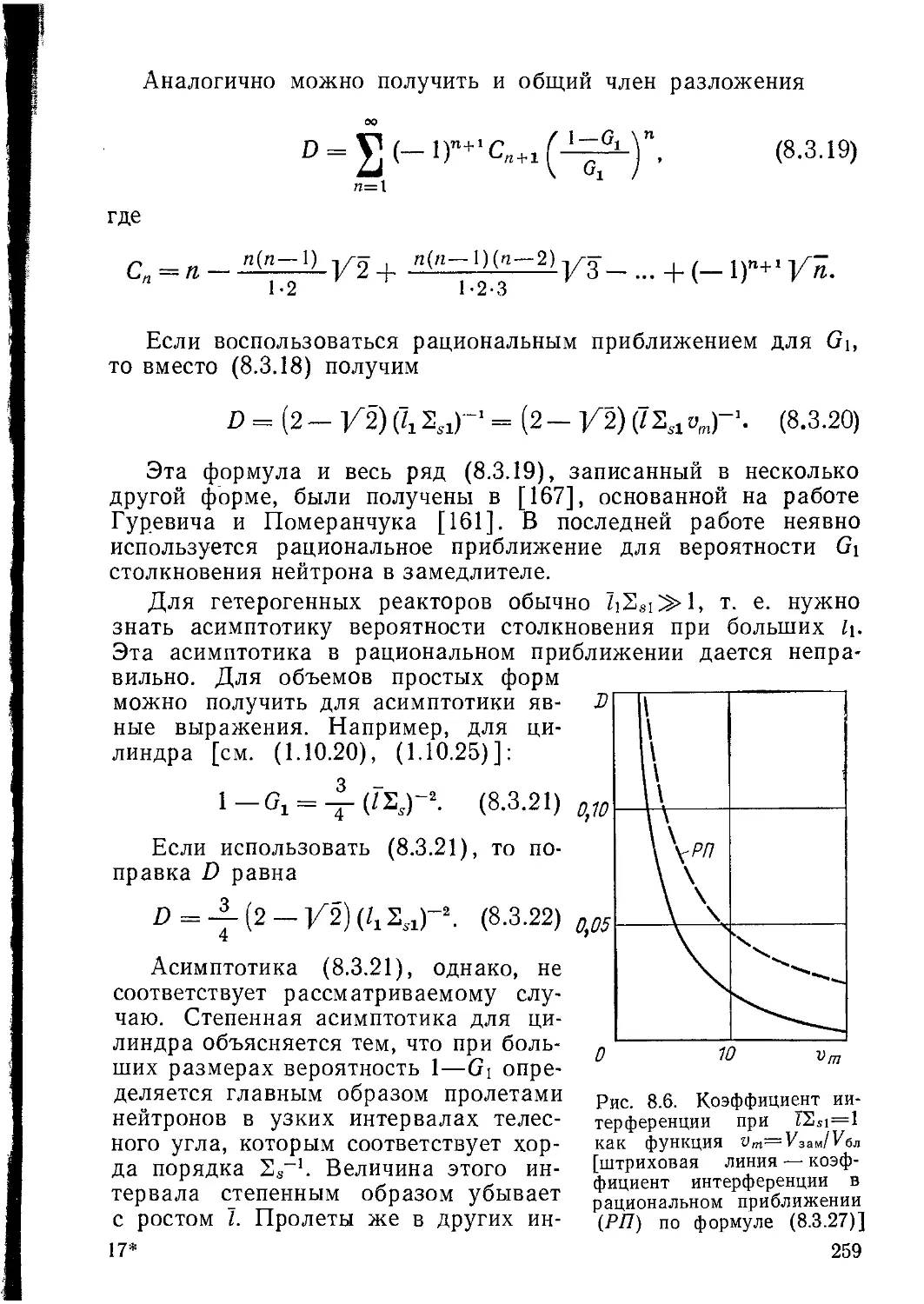
6 В 10 12 14 16 ЕМэР
Рис. 1.14. Сечения реакций (и, 2/г) и о-0
(и, Зл) для 238U [штрихпунктнром ’
дано произведение (Tn.zn (£)Х(£)Х V
Х200, где /(£)—нормированный
спектр нейтронов деления (1.2.1)]
где /(£') вычисляется по 1
(1.2.1) или (1.2.11). В ^габл.
1.15 приведены значения о для
некоторых нуклидов. Величи-
на (1.8.1) чувствительна к ви- 0,5
цу спектра %(Е), который для
различных нуклидов несколь-
ко различен (см. табл. 1.15, о
для 237Np). Спектр нейтронов о
при Е>6 МэВ в реакторе
может несколько отличаться от х(^)- Поэтому данные табл.
1.15 надо рассматривать только как ориентировочные.
Сечение реакции (п,2п) на 237Np приведено для образования
2a0’"Np, который с вероятностью 52% переходит в 236U и с ве-
роятностью 48% — в 23вРи [7’1/2=22,5 ч; полное сечение реак-
ции 237Np (и, 2п) 23e<g+m)Np на 36% больше].
В термоядерном реакторе реакция (и, 2п) играет большую
роль, поскольку в реакции T(D, и)4Не возникают нейтроны,
энергия которых (14 МэВ) значительно больше, чем при делении.
1.9. УСЛОВИЯ ОСУЩЕСТВЛЕНИЯ ЦЕПНОЙ РЕАКЦИИ ДЕЛЕНИЯ*
Рассмотрим историю нейтрона от его рождения при делении
235U до поглощения каким-либо ядром. Для простоты будем
считать, что в реакторе нет изотопов плутония.
Пусть ядро 235U поглотило нейтрон и разделилось. При этом
в среднем возникает v нейтронов. Сталкиваясь с ядрами окру-
жающей среды, эти нейтроны частично поглощаются, но глав-
ным образом рассеиваются, теряя при этом часть кинетической
энергии. До тех пор пока их энергия выше порога деления 238U,
существует вероятность того, что при столкновении с ядром
238U произойдет деление. В результате число нейтронов возра-
стет до ve. Величину е будем называть коэффициентом размно-
жения па быстрых нейтронах (см. § 9.1; вместо е используют
также обозначение ц).
Если в реакторе имеется замедлитель, т. е. вещество с малой
атомной массой, то в результате столкновений с легкими ядра-
ми нейтроны начнут быстро терять свою энергию (см. § 2.2).
Сечение поглощения 238П имеет при энергии выше 6 эВ весьма
* См. первые работы по теории ядерных реакторов [60—62].
29
большое число узких максимумов (резонансы, см. гл. 8). Поэто-
му некоторое число нейтронов в процессе замедления будет по-
глощено 238U. В результате образуется ядро 239U', которое после
двух p-распадов превращается в ядро 239Ри (см. гл. 13). Обо-
значим <р вероятность того, что нейтрон в процессе замедления
не будет захвачен ядром 238U (эту вероятность обозначают так-
же р). Когда энергия нейтрона станет соизмерима со средней
энергией теплового движения молекул замедлителя, дальней-
шее замедление прекратится. Такие нейтроны будем называть
тепловыми (см. § 2.4 и 7.5). Количество тепловых нейтронов
равно veep.
Тепловой нейтрон диффундирует в среде до тех пор, пока не
будет поглощен каким-либо ядром. Свободный нейтрон неста-
билен и распадается на протон, электрон и антинейтрино. Вре-
мя жизни свободного нейтрона около 15 мин, что на несколько
порядков больше, чем время жизни нейтрона в конденсирован-
ных средах (см. § 2.1). Поэтому всюду ниже не будет прини-
маться во внимание распад нейтрона.
Обозначим 0 вероятность того, что нейтрон будет поглощен
235U, а не каким-либо другим ядром (используется также обо-
значение/; часто 0 обозначают вероятность поглощения не 235U,
а любым изотопом урана). Обозначим 1/(1-фа) (см. § 1.5) ве-
роятность того, что поглощенный 235U нейтрон вызовет деление.
Тогда количество нейтронов, вновь вызвавших деление, равно
k = —-— вфО = теф 6. (1,9.1)
1 -j- а
Величину k будем называть коэффициентом размножения.
Если реактор достаточно большой, так что вероятность вылета
нейтрона из реактора пренебрежимо мала, то при k=1 весь
рассмотренный выше цикл повторится, т. е. будет осуществлять-
ся стационарная цепная реакция деления. Если &>1, то коли-
чество нейтронов будет возрастать, если &<1, то убывать со
временем (см. гл. 14). Часто k называют коэффициентом раз-
множения бесконечно большого реактора и обозначают kx.
Если реактор имеет конечные размеры, так что с некоторой
вероятностью Р нейтроны выходят из объема реактора и погло-
щаются где-то в окружающей среде, то для осуществления ста-
ционарной цепной реакции должен равняться единице эффек-
тивный коэффициент размножения
Йэф=^(1-Р). (1.9.2)
Каждому значению объема (при фиксированной форме) со-
ответствует определенное значение Р. Если при этом йЭф= 1, то
этот объем будем называть критическим.
Формула (1.9.1) называется формулой «четырех сомножи-
телей». В первые годы развития теории ядерных реакторов она
30
(1.9.3)
была чрезвычайно популярна. Впоследствии, однако, все более
К отчетливо стали понимать ее условный характер. Например, де-
Е ление 235U происходит при поглощении не только тепловых ней-
К тронов, по и резонансных, и быстрых; в резонансной области
К нейтроны поглощаются не только 238U, но и всеми другими ядра-
МИ и т. д. Кроме того, что более существенно, появилась реаль-
jf’ мая возможность с помощью расчетов на ЭВМ. получать баланс
I' нейтронов сразу для всего процесса замедления и диффузии.
? Поэтому в настоящее время чаще определяют коэффициент раз-
множения как отношение числа нейтронов, возникших от всех
актов деления в единицу времени, к числу всех поглощенных
нейтронов в единицу времени:
_ Число рожденных нейтронов
Число поглощенных нейтронов'
Если в знаменатель (1.9.3) добавить число нейтронов, вы-
шедших из реактора, то получим эффективный коэффициент
размножения.
Тем не менее надо все же отметить, что физические процессы
в быстрой, резонансной и тепловой областях энергии нейтронов
имеют специфические особенности, которым соответствуют
определенные вычислительные методы, оптимальные для одной
области энергии и менее выгодные для другой. Поэтому полезно
сохранить формулу (1.9.1) и термины, которые с ней связаны,
помня только об известной условности, которая в ней содер-
жится.
Условие баланса нейтронов (/<5ф=1) можно записать в не-
сколько иной форме. Пусть при делении возникло v нейтронов.
Эти нейтроны расходуются следующим образом: а нейтронов
захватываются делящимися ядрами, qt поглощаются замедли-
телем, конструкционными элементами, продуктами деления
(как в самом реакторе, так и вне его, т. е. в qt включается и
утечка нейтронов из реактора), X/ поглощаются 238U, в резуль-
тате чего возникает делящийся нуклид 239Рц (см. гл. 13). Для
осуществления стационарной реакции необходимо, чтобы остал-
ся один нейтрон, т. е.
v—а—qf—Xf—1, (1.9.4)
или иначе
П = 1+<7а+ха; qa=qf/(l + a); xa=xf!(1-Ьа). (1.9.5)
Величину ха можно назвать коэффициентом конверсии Кк,
так как она равна числу появляющихся ядер плутония при ис-
чезновении одного ядра 235U (см. гл. 13). Реактор, где осущест-
вляется такой процесс, называется конвертером. Максимальное
значение Кк равно
(Як)макс = Т1-1. (1-9.6)
31
Если в реакторе производятся те же ядра, что и делятся
(239Pu, 24IPu в плутониевом цикле, 233LP в ториевом цикле, см.
гл. 13), то коэффициент конверсии правильнее называть коэф-
фициентом воспроизводства (Ав).Если воспроизводство расши-
ренное, т. е. Кв>1, то реактор называется размножителем. Ус-
ловие осуществления размножения
Ха=^в>1; П-?а>2. (1.9.7)
Из рис. 1.9 видно, что размножение можно осуществить
только на быстрых нейтронах, поскольку только в этой области
энергии г] заметно превышает 2 (см. также § 13.4).
Определим еще некоторые термины, которыми будем в даль-
нейшем пользоваться. Активной зоной реактора будем называть
ту его часть, которая содержит ядерное топливо. Часть реакто-
ра, в которой топлива нет, будет называть отражателем. За
отражателем располагается защита от излучений, хотя и отра-
жатель частично выполняет роль защиты (и наоборот). По-
скольку в настоящей книге рассматривается только теория крити-
ческих размеров и не будут излагаться методы расчета защиты,
отражателем надо называть ту часть внешней по отношению
к активной зоне среды, которая оказывает влияние на крити-
ческие размеры активной зоны.
Гомогенным будем называть такой реактор, в котором ядер-
ное топливо равномерно распределено по активной зоне. Точ-
нее, размеры блоков топлива столь малы, что поток нейтронов
(всех энергий, существенных для определения критических раз-
меров) одинаков в топливе и в среде между блоками. Если это
условие не выполнено, то реактор называется гетерогенным.
Влияние гетерогенной структуры реактора на его физические
характеристики называется блок-эффектом. Количественно
блок-эффект может быть весьма различным. Несмотря на боль-
шую роль блок-эффекта, в большинстве случаев оказывается
возможным ввести такие эффективные параметры, крторые поз-
воляют свести задачу о критичности гетерогенного реактора
к задаче о критичности гомогенного реактора с указанными эф-
фективными параметрами. Такая процедура замены гетероген-
ного реактора гомогенным с эффективными параметрами назы-
вается гомогенизацией.
Существующие в настоящее время реакторы классифициру-
ются по самым различным признакам: по назначению реактора
(получение энергии, производство новых нуклидов, постановка
физических, химических, биологических исследований); по виду
замедлителя (Н2О, D2O, Be, С, отсутствие замедлителя); по
виду теплоносителя (Н2О, D2O, газ, органические жидкости,
расплавленный металл); по виду топлива (естественный уран,
слабообогащенный, чистый делящийся нуклид, смесь урана и
плутония; металлический уран, диоксид урана, карбид урана);
32
jo конструкционным особенностям (корпусной, канальный). Для
теории важны только две особенности реактора — это гетеро-
генность в том смысле, как было разъяснено выше, и характер
нейтронного спектра, а именно нейтронами каких энергий вызы-
вается основная часть делений. В настоящей книге рассматри-
ваются реакторы на тепловых нейтронах, когда подавляющая
часть делений производится тепловыми нейтронами.
1.10. ВЕРОЯТНОСТЬ СТОЛКНОВЕНИЯ
Рассмотрим нейтрон, возникший в начале координат и дви-
жущийся по направлению оси х. Пусть р(х) — вероятность
того, что нейтрон прошел путь х и не испытал на этом пути
столкновения. Вероятность столкнуться на пути Ах равна, по
определению сечения, 2/Ах. Следовательно,
p(x-j-Ax) —р(х) =—2;Ах
или при Ах->0
^ = -2г, (1.10.1)
dx
где 2j — полное макроскопическое сечение (в дальнейшем бу-
дем писать 2 вместо 2«). Решая уравнение (1.10.1) с началь-
ным условием р(0) = 1, получаем вероятность пройти путь х
без столкновения
р(х) =ехр (—2х). (1.10.2)
Вероятность того, что нейтрон пройдет путь х, не столкнув-
KSCli, а затем на отрезке Ах испытает столкновение, равна
•хр (—2х)2Ах, т. е.
ро(х)=2ехр(—2х) (1.10.3)
есть плотность вероятности столкновения. Очевидно, что ро(х)
(1.10.3) имеет правильную нормировку
J po(x)dx = 1.
о
С помощью (1.10.3) определим средний путь, проходимый
нейтроном без столкновения,
I = хр0 (х) dx — 2 у х ехр (— 2х) dx = 2~’. (1.10.4)
! ° °
Величину /=2-1 называют средней длиной свободного про-
бега или просто длиной пробега. Соответственно величины
la=2a~}; /S=2S-1 (1.10.5)
3—6053 33
будем называть длиной поглощения и длиной рассеяния (см.
приложение). В конденсированных средах ls равно нескольким
сантиметрам, а 1а имеет разный порядок величины — от долей
миллиметра до 100 м (для D2O).
Пусть в точке г' расположен точечный источник нейтронов,
который испускает 1 нейтрон в 1 с, причем все направления
скорости равновероятны (изотропный источник). Рассмотрим
точку г. Вероятность того, что нейтрон дойдет до точки г, не
столкнувшись, а затем произойдет столкновение на пути ds,
равна
Sds exp [—21 г—г' | ].
Подсчитаем вероятность столкновения в элементе объема
dV, расположенном около точки г. Записывая dV= |г—
—r'^dQds, где dQ — телесный угол, под которым виден объ-
ем dV из точки г', и учитывая, что внутри угла в 1 с ис-
1 4
пускается —dQ нейтронов (изотропный источник), получаем
4п
для вероятности столкновения в объеме dV
2[4л(г—г')2]-1ехр [—2|r—r'|]dV.
Функцию
К(г) = (4№)-1 ехр (—2г) (1.10.6)
назовем ядром первого столкновения для точечного источника,
а произведение 2К — плотностью столкновений. Если имеется
протяженный источник Q(r'), то создаваемая им плотность
столкновений равна
К (г) != — f (г — г')-2 ехр [— 2 | г — г' | ] Q (г') dV'. (1.10.7)
Вычислим ядро первого столкновения для плоского источ-
ника. В этом случае Q (г') =6(х0—х') и
К (г — г0) = С(г —г')-2ехр(—2 | г — г' [ ] 8 (х0 — х’) dV.
4л J
(1.10.8)
Вводя в плоскости у', z' полярные координаты, получаем
= 1 ?ехр[— S|/(x —У-0)2+р2]
~ 2 ,) (х-х0)2 + Р2
о
или
К(х — х<)) = —Е1( | х — х0 | ),
(1.10.9)
34
где Ei(z) —интегральная экспонента:
E1{z)^^S^Ldx,
z
(1.10.10)
В математической литературе под интегральной экспонен-
той обычно понимают несколько другую функцию Ei (г), рав-
ную
—Ei(—г) =Ei (г),
но в теории переноса нейтронов обозначение (1.10.10) обще-
принято.
В случае нитевидного источника Q = 6(%o—x')b(yo—у'),
поэтому (р= [ (х—х0)2+(у—Уо)2]1/2):
оо ____
2 - I гг + р*
О
что заменой переменных г=р ctg <р приводится к виду
^(p) = TLKi1(2p), (1.10.11)
2лр
где
тг/2
KL(z)= С sin”-1 ф exp (———(1.10.12)
J \ sin <p )
o
— функция Бикли [63].
Пусть в объеме V имеется однородный изотропный источ-
ник нейтронов, т. е. Q(r) = l. Вероятность столкновения в
объеме V равна
Рс = — f f expl~--Lr—r' 1 1 dVdV. (1.10.13)
J J (r — r')® 4 ’
V V
Вероятность для нейтрона, рожденного в объеме V одно-
родным изотропным источником, выйти из объема V, не испы-
тав ни одного столкновения, равна
Р=1— Рс. (1.10.14)
Вероятность Р для тел различной формы табулировалась
многими авторами (см., например, [64] и приложение). Для
бесконечной пластины
1 —2Д —
\ 2
а = 2/,
а
(1.10.15)
3*
35
где I — средняя хорда пластины, равная удвоенной
толщине;
£3 (Л) = У ехР (— xu)u~3du.
При малых и больших а имеем:
Гт„ 2 , 3 1 1 ,
- In—4-------у------а3;
[ а 1 2 J 48
у=0,577; Р = —; а>
а
Р= 1-
(1.10.16)
Для сферы
Р = а~' 1 —
а = 2/,
(1.10.17)
8 \
Р =
где I = —R, R—йрадиус сферы. При малых и больших
3
р = \ — —,
16
Для бесконечно длинного цилиндра (см. [64]; вывод этой
формулы имеется в [65]):
р=~ +v - w+4
о о о о
(1.10.19)
где Ц, Ki — стандартные обозначения для цилиндрических функ-
ций, их аргумент равен а/2, а=27, I равно диаметру цилиндра.
При малых й больших а имеем:
р = 1 । | — 4-
3'8 а 32
Со= 1,12; Р = ----2-
0 а 44
Часто для вероятности Р используют рациональное прибли-
жение Вигнера [66]:
Р=1—РСМ1-Н)-1- (1.10.21)
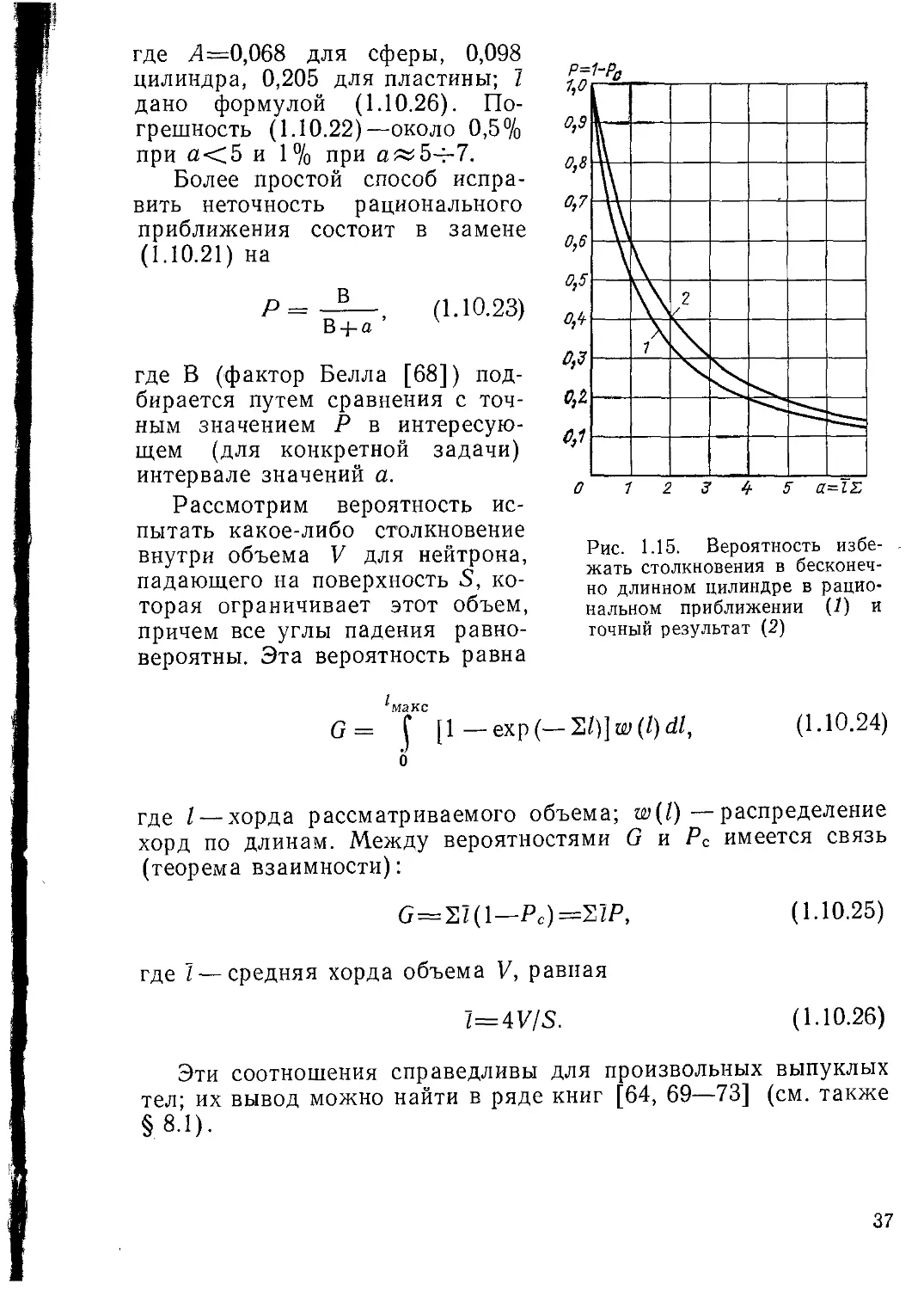
На рис. 1.15 приближение (1.10.21) для цилиндра сравнивается
с точным результатом [64]. Ошибка (1.10.21) достигает 10—20%
(см. также приложение). Значительно более точная формула
предложена в [67]:
Р = Lz^P.(-a) _ Аа exp (— a); a = TS, (1.10.22)
а имеем:
(1.10.18)
(1.10.20)
а
36
где Л=0,068 для сферы, 0,098
цилиндра, 0,205 для пластины; 1
дано формулой (1.10.26). По-
грешность (1.10.22)— около 0,5%
при а<5 и 1% при а «5=7.
Более простой способ испра-
вить неточность рационального
приближения состоит в замене
(1.10.21) на
, (1.10.23)
В-ра v
где В (фактор Белла [68]) под-
бирается путем сравнения с точ-
ным значением Р в интересую-
щем (для конкретной задачи)
интервале значений а.
Рассмотрим вероятность ис-
пытать какое-либо столкновение
внутри объема V для нейтрона,
падающего на поверхность S, ко-
торая ограничивает этот объем,
причем все углы падения равно-
вероятны. Эта вероятность равна
Рис. 1.15. Вероятность избе-
жать столкновения в бесконеч-
но длинном цилиндре в рацио-
нальном приближении (7) и
точный результат (2)
G = "["[I — ехр(—SZ)]ay (Z)dZ, (1.Ю.24)
b
где I — хорда рассматриваемого объема; w(l)—распределение
хорд по длинам. Между вероятностями G и Рс имеется связь
(теорема взаимности):
6=27(1—РС)=^1Р,
(1.10.25)
где I — средняя хорда объема V, равная
1=4V/S.
(1.10.26)
Эти соотношения справедливы для произвольных выпуклых
тел; их вывод можно найти в ряде книг [64, 69—73] (см. также
§8.1).
37
Глава 2
ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ДИФФУЗИИ И
ЗАМЕДЛЕНИЯ НЕЙТРОНОВ
2.1. УРАВНЕНИЕ ДИФФУЗИИ НЕЙТРОНОВ
Уравнение диффузии является следствием условия баланса
нейтронов. Количество нейтронов в элементе объема ДУ и энер-
гетическом интервале ДЕ запишем так: N(r, Е, f)&V&E, где
W(r, Е, t) —плотность нейтронов*. Произведение плотности ней-
тронов на скорость будем называть плотностью потока нейтро-
нов:
Ф(г, Е, t)—vN(r, Е, t). (2.1.1)
Составим уравнение баланса нейтронов в элементе объема
ДУДЕ. Убыль нейтронов из элемента ДУДЕ обусловлена следу-
ющими причинами: поглощением, изменением энергии при стол-
кновении, выходом цз объема ДУ за счет диффузии. Число по-
глощенных нейтронов за время Д/ равно
2я(г, Е)Ф(г, Е, t)AV&EM, (2.1.2)
где 2а(г, Е)—макроскопическое сечение поглощения (предпо-
лагается, что среда неподвижна и 2Я не зависит от времени).
Число нейтронов, ушедших из энергетического интервала ДЕ из-
за изменения энергии при рассеянии, равно
2уВ(г, Е)Ф(г, Е, t)AVAEM, (2.1.3)
где 2ув — сечение увода (см. § 2.2 и гл. 3). Убыль нейтронов из
объема ДУ из-за диффузии равна
J j (г, Е, t)ds^EM, (2.1.4)
S
где s — поверхность, окружающая объем ДУ; j (г, Е, t)—плот-
ность тока нейтронов [выражение (2.1.4) фактически определя-
ет величину j]. Преобразуя интеграл (2.1.4) в объемный, полу-
чаем (если ДУ достаточно мало) число ушедших нейтронов:
div j(r, Е, ОДУДЕДЕ (2.1.5)
Поступление нейтронов равно S(r, Е, /)ДУДЕД/, где S —
мощность источников нейтронов. Разность между поступлением
* Здесь имеется в виду среднее число нейтронов в единице объема. Фак-
тически всегда наблюдаются флуктуации числа нейтронов. Если число ней-
тронов в единице объема велико, то флуктуациями можно пренебречь. В кри-
тических сборках «нулевой» мощности (порядка или менее 1 Вт), или в под-
критических сборках, особенно при малой подкритичности, флуктуации могут
быть существенными. По этому вопросу см., иапример, [74] и цитированную
там литературу.
38
и убылью равна приращению числа нейтронов в объеме ДУ и
энергетическом интервале АЕ. Составив эту разность и поделив
па ДИАЕД/, получим уравнение для потока нейтронов
+ div j (г, Е, t) + [Sa (г, Е) + S в (г, Е)] Ф (г, Е, t) =
dt
= S(r,E,f). ' (2.1.6)
В соответствии с различным происхождением источников S
н (2.1.6) энергетический спектр нейтронов можно разделить на
три области: быстрые нейтроны, замедляющиеся и тепловые.
Быстрыми будем называть нейтроны, энергия которых выше
/;'гр•—практической границы спектра нейтронов деления (см.
§ 1.2). Для быстрых нейтронов S(r, Е, t) [см. (2.1.6)] есть
сумма двух слагаемых: нейтронов, возникших при делении, и
нейтронов, получивших энергию Е в результате столкновений
более энергичных нейтронов с ядрами среды (всюду ниже пред-
полагается, что нейтроны возникают в среде в результате деле-
ний, хотя, конечно, общая теория справедлива для любых источ-
ников) .
Энергия замедляющихся нейтронов заключена в пределах
ЕС<Е<ЕТР, (2.1.7)
где Ес —верхняя граница энергии тепловых нейтронов (см.
§ 2.4, 7.5). Для замедляющихся нейтронов источники в урав-
нении (2.1.6) возникают только за счет замедления более энер-
гичных нейтронов (если не считать запаздывающих нейтронов,
спектр которых несколько мягче, чем мгновенных, см. § 1.3).
Для тепловых нейтронов величина S описывает поступление
в данный энергетический интервал АЕ не только за счет замед-
ления более «горячих» нейтронов, но и за счет «нагревания»
более «холодных» при столкновении с достаточно быстро движу-
щимися ядрами среды.
Поскольку величина S зависит от плотности потока нейтро-
нов, запись уравнения (2.1.6) еще не закончена — надо явно
сформулировать эту зависимость. Отложим эту задачу до гл. 3.
Уравнение (2.1.6) записано для малого энергетического ин-
тервала АЕ. Часто этот интервал можно сделать достаточно
большим и тогда под Ф(г, Е, OS (г, Е) следует понимать сред-
ние значения по рассматриваемому интервалу. Для фактическо-
го вычисления средних значений надо иметь информацию о ви-
де спектра нейтронов внутри этого интервала (см. гл. 3). Пре-
дельный случай такого «укрупнения» интервалов — две группы
нейтронов: тепловые и замедляющиеся [спектр нейтронов деле-
ния в этом случае заменяется моноэнергетическим с энергией Е
(1.2.3)].
39
Для тепловой группы надо положить 2ув = 0, поскольку
столкновения, уменьшающие энергию нейтрона, оставляют его
в тепловой группе, а вероятность такого столкновения, при
котором нейтрон приобретает энергию выше Ес, при достаточно
большом значении Ес пренебрежимо мала. Поэтому для тепло-
вой группы
+ div j (г, 0 + 2О (г) Ф (г, t)=S (г, t), (2.1.8)
где (г) —среднее сечение поглощения; S(r, t) —источник те-
пловых нейтронов, т. е. число нейтронов, замедляющихся в точ-
ке г в единицу времени до энергии ниже Ес (см. § 2.2 и гл. 3).
Уравнения (2.1.6) и (2.1.8) надо дополнить связью между
плотностью тока j (г, t) и плотностью потока Ф(г, t). Такая
связь может'быть установлена только приближенно, когда гра-
диент Ф достаточно мал (см. также дополнение):
[2Л1>(г) J”1 |grad Ф(г) | <€Г1; 2h=Xa+2s, (2.1.9)
и, следовательно, только в этом случае можно использовать
уравнения (2.1.6), (2.1.8) для определения плотности потока
нейтронов.
Плотность тока / можно представить как разность плотности
«односторонних» токов /+ и
/=/+-/- (2.1.Ю)
Рассмотрим площадку As, расположенную в начале коорди-
нат, и подсчитаем число нейтронов, пересекающих ее в одном
направлении (односторонний ток). Число рассеяний нейтронов
в единицу времени в точке г равно ХяФ(г, t) (при этом не ука-
зывается энергетическая переменная, поскольку она нас не ин-
тересует). Число нейтронов, появившихся в точке г и прошед-
ших путь |г| до площадки As без столкновений, на единицу те-
лесного угла .равно [см. (1.10.6); предполагается, что рассеяние
изотропно, т. е. все направления движения нейтрона после рас-
сеяния равновероятны; среда однородна]:
Дехр(- г2г)Ф(г, t). (2.1.11)
Интегрируя (2.1.11) по полупространству, расположенному
с одной стороны от площадки As, получаем для проекции плот-
ности тока j+s на направление As следующее выражение:
j+s = —- С г-2£\ехр (—г 2г)Ф f г, t-—r'2drdQ,
4~ J \ v /
где Q.s— проекция вектора v/|v| на нормаль к площадке. Вве-
дем полярную систему координат с осью, направленной по нор-
40
мали к площадке. Тогда Q5=cos,fl', dQ = sin 'M’&dq,
oo л/2 2 ТС
j+s — — C exp (—r2f) dr f sin 9- cos&dft f Ф f r, t-— dtp.
4л J J J \ v J
ooo
. (2.1.12)
Предположим, что плотность потока ф(г, t) мало изменяет-
ся, если г изменяется на величину S;-1, а время — на (uS;)-1.
Тогда в первом приближении можно под интегралом (2.1.12)
сделать замену:
Ф (г, t-----=5= Ф (0, t).
У V ]
Выполнив интегрирование, получим
(о, t)
- 4Sf
Если Sa=7^0, то, как правило, поток зависит от координат.
Поэтому надо в (2.1.13) положить
/±=Ф/4,
(2.1.13)
(2.1.14)
т. е. плотность одностороннего тока, или число «ударов» нейтро-
нов о площадку, равна 1/4 плотности потока нейтронов. В сле-
дующем приближении надо разложить Ф (г, t------— ) в ряд
ф(г, t------- =Ф(0, /) + г grad Ф (0, 0 — — -Ф . (2.1.15)
\ v / v dt
Подставив (2.1.15) в (2.1.12) и проинтегрировав, получим
[знак минус перед ^габФ^ означает, что ток по направлению
As отрицателен; /_5 отличается от j+s только тем, что направле-
ние As изменяется на противоположное]:
= 5уФ(0, 0-----дФ (0J) _ (grad(D) (2.1.16)
±s 4Sf 4&S/2 dt ' 6Sf2
Из (2.1.16) получим вектор плотности полного тока
j=j+—j-=— -О grad Ф, (2.1.17)
где коэффициент диффузии
D = -^-. (2.1.18)
3Sf2 v 7
Разложение (2,1.15) можно применять для вычисления ин-
теграла (2.1.12) только в том случае, если функция Ф(г, t) из-
меняется существенно медленнее, чем ехр (—rSt), т. е. если вы-
41
полнено условие (2.1.9). Как показано ниже, это условие вы-
полняется, только если
Sa«Xs. (2.1.19)
Поэтому коэффициент диффузии можно записать и так:
D=(3Zt)-' (2.1.20)
или
D=(3Ss)~>. (2.1.21)
В дальнейшем под коэффициентом диффузии будет пони-
маться (2.1.20), если не оговорено противное (см. также допол-
нение) .
Выше предполагалось, что среда однородна. Из вывода
(2.1.16) следует, что результат справедлив и для неоднородной
среды, если только Sf(r) мало изменяется на расстояниях по-
рядка 2гл. Таким образом, уравнение диффузии (2.1.8) запи-
шется так:
— —div D grad Ф + 2аФ = S (2.1.22)
dt
или для стационарного случая и однородной среды
(А — Е2)Ф(г) = — (2.1.23)
где А = div grad — оператор Лапласа и L — длина диффузии,
равная
L=(32a2;)~1/2- (2.1.24)
Если рассеяние неизотропно, то (см. дополнение) S; надо за-
менить транспортным сечением Sfr (1.4.7).
Можно записать уравнение диффузии не относительно плот-
ности потока нейтронов, а относительно плотности М(г). Тогда
(для однородной среды) получим
DAN—N/iT = — S, (2.1.25)
где
tT=(VT^a)~l (2.1.26)
— время жизни нейтронов в среде; vT — средняя скорость ней-
трона в тепловой группе. Величину
D=vT/(3Ztr) (2.1.27)
часто называют коэффициентом диффузии вместо (2.1.20). По-
лезно отметить порядок величины tT. Наименьшим макроскопи-
ческим сечением (из конденсированных сред) обладает тяже-
лая вода: Sa—10-4 см. Так как Vr=2,5-105 см/с (см. § 2.4), то
для тяжелой воды ^=0,04 с. В реакторах на тепловых нейтро-
нах 6г= 10-4-4-10-3 с.
42
Рассмотрим решение уравнения диффузии для однородной
неограниченной среды, причем S—0 всюду, кроме начала коор-
динат (точечный источник тепловых нейтронов), т. е.
(A-A-2)Gs(r) = --^S(r), (2.1.28)
где 6(г)—дельта-функция Дирака*. Функция Gs называется
функцией Грина уравнения диффузии. Уравнение (2.1.28) фор-
мально имеет один и тот же вид для одномерного (источник —
бесконечная плоскость), двухмерного (источник — бесконечная
нить) и трехмерного (источник — точка) случаев. Необходимо
только под г понимать соответственно одну (х), две (х, у) или
три (х, у, z) координаты, а дифференциальный оператор Д за-
писывать так:
. d2 д2 д2 д2 д2 д2
А =----; ----4---; -----4----4------.
dx2 дх2 1 ду2 дх2 ду2 ' дг2
Для решения уравнения (2.1.28) применим метод Фурье, по-
ложив
Gs (г) = (2тг)_/г J Gs (k) exp (i кг) dk, (2.1.29)
где п=\, 2, 3 и dk=d/sb dk\dkz, dk^dk^dk^ для одно-, двух- и
трехмерного случаев соответственно. Воспользовавшись фурье-
представлением б-функции
8 (г) = (2тг)~п J exp (i кг) dk,
получим
J | (Л2 + L~2) Gs (к) — -A-j exp (i кг) dk = 0. (2.1.30)
Умножим (2.1.30) на exp (—ik'r) и проинтегрируем по всему
пространству. Под интегралом возникнет б (к—к'), и в силу
свойств б-функции получим фурье-образ функции Грина:
Gs(k) =-^-(&2 + £~2)~'. (2.1.31)
Подставив (2.1.31) в (2.1.29), получим для функции Грина
следующее выражение:
Gs (г) = [(2t)"D] J (й2 + Г-2)"1 exp (i kr) dk. (2.1.32)
* Дельта-функция Дирака определена равенствами б(х)=0 при х#=0
и j f(x)S(x)dx=f(O)—для любой непрерывной при х=0 функции; <5(г) =
=6(x)6(z/)6(z).
43
В одномерном случае (см. [75, формула (3.723.2)]):
Gs(x) = -5- У ^1-2 еХР (—НН' (2Д-33)
о
Полезно проверить непосредственной подстановкой, что (2.1.33)
удовлетворяет уравнению (2.1.28). Имеем
AGs(x) = -A-exp
dx D \ L / х
— Gs(x) = (2OL)-Iexpf_-l^-') 11 —L —1^1],
dx2 \ L ) [ dx х j
и так как
то уравнение (2.1.28) удовлетворяется. Отметим, что Gs(x) нор-
мирована следующим образом:
+ °о
Sa f Gs(x)dx= 1, (2.1.34)
—00
т. е. число поглощенных нейтронов во всем пространстве равно
единице.
В двухмерном случае функция Грина имеет вид [после ин-
тегрирования (2.1.32) по углу между векторами к и г]:
Gs (г) = (2ТГО)-1 J (й2 -ф Г-2)-1 kjo (kr) dk,
о
или после вычисления интеграла (см. [75, формула (6.566.2)]):
Gs(r) = (^D)-'K0^, (2.1.35)
где Jq и Ко — стандартные обозначения цилиндрических функ-
ций.
Проверим правильность коэффициента в формуле (2.1.35).
Для этого окружим нить источников цилиндрической поверхно-
стью малого радиуса р и определим полный ток нейтронов J
через эту поверхность на единицу длины:
7 = —2тгОр
5р L \ L )
При p/L 1 имеем Кл = -^/Р и поэтому 7=1, т. е. коэф-
фициент в (2.1.35) написан правильно и Gs соответствует источ-
нику единичной мощности. Так же как и в одномерном случае,
44
число поглощенных нейтронов во всем пространстве равно еди-
нице:
Jos(r)rdr = 1.
о
В трехмерном случае имеем (см. [75, формула (3.723.3)]):
Gs{r) = {^Drrl = (2.1.36)
о
Таким же способом, как для Gs (2.1.35), легко проверить пра-
вильность коэффициента в (2.1.36).
Рассмотрим нейтронное поле, возникающее от точечного ис-
точника (2.1.36), и выясним, при каких условиях выполняется
неравенство (2.1.9). Если оно выполняется, то (2.1.36) правиль-
но описывает плотность нейтронного потока, если нет, то урав-
нение диффузии несправедливо и (2.1.36) не дает правильного
распределения нейтронного потока (см. дополнение). Если Ф(г)
дано (2.1.36), то условие (2.1.9) выглядит так (S< заменено на
Sfr)
=(r^r)-+№,)- < 1. (2.1.37)
Условие (2.1.37) выполняется, если одновременно выполняет-
ся как неравенство
г2/г>1, (2.1.38)
так и неравенство
Л2^ = -|/ — Ъ
V 3 S,
т. е. кроме выполнения условия (2.1.19) необходимо, чтобы рас-
стояние от источника было много больше S"1.
В неоднородной среде возникает еще одно условие приме-
нимости уравнения диффузии: размеры неоднородностей долж-
ны быть много больше (см. гл. 10).
Вычислим средний квадрат перемещения нейтрона при диф-
фузии, т. е. среднее расстояние от точки, где появился тепловой
нейтрон, до точки, где он поглощен:
—_ jr2Gs (г) dr
J Os (г) dr
Подставив (2.1.36) в (2.1.40) и вычислив интеграл, получим
? = 6L2; х2 = у2 = ? = 2L2- ? = х2 + у2 + ?. (2.1.41)
(2.1.39)
(2.1.40)
45
Если источник расположен не в начале координат, а в про-
извольной точке г', то для однородной бесконечной среды
Gs(r, r') = Gs(|r—r'|),
т. е. функция Грина зависит только от модуля разности г и г'.
Пусть источники S в уравнении для тепловых нейтронов обу-
словлены только рождением быстрых нейтронов при делении
и их последующим замедлением. Тогда, если пренебречь деле-
* ниями, которые вызваны замедляющимися нейтронами (см.
гл. 3), число быстрых нейтронов, возникающих в точке г' за
единицу времени, равно vSf (г')Ф(г'), а мощность источников
для тепловых нейтронов равна
S(r)= j v2f(r')IF (г', г)Ф(г'Иг', (2.1.42)
где W (г', г) — вероятность того, что рожденный в точке г' бы-
стрый нейтрон в результате замедления становится тепловым
в точке г. Таким образом, в этом случае уравнение диффузии
надо записать так:
— = div D grad Ф (г) — Sa (г) Ф (г) + С (г') W (г\ г) Ф (г') dr',
di J
(2.1.43)
или для однородного реактора и в стационарном случае
£)ДФ — 20Ф + vS; Г W (г', г) Ф (г') dr' = 0.
(2.1.44)
Предположим, что функция Ф(г') изменяется медленно по
сравнению с W(r', г). Этот случай имеет место, если размер
реактора [масштаб изменения Ф(г')] много больше длины за-
медления [масштаб изменения W(r', г), см. § 2.2, 3.3]. Тогда
можно разложить Ф(г') в ряд:
з
ф (Г’) - Ф(г) + j (Х,— X,’) £(Х,- X,') (Xх/)^.
Z=1 if
(2.1.45)
В большом реакторе надо положить
J W (г', г) dr' = <р; j’ (xt — Xt')W(r', r)dr' = O;
f (*i~ x}')W (r\ r)dr' = <p£728M,
(2.1.46)
где q> — вероятность того, что быстрый нейтрон, не поглотив-
шись, замедлится и станет тепловым (см. § 2.3); х2-2— средний
46
квадрат перемещения нейтрона вдоль_оси Х{ в процессе замед-
ления. Обозначим (см. § 2.2, 3.2; Ут — длина замедления)
з __ _
2хг2=г2 = 6т (2.1.47)
г=1
и получим
JlF (г', г)Ф(г')Л'= <р(1 + ^Д)Ф(г).
Введя коэффициент размножения бесконечной среды (см.
§ 1-9)
vSf
= k (2.1.48)
и эффективный коэффициент диффузии
D(l+fe-M=D3.3, (2.1.49)
\ L? I
получим
£>эфДФ+2а(&— 1)Ф=0 (2.1.50)
или
(Д+а2)Ф=0, (2.1.51)
где
= (2.1.52)
L2 + kx. ’
В уравнение (2.1.51) входит только поток тепловых нейтро-
нов. Поэтому это уравнение будем называть уравнением одно-
группового приближения (см. гл. 4) или уравнением с эффек-
тивным коэффициентом диффузии. Величину а2 называют «лап-
ласианом» или «материальным параметром» в том смысле, что
для определения а2 по (2.1.52) надо знать характеристики среды:
коэффициент размножения, длину диффузии и замедления. Ча-
сто величину а2 обозначают В2 и называют «баклингом» (от
англ, buckle, что означает «изгиб»; такое название связано с тем,
что В2 характеризует кривизну нейтронного поля, см. гл. 4).
Как будет показано ниже (см. гл. 3, 4), уравнение (2.1.51)
справедливо только при k—1<С1 и поэтому вместо (2.1.52) мож-
но написать
ct2= (Те—1)/Л42; M2=L2+x, (2.1.53)
где М — длина миграции, характеризующая среднее расстояние
между точками рождения и поглощения нейтрона.
К уравнению диффузии (2.1.23) надо добавить граничные
условия, которые должны соблюдаться на границах сред с раз-
47
личными свойствами: равенство плотностей потоков на границе
раздела
Ф1=*Ф2 (2.1.54)
и равенство токов (следствие закона сохранения нейтронов, при-
мененного к приграничному слою)
(2.1.55)
где штрихом обозначена производная по нормали к границе
раздела.
Поскольку выражение для тока (2.1.17) приближенно, то и
граничное условие (2.1.55) выполняется только приближенно.
В ряде случаев удается увеличить точность решения задачи, со-
хранив диффузионное уравнение, но изменив граничные условия
(2.1.54), (2.1.55), что очень удобно для приложений (см., напри-
мер, [76]). В некоторых приближенных методах не выполняется
условие (2.1.54)—на границе раздела возникает скачок плот-
ности потока нейтронов (см. § 7.3).
Специально надо остановиться на граничных условиях, кото-
рые должны выполняться на границе с вакуумом (или абсолют-
но черным телом, поглощающим все нейтроны, падающие на его
поверхность). Пусть вакуум занимает полупространство х>0,
а полупространство х<0 занято средой, которая не поглощает
нейтроны. Вакуум не возвращает нейтроны, падающие на гра-
ницу раздела. Поэтому на границе раздела надо положить /_==
= 0 или [см. (2.1.16)]
-?-2,гФ(0) = — . (2.1.56)
2 \ dz / г=0
Если решить уравнение диффузии при 2й=0 и с граничным
условием (2.1.56), то получим
Ф(г)=С’(г0 — z); г0 = —S//1; С = const. (2.1.57)
3
Если экстраполировать выражение для плотности потока
нейтронов (2.1.57) из области г<0 в область х>0, т. е. в сторо-
ну вакуума, то экстраполированная плотность потока обратится
в нуль на плоскости, которая отстоит от истинной границы раз-
дела на расстоянии г0. Эту плоскость будем называть экстрапо-
лированной границей среды. Точное решение задачи [77—79]
показывает, что вдали от границы на расстояниях, много боль-
ше Sir, справедливо диффузионное решение (2.1.57), но с заме-
ной коэффициента 2/3 на 0,710446. Вблизи границы уравнение
диффузии нарушается и плоскость потока нейтронов отлична от
(2.1.57).
Таким образом, можно исключить из рассмотрения область,
заполненную веществом с сильным поглощением, где наруша-
48
ется уравнение диффузии, если известно граничное условие на
ее поверхности:
2Ф. (2.1.58)
Для цилиндрической и сферической поверхностей удобно вве-
сти в (2.1.58) радиус, так чтобы X было безразмерной, величи-
ной:
р^®=ЯФ(р). (2.1.59)
др
Граничное условие X для черного цилиндра (или сферы) за-
висит от его радиуса (см. § 6.1).
Вместо граничного условия X можно рассматривать альбедо
(коэффициент отражения), определив его равенством
₽=/-//+, (2.1.60)
где J+ — ток из первой среды во вторую; /_ — ток в обратном
направлении (р — альбедо второй среды; 1—р — коэффициент
поглощения). Если /_=0 (вторая среда вакуум), то альбедо рав-
но нулю. Если использовать для /± диффузионные значения, то
получим для плоской границы раздела
(2.1.61)
где X определено (2.1.58). Пусть область z>0 заполнена средой
с малым сечением поглощения, к которой применимо уравнение
диффузии. Тогда при z>0 [если на бесконечности нет источни-
ков нейтронов, то Ф(з) =0 пр'и z->-oo];
Ф(х)— А ехр (—z/L),
откуда
Подставляя этот результат в (2.1.61), получаем
При ай<С(Тз имеем (ц=0):
т. е. коэффициент поглощения пропорционален корню квадрат-
ному из отношения Galas- Например, если <ja/<js= 10"3, то 1—р=
= 0,07.
Выше предполагалось, что среда, в которой происходит диф-
фузия нейтронов, неподвижна. При больших скоростях движе-
4—6053 49
ния среды имеет место частичное увеличение нейтронов, что на-
до учитывать. Теория переноса нейтронов в движущейся среде
изложена в [80].
Задача 1. Определить плотность потока тепловых нейтронов, среднее зна-
чение и отношение максимальной плотности потока к средней (источники ней-
тронов расположены во внешней среде) для: однородной пластинки; однород-
ного цилиндра бесконечной длины; однородной сферы.
Решение. Пластинка. Пусть ось х направлена перпендикулярно пла-
стинке, начало координат в середине пластинки. По соображениям симметрии
плотность потока зависит только от х, причем Ф(х)=Ф(—х). Уравнение
(2.1.23) надо записать так:
(РФ Ф
dx?
Его решение будет Ф=ЛсЬ(х/£). Средняя плотность потока по объему
пластинки (толщиной 2d) равна
d
-If L d
ф=— 4>(x)dx= A—sh —.
d J d L
о
Отношение максимальной плотности потока к средней
~ Фмакс d d
Q=—=— = —cth—, (2.1.63)
или при d^L
(2.1.64)
Цилиндр. Введем цилиндрическую систему координат, ось которой сов-
падает с осью цилиндра. Плотность потока нейтронов зависит от р, и урав-
нение (2.1.23) записывается так:
1 d / _d®_\ Ф
р dp \ dp J L*
(2.1.65)
Общее решение уравнения (2.1.65) есть линейная комбинация цилиндри-
ческих функций /о(р/Е) и Ло/(р/£) (см., например, [75]). Функция Ло(р/Л)
обращается в бесконечность при р->0, и поэтому решение ее не содержит.
Следовательно,
Ф(р)=.4/0(р/Л).
Средняя плотность потока по объему цилиндра (радиус равен г)
2 С 2L / г
Ф = -Г Ф(Р)Р<*Р= А--------Ц —
г2 J г \ L
о
отношение максимальной плотности потока к средней равно
Q__ Фмакс/р(г jL)
ф VLlr)I1(rlL)
или при малых r/L
(2.1.66)
1 / Г \2 1 / г \4 1 / г \в
~ 1 + 2 (. 2L ) ~ 12 \ 2Z, ) \~2E~) (2Л-67>
50
Сфера. Уравнение в сферических координатах имеет вид
1 d / „ с/Ф \ Ф
---. --- ( г2 --- I _ —— = 0 ,
г2 dr \ dr / L2
или, если ввести вспомогательную функцию /=гФ,
dr2 L2
(2.1.68)
Решение, не обращающееся в начале координат в бесконечность, будет таким:
А г
Ф =-----sh —.
г L
Среднее значение по объему равно (радиус сферы R)
3 С 3AL [ R L R 1
Ф — —I Ф (г) r2dr = -------- ch —— —-----sh —— ;
R J R2 [ L R L J
0
отношение максимальной плотности потока к средней
- Фмакс I nth 1
и — —=-----—-------- ---cth-------— 1
4 Ф 3L2 L L L
или при R<g.L
Q =
1 / К V ,
525 \ L ) +
(2.1.69)
(2-1.70)
Задача 2. Рассмотреть поле тепловых нейтронов вне пластинки; цилинд-
ра; сферы, если источники тепловых нейтронов однородны, расположены во
внешней неограниченной среде.
Решение. Пластинка. Решение уравнения (2.1.23) с постоянными
источниками имеет вид
S Г ' / I х I \1
Ф = —ll-Cexp^-y^JJ, (2.1.71)
где С — постоянная, определяемая из граничных условий на поверхности
пластины.
Цилиндр. Решение уравнения (2.1.23) следующее:
(2.1.72)
Вторая цилиндрическая функция исключается, так как она неограниченно
возрастает с ростом р.
Сфера. Уравнение (2.1.23) имеет решение:
Ф= —
[j-^-expf--^].
(2. 1-73)
Задача 3. Между двумя средами расположена тонкая пластинка толщи-
ной d, слабо поглощающая нейтроны. Ее влияние на плотность потока
нейтронов можно свести к изменению граничных условий между двумя сре-
дами. Получить эти условия.
Решение. Если пластинка достаточно тонкая, то она слабо деформи-
рует нейтронный поток. Поэтому условие (2.1.54) не изменяется. Изменение
условия (2.1.55) следует из закона сохранения нейтронов:
—£i®i'4-ZW=2ad<i», (2.1.74)
А
где 2а — макроскопическое сечение поглощения_в пластине; Ф —средний
поток нейтронов в пластине. Если 2ad<Sl, то Ф можно заменить Ф1=Ф2.
Если градиенты Ф/, Фа' малы, то (2.1.74) может заметно отличаться от
(2.1.55) даже прн малых значениях 2ad.
Задача 4. Цилиндр радиусом р из материала, поглощающего, но не за-
медляющего нейтроны, окружен оболочкой толщиной d из материала, слабо
поглощающего и не замедляющего нейтроны. Определить отношение плот-
ностей потока нейтронов на внешней и внутренней поверхностях оболочки.
Решение. Если оболочка слабо поглощает нейтроны и источники рав-
ны нулю (оболочка не замедляет нейтроны), то общее решение уравнения
(2.1.65) будет
Ф(г) =4+В1п г. (2.1.75)
Составим условие баланса на внутренней поверхности оболочки:
2лрРеФ/(р) =mp22aiQ-1®(p),
где Q — отношение максимальной плотности потока к средней для внутрен-
него цилиндра (индекс е относится к оболочке, i — к внутреннему цилин-
дру). Из этого равенства можно определить В/A и подставить в искомое
отношение:
4 + filn(p+d) 3 ( d \
Р = Л+В1„р - 1 +1 + -) <2-1-76)
Пусть тогда
3
^-l= — dStre. (2.1.77)
Если, например, d=0,2 см и оболочка изготовлена из алюминия (2/гв =
=0,1), то р—1 <g 1. Если же оболочка представляет собой слой простой
воды (теплоноситель), то 2;,е=2 см-1 и |3—1^0,6, т. е. на тонком слое
воды возникает заметный скачок плотности нейтронного потока (в этом слу-
чае надо еще учесть источники тепловых нейтронов в воде).
Задача 5. Вычислить среднее значение г2т с помощью фурье-образа
функции Грина.
Решение. Пусть G(r)—функция Грина и G(k2)—ее фурье-образ.
Тогда
j r2G(r)dr J exp (i kr)r2G(ft2)dkdr
J G(r)dr J exp (i kr)G(ft2)dkdr
з
LS2 d2
2 exp (i kr) s= — -0&2Г exp(i kr) , то интегрируя
по частям no k, а затем по г, получаем
Г d2 1
г2 = — G-Чй2) G(W)
L dkj2 'jA:2=0
Аналогично
rzm — (_________1)',г
/ д2 \'n 1
\ ОЙ;2 / Jft==0
(2.1.78)
„ &
Так как —•—
dkj2
О(й2) = бОв(й2)+ bk2G*'(k2), то г2= — 6[О-1(й2)С*(й2)]А2=0;
52
r* = 60 [G-!(Й2)G"(й2)]ft2=0. (2.1.79)
Если G(r) — диффузионная функция Грина (2.1.31), то
^ = 6Г2; ri = 120L4; =(2т +1)! РТ (2-1.80)
Задача 6. Определить поле тепловых нейтронов, возникающих от еди-
ничного точечного источника, расположенного в правом полупространстве;
левое полупространство — вакуум.
Решение. Используем метод изображений. Пусть г0 — радиус-вектор
источника. В вакууме расположим фиктивный отрицательный источник, явля-
ющийся зеркальным изображением реального источника в экстраполирован-
ной границе. Пусть начало координат расположено на экстраполированной
границе на линнн, соединяющей истинный и фиктивный источники. Тогда ра-
диус-вектор фиктивного источника будет —г0. Плотность потока нейтронов
в правом полупространстве
Ф(г) 1 r-r»|-lexP (-ILT^L) -
— I г + Го |~хехр - Г~£'~ J]- (2.1.81)
Написанное выражение удовлетворяет следующим условиям: уравнению
диффузии в правом полупространстве, граничному условию на экстраполи-
рованной границе: Ф(г)=0 и соответствует единичному источнику в точке
Го (последнее можно сформулировать также в виде граничного условия на
поверхности бесконечно малой сферы, окружающей точку го). Так как урав-
нение н граничные условия однозначно определяют решение, то (2.1.81)
является единственным решением задачи.
2.2. ЗАМЕДЛЕНИЕ НЕЙТРОНОВ
Если энергия нейтрона заключена в интервале (2.1.7), то
замедление происходит в результате упругих столкновений с яд-
рами, поскольку ЕГр приблизительно совпадает с порогом не-
упругого рассеяния (см. § 1.4). При этом ядра можно считать
неподвижными (вследствие того, что скорость нейтронов много
больше скорости ядер) и свободными, т. е. не учитывать связей
атомов в молекуле или кристаллической решетке (так как энер-
гия нейтрона много больше энергии связи).
Рассмотрим некоторые следствия из механики упругих столк-
новений. Пусть v, у' — скорости нейтрона до и после столкнове-
ния; V' — скорость ядра после столкновения. Законы сохране-
ния импульса и энергии дают
v^=4V'+v'; v2=AV'2-\-v'2, (2.2.1)
где А — относительная атомная масса ядра, точнее, отношение
массы ядра к массе нейтрона. Обычно можно пренебречь раз-
личием между этим отношением и атомной массой. Скорость
системы координат, в которой покоится центр инерции нейтрона
и ядра, равна
Уо=(1+Л)-’у.
53
сводится только к повороту
между векторами у'—v0 и
В этой системе координат рассеяние
относительной скорости на угол <р
v—Vp, причем
! v' — v0 | = | v — v0 |
Поэтому, возводя в квадрат равенство v'=(v'—v0)—Vo и ис-
пользуя определение vo, получаем
О 7)2
=-^7^г(1+2Лсо8Ф + Л2), (2.2.2)
откуда определяем отношение энергий после (Е') и до (Е) стол-
кновения:
Е7 1
-^7=4-[1 + ®0+ (1 -e0)cos<p], (2,2.3)
Е 2
где
Из равенства (2.2.3) следует, что
еоЕ^Е'^Е, (2.2.5)
т. е. 1—ео есть максимально возможная доля энергии, потерян-
ной нейтроном в результате одного упругого столкновения. Из
(2.2.3) следует, что среднее значение отношения Е'/Е равно
(1+ео)/2.
Если Л^>1, то из (2.2.4) получаем
1—ео==4/Л. (2.2.6)
Обозначйм w(E, Е') вероятность того, что нейтрон, энергия
которого до столкновения равна Е, после столкновения будет
иметь энергию Е'. Количество нейтронов в энергетическом ин-
тервале .равно w(E, E')\dE'\, или с использованием (2.2.3)
w(E, Е') | dE' \ =w(E, Е')—dQ = sin<pt/<p. (2.2.7)
Если рассеяние в системе центра инерции изотропно (при
E<EYp анизотропия упругого рассеяния мала [38]), то количе-
ство нейтронов, рассеянных в единицу телесного угла, не зави
сит от <р, т. е. правая часть (2.2.7) не зависит от <р, а значит, и
от Е'. Таким образом, w(E, Е') не зависит от Е' и может быть
определено из условия нормировки:
Е
\w(E, E')dE’ = 1,
е0£
54
т. е.
w(E, £') = [(!— е0)£]-‘; е0Е<Е'<Е;
w (Е, Е') = 0; Е' > Е; Е' < е0Е.
(2.2.8)
Минимальные значения энергии после первого, второго, тре-
тьего столкновений и т. д. равны еоЕ, ео2Е, 8о3Е ..., т. е. образу-
ют геометрическую прогрессию. Логарифмы этих значений об-
разуют арифметическую прогрессию, и поэтому логарифмиче-
ская шкала энергии часто оказывается более удобной. Лога-
рифм отношения энергий называется летаргией:
и=1п (Ео/Е). (2.2.9)
В качестве Ео можно взять любую энергию: обычно полага-
ют Е0=2 МэВ (средняя энергия спектра нейтронов деления, см.
§ 1.2), хотя это не всегда удобно, поскольку часть нейтронов
деления будет иметь отрицательную летаргию.
Вычислим среднее изменение летаргии при одном столкно-
вении:
_____ Е
Е = In J In А. w (Е, Е') dE' = 1 + (2.2.10)
Приближенно при Л^>1 имеем (при Л = 2 эта формула имеет
погрешность <—4 %):
_1__А 1 1
Е — 2' + 3 + 18 А ‘
Среднее число столкновений нейтрона при замедлении от
энергии Ео до Ес обычно определяют так:
Nc' = [1п(Е'/Е)]—1 In (Е0/Ес) = Г1 In (Е0/Ее).
Однако в работе [81] показано, что правильное выражение
для среднего числа столкновений следующее (см. также приме-
чание в книге [82] на с. 165; в Дополнении 2 приведен вывод
этого результата):
Л?с=[1п(Е'/Е)]-11п(Е0/Ес)= (in—М 1п(Е0/Ес). (2.2.11)
В табл. 2.1 приведены значения g-1, N'c и Nc при Е0=2 МэВ,
Ес = 0,2 эВ для некоторых элементов. Различие между Nc и N'.-
существенно только для легких ядер. Отметим, что разность
Nc—N'c при Л>1 равна
Nc — Nc' = —
6
77) Ш (Efl/Ec),
0-71 f
55
Таблица 2.1. Среднее число столкновений при замедлении
Нуклид 1Н 2D ®Ве 1!С S7A1 2OSpb
Г1 1 1,38 4,84 6,34 13,8 104,3
7V% 16 22 78 102 223 1682
23 27 81 105 226 1685
т. е. Nc—N'c при Л->оо не равно нулю, а стремится
Из табл. 2.1 видно, что даже для водорода среднее число
столкновений нейтрона в процессе замедления много больше
единицы.
Найдем связь между углом рассеяния в лабораторной систе-
ме координат '0' (т. е. углом между векторами v и v' и углом
рассеяния в системе центра инерции <р). Исключая V' из (2.2.1),
получаем
cos '&= (2vv')-1 [у'2(Л—1)—у2(Л+1)]
или, используя (2.2.2), имеем
.. 1 + A cos <р
COS& = : =
]/ 1 -j- 2А cos <р -f- А2
(2.2.12)
Среднее значение cos'© получаем интегрированием (2.2.12)
по d[i=d со&ср:
—г- 1 г 1 + Лр, , 2
COS & =- -77- ар. .
2 Jl/l+24p+42 34
(2.2.13)
Таким образом, для замедляющихся нейтронов транспортное
сечение (ога=0)
o"=(1_srh- (2,2,14)
Из (2.2.12) следует, что при столкновении нейтрона с прото-
ном (Л —1) имеем т9’=<р/2, т. е. максимально возможное значе-
ние угла рассеяния в лабораторной системе координат равно
л/2*.
* Выражения для § и cos в случае анизотропного в системе центра
инерции упругого рассеяния приведены, например, в [83].
56
Рассмотрим замедление нейтронов в бесконечной однородной
среде, состоящей из тяжелых атомов (Л^> 1), сечение поглоще-
ния которых равно нулю. При каждом столкновении нейтрон
будет терять незначительную часть своей энергии и поэтому,
пройдя за время Д/ путь оД/, испытает vAt^s столкновений (если
Л^>1, то скорость нейтрона при этом изменится мало). Среднее
относительное изменение энергии при одном столкновении со-
гласно (2.2.8) равно (/\Е/Е)=\п (Е/Е')—^, а при иД/25 столк-
новениях это изменение будет (&.Е/Е) =v&jSM, откуда
(2.2.15)
v&s Е ' ’
Пусть каждую секунду в среду попадает один нейтрон с энер-
гией Еа. Через время t в среде будет находиться t нейтронов.
Если записать /=2(Д/)ъ воспользоваться выражением (2.2.15)
i
и заменить сумму интегралом, то получим
Левая часть равенства (2.2.16) есть полное число нейтронов,
а подынтегральная функция описывает спектр нейтронов, уста-
новившийся в непоглощающей среде под действием нейтронного
источника единичной мощности. Таким образом, в тяжелом за-
медлителе плотность потока замедляющихся нейтронов зависит
от энергии следующим образом:
ф<£’=тЬ-- <2-2-,7>
где S — мощность источника, т. е. количество нейтронов, появ-
ляющихся в единицу времени в единице объема.
Если среда состоит из ядер с различной атомной массой, то
в (2.2.17) надо заменить суммой по всем сортам ядер:
(2-2.18)
Спектр (2.2.17) называется спектром Ферми, а величина
— замедляющей способностью среды. Если не зависит
от энергии, то из (2.2.16) получим время замедления
(yo»yJ; <2-2-19)
где ц0 и vc — скорости нейтронов, соответствующие энергиям Eq
и Ес.
57
Сравним время замедления t3 с временем жизни тепловых
нейтронов Е (2.1.26):
Поскольку величина 2vT/vc порядка единицы (см. § 2.4), время
замедления много меньше, чем время жизни теплового нейтро-
на, если [всюду надо понимать в смысле (2.2.18)]
T=S^X)<1 (2.2.21)
Параметр у будем называть «жесткостью» нейтронного спектра.
Реакторы на тепловых нейтронах характеризуются малой жест-
костью, у<С1 (см. такж-е § 2.4).
Обычно определяется свойствами замедлителя (и, воз-
можно, теплоносителя), а сечение поглощения — количеством
ядерного топлива в единице объема. Численные значения gSj
приведены в приложении.
Из формулы (2.2.16) видно, что время пребывания нейтрона
в среде однозначно связано с его энергией. Время пребывания
нейтрона в замедлителе можно назвать его «возрастом». Отсю-
да произошло название рассматриваемого приближения — воз-
растное. Это приближение можно назвать также моделью не-
прерывного замедления, поскольку предполагается, что нейтрон
теряет свою энергию только очень малыми порциями.
Приведенные выше рассуждения имеют полукачественный
характер. Рассмотрим теперь точное уравнение для плотности
потока замедляющихся нейтронов в бесконечной однородной сре-
де с однородными источниками. Будем учитывать только упру-
гие рассеянйя. Число столкновений, происходящих в единицу
времени с нейтронами, энергия которых заключена в интервале
(EE~dE; Е), равно 2/(£')Ф(Е)<7£'. Если dE достаточно мало, то
любое столкновение выводит нейтрон из рассматриваемого ин-
тервала энергии. Приход нейтронов в этот интервал из-за столк-
новений при более высоких энергиях (для простоты записи рас-
сматривается случай, когда среда содержит ядра одного сорта)
равен
£/во
dE J Zs(E')4>(E’)w(E', E)dE',
Е
где w(E', Е) определено (2.2.8). Добавляя еще нейтроны, появ-
ляющиеся от источника S(E), получаем, используя (2.2.8):
2 ДЕ) Ф (Е) = —f 2ДЕ')Ф(Е')^ + Е(Е). (2.2.22)
1—е0 J Е
58
Если Е/ео больше предельной энергии Е *, выше которой
3(E) =0, то Е/ео надо заменить Е*.
Кроме плотности потока нейтронов удобно рассматривать
плотность замедления, т. е. количество нейтронов, пересекающих
в процессе замедления за единицу времени в единице объема
данное значение энергии. Пусть Е — энергия, при которой надо
определить плотность замедления. Если E<E'<E/go, то нейтрон
с энергией Е' может получить энергию меньше Е в результате
одного столкновения. Вероятность такого события равна
Е
J w(E',E")dE".
*QE'
Так как число рассеяний нейтронов с энергией Е' равно
Ф(Е/)Ез(Е'), то для плотности замедления п(Е) получим сле-
дующее выражение:
£/е0 Е
п(Е)= J Ф(Е')2ДЕ')йЕ' J w(E’,E")dE",
Е
или, используя (2.2.8),
Е/ео
п(Е)=—^— С Ss(E') Ф (E')dE'. (2.2.23)
1 —е0 ,J \ Е’ )
Е
В логарифмической шкале энергии вместо (2.2.23) получим
и
п(и) = —?— С [ехр(и' — и) — e0]Ss («')$ (“') du';
1— Ео J
и + 1пг0
п(и) = п[Е(и)], (2.2.24)
где Ф(и)=Ф(Е)№Е№и\=ЕФ(Е)—поток в шкале летаргии.
Дифференцируя (2.2.23) по Е и используя (2.2.22), устанавли-
ваем связь между плотностью потока и плотностью замедления:
^^- = 2а(Е)Ф(Е)—3(E). (2.2.25)
дЕ
Эта формула имеет ясную физическую интерпретацию и следует
прямо из определения плотности замедления. Если Sa(E) —
=3(Е)=0, то плотность замедления не зависит от энергии, что
согласуется с наглядными соображениями.
Пусть источник нейтронов — моноэнергетический 3(E) =
= Зб(Е—Ео) и поглощение равно нулю. Тогда вместо (2.2.22)
59
запишем
мин (£0, В/в0)
(Е) Ф (£) = (1 - ео)-> J Д (£') Ф (Е’) + S5 (Е — Ео),
Е
(2.2.26)
а вместо (2.2.25)
-^ = -58 (Е~Е0). (2.2.27)
Уравнение (2.2.26) для водородного замедлителя легко ре-
шается (см. § 2.3). Для произвольного замедлителя уравнение
(2.2.26) было впервые решено Плячеком [84] путем последова-
тельного рассмотрения интервалов (EQ, ео£о), (еоЕф ео2£о) и т. д.
Было показано, что поток нейтронов (в логарифмической шка-
ле) сначала испытывает колебания'(с разрывом при Е=еоЕо),
а затем стремится к постоянной величине S/(^Ss). Функция,
удовлетворяющая уравнению (2.2.26), называется функцией
Плячека, а колебания потока — осцилляциями Плячека (см. по-
дробнее, например, [69—71, 73—77]).
Если пренебречь осцилляциями Плячека и не рассматривать
энергий, близких к Ео, то уравнение (2.2.26) удовлетворяется,
если (при Ss=const) положить Ф(Е)—а/Е, где а — произволь-
ная константа. Подставив этот результат в (2.2.23), получим
n(E)=a^s. (2.2.28)
Так как при Е>Е0 должно быть п(Е)=0, то (2.2.28) совме-
стимо с (2.2.27), если что подтверждает формулу
(2.2.17) для плотности потока [это рассуждение, конечно, не
является строгим доказательством, поскольку, получив решение
вдали от Ео, нельзя продолжить (2.2.28) вплоть до Е0’, полное
доказательство можно получить, построив функцию Плячека].
Для смеси различных ядер уравнение (2.2.26) надо записать
так:
Е/е0/
2Д£)Ф(£) = JJ(l-eojr J ^i(-^(E-} dE'+S^E-EQ).
i е
(2.2.29)
Асимптотическая плотность потока, т. е. при Е<^_Ео, равна
(при Ss = const)
Ф(Е) = Л^, (2.2.30)
где определено (2.2.18). Таким образом, между потоком
и плотностью замедления в асимптотической области имеется
60
Рис. 2.1. Спектр нейтронов, замед-
ляющихся в различных средах
(Н2О, D2O, С) и возникших при
делении 235U; сечение деления
235U, усредненное по интервалам,
которые много больше расстояния
между уровнями: штриховая —
спектр нейтронов деления %(«);
штрихпунктирная — сечение, под-
чиняющееся закону 1/а
связь [в дальнейшем под всегда будет пониматься величи-
на (2.2.18)]:
n(E)=gSs(D(£)£; п(и) =gSsO(u). (2.2.31)
На рис. 2.1 изображен спектр нейтронов, возникших при
делении 235U, устанавливающийся в различных замедлителях:
обычной и тяжелой воде, графите. Спектр получен путем чис-
ленного решения мнбгогрупповых уравнений (см. гл. 3). Коли-
чество 235U подобрано так, чтобы параметр жесткости у
(2.2.21) равнялся примерно 0,05. Из рисунка видно, что в обыч-
ной воде спектр нейтронов при и<4 повторяет спектр нейтро-
нов деления, а при и~4ч-5 переходит в спектр Ферми. Абсо-
лютное значение потока в асимптотической области обратно
пропорционально £Ss, как и должно быть (нормировка кривых
на рис. 2.1 проведена на одинаковую мощность источника).
Незначительные отклонения от прямых линий при и>5 связа-
ны с поглощением нейтронов 235U (см. § 2.3). Различный ха-
рактер спектра при больших энергиях связан не только с раз-
личной атомной массой замедлителей, но и с различным харак-
тером зависимости Ss от энергии.
На рис. 2.1 приведено и сечение, следующее закону l/v
[см. (1.5.8) и § 2.3] в произвольной нормировке, а также се-
чение деления 235U, усредненное по интервалам летаргии
~0,2—0,1. Видно, как резко падает число поглощенных ней-
тронов 2а(н)Ф(и) на интервал летаргии. Осцилляций Пляче-
ка здесь не заметно, поскольку, во-первых, источник не моно-
энергетический, а, во-вторых, энергетические группы слишком
широкие (25 групп на весь интервал летаргии). На рис. 2.1
изображен спектр нейтронов при Е>0,2 эВ. При меньших
61
энергиях начинается переход к спектру тепловых нейтронов.
Максимум распределения тепловых нейтронов значительно
превышает (если у<С1) значение плотности потока при Е=
= ЕС (см. § 7.5).
Пусть Ес — верхняя граница тепловой группы. По физиче-
скому смыслу плотности замедления п(Ес) есть мощность ис-
точника для тепловых нейтронов. Поэтому в уравнении
(2.1.23) надо положить S = n(Ec), т. е. уравнение диффузии
нейтронов будет следующим:
£>ЛФт (г) —2атФт (г) = — п (г,Ес). (2.2.32)
Обратимся теперь к выводу уравнения, определяющего за-
висимость плотности замедления от координат. Уравнение ба-
ланса (2.1.6) можно переписать, выделив в качестве источни-
ков только те нейтроны, которые возникают в результате де-
ления. По определению ^плотности замедления, число нейтро-
нов, появляющихся в данном энергетическом интервале dE
и элементе объема dr в результате замедления, можно запи-
сать так:
fn (г, Е + dE) — п (г, £)] dr = dEdr,
поэтому вместо (2.1.6) получим
^+divj+SaO + ^- = S(r, Е). (2.2.33)
ot дЕ
Воспользовавшись связью между плотностью тока j и плот-
ностью потока Ф в диффузионном приближении (2.1.17) и фор-
мулой (2.2.31), получим при Sa = 0 в стационарном случае
— =A/z + S(r, т), (2.2.34)
где
^ = -(З^ЛгГ’^ (2.2.35)
Е
и S(r, т) — источник в шкале т, т. е. S(r, r)dr——S(r,E)dE.
Из (2.2.35)
Еа
т (£) = — С ——t (2.2.36)
Е
где Ео — произвольная энергия. Удобно выбрать Е0=2 МэВ.
Если gSs и не зависят от энергии, то из (2.2.36) получаем
.(Е) = (3^/г)-Чп-^=^- и(Е), (2.2.37)
где и(Е) — летаргия (2.2.9).
62
/г (г, т)\ /п(г, т)\ (Dn' (г. т) \
.. (2.2.38)
2
Поскольку плотность потока Ф(г, Е) в диффузионном при-
ближении удовлетворяет граничным условиям (2.1.54),
(2.1.55), плотность замедления удовлетворяет граничным усло-
виям (для всех значений т):
Dnr (г, т)
Рассмотрим уравнение (2.2.34) с моноэнергетическим ис-
точником, причем значение т, соответствующее энергии источ-
ника, равно нулю:
— = Д/г + S (г) 8 (г). (2.2.39)
dt
Интегрируя (2.2.39) по малому интервалу около т = 0, по-
лучаем
п (г, 0)=S(r), (2.2.40)
т. е. можно рассматривать уравнение (2.2.34) без источников,
дополнив его «начальным» условием (2.2.40).
Уравнение (2.2.34) формально совпадает с уравнением теп-
лопроводности.
Величина т(£), определенная (2.2.36) при Е=ЕС, назы-
вается «возрастом» нейтронов, возникших от источника с энер-
гией Ео, хотя она имеет размерность см2, а не с. Величину
х(Е) для произвольного Е называют возрастом, соответствую-
щим энергии Е. Уравнение (2.2.34) есть уравнение возрастно-
го или, точнее, диффузионно-возрастного приближения.
Определим нейтронное поле, возникшее в бесконечной од-
нородной среде от точечного источника моноэнергетических
нейтронов, т. е. рассмотрим решение уравнения
dW (г’.2> _ (Г; т) (2.2.41)
dt
с начальным условием
F(r, 0)=6(г). (2.2.42)
По аналогии с решением уравнения (2.1.28) перейдем к
фурье-образу (п=1, 2, 3 для одно-, двух- и трехмерного слу-
чаев соответственно):
W (г, -) = (2т)-" J W (k2, t) exp (i kr) dk.
Функция W(k2, т) удовлетворяет уравнению
dW<£2’ z> = — k2W (k2, t) (2.2.43)
с начальным условием W(k2, 0) = l. Уравнение (2.2.43) с этим
начальным условием имеет решение
W(k2, т)=ехр (—k2x). (2.2.44)
63
Выполнив обратное преобразование Фурье
й-7 (г, <t) = (2т)“п j exp (— k2-i + i kr) dk,
получим
W (г, т) (4itt)_"/2exp (— — 'j. (2.2.45)
\ 4т )
Функция W (г, т) нормирована на единицу:
JlT(r, %)dr = 1
и может быть интерпретирована как вероятность того, что
быстрый нейтрон, рожденный в точке г=0, замедлившись до
возраста т, окажется в точке г. Средний квадрат перемещения
при замедлении равен
F= Jr2lF(r, т)б/г = 2/гт, (2.2.46)
где п— 1, 2, 3 для источника в виде плоскости, нити и точки
соответственно. Поэтому величину Ут называют также длиной
замедления [ср. с (2.1.41)]. Если источник расположен не в
начале координат, а в произвольной точке г0, то в силу одно-
родности среды получим
W (г, х) = (4itT)~~n/2exp | —(г~~г<1—I. (2.2.47)
L 4т J
Если блоки ядерного топлива имеют малые размеры по
сравнению с /г, то их можно рассматривать как точечные ис-
точники быстрых нейтронов. Пусть число нейтронов, возни-
кающих в единицу времени в блоке с номером т, равно Sm.
Если замедлитель бесконечен, точнее, если расстояние крайних
блоков от границы замедлителя много больше ]/т, то плот-
ность замедления в точке г равна
Mr,T) = (4zT)-1Vsmexp[--(2.2.48)
L 4т J
т
где предполагается, что блоки имеют вид бесконечно длинных
нитей; rm — двухмерный вектор, определяющий положение
m-го блока. Рассмотрим более подробно зависимость плотно-
сти замедления от координат внутри ячейки большой однород-
ной решетки блоков. Если число блоков достаточно велико и
рассматривается не крайняя ячейка, то вместо конечной ре-
шетки можно рассмотреть бесконечно большую решетку. Тогда
сумму (2.2.48) надо распространить до бесконечности и мож-
64
но положить Sm=l. Обозначив х, у компоненты вектора г,
получим
+ оо
n(x,y;x) = (4.x)- £ (2.2.49)
m1;m2=—оо
где а — шаг решетки, которая предполагается квадратной.
Для вычисления суммы (2.2.49) используем формулу сумми-
рования Пуассона [85]
2 И^)= 2 exp(2itfnfci)f(£)dfc (2.2.50)
Л=—оо т=—оо —оо
и получим
« (х, у; х) = (4ттх)-1 J exp ^2itnk i— 'Г -j dk,
n
где суммирование проводится по всем целочисленным компо-
нентам двухмерного вектора п от —оо до Ч-оо, а интегриро-
вание — по двухмерному пространству от —оо до +:оо. Вы-
полнив интегрирование, получим
п (г, х) = -у У[exp f~ — п~] cos ^5. (2.2.51)
л2 W \ а2 / а
п
Если справедливо неравенство
то в сумме по и можно оставить слагаемые с минимальным
значением |п|, т. е. /г1 = и2=0; «1 = 0, «2=±1; «2=0,
«1 = ±1. Сравним значение и(г, т) на поверхности блока (т. е.
при х=у=О) и в центре ячейки = у =
„ \ 1 Г1 1 л ! 4"т \ I /а а \
п (U, (J; х) = — 1+4 ехр — — ; п \ — —: х ] —
а2 [ \ а2 / J \ 2 ’ 2 /
Таким образом, амплитуда колебаний плотности замедле-
ния в ячейке мала, если выполнено неравенство
4ехр(- ^<<1, (2.2.53)
5—6053
65
и тогда плотность замедления в ячейке не зависит от коорди-
нат. Если (2.2.53) справедливо при т=тс, то источники для
тепловых нейтронов, равные п(г, тс), не зависят от координат.
Обычно неравенство (2.2.53) для т=тс выполняется очень хо-
рошо. Так, если т для D2O равно 125 см2, а для графика
320 см2, то левая часть (2.2.53) меньше 10-2, если а<29 см
и а<46 см соответственно. Физическая причина того, что плот-
ность замедления не зависит от координат, заключается в том,
что в формировании нейтронного поля в данной точке прини-
мает участие большое число соседних блоков.
Отметим, что первое слагаемое в (2.2.51), т. е. 1/а2, полу-
чается, если в сумме (2.2.49) суммирование заменить интегри-
рованием. Поэтому для произвольной формы ячейки, если ее
максимальный размер характеризуется величиной а, удовлет-
воряющей условию (2.2.52), имеем
n(r, т) = 1/«, (2.2.54)
где s — площадь ячейки. Далее, если в сумме (2.2.48) зави-
симость Sm от т достаточно плавная и выполнено условие
(2.2.52), то сумму можно заменить интегралом:
« (г> т) = Уw (r — rrn> т) sm = — f IE (г — г', X) s (г') dr'. (2.2.55)
La $ tJ
т
Рассмотрим теперь уравнение (2.2.32), в котором плот-
ность замедления равна 1Ё(г, т) (2.2.45) при т = тс (ниже ин-
дексы у D и т опускаем);
r>AGf(r)-SaG/(r)=—1Е(г, т). (2.2.56)
Очевидно, функция G/(r) описывает поле тепловых нейтро-
нов, возникшее от единичного точечного источника быстрых
нейтронов/ помещенного в начало координат. Зная фурье-об-
раз W(k2, т) (2.2.44), получаем фурье-образ от Gf.
exp (—62т), (2.2.57)
откуда
G (г) = -М _е*Р L-fe2l+i^r2- dk. (2.2.58)
' (2n)«Dj &2 4-L-2 v
В одномерном случае *
00
, f cos kx exp (— dk L t Г, . x
Gf(x) = --------=—exp— 2ch—4-
M J k2 + L-3 40 F £.2 [ £
0
* Обратим внимание, что в распространенном справочнике [75] формулы
(3.954.1) и (3.954.2) для интегралов (2.2.59), (2.2.61) содержат опечатку, ко-
торая, к сожалению, перешла в книгу [86]. Автор признателен Б. П. Кочу-
рову за указание на эту опечатку.
66
(2.2.59)
где erf z— интеграл вероятностей:
erf z = -Д= f exp (— Z2) dt. (2.2.6C)
V " J
0
В трехмерном случае G/(r) также выражается через функ-
цию (2.2.60):
00
„ , . 1 С ^sinArexof—k2z) dk 1 т Г г _</ г ।
G, (г) = —— -------------------—=-----ехр — ехр — erf —7^+
n 2~2DrJ &2+L-2 8л0г *L2 |_ L \2|/т
о
, 1/т \ , ( г \ г
+4- + ехр —г erf ——
L > ' L > \2 l/т
Наконец, для двухмерного случая
2sh (2.2.61)
kJ0 (kr) ехр (— k2~)dk
k2-\-L~2
(2.2.62)
о
Этот результат можно записать в несколько иной форме. Лег-
ко обнаружить, что Gf (2.2.62) удовлетворяет дифференциаль-
ному уравнению
д
dz
1
L2
1
4~Dr
г2
4г
с начальным условием
Решив это уравнение, получим
Gf (г) = —-— ехр —
п ’ 2~D L2
dz
4L2z) J г
г2
о
(2.2.63)
Для тяжелой воды и графита выполняется неравенство
т<£2. (2.2.64)
67
5*
В этом случае в (2.2.63) можно под интегралом разложить
в ряд ехр (—z). Тогда
Gf (г) = —— ехр — 1/(0 [——— Ех I— j — Гехр (——'j —
М ’ 2~D f £2 1 *4 L J 2 \ 4т / 2L2 [ Ц 4т /
(2-265)
где £i — интегральная экспонента (1.10.10). Очевидно, что
если т=0, то Gf переходит в Gs (2.1.35), что и соответствует
физическому смыслу этих функций. Если выполнено условие
(2.2.64) и г2^>4т, то Gf также совпадает с Gs. Иногда выгод-
нее Gf записывать так:
ехрНг+Д)Н“-
Интеграл (2.2.62) выражается через неполные цилиндриче-
ские функции [87].
Есть источник нейтронов не моноэнергетический, то его
можно представить как суперпозицию моноэнергетических ис-
точников
S(t) = JS(t — T')8(V)tfc'. (2.2.67)
Поскольку уравнение возрастного приближения линейно, реше-
ние в этом случае можно записать так:
л(г, г) = Js(x—г)1Г(г, 1,)^\ (2.2.68)
где W(r, т') определяется по (2.2.47). Пусть в (2.2.68) S = % —
спектр деления в шкале т. Определим средний квадрат пере-
мещения нейтрона от точечного источника нейтронов деления
rf = Jx(T,)r5(t — jjdz' = ^(E'fr^ — ^dE', (2.2.69)
где г2(т—т') — средний квадрат перемещения нейтрона, рож-
денного моноэнергетическим источником с энергией Е' при за-
медлении до энергии Е. Рассмотрим случай, когда cSs и
не зависят от энергии (фактически такая зависимость при боль-
ших энергиях существенна, причем в среднем убывает с
ростом энергии). Положим
---In—; ?(т — т') =---------In—, (2.2.70)
68
где Es — искомая эффективная средняя энергия спектра де-
ления. Из (2.2.69) получим
ln£s = ^X(£,)ln£'d£'. (2.2.71)
б
Подставив в (2.2.71) спектр (1.2.1), получим (см. [75, форму-
ла (4.355.1)]):
ln£„ = —=fx lnxexp ( ——'l dx = In------------|- 2 — С;
s |/л9» J \ в / 4
О
или
£„ = -ехР £ = 0,69 Е,
s 6
С = 0,577,
(2.2.72)
где Е — средняя энергия нейтронов деления _(£=2 МэВ).
Если учесть, что Ss падает с ростом энергии, то Ё8 возрастает
по сравнению с (2.2.72).
Соотношение (2.2.46) позволяет экспериментально опреде-
лить т, измеряя активацию детектора на различных расстоя-
ниях от источника. При этом детектор должен поглощать ней-
троны только определенной энергии, т. е. иметь один сильный
резонанс. Обычно определяют т с помощью детектора из1151п,
который имеет резонанс при £=1,46 эВ. Если источником слу-
жат делящиеся ядра, то автоматически происходит усреднение
типа (2.2.69) с нужным весом. Добавка Ат, связанная с замед-
лением от 1,46 до £с, мала по сравнению с т и может быть
вычислена приближенно по формуле, аналогичной (2.2.36):
(2.2.73)
Следует, однако, иметь в виду, что при энергии 0,3—0,5 эВ
уже надо учитывать влияние химических связей на процесс пе-
редачи энергии от нейтронов к ядрам замедлителя. По этой
причине значение Ат, вычисленное по (2.2.73), будет меньше
фактического. Например, в [88] приведены результаты изме-
рения т для ВеО до £=1,46 эВ и £=0,3 эВ. Эксперимен-
тально найденное значение (2.2.73) при £с=0,3 эВ оказалось
69
равным (при плотности ВеО 2,79 г/см3) (Ат) э= 12,5 (25) см2,
а теоретическое значение (Ат)т = 7,35 см2 *.
Средний квадрат перемещения нейтрона, или длина замед-
ления, играет большую роль в теории критических размеров
(см. гл. 4). Ниже под возрастом т(£с) всегда будет понимать-
ся величина, определенная по (2.2.46) из измеренного значе-
ния г2 или вычисленного по более точным методам, чем изло-
женные здесь. Значение т для смеси легкого замедлителя с
тяжелыми ядрами нельзя вычислять по (2.2.36), поскольку
большую роль играют неупругие столкновения и анизотропия
рассеяния на тяжелых ядрах при больших энергиях. Экспе-
риментальные значения для чистых замедлителей и некоторых
смесей с более тяжелыми веществами приведены в приложе-
нии.
Остановимся на условиях применимости возрастного при-
ближения. Некоторые условия применимости уже были пере-
числены выше: достаточно слабое поглощение (см. подробнее
§ 2.3); изотропия рассеяния в системе центра инерции; энер-
гия нейтрона существенно больше, чем энергия связи в моле-
куле или кристаллической решетке. Кроме того, для приме-
нимости возрастного приближения должны быть выполнены
два условия: расстояния от источника не должны быть слиш-
ком большими, и нейтрон в процессе замедления должен ис-
пытать много столкновений. На больших расстояниях от ис-
точника нарушается условие применимости диффузионного
приближения (2.1.9). В самом деле, если в (2.1.9) подставить
(2.2.45), то получим
dW I г
dr | 2-.S/r
1
W'Sfr
< 1-
(2.2.74)
Очевидно, что на больших расстояниях и\ условие
(2.2.74) должно нарушаться. На больших расстояниях быстро
затухающая функция (2.2.45) становится меньше, чем функ-
ция вида ехр (—Ssr), которая описывает «прямые прострелы»
нейтронов без столкновений [см. (1.10.6)], в то время как
(2.2.45) возникает в результате многократного рассеяния (на-
помним, что вблизи источника на расстоянии диффузи-
онное приближение также нарушается).
Если недостаточно хорошо выполняется условие Ас1§>1, где
Nc — среднее число столкновений, определенное (2.2.11), то
средний квадрат перемещения нейтрона при замедлении надо
записать так:
/5=6 (т+С), (2.2.75)
* Если учесть движение ядер (см. § 2.4), то (Дт)т возрастет до 8 см2.
70
где т определено (2.2.36), а величина С равна [89]
с = (зад-1 (2 - г1 V. f/Sp/-(ln--z)2 -
| LA 1 — ^о/
,fr
(6/1,)-’ (2 + Л,•) (Лу - I)2 Ш еоу
УЯу
Лу — атомная масса ядра сорта /; с} = ^-г и Ss, Szr — полные
макроскопические сечения среды. Если Ss зависит от энергии,
то в (2.2.76) надо подставлять значения Ss для энергии, близ-
кой к энергии источника. При Л^>1 из (2.2.76) получим
С = А(2ЛгГ(1 + _2_). (2.2.77)
Происхождение добавки С в (2.2.75) проще всего понять
следующим образом. Рассмотрим точечный изотропный источ-
ник нейтронов. Замедление испущенных источником нейтронов
начнется только тогда, когда начнутся их столкновения с' яд-
рами окружающей среды. Поэтому физически точечный источ-
ник является с точки зрения теории возраста протяженным.
Вместо функции Грина (2.2.45) надо написать
1Г (г, 'О = Г K(r')(4ir-t) 3/2 exp
(£гг2а_] (2.2.78)
4т I
где К (г') — ядро первого столкновения (1.10.6). Определим
средний квадрат перемещения, исходя из функции (2.2.78):
г2 — J W (г, т) гЧг = 6 [Т + (3S/)-1]. (2.2.79)
Возникшая при этом добавка к т близка к С (2.2.П).
Несколько слов надо сказать о замедлителях, содержащих
водород. Сечение рассеяния водорода и его замедляющая спо-
собность значительно больше, чем у других элементов, входя-
щих в состав замедлителя (например, у кислорода в воде).
Поэтому можно рассматривать в первом приближении только
рассеяние на водороде. Сечение рассеяния водорода при боль-
ших энергиях существенно меньше, чем при средних и тем бо-
лее тепловых (рис. 2.2, где приведены полные сечения, прак-
тически совпадающие с сечениями рассеяния для нескольких
легких ядер). Поэтому, хотя общее число столкновений при
замедлении на водороде достаточно велико (см. табл. 2.1),
основное перемещение нейтрон совершает при больших энер-
гиях, испытывая при этом малое число столкновений. Отсюда
следует, что пространственное распределение нейтронов в во-
дородсодержащих замедлителях плохо описывается возраст-
ным приближением (см. также § 4.6).
71
Рис. 2.2. Полные сечения изотопов водорода
(Н, D), углерода (С), кислорода (О) как функ-
ции энергии нейтрона (для углерода и кисло-
рода при больших энергиях приведены сред-
ние значения по группам)
Рис. 2.3. График функции
ф(0, £„) (2.3.24)
Задача 1. Определить мощность источников в тепловой группе в интер-
вале энергий между Ej и Ei+i, возникающих из-за замедления нейтронов
с энергией больше Ес, если при Е'>ЕС имеет место спектр Ферми.
Решение. Пусть Е—энергия внутри интервала (Ej, Е/+1), причем
Е^>е.0Ес. В этом случае нейтрон с энергией выше Ес может попасть в рассма-
триваемый интервал в результате одного столкновения. Мощность источников
с энергией Е равна
£/е0
q(E) = j £s9(E')w(E', E)dE',
Ec
или, если подставить w(E', Е) по (2.2.8) и Ф(Е')=с/Е', где С—постоянная,
q (£) (Е-^-е.Е-^. (2.2.80)
1 —е0
Интегрируя (2.2.80) по интервалу (Ej, Ej+1), получаем (при Ej>e0£c):
cXs Г£;-1—-Е: Е,-.-, 1
q, = ----— -LLi-------' —eoln . (2.2.81)
1 L Ec Ej J 1
Мощность источников для всей тепловой группы получится из (2.2.81),
если положить Е/+\=ЕС и Ei=e,0Ec, т. е. q=&,Es. Следовательно, мощность
источников в тепловой группе пропорциональна значению в данной точке
(можно рассматривать среду с неравномерным распределением замедляющей
способности по пространству). Если замедляющиеся нейтроны распределены
по ячейке равномерно, то фермиевский спектр определяется средним значе-
нием заземляющей способности и c=S/gSs, где S— число нейтронов де-
ления на единицу объема ячейки.
Задача 2. Определить г2 и г4 для перемещения нейтрона от рождения
при делении до поглощения в тепловой группе. __
Решение. Исходя из формул для г2 и г4, приведенных в задаче 5
§ 2.1, и формулы (2.2,57) для фурье-образа Gj, получим
Н = 6(т+£2); ^=120(£44-т£2-{-т2/2).
72
Задача 3. Определить поле замедляющихся нейтронов, возникших от
единичного источника быстрых нейтронов, расположенного в среде, занимаю-
щей первое полупространство (левое полупространство — вакуум).
Решение. Применим метод изображений. По аналогии с задачей 6
в § 2.1 получим
п(г, -г) = (4лг)~3/2[ехр(--(Г~-о)2-]-ехр ( - "R (2.2.82)
I. \ 4т / V 4т ) I ’
где Го — радиус-вектор источника. Построенная функция (2.2.82) удовлет-
воряет следующим условиям: а) уравнению (2.2.34) в правом полупростран-
стве, причем точечный и моноэнергетический источники расположены в точке
го; б) равна нулю на экстраполированной границе. Поскольку уравнение и
граничные условия однозначно определяют решение, то (2.2.82) является
единственным решением задачи.
Задача 4. Пространство вне сферы радиусом р занято непоглощающнм
замедлителем. Внутри сферы находится делящееся вещество в таком состоя-
нии, что можно пренебречь замедлением нейтронов внутри сферы. Опреде-
лить поле замедляющихся нейтронов вне сферы.
Решение. Вне сферы плотность замедления удовлетворяет уравнению
(2.2.34) при 5=0. На границе сферы должны выполняться:
граничное условие
дп |
— =0; (2.2.83)
дг |г=р
начальное условие
п(г, О)=сб(г—р), (2.2.84)
где с постоянная, зависящая от числа делений внутри сферы. Выполняя
преобразование Лапласа над (2.2.34) при 5 = 0, но с учетом (2.2.84), полу-
чаем
Дп(г, X)—Хя(г, Х)=—сб(г—р), (2.2.85)
где
00
п(г, Л) — | п(г> т)ехр( — ?.т)с/т.
О
Решение уравнения (2.2.85) имеет следующий вид:
ЛА)
я(г, X) =.= --— ехр[ —J/А (г—р)]; г>р. (2.2.86)
г
В точке г=р имеется скачок производной: по условию (2.2.83)
д I
—-— п (г Л) =0,
or |т=р—о
а дифференцируя (2.2.86), имеем
-у—я(г, X)! = - ^-“-0+1/Тр).
or |г=р + О р2
Подставляя этот результат в (2.2.85), получаем в левой части 6-функ-
цию. Приравнивая коэффициенты при 6-функциях, находим связь между
Л (Л) и .с:
, рс
Л(л) = р-г + КГ •
73
= l-L-Гн
р L
Таким образом:
n(r, X) =—(р-1+|/^)-1ехр[-/л(г —р)]. (2.2.87)
г
Обратное преобразование Лапласа дает (см., например, [90, с. 221]):
п(г, т) —--ехр — ——I 1— ~ ехрх2- (1 — erfx)], (2.2-88)
г [/ лт [ 4т: J р J
где
г—Р) I
2т ]'
Легко проверить, что (2.2.88) удовлетворяет условию •(2.2.83), хотя
(2.2.87) этому условию не удовлетворяет. Здесь нет противоречия, поскольку
при обратном преобразовании Лапласа необходимо выполнить интегрирова-
ние скачка функции (2.2.87) на разрезе в комплексной плоскости X от
—оо до 0. Производная по г от скачка равна нулю при г-*-р.
При больших значениях аргумента х имеем
J 1/1
ехр(х2)-(1 —exfx) = 1 — —
Подставляя этот результат в (2.2.88) и учитывая, что для еди-
ничного источника надо положить с=[4лр2]-1, получаем, что
при р—>0 (2.2.88) переходит в (2.2.45).
2.3. ПОГЛОЩЕНИЕ НЕЙТРОНОВ ПРИ ЗАМЕДЛЕНИИ
Сечение взаимодействия нейтронов с тяжелыми ядрами
имеет сложный характер, поскольку тяжелые ядра обладают
большим числом резонансов. Например, среднее расстояние
между резонансами 238U составляют 20 эВ и число их в ин-
тервале 0<£<10 кэВ ~500. Число резонансных уровней де-
лящихся ядер в несколько раз больше. Отсылая за подроб-
ностями и выводом к общим курсам ядерной физики или более
прикладным монографиям [71, 91], приведем здесь только
простейшее описание зависимости сечения от энергии (одно-
уровневое приближение).
Сечение радиационного захвата изолированным резонансом
описывается формулой Брейта — Вигнера (эта форма резо-
нансной линии называется естественной)
(£•) = c0Zl_ j/^(l + л;3)-1; х = -1(£-£г), (2.3.1)
г
где с0 — полное сечение в максимуме (т. е. при Е — Ег); °0^-=
= с (Ег) = от0—сечение радиационного захвата в максимуме;
4,У.», 2'6М'°' Ы+1Г. (2.3.2)
Г 1 Ег \ А )
74
Er — энергия, эВ; 2лХ— длина волны нейтрона с энергией Ег
в системе центра инерции нейтрона и ядра; численный коэффи-
циент в (2.3.2) подобран так, чтобы о0 получилось в барнах; А—
атомная масса ядра; Г7— радиационная ширина; Гп—нейтрон-
ная ширина; Г — полная ширина:
Г = Г„ + Г7; (2.3.3)
g— статистический фактор:
12/4-1
S 2 2/41'
(2.3.4)
Здесь / — спин ядра; J — полный момент рассматриваемого
уровня. Для низких энергий преобладают s-уровни, т. е. с мо-
ментом, равным нулю (поскольку длина волны нейтрона много
больше размера ядра). Для s-уровней 7= / ± .Если 1=0, то
для s-уровней g=l. Экспериментально обычно определяются
£Г„ и Г7 (см., например, [7]), поэтому g надо знать только для
вычисления полной ширины Г. Чаще всего ГИ<^;Г7, и тогда до-
статочно знать произведение gTn.
Формула (2.3.3) более точно должна быть записана так:
г = г1 + г„кд/дг.
(2.3.5)
Это уточнение имеет смысл делать только для низкорасполо-
женных уровней, как, например, уровень 135Хе при энергии
£=0,085 эВ (см. § 12.1). Однако и здесь влияние этой поправ-
ки на практически интересные результаты весьма мало [92].
Ниже поправка (2.3.5) не будет использоваться.
Сечение рассеяния зависит от энергии более сложным об-
разом, поскольку существует интерференция между амплитуда-
ми резонансного рассеяния (происходящего с образованием
составного ядра) и потенциального рассеяния (рассеяние на
потенциальной яме). Сечение рассеяния имеет вид
os(£) = ор 4 (2-3'6>
\ Г ]/ п X / 14 х2
где X определено (2.3.2); ор — сечение потенциального рассея-
ния. Если х^>1, то os=Op, т. е. вдали от изолированного ре-
зонанса рассеяние равно потенциальному. Потенциальное рас-
сеяние приближенно выражается через радиус ядра:
Ор = 4л7?/2=4л£2(1—А)2, (2.3.7)
где /?=1,35Л1/3-10-13 см — радиус ядра; Л — поправка, дости-
гающая довольно заметной величины ±1/4 [7].
Так как х>0 при Е>ЕГ и х<0 при Е<.ЕГ, то интерфе-
ренция уменьшает сечение при Е<ЕГ и увеличивает при £>
>ЕТ.
75
Если кроме процессов радиационного захвата и рассеяния
может происходить деление (другие процессы нас, как прави-
ло, не будут интересовать), то для о?(Е) надо написать фор-
мулу, аналогичную (2.3.1):
«,(£) = ». (2-3.8)
а вместо (2.3.3) — формулу
Г=Г?+Г„+Гу, (2.3.9)
где Г/ — делительная ширина уровня.
Если имеется несколько неперекрывающихся уровней, то
сечение равно сумме отдельных слагаемых вида (2.3.1), (2.3.6),
(2.3.8) (более точное описание см. в [71, 91]).
Сечение взаимодействия нейтрона с ядром зависит не от
энергии нейтрона в лабораторной системе координат, а от энер-
гии относительного движения. Поэтому тепловое движение ядер
приводит к изменению сечений. Хотя скорость движения ней-
трона, энергия которого лежит в резонансной области, много
больше скорости движения ядер, тем не менее влияние тепло-
вого движения вполне заметно, что связано с малой шириной
резонансных уровней. Энергия относительного движения
£' = y(v-V)! = £-m'vV+yV2; Е = (2.3.10)
где т! = т —----приведенная масса нейтрона; v, V — скорости
1А
нейтрона и ядра. Если обозначить f(V) нормированную функ-
цию распределения ядер по скоростям, то среднее сечение
равно
ЦЁ) = j О (£') f (V) dV. (2.3.11)
Пренебрегая квадратом V в (2.3.10), получаем [если энер-
гия нейтрона 1 эВ, температура среды 300 К, атомная масса
ядра 240, то (V/v)2 -10 4]:
Е' = Е — V2tn/EV, (2.3.12)
где V — проекция V на направление движения нейтрона.
Предположим, что f(V) есть максвелловское распределение*
/ т д / mA \ с*
ехР (“^7 П ; р (у)dV = 1 > (2-3. !3)
* Это предположение справедливо, если Т>0, где 0 — характеристическая
(дебаевская) температура. Обычно это условие выполнено достаточно хо-
рошо [71].
76
где Т — абсолютная температура; k — постоянная Больцма-
на. При выполнении усреднения (2.3.11) обычно пренебрегают
медленно изменяющимися множителями, полагая в них £'=
~Е. Тогда, если о(Е) дано (2.3.1),
— оо
mA WdV
--- v --------------
2kT ) Г2+4 (Ег—Е’)2
(2.3.14)
Обозначим
±(Е'-Ег) = у, A(£-£f) = x
и
4 = С,= 4=Д^, (2.3.15)
' А; т л Л 21/ kTEr
где А — доплеровская ширина уровня (такое название связа-
но с тем, что рассматриваемое здесь изменение сечения обус-
ловлено эффектом Доплера). Из (2.3.14) получим (при Л^-1,
m = m'):
(£) = 3о-^г ]/^-<p(x, Q, (2.3.16)
где
Z у exp Г-^- (х-у)21
ф (X, Q = -М -т5,-,--------------J dy. (2.3.17)
2 / " Д 1 + У2
Очевидно, что усредненное значение зависит от температу-
ры. Так как £0 обратно пропорционально фТ, то малым темпе-
ратурам соответствуют большие значения £0. Усреднение сече-
ния рассеяния приводит к следующему результату:
М*) = ор + °о V Ж Q + и]’ (2.3.18)
1 у Я Л
где ф определено (2.3.17), а х равно
Г J 2
f уехр (х—у)2
dy.
(2.3.19)
77
Функции ф, х могут быть выражены через табулированную
функцию — интеграл вероятностей от комплексного аргумен-
та [93, 94]:
Ф (•*> Q = ^- C0Re w + i) ’
М*, Q = Со1га® [4“ (х + *)];
(2.3.20)
w(z) = ехр(—z2)
Для численного определения функций ф и % можно исполь-
зовать также тот факт, что ф удовлетворяет дифференциаль-
ному уравнению
4 4х Дф . 2 I 2 \
---- * ' “ -4— ---- "" —I— I 1 -г- Л —г- ——
?04 dx* V dx ?о2 /
(2.3.21)
1
с такими начальными условиями: ф(0, Q дано (2.3.24); -^-1
dx |х=0
= 0, а х равно
х(%> = + Q.
*Q dx
Более точная запись доплеровского сечения исследовалась
многими авторами (см., например, [92, 95]); отклонения от
рассмотренных здесь формул для условий, реализующихся в
реакторе, незначительны.
Если температура достаточно низка, то ^03>1. Отметим,
что, например, для первого уровня 238U и температуры 300 К
получим (см. 8.1) £о=0,5, т. е. значения соответствуют
более низким температурам. Если £о^>1, то подынтегральное
выражение в (2.3.17) мало всюду, кроме окрестности точки
х=у. Полагая в знаменателе х=у, получаем
ф(х, £0) - (14-х2)-1; £о>1, (2.3.22)
т. е. при низких температурах форма резонансной кривой ста-
новится естественной, как, очевидно, и должно быть.
В случае высоких температур, когда Со->О, можно записать
—00
и разложить в ряд
ехр (у V ху\ = 1 + + •••
78
В первом приближении по £0 получим
Ф (*, Q = ехр ( - 4 V -И > (2.3.23)
т. е. резонансная линия имеет гауссову форму. В этом пре-
дельном случае линия называется чисто доплеровской.
При х=0, т. е. в центре линии, имеем (рис. 2.3)
l/о Г х °<Ег. Т) |/п » (1 Г \ /Г) О ЛЛД
Ф(°. Со) - СТ(ЕГ> 0) — ~2~ £оеХР 4 \ ~erf 2 г (2-3-24)
При £0> 1
Ф(0, с0) = 1—4,
т. е. под влиянием эффекта Доплера сечение в центре линии
понижается. Площадь под резонансной кривой при этом сохра-
няется:
+ оо 4-оо
J <р(х, C0)dx= j = (2.3.25)
— 00 —оо
На рис. 2.4 изображена резонансная линия первого уровня
238U (£=6,67 эВ, см. § 8.1) при различных температурах (при
этом полагается ~^ЕГ1Е=\). Точка х=8 отстоит от центра
резонансной линии всего на 0,1 эВ. Поскольку в центре линии
естественной формы сечение поглощения для этого уровня со-
ставляет 2-104 б, то при х=8 сечение еще не мало (при Т =
= 300 К Ох=8 = 800 б). При очень больших х форма линии
становится естественной. Действительно, (2.3.17) можно запи-
сать так:
- ~ ?02Z2
4
U2) (1+--) ’ 1+*2 ’ ' ' ’ '
или, разложив в ряд по е,
(2Л27)
т. е. при условии х2^>6/^02 действительно имеем естественную
форму линии (см. также задачу 1 в конце § 2.3).
Если поглощение нейтронов достаточно слабое, то в первом
приближении можно считать, что спектр нейтронов сохраняет-
ся таким же, каким он был бы в отсутствие поглощения. Тогда
79
+°° ехр
Рис. 2.4. Форма резонансной линии
поглощения для первого уровня 238U
при различных температурах урана
Рис. 2.5. График функции У£/£НХ
для 238U и 23sPu
количество захваченных нейтронов с энергией больше Е равно
[см. (2.2.17)]
Еа Е,
J a (E)$(E)dE = S j
^(E)dE
£ Ss£
Величина обычно не зависит от энергии, и количество
захваченных нейтронов определяется интегралом
Е° (Е'\
A(£)=J-^d£, (2Л28)
Е
который называется резонансным интегралом радиационного
захвата до энергии Е, точнее, резонансным интегралом беско-
нечного разведения, т. е. для очень малых концентраций по-
глощающего вещества. Аналогично определяются резонансные
интегралы деления или поглощения, если а? заменить щ
или оа.
Если нижний предел в (2.3.28) не указывается, то подразу-
мевается, что он равен «кадмиевой границе», т. е. энергии,
выше которой фильтр из кадмия становится прозрачным для
нейтронов. Эта граница незначительно зависит от толщины при-
меняемого фильтра, но в большинстве справочников и обзоров
проводится пересчет на одно и то же значение нижнего пре-
дела Е=0,5 эВ. Кадмиевая граница близка в той границе Ес,
которую можно провести между замедляющимися и тепловыми
нейтронами, но не совпадает с ней (см. подробнее § 2.4 и 7.5).
Вдали от резонанса, когда E<^iEr, сечение поглощения про-
порционально l/yE^l/o (закон 1/о). Действительно, из (2.3.1)
80
следует, что при Е<^ЕГ
/ 4£г2 х-1 /"Г
от (£) = от0 (1 + у >• (2.3.29)
Если имеется только один резонанс, то сечение при скоро-
сти нейтрона 2200 м/с, Е=£н=0,0253 эВ равно
/ 4ЕГ2 \~1 Г~р
М£н) = <Ц1 + -гН (2.3.30)
Если резонансов несколько, то
МД.)-£°,ф+^] (2-3.31)
j
Легкие ядра, например 6Li, 10В, имеют широкий интервал
энергии, на котором справедлив закон \/v (6Li имеет первый
резонанс при Е = 252 кэВ, 10В — при £'=170 кэВ). Если закон
1/и справедлив на интервале Е^<Е<Е', то резонансный ин-
теграл на этом интервале равен
А(Ес,£) = у^|^ = 2|/2|^(Ен)(1--|/ф). (2.3.32)
Ес
Если Е'^>ЕС, то можно пренебречь вторым слагаемым в
(2.3.32) и тогда
Л (Ш = 2 /4- = °>45^ <2-3-33*
" сс
где численное значение соответствует Ес=0,5 эВ.
Как левая часть, так и параметры, входящие в правую часть
равенства (2.3.31), измеряются на опыте. Если эксперименталь-
ные данные не удовлетворяют равенству (2.3.31), то это озна-
чает, что существует уровень при отрицательной, но близкой к
нулю энергии (связанный уровень). В этом случае в проме-
жутке EK<zE<zEri, где Ег\ — энергия первого положительно-
го уровня, закон 1/и не справедлив и резонансный интеграл
по этому интервалу энергии не определяется формулой (2.3.32).
тт ок °т
Для примера на рис. 2.5 приведена величина —------- для
|/£н ат(£н)
238U, когда выполняется закон 1/и и отклонения от него наблю-
даются только при приближении к резонансу при Е=6,67 эВ*,
* В [96] показано, что экспериментальные данные для 0т(Е) при малых
энергиях согласуются с предположением, что 238U не имеет резонансных уров-
ней при отрицательной энергии. В справочнике [32] приводится уровень при
Е=—137 эВ, который не оказывает заметного влияния 0у(Е) при Е поряд-
ка Ея.
6—6053 81
и для 238Pu, когда имеется отрицательный уровень и закон 1/и
не справедлив. Видно, что кривые имеют разный характер.
Вычислим резонансный интеграл, если сечение описывается
изолированным резонансом (2.3.1):
_ f ^(E)dE = Г7 “• 7-^7 dE . _ £_gf -
J Е ° Г J V Е (1+х2)£’ Г/2 ’
Ес Ес
Если Ег—Ес»Г/2, то в медленно изменяющемся множителе
Е~3/2 можно положить Е=ЕГ и распространить интегрирование
по х до —оо. Тогда получим
А ~х~ ~Ё~ = ~2 Е~ а°’ (2.3.35)
Если имеется несколько неперекрывающихся уровней, то
полный резонансный интеграл равен сумме резонансных инте-
гралов по всем уровням:
А = 2 Ад (2.3.36)
I
Аналогично записывается резонансный интеграл деления и
поглощения, если заменить в (2.3.35) Гт на Г/ или Г?+Г/.
При таком приближенном вычислении интеграла (2.3.34) се-
чение вдали от резонанса, где справедлив закон 1/и, описы-
вается неправильно. Поэтому обычно к резонансному интегра-
лу (2.3.36) добавляют часть 1/и (2.3.33) и полный резонансный
интеграл записывают следующим образом:
7,1/и-
(2.3.37)
Такой способ записи справедлив, если ЕссЕг. В противном
случае надо в (2.3.37) ввести поправку:
(2.3.38)
где Afi/" — часть резонансного интеграла I/O, возникающая от
j-ro уровня. Функция f{EJEr) в формуле (2.3.38) изображена
на рис. 2.6 [аналитическое выражение для j (г) получено в за-
даче 2 в конце настоящего параграфа]. Из рисунка видно, что
при Ес/Ег>0,4 функция f становится отрицательной. Комбини-
руя (2.3.30), (2.3.33) и (2.3.35), получаем связь Ir,nv и А Для
данного уровня:
7</> Г
JV. Vv —
лр ЕГЕС
2
(2.3.39)
82
Во многих случаях (232Th, 238U,
240Pu и др.) резонансный интеграл
много больше, чем сечение при v =
= 2200 м/с, и тогда E/v в (2.3.37)
играет малую роль. Но если главные
резонансы сильно блокируются
из-за гетерогенной структуры ре-
актора (см. § 8.1), то относитель-
ная роль Ц/v возрастает и правиль-
ный учет этой части резонансного
интеграла становится существен-
ным.
Как следует из (2.3.25), допле-
ровское уширение резонансной ли-
нии не влияет на величину резо-
нансного интеграла бесконечного
разведения, и поэтому при малых
концентрациях поглощающего ве-
щества температура не влияет на
величину резонансного поглощения
(см. § 8.2).
Учтем теперь влияние поглощения нейтронов на спектр Фер-
ми. Если плотность потока нейтронов не зависит от координат,
то плотность замедления связана с плотностью потока уравне-
нием (2.2.25). Поглощение будем считать малым, и поэтому в
правой части (2.2.25) выразим Ф(Е) через п(Е) по формуле
(2.2.31), которая справедлива, если поглощение равно нулю.
Тогда получим
дп___Sa(E)
дЕ ~ №
^ + S(£).
Е
(2.3.40}
Интегрируя (2.3.40), будем считать, что Sa(E)=0 в той об-
ласти энергии, где S(E)#=0. В этом случае
n(E)=Sexp (—w(E')), (2.3.41)
где S — мощность источников, т. е.
S = J S (Е)
® (Е) = Г AIL _ bSEt, (2.3.42)
J Е
Е
где Ja(E)—макроскопический резонансный интеграл поглоще-
ния до энергии Е.
6* 83
В первом приближении можно (2.3.41) подставить в (2.2.31)
и тогда получим спектр нейтронов
ф (Е) = = S exp(-w(£)) (2 3 43)
i£s(£) tfsE
Это приближение будем называть возрастным (его называют
также приближением Ферми). Поглощение нейтронов нуклидом
1 теперь будет характеризоваться эффективным резонансным ин-
тегралом
£о
7‘ДЕ)=у 2£^1ехр[-®(Я)Ж (2-3.44)
Е
В некоторых случаях 1ад легко вычислить явно. Пусть име-
ется только один поглощающий нуклид, т. е. сечение оаг
в (2.3.44) совпадает с сечением поглощения в (2.3.42). Тогда,
вводя в (2.3.44) величину уи(Е) в качестве переменной интег-
рирования, получаем эффективный макроскопический резонанс-
ный интеграл поглощения (Ео) =0]:
а>
Ja3(E)^s\exp (—да) dw = (1 - exp (-w)) - Ja (£) S (£), (2.3.45)
о
где /а(Е)—макроскопический резонансный интеграл бесконеч-
ного разведения, а
С(£) = l-exp(-w(£))_ (2 3 46)
w (Е)
Если все сечения поглощения подчиняются закону 1/и, то
да(Е) = -^2, (£„)/-%; Sa‘'(£) = Sai(^I)]/4L’ (2-3-47)
поэтому
7:Э(£) = Л(Е)ЧЕ), (2.3.48)
где £(Е) совпадает с (2.3.46). Значение w(E) при Е—Ес будем
обозначать wc * Очевидно, что wc в этом случае пропорциональ-
но параметру жесткости у (2.2.21); если Е'с = 0,5 эВ, то
дас=0,45у. (2.3.49)
Диффузионное уравнение справедливо при выполнении усло-
вия (2.1.19). Если сечение поглощения удовлетворяет закону
* Не следует индекс с воспринимать как указание на то, что wc зави-
сит только от ос; в определение (2.3.42) входит сечеиие поглощения ва=
— Oc-j-Of.
84
l/v, то это условие приводит к неравенству
(2Л5О>
Для Л>1 должно быть дас<сЛ/4. Для тяжелой воды •0,5 и
условие применимости будет ьус<С1- В случае малых w имеем
С(Е) = 1-^(2:)+ J_W* (2.3.51)
2 6
Если нуклид I имеет один уровень при Е—Ег, а поглощение
выше этого уровня достаточно слабое, множитель ехр (—w) в
(2.3.44) можно вынести за знак интеграла при Е—Ег, т. е.
4 = Дехр(-ю(Д)). ' (2.3.52
Величина
<р(£)=ехр (—w(E)) (2.3.53)
во всех приведенных выше формулах имеет простой физический
смысл: это есть вероятность того, что нейтрон в процессе замед-
ления до энергии Е не будет поглощен [это определение следует
из (2.3.41)]. Величину <р(ЕД будем обозначать просто <р (см.
§ 1.9). Из (2.3.46), (2.3.42) и (2.3.45) имеем
1 — ? = w£c = = /аз{-Е} , (2.3.54)
т. е. 1—<р пропорционально эффективному резонансному инте-
гралу поглощения, что и соответствует физическому смыслу ве-
личины 1—ср.
Поскольку возрастное приближение справедливо только при
достаточно слабом поглощении, а сечения в максимумах резо-
нансных линий могут быть очень большими, необходимо рас-
смотреть более точную теорию. Полное рассмотрение задачи до-
статочно сложно. Здесь мы рассмотрим только основные момен-
ты, отсылая читателя за подробностями к специальной литера-
туре (см. [71] и указанную там обширную библиографию).
Пусть в сумме по / в уравнении (2.2.29) имеется два слагае-
мых: /=1 —легкие ядра, /=2— тяжелые:
2ДЕ)Ф(Е) =-----!--- I Г81Ф(£')4£' +
1 — soi ’ Е'
Е
-J-—1— f +iS(£). (2.3.55)
1— е02 а Е’
Е
85
Предположим, что масса тяжелого ядра столь велика, а
энергетический интервал Е<Е/<Е/е02 настолько мал, что вы-
ражение SsaO/f можно считать внутри этого интервала посто-
янным (приближение бесконечной массы поглотителя; ниже ус-
ловие применимости будет сформулировано более точно). Тогда
£/80 2
—С Zs&№\dE,^ ^2Ф(£) ф(£)
1 —*02 J Е’ е02
Е
и вместо (2.3.55) получим (eoi^eo):
£/8°
(Е) Ф (Е) = —— ( +S(E), (2.3.56)
1—ео J £
Е
где S;(E)=Sa(E)+Ss(E), причем S.s(E)—сечение рассеяния
только легких ядер, a Sa(E]—суммарное сечение поглощения
всеми ядрами.
Уравнение (2.3.56) легко решается для водорода, когда ео=
= 0 (этот результат был получен Г. Бете в 1937 г. [97]). Вместо
(2.3.56) имеем
2ДЕ)Ф(Е) =
Е'
+ S(E),
(2.3.57)
где Ео— максимальная энергия, выше которой S(E) и Ф(Е)
равны нулю.
Дифференцируя (2.3.57) по Е, получаем
— 2ДЕ)Ф(Е) =-----^(£)Ф(£) + S' (Е). (2.3.58)
dE Е
Если S/(E)=0, то (2.3.58) можно проинтегрировать:
(Е) Ф (Е) = (Ео) Ф (Ео) ехр f . (2.3.59)
,) Zt(E')Е
Е
Пусть источник S(E) моноэнергетический, т. е. S(E) =
= S6(E—Ео). Добавим в правую часть (2.3.59) Л6(Е—Ео) и
подставим в интегральное уравнение (2.3.57). Уравнение удов-
летворяется, если
X = S; Ф(ЕО) = —SSs(£o) -. (2.3.60)
W(E0)Et
Заменим в подынтегральной функции (2.3.59) Ss(E')=-
= Sz(E')—Sa(E') и положим Sa(Eo)=O. Тогда (при Е^Е0)
С
Ф(Е) = —exp(-w(E)),
bf(c) Е
(2.3.61)
86
где
w
С____Sg(E')
,) 2И£')+2а(Е')
dE'
Е' ’
(2.3.62)
что отличается от (2.3.42) только заменой полным сечением
Sa+Ss (для водорода £—1). Таким образом, в случае бесконеч-
ной массы ядра поглотителя и водородного замедлителя веро-
ятность избежать резонансного поглощения при замедлении до
энергии Е дается выражением
Ф (£) = ехр
Sa(E')dE'
J [Ss(£') + Sa(£')J Е'
(2.3.63)
где Ss учитывает только рассеяние в водороде.
Перейдем теперь к случаю произвольного замедлителя и рас-
смотрим только наиболее важные приближенные результаты.
Следующее рассуждение заимствовано из монографии Вейнбер-
га и Вигнера [69]. Заменим поглощение рассеянием. Тогда
плотность полного потока нейтронов, возникших от единичного
источника быстрых нейтронов в асимптотической области энер-
гии, будет
Фт=(£2^)-!.
Плотность потока Фт есть сумма плотности действительного по-
тока нейтронов, условно назовем их «белыми», и плотности фи-
ктивного потока, вызванного заменой поглощения рассеянием,—
эти нейтроны назовем «черными» *. Вероятность того, что в про-
цессе замедления нейтрон, белый или черный, примет значение
энергии в интервале (E-^-dE, Е), равна (в силу стационарности
процесса) числу нейтронов, покидающих этот интервал, т. е.
Фт2/^£= (сЕ)~]с1Е. Вероятность того, что нейтрон станет чер-
ным при уходе из этого интервала, т. е. поглотится, равна
dE Sa
——• Следовательно, вероятность того, что нейтрон не ста-
1 dE о
нет черным, т. е. не поглотится, равна 1----Предпола-
гая, что вероятности попадания нейтронов в различные энерге-
тические области статистически независимы, получаем вероят-
ность избежать резонансного поглощения при замедлении до
энергии Е:
г Е°
-гт /i dE \ f S0(E')dE' ,o Q д.,
<p (E) = П 1----------) =sexp — --------—— --------- . (2.3.64)
u E J
* Вейнберг и Вигнер в своей монографии указывает, что схема этого
рассуждения принадлежит Эйнштейну.
87
Этот результат обычно называют приближением Вигнера.
Независимо он был получен Ахиезером и Померанчуком [98J
путем приближенного решения точного уравнения для величины
ф(£).
В дополнении III показано, что формула (2.3.64) справедли-
ва, если выполнены следующие два предположения: а) замед-
лением на ядрах поглотителя можно пренебречь (приближение
бесконечной массы поглотителя) и б) поглощение обусловлено не-
перекрывающимися уровнями, причем поглощение в каждом
уровне мало, т. е. если представить In [<р(Е) ]_ 1 = w (Е) в виде
суммы по уровням
/
то должно быть
(2.3.65)
но не обязательно г^(Е)С1.
Очевидно, что если 2a<CSs, то (2.3.64) переходит в (2.3.53),
где w(E) определяется (2.3.42). Если возрастное приближение
применить к случаю, когда SQ=oo в некоторой узкой области
энергии, то получим <р=0. На самом деле при этом ср^О, по-
скольку нейтрон может «перескочить» опасную зону, если она
достаточно узка. Однако если Sa=oo в интервале (Е, Е'), та-
ком, что (Е—Е')/Е>е.о, то нейтрон не может перескочить зону
сильного поглощения при одном столкновении и поэтому долж-
но быть <р=0. Между тем из приближения Вигнера (2.3.64) сле-
дует, что, если (Е—Е')/Е=го, то
Г
J sa + z; IE
dE ____ ln( 1 — e0)
~Ё I
(2.3.66)
При A^>1 правая часть (2.3.66) равна 2, т. е. вместо <р = 0 по-
лучим <р=ехр (—2)<С1. Отсюда можно заключить, что прибли-
жение Ферми завышает, а приближение Вигнера занижает ре-
зонансное поглощение. Очевидно, что согласно критерию
(2.3.65) формула (2.3.64) и не обязана давать правильный ре-
зультат в этом случае, поскольку поглощение в некотором узком
интервале не мало.
Проанализируем более подробно формулу (2.3.64). Вычис-
лим W, для изолированного уровня с естественной формой ли-
нии (индекс / опустим):
(2.3.67)
88
Полагая, как и ранее, в медленно изменяющихся функциях
Е=ЕГ1 распространяя интегрирование по х до — оо, получаем
= . ^гай0 + (2.3.68)
2g£rSs \ Ss / ’
или, обозначая
= (2.3.69)
имеем для микроскопического резонансного интеграла
Лэ = 4(1 + ^;“1/2, (2.3.70)
где резонансный интеграл 1а определен (2.3.35). Очевидно, что
при малых концентрациях поглощающего вещества 1аэ=1а,
а при больших, когда Eao2>Ss,
» = (2.3.71)
т. е. резонансное поглощение при малых концентрациях растет
пропорционально первой степени, а при больших'—корню квад-
ратному из концентрации поглощающего вещества.
Сформулируем более точно условия применимости приближе-
ния бесконечной массы поглотителя. Назовем шириной опасной
зоны АЕ энергетическую область, где поглощение существенно
(эту величину называют также практической шириной резонан-
са). Величину ДЕ определим из следующего условия: при Е—
= Ег-(-АЕ/2 подынтегральная функция в (2.3.67) в 2 раза мень-
ше, чем в максимуме, т. е. при Е=ЕГ (в медленно меняющихся
функциях положено Е=ЕГ):
+ 1. (2.3.72)
Условие применимости состоит в том, чтобы, с одной сторо-
ны, АЕ было много меньше расстояния между уровнями D
(в противном случае их нельзя считать неперекрывающимися),
а с другой, АЕ — много больше скачка энергии при столкнове-
нии с ядром поглотителя:
(1—е0)Ег<ЛЕ«Е>. (2.3.73)
Если считать, что для нижних уровней D—'Ег, то должно
быть
+ 1 ^1. (2.3.74)
При увеличении энергии резонанса Ет левое неравенство бу-
дет нарушено (ширина Г практически мало меняется при уве-
89
личении энергии резонанса, а £а0, как правило, уменьшается),
т. е. приближение бесконечной массы поглотителя не будет спра-
ведливо. Роль этих уровней 238U в реакторе на тепловых ней-
тронах невелика (более детальное обсуждение проведено
в гл. 8 применительно к резонансному поглощению в гетероген-
ном реакторе).
Рассмотрим теперь противоположный случай, когда резонанс
можно считать узким по сравнению со скачком энергии нейтро-
на при столкновении с ядром поглотителя (приближение узкого
резонанса). В этом случае плотность потока нейтронов возму-
щается только в интервале, малом по сравнению с областью
интегрирования в обоих интегралах в правой части (2.3.55). По-
этому можно в правую часть (2.3.55) подставить вместо плот-
ности потока Ф ее асимптотическое значение
Ф (Е') = [ (^Ssi+g2SP) £']->, (2.3.75)
где индекс 1 относится к замедлителю, 2 — к поглотителю, при-
чем учитывается только потенциальное рассеяние на поглотите-
ле (вдали от резонанса os=oP). В результате из уравнения
(2.3.55) получаем
Ф(Е) = [^(Е)Е]-1; 1= (giS^+^Sp)^-1; S.=Ssl+SP, (2.3.76)
где S(E)—полное сечение, т. е. включающее в себя резонанс-
ное рассеяние на поглотителе. Количество поглощенных нейтро-
нов будет равняться
w = j 2Й (Е) Ф (Е) dE = 4- J-|^ . (2.3.77)
Эффективный резонансный интеграл для одного уровня, се-
чение которого описывается формулами (2.3.1), (2.3.6), получа-
ется равным
+ о°
./ = f ---------------= , (2.3.78)
ЧЕГ I х2 + 6х+с |/с —&2
—оо
где 1а дано (2.3.37); 6 = }AypS0/(]A с = 1 + S0/Ss.
Формулу (2.3.78), если учесть (2.3.2), можно переписать так:
Г 20 / 2, \ 1-1/2
I аз - 1а [1 +-27(1 • <2-3-79)
Этот результат отличается от (2.3.70), во-первых, заменой
Оао на со в отношении 7аэ//а, т. е. сечение поглощения в макси-
муме заменяется полным сечением, и, во-вторых, поправкой,
пропорциональной потенциальному рассеянию (она является
следствием интерференции потенциального и резонансного рас-
90
сеяний). В реакторах на тепловых нейтронах последняя поправ-
ка мала, хотя в некоторых случаях она становится существен-
ной. Например, интерференция играет большую роль для уровня
Fe при Е=27,7 кэВ или для уровня 238U при £=190 эВ (см. по-
дробнее [71]).
Если учитывать доплеровское уширение резонансных линий,
то эффективный резонансный интеграл (при пренебрежении ин-
терференцией потенциального и резонансного рассеяний) надо
записать так:
V = A№0); 0 = -К (2.3.80)
"а о
где 1а определено (2.3.35) и
4- оо
] (С Р) = j- f —dx, (2.3.81)
° ' "J Р+Ф(х, ?о) 1 ’
—00
причем ф дано (2.3.17). Исследованию функции J(£0, Р) посвя-
щено много работ (см. [70, 71, 99] и, например, [100]). График
функции J имеется, например, в [99].
Отметим, что для чисто доплеровской формы линии [см.
(2.3.24)], когда фо^О, получим
-hoo
;<°'р>=дМ
—оо
и IaD—Ia, т. е. при очень высокой температуре сечение в макси-
муме линии столь сильно уменьшается, что поглощение стано-
вится слабым. Поведение функции J(£0, Р) при р^>1 разобрано
в задаче 4 в конце настоящего параграфа.
Случай малых 1/р (см. задачу 4 в конце этого параграфа)
реализуется в реакторах на тепловых нейтронах, если вычисля-
ется резонансное поглощение 235U или 239Ри. Тогда эффект гете-
рогенности невелик и можно пользоваться гомогенным прибли-
жением.
Наиболее общий случай промежуточного резонанса с учетом
доплеровского уширения и интерференции резонансного и по
тенциального рассеяния рассмотрен, например, в [101].
Остановимся еще на одном методе определения плотности
потока замедляющихся нейтронов в среде с поглощением (ме-
тод Грюлинга — Герцеля [71, 102, 103]. Запишем уравнение для
плотности замедления (2.2.24):
п(и) = С exp(u'~u)~ ^ф(ц')^'; (2.3.82)
J 1—ео
и—г
ф (и') = S/D (и'); г = 1п —.
о
91
Если плотность потока не сильно изменяется внутри проме-
жутка интегрирования (т. е. если поглощение не слишком силь-
ное), то можно разложить в ряд
ф(и') = ф (и)+ («' — «)—. (2.3.83)
ди
Подставив разложение (2.3.83) в (2.3.82), получим
п (и) = ? ф (и) — , (2.3.84)
ди
где
£'= f exP«-M).-£-0- (ц' _ и) du' = ! — — —(1пе0)2. (2.3.85)
J 1— ео 2 1 —е0
и—г
Плотность замедления^ удовлетворяет уравнению [см.
(2.2.5), где надо перейти к логарифмической шкале; S(u)=0]:
-J- = _SaO(u) (2.3.86)
ди
или при использовании (2.3.84)
^-£'-^- + 2аф(«) = о. (2387)
ди ди2
Для оценки второй производной, которая по условию мала,
можно воспользоваться приближенной связью п=£ф, т. е.
ди, g ди2 £ ди а
или, подставляя в (2.3.87),
^-[('^ + -^2а')ф] + 2цФ-0. (2.3.88)
ди [\ § / J
Сравнивая (2.3.88) с точным уравнением (2.3.86), получаем
и(ц)=?(25+?12й)Ф(ц); £1 = ГГ2 (2.3.89)
или, выражая отсюда Ф(и) через п(и) и подставляя в (2.3.85),
имеем уравнение для плотности замедления
дп 2а / \
-- _---------2----п (и\
ди g(Sa + ^Sa)
решение которого дает вероятность избежать резонансного по-
глощения:
г Е°
= п(Е) _ С ----------?a(E)dE— (2.3.90)
u Е J
92
При А=1 параметр £1 = 1, а при А»1
(2.3.91)
Для тяжелого поглотителя возникает отклонение от формулы
(2.3.64). В самом деле, для смеси элементов надо записать [см.
(2.2.18)]:
+ Xso so. (2.3.92>
Если для поглотителя Д^-оо, то £д = 0, £'л=0 и из (2.3.92)
выпадает сечение рассеяния на поглотителе. Поэтому в (2.3.90)
как g, так и gi надо вычислять только для замедлителя. Для
водородного замедлителя gi = l и результат совпадает с точным
решением, но, например, для дейтерия gi=0,8 и сечение погло-
щения, в отличие от (2.3.64), входит с множителем £1<1.
Это приближение нельзя применять буквально к вычислению
резонансного поглощения сильным уровнем, но оно может слу-
жить отправной точкой для построения вычислительных схем,
которые отписывают более сложные случаи резонансов с про-
межуточными свойствами (между приближением бесконечной
массы поглотителя и приближения узкого резонанса [71]).
Поскольку теория резонансного поглощения в гомогенной
среде непосредственно не применима к гетерогенному реактору,
здесь не сравниваются теория с экспериментом и приближенные
формулы с результатами численных расчетов. Для гетерогенно-
го реактора такое сравнение проведено в § 8.6.
Задача 1. Рассмотреть функцию ф(х, £0) при £0»1.
Решение. Заменив в (2.3.17) //=x-'-2Lj-'‘z, получим
+ оо
Ф(х, ?о) = ~~7-~ I ехр( —г2)[1 4-х24-4хг?0-1 + 4г2?0—2]-1<iz,
У 7С J
— 00
откуда, разложив в ряд по 1/£0 и вычислив интегралы, имеем [см. также
формулу (2.3.27), полученную при х2> 1]:
Ф(х, ?о) = (1+^)"1
Таким образом, при малых х (т. е. в центре линии) поправка к естест-
венной форме _лииии отрицательна — сечение в центре линии уменьшается,,
а при x>l/V3 поправка положительна — линия делается более широкая
(см. рис. 2.4).
Задача 2. Определить функцию f(z) в формуле (2.3.38), считая е =
=Г/(2£л) малым параметром.
_ 2 1 —Зх2 ]
?оа (1+х2)2]
93-
Решение. Формула (2.3.34) дает 71 = 7[СС, где /т° определено
(2.3.35), а
00 оо
С = — ( х~3,2[(х—1)2+ е2]~1 dx = —Im х~3/2 (х—а2) i>;
7С J ТС J
г г
е=Г/(2£г); z=£c/£,; a2=I-|-ie.
Сделав замену переменных х=у~2, получим
1//Г
г Ат 1 f У^У
С~~ я Im .) /,8-а-2 “
о
причем под In понимается главна^ ветвь: если М— |Л41 exp (icp), то 1п М =
=1п |Л4|-|-1ф, ]ср | <л. При е<^1 из (2.3.93) имеем
C=l+ — f(z), (2.3.94)
те
где
Используя формулу
.дующий результат (см.
(2.3.39), получаем для функции f(z) в (2.3.38)
рис. 2.6; формула справедлива и при г>1):
сле-
/ г - 1 / 1 \ 3 , г—
= Т1/г п
1 + |Л_
1 —/г
Можно получить формулу для С и без разложения по е:
2 2 + п /2г (1 + «) ,
теи2 [ |/г и 1/2(1 -j-u) u-j-z
(2.3-95)
2 — и
u|/2(u — 1)
К 2г(и— 1)
те—arctg----------
и—г
U2=14-e2. (2.3.96)
Задача 3. Решить задачу 2 для формы линии (2.3.16).
Решение. В этом случае имеем
Е
dE
---— / of
£ I л’
где /у0 определено (2.3.35), a CD равно
4-оо оо
4 р / 1 \ р dx
С п =--------т=т I ехр — — Ёп2 у2 Im I —7^5--------------du.
D 2тт/те J 4 ° У / .) х3/2 (х-а2) у’
—оо г
причем введены те же обозначения, что и в задаче 2, за исключением
a2=l+O+i)e2-
94
Из (2.3.93) следует
+ оо
1 1 (, a +|/z \
Xlm — /-— — ——I In---------------j dy. (2.3.97)
. а2|/ z 2a3 \ а — ]/г
При разложении (2.3.97) по e надо опустить линейные члены по у, по-
скольку при интегрировании они обратятся в нуль. Линейные поправки
к (2.3.94) отсутствуют. Квадратичные члены по е дают
15 _/2 \
77-1 . (2.3.98)
16 \ Со /
где /о (г) дано (2.3.95). Например, для первого уровня 238U имеем (при
7=400 К, go=O,39, см. § 8.2): е=0,002, У?=0,274 и f(z)—f(z0) =0,02.
Задача 4. Вычислить функцию 7(^о, ₽) (2.3.81) при малых ₽-1 =
===SaO /2s-
Решение. При малых 1 /р можно разложить в ряд
+ 00
ЦЪ, ₽) = — f ф(х, ?о) 1 - 77 ф(х, ?о) dx
л J L Р
и проинтегрировать
'(?о, Р)= 1--^гЖ), (2.3.99)
2р
где
F(?o) =-l^-?oexp (у ?02) [1 —erfp^[. (2.3.100)
При ^0-+-°° (естественная форма линии) 7(£о) = 1 и (2.3.99) согласуется
с (2.3.70) при S0/Ss«l.
2.4. СПЕКТР НЕЙТРОНОВ В РЕАКТОРЕ.
СКОРОСТЬ РЕАКЦИЙ
Если поглощение нейтронов очень мало, а размеры реактора
велики, так что утечка нейтронов не играет роли, то нейтроны
можно рассматривать как газ, находящийся в термодинамиче-
ском равновесии со средой*. В этом случае энергетический
* Плотность потока тепловых нейтронов в реакторе обычно находится
в интервале 1013—1015 нейтр/(см2-с). Если скорость нейтронов 105 см/с, то
плотность нейтронного газа 10s—1010 см-3, т. е. нейтронный газ чрезвычай-
но разреженный (число молекул в 1 см3 газа при нормальных условиях
«IO19). Поэтому можно пренебречь влиянием нейтронов на термодинамиче-
ские характеристики среды. Но в то же время плотность потока нейтронов
в реакторе надо считать очень большой, если сравнивать ее с плотностью
потока нейтронов в космических лучах на поверхности Земли, которая по-
порядку величины равна 10-3 нейтр/(см2-с).
95-
спектр нейтронов описывается максвелловским распределением
р / F \
Ф(Е) = ц¥(Е) = Фм —ехр (2.4.1)
Су \ £у /
где Er=kT', k — постоянная Больцмана; Т — абсолютная темпе-
ратура среды и нейтронов. Спектр (2.4.1) нормирован так:
[ф(£)й£ = Фм.
б
Напомним, что среднее значение энергии в максвелловском
•спектре равно
оо
J EN(E) dE
Ё = = А Ет, (2.4.2)
£ N(E)dE
о
а среднее значение И Е
(2.4.3)
Функция Ф(£) (2.4.1) максимальна при Е = ЕТ, т. е. £т —
наиболее вероятное значение энергии. Определяя среднее сече-
ние в максвелловском спектре, надо интегрировать произведе-
ние о(£)Ф(£), а не o(E)N(E), поскольку число реакций, вы-
званных нейтронами с энергией Е, пропорционально gvN=
=о(£)Ф(£). Следовательно,
[а(Е)Ф(£)<|Е
S = -----------=p(£)JLexp(-£).|£. (2.4.4)
J®(E)dE °
О
Пусть о(Е) удовлетворяет закону 1/и. Тогда
(2.4.5)
Л г Е у
В качестве стандартной энергии нейтрона обычно берут £н—
= 0,0253 эВ. Скорость нейтрона, кинетическая энергия которого
равна £н, будет ин=2200 м/с. Если записать kTK=EK, то Т,,-—
= 293,6 К=20,4°С, т. е. 2200 м/с — наиболее вероятная скорость
нейтрона при температуре 20,4°С. Средняя квадратичная ско-
рость при этой температуре равна
v2 = ]/'~yvh = 2694 м/с,
96
а средняя арифметическая равна
v = пн = 2482 м/с. (2.4.6)
[/ л
Если сечение отклоняется от закона 1/ц, то вместо (2.4.5)
напишем
а = -у/ JEl а (Ен) g, (2.4.7)
где g равно (фактор Весткотта [104])
ОО
g = fo(£’)£'exp (2.4.8)
у л I \ Ет /
О
Множитель g является удобной характеристикой отклонения
сечения от закона l/v. Например, для 235U g всего на несколько
процентов меньше единицы, а для изотопов плутония (239Ри,
241Pu) g заметно превышает единицу. Множитель g является
функцией температуры нейтронов (см. приложение IV и гл. 12).
Учет поглощения приведет к тому, что спектр нейтронов бу-
дет отличаться от максвелловского (см. § 7.5). При этом, по-
скольку нейтроны приходят в тепловую группу, замедляясь,
а медленные нейтроны более интенсивно поглощаются, быстрых
нейтронов будет больше, чем по распределению Максвелла, а
холодных меньше. Тем не менее если поглощение не очень силь-
ное, то можно в некотором приближении по-прежнему описы-
вать спектр нейтронов в тепловой группе распределением Мак-
свелла, но с более высокой температурой, чем температура за-
медлителя Е3:
Ет=гЕ3. (2.4.9)
При больших энергиях (по сравнению с Ет) спектр Максвел-
ла должен переходить в спектр Ферми (см. § 2.2). Поэтому Ет
не является ни средней энергией по всему спектру нейтронов
(средняя энергия по спектру Ферми близка к энергии нейтронов
деления и не имеет никакого отношения к тепловой группе), ни
средней энергией по тепловой группе, поскольку верхняя грани-
ца тепловой группы обычно проводится так, что захватываются
часть спектра Ферми и переходная область между максвеллов-
ским и фермиевским распределениями. Величина Ет является
просто удобным параметром для описания спектра, который пе-
реходит в температуру при достаточно малом поглощении. Сде-
лав такие оговорки, мы для краткости будем называть
Ет температурой нейтронов.
7-6053 97
Таким образом, будем описывать спектр нейтронов в реакто-
ре двумя функциями:
Ф1(£)=-±_£ехр(--|-), Е<ЕС; (2.4.10)
ф (£) = Sexp[-a)(E)] Е>Е (2.4.11)
$SsEx(E) с' v '
причем должно соблюдаться условие непрерывности
Ф1(Ес)=Ф2(£с), (2.4.12)
где Ес — верхняя граница тепловой группы нейтронов. В фор-
мулах (2.4.10), (2.4.11) С — нормировочная постоянная; S —
мощность источника замедляющихся нейтронов, множитель
ехр (—w) учитывает отклонение от спектра Ферми,’ вызванное
поглощением нейтронов [см. (2.3.43)], множитель х(Е)—от-
клонения от спектра Фермщза счет движения ядер (см. ниже).
Влиянием утечки на спектр по-прежнему будем пренебрегать,
т. е. будем рассматривать достаточно большой реактор.
Мощность источников пропорциональна числу делений в еди-
нице объема (в реакторах на тепловых нейтронах можно счи-
тать, что v не зависит от энергии):
оо
S = v J (Е) Ф (Е) dE. (2.4.13)
о
Если имеется несколько делящихся нуклидоЁ, то (2.4.13)
надо заменить суммой аналогичных выражений по всем сортам
делящихся нуклидов или заменить v средним значением
2 V/ Jsf/(E)<I>(E)rfE
v = —'----------------, (2.4.14)
2 ]\/(£)Ф(Е)4£
/
а под Sf в (2.4.13) понимать суммарное макроскопическое сече-
ние деления.
Поскольку утечкой пренебрегается, количество рожденных
нейтронов должно равняться количеству поглощенных. Поэтому
вместо (2.4.13) можно написать
ОО
5= [%а(Е)Ф(Е)с1Е. (2.4.15)
о
Подставим (2.4.10), (2.4.11) в интеграл (2.4.15). Имея в ви-
ду, что
dw=-^d\
%EsEn.(E)
98
получаем
00
( 2а (Е) Ф2 (Е) dE = S(1 — ехр(—®)); w = w(Ec). (2.4.16)
К
Интеграл по тепловой группе обозначим так:
СГ2а(Е)Ф1(Е)^Е = 2аФт, (2.4.17)
6 ' I '
где 2а — среднее сечение поглощения в тепловой группе; Фт —
плотность потока в тепловой группе, т. е.
Ес
Фт = Фх (£) dE == С [1 — (* + 1) ехр (— л)]
о
(2.4.18)
и
х=Ес[Ег. • (2.4.19)
Таким образом, из (2.4.15) находим
5=2аФт ехр (®). (2.4.20)
Это равенство имеет простой смысл и может быть написано
без каких-либо вычислений. Если утечка отсутствует, то количе-
ство нейтронов, поглощенных в тепловой группе, т. е. 2аФт, рав-
няется мощности источника, умноженной на вероятность того,
что нейтрон не будет поглощен при замедлении <р=ехр (—w).
В результате получаем формулу (2.4.20).
Условие непрерывности (2.4.12) дает
х2ехр( — х)*(Ес) _ 2а ______
1 — (х+ 1)ехр(— х) ~ = ^т'
(2.4.21)
Если справедлив закон 1/и, то
2а = -^ 2а (Ен) Уf0 (х), (2.4.22)
где
2 Л-
erf I/ х — , у х ехр(—х)
|/ л
1 —(х+ 1)ехр(— х)
у*
(2.4.23)
99
При х>1 функция fo(x) близка к единице: f0(3) = 1,11; fo(5) =
= 1,024. Если закон l/v не справедлив, то
So= -^SO(£H) (2.4.24)
2 Г Er
где множитель fa аналогичен множителю g в (2.4.8). При х^>1.
fa совпадает с g. Введем отношение
хз = “ = Лг> (2.4.25)
где Е3— температура замедлителя в энергетических единицах
и z определено (2.4.9). Обозначим величину
Ь = = (Ен) Уfa (^Г- (2.4.26)
Естественно сделать предположение, что отклонение эффек-
тивной температуры нейтронов Ет от температуры замедлителя
пропорционально поглощению Sa, т. е.
z=l-)~ay3, (2.4.27)
где а — некоторая постоянная (а^2^-3, см. ниже).
Уравнения (2.4.21), (2.4.27) с учетом (2.4.25), (2.4.26) позво-
ляют построить зависимость х3 от у3. Такая зависимость (при
и=1, fa—1, а=2) представлена на рис. 2.7. Из рисунка видно,
что х3 заключено в сравнительно узком интервале (если у3<
<0,7):
Рис. 2.7. Зависимость Хз=Ес1Е3 и
и х--Ес!Е3 от у3 (2.4.26) (штри-
ховой линией показан результат
решения задачи в § 2.4)
7<л3 = -^-<8. (2.4.28)
Е3
Таким образом, верхняя гра-
ница тепловой группы Ес сравни-
тельно слабо зависит от жестко-
сти спектра и определяется глав-
ным образом температурой за-
медлителя. Если температура за-
медлителя равна 300 или 1000 К,
то Ес равно соответственно 0,2
или 0,6—0,7 эВ.
Определим отношение плот-
ности потока на границе тепло-
вой группы Ф(ЕС) к средней
плотности потока в тепловой
группе. Используя (2.4.20), полу-
чаем (при оу<С1):
= = гт, (2.4.29)
Ф1 |т
100
т. е. при ут<1 плотность потока замедляющихся нейтронов мно-
го меньше плотности потока в тепловой группе. При у3—1 имеем
х—-3 (при этом уТ‘—1/2). В этом случае
Ес °°
[ Ф! (Е) dE = 0,8 [ Ф (Е) dE-, Oj (Ес) = 0,4®! (Ет).
о 6
При еще больших значениях у3 спектр в тепловой группе может
сильно отличаться от максвелловского и простая аппроксима-
ция (2.4.9), (2.4.10) теряет смысл.
Чаще, однако, надо сравнивать интегральные плотности по-
токов в тепловой группе и группе замедляющихся нейтронов
(при а'С 1):
Е,
= ф->Г ф2(Е)dE = Тт In-А . (2.4.30)
Фт J Ес
Ес
Поскольку In (Ео/Ес) ~ 16, даже при ут = 0,14-0,2 отношен
(2.4.30) порядка или больше единицы.
Зависимость х3 от у3, изображенная на рис. 2.7, получена на
основании двух неравноценных по своему значению утвержде-
ний: закона сохранения нейтронов, который содержится в ра-
венстве (2.4.15) и для достаточно больших реакторов всегда
выполняется, и предположения (2.4.27) с конкретным значени-
ем а=2. Второго предположения можно не делать, если исполь-
зовать другой точный закон—закон сохранения энергии: кине-
тическая энергия всех рожденных нейтронов равна сумме энер-
гии, переданной нейтронами ядрам замедлителя при столкнове-
ниях, и кинетической энергии поглощенных нейтронов. При вы-
числении надо воспользоваться какой-то моделью, описывающей
столкновения нейтронов с ядрами замедлителя. В [105] полу-
чены конкретные результаты для простейшей модели столкно-
вения упругих шаров (см. задачу в конце параграфа). Линей-
ная зависимость (2.4.27) подтвердилась с хорошей точностью,
причем а=2,5 для атомной массы замедлителя А=4 и а=3 для
А = оо.
Надо иметь в виду, что гетерогенная структура реактора мо-
жет внести существенные поправки в полученные здесь резуль-
таты (см. § 7.5). При этом нейтроны в блоке топлива оказыва-
ются заметно более горячими, чем по расчету с применением
изложенных здесь соображений, относящихся к гомогенному ре-
актору.
В [105], кроме того, получена функция
X (£) = [1 -2 (1 --М 4-1 + ^44. (2.4.31)
L \ 2Д / £ J
101
где А — атомная масса замедлителя;
£1=2(1—ео)-1—^1, (2.4.32)
что близко к параметру Грюлинга — Герцеля (2.3.89), а при
Л=1 и Л^>1 совпадает с ним. Первое слагаемое с (2.4.31) обу-
словлено движением ядер замедлителя.
Применим аппроксимацию спектра (2.4.10), (2.4.11) к опре-
делению скорости образования или уничтожения нуклидов в ре-
акторе. В каждом реакторе «сгорают» одни нуклиды и появля-
ются другие. Это могут быть как превращения в специальных
Мишенях, предназначенных-для производства искусственных ну-
клидов, так и изменения в составе топлива [«сгорание» 235U, по-
явление и сгорание изотопов плутония (см. подробнее гл. 13)].
Скорость образования или уничтожения нуклида определя-
ется величиной F (число реакций в,единице объема в единицу
времени в расчете на одно ядро мишени):
F = J о (Е) Ф (Е) dE. (2.4.33)
. о
Подставив (2.4.10), (2.4.11) в (2.4.33), получим
F = OTa + S-^-C, (2.4.34)
где Фт — поток нейтронов в тепловой группе (2.4.18); ст—сред-
нее значение о(Е) в тепловой группе; S — мощность источников
замедляющихся нейтронов; I — резонансный интеграл бесконеч-
ного разведения, а в множителе £ содержатся все поправки
к идеальному спектру Ферми не только за счет искажения энер-
гетического спектра, но и за счет гетерогенной блокировки резо-
нансного поглощения (см. гл. 8). В такой общей форме, пока не
использованы конкретные приближения для <т и £, формула
(2.4.34) является точной. Фактически от аппроксимации (2.4.10),
(2.4.11) здесь заимствована только целесообразность разбиения
спектра'нейтронов на две области — тепловые нейтроны и за-
медляющиеся. Поэтому Ес не обязано совпадать с концом мак-
свелловского спектра, как в (2.4.12), а просто является верхней
границей тепловой группы, например Ес==0,5 эВ (см. § 2.2).
Мощность источников S можно выразить через удельную
мощность реактора, т. е. мощность, выделяющуюся в единице
объема W:
S=vW/Ef, (2.4.35)
где Ef — энергия, выделяющаяся в одном акте деления (см.
§ 1.7). Если в реакторе имеется несколько делящихся нуклидов,
102
то v и Ef надо заменить средними значениями:
\2п(Е)Ф(Е)аЕ
—г—;--------------’ (2-4-36)
f f %Ef/ j2r/(E)<P(E)dE
i
a v определено формулой (2.4.14). Из данных § 1.7 видно, что
Е^ почти одинаковы для всех делящихся нуклидов, и поэтому
в большинстве случаев можно положить Ef!=Ef. Формулу
(2.4.34) можно применить и для определения числа делений:
W ~ W
— — Фт,- Н------------wf,
Ef т' ' т E[ f’
(2.4.37)
где
wf= ls7
(2.4.38)
Фт/ — плотность потока тепловых нейтронов в топливе; Sf —
среднее макроскопическое сечение деления в тепловой группе;
Jf — макроскопический резонансный интеграл бесконечного раз-
ведения; &— множитель, аналогичный £, но относящийся к ре-
зонансному интегралу деления. Из (2.4.37) получим
(2.4.39)
Если обозначить- 3 отношение
нейтронов в мишени и топливе
плотностей потоков тепловых
Р=фт/фтГ, (2.4.40)
то для скорости реакции F (2.4.34) имеем следующий результат:
Формулу (2.4.41) можно записать и так:
Е^ФтО,
где
° =° + тЛ; Л =
vS;
(2.4.41)
(2.4.42)
(2.4.43)
(2.4.44)
ioa
Если в реакторе присутствуют несколько различных деля-
щихся нуклидов, то (при Efi=Ef)
^'1'4 }fi^fi
T = ' (2.4.45)
Таким образом, эффективное сечение а состоит из двух сла-
гаемых: среднего сечения в тепловой группе сг и произведения
эффективного резонансного интеграла, /Э=/С на параметр жест-
кости у [ср. формулу (2.2.21); новое определение у (2.4.44) яв-
ляется более точным; здесь всюду понимается в смысле
(2.2.18)].
Из формулы (2.4.41) видны основные факторы, определяю-
щие скорость реакции Е; удельная мощность реактора W/Ef,
тепловое сечение о, резонансный интеграл It,, замедляющая спо-
собность среды Для получения максимальной скорости ре-
акции надо иметь максимально высокое удельное энерговыделе-
ние в реакторе. Первое слагаемое в (2.4.41) растет при умень-
шении Sf, т. е. при уменьшении количества топлива в единице
объема (а значит, и при уменьшении жесткости). Однако если
/э^>о, то даже при малых у первое слагаемое в (2.4.41) не иг-
рает заметной роли и уменьшение S; не приводит к сильному
росту F (очень значительно уменьшать нельзя, так как при
этом возрастает относительная роль вредных потерь в реакто-
ре). В этом случае надо уменьшать т. е. использовать пло-
хие замедлители, если только это разрешается условиями кри-
тичности (при уменьшении возрастают длина замедления и
резонансное поглощение). Наоборот, если сг^/э, то надо стре-
миться к возможно более мягкому спектру в реакторе.
Коэффициент при резонансном интеграле в (2.4.41)
ф==_2_ JL
Ef
равен плотности потока замедляющихся нейтронов на единич-
ный интервал летаргии (если не учитывать поглощения). Для
235U имеем
Ф=7,5-lO13(^Ss)“4Fo, (2.4.46)
где измеряется в см-1; IFo — удельное энерговыделение,
МВт/л.
Отметим, что в согласии с (2.4.43), (2.4.44)
Sf = 2f(l— wf)-\ (2.4.47)
Поэтому формулу (2.4.39), которая устанавливает связь между
плотностью потока тепловых нейтронов и удельной мощностью,
104
можно записать так:
Фт=4-(%)-’. (2.4.48)
Пусть в реакторе имеется один делящийся нуклид — 235U.
Подставляя числа в (2.4.48), получаем
Фт =2,07-1013Р Ч(£— нейтр/(см2-с), (2.4.49)
где Р — мощность, МВт, выделяющаяся в реакторе на 1 кг 235U.
Используя формулы (2.4.24), (2.4.47), находим
2^ = -L- 1/-^ (2.4.50)
°f5 |/"я F Ен ff5
где ff5 — множитель, аналогичный fa в (2.4.24), но для сечения
деления 235U. Таким образом, плотность потока в тепловой груп-
пе, или просто плотность потока тепловых нейтронов, зависит не
только от удельной мощности Р, но и от эффективной темпера-
туры нейтронов. Удобно условиться, что значение Фт использу-
ется для вычисления числа реакций с нуклидом, сечение кото-
рого подчиняется закону 1/у. Это сечение содержит множитель
у/. и поэтому если положить
2 Г £т
ф = ф«= 2,07-1013Р(£-2^) нейтр/(см2-с), (2.4.51)
т т
то надо всегда умножать Фт° на сечение, взятое при энергии
Ев *. Выражение (2.4.51) содержит множитель 1—Wf, учитыва-
ющий деления, вызванные замедляющимися нейтронами, и мно-
житель )f5. Последний для 235U близок к единице и мало зависит
от эффективной температуры нейтронов (см. приложение IV, где
приведены множители g, которые при х^>1 мало отличаются от
множителей f). Если £т=400ч-600 К, то g'/s=0,95 и
Фт°=2,18- 1013Р(1—twf). (2.4.52)
Если жесткость спектра нейтронов мала, то можно прене-
бречь в (2.4.52) множителем 1—wf. В этом случае плотность
потока в тепловой группе полностью определяется удельной
мощностью реактора Р, МВт/кг 235U.
В реакторах, в которых используется в качестве топлива
естественный или слабообогащенный уран, некоторую, хотя и не
очень большую, роль играет деление 238U быстрыми нейтронами.
* Если закон l/v не выполняется, то Фт° надо умножать на o(E№)gr.
105
Обозначим §28 отношение числа делений 238U к числу делений
235U. Применяя формулу (2.4.34) к делению 235U, получаем
Г5 - г5
= фт2<5 + v5 ~
Е;^ Т ' Ef5
Ч 5ге) &S ’
где IF5 — энергия, выделяющаяся за счёт деления только 235U
(v8/v5= 1,16, см. § 1.1). Выражая №5 через полную мощность
(отношение EfS/Ef5 весьма близко к единице: Е?8/Е?5= 1,016, см.
§17):
Г5 = Г (1 + '>
5 \ £/5 28/
имеем
Фт=2,07-1013Р(14~1,01662s)-1 (1—(2.4.53)
причем
= vE (1 + 1,16828)-Д-- (2.4.54)
Учет делений 238U уменьшает плотность потока тепловых
нейтронов при заданном Р, поскольку дополнительные деления
вызываются не тепловыми нейтронами. Способы вычисления 628
изложены в гл. 9.
Используем формулу (2.4.49) при Х';<С1 для определения
плотности потока нейтронов в сборке «нулевой» мощности.
Пусть мощности сборки 0,1 Вт, количество 235U 10 кг. Тогда
плотность потока примерно равна 2-105 нейтр/(см2-с) и число
нейтронов около 1 см-3. Число делений в сборке примерно равно
3-109. с-1. Если ее объем 1 м3, тр число делений в 1 см3 около
3000. Поэтому в такой сборке будут вполне заметные, порядка
30001/2, около 2% флуктуации («шумы») удельной мощности
(подробнее о флуктуациях в ядерных реакторах см., например,
в [74]).
’’ Задача. Использовать закон сохранения энергии нейтронов^ для под-
тверждения формулы (2.4.27) [105].
Решение. Пусть £i — энергия, удовлетворяющая неравенству Ес<£.
<£i<7,o=2 МэВ, причем So(£i)=0, при £1 справедлив спектр Ферми и
при энергии ниже Е\ сечение неупругого рассеяния равно нулю. Закон со-
хранения энергии нейтронов запишем так:
£1(£1)+£2(£1)=£o(£i), (2.4.55)
где У1(£1)—кинетическая энергия нейтронов, поглощенных при энергиях
ниже Е\.
Е1
К^Е.) = J £Sa(£)$(£)dE; (2.4.56)
о
энергия, переданная от нейтронов к ядрам замедлителя:
оо £3
К2(Е1) = pV0(H)du J М(£) (SEv^dE, (2.4.57)
о о
106
где No(u)—число ядер с энергией u[No(u) нормировано на 1]; N(Е)—
число нейтронов с энергией Е; г’,?—относительная скорость нейтронов; &Е—
энергия, переданная от нейтрона к ядру при одном столкновении; угловые
скобки означают усреднение по всем углам рассеяния. Наконец, Ko(Ei) —
энергия тех нейтронов, которые испытали последнее столкновение, обладая
энергией выше Ei, причем после столкновения энергия стала меньше Ег.
Et/ea Е,
(• С 1___е
dE dE'$(E)w(E, Ef)E' =------------EXS (-2.4.58>
»J »J 2 £
Et *aE
[использованы формулы (2.2.8), (2.2.17)]. Если можно пренебречь движе-
нием ядер, то
(2.4.59}
При Е>ЕС учет движения ядер представляет собой малую поправку
к (2.4,59), и поэтому
(AEt^Ss) Е>Ес- (2.4.60}
где с — некоторая постоянная. Составим теперь баланс энергии при Е=ЕС.
Из (2.4.55) следует тождество
Кл (Ес)+К2(Ес) = (Ei) —[51 (51) -51 (Ес) ]- [К2 (Ei) -К2 (Ес) ].
Применяя (2.4.57), (2.4.58), (2.4.60), получаем
Et
1—ео f [1 — ео 7 Зс Е3\ '
КАЕс) + Ка(Ес) = EXS-J Е |^—° SД 1 - — ) + Sa(E)ji>(E)dE „
Е
(2.4.61))
где для N(и) использовано максвелловское распределение с температурой
Е3. Из физических соображений очевидно, что энергетический баланс при
Е = ЕС (2.4.61) не может зависеть от значения энергии ЕЕ^>Ес. Поэтому пра-
вая часть (2.4.61) не должна содержать £;. Если 2а = 0, то правая часть
(2.4.61) содержит InEi/E}. Зависимость от Ei исчезает, если заменить £
в Ф(Е) (2.2.27) на £и0(Е), где
z0(£) = 1- ~ (2.4.62)1
2 Е
Если в (2.4.61) учесть поглощение, причем 2а(Е)~Е_“, а<1, то зави-
симость правой части от Ei исчезает, если и0(Е) заменить на
. Зс „ Sg(E) 2
2 Е + 1 Ss ’ 1—е0
Теперь интеграл в правой части (2.4.61) можно вычислить, если ввести:
в качестве независимой переменной величину w [см. (2.4.16)]:
, 5х(Ес) +Кг[Ес) =-Ц--^5Есехр( — w). (2.4.63)"
Далее имеем [использовано (2.4.10)]:
5Х(ЕС) = сХа (Ен) [Е£'н£т fla 3 (х),
107-
где
ил(х) = erf ]/х —
ехр(—х);
(2.4.64)
fia
Ес
%а(Ен) J Е3/2ехр
О
-1 Ес
^Е22а(Е)ехр
О
_Е_\
Ет I
dE.
Для вычисления Лг(Ес) надо выбрать какую-либо модель для динамики
столкновения нейтрона с ядром. Используем самую простую модель: стол-
кновение упругих шаров. Пусть v, V — скорость нейтрона и ядра до стол-
кновения. Скорость нейтрона после столкновения равна (см., например,
[Ю6]):
А____
1-4- А
I V—V | п04
v 4- XV
1 + А
(2.4.65)
где по — единичный вектор скорости нейтрона после столкновения в системе
центра инерции. Разность энергий нейтрона до и после столкновения равна
ДЕ =
А
(1-М)*
— AV2 + (А— 1) vV — | v — V | (nov + Лп0У)].
(2.4.66)
Считая, что в системе центра инерции рассеяние изотропно, получаем
4-1
(AE^Ss) = 9/1'т5г2 I - -41/2 + ( А - 1)v/y2 + V2_2t,Vp dp =
= ^SsF(E, u), (2.4.67)
где
F(E, u) =
и 4 I
vF\(E,v); E>~^’ Fi = E— — M
c '
— VF2(E, u); E<-^-; F2 = «--|-
U2 I 1 \
--- 1 J----- ;
AE \ 4Л J
1 \ 4
— —7" “ — ----
24 ) 15
A \ 4 AE2
— I E —--- ---
2 / 15 и
Из (2.4.67) .определяется постоянная с в формуле (2.4.62):
с =-^-(1-1/(24)),
О
чем оправдывается формула (2.4.31). Оставшиеся интегралы можно вычис-
лить при условии ЕсЛэ>Е3. В результате получается уравнение
R(z, х) = Гт/х[1 — (х4- 1)ехр( — х)]—~ ——- Ц1 (х)1, (2.4.68)
I fa 1 — е0 I
ГДе п, . 2(2- 1)г3/г Г , 4 , г+12 1 + 6г 1
(г’ Х) (г-+-1/Л)7/2 [_г-Г -4 ' 2г2А2 + 2z343 j
Г х2 1 + х / 1 \ 1/ 1\1
—2 ехр( —х) 1 + х +— —----------- 1 — —- — —— [ 1 +-----------) .
' L 2 г \ 2Л/ 2Лг2 \ 4+ / J
108
Уравнения (2.4.21) и (2.4.68) позволяют определить х и г как функцию
ут или уз. Результат численного анализа этих уравнений показал [105] (ве-
личины ут и fa, введенные здесь, несколько^ отличаются от определений
(105]), что линейная зависимость z от у3 выполняется с хорошей точностью.
Зависимость х3 от у3, полученная из (2.4.68) и (2.4.21), приведена (при
А=4) на рис. 2.7. Основной вывод о слабой зависимости х3 от у3 (см. нера-
венство (2.4.28)] сохраняется.
Глава 3
ГРУППОВЫЕ УРАВНЕНИЯ
3.1. МНОГОГРУППОВЫЕ ДИФФУЗИОННЫЕ УРАВНЕНИЯ
Уравнение баланса нейтронов в диффузионном приближении
было записано в § 2.1. В уравнении (2.1.6) не конкретизирова-
лось выражение для источников нейтронов S(r, Е). Нейтроны
с энергией Е могут возникать либо в результате деления, либо
в результате столкновений с ядрами среды. Источники нейтро-
нов, возникших в результате деления, запишем так:
Х(Е) j' v(E')Sf(E')4>(r, E')dE', (3.1.1)
6
где учитывается зависимость v от энергии (см. § 1.1); %(f) —
нормированный на единицу спектр нейтронов деления (см.
§ 1.2). Для нескольких делящихся нуклидов надо написать сум-
му
00
2 Zi (Е) [ v; (Р) (Р) Ф (г, Е’) dE’. (3.1.2)
I 0
Обычно можно считать, что спектр %i(E) одинаков для всех де-
лящихся нуклидов, присутствующих в реакторе.
Число нейтронов с энергией Е, появляющихся в результате
столкновений с ядрами среды, равно
Jss(P)ay(P, £)Ф(г, E’)dE’, (3.1.3)
6
где w(E', Е) —вероятность того, что в результате столкновения
с ядром энергия нейтрона изменится от Е' до Е. Фактически
произведение в (3.1.3) надо писать в виде суммы
SSsi(P)^(P, Е) (3.1.4)
i
по различным ядрам. Чтобы не загромождать формул, сумму
(3.1.4) не будем явно выписывать. Учитывая (2.1.6), (2.1.17),
109
(3.1.1), (3.1.3), получаем стационарное уравнение диффузионно-
го приближения (сечения могут быть функциями координат, что
явно не отмечено):
divD(E) grad<D(r, Е)—2г(Е)ф(г, Е) +
оо оо
+ ^s(E')w(E', Е)Ф(г, E')dE' = —x(E) f v(E')Zf(E’)$(r, E')dE'.
о о
(3.1.5)
Если при столкновении с ядрами энергия нейтрона не изме-
няется, то член 25Ф компенсируется в левой части (3.1.5) и се-
чение рассеяния входит в уравнение только в коэффициенте диф-
фузии.
В области замедляющихся нейтронов функция w(E', Е) да-
ется формулой (2.2.8). При энергии Е^> 100 кэВ w(E', Е) отли-
чается от (2.2.8), поскольку нарушается предположение об изо-
тропии рассеяния в системе центра инерции, лежащее в основе
(2.2.8). Кроме того, при больших энергиях функция w(E', Е)
должна учитывать неупругие столкновения (см. § 1.4). При ма-
лых энергиях нейтронов, сравнимых с кинетической энергией
движения молекул среды, функция w(E', Е) учитывает перехо-
ды как с уменьшением, так и с увеличением энергии нейтрона.
Здесь мы ограничимся формальной записью многогрупповых
уравнений, не конкретизируя вид w(E', Е).
В уравнении (3.1.5) не учтены процессы (и, 2/г). В реакторах
на тепловых нейтронах эти процессы играют малую роль (ис-
ключением является случай, когда замедлителем является бе-
риллий) . Можно считать, что процессы (п, 2п) эффективно вклю-
чены в правую часть (3.1.5).
Весь интервал энергии 0<Е<ЕмаКс, где EMaKc^10 МэВ —
практическая верхняя граница энергии нейтронов, возникающих
при делении, разделим точками Е, на G интервалов. Совокуп-
ность нейтронов, энергия которых принадлежит /-му интервалу,
назовем '/-й «энергетической группой нейтронов» или просто /-й
«группой». Нумеруют группы обычно начиная с больших энер-
гий. Разбиение на группы удобно проводить так, чтобы отно-
шение Ej/Ej+\ не зависело от номера группы. Тогда интервал
летаргии \и не зависит от номера группы:
Д«=«/—u;+i.=const.
Конечно, могут быть задачи, где нецелесообразно все интер-
валы Ди считать одинаковыми. Например, если имеется один
узкий резонанс и желательно детально описать зависимость по-
тока от энергии внутри опасной зоны этого резонанса, где поток
существенно зависит от энергии, то надо взять узкие группы
внутри резонанса и значительно более широкие вне его. Если
ПО
желательно детально описать поток нейтронов в тепловых груп-
пах, а реактор имеет мягкий спектр [т. е. у<С1, см. (2.2.21)1 то
тепловые группы надо взять узкими, а замедляющиеся нейтро-
ны можно объединить в одну или несколько групп. Разбиение на
группы при Е<ЕС выгоднее проводить равномерно в шкале ско-
ростей (или энергии), а не летаргии. Рассматривая реактор на
быстрых нейтронах, надо провести более мелкое разбиение на
группы при больших энергиях (порядка МэВ), а тепловые ней-
троны можно описывать одной группой (или совсем не учиты-
вать). Широкое распространение получило 26-групповое разбие-
ние всего энергетического интервала [34, 35]. При этом две
последние группы (25, 26) описывают тепловые нейтроны. При
детальном расчете реактора на тепловых нейтронах, когда уЧИ.
тывается термализация (см. гл. 7), они должны быть заменены
большим числом более мелких групп. Границы энергетических
интервалов в 26-групповом разбиении приведены в приложе-
нии IX.
Проинтегрируем уравнение (3.1.5) по энергии в интервале
E]+i<E<Ej и обозначим
Ф7(г)=у Ф(г, E)dE-, (3.1.6)
^• = [ФДг)Г j 2а(£)Ф(г, E)dE; (3.1.7)
с. .
Dj = ^(r)J- р(Е)Ф,(г,Е)Ж.
£/+i
Если предположить, что плотность потока в группе j можно
представить в виде произведения
Ф(г, Е) = С/Ф/(г) Ф/(Е), (3.L8)
то групповые константы (3.1.7) не будут зависеть от координат
если исходные константЬ не зависят от них. Если исходные
константы зависят от координат, то надо аппроксимировать эту
зависимость кусочно-постоянными функциями. Тогда и группо-
вые константы будут кусочно-постоянными. Интеграл в правой
части (3.1.4) представим в виде суммы
00
J v(E)Sf(E)®(r, E)dE = ^\ vjSp-ФДг), (3д 9)
b i
111
где
Ei
v;Sfy = [Oy(r)]-* j v (E) (E) Ф(г, E)dE, (3.1.10)
Ei+i
и обозначим
E.
Xi = J X (E) dE.
Ei+i
Интеграл в левой части (3.1.4) запишем так:
Е! оо
| dE\ Zs(E')w(E', Е)Ф(г, E')dE' = 2Г>/-ФГ (г) + Sz>/ФДг),
£/+i 0
(3.1.11)
где Sy-, j — сечение перехода из группы j' в группу /; S/, /— се-
чение рассеяния, оставляющего нейтроны в данной группе. Раз-
ность
Ss/Ф/—S/, ;Ф/ = 2уВ;Фу (3.1.12)
дает число нейтронов, уходящих из данной группы во все ос-
тальные (сечение увода).
Таким образом, многогрупповые диффузионные уравнения
запишутся следующим образом:
div [D} grad Ф> (г)] — (2aj 4- SyB}) Ф; (г) +
+ S S/s/O/'(r)=-yJSviSf(^(r). (3.1.13)
Если групповые сечения, входящие в (3.1.13), записаны в ви-
де (3.1.7), (3.F.10), (3.1.11), куда входит неизвестная плотность
потока ф (г, Е), то уравнения (3.1.13) тождественно совпадают
с (3.1.5), однако коэффициенты его неизвестны. Надо либо пред-
положить, что группы столь узки, что плотность потока в фор-
мулах (3.1.7), (3.1.10), (3.1.11) можно заменить средним значе-
нием по энергии, вынести за знак интеграла и сократить
с Ф/(г), либо надо иметь какую-то информацию о зависимости
плотности потока от энергии внутри группы.
Если поглощение замедляющихся нейтронов достаточно сла-
бое, то можно считать, что плотность потока в шкале летаргии
внутри каждой группы постоянна:
Ф(м)=сопз1; Ф(Е)=сопз1/Е; wz<m<M/+i.
Тогда для сечения поглощения
“/+1
= (“j+1 — «/) ’ J %a(u)du, (3.1.14)
112
и аналогично для других сечений. Это означает, что сумма
(Gi — число групп в области Е>ЕС)
Gt
+ l из) = (3.1.15)
/=1
равна резонансному интегралу поглощения бесконечного разве-
дения. Аналогично записываются и резонансные интегралы де-
ления и радиационного захвата.
Многогрупповые уравнения как в диффузионном, так и в бо-
лее точных приближениях рассмотрены в ряде монографий (см.,
например, [70, 103]). К этим монографиям мы и отсылаем чи-
тателя для более подробного ознакомления.
3.2 УРАВНЕНИЯ С ДВУМЯ ГРУППАМИ НЕЙТРОНОВ
Увеличивая энергетическую ширину групп и уменьшая их
число, приходим к предельному случаю двух групп: первая груп-
па — замедляющиеся нейтроны, вторая — тепловые. Для расче-
та больших реакторов на тепловых нейтронах двухгрупповое
приближение обладает в большинстве случаев достаточной точ-
ностью и поэтому используется во многих практических расче-
тах. Запишем уравнения двухгруппового приближения так (для
однородной среды):
7)1АФ1—(Si2-|-Sai) Ф1=—у(2Г1Ф1+2Г2Ф2) ; (3.2.1)
/)2АФ2—2а2Ф2=—212Ф1. (3.2.2)
Под vSf1>2 понимается сумма SyV^S|i,2 по всем делящимся нук
лидам.
Рассмотрим сначала смысл коэффициентов второй группы.
Для тепловых нейтронов х(£)=0 и поэтому из (3.1.5) получим
D (£) ДФ (г, Е) — (£) Ф (г, Е) = — J (Е') w (Е', Е) Ф (г, Е') dE'.
о
(3.2.3)
Предположим, что плотность потока ф(г, Е) может быть
представлена в виде
Ф(г, £)=Ф2(г)Ф2(Е), (3.2.4)
где Ф2(Е) нормировано так, что
(X(E)dE = 1,
6
8—6053
113
Т. е. предполагается, что форма спектра ней’грондв не зависит от
координат. Это не означает, что вб всем реакторе справедливо
(3.2.4). Можно считать, что реактор разбит на несколько обла-
стей, для каждой области справедливо (3.2.4), но с разными
спектрами нейтронов Ф2(£).
Подставим (3.2.4) в (3.2.3) и проинтегрируем до верхней гра-
ницы тепловой группы Ес. Если ЕГ>ЕС, а Е<ЕС, то интеграл
Ео
J dE J (£') w (Е’, Е) Ф (г, £') dE' = п (г) (3.2.5)
0 ' Ес
равен плотности замедления при Е—Ес и мощности источников
в тепловой группе (см. § 2.2).
Если Ес много больше средней кинетической энергии моле-
кул замедлителя, Ec^>kT (см. § 2.4), то вероятность таких
столкновений, при которых нейтроны тепловой группы получат
энергию больше Ес, пренебрежимо мала, т. е.
Ес
J ш(£', £)d£= 1, £'<£с.
о
Тогда
Ес Ес Ес
j dE J (£') w (E\ E) Ф (r, £') dE' = J (£') Ф (r, £') dE'. (3.2.6)
CO о
• Следовательно, вместо (3.2.3) получим
£2АФ2(г) — 2агФ2(г) =— n(r), (3.2.7)
где
Ес
= ^г(£)Г1фД^)^ (3.2.8)
О tJ
о
и
Ес
= J (£)Ф2(£)</£. (3.2.9)
о
Если спектр нейтронов в реакторе аппроксимируется форму-
лами (2.4.10), (2.4.11), то Ес должно совпадать с энергией пере-
хода от максвелловского спектра к фермиевскому (2.4.12). Если
ф2(£) определяется каким-либо численным методом (см. §7.5),
ю выгоднее выбрать Ес несколько больше, например Ес=0,5 эВ.
Тогда переходная область между максвелловским и фермиев-
ским спектрами будет включена в тепловую группу.
114
Рис. 3.1. Зависимость сечения'рас-
сеяния нейтронов as для Н2О,
D2O, С от энергии
Рис. 3.2. Зависимость среднего косинуса
рассеяния для Н2О и D2O от энергии
нейтрона (значение для D2O дано
штриховой линией; для Н2О 1100=0,61)
Можно записывать уравнение диффузии не относительно
плотности потока нейтронов, а относительно-плотности N = — Ф..
и
Тогда получим уравнение (2,1.25), причем
D=vDz, tt= (uSe2)~1, (3.2.10)
где D2, определены (3»2.8) и (3.2.9), a v— средняя арифме-
тическая скорость нейтронов в тепловой группе. Если справед-
ливо максвелловское распределение тепловых нейтронов с эф-
фективной температурой ЕДсм. (2.4.6)], то
(3,2,11).
Е л ! 7 £ч
Усреднение сечения поглощения (3.2.9) рассматривалось в
§ 2.4. Сечение рассеяния и средний косинус угла рассеяния ц
[см. (1.4.7), (2.2.13)] в тепловой группе зависят от энергии. На
рис. 3.1 приведена зависимость щ от энергии для наиболее рас-
пространенных замедлителей (Н2О, DsO, графита С). Колеба-
ния os для графита при малых энергиях связаны с кристалличе-
ской структурой (см. подробнее, например, [107]). Сечение рас-
сеяния’ при энергии порядка 1 эВ обозначают oSf, это сечение
рассеяния на свободном ядре, когда можно не учитывать хими-
ческих связей в молекуле или кристалле. Йри малых энергиях
(порядка 0,01 эВ) ядро можно рассматривать жестко связанным
в молекуле или кристалле; соответствующее сечение обозначим
cTs- Связь между сь- и oSf дается выражением
• °‘= (3-2-12)
\ дп ]
8*
115
где А — атомная масса рассеивателя. Различие между os и oSf
особенно велико для водорода: os = 4osf (см. рис. 3.1). Менее
существенный эффект для дейтерия:
9
а = —а
s 4 '
(см. рис. 3.1);
вклад кислорода несколько уменьшает эффект. На рис. 3.2 при-
ведена зависимость среднего косинуса угла рассеяния для Н2О
и D2O [108]. Асимптотическое значение р, [см. (2.2.13)]:
(3-2ЛЗ)
достигается при энергии в несколько десятых электрон-вольта.
Усреднение коэффициента диффузии (3.2.8) можно провести
аналогично усреднению сечения поглощения [см. (2.4.7)]. Целе-
сообразнее, однако, исходить из макроскопических эксперимен-
тов по определению коэффициента диффузии, когда автомати-
чески проводится усреднение по максвелловскому спектру (из-
мерению диффузионных характеристик для веществ, которые
используются в реакторах как замедлители, посвящена обшир-
ная литература, см., например, [109—111]). В обзоре [112]
приведены следующие формулы. Коэффициент диффузии для
Н2О
D (Т, Тп) = D(T0, То) [0,06 + 0,94 /-^] (3.2.14)
где
О(Г0, То) =0,1423(19) см;
р — плотность воды; Т и Тп — температура воды и нейтронов;
То=293 К.
Квадрат1 длины диффузии (2.1.24) равен
L2=Dj^a, (3.2.15)
причем
L2(T0, То) =7,34(10) см2,
а среднее сечение поглощения вычисляется по (2.4.5).
Для D2O
D(T, Т„) = Ь(Т0, То) [о,69+0,31 /У (3.2Д6)
где (по данным обзора [ИЗ])
Д(Т0, То)=0,84(1) см. (3.2.17)
Для тяжелой воды большую роль играет поглощение в при-
месях простой воды. Сечение поглощения равно
2а(^№ Т, Тп) = Ха(0, То, Т0)^П + 457,8 сн), (3.2.18)
116
где (см. приложение V, где приведены несколько другие дан-
ные, основанные на измерении микроскопических сечений погло-
щения D и О, [31])
Sa(0, То, Го) =0,406(16)-10-4 см-';
сн — отношение числа ядер Н к сумме D и Н. Коэффициент
диффузии равен
D (сн, Т, Тп) = D (0, То, То) — Г--_= ।
Н р(Г) 0,69+0,31 |/Г„/Г» '
5,946сн
Г 0,06+0,94
(3.2.19)
где D(0, То, То) дано (3.2.17). Длина диффузии получается по
(3.2.15), причем (см. также табл. V.3 приложения V)
Г2(0, То, Го) =2,07 (8)-104 см2.
Сечения рассеяния других веществ, используемых в реакто-
рах, приведены в приложении.
Рассмотрим теперь коэффициенты, входящие в уравнение
(3.2.1). В согласии с общим определением § 3.1 имеем
ФДг) = J°O(r, = [Фх (г)]-1 J° j (£) Ф (г, E)dE.
Ес Ес
(3.2.20)
Когда энергетическая группа столь широка, как в рассматри-
ваемом случае, необходимо использовать дополнительную ин-
формацию о виде спектра Ф(г, Е). Запишем плотность потока
нейтронов так [см. (2.3.43)]:
Ф (г, Е) = п* (г) ехр[~эд<£)1 (3.2.21)
где
Ф = ехр (—&+); пс(г)=п(г, Ес); wc = w(Ec), (3.2.22)
т. е. ф — вероятность избежать резонансного поглощения при
замедлении; пс — значение плотности замедления на границе
тепловой группы. Тогда (предполагается, что не зависит от
энергии, хотя это и не принципиально):
f Sa (Е) Ф (г, Е)dE = [ exPbj?.(£)) 2°..<£) dE =
J gSsf ’ E
117
W
[exp (-да)dw =
¥ J . f
о
£<>
V f 2Z (E) Ф (r, E)dE = —nc (r),
(3.2.23)
(3.2.24)
где Wf дано (2.4.38). Отметим, что формулы (3.2.23), (3.2.24)
можно считать точными в том смысле, что они определяют ве-
личины ф и Wf. Приближение тогда заключается только в том,
что ср и Wf не зависят от координат.
Далее надо вычислить фДг):
Eq Ко _
ФДг)= [ Ф(г, (3.2.25)
Е„
где
— среднее
Ф= —(* ехр(—да (u)) du; ис = 1п — (3.2.26)
Че J Ес
о
значение ф по летаргии. Таким образом,
2а1 = . V£fi = (3.2.27)
Т“с
Источником “для тепловой .группы должна быть плотность
замедления при' Е—Ес, т. е. 212Ф1==Пс,-и. поэтому из (3.2.25)
получим
S12=^?. ' (3.2.28)
«с?
Теперь уравнения (3.2.1), (3.2.2) можно переписать так (вме-
сто п'с'будем писать и):
Д;(Д-Е2-)Ф2 = -п;
где
= D1 (S12 + Sal- = ^-, ’ = fg- (3.2.30)
118
Если вместо Ф4 во второе уравнение (3.2.29) ввести плот-
ность замедления, то это уравнение перепишется таким обра-
зом: ..
(Д-^)«=-^-2а2Ф2, (3.2.31)
где
£ = (3.2.32)
Если в (3.2.29), (3.2.30) Ф2 и п не зависят от координат, то
получаем k*=\, т. е. k* имеет смысл коэффициента размноже-
ния бесконечной среды, причем множитель (1—wf)~x учитывает
влияние делений, вызванных замедляющимися нейронами. Если
определить коэффициент размножения по (1.9.3) в виде
и использовать формулы (3.2.25), (3.2.27), то получим
k = ...2 ----- (3.2.34)
2П2Ф2 Ч----- п
V
т. е. Я зависит от отношения плотностей групповых потоков и
поэтому не может быть коэффициентом в уравнениях (3.2.29) —
(3.2.31). Подставив в (3.2.34) п из (3.2.29), получим
~ k<Z2 + wf(l—L.?b)&2 _k + wf — WjL2*b®2l®2
тФ2Ч-(1-т)(1-£22А)Ф2 1-(1-¥)£22ДФ2/Ф/
Если Д22ДФ2/Ф2<1 (большой реактор), то
£=k + w}. (3.2.36)
Этот результат отличается от (3.2.32),. однако если ввести /г3ф
как число, на которое надо разделить v, для того чтобы коэффи-
циент размножения стал равным единице, то получим
йэФ=^Ч~®/ . (3.2.37)
как из (3.2.32), так и из (3.2.36). Отклонение йЭф от единицы
характеризует степень подкритичности или надкритичности (см.
также § 4.6).
Обратим внимание на. отличие т* от т. Во-первых, это отли-
чие связано с тем, что в процессе замедления нейтрон может
вызвать деление, в результате чего он исчезает, но появляется
новый быстрый нейтрон, который снова может вызвать деление.
Возникает геометрическая прогрессия, суммирование которой
приводит к множителю (1—а^)-1С Во-вторых, т* содержит мно-
119
житель ф, который уменьшает длину замедления за счет того,
что в процессе замедления нейтрон имеет некоторую вероятность
поглотиться (см. также § 4.6, где дано другое определение-дли-
ны замедления).
Если справедлив закон 1/и, то
ф = А[ ехр(— г) — = 1— (3.2.38)
Uc J Z ис 2ис
Если при Е—Ег, и=иг имеет место резонансный уровень, так
что ехр (—®(£)) = 1 при Е>ЕГ и ехр (—®(£))=ф при Е<.ЕГ,
то
Ф= 1 — (1 — ф) fl — -М (3.2.39)
\ /
Для 238U можно получить следующую формулу (при этом ис-
пользованы данные по резонансному поглощению, см. гл. 8):
Ф=1—0,13®1/v—0,27® б л—0,68®Иб, (3.2.40)
где ®!/а — резонансное поглощение, обусловленное той частью
сечения, которая подчиняется закону 1/и; ®бл— блокированное,
®нб— неблокированное резонансное поглощение (см. гл. 8).
Граничные условия для плотности потока в тепловой группе
имеют обычный вид (2.1.54), (2.1.55), где коэффициент диффу-
зии определен (3.2.8). Граничные условия для плотности потока
в первой группе получаются, если проинтегрировать по энергия
граничные условия для плотности потока Ф(г, Е), т. е.
Фь £1Ф'1 непрерывны на границе раздела. (3.2.41)
Если использовать в уравнениях плотность замедления, то
в силу (3.2.25) получим, что
непрерывны на границе раздела. (3.2.42)
Уравнения (3.2.29), (3.2.31) описывают распределения плот-
ностей нейтронных потоков в гомогенной размножающей среде. -
Двухгрупповое приближение можно использовать и для описа-
ния плотности потока в замедлителе гетерогенного реактора.
Тогда У т*=У % и L2=L— длины замедления и диффузии в
замедлителе.
Рассмотрим функцию Грина для замедляющихся нейтронов
^п(г)
(д----LW . (г) = — — 3 (г) (3.2.43)
\ Т I 11 т
120
и функцию Gf11, определенную уравнением
(Д — (г) - (г). (3.2.44)
Ограничимся рассмотрением двухмерного случая. Повторяя
рассуждения § 2.1, которые привели к формуле (2.1.35), полу-
чаем
(г) = (3.2.45)
Решение уравнения (3.2.44) с (3.2.45) в правой части имеет
вид
Gp(r) = AK0(r/L)-[2W(l-x/L2)]~lK0(r/^), (3.2.46)
где константу А проще всего определить из условия: функция
G/11 не имеет особенности при г=0. Этому условию удовлетво-
ряет функция
GP (г) = I2tZ)(1—т/Т2)]”1 [K0(r/L) -К0(г/Г?)]. (3.2.47)
3.3. ДВУХГРУППОВОЕ И ВОЗРАСТНОЕ ПРИБЛИЖЕНИЯ
Уравнения двухгруппового приближения могут быть получе-
ны из уравнения возрастного приближения. Рассмотрим сначала
случай без поглощения при замедлении. Тогда уравнения воз-
растного приближения записываются так (индекс 2 в тепловой
группе опускается; величина гс обозначалась в § 3.2 просто т):
Z) (A—L-2) Ф (г) =—л (г, тс); (3.3.1)
Дл (г, т) = (3.3.2)
с начальным условием
л (г, 0)=vS/O(r). (3.3.3)
Разложим л(тс) в ряд по тс:
” <0) -" <'> - т <ЗЛ4>
Второй производной в (3.3.4) можно пренебречь, если
тс д2п дп.
V а.2 ^"аГ’
или, используя .(3.3.2),
Ап <&Ап; Д (fin) « Дл. (3.3.5)
Из соображений размерности (более точный критерий см.
в гл. 4) имеем Ап—nlR2, где R — характерный размер реактора.
121
Поэтому в (3.3.4) можно пренебречь второй производной, если
i«R2: (3.3.6)
т. е. размеры реактора много больше длины замедления.
Пренебрегая в (3.3.4) второй производной, определяем пер-
вую и подставляем в (3.3.2). Используя начальное условие
(3.3.3), получаем
- Д/г--- (3-3.7)
хс хс
что совпадает с уравнением (3.2.31), если там положить /а~
r=Jf=O.
Разделим весь интервал 0Ст<тс на G частей точками т3-, за-
дп
меним в каждом интервале производную отношением ко-
нечных разностей. В результате получим систему многогруппо-
вых уравнений
Д/г,----(3.3.8)
х/—x/-i . Л —x/-i
причем rto=v2fG>, а па—п(хс) является источником для нейтро-
нов тепловой группы. Система многогрупповых уравнений
(3.3.8) отличается от сформулированных в § 3.1 тем, что источ-
ником в группе / служит только поток в соседней группе /—1.
Это справедливо для достаточно широких групп, когда нейтрон
не может перескочить через группу при одном столкновении
с ядром замедлителя.
Для замедлителей, содержащих водород, это приближение
незаконно, поскольку нейтрон любой энергии при столкновении
с протоном имеет некоторую вероятность получить энергию вну-
три тепловой группы. Для дейтерия максимально возможное из-
менение летаргии при одном столкновении равно
In (£'7£')макс=1п 9=2,2.
Так как полный интервал изменения летаргии равен 15,2, то
максимальное число групп в уравнении (3.3.8) равно 7. Поэтому
систему (3.3.8) в этом случае можно назвать «малогрупповым»
приближением. Для графита In (£'7£')макс=0,3 и в уравнении
(3.3.8) законно использовать большое число групп.
Учтем теперь поглощение. Точное (в пределах диффузионно-
го приближения) уравнение имеет вид [см. (2.2.33)]:
(ОД — 2а) Ф (г, Е) = — (3.3.9)
122
Если использовать связь между плотностью потока и плотностью
замедления (2.3.43), то получим
[Д — £-2(г)]л(г, t) = (3.3.10)
с начальным условием
Ео
п(г, 0) = v2/2o2 (г) + у j 2ДЕ)Ф(г, E)dE. (3.3.11)
Е„
Проведем замену переменных:
п (г, t) = п (г, т) exp [®с — w (х)];
Г dt
J £2W ’
о
w
(3.3.12)
Вместо (3.3.10), (3.3.11) получим
вие:
уравнение и начальное усло-
л ~ дп
Д« =
5т
Е«
и (г, 0) = vS/2<pO2(r) + v<p^ 2ДЕ)Ф(г, E)dE. (3.3.13)
Ес
Используя разложение (3.3.4) для функции п и опуская вто-
рую производную, имеем [й(тс)=п(тс)]:
— ¥Е/2фФ2(г) + v<p
2ДЕ)Ф(г,’Е)^Е .
(3.3.14)
Подставляя теперь вместо Ф(г, Е) выражение (3.2.21), получаем
га(г) =----[у2/2<рФ2(г) +wfzz(r)], (3.3.15)
т
что совпадает с (3.2.31), за исключением множителя <р при т.
Причина расхождения заключается в том, что использованная
связь между плотностью потока и плотностью замедления на-
рушается, если одновременно учитываются резонансное погло-
щение и утечка нейтронов (см. также § 4.6).
Сравним функции Грина двухгруппового приближения б/11
(3.2.47) и возрастного G; (2.2.63). Обе функции имеют одина-
ковую нормировку, одинаковый средний квадрат перемещения
123
(см. задачу в конце настоящего параграфа), одинаковый вид
при г—>-оо, если т<СА2:
б" (г)= [2тг£) (1 - Ко (r/L); Gf (г) = Ко(r/L).
2^Lf
(3.3.16)
При г—0 обе функции конечны и равны [функция Е[ опре-
делена (1.10.10)]:
С” (0) = \2тЕ> (1 — х/Г2)]-1 In ~ ; G; (0) = 'хр^2) Ег (z/L2).
(3.3.17)
Если т<сЕ2, то Gfn(0) близко к Gf(0). Например, для D2O и
графита имеем т/Л2=0,015 и 0,14. Подставляя эти значения в
(3.3.17), получаем для D2O
для графита
, о
Gf(0)
В теории гетерогенного реактора функция Gf играет боль-
шую роль (см. гл. 11). Сравнительно небольшая разница между
G; и Gf11 позволяет без большой погрешности заменить возраст-
ное приближение более простым двухгрупповым [или малогруп-
повым в смысле уравнения (3.3.8)].
Задача. Сравнить г2 и г4 для G;11 и Gf.
Решение. Фурье-образ функции G?n равен [см. (2.1,31), (3.2.47)]:
G?">) =[£>(1—т/7.2)]->[ l^+T.-2)-1-(^-pr-i)-1].
Исходя из формул, приведенных в задаче 5 § 2.1, получаем для Gf" (трех-
мерный случай):
Гп=6(£2 + т),
т. е. г2[ и г203 равны. Для г4 получим = 120(7.4 + xL2 + т2) иль (см. за-
дачу 2 в § 2. 2)
1 т \2 Г т 1 / т \21—1
Р)воз ~1+ 2 L3 И1 + L2 Л
Для графита отличается от г%03 примерно на 0,5%, для D2O отличие еще
меньше.
Глава 4
КРИТИЧЕСКИЕ РАЗМЕРЫ ГОМОГЕННОГО РЕАКТОРА
4.1. ОДНОРОДНЫЙ РЕАКТОР БЕЗ ОТРАЖАТЕЛЯ.
ОДНА ГРУППА НЕЙТРОНОВ
Задача об определении критических размеров реактора яв-
ляется одной из центральных задач теории. В большинстве слу-
чаев реактор является гетерогенным (см. § 1.9). Теория крити-
ческих размеров гетерогенного реактора изложена в гл. 11. Если
реактор содержит достаточно большое число блоков, свойства
которых не сильно отличаются друг от друга, то можно вместо
гетерогенного реактора рассматривать гомогенный, но с эффек-
тивными значениями параметров (гомогенизация гетерогенного
реактора). Вычислению этих эффективных значений параметров
посвящены гл. 7—10. В настоящей главе параметры гомогенно-
го реактора будут считаться заданными.
Начнем с рассмотрения простейшего случая однородного ре-
актора без отражателя. Строго говоря, реактора без отражате-
ля не бывает. Всегда имеется защита от излучения или какие-то
конструкционные элементы, которые играют роль отражателя.
Однако такой отражатель мало влияет на критический размер
реактора. В этом случае можно определить эффективную тол-
щину отражателя Аэф и считать, что граница реактора проходит
на расстоянии Аэф от фактической границы его активной (т. е.
содержащей размножающую среду) зоны. При этом Аэф не за-
висит от размеров и формы реактора. В идеальном случае, когда
активная зона граничит с вакуумом, Дэф= 0,712^' (см. § 2.1),
если размеры реактора много больше 2^’.
В дальнейшем, говоря о границе реактора, мы всегда будем
подразумевать его эффективную границу.
В настоящей главе рассмотрены условия критичности реак-
тора, находящегося в стационарном состоянии. Процесс установ-
ления стационарного состояния рассмотрен в гл. 14.
Большой однородный реактор без отражателя хорошо описы-
вается уравнением с одной группой нейтронов (см. § 2.1). В этом
случае плотность потока нейтронов удовлетворяет уравнению
(А+а2)Ф(г)=0, (4.1.1)
где а2 определено (2.1.52).
Уравнение (4.1.1) в математической литературе (см., напри-
мер, [85]) называется уравнением Гельмгольца. В литературе
по теории реакторов уравнение (4.1.1) часто называют «волно-
вым уравнением» [69] на том основании, что если искать реше-
125
ние волнового уравнения
в виде <p(r, t) =<p0(r) ехр (ia/), то, для <ро(г) получим уравнение
(4.1.1). Мы не будем использовать такое название, поскольку
волновое уравнение, описывающее распространение и излучение
волн, принадлежит к гиперболическому типу, а уравнение диф-
фузии (2.1.43), из которого было получено в § 2.1 уравнение
(4.1.1), принадлежит к параболическому типу.
Решение уравнения (4.1.1) должно удовлетворять гранич-
ному условию Ф(г)—О на границе, реактора (см. § 2.1). Такое
решение существует не при всех значениях а2. Те значения а2,
при которых решение существует, называются собственными
значениями, а соответствующие функции — собственными функ-
циями (см. любой курс по уравнениям математической физики).
Пусть a?n — собственные значения; Ф„(г)—собственные функ-
ции уравнения (4.1.1). Суперпозиция вида
Ф(г) = ЗЛ„Ф„(г),1 ’ (4.1.2)
п
где Ап — произвольные постоянные,, удовлетворяет уравнению
(4.1.1). В гл. 14 будет рассмотрено нестационарное уравнение и
показано, что при приближении к стационарному состоянию,
если эффективный коэффициент размножения равен единице,
все слагаемые (4.1.2), кроме того, которое соответствует мини-
мальному собственному числу, содержат множители, неограни-
ченно убывающие во времени. Таким образом, нас должно ин-
тересовать только минимальное собственное число. Условия сим-
метрии задачи часто облегчают написание нужного решения.
Рассмотрим ряд примеров.
Если реактор имеет вид однородной пластины, то плотность
потока нейтронов зависит только от координаты х (ось х пер-
пендикулярна" пластине, начало координат — в середине пласти-
ны). Уравнение (4.1.1) надо записать так:
^5- + а2ф = 0. (4.1.3)
dx2
Уравнение (4.1.3) имеет решение
Ф(х) — Л cos ах, (4.1.4)
где А — произвольная постоянная (по соображениям симметрии
решение не содержит sin ах). Граничное условие (d — толщина
пластины)
Ф(±б//2)=0 (4.1.5)
будет выполнено, если
а=—п' «=1,2,3..., (4.1.6)
126
Минимальное значение а имеет при п=1, т. е. реактор будет
критичен, если толщина пластины удрвлетворяет условию ,
a=n/d. ' (4:1:7)
Величину а, определенную из'(4.1.7) по заданному значению
d, называют геометрическим параметром, а величину а, опреде-
ленную по (2.1.53) через характеристики размножающей сре-
ды, — материальным параметром. Условие критичности состоит
в равенстве материального и геометрического параметров:
k — 1_ - й.
^=-~М---------d-SareoM- (4.1.8)
Пусть реактор имеет форму параллелепипеда со сторонами
а, Ь, с. Уравнение (4.1.1) в более подробной записи имеет вид
ч,и0 (4.1.9)
дх* ду2 дгг v
Уравнение (4.1.9) решается методом разделения переменных
(см. ниже пример цилиндрического реактора). Решение имеет
вид
Ф(х, у, г)=Л cos otxxcos ay у cos аг г\
ах=п/а-^ ay=n/b-, аг=п/с, ах2 +iav2-j-az2=a2. (4.1.10)
Объем реактора равен-
У=аЬс—л3/(ахауаг). (4.1.11)
Минимальный объем при заданном а имеет реактор в виде куба
(если сравниваются между собой только параллелепипеды):
VK = 3y3V/a3. (4.1.12)
Рассмотрим сферический реактор. Уравнение (4.1.1) запи-
шем в сферической системе координат; при этом учтем, что плот-
ность потока нейтронов не зависит от углов:
(4-МЗ)
\ г2 дг дг /
Если положить Ф(г) = —f(r), то получим
г
— + «7 = о
dr2
и, следовательно,
Ф (г) = — (A sinar + В cos ar), (4.1.14)
г
где А и В — произвольные постоянные. Плотность потока при
г=0 должна быть конечна, что возможно, только если В=0
127
(фактически (4.1.14) при В^=0 не является решением уравнения
(4.1.13) при г—0, поскольку 1/г имеет бесконечные производные
при г=0]. Таким образом,
Ф (г) = — sinar. (4.1.15)
Г
Граничное условие ф(/?)=0, где R— эффективный радиус
реактора, дает sina/? = 0, т. е. минимальное собственное значе-
ние а равно
a=n/R. (4.1.16)
Критический объем реактора равен
V = — R3 = —. (4.1.17)
3 3«3 ' ’
Рассмотрим цилиндрический реактор радиусом R и высотой
Н. В силу симметрии плотность потока не зависит от азиму-
тального угла. Поэтому уравнение (4.1.1) в цилиндрической си-
стеме координат запишем так:
(—4г 4-+4т+а2)ф (г>г)=°- (4Л-18)
\ г дг дг дг2 j
Будем решать (4.1.18) по методу разделения переменных. По-
ложим Ф(г, z)=/7(r)Z(z), подставим в (4.1.18) и разделим на
Г(г)7(г): .
1 d2Z <Z)_ — — g2; Л =_LjLr_L (4.1.19)
Z (z) dz2 F (r) r dr dr
Поскольку левая часть (4.1.19) зависит только от z, а правая —
только от г, (4.1.19) равно постоянной, которую обозначим —аг2.
Тогда из (4.1:19) получим
— + a/Z = 0; ArF + ar2F = 0; аг2 + ar2 = a2. (4.1.20)
dz2
Решением первого уравнения (4.1.20) будет
Z(z) =cos azz; az—п/Н. (4.1.21)
Решением второго уравнения (4.1.20) являются функции Бессе-
ля и Неймана нулевого порядка (см., например, [75]):
К(г)-Л/о(агг)+ВЛ^о(агГ). (4.1.22)
Функция ?/0(г) = У0(г) обращается в бесконечность при г —
= 0 и поэтому В=0, т. е.
F(r)—AJ0(arr); Ф(г, г)=Л cos (a2z)/0(arr). (4.1.23)
Граничное условие Ф(/?)=0 дает J0(a,R) = 0, откуда
ar=ai°/R, (4.1.24)
128
где cti°=2,4048 — первый корень бесселевой функции нулевого
порядка.
Таким образом, объем цилиндрического реактора равен
V = VR*H = — (4.1.25)
«г \ “г /
или, если выразить объем через а2 и отношение H]R,
0,58бГ/2—
\ а J R L \ Н / ' ]
= Vo^[(^)2+ °,586]3'2 , (4.1.26)
где Vo — критический объем сферы при том же значении а2.
Минимальный критический объем при фиксированном а2 имеет
цилиндр при —— = 1,083, причем этот минимальный объем ра-
вен Уод= 1,142 Vo. Сравним между собой объемы реакторов
в виде сферы, цилиндра и куба при одинаковых значениях а2:
Vo=O,876 Vo4=0,806 VK,
т. е. объем уменьшается, по мере того как форма реактора ста-
новится более «правильной» и уменьшается отношение поверх-
ности к объему:
(А \ =3,46—; = 3,29—; (—= 3—.
\ V / куб а \ /оц а \ V / сфера а
Можно определить критический объем и для некоторых дру-
гих форм реактора. Так, в работе [114] приведены результаты
для правильных многоугольных призм бесконечной высоты:
а^==Л«ао2, (4.1.27)
где ао соответствует цилиндру равновеликого объема; N— чис-
ло граней призмы; постоянные Ак равны: Аз—1,2545, А4—
=1,0865, А5= 1,0413, Л6=1,0232, Л7=1,0144, Л8 = 1,0096 (более
подробные данные для N от 3 до 20 опубликованы в [115]).
Для эллиптического цилиндра в [116] получено
где ао2 имеет тот же смысл, что в (4.1.27); е — эксцентриситет
эллипса [хотя (4.1.28) получено для малых е, точность этой фор-
мулы удовлетворительна вплоть до отношения осей эллипса
примерно 5] *.
* См. [116, 117]; автор признателен Ю. В. Петрову и Э. Г. Сахновско-
му за сообщение по этому вопросу. Результаты для эллиптического цилиндра
в [85] ошибочны.
9—6053 129
Задача о критичности полусферы решена в книге [118]:
а=4,4934/7?,
где 7?— радиус полусферы.
Критичность вытянутого эллипсоида вращения рассмотрена
в [119, 120].
Можно выразить а через среднюю хорду объема реактора
(1.10.26). При этом получим
а=соп/7, (4.1.29)
где коэффициент с0 изменяется от —'1,2 до 2 для разной гео-
метрии:
Шар.................................. 1,33
Полусфера.............................1,27
Куб.................................. 1,16
Пластина.............................2
Бесконечный цилиндр...................1,53
Шестигранная призма..................1,48
Конечный цилиндр...................1,216^Со= - 2|/0,586 + (7?///)2
Формула (4.1.29) может быть полезна для ориентировочной
оценки критического объема.
Из (2.1.53) следует, что критический объем обратно про-
порционален (k—1)3/2 и прямо пропорционален кубу длины ми-
грации:
1/~(й—1)-з/2М3. (4.1.30)
Пусть плотность вещества в реакторе изменяется таким об-
разом, что сохраняется геометрическое подобие его конструк-
ции. Тогда коэффициент размно-
жения не изменяется (если пре-
небречь возможным изменением
блок-эффектов, см. гл. 7—10), а
длина миграции обратно пропор-
циональна плотности 1/р_ По-
этому объем реактора изменяет-
ся как р~3, а критическая мас-
Рис. 4.1. Распределение плотности
потока нейтронов в однородном
реакторе в виде сферы, цилиндра,
пластины
са — как р .
На рис. 4.1 приведено распре-
деление плотности потока ней-
тронов в реакторах различных
форм: сфера, цилиндр, пластина.
Эти распределения очень похожи.
В приложениях важное зна-
чение имеет коэффициент усред-
нения плотности потока (обрат-
ную величину называют коэффи-
130
Таблица 4.1. Коэффициенты усреднения плотности потока
Геометрия Hi |Л2
Пластина 2 — = 0,637 п 0,5 •
Шар 3 — = 0,304 л2 3 — = 0,152 2л2
Цилиндр (по радиусу) Л(2-405) „ „ 1,2 -0’433 [Л (2,405)]2 = 0,27
Цилиндр (по высоте; 2 — = 0,637 ге 0,5
Параллелепипед -~ = 0,258 л3 0, 125
циентом неравномерности):'
= (W* I Ф(г)</г, (4.1.31)
где V — объем реактора; Фт — максимальное значение плотно-
сти потока; интегрирование ведется по объему активной зоны.
Существенно также среднее значение квадрата плотности по-
тока:
!л2 = (УФ^)-1 j* Ф2 (Г) d г. (4.1.32)
Значения pi и цг для реакторов различных форм без отра-
жателя приведены в табл. 4.1. Коэффициенты усреднения раз-
личаются между собой гораздо сильнее, чем кривые на рис.
4.1, — это следствие различной размерности задачи: для пласти-
ны интегрируется Ф(г), для цилиндра гФ(г), для сферы г2Ф'(г).
Поэтому для цилиндра и тем более для сферы внешние слои,
где плотность потока нейтронов мала, играют значительно боль-
шую роль, чем для пластины.
Выше рассматривался реактор, находящийся в критическом
состоянии. Если реактор находится в подкритическом состоя-
нии, то для поддержания стационарных условий необходим
внешний источник нейтронов. Плотность потока нейтронов при
этом удовлетворяет уравнению
РДФ+(£— 1)2аФ=—q, (4.1.33)
где q — мощность источника нейтронов. Проинтегрируем это
уравнение по объему и обозначим: Q = J qdr — интегральную
мощность источников; N= J Ф2айг — общее число нейтронов,
9* 131
поглощенных в реакторе; S=—D j gradOds — число нейтро-
нов, вышедших из реактора. Тогда вместо (4.1.33) получим
(k—\)N— S=—Q. (4.1.34)
Эффективный коэффициент размножения определен формулой
(1.9.2), где Р по физическому смыслу равно P—S/(N-irS'). За-
меним в (4.1.34) /г==/гэф/(1—P)^k3<p(N-\-S)lN и получим
ЛН-5=<2/(1-йЭф), (4.1.35)
т. е. полное число поглощенных нейтронов, включая утечку,
в 1/(1—&Эф) раз больше, чем интегральная мощность источни-
ков. Поэтому величину 1/(1—&Эф) называют коэффициентом
умножения подкритического реактора. Если йЭф близко к едини-
це, то коэффициент умножения весьма велик.
4.2. НЕОДНОРОДНЫЙ РЕАКТОР БЕЗ ОТРАЖАТЕЛЯ.
ОДНА ГРУППА НЕЙТРОНОВ
Рассмотрим цилиндрический реактор без отражателя беско-
нечной высоты, состоящий из двух областей: выравненной зоны
0<г<п и внешней зоны rx<r<R. В выравненной зоне положим
а=0; во внешней зоне задано а2>0. Требуется определить от-
ношение и//?, коэффициенты усреднения по радиусу pi и ц2 как
функции aR.
Уравнение (4.1.1) при «2=0 для цилиндра имеет общее ре-
шение:
ф(г)=с04~С1 In г.
Из условия, конечности Ф при г=0 получим Ci==0, т. е. Ф=
=const. Решение уравнения (4.1.1) во внешней области дано
(4.1.22), причем надо сохранить обе функции J0(ar) и Na(ar),
так как No(ar) не обращается в бесконечность при Г1<г<£.
Плотность потока в выравненной зоне положим равной едини-
це. Решение для внешней зоны:
ф 0 = Л"1 [М, («/?) Jo (аг) - /0 (aR) No (аг)], Н < г < /?;
о = ЛГ0(а/?)7о(аГ1)-70(^)У0(аГ1)
удовлетворяет граничным условиям Ф(/?)=0, ф(Г1)=1. Вто-
рое граничное условие при r=rj
Ф'(Г1)=0 (4.2.2)
приводит к условию критичности
No(aR)Ji(ari)—Jo(aR)Ni(ari) =0. (4.2.3)
132
(4.2.1)
На рис. 4.2 изображена по-
лученная из (4.2.3) зависи-
мость n/R от aR. Чтобы пло-
щадь выравненной зоны пре-
вышала половину всей площа-
ди активной зоны, т. е. (п//?) >
>0,7, значение aR должно быть
больше 5,5. Это означает, что
а2, более чем в 4 раза превы-
шает то значение а2, при кото-
ром критичен однородный ре-
актор того же радиуса R (т. е.
реактор без выравненной зоны,
когда а/? = 2,405). Если длины
миграции в выравненной и
внешней зонах близки, то k—
—1 во внешней зоне должно
быть в 4 раза больше, чем для
однородного реактора тем же
радиусом.
Коэффициент усреднения
Рис. 4.2. Зависимость радиуса вырав-
ненной зоны Г1 и коэффициентов вы-
равнивания (12 от aR
К
(4.2.4)
С помощью (4.2.3), воспользовавшись известным соотноше-
нием между цилиндрическими функциями
J0(z)N1(z)-J1(z)N0(z)=-2l(nz), (4.2.5)
получим
к
R
2 Л(«Г1)1
а/? /0(“Я)]
'1
R
(4.2.6)
Для вычисления ц2 используем формулу (см. [75, формулы
(5.54.1), (5.54.2)]):
«а
J х [aJ0 (х) — bN0 (x)j2 dx —
xt
’ {[aJ0 (х) - bN0 (х)]2 + [aJ1 (л) - bN, (x)]2}, (4.2.7)
условие критичности (4.2.3) и формулу (4.2.5). В результате вы-
числений находим (см. рис. 4.2)
Г гх Л(а^1) I2
I R Д(о-Ю J
_ W2
— 4
(4.2.8)
133
Рассмотрим полный ток нейтронов через боковую поверх-
ность реактора (на единицу высоты)
J=2nDR(tf (/?) = 2n.DaRA0~1 [ЛЛ0 (а/?) Л (а/?) — Jo (а7?) М (а7?) ].
(4.2.9)
Используя (4.2.5) и выражая Ло в (4.2.1) через ри:
A-'=^-(aRy[^-(rilRy],
4
получаем
7=лР(а/?)2 [Щ-(П//?)2]. (4.2.10)
Сравним Т с током нейтронов 70 через поверхность однород-
ного реактора тем же радиусом R и с тем же коэффициентом
диффузии:
_£Pi (ri/B)2 / а \2 Ф(0) _ 2,405 (4 2 11)
Jo Pio \ “о J Фо(О) R
где цю — коэффициент выравнивания; Фо(О)—плотность пото-
ка в центре однородного реактора. Если сравниваются реакто-
ры с одинаковой мощностью, то (предполагается, что Sf одина-
ково и не зависит от координат)
Ф(0) _ Рю
Фо(0) — Щ
и тогда
J =;0[1- — М2] (—у. (4.2.12)
Pl \ R 1 J \ “п J
Из рис. 4.2 получим, например, при aR—6, щ = 0,805; r^R—
= 0,72 и 7/76=2,2, т. е. выход нейтронов при той же мощности
реактора изменился в результате выравнивания потока в 2,2
раза.
Если реактор имеет конечную высоту Н, но не имеет на ос-
нованиях отражателей, то сохраняются все приведенные выше
формулы с заменой
а—> ar = ]Za2—а22; аг = ~!Н. (4.2.13)
Рассмотрим аналогичную задачу для высотного выравнива-
ния. Пусть реактор имеет высоту Н и бесконечен в радиальном
направлении (т. е. реактор в вид пластины). В выравненной
зоне положим (начало координат расположено в центре реак-
тора)
Ф(г) = 1; |z|<zi. (4.2.14)
При zj< Iг| <77/2
ф (г) =Л sin az-J-B cos az. (4.2.15)
134
Граничные условия Ф(Я/2)=0, <D(zi) = l, O'(zi)=0 дают
условие критичности
(4.2.16)
откуда
— «>«„ = —. (4.2.17)
2 .2а /7
Коэффициенты усреднения равны
и1 = — + (1 — АА = 0,637 + 0,726-^-;. (4,2.18)
п \ я / н н
р'2==т(1 +^)- (4-2Л9>
Чтобы получить коэффициент усреднения, например pi=-
=0,8, т. е. увеличить его на 25% по сравнению с коэффициен-
том для однородного реактора, надо иметь 2zi = 0,447/, т. е.
а=1,8ао, или если длины миграции в зонах близки, то k—1 во
внешней зоне надо увеличить в 3,3 раза по сравнению с k—1
для однородного реактора той же высоты.
Если реактор имеет конечные размеры в радиальном на-
правлении и не имеет отражателя на боковой поверхности, то
все формулы сохраняются с заменой (/? — радиус реактора):
а—>аг = |/аг— аг2; аг = ——-. (4.2.20)
R
Следует иметь в виду, что отражатель, даже не очень хоро-
ший, заметно изменяет коэффициенты усреднения (см. § 4.3).
Задача I. Сравнить ток J (4.2.10) с общим количеством нейтронов, по-
глощенных в зоне г,<г<Я.
Решение. Количество нейтронов, поглощенных в зоне ri<r<R, равно
[при Ф(0) = 1]:
R г R
Принимая во внимание, что в теории с одной группой нейтронов M2 = D/Sa,
получаем
J=a2M2N= (k— V)N,
где k — коэффициент размножения при ri<r<R. Этот же результат следует
из (1.9.2). В самом деле, так как йЭф=1, то число выходящих нейтронов
k — 1
равно PN0——-—No, а число поглощенных У=(1—P)N0=No/k, где No —
k
число нейтронов, родившихся в зоне г;<г<Р. Поскольку ток в сторону вы-
равненной зоны равен нулю, получим J=(k—l)N.
Задача 2. Показать, что прн ап1 из формулы (4.2.3) следует
условие критичности для плоского реактора, т. е. (4.2.17), и оценить погреш-
ность в первом порядке по (а/?)-1.
135
Решение. Используя асимптотическое разложение цилиндрических
функций и учитывая два члена разложения по параметрам (а/?)-1 и (ап)-1,
получаем из (4.2.3)
1 / ! , 3 \
Если положить а(/?—Г])=л/2-)-Д, то надо считать, что Д<1. Тогда
" , 1 / 1 , 3 \
a(R—ri)=-----4-— ——4-------- . (4.2.21)
Пренебрегая в (4.2.21) вторым слагаемым в правой части, получаем (4.2.17).
Подставляя в правую часть (4.2.21) вместо afi результат, полученный
в первом приближении, т. е. art = aR—л/2, имеем
a(^-fi)=V+ оЬ"- (4.2.22)
Таким образом, уже при а7?>5 можно использовать формулу (4.2.17) для
цилиндрической задачи, так как погрешность определения а или R при этом
меньше 6 %.
4,3. РЕАКТОР С ОТРАЖАТЕЛЕМ.
ОДНА ГРУППА НЕЙТРОНОВ
Применение уравнения с одной группой нейтронов к расче-
ту реактора с отражателем не приводит к заметным ошибкам
только в тех случаях, когда отражатель «достаточно плохой»,
а реактор «достаточно большой». Тем не менее рассмотрение
простейших задач в этом приближении может быть полезным.
Уравнение (2.1.44) справедливо и в том случае, когда точка
г принадлежит отражателю. Надо только считать, что vSf есть
функция координат, не выносить ее в (2.1.44) за знак интегра-
ла и учитывать, что v2f=O вне активной зоны. Если точка г'
расположена в отражателе достаточно далеко от границы ак-
тивной зоны, так что функция U?(r, г') достаточно мала, то по-
следним слагаемым в (2.1.44) можно пренебречь. Условием ма-
лости является неравенство
(4.3.1)
РЧ
причем г' — точка в отражателе, г — в активной зоне, вблизи
ее границы; х2— значение возраста для отражателя.
Таким образом, будем считать, что в активной зоне справед-
ливо уравнение (4.1.1), а в отражателе — уравнение
(А—Е2-2)'Ф2=0, (4.3.2)
где Ф'г — плотность потока нейтронов в отражателе; L2—
=Y D2/ Sa2— длина диффузии тепловых нейтронов в отража-
теле. Фактически уравнение (4.3.2) справедливо только вдали
от границы активной зоны; в одногрупповом приближении пре-
136
небрегают этим обстоятельством. Из (4.3.1) и (4.3.2) следует,
что это приближение законно, если Этому условию удов-
летворяют все замедлителил, кроме Н2О.
Уравнения (4.1.1) и (4.3.2) надо дополнить граничными ус-
ловиями на границе активной зоны и отражателя
-Ф1=Ф2; (.4.3.3)
где Z>i, Z>2 — коэффициенты диффузии тепловых нейтронов
в активной зоне и отражателе. В § 2.1 был введен эффективный
коэффициент диффузии (2.1.49). Однако уравнение (2.1.50) не
справедливо, если точка г расположена на границе активной зо-
ны. Поэтому в (4.3.3) под коэффициентом диффузии Di надо
понимать нечто среднее между D3$ и истинным коэффициентом
диффузии. Эта неопределенность уменьшается, если т в актив-
ной зоне мало по сравнению с L2. После этих оговорок решим
две простейшие задачи по определению критических размеров
реактора с отражателем.
Рассмотрим сферический реактор. Радиус активной зоны R,
толщина отражателя А. Плотность потока нейтронов в активной
зоне равна [решение уравнения (4.1.1)]
ф1 = Л^^-, (4.3.4)
а в отражателе [решение уравнения (4.3.2)]
Ф2 = — [В ехр (— r/L2) С ехр (r/L2)]. (4.3.5)
г
Используя граничное условие на внешней поверхности отра-
жателя Ф2(Р+А)=0, можно исключить из (4.3.5) постоян-
ную С:
Ф2 =— [ехр(— гЩ) — ехр(— + (4.3.6)
Граничные условия (4.3.3) приведут к условию критичности
^- = Г1 —?(1 + —)] 1 . (4.3.7)
a R [ К ^3' / J
где
Положим
Р = -£-; L2'=A2th-A_. (4.3.8)
^2 ^2
R=Ro—АЭф; Ro=nja, (4.3.9)
т. е. Ro — радиус реактора с тем же материальным параметром
а, но без отражателя; Аэф — экономия в радиусе активной зоны
137
реактора, обусловленная применением отражателя. Из (4.3.7)
получим
tgаДэф = 1 — -L*- Г* . (4.3.10)
Р L р г. схДэф J
Если р=1, то из (4.3.10) следует
дЭф =— arctgaL/. (4.3.11)
а
Из (4.3.11) видно, что если аДэф<^1, т. е. если экономия за счет
отражателя много меньше размеров реактора, то и ctL'aCl-
Тогда из (4.3.10) получим
Д = _L arctg У-. (4.3.12)
“ Р Р
Равенство (4.3.12) показывает, что экономия в размерах ре-
актора, связанная с применением отражателя, пропорциональна
длине диффузии в отражателе. Она увеличивается, если исполь-
зуется отражатель с малым коэффициентом диффузии (т. е.
если р<1). Экономия уменьшается, если толщина отражателя
уменьшается и делается меньше длины диффузии. Так как
th 1 — 0,73, a th 1,5=0,90, то увеличение толщины отражателя
сверх (1 —1,5)12 не приводит к заметному возрастанию ЛЭф-
Поэтому не имеет смысла делать отражатель очень толстым.
Напомним, что было сделано предположение Дэф,~'£/2<С/?,
т. е. реактор достаточно большой. Исследование случая, когда
это предположение не выполняется, нецелесообразно, поскольку
точность одногруппового уравнения уменьшается при уменьше-
нии размеров реактора. Из (4.3.11) следует, что при а£'2<^1,
р—\ справедливо разложение
Дэф = L/[l - -2- (aL/)^ (4.3.13)
т. е. поправка, учитывающая следующие члены разложения по
aL'2, уменьшает эффективную добавку Аэф.
Рассмотрим теперь цилиндрический реактор с отражателем
на боковой поверхности, но без отражателей на основаниях ци-
линдра. Пусть высота реактора равна Н. Положим
Ф(г, з)=Ф(г) cosotzZ; v.z=n!H (4.3.14)
и получим уравнения в активной зоне
(АЛ+а,2)Ф1=0; а,2=а2—аг2 (4.3.15)
и в отражателе
(Дг — х2) Ф2 ='); х2=-^-+аД (4.3.16)
138
где Аг определено (4.1.19). Решение уравнения (4.3.16), удов-
летворяйте граничному условию Ф2(/?1) =0, А, где А —
толщина отражателя, имеет вид
Ф2 = С[К0(хг)-Ф/0(хг)|; Ф = (4.3.17)
Если отражатель имеет бесконечную толщину, то W=0. Реше-
ние уравнения (4.3.15) дано (4.1.23). Граничные условия (4.3.3)
приводят к уравнению критичности
Jp(arR)____' К, (х^) (4 3 18)
“гЛ(“гй) ~ ?х Ki (*Я)-Ф/1 (*/?) f
Пусть R-=Rq—АЭф и АЭф<^/?о. Тогда левую часть (4.3.18)
можно разложить в ряд по малой величине а,-Аэф. В первом при-
ближении
1 К0(х/?)-Ф/0(х/?)
рх KiivR) -f-w^x/?)’
(4.3.19)
В том же приближении надо считать, что %R^cR0^> 1, по-
скольку из (4.3.19) следует, что Аэф и Т2 — одного порядка. Тог-
да можно воспользоваться асимптотическим разложением функ-
ций Ki, Ц [75, 93]. В результате получим [сохранен один член
асимптотического разложения; если учитывать следующие чле-
ны, то надо одновременно учесть и следующие члены в разло-
жении левой части (4.3.18)]:
** - ‘Ь (й ГТ+^Т?). (4.3.20)
Полученный результат практически совпадает с (4.3.12), так
как в рассматриваемом приближении аг2Е22<с1 (если 2R ^.Н).
Таким образом, в этом приближении экономия в размерах ре-
актора не зависит от конкретной геометрии, что можно было,
конечно, предвидеть заранее.
Рассмотрим еще случай совсем малых толщин отражателя
A <Z,2.
(4.3.21)
Длина диффузии хороших замедлителелй (графита, D2O)
около 50—100 см. Поэтому отражатель толщиной 10—15 см
можно считать тонким в смысле неравенства (4.3.21). Из (4.3.8)
в этом случае следует L/2=A и тогда из (4.3.10) при aA<gl по-
лучим
АэФ=А/р, (4.3.22)
т. е. тонкий отражатель экономит в размерах реактора (если
у~1) величину, равную своей толщине.
Задача 1. Определить коэффициенты pt и ц2 для плоского реактора, если
отношение эффективной толщины отражателя к высоте реактора равно г
(отражатели с обеих сторон одинаковые; г=ДЭф/Н0, где ДЭф—эффективная
толщина одного отражателя; Но — высота активной зоны).
139
Решение. По определению ьц имеем
я„/2
Pi = J Ф(х)</Х.
° -Яо/2
п
Положив Ф(х) = cos ах, где а =--(1 -f- 2z)-1, и
но
проинтегрировав, полу-
чим
2 лг
Pi = — (1 + 2z)cos — .
л 1 -f- 2г
2 Г л2 z2
При г<^ 1 отсюда имеем =— 1 +2г—-------------------------
7^ |_ 2 14—
(4.3.23)
с точностью до членов
2
—, т. е. коэффициент
порядка г4. Пусть, например, 2 = 0,1, тогда jii=l,16
16 % по сравнению с коэффициентом для реактора без
усреднения возрос на
отражателя.
По определению,
После интегрирования
Яо/2
p.2 = -^- J ®2(x)dx.
° -Яо/2
получим
1 4- 2z 2nz 3
--------sin----------- ,
л 1 -J- 2z J
(4.3.24)
2 14
или при малых г
1 (
Рг — 2 + 2г
Если, например, 2 = 0,1, то ц2 на 19 % больше, чем для реактора без отра-
жателя.
Задача 2. Решить задачу 1 для цилиндрического реактора бесконечной
высоты, если отношение эффективной толщины отражателя к радиусу рав-
но г.
Решение. По определению jii имеем (Ro— радиус реактора)
Ко
2 (“ 2
Pi=-^r j h(*r)rdr = -^J1(aRQ),
О
или
/ ccr,Rn \
Pi = Pi°(l 4z)[J1(a0/?0)]-iJ1 44 ; а0/?0 = 2,405,
\ 1 -t-z /
(4.3.25)
где pt0 — коэффициент усреднения для реактора без отражателя. При z<Cl
Hi=|ii0(l-)-2z).
Коэффициент ц2 равен [см. (4.2.7)]
Ко
Рг = С JQ2(ar)rdr = /02
Ко2 J
0
“о^о \ , » I “оРо \
l+z/T 1 U+z )
(4.3.26)
140
При Z<1
Н2=Н2°(1+2г).
Сравнение с результатами решения задачи 1 показывает, что линейные
члены по г не зависят от геометрии.
Задача 3. Определить условие критичности сферического реактора ра-
диусом R, в центре которого расположена черная сфера радиусом р; то же
при замене черной сферы пустотой.
Решение. Плотность потока в активной зоне равна
sinar cos ar
Ф (г) =А-------j-В------
Граничные условия Ф(В)=Ф(р)=0 приводят к уравнению критичности
tg aR=tg ap.
Если ap< 1, а/? = л4-6, 6<C 1, то 6=ap, R = — -J-p.
a
В случае пустой сферы ток нейтронов при г=р равен нулю, т. е. Ф' (р) =
=0. Условие критичности будет
. „ tg“P~“Р
tg aR —----------
1 -j- ap tg ap
При apCl, aR=K—6, 6<1 имеем
D « (ap)2
R = — + p—
a 3
t. e. поправка к радиусу однородного реактора значительно меньше, чем
в случае черной сферы.
4.4. РЕАКТОР С ОТРАЖАТЕЛЕМ. ДВЕ ГРУППЫ НЕЙТРОНОВ
Уравнения с двумя группами нейтронов запишем так [см.
(3.2.29), (3.2.31)]:
Чд--тг1ф(г) = -«(г); (4-4Д)
\ ь2 /
/ 1 \ ь*
( Д - 4-)« W = - -V Ф (г), (4.4.2)
\ и* / т*
где т*, k* определены (3.2.30), (3.2.32). Применив к (4.4.1)
оператор А—1/т*, получим
Разложим квадратный трехчлен относительно А на множители:
(А+й!2) (А—а22)Ф (г) =0, (4.4.4)
где
4(й*—1)т*Д?
(Д24-Т*)2
(4.4.5)
141
Если k*—1<^1, то радикал в (4.4.5) можно разложить в ряд.
Сохранив главные члены, получим
ai2 = k—=Ll; M2 = L2 + г*; (4.4.6)
т. е. k*—1<С1, параметр сц2 совпадает с лапласианом (2.1.53),
в котором учтено поглощение и размножение нейтронов при
замедлении путем замены k и т на k* и т*.
Обозначим ЛГ] и N2 решения уравнений
(A4-a12).Vi = 0; (А—а22)Лт2=0. (4.4.8)
Общее решение уравнения (4.4.4) будет
Ф^С^+С^, (4.4.9)
где Сь С2— произвольные постоянные. Из (4.4.1) получим
(4.4.10)
где
T1=l+ai2L2; y2=a22L2— 1, (4.4.11)
причем
(4.4.12)
Если справедливо разложение (4.4.6), (4.4.7), то
V1=l; Y2=£7t*. (4.4.13)
Запишем уравнения (4.4.1), (4.4.2) для цилиндрического ре-
актора. Если на основаниях цилиндра нет отражателей, то мож-
но разделить переменные, выделить зависимость от z в виде
множителя cos azz. Для функций, зависящих только от радиу-
са, получим следующие уравнения:
D(^r---Л- ) Ф (0 = - « (Г); (дг-М п (г) = - 2аФ (г),
\ L' J \ т' / т
(4.4.14)
где
z/ =
При этом формула
мену:
^'^(l-h^-'OHV)-1. (4.4.16)
(4.4.5) сохраняется, но надо сделать за-
£2^£'2.
142
Рассмотрим реактор без отражателя. На границе реактора
должно быть ф(R)=n(R) —0. Выражая CiNi(R) из (4.4.9) и
подставляя в (4.4.10), получаем
(Yi+Y2)C2AA2(/?)=0. (4.4.17)
Функция JV2(r) > например, для сферического реактора имеет
вид
У2(г) = ДйДзЦ
г
т. е. не обращается в нуль при г=Д и действительных аг- По-
скольку у1+у2#=0> то из (4.4.17) следует, что С2=0. Таким об-
разом, для реактора без отражателя справедливо уравнение
с одной группой, но с заменой а2 (2.1.52) на щ2 (4.4.5) (см. так-
же § 4.6). Для реактора с отражателем Сг#=0. Отметим, что
N2(r) —функция, монотонно растущая с ростом г, т. е. она до-
стигает максимума на границе с отражателем. По мере удале-
ния от границы отражателя N2 убывает, причем характерная
длина равна 1/сс2- В большом реакторе 1/а2, и поэтому в цен-
тральной части активной зоны большого реактора справедливо
уравнение, совпадающее с одногрупповым приближением.
Уравнения для отражателя получаются из (4.4.1), (4.4.2),
если положить там 2f=0, т. е. й*=0:
D (Д — Ф = — п; (д—= (4.4.18)
Если «(г) есть решение второго уравнения (4.4.18), то
Ф (г) = Фо (г) - (1 - -Д-Г1 ц (г), (4.4.19)
и \ L* j
где Фо(г)—решение однородного уравнения для Ф(г). Напри-
мер, для сферического реактора и бесконечного отражателя
/ \
ф (г) = — ехр ( - - (4.4.20)
Граничные условия для Ф1 имеют обычный вид (2.1.54),
(2.1.55), для плотности замедления п— (3.2.42).
Условие критичности даже для простейших случаев одно-
родного реактора с бесконечным отражателем получается гро-
моздким, и его подробный анализ затруднителен. Для более
сложных случаев, когда активная зона (и отражатель) состоит
143
из нескольких слоев, возможно только численное решение за-
дачи. Вопросы численного определения критических размеров
в двух- или многогрупповом приближении изложены во многих
монографиях (см., например, [70, 103, 121, 122]); математиче-
ские вопросы теории реакторов рассмотрены в [123]. Большой
экспериментальный и теоретический материал о критических
объемах и массах различных делящихся нуклидов приведен в
справочнике [124].
Известен только один случай, когда в двухгрупповом при-
ближении можно получить простую формулу для критического
размера реактора с отражателем. Хотя этот случай редко мож-
но использовать на практике, приведем здесь результат ввиду
его красоты и возможности простого качественного анализа.
Если замедлитель в активной зоне и отражателе один и тот же
(т. е. Ti=T2, Di~D2, индексы 1, 2 обозначают активную зону и
отражатель), толщина отражателя бесконечна, можно ие учи-
тывать поглощения нейтронов при замедлении и реактор до-
статочно большой, так что справедливо неравенство
а^3>1, то радиус сферического реактора равен [125,
с. 147]
R=Ro—Аэф; 7?o=n/ai,
где
дэф = “ farctg a1E2 + arctg ax — arctg .
I a2 .
(4.4.21)
Если т=0, to (4.4.21) совпадает c (4.3.11). Если
ai/a2<Cl,
TO
Дэф L2 + /7- l/a2 = L2 + /7(1-1^), (4.4.22)
где использовано (4.4.7). Если т—L^2, то т. е. эконо-
мия в размере возрастает по сравнению с оценкой в одногруп-
повом приближении на 0,3 ]/ т, что обычно мало по сравнению
с 7-2 (кроме обычной воды). Если сохранить в разложении
(4.4.21) еще один член, то получим
Дэф = «Г’----(Д23 + ~ «г3), (4.4.23)
О
т. е. величина Лйф уменьшается. Учет конечности толщины от-
ражателя также уменьшает ДЭф. Формула (4.4.21) справедлива
и для эффективной толщины отражателя реактора в виде пла-
стинки (при тех же условиях).
Если в центральной части реактора расчет по одной или
двум группам дает одинаковое распределение плотности пото-
ка, то вблизи границы активной зоны с отражателем двухгруп-
повые уравнения приводят к большему значению плотности по-
144
тока, чем одногрупповое. Если отражатель хороший (слабо
поглощающий нейтроны), а активная зона маленькая, то в отра-
жателе возникает максимум потока. По мере уменьшения ак-
тивной зоны и увеличения сечения поглощения в ней максимум
плотности потока тепловых нейтронов в отражателе возрастает
и может значительно превосходить плотность потока в активной
зоне. Такое распределение плотности потока осуществляется в
исследовательских высокопоточных реакторах [126]. Количе-
ственный расчет малой активной зоны с хорошим отражателем
может быть сделан только в многогрупповом приближении. Од-
нако качественные особенности распределения плотности пото-
ка в отражателе можно понять и из двухгрупповых уравнений.
Рассмотрим сферический реактор с бесконечным отражате-
лем. Плотность потока в отражателе дается формулой (4.4.20).
Как указывалось в § 2.1, можно исключить из рассмотрения
область, где нейтроны сильно поглощаются (в данном случае
это активная зона), если ввести эффективное граничное усло-
вие. Это условие можно сформулировать как обращение в нуль
плотности потока, экстраполированной внутрь поглощающей об-
ласти, на эффективной границе, которая расположена на рас-
стоянии порядка Ss-1 от геометрической (см. § 2.1 и 6.1). По-
скольку радиус активной зоны значительно больше Ss-1, в пер-
вом приближении можно не делать различия между эффектив-
ной и геометрической границами. Таким образом, вместо
(4.4.20) надо написать (R— радиус активной зоны):
Ф(г) = — [ехр ( — -—— — exp f — > 'К'6 Ф(^) = 0.
г L \ Д / ' |/ г ) J
(4.4.24)
Плотность потока (4.4.24) максимальна при г=го, где го
определяется из уравнения
Г1 + —^expf_*-\ = (1 +-^ ехр (4.4.25)
\ L J у L j \ |/ т J \ |/ т /
или
r0—R =
|Л Д
д-/7
In
1 + Го/1Лт
1 + г о/Д
(4.4.26)
Если у х (этому условию удовлетворяют все хорошие
замедлители, кроме обычной воды), то
г0 - R ъ /7 In Гх 1П (2 + у- ) . (4.4.27)
Так как размеры активной зоны исследовательского реактора
невелики, например /?=( 1-^-2) т0 Го~/т, т. е. макси-
мум плотности потока в отражателе расположен на расстоянии
порядка "Кт от границы активной зоны. Значение плотности
10—6053
145
потока в максимуме равно
ф« = ТТТ^(1-е“1); (4.4.28)
Абсолютное значение плотности потока тепловых нейтронов
в отражателе можно определить из условия баланса нейтронов.
Вероятность выхода из активной зоны равна [см. (1.9.2)]
(4.4.29)
а число вышедших нейтронов
(4.4.30)
где W — мощность; Ef — энерговыделение в одном акте деления
(см. § 1.7). Все вышедшие из активной зоны нейтроны погло-
щаются в отражателе, т. е.
N = 4т2д J г2Ф (г) dr — 4ъА2а [L2 ехр (R/L) — т ехр (/?/Кх)] AnDA.
(4.4.31)
Таким образом,
_ г k~ 1 1—е~1_____
m~V Ef k (Z?4-
= 4,7• 1015 v нейтрДсм2-c), (4.4.32)
k R + у т
где W—мощность, МВт; S/r — транспортное сечение в отража-
теле. Положим для примера &=1,6, v=2,4, S/r-1 = 2,5 см, R=
=20 см, ]/"т=10 см и получим
Ф’т=5,6-1013 Й? нейтр/(см2-с). (4.4.33)
Для достижения плотности потока нейтронов 1015 нейтр/
(см2-с) необходима мощность около 20 МВт. Более точные вы-
числения показывают, что мощность должна быть несколько
больше [126, 127].
Отношение максимальной плотности потока нейтронов
к мощности реактора называют качеством исследовательского
реактора [126]:
К = 4^- = 4,7 10‘°v k-^ —----------. (4.4.34)
W k 7? + [А (см2-с-МВт)
Из (4.4.34) видно, что качество возрастает при увеличении
k и уменьшении R, /ти Itr- Следует, однако, иметь в виду, что
качество — не единственный параметр, характеризующий иссле-
146
довательский реактор. Важен также большой объем того про-
странства, где достигается максимальный поток, для того чтобы
можно было разместить каналы для вывода нейтронных пучков
(если реактор предназначен для нейтронных исследований вне
реактора) или мишени для облучения нейтронами. Объем этого
пространства пропорционален /?. Если качество (4.4.34) умно-
жить на /?, то размер активной зоны практически выпадает. Это
означает, что не следует стремиться к очень малым активным
зонам. Для более полного анализа свойств исследовательского
реактора необходимы подробные расчеты (с примерами таких
расчетов можно ознакомиться, например, в работах [128, 129]).
Задача 1. Получить условие критичности для цилиндрического реактора
радиусом 7? бесконечной длины с отражателем толщиной Д.
Решение. Плотности потоков в реакторе [см. (4.4.9) — (4.4.11),
(4.4.19)]
Ф1=А1/о (ct2r)',
«1 = -ту [А1у1Д( axr) — Aj-p/oltV)]
и в отражателе
где
При этом Ф2(г) и п2(г) удовлетворяют условиям Ф2(/?+Д)=0, n2(R-l~
-|~А)=0. При r=R, т. е. иа границе реактора с отражателем, должны выпол-
няться условия [см. (3.2.41), (3.2.42)]:
Ф1(/?) = Ф2(Я); Ф/ (/?) = рФ2' (R); p=£>2/£>i; ni(R)=sn2(R)-
пг'(R) = sn2'(R); s=(£Ss4-') / ; F=s-^-.
\ 9 /a / ' 9/1 Д
где Di, Di — коэффициенты диффузии для тепловых и замедляющихся ней-
тронов. В отражателе обычно можно положить <р2=1, поскольку поглощение
замедляющихся нейтронов там мало. Граничные условия дают четыре урав-
нения для коэффициентов А/. Условие критичности получится, если детерми-
нант этих уравнений приравнять нулю (условие существования нетривиаль-
ного решения однородной системы линейных уравнений). Надо найти мини-
мальное значение коэффициента размножения или размера реактора, кото-
рые обращают этот детерминант в нуль.
Задача 2. Полупространства х>0 и х<0 заполнены различными размно-
жающими средами с коэффициентами размножения, равными единице. Опре-
делить отношения тепловых Ф+/Ф_ и замедляющихся и+/и_ нейтронов вдали
от границы раздела.
Ю* 147
Решение. Если k*—l, то ai = 0, Yi=l, а22 и у2 даны (4.4.7) и (4.4.13).
Решения уравнений (4.4.1) и (4,4.2) при х>0
Ф+(х) =А+-|-Л+х—В+ ехр (—а2+х);
n+(.v)=Sa+[A+4 Л+х-(-В+у2+ ехр (—а2+х)]
и при х<0
ф_(х) =А_-|-Л_х-|-В_ ехр (—а2-Х);
n_(x)=Sa-[A_-|-A-x—В_у2_ ехр (—а2_х)].
В общем случае нельзя положить Л+ = Л_=О, поскольку условие баланса
нейтронов в каждом элементе объема дает равенство fe'=l [см. (3.2.35)],
а не k*=l. Вблизи х=0, в области шириной порядка 1 /а2, где ДФ=А0, &—1
различного знака, и поэтому при Л±=0 система в целом может быть как
иадкритичной, так и подкритичной. Положим Х_=0, а Л+ будем считать
малым; |Л+/В+1 <«г_. Тогда на расстояниях от точки х=0, больших по
сравнению с 1/а2±, но малых по сравнению с 1 /Л+, отношение плотностей
потока нейтронов равно: Ф+/Ф_=Л+/А_.
Запишем граничные условия для Ф и и:
А_-т В_=А+—В+; У-(А-—?2-В_) =у+(А+-1у2+Р+),
где [см. (3.2.42); параметры у+ близки к параметру жесткости (2.2.21)]
Для отношения А±/А_ получим
_d+_ = Ч'- 1 + ?2-С
А_ Y+ 1+Г24-Се-1’
где
С = 1 + sB'r !В~ е = Т+ Та+ = S~'~ е = / £ ^Wf \
1 + В+/В_’ е Y—Ya- е- ’ ± у ) ±‘
D и D — коэффициенты диффузии тепловых и замедляющихся нейтронов.
Результат существенно упрощается, если е близко к единице. Тогда
А, = Y— 1 + (L2/t*)
А_ Y+ 1+(^Л*)+’
а если е± близки к единице, то
Ф+ Y—+ иг--1 Ф| + ис +
—I -~ =-----------------------------27» (4.4.35)
Ф- Y+A-Uc $i— «c + Y+!
где uc=ln (Ео/ЕД, а Ф-,— плотность потока в первой группе (3.2.25). Из
формул (4.4.35) следует, что если в большом реакторе активная зона состоит
из двух областей с £*=1 и различными жесткостями, то плотность потока
тепловых нейтронов больше в той области, где жесткость меньше. При этом
если и хотя бы одна из областей имеет у^>ис~', то Ф+/Ф_<С1. На-
оборот, плотность потока замедляющихся нейтронов больше там, где жест-
кость больше, причем если у+^>у_ и хотя бы в одной области y<guc_|, то
Ф1+/Ф1_>1. Таким образом, возникает естественная единица для жесткости
"l>=Uc_1=0,07, когда £2/т=&1. Чем больше у превышает ис-1, тем легче воз-
никают сильные неравномерности плотности потока в неоднородной актив-
ной зоне.
148
Если использовать два Других граничных условия, то можно опреде-
лить Х+:
Х4. (7)а2В) Ya—(1 gf)
Я+а2+ (D«as)+ I+Ya-e'
где
/ D X / D \ e- , ( l~wf \ , , . •.
e' = I— ) I --- e =------; e = I -------- 1 -f- (w — Wf) .
\D J_\Dj+ ' ± X ? U
Если при x>0 расположена более мягкая среда (т. е. с меньшим зна-
чением у), то В+>0 и В->0 (увеличение потока в более мягкой среде, см.
также § 4.5). В мягкой среде величина w—Wf меньше, чем в жесткой. По-
этому Х+<0, т. е. при х>0 должен быть расположен сток нейтронов; на-
пример, при х=А+/Л+ активная зона должна граничить с вакуумом. Можно
явно вычислить интегралы по объему от vSf<D и 20Ф и убедиться, что при
Л± = 0
J vSf&dEdx>§ ^dEdx,
т. е. система при Л± = 0 иадкритичиа.
Задача 3. В области |x|<d расположен замедлитель, а при \x\>d—•
размножающая среда с коэффициентом размножения, равным единице. Опре-
делить отношение потоков тепловых нейтронов при х=0 и вдали от границы
jx|=d.
Решение. Пренебрегая поглощением в замедлителем при |x|<d, за-
пишем решения уравнений (4.4.18) так:
, . ат, / х
Ф1(х) = Л + —— ( 1—ch
X V
гах(х) = a ch / ~, (4.4.36)
V "h
а решения уравнений (4.4.1), (4.4,2) при |х|>й!
Ф2(х) =ci-|-X(x—d)-(-C2 ехр (—а2(х—d));
a2(x)=Sa2[Ci-|-X(x—d)— у2сгехр (—а2(х—d))]. (4.4.37)
Если Л мало, то искомое отношение равно А/с\. Граничные условия дают:
л + О —с) = -Ьс2; C=y(C1— c2r2); C = ch-^L-;
Di (^)i l/Ti
(4.4.38)
-% ?
—a|A1S = D2(X—a2c2); Y D2(XY2a2c2); S = sh—^=-.
uc . |/ tx
(4.4.39)
Исключая а из (4.4.38), имеем
М D1 cY С + Cj [ £>! D4 ? С
(4.4.40)
причем использовано соотношение (см. задачу 2): исуу2= (£)2/£>2) (1—tof)/q).
Из условий (4.4.39) получим
А
а2<?2
(4.4.41)
149
т. е. Х<0 (если <р<1—te>f). По модулю (4.4.41) мало либо в_силу малости
резонансного поглощения (для мягкого спектра), либо, если у~1, из-за боль-
шого знаменателя. Так как Л<0, то система бесконечного размера будет иад-
критичиой, т. е. введение непоглощающего замедлителя при | х | привело
к увеличению реактивности. Причина такого увеличения состоит в том, что
имеется некоторая вероятность для замедляющегося нейтрона попасть в за-
медлитель при |x|<d, замедлиться там до тепловой энергии и вернуться
в активную зону, избежав тем самым резонансного поглощения (если резо-
нансное поглощение равно нулю, то ср=1, Wf—0 и Л=0).
Комбинируя второе равенство (4.4.38) с первым (4.4.39), получаем
X С cz2D2
<?2 + k «2С2 / S 1 k\(Sss)i
d2 С 1/7
или, используя малость (4.4.41) и заменяя, при -<1, ------= ——i-;
2тх S d
ct _ [ £>2 Т1 d
q ~ Л D2 L ¥ + Di d* Z2
Если все коэффициенты диффузии одного порядка, d2~2t'i, d>2L2, то
для оценок последним слагаемым в (4.4.40) можно пренебречь. Тогда
Л п, - С—1
— = 1 + ис1 —р--------- (4.4.42)
£ 1 D£ С
Пусть размножающая среда имеет жесткий спектр (при этом двухгруппо-
вое приближение качественно еще правильно), например: (So/£Ss)2~1, ш=0,5,
Ф=1, й!2=2т1, (С—1)/С=0,5 и Тогда А/щ~6, т. е. в замедлителе
возникает значительный всплеск тепловых нейтронов («ловушка нейтронов»).
Для других геометрий (цилиндр, сфера) изменяются только численные ко-
эффициенты. Поглощение в замедлителе, стенках, мишеиях, которые могут
помещаться в ловушку, утечка нейтронов в боковых направлениях из-за ко-
нечного размера реактора уменьшают значение плотности потока в ловушке.
4.5. МЕТОД ЭФФЕКТИВНЫХ ГРАНИЧНЫХ УСЛОВИЙ
Пусть размеры реактора много больше V т. Вдали от отра-
жателя справедливо уравнение с одной группой нейтронов. Об-
ласть, где нарушается это уравнение, мала по сравнению с раз-
мером реактора. Представим плотность потока нейтронов в ви-
де суммы двух слагаемых:
ф(г)=ф0(г)+Ф1(г), (4.5.1)
где Фо (г) удовлетворяет уравнению с одной группой
ДФо(г)+а2Фр(г)=О, (4.5.2)
а Ф1 (г) стремится к нулю по мере удаления от границы с от-
ражателем. Таким образом, в основной части объема активной
зоны Ф(г)=Ф0(г). Существование отражателя приводит к из-
менению граничного условия, которому удовлетворяет функция
Фо, если ее продолжить до границы с отражателем. Вместо ус-
150
ловия Фо=О для реактора без отражателя теперь на границе
активной зоны надо поставить условие
1 аФ0
Фо dx
(4.5.3)
где X — некоторая величина (размерностью см-1), которая опре-
деляется свойствами отражателя и активной зоны, но для до-
статочно большой активной зоны не зависит от ее размеров.
Последнее обстоятельство позволяет определить X, если рас-
смотреть в двухгрупповом приближении распределение плотно-
сти потока тепловых нейтронов вблизи плоской границы беско-
нечной активной зоны и отражателя (в принципе можно опре-
делять X и в более точных приближениях, но аналитические
формулы становятся слишком громоздкими).
Пусть при х<0 расположена бесконечная активная зона,
а при 0<х<Д— отражатель. Можно учесть утечку нейтронов
вдоль границы раздела, введя величины
С = VL^ + Р = /х-> + а/; р = Уага + аД (4.5.4)
где аг=л/Я; Н — высота активной зоны и отражателя по на-
правлению, перпендикулярному оси х. Решения уравнений
(4.4.1), (4.4.2) для активной зоны следующие:
Фх = 1—Хх + b ехр фл); /z1 = -^J-(l—2х— Ьу2ехр(Рл)), (4.5.5)
Д.2
«I- ст
а для отражателя
Фг = Лг[ехр(— £х) — ехр(— С(2Д— л))]—^-(1 —-М ‘ п2\
О2 \ Z-22 /
п2=Л2 [ехр (—рх)—ехр (—р(2Д—х))], (4.5.6)
где X — искомое граничное условие; а2 определено (4.4.7), у2—
(4.4.13). Граничные условия при х=0:
Ф!=Ф2; ф'1 = рф'2; m=sn2; n'i — psn'2;
P^DJD,- p^DjDi, (4.5.7)
позволяют определить X. Опуская очевидные вычисления, при-
ведем результат [125]:
Х=р|/—у2(Р+рр/)£, (4.5.8)
где
ь =(4 5 9)
₽ G + y2) + +WT3 (И'—?')’
Z'—Z cth £Д; p'=p cth рД;
Y = J_
Mi2 k L22 ) s’
151
Коэффициент b дает представление об отклонении истинной
плотности потока от экстраполированной вблизи отражателя.
Приближенно можно записать
Ф(г)=Фо(г)Ч'ЬФо(7?) ехр (—Р(7?—г)), (4.5.10)
где ф'о(г) —плотность потока, полученная из уравнения (4.5.2)
с граничным условием (4.5.3). Соответственно коэффициент ус-
реднения равен
«•1 = РюОФ0(Я)-^-, (4.5.11)
Р к
где рю вычислено для Ф0(г) [см. § 4.1 и задачи в § 4.3; п=1,
2, 3 для пластины (/? — ее полутолщина), цилиндра и сферы
соответственно].
Если замедлители в активной зоне и отражателе одинаковы
и можно не учитывать поглощение нейтронов при замедлении,
то вместо (4.5.8) получим
1 = Iх') — (Р _ а2аЛ22— * мд |2)
Л?'(р + р')-р'(₽+?') ’ «22т-1 ’ ( ’ 1
Если толщина отражателя стремится к бесконечности, то из
(4.5.12) имеем
Я,-1 = 14~Р 1 -Р 1 (4 5 13)
1 (?₽)-х-ФРГ1]
или при az2=0
Z-' = LS + Vx-l/a2. (4.5.14)
Из формулы (4.5.5) следует, что экстраполированная плот-
ность потока, т. е. функция Ф1(х) при Ь—0, обращается в нуль
при х=1/Х. Таким образом, 1/Х равна эффективной толщине от-
ражателя. Поэтому (4.5.14) совпадает с (4.4.22).
Если толщина отражателя мала, так что выполняются нера-
венства
А2
зд22
<1;
А2
Зт2
(4.5.15)
< 1
и аг2=о, то из (4.5.8), (4.5.9) получается следующий результат
[используется (4.4.13) прит*=т]:
= дГ=Х-1-Ь!-------А, f+
1_рЛ12 рМ2 М М2 \ РР 1
(4.5.16)
Если граничное условие известно, то на плоской поверхно-
сти положим
/1 аФ(г) \
\Ф (z) dz )г=Н
(4.5.17)
152
на сферической
Г 1
[гФ(г)
_^_(гф(г))1 =-i;
dr Jr=£
на цилиндрической
[ ------— /г Ф (Г)
[|/гФ(г) dr
(4.5.18)
(4.5.19)
Множители г и К г в (4.5.18), (4.5.19) под знаком произ-
водной введены для частичного учета кривизны поверхности.
Используя формулы (4.5.17) — (4.5.19), получаем уравнения для
определения критических размеров:
1) плоского реактора высотой 2Н
a tg аЯ=Х; (4.5.20)
2) плоского реактора высотой И с различными отражателя-
ми на основаниях
1g аН = — (4.5.21)
Х^ Xg ~
3) сферического реактора радиусом R
a ctg aR——X; (4.5.22)
4) цилиндрического реактора радиусом R
a^a.rR) _ 2 + J (4.5.23)
Рассмотрим цилиндрический реактор, окруженный отража-
телем со всех сторон. Будем искать приближенное решение в
виде произведения
ф(г, z)=O(r)Z(z). (4.5.24)
Гранйчное условие на боковой поверхности Хг определим как.
функцию аг, а граничные условия на основаниях Х[2, Хгг— как
функции аг (в этом случае во всех формулах для X надо заме-
нить агг->а,). Тогда
-гЛ(К^) = ( ) + _1_
J0(<*rR) 2R
tg аН = — [Х1г(Кг) + аг2 + агг = а2. (4.5.25)
В уравнения (4.5.25) входят четыре неизвестные величины:
R, И, az, аг, т. е. можно определить, например, R как функцию
Н. Практически удобна такая последовательность действий.
Найдя функции Xr(az), X]z(ar), Хгг(аг), получим из первого урав-
нения (4.5.25) при заданном R аг как функцию az, а из второго
при заданном Н а2 как функцию а'г. Отложив по осям а2, аг, по-
153
строим обе функции аг(аг) и az(ar). Точка пересечения дает
искомые значения az, аг и a2=ar2-|-az2. Если это значение а2 не
совпадает с материальным параметром, то надо повторить рас-
чет при других значениях R, Н.
Такой метод приближенного разделения переменных можно
применять и при численном определении критических размеров,
если только роль отражателя не слишком велика, активная зона
однородна, так что параметры az. аг имеют смысл, а область,
где аппроксимация (4.5.24) удовлетворительна, занимает зна-
чительную часть объема активной зоны.
Можно оценить точность метода эффективных граничных
условий, сравнив (4.5.22), где X дано (4.5.14), с формулой
(4.4.21). Из (4.5.22) находим
ДЭф = — arctg -у- = — arctg |'а1Т2 + aj/7-— ) . (4.5.26)
“1 К “1 \ “2 /
В первом приближении, когда си мало, (4.5.26) совпадает
с (4.4.21). В следующем приближении из (4.5.26) получим
Дэф = Ег + )Л- — —k+jA-— > (4-5-27)
«2 3 \ «2 /
что отличается от (4.4.23). Заменяя и2 по (4.4.7), находим ошиб-
ку приближенного решения
_ Дпр-Дт = __ 2 (4.5.28)
д дт
где
(1 — —(1 +-f-^= -
f = з------------- А/ у А-------= VL,2 + t. (4.5.29)
+ ГТ
Если ъ—-Li2, LJMt—0,7, то f (4.5.29) изменяется от 0,7 для
графитового замедлителя до 2,4 для тяжеловодного. Если сц2т—
= 0,1, то погрешность в значении экономии размеров за счет
отражателя составит 7—24%. Таким образом, условие приме-
нимости метода эффективных граничных условий
а.12т<1, (4.5.30)
что совпадает с условием применимости двухгруппового при-
ближения. Пусть для большого реактора /? = 400 см, Дэф=50см.
2 4
Погрешность 20% в Дэф составит 2,5% в /?эф. Если /?эф = —-—, то
“г
37?эф Sar Sar2 Sa2 dk
7?эф ar 2ar2 2а2 2(k — 1)
154
Если £—1=0,02, то б£ порядка 1 • 10“3, что меньше погреш-
ностей, связанных с погрешностью, например, величины v (см.
§ 1.1). Для реактора меньших размеров погрешность более су-
щественна.
Задача. Определить радиус выравненной зоны г, и коэффициент усред-
нения pi для цилиндрического реактора, если при г=7? задано граничное
условие (d<b/dr) /Ф=—Д-].
Решение. Так же как в § 4.2, запишем: Ф(г) = 1 при г<гр, Ф(г) =
=Л70 (аг)—|—.BjVq (аг) при пСгСЯ.
Граничные условия при г=Л н г=Р приводят к условию критичности
(коэффициенты диффузии одинаковы):
70(х)—exZjX) _ Л(РХ) х==а„. _£1_. 6 = А
N0(x) — ехЛ\ (х) ’ R ’ R ’
откуда при заданных хне можно найти p=r\/R. Коэффициент усреднения
определяется формулой
.
X Zo (X) — exjy (х)
Плотность потока на краю активной зоны равна
Ф(Р) ==-у- хр[4(рх)^(х)— ^(px)Z0(x)J.
Легко вычислить щ:
Щ= (1—|—х2еа) р2°,
где р2° — значение |т2 при е=0 (4.2.8). При е=0 получим формулы § 4.2.
Отметим, что даже малые значения е заметно изменяют значения ц, и р.
Например, если а/? = 3, то при е=0 имеем gi = 0,59, р—0,37, а при е=0,1
получим gi=0,74, р = 0,49 и <р(Р)=0,22. Если р=0, т. е. выравненная зона
отсутствует, то при 6 = 0,1 q>(P)=0,12.
t
4.6. РЕАКТОР БЕЗ ОТРАЖАТЕЛЯ. ОБЩИЙ МЕТОД
Рассмотрим однородный реактор без отражателя в много-
групповом или возрастном приближении. Будем считать, что
для всех групп положение экстраполированной границы оди-
наково, т. е. будем пренебрегать зависимостью от энергии
нейтронов. В этом случае геометрический параметр можно оп-
ределить следующим образом. Пусть символическая запись мно-
гогруппового уравнения такова:
Е(Д)Ф = 0, (4.6.1)
где £(Д)—матрица, зависящая от оператора Лапласа; Ф —
вектор, компонентами которого являются групповые плотности
потоков. Рассмотрим одну фурье-компоненту вектора плотно-
сти потока
Ф=Л?о ехр (iar). (4.6.2)
155
Подставляя (4.6.2) в (4.6.1), получаем условие критичности
в виде равенства нулю детерминанта
|L(—а2)|=0. (4.6.3)
Определим из (4.6.3) минимальное значение а2 и составим
такую линейную комбинацию решений (4.6.2), которая удовлет-
воряет граничным условиям, положительна и не обращается
в бесконечность внутри реактора. Например, для плоского ре-
актора
Ф = Фо [ехр (i аг) + ехр (— i аг)] = Фо cos аг;
для цилиндрического
2*
Ф = — Фо f ехр (i аг cos &) d& — Ф070 (аг).
2л J
о
В случае двухгруппового уравнения из (4.4.3) получим кон-
кретный вид уравнения (4.6.3) в этом приближении
(1+а2Л2) (1-НА*)=&*. (4.6.4)
Пусть (4.6.4) не удовлетворяется. Введем 1гЭф как число, на
которое надо разделить v, для того чтобы (4.6.4) удовлетвори-
лось. Используя определения (3.2.30), (3.2.32), получаем из
(4.6.4)
Эф (1 -J- а2/,2) (1 а2ту) 1 Н~а2т<?
ИЛИ
й = 2^.--------------?-------_ + _2пГ_. (4.6.6)
L 2а (1 -j-a2Z.2)(l + а2ту) Ja3
В записи (4.6.6) ясно видна структура условия критичности.
Число нейтронов, возникших при поглощении одного теплового
нейтрона (vSf/Sa), умножается на вероятность избежать резо-
нансного поглощения (<р), вероятность избежать утечки при за-
медлении (1+а2т<р)-1 и при диффузии (1-|~а2Л2)-1. К получен-
ному числу надо добавить число нейтронов, возникших при
поглощении одного замедляющегося нейтрона (vJfJ/аэ), умно-
женное на вероятность поглощения при замедлении (1—ф), и
вероятность избежать утечки при замедлении (1-|-а2т<р)_1. Если
сумма равна единице, то реактор находится в критическом со-
стоянии.
Равенство (4.6.5) можно переписать и таким образом:
).ЧЧ 7
ф (1 + a2L2) (1 + аЧр) '
156
где /г определено (3.2.35) с заменой ЛФ2=—сс2Ф2, как это тре-
буется равенством (4.6.3). В линейном приближении по а2
^эф = j ’ (4.6.8)
где длина миграции М определена так [формула (4.6.9) полу-
чена в [130] непосредственно из кинетического уравнения]:
Л42=Л2ф-|-Тф. (4.6.9)
В § 3.2 была дана наглядная интерпретация величины т*.
Теперь, однако, в (4.6.9) длина замедления входит без множи-
теля (1—®f)-1. Разница объясняется разными нормировками:
в § 3.2 рассматривался нейтрон, рожденный при поглощении
теплового нейтрона, и поэтому его размножение при замедле-
нии интерпретировалось как увеличение длины миграции. Те-
перь в формулах (4.6.7) — (4.6.9) рассматривается нейтрон, рож-
денный при поглощении нейтрона любой энергии. Поэтому
захват или поглощение с делением надо интерпретировать толь-
ко как уменьшение длины миграции. Длина замедления отли-
чается от введенной в § 2.2 только множителем ф. При этом
появляется множитель ф при квадрате длины диффузии, кото-
рый имеет наглядную интерпретацию: уменьшение числа ней-
тронов, достигших тепловой энергии. При использовании фор-
мулы (4.6.9) для длины миграции надо иметь в виду, что вели-
чина /г описывает баланс нейтронов с учетом утечек [см.
(3.2.35)]:
kfi + Wf a2L2
1 + (1 — <f)a2L2 ’
(4.6.10)
где значение для бесконечной однородной среды,
т. е.
С vSf<I>odE
k0 = -------------
f ^0 dE
(4.6.11)
причем Фо — плотность потока нейтронов в бесконечной среде.
Как мы увидим в гл. 7—9, в гетерогенных реакторах обычно
вычисляют именно величину ko исходя из баланса нейтронов
в ячейке, на поверхности которой ток нейтронов равен нулю.
Подставляя (4.6.10) в (4.6.7), получаем в линейном приближе-
нии по а2:
*эФ=т+^; Af2 = P(l-wf) + ^- (4.6.12)
Таким образом, при определении длины миграции в среде,
где происходит поглощение и размножение нейтронов в процес-
се замедления, необходимо всегда обращать внимание на точ-
157
ное определение, которое дается коэффициенту размножения.
Рассмотрим теперь возрастное приближение, сначала без
учета поглощения нейтронов при замедлении:
Р(Д-£-г)Ф = -Л(гс);
М (:)=—; /г(С) = т2;Ф.
д-с '
(4.6.13)
Переходя к фурье-компонентам (они обозначаются теми же
буквами), имеем
(14-а2£2)Ф=Еа-1п(тс); (4.6.14)
а2Л(т); n(0) = v2f®. (4.6.15)
Решая уравнение (4.6.15), находим
n(xc)=vSf ехр(—а2тс)Ф (4.6.16)
и, подставляя в (4.6.14) (опускаем индекс с у т), получаем
vSf
k = =(1 + а2!2) ехр (аат). (4.6.17)
Из (4.6.17) определяем эффективный коэффициент размно-
жения
*эф = - sf- (1 +а2АТ,ехр(-«Ч (4.6.18)
Выражение (4.6.18) отличается от (4.6.6) заменой [если
в (4.6.6) положить ф=1]
1-|-а2т->ехр (а2т) (4.6.19)
или
е-р(а2г)-1^ /1+а^+ (а^+ (4 g 2Q)
а2 \ 2 6 /
Если решена какая-либо задача о критичности реактора
в двухгрупповом приближении, причем отражатель не играет
слишком большой роли, а активная зона близка к однородной,
то можно найти разницу 6£Эф между двухгрупповым и возраст-
ным приближениями, предположив, что а2 в этих двух расчетах
должны совпадать, как они совпадают для однородного реак-
тора без отражателя, и различие состоит только в разной связи
между k и а2. Таким образом, имеем
^эф (М)ц — (Мв ехр(а2т) fa2-)2 / 2 2
-г = -----тт—;----- = -г-;—-----1 ——- 1-----— a• (4.6.21)
&эф (^эф)в 1-рах 2 \ 3 /
При а2т=0,1 получаем б£Эф=0,005, т. е. при а2т>0,1 поправ-
ку (4.6.21), как правило, надо учитывать. Обратим внимание
на то, что &Эф по возрастной теории получается меньше, чем по
158
двухгрупповой (или объем реактора при одинаковых k, L2, т по
возрастной теории получается больше). Если приближенно из-
вестно а2, то, решая двухгрупповые уравнения с т (4.6.20), по-
лучаем результат, совпадающий с результатом возрастного при-
ближения (если активная зона достаточно однородна и эконо-
мия за счет отражателя много меньше размеров реактора).
Из (3.3.8) можно получить выражение для &Эф в многогруп-
повом приближении (в смысле § 3.3; это приближение лучше
называть «малогрупповым»):
Пусть все Xi равны между собой. Тогда Xi=x/n, если общее
число группы равно п-|-1. Очевидно, что при и->оо (4.6.22) пе-
реходит в формулу возрастного приближения (4.6.18). Пусть п.
конечно. Составим разность между k3$ в и-|-1-групповом и воз-
растном приближениях:
(^эф)п-И (^эф)оо
(^эф)
ехр(х)----1; х = (4.6.23)
(! + %/<
При 1 получим
(4.6.24)
т. е. сходимость метода многих групп медленная — как 1//г. Из
(4.6.24) можно определить dfe между двух и трехгрупповыми
расчетами j
/ \ _ /sk_\ f5k\___________
\ k /2;3 \ k /2;оо V k /3;оо 4
в то время как
/ 8k X2
\ k ]2; оо 2
Таким образом, переход от двух- к трехгрупповому прибли-
жению исправляет только половину погрешности двухгруппо-
вого приближения. Эти оценки в реальных задачах, когда
реактор неоднороден и существует отражатель, не могут претен-
довать на количественную достоверность, но тем не менее по-
лезны для предварительной оценки числа групп, которое необ-
ходимо для решения данной задачи с определенной точностью.
Рассмотрим решение уравнения (4.6.17) относительно а2.
Приближенные формулы получаются либо разложением
ехр (—а2т) в ряд, либо предварительным логарифмированием
159-
и разложением в ряд In (1-|-а2Е2). Таким образом, находим сле-
дующие приближенные решения уравнения (4.6.17):
(4.6.25)
(4.6.26)
При и а2£2=а2т^=0,4 погрешность (4.6.26) около 0,5%,
а (4.6.25) несколько больше 1%. При меньших значениях k по-
грешность уменьшается. Поэтому в большинстве случаев точ-
ность (4.6.25) или (4.6.26) вполне достаточна. В [131, 132] по-
казано, что можно построить точное аналитическое решение
уравнения (4.6.17), однако оно имеет сложный вид.
Отметим, что функция (1 -}-а2т) в двухгрупповой теории
или ехр (—а2т) в возрастной есть не что иное, как фурье-образ
функции Грина соответствующего уравнения. Этим обстоятель-
ством можно воспользоваться, чтобы построить уравнение, ана-
логичное (4.6.17), исходя непосредственно из эксперименталь-
ных данных о распределении замедляющихся нейтронов от то-
чечного источника нейтронов деления. Например, в [133] экс-
периментальные данные о распределении по пространству ней-
тронов с энергией £=1,46 эВ, возникших от точечного источника
деления в тяжелой воде, аппроксимируются формулой (анало-
гичная аппроксимация для ВеО приводится в [88]):
W (г) =----==-ехр f------— 'j 4-----==ехр ( — V (4.6.27)
V ' (4m;1)3/2 \ 4^ ) Г (4лт2)3/2 4т2 )’
+ ^2Х2 = Т>
где Ti= 147,9; т2=61,9; Ci = 0,56. Фурье-образ функции (4.6.27)
равен
IF(ci2)=Ci ехр (—а2Т1)4-с2 ехр (—аЧг), (4.6.28)
и поэтому условие критичности вместо (4.6.18) будет
k'^ = 1С1 ехР “2 + Сг ехр (4-6-29>
1 -j-
Легко определить разницу между (4.6.18) и (4.6.29). При
а2т< 1 имеем
+ с 23t\] = —0,076аМ. (4.6.30)
&эф 2 [ у т2 т2 J \
Если а2т=0,2, то dk—3-10-3.
160
Таблица 4.2. Значения четвертого и шестого момейтов
для Н2О, графита и D2O
Замедлитель с.
н2о 1,13(3) 1,85(26)
Г рафит 0,58(1) 0,26 (2)
d2o 0,58 0,24
Поскольку обычно cAr^l, достаточно знать несколько чле-
нов разложения функции Грина:
оо
№(а\)= 2 (-1ГСОТ(«2Т- (4.6.31)
т—0
Коэффициенты Сгт связаны с моментами функции распределе-
ния, т. е. со средними значениями г2т [см. формулу (2.1.78);
выражения для С2та в различных теориях приведены в [134]]:
С31,1 == (2/n-J- 1)1 т’" ’ — С2 = 1. (4.6.32)
Для возрастного приближения C2m= (т!)-1 для одногруп-
повой теории замедления С2т=1. В [135] приведены экспери-
ментальные значения для коэффициентов С4 и С6 для Н2О, гра-
фита н смесей Н2О с металлами. Данные для Н2О, графита и
D2O [полученные из формулы (4.6.28)] приведены в табл. 4.2.
Из табл. 4.2 следует, что к обычной воде возрастное прибли-
жение не применимо (для возрастного приближения должно
быть С4=0,5; Сб=0,16). Для графита и D2O согласие с возра-
стным приближением более удовлетворительно [см. (4.6.30)].
Как указывается в [134], во всех диффузионных теориях С2т
падает с ростом т. Поэтому неравенство С6>С4 для обычной
воды означает, что диффузионное приближение для нее обла-
дает большой погрешностью. Для смеси обычной воды с метал-
лами применимо диффузионное малогрупповое (2—3 группы)
приближение.
Учтем теперь поглощение при замедлении в возрастном
Запишем еще раз соответствующие уравнения:
П(Д—Д-2)Ф(г) = п(г, тс); )
[Д—Д-2(г)]/г(г, г) = ;
dz
Е.°
п(г, 0) = vSpI>(r) + vj n^-sP-Yf(E)dE.
Ес
приближении.
(4.6.33)
11—6053
161
Переходя к фурье-образу, получаем
(1+ а2Е2)Ф(а) = Sa~1n(a, тс);
дп(а, т)
[a2+L-2(t)]n(a, г) = - —
(Л
Ео
Г п(<х, Е)
п(я, 0) = >2рФ(а) 4-v \ ———Sf(E)dE.
J
E„
(4.6.34)
Дифференциальное уравнение для n(a, т) имеет решение
т Ео
п(а, т) = n(a, 0)ехр [ — а2т—о>(т)]; а»(т) = J —jy = J £LSE
О Е
Подставляя (4.6.35) в последнее уравнение (4.6.34), определяем п(а, 0).
Таким образом, вместо (4.6.16) получаем
я (“, "с) =
vSf<I>(a)exp( — а2тс— а»с)
- fVf(E)
1 — v -—-ехр (— а2т (Е) — w(E)) dE
J &SE
E„
(4.6.36)
или, подставляя (4.6.36) в первое уравнение (4.6.34), находим условие кри-
тичности (индекс с у тс опускаем):
vSf f 4(4
k = —— <f = (1 + a2E2)exp(a2t) 1 — v I ——— exp( — a2t(E) — ai(E))dE ,
J 5
EC J
(4.6.37)
откуда эффективный коэффициент размножения
Ь руп / _<у2-г"I (* f ( )
M=-,4t2/a +И 777- exp[-a2x(E)-w(E)]dE. (4.6.38)
J <;Lsc.
Ec
Пользуясь тем, что подынтегральная функция в (4.6.38) максимальна при
Е — Ес, заменяем
ехр (—а2т(Е))->ехр (—а2т(Ес)); t(Ec)=t. (4.6.39)
Тогда
I' k \
кэф=\^ + ехр( —а2т), (4.6.40)
что отличается от (4.6.5) заменой 1-{-и2т->ехр (а2т), а также тем, что т не
умножается на (р. Отсутствие множителя tp объясняется тем, что исполь-
зованная связь между плотностью потока н плотностью замедления (2.3.43)
нарушается, если одновременно учитываются утечка нейтронов и резонанс-
ное поглощение [см. также (3.3.15) ]. Надо учесть, что вышедшие из реактора
нейтроны не испытывают резонансного поглощения. Плотность замедления
162
при этом возрастает следующим образом (для фурье-компонент и в шкале
летаргии):
«(«) = -—? = ехр( —а»(«)), (4.6.41)
1—Р(и)(1—?)
где Р(и) — вероятность
выхода из реактора:
сШ(и)
Р'и)= 1 + а2£2(и)
(4-6-42)
Таким образом,
Г 1 1
a2 _L-------
и вместо (4.6.35) получим
Г 1 1
Ф(а)52, = ехр( —w(a))a® + —— n(t) = —
L L W.
дп
dt
(4.6.43)
и
n(z) — n(0)exp [ — a2t(u)y(u) —и>(и)]; <f(u) = — j* exp( — w)da,
о
(4.6.44)
т. е. при т появляется множитель (р.
Замена (4.6.39) означает, что пренебрегается влиянием утечки на спектр
замедляющихся нейтронов. В первом приближении влияние утечки можно
учесть, если вместо (4.6.39) записать
ехр(~-аат(Е)) — ехр( —а2т)ехр( —а2 [т(Е) —т])
a2 Е •
3Sfr £Ss Ес
ехр ( —а2т) [1 -|-а2(т—т(£))] =г ехр(—а2т) 1 +
Тогда второе слагаемое в (4.6.40) будет
а»; ехр (—а2Т(р) (1—|—са2т),
где (здесь положено <р=1)
1 Ъ(Е) Е
С==Т^С\ ~Ё~ ехр(-ш(Е))1п —dE.
£„
. (4.6.45)
(4.6.46)
(4.6.47)
Для оценки величины с рассмотрим случай, когда выполняется закон
” . > вычислить, если разложить в ряд по а»:
_ 1 а'с
2 ис
заменить 1-(-са2т->ехр (са2т) и вместо
1 /о. Тогда интеграл (4.6.47) можно
2
с =-----
(4.6.48)
-|- Wf ехр [ — а2х(у — с)].
(4.6.49)
т. е. c<g;l. Следовательно, можно
(4.6.40) получить
. k ехр(—а2ту)
Эф 1 + а2£2
Если ввести ka, то вместо (4.6.12) имеем
Л42 = Т2(1—Wf) -1-т (<р—Wfc)
или если воспользоваться (3.2.38) и (4.6.48), то
(4.6.50)
ЛР = Л2(1 — wf) + т 1
«с
(4.6.51)
11*
163
Таким образом, учет влияния утечки на спектр замедляющихся нейтро-
нов приводит к дополнительному уменьшению эффективного значения т.
Отметим, что во всех формулах этой главы под ср понимается вероятность
избежать резонансного поглощения всеми нуклидами, в том числе и деля-
щимися, т. е. в wc входит резонансный интеграл не только радиационного
захвата, но и деления.
До сих пор рассматривался изотропный реактор. Между тем
кассеты с топливом и теплоносителем, расположенные, как пра-
вило, параллельно друг другу, могут привести к анизотропии.
Формально можно ввести анизотропию, заменив в выражении
для тока (2.1.17) скалярный коэффициент диффузии тензорной
величиной Dik = Dki-.
= (4.6.52)
k
Ограничиваясь возрастным приближением без учета .погло-
щения нейтронов при замедлении, получаем условие критично-
сти
(4.6.53)
В частности, если все кассеты параллельны и решетка кассет
однородна, то все направления, перпендикулярные кассете, рав-
ноправны. Тогда
£эф = &J1 + («г2^ + «г2^)Г*ехр[— (а22т(| +а/т±)], (4.6.54)
где
п 2,4
я, = ---• аг =------•
2 Н R ’
Н, R — высотами радиус (эффективные) реактора; т^, 7.2, т
значения т и L2 для параллельного и перпендикулярного на-
правлений. Для одногруппового приближения
= k [1 + я/442 + a/M2J. (4.6.55)
Количественно анизотропия длины миграции рассмотрена в гл. 10.
Задача. Показать, что учет немоноэнергетичности нейтронов деления при-
водит к пренебрежимо малым поправкам в условии критичности.
Решение. Вместо (4.6.17) надо написать
6(1+а2£2)-1= рх(£0)ехр(а2т(£0, Ес)) dE0 = ехр(а<), (4.6.56)
где х(£о)—спектр нейтронов деления (1.2.1); т(£о, Ее)—возраст нейтронов,
родившихся с энергией Ео, при энергии Ес- Надо найти разницу между т
и т0, где
^о = ^(Е0)ЦЕа, Ec)dE0. (4.6.57)
164
Разложив (4.6.56) в ряд по а2т и использовав (4.6.57), получим
(4.6.58)
где
^2 = $ Ec)dE0.
Для приближенной оценки можно предположить, что
, Ей
^(Eq, Ес) = Д1п ,
Е с
где А — константа. Все интегралы можно вычислить, если воспользоваться
формулой (1.2.1) для % (До). В результате
т — то
*0
а2т„ —
----- = — 2-10—3а2т0.
2«с2
Величинами такого масштаба следует пренебрегать.
Глава 5
ТЕОРИЯ ВОЗМУЩЕНИЙ
5.1. ТЕОРИЯ ВОЗМУЩЕНИЙ ДЛЯ УРАВНЕНИЯ
С ОДНОЙ ГРУППОЙ НЕЙТРОНОВ
Допустим, что решена задача о критичности некоторого ре-
актора и найдено распределение плотности потока нейтронов
по пространству. Рассмотрим другой реактор, характеристики
которого мало отличаются от характеристик первого. Эти ма-
лые отклонения будем называть возмущения. О первом реак-
торе будем говорить как о невозмущенном, а второй называть
возмущенным. С помощью теории возмущений можно опреде-
лить условие критичности второго реактора.
Уравнение с одной группой нейтронов (см. § 2.1) для невоз-
мущенного реактора запишем так:
vDoVOo + 2ao<-A-- 1Афо=О, (5.1.1)
Нф J
а для возмущенного
V-DV<D + S -----1)ф = 0, (5.1.2)
\ &эф /
причем все коэффициенты могут быть функциями координат,
но поверхности, где плотность потока обращается в нуль или
коэффициент диффузии испытывает скачок, одинаковы для
уравнений (5.1.1) и (5.1.2). В уравнениях (5.1.1), (5.1.2) введен
множитель .^эф-1, как это делалось в § 4.6.
165
Умножим (5.1.1) на Ф, а (5.1.2) на Фо, вычтем (5.1.2) из
(5.1.1) и проинтегрируем по всему пространству. Используя ра-
венство
ФУ0о?Фо=У [Ф-О0УФ0] — Оо(УФ) (УФо), (5.1.3)
получаем
j di v [ФРоуФо — Ф0£>уФ] d г 4- J 8D (\?Ф) (v®0) dr —
(5.1.4)
1'Де
5D=D — D0;
8 2а
В силу граничных условий (2.1.54), (2.1.55) величина
ФОоУФо—Фо-РУФ непрерывна на границах областей с различ-
ными коэффициентами диффузии (по предположению, эти гра-
ницы одинаковы для возмущенного и невозмущенного реакто-
ров). Поэтому после преобразования первого интеграла
в (1.5.4) в поверхностный останется только интеграл по внеш-
ней поверхности реактора, который равен нулю, поскольку на
этой поверхности ф=ф0—0. Таким образом,
о1
аГ2а/—--------1У|фФо</г = О, (5.1.5)
L \ &Эф /I
откуда
Г / _ 82д)ф0Ф4г— | 8£»(уфо)(уф)йг
8/гэф J \ %ф
--------------------------. (6.1.6)
2,/1 *офоФй г
Если изменения bD, 6Sa, bk достаточно малы, то можно по-
ложить в (5.1.6) Ф0=Ф. Кроме того, будем считать, что = 1 •
т. е. невозмущенный реактор находится в критическом состоя-
нии. Тогда
f 8[2а(^-1)]ф02йг- f ад(?Ф0)2^г
^Эф = ~J. (5.1.7)
j Sa0 k0 Фо2 d Г
Если 2а° и kQ не зависят от координат, то, предполагая, что
166
6v=0, получаем
/ f V1 Г С / 1 \
5Йэф= (J Ф02^г) [J — X Х
хФ02^г—-1— (5Р(?Ф0)2аг]. (5.1.8)
J J
Отметим существенную разницу между возмущением сече-
ний поглощения или деления, с одной стороны, и сечения рас-
сеяния, с другой. Влияние первых на реактивность пропорцио-
нально квадрату невозмущенной плотности потока нейтронов
в том объеме, где возмущение отлично от нуля, а влияние сече-
ния рассеяния пропорционально квадрату градиента плотности
потока. Поскольку градиенты плотности потока нейтронов
в большом реакторе малы, Л2 (V Фо)2 «С Фо2:
_ = L2 (^ Фо)2 « Фо2-
Поэтому изменение сечения рассеяния влияет на реактивность
много меньше, чем изменение сечения поглощения или деления
(при одинаковых 6S/S).
Пусть 6O=6Sf=0, а 62о#=0 в малом объме AV. Тогда
tk = — Л _фо2(го)АК. (5.1.9)
эф ь у р ’ ' >
а Ф02(г)йг
где г0 — точка, принадлежащая объему AV. С помощью равен-
ства (5.1.9) можно вычислить сечение 6Sa вещества, вносимого
в объем AV, или сравнить между собой различные 6Sa, если из
эксперимента известны возникающее при этом изменение реак-
тивности ц плотность потока Ф02. Можно, наоборот, определить
с помощью (5.1.9) распределение плотности потока Фо (г) по
реактору, если один и тот же поглотитель вносить в разные
точки реактора и измерять возникающее при этом изменение ре-
активности (измерять изменение реактивности можно по перио-
ду разгона реактора, см. гл. 14). Отметим, что реактивность
пропорциональна квадрату плотности невозмущенного потока
Фо2 только в этой области реактора, где справедливо уравнение
с одной группой нейтронов (см. § 5.2).
Из формулы (5.1.7) при 60=0 и k—1-Cl следует
Чф = JФо2 (О dr / JФо2 (г) dr, (5.1.10)
т. е. наибольшее влияние на реактивность реактора оказывает
изменение коэффициента размножения в той области, где плот-
ность потока максимальна, — в этой области нейтрон имеет наи-
большую «ценность».
167
Выше предполагалось, что возмущенное уравнение отлича-
ется от невозмущенного значениями коэффициентов, а гранич-
ные условия для Ф и Фо одинаковы (в том смысле, что Ф и Фэ
обращаются в нуль, а ?Ф и ?Ф0 терпят разрыв на одних и тех
же поверхностях). Рассмотрим теперь возмущение граничных
условий. Пусть (5.1.2) справедливо только вне объема, ограни-
ченного поверхностью 5, а (5.1.1)—во всем объеме. Тогда в
(5.1.4) первый интеграл отличен от нуля и после преобразова-
ния в поверхностный равен
+ ГГфОо^-ФоР^.]^, (5.1.11)
J [ on дn J
где производная берется по нормали, направленной внутрь объ-
ема реактора. Если невозмущенный ток нейтронов через поверх-
ность S мал, то можно пренебречь первым слагаемым в (5.1.11).
Тогда, полагая 8D=d[(k—l)Sa]=0, считая, что feo=const,
Sa°==const и учитывая равенство D=2aM2 (см. § 2.1), полу-
чаем
_ №
k0
(5.1.12)
J<I>o (г)Ф(г)4г
распространен на объем реактора
где интеграл в знаменателе
за вычетом объема, ограниченного поверхностью 3. Если вну-
три поверхности 5 расположено тело, сильно поглощающее ней-
троны (например, регулятор, см. гл. 6), то вблизи поверхности
3 плотность потока Ф может сильно отличаться от Фо. Однако
если возмущение в определенном смысле слабое (см. гл. 6), то
объем, где Ф существенно отличается от Фо, мал по сравнению
со всем объемом реактора. Тогда в знаменателе (5.1.12) можно
положить Ф=Ф0 и распространить интеграл на весь объем ре-
актора. В этом случае
S/M>~ k„
J Ф02(г)4г
(5.1.13)
поверхность цилиндра радиусом
р — радиус регулятора, располо-
Пусть поверхность S есть
(/? — радиус реактора;
женного параллельно оси цилиндрического реактора). Тогда из
(5.1.13) получим (~^— =--------Y
\ дп о р /
—
дФ
2Л42Ф0(г0)р—
др
(5.1.14)
168
где ц2 — коэффициент усреднения квадрата плотности потока
[см. (4.1.32)]; Фо(го) —плотность невозмущенного потока в том
месте, где поставлен регулятор. В числителе (5.1.14) замена Ф
на Фо в этом случае, конечно, недопустима. В гл. 6 формула
(5.1.14) будет использована для определения эффективности ре-
гулятора в гомогенном реакторе.
Влияние малого изменения формы реактора на его критич-
ность рассмотрено в [116]; заимствованные из этой работы
результаты для эллиптического цилиндра приведены в гл. 4.
Выше рассматривалось только изменение собственного чис-
ла (йЭф), возникающее при возмущении и только в первом при-
ближении. Теперь кратко сформулируем общий аппарат теории
возмущений, позволяющий, в принципе, вычислять собственное
число и собственную функцию в любом приближении. Для про-
стоты в качестве невозмущенного реактора будем рассматри-
вать однородный реактор без отражателя. Собственные функ-
ции фт° удовлетворяют уравнению
ДФт°+Ет°Фт0=0, (5.1.15)
где Е,п°— соответствующее собственное число. Запишем урав-
нение для другой собственной функции:
ДФЯЕЛ°=0. (5.1.16)
Умножим уравнение (5.1.15) на Ф^°, а (5.1.16) на Фт°, вычтем
одно из другого и проинтегрируем по объему. В результате
j (Ф°ДФ„ - Ф^ДФ°) dv = J div (ФД?Ф* - Ф°dv. (5.1.17)
На границе реактора фЛ°=фт°=0. Преобразуя объемный инте-
грал в поверхностный, убедимся, что (5.1.17) равно нулю. По-
этому
(Е,£-Е2) ^,^^ = 0,
откуда
= (5.1.18)
Постоянную ат можно считать равной единице.
Запишем теперь возмущенное уравнение
ДФ+[Е— У(г)]ф=0 (5.1.19)
и будем искать его приближенное решение. Для этого разложим
Ф в ряд по функциям Фт°:
Ф = 2^Фт- (5.1.20)
169
Подставив (5.1.20) в уравнение (5.1.19), получим
3^(^ + У)Ф^ = 2ст£Фт°. (5.1.21)
т т
Умножим (5.1.21) на Ф^° и проинтегрируем по объему реактора.
Принимая во внимание (5.1.18), получаем
(£ — Ek)ck = ^Vkmcm, (5.1.22)
т
где
Vkm = уУ(г)Ф°АФ^. (5.1.23)
Представим Е и ск в виде рядов:
Е=Е°+ЕМ+ЕСЦ- ...; cfe=cft°+^<I)+^(2)+ ..., (5.1.24)
где и имеют тот же порядок малости, что и возмущение
V; EW и имеют порядок малости V2 и т. д.
Для определения поправки первого порядка к ф„° и En° по-
ложим сп°=1, ст°~0 (т=£п) и подставим в уравнение (5.1.22):
E=En°-|-En(I); Cfe=Cfe°+cfe<1). Отбрасывая слагаемые второго по-
рядка малости, получаем, если k = n:
£p = Vn„ = jV(r)№«, (5.1.25)
результат, который был получен выше. Если n=£k, то из (5.1.22)
имеем
с .().=k^n, (5.1.26)
k Eno-Ek<> ’ ' ’ v
a cn(1) остается произвольным. Если положить cn(I)=0, то
где штрих у суммы означает отсутствие члена п—т.
Легко проверить, что условие сп(|) = 0 вытекает из требова-
ния нормировки:
j [Ф„° 4- Ф„']Мп = 1
с точностью до членов второго порядка малости.
Из формулы (5.1.27) вытекает условие применимости теории
возмущений:
Vnm < | Еп°—Ет° I.
(5.1.28)
170
Аналогично можно определить поправки более высокого по-
рядка. Ограничимся вычислением Еп2- Полагая в уравнении
(5.1.22) Е=Еп°-[-Еп^'>-гЕп<.2\ получаем
(при сп<’>=0; k = n):
£„(2) = Мтст(1)-
т
Используя равенство (5.1.26) и учитывая, что VHm=Vmn, полу-
чаем
Е„ (2> = V—— (5.1.29)
U Еп°-Ет°
т
Если Еп° — наименьшее собственное число, то Еп°<Ет°, и по-
правка второго порядка всегда отрицательна.
Все приведенные выше рассуждения справедливы и для не-
однородного реактора, если только заменить АФ на [А4~/(г)]Ф.
Однако в этом случае определение всех собственных функций
будет достаточно сложной задачей (см. также § 5.3).
5.2. ТЕОРИЯ ВОЗМУЩЕНИЙ ДЛЯ УРАВНЕНИЙ
С ДВУМЯ ГРУППАМИ НЕЙТРОНОВ
.Уравнения с двумя группами нейтронов (3.2.1), (3.2.2) удоб-
но записать в матричном виде:
М ф (г) =-----— мг Ф (г), (5.2.1)
где Ф — двухмерный вектор с компонентами Фь ф2, а М и Mi—
матрицы:
= l 212 1 \ 0; 0/
(5.2.2)
Уравнение (5.2.1) можно получить из вариационного прин-
ципа так же, как получают уравнения механики или теории по-
ля .Составим функцию Лагранжа
X = С Ф+(г) (Мф —— мЛ Ф (г) dr, (5.2.3)
J \ /гэф /
где вектор Ф+ удовлетворяет тем же граничным условиям, что и
Ф. Воспользуемся равенством
f Ф+ ?£>?Ф4г = J Ф+ОуФ^З —\D (?Ф+) (?Ф) dr, (5.2.4)
Й S V
где S — поверхность, ограничивающая объем V [если внутри
объема имеются поверхности разрыва производных, то надо по-
171
требовать выполнения условий (2.1.55) для ф и Ф+]. Так как на
внешней поверхности реактора Ф+=0, то первый интеграл в
правой части (5.2.4) равен нулю. Поэтому функция Лагранжа
(5.2.3) может быть записана так:
2
^ = - f (S к + Фг+ Sai Ф/ - ~ Ф1+ 2МФг1 +
<) I L ^эф J
+ (Ф1+-Ф2+)212Ф1^г. (5.2.5)
Теперь если за обобщенные координаты взять компоненты
вектора Ф+, то уравнение Эйлера—Лагранжа, дающие экстре-
мум функции Лагранжа
_ V д . д'£ о /5 о 6)
аФ(+ Ъ dXj д ( ЭФЛ \ (‘ '
/-1 \ дх, )
совпадают с (5.2.1). Если же за обобщенные координаты взять
Ф,, то получим уравнение
М + Ф+ (г) =----— AV Ф+ (г), (5.2.7)
&эф
где /И+ и М1+ — матрицы, транспонированные по отношению
к матрицам М и Mi, т. е. Mlk+~Mhi. Компоненты вектора Ф+
будем называть сопряженной плотностью потока, а уравнение
(5.2.7) — сопряженным уравнением.
Если бы матрицы М, М были симметричными, то они совпа-
дали бы со своими транспонированными Л1+=Л1. В этом случае
уравнения называются самосопряженными [т. е. (5.2.7) совпадает
с (5.2.1)]. Как видно, уравнения двухгруппового приближения
не являются самосопряженными. Несамосопряженность являет-
ся характерной особенностью уравнения переноса и большинст-
ва приближений, которые из него вытекают. Это свойство от-
личает уравнение переноса от большинства уравнений других
разделов теоретической физики (о математических следствиях
этого обстоятельства см., например, [123]).
Условие критичности есть условие существования нетриви-
ального решения у однородной системы уравнений (5.2.1), ко
торое символически можно записать так:
---— М 111 = 0, (5.2.8)
I &эф 11
где двойная черта означает детерминант матрицы [чтобы это
символическое равенство приобрело точный смысл, надо запи-
сать производные в виде конечных разностей, а функцию Ф(г)
заменить конечным числом значений в дискретных точках], По-
172
скольку замена 10, 201 на 20+, 201+ приводит в (5.2.8) к замене
строк детерминанта столбцами, условие критичности уравнения
(5.2.7) совпадает с условием критичности уравнения (5.2.1).
Поэтому йэф в (5.2.1) и (5.2.7) совпадают.
Напишем уравнение для возмущенного реактора:
(Д + Ф (г) = — + Ф(г)^
Д5ГЛ1)Ф(Г)’ (5'2'9)
а невозмущенный реактор будем описывать сопряженным
уравнением
Л4 4~ ф0+=----!_Уих+Ф0+. (5.2.10)
*э°ф
Умножим уравнение (5.2.9) на Фо+, а (5.2.10) на Ф, вычтем
(5.2.10) из (5.2.9) и проинтегрируем по всему объему:
J (Фо+ Л?Ф— Ф7И+ Фо+) dr + j Фо+ З/ИФ^г =
= — — С (Фи+ Л^Ф — фЯ+ Фо+) —
— _L Сф0+8М1Фс/г+_^!*1Сф+М1Фс/г. (5.2.11)
J (*эФ)2 J
Наша цель — получить соотношение между 6£Эф и 67Й, 6201.
Поэтому из (5.2.11) надо исключить члены, не содержащие
бйЭф, 610, 610]. Очевидно, что
Фо+Дф-ФМ^ Фо+ = 3(Фо+*МшФг-ФХ*Фо*) = О
ik
в силу равенства Mki = M/k. Точно так же из первого слагаемого
в левой части (5.2.11) исключаются члены, не содержащие про-
изводных. Члены, содержащие производные, преобразуются с по-
мощью равенства (5.2.4), так что получается
у, j div [Фо+/ Di^i — ФгР^Фо) ]dr. (5.2.12)
( = 1,2
Поскольку Ф и Ф+ удовлетгоряют граничным условиям (2.1.54),
(2.1.55), то Фо+/ОгуФг и Ф^Пд/Фо) непрерывны на границах с раз-
личными коэффициентами диффузии и обращаются в нуль на
внешней поверхности реактора и на поверхности черных тел,
которые могут быть помещены в реактор. Поэтому, преобразуя
173
(5.2.12) в поверхностный интеграл, получаем Руль. Таким обра-
зом, из (5.2.11) получим 8£Эф(&эф= 1):
С Ф0+(8Л? +
^эф — ~ —
Фа+мг+Фаг
(5.2.13)
Заменяя в первом приближении ф на Фо и раскрывая сокра-
щенную запись (5.2.13), находим (при этом потребуем непрерыв-
ности не только DiVcbi, но и бОг?Ф;; поэтому Ф^уоО^Ф^ заме-
няем на — бД^Фо) 7Фо;):
JJ2 vS5W уФо>+й212Фо1(Ф^-Фо1Фг
8£зф=—---------------р------------------------------------
J ф+ (vSh®01+ vS/2®02)dr
(5.2.14)
Рассмотрим случай, когда Sfli=Sfl=6Z\=6S12=0, Sf2=
= const. Из (5.2.14) получим
8^эФ —
J I ^2 vlf2 J
(5.2.15)
Выпишем второе уравнение (5.2.10):
(у£>2? -2а2) Фо+2 = - vS^, (5.2.16)
откуда (ц, = const, k = -^-> так как SO1 = — oY
Фо! = 4- (1 - Ф0+2- (5.2.17)
k
Следовательно, вместо (5.2.15) имеем
[ [Ф02( ’ ~ Фо+2 фJ
J L z/2 2-02
/Фе2(1-А22Д)Ф^Рг
(5.2.18)
Если реактор достаточно большой и в нем нет областей
с большими градиентами, то Т2®ДФ^ С Фог-Приближенно мож-
но записать
Фо+1 ^-£-(1 + т22 а2) Фог = ехр (- Л) Ф0+2, (5.2.19)
174
где а2 — некоторое среднее значение лапласиана (а2т<С1). Тог-
да (5.2.18) запишем так:
’82'3 ехр(а2т) «2аа 1
J Ф02 Ф02^Г
(5.2.20)
что отличается от (5.1.8) (при 60 = 0) заменой Фо2 на Ф02Ф02 и
не очень существенным множителем ехр (а2т). Таким образом,
уменьшение (или увеличение) реактивности при внесении в ре-
актор дополнительного поглощения (или деления) пропорцио-
нально произведению плотности невозмущенного потока Ф02 и
плотности сопряженного потока Фог- В знаменателе (5.2.20) в
отличие от (5.1.8) также стоит интеграл от произведения плот-
ности потока на плотность сопряженного потока.
Пусть в объеме ДУ произошло дополнительное поглощение
одного нейтрона, т. е. б2аФо2ДУ=1- Уменьшение реактивности
пропорционально значению плотности сопряженного потока
Фо+ в объеме ДУ. По этой причине плотность сопряженного по-
тока называют «ценностью» нейтронов — нейтрон более «ценен»
(т. е. вносит большой вклад в реактивность) там, где больше
плотность сопряженного потока.
Рассмотрим случай, когда б2аг= 6S/2=6Sai = 6S/i = 62i2=0.
Из (5.2.14) получим
f I SDi 7фoi 7ф01 + 8О2 у Ф+ уф02] dr
86эф = 2, (5.2.21)
vS/2J4+®02dr
т. е. изменение реактивности, вызванное изменением коэффици-
ентов диффузии, пропорционально произведению градиентов
плотности потока и плотности сопряженного потока. В большом
реакторе можно положить (а2т<С1):
vSf» v2f,
Ф01 =ss -=-^- (1 — aS) Ф02 Ф02 (5.2.22)
^12 ^12
и [см. (5.2.19) при Л < 1] Фо1 Фог- Тогда
Чф =
С [ SD, SD, \ „
J Ф02 Ф02
(5.2.23)
175
В частном случае, когда bDJDi, не зависят от коорди-
нат:
[ ^Ф+ ^Фб/г = J div (Ф+ ^Ф)<Д— Ф+ДФб/г =«= a2 j Ф+Фб/г
и
(5.2.24)
Чф = 4-ДГЛ2 + Цг-х
\ 'Л U1
что, очевидно, сразу можно написать из условия критичности
однородного большого реактора.
В двухгрупповом приближении можно получить формулу,
аналогичную (5.1.13). Из (5.2.11) в этом случае находим (все
6S —0; градиент плотности невозмущенного потока на поверх-
ности S равен нулю):
РФ, _ , РФ2
+«<£“=
(5.2.25)
Чф =
]фсн (^НФ1 + ^:'2Ф2ДГ
Пусть внутри поверхности S находится вещество, которое
поглощает только тепловые нейтроны. Тогда <9Ф1/<9п=О. Пре-
небрегая vSfi, используя (5.2.19) и заменяя в знаменателе Ф2^=
«ьФо2, получаем
Г 2
8/г.,ь = —Д-
1+“2/-22 Уф+ФозРг
что отличается от (5.1.13) заменой М2 на Л22 и Фо2 на Ф(иФв2
(см. также гл. 6; для большого реактора а2Т22<Д)-
Отметим, что для однородного реактора без отражателя
ф2+=ф2. В самом деле, если положить
Ф2+=ЛФ2; Ф1+=ВФь (5.2.27)
то сопряженное уравнение (5.2.7) совпадает с (5.2.1), если вы-
полнено условие
(5.2.26)
(5.2.28)
А _ vS/2
212
Если выбрать Л = 1, то ф2+=ф2, а Ф;+ отличается от Ф; по-
стоянным множителем B=Si2/vSf2- Для неоднородного реакто-
ра (или реактора с отражателем) замену (5.2.27) сделать нель-
зя. Отсюда следует, что Ф2+ близко к Ф2, если неоднородности
в активной зоне малы и отражатель играет малую роль. Напро-
тив, если активная зона неоднородна или имеется хороший от-
ражатель, то Ф2+ заметно отличается от Ф2.
176
Рассмотрим простейший пример: однородное полупростран-
ство (х<0), заполненное размножающей средой, граничит с бес-
конечным отражателем (х>0). Будем для простоты считать, что
замедлитель в активной зоне и отражателе одинаковый (одина-
ковы значения т и коэффициентов диффузии). Кроме того, пре-
небрегаем поглощением нейтронов при замедлении.
Вместо плотности потока Ф] введем плотность замедления.
Индексы 1, 2 обозначают активную зону и замедлитель. Сопря-
женное уравнение в этих обозначениях имеет вид
£>(Д —£“2)Ф+ = — — Ъап+-,
т
(Д — т-1) п+ = — Ф + .
(5.2.29)
Решение сопряженного уравнения нормируем так, чтобы при
—оо было Ф1 = Ф1+, П1 = П1+. Решения имеют вид [см. (4.5.5),
(4.5.6)]:
Фх = а—хф-5ехр(|3л);
Ф2 = А ехр (— х/Ь2)-(1 — т/L/)-1 п2;
D . , ,Q (5,2.30)
«1 =-—[а —л —5у2ехр(₽х)];
L1
п2 = (9-^ехр (— х/У^);
Ф|+=а+—х-\-Ь+ ехр (|3х);
Ф2+=Л+ехр(—х/Лг); (5.2.31)
П1+=т[а+—х—Ь+у2 ехр (₽х)];
п2+ = В+ т ехр (— х/]Л) + -—1— ф2+,
1 L2‘1
Если ]/~т <Б2,
как ехр
Ф„+ (оо) л*1- , ,
то , а отношение nA п
Ф2(оо) А
1 \ 1 т-
----— х . Граничные условия
^-2 / J
возрастает
Ф1 = Фг; П1=П2', Ф/=Ф2'; П\=П2
и такие же условия для сопряженных функций приводит к урав-
нениям, из которых можно определить А и Л+:
А = Ь2
1 ,
+ L. + (-(Л"//,
12—6053
177
1А~£2___________t/Z^________
14-|A/z2 1 +W +|/1 + W
(5.2.32)
В частном случае, когда выполняется неравенство т, Li2C
-СЛ22, получаем
Ф2+(°°) _ А+ _ /1 ._______L_\~x
Фа(оо) “ А ~ ( Lf)
(5.2.33)
т. е. если активная зона имеет малую жесткость, то Ф и Ф+
близки, а если активная зона имеет большую жесткость, так
что r/L^^l, то плотность сопряженного потока Ф+ в отра-
жателе существенно меньше, чем плотность потока Ф.
Теория возмущений находит применение при решении боль-
шого числа задач. Здесь рассмотрены только простейшие ее
аспекты. Построение теории возмущений для многогрупповых
уравнений и для кинетического уравнения, а также разнооб-
разные ее применения можно найти в [73, 136, 137].
Задача. Определить зависимость эффективности регулятора от глубины
погружения в активную зону. Считать, что в активной зоне Ф+=Ф, а в отра-
жателе Ф+ = 0. Эффективность полностью погруженного регулятора считать
заданной.
Решение. Если регулятор погружен в активную зону не полностью,
то в формуле (5.1.13) возникнет множитель
У Ф2(г)Дг
д________
я-д
j Ф2(г)&
д
= f(z),
где Д — эффективная толщина от-
ражателя; г — координата нижне-
го конца регулятора (ось z на-
правлена вниз); Н—Д-—коорди-
ната ннжнего конца активной зо-
ны, регулятор опускается в актив-
ную зону сверху. Положив
Рис. 5.1. Зависимость эффективно-
сти регулятора от глубины погру-
жения в активную зону:
д=0 — нет отражателя; 2Д/Я=0,2 —
отражатель экономит 20% высоты ре-
актора; Н-к/а. — эффективная высо-
та реактора
178
®(z)=sinaz, получим
где
f(x) =
1 ( г e 1 1
x— —:----------<sin2л (l-s)x + — —sinne
2л(1 —e) I j/ 2 J J
sin ns
n(l—s)
г — Д 2Д
X= //-2Д ’ e = H '
На рис. 5.1 изображена функция f(x) при e=0 и e=0,2. Функция f(x)>
имеет довольно значительный участок, где она близка к прямой линии, при-
чем 6k на этом участке равно 70—80 °/о 6k полностью погруженного регуля-
тора. Регулирование обычно проводится в этой «линейной области». Запас
реактивности тогда можно выражать в метрах погруженных стержней (если
не учитывать интерференции, см. гл. 6). Необходимо отметить, что кривая
на рис. 5.1 правильно описывает зависимость 6k(z), только если выполнено’
условие применимости теории возмущения, которое в данном случае имеет
вид: 6k(z) <Са22Л42. Если это условие не выполнено, то регулятор сильно де-
формирует поток нейтронов. В этом случае 6k(z)/k на начальном участке
значительно меньше, чем на рис. 5.1.
5.3. НЕЛИНЕЙНАЯ ЗАПИСЬ ОДНОГРУППОВОГО УРАВНЕНИЯ
И ТЕОРИЯ ВОЗМУЩЕНИЙ
За последние годы (см. [138]) в квантовой механике раз-
работана новая теория возмущений, имеющая ряд преимуществ
перед классической (последнюю обычно называют теорией
возмущения Рэлея—Шредингера; в § 5.1 она использовалась
для вычисления поправки первого порядка). Поскольку ста-
ционарное уравнение Шредингера по форме совпадает с урав-
нением одногруппового приближения, то можно непосредствен-
но перенести метод, разработанный для уравнения Шрединге-
ра, на уравнение с одной группой нейтронов (см. [139, 140]).
Уравнение с одной группой для неоднородного реактора за-
пишем так:
ЛФ+[£— У(г)]Ф=0, (5.3.1)
где Е — собственное число; Е—У(г) — зависящий от коорди-
нат лапласиан. Уравнение для невозмущенной плотности по-
тока Фо будет
ЛФо+£'оФо=0. (5.3.2)'
Введем новую переменную
у(г) = —[Ф(г)]~‘ grad®(r) =
= —-grad In Ф(г). (5.3.3)
Величина у совпадает с граничным условием, например
(2.1.58). Основная идея рассматриваемой теории состоит в том,
чтобы записать уравнение для «граничного условия» во всем
12* 179<
объеме реактора. Подставив (5.3.3) в уравнение (5.3.1), по-
лучим
div у—у2~Е— У (г). ' (5.3.4)
Одного скалярного равенства (5.3.4) недостаточно, чтобы опре-
делить вектор у. Однако из (5.3.3) следует, что вектор у по-
тенциален, т. е. является градиентом некоторого скаляра. С этим
дополнительным условием (5.3.4) эквивалентно исходному
уравнению (5.3.1).
Теперь запишем:
ОО 00
У=2^"У«; Е=2^пЕ,г. Vtr^zVHr), (5.3.5)
п =0 п=0
где % — формальный параметр, который положим равным еди-
нице в конце вычислений. В (5.3.5) принято Vo=0 в согласии
с (5.3.2). Подставив (5,3.5) в (5.3.4) и приравняв члены с оди-
наковыми степенями X, получим
div Фо2уи= (£„—Qn) Фо2, (5.3.6)
где
п—1
Qi = V; Q„ = - 5у/У/,_г., п^2. (5.3.7)
(=1
Если Фо=О на границе реактора, то, проинтегрировав
(5.3.6) по объему, получим
Е1г = (J Ф02 dr)-1 J Qn Ф02 dr. (5.3.8)
При п=1 ‘(5.3.8) совпадает с обычным выражением [см.,
например, (5.1.10)]. Поправка Е2, как и в обычной теории
[см. (5.1.29) ], всегда отрицательна:
Е2 = - (J Фо2 dr)-1 J у* Ф02 dr < 0. (5.3.9)
Пусть до внесения возмущения справедливо уравнение
(5.3.2), т. е. невозмущенный реактор критичен. После внесения
возмущения, т. е. после замены Ео на Ео—У (г), реактор не
будет критичным. Следовательно, плотность потока Ф(г, /)
удовлетворяет нестационарному уравнению
-L ^>=ДФ(г, О + (Ео-ЮФ(г, 0- (5-3.10)
Ищем решение уравнения (5.3.10) в виде Ф(г,/)=Ф(г) ехр At.
Получим
ЛФ(г) + (Е—У)Ф(г)=0, (5.3.11)
180
где Е=Е0—К/D. Пусть новое значение собственного числа
приближенно равно E = EQ-\-E{-\-E2. Тогда
Л/О=-£'1—Е2. (5.3.12)
Если Е\ = 0, то в силу (5.3.9) Л>0, т. е. если возмущение та-
ково, что /?| = 0, то поток возрастает со временем, т. е. реактор
надкритичен [разумеется, если ряды (5.3.5) быстро сходятся
и возмущение не изменяет граничных условий].
Отметим, что в новой теории возмущений не надо знать
ни собственных значений, ни собственных функций невозму-
щенной задачи, кроме основной. Особенно просты случаи одно-
мерной геометрии, когда все результаты даются в виде квад-
ратур. В многомерных случаях надо решать уравнение (5.3.6)
с дополнительным условием уп = grad cpn, причем от номера
приближения зависит только правая часть. При этом в отли-
чие от исходного уравнения (5.3.1) не надо решать задачу на
собственные значения.
В случае плоской геометрии решение уравнения (5.3.6)
будет
г
(z) = [Фо (z)]~2 J (E’rt-Q„)O02(z)rfz, (5.3.13)
—п/2
причем высота реактора принята равной л, Фо(±л/2)=О. Ес-
ли вычислены уп, то плотность потока нейтронов равна
Если Фо(г)=Фо(О) cos z, то z/0=tg и и, очевидно,
(Z X
— [ у0 dz = ехр (In cos z) = cos z.
5 /
Теперь ^рассмотрим два примера. Пусть возмущение равно
— а——, т. е. уравнение (5.3.1) имеет вид
I г |
Ф" (г) ф- (£ + а-£-\ф(г) = 0;-
\ | г | / 2 2
Ео = 1; а = const. (5.3.15)
Этот пример интересен тем, что можно написать точное реше-
ние и определить погрешность приближенного решения. Имеем
условие критичности
(£ — а)~1/2= — (£ + «)-1/2(5.3.16)
181
и плотность потока
Ф(г) = cos (z]ZЕ—а] + ctg —a) sin (z]/E—a), z<0;
(5.3.17)
Ф (z) = cos (z]/E -фа) —cfg ^-—J^E-i-a} sin (z ]/E ф-a), z >0.
Первая поправка к собственному числу равна нулю (возму-
щение — нечетная функция z). Первое приближение для у
будет
а р z , , а Г ” I zI l-ni,!
у-, = —I ------cos2 zdz =--- — — 4- J—L + — sin 2 z .
cos2 z J | z | cos2 z 4 ~ 2 4 1 ]
—k/2
(5.3.18)
Отметим, что У\ конечно при всех z, включая ±л/2. Плотность
потока в первом приближении равна
Фх (z) = cos z ехр \а ( —
I \ 4
(5.3.19)
Во втором приближении получим
п/2
Е.. = — (jcos2zdz} J у*cos2zdz =
—тс/2
it/2
4 » p / x 1 • c \2 dx a2 zro orii
=----------a2 I---------------sin2x ----------= — —. (5.3.20)
л J \ 2 4 / sin2x 4
0
При a=0,5 имеем E2=—0,0625, E=E04-E2=0,9375, что отли-
чается от точного значения [полученного численным решением
уравнения (5.3.16)] Е = 0,9386 только на 0,12 %’. С ростом а
ошибка растет примерно как а4.
Второе приближение для потока имеет следующий вид:
Ф (z) = Фх (z) ехр f— J у2 (z) dz'), (5.3.21)
\ о j
где
^2
COS2 Z
У 2 (z) =
— + — -j—— sin 2z ) -f-
4 2 4 )
+ _5!_f(2L__Lsin2xV-^-. (5.3.22)
cos2 2 j \ 2 4 / sin2 x
о
На рис. 5.2 приведены Фо(г) и Ф(г) [при а=0,5, причем
фо(О) =Ф(0) = 1]. Отклонения Ф1 и Фз от Ф столь малы, что
182
Рис. 5.2. Невозмущенное рас-
пределение потока Фо и точ-
ное решение задачи ФТОЧн с
возмущением V(z)=z/(2|z|):
+ —> первое приближение для за-
дачи с возмущением V(z)=z/n (см.
задачу в конце параграфа)
их трудно изобразить на рисунке. Поэтому на рис. 5.3 приве-
дены разности (Ф1— Ф)/Ф и (Ф2—Ф)/Ф. Видно, что ошибка
первого приближения не превосходит 1,8%, а второго 0,3%,
причем относительная ошибка максимальна на краю реактора,
где требования к точности минимальны.
Теперь рассмотрим реактор со случайными неоднородностя-
ми. Такие случайные неоднородности могут быть из-за неопре-
деленности в обогащении и количестве топлива, разброса в
свойствах конструкционных материалов, кипения теплоносите-
ля, 'неточности в геометрических характеристиках ячеек реак-
тора. Реактор по-прежнему будем считать плоским. Плотность
потока нейтронов удовлетворяет уравнению
Ф"(з) + [Е—V(z)]®(z)=0, (5.3.23)
причем вероятность того, что V(z) имеет данное значение,
равна
р[У(г)] = -^ехр(— a2V2(z)); f pdV = 1. (5.3.24)
Vп J
— 00
Средние значения равны
V(z) = 0, V^z) = 1 /2а2, (5.3.25)
а корреляция равна нулю:
V(z)V(z')=O, z=£z'. (5.3.26)
Условие (5.3.26) следует понимать как некоторую идеали-
зацию. Если V(z) V(z') У=0 только в том случае, когда \z—z'{
много меньше высоты реактора, то приближение (5.3.26) до-
пустимо.
Спрашивается, каковы наиболее вероятное значение соб-
ственного числа Ё и наиболее вероятное распределение потока
183
Рис. 5.3. Отклонение первого
1 и второго 2 приближений от
точного решения задачи для
возмущения V (z) —г/ (21 z |)
Ф(г). Чтобы это выяснить, надо решить (приближенно) урав-
нение (5.3.23) для произвольного V(z), а затем провести усред-
нение по всем возможным значениям V(z). Пусть решение
получено в виде функционала от V(z): Ф[Р(г)]. Тогда сред-
нее значение Ф дается континуальным интервалом *
ф“(5) — -A-J ф [V (2)] ехр (—«2 JvVW)JJ-~dV(z), (5.3.27)
г
где П — произведение по всем значениям z, а С — нормиро-
Z
вочный делитель, равный значению интеграла при Ф=1. Мно-
житель 1/С обеспечивает выполнение равенства (5.3.27) при
® = const. При реальном вычислении континуального интегра-
ла надо промежуток интегрирования по z разбить на N интер-
валов, обозначить среднее значение V в fe-м интервале Vk, вы-
числить получившийся Л^-кратный интеграл и устремить N к
бесконечности. При этом С= (Az)~N/2.
Первая поправка к собственному числу равна
«/2
Ei — — J V (z) cos2 zdz.
—п/2
Очевидно, что среднее значение £1 = 0 и надо вычислять по-
правку второго порядка. Рассмотрим сначала первое прибли-
жение для плотности потока. Имеем из (5.3.13)
z/i(z) = (cosz) 2
(ти + 2z + sin 2z) — J V (z') cos2z’dz'
'—тс/2
и далее
Ф1 (г) =Ф1 (0) cos z ехр F (г), (5.3.28)
* Континуальным интегралом называется интеграл, кратность которого
равна бесконечности, причем ие счетной, а континуальной (т. е. равна «числу
точек» непрерывного отрезка). Такое понятие впервые введено в теоретиче-
скую физику Р. Фейимаиом (1951 г.) при построении квантовой теории поля.
184
тде
z z
Fй7rtl* - j "+2Lt^' -
0 0
— I _— (" V (z”) cos2z”dz", (5.3.29)
J cos2г' J
0 —it/2
а Ф1 (0) — произвольная постоянная интегрирования, поэтому
не зависит от V. В дальнейшем положим Ф1(0) = 1. Первый
интеграл в (5.3.29) вычисляется, а во втором изменим поря-
док интегрирования. Тогда (при г>0):
к/2
f(z)= J f(z')V(z')dz', (5.3.30)
тде
(4г —-7)tg2cos22';
f(z')sf2=[M-----)tgZ — tg Z'l
L \ 2 л / J
cos2z';
0<z'<z; (5.3.31)
f(z') = f> = — (-y + -7) tgzcos2z'; z<z'<-y.
При выполнении усреднения (5.3.27) надо вычислить инте-
грал по V от выражения [Дг' — величина интервала по г', на
которые разбивается интервал (—л/2, л/2) при аппроксимации
континуального интеграла конечномерным]:
exp[/(z') V(z')— с№(г')] Дг' =
[/ т . f \ 2 1 / [2
— а V----— Az' ехр | —-— Дг'
\ 2а / J V 4а2
Интегрирование по каждому V(z') дает
В результате получаем произведение экспонент. В пределе при
Az'—rO в показателе будет стоять интеграл от /2/(4а2), а мно-
житель 1/С сократится. Следовательно,
Ф1 (г) =cos z ехр [ф (г) / (4а2) ], (5.3.32)
тде
0 г л/2
ф (г) = J dz + J // dz + J f32 dz. (5.3.33)
— */2 0 z
185
Таблица 5.1- Значения функции ф (г)
г Ф (г) г Ф (г)
0,2 0,01 1,0 0,13
0,4 0,036 1,2 0,147
0,6 0,07 1,4 0,155
0,8 0,099 п/2 0,1566
Интегралы в (5.3.33) вычисляются:
, , , Зп . 4гЕ, 2 16г [ . n . 1 . . \ 1 , , ,
Ф (г) =--- 1---------------- sin 2z И-sin 4г tg г +
Т 32 л2 З'2 \ 8 /1
+ -у (г---~-sin4zj — "Y (1-----7“) U —cos“z)tgz. (5.3.34)
Значения функции <р(г) приведены в табл. 5.1. Если 1/(4аг)=^1
или уГу2 1,4, До среднее значение Фх(г) больше, чем Ф0(г),
примерно на 10% (напомним, что за единицу принято зна-
чение собственного числа в нулевом приближении).
Нетрудно вычислить среднее значение [Ф1 (г) ]п. Действи-
тельно,
(Ф1/Ф0)п — ехр (nF), -'(5.3.35)
где F дано (5.3.30). Таким образом, функции ft (5.3.31) воз-
растают в п раз, а ф(г) (5.3.34) в п2 раз. Поэтому
(ф1/ф0)«=(ф1/фо)'!\ (5.3.36)
В аналогичных задачах часто вычисляют среднюю флуктуа-
цию:
- бФ2=[Ф1(г)—Фо(г)]2/[Фо(г)]2. (5.3.37)
Используя (5.3.36), получаем
6Ф2=Ф12(О) ехр (ф(г)/а2) —
-2Ф1 (0) ехр (ф (г)/(4а2)) +1, (5.3.38)
где восстановлен множитель ФДО), поскольку, очевидно, 6Ф2
зависит от нормировки Фь
Определим теперь среднее значение поправки второго по-
рядка к собственному числу. Имеем
Е, =----— J у-,2 cos2 zdz. (5.3.39)
—n/2
186
В выражение у\2 входит произведение V(z')V(z"). При усред-
нении по V отличный от нуля результат возникнет только,
«если г’ — г". Так, например,
я/2 */2
Ei=-~ J cos2z'tfe' J cos2z"dz"X
—п/2 — тс/2
dV (z)
С
я/2
—— f cos4zcfe = 3/(4тга2),
л2а2 J
—«/2
-г. е. усреднение по V эквивалентно замене V (z') V (г") на
—1—б (г'—г"). Используя этот результат, легко вычислить сред-
2а2
лее значение Е2. После вычисления элементарных интегралов
получим
£г = --/т- (5.3.40)
16ла2
Если, например, 1/(4а2) = 1, то Е2 ——0,24. Это число со-
ответствует очень большим возмущениям, когда ур2яа1,4, т. е.
больше, чем невозмущенное собственное число, равное едини-
це. Как было показано выше, отрицательный знак Е2 (при
условии, что £1 = 0) означает, что случайные флуктуации в
свойствах размножающей среды реактора всегда приводят
к положительной реактивности. Или, иначе, если однородный
реактор находится в критическом состоянии, то реактор тех
же размеров со случайными неоднородностями, такими, что в
среднем значение лапласиана не изменяется, в большинстве
случаев будет надкритичным и плотность потока нейтронов в
нем будет возрастать со временем.
Задача. Получить первое приближение для плотности потока нейтронов,
если У(г)=г/эт.
Решение. Из уравнения (5.3.13) при я=1, Ei=0
получим
У1 (г) = (я cos г)-1[г2/4—л2/16 г (г/4) sin 2z-p(cos 2z)/8-J-1/8],
.а из (5.3.14) при п= 1:
Фх(г) = cos г ехр
г
— (l/i(z)dz
6
Результаты вычислений показаны на рис. 5.2 крестиками. Видно, что они
лежат между невозмущенным потоком Фо (г) н Ф(г) (5.3.17). Этот результат
понятен, так как возмущение У(г)=г/я менее сильное, чем рассмотренное
.в тексте.
187
Глава 6
РЕГУЛЯТОР В ГОМОГЕННОМ РЕАКТОРЕ
6.1. ЭФФЕКТИВНОЕ ГРАНИЧНОЕ УСЛОВИЕ ДЛЯ ЧЕРНОГО ЦИЛИНДРА
Регулирование плотности нейтронного потока, а значит, и
мощности реактора чаще всего осуществляется путем погруже-
ния в активную зону цилиндрического стержня, изготовленного
Из материала, сильно поглощающего нейтроны (например, кад-
мия, бора).
Плотность нейтронного потока вдали от сильно поглощаю-
щего тела, помещенного в слабо поглощающую среду, можно
определить, если известно граничное условие (2.1.59). Запишем
это условие в несколько другой форме:
Т(р) =-------------- Y(p)==JisP_ (6.1.1)
1 ' ’ дФ | 1 v ’ Х(р) ’ v z
л
дг |г=р
где р — радиус цилиндра (ниже будет рассматриваться толь-
ко граничное условие для цилиндра); Х(р) определено (2.1.59).
Изложим простейший способ * определения граничного усло-
вия («метод баланса», см. [141]).
Пусть бесконечно длинный, черный (т. е. поглощающий каж-
дый нейтрон, ударившийся о его поверхность) цилиндр поме-
щен в неограниченную, однородную, непоглощающую среду. Бу-
дем считать, что источники нейтронов в среде отсутствуют. На
бесконечности задан ток нейтронов по направлению к цилинд-
ру. Вдали от цилиндра справедливо уравнение диффузии, ко-
торое в данном случае сводится к уравнению
ДГФ=О. (6.1.2)
Общее решение уравнения (6.1.2) можно записать так:
Ф(г) = у + 25р1п—. (6.1.3>
Р
Если экстраполировать (6.1.3) до поверхности цилиндра, то
легко проверить, что у в (6.1.3) совпадает с (6.1.1). Ток ней-
* В свое время были разработаны более точные методы, однако теперь
получение граничного условия путем непосредственного решения кинетиче-
ского уравнения на ЭВМ не представляет большого труда и поэтому отпала
необходимость в разработке приближенных, но все же достаточно сложных
аналитических методов определения у(р). Некоторые результаты численного
определения граничных условий приведены, например, в [142]. Наиболее точные
результаты получены в [143] (см. также [130]).
188
тронов вдали от цилиндра, отнесенный к единице поверхности
цилиндра, равен
or р 3
Поскольку среда не поглощает нейтронов, а источники от-
сутствуют, такое же число нейтронов поглощается единицей
поверхности цилиндра. Но это число равно также числу ударов
нейтронов о поверхность цилиндра, поскольку каждый нейтрон,
пересекающий поверхность цилиндра, будет поглощен. Поэто-
му (см. также § 2.1)
/ [Ф(г)] = f exp[-^r°-r''] совфф(f) dr' = -1-, (6.1.5)
4п J ] r0 — г' ]2 3
где r0 — точка на поверхности цилиндра; cos <р — проекция
единичного вектора скорости нейтрона на нормаль к поверх-
ности цилиндра. Запись в левой части (6.1.5) подчеркивает,
что ток / является функционалом от плотности потока Ф (г).
Таким же образом будет записываться ток, связанный с плот-
ностью потока нейтронов, если последняя имеет какое-либо кон-
кретное функциональное выражение.
' Пусть точное выражение для плотности потока нейтронов
следующее (буквой г обозначается расстояние точки г от оси
цилиндра):
Ф(г) = у + Sspln —+ Ф/(г), (6.1.6)
Р
где ФДг) убывает по мере удаления от поверхности цилиндра
приблизительно по закону ехр [—, где R — расстояние
от поверхности черного тела (см. дополнение). Обычно Ф* на-
зывают переходной, а ф—Ф; — асимптотической частью точ-
ного решения. Подставляя (6.1.6) в (6.1.5), получаем
y = 14- - р/ [1п - - нф, <г) 1} 11 и”- (6-1 -7)
I з L р 1 J
Ток j [1] равен числу ударов о поверхность, если плотность
потока нейтронов не зависит от координат и равна единице.
Как было показано в § 2.1,
= (6.1.8)
4
Пренебрегая в (6.1.7) функцией Ф/ (в этом и состоит исполь-
зуемое приближение), находим
Т = 4-~ 4Р2лГ1п—1. (6.1.9)
3 L Р J
Для вычисления / In— введем декартову систему координат
L р 1
с началом на поверхности цилиндра, ось х направлена по нор-
189'
•Мали, г — по образующей. Тогда coscp = x/|r—г'|, проекция
ir' на плоскость (ху) равна
s = Т'р3 + R2 + 2?R cos ф; R2 = л2 + у2,
где ф — угол между нормалью и направлением на точку (х, у).
Плотность потока зависит только от s. Поэтому
ЛФ(г)1-> У <ty Jfeexp [- S,r?+^J (ДУ)37г-.
•—оо 1—оо О
(6.1.10)
Вводя в плоскости (х, у) полярные координаты R, ф и обозна-
чая [см. (1.10.12)]
г & = 1 sin8exp[_ «^1 =
J (z2-J- /?2)3/2 IF I [ sin 9]
—оо 0
получаем
j [ф (г)] = А- cos фс/ф J Ф (s) Ki2 (R2S) dR. (6.1.11)
о о
Таким образом,
T = 4-pS/(pSs), (6.1.12)
О
где
F(z)— — cos ф4ф J In — Ki2(R)dR; s2 = z2 + R2 + 2Rzcos ф
о о
или, интегрируя по ф, имеем
оо
F(2) =-2- fKi2(A)Fx (— }d>;
71 J \ 2 /
о
(6.1.13)
Fi (л) = — х — 1 + f— — x'i
2 V х ]
arctg x + In (1 + a2).
190
Нетрудно проверить, что
при р—*-0 получим у=4/3, а
при р->оо 7=2/3. Значение
7=4/3 является точным. В са-
мом деле, бесконечно малый
цилиндр не возмущает ней-
тронного поля, и поэтому диф-
фузионное решение справедли-
во вблизи блока, т. е. пренебре-
жение Ф/ является законным.
Значение 7=2/3 для плоско-
сти (р->оо) было получено в
§ 2.1, по существу, точно таким
же способом. Поскольку из-
вестно точное значение для
плоскости (см., например, [77,
78] 7=0,7104, можно предло-
жить интерполяционную фор-
мулу, уточняющую значения 7:
л,* / \ t \ 1 0,7104 —2/3 Г 4
Y*(P) = Y (Р) + --— -
z/ о о
Рис. 6.1. Зависимость эффектив-
ного граничного условия на по-
верхности черного цилиндра от
геометрического радиуса:
---— по формуле (6.1.15); О — по
формуле (6.1.14)
— Т(Р) , (6.1.14)
где 7(р) дано (6.1.12). Ошибка формулы (6.1.14) максимальна
в интервале 0,2<pSs<0,6 и равна 7 %.
Наиболее точные результаты получены в [143]. Там же при-
ведены значения у(р) для поглощающей среды. Результаты в
[143] аппроксимированы формулой (для случая Sa=0; по-
грешность в десятых долях процента; другие аппроксимации
см., например, в [144]):
V (pS ) = 0:7104fpSs)2 +0,6939pSy+0,01147 ,g j 15,
' s> (pSsp+o,5416p2s +0,0086 ’ 1 ,
На рис. 6.1 (см. также Приложение VII) приведены дан-
ные [143] для непоглощающей среды и результаты вычислений
по (6.1.14).
Нетрудно распространить приведенные выше рассуждения
на случай «серого» цилиндра, т. е. поглощающего не все па-
дающие на его поверхность нейтроны. Пусть £ есть вероятность
того, что нейтрон, ударившийся о поверхности цилиндра, будет
им поглощен. Так как внешняя среда не поглощает нейтронов,
то ток при г-^-оо равен числу поглощенных нейтронов, т. е.
£/[Ф(г)] = 1/3. (6.1.16)
191
Подставляя вместо Ф(г) в (6.1.16) выражение (6.1.6) и
пренебрегая по-прежнему Ф/, получаем
с* ч
где учерн определено для черного цилиндра. Приближенные ме-
тоды определения С изложены, например, в [145, 146]. Если
можно пренебречь рассеянием в цилиндре, то С совпадает с G
(1.10.24) и с помощью (1.10.25) выражается через табулирован-
ную функцию Р (см. § 1.10 и Приложение VI).
Формула (6.1.17) справедлива и для другой геометрии, на-
пример, для серой сферы. Величина уЧерн для сферы малого
радиуса приведена в § 13.6.
6.2. РЕГУЛЯТОР В ОДНОГРУППОВОМ ПРИБЛИЖЕНИИ*
Начнем рассмотрение эффективности регулятора с простей-
шей задачи: в центре гомогенного цилиндрического реактора
без отражателя с радиусом R помещен на всю высоту реакто-
ра цилиндрический черный регулятор. Требуется определить
изменение реактивности, реактора при извлечении регулятора.
Распределение плотности потока нейтронов будем описывать по
теории с одной группой нейтронов. Общее решение уравнения
(4.1.1.), обладающее аксиальной симметрией, запишем так:
Ф(г) —AJo(ar)-}-BNo(ar). (6.2.1)
На границе реактора должно быть Ф(Р)=0, откуда мож-
но выразить В через А:
Ф (0 = А р0 (ar) - No (аг)1. (6.2.2)
Будем называть эффективным радиусом регулятора р то
значение радиуса, на котором экстраполированное диффузион-
* В настоящей главе рассматривается регулятор в гомогенном реакто-
ре. Возникает законный вопрос, в какой мере полученные формулы можно
применять к гетерогенному реактору с большим расстоянием между блоками
[см. ниже условие (11.1.1)]. В [86] оценена погрешность гомогенных формул
для эффективности кадмиевого (т. е. черного для тепловых нейтронов) ре-
гулятора, поставленного в центр квадратной ячейки. Оказалось, что гетеро-
генные поправки весьма малы (5—10 %). Сравнение с экспериментом, вы-
полненным на критической сборке, также показывает, что погрешность го-
могенного приближения невелика (примерно 20 %, причем сюда входит по-
грешность определения длины миграции в решетке). Существенно, что рас-
сматривался регулятор в центре ячейки; если регулятор заменяет собой
тепловыделяющую кассету, то погрешность гомогенного приближения сущест-
венно возрастает. Современная теория гетерогенного реактора (см. [130]
и гл. 11) позволяет рассчитать эффективность регулятора, не прибегая к го-
могенному приближению.
192
Рис. 6.2. Зависимость отношения
эффективного радиуса к геомет-
рическому радиусу черного ци-
линдра от его геометрического ра-
диуса (при p0Ss=l масштаб по
оси абсцисс изменен)
ное распределение (6.2.2) обращается в нуль:
Ф(р) = А р0(ар)—(ар)] = 0.
L М>(«Я) j
(6.2.3)
Предполагая, что ар<С1 и заменяя в (6.2.3) приближенно
/0(ар) = 1, М0(ар) =------— 1п-^- [где С0=2ехр(—С) = 1,123;
ар
С=0,5772 — постоянная Эйлера], получаем условие критич-
ности в виде
Л (^) = - -Mln Луо (а/?). (6.2.4)
, 2 \ ар /
Если вместо условия (6.2.3) на эффективном радиусе р по-
ставить граничное условие (6.1.1) на истинном радиусе ро, то
вместо (6.2.4) имеем
h №=- 4 —?— N* <6-2-5)
Л1П—+1
«Ро
или, сравнивая с (6.2.4), находим связь р и ро’.
Р = роехр
М = роехр Г—
А ) ™ 2,Ро J
(6.2.6)
где использовано (6.1.1). Таким образом, эффективный радиус
р является функцией геометрического радиуса р0. На рнс. 6.2
дан график отношения р/ро, если для у(р0) используется фор-
мула (6.1.15).
Пусть а = а0 ба, a.0R = 2,4048, -^-<^1, т. е. а0 есть мате-
«0
риальный (он же геометрический) параметр реактора без ре-
гулятора, а а — с регулятором. Найдем ба/а0 из условия кри-
тичности. По определению ба/а0 всегда положительно. Малым
параметром является величина
/ С \ ”1
S = [1П -М .
\ «оР /
(6.2.7)
13—6053
193
Представим ба/ао в виде ряда:
— =c1S + c2e2+c3e3 (6.2.8)
«о
и разложим все функции, входящие в равенство (6.2.4), в ряд
по
= е + 8а-^-fin —=e(l+<?1s2);
\ ар / да \ ар /
/0(а/?) = (с1е+с2е24-с3е8) a0RJ0' (aQR) Х-^-(с12г2+2с1сХ)Х
х («0Ryj0" м)+y ci3s3 (a«^3 z«''' <“•>*);
(a/?) = No (aQR) + (схе + c2s2) aQRN0' (a0R) +
(6.2.9)
Подставляя (6.2.8), (6.2.9) в (6.2.4) и приравнивая коэф-
фициенты при одинаковых степенях е, получаем [Ji (a0/?) =
= 0,5191, У1 (aoR) =0,1028]:
Ci = [a0Wi Ы)]~2=0,6417;
са __ Ci ” («о#) _ q 0098-
сг 2 2
_С1+ <_£2.у — _£11 r_L + (ао^1 = _ 0,1863.
Ci \ Ci / 3 4 I
Таким образом, возникает ряд
— = [a0Z?/x (a0/?)]-2 s (1 + 0,Ole — 0,19s2). (6.2.10)
a0
Если воспользоваться (2.1.53), то при а2Л42<С1 получим
(тривиальный множитель 1 -|—!——, который формально дол-
2 а0
жен присутствовать, если учитываются высшие степени е, остал-
ся не раскрытым):
— - _ 2(/.2 + г)---- t +0 01s_019g2j 6 _L ±L\ (6.2.11)
k /?%ln(Co/aop)V Ц 2 «о / '
где Ц2 определено в § 4.1. Отметим, что, поскольку
8a 1 Sk
а 2 k— 1
малость 5a/a означает, что выполнено неравенство
6А<2(£—1).
(6.2.12)
194
Сильная компенсация в коэффициентах с2 и Сз приводит к
тому, что первое приближение в разложениях (6.2.10), (6.2.11)
обладает высокой точностью. Например, если g—1/4, то по-
грешность первого приближения не 25 %, как можно было бы
ожидать, а всего 1 %, причем не за счет второго, а за счет тре-
тьего члена разложения. Однако, как будет видно ниже, эта
компенсация случайна в том смысле, что она нарушается для
эксцентрично расположенного регулятора.
Из (6.2.2) можно найтн точку гт, где плотность потока максимальна:
Если агт<С1, то в первом приближении по е получим
где использовано следующее из (6.2.10) равенство
1 8fe
* = — [аоЯЛ(аоЯ)]2 "
Если эффективность регулятора мала, т. е. 8k<^k—1, то rm^iR и макси-
мум плотности потока расположен близко от центра реактора. Значение
плотности потока в максимуме равно
Фт — А
+ — eN0(arm)
(6.2.15)
Постоянную А определим из условия равенства средних потоков по объему:
г7о(аог)^
7?
rN0(w)dr
0 р
что при малых е дает А = 1 -|-0,17е. Изменение плотности потока
в точке гт из-за введения регулятора равно
—— = 1 + 0,4s — — In —,
Z0(arm) 2 е
(6.2.16)
а отношение Фт к плотности потока в центре реактора без ре-
гулятора
-^- = 1— 0,Is In— 4-—. (6.2.17)
/о(О) 2 * / ’
Оба отношения (6.2.16) и (6.2.17) при е<С1 меньше единицы. Найдем
точку гь а0Г1=х, такую, что при r>ri плотность возмущенного потока боль-
13* 195
ф
Рис. 6.3. Распределение плотности потока
нейтронов в цилиндрическом однородном
реакторе с регулятором в центре и отно-
сительное изменение плотности потока ней-
тронов по сравнению с плотностью потока в
реакторе без регулятора [6й=0,1 (k—1)]
Рис. 6.4. Зависимость эффек-
тивности от геометрического
(------) и от эффективного
(--------)радиуса (радиус ре-
актора равен lOOSs-1, норми-
ровка в точке p2s=l)
ше плотности невозмущенного, т. е.
При е<С1 это''уравнение не содержит 8:
0,17J0(x) +0,642Z1(%) +-^- N0(x) =0.
Численное решение дает х=0,7; ri//?=0,29, т. е. на расстояниях, больше 1/3
радиуса, плотность потока при введении регулятора возрастает, а при мень-
ших расстояниях уменьшается. Пусть, например, §k/(k—1)=0,1. По (6.2.15)
имеем 8 = 0,078, по (6.2.14) rm//?=0,164 и Фт=0,893. На рис. 6.3 приведены
распределение плотности потока Ф(г) и относительное изменение плотности
потока
А
J0(af,r)
Ф(г)
Фо(г)
f о (w) + —Wo(ar)
(6.2.18)
— 1
(а/?=2,2552; А = 1,0079). Если ^=1002s-‘, то из (6.2.7) и (6.2.6) находим
Po=O,172s-1.
Следует иметь в виду, что полученные здесь результаты имеют только
качественный характер, поскольку теория с одной группой является при-
ближенной, а реактор редко имеет однородную активную зону и не имеет
отражателя.
196
Зависимость 8k от эффективно-
го радиуса регулятора слабая, по-
скольку в (6.2.11) радиус входит
под знаком логарифма. На рис. 6.4
эта зависимость (нормированная на
8k при pSs=l) дана штриховой ли-
нией. Эффективный радиус экспо-
ненциально зависит от геометриче-
ского радиуса р0 [см. (6.2.6)]. Вид-
но, что зависимость 8k от геометри-
ческого радиуса более сильная,
особенно при малых радиусах регу-
лятора.
Рассмотрим теперь регулятор,
поставленный на расстоянии г0 от
Рис. 6.5. К задаче об эксцен-
трично поставленном регу-
ляторе (го — радиус-вектор
регулятора)
центра реактора. Плотность потока
нейтронов зависит от угла 0 (рис. 6.5), причем только от cos 0
(в силу симметрии). Общее решение уравнения (4.1.1) выглядит
следующим образом:
00 00
Ф(г, 0)= 5^„/„(ar)cos«0+ I r-r'|)cos«e. (6.2.19)
п=0 п=0
Будем предполагать, что поле нейтронов вблизи регулятора
можно описать только одной гармоникой, т. е. положить Вп — 0
при ra^sl. Такое ограничение возможно при достаточно малом
р. Воспользовавшись теоремой сложения (см., например, [75])
А^о(« I г —г' I) = ^о(а'')/о(аго) +
00
+ 2 S (аг) (аг0) COS «9 (г>г0),
М=1
(6.2.20)
перепишем (6.2.19) в виде ряда по гармоникам cosn0. На гра-
нице реактора при r=R должны равняться нулю коэффициен-
ты при cos п0 для всех значений п. Поэтому
_____ No(aR) Jo (ar0) ._______ ____2Nn(<xR)Jn(ar0) , / q\ (6 2 21)
70 (a/?) ’ " Лг(“#)
Воспользовавшись этими равенствами, можно условие кри-
тичности Ф(р) =0 записать следующим образом:
/о (a/?) = —J-------------------------No (а/?), (6.2.22)
1п —— -4- TcS-Aa)
ар
197
где
00
sx (а) = 2 Nn (aR) 1* (ar0) [Jn (aR)]~>.
n=l
Возьмем за малый параметр величину
s’ = Fin -^5- + itSx (a0)l
L «oP J
(6.2.23)
(6.2.24)
и повторим проведенное выше вычисление для центрально рас-
положенного регулятора (ограничиваясь двумя членами разло-
жения по е'):
Л)8(<Уо) 5, Л , С2 Л
a [«o^i (“о^)]2 \ Ci /’
(6.2.25)
где
~ = vlfao^ (“о*)]"2- 11 -77^гК (Vo) -
ci 2 ( Л(аоЮ J
гр
М)(«0#)
Л(“ой)
J О (aoro) 11 (a(/o) —
= 0,01702 (aoro) - 3,09 ^-70 (aoro) 7Х (a0r0). (6.2.26)
А
Из (6.2.26) видно, что коэффициент Сг/С], который теперь
является функцией Го, мал только при го=О. Например, при
aoro=l имеем с%1с\ = —0,426.
Если малым параметром считать е (6.2.7), то вместо (6.2.25)
получим
— = ( — 'j 11 +Е, ( —} 1 (6.2.27)
“ \ а /о L \ a /oJ
где
(—) =/о2(«о/-о)|—) (6.2.28)
\ а / О \ a /00
/ 8a \
— результат первого приближения по е; ----- — значение, по-
\ a ' 00
лученное в первом приближении по е для регулятора, распо-
ложенного в центре реактора, т. е. первый член в (6.2.10), а
F\ равно
р _ [«о^Л!^)!2 f Cj
7q2 («о ro) V ci
= 0,015 — 2a0r0 _ 4,9 —,
7o(aoro) 702(a0r0)
(6.2.29)
198
где Si определено (6.2.23) при а = а0. При малых аого в сум-
ме Si можно сохранить только первое слагаемое, и тогда
Л«0,015—7,17(г0/Я)2. (6.2.30)
Обратим внимание, что 6а/а в первом приближении, т. е.
(6.2.28), пропорционально квадрату невозмущенной плотности
потока в том месте, где поставлен регулятор. Этот результат
согласуется с формулами теории возмущений (см. § 5.1). Вто-
рое слагаемое в (6.2.27) дает поправку к первому приближе-
нию теории возмущений.
6.3. ИНТЕРФЕРЕНЦИЯ ДВУХ РЕГУЛЯТОРОВ
Рассмотрим интерференцию двух регуляторов, расположен-
ных по одному диаметру на расстоянии го от центра реактора
(рис. 6.6). Пренебрегая, как и в § 6.2, гармониками в описа-
нии собственного поля регуляторов [т. е. коэффициентами Вп
при в (6.2.19)], запишем плотность потока нейтронов сле-
дующим образом (см. обозначения на рис. 6.6):
ОО
Ф(г, е)= 5 Ап J2n (ar) cos 2пЬ + N0(ar') + N0(ar"). (6.3.1)
n=0
Используя формулу (6.2.20), получаем
No (ar') + No (ar") = 27 о (aro) No (ar) +
00
+ 4 2 hn M N2n fa) cos 2/z0 (r > r0). (6.3.2)
n=l
Граничное условие на поверхности реактора позволяет опре-
делить постоянные Ап, а граничное условие на эффективной по-
верхности регуляторов приводит к условию критичности [см.
(6.2.22)]:
Jo(aR) =—л2Уо(с^?)/о2(аго)е", (6.3.3)
где малый параметр е" равен
s" = Г1п -----дго (2ar ) + 2TTSJ-1 (6.3.4)
ap 2 J
И
N^aR)
^2tl(aR)
2
J2n (аГо).
(6.3.5)
С точностью до квадратичных членов по е" имеем
__ 270а (a0 r0) sv /1 | 2 —2
«о — 1«о^Л(ао^)]2 \ С1 /’
(6.3.6)
199
где c2/ct имеет прежнее значение, т. е. (6.2.26), а е" равно вы-
ражению (6.3.4) при а=ао- Формулу (6.3.6) можно переписать
в виде ряда по е (6.2.7). В результате
= — \ \ Y (6.3.7)
“о \ й0 / 10 \ V “о / 1OZ
где (6a/ao)io совпадает с (6а/ао)о (6.2.28), т. е. определяет эф-
фективность одного регулятора в первом приближении по е,
а F2 равно
Р = _[«og£i Г (2a r0)l. (6.3.8)
[ C1 2 01 0°7J k ’
Определим «коэффициент интерференции» двух регуляторов § с
помощью равенства
где (ба/ао)1 — эффективность одного регулятора (6.2.27), вы-
численная с точностью до квадратов е. Подставляя (6.3.7) и
(6.2.27) в (6.3.9), получаем с точностью до линейных членов
по (6a/ao)io:
’ х = аог<» (б3-10)
V “о /10 \ “о /10
где
?0(х) = 2,448 ^о(-2—} +0,0153 —2% ЬМ 4- (6.3.11)
oV ' VW '.W VW
a Si и S2 определены формулами (6.2.23) и (6.3.5) при а = а0.
При малых х=аоП) главным чле-
ном в 1о(х) является первый, содер-
жащий функцию 2Vq(2x), которая об-
ращается в бесконечность при х->0 и
описывает «непосредственное влия-
ние» одного регулятора на другой.
При малых х функция Д/0(2х) отрица-
тельна, т. е. коэффициент интерферен-
ции отрицателен. Это означает, что
эффективность двух одновременно дей-
ствующих регуляторов меньше, чем
сумма эффективностей двух регулято-
ров, действующих порознь. При х=
=0,47, т. е. при Го//? = О,195, функция
N0(2x) обращается в нуль, и при даль-
200
Рис. 6.6. К задаче об интер-
ференции регуляторов в точ-
ках Го и —Го
Рис. 6.7. Зависимость коэффициента интерферен-
ции двух регуляторов, расположенных на одном
диаметре,, от расстояния между ними. Стрелкой
показано положение корня уравнения Л?о(2х)=0.
По оси ординат отложено произведение коэффи-
циента интерференции go на квадрат невозмущен-
ного потока в той точке, где поставлен регулятор
нейшем увеличении расстояния между
регуляторами коэффициент интерферен-
ции становится положительным. Нагляд-
ное объяснение положительности коэф-
фициента интерференции состоит в том,
что второй регулятор попадает в область,
где первый вызвал повышение плотности нейтронного потока.
На рис. 6.7 приведен график функции Л>2 (х) go (х); х=аого,
построенной по формуле (6.3.11). Коэффициент интерференции
обращается в нуль при х=0,485, что очень близко к корню
функции N0(2x), который расположен при х=0,47. При увели-
чении х становятся существенными и другие слагаемые форму-
лы (6.3.11) *.
Таким, образом можно рассмотреть и более сложные случаи.
Предельным случаем большого числа регуляторов является «ре-
шетка» регуляторов, равномерно заполняющая всю активную
зону. На практике такая решетка регуляторов используется, во-
первых, для компенсации того уменьшения реактивности, кото-
рое возникает при выгорании топлива (см. гл. 13), во-вторых,
для компенсации положительной реактивности, которая возни-
кает при остановке реактора из-за распада 135Хе (см. гл. 12)
и температурного эффекта (см. гл. 14). В последнем случае
регуляторы (они обычно называются СУЗ — стержни управ-
ления и защиты) опускаются на всю глубину, чтобы надежно
запереть реактор. Наконец, с помощью большого числа регуля-
торов можно, опуская их на различную глубину, оказывать
влияние на уровень мощности в каждом канале с топливом.
6.4. РЕГУЛЯТОР В ДВУХГРУППОВОМ И ВОЗРАСТНОМ ПРИБЛИЖЕНИЯХ
Решение уравнений двухгруппового приближения (4.4.1),
(4.4.2) для случая, когда в центре реактора расположен регу-
лятор, имеет следующий вид [см. (4.4.9), (4.4.10); изменены
* Автор пользуется случаем отметить, что в [125] в формуле (3.1.27)
была допущена ошибка и поэтому данные табл. 19 для коэффициента интер-
ференции неправильны. Автор признателен П. П. Благоволину за указание
на эту ошибку.
201
обозначения: оц-э-а; аг-НЗ]:
ф (Г) = AJ0 (ar) + BN0 (ar) + Л/о (М + (₽'')'>
п(г) = ТтНИ-Маг)— Y2^i/o(Pr)+Yi^o(ar)— уА/СвФО].
(6.4.1)
где уь уз определены формулами (4.4.11). Если реактор не
имеет отражателя, то условия Ф(R) = п(В) =0 на границе ре-
актора позволяют исключить из (6.4.1) коэффициенты Д и В:
ФИ=л[/0(«г)-^.^(„)] +
+ Вх|--Т®7Л(РИ + ^(М1;
°w=-ц Н р. <") - "•<»)]-
(6.4.2)
Если 1 и рассматривается область, далекая от границы
реактора, то можно пренебречь слагаемыми, которые содержат
До(₽^), т. е. положить
ф (г) = А / о (аг)
^-^0(аг)1 + В^0(₽г);
п(г) = [/„(аг)-2^_ДГ0(аг)] -уДКо(₽г)}.
(6.4.3)
Рассмотрим сначала случай, когда регулятор не поглощает
замедляющихся нейтронов (например, кадмий). Тогда плот-
ность замедления п(г) не должна иметь особенность при
г=0. Поскольку при г->0 имеем
y0(ar) = -Ain_£a.. Ko(₽r)=inJk
п аг рг
особенность при г=0 исчезает, если выполнено условие
2 71 J0(aR) д
" r2 No(aR)
(6.4.4)
Поэтому плотность потока в тепловой группе равна
Ф (г) = л k (ar) - к (ar) —1 Ко (₽г)11.
I N0(aR) L 71 Га JJ
(6.4.5)
202
Условие критичности, следующее из равенства Ф(р)—О,
имеет вид (при условиях ар<С1, рр<С1):
/0 («/?) = -
^Г1П_£о. + Л1п-£»_1 1
2 1 ар Ya РоР .
Уо (а/?)-
(6.4.6)
Из равенства (6.4.6) следует, что разложение для Sa/aa по сте-
пеням е, полученное в § 6.2, сохраняется, но с новым значени-
ем е (только до е2, члены порядка е3 изменяются):
I 1 Cn 1 + 1 Со "I*-! //? л ’~7\
е = 1п -2- -U 0-------1П -2- . (6.4.7)
L “оР ₽о2/-2—1 РоР J
Если k—1 <С 1, то (см. § 4.4; т* заменено т):
a02L2«l; ₽2 = ₽02 = ± + -i;
P02L2—1=L2/t (6.4.8)
и (6.4.7) можно переписать так:
s= fl —Г' Fln-i-—— ln-2-l-1. (6.4.9)
\ ;-2 / L “оР Z.24-t a0 J
Поэтому вместо формулы (6.2.11) получим (в первом при-
ближении по е)
Sk _ 2Л2
k ~~ W2
(6.4.10)
где
еЭ-*=1П-^- ———Ini. (6.4.11)
“оР £2-Н «о
Поскольку обычно р<1/₽, второе слагаемое в (6.4.11) за-
метно меньше первого. Поэтому единственное существенное из-
менение, связанное с переходом к двухгрупповому приближе-
нию, состоит в замене r-j-A2->ZA Такое изменение вполне есте-
ственно с физической точки зрения, если регулятор не погло-
щает замедляющихся нейтронов.
Пусть теперь регулятор поглощает и замедляющиеся ней-
троны, причем эффективный радиус регулятора для замедляю-
щихся нейтронов равен р'. Тогда из (6.4.3) получим условие
критичности (при р, р'<С1/Р, 1 /а):
(6.4.12)
203
где
8 г г
I , , , ьо
In-----+ b In--------
“о? “о ₽'
b
т
£2
Ш-р
РР
1п-^-
0?'
(6.4.13)
или
е —
р \-‘
(6.4.14)
Если р'->0, то 6->0, но
6 In (р/р') —*-р In
и (6.4.14) переходит в (6.4.6), как и должно
то из (6.4.14) получаем формулу одногрупповой теории. Этот
случай реализуется, если регулятор черный как для тепловых,
так и для замедляющихся нейтронов и величины S.s одинаковы
в обеих группах.
Вместо введения эффективных радиусов можно задать на
геометрическом радиусе регулятора граничные условия следую-
щего вида (при этом Л/й безразмерны):
/г-дФ) — АФ-----------—Ллп-,
dr }r=9„ D
быть. Если р = р',
— Лп п.
Г=Ро
(6.4.15)
(6.4.16)
Подставив в (6.4.15) Ф, п в виде (6.4.3), получим условие
критичности (аро<^1, ₽ро<1):
/о(а/?) = ___2_ ад
и следующее из него выражение для эффективности регулято-
ра (в первом приближении по е*)
6k 2 (А2 + т) *
--------------S ‘,
k /?2Ц2
где [если выполнено (6.4.8)]
s* = fln + дГ1 .
\ “Ро /
Д2
---Ли
т
(6.4.17)
(6.4.18)
Z.2 /
1 + ~ + I Л-22 + -Л-21 + ~
д = ______
Ajx—-Л-21 + А22 + ЛПЛ22 ( 1 +
т \
(6.4.19)
204
Если Лц=Л21 = 0, то
д ^0=-ЪГln + 4ir л^‘- (6Л2°)
Д2 Рр0 £2
Заменяя геометрический радиус эффективным по (6.2.6)
— = — expf — —— 'j; (6.4.21)
Ро ? \ -Л-22 /
получаем, что е; (6.4.18) в этом случае совпадает с (6.4.9), как
и должно быть.
Рассмотрим регулятор, замедляющий нейтроны, но погло-
щающий только тепловые нейтроны, например, из кадмия с
внутренним теплоносителем. Тогда, применяя для внутренней
полости регулятора уравнение (3.2.31), не будем учитывать по-
глощение. Решение уравнения (3.2.31) в этом случае будет
ni = ^оСр/К'ч).
откуда
dtit
Фо
ii
Ро Л (ро/РЧ)
ЛЛРо/ГЧ)
Ро2 .
Pos«2x;. (6.4.22)
Переходя от внутренней среды (индекс i) к внешней (индекс е)
с помощью граничных условий (2.2.38), находим
Ли = ^--^-, (6.4.23)
‘-'е
где D — коэффициент диффузии замедляющихся нейтронов.
Применяя закон сохранения нейтронов в тепловой группе,
получаем .
Ро~ ~ Ро2 Че ~ 77Г ’ <6-4-24)
Фо 2 2De
где черта означает усреднение по объему регулятора. Первое
слагаемое в правой части (6.4.24) эквивалентно слагаемому
Л22Ф в (6.4.15). Заменив приближенно nt- на п,(ро), получим,
используя граничные условия (2.2.35):
т. е. в этом приближении Лц=Л21. Тогда
Д=ДО-ДЬ (6.4.26)
205
где Ао определено (6.4.20), a Ai равно
Если использовать (6.4.21), то
Р?о
^22
₽Р
Так как Ai>0, то замедлитель внутри регулятора увеличи-
вает его эффективность, как и должно быть из наглядных со-
ображений: нейтроны, замедлившиеся внутри регулятора, по-
глощаются внутренней поверхностью черного для тепловых ней-
тронов поглощающего слоя. Это дополнительное поглощение и
увеличивает эффективность регулятора. Различие в эффективно-
сти между «мокрым» и «сухим» регуляторами (замедлитель
внутри регулятора — это либо простая, либо тяжелая вода)
равно
(6.4.28)
Обычно либо ро2<с2т,, либо Dt^De (например, внутри про-
стая вода, снаружи графит или тяжелая вода). Тогда
Лп<1 и
К
Рассмотрим, наконец, возрастное приближение. Если огра-
ничиться первым приближением по 8, то всегда справедлива
формула [см. также (5.1.14)]:
где
Sk 2L2
--- = s,
k--R2H2
®oPo)
(6.4.29)
(6.4.30)
причем Форо) — плотность невозмущенного потока, т. е. потока
в точке г0 до постановки там регулятора. Воспользуемся теперь
/ дФ \
для вычисления градиента (---- уравнением (2.1.44), при-
\ дг / г=?
206
чем предположим, что
IF (г, г') = (4^)-1expJ— (Г4тГ )8]- (6.4.31)
В этом случае (2.1.44) эквивалентно возрастному приближе-
нию. Введем в уравнение (2.1.44) точечное возмущение:
Дф (г) — + _L f Г (г, г') Ф (г') dr' — ДЗ (г — г0) = 0. (6.4.32)
Д2 L2 J
С помощью преобразования Фурье легко получить решение
уравнения (6.4.32)
ф (Г) = ф (г)---— С-----exp[t(r-rB)x]dx-- (6.4.33)
0 4-2 J №-J-Д-2 [1—6 ехр(—Л)] ’ 4 7
где Фо (г) — решение однородного уравнения (6.4.32). Инте-
грируя в (6.4.33) по углам и учитывая, что Ф(р)=0 (рассмат-
ривается черный регулятор с эффективным радиусом р), за-
пишем (6.4.33) так:
Ф (г) = Фо (г) - Фо (г0) (6.4.34)
где*
Р(Г)= (6Л35)
о
Интеграл (6.4.35) при г->0 расходится на верхнем пределе.
С помощью равенства
f (rx)dx = /_г_\ (6.4.36)
J Х2 + £-2 ° \. Д У 4
О
можно переписать (6.4.35) так:
Ptf-^^+kP^r), (6.4.37)
где
* Подынтегральное выражение в (6.4.35) имеет полюс при х2=а2; инте-
грал надо понимать в смысле главного значения (см. [86]).
207
Производная от (6.4.38) по г при г=0 имеет порядок ве-
личины 1/L, и поэтому, пренебрегая величинами порядка p/L,
находим
Тогда 8 (6.4.30) равно
е = [Р(р)]->= К.
1—1
(6.4.39)
Интеграл Л(0) проанализирован в [86] (а2т<1):
Р1(0)=-------------In-^ + Z?! +0(<А). (6.4.40)
V ’ 2(L^+kz) 2и2т 1 V т / V 7 ' ’
График функции приведен в [86, с. 222]. При a=L2/x=
= 1 7?i = —0,1. Сравним 8"1 (6.4.11), обозначив эту величину
зП1 и s—](6.4.39), обозначив ее е^1:
As-’ = еГ1 — ей1 = R-L (а) + -i- In а —
ь 0,577а .
1 h о,
-----------In-----
2(1 —а) [ 1 +
Если а=\, то Аб-1 = —0,07; так как е~1 = 2-ь4, то |Ае~Ч<С
С8_', т. е. при а2т<С1 двухгрупповое приближение 8ц (6.4.11)
мало отличается от возрастного 8В (6.4.39).
(6.4.41)
Часть II
ГЕТЕРОГЕННЫЙ РЕАКТОР
Глава 7
ПОГЛОЩЕНИЕ ТЕПЛОВЫХ НЕЙТРОНОВ
7.1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
Вероятность поглощения теплового нейтрона 235U в гомоген-
ном реакторе можно записать так:
б=(1 + 2<7>)-1 = (1+7Г’; 9 = 2^-, (7.1.1)
где суммирование проводится по всем сортам нуклидов, кро-
ме 235U;
- _ Ес
q. = ^L. Оа = С Оа (£)ф (£) dE, (7.1.2)
с5аа5 J
О
Ес — верхняя граница тепловой группы; с,, — число ядер
нуклида / и 235U в единице объема реактора. Ниже, чтобы не
загромождать формулы, будем предполагать, что имеется толь-
ко один сорт делящихся нуклидов. Распространение на общий
случай достаточно очевидно.
В гетерогенном реакторе концентрации с/ и плотность по-
тока нейтронов Ф зависят от координат. Поэтому в (7.1.2) на-
до добавить интегрирование по объему:
Ес
J Cj(r)dr j aaj(E, г)Ф(Е, r)dE
-----------------• (7.1.3)
В настоящей главе будут рассматриваться реакторы с пра-
вильной решеткой одинаковых блоков топлива. Тогда, если реак-
тор достаточно большой, интегрирование в (7.1.3) можно рас-
пространить только на объем одной ячейки, поскольку все ячей-
ки одинаковы. На границе ячейки плотность тока нейтронов
по соображениям симметрии равна нулю.
Если ячейка обладает высокой симметрией, например квад-
ратная или, лучше, шестигранная, то истинную границу ячейки
14—6053 209
можно заменить окружностью, причем площадь, которую она
ограничивает, равна площади ячейки (всюду ниже рассматри-
ваются однородные по высоте цилиндрические блоки и под пло-
щадью блока, ячейки и т. п. подразумевается площадь сечения'
в плоскости, перпендикулярной оси блока). На граничной
окружности плотность тока нейтронов равна нулю. Такую ци-
линдрическую ячейку будем называть «эквивалентной цилинд-
рической ячейкой» или «ячейкой Вигнера—Зейтца» (по имени
авторов, которые использовали этот прием в теории твердого
тела задолго до создания реакторов). Как будет показано в
гл. 11, такая аппроксимация для однородной решетки обладает
очень высокой точностью.
В односкоростном приближении интеграл по энергии заме-
няется средним значением (в § 7.5 мы откажемся от этого при-
ближения) . Тогда
’/ f с/(г)Ф(г)4г
q} = —-------------=....JJJ ' , (7.1.4)
Oj J с6(г)Ф(г) dr овс»ф»у|»
где Vj — объем, содержащий нуклид /; С/ — среднее значение
концентрации (обычно С/ постоянно внутри объема Vj); Ф;- —
среднее значение плотности потока тепловых нейтронов по объ-
ему Vj. Запишем [<7/ГОм дано (7.1.2)]:
<7/—^/гом^/ (7.1.5)
и будем называть коэффициентом блокировки для тепловых
нейтронов или коэффициентом неравномерности. Если рассмат-
риваемый нуклид равномерно размешан вместе с 235U (напри-
мер, 238U), то для него £=1. Плотность потока нейтронов мак-
симальна в замедлителе. Поэтому £ для замедлителя принимает
максимальное значение. Если блок топлива сплошной, то
^1 (если решетка неоднородна, например, имеются сильно по-
глощающие стержни регулирования, то, конечно, для них £<1).
Если блок топлива имеет вид полого цилиндра, внутри которого
нет (или мало) замедлителя, то для нуклидов, расположенных
во внутренней полости может быть меньше единицы.
В гетерогенном реакторе (по определению, принятому в на-
стоящей главе) расстояние между блоками а много больше
длины рассеяния в замедлителе;
a^>ls; aSs>l. (7.1.6)
Тогда в замедлителе имеется большая область, где справед-
ливо уравнение диффузии. Для вычисления плотности потока
нейтронов в этой области надо задать на поверхности блока
граничные условия, которым удовлетворяет диффузионный по-
210
ток, если его экстраполировать до поверхности блока. Гранич-
ные условия запишем так (р — радиус блока) :
== ЛФ (р) — Л'—(р), (7.1.7)
\ дг /г=р 1)е
где пе — плотность источников тепловых нейтронов, т. е. плот-
ность замедления при Е=ЕС, а X и 7/ — некоторые безразмер-
ные коэффициенты. Плотность потока Ф(г) удовлетворяет урав-
нению
РДФ—ЕаеФ = — пе, (7.1.8)
где индекс е означает внешнюю по отношению к блоку среду.
Здесь и далее будем считать, что пе не зависит от координат
(см. § 2.2 и 9.3). Решение уравнения (7.1.8) в цилиндрической
ячейке можно записать так:
ф __ пе ___Д /Le) 4- CI0(r/Le) .у | 9)
KB(?ILe) +C/0(p/Le) ’
где /Со, /о — стандартные обозначения цилиндрических функ-
ций мнимого аргумента. На внешней поверхности ячейки плот-
ность тока нейтронов равна нулю (радиус ячейки R) :
=0, (7.1.10)
\ dr Jr=R V
откуда'получим значение постоянной С в (7.1.9):
C^K^R/LgjlhtR/Lg). (7.1.11)
Поглощение нейтронов в замедлителе в большинстве случаев
мало. Тогда можно положить поглощение равным нулю, найти
распределение нейтронов и вычислить поглощение замедлите-
лем в этом невозмущенном потоке. Предельный переход к рав-
ному нулю сечению поглощения можно провести в (7.1.9), но
проще заново написать решение. Общее решение однородного
уравнения в этом случае содержит константу и логарифм, а
частное, как нетрудно убедиться, если записать оператор Ла-
пласа в цилиндрических координатах (см. 4.1.18), равно
(7.1.12)
De 4
Поэтому решение уравнения (7.1.8) при 2ае=0, удовлетво-
ряющее граничному условию (7.1.10), имеет вид
Ф('') = Ф(Р) + -^(-у-1Пу--±^) (7.1.13)
ИЛИ
Ф(г)=Ф(/?)—Л*!.in21—(7.1.14)
De \ 2 г 4 J
14* 211
Граничное условие (7.1.7) однозначно определит постоян-
ную А в (7.1.9) или Ф(р) в (7.1.13):
A = J±- (х—X-2e_\[_L_ яГ1 (7.1.15)
\ Le2 / \ Le Kt>(?/Le) Г/0(р/Де) /
где С дано (7.1.11) и
Ф(р) = ^(^=124-Г А (7.1.16)
We \ 2 У
Обратное утверждение, однако, неправильно: если известно
из каких-то соображений диффузионное решение, то постоян-
ные X, V не определяются однозначно, поскольку в (7.1.9) или
(7.1.13) только одна постоянная, а граничных коэффициентов
два. Этим произволом можно воспользоваться для того, чтобы
сделать коэффициенты X, V максимально универсальными, на-
пример чтобы они зависели только от свойств блока и замед-
лителя, но не от размеров ячейки.
7.2. ДИФФУЗИОННОЕ ПРИБЛИЖЕНИЕ
Применение диффузионного приближения для определения
плотности потока тепловых нейтронов во всем объеме ячейки
приводит, как правило, к слишком большим ошибкам. Тем не
менее качественные закономерности сохраняются. Поэтому рас-
смотрим эту задачу.
Предположим, что источники тепловых нейтронов заданы ку-
сочно-постоянной функцией: пе — вне блока, /г, — внутри бло-
ка (индекс i относится к характеристикам среды внутри блока,
индекс е — вне блока), причем [см. (2.2.38)]:
(4>^s)e
Будем считать, что блок однороден. Присутствие легких ядер
(теплоноситель, кислород в составе оксида урана, покрытия)
внутри блока -характерно для реакторов атомных электростан-
ций. При этом, конечно, блок фактически неоднороден. Однако
в некоторых условиях, особенно когда размеры неоднородностей
малы по сравнению с длинами la, ls, замена неоднородного бло-
ка однородным с некоторыми средними значениями Ss, не
меняет качественной картины.
При решении задачи в диффузионном приближении не обя-
зательно вводить граничные коэффициенты X, V. Однако в даль-
нейшем (см. гл. 11) граничные условия (7.1.7) будут использо-
ваться, и поэтому полезно получить значения коэффициентов
%, %' в диффузионном приближении.
Составим уравнение баланса нейтронов в блоке: суммарный
ток на блок равен разности числа нейтронов, поглощенных бло-
212
ком, и суммарной мощности источника тепловых нейтронов в
блоке:
2тгрПе^- = тр22агФ; —тгрЧ, (7.2.2)
д?
где фг — среднее значение плотности потока нейтронов по объ-
ему блока. Заменим в (7.2.2) и, по (7.2.1.) и обозначим
Ф»=ф(р)/<Э, (7.2.3)
где величину Q, фактически определенную этим равенством, на-
зовем коэффициентом экранировки блока. Вместо (7.2.2) имеем
дФ _ p2St.t- ф _ _тгр2_ (gSs)(-
dp 2DeQ V 7 2De
откуда, сравнивая с (7.1.7),
Л = = — p2SZre So(- Q-';
2DeQ 2
,, P2 (^s)z 3 (&)<
A = ------- --- ~ ------p Zj ire-------
2v 2 uc
(7-2.4)
(7.2.5)
где Sfre> Stre — транспортные сечения для тепловых и замедляю-
щихся нейтронов. Здесь и далее блок топлива будем рассматри-
вать как целое и характеризовать средними макроскопическими
сечениями поглощения и рассеяния. Буквой q обозначим теперь
отношение числа нейтронов, поглощенных в замедлителе, к
числу нейтронов, поглощенных в блоке:
п — Р2) Г — П Г — а I п • Г — п I 41 . п — п Г)
Я х, о ------ 7ГОМ * Яа i VI’ * "Т" » V0 9гом Я*
^ai Рг Я гем
(7.2.6)
Величину 71 будем называть внешним блок-эффектом, поскольку
она характеризует неоднородность нейтронного потока вне бло-
ка, а £ — полным блок-эффектом (употребляется также термин
«коэффициент проигрыша»). Полный блок-эффект показывает,
во сколько раз возрастает отношение числа нейтронов, погло-
щенных в замедлителе, к числу нейтронов, поглощенных в бло-
ке при переходе от гомогенного к гетерогенному реактору с той
же средней концентрацией топлива и замедлителя. Введем еще
обозначение
— отношение суммарной замедляющей способности блока и за-
медлителя вне блока. Величины X, X' (7.2.5) можно выразить
213
через qQ и q:
R3—?2 . = #2-р2 с
(7.2.8)
Формулы (7.1.9), (7.1.15) и (7.2.8) позволяют записать зна-
чение плотности потока на поверхности блока Ф(р) и средней
плотности потока в замедлителе Фе следующим образом:
Ф(Р) = -^- 1-
^ае
пе <7о[1 +^(1 + ?i°)].
2де 1 + <7о + <7i°
(7.2.9)
(l+^m
пе । Le2 __ пе 9i° + <7о(1 + ci)
^ае (j ^0) X р2 ^ае 1 + Яо + ^1°
2Де2
(7.2.10)
где
л о — Р2 Rp(?/l-e) 4~ б^/о(р/Де) _। (7 2 11)
41 2?Le K^/^-CI^p/L^ ’ '
а С дано (7.1.11). По определению (7.2.6), отношение величин
<71 и q0 должно быть
£х_ = Фе
?о Ф(?)
откуда, используя (7.2.9) и (7.2.10), получаем
п _ п о_____™
Чг~Ч1 1 + ^(i + 9io)-
(7.2.12)
(7.2.13)
Если в блоке нет легких ядер и С|=0, то внешней блок-
эффект дается величиной q^ (7.2.11). Обычно ?о<^1, ?1°<С1 и
тогда вместо .(7.2.13) получим
^^(l+cg)-1.
(7.2.14)
Из (7.2.13) и (7.2.14) следует, что замедлитель внутри бло-
ка уменьшает внешний блок-эффект, что вполне понятно, так
как источники нейтронов в блоке повышают там плотность по-
тока тепловых нейтронов.
Как уже указывалось выше, в случае слабого поглощения
легче получить результат, непосредственно обратившись к ис-
ходным уравнениям, чем проводить разложение q\° по малым
параметрам Я/Ье и pJLe. Из (7.1.13) получим
Фе = Ф(Р) + ^Е(С), (7.2.15)
214
где
F(c) =
In —
с
\ — c
A + JL. c=p_y
2 2 \R )
(7.2.16)
ffi _ Фе _ । _ __Щс)_____
<7o Ф(Р) 2(1—c)(l+c5)
Плотность потока при r—R равна
Г /1п— \
ф(^) = ф(р)[1+2(ТТЧ)^-1>1
(7.2.17)
(7.2.18)
Подставляя X (7.2.8) в (7.2.17) и используя (7.2.14), получаем
91» = -^-Е(с).
v 4/-/
(7.2.19)
Если (7.2.11) разложить по p/Le и RlLe, то получим
(7-2-20)
где F('c) дано (7.2.16), а
Г in— "]
Fx(c) = ——+ — Id--------------— In—— Y (7.2.21)
' 24 1 - c L 1 - c J c \ 24 12 / ' '
Первый член в (7.2.20) совпадает с (7.2.19); поправочный
член обычно весьма мал.
Теперь надо определить коэффициент экранировки Q. Ре-
шение уравнения диффузии внутри блока будет
ф. (Г) = -HL- + А' JAL/М. > (7.2.22)
^ai ^о(Р/^т)
где А' — константа, определяемая совместно с Л в (7.1.9) из
граничных условий
ф/ (р) = Фе (р); ^ = De (7.2.23)
др др
Определив среднее значение Фг- из (7.2.22), можно запи-
сать коэффициент экранировки так:
Q-1 = (QO-1)[1 + -^-
(7.2.24)
215
где (см. § 2.1, задача 1)
Q = 7о(Р
40 ’
(7.2.25)
Очевидно, что если (£28)г = 0, то Q — Qo. В этом случае коэф-
фициент экранировки не зависит от свойств внешней среды.
В общем случае, когда (£28)г=#0, надо воспользоваться гра-
ничными условиями (7.2.23). Выражая комбинации цилиндри-
ческих функций, входящие в граничные условия, через Qo и qi°,
записываем равенства (7.2.23) так:
п1 । Д’ _ пе д. А!___________Угри д
^•al -%ае Qo 1 + Ух0
Определяя отсюда А' и подставляя в (7.2.24), получаем
О__1 =______________Фо-1______________ (7 о 261
4 1 + С^(1+УгомС<) + 4l°)(l ~^Угом)-1 >
или при малых qi°, g-ox
Q-1=(Q0-1)(1+q)-1, (7.2.27)
т. е. коэффициент экранировки уменьшается, если блок содер-
жит легкие ядра (сравниваются блоки с одинаковыми и Ss,
но разными |Ss). Для полного блок-эффекта из (7.2.6), (7.2.14)
и (7.2.27) получаем
_ I __Ч_ __ f I ___________ О-
14-Cj, “Г 1 + с^ Ч° [ 1 4-^
(7.2.28)
где £о>1 — полный блок-эффект при q=0.
Практически коэффициент экранировки Qo не бывает боль-
шим (значение Q0=2 следует считать большим). Тогда цилинд-
рические функции, входящие в (7.2.23), можно разложить в
ряд и получить (см. задачу 1 в § 2.1):
Qo=1 + Т (М - +• • • (7-2-29*
о \ i-j у 1У2 \ i-j у
Как видно из формул (7.2.4), (7.2.25), (7.2.27), величина
V не зависит от размеров ячейки, a 7) зависит через величину
с§, входящую в формулу (7.2.27). Как отмечалось в § 7.1, гра-
ничные коэффициенты %, V не определяются однозначно по
заданной плотности потока. Можно предположить другой спо-
соб определения граничных коэффициентов, при котором они
не зависят от размеров ячейки *.
Пусть источники тепловых нейтронов представлены в виде
* Автор признателен Б. П. Кочурову за обсуждение этого вопроса.
216
суммы двух функций: пе, отличной от нуля только вне блока,
и nt, отличной от нуля только внутри блока. Плотность потока
тепловых нейтронов от источника пе обозначим Фь а от источ-
ника nt—Ф2, причем обе функции удовлетворяют граничному
условию (7.1.10). В силу линейности уравнения, которому под-
чиняются ПЛОТНОСТИ ПОТОКОВ Ф1 и Ф2, плотность полного потока
равна
Ф=Ф1+Ф2. (7.2.30)
Из условия баланса нейтронов для Ф1 получим граничное
условие
Р^-==2ФХ, (7.2.31)
др
где
<7-2-32>
и Qo определено (7.2.25), если использовать диффузионное при-
ближение для плотности потока внутри блока. Если плотность
потока определяется каким-либо более точным способом, то Qo
есть коэффициент экранировки (7.2.3), вычисленный для случая,
когда источник тепловых нейтронов внутри блока равен нулю.
Поскольку сумма (7.2.30) должна удовлетворять уравнению
(7.1.8), то из (7.2.31) следует
р-^- = 2Ф2 (р) — (7.2.33)
dp De
Если поглощение в замедлителе вне блока равно нулю, то,
поскольку источники для Ф2 вне блока отсутствуют, с?Ф2/б1р = 0,
откуда
Г = 2-^^-. (7.2.34)
Из (7.2.22) для Ф2 следует А'=0, т. е. Ф2=п(/2ог, и по-
этому
Qo- = V р2^tre Qo-- (7.2.35)
2хе (£SJe 2 ис
Если замедлитель вне блока поглощает нейтроны, надо вос-
пользоваться (7.2.23), подставив в (7.2.33) выражение (7.2.22).
Нетрудно убедиться, что (7.2.35) не изменится. Обратим вни-
мание на то, что V (7.2.35) отличается от Z (7.2.32) только за-
меной сечения поглощения 2О,- сечением увода ис-л t. Гра-
ничные условия (7.2.32), (7.2.35) не зависят от радиуса ячейки,
что делает их более универсальными, чем (7.2.5).
Задача 1. Непосредственной проверкой убедиться, что граничные коэф-
фициенты (7.2.5) и (7.2.32), (7.2.35) приводят к одной и той же плотности
потока нейтронов вне блока.
217
Решение. Плотность потока нейтронов вне блока дается формулой
(7.1.9), где А определено (7.1.15). Применяя формулы (7.2.5)—(7.2.7), по-
лучаем
___ пе (1 Ч- *7]°) (1 Сь <7го.м *5)
— ------ —............................
Sai
1 + -Ь <7гом Q
а если вместо (7.2.5) использовать (7.2.32), (7.2.35), то
(7.2.36)
Пе (1 +?1°)(1~ С^<7гом)
Л = .________________________________
Sai 1 + ‘71° 4" б/гом Qo
(7.2.37)
Легко проверить, что в силу (7.2.26) выражения (7.2.36) и
Задача 2. Определить коэффициент экранировки блока
(7.2.37) равны.
в виде полого
цилиндра, если внутренняя полость заполнена непоглощающим замедлителем
(внешний замедлитель также можно считать непоглощающим).
Решение. Плотность потока тепловых нейтронов во внутренней полости
равна
, П[ г2
ф. = а— -----------, О
а- 4
в стенке цилиндра
Ф(г)
+ В1а
Р
в замедлителе
г2 —р!2
4
De L 2 Pi
Интегрируя Ф(г) по области p<r<pi, выразим Q так:
(Р12-р2)[ Ж0(Р1 /L) + B/0(P1/L)J
О =----------------- ---------
2L {Pi 1^Л(Р1/^) ^^iXPi/Ml Р [^Л(Р/^) AKi(р/^-)]}
Используя граничные условия для Ф при г=р и г=рь полагая ni/ne =
= (g2s),/(gSs)<., получаем
где Zi=/i(p/L); /.(pi/L)
- - L
2 г.2 АЛ1 +^(/1+ СЧ,
п _ Pl2 —Р2____________________Р *
У 2р1Е(1 + с$) —
и аналогично определены Ki, Л’ь а
• Р2 (SSs)i
(7.2.38)
Если Ap=pi—
в ряд по кр/L. Тогда
СЕ = -------
Я2-Р!2
р, ТО можно
(£Ss)e
разложить цилиндрические функции
45
Др \2 / Др \ 2
СТ/
_1_
4
Ар \2 1
Р / ~ 12
1 +
218
Если Л,о/p положить равным нулю, то полый цилиндр превращается в блок
в виде двух пластин толщиной Др, расположенных на расстоянии 2р. Для
такого блока коэффициент экранировки равен
Q^L(1 + ^)
Др / Др г
cth -у- + с Л sh -у- I
Р
R—Pi (^s)/
Разложив Q по Др/L, получим формулу (7.2.39), в которой положено
Др/р=0.
7.3. ПРИБЛИЖЕНИЕ Р2
Простейшим аналитическим методом, уточняющим диффу-
зионное приближение, является приближение Р? метода сфери-
ческих гармоник (см. Дополнения 1, 3; более полное изложе-
ние см. в [86, 147]).
В Дополнении 1 показано, что для задач, в которых плот-
ность потока нейтронов зависит от одной переменной, уравне-
ние приближения Р2 совпадает с уравнением диффузионного
приближения, но с другим значением коэффициента диффузии:
D = (32J-1 (1 + А -М S = 2а + Ss; = Sa + Ss (1 - сЪ^).
(7.3.1)
Длина диффузии по-прежнему определяется равенством
L = /Д2, (7.3.2)
Поэтому справедливы формулы (7.2.22) и (7.1.13) для плот-
ности потока нейтронов внутри и вне блока (здесь будет рас-
смотрен только случай малого поглощения в замедлителе).
Основное отличие приближения Р% от диффузионного — другая
запись граничных условий. В приближении Р% на границе сред
с различными свойствами требуется непрерывность величин *
О— (7.3.3)
dr ’
и
Ф = Л _ + _^Ф_ + _2л_. (7.3.4)
\ 5S / 5S dr2 5S v '
Из формулы (7.1.13) определим, при Sae—0, величину
^=фе(р)-^Н—+4У <7-3-5)
\ С О у
а ид формулы (7.2.22) величину 4*7:
* В первом издании было опущено последнее слагаемое в формуле
(7.3.4); учет этого слагаемого приводит к незначительному изменению вели-
чины f (7.3.11).
219
IF =ф (Р)(1__^\-----------------------М (7.3.6)
( 5St. ) 5St- \ 2<Э0 / 5S, V 7
Для определения А' надо воспользоваться условием (7.3.3),
формулами (7.1.13) и (7.2.22):
А' = »е(1-Д qq (7.3.7)
с2<ц
причем для вычисления Qo по формуле (7.2.25) надо использо-
вать новое определение L (7.3.1), (7.3.2). Теперь для Фг(р)
получим [использовано граничное условие (7.2.25) ]:
Фг(р) (7.3.8)
cSai S
Среднее значение Ф(-(г) определим из (7.2.22):
Фг = + — - Л(1~с)(14-С ), (7.3.9)
1 20i Qo с2а{ ' ( >
откуда получим коэффициент экранировки
Qfi "4” Ct
ф;(Р)/Фг=4тг- = Q-
1 ~г Д
что совпадает с (7.2.27), но только L имеет другое значение.
Приравнивая (7.3.5) и (7.3.6), используя (7.3.8) и (7.2.22),
определяем скачок плотности потока нейтронов на границе меж-
ду блоком и замедлителем:
Скачок плотности потока на границе сред с различными свой-
ствами является характерной особенностью Р2-приближения (и
вообще всех четных приближений). При более точном решении
задачи (см. § 7.4) скачок превращается в более или менее рез-
кий подъем, развивающийся на длине порядка (2S/r)-1 (рис. 7.1).
Отношение Фе/Ф(р) равно
= 1 + f + 2(12ю!сЛ с) . (7-3.11)
Ф; (f>) 1 С)\ 1 I С^1
где X определено (7.2.5), (7.2.7), (7.2.25), (7.2.27).
220
Формулы (7.3.1), (7.3.10),
(7.3.11) позволяют вычислить q
(7.2.6) в /^-приближении. Скачок
плотности нейтронного потока на
границе двух сред, имеющийся в Р2-
приближении, в известной мере пре-
пятствует использованию этого ме-
тода в практических расчетах, по-
скольку на границе между блоком
и замедлителем обычно расположе-
на тонкая защитная оболочка из
материала, поглощение в котором
составляет заметную часть всех
вредных поглощений тепловых ней-
тронов в реакторе. Скачок плотно-
сти нейтронного потока на грани-
це блок — замедлитель не позво-
ляет определить значение плотности
потока на оболочке и вычислить
поглощение нейтронов. Однако
сравнение с точными расчетами
(см. § 7.4) показывает, что полу-
сумма (Фе4-Ф,)/2 очень близка к
точному значению плотности потока
цепт полезно иметь в виду при использовании Рг-приближения.
Из данных, приведенных в § 7.4, видно, что точное решение
лежит между результатами Pi- и Рг-приближений (это общее
свойство Рп-приближений: четные и нечетные приближения с
разных сторон приближаются к точному решению, см. также
Дополнения 1, 4). Поэтому оценка величины 0 по Pi- и Р2-
приближениям может быть весьма полезной (и достаточно точ-
ной) в тех случаях, когда более последовательный и точный
расчет на ЭВМ по каким-либо причинам затруднителен.
Примеры, где сравниваются результаты в Pi- и /^-прибли-
жениях с точным решением задачи в односкоростном прибли-
жении, приведены в .§ 7.4.
Рис. 7.1. Распределение плотно-
сти потока нейтронов в ячейке,
вычисленное в Р,- н /^-прибли-
жениях [Фр (г), Фр2(г)], а так-
же полученное путем решения
интегрального уравнения пере-
носа [Ф(г)]
на границе блока. Этот ре-
7.4. ОДНОСКОРОСТНОЕ ПРИБЛИЖЕНИЕ
Существует большое число методов решения кинетического
уравнения, которое описывает распределение плотности нейтрон-
ного потока по ячейке в односкоростном приближении. В пер-
вые годы развития теории ядерных реакторов наибольшее вни-
мание уделяли методу сферических гармоник (см. [69, 70, 77,
103, 125, 148]). С современной точки зрения, однако, кажется,
что целесообразнее непосредственно численно решать кинети-
ческое уравнение, записанное в той или иной форме. Если рас-
221
сеяние нейтронов сферически-симметрично в лабораторной си-
стеме координат, то наиболее естественно записать кинетиче-
ское уравнение в интегральной форме (часто эту форму записи
кинетического уравнения называют уравнением Пайерлса [149]).
Анализ, проведенный в [150], показывает, что учет анизотропии
рассеяния в тепловой группе вносит очень малые поправки. Из
других методов решения кинематического уравнения отметим
как наиболее точный и перспективный метод поверхностных
псевдоисточников [151].
Рассмотрим число нейтронов, появившихся в элементе объ-
ема dr' как от внешнего источника S(r'), так и в результате
столкновения нейтронов в этом элементе объема. Это число
равно
[2/D(r')+S(r')]rfr'. (7.4.1)
Если рассеяние сферически-симметрично, то число нейтронов,
достигших точки г, не испытав при этом столкновения, полу-
чится умножением (7.4.1) на ядро первого столкновения (1.10.6):
Я (г, г') = (4л/?2)-1 ехр (-2/?), (7.4.2)
где 2/? — «оптический» путь между точками г и г':
я
2R = j2(x)dx; /? = | г — г' | , (7.4.3)
о
и интеграл берется по лучу, соединяющему точки г и г'. Если
среда однородна, то
2/? = 2/?. (7.4.4)
Из (7.4.2) следует, что ядро К симметрично:
К(г, г')=К(г', г). (7.4.5)
Плотность потока нейтронов в точке г получится интегрирова-
нием по всему объему:
Ф (г) = J К (г, г') [2S (г') Ф (г') + S (г')] dr'. (7.4.6)
Удобно вместо плотности потока Ф(г) ввести плотность
эмиттированных нейтронов:
ЛГ(г)=2Дг)Ф(г)+5(г). (7.4.7)
Подставляя (7.4.7) в (7.4.6), получаем
N (г) = 2, (г) J К (г, г') N (г') dr' + S (г). (7.4.8)
На границе ячейки ток нейтронов должен равняться нулю.
Один из возможных способов записи этого граничного условия,
222
дающий хорошую точность, если слой замедлителя в ячейке
больше Ss-1, состоит в том, что все пространство вне ячейки
заполняется средой без источников и без поглощения. Такая
среда возвращает все падающие на нее нейтроны. Граничное
условие в такой формулировке называется «белым».
Представим интеграл (7.4.8) в виде суммы интегралов по
объемам Vj, внутри которых сечения можно считать постоян-
ными. В случае цилиндрической ячейки объемы V, — это коль-
цевые слои, ограниченные коаксиальными цилиндрами. Проин-
тегрировав (7.4.8) по объему Vj, получим
S?' = ^V7S?"S'v, + ^’ (7-4-9)
/
где Ni, Si — средние значения:
Ni = Vr' §N(r)dr, St = У"1 J S(r)dr, (7.4.10)
vi vi
a
Pi} = Л A7(r)dr'\—1 J dr J dr'SzK(r, r')W(r') (7.4.11)
V/ J vt vt
есть вероятность для нейтрона, рожденного в объеме У/, испы-
тать первое столкновение в объеме У,-. Если объемы У,- доста-
точно малы, то 7V(r) в (7.4.11) можно вынести за знак инте-
грала. Тогда
p.j = pi} = V.^ JdrJdr'SzK(r, г') (7.4.12)
vi vi
есть вероятность первого столкновения в объеме У; для ней-
трона, рожденного в объеме У/ однородным, изотропным, еди-
ничным источником. Поэтому излагаемый здесь метод называ-
ют также методом «вероятности первого столкновения». Следо-
вательно, уравнение (7.4.8) переходит в систему линейных урав-
нений
= + (7.4.13)
i
Полная вероятность столкновения во всем объеме равна еди-
нице, т. е.
Js(r)K(r, г') dr = 1, (7.4.14)
откуда
ЕАц = 1. (7.4.15)
223
Из условия симметрии (7.4.5) следует равенство
(7.4.16)
Пусть ячейка имеет М слоев, а индекс Л4+1 присвоим слою
вне ячейки (отражателю). Плотность потока в отражателе Фм+i
можно исключить следующим образом. Так как Sm+i=
= Ss,m+i, Sm+i = 0, Фм+1=const (толщину слоятИ+1 можно счи-
тать конечной, но большой по справнению с 2м+ь тогда объ-
ем Ум+i конечен), то, положив в (7.4.13) г=Л4+1, можно
выразить jVm+iVm+i так:
где использовано условие нормировки (7.4.15). Подставив
(7.4.17) в (7.4.13), получим
м
/=1
где
D' n । Pi,M + lPM+l,i П , PM + l,i Vi^iPM+l,j
У — H M ~ И Н М
S Pk,M+l 5j PM+l,k^k^h
k=l k=l
(7.4.18)
(7.4.19)
причем использовано (7.4.16). Таким образом, в уравнение
(7.4.18) входят только плотности потоков в ячейке. Суммируя
(7.4.19) по i -и используя (7.4.15), находим
м м
= ^Pij + Pm+u = 1, (7.4.20)
Г = 1 1 = 1
т. е. P'ij удовлетворяют условию нормировки. Выполняется так-
же и условие симметрии
которое позволяет вычислять Р'ц только при i:>/.
В [130, 152] приведены конкретные выражения для Рц
в случае бесконечного цилиндра [Рц выражаются через одно-
кратные интегралы от функции Кдз (1.10.12)].
Источник S(r) в уравнениях (7.4.6) или (7.4.8) пропорцио-
нален значению £2S в точке г (см. § 2.2, задача 1). Отметим
еще, что заменой можно приближенно учесть анизотро-
пию рассеяния. Такое приближение называют транспортным.
224
В [152] приведено описание программы* и сравниваются
результаты, полученные этим методом, с результатами, полу-
ченными другими, наиболее точными методами. Различие
в значении полного блок-эффекта в большинстве случаев не
превосходит 1%.
Теперь перейдем к сравнению приближений Pi и Р2 с ре-
зультатами, которые получены по программе [152] (последние
для краткости будем называть точными).
На рис. 7.1 представлено распределение плотности потока
нейтронов в ячейке с параметрами p=Sai=2s.=Sse=l, Хае=
= (gSs)i=O, R=4 (р — радиус блока; R— радиус ячейки), по-
лученное в Рг, Р2-приближениях и при точном решении задачи
(Ф(г)). Все распределения нормированы так, что совпадают
средние значения плотности потока внутри блока. Из рис. 7.1
видно, что вне блока
Фр, ОХ Ф ОХ Фр. (О- (7.4.21)
Внутри блока все три кривые пересекаются, но в централь-
ной части блока справедливо неравенство (7.4.21). Из рис. 7.1
видно, что кривая, соответствующая точному значению Ф(г),
поднимается значительно круче, чем кривые, соответствующие
приближенным, — это и есть «недиффузионный скачок», кото-
рый в точном решении заменяет разрыв Ф(г) в Р2-приближе-
нии. Разрыв Ф (г) в Р2-приближении значителен, но полусумма
4-[ФДр) + фДр)ХФ(р)
близка к точному решению (кружок на рис. 7.1). Поэтому ко-
эффициентом экранировки в Р2-приближении целесообразно
считать величину
Q;2= Л+ _Х\ (7.4.22)
Ф/ \ Z /
где Qp2 и f даны (7.3.7), (7.3.10). Полусумма
4"1Ф/>8 (р) + Ф/>. (р)]
всего на 2% больше точного решения. На рис. 7.1 видно, что
Фе в Р2-, Pi-приближениях [равное £ (7.2.6) в используемой
нормировке] на 10—16% отличается от точного решения. По-
лусумма
* Впервые результаты вычислений по программе, основанной на этом
методе, были опубликованы в [153].
15—6053 225
Рис. 7.2. Сравнение коэффициентов экранирова-
ния в Pt- и Рг-приближениях с точным значе-
нием, полученным при решении интегрального
уравнения переноса (см. текст)
Рис. 7.3. Зависимость Q—1
от разных параметров (см.
текст)
отличается от точного значения только на 1 %. Поглощение
в замедлителе q (для графита или тяжелой воды) редко суще-
ственно превышает 5%, и поэтому погрешность 1% в £ озна-
чает, что в коэффициенте размножения может быть ошибка
0,05%, что меньше ошибки из-за неточности значений v и ояд
для делящихся нуклидов (см. § 1.1; 1.5).
На рис. 7.2 сравниваются значения коэффициентов экранировки
Q₽1, О-'р, и точное значение Q для случая р = 2^=2^=!, (£2Д =
= 0, R — 4 при разных значениях 2а,/2,-. Если Q—1 = 0,15—г-0,5,
то точное значение Q практически равно полусумме (Qp, 4-Qj,a)/2,
причем (Q —Qp,)/(Q —1) не превышает 20 — 30%, a (Q + Q'Pi)IQ
4 — 7%. При больших значениях Q ошибка ^..-приближения воз-
растает и ^полусумма (Qp, + Qp3)/2 становится больше Q. При
уменьшении р2(;е ошибка ^..-приближения возрастает. Например,
при р = 2^ = 2а/ =1, 2те = 0,25, R = 4 имеем (%, = 1,613; =
= 2,96; (QP1 4-Qy/2 = 2,286; Q= 1,791. Таким образом, для ма-
лых блоков р2зе<С1 использование ^-приближения приводит
к заметным ошибкам.
226
В диффузионном приближении коэффициент экранировки
определяется только свойствами блока и не зависит от харак-
теристик среды вне блока. В приближении Р2 величина Qp2
также определяется только характеристиками блока, однако
значение скачка плотности потока и, следовательно, Q'Pi
(7.4.22) зависит от свойств внешней среды. На рис. 7.3 пред-
ставлена зависимость точного значения коэффициента экрани-
ровки Q от pSse при ,p=Sai=2S(=l, R=4 (вариант I) и при
EaZ=0,5, p=SSi=l, R~4 (вариант 2); всюду (jSs)(— 0 (шкала
абсцисс /). Видно, что при изменении pSse в 8 раз величина
Q—1 изменяется всего на 13—15%, т. е. точное решение зада-
чи показывает, что зависимость Q от свойств внешней среды
весьма слабая. На рис. 7.3 для варианта 1 штриховыми линия-
ми даны значения Qp и Qp. Видно, что в Р2-приближении
зависимость Qp2 от параметра pSse оказывается слишком силь-
ной. Там же приведена зависимость Q—1 от р/7? при p=2S(=
==Sm=2se=l (вариант 1) и Sai=0,5, p=Ssi=Sse = l (вари-
ант 2); для обоих вариантов (g3s)x=O (шкала абсцисс II), Из
рисунка следует, что при изменении p/R в 4 раза Q—1 изменя-
ется очень незначительно, всего на 6—8%.
На рис. 7.4 приведены значения полного блок-эффекта, т. е.
Фе/Ф; = С, в диффузионном приближении (CpJ и при точном вы-
числении (Q. Кривые I дают зависимость Q(,Pi от 2ai/S; при р =
= Sse= 1, R = 4; кривые II — зависимость C/CPt от p2se при р =
= Sa; = 2s( = l, R = 4, а кривые III — зависимость С/Ср, от /?/р
при р = = 1 [всюду (ЙУ/ = 0J.
Из рис. 7.4 видно, что отношение всегда больше единицы,
причем это превышение составляет примерно 10 — 30%. Величина
QCPl растет при уменьшении R/?, pSse, 2г/2а,. На этом рисунке
штриховыми линиями даны отношения
(7.4.23)
как функции тех же параметров. Видно, что отношение (7.4.23)
близко к единице за исключением малых значений р2%, причем
при р2%'--'0,5 величина (7.4.23) становится меньше единицы.
Для малых значений р2% ошибка Рг и /^-приближений мак-
симальна.
Формулу диффузионного приближения для внешнего блок-
эффекта qx (7.2.19) часто уточняют так:
<71° = ^-^^+ 8].
(7.4.24)
15*
227
Рис. 7.5. Зависимость недиффу-
зионной поправки к внешнему
блок-эффекту от различных
параметров (см. текст)
Рис. 7.4. Зависимость отношения полных
блок-эффектов при точном решении (сплош-
ные линии) и в Pi-приближеиии от различ-
ных параметров (см. текст)
где в 6 заключены все недиффузионные поправки к внешнему
блок-эффекту. На рис. 7.5 дано произведение pSse6 как функ-
ция pSse (для случая p=SO!=Sst=l, 7?=4; шкала абсцисс 1,
кривая 7). При pSse—>0 произведение pSse6 должно равняться
л/З [86, с. 57]. Из рис. 7.5 видно, что это значение согласуется
с результатами численного решения задачи, однако уже при
pSse=0,25 расхождения с оценками, которые приведены в [86]
и справедливы при pSse<Cl, становятся большими.
Кривые 11, III на рис. 7.5 описывают зависимость pSse6 от
Sai/Ss при p=Sse=l, /?=4 и ОТ R/p при p=Saf=SSi=2se=l.
Видно, что зависимость pSSf(5 от параметров pSse, Sai/St, R/р
приблизительно одинаково существенна. Этот вывод не со-
гласуется с данными [145], где считается, что 6 есть функция
только p2se.
Вычисления коэффициента экранировки при с^=0 с хоро-
шей точностью подтверждают формулу (7.2.27), в которой под
Qo надо понимать значение коэффициента экранировки при
<^=0, но при одинаковых других параметрах, включая Ssi-. По-
грешность формулы (7.2.27) при с^^0,15 и Q—1^0,3 не более
1-2%.
228
7.5. ТЕРМАЛИЗАЦИЯ НЕЙТРОНОВ
Задача о термализации нейтронов, т. е. определение спектра
нейтронов в тепловой группе, принадлежит к числу самых слож-
ных задач теории реакторов. Эта сложность обусловлена не-
сколькими моментами. Во-первых, плотность потока нейтронов
(]•(!', Е) зависит не только от координат, но и от энергии, что
существенно усложняет задачу по сравнению с односкоростным
приближением, рассмотренным в § 7.4. Во-вторых, нейтрон при
столкновении с движущимся ядром может как терять, так и
приобретать энергию. Это обстоятельство существенно отли-
чает задачу о термализации от задачи замедления, когда ней-
трон при столкновениях может только терять энергию*, что де-
лает задачу более сложной для численного решения. Наконец,
вероятность перехода нейтрона от энергии Е к Е' и от направ-
ления движения й кй'
w(E—+E'\ Q^-Q') =w(E, E’\ ft), (7.5.1)
где — угол между векторами Q, Q', является сложной функ-
цией аргументов. Эта сложность связана с тем, что необходимо
учитывать влияние химических связей ядра в молекуле или
кристаллической решетке на процесс передачи энергии от ней-
трона к ядру и от ядра к нейтрону. Функция (7.5.1) измеряет-
ся на опыте, как и все другие сечения взаимодействия нейтро-
нов с ядрами, которые используются в теории реакторов. Со-
ответствующие измерения, однако, более сложны: функция
(7.5.1) зависит от трех аргументов и, кроме того, еще от тем-
пературы среды. Фактически мы не располагаем полным набо-
ром необходимых данных. Поэтому общепринятым является
прием создания приближенной модели для столкновения ней-
трона с молекулой или кристаллической решеткой. Эта модель
апробируется на имеющихся экспериментальных данных, а не-
достающие данные получаются при помощи выбранной мо-
дели путем интерполяции или экстраполяции. В простейшем
случае достаточно проверить, что модель правильно описы-
вает зависимость полного сечения рассеяния от энергии ней-
тронов и температуры среды
as (Е, Т) = $w (Е, Е', Q; Т) dOdE’. (7.5.2)
В большинстве случаев представляют интерес интегральные
величины типа
(г) = У az (г, Е) Ф (г, Е) dE (7.5.3)
* Интересная возможность ускорения нейтронов в среде, содержащей
изомерные ядра, рассматриваются в работе [154].
229
или интеграл от (7.5.3) по объему
= Jaz(r> £)Ф(г, E)dEdr. (7.5.4)
Это обстоятельство облегчает создание теоретических мо-
делей, описывающих столкновение нейтрона с молекулой.
Часто оказывается, что простая модель приводит к достаточ-
но точным результатам для интегралов (7.5.3), (7.5.4) [155].
В тех случаях, когда рассматриваются разностные эффекты,
например зависимость коэффициента размножения от темпе-
ратуры среды, приходится использовать более сложные и' точ-
ные модели.
Здесь не будет излагаться теория термализации, поскольку
эта тема очень обширна и рассмотрена в специальных моно-
графиях (кроме цитированных выше книг по теории реакторов
[69, 70, 103, 148] отметим монографию, посвященную физике
медленных нейтронов [Ю7], материалы конференций [109],
сборник [111]; с прикладной точки зрения полезно краткое
изложение вопроса в [155]).
Конструкция твэлов в современных реакторах весьма разно-
образна, и невозможно привести результаты численных расче-
тов, которые давали бы ответы на вопросы, касающиеся всех
типов реакторов. Поэтому ограничимся рассмотрением двух
примеров: реактора с мягким спектром — тяжеловодного с га-
зовым охлаждением на естественном уране [156] и реактора
с более жестким спектром — ВВЭР [157].
В рассматриваемом примере блоки тяжеловодного реактора
имеют радиус 10 см, а ячейка — радиус 22 см. Блок состоит из
большого числа тонких стержней, которые при расчете заменя-
лись сплошной средой. Содержание ядер в такой гомогенной
смеси следующее: 1024 ядро/см3; 238U—1,41-10-2; 235U—1,02-10~4;
Mg—6,5-10~3; СО2—6,6-10“4. Замедлитель — D2O, его темпера-
тура 343 К.
Расчеты проводились по программе, которая решает много-
групповое интегральное уравнение, являющееся обобщением
односкоростного уравнения, описанного в § 7.4 (описание про-
граммы см. в [158]; впервые результаты подобных расчетов
опубликованы в [159]). Эта программа ограничивается транс-
портным приближением, когда не учитывается корреляция
между углом рассеяния и изменением энергии, т. е. в качестве
вероятности перехода от энергии Е к Е' используется величина
Jw(E->E'; Q->Q')dQ'. (7.5.5)
Анизотропию рассеяния приближенно учитывают заменой
Ss(£) на Sa (£)=Ss (£) [1—ц(Е)]. В большинстве случаев
это приближение достаточно. В качестве источника нейтронов
230
Рис. 7.6. Зависимость плотности пото-
ка нейтронов в тепловой группе
Г)ф (и) ОТ скорости V/VH (Пк=
=2200 м/с) или энергии Е для цен-
тра блока и края ячейки тяжеловод-
ного реактора:
X •— максвелловское распределение при
температуре 362 К; О — то же при 518 К
Рис. 7.7. Зависимость плотности пото-
ка нейтронов в тепловой группе от
скорости и энергии для центра блока
с плутонием и для края ячейки тя'
желоводного реактора:
Ч- — максвелловское распределение при
температуре 460 К
в тепловой группе принимается невозмущенный спектр Ферми
(см. задачу в § 2.2).
На рис. 7.6 изображен спектр нейтронов для центра блока
и для края ячейки. Видно, что максвелловское распределение
хорошо аппроксимирует спектр нейтронов. При этом эффек-
тивная температура этого распределения заметно выше, чем
температура замедлителя 343 К; в центре блока эффективная
температура примерно на 150 К выше, чем на краю ячейки.
При энергии около 0,2 эВ спектр переходит в спектр Фер-
ми* (штриховой линией показано продолжение максвелловско-
го спектра при энергии больше 0,2 эВ). Спектр Ферми в блоке
несколько искажен поглощением нейтронов. Точка пересечения
экстраполированных спектров Ферми и Максвелла находится
при Ес=0,24-0,25 эВ, что хорошо согласуется с выводами § 2.4:
£с=(74-8)£3=0,214-0,26 эВ.
* На рисунках приведен спектр в шкале скоростей, так как $(E)dE=
=®(n)dn, то иФ(а) =const для спектра Ферми.
231
На рис. 7.7 приведен спектр нейтронов для той же ячейки,
только 235U заменен изотопами плутония (концентрация,
1024 ядро/см3: 239Ри—4,35-IO-5; 240Ри—3,7-10~5; 24Ти—
1,14-10's).
Спектр на краю ячейки мало отличается от спектра на
рис. 7.6. Спектр в центре блока имеет заметный провал в райо-
не 0,3 эВ, где 239Pu, 241Ри имеют резонансы (см. § 1.5). Резо-
нанс 235U значительно слабее, и он оказал малое влияние на
спектр рис. 7.6. Из рис. 7.7 видно, что при верхней границе
тепловой группы Ес=0,5 эВ весь резонанс 239Ри помещается
в область, для которой решается задача о термализации. Резо-
нанс 240Ри, расположенный при £=1 эВ, находится уже в той
области энергии, где устанавливается спектр Ферми, и поэтому
его влияние на спектр нейтронов можно учитывать с помощью
более простой программы расчета спектра замедляющих ней-
тронов (см. § 8.6).
Если усреднение сечений проводится до энергии 0,5 эВ, то
при этом захватывается часть фермиевского спектра. Поэтому
средние сечения сильнее отличаются от <т(Ен), чем при усред-
нении по чисто максвелловскому спектру. На рис. 7.8 приведены
отношения о/а(Ев) как функции жесткости спектра у (для бло-
ка, соответствующего рис. 7.6). Изменение жесткости дости-
галось изменением радиуса ячейки, а сама жесткость опреде-
лялась так:
У==Еа/'Е£з,
где Sa — среднее сечение поглощения по всей ячейке. На
рис. 7.8 приведено также среднее значение (1/и). Если сечение
следует закону 1/и, то кривая a/a(EH) не отличается от (1/и).
Для 238U отклонения от закона 1/v очень малы и кривая
о/о(Ен) практически не отличается от (1/и) (по этой причине
она не нанесена на рисунок). Для 235U отношение о/о(Ен)
близко к (1/п): Для 239Ри сечение а заметно растет с увеличе-
нием у, что объясняется влиянием резонанса при Е=0,3 эВ.
Для 241Ри среднее значение почти постоянно— влияние резо
нанса компенсируется увеличением средней скорости. На
рис. 7.8 изображена и зависимость а от у (см. § 1.5).
Значение ТЭф просто связано с максимумом кривой иФ(у).
Если аппроксимация максвелловским распределением доста-
точно хорошая, то
uO(y)=const и4ехр (—v2/v02) (7.5.6)
и тогда
цмакс = -|/2ц0; ^ = (293/0^,
232
Рис. 7.8. Зависимость эффективной
температуры нейтронов Тэф (кривая
I — по блоку, кривая II — по ячейке),
средних сечений а/о(£н); а для 235U,
2зэри, 24ipu и среднего значения
(1/п) от жесткости спектра в ячейке
тяжеловодного реактора
Рис. 7.9. Зависимость превышения эф-
фективной температуры нейтронов
над температурой замедлителя
ДТ/ТзУз от жесткости спектра в
ячейке:
I — для среднего спектра в ячейке: II —
для среднего спектра по блоку
где v, v0 измерены в единицах vH. Более точно v0 определяется
по двум значениям v2, близким к максимуму (7.5.6):
и02 = (rf-v*) [in • (7Д7)
L \ /J
Фактически плотности групповых потоков есть интегралы от
искомого распределения. Поэтому если аппроксимировать расп-
ределение Ф(и), полученное при решении многогруппового
уравнения, максвелловским распределением, то с расчетом надо
сравнивать величину
о+До/2
Ф(и)==Т J (7.5.8)
z V—Ли/2
где Ди — ширина группы в шкале скоростей. Если число групп
(до энергии 0,5 эВ) достигает 15—20, то ширина групп доста-
точно мала и поправкой, связанной с формулой (7.5.8), можно
пренебречь.
233
Рис. 7.10. Спектр нейтронов в
тепловой группе для реактора
ВВЭР:
/ — спектр в начале кампании;
// — спектр при значительном вы-
горании, когда в блоке накоплено
большое количество плутония; X—
максвелловское распределение при
температуре 720 К; О — то же при
660 К
На рис. 7.9 приведено отношение
Гэф т3 ьт
?з 7з TgYg
как функция уз (2.4.26). По приближенной теории § 2.4 отно-
шение (7.5.9) должно быть постоянным и равняться примерно
двум [см. формулу (2.4.27)]. Из рис. 7.9 видно, что для среднего
значения по ячейке (кривая /) этот результат подтверждается.
Однако более существенное значение имеет средняя эффектив-
ная температура по блоку (кривая II), для которой отношение
(7.5.9) совсем не постоянно и значительно больше двух. Таким
образом, гетерогенные поправки к выводам § 2.4 для реактора
с большей гетерогенностью оказываются значительными.
На рис. 7.10 приведены спектры для ВВЭР (радиус блочка
из оксида урана равен 0,39 см, оболочка циркония толщиной
0,092 см, слой воды 0,206 см, температура воды 558 К, плот-
ность 0,75). Кривая 1 характеризует средний спектр нейтронов
по блоку в начале кампании (концентрация ядер, 1024 ядро/см3:
235U—7,68-Ю-4; 238U—2,06-Ю-2) Спектр нейтронов в замедли-
теле не сильно отличается от спектра в блоке (тонкий слой за-
медлителя). Крестиками на рис. 7.10 дано максвелловское рас-
пределение с температурой 720К. Отклонение иФ(г>) от макс-
велловского распределения при энергии больше Ет более суще-
ственно, чем на рис. 7.6. Отношение максимума спектра
к фермиевской части значительно меньше, чем на рис. 7.6. Пе-
реход к спектру Ферми происходит при энергии Ес—0,35 эВ,
что близко к рекомендации § 2.4: £'с=(74-8)Е3=(0,344-0,38) эВ.
Сравнение результата численного расчета с формулой (7.5.9)
234
не следует проводить, поскольку для жестких спектров она не
справедлива.
Кривая II относится к блоку, содержащему значитель-
ное количество изотопов плутония (концентрация ядер,
1024 ядро/см3: 235U —3,11-Ю-4; 236U — 8,2b 10~5; 238U —
2,02-10-2; 239Pu —1,11-Ю-4; 240Pu — 3,16-10~5; 241Pu —
1,91-10~5; 242Pu— 4,25-10-6). На кривой виден провал при
£=0,3 эВ, однако менее сильный, чем на рис. 7.7, поскольку
относительное поглощение нейтронов 239Ри в этом примере
меньше. Кружками дано максвелловское распределение при
7\,ф=660 К. Эта температура меньше, чем для первого примера,
поскольку второй случай соответствует меньшему значению пол-
ного сечения поглощения 2Д(£Н). Кроме того, резонанс при
£=0,3 эВ несколько деформирует правую часть максвелловско-
го распределения, что приводит к эффективному уменьше-
нию Т.
Сравнение спектров тяжеловодного реактора (см. рис. 7.6,
7.7) и ВВЭР (см. рис. 7.10) показывает, что если в первом слу-
чае предположение о максвелловском распределении нейтронов
в тепловой группе выполняется хорошо, то для ВВЭР согласие
с максвелловским распределением значительно хуже. Поэтому
для реактора типа ВВЭР обязателен термализационный рас-
чет, так как иначе нельзя определить средние сечения, условия
критичности и закон выгорания топлива (см. гл. 13). Более
того, для реактора с большим значением у роль надтепловой
части спектра столь значительна, что необходим многогруппо-
вой расчет, охватывающий весь энергетический интервал от
спектра деления до тепловой группы (такая программа описана
в [160]).
Глава 8
РЕЗОНАНСНОЕ ПОГЛОЩЕНИЕ
8.1. БЛОК-ЭФФЕКТ ДЛЯ РЕЗОНАНСНОГО ПОГЛОЩЕНИЯ
Блок-эффект для резонансного поглощения, т. е. отношение
резонансного интеграла бесконечного разведения к эффектив-
ному резонансному интегралу гетерогенной среды, может быть
весьма существенным. Поэтому правильное вычисление коэф-
фициента блокировки имеет важное значение.
Если при определении блок-эффекта для тепловых нейтро-
нов первым приближением является диффузионный расчет, то
при вычислении блок-эффекта для резонансных нейтронов бу-
дет использоваться «антидиффузионное» приближение, когда
235
рассматривается поглощение при прямых пролетах нейтрона
через блок [161].
Пусть сечение поглощения описывается формулой Брен-
та-Вигнера (2.3.1). Определим «ширину опасной зоны» ЛЕГ
(или «практическую ширину резонанса») с помощью равенства
oa(Er + -^PJ=l, (8.1.1)
где р8 — число ядер 238U в 1 см3 блока (для определенности бу-
дем иметь в виду резонансное поглощение в 238U); I — средняя
хорда блока (1.10.21). Так как ДЕг^>Г/2 и в большинстве слу-
чаев \Ег^Ег, то из (8.1.1) и (2.3.1) получим
ДЕГ = Г У~а\ а = оа (Er) psl. (8.1.2)
Для 238Ua>l и А^г^Г. Это означает, что основное погло-
щение нейтронов происходит не в центральной части резонанс-
ной линии шириной Г, а в значительно более широкой области
АЕГ, т. е. фактически на «крыльях» резонансной кривой. При
увеличении концентрации поглощающего вещества ширина
опасной зоны растет пропорционально корню квадратному из
концентрации.
Сравним АД со скачком энергии при столкновении нейтро-
на с ядром замедлителя (см. § 2.2):
ДЕ=Е —Е' =—Е. (8.1.3)
Предположим, что резонансный поглотитель имеет только
один уровень, а сечение поглощения остальных нуклидов доста-
точно мало. Тогда плотность потока нейтронов с энергией Е не
зависит от ^координат, если выполняется неравенство
Е—ЕГ^>ДЕГ (если поглощение равно нулю, то плотность пото-
ка нейтронов в ячейке не зависит от координат, см. § 2.2). По-
этому если
ДЕ>АЕ„ (8.1.4)
то генерация нейтронов в замедлителе внутри опасной зоны
будет происходить однородно по пространству и изотропно по
скоростям. Если энергия нейтрона лежит внутри опасной зоны,
то после столкновения с ядром замедлителя энергия нейтрона
по-прежнему останется внутри опасной зоны только с вероят-
ностью AEr/AEcl. При этом надо учесть, что малые потери
энергии происходят при «косых» столкновениях, когда направ-
ление движения нейтрона мало изменяется. Поэтому на блок
попадут только те нейтроны, которые и до столкновения дви-
гались по направлению к блоку. Ясно, что пространственное
распределение нейтронов, движущихся по направлению к бло-
236
ку, меньше подвергается воздействию резонанса, по сравнению
с движущимися по направлению от блока. Из этого качествен-
ного рассуждения можно сделать вывод, что генерация нейтро-
нов внутри опасной зоны, точнее, тех нейтронов, которые дви-
жутся по направлению к блоку, происходит равномерно по
пространству и изотропно по скоростям не только при выпол-
нении (8.1.4), но и при более слабом условии
АЕ. (8.1.5)
В табл. 8.1 приведены параметры наиболее сильных резо-
нансных уровней 238U, сечения поглощения в максимуме <тг=
= ov(Er), резонансный интеграл бесконечного разведения
(включая часть 1/и) и вклад данного уровня в блокированную
часть резонансного поглощения [см. (8.1.27); в таблице даны
уровни с 0,25 %; а при вычислении ft учтены уровни до энер-
гии 6 кэВ], а также значения АЕГ для блока из металлическо-
го урана при /=4 см и скачки энергии при столкновении с
ядрами D, С, U.
Из табл. 8.1 видно, что условие (8.1.4) выполняется для всех
уровней при столкновении нейтрона с D, а при столкновении с
ядром С для первого уровня выполняется только условие
(8.1,5). При увеличении энергии уровня условие (8.1.4) выпол-
няется лучше.
Полезно определить «центр тяжести» резонансных уров-
ней Е:
lnE=^fi In Eri,
(8.1.6)
где ft приведены в табл. 8.1. Если недостающие 8 % в сумме
S f‘ аппроксимировать одним уровнем £‘=1,5-?-2 кэВ, то £?=
= 32 эВ.
В дальнейшем будем считать, что нейтроны генерируются в
замедлителе однородно по пространству и изотропно по углам
(это приближение называют «приближением плоского потока»).
Кроме того, будем предполагать, что блок не замедляет ней-
троны. Это предположение выполняется, если блок состоит
только из урана (см. § 8.4) и справедливо хотя бы одно из
следующих неравенств:
AE(238U)«AEr; (8.1.7)
Г„<Г. (8.1.8)
Из табл.8.1 видно, что для первого уровня 238U выполняются
оба неравенства, а затем с ростом энергии они выполняются
все хуже или даже не выполняются вовсе. Однако роль этих
уровней в суммарном резонансном поглощении и требования
237
Таблица 8.1. Параметры Основных резонансных уровней 238U
Ег, эВ Г, мэВ V V б 1<х>. б ff % ДЕГ, эВ ДЕ, эВ
D 1 с и
6.67 24,89 0,06 22190 130,51 37,91 1,6 5,9 1,9 0,1
20,87 33,7 0,303 26600 67,66 17,96 2,4 18,5 5,9 0,35
36.68 57,3 0.59 17350 42,74 14,03 3,3 32,7 10,5 0,6
66,02 48.1 0,507 9960 11,42 4,95 2,1 59 19 1,1
80.73 26,9 0,071 2140 1,12 1,05 0,5 72 23 1,3
102,5 94,4 0,742 4920 7,14 4,40 2,9 91 29 1,7
116,9 47,8 0,527 5610 3,61 2,08 1,6 104 33 1,9
145,6 23,1 0,039 670 0,17 0,28 0,3 129 41 2,4
165,3 26.4 0.129 1790 0,45 0,47 0,5 147 47 2,7
189,7 197 0,883 1430 2,35 2,68 3,2 169 54 3,2
208,5 72,8 0,685 2720 1,49 1,24 1,7 185 59 3,5
237,6 52,8 0,53 2760 0,97 0,80 1,2 211 67 3,9
273,6 47.9 0,522 2390 0,66 0,58 1,0 243 78 4,6
290,9 40,0 0,407 2090 0,45 0,43 0,8 259 83 4,8
347.7 102,7 0,779 1300 0,61 0,73 1,6 309 99 5,8
410,2 42,1 0,466 1590 0,26 0,28 0,7 364 116 6,8
518,3 72,6 0,675 1110 0,25 0,32 1,0 460 147 8,6
535,3 67,8 0,648 1120 0,22 0,29 1,0 475 152 8,9
580,1 66,8 0,629 1060 0,19 0,25 0,9 516 165 9,7
595,0 108,1 0,786 743 0,21 0,34 1,3 529 169 9,9
661,1 149,2 0,838 541 0,19 0,36 1,5 [588 188 11
958.6 225,7 0,899 248 0,09 0,25 1,5 851 272 16
991,6 404,7 0,938 152 0.1 0,34 2,2 882 282 16,5
Сумма
272,86 92,02%
Примечание. Таблица составлена по данным [32]; /до/ составляет 98.2%
полного резонансного интеграла бесконечного разбавления.
к точности вычисления эффективного резонансного интеграла
уменьшаются (см. § 8.6).
Число нейтронов с энергией Е, возникающих в единице объ-
ема замедлителя в единицу времени, равно
Е/в0
J Ф(£')251да(Р, E)dE'.
Е
Подставляя сюда w(E', Е) = [(1— ео)£']-1 и Ф(Е')~
= (^sE'Vi)~* l (мощность источников равна: 1 нейтрон в ячей-
ке в 1 с), получаем для числа нейтронов, появляющихся в еди-
ницу времени во всем объеме замедлителя:
^31^1
(8.1.9)
238
Рис. 8.1. Граница замедлителя в квадратной ячейке
где Vi — объем замедлителя; V — объем
ячейки; — среднее значение (так
как блок не замедляет, то £Ss = £SsVi/V).
Рассмотрим нейтрон, получивший энер-
гию Е в результате столкновения с яд-
ром замедлителя *. Пусть Р — вероятность испытать сле-
дующее столкновение опять в замедлителе, причем допу-
скается многократное пересечение блоков и рассеяние (но
не поглощение) в них. Если выполнено условие (8.1.4), то после
столкновения в замедлителе нейтрон выйдет из опасной зоны.
Поэтому число поглощенных нейтронов равно (Р зависит от
энергии, £Ss=const):
ф = JjZkpl—Pj (8.1.10)
Пусть Pi — вероятность столкновения в замедлителе для
нейтрона, возникшего внутри замедлителя, при условии что он
не пересекает границу замедлителя. Под границей замедлителя
надо понимать границу блока (рис. 8.1, сплошная линия), а не
границу ячейки (штриховая линия), поскольку нейтрон, пере-
секший границу ячейки, не рассматривается и заменяется дру-
гим нейтроном, пришедшим из соседней ячейки с той же энер-
гией, в той же точке, но с зеркально отраженной скоростью.
Пусть далее Go — вероятность поглощения нейтрона, пада-
ющего на блок, a Gi — вероятность столкнуться в замедлителе
для того нейтрона, который попал в замедлитель, пересекая
границу блока. Тогда число нейтронов 1—Р складывается из
тех, которые, не столкнувшись в замедлителе (вероятность
1—Pi), поглотились в блоке (вероятность Go), тех, которые не
столкнулись в замедлителе, не поглотились блоком [вероят-
ность (1— Pi) (1—Go)], вернулись в замедлитель из блока, но,
не столкнувшись в нем (вероятность 1—GJ, поглотились в
блоке (вероятность Go) и т. д. В результате получим геомет-
рическую прогрессию
l_p-=(l_P1)Go +
+ (1 - Л) (1 - Go) (1 - GJ Go + ... = . (8.1.11)
Gx -4- (1 — GJGq
Вёроятности Gi и Pi связаны между собой соотношением
(1.10.25):
G^S.J^l-A); 71=4V1/S1,
См. также [162].
239
где Si — поверхность замедлителя (равная поверхности блока,
см. рис. 8.1); 7] — средняя хорда объема замедлителя. Таким
образом, формулу (8.1.9) надо записать так:
Если размеры ячейки много больше З^1 = lsl, то Gx близко
к единице и вместо (8.1.12) получим (приближение изолирован-
ного блока)
Ео
-A- f Go^
J ° E
Ec
(8.1.13)
Различие между (8.1.13) и (8.1.12) обусловлено интерферен-
цией блоков.
Формулу (8,1.13) можно получить значительно более про-
стым путем. Количество ударов нейтронов, приходящихся на
единицу поверхности, если нейтроны распределены в простран-
стве однородно и их скорости изотропны, равно Ф/4 (см. §2.1).
Умножая Ф/4 на вероятность поглощения Go, учитывая, что
плотность потока равна (дЗ^)”1, и интегрируя по энергии, по-
лучаем формулу (8.1.13).
При выводе (8.1.12) предполагалось, что в блоке может про-
исходить рассеяние нейтронов, но при этом энергия будет из-
меняться на величину, много меньшую, чем ширина опасной
зоны. В противном случае Go в первом, втором слагаемых и т. д.
в (8.1.11) будут иметь различные значения. Из табл. 8.1 видно,
что это предположение выполняется только для первых уров-
ней. Однако роль более высокорасположенных уровней не ве-
лика и ошибка в вычислении резонансного поглощения этими
уровнями не столь существенна.
Обратимся теперь к вычислению вероятности Go. Предпо-
ложим сначала, что рассеяние в блоке отсутствует. Пусть ней-
трон падает на поверхность блока под таким углом, что хорда,
проведенная под этим же углом, имеет длину I. Вероятность
поглотиться для этого нейтрона равна
1—ехр [—За (£)/],
а полная вероятность получается при интегрировании по всем
хордам:
^макс
Go(£)= j [1—ехр (—Зй (Е)/)]©(/) d/s (|1— ехр (—За (£)/)]),
о
(8.1.14)
240
где w(l) — распределение хорд по длинам, нормированные Иа
единицу: f w(l)dl=l. (8.1.1й) о
Переставляя порядок интегрирования по Е и 1, получаеМ
<1 (8.1.16>
Ее
где Vo — объем блока (блок предполагается однородным) - Ра"
венство (8.1.16) является определением эффективного резонанс"
ного интеграла
(8.1-17>
где I — средняя хорда блока:
7=4VO/So- (8-llS>
Пусть оа(Е) в (8.1.17) определено формулой (2.3.1). Считая»
что медленно изменяющиеся множители 1/Е, \ЕГ/Е можно за’
менить их значениями при Е=ЕГ, получаем
00
(8.1.19)
4-Х2 yj /’
a(Z) = ov(E'r) р81.
Если 2(ЕГ—Ес)/Г^>1, то нижний
(8.1.9) можно заменить на —оо. Тогда
предел в интеграЛе
г —
эф ~ 2ЕГ а
4ОфД = /яр, (8.1-2°)
l-t-x2 /J /
где а = а(Т); — резонансный интеграл бесконечного развеДе'
ния, определенный формулой (2.3.35), а₽ — коэффициент бл°
кировки, равный
1 /
1 — ехр — ———
k 1 + х2
-1-</(а)). (8.1-21)
п а
Особенно интересен случай, когда а^>1. Из данных табЛ-&-1
видно, что для первого уровня 238U при 7=1 имеем
16—6053 241
(блок из металлического урана). При в интеграле J(а)
(8.1.21) играет роль область интегрирования х2^>1. Поэтому
приближенно.
— —Шх,
х2 /J
а» 1.
(8.1.22)
Дифференцируя по а, получим
J' (а) = J ехр (— а/х2) = 2 J ехр (— аг2) dz = —.
о о
Интегрируя по а в пределах 0, а и принимая во внимание, что
из (8.1.21) следует 7(0) = 0, получаем
J(a) = 2]/~Tta, а>1. (8.1.23)
Тогда
Р = 2 (8124)
]/и а У та У I
И
л а,Г г 1/п-
=-- -г = с (8Л-25)
где
с = 1 / п ,
V ?8i Ут
Таким образом, эффективный резонансный интеграл зависит
как от геометрических характеристик блока и концентрации по-
глощающего вещества [множитель С в (8.1.25)], так и от ха-
рактеристик уровня, которые входят в комбинации (ее будем
называть «весом» уровня):
f = rVTr/Er. (8.1.26)
В табл. 8.1 приведены нормированные веса уровней
Г» Уari (уч г/ Уяг1 \ 1
Eri ^ri J
(8.1.27)
где суммирование проводится до уровня при £=6 кэВ. Обра-
тим внимание, что С в (8.1.25) обратно пропорционально
]/р8/, т. е. эффективный резонансный интеграл уменьшается при
увеличении размеров блока.
242
Интеграл по х в формуле (8.1.21) можно вычислить точно
(см. задачу 1 в конце параграфа):
1(а)=лаехр (—ц/2) [70(«/2) +
+Л(а/2)]. (8.1.28)
При больших а, воспользовавшись асимптотическим разло-
жением цилиндрических функций, получим
J (а) = 2]/^(1 — (8.1.29)
т. е. приа ^10-4-20 можно ограничиться первым членом асимп-
тотического разложения, и тогда справедлива формула (8.1.23).
Для окончательного вычисления эффективного резонансного
интеграла надо определить отношение
В большинстве интересных случаев это отношение близко
к единице. Рассмотрим подробнее случай цилиндрического бло-
ка. Расположим центр сферической системы координат на по-
верхности цилиндра, а ось направим по образующей. Длина
хорды выражается через углы ф, ф так:
/(&, ф)= ..,2j?cos? , (8.1.30)
sin 0
где R — радиус цилиндра, a ф) равно (w пропор-
ционально проекции скорости нейтрона на нормаль к цилиндру)
w($, ф) = (1/л) sin Ф cos ф, (8.1.31)
причем выполняется условие нормировки (8.1.15):
тс тс/2
J sinMft J w (&, <р) dtp = 1.
0 —<2
Таким образом, имеем [использована формула (8.1.18), 1=
= 27?] *:
/ г—\ u ”/2 г-------
-ЦТ = T.isinMS [
0 — к/2
_4
и
^/2 -,2
J cos3/2 tpdtp
Lo J
[Г(1/4)Н
l&r2
ИЛИ
(]/Т) / /I = 0,9726.
(8.1.32)
* Здесь Г — гамма-функция [75].
16* 243
Таблица 8.2. Значения функции Р (п)
п 0 1/2 3/4 1 3/2 2 5/2
F(n) Подстав 0,973 ЛЯЯ ЭТО! 1 резулы 1,037 гат в (8. р= 1,0$ 1,098 1.24), по 17—^. К а 1,333 лучаем 2,08 со (8.1.33)
Аналогичные вычисления для шара и пластинки дают со-
ответственно
(У Г) /Vi = 0,9798; 0,9428. (8.1.34)
Полезно для цилиндра вычислить функцию (см. также
[163])
/«л+1/2\
F(n)=FH») = X—(8.1.35)
Аналогично (8.1.31) получаем
те те/2
F (п) = — Jsin2M& J + 1/2 COS 4>dq> =
0 —п/2
(8.1.36)
В табл. 8.2 приведено несколько значений функции F(n).
С помощью табл. 8.2 можно уточнить формулу (8.1.33). Ис-
пользуя разложение (8.1.29), получаем
= 2 [F(0) — 1 — 1’097 Г1 — 0)292
I 4а J I/tT L а
у та L J у a L
На рис. 8.2 дан график р(а), полученный численным интегри-
рованием по формуле (8.1.21); там же приведены графики, по-
строенные по асимптотическим формулам (8.1.33) и (8.1.37).
Малое отличие{VI) от V Т (всего 2—6%) позволяет пренебречь
множителем {/!)/// в (8.1.24). Тогда
р = 2/1/™ = 1,128//а. (8.1.38)
244
При этом эффективный резо-
нансный интеграл зависит толь-
ко от средней хорды t, которая
для тел произвольной формы (но
выпуклых) определяется форму-
лой (8.1.18). Для вывода форму-
лы (8.1.18) кроме чисто геомет-
рических соображений (см. ссыл-
ки на литературу в § 1.10) мож-
но использовать и физические
[125] (этот вывод принадлежит
И. И. Гуревичу). Рассмотрим
объем V, ограниченный поверх-
ностью S и заполненный рассеи-
вающей, не поглощающей средой.
Пусть плотность потока нейтро-
нов вне объема однородна и изо-
тропна. Односторонний ток ней-
тронов внутрь объема равен
Рис. 8.2. Коэффициент блоки-
ровки резонансного интеграла
в различных приближениях
[цифры у кривых—номера фор-
мул; a=7S7(£’r)]
(Ф/4)5. (8.1.39)
Но этот ток должен равняться
Q/T, (8.1.40)
где Q — общее количество нейтронов в объеме V, т. е. Q=
= (1/о)ФК a T"=Z/t7 — среднее время пребывания в объеме,
где 7 — средний путь, проходимый нейтроном в объеме V. Если
рассеяние отсутствует, то 7 совпадает со средней' хордой объ-
ема V. Приравнивая (8.1.39) и (8.1.40), имеем
(1/4)Ф5=ФУ/7, (8.1.41)
откуда для 7 получим (8.1.18).
Из этого рассуждения видно, что под 7 можно понимать сред-
ний путь, проходимый нейтроном в блоке с учетом излома тра-
ектории при рассеянии. Тогда полученные выше формулы при*
менимы, если только пренебречь различием между(]Л/) и ]/Т,
и для блока с рассеянием (но без замедления). Таким образом,
если выполнено условие (8.1.7), то от (8.1.8) можно отка-
заться;
Во многих приложениях возникают значительные упроще-
ния, если приближенно считать, что
(8.1.42)
Надо только проверить, что при 7->оо и Z->0, |f (/) | <;71/2±5/2
(см. табл. 8.2).
245
Для упрощения вычисления резонансного поглощения часто
используют рациональное приближение [см. (1.10.21) и
(1.10.25)]:
Выполнив интегрирование по х [см. (8.1.21)], получим
₽рп= (1+а)-1/2. (8.1.44)
Если воспользоваться другой, более точной, приближенной
формулой (1.10.22), то после интегрирования по х получим (см.
задачу 1 в конце параграфа):
рсм = ехр (--1-) +Л -
- О,О49а[/о(-|) - Л (-j-)]}- (8.1.45)
При а^>1 из (8.1.44) имеем
pPn = -L(i-4-)> (8Д-46)
У а ' 2а /
что отличается от (8.1.37) на 10 % в главном члене и значи-
тельно сильнее во втором. Из (8.1.45) при й}>1 получим
что отличается от (8.1.37) совсем незначительно.
Для уровней 238U почти всегда ц^>1. Однако в реакторе
накапливаются другие нуклиды, имеющие сильные резонансные
уровни, например 240Pu, 236U и др. (см. гл. 13). Концентрация
их в начале работы реактора весьма мала, и тогда осущест-
вляется случай ц<с1. Из (8.1.21) и (8.1.28) получим
р=1—й/3. (8.1.48)
Следующие члены по степеням а вычислить простым разло-
жением (8.1.28) нельзя, так как соответствующие интегралы
расходятся. Если использовать приближение (8.1.44), то при
а<^_ 1 получим
ррп=1--|- + 4-а2, (8.1.49)
что заметно отличается от (8.1.48). Из (8.1.45) при й<С1 имеем
рсм=1—0,299а+0,099а2, (8.1.50)
246
что очень близко к (8.1.48). Можно исправить рациональное
приближение по (1.10.23). Тогда
В .
В + а ’
[4 = (В/а)1/2, а>1;
Ррп — 1 Ct-, о ’С 1.
(8.1.51)
Из сравнения с (8.1.33) получим В= 1,203, а из сравнения с
(8.1.48) 8=3/2. Взяв среднее значение 8=1,39 получим, что
0'рп при а^> 1 и 1—р'рп, при а<С1 отличаются от точного зна-
чения на 7,5—8 % •
Сравним эффективный резонансный интеграл в рациональ-
ном приближении
(4ф)рп = // /1+20(^)/ (8-1.52)
с эффективным резонансным интегралом гомогенной среды
(2.3.70). Очевидно, что (2.3.70) переходит в (8.1.52) при за-
мене («теорема эквивалентности», см. подробнее [71, 99]):
1 - V
(s-1-53)
Множитель V/Vo возник в (8.1.53) потому, что в (8.1.52) Sa —
макроскопическое сечение в блоке, а в (2.3.70) — в ячейке.
Теорему эквивалентности часто используют при расчете резо-
нансного поглощения: численное решение уравнения замедления
проще выполнить для однородной среды. Определив эффектив-
ный резонансный интеграл и сделав замену (8.1.53), получим
эффективный резонансный интеграл для гетерогенного случая.
Погрешность такого способа вычисления резонансного интегра-
ла не выше 10—15%; она может быть уменьшена введением
дополнительных поправок, например, вида (1.10.83).
Поскольку в исходной формуле (8.1.9) источник нейтронов
нормирован на единицу, вероятность избежать резонансного по-
глощения, если поглотитель имеет один уровень, равна
Ф=1- Ф; Ф=-^-4ф. (8.1.54)
Если имеется несколько неперекрывающихся уровней, то
Г=П(1-«; 'h = T=pUl. (8.1.55)
247
где /эф — эффективный резонансный интеграл i-го уровня. Если
а число уровней велико, то
Ф = ехр (— ф); <p = S<pj. (8.1.56)
В таком виде результат формально совпадает с формулами
для резонансного поглощения в гомогенной среде (см. § 2.3).
Отклонение 1—iq> от суммы ф. связано с искажением фер-
миевского спектра, вызванным резонансным поглощением.
С этой точки зрения очевидно, что пока выполнено условие
(8.1.4) и данный уровень не деформирует поле падающих на
блок нейтронов, из (8.1.56) надо исключить «самодействие»
уровней, т. е. вместо (8.1.56) записать (практически достаточно
рассмотреть квадратичные члены по ф):
ф 1 — ф -4- ф/ Ф, = ехр (—ф)----------------фЛ (8.1.57)
i
Введя нормированный вес уровней (8.1.27), можно за-
писать
£ф/2 = ЕЛаФ2,
тогда
(8.1.58)
Подставив в (8.1.58) значения ft по табл. 8.1, получим
£М = 0,2. (8.1.59)
Если ф~0,1, то исключение самодействия означает умень-
шение ср (или увеличение ф) на 0,001.
Задача 1. Проверить формулу (8.1.28).
Решение. Дифференцируя (8.1.28) по а, получаем J'a(a) = л/0(л/2)Х
Хехр (—а/2), а дифференцируя 7(а)=лаР (8.1.21) по а, находим
00
(* / а \ dx
1’(а) = 2 ехр - — „ = л/0(а/2)ехр(—а/2).
J \ 1 н- х2 / 1 + х2
о
Таким образом, (8.1.28) может отличаться от лар только на постоянную. Но
при а=0 имеем 7(а)=0 и лаР=0, откуда следует, что эта постоянная равна
нулю и формула (8.1.28) правильна.
248
Задача 2. Провести исследование интеграла по энергии (8.1.19), не за-
меняя нижнего предела на —оо и не пренебрегая медленно изменяющимися
множителями под интегралом (см. задачу 2 в § 2.3).
Решение. Коэффициент блокировки (8.1.21) запишем так:
ОО
„ 1 / (• Г ( а \ 1 dx \
В = -^( 1— ехр -------------==- -------------— ), (8.1.60)
ла \ J [ \ ( 1 + X2) 1/ 1 -}- / J 1 -f- еХ /
'-(1-г)/г
где е=Г/(2£г); z=EdEr. Будем считать, что е<С1, а»1, но a=eVa<Cl.
Пренебрегая единицей по сравнению с х2 в (8.1.60), записываем
₽=—^ (|/а£), (8.1.61)
ла
где
(* Г / 1 \ 1 dx
F = I 1—ехр ( — -------------------_ I -------. (8.1.52)
J [ \ х21/1 -f- ах / J 1 + ах
—(1—г)/а
Выберем число М, такое, что 1<СЛ1<С1/а. При |х| >М
ехр
== 1 - (%2 |/1 + ах)”* +-|- [*4(‘ +
1 + ах / 2
а при |х| <М
(14-ax) “ *= 1 — ах-|-а2х2;
/ 1 \ / 1 \ Г а
еч> Г «ГГТ^/ “ “р Г Тг) ['
Тогда F = F± 4- f2, причем
1/(«М)
= а
0
a2 xS/2 I
~ ~ dx4-
2 к 1 4-х _
!/(«*!)
(8.1-63)
f Г 1 —ехр( — х2)
dx+ 2а2 ------—
.) L х2
1/М
+
(8.1.64)
7 х2
4~— ехр (—х2)— ------ехр(—х2)
8 8
Интегралы (8.1.63), (8.1.64) могут быть вычислены. Сохраняя члены по-
рядка 1/Л4, аЛ-1, а2Л42, 1/Л43, а2, получаем
9 15 1
F, =------- — а2Л42—-------4
1 М 4 3MS
~ ! 5
f2 = 2 |Л л fl — а2
2—Зг
3 1 *-
Л L (1-г)|/7 2 1-
- — 4- — а2Л424- ——.
М ~ 4 ЗЛ42
249
Сумма F = Fj 4- F2 не содержит M:
(8.1.65)
Так как <а> — а, <а3/2> = 1,098(a)-3/2 (см. табл. 8.2), то
Аф=-/°эф(1-1,88а'е2) + /1/Л(г),
(8.1.66)
где — эффективный резонансный интеграл, причем р ^определено (8.1.33),
/(г) совпадает с функцией, полученной в задаче 2 § 2.3. Такое согласие не
удивительно, поскольку функция f(z) возникает при разложении экспоненты
в (8.1.60) в ряд, что соответствует гомогенному приближению для этой части
эффективного резонансного интеграла. Вторая поправка в (8.1.66), пропорцио-
нальная VI , обычно невелика: для первого уровня 238LJ и блока из ме-
таллического урана радиусом 1,3 см имеем а=2500, е2=4-10'6 и поправка
составит 1,9 % /°ф.
Задача 3. Определить влияние нерезонансного поглотителя на значение
эффективного резонансного интеграла.
Решение. Пусть сечение, нерезонансного поглотителя равно оДЕ).
Обозначим ai = oi(£r)c1Z, где с,— число ядер нерезонансного поглотителя
в 1 см3. Если считать, что сечение Oi (Е) постоянно внутри опасной зоны
резонанса, то при а^>1 вместо (8.1.21) имеем
Ца) = I 1—ехр
(8-1.67)
Здесь первый множитель под интегралом — вероятность поглощения
на пути Z, второй — вероятность поглощения резонансным поглотителем.
Интеграл (8.1.67) равен
J (a) = 70(а) _L -|ZjL erf l/aj,
F Cl-t
(8-1.68)
где Д (а) =2|л«— значение J прн «1=0. Обычно можно считать, что ai<^l.
Тогда нз (8.1.68) получаем
[я, a,2 1
(8.1.69)
Проводя усреднение по хордам, воспользуемся табл. 8.2:
;эф = Т°ф [ 1 -0,376«i + 0,214ai2],
(8.1.70)
где /Оф — эффективный резонансный интеграл, вычисленный без учета нерезо-
нансного поглотителя. Поскольку нерезонансное поглощение падает с ростом
энергии, эффект может быть заметен только для низкорасположенных уров-
ней. Пусть поглощение в 235LJ таково, что Sa(EH)Z=l. При энергии первого
резонансного уровня 238LJ (считаем, что сечение 235U приближенно следует
закону 1/о) получим Ai = 0,06. Тогда по (8.1.70) получим, что резонансный
интеграл первого уровня 238U уменьшится на 2,2 %. Для резонансного уров-
ня 240Ри, расположенного при Е—1 эВ, эффект в 2 раза больше.
Задача 4. Решить задачу 3, используя формулы (1.10.22), (1.10.25).
250
Решение. В этом случае вместо (8.1,67) получим (по-прежнему счи-
таем х2» 1):
/(а) =
1-М
а \2 ( - а \) adx
а, 4---- ехр — а.— -------> ——=——.
х3 / J \ х2 /У а + а±х2
Вычислив интегралы, имеем
7эф='°ф [4"erfа±
А / 1 - \ ' _
(8.1.71)
где А для цилиндра равно 0,098. Разложив (8.1.71) в ряд по аь получим
4ф = /°ф[ 1 — 0,367^4-0,140а!2 —0,045а!3 + 0,013а!4—...]. (8.1.72)
При малых 01 (8.1.72) мало отличается от (8.1.70). В отличие от (8.1.70)
формулу (8.1.71) можно применять и при ai>l.
8.2. ЗАВИСИМОСТЬ РЕЗОНАНСНОГО ПОГЛОЩЕНИЯ
ОТ ТЕМПЕРАТУРЫ
Теоретическое определение температурной зависимости эф-
фективного резонансного интеграла 238U является сложной за-
дачей, поскольку, как показывает анализ (см. § 8.6), не су-
ществует сколько-нибудь узкой энергетической области, кото-
рая отвечала бы за основную часть температурного эффекта.
Почти все резонансные уровни, в том числе неразрешенные,
расположенныё при энергии в несколько килоэлектрон-вольт,
вносят вклад в температурный коэффициент резонансного инте-
грала. Здесь будет проведено приближенное (полукачественное)
рассмотрение. Более точные результаты, полученные численны-
ми методами, и экспериментальные данные приведены в § 8.6.
Если оставаться в рамках тех же предположений, что и в
§ 8.1, то учет уширения резонансной линии из-за эффекта Доп-
лера (см. § 2.3) приведет к следующему выражению для коэф-
фициента блокировки [см. (8.1.21)]:
₽(а,Ч0)=-^< f [1-ехр(-«(/)ф(х, Q)]dx\, (8.2.1)
па \ J /
где (см. § 2.3)
+ “ ехр[- (х— </)21 dy
= <8-2-2’
* —00
а (/) = Г£а (Ег\, С0 = Г/Д; Д = 2]/ЁДМ; а = а(1). (8.2.3)
Значения g0 Для первых резонансных уровней 238U приведе-
ны в табл. 8.3. Значения £0~ 0,24-0,4 следует считать больши-
ми. На рис. 8.3 представлена зависимость р(£о), полученная
251
но записать:
Рис. 8.3. Зависимость коэффи-
циента блокировки от £о=Г/Д
при а=10 и а=40
численным интегрированием
(8.2.1), при а=10 и а=40. Вид-
но, что если а— 10, то$(£о) близко
к ;(3(оо) при £о^1, а если а=40,
то при £о^О,5. При еще больших
значениях а (реальные значения
а для первых уровней 238U при
/>1 больше 500) кривая ₽(£о)
еще ближе подходит к оси орди-
нат и Р(£о) близко к р(°о) при
еще меньших значениях £0-
Как показано в § 8.1, приближенное равенство (8.1.42)
имеет удовлетворительную точность. Тогда вместо (8.2.1) мож-
4-оо
Р(«, Q=-L [ [1— ехр(— аф(х, Q)]dx.
rta J
—-ОО
(8.2.4)
На рис. 8.3 штриховой линией дано р(£о), вычисленное по
(8.2.4) при а=10. Видно, что разница между точным значе-
нием (8.2.1) и приближенным (8.2.4) достаточно мала.
Рассмотрим случай столь сильных уровней, что не только
а^>1, но и Эти уровни 238U (при Т=400 К и 1=3 см)
приведены в табл. 8.3.
Таблица 8.3. Наиболее сильные уровни 238U
Ег, эВ <0 %
6,67 0,40 504 37,9
20,87 0,31 354 18,0
36,7 0,39 374 14,0
66,0 0,25 85 5,0
102,5 0,39 104 4,4
116,9 0,18 27 2,1
189,7 0,59 71 2,7
208,5 0,21 17 1,2
2 fi = 85,3
252
Так как <р(х, £0) — ф(—х, £0), то р (8.2.1) можно запи-
сать так:
00
Р = -Л- / Г [1 — ехр (— Яф (х, Со))] dx\. (8.2.5)
ла \J /
о
Заменим переменные интегрирования х—>2у а (Сох) а затем в
(8.2.2) у—>2 Vа (Сох)-1 + 2yZ0~1 и получим
+ <»
о Vя С / 2\ Г1 I / '+ I 2\ X2 2ху I-1 .
$= Л-- exp(-t/2) 1 + + ^ + ~т= dy.
4у^а J L \ 4 ) a ]/ a J
-00
(8.2.6)
Разложим S в ряд по 1/a и выполним интегрирование:
S = + f—— (—--------L;; 2+Л _^_1
'4 L \ 2 4 / а \ 4 4 16 / аа J
(8.2.7)
Подставив (8.2.7) в (8.2.6), разложив в ряд по 1/а и про-
интегрировав, получим (для усреднения по хордам использо-
ваны данные табл. 8.2):
= Ро 1 + 1,69
1 — — £ 2
_б , _12 А______________LS2_.
а?02 а2?04 \ 3 °
—-С Л], (8-2-8)
60 / J
где ро — коэффициент блокировки при $о=°°, а^>1, т. е. при
7=0. Если £о2<С1, а£о2>ЗО, то в (8.2.8) можно опустить ряд
слагаемых:
(8.2.9)
Складывая резонансные интегралы для уровней, указанных
в табл. 8.3, получаем
7^(Т) = 7Я’(0) [1 + 1,7?]^
Ьм ai ’fl
(8.2.10)
где fi'= (0,853) -'ft — вес уровня (см. табл. 8.3). Подставляя
числа, находим
3 \ т 1
7 / т0 J’
Лф(П =/$ (0) 1 + 0,0066
Т0 = 293 К; (8.2.11)
253
I измеряется в см, т. е. эффективный резонансный интеграл
этой группы уровней линейно зависит от температуры, однако
коэффициент при Т/То весьма мал. Таким образом, группа
сильных уровней, вносящая основной вклад в эффективный ре-
зонансный интеграл, играет малую роль в температурной зави-
симости резонансного интеграла (см. более точные данные в
§8.6).
При увеличении энергии уровня £0 и а уменьшаются. По-
этому рассмотрим противоположный случай, когда не только
£о<С1, но и й£о2<С1. В этом случае резонансная линия имеет
чисто доплеровскую форму (2.3.23). Разложив экспоненту в
(8.2.2) по 'ttfxyl'l, получим
Ж Со)=фехр(
Тогда (8.2.4) дает
00
f\dx
4 /] f
где
f = ехр
?о2х2 \ Л , V*" \
4 / \ 4 |/”тс /
ехр
(8.2.12)
(8.2.13)
(8.2.14)
8
b = а^.
Показатель экспоненты в (8.2.14) максимален по модулю
при ^о2л:2/4=1 и при этом равен а£о2/(2е) «а£о2/5. Таким об-
разом, при а£о2<Сб множитель f в (8.2.13) можно заменить
(Г 2%2 \
-------= и и проинте-
4 )
грировав по частям, получим
₽= 4 F(6)> (8215)
где
Ь г~
F(&) = VTir&Je-2 |/ 1(8.2.16)
О
Если, например, а=100, £о=О,1, то а^о2=1<С5, аС0 =
= 9>1. При Ь»1 можно разложить радикал в (8.2.16) в ряд
и проинтегрировать до бесконечности:
F (b) ~ VWh + -----(8.2.17)
' ' L 1п b (In У;2 (In Ь)3
254
где S1 = = 0,288;
= J_ 4- C2^ = 0,247;
8 \ 6 /
S3
— |c3
16
+ — C + 2,41 = 0,34;
2 I
C = 0,5772.
Функции F(b) (8.2.17) при а£о>1 слабо зависит, от £0.
Пренебрегая этой зависимостью, получаем, что эффективный
резонансный интеграл группы уровней, параметры которых
удовлетворяют неравенствам
£0<С1, п&)2<1, (8.2.18)
пропорционален корню квадратному из температуры [161]:
/Д’ (Т) = /Д’ (То) УТ/Т0. (8.2.19)
Если &»сг^0<1. то из (8.2.15) следует, что
[5= 1 — J/ “V"’ (8.2.20)
т. е. температурная зависимость и блокировка исчезают. Уров-
ни, для которых а£о<С1, дают вклад в неблокируемую часть
резонансного интеграла (см. § 8.6). Таким образом, примерно
85 % блокированного резонансного интеграла практически не
зависит от температуры. Если считать, что остальные 15% при-
надлежат уровням, которые удовлетворяют условиям (8.2.18),
то получаем
4ф(П = ^эфГо) [0,85 + О,15/77То]. (8.2.21)
Формула (8.2.21) получена путем приближенных оценок и
поэтому нуждается в проверке более точными вычислениями.
В § 8.6 приведены результаты таких вычислений и сопоставле-
ние их с экспериментальными данными. Отличие от (8.2.21)
оказывается незначительным.
На рис. 8.4 и 8.5 приведены зависимости р(а, £0) Для раз-
ных £0, полученные путем численного интегрирования по фор-
муле (8.2.1). Этими зависимостями можно пользоваться, когда
блокировка не очень сильная (а не очень велико) и выполня-
ются условия, сформулированные в § 8.1 (например, нижние
уровни 236U, 240Pu, 242Ри, которые накапливаются при выго-
рании топлива).
Поскольку доплеровское сечение описывается достаточно
сложными формулами, то иногда целесообразно заменять их
более простыми, которые тем не менее сохраняют наиболее
существенные свойства. Такие аппроксимации предложены в
ряде работ (см., например, [164]).
255
Рис. 8.4. Коэффициент блокировки
|3(а, go), полученный численным инте-
грированием по формуле (8.2.1) (ма-
лые значения а)
Рис. 8.5. Коэффициент блокировки
Р(а, go), полученный численным инте-
грированием по формуле (8.2.1)
(большие значения а)
В энергетических реакторах, особенно использующих оксид
урана, возникает сильная неоднородность температуры по твэ-
лу. Можно показать, что замена твэла с, неоднородным рас-
пределением температуры однородным с температурой, равной
средней температуре по объему, не приводит к заметным по-
грешностям [165, 166].
8.3. ИНТЕРФЕРЕНЦИЯ БЛОКОВ
Из формул (8.1.21), (8.1.28) следует, что блокировка ре'
зонансного поглощения исчезает, если
а=72г<1. (8.3.1)
Для металлического 238U при 1=1 имеем а ~ 1000 (см.
табл. 8.1), т. е. блокировка исчезает, если радиус блока
р<10-3см. (8.3.2)
Если рассматривать не один изолированный блок урана, а
решетку, шаг которой уменьшается при уменьшении радиуса
блока, то, как оказывается, блокировка исчезает при значи-
тельно больших размерах блока. Из формул (8.1.12), (8.1.20),
256
(2.3.35) следует, что коэффициент блокировки надо записать
так:
g__ Р Gq dE 1 Р Godx /g
1 = 7rTJ i-A F = J i-Gj ' ‘ ’
' + „ Go —oo l-J- _ Go
Gi Gi
Применим рациональное приближение (8.1.43) для Go и G]
и запишем р следующим образом:
В = —!— [ ---------. (8.3.4)
J Sa(x)/ -
-о» 1 +—“L_2_ + 2a(x)z
11
Пусть резонансная линия имеет естественную форму
2a(x)=2r/(l+x2). (8.3.5)
Тогда интеграл (8.3.4) легко вычисляется:
(8.3.6)
где 2г — сечение поглощения в центре линии для равномерно
размешанного по ячейке поглощающего вещества;
/1=4 Vi/So—lVm", (8.3.7)
Vm=VJV0 (8.3.8)
— отношение объемов замедлителя и блока. При SslZi^> 1 фор-
мула (8.3.6) переходит в (8.1.44), как и должно быть. Сравни-
вая (8.3.6) с формулой для гомогенной смеси (2.3.70), полу-
чаем условие гомогенизации
(8.3.9)
Пусть, например, /sl = 3 см, vm—20; гомогенизация про-
исходит при радиусе блока р<с0,075 см вместо р<с0,001 см
по (8.3.2). Назовем радиусом гомогенизации величину
p0=ZSI/(2ura). (8.3.10)
Пусть р=р0; считая vm^> 1, находим шаг решетки
(8.3.11)
т. е. при vm^> 1 имеем a<^.lsi. Таким образом, гомогенизация воз-
никает, если размеры ячейки малы по сравнению с длиной рас-
сеяния в замедлителе. Поскольку основное поглощение про-
исходит на крыльях резонансной кривой (ширина опасной зоны
17—6053 257
много больше Г), нейтрон сможет несколько раз пройти через
блоки, прежде чем будет поглощен. В этом состоит физическая
причина гомогенизации в том случае, когда радиус блока мень-
ше радиуса гомогенизации, а условие (8.3.1) еще не выпол-
нено.
Рассмотрим теперь поправки к модели изолированного бло-
ка, которая изложена в § 8.1 (эта поправка на интерференцию
блоков обычно называется поправкой Данкова—Гинзбурга
[69—71,99]).
Разложим (8.1.12) в ряд по 1 —Gi:
ф = ф0(1-Д), (8.3.12)
где фо определяется по (8.1.13), a D в первом приближении
равно
Г
1 г 1 —F
D = —. (8.3.13)
Gi С г dE
J °0 Е
Следуя (8.1.14), имеем
J G„2 М = dldl'w(/) w(I') [1 - exp (-ZSa (£))] x
X[l-exp(-/'S0(£))]
или
J G02 = J dldl'w (I) w (/') {[1 - exp (—ZSa (£))]+
+ J1 - exp (/' 2a (£))] - [1 - exp [- (/ + /') 2a (£)]]}. (8.3.14)
Исполь&уя условие нормировки (8.1.15), учитывая, что для
сильной блокировки
J [1 — ехр (- (Z + /') 2Й (£))] = const КГфТ7, (8.3.15)
и основываясь на формуле [см. (8.1.42)]
iyT+Г} ^Kr+F^/27, (8.3.16)
получаем
Следовательно,
(2—]/2)-^-. (8.3.18)
Gi
258
Аналогично можно получить и общий член разложения
00
(8.3.19)
где
Сп = п - ]/2 + з _ + (_ 1)"+’ уп.
Если воспользоваться рациональным приближением для Gi,
то вместо (8.3.18) получим
D = (2- ]/2) C^sly~l = (2- ]/2) (72s1^)-’. (8.3.20)
Рис. 8.6. Коэффициент ин-
терференции при ZSsi=l
как функция vm=Vзам/Гел
[штриховая линия — коэф-
фициент интерференции в
рациональном приближении
по формуле (8.3.27)]
Эта формула и весь ряд (8.3.19), записанный в несколько
другой форме, были получены в [167], основанной на работе
Гуревича и Померанчука [161]. В последней работе неявно
используется рациональное приближение для вероятности Gi
столкновения нейтрона в замедлителе.
Для гетерогенных реакторов обычно /iSsi^>l, т. е. нужно
знать асимптотику вероятности столкновения при больших h.
Эта асимптотика в рациональном приближении дается непра-
вильно. Для объемов простых форм
можно получить для асимптотики яв-
ные выражения. Например, для ци-
линдра [см. (1.10.20), (1.10.25)]:
3 -
1 — Gi = — (8.3.21)
Если использовать (8.3.21), то по-
правка D равна
D =А(2_]/2)(/12ЛГ. (8.3.22)
Асимптотика (8.3.21), однако, не
соответствует рассматриваемому слу-
чаю. Степенная асимптотика для ци-
линдра объясняется тем, что при боль-
ших размерах вероятность 1—Gi опре-
деляется главным образом пролетами
нейтронов в узких интервалах телес-
ного угла, которым соответствует хор-
да порядка Ss->. Величина этого ин-
тервала степенным образом убывает
с ростом I. Пролеты же в других ин-
17* 259
тервалах телесного угла дают экспоненциально малый вклад
в вероятность 1—Gj. Для объема замедлителя (см. рис. 8.1)
главный вклад в 1—Gi дают пролеты с минимальным расстоя-
нием между блоками, причем этот вклад экспоненциально убы-
вает с увеличением шага решетки.
Удовлетворительная формула предложена в [163]:
। _q ___ ехр [ с ^il
1 ~ 1 + (1 - c)SsЛ ’
где
С—“/'МИН//1 С],
(8.3.23)
(8.3.24)
причем /мин — минимальное расстояние между блоками в ре-
шетке; Ci=0,08 для квадратной решетки; Ci=0,12 для шести-
гранной. Если блоки заключены в оболочку с малым полным
сечением, то [163]
Ус
1 + vc .
(8.3.25)
где vc — отношение объема оболочки к объему блока; с^—
= 0,886 для квадратной решетки и сг=0,952 для шестигранной.
Сравнение формулы (8.3.23) с расчетами по методу Монте-Кар-
ло показало, что ее погрешность не превышает 1,5—2% [163].
На рис. 8.6 для примера приведен график функции D при
/Ssi — 1, Пс=0, вычисленной по формулам (8.3.23) и (8.3.19)
(сплошная линия). При малых vm поправка,/) становится зна-
чительной.
Если применять рациональное приближение, то коэффици-
ент блокировки описывается (8.3.6). Комбинируя эту формулу
с (8.1.44), получаем
- Ррп = 1 - ~ (8.3.26)
]/ 1 а [ 1 + (/ Ssl vm) ]
Для слабых уровней D зависит от параметров уровней. Для
сильных, когда а->оо, D не зависит от параметров уровней
[так же как (8.3.19) ]:
Ррп=1- 1 +
1 1/2=1 — (1 + ~----------) ’/2. (8.3.27)
@1 /рп] х ^sivm /
Разложив (8.3.27) по (1—Gi)/Gi, получим ряд, очень по-
хожий на (8.3.19). На рис. 8.6 штриховой линией дана функ-
ция (8.3.27) при ZSsl = l. Видно, что при больших vm формула
(8.3.27) завышает поправку в несколько раз по сравнению с
(8.3.19).
260
Отметим, что иногда при вычислении поправки D заменяют
блок черным телом для энергии нейтрона внутри опасной зо-
ны. Тогда получаются формулы, которые отличаются от при-
веденных здесь численными коэффициентами.
8.4. РЕЗОНАНСНОЕ ПОГЛОЩЕНИЕ СЛОЖНЫМИ БЛОКАМИ
Рассмотрим цилиндрический блок, состоящий из двух областей: 0<г<рь
где сечение равно Si(-E) и pi<r<p2, где сечение равно S2(E). Пусть отно-
шение Si(£,)/S2(5) постоянно, т. е. резонансное поглощение обусловлено
одним и тем же нуклидом и две указанные области отличаются только кон-
центрацией ядер. Определим среднее сечение:
S = S2(l+z2e); z=pi/ip2; е= (Si—’S2)/S2. (8.4.1)
Если е=—1, то Si = 0, что соответствует полому цилиндру. Если е = оо,
то S2=0, т. е. цилиндр имеет радиус Pi вместо р2. Обозначим эффективный
резонансный интеграл, вычисленный по средней плотности поглотителя, 7,
а истинный интеграл 7. Вычислим отношение 7/7. Будем рассматривать силь-
ный резонас, когда можно ограничиться первым членом асимптотического
разложения (8.1.23). В .этом случае резонансный интеграл определяется сред-
ним значением <VSZ>. Тогда
(Ksz)
Vs <ГГ)
(8.4.2)
При вычислении средних значений в (8.4.2) интегралы по О сокращаются
(см. вычисление <}'/> в § 8.1). При интегрировании по ф в числителе надо
заменить
SZ -» 2Stp2 г2—sin2 <р2S2p3 [cos <р—|/z2—sin2 ср],
0<sin (p<pi/p2;
SZ->2S2p2 cos ф, pi/p2<sin ф<1,
а в знаменателе
SZ->2p2S cos ф.
Интегрируя с весом (8.1.31), получаем
7 _ Ф0(г) + гФ1(г, е)
Т ~ 1/1 + ег2Фо(О) ’
где
Фо(г) = f (1 -х2)1/4 dx; Фо(О) = 77Х [Г(0,25)]г;
(8.4.3)
(8.4.4)
1
Фх(г, е) = J [|/1—г2х24-ег|/1—х2]^2 dx. (8.4.5)
о
На рис. 8.7 приведены отношения_ 7/7 как функция z для нескольких
значений е. Из рисунка видно, что 7/7 очень близко к единице в широком
интервале изменения в от —1 до ~10. Только при е-*-оо, когда во внешней
261
Рис. 8.7. Зависимость отношения 1/1
от 2=pi/p2 [при 0<r<pi сечение по-
глощения 21, при р1<г<Ра сечение по-
глощения S2, e=(Si/S2)—1]
Рис. 8.8. Зависимость отношения
</г>/Кг для полого цилиндра от
2= Р1/Р2
области концентрация поглощающего вещества стремится к нулю, величина
1/1 существенно отличается от единицы. В этом случае
z/7=l/T = |/K7S. (8-4.6)
как и должно быть. Таким образом, неравномерное распределение погло-
щающего вещества по блоку очень слабо сказывается‘на значении эффектив-
ного резонансного интеграла, т. е. вычисления можно, проводить, заменяя
неоднородный блок однородным со средним значением концентрации.
Если z->-l, то 1/1=1 за исключением случая е=—1 (т. е. случая полого
цилиндра), когда в (8.4.3) возникает определенность. Раскрывая ее, по-
лучаем (см. рис. 8.7):
/ А----1.3=1 3 Lr(l,2S)J
Для полого цилиндра в согласии с формулами (8.1.20),
имеем
/ =
(8.1.24), (8.1.32)
[Г(0,25)]2 /0
9*2 |А у2р3 S
3 = sa(l—22);
1___г__«Д1,
/57 /Г "
(8.4.7)
(8.4.8)
где /о—резонансный интеграл бесконечного разведения; 7-—средняя хорда
полого цилиндра, т. е. 7=2р2(1—г2). Разделив (8.4.8) на (8.4.7) и сравнив
с (8.4.3), для полого цилиндра имеем
(КГ> С
у^ = ут^Г[Фо(г) + гФ1(г- -l)]^f(z), (8.4.9)
262
где
1/2
С = —е-7^-[Г(0,25)]2= 1,112.
Зл[/п
На рис. 8.8 представлена функция f(z). При z=0 f(z) совпадает
с (8.1.32), а при z=l полый цилиндр превращается в пластинку и поэтому
f(l) равно 0,9428 [см. (8.1.34)]. Из рис. 8.8 видно, что отношение (8.4.9)
при всех значениях z очень близко к единице.
Пусть внутренняя полость г<р. в полом цилиндре заполнена легким за-
медлителем. Будем считать, что каждое столкновение нейтрона с ядром за-
медлителя выводит его из опасной зоны резонанса. Ограничимся выводом
приближенной формулы (формула Карлвика— Першагена [168]), которая
справедлива при замене (]/1 ) на j/1 . Как было показано выше на мно-
гочисленных примерах, точность такого приближения достаточно высока.
Применим к полому цилиндру рассуждение, использованное в § 8.1 при
выводе формулы Для средней хорды (8.1.18). Число ударов нейтронов о внеш-
нюю поверхность равно ®Se/4, а число ударов о внутреннюю Ф5,у/4, где
Se, S; — внешняя и внутренняя поверхности и
/1° г
7= / j Ssexp( — Zsx)dx\ = <1 —ехр( — z0Ss)>, (8.4.10)
причем /о — хорда внутреннего объема; < > — усреднение по всем хордам
внутреннего объема. Используя (1.10.25), имеем
у=^Ла(\-Рс), (8.4.11)
где /о — средняя хорда внутреннего объема; Рс—-вероятность испытать стол-
кновение
во внутреннем объеме (см. § 1.10). Аналогично (8.1.41) запишем
Ф „ „ ФК
(Sf Y ~Ь$е) = - ,
откуда
7=4У/59ф; 5Эф=$е+т$/.
(8.4.12)
Если Ss?o>i, большой внутренний объем, то т~1 и обе поверхности
(внешняя и внутренняя) входят в определение средней хорды с одинаковым
весом. Если SsZo<Cl, малый внутренний объем, то прн определении средней
хорды надо учитывать только внешнюю поверхность.
Зная среднюю хорду (8.4.12), можно определить коэффициент блоки-
ровки (8.1.38) и эффективный резонансный интеграл (8.1.20).
Выше предполагалось, что скачок энергии при столкновении с ядром
замедлителя во внутренней полости (8.1.3) много больше ширины опасной
зоны (8.1.2). Определим атомную массу замедлителя, для которой эти шири-
ны равны. Приравнивая (8.1.2) н (8.1.3), получаем (при Ао»1):
1 _ Г|/ог Vpsl
Ei- 4
(8.4.13)
т. е. А о зависит как от параметров уровня, так и от размеров блока. Значе-
ние Ао для основного уровня 238и и 7~1 равно примерно 30. Поэтому такие
вещества, как графит, кислород, магний, алюминий и др., нельзя считать до-
263
статочно легкими. Можно предположить интерполяционную формулу, напри-
мер, вида *
_» s3(b =-----4—---, (8.4.14)
5 ф (14-^/Л0)з ’ v
где До определено (8.4.13); А—атомная масса рассматриваемого замедли-
теля. Формула (8.4.14) эффективно учитывает неполное выбивание нейтрона
из опасной зоны резонанса. Усреднив (8.4.13) с весом fi (8.1.27) по всем уров-
ням 238U, которые блокируются, получим [прн этом используется формула
(8.1.25) и считается, что ]:
4 - 2 -т-=(2 Н4ф -гр*’ (8-4-!5)
71 о «« \ / 4 V л
i 4 / '
где /Эф — блокируемый резонансный интеграл 238U, вычисленный для плотно-
сти рв°, а рз— плотность урана в блоке с замедлителем. Подставляя
в (8.4.15) Е/?=0,2 [см. (8.1.59)] и экспериментальное значение /Эф (см. § 8.6),
находим
До = 5L- 1/ _PsL, (8.4.16)
УТ Г р8
где р8° = 0,04 73-1024; р8— число ядер 238U в 1 см3 блока в замедлителе;
1 выражено в см. Если этот результат подставить в (8.4.14) и (8.4.11), то
формула (8.4.12) превратится в уравнение для определения /. При этом,
однако, правая часть слабо зависит от Z и первая же итерация приводит
к достаточно точному результату.
Отметим, что формула (8.4.16) применима для вычисления суммарного
резонансного поглощения. Если же надо определить поглощение отдельным
уровнем или группой уровней, то следует заново определить величину До.
Теперь рассмотрим однородный блок, в котором наряду с резонансным
поглотителем имеются легкие ядра, причем каждое столкновение нейтрона
с таким ядром выводит его из опасной зоны резонанса **. Надо рассмотреть
два эффекта: вывод нейтронов из опасной зоны и дополнительный источник
нейтронов в блоке, связанный с наличием там легких ядер. Первый эффект
уже рассматривался в задаче 3 § 8.1, поскольку влияние легких ядер на
резонансное поглощение, если каждое столкновение выводит нейтрон из опас-
ной зоны, эквивалентно влиянию нерезонансного поглотителя. Результат
дается формулой J8.1.70) [см. также (8.1.71)]:
4ф =/эф ['-0.376^1 + 0,214а?]; (8.4.17)
где /дф — эффективный резонансный интеграл блока без легких ядер, но с тем
же количеством резонансного поглотителя; — макроскопическое сечение
рассеяние на легких ядрах в блоке.
Обратимся ко второму эффекту. Число нейтронов с энергией Е, появля-
ющихся в единицу времени в единице объема блока, равно
Is f Ф(Е')ш(Е', E)dE’. (8-4.18)
* Идея подобной интерполяции принадлежит В. В. Орлову [73, 169].
** Впервые эта задача была рассмотрена А. П. Рудиком в 1950 г. (см.
[125], а также [71, 73]).
264
Если скачок энергии при столкновении с легким ядром много больше ши-
рины опасной зоны, то в (8.4.18) можно поставить невозмущенную плотность
потока. Используя формулу (2.2.8) для w, получим вместо (8.4.18):
^/®0
Г dE' _
ПЕ, .) (1-е0)Е'2 t£sVE ’
Е
(8.4.19)
Количество поглощенных нейтронов равно
SsV о
VEr
J G(E)dE^s
(8.4.20)
где G (£) — вероятность того, что возникший в блоке нейтрон будет там
поглощен; 61 — соответствующий резонансный интеграл; р8° — число ядер
поглотителя в 1 см3 блока. Вводя в (8.4.20) резонансный интеграл бесконеч-
ного разведения /о, получаем
5/ = [ G (х) dx.
(8.4.21)
Вероятность поглощения G(x) может быть выражена с помощью фор-
мулы (1.10.25) через вероятность поглощения падающего на блок нейтрона,
а последняя записана так же, как (8.1.14). В результате получим
S (х) Г 1 Г 1
<?(*) = у Л М 1 - Ъ Zxl ~-4- Е 1~/~ О-е^-^ВД+ад))^)^ ,
+ “a W L “Ь 4$J * J J
(8.4.22)
где первый множитель превращает вероятность столкновения в вероятность
поглощения. Положим для сильного уровня 2а(х) =2г/х2; х2»1 и запишем
интеграл от G(x): так:
С С ^rdx 1 С С %rx2dx
\dxG(x)= ' - у w(l)dl \ [1 —ехр(—<z/x2—<Zj)J ,
J J ^r + x I J J (2r4-2sx2)2
где а=242>1; ai = 2sZ.
Интегрирование может быть выполнено:
(1—2л1)(1—erfj/л!) -)-2 1/ — ехр(—аг)
г л
(8.4.23)
Подставляя (8.4.23) в (8.4.21) и используя выражение для коэффициента
блокировки (8.1.33), находим
—-^2—+ -^- /(! —2^1) (1 — erf |Z«i) 4-
4-2 ехр(— «1)/1- (8.4.24)
Разлагая (8.4.24) в ряд по at и используя данные табл. 8.2, получаем
=/°ф [0,753^1 —0,285Лх21- (8.4.25)
265
Объединяя (8.4.17) н (8.4.25), находим окончательный результат (см. также
задачу в конце параграфа):
/эф = 4ф’ = /°ф[1 + 0,377ai — 0,07Й12] =
= ^ф [1 +0,754pSs—0,284p2Ss2]_ (8.4.26)
Если в рассматриваемой задаче применить рациональное приближение,
то надо сделать замену:
с 7s
J [l-exp(-/S)M/)dZ-—
Если считать, что л»1, то первый эффект дает
=/$ (* +«!Г1/2,
а второй
Складывая, имеем
Лф = 4°ф>/1+«1.
(8.4.27)
При малых а1г когда применимо разложение (8.4.26), разность (Уэф//2ф)—
— 1 в рациональном приближении примерно на 30 % больше, чем дает фор-
мула (8.4.26) (см. также задачу в конце параграфа). Такая разность возни-
кает, например, при вычислении изменения реактивности в результате потери
теплоносителя внутри сложного блока. При вычислении таких разностных
эффектов желательно не использовать рациональное приближение.
Если атомная масса легких ядер не удовлетворяет условию А<^А0, где
Ао определено (8.4.13), то надо ввести £3ф по (8.4.14) или для резонансного
поглощения в 23SU по (8.4.16) (Z выражено в см):
(8.4.28)
Проверкой формул (8.4.26), (8.4.28) может служить определение резо-
нансного интеграла для блока из оксида урана по экспериментально найден-
ному резонансному интегралу для металлического урана (см. § 8.6).
В энергетических реакторах используются, как правило, блоки в виде
прутков нз урана или оксида урана, собранные вместе в одной кассете
(«кластере»). Эффективный резонансный интеграл такого сложного блока
определяется эффективной поверхностью [так же, как в (8.4.12)]:
*S==Se-|-'yS/, (8.4.29)
где Se — внешняя поверхность, в качестве которой надо рассматривать по-
верхность «резиновой пленки», натянутой на кластер (без учета покрытий);
S; — суммарная поверхность,
Si = 2n()N~Se-, (8.4.30)
р — радиус прутка (без покрытия); W— их число. Величина у в (8.4.29) имеет
такой же смысл, как в (8.4.10), (8.4.11), и совпадает с величиной Gb которая
рассматривалась в § 8.3. Поскольку для замедлителя в кластере
266
(теплоноситель, а иногда и покрытие) невелико, можно использовать рацио-
нальное приближение, когда
^S1 ^1
* 4* 11
(8.4.31)
причем 7i = 4Vi/Si, где Vi — объем замедлителя в кластере; Si — его поверх-
ность, равная Si=2npW-4-Ss; р'— радиус прутка с покрытием. Сечение
можно заменить 2Эф по (8.4.14). Обычно такая замена мало влияет на ре-
зультат. Сравнение с экспериментальными данными проведено в § 8.6.
В [170] получена приближенная формула для эффективной хорды класте-
ра с большим количеством прутков. Отсылая за подробностями к (170], при-
ведем окончательный результат:
/эф = "7" + / ( 1 ) у г , о г/г —j no I п-1’ (8.4.32)
Ь '. 81 / 4* В [(“1 1)5 4*1]
где I — средняя хорда прутка; L — средняя хорда кластера; vm, — объем-
ная доля и макроскопическое сечение замедлителя в кластере между прут-
ками; Gi совпадает с величиной, введенной в (8.1.11); gi— аналогичная ве-
личина для замедлителя внутри кластера; В, b -— поправки к рациональному
приближению для кластера и прутка [см. (1.10.23)]. Предполагалось, что
одно столкновение с ядром замедлителя выводит нейтрон из опасной зоны.
Если это не так, то можно ввести поправку по (8.4.14).
Если положить В=Ь—1 и предположить, что кластеры не интерферируют
друг с другом, т. е. 0=1, то формула (8.4.32) упрощается:
/ЭФ = /+ Z f-L —j) . (8.4.33)
\ 81 / 14*
Особенно просто выглядит результат для кластера, в котором нет замед-
лителя, т. е. Используя рациональное приближение для gi, полу-
чаем
—-1=— =
81 Im
где По — объемная доля прутков в кластере. Тогда
/эф= У оЕ--;-/
(8.4.34)
(8.4.35)
Первое слагаемое в (8.4.35) соответствует равномерному «размешиванию»
прутков по кластеру, а второе дает поправку к такому «размешиванию».
В формулах (8.4.32), (8.4.35) никак не отражается конкретная расстановка
прутков по кластеру. Поэтому формулы справедливы и для хаотического
распределения. Тогда (8.4.35) можно получить следующим образом. Эффек-
тивная хорда кластера равна хорде прутка, умноженной на число «столкно-
вений частицы», движущейся по хорде и проходящей через прутки без рас-
сеяния: /Эф = /Л4. Число «столкновений» М равно
M=L/h+l, h=(oc)-\ (8.4.36)
где c=N/(лВ2)—концентрация прутков; N — их число в кластере; R— ра-
диус кластера; о — «эффективное сечение». Единица в (8.4.36) прибавлена,
поскольку число промежутков между прутками на единицу меньше, чем
число прутков вдоль хорды. Эффективное сечение надо определить как отно-
шение лр2//. Тогда из (8.4.36) получим (8.4.35). Таким образом, второе сла-
гаемое (8.4.35) связано с «краевым эффектом», т. е. для очень большого
кластера оно не играет роли. Если записать с’0 = (р/7?)2N, то
/ р \а
/эф=[~ Л/^4*/,
\ к /
(8.4.37)
267
т. е. формула (8.4.35) учитывает два главных члена при /V3>1. Следующие
члены разложения по 1 /N, вероятно, будет зависеть от конкретной расстанов-
ки прутков. Если в (8.4.37) р—>-0 при сохранении N, то первое слагаемое
убывает быстрее второго и для очень малых прутков остается только вто-
рое слагаемое. Так и должно быть, если почти каждая хорда кластера либо
совсем не пересекает прутков, либо пересекает только один.
Более точное вычисление резонансного поглощения блоками такой слож-
ной геометрии целесообразно проводить методом Монте-Карло. Методу Мон-
те-Карло применительно к расчету ядерных реакторов посвящена обширная
литература (см., например, [171, 172] и приведенную там библиографию).
Задача. Определить, используя формулу (1.10.22), эффективный резонанс-
ный интеграл блока, содержащего легкие ядра.
Решение. Вместо формулы (8.4.21) получим
№
Sa(X)
“Г
Pc(x)dx,
где
1 — exp [—(Sa(x)-f-S-)/] - -
Pc(X) = 1 --------+ A [Sa(x) + Ss] I exp [ - (Sa(X) + Ss) /].
l+i(X/ -j- +J I
Полагая 2a(x)I=a/x2, x!>l, Ssl=ai и интегрируя по x, имеем
o/ = /° ^21 (1 - 1 17 1 - —'l erf |/ax +
ф 2 \ 4 ) L\ v 1
+ ,z— (1+A»i) ехр ( —aj], (8.4.38)
|/ Яйх J
где /°ф—эффективный резонансный интеграл без учета легких ядер в блоке.
Складывая (8.4.38) и (8.1.71), находим (Л-=0,098 для цилиндра):
'эф=/э°ф (1 - 4)-1 [4 ~(i+e"f +
+ "у (1 — -у) exP(~ai)]’ (8.4.39)
Разложение (8.4.39) в ряд по степеням ai имеет вид
/эф = /э°ф[1 + 0,3668ах-0,04б7а? + 0,0091a/—0,00170?+ ... ]. (8.4.40)
Если ax= 1, то по формуле (8.4.39) получим /эф = 1,328/°ф, в то время как
рациональное приближение (8.4.27) дает /эф = 1,414/°ф, т. е. (/Эф—/°ф)//°ф
в рациональном приближении на 30 % больше, чем при использовании зна-
чительно более точной формулы (1.10.22).
8.5. РАСПРЕДЕЛЕНИЕ ПОГЛОЩЕННЫХ НЕЙТРОНОВ ПО БЛОКУ
Рассмотрим однородный цилиндрический блок. Количество
нейтронов, поглощенных в слое (г, г-}-Аг), обозначим J(r)rAr.
Для изолированного уровня с естественной формой линии в
268
Рис. 8.9. К формуле (8.5.1)
тех же предположениях, которые ис-
пользовались в § 8.1, получим
7 (г) r&r = const J Jexp - j 4-
(8.5.1)
4-ехр
A/u)(Q)dQdx,
где (см. рис. 8.9)
а
b+ = —l±; а = 2Srp; /±
cos <р + |/z2—sin2 <р .
sin ft
А/ = ---------r-^r -; 0 < <р < <р0;
р sin ft у z2—sin2 <р
sin<p0 = z — —.
?
(8.5.2)
Полное число поглощенных нейтронов равно
р
J J (г) rdr = const I (а) = const 2]/ад, а^>1, (8.5.3)
о
где постоянная совпадает с постоянной в (8.5.1). Поэтому нор-
мированная плотность поглощенных нейтронов будет
J (г) = —т=^“ f [ехР ( ~~ ~ Ь+~ +
2|/мр JL к 14-х2/
+ ехр (----— \ 1-------— (8 5 4)
1 1 4-x2/J (1 -j-x2) sin ft (/z2—-sin2 ft
J (r) rdr = 1.
о
Воспользуемся тем, что интегралы по х в (8.5.4) получа-
ются из интеграла (8.1.28) путем дифференцирования по Ь:
Ч-оо
[ ехр (--------—'j——— = irexp(-------(8.5.5)
J ij-x2/ 1-f-х2 V 2/ \2/
— 00
Таким образом,
, -------------х/2 4>о
7 (г) = — 1/ — [ sin&i& ( 2C0S ¥ г lexp f-±) /0 Г—) ф-
р2 V " J J |/z2 —sin2? L \ 2 ) \ 2 )
о о
4-ехр -----(8.5.6)
269
Рассмотрим сначала такую область значений г, что (р—
—r)a/p<t:l, хотя а^>1. Тогда
, cos w ... . , -
b+= а------>1;
sin О
Обозначим часть J(r), куда входит Ь±, через J±. При вычис-
лении /+ можно положить фо=л/2, 2=1,
ехр (— 4-М 7° (vM = н)-1/2-
\ / \ ^ /
Тогда
]+ = —; с = -[Г(0’25-)]4 = 0,729. (8.5.7)
р2 24п2
При вычислении /_ сохраним линейный член по Ь-.
*12 <Ро , ------
j_(r)=_LC sin ш [ Г1 — — со-?-у-~ ^a~sina Ч d<p.
р2 J J |/z2—sin2 <р [ 4 sin 0 J
о о
(8.5.8)
В первом слагаемом (8.5.8) можно положить <р0=л;/2,
z=l. Тогда получим
, г— г /Фо
J (Г) = !----£. ( Г 22s...!_ dy — z | . (8.5.9)
' 2р2 4 \ J |/z2—sin2<p / '
L \0 / J
При a^> 1 можно пренебречь J+ по сравнению c Вычислив
интеграл в (8.5.9) при 1—2<С 1, найдем
> z \ |Ata Fi 11 , . 8 XT _ n
J (H = Vr- 1--------i 1 + In—; 7— • (8.5.10)
' ’ 2p2 4 \ 1 1—Г/р /J '
Таким образом, плотность поглощенных нейтронов макси-
мальна на краю блока и убывает на расстояниях порядка ИЛ1.
Общее количество нейтронов, поглощенных в слое порядка
2г-1, определится интегралом от (8.5.10) в пределах от р—
—2г-1 до р. Этот интеграл легко оценить сверху:
р . —
J rJ(r)dr< У^-«1, (8.5.11)
p-V1
т. е., несмотря на очень высокий максимум функции /(г) на
краю блока, количество нейтронов, поглощенных в узком слое
порядка Sr1, составляет малую долю общего числа поглощен-
ных нейтронов.
270
Таблица 8.4. Значения функции f (г)
Z 0 0,2 0.4 0,6 0,8 0.9 0,94 0,98 1,0
f(z) 1 0,992 0,968 0,922 0,839 0,766 0,721 0,650 0,539
Теперь рассмотрим область, далекую от границы блока, ко-
гда Ь±У>1. Из (8.5.6) получим
У(г) = -!Ц- fsin&d» l C0S<P . + -/U') d<₽. (8.5.12)
' ЯР J J |/z2 —Sin2<p ^|Л> + |/&_J ' ’
Q о
Так как b± пропорциональна а, то параметры уровней не
входят в 1 (г) (8.5.12). После интегрирования по 6 получим
J(r) = —Г(г); Т(г) = -Д^; с' = . [Г-^-25)1'2- =1,236,
V ' f2 - |/ 1-z2 6л ’ ’
(8.5.13)
где
п/2
f(z) = —( [((/1 — z1 sin2 <р 4- z cos <р)1/2 +
Л J
о
+ (к 1 — z2 sin2 ф — 2 cos <р)1/2 ] dtp. (8.5.14)
Функция f(z) приведена в табл. 8.4. При z<Cl и 1—z<Cl /(z)
может быть разложена в ряд:
/(z) = l—0,1875z2—0,0615z4-0,0263z6+...; z<l;
f(z) = 0,539+0,835/1=7+ ...; 1—z<l.
Функция F (z) изображена на рис. 8.10. Резкий подъем при
2—х1 обусловлен множителем 1/1—z2.
Так как F(0) = 1, то из (8.5.10) и (8.5.13) получим отноше-
ние плотностей поглощенных нейтронов на краю блока и в
центре:
0,7 Va > 1. (8.5.15)
Таким образом, плотность поглощенных нейтронов состоит
из двух частей: плавной кривой (8.5.13), одинаковой для всех
уровней, удовлетворяющих условию а^>1, и узкого пика шири-
ной порядка 2г-1, высота которого обратно пропорциональна
коэффициенту блокировки (1 (8.1.24), т. е. различна для раз-
ных уровней. Для металлического 238U (для главных уровней)
Sr-1~l О-3 см.
271
Рис. 8.10. Универсальная функция
F(z)
Рис 8.11. Распределение поглощенных
нейтронов по блоку:
X — эксперимент;-------теория
Рассмотрим, как изменяются полученные результаты при
учете доплеровского уширения линии. Вблизи края блока вме-
сто (8.5.5) получим (Ь_<С1):
J ехр[— Q]<[>(х, Q[ 1 — -у fо) C°S¥ Sln2~ .
(8.5.16)
где
HQ = -^р-^ехр (^-Q) [1 — erf (8.5.17)
Таким образом, вместо (8.5.10) имеем
7(г) = 7 (р) Г1 — JM(Q(i-z)/i+in-§-Y|, (8.5.18)
где
Цр) = V^a/(2p2); а>1.
Формула (8.5.18) отличается от (8.5.10) заменой [см.
(2.3.35)]:
2r->2J(Co) = 2r<HO,/2Q, (8.5.19)
272
т. е. высота пика сохраняется, а ширина возрастает [однако
фактически нормировка (8.5.3) должна быть изменена и вы-
сота пика уменьшается в отношении /эф(0)//Эф(Т), где h$(T) —
эффективный резонансный интеграл при температуре Т]. Функ-
ция ф (0, go) представлена на рис. 2.3. Из этого рисунка видно,
что для главных уровней 238U ширина пика возрастает в не-
сколько раз по сравнению с естественной формой линии, т. е.
с температурой, равной нулю. Что касается внутренней области
блока, то при а^>1 и для главных уровней, когда ngo23> 1, эф-
фект Доплера не сильно изменяет резонансное поглощение (см.
§ 8.2). Поэтому влияние температуры на функцию F (z) для
главных уровней не сильное. Для более слабых уровней влия-
ние температуры существенное, но роль самих уровней умень-
шается.
Очевидно, что неблокируемое поглощение приводит к рав-
номерному распределению поглощенных нейтронов по объему
блока. Пусть р — доля неблокированного поглощения; 1—р —
блокируемого. В принятой нормировке плотность неблокируе-
мого поглощения равна
t*Lrdr = p.
О
Таким образом, полная плотность поглощенных нейтронов
ф(г), нормированная так, что общее число поглощенных ней-
тронов равно фо, будет
Ж=^[р+у O-W-Ur)]. (8.5.20)
Вдали от края блока имеем
Ф (0 = А [Р + °>658 (1 ~ Р) F (Z)]. (8.5.21)
тер4
На краю блока вместо (8.5.10) надо написать
/
где /у—вес уровня (8.1.26). Вычисление суммы для 20
i
первых уровней 238U дает ]/ау= 118 и (для металлического урана)
]/га = 2б)//1 (I измеряется в см.) (8.5.22)
18—6053 273
Следовательно, отношение плотностей поглощенных нейтро-
нов на краю и в центре блока равно (7 — в см)
-11PL == л (р) ^+L1’5.L1-£)Kf ... (8.5.23)
ф(0) 0,618 + 0,382р
В [173] приведены экспериментальные данные о распреде-
лении поглощенных нейтронов для блока радиусом 0,4915 см
из металлического урана. Этому радиусу соответствует (см.
§ 8.6) р—0,254. Формула (8.5.23) дает ipi (р) = 12,2. Как отме-
чалось выше, эффект Доплера приводит к изменению норми-
ровки. В данном случае эта поправка уменьшает фДр) до
ф1(р) = 11. Экспериментально получено ф1(р) = 10,5. Формула
(8.5.21) дает в этом случае
-^2- = ^ (г) = 0,355 + 0,645т7 (г), (8.5.24)
где F(z) определено (8.5.14) (см. рис. 8.10). На рис. 8.11 при-
ведены теоретическая кривая (8.5.24) и экспериментальные точ-
ки из [173]. Видно, что рассмотренное здесь простейшее при-
ближение удовлетворительно согласуется с экспериментом. На
рис. 8.11 изображен резкий подъем кривой при г->р. Фактиче-
ски подъем еще более высокий, так как фДр) в 4 раза больше,
чем значение ф1 в последней точке на рисунке, отстоящей от
границы блока на 0,01 см.
Неравномерное распределение поглощенных нейтронов при-
водит к неравномерному накоплению 239Рц при выгорании топ-
лива (см. гл. 13), правда, не столь сильному, как это изобра-
жено на рис. 8.11, поскольку тепловые нейтроны распределены
по блоку почти равномерно и суммарная плотность поглощен-
ных нейтронов не столь сильно зависит от расстояния до края
блока.
Полную плотность нейтронных захватов запишем так:
Р(г) = СФ(г)-Н(г),
где Ф(г) — плотность потока нейтронов в тепловой группе;
ф(г) определено (8.5.20), а постоянная С получается из усло-
вия нормировки:
р
2irC J гФ (г) dr = 1 — ф0.
о
Таким образом,
= (8-5.25)
лр2 ф
274
где Ф — средняя плотность потока в тепловой группе. Опреде-
лим отношение Р(р)/Р(0):
Р(р) _ (1-Фо)<Э+Фо [/ + 11,5(1-/) /Г] (8 5 26)
Р(0) ’ (1-ф0)<2-1+ Фо(0,618+0,382/) ’ v • • ;
где Q — коэффициент экранировки [приближенно считается,
что Ф(0)/Ф=(2-1]. Рассмотрим для примера блок радиусом
0,5 см (см. рис. 8.11), для которого р=0,254. Пусть фо=0,2,
Q = 1,05. Тогда из формулы (8.5.26) получим
= 2,88.
Р(0)
Отступим от края блока на 0,01 см. Тогда z=0,98, F(z) =
= 3,266 и, полагая приближенно Ф(г)/Ф=(2[1—2Q(1 —
—г2/р2) ] = 1,045, получаем
Ф(г)
о, , (1-Фо)-^ + Фо[Р + О,618(1-р)Т(г)1
—?----------------------------------------=1,31.
Р(0) (1 —+o)Q“4-+о [0,618 + 0,382/?]
Если отойти от края блока на 0,1 см, то Р(г)/Р(0) = 1,09.
8.6. ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ О РЕЗОНАНСНОМ ПОГЛОЩЕНИИ
И РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ
Экспериментальные данные о резонансном поглощении мож-
но разделить на несколько качественно различных уровней.
Наименее информативные данные получаются при измерении
резонансных интегралов для бесконечного разведения (см., на-
пример, [7, 13, 32, 33] и Приложения IV и V). В практических
реакторных расчетах резонансные интегралы бесконечного раз-
ведения можно непосредственно использовать в тех случаях,
когда, во-первых, спектр замедляющихся нейтронов не сильно
отличается от фермиевского (т. е. у<С1) и, во-вторых, резо-
нансное поглощение данным нуклидом не блокируется. В боль-
шинстве реакторов на тепловых нейтронах к таким нуклидам
можно отнести ядра замедлителя, теплоносителя, А1 (но не
Zr, резонансное поглощение которого заметно блокируется) и
в реакторах с мягким спектром, когда 0,1+0,2, ядра 235U,
239Pu и 241Pu.
Следующий уровень данных — это параметры резонансных
уровней (см. [7, 32], основные уровни 238U приведены в табл. 8.1,
параметры нижних уровней ряда трансактинидов указаны в
Приложении IV). Если известны параметры всех резонансных
уровней, то эффективный резонансный интеграл можно полу-
18* 275
чить теоретически (простые формулы приведены в § 8.1—8.4,
результаты численных расчетов см. ниже). Основной вклад в
эффективный резонансный интеграл 238и вносят несколько
нижних уровней, для которых изложенная выше простая теория
не содержит больших ошибок. Тогда согласно § 8.1 эффектив-
ный резонансный интеграл определяется комбинацией парамет-
ров (8.1.26) и ошибка эффективного резонансного интеграла
определяется ошибками величин, входящих в (8.1.26).
Наиболее употребительная запись эффективного резонанс-
ного интеграла учитывает основной результат теории, изложен-
ной в § 8.1: блокированная часть резонансного интеграла’ об-
ратно пропорциональна корню квадратному из размеров блока.
Обычно этот результат записывают так:
/эФ = Л + 5/Ж (8.6.1)
где S — поверхность блока, см2; М — масса, г; Л — неблоки-
руемая часть резонансного интеграла; постоянная В, если ис-
пользовать результаты теории § 8.1, равна
s=/ir <8-6-2’
с& — число ядер 23f8,U в 1 см3; р — плотность урана, г/см3;
остальные величины определены формулами (8.1.26) и (8.1.32).
Наиболее полный список уровней 238Uопубликован в [32].
При обработке этих данных к неблокируемым причислялись такие
уровни, которые имеют сечение в центре линии (с учетом допле-
ровского уширения при температуре 293 К) меньше 10 б. Если
1 — 2 см, то величина Zy(Er)l для таких уровней близка к еди-
нице. Поскольку для этих уровней £0<0,14-0,2, то, как следует
из рис. 8.4, коэффициент блокировки р>0,95, т. е. действительно
такие уровни практически не блокируются.
В результате обработки данных по уровням 238U получено:
резонансный интеграл бесконечного разведения до энергии Et=
= 0,5 эВ [с учетом l\/v по формуле (2.3.38)] /оо=278(2), коэф-
фициенты в формуле (8.6.1)
2 А-= 1,466(10); В = 25,1 (2), (8.6.3)
I
неблокируемый резонансный интеграл до E=10 кэВ, /н.б=
= 2,72 б.
Распределение V ft и 7Нб по энергетическим группам при-
I
ведено в табл. 8.5. Неблокируемое резонансное поглощение
состоит из поглощения слабыми s-уровнями, р-уровнями (все
р-уровни не блокируются) и 7i/t>. Резонансный интеграл Л/о со:
276
ответствует сечению, подчиняющемуся закону 1/и только при
энергиях, много меньше, чем первый резонансный уровень. Если
же вычисляется резонансный интеграл по произвольному ин-
тервалу (Еь Ej+l), то в согласии с (2.3.38) или (8.1.66)
71/0 (Е}, Ej+1) = /{‘,1 (Ес) [ Уf ,
(8.6.4)
где l[‘/l (Ес)— „истинный" резонансный интеграл от части сечения,
подчиняющегося закону 1/и, соответствующей i-му уровню. Функ-
ция f(z) дана (2.3.95). Как указывалось в § 2.3, f(z)<0, если
0,4<г<1. Если же г—1<С1, то —/(г)^>1. Поэтому если Е, или
Е/+1 оказывается вблизи уровня, то E/v(Ei, El+i) отрицательно.
Так и происходит в 21-й группе (граница группы 4,65 эВ, уро-
вень 6,67 эВ), в 20-й группе (граница группы 21,5 эВ, уровень
20,87 эВ) и в 17-й группе (граница группы 100 эВ, уровень
102,5 эВ). Поскольку в этих группах имеются сильные уровни,
то суммарное сечение, конечно, будет положительным. Здесь
подразумевается, что блокируемая часть резонансного интегра-
ла вычисляется с помощью приближенно записанного инте-
грала (8.1.21). Если же проводится численное вычисление ре-
зонансного поглощения, то отрицательный член (а7) может воз-
никнуть (если условия применимости теории § 8.1 не сильно
нарушены) при аппроксимации резонансного интеграла форму-
лой вида
I (Ej, EJ+1) = а,} + Ь} / I + В} j/S/Af. (8.6.5)
Разделение на s- и р-уровни достоверно только при малых
энергиях (Е<1 кэВ). Особенно большая неопределенность воз-
никает при Е>5 кэВ. Поэтому в табл. 8.5 в этом случае приве-
дено только суммарное значение по 5- и р-уровням. Величина
Г7 для р-уровней не измерялась; она принималась равной сред-
ней ширине для з-уровней в том же энергетическом интервале
(Г7 монотонно возрастает от 23 до 30 М.эВ). В интервале 6—
10 кэВ вычисления проводили по среднему значению £ТИ =
= 74 мэВ и среднему расстоянию между уровнями 0=12,8 эВ.
Суммарные значения Л/о и 7нб приведены в табл. 8.5 до энер-
гии 0,465. Пересчет до энергии 0,5 эВ дает: Ц/о (0,5) = 1,09 б,
7нб(0,5) =2,89 б. Отметим, что при вычислении о’с(Е'н) и 7i/0 по
параметрам уровней надо учитывать отрицательный уровень
(см. [32]): Ег=-—137 эВ, Г7=21,5 мэВ, £ГП — 720 мэВ. Его
вклад в Ос (Ен) и I\/v около 10 По-
следующая группа экспериментов — интегральные экспери-
менты по определению эффективного резонансного интеграла
277
Ь? Таблица 8.5. Распределение резонансного интеграла по группам
Номер группы Энергия, эВ Интервал летаргии Доля f.. % (чнс- ло уровней) ^нб (число уровней) ^нб (Р) (число уровней) 71/о(Е/> £/н> /нб’ 6 (суммар- ный)
24 0,465—1 0,7657 0 0 0 0,447 0,447
23 1—2,15 0,7655 0 0 0 0,30 0,30
22 2,15—4,65 0,7714 0 0 0,023(1) 0,545 0,568
21 4,65—10 0,7657 37,91 (1) 0 0 —0,251 —0,251
20 10—21,5 0,7655 17,96(1) 0 0,092 (3) —0,407 —0,315
19 21,5—46,5 0,7714 14,03(1) 0 0,002 (1) 0,466 0,468
18 46,5—100 0,7657 6,01(2) 0 0,061 (7) 0,068 0,129
17 100—215 0,7655 11,15(6) 0 0,046 (12) —0,052 —0,006
16 215—465 0,7714 3,49(10) 0,009(1) 0,086 (17) 0,002 0,097
15 465—1000 0,7657 4,0(21) О',012(1) 0,162 (43) 0 0,174
14 1000—2150 0,7655 3,42(42) 0,094(13) 0,1396 (70) 0 0,2336
13 2150—4650 0,7714 1,91 (45) 0,2557(61) 0,1485(89) 0 0,4042
12 4650—10 000 0,7657 0,12(4) 0,70 ( —•400) 0 0,70
Сумма 100 100(133) 1,80 ( -.700) 1,118 2,92
Таблица 8.6. Экспериментальные значения постоянных в формуле (8.6.1)
Резонансный поглотитель А В Погрешность Сф. % Интервал VsIm
и 4,21 26,5 3,5 0,25—0,65
ио2 5,55 26,0 3,5 0,3—0,9
Th 5,00 15,4 4,5 0,3—0,9
ThO2 5,79 16,0 4,5 0,3—0,9
для блоков урана во всем интервале энергии Е>0,5 эВ. В боль-
шинстве случаев эти эксперименты сводятся к определению ак-
тивации образцов, покрытых слоем кадмия, чтобы исключить
поглощение тепловых нейтронов. Геометрия образцов должна
быть'по возможности ближе к геометрии твэлов, используемых
в реакторе. Здесь приводятся результаты измерений для сплош-
ных цилиндрических образцов из урана, тория и их оксидов (для
оксидов М масса не только поглотителя, но и кислорода). Эф-
фективный резонансный интеграл записывается в виде (8.6.1).
Экспериментальные значения постоянных А и В приведены в
табл. 8.6 по данным [174] (в эти данные введена поправка в
связи с изменением резонансного интеграла золота, который ис-
пользовался в [174] в качестве стандарта: по [174] 7(Аи) =
= 1565(40) б, по [32] /(Au) = 1550(28)). Постоянная А учиты-
вает также и поглощение по закону l/v. Приведем значения по-
стоянных по [175]: для металлического урана А = 2,92; В = 25,6;
для оксида урана А = 4,11; В = 26,3 [погрешность 5 %; без уче-
та поглощения по закону l/v; введена перенормировка /(Au)].
Температурную зависимость резонансного интеграла целесо-
образно записывать так:
/эф(Л = А+в[1 + а -^--1)] <8-6-6)
поскольку слабое неблокируемое поглощение не должно зави-
сеть от температуры (см. § 8.2). В формуле (8.6.6) Т0=293 К,
а коэффициент а равен 0,125(10) для металлического урана и
0,155(10) для оксида урана.
Отметим, что часто (см., например, [174]) температурный
коэффициент относят к полному резонансному интегралу, а не
только к блокированной части, как это сделано в (8.6.6). При-
веденные здесь значения а получены пересчетом данных [174],
причем оказалось, что а не зависит от S/М в том интервале
значений, для которых выполнены эксперименты (см. табл. 8.6-
при другой записи температурный коэффициент зависит от раз-
меров блока).
Следующий уровень экспериментальных исследований — это
опыты на критических сборках. Сопоставление теоретического
279
и экспериментального критических объемов, а также отношений
активаций детекторов с различными спектральными характе-
ристиками позволяет проверить правильность всей совокупно-
сти констант и методов расчета. Как правило, из одного или
малого числа опытов нельзя однозначно определить, какая
именно константа нуждается в исправлении, если наблюдается
расхождение в критическом объеме между теорией и экспери-
ментом. Однако, проведя достаточное число опытов, можно ука-
зать такую константу или группу констант. Мы не будем по-
дробно освещать здесь эти вопросы.
Перейдем к изложению некоторых результатов численных
расчетов блокированной части резонансного поглощения (см.
[176—178]; аналогичные вычисления проводились и другими
авторами [179]).
"Эффективный резонансный интеграл определялся путем ре-
шения многогруппового интегрального уравнения переноса, запи-
санного в транспортном приближении (см. § 7.4) для энерге-
тической области Еп—ДЕ1<£<£'п-]-Д£,2, где Eri — положение
i-ro резонансного уровня; ДЕЬ &Е%— такие величины (в боль-
шинстве случаев ДЁ^ДЕг). что вне рассматриваемого интер-
вала поглощение слабое и его можно вычислять, как в случае
бесконечного разведения. Вычисления проводились для цилинд-
рического блока из металлического урана и цилиндрической
ячейки (с белым граничным условием, см. § 7.4). В большинстве
случаев замедлителем служила тяжелая вода, однако влияние
замедлителя на резонансный интеграл пренебрежимо мало —
это специально проверялось. Сечение поглощения и рассеяния
238U вычислялось по параметрам уровней (использовались дан-
ные [7]) в одноуровневом приближении с учетом эффекта Доп-
лера и интерференции потенциального и резонансного рассея-
ния (см. § 2.3).
Численно решая уравнения переноса, можно определить за-
висимость плотности потока нейтронов от координат. На
рис. 8.12 представлена зависимость плотности потока нейтронов
в замедлителе от расстояния до блока при энергиях нейтронов
6,6 и 4,6 эВ, т. е. вблизи первого резонанса (блок тяжеловодного
реактора с газовым охлаждением [180], радиус блока
6,3 см, радиус ячейки 14,8 см). Видно, что в плотности нейтрон-
ного потока имеется довольно глубокая «воронка». Наличие та-
кой воронки, однако, не означает, что нарушается гипотеза
«плоского потока» (см. § 8.1), которая требует постоянства не
полной плотности, а плотности только тех нейтронов, которые
движутся по направлению к блоку. Получающаяся в расчетах
воронка имеет характер «тени», т. е. ослабления плотности по-
тока за счет поглощения тех нейтронов, которые проходят че-
рез блок. Истинное отклонение от гипотезы плоского потока
должно обнаружиться в зависимости резонансного интеграла
280
от площади ячейки. Для обыч-
но используемых блоков такая
зависимость отсутствует (точ-
нее, для изолированного уров-
ня она заметно меньше 1 %;
см. ниже данные по интерфе-
ренции уровней).
Поучительно сравнить ре-
зонансные интегралы для не-
скольких первых уровней 238U,
полученных численным мето-
дом и по приближенным ана-
литическим формулам, приве-
денным в § 8.1, 8.2 (табл. 8.7).
При вычислении резонансного
интеграла данного уровня учи-
тывалось поглощение по зако-
Рис. 8.12. Распределение нейтронов
в замедлителе при энергиях, близких
к энергии первого резонансного уров-
ня 238U
ну 1/и, связанному с этим уровнем. Поэтому в резонансный инте-
грал включено поглощение не только вблизи Ег, но и во всей
области £>0,5 эВ. При вычислении учитывалась поправка
(8.1.66), а при вычислении температурной зависимости исполь-
зовалась формула (8.2.8) (в табл. 8.7 приведены данные для
температуры 293 К).
В табл. 8.7 приведены данные по уровням, составляющим
85 % блокированной части резонансного поглощения. Видно, что
поглощение первыми уровнями удовлетворительно описывается
Таблица 8.7. Сравнение аналитического и численного вычисления
резонансных интегралов для первых уровней 2381)
Ег, эВ р, см а I по формуле (8.1.66) I (Т) по фор- муле (8.2.8) / (Т) (числен- ный расчет) ^ан ^числ rt,
/ ’ 'и 1 ан
6,67 0,5 970 5,185 5,215 5,110 2,0
1,4 2720 3,281 3,287 з,ио 5,7
2,6 5050 2,512 2,514 2,297 9,5
20,9 0,5 1137 2,175 2,198 2,180 0,8
1,4 3185 1,374 1,379 1,353 1,9
2,6 5910 1,056 1,058 1,024 3,3
36,8 0,5 830 1,804 1,820 1,742 4,5
1,4 2330 1,147 1,150 1,120 2,7
2,6 4320 0,887 0,888 0,864 2,8
66,1 0,5 466 0,601 0,633 0,593 6,8
1,4 1300 0,371 0,377 0,386 —2,3
2,6 2420 0,280 0,282 0,300 —6,0
102,5 0,5 239 0,561 0,580 0,482 20
1,4 670 0,348 0,352 0,328 7,3
2,6 1240 0,264 0,265 0,261 1,5
189,7 0,5 66 0,315 0,334 0,192 74
1,4 186 0,194 0,198 0,134 47
2,6 345 0,146 0,147 0,111 32
281
Рис. 8.13. Зависимость резонансного
интеграла 238U и его температурной
поправки от энергии (для блока из
металлического урана радиусом
1,4 см)
простой теорией, изложенной
в § 8.1, 8.2. Большое расхожде-
ние имеется только для уров-
ня 189,7 эВ, который имеет
особо большое отношение Гп/Г,
и поэтому для него надо учи-
тывать резонансное рассеяние.
Суммарное отклонение анали-
тического расчета резонансно-
го интеграла шести уровней
(табл. 8.7) от численного со-
ставляет около 5% (для бло-
ка р= 1,4 см). Удовлетворительно описывается и температур-
ная поправка, однако роль этих уровней в температурной зави-
симости суммарного резонансного интеграла невелика.
Сравним результаты вычислений с экспериментальными дан-
ными. Вычисления проводились для радиусов блоков 0,5; 1,4;
2,6 см и температур 293, 500, 800 К. До энергии 2 кэВ учиты-
вались все уровни (всего 68 уровней; некоторое число слабых
уровней не обрабатывалось численно и учтено по приближен-
ной оценке; они дают вклад 0,7 % в суммарный резонансный
интеграл). Параметры уровней брались из [7]. В интервале
2<£<10 кэВ вычисления проводили по средним параметрам
(которые брались также из [7]). На рис. 8.13 дано отношение
ЦЕ)/I, где ЦЕ) — резонансный интеграл до энергии Е, а I —
до 10 кэВ и отношение температурных поправок
Д/ (Е) =• 7 (£' .Т)~7£-£’-г»Ц Т = 800 К, То == 293 К.
v ’ /(Г)—/(То)
Из рисунка видно, что если 80 % блокированного резонанс-
ного интеграла лежит ниже 200 эВ, то в температурную зави-
симость эта область энергии вносит только 27 %. Вообще нель-
зя указать сколько-нибудь узкую область энергии, которая бы-
ла бы ответственна за основную часть температурной зависи-
мости. В области £<6,7 эВ и между резонансами 6,7 и 20,9 эВ
резонансный интеграл возрастает за счет учета сечения, под-
чиняющегося закону 1/v.
Результаты вычислений могут быть аппроксимированы фор-
мулой
ЛФ=а+Д1 + «(/77- (8.6.7)
282
где
а= 1,16± (0,02);
5=26,4± (0,03) ±0,5;
а=0,119 ± (0,002) ± 0,005,
причем в скобках указана примерная ошибка аналитической
аппроксимации численных данных, а последнее число — погреш-
ность, связанная с неточностью параметров уровней. Если вме-
сто [7] принять данные [32], то окажется, что изменения ка-
саются главным образом двух первых уровней, причем сумма
2\fi уменьшается на 1,5 % > что приводит по (8.1.2) к <55 =
Г
=—0,4. Таким образом, использование новых данных, по
сравнению с расчетом [176], дает значение 5=26,0(3).
Сравнение этих результатов с формулой (8.6.2) и данными
табл. 8.6 показывает, что между вычислениями и измерениями
имеется вполне удовлетворительное согласие, причем погреш-
ность вычислений по параметрам уровней меньше, чем по-
грешность интегральных экспериментов (погрешность 5 в
табл. 8.6 для урана равна ±0,9). Погрешность численного сче-
та оценивается 0,2 % (без учета систематической погрешности,
которая связана с неточностью самой теоретической схемы, а
именно использование транспортного приближения и пренебре-
жение интерференцией уровней, см. ниже).
Величина а в (8.6.7) близка к сумме (см. табл. 8.5)
/i/b(0,5)-|-/h6(s)£< 2кэв=1,2 б. Поглощение р-уровнями прини-
малось в [176]: /Нб(р) = 1,38 б, т. е. суммарное неблокируемое
поглощение от 0,5 эВ до 10 кэВ получалось равным 2,54 б, что
на 0,35 б меньше, чем следу-
ет из табл. 8.5. Чтобы срав-
нить результат с коэффици-
ентом А в табл. 8.6, надо
учесть поглощение при £>
>10 кэВ.
Зависимость от энергии
сечения поглощения 238U
при энергиях больше 10 кэВ
показана на рис. 8.14 (см.,
например, [13]). Характе-
ризовать поглощение при
этих энергиях резонансным
Рис. 8.14. Сечение поглощения 238U при
больших энергиях
интегралом не совсем пра-
вильно, поскольку спектр
283
Т аблица 8-8. Параметры эффективного уровня
Номер группы Е, эВ Г„, ЭВ г7, эВ L ег, б
11 14880 315,8 16,73 131,8 0,171
12 5965 113 3,734 73,32 0,2688
13 3260 49,96 1,933 45,45 0,0643
14 1714 1,305 2,781 13,67 0,1365
15 872,8 0,643 1,059 11,45 0,1448
16 369,0 0,169 0,165 6,45 0,2782
17 169,6 0,775 0,0757 5,74 0,0501
Ферми здесь еще не установился (см. рис. 2.1). Если тем не ме-
нее вычислить резонансный интеграл I, б, то получим
1МэВ
/£>10кэв = С ° (Е) = 1,55.
j Е
10 кэВ
Таким образом, неблокируемая часть резонансного интегра-
ла /1/о(0,5), б, состоит из слагаемых:
/1/о (0,5)-|-/Нб (s)(р)10 кэВ) — 4,44 б,
что отличается от коэффициента А в табл. 8.6 на 0,23 б, или
на 5 %. Учитывая, что часть уровней, причисленных к небло-
кируемым, на самом деле на несколько процентов могут бло-
кироваться, следует признать, что согласие между интеграль-
ным экспериментом и расчетом по параметрам уровней весьма
хорошее.
Формула (8.6.6) дает резонансный интеграл во всей энерге-
тической области выше 0,5 эВ. Можно построить такие же фор-
мулы для более узких энергетических интервалов. Целесооб-
разнее, однако, особенно если иметь в виду программы, осно-
ванные на микроскопических константах (как, например,
программа TRIFON [160]), аппроксимировать совокупность резо-
нансных уровней, расположенных в данной энергетической груп-
пе, одним эффективным уровнем. Такая аппроксимация пред-
ложена в работе [181]. В табл. 8.8 представлены эффективные
параметры уровней в группах 12—17, полученные в [182] на
основе теории, изложенной в [181].
В качестве эффективных параметров использовались энер-
гия резонанса Е, нейтронная ширина Гп, радиационная шири-
на Г7, параметр L, определяющий доплеровское уширение по
формуле ^==Г/ДЕ, а также неблокируемое сечение о.
Данные табл. 8.8 получены для интервала: 20 6<(/cs)-1<
<200 б, где се — число ядер 23€U, 1024 см3. В других интер-
валах (/Cs)-1 эффективные параметры могут существенно изме-
284
Таблица 8-9. Интерференция резонансных уровней
Радиус бло- ка, см Уо V1 _ ДФ % ф • 1 Радиус бло- ка, см уо Vi _ДФ о/ Ф • /" Радиус бло- ка, см Vj _ 0/ ф ’ /»
d2o Гра- фит d2o Гра- фит d2o Гра- фит
1,5 0,125 1,45 1,48 2,0 0,125 2,14 2,22 2,5 0,125 2,9 3,13
0,0667 1,73 1,79 0,0667 2,58 2,84 0,0667 3,49 4,10
0,0417 1,99 2,15 0,0417 2,93 3,49 0,0417 3,87 4,97
ниться. Результаты расчета коэффициента размножения (и дру-
гих характеристик решеток) по программе TRIFON с исполь-
зованием эффективных уровней сравнивались с расчетами по
другим программам (главным образом с расчетами, выполнен-
ными методом Монте-Карло, см. подробнее [182]).
Неблокируемый резонансный интеграл /нб=2°^и» вычис-
I
ленный по данным табл. 8.8, отличается от данных табл. 8.5.
Различие объясняется тем, что при составлении табл. 8.5 ис-
пользовался определенный критерий неблокируемости [<тоХ
Х(Ег)<10 б]. Расчет по эффективным уровням табл. 8.8
может привести к резонансному интегралу, часть которого фак-
тически надо отнести к неблокируемому.
Вычисления в [176—178] проводились для отдельных уров-
ней, а затем суммировались резонансные интегралы по всем
уровням:
/=2Л- (8-6.8)
/
Фактически, однако, деформация потока, вызванная погло-
щением /-м уровнем, может повлиять на резонансное погло-
щение нижележащими уровнями. Для оценки этого эффекта
надо вычислить вероятность избежать резонансного поглоще-
ния каждым уровнем в отдельности ср/, а затем всеми уровнями
сразу <р2 и составить отношение
Дср/ср = (фЕ — [[ фЛ / П Ч> (8 -6.9)
\ j ! / j
Изменению Дер можно сопоставить изменение резонансного
интеграла
Д///=Дф/ф; <р = ехр (—ф). (8.6.10)
Результаты такого расчета [183] для трех нижних уровней
238U и различных ячеек приведены в табл. 8.9. Как и следо-
вало ожидать, Дф/ф<0 и растет по модулю с ростом радиуса
285
ячейки. Для графита эффект несколько больше, чем для тяже-
лой воды.
Расчет по пяти уровням (для р—2 и Vo/Vi = 0,0667) привел
к увеличению эффекта на 14 %!. Поэтому можно ожидать, что
полный эффект интерференции всех уровней несколько больше,
чем указано в табл. 8.9. Таким образом, вычисление полного
резонансного интеграла как простой суммы (8.6.8) завышает
резонансный интеграл на 2—6 %.
Пример интерференции между резонансными уровнями
различных нуклидов приведен в [184]. Среди продук-
тов деления имеется 133Cs (см. рис. 12.9), поглощающий
нейтроны главным образом в резонансной области. Глав-
ный уровень 133Cs, расположенный при энергии 5,9 эВ,
подавляется резонансным уровнем 238U при 6,7 эВ (см.
табл. 8.1). В результате эффективное сечение сизз уменьшается,
по данным [184], на 4—5%. Значение сп33 надо знать
с хорошей точностью, поскольку одним из способов из-
мерения интегрального потока в реакторе является измерение
отношения чисел распадов 134Cs и 137Cs в образце выгружен-
ного топлива (период полураспада 134Cs равен 2,06 года, а
137Cs — 30,2 года; 137Cs получается непосредственно при деле-
нии, a 134Cs — только при захвате нейтрона 133Cs). Прибли-
женно отношение числа распадов равно
t
Д13£ __ Д_ У133 N.34 ~ зз Г ф df^
-4137 2 yi3i Х137 J
0
где у — выходы (приблизительно одинаковые для изотопов
урана и плутония); — постоянные распадов; t — время пре-
бывания топДива в реакторе.
Для иллюстрации возможности численного расчета на
рис. 8.15 приведена зависимость плотности потока нейтронов
от летаргии, полученная по программе TRIFON [160], с явным
учетом всех резонансных уровней 238U в 16—21 группах. От-
метим всплески плотности нейтронного потока около уровней,
обладающих особенно большими нейтронными ширинами (£7=
= 189; 347 эВ и др.). Эти всплески объясняются тем, что мак-
симум резонансного рассеяния смещен относительно максиму-
ма поглощения в сторону больших энергий [см. (2.3.6)]. Резо-
нансное рассеяние на уране столь велико, что возникает зна-
чительное возрастание потока нейтронов с энергией меньше,
чем максимум рассеяния на величину скачка энергии при столк-
новении с ядром урана. При энергии Е^200 эВ величина это-
го скачка больше (или порядка), чем ширина опасной зоны
резонанса. Поэтому минимум и максимум потока не компен-
сируют друг друга. Неудивительно, что для таких резонансов
286
ф
Рис. 8.15. Пример зависимости плотности потока Ф от летаргии и=1п(1,05Х
ХЮ7/£) в блоке 238U 1 в замедлителе 2 (масштаб по шкале абсцисс нерав-
номерный)
изложенная в § 8.1 теория, по которой пренебрегается замед-
ление на уране, приводит к большим погрешностям (см. бо-
лее'общую теорию в [71]).
Сравним экспериментальные данные о поглощении в бло-
ках из оксида урана с теоретическими формулами, описываю-
щими влияние легких ядер на блокированную часть резонанс-
ного интеграла [см. (8.4.26), (8.4.28)]. На рис. 8.16 приведены
соответствующие результаты. По оси ординат отложено отно-
шение
а/ /ио ~ /тмеор
I ^ио2
(8.6.11)
где /ио2 — экспериментальное значение резонансного интеграла для
блока из оксида урана радиусом р; /^еор — экспериментальное зна-
чение для металлического урана с теоретическим учетом при-
сутствия легких ядер. Кривая 1 вычислена без учета столкно-
вений с кислородом. Кривая 3 учитывает столкновение с кис-
лородом, причем считается, что каждое столкновение выводит
нейтрон из опасной зоны. В соответствии с § 8.4 для этого блсь
кированную часть резонансного интеграла [т. е. второе сла-
гаемое в (8.6.1)] надо умножить на множитель, определенный
формулой (8.4.26) или (8.4.39). Кривая 2 вычислена так же,
как 3, но 2S заменено 2Эф по (8.4.28), где р8° — число ядер ура-
на в металле; р8 — в составе оксида. Из рисунка видно, что
кривая 2 почти вся лежит внутри полосы экспериментальной
погрешности ±3,5 %!. При малых радиусах различие между все-
ми кривыми несущественно. Прямоугольник на рис. 8.16 озна-
чает следующее: горизонтальные линии — полоса ошибок экс-
287
Рис. 8.16. Сравнение экспе-
риментального значения ре-
зонансного интеграла для
оксида урана с теоретиче-
ским значением в различных
предположениях
перимента, вертикальные — границы
радиусов измеренных блоков.
Ошибка отношения (8.6.11), если
измерения /ио2 и 7М независимы, рав-
на 3,5У2=5%. Однако при измерении
использовался один и тот же стандарт
(резонансный интеграл золота), не-
точность которого выпадает из отноше-
ния. Поэтому экспериментальная
ошибка отношения (8.6.11) равна
(3,5-М) %.
Рассмотрим теперь эксперименты
[185] по определению резонансного
интеграла для блока в виде полого ци-
линдра («втулки»), причем внутрен-
ний объем может быть заполнен раз-
личными замедлителями. Измерения
проводились для металлического ура-
на, внутренний диаметр во всех опы-
тах был равен 3 см, внешний диаметр
изменялся от 4,6 до 5,4 см. Внутренняя полость заполнялась воз-
духом, водой, графитом, магнием, висмутом. Значение резонанс-
ного интеграла 10 для втулки внешним диаметром 5 см с возду-
хом в полости являлось нормировочным. В табл. 8.10 приведены
разности, %:
(7/Л)) теор (7/7о) эксп-
(8.6.12)
Поглощение по закону 1 Ди включалось в резонансный интеграл,
а постоянные А и В брались из табл. 8.5. Расчет проводился по
формулам (8Д.1), (8.4.12), (8.4.14), (8.4.16).
Для тяжелых замедлителей использование формул (8.4.14),
(8.4.16) существенно улучшает согласие: если положить для
висмута 2эф=28, то получим, что разность (8.6.12) равна +8 %'.
Более точный численный расчет без использования равенства
(]//) = 1^/ увеличивает теоретическое значение резонансного
интеграла для тяжелых замедлителей на 1—2%, что улучшает
согласие теории с экспериментом.
Таблица 8.Ю. Экспериментальные и расчетные данные по резонансным
интегралам 238U полых цилиндрических втулок с замедлителем
Внешний диаметр» см Воздух Н2О Г рафит Магний Висмут
4,6 0,0(12) 2,0(17) —3,8(15) —5,3(15) —2,9(14)
5,0 — 1,7(15) 3,5(15) —2,4(15) -1,9(8) -2,6(8)
5,4 1,4(11) 0,4(12) — —1,8(10)
288
Таблица 8.11. Исходные данные для расчета резонансного поглощения
в кластерах
Число прутков Расстояние между центрами прутков, см Диаметр по и03, см Диаметр по покры- тию, см Масса на 1 см вы- соты, г sg, см2 Vj, См2 /1, СМ
7 1,89 1,48 1,7 122,8 15,99 4,09 0,306
19 1,89 1,48 1,7 333,4 27,33 13,08 0,406
27 1,5 1,18 1,36 301,2 26,21 11,58 0,327
Таблица 8.12. Экспериментальные и расчетные значения резонансного
интеграла в кластерах
Число прут- ков Воздух ню d2o
^экс ^теор т ^экс ^теор т ^экс Л-еор
7 13,8(3) 13,98 0,313 15,6(5) 15,41 0,0766 14,5(3) 14,44
19 12,1(3) 12,02 0,376 13,8(3) 14,70 0,0952 12,8(3) 12,78
27 11,8(3) 12,25 0,327 14,9(3) 15,24 0,0786 12,5(3) 13,06
О,
Теперь проведем сравнение теории с экспериментом для эф-
фективного резонансного интеграла твэла в виде пучка стерж-
ней (кластер). Экспериментальные данные имеются в [168].
В табл. 8.11 приведены основные исходные данные для расчета.
В табл. 8.12 приведены результаты измерений и вычислений
резонансных интегралов. При вычислении использовались фор-
мула (8.6.1) с постоянными для оксида урана из табл. 8.5 (по-
глощение по закону 1 /и исключено), а также формулы (8.4.29) —
(8.4.31). Для D2O использовалась формула (8.4.28); ее влияние
на результат: —(14-2) %.
Из табл. 8.12 видно, что между тео-
рией и экспериментом имеется достаточ-
но хорошее согласие.
Выше подробно рассмотрены экспе-
риментальные данные по резонансному
поглощению в 238U. Из других нуклидов,
резонансное поглощение в которых бло-
кируется, надо отметить в первую очередь
240Ри, затем 236U и 242Ри (см. гл. 13).
Почти все трансактиниды, появляющиеся
в реакторе при выгорании топлива (см.
гл. 13), имеют один главный резонанс-
ный уровень (см. Приложение IV), по-
глощение которым хорошо описывается
приближенной теорией, изложенной
в § 8.1, 8.2. Как правило, величина
О 0,1 0,2 0,3 Д',.см
Рис. 8.17. Зависимость
эффективного резонанс-
ного интеграла циркония
от толщины пластинки d
19—6053
289
a=lGrc, где с — концентрация ядер рассматриваемого нуклида,
не очень велика или даже порядка единицы. Тогда резонансное
поглощение можно определить с помощью рис. 8.4 и 8.5.
Из конструкционных материалов, используемых в реакторах,
надо отметить цирконий. Резонансный интеграл циркония ра-
вен ~ 1 б, и он складывается из поглощения несколькими изо-
топами. Главные уровни выделить затруднительно. В большин-
стве случаев можно воспользоваться экспериментальными дан-
ными [186, 187] по измерению эффективного резонансного инте-
грала пластинки в зависимости от ее толщины. Результаты
приведены на рис. 8.17 (средние из данных [186, 187]; погреш-
ность дана ориентировочно). Для толщины пластинки 4—5 мм
резонансное поглощение сильно блокируется. В этом случае для
пересчета к другой геометрии можно считать, что эффективный
резонансный интеграл обратно пропорционален I .
Глава 9
БЫСТРЫЕ НЕЙТРОНЫ
9.1. РАЗМНОЖЕНИЕ НА БЫСТРЫХ НЕЙТРОНАХ
Рассмотрим сначала простейший способ вычисления коэффи-
циента размножения на быстрых нейтронах, когда все нейтро-
ны, обладающие энергией выше порога деления 238U, объеди-
няются в одну группу. На рис. 1.10 штриховой линией показа-
но произведение f (Е) =<jf (£’)%(£'), где в/(Е) — сечение деле-
ния 238U; х(Е) — спектр нейтронов деления (1.2.1). Видно, что
f(E) имеет сравнительно узкий максимум, что и оправдывает
применение одногруппового приближения. Будем считать, что
каждое столкновение нейтрона с ядром замедлителя настолько
сильно уменьшает энергию нейтрона, что она оказывается ниже
порога деления 238U. Расстояние между блоками будем считать
достаточно большим (а^>/«), и поэтому можно рассматривать
изолированный блок урана.
В качестве групповых сечений надо взять средние значения
по спектру деления
а= J <j(E)%(E)dE, (9.1.1)
^пор
где %(£) — нормированный спектр деления (1.2.1); Епо? — по-
рог деления 238U.
290
В большинстве случаев можно считать, что рождение ней-
тронов, главным образом в результате делений 235U, вызванных
тепловыми нейтронами, происходит равномерно по объему бло-
ка. Тогда вероятность столкновения быстрого нейтрона внутри
блока Рс (см. § 1.10) является функцией только 2ф, где 2< —
полное макроскопическое сечение; р — радиус блока.
Пусть в результате деления в блоке возник один быстрый
нейтрон. Подсчитаем число нейтронов, вышедших из блока и
начавших процесс замедления. Вероятность для нейтрона выйти
из блока без столкновения равна
/о=1-Рс. (9.1.2)
Число нейтронов, вышедших из блока, если первоначальный
нейтрон испытал одно столкновение в блоке, равно
h = J4—+ ^ = ^ + ^ + ^ + 2^, (9.1.3)
где v8 — среднее число вторичных нейтронов при делении 238U;
2S — сечение упругого, а 21П — неупругого рассеяния. При
этом считается, что при неупругом столкновении энергия ней-
трона падает ниже порога деления, а при упругом столкнове-
нии, наоборот, совсем не изменяется [при упругом столкновении
с ядром урана максимальное изменение энергии равно 2%, что
мало по сравнению с шириной максимума кривой f(E) на
рис. 1.10]. Если в составе блока имеются легкие ядра, то сече-
ние рассеяния на них можно присоединить к сечению неупру-
гого рассеяния. Все сечения понимаются в смысле средних зна-
чений по (9.1.1).
Число нейтронов, вышедших из блока после двух столкно-
вений, равно
-Ц S,. \2 v8Sf4-Ss S,-n
8 ' s р 2 /1 _____р \ । 8 г 1 s р р
) с ' с с
(9.1.4)
OQ
и т. д. для произвольного числа столкновений. Сумма jn
п=0
равна коэффициенту размножения на быстрых нейтронах. Эта
сумма сводится к геометрической прогрессии, суммируя кото-
рую, получаем
[(v8-l)2f-ST]Pc
+ 2z-(v8Sz+2s)Pc
(9.1.5)
Для малых радиусов (р2/<^1) имеем (см. § 1.10):
«5
19
291
и поэтому
4
е=1 + [(^-O^-Sjp. (9.1.6)
О
Подставляя в (9.1.6) v8=2,8; of = 0,313; ov=0,06 [средние
в смысле (9.1.1)], получаем для металлического урана (р из-
меряется в сантиметрах).
е=1+0,032р. (9.1.7)
Из (9.1.6) видно, что при малых р величина е не зависит от
сечения рассеяния. В общем случае (9.1.5) 8 зависит от os, но
эта зависимость не очень существенна. Приняв [13] для сред-
них значений о5=4,2; о<=6,6, получим
Для гомогенной среды надо положить Рс=1. Тогда из
(9.1.8) находим 8=1,33, что не согласуется с результатами экс-
периментов: 8=1,173(2) (см., например, [44] и цитируемую там
литературу). Причина состоит в том', что в большом объеме
урана спектр нейтронов из-за неупругих столкновений стано-
вится более мягким и средние сечения изменяются (в основном
уменьшается среднее сечение деления). Отсюда следует, что для
больших блоков формула (9.1.8) должна завышать значение е.
Более точно коэффициент размножения на быстрых нейтро-
нах можно вычислить численными методами путем решения
многогруппового уравнения переноса*. Так же как в § 7.4, 7.5,
рассмотрим интегральное уравнение переноса в транспортном
приближении для цилиндрической ячейки (подробнее см. [188,
160]):
Ф,(г) = J^(r> г'ИФДг^ + ЗДНИг'; /=1,2,...,/?, (9.1.9)
где /— индекс энергетической группы; К/ (г, г')—ядро первого
столкновения в /-й группе (см. § 1.10, 7.4); Ss/ — сечение рассе-
яния (сумма упругого и неупругого рассеяний). Источники S,
складываются из трех составляющих:
Sj=Sje-]-Sif-\-Sjt, (9.1.10)
где Sje — источники, обусловленные делениями в группах ниже
n-й; S/f — источники делений, вызванных захватом нейтронов
в группах 1, 2, ..., п, т. е.
п
Sjf = ф»;
! = 1
* Можно, оставаясь в рамках одногруппового приближения, внести в тео-
рию уточнения, связанные с влиянием соседних блоков и отражением вы-
шедших из блока нейтронов от замедлителя. Такая теория построена в § 9.2
для определения эффективного сечения реакции (п, Чп).
292
%j— доля нейтронов спектра делений в j-й группе (предполага-
ется, что спектр нейтронов одинаков для делений, вызванных
нейтронами разных энергий); S/t— источник, связанный с пере-
ходами в данную группу из более высоких:
п—1
i =1
Источник
gi(r)=Sie+S!f=7jF(r)
будем считать нормированным, так что
= jF(r)dr=l,
(9.1.11)
(9.1.12)
т. е. в ячейке появляется один нейтрон, распределенный по
энергии по’закону (1.2.1) и по пространству с плотностью F(r).
Функцию F(r) в первом приближении можно считать пропор-
циональной плотности делений в тепловой группе и в случае
необходимости уточнить итерациями.
Напишем условие баланса для рассматриваемых п энерге-
тических групп [это соотношение может быть написано непо-
средственно, а может быть получено интегрированием уравне-
ния (9.1.6) с учетом нормировки ядра, см. § 7.4]:
x[<SeV>+<vSfOV>]=<S^OV>+<S"+1OV>+<SfOV>, (9.1.13)
где х — доля спектра нейтронов с энергиями больше Еп\ 2и+1 —
сечение перехода в энергетическую область ниже Еп', скобки
<> — суммирование по группам и зонам ячейки; V — объем зо-
ны. Условие (9.1.13) можно переписать так:
(SeV) = — (2ЙФУ)= 1— (vSfOV), (9.1.14)
%
где
Sg;-=Sc;.+2/.n+i+(i_XV/)2f/. (9.1.15)
Определим отношение числа делений, вызванных нейтронами
с энергиями выше и ниже Еп:
(^ФУ) ФИ)
S2s — 1 ~ XVe /£ ф|/\
— <sey>
(9.1.16)
Обозначим отношение числа нейтронов в ячейке с энергией
ниже Еп к числу нейтронов, возникших от делений в группах
ниже Еп, еф(Еп)
еФ(^) = —1— [(1—Х) (SeV) + (1-xXvS^V) + (2"+’ФУ)], (9.1.17)
W2' )
293
или, исключив Sn+I с помощью (9.1.15) и заменив Se по (9.1.14),
получим
(V — 1)2,—Sc (V—l)Sf—Sc„ , „
sq,(£„) = i+_<—ч=1+-—Ц—48, (9.1.18)
2g 2f
где черта означает среднее значение по энергетическим группам.
В формулах (9.1.17) и (9.1.18) величина <р(Еп) есть вероят-
ность избежать поглощения при энергии выше Еп. В прибли-
женном одногрупповом подходе, который был изложен выше,
полагали, что Еп равно порогу деления 238U, и вместо eq>(En)
записывали просто е, Если подставить в (9.1.18) значения по-
стоянных в одногрупповом приближении, то получим
е=1+0,62628. (9.1.19)
Располагая многогрупповой программой, которая дает пол-
ный баланс нейтронов при замедлении, нет нужды отдельно вы-
числять 8 и <р(Е'п). Однако расчет резонансного поглощения
в 238U с явным учетом блокировки большого числа уровней тре-
бует большого числа групп и, следовательно, большого времени
на ЭВМ. Значительно проще ограничиться вычислением группо-
вых потоков и баланса нейтронов в энергетической области £>
>10 кэВ, где блокировка уровней 238U не существенна, а резо-
нансное поглощение при Е<;10 кэВ опре-
Рис. 9.1. Теоретическая и
экспериментальная зави-
симости баз от шага ре-
шетки а (/) и от радиуса
блока из металлического
урана р (2)
делить по эмпирическим формулам. При
этом величина ыр(Еп) есть произведение
коэффициента размножения на быстрых
нейтронах и вероятности избежать резо-
нансного поглощения при замедлении до
энергии 10 кэВ. Поэтому при использова-
нии эмпирической формулы для эффек-
тивного резонансного интеграла надо ис-
ключить из нее резонансное поглощение
при энергии выше 10 кэВ, чтобы не учи-
тывать его дважды.
Многогрупповая программа учитывает
влияние на 8 многих факторов, опущен-
ных в приближенном одногрупповом под-
ходе: отклонения реального спектра в
ячейке от спектра нейтронов деления, за-
медления на ядрах, входящих в состав
блока, отражения нейтронов от замедли-
теля и возвращения их в блок, интерфе-
ренцию между соседними блоками. Кро-
ме того, многогрупповая программа учи-
тывает пространственные неоднородности
плотности потока при Е> 10 кэВ, которые
294
могут быть значительными для достаточно больших расстояний
между блоками, поскольку^ плотность замедления не успевает
выравняться по объему ячейки (см. § 2.2 и [188, 189]). Эта про-
странственная неоднородность вносит поправку в эмпирические
формулы для эффективного резонансного интеграла, зависящую
от шага решетки (эмпирическая формула была получена путем
обработки опытов на решетках с достаточно малым шагом, ко-
гда этот эффект несуществен).
В качестве примера использования многогрупповой програм-
мы [188] приведем результаты расчетов коэффициента размно-
жения на быстрых нейтронах для сплошного блока из металли-
ческого урана (замедлителем служила тяжелая вода; вычисле-
ния проводились до энергии 1,1 МэВ — практического порога
деления 238U). Полученные результаты можно аппроксимиро-
вать аналитической зависимостью (погрешность аппроксимации
порядка 0,001)
s= 1 +(3,36р — 0,235р2) 10-2+ 0,027ехр-у-), (9.1.20)
где р — радиус блока, см; а — шаг решетки (квадратной); /=
— 7 см для D2O. Первый член в (9.1.20) почти совпадает
с (9.1.7), последний дает представление о величине интерферен-
ции между блоками (а>/).
В многогрупповых расчетах учитывается также размножение
нейтронов по реакции (п, 2п.) на дейтерии или бериллии. Этот
эффект для D2O приводит к увеличению коэффициента размно-
жения на (1—2)-10-3 (он практически полностью компенсиру-
ется поглощением в кислороде при больших энергиях). Реакция
(п, 2п) на 238U дает незначительный вклад в реактивность
(около 1% 8—1).
На рис. 9.1 приведены результаты расчета по многогруппо-
вой программе [188] и экспериментальные [190]. Кривая 1 дает
зависимость fos от шага решетки (блок в виде кластера из 19
прутков с воздухом между прутками; в расчетах заменялся
сплошным блоком; замедлитель D2O); кривая 2 — зависимость
628 от радиуса блока (замедлитель D2O). Видно, что имеется
удовлетворительное согласие между теорией и экспериментом
(расхождение в 628^0,003 означает расхождение в коэффициен-
те размножения около 0,002).
9.2. РЕАКЦИЯ (п, 2п)
Сечение реакции (п, 2п) для 238U (см. § 1.8) изображено на
рис. 1.12. Там же штриховой линией изображено произведение
f(E)=an,2n(£)x(E), (9.2.1)
295
где %(h) — спектр нейтронов деления (1.2.1). Из рисунка вид-
но, что /(£) имеет сравнительно узкий максимум при энергии
7—9 МэВ. Поэтому можно использовать одногрупповое прибли-
жение. Поскольку погрешности сечения оп,2п довольно значи-
тельные (см. рис. 1.12), то более точное рассмотрение в боль-
шинстве случаев нецелесообразно. В дальнейшем под ап,2п бу-
дем понимать среднее значение по (1.8.1); Sn,2n— соответству-
ющее макроскопическое сечение.
Вычислим число реакций (п, 2п), происходящих в блоке то-
плива, если в нем происходит Nf делений. В первом приближе-
нии можно считать, что деления равномерно распределены по
блоку. Тогда вероятность столкновения нейтрона, родившегося
в блоке, равна Рс. Вероятность того, что при столкновении про-
изойдет реакция (п, 2п), равна отношению Sn,2n и если пол-
ное сечение усреднено по интервалу энергии 7—9 МэВ. Таким
образом, число реакций
(9.2.2)
Sf
Определим эффективное сечение оп,2п с помощью равенства
Л^=ап,2пФтУс, (9.2.3)
где V — объем блока; Фт — плотность потока тепловых нейтро-
нов; с — концентрация ядер 238U (или другого нуклида, для ко-
торого вычисляется о). Число делений в блоке равно Nf=
=Sf<DTV, где Sf определено в § 2.4 (Sf = OfC, где с — концентра-
ция делящихся ядер в блоке). Сравнивая (9.2.2) и (9.2.3), по-
лучаем
vSf
с 2„----Рс. (9.2.4)
Можно характеризовать реакцию (п, 2п) не эффективным
сечением ап,2п_, а эффективным резонансным интегралом Zn,27l.
Тогда вместо (9.2.3) надо написать
N=y~In,2n^iVc, (9.2.5)
где у — жесткость спектра, определенная (2.4.44). Тогда вместо
(9.2.4) получим [см. (2.4.44), (2.4.47); Р=1]:
vSf ЕЕ, I/
In 1П = ---- Рс°п = — — Рс 2П, (9-2.6)
И
где gSs — средняя замедляющая способность среды в ячейке;
V — объем блока; Vo — объем ячейки. Такая запись в некото-
рых случаях обладает преимуществом перед (9.2.4), поскольку
правая часть (9.2.6) не изменяется при выгорании ядерного то-
плива (это изменение переносится на у).
296
Учет упругого рассеяния и интерференции между блоками
приводит к замене Рс эффективной вероятностью Р. Так же как
в § 9.1, будем пренебрегать изменением энергии при упругом
столкновении с ядрами урана. При неупругом столкновении
энергия нейтрона изменяется столь сильно, что он выходит из
интересующего нас энергетического интервала. Вероятность
упругого столкновения равна (Ss/Sf)Pc, где Ss — среднее зна-
чение в интервале 7—9 МэВ. Вероятность столкновения однаж-
ды рассеянных нейтронов равна (Ss/Sf)Pc2, вероятность столк-
новения после двух упругих рассеяний равна (2s/Sf)2Pc3 и т. д.
Суммируя возникающую геометрическую прогрессию, получаем
вероятность столкновения нейтрона в данном блоке после про-
извольного числа упругих рассеяний
w0=Pc/(l—$Pc); (9.2.7)
а вместо (9.2.4) имеем
= ®0- (9.2.8)
В формуле (9.2.8) пренебрегается размножением нейтронов:
следовало бы заменить vSfx+Ss, где v — число вторичных ней-
тронов; Sf — среднее значение сечения деления; % — доля ней-
тронов спектра деления, приходящаяся на интервал 7—9 МэВ.
Так как % порядка 0,01, то размножение можно не учитывать.
Теперь проследим судьбу нейтронов, вышедших из блока.
Вероятность выхода как без столкновения, так и после произ-
вольного числа упругих столкновений равна
ЙУ0=1-Рс+рЛ(1-^)+(рРс)2(1-^)+ ... = (1-Рс)/(1- РРс).
(9.2.9)
Будем считать, что каждое столкновение с ядром замедли-
теля уменьшает энергию нейтрона ниже порога реакции (п, 2п).
Тогда вероятность пересечения границы второго блока равна
(1—Рс)(1—рРс)-’(1—Gi), а вероятность столкновения во вто-
ром блоке (см. § 8.1, где введены аналогичные величины Go и
Gi) будет
±zJk(i-Gi)G0. (9.2.10)
Во втором блоке также могут происходить упругие столкно-
вения, которые не выводят нейтрон из интересующей нас обла-
сти энергии. Вероятность столкновения во втором блоке равна
_ (l-PcHl-GxlGo
W1~ (1-PPC)2
(9.2.11)
297
Число нейтронов, вышедших из второго блока, равно
X-[l “Go + PG0 (1 -Рс) + ^?0.рРс(1 -Рс) +...]=
= (1 -Pc) (1 - GJ [1 - $РС - (1 -₽) Gol (1 - №сГ\ (9.2.12)
а вероятность столкновений в третьем блоке будет
йУ2=аУ1(1—GJ [Go+pGoPc4-pGo• ^Рс-РгД- ...]=u>i&, (9.2.13)
где
*> = (1-GO [1-PPC-(1-P) Go] (1-рРс)-1. (9.2.14)
Очевидно, что число столкновений в следующем блоке будет
содержать еще один множитель b и т. д. Общее число столкно-
вений во всех блоках, кроме первого, равно
(9-2Л5)
Используя равенство (см. § 1.10; /—средняя хорда блока)
G0=Si/(l—Рс), получаем
А = a Г1 + Г* . (9 2Д6]
1-VPJ L Gt 1-₽PC J V '
д = 2Д
Таким образом, вместо (9.2.4) или (9.2.8) имеем
vs, ~ ~ р; г ~
о„ s = а г„-----------Р, [ 2П ---------Ро гп (9.2.17
fir, т Hr Hl » Tit al I 5p r » lh ill/ \ ,
X/ X/ ]/0
где
P=—(9.2.18)
А определено (9.2.16). Если расстояние между блоками много
больше длины рассеяния в замедлителе, то А является малой
поправкой, и поэтому в ней можно использовать рациональное
приближение для величины Рс, т. е. Рс=а/(1+а). Тогда
а 1—Gt
!+«(!-₽) «(l-p) + G1
(9.2.19)
Если и для первого слагаемого (9.2.18) использовать рацио-
нальное приближение, то
а(1_₽)+С1 •
(9.2.20)
Для решеток с большим шагом величина Gi в (9.2.14),
(9.2.19) или (9.2.20) может быть вычислена по формуле (8.3.23).
298
Для решеток с малым шагом (по сравнению с длиной пробега
в замедлителе при энергии 7—8 МэВ) можно и для О1_приме-
нить рациональное приближение, когда 1—Gi=(l+/iSsi)-1;
~l1==lvm. В этом случае ,
р __ (9.2.21)
2/(1 — Р) + ^sivm(1 + I ^si vm)~1
где Ssi — сечение рассеяния в замедлителе; vm — отношение
объемов замедлителя и блока. Если 7—>0 при ym=const, то из
(9.2.21) получим
Р _--------------- (9.2.22)
2/—2V -4- 251 vm
— результат, справедливый для однородной смеси тяжелых
ядер и замедлителя (Р— вероятность столкновения с тяжелым
ядром с учетом того, что при упругом рассеянии нейтрон не вы-
ходит из интересующей нас области энергии). Формулы (9.2.17)
удобны для вычислений по программам, в которых входной ин-
формацией являются сечения, связанные с числом реакций фор-
мулами типа (9.2.3). С физической точки зрения интересно чис-
ло реакций (и, 2п) в ячейке, отнесенное к одному быстрому ней-
трону, возникшему в ячейке [см. (9.2.2)]:
NO=^LP. (9.2.23)
2/
Рассмотрим два примера. Вычислим оп, in для 238U в тяжеловодном
реакторе с газовым охлаждением: радиус блока 10 см, шаг квадратной ре-
шетки 39 см, металлический естественный уран занимает 15 % объема блока,
15 % объема блока занято магнием. Принимаем следующие значения по-
стоянных: о/и=6,3; <Ъи=3,5; <Т/ме=1; Ssi = 0,12; Ss0 = 0,025 (только уран);
2/о = 0,051. Точное значение Рс=0,409 (рациональное приближение Рс=
=0,505). По формуле (8.3.23) получаем 1—Gi = 0,0243; по (9.2.16) имеем
Д=0,015, т. е. влияние соседних блоков весьма мало (сильно гетерогенный
реактор). По (9.2.18) находим Р=0,544. Применение формулы (9.2.19) воз-
можно, поскольку Л мало, и тогда Д=0,012. По (9.2.20) Р=0,714, что на
31 % больше точного значения. По (9.2.21) Р=0,752, что на 38 % больше
точного значения.
Подставляя в (9.2.17) ап, 2п = 15,7-10-3 (см. табл. 1.15) и v2f для
естественного урана с плотностью 15 % плотности металлического урана, по-
лучаем (у=0,1, 628=0,05):
<т„, 2п=0,0126 б.
Другой пример—тесная решетка реактора ВВЭР-1000 [157]. Используя
данные по сечениям в первой группе (6,5—10 МэВ, см. [35]). находим (ра-
диус таблетки UO2 0,37 см):
Рс=0,088; Рс/ (1—Рс) = 0,091.
При этом считается, что упругое столкновение с кислородом выводит нейтрон
из интересующей нас области энергии. Фактически это не всегда так, по-
скольку среднее изменение энергии при таком столкновении около 1 МэВ.
Противоположное допущение, когда считается, что энергия нейтрона при
столкновении с кислородом не изменяется, увеличивает величину Рс/(1—Рс)
до 0,0925.
299
Величина A (9.2.16) равна 0,563, если упругое столкновение на кислороде
выводит нейтрон из области энергии 7—8 МэВ, и 0,742— в противоположном
случае. Таким образом, основное число реакций (п, 2п) происходит не в том
блоке, где возник первоначально нейтрон, а в соседних. При этом различные
предположения об упругом столкновении с кислородом приводят к несколько
различным результатам. Взяв среднее значение, получим для Р:
Р=0,74±0,1.
Применение формулы (9.2.21) для тесной решетки реактора ВВЭР не дает
большой ошибки Р=0,79.
Если концентрация 235U равна 4,4 %, то по (9.2.17) получаем (при этом
для оценки используется формула vaf=v[(jfпри f=0,95,
7=0,5, 62S=0,05; для более точного определения v2f надо получить баланс
нейтронов в ячейке, например, с помощью программы [160]) :
Стп, 2п=0,104 б,
что существенно больше, чем для предыдущего примера.
Большое значение оп, гп для реактора ВВЭР, по сравнению со значе-
нием ап, 2П в первом примере, связано главным образом с множителем
Если же сравнивать величины Л'о (9.2.23), то их отношение, равное
отношению Р, значительно ближе к единице: 1,36x0,18.
Глава 10
ДЛИНА МИГРАЦИИ И ЛАПЛАСИАН
10.1. КАЧЕСТВЕННЫЕ СООБРАЖЕНИЯ И
ДИФФУЗИОННОЕ ПРИБЛИЖЕНИЕ
В однородной среде длины диффузии и замедления опреде-
ляются формулами
L2=D^=(3^a)~\ (10.1.1)
‘ T=.D(gSs)-]U=(3S^)->U. (10.1.2)
_ В неоднородной среде можно ввести средние значения L2 и
т, которые определяют усредненную плотность потока нейтро-
нов и входят в гомогенизированные уравнения и условия кри-
тичности:
Z? = Z)(Sa)-’; (10.1.3)
г = ц(^)-1и. (10.1.4)
Среднее значение сечения поглощения (или увода) опреде-
ляются так:
— ^2а(г)Ф(г)4г
J - (10.1.5)
I Ф(г)4г
300
Если 2а в блоке и замедлителе не зависят от координат, то
2агФг Уг + 2аеФе Уе = 2 1 + ? 1
Ф/^+ФеУе ае 1
1 — с
(10.1.6)
то q и £ определены (7.2.6). При усреднении gSs можно считать,
что £=1:
gSs= (|Ss)e(l-c) + (gSs)iC. (10.1.7)
Что касается коэффициента диффузии, то можно предло-
жить два способа усреднения: усреднять коэффициенты диффу-
зии (длины рассеяния) или сечения рассеяния (точнее, транс-
портные сечения). Будем рассматривать ячейку, в которой как
блок, так и замедлитель однородны. При первом способе усред-
нения имеем Dr = (1~-с) Dg-^— , (10.1.8) 1 — С + с? 1
а при втором D, = 1~с + с^~1 . (10.1.9)
Очевидно, что в (10.1.9) можно привести переход к гомоген-
ному размешиванию, если размеры блоков стремятся к нулю
U=l):
Str— (1—c)Htre~lrCHtri,
(10.1.10)
а (10.1.8) при этом не дает правильного результата.
Перейдем теперь к более строгим, но все еще качественным
рассуждениям, которые покажут, что ни (10.1.8), ни (10.1.9) не
являются правильными способами усреднения.
Пусть размеры неоднородностей велики по сравнению с дли-
ной рассеяния, а поглощением нейтронов можно пренебречь.
Тогда плотность потока нейтронов в среде без источников удов-
летворяет уравнению и граничным условиям
ДФ = 0; = дФ(_дФ^ (Ю.1.11)
1 дп дп dt dt v ’
где n — нормаль; t — касательная к границе раздела сред i и е.
Уравнение и граничные условия (10.1.11) совпадают с урав-
нениями и граничными условиями для электрического потенци-
ала в диэлектрике, причем роль диэлектрической постоянной
играет коэффициент диффузии. Поэтому для определения сред-
него коэффициента диффузии в неоднородной среде можно вос-
301
пользоваться приемом, который хорошо известен в теории ди-
электриков [191].
Каждый блок в решетке реактора будем рассматривать как
«молекулу» диэлектрика, в которой под влиянием внешнего по-
ля индуцируется дипольный момент. Пусть блок имеет форму
сферы, цилиндра или пластинки, причем внешнее поле (вместо
градиента плотности нейтронного потока будем говорить об
электрическом поле Е) однородно. Поле внутри блока, помещен-
ного во внешнее однородное поле Е, равно [191] (для пластин-
ки и цилиндра речь идет о перпендикулярной составляющей
поля к поверхности пластинки или оси цилиндра):
Б‘-уу,Е- (ЮЛ.12)
где gj — диэлектрическая постоянная блока, т. е. отношение
D-ilDe, а п=3, 2, 1 для сферы, цилиндра и пластинки соответст-
венно. Блок будет поляризоваться, причем поляризация едини-
цы объема равна
Р^-^-Е^-^-------------^——Ее. (10.1.13)
4л 4л п— 1 + е,-
Если имеется не один блок, а много, причем концентрация бло-
ков с= VJ(Vi-\-Vе) не мала, то надо учитывать отличие сред-
него поля от «действующего» [191]:
ЕД = Е+— Р, (10.1.14)
п.
где Р—средняя поляризация среды [в теории диэлектриков
обычно рассматриваются сферические молекулы и в (10.1.14)
полагают п=3]. В то же время средняя поляризация среды рав-
на
Р = cP, =
Подставив Ед (10.1.14) в
р — сп 0г—1)
4л(я—l-f-s
1) g
4п(п—1 + ez) Д
(10.1.15), определим Р:
__Г1 с(ег— 1) '
i) Я—14-е/
(10.1.15)
Е.
(10.1.16)
Так как е=1-|-4лР/Е, то, заменяя g на D/De и е(- на Di/De,
получаем (другим способом этот результат получен в [192]):
D = De
(я—1) (Р,- — Ре)
(я—1)Ре-гО1
Dj-De
(Ч—
(10.1.17)
302
В частности, для цилиндрических блоков п—2 и из (10.1.17)
находим для коэффициента диффузии в направлении, перпенди-
кулярном оси цилиндра (эта формула применительно к диффу-
зии нейтронов в реакторе впервые была получена в [193]):
DJ- = P‘-Sr (10ДД8)
где р — коэффициент поляризации [с точностью до множителя
с/(2л) р является коэффициентом пропорциональности между
Р и Ед, см. (10.1.15)]:
Р=(Е—Ее)/(Е;+Ее). (10.1.19)
Для блоков в виде пластин коэффициент диффузии в пер-
пендикулярном направлении получим из (10.1.17) при п=1:
= <10л-20>
Теперь найдем выражение для коэффициента диффузии в па-
раллельном направлении. Запишем суммарный ток нейтронов
в ячейке по направлению вдоль оси цилиндра или поверхности
пластинки:
с п <ЭФ(- , ,, , п дФе \ сп дФ
S \cDi~^—+ U— c)De-~^- \=SDn —,
\ дг дг j дг
где S — площадь ячейки; ф— средняя плотность потока в ячей-
ке; Du — по определению, коэффициент диффузии в параллель-
ном направлении. Пренебрегая зависимостью плотности потока
от перпендикулярной координаты, получаем
D„ =De[l + c(®-l)], (10.1.21)
где
a^Di/De (10.1.22)
будем называть коэффициентом продольной поляризации.
Полученные формулы показывают, что в реакторе возникает
анизотропная диффузия (см. § 4.6). Но эти формулы нуждают-
ся в уточнении, поскольку предельный переход к гомогенному
размешиванию для сколь угодно малых блоков возникает толь-
ко для перпендикулярного направления в случае пластинчатых
блоков. В самом деле, из (10.1.20) следует
Ytr=C^tri+(l — C)^tre, (10.1.23)
что справедливо в случае сколь угодно малых блоков. Ниже по-
казано, что из более точных выражений для коэффициентов по-
ляризации следует при с <gc 1, предельный переход к малым бло-
кам во всех случаях. Введение вспомогательных понятий о ко-
303
эффициентах поляризации помогает учесть влияние блок-эф-
фекта на длину миграции. Рассмотрим эту задачу в диффузион-
ном приближении для диффузии в перпендикулярном направ-
лении и цилиндрических блоков. z
Прежде всего вычислим поле точечного диполя, т. е. рас-
смотрим два параллельных нитевидных источника мощностью
/ и —/, расположенных в точках Го и —г0 (эти векторы распо-
ложены в плоскости, перпендикулярной нитевидным источни-
кам).
Источники ±/ создают нейтронный поток
Gi(r)
! Г К- ( I г — го I \ w I ! г+ r0 I
2кОе[ЛЛ Le ) К Л
Пусть теперь г0 стремится к нулю, но произведение Р=
——2/|го], т. е. дипольный момент остается конечным. Если
г0<^г, то | г+Гц | =гТ/'о cos ф, где <р — угол между вектором г и
осью диполя. Поэтому
Gi{r, <р) =
Ki —
2"DeLe \ Le
COS ф.
(10.1.24)
Пусть теперь вместо точечного диполя имеется блок радиу-
сом р, причем вдали от блока градиент плотности потока постоя-
нен, т. е.
Фе=Сх=Сг cos <р; г->-оо.
Под влиянием этого внешнего поля в блоке индуцируется ди-
польный момент, так что плотность потока нейтронов вне блока
равна (здесь выписывается только та часть плотности потока,
которая пропорциональна cos <р; кроме того, имеется слагаемое,
не зависящее от угла ф):
Фе (г» ф) = Cr COS ф -j- Gt (г, ф) = (Сг
—— Кг
2nDeLe
— | COS ф,
К J J
(10.1.25)
где P — пока неизвестный дипольный момент блока. Вместо Р
можно ввести коэффициент поляризации р, определив его ра-
венством
P = 2^De^, (Ю.1.26)
где Ф — плотность внешнего потока, т. е. Ф=Сх. Тогда плот-
ность потока вне блока будет
фе (г, ф) = С р
---(-7—)] C0S ф»
\ / J
(10.1.27)
304
или при r^L,
Фе {г, ф) = С г
(10.1.28)
Плотность потока внутри блока (тоже только та часть, которая
содержит coscp) в диффузионном приближении равна
Фг(г, ф) = А1г (-J-) cos ф.
\ /
(10.1.29)
Граничные условия (2.1.54), (2.1.55) позволяют определить
коэффициент р:
Рис. 10.1. Поведение слагае-
мого плотности потока ней-
тронов, пропорционального
cos <р (при ф=0 и 180°) в
блоке и вблизи него
где
^ = -^-(220-1) (10.1.31)
и Qo определено (2.1.66).
Величина Xi имеет простой смысл — она является граничным
коэффициентом первой гармоники (т. е. части потока, пропор-
циональной costp) внешнего нейтронного потока:
р-^ = Я1Ф1; ^=-^-±1. (10.1.32)
dp 1 — р
Таким образом, зная коэффициент поляризации р (не обя-
зательно в диффузионном приближении), можно определить
граничный коэффициент для первой
гармоники. При Q0=l (10.1.30) пе-
реходит в (10.1.19).
Коэффициент р определяет, на-
сколько возмущается блоком пер-
вая гармоника внешнего поля. На
рис. 10.1 штриховой линией показа-
но продолжение внешнего поля вну-
три блока, а сплошными — диффу-
зионное распределение плотности
потока внутри блока (напомним,
что Ф описывает только то слагае-
мое плотности потока, которое про-
порционально cos<p; плосксоть чер-
тежа разрезает блок по линиям
<р=0 и <р= 180°; принято р = Т( =
= С=1, р=1/2 и р= —1/2). При
20—6053 305
₽>0 средний градиент плотности потока внутри блока меньше,
чем у внешнего поля, при ,р<0, наоборот, больше. В § 10.2 при-
ведены более точные формулы для коэффициентов поляризации
и проанализировано влияние коэффициентов поляризации на
длину миграции.
10.2. ДЛИНА МИГРАЦИИ
Можно дать несколько определений длины миграции в ге-
терогенном реакторе. Мы примем определение, основанное на
условии критичности реактора. Если эффективный коэффициент
размножения однородного гетерогенного реактора можно запи-
сать в виде
где а®, а2^ — параллельная и перпендикулярная каналам компо-
ненты геометрического параметра, то величины А4ц и —Дли-
ны миграции в параллельном и перпендикулярном направле-
ниях.
Как показано в [86], из теории гетерогенного реактора вы-
текают следующие результаты (см. также [194]; основная идея
сформулирована в гл. 11, конкретные вычисления см. в [86]).
Длина миграции в параллельном направлении определяется ра-
венствами
+г„; (10.2.2)
С
Q 4" " © <7гом
^11 = ---------------L/; (10.2.3)
1 +q
г = (1 r——F(.c), (10.2.4)
где Le2, Хе относятся к чистому замедлителю; со, со — коэффи-
циенты продольной поляризации блока для тепловых и замед-
ляющихся нейтронов [в диффузионном приближении (10.1.22),
более точные формулы см. ниже]; величины q, дГОм, eg, с, F(c)
определены в § 7.2 формулами (7.2.6), (7.2.7), (7.2.16).
Длина миграции в перпендикулярном направлении опреде-
ляется равенствами
М\ + ДЛ42; (10.2.5)
4 = (Ю.2.6)
1—с
306
V
(1_С)(1+<Ч)
(10.2.7)
= 1 + Рс -= 1 +рс
1 — Рс ’ 1 — рс ’
(10.2.8)
где р, р — коэффициенты поперечной поляризации блоков для
тепловых и заземляющих нейтронов [в диффузионном прибли-
жении (10.1.30), (10.1.31), более точные формулы см. ниже].
Поправочный член ДЛ42 зависит от характеристик как тепловых
нейтронов, так и замедляющихся. Для незамедляющего блока
АЛ42 равно [86, 195]:
ДЛ!2
где
-----Р Р _ 21 р _ . CL—PH1 Р) + р) 21 (10.2.9)
(1-Рс)(1-Рс) 2 и (1-рс)(1-рср 4 ’ 1
р = (1-с) 1
с(1 + Р—2Рс) р .
(1-рС)(1_с)2
(10.2.10)
а коэффициент pi в диффузионном приближении равен
;i = 22l(q0_ 1). (10.2.11)
Поправка АЛ!2 содержит множитель р2/4. Величина поряд-
ка р2/4 является естественной границей точности рассматривае-
мой теории. В (10.2.9) собраны главные члены такого порядка.
Теория, развитая в [86], не учитывает поглощение нейтро-
нов при замедлении. Если это поглощение не сильное, то его
можно учесть, вводя в формулы (10.2.2), (10.2.5) множители
по аналогии с результатом, который получен в § 3.2, 4.6 для
гомогенного реактора [см. (4.6.12)]:
Л!^| — (1 — Wf) -J- 11| <pj Л!= £,д_ (1 — Wf) -|- 'c_lcP ‘-,-4!2.
(10.2.12)
При этом, как отмечалось в § 4.6, коэффициент размножения
должен определяться по (4.6.11), т. е. для бесконечной среды
(без утечек) или, если иметь в виду гетерогенный реактор, для
ячейки с граничным условием Ф'(/?)=0 на ее внешней поверх-
ности. При других определениях коэффициента размножения
множители при L2 и т, связанные с поглощением замедляющих
нейтронов, могут иметь другой вид (см. § 3.2, 4.6). В дальней-
шем анализе формул для длины миграции положим Wf=0 и
<р=1.
20* 307
Формулам (10.2.3), (10.2.6) соответствуют средние значения
коэффициентов диффузии (см. (10.1.3) и (10.1.6); для замед-
ляющихся нейтронов надо положить £=1 и заменить со, р на
со, р; поправочным членом ДЛ12 пренебрегаем):
£> = 1 1) D (10.2.13)
Dj_ = Dev(\ — с + Л~Т'- (Ю.2.14)
Прежде чем обсуждать более точные по сравнению с диф-
фузионным приближением методы вычисления р и со, надо по-
смотреть, какова по порядку величины поправка к простым спо-
собам усреднения (10.1.8), (10.1.9). Очевидно, что разница меж-
ду различными способами усреднения будет возрастать при уве-
личении с и различия в коэффициентах диффузии замедлителя
и блока. В этом смысле хорошим примером является тяжеловод-
ный реактор с газовым охлаждением [86, 180, 195], для кото-
рого с=0,19, J]fre/Scrz=2,5, р = 0,498, р=0,336. Для этого при-
мера имеем [£>i и £>2 определены (10.1.8), (10.1.9)]:
= 0,89; D2/D± = 0,82, (10.2.15)
т. е. погрешность простого усреднения составляет 11 —18 % , при-
чем усреднение длин рассеяния дает несколько лучший резуль-
тат. Для замедляющихся нейтронов имеем
Йх/Д± = 1,06; DJDl = 0,97, (10.2.16)
т. е. погрешность меньше и лучший результат дает усреднение
сечений. Следовательно, существенную роль играет блок-эф-
фект, который для замедляющихся нейтронов отсутствует, а для
тепловых достаточно велик (£=1,7).
Разность перпендикулярной и параллельной длин диффузии
равна
Для упомянутого выше реактора имеем
L2JL\ = 1,144,
однако если в (10.2.17) не учитывать блок-эффекта, т. е. поло-
жить £=1, то знак анизотропии изменится. Для длины замед-
ления получим
т,— т----------------------------со +1\ (10.2.18)
1 II (1 — с)(1 + сг) рс )
308
и
= 0,86.
Поскольку анизотропии длины диффузии и длины замедле-
ния имеют разный знак, результирующая анизотропия длины
миграции в этом примере оказывается незначительной, несмот-
ря на большой размер блока и большую разность коэффициен-
тов диффузии замедлителя и блока.
Величина ДМ2 (10.2.9) порядка р2/4, что для рассматривае-
мого примера составляет 10 см2, или 3 % М2±. Можно уточ-
нить возрастное приближение учетом первого пробега [см.
(2.2.78), (2.2.79)]. При этом оказывается [86], что получаю-
щаяся дополнительная поправка состоит из двух слагаемых раз-
ного знака и поэтому чувствительна к значению констант для
быстрых нейтронов. По порядку величины она равна р2/4. По-
этому, чтобы надежно вычислять поправки порядка р2/4 к дли-
не миграции, необходимы численные многогрупповые расчеты,
при которых учитывалось бы влияние гетерогенной структуры
реактора на перемещение нейтрона, испытавшего несколько
столкновений. Особенно большую роль этот эффект должен
играть для реактора РБМК [196], замедлителем в котором слу-
жит графит, а теплоносителем — кипящая обычная вода, и зна-
чительная часть замедляющей способности среды определяется
водой внутри тепловыделяющей кассеты.
Пусть погрешность коэффициентов поляризации есть 6р и
бсо. Определим возникающую из-за этого погрешность в дли-
нах диффузии:
_ 2сар = с
л2± 1-Рас2 ’ л2 (1-с)К
Аналогичные формулы справедливы для и (если
С = 1). Пусть с — 0,2, £ = 1,6. Тогда
6V2 г. . 8Л,,
—=L_ = 0,488; ---L = 0,168®.
L2 /2
Чтобы определить погрешность величин р и ®, надо
между собой (и, если возможно, с экспериментальными резуль-
татами) значения ip и ®, полученные разными методами. Здесь
мы ограничимся формулами в Р2-приближении (подробности
см. в [86]; более точные методы см. в [130]). Использование
результатов Р2-приближения удобно в том отношении, что ис-
тинное значение р и ® находится между результатами Pi- и
Р2-пр"иближений.
(10.2.19)
положить
сравнить
309
Коэффициент продольной поляризации и определяется в Р2-
приближении формулой
I. \ J
U \ Zjq / J
(10.2.20)
где
xi Л>(*() . д _ хе Кр(хе).
2 7j(xt-) ; е 2 К^Хе)’
ч = (5SzrMsM)I/2p; 2i>e=(Ss + 2flb; s^tri/2tre-\ (Ю.2.21)
Q=Qofi + 4
\ 5
Qo определено (7.2.25), a D и L — (7.3.1), (7.3.2). Формула
(10.2.20) сильно упрощается, если можно пренебречь поглоще-
нием (Sai = 0, Q=QO=1):
(0 = ±[1-
(1-S)8
Д(- -f-
(10.2.22)
Если размер блоков стремится к нулю, т. е. х(>е^1, то Д,=
= 1, Де=0 и
(о = 2—з. (10.2.23)
Подставив (10.2.23) в (10.2.13) и положив £=1, получим
при £<С 1:
ftr={l-c)^tre+c^tri, (10.2.24)
т. е. выполняется переход к гомогенному случаю (чего не было
в Pi-приближении). Для пустых каналов имеем
со=2+Де, (10.2.25)
в то время как в диффузионном приближении го = оо. Из
(10.2.25) следует для пустых каналов
Dn =De[l +с (со— l)] = De[l +*(1+A,)1- (Ю.2.26)
Коэффициент поперечной поляризации р в Р2-приближении
определяется следующим образом (эта формула записана не-
сколько иначе, чем в [86]; отметим опечатку в [86]: в формуле
(7.90) 2Qo-H надо заменить на 2Q0—1):
р = + , (10.2.27)
1 + «' +®2
310
где
s'= s (2Q0—1)~’;
8i = A"1 KQo- *) (* - l)(2Qo -1)"1 + GA (Hl;
32 = A-1 [Qo (s - 1) (2Q0 —)-’ 4- САг (s')];
A=^ + sAe; C = A£ (1--J-V
A (s') = (14-Ae)[(l-A.) (1—s')—(Qo—1) (1-s) (2Q0— 1)-].
A2 (s') = Ax(- s') + Qo (2Q0 - I)"1 - Дг - s' (2 - At - Qo),.
причем A;, Ae, Xi, определены (10.2.21), Qo — (7.2.25), L —
(7.3.1).
Формулу (10.2.27) можно применять и для пустых каналов,
когда s=s'—Xt=O:
(10.2.28)
(10.2.29)
(10.2.30)
(10.2.31)
2+ Ае
вместо (3=1 в /^-приближении. Если радиус блока стремится
к нулю, то Ае=0, Д(= l+x(-2/8. Тогда из (10.2.27) получим (в
[86] имеется опечатка: пропущен множитель 1/2):
р = А(1 -S).
Подставив этот результат в (10.2.14), получим при £=1:
G / Sf»-/
1 —-- 1 — —~
SV 2 \ ^tre
tr —^tre ~ ~ «
1 -1— 1 —-^£L
2 \ ^tre
Если выполнено неравенство (с/2)[1—<1, то
(10.2.31) переходит в формулу для гомогенной смеси.
Интерполяция между Р\- и Рг-приближениями
₽ = (1-а)рРх + а₽Р2 (10.2.32)
приводит к весьма точным результатам. При этом а>0,5, по-
скольку приближение Р2 является более точным. Сопоставле-
ние (10.2.32) с результатами, которые получены по методу ба-
ланса [86], показывает, что (10.2.32) при а—2/3 имеет погреш-
ность не более 2—3 %.
Для пустых каналов
щая хорошей точностью
существует очень простая и обладаю-
интерполяционная формула [197]:
= — 1+2pSfre . (10.2.33)
2 1 +?Ztre ’
Формула (10.2.32) при а=2/3 совпадает с (10.2.33) с по-
грешностью 0,2 % при (£>±/Де)<2.
311
Для пустых каналов выполнено большое количество экспе-
риментов по определению средних коэффициентов диффузии
[198, 199] (более старые экспериментальные работы по диффу-
зии в неоднородных средах цитируются в [200]).
Формула (10.2.32) и аналогичная формула для со
— =(1—. а)(-Ц +а(—) (10.2.34)
Ш \ “ JP1 \ W / А
при а=2/3 вполне удовлетворительно согласуются с экспери-
ментальными данными. В приближении Pi для пустых кана-
лов 1/со=О. В [86] рекомендуется использовать в (10.2.34)
<2=3/4; однако после уточнений в обработке экспериментальных
данных, которые указаны в [199, 201], значение а—2/3 лучше
согласуется с опытом. Формула (10.2.34) для пустых каналов
дает более точный результат [86], чем широко используемая
формула Биренса [202] (вывод этой формулы см. в [200, 130];
такие же результаты были независимо получены В. С. Фурсо-
вым и С. Л. Соболевым в 1948 г., см. цитаты в [203, 199]):
Ои=Ое[14-С(1+2рад]. (10.2.35)
Точность формул (10.2.32), (10.2.34) такова, что погреш-
ность в М2 в этой модели [см. (10.2.19)] не более 1 %. Значи-
тельно большая ошибка может возникнуть из-за того, что в
двухгрупповом подходе неточно учитываются процессы при
больших энергиях, когда пробег нейтрона сильно зависит от
энергии. Кроме того, реальные блоки обычно неоднородны и
замена их однородными со средними значениями концентраций
ядер может вносить некоторую погрешность. Наконец, поправ-
ка, связанная с поглощением и размножением нейтронов при
замедлении [см. (10.2.12)], получена в гомогенном приближе-
нии. Все эти погрешности можно существенно уменьшить при
численном решении задачи. Численным методам в теории гете-
рогенного реактора посвящена монография [130].
Другие теоретические подходы к диффузии нейтронов в не-
однородных средах изложены в [200, 204—207].
10.3. ЗАВИСИМОСТЬ КОЭФФИЦИЕНТА РАЗМНОЖЕНИЯ И
ЛАПЛАСИАНА ОТ ШАГА РЕШЕТКИ И РАДИУСА БЛОКА
Теория, развитая в гл. 7—10, позволяет учесть влияние гетерогенной
структуры реактора на параметры, входящие в гомогенизированные уравне-
ния и определяющие критические размеры. Решетки современных ядерных
реакторов имеют сложную структуру и характеризуются многими параметра-
ми. Однако в первых опытах по осуществлению цепной ядерной реакции деле-
ния решетка была максимально простой: блоки в виде однородных цилиндров
из металлического урана, заключенные в тонкую защитную оболочку из алю-
миния. Такую решетку характеризуют три параметра: шаг решетки, радиус
блока, толщина оболочки. Если фиксировать толщину оболочки, то остается
312
Рис. 10.2. Зависимость k™ от шага ре-
шетки а и радиуса блока р для тяже-
ловодной сборки с естественным ура-
ном (при I % Н2О; штрихованной ли-
нией показана кривая для р= 1,4 см
при 0,1% Н2О)
Рис. 10.3. Зависимость лапласиана а2
от шага решетки а и радиуса блока р
для тяжеловодной сборки с естествен-
ным ураном (при I % Н2О; штрихо-
вой линией показана кривая для р=
= 1,4 см при 0,1% Н2О)
два параметра. В то время, когда проводили первые опыты, было очень важно
получить зависимость коэффициента размножения и лапласиана от этих пара-
метров, чтобы выбрать оптимальные их значения (например, дающие мини-
мальный объем реактора или минимальную критическую массу).
В настоящее время такие зависимости имеют значения для планирования
эксперимента иа критических сборках, которые ставятся в целях проверки
всей совокупности констант и методов вычислений. Чтобы погрешность вы-
числений была минимальной, необходима максимально простая сборка: блок
простой конструкции, однородная решетка без отражателя. Проведя доста-
точное количество опытов на критических сборках, которые по возможности
сильнее отличаются друг от друга по шагу и радиусу блока, можно уточнить
ряд фундаментальных характеристик, таких, как число вторичных нейтронов,
резонансный интеграл 23SU, длина миграции и др. Обычно кроме критического
объема и распределения плотности потока нейтронов по объему измеряются
различные спектральные характеристики: активация детекторов с различными
зависимостями сечений от энергии (например, 235U, Lu, Dy, отношение числа
делений выше и ниже порога деления 238U и т. д.).
Рассмотрим качественно зависимость и а2 от шага решетки и радиуса
блока. При увеличении шага решетки, если радиус блока фиксирован, падает
резонансное поглощение и растет поглощение в замедлителе, т. е. <р растет,
а 0 падает. Поэтому при некотором значении шага решетки k^, имеет макси-
мум. С ростом радиуса при фиксированном шаге уменьшается ср, а 0 и е
растут. Поэтому к™ растет с ростом радиуса, если шаг решетки большой, ср
близко к единице и главную роль играет изменение 0. Наоборот, при малом
шаге, когда главную роль играет изменение ср, коэффициент размножения
уменьшается с ростом радиуса.
На рис. 10.2 приведена зависимость от шага а при разных радиусах р
для решетки из металлического естественного урана и тяжеловодного замед-
лителя. При этом толщина защитной оболочки из алюминия равна 1 мм,
313
примесь обычной воды составляет 1 % и только для радиуса 1,4 см 0,1 %.
Из рисунка видно, как сильно влияют на малые примеси простой воды
в тяжелой.
Величина а2, определяющая критический размер реактора без отражате-
ля, зависит от длины миграции, которая возрастает при увеличении шага за
счет роста Л2 (т падает с ростом шага за счет незначительного изменения
. Поэтому максимум кривой а2 (а) сдвигается в сторону меньших шагов,
по сравнению с кривой А’™ (а). На рис. 10.3 приведена серия кривых а2 (а)
при разных радиусах блока (те же условия, что иа рис. 10.2). Максимальные
значения а2 соответствуют решетке, имеющей минимальный объем. Для тя-
желоводной сборки иа естественном уране оптимальной решетке соответст-
вует шаг 13—14 см и радиус блока 1,4 см. Объем критической сборки в виде
цилиндра без отражателей равен 6,7—7,2 м3 (цилиндр при этом имеет опти-
мальное отношение высоты к радиусу, см. § 4.1).
Тяжеловодная сборка является наиболее удобным инструментом для про-
верки констант с помощью интегральных экспериментов. Это связано с тем,
что замедлитель жидкий и ему легко придать форму идеально правильного
цилиндра, практически полностью заполненного однородной решеткой, шаг
которой легко изменять. Размеры тяжеловодной сборки достаточно велики,
так что неточности в положении экстраполированной границы играют малую
роль. Кроме того, сравнительно большое значение шага решетки позволяет
определить лапласиан не только из геометрических соображений, когда надо
учитывать поправки на небольшой, но все-таки всегда имеющийся отража-
тель, но и путем измерений распределения плотности потока нейтронов по
высоте и радиусу сборки.
Глава 11
ТЕОРИЯ ГЕТЕРОГЕННОГО РЕАКТОРА
11.1- ГЕТЕРОГЕННЫЙ РЕАКТОР С МАЛЫМИ БЛОКАМИ
Основная идея теории гетерогенного реактора состоит в пред-
положении, что каждый блок топлива может быть охаракте-
ризован некоторым количеством постоянных, определяемых
только свойствами данного блока, т. е. не зависящих от свойств
и расположения остальных блоков. Это предположение позво-
ляет разделить теоретическое описание реактора на две части:
1) определение постоянных, характеризующих данный блок;
2) определение свойств совокупности блоков с заданными по-
стоянными. Такое разделение задачи существенно упрощает тео-
рию *.
Сформулированное предположение выполняется, если длина
рассеяния нейтрона в замедлителе много меньше расстояния
между блоками:
lse = ^7e (11.1.1)
* Такая постановка задачи была сформулирована Л. Д. Ландау. Первое
систематическое изложение теории гетерогенного реактора содержится в не-
опубликованной рукописи А. И. Ахиезера и И. Я. Померанчука [208].
314
Фактически требуется выполнение неравенства ехр (—Ssea) С
<1 и поэтому практически достаточно выполнения более сла-
бого условия
Ъ7е<а. (11.1.2)
Начнем изложение с теории гетерогенного реактора с ма-
лыми блоками [86, 125, 195, 209, 210]. Под малыми блоками
будем понимать блоки, размеры которых р много меньше рас-
стояния между блоками (для цилиндрических блоков, которы-
ми мы ограничимся, р — радиус блока):
р,<а. (11.1.3)
Если блок имеет достаточно малые размеры, то плотность
потока нейтронов на поверхности не зависит от азимутального
угла (для бесконечно высокого реактора не зависит и от коор-
динаты г) и можно говорить просто о плотности потока ней-
тронов на данном блоке.
Рассмотрим идеальный реактор на тепловых нейтронах, в ко-
тором замедляющиеся нейтроны не поглощаются. В таком ре-
акторе блок характеризуется двумя постоянными: постоянной
размножения tj*, которая равна числу быстрых нейтронов, рож-
денных в блоке k при поглощении им одного теплового нейтро-
на, и тепловой постоянной уь равной отношению числа ней-
тронов, поглощенных блоком в единицу времени /*, к плотно-
сти потока нейтронов на его поверхности:
Т*=Л/Ф*. (Н.1.4)
Основное уравнение гетерогенного реактора сформулируем
с помощью двух функций Грина Gf(r, г') и Gs(r, г'). Под
Gf(r, г') будем понимать поток тепловых нейтронов в точке г,
возникший от единичного источника быстрых нейтронов в точке
г'; под Gs(r, г') — поток тепловых нейтронов в точке г, возник-
ших от единичного точечного источника тепловых нейтронов в
точке г'. Если в точках гк расположены блоки, обладающие ха-
рактеристиками г]* и y.k, то в точке г под влиянием этих источ-
ников возникнет поток нейтронов плотностью
Ф(г) = Ж^ (г, rk)-Gs(r, гА)]ЬФ6, (11.1.5)
k
где Ф* — плотность потока нейтронов на поверхности блока k,
центр которого расположен в точке г*. Пусть в (11.1.5) г стре-
мится к точке на поверхности блока k. Тогда
Ф*= 2Ж гй,)Ф;г', (И.1.6)
k'
где ядро Н (гъ гй,) равно
н (гь rk,)~Gs(rk, г,,)], (И.1.7)
315
причем под Gs(rk, щ) понимается значение Gs(r, rk), если точ-
ка г расположена на поверхности блока k [такую оговорку не-
обходимо сделать, поскольку для цилиндрического блока Gs(r,
г')->°о при г-н-'].
Равенство (11.1.6) является системой линейных однородных
уравнений относительно Ф*. Приравняв детерминант этой си-
стемы нулю, получим условие существования нетривиального ре-
шения, которое с физической точки зрения является условием
критичности. Оно связывает постоянные г]^, уь с параметрами,
входящими в функции Gf и Gs. Систему (11.1.6) можно записать
в матричной форме:
Ф=ЯФ, (11.1.8)
где Ф — вектор, компоненты которого равны Ф/г, а матричные эле-
менты Hkk> равны Н (rft, rfeI). Условие критичности имеет, очевид-
но, вид
det (7? —1) = 0. (11.1.9)
Если выполнено условие (11.1.1), то для большей части ячей-
ки справедливо уравнение диффузии. Поэтому для определения
функций G можно воспользоваться формулами (2.1.35) и
(2.2.66). Тогда ядро (11.1.7) запишется так:
Н (г*> >» = [~2“ ехР (ту) х
(11.1.10)
При этом Ф/г равно экстраполированному на поверхность блока
значению плотности диффузионного потока.
Если реактор имеет высоту Н и не имеет отражателей на
основаниях, то в (11.1.10) надо сделать замену L-+L'-.
L'=L(\+a^L2)-^2-, az—n!H (11.1.11)
всюду, кроме множителя ехр (т/Л2).
Возрастное приближение можно использовать только для
ограниченного круга задач. В большинстве приложений необ-
ходимо применять многогрупповой (см. § 3.3) метод. Здесь мы
ограничимся двухгрупповым приближением. В этом случае
функция G; дается формулой (3.2.47), а ядро (11.1.7) надо за-
писать так:
(11.1.12)
\ Vт / J \ ь )}
316
Если применить оператор Д—L2 к уравнению (11.1.5) и счи-
тать, что функции Gf и Gs определены формулами (2.2.66) и
(2.1.35), то получим
ГДФ (г) - ЕФ (г) 4- 2 -n^kW (г, гк) Ф* — S ьЗ (г — гА) Фй = О,
k k
(11.1.13)
где W определено (2.2.47), aS — макроскопическое сечение по-
глощения замедлителя.
На первый взгляд кажется, что уравнение (11.1.5) имеет
значительно большую область применимости, чем (11.1.13), по-
скольку (11.1.5) не обязательно предполагает использование
диффузионного приближения для Gs. Однако если у определено
правильно, т. е. без использования диффузионного приближе-
ния, то баланс нейтронов в (11.1.13) найден правильно и усло-
вия критичности, следующие из (11.1.13), не будут содержать
погрешности диффузионного приближения [при выполнении ус-
ловия (11.1.1) или (11.1.2)].
Рассмотрим реактор, содержащий много ячеек. Предполо-
жим также, что нет резких нарушений однородности решетки.
В таком реакторе можно провести усреднение плотности пото-
ка Ф(г) в уравнении (11.1.13) и перейти к уравнению для сред-
ней плотности потока по ячейке. Плотность потока Ф(г) мож-
но представить как произведение медленно меняющейся функ-
ции Ф(г) и быстро меняющейся функции / (г), т. е.
ф(г) =f (г)Ф(г). (11.1.14)
Функция f(r) описывает ход плотности потока нейтронов
в ячейке, а Ф(г) — общий ход средней плотности потока по
реактору. Поэтому надо считать, что f(r) есть периодическая
функция с периодом, равным расстоянию между блоками. Ее
среднее значение равно единице, а среднее значение производ-
ных равно нулю. Тогда среднее значение Ф(г) по ячейке рав-
но Ф(г), где г теперь означает центр того объема, по которому
проведено усреднение. Следовательно,
дф(?)=7(Р)дф(7)=дф7Г). (11.1.15)
Далее из формулы (2.2.55) следует, что
21Г(г, гА)Ф(гА) = (У0С0)--* J 1^(г, г')Ф(Р)*', (11.1.16)
k
где Уо — объем ячейки, а
^ад/Ф^), (11.1.17)
317
и предполагается, что величина £о не зависит от г и может быть
вынесена в (11.1.16) за знак интеграла. Далее имеем
VJ 8 (г - rfe) Ф (rj = 4- Ф (rj =44. (11.1.18)
k
Теперь результат усреднения уравнения (11.1.13) можно за-
писать так:
ДДФ (г) - 2 f 1 4-—М Ф
\ W/
С w (г, г')Ф(г'Мг' = 0
*'AJ 1.1.
Поскольку у есть отношение тока нейтронов на блок к пото-
ку на его поверхности, VoS/y равно отношению числа нейтро-
нов, поглощенных замедлителем в ячейке, к числу нейтронов,
поглощенных в блоке, которое получилось бы в том случае,
если бы поток нейтронов в замедлителе равнялся потоку на по-
верхности блока, т. е. [см. (7.2.6)]
1/о2/у=^о.
(11.1.20)
Определим величину qt равенством
г = 1 _i_______________________д_____L
° + <7о “ Q ’
(11.1.21)
где £0 дано (11.1.17); £ — полный блок-эффект; Q — коэффи-
циент экранировки. Величина qi отличается от аналогичной ве-
личины, введенной в § 7.2, поскольку там для определения qi
использовалась эквивалентная цилиндрическая ячейка. Введя
обозначения (Д — длина диффузии в замедлителе)
r = -£-Le2; q^q. + qf, L?= А, (11.1.22)
1 +<7 1 +<7 S
получим уравнение гомогенного реактора [см. (2.1.44)]:
ДФ(г)-_Щ._|__А- Г'П1’. r')W)dr' = 0- (И.1.23)
Переход к физически гомогенному реактору можно выпол-
нить либо в уравнении (11.1.23), положив там £о=1, либо в
(11.1.6). Для этого надо явно выписать у для малых блоков:
'р=лр22г-,
где 2, — сечение поглощения внутри блока. Переходя в (11.1.6)
от суммирования к интегрированию, получаем
Ф(г) = 2t- JhGf(r, r')-Gs(r, г')]Ф(г')б/г', (11.1.24)
318
где 2г — — среднее по ячейке макроскопическое сечение по-
а2
глощения топлива. Применяя к уравнению (11.1.24) оператор
A—Le~2 и учитывая уравнения, которым удовлетворяют функ-
ции Gf и Gs, находим
DeAO(r)—2аФ(г) + ^2а JlF(r, г')Ф(г')Л' = 0, (11.1.25)
где
Sa=2e+S,-;
Очевидно, что (11.1.25) совпадает с (11.1.23), если в послед-
нем положить £о=1.
Рассмотрим уравнение (11.1.6) для однородной решетки,
причем определим Gf и Gs для бесконечной однородной среды.
Тогда Н будет зависеть только от разности г—-гк, т. е.
Ф(г) = £Я(г-г*)Ф(гД (11.1.26)
k
Распространим сумму, стоящую в правой части (11.1.26),
до бесконечности. При этом вне реактора вводятся фиктивные
источники и стоки нейтронов, которые нужны только для вы-
полнения граничных условий на поверхности реактора (предпо-
лагается, что реактор не имеет отражателя). Положим
Ф(г*)= SC(a)exp(iarfe), (11.1.27)
a
где суммирование проводится по различным направлениям век-
тора а, т. е. при постоянном а2. Подставляя (11.1.27) в (11.1.26),
получаем
Ф(г) = 2 с (a) ехр (i ar) F (г, а), (11.1.28)
а
где
F(r, а)~2я (г-г*)ехр(—ia(r—rft)). (11.1.29)
k
Плотность замедления равна
п (г, ^)=11т2г(г—г*; х)ф <г*)=2 с exP(iar) Fi (r>«;x)»
k a
(11.1.30)
где
Fi(r, a; х) = т1у2й7(г— rk> ^) exp (-ia (r - rj). (11.1.31)
k
319
Функции Ф(г) (11.1.28) и п (г, т) (11.1.30) удовлетворяют
следующим условиям: 1) Ф(г) удовлетворяет уравнению диф-
фузии, а ц(г, т) — уравнению замедления, если точка г лежит
внутри реактора; 2) Ф(гй) и /г(г*, т) имеют особенности, если
точка г* лежит внутри реактора, причем мощность источников
и стоков нейтронов в точке гк соответствует числу испущенных
быстрых нейтронов и числу поглощенных в блоке k медленных
нейтронов; 3) если дополнительно предположить, что функции
F(r, а) и F\ (г, а; т) (последняя для всех значений T<ii) за-
висят только от а2, то
Ф (г) = F (г, а2) С (a)exp(iar);
а
ft (г, = ^i(r, a2; "О S С (a) exp (iar). (11.1.32)
а
Поэтому Ф(г) и п(г, т) удовлетворяют граничному условию
Ф = п=0 на поверхности реактора, если этому условию удов-
летворяет сумма
2C(a)exp(iar). (11.1.33)
Например, для цилиндрического реактора С (a)—const и
сумма (11.1.33) равна (в этом случае а — двухмерный вектор
и сумму надо заменить интегралом по углу между а и г):
2 С (a) ехр (iar) = const Jo (ar),
a
Тогда Ф(7?) —n(R, т) =0, если Jo(aR) =0.
Таким образом, если выполнено (11.1.32), то Ф(г) (11.1.28)
и п(г, т) (11.1.30) суть решения уравнений дуффузии и за-
медления, удовлетворяющие надлежащим граничным условиям
на поверхности реактора и поверхностях всех блоков внутри
реактора. Особенности функций Ф и п вне реактора — это
фиктивные источники, с помощью которых удовлетворяются
граничные условия на поверхности реактора.
Поскольку исходное уравнение линейно, для определения а2
достаточно рассмотреть одно слагаемое в сумме (11.1.27). По-
ложим r=rfe в (11.1.28). Тогда
Ф(Гй)=ехр (iar*) = F(rk, a2) ехр (iar*)
и для определения а2 получаем уравнение
P^k, “2)= 2^(^')ехр(—iarftft,)=l- (11-1-34)
k'
320
Так как сумма в (11.1.34) распространена до бесконечности,
то, изменяя индекс суммирования, получаем [это означает, что
F(rk, а2) не зависит от г*]:
2//(гй)ехр(—iarfe) = L (11.1.35)
k
Уравнение (11.1.35) будем называть характеристическим
уравнением гетерогенного реактора. Рассмотрим подробнее
функцию F(r, а) (11.1.29). Если функция Gf задана (2.2.66),
то, применяя формулу суммирования (2.2.50), находим (решет-
ка квадратная с шагом а; т=тс; L=Le):
2 Gf (r — ra) exP (— i« (r — rJ) =
k
= ехр(т/Л2) Г e~z &
4?tD J г
t/Z.2
П
(r—ok)2 .
4L2z
2rnki—a(r — ak)i dk.
Интегралы no dk и dz легко вычисляются:
SG/(r~ r*)exp(— ia(r — rft)) =
Для большого реактора выполнено условие (оно означает,
что число ячеек велико)
-1^-<1. (11.1.37)
Поэтому если выполнено условие (2.2.53), то в сумме
(11.1.36) можно оставить одно слагаемое п = 0. Тогда
S <3( (г - г»)ехр (- i<x (г - г»)) = . (11.1.38)
k
т. е. эта часть функции F не зависит от направления векто-
ра а. Для функции Fi(r, а: т)аналогично получим (0<т^Тс):
Fi(r, а; г) = _Д_^ехр(—a2t)-j_
1 4я2т / । аа \2 , 2тгп •'
ехр------/„+— +------------1
J а2 \ 2г. I а
п/-о
21—6053
321
Если выполнено условие (11.1.37), то (11.1.39) не зависит
от направления а независимо от того, выполняется условие
(2.2.53) или нет.
В самом деле, если условие (2.2.53) заменить противополож-
ным: 4л2гп2/а2<^1, то зависящая от угла часть выражения
(11.1.39) приближенно равна
S' । __ 4л2тп2 /1 . аа, cos G \ ’
а2 \ | и | / ’
где -О — угол между векторами а и п. При выполнении усло-
вия (11.1.37) эта величина не зависит от О.
Теперь рассмотрим сумму
2<Л(Г —rfe)e4>(— ia(r~ гА)) =
А
- ъЬ- S (1£т£41)ех₽ “ <г - г>»-
k
(11.1.40)
Если здесь заменить сумму интегралом, то получим (см.
[75, формула (6.521.2)]):
ОО
J]Gs(r —rA)exP(-i«(r —Гй))^2^у rKo[j-yo^ г)dr =
k о
^(Н^Г (П-1.41)
Поэтому запишем
У] GДг “ rk) ехр(- ia (г — гJ) = ~- R1 + + <7i (s, а)],
k
(11.1.42)
где <7i (s, а) учитывает отклонение рассматриваемой суммы от
интеграла (11.1.41); s — вектор, проведенный в точку г из цен-
тра ближайшего блока [сумма (11.1.40) зависит только от это-
го вектора]. Сумма (11.1.40) может быть получена из (11.1.36),
если положить т=0. Рассмотрим реактор конечной высоты и
сделаем замену (11.1.11). Тогда для <?i(s, а) получим
, , 7 2Ttns Л
(s, а) = ехр — i j х
п
( 1 I Г f . dttr \ 2 1 /1 | ОГ О. . 1 /11 1 А О \
XV + — + (v) 1} ~(1+аЛ) (11л-43>
322
или при условии (напомним, что L обозначает длину диффузии
в замедлителе)
е = -51-<£1 (11.1.44)
имеем (штрих у суммы означает отсутствие слагаемого с п=
=0)
Такая запись не вполне удовлетворительна, так как сумма
(11.1.45) сходится не абсолютно и результат может зависеть
от порядка суммирования. Однако если вычислять разность
= </! (s, а)—<?! (s, 0), то для нее получим абсолютно сходя-
щийся ряд
п
(11.1.46)
Пусть точка s расположена на поверхности блока [именно
такая сумма входит в (11.1.35)]. При малых р можно положить
в (11.1.46) [но не в (11.1.45)] р —0. После этого разложим
(11.1.46) в ряд по аг и аг:
= (Ц.1.47У
4я3 [и6 п4 j
п
Сумму в (11.1.47) легко оценить (см. [86]; отметим, что
(11.1.47) не зависит от направления вектора а):
5^ еа2-(-а^о аг'2). (11.1.48)
Если az2=0, то 6<7i можно выразить через число ячеек в реак-
торе N:
bq^z/N. (11.1.49)
Для больших реакторов 1 и величина (11.1.49) весь-
ма мала. Еще меньше следующие члены разложения по аг, даю-
щие зависимость 6<7i от направления вектора аг (они содержат
более высокие степени малой величины а2аг2). В функцию
F(r, а) входит сумма (11.1.46) для произвольного г. Однако
наличие осциллирующего множителя ехр (2nnsi/a) не может
усилить зависимость 671 от направления вектора аг. Таким об-
21* 323
разом, доказано, что функции F(r, а) и F{(r, а; т) не зависят
от направления а.
Из (11.1.20), (11.1.38) и (11.1.40) получим явный вид ха-
рактеристического уравнения (возвращаемся к обозначениям тс
и Le для возраста и длины диффузии в замедлителе):
?;ехр( — а2тс)—1 _ .
sr~s ~ Чо~Г Vl>
1 + “2^-е2
(11.1.50)
где <71 — значение функции <?i(s, а2), если точка s расположе-
на на поверхности блока:
<71 —<7i(p> а2) (11.1.51)
или
k= (l-J-ct2/.2) ехр (а2тс), (11.1.52)
где k и L2 определяются по (11.1.22). Если qi (11.1.51) совпа-
дает с <7ь введенной в § 7.2 для цилиндрической ячейки, то
(11.1.52) совпадает с характеристическим уравнением гомоген-
ного (точнее, гомогенизированного) уравнения. В § 11.2 приве-
дены значения qi (11.1.51) для различных решеток. Из фор-
мул (11.1.49), (11.1.48) следует, что внешний блок-эффект весь-
ма слабо зависит от размеров реактора, если число ячеек доста-
точно велико и (а/Н)2-^!.
11.2. ВНЕШНИЙ БЛОК-ЭФФЕКТ
Как показано в § 11.1, величина <71 (р, а2) имеет порядок е,
a 6<7i — порядок еа2а2, т. е. для больших реакторов, когда
а2а2<С1, <71 не зависит от а2. Поэтому рассмотрим бесконечно
большой однородный реактор и блоки конечного радиуса.
В § 2.2 было показано, что плотность замедляющихся нейтро-
нов обычно .постоянна по объему ячейки. Объемная мощность
источников для тепловых нейтронов равна
ЛуФо/Зо, ' (11.2.1)
где So — объем замедлителя в ячейке на единицу высоты (для
кратности будем говорить «площадь замедлителя»); Фо — сред-
нее значение плотности потока на поверхности блока (как от-
мечалось в § 11.1, Фо — экстраполированное на поверхность
блока значение плотности диффузионного потока). Поскольку
блок теперь имеет конечные размеры, нельзя воспользоваться
формулами § 11.1.
Дифференциальное уравнение для плотности потока нейтро-
нов в замедлителе запишем так:
£>ДФ (г) -2аФ (г) —q уФо/5о=0. (11.2.2)
Поскольку реактор бесконечен,
q=l+?o+<7i, (11.2.3)
324
Рис. 11.1. Обозначения к
формуле (11.2.6)
где <71 и подлежит определению. Общее решение уравнения
(11.2.2) с учетом (11.2.3) и (11.1.20) запишем следующим об-
разом:
Ф (г) = l+'fr + ft фо - V V АпКп (ехр (i <fkn), (11.2.4)
Ча L-A L4 \ L J
п k
где — азимутальный угол вокруг блока k\ Ап — постоянные,
одинаковые для всех блоков, поскольку решетка бесконечна и
однородна (и ток на бесконечности равен нулю). Если решетка
симметрична, то в сумме по п в (11.2.4) присутствуют кроме
нулевой только высокие гармоники (например, для квадратной
ячейки — кратные четырем). В первом приближении учтем в
сумме по п только один член «=0. Такое ограничение означа-
ет, что «собственное» поле данного блока не зависит от угла
Ф& и зависимость плотности потока от угла возникает в ячейке
только под влиянием соседних блоков. Иначе можно сказать,
что действие окружающих блоков на данный не приводит к его
поляризации (см. гл. 10). Равенство (11.2,4) при этом будет
справедливо, если его усреднить по углу около некоторого вы-
бранного блока:
<Ф(г)) = _L±^l+^. Ф0-А0/у]к(11.2.5)
k'
где скобки < > означают усреднение по углу; г — точка вблизи
поверхности блока k. Представим Ко в (11.2.5) с помощью тео-
ремы сложения цилиндрических функций (см. [75, формула
(8.530.2)]) (рис. 11.1):
/<. (-ЦрШ) = £/„ ехр^».);
k=£k'. (11.2.6)
325
Приняв центр блока k за начало координат, получим
<2«. (Л?£1)> - ) +/«(т) 2. = ^.W. О1-2-7)
k'
где (штрих у суммы означает отсутствие слагаемого &=0)
(11.2.8)
k
Постоянную Ао в (11.2.5) можно связать с у:
Y<D0 = 2irpD/—\
и, используя (11.1.20), имеем
__ __________Фр
° 2п£290 [—pF0'(p)]’
(11.2.9)
где
-р^о'(р)=-^[К1(4-)-Л (-£-) So]- (Н-2.10)
Пусть точка г в (11.2.5) расположена на поверхности блока k.
Тогда <Ф(г) >=Фо и из (11.2.5) определяем <?i:
<7i = -----------------1. (11.2.11)
2л£2 [-р/7(р)1 ’
Ниже будем считать, что выполняется неравенство (11.1.44).
Тогда при вычислении (11.2.8) в первом приближении по е мож-
но заменить сумму интегралом, а в следующем приближении
запишем
Зо = -!-(1+еДо), (И-2.12)
2е
где До характеризует отклонение суммы от интеграла. Величина
До вычислена в [86] для ячеек различных форм (S — площадь
ячейки):
До = -1П^-Т + 8’ Y = 1,78..., (11.2.13)
причем & зависит от формы ячейки (табл. 11.1). Разложив
Fo(p) и рГо(р) в ряд по е, получим
^о(Р)=^(1+71о + ^); (Н-2.14)
-рЛ/ (Р) = (1 -с)[1 - ~~с (1 +-f) ~ <7юj , (Н.2.15)
где
7ю = ® f До+21п-^-) =е (in-L- 4 +И (11-2.16)
\ Y ? / \ с 2 )
326
Таблица 11.1. Значения коэффициента 6
Ячейка г Ячейка г
Треугольная Квадратная Шестиугольная 0,1464 0,0237 0,0025 Прямоугольная с отно- шением сторон: 1,25 1,5 2,0 3,0 5,0 0,058 0,134 0,370 0,712 2,60
И
Подставив
лучим *
c=np2/S.
разложения (11.2.14), (11.2.15) в
<71 = ®
1
1п —
с 3 с 5
1 -с — 2 + 2 + 1 — с
(11.2.17)
(11.2.11), по-
(11.2.18)
При 6 = 0 (11.2.18) совпадает с (7.2.19). Таким образом, ве-
личина ,6 характеризует отклонение блок-эффекта в реальной
ячейке от блок-эффекта в эквивалентной круглой (цилиндриче-
ской) ячейке. В табл. 11.1 приведены значения 6 для трех сим-
метричных ячеек (рис. 11.2) и прямоугольной ячейки с различ-
ным отношением сторон [86]. Видно, что при увеличении сим-
метрии ячейки величина 6 уменьшается (три ячейки на рис. 11.2
можно характеризовать углом 2л//г, /2=3, 4, 6, при повороте на
который решетка совпадает с первоначальной; 6 падает с рос-
том п). Для сильно вытянутых ячеек значение 6 становится су-
щественным.
В приведенных выше формулах величина с не считается ма-
лой. Формально это неправильно, так как если с не мало, то
в (11.2.4) надо учесть члены с /г=#0. Однако чем выше симме-
трия ячейки, тем более высокая степень с правильно учитывает-
* Погрешность разложения по е можно оценить по формуле для ци-
линдрической ячейки (7.2.20): если с=0,1, то при a=L погрешность равна
5%; если с=0,05, то при a = L погрешность составит 2 %. Поэтому получен-
ные здесь формулы можно использовать вплоть до значений L порядка а.
Рис. 11.2. Треугольная (а),
квадратная (б) и шестиуголь-
ная (в) симметричные реше.тки
(штриховыми линиями показа-
ны границы ячеек)
О а)
О
о f о ! о
I______I
О S)
о
О глО
< о >
о <---/ о
О в)
327
ся с полученными формулами. Поэтому в формулах для </i
сохранены все степени с. Поправка для квадратной ячейки ока-
зывается весьма малой (см. § 11.4).
Если в формуле (11.2.4) пренебречь Ап при п=#0 и восполь-
зоваться (11.2.9), то получим распределение плотности диффузи-
онного потока нейтронов по замедлителю в ячейке:
где
S(4^)
91 =“iSZ2 [ — pF0'(₽)] (11.2.20)
Величина ^i(r) (11.2.20) вычислена в [86]. При малых г при
этом получено
Ф(г)
Фо
е Г, г2 л(р2 — г2) п4
— In — -к — —
<7о L Р2 а2 90
г \ 4 .
— cos 4<р
, а )
(11.2.21)
Если в (11.2.21) пренебречь последним слагаемым, то резуль-
тат совпадает с распределением в круглой ячейке [если можно
пренебречь поглощением нейтронов в замедлителе, см. формулу
(7.1.13)]. Гармоника cos4<p отлична от нуля и на поверхности
блока; она обусловлена другими блоками. Однако это внешнее
поле должно приводить к поляризации блока (см. гл. 10), в ре-
зультате чего амплитуда гармоники изменится по сравнению
с (11.2.21). Если 1, то амплитуда гармоники cos4<p мала.
Мала будет и поляризация. Поэтому при малых с формулы
(11.2.19), (11.2.20) дают правильное распределение плотности
потока (диффузионного) по объему замедлителя. Распределение
плотности потока в круглой ячейке запишем так:
4Р-=1 +—Е0(г); Е0(г) = 21п—— (11.2.22)
Фо Фо р \ R J
а в квадратной
-^-=1 +—Р(Г1, гг), (11.2.23)
Фо Фо
где Г1, г2 — координаты точки, г. На рис. 11.3 приведена кривая
F0(r) для с=0,1 и точками обозначено несколько значений
/?(гь г2). Видно, что в точках, лежащих на стороне ячейки, плот-
ность потока ниже, а на диагонали—выше, чем в круглой ячейке
(если сравнивать точки, находящиеся на одинаковом расстоя-
нии от центра ячейки). Если £~2, с=0,1, то е/go порядка еди-
ницы, и поэтому различие между Ео(т) и Е(гь г2) дает представ-
ление о различии в плотностях потоков. В данном примере ма-
ксимальная плотность потока в центре квадратной ячейки отли-
чается от максимальной плотности потока на краю круглой
328
Рис. 11.3. Распределение плотности потока
нейтронов в цилиндрической (/•'о(г)) и квад-
ратной (F(rh г2)) ячейках [см. формулы
(11.2.22), (11.2.23)]. Цифры в скобках — ко-
ординаты точек, если шаг решетки принят
за единицу; г — расстояние от центра ячей-
ки; 7?— радиус цилиндрической равновели-
кой ячейки
ячейки на 8%. Такое незначитель-
ное различие, к тому же разного
знака, и объясняет тот факт, что
средние значения плотности потока
по круглой и квадратной ячейкам
мало различаются между собой.
11.3. СЛОЖНАЯ РЕШЕТКА
В большинстве случаев решетка ядерного реактора содержит
различные блоки: каналы с различным содержанием топлива,
регуляторы. Рассмотрим случай, когда решетка, содержащая раз-
личные блоки, обладает симметрией, а именно состоит из периоди-
чески повторяющихся элементарных ячеек, каждая из которых
содержит несколько различных каналов. Такую решетку будем
называть сложной. Сложная решетка является удобной моделью
для изучения различных локальных эффектов, например измене-
ния плотности потока нейтронов на поверхности каналов с топ-
ливом при движении регулятора или взаимного блок-эффекта
для каналов с разным содержанием делящихся ядер. В таких
случаях можно не стремиться к точному выполнению условия
критичности для всего реактора в целом и не интересоваться
распределением плотности потока нейтронов по всему реактору,
а определять только отношения средних плотностей потоков для
блоков, входящих в состав одной элементарной ячейки, считая
всю решетку бесконечно большой.
Ниже рассмотрена сложная решетка в простейшем случае
малых блоков (более общие случаи представлены в [86, 211],
а численные методы — в [130]).
Пусть Г/ — радиус-вектор /-го блока в ячейке относительно
какого-то блока, выбранного за начало координат в каждой ячей-
ке, a Rfe — радиус-вектор начального блока k-й ячейки. Уравне-
ние (11.1.6) можно записать так:
S H(Rft + rj; R^ + r.,)Ofe,,r. (11.3.1)
k',j'
Если реактор не имеет отражателя, то, вводя фиктивные источ-
ники вне реактора, распространяем сумму в (11.3.1) до беско-
329
нечности и ищем решение в виде
Фу=Ф/ ехр ia (Rfe+r/). (11.3.2)
Подставляя (11.3.2) в (11.3.1), получаем
х
ф;= 2 г )ФГ, (11.3.3)
/>=1
где W число блоков в ячейке и
Н (г;, г )= 2^(Ra + h—r,,)exp(ia(Rfe4-r> —г.,)). (11.3.4)
k ‘ ‘
Очевидно, что из отношения Ф^/Ф/» исключается множитель
[iaR*], характеризующий изменение плотности потока по реак-
тору, и поэтому эти отношения описывают только локальные эф-
фекты. Часто в элементарной ячейке некоторые блоки одинаковы
и одинаково расположены по отношению к соседним. Такие бло-
ки будем называть эквивалентными. Плотность потока нейтро-
нов на эквивалентных блоках одинакова, и поэтому число неиз-
вестных в (11.3.4) уменьшается:
м
ф>= 2 (н.э.5)
/'=1
где М — число неэквивалентных блоков; т, — число эквивалент-
ных блоков сорта /.
Если размер ячейки а не слишком велик, так что выполняют-
ся условия (11.1.44) и (2.2.53), то справедливы формулы
(11.1.38), (11.1.42). Тогда
1
T)j, ехр( —а2т) — 1
14-^2V
(11.3.6)
где
70;, = ssae/rr; (11-3.7)
/ \ е VI' 1 Га п(г/ —Г/'1 /11 оо\
<71 1/, ту — ехр 2iti------------; (11.3.8)
' л n2 L а
п
S — площадь сложной ячейки; e=S/(4лЬе2) и 71(4, r/)=<7i(p;),
где р/ — радиус /-го блока. Вычисление суммы (11.3.8) рассмо-
трено в [86, 211]. Если число неэквивалентных блоков равно
330
двум, то можно явно решить уравнения
(11.3.5) и проанализировать результат.
В противном случае формулы слишком
громоздки и необходимо численное ре-
шение.
На рис. 11.4 приведены примеры
сложных решеток с М=2, когда в каж-
дой ячейке имеется один блок второго
сорта и п=1, 2, 3, 4 блоков первого сор-
та, т. е. в уравнении (11.3.5) 714=2, mi =
= п, т2=1- Отметим, что азимутальная
зависимость плотности нейтронного по-
тока на поверхности блока первого сорта,
которая не, может быть правильно полу-
чена в приближении малых блоков, дает-
ся выражением
Ф=Фо [ 1+Л cos (5—п) <р].
При этом начало отсчета угла <р для раз-
ных эквивалентных блоков различно.
Поэтому приближение, которое не учиты-
вает угловую зависимость собственного
нейтронного поля, по мере роста п стано-
вится все менее точным.
Переопределив величины q0]- и'^х (щ, г.,):
S/^ae
4oi = ’
si> VY 1 Г . n(n—г,-=)
ft (П> '•/’)=-г £ -^ехр|27П—
п
ООО
• •
о о о W
• •
ООО
0 0 * 0 0 *
• 00*00
о о • о о •
0*00*0
0 0 * 0 0 *
*0*0*0
о о о о о о о
0*0*0* /2=3’
о о о о о о о
• 0*0*0
0 0 О О о о
о о о о о о
о о о о о о л=
О О О О 0*0
Рис. 11.4. Примеры
сложных решеток
(11.3.9)
= (Н.З.Ю)
где S/ — площадь, приходящаяся на блок сорта /, можно исклю-
чить числа эквивалентных блоков т, из (11.3.5). Тогда для М =
=2 получим уравнения
Ф1 = Я(г1, + П)Ф2; 1 з
Фе = ^(г2, Г1)Ф1 + ^(Г2, г2)Ф2. /
Вычитая уравнения (11.3.11) одно из другого, находим отно-
шение Ф2/Ф1:
Л J+A_ (11.3.12)
1 + ’
где
/?г = /7(гг, гг)— Н(г}, г^ = д^[д1 (рг) —?i(r;, гг)]; j=£i.
(11.3.13)
331
Таблица 11.2. Значения коэффициентов А,;
Дд п=1 п=2 п=3 п=4
Ди 0,0237 0,1464 0,177 0,0237
Д12 0,0237 0,0025 0,0025 0,0237
Д12 —0,693 —0,549 —0,46'2 —0,173
Д21 —0,693 — 1,099 —1,386 —0,693
Величины Qi(r;-, г() вычислены в [86]:
9i(H, П) = ег[(1п-^_ А.) §г7 + ДУг], (11.3.14)
где значения коэффициентов Д!,-( приведены в табл. 11.2.
Формула (11.3.12) допускает простую интерпретацию: 1-H?i
есть отношение плотности невозмущенного потока в той точке
ячейки решетки из первых блоков, где помещен блок из второй
решетки, к плотности потока (также невозмущенного) на по-
верхности первого блока.
Отметим, что в случае п=1, 2, 3 выполняются равенства
(Р1 = Рг):
Дн—Д21 = Д22—Д!2+1п«; qx (rb п)— 9i (r2, п) =
= 91(<2, г2) — <71(Г1, г2), (11.3.15)
что обеспечивает выполнение очевидного условия ф1=ф2 при
71=72 и р1 = р2. При «=4 блоки 1 и 2 находятся в различных
условиях и Ф1=#Ф2, даже если все блоки в решетке
Условие критичности, следующее из обращения в
минанта уравнений (11.3.11), можно записать так:
(1+а2Л2)ехр (а2т) =k,
где
к= [П1 (q(2)_^12) _|_П2 (q(1>—q21) ] 0-1;
^=(qWq^-qX2q2x)D-'Le2,
причем
9// = 910ь О); 9(г> = 9ог + 91(г.> П) = 9о1 + 9р;
D = </(’> 9(2> -j- 9(,) + 9(2) — 912 9г, — 912 9г1-
В [86, 211] приведены формулы, в которых учитывается как
конечность радиуса, так и наличие замедлителя внутри блока.
Использованный здесь и в [86] метод можно применить и
при анализе сложной решетки в Р3-приближении [212, 213].
Применим полученные формулы к тому случаю, когда бло-
ки 2 являются абсолютно черными (решетка регуляторов).
332
одинаковы,
нуль детер-
(11.3.16)
(11.3.17)
(11.3.18)
Тогда т]2=0, S,a2->oo, т. е. ^02=0, а ,р2 — эффективный радиус
регулятора. В этом случае коэффициент размножения при нали-
чии регуляторов равен
k----. p = q<’>(l+ qf)) + (*> - Q12 - 7ai - q12 q21,
(11.3.19)
а в отсутствие регуляторов надо положить д0&>=оо, и тогда ко-
эффициент размножения равен
й0=тц [1 '•
Разность 1—(й/й0) дает эффективность решетки регуляторов:
+q12)D-', (11.3.20)
Kq
где D определено (11.3.19). Если 1, то можно пренебречь qi2
и по сравнению с единицей. Тогда
fe-0~fe = (1 4- . (Н .3.21)
k0 \ qW — q2l )
Сравним этот результат с эффективностью решетки регуля-
торов, которая поставлена в гомогенную размножающую среду.
Представим плотность потока нейтронов в виде
Ф(г)=Ф+/(г),
где Ф — среднее значение плотности потока по ячейке решетки
регуляторов. Если размеры ячейки достаточно малы, так что вы-
полнено условие [см. уравнение (2.1.44)]
J W (г, r')f (rf) dr' = 0,
то плотность потока нейтронов в ячейке с регулятором удовле-
творяет уравнению
ОЛФ—2аФ+йо2аФ = О, (11.3.22)
где й0 — коэффициент размножения гомогенной среды до введе-
ния регуляторов. Для бесконечной решетки должно быть й=1.
Используя формулу (7.2.10) для среднего значения плотности
потока по ячейке, получаем [при q=0 в (7.2.10) надо положить
яе=й02аФ]:
ЛгтА-ЛгтЬ-Ц-^)-1. (11.3.23)
&0 ^0
333
Для черного регулятора 2а£=оо и ^о=О. Если
(11.3.24)
где Lo — длина диффузии
ячейки регуляторов, то
S
q
S
4л£0г
в гомогенной среде и 5 — площадь
S __3
4л£02 \ пр2 2
Этот результат совпадает с (11.3.21), если пренебречь qi2, <721 и
<?2(1)<^1- В самом деле, при д(1)<С1 имеем L02=qt-1'>Le'2, и поэтому
q/2) равно q (11.3.25). Таким образом, коэффициенты q{j харак-
теризуют поправки к гомогенному приближению. Из табл. 11.2
видно, что Дц порядка единицы и поправки малы, если только
логарифм в формулах для qi велик по сравнению с единицей,
т. е. эффективный радиус регулятора очень мал. Отметим, что
при выводе (11.3.21) требовалось выполнение неравенств 1,
но не равенства которое эквивалентно (11.3.24).
(11.3.25)
Задача. Бесконечная решетка состоит из размножающих (1) и погло-
щающих (2) блоков с одинаковым радиусом (п=/=4). Определить зависимость
реактивности от шага решетки (замедлитель не поглощает нейтронов, резо-
нансное поглощение равно нулю, источники тепловых нейтронов равномерно
распределены по ячейке).
Решение. Аналогично (11.3.21) имеем
k0—k = g<2) —giaV1
k0 \ (К1)—<7217
где k0 — коэффициент размножения решетки без поглощающих блоков; k —
с поглощающими. Выразим #о(1,2> через yi ,2 по формулам (11.3.9) и исполь-
зуем (11.3.14):
k0 — k
k0
Г S2 3
f2-i + (4nD)-i pn - — + Д22-Д12
Г S, 3
T1-1+(4nD)-1 In — - —+Ди—Д21
где п—8з/81 = const. Применяя (11.3.15), получаем
k0 — k [ . n__________7i~7г__________'
L + ” ^”72+7172 l(4^O)~'In S,4- Л]
(11.3.26)
где
[1 3
ln “+Г - V + All — Д21
лр2 2
Если y2<Yi, то правая часть (11.3.26) возрастает с ростом Si, а если y2>yi,
то убывает, т. е. если поглощающие блоки менее серые, чем размножающие,
то реактивность убывает с ростом шага решетки, а если более черные, то
возрастает. Этот результат может быть истолкован более наглядно. Если
блоки 2 слабо поглощают нейтроны, то справедлива теории возмущений и
эффективность поглотителей возрастает прн увеличении шага, поскольку
возрастает плотность невозмущенного потока нейтронов в том месте, где по-
334
ставлен блок 2. Сильные поглотители находятся в более глубоком минимуме
нейтронного поля, чем размножающие блоки, причем этот минимум становит-
ся еще более глубоким при увеличении шага решетки, т. е. эффективность
поглотителей убывает.
11.4. ГЕТЕРОГЕННЫЙ РЕАКТОР С БОЛЬШИМИ БЛОКАМИ
Теория гетерогенного реактора с большими блоками изложе-
на в [86] и в более современной форме — в книге Б. П. Кочуро-
ва [130]. Поэтому здесь будут отмечены только основные исход-
ные моменты и главные результаты теории. Чтобы не усложнять
запись формул, ограничимся двумя группами нейтронов. Обоб-
щение на большее число групп не представляет принципиальных
трудностей [130]. Общее решение двухгрупповых уравнений
(см. § 3.2) в замедлителе в окрестности некоторого произволь-
ного блока k можно записать так:
Ф1 (г) = 2 (*1 ! г - rft) ехр (i <pftn) +
k>n
+ San,/»(xir)exp(inS);
" „ (11.4.1)
Ф2 (г) = 2 Ak.nKa (*г I Г - г* I ) ехр (1п) —
k,n
_ А. (1 _ т/£2)-1 Ф1 (Г) JI a2Jn ехр (i
2 « )
где О, ф/г — полярные углы-точки г в системах координат с на-
чалами в центре реактора и в центре блока k\ xi2=r-1-|-az2; х22=
=L~2-j-az2; постоянные /)д‘п, CLn, удовлетворяющие условию
вещественности потоков:
лц=(л^_п)*; 4 = (А)*, (н.4.2)
где * — знак комплексного сопряжения, должны определяться
из граничных условий на внешней границе реактора (коэффи-
циенты а„) и на поверхностях всех блоков (коэффициенты
^4а,л). Для определения коэффициентов ап1 надо, применял
теорему сложения цилиндрических функций, переписать Ф»(г)
как функции только одного угла О’. Чтобы использовать гранич-
ные условия на поверхности фиксированного, но произвольного
блока k, следует записать ФДг) как функции только одного уг-
ла ф£. Результат такого исключения может быть записан в со-
кращенной матричной форме так [130] (г — радиус-вектор точ-
ки в окрестности блока k):
ф(г) = С(7<+777)С-1В, (11.4.3)
335
где Ф(г) —вектор, компоненты которого равны амплитудам
разложения плотности потока в группе i по азимутальным гар-
моникам около блока k, Фл‘п (г); К. — диагональная матрица
с элементами Кп (х(г) ппг'-> I— диагональная матрица с элб~
ментами In(Kir)5kk'6nn'‘, Г —матрица с элементами (эта матри-
ца выписана здесь только для случая бесконечно большого ре-
актора [86, 130]):
Fkk',nn> = (i — 8*fe/)(— 1 (хг I rk — rk, I )expi (n' —
(11.4.4)
где — угол между линие'1, соединяющей центры блоков k и k',
и некоторым фиксированным направлением; наконец, матрица
С равна
и С~'!В=А. Записанное в виде (11.4.3) решение справедливо и
для произвольного числа групп. Структура матрицы С в этом
случае приведена в [130].
Гетерогенное уравнение реактора возникнет, если в (11.4.3)
положить r—pk и установить связь между Ф и В с помощью
граничных условий. Граничные условия можно задать с помо-
щью Л матрицы (ф = ф(рА)):
р^Ф-ЛФ, (11.4.6)
д?
или с помощью связи между В и Ф:
В=уФ, (11.4.7)
или между В и ЧГ=СГС"1В:
B=U'V. (11.4.8)
Уравнение соответственно имеет вид [130]
Ф = С(К4-7Г)С-1 (- С/С-’Л + Ср —Ф, (11.4.9)
\ Ф /
или
1ф = С(/С+//?)С-1?Ф, (11.4.10)
или ,
4r=CFC-W, (11.4.11)
а между матрицами Л, у, U имеются соотношения
у = — С1С~'ЛА-С? — С-1; (11.4.12)
Ф
336
(11.4.13)
C7=y(l—CKC-^^CIC-1. (11.4.14)
Если явно записать выражение СК (г) С~}В в двухгрупповом
приближении, то получим
СК(г)С-’В= г„ , . “ ' . ,R , (11.4.15)
т. е. если положить Вг= (2л7)1)-1В/1 и В2= (2n,D2)~1B,2, то
(С7СС-1В')г равно плотности потока в i-группе, который возник
от точечного источника с интенсивностью B'i. Таким образом,
СКС-гВ есть «собственное поле» блоков. Наоборот, вектор
С7С-ПР дает поле внешних источников в центрах блоков. По-
этому матрицу U можно назвать матрицей «отклика» или ма-
трицей «реакции», показывающей, какие амплитуды собствен-
ного поля индуцируются внешним полем.
Для точечных блоков, когда 1 = 1 и р — 0, имеем v = —Л.
бр
Связь между U и у остается нелинейной и в этом случае.
Полезно получить значения матричных элементов Аг/ для
нулевой гармоники в диффузионном приближении. Компоненты
Л22, Л21 найдем, интегрируя уравнение (3.2.2) по объему блока
и используя граничные условия для групповых потоков [см.
также (7.2.5), (7.1.7)]:
К2г=-lP2S„e2Sai2Q-; Л21 =----3-?^ire2^s)iU-\ (Н.4.16)
Компоненты Ли, AJ2 получим, интегрируя уравнение (3.2.1) по
объему блока:
Лп = [- v 4- Sail + (?Ss)f u~'\\
Л1а = - P22/reiv2/i2 Q- = -7jA22 (11.4.17)
~tre\
При этом использована формула (3.2.28) при <р=1.
Таким образом, компонента Л12 пропорциональна числу де-
лений, вызванных тепловыми нейтронами, Л22 пропорциональна
поглощению тепловых нейтронов, А21 отлична от нуля, только
если внутри блока имеется замедлитель, Ли описывает погло-
щение, размножение и замедление нейтронов первой группы.
Если пренебречь поглощением замедляющихся нейтронов, то
—Aii=|^A2i. Эти качественные особенности компонент Л-ма-
трицы сохраняются и в общем случае, когда уравнение диффу-
22—6053 337
зии несправедливо внутри блока. Если а22#=0, то, раскладывая
в ряд по а22, получаем
Л=Ло+а22Л2, (11.4.18)
где Л2 связана с миграцией в параллельном направлении. Для
компоненты Л22 в диффузионном приближении имеем
02
Л2 = -^-®, (11.4.19)
где &—Di!De (см. § 10.1).
Диагональные компоненты Л-матрицы для первой гармоники
выписаны в § 10.1 [см. (10.1.32)].
В теории гетерогенного реактора с малыми блоками не учи-
тываются поглощение замедляющихся нейтронов и замедление
внутри блока. Тогда отличны от нуля только Л22 и Aj2, причем
постоянная у (11.1.4) равна у=2л£)2Л22.
Метод определения U- и Л-матриц, основанный на числен-
ном решении многогруппового интегрального уравнения пере-
носа, изложен в [130]. При этом Л-матрица определяется для
изолированного блока, помещенного в неограниченный замед-
литель. Влияние на данный блок других соседних блоков при
этом заключается не в том, что изменяется Л-матрица, а в том,,
что изменяются плотности групповых потоков на поверхности
данного блока. Эти плотности потоков определяются при реше-
нии гетерогенного уравнения и в этом смысле зависят от рас-
положения и свойств ближайших блоков решетки. В практиче-
ских расчетах для определения Л-матрицы можно использовать
методы расчета цилиндрической ячейки конечным радиусом
[130].
В работе [214] изложен алгоритм определения Л-матриц. При
этом достигнута такая форма записи гетерогенного уравнения,
что собственное число совпадает с эффективным коэффициен-
том размножения. Это обстоятельство очень важно для прило-
жений (в других записях собственное число совпадает с коэф-
фициентом размножения только, если последний равен едини-
це) .
Аналитические методы в теории гетерогенного реактора
с большими блоками применимы к решению ограниченного чис-
ла задач. Среди них отметим задачу об однородной квадратной
бесконечной решетке. В [86] получена поправка к внешнему
блок-эффекту, связанная с учтом гармоники cos4cp в собствен-
ном поле блока:
891 = — с4 ^е—°C. с = ^-, (11.4.20)
71 De+D; а? ' ’
338
где е дано (11.1.44). Эта поправка с практической точки зрения
пренебрежимо мала для сколь угодно больших блоков (макси-
мальное значение с=л/4).
Другая задача, допускающая аналитическое решение, — это
определение длины миграции в решетке. Если для определения
длины миграции в параллельном направлении можно не при-
влекать теорию гетерогенного реактора, а ограничиться рассмот-
рением одной ячейки [86, с. 98], то для вычисления перпенди-
кулярной длины миграции применение теории гетерогенного
реактора обязательно. Общая идея заключается в том, что гра-
ничные условия на поверхности реактора выполняются с помо-
щью фиктивных источников, заполняющих все пространство вне
реактора, и решение гетерогенного уравнения ищется в виде
Фл.^Ф^ехрСаг^),
причем сохраняются члены с и=0, ±1 (нулевая и первая гар-
моники). Условие критичности, полученное из гетерогенного
уравнения, записывается в первом порядке по а2 так (аг2=0):
А? = 14-ааЛ4, (11.4.21)
где k — значение коэффициента размножения, полученное из
того же уравнения при а2=0, а Му —искомая длина миграции.
Результаты такого вычисления [86] обсуждались в § 10.2. По-
путно определяется зависимость плотности потока тепловых ней-
тронов на поверхности блока от азимутального угла:
Ф(<р) =ф(1-]-а1 coscp), (11.4.22)
где Ф — среднее значение плотности потока на поверхности бло-
ка; угол ф отсчитывается от направления на центр реактора,
амплитуда ау равна
5 -.
р-д-AiM
дг 1 — р (j
Z0(w) Jr=rk 1—I
1 — с ]
?o(l+^/Qo) J Х
1 —20с 1/1 ч
(11.4.23)
где 7о, 71, Qo, с, с$, е определены в § 7.2, а р, р —в § 10.2. Ампли-
туда пропорциональна градиенту среднего поля в том месте,
где расположен блок, и зависит от коэффициентов поляризации
и внешнего блок-эффекта. Если р>0, т. е. блок менее плотный,
чем замедлитель, то два последних множителя в (11.4.23) могут
в значительной степени компенсировать друг друга и тогда ам-
плитуда а\ характеризуется только градиентом среднего поля.
В общем случае неоднородного реактора гетерогенные урав-
нения надо решать численно. Основная трудность решения свя-
22* 339
зана с тем, что длина диффузии в замедлителе (графит, тяже-
лая вода) много больше шага решетки, и поэтому матричные
элементы Fkk- в уравнениях (11.4.9) — (11.4.11) оказываются от-
личными от нуля практически для всех k, k' даже для больших
реакторов. Счетное время для решения таких уравнений квад-
ратично растет с ростом числа блоков и для больших реакторов
(с числом блоков порядка 1000) становится слишком большим.
С физической точки зрения такого «дальнодействия» не должно
•существовать; блоки влияют друг на друга, если расстояние
между ними порядка длины диффузии в решетке, а не в чистом
замедлителе. Длина диффузии в решетке порядка шага. По-
этому фактически матричные элементы Fkk должны быть от-
личны от нуля только вблизи диагонали.
В [130] используется это с физической точки зрения очевид-
ное обстоятельство. Основная идея метода состоит в следую-
щем. Если в матрице Fkk- вместо щ ввести произвольный вектор
г, то для тепловой группы справедливо уравнение
А----^U(r, гА) = 0. (11.4.24)
Приближенно уравнение (11.4.24) будет выполняться, если опе-
ратор Лапласа заменить разностным оператором на сетке, со-
стоящей из узлов решетки. Это означает, что применение та-
кого оператора к уравнению типа (11.4.9) — (11.4.11) обратит
в нуль, точнее, сильно уменьшит матричные элементы с больши-
ми значениями |г/г—rfe-|. Фактически применение конечно-разно-
стного оператора Лапласа означает, что берется некоторая ли-
нейная комбинация исходных гетерогенных уравнений, причем
такая простаяь операция уничтожает формально присутствовав-
шее в уравнениях дальнодействие.
При реализации этой идеи в [130] конечно-разностный опе-
ратор Лапласа заменяется похожим оператором, который содер-
жит несколько свободных параметров. Эти параметры выбира-
ются из условия наилучшего обращения в нуль матричных эле-
ментов вне некоторой окрестности данного блока. Для решения
полученных уравнений можно применить методы, близкие к ме-
тодам, разработанным для численного решения гомогенных
уравнений. Точность результата можно проверить, сравнив
с численным решением исходных уравнений. Эта точность ока-
зывается вполне достаточной для практических целей [130].
Если замедлитель в реакторе заключен в цилиндрический сосуд
(тяжеловодный реактор), то границу реактора приходится за-
менять ломаной линией, что и вносит максимальную ошибку
в результаты. Для больших реакторов эта ошибка несуществен-
на, а для малых в этом случае можно применять метод непо-
средственного решения исходных гетерогенных уравнений.
340
Если реактор неоднороден по высоте, то можно использовать
разложение плотности потока в ряд Фурье и распространить
метод на трехмерные задачи. За дальнейшими подробностями
решения гетерогенных уравнений отсылаем к [130] *. Альтерна-
тивный метод решения гетерогенных уравнений, успешно заре-
комендовавший себя, предложен С. С. Городковым [215, 216].
В настоящей главе предполагалось, что выполнено условие
(11.1.1) или хотя бы условие (11.1.2). В противном случае нет
области, где справедливо уравнение диффузии, и изложенный
здесь метод, если поглощение в блоках мало, неприменим**.
Разработаны и другие методы, не использующие предполо-
жения (11.1.1). По этому вопросу мы вынуждены отослать чита-
теля к оригинальным работам [217, 218].
* Дальнейшее развитие этот метод получил в следующих работах:
1) Малофеев В. М. Алгоритм и программы трехмерного расчета гетеро-
генного реактора (программы TREC и TREC-6). М. Препринт ИТЭФ. 1985.
№ 34.
2) Малофеев В. М. Метод трехмерного расчета гетерогенного реактора
в дипольном приближении. М. Препринт ИТЭФ. 1987. № 73.
3) Малофеев В. М., Смирнов С. Е. TREC-программа трехмерного расчета
гетерогенного реактора в дипольном приближении. М. Препринт ИЭФ. 1988.
№ 164.
** Если граничное условие ставить не на поверхности блока, а на гра-
нице эквивалентной ячейки, то область, где нарушается уравнение диффузии
попадает внутрь такого увеличенного блока. Тогда требования в условиях
(11.1.1) и (11.1.2) смягчаются. Практика расчетов (см. {130, 183]) показала,
что при этом гетерогенные уравнения хорошо описывают также и сборки
с тесными решетками.
Часть III
ИЗМЕНЕНИЕ СВОЙСТВ РЕАКТОРА
ВО ВРЕМЕНИ
Глава 12
ВЛИЯНИЕ ПРОДУКТОВ ДЕЛЕНИЯ НА РАБОТУ РЕАКТОРА
12.1. ОТРАВЛЕНИЕ РЕАКТОРА
РАДИОАКТИВНЫМИ ПРОДУКТАМИ ДЕЛЕНИЯ
При работе реактора в ядерном топливе накапливаются про-
дукты деления. Влияние их на реактивность реактора называ-
ется отравлением и зашлаковыванием. При этом обычно отрав-
лением называют влияние на реактивность радиоактивных про-
дуктов деления, а зашлаковыванием — стабильных. Основную
роль в процессе отравления играет 135Хе, обладающий исключи-
тельно большим сечением поглощения тепловых нейтронов (ма-
ксимальное сечение среди всех ядер). При делении 238U и изо-
Таблица 12.1. Характеристика 135Хе и 105Rh
Параметр I3sXe ,,5Rh
Сечение поглощения при Е—Ен, б 2,65(11).106 1,6(3)-ю*
Резонансный интеграл поглощения, б 7,6(5) • 10» 1,7(3)-104
Период полураспада, ч 9,083 35,35
Период полураспада предшественни- ка, ч с Выходы цепочки при делении, %: 6,61 4,4
нейтронами спектра деления, 232^ 7,18 0,038
тепловыми нейтронами, 233U 6,01(34) 0,55(11)
тепловыми нейтронами, 235U 6,58(13) 0,98(4)
нейтронами спектра деления, 238{J 6,71(39) 3,5(4)
тепловыми нейтронами, 239Ри 7,14(29)* 5,5(5)
тепловыми нейтронами, 241Ри Независимый выход, % выхода це- почки: 7,47(53) 6,2(3)
23271! 21**
233JJ 23
235и 8,5
аази 4,9
23ЭрЦ 17,5
241рц 3,8
* Полный выход 7,18 %; выход 133Cs — 0,04 %.
** См. [219].
342
топов плутония некоторый
вклад в отравление вносит s’s
105Rh. Имеется еще мно-
жество радиоактивных про-
дуктов деления, но их мо5
роль в отравлении весьма
мала.
В табл. 12.1 приведены 10s
основные характеристики
135Хе и 105Rh [31, 32, 45, 46].
135Хе имеет резонансный
уровень со следующими па- 0 °>05 °>1 V5
раметрами [31]: Ег—
— 0,084(1) эВ; 2gPn— Рис. 12.1. Сечение поглощения 135Хе
= 24(2) • 10-3 эВ; Гу= off); среднее сечение по максвелловско-
=95(5)-10-3 эВ; Г= му распределению с(Ет) и g(E-r)-фактор
= 114(5) ov(Er) = 2,8(2) X (X —сечение для скорости 2200 м/с)
ХЮ6. На рис. 12.1 приве-
дены зависимости сечения
поглощения 135Хе от энергии нейтронов, среднего сечения
по чисто максвелловскому спектру от эффективной температуры
Ет [см. (2.4.4)] и g-фактора также от Ет [см. (2.4.8)]. Видно,
что при энергии 0,2—0,3 эВ сечение поглощения на порядок
меньше, чем сечение в области 0,02—0,03 эВ. Максимум в сече-
нии приводит к тому, что с ростом Ет сначала g растет, а затем
падает, т. е. сечение 135Хе при малых энергиях падает медлен-
нее, чем по закону 1/п, а затем — быстрее (если сечение подчи-
няется закону 1/v, то g—1, см. § 2.4).
Схема образования 135Хе выглядит следующим образом [46,
220] (числа под стрелками — периоды полураспада Г1/2):
Хещ
/ I
16,5% / 15.65МИН
/ I
83,5%
Sn—>Sb ——>Тс--------->1----> Хе--> Cs-------^Ва.
1,7с 18с 6,61ч 9,083ч 3 ,з.Ю6лет
Обычно можно не учитывать короткоживущих предшествен-
ников иода, продуктов распада 135Хе, изотопа 13еХе, который
возникает при захвате нейтрона 135Хе и Хет в метастабильном
состоянии (при некоторых переходных процессах пренебреже-
ние Хет может привести к погрешности около 5%! [220]). Тогда
схема распада упрощается (изменение Ту2 для иода прибли-
женно учитывает наличие Хет [220]):
Уг | Л
>Хе-
6,65ч-------9,083ч
343
где z/i — кумулятивный выход иода, а у2 — независимый выход
ксенона (см. § 1.6). Значения y\-\-yi=y и у2/у приведены в
табл. 12.1.
Система уравнений, описывающая образование и уничтоже-
ние иода и ксенона, имеет следующий вид:
at
—-—Я//— (охФ + ^х)^>
(12.1.1)
где I, X — числа ядер 1351 и 135Хе; %i, лх— постоянные распада
(Xi = 2,895-10-5 с-*=0,1042 ч"1, %х=2,12-Ю"5 с-^0,0763 ч-!);
У\—средний выход иода; у2 — средний выход ксенона, т. е.
2^/А
А—
2/
2 /
У 2 =----
(12.1.2)
2/
1/1,2/—выходы при делении нуклида /; Sf/—его макроскопическое
сечение деления; if —суммарное макроскопическое сечение де-
ления [см. (2.4.47)]. Резонансный интеграл 135Хе можно не учи-
тывать, и поэтому ох — сечение в тепловой группе; Ф — плот-
ность потока тепловых нейтронов (см. § 2.4).
Прежде всего рассмотрим стационарное состояние реактора,
когда-А _ о. Из уравнений (12.1.1) получим стационар-
d t dt
ные концентрации I и Хе:
= ’ 2 Ф; Хо = —;
л.« I ^Х
У = У1 + У2-
Из (12.1.3) имеем макроскопическое сечение Хе:
у __ у _ А Ф
2Х Х%° 1+М(*хФ) ’
(12.1.3)
(12.1.4)
т. е. при достаточно большой плотности потока макроскопиче-
ское сечение Хе не зависит от его микроскопического сечения.
В этом случае каждое ядро Хе погибает не в результате распада,
344
а в результате захвата нейтрона [получающийся изотоп 13еХе
стабилен и имеет малое сечение захвата: о(136Хе)=0,16(3)].
Характерное значение плотности потока, когда знаменатель в
(12.1.4) равен двум, следующее:
Фх=Хх/пх=0,8-1013 нейтр/(см2-с). (12.1.5)
При этом использовано значение ох при скорости 2200 м/с; фа-
ктически же Фх определяется средним значением сечения в те-
пловой группе и зависит от эффективной температуры нейтро-
нов. Из рис. 12.1 видно, что эта зависимость не очень сильная;
при больших плотностях потока [Ф^Ю14 нейтр/(см2-с)] ее
можно не учитывать, поскольку Хх уже почти не зависит от ох.
Изменение реактивности, вызванное накоплением ксенона,
равно
~~ (1 (12.1.6)
Sa
где Ха — полное макроскопическое сечение поглощения, и пред-
полагается, что плотность потока нейтронов не зависит от коор-
динат. Фактически, конечно, такая зависимость существует.
Пользуясь теорией возмущений (см. гл. 5), получаем
ДА ______f У Ф+ (г)Ф(г)
А “ J £ 1 + (Фх/Ф(г))
(12.1.7)
где
С= У Ф+(г) Ф (г) dr.
Если плотность потока нейтронов столь велика, что
Фх/Ф(г)«1, то в (12.1.7) можно провести разложение в ряд.
Тогда, предполагая, что Xf/Xa не зависит от координат и что
ф+=ф, находим
(12.1.8)
где (ДА/А)оо — изменение реактивности при бесконечно большой
плотности потока, а (ДА/А) —изменение реактивности, вычис-
ленное для средней плотности потока, т. е.
/ ДА \ ~
----) = — у-^—,
\ А /оо Sa
(12.1.9)
345
Пусть, например, коэффициент выравнивания по радиусу ра-
вен 1, а распределение плотности потока по высоте дается за-
висимостью Ф(г)=соэaz. Тогда (Ф)2=0,405, Ф2=0,5 и*
— = W1 +0,19(12.1.10)
А \ k )\ Ф ) к '
Таким образом, учет неравномерности плотности нейтрон-
ного потока по реактору увеличивает эффект отравления по срав-
нению с вычисленным по средней плотности потока. Физическая
причина этого состоит в том, что отравление максимально в цен-
тре реактора, где ценность нейтронов наибольшая. Поскольку
Ф'хСФ, различие между Afe/fe и (Afe/fe) невелико. Например,
если Ф=5-1013 нейтр/(см2-с), то из (12.1.10) получим (А&/&) =
= 1,03 (Afe/fe).
Если в реакторе имеется один делящийся нуклид, например
235U, то удобно ввести величину <7fx=Sx/S/5:
<7/х=г/5(1+Фх/Ф)~1.
Коэффициент размножения можно записать так:
k = ^-------------------------.
(12.1.11)
(12.1.12)
где <7f=Sc/Sf; 2С — полное макроскопическое сечение радиаци-
онного поглощения (кроме 135Хе). Тогда изменение коэффици-
ента размножения при появлении ксенона равно
k
~qfx-
k
(12.1.13)
Стационарное отравление 105Rh может быть вычислено по
аналогичным формулам, если заменить и ох-^-Оци. Ха-
рактерное значение плотности потока нейтронов для 105Rh равно
3,4-1014 „ ,, з ,
Фд =—----------- неитр/(см-с),
l + v
(12.1.14)
где у — жесткость спектра. Обычно у 0,5, и поэтому Фц >
> 2,3-1014 нейтр/(см2-с), что примерно в 30 раз больше, чем
Фх (12.1.5). Поэтому для реакторов с не очень большой плотно-
стью потока существенно меньше, чем 7fX- Для 235U выход
родия в несколько раз меньше, чем ксенона, что еще уменьшает
по сравнению с qfx-
* К этой задаче удобно применить ту форму теории возмущений, ко-
торая изложена в § 5.3. При этом легко определить ие только изменение
собственного числа, но и собственной функции (см. задачу в конце этого
параграфа).
346
Если учитывать неравномерность плотности нейтронного по-
тока по объему реактора, то надо пользоваться формулой
(12.1.7). При этом чаще всего осуществляется неравенство
Ф(г) СФк- В этом случае имеем
f—) XL1G-XU (12.1.15)
\ k Jr \ k )r Фф2 L ФЯ \ ФФ»/] ' '
где (Afe/fe)R вычислено для средней плотности потока. Аналогич-
ной формулой надо пользоваться и для ксенона в тех случаях,
когда Ф<сФх- Если Ф (г) = cos az, то
(—) = — [— 'J f 1 — 0,389-f-Y (12.1.16)
k k Jr 3 \ k Jr фк J’ ' 7
t. e. (&k/k)R отличается от (Д£/£)и уже в нулевом порядке по
малому параметру Ф/Фи (см. задачу в конце параграфа). Обыч-
но можно ограничиться одним слагаемым в (12.1.15), (12.1.16).
В большинстве случаев хорошая точность получается, если в
(12.1.15) положить
JL = Фмакс + ф . (12.1.17)
ф фа 2Ф ' '
Например, если Ф(г)=соэа2, то (12.1.17) равно 1,285 вме-
сто точного значения 4/3.
Выше рассматривалось влияние неравномерности плотно-
сти потока по реактору на величину отравления ксеноном. Иног-
да значительная неравномерность плотности потока может воз-
никать и в каждой тепловыделяющей сборке (ТВС). Тогда се-
чение Хх(Ф) надо усреднить по объему ТВС (k— коэффициент
размножения ячейки):
v f 2/Ф</у
£ =---------z------------,
j 2аФ<2о 4- J Sx (Ф) $du
где 2а — сечение поглощения всеми нуклидами, кроме 135Хе.
Считая, что 2f и 2а не зависят от координат, и используя
(12.1.4), получаем
2ПФ) = ?2х(Ф), (12.1.18)
где
1+Фх/Ф / ф \
5 Ф \ 1+Фх/Ф /'
Считая, что Фх/Ф<^1, разложим в ряд. Тогда для £ получим
/ Фх V - /Тх
£=!+(-=р-р; / = Ф^-1А —1. (12.1.19)
347
Если Ф(г) аппроксимировать параболой, то легко вычислить
® (4) -1 =4141п*-1; <I2J'2O)
где — радиус ТВС.
Даже при больших Ф(/?)/Ф(0) значение f мало; например,
если х=3, то /=0,1. Таким образом, даже при очень значитель-
ной неравномерности плотности потока тепловых нейтронов по
ТВС можно вычислять 2Х(Ф), пользуясь средним значением Ф.
Обратимся теперь к переходным процессам, которые описы-
ваются уравнениями (12.1.1). Решение этих уравнений, если
плотность потока и Sf постоянны во времени, при произвольных
начальных условиях /(0), Х(0) имеет следующий вид:
/(О=/о+[/(О)-/о] ехр (-М0;
X (0 = Хо + ч [/ (0) - 10] [ехр (- 2, 0 - ехр (- 2XQ] +
Лх — Лг
+ И(0)-Х0]ехр(-2хО, (12.1.21)
где /о, Хо определены (12.1.3) и
7/х=2.х и“ОхФ. (12.1.22)
Если в (12.1.21) положить /(0)=Х(0) =0, то получим закон
увеличения концентраций I и Хе при пуске реактора в момент
/ = 0, причем плотность потока нейтронов изменяется скачком
от ф—0 при 7<0 до Ф при />0. Зная концентрацию Хе, можно
определить макроскопическое сечение и величину qfX как функ-
цию времени. На рис. 12.2 приведена зависимость <7fx(0/<7fx(o°)
для различных плотностей потоков. Если пренебречь независи-
мым выходом Хе, то /o/Xo=2,x/Xi и значение У] исчезает из
отношения <7fx.(0/^fx(oo), т. е. это отношение одинаково для
всех делящихся нуклидов.
При малых временах, когда 2Д<С1, //xi<l, можно (12.1.21)
разложить в ряд:
/2 Р '
^(0=А% + [Х(О)-Хо] 1-2^ + 2
6
+ 2^[7(О)-/о]Г1 -(2x + 2i)4- +V (2х+^М +2р/2’.
L 2 о 1
(12.1.23)
При Х(0)—Ц0) =0, т. е. для пуска реактора, получим
У 2
^Г1-±(21 + 2х)'.
О
(12.1.24)
Рассмотрим теперь поведение X(t) при остановке реактора,
который долго работал на постоянной мощности. Для этого на-
348
Рис. 12.2. Зависимость <7х (/)/<7х(о°)
от времени при различных плотностях
потоков нейтронов Ф
Рис. 12.3. Зависимость глубины
иодной ямы (по отношению к ста-
ционарному отравлению) от вре-
мени при различных плотностях
потоков Ф до остановки реактора
[штриховой линией дана аналогич-
ная зависимость для 105Rh (235U)
при плотности потока 1015 нейтр/
/(см2-с)]
до найти решение уравнений (12.1.1) при Ф=0 с начальными-
условиями /(О)=/о, X(O)=Xo, где /о, Хо— концентрации иода,
и ксенона при /<0. Это решение получится из (12.1.21), если
там положить <D=Zo=JV0=O и заменить /(0), Х(0) на 10, Хо,
т. е.
Л0 = Л>ехР(—М): Аг(0 = А'оехр(—2x0 +
X.
+ -т—Ц—/0(ехр(—21 f) — ехр (—2х 0)- (12.1.25>
Определим отношение qfx(t)fqtxffi), т. е. отношение отри-
цательной реактивности, вносимой 135Хе после остановки реак-
тора, к стационарному значению qfx до остановки:
= ехР (— + 0 + х X (ехр (— 2j 0 — ехр(— 2Х О)-
4fX'v> '-х Л1 у
(12.1,26).
При малых t можно разложить (12.1.26) в ряд:
-^S-=l + К - ^-Ях V = 1 + 0,07 - 0,093V,
<7/х(и1 \ у у / \ у х /
(12.1.27)?
349
где t — время, ч; конкретные цифры относятся к 235U. Из
(12.1.27) видно, что z?fX растет со временем линейно и тем бы-
стрее, чем больше плотность потока нейтронов до остановки.
При плотности Ф<у2Фх/У1=7 •1011 нейтр/(см2-с) производная
отрицательная, т. е. убывает (численное значение дано для
235U; для 239Ри оно в 2 раза больше). Отметим, что qfx(t)
в (12.1.26) в отличие от <7fx(0) зависит от стх при любых плот-
ностях потоков.
Увеличение отрицательной реактивности после остановки ре-
актора называют «иодной ямой». Физическая причина появле-
ния иодной ямы состоит в следующем. При уменьшении плотно-
сти потока уменьшается главная причина исчезновения ядер Хе
(захват нейтрона), а появление их при распаде иода некоторое
время происходит с прежней скоростью. Затем количество иода
начинает уменьшаться, накопившийся Хе распадается, и 2х(0
стремится к нулю.
На рис. 12.3 приведена зависимость Хх(/)/Хх(0) для 233 U
[для других нуклонов зависимость Хх(0/2х(0) близка к изо-
браженной на рис. 12.3, поскольку отношение yi/y для всех
.делящихся нуклидов близко к единице]. Из рис. 12.3 видно, что
глубина иодной ямы при плотностях потоков 5-Ю13—1014 в 2—4
раза превосходит стационарное значение <?/х, а продолжитель-
ность достигает 30—40 ч. Для пуска реактора в этот промежу-
ток времени необходимо иметь значительный запас реактивности
в органах регулирования. Очевидно, что такое же явление, но
меньших масштабов возникает в том случае, когда мощность
реактора падает не до нуля. Соответствующие формулы можно
получить из (12.1.21).
Величина (12.1.26) зависит от координат, поскольку плот-
ность потока нейтронов до остановки зависела от координат.
.Можно усреднить 2Х(/) аналогично (12.1.7), но такая величина
не будет иметь физического смысла, поскольку распределения
плотности потока нейтронов до остановки и в момент последую-
щего пуска могут быть существенно различными, например, за
счет движения органов регулирования или других изменений в
состоянии реактора.
В связи с процессами накопления иода и ксенона возникло
-много задач по оптимизации различных характеристик этого
переходного процесса. Эти интересные задачи изложены в мо-
нографии А. П. Рудика [221], к которой мы и отсылаем чита-
теля (см. также [222]).
Явление, аналогичное иодной яме, происходит и в результа-
те накопления 105Rh, однако его масштаб значительно меньше
(см. рис. 12.3).
В табл. 12.2 приведены характеристики нескольких других
нестабильных продуктов деления, которые надо учитывать, если
ллотность нейтронов существенно превышает 1014 нейтр/(см2-с).
-350
Таблица 12.2. Характеристики с лабопоглощающих нестабильных
осколков
Нуклид б I, б Г1/2- сут Выход, %
23 3|J 235CJ 23 8U seepu 141PU
1ззхе 190(90) 52* 5,29 5,96 6,75 6,47 6,97 6,55
М1Се 29(3) 0,48 32,5 6,74 5,81 6,76 5,34 4,79
143рг 90(10) 190(25) 13,58 5,92 5,94 4,68 4,47 4,42
127шТе 3380(500) 1140(170) 109 0,5 0,12 0,12 0,52 0,24
*По [219].
Суммарное значение qf для нуклидов, перечисленных в табл.
12.2 (кроме Те) при плотности потока 1014 нейтр/(см2-с) и у=
=0,1 равно при делении 235U, 238U, 239Pu, 241Pu соответственно
%: 0,26; 0,24; 0,23; 0,21.
Промежуточное положение между 135Хе и слабопоглощаю-
щими нуклидами занимает 127тТе. Большой период полураспада
и не очень большое сечение приводят к тому, что равновесная
концентрация наступает при сравнительно больших выгораниях:
если Ф=2-1013 нейтр/(см2-с), то время когда (оФ-)-А,)/1—-1,
равно 80 сут; если Ф=1014 нейтр/(см2-с), то /1 = 30 сут. При
t>ti имеем qf=yl(1+Ф*/Ф), где ф*=2-1013 нейтр/(см2-с). По
своему влиянию на реактивность при t>ti 127mTe сравнивается
с 105Rh при плотностях потоков порядка 1013 нейтр/(см2-с) и ра-
за в 2—3 меньше при плотности потока порядка 1014 нейтр/
(см2-с).
Радиоактивные изотопы Pm входят в цепочку Pm—Sm—Eu,
которая рассмотрена в § 12.3.
Задача. Используя теорию возмущений, которая изложена в § 5.3, вычис-
лить 6k и искажение плотности потока нейтронов в плоском реакторе без
отражателей за счет отравления 135Хе и 105Rh.
Решение. В качестве возмущения возьмем разность между отравле-
нием в данной точке z и отравлением, вычисленным по среднему потоку.
Если первое приближение собственного числа (когда возмущение равно ну-
лю) нормировано на единицу, то возмущение надо разделить на k—1 =
У Г Ф(г)
V(2)=v(fe_l) Ф(г)+Фх
Ф
Ф±4
Ф(г)=Фтсозг, (12.1.28>
где у — выход 135Хе; v — число вторичных нейтронов; Фх — характерная плот-
ность потока (12.1.5); Ф=2Фт/л— средняя плотность потока. Возмущение
(12.1.28) зависит от плотности потока, и поэтому необходимо делать итера-
ции. Однако в данном случае искажение потока столь незначительно, что
итераций можно не делать. Перепишем (12.1.28) так:
V (z) = А 1
2/п -f- а
a -j- cos г
. У а Фх
А =—гт—;--------------1 а = (12.1.29}
v(fe—1) a-f-2/п Фт
351
Для численных опенок положим #=7,14 %: v=2,86 (делящийся нуклид —
239Рц); k—1=0,01; а = 0,2; А = 0,5968; Фт = 4-1013 нейтр/(см2-с).
Первая поправка к собственному числу равна [см. (5.3.9)]:
«/2
4 Г Г 8
£, = — I Р(г) cosa zdz = А 1 — — + с
л J л2
о
(12.1.30)
тде
» Г 8
с = 2а2 1 ———
) л2
1+-аг1/'2.. Arth 1/
|/1 — а2 ' 1 + а
(12.1.31)
Чтобы сопоставить результат с (12.1.10), надо добавить к (12.1.30)
Л/г \ у Ф у________1
k / v(A —1) Ф-рФд v(A —I) l+«/2e’
Тогда
т. е. формула (12.1.10) соответствует случаю с=0. Пренебрежение с при а=
= 0,2 означает ошибку около 10 % в значении коэффициента при Фх/Ф в фор-
муле (12.1.10). При а=0,2 £1=0,1, т. е. изменение собственного числа со-
ставляет 10 % k—1.
Первое приближение для плотности потока [см. (5.3.11), (5.3.12)]:
Фх(г) = cos г ехр I — J #х (z)dz I, (12.1.32)
\ о /
тде
(£, — А { sin 2z\ ,
' #1(z) = (cosz)-M—-— z+—— 4-
\ хЬ \ X* /
/ 2 \| 2а2 Г\ — a z \ 1] ,
-4- А I—+а| sinz—a? + T7===-Arth 1/ —— tg — >. (12.1.33)
1 \ я у.[ 1/1 —а2 V 1-]-а 2/JJ
Аналогичные формулы справедливы для отправления 105Rh. При у=0,1
.имеем [см. (12.1.14)] ФЛ=3,1 • Ю14' нейтр/(см2-с). Поэтому при плотности
потока Фт=4-1013 нейтр/(см2-с) получим а=7,73, А=1,777 (для 239Ри). При
а>1 в формулах (12.1.31), (12.1.33) надо сделать замену:
При а»1 можно разложить (12.1.30) в ряд по степеням 1/а. Однако
проще это сделать для (12.1.29). Результат такого разложения
Л/г 4 / АА: \ / 9я2 \ Ф
k 3 \ k J _1+ V ~ 64 j
совпадает с (12.1.16).
.352
На рис. 12.4 приведено относительное изменение плотности потока (Ф]—
—Фо)/Фо, вызванное отравлением 135Хе и 105Rh (делящийся нуклид 239Ри),
для двух значений Фт: 4-Ю13 нейтр/(см2-с) (кривые 2, 4) и 1,6Х
ХЮ14 нейтр/(см2'С) (кривые 1, 3). Кривые 1, 2 учитывают только влияние
135Хе, кривые 3, 4 — суммарное влияние 136Хе и I05Rh. Видно, что (Ф]—
—Фо) /Фо слабо зависит от Фт, поскольку с ростом плотности потока влияние
,35Хе уменьшается, a 105Rh — возрастает (для 235U выход 105Rh существенно
меньше и его роль незначительна). Максимальное изменение плотности пото-
ка ~8 % происходит на краю реактора (надо учитывать, что даже плохой
отражатель может привести к изменению плотности потока того же, или даже
большего, порядка). Увеличение коэффициента усреднения igi для кривой 3
составляет примерно 2 %.
12.2. СТАБИЛЬНЫЕ СИЛЬНОПОГЛОЩАЮЩИЕ ПРОДУКТЫ ДЕЛЕНИЯ
Если продукт деления стабилен, то его концентрация с(- оп-
ределяется из уравнений
= (12.2.1)
i
где t/ij — выход i-ro продукта при делении /-го нуклида. Если
сггЗ>сг[, то быстро устанавливается равновесная концентрация
(наступает насыщение). За это время не успевают существенно
измениться состав топлива и плотность потока нейтронов. По-
этому надо написать решение уравнения (12.2.1) при O = const,
2f = const и начальном условии Cj(O)= 0:
G (0 = S (Уа%Л) [1 -ехр (-«(ф/)]. (12.2.2)
/
Макроскопическое сечение всех продуктов деления, которые
Рис. 12.4. Относительное изменение
плотности потока по высоте плоского
реактора (делящийся нуклид 239Ри)
ДФ/Ф, вызванное отравлением 135Хе
и 105Rh:
1, 3— поток 1,6*1014 нейтр/(см2*с); 2, 4 —
поток 4*1013 нейтр/(см2*с); 1, 2 — только
i35Xe; 3, 4 — 135Хе н 105Rh
23—6053
353
w Таблица 12.3. Характеристики стабильных сильнопоглощающих продуктов деления [31—33,45,46]
Параметр 149Sm lslSm 113Cd * = ’Gd i
а, б 4,014(60)•104 1,52(3) • Ю4 2,06(4)-104 2,540(8) -Ю6
/, б 3,4-103 3,52(16) Ю3 390 720(20)
годы 90
°, б 1,4(3)-10s 173
Л б для предшественника 1,2-10® 1830
4 54,81 28,4 5,37 15,15
Выход, “/о
2327^ 1,22 0,80 0,046 0,0006 2,13
233JJ 0,77(3) 0,35(3) 0,013(3) 0,0067(7) 1,14(4)
235JJ 1,08(6) 0,424(12) 0,010(2) 0,0063(5) 1,52(6)
238JJ 1,67(6) 0,83(5) 0,056(11) 0,031(6) 2,59(8)
239ри 1,28(8) 0,80(5) 0,077(8) 0,076(8) 2,23(9)
24ipu 1,46(6) 0,90(6) 0,155(15) 0,131(13) 2,64(9)
удовлетворяют условию при ^(ОгФ)-1 равно
UljEfj,
ч
т. е. поглощение нейтронов этими продуктами зависит только от
выходов уц, а не от сечений <ц. В табл. 12.3 приведены -сечения
и выходы соответствующих нуклидов (151Sm радиоактивен, но
его распадом можно пренебречь).
Вычислив по данным табл. 12.3 значение qf для сильнопогло-
щающих нуклидов, получим ^^1,5^-2,5%, причем главным ну-
клидом является I49Sm. Схема распадов в цепочке с массовым
числом Л=149 следующая:
Ba —- La —► Се-> Рг------> Nd---► Pm-------► Sm.
0,9с 2,9с 5(1)с 2,5(2)мин 1,73(1)4 53,03(5)4
Обычно можно ограничиться рассмотрением только одного
предшественника — 149Рт с эффективным периодом полураспа-
да [220]
Т3& = Tm (Nd) + Г1/2 (Pm) = 54,81 ч.
Уравнения, описывающие изменения концентрации 149Sm
(или других нуклидов из перечисленных в табл. 12.3), с учетом
предшественника 149Рт записываются так:
-^- = у2гФ — ХрР\ ~ = 1РР — ?38Ф; Хр=1Р + арФ, (12.2.3)
где Р и S — концентрации Pm и Sm. Стационарное значение
суммы макроскопических сечений поглощения Pm и Sm равно
Sp+Ss=ySf, т. е. определяется только выходом рассматривае-
мой цепочки. Накопление Pm и Sm, если плотность потока в ре-
акторе в момент t=0 скачком возрастает от нуля до Ф, проис-
ходит по закону
p=(t/2z®/2p)[i — ехр(—
S= (yfzM^os)[l-ехр(-о5Ф/)] +
л'
+ yS)ф , р [ехр(— Xpt) — ехр(— o/W)]-
Лр — а5Ф
Сечение 149Рт сравнительно невелико, и при Ф<1014 нейтр/
(см2-с) можно положить 'к'р=ХР. Надо учитывать, что 149Sm
имеет резонанс при £’=0,1 эВ, и поэтому его сечение в тепловой
группе зависит от состава ячейки реактора и должно быть опре-
делено одновременно с термализационным расчетом ячейки (см.
§ 7.5). На рис. 12.5 представлены зависимости oa(f), среднего
23* 355
Рис. 12.5. Зависимость сечения погло-
щения о(£) 149Sm, среднего сечения
по максвелловскому распределению
а(Ет) и ^-фактора от температуры
(X — сечение при скорости 2200 м/с)
Рис. 12.6. Зависимость сечеиия погло-
щения 151Sm от энергии <т(£), сред-
него сечения по максвелловскому рас-
пределению о(£т) и ^-фактора от
температуры (X — сечение при ско-
рости нейтронов 2200 м/с)
сечения по чисто максвелловскому спектру а(Ет), ^-фактора
для 149Sm, а на рис. 12.6 — те же величины для 151Sm.
Если положить 05=66 000 [g=2,2; Ет=0,04; см. (2.4.7)],
то характерное значение плотности потока Ф$ равно
Os=W<Js=5,3-1013 нейтр/(см2-с). (12.2.5)
При этой плотности потока обе экспоненты в (12.2.4) затухают
за время порядка 3 сут. Суммарное макроскопическое сечение
Pm и Sm равно
^s+p=y^f [1 —(1—е)-1 ехр (—<у$Ф04-е(1— 8)-1 ехР (—%'₽/)],
(12.2.6)
где 8=(os—<тр)Ф%р-1. При g=l в (12.2.6) возникает неопреде-
ленность, которую, однако, легко раскрыть. Изменение коэффи-
циента размножения, вызванное накоплением Pm и Sm, равно
=----= —-^-[1 — (1 — е)-’ехр(—о^Ф/)
е (1 — s)_I ехр (—Xj,^)]. (12.2.7)
Аналогичными уравнениями описывается изменение реак-
тивности, вызванное накоплением других продуктов деления,
356
перечисленных в табл. 12.3. Для 15ISm характерное значение
плотности потока равно (если £т=0,04, а=6000):
Яс,
Фз1 =-------= 10” нейтр/(см2-с).
При этом обе экспоненты затухают за время порядка 1 сут. Для
других продуктов деления характерное значение плотности по-
тока Фса=1,8-1015 нейтр/(см2-с); Фоа = 5-1013 нейтр/(см2-с).
При остановке реактора возникает явление, похожее на иод-
ную яму. Концентрации Pm и Sm изменяются по закону
Р (f) = Р (0) ехр (- Я/> Q; Р (0) у^Ф/Я^;
S (0 = S (0) + Р (0) [ 1 — ехр (- Яр /)];
5(0)=ДЯр/(Я>5).
(12.2.8)
Сумма макроскопических сечений Pm и Sm равна
Ss+P = 2S(0) + Sp(0) [ехр(- Яр 0 + -^ (1 -ехр(- Яр0)], (12.2.9)
L °р
т. е. разница сечений при t=eo и t—О составляет
<т2 = Р(0) (<ts—<тр). (12.2.10)
Таким образом, при остановке реактора реактивность умень-
шается на величину
Ak = J- (12.2.11)
Ч l-i-ОрФАр Ф5 v 7
где у — выход цепочки с Л = 149; Фз—характерная плотность
потока (12.2.5). В этом случае реактивность не восстанавлива-
ется, поскольку Sm не распадается. Накопившийся Sm прихо-
дится сжигать при повторном включении реактора.
Аналогичные уравнения описывают накопления других нук-
лидов, перечисленных в табл. 12.3. После остановки реактора
возникает отрицательная реактивность:
V Ф/ 1 +а/ Ф/Хг
(12.2.12)
где у;-—выходы, а а,—сечения 149Sm, 151Sm, 113Cd, 157Gd; a';, 2Л—
сечение и постоянная распада предшественника. Характерные
значения Ф, были приведены выше. На рис. 12.7 показана за-
висимость Ak (12.2.12) для 235U от Ф. Основной вклад в Ak вно-
сит 149Sm [поскольку а для 149Sm существенно зависит от эф-
357
Рис. 12.7. Зависимость отрицательной
реактивности, вносимой сильнопогло-
щающими стабильными продуктами
деления после остановки реактора,
от плотности потока тепловых ней-
тронов до остановки
Рис. 12.8. Зависимость поглощения
нейтронов Pm и Sm от глубины выго-
рания (если не учитывать последова-
тельных поглощений Pm, Sm, то
qi, Sm+Pm=i/ Sm)
фективной температуры нейтронов, в каждом конкретном слу-
чае \k (12.2.12) надо вычислять заново]. Из рис. 12.7 видно,
что если Ф>1015 нейтр/(см2-с), то при остановке реактора воз-
никает столь большая отрицательная реактивность, что повтор-
ный запуск может оказаться невозможным. Таким образом, вы-
сокопоточный реактор нельзя останавливать («самариевая
смерть» [223]-). Задача об оптимальном выжигании образовав-
шегося 149Sm рассмотрена в [221, 223].
В группе нуклидов Pm, Sm, Ей, образующихся при делении,
большинство обладает большими сечениями поглощения и поэто-
му возникает длинная цепочка последовательных захватов ней-
тронов (см. § 12.3). Последовательные захваты нейтронов при-
водят к тому, что поглощение, например 151Sm, значительно
больше, чем это следует из уравнения (12.2.1). На рис. 12.8 для
примера приведены отношения QfSm+Pm/t/sm, равные единице,
если справедливо (12.2.1) как функции и величины д=о0Ф^ гДе
<то=1ООО б при O = const, у=0,1.
Последовательные захваты приводят к тому, что эффектив-
ное сечение некоторого символического продукта деления (см.
§ 12.3), которым можно аппроксимировать поглощение нейтро-
нов нуклидами всей цепочки, оказывается аномально малым.
Поясним это явление на простом примере последовательного за-
хвата двумя нуклидами, концентрации которых обозначим Ci,
358
Рис. 12.9. Зависимость погло-
щения нейтронов продуктами
деления (по отношению к чис-
лу делений) от времени при
малых выгораниях [плотность
потока Ф=3-1013 нейтр/
(см2-с)1
с2, выходы У1, у2, сечения по отношению к сечению деления th,
о2- Уравнения для с, следующие :
— ~ — <з2с2. (12.2.13)
ds as
Решив уравнения (12.2.13) с начальными условиями Ci=c2=0,
составим величину
^ = 0^1 Н-о2с2 = 1/1[1 — ехр(— о^)] + (Ут_ + У[1 — ехр(—o2s)] +
+ —[ехр(—отв) —ехр(—o2s)]. (12.2.14)
°2
Разложим (12.2.14) в ряд по Oi« и o2s:
^ = pos(l— (12.2.15)
где
у У1°1 4~ Уг°2 . 0 _ У1°12 4- Уга2а У1а1а2 (12 2 16)
° У1°1~Ь У2°2
имеют смысл выхода и сечения эффективного осколка, которым
заменены два продукта деления (12.2.13). Если y2<yi, а такое
соотношение справедливо для всех звеньев цепочки Pm, Sm, Eli,
то o' может быть много меньше, чем аь о2- Пусть, например,
О1—О2=о. Тогда
0=01/2/(1/14-1/2).
Если t/2=t/i/3, то о=о/4. В результате оказывается, что функция
Qf(s), описывающая поглощение нейтронов всеми членами це-
почки Pm, Sm, Ей, является почти прямой линией [кроме на-
чального участка (12.2.1)), когда существенно только поглоще-
ние 149Sm, 151Sm], хотя сечения почти у всех нуклидов цепочки
достаточно велики.
На рис. 12.9 для примера изображена зависимость qf(t) по-
глощения всеми продуктами деления в начальный период рабо-
359
ты реактора. Резкий подъем в течение первых двух суток — это
поглощение нейтронов 135Хе. Поскольку пример взят для 235U
с начальной плотностью потока 3-1013 нейтр/(см2-с), роль 105Rh
очень мала. Далее наступает более медленный рост за счет по-
глощения изотопами Sm. Если не учитывать остальных продук-
тов деления (см. § 12.3), то кривая qf должна была бы асимп-
тотически приближаться к самой верхней горизонтальной ли-
нии. Видно, что при ^=20 сут qf(t) пересекает эту линию.
Задача. Оценить влияние 147Рт, 148Рт на реактивность при самариевой
смерти (рис. 12.10).
Решение. Величина реактивности после остановки реактора пропор-
циональна концентрации 149Рт в момент остановки (остальные нуклиды
в табл. 12.3 вносят малый вклад). Поскольку явление самариевой смерти
существенно только при больших значениях потока нейтронов, пренебрегаем
распадом 147Рт и 147Nd, см. рис. 12.10). Тогда концентрация |47Рт определя-
ется уравнением
dc7
— = I/7SfO—О,С,Ф,
откуда при постоянной плотности потока и с7(0)=0
с7 = ~~ I [1—ехр( — <т7Ф/)].
ст7
Обозначим величины, относящиеся к 14SmPm, одним штрихом, а к 148гРт —
двумя. Тогда
~ = с7Ф (Xg7 о8'Ф) .
dt
Если (Z's-pT's®)/» 1 и (Х'б/Ф-Ес'б) >о',7, то концентрация с'8 равна
с'8=у72, (сб/оу) {(Vs/Ф) Н-ст'в]“ *[ 1 —ехр (—о7Ф1) ]
и аналогично
c',8=i/72f(o"7/O7)[(V's/®)+47"8]_1ll—ехр (—<т7Ф/)].
Уравнение для концентрации 149Рт
~ = y0Sf®+ (о8'с8' + о8"с8")Ф— (Х9 + о9Ф)с9-
при (Хд-|-ст9Ф)1 имеет решение
c9=^!i+— (—,°8' ф
I Уз \ °7 V+^s' Ф
Ц8"Ф \
К" + о8"Ф/
[1— ехр(— ст7Ф#) ]
где Сд—концентрация 149Рт без учета 147Рт и 14SPm. При плотности пото-
ка Ф=1014 нейтр/(см2-с) имеем <т"8Ф/Х"8=10; </8ФД'8=0,2. Считая приближен-
но, что o,'7 = o'"7=0,5<j7 и полагая (/7=2,31; (/9=1,08; получаем при Ф> 1014:
с -с°
с9 — <-9
1+1,071 1
0,2Ф
1 +0,2Ф
(1 — ехр(— о7Ф/))
361
где Ф=Ф/1014. Если у~0,1, то 400 б. Пусть продолжительность работы
реактора характеризуется величиной a5®/=s5<0,5. Тогда можно разложить
в ряд по О/ФТ
с9 — с°9
1+0,6 1 +
0,2Ф \
------= ) s.
1 + 0,2Ф /
Если например, s5 = 0,3, Ф=1, то сэ = 1,2со°, а при Ф=10 имеем С9 = 1,3с9°.
Таким образом, отрицательная реактивность за счет иакоплеиия 149Sm после
остановки реактора при плотностях потока 1014—1015 нейтр/(см2-с) и глуби-
не выгорания 235U около 30 % возрастает при учете нуклидов 147Рт и 148Рт
на 20—30 %.
12.3. ЭФФЕКТИВНЫЙ ОСКОЛОК
Макроскопическое сечение поглощения всеми продуктами
деления, отнесенное к макроскопическому сечению деления,
qt(t) можно записать так:
(12.3.1)
где qp— поглощение распадающимися продуктами деления (см.
§ 12.1); i?cn — сильнопоглощающими стабильными продуктами
деления (см. § 12.2); q(t) —всеми остальными. Проще всего
характеризовать q средним сечением и средним резонансным
интегралом на пару осколков. В табл. 12.4 приведены средние
значения, рекомендованные в [224, 225]. При этом выход пары
осколков считался равным единице, хотя фактически этот выход
равен 1--— (г/р+усп), где уР— выход радиоактивных; усп —
стабильных сильнопоглощающих продуктов деления.
Погрешность, которая возникает в величине q(t) при ис-
пользовании Данных табл. 12.4, при плотностях потоков 1013—
1014 нейтр/(см2-с) составляет 10—15%.-
Для более точного вычисления влияния продуктов деления
на реактивность реактора надо рассмотреть значительное (по-
рядка сотни) количество нуклидов. В [224] показано, что вся
совокупность продуктов деления, кроме распадающихся и
сильнопоглощающих, может быть заменена одним «эффектив-
ным нуклидом», который будем называть «эффективный оско-
аблица 12.4. Среднее сечение и резонансный интеграл пары осколков, б
[Нуклид У Нуклид а I
233(J 40 180 241рц 49 320
235(J 40 210 232Th 43 215
239рц 47 280 238(J 46 270
362
лок» (ЭО). При этом надо учесть, что большинство нуклидов,
возникающих при делении и поглощающих нейтроны, имеют
предшественников с периодами полураспада от нескольких ча-
сов (более короткие периоды можно не учитывать) до несколь-
ких лет. Поэтому правильной моделью ЭО является модель
с предшественником. Концентрации ЭО с и его предшественни-
ка Со определяются из уравнений
Яс0; — = Яс0 — оФс; 7=о + у/. (12.3.2)
dt dt
Если плотность потока и жесткость постоянны, то уравнения
(12.3.2) легко решаются и для q(t) получаем
!— expf---------------+ у2-ехр (—Л/) , (12.3.3)
L 1 — “ \ of J 1 — “ J
где а=оФД; 5=дФ(; Х=1п 2/7’1/г-
В [224] величина q{t) вычислялась на ЭВМ с учетом основ-
ных предшественников и взаимных превращений нуклидов при
захватах нейтронов. Параметры ЭО, входящие в (12.3.3), под-
гонялись так, чтобы наилучшим образом аппроксимировать q{t}
(табл. 12.5).
Параметры ЭО зависят от плотности потока нейтронов. Для
определения параметров при промежуточных значениях плот-
ности потока в [224] предложены следующие интерполяцион-
Таблица 12.5. Параметры эффективного осколка
Нуклид Плотность потока, иейтр/(см2-с) У, % О, б I, б 71/2’ сут
233 [J 1043 35,4 118 600 5,1
1044 47,6 90 470 5,1
1043 43,97 95,68 575,2 10,73
235Ц 1044 52,41 85,01 515,2 9,13
1015 75,97 45,71 275,7 3,66
1043 59,20 84,86 590,7 11,27
239рц 1044 68,75 75,95 517,5 8,67
1045 97,69 40,55 272,5 2,62
1043 63,84 82,17 600,6 10,46
2UPu 1044 73,56 74,27 532,7 8,1
1045 98,0 43,16 309,5 2,49
1013 43,4 100 554 4,4
232Tft 1044 56,9 62 449 4,4
1043 58,67 82,98 560,5 15,5
Ю44 64,51 81,47 552,1 1,09
238 [J 1045 100,9 40,73 256,5 -2,87
363
Таблица 12.6. Параметры интерполяционных формул
Нуклид Ф1 ф'1 Фз ф'2 Ф’. ф4
235Ц 19.08 38,34 333,3 57,73 512,2 66,46 51,22
23spu 22,27 43,05 488,4 65,26 261,7 49,81 29,97
24фц 19,39 33,25 296,6 64,31 174,4 43,48 30,96
238Ц 56,25 163,7 —121,1 -157,4 —113,8 —138,3 22,42
ные формулы:
1 + (Ф-1)/Ф! .
Voi + (Ф-и/Ф/ ’
/ = / 1 +(Ф-1)/Ф3 .
°1 + (Ф-1)/Ф3'’
7\/2 =7?/2[1 + (Ф-1)/Ф4Г\
1 + (Ф-1)/Ф2
1 + (Ф-1)/Ф2'’
(12.3.4)
где Ф — плотность потока, деленная на 1013 нейтр/(см2-с), а
параметры Фг- приведены в табл. 12.6. Отрицательный знак
у некоторых Ф/ означает, что соответствующими формулами
нельзя пользоваться при плотностях потоков, заметно превы-
шающих 1015 нейтр/(см2-с).
Зависимость параметров эффективного осколка от плотно-
сти потока достаточно слабая, и в большинстве практических
расчетов можно считать их постоянными, вычисленными по сред-
нему значению плотности потока.
Произведения уст и yl, которые в основном определяют по-
глощение нейтронов ЭО, значительно слабее зависят от потока,
чем ст и I. Например, для 235U сечение ст изменяется более чем
в 2 раза при изменении плотности потока в 100 раз (см.
табл. 12.5), в то время как произведение уст изменяется толь-
ко на 20 %.
Точность подгонки параметров ЭО такова, что погрешность
определения qt составляет 2—3 %. Того же порядка погреш-
ность qt из-за погрешностей в выходах и сечениях продуктов
деления. При плотности потока 1015 нейтр/(см2-с) погреш-
ность может быть несколько больше, поскольку возрастает роль
предшественников и аппроксимация одним ЭО недостаточно
точна.
Предложенная в [224] модель ЭО справедлива для реакто-
ров с мягким (у<0,3) спектром нейтронов.
В тех случаях, когда точность аппроксимации одним ЭО не-
достаточна, надо выделить группу слабопоглощающих нукли-
364
Таблица 12.7. Параметры эффективного слабопоглощающего осколка
Параметр газу 235U 2Э9ри 2*ipu 282ТЬ
Выход у 1,53 1,46 1,37 1,37 1,55 1,40
ч, б 2,0 1,54 1,96 2,28 2,3 1,79
Z, б 8,4 9,4 16,9 21,4 7,5 12,3
Таблица 12.8. Выходы основных продуктов деления, %
Нуклид 233(J 2sspu 2“Pu sa2Th «Э8Ц
«3Кг 1,01 0,53 0,301 0,202 : 2,0 0,395
»3Мо 6,22 6,51 4,98 4,02 5,73 5,28
99Тс 5,1 6,14 6,19 6,17 2,98 6,20
103Rh 1,71 3,15 6,79 6,87 0,167 6,38
108Ag — 0,03 1,10 2,48 — 0,13
1297?'J'g 0,087 0,102 0,26 0,155 0,013 0,043
129 J 0,425 0,51 1,28 0,78 0,065 0,218
131Xe 3,48 2,78 3,78 3,20 3,78 3,19
l33Cs 5,96 6,75 6,97 6,55 6,97 6,47
i«pr 6,74 5,81 5,34 4,79 5,34 6,76
148Nd 5,92 5,94 4,47 4,42 4,47 4,68
145Nd 3,38 3,92 3,12 3,14 3,12 3,90
i47Pm 1,87 2,31 2,11 2,27 2,H 2,56
i62Sm 0,196 0,266 0,593 0,731 0,593 0,537
i63Eu 0,104 0,159 0,395 0,521 0,395 0,439
iS6Eu 0,023 0,0324 0,218 0,232 0.218 0,116
i56Eu 0,0112 0,0127 0,0112 0,165 0,002 0,0663
Примечание. Таблица составлена по данным [45]; выходы ,S5Xe, ,05Rh, l49Sm,
lslSm приведены в табл. 12.1, 12.3.
дов, аппроксимировать только их эффективным осколком, а
остальные учитывать точно. Параметры слабопоглощающего
осколка приведены в табл. 12.7.
На рис. 12.10 приведены основные нуклиды, их предшествен-
ники и цепочки нейтронных захватов, которые надо учитывать
при более точном определении нейтронного поглощения про-
дуктами деления. На этой схеме указаны сечения (цифры над
стрелками), резонансные интегралы (цифры под стрелками) в
барнах и периоды полураспада (цифры рядом с вертикальны-
ми стрелками). Выходы при делении приведены в табл. 12.8.
Численные расчеты по схеме рис. 12.10 позволяют устано-
вить влияние на реактивность различных нуклидов. Они рас-
положены в порядке уменьшения этого влияния: I43Nd, 149Sm,
I03Rh, 147Pm, 133Cs, 131Xe, "Tc, lsISm, 152Sm, 145Nd (в зависимо-
сти от жесткости спектра, плотности потока, глубины выгора-
ния порядок в этом списке может несколько изменяться; при
365
Рис. 12.11. Зависимость поглощения ней-
тронов продуктами деления от количе-
ства разделившегося 235U (кроме 135Хе;
мощность постоянна):
-----— расчет с учетом всех продуктов деле-
ния, приведенных на рис. 12.10 и слабопогло-
щающего ЭО с параметрами, указанными
в табл. 12.7; X-—расчет с одним ЭО> пара-
метры которого изменяются по мере измене-
ния плотности потока; О — расчет с одним
ЭО, параметры которого соответствуют сред-
ней плотности потока
делении 239Ри увеличивается значение i03Rh, 105Rh и умень-
шается i43Nd). На перечисленные нуклиды приходится пример-
но 70 % всего поглощения (если исключить 135Хе). Основной
вклад в резонансное поглощение вносят 133Cs, 147Pm, "Тс, I03Rh,
•131Хе, 152Sm, 155Eu, 154Eu, 145Nd (70%' всего резонансного погло-
щения) .
На рис. 12.11 приведены значения qt—qx.e при делении 235U
с постоянной мощностью. Начальное значение плотности пото-
ка 3-Ю13 и 3-1014 нейтр/(см2-с), жесткости у=0,2. При началь-
ной плотности потока 3-1013 нейтр/(см2• с) погрешности при-
ближенного расчета достигают 3 % только при больших глуби-
нах выгорания^ урана (~60%). Для начальной плотности
потока 3-1014 нейтр/(см2-с) погрешность составляет2—5%, одна-
ко при таких больших плотностях потоков схема на рис. 12.10
[слабопоглощающий ЭО (см. табл. 12.7)] дает значения q, не-
сколько завышенные по сравнению с более точным расчетом,
когда явно учитывалось 115 нуклидов (к схеме рис. 12.9 надо
добавить следующие нуклиды: 144Nd, 146Nd, I48Nd, 150Nd, l55Gd,
156EU; 1560(1, 140Ce> 141Ce> 142Ce> 143Ce> 100Ru> 135(2Si Юбр^
89Y, 9lZr, 1I5In, H0Cd, IHCd [224]). Из нуклидов, включенных
в эффективный слабый осколок (см. табл. 12.7), наибольшее
значение имеют: 93Zr, 97Мо, 101Ru, 107Pd, 108Pd, 127La.
На рис. 12.10 сечения и резонансные интегралы приведены
по [31, 32], а в расчете [224] использовались сечения [7]. Но-
вые данные приводят к увеличению сечения пары осколков на
~ 1 %’ для 235U и ~3 % для 239Рш
Выше рассматривалось поглощение нейтронов продуктами
деления в одной точке реактора. Рассмотрим для простоты плос-
кий реактор, в котором плотность потока нейтронов зависит
366
только qt координаты z. Пренебрегая выгоранием ЭО и пред-
шественником, имеем
2эо(г) = г/^оэоФ(г)/. (12.3.5)
Изменение коэффициента размножения в точке z из-за появ-
ления ЭО равно
где Sa — суммарное поглощение всеми нуклидами, кроме ЭО.
Изменение эффективного коэффициента размножения реактора
из-за появления ЭО определим по теории возмущений
JdA(z)O2(z)d?, (12.3.7)
или, подставив (12.3.6),
ДА = Дй/'; f = (Ф3)/Ф (Ф2), (12.3.8)
где Ak вычисляется по среднему значению; 2эо = у2^°эоФ^. Если
Ф(г)=созг, то [см. (12.1.16)] f—413. По мере выгорания ядер-
ного топлива распределение Ф(з) становится более плоским и
f приближается к единице (см. § 13.3).
12.4. АКТИВНОСТЬ И ЭНЕРГОВЫДЕЛЕНИЕ
ОСКОЛКОВ ДЕЛЕНИЯ
Если время жизни нуклидов, входящих в одну цепочку по-
следовательных распадов, много меньше времени работы реак-
тора, то концентрации этих нуклидов определяются из условий
равновесия:
Х)С1—у>°Х/Ф; Х2С2=/ч с 1 -1- у2° S/Ф;
tac3—^гСг-ЬУзО^цФ ..., (12.4.1)
где X, — постоянные распада; у? — независимые выходы (см.
§ 1.6). Активности (число распадов в 1 с) равны
А1 = Xi С\=У1ХуФ; А2==7.2С2=:=У2^/Ф;
Аз=ХзСз=уз2/Ф ..., (12.4.2)
где у, — кумулятивные выходы (т. е. У/ = У1°+У2°+ - +yz°).
Таким образом, активность пропорциональна кумулятивному
выходу (чем и определяется значение кумулятивного выхода,
вопреки некоторой «нефизичности», которая отмечалась в § 1.6
при определении этого термина).
Если в некоторый момент времени (/=0) реактор останов-
лен (или некоторая порция топлива извлечена из реактора), то
367
активности изменяются так: ;
Л! (0=^0 ехр (-W);
А„ (/) = у^Ф ехр (— Я2 0 +
+ Z/iSfO2 — [ехр (— Ях t) - ехр (- Я2 /)]. (12.4.3)
л2—
Обычно кумулятивные выходы последних членов цепочки почти
одинаковы. Если лД;>1 и Xi^>X2, то Ai(t) можно пренебречь,
a A2(t) равно
Дг(О =Уг2/Ф ехр (—W),
т. е. нуклид 2 можно считать первым в цепочке распадов. Если
же, наоборот, то Л2=У1ДФехр (—W) =ЛЬ т. е.
короткоживущий нуклид 2 удваивает суммарную активность.
Физически это очевидно, так как долгоживущий нуклид 1 пе-
реходит в нуклид 2, который тут же распадается, удваивая чис-
ло распадов. Поэтому если интересоваться активностью при
i>t*, то можно пренебречь всеми нуклидами в начале цепочки,
для которых Тц2<^Ц* (обычно короткоживущие нуклиды рас-
положены в начале цепочки), но необходимо учесть коротко-
живущие нуклиды (если они существуют), возникающие при
распаде долгоживущих.
Если 7’1/2>7', где Т — время работы реактора, то
А (/) = Х1С1 (Г) ехр (— Лх /); сх (Т) = [ 1 - ехр (- Лх Г) J.
(12.4.4)
Если нуклид 1 имеет большое сечение поглощения нейтронов,
то Ci(T) изменяется так:
сЛТ)= ехр(- А/Г)]; Я/ = Ах + охФ. (12.4.5)
Для второго члена цепочки имеем
Д2 (0 = Я2с2 (Г) ехр (— Я2 /) +
+ Ахсх (Т) \ [ехр (— Ях t) — ехр (— Я2 /)], (12.4.6)
Л2 Aj
где Ci(T), с2(Т) — концентрации нуклидов в момент остановки
реактора; сДГ) дано (12.4.5), а с2(Т) равно
(т7 - 2/Ф[1 — ехр(—А/ Т)] +
\ Л2 ^2 /
+ ух^Ф,- -А [ехр (- Я/ Т) - ехр (- Я/ 7)]. (12.4.7)
Лх —Л2 )
368
В (12.4.7) учтено поглощение нейтронов обоими нуклидами.
В некоторых случаях (например, I34Cs) выход нуклида 2
практически равен нулю (например, выход 134Cs порядка
10-5 %), и он возникает в реакторе только в результате погло-
щения нейтрона нуклидом 1. Тогда Ai(^) сохраняет прежний
вид (12.4.4), (12.4.5), а
A2(t) —К2с2(Т) exp (—k'2t);
с2(Т)= -^[1 — ехр(—Я/Т) +
+ 77^75 (ехР С” - ехР (” <12Л8>
Л1 — л2'
Если нуклид 1—стабильный (как 133Cs), то Х( = 0, ЯЛ =
= одф.
Удобно рассматривать удельную активность, относя ее к
единице массы разделившихся ядер (эта масса примерно на
1 °/о больше массы всех продуктов деления, поскольку нейтро-
ны, испущенные при делении, поглощаются главным образом
не в продуктах деления, а число нейтронов v близко к 1 % от
атомного номера). Тогда надо заменить
^Ф = ^ФТ/Т=М}/Т,
где Nf — число разделившихся ядер за время Т. Нормируя это
число на 1 г, получаем
27Ф^2,94-1016/Т, (12.4.9)
где Т — время работы реактора, сут; удельная активность при
этом будет выражаться в Бк/г (беккерель на грамм равня-
ется 2,7-10-11 Ки/г (кюри на грамм)). В (12.4.9) предпола-
гается, что число делений 235U и 239Ри примерно одинаково и
средняя атомная масса разделившихся нуклидов равна 237.
Энерговыделение при распаде нуклида i равно
q^AiEi,
где Ei — средняя энергия электронов и у-квантов. При опре-
делении qi надо во всех формулах заменить
A^qr, ^Ф^П-МРЕ^Т,
где Ei — энергия, МэВ; Т — время работы реактора, сут; qi —
энерговыделение, Вт/г.
Можно иначе нормировать энерговыделение (см. § 1.6):
энергия, МэВ на одно деление. В этом случае следует сделать
замену:
Ai-^qc, И^Ф^-Ei.
Из (12.4.4) — (12.4.8) видно, что формула (1.7.8) справед-
лива только в том случае, когда можно пренебречь поглоще-
24—6053 369
нием нейтронов. Поглощение нейтронов существенно для 134Cs,
148Pm, 135Хе, 105R'h, 147Рго, 154Eu, l55Eu и приводит к незначи-
тельным поправкам (если Ф^Ю14 см~2с-1) для 147Nd, 149Pm,
143Pr, ,33Хе.
В табл. 12.9 приведены удельные активности нуклидов через
время t после остановки реактора, для которых 1 ч<Т1/2<1 сут,
в табл. 12.10: 1 сут<Т1/2<0,5 года, в табл. 12.11: 0,5 года<
<Т’1/2<100 лет. Принято Т=3 года, у=0,5(г/гзз+г/гзэ), учтены
нуклиды с у>0,05 %, плотность потока тепловых нейтронов
принята 3-1013 нейтр/(см2-с), жесткость спектра у;=0,2.
Суммарная активность в табл. 12.9 для t=\ ч занижена,
так как не учитываются короткоживущие нуклиды. При /=3 ч
эта неточность уже не существенна.
При 1000 лет активность определяется главным образом
распадами:
"Тс-------->99Ru; 93Zr------->93mNb------->93Nb;
2,13-105лет 1,510рлет 13,6 года
,26Sn------> 12SmSb---> ,26Те.
1-10’лет 19 мин
Суммарная активность (/~1000 лет) равна ~2-107 Бк/г=
= 6-10“4 Ки/г (~75% активности приходится на "Тс). Эта
активность примерно на два порядка больше, чем удельная ак-
тивность естественного урана, находящегося в равновесии со
своими продуктами распада.
Много это или мало? Предположим, что на Земле работает
1000 реакторов мощностью 1 ГВт (эл.) каждый в течение
100 лет (в открытом цикле, см. § 13.4). Общее количество про-
дуктов деления, произведенное за это время, составляет при-
мерно 10й г=105 т. Через 1000 лет их активность будет того
же порядка, что и активность 107 т естественного урана, нахо-
дящегося в равновесии с продуктами распада. Если учесть, что
в земной коре около 1011 т урана, то видно, что дополнительная
активность, вносимая атомной энергетикой в отдаленные эпохи,
ничтожно мала (здесь еще не учтена естественная радиоактив-
ность тория и 40К).
В табл. 12.12 приведена суммарная активность всех оскол-
ков, а также некоторых групп осколков: «главные осколки»
(89Sr, 90Sr+90Y, 95Zr+95Nb, l03Ru+l03mRh, I06Ru+106Rh,
1Э11, !34Cs> !37Cs> i37mBa> 140Ba+140La, i41Ce, 144Ce+l44Pr),
нуклиды I, Kj-j-Xe, Cs, Sr. При этом учитывается активность
дочернего нуклида. Из табл. 12.12 видно, что I, Кг, Хе практи-
чески полностью распадаются при /~30 сут, через 0,5 года
«главные нуклиды» дают почти всю активность, а через 10 лет
остаются только Cs и Sr.
370
Таблица 12.9. Активность осколков деления , 1 ч< ' Т 1/2< 1 сут, ГБк/г*
Время t ч
Нуклид Tl/2’ 4 у, % E. МЭВ Последующие распады**
1 3 10 24 72
87Кг 1,27 1.77 2,1 275 92 2
100 % 88
88Кг 2,84 2.46 2,16 1035 635 115 3,8 — * Rb (17,8 мин; 2,7)
57,6 % 91m
91Sr 9,63 4,22 1,35 1660 1440 870 317 10 -> Y(50 мин; 0,56;
92Sr J, 2,71 4,45 1,53 925 555 93 2,6 —
92у 3,54 4,45 1,7 1170 ИЗО 415 38 —
93у 10,2 5,14 1,26 1290 ИЗО 700 270 10
97,3 % 97m
97Zr 1 16,9 5,62 1,19 3050 2810 2110 1190 166 * Nb (1 мин; 0,72)
97Nb 1,2 5,62 1,12 1590 1510 1150 650 90
28 % 105m
106Ru 4,44 3,18 1,17 935 685 230 25 — —► Rh (45 с; 0,19)
100 % 109m
iospd 13,43 1 ,o 0,36 5Ю 460 320 155 13 ► Ag(40 c; 0,09)
129Sb J. 83,4 % 4,4 1,1 1 7 252 184 61 7 —
129Te 1,16 0,92 0,6 238 194 69 8 —
133J 2,09 4,75 1,02 915 470 46 0,4 —
13«Te ; 0,69 5.7 1,07 560 75 — — ——
134J 0,88 7,5 3,14 1410 440 3 — —
136u 6,65 5,95 2,0 1440 1170 560 130 1
136Xe 9,1 1,44 0,56 340 336 230 96 3 Эффективный кумулятивный выход при
Ф=3-1013 нейтр/(см2-с)
139Ba 1,38 6,01 0,91 975 360 И — —
141La 3,92 5,56 0,98 1250 880 255 21 —
145pr 5,98 3,52 0,7 840 670 295 58 —
149Nd 1,72 1,18 0,83 210 95 6 — —
Другие нуклиды*** 263 180 41 2 — '—
Сумма 21 100 15 500 7580 3000 293
* Периоды полураспада н вероятности ветвления даны по [278], выходы
** В скобках: Т1/2И £; число над стрелкой — вероятность распада.
*** 83Br-|-83"iKr> 85/T1Kr, ll2Ag, 1,3Ag.
по [219], эиерговыделеиия — по [46].
У Таблица 12.10. Активность осколков делении, ( сут<7’1/2<0,5 года, ГБк/г
Нуклид Tl/2, сут У- % Е, МэВ Время t, сут Предшественники и последующие расходы
10 ч 1 3 Ю 30 182,5 365
»8Sr 50,62 3,27 0,58 873 866 843 766 582 72 6
58,5 4,22 0,61 изо 1126 1100 1015 800 131 15 Распад 91Sr и 91mY (см. табл, 12.9)
94Sr 3,14 4,95 1,62 2425 2130 1370 290 3 100 % 94 * Y(19 ми»; 2,66)
88Zr | 64,02 5,69 0,85 1520 15Ю 1480 1370 1100 210 30
98Nb 34,98 0,81 1530 1530 1525 1515 1420 420 63
8°Mo 2,75 6,14 0,56 2870 2510 1520 260 2 — — 87,5 % 99/н * Тс (6 ч; 0,14)
103Rll 39,25 5,0 0,54 2660 2630 2540 2250 1580 105 4 100 %103т ► Rh (56 мин; 0,04) Эффективный выход при Ф=
106Rh 1,64 2,9 0,23 650 510 220 12 — — —
13Ц 8,01 3,38 0,58 875 835 700 380 68 — — =3-1013 нейтр./ (см2-с)
132 Те 3,27 4,75 0,34 2370 2100 1370 310 4 - 100 % 132 * I (2,3 ч; 2,72) Распад 1331 (см. табл. 12.9)
133Xe 140Ba | 5,25 12,75 4,75 5,93 0,18 0,47 1225 1555 1135 1510 875 1350 345 925 25 ЗЮ — —
14ULa 1,68 2,83 1590 1575 1490 1060 360
141 Ce 143Ce | 32,5 1,37 5,56 5,19 0,24 0,73 1490 ИЗО 1470 840 1410 305 1210 9 790 31 1 Распад I4ILa (см. табл. 12.9)
143pr 13,56 0,31 1390 1380 1295 930 335
117Nd 11,05 2,21 0,39 580 555 490 315 90
lasmpm 148gpm 41,29 5,37 2,15 1,38 53 200 52 180 50 140 45 60 32 4 2 — / Захват нейтрона 117Рт при Ф=ЗХ I ХЮ13 нейтр/(сма-с)
u’Pm 2,21 1,18 0,39 280 240 130 14 — — — f Распад 118Nd (см. табл. 12,9), без
Другие 510 448 308 181 85 5 ( учета 148Рт
нуклиды* Сумма 26 900 25 130 20510 13 250 7590 976 120
*lnAg, 127Sb, 127Те. I27-"!Te, 128mTe, 128Те, 181Pm, 183Sm, 188Eu.
Таблица 12.11;. Активность осколков
деления, 0,5 года<Т1/2<10» лет, ГБк/г
Нуклид Tl/2> годы % Е, МэВ Время t, годы Последующие распады
30 сут | 0-5 | 1 з 10 30 100 300
®°Sr 29,2 4,52 0,19 167 166 163 155 132 82 15 0,1 100 % 90 —- Y (64,3 ч; 0,93)
iO6Ru 1,017 2,36 0,01 1040 785 560 143 1 — — — 100 % 106 —* Rh (30 с; 1,62)
134Cs 2,062 1,72 160 140 120 60 6 — — — Захват нейтрона 133Cs
13?Cs 30 6,4 0,18 228 225 223 213 181 114 23 0,2 100 % 137 * Ва (2,55 мин; 0,66)
114Ce 0,782 4,61 0,11 2140 1480 950 160 -— — — — 100 % 144 * Рг (17,7 мин; 1,24)
w’Pm 2,623 2,21 0,06 172 154 135 80 12 — — — С учетом поглощения нейтронов; рас- пад 147Nd (см табл. 12.10)
Другие нукли- ды* 23 23 21 16 8 2 — —
Сумма 3930 2970 2160 830 340 198 38 0,3
а *86Кг, 126sb, 12б"'Те, lMEu.
Таблица 12.12. Суммарная активность осколков и некоторых групп
нуклидов ,
Время Суммарная актив- ность, «Главные ОСКОЛКИ" , ГБк/г Нуклиды, ГБк/г
ГБк/г Ки/г I* Кг+Хе** Cs***
1 ч 51 900 1400 6200 3030 7200
3 ч 46 300 1250 4510 2410 6600
10 ч 38 400 1040 15 800 2940 1610 4800
1 сут 32 100 870 15 600 2200 1250 3500
3 сут 24 700 667 14 300 1580 890 2400
10 сут 17 200 465 13 200 720 350 1200
30 сут 11 200 316 9900 93 35 390 750
0,5 года 3950 107 3530 — 9,5 365 240
1 год 2980 62 2120 — 9 340 170
3 года 830 22 730 — 8 270 155
10 лет 340 9,2 323 — 5 180 130
30 лет 200 5,1 197 — 1,4 110 32
100 лет 40 1,1 38 — — 23 15
300 лет 0,3 0,008 0,3 — — 0,2 0,1
# 1311 133J^_133ye 134J f
i3sI+’i3sXe.
м 83тКГ1 83КГ] 85тКг> 88Кг + 88КЬт 133Хе> 133Хе.
*** i34Cs I37Cs + 137Ba
•*** "Sr,' MSr+90Y, ,1Sr+s,mY 92Sr+MY, MSr+MY.
Таблица 12.13. Энерговыделение осколков деления
Время Энерговыде- ление, Время Энерговыделе- ине, Время Эиерговыделение,
МэВ/дел, Вт/г МэВ/дел. Вт/г МэВ/дел. Вт/г
1 ч 2,04 8,8 10 сут 0,48 2,1 10 лет 6,1-Ю-з 0,026
3 ч 1,65 '7,1 30 сут 0,3 1,3 30 лет 3,5-10-3 0,015
10 ч 1,3 5,6 0,5 года 0,11 0,5 100 лет 6,8-10~ « 2,9-10-з
1 сут 1,03 4,5 1 год 0,061 0,26 | 300 лет 5-10-е 2- IO—5
3 сут 0,76 3,3 3 года 0,02 0,085 1000 лет 7-Ю-8 3-10-7
Используя табл. 12.9—12.12, можно определить энерговыде-
ление осколков. Результат приведен в табл. 12.13. Энерговы-
деление осколков можно найти также по таблице Приложе-
ния VIII. Разница в значениях энерговыделения с табл. 12.13
не превосходит 15 % (напомним, что рассматривается реактор,
в котором половина делений 235U и половина 239Рп; время ра-
боты 3 года). Надо еще учесть, что формула (1.7.9) не при-
менима к энерговыделению тех нуклидов, для которых суще-
ственно поглощение нейтронов. Их вклад в общее энерговыде-
ление от 2 % при t~l ч до 20 % при /—10 лет.
Чтобы от удельной активности (Бк/г) перейти к полной ак-
тивности (Бк), надо удельную активность умножить на массу
374
осколков (г). Поскольку каждый грамм разделившегося ве-
щества выделяет энергию приблизительно 1 МВт-сут, то
А [Бк] = А Г—lWmf>
L г J
где W — мощность, МВт; Т — время работы реактора, сут;
nif — переводной множитель, г/(МВт-сут), близкий к единице
(см. § 1.7). В (12.4.9) время входит в знаменатель, поэтому
активность короткоживущих нуклидов, успевающих достичь рав-
новесия, зависит только от мощности реактора (а не от глу-
бины выгорания или потока нейтронов, кроме, разумеется 135Хе,
105Rh).
Выше рассматривалась активность продуктов деления. Кро-
ме того, при работе реактора возникают радиоактивные транс-
урановые элементы. Ограничимся по этому вопросу только
краткими замечаниями. Из табл. 13.1 (рассматривается откры-
тый цикл, но с извлечением изотопов плутония) можно полу-
чить, что через 1000 лет после выгрузки наибольшую актив-
ность имеют 241Am, 243Ат, 240Ри (последний образуется при рас-
паде 244Ст). Их суммарная активность для реактора типа
ВВЭР равна примерно 5-10'12 Бк на 1 т загруженного топлива.
Если взять приведенный выше пример: 1000 реакторов, загруз-
ка каждого порядка 100 т, продолжительность кампании 3 года,
то общее количество выгруженного за 100 лет топлива составит
3 - 10б т, а суммарная активность трансурановых элементов (кро-
ме плутония) — 1,5-1019 Бк. Удельная активность естествен-
ного урана 2,6-105 Бк/г. Суммарная активность урана в зем-
ной коре примерно 1022 Бк, т. е. значительно больше, чем ак-
тивность выгруженных трансурановых элементов. Конечно, с
практической точки зрения существенно, что естественная ра-
диоактивность распределена по большому объему, а продукты
работы реакторов сосредоточены в небольшом числе пунктов.
Глава 13
ВЫГОРАНИЕ ЯДЕРНОГО ТОПЛИВА В РЕАКТОРЕ
13.1. МАЛАЯ ГЛУБИНА ВЫГОРАНИЯ
Главной реакцией для ядерного реактора является, конечно,
реакция деления. Большую роль в работе реактора играет так-
же реакция радиационного захвата на тяжелых ядрах. В ре-
зультате образуются более тяжелые нуклиды, которые, испы-
тывая [К-превращения, дают начало образованию нуклидов со
все увеличивающимся порядковым номером.
375
В настоящем параграфе рассмотрены процессы, играющие
роль при малых глубинах выгорания, в следующих парагра-
фах — при больших, а в § 13.5 — процессы образования ну-
клидов, которые, не оказывая заметного влияния на реактив-
ность реактора, интересны по каким-либо другим причинам.
Начнем с выгорания 23SU. Ниже под концентрацией нукли-
да будем понимать отношение числа его ядер к числу ядер
238U, выгоранием которого в этом параграфе пренебрегаем.
Уравнение, описывающее изменение концентрации 235U, имеет
следующий вид (количество 234U обычно столь мало, что пе-
реходы 234U—>-23sU можно не учитывать):
^=-о6с6Ф, (13.1.1)
где о — сечение поглощения 235U, определенное по (2.4.43)
(в дальнейшем не будем употреблять знак Д). Решение урав-
нения (13.1.1) можно записать так:
t
с5 = с5°ехр(—s); (13.1.2)
о
где С5° — начальная концентрация 235U. При малых глубинах
выгорания получим (<D=const, O5=const):
С5 = ^5°(1— Зб); з5=о5Ф^. (13.1.3)
При радиационном захвате нейтрона ядром 235U образует-
ся 236U; его концентрация определяется уравнением
^ = Ос6С6Ф-О.6С6Ф.
и, с а а оо
at
(13.1.4)
При малых глубинах выгорания с6 линейно растет со вре-
менем [предполагается, что Се(О)=О]:
Гб = Ос5Г5°Ф/.
Поскольку сечение 236U мало, его влиянием на реактивность
при малых глубинах выгорания можно пренебречь.
В цепочке превращений (см. § 13.2), которая начинается с
238U, можно пренебречь 239U, 240Np, поскольку их периоды полу-
распада малы, а учесть только 239Np, 239Pu, 240Pu (более тяжелые
изотопы плутония надо учитывать при больших глубинах вы-
горания). Уравнения для концентраций записываются так (cs=
= const; CilCs-^Ci', индекс N относится к 239Np):
de de9
°8Ф cn’ ^cn °в£?оФ;
У = Я + Од,Ф; = ослф + aNcN^ ~ °ософ-
(13.1.5)
376
Решая первые уравнения из (13.1.5), получаем [при (D=const,
щ = const, Cjy(O) =сэ(0) =0]:
с№’Т7’[1“ехр Я'
Л/
А. ая Г, i , /к 1—ехр(—/Щ)
_L 1 _ еХр (— s9) - о9Ф--------------L
-а9Ф а9 L А'
1
I
(13.1.6)
S, = о.Ф/.
При совсем малых временах, когда Л'/<С1 (т. е. t<C3 сут),
концентрация плутония растет квадратично, а если At'^>l, но
Sg<l,— то линейно. Будем считать, что выполняются неравен-
ства
s9<Cl; о9Ф/Х<1; щуФД<1.
(13.1.7)
Имеем приближенно
Ст9ф/Х=3- 10-3Ф,
где Ф — плотность потока, деленная на 1013 нейтр/(см2-с); ве-
личина щуФ/Х на порядок меньше, чем ст9Ф/Х. При условиях
(13.1.7) имеем
Г. , (^9—<7v)$ I Г, з, 1—ехр(— V/)
со=s« L1-----X----J L1 - т--------к!-----
Коэффициент размножения запишем так:
+ 2e-j-S8-j-65 ’
s8 = а8ФЛ
(13.1.8)
(13.1.9)
где SS — макроскопическое сечение поглощения всеми нукли-
дами, которые не выписаны явно. В начальный момент време-
ни &=т]50, где 0 = 25°/Sa°, причем 2а° — полное сечение погло-
щения в начальный момент времени (включающее и резонанс-
ное поглощение). В § 1.9, гл. 7, 8 вместо 0 использовалось обо-
значение 0<р. Поскольку т]5~2, а для большого реактора 6=1,
0 близко к 0,5. Определим изменение коэффициента размноже-
ния в такой модели, когда быстро насыщающиеся продукты де-
ления (Хе, Sm) приходят к стационарному состоянию мгновен-
но, а слабопоглощающие еще не оказывают влияния на реак-
тивность. Из (13.1.9) получим
ЗЛ / ^79 • \ По Со (Тд; С bj
——е — -Ц—(1 — 6)s5—е— -4-. (13.1.Ю)
А \Ч6 / а6 с6» ' ' 5 <т6 с6» ' >
Три слагаемых в (13.1.10) имеют ясный физический смысл.
Первое слагаемое — увеличение реактивности, вызванное появ-
лением 239Ри (так как т)9/т]5~ 1, а 0<1, то слагаемое положи-
377
тельно), второе — уменьшение реактивности, связанное с вы-
горанием 235U, и третье — поглощение нейтронов Np.
Назовем начальным плутониевым коэффициентом сумму чи-
сел ядер 239Ри и 239Np, появляющихся в реакторе взамен од-
ного уничтоженного ядра 235U:
р~
\ ст8
1
(13.1.11)
В формуле (13.1.11) сечение щ надо понимать в смысле
(2.4.43), т. е. о» включает в себя резонансное поглощение. Если
у~0,1, а резонансный интеграл равен 10 б, то резонансная
часть сечения составляет 1 б, а тепловая 2,7 б. Если жесткость
спектра нейтронов возрастает или блокировка резонансного ин-
теграла падает, то роль резонансной части сечения еще больше.
Обратим внимание, что в (13.1.11) в знаменателе стоит С50.
Это, однако, еще не означает, что с ростом обогащения 235U
начальный плутониевый коэффициент автоматически падает; од-
новременно с ростом обогащения обычно растет резонансное по-
глощение в 238U. Если исходить из формулы (1.9.5), которая
учитывает условие критичности, то
1- qa, (13.1.12)
где qa — суммарные вредные потери нейтронов (отнесенные к
поглощению в 235U) в замедлителе, теплоносителе, конструк-
ционных материалах, продуктах деления, в отражателе и за-
щите. Обычно в реакторах на обогащенном уране нет столь
жесткой экономии нейтронов, как в реакторах, использующих
в качестве тойлива естественный уран. Поэтому qa в них боль-
ше и хр меньше. Кроме того, хр уменьшается, если падает т]5—1,
что происходит при увеличении жесткости спектра нейтронов.
В формуле (13.1.12) не учитывается деление 23SU. Фактически
под т]5 надо понимать эффективное значение
Т|5эф=3 (VsS f 5 + VgSfs) /Sa5-
Ясно, что рост числа делений 238П увеличивает хр.
В § 1.9 величина хр, определенная равенством (13.1.12),
была названа коэффициентом конверсии. Теперь будем
различать эти два термина: коэффициент конверсии есть
отношение выгруженного из реактора Ри к разделивше-
муся 23SU. Поскольку образующийся в реакторе Ри ча-
стично сгорает, коэффициент конверсии всегда меньше, чем на-
чальный плутониевый коэффициент. Они равны друг другу
только при бесконечно малой глубине выгорания.
378
Используя (13.1.3) и (13.1.8), получим вместо (13.1.10):
Ц = s U ( % _ Q\ ^9 /1 ! пэФ \ [1 _ Л-_ 1—ехр(—Х7) 1 _
А I Р \ 4s / Щ \ л / 2 K't J
„ Стм 1—ехр(— Х7) 1
-----F7----- — (1—9)}. (13.1.13)
При малых временах, когда Х7<С1, имеем [пренебрегая ма-
лыми параметрами (13.1.7)]:
ЗА /о.. \
— = —Ss 6-^4- 1 — 6) , (13.1.14)
т. е. реактивность убывает пропорционально выгоранию 235U
(этот эффект усиливается одновременно происходящим накоп-
лением 135Хе и изотопов Sm). Для примера рассмотрим реак-
тор на естественном уране, когда хр = 0,8, 0 = 0,5. Приняв
Ox/tfs — O.l, 05=680 б, получим
в6 = 5,9-10-^Ф; — = —3,2-10-4/Ф.
k
где t — время, сут; Ф — плотность потока, 1013 нейтр/(см2-с).
Если Х7»1, по-прежнему не учитывается 240Ри и прене-
брегается малыми величинами (13.1.7), то
ЗА
--- — S 5
А 5
. 49 \
'р — I ;
лр
если принять Т]9 = Т]5, ТО
= S6(l — 6) fxp— — 1'j.
Положив приближенно 0=0,5; оэ/о5~2, получим
-у- = 6-10-4/Ф(хр —0,5).
(13.1.15)
(13.1.16)
(13.1.17)
Реактивность возрастает, если х„>——-v0,5. Причина роста
s9
состоит в том, что ядро 235U заменяется ядром 239Рп с тем же
значением т], но большим сечением, и поэтому роль вредных
поглощений уменьшается. Отметим, что при выводе формулы
(13.1.17) было сделано так много приближений, что ее нельзя
применять для количественных оценок. Более точные вычисле-
ния, учитывающие выгорание 239Ри, накопление продуктов де-
ления и 240Ри, показывают, что fok/k в начальный период ра-
боты реактора отрицательно за счет накопления Хе и Sm. По-
сле того как Хе и Sm пришли в равновесие, 8k/k положитель-
но, если хр > 0,74-0,75. При хр~0,75 разница между макси-
379
мумом и минимумом k(s) составляет примерно 0,5%, а при
хр—0,9 она возрастает до 2% (эти данные относятся к тяже-
ловодному реактору с малыми вредными потерями и мягким
спектром нейтронов).
Уменьшение реактивности при [см. (13.1.14)] можно
назвать «нептуниевой ямой». Минимальное значение k опреде-
лится дифференцированием (13.1.13) по времени. Пренебрегая
оэФ/Х, получаем
Хр Г (Л - е) А _ е 2^1
U= ^1П Л? л й, (13лл8)
Хр[——в)-2-—1 + 9
\ % / о6
При тех же значениях параметров, которые выше были ис-
пользованы в примерах, получим £МИн=3,1 сут. Значение 6k при
равно 6k=—4-Ю-4 Ф. Практически нептуниевая яма
маскируется более сильным эффектом, связанным с накопле-
нием 135Хе и изотопов Sm (см. гл. 12 и рис. 13.1).
При остановке реактора 239Np распадается и образующий-
ся при этом 239Ри увеличивает реактивность. Если реактор ра-
ботал время /Ой,-1, то добавочное количество 239Ри равно
овФ/Х. Изменение реактивности при этом будет
— = хр-^. (13.1.19)
k и л
При тех же значениях параметров получим 6&—10-3 Ф.
Практически этот эффект происходит одновременно с более
сильными эффектами: «иодная яма» (см. § 12.1) и накопление
Sm при распаде Pm (см. § 12.2).
В реальном реакторе плотность потока нейтронов зависит
от координат. Применяя теорию возмущений (см. гл. 5), нахо-
дим
_^_ = J ф(/г ^ф+фе/г^1 t (13.1.20)
где дано (13.1.13). Если пренебречь малыми величинами
k
оэФ/Х, ЩуФД, то 6k линейно зависит от плотности потока. По-
этому, положив Ф+=Ф, получим
где (6&/А) вычислено по средней плотности потока. Пусть, на-
пример, Ф=Л cos аг, тогда Ф = 2/л, Ф2 = 0,5, Ф3 = 4/3л и
380
[ср. формулы (12.1.15) и (12.1.16)]
4 f ik \
3 \ k J
k
(13.1.22)
Выше рассмотрен случай, когда плотность потока не изме-
няется во времени. Другой часто встречающийся случай — по-
стоянство мощности данного твэла. Плотность потока нейтро-
нов при этом зависит от времени. Решение (13.1.2) справедливо
при любой зависимости плотности потока от времени. Если
ограничиться случаем Л/:^>1, то dcN/dt=G и уравнение для кон-
центрации 239Ри запишем так:
dss
(13.1.23)
где в качестве независимой переменной взято S5:
t
s-=§<I)s.dt.
о
(13.1.24)
Если отношение сечений не зависит от времени, а в множи-
теле Л/Л', который близок к единице, плотность потока заменить,
средним значением по времени, то (13.1.23) будет уравнением
с постоянными коэффициентами и его решение можно сразу за-
писать:
с,=А- “ [1—ехр (—sВ)1; (13-1 -25)'
Л а9 о6
Считая, что при делении разных нуклидов выделяется (на
одно деление) одна и та же энергия (см. § 1.6), запишем усло-
вие постоянства мощности:
Ф (S5)![CF/5C5 (S5) +Of9 X
X Сд (s5) ] =Ф0О/5С5°. (13.1.26)
Используя определение ds5=C5$(s5)dt и (13.1.2), (13.1.25),.
имеем
s5° = O0sff = O0J-^- =1-ехр(—s6) +
О
OeGfo ( бе 1
+ ХР Ь - -Г- 11 - еХР (- (13-1 -27>
или при малых S5
s5 = s5° (1 — as5°); а= 2-(Хр-^--1). (13.1.28)
381
Из (13.1.25) получим для концентрации cg(X=V):
^ = ^c5°s6»(l-te5»); (13.1.29)
2 = 5
Если учесть конечность времени жизни Np, пренебречь
ехр (—М), но сохранить 1/М, то получим вместо (13.1.29) [см.
(13.1.6)]:
cs = xpc°s° (1 (13.1.30)
Зависимость плотности потока от времени получим из
(13.1.26):
= a0-f-aiS5°а2 (s50)2; (13.1.31)
где
. = 19 Ф0°5 . ’М 1 1 1 = 19 ,
а0=1-Хр—-j—> «1 = хр— -1; а2~ +<*- — ХрЬ.
(13.1.32)
Обратимся теперь к накоплению 240Ри, ограничиваясь по-
прежнему малой глубиной выгорания s5C 1. Уравнение для кон-
центрации 240Ри запишем так (Х7^>1, Х=Х' и считаем, что при
поглощении нейтрона 239Np сразу возникает 240Ри, см. § 13.2):
Будем искать решение уравнения (13.1.33) в виде ряда по сте-
пеням s5o:
Co=='₽OS5O + ₽1(S5°)2+ ... (13.1.34)
В результате подстановки (13.1.34) в уравнение (13.1.33) по-
лучим
Определим среднюю концентрацию 240Ри в выгружаемом
плутонии. Для этого найдем сначала сумму с9+сЛ- [см. 13.1.30)]:
C9+Cn = XpC5°S5°(1 — bs5°). (13.1.36)
Усреднив (13.1.35) и (13.1.36) по объему реактора или по ча-
сти этого объема, откуда выгружено топливо, получим
со °С9 - ф2 Г. 2(1—-Од,/ Осв)
ct Б CN 2a5 5 (ф)2 L М
(13.1.37)
Оценим концентрацию 240Ри при s5°=0,2. Пусть х/>=0,8;
,с5° = 7• 10~3; <jc9/<j5=0,5; <т^9/сг/5=2; Фо=5-1О13 нейтр/(см2-с);
1/М = 0,05; on/os—0,1. Получим Cg=8-10“4; C’o=5-lO-s. Опре-
282
делим резонансное поглощение в 240Ри. Предположим, что =
=0,15; Лзэф==10 б. Резонансный интеграл 240Ри без учета бло-
кировки равен 8000. Поэтому имеем
A- АД. _ 0,04; <р0 = 0,006,
Фе Дэф
т. е. при глубине выгорания s5=0,2 уже надо учитывать резо-
нансное поглощение 240Ри. Оценим блокировку резонансного
интеграла. Для этого надо (см. § 8.1) вычислить величину а=
= Grcol. Если рассматривать блок из металлического урана и
принять ог=1,6-105 б, то 0=0,37, где 7 — средняя хорда бло-
ка. При 7=3 о=1. При этом коэффициент блокировки равен
0,8 (см. рис. 8.4). Следовательно, учет блокировки увеличивает
коэффициент размножения на 1 • 10-3. Таким образом, блоки-
ровка резонансного интеграла 240Ри должна учитываться при
глубине выгорания ss>0,2 (см. рис. 13.1).
Концентрация 241Ри растет при ss<CZl пропорционально t3:
Выделение энергии в реакторе равно (предполагается, что
Ef одинаково для всех делящихся нуклидов, см. § 1.7):
t
W = Ef (1 + 628) f (af Д6 + aMV9) ФЛ =
О
t
= Ef (1 + J ФоДЛ°Л = Ef (1 + М Л° (13.1.39).
о
где Ni — числа ядер в рассматриваемом объеме реактора; 62s
определено в § 9.1. Полагая, что при делении 1 г выделяется
энергия 1 МВт-сут (более точные данные см. в § 1.7), полу-
чаем количество энергии, выделяющейся на 1 кг 238U, 103 МВтХ
Хсут/кг:
Г = (1+а28)^5 0 (13.1.40).
°5
Положив 075/05=0,85; 628 = 0,04; с5°=7,2-10~3, получим
IF=6,4$5° МВт-сут/кг,
т. е. малой глубине выгорания s5°^0,2 соответствует энерговы-
деление lFsgU,3 МВт-сут/кг.
Из приведенных выше формул видно, что большую роль при
определении k(s) играет отношение 09/05. Это отношение в
сильной степени зависит от температуры нейтронов. Например,
при Т=300 К и жесткости спектра у=0,1, используя данные
38а
Рис. 13.1. Изменение реактивности реакто-
ра на естественном уране и коэффициента
конверсии при малых выгораниях:
—------ с учетом поглощения нейтронов продук-
тами Деления:--------— без учета поглощения;
-------- без учета блокировки резонансного ин-
теграла 240Ри
ло ^-факторам приложения IV.2, получим а9/о5=1,62. При тем-
пературе 500 К 09/05=2,17. Отсюда видно, что невозможно вы-
числить зависимость k(s), если предварительно не решить зада-
чу о термализации нейтронов (см. гл. 7) и не определить эф-
фективные сечения 239Ри и 235U.
На рис. 13.1 представлены результаты численного решения
уравнений выгорания для естественного урана. При этом учи-
тывались нуклиды 236U, 236U, 237U, 238U, 237Np, 239Np,
239Pu, 240Pu, 241Pu, продукты деления 235U и 239U: 135Xe, i06Rh,
149Sm, 161Sm с их предшественниками и эффективный осколок
ло § 12.3. Начальное значение плотности потока равнялось
7-Ю13 нейтр/(см2-с), мощность считалась постоянной, плот-
ность потока и жесткость соответственно изменялись, сечение
задавалось по § 2.4 в приближении двух групп, эффективный
резонансный интеграл 238U был равен 10,6 б, сечения в тепло-
вой группе определялось путем решения термализационной за-
дачи (см. § 7.5). На рис. 13.1 штриховой линией показано из-
менение реактивности без учета поглощения нейтронов продук-
тами деления, сплошной — с учетом поглощения продуктами
деления (абсолютные значения k даны приближенно, посколь-
ку они зависят от конкретных параметров ячейки).
Минимум штриховой кривой лежит примерно при t=
= Зч-4 сут, что согласуется со сделанной выше оценкой. Ми-
нимум сплошной кривой расположен при /=7-4-8 сут. Штрих-
пунктирная кривая проведена без учета блокировки резонанс-
ного интеграла 240Ри. Видно, что блокировку надо учитывать
начиная с выгораний порядка 1 МВт-сут/кг.
Учет поглощения нейтронов в 236U, 237U, 237Np, 239Np,
240Pu при /=54 сут приводит к значениям 6k, соответственно
•384
равным IO-3, 6-IO-5, IO-4, 4-10~4, 7-10-3. По ним можно су-
дить о необходимости учитывать тот или иной нуклид при рас-
чете реактивности с заданной точностью.
На рис. 13.1 приведен еще коэффициент конверсии, опреде-
ленный как отношение количества делящихся изотопов плуто-
ния к уничтоженному количеству 235U в момент времени t, т. е.
[C9(0+Cn(0+C1(0]/[^50-C5(0]- (13.1.41)
При малых временах Кк равен начальному плутониевому коэф-
фициенту, а затем несколько уменьшается (см. также § 13.2).
13.2 БОЛЬШАЯ ГЛУБИНА ВЫГОРАНИЯ
Уравнения, описывающие изменения концентраций нуклидов
со временем, при глубоких выгораниях становятся нелинейны-
ми. Основные причины нелинейности следующие. Во-первых,
она возникает из-за блокировки резонансных интегралов. Наи-
более сильное резонансное поглощение из трансурановых ну-
клидов имеет 240Ри, причем главный резонанс дает 90 %' всего
резонансного поглощения и обладает очень большим сечением
поглощения в центре резонансной линии (о>= 1,6 • 105 б).
Содержание 240Ри в энергетических реакторах доходит до
2 кг на 1 т 238U. Оценим отношение параметров а (8.1.2) для
240Ри и главного резонанса 238U. При концентрации 240Ри, рав-
ной 2-10-3, имеем
— 0,002 (Дг)г<10 — 0,016.
и238 (°г)238
Поскольку значение а для главного уровня 238U составляет
примерно 2000, для 240Ри получим п=30, т. е. величина резо-
нансного интеграла уменьшается из-за блокировки примерно в
5 раз (см. гл. 8). Поскольку для 240Pu Zc=8000 б, а ас(£н) =
= 290, при жесткости у>0,1 имеем у/с^>Ос(£н). Поэтому при
изменении концентрации 24<|Ри от 0 до 2-Ю-3 эффективное се-
чение о изменится в несколько раз.
Блокировку главных резонансных уровней надо учитывать
также у 242Ри и 236U.
Вторая причина нелинейности состоит в зависимости пара-
метра у от концентрации делящихся ядер. Этот эффект наибо-
лее существен для реакторов, работающих на сильно обогащен-
ном уране, когда сгорающий 235U не компенсируется появле-
нием плутония. Наоборот, если начальный плутониевый коэф-
фициент близок к единице, то уменьшение концентрации 235U
компенсируется появлением 239Ри и жесткость спектра почти
постоянна.
Наконец, от концентрации нуклидов может зависеть сечение
в тепловой группе от, поскольку изменение концентрации при-
25—6053 385
водит к изменению эффективной температуры нейтронов (сред-
ней скорости), от которой зависит от (существенно, что от кон-
центрации зависит отношение сечений). Этот эффект особенно
существен для 239Pu, 241Ри, имеющих резонанс при £=0,3 эВ
(см. §7.5).
Несмотря на то что нелинейность существенна и должна
учитываться в расчетах, претендующих на высокую точность,
полезно рассмотреть и линейную модель выгорания. Рассмот-
рим прежде всего самый простой случай выгорания одного 235U,
,т.. е. когда концентрация 238U мала и образующимся 239Ри
можно пренебречь. Уравнение (13.1.1) и его решение (13.1.2)
справедливы при любой зависимости плотности потока и се-
чения от времени. Наиболее часто встречающийся случай —
постоянство мощности данного твэла:
О7бФс5=с=const. (13.2.1)
Тогда вместо (13.1.1) имеем (так же как в § 13.1, не будем
писать знак Д над oj:
= — -^-с. (13.2.2)
Л
Отношение об/ст/б может зависеть от времени за счет изме-
нения -у при выгорании. Однако эта зависимость достаточно сла-
бая: при изменении у в 2 раза отношение 05/0/5 изменяется
всего на 1,5—2%. Зависимость 05/0/5 от эффективной темпера-
туры нейтронов также слабая. Поэтому можно считать, что от-
ношение 05/0/5 постоянно. Тогда
С5=С50(1—П5°ФоО>
(13.2.3)
где Фо, 05° — плотность потока и сечение при t = 0. Таким об-
разом, концентрация 236U линейно зависит от времени (естест-
венно, что с5 не может убывать до нуля, так как гораздо рань-
ше реактор станет подкритичным). Подставляя (13.2.3) в
(13.2.2), получаем закон изменения плотности потока нейтро-
нов
ф(0
_ Фо °5°
1 — ®8° Фо t °f А '
(13.2.4)
Подставляя (13.2.4) в определение S5 (13.1.2), имеем
5, = -1п(1-о6»Ф00; Ф(55) = Фо — exp(s5). (13.2.5)
’/в
386
Рис. 13.2. Схема превращений нуклидов при выгорании топлива. Квадраты и
стрелки, выделенные жирными линиями, относятся к основным нуклидам
и основным реакциям; двойные линии — к второстепенным. Тонкие и штрихо-
вые линии обозначают нуклиды и реакции, которые в большинстве случаев
можно не учитывать (см. также рис. 13.11—13.13). Цифры над горизонталь-
ными стрелками — сечения радиационного захвата в тепловой группе, под
стрелкой — резонансные интегралы. Цифры рядом с вертикальными стрелка-
ми— сечения и резонансные интегралы деления (см. Приложение IV); рядом
с наклонными стрелками — периоды полураспада
Обратимся теперь к более сложному случаю накопления
изотопов плутония. При больших глубинах выгорания можно
па схеме рис. 13.2 опустить все короткоживущие нуклиды*.
Тогда система уравнений, описывающих изменение концентра-
ции 239Pu, 240Pu, 241Ри, будет выглядеть так:
~~ = ° Л — = °СА — о0с0; \ = f Ф (/) dt-,
о
ilC Г f < X.’
dtt с0 ° 1 1 1 1 г ф(Ц
или, если ввести вектор с с компонентами с$, с0, С\,
de .
---- — о£а С, г — АС,
dtT
(13.2.6)
(13.2.7)
* См. задачу в конце параграфа.
25* 387
где
/1 \ / с, 0 0 \
е==1 О ь Л = 1—°С9 °0 О /‘ (13.2.8)
\О/ \ О — <зс0 о//
Сечение сцо только незначительно отличается от полного се-
чения поглощения, поскольку в реакторах на тепловых нейтро-
нах деление 240Ри играет малую роль. Поэтому положим ос0=
= оо- В (13.2.6) учитывается распад 241Ри. Обычно этот распад
играет малую роль (7’1/2=14 лет); поэтому можно в а/ заме-
нить Ф(0 средним значением плотности потока. Выгоранием
238U пренебрегаем, т. е. считаем а константой. Тогда если счи-
тать, что ot=const, то система уравнений (13.2.6) является
системой с постоянными коэффициентами. Решение системы
(13.2.6) есть сумма частного решения
ср=Л ‘eacsCg (13.2.9)
и общего решения
с=ехр (—Л^1)Л, (13.2.10)
где А — произвольная постоянная. Если начальные концен-
трации заданы вектором с0, то решение можно записать так:
с=сР+ехр (—Ati) (с0—ср).
(13.2.11)
При /->оо имеем с=сР, т. е. ср есть равновесная концентра-
ция, которая устанавливается, если реактор работал достаточ-
но долго. Компоненты вектора ср легко получаются из (13.2.6),
d п
если положить — = 0;
dt
°s Cgp ^-8» ^ор 3С9 „ С9р — 3Й » /• * С 8>
°9 °о ®э а0
__ сС9 ав Z,
с1р . с0р 3 1 , С8* ’» ° 1
(13.2J2)
Матрица exp (—Afj) равна
/ аи О О
ехр(—Л^) = 1 а12 а22 О
\ а23 а33
(13.2.13)
388
где
au = ехр (—$„); a2S = exp(—s0); a33 = exp (—sx);
t
S( — j o£ Ф (/) dt;
о
«и = Jexp (— s0) — exp (— s„)];
°9 —a0
«23 = —-— [exp (— s0) — exp (— sj];
°1 °0
«13 = J—--------[exp (— s0) — exp (— sx)] —
°Э—°0 I °1 — °0
— [exp (— s„) — exp (- Si)] J.
(13.2.14)
Нетрудно написать общее решение уравнений, аналогичных
(13.2.6), для произвольного числа последовательных переходов
[226]:
^- = Жсг_1-Дсг; co(f) = O; сх(0)= 1; сг(0) = 0 г>2;'
с„(0 = А(2)А2(’)...А<'21у]
ехр( —4(0
П(А-Л)’
i^=k
(13.2.15)
Как указывалось в начале параграфа, блокировка резонанс-
ного интеграла 240Ри быстро достигает асимптотической обла-
сти, когда справедлива формула (8.1.33) (эффект Доплера игра-
ет малую роль для первого уровня 240Ри). В этом случае сече-
ние поглощения 240Ри надо записать так:
°о~ а +
(13.2.16)
где
« = + & = 1,097Т(/-/В)/-/Од (13.2.17)
и /н — часть резонансного интеграла, которая не блокируется.
Условие равновесия для 240Ри (13.2.12) дает уравнение для
определения Со (и, следовательно, о0):
<зсдсд = acQ-^-bVcg,
(13.2.18)
389
откуда
1/с = 1/~ 1 -I- 4аа<:»Са _ 1
V С» 2а V 1 i 68 1
a0 = fl[l+2(/l+^M-l)
(13.2.19)
Из условия (13.2.12) можно получить соотношение концен-
траций изотопов плутония в равновесии:
е,р:сор:с1р = 1:-^~ (13.2.20)
со °1
причем под Со надо понимать (13.2.19). Время установления
равновесной концентрации 239Ри порядка
Тъ-2- _3000_ лет, (13.2.21)
аэФ а9ф
где Ф — плотность потока, деленная на 1013 нейтр/(см2-с). По-
ложив 09=1000, Ф = 5, получим Г»0,6 года. Для 240Pu, 241Ри
время установления равновесной концентрации в несколько раз
больше. В энергетических реакторах концентрация 239Ри успе-
вает достичь равновесия, а концентрация других изотопов Рц
достигает равновесия, только если повторно использовать топли-
во (после химической переработки и очистки от продуктов де-
ления).
Значение равновесной концентрации 239Ри обычно порядка
с9р/с8= (3—6)-10~3. Величина сдр зависит от жесткости спек-
тра, степени блокировки резонансного интеграла 238U и эффек-
тивного сечения 239Ри, которое растет с ростом температуры
нейтронов в тепловой группе (см. § 7.5). Сечение 240Ри опре-
деляется главным образом резонансным интегралом и поэтому
.зависит от жесткости спектра. В реакторах с мягким спектром
^0,2) сор близко к Сэр, а в реакторе с жестким спектром
(например, в реакторе ВВЭР) сор меньше, чем с9Р.
Равновесная концентрация 242Ри не достигается даже при
нескольких повторных циклах использования топлива (име-
ются в виду реакторы на тепловых нейтронах с глубиной вы-
горания 10—40 МВт-сут/кг). Поскольку сечение 242Ри мало, его
влияние на реактивность не слишком велико даже при концен-
трациях, близких к равновесным. Оценить равновесную концен-
трацию можно, используя формулы, аналогичные (13.2.16),
(13.2.19).
Рассмотрим теперь цепочку превращений, которая начинает-
ся с 235U (см. рис. 13.2). В этой цепочке имеются два нукли-
да — 237U и 238Np с малым временем жизни и большим сече-
нием поглощения (см. рис. 13.2).
390
Отношение числа поглощенных нейтронов и числа распадов
определяется величиной стФ'Д, которая равна (для у=0,1): для
237U — 0.0037Ф, для * 238Np — 0.0057Ф, где Ф — плотность по-
тока нейтронов, деленная на 1013 нейтр/(см2-с). Если Ф^Ю,
то можно не учитывать 237U и 238Np и считать, что 236U пере-
ходит в 237Np, а последний — в 238Ри *. Тогда, вводя вектор
с'(с6, с7, Се) и учитывая (13.2.1) записываем- уравнение, опре-
деляющее концентрации 236U, 237Np, 238Pu:
= soc5 ехр (- s5) - Д'с(13.2.22)
at
где е равно (13.2.8), а Л' выражается так:
/ об 0 0 \
Л'=1 — 0g о, О I. (13.2.23)
\ 0 —о, о8/
Решение уравнения (13.2.22) по форме почти совпадает
с (13.2.11):
c'—c'p(t) +ехр (—Л71) (с'о—с'р(О)), (13.2.24)
где ехр (—Л71) получается из (13.2.13), (13.2.14) заменой од,
Сед—°0—о'1~а
с'р(О = (Л'—о5)-1е<тС5С50ехр (— $5), (13.2.25)
причем
/ (°. - фг1 \
(A'-o5)-’s=I о6[(о, —05)(0g —Og)]-1 I. (13.2.26)
' [(°8 — (°7 “ °5) (’. — °5)]-’ >
Выпишем явно c5:
(0 = Ф (0) exp (- Sg) + [exp (— s.) — exp (— s5)] c5°. (13.2.27)
°s —°e
Если 7=0,1 и резонансный интеграл 236U не блокируется, то
о6=40. При с6(0)=0 получим
се=Ас5° [ехр (—s6)—ехр (—s5)]; s6=0,056s3,
где А=а5/[1+а5—(ов/фб)]- При as=0,2, of5=600, «6=40 имеем
А = 0,176. Если s5=3 (т. е. почти полное выгорание 235U), то
с6=0,14 Cs0. Влияние 236U на реактивность можно характеризо-
вать величиной <7б=—, равной в этом случае (если у=0,1, 18=
28
* Исключением является случай, когда время пребывания урана в реак-
торе невелико, например, 1—2 мес; тогда надо учитывать задержку в обра-
зовании S37Np на время порядка Т237=Тцг(\п 2~10 сут. Если в реакторе
имеется значительное количество 24IPu, то надо учитывать образование
238Ри по схеме рис. 13.13.
391
=106) q6= 1,5c5°/c8. Видно, что это влияние мало. При увели-
чении жесткости Сб и q8 растут примерно пропорционально у.
Существенное отличие урановой цепочки от плутониевой со-
стоит в том, что, во-первых, здесь исчезает делящийся нуклид,
а в плутониевой, наоборот, появляется (239Ри). Во-вторых, сече-
ние 235U значительно больше, чем сечение 238U. Поэтому выгора-
ние 235U всегда существенно, в то время как выгоранием 238U
часто можно пренебречь.
Заметим, что некоторый вклад в образование 237Np вносит
реакция (п, 2п) на 238U. Сравним количество образовавшегося
237Np через 236U и по реакции 238U (п, 2п) 237U->237Np. Прибли-
женно, пренебрегая 237U и выгоранием 237Np, имеем по первой
цепочке
б ОСО ’ 7 2 ® С ®
и по второй
С7(2) = С80<Гя,2пФ/,
где оп,2п—эффективное сечение, определенное в § 9.2.
Отношение
. С5° ДС5 дбФ'< _ J6 aCS g (13 2 28)
Cg° СП,2П 2 2cs° ап,2П Д5
При больших глубинах выгорания вклад первой цепочки,
квадратично зависящий от времени, всегда больше, чем второй
Наоборот, при малых глубинах выгорания реакция (п, 2п) иг-
рает главную роль. Подставим в (13.2.28) числа. Для реактора
с мягким спектром (у=0,1)стс5= 110, 05=720, <у6=40, аП;2п =
= 0,01 (см. §„9.2, пример тяжеловодного реактора с естествен-
ным ураном). Если c5°/cs°=7,2 -10~3, то
c7(i)/c7(2) = 2,2s5,
т. е. равенство обеих цепочек достигается при глубине выгора-
ния 35=0,45 (что соответствует энерговыделению W=
=3 МВт-сут/кг). Для реактора с жестким спектром (у=0,51
Oc5= 160, 0’5=890, сг6=190, ап,2п=0,09 (см. § 9.2, пример реак-
тора ВВЭР). Тогда при С50/с8°=0,03 получим
Ст(1)/С7<2)=635,
т. е. обе цепочки сравниваются при 35 = 0,16, что по энерговы-
делению не сильно отличается от первого случая.
Поскольку глубина выгорания 3 МВт-сут/кг составляет при-
мерно 1/3 полной" глубины выгорания для реактора на естест-
венном уране и 1/10 — для реактора ВВЭР, роль цепочки с ре-
акцией (п, 2«) для ВВЭР оказывается меньше, чем для реак-
тора с естественным ураном.
392
Рис. 13.3. Изменение k□о реактора на
естественном уране при глубоком вы-
горании топлива:
Кк — коэффициент конверсии в делящиеся
изотопы плутония; К'к — коэффициент кон-
версии во все изотопы плутония; Afe/fe —
изменение из-за поглощения нейтронов
продуктами деления [начальная плотность
потока 7*1013 нейтр/(см2-с); 7=0,097]
Точный расчет выгорания
ядерного горючего и образования
трансурановых элементов в реак-
торе можно произвести только
численно. В качестве первого эта-
па при этом производится расчет
в «точечном приближении», когда
не учитывается пространственная
неоднородность нейтронного по-
тока по реактору (см. § 13.3).
Приведем в качестве первого
примера результаты расчета
глубины выгорания для тяжеловодного реактора на естествен-
ном уране*. Схема учитываемых нуклидов приведена на
рис. 13.2.
Расчет проводился в двухгрупповом приближении для сече-
ний [см. (2.4.43)] при условии постоянства мощности. Плот-
ность потока нейтронов и жесткость спектра изменялись во
времени.
Начальное значение плотности потока 7-Ю13 нейтр/(см2-с),
жесткости у=0,097. Эффективный резонансный интеграл
238U принят 10,66. Вредные поглощения нейтронов (замед-
литель, конструкционные материалы) составляют 11% поглоще-
ния в 238U. Сечения изотопов урана и плутония в тепловой груп-
пе определялись путем решения термализационной задачи для
начальной загрузки (см. § 7.5; средние сечения изотопов плуто-
ния определялись в спектре нейтронов, который устанавливает-
ся в отсутствие плутония). Блокировка главных резонансов
240Pu, 242Pu, 236U определялась по теории, которая изложена в
гл. 8 (см. рис. 8.4, 8.5).
Зависимость коэффициента размножения от глубины вы-
горания, полученная в этом приближении, приведена на рис.
13.3 (сплошная линия). Затем при глубине выгорания
4,4 МВт-сут/кг, когда концентрация 239Ри составила 80% рав-
новесной, был проведен новый расчет сечений в тепловой груп-
* Многочисленные результаты расчетов накопления трансурановых эле-
ментов в реакторах различного типа приведены в [227], см. также [228].
393
пе уже с учетом того количества изотопов плутония, которые
образовались к этому моменту. Новая зависимость k от глубины
выгорания приведена на рис. 13.3 штриховой линией. Уменьше-
ние k при таком пересчете вызвано тем, что плутоний деформи-
рует спектр нейтронов в области 0,3 эВ, и поэтому его сечение
в тепловой группе уменьшается (см. § 7.5, рис. 7.7). Чтобы по-
грешность определения k не превышала 0,5—1%, необходимо
несколько раз пересчитывать сечения плутония, причем это надо
делать при сравнительно малых глубинах выгорания, когда кон-
центрация 239Ри еще не достигла равновесного значения.
В промежутках между двумя пересчетами сечений необхо-
димо учитывать изменение жесткости спектра и блокировки ре-
зонансных интегралов для тех нуклидов, концентрация которых
заметно изменяется на данном интервале времени. В противном
случае кривая k (IF) будет иметь «скачки», которые приходится
сглаживать, основываясь только на интуитивных соображениях.
На рис. 13.3 виден максимум реактивности, который более
подробно обсуждался в § 13.2.
Если запас на регулирование и утечку нейтронов равен 3%,
то при l¥zo=6,8 МВт-сут/кг запас реактивности оказывается ис-
черпанным. Дальнейшее выжигание твэла возможно, если рядом
с ним имеются твэлы с менее выгоревшим топливом. Так об-
стоит дело, если реактор работает в режиме непрерывной пере-
грузки, когда в нем присутствуют твэлы с различной глубиной
выгорания вплоть до некоторого W, так что средняя глубина
выгорания равна ТГ0 (см. § 13.3).
На рис. 13.3 показана также зависимость потерь реактивно-
сти из-за поглощения нейтронов в продуктах деления от глуби-
ны выгорания. При глубине выгорания 10 МВт-сут/кг эти по-
тери составляет 10%.
На рис. 13.4 приведены зависимости концентраций делящих-
ся нуклидов от глубины выгорания (штриховой линией показано
изменение концентрации 239Ри, которое возникло из-за пересчета
сечений в тепловой группе при W=4,4 МВт-сут/кг). Концентра-
ция 239Ри достигает насыщения при W-—5-*-7 МВт-сут/кг. На
рис. 13.4 изображена, кроме того, зависимость отношения пол-
ного макроскопического сечения деления к начальному значе-
нию от глубины выгорания. Изменения Sf незначительны
(-10%).
На рис. 13.5 даны концентрации неделящихся нуклидов. Вид-
но, что концентрация 240Ри еще далека от насыщения. Рост кон-
центрации 236U замедляется в связи с уменьшением концентра-
ции 235U.
Сравним количество делений разных нуклидов за все время
работы реактора. Имеем следующие соотношения (М, — число
делений в единице объема; Сг — число ядер в единице объма;
cN— концентрация 239Np, делением 240Pu, 242Ри пренебрегаем,
394
Рис. 13.4. Зависимость концентрации
делящихся нуклидов в реакторе с
мягким спектром нейтронов от эиер-
говыделеиия
Рис. 13.5. Зависимость концентрации
неделящихся нуклидов в реакторе с
мягким спектром нейтронов от эиер-
говыделения
«5, аэ — средние значения этих величин по времени; 628=0,077):
=U+
1+ «5
^8=628 (М54“N9-|-Ni) ; N\=<J.gNg—Cq—Cl—C2,
откуда
A7g= ( 1 —Ctg) ~] ( 1 —бае) —1 [C8°—Cg—Cg—Cy—628 (A/5—c0—C\—C2) J •
(13.2.29)
Здесь ег — суммарная концентрация 242Pu, 24lAm, 243Am, 244Cm.
При выгорании 10,3 МВт-сут/кг получим относительные числа
делений (n^Ni
/25=45,7%; n9=41,3%; ш=5,9%; я8=7,1%. (13.2.30)
Отношение М5 / S равно доле энергии, выделившейся при
делении 235U. Чем меньше это отношение, тем лучше использует
реактор единственный имеющийся в природе делящийся нуклид
235U. На рис. 13.6 изображена величина 1 —М5 /2^/ как Функ-
ция выгорания.
395
Рис. 13.6. Зависимость отношения
числа делений изотопов Ри и
238U к полному числу делений для
реактора с мягким спектром (/)
и для реактора ВВЭР (3) и удель-
ного расхода топлива от эиерго-
выделения [см. (13.2.34)] для реак-
тора с мягким спектром (4) и для
реактора ВВЭР (2)
Общее выделение энергии в реакторе равно (Nt— число де-
лений нуклида t в реакторе)
W=E f5N^~\-EfgN^-\-EfiN l -\-EfgNg — Ef^ (jVg—|— 1,042Ng-1,052^-)-.
+ l,016/V8). (13.2.31)
В (13.2.31) коэффициенты при Nt близки к единице. Они будут
еще ближе к единице, если от числа ядер перейти к массе раз-
делившихся нуклидов (см. § 1.7):
(Р5+ 1,025Р9+1,026Pj-H ,00Р8). (13.2.32)
Поэтому с большой точностью можно характеризовать общую
энергию, выделившуюся в реакторе, общей массой разделивше-
гося вещества Р (см. табл. 1.13):
1Г=Е;5Р=(0,96-;-0,98)Р, МВт-сут/кг, (13.2.33)
где Р — масса "разделившегося вещества, г/кг топлива. С по-
грешностью 0,1—0,2% Р совпадает с массой всех продуктов де-
ления (различие возникает, во-первых, потому, что надо учесть
массу тех нейтронов, которые поглощаются не в топливе, и, во-
вторых, потому, что выделившаяся энергия эквивалентна 0,1%
массы продуктов деления). Поскольку 1 г разделившегося ве-
щества выделяет энергию приблизительно 1 МВт-сут, 0,1 W чис-
ленно равно (если W выражать в МВт-сут/кг) количеству раз-
делившегося вещества (%), например при энерговыделении
10 МВт-сут/кг разделился 1% урана.
В рассмотренном выше примере при выгорании
10,3 МВт-сут/кг в выгружаемом топливе содержится 4,12 кг
изотопов плутония на 1 т топлива. Изотопный состав плутония
следующий, %: 239Ри — 59,8; 240Ри — 30,8; 241Ри—6,8; 242Ри—2,4;
гз8ри — 0,2. Поскольку концентрация изотопов плутония нели-
нейно зависят от глубины выгорания, при усреднении по объему
реактора данные, полученные в «точечном приближении», могут
несколько измениться.
396
Концентрация 239Pu достигает насыщения, и поэтому коли-
чество полученного в реакторе плутония в единицу времени воз-
растает, если глубина выгорания уменьшается.
Отметим еще, как изменяются коэффициенты конверсии:
Кк — конверсия только в делящиеся изотопы плутония; К'к— во
все изотопы плутония:
к = co+£i. к , = с9 + С1 + с0 + са .. (13.2.34)
С5°-с6 с5° —С5
На рис. 13.3 изображены обе зависимости KX(W) и K'K(W).
При Ц7=0 коэффициент конверсии Кк(0) равен начальному плу-
тониевому коэффициенту (хр=0,765), а затем с ростом выгора-
ния монотонно падает. Коэффициент К'к имеет минимум при
Ж—7 МВт-сут/кг, а далее возрастает: начинает интенсивно на-
капливаться 240Ри. Одна из важнейших характеристик реакто-
ра— это «удельный расход топлива»*
q pH_К
= (13-2-35)
где qh’k — начальная и конечная концентрации делящихся ну-
клидов. Если Cf — концентрация, г/кг, a W' — энергия, МВт-сут/
кг, то размерность g0— г/(МВт-сут). Если разделить go на т?
(см. табл. 1.13; не совершая большой ошибки, можно считать,
что Ш( одинаково для всех нуклидов; при желании можно вве-
сти усредненное значение), то получим безразмерную величину
g0’= — g0. (13.2.36)
tnf
Так как m.f близко к 1 г/(МВт-сут), то численно go и g'o прак-
тически совпадают. Если реактор работает на чистом 235U, то
g'o=l + ct5=l ,2^-1,3.
В таком реакторе наименее экономично расходуется топливо.
Для рассмотренного примера величина g0 (13.2.35) приведена на
рис. 13.6 (кривая 4). Видно, что go^O,3, т. е. существенно мень-
ше единицы. Это замечательное свойство ядерных реакторов:
общее число делений больше, чем разность начального и конеч-
ного числа делящихся ядер, —делящиеся ядра частично воспро-
изводятся. Для бридера g0 отрицательно.
Обратимся теперь к другому реактору — ВВЭР. В качестве
топлива в реакторе ВВЭР используется оксид урана с содержа-
нием 235U 3—4%. Таблетки из оксида урана заключены в цир-
* Этот коэффициент полностью аналогичен коэффициенту; который всег-
да используется для оценки работы обычных электростанций: количество
сожженного топлива для производства единицы энергии. Автор-признателен
Б. И. Ильичеву, обратившему внимание на наглядный смысл величины g'o.
397
кониевую оболочку. Теплоносителем служит обычная вода под
давлением (она же выполняет функции замедлителя). Подобные
физико-технические характеристики реактора ВВЭР приведены
в [157]. Поскольку реактор ВВЭР имеет более жесткий спектр
нейтронов (у=0,4-М),5), двухгрупповая модель для эффектив-
ных сечений (см. § 2.4) может приводить к погрешностям. По-
этому расчет проведен на основе программы [160], которая
дает полный баланс нейтронов в ячейке и вычисляет скорости
всех реакций с учетом блокировки резонансных интегралов
[228].
На рис. 13.7 и 13.8 приведены зависимости концентраций
изотопов урана и плутония от глубины выгорания (расчет про-
веден для реактора ВВЭР-365 [157]). Отметим, что равновес-
ная концентрация 239Ри примерно в 2 раза выше, чем в реакторе
с мягким спектром (см. рис. 13.4). Причина такого увеличения
равновесной концентрации состоит в том, что сечение 238U воз-
растает из-за уменьшения блокировки резонансного интеграла
и увеличения жесткости спектра нейтронов сильнее, чем сечение
239Ри. Концентрация 240Ри еще не достигла равновесия, но все
же видно, что отношение с0/с9 в реакторе с жестким спектром
меньше, чем в реакторе с мягким спектром. Это происходит по-
тому, что 240Ри сильнее выгорает, так как в жестком спектре его
среднее сечение существенно больше. По этой же причине кон-
центрация 241Ри выше в реакторе с жестким спектром, чем в
реакторе с мягким спектром.
На рис. 13.7, 13.8 приведены также экспериментальные дан-
ные о содержании в топливе изотопов урана и плутония [229];
более подробное сравнение расчета с экспериментом см. в [228,
230]. В расчетах рассматривалась только одна ячейка с усло-
вием полного отражения нейтронов на границе (см. § 7.4, 7.5).
Фактически же в реакторе возможны перетечки нейтронов из
одной ячейки, обладающей большим коэффициентом размноже-
ния, в другую, коэффициент размножения в которой меньше.
Поэтому спектр" нейтронов в расчете мог несколько отличаться
от фактического. Принимая во внимание допущенные идеализа-
ции, следует признать, что согласие между расчетом и экспери-
ментом вполне удовлетворительное.
На рис. 13.8 приведены также коэффициенты конверсии
(13.2.34). Видно, что Кк существенно ниже, чем в реакторе иа
естественном уране. Коэффициент К'к не имеет минимума (как
было на рис. 13.3); это следствие меньшей концентрации 240Ри.
Удельный расход топлива go (13.2.35) в реакторе ВВЭР при-
мерно в 2 раза выше, чем в реакторе с естественным ураном
(см. рис. 13.6, кривые 2 и 4). Отношение числа делений 239Ри
к полному числу делений в реакторе ВВЭР меньше, чем в реак-
торе с естественным ураном (см. рис. 13.6, кривые 1 и 5).
Глубина выгорания топлива в реакторе ВВЭР, работающем
398
Рис. 13.7. Зависимость эксперимен-
тальных (точки) и теоретических
(кривые) концентраций делящихся
нуклидов в реакторах ВВЭР от глу-
бины выгорания
Рис. 13.8. Зависимость эксперимен-
тальных (точки) и теоретических
(кривые) концентраций неделящихся
нуклидов в реакторах ВВЭР от глу-
бины выгорания
на обогащенном уране, конечно, много выше, чем в реакторе на
естественном уране. Если начальное содержание 235U составляет
3%, то глубина выгорания равна 30 МВт-сут/кг, что в 3 раза
больше, чем в реакторе на естественном уране. Это, однако, еще
не означает, что в реакторе ВВЭР делится больше ядерного
топлива, чем в реакторе с естественным ураном. В самом деле,
для получения некоторого количества обогащенного урана надо
переработать большее количество естественного урана. При
этом кроме обогащенного урана образуется обедненный уран
с концентрацией 235U 0,2—0,3% (отвал).
Определим, сколько естественного урана надо затратить,
чтобы получить обогащенный уран с концентрацией 23SU, рав-
ной с. Пусть ре — масса естественного урана, из которого при
обогащении получено р кг обогащенного урана с концентрацией
235U, равной с, и направлено в отвал р0 кг урана с концентра-
цией 235U с0. Составим баланс 235U и 238U:
реСе—рС-^р0С0; ре ( 1 — Се) =р(1 —С) -\-р0 ( 1—Со) ,
откуда получим
ро==_£г^р. (13.2.37)
Cg—” Cq Cq Cq
Если c=3%, ce=0,71% и cQ=0,3% или 0,2%, то pe=6,6p или
pe=5,5p. Таким образом, при глубине выгорания30 МВт-сут/кг
«сгорает» не 3% всего добытого урана, а только 3/6=0,5%.
Следовательно, в реакторах на тепловых нейтронах сжига-
399
Таблица 13.1. Состав выгружаемого топлива из реакторов ВВЭР и ТВР, кг/т
Нуклид ВВЭР TBP Нуклид ВВЭР TBP
238[J 942,5 981,6 2i2«Am 9,2-10-1 4,0-10-5
235[J 8 1,1 «sCm 2,2-10-i 5,7-10-6
239рц 5,2 2,6 242С1П 1,0-10-1 1,8-10-5
236{J 4,5 9,4-10-1 2«Cm 6,7-10-5 2,7-10-5
240 рц 2,1 1,5 233Ц 5,3-10-» 5,2-10-7
24ipu 8,7-ю-1 2,9-10-i 247Cm 2,9-Ю-з 2,7-10-3
237Np 4,9-10-! 6.8-10-2 230Th 1,9-10-6 4,4-10-’
242 рц 3,7-10-i 1,4-10-1 232Th 6,2-10-7 1,0.10-’
238рц 1,7-10-1 1,7-10-2 232Ц 6,1-10-7 3,6-10-»
2«Am l,6-10-i 4,9-10-2 23ipa 5,4- IO-’ 2,4-10-8
234Ц 1,2-10-1 3,7-10-2 »Cm 1,9- IO-’ 1,3-10-9
2 «‘Am 1,0-10-1 1,1-10-2 23брц 1,5-10-7 1,9-10-8
2«Cm 2,5-10-2 1,6-10-3 250Cf 2,2-10-о l,4-10-i2
2«Cm l,9-10-3 3,5-10-1 252Cf 4,0-10-u 1,6- 10-13
ется 0,5—1 % всего урана. Увеличить глубину выгорания можно
при повторном использовании топлива после очистки от про-
дуктов деления и выделения изотопов урана и плутония (см.
§ 13.4). Еще более глубокого выгорания можно достичь в реак-
торах на быстрых нейтронах (см. [231, 232] и цитированную
там литературу).
В табл. ”13.1 приведены приблизительные данные о составе
выгружаемого топлива из реактора типа ВВЭР (плотность по-
тока 3-1013 нейтр/(см2-с), глубина выгорания 30 МВт-сут/кг,
выдержка отработавшего топлива 3 года, начальный состав на
1 т: 966,875 кг 238U, 32,875 кг 233U; 0,25 кг 234U; данные для
ВВЭР взяты из [233]) и тяжеловодного реактора [начальная
плотность потока 7-Ю13 нейтр/(см2-с), выгорание 10 МВт-сут/
кг, выдержка 3 года, начальный состав на 1 т: 992,847 кг 238U;
7,1 кг 235U; 0,057 кг 234U].
С удельным, расходом топлива тесно связана другая величи-
на— коэффициент воспроизводства (КВ). Коэффициент воспро-
изводства определим как отношение средних по объему и по
времени скоростей появления и исчезновения делящихся нукли-
дов (под делящимися здесь понимаются нуклиды, делящиеся
нейтронами всех энергий, в отличие от «неделящихся», которые
делятся только нейтронами с энергией выше определенного по-
рога):
КВ = 2С80/2'591 (13.2.38)
или
1 -КВ= (2;591 -2С80)/2а591, (13.2.39)
400
ГДе 2С8О — Scs4-Sc0; S(J59I — 2я6+2й»4-2а1; 2al — Sal[l 4-Л1/(°nl®)].
причем под S понимается усредненная по объему и времени
скорость реакции.
В знаменателе (13.2.39) заменим
2a591 = 2f/^; с = (14-3)/(1 +«),
где — среднее значение полного числа делений; a = Sf59i/2f5ei;
3 = SfsO/S^91. Концентрация делящихся ядер удовлетворяет урав-
нению
4^ = 2С80-2;951. (13.2.40)
at
Среднее значение правой части (13.2.40) между перегрузками
равно
у- [&591 -2cs0)d/ = (13.2.41)
о
где Т — среднее время между перегрузками; cf и cfK — началь-
ная и конечная концентрации делящихся нуклидов. Таким об-
разом, КВ реактора равен
KB=l-^'0=l-£g0/mf) (13.2.42)
где go — удельный расход топлива (13.2.35), a g'o определено
(13.2.36).
Пусть реактор состоит из нескольких зон с различными вре-
менами между перегрузками Т/. Тогда
3 ^«591 2/во)
1—КВ==—i----------------, (13.2.43)
/
где —полное число делений в зоне /. Концентрация деля-
щихся нуклидов в зоне /, с учетом перегрузок при t=nTj (п —
целое число), определяется уравнением
- S'59I + 8 (t - nT}) (cf« - cf).
Поэтому среднее значение по любому интервалу времени, крат-
ному Tj, равно
Жил -%о=~(cHf-cKf)- (13.2.44)
’ 1
26—6053
401
Следовательно, КВ определяется равенством
1—КВ = —4----------- (13.2.45)
i
где Pj — мощность зоны /; g'Qj— безразмерный удельный рас-
ход топлива в зоне / (13.2.36). Если ввести среднее значение
где Р — полная мощность реактора, то
1-КВ=^70>
где g'o — среднее значение,
— Pi ,
£o'=2j—
(13.2.46)
(13.2.47)
т. е. усреднение удельных расходов по зонам надо производить
с весом, равным относительной мощности зоны.
Можно получить для КВ другое выражение, если исходить
из условия баланса нейтронов типа (1.9.4), а именно:
(v2f) 591Н- (vSf)eo—S0,591-[-S/SO'r^cSo+S, (13.2.48)
где 2 включает в себя все вредные потери нейтронов, в том чис-
ле и утечку. Такое же равенство можно написать для каждой
зоны реактора. Тогда 2 будет включать перетечки из одной зоны
в другую (т. е. утечка может быть и отрицательной). Если раз-
делить (13.2.48) на 2Я59ь то получим
. КВ = цеЭф—1—2'; 2,=2/2й591, (13.2.49)
где
_ (V^/)591 . . . 1(V l)2/JsO
4 у ’ гэф 1 "т" f’jT-1 "
^0591 lV2,/1591
(13.2.50)
Величина ц имеет смысл среднего значения v2f/2a по делящим-
ся нуклидам, а еЭф близко, но не совпадает с величиной е, вве-
денной в гл. 9. Все величины в (13.2.49), (13.2.50) надо пони-
мать как средние значения по пространству и времени.
Ясно, что КВ возрастает, если 2' падает, a 2/so и т] растут.
Из формулы (13.2.42) и определения £, на первый взгляд, сле-
дует, что КВ убывает с ростом d=2fso/Sf59i в противоречии
с формулой (13.2.49). Однако в (13.2.42) входит еще удельный
402
расход топлива go, который растет при увеличении Sf8o за счет
роста реактивности и глубины выгорания. В формуле (13.2.49)
явно учитывается условие критичности, в чем и состоит ее из-
вестное преимущество перед формулой (13.2.42).
Величину
60 = — --Щ- —— (13.2.51)
mt 1 + a пи
можно назвать «теплотворной способностью» ядерного топлива,
так как она равна энергии, выделяющейся при уничтожении 1 г
смеси 235U, 239Ри и 241Рп. Она слабо зависит от вида реактора
на тепловых нейтронах и равна (с точностью до нескольких про-
центов) £>о=0,8 МВт-сут/г. Принимая это значение, получаем из
табл. 13.7: для реактора ВВЭР КВ=0,5, для тяжеловодного ре-
актора КВ = 0,75 (см. также § 13.4).
При увеличении концентрации делящегося вещества в еди-
нице объема реактора и сопровождающемся увеличении жест-
кости спектра нейтронов 2' падает (за исключением поглоще-
ния нейтронов в тех продуктах деления, которые обладают
большими резонансными интегралами), 2/so растет, т) сначала
несколько падает, а при переходе к спектру реактора на быст-
рых нейтронах растет.
Следуя этим соображениям, можно поднять КВ для реакто-
ра ВВЭР, если использовать металлическое топливо вместо
оксидного. При этом коэффициент воспроизводства поднимает-
ся до 0,77 [234]. Другой путь — значительное уменьшение отно-
шения объема замедлителя и топлива (до 0,5 вместо 2). При
этом, используя топливо (U—Ри)О2, можно поднять КВ до 0,9—
0,95 [235]. При этом, однако, содержание делящихся ядер до-
ходит до 80 г/кг, а общая загрузка Ри в реактор (мощностью
1 ГВт) составит ^7 т [235].
Из (13.2.49) следует, что если 2' изменилось на 62', то из-
менение КВ равно 6КВ=—62'. При этом предполагается, что
изменение 62' компенсировалось, например 2С8о, так, что
реактор остался в критическом состоянии. Наиболее удобным
способом сопоставить различные изменения в характеристиках
реактора — это привести их к изменению реактивности. Поэтому
полезно получить соотношение между и 6КВ. Запишем ко-
эффициент размножения так (если 2 включает утечку, то это
эффективный коэффициент размножения):
t)aai ~4~ (V^v)so _________ + (v2;)80/2Q691 (13 2 52)
2й591 4* ^cso + 80 -f- 2 1 -f- KB -f- 2' -f- (2180/2a 5!)1)
Из (13.2.52) получим
6KB = —^-h + (v2f)80/2fl591],
я2
26*
403
ИЛИ При k=l И v2f80^CSa591
6КВ=— ^bk. (13.2.53)
Знак минус в (13.2.53) возник потому, что увеличение 2с8»
увеличивает КВ, но уменьшает реактивность. Если же bk обу-
словлено изменением других величин (2' или т]), то в (13.2.53)
должен стоять знак плюс.
Задача 1. Реактор на высокообогащенном 23SU работает при постоянной
мощности, причем через время Т после начала работы с5(Г) =ас8(0). Опре-
делить отношение средней по времени плотности потока Ф(/) к потоку в мо-
мент времени 1=Т/2.
Решение. Из формул (13.2.3) и (13.2.4) имеем (прн OfS=const):
ОдФ^Т — 1—я; Ф (?) = 2Ф0/ (1-]-п)
и
Т
--- Фо С * Фо 1
Ф(0 = —j (1—^ФоО-1^ = ттг^1п“-
о
Таким образом,
Ф(0 = 1+« 1п /_!\
Ф(0 2(1 - а) П \ а )'
Например прн а=0,5 это отношение равно 1,04, а прн я=0,25 — равно 1,15.
Задача 2. Определить внд уравнения для концентрации 239Ри, записан-
ного без явного учета 239Np, решение которого совпадало бы при
с решением (13.1.6).
Решение. Если то из уравнения для 239Np (13.1.5) получим
cn = о6с5Ф/?.', поэтому
= (о8г8—Ол'Сл')Ф—о9с9Ф. (13.2.54)
Кроме того, надо изменить начальное условие. Если с«(0)=0, сэ(0)#=0,
то к решению (13.1.6) следует добавить с9(0) ехр (—s9). Тогда при
решение (13.1.6) можно переписать так:
с9(0 ь= c9(0)exp(—s9) -F- — ехр (— s9)], (13.2.55)
а9
где
7.(0) - с,(0)[1 ~ Г‘
л \ л / L j
илн, при условии ОлФ/Х<С1,
с7(0) = с9 (0) — о8с8Ф/ (?.—с8Ф). (13.2.56)
Очевидно, что (13.2.55) является решеньем уравнения (13.2.54) с началь-
ным условием (13.2.56). Изменение начального условия возникает потому,
что в приближенном уравнении (13.2.54) накопление 239Ри начинается с мо-
мента /=0, в то время как фактически в интервале 0<?<1/Х плутоний
только сгорает и не появляется вновь. Поэтому эффективная начальная кон-
центрация 239Ри для уравнения (13.2.54) должна быть меньше истинной.
Отметим, что если пренебрегать величиной о9Ф/Х, то сумма Cg-j-Cy удовлет-
404
воряет уравнению (13.2.54) при ал'=0 с начальным условием Сд(0), а не
с9(0).
Задача 3. Определить влияние 239Np на коэффициент размножения, если
установилась равновесная концентрация 239Ри. Оценить концентрацию 239Np.
Решение. В случае равновесия имеем (см. § 13.1):
Oaacs-----ф-----а8с8 с.\'-
Суммарное поглощение 2а9-)-2\=28 не изменилось по сравнению с тем слу-
чаем, когда Ол = 0. Сечение деления изменилось: 6Sf=—S^l-j-ctg)-1. Поэтому
8k——т]92л/2а. Из уравнения для cN получим
Пусть Ф=5-1013 см-2-с-\ у=0,1. Тогда SJV = 7,3-10-'1Ss. Если S8=0,3Sa и
т]9=2, то 8k=—4,4-10-4. Таким образом, при плотностях потока меньше
1014 см-2-с-1 поглощение в 239Np можно не учитывать. Концентрация 239Np
в этом примере равна c«/c8 = 5-10-2 кг/т. Если равновесная концентрация
?39Ри равна 3 кг/т, то после остановки реактора концентрация 239Ри воз-
растает за счет распада Np на 1,7 %.
13.3. НЕПРЕРЫВНАЯ ПЕРЕГРУЗКА ТОПЛИВА
Выше рассматривалось выгорание топлива и связанное с ним
изменение реактивности реактора в том случае, когда плотность
потока не зависит от координат. Можно интерпретировать эти
результаты иначе: вычислено изменение состава топлива и ре-
активности в некоторой точке реактора. В другой точке, при
другом значении плотности потока выгорание будет происхо-
дить по другому закону. Поэтому говорят о выгорании в «точеч-
ном приближении». Если выгорание не изменяет распределения
плотности потока в реакторе, то можно усреднить &Эф, исполь-
зуя теорию возмущений.
Если весь реактор загружается одновременно и выгружают-
ся все твэлы также одновременно, то сначала йЭф>1 и необхо-
димо гасить излишнюю реактивность дополнительными погло-
тителями. Топливо выгружают, когда йЭф без поглотителей ста-
новится равным единице. Такая работа реактора называется
работой кампаниями. При другой схеме работы в реактор не-
прерывно загружаются свежие твэлы и выгружаются наиболее
выгоревшие — работа в режиме непрерывной перегрузки. В этом
случае в каждый момент времени в реакторе находятся твэлы
с различной глубиной выгорания (всех возрастов) и состояние
реактора не зависит от времени. Поскольку реактивность реак-
тора определяется средним значением k по объему, а выгружа-
ются твэлы с минимальным k, при непрерывной перегрузке
можно получить более глубокое выгорание, чем при работе кам-
паниями. Здесь будет рассмотрен только случай, когда режим
непрерывной перегрузки уже достигнут и реактор находится
405
в стационарном состоянии. Вопрос об оптимальном выходе в
стационарное состояние более сложен и рассматриваться не
будет.
Пусть твэлы в реакторе расположены в решетке с шагом а.
Если внутри окружности радиусом R. (R.—среднее расстояние,
проходимое нейтроном в процессе миграции) расположено мно-
го твэлов, то поток нейтронов на данном твэле формируется не
только им самим, но и многими окружающими, которые из-за
непрерывной перегрузки имеют все возможные глубины выго-
рания. Так как /?2=4Л12, то условие применимости данной мо-
дели следующее:
4лЛ42»а2. (13.3.1)
Предположим, что плотность потока зависит только от коор-
динаты z (а по радиусу реактора плотность потока достаточно
хорошо выравнена). Тогда, используя уравнение с одной груп-
пой нейтронов, запишем
-^Ф- + -А<г1~1-ф = 0) (13.3.2)
где М можно считать постоянной, a k(z) — среднее значение ко-
эффициента размножения на данной высоте z*:
s(z)
J k^ds> (13.3.3)
о
где 5 — глубина выгорания; s(z)—максимальная Глубина вы-
горания для точки г. Запишем
ds=G(z)2f(z, t)dt,
причем Ф(г) не зависит от t в силу стационарности задачи. Ин-
тегрируя, получаем
s(z, Т’)=Ф(г)27(5)Т,
где Т — время нахождения твэла в реакторе; Sf(z)—среднее
по времени от Далее будем предполагать, что Sf(z) не за-
висит от z. Справедливость этого предположения можно оце-
нить на простой модели, когда уравнения выгорания линейны
и учитываются только 235U и 239Ри:
ехр(—s8) + Po44^'(1 —-ехР(—s»))
1 + И9
Идея последующих рассуждений заимствована из [236].
406
где Ро=2с8/2°5 —начальный плутониевый коэффициент
(13.1.11). Усреднение по времени дает
2 2о5 Г1 -ехр(-s8) Ij-ag /j---1—ехр(—s9) \~1 (13.3.4)
s5 1 ~Ь а» \ St / J
где 55 зависит от г. Следовательно, требуется, чтобы Sf (13.3.4)
не зависело от 55. Положим для оценки s9=2s5; 05=0,2; аэ=0,4;
Ро—0,8. Тогда 2f/2°5 отклоняется от 1 не более чем на 11% при
изменении $5 от 0 до 3. Таким образом, 2/ почти не зависит от
z. Следовательно, для максимальной глубины выгорания
можно записать
s(z) = const Ф(г). (13.3.5)
Подставляя (13.3.5) в (13.3.2), получаем
S
-^r-+(^)2F(5) = 0; F(s)=^(s')ds'-,
о
f(s) = а = —. (13.3.6)
Функция s(z) удовлетворяет следующим граничным условиям
(для простоты рассматриваем симметричный по высоте реак-
тор; Н — полная высота активной зоны):
=0; (13.3.7)
dz \г=Щ2
=2, (13.3.8)
V 5 dz /г=0
где % — некоторая постоянная (см. § 4.5). Если Х=оо, то реак-
тор не имеет отражателя и при z=0 глубина выгорания равна
нулю: $(0) =0.
Уравнение (13.3.6) может быть решено в квадратурах мето-
дом понижения порядка. Положим
ds ~^ = Р- (13.3.9)
Тогда Подставляя d*s dp dp ds _ dz* dz ds dz ~ (13.3.10) в (13.3.6) и = (13.3.10) интегрируя с учетом гра-
ничного условия (13.3.7), получаем
р (s) = V Ф — ф (s), (13.3.11)
407
где
s
tp(s) = j* F(s')ds'-,
о
(13.3.12)
F(s) определено (13.3.6) и sm — максимальная глубина выго-
рания, т. е. глубина выгорания при z=H/2. Из (13.3.9) следует
z (s) = С ,
V ’ J P(s’) ’
«о
(13.3.13)
где 5о — глубина выгорания при z=0 (если отражателя нет, то
5о=О). Обращая равенство (13.3.13), находим зависимость s от
z. Подставим в (13.3.13) р($) из (13.3.11) и положим z(sm) =
—HJ2. При этом возникает условие критичности
т
ds 7С
1/ф(5ОТ)-Ф(«) “ 1/2
(13.3.14)
Второе граничное условие (13.3.8) с помощью (13.3.9) запишем
так:
с 2
= + Л= 1/Д, (13.3.15)
2л2
причем А — эффективная толщина отражателя. Из уравнений
(13.3.14), (13.3.15) следует определить sm и sq. Средняя глуби-
на выгорания s связана с максимальной:
s=p,sm, (13.3.16)
где ц — коэффициент выравнивания по высоте:
Н/2 . г- sm
f s(z)dz = f - . (13.3.17)
7Zsm J 7tsm J !y 4(sm) — ф(в)
о s0
Средняя концентрация какого-либо нуклида c(s) равна
Я/2 sm
c~^j = — f c(z)dz = ^-{ r-c(s}ds - . (13.3.18)
V ’ Н J Я J 1/ф(М-Ф(О
О So
Если зависимость c(s) линейна, то
c(s)=c(s). (13.3.19)
Если зависимость с($) нелинейна, то (13.3.19) не имеет места.
В общем случае уравнения (13.3.14), (13.3.15) можно ре-
шить только численно. При этом надо иметь в виду, что подын-
408
тегральная функция в (13.3.14) обращается в бесконечность на
верхнем пределе. Можно сделать замену переменных:
£2=ip(sm)—ф(х); 2tdt——F(s)ds.
При s=s0. t=tQ= ф($о), при s—sm t=0. Тогда вме-
сто (13:3.14) получим
о
Г dt_______п
J F(s) ~ 2|/Г’
о
где в F(s) переменная s выражена через t. В интервале 0<£<
</0, s0<s<sm, F(s)^=0, если s0>0 и sm<s'm, где dty(s'm)/ds =
=F(s'm)=0. Если sm=s'm, интеграл в формуле (13.3.14) рас-
ходится и равенство (13.3.14) не может выполняться. Если $о=
=0, то такая замена не приводит к цели, так как F(0)=0.
Введем еще функцию
S
z(5)=[[Ms)-i]^; fer = 7-^fe; <13Л2°)
J 1 + a Al2 НЭф
0
Если перегрузки проводились бы не целыми каналами, а в каж-
дом элементе объема, то среднее значение kr должно было бы
равняться единице, т. е.
Х(«о)=О, (13.3.21)
где So — максимально возможная глубина выгорания. Требуется
определить, насколько s=smp, отличается от s0.
Отметим, что глубину выгорания во внешней зоне реактора,
где имеются радиальные утечки, можно определить таким же
способом, если заменить
k(s)^k(s)—ar2M2.
При этом, однако, граничное условие между зонами будет вы-
полнено только в среднем, поскольку зависимости Ф(а) в раз-
ных зонах будут различными.
Рассмотрим теперь наиболее простой случай, когда k линейно
зависит от s. В этом случае можно провести более полный ана-
лиз. Пусть
и, следовательно, F (s) = s ( а — f(s)=a—bs (13.3.22) — bs\- 'Hs) = — а $|; 2 J т 2 \ 3 /
409
t , a2M2s
Z "" 1 -}-a2M2
л b
a — 8--------s •
2
1
2 *
2
(13.3.23)
Очевидно, что а равно запасу реактивности при s=0, деленному
на а2Л12.
Из выражения для %($) получим
Г _ 2(л-»)
О Л — " "" .
Непосредственной проверкой можно убедиться, что
т. е. глубина выгорания при работе кампаниями «1 в 2 раза
меньше, чем в случае идеальной непрерывной перегрузки.
Если считать, что плотность потока нейтронов при выгора-
нии не деформируется, т. е. Ф (z) —Фо cos az, то можно опреде-
лить среднее значение kr(s) по теории возмущений (см. гл. 5;
здесь положено Д=0):
Ms)
Н/2
£r(z) cos2 azdz
О
Н/2
J cos2 azdz
О
(13.3.24)
В нашем приближении [см. (13.3.3)] kr(z)~ IJ-f-oAVPa
X bsm cos az (1 ,-f- a2Al2) 1
то, вычисляя интеграл в
7-_Ls -
те
и поэтому если потребовать
(13.3.24), имеем
3(Л —1) 3 - 3
= —------- ~ — s0 = — $1,
2b 4 0 2
a2 Л-12
-J-X
kr (s) = 1,
(13.3.25)
t. e. если при выгорании не происходит деформации плотности
потока, то средняя глубина выгорания в выгружаемом топливеs
составляет 75% максимально возможного значения при идеаль-
ной непрерывной перегрузке s0 и в 1,5 раза больше, чем при
работе кампаниями.
Теперь обратимся к полученным выше формулам, в которых
учитывается искажение плотности потока нейтронов под влия-
нием выгорания. Подставим (13.3.22) в (13.3.11) и (13.3.13) и
410
обозначим x=s/sm, y=2zjH-.
где
Полагая в (13.3.26) х=у=Л, получаем условие критичности
(13.3.14) для частного случая (13.3.22). Сделаем в (13.3.26) за-
мену переменных х = 1---— (1 — и1 2):
ьоу (1-«212иа + у(1-ва)(1+Зи«)
(13.3.28)
где Ь = У(1 —2_г)/3; Ьо = У(1 -|-2х0)/3. Интеграл (13.3.28) так
же, как (13.3.26), расходится при е->0, х—Ь—1. Поскольку ле-
вая часть конечна, то при е->0 должно быть а->оо, т. е. малые
е означают большой запас реактивности в свежем топливе (за
единицу реактивности принята утечка а2Л12). В дальнейшем
будем рассматривать случай малых 8 и больших а. Если 1—
;>3е, то в (13.3.28) можно положить 8=0. Тогда
у (х) = —[Arth b — Arth Ьо].
л|/ а
(13.3.29)
Разрешая (13.3.29) относительно х, имеем
/ \ ЗГ / "\^а . .Д12 1 _. 3 1,/п/а . ,Л1 2
*(y)=^[th(—z/4-CjJ У + ’
(13.3.30)
где
или
х (у) = 1 — 6А
М-4Ч
Ц-Лехр -lEk-z/Jj2
1 —6р 1—х0
1 ~Ь 2 -(- Хр -Ь |/3 \/~ 1 -(- 2х0
(13.3.31)
411
Рис. 13.9. Зависимость плотности
потока (глубины выгорания) от
координаты в реакторе с непре-
рывной перегрузкой:
1 — невбзмущенный поток; 2 — а=10;
3 —а=20; y—2z/H: x=s(y)/sfn
Зависимость x(t/) при хо=0, а=10; 20 приведена на рис. 13.9.
Для сравнения там же приведена зависимость плотности пото-
ка нейтронов от координаты для однородного реактора х=
= sin (пу/2) (кривая 1). Решение при z>H!2 получим с помо-
щью замены: Z-+H—z. При у=1 по формуле (13.3.31) имеем
(а=10) х(1)=0,989 вместо х(1) = 1, т. е. погрешность доста-
точно мала, хотя теоретически формула не справедлива при
х^1.
Для более точного вычисления интеграла (13.3.28) запишем
У№ = —» [(/х — /8)4-/в],
а
где
6
j __ р__________du________
2 J 21/'(1-«)8+*(!-«)
f>0
Интеграл 12 элементарно вычисляется, а при вычислении
разности Ц—12 можно положить е=0. В результате
у (Л) = —[ArthЬ — ArthЬй — In-1 + >41+5/(1 Дй) ]. (13.3.32)
1+/1+ е/(1-М J
Если в правой части (13.3.31) заменить
у - у + la ,
«/а 1+1/1+е/(1 + &0)
то функцию х(у) вблизи значения х=1 можно получиь путем
быстро сходящейся итерационной процедуры. Из (13.3.32) най-
дем условие критичности (надо положить y=x—b=V):
= — inf—V (13.3.33)
7? \ 6 /
412
В частности, при хо=О
У а = —(in —+ 0,7625 V. <13.3.34)
П \ S /
Например, при а=10 получим е==0,015, т. е. формула Д13.3.29)
теоретически справедлива только при 1—хУ 0,045, однако
(13.3.31) даже при х=1 имеет ошибку около 1%.
Второе условие критичности (13.3.15) запишем так:
К у а У (1 — x0)2(l+2x0) + 3s(l—х03) = HlxQ. (13.3.35)
При х0<1, е<1
х0 = -УУ...= -У— (In J- + 0,7625 \.
0 Узнх УзНК \ е 1 J
Из (13.3.17) получим для коэффициента выравнивания сле-
дующее выражение:
|Х-=1------* f z . -
пУ a J У1 — х3—с (1— х3)
= 1-------Г —- .— . (13.3.36)
J/“’О—к2)2+-у(1—“2) (1—3“4)
Положив е=0, найдем
|х = 1-----±^(1 —г>). (13.3.37)
п\/ а
Чтобы провести более точное вычисление, добавим и вычтем
из интеграла формулы (13.3.36)
1
р______(1 —u)du
J 1/-(1-и)2 + е(гзу) •
Разность интегралов можно разложить в ряд по 8 (только ли-
нейный член) и оставшуюся часть вычислить точно, а затем
разложить в ряд по 8. В результате имеем
ц=1-----^о) + е[—-----------------З~7=~(3-----М]. (13.3.38)
«Уа ' 0/1 <2 2п\/а V /]
При %о=О, Ьо=1/У 3 и
ц=1--р=( 1,268+ 0,951s)-)~е. (13.3.39)
Из (13.3.16), (13.3.27), (13.3.29) при хо=О, 8<С1 получаем
sls1 = ixsm/s1 = (2al(a— 1))(1 + 0,807/1+а).
413
Таблица 13.2. Влияние выгорания на различные средние
характеристики высотного распределения плотности потока
а t 2Д Н 1* s/s. (*'/*'о)г=0 фЗ/ф ф2
5 0,064 0 0 0,702 1,59 1,28 1,25
10 0,0149 0 0 0,761 1,65 1,56 1,18
15 0,0049 0 0 0,797 1,69 1,80 1,15
20 0,0019 0 0 0,821 1,72 2,01 1,13
5 0,045 0,1 0,2 0,775 1,73 1,30 1,14
10 0,0094 0,1 0,26 0,836 1,80 1,56 1,084
15 0,0028 0,1 0,31 0,872 1,84 1,74 1,065
20 0,001 0,1 0,35 0,895 1,87 1,89 1,051
Например, при а=10 s/si=l,66, т. е. средняя глубина выгора-
ния в 1,66 раза больше, чем при работе реактора кампаниями
(табл. 13.2).
Численные вычисления интегралов (13.3.26), (13.3.36) пока-
зали, что погрешность приближенных формул для коэффициен-
та выравнивания при а=5 составляет примерно 2%', а при а=
= 10— уже менее 0,5%. В табл. 13.2 приведены значения у, и
s/si при разных а и при Д=0 или 2Д/Я=0,1.
Из полученных выше формул можно определить, насколько
увеличивается утечка нейтронов, или, иначе, градиент плотно-
сти потока нейтронов, в результате выгорания. Из (13.3.9) на-
ходим, используя аппроксимацию (13.3.22):
dФ \
— = р(0) =
dz lz=tl I K !
KSm |Z5" /". 2 (
н У 1— Хо \3~
s)(l—х03), (13.3.40)
а для невозмущенного потока
«/Фр \ _
dz /г=0 Н Ч-2Д
Будем считать, что сравниваются реакторы с одинаковыми
т. е.
где ц определено (13.3.36), а б— (13.3.23). В табл. 13.2 приве-
дены значения отношения (13.3.41).
414
Нетрудно вычислить среднее значение любой степени плот-
ности потока:
1 - — =1-------— - -4= f - (l~xn)dx—. (13.3.42)
ф" J 1Л1—Xs—С(1—х3)
m
Ло
В § 12.1, 12.3 при усреднении поглощения нейтронов в продук-
тах деления возникала комбинация ф3/(ФФа) [см. (12.1.15),
(1.2.3.8)]. В табл. 13.2 приведены значения этой комбинации,,
вычисленной по формуле (13.3.42) путем численного интегриро-
вания. Поправку такого вида не следует вводить в условие кри-
тичности (13.3.14), поскольку все уже учтено в f(s) и в способе
усреднения. Оценка величины Ф3/(ФФ3) полезна для предвари-
тельных расчетов, когда еще не проведено усреднение выгора-
ния по высоте реактора.
Из данных табл. 13.2 видно, что при Д=0 отношение s/si
равно 1,6—1,7, а при 2Д/Я=0,1—около 1,7—1,8, т. е. глубина
выгорания s меньше, чем при идеальной непрерывной перегруз-
ке So [см. (13.3.21)] на 15—20%.
Уплощение нейтронного потока из-за выгорания топлива
увеличивает утечку из реактора в 1,5—1,8 раза. Отношение
Ф3/(ФФ2), равное 4/3 для невозмущенного реактора без отра-
жателя заметно приближается к единице, особенно для реак-
тора с отражателем.
В табл. 13.2, кроме того, приведена величина хо, т. е. отно-
шение глубины выгорания на краю реактора при z=0 к макси-
мальному значению. Видно, что при 2Д/Я=0,1 х0 достигает
0,2—0,3.
Выше предполагалось, что коэффициент размножения k(z)
зависит от z только через s(z) по формуле (13.3.3). Можно
рассмотреть более общий случай:
S(2)
£[s(z); z]=yj- J k (s) ds + bk (z), (13.3.43)
о
где &k(z) учитывает дополнительную зависимость k от коорди-
нат. Такая зависимость может возникнуть, например, из-за дви-
жения органов регулирования, которые перемещаются на корот-
кое время так, что это не сказывается на зависимости k(s) илн
из-за влияния температуры топлива и замедлителя, которая
учитывается при определении k(s) только в виде среднего зна-
чения.
Вместо уравнения (13.3.6) получим
— + (— V f-^-4- -fe(2) + A]s = 0, (13.3.44 )
dz2 \ Н ) s a2Af2 1
415
или, если считать 8>k(z) малой величиной,
[£<££> + 6fe-(2l+А'|ф = р (13.3.45)
dz* \ Н J [ зв «2Д42 J ’
где А — собственное число [его надо вводить, чтобы компенси-
ровать 6x(z)]; so(z)—решение уравнения (13.3.44) при 8k(z) =
= 0. Подчеркнем, что возмущение входит в уравнение (13.3.45)
линейно. В работе [237] получена система собственных функ-
ций для уравнения (13.3.45) [при линейной аппроксимации
(13.3.22)] и построена теория возмущений. Можно применять
к этому уравнению и ту форму теории возмущений, которая из-
ложена в § 5.3. При этом надо знать только основную собствен-
ную функцию; ее можно определить численно для любой зави-
симости k(s) [см. (13.3.13)]. При этом интегралы, входящие
в формулы теории возмущений § 5.3, также вычисляются чис-
ленно. Пример применения нелинейной теории возмущения
§ 5.3 к нелинейному уравнению приведен в задаче § 15.2.
13.4. замкнутый топливный цикл
Как было указано в § 13.2. в реакторе на тепловых нейтронах может
разделиться только 0,5—1 % урана. Это количество можно существенно уве-
личить, если выгруженное топливо после химической переработки и очистки
от продуктов деления и трансплутониевых элементов возвращать обратно
в реактор. Такой топливный цикл называется замкнутым, в отличие от откры-
того цикла, когда облученное топливо больше не используется в реакторе *.
Так как реакторы на тепловых нейтронах имеют коэффициент конверсии
меньше единицы, то реактивность возвращенного в реактор топлива будет
недостаточна для поддержания цепной реакции. Поэтому некоторая часть
выгруженного урана должна быть заменена ураном, который содержит 235U
больше, чем в отработавшем топливе.
Будем рассматривать идеализированную схему, когда плутоний, выгру-
женный из реактора, возвращается в тот же реактор (под реактором можно
понимать группу одинаковых реакторов, имеющих общее предприятие по пе-
реработке топлива).
После нескольких кампаний содержание 239Pu, 240Ри и 24,Ри достигает
равновесных значений и, следовательно, уже не зависит от времени. Кон-
центрация 235U в каждом твэле изменяется со временем. Однако если реак-
тор работает в режиме непрерывных перегрузок, то среднее значение кон-
центрации 235U по объему реактора не зависит от времени. Таким образом,
если отвлечься от медленно накапливающихся 242Ри и 236U, то средний по
реактору состав топлива не зависит от времени.
Основные характеристики замкнутого цикла можно получить, используя
только соотношение баланса нейтронов. Запишем это соотношение так:
X = ^а> (13.4.1)
/
* Часто под топливным циклом понимают все этапы производства — от
добычи урана до захоронения радиоактивных отходов; здесь мы понимаем
этот термин более узко, рассматривая только работу реактора. По поводу
переработки топлива см., например, [42, 238]. Содержание этого параграфа
в значительной степени основано на работе П. И. Христенко [239].
416
где сумма берется по всем делящимся ядрам, к которым причисляются также 238U
и 240Pu; Sa — сечение поглощения нейтронов конструкционными материалами,
теплоносителем, замедлителем, продуктами деления, а также нуклидами 236Lf,
242Pu и др., которые не включены в сумму по j. В (13.4.1) включена также
утечка нейтронов. Все сечения в (13.4.1) понимаются как интегралы по ней-
тронному спектру реактора.
Разделим (13,4.1) на S-е и учтем условия равновесия [см. (13.2.12)]:
^с8 = ^аэ> Sce = Sa0; Sco = Sal = Sal [1 -|-^1/(оа1Ф)], (13.4.2)
где Л,— постоянная распада 24,Pu. В результате преобразований получим
(’Is—1)?5=?—z, (13.4.3)
где
z = z0 + z1 —z2;
го = % — 2 + ae'a0'(4i — 2); z, = (v8 — l)/a8 + ae'a0' (>0 — l)/a0;
(13.4.4)
Z2=a,4' (41—l)/[l+Oai®Ail; “/' = “/7(1+“/);“/ = Ocy/a/;; I
4/= V/7(1 + “/)-
Далее,
<75=^ = —-^-; = (13.4.5)
“cs °C8 c8 ^CS
причем черта означает усреднение по объему реактора или по времени для
данного твэла.
Очевидно, что реактор будет потреблять минимальное количество посту-
пающего в цикл топлива, если cs/c8 минимально, т. е. q минимально, z и
(4s—1)Оаи/Ос8 максимальны. Величина q минимальна, если в реакторе хоро-
ший баланс нейтронов: малый захват в конструкционных материалах, замед-
лителе, продуктах деления.
Рассмотрим величину z. Если пренебречь распадом 24,Ри и делением
24ори, т0
z=z0-4-(V8— l)/a8; 20=119—2-|~а'9(т) 1—2). (13.4.6)
Значение гр практически не зависит от жесткости спектра и равно
2,2—2,25. Значение а9 растет с увеличением жесткости спектра. Если 0,45<
<а9<0,55, то
—О,О15<го<О,О7.
(13.4.7)
слагаемое в z (13.4.6) обусловлено делением 238U. Использовав
условия равновесия (13.4.2), получим v8—1 (v8—l)Sf8 _8 = (_8 >_Г8 > (13.4.8) “8 Sf9+Sh(l+“1)
или, приближенно, v8 1 -(>8-1) ^28, (13.4.9) “8
где б28 определено в § 9.1. Таким образом, Zi возрастает с ростом числа де-
лений 23811. Для увеличения 628 необходимо поместить в единицу объема
реактора много 238U, что повлечет за собой в силу условий (13.4.2) большое
количество 239Ри, т. е. приведет к увеличению жесткости спектра и уменьше-
нию z0. Величина q [см. (13.4.5)], как правило, падает при увеличении жест-
27—6053 417
кости, поскольку при этом растет как концентрация 288U, так и его сечение.
Если определены q и z, то средняя концентрация 235U равна
°cs q — z
с6------------------ с8.
°Я5 % 1
(13.4.10)
Отношение сечений оС8/оа5 увеличивается с ростом жесткости, поскольку роль
резонансного поглощения в 238U (даже с учетом блокировки резонансного по-
глощения) больше, чем роль резонансного поглощения в 235U. Значение т]5—1
уменьшается при увеличении жесткости спектра, хотя и не сильно. Таким
образом, множитель оС8/аО5(г)5—1) в (13.4.10) увеличивает преимущества
реактора с мягким спектром.
Из этого качественного анализа видно, что зависимость c5/cs от жестко-
сти спектра достаточно сложна. Поэтому мы ограничимся примером, основан-
ным на численных расчетах. Он приведен в конце этого параграфа.
Среднее значение с5 легко связать с начальными cs" и конечным с5к зна-
чениями концентрации 235U:
С5к=С5нехр (—s5); с5н=ё5$5[1—ехр (—S5)]-1; s5 = oO5®7’. (13.4.11)
Будем считать, что при повторных изготовлениях твэла после химиче-
ской переработки в единице объема всегда находится одно и то же число
ядер топлива С5°-|-с80. Тогда если x(cs°4-cs0)—число ядер ураиа, которое
необходимо добавить для поддержания реактивности, а у — доля ядер ура-
на, которые остались неиспользованными при изготовлении твэлов (т. е. оста-
лись в отвале), то
(1—f/)c5K4-xcs° = c5"; (1—у) (с8+с5-^б)Ч--Чс8°+с5°)+г’рн =
= с8°+с5», (13.4.12)
где сР" — начальная концентрация изотопов плутония. Решив уравнения
(13.4.12), получим
х = х = с8° + с6° —Срн _ = cs° + с6°
с6°+Х'с6к ’ (С8 + с6+ с6)к (с8 +с6+с6)к
1— у=К—хК'. (13.4.13)
Поскольку С8»с5, с6, Ср, то А и А' близки к единице.
Пусть энерговыделение на единицу массы топлива в реакторе в одной
кампании равно, 1Ео. Тогда энерговыделение на единицу массы урана, посту-
пающего извне в цикл, равно
W=W0/x. (13.4.14)
Если рассматривать не равновесное состояние, а работу реактора, начиная
с первой кампании на уране, то для N кампаний получим суммарное энерго-
выделение (на единицу массы урана, поступающего в цикл)
W / N
<•=1 / i=i
где Woi — энерговыделение для t-й кампании; х,- определяется по (13.4.13).
Очевидно, что для первой кампании (естественный уран) xi = l, а затем
х;<1, причем желательно иметь х;<К1. Предположим для простоты, что
1Ео;=1Ео для всех i, хг=х, !#=!. Тогда для N кампаний
Wn=W0/(x+N~1). (13.4.16)
При 7V—>оо получаем формулу (13.4.14). Следовательно, если х<К1, то в за-
мкнутом цикле можно сжечь значительно больше урана, чем в открытом, но
только за большое число кампаний. Пусть, например, х=0,1; N—10. Тогда
энерговыделение с единицы массы урана, поступившего в цикл, будет 51Ео.
Только при Л'^>10=1/х получим W= W/x0= 1О1Ео.
418
Следует, конечно, иметь в виду при рассмотрении работы реактора за ко-
нечное время, что выгруженное из него топливо еще обладает потенциальной
возможностью энерговыделения и если его поместить в другой реактор, то для
него величину W надо уже определять по формуле (13.,4.14), а ие по
(13.4.16).
Если в (13.4.13) положить Л=Х'=1 и использовать (13.4.11), то
л = = ; • । 1 о. ч. ч)
с5° — C5S5 fexp(sB) — 1]—1
Минимум х совпадает с минимумом с5 (если s5 фиксировано).
Учтем теперь потери плутония при переработке твэлов. Эти потери при-
водят к тому, что концентрация изотопов плутония в твэлах несколько отли-
чается от равновесной. Отклонения от равновесия создаются еще и в том
случае, если вылетающие из активной зоны нейтроны поглощаются специаль-
ными твэлами, которые содержат уран с минимальным содержанием 235U
(экран). В твэлах экрана ие допускается большого накопления 239Ри, чтобы
не происходило большого числа делений, так как в противном случае экран
потеряет свои функции улавливателя нейтронов. Поэтому содержание плу-
тония в экране далеко от равновесного. Добавление этого плутония после
переработки в твэлы активной зоны приводит к отклонению от равновесия.
В соотношение баланса (13.4.1) входят средние по объему реактора кон-
центрации. В режиме непрерывной перегрузки их можно заменить средними
значениями по времени для одного твэла. Усредняя по времени уравнение
dCa
—Г-= (2с8-2а9)Ф, (13.4.18)
at
получаем
(^а9 ^аэ) /s9 = ^С8— 2а9; 39 — ОадФУ,
где Т — продолжительность кампании. Если потери при химической перера-
ботке и изготовлении твэлов равны е, то
с9н = с9к(1—е); сон = сок(1—е); dH=CiK(l—е—%iT2), (13.4.19)
где Т?— время переработки и изготовления твэлов (%1Тг<С1). В первом
порядке по е получим новые условия равновесия:
Sa9=Sc8 (1—e/s9); e/s9«l. (13.4.20)
Аналогично при е/з0, e/si < 1:
= ^с9( 1 s/5o) == ag/ ^с8 [ 1 s/59( 1 “1" °Я9/®аоП> 'j
Sal = sco(l— е'/д) = “9'“o'Sc8 [1 — (е/«9)(1 + W W (13.4.21)
где e/==8—f-XiTg.
Используя новые условия равновесия (13.4.20), (13.4.21), получаем вме-
сто (13.4.3):
(%— 1)?5 = ?к + <7зам + Яе + ?пД 4" 4" 41 + ?з + 4в— (zo 4” г1 — гг) > (13.4.22)
где г0, Zi, z2 даны (13.4.4);
4а = -S9-1(e?' -Нх);
Я' ~ 1 +го+а9'ао'^(»li — 2)(оЯ9/оа0) +
, v0—1 ]
4- (’ll— 1) (oa9/aal) 4" (1 + (Оа9/°ао))
“о J
27* 419
и q, (определяется распадом 24IPu за время переработки)
У\ = “/“оЧ7)! I)°a9^i^2/°ai j (13-4.24)
qK — потери в конструкционных материалах; q33ls — в замедлителе (все поте-
ри отснесены к Sc8); qu~^ —потери в продуктах деления; q2, qi, q3, q3— по-
тери в 242Pu, 24lAm, 243Am, 236U. Черта означает усреднение по времени. По-
тери в других трансурановых нуклидах менее существенны. Потери
в продуктах деления можно разделить на две части: поглощение сильнопо-
глощающими (I35Xe, Sm—qxe, sm) и слабопоглощающими продуктами деле-
ния. Последние аппроксимированы в § 12.3 одним эффективным осколком.
Пренебрегая предшественником, запишем уравнение для концентрации ЭО,
возникающего при делении нуклида /:
(13.4.25)
Если плотность потока нейтронов не зависит от времени, то
2/s(O=f//Sf/[l—ехр (—S/3)]; (13.4.26)
Усреднив по времени, получим при s/s = a,s®7'<g 1:
2/э = -у«//2//^э- (13.4.27)
Используя условия равновесия (13.4.2) и пренебрегая делением 240Ри,
получаем
I
Чэо = 2 S9<*’
где
УчРъ* , У1°1* । .
Q =т;— + ТП----------, "Г,—гм + y»°s аа±У5°5 Уб (1 +“s); »/* =
1+“» 0 +“1)(1 +Х1/°а1Ф)
= ч/э/оа9. (13.4.28)
Теперь рассмотрим сц и q3. Если концентрация 24,Ри достигла равнове-
сия, то в уравнении, которое описывает накопление 24,Ат,
= сЛ1Ф (13.4.29)
концентрация Ci "не зависит от времени. Решая (13.4.29), находим (предпо-
лагается, что при химической переработке америций удаляется, так что в каж-
дой кампании начальное значение сА^ равно нулю):
Ч = (13.4.30)
Усредняя (13.4.30) по времени, напишем (а0»1, «Л1 1):
У1~ 0 5Л / (1 + j 'j • (13.4.31)
2 Л1 / \ Л-1 /
Точно так же можно определить q3t если считать, что концентрация 242Рп
мало изменяется на протяжении одной кампании:
(13.4.32)
420
где q2— среднее значение q2 за кампанию.
В правой части (13-4.22) величины <?э0, qlt q3 пропорциональны, a qe об-
ратно пропорционально продолжительности кампании. Поэтому при некотором
значении з9 правая часть (13.4.22) достигает минимума, т. е. концентрация
235U будет минимальна. Если обозначить
Чэо + 91 + 9з =
то минимум qs будет при з9, равном
(5э)мин = |/^(e9/+ 91)/-®> (13.4.33)
и при этом
?ЭО + 91+ 9з = + 9х) (13.4.34)
Практически оказывается, что если потери при переработке малы (поряд-
ка 1 %), а Г составляет примерно 2 года, то минимум с5 осуществляется при
очень коротких кампаниях и стоимость переработок будет слишком велика.
Поэтому надо находить компромиссное решение.
Из формулы (13.2.38) получим, если учесть равенства (13.4.2), коэффи-
циент воспроизводства
КВ = 1—-------(13.4.35)
1 + <?5 + а9 “О
В качестве примера рассмотрим тяжеловодный реактор с газовым охлаж-
дением [239]. Хотя этот пример имеет иллюстративный характер, следующие
из него качественные выводы представляются достаточно достоверными. Вы-
числения проводились по идеализированной схеме: рассматривалась одна
ячейка *, причем непрерывная перегрузка топлива учитывалась только тем,
что кампания кончалась не когда йЭф= 1, а при условии
Т
М= k^(t)dt= 1. (13.4.36)
о
После окончания кампании плутоний возвращался в реактор, при этом
учитывались потери (1 %) и распад 24,Ри за время переработки (7’2 = 2 года).
Считалось, что 75 % нейтронов, выходящих из активной зоны реактора, по-
глощаются в экране из 238U, причем 8 % образовавшегося в экране 239Ри
разделилось, а 4 % перешло в 240Ри. Такая смесь изотопов плутония присо-
единялась к основному топливу в каждомй кампании. Количество 235U в на-
чале каждой кампании выбиралось так, чтобы следующая кампания была
примерно той же продолжительности, что и предыдущая.
Глубина выгорания топлива вычислялась по программе [228]. В этой про-
грамме скорости реакций рассчитываются по программе [160], которая
решает интегральное уравнение переноса в транспортном многогрупповом
приближении. При этом явно учитывались резонансные уровни 238U, располо-
женные ниже 215 эВ, и по одному главному уровню 240Pu, 242Pu, 286U. По-
глощение резонансными уровнями 238U, расположенными в интервале 215<
<£<10 000 эВ, оценивалось приближенно.
* Радиус ячейки 26 см, радиус блока 12,5 см, две трубы из Zr общей
толщиной 0,71 см расположены на расстоянии 12,5—14 см от центра блока.
Металлический уран занимает 30 % блока, покрытие из Mg—13 %. В рас-
чете блок считался однородным. Замедлитель—D2O с примесью 0,3 % Н2О.
Энерговыделение составляло 0,02 МВт на 1 см длины. Средняя температура
урана 723 К, замедлителя 353 К.
421
Рис. 13.10. Зависимость концентраций нуклидов при повторном использовании
топлива в тяжеловодном реакторе от энерговыделения
На рис. 13.10 представлены концентрации изотопов ураиа и плутония
как функции суммарного выгорания на 1 кг топлива. Разрывы в с9 возни-
кают из-за добавки плутония, накопившегося в экране, разрывы в с, обу-
словлены распадом 241Рц за время переработки; разрывы в а— поступлением
урана в топливный цикл извне. Поскольку часть урана остается в отвале,
то разрывы возникают и в с6. Из рис. 13.10 следует, что концентрации 239Ри,
24«Pu, 241Ри практически достигли равновесия. Концентрация 242Рп еще
далека от равновесной (на рисунке показана равновесна^ концентрация
242Рц —ср).
В том спектре нейтронов, который существует в блоке топлива, величи-
ны а< и г), имеют следующие значения: а5=0,208, г)д = 2,0; «9=0,461, ц9=1,96;
«1 = 0,316, т|! = 2,22; а8=7,11; ыо = 8О. Отношения сечений равны: Оа9/оао = 3,16;
oa9/Oai=0,86; Оа9/Оа5=2,0; Оаб/Ос8=110. Важными характеристиками спек-
тра являются также отношения (Sf8~|-2fo)/2f = O>137; Sf(£>0,465 эВ)/2г=
=0,195; Sc8(£> 0,465 эВ)/Sc8 = 0,59. Конкуренция между распадом и погло-
щением нейтронов 241Ри характеризуется величиной Л]/о£11Ф=0,075, а про-
должительность кампании — величиной s9=l,65.
Из приведенных значений параметров следует:
zo=O,O28; Zi = 0,263; г2 = 0,028; 2=20+2,—г2=0,262. (13.4.37)
Вредные потери нейтронов характеризуются величинами: </к = 0,062;
?зем = 0,032; <?хе, sm = 0,077; </6 = 0,006; </2=0,027; </1 = 0,011; </3=0,004; <?эо=
= 0,059.
Потери нейтронов из-за неполного улавливания экраном равны
</yT=a2.M2Sap/Sc8,
где Sa — полное сечение поглощения; р — доля нейтронов, которые не улав-
ливаются и уходят в защиту (принято р=0,25). Величины </в=0,028,
<7Л = О,ОЗ (при е=0,01 и Тг=Ч года). Полная сумма всех вредных потерь
S <7<=0,33. На основании этих численных значений получим
I
G/6-l)76= S<7i-z = 0,066, (13.4.38)
422
откуда находим концентрации 235U (по отношению к 238U): с5=0,6-10-3,
С5н = 088-10-3, с5к = 0,39- 10“3. Значение х (13.4.13) равно 0,072 (можно по-
ложить Х=Х'=1). При энерговыделении за кампанию Ц70 = 7,9 МВт-сут/кг
получим долю (%) разделившегося урана [по (13.4.14)]:
О,1Г=О,1Го/х=11 %.
Используя (13.4.38), получаем КВ=0,935 [см. (13.4.35) при rjg—1 = 1,
а'9а'о=О,31].
Обратим внимание на большую роль делений 238U. Если исключить из
(13.4.22) zb то концентрация с5 увеличится в 5 раз. Большое значение 62s
достигается тем, что ТВС имеют большие размеры и высокий коэффициент
заполнения ураном.
Отметим также большую роль распада 24Фи: если величины z2, qt и
<7, положить равными нулю (Ai = 0), то с5 уменьшится в 6 раз [такие
сильные изменения связаны с тем, что в (13.4.38) происходит очень
сильная компенсация между различными слагаемыми, поэтому в более точ-
ном расчете эти оценки могут существенно измениться]. Потери плутония
при переработке (е=0,01) приводят к увеличению с5 на 15 %.
Отметим, что с5" меньше, чем концентрация 235U, в отвале заводов по
разделению изотопов урана, Поэтому реактор можно подписывать не естест-
венным ураном, а отвалами разделительных заводов. Возможность исполь-
зования отвалов является существенным преимуществом тяжеловодных
реакторов перед другими типами реакторов на тепловых нейтронах.
В заключение отметим, что рассмотрение равновесного состава топлива
привлекательно тем, что можно легко проанализировать влияние различных
факторов на коэффициент воспроизводства, величину х (13.4.13), концентра-
цию с5.
13.5. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ СЛУЧАИ
ПРЕОБРАЗОВАНИЙ НУКЛИДОВ В РЕАКТОРЕ
13.11. Схема преобразования
Ториевый цикл (рис. 13.11) очень похож на плутониевый:
238U заменяется 232Th, 239Np — 233Ра, Wu — 233U, 240Ри—234U,
24ipu — 235ц, 242ри — 236]j (На рИС 13 ц приведены еще 233Th и
234Ра; их можно не учитывать, поскольку они обладают малым
периодом полураспада).
Основное отличие ториево-
го цикла от плутониевого со-
стоит в том, что 238U нет в осно-
ве природного урана (период
полураспада 233U Т'1/2= 1,6-105
лет много меньше возраста
Земли, и поэтому весь 233U
распался). Чтобы осуществить
ториевый цикл, надо сначала
получить 233U в реакторе, ко-
торый работает на 235U или
239Ри и содержит 232Th в каче-
стве поглотителя нейтронов.
232Th, так же как 238U, име-
ет много резонансных уровней,
Рис.
нуклидов в ториевом цикле (обозна-
чения см. на рис. 13.2)
423
которые сильно блокируются (см. § 8.6). Сечение поглощения
в тепловой группе у 232Th заметно больше, чем у 238U. Сечение
деления быстрыми нейтронами и число вторичных нейтронов
для 232Th существенно меньше, чем для 238U. Поэтому роль
размножения на быстрых нейтронах в ториевых реакторах
меньше, чем в урановых (см. § >1.1, 1.5).
Период полураспада 233Ра примерно в 10 раз больше, чем
239Np. Сечение и особенно резонансный интеграл протактиния
также больше, чем нептуния. Поэтому в реакторах с большой
плотностью потока или с жестким спектром потери нейтронов
в 233Ра будут существенны.
Влияние 233Ра на коэффициент размножения в равновесном
состоянии может быть вычислено так же, как вычислялось вли-
яние 239Np в задаче 2 § 13.2. Имеем
S А v ( ^р \ 1 у
S/ 2а ’ + Орф )
и отношение концентраций 233Ра и 233U:
СР аз ^р \~х
Положим Ф=2,5-1013 нейтр/(см2-с); у=0,1; Ti/2—27 сут,
Тогда
|Л.р/(аРФ) =91.
Если т|з=2,28, 2а=2,52г, то —б&=0,01 вместо 2-Ю-4 в случае
239Np (см. задачу 2 § 13.2). Отношение концентраций 233Ра и
233U равно для этого примера ср/с3=0,056.
После остановки реактора, когда весь 233Ра распадается (т. е
через несколько месяцев), концентрация 233U возрастет на5,6%.
Если топливо при этом останется в реакторе, то его реактив-
ность увеличится на 3,7%.
Коэффициент ц 233U в тепловой группе больше, чем у всех
других нуклидов (см. табл. 1.8), причем ц слабее зависит от
энергии, чем у 239Рц или 235U (см. рис. 1.8; 1.9). Сечение радиа-
ционного захвата 233U (величина а) существенно меньше, чем
у 239Ри. Поэтому роль 234U, 235U, 236U значительно меньше, чем
240Ри, 241 Ри и 242Ри в плутониевом цикле. Поглощение нейтронов
продуктами деления 233U заметно меньше, чем продуктами де-
ления 239Ри.
Это сравнение показывает, что с точки зрения баланса ней-
тронов ториевый цикл имеет как преимущества, так и недостат-
ки по сравнению с плутониевым циклом. Используя ториевый
цикл, теоретически можно получить реактор-размножитель на
тепловых нейтронах, однако практически потери в конструк-
ционных материалах, замедлителе, продуктах деления, протак-
тинии приводят к тому, что нельзя надежно гарантировать
424
сколько-нибудь заметное повышение КВ над единицей. В за-
мкнутом цикле, аналогичном циклу, рассмотренному в § 13.4,
можно получить КВ=1. Чтобы иметь КВ>1, надо в процессе
работы непрерывно извлекать продукты деления и протактиний.
Принципиально возможна такая очистка в гомогенном реакторе
с тяжелой водой [240] или в реакторе на расплавленных солях
[241]. Более подробно вопросы использования тория в ядерных
реакторах рассмотрены в [242].
Задача. Пусть гомогенный реактор U—Th находится в равновесном со-
стоянии, т. е. 22=S3 (Ра пренебрегаем). Предположим, что для поддержания
реактивности, которая падает из-за накопления продуктов деления, можно
непрерывно подпитывать ураном или непрерывно выводить торий. Что выгод-
нее [243]?
Решение. Так как реактор находится все время в критическом состоя-
нии, то
^з+ sa(l + ? + '7i)
где <71 = ct — поглощение в продуктах деления (кроме быстронасыщающих-
ся); <7—все остальные потери нейтронов, включая утечку. Пренебрегая выго-
ранием тория и учитывая условие равновесия, получаем
23=23°(1+ТзО; S2=22o(1—У20,
где у3, у2 — соответствующие скорости подпитки и увода. Подставляя S2, 23
в выражение для k и приравнивая выражения при одинаковых степенях вре-
мени, получим
с сх с(1—х)
Г2+тз = 77—; Тз=тт—; ъ=~—>
14-<7 1 +<7 1 +<?
т. е. при х=0 происходит только увод тория, а при х=1—только подпитка
ураном. Составим коэффициент воспроизводства КВ (х) =S2(x)/Ss(x) и опре-
делим отношение КВ(0)/КВ(1):
кв<»>кв<°>-
т. е. КВ всегда выше в том случае, когда осуществляется подпитка ураном.
Калифорний-252 интересен как очень мощный источник ней-
тронов, возникающих в результате спонтанного деления. Пусть
п — число ядер в 1 г вещества. Число делений (спонтанных) Nf
и число а-распадов Na в 1 с равны
Nf=Kfti; Na==kan,
причем
= Т\Г2 = —
Л
Число нейтронов спонтанного деления, очевидно, равно
Nv=vNf, (13.5.1)
425
Таблица 13.3. Число нейтронов спонтанного деления
Нуклид Nv, нейтр/(гс) Нук- лид нейтр/(г-с) Нуклид нейтр/(г-с) Нук- лид нейтр/(г-с)
235Ц 2,7-10~4 239рц 2,3-10-2 242ШАгп 1,5-102 244Ст 1,1-10’
236Ц 5-Ю-3 240рц 9-Ю2 243Дт 4,2 243 Ст 39
238U 1,1.10-2 241 рц 5-Ю-2 242CIT1 2-10’ 24«Ст 9-10е
23брц 3,5- Ю4 242рц 1,6-10» 243 Ст 1 2-Ю3 232Cf 2,3-1012
2§8Рц 2,5-103 241Агп 5,7-10-1
а энерговыделение
W=EfNf+EaNa= 1,6- 10~13Х
X(EfNf+EM Вт/г, (13.5.2)
где Ef, Еа — энергии, МэВ; Nf, Na — число делений или «-распа-
дов в 1 г вещества.
В табл. 13.3 приведены Nv для ряда нуклидов. Видно, что
интенсивность нейтронного излучения 252Cf на несколько поряд-
ков выше, чем у других нуклидов. Обычно энерговыделение за
счет а-распада много больше, чем за счет спонтанного деления.
Исключение составляет 252Cf, для которого оба слагаемых
в (13.5.2) одного порядка.
Схема образования 252Cf из 244Сш приведена на рис. 13.12
(до 244Ст, см. рис. 13.2). Количество образующегося при работе
реактора 252Cf очень мало (см. табл. 13.1). Поэтому 252Cf полу-
чают в несколько этапов. Сначала специально выделенные для
этой цели твэлы оставляют в реакторе для более глубокого выго-
рания плутония с целью накопить 242Рп. Далее из этих твэлов
извлекают плутоний и в другом реакторе с более высокой плот-
ностью потока облучают до образования 244Сш. Наконец, после
вторичной переработки извлеченные из образца изотопы кюрия
облучают с целью получить 252Cf.
Из рис. 13.12 видно, что имеются «узкие места», задержи-
вающие образование 252Cf из 244Сш: во-первых, это малые сече-
ния поглощения 246Ст, 248Ст и, во-вторых, большие сечения де-
ления у 245Ст, 247Ст и 249Cf. В результате деления значительная
часть исходного 244Ст превращается в продукты деления, а не
в более тяжелые трансплутониевые нуклиды.
Отметим, что первое обстоятельство можно устранить, если
проводить облучение в реакторе с жестким спектром, поскольку
резонансный интеграл у всех изотопов кюрия достаточно велик.
Более подробные данные о производстве 252Cf можно найти
в [227] и цитируемой там литературе.
Плутоний-238 представляет интерес как изотопный источник
энергии [227], в частности как источник энергии для стимуля-
тора сердечной деятельности. Энерговыделение 238Рц составляет
0,6 Вт/г. В реакторе 238Ри получается по схеме, приведенной на
426
Рис. 13.12. Схема образования 252Cf из 24',Ст
рис.13.2. При этом он является малой примесью к тяжелым изо-
топам плутония (см. табл. 13.1). Для получения чистого 238Ри
надо предварительно выделить из топлива 237Np и поместить его
в реактор в виде специальной мишени. Как видно из рис. 13.2,
накопление 237Np происходит двумя путями: через 235U, 236U, 237U
и по реакции 238U(/z, 2/z) 237U (см. § 13.2).
Поскольку 238Pu имеет довольно значительное сечение захва-
та, возникают (в небольшом количестве) и более тяжелые изото-
пы плутония, которые в данном случае являются нежелатель-
ным балластом. Другим недостатком этого способа является на-
копление 236Ри и 232U по реакции (/г, 2п) и (у, п) на 237Np (см.
ниже).
Схема другого способа получения 238Ри изображена на
рис. 13.13 [227, 244]. Для осуществления этого способа надо
извлечь из отработавшего топлива 24iAm, образующийся при рас-
паде 24iPu как в реакторе, так и при хранении отработавшего
топлива. Количество 241Ат через 3 года после выгрузки состав-
ляет 0,05 кг/т для тяжеловодного реактора и 0,16 кг/т для реак-
тора ВВЭР (см. табл. 13.1). После облучения Ат в реакторе
возникает 242Аш (16 ч), который, распадаясь, переходит в 242Сш
и 242Ри (см. рис. 13.13). 242Сш, распадаясь как в реакторе, так и,
главным образом, вне реактора, переходит в 238Ри (с некоторой
примесью 242Ри, который образуется при распаде 242Ат).
Очень небольшие примеси 236Ри могут возникать по реакции
(n, 2/z) на 237Np, который накапливается в небольших количест-
вах в результате распада 24iAm. Другой возможный путь — реак-
ция 241Am(/z, 2/z)240Am, причем 240Am, превращающийся в 240Pu,
427
Рис. 13.13. Схема образования 238Ри из 241Ат.
Рис. 13.14. Радиоактивные превращения продуктов распада 236Рц и 232U
имеет очень небольшую вероятность испытать а-распад с обра-
зованием 236Np.
Плутоний-236 и уран-232 накапливаются в реакторе в очень
малых количествах, поскольку эти нуклиды возникают либо
в результате реакции (п, 2п), которая имеет малое сечение, либо
при захвате нейтронов малыми примесями тория и протактиния.
Тем не менее концентрацию 236Рц и 232и надо знать, потому что
при распаде 232U накапливаются дочерние продукты, обладаю-
щие жестким у-излучением. Схема распада 236Рц и 232и приве-
дена на рис. 13.14. Основные у-кванты испускаются 208Т1 (их
энергия 2,62 МэВ). Поскольку все нуклиды после 228Th облада-
ют малым периодом полураспада, для них можно написать
(13.5.3)
Поэтому число распадов 208Т1 в 1 с равно
^08^08=6^28^28, (13.5.4)
428
где е—0,36 — коэффициент разветвления в распаде 212Bi; %08, ^28
и Сое, с28— постоянные распада и концентрации 208Т1 и 226Th.
Пусть в выгруженном из реактора топливе содержатся 236Ри и
232U с концентрациями с6о, с2о- Для определения зависимости
ц08 (0 надо решить уравнения
—^- = —-^- = V-V2; -^- = Л2с2 —Л28^„ (13.5.5)
at at at
с начальными условиями с6(О)=Сбо; <7г(О)=с2о, и если продол-
жительность кампании реактора мала по сравнению с перио-
дом полураспада 232U, то с2в(0) =0.
Решив уравнения (13.5.5), получим число распадов aos-pj
htfCos—C20F i (t) -{-CeoFzft), (13.5.6)
где Fi и F? — универсальные функции:
F1(/) = SA2['1--M 1 [ехр(—-ЛД) —ехр(—Я2гД)]; (13.5.7)
\ “23 /
F2(0 = a2fi —M"4(i -4Ч~11ехР(-^)-ехР(-М)]-
— f1 — -рЧ Х(ехр(— М) — ехР(— Л280]1. (13.5.8)
\ ^28 / J
На рис. 13.15 приведены функции Л, F2- Для получения чис-
ла распадов 208Т1 в 1 с надо умножить Fi, F2 на число ядер
232ц1 и 23бри в рассматриваемом
объеме в начальный момент вре-
мени, т. е. в момент выгрузки из
реактора.
Все возможные пути образо-
вания 232U и 236Ри показаны на
рис. 13.16 (штриховой линией
обозначены нуклиды с малыми
временами жизни, которые обыч-
но можно не учитывать). В раз-
ных условиях главное значе-
ние имеет та или иная це-
почка. В ториевом цикле ос-
новную роль играет реакция
232Th(n, 2n)231Th; при получении
238Ри из 237Np — реакции (п, 2п)
и (у, п) на 237Np (у-кванты
возникают в конструкционных
материалах при захвате ней-
тронов, и их количество и энер-
гия зависят от конкретных об-
стоятелььств [227]). Если 238Ри
Рис. 13.15. Универсальные
функции для определения чис-
ла распадов 208Т1
429
Рис. 13.16. Схема цепочек, приводящих к образованию в реакторе 232U и
236Рп (сечения и периоды полураспада см. в Приложении IV)
предназначен для медицинских целей, то количество 236Ри
ограничено условием
-^-<3-10-’,
С238
Если в топливе реактора имеются хотя бы незначительные
примеси тория и протактиния, то надо учитывать цепочки, на-
чинающиеся с этих нуклидов. Если при изготовлении твэлов
концентрация тория и протактиния равна нулю, то все же за
время их хранения и за время работы реактора накапливается
достаточное количество изотопов тория за счет а-распада 234U,
235U, для того чтобы эти цепочки вносили заметный вклад в на-
копление 232U.
О накоплении 232U и 236Ри в реакторном топливе см. [245,
246].
13.6. ПОЛУЧЕНИЕ ИСКУССТВЕННЫХ НУКЛИДОВ И
ВЫГОРАНИЕ ПОГЛОТИТЕЛЕЙ
В предыдущих параграфах речь шла об изменении концен-
траций нуклидов, связанных с топливным циклом. Преобразо-
вание одних нуклидов в другие, кроме того, может происходить
в специальных мишенях, помещенных в реактор для получения
искусственных нуклидов, а также в органах регулирования или
в выгорающих добавках, служащих для компенсации излишней
реактивности.
430
Большинство искусственных нуклидов производится в реак-
торе по схеме:
Стабильный нуклид Ci в результате радиационного захвата
нейтрона переходит в радиоактивный нуклид Сг, который мо-
жет еще и захватывать нейтрон. Нуклиды, получающиеся при
распаде и захвате нейтрона нуклидом Сг, обычно не представ-
ляют интереса и их концентрации можно не вычислять.
Запишем уравнения, определяющие концентрации нуклидов
Ci и с2:
01ф(?1; -^- = о1Фс1 —о2'Фс2; о2'=а2[1 4-Л2/Фо2],
dt dt
(13.6.1)
где oi, о2 понимаются в смысле (2.4.43). Если сечения и поток
нейтронов не зависят от времени, то уравнения (13.6.1) имеют
решения:
б?1 = С1° ехр (— s2); сг = —— ехр (— s2) — ехр (-LA- ,
°2'—°1 L \ °1 Ji
(13.6.2)
где 51 = щФ/ и предполагается, что с2(0)=0. Дифференцируя
c2(si) по Si, определяем максимум с2 и значение Si = s1TO, при
котором этот максимум достигается:
slm=(lna)/(a-1); а = -2~ = ;
а В1 01Ф
(13.6.3)
c2(Sim) = Ci° ехр [—/(а)]; /(а) = ^-^. |
Очевидно, что c2(sim) монотонно убывает с ростом а, при-
чем обратно пропорционально а при больших а. Практически
нецелесообразно накапливать максимальное количество нукли-
да с2, так как при приближении к максимуму концентрация
возрастает медленно и затрачивается много времени для незна-
чительного ее увеличения.
Активность получаемого нуклида в международной системе
единиц (СИ) измеряется в беккерелях (Бк) — число распадов
в 1 с, т. е.
А=КгС2=Сг In 2/7i/г,
где Сг — общее число ядер нуклида 2 в мишени. Часто пред-
ставляет интерес удельная активность, Бк/кг,
Л0=(Л/р),
431
г
Рис. 13.17. Удельная активность и относительная концентрация Сц1с° 60Со при
облучении в реакторах с различной плотностью потока нейтронов, в зависи-
мости от флюенса ФЛ Жесткость спектра у==0,1 (штриховая линия: у=0,2,
Ф=1014 см-2-сч)
где р — масса мишени. Используется также и внесистемная
единица активности кюри: Ки=3,7-1010 Бк.
В формулах (13.6.1), (13.6.2) не учитывались блокировка
резонансного интеграла и блокировка в тепловой группе. Эти
уточнения целесообразно рассматривать конкретно для каждо-
го нуклида *.
Рассмотрим два примера: получение 60Со из 59Со и 1921г из
1911г. На рис. 13.17 представлено отношение концентрации 60Со
к первоначальной концентрации 59Со cdcxQ в зависимости от
флюенса (т. е. от произведения плотности потока нейтронов на
время облучения) при жесткости спектра у=0,1 (штриховая
линия при у=0,2). На рис. 13.18 приведена зависимость вре-
мени, необходимого для достижения удельной активности
1013 Бк/г от плотности потока при разных значениях у (удель-
ная активность определена для массы всей мишени; химически
очищая ее от никеля, образующегося при распаде 60Со; можно
несколько увеличить удельную активность).
Из рис. 13.18 видно, что для достижения больших активно-
стей (больше 1013 Бк/г) необходимы значительные плотности
потока нейтронов и промежутки времени.
При плотности кобальта 8,9 г/см имеем Sa=3,38 см-1. По-
этому если мишень имеет размеры порядка 1 мм, то блокиров-
* Подробнее об образовании нуклидов в реакторе см., например,
[227, 247].
432
Рис. 13.18. Зависимость времени,
необходимого для достижения
удельной активности 60Со
1013 Бк/г=270 Ки/г от плотности
потока нейтронов при различных
значениях жесткости спектра у
ка тепловых нейтронов незна-
чительна (см. ниже пример с
иридием). Основной резонанс-
ный уровень 59Со находится
при энергии 132 эВ и имеет
сечение поглощения в макси-
муме около 9006. Для этого
уровня ГП^>Г7 и поэтому тео-
рия, изложенная в гл. 8, непри-
менима. Однако качественные
соображения показывают, что
блокировка при средней хорде’
мишени, примерно равной или
больше 0,1 см, должна быть
сильной. Формально блоки-
ровку можно учесть изменени-
ем жесткости спектра. Из
рис. 13.18 видно, что измене-
ние жесткости от 0,1 до 0 (что
эквивалентно бесконечно силь-
ной блокировке) при потоке
больше 6-1013 см~2-с-1 не очень
сильно влияет на результат.
Переходим теперь к иридию
(рис. 13.19). Если не учитывать
блокировку в тепловой группе,
то можно не учитывать 1931г.
На рис. 13.20 приведены отношение c2/ci° и удельная актив-
ность (масса мишени с учетом 1931г и продуктов распада) в за-
висимости от флюенса при у=0 и у=0,1. Заштрихованная об-
ласть — полоса ошибок из-за неточности сечений. Видно, что
ошибки сечений сильно влияют на результат только при актив-
ностях, близких к максимуму. На рис. 13.21 приведена зави-
симость времени, необходимого для достижения активности
1,5-1014 Бк/г, от плотности потока.
Рассмотрим подробнее блокировку резонансного интеграла.
Таблица 13.4. Первые резонансные уровни 19Чг [32]
Ег, эВ 2grn, мэВ гт, мэВ Г, мэВ V б /оо б
0,6528 (50) 0,547 (6) 72,2(5) 72,6 (5) 15120 2384(48)
5,36(1) 6,0(1) 82(2) 87(2) 15980 413(7)
6,13(1) 6,37(5) 83(11) ЭЦП) 13720 324(3)
Сумма 3120(50)
28—6053
433
Рис. 13.19. Схема нуклидных превращений при облучении иридия
Рис. 13.20. Зависимость удельной активности и относительной концентрации
192Ir c2/ci° при облучении в реакторе с различной плотностью потока тепло-
вых нейтронов от флюенса Ф/ [сплошные линии — у=0,1, штриховые у=0.
заштрихованная область — полоса ошибок в исходных данных (главным
образом сечение |921г). Кривая Б — с учетом блокировки (см. текст)]
В табл. 13.4 приведены параметры первых трех резонансных
уровней 1911г. При вычислении резонансного интеграла беско-
нечного разведения /«, надо использовать формулу (2.3.38), где
f(z) дано (2.3.95). При этом поскольку Ег для первого уровня
только незначительно превышает Ес, то f(z)<0. Считая, что
остальные (£г>6,1 эВ) уровни не блокируются, получаем ве-
434
личину неблокируемого резо-
нансного интеграла 7Нб=
= 380((110). При плотности
иридия 22 г/см3 и средней хор-
де 0,1 см имеем (надо учесть,
что содержание изотопа 1911г
составляет 37,3%) а=
=—ISa(Er) =39. По формуле
(8.1.37) имеем £1=0,175, /бл =
= 546, полный резонансный ин-
теграл /нб-Нбл = 926, т. е. 25%
от 7оо=3500.
Блокировка в тепловой
группе определяется значением
макроскопического сечения по-
глощения при энергии Ен —
= 0,0253 эВ, которое для ме-
таллического иридия равно
Sa(EH)=30 см-1. Поскольку
1911г, сгорая, заменяется 1921г,
который также имеет большое
сечение, а ,931г выгорает мало,
можно считать в первом при-
ближении, что Sa не зависит
Рис. 13.21. Зависимость времени, не-
обходимого для достижения актив-
ности 1921г 1,5-1013 Бк/г=400 Ки/г
от плотности потока тепловых ней-
тронов при разной жесткости спект-
ра (без учета блокировки)
от времени.
Дальнейшее рассмотрение проведем для сферических мише-
ней малого радиуса p<^Ss-1, где Ss — макроскопическое сечение
рассеяния замедлителя, окружающего мишень. Для определе-
ния среднего значения потока в тепловой группе Ф используем
граничное условие для малой черной сферы [248]:
о 16 J
Если мишень не черная, то можно воспользоваться формулой
(6.1.17), положив там £=G = IS,P, и использовать для Р раз-
ложение (1.10.18). Тогда
4 Г 5 - 8 -
7S. «1; /%> 1, (13,6,6)
т. е. поправки на конечность мишени и ее не полную черноту
частично компенсируют друг друга. .
Если мишень с граничным условием у помещена в/СЛвбо-
поглощающую среду без источников, то плотность потоки ней-
тронов вне мишени равна
Ф(Г) = сГт+_^_ек
г
Ф (?) = £?! Ф00 = с(у + р21), (13.6.6)
28*
435
где Фоо — плотность потока нейтронов вдали от мишени. Пол-
ное число нейтронов, поглощенных мишенью в единицу време-
ни, равно
У2Гф= - S - <?-ф-р-
а 32s др ’
где V — объем; S — поверхность мишени. Если 2а не зависит
от координат, то
5 дФ(р) 1 1 з -
(13.6.7)
Теперь учтем, что мишень не содержит легких ядер и по-
этому каждая компонента максвелловского распределения по-
глощается мишенью независимо. Тогда (здесь не учитывается
резонансное поглощение)
.- Ъ ______________
= (E)c1<t>(E)dE, (13.6.8)
dt J
о
где Ci — среднее число ядер нуклида 1 в мишени. Считая, что
выгорание не очень сильное, приближенно заменяем <?!©(£) =
= С1Ф(Е). Используя (13.6.7), получаем (p2s<Cy):
Ес
f Ф (Е) dE, (13.6.9)
dt V J 2(E) ’
о
где Ф (Е) — плотность потока нейтронов с энергией Е в реак-
торе. Если 2(E) и оДЕ) подчиняются закону l/v, то
df;
17
С1°1 (Ен) ф
/'2 (Ен) °’
(13.6.10)
где Фо — плотность потока нейтронов тепловой группы. Таким
образом, блокировка тепловых нейтронов учитывается множи-
телем [Z'2(EH)]_1. Такой множитель надо вводить в сечения
нуклидов 1 и 2. Для иридия этот множитель равен ^0,033/-1
[если пренебрегать малыми поправками в (13.6.5)].
При сильных выгораниях (вблизи максимума с2) надо учи-
тывать, во-первых, что 2 зависит от времени и, во-вторых, что
выгорание 1911г происходит неравномерно по мишени (см. ниже
выгорание Gd). Для приближенной оценки достаточно приве-
денных формул. Для примера на рис. 13.20 приведена зависи-
мость c2/ci° для мишени с 7=0,1 см; у=0,1; Ф=5-1013 см~2-с-1
(кривая Б). По приведенным выше формулам оЭф(191) =315,
436
/эф((191)=930; оЭф(192) =470; /(192) =3200 (1921г имеет силь-
ные резонансные уровни, но, поскольку его концентрация много
меньше, чем 1911г, блокировку резонансного интеграла можно
не учитывать). Видно, что учет блокировок уменьшил актива-
цию более чем в 2 раза.
Если в мишени имеется только один нуклид, обладающий
большим сечением (Si=S), то
= ^ = 6?!°--Ъ-t, (13.6.11)
dt I I
причем Ф<Ж <С 1, поскольку выгорание считалось малым. Роль
макроскопического сечения здесь играет I-1. Такой закон спра-
ведлив для мишени, «обгорающей» с поверхности. Пусть за
время At сгорает слой толщиной Аг, содержащий 4№ДгС1° ядер
нуклида 1. Тогда (число сгоревших ядер приравниваем к числу
ударов нейтронов о поверхность мишени);
dr/dt=—Фо/4С1°.
Откуда получаем закон изменения радиуса поглощающей ча-
сти мишени:
г-р-^Е (13.6.12)
При этом средняя концентрация нуклида 1 в мишени радиусом
р равна
что совпадает с (13.6.11) при малых выгораниях. Предположим,
что нуклид 2 имеет малое сечение поглощения, так что сгорев-
шая часть мишени делается прозрачной. В момент Z(r) = (p—
—г)4с1°/Фо все ядра нуклида 1 на радиусе г превращаются
в ядра нуклида 2, который затем распадается. Поэтому концен-
трация нуклида 2 описывается формулами
с2(Г1/) =0, /</(г); с2(г^) =
= Ci° ехр [—jA<2(Z'—Z(r))], t>t(r). (13.6.13)
Нарисованная выше картина обгорающего поглотителя фа
ктически осуществляется только при очень малых у, когда по-
глощением нейтронов при Е>ЕС можно полностью пренебречь.
Фактически всегда такое поглощение существует и приводит
к объемному выгоранию.
Наибольшим сечением поглощения в тепловой группе (кроме
135Хе) обладает 157Gd. На рис. 13.22 и 13.23 приведены распре-
деления концентраций 155Gd и 157Gd по радиусу стержня, содер-
жащего гадолиний, для разных моментов времени [249] (рас-
437
Рис. 13.22. Распределение концентра-
ции 155Gd по радиусу стержня при
различных выгораниях 235U (s5=
=о5Ф^=1—с5/с5°)
Рис. 13.23. Распределение концентра-
ции 157Gd по радиусу стержня при
различных выгораниях 235U
чет проводился по программе TRIFOB [228]). Моменты време-
ни определялись выгоранием 235U: Х5=озФ(=1—Cs/fs0- Началь-
ные концентрации: 155Gd—0,369-1020 см~3, 157Gd—0,384-1020 см-3.
Поглотитель из смеси гадолиния и алюминия помещался внутри
трубчатого твэла из обогащенного урана. Жесткость спектра
нейтронов около 0,25. Из рисунков видно, что выгорание по
Рис. 13.24. Схема превращений нуклидов при выгорании европия (штриховыми
438
объему достаточно интенсивно
и о преобладании поверхност-
ного выгорания можно гово-
рить лишь в начальные момен-
ты времени.
Наиболее распространен-
ные материалы для регулято-
ров и поглотителей — бор и
кадмий. Их выгорание вычис-
ляется просто, поскольку вто-
ричные нуклиды не имеют
больших сечений.
Большим сечением погло-
щения обладает также евро-
пий. В этом случае образуется
большое количество вторичных
стабильных и радиоактивных
нуклидов, многие из которых
имеют большие сечения (рис.
Рис. 13.25. Зависимость суммарного
макроскопического сечения поглоще-
ния при выгорании европия (по отно-
шению к начальному сечению) от
флюенса при различных жесткостях
спектра нейтронов
13.24).
На рис. 13.25 представлена
зависимость макроскопического
сечения поглощения, отнесен-
ного к начальному, от флюенса
при плотности потока 5-Ю13
см 2-С’4 при различных жест-
костях спектра нейтронов. Расчет выполнен без учета блокиро-
вок и поэтому может служить только для первой ориентировки.
Хотя в цепочке превращений имеются распадные звенья, расчет
при других потоках (в 2 раза больше и в 2 раза меньше) привел
к очень близким результатам.
Из рис. 13.25 видно, что макроскопическое сечение резко па-
дает при флюенсах порядка 3-1020 см~2, а затем остается почти
постоянным на уровне 15—25% первоначального. После 1 года
эксплуатации при плотности потока 5-Ю13 см-2-с-1 и жесткости
у=0,2 нуклидный состав поглотителя следующий, %: 153Еи — 36,
линиями даны нуклиды, играющие малую роль)
439
Рис. 13.26. Схема превращения нуклидов при выгорании гафния
!54Eu_i7i 155EU — 3, 156Eu —2, 152Sm — 1, 132Gd-~ 2, 153Gd —9,
156Gd — 27, 158Gd — 2. 15IEu и 152Eu выгорают полностью.
В качестве конструкционного материала в реакторах широко
используется цирконий. В цирконии всегда имеются, хотя и
очень незначительные, примеси гафния, который является хими-
ческим аналогом циркония. Поскольку изотопы гафния имеют
довольно большие сечения и резонансные интегралы, то по мере
Рис. 13.27. Зависимость макроскопи-
ческого сечения гафния при выгора-
нии (по отношению к начальному се-
чению) от времени (плотность пото-
ка нейтронов 5-1013 см-2-с-1)
работы реактора гафний выго-
рает. На рис. 13.26 приведена
схема нуклидных превраще-
ний. Цифры внутри прямо-
угольников означают массовое
число и распространенность
данного изотопа (или период
полураспада).
Не учитывается 174Hf, со-
держание которого составляет
0,17%. Расчет проводился при
постоянной плотности потока
5-Ю13 нейтр/(см2-с) и при по-
стоянной жесткости (0,05<
<у<0,5). Результаты пред-
ставлены на рис. 13.27, где по
оси ординат отложено отноше-
ние полного макроскопическо-
го сечения поглощения всей
цепочкой нуклидов (см. рис.
13.26) к начальному значению
этого сечения. Поскольку в
рассматриваемой цепочке роль
распадов мала, результат за-
висит главным образом от
флюенса. Поэтому приближен-
но данные при других значени-
440
ях плотности потока можно получить, соответственно изменив
масштаб по оси абсцисс.
При плотности потока 5-Ю13 нейтр/(см2-с) сечение умень-
шается в 2 раза примерно за 1,5 года в мягком спектре (у=
=0,05) и за 0,5 года в жестком (у=0,5). Дальнейшее уменьше-
ние происходит значительно медленнее.
Глава 14
КИНЕТИКА РЕАКТОРА
14.1. КИНЕТИКА НА МГНОВЕННЫХ НЕЙТРОНАХ
Выше рассматривались изменения параметров реактора во
времени, связанные с изменением состава топлива. Эти процес-
сы протекают медленно: наиболее быстрый, связанный с накоп-
лением !35Хе, имеет характерное время порядка 10 ч. Теперь
рассмотрим значительно более быстрые процессы, характеризую-
щиеся минутами и секундами. В этом случае надо учитывать
запаздывающие нейтроны. Начнем, однако, со случая, когда
можно не учитывать запаздывающих нейтронов. Как показано
в § 14.2, это случай еще более быстрых процессов, которые воз-
никают, если отклонение эффективного коэффициента размно-
жения от единицы больше, чем доля запаздывающих нейтронов
Р (1.3.1).
Запишем уравнение замедления в возрастном приближении
и уравнение диффузии (см. гл. 2, 3):
* г_____2 / dti 1 dti
Ьп — L 2(Е)П= ------- 4-----------;
' d-. vD dt
ДтДФ-2атФ = -/г(г, гс, t)+ —
vT ot
(14.1.1)
Будем искать решение уравнений (14.1.1) в виде
п(г, т, t)=n(r, т) ехр (ЛО; Ф(г, 0=Ф(г) ехр (Л0. (14.1.2)
Очевидно, что функции п и Ф удовлетворяют уравнениям
A»-[L-(£) + W]«=^-; (14ЛЗ)
ДТДФ - (SaT + Z/uT) Ф = - п (г, гс).
В первом уравнении (14.1.3) сделаем замену переменных
[см. (3.3.12)]:
п(г, т)=п'(г, т) ехр [—w'(т)], (14.1.4)
441
где
Е°
W (г) = W (г) + Я f = W (г) + -Л_ f = w (т) + 2Я/(ВД,
Е
(14.1.5)
ау(т) определено (3.3.12) и предполагается, что gSs и D не за-
висят от энергии. Начальное условие по т для функции п
n(r, 0)=n'(r, 0)=vSfO(r) (14.1.6)
при этом не изменится (для простоты пренебрегается размно-
жением нейтронов при замедлении). Таким образом,
л I дп'
Д/г =-------;
дх
РТДФ — (2„т + Я/г?т) Ф = —п (г, хс) ф ехр (- 2Z/?Ssoc),
(14.1.7)
где vc — скорость, соответствующая энергии Ес — верхней гра-
нице тепловой группы; ср — вероятность для нейтронов при за-
медлении достичь тепловой группы, не поглотившись. Пусть при
/.=0 имеем
О vSpf ехр( —а%)
Йэф — SaT 1 + a2i2 1 ’
(14.1.8)
1. е. при 7,=0 уравнение (14.1.7) не имеет решения или, други-
ми словами, реактор не находится в критическом состоянии.
Очевидно, что уравнение (14.1.7) имеет решение, если
ехр [~ “ a%](1 + ) 1 =1 = й°ф + ЧФ,
(14.1.9)
где L'— [32/Л(2а-|-Х/Пт)]_1/2, т. е. заменяется на Sa-J-A-M-
Пусть X достаточно мало; тогда, разлагая (14.1.9) в ряд по
получаем
5йзф _ _ A/(^SaT) 21, \ __ / tx \ 0
/г° ~ ~ 1 \ Ч-«2/.2
эф
где tT — время жизни теплового нейтрона (2.1.26); tB—время за
медления (2.2.19). Таким образом, при а2£2-<1, 6йэф<^1 имеем
При этом б^эф показывает, насколько надо изменить &°ф ре-
актора, чтобы он оказался в критическом состоянии. Если >
>1, то бйЭф<0 и Х>0, т. е. плотность потока нейтронов возрас-
442
тает. Если й°ф <1, то 6йЭф>0, Х<0, и плотность потока умень-
шается. Если у<<1 [см. (2.2.20), (2.2.21)], то можно пренебречь
t3 по сравнению с /т:
8&эф
(14.1.12)
Формулы (14.1.8), (14.1.9) и следующий из них результат
(14.1.11) справедливы для однородного реактора без отража-
теля. Если реактор неоднороден, в том числе с отражателем, то
для определения связи между 6/гЭф и А, можно использовать тео-
рию возмущения. Для простоты пренебрежем временем замед-
ления. Тогда надо определить величину 6&эф, которая соответ-
ствует замене в тепловой группе на Еа+62Я, причем 6Sa=
—А/
Применяя формулу (5.2.14) при 6Sfj=6Z)(=6Si2=6Sai=0,
получаем
( (1/ит)Ф(цФо2
8^эФ = — Я ------------------------
J Ф(И (v^fi4’oi+ v2f2O02)dl/
Пренебрегая делением в первой группе и считая, что в активной
зоне vSf=const, находим
(14.1.13)
j (1/ут)Ф+Ф02ДТ
8^.ь =------------------------------, (14.1.14)
J Ф+ Ф02ДР
причем Vj — объем активной зоны, где S/2¥=0; V2 — объем от-
ражателя.
Если, как это делалось в гл. 5, приближенно заменить Фш на
Фо2/6, £ = vSf„/Sa2, то
8^эф ~ ^эф=
{ф<ф02дт
| РТ1 ^2_________
$ф+ф02ДУ
Г1
(14.1.15)
где G — время жизни тепловых нейтронов в активной зоне; оть
vт2 — средние скорости тепловых нейтронов в активной зоне и
отражателе. Таким образом, время жизни нейтрона в отража-
теле входит в эффективное время с множителем, зависящим от
плотности потока Ф02 и сопряженнного потока Ф<и в отража-
443
теле. Если S02 велико, то Ф02 в отражателе много меньше, чем
в активной зоне. При этом /эф мало отличается от tT. Если
в отражателе мало, то Ф02 в отражателе того же порядка или
даже больше, чем в активной зоне (см. § 4.4; сопряженный
поток падает в отражателе быстрее, чем Фог)- Таким образом,
хороший отражатель увеличивает эффективное время жизни,
определяющее постоянную разгона (затухания) X.
Некоторые примеры, относящиеся к кинетике реакторов с от-
ражателем, будут рассмотрены ниже.
Выше было найдено только частное решение уравнений
(14.1.1). Теперь обратимся к общему решению. Чтобы не загро-
мождать запись, рассмотрим уравнение с одной группой ней-
тронов
£>(ДФ4-а2Ф) = — (14.1.16)
где D — эффективный коэффициент диффузии (2.1.50). Под-
ставляя в (14.1.16) частное решение (14.1.2), получаем
ДФЧ-fa2-----Мф=0. (14.1.17)
\ vD )
Общее решение уравнения (14.1.17) надо записать так. Пусть
Ф„(г)—собственные функции уравнения (14.1.17), а
ari2=a2—Xn/(aD) (14.1.18)
— соответствующие собственные значения. Тогда общее реше-
ние уравнения (14.1.16) будет
Ф(г, 0-2ЛЖ(г)ехр(М), (14.1.19)
п=0
где Ап определяются из начальных условий. Выражая с по-
мощью (14.1.18), имеем
00
Ф(Г, 0=3 Л„Ф„(г)ехр^(а2-а„2)О. (14.1.20)
п=0
Пусть ао2 — наименьшее собственное число и пусть |а2—ао2|
много меньше, чем расстояние до следующего собственного чис-
ла, т. е. (для самосопряженных уравнений все собственные чис-
ла действительны)
|а2—а02| «Cai2—а02.
Тогда из (14.1.20) и (14.1.12) следует
Ф (г, 0 = Афо (г) ехр ( — *) + 2 Апфп (г) ехр [— vD (а„2—а2)0,
тг=1
(14.1.21)
444
причем, поскольку а2<аи2, п=/0, второе слагаемое в (14.1.21)
обязательно затухает. Таким образом, независимо от значений
коэффициентов Ап, т. е. независимо от начального состояния,
через некоторое время пространственное распределение плотно-
сти потока будет описываться первой собственной функцией, со-
ответствующей минимальному собственному числу. При этом
скорость убывания второго слагаемого в (14.1.21) много больше,
чем скорость изменения первого.
Рассмотрим такой пример: цилиндрический реактор беско-
нечной высоты без отражателя. Основная собственная функция
Фо (г) = /0 (2,405/77?),
а следующая
Ф1 (r) = (cos ф+а sin ф) Ji (3,832 r/R),
Тогда (ai2—a02)/ао2= 1,54. Поэтому отношение показателей пер-
вой и второй экспонент в (14.1.21) равно
-A [»D (ax2 - a02)]-1 б/fe [М2 (a,2 - О]”1 8k [ A (k — 1)]"’.
tT [21
Таким образом, при условии
Sfc^A^-i) (14.1.22)
вторая экспонента в (14.1.21) и все следующие затухают значи-
тельно быстрее, чем первая. Пусть, например, k—1=0,1;
= 0,01; 7=4,10-4 с. Через 0,01 с после возникновения возмуще-
ния первая экспонента изменилась незначительно: ехр (±0,25)^
я«1±0,25, а вторая равна ехр [—3,75]=0,02. Если 6k еще мень-
ше, то различие будет сильнее, но при 6й<0,01 надо учитывать
запаздывающие нейтроны (см. § 14.2). Для больших реакторов
k—1 мало и для точного расчета кинетики уже нельзя ограни-
чиваться одной собственной функцией.
Полученный результат очень важен. Он показывает, что при
выполнении условия (14.1.22) плотность потока нейтронов в ре-
акторе описывается только одной собственнной функцией
Ф(г, П=ф0(г) ехр (М).
Например, при пуске реактора начальное распределение плот-
ности потока определяется внешним источником нейтронов и
может очень сильно отличаться от основной собственной функ-
ции. После введения положительной реактивности, достаточной
для того, чтобы йЭф незначительно превышало единицу, начина-
ется рост плотности потока, причем растет основная собствен-
ная функция, а другие составляющие первоначального распре-
деления плотности потока убывают.
445
Если при определении поведения реактора во времени огра-
ничиваются одной собственной функцией, то такое приближение
называют «точечным». В этом приближении несущественно, ка-
ким образом в реактор вводится реактивность: локально в ка-
ком-либо месте или равномерно по всему объему — плотность
потока будет расти (убывать) по закону, который определяется
только величиной введенной реактивности.
Отметим, наконец, что из кинетического уравнения следует
не уравнение диффузии, а телеграфное уравнение, содержащее
также вторую производную по времени (см. [69, с. 223]):
ОДФ — 2аФ-|-/г= — — + — —. (14.1.23)
о dt v2 dt2
Если Ф=Ф0 ехр М, то отношение второго слагаемого в правой
части (14.1.23) к первому равно
3D д2Ф
-4£- (14.1.24)
v dt
где TCT-I=oSfr — время между двумя последовательными столк-
новениями нейтрона. Если п = 2500 м/с, 277 =3 см, то ТСт=
=1,3-10~5 с. Для процессов, медленных по сравнению с Тст, от-
ношение (14.1.24) много меньше единицы и справедливо обыч-
ное уравнение диффузии.
Задача 1. Определить эффективное время жизни тепловых нейтронов
в ячейке гетерогенного реактора (в точечном приближении).
Решение. В стационарном случае для бесконечно большого реактора
^эф = 4<р(1 + 7о + ?1)~х,
где q0, qi определены (7.2.6), (7.2.14), (7.2.19). В нестационарном случае
уравнение для плотности потока в точечном приближении отличается от ста-
ционарного случая заменой Поэтому надо заменить
<?ГОМ—*-</гом[1-{-7./(nSae)]/[l-[-A./ (nSai)]; <71—><ц[1-|-А./(а2ае) ];
Q-*Q4-(Q-i)V(t'S«<)-
Эффективное время жизни определим с помощью равенства /Эф = бА/Х. Если
\/ (uSa) <1, <?0-С1, ?1«;1, то
^эф = t f 1 + " ? 1 >
\ 1 — С /
где t=(uSa)-1; определено (10.1.6), с и t,— (7.2.16), (7.2.6). Так как в гете-
рогенных реакторах обычно с< 1, то /Эф близко к t.
Задача 2. Определить эффективное время жизни теплового нейтрона
в реакторе с отражателем.
Решение. В качестве модели возьмем сферический реактор с беско-
нечным отражателем. Условие критичности дается формулой (4.3.7), где
Д = оо и р=1. В согласии с (14.1.9) надо заменить a2->a2-—to!(vD) и, кроме.
446
того, L2->-i-2[l-l-X/(vSa2)]~’/2- Положив а2 = а02-|ч6А/Л42=а02-|-бА2а1/£> и опре-
делив /Эф=6/гД, получим при 6k<^i, Х/(и2а)<С1:
(k — \)t2 1 . R ,
^эф = 1 Ч- . р а—1 Ч- - (1 + «о2 ^-2) > (14.1.25)
Htj. J *-'2
где ii, t2 — время жизни нейтрона в реакторе и отражателе. Таким образом,
время жизни нейтрона в отражателе умножается на k—1, т. е. на долю ней-
тронов, выходящих из активной зоны.
Задача 3. В плоский реактор высотой Н, ие ограниченный в других на-
правлениях, при t=0 мгновенно вставлен тонкий размножающий или погло-
щающий плоский блок. Его координата 2=0. Определить зависимость плот-
ности потока от времени и координаты z.
Решение. Ограничиваясь одногрупповым приближением, имеем урав-
нение для плотности потока при КО
— +«о2 Ф» = 0, (14.1.26)
\ dz2 /
а при t>0
/ d2 \ С 1 ЭФ
— + «02 Ф(г, 0 +77 Ф(0, П3(г) = —------------—, (14.1.27)
\ dz2 / Н Dv dt
где С—безразмерная постоянная. Сначала рассмотрим стационарное урав-
нение
(тт + “2') ф(г)+-7Гф(°)а(г) = °, (14.1.28)
\ dz2 / п
где а—новое значение лапласиана, которое надо определить из условия кри-
тичности при t>0. Уравнение (14.1.28) имеет решение
С
Ф(?) = A cos az— Ф(0) sin а | z | , (14.1.29)
откуда Ф(0)=А. Граничное условие Ф(///2) =0 приводит к условию критич-
ности
2a// . a// .
------ ctg ---= 1,
С Ч s 2
причем надо найти минимальное значение а Если
|a/a0—1| = |Д|<£1; ааН=л; k = k0-\-8k; 6/г<§;1,
то
л2 6k
С = —тс2 А = —— —------
2 k— 1
Решение (14.1.29), если учесть (14.1.30), можно записать так:
Ф (?) = Ф(0) (sin j sin a (_^
(14.1.30)
(14.1.31)
(14.1.32)
Теперь рассмотрим уравнение (14.1.27). Для разности Ф—Ф0=Ф имеем
[положено Фо(О) = 1]:
Ч2Ф С 1 ЭФ
+ а02 Ф[1 Ч-Ф(0> £)] 3(z) = —— ——
dz2 Н Dv ot
447
Проводя преобразование Лапласа, получаем (’Fp — функция, сопряженная по
Лапласу с Чг):
। </2Ф’ С / 1 \ /--------
_Д+а2фр+__ ^__ + Фр(0)р(г)=0; а = ]/ а02 — (14.1.33)
Решив уравнение (14.1.33) с ограниченным условием Чгр(///2)=0, найдем
sin a
(14.1.34)
Ф (Z) _ C_________________________
p 2aHp <M C a,H
cos —-— — ---------------—- sin---
2 2a// 2
Для выполнения обратного преобразования надо знать полюсы ЧСДг).
Полюс р=0 дает вклад, который полностью компенсирует Ф0(г). Таким обра-
зом, надо учесть только корни уравнения
2a// a//
— =tg—.
Это уравнение совпадает с (14.1.30). Поэтому первый корень совпадает с а.
При малых С следующие корни расположены вблизи аН=тг, и=3, 5, 7 ...,
т. е.
(14.1.35)
, , „ (и2—l)(fe—1)
Рп = — (п2~ 1 )a02 uD = —------------
‘т
Вблизи корня
имеем
a// _ __
C0ST " ^sinT = (/’_/’n)/7(Pn):
F (Pn)
C a,H
2aH““' 2
д Г a,H C aH 1
—— cos ——------------ sin —
dp L 2 2a// 2 ]/> = Pn
и поэтому
exp (Pnt)
-------(14.1.36)
sin an
2CD
7/2
S . «»// L С
п=1,з,5... Pnsm—[1- —
Если —pnt— (я2—1)(й—1)///-гЗ> 1, то в (14.1.36) остается одно слагаемое:
- / И \
sin a •— - | г | ехр(рД)
Ф(г, t) = В--------------------------------
a H
sin-----
2
где a — минимальный корень (14.1.30) и
2С — ГС
В =------(“о2 — a2)-1 11 — -£ —
//2 f [ а2//2
Если |С|«1, то, принимая во внимание (14.1.31), получаем В=1. Таким
образом, статическое распределение плотности потока (14.1.32) растет (если
С>0) или убывает (если С<0), не изменяя своей формы. Этот результат
соответствует точечному приближению. В данном случае критерий примени-
мости имеет вид |Рз/| >1; |Рз| 3>Pi или ^2>/т/[8(/г—1)]; 6&<g8(6—1). Более
полное исследование имеется в [250].
448
Ф(г, t)
p1 = (14.1.37)
C
1 — —
4
14.2. КИНЕТИКА С УЧЕТОМ ЗАПАЗДЫВАЮЩИХ НЕЙТРОНОВ*
В одногрупповом приближении уравнения для ф и концен-
траций Ci нейтронных излучателей (число групп запаздываю-
щих нейтронов произвольно; в приложениях обычно использу-
ются шесть групп; см. § 1.3) запишем так:
ДДФ + (vp2z - SJ Ф + V liCi = -L ; (14.2.1)
i
= (14.2.2)
где vp — среднее число мгновенных нейтронов при делении; (3»—
доля запаздывающих нейтронов i-й группы. В стационарном со-
стоянии имеем
В * v
= (14.2.3)
и vp заменяется в (14.2.1) на vt‘.
Vp-^ = vp(l+₽); Р = (Н.2.4)
Если ограничиться точечным приближением, то пространст-
венная зависимость плотности потока описывается основной соб-
ственной функцией. Поэтому положим в (14.2.1) Дф=—а2Ф и
запишем
tT = (ka - 1 - а2М2) Ф + Sa- У С
dt ьл
I
^- = ^02аФ-^с^
(14.2.5)
где k0 = yq-p — коэффициент размножения на мгновеннных нейт-
ронах. Для стационарного случая имеем й=й0(1+₽) = 1-^-а2Л12.
Пусть
&=l+a2M2+6A!,
причем 8k не зависит от времени. В этом случае решение урав-
нений (14.2.5) проще всего получить с помощью преобразования
Лапласа. Обозначая сопряженную по Лапласу той же буквой,
но с чертой сверху, получаем
tr [рФ - Ф (0)] = (k0 - k + 3 k) Ф + 2a-' 2 ci,
i
PCi—Ci (0) =Р^0Ф Sa — 2,tCi,
(14.2.6)
* Уже в первых работах по теории ядерных реакторов была отмечена
большая роль запаздывающих нейтронов для кинетики реактора [251].
29—6053 449
где Ф(0), С;(0) —начальные значения плотности потока и кон-
центраций. Исключив Ci из равенств (14.2.6), получим
*тф (0) + 2 Л,сг(О)/ (р + М
Ф =---------------------------------(14.2.7)
fTp— 6k -t-koP^^i/ (р+ )
i
Обратное преобразование дает
Ф(0 = ^Лехр(р/), (14.2.8)
где
/тФ(0)+Sa-i 2 Mf(0)/(P/+^i)
Aj~---------------------------------(14.2.9)
zT-}- ka 2 РА» / (pj 4" ^-i)2
i
и pj — корни уравнения
— 8fe — (14.2.10)
P
i
Если при Z<0 реактор находился в стационарном состоянии,
а затем реактивность скачком изменилась на величину 8k, то
(6k<^k)
Ci(0)= ^k,> Ф(0)
и тогда [Ф(0)=1]
Г 0/ I-1 Г d I'1
Л = 6^[8^ —М (l + Xy/P/Js] = 8^[8^ 5(1/Ру) fto)] ’
(14.2.11)
причем
2Л=1- (14.2.12)
/
Отметим, что всюду 8k понимается как 8koo, а не 6&Эф- В про-
стейшем случае 6&Эф — 6&оо/(1-|-а2Л12).
При анализе этого результата весьма полезно сделать гра-
фическое построение для определения корней pj. На рис. 14.1,
450
Рис. 14.1. График для на-
хождения корней уравне-
ния (14.2.10) (корни Тр,
Хо, Xi, Х2, Хз; величины Л/
пронумерованы в обратном
порядке по сравнению с
табл. 1.6)
14.2 приведены зависимости y=f(x), х—1/р и y—x6k—tT. Кри-
вая у=/(.г) имеет асимптоту при х->±оо:
(14.2.13)
I
и разрывы с бесконечным скачком при х=—Л.,--1 (на рис. 14.1
приведены три первые группы запаздывающих нейтронов, на
рис. 14.2 — три остальные группы). Если 6й>0, то прямая у=
=x6k—tr пересекает кривую y=f(x) в одной точке при х>0 и
в шести точках при х<0. Положительный корень описывает уве-
личение плотности потока нейтронов в реакторе, который был
критичен при ^<0 и получил мгновенное приращение реактив-
ности 6k при t=0. Отрицательные корни x=Xj описывают пере-
ходный процесс. Производная f (х) при х=0 равна
f(0) = SfW, (14.2.14)
t
а тангенс угла наклона прямой y=x6k—равен 6k. Если 6k<^
<§С|3, положительный корень Тр много больше, чем |х/|. Пусть
Рис. 14.2. График для на-
хождения корней уравне-
ния (14.2.10) (корни Тр,
х4, хз; величины X/ прону-
мерованы в обратном по-
рядке по сравнению с
табл. 1.6)
. 29*
451
Таблица 14.1. Значения постоянной в формуле обратных часов
Нуклид 2”U 235Ц 238ри 24ipU 2S2Th 2 38(J
«г 8 II W [з° о । со о 1 50 87 32 61 230 128
8k столь мало, что
(14.2.15)
Тогда из (14.2.10) следует
= = (14.2.16)
Формула (14.2.16) называется формулой «обратных часов»:
8k обратно пропорционально времени разгона реактора. В табл.
14.1 приведены значения ух для различных нуклидов.
Отметим, что постоянная ух для 239Рц значительно меньше,
чем для 235U: период разгона для реактора с 239Ри при задан-
ном 8k значительно меньше, чем для реактора с 235U. В табл.
14.2 приведены зависимости 8k от Тр по точной формуле
(14.2.10) при ZT=10~3 с, йо=1, а также значения, полученные по
(14.2.16) (для 235U). При Тр>5 мин, 6&<2,6-10*~4 погрешность
формулы (14.2.16) менее 10%.
Для тяжеловодного реактора надо учесть еще фотонейтро-
ны, возникающие при расщеплении дейтона у-квантами оскол-
ков деления (см. § 1.3):
\k—8k-\-P (8k)v, (14.2.17)
где 8k и (8k)v приведены в табл. 14.2, а Р — вероятность того,
что у-квант не будет поглощен в твэле или других конструкци-
ях. Из данных табл. 14.2 видно, что добавление (8k) v сущест-
венно изменяет период разгона, особенно при больших Тр.
Если 8k возрастает и становится больше 0, то положитель-
ный корень Тр уменьшается и неравенство (14.2.15) заменяется
противоположным. Тогда из (14.2.10) следует
= = (14.2.18)
тр и 6k — ₽
что при б&>0 совпадает с (14.1.12). Таким образом, условие
характеризует границу применимости формул без учета
запаздывающих нейтронов.
Графическое построение (см. рис. 14.1 и 14.2) облегчает ана-
лиз переходного процесса. Из формул (14.2.11) и рис. 14.1, 14.2
452
Таблица 14.2. Зависимость периода разгона реактора
от внесенной реактивности (для 235U)
ТР ik 8й по (14.2.16) (8fe)7
0,25 с 1,03-10-2 9,64-10~4
0,5 с 7,90-10-з — 9,27-10~4
1 с 6,35-Ю-з — 8,63-10“4
2 с 5,14-10-з — 7,68-10-4
3 с 4,50.10-3 — 7,01-Ю-4
5 с 3,73-10-з — 6,12-10-4
10 с 2,79-Ю-з — 4,96-10—4
20 с 1,96-Ю-з — 3,97-10_4
40 с 1,29-10-з — 3,14-10—4
60 с 9,83-10-4 1,46-Ю-з 2,62-10—4
80 с 7,97-10~4 1,09-Ю-з 2,43-10_4
100 с 6,71 -10—4 8,74 • 10—4 2,14-10—4
200 с 3,78-10—4 4,37-10—4 1,66-ю—4
300 с 2,64-10“4 2,91-Ю-4 1,39-10_4
400 с 2,03-10-4 2,18-10~4 1,22.10“4
500 с 1,65-10-4 1,75-10~4 1,10-10—4
10 мин 1,39-10—4 1,46 - Ю—4 1,01 -io—4
20 мнн 7,15-10-3 7,28-Ю-з 7,27-Ю-з
30 мин 4,81-10-8 4,85-10-з 5,97- IO-6
1 ч 2,44-10-з 2,43-10-» 4,18-Ю-з
5 ч 4,90-10-» 4,85-10-» 1,60-Ю-з
20 ч 1,23-Ю-з 1,21-10-» 5,92-10-»
50 ч 4,91-Ю-7 4,85-10“7 4,88- IO-6
100 ч 2,46-10—7 2,43-10—’ 1,87-10-6
следует, что коэффициент Д/ в (14.2.8), соответствующий поло-
жительному корню Тр (обозначим его Ар), положителен, а все
остальные коэффициенты Д/ отрицательны. Поэтому
Ф (0 = Ар ехр (tJTp) —F (/), (14.2.19)
где F(t)—сумма экспонент с отрицательными показателями,
причем /?(0)=1—Др [принято Ф(0) = 1]. Если то Тр»
>|х/|, и тогда рост Ф(/) сначала происходит за счет убывания
F(t), а затем, когда Е(/)<^1, начинается рост первой экспонен-
ты в (14.2.19). Величину Ар можно определить из формулы
(14.2.11):
Ар = 8k Гзб - 2 ₽,-/(1 + Vp)<-1 , (14.2.20)
L i J
или если Tptkt^A и справедлива формула (14.2.16), то
Лр = [1-8£(S Pi/V) / (Ж/<)2] 1- (14.2.21)
453
Из табл. 1.5, 1.6 следует (для 235U):
T-^Pz/Zz=12,7 с; £ W = 3,19 с2 (14.2.22)
i I
и поэтому
Д =71-2,9 —V . (14.2.23)
\ ₽ /
Например, при 6й=10~4 имеем Ар= 1,04 при 6/г=5-10~4 Ар=
=1,27. При бй=10_3 приближенная формула (14.2.23) дает
Др=1,73, а точная (14.2.20)—Др=1,42. Таким образом, при
6/г<10_4 увеличение плотности потока происходит практически
по экспоненте с периодом разгона Тр (который составляет бо-
лее 10 мин). При 10-4 плотность потока возрастает на де-
сятки процентов за время порядка времени жизни запазды-
вающих нейтронов, а затем растет экспоненциально с пе-
риодом разгона Тр. Среднее время жизни запаздывающих
нейтронов равно 12,7 с (14.2.22). Из рис. 14.1 и 14.2 видно, что
I | > 1/Aj.
Для тяжеловодных реакторов условие ТрХ/^>1 для всех
групп фотонейтронов обычно не выполняется (см- табл. 1.7).
Приближенно фотонейтроны можно разделить на две группы:
для первой ТРХ/3>1, а для второй ТРХ/С1. Тогда первую группу
можно присоединить к запаздывающим нейтронам деления, а
второй группой пренебречь. Например, учитывая три группы
наиболее короткоживущих фотонейтронов, получаем для них
2 (Рг/М = 29 • 10-3 с, 2 (IW) = 3,75 с2,
i i
и если /’=0,5 [см. (14.2.7)], то для суммы всех запаздывающих
нейтронов имеем
2(W) / 2(fW = 3,8/P; (3 = 7,77.10-3,
i j i
т. e. Ap—1 возрастает по сравнению с (14.2.23) на 15%.
Рассмотрим теперь остановку реактора, когда при t—Q мгно-
венно вводится отрицателная реактивность. Если 6й<0, то по-
ложительный корень Тр исчезает, но появляется один дополни-
тельный отрицательный корень, когда прямая y=x6k—tT пере-
секает асимптотическую ветвь кривой у—f(x) при х->—оо (на
рис. 14.2 эта ветвь не нанесена). Все формулы при этом сохра-
няются. Минимальный по модулю корень (обозначим его х0—
——То) определим из (14.2.10) при Т0%г-С1:
То — t-ri( I 6k I -фр) .
454
Если, например, |<Уг|^р и tT—4-10-4 с, то То—0,03 с, что в не-
сколько раз меньше, чем минимальное значение 1/Л/. Поэтому
соответствующий коэффициент Ло равен
Л0=|б£|/(|&Ч+₽). (14.2.24)
Можно записать
Ф(0 = Лоехр[-^-)+Е(0, (14.2.25)
где F (t) —сумма экспонент с отрицательными показателями,
причем Е(0) = 1—Ло=р/(р+|бй|). Рассмотрим случай больших
18k |, когда |бй| 3>р. При этом прямая y=x8k—/т проходит
очень круто и пересекает кривую y=f(x) вблизи разрывов Xi=
=—Кг1 (кроме первого корня То). Пэтому положим
^=-(4-+е^; (14.2.26)
Уравнение (14.2.10) запишем так:
(V + I 8* I - *т = S 1-М^ + е,.)-
i
и разложим в ряд по е/. Сохранив только главный член, полу-
е/=р//(%/|^|). (14.2.27)
Подставив (14.2.26), (14.2.27) в общую формулу для Л/, име-
ем приближенно
Л7=р//|бй|. (14.2.28)
Таким образом, при 18k 1Р плотность потока нейтронов
описывается универсальной функцией <р(^) [первое слагаемое
в (14.2.25) можно не учитывать, поскольку оно мало при
Ф^ = ТЖ ф(0; ^) = S~T (Н.2.29)
Если учитывать фотонейтроны, возникающие в тяжелой воде,
то вместо (14.2.29) получим
®(0=тжф('>+'’тят^№ (14-2-30)
Тт(() = 5 (у')техр(_4"ф
/
В табл. 14.3 приведены значения функций <р(0 и <pv(0-
Можно, конечно, и более точно определить изменение плотно-
сти потока нейтронов при введении отрицательной реактивности
непосредственно из уравнений (14.2.8) — (14.2.11). Однако надо
455
Таблица 14.3. Значения функций <р (Z) и <Рт(О
t, с ч> (О Ф-f (О t, с ч> (t) ч>т (0 t, с <Р (О фт (О
1 0,74 0,84 20 0,16 0,29 75 0,034 0,18
2 0,61 0,71 30 0,11 0,26 100 0,020 0,15
5 0,41 0,50 40 0,085 0,23 150 0,0075 0,12
10 0,25 0,36 50 0,064 0,22 200 0,0034 0,10
иметь в виду, что мгновенное введение реактивности (т. е. за
время много меньше, чем 1/Z/) практически никогда не реали-
зуется. Поэтому надо либо использовать грубые оценки (см.
табл. 14.3), либо численно решать уравнения (14.2.5) при за-
данной зависимости 8k от времени.
Часто возникает необходимость заменить шесть групп запаз-
дывающих нейтронов более простой аппроксимацией, уменьшив
число групп, а в предельном случае — одной группой с пара-
метрами р и X. Чтобы сохранить правильный переход к быстрой
кинетике (т. е. к кинетике без учета запаздывающих нейтронов)
и правильное значение периода разгона, надо удовлетворить ра-
венствам
T=vse-
I i
В этом случае уравнение (14.2.10) имеет явное решение
dk
[1 ±
+--(РЛ+м>.] <14-2-31)
или при /т7<С₽ получим правильное значение положи-
тельного корня [см. (14.2.16)]
Xi=Tp=$l (7.8k),
а отрицательный корень
х2=-Т0=-^/р (14.2.32)
приводит к слишком быстро протекающему переходному про-
цессу: G^IO-3 с, 3^=7-10 3, |х2| = 0,13 с-С (1/%)=12,7 с. Поэто-
му для правильного описания не только разгона, но и переход-
ного процесса необходимо использовать по крайней мере две
группы запаздывающих нейтронов. При этом должны выпол-
456
няться условия (для 235П и если не учитываются фотонейтроны)
₽1+₽г=₽-6.85-10~3;
1 / Р1 , Рг \ _ / 1 \ _ 10 7
’ 1 } (14.2.33)
-5-(т7+тт)=Ю?> = 466Л I
Р \ V ?'2 / J
Условия (14.2.33) дают
гг1 = 12,7+17,5= 12,7 — 17,5]ИШ. (14.2.34)
Например, если Pi=0,26p, р2=0,74р, то 1/%=42.2 с, 1/%2=
= 2,35 с, т. е. более интенсивная группа имеет меньшее время
жизни (что качественно согласуется с шестигрупповым описа-
нием).
Плотность потока нейтронов в этом приближении равна
(бй>0):
Ф(/)=Лрехр (£/Тр)+Лоехр (—^/70)+Л1 ехр (—t/Ti), (14.2.35)
где Тр определяется (при б/г<р) формулой (14.2.16);
То—1т/$
(это соотношение при 6&<СР справедливо при любом числе
групп) и
Коэффициенты А{ описываются формулами (при бй<ср и без
учета фотонейтронов)
+ =1+2,9 —; Ло = — —; + = —1,9 — ,
р ' ’ р ’ 0 р р
т. е. |Л1| больше, чем |Л0|, и, следовательно, в переходном
процессе большую роль играет экспонента с временем жизни
порядка Лг1, а не с временем Т0=МР (при бй<^р коэффициен-
ты Аг не зависят от выбора рг).
Все численные данные, кроме приведенных в табл. 14.1, от-
носятся к реактору с 235U. Если реактор содержит несколько
делящихся нуклидов, то среднее значение р равно
Р = 2>Мь
I
где Пг — доля делений i-ro нуклида. Для примера (13.2.30) по-
лучим р=5,5-10-3, что на 20% меньше, чем для 235U. Отметим,
что р для 239Рц в 3 раза меньше, а для 238U в 2,5 раза меньше,
чем для 235U. Поэтому для реактора с глубоким выгоранием,
457
когда накапливается много плутония, и тем более для реактора,
работающего в замкнутом цикле, совершенно необходимо учи-
тывать зависимость р от состава топлива.
Отметим, что только «мгновенное энерговыделение» (кине-
тическая энергия осколков, мгновенное у-излучение) пропорцио-
нально потоку нейтронов в данный момент времени. К мгновен-
ному энерговыделению надо еще присоединить кинетическую
энергию нейтронов. Если характерное время много больше F,
то к мгновенному энерговыделению можно добавить энергию,
выделяющуюся при захвате нейтрона Wn (1.7.5). Остальная
часть энергии ^72 (см. табл. 1.11), составляющая пример-
но 9% полной энергии, изменяется со временем не пропорцио-
нально потоку нейтронов.
Пусть с — концентрация какого-либо осколка:
-^- = гм(0-яс,
dt
где WM(t) —величина, пропорциональная потоку нейтронов или
мгновенному энерговыделению. Имеем, очевидно,
t
c(t) = $ WM (f) exp [- A (t — t')] dt’. (14.2.36)
о
Энерговыделение осколков равно ^3 = 2(7/'|чсг(0- Из (14.2.36)
i
получим
t
^(0 = [wjt')^F(t-t’)di',
о
где F определяется (1.7.9) и протабулировано в приложении
VIII. Если где Т — время стационарной работы реакто-
ра, то
t + T
W3(t) = Wu°[F(t)-F(t-[-T)]~\- J WM(t')-^-F (t-{-Т — f) dt’.
т
(14.2.37)
Если 1Ем=0 при t>T, то получим формулу (1.7.8).
Таким образом, если численно решить уравнения (14.2.5) при
заданной зависимости &о(О> то> определив WM(t), при t>T по-
лучим по формуле (14.2.37) запаздывающую часть энерговы-
деления. Если к моменту времени t мгновенное энерговыделение
значительно уменьшилось, то вклад W3 (1.7.8) становится опре-
деляющим.
458
14.3. КИНЕТИКА РЕАКТОРА С ОТРАЖАТЕЛЕМ
Уравнение (14.2.5), послужившее основой для всех результа-
тов, полученных в § 14.2, справедливо для реактора без отра-
жателя. Кинетика реактора с отражателем много сложнее. Рас-
смотрим простейший случай сферического реактора с бесконеч-
ным отражателем в одногрупповом приближении. Пусть при t<zO
реактор находился в стационарном состоянии. Плотность пото-
ка нейтронов при /<0 удовлетворяет уравнениям (D1 = D2=D):
[DA + (^-l)Sfll]®o(r)-O, г<Я;
(DA —2аг)Фо(г) = О, r>R.
Эти уравнения имеют решения
(14.3.1)
Ф0(г) = -5^- г<Я; a02 = (^-l)/M2;
г sin а0Я
фо (г) = — ехр ( — , r>R.
Г ' /
(14.3.2)
Условие критичности [см. (4.3.7) при р=0, Д=оо] будет
UoL2 ctg cto/?—f—1—0. (14.3.3)
При t=0 мгновенно вносится возмущение bk=k—kx==
=й0(1+р)—При t>0 справедливы уравнения
V = рД + (^0-1)2а1]Ф + VVa;
V ot
i
^ = ₽А201Ф-^ь r<R- (14.3.4)
at
- _^. = (ОД-2о2)Ф, r>R. (14.3.5)
v at
После преобразования Лапласа (преобразованные функции
обозначаются теми же буквами, но с чертой сверху) получим
G№(r)-®i(r, О)] = [М2Д + йо-1]Ф1+2а71 2КС1,
t
r<R
P?i (г) - Ci (г, 0) = рД2а1 Ф> — Аг Ct,
(14.3.6)
/2[рФ2(г)—Ф2(г, 0)] = (Л22Д— 1)Ф2(г); r>R, (14.3.7)
459
где tx, t2 — времена жизни нейтронов в реакторе и отражателе.
Исключив Ci и С{(г, 0) (при bk^k), получим вместо (14.3.6):
[ЛРД + k. - 1 + D (р)] Фг (г) = - к + k. V -М Фо (г); Г < R,
\ Р А~ч. I
(14.3.8)
где Фо (г) =Ф1(г, 0) и
D(p) = M- + +
(14.3.9)
Подставив (14.3.2) в (14.3.8), (14.3.7) и решив уравнения, най-
дем
гф (г) = A sin ar — Sk ~ D<<p^ sin a°r
1 sin aR D(P) sina0R
(14.3.10)
где
tf=a02+D(p)/M2
(14.3.11)
и
гФ2(г) = Вехр Г— А
L ^2
r—R
+ + —ехр (14.3.12)
Граничные условия позволяют определить А и В. В резуль-
тате
ГФ!(Г) =
afe Г/Р(р) _ j
pD(p) fife
sin aor
sin a0R
1 -|- /#2 — 1___sin ar )
at2 ctg aR /1 + pt2 sin aR
(14.3.13)
/Ф2 (r) = — exp
P
r—R \
Sfe______i -Ь a£-2 Ctg a-R ex _ (r — R) ]/1 + pt2
pD(p) aL2ctgaR-}-|/'l + pt2 L2
(14.3.14)
При обратном преобразовании Лапласа полюс р=0 не дает
вклада, поскольку соответствующий вычет в силу (14.3.9) обра
щается в нуль. Поскольку при Z)(p)=O имеем a2=ao2 и
aoT-2 ctg ao-R=—1, то и нули £)(р) не являются полюсами. Таким
образом, в качестве полюсов надо учесть только нули выраже-
ния
aL2ctga/? + ]/T+^2 =0. (14.3.15)
Будем рассматривать только минимальный корень уравнения
(14.3.15), что соответствует точечной кинетике. Сначала будем
460
предполагать, что Rep>—l/tz- Разложив в ряд по 6а/ао=
— (а—ао)/ао<^ 1 и учитывая, что согласно (14.3.11)
8а __ Р(р)
“о ~ 2(fej—1) ’
получаем
aL2ctga/?=-l--^-a; а=1 + ^_(1+а^), (14.3.16)
т. е. р является корнем уравнения
D (р) _ 2(^1) _ 1) = о
или «-ркф-н.Я-М-о, L Р 4- j i (14.3.17)
где / -- / _1_2 |/1 + ^2-1 а р ’ (14.3.18)
причем при р/2<С1: ^=^+(^—1)^, (14.3.19) что совпадает с (14.2.25). В результате обратного преобразова- ния
Ф1 (г, 0 = Фо(г) 2>Ae<p(PjO> / (14.3.20)
где pj — корни уравнения (14.3.17), а А/ при ptz<^i\ совпадают
с (14.2.21). Если учесть следующий член разложения по pts, то
к А, (14.2.21) прибавится добавка бА/, равная (А/=А;°-|-бА/):
' 4(6-1)1 ' £ (₽/ + >.,) J
i
X (14-А ^—\~2\8k — kopfY--------------—Г , (14.3.21)
\ t2 k-ij L 01 и {Pj+m2J
i
fa__ 1
или если | pj | 3>2г и , то
8Aj = -^-—. (14.3.22)
1 4(fe—1)
Аналогично в отражателе
Фг (г, 0 = 7" А- ехр [р/ — -Г , (14.3.23)
461
т. е. в отражателе зависимость плотности потока от координат
совпадает со стационарным случаем только при p/^^l. Если
разложить в ряд по pjt2, то при получим
ф2 О'» О = 7 2 (Л° + М') ехр (к t ;
8А' = - Г1 - 2(r~^ 1. (14.3.24)
4(£—1) L L2 J
При обратном преобразовании надо учесть особенность при
р=—1/^2- В комплексной плоскости р проведем разрез вдоль
действительной оси от —оо до —\Ц2. Интегрирование по этому
разрезу внесет в (14.3.20) дополнительное слагаемое бФь рав-
ное
8Фх(г, f)=-L- f (Ф1_-Ф1+)еХр(рО^р, (14.3.25)
2л 1 J
— 00
где Ф1+ — значения (14.3.13) при замене l-}-pt2-+
—► ± —1—pt2. Будем по-прежнему считать, что ба<Сао и ис-
пользовать формулу (14.3.16). Кроме того, будем считать, что
a8k<^k—1. Делая в (14.3.25) замену —1—pt2=z, имеем
8Ф1(г, О = -777^-77 фо О') ехр (-70 Л (О, (14.3.26)
где
°
Аналогично для отражателя имеем
8фг (К 0 = - ехр (- 70 Л (г, 0, (14.3.27)
где
Ц (г, t) = — I --------------Гх cos f —— х —
v ’ л .) (1-t-x2)2 L \ L J
о
— sin 7"Л j j exp (— tx2/t2) dx.
Интегралы Д, I2 выражаются через функции erf. Ограничимся
только асимптотикой. При t<g.tz имеем
/1 = 1/2; Z2--M1 -^=^]ехр
2 bg \ Z/g /
462
а при />/2:
/=/=_□_ (^7 )3/2 .
2 |Z«
При t<^t2 добавки 6Ф1 и 6Ф2 уничтожают 6Л/ (14.3,22) и
6А' (14.3.24). Таким образом, в отражателе при t<^t2 простран-
ственное распределение плотности потока сохраняется таким жв|
как и при t<0. Нарушение этого условия с физической точки
зрения недопустимо. По мере роста t возникают отклонения от
распределения Ф0(г), причм добавка к Ф2(г, t) отличается от
экспоненты как по пространству, так и по времени.
Уравнения с двумя группами значительно сложнее, чем с од-
ной. Поэтому столь же полное исследование кинетики реактора
с отражателем было бы слишком громоздким. Ограничимся
только определением значений параметра р при заданном б/г
для простейшего случая, когда можно явно написать условие
критичности [см. формулу (4.4.21) и сформулированные в § 4.4
условия, при которых она справедлива].
Запишем основные уравнения
t3 = од-1) П1 +
i
dt
(14.3.28)
где — время жизни теплового нейтрона; t3 — время замедле-
ния. Будем искать решения уравнений (14.3.28), пропорциональ-
ные ехр (pt). Исключая ci, получаем
[А-(1+р^1)/Л12]Ф1=-и1/£)1; (14.3.29)
[Д - (1 + fW п = - A*-\k + 8/г - kjp V -М ф1( (14.3.30)
•С L
где k — коэффициент размножения в стационарном состоянии;
б/г— возмущение. Применим оператор Л—(1+р/3)/т к уравне-
нию (14.3.29), используем (14.3.30) и получим, так же как в
§ 4.4:
(A+ai2) (А—а22)Ф1=0, (14.3.31)
где
а1.2 = + -^~(Д14+ Ъф) +
/k -f- fife — feop 2j Pi/(P +
4-(L]4+«2+----------------n-------------(lUm)-’-
4 LpZ
(14.3.32)
463
и
^ = L?/(l+pM; тэф = г/(1 +Л). (14.3.33)
По-прежнему справедливы формулы (4.4.8) — (4.4.11) с за-
меной (14.3.33). Справедливо также равенство
(14.3.34)
Для отражателя справедливы прежние уравнения, только
с заменой:
L22-AU-L22/(1+pQ; (14.3.35)
где t2 — время жизни теплового нейтрона в отражателе (время
замедления в активной зоне и в отражателе одинаково). Усло-
вие критичности (4.4.21) запишется так [для вывода этой фор-
мулы кроме условий, сформулированных в § 4.4, требуется вы-
полнение (14.3.34)]:
tg “i# = — tg [arctg ах/,2эф -|- arctg ax — arctg (ax/a2)]. (14.3.36)
Решение уравнения (14.3.36), сооответствующее минималь-
ному собственному числу, будет
aiR = it — [arctg ахЛ2эф-|- arctg ах]Лэф — arctg (ах/а2)], (14.3.37)
где под arctg понимается главная ветвь. Пусть 8аХ;2 = аХ12—
где а°_2 соответствует стационарному состоянию. Тогда (ниже
вместо а® будем писать ах 2):
8аXR = - (14.3.38)
1 -WL22 l-W* l+(“i/“2)2’
причем, если ph, ptz, pts,<^A,
8 («Аэф) = L^ai —5- «18 (®i/«a) = — -
2 a2
8 (ai V m) = V* 8ai — — ai V* pts.
Таким образом, из (14.3.38) следует
5al2 . д Sa22 ~ P I Z2L2 , tg|A )
ax2 “Г Л a22 R' \ l-f-ax2£22 ф 1 J
(14.3.39)
(14.3.40)
где
A = ”2 1 • /?' — /? _l __£l_ j-____”2
V+a22 R' ’ 14-ax2t-22 l+ax2T~ a^ + a,2’
(14.3.41)
464
Разложив а2 2 (14.3.32) по малым параметрам р\, р/г, pts, bkt
р, получим
2 8k—+
а2 2 ах2Л42
Подставляя этот результат в (14.3.40), находим
для определения р:
bk — kop 2 рг7 (р -|- ^г) — Р (^эф + ^зэф) = 0>
i
где
G (1 + аЛС) + “i2M2-------;
Эф ~Г 1 /~Г 1 £„(1 + aj2L22) ’
'зэф = ta (1 +a?A12C) + ^2^^^
(14.3.42)
уравнение
(14.3.43)
(14.3.44)
(14.3.45)
1 wj £>g 1 •‘f- CAj U
(1 (14.3.46)
a2 \ 1 Л42 /
В уравнении (14.3.43) так же, как и в уравнениях § 14.2, 8k
означает изменение kx, а не k3$. Используем связь между kx и
/г:1ф (4.6.22):
£эФ=М1+а12Ь12)-1(1^т)~1-
Тогда вместо (14.3.43) имеем
^эф ^ОэфР Pi/(P4“^i) —Р (^эф-J- ^Зэф) = 0, (14.3.47)
где
^=(l + a1V)*i + »i*«) ' (14-3-48)
При т=0 (14.3.44) превращается в результат одногруппо-
вого приближения (14.3.19). Обычно С<=»1 и тогда Л в формуле
(14.3.48) входит со множителем (l-f-a^Li2)-1, а 1з — с множи-
телем (l-J-di2?)-1. Последний результат не согласуется
с (14.1.10), где такой множитель отсутствует. Это объясняется
30—6053 465
неточным описанием процесса замедления в теории с двумя
группами: время замедления определяется интегралом (2.2.16),
который сосредоточен на нижнем пределе, а вытекают из ак-
тивной зоны более быстрые нейтроны, время замедления кото-
рых значительно меньше. Время жизни нейтронов в отражателе
/2, так же как и в теории с одной группой нейтронов, умножа-
ется на величину утечки сцШ2.
Рассмотрим численный пример: реактор ТВРМ [129]. Актив-
ную зону реактора аппроксимируем сферой радиусом 34 см.
Активная зона характеризуется следующими значениями пара-
метров: &=1,71; Ai2=52 см2; т=123 см2; Sai = 0,0144 см-1; t\ =
= 2,2-10-4 с; 1з=10_5 с. Отражатель D2O имеет толщину 70 см.
Аппроксимация его бесконечным отражателем должна увели-
чить эффективное время жизни. Для отражателя Z,22=4800 см2,
/2=0,02 с. Из этих данных получим: cti2=0,003587; a22=0,03095;
а12Л42=0,6277. Величина R" равна [выписаны слагаемые в том
же порядке, как и в формуле (14.3.46)]: /?"=34+3,8+
4-7,7—4,5=41; С=0,861. Таким образом, /Эф=14,6-10~4 с; 1'0ф=
= 8,5-10-4 с; /3эф=0,13-10-4 с; Г3эф=0,08-10~4 с.
Экспериментально на критической сборке, имитирующей ре-
актор, было получено /'Эф=6,5-10~4 с, что на 30% меньше, чем
вычисленное значение. Знак расхождения соответствует сделан-
ным аппроксимациям. Расчет того же примера по формулам
одногруппового приближения дает ^Эф=9,6 • 10~4 с, что не силь-
но отличается от двухгруппового результата.
В более сложных случаях, например для гетерогенного ре-
актора, необходимо использовать численные методы. При этом
оказывается, что если рассматривать решения вида
Ф(г) ехр (pt), то можно получить зависимость между р и йЭф,
решая ряд стационарных задач. Запишем диффузионное урав-
нение (3.1.5) для нестационарного случая и с учетом запазды-
вающих нейтронов (полученные ниже результаты справедливы
не только для диффузионного приближения, но и для общего
случая):
= di v D grad Ф - (Sc 4- SJ Ф +
v dt
+ [%s(EF)w(Ef, E)<S(t, r, E')dE' +
+ /(£)[ vp (E1) (Д') Ф (t, r, E') dE' + ck (t, r) (E), (14.3.49)
J к
где x(E) —спектр мгновенных нейтронов; %ДЕ) —спектр запаз-
дывающих нейтронов й-й группы (нормированный на единицу,
см. гл. 1). Уравнение для концентраций нейтронных излуча-
466
телей имеет вид
А = ₽фдВДЕ')Ф(1,г, E')dE'-Xkck. (14.3.50)
В стационарном случае имеем
2 С^Ъ. = 2 (£) Г vp (£') 2, (£') Ф (г, £') dE',
k k
т. е. два последних слагаемых в правой части (14.3.49) запи-
шутся так:
[x(^) + 2₽&xH^)]f ^(£')2Д£')Ф(г, E')dE'. (14.3.51)
Если Ф(^, г, £)=ехр (р/)Ф(г, Е), ck(t, г) = ехр (р/)с*(г), то
уравнение (14.3.49) превратится в стационарное уравнение, но
с заменой
2с(£)->2с(£)+р/п, (14.3.52)
где v — скорость нейтрона, энергия которого равна Е, и в
(14.3.51) надо заменить
X (Я) + У Рл П (Е) / (£) + V - W_ ь {Е) =
лвЛ P-th
k k
= [х (Я) + 2 р* (£)] - Р 2 М> + ^)] п (Е). (14.3.53)
k k
Особенно просто выглядит такое приближение, когда разли-
чие между %(£) и х&(£) можно учесть, вводя эффективное зна-
чение (к:
^=₽/Ы£)/хЖ (14.3.54)
где черта означает усреднение по фактическому спектру нейтро-
нов в реакторе. Тогда замена (14.3.53) сводится к
Х(£) + У ^(Е)-xW +₽) [1 (14Л55>
L 1 + Р Р + Хй J
Пусть &Эф—эффективный коэффициент размножения при р—
= 0, a k3$— то же, если выполнена замена (14.3.52). Опреде-
лим эффективное время жизни нейтрона t с помощью равенства
(йэф—йэф)/йэф = р^. (14.3.56)
Замена (14.3.55) сводится к множителю при vp. Если значение
р действительно соответствует разгону реактора с временем 1/р,
30* 467
i
то после замен (14.3.52), (14.3.55) эффективный коэффициент i
размножения должен равняться единице. Поэтому
1 r 1_____Рй
*эф i+pZjp + V
или, используя (14.3.56), получим
+ -Л-, (14.3.57)
^эф ^эф 1 "Ь Р mJ Р "Ь ~^k
k
что совпадает с (14.3.47), если ^ = ^ф + ^зэф- Таким образом, в ’
этом приближении достаточно сделать два расчета: при р=0 ]
для определения йЭф и после замены (14.3.52) для определения 1
^8ф> затем t — по (14.3.56). Истинное значение р, соответству-
ющее йЭф, получится при решении уравнения (14.3.57).
Если речь идет о расчете гетерогенного реактора, то замену
(14.3.52) надо вводить как при вычисленииЛ-матриц (см.§ 11.4), 4
так и во всех функциях Грина, с помощью которых строится
гетерогенное уравнение (см. гл. 11).
Глава 15
УСТОЙЧИВОСТЬ РЕАКТОРА
15.1. ПРОСТРАНСТВЕННЫЕ КСЕНОНОВЫЕ КОЛЕБАНИЯ
Очень большое сечение поглощения 135Хе и существование
радиоактивного предшественника приводят в известных усло-
виях к возникновению пространственных колебаний плотности
нейтронного потока в реакторе. В самом деле, пусть в некото-
ром объеме реактора по каким-либо причинам произошло уве-
личение плотности потока нейтронов по сравнению со стацио-
нарным значением. В этом объеме 135Хе начнет выгорать быст-
рее, чем образовываться при распаде иода, поскольку концен-
трация последнего еще не успела установиться в соответствии
с новым значением плотности потока нейтронов. Уменьшение
концентрации 135Хе приведет к увеличению реактивности в этом
объеме реактора, и в результате плотность потока нейтронов
возрастет еще сильнее. Таким образом, реактор потеряет устой-
чивость. Очевидно, что реактор больших размеров должен быть
менее устойчив, поскольку qx делается сравнимым с kx—1 или
даже превышает эту величину и, следовательно, малые измене-
ния qx могут приводить к заметным изменениям в распределе-
нии плотности потока по объему реактора. Характерной длиной
468
является длина миграции. Поэтому условия устойчивости долж-
ны накладывать ограничения на величину MfH, где Н — ха-
рактерный размер реактора.
Обратимся к выводу критерия устойчивости по отношению
к ксеноновым колебаниям. Уравнения (12.1.1) нелинейны — в
них содержится произведение Ф и X. Для анализа устойчиво-
сти в малом, т. е. исследования границы устойчивости, доста-
точно рассмотреть линейное приближение. Положим в (12.1.1)
/(г, t) =/0(r)+i(r, f)A«,; Х(г, /)=Ао(г) +
+x(r, t)Xx-, Ф(г, t) = Фо(r) +<p(r, 0®o> (15.1.1)
где Хсо= (У1+У2)2?/ох — значение Хо (12.1.3) при Ф->оо; ф0 —
среднее значение Ф0(г); /о. Хо, Фо — стационарные значения
концентраций и плотности потока, a i, х, <р — величины, малые
по сравнению с 1. Для простоты предположим, что имеется
только один сорт делящихся нуклидов. Для i и х получим си-
стему уравнений (постоянные распада I и Хе обозначаем Ai
и кх, сечение Хе—оД:
-37 = Ух0 схФ0 <р — У1° = У1/(у1 + уг);
at
~~х~ = "I-—(°*фо(г)Н_Мл:’ |
dt \^х + охФ0(г) } 1
(15.1.2)
Применим к уравнениям (15.1.2) преобразование Лапласа.
Обозначим
i (г, р) = z(r, i)exp(—pt) di (15.1.3)
6
и аналогично х и <pi. Если начальные условия i (г, 0)=0,
х(г, 0)=0, то из (15.1.2) получим
i(r, р) =У1°оЛ>о<р(г, p)/(p+A,i);
х (г, р) = ------^—5--------Г-------------
Р + 4- °x®o(z) l^x-b°x®o(r)
У1°—Мф(г, Р)-
Р + ^iJ
(15.1.4)
Теперь обратимся к уравнению для плотности нейтронного
потока. Поскольку неустойчивость возникает в больших реак-
торах, можно ограничиться уравнением с одной группой ней-
тронов. Далее можно ограничиться линейным приближением в
зависимости k от концентрации 135Хе:
Чг, О = йо-₽хХ; ₽х=-^.
(15.1.5)
469
Поскольку характерные времена в рассматриваемой задаче
много больше, чем времена жизни запаздывающих нейтронов
(см. § 1.3 и гл. 14), их можно не учитывать. Таким образом,
Ф удовлетворяет уравнению
(ЛГД + £0-1_р^)ф(Г, о = е(г, 0Ф(г,04Л-зр (15.1.6)
где e(r, t) описывает влияние органов регулирования на реак-
тивность. В уравнении (15.1.6) не учитывается зависимость
реактивности от мощности реактора (мощностной коэффициент
реактивности, см.§ 15.2). Для анализа явлений, связанных
только с 135Хе, учет мощностного коэффициента не обязателен.
После линеаризации уравнения (15.1.6) получим
(Л12Д + k - 1) ф (Г, t) - М X (г, t) = Еф0 (г)/Ф0 + tT
Фо dt
(15.1.7)
где
k=k0—₽хХ0. (15.1.8)
В практических расчетах следует учесть зависимость k и
е от координат. Это можно сделать только численными мето-
дами. Для анализа качественных особенностей достаточно сде-
лать простейшее предположение: &=const и е=е(£), т. е. рас-
смотреть однородный реактор, в котором регулирование изме-
няет реактивность равномерно по всему объему реактора. Ди-
намику самого процесса регулирования рассматривать не
будем. Предположим только, что регулирование происходит до-
статочно быстро и таким образом, что поддерживается постоян-
ной общая мощность реактора, т. е.
J<р(г, £)dr = 0. (15.1.9)
После преобразования Лапласа уравнения (15.1.7) полу-
чим
[M2^k-1-F(p, г)]ф(г, р) =
= е(р)Фо(г)/Фо+р/т<р(г, р)—£т<р(г, 0), (15.1.10)
где <р(г, 0) — начальное значение <р (г, t) и
F (Р, г) =-------------Г-----Ь------1. ах = йо2y/V)
p-j-^x + ffx®o(r) [Ах+а^Фо(г) Z’ + ^iJ
(15.1.11)
а величина е(р) определяется из условия (15.1.9). Так как
|р| ~‘кх~ 10-1 ч-1, то pt-^k—1. Таким образом, второе сла-
гаемое в правой части (15.1.10) можно опустить.
470
Рассмотрим простейший случай, когда плотность потока ней-
тронов зависит только от координаты z. Тогда <р, F зависят
только от z (кроме параметра р). В самом грубом приближе-
нии заменим Фо (г) в F(p, z) средним значением Фо, т. е.
F{z, p)-^F(p)
Г ^-х
Р + '-х -Г °x®0 |Л + °хФо
У1аР 1
Р+ м
(15.1.12)
Если начальное возмущение произошло в первой гармонике,
т. е. <р(г, 0)=<росоэаг, то по условию (15.1.9) органы регули-
рования сразу возвратят реактор в исходное состояние <p(z, /) =
= 0. Рассмотрим начальное возмущение в виде <р(г, 0) —
— (ро cos anz; п^2. Если п — четное, то условие (15.1.9) авто-
матически выполняется и уравнение (15.1.10), если в нем сде-
лать замену (15.1.12) удовлетворяется предположением
<p(z, р) = ап (р) cos naz; e(p) = 0; [(«2 — 1) а2 + ^-] ап =
(15.1.13)
откуда
= + (15.1.14)
После подстановки F(p) (15.1.12) в (15.1.14) в знамена-
теле ап(р) возникает полином второго порядка, корни которого
после обратного преобразования Лапласа определяют частоты
колебаний. Эти корни определяются из уравнения
p2+bp+c= (p—pi) (р—р2) =0,
где
b — 21 -|- Хх охФ0 -|-
^уН^хФ0
(ft2 — 1)Л№’
С =Я1(Ях + ахФ0) + -А^.
а*Ф|
Р2уР/2-хФ0
(ft2—1)лЛ42 ’
(15.1.15)
где а заменено на njH-, Н — высота реактора и ах подставлено
по (15.1.11).
Условие устойчивости (Rep/CO) содержится в неравенствах
с>0, &>0.
(15.1.16)
Очевидно, что с всегда положительно. Поэтому неустойчивость
может возникнуть только при нарушении неравенства Ь>0.
Таким образом, критерий устойчивости можно записать так
(впервые критерий устойчивости был получен в [252]):
— >---------------Г -уг/у} [ 1 + +_А* Г1 . (15.1.17)
Р/2 \\Х + 1ХФО 1 0л.Фо ] ' ’
471
Рис. 15.1. Границы устойчи-
вости для ксеноновых коле-
баний:
---------- 235ц с учетом--независи-
мого выхода 135Хе;-------- — без
учета независимого выхода;
——-------для »»Ри с учетом не-
зависимого выхода; X — расчет
с приближенным учетом непре-
рывного участка спектра
Если п^З и нечетно, то из условия (15.1.9) следует ах=
— —а-п/п, т. е. плотность возмущенного потока обязательно со-
держит также и первую гармонику. Из (15.1.10) следует, что
ап по-прежнему дается (15.1.14) и условие устойчивости (15.1.17)
сохраняется.
Из (15.1.17) следует, что при малых плотностях потоков,
когда г/г/У'Со’хФоДл:^!, критическое значение Л42/№ растет
как Ф02, а при больших Фо стремится к постоянной (численное
значение получено при n=2, k=l, v=2,42, yi = 0,06):
(-S-) = — V Г 2^ Г = 0,029. (15.1.18)
\ Н /со П Т (я2—1)> ’ ' '
При плотностях потоков Ф<ФЖ г/2/*/=7,4 • 1011 нейтр/(см2-с)
для 235U или Ф<1,5-1012 нейтр/(см2-с) для 239Ри правая часть
(15.1.17) становится отрицательной, т. е. реактор устойчив при
любых значениях М/Н. На рис. 15.1 показана кривая М./Н (при
п=2) как функция Ф. Области устойчивости расположены
сверху от кривых.
Если условие (15.1.17) не выполнено, то начинаются колеба-
ния с частотой порядка Мг1 и возрастающей амплитудой. По
мере роста амплитуды точность линейного приближения падает,
и, чтобы проследить дальнейшее развитие колебаний, надо обра-
титься к точным нелинейным уравнениям.
На границе области устойчивости, когда Ь = 0, имеем р2 =
= —с, т. е. происходят незатухающие колебания с частотой
со0=ус (при Ь>0 они будут затухать, а при Ь<0 — нарастать).
472
Используя (15.1.15), легко определить частоту соо:
%2 — Мх Ф 1 4
1+(1-4-*1Дх)/Ф
1 о
1 — Уг°
Ф
ф = (15.1.19)
f-x
где ф — отношение Фо к ^характерному потоку Фх (12.1.5). При
больших потоках, когда ф^> 1, получим
а>р2=А1Уф. (15.1.20)
Используя формулы (15.1.15), можно найти частоты (ком-
плексные) в общем случае.
Еслиф^>1, то условие (15.1.17) дает
[1 2 +МУ
№ \ //2 У «, [ 3-
(15.1.21)
т. е. приближение к предельному значению (М21Н2)ОО проис-
ходит по закону ~ 1 /ф.
Аналогично можно рассмотреть критерий устойчивости по
отношению к радиально-азимутальным колебаниям. Колебания
по п-й радиальной и т-й азимутальной гармоникам в реакторе
без отражателя возникают, если
М <_______________ °х Фр/(^х 4- °х Фр) у%1у (15 1 22)
Н , (an,m—£zo,l)v 1 + (^1 + М/ ’хФр
где а0,] = 2,405; ап,т — п-й корень функции Бесселя m-го по-
рядка.
Более точное исследование устойчивости можно провести,
только в той или иной степени привлекая численные методы.
Здесь мы ограничимся указанием на некоторые новые принци-
пиальные моменты. Рассмотрим колебания по оси z и положим
Ф = Ф0созаг. Уравнение (15.1.10) перепишем так:
+ l^1 + Фосоз«г)] -
~ В (/?)(« + cos аг)-11 ф(г, р) = — <Р(г^г°—, (15.1.23)
где
р-^-рКх', X—Zi/У а= (р+1)/фр;
фо=ахФо/М, В(р) =а[1+р2/(р+А)]//? (15.1.24)
и положено г/2° = 0.
Представим решение уравнения (15.1.23) в виде ряда Фурье
(это решение удовлетворяет граничным условиям):
4- оо
<P(z,p) = 2 А„(р)ехр(iaraz); Ап(р) = А_п(р); Ao = 0. (15.1.25)
П=—00
473
Подставим (15.1.25) в уравнение (15.1.23), умножим обе
части на ехр (—ia/nz) и проинтегрируем по г:
1 яд]А~м+ЯЯ7ЕF“<°>А"w“
п
Н/2
-j^B(P)^Pmn(p)An(p) = —^^- j <p(z, О)ехр(--iamz)dz,
n —Hj2
(15.1.26)
где
it/2
j iz- <15л-27)
—тс/2
Очевидно, что Fk(p) =F-k(p) и действительно при действи-
тельном р. Все функции Fk(p) выражаются линейно через F0(p)
и полиномы от р. Функция Fo(p) равна
"/2 -----
РЛР)=- (' —— = -7=1п1 + 1Л1~д2 . (15.1.28)
тс J а + cos z тс J/ 1 — а2 а
—тс/2
Функция Fo (а) аналитична всюду в комплексной плоскости
а, за исключением отрезка действительной оси —1<а<;0, на
котором подынтегральное выражение в (15.1.28) может обра-
щаться в бесконечность. Аналитически продолжая функцию
Ао(а) из области 0<а<;1 на отрицательные значения —1<а<
<0, получаем
f0(fl) = —i=[lnl-±pH«!: + iJ; —1<а<0, (15.1.29)
причем знак «—» относится к верхнему берегу разреза, а «+»
к нижнему.
Существование разреза в комплексной плоскости а, а зна-
чит, и в комплексной плоскости р означает, что имеется участок
непрерывного спектра частот в колебаниях плотности нейтрон-
ного потока *.
Уравнение (15.1.26) содержит бесконечно много ампли-
туд Ап- Однако при больших \т—п\ подынтегральная функция
в (15.1.27) содержит быстро осциллирующий множитель. Поэто-
му Fmn убывает при росте \т—п\ и можно ограничиться рас-
смотрением небольшого числа амплитуд. Не претендуя на вы-
сокую точность результата, проанализируем нулевое приближе-
* Впервые существование непрерывного спектра частот установлено в ра-
боте [253].
474
ние, когда в (15.1.26) сохраняется одна амплитуда, соответ-
ствующая начальному возмущению. Пусть
<р (z, 0) = -^-{exp(2azi) + exp(—2а.г i)]
и Лт=0 при |т|#=2. Тогда
А (р) = [— - - 4г (°) + в (р) Fo (р) Г1.
2ах L “х Р Ч~ X РФо
(15.1.30)
где (будем считать, что ф0> 1)
А(0) = 1п ]• (15-1-31)
"И Фо —1
При обратном преобразовании Лапласа получим
<р (z, t) = А2 (t) cos 2az,
где
—i
A(0 = J] Res A (ft) exp (p, о+4; j МГ(в)—A+(ft]exp(ft)d^,
i - (1+Ф0)
(15.1.32)
причем Res/12(p/) — вычеты в полюсах р;; А^ — значения
А2 (р) на верхнем и нижнем берегах разреза. Интегрирование
в (15.1.32) происходит по отрицательным значениям р, т. е.
часть функции A2(t), связанная с непрерывным спектром ча-
стот, всегда апериодически затухает.
Если невозмущенное значение плотности потока отличается
от cos az, то конкретные формулы изменяются, но сохраняется
разрез на участке действительной оси р:
—[1+тах тр (z) ] <р< — [1+min -ф (z) ]
или в исходных единицах
— (Ах+ох max O(z)) <р<—(Zx+ax min O(z)). (15.1.33)
Граница устойчивости соответствует обращению в нуль ре-
альной части р полюса А2(р) (15.1.30), т. е. (р=1со):
ах “F1® “Фо “Фо
X (1 [ReBo(ico) + iImEo(ico)] = 0. (15.1.34)
\ X-t- ico/
475
Приравнивая нулю действительную и мнимую части (15.1.34),
получаем
Ж2 / Л42 \ ( св2
я2"- ^//U-h2
1
Фо
[(м
<о2( 1 —
ш2 + Х2 )
Re Fo (ко) —
/ м4
\ co2 + X2
— 1 j ImEo(ico)
(15.1.35)
ш
>аФо _ fo(O)
X2 4- м2 св
(15.1.36)
Исключая с помощью (15.1.36) co из равенства (15.1.35), на-
ходим как функцию соо или Фо. Рассмотрим случай
фЗ>1. Из равенства (15.1.20) видно, что со2 порядка ф0. По-
этому |а| = | (1-f-ico)/-фо| 1 и /7o(ico) логаримически зависит
от со, ф0. Учитывая главные члены, получаем из (15.1.35)
М2____/ М2 \ Tj X2 (2—~X)Re F0(i <в) — m Im Fo(im) 1 j
Я2 ~(, Я2 J00L M2 — ф0 j- I • • 1
Так как Re Fo и Im Fo входят в (15.1.37) с малым парамет-
ром, то в (15.1.36) можно оставить только главный член:
ReFo(ico) =Афо/со2. (15.1.38)
Мнимая часть T’o(ico) равна (|а2|<С1):
Im Fo (ico) = — Im In..— — Im In [ /-2t'° exp (— i arctg co) =
л 1 + i(B at [ У 1 + св2
-- ---— arctg co == — 1 —; co»l. (15.1.39)
at 7ИВ
Подставляя (15.1.38) и (15.1.39) в (15.1.37), имеем
2» [1 - —Ч--2-!- (15.1.40)
№ \ Н2 / оо L Фо яФо J
Из (15.1.38) имеем
_2_1п_2^о =2К (15.1.41)
л ш (В2
Если обозначить со/фо^-^С 1, то
Фо = -^т11п(2/х)Г. (15.1.42)
2х2
Задавая х, находим ф0 и со. Полученные таким образом зна-
чения М/Н на границе устойчивости отличаются от (15.1.22)
при у21у=0 и Фо> 1014 нейтр/(см2-с) на несколько процентов
(см. рис. 15.1). Закон приближения (M/FF)2 к асимптотическо-
му значению (М/Я)2^ в (15.1.21) и (15.1.40) различен: в
476
(15.1.21) отклонение от асимптотики пропорционально 1/-фо, а в
(15.1.40)
Уравнение (15.1.26) решено здесь в грубом приближении,
поэтому не следует придавать значение расхождению в несколь-
ко процентов. Важно, что различные подходы к решению зада-
чи не привели к существенному расхождению.
В уравнении (15.1.6), как уже указывалось, не включены
температурный и мощностной коэффициенты реактивности. По-
дробное рассмотрение этих эффектов выходит за рамки настоя-
щей книги. Поэтому ограничимся кратким замечанием. Если из-
менение реактивности связано с изменением потока нейтронов
(мощности) таким образом:
8k = dw (Ф--Фо) /Фо,
то в уравнение (15.1.10) надо внести замену
F(p, r)-+F(p, г)—aw (15.1.43)
и условие устойчивости (15.1.17) следует переписать так:
(/Z2 - 1) - ^ > М - yjy] [ 1 + Г
v \^х + sx®o / L ахФо I
(15.1.44)
Если aw положительно, то очевидно, что устойчивость ухуд-
шается.
Фактически температура и реактивность не мгновенно сле-
дуют за изменением потока нейтронов. В простейшем случае
надо вместо (15.1.43) ввести более сложную замену
F(p, r)-^(Ar)--V-^—, (15.1.45)
4^ 1 + ^iP
i
где сумма описывает вклады в коэффициент размножения от
изменения потока нейтронов в различных частях объема реак-
тора (топливо, теплоноситель, замедлитель и др.), а т/ — па-
раметры размерности времени, определяющие запаздывание в
изменении реактивности. Поскольку замена (15.1.45) содержит
р, то условия устойчивости необходимо определить заново.
Обычно тг<С1/Ах, и тогда (15.1.45) сводится к (15.1.44). Одна-
ко существуют и достаточно медленные процессы, например на-
гревание графита в реакторе РБМК. [254], когда параметры
нельзя считать равными нулю.
15.2. ТЕМПЕРАТУРНЫЙ КОЭФФИЦИЕНТ РЕАКТИВНОСТИ
Для устойчивой работы реактора большое значение имеет
знак температурного коэффициента реактивности. При положи-
тельном знаке температурного коэффициента реактивности экс-
477
плуатация реактора сильно затрудняется и к органам регули-
рования предъявляются специальные более жесткие требования.
Температурным коэффициентом реактивности будем назы-
вать величину
1 д&эф
= “м" ~дГ ’
(15.2.1)
где Т — температура реактора (в дальнейшем будем считать,
что /гЭф=1). Для практики большее значение имеет мощност-
ной коэффициент реактивности
06147 =
(15.2.2)
однако для выяснения связи aw с а* надо анализировать усло-
вия теплосъема в реакторе, что выходит за рамки настоящей
книги. Величина а* (15.2.1) имеет несколько условный смысл,
поскольку температура в разных частях реактора различна и
ее изменение при переходных процессах в разных областях ре-
актора происходит по разным законам. Можно различать тем-
пературные коэффициенты реактивности при изменении темпе-
ратуры топлива, теплоносителя и замедлителя.
Вычисление температурных коэффициентов реактивности яв-
ляется сложной задачей, поскольку, как правило, они обуслов-
лены несколькими причинами и имеют составляющие разных
знаков. Ввиду компенсации между различными составляющими
требования к точности расчета повышаются. Поэтому ограни-
чимся перечислением различных факторов, оказывающих влия-
ние на зависимость эффективного коэффициента размножения
от температуры, и оценкой их по порядку величины.
Начнем с рассмотрения влияния температуры топлива на
реактивность. Это влияние почти целиком обусловлено эффек-
том Доплера при резонансном поглощении 238U. Соответствую-
щее изменение коэффициента размножения получим из полу-
эмпирической формулы (8.6.2):
— - _ §ф =--------^^==ф8Г, (15.2.3)
где I — полный эффективный резонансный интеграл; /бЛ —
его блокируемая часть; 7’0=293 К; Т — абсолютная темпера-
тура топлива; а — коэффициент из формулы (8.6.2). Подставив
в (15.2.3) а=0,125, /бл//=0,6, Т=500 К, ф = 0,12, получим
— - — 10-3 Д-1. (15.2.4)
дТ
Внутри твэла может возникать значительный градиент тем-
ператур, особенно для твэлов из оксида урана. Тем не менее
удовлетворительная точность получится, если в (15.2.3) под-
478
ставлять среднее значение температуры по объему твэла [165,
166]. Незначительная добавка к (15.2.3) может возникать из-за
резонансного поглощения другими нуклидами, например 240Ри.
Если в составе твэла имеются легкие ядра (водород, углерод,
кислород или даже более тяжелые — магний и алюминий), то
при нагревании твэла возрастает эффективная температура ней-
тронов тепловой группы, что приводит к дополнительному сла-
гаемому в температурной зависимости реактивности при изме-
нении температуры топлива. Для расчета этого эффекта надо
решить термализационную задачу (см. § 7.5).
При изменении температуры замедлителя (и теплоносите-
ля) возникает изменение реактивности как непосредственно
из-за изменения температуры (изменение эффективной темпе-
ратуры нейтронов тепловой группы), так и из-за изменения
плотности теплоносителя и замедлителя, если последний
жидкий. Если замедлитель твердый, то, во-первых, его темпе-
ратурный коэффициент расширения значительно меньше, чем
жидкого, и, во-вторых, твердый замедлитель выполняется в
виде отдельных блоков и при тепловом расширении уменьша-
ются зазоры между блоками, так что общее количество ядер
в активной зоне не изменяется.
Самый простой эффект реактивности из-за изменения плот-
ности замедлителя и теплоносителя состоит в изменении по-
глощения нейтронов в тепловой группе:
6k
k
^*7зам ___ _ ^*7заМ
1 + 2^ ~
?зам др
V р
(15.2.5)
- - аЬТ,
Р
где «/зам отнесено к сечению деления (см. гл. 7) и бр/р — от-
носительное изменение плотности. Если
(15.2.6)
то
_ Дзам аЬТ. (15.2.7)
Пусть, например, q3!M=2,5-10-2, ц»10-3 (а является функ-
цией температуры); тогда
(15.2.8)
— - КГ5 к-1,
дТ
т. е. порядок температурного коэффициента такой же, как за
счет эффекта Доплера, но знак его другой.
Следующий эффект — влияние плотности замедлителя на
утечку нейтронов. Если твэл вносит малый вклад в замедляю-
479
щую способность, то т изменяется пропорционально квадрату
изменения плотности замедлителя, a L2 — пропорционально
первой степени. Поэтому
/ 2х L2 \ 6р Г / L2 х-1
XT = “м U+~ ~ I1 + (‘ +—,) И-
(15.2.9)
Для небольших реакторов, когда утечка большая, k—1 >0,1,
этот эффект значителен:
-^^_>10~4К-1 (15.2.10)
(при а»10-3). Поэтому исследовательские реакторы, имеющие
большую утечку, обладают отрицательным температурным ко-
эффициентом.
Для больших реакторов, когда k—1^0,014-0,02, имеем
(£2^>т или А2Ст):
— (1-^4)-10-3К“’, (15.2.11)
т. е. это слагаемое температурного эффекта того же масштаба,
что (15.2.4) и (15.2.8).
Плотность замедлителя (и теплоносителя) влияет также на
величину резонансного поглощения. Если записать коэффициент
размножения большого реактора (а2 = 0) в виде (4.6.5), т. е.
&=т]0 ехр (—wa)+&yf,
то получим
= (wa — wf)—; wa, ayf<l. (15.2.12)
k P
При этом предполагается, что
»(&) _ SP
p
Если в (15.2.12) учитывается только резонансное поглощение
238U, то Wf = 0; пусть при этом йУо=ф=0,1. Тогда при а=10~3
имеем
~ — Ю-’К"1. (15.2.13)
Если все сечения подчиняются закону 1/и, то из условия
&Эф=1 (при а2 = 0) получим wa—wf, т. е. в этом случае изме-
нение реактивности равно нулю. Отношение Wf/wa=vlf/la для
основных делящихся нуклидов приведено в табл. 15.1.
480
Таблица 15.1. Значения vlflla Для делящихся нуклидов
Нуклид
233 (J 2,10
235U 1,59
239 рц 1,72
241рц 2,28
Из табл. 15.1 следует, что для всех делящихся нуклидов
Wf>wa и поэтому учет делящихся нуклидов в (15.2.12) несколь-
ко уменьшает (по модулю) значение (15.2.13).
Если ТВС имеет вид кластера или многокольцевого твэла,
то теплоноситель находится внутри блока. При уменьшении
плотности теплоносителя из-за нагревания резонансный инте-
грал такого сложного блока уменьшается (см. § 8.4). Поэтому
возникает дополнительное (положительное) слагаемое в тем-
пературном коэффициенте реактивности. В грубой модели, когда
справедлива формула (8.4.27), имеем
________а! ^ai_________ai др (15 2 14)
/ ~ 2(1 +«х) ~ 2(1+^) р ’ k ’ 7
где ai = 7Ssi; 7 — средняя хорда блока; Ssi — среднее макро-
скопическое сечение рассеяния теплоносителя. Положим ф — 0,1,
коэффициент а в (15.2.6) равен 10~3; 7=8 см; Ss = 0,5 см-1
(Н2О при плотности 0,7 занимает половину объема):
= + 0,4-1 О-ЧТ1. (15.2.15)
Другую оценку эффекта получим, если используем экспе-
риментальные данные, приведенные в табл. 8.12. Для боль-
шого кластера (27 прутков) имеем 67//=0,26бр/р и при тех же
условиях, что (15.2.15), находим
— = 0,25-1СГ4К-1.
дТ
Если замедляющая способность ячейки наполовину обуслов-
лена теплоносителем (теплоноситель — простая вода, замедли-
тель — графит), то вместо (15.2.13) получим
— = — 0,5- 10-4К~'.
дТ ’
Добавляя еще положительный коэффициент (15.2.7), видим,
что происходит существенная компенсация слагаемых разного
знака. Величину и даже знак температурного коэффициента
31—6053 481
по теплоносителю в этом случае можно получить только в ре-
зультате весьма детального расчета с использованием числен-
ных методов.
Наконец, обратимся к влиянию температуры нейтронов на
реактивность (см. § 2.4, 7.5). Связь между температурой ней-
тронов в блоке и температурой замедлителя (и теплоносителя)
можно получить только численно, решая уравнения, описываю-
щие термализацию нейтронов (см. § 7.5, где указано, что оцен-
ки по формулам, полученным для гомогенной среды в § 2.4,
могут приводить к заметным погрешностям). Поэтому получен-
ные ниже оценки нельзя непосредственно использовать, но тем
не менее они полезны, так как дают известную ориентировку
о порядке величины эффекта.
Если зависимость сечения делящихся нуклидов от темпера-
туры характеризовать множителем g (2.4.8) и записать k так
[см. (4.6.5) при а2 = 0]:
^ = ^т(1 — + = (15.2.16)
то, дифференцируя множители g по температуре, получаем
[при k= 1, йт= (1—Wf) I (1—йУа)]:
= (15.2.17
i i
где
(^) О' ' Wf) gfi д-р (^igai) 1______Wa др (15.2.18)
и T],=vz2/>7S«^ вычислено для температуры Т. Если wf,
то &(Т) становится универсальной функцией температуры, ко-
торая не зависит от типа реактора:
k (Л = -W- - te)” (15.2.19)
Температурный коэффициент определяется средним значе-
нием по делящимся нуклидам, которое вычислено с весом по
(15.2.17). Для основных делящихся нуклидов значения функции
£(Т) приведены в табл. 15.2 Из таблицы видно, что для реак-
тора с 235U рассматриваемая составляющая температурного эф-
фекта отрицательна и невелика по модулю. При накоплении изо-
топов плутония, когда число нейтронов, возникающих при де-
лении плутония, составляет примерно 10% числа нейтронов, воз-
никающих при делении урана, эта составляющая температур-
ного эффекта изменяет знак и становится положительной. При
значительном накоплении плутония она сравнивается (по мо-
48 2
Таблица 15.2. Функция ^(7), 10-4 К-1
Т, °C 23 5U 239Ри 24LPl1 Т. °C 23 5Ц 2 39ри 24ipu
20 —1,2 1 ,8 2,6 600 —0,35 5,2 3,0
100 — 1,1 3,0 3,9 700 -0,3 4,1 2,2
200 —0,9 6,4 5,0 800 —0,3 3,2 1,5
300 -0,6 6,0 4,5 900 -0,3 2,5 1,2
400 —0,45 6,0 4,2 1000 —0,3 2,1 1,2
500 —0,35 5,7 3,5
дулю) с другими составляющими или даже превосходит их.
Таким образом, большой реактор, для которого эффект утечки
мал, при значительном накоплении изотопов плутония может
приобрести положительный температурный эффект реактивно-
сти. Реактор с положительным коэффициентом реактивности
не должен допускаться к эксплуатации.
Некоторый дополнительный вклад в (15.2.17) вносят продук-
ты деления (главным образом135Хе, 149Sm, 151Sm):
где
ле _ ' „—1 „* ^aj .
л ' v(. gai УУ ST ’
(15.2.20)
— эффективный выход /-го продукта деления при делении t-ro
нуклида; ga)- относится к сечению поглощения /-го продукта
деления (см. § 12.1, 12.2). Главный вклад в сумму (15.2.20)
вносит 135Хе. По порядку величины Д| для 135Хе равно 10 5 К-1,
причем Ас, изменяет знак при 7==500 :—600 К (при Г<500 К;
Л£<0).
Приведенные здесь данные по составляющим температурного
коэффициента реактивности носят ориентировочный характер.
Для каждого реактора температурный коэффициент реактивно-
сти должен быть определен численно, причем ввиду компенса-
ции между различными составляющими вычисления должны
быть проведены с максимальной тщательностью.
Задача. Рассмотреть плоский реактор без отражателя, материальный па-
раметр которого линейно зависит от температуры, а разность температур на
участке (0, г) пропорциональна интегралу от плотности потока нейтронов от
0 до z,
31* 483
Решение. Применим теорию возмущений, изложенную в § 5.3. В одно-
групповом приближении плотность потока нейтронов удовлетворяет урав-
нению
Ф"(х)4-[£-У(х)]Ф(х)=0, (15.2.21)
где
х
V(x) = —j" Ф(х)<1х
6
рассматриваем как возмущение. Выберем единицу длины так, чтобы высота
реактора равнялась л. Тогда плотность невозмущенного потока равна
®o=cosx, (15.2.22)
а собственное число £'о=1. В первом приближении теории возмущений со-
гласно формулам (5.3.8), (5.3.13), (5.3.14) имеем
£i = 0; j/i= (Vo/6) cos х
и плотность потока нейтронов
Ф, (х) =4i cos х ехр[—(Vo/6) sin х], (15.2.23)
где Д— нормировочный множитель; если сохранять такую же нормировку, как
в (15.2.22), то Д=~
6
. Имеем, очевидно, V|
= Уо, т. е. Уо=1 соответствует случаю, когда разность материальных парамет-
ров внизу и вверху реактора равна геометрическому параметру однородного
реактора.
Легко определить максимум (15.2.23). Дифференцируя по х, получаем
приближенно
sin хт = — У0/6;<Ф/ (хт) = Д £ 1 + ~'
т. е. при 17=1 искажение невозмущенного потока невелико.
Поправка второго порядка состоит из двух слагаемых. Во-первых, надо
вычислить второе приближение, сохранив Ф=Ф0 в V(x), во-вторых, под-
ставить (15.2.23) в V(x) и вычислить квадратичный член no Vo. Затем
по отношению к этому члену построить первое приближение. Опуская вы-
числения, приведем результат во втором приближении
£2=—Уо732 (15.2.24)
и
Г[/ ] / у \ 2 1
— —j7~sinx—~Тб~ ~6 / s'n2% | (15.2-25)
Из (15.2.24) следует, что если Vo порядка 1, то при вычислении соб-
ственного числа можно пренебречь возмущением, т. е. проводить вычисления
для средней температуры. Совершаемая прн этом погрешность в коэффи-
циенте размножения составляет примерно 3 % величины утечки.
Если разложить (15.2.25) до квадратичных членов по Vo, то
Ф2 =-- 4„cosx/Г1 — —~sinx+—f—— Y»sin2x ——( — j sin2xl,
U 6 2)67. j 16 \ 6 / J
откуда видно, что почти 90 % квадратичных членов содержится уже в пер-
вом приближении, что свидетельствует о его высокой точности.
484
Аналогичную задачу можно решить и для случая, когда реактор при
Уо=О имеет выравненную зону. При этом оказывается, что возмущенный по-
ток тем сильнее отличается от невозмущениого, чем шире выравненная зона.
Уравнение (15.2.21) может быть решено и без применения теории воз-
мущения. Обозначим (начало координат перенесено на основание реактора)
г
Ф(х)(1х = 3
о
г/Ф d(I> 1
и введем з в качестве независимой переменной, так что ---------= Ф--------= — X
dz ds 2
t/Ф2
X ------. Тогда вместо (15.2.21) получим
ds
d2 /_ФЦ Уоз
ds2 \ 2 / 2
(15.2.26)
Решение уравнения (15.2.26), очевидно, имеет вид
Ф2 = 2[ V»s3/12—£з2/24-сз4-с'].
Из условия Ф(0)=з(0)=0 находим с'=0, а из условия s(n)=2, Ф(п)=0
определяем с. В результате
Ф2 = ^— Г = — s(2—з) (— — 2—sV (15.2.27)
\ dz / 6 \ Pq /
откуда
С ds \/ 1/0 z
J ,---------------------------~ Г 6
° 1/ 2(2 —s) - 2 — s)
Г \ Vo /
или, заменяя з = 2sin2<р,
arcsin Ks/2 ________
J (l-ft2sin2¥)_|/2d<p = -|- j/fi — Jkz, (15.2.28)
о
где
(3£ \ -1
— -1 . (15.2.29)
l'o /
Интеграл (15.2.28) является эллиптическим интегралом первого рода, его
верхний предел называется амплитудой, а синус амплитуды — эллиптическим
синусом от правой части (15.2.28):
3 = 2sn2(uz; ft); и = (1/2) |/Е —V0/3z, (15.2.30)
где k — модуль, определенный (15.2.29). Подставляя (15.2.30) и используя
соотношения между эллиптическими функциями (см., например, [93])
1—sn2 х=сп2 х; 1—ft2 sn2 x=dn2 х; sn x-cn x-dn х=—(1—k2 sn4 x) sn 2x,
получаем
®(z)=2u[l—k2 sn4 (uz; ft)]sn(2«z; k). (15.2.31)
Условие критичности Ф(л)=0 дает Г93]
nu=K{k2), (15.2.32)
32—6053 485
где К — полный эллиптический интеграл Первого рода. Из (15.2.32), (15.2,30),
(15.2.29) имеем
ЙК(Й2)= " 1/
А г □
откуда, задавая k2, можно определить Vo, а затем Е. Если снова перенести
начало координат в центр реактора, то (15.2.20) запишется так:
Ф"(х) + (Ео—Д)Ф (х) — Ф (х) J Ф (x)rfx = О,
ления показывают, что при Vo~l величина Д очень близка к •—E2=Vo2/32,
т. е. подтверждается результат теории возмущений. Сравнение точного ре-
зультата с первым приближением теории возмущений показывает, что при
Vo=l ошибка первого приближения меньше 0,5 %, прн V0 = 3 она возрастает
примерно в 3 раза.
В более сложных случаях высотное распределение плотности потока
Фо (z) определяется численно при постоянной температуре. Затем можно
определить возмущенный поток Ф(г) и зависимость температуры от высоты,
численно находя все величины, фигурирующие в формулах теории возму-
щений.
15.3. РЕГУЛЯТОР, ДАТЧИК И УСТОЙЧИВОСТЬ
В неравенстве (15.1.17) или (15.1.22) знаменатель правой
части содержит собственное число ап2—п2л2/Н2, т. е. чем больше
ап2, тем устойчивее гармоника пространственного распределе-
ния cos anz. С физической точки зрения это понятно: увеличение
утечки (или перетечки из области с максимальным потоком в
область, где поток минимален) способствует устойчивости, так
как чем больше утечка, тем меньшее влияние оказывает погло-
щение нейтронов ксеноном на распределение плотности потока.
Это обстоятельство можно использовать для качественного ана-
лиза ряда задач на устойчивость [255].
Кроме регулятора в реакторе должны быть приборы (каме-
ры деления, ионизационные камеры [74]), показания которых
пропорциональны плотности потока нейтронов в том месте ре-
актора, где размещен прибор. В дальнейшем такой прибор бу-
дем называть «датчиком». Движение регулятора управля-
ется сигналами, поступающими от датчиков. Алгоритм управ-
ления может быть различным: поддержание постоянной средней
мощности реактора, потока нейтронов в том месте, где разме-
щен датчик, и т. п.
Рассмотрим плоский реактор высотой Н. Пусть в точке z0
расположен датчик, служащий для поддержания постоянного
потока в этой точке, т. е. если ср (г) — отклонение плотности
потока от невозмущенного, то
<p(zo)=O.
(15.3.1)
486
Если вместо преобразования Лапласа, как это было сделано
в § 15.1, искать решение, пропорциональное ехр (pt), то полу-
чим [см. (15.1.10) без двух последних слагаемых в правой ча-
сти) :
уиг-Я-+^-1)ч,+^г’гр)-?^)<р=0> <15-3-2)
dz2
где F(p) определено (15.1.12), a f(z, гр) характеризует действие
регулятора. Будем считать, что до возмущения регулятор вносит
р реактор реактивность по закону:
Ak=C6(z—2Р)ФО; 0(г) —1, z>0; 0(г)=0; з<0.
Возмущение состоит в том, что Фо заменяется Фо-НфФо, а ко-
нец регулятора смещается на Аг, т. е. в уравнении для q> появ-
ляется разность:
С [0 (z—гр—Аг) (Фо+Фоф) —0 (г—гр) Фо] —
= С [0 (г—гР—Аг) —0 (г—гР) J ФоЛ С0 (г-—гр) Ф0<р. (15.3.3)
Заменим теперь
С [0 (г—гр—Аг) —0 (г—zp) ] Фо= САгб (г—гр) Фо==
= рб(г—гр), (15.3.4)
где р характеризует реактивность, вносимую регулятором. По-
следнее слагаемое в (15.3.3) можно включить в (k—1)<р в урав-
нении (15.3.2). При этом будем считать тем не менее, что k не
зависит от координат. Это означает, что движение данного ре-
гулятора как-то компенсируется другими, явно не входящими
в (15.3.2) регуляторами, так что их совокупное действие сводит-
ся к условию &=const. Таким образом, отклонение плотности
потока от невозмущенного <р(г) удовлетворяет уравнению
М2(р"+ [k—1— F (р) ] <р+рб (г—гр) =0 (15.3.5)
и условию (15.3.1). Решение уравнения (15.3.5) должно удов-
летворять граничным условиям <р(0) =ip(И) =0, условию не-
прерывности в точке z—Zp и условию (15.3.1). Величина р при
этом определяется равенством:
Р = Л42
д<р(гр4-0)
дг
d<t (гр - 0)
дг
(15.3.6)
Легко обнаружить, что уравнение (15.3.5) имеет две серии
собственных функций, удовлетворяющих всем перечисленным
условиям (принято для определенности, что г0<гр):
sin ад
0,
Н-г
Н—zp
0 < г < гр;
zp <г<Н,
(15.3.7)
32*
487
причем
^(Р) + [«277~^-2-1](^-1) = о, *~1=(^гГ’ (l5-3.8)
(1 * ^р) J \ п /
и вторая серия:
sin(wz/z0), 0<z<zp;
Ф«,2 =
___— (ny°j___Sin ('I, zp<z</7, (15.3.9)
. / H-zp\ \ z0 )’ p v '
Sin ТЛ------
\ 4 1
причем - •
— / Ha \
F+lri2—-------1 (£ — l) = 0. (15.3.10)
\ z02 /
Случай, когда (H—zp)/z0 равно целому числу, надо исклю-
чить. В этом случае последовательность <р„,2 является частью
последовательности сри,ь т. е. возникают кратные корни и реше-
ние имеет другой вид.
Сравнение (15.3.8), (15.3.10) с (15.3.13) показывает, что
в условии устойчивости (15.1.17) надо заменить п2—1 [в том
случае, когда вместо выполнения преобразования Лапласа
ищется решение вида ехр (pZ)<p(z), уравнение (15.1.13) заме-
няется однородным, т. е. правая часть равна нулю] следующим
выражением:
га2- 1
2 / И \2
га2 -------------
н—Zp
га2
(15.3.11)
Из (15.3.11) видно, что граница устойчивости зависит от рас-
положения регулятора (zp) и датчика (г0). Если zp близко к ну-
лю или z0 близко к Н, т. е. регулятор и датчик расположены
близко к одному краю реактора (напомним, что z0<zp), то ми-
нимальное значение F можно сделать сколь угодно близким
к нулю и устойчивость реактора теряется. Наоборот, если zq
близко к нулю, a zp-—Н, т. е. датчик и регулятор расположены
на разных концах реактора, то минимальное значение Г можно
сделать сколь угодно большим. В этом случае реактор, неус-
тойчивый по критерию (15.1.17), можно сделать устойчивым.
Например, если по условию (15.1.17) реактор неустойчив при
га^З (т. е. могут возникать и расти колебания с пространствен-
ным распределением cosnaz при га^З), то достаточно располо-
488
жить датчик и регулятор так, чтобы z0, Н—— Н, и реактор
3
станет устойчивым по отношению ко всем собственным функ-
циям фп,1 и фп,2- Из этого примера видно, что результаты ана-
лиза устойчивости реактора без учета взаимного расположения
регулятора и датчика могут не иметь ничего общего с действи-
тельностью.
Аналогичный анализ можно провести и для цилиндрического
реактора. При этом формально анализ сильно усложняется, но
по существу, он остается таким же простым [256]. Весьма удов-
летворительной оказывается система из семи регуляторов (один
в центре, шесть равномерно расположены на окружности ради-
усом около 2/3 радиуса реактора). Каждый регулятор управля-
ется датчиками, которые расположены на окружности радиу-
сом —4/4 радиуса реактора с центром в точке, где расположен
регулятор. Сближение регулятора и датчика существенно ухуд-
шает устойчивость. Регулятор должен поддерживать минимум
среднего значения отклонения потока в точках, где расположе-
ны датчики, управляющие данным регулятором. Такая система
называется локальными автоматическими регуляторами (ЛАР).
Она применяется на реакторах РБМК [196].
Численные методы исследования устойчивости подтвердили
основные результаты, полученные с помощью описанного здесь
на простейшем примере, метода оценки устойчивости по вели-
чине собственных чисел [257]. За дальнейшими подробностями
мы вынуждены отослать читателя к оригинальной литературе.
В настоящей граве рассмотрены только некоторые вопросы
динамики реактора. Более подробное изложение динамики ре-
акторов можно найти в специальной литературе (см., например,
[258—261]).
Дополнение 1. ОДНОСКОРОСТНОЕ КИНЕТИЧЕСКОЕ УРАВНЕНИЕ
1. Формулировка уравнения. Односкоростное кинетическое уравнение
описывает перенос нейтронов в том случае, когда можно пренебречь изме-
нением энергии нейтрона при столкновениях с ядрами среды. Если такого
пренебрежения сделать нельзя, а в большинстве случаев это именно так, то
надо рассматривать многоскоростное кинетическое уравнеине. Переходя к мио-
гогрупповому приближению, сечение увода в каждой группе можно присоеди-
нить к сечению поглощения, а источниками (кроме нейтронов, непосредствен-
но возникающих при делении) служат те нейтроны других групп, которые
при столкновении приобрели энергию, принадлежащую данной группе. Тогда
в каждой группе формулируется односкоростное уравнение переноса, причем
источники зависят от потоков в других группах, т. е. многогрупповое кине-
тическое уравнение сводится к системе связанных односкоростных уравнений.
Таким образом, односкоростное приближение является необходимым элемен-
том наиболее общего случая. Ниже при рассмотрении односкоростного при-
ближения источники будут считаться заданными.
Пусть N(г, Sl)drdQ— число нейтронов в элементе объема dr, скорость
которых расположена внутри элемента телесного угла dQ (Я — единичный
вектор направления скорости). Кинетическое уравнение является следствием
баланса нейтронов в элементе фазового объема drdQ. Во-первых, нейтроны
уходят из рассматриваемого элемента объема из-за поглощения н рассеяния
(при рассеянии изменяется направление скорости); число таких нейтронов
равно
2Ф(г, Q)drdQ; Ф(г, Q)=vN(r, Я),
где v — абсолютное значение скорости; 2 = 2и-|-2з (в многоскоростных зада-
чах в 2 входит также н сечение увода). Во-вторых, число нейтронов, выхо-
дящих из элемента dr, не равно числу входящих; их разность есть
Я\7Ф(г, £l)drdSh, причем оператор \7 действует на координату г. Наконец,
нейтроны могут входить в элемент ЙЯ в результате столкновений, при кото-
рых направление скорости изменяется от Я' до Я; число таких нейтронов
равно
У р
— |х(ф)Ф(г, Q')dQ'drd£i,
4л J
где ср—угол между Я и Я'; pi (ср) —вероятность того, что при столкновении
направление скорости изменится на угол ср. Величина pi (ср) нормирова-
на так:
-7- С р. (ф) dti = I.
4л J
490
Если рассеяние изотропно, то ц(ф) = 1. Наконец, нейтроны могут появиться
за счет источника 5 (г, ft)drdil/(4л). Таким образом, получаем уравнение
— Аф(г.’_й). _ _ (йу S) Ф (Г, Й) +
v dt
+ —Гр(ф)Ф(Г, ------------------— 5(г, Й). (Д.1.1)
4л J 4п
Плотности потока и тока нейтронов равны соответственно
ф (г) = J Ф (г, й)«/й; J(r) = J ЙФ(г, Й)бШ. (д.1.2)
2. Диффузионное приближение. Решение уравнения (Д. 1.1) можно искать
в виде ряда по степеням вектора Й. Ограничиваясь линейными членами, за-
писываем
Ф(г, Й)=Д4-ВЙ. (Д.1.3)
В дальнейшем будут использованы формулы
йгДЙ = 0; Jйгй/й2 = -у 8О. (Д. 1.4)
Коэффициент 4/3 в (Д.1.4) проверяется путем свертки по индексам (по
повторяющимся индексам проводится суммирование от 1 до 3): й/й<=1;
6,г=3. Интегрируя (Д.1.3) по И, определяем Д, а умножая на й и интегри-
руя, воспользовавшись второй формулой (Д.1.4), находим В:
Ф(г, Й) = — [Ф(г)+'ЗЛ(г)Й]. (д.1.5)
4л
Уравнение (Д.1.1) в стационарном случае запишем так:
(йу + 2)Ф(г, Q)=-Ls(r) +
4л
+ —S [р.(ф)Ф(г, Й')^; c = S5/S. (Д.1.6)
4л J
Подставив (Д.1.5) в (Д.1.6), воспользовавшись (Д.1.4) и определением
среднего косинуса рассеяния ,и:
йгЙ/ |л(Ф) с/Й dQ' = -у- ^ij,
получим после интегрирования по й
(1- C)20(r) + VJ(r)=S(r), (Д.1.7)
а умножая (Д.1.6) иа Й и интегрируя (предполагается, что S не зависит
от Й), находим второе уравнение:
J-уф (г)-)-S(1 -q*)J(r) = 0. (Д.1.8)
Q
191
Из (Д.1.8) определим вектор плотности тока J(r) и коэффициент диф-
фузии D:
J (г) = - О7Ф (Г); D = [32 (1 - с 12Я + 2,(1 - ЙОГ' =
О
= (32,г)-’. (Д.1.9)
Дифференцируя (Д.1.8) и используя (Д.1.7), получаем уравнение диффузии
VDV®(r)-2o®(r)=-S(r). (Д.1.Ю)
Из (Д.1.10) получим для длины диффузии выражение (2.1.20).
В уравнении (Д.1.6) сечения могут быть функциями координат, причем ,
также и разрывными, например кусочно-постоянными. Уравнения (Д.1.7) и
(Д.1.8) остаются при этом справедливыми. Отсюда следует, что nJ и Ф
непрерывны на границах раздела сред с различными свойствами (кроме
границы с вакуумом, п — вектор нормали к границе раздела), так как в про-
тивном случае эти уравнения содержали бы 6-функции, возникающие от диф-
ференцирования разрывных функций. Менее формально этот результат можно
получить, если проинтегрировать (Д.1.7) и (Д.1.8) по малому цилиндру
с высотой h и площадью основания ДЗ, причем граница между средами
проходит внутри цилиндра параллельно основанию. Если А->0, то интеграл
от членов, которые не содержат производных, стремится к нулю. Интеграл
от div J равен n(Ji—J2) ДЗ=0, где индексы 1,2 различают две среды. Таким
образом, на границе раздела справедливо
(nJ)l=(nJ)2. (Д.1.11)
Точно так же при интегрировании (Д.1.8) получим (Ф2—Ф1)п,ДЗ=0, где
п{ — проекция вектора п на направление оси xi. Умножая на п,, и сокращая
на ДЗ, имеем
Ф^Фг, (Д.1.12)
т. е. непрерывность Ф на границе.
3. Приближение Р2. Продолжим разложение (Д.1.5) и учтем еще одно
слагаемое:
Ф(г, О)= — [<D(r)4-3J(r)fi4-fiP(r)Ql. (Д.1.13)
4л
Добавленное в (Д.1.13) слагаемое
QP(r)fi=QsQ/P0(r) (Д.1.14)
является однородным полиномом 2-го порядка от компонент вектора й.
В методе сферических гармоник этот полином должен быть гармоническим
(тогда разложение по полиномам от й совпадает с разложением по сфери-
ческим функциям), т. е.
= (Д.1.15)
492
откуда
Pw=0.
(Д.1.16)
Из (Д.1.14) следует, что тензор Рц симметричен: Рц=Рц.
Если в разложении :р(<р) по степеням cos<p=1212' сохранить два слагае-
мых, то в силу (Д.1.4), (Д.1.16) получим
р,(<р)ф (г, О') dQ' = Ф(г) -{-3 ti J (г) О.
Первое слагаемое в (Д. 1.6) запишется так:
1 Г dZ,-(r) &Рц 1 „ , .
Й?Ф(г, й)= (д-и7>
Последнее слагаемое в (Д.1.17) не является гармоническим полиномом, ио
его можно представить как сумму двух гармонических (общее правило см.,
например, в {86, 147]):
дРц (Г 2 ] ,21 дРи
= ([адо(—5-°«Л)о>-1 + isf
(Д.1.IS)
В приближении Р-2 гармонический полином 3-го порядка следует опустить.
Таким образом, получим из (Д.1.6):
2 дРц(г)
2„Ф (г) + Й?Ф (г) + 3Szr Ш (г) + +
ЭЛ(г)
+ зад-^—hW^(r)Z = s. (д.1.19)
Будем считать, что источник 3 не зависит от 12. Интегрируя (Д.1.19) по
12 и используя (Д.1.4), (Д.1.16), находим
Sa®-J div J=S. (Д.1.20)
Умножая (Д.1.19) на £2* и интегрируя, имеем
7 Н + 7 d+M - 0. (Д• 1.21)
о ufy \ Ь /
Умножая (Д.1.19) на ----------- ?Jki [добавление — (Sfei£2a)Ra_1
3 { 3
делает полином 12*12/ гармоническим и ортогональным ко всем полиномам
других порядков], интегрируя и используя формулу (структура этой форму-
лы диктуется соображениями симметрии, а коэффициент определяется путем
свертки по индексам):
—— ГййЙгЙД;с(О — — -|- bkibu Skj8H), (Д. 1.22)
4тс J 15
получаем
р у—1 [\ <• 3 / dJi д/1 \
Pii-^ [SydlvJ--+—)]. (Д.1.23)
493
Из (Д.1.20), (Д.1.21) находим условия непрерывности на границе сред
С различными свойствами для следующих величин:
nJ; ф = Ф-|- —nPn. (Д.1.24)
5
Подставляя (Д.1.23) в выражение для ф (Д.1.24), получаем
ф=ф(1—§)+1i“_"sHnv)(nJ)- г(д-’-25)
С помощью (Д.1.23) и (Д.1.20) исключим из (Д.1.21) Pi, и div J (здесь
и далее будем считать, что источники не зависят от координат):
VaJ —x2J= — (52 -j- Sa) ?Ф = D (x2 — L'3)v(I), (Д.1.26)
3
где
D = (3S<r)-*(l b2 = D/L(1; x3 = 5SS<r. (Д.1.27)
\ 5^ /
Дифференцируя (Д.1.21) и исключая Рц и J, имеем
ОД|Ф—2„Ф=— S. (Д.1.28)
Положим
J = — £>V®+J*- (Д.1.29)
Подставляя (Д.1.29) в (Д.1.26), убеждаемся, что J* удовлетворяет одно-
родному уравнению (Д.1.26). Подставляя (Д.1.29) в (Д.1.20) и учитывая
(Д.1.28), находим дополнительное условие, которому должно удовлетво-
рять J*:
divJ*=O. (Д.1.30)
Из (Д.1.29) видно, что ток J можно разделить на две части: —£)\7Ф>
связанный с плотностью потока так же, как в Pi-приближении, но с другим
значением коэффициента диффузии, и второе слагаемое J*, изменяющееся на
расстояниях порядка х-1. При Sa<gSs имеем x-1<gL.
В одномерных случаях J*=0. В самом деле, из условия divJ* = O имеем
/* = с; J*=c/r\ J*=c/r2\ c=const
для плоского, цилиндрического и сферического случаев соответственно. Оче-
видно, что эти функции не удовлетворяют однородному уравнению (Д.1.26)
и поэтому с=0. В этом причина того, что в одномерном случае Р2-прибли-
жеиие по сложности эквивалентно Pi-приближению. В многомерных задачах
это не так (см., например, [86]).
В одномерном случае Пу =nJ==J, J = —D-^-. Поэтому из (Д. 1.25)
dr dr
следует
2Sa \ 6П <Рф 2S
5S / + 5S dr2 + 5S ‘
(Д.1.31)
494
4. Функция Грина одиоскоростного кинетического уравнения. Рассмотрим
стационарный случай. Пусть среда бесконечна и однородна. Рассеяние счи-
таем изотропным (см. ниже), источник — не зависящим от й. Решение урав-
нения (Д.1.1) ищем в виде разложения в ряд Фурье:
Ф(г, Q) = Jexp(ikr)<D(k, O)dk;
S(r) = J exp(i kr) s (k) dk;
ф (r) = J exp (i kr) Ф (k) dk.
Очевидно, что
ф(к) = £Ф(к, Q)dQ.
Подставляя (Д.1.32) в (Д.1.1), имеем
1 i ф(к> О)----------?5-ф(к) =
X / 4лХ 4лХ
(Д.1.32)
(Д.1.33)
(Д.1.34)
Определяя из (Д.1.34) Ф(к, й) н интегрируя по й, получаем Ф(к):
Ф(к)
J_[s(k) + S^(k)]f[l + z
4лХ J _
—1 1 dQ.
X
(Д.1.35)
При вычислении интеграла в (Д.1.35) направим полярную ось по направле-
нию вектора к. Тогда
+1
(* d(l п С dx 2пХ . 1 + i k/Я 4лХ , k
I i । .mW = 2lt ---------------==------ln —-—— -----------arctg —.
J l + ifik/S J 14-ifex/X Ik 1 —ife/X k X
—i
Таким образом,
Ф (к) = s (к) Г (/г/arctg-M - 2 J \
L \ « / J
и после обратного преобразования Фурье:
Л Г s(k)exp( — ikr)dk
ф(г)=]~7-----------' {ДЛ,36)
Ц arctg — j — ХЛ.
Рассмотрим точечный изотропный источник нейтронов
S(r)=a(r); s(k) = (2n)-3. (Д.1.37)
Подставив (Д.1.37) в (Д.1.36) и выполнив интегрирование по углам, полу-
чим функцию Грина односкоростного кинетического уравнения
G (г) = (4ла i г)-' ----feexp^rLf- . (Д. 1.38)
-оо fe^arctg— j —Xs
Рассмотрим комплексную плоскость переменной k. В верхней полуплоско-
сти k=a\\b, b>0, при [fej->oo подынтегральная функция затухает. Поэтому
495
можно замкнуть контур интегрирования по большому кругу в верхней по-
луплоскости, выделив при этом две особые точки: полюс при k=i/L и точку
ветвления при fe=iS. При этом L определяется из уравнения
Arth(SL)-i=(2sL)-’.
(Д.1.39)
Интеграл (Д.1.38) равен вычету в полюсе и интегралу по берегам раз-
реза в комплексной плоскости от точки fe=iS до бесконечности. Опуская
дальнейшие вычисления, приведем окончательный результат:
G(r) = Gas(r)-^Gt(r), (Д.1.40)
где
Gas (г) = -у ~ (-gL)y 2,у ехр (— r/L); (Д. 1.41)
(St) 2—Sa/S
со
г2 ехр ( —rSz) dz
(Д.1.42)
Для источника в виде нити надо сделать замену:
— ехр (------. _L ехр (— rSz) — K0(rz£).
г \ L / \ L ) г
Очевидно, что Gt затухает иа расстояниях порядка 2-1, a Gas — поряд-
ка L. Если SaCSs, то из (Д.1.39) следует (см. ниже). В этом слу-
чае при r»S-1 можно пренебречь Gt. Поэтому G„s называют асимптотиче-
ской частью функции Грина, а Gt — переходной. В противоположном случае,
когда So5>Ss, из (Д.1.39) следует
I
т. е. L~S-1, и разделение иа Gas н Gt теряет смысл, поскольку обе функции
затухают на расстояниях одного порядка.
5. Сравнение точной функции Грина с диффузионной. Если SL3>1, то
решение уравнения (Д.1.39) можно построить в виде ряда по степеням е=
=SO/S5. Разложив Arth (St)-1 в ряд, получим
[1 + Т(SLr +Т (ЕЛ)“4 + -]: L°~2 = 3SA-
(Д.1.43)
Представив 1/L2 в виде ряда по е, найдем
— = —[1
L2 tj2 |_
4 । 144 2
--------е -4-------е
5 175
(Д.1.44)
где L1~2 = 3SSO [см. (2.1.24)]. Из формул (Д.1.27) при р=0 получаем
L-2 = L?2 1
Зб_е2
25
(Д.1.45)
496
Таблица ДЛ. Отношение Gas(r)/G(r) для Изотропного
рассеяния при отсутствии поглощения
rl Grt /G as1 ГЕ °ЯЛ/°
0,1 0,2 0,3 0,4 и, сравнивая 0,2574 0,4428 0.5762 0,6734 с (Д.1.44), и 0,5 0,6 0,7 0,8 меем 0,7451 0,7988 0,8396 0,8710 0,9 1,0 2,0 з,о 0,8954 0,9147 0,9854 0,9967
= (ДЛ-46)
A/D AJj
Из формул (Д.1.44% (Д.1.46) следует, если e<S 1, неравенство
L~2< 1^2<АГ2. (Д-1-47)
Поэтому плотность потока нейтронов вдали от точечного источника, вычис-
ленная в различных приближениях, удовлетворяет неравенству Ф > Фр1 >
>Фр,. Однако, например, в ячейке реактора кривые Ф(г), Фра (г), Фр1 (г)
(см. рис. 7.1) расположены в другом порядке.
Сохраняя линейные по е члены в предэкспоненциальном множителе Gas,
получаем
= ехр =Q^Gd(r), ‘(Д.М8)
где Ga(r)—диффузионная функция Грина (2.1.36); £>=(3Ss)-1 и
$эф=1------(Д.1.49)
о
Таким образом, единичный источник нейтронов воспринимается иа боль-
ших расстояниях как имеющий уменьшенную интенсивность <?Эф<1. Такое
уменьшение мощности источника связано с дополнительным поглощением
нейтронов на расстоянии Г'—S-1 от источника, поскольку плотность потока
там увеличивается за счет Gt.
Аналогично п. 4 можно получить функцию Грина кинетического урав-
нения в случае анизотропного рассеяния. Ограничимся уравнением для L,
которое заменяет собой (Д.1.39). Если
Р-(ф) = 14-Зц cos <р,
то вместо (Д.1.39) получается
Arth(Zb)— - (ЗД- ; L,’=(3Z.8J-. (Д.1.50)
l+H(! + e)L2/Le2
497
Разложение (Д.1.50) в ряд по в приводит К следующему результату^
£-3 = £1-2 / 1 _ А е\. = (3Sfl2/r)->. (Д.1.51 )
\ о /
В табл. Д.1 приведены значения Gas(r)/G(r) при 2о==0; р=0 (см. по-
дробнее в [72]).
Из табл. Д.1 видно, что уже при г~0,52-1 асимптотическая часть функ-
ции Грина Gas составляет 75 % полной функции Грнна G, т. е. переходная
часть в 3 раза меньше асимптотической.
Дополнение 2. СРЕДНЕЕ ЧИСЛО СТОЛКНОВЕНИЙ ПРИ ЗАМЕДЛЕНИИ*
Обозначим Nn-i(x')—число нейтронов, испытавших п—1 столкновение
и имеющих энергию Е'=Еох', где Ео — энергия моноэнергетического источ-
ника. После того как эти нейтроны испытают еще одно столкновение, число
столкновений будет равно п, а энергия упадет до Е=ЕоХ. При этом Nn_t(x')
и Nn(x) связаны между собой вероятностью w{E', Е) (2.2.8):
E/$q X/Sq
Nn(x)= j w(E', E)Nn_1(x’)dE' = (l-^~' J
E x
(Д2.1)
Умножим обе части уравнения (Д.2.1) на Xs-1 и проинтегрируем по х (пре-
образование Меллина). В левой части получим
ОО
Фл(«) = 1 (Д-2.2)
о
В правой части сначала изменим порядок интегрирования, что даст
(Д.2.3)
(1— eo)s
Если учтем моиоэнергетичность источника Мо(х)=6(1—х), то из (Д.2.2)
получим фо=1. Применяя последовательно (Д.2.3), определяем фп(з):
фп(«)=[(1—eos)/s.(l—ео)]п. (Д-2.4)
Обратное преобразование дает
г+ 1оо ч
fri(f=«8F J 1(1 - 8оЭ/«1" x-sds. (Д.2.5)
C—ioo
Можно проверить, что из (Д.2.5) следуют обязательные свойства Nn: Nn(x) =
=0 прн х>1; JVn(x)=O при x<eon; Nt{x)=6{l—х),
* См. [81].
498
С помощью (Д.2.5) вычислим среднее значение Х? пбсле п столкновений:
t
(x0„ = ( xpNn(x)dx.
* п
®0
(Д.2.6)
Подставляя (Д.2.5) в (Д.2.6) и изменяя порядок интегрирования, по-
лучаем
c+ia
с— la
1—е»(1 + /’-«)
—V-----------ds- (Д-2-7)
1 Т~ Р—s
Первый миожитель в подынтегральной функции (Д.2.7) не имеет особен-
ности при s=0. Второй множитель надо разбить иа два слагаемых. В пер-
вом можно замкнуть контур интегрирования через Res>0, так как ео<1 и
е0®->-0 при Res->oo. Тогда интеграл равен вычету в полюсе s= 1-}-р. Второе
слагаемое неограниченно растет при Re s->oo, но падает при Re s-> —оо.
Поэтому контур интегрирования в этом случае можно замкнуть по большому
кругу в сторону Res<0. Так как внутри этого контура нет особых точек, то
эта часть интеграла равна нулю. Таким образом, получим
(хр)п=[(1_8о>+р)/(1-6о)(1+р)]’>. (Д.2.8)
В частности, при р=1
— - 1 in
хп= ~ (1 +«о) I
(Д.2.9)
или
П = 1П (Е0/Еп)/1п [ ——
\ 1 + ео
(Д.2.10)
где Ёп — средняя энергия нейтрона после п столкновений. Результат (Д.2.9)
весьма нагляден: средняя энергия после одного столкновения соответствует
середине интервала (£о, ВоЕо), после второго — середине интервала
(Lifeр 1+ео г \ и
I 2 с°’ ~2—и Т. Д.
С помощью (Д.2.5) можно вычислить среднее значение 1пх [81]
/г = -^-1п(1/х„),
е
как и должно быть по определению g, но In (1/л(п)^1п (1/х„). Таким
образом, среднее число столкновений можно определить либо как п=
= 1п (£о/£п)/1п (Е'/Е), либо как п=1п (£0/£)/1п (£'/£)•
499
Дополнение 3. РЕЗОНАНСНОЕ ПОГЛОЩЕНИЕ В ОДНОРОДНОЙ СРЕДЕ
[ВЫВОД ФОРМУЛЫ (2.3.64)] *
Пусть нейтрон при замедлении достиг энергии Е. Вероятность замедлить-
ся до тепловой энергии без поглощения обозначим у(Е). Очевидно, что
Ф(£) отличается от tp(£) (2.3.53) постоянным слагаемым: ф(Е)-]-ф (Е) =
=<р(£«)=ф(££)з(р. Вероятность столкнуться и не поглотиться, приобрести
в результате столкновения энергию Е' н замедлиться до тепловой энергии
без поглощения равна
<д-зл>
i
где Wi дано (2.2.8), Проинтегрировав по всем возможным значениям Е',
получим уравнение для ф(Е):
*<£) ” Е вдттйЬе ! ‘Т(£,) dE-
i е01Е
Если масса ядер поглотителя достаточно велика, то ф(£') можно выне-
сти за знак интеграла в том слагаемом (Д.3.2), который соответствует погло-
тителю. Тогда аналогично (2.3.56) получим
Е _
Ф № = IT Vf f ф (£,) dE’> (Д-33)
aJ SZ(E)(1 —е0/)Е J
‘ eoiE
где не содержит Ss поглотителя и суммирование проводится только по
ядрам замедлителя (что отмечено штрихом при знаке суммы), поглощением
в котором пренебрегаем. Поэтому Ssl/Ss не зависит от энергии. Из уравне-
ния (Д.3.3) надо определить ф(Ео)=ф.
Рассмотрим один уровень. Введем вероятность поглощения при столкно-
вении
Г(Е) = 2а(Е)/ЕДЕ); 1 - W (Е) = (Д.3.4)
где Ss не включает рассеяния на ядрах поглотителя. Вместо (Д.3.3) на-
пишем
. ^(E')dE’. «ад
Е ЬЛ eof) J
•oiE
Будем считать малым параметром величину
(Д.з.в)
См. [98, 125].
500
Положим W(E)=fiWa(E) и ф= 1-[—Рф1 (при P=0 поглощение отсутст-
вует и q>— 1). Из (Д.3.5) в первом порядке по § получим
В
Фт (Е) = 2's - [ Ф1 (Е') dE' - Гв (Е). (Д.3.7)
eoiH
Применим к (Д.3.7) преобразование Меллина. Обозначим
us = f Es“' Ф1 (Е) dE; vs = J Es~' Wo (E) dE. (Д.3.8)
о о
Умножим обе части (Д.3.7) на Es~' и проинтегрируем по Е (при этом в пра-
вой части надо изменить порядок интегрирования). В результате получим
ws=t»s[A,(s)]-1,
(Д.3.9)
где
Обратное преобразование дает
Ф1(£)
2л1 J
(Д.3.11)
где с лежит левее всех особенностей подынтегральной функции. Особенно-
стями подынтегральной функции являются нули A(s). Очевидно, что Д(0)=>
= 0. Покажем, что нет нулей А(з) при Res<0. Если Ims = 0, то это сразу
видно из (Д.3.10). Пусть s=a-|-i&, а<0. Запишем A(s) так:
д (5) = (Re At + i Im Л{),
где
1т/г =bLt
ехр(а£.)^Ь-(1_^)-11;
bL{ J
L[ -= In ——.
eoi
При a<0 первое слагаемое в квадратных скобках по модулю <1,
а (1—£;)-1>1. Поэтому Im A/=bCi, а<0. Так как 1m Л, входит в сумму по
I с положительными коэффициентами, то мнимая часть (з—1)А не равна
нулю при Таким образом, A(s)y=0 при а<0, т. е. A(s) не имеет нулей
₽ левой полуплоскости.
501
Если Ei больше верхней границы опасной зоны резонанса, то можно
считать, что IFo(E'i)=0. Тогда при Re s>0 имеем |os| <EiRe s. Отсюда сле-
дует, во-первых, что можно замкнуть контур интегрирования по большому
кругу при Res>0 и, во-вторых, что при вклад полюсов с Res>0 не
существен. Таким образом, интеграл (Д.3.11) равен вычету в полюсе s=0;
Ф1 (^о) = ,----= — , (Д.3.12)
L ds ]
где g = — среднее значение g,- для замедлителя [см. (2.2.18)].
i
Так как
Е„
v0 = ~^^dE-, ф(£0) = ф=1+рФ1(Е1),
I
Ес
то из (Д.3.12) получим
ф= 1 _ 2 f la(E} dE
g J ZO(E)+2S E
Ec
Если имеется много неперекрывающихся уровней, то
1 Ес J
г Ео
^ехр ,
g J Sa(E) + Ss Е
L Е„ J
что совпадает с (2.3.64).
Приложение I. НЕКОТОРЫЕ ФИЗИЧЕСКИЕ ПОСТОЯННЫЕ * **
Масса покоя протона тр= 1,6726485(86) 10~24 г= 1,007276470(11) а. е. м =
=938,2796(27) МэВ.
Масса покоя нейтрона тп=1,67495443(86) • 10~24 г = 1,008665012(37) а. е. м.=
=939,5731(27) МэВ.
Масса покоя электрона пге = 9,109534(47) • 10~27 г=5,4858026(21)Х
ХЮ-4 а. е. м.=511,0034(14) кэВ.
Атомная единица массы (а. е. м.) =931,5016(26) МэВ=1/12 массы 12С.
Скорость света в вакууме с=2,99792458(1) • 1010 см/с.
Заряд электрона е= 1,6021892 (46) 10 19 Кл.
Постоянная Планка Й =й/(2л) = 1,0545887(57) • Ю'34 Дж-с.
Постоянная Авогадро Na —6,022045(31) • 10~23 моль-'.
Постоянная Больцмана k = 1,380622(44) • 10~23 Дж-К-1.
Объем моля идеального газа Vm=2,241383(70) 10~2 м3-моль~‘,
Абсолютная температура Г, К=273,15-|-7’ °C.
1 электрон-вольт=АГ при Т=1,160450(36) • 104 К.
1 МэВ = 106 эВ = 1,602143(44)-10-6 эрг = 1,60214-10“13 Дж = 4.4504Х
ХЮ-20 кВт-ч=1,8543-Ю-24 МВт-сут=3,8216-10->7 ккал.
Длина волны нейтрона Х=0,287У£, где Е—энергия, эВ; X, 10~8 см,
4пХ2=2,604-106/£, б.
Время жизни нейтрона 893,0(63) с [263].
Приложение II. ДЕФЕКТ МАССЫ НЕКОТОРЫХ АТОМОВ а. е. м. ”
Дефект массы, а. е. м„ равен ДЛ4=Л1(А, Z) —А, где М(А, Z) — масса
атома с атомным числом А и порядковым номером Z.
Легкие атомы
>Н 0,007825037(10) 2Н 0,01410787(10) 3Н 0,016049286(37)
3Не 0,016029297(33) 4Не 0,00260325(5) "Li 0,0151232(8)
Некоторые тяжелые атомы
aospb —0,023359(5) 239Pu 0,0521578(25)
22sTh 0,028726(6) 24«Pu 0,0538087(25)
* По [1, 262].
** См. [264].
503
229Th 0,031756(7) 24]Pu 0,0568469(24)
азоть 0,0331307(31) 2«PU 0,0587385(24)
232Th 0,0386538(25) 2«pu 0,064200(5)
231Ра 0,0358809(33) 241Am 0,0568246(24)
232£J 0,037141(6) 243Am 0,0613741 (34)
233(J 0,0396293(35) 242Cm 0,0588313(26)
234Ц 0,0409474(26) 243Cm 0,0613820(28)
235£J 0,0439252(26) 244Cm 0,0627477(25)
236Ц 0,0455629(25) 245Cm 0,0654870(31)
23S(J 0,0507858(24) 246Cm 0,0672205(37)
237Np 0,0481688(24) 247Cm 0,070349(5)
236pu 0,046043(6) 248Cm 0,072345(6)
2Э8Рц 0,0495552(26) 252Cf 0,081622(6)
Приложение 111. ВЫДЕЛЕНИЕ ЭНЕРГИИ ПРИ РАДИОАКТИВНОМ
РАСПАДЕ НЕКОТОРЫХ ТЯЖЕЛЫХ АТОМОВ (получена из таблицы
Приложения II)
Нуклид Энерговыделени e Нуклид Энерговыделеиие
кэВ Вт/г кэВ Вт/г
232g 40780* 5,34* 242pu 4983 1,16-10-4
233g 4909 2,8-10-4 24ipu 6233** 6,68-10-?**
234 g 4856 1,8-10-4 241АГП 5638 0,115
235g 4557** 5,8-10-s** 243ДШ 5648** 6,68-Ю-з**
236g 4011 1,54-Ю-о 242Cm 6216 122
238g 5718** l,14-10-8** 243СГП 6167 1,89
237Np 5019** 2,1-1О-о** 244Cm 5902 2,83
236pu 5867 18,5 24?cm 5623 5,72-10-3
238pu 5593 0,568 24ocm 5476 0,01
239pn 5244 1,91-Ю-з 24’Cm 5424** 2,9- Ю-о**
240рц 5256 7,07-10-? 24scm 5162 5,22-10-4****
241PU 5,6*** 3,4-10-9 252Cf 6217 40****
* В равновесии со всеми продуктами распада.
** В равновесии с короткоживущими продуктами распада.
*** Максимальная энергия р-частиц 20,8 кэВ; а-распад, происходящий с вероят-
ностью 2,5-1О~5, дает вклад в энерговыделеиие ^2%.
**** с учетом энерговыделения при спонтанном делении; энерговыделеиие, кэВ,
Относится только к а-распаду.
33—6053
Приложение IV. НЕЙТРОННЫЕ СЕЧЕНИЯ И РЕЗОНАНСНЫЕ ИНТЕГРАЛЫ ТРАНСАКТИНОИДОВ
Таблица IV.1. Сечения в тепловой группе (и=2200 м/с), периоды полураспада [2781, число вторичных нейтронов
Элемент А Т U2 б О-p б V б V
Торий 90Th 227 18,72 сут 202(13)
228 1,913 года <0,3 123(15)
229 7.34-103 лет 30,8(15) 2,14(4)
230 7,52•104 лет <1,2-10—3 61 (6)
231 25,6 ч 23,0(3)
232 1,405-1010 лет <2,5-10-в 7,37 (6) 12,97(10)
233 22,3 мин 15(2)
234 24,1 сут <0,01 1500(100) 1,8 (5)
Протактиний 81Ра 230 17,4 сут 1500(250)
231 3,28-104 лет 0,020 (1) 200,6(23) 10,6
232 1,31 сут 700(100)г 464 (95)
233 27,0 сут 1,17 мин <0,1 20,1 (32) (1,2 мин) 19,4 (30) (6,7 ч) 15,5(30)
234m <500
234£ 6,7 ч <5000
Урая „U 230 20,8 сут 25(10)
231 4,2 сут 400(300)
232 68,9 года 76,8(48) 74,9(16) 13,3(22) 3,15(4)
233 1,593-105 лет 529,1 (12) 45,5 (7) 12,6 (3) 2,4933(39)
234 2,45-10* лет <0,65 99,8(13) 19,6(10)
235 7.038-10® лет 582,6(11) 98,3(8) 14,0(5) 2,4251 (34)
236 2,342-107 лет 0,07 5,Н (21) 13,7(17) 2,338 (22)
237 6,75 сут <0,35 443(167)
4,468-109 лет 4-Ю-6 2,680 (19) 9,38(9) 1,98(3)5/»
.23,5 мин йй,1 4 14(3) 22(5)
сл
о
о
Элемент А Т 1/2 Оу » б
Нептуний 93Np 234 4,4 сут 900(300)
235 396,2 сут
236g ls15-105 лёт (2760(170)** 12500(150)
236т 22,5 ч 2740 (140)***
237 2,14-Ю6 лет 0,0215(24)
238 2,117 сут 2088(30)
239 2,3 сут
Плутоний 94Рц 236 2,851 лет 170 (35)
237 45,1 сут 2455 (295)
238 86,96 года 17,9(4)
239 24 113 лет 748,1 (20)
240 6569 лет 0,056(30)
241 14,38 года 1011,1 (62)
242 3,763-105 лет <0,2
243 4,956 ч 196(16)
244 8,08-Ю7 лет
245 10,5 ч
Америций 95Ат 241 432,2 года 3,20(9)
242т 141,2 года 6950 (280)
242g 16,02 ч 2100(200)
243 7348 лет 0,198(4)
244т 26 мин 1600 (300)
244g 10,1 ч 2300(300)
Кюрий 96Ст 242 161,4 сут <5
243 28,5 года 617 (20)
244 18,1 года 1,04(20)
Продолжение табл. IV.1
СПр б а5. б V
150(2) (22,5 ч) 3,12(14)
175,9(29) 2,252 (16)
32 (6) (7,5 мин) г**** 36 (8) (67 мин) г
2,21 (18) Sp
540 (7) 25,0(18) 2,90(2)
269,3(22) 7,3(4) 2,8768(57)
289,5 (14) 1,64 (9) 2,17(1) Sp
358,2(51) 9,1 (Ю) 2,9369 (73)
18,5(5) 87(10) 8,44 (21) 2,153(19) Sp
1,7 (1) 150(30) 2,3(2) Sp
54 (5) (141 года) 533(13) (16 ч) 3,213(32)
2000 (600) 3,260(24)
75,1 (18) 3,8(4) (10,1 ч)
16(5) 2,538(12) Sp
130 (10) 3,430(47)
15,2(12) 11,6(7) 2,696(10) Sp
Продолжение табл. IV.1
Элемент А т ’ б а.р б 6 V
Кюрий 96Ст 245 8,52 103 лет 2145(58) 369(17) 3,717(60)
246 4,73-103 лет 0,14(5) 1,22(16) 11,1(2) 2,950 (14) Sp
247 1,56- Ю7 лет 81,9(44) 57(10) 3,79(15) Sp
248 3,40-105 лет 0,37(5) 2,63 (26) 7,65(40) 3,157(15) Sp
249 64,15 мин 1,6(8)
250 ~7400 лет 3,17(8) Sp
Берклий 97Вк 249 329 сут 746 (40) 7.7 3,395(26) Sp
250 3,22 ч 960(150) -.350
Калифорний 98С1 249 350,7 года 1642(33) 497(21) 4,06 (4)
250 13,08 года 2034(200) 3,51 (4) Sp
251 898 лет 4895(250) 2850(150)
252 2,368 года 32 (4) 20,4(15) 3,7Q75 (40) Sp
253 17,8 сут 1300 (240; 17,6(18)
254 60,5 сут 4,5(15) 3,83(5) Sp
Энштейнпй 99Es 253 20,47 сут 178 (15) (39,3 ч) 5,8 (7) (276 сут)
254m 39,3 ч 1826(80)
254g 276 сут 1966(160) 28,3(25)
255 39,8 сут 55(Ю) г
Фермий шорт 254 3,24 ч 1400 г (а) -.76 3,98(19) Sp
255 20,1 ч 3360(170) 26(3)
256 2,63 ч -.45 3,74(18) Sp
257 100,5 сут 2950 (160) 3,796(14) Sp
* По данным [32, 33[; г — для реакторного спектра; а — сечение поглощения; Sp — для спонтанного деления (периоды полураспада
для спонтанного деления см., например, в [13]).
** Данные [265].
*** Данные [2661.
**** В [267] приведено: 0^=37; /т=126.
***** Данные [131.
507
Таблица IV.2. Резонансные интегралы бесконечного разведения
Элемент А 7?. 6 7^, 6
onTh 228 1014
229 466(75) 1000(175)
230 1007 (35)
232 85(3)
233 400(100)
о, Ра 231 525(60)
232 233 3,0 300(70) 438(70) (1,18 мин)
432(70) (6,75 ч)
9„и 232 350(30) 280(15)
233 760(17) 137(6)
234 6,5 660(70)
235 275 (5) 144 (6)
236 7,8(16) 360 (15)
237 1200(200)
238 1,54 (15)-10—3 277(3)
93NP /236g 1030(100)*
(236m 700(400)** 640 (50)***
237 6,9(10)
238 883 (70) 1500(500) a
239 126****
Q.PU 236 960***** 197*****
238 33 (5) 162(15)
239 240 301(10) 8,8 220 (20) 8100(200)
241 570(14) 162 (8)
242 5(2) 1115(40)
243 550 (80) 270 (35)
244 40,6(29)
245 220 (40)
osAm 241 14,4(10) 195(20) (141 года)
1230 (100) (16,1 ч)
242m 1800(65) 230(100)
242g <300 1820(70); 94(9) (Ю,1 ч)
243 10(6)
9eCm 242 110(20)
243 1570(100) 215(20)
244 18(2) 650(30)
245 840 (40) 101 (8)
246 10,2 (4) 121 (7)
247 760 (50) 530 (30)
248 15 270(15)
* Данные [265].
** Данные [266]. ГЛ_О,.
*** Резонансный интеграл 237Np зависит от энергии (см U68J):
£,эВ. . . . 0,625 0,525 0,500 0,475 0,450 0,400
/ТС, б..... 550 582 635 733 788 817
**** Данные [267].
***** Данные [13].
508
Продолжение табл. IV.2
Элемент А ГГ 6 Пр б
97Вк 249 1100(100)
sgCf 249 2380 (85) 765 135)
250 11 600 (500)
251 5900(100) 1600(30)
252 110(30) 43,5(30)
253 2000(400) 13(3)
99I-S 253 3750 (200) (39,3 ч) 114 (7) (276 сут)
254 1000
254 1200(250) 18,2(15)
iooFm 257 5000 а
Таблица IV.3. ^-Факторы 235U, 239Pu, 241Pu как функция
температуры нейтронов *
т, к 23 »и 238ри 24ipu
ef Sf Sf
293 0,976 0,979 1,056 1,078 1,044 1,044
300 0,974 0,976 1,059 1,084 1,050 1,044
400 0,953 0,955 1,153 1,211 1,119 1,099
500 0,937 0,941 1,ЗЮ 1,415 1,216 1,187
600 0,926 0,931 1,524 1,690 1,327 1,295
700 0,918 0,925 1,777 2,010 1,439 1,406
800 0,912 0,921 2,044 2,347 1,542 1,512
900 0,908 0,918 2,307 2,676 1,629 1,604
1000 0,904 0,916 2,551 2,981 1,701 1,681
1100 0,900 0,913 2,771 3,255 1,755 1,741
1200 0,896 0,910 2,962 3,493 1,796 1,787
1300 0,892 0,907 3,125 3,695 1,824 1,819
* Определение g-фактора см. в (2,4,8); данные по изотопам плутония заимствованы
из [16], где приведены более подробные данные; для урана g-фактор вычислен по сече-
ниям [15, 16]; ga и gf при 20 °C совпадают с приведенными в табл. 1.8.
Таблица IV.4. Параметры первого резонансного уровня
некоторых трансактинондов *
Нуклид Ef, эВ gTn, мэВ Г7> мэВ ау(Ег), б , б
234U 5,16(1) 3,92(2) 24,6(38) 60 400 525(13)
236Ц 5,45(3) 2,16(8) 24,5(10) 36 000 277 (14)
240 рц*** 1,056(1) 2,45(2) 30,3 (3) 155 000 8000 (200)
24 2рц 2,676(2) 2,00 (8) 25,0(15) 67 400 1070(40)
244Ст 7,67(1) 10,4(4) 37,2(33) 58 500 570 (30)
* По данным [32].
** /у — резонансный интеграл поглощения первым уровнем.
*** Данные [2791.
509
Приложение V. НЕЙТРОННЫЕ СЕЧЕНИЯ
И ДИФФУЗИОННЫЕ ХАРАКТЕРИСТИКИ НЕКОТОРЫХ ВЕЩЕСТВ
Таблица V.I. Сечения и резонансные интегралы*
Элемент Изотоп Содержание в ес- тественной смеси % (или Т1/2) <5^ , б °s- б** !у, б
1Н 1H 99,985 0,3326(7) 20,491(14)
2H 0,015 0,519 (7) X 3,390(12)
10"~3***
3H 12,323 года <6-10-8 1,70(3)
2Не 3He 1,38-10-“ 0,031 (9) 10“3 3,10(13)
5333 (7)р 2400 (7) р
Ше 0,76(1)
3Li Ест. 44,8 (30) -10-3 0.95 (4)
70,5(19)а
«Li 7,5 38,5 (30). 10-3 0,75 (2)
940 (4) а
7Li 92,5 45,4 (30). IO"3 0,97 (4) 4,0 (4)-IO-3
4Ве 8Be 100 7,6 (8)-IO-3 6,151(5)
6в Ест. 0,10(4) 4.27(7) 1722 (5) а
767(8)а 2,23 (6)
k>B 20,0 0,5(2)
3837 (9)а
nB 80,0 5,5 (33). IO-3 4,84 (4)
«с Ест. 3,50 (7)-Ю-з 4,740 (5) 1,57 (5)-Ю-з
12c 98,9 3,53 (7)-IO-3 4,746(2) 1,7 (2)-Ю-з
isc 1,1 1,37 (4)-IO-3 4,19(12)
7n Ест. 74,7 (73)-Ю-з 10,03(8)
1,90 (3)я 10,05(12) 34-Ю-3
14N 99,63 75,0 (75)-Ю-з
1,83 (3)Р
16N 0,37 2,4 (8) 10-е 4,59(5) 0,11-10-з
8О Ест. 0,19(2)10-3 3,761 (6)
0,279 (19) 10- ’я 0,4-10—За
ie0 99,762 0,190 (19)-Ю-з 3,761 (6) 0,36-Ю-з
170 0,038 0,538 (65)-Ю-з 3,61 (6) 0.39-Ю-з
0,235 (10) а 0,105(10) а
iso 0,2 0,16(1)10—8 0,87(4)- IO-3
nNa 23Na 100 0,530(5) 3,025 (20) 0,311 (10)
i2Mg Ест.. 0,063(3) 3,4140 (24) 0,038 (4)
13AI 27A1 100 0,231 (3) 1,4134(10) 0,17 J)
14 Ы Ест. 0,171 (3) 2,0437(17) 0,127 (14)
22Ti Ест. 6,09(13) 4,09(3) 3,1 (2)
Ест. 2.56(3) 11,35 (3) 1,4(2)
27Со 68Co 100 37,18 (6) 6,00 (6) 74 (2)
e°Co 5,27 года 2,0(2) 4,3(9)
28^1 Ест. 4,49(16) 17,8(4) 2,15(20)
29^4 Ест. 3,78 (2) 7,78 (3) 4,1 (1)
4()Zr Ест. 0,185(3) 6,40 (4) 0,95(15)
41 Nb 83Nb 100 1,15(5) 6,37 (71 8,5(5)
42^0 Ест. 2,55(5) 5,59 (4) 24(2)
72Hf Ест. 104,1(5) 10,3(4) 1992(50)
77Ir Ест. 425,3(24) 14,2(28) 2150(100)
191Jr 37,3 954 (10) 15 3500(100)
510
Продолжение тгбл. V.1
Элемент Изотоп Содержание в ес- тественной смеси, % (или Т1/2) <5^, б б“ , б
79Au 1821г ISSJr 197Аи 74,2 сут 62,7 100 645(32)( 1,45 мин) 309(30)(74,2 сут) 1420(200) 1И (5) 98,65 (9) 7,84 (13) 3242 1350 (100) 1550 (28)
82?Ь Ест. 0,170(2) 11,4(2) 0,16(4)
20SB1 100 0,0338 (7) 9,300 (3) 0,19(2)
* По данным обзоров [31—33]; сечения реакций (па) и (пр) отмечены буквами а и
р, сечение поглощения — буквой а; ест. — естественная смесь изотопов.
* * Приведены сечения рассеяния для свободного ядра (см.§ 3.2); если Л>>1, то
этими данными можно пользоваться и для тепловых нейтронов. Для элементов с малыми
А и их химических соединений надо использовать табл. V.2.
* ** По данным [269] Оу=0,476(20)-10-3.
сл
ьэ
Таблица V.2. Макроскопические сечения некоторых веществ*
Элемент (химиче- ское соединение) Атомная масса Плотность,г г/см8 Число атомов (молекул) в 1 см8, 1024 V см 1 1а* см СМ-' ls, см
Н2О 18,015 1,0 0,03343 1,972 (4). IO-2 50,73 (11) 1,496(1) 0,6684 (4)
D3O 20,028 1,105 0,03323 3,88 (7)-10-6** 2,57 (5)-IO4 0.3503(8) 2,855(7)
Be 9,012 1,84 0,123 8,2 (9)-10-4 1,21 (12)-103 0,7566 (6) 1,3217(10)
ВеО 25,011 2,79 0,0672 4,7 (4)-IO-4 2,12(2) • 10® 0,666 (8) 1,50(2)
С 12,011 1,67 0,0837 2,60 (5) 10-4 3,85(8)-Ю8 0,3967 ( 4) 2,521 (3)
Na 22,99 0,97 0,0254 1,196 (9)-IO-2 83,5(11) 0,0768 (5) 13,02(8)
Mg 24,31 1,74 0,0431 2,41 (12)-IO-8 415(19) ' 0,1471 (1) 6,796 (5)
Al 26,98 2,70 0,0603 1,23(2)- IO-2 81,3(11) 0,08523 (6) 11,733 (8)
Fe 55,85 7,87 0,0849 l,92(3)-10-x 5,20(6) 0,9636 (25) 1,038 (3)
Zr 91,22 6,44 0,0425 6,97 (12)-IO-» 143 (2) 0,272 (2) 3,68(3)
Pb 207,2 И ,34 0,033 4,97 (6)-IO-8 201 (2) 0,376 (7) 2,66 (5)
Bi 209,0 9,75 0,0281 8,42 (2)-10-4 1190 (20) 0,2613(1) 3,827 (1)
Th 232,04 И,1 18,7 0,0288 0,189(2) 5,37 (6) 0,374 (3) 2,67(2)
238,03 0,0473 0,313(1) 3,19(1) 0,445(4) 2,25 (2)
* I = z 1 — a 1 a — (£и>- где Sa(£H) вычисляется по ffa из табл. V.I.
** Если использовать данные [269], то Sa=3,62(13)-IO-5; la=2,76(10)• 10*.
*** Естественная смесь изотопов урана; учтены g-факторы при 20 °C.
Таблица V.3. Диффузионные характеристики некоторых веществ
Элемент (химическое соединение) D, cm L, CM cm-1 CM~‘ T*, CM2 T, CM2
Н2О 0,1423 (19) 2,69 (2) 1,385 (1) 0,577 26,48 (32) 26,9 (4)
d2o 0,84(1) 147(2) 0,1/й4 0,27 Hl(l) 118(2)
Be 0,487 (5) 24,4 (13) 0,1561 (1) 0,70 86,6(24) 90(3)
ВеО 0,627 (7) 36,5(3) 0,1156 (1) 0,625 92,0(15) 95 (2)
С 0,828(8) 56,4(6) 0,06259 (6) 0,375 282,5(18) 297 (2)
Na 3,755(6) 17,7(1) 0,00649(4) 0,0746
Mg 2,229(2) 30,4(8) 0,01178(1) 0,143
Al 3,418(7) 16,7(1) 0,006165(5) 0,0831
Fe 0,288(1) 1,22(1) 0,0341(1) 0,952
Zr 1,195 (9) 13, i (i) 0,00592 (4) 0,270
Pb 0,875(16) 13,311) 0,00361 (7) 0,375
Bi 1,2716(5) 38,9 (4) 0,002494(1) 0 260
Th 0,593(2) 1,78(1) 0,00325(3) 0,373
U 0,440 (2) 1,186(6) 0,00372 (4) 0,444
Примечание. Коэффициент диффузии тепловых нейтронов D и возраст т* доэнергии 1,46 эВ приведены по экспериментальным
цаииым для Н2О из [112, 270], для D2O — из [113, 133. 271, 272], данные для Т* приведены к 100% D2O и усреднены; для Be — из [88,
273], для ВеО —из [88, 274], для С — из [275, 276]. Поправка Лт=т—Т* определена по формуле (2.2.73) до энергии 0,5 эВ. Если для аа D2O
использовать [269], то£р2о = 152(3). Все данные приведены для той плотности, которая указана в табл. V.2. Для остальных веществ коэф-
фициент диффузии вычислен по формуле D= [3(2а+25)]-1,где 2О и 2^ приведены в табл. V.2. Длина диффузии вычисляется по формуле
где У-а указано в табл. V.2. Транспортное сечение для замедляющихся нейтронов 2^= (1 — Ц) где см. в табл. V. 2, ц=
=2/(ЗД) (см. § 2.2). Возраст нейтронов для тяжелых элементов ие приводится, так как обычно они прусутствуют в реакторе в смеси с
легкими веществами (см. табл. V.5).
513
Таблица V.4. Возраст нейтронов для смеси D,0 и Н,0 (до энергии
1,46 эВ, см2. [272])
CDSO- % 99,8 99 98,4 95,3 94 91,8 48,6
Т, СМ2 109(3) 107(5) 106(3) 93 (3) 86 (3) 78(3) 38,6(10)
Таблица V-5. Возраст нейтронов дл’я смеси Н20 с металлами (до энергии
1,46 эВ, см2. [135, 277])
VM/V0 0,2 °,з °, 4 0,5 0,6 0,7 0,8
Al 33 37 45 59 75 101 159
Zr 29 33 40 47 57
Fe 30 34 40 45 51 76
Таблица V.6, Возраст нейтронов для смеси D20 с алюминием (см. [277];
т0 — возраст чистой D2O)
0,05 o,i 0,15 0,2 0,25
t/-t0 1,07 1,13 1,25 1,35 1,47
Данные табл. V.4 приведены на рис. ПУЛ. Сплошная линия — парабола,
проведенная по методу наименьших квадратов (при концентрации D2O>
>90%), т=[110,5—3,5с—0,07с2] см2, с — концентрация D2O, %.
Рис. ПУЛ. Зависимость воз-
раста нейтронов деления в
тяжелой воде от ее концен-
трации (до £=1,46 эВ)
514
Приложение VI. ВЕРОЯТНОСТЬ СТОЛКНОВЕНИЯ ДЛЯ
БЕСКОНЕЧНО ДЛИННОГО ЦИЛИНДРА
zs р=1-рс Погреш- ность РП (1.10.21), % Погреш- ность фор- мулы (1.10.22), % Р=1 — Рс Погреш- ность РП (1.10.21), % Погреш- ность фор- мулы (1.10.22), %
0,2 0,8850 —5,8 0,59 2,8 0,3186 — 17,4 —0,03
0,4 0,7930 -9,9 0,61 3,0 0,3016 — 17,1 0,15
0,6 0,7165 —12,8 0,43 3,2 0,2861 — 16,8 0,29
0,8 0,6516 —14,7 0,21 3,4 0,2720 — 16,4 0,42
1,0 0,5960 —16,1 0 3,6 0,2591 — 16,1 0,54
1,2 0,5478 —17,0 —0,17 3,8 0,2473 — 15,8 0,65
1,4 0,5057 — 17,6 —0,29 4,0 0,2365 — 15,4 0,73
1,6 0,4687 — 17,9 —0,36 5,0 0,1932 —13,7 1,И
1,8 0,4361 —18,1 —0,37 6,0 0,1629 —12,3 1,16
2,0 0,4072 — 18,1 —0,36 7,0 0,1405 — 11,0 1,14
2,2 0,3813 —17,9 —0,29 8,0 0,1235 —10,0 0,97
2,4 0,3582 —17,9 —0,19 9,0 0,1100 —9,1 0,95
2,6 0,3374 —17,7 —0,09 10,0 0,0992 -8,4 0,81
Приложение VII. ЭФФЕКТИВНОЕ ГРАНИЧНОЕ УСЛОВИЕ
ДЛЯ ЧЕРНОГО ЦИЛИНДРА*
р£ т рЕ Т Р- Т
0 001 1,32998 1.0 0,91581 5,0 0,76225
0,01 1,31031 1,2 0,89151 6,0 0,75368
0,1 1,20566 1,4 0,87205 7,0 0,74750
0,2 1,13608 1,6 0,85614 8,0 0,74284
°,з 1,08571 1,8 0,84291 9,0 0,73921
0,4 1,04649 2,0 0,83175 10 0.73630
0,5 1,01474 2,5 0,81031 15 0,72758
0,6 0,98840 з,о 0,79503 20 0,72325
0,7 0,96610 3,5 0,78365 50 0,71552
0,8 0,94697 4,0 0,77481 100 0,71297
0,9 0,93036 4,5 0,76970
По данным [143]
Приложение VIII. ЗНАЧЕНИЯ ФУНКЦИИ F(t) (1.7.9), МэВ/дел*.
t, с 2 33U аззу 338U 239pU 232ТИ
1 9,605 12,31 14,19 10,27 14,53
1,5 9 449 11,98 13,61 10,03 14,05
2 9,317 11,69 13,16 9,816 13,66
4 . 8,915 10,83 11,96 9,206 12,57
6 \ 8,629 10,26 11,23 8,795 11,87
8 8 404 9,830 10 70 8,488 11,35
10 8,218 9,494 10,29 8,243 Ю,95
15 7,856 8,882 9,546 7,794 Ю,19
20 7,584 8,455 9,012 7,476 9,649
40 6,888 7,459 7,755 6,707 8,346
60 6,459 6,888 7,052 6,251 7,600
80 6,150 6,493 6,572 5,929 7,091
100 5,912 6,198 6,217 5,685 6,715
150 5,491 5,696 5,621 5,262 6,087
200 5,205 5,369 5,241 4,982 5,689
400 4,570 4,667 4,464 4,357 4,880
600 4,218 4,283 4,072 3,993 4,474
800 3,970 4,009 3,804 3,726 4,198
1000 3 778 3,796 3,598 3.516 3,989
1500 3’,429 3,408 3,220 3,128 3,610
2000 3,180 3,137 2,954 2,857 3,340
4000 2,609 2,534 2 366 2,276 2.704
6000 2,314 2,234 2,078 2,002 2,372
8000 2,123 2,044 1,901 1,839 2,158
1.104 1,984 1,908 1,777 1,727 2,002
1,5-Ю4 1,750 1,685 1,578 1,548 1,744
2-Ю4 1,600 1,545 1,455 1,437 1,582
4-104 1,289 1,258 1,204 1.204 1,259
6-Ю4 1,140 1,117 1,077 1,081 1,114
8-Ю4 1,051 1,030 0,9955 1,000 1,031
1-10® о 0,9906 0,9691 0,938з 0.9421 0 9778
1,5-Ю® 0,8956 0,8734 0,8459 0,8480 0,8975
2-Ю® 0,8374 0,8154 0,7884 0,7890 0,8507
4-Ю® 0,7174 0,6975 0,6673 0,6634 0,7559
6-Ю® 0,6508 0,6331 0,6002 0,5944 0,7007
8-Ю5 ’0,6029 0,5868 0,5530 0,5462 0,6582
1.10е 0,5657 0,5509 0.5171 0 5097 0,6234
1,5-Ю6 0,4993 0,4866 0,4544 0,4464 0,5569
2-Ю6 0,4538 0,44’5 0,4125 0,4046 0,5089
4-Ю6 0,3549 0,3457 0,3224 0,3163 0,4023
6-Ю6 0,3071 0,2983 0,2784 0,2741 0,3516
8-Ю6 0,2770 0,2680 0,2503 0,2477 0,3199
1-Ю7 0,2549 0,2457 0 2296 0 2282 0,2965
1,5-Ю7 0,2179 0,2078 0,1941 0,1945 0,2565
2-Ю7 0,1956 0,1846 0 1717 0,1728 0,2313
4-Ю7 0,1596 0,1457 0 1299 0,1302 0,1861
6-Ю7 0,1464 0,1308 0,1113 0,1099 0,1671
8-Ю7 0,1387 0 1222 0,1001 0 09741 0,1559
1 - 10s 0,1334 0,1165 0,09'80 0,08931 0,1485
1,5-Ю3 0,1253 0,1082 0,08307 0,07859 0,1378
516
Продолжение при гож. VIII
t, 0 23 3JJ 235U 238U J3»pu ••Th
2-Ю3 0,1198 0,1032 0,07810 0,07344 0,1312
4-10s 0,1032 0,08836 0,06647 0,06269 0,1121
6-10s 0,08937 0,07613 0,05746 0,05466 0,09641
8-lOs 0,07760 0,06570 0,04979 0,04783 0,08209
1 • IO9 0,06749 0,05678 0,04321 0,04195 0,07149
* По данным [57].
Приложение IX. ЭНЕРГЕТИЧЕСКИЕ ГРАНИЦЫ
НЕЙТРОННЫХ ГРУПП В 26-ГРУППОВОЙ СИСТЕМЕ
Номер группы Энергетические границы Интервал летаргии Номер груп- пы Энергетические границы Интервал летаргии
1 10,5—6,5 МэВ 0,4796 14 2,15— 1 кэВ 0,7655
2 6,5—4 МэВ 0,4855 15 1000—465 эВ 0,7657
3 4 — 2,5 МэВ 0,4700 16 - 465—215 эВ 0,7714
4 2,5—1,4 МэВ 0,5798 17 215—100 эВ 0,7655
5 1,4—0,8 МэВ 0,5596 18 100—46,5 эВ 0,7657
6 0,8—0,4 МэВ 0,6931 19 46,5—21,5 эВ 0,7714
7 0,4 — 0,2 МэВ 0,6931 20 21,5—Ю эВ 0,7655
8 0,2—0,1 МэВ 0,6931 21 10—4,65 эВ 0,7657
9 100—46,5 кэВ 0,7657 22 4,65—2,15 эВ 0,7714
10 46,5—21,5 кэВ 0,7714 23 2,15—1 эВ 0,7655
11 21,5—Ю кэВ 0,7655 24 1—0,465 эВ 0,7657
12 10—4,65 кэВ 0,7657 25 0,465—0,215 эВ
13 4,65—2,15 кэВ 0,7714 26 0,215—0 эВ
/
СПИСОК ЛИТЕРАТУРЫ
1. Обозначения, единицы измерений и терминология в физике, документ
U. I. Р. (1978)// Усп. физ. наук. 1979. Т. 129. Вып. 2. С. 290—325.
2. Харвей Дж., Сандерс Дж. Обзор данных по эффективным сечениям и
выходам нейтронов// Успехи в области ядерной энергии: Пер. с англ. М.:
Изд-во иностр, лит., 1958. С. 9.
3 Hughes D. J., Schwartz R. В. Neutron Cross Sections// BNL-325. 2 ed.
1958.
4. Neutron Cross Sections/ J. R. Stehn, M. D. Goldberg, R. Wiener-Chas-
man e. a.// BNL-325. 2 ed. 1965. Suppl. N 2.
5. A survey of values of the 2200 m/s constants for four fissile nuclides/
С. H Westcott, K. Ekberg, G. C. Hanna e. a.// Atomic Energy Rev. 1965.
Vol. 3, N 2. P. 3—61.
6. Revision of values for the 2200 m/s neutrons constants for four fissile
nuclides/ G. C. Hanna, С. H. Wescott, H. D. Lemmel e. a.// Ibid. 1969.
Vol. 7, N 4. P. 3—93.
7. Mughabghab S. F., Garber D. I. Neutron Cross Sections// BNL-325.
1973. 3 ed. Vol. 1.
8. Stehn J. R. Thermal Data for fissile nuclei in ENDF/B-IV// Trans. Amer.
Nucl. Soc. 1974. Vol. 18. P. 351.
9. Lemmel H. D. The third IAEA evaluation of the 2200 m/s and 20°C ma-
xeellian neutron data for 233U, 235U, 239Pu and 24IPu// Proc, of the Conf, on
Nuclear Cross Sections and Technology, Washington. 1975. Vol. 1. P. 286.
10. Lemmel H. D. Thermal parameters for 233U, 23SU, 239Pu, 24IPu// Nuc-
lear Data Standarts for Nuclear Measurements: Techn. Rep. N 227. IAEA.
Vienna, 1983.
11. Divadeeman M., Stehn J. R. A least-squares fit of thermal data for fis-
sile nuclei// Ann. Nucl. Energy 1984. Vol. 11, N 8. P. 375.
12. Howerton R. J. v Revisited// Nucl. Sci. Engng. 1977. Vol. 62, N 3.
P. 438.
13. Горбачев В. M., Замятин Ю. С., Лбов А. А. Взаимодействие излуче-
ния с ядрами тяжелых элементов и деление ядер. М.: Атомиздат, 1976.
14. Малиновский В. В., Воробьева В. Г., Кузьминов В. Д. Обзор резуль-
татов измерений среднего числа мгновенных нейтронов деления// ВАНТ. Сер.
Ядерные константы. 1983. Вып. 5(54). С. 19—56.
15. Оцененные нейтронные константы урана-235/ В. А. Коньшин,
Г. В. Анципов, Е. Ш. Суховицкий и др. Минск: Наука н техника, 1985.
16. Коньшин В. А. Ядерно-физические константы делящихся ядер. М.:
Энергоатомиздат, 1984.
17. Большов В. И., Смиренкин Г. Н. Измерение разности средних энер-
гий спектров нейтронов 233U, 23SU, 239Pu и 2S2Cf// Атомная энергия 1985.
Т. 59. Вып. 5. С. 343—345.
18. Бойцов А, А., Старостов Б. И. Оценка формы спектра мгновенных
нейтронов спонтанного деления 2s2Cf// Нейтронная физика. М.: ЦНИИатом-
ннформ, 1984. Т. 2. С. 301—306.
518
19. Крошкии Н. И., Замятиин Ю. С. Измерение энергетических спектров
и среднего числа v мгновенных нейтронов деления// Атомная энергия. 1970.
Т. 29. Вып. 2. С. 95.
20 Watt В. Е. Energy spectrum of neutrons from thermal fission of 23SU//
Phys. Rev. 1952. Vol. 87, N 6. P. 1037.
21. Григорьев E. И., Ноздрачев С. Ю., Ярына В. П. Оценка спектра ней-
тронов деления 235Ц по результатам интегральных экспериментов// Атомная
энергия. 1978. Т. 45. Вып. 3. С. 225.
22. Старостов Б. И., Семенов А. Ф., Нефедов В. Н. Оцененные данные
по спектрам мгновенных нейтронов деления 233U, 235U, 239Pu, 24IPu// Ней-
тронная физика. Т. 4. М.: ЦНИИатоминформ, 1980. С. 47.
23. Гангрский Ю. П., Далхсурэн Б., Марков Б. Н. Осколки деления ядер.
М.: Энергоатомиздат, 1986.
24. Маневич Л. Г., Немировский П. Э., Юдкевич М. С. Константы за-
паздывающих нейтронов// Препринт ИАЭ-4308/4. М.: ЦНИИатоминформ,
1986.
25. Кипин Дж. Р. Физические основы кинетики ядерных реакторов: Пер.
с англ. М.: Атомиздат, .1967.
26. Tuttle R. J. Delayed-neutron data for reactor physics analysis// Nucl.
Sci. Engng. 1975. Vol. 56. P. 37.
27. Synetos S. Integral measurements of delayed neutron average energies
for 235U// Nucl. Data Sci. and Technol. (Proc. Intern Conf., Antwerpen). 1982.
P. 268—271.
28. Evaluated delayed neutron spectra and their importance in reactor
calculations/ D. Sapihier, D. Ilberg, S. Shalev, S. Yiftah// Nucl. Sci. Engng.
1977. Vol. 62, N 4. P. 660.
29. Случаевская В. M., Матвеенко И. П. Основные данные по запазды-
вающим нейтронам// Вопросы атомной науки и техники. Сер. Ядерные кон-
станты. Вып. 3(38). М.: ЦНИИатоминформ, 1980. С. 29.
30. Иванов В. И., Машкович В. П., Центер Э. М. Международная система
единиц (СИ) в атомной науке и технике. М.: Энергоиздат, 1981.
31. Mughabghab S. F., Divadeenan М., Holden N. Е. Neutron Cross Sec-
tions. Vol. 1. Part A. N. Y. — London: Academic Press, 1981.
32. Mughabghab S. F. Neutron Gross Sections. Vol. 1. Part B. N. Y.—
London: Academic Press, 1984.
33. Радиационный захват нейтронов: Справочник/ Т. С. Беланова,
А. В. Игнатюк, А. Б. Пащенко, В. И. Пляскин. М.: Энергоатомиздат, 1986.
34. Групповые константы для расчета ядерных реакторов/ Л. П. Абагян,
Н. О. Базазянц, И. И. Бондаренко, М. Н. Николаев. М.: Атомиздат, 1964.
35. Групповые константы для расчета реактора и защиты/ Л. П. Абагян,
Н. О. Базазянц, М. Н. Николаев, А. М. Цибуля. М.: Энергоиздат, 1981.
36. Абагян Л. П., Юдкевич М. С. Библиотека нейтронных данных для
расчета тепловых реакторов// Вопросы атомной науки и техники. Сер. Ядер-
ные константы. Вып. 1(40). М.: ЦНИИатоминформ, 1981. С. 39.
37. Сечения пороговых реакций, вызванных нейтронами/ В. М. Бычков,
В. Н. Манохин, А. Б. Пащенко, В. И. Пляксин. М.: Энергоиздат, 1982.
38. Николаев М. Н., Базазянц Н. О, Анизотропия упруго рассеянных
нейтронов. М.: Атомиздат, 1972.
39. Шуколюков Ю. А. Продукты деления тяжелых элементов на Земле.
М.: Энергоатомиздат, 1982.
40. Петров Ю. В. Естественный ядерный реактор «Окло»// Усп. физ.
наук. 1977. Т. 123. Вып. 3. С. 473—486.
41. Bigham С. В., Durham R. W., Ungrin J. A direct measurement of the
thermal neutron conversion ratio of natural uranium// Canad. J. Phys. 1969.
Vol. 47. P. 1317.
42. Report of the american society by the study group on nuclear fuel cyc-
les and waste management// Rev. Mod. Phys. 1978. Vol. 50, N 1. Part II.
519
43. Групповые нейтронные сечения деления и радиационного захвата
трансактинидов/ А. И. Воропаев, А. А. Ваньков, В. В. Возняков и др.// Во-
просы атомной науки и техники. Сер. Ядерные константы. Вып. 3/34. 1979.
С. 34—60.
44. Горбачева Л. В., Мантуров Г. Н., Цибуля А. М. Оценка результатов
измерения средних сечений 235U, 238U и 239Pu на спектрах нейтронов деления
235U, 2S2Cf// Атомная энергия. 1980. Т. 49. Вып. 4. С. 256.
45. Crouch Е. А. С. Fission-product yields from neutron-induced fission//
Atomic Data and Nucl. Data Tables. 1977. Vol. 19, N 5. P. 417.
46. Бета-/и антннейтринное излучение радиоактивных ядер: Справочник/
В. Г. Алексанкин, С. В. Родичев, П. М. Рубцов и др. Под ред. П. М. Рубцо-
ва.: М.: Энергоатомиздат, 1989.
47. Nuclear charge distributions in the isobar 92 to 100 resulting from
thermal neutron fission of uranium 235/ G. Sieget e. a.// Phys. Rev. Lett.
1975. Vol. 34, N 16. P. 1034.
48. Радиационные характеристики продуктов деления/ Н. Г. Гусев,
П. М. Рубцов, В. В. Коваленко, В. М. Колобашкин. М.: Атомиздат, 1974.
49. Wagemans С., D’hondt Р., Schillebeck Р., Brissot R. Triton and alpha
emission in the thermal-induced ternary fission of 233U, 23SU, 239Pu and 241Pu//
Phys. Rev. C. Nucl. Phys. 1986, Vol. 33, N 3. P. 943—953.
50. James M. F. Energy release in fission// J. Nucl. Energy. 1969. Vol. 23.
P. 517.
51. Немировский П. Э. Энергия деления изотопов урана и трансурановых
элементов// Препринт ИАЭ-3230/3. 1980.
52. Копейкин В. И. Энергия, выделяемая на акт деления урана и плуто-
ния в ядерном реакторе// Препринт ИАЭ-4305/2. 1986.
53. Jedruch J., Nodrik R. J. Verification of energy release in fission from
power plant calorimetries and isotopic composition of spent fuel// J. Nucl.
Energy. 1973. Vol. 27, N 4. P. 195.
54. Shure K-, Wallance O. J., Conner J. C. Comparison of calculations and
measurements of fission product decay heat for uranium 235 and plutonium 239
for cooling times>5-104s// Nucl. Sci. Engng. 1979. Vol. 71, N 3. P. 327.
55. Fission-product energy release for times following thermal neutron fis-
sion of 235U between 2 and 1400 s/ J. K. Dickens e. a.// Ibid. 1980. Vol. 74,
N 2. P. 106.
56. Грибии А. А., Пологих В. Г. Остаточное энерговыделение продуктов
деления 23SU тепловыми нейтронами// Атомная энергия. 1981. Т. 51. Вып. 1.
С. 16.
57. Shure К. Decay rate and decay heat data from fission products// Nucl.
Sci. Engng. 1981. Vol. 78, N 1. P. 185.
58. Сечение реакции 237Np(n, 2n) 236Np (22,5 ч), вызываемой нейтронами
спонтанного деления 252Cf/ Е. А. Громова, С. С. Коваленко, Ю. А. Немилое
и др.// Атомная энергия. 1986. Т. 60. Вып. 1. С. 68—69.
59. Pearlstein S. Analysis of (п, 2л) cross sections for medium and heavy
mass nuclei// Nucl. Sci. Engng. 1965. Vol. 23, N 3. P. 238.
60. Зельдович Я- Б., Харитон Ю. Б. Деление н цепной распад урана//
Усп. физ. наук. 1940. Т. 23. С. 329.
61. Смит Г. Д. Атомная энергия для военных целей: Пер. с англ. М.:
Трансжелдориздат, 1946.
62. Ферми Э. Элементарная теория котлов с цепными ядерными реакция-
ми// Усп. физ. наук. 1947. Т. 32. Вып. 1. С. 54.
63. Makino К. Some rational approximations for Bickley functions Kiu
(N=l, 2, 3, 4, 5)// Nukleonik. 1967. Rd. 9, N 7. S. 351.
64. .Case К. M., de Hoffmann F., Placzek G. Introduction to the theory
of neutron diffusion. Vol. 1. Los Alamos, 1953.
65. Лалетин H. И. Метод поверхностных псевдоисточников для решения
уравнения переноса нейтронов// Методы расчета полей тепловых нейтронов
в решетке реактора. М.: Атомиздат, 1974.
520
66. Resonance Absorption of neutron by spheres/ E. R. Wigner e. a.//
J. Appl. Phys. 1955. Vol. 26. P. 260.
67. Chao Y. A., Martinez A. S. On Approximations to the neutron escape
probability from an absorbing body// Nucl. Sci. Engng. 1978. Vol. 66. P. 254.
68. Leslie D. C., Hill J. G., Jonsson A. Improvements to the theory of re-
sonance escape in heterogeneous fuel// Nucl. Sci. Engng. 1965. Vol. 22, N 1.
P. 78—86.
69. Вейнберг А., Вигнер E. Физическая теория ядерных реакторов: Пер.
с англ. М.: Изд-во иностр, лит., 1961.
70. Белл Д., Глесстон С. Теория ядерных реакторов: Пер. с англ. М.:
Атомиздат, 1974.
71. Лукьянов А. А. Замедление и поглощение резонансных нейтронов. М.:
Атомиздат, 1974.
72. Кейз К., Цвайфель П. Линейная теория переноса: Пер. с. англ. М.:
Мир, 1972.
73. Фейнберг С. М., Шихов С. В., Троянский В. Б. Теория ядерных реак-
торов. Т. 1. М.: Атомиздат, 1978.
74. Казанский Ю. А., Матусевич Е. С. Экспериментальные методы физи-
ки реакторов. М.: Энергоатомиздат, 1986.
75. Градштейн И. С., Рыжик И. М. Таблицы интегралов, сумм, рядов и
произведение. Изд. 5-е. М.: Наука, 1971.
76. Pomraning G., Clark М. A new asymptotic diffusion theory// Nucl.
Sci. Engng. 1963. Vol. 17, N 2. P. 227.
77. Девисон Б. Теория переноса нейтронов: Пер. с англ. М.: Госатомиздат,
1960.
78. Placzek G., Seidel W. Milnes problem in transport theory// Phys. Rev.
1947. Vol. 72. P. 550.
79. Cohen E. R. A Numerical Calculation of the milnes problem extra-
polation length// Nucl. Sci. Engng. 1970. Vol. 42, N 2. P. 231.
80. Кострица А. А. Теория переноса нейтронов в движущейся среде. М.:
Атомиздат, 1981.
81. Ruby L. Dancoff’s solution for the number of collisions necessary to
slow down// Nucl. Sci. Engng. 1984. Vol. 86, N 1. P. 110—111.
82. Глесстон С., Эдлунд M. Основы теории ядерных реакторов: Пер.
с англ. М.: Изд-во иностр, лит., 1954.
83. Кулик В. В. Влияние анизотропии упругого рассеяния на параметры
замедления нейтронов// Атомная энергия. 1985. Т. 58. Вып. 2. С. 135—137.
84. Placzek G. On the theory of the slowing down of neutrons in heavy
substances// Phys. Rev. 1946. Vol. 69, N 9. P. 423.
85. Морс Ф. M., Фешбах Г. Методы теоретической физики. Т. 1: Пер.
с англ. М.: Физматгиз, 1962.
86. Галанин А. Д. Теория гетерогенного реактора. М.: Атомиздат, 1971.
87. Агрест М. М., Максимов М. 3. Теория неполных цилиндрических
функций. М.: Гостехиздат, 1965.
88. Измерение длины замедления нейтронов деления в спеченной окиси
бериллия до энергии 1,44 и 0,3/ И. Ф. Жежерун и др.// Атомная энергия.
1962. Т. 13. Вып. 3. С. 258.
89. Ахиезер А. И., Померанчук И. Я. Некоторые вопросы теории ядра.
Изд. 2-е. М.: Гостехиздат, 1950.
90. Бейтман Г., Эрдейн А. Таблицы интегральных преобразований. Т. 1:
Пер. с англ. М.: Наука, 1969.
91. Лукьянов А. А. Структура нейтронных сечений. М.: Атомиздат, 1978.
92. Accurate doppler broadened absorption/ G. W. Hinman, G. F. Kuniciz,
J. B. Sampson e. a.// Nucl. Sci. Engng. 1963, Vol. 16, N 2. P. 202.
93. Справочник по специальным функциям: Пер. с англ. М.: Наука, 1979.
94. Фаддеева В. Н., Терентьев Н. М. Таблицы интеграла вероятности от
комплексного аргумента. М.: Гостехиздат, 1954.
34—6053 521
95. Ishiguro Y. A rigorous expression for shape of a doppler-broadened re-
sonance// Nucl. Sci. Engng. 1966. Vol. 24, N 3. P. 375.
96. Baumann N. P., Owais M. Energy dependence of the 238U thermal
capture cross section// Trans. Amer. Nucl. Soc. 1980. Vol. 34. P. 767.
97. Бете Г. А. Физика ядра. Ч. 2: Пер. с англ. М. — Л., 1948.
98. Ахиезер А. И., Померанчук И. Я. Резонансное поглощение// Поме-
ранчук И. Я. Собрание научных трудов. Т. 1. М.: Наука, 1972. С. 284.
99. Дреснер Л. Резонансное поглощение в ядерных реакторах: Пер.
с англ. М.: Атомиздат, 1962.
100. Steen N. М. Approximate 7(0, ₽) function// Nucl. Sci. Engng. 1969.
Vol. 38, N 3. P. 244.
101. Goldstein R. Intermidiate resonance absorption including interference
scattering and Doppler broadening// Trans. Amer. Nucl. Soc. 1975. Vol. 21.
P. 493.
102. Goertzel G., Grenling F. An approximate method for treating neutron
slowing down// Nucl. Sci. Engng. 1960. Vol. 7, N 1. P. 69.
103. Марчук Г. И. Методы расчета ядерных реакторов. М.: Атомиздат,
1961.
104. Westcott G. Н-, Walker W. Н., Alexander Т. К. Effective cross sections
and cadmium ratios for the neutron spectra of thermal reactors// Proc. 2nd.
Intern,. U. N. Conf. Peaceful Uses Atomic Energy. Geneva, 1958. Vol. 16.
P. 70.
105. Галанин А. Д. Некоторые замечания о спектре тепловых нейтронов
в реакторе// Препринт ИТЭФ № 23. 1974.
106. Ландау Л. Д., Лифшиц Е. М. Механика. М.: Физматгиз, 1958.
107. Гуревич И. И., Тарасов Л. В. Физика нейтронов низких энергий.
М.: Наука, 1965.
108. Kornbichler S., Lemmel Н. D. Bestimmung der Diffusions Konstanten
D(E0, T) and Dv (T) thermischer Neutronen in H2O, Phenylen, ZrHi.92 and D2O
durch Messung der Streuwinkelverteibungen// Nukleonik. 1965. Bd. 7. S. 265.
109. Термализация нейтронов. Труды Брукхейвенской конференции, США,
30 апр. — 2 мая 1962 г.: Пер. с англ. М.: Атомиздат, 1964.
ПО. Спектры медленных нейтронов: Сб. статей: Пер. с англ. М.: Атом-
издат, 1971.
111. Методы расчета полей тепловых дейтронов в решетке реакторов: Сб.
статей/ Под ред. Я. В. Шевелева. М.: Атомиздат, 1974.
112. Jarvis R. ,G. A Review of Diffusion Parameters for Thermal Neutrons
in Light and Heavy Water// AECL, 1964. N 2072.
ИЗ. Попков В. H., Бологов В. Ф. Обзор экспериментальных работ па
измерению длины диффузии в D2O и оценка рекомендованного значения//
Препринт ИТЭФ № 92. 1957.
114. Геометрический параметр правильных многоугольных призм/
И. Э. Исакас, В. В. Кузьминов, Ю. В. Петров и др.// Атомная энергия. 1983.
Т. 54. Вып. 5. С. 371.
115. Murray R. L., Hirons J. J., Reith R. J., Smith O. J. Geometric backling
of polygonal reactors// Nucl. Sci. Engng. 1968. Vol. 34, N 1. P. 86—87.
116. Петров Ю. В., Сахновский Э. Г. О влиянии малого изменения фор-
мы реактора на его критичность// Атомная энергия. 1980. Т. 49. Вып. 2.
С. 127.
117. Gast Р. F., Bournia A. Finding the backling of an elliptic cylinder//
Nucleonics. 1956. Vol. 14, N 4. P. 109.
118. Цвайфель П. Физика реакторов: Пер. с англ. М.: Атомиздат, 1977.
119. Liu Т. С., Liu С. С., Chien J. Р. Spheroidal reactor analysis// J.
Nucl. Energy. 1966. Vol. 20. P. 779.
120. Chen W. L., Isbin H. S. The Prolate ellipsoidal nuclear reactor with
finite reflector// Nukleonik. 1967. Bd 9, N 3. S. 145.
121. Лебедев В. И., Марчук Г. И. Численные методы в теории переноса
нейтронов. Изд. 2-е. М.: Атомиздат, 1981.
522
122. Вычислительные методы в физике реакторов: Сб. статей/ Под ред.
X. Гринспена, К. Келбера, Д. Окрента: Пер. с англ. М.: Атомиздат, 1972.
123. Шихов С. Б. Вопросы математической теории реакторов (линейный
анализ). М.: Атомиздат, 1972.
124. Критические параметры делящихся материалов и ядерная безопас-
ность: Справочник/ Л. Д. Диев, Б. Г. Рязанов, А. П. Мурашов и др. М-<
Энергоатомиздат, 1984.
125. Галанин А. Д. Теория ядерных реакторов на тепловых нейтронах.
М.: Атомиздат, 1959.
126. Бать Г. А., Коченов А. С., Кабанов Л. П. Исследовательские ядер-
ные реакторы. Изд. 2-е. М.: Энергоатомиздат, 1985.
127. Экспериментальные возможности реактора ПИК/ А. Н. Ерыкалов,
И. А. Кондуров, К. А. Коноплев и др.// Препринт ЛИЯФ № 376. 1977.
128. Петров Ю. В. Выбор параметров реакторов для физических иссле-
дований// Препринт ЛИЯФ № 802. 1982.
129. Михайлов В. М., Мырцымова Л. А. Гетерогенный расчет реактора
ТВР// Препринт ИТЭФ-15. 1985.
130. Кочуров Б. П. Численные методы в теории гетерогенного реактора.
М.: Атомиздат, 1980.
131. Siewert С. Е. Ап exact analytical solution of an elementary critical
condition// Nucl. Sci. Engng. 1973. Vol. 51, N 1. P. 78.
132. Siewert С. E., Burniston E. E. On a critical condition// Ibid. Vol. 52,
N 1. P. 150.
133. Graves W. E. Measured slowing down distribution at the indium re-
sonance from a line source of fission neutron in heavy water// Ibid. 1962.
Vol. 12, N 3. P. 439.
134. Гарусов E. А., Петров Ю. В. Малогрупповая расчетная модель за-
медления для водо-алюминиевых активных зон// Атомная энергия. 1972
Т. 32. Вып. 3. С. 225.
135. Гарусов Е. А., Петров Ю. В. Моменты функции замедления и ее
малогрупповые модели для водо-металлнческих смесей// Атомная энергия.
1974. Т. 36. Вып. 2. С. 143.
136. Стумбур Э. А. Применение теории возмущений в физике ядерных
реакторов. М.: Атомиздат, 1976.
137. Льюис Дж. Ценность, сопряженная функция: Пер. с англ. М.: Атом-
издат, 1972.
138. Турбинер А. В. Задача о спектре в квантовой механике и процедура
«нелинеаризации»// Усп. физ. наук. 1984. Т. 144, № 1. С. 35—79.
139. Галанин А. Д. Теория возмущений для уравнения с одной группой
нейтронов// Атомная энергия. 1986. Т. 60. Вып. 4. С. 267.
140. Сахновский Э. Г. Об ускорении сходимости в задачах теории воз-
мущений для ядерных реакторов// Атомная энергия. 1977. Т. 42 Вып 2
С. 141.
141. Бать Г. А., Зарецкий Д. Ф. Эффективные граничные условия в тео-
рии диффузии нейтронов (обзор)// Атомная энергия. 1958 Т. 4. Вып 6
С. 510.
142. Исакова Л. Я. Эффективные граничные условия на поверхности
черного поглощающего стержня// Там же. 1968. Т. 25. Вып. 3. С. 229.
143. Kavenoky A. The Cw-method of solwing the transport equation; appli-
cation to cylindrical geometry// Nucl. Sci. Engng. 1978. Vol. 65. P. 514,
144. Песков P. А., Самойлов О. Б. К вопросу об эффективных граничных
условиях на поверхности поглощающих стержней// Атомная энергия 1974
Т. 37. Вып. 5. С. 417. '
145. Амуял А., Бенуа П., Горовиц Д. Новый метод определения коэффи-
циента использования тепловых нейтронов в элементарной ячейке// Некото-
рые вопросы ядерной энергетики/ Под ред. М. А. Стыриковича М : Атом-
издат, 1959. С. 237.
34* 523
146. Галанин А. Д. О вычислении коэффициента теплового использова-
ния// Нейтронная физика. М.: Госатомиздат, 1961. С. 125.
147. Румянцев Г. Я. Граничные условия в методе сферических гармоник//
Атомная энергия. 1961. Т. 10. Вып. 1. С. 26.
148. Смелов В. В. Лекции по теории переноса нейтронов. Изд. 2-е. М.:
Атомиздат, 1978.
14 9г Peierls R. Critical conditions in neutron multiplication// Proc. Cam-
bridge Philos. Soc. 1939. Vol. 35. P. 610.
150. Лалетин H. И. Чувствительность коэффициента использования теп-
ловых нейтронов к вариациям макроскопических сечений// См. [111]. С. 289.
151. Лалетин Н. И. Метод поверхностных псевдоисточников для решения
уравнения переноса нейтронов// См. [111]. С. 187.
152. Бурмистров А. Я-, Кочуров Б. П. Решение интегрального уравнения
Пайерлса в многозонной цилиндрической ячейке// Препринт ИТЭФ № 49.
1976.
153. Распределение плотности нейтронов в серых цилиндрах/ А. М. Во-
ронина, А. С. Кронрод, 3. С. Рябова и др.// Тр. Второй международной
конф, по мирному использованию атомной энергии (Женева, 1958). Докл.
советских ученых. Ядерные реакторы и ядерная энергетика. М.: Атомиздат,
1959. С. 207.
154. Петров Ю. В. Многократное ускорение нейтронов в инверсно засе-
ленной среде// ЖЭТФ. 1972. Т. 63, № 3. С. 758—760.
155. Neutron thermalization in reactor lattice cells/ R. J. J. Stammler e. a.
Vienna, 1966.
156. Jaderna energie. 1975. Vol. 21, N 4.
157. Семенов В. В. Основные физико-технические характеристики реак-
торной установки ВВЭР// Препринт ИАЭ № 3104. 1979.
158. Михайлов В. М. TERMIT — программа решения многогрупповых
интегральных уравнений переноса нейтронов в тепловой области для цилин-
дрической ячейки// Препринт ИТЭФ № 119. 1978.
159. Honeck Н. С. The calculation of the thermal utilization and disadvan-
tage factor in uranium-water lattices// Nucl. Sci. Engng. 1964. Vol. 18, № 1.
P. 49.
160. Бурмистров А. Я., Кочуров Б. П. Пространственно-энергетическое
распределение нейтронов в цилиндрической ячейке реактора (программа
TRIFON)// Препринт ИТЭФ № 107. 1978.
161. Гуревич^И. И., Померанчук И. Я. Теория резонансного поглощения
в гетерогенных системах// См. [98]. С. 270.
162. Bell G. I. A simple treatment for effective resonance absorption cross
sections in dense lattices// Nucl. Sci. Engng. 1959. Vol. 5. N 2. P. 138.
163. Sauer A. Approximate escape probabilities// Nucl. Sci. Engng. 1963.
Vol. 16, № 3. P. 329.
164. Колесов В. В., Лукьянов А. А. Метод оценки доплеровского ушире-
ния резонансов// Атомная энергия. 1979. Т. 47. Вып. 3. С. 205.
165. Dresner L. Some remark on the effect a nonuniform temperature di-
stribution in the temperature dependence of resonance absorption// Nucl. Set
Engng. 1961. Vol. 11, N 1. P. 35.
166. Pettus W. G., Baldwin M. N. Doppler coefficient measurements on Th
and ThO2 rods with nonuniform temperature distributions// Ibid. 1961. Vol. 26,
N 1. P. 34.
167. Петров to. B. Резонансное поглощение в тесно расположенных ма-
лых блоках// Атомная энергия. 1957. Т. 2. Вып. 4. С. 357.
168. Hellstrand Е. Measurements of the effective resonance integral in
uranium metal and oxide in different geometries// J. App. Phys. 1957. Vol. 28,
N 12. P. 1493.
169. Шихов С. В. Учет гетерогенного резонансного блок-эффекта при со-
ставлении многогрупповых констант для расчета тепловых реакторов// Атом-
ная энергия. 1966. Т. 20. Вып. 1. С. 17.
524
15—2Э
170. Segev М. An equivalence relation for a doubly heterogeneous lat-
tice// Nucl. Sci. Engng. 1982. Vol. 81, N 1. P. 151.
171. Спанье Дж., Гелбард Э. Метод Монте-Карло и задачи переноса ней-
тронов'. Пер. с англ. М.: Атомиздат, 1972.
172. Франк-Каменецкий А. Д. Моделирование траекторий нейтронов при
расчете реакторов методом Монте-Карло. М.: Атомиздат, 1978.
173. Experimental studies of 23SU resonance neturcn capture in UO2 fuel
rods/ G. C. Smith, J. Hardy, D. Klein e. a.// Nucl. Sci. Engng. 1961. Vol. 9,
N 4. P. 421.
174. Hellstrand E. Measurement of resonance integrals// Reactor physics
in the resonance and thermal regions: MIT Press, 196Q. Vol. 2. P. 151.
175. Hellstrand E., Lundgren G. The resonance intergral for uranium metal
and oxide// Nucl. Sci. Engng. 1962. Vol. 12, N 3. P. 435.
176. Благоволин П. П., Галанин А. Д. Определение блокированного ре-
зонансного поглощения в 238U н его температурной зависимости путем ре-
шения интегрального уравнения переноса// Препринт ИТЭФ № 106. 1978.
177. Благоволин П.- П. Многогрупповая программа вычисления эффек-
тивного резонансного интеграла в многослойной цилиндрической ячейке теп-
лового реактора// Резонансное поглощение нейтронов. Материалы Всесоюз-
ного семинара по резонансному поглощению нейтронов, июнь 1977. М.: Изд.
МИФИ, 1978. С. 29.
178. Благоволин П. П., Галанин А. Д. О масштабе погрешности вычисле-
ния эффективного резонансного интеграла в тепловом реакторе// См. [177].
С. 79.
179. Seminar on 23SU Resonance Capture. Ed. S. Pearlstein. 1975.
BNL-NCS-50451.
180. Метод расчета физических параметров однородных решеток тяже-
ловодных реакторов с газовым охлаждением типа КС/ А. Д. Галанин,
Б. И. Ильичев, Б. П. Кочуров и др.// Jaderna energie. 1975. С. 21. С. 134.
181, Кочуров Б. П. Эффективные резонансные уровни// Атомная энер-
гия. 1986. Т. 60. Вып. 3. С. 176.
182. Акимушкин С. В., Кочуров Б. П. Эффективные уровни урана-238.
ВАНТ. Сер. Физика ядерных реакторов. 1990. № 1.
183. Кочуров Б. П. Тестовые расчеты физических параметров критиче-
ских сборок TRX, BETTIS и MIT по программе TRIFON// Препринт ИТЭФ
№ 164. 1980.
184. Takano Н., Ishiguro V., Matsura S. Effect of resonance interference
between 238U and 133Cs on isotope correlation of fission product// Nucl. Cross
Sections for Technology. Proc. Intern. Conf., Knoxville, 1979: U S. Dep ol
Com. NBS, Spec. Publ. 1980. N 594. P. 224.
185. Шведов О. В., Белкин В. Ф., Попков В. Н. Эффективный резонанс-
ный интеграл втулочных тепловыделяющих элементов, содержащих замедли-
тель во внутренней полости// Бюл. информ, центра по ядерным данным. М.:
Атомиздат, 1968. Вып. 5. С. 176.
186. Hellstrand Е,, Lindahl G., Lundgren G. Studies of the effictive total
resonance absorption cross sections for zircaloy 2 and zirconium// Arkiv Fysik.
1962. Vol. 20. P. 559.
187. Kocic A., Markovic V. Experimental determination of resonance ab-
sorption cross section for zircaloy and zirconium// Bull, of the Boric Kidric
Inst, of Nucl. Sci 1968. Vol. 19, N 2.
188. Бурмистров А. Я-, Кочуров Б. П. Эффективный резонансный инте-
грал прн больших шагах решетки и размножение на быстрых нейтронах//
Атомная энергия. 1973. Т. 35. Вып. 2. С. 122.
189. Наумов В. И., Юрова Л. Н. О поправках к эффективному резонанс-
ному интегралу прн больших шагах гетерогенной решетки// Физика ядерных
реакторов. Вып. 1. М.: Атомиздат, 1968. С. 133.
190. Markl Н., Fowler A. G. Generalized method for calculating the fast
fission effect in coacsial cylindrical lattice cells// Nukleonik. 1964 Bd 6 N 1
S. 39, . . .
525
191 Тамм И. Е. Основы теории электричества. Изд. 5-е. М.: Гостехиздат,
1954.
192. Илиева К. Д., Степанов А. В. К теории диффузии тепловых нейтро-
нов в среде со случайными неоднородностями// Краткие сообщения по фи-
зике./1972. № 4. С. 65.
193. Выгорание горючего в водо-водяных энергетических реакторах н
эксперименты с уран-водной решеткой/ С. М. Фейнберг, Е. С. Анциферов,
В. П. Катков н др.// См. [153]. С. 411.
194. Беднаж Р., Кочуров Б. П. Условие критичности гетерогенного реак-
тора с блоками конечного радиуса// Nukleonika. 1964. Bd 9, N 6. S. 439.
195. Галанин А. Д. Развитие теории гетерогенных ядерных реакторов//
Проблемы ядерной физики и физики элементарных частиц (памяти акад.
А. И. Алиханова). М.: Наука, 1975. С. 330.
196. Доллежаль Н. А., Емельянов И. Я- Канальный ядерный энергетиче-
ский реактор. М.: Атомиздат, 1980.
197. Carter С., Jarvis R. Influence of a cylindrical channel on a neutron
flux which varies linearly in a direction perpendicular to the axis of the chan-
nel// Reactor Sci. and Techn. 1961. Vol. 15. P. 113.
198. Deniz V., Le Ho J. G., Sagot M. Study of lattices of graphite with
empty channels by means of the pulsed source technique// Nucl. Sci. Engng.
1968. Vol. 32, N 2. P. 202.
199. Жежерун И. Ф. Проверка теории диффузии нейтронов в среде с ка-
налами импульсным методом (решетка каналов большого поперечного раз-
мера)// Атомная энергия. 1972. Т. 32. Вып. 2. С. 143.
200. Григорьев И. С., Новиков В. М. Диффузия нейтронов в гетероген-
ных средах. М.: Атомиздат, 1966.
201. Лалетин Н. И. Заметки о диффузии нейтронов в среде с каналами//
Атомная энергия. 1972. Т. 32. Вып. 4. С. 328.
202. Behrens D. J. The effect of holes in a reacting material on the pas-
sage of neutrons// Proc. Phys. Soc. 1949. Vol. Аб2. P. 107.
203. Лалетин H. И. Влияние цилиндрического канала на диффузию ней-
тронов// Атомная энергия. 1959. Т. 7. Вып. 1. С. 18.
204. Benoist Р. Streaming effects and collision probabilities in lattices//
Nucl. Sci. Engng. 1968. Vol. 34, N 3. P. 285.
205. Степанов А. В. Вычисление коэффициента проигрыша методом тео-
рии возмущений// Атомная энергия. 1969. Т. 26. Вып. 3. С. 281.
206. Степанов Д, В. К теории переноса нейтронов в неоднородных сре-
дах// Тр. ФИАН. Т. 44. М„ 1969. С. 204.
207. Лалетин Н. И. Распространение нейтронов в гетерогенной среде//
См. [153]. С. 634.
208. Ахиезер А. И., Померанчук И. Я. Введение в теорию нейтронных
мультиплицирующих -систем// См. [98]. С. 284.
209. Фейнберг С. М. Гетерогенные методы расчета реакторов// Тр. меж-
дунар. конф, по мирному использованию атомной энергии (Женева, 1955).
Реакторостроение и теория реакторов. Докл. советских ученых Т. 5. М.:
Изд-во АН СССР, 1955. С. 578.
210. Auerbach Т. A consistent heterogeneous theory of reflected lattices//
Nucl. Sci. Engng. 1967. Vol. 29, N 3. P. 317.
211. Галанин А. Д. К теории сложной решетки ядерных реакторов//
Препринт ИТЭФ № 943. 1972.
212. Галанин А. Д., Торлин Б. 3. Сложная решетка в Р3-приближении//
Атомная энергия. 1974. Т. 36. Вып. 2. С. 125.
213. Раевская В. Е., Торлин Б. 3. Метод матричной прогонки для расче-
та сложной решетки в Рз-приближении// Там же. 1980. Т. 49. Вып. 5. С. 310.
214. Кварацхели А. Ю., Кочуров Б. П. Метод вычисления физических
характеристик ячейки гетерогенного реактора// Там же. 1985. Т. 58. Вып. 2.
С. 183.
526
215. Городков С. С. Новый метод расчета гетерогенных реакторов// Пре-
принт ИАЭ № 2251. 1973.
216. Городков С. С. Трехмерная формулировка квазиальбедного метода
расчета гетерогенного реактора// Препринт ИАЭ № 2729. 1976.
217. Лалетин Н. И., Ельшин А. В. Уточнение метода гомогенизации ге-
терогенного реактора// Атомная энергия. 1977. Т. 43 Вып. 247.
218. Лалетин Н. И., Ельшин А. В. Вывод конечно-разностных уравнений
гетерогенного реактора// Препринт ИАЭ № 3280/5. 1980.
219. JNDC FP decay and yield data/ H. Ihara, Z. Matumoto, K. Tasaka
e. a.// JAERI-M, 9715, 1981.
220. Ottewitte E. H. Signifficance of expanded xenon and samarium infor-
mation// Trans. Amer. Nucl. Sci. 1977. Vol. 27. P. 921,.
221. Рудик А. П. Оптимизация физических характеристик ядерных реак-
торов. М.: Атомиздат, 1979.
222. Герасимов А. С., Рудик А. П. Отравление реактора ксеноном-135.
М.-. Атомиздат, 1982.
223. Зарицкая Т. С., Рудик А. П. Оптимальное выжигание I49Sm при
остановке высокопоточного реактора// Атомная энергия. 1969. Т. 26. Вып. 5.
С. 448.
224. Галанин А. Д. Аппроксимация поглощения нейтронов продуктами
деления одним эффективным осколком// Там же. 1981. Т. 50. Вып. 1. С. 3.
225. Галанин А. Д. Эффективные осколки при делении урана-223 и то-
рия-232/ Препринт ИТЭФ № 183. 1983.
226. Кривохатский А. С., Романов Ю. Ф. Получение трансурановых и
актиноидных элементов при нейтронном облучении. М.: Атомиздат, 1970.
227. Круглов А. К., Рудик А. П. Реакторное производство радиоактив-
ных нуклидов. М.: Энергоатомиздат, 1985.
228. Востриков М. В., Кочуров Б. П. TRIFOB — программа расчета изме-
нения изотопического состава топлива в цилиндрической ячейке реактора
с детальным учетом пространственно-энергетического распределения нейтро-
нов// Препринт ИТЭФ № 106. 1981.
229. Определение содержания изотопов урана и трансурановых элемен-
тов в отработанном топливе ВВЭР-365/ В. Я. Габескирия, В. В. Грызина,
А. А. Зайцев и др.// Атомная энергия. 1978. Т. 44. Вып. 5. С. 440.
230. Зарицкая Т. С., Рудик А. П. Комбинированно-итерационный метод
расчета выгорания топлива в ядерных реакторах// Препринт ИТЭФ № 99.
231. Петросьянц А, М. Современные проблемы атомной науки и техники
в СССР. Изд. 4-е, перераб. и доп. М.: Атомиздат, 1979.
232. Троянов М. Ф. Развитие научно-технических основ энергетических
быстрых реакторов// Атомная энергия. 1981. Т. 50. Вып. 2. С. 102.
233. Raman S. General survey of applications which require actinide nuc-
lear data// Transactinium Isotope Nuclear Data (TND) IAEA, Vienna, 1976
Vol. 1. P. 39,
234. Левина И. K-> Сидоренко В. А. Некоторые нейтронно-физические
аспекты улучшения использования топлива в водоохлаждаемых энергетиче-
ских тепловых реакторах ВВЭР и РБМК// Атомная энергия. 1986. Т. 60.
Вып. 4. С. 243.
235. Kuczera В., Goetzmann С. A., Brogli R. Der Fortgeschrittene Druck-
wasserreaktor (FDWR)// Atomwirtschaft —Atomtechnik. 1986. Vol 31 N 6
P. 290—296.
236. Торлин Б. 3. Распределение плотности нейтронов в реакторах с глу-
боким выгоранием топлива// Препринт ИТЭФ № 242. 1964.
237. Орлов В. В. Нелинейная одногрупповая теория большого реактора//
Вопросы атомной науки и техники. Сер. Физика и техника ядерных реакто-
ров. 1987. Вып. 2. С. 3—11.
527
238. Никифоров А. С., Землянухин В. И., Шмидт В. С. Вопросы регене-
рации отработавшего топлива АЭС// Атомная энергия. 1981. Т. 50. Вып. 2.
С. 122.
239. Христенко П. И. Повторное использование энергетического плутония
и урана и регенерация нейтронов в тепловом реакторе// Там же. 1977. Т. 42.
Вып./4. С. 272.
240 Бяков В. М., Иоффе Б. Л. Гомогенный реактор на естественном ура-
не// См. [153]. С. 398.
241. Блинкин В. Л., Новиков В. М. Жидкосолевые ядерные реакторы.
М.: Атомиздат, 1978.
242. Мурогов В. М„ Троянов М. Ф., Шмелев А. Н. Использование тория
в ядерных реакторах. М.: Энергоатомиздат, 1983.
243. Зависимость удельной энергии от режима эксплуатации энергетиче-
ских реакторов// Т. С. Зарицкая, Г. В. Киселев, А. П. Рудик, Э. М. Цен-
тер/ Препринт ИТЭФ-26. М., 1986.
244. Harbour R. М., MacMurdo R. W., Crosson F. J. Thermal neutron cap-
ture cross sections and cature resonance integrals of americium-241// Nucl.
Sci. Engng. 1973. Vol. 50, N 4. P. 364.
245. Матвеев Л. В., Центер Э. М. Проблема накопления 232U и 236Ри
в ядерном топливе// Атомная техника за рубежом. 1980. № 4. С. 10.
246. Зависимость образования 232U в ядерном топливе от спектра нейтро-
нов/ Т. С. Зарицкая, С. М. Зарицкий, А. К. Круглов и др.// Атомная энер-
гия. 1980. Т. 48. Вып. 2. С. 67.
247. Киселев Г. В., Рудик А. П. Теория оптимизации процессов образова-
ния нуклидов// Препринт ИТЭФ № 134. 1985.
248. Davison В. Influence of a black sphere and of black cylinder upon the
neutron density in an infinite non-capturing medium// Proc. Phys. Soc. 1951.
Vol. A64. P. 181.
249. Михайлов В. M., Мырцымова Л. А. Расчет выгорающего поглотите-
ля в цилиндрической ячейке тепловыделяющей сборки реактора ТВР-М//
Препринт ИТЭФ № 63. 1985.
250. Афанасьев А. М., Торлин Б. 3. Поведение реактора после скачка
реактивности, введенной локально// Препринт ИТЭФ № 83. 1981.
251. Зельдович Я. Б., Харитон Ю. Б. Кинетика цепного распада урана//
ЖЭТФ. 1940. Т. 10. С. 477.
252. Randall D., John D. S. Xenon spatial oscillations// Nucleonics. 1958.
Vol. 16, N 3. P. 82.»
253. Афанасьев A. M., Торлин Б. 3., Трубенко A. M. Об устойчивости и
частотах пространственных ксеноновых колебаний// ВАНТ. Сер. Динамика
ядерных энергетических установок. 1977. Вып. 1. С. 15.
254. Крамеров А. Я., Шевелев Я. В. Инженерные расчеты ядерных реак-
торов, М.: Энергоатомиздат, 1984.
255. Афанасьев А. М., Торлин Б. 3. Автоматический регулятор и ксено-
новые колебания// Атомная энергия. 1977. Т. 43. Вып. 4. С. 21
256. Торлин Б. 3. Влияние размещения датчиков на азимутальную и
радиальную устойчивость реактора// Атомная энергия. 1980. Т. 48. Вып 5.
С. 297.
257. Конев В. Н., Торлин Б. 3. Методика двумерного анализа устойчиво-
сти распределения нейтронов в реакторе// Атомная энергия. 1983. Т. 54
Вып. 6. С. 390.
258. Хитчкок А. Устойчивость ядерных реакторов: Пер. с англ. М.: Гос-
атомиздат, 1963.
259. Горяченко В. Д. Методы теории устойчивости в диапазоне ядерных
реакторов. М.: Атомиздат, 1971.
260. Хетрик Д. Динамика ядерных реакторов: Пер. с англ. М.: Атом-
издат, 1975.
261. Емельянов И. Г., Гаврилов П. А., Селиверстов Б. Н. Управление и
безопасность ядерных энергетических реакторов. М.: Атомиздат, 1975.
528
чнниими;
262. Рекомендуемые согласованные значения фундаментальных
ских постоянных (Доклад рабочей группы CODATA по фундамеитЫМИЙ
физическим постоянным, август 1973)// Усп. физ. наук. 1975. Т. 115. ВЫГЬ
С. 623.
263. Франк А. И. Фундаментальные свойства нейтрона: пятьдесят лет
исследований// Там же. 1982. Т. 137. Вып. 1. С. 5.
264. Wapstra А. Н., Bos К. The 1977 atomic mass evaluation, part 1. Ato-
mic mass table// Atomic Data and Nuclear Data Tables. 1977. Vol. 19, N 3.
P. 177.
265. Сечение деления долгоживущего изомера 236Np тепловыми нейтро-
нами/ Б. Н. Беляев, Е. А. Громова, С. С. Коваленко и др.// Атомная энергия.
1986. Т. 60. Вып. 2. С. 146.
266. Сечение деления короткоживущего изомера 236Np тепловыми ней-
тронами/ Е. А. Громова, С. С. Коваленко, Ю. С. Немилов и др.// Атомная
энергия. 1984. Т. 56. Вып. 4. С. 212—214.
267. Japanese evaluated nuc. data library. JENDL-1, March, 1979.
268. Benjamin R. W. Status of measured neutron cross sections of trans-
actinium isotopes for thermal reactors// In (233]. Vol. 2. P. 1.
269. Прямые измерения эффективного сечения радиационного захвата
тепловых нейтронов дейтронами/ В. П. Алфименков, С. Б. Борзаков,
Э. В. Васильева и др.// Ядерная физика. 1980. Т. 32, № 6. С. 1491.
270. Paschall R. К. The age of fission neutron to indium resonance energy
in water// Nucl. Sci. Engng. 1964. Vol. 20, N 4. P. 436.
271. Olcott R. N. Homogeneous heavy water moderated critical assemblies.
Part I. Experimental// Ibid. 1956. Vol. 1, N 4. P. 327.
272. Wade J. W. Neutron Age in Mixture of D2O and H2O// Ibid. 1958.
Vol. 4, N 1. P. 12.
273. Жежерун И. Ф. Изучение диффузии нейтронов в бериллии импульс-
ным методом// Атомная энергия. 1964. Т. 16. Вып. 3. С. 224.
274. Жежерун И. Ф.' Изучение диффузии нейтронов в спеченной окиси
бериллия импульсным методом// Там же. 1963. Т. 14. Вып. 2. С. 193.
275. Жежерун И. Ф. Проверка теории диффузии нейтронов в среде с ка-
налами импульсным методом (тесная решетка каналов малого диаметра)//
Там же. 1968. Т. 24. Вып. 1. С. 33.
276. Campbell R. W., Paschall R. К., Swanson V. A. The Age of fission
neutron to indium resonance energy in graphite// Nucl. Sci. Engng. 1964.
Vol. 20, N 4. P. 445.
• 277. Марченко Л. В., Сергеев Ю. А. Расчет квадрата длины замедления
для различных сред в 18- и 26-групповых /^-приближениях и их сравнение
с экспериментальными данными// Бюл. центра по ядерным данным. М.:
Атомиздат, 1969. Вып. 6. С. 319.
278. Гусев Н. Г., Дмитриев П. П. Радиоактивные цепочки: Справочник.
М.: Энергоатомиздат, 1988.
279. Parametres of the 1.056 eV resonance in 240Pu and 2200 m/c neutron
total ceoss sections of ?35U. 23?Pu and 241Pu/ R. R. Spencer, J. A. Harwey e. a.//
Nucl. Sci. Engng. 1987._Vol. 96, № 9. P. 318—329.
280. Evaluation of v0 for 239Pu: impact for applications of the fluctuations
at low energy/ E. Fort, J. Frehaut e. a.// Ibid. 1988. Vol,. 99, № 8. P. 375—389.
АЛФАВИТНО-ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Активна^ зона 32
Альбедо 49
Анизотропная диффузия 164, 302, 306
Асимптотическая часть функции Гри-
на 496
Асимптотический поток замедляю-
щихся нейтронов 60
Баклинг 47
Белое граничное условие 223
Блок-эффект 32
— при поглощении тепловых ней-
тронов 210
-------------внешний 213, 227,
324
— полный 210, 213,
216, 227, 318
— при резонансном поглощении
241, 256, 279
Вероятность выхода нейтрона 30, 35
— избежать резонансного погло-
щения 30, 87, 500
—-------— в гетерогенном реак-
торе 247
— изменения энергии при упру-
гом столкновении 54
— первого столкновения 35, 223
------для цилиндра 35, 515
— поглощения теплового нейтро-
на ураном 30, 209
— столкновения 33
— утечки 30
Вес уровня 242
Возмущение в реакторе 165
Возраст нейтронов 58, 514
•-----до индиевого резонанса 69,
514
Время жизни свободного нейтрона
503
— — теплового нейтрона 42
— замедления 57
Выгорание гадолиния 438
— гафния 440
— европия 438
Высокопоточный реактор 146
530
Выход основных продуктов деления
365
— радиоактивных продуктов де-
ления 342, 351
Выход сильнопоглощающих продук-
тов деления 354
— цепочки 22
Геометрический параметр 127
Гетерогенный реактор 30, 314
— — , численные методы 340
Глубина выгорания топлива 383, 393
Гомогенизация реактора 32, 257, 317
Граница тепловой группы нейтронов
39, 98, 100, 229
Граничное условие в Р2 приближе-
нии 219, 494
— — для плотности замедления
63, 120
— — — потока тепловых ней-
тронов 48, 120
-----на поверхности блока 211,
337
----------, граничащей с ваку-
умом 48
—------серого цилиндра 192
-------черного цилиндра 191,
515
—•-----черной сферы 435
Группы запаздывающих нейтронов 12
— нейтронов ПО
Двухгрупповое представление сече-
ний 103
Дипольный момент блока 304
Длина диффузии 42, 496
----- в воде 116
-----в гетерогенном реакторе 306
— — в тяжелой воде 117
— замедления 64
----- в гетерогенном реакторе
306
— миграции 47, 157, 302, 307
— поглощения 34
— рассеяния 34
Доплеровское уширение уровней 76,
251
Жесткость нейтронного спектра 58,
104
Закон l/v 80
Замедляющая способность 57
Замкнутый топливный цикл 416
Запаздывающие нейтроны деления 11
— фотонейтроиы 13
Изотропия рассеяния 15
Интерференция резонансных уровней
285
Иодная яма 350
Кадмиевая граница 80
Калифорний-252 425
Качество исследовательского реакто-
ра 146
Коэффициент блокировки резонанс-
ного интеграла 241
--------- тепловых нейтронов 210
— воспроизводства 400
— диффузии 41
-----в Р2 приближении 219, 494
— диффузии в воде 116, 117
— интерференции регуляторов
200
— конверсии 31, 384, 393
— поляризации 303, 310
— проигрыша 213
— размножения 30, 119, 157
— усреднения потока 131, 133,
140
— экранировки 50, 216, 225
— — полого цилиндра 218
Критерий устойчивости 471
Критическая сборка 313
Критический объем 30, 129, 144
Кумулятивный выход 21
Лапласиан 47
Летаргия 55
Ловушка нейтронов 150
Материальный параметр 47, 127
Матрица граничных коэффициентов
336
Метод баланса 188
— вероятности первого столкно-
вения 223
— Грюлинга — Герцеля 91
— эффективных граничных усло-
вий 150
Моменты функции Грина 124, 161
Независимый выход 21
Нейтроны быстрые '39, 290
— деления запаздывающие 11
-мгновенные 6
Нейтроны деления спонтанного 426
— замедляющиеся 39
— тепловые 39
Нептуниевая яма 380
Неупругое рассеяние 15
Односторонний ток 40
Оптический путь 222
Отражатель 32, 136, 141
Параметры резонансных уровней ура-
на 238 238, 281
Период разгона реактора 442, 453
Плотность замедления 59
— потока нейтронов 38
— тока нейтронов 38
Плутониевый коэффициент 378
Плутоний-236, образование в реакто-
ре 428
— — 238, получение в реакторе
426
Поляризация блоков 303
Поправка Белла 37, 247
—• Данкова — Гинзбурга 258
Потенциальное рассеяние 75
Приближение бесконечной массы по-
глотителя 86, 500
— Вигнера 88
— возрастное 57, 84, 121, 158
— двухгрупповое 113, 141
— диффузионное 41, 491
— изолированного блока 240
— малогрупповое 122
— многогрупповое 109
— одногрупповое 47, 125
— односкоростное 221, 490
— рациональное 36, 246, 515
— точечное 446
— узкого резонанса 90
— Ферми 84
Продукты деления 20
----основные 365
----радиоактивные 342, 351
----сильнопоглощающие 354
Равновесная концентрация плутония
388, 417
Реактор гетерогенный 32, 314, 335
— гомогенный 32, 125
— на тепловых нейтронах 32
Резонансная линия доплеровская 76,
79
-------- естественная 74
Резонансный интеграл 80
— — бесконечного разведения
80, 82
— — блока с легкими ядрами
264
----блокированный 88, 241,276
531
Резонансный интеграл для закона
1/у 81
--------кластера 266, 267, 289
--------неблокированный 82, 241,
279
--- полого цилиндра 263
— — с учетом доплеровского
уширения 91, 251
---урана 238, 275
------- теоретический 275, 281
— — — экспериментальный 279
циркония 289
Решетка регуляторов 332
Самариевая смерть реактора 358
Сечение деления 14, 17, 505
— доплеровское 78
— макроскопическое 14, 512
— неупругое 14, 16
— поглощения 14, 505, 510
— рассеяния 14, 505, 510
— транспортное 16
— увода 112
Скорость реакции 103
Сопряженный поток 172
Спектр замедляющих нейтронов 57,
84
— запаздывающих нейтронов 13
— максвелловский 96
— мгновенных нейтронов деле-
ния 9
— нейтронов в реакторе 98, 231,
234
— Ферми 57
Среднее сечение пары осколков 362
— число столкновений при за-
медлении 56, 498
Средний квадрат перемещения при
диффузии 45 с
------------ при замедлении 64
— косинус угла рассеяния 16,
115
Средняя длина пробега 33, 512
— скорость нейтронов в максвел-
ловском спектре 96
— хорда 37, 245
— — кластера 267
— энергия нейтронов деления 9
запаздывающих 13
Теплотворная способность ядерного
топлива 403
Ториевый цикл 423
Удельный расход топлива 397
Уравнение Гельмгольца 125
— Пайерлса 222
— самосопряженное 172
— сопряженное 172
Уран 232, образование в реакторе 428
532
Условие применимости возрастного
приближения 70
— — двухгруппового уравнения
122, 159
--------уравнения диффузии 45
Фактор Весткота 17, 97, 509
Формула Биренса 312
— Брейта и Вигнера 74
— Карлвика и Перш'агена 263
— «обратных часов» 452
— суммирования Пуассона 65
— четырех сомножителей 30
Функция Грина уравнения диффузии
43
----------- замедления возрастная
63
-----------двухгрупповая 121
— --------- односкоростного 495
Ценность нейтрона 175
Ширина опасной зоны 89, 236
— уровня доплеровская 77
— — естественная 74
практическая 236
Экстраполированная граница 48
Энерговыделения в топливе после вы-
грузки 27, 374, 516
— при делении 23
— при распаде трансактиноидов
27, 504
Эффективная температура нейтронов
97
— толщина отражателя 152
Эффективное сечение рассеяния 264
Эффективность регулятора 192
— — в возрастном приближении
206
— — в двухгрупповом прибли-
жении 201
Эффективные резонансные уровни
урана-238 284
Эффективный коэффициент диффузии
47
— — размножения 30, 157, 158,
163
— осколок 363
— — слабопоглощающий 365
— радиус черного цилиндра 193
Ядро гетерогенного уравнения 315
— первого столкновения 34
Ячейка Вигнера — Зейтца 210
— сложная 329
— цилиндрическая 210
— шестигранная 327
ОГЛАВЛЕНИЕ
Предисловие к первому изданию...................................... 3
Предисловие ко второму изданию..................................... 5
ЧАСТЬ I
ГОМОГЕННЫЙ РЕАКТОР
Глава 1. Некоторые сведения из нейтронной физики................... 6
1.1. Число вторичных нейтронов при делении ядер....... 6
1.2. Спектр мгновенных нейтронов деления............... 9
1.3. Запаздывающие нейтроны........................... 11
1.4. Взаимодействие нейтрона с ядрами..................14
1.5. Сечения основных нуклидов........................ 17
1.6. Продукты деления*.....................................= 20
1.7. Энерговыделение при делении.......................23
1.8. Реакция (п, 2п)...................................28
1.9. Условия осуществления цепной реакции деления .... 29
1.10. Вероятность столкновения.................................33
Глава 2. Элементарная теория диффузии и замедления нейтронов 38
2.1. Уравнение диффузии нейтронов......................38
2.2. Замедление нейтронов..............................53
2.3. Поглощение нейтронов при замедлении...............74
2.4. Спектр нейтронов в реакторе. Скорость реакций .... 95
Глава 3. Групповые уравнения..............................109
.' ’3.1. Многогрупповые диффузионные уравнения................К109’
3.2. Уравнения с двумя группами нейтронов......................113
3.3. Двухгрупповое и возрастное приближения....................121
Глава 4. Критические размеры гомогенного реактора.................125
4.1. Однородный реактор без отражателя. Одна группа нейтронов 125
4.2. Неоднородный реактор без отражателя. Одна группа нейтронов 132
4.3. Реактор с отражателем. Одна группа нейтронов .... 136
4.4. Реактор с отражателем. Две группы нейтронов...............141
4.5. Метод эффективных граничных условий.......................150
4.6. Реактор без отражателя. Общий метод.......................155
к/'
/ Глава 5. Теория возмущений.......................................165
5.1. Теория возмущений для уравнения с одной группой нейтронов 165
V 5.2. Теория возмущений для уравнений с двумя группами нейтронов
5.3. Нелинейная запись одногруппового уравнения и теория воз-
мущений ..................................................179
Глава 6. Регулятор р гомогенном реакторе...........................188
6.1. Эффективное граничное условие для черного цилиндра . . . 188
6.2. Регулятор в одногрупповом приближении....................192
533
6.3. Интерференция двух регуляторов........................ 199
6.4. Регулятор в двухгрупповом и возрастном приближениях . . 201
ЧАСТЬ II
ГЕТЕРОГЕННЫЙ РЕАКТОР
Глава 7. Поглощение тепловых нейтронов..............................209
J.I. Основные определения . . . . . ................ 209,
^.2. Диффузддвдоа^прибщжение . а,Т*.............................J12.
7,-3. Приближение .............................................219
* 7.j. Односкоростное приближение............................221
7.5. Тер^ЛйзаТ1ИЯ*“неитронов“..............................229
Глава 8. Резонансное поглощение.....................................235
8.1. Блок-эффект для резонансного поглощения...............235
8.2. Зависимость резонансного поглощения от температуры . . 251
8.3. Интерференция блоков..................................256
8.4. Резонансное поглощение сложными блоками...............261
8.5. Распределение поглощенных нейтронов по блоку .... 268
8.6. Экспериментальные данные о резонансном поглощении и ре-
зультаты численных расчетов...............................275
Глава 9. Быстрые нейтроны...........................................290
9.1. Размножение на быстрых нейтронах.................... . 290
9.2. Реакция (п, 2га)..........................................295
Глава 10. Длина миграции и лапласиан................................300
10.1. Качественные соображения и диффузионное приближение 300
10.2. Длина миграции...........................................306
10.3. Зависимость коэффициента размножения и лапласиана от ша-
га решетки и радиуса блока...............................312
Глава И. Теория гетерогенного реактора...........................314
11.1. Гетерогенный реактор с малыми блоками....................314
11.2. Внешний блок-эффект......................................324
11.3. Сложная решетка..........................................329
11.4. Гетерогенный реактор с большими блокамц..................335
ЧАСТЬ III
ИЗМЕНЕНИЕ СВОЙСТВ РЕАКТОРА ВО ВРЕМЕНИ
Глава 12. Влияние продуктов деления на работу реактора .... 342
12.1. Отравление реактора радиоактивными продуктами деления 342
12.2. Стабильные сильнопоглощающие продукты деления . . . 353
12.3. Эффективный осколок....................................362
12.4. Активность и энерговыделение осколков деления .... 367
Глава 13. Выгорание ядерного топлива в реакторе...................375
13.1. Малая глубина выгорания................................375
13.2. Большая глубина выгорания..............................385
13.3. Непрерывная перегрузка топлива.........................405
13.4. Замкнутый топливный цикл...............................416
13.5. Некоторые специальные случаи преобразований нуклидов
в реакторе...................................................423
13.6. Получение искусственных нуклидов и выгорание поглотителей 430
534
»тпи»|инш;
Глава 14. Кинетика реактора..................................‘WWInMli
14.1. Кинетика на мгновенных нейтронах...................
14.2. Кинетика с учетом запаздывающих нейтронов..........44ГО^М
14.3. Кинетика реактора с отражателем....................459 НтЦ
Глава 15. Устойчивость реактора.............................. 468
15.1. Пространственные ксеноновые колебания..............46 8
15.2. Температурный коэффициент реактивности.............47 7
15.3. Регулятор, датчик и устойчивость...................48 6
Дополнение 1. Односкоростное кинетическое уравнение .... 490
Дополнение 2. Среднее число столкновений при замедлении . . 49 8
Дополнение 3. Резонансное поглощение в однородной среде [вы-
вод формулы (2.3.64)]......................................500
Приложение 1. Некоторые физические постоянные................503
Приложение II. Дефект массы некоторых атомов..............503
Приложение III. Выделение энергии при радиоактивном распаде
некоторых тяжелых атомов..................................50 4
Приложение IV. Нейтронные сечения и резонансные интегралы
трансактиноидов .......................................... 505
Приложение V. Нейтронные сечения н диффузионные характери-
стики некоторых веществ....................................510
Приложение VI. Вероятность столкновения для бесконечно длин-
ного цилиндра..............................................515
Приложение VII. Эффективное граничное условие для черного
цилиндра...................................................515
Приложение VIII. Значения функции F(t) (1.7.9), МэВ/дел. . . 516
Приложение IX. Энергетические границы нейтронных групп в 26-
групповой системе...................................... . 517
Список литературы...........................................518
Алфавитно-предметный указатель.............................530
Научное издание
Галанин Алексей Дмитриевич
ВВЕДЕНИЕ В ТЕОРИЮ ЯДЕРНЫХ РЕАКТОРОВ
НА ТЕПЛОВЫХ НЕЙТРОНАХ
Заведующий редакцией В. В. Климов
Редактор О. М. Малявина
Редактор издательства Г. Б. Казьмина
Художественный редактор Б. Н. Тумин
Технический редактор Г. С. Соловьева
Корректор Г. А. Полонская
ИБ № 3418
Сдано в набор 23.04.90 Подписано в печать 24.09.90
Формат 60Х88'/ц Бумага типографская № 2 Гарнитура литературная
Печать высокая Усл. печ. л. 32,83 Усл. кр.-отт. 32-83 Уч.-изд. л.35,57
Тираж 1Ю0 экз. Заказ 6053 Цена 7 р. 40 к.
Энергоатомиздат. 113114, Москва, М-114, Шлюзовая наб., 10
Ордена Октябрьской Революции и ордена Трудового Красного Знамени
МПО «Первая Образцовая типография» Государственного комитета
СССР по печати. 113054, Москва, Валовая, 28