Автор: Андронов В.В.
Теги: общая механика механика твердых и жидких тел физика механика теоретическая механика
Год: 2003
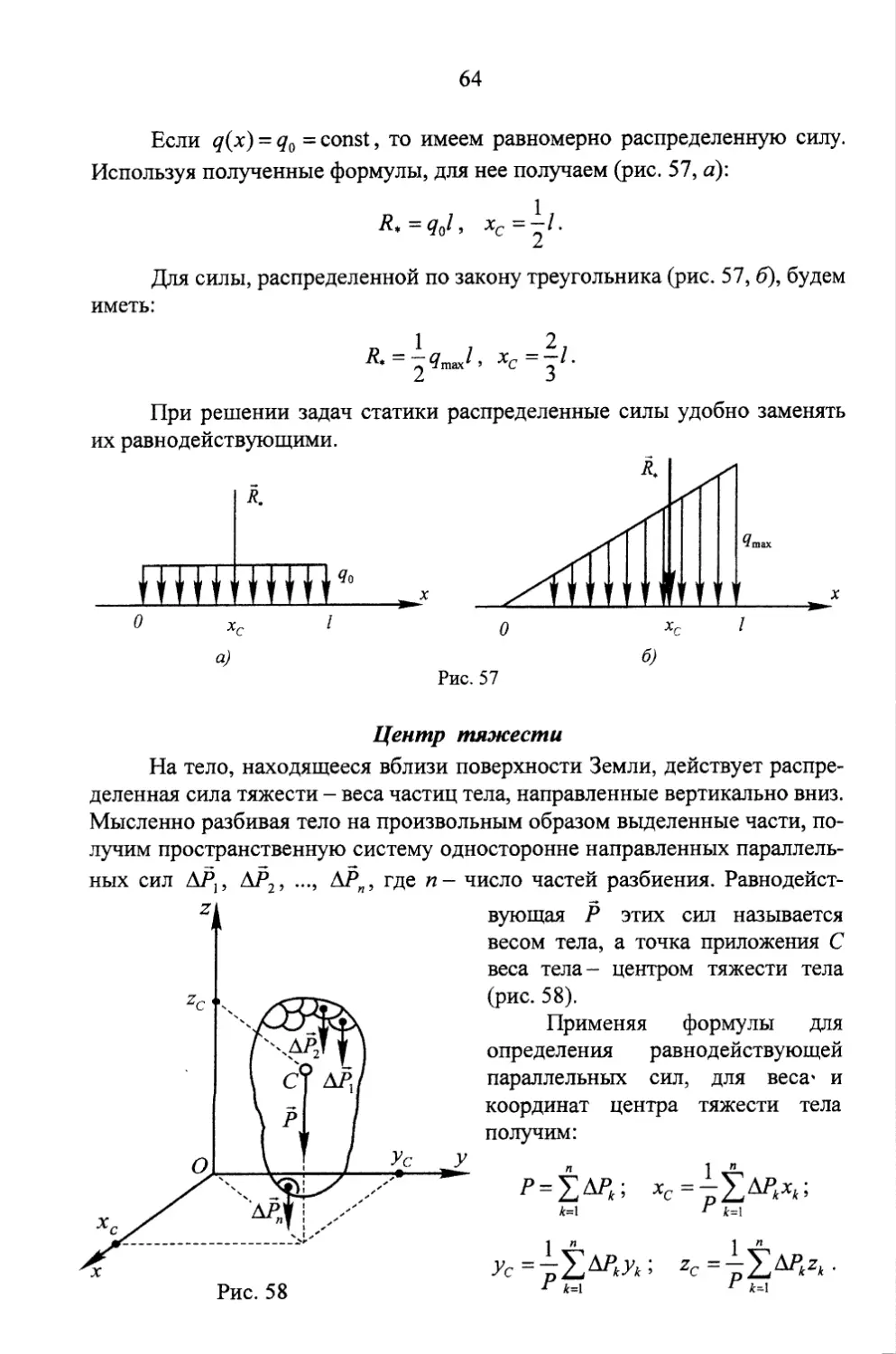
Текст
Министерство образования
Российской Федерации
Московский государственный университет леса
В.В. Андронов
ТЕОРЕТИЧЕСКАЯ
МЕХАНИКА
20 лекций
Часть!. Лекции!...10
Статика. Кинематика
Учебное пособие
Для студентов очного и заочного обучения
Издание второе, дополненное и исправленное
Допущено УМО по образованию в
области Лесного дела в качестве учебного
пособия для студентов вузов, обучающихся
по специальностям 260100 и 260200.
Издательство Московского государственного университета леса
Москва - 2003
УДК 531
6Л2 Андронов В.В. Теоретическая механика. 20 лекций. Ч. 1. Статика.
Кинематика: Учебное пособие для студентов очного и заочного обу-
чения. Спец. 260100 и 260200. 2-е изд., доп. и испр. - М.: МГУЛ,
2003.- 137 с.
Книга содержит материал лекций, которые автор читает в Московском госу-
дарственном университете леса студентам технологических специальностей. На-
стоящая, первая часть книги, включает статику и кинематику. Для лучшего усвоения
материала в конце каждой лекции приводятся вопросы для самопроверки и упражне-
ния.
В интересах студентов заочных форм обучения в книге большое внимание уде-
ляется поясняющим примерам и решению задач.
Одобрено и рекомендовано к изданию в качестве учебного пособия
редакционно-издательским советом университета.
Рецензенты: д. ф.-м. н., профессор В.Ф. Журавлёв, МФТИ;
д. т. н., профессор Л.В. Божкова, МАМИ
Кафедра теоретической механики
Автор - Вячеслав Васильевич Андронов, профессор, доктор
технических наук
© В.В. Андронов, 2000
© Московский государственный университет леса, 2003
ПРЕДИСЛОВИЕ
Настоящая книга содержит расширенный материал лекций по
теоретической механике, которые автор читает в Московском
государственном университете леса студентам технологических
специальностей лесного комплекса. Для лучшей связи непосредственно с
учебным процессом материал книги разделен на лекции (вместо глав), а
заголовки внутри лекций совпадают с соответствующими пунктами
рабочей программы дисциплины.
Первая часть книги включает в себя статику (лекции 1...6) и кинема-
тику (лекции 7... 10). В Добавлении, призванном подчеркнуть значение
предмета для дисциплин специальной подготовки, рассматривается кине-
матика формирования поверхности изделий из древесины путем фугова-
ния. Профилированный материал содержится также в ряде предлагаемых
упражнений.
Вторая часть книги посвящена динамике и издается отдельно.
В книге большое внимание уделяется примерам и кратким задачам,
поясняющим суть вводимых определений и устанавливаемых теорем. По-
следнее очень важно для успеха в самостоятельной работе, которой в соот-
ветствии с современными тенденциями в высшей школе отводится все
большее место.
В расчете на использование книги студентами-заочниками большое
внимание уделяется примерам и кратким задачам, поясняющим суть вво-
димых определений и рассматриваемых теорем. С этой же целью в конце
каждой лекции приводятся вопросы для самопроверки и специально со-
ставленные упражнения либо указания по выбору задач из Сборника
И.В. Мещерского. Продумывание ответов на эти вопросы и вдумчивое,
неформальное решение рекомендованных задач позволят обучающемуся
надежно подготовить себя по теоретической механике - одной из базовых
дисциплин высшей технической школы.
4
ВВЕДЕНИЕ
ПРЕДМЕТ И ОСНОВНЫЕ ПОНЯТИЯ
ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ
В окружающем нас мире мы постоянно встречаемся с механическим
движением, то есть с перемещением материальных тел в пространстве.
Одни механические движения совершаются в природе сами собой, незави-
симо от человека (суточное вращение Земли, движение планет и комет,
приливы и отливы, извержения вулканов и др.). Другие виды механическо-
го движения специально создаются человеком и используются для различ-
ных целей (механические движения в механизмах и машинах, измеритель-
ных приборах, испытательных стендах, разнообразном технологическом
оборудовании). Несмотря на гигантское разнообразие проявлений механи-
ческого движения, в их основе лежат некоторые общие, и притом доста-
точно немногочисленные, закономерности. Эти общие фундаментальные
закономерности и служат предметом изучения в теоретической механике.
Частным случаем движения является равновесие (покой). Равновесие так-
же подчинено строгим количественным соотношениям, которые тоже рас-
сматриваются в теоретической механике. Таким образом, теоретическая
механика - это наука, изучающая общие закономерности движения и рав-
новесия материальных тел.
В основе теоретической механики, как и любой другой естественной
науки, лежит опыт, наблюдение изучаемых явлений. В особенности это
относится к начальному периоду развития теоретической механики, когда
основные законы движения только еще формировались. В результате мно-
гочисленных наблюдений над движением тел было установлено, что не все
физические свойства тел, такие как масса, размеры, форма, твердость, цвет
и т.п., играют одинаково важную роль в процессе движения. Некоторые из
свойств оказываются второстепенными, а подчас и вовсе не влияют на ха-
рактер наблюдаемого движения. Отвлекаясь от учета второстепенных в
данных условиях факторов и оставляя в предмете исследования лишь
главные, определяющие его свойства, получают ту или иную расчетную
схему или, иначе, теоретическую модель изучаемого явления. Этот прием
познания действительности называется абстрагированием и является ос-
новным методом научного исследования. Метод абстрагирования широко
используется в теоретической механике.
5
Одной из основных моделей материальных тел в теоретической ме-
ханике является абсолютно твердое тело*. Абсолютно твердым называет-
ся такое воображаемое твердое тело, у которого расстояния между точками
остаются неизменными при любых условиях. Кроме абсолютно твердого
тела в теоретической механике используется понятие материальной точ-
ки. Материальная точка - это твердое тело или частица твердого тела, раз-
мерами которых в данных конкретных условиях можно пренебречь. Наря-
ду с абсолютно твердым телом и материальной точкой в теоретической
механике изучают движение и равновесие механической системы, то есть,
выделенной некоторым образом совокупности материальных точек.
Материальные тела, как правило, находятся в состоянии взаимодей-
ствия (одна часть машины давит на другую, планеты притягиваются
Солнцем, электрически заряженные тела притягиваются или отталкивают-
ся и т.д.). Для количественной характеристики взаимодействия тел вводит-
ся понятие силы. Силой называется физическая величина, характеризую-
щая интенсивность и направление взаимодействия тел. Для полной харак-
теристики силы требуется задать следующие ее элементы:
1) точку приложения силы;
2) направление силы;
3) численное значение (модуль) силы.
Совокупность направления и численного значения силы образуют
вектор силы. Вектор силы является свободным вектором и к нем}7 приме-
нимы правила обычной векторной алгебры. Что же касается силы как та-
ковой, то она является закрепленным (связанным) вектором, так как имеет
вполне определенную точку приложения. Поэтому задать силу - значит
задать два вектора: вектор силы F (свободный вектор) и радиус-вектор г
точки приложения силы, проведенный из произвольно выбранной в теле
точки отсчета О.
Векторы F и г можно задавать геометрически или аналитически.
При геометрическом способе задания приводится рисунок, на котором
указываются точки приложения сил и соответствующие направленные от-
резки, изображающие векторы сил. При этом точку приложения силы
можно совмещать как с началом вектора силы (рис.1, а), так и с концом
вектора силы (рис.1, б). При аналитическом способе задания сил с телом
связывается прямоугольная декартова система координатных осей Oxyz
(рис. 2), и векторы F и г задаются своими проекциями на выбранные оси:
F = (Fx,Fy,Fz), г =(rx,ry,r2)~ {х,у,z). Как видим, сила задается посредст-
В дальнейшем для краткости будем говорить также "твердое тело", "тело".
6
вом упорядоченной системы шести чисел (Fx,Fy,Fz,x,y,z) - шести коор-
динат закрепленного вектора.
Соответствие силы
закрепленному вектору, во-
обще говоря, должно отра-
жаться и в системе обозна-
чения сил, в которой долж-
ны присутствовать элемен-
ты как вектора силы, так и
точки приложения силы.
Например, можно исполь-
зовать обозначение сил в
виде: F(a) - сила, определя-
емая вектором силы F и
точкой приложения силы А,
или (F, г) - сила, опреде-
ляемая вектором силы F и
радиусом-вектором г точки
приложения. Однако для
простоты изложения, как
это обычно и делается в большинстве учебников, будем пользоваться для
сил упрощенными обозначениями, совпадающими с обозначениями векто-
ров этих сил, прибегая к полным обозначениям лишь в отдельных случаях.
Наряду с материальной точкой и абсолютно твердым телом сила яв-
ляется одним из основных понятий теоретической механики. Если матери-
альная точка и абсолютно твердое тело служат моделями материальных
тел, то сила служит моделью, характеризующей взаимодействие тел.
7
На твердое тело могут одновременно действовать несколько сил; то-
гда говорят, что к телу приложена система сил.
Приведем еще несколько общих определений.
1. Если абсолютно твердое тело может получить перемещение в лю-
бом направлении в пространстве, оно называется свободным твердым те-
лом.
2. Система сил, под действием которой свободное абсолютно твер-
дое тело может находиться в состоянии покоя, называется уравновешенной
системой сил.
3. Две системы сил такие, что замена одной из них на другую не из-
меняет состояния покоя или движения тела (кинематического состояния
тела), называются эквивалентными системами сил.
4. Одна сила, эквивалентная данной системе сил, называется равно-
действующей системы сил.
Курс теоретической механики обычно разделяется на три части-
статику, кинематику и динамику. В статике излагается общее учение о
силах, и рассматриваются условия равновесия сил. В кинематике изучают-
ся математические способы описания движения тел и определение кинема-
тических характеристик движения. При этом связь движения с действую-
щими силами не рассматривается. Причинные связи движения с дейст-
вующими силами рассматриваются в динамике- основной части курса
теоретической механики.
9
СТАТИКА
ЛЕКЦИЯ 1
ЗАДАЧИ СТАТИКИ. АКСИОМЫ СТАТИКИ.
СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ
Статикой называется раздел теоретической механики, в котором
изучаются общие правила действия с силами и условия равновесия абсо-
лютно твердого тела под действием приложенных сил. В статике решаются
две основные задачи - задача о преобразовании сил и задача о равновесии
сил, приложенных к абсолютно твердому телу.
Задача о преобразовании сил состоит в решении следующего вопро-
са: как данную систему сил заменить другой системой сил, ей эквивалент-
ной? С задачей такого типа мы неоднократно встречаемся уже в школьном
курсе физики, когда требуется сложить две силы или разложить данную
силу на составляющие по двум заданным направлениям. Данная сила и ее
составляющие- суть две эквивалентные системы сил. Часто требуется
отыскать простейшую систему сил, эквивалентную данной.
В задаче о равновесии выводятся условия, которым должны удовле-
творять действующие силы, чтобы твердое тело под их совокупным
действием могло находиться в состоянии равновесия.
При решении этих задач руководствуются аксиомами статики - не-
которыми основополагающими исходными положениями, справедливость
которых принимается без доказательства. Вот эти аксиомы.
Аксиома 1
Свободное абсолютно твердое тело под действием двух сил может на-
ходиться в равновесии тогда и только тогда, когда эти силы равны по вели-
чине и направлены вдоль одной прямой в противоположные стороны (рис. 3).
- I Эта аксиома устанавливает
2^^ простейшую уравновешенную сис-
тему сил в виде совокупности двух
А В \ сил Fu и F2B\ равных по модулю и
- \^х***^ S противоположно направленных
вдоль общей линии действия Z. Для
уравновешенной системы сил будем
использовать обозначение О”
* Цифровая часть индексов обозначает номер силы, буквенная - точку приложе-
ния силы. Обозначение FiA следует читать так: сила, определяемая вектором F\, прило-
женным в точке А, и т. д.
10
(символ эквивалентности нулю). Тогда содержание первой аксиомы запи-
шется так:
(^,Ks)~0,
если^2 = -^ ъАе1,В&1.
Аксиома 2
Если к системе сил, приложенной к абсолютно твердому телу, до-
бавить или исключить из нее уравновешенную систему сил, то получим
новую систему сил, эквивалентную первоначальной.
Рис. 4
рис. 4, б, и исходная система из
лентны. Это можно записать так
Поясним смысл этой аксиомы при-
мером. Пусть к твердому телу прило-
жены силы F1A9F2B,F3C (рис. 4, а).
Дополнительно приложим к телу две
силы Pw и Р2Е, равные по величине,
противоположные по направлению и
действующие вдоль одной прямой DE
(рис. 4, б). Согласно аксиоме 1, силы
Pw и Р2Е образуют уравновешенную
систему сил: (PXD,P2E)~Q- Тогда из
аксиомы 2 следует, что полученная
система из пяти сил, показанная на
х сил, показанная на рис. 4, а, эквива-
(Лл ’ Fib •> F'ic) ~ (ЪА, F2B, F3C, PlD, P2E).
Данная аксиома используется при доказательстве многих теорем ста-
тики. В частности, из нее вытекает следующая важнейшая для построения
статики теорема.
Теорема (о соответствии силы скользящему вектору)
Не изменяя действия данной силы на абсолютно твердое тело, точ-
ку приложения силы можно перемещать вдоль линии действия силы.
Доказательство. Пусть к абсолютно твердому телу приложена сила
FA9 то есть сила, определяемая вектором <с илы F и точкой приложения си-
лы А (рис. 5, а). Проведем линию действия силы I и выберем на ней произ-
вольную точку В (рис. 5, б). Приложим в точке В две силы FB и - FB, рав-
ные по модулю заданной силе FA и направленные вдоль прямой / в проти-
воположные стороны (рис. 5, в). Силы FB и - FB образуют уравновешен-
11
ную систему сил, поэтому, согласно аксиоме 2, система сил (FA,FB-FB) и
заданная сила FA эквивалентны:
(FA,FB,-FB)~FA.
Но силы Fa и - FB также образуют уравновешенную систему сил, и
на основании той же аксиомы 2 могут быть отброшены. Отбрасывая эти
силы, приходим к эквивалентной системе, состоящей только из одной си-
лы FB (рис. 5, г):
{Fa,Fb-Fb)~Fb.
а) б) в) г)
Рис. 5
В полученных отношениях соответствия левые части одинаковы, от-
куда следует
что и доказывает нашу теорему.
Из этой теоремы следует, что точка приложения силы в статике не
имеет значения, достаточно указать только линию действия силы. Вектор-
ные величины, смысл которых не изменяется при переносе вдоль линии
действия, называются скользящими векторами. Следовательно, сила в ста-
тике твердого тела является скользящим вектором.
Линию действия силы можно задавать непосредственным описанием
(например: сила приложена к свободному концу балки перпендикулярно к
ее оси), геометрически (при помощи чертежа), заданием уравнения прямой
линии. Однако в статике более удобным оказывается задание линии дейст-
вия силы при помощи новой физической величины - момента силы отно-
сительно точки (центра).
12
Момент силы относительно точки
Моментом силы относительно данной точки О (центра О) называ-
ется векторное произведение радиуса-вектора точки приложения силы,
проведенного из точки О, на вектор силы:
M0(F) = rxF.
Согласно данному определению, момент есть векторная величина,
называемая также вектором-моментом силы. Точкой приложения момента
служит центр момента - точка О. Направление момента и его модуль уста-
навливаются соответствующим правилом векторной алгебры. Момент на-
правлен перпендикулярно плоскости, образованной точкой О и вектором
силы, в ту сторону от этой плоскости, из которой сила F видна ориенти-
рованной против движения часовой стрелки. Модуль момента равен
|М0(/)| = |/jjf|-sina = F-h.
Величина h = |r|-sina, равная кратчайшему расстоянию от центра
момента (точки О) линии действия силы (прямой /), называется плечом
силы относительно точки О.
Сказанное поясняет рис. 6. Если линия действия силы проходит че-
рез центр момента ОК - 0 и, следовательно, вектор-момент также
равен нулю.
Из определения момента следует, что он не изменяется, если точку
приложения силы (А) перемещать вдоль линии действия силы (/). Более то-
го, момент задает эту линию действия. Поэтому сила FA, как скользящий
вектор, вполне определяется своим вектором F и вектором-моментом
M0(F). В этом смысле обозначения силы в виде (F,r) и (F,M0(F))
вполне тождественны.
Алгебраический
момент силы
Наряду с общим понятием
момента силы относительно точки
как вектора, в статике широко ис-
пользуется понятие алгебраичес-
кого момента силы. Алгебраичес-
ким моментом силы относитель-
но данной точки О (обозначается
M0(F)) называется произведение
модуля силы на плечо, взятое со
знаком плюс или минус. Правило
знаков принимается следующее:
если плоскость, образованная век-
13
тором силы и точкой О, стремится повернуться под действием силы вокруг
точки О против движения часовой стрелки, то следует брать знак плюс, ес-
ли по движению часовой стрелки - то знак минус.
Алгебраический момент силы используется, например, в случае сис-
темы сил, линии действия которых расположены в одной плоскости (пло-
ской системы сил).
Пример.
Силы FlA, F2B, F3C расположены в одной плоскости. Найти алгеб-
раические моменты этих сил относительно точки О, взятой в той же плос-
кости (рис. 7).
Из моментной точки
опускаем перпендикуляры на
линии действия сил и полу-
чаем: hi = OL- плечо силы F\A
относительно точки О; h2 =
ОК - плечо силы F2B отно-
сительно той же точки. Линия
действия силы F3C проходит
через точку О, поэтому h3 = 0.
Учитывая правило знаков, для
алгебраических моментов нахо-
дим:
Мо^ = ^ M0(F2)--F2-h2; Mo(F3) = O.
Аксиома 3 (правило параллелограмма сил)
Равнодействующая двух сил, приложенных к твердому телу в одной
точке, приложена в той же-точке и равна их геометрической сумме
(рис. 8):
(FU,F2A)~RA, r = fi+f2.
Аксиома 4 (о равенстве действия и противодействия)
Силы взаимодействия двух тел равны по величине и направлены по
одной прямой в противоположные стороны (рис. 9).
Однако эти силы не образуют уравновешенную систему, поскольку
приложены к разным телам.
14
Рис. 9
Рис. 8
Все реальные твердые тела несколько изменяют свою форму (де-
формируются) под действием приложенных сил. Могут изменять форму
(взаимное положение) и несколько абсолютно твердых тел, сочлененных в
единую систему (например, цепь, которая состоит из отдельных шарнирно-
сочлененных звеньев). Следующая аксиома относится именно к таким ма-
териальным телам.
Аксиома 5 (о затвердевании)
Равновесие деформируемого твердого тела не изменится, если оно
станет абсолютно твердым (неизменяемым).
Смысл этой аксиомы состоит в следующем. Пусть имеем изменяе-
мую систему абсолютно твердых тел, находящуюся в покое под действием
приложенной системы сил (рис. 10, а). Из данной аксиомы следует, что со-
стояние покоя системы не нарушится, если ее превратить в неизменяемую
систему (например, дополнив шарнирное соединение тел сварным швом,
как показано на рис. 10, б). Эта аксиома широко используется в статике
при исследовании равновесия систем, состоящих из нескольких абсолютно
твердых тел, а также в курсе сопротивления материалов, где изучается
равновесие упругого (деформируемого) тела.
Чтобы сформулировать следующую аксиому, потребуется познако- •
миться с новыми понятиями. Во введении уже было дано понятие свобод-
ного твердого тела - это тело, которое можно переместить в любом на-
правлении в окружающем пространстве. Часто, однако, приходится встре-
чаться со случаем, когда перемещения тела в некоторых направлениях ока-
зываются невозможными, так как этому препятствуют другие тела, с кото-
рыми рассматриваемое тело скреплено или соприкасается. Такое тело на-
зывается несвободным.
15
В случае несвободного тела мы имеем, с одной стороны, выделенное
тело, состояние которого нас интересует, и, с другой стороны, имеем тела,
которые ограничивают перемещения выделенного тела. Эти последние на-
зываются связями, а силы, с которыми связи действуют на выделенное те-
ло, называются реакциями связей. Сформулируем теперь аксиому, назы-
ваемую аксиомой освобождаемости от связей.
Аксиома 6 (освобождаемости от связей)
Состояние покоя или движения несвободного тела не изменится, ес-
ли связи отбросить, а их действие на тело заменить реакциями.
Из этой аксиомы следует, что любое несвободное тело можно рас-
сматривать как свободное. Для этого достаточно связи мысленно отбро-
сить, а их действие на тело заменить реакциями отброшенных связей.
Полученное в результате освобождения от связей свободное тело на-
ходится под действием двоякого рода сил - сил задаваемых и реакций свя-
зей. Задаваемые силы называются также активными силами, а реакции свя-
зей - пассивными силами, поскольку они заранее неизвестны и всецело за-
висят от величин, направлений и точек приложения активных сил.
Пример.
Дана балка АВ, закрепленная одним концом к неподвижному осно-
ванию при помощи цилиндрического шарнира А и удерживаемая в равно-
весии в горизонтальном положении невесомой нитью ВС, прикрепленной к
наклонной стене в точке С. На балку действуют собственный вес G и сила
Р (рис. 11, а). Освободить балку от наложенных связей.
16
В данном случае выделенным телом является балка АВ. Ее переме-
щения ограничены шарниром А и нитью ВС, которые являются связями.
Мысленно отбрасываем связи и прикладываем к балке соответствующие
реакции. Реакция нити направлена всегда вдоль нити. В самом деле, выде-
лив отдельно нить, видим, что она находится в равновесии под действием
двух сил - силы Т'в, действующей со стороны балки, и силы Т'с, дейст-
вующей со стороны стены (рис. 11, б). Нить, таким образом, находится в
равновесии под действием двух сил, и из аксиомы 1 следует, что эти силы
направлены вдоль прямой ВС. Сила Т’в, по смыслу, представляет собой
силу, с которой балка действует на нить. Реакция же нити суть сила, с ко-
торой нить (связь) действует на балку. Отсюда, в полном соответствии с
аксиомой 4 о равенстве действия и противодействия, приходим к выводу,
что реакция нити Тв направлена вдоль нити от точки В к точке С, что и
показано на рис. 11, г.
Относительно реакции шарнира ^известно только то, что она:
1) проходит через центр шарнира А и 2) лежит в плоскости, перпендику-
лярной оси шарнира. Следовательно, это есть неизвестный вектор в плос-
кости Аху, перпендикулярной оси шарнира. Его удобно представить в виде
суммы двух составляющих ХА и YA, приложенных в центре шарнира и на-
правленных вдоль координатных осей (рис. 11, в).
Теперь можно изобразить полную систему сил, приложенную к бал-
ке (см. рис. 11, г). Она состоит в данном случае из пяти сил, из которых две
силы - Р и G являются активными, а три силы - ХА, YA, Тв - реакциями
17
связей. Численные значения реакций, то есть величины ХА, YA, Тв наперед
неизвестны и определяются в ходе решения задачи на равновесие. В этой
связи заметим, что цилиндрический шарнир порождает в задачах статики
две скалярные неизвестные: ХА, YA. Если XAf YA стали известны, то величи-
ны Ra и а, определяющие модуль и направление реакции RA, однозначно
определяются по формулам (см. рис. 11, в)
Ra = JxA + У? , sina = —, cosa = “.
В дальнейшем условия равновесия будут формулироваться примени-
тельно к свободному твердому телу. Чтобы воспользоваться этими усло-
виями при изучении равновесия несвободного тела, прежде всего, требует-
ся освободить тело от наложенных связей, как это было сделано в приве-
денном примере. Для решения этой задачи ниже приводятся наиболее час-
то встречающиеся типы связей и их реакции. При этом общее правило на-
правления реакций состоит в следующем: реакция связи всегда направлена
противоположно движению, запрещаемому телу этой связью.
Основные типы связей и их реакции
1. Гладкая (без трения) плоскость или поверхность. Такие связи
препятствуют перемещениям тела только в направлении общей нормали в
точке касания, вдоль которой и будет направлена соответствующая реак-
ция. Поэтому реакция гладкой плоской опоры перпендикулярна этой опоре
(реакция NA на рис. 12, а); реакция гладкой стенки перпендикулярна этой
стенке (Л^на рис. 12, б); реакция гладкой поверхности направлена по нор-
мали к этой поверхности, проведенной в точке касания (N2 на рис. 12, в).
Рис. 12
18
2. Острый выступ. В этом случае можно считать, что опирается сам
выступ, а опорой служит рассматриваемое тело. Это приводит к случаю 1
и выводу, что реакция гладкого выступа направлена по нормали к поверх-
ности опирающегося тела (сила N{ на рис. 12, в).
3. Гибкая связь (невесомые нить, трос, цепь и т.п.). Соответствующая
реакция направлена вдоль связи от точки крепления нити к точке подвеса
(сила Тв на рис. 11, г, сила ТА на рис. 12, б).
4. Невесомый прямолинейный стержень с шарнирами на концах. Ре-
акция направлена вдоль стержня. Поскольку стержень может быть как
сжат, так и растянут, реакция может иметь направление как к точке подве-
са стержня, так и от точки подвеса (реакции 5, и S2 на рис. 13, а).
5. Невесомый коленчатый или криволинейный стержень. Реакция
направлена вдоль прямой, проходящей через центры концевых шарниров
(сила §3 на рис. 13, а; сила S на рис. 13, б).
6. Подвижная шарнирная опора. Реакция направлена перпендику-
лярно плоскости опоры (плоскости катания) (рис. 14, я, б).
Рис. 14
7. Цилиндрический шарнир (рис. 15, а), радиальный подшипник
(рис. 15, б). Реакция проходит через центр шарнира (центр срединного се-
чения подшипника) и лежит в плоскости, перпендикулярной оси шарнира
(подшипника). Она эквивалентна двум неизвестным по модулю силам-
19
составляющим этой реакции вдоль соответствующих координатных осей
(силы Хо, Yq на рис. 15, а; XА, ZA и Хв, ZB на рис. 15, б). (Разъяснения
по этому поводу см. также в примере на стр. 16).
а)
8. Сферический шарнир (рис. 16, а), подпятник (или радиально-упор-
ный подшипник) (рис. 16, б). Реакция состоит из трех неизвестных по мо-
дулю сил - составляющих реакции вдоль осей пространственной системы
координат.
9. Жесткая заделка (рис. 17). При действии на тело плоской системы
сил полная реакция заделки складывается из силы с составляющими ХА и
Ya , и пары сил* с моментом МА, расположенных в той же плоскости, что и
действующие силы.
10. Скользящая заделка (рис. 18). В случае плоской системы сил и
отсутствия трения реакция состоит из силы N и пары сил с моментом М,
расположенных в одной плоскости с действующими силами. Сила N пер-
пендикулярна к направлению скольжения.
* Понятие пары сил и свойства пары будут даны в лекции 2.
20
Рис. 17
Вопросы для самопроверки
1. Что называется абсолютно твердым телом, материальной точкой?
2. Укажите элементы силы. Какими способами можно задать силу?
3. Что называется векторным моментом силы относительно точки
(центра)? Что такое алгебраический момент силы?
4. В каком случае момент силы относительно точки равен нулю?
5. Что называется системой сил? Какие системы сил называются эк-
вивалентными?
6. Что называется равнодействующей системы сил?
7. Дайте определение несвободного твердого тела, связи, реакции
связи?
8. Можно ли несвободное тело рассматривать как свободное?
9. На какие две группы делятся силы, действующие на несвободное
твердое тело?
21
Упражнения
1. Найти равнодействующую R сил Fr и F2 (рис. 19). Задачу решить
геометрически (решая треугольник) и аналитически (выбрав подходящую
систему координат и действуя с проекциями сил на выбранные оси).
Рис. 19
2. Вычислить и построить векторы-моменты сил Р и Q относитель-
но центра О (рис. 20). Величины а, b обозначают длины соответствующих
ребер прямоугольной призмы.
3. Вычислить алгебраические моменты сил Р, Т , G относительно
точки О, если О А - 2а, АВ = ВС = а (рис. 21).
4. Изобразить полную систему сил, приложенных к балке АВ (рис. 22).
Какие из них являются активными силами и какие - пассивными?
5. Назовите типы связей и укажите направления реакций в приведен-
ных ниже примерах (рис. 23).
Рис. 23
22
ЛЕКЦИЯ 2
СХОДЯЩИЕСЯ СИЛЫ И ПАРЫ СИЛ
Сходящиеся силы. Приведение сходящихся сил к простейшему виду
Сходящимися называются силы, линии действия которых пересека-
ются в одной точке (рис. 24, а). Так как силы - векторы скользящие, схо-
дящиеся силы можно перенести вдоль их линий действия в общую точку О
и рассматривать систему сил, приложенных в одной точке - точке пересе-
чения линий действия сил (рис. 24, б).
Пусть дана система сходящихся сил (^,F2,...,FW), приложенных в
точке О (рис. 25, а). Можно ли эту систему сил привести к более простому
виду? Чтобы ответить на этот вопрос, будем последовательно складывать
заданные силы, применяя каждый раз аксиому 3. Сначала находим равно-
действующую Rl2 сил и F2 *. Заменяя эти силы их равнодействующей
Д2, получаем новую систему сил (7?12,jF3,...,F„), эквивалентную исходной
системе:
(Л.Л.-Л) ~ ЛЛ-Л, 4 =Л+Л-
Далее можно найти равнодействующую Я13 сил Я12 и F3 и прийти к
системе сил (J?13,F4,...,F„), также эквивалентной исходной системе:
(Л,Л.-.Л) ~ ЛЛ---Л), ri3 = Ra+л=Л+Л + Л-
* Сложение векторов коммутативно, поэтому силы можно складывать в любом
порядке.
23
Видно, что после каждого такого преобразования получается эквива-
лентная исходной система сил, в которой на одну силу меньше, чем в пре-
дыдущей системе. Поэтому, выполнив указанное преобразование п - 1 раз,
приходим к одной силе, RX n, для которой получаем
=А, л-1+Л=+ Л+-+Я-1 + р’п = •
*=!
Таким образом, заданная система сил оказалась эквивалентной од-
ной силе R = Rln, которая и является для нее равнодействующей:
(ЛЛ,...Л)~Й,Л = ХЛ-
*=1
Этим доказана следующая важная теорема статики о приведении
системы сходящихся сил к простейшему виду: система сходящихся сил в
общем случае эквивалентна одной силе - равнодействующей. Эта равно-
действующая приложена в точке пересечения линий действия сил и равна
их геометрической сумме.
Вычисление и построение равнодействующей
Вычисление и построение равнодействующей сходящихся сил осу-
ществляется по правилам векторной алгебры. Это можно сделать геомет-
рическим и аналитическим способами.
При геометрическом способе строится векторный (силовой) много-
угольник, замыкающая сторона которого и определяет вектор равнодейст-
вующей (рис. 25, б). Перенеся этот вектор параллельно себе в точку О пе-
ресечения линий действия сил, получаем искомую равнодействующую
(см. рис. 25, а).
Рис. 25
При аналитическом способе равнодействующая определяется через
ее проекции на оси декартовой системы координат, которую удобно вы-
брать с началом в точке приложения сил О. По теореме векторной алгебры
24
о проекции суммы векторов на ось.
выбранные оси получаем:
|я| = Д2+Я2+Я2, cosa
для проекции равнодействующей на
4=1 4=1
Эти равенства выра-
жают правило: проекции
равнодействующей сходя-
щихся сил на выбранные
координатные оси равны
алгебраическим суммам про-
екций заданных сил на со-
ответствующие оси. Да-
лее, вспоминая правило
построения вектора по его
_____ж проекциям на координат-
у ные оси, строим равно-
действующую R (рис. 26).
Модуль и направляющие
косинусы равнодействую-
щей определяются по фор-
мулам
1-4, 0080 = 7^-, COSV = -dr.
W И w
Условия равновесия сходящихся сил
Сходящиеся силы находятся в равновесии, если их равнодействую-
щая равна нулю. В математической форме это условие выражается вектор-
ным равенством
4=1
называемым векторным условием равновесия сходящихся сил. Это усло-
вие можно выразить в геометрической форме (в терминах силового много-
угольника) и в аналитической форме (через проекции сил на координатные
оси).
Применительно к силовому многоугольнику равенство (1) означает,
что длина замыкающей стороны силового многоугольника равна нулю.
Следовательно, в силовом многоугольнике конец вектора последней силы
(^) совпадает с началом вектора первой силы (^). Такой силовой много-
угольник называется замкнутым. Отсюда вытекает следующее геометри-
ческое условие равновесия сходящихся сил: чтобы сходящиеся силы нахо-
25
дились в равновесии, необходимо и достаточно, чтобы силовой много-
угольник, построенный из этих сил, был замкнутым.
Аналитические условия равновесия представляют собой покоорди-
натную запись векторного равенства (1):
2Ж = о,2Л=о,£^ = о. (2)
А=1 Л=1
Из равенств (2) следует, что для равновесия сходящихся сил необхо-
димо и достаточно, чтобы алгебраические суммы проекций всех сил на
координатные оси были равны нулю.
Если сходящиеся силы расположены в одной плоскости, то имеем
плоскую систему сходящихся сил. Воспользуемся произволом в выборе
координатных осей и выберем их так, чтобы координатные оси Ох, Оу ока-
зались в одной плоскости с заданными силами. Тогда третье условие в (2)
будет выполняться тождественно (всегда, при любых силах). Следователь-
но, для плоской системы сходящихся сил имеют место только два анали-
тических условия равновесия:
2X = o,£^ = o. (3)
А=1 к=1
Два условия равновесия плоской системы сходящихся сил остаются
и при произвольном выборе осей. Кажущаяся возможность составить в
этом случае также и третье условие оказывается несостоятельной: третье
условие будет простым следствием первых двух, то есть не будет являться
независимым.
Если среди сил, удовлетворяющих условиям равновесия, имеются
неизвестные силы, тогда условия равновесия служат для определения этих
сил и называются уравнениями равновесия. Такими неизвестными обычно
являются реакции связей: заранее мы можем указать только направления
реакций, а численные значения реакций определяются в результате состав-
ления и решения уравнений равновесия.
Пример 1.
Определить давление однородного шара на гладкую стенку и натя-
жение нити, если шар находится в равновесии (рис. 27, а). Вес шара
Р = 20 Н, угол наклона нити к вертикали а = 30°.
Мысленно освободим шар от наложенных связей. Для этого связи
отбросим, а их действие на шар заменяем реакциями. Реакция стенки N
направлена перпендикулярно стенке (от точки касания С к центру шара О),
реакция нити t - вдоль нити от точки А к точке В. Тем самым выявляется
полная система сил, приложенных к покоящемуся шару. Это система сил,
сходящихся в центре О шара, и состоящая из веса шара Р (активная сила),
реакции стенки N и реакции нити Т (рис. 27, б). Реакции N и Т по вели-
26
чине неизвестны. Для их определения следует воспользоваться условиями
равновесия (в той или иной форме - геометрической, аналитической).
При геометрическом способе решения строится замкнутый много-
угольник сил и используются соотношения школьной геометрии (теорема
синусов, теорема косинусов, теорема Пифагора и т.д.). В данном случае
это замкнутый силовой треугольник (рис. 27, в), из которого получаем:
jV = Ptga, 7 = P/cosa,
или, после подстановки числовых значений:
1 л/З
N = 20 • = 11,547Я; Т = 20:— = 23,094Я.
Л 2
При аналитическом способе решения выбирается подходящая систе-
ма координат, и уравнения равновесия составляются в форме (2) или (3).
Выбирая оси, как показано на рис. 27, б, составляем для данной плоской
системы сходящих сил два уравнения равновесия:
=0: Tsina-jV==0,
ji=i
£7^ = 0: rcosa-P = 0. (2)
*=i
Решая эти уравнения, приходим к тем же значениям для неизвестных
сил: N = Ptga, Т = Р/ cosa.
Отметим, что реакция N - это сила, с которой стенка действует на
шар. Давление шара на стенку суть сила N', приложенная от шара к стен-
ке. Она равна по модулю силе N, но направлена в противоположную сто-
рону - от шара к стенке (показана штрихами на рис. 27, а).
27
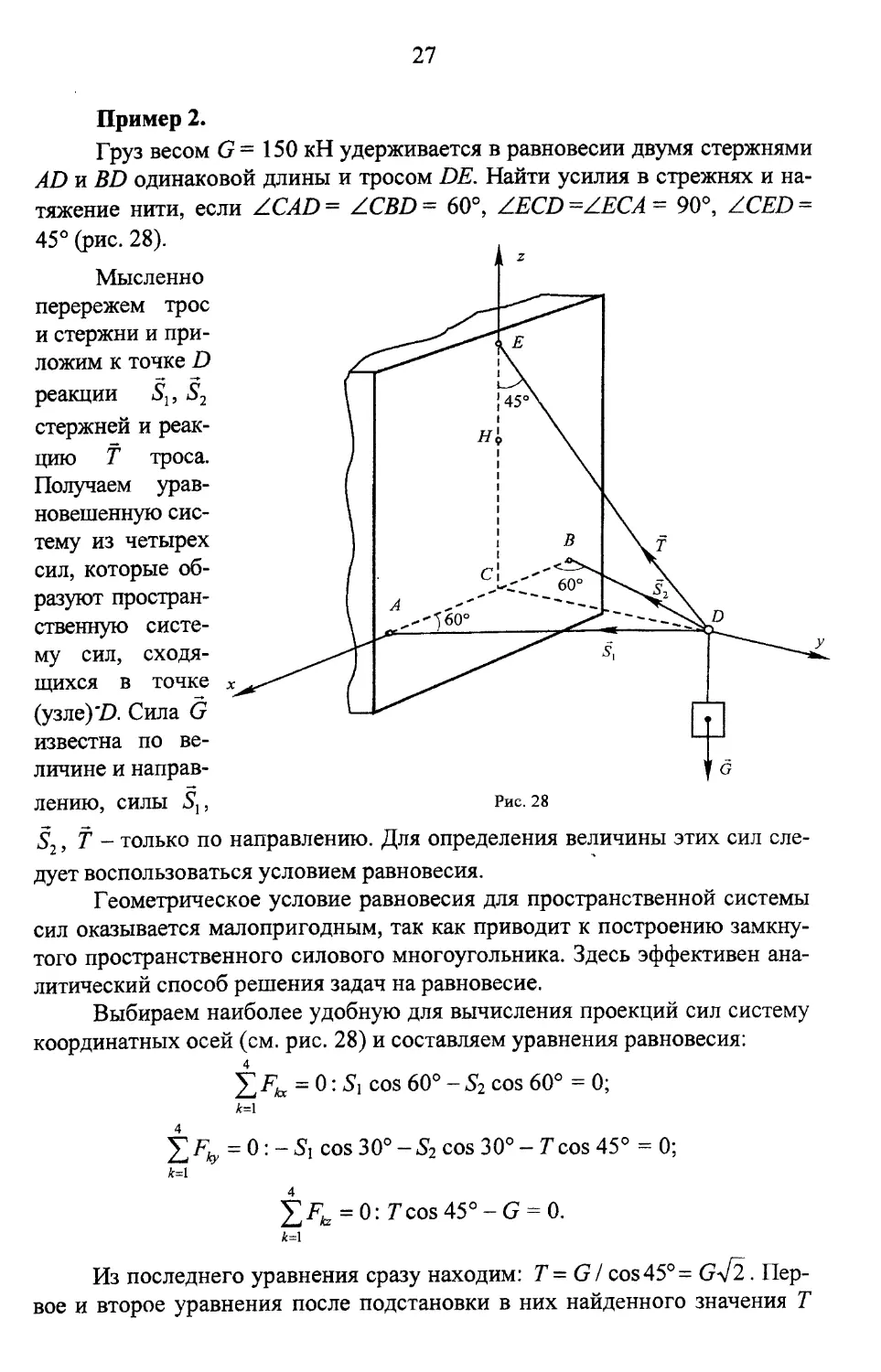
Пример 2.
Груз весом G = 150 кН удерживается в равновесии двумя стержнями
AD и BD одинаковой длины и тросом DE. Найти усилия в стрежнях и на-
тяжение нити, если /CAD = Z.CBD ~ 60°, /ECD -/.ЕСА = 90°, /CED =
45° (рис. 28).
Мысленно
перережем трос
и стержни и при-
ложим к точке D
реакции Д, S2
стержней и реак-
цию Т троса.
Получаем урав-
новешенную сис-
тему из четырех
сил, которые об-
разуют простран-
ственную систе-
му сил, сходя-
щихся в точке
(узле)!). Сила G
известна по ве-
личине и направ-
лению, силы Д,
Д, t - только по направлению. Для определения величины этих сил сле-
дует воспользоваться условием равновесия.
Геометрическое условие равновесия для пространственной системы
сил оказывается малопригодным, так как приводит к построению замкну-
того пространственного силового многоугольника. Здесь эффективен ана-
литический способ решения задач на равновесие.
Выбираем наиболее удобную для вычисления проекций сил систему
координатных осей (см. рис. 28) и составляем уравнения равновесия:
^F^ = 0: 5i cos 60° - S2 cos 60° = 0;
Ar=l
£ = 0: - 5i cos 30° - S2 cos 30° - T cos 45° = 0;
£=i
XFfe = 0:Tcos 45°-G = 0.
a=i
Из последнего уравнения сразу находим: Т = G / cos 45°= G^2. Пер-
вое и второе уравнения после подстановки в них найденного значения Т
28
образуют систему для определения неизвестных Si и S2. Выражая из перво-
го уравнения неизвестное S2 и подставляя во второе уравнение, приходим к
уравнению с одним неизвестным (Si):
- 2S, cos 30o-GV2 cos 45°= 0.
Из него находим:
g72cos45° _ Ga/3
2cos30° “ 3
Теперь легко определяется и оставшееся неизвестное (S2):
^ = ^ = -^73/3.
После подстановки значения G =150 кН, находим численные значе-
ния реакций: Т- 212,13 кН; Sj = S2 --86,60 кН.
Отрицательные знаки у реакций Sb S2 указывают на то, что эти силы
имеют направления, противоположные указанным на рис. 28. Можно было
бы сразу указать точное направление этих сил, так как видно, что стержни
испытывают сжатие. Мы не сделали этого только потому, что избранный
вариант зрительно более удобен для вычисления проекций сил на оси.
Представим себе, что груз G в приведенном примере поддерживался
бы еще одной или несколькими связями - еще одним стержнем (например,
вдоль CD)), еще одним тросом (например, протянутым из точки D в точку
Н). Тогда в уравнения равновесия вошли бы и реакции этих дополнитель-
ных связей, и мы имели бы не три, а четыре, пять и более неизвестных.
Однако число уравнений равновесия остается при этом неизменным - три
независимых уравнения для пространственной системы сходящихся сил и
два - для плоской. Следовательно, не всякая задача на равновесие может
быть рещена при помощи уравнений статики. В статике могут быть одно-
значно решены лишь задачи, в которых количество неизвестных совпадает
с числом независимых уравнений равновесия. Такие задачи называются
статически определенными. Если количество неизвестных превышает
число независимых уравнений статики, то задача не может быть однознач-
но решена методами статики и называется статически неопределенной.
Методы решения статически неопределенных задач рассматриваются в
курсе сопротивления материалов.
В заключение раздела о сходящихся силах приведем две теоремы,
весьма полезные при решении задач.
Теорема о трех силах
Если свободное твердое тело находится в равновесии под действи-
ем трех непараллельных сил, то эти силы лежат в одной плоскости, а ли-
нии действия сил пересекаются в одной точке.
Эта теорема позволяет в ряде случаев определить направление реак-
ции связи.
29
Пример.
Указать направление полной реакции шарнира А трехшарнирной ар-
ки АВС (рис. 29). Арка нагружена силой Р, весом полуарок пренебречь.
Рассматриваем отдельно
каждую полуарку. Полуарка ВС
служит для полуарки АС колен-
чатой стержневой связью (см.
рис. 13, б на стр. 18), поэтому ее
реакция Rc направлена вдоль ВС.
Теперь видно, что для полуарки
АС выполняются все условия
теоремы о трех силах (третьей
силой является полная реакция RA
неподвижного шарнира А). Линии
действия сил Р и Rc пересекают-
ся в точке С, следовательно, через эту точку пройдет и линия действия
реакции RA.
Теорема Вариньона
Момент равнодействующей сходящихся сил относительно некото-
рого центра равен сумме моментов всех заданных сил (составляющих)
относительно того же центра.
. Теорема справедлива как для векторных, так и для алгебраических
моментов.
Доказательства теорем предлагается разобрать самостоятельно по
полным учебникам.
Пара сил и ее момент
Парой сил (или просто парой) называется совокупность двух парал-
лельных сил, равных по модулю, противоположных по направлению и при-
ложенных в разных точках тела (рис. 30). Пару сил будем обозначать
символом (Л»-^с)- Силы !
Fd, -Fc называются силами'
пары; плоскость, в которой
лежат силы, называется
плоскостью действия пары.
Кратчайшее расстояние
между линиями действия сил
пары называется плечом пары
(длина h отрезка АВ на рис.
30). Так как силы можно пе-
ремещать вдоль их линий дей-
ствия, в дальнейшем силы
пары будем изображать при-
30
ложенными к концам плеча пары. Будем также пользоваться более про-
стым обозначением пары в виде (F, -F), не содержащем обозначений
точек приложения сил.
Пара сил характеризует особый вид взаимодействия тел, который
нельзя выразить одной силой. Поэтому в статике, наряду с силами, рас-
сматриваются отдельно также пары сил с их специфическими свойствами,
правилами сложения и усло-
виями равновесия.
Изначально пара сил
задается четырьмя векторами
F, rA, -F\ гв (рис. 31) - двумя
векторами сил пары и двумя
радиусами-векторами их точек
приложения*. Возьмем какую-
либо точку пространства в
качестве центра моментов О и
вычислим моменты сил пары
относительно этого центра
4(^)=^xF; M0(-F)=r£x(-F).
Тогда предыдущее утверждение можно выразить и в такой форме:
пара сил может быть задана векторами сил пары и моментами этих сил от-
носительно произвольного центра О. Теперь зададимся вопросом: нельзя
ли пару сил задавать по-другому, желательно меньшим числом опреде-
ляющих элементов?
Геометрическая сумма векторов сил пары всегда равна нулю, поэто-
му она не может использоваться для характеристики пары. Вычислим
сумму моментов сил пары относительно точки О:
Mq(F) + M0(-F) = rAxF + rBx(-F) = rAxF-rBxF =
= (rA - rB)x F = BA x F.
В полученном результате обращают на себя внимание два обстоя-
тельства.
1. В то время как сумма векторов сил пары всегда равна нулю, сумма
моментов сил пары отлична от нуля.
* Точнее - тремя векторами, поскольку задание вектора F одновременно опре-
деляет и вектор — F. Напомним также, что в качестве точек приложения могут быть
выбраны любые точки на линиях действия сил пары.
31
2. Сумма моментов сил пары не зависит от выбора центра момен-
тов- векторы гА,гВ9 зависящие от выбора точки О, выпали из окончатель-
ного выражения для искомой суммы.
Таким образом, сумма моментов сил пары оказывается зависящей
только от элементов самой пары - плоскости действия пары, модуля сил и
плеча пары. Это наводит на мысль использовать эту величину в качестве
характеристики пары сил. В дальнейшем сумму моментов сил пары будем
называть моментом этой пары. Поскольку момент пары не зависит от вы-
бора центра моментов, то он является свободным вектором - его можно
прикладывать в любой точке твердого тела, на которое действует данная
пара сил.
Итак, на вопрос о том, можно ли задавать пару сил более простым
способом, получен утвердительный ответ: пару сил можно характеризо-
вать, задавая лишь один вектор - момент пары. Моментом пары сил назы-
вается свободный вектор M(F9-F), равный геометрической сумме мо-
ментов сил пары относительно произвольно выбранной точки О простран-
ства
M(F,—F) = M0(F) + Mg(—F).
Здесь следует заметить, что приведенные рассуждения имеют скорее
наводящий характер и не являются строгим доказательством только что
сформулированного вывода. Однако в статике имеется ряд теорем, в кото-
рых'сделанный вывод получает строгое обоснование. С этими теоремами
можно познакомиться по полным учебникам по теоретической механике.
Воспользовавшись произволом в выборе точки О в определении мо-
мента пары, можно прийти к более простому способу вычисления момен-
та. Примем в качестве центра моментов точку приложения силы - F (точку
В на рис. 31). Тогда можно написать
M(F, -F) = Мв (F) + Мв (-F) = Мв (F).
Здесь учтено, что MB{-F) = 0, так как сила -F проходит через точ-
ку В. Если за центр моментов принять точку А, в которой приложена сила
F, то в нуль обращается момент силы F, и мы получаем
M(F, -F) = МА (F) + МА (-F) = МА (-F).
Это приводит к еще одному правилу для вычисления момента пары:
момент пары сил равен моменту одной из сил пары относительно точки
приложения другой силы.
Тем самым определение момента пары сводится к вычислению и по-
строению момента силы относительно точки, подобно рассмотренно-
му ранее (см. стр. 12). В итоге приходим к следующему выводу: момент
пары сил есть вектор, численно равный произведению модуля сил пары на
32
плечо пары и направленный перпендикулярно плоскости действия пары в
ту сторону, из которой "вращение" пары видно происходящим против
движения часовой стрелки (правило буравчика); в качестве точки прило-
жения момента пары может быть взята любая точка тела.
Алгебраическим моментом пары называется произведение модуля
сил пары на плечо пары, взятое со знаком плюс, если пара ’’вращает" свою
плоскость против движения часовой стрелки, и со знаком минус, если
наоборот.
Примеры.
На рис. 32 изображена пара сил (Р,-Р), действующая в плоскости
диска радиуса R, установленного перпендикулярно к оси вращения. Плечо
пары равно диаметру диска, модуль момента пары равен
М = |Л/(Л-Р)|=2РЙ.
Момент пары М = М(Р-Р) направлен перпендикулярно плоскости
диска и может быть приложен в любой точке диска.
На рис. 33 показан аналогичный случай, но изображенный в плоской
проекции. Здесь силы пары (F,-F) направлены перпендикулярно плоско-
сти чертежа (знаком ® изображаются векторы, направленные "на читате-
ля", знаком ® - от читателя). Момент пары М= M(F-F) по модулю ра-
вен 2FR, перпендикулярен плоскости диска и лежит в плоскости чертежа
(точнее, может быть перенесен параллельно себе в плоскость чертежа).
Еще два примера построения момента пары содержатся на рис. 34.
Модули моментов изображенных пар имеют значения:
М, = |л/( Л ,~Л)| = (Ь - 6'), М2 = |м(Л -Л)| = аР2.
33
Векторы-моменты пар
имеют проекции:
Л?,(0, О, (Ь-Ь')Р,),
М2(0,-аР2,0).
Свойства пары сил
I. Можно изменять ве-
личину сил и плечо пары, ос-
тавляя без изменения величину
момента и направление "вра-
щения" сил пары.
2. Пару сил можно как
угодно перемещать в своей
плоскости действия.
3. Пару сил можно
перемещать параллельно себе в любую плоскость, неизменно связанную с
телом, к которому она приложена.
Перечисленные в этих свойствах действия не изменяют ни величину,
НИ направление момента пары, поэтому являются эквивалентными преоб-
разованиями пары.
В приведенных выше примерах речь шла о построении момента по
заданным элементам пары- плоскости действия, силам и плечу пары.
Можно ставить и обратную задачу - построить пару сил по ее моменту.
Пусть требуется построить пару сил по ее моменту М (рис. 35, а). Для
этого строим плоскость 77, перпендикулярную линии действия Г момента
(рис. 35, б). Эта плоскость будет служить плоскостью действия пары. В
этой плоскости располагаем две силы {Р-Р} по следующему правилу. На-
правление сил выбирается так, чтобы из конца вектора-момента М силы
были видны ориентированными против движения часовой стрелки. Вели-
чина сил и плечо пары могут быть любыми (свойство 1), но чтобы их про-
Рис. 35
34
Согласно свойству 3 плоскостью действия пары будет являться и
любая другая плоскость П\ П", ..., параллельная плоскости П.
В дальнейшем, имея дело с парами сил, мы будем указывать только
их векторы-моменты М2 и т.д., прибегая к построению самой пары
лишь при необходимости.
Приведение системы пар сил к простейшему виду или сложение
пар сил
Пусть к твердому телу приложены одновременно несколько пар сил
с моментами Мг, М2, ... , Мп, действующих в различных плоскостях.
Можно ли эту систему пар привести к более простому виду? Оказывается,
что можно, и ответ подсказывается следующей теоремой о сложении двух
пар.
Теорема. Две пары сил, действующие в разных плоскостях, эквива-
лентны одной паре сил с моментом, равным геометрической сумме мо-
ментов заданных пар.
М
Рис. 36
Пусть пары заданы своими моментами М} и М2 (рис. 36, а)*. По-
строим две плоскости, перпендикулярные этим векторам (плоскости дей-
ствия пар) и, выбрав некоторый отрезок АВ на линии пересечения плоско-
стей за плечо, общее для обеих пар, построим соответствующие пары:
* Для большей выразительности вектор-момент пары иногда снабжают круговой
стрелочкой, дополнительно подчеркивая этим вращательный характер оказываемого
воздействия.
35
(Д,-Д^ (Д, - Д) (Рис- 36, б). В соответствии с определением момента
пары можем написать
= М (Д, - Д) = Мв (Д) = В А X Д
м2=м(Д,-Д)=мДД)=влхД.
В точках А и В имеем сходящиеся силы. Применяя правило паралле-
лограмма сил (аксиома 3), будем иметь:
(fx,f2)~r, (-Fx-F2)~-R, R = Fx+F2.
Заданные пары оказываются эквивалентными двум силам R, -R,
также образующим пару. Тем самым первая часть теоремы доказана. Вто-
рая часть теоремы доказывается прямым вычислением момента результи-
рующей пары:
M = M(R,-R) = BAxR = BAx(Fx + F2) = BAxFx + baxf2 = мх + м2.
Если число пар п > 2, то, попарно складывая их в соответствии с этой
теоремой, можно любое число пар привести к одной паре. В результате
приходим к следующему выводу: совокупность (систему) пар сил, прило-
женных к абсолютно твердому телу, можно привести к одной паре с мо-
ментом, равным геометрической сумме моментов всех заданных пар.
Математически это можно записать следующим образом:
(мх,м2,...,м„)~м,м =
*=1
На рис. 37 дается геометрическая иллюстрация полученного вывода.
Для равновесия пар сил требуется, чтобы момент результирующей
пары был равен нулю, что приводит к равенству
ЕЯ=о-
*=1
Рис. 37
36
Это условие можно выразить в геометрической и аналитической
форме.
Геометрическое условие равновесия пар сил: чтобы система пар
сил находилась в равновесии, необходимо и достаточно, чтобы векторный
многоугольник, построенный из моментов всех пар, был замкнутым.
Аналитическое условие равновесия пар сил: чтобы система пар сил
находилась в равновесии, необходимо и достаточно, чтобы алгебраиче-
ские суммы проекций векторов-моментов всех пар на произвольно выбран-
ные координатные оси Oxyz были равны нулю:
5Х=0; УМ, =0; УМ^=О.
к=\ к=\ *=1
Если все пары лежат в одной плоскости, то есть образуют плоскую
систему пар, получается лишь одно аналитическое условие равновесия -
сумма алгебраических моментов пар равна нулю.
Вопросы для самопроверки
1. В чем состоит правило силового многоугольника? Для чего слу-
жит силовой многоугольник?
2. Как найти равнодействующую сходящихся сил аналитическим
способом?
3. В чем состоит геометрическое условие равновесия сходящихся
сил? Как формулируется это же условие аналитически?
4. Сформулируйте теорему о трех силах.
5. Какие задачи статики называются статически определенными и
какие - статически неопределенными? Приведите пример статически не-
определенной задачи.
6. Что называется парой сил?
7. Что называется моментом (вектором-моментом) пары сил?
Каковы направление, модуль и точка приложения момента?
8. Что называется алгебраическим моментом пары?
9. Сформулируйте правило сложения пар, произвольным образом
расположенных в пространстве.
10. В чем заключаются векторное, геометрическое и аналитическое
условия равновесия системы пар сил?
Упражнения
1. При построении силового многоугольника силы можно распола-
гать в любом порядке (свойство коммутативности сложения векторов). По-
стройте все силовые многоугольники, определяющие равнодействующую
сил Р\9 Р2, Р3 (рис. 38). Принять Pi = Р3.
37
2. Три сходящиеся силы заданы своими проекциями на координатные
оси Oxyz\ F\ (2 Д-5); F2 (-1,2,3} F3 (4,3,1). Найти проекции равнодействующей.
3. Будет ли уравновешенной следующая система сходящихся сил,
заданных своими проекциями на оси декартовой прямоугольной системы
координат Oxyz\ Д(-3,4,1); F2 (1,0,5}, F3(2,-4,-6)?
4. Пренебрегая трением на блоке, определить реакции стержней АВ и
ВС, поддерживающих груз весом Q = 80 кН (рис. 39).
5. Вайма для получения клеёных заготовок включает в себя шарнир-
но-стержневой механизм (рис. 40), в котором стержни АВ, ВС и CD совпа-
дают со сторонами квадрата, а стержни АЕ, BF, CG и DH равны между со-
бой и направлены по диагоналям того же квадрата. Определить усилия во
всех стержнях, если сжимающие силы равны Р = 15 кН.
6. Пакет хлыстов весом Q = 150 кН удерживается в равновесии стой-
ками АВ и АС А-образной стрелы и канатом AD (рис. 41). Пренебрегая ве-
сом каната и стоек и считая крепления стоек шарнирными, найти натяже-
ние каната и сжимающие силы в стойках.
Рис. 40
Рис. 41
38
ЛЕКЦИЯ3
ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ
ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ
СИСТЕМЫ СИЛ
Момент силы относительно оси
Моментом силы F относительно оси £ называется проекция на
эту ось вектора-момента силы относительно любой точки О, взятой на
данной оси (рис. 42). Вводя для момента относительно оси обозначение
(f), для проекции вектора-момента на ось £ - обозначение \^М0 ,
в соответствии с данным определением запишем:
M,(F) = [M0(F)]e 0^.
Для моментов силы F относительной осей декартовой прямоуголь-
ной системы координат Oxyz, по определению, имеем:
Для большей ясности эта ситуация дополнительно показана на
рис. 43 (на рисунке изображен случай, когда Мх и Mz положительны, а Му
отрицательна).
Рис. 42
Рис. 43
39
В статике, однако, применяют способы вычисления осевых момен-
тов силы, не требующие предварительного построения вектора-момента
силы Мо (f\. При этом пользуются одним из следующих способов.
Аналитический способ вычисления момента
В основе способа лежит известное из векторной алгебры представ-
ление векторного произведения в виде определителя, что позволяет запи-
сать для вектора-момента силы следующее выражение
J к
У 2
F> F>
Здесь i.j.k - орты координатных осей; х, у, z~ координаты точки
приложения силы; FxiFyiFz - проекции силы на координатные оси. Вспо-
миная, что в формуле разложения вектора на составляющие по координат-
ному базису коэффициенты при ортах являются проекциями этого вектора
на соответствующие оси, а в данном случае, по определению - моментами
силы F относительно координатных осей, приходим к равенствам:
Mx(F) = yF2-zFy-,
My(F) = zFx-xFz;
M2(F) = xFy-yFx.
Полученные формулы называются аналитическими выражениями
для моментов силы относительно координатных осей. Они позволяют
вычислять моменты силы относительно координатных осей без предвари-
тельного построения момента относительно начала координат.
Геометрический способ
вычисления момента
Пусть даны сила F и ось £
(рис. 44). Проведем плоскость Н, пер-
пендикулярную оси £, и отметим
точку О пересечения оси с этой плос-
костью. Из начала и конца вектора
силы опустим перпендикуляры на
плоскость Н. Вектор FH = А'В' назы-
вается проекцией силы F на плос-
кость Н. В отличие от проекции силы
на ось, являющейся алгебраической
40
величиной, проекция силы на плоскость является вектором, и с ней можно
обращаться как с обычной силой - проектировать на оси, вычислять век-
торный и алгебраически моменты. Так, алгебраический момент проекции
FH относительно точки О имеет значение
M0(FH) = ±FH-h.,
где h* ~ плечо этой проекции относительно точки О.
Изобразим момент силы F относительно точки О и заметим для
дальнейшего, что для модуля момента справедливо равенство
|^О(/)| = 25ОЛ£,
устанавливающее, что модуль момента Мо (f) равен удвоенной площади
треугольника ОАВ (доказать самостоятельно). Вычисляя теперь момент
силы относительно оси в соответствии с определением, последовательно
находим
Я (г) = \мо (f)|cosy = 2S0M cosy = +2S0A.B. =
= F2[±FH-h^ = +FH-h.=M0(FH\
В третьем из написанной цепочки равенств использована теорема
геометрии о том, что площадь проекции плоской фигуры на некоторую
плоскость (в нашем случае площадь треугольника ОА’В’) равна площади
проектируемой фигуры (треугольника ОАВ), умноженной на косинус угла
между плоской фигурой и ее проекцией. Знак плюс соответствует острому
углу между M0(f^ и осью £, знак Йину с - тупому' углу между ними (на
рис. 44 изображен первый случай).
Отбрасывая в полученной цепочке равенств промежуточные значе-
ния, получаем:
л/5(/)=л/0(4)=±^-/ь.
Этим равенством устанавливается следующее правило для вычисле-
ния момента силы относительно оси. Момент силы относительно оси ра-
вен алгебраическому моменту проекции этой силы на плоскость, перпен-
дикулярную оси, вычисленному относительно точки пересечения оси с
плоскостью. При этом правило для определения знака алгебраического
момента остается прежним, если на силу FH и точку О смотреть с
положительной стороны оси £.
Из полученного правила ясно видны случаи, когда момент силы от-
носительно оси равен нулю. Это имеет место в двух случаях:
41
1) когда сила параллельна оси (в этом случае имеем FH - 0);
2) когда сила пересекает ось (в этом случае Л* = 0).
Заметим, что данный (геометрический) способ вычисления момента
силы относительно оси находит преимущественное использование при
решении задач статики.
Пример.
Вычислить моменты относительно координатных осей силы F, дей-
ствующей по диагонали грани DEKL параллелепипеда. Угол наклона силы
к основанию параллелепипеда равен а, длины ребер составляют: ОА=а,
OL=b (рис. 45).
Воспользуемся сначала более употребительным геометрическим
способом. Для определения момента относительно осих силу F следует
спроектировать на какую-либо плоскость, перпендикулярную осих. На
рис. 45 уже имеются две такие плоскости - плоскость Oyz и плоскость гра-
ни ABDK. Выбираем эту последнюю за плоскость Я находим проекцию
FH =Fl силы F на эту плоскость = F sin а), отмечаем точку А пересе-
чения выбранной плоскости с осьюх. Далее, вычисляя алгебраический
момент силы F\ относительно точки Л, находим момент силы F относи-
тельно оси х:
Mx(f) = Ma(F}) = Fbsma.
При вычислении момента относительно оси у замечаем, что сила F
уже лежит в плоскости, перпендикулярной оси у и пересекающейся с этой
осью в точке L. В этом случае проекция FH равна самой силе F, и момент
силы F относительно оси у совпадает с алгебраическим моментом силы F
относительно точки Я
Му (г) = ML (f) =-F-h.= -Fa sin a.
42
Для определения момента относительно осиг в качестве плоско-
сти Н удобно принять координатную плоскость Оху. Проекция силы F на
эту плоскость равна вектору F2 с модулем F2 = F • cos а. Вычисляя алгеб-
раический момент этой проекции относительно точки О, находим:
мг (г) = Мо (F2) = Fbcosa.
При аналитическом способе вычисления осевых моментов прежде
всего определяем проекции силы на координатные оси и проекции радиу-
са-вектора точки приложения силы (координаты точки К):
F = (-Fcosa; 0; Fsina);
г = (я, Ь, 0).
Применяя теперь аналитические выражения для моментов силы от-
носительно координатных осей, находим:
Mx(f} = yFz -zFy = 6(Fsina)-0-0 = F6sina;
My^F} = zFx -xFz =0-(-Fcosa)-a(Fsina) = -Fasina;
Mz (f) = xFy - yFx = a-0- 6(-Fcosa) = Fbcosa.
Преобразование пространственной произвольной системы сил
В предыдущей лекции были рассмотрены правила преобразования и
условия равновесия сходящихся сил и пар сил. Полученные результаты от-
крывают возможность перейти к рассмотрению наиболее общего случая -
совокупности сил, линии действия которых как угодно расположены в
пространстве- пространственной произвольной системы сил. Для про-
странственной произвольной системы сил также будем решать две основ-
ные задачи - задачу о преобразовании в эквивалентные системы сил и за-
дачу о равновесии сил.
Сначала рассмотрим вспомогательную теорему о параллельном пе-
реносе силы.
Лемма о параллельном переносе силы
Лемма. Всякую силу, приложенную к абсолютно твердому телу,
можно перенести параллельно себе в любую точку тела, добавляя при
этом некоторую пару.
Пусть Fa - сила, приложенная к телу в точке А (рис. 46, а). Произ-
вольно выберем в теле точку О и приложим к телу в этой точке две урав-
новешенные силы, одна из которых векторно равна данной силе, другая -
равна ей и противоположно направлена (рис. 46, б). Данная сила FA и по-
лученная система сил [fa9 FOi -Fo}9 согласно аксиоме 2, эквивалентны:
fa~(fa, f0, -f0).
43
Но векторы сил FA и Fo равны, поэтому силу Fo можно рассматри-
вать как силу Fa , только перенесенную в другую точку тела (точку (?); си-
лы же Fa и - Fo образуют пару ^F, —Fj. Из этого следует, что предыду-
щее отношение эквивалентности можно выразить в форме: сила FA эквива-
лентна cwieF0 и паре (f, -F), что и доказывает лемму.
Пара сил ^F, -F) называется присоединенной парой. Момент при-
соединенной пары, по определению момента пары, можно представить в
виде
m(f\ -f)=mo(f).
Откуда следует, что момент присоединенной пары равен моменту
данной силы относительно новой точки приложения силы.
Приведение пространственной произвольной системы сил к
данному центру. Главный вектор и главный момент. Основная
теорема статики
Пусть даны силы FJ, F2,.. .,F„, приложенные к телу соответственно в
точках 4, А2,...,Ап (рис. 47, а). Осуществим преобразование данной про-
странственной произвольной системы сил, называемое приведением сил к
данному центру. Выберем в теле произвольную точку О и в соответствии с
леммой перенесем в эту точку все заданные силы. В результате получим
новую систему сил, эквивалентную данной и состоящую из таких же сил,
только приложенных в точке О, то есть сил F10, F2Q,...9Fn^ и присоеди-
ненных пар (Fp -Fj), (F2, -F2),...,(f„, -Fn) (рис. 47, б).
Силы Fj0, F2o’---’^o являются сходящимися в точке О, и их можно
заменить одной силой R (равнодействующей), приложенной в той же точ-
ке и равной геометрической сумме сил:
(4> ^20’-• ~ =
44
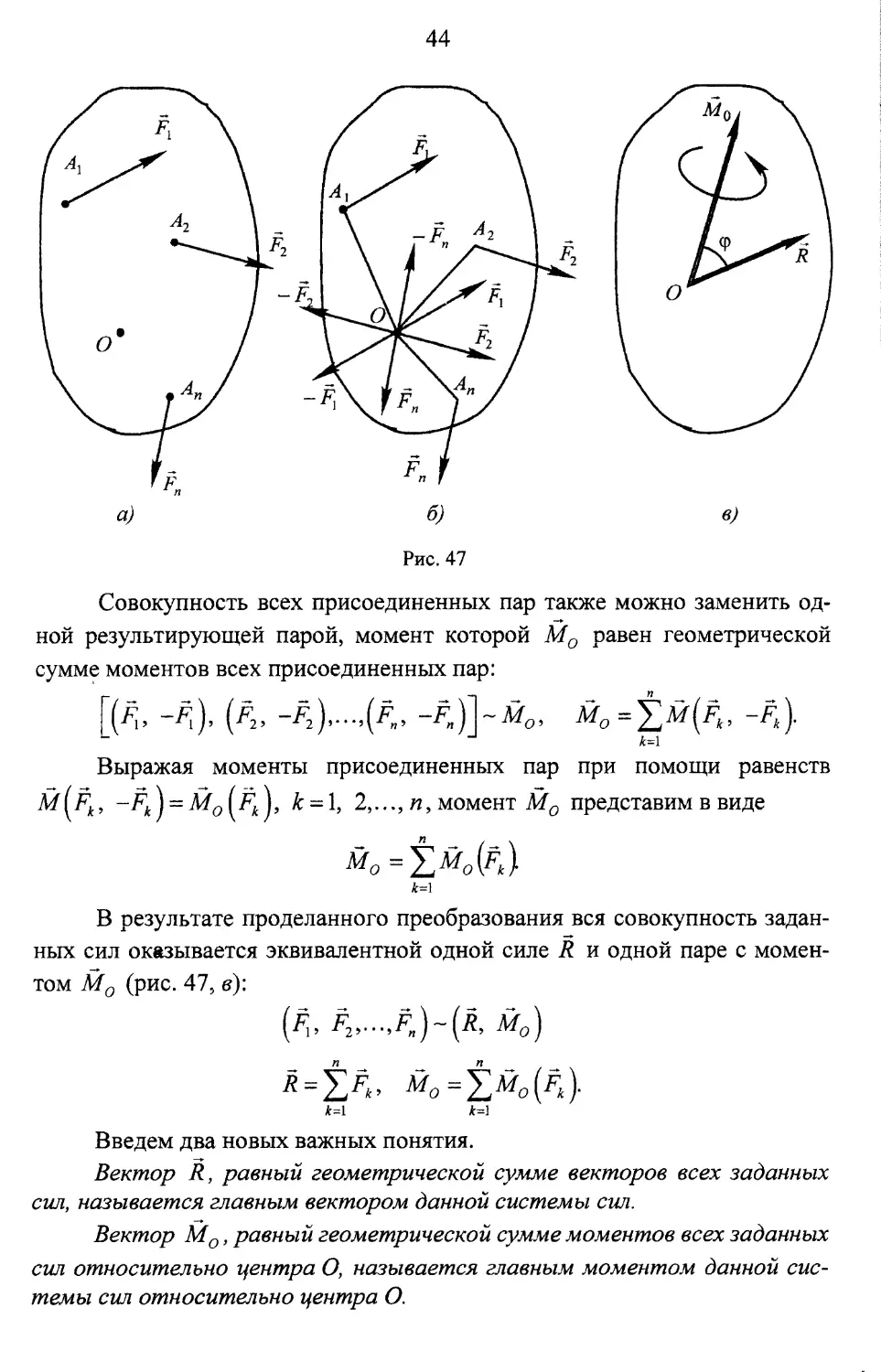
Совокупность всех присоединенных пар также можно заменить од-
ной результирующей парой, момент которой Мо равен геометрической
сумме моментов всех присоединенных пар:
[(/?, -/?), (Л, -Ft).
Выражая моменты присоединенных пар при помощи равенств
M^Fk, -Fk j = Мо (Fk к = 1, 2,..n, момент Mo представим в виде
m0 = £w0(fJ
к=1
В результате проделанного преобразования вся совокупность задан-
ных сил оказывается эквивалентной одной силе R и одной паре с момен-
том Мо (рис. 47, в)\
(Ft,
R = XFt, Мо = £л/ДЛ)-
*=1 Ъ=1
Введем два новых важных понятия.
Вектор R, равный геометрической сумме векторов всех заданных
сил, называется главным вектором данной системы сил.
Вектор Мо, равный геометрической сумме моментов всех заданных
сил относительно центра О, называется главным моментом данной сис-
темы сил относительно центра О.
45
Теперь итоги выполненного преобразования можно сформулировать
так. Всякую пространственную систему сил в общем случае можно заме-
нить эквивалентной ей системой, состоящей из одной силы, равной глав-
ному вектору этой системы сил и приложенной в произвольно выбранной
точке тела (центре приведения) и одной пары сил с моментом, равным
главному моменту системы сил относительно выбранного центра
приведения.
Это утверждение носит название основной теоремы статики.
Примечание. Не следует смешивать понятия главного вектора и рав-
нодействующей системы сил. Равнодействующая, по определению, это си-
ла, эквивалентная данной системе сил. Главный вектор представляет собой
просто векторную сумму всех заданных сил. Как следует из основной тео-
ремы статики, главный вектор эквивалентен данной системе сил только в
совокупности с парой сил с моментом Мо, и поэтому не может служить
для нее равнодействующей. В дальнейшем будем пользоваться для равно-
действующей обозначением А.
Вычисление и построение главного вектора и главного момента
Выбираем систему координатных осей Oxyz (рис. 48)и вычисляем
проекции главного вектора как алгебраические суммы проекций всех за-
данных сил на выбранные оси:
По найденным проекциям, откладывая соответствующие отрезки
вдоль координатных осей (с учетом знака проекции), строим прямоуголь-
ный параллелепипед. Направленная диагональ, проведенная из начала ко-
46
ординат в противоположную вершину параллелепипеда, определяет глав-
ный вектор R (см. также рис. 26). Модуль и направляющие косинусы
главного вектора определяются следующими вытекающими из построения
формулами:
|я| = Jr2x + Лр + К?, cosa = &, 0053 = 7777, cosy = .
1*1 1*1 1*1
Совершенно аналогично определяются проекции, модуль и направ-
ляющие косинусы главного момента:
= ±мх (Л), = Xму (Л), (Л)>
/1=1 /Ы к=\
^^М^+М^+М^, cosA = ^, cosB = i^, cosr = ^.
\Mo\ R |^o|
К формулам для вычисления проекций главного момента необходи-
мо привести следующие пояснения.
Главный момент, по определению, есть векторная сумма моментов
всех сил Fk(k = 1, 2,...,^относительно центра О. Следовательно, его про-
екции на координатные оси равны алгебраическим суммам проекций на
эти оси векторов-моментов сил относительно центра (9, то есть величин
[м0(л)]х> [л/ДЛ)],. [Я(Л)1 (*=1, 2,...,«)•
Но эти величины, по определению момента силы относительно оси,
являются моментами сил относительно соответствующих координатных
осей:
[л/0(Л)]х=л/ДЛ);
[лЛ(Л)]^=ч(Л)> [Я>(Л)1 =^(Л) 2,.
Отсюда непосредственно следуют написанные выше выражения для
величин МОх, МОу, MOz.
Косинус угла ср между главным вектором и главным моментом опре-
деляется так:
Rx'M0x + Ry 'М0у +Rz ‘M0z
COS(p= -------Д-7-Д .------
1*1-KI
Формула получается следующим образом. По определению скаляр-
ного произведения векторов R и Мо имеем:
R • Мо - |я| • \мо1 • cos ср.
47
С другой стороны, эта же величина может быть вычислена через
проекции векторов-сомножителей:
R • Мо = Rx • МОх + Ry • + Rz • MOz.
Приравнивая правые части и разрешая полученное уравнение отно-
сительно coscp, приходим к написанной формуле.
Перемена центра приведения
Выберем в качестве центра приведения другую точку О' тела. Изме-
нятся ли главный вектор и главный момент при замене центра приведе-
ния О на 01
Главный вектор останется без изменения, так как при переносе сил
параллельно себе в другую точку не изменяются ни модули, ни направле-
ния сил.
Вычислим новое значение главного момента. Пусть гк - радиусы-
векторы точек приложения сил Fk относительно точки О' («нового» центра
приведения), гк - то же самое относительно точки О («старого» центра
приведения). Эти величины связаны очевидными равенствами гк = 0'0 + гк
(к= (рис. 49). Для нового главного момента можем написать:
к=1 к=1 к=1 \ к=1 ) к=\
Рис. 49
48
При учете очевидных равенств
к=\ к=\
полученный результат запишется в форме
Мо, = Мо + 0'0 х А,
или, что то же самое:
M0.=M0+Mff(R).
Таким образом, получено следующее правило: при перемене центра
приведения новый главный момент системы сил равен геометрической
сумме старого главного момента и момента главного вектора, прило-
женного в старом центре и вычисленного относительно нового центра
приведения.
На рис. 49 показано соответствующее геометрическое построение
(параллелограмм моментов при точке О').
Однако проекция главного момента на направление главного вектора
остается неизменной. Действительно, проектируя полученное равенство на
ось £, совпадающую по направлению с главным вектором (рис. 49), получаем:
Мо. coscp' - Мо coscp + (^)] •
Но Мо, (r} ± £, поэтому последнее слагаемое всегда равно нулю. В
итоге имеем равенство
Мо, cos ф' = Мо cos ф = М' = const.
Таким образом, при всевозможных переменах центра приведения
для данной системы сил две величины остаются неизменными - её глав-
ный вектор R и проекция М' главного момента на направление главного
вектора. Эти величины называются инвариантами системы сил (А - век-
торный инвариант, М' - скалярный инвариант). Величину М’ называют
также наименьшим главным моментом системы сил.
Вопросы для самопроверки
1. Что называется моментом силы относительно оси?
2. Изложите способы вычисления момента силы относительно оси
(аналитический способ, геометрический способ).
3. В каких случаях момент силы относительно оси равен нулю?
4. Что называется пространственной произвольной системой сил?
5. Что называется главным вектором и главным моментом системы
сил?
6. В чем состоит различие между главным вектором и равнодейст-
вующей системы сил?
7. Сформулируйте основную теорему статики.
8. Зависят ли главный вектор и главный момент от выбора центра
приведения сил?
49
ЛЕКЦИЯ 4
ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ
ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ
СИСТЕМЫ СИЛ (продолжение). ЧАСТНЫЕ
СЛУЧАИ СИСТЕМЫ СИЛ
Случаи приведения к простейшему виду
Приведение к паре
Пусть в результате приведения сил (/], F2,...9Fn) к центру О оказа-
лось, что главный вектор равен нулю, а главный момент отличен от нуля:
R = О, Мо * 0. Тогда в силу основной теоремы статики можем написать
(Я Я-ЛН-
Это означает, что исходная система сил в этом случае эквивалентна
паре сил с моментом Мо .
Момент пары не зависит от того, какая точка выбрана в качестве
центра моментов при вычислении момента пары. Следовательно, в данном
случае главный момент не должен зависеть от выбора центра приведения.
Но именно к этому выводу и приводит соотношение
Мо> - Мо + О'О х R,
связывающее главные моменты относительно двух различных центров.
При R = 0 добавочный член также равен нулю, и мы получаем
Мо, - Мо = const.
Приведение к равнодействующей
Пусть теперь главный вектор не равен нулю, а главный момент равен
нулю: R Ф 0, Мо = 0. В силу основной теоремы статики имеем
(Я Я-Л)~Я
то есть система сил оказывается эквивалентной одной силе - главному
вектору. Следовательно, в этом случае исходная система сил приводится к
равнодействующей, и эта равнодействующая совпадает с главным векто-
ром, приложенным в центре приведения: R*=R0.
50
Система сил приводится к равнодействующей и в том случае, когда
главный вектор и главный момент оба не равны нулю, но взаимно перпен-
дикулярны: R&0, Мо*0, RA-M0, Доказательство осуществляется при
помощи следующей последовательности действий.
Через центр приведения О проводим плоскость, перпендикулярную
главному моменту Мо (рис. 50, а). На рисунке эта плоскость совмещена с
плоскостью чертежа, в ней же расположен главный вектор R . В этой
плоскости строим пару с моментом Мо, причем силы пары выберем рав-
ными по модулю главному вектору R ; тогда плечо пары будет равно
h = Мо /R. Далее переместим пару в ее плоскости таким образом, чтобы
одна из сил пары оказалась приложенной в центре приведения О противо-
положно главному вектору R ; вторая сила пары будет приложена в точ-
ке С, отстоящей от центра О в нужную сторону, определяемую направле-
нием Мо, на расстоянии ОС, равном плечу пары h (рис. 50, б). Отбрасывая
теперь уравновешенные силы R и -R , приложенные в точке О, приходим
к одной силе R , приложенной в точке С (рис. 50, в). Она и будет служить
равнодействующей данной системы сил Л = Rc.
Рис. 50
Видно, что равнодействующая 7?» по-прежнему равна главному век-
тору R , однако отличается от главного вектора своей точкой приложения.
Если главный вектор приложен в центре приведения О, то равнодейст-
вующая R* - в точке С, положение которой требует специального опреде-
ления. Геометрический способ нахождения точки С виден из проделанного
выше построения.
Для момента равнодействующей относительно центра приведения О
можно написать (см. рис. 50):
Мо (л) = ОС X R = м(-О) = Мо = ±М0 (Д),
£=1
51
или, опуская промежуточные значения:
^0(л.)=Ж(Л)-
к=1
Если спроектировать это векторное равенство на какую-либо ось £,
проходящую через точку О, получаем соответствующее равенство в про-
екциях:
к=4
Вспоминая, что проекция момента силы относительно точки на ось,
проходящую через эту точку, является моментом силы относительно оси,
перепишем этой равенство так:
Полученные равенства выражают теорему Вариньона в ее общем ви-
де (в лекции 2 теорема была сформулирована только для сходящихся сил):
если система сил имеет равнодействующую, то момент этой равнодей-
ствующей (относительно точки, относительно оси) равен сумме моментов
всех заданных сил - составляющих (относительно той же точки, той же
оси). Понятно, что в случае точки суммирование моментов векторное, в
случае оси - алгебраическое.
Приведение к динаме
Динамой или динамическим винтом называется совокупность пары
сил и силы, направленной перпендикулярно плоскости действия пары.
Можно показать, что в общем случае приведения, когда R * О, Мо ф 0 и R
не перпендикулярен Мо, исходная система сил эквивалентна некоторой
динаме.
Условия (уравнения) равновесия пространственной произвольной
системы сил
Если система сил находится в равновесии, то ее главный вектор и
главный момент равны нулю:
Я = 0; М = 0.
Эти векторные равенства приводят к следующим шести скалярным
равенствам:
t^=0; £Х=0; XFfa=0;
Л-1 k=\ k=l
Ж&)=0; 1>X)=O; £ч(Л)=о,
k=\ k=l Л-1
52
которые называются условиями равновесия пространственной произволь-
ной системы сил. Первые три условия выражают равенство нулю главного
вектора, следующие три - равенство нулю главного момента системы сил.
В этих условиях равновесия должны учитываться все действующие
силы - как активные (задаваемые), так и реакции связей. Последние зара-
нее неизвестны, и условия равновесия становятся уравнениями для опре-
деления этих неизвестных -уравнениямиравновесия.
Поскольку максимальное число уравнений равно шести, то в задаче
на равновесие тела под действием произвольной пространственной систе-
мы сил можно определить шесть неизвестных реакций. При большем ко-
личестве неизвестных задача становится статически неопределенной.
И еще одно замечание. Если главный вектор и главный момент отно-
сительно некоторого центра О равны нулю, то они будут равны нулю от-
носительно любого другого центра. Это прямо следует из материала о пе-
ремене центра приведения (доказать самостоятельно). Следовательно, если
условия равновесия тела выполняются в одной системе координат, то они
будут выполняться и в любой другой неподвижной системе координат.
Иными словами, выбор координатных осей при составлении уравнений
равновесия совершенно произволен.
Пример.
Прямоугольная плита (рис. 51, а) весом G - 5 кН удерживается в го-
ризонтальном положении сферическим шарниром О, подшипником А и
тросом BE, причем точки О и Е находятся на одной вертикали. В точке D к
плите приложена сила Р (Р = 3 кН), перпендикулярная стороне OD и на-
клоненная к плоскости плиты под углом 45°. Определить натяжение троса
и реакции опор в точках О и А, если а = Р = 30° и ОА = 2 • OD.
Рис. 51
53
Для решения задачи рассматриваем равновесие плиты. К активным
силам Р9 G добавляем реакции связей - составляющие XQ, Уо, Zo реак-
ции сферического шарнира, реакции ХА, ZA подшипника, реакцию f
троса. Одновременно вводим координатные оси Oxyz (рис. 51, б). Видно,
что полученная совокупность сил образует произвольную пространствен-
ную систему, в которой силы XQ9 YQ9 ZQ, ХА, ZA, f неизвестны.
Для определения неизвестных составляем уравнения равновесия.
Начинаем с уравнения проекций сил на ось х:
j>X=0: Хо + ХА-Т-sin2 30° = 0.
Поясним определение проекции Тх. Её вычисление осуществляется в
два приема- вначале определяется проекция силы Т на плоскость
Оху =rsinp), далее, проектируя на осьх (удобнее на ось Ах', па-
раллельную Ох), находим Тх (см. рис. 51,6):
= -Т^ sin а = -(Тsin Р) sin а = -Г sin2 30°.
Этим способом двойного проектирования удобно пользоваться, ко-
гда линия действия силы и ось не пересекаются. Далее составляем:
у = 0: Уо + Pcos45° - Гзт30° cos30’ = 0;
у Г, =0: ZQ+ZA +rcos30°-G!-Psin45D=0.
KZ U /1
к=1
Уравнение моментов сил относительно оси х имеет вид:
У Л/ДД) = О: -G — + Tcos30°-OA + Z, ОА = 0.
k=i 2
Моменты сил XQ, Уо, Zo., ХА, Р в уравнении отсутствуют, так как
эти силы либо пересекают ось* (р, ZQ, Foj, либо ей параллельны
(хо, Хл). В обоих этих случаях момент силы относительно оси равен ну-
лю (см. с. 41).
Вычисление момента силы часто облегчается, если силу разложить
подходящим образом на составляющие и воспользоваться теоремой Варинь-
она. В данном случае это удобно сделать для силы f. Разлагая её на гори-
зонтальную (т^) и вертикальную составляющие, можем написать:
мх(г)=мх(^)+мДг).
54
Но Мх^)- 0 (сила пересекает осьх), второе же слагаемое легко вы-
числяется:
Мх (г) = Г • DB = Г • ОА = rcos30° • ОА.
Далее составляем остальные уравнения моментов:
£Х,(^)=0: G- — -Tcos30°-AB + Psin45°-АВ =0;
*-i
Ja/z(f*)=O: Рсо845”-ЛВ-^л-Л(?=0.
k=L
Момент силы Т в последнем уравнении отсутствует, так как линия
действия силы пересекается с осью z (в точке Е).
Мы получили шесть уравнений, содержащих шесть неизвестных.
Решая их, определяем все искомые реакции.
Из последних двух уравнений, содержащих лишь по одной неизвест-
ной, сразу находим ХА и Т:
_ РуДУ .ДР = 32 л8 _ ЗЛ ,
А АО 2-АВ 4
| G-- + Psin45"
Т = -Ь—--------
АВ' cos 30е
5 + Зд/2
----г=— = 5,336 кН.
7з
Подставляя найденные значения реакций в остальные уравнения, оп-
ределяем значения других неизвестных:
7 ТТ 7 5 + 3>/2
7 --------= -2,121 кН, Zc, =-------= 4,621 кН,
2 0 2
Y° = 89 кН, хо = 0,273 кН.
Отрицательный знак реакции ZA означает, что ее действительное на-
правление противоположно принятому в расчетах (указанному на
рис. 5\,бу.
Частные случаи системы сил
Плоская система сил
Совокупность сил, расположенных в одной плоскости, называется
плоской системой сил. Выберем центр приведения О и координатные
оси х, у в той же плоскости, ось z направим перпендикулярно к ней. Для
проекций главного вектора и главного момента на эти оси будем иметь:
55
R = (Лх,7?у,0), Mo = (0,0,Л/Ог). Величины Rz, МОх, Моу равны нулю (поче-
му?), а значащие проекции определяются по формулам:
R, = Ry = 1л> мОг = ±м0 (т?).
к=1 к-\
Заметим, что моменты сил относительно оси z в данном случае сов-
падают с алгебраическими моментами сил относительно точки О, что и уч-
тено в формуле для Mqz^
Видно, что скалярное произведение R • Мо = 0, поэтому главный
вектор и главный момент, если не равны нулю, то взаимно перпендику-
лярны. Отсюда следует, что для плоской системы сил возможны только
два случая приведения к простейшему виду - к паре сил (если R =0) и к
равнодействующей (если R 0).
Условия равновесия, представляющие собой координатную запись
векторных равенств R = О, Мо =0, запишутся так:
2Л=о, $Л=°> Хм0(Л)=о.
А=1 Л=1
Следовательно, для плоской произвольной системы сил имеются три
независимых условия (уравнения) равновесия - должны равняться нулю
алгебраические суммы проекций сил на две координатные оси и сумма ал-
гебраических моментов сил относительно произвольной точки, взятой в
плоскости действия сил.
Пример.
Найти реакцию цилиндричес-
кого шарнира А и натяжения ветвей
троса, удерживающих в равновесии
ступенчатую балку АВС (рис. 52, а).
К балке приложены пара сил с
моментом М = 30 кНм, сосредо-
точенная сила Р = 80 кН и равно-
мерно распределенная сила интен-
сивностью q - 8 кН/м, действую-
щие в одной плоскости. Принять
АЕ = ED = DB = ВС = а= 2м,
а = 60°, блок считать идеальным.
Распределенную силу, пред-
ставляющую собой плоскую сис-
тему параллельных сил, заменяем
равнодействующей - сосредоточен-
Л
Рис. 52
56
ной силой Q, приложенной посередине участка ВС балки и равной по мо-
дулю 2 = да = 8- 2 = 16 кН. Мысленно отбрасываем связи, заменяя их дей-
ствие реакциями - силами ХА, YA, ТЕ, TD. Вследствие идеальности блока
(отсутствия трения в оси блока) натяжения ветвей троса по величине оди-
наковы: ТЕ =TD =Т.
В полученной плоской системе сил (рис. 52, б) неизвестными явля-
ются силы ХА, Ya и величина Тсил ТЕ и fD. Для их определения восполь-
зуемся условиями равновесия плоской произвольной системы сил. Выби-
раем координатные оси и составляем уравнения равновесия:
VF =0: ХА -7\cos30°+Psin45° =0;
k=l
=0: r4+7’£+7’Dsin30”-e-Pcos45"=0;
k=\
T£acos30° +TD -2acos30°-М-^ЗасозЗО1 +-|-
k=] < 2 J
-Fcos45°(3tfcos30° + a)- Pcos45° - Зя sin 30° = 0.
Для удобства определения момента сила Р разложена на состав-
ляющие вдоль координатных осей (на рис. 52, б показаны штриховыми ли-
ниями), после чего применена теорема Вариньона.
Из последнего уравнения, содержащего одну неизвестную
(T = TE-TD), находим Т=135,86 кН. После подстановки значений
Г£ = TD =135,86 кН в первое и второе уравнения определяем остальные
неизвестные: YA = -131,22 кН, ХА= 61,09 кН. Отрицательный знак ве-
личины Ya означает, что реакция YA направлена в противоположную сто-
рону.
Система параллельных сил
Выберем ось Oz параллельно силам, тогда оси Ох, Оу расположатся
в плоскости, перпендикулярной силам. Проекции сил Fk (£ = 1, 2,...,и) на
оси Ох, Оу и моменты сил относительно оси Oz будут равны нулю, по-
этому главный вектор и главный момент получаются в следующем виде:
Я = (0,0,Лх) ; М0=(М01, М^, о),
4=1 4=1 4=1
Вычисляя скалярное произведение главного вектора и главного мо-
мента, обнаруживаем, что опа равна нулю, поэтому главный вектор и глав-
ный момент взаимно перпендикулярны. Следовательно, параллельные си-
лы имеют, как и плоская система сил, только два случая приведения к про-
стейшему виду - к пире (при R = 0; и к равнодействующей {при Я 0 j.
Уравнения равновесия параллельных сил имеют вид;
-°; £a/,(fJ=o, 2Х1ЛН.
;-i l-i >-|
то есть d.'Vf рцкшмныин жт&ш пириыМъных сия »£
О&содшю гг ЛхзлкюточлЛ), (ъд.тм ДчЛечьг мулю «-ь-гебраическая cv^tntJ
c’w-r cU'rO-Hr и атг!еб^гнчь|£г.К|-гс' oj.mjhw .чсшйн-
с к ? олт/еачггг^.'сьчо осей пе/>лен^ик>у1у<^чых гнетам.
Можно выделить еще более- частимй случай- гх-гсх^та слсюслгу па-
раллельных сил. Дам иСс существуют два независимых ус-.товпя равновесия:
£Х-0; XMuWl-0-
<*1 i-1
Здесь точка О и ось г лежат в одной плоскости с силами, причем оску рас-
положена параллельно силам.
НацоМНИМ езпе о схг^гЭлт^щ.-ея ^плих (в пространстве и на плоскости),
для которых вопросы приведения п равновесия были рассмотреть! ранее и
лекции 2.
Пример.
Круглый стол весом £>- 2Ю Н имеет три ножки, расположенные в
вершинах равностороннего треузозхьника АйС со стороной а. В точке/?,
посередине расстояния между' носкими, к столу приложена вертикальная
сила Р- ЮО II- Определить давления ножек стола на гладкую горизон-
тальную опорную плоскость (рис. 53,«).
Реакции ,УЛ, Ar-, Л'. гладкой плоскости |»ерпвн;п1к.у;(ярАЫ -пой
плоскости. Добавляя их к активным сипам Л £?, ламечаем, что к столу
приложена ирсю1ранствсниам система т1аралйе.:£ьных сил. Составляем для
лес равнения равновесия- Дн* удобства вычисления ьюме^тов основной
рисунок до[Юиняом плоской проекции (рнс. S3, б), на которой реакции на-
правлены «на читателя», силы Р> Q - «ог щпатмя», а трву^орьчик
отображается без искажения. Будем иметь;
=^0; Л'^асиаЗО' -Q^ сгсозЗО' - Р a cos ? О’ -<!'
Af. f УС 1 = U: -.V-a - N = - с О - -I Р —лепя 60' =0.
58
Решая эти уравнения, найдем:
N ,=N„ =^ + - = 120 Н, ДГ =2 = 70 Н.
' в 3 2 3
Заметим, что определение давлений стола на четырех ножках приво-
дит к статически неопределенной задаче - неизвестных становится четыре,
а количество уравнений остается прежним, равным трем.
Равновесие системы тел
Наряду с задачами на равновесие отдельного тела в статике встреча-
ются задачи, в которых требуется рассмотреть равновесие нескольких
твердых тел, образующих единую конструкцию. В этих случаях прежде
всего требуется выяснить, будет ли такая система тел статически опреде-
лимой. Ответ на данный вопрос получаем, сравнивая число неизвестных с
числом независимых уравнений равновесия.
Для этого система тел мысленно расчленяется на отдельные тела, из
которых она составлена, и подсчитывается общее число уравнений равно-
весия для тел системы. Если общее число уравнений совпадает с числом
неизвестных, система тел статически определима; если неизвестных боль-
ше, чем уравнений, система тел является статически неопределимой.
Пример.
Будет ли статически определимой система, состоящая из балки АВ и
опирающегося на нее цилиндра (рис. 54, я)? Активные силы Р, Q, G, уг-
лы а, р и все размеры считать заданными.
Мысленно расчленяем систему, изображаем отдельно цилиндр
(рис. 54, б) и балку (рис.54, в) со всеми приложенными к ним силами. Для
данной системы неизвестными являются реакции связей: составляющие
реакции заделки ХА, YA, МА , реакция стены N и величина взаимного
59
давления балки и цилиндра N12 = N2{ = N. - всего пять величин. Общее
число независимых уравнений равновесия также равно пяти - два уравне-
ния равновесия для плоской системы сходящихся сил, приложенных к ци-
линдру, и три уравнения для плоской произвольной системы сил, дейст-
вующих на балку. Следовательно, система статически определима. Стоит,
однако, добавить хотя бы одну новую связь, например, невесомый стер-
жень CD (рис. 54, г), как система становится статически неопределимой.
Рис. 54
Статически определимая система может быть до конца исследована
методами теоретической механики. При этом можно пользоваться двумя
способами решения задачи.
При решении первым способом уравнения равновесия выписывают-
ся для каждого тела; в эти уравнения, в числе прочих сил, входят и силы
взаимодействия между телами (реакции внутренних связей). При втором
способе решения вначале составляются уравнения равновесия для всей
системы (конструкции), рассматриваемой как единое твердое тело. Эти
уравнения не содержат сил взаимодействия между телами и поэтому со-
держат меньшее число неизвестных. Если полученных таким способом
уравнений недостаточно для решения задачи, то система расчленяется, и
недостающие уравнения составляются для какой-либо из частей (тел) сис-
темы. Заметим, что второй способ часто предпочтительнее, так как приво-
дит к более простым системам уравнений.
60
Вопросы для самопроверки
1. В каком случае данная система сил приводится к паре? К равно-
действующей?
2. Сформулируйте теорему Вариньона в ее векторной и скалярной
формах.
3. Каковы случаи приведения плоской системы сил?
4. Когда параллельные силы эквивалентны одной силе? Одной паре?
5. В чем состоят условия равновесия пространственной произволь-
ной системы сил?
6. Запишите условия равновесия пространственной системы парал-
лельных сил.
7. Сколько независимых уравнений равновесия можно составить для
плоской произвольной системы сил? Как запишутся эти уравнения?
8. Каковы условия (уравнения) равновесия плоской системы парал-
лельных сил?
9. Как определить, является ли данная система твердых тел статиче-
ски определимой?
10. Приведите примеры статически определимых и статически неоп-
ределимых систем тел.
11 .Какими двумя способами можно составлять уравнения равнове-
сия для системы тел?
Упражнения
Решить следующие задачи из сборника задач по теоретической ме-
ханике И.В. Мещерского (номера задач приводятся по книге 1981 года из-
дания).
По теме «Равновесие плоской произвольной системы сил»: 4.7, 4.9,
4.10,4.15,4.28.
По теме «Равновесие системы тел»: 4.33, 4.35, 4.58.
По теме «Равновесие пространственной произвольной системы сил»:
8.13,8.17, 8.27,8.29.
По теме «Равновесие пространственной системы параллельных сил»:
8.5, 8.8.
61
ЛЕКЦИЯ 5
ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ И ЦЕНТР
ТЯЖЕСТИ
Центр параллельных сил
Пусть дана система параллельных сил (/J,F2,...,F„) с отличным от
нуля главным вектором R. Как следует из предыдущей лекции, такая сис-
тема сил приводится к равнодействующей R*, равной
R. = R = ±Fk.
к=\
Будем считать, что точки приложения сил А2,..., Лп фиксированы.
Тогда равнодействующая А также будет иметь вполне определенную точ-
ку приложения С, называемую центром данной системы параллельных
сил. Выведем формулы, определяющие положение этого центра.
Пусть точка О - произвольно выбранная точка отсчета,
гк(к = 1,2,..., я) - проведенные из точки О радиусы-векторы точек прило-
жения сил, гс - радиус-вектор центра параллельных сил, ё (|е| -1) - еди-
ничный вектор общего направления сил (рис. 55). В силу параллельности
векторы сил и вектор их равнодействующей могут быть записаны в сле-
дующем виде:
Fk=Fk,e, R, = ±Fk=(±Fk,)e,
к=1 к=\
величины F& обозначают алгеб-
раические значения сил, то есть
взятые со знаком ”+” или модули
сил. Знак "+” берется в случае, когда
сила и вектор е направлены в одну
сторону, знак если эти направ-
ления противоположны.
Для определения положения
центра параллельных сил восполь-
зуемся теоремой Вариньона, согласно
которой имеем равенство
м0(А)=ХЧ(Л).
к-\
62
Вспоминая выражение для момента силы относительно точки и
свойства векторного произведения, представим левую и правую части ра-
венства в следующем виде:
Л?0(А) = rc X Л = Гс X е = (^Ft.)rc X ё;
Л=1 *=1
X м0 (Л)=Z х =(£ )х«
Л=1 к=1 к=1
После этого равенство примет вид
(ХЛ-)?с х ё = х ё •
Л=1 к=1
Вторые сомножители в левой и правой частях равенства одинаковы,
следовательно, будут равны и первые сомножители:
к=1 к=1
Отсюда следует формула
п
к=\
определяющая положение точки С - центра параллельных сил.
Заметим, что вектор е, задающий общее направление сил, не входит
в полученное выражение. Это означает, что центр параллельных сил не за-
висит от направления сил, а зависит только от их алгебраических значений
и точек приложения.
Выберем с началом в точке О декартову систему координатных осей
Oxyz. Проектируя обе части полученной векторной формулы на выбранные
оси, получим выражения для координат центра параллельных сил:
Если все силы направлены в одну сторону, то величины F^ либо все
равны Fh либо все равны -Fk (к = 1,2,..., п). В этом случае формулы упро-
щаются:
Здесь Fk (к = 1,2,..., и) - просто модули сил.
63
Распределенные силы
Частным случаем параллельных сил служат распределенные силы. В
отличие от силы, приложенной в одной точке и называемой сосредоточен-
ной силой, распределенная сила приложена в каждой точке некоторой ли-
нии, поверхности или объема. Распределенная сила характеризуется своей
интенсивностью- величиной силы, приходящейся на единицу длины,
площади или объема.
Пусть имеем распределен-
ную силу, действующую на
отрезке [0, /] оси х и пусть
q = q(x) - ее интенсивность
(рис. 56, а). Мысленно разобьем
отрезок [О, Z] на п произвольных
элементарных участков [0, xj, а)
[хь х2], [хл_1, Z] и вычислим
силу, действующую на каждый
участок, по формуле
Д/\ = д(хк*)Дхк (£ = 1,2,л),
где &хк — хк — хк^ - длина соот-
ветствующего участка, а хк* -
абсцисса точки, произвольно
взятой внутри или на границе
Рис. 56
соответствующего интервала. В результате получим систему параллель-
ных сил, приложенных в точках с абсциссами хк (к = 1,2, ..., п) и направ-
ленных в одну сторону. Такая система сил всегда имеет равнодействую-
щую. Величина 7?* и точка приложения С равнодействующей, в соответст-
вии с полученными выше результатами, будут определяться выражениями
(приближенно):
к=\ к=\
хс=•
, А=1 к=1
Устремляя в этих формулах число отрезков разбиения п к бесконечности и
переходя к пределу, приходим к следующим точным формулам, опреде-
ляющим величину и точку приложения равнодействующей распределен-
ной силы (рис. 56, б):
R* = Jq(x }dx , хс= — ^xq(x)dx.
о О
64
Если q(x) -qQ= const, то имеем равномерно распределенную силу.
Используя полученные формулы, для нее получаем (рис. 57, а):
R* = 1 хс =~^ •
Для силы, распределенной по закону треугольника (рис. 57, б), будем
иметь:
ХС=|/-
При решении задач статики распределенные силы удобно заменять
Рис. 57
Центр тяжести
На тело, находящееся вблизи поверхности Земли, действует распре-
деленная сила тяжести - веса частиц тела, направленные вертикально вниз.
Мысленно разбивая тело на произвольным образом выделенные части, по-
лучим пространственную систему односторонне направленных параллель-
ных сил ДР, ЛР2, ..., ДР , где п — число частей разбиения. Равнодейст-
Рис. 58
вующая Р этих сил называется
весом тела, а точка приложения С
веса тела- центром тяжести тела
(рис. 58).
Применяя формулы для
определения равнодействующей
параллельных сил, для веса* и
координат центра тяжести тела
получим:
Л=1 * k=i
Ус=; zc =
* Л=1 * л-1
65
В этих формулах хк, ук, - координаты точек приложения Ак сил
&Pk(k = l,2,...,ri).
Из полученных формул, в частности, вытекает следующая теорема о
положении центра тяжести симметричного тела. Если однородное тело
имеет плоскость, ось или центр симметрии, то центр тяжести тела
лежит соответственно в этой плоскости, на этой оси, в этом центре.
Предлагаем провести соответствующее доказательство самостоятельно.
Интегральные формулы для координат центра тяжести
сплошных тел полученные формулы приъодлл\л^^^т^
му ввду.
Тело называется сплошным, если вещество в теле распределено не-
прерывно. В сплошном теле можно неограниченно уменьшать размеры
выделенных материальных элементов и осуществлять предельные перехо-
ды. Пусть Emk, EVk(k = 1,2, ..., п)~ массы и объемы элементов, выделен-
ных в сплошном теле, Ак- точки внутри этих элементов. Отношение
I EV * называется средней плотностью тела в точке Ак. Предел, к кото-
рому стремится средняя плотность при неограниченном уменьшении объ-
ема A Vk, называется плотностью тела в точке Ак.
р(А,)= lim
* ДР*->0 Д)/
Тело называется однородным, если его плотность одинакова во всех точ-
ках: р(Ак) = р = const.
Для сплошных однородных тел, полагая Emk=pEVk,
ЕРк ~ Emkg = pEVkg, Р = pVg (g- ускорение силы тяжести) и переходя в
формулах для координат центра тяжести к пределу при п -> <х>, получим:
Хс = у Vdv ’ yc=^Vdv’ Zc=^Vdy-
Г (Г) K (У) У (V)
В этих формулах И- объем тела, dV- объем выделенного элемента ин-
тегрирования, х, у, z - декартовы координаты какой-либо точки внутри или на
границе элемента. Знак J обозначает интегрирование по всему объему тела.
(Г)
Для однородных поверхностных тел (мембраны, оболочки) и мате-
риальных линий (стержни, нити) эти формулы преобразуются к следую-
щему виду:
для поверхностных тел
= zc=^\zds,
d (S) d (S) d (5)
для материальных линий
у jxdl; yc =y $ydl; zc = y jzdl.
1 (/) 1 (I) 1 (I)
66
В этих формулах 5 - площадь поверхности тела, dS - площадь выде-
ленного на ней элемента интегрирования, I - длина линии, dl - длина ее
элемента, х, у, z - декартовы координаты какой-либо точки, принадлежа-
щей элементу интегрирования, хс, у& zc - декартовы координаты центра
тяжести данного поверхностного тела или материальной линии.
Пример 1.
Найти центр тяжести однородного полушара радиуса R.
Выберем начало координат в центре
основания полушара, проведем координат-
ные оси (рис. 59). Полушар симметричен
относительно оси Oz, поэтому его центр
тяжести С лежит на этой оси: хс= ус= 0.
Остается определить величину zc = ОС.
В качестве элемента интегрирования
выбираем в полушаре слой толщиной dz и
круглым основанием радиуса г - 7?coscp.
Далее находим (с точностью до величин
первого порядка малости относительно dz):
z = 7? sin ср, dz = Rcosqxkp,
2
dV = 7ir2d!z = 7i(jRcos(p)2J?cos(p6/(p = 7t7?3cos3q) Лр, V = -л7?3.
Подставляя найденные значения в интегральную формулу для коор-
динаты zc, вычисляем
1 3
zc = — |zdV =--------- j*J?sinq) • itR3 cos3 фб/ф =
F (r) 2tiR o
3 л/?4 71 p 3 . 3R f cos^
=-----7 COS ф8Шфб/ф =-----------------
2л/?3 oj 2 I, 4 J
я/2 ~
= -я.
о 8
Таким образом, центр тяжести однородного полушара находится на
его оси симметрии на расстоянии 3/?/8 над центром основания.
Пример 2.
Найти центр тяжести дуги АВ окружности с радиусом R и централь-
ным углом 2а (рис. 60).
Поместим начало координат в центр соответствующей окружности,
ось Ох проведем через середину дуги, оси Оу - перпендикулярно к ней. По
теореме о положении центра тяжести симметричного тела будем иметь
ус = 0. Координату хс = ОС вычисляем по соответствующей формуле для
67
координат центра тяжести материальной
линии. Примем за элемент интегри-
рования бесконечно малый участок дуги,
определяемый конечным углом (р и
бесконечно малым углом dtp. Будем
иметь: dl - Rd<p, х = Kcoscp, I = 2Ra (I -
длина дуги AB). Далее вычисляем хС'.
1 1 “
хс = - ^xdl =-----JR2 cosqxZcp =
I (/) ZRa _а
R1 аг
=----- |coscpd(p =
2Яа_{
R R
=—sin(p =—[sin a- sin(-a)] =
-a
sin a
= R-----.
a
В этой формуле а выражается в радианах.
Придавая углу а значение a = л / 2, найдем абсциссу центра тяжести
полуокружности:
_sinK/2 2R
xr = R-----= —
л/2 л
Аналогичным образом могут быть найдены центры тяжести других
тел простой геометрической формы - отрезка прямой, площади треуголь-
ника, площади кругового сектора, объема конуса и т.д. А как быть в более
сложных случаях? Из вычислительных способов (существуют еще экспе-
риментальные способы) часто можно воспользоваться методом разбиения.
Метод разбиения
Он состоит в том, что рассматриваемое тело мысленно разбивается
на части, центры тяжести которых известны либо легко могут быть опре-
делены, после чего применяются формулы для определения координат
центра системы параллельных сил
; Ус-—„—
5?*
В этих формулах Рк и хк, ук, zk - веса и координаты центров тяжести
Ск (к = 1, 2,..., п) выделенных частей тела.
68
Для однородных тел в этих формулах вместо весов можно использо-
вать пропорциональные им величины - объемы Vk (для пространственных
тел), площади Sk (для плоских и поверхностных тел), длины 1к (для одно-
мерных тел).
Пример.
Найти центр тяжести детали из тонкой однородной проволоки, изо-
браженной на рис. 61. Принять BD
АВ.
Видно, что деталь может
быть разбита на два простых
тела - прямолинейный стержень
BD длиной 2R (тело 1) и
половинку кольца (полуок-
ружность АВ) радиуса R (тело 2).
Выбираем оси координат, опре-
деляем длины и координаты цент-
ров тяжести выделенных частей
детали:
71 = 27?, Xi = -R, yi = -R;
2R
12 = tiR, х2 - —, у2 = 0.
п
Далее по формулам способа разбиения, в которых веса заменены в
данном случае длинами, вычисляем координаты центра тяжести детали:
2 2R
lx+lx 2R<~R) + *R-----------
„ _ «=1 _ >1Л1 ' >2Л2 _____________7Г а .
с lx+l2 IR + tiR
к=\
Yltyt 2Л(-Л) + —-0
ус = ---= —— = -0,3897?.
2R + nR 2 + п
к=]
По найденным координатам строим точку С на чертеже. Следует
иметь в виду, что центр тяжести может оказаться вне пределов самого те-
ла. Тогда следует считать, что он жестко присоединен к телу.
Способ разбиения распространяется и на тела, содержащие вырезы и
пустоты. В этом случае величины Рк (или пропорциональные им Vk, Ski lk),
относящиеся к пустотам и вырезам, следует считать отрицательными, а
сам способ называется способом отрицательных масс.
69
Пример.
Определить положение центра тяжести плоской шайбы с прямо-
угольным вырезом (рис. 62).
Тело симметрично относительно оси Ох,
откуда сразу следует, что ус - 0. Для определения
хс шайбу считаем состоящей из двух тел - сплош-
ного круга радиуса R с центром в начале координат
(тело 1) и прямоугольника со сторонами 2а, 2Ь и
отрицательной площадью (тело 2). Вычисляем
нужные величины:
= TtR2, Xi - 0, S2 = -4ab, x2~a
и определяем абсциссу центра тяжести шайбы:
2
у s х
5Г”' ~ Si 4- $2 TtR2 — 4ab
2^к
*=1
Вопросы для самопроверки
1. Что называется центром системы параллельных сил? Приведите и
поясните формулы для координат этого центра.
2. Запишите формулы для координат центра параллельных сил, на-
правленных в одну сторону. В чем их отличие от формул общего случая?
3. Какие силы называются распределенными? Поясните переход от
распределенной силы к силе сосредоточенной.
4. Что называется центром тяжести тела? Приведите общие формулы
для определения координат центра тяжести.
5. Вывести интегральные формулы для координат центра тяжести
объемного, поверхностного и одномерного тела.
6. Сформулируйте теорему о расположении центра тяжести симмет-
ричного тела.
7. В чем состоит способ разбиения при нахождении центров тяжести
тел?
8. Поясните способ отрицательных масс. Как показать, что в форму-
лах метода разбиения объемы (площади, длины), относящиеся к пустотам
и вырезам, следует считать отрицательными?
70
ЛЕКЦИЯ 6
ТРЕНИЕ ТВЕРДЫХ ТЕЛ
Трение покоя и трение скольжения
В лекции 1, говоря о взаимодействии выделенного тела со связями,
мы считали поверхности тел идеально гладкими. Это выражалось в том,
что, характеризуя действие опорной поверхности на некоторое тело, мы
вводили в рассмотрение только нормальную реакцию N. Между тем эле-
ментарный опыт показывает, что соприкасающиеся тела взаимодействуют
также в касательной плоскости, то есть поверхности тел являются шерохо-
ватыми.
Сила Т, возникающая при соприкосновении тел в плоскости касания
тел, называется силой трения.
Добавляя силу трения Т к нормальной
реакции N и складывая эти силы, получаем
полную реакцию R поверхности (рис. 63). Полная
реакция направлена под некоторым углом ср к
направлению нормали. Только при очень хорошо
обработанных поверхностях, когда величина силы
Т мала по сравнению с силой N, бывает
допустимо в расчетах пренебречь трением и
считать поверхности тел идеально гладкими.
Кратко остановимся на законах трения.
Рассмотрим тело весом Р, лежащее на горизонтальной плоской по-
верхности (рис. 64). Будем действовать на тело горизонтальной силой S и
следить за его состоянием. Если S = 0, то тело находится в покое. Увели-
чивая силу S от нуля, можно обнаружить, что до некоторых пор состояние
s
f —
7777777Т777777ТП ТТ7ГШ77
Рис. 64
71
покоя сохраняется - возникающая сила трения Т, называемая силой тре-
ния покоя (силой сцепления), будет уравновешивать приложенную силу S:
Т = —S. Наконец, наступает такое пороговое состояние, когда малейшее
приращение силы 5 приводит к троганию тела из состояния покоя. Это
состояние тела, пограничное между покоем и движением, называется пре-
дельным равновесием.
В состоянии предельного равновесия сила трения покоя достигает
своего максимального значения Т = Tmax. При дальнейшем увеличении си-
лы S состояния покоя нарушается, и тело начинает скользить в направле-
нии силы S. При этом касательная составляющая силы взаимодействия
тела с опорной поверхностью продолжает существовать и называется си-
лой трения скольжения.
Многочисленными опытами установлено*, что величина максимальной
силы трения покоя пропорциональна нормальной реакции (нормальному
давлению) Nи в первом приближении не зависит от площади касания:
^rnax “ W
Это соотношение носит название закона Кулона (точнее, закона
Амонтона-Кулона). Безразмерная величина /0 называется коэффициентом
трения покоя (коэффициентом сцепления). Значения fQ для различных ус-
ловий берутся из технических справочников, либо определяются экспери-
ментально.
Из всего сказанного выше следует, что для величины силы трения
покоя Т можно написать:
0<т<ттах=ж.
Это означает, что сила трения покоя не имеет какого-то определен-
ного значения - она зависит от приложенных сил и должна определяться,
как и нормальная реакция N, из уравнений равновесия тела.
В задачах статики с учетом сил трения оказываются весьма полез-
ными также понятия угла трения и конуса трения.
Углом трения (р) называется значение угла ср между направлением
полной реакции шероховатой поверхности R и нормалью к этой поверх-
ности в момент достижения предельного равновесия:
P = <p|7=rmax=arCtg/0.
* Законы трения изучались еще Леонардо да Винчи (1452 - 1519), а в XVII веке -
французским физиком Г. Амонтоном (1663 - 1705). В наиболее систематической форме
законы трения твердых тел сформулированы UI.O. Кулоном (1736 - 1806) - также
французским физиком.
72
Конусом трения называется геометрическое
место линий действия полной реакции шероховатой
поверхности при всевозможных направлениях силы
трения покоя (рис. 65).
Для силы трения, возникающей при сколь-
жении тела - силы трения скольжения, основные за-
кономерности таковы.
1. Сила трения скольжения направлена в
сторону, противоположную вектору скорости
скольжения б.
2. Величина силы трения определяется зависи-
мостью
где f - коэффициент трения скольжения, N - нормальное давление.
3. Коэффициент трения скольжения слабо зависит от скорости
скольжения и (рис. 66, а).
I/
Рис. 66
В силу последнего свойства в расчетах движения с учетом трения за-
висимостью flu) часто пренебрегают и коэффициент трения скольжения
принимают постоянным: f = const = f' (рис. 66, б). Обычно /' < /0, одна-
ко нередко для простоты принимают f - f^= f.
Трение качения
Рассмотрим цилиндрический каток, покоящийся на горизонтальной
плоскости (рис. 67, а). Приложим к его центру силу S и будем наблюдать
за состоянием катка при постепенном увеличении этой силы. Опыт пока-
зывает, что движение катка начинается не сразу, а лишь после достижения
силой S некоторого предельного значения.
Однако из уравнений равновесия катка, составленных даже при уче-
те силы трения покоя, следует совершенно другой вывод- движение
должно начинаться при сколь угодно малой силе S. Действительно, для
плоской системы сил: Р (вес катка), N (нормальная реакция опоры), t -
сила трения покоя и приложенной силы S в состоянии равновесия должны
73
удовлетворяться все три уравнения равновесия: £7^ = 0; £7^=0;
£мо (7^) = 0. В нашем же случае третье уравнение имеет вид 57? = 0 (7? -
радиус катка) и удовлетворяется только при 5=0; при 5^0 равновесие не-
возможно, и каток приходит в движение при сколь угодно малой силе S.
Рис. 67
Причина противоречия кроется в том, что были учтены не все силы,
действующие на каток со стороны опорной поверхности. Контакт реаль-
ных тел всегда осуществляется по некоторой площадке, в результате чего
возникает еще пара сил с моментом Мс, противоположным направлению
возможного качения тела по опорной поверхности (рис. 67, б).
При учете момента трения качения уравнение моментов относитель-
но точки О приобретает вид SR- Мс- 0, снимающий возникшее противо-
речие. Из этого уравнения следует, что пока качения нет, момент трения
Мс равен моменту движущейся силы S: Mc-SR. Постепенно увеличивая
силу S, можно прийти к такому предельному состоянию, когда малейшее
приращение силы 5 вызывает качение катка по опоре. В этом состоянии
предельного равновесия момент трения качения принимает свое наиболь-
шее значение
МС = М™ =kN.
Величина к, имеющая размеренность длины, называется коэффици-
ентом трения качения и определяется из эксперимента либо по техниче-
ским справочникам.
Момент трения качения, таким образом, изменяется в пределах
0<Мс<М™ = kN,
принимая значение Mc=kN только при возникновении качения.
Вообще говоря, под действием силы 5 каток может как катиться, так
и скользить. Если при постепенном возрастании S сначала устанавливает-
ся равенство S = fQN = /0Р, каток начинает скользить; если сначала уста-
74
Рис. 68
навливается равенство £ = — Р, начинается качение. Поскольку k!R<f^
R
то сила S, необходимая для качения, много меньше значений этой же си-
лы, необходимой для скольжения. Этим, например, объясняются преиму-
щества подшипников качения (шариковых, роликовых, игольчатых) по
сравнению с подшипниками скольжения.
Решение задач статики при учете сил трения
Общие правила решения задач на равновесие с учетом сил трения
остаются теми же самыми, что и при отсутствии трения. Некоторое отли-
чие состоит только в том, что в уравнения равновесия будут входить, на-
ряду с нормальными реакциями, также и силы трения шероховатых связей.
Это увеличивает общее число неизвестных, так как силы трения покоя за-
ранее неизвестны. В результате задача статики, будучи статически опреде-
ленной при гладких связях, может оказаться при учете трения статически
неопределенной.
Если рассматривать не произвольное, а предельное состояние равно-
весия системы с трением, то число неизвестных уменьшается - в этом слу-
чае все или некоторые силы трения принимают свои максимальные значе-
ния и могут быть выражены при помощи закона Кулона:
Ft = /У, (z - 1, 2,..., т\т< п).
Здесь п - число всех связей (контактов) с трением, т - число связей в
состоянии предельного равновесия, /, Nt - соответствующие коэффициен-
ты трения и нормальные реакции. В задачах с трением качения то же самое
можно сказать относительно моментов трения качения.
При определении направления сил трения и моментов трения руко-
водствуются физическими соображениями.
Пример.
Исследовать равновесие стержня АВ весом
Р, удерживаемого силами трения под углом а к
вертикали (рис. 68). Стержень однородный,
коэффициент трения покоя между стержнем и
стенкой равен/ь между стержнем и полом -f2.
Прикладываем к стержню действующие
силы - вес Р, нормальные реакции связей NA,
NB, силы трения ТА, Тв. Это плоская произволь-
ная система сил, следовательно, мы можем
составить для стержня три независимых
уравнения равновесия.
75
Обозначив для удобства длину стержня 2/, запишем эти уравнения в
следующем виде:
tFb=0-~TB+NA=0-
*=1
t^, = 0:r<+^-P = 0;
к-1
^MB(Fh) = 0: -21ТА sina - 21NA cosa + Plsina = 0.
При произвольном a в этих уравнениях содержатся четыре неиз-
вестные - №, Nв, ТА, Тв. Следовательно, задача не имеет однозначного ре-
шения (является статически неопределенной).
Ситуация меняется, если рассматривать значение a = а*, соответст-
вующее предельному равновесию. В этом случае для сил трения справед-
ливы равенства
TB = f2NB.
Подставляя их и значение а ~ а* в написанные уравнения равнове-
сия и разделив все члены третьего уравнения на Zcos а*, приходим к сле-
дующим уравнениям предельного равновесия стержня:
/Л^+^-Р^О;
- 2J\N А tga* - 2NA + Ptga* = 0.
В этой системе три уравнения и три неизвестные - NА, NB, tga*, что
открывает возможность для получения однозначного решения.
Из первого уравнения имеем
^=/Л.
Подставляя это значение во второе уравнение, получим
NB=—-----.
1 + /1Л
После этого определяется и реакция NA:
Na=—----•
Подставляя найденные значения реакций в третье уравнение, нахо-
дим tg a*:
2/2
tga* - ———
1-ЛА
16
При углах наклона, больших а*, равновесие невозможно - стержень
соскальзывает под действием силы тяжести.
При а < а* стержень находится в равновесии. Однако положения
равновесия при а < а* уже не будут предельными, и найденные значения
реакций на эти положения не распространяются. В этих положениях задача
остается статически неопределенной.
Таким образом, стержень имеет бесконечное множество непрерывно
расположенных положений равновесия. Соответствующий им интервал
О < а < а* значений угла а определяет область равновесия.
Если трения нет (/i “ 0), область равновесия стягивается в точку
а = 0 - покой становится возможным только для вертикально поставлен-
ного стержня. Эта ситуация сохраняется и в случае/2 = 0, f\ 0. Поэтому
поддержание равновесия в наклонном положении за счет шероховатости
стенки невозможно (даже при очень больших значениях/i).
Заклинивание
В заключение познакомимся еще с явлением заклинивания, возни-
кающим при определенных условиях в системах с трением.
Пусть тело, весом которого для простоты пренебрегаем, хотят вы-
вести из состояния покоя на шероховатой опоре силой Р, составляющей
угол а с нормалью (рис. 69). Всегда ли это возможно осуществить?
Составим условия равновесия сходящих-
1 у ся сил, приложенных к телу:
. /р =
Лау *=1
х I I? ^2^ = 0: N“^cosa = 0.
///7777777/,
Отсюда для силы трения и нормальной
Рис. 69 реакции получаем:
T = Psina, jV = Pcosa.
Покой тела сохраняется, пока сила трения находится в пределах
0 < Т < fQN, гдеУо ~ коэффициент трения покоя. Подставляя сюда найден-
ные значения Г, N и решая полученные неравенства относительно угла а,
получаем следующее условие покоя тела на плоскости:
0 < a < arctg /0.
Примечательно, что полученное условие не содержит величины си-
лы Р. Следовательно, покой сохраняется при любой, даже сколь угодной
большой силе Р, если угол а находится в указанных пределах. Тело мож-
но разрушить, но привести в движение невозможно.
77
Этот эффект, называемый явлением заклинивания, проявляется и в
более сложных системах с трением.
Вопросы для самопроверки
1. Что такое трение покоя? В каких пределах изменяется сила трения
покоя?
2. Как направлена полная реакция негладкой (шероховатой) связи?
3. Объясните понятия "угол трения", "конус трения".
4. В чем состоит явление заклинивания?
5. В чем проявляется трение качения? В каких пределах изменяется
момент трения качения?
Упражнения
1. Плоское тело весом Р находится в равновесии на наклонной плос-
кости с коэффициентом трения покоя /о- Найти, при каком значении угла
наклона а тело начнет соскальзывать с плоскости.
2. При каких значениях угла а каток весом Р- ЮН, ось которого
расположена горизонтально, может находиться в равновесии на наклонной
плоскости (рис. 70)? Радиус катка R = 5 см, коэффициент трения качения
к - 0,2 см.
Рис. 70 Рис. 71
3. При каком условии на углы ось аг (рис. 71) верхнее бревно может
быть вытеснено горизонтальными сжимающими силами Р путем скольже-
ния по нижележащим бревнам (без вращения), если коэффициент трения
покоя для бревен равен/о?
4. По условиям предыдущего примера рассмотреть случай, когда вы-
ход из равновесия происходит путем качения в одной точке опоры и каче-
ния со скольжением в другой. Коэффициент трения качения равен к.
79
КИНЕМАТИКА
Кинематикой называется раздел теоретической механики, в котором
механическое движение изучается без выяснения его причин, с чисто гео-
метрической точки зрения. Название раздела происходит от греческого
слова aetvepa (движение).
Слово "движение" как философская категория обозначает всякое из-
менение в окружающем нас материальном мире. Механическое движе-
ние - это наиболее простой вид движения материи, состоящий в простом
изменении взаимного положения тел.
Скажем более полно и точно: механическим движением называется
изменение положения тела в пространстве, происходящее с течением
времени и наблюдаемое относительно некоторого другого тела, условно
принятого за неподвижное.
Условно неподвижное тело, по отношению к которому фиксируются
положения движущегося тела в различные моменты времени, называется
телом отсчета. Система координатных осей, неизменно связанная с телом
отсчета, будет определять пространство, в котором происходит движение.
Физическое пространство трехмерно и евклидово. Это означает, что
все измерения в нем осуществляются на основе правил обычной (школь-
ной) геометрии - планиметрии и стереометрии. Основной единицей для
измерения расстояний служит 1 метр (м), для измерения углов - 1 радиан
(рад)-
Время рассматривается в кинематике как непрерывно изменяющаяся
скалярная величина /, играющая роль независимого переменного (аргумен-
та). Все другие кинематические величины (расстояния, углы, скорости и
т.д.) считаются зависящими от времени (функциями времени). Считается,
что течение времени не зависит от выбора тела отсчета и происходит оди-
наково во всех точках пространства. За основную единицу времени при-
нимается 1 секунда (с).
Указанные представления (модели) пространства и времени были
разработаны великим основоположником теоретической механики
И. Ньютоном (1642 - 1727) и носят названия абсолютного пространства и
абсолютного времени. Эти понятия и сегодня остаются одними из основ-
ных в теоретическом естествознании, хотя последующее развитие науки
привело к их некоторому пересмотру и уточнению.
Совокупность системы координат и прибора для отсчета времени
(часов) образуют систему отсчета. Поскольку, однако, ход времени в ки-
нематике не зависит от выбора системы координат (имеется одно время
для всех систем координат), под системой отсчета часто понимают только
саму систему координат.
80
В кинематике решаются две основные задачи.
Первая задача кинематики состоит в установлении способов задания
движения. Задать (описать) движение тела - значит указать способ, позво-
ляющий определить положение тела в любой наперед заданный момент
времени. В общем случае это делается при помощи кинематических урав-
нений движения. Вторая задача кинематики состоит в определении по
уравнениям движения всех кинематических величин, характеризующих
как движение всего тела в целом (скорости и ускорения поступательной
части движения, угловой скорости и углового ускорения тела), так и дви-
жения отдельных точек тела (траекторий точек, скоростей и ускорений то-
чек и т.д.).
81
ЛЕКЦИЯ 7
КИНЕМАТИКА ТОЧКИ
Поскольку в кинематике действие сил не рассматривается, то ос-
таются в стороне также и инертные свойства тел. В частности, остается
без всякого применения мера инертности материальной точки - ее мас-
са. По этой причине понятия материальной точки и геометрической точ-
ки в кинематике не различаются, можно говорить просто о точке. С во-
просов движения этого самого простого объекта мы и начнем изложение
кинематики.
Способы задания движения точки
Различают векторный, координатный и естественный (натуральный)
способы задания движения.
Векторный способ задания движения состоит в следующем.
Пусть М- движущаяся точка, А - тело отсчета (рис. 72). Выберем в
теле А произвольную точку О - точку отсчета, построим вектор г = ОМ.
Этот вектор, начало которого совпадает с точкой отсчета О, а конец - с
точкой М9 называется радиусом-вектором точки М. При движении точки М
радиус-вектор г непрерывно изменяется во времени, поэтому существует
некоторая вектор-функция времени
r = r(Z). (1)
Если эта функция известна, то для каждого
момента времени t может быть построен вектор г и тем
самым найдено положение движущейся точки в этот
момент.
Функция (1) называется векторным законом
(векторным уравнением) движения точки М.
При координатном способе задания движения с
телом отсчета связывается какая-либо, например
декартова прямоугольная, система координат (рис. 73).
Движение точки будет задано, если ее координаты
будут известны как функции времени
(2)
x = x(Z), y = y(t), z = z(t).
82
Рис. 73
Зависимости (2), выражающие текущие координаты движущейся
точки в виде функций времени, называются уравнениями движения точки
в декартовых координатах.
Если точка движется, оставаясь все время в одной плоскости, то оси
Ох, Оу можно расположить в той же плоскости и ограничиться двумя
уравнениями движения
x = x(Z), y = y(t). (3)
При движении в плоскости часто удобно пользоваться полярной сис-
темой координат, задавая положение точки ее полярным углом 0 и полярным
радиусом р (рис. 74). В этом случае уравнения движения точки имеют вид
0 = 0(r), p = p(t).
Линия, описываемая движущейся точкой в пространстве, называется
траекторией точки. Естественный способ задания движения состоит в
задании траектории точки и закона движения по траектории.
Пусть траектория точки М суть
заданная кривая, М- положение точки на
ней (рис. 75). Будем рассматривать траек-
торию как криволинейную координатную
ось, для чего выберем на ней начало отсчета
дуг (точку О]) и направление отсчета дуг (на
рис. 75 направление отсчета дуг выбрано
вправо от точки О}). Длина дуги О\М, взятая
со знаком плюс или минус в зависимости от
положения точки Мотносительно начала отсчета дуг О], вполне определя-
ет положение точки в пространстве и называется дуговой координатой
точки. Движение точки будет задано, если ее дуговая координата s будет
выражена в виде функции времени
s = s(t). (4)
Зависимость (4) называется законом движения точки по траекто-
рии или, что то же самое, законом движения точки в естественной форме.
83
Пример.
Написать уравнения движения точки, движущейся равномерно по
окружности радиуса R и делающей п оборотов за одну минуту.
Начнем с естественного способа описания
движения. Изображаем траекторию - окружность
радиуса R с центром в точке О (рис. 76). Начало от- q
счета дуг (91 совместим с положением точки в мо-
мент начала наблюдения, то есть при t = 0; за поло- ( )
жительное направление отсчета выберем направле- \ )
ние в сторону движения точки.
Пусть М~ положение движущейся точки в
текущий момент времени t(t > 0). Для центрального
угла который будем отсчитывать в сторону движения точки,
согласно условию, можем написать
Ф =
2пп пп
---/ = —t.
60 30
Рис. 77
Здесь ф измеряется в радианах, t - в секундах.
Длина 5 дуги О\М, радиус окружности R и центральный угол ф свя-
заны геометрическим соотношением
5=Лф.
Подставляя сюда найденное значение ф, получаем
nRn J?
s —---1. /
30
Это и есть закон движения точки в
естественной форме.
Для описания движения в координатной
форме прежде всего следует выбрать подходящую
систему координат, например, изображенную на
рис. 77. Далее строят координатные отрезки и
определяют соответствующие переменные
расстояния. В нашем случае будем иметь:
х = 0{М' = <91О+ОЛГ=7?4-Асо8(180°~ф) = A(l-coscp);
у = ОХМ"- М' М = 7?sin(180°-4p) = Азтф.
Подставляя сюда угол ф как функцию времени, получаем уравнения
движения в координатной форме
W) D . Tint
x-R 1-cos— , y = Rsm—.
V 307 z 30
84
Пусть 7, j - координатные орты. Тогда для радиуса-вектора точки
г -ОХМ будем иметь:
~ -г г» I 1 ( . ЯИП-г
г = XI + VI = Л 1- COS- 7 + Sin----- 7
V 307 < 307
Полученное равенство, выражающее радиус-вектор точки М как
функцию времени, служит векторным уравнением ее движения.
Определение траектории, скорости и ускорения точки при
векторном способе задания движения
Пусть движение точки М задано векторным способом, то есть задан
радиус-вектор точки как функция времени
r = r{t). (5)
т Линия, описываемая концом пере-
_ менного вектора, начало которого нахо-
Му дится в заданной неподвижной точке,
^^**^*НГ называется годографом этого вектора.
7 Xs* Отсюда и из определения траектории
/Ч / Годограф г следует правило: траектория точки
/ \ / есть годограф ее радиуса-вектора.
\ / г} Пусть в некоторый момент t точка
П / занимает положение М и имеет радиус-
\ / вектор г , а в момент tx - t + Дг - поло-
\ / жение М\ и радиус-вектор гх (рис. 78).
° Вектор ММ\, соединяющий последо-
Рис. 78 вательные положения точки в указанные
моменты, называется вектором перемещения точки за время Д/ = tx -1.
Вектор перемещения следующим образом выражается через значения век-
тор-функции (5):
ММ\ - гх - г ~r(t + Дг)- r(t) = Аг .
Если вектор перемещения поделить на величину промежутка Дг, по-
лучим вектор средней скорости точки за время Д/
_ = ММх = Д7
Ucp~ ДГ ”дГ
Будем теперь уменьшать промежуток Дг, устремляя его к нулю. Пре-
дел, к которому стремится вектор средней скорости бср при неограничен-
ном уменьшении промежутка Дг, называется скоростью точки в момент t
или просто скоростью точки б. В соответствии со сказанным для скорости
получаем:
_ v _ .. Дг .. г(г + Дг)-г(О dr
t> = lim и= lim — = lim —----------------- —
р д/->о Д/ д/->о Д/ clt
85
Итак, вектор скорости точки равен производной по времени от ее
радиуса-вектора:
dr
— = г.
dt
(6)
Поскольку секущая ММ\ в пределе (при Д/—>0) переходит в каса-
тельную Л/т, приходим к выводу, что вектор скорости б направлен по ка-
сательной к траектории в сторону движения точки.
В общем случае скорость точки также переменна, и можно интересо-
ваться быстротой изменения скорости. Скорость изменения скорости на-
зывается ускорением точки.
Для определения ускорения а
выберем какую-либо неподвижную точку А
и будем откладывать из нее вектор
скорости б в различные моменты времени.
Линия, которую опишет конец 7V вектора ~ / f
скорости, представляет собой годограф Годограф и / /-
скорости (рис. 79). Изменение вектора /
скорости выражается в том, что *А
геометрическая точка N движется по Рис
годографу скорости, а скорость этого
движения служит, по определению, ускорением точки М.
Применив для переменного вектора б все те рассуждения, которые
были использованы выше для переменного вектора г, для ускорения а
получаем:
_ J6 d2r
а — — — —,
dt dr
(7)
или, при обозначении производной по времени точкой:
а = 6 = г . (8)
Формулы (6) - (8) являются наиболее общими формулами кинемати-
ки для определения скорости и ускорения.
Определение траектории, скорости и ускорения точки при
координатном способе задания движения
Пусть движение точки задано уравнениями движения в декартовых
координатах: x = x(t), y~y(j), z = z(t).
Для каждого момента времени t по этим уравнениям можно определить
координаты точки в этот момент и указать ее положение в пространстве.
Придавая t всевозможные значения, получим множество положений дви-
жущейся точки в пространстве - ее траекторию. Следовательно, уравнения
движения одновременно являются уравнениями траектории точки в пара-
86
метрической форме, причем параметром служит время t. Чтобы получить
уравнение траектории в виде зависимости между координатами точки,
достаточно из уравнений движения исключить время.
Пример 1.
Движение точки задано уравнениями х = 2sin/, у = 4cos2/ (х, у - в
сантиметрах, t - в секундах). Найти уравнение траектории точки в коорди-
натной форме.
Для определения уравнения траектории из уравнений движения ис-
ключаем время t. Для этого из первого уравнения выражаем
х
sm t = —
2
и подставляем это значение во второе уравнение, преобразованное к функ-
циям одинарного угла:
= 4 cos 2/ =
4(cos21 - sin2t)= 4(1 - 2sin2 /) = 41 1 - 2 • = 4 - 2x2.
Рис. 80
Опуская промежуточные выражения,
получаем уравнение траектории
у = 4-2х2.
Уравнение определяет параболу, рас-
положенную симметрично относительно оси у,
с вершиной в точке (0,4). Траекторией служит
кусок этой параболы, заключенный между
точками с координатами (-2,-4) и (2,-4)
(рис. 80).
Пример 2.
Определить уравнение траектории, если
точка движется согласно уравнениям (х-в
сантиметрах, t - в секундах):
x = 2 + 5sin2r, у = 3(1 + cos2/).
Для исключения времени t из уравнений движения выразим из этих
уравнений sin2/ и cos2/:
sin 2t = -—-, cos 2t = ——-.
5 3
Возводя эти равенства в квадрат и почленно складывая, получаем
уравнение траектории в координатной форме:
(х-2)2 . (у-3)2
52 З2
Это уравнение эллипса с центром в точке А (2,3) и с полуосями а =
5 см, b = 3 см (рис. 81). Траекторией служит вся кривая эллипса.
87
Рис. 81 Рис. 82
Займемся теперь определением скорости и ускорения.
Зная уравнения движения точки, можно выразить в функции време-
ни радиус-вектор точки (рис. 82):
г = x(j)i + y(t)j + z(t)k .
Теперь находим скорость, дифференцируя радиус-вектор по времени:
При дифференцировании учитывается, что оси Oxyz неподвижны,
поэтому координатные орты являются постоянными векторами, и их про-
изводные равны нулю.
Полученная формула определяет скорость точки в виде разложения
по координатному базису i, j, к . Так как коэффициенты при ортах равны
проекциям скорости на соответствующие координатные оси, отсюда сле-
дуют формулы
dx . dy . dz .
о =— = х, о= —=у, о. = — -z.
dt dt 4 dt
По известным проекциям находим модуль и направляющие косину-
сы скорости:
м=7и*+и2+и' ’
А "Л "у Т\ °;
cos(o, I ) = 7-7, COS IO, J I = 77, COS О, К =77.
|u| |o| v 7 |v|
Аналогичным образом определяется и ускорение. Дифференцируя
выражение для вектора скорости, получаем:
_ <76 d (dx : dy ~ dz ~\ d2x- d2y~ d2z-
a= — = — —1 + —J 4-—к =—+—7-j + —-k .
dt dt < dt dt dt ) dt dt dt
88
Откуда для проекций ускорения следуют формулы
d2x .. d2y .. d2z
a’ = ~d7=z
Проекции ускорения можно выразить также через проекции скорости:
dv . d\) , d\)r
а =—£ = ur, а =—~ = т> , а =—- = и .
х dt х ' dt у z dt
Модуль и направляющие косинусы ускорения выражаются равенст-
вами
\а\ = ^а2 + а2+а2,
cos[a,z) = ^-, cos(Xj) = -y, costa =
v 7 |a| v 7 |я| v
Пример.
Точка движется в плоскости ху согласно уравнениям
07 2^ ; . .
X = 2/ cos —, у = I Sin COt,
2
где х, у - заданы в сантиметрах, время t - в секундах, а величины /, (о - за-
данные постоянные. Найти скорость и ускорение точки в момент, когда
она впервые после начала движения пересекает ось х.
Скорость и ускорение находим, вычисляя их проекции на коорди-
натные оси. Сначала это сделаем для произвольного момента t:
. COt f . COt^ co , .
= x = 2/ • 2 cos--sm— • — = -/cosin cot,
x 2 [ 2 J 2
= у =/cocoscot,
у У 7
ax = —/co2 cos cot,
= -/co2 sin cot.
Когда точка находится на оси х, выполняется равенство у = 0. Под-
ставляя это значение во второе уравнение движения и решая полученное
уравнение относительно t, находим
Л я 2л Зл
t = О, —, —, —,...
со со со
Момент t = 0 соответствует началу движения, а первое после начала
движения пересечение оси х происходит при t = tj = л/со. Подставляя это
значение в предыдущие формулы, найдем
л
(tj) = -/со sin со • — = -/со sin л = 0, и (t.) = /со cos л = -/со,
со
<3x(tj)= -/со2 с°8л = /со2, сГу (tj) = —/со2 sin л = 0.
89
Таким образом, в расчетный момент времени t = tx скорость 6 = 6^
ускорение а = ах имеют модули
и = ц = /со, а = ах = /со2
и направляющие косинусы
cos(6,,H = 0, cos(d1,7) = -1,
COS(a1,lJ = l, C0S^1;
На рис. 83 показана геометрическая
картина движения. Траекторией точки слу-
жит окружность радиуса I с центром в точке
С (/,0). Подставляя в уравнения движения
t = 0, находим, что в начальный момент
точка находится в положении Мо (2/, 0).
Придавая времени t малое положительное
значение t = 8 и определяя знаки координат
х, у, получаем х(е) > 0, Xе) > 0, из чего сле-
дует, что точка движется из положения Мо
против хода часовой стрелки. В расчетный
момент t = t\ = тт/со она находится в начале
координат, имея скорость б = ц и ускорение а
Рис. 83
а.
Определение скорости и ускорения точки при естественном
способе
задания движения
Естественные координатные оси и их орты
Пусть заданы траектория точки, начало и направление отсчета дуг.
Выберем на траектории произвольным образом точку М и проведем каса-
тельную Л/т. Плоскость, проходя-
щая через точку М перпендику-
лярно к касательной Л/т, называет-
ся нормальной плоскостью траек-
тории в точке М(рис. 84).
Придадим дуговой коорди-
нате s приращение Ду и отметим
точку М' с координатой s + As.
Пусть Л/'т' - касательная к траек-
тории в точке М'. В общем случае
траектория точки - пространст-
венная кривая, поэтому касатель-
ные Л/т и Л/'т’ суть скрещиваю-
Рис. 84
щиеся прямые.
90
Проведем прямую Л/t”, параллельную касательной М'т\ Прямые Mi
и Л/т” образуют плоскость Мтг". Предельное положение плоскости Л/тт”,
когда точка М неограниченно приближается к точке М, называется сопри-
касающейся плоскостью траектории в точке М. Соприкасающаяся плос-
кость представляет собой ту из бесконечного множества плоскостей, про-
ходящих через касательную Mi, которая наиболее тесно примыкает к тра-
ектории в окрестности точки М. В случае плоской траектории соприка-
сающаяся плоскость совпадает с плоскостью траектории.
Нормальная и соприкасающаяся плоскости взаимно перпендикуляр-
ны. Проведем через точку М третью плоскость, перпендикулярную к обе-
им указанным плоскостям - так называемую спрямляющую плоскость. В
итоге получаем прямой трехгранный угол с вершиной в точке М, называе-
мый естественным трехгранником траектории в этой точке. Ребрами ес-
тественного трехгранника являются касательная Mi, главная нормаль
Мп - линия пересечения нормальной и соприкасающейся плоскостей и би-
нормаль (вторая нормаль) Mb - линия пересечения нормальной и спрям-
ляющей плоскостей (рис. 85).
Касательная, главная нормаль и бинормаль взаимно перпендикуляр-
ны и после установления на них направлений образуют естественную сис-
тему координатных осей. Положительное направление касательной
выбирается в сторону возрастания дуговой координаты 5 и задается ортом
касательной т° (|то| = 1).
Положительное направле-
ние главной нормали за-
дается ортом п° (|л°| = 1),
который направляют от
точки М в сторону во-
гнутости траектории. Орт
бинормали Ь° = 1 j
выбирают согласно пра-
вилу 6°=т°хй°, чем обес-
печивается правосторон-
ность естественного коор-
динатного базиса т°, п°,
Ь° (см. рис. 85).
Рис. 85
91
Определение скорости
Вспомним основную формулу кинематики для определения скорости
_ dr AF
и =— = lim—.
dt Ar
Здесь AF - вектор перемещения точки, Аг- время перемещения
(рис. 86). Обозначим As перемещение вдоль траектории за этот же проме-
жуток времени и представим правую часть этого равенства в виде произ-
ведения двух пределов:
AF .. AF As .. AsAF
lim — = lim------= hm — hm —.
AZ->0 Д/ A/->0 A.y А/ Л/“>0 Ar As~>0 A.s
As->0
Первый из этих пределов равен
производной ds/dt и может быть вы-
числен, поскольку закон движения по
траектории s = s(t) при естественном
способе описания движения задается.
Далее, простые рассуждения показывают,
что второй предел равен по модулю
единице (как предел отношения длины
хорды к длине дуги) и направлен по каса-
тельной в сторону возрастания s.
Следовательно, он определяет орт
касательной т°, для которого попутно
получаем формулу
_о AF dr
т = lim — = —
As ds
Таким образом, при естественном способе задания движения ско-
рость точки определяется формулой
Формулу можно рассматривать как результат разложения вектора б
на составляющие по естественному координатному базису. Величина
от = ds / dt равна проекции скорости на направление касательной, а проек-
ции скорости на главную нормаль и бинормаль равны нулю. В общем слу-
чае ит = ±и, где и - модуль скорости. Если точка движется в положитель-
ном направлении, то = и, и можно записать
б = и • т°.
92
Определение ускорения
Будем исходить из общей формулы для ускорения
_ dv
а =—.
dt
Пусть, для определенности, точка движется в положительную сторо-
ну отсчета дуг; тогда вектор скорости выражается формулой
б = о-т°,
где и - модуль скорости, т° - орт касательной. В общем случае криволи-
нейного движения переменны оба сомножителя в этой формуле; послед-
ний- вследствие изменения направления касательной. Поэтому орт т°
имеет производную по времени, которая выражается формулой
dt р
где п° и р - соответственно орт главной нормали и радиус кривизны тра-
ектории в рассматриваемом положении движущейся точки.*
Дифференцируя по времени выражение для скорости, получим
_ d\5 d< dx° d\)^Q и2
dt dt dt dt dt p
Формула выражает ускорение точки в виде суммы составляющих по
осям естественной системы координат. Из нее следует, что ускорение име-
ет на эти оси проекции
Jv и2 л
а=—; а=—; а, =0.
’ dt " р 6
Первая из них есть проекция ускорения а на касательную и называ-
ется касательным ускорением. Вектор касательного ускорения
а, = ахт°
направлен в сторону скорости, если движение ускоренное (dvldt> 0), и
против скорости, если движение замедленное (dv/dt < 0).
Проекция ускорения на главную нормаль называется нормальным
ускорением. Модуль (ап) и вектор (ап) нормального ускорения выражают-
ся формулами
U2 _ и2 _0
—; а„=—п°.
Р Р
a,
* Вывод этой формулы можно найти, например, в книге: Н.В. Бутенин, Я.Л. Лунц,
Д.Р. Меркин. Курс теоретической механики. Т. 1. - М.: Наука, 1985.
93
Так как величина и2 /р положительна, нормальное ускорение всегда
направлено в сторону орта п°, то есть по главной нормали в сторону во-
гнутости траектории.
Проекция ускорения на бинормаль (аь) равна нулю, что означает, что
вектор ускорения лежит в соприкасающейся плоскости. Таким образом,
ускорение при естественном способе задания движения точки определяет-
ся как сумма касательного и нормального ускорений:
_ _ _ | _ о2
а = ат+аи а=—т; а=—п .
\ at р )
Это правило дополнительно проиллюстрировано на рис. 87, где слу-
чай а) соответствует ускоренному движению точки, а случай б) - замед-
ленному движению. Модуль ускорения в обоих случаях определяется по
теореме Пифагора:
Рис. 87
Если точка движется прямолинейно, то нормальное ускорение не
f °2
возникает \а = — = 0 , и ускорение состоит только из касательного:
\ ” 00 )
а = ах.
При равномерном криволинейном движении (и = const), наоборот,
отсутствует касательное ускорение (ах - dv/dt = 0), и полное ускорение
точки равно ее нормальному ускорению: а = ап.
Пример.
Точка движется по окружности радиуса R = 10 см согласно закону
5 = 10^2, см. Вычислить и построить скорость и ускорение точки в момент
когда она пройдет половину окружности.
94
В момент t=t\ дуговая координата точки 5 =54= 10/2 равна половине
длины окружности: 10/2 = nR, откуда находим
Определяем скорость точки в момент /ив расчетный момент :
о = — = 20/, см/с; о(/!) = и, = 20/j =20л/к =35,45 см/с.
Определяем касательное ускорение
а. __ ^2 = 20 см/с2.
т dt
Видно, что оно не изменяется с течением времени - точка движется
равноускоренно. Это же значение касательное ускорение имеет и в расчет-
ный момент:
ат(/1) = л1т =20 см/с2.
Определяем нормальное ускорение
я = 2_ - 2_ - 40/^ см/с2; ап(/1) = а1п =40тс = 125,66 см/с2.
Р *
Определяем полное ускорение в момент / = /р
<7(/j) = а} = + а2п = 127,24 см/с2.
На рис. 88 показаны положения точки в
текущий (М) и расчетный (М^) моменты
времени, а также векторы скорости и ускорений
точки в момент / = /ь
В заключение заметим, что от одного
способа задания движения можно перейти к
другим способам. Например, при определении
скорости в случае координатного способа
описания движения был предварительно сделан
переход к векторному способу в виде
г = х(/)/ + y(t) j + z(t)k.
Чтобы перейти от координатного способа к естественному, прежде
всего требуется найти уравнение траектории. Как было показано выше, это
делается исключением из уравнений движения времени /. Закон движения
по траектории можно получить на основе равенств
ds , Г2 Т
и =— И V = ±yJX + у ,
dt
95
определяющих скорость точки при естественном и координатном способах
задания движения. Приравняв правые части равенств, разрешая получен-
ное соотношение относительно ds и интегрируя, находим
s = s0 ± jjx2 +y2dt.
О
Это выражение определяет закон движения по траектории в общем
виде.
Если отсчет дуговой координаты вести от начального положения
точки в сторону движения, то s0 = 0, радикал положителен, и закон движе-
ния примет вид
5= ^х2 + у2 dt.
о
Вопросы для самопроверки
1. Что значит задать движение точки? Опишите координатный спо-
соб задания движения.
2. В чем состоят естественный и векторный способы задания движе-
ния точки?
3. Приведите общие (векторные) формулы для определения скорости
и ускорения точки.
4. Что называется траекторией точки? Как получить уравнение тра-
ектории по уравнениям движения точки в декартовых координатах?
5. Поясните определение скорости и ускорения точки при коорди-
натном способе задания движения.
6. Что называют естественными координатными осями? Как выби-
раются положительные направления этих осей?
7. Как определяются величина и направление скорости при естест-
венном способе задания движения?
8. Как называются и как вычисляются проекции ускорения точки на
естественные оси?
9. В каких случаях нормальное ускорение точки равно нулю?
10. Когда точка не имеет касательного ускорения?
Упражнения
Решить в указанном порядке следующие задачи из сборника
И.В. Мещерского 1981 года издания: 10.2, 10.6, 10.12, 11.3, 11.5, 12.13,
12.19, 10.19, 10.4.
96
ЛЕКЦИЯ 8
ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Вначале докажем одну теорему, справедливую при любом движении
твердого тела.
Теорема. Проекции скоростей двух точек тела на ось, проведенную
через эти точки, равны.
Доказательство. Пусть гх, г2 - ра-
б^\ диусы-векторы двух произвольно выбран-
/ л/ных точек Мь М2 тела (рис. 89). Так как тело
I / абсолютно твердое, то вектор М}М2,
\ I соединяющий эти точки, постоянен по
\ / >X/otл Д' 2
X \2 / модулю:
rx I / \МХМ21 = / = const.
/г 11
q V Будет постоянен при движении тела и
скалярный квадрат вектора М}М2:
Рис. 89 2
^МХМ2^ -I2 = const.
Выражая это равенство через радиусы-векторы точек
и дифференцируя по времени, последовательно получаем:
=0; Л/)Л/2(и2-и,) = 0;
\ at at J
/и2 cosa2 - /Vj coso^ = 0; ц cosa^ = u2 cosa2.
Но произведение UjCosoii есть проекция скорости Gj на ось
проходящую через точки М\, М2, а произведение u2cosa2 - проекция и2;
скорости б2 на эту же ось. Следовательно
0^=0^,
что и доказывает теорему.
Данная теорема используется при доказательстве других, более ча-
стных теорем кинематики, а также при решении задач на определение ско-
ростей.
97
Пример.
Стержень АВ движется так, что его конец А скользит вдоль верти-
кальной стенки, а конец В - по горизонтальному полу. Определить ско-
рость точки В в момент, когда стержень наклонен к стенке под углом а -
30°, если точка А имеет в этот момент скорость = 1 м/с (рис. 90).
Так как точка А стержня не отделяется при движении от стенки, а
точка В - от пола, скорости точек направлены
так, как показано на рисунке. В соответствии с
теоремой имеем . Вычисляя
ил4=илсо8а, uB^=D5sina и подставляя в
написанное равенство, получаем
cos a = \эв sin а,
откуда следует
~ ct8a ~ ’ >/? = 1,73 м/с.
Перейдем теперь к изучению простейших
движений твердого тела- поступательного и
Рис. 90
вращательного.
Поступательное движение
Поступательным называется такое движение твердого тела, когда
всякая прямая, мысленно проведенная в теле, перемещается параллельно
самой себе.
Теорема. При поступательном движении все точки тела описыва-
ют одинаковые (конгруэнтные) траектории и имеют в каждый момент
времени геометрически равные скорости и ускорения.
Доказательство. Пусть тело движется поступательно (рис. 91). Про-
извольно выберем в теле две точки М\ и М2. Вектор г ~ М}М2, соединяю-
щий эти точки, при поступательном движении тела
является постоянным вектором - его направление
остается постоянным в соответствии с опреде-
лением поступательного движения, модуль - в
силу неизменности расстояний между точками
абсолютно твердого тела. Следовательно, для ра-
диусов-векторов гх, г2 выделенных точек в любой
момент времени выполняется соотношение
__________________. Рис. 91
г2 = 1\ + Г , Г = const.
98
Это равенство означает, что если положение точки М\ в какой-то мо-
мент времени стало известно, то положение точки М2 в этот момент найдет-
ся путем смещения точки на векторную величину г , одинаковую во все
моменты времени. Поэтому, если известно геометрическое место положе-
ний (траектория) точки Mi, то геометрическое место положений (траекто-
рия) точки М2 получается путем сдвига траектории точки М\ в направлении
и на величину вектора г = МХМ2. Что и доказывает конгруэнтность траек-
торий точек М\ и М2. Поскольку точки М\, М2 выбраны произвольно, то
конгруэнтны траектории всех точек тела.
Дифференцируя написанное равенство последовательно два раза по
времени, убеждаемся в справедливости и второй части теоремы:
ц = б2, ах - а2.
Общая для всех точек тела скорость ц = б2 = ... = и называется ско-
ростью тела; общее для всех точек ускорение ах = а2=...= а - ускорением
тела. Сразу заметим, что эти термины имеют смысл только при поступа-
тельном движении; во всех других случаях движения тела отдельные точки
тела имеют разные скорости и ускорения.
Из всего сказанного следует, что изучение поступательного движе-
ния тела сводится к задаче кинематики точки. Именно, в теле выбирается
точка, движение которой определяется наиболее просто, и методами кине-
матики точки определяются ее траектория, скорость, ускорение. Траекто-
рии, скорости и ускорения остальных точек определяются простым пере-
носом кинематических характеристик выделенной точки.
Пример.
Определить траекторию, скорость и ускорение точки М, жестко свя-
занной со звеном АВ механизма спарника (рис. 92), если О\А = О2В = г =
0,5 м, а угол ф = ZAO\O2 = ZBO2x = 10t, рад.
Замечаем, что звено АВ механизма движется поступательно. Движе-
ние его точки А, которая одновременно
служит концом кривошипа О\А, легко
определяется. Выделим эту точку и най-
дем ее кинематические характеристики.
Непосредственно видно, что
траекторией точки А является окруж-
jc ность с центром в точке О\ и радиусом
г. Сместив эту окружность так, чтобы ее
центр оказался в точке О, причем
0}0 = АМ, получаем траекторию точ-
ки М.
ние. 92
99
Для определения скорости и ускорения точки М сначала найдем эти
величины для точки А, для которой уравнения движения имеют особенно
простой вид:
хА = гcoscp = 0,5cosl0z, м;
уА = rsincp = 0,5 sin 10z, м.
Определяем скорость vA(vAx,vAy) и ускорение аА (аАх,аА ), вычисляя
их проекции на координатные оси:
= хА =-5 sin 10Z, м/с; = уА = 5 cos 10Z, м/с;
алх = = -SOcoslOz, м/с2; аАу = = -50sinl0z, м/с2.
По найденным проекциям строим при точке А ее скорость \5А и ус-
корение аА. Скорость и ускорение точки М геометрически равны скорости
и ускорению точки А. Остается перенести эти векторы в точку Л/и поме-
нять индекс.
Вращательное движение
Уравнение вращательного движения. Угловая скорость и угловое
ускорение тела
Движение тела называется вращательным, если по крайней мере две
точки тела остаются неподвижными. Фактически неподвижной будет це-
лая прямая, проходящая через эти неподвижные точки и называемая осью
вращения тела.
Прежде всего выясним, как можно задать вращательное движение
математически. Для этого через ось вращения О]О2 проведем две полу-
плоскости - неподвижную (77]), связанную с
окружающими неподвижными предметами, и
подвижную (77), неизменно (жестко) связанную с
телом (рис. 93). Для определения положения тела 1
будет достаточно знать положение полуплоскости
П относительно полуплоскости П\, которое можно
задавать, указывая линейный угол ср между этими
полуплоскостями, называемый углом поворота
тела.
Если угол поворота задан как функция
времени
Ф = Ф(О,
то вращательное движение тем самым будет опи-
сано, а зависимость <р = <p(Z) называется уравнени-
ем (законом) вращательного движения.
Рис. 93
100
Положительное направление отсчета угла ср выбирают обычно в сто-
рону вращения тела и измеряют в радианах.
Основными кинематическими ’ величинами, характеризующими
вращательное движение, являются угловая скорость тела
и угловое ускорение тела
Если со = const, вращение называется равномерным, а закон враща-
тельного движения имеет вид: ср = ср0 +со/. Если полуплоскости П и П} в
начальный момент (t = 0) совпадают, то ср0 = 0 и ср = со/.
При условии е = const вращение называется равнопеременным - рав-
ноускоренным, если 8 и со имеют одинаковые знаки, и равнозамедленным,
если знаки 8 и со противоположны. При равнопеременном вращении угло-
вая скорость и угол поворота тела выражаются формулами
со = со0+8/; ср = ср0 + со0/ + —.
Здесь соо, Фо - начальные (при t = 0) значения угловой скорости и уг-
ла поворота тела. Если движение начинается из состояния покоя и угол ср
отсчитывается от начального положения тела (полуплоскости П и П\ в на-
чальный момент совпадают), то соо = Фо= 0, и формулы для определения оо
и ф принимают особенно простой вид: ® = 8/, ср = 8/2 / 2.
Траектории, скорости и ускорения точек тела
Траектории точек тела при вращательном движении - это окружно-
сти с центрами на оси вращения, лежащие в плоскостях, перпендикуляр-
ных оси вращения. Радиусы окружностей (радиусы вращения) равны крат-
чайшим расстояниям точек до оси вращения (см. рис. 93).
Пусть М- произвольная точка тела,
окружность радиуса ОМ = R- ее
траектория (рис. 94). Для длины 5 дуги
О\М, отсчитанной от точки О\ пересечения
с неподвижной полуплоскостью, будем
иметь:
s = Я(ф + а).
Здесь угол а является постоянным
(как угол между двумя прямыми в
абсолютно твердом теле), а угол ф
Рис. 94
101
изменяется с течением времени в соответствии с законом движения
Ф = ф(О-
Написанное равенство при учете зависимости ср = ср(7) представляет
собой закон движения точки М по траектории. Применяя правило опреде-
ления скорости при естественном способе задания движения и учитывая,
что а = const, получаем
и = — = — Г/? (ф + а)"1 = R— = Асо.
dt dtL 7J dt
Таким образом, скорость (линейная) точки вращающегося тела равна
по модулю произведению радиуса вращения на величину угловой скорости
тела. Для направления скорости получаем следующее правило: скорость
направлена перпендикулярно радиусу вращения (в плоскости траектории
точки) в сторону вращения тела.
Продолжая и далее пользоваться естественным способом задания
движения, для ускорения точки М получаем
а = ах + ап,
где
а = — = —(Ra)) = R— = Re,
х dt dC 7 dt
и2 (T?co)2 2
а ----_ v---
Р R
Касательное ускорение ах направлено в одну сторону со скоростью
б, если вращение тела ускоренное, и противоположно б, если вращение
замедленное. Нормальное ускорение ап, называемое также осестремитель-
ным ускорением, направлено по радиусу к оси вращения. Величина полно-
го ускорения определяется по формуле
а = ~ + со4 .
Сказанное проиллюстрировано на рис. 94, где показан случай уско-
ренного вращения против часовой стрелки.
Векторы угловой скорости и углового ускорения тела
Полученная выше формула для угловой скорости тела
б/ср
СО = — = ф
dt
определяет эту величину алгебраически - содержит величину угловой ско-
рости и знак (направление вращения), но не определяет положения оси
вращения в пространстве. Чтобы угловая скорость указывала также поло-
жение оси вращения, вводится понятие вектора угловой скорости.
102
Вектором угловой скорости тела называется скользящий вектор Й,
численно равный абсолютной величине угловой скорости |со| = |ф| и на-
правленный вдоль оси вращения в ту сторону, из которой вращение тела
видно происходящим против часовой стрелки.
В соответствии с этим определением вектор угловой скорости выра-
жается формулой
со = со Л — ф£,
где к - орт координатной оси z, проведенной вдоль оси вращения тела,
со = ф - алгебраическое значение угловой скорости.
Производная по времени от вектора
угловой скорости тела называется вектором
углового ускорения тела:
8 = — = сяк = фк .
dt
Из приведенных формул следует, что
векторы й и 8 оба направлены вдоль оси
вращения - в одну сторону, если вращение
ускоренное (рис. 95, а), и в противоположные
стороны, если вращение замедленное (рис. 95, б).
На рисунках круговой стрелкой показано
направление вращения.
Векторные формулы для линейной
скорости, касательного и нормального
ускорений точки тела
Векторное представление угловой скорости
и углового ускорения тела позволяют записать
линейную скорость, а также касательное и нор-
мальное ускорения произвольной точки тела в
виде следующих векторных произведений:
б = йхг ,
ах = 8 х г ,
ап=Йхб = ЙхЙхГ.
В этих формулах й, 8 - векторы угловой
скорости и углового ускорения тела, приложен-
ные в произвольной точке О оси вращения, г -
радиус-вектор рассматриваемой точки, прове-
денный из точки О (рис. 96). Справедливость
формул проверяется непосредственно.
103
Формулы широко используются при изучении кинематики более
общих случаев движения твердого тела.
Вопросы для самопроверки
1. В чем состоит теорема о проекциях скоростей двух точек абсо-
лютно твердого тела?
2. Что называется поступательным движением тела?
3. Сформулируйте теорему о траекториях, скоростях и ускорениях
точек тела при его поступательном движении.
4. Какое движение тела называется вращательным? Запишите и по-
ясните уравнение (закон) вращательного движения.
5. Что называется угловой скоростью и угловым ускорением?
6. В каком случае вращательное движение называется равномерным?
Запишите закон (уравнение) равномерного вращения.
7. Приведите формулы для угловой скорости и угла поворота тела
при его равноускоренном вращении.
8. Что называется вектором угловой скорости тела? Приведите фор-
мулу для вектора угловой скорости.
9. Что называется вектором углового ускорения? Как направлен век-
тор углового ускорения?
10. Запишите и поясните векторные формулы для линейной скоро-
сти, касательного и нормального ускорений точки вращающегося твердого
тела.
Упражнения
Решить в указанном порядке следующие задачи из сборника
И.В. Мещерского 1981 года издания: 13.2, 13.3, 13.13, 13.4, 13.7, 13.15,
13.18.
104
ЛЕКЦИЯ 9
ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ
ТВЕРДОГО ТЕЛА
Уравнения движения
Плоскопараллельным (плоским) называется такое движение твер-
дого тела, при котором все точки тела перемещаются в плоскостях, па-
раллельных некоторой заданной неподвижной плоскости (основной плос-
кости). Примерами тел, совершающих плоскопараллельное движение, яв-
ляются: тело с плоской гранью, соприкасающееся при движении всей этой
гранью с неподвижной плоскостью (рис. 97, а); шатун АВ кривошипно-
ползунного механизма (рис. 97, б)\ отдельные звенья роботов-манипулято-
ров (звено АВ на рис. 97, в); зубчатые колеса в сложных зубчатых переда-
чах (колесо с осью А на рис. 97, г) и др.
Пусть имеем тело, которое совершает плоскопараллельное движение
(рис. 98). Проведем вспомогательную плоскость 77, параллельную основ-
ной плоскости 77] так, чтобы она пересекла тело. В сечении получим неко-
торую плоскую фигуру S. При движении тела его плоская фигура 5 будет
105
перемещаться, оставаясь все время в
своей плоскости П. Выберем на пло-
ской фигуре точки А, В, С, ... и
проведем через эти точки прямые 1-1,
2-2, 3-3, ... , перпендикулярные
плоской фигуре. Поскольку плоская
фигура движется в своей плоскости,
указанные прямые будут перемещать-
ся, оставаясь все время параллельными
самим себе, то есть будут двигаться по-
ступательно. Следовательно, все точки
прямой 1-1 будут двигаться одинаково,
точно так же, как точка А этой прямой,
принадлежащая плоской фигуре S, все
точки прямой 2-2 - точно так же, как
точка В плоской фигуры S и так далее.
2
Рис. 98
Отсюда следует вывод: при изучении плоскопараллельного движения тела
достаточно ограничиться изучением движения какой-либо плоской фигу-
ры этого тела, движущейся в своей плоскости.
Пусть S - какая-либо плоская фигура тела, Оух^у^ - неподвижные ко-
ординатные оси, расположенные в той же плоскости (рис. 99). Выясним,
каким образом можно задавать движение плоской фигуры при помощи
уравнений.
Выберем на фигуре произвольную точку О, которую будем называть
полюсом, и построим координатные оси Оху, неизменно связанные с этой
фигурой и движущиеся вместе с ней. Положение плоской фигуры 5 будет
однозначно определено, если будет известно положение осей Оху относи-
тельно осей О1Х1У1- Но положение
одной плоской системы координат
относительно другой, расположенной в
той же плоскости, будет определено,
если задать три скалярные величины -
координаты х\0, Ую подвижного начала
(полюса О) и угол ф, который ось х
подвижной системы координат обра-
зует с осью Xi неподвижной системы
координат. А если эти величины
известны как функции времени
Хю = Х1о(0, Ую =yio(i), ф = ф(0>
106
то положение подвижных осей, а, следовательно, и положение плоской
фигуры, будет известно для каждого момента времени. Поэтому эти равен-
ства есть не что иное как уравнения движения плоской фигуры, движущей-
ся в своей плоскости, или, что то же самое, уравнения плоскопараллельного
движения тела.
Угловая скорость и угловое ускорение тела при
плоскопараллельном движении
Если бы в уравнениях плоскопараллельного движения изменялись
только величины х10, Ую, а угол (р оставался постоянным, то движение тела
было бы поступательным. Если же были бы постоянными хю, ум, а изме-
нялся во времени только угол ср, мы имели бы чисто вращательное движе-
ние. Так как в общем случае переменны все три указанные величины, то
следует вывод: при плоскопараллельном движении тело участвует одно-
временно в двух движениях- поступательном, определяемом движением
произвольно выбранного полюса О, и вращательном вокруг этого полюса
(точнее - вокруг оси, перпендикулярной плоской фигуре и проходящей через
полюс О).
Величины
со — ср и s = (Ь =ср
называются угловой скоростью и угловым ускорением тела при плоскопа-
раллельном движении. Определим также векторы угловой скорости и уг-
лового ускорения тела
ю = ф£, 8 = О) = ф£,
где к - единичный вектор, приложенный в полюсе О и направленный
перпендикулярно плоской фигуре тела в ту сторону, из которой отсчет уг-
ла (р виден происходящим против часовой стрелки.
Одно из замечательных свойств плоскопараллельного движения со-
стоит в том, что угловая скорость и угловое ускорение не зависят от выбо-
ра полюса - вокруг любой своей точки плоская фигура вращается с одной
и той же угловой скоростью и одним и тем же угловым ускорением.
Определение скоростей точек тела. Метод полюса
По заданным уравнениям плоскопараллельного движения можно
вычислить и построить скорость б0 полюса О и определить направление
вращения и величину угловой скорости со (рис. 100, а).
Нас будет интересовать величина и направление скорости \эм произ-
вольной точки М плоской фигуры. Для решения этой задачи выразим ра-
диус-вектор точки М в виде суммы векторов, законы изменения которых в
силу уравнений движения известны (см. рис. 99):
ГуМ=гю+7 (г=0М).
107
Дифференцируя это выражение по
времени и имея в виду очевидные ра-
венства
dt м
получим
Выясним смысл производной dr/dt.
С этой целью заметим, что вектор dr/dt
совпадает с производной вектора гш,
вычисленной при условии, что гю - const.
Рис. 100
Но при этом условии полюс О неподвижен, а плоская фигура только вра-
щается вокруг полюса О. Следовательно, производная dr/dt выражает ли-
нейную скорость точки М в этом вращательном движении. Обозначив ее
через (произносится так: линейная скорость точки М в ее вращении
вместе с плоской фигурой вокруг полюса О\ запишем:
dr
dt
d _
dt Г'
r\o
= const}
~ ^MO '
Величина и направление uw определяются в полном соответствии с
правилом определения скорости точки вращающегося тела. В частности,
имеет место векторная формула
>
где (Ь - вектор угловой скорости тела (плоской фигуры).
В результате выражение для скорости произвольной точки М пло-
ской фигуры принимает вид
Полученная формула выражает метод полюса, служащий наиболее
общим методом определения скоростей точек тела при плоскопараллель-
ном движении. Ему соответствует следующая словесная формулировка:
скорость произвольной точки плоской фигуры равна геометрической сум-
ме скорости точки, принятой за полюс, и линейной скорости во враща-
тельном движении этой точки вместе с плоской фигурой вокруг полюса.
На рис. 100, б приводится геометрическая интерпретация полученно-
го правила.
108
Пример.
Вычислить скорость точки В стрежня в примере на с. 97.
Движение стержня является плоскопараллельным. Выберем за по-
люс точку А стержня, тогда для точки В в соответствии с методом полюса
можем написать:
Направления векторов б5, vBA известны, неизвестными являются
Полученное векторное уравнение
можно решать геометрически или анали-
тически. Геометрический способ состоит в
построении и последующем решении тре-
угольника (или параллелограмма) ско-
ростей. Из точки В проводим вектор,
геометрически равный скорости полюса б4,
а из конца этого вектора проводим прямую,
параллельную вектору б5л (рис. 101). Точка
пересечения этой прямой с осью Ох, вдоль
которой направлен искомый вектор бй,
решает поставленную задачу геомет-
рически. Остается решить полученный треугольник и вычислить Бу-
дем иметь:
ctg30° = 1 • >/з = 1,73 м/с.
При аналитическом способе решения составляют и решают два ска-
лярных уравнения, получаемые путем проектирования векторного уравне-
ния для скоростей на подходящим образом выбранные координатные оси.
Выбрав координатные оси как показано на рис. 101, получаем два уравне-
ния с двумя неизвестными - и
= vBA - cos30°;
0 = -ил + dba sin30°.
Решая их, получаем для vB тот же самый
результат.
Мгновенный центр скоростей
Пусть известны угловая скорость со и
линейная скорость б0 некоторой точки О
плоской фигуры (рис. 102). Повернем луч OL,
вдоль которого направлена скорость б0, на
109
прямой угол в сторону вращения фигуры и отложим вдоль него отрезок ОР
длиной
ОР = ^.
со
Вычислим скорость построенной таким образом точки Р плоской
фигуры. Приняв за полюс точку О, для скорости точки Р будем иметь
Vp = + Vp0 .
Непосредственно видно, что вектор бР0 направлен противоположно
вектору б0. Кроме того, он имеет тот же модуль:
иР0 - со • ОР = со • — = .
со
Таким образом, скорость точки Р складывается из двух равных и про-
тивоположно направленных векторов и поэтому равна нулю. Из построе-
ния следует, что этим свойством обладает одна-единственная точка Р.
В результате установлено следующее свойство плоскопараллельного
движения: у движущейся плоской фигуры в каждый момент времени име-
ется единственная точка, скорость которой равна нулю. Эта точка на-
зывается мгновенным центром скоростей.
Определение скоростей точек плоской фигуры через
мгновенный центр скоростей
При определении скоростей за полюс можно лринять любую точку
плоской фигуры. Примем за полюс мгновенный центр скоростей Р. Тогда
для скорости произвольной точки М плоской фигуры будем иметь фор-
мулу
= + ^мр ’
Но бр = 0, поэтому
= ^МР •
Полученное равенство означает, что скорости точек плоской фигу-
ры равны линейным скоростям этих точек при их вращательном движе-
нии вместе с плоской фигурой вокруг мгновенного центра скоростей".
~vMP, ~vNP и т.д. (рис. 103). Направления скоростей перпендику-
лярны мгновенным радиусам (отрезкам, соединяющим точки с мгновен-
ным центром скоростей), модули скоростей равны произведениям мгно-
венных радиусов на угловую скорость тела: = РМ • со, иN = PN • со и
Т.д.
по
Рис. 103
Отметим два свойства
распределения скоростей точек
плоской фигуры, вытекающие
из установленного правила:
1) мгновенный центр ско-
ростей лежит на пересечении
перпендикуляров, восставленных
в соответствующих точках к их
скоростям (рис. 103, а);
2) концы скоростей точек
плоской фигуры, расположенных
на некоторой прямой, проходя-
щей через мгновенный центр скоростей, также лежат на одной прямой,
проходящей через мгновенный центр скоростей (рис. 103, б).
Различные случаи определения положения мгновенного
центра скоростей
Из предыдущего пункта видно, что вычисление скоростей при плос-
копараллельном движении сильно упрощается, если положение мгновен-
ного центра скоростей известно. Общий способ определения его положе-
ния рассмотрен выше. Ниже приводятся характерные частные случаи, ко-
гда положение мгновенного центра скоростей (сокращенно м.ц.с.) легко
определяется.
Рис. 104
Рис. 105
1. Одна цилиндрическая поверх-
ность катится без скольжения по
другой цилиндрической поверхности
(или плоскости), остающейся непод-
вижной. М.ц.с. находится в точке
соприкосновения плоских фигур под-
вижной и неподвижной поверхностей
(рис. 104, а} б). Если при этом известна
скорость какой-либо точки под-
вижного цилиндра, то это позволяет
определить также направление вра-
щения и величину угловой скорости
(по формуле о = t)j / АР).
2. Известны скорость одной
точки тела (по величине и направле-
нию) и направление скорости другой
точки (штриховые линии на рис. 105).
Ill
2.1. Направления скоростей не параллельны (рис. 105, а). Тогда м.ц.с.
находится в точке пересечения перпендикуляров, восставленных в этих
точках к направлениям скоростей. Основанием к такому построению слу-
жит свойство 1) распределения скоростей в плоской фигуре (см. с. 110).
2.2. Направления скоростей
параллельны (рис. 105, б). В этом
случае указанные перпендикуляры не
пересекаются, и м.ц.с. не существует.
Можно показать, что в этом случае
угловая скорость тела равна нулю, а
скорости всех его точек геометри-
чески равны. Мы имеем так называ-
емый случай мгновенного поступа-
тельного движения. В состоянии
мгновенного поступательного движе-
ния, например, оказывается шатун АВ
кривошипно-ползунного механизма
каждый раз, когда кривошип ОА
перпендикулярен направляющей пол-
зуна В (рис. 106, а, б).
3. Известны скорости концов
некоторого отрезка АВ плоской фи-
гуры; направления скоростей перпен-
дикулярны к этому отрезку. М.ц.с.
находится построением, показанным
на рис. 107, а, б, вытекающим из
свойства 2) распределения скоростей
плоской фигуры (см. с. 110).
Рис. 107
Определение ускорений точек тела
Формулу для определения ускорений при плоскопараллельном дви-
жении получим, дифференцируя по времени выражение для скорости про-
извольной точки М тела:
— d\)
at at
~ ч d d(b ~ ~ dr
+ uw) = — (u0+a>xr) = —f- + — xr +ЮХ —
dt dt dt dt
Смысл отдельных слагаемых в полученном равенстве вполне очевиден:
—= ао - ускорение полюса О;
dt
112
— х г = г х г = а^о - касательное ускорение во вращательном дви-
dt
жении точки М вместе с плоской фигурой вокруг полюса О\
_ dr _
сох — = со х o w = со х со х г = амо - нормальное ускорение во враща-
dt
тельном движении точки М вместе с плоской фигурой вокруг полюса О.
Модули и направления ускорений ахмо, а^о находятся как при простом
вращательном движении вокруг центра О.
Используя введенные обозначения, приходим к следующей формуле
для определения ускорений:
^м + ^мо + а мо •
Одновременно получено правило для определения ускорений при
плоскопараллельном движении методом полюса - ускорение любой точки
плоской фигуры равно геометрической сумме ускорения произвольно вы-
бранного полюса и касательного и
нормального ускорений во вращательном
движении этой точки вместе с плоской
фигурой вокруг выбранного полюса.
На рис. 108 показаны направления
составляющих и векторный многоугольник
ускорений, определяющий ускорение точки
М согласно данному способу.
Модуль ускорения ам удобно нахо-
дить методом проекций. Выбрав коорди-
натные оси Мху (например, так, как это
принято на рис. 108) и проектируя век-
торную формулу для ам на эти оси,
последовательно находим:
^=^sina + <4,; аМу = а0 cos а - апм0;
“м
2
Пример.
В механизме эллипсографа (рис. 109) скорость и ускорение ползуна
А направлены к точке О и имеют значения = 0,5 м/с, аА = 2 м/с2. Найти
ускорение ползуна В, если АВ = 1 м, а угол а составляет в этот момент 30°.
113
Примем точку А за полюс, тогда для ускорения точки В можно запи-
сать:
«В = &А + &ВА + &ВА •
Это - векторное уравнение для определения ускорения точки В, ко-
торое можно решать геометрически или аналитически.
Воспользуемся аналитическим способом решения. Для этого, прежде
всего, изображаем при точке В все составляющие её ускорения
(рис. 109, а). Ускорение аА известно по величине и направлению; ускоре-
ние аВА - только по направлению (от точки В к полюсу А); ускорения аВА и
ав, известные только по своим линиям действия, направляем вдоль этих
линий в ту или иную сторону (точное направление станет известно в ходе
решения задачи).
Как ранее упоминалось, векторное уравнение на плоскости эквива-
лентно двум скалярным уравнениям, которые получим, проектируя век-
торное уравнение на подходящим образом выбранные координатные оси.
Проектируя обе части векторного уравнения ускорений на оси Ох, Оу
(рис. 109, а), получаем:
~ав~ авА sin ^°~авА cos 30°;
0 = -аА + аВА cos30°+a^ sin 30°.
В полученной системе двух уравнений содержатся три неизвестные:
ав, авА> аВА’ поэтому одну из них требуется предварительно определить.
Обычно удается найти величину аВА. Для этого строим мгновенный центр
скоростей Р звена АВ, после чего находим угловую скорость:
vA 0,5 1 1
АР ЛВ-cosa 1 V3 у/3 с
'~2
114
Направление угловой скорости показано круговой стрелкой (опреде-
ляется по направлению скорости ).
Теперь не представляет труда вычисление апВА :
о ( 1 V 1 7
а" = а>2-АВ = -1 = -, м/с2.
ВА з
Зная апВА, решаем полученную систему. Из второго уравнения сразу
находим
2-1.1
ахВА = ал =--^2, = JL= 2,117, м/с2.
ВА cos 30° 7з зТз
2
Положительный знак величины аВА указывает, что принятое направ-
ление вектора аВА совпадает с его истинным направлением.
По найденному ускорению аВА определяем величину и направление
углового ускорения звена АВ. Величина углового ускорения равна
е = £м= 2Д12 = 2,117, 4-,
АВ 1 с2
направление показано на рисунке круговой стрелкой.
Подставляя значение аВА в первое уравнение, вычисляем ускорение
ползуна В:
ав = a" cos 30°-а' sin 30° = 1 • — —11= - = -0,770, 4 •
в ВА ВА 3 2 313 2 с2
Отрицательный знак величины ав указывает на то, что вектор ав
имеет направление, противоположное принятому.
Примечание. Установив отрицательный знак величины ав (или ал-
гебраического значения какого-либо другого неизвестного вектора) не
следует потом изменять его направление и переделывать расчеты. Ведь ис-
тинное направление вектора и его модуль стали известны!
Этим решение поставленной задачи заканчивается.
Заметим, что теперь мы располагаем данными, позволяющими опре-
делить скорость и ускорение любой точки стержня АВ. Дополнительно
найдем, например, скорость и ускорение его средней точки (точки Q.
Скорость наиболее просто определяется при помощи мгновенного
центра скоростей. Применяя соответствующее правило, получаем, что ско-
рость бс равна по модулю
115
ur =a-PC = a- — = -7=- —= 0,289, м/с
c 2 7з 2
и направлена перпендикулярно к мгновенному радиусу PC в сторону угло-
вой скорости (рис. 109, б).
Для определения ускорения воспользуемся формулой
&С — &А + &СА + &СА •
Направления слагаемых векторов показаны на рис. 109, б, модули
ускорений ахСА, апСА легко могут быть вычислены, так как и со, и е теперь
известны:
дъ
ах =е-СА = е~ = 2,117-0,5 = 1,058 м/с2;
СА 2
( 1 \2 1 1
а* = а2СА = Н= • —= —= 0,167м/с2.
с 2 6
Проектируя векторное уравнение для ас на оси Ох, Оу, находим
проекции искомого ускорения
аСх ~ асА sin30° - апСА cos 30° = 0,384 м/с2 ;
aCv = -аА + ахСА cos30° + a” sin30° = -1,001 м/с2,
/1 Czi С/Л 7 7
а далее и численное значение ускорения
ас = у]асх + асу = 1,072, м/с2.
В некоторых задачах на плоскопараллельное
движение угловое ускорение тела может быть
вычислено непосредственно по формуле
8 = da / dt, определяющей понятие углового
ускорения. Например, так обстоит дело в случае с
колесом, катящимся без скольжения со скоростью
центра б0 и ускорением центра а0 (рис. 110).
М.ц.с. колеса находится в точке касания Р, поэтому
для угловой скорости получим (R - радиус колеса):
Поскольку R = const, то угловое ускорение найдется прямым диффе-
ренцированием угловой скорости по времени:
и0 у 1 dv0 _а0
R)Rdt R
da _ d
dt dt
116
Вопросы для самопроверки
1. Какое движение твердого тела называется плоскопараллельным?
Приведите примеры плоскопараллельного движения.
2. Как задать плоскопараллельное движение при помощи уравнений?
3. В чем состоит метод полюса при определении скоростей точек те-
ла при плоскопараллельном движении? Приведите пример применения ме-
тода.
4. Что называется мгновенным центром скоростей? Как определяют-
ся величины и направления скоростей точек тела при помощи м.ц.с.?
5. Укажите способы определения положения м.ц.с.
6. Приведите векторную формулу, связывающую ускорения двух то-
чек плоской фигуры. Как называются отдельные слагаемые в этой форму-
ле?
7. Как найти угловую скорость и направление вращения плоской фи-
гуры? Укажите характерные случаи.
8. Как вычисляется угловое ускорение при плоскопараллельном
движении тела?.
Упражнения
Решить следующие задачи из сборника И.В. Мещерского 1981 г. из-
дания: 16.2, 16.3, 16.4, 16.10, 16.15, 16.28, 16.32, 16.33, 18.11, 18.22, 18.40.
117
ЛЕКЦИЯ 10
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
Основные понятия и определения
До сих пор при изучении движения точки (отдельной точки, точки
тела) мы всегда предполагали, что система координат Oxyz, относительно
которой рассматривается движение, является неподвижной. Теперь рас-
смотрим случай, когда система координат Oxyz также движется, так что
движутся как точка М, так и система координат Oxyz- по отношению к
другой системе координат OpciyiZi, являющейся неподвижной (рис. 111).
Этот случай, когда движение точки М рассматривается одновременно в
двух системах координат - подвижной и неподвижной, называется
сложным движением точки.
Движение точки относительно
неподвижной системы координат на- % /
зывается абсолютным движением. Ее \ /
скорость б и ускорение а по отно- 2 \/М
шению к неподвижным осям назы- м Y У
ваются соответственно абсолютной »
скоростью и абсолютным ускоре- /
нием. J
Движение точки относительно
подвижной системы координат назы- q___________
вается относительным движением. jx " **
Скорость и ускорение точки по отно- х
шению к подвижным осям назы-
ваются относительной скоростью
(обозначается бг) и относительным Рис. 111
ускорением (аг). Индекс г - от латинского слова relativus (относительный).
Движение подвижной системы координат вместе с неизменно свя-
занными с ней геометрическими точками относительно неподвижной сис-
темы координат называется переносным движением. Переносной скоро-
стью (бе) и переносным ускорением (ае) точки М называются скорость и
ускорение относительно неподвижной системы координат точки М', неиз-
менно связанной с подвижными осями, с которой совпадает в данный мо-
мент времени движущаяся точка М. Индекс е - от латинского enteiner (ув-
лекать с собой).
Понятия переносной скорости и переносного ускорения являются
более тонкими. Приведем следующее дополнительное пояснение. В про-
118
цессе относительного движения точка М оказывается в различных местах
(точках) подвижной системы координат. Обозначим М' ту точку подвиж-
ной системы координат, с которой совпадает в данный момент движущая-
ся точка М. Точка М' движется вместе с подвижной системой координат
относительно неподвижной системы с некоторой скоростью и ускоре-
нием ам,. Эти величины и служат переносной скоростью и переносным
ускорением точки М\
-» — -- — М'
ае=аМ'=-Г--
at
Сделаем еще два замечания.
1. Подвижные и неподвижные координатные оси, фигурирующие в
постановке задачи о сложном движении, нужны лишь для общности по-
становки задачи. На практике роль систем координат выполняют конкрет-
ные тела и предметы - подвижные и неподвижные.
2. Переносное движение или, что то же самое, движение подвижных
осей относительно неподвижных, сводится к одному из движений твердого
тела - поступательному, вращательному и т.д. Поэтому при вычислении
переносной скорости и переносного ускорения следует пользоваться соот-
ветствующими правилами, установленными для различных видов движе-
ния тела.
Скорости и ускорения в сложном движении связаны строгими мате-
матическими зависимостями - теоремой сложения скоростей и теоремой
сложения ускорений.
Теорема сложения скоростей
Вначале получим общие выражения для абсолютной, относительной
и переносной скоростей, основываясь на введенных выше определениях и
результатах кинематики точки, изложенных в лекции 7. Однако предвари-
тельно сделаем одной замечание.
Один и тот же переменный вектор (радиус-вектор, вектор скорости и
т.д.) в различных системах координат, движущихся относительно друг
друга, изменяется по-разному. Соответственно, отличными друг от друга
будут и его производные, вычисленные по отношению к разным системам
координат. Поэтому в кинематике всегда следует отдавать себе отчет в
том, относительно какой системы координат вычисляется та или иная век-
торная производная.
Пусть г - радиусы-векторы точки М, проведенные из начала не-
подвижной и подвижной систем координат соответственно, г0 - радиус-
вектор подвижного начала относительно неподвижного (рис. 112).
119
Абсолютная скорость точки М9 в
соответствии с определением, будет выра-
жаться производной по времени от радиуса-
вектора г}, вычисленной относительно
неподвижной системы координат:
Относительная скорость выражается
производной от радиуса-вектора г,
вычисленной относительно подвижной сис-
темы координат. Вводя для производных
относительно подвижной системы коор-
динат знак ~ (тильда), запишем:
dr
и г-—.
dt
Рис. 112
При вычислении производной относительно подвижной системы ко-
ординат (ее называют также относительной производной, локальной про-
изводной) движение подвижных осей игнорируется - оси считаются как
бы неподвижными (остановленными).
Пусть х, у, z - текущие координаты точки М в подвижных осях,
z, j.k - орты этих осей. Тогда, учитывая сказанное о вычислении локаль-
ной производной, для относительной скорости получим:
dr _ d
dt dt
xi + yj + zk
i = const
j = const
к = const
dx т dy - dz r
— i + —j +—к
dt ' dt dt
Переносная скорость точки M, в соответствии с определением, вы-
ражается производной от радиуса-вектора точки М’ подвижной системы
координат, вычисленной относительно неподвижной системы координат:
dru, d хгтк
Ч = = -f- = —(r0 + °M) =
at dt
£
dt
x - const
r0 + (xi + yj + zk) у = const
z = const
dfn di di
— + x— + y—
dt dt dt
dk
z—.
dt
Здесь учтено, что вектор ОМ’ имеет в подвижном координатном ба-
зисе то же представление, что и вектор г, только координаты х, у, z явля-
ются для него постоянными (так как точка М’ неизменно связана с под-
вижной системой координат).
120
Найдем теперь зависимость между абсолютной, относительной и пе-
реносной скоростями. Для этого продифференцируем относительно непод-
вижной системы координат обе части равенства
zj = r0 + г = r0 + xi + yj + zk ,
учитывая, что по отношению к неподвижной системе все величины в нем
являются переменными: г0, а также i,у,к - от движения подвижных осей,
х,у, z - вследствие относительного движения. Будем иметь:
dr, drn di di dk dx~ dy ~ dz
dt dt dt dt dt dt dt dt
или, используя введенные выше обозначения:
Мы получили, что абсолютная скорость точки при ее сложном
движении равна геометрической сумме переносной и относительной ско-
ростей.
В этом и состоит теорема сложения скоростей при сложном движе-
нии точки. Геометрически это означает, что абсолютная скорость выража-
ется направленной диагональю параллелограмма, сторонами которого
служат векторы относительной и переносной скоростей (см. рис. 122;
штриховыми линиями на рисунке показаны абсолютная и относительная
траектории точки).
Теорема сложения ускорений
Предварительно получим общие выражения для относительного и
переносного ускорений.
Относительное ускорение характеризует скорость изменения отно-
сительной скорости по отношению к подвижной системе координат. Сле-
довательно, оно выражается локальной производной по времени от отно-
сительной скорости точки:
dvr _ d
dt dt
dx -r dy - dz -
— i + —j +—к
dt dt dt
i - const
j - const
к = const
d2x~ d2y~ d2z
dt2 dt dt
Переносное ускорение, в соответствии с его определением и смыс-
лом, выразится так:
ае=а^'
dt
х = const
у = const
z = const
d2ro d2i
---r- + *—v
dt-dt
d2j d2k
---T“ + z--
dt dt
121
Абсолютное ускорение точки характеризует скорость изменения аб-
солютной скорости по отношению к неподвижным осям и поэтому будет
равно
_ d\5 d _ _ ч бЛЗ dvr
(2=----= “ (Ч +D ) =-------~ +----- .
dt dt е r dt dt
Производные вычисляются по отношению к неподвижным осям, по-
этому при дифференцировании выражений для бе и бг будут переменны-
ми как координаты х, у, z, так и орты 7, у, к . Выполнив дифференцирова-
ние, с учетом полученных выше выражений для переносного и относи-
тельного ускорений можем записать:
dx di _^dy dj dz dk
dt dt dt dt dt dt,
Видно, что абсолютное ускорение складывается из переносного и
относительного ускорений и из дополнительного слагаемого, которое по-
лучило название ускорения Кориолиса* (кориолисова ускорения). После
некоторых преобразований, которые здесь не приводятся, ускорение Ко-
риолиса представляется в виде следующего выражения:
dx di dy di dz dk | .
+ —— + =2(0 xn ,
dt dt-dt dt dt dt I
где 6 e - вектор переносной угловой скорости, бг - вектор относительной
линейной скорости точки.
Таким образом, приходим к теореме сложения ускорений, которую
можно записать в виде следующих двух векторных равенств:
а = ае + аг + ак; ак = 2(бе х бг).
Словесная формулировка теоремы такова: абсолютное ускорение
при сложном движении точки равно геометрической сумме ее относи-
тельного, переносного и кориолисова ускорений. Ускорение Кориолиса
равно удвоенному векторному произведению вектора переносной угловой
скорости на вектор относительной линейной скорости точки.
Причины появления ускорения Кориолиса
Из определения переносного и относительного ускорений следует,
что первое из них учитывает изменение переносной скорости в переносном
движении, второе - изменение относительной скорости в относительном
движении. Однако переносная скорость может зависеть от относительного
движения, а относительная скорость - от переносного движения.
* Кориолис Гаспар Гюстав (1792 - 1843) - французский ученый-механик.
122
Сказанное хорошо видно на примере сложного движения точки М
(рис. 113, а), которая движется вдоль стержня О А со скоростью (отно-
сительное движение), а стержень, в свою очередь, вращается с угловой
скоростью сое вокруг центра О (переносное движение). Пусть оба движения
равномерные: = const, = const. Так как относительное движение рав-
номерное и прямолинейное, относительное ускорение равно нулю. Тем не
Рис. 113
менее относительная скорость
изменяется, что видно из
рис. 113, б, на котором показаны
два положения точки Ми стержня
в последовательные моменты вре-
мени t и f = / + А/. Приращение
относительной скорости Абг
(Aur = 2ur sin(A(pe / 2)) вызвано
изменением направления относи-
тельной скорости вследствие вра-
щения стержня (из-за наличия
переносного движения).
Далее, переносное каса-
тельное ускорение точки М
равно нулю (ое = const; =
ckbe/dt = 0; сгг =0). Однако переносная скорость не остается постоянной по
модулю, а изменяется за время Аг на величину
Аое = и' - ц, = (5 + Ау)ое - 5 • ое = As • ое.
Причиной изменения служит смещение точки в зону больших значений
переносной скорости из-за наличия относительного движения.
Указанные приращения, не учитываемые ни переносным, ни относи-
тельным ускорениями, и приводят в итоге к возникновению кориолисова
ускорения.
Вычисление и построение ускорения Кориолиса
Для определения величины и направления кориолисова ускорения
прежде всего следует вычислить и направить относительную скорость бг.
Далее строится вектор переносной угловой скорости со е и переносится па-
раллельно себе в точку М. После этого остается воспользоваться правилом
векторной алгебры для определения векторного произведения.
Ускорение ак направлено перпендикулярно плоскости, в которой
лежат векторы б е и , в ту сторону, из которой кратчайший поворот от
123
вектора к вектору бг виден про-
исходящим против часовой стрелки
(рис. 114). Модуль ускорения Ко-
риолиса определяется по формуле
ак = 2|Se|-|6,|-sin<x,
где а - угол между векторами йе и
бг.
Ускорение Кориолиса равно
нулю в следующих случаях.
1. Когда один из векторных со-
множителей равен нулю (пг= 0 или
Ше = 0).
2. Когда векторы йе и бг
коллинеарны. В этом случае угол а
равен либо 0 (рис. 115, л), либо 180°
(рис. 115,6), поэтому sina, а вместе
с ним и ak, равны нулю.
3. Когда переносное движение
является поступательным. В этом
случае движение подвижных осей не
имеет вращательной составляющей,
поэтому переносная угловая скорость
равна нулю в любой момент времени:
йе = 0. В любой момент времени бу-
дет равно нулю и кориолисово уско-
рение, и теорема сложения ускорений
при поступательном переносном
движении принимает такой же вид,
как и теорема сложения скоростей:
а = ае + аг.
Так обстоит дело, например, Рис- 116
при сложном движении точки М, показанном на рис. 116. Переносным
движением является движение стержня АВ (спарника), которое при усло-
вии О;А = О2В = R является поступательным. Ускорение Кориолиса в дан-
ном случае отсутствует.
124
Пример.
Жесткая рамка в виде прямо-
угольного треугольника ОАВ вращается
вокруг неподвижной оси с угловой
скоростью со = 4/, 1/с (рис. 117). По ги-
потенузе ОВ движется точка М согласно
уравнению 5 = ОМ= см. Найти абсо-
лютную скорость и абсолютное ускорение
точки М в момент времени t = t\ = 1 с.
Точка М совершает сложное движе-
ние- одновременно движется относитель-
но рамки (подвижная система координат) и
окружающих неподвижных предметов (не-
подвижная система координат). Перенос-
ным движением является вращательное
движение рамки, относительным - прямо-
линейное движение точки М вдоль прямой ОВ. Пусть М- положение точ-
ки в текущий момент /, М\ - в расчетный момент t = t\.
Переносная скорость точки М найдется как линейная скорость точки
М' рамки, совпадающей в данный момент с движущейся точкой М. (При
определении переносной скорости можно пользоваться следующим прие-
мом: мысленно остановить относительное движение и найти скорость в ос-
тавшемся движении). Так как рамка вращается, переносную скорость
вычисляем по формуле
ve=Re($e, где Re = МК = ОМ sin30°, =
Подставляя данные из условия задачи, находим:
ц,(Z) = 5Г2 sin30° • 4/ = 10?, см/с;
ие(1) = 10 см/с.
Примем, что в расчетный момент плоскость рамки совпадает с плос-
костью рисунка. Тогда вектор бе будет направлен перпендикулярно к
плоскости рисунка "от нас".
Величину относительной скорости находим, дифференцируя закон
относительного движения
ds
ur(z) = —= 10^, см/с; иг(1) = 10, см/с.
Вектор бг направлен вдоль прямой ОВ в сторону движения (к точке В).
Складывая векторы и бг, известные теперь по величине и на-
правлению, находим абсолютную скорость точки М. Так как слагаемые
125
векторы взаимно перпендикулярны, модуль абсолютной скорости вычис-
ляем по теореме Пифагора:
и(1) = ^(ve(l))2 + (и,(1))2 = 10V2 = 14,1, см/с.
Абсолютное ускорение находим по теореме сложения ускорений:
а = ае + ar + ак = aJ + а" + а' + а ” + ак.
Дальнейшее решение состоит в вычислении и построении каждого
из составляющих ускорений и последующем их суммировании.
Для определения переносного касательного ускорения сначала вы-
числяем переносное угловое ускорение
dca л ,, 2
8 =—- = 4, 1/с ,
dt
а далее и само ускорение:
axe(t)-Re • 8е = ОМ• sin30°-8e — Юг2, см/с2.
aJ(l) = 10, см/с2.
Направление вектора ахе совпадает с направлением вектора ("от
нас").
Вычисляем переносное нормальное ускорение:
ane(t) = Re®2 = 5t2 • sin30° • (402 = 40г4, см/с2;
<(1) = 40, см/с2.
Направлено а" по радиусу переносного вращения к оси вращения (к
точке К\).
Относительное касательное ускорение равно
т dv(t) d . 2
а = —г-—- = — (1 Or) — 10, см/с
r dt. dt
и направлено в одну сторону с относительной скоростью . Так как отно-
сительное движение прямолинейное, относительное нормальное ускорение
равно нулю (а” = 0).
Условно переносим вектор переносной угловой скорости =6 в
точку М и определяем модуль ускорения Кориолиса:
ак (?) = 2юе t>r sin 30° = 2 • 4? 10? • 1 / 2 = 40?2, см/с2;
at(l) = 40, см/с2.
Вектор ак направлен перпендикулярно плоскости рисунка "от нас".
126
Выбираем с началом в точке Мвспомогательные оси ц, £ и вычис-
ляем методом проекций абсолютное ускорение а (а^ ац, в расчетный
момент t = = 1 с:
= -а] -ак = -10 - 40 = -50, см/с2;
1 О
= a’ sin30° - а”=10• — 40 = -35, см/с2;
л Г 2
а, = < cos 30° = 10 • — = 5 7з = 8,66, см/с2;
_______2_____________
а = ^а2+а2+а2 = 7(-50)2 +(-35)2 + (5л/з)2 = 61,64, см/с2.
Вопросы для самопроверки
1. Что называется сложным движением точки? Приведите примеры
сложного движения.
2. Что называется абсолютным, относительным и переносным дви-
жением?
3. Дайте определение абсолютной, относительной и переносной ско-
рости точки. Приведите для них общие выражения в виде производных.
4. Получите и поясните общие выражения для относительного и пе-
реносного ускорений.
5. В чем состоит теорема сложения скоростей?
6. Сформулируйте теорему сложения ускорений.
7. Запишите векторную формулу для определения ускорения Корио-
лиса. В каких случаях ускорение Кориолиса обращается в нуль?
8. Как определяются модуль и направление ускорения Кориолиса?
9. Поясните причины возникновения кориолисова ускорения.
Упражнения
Решить в указанном порядке следующие задачи из сборника
И.В. Мещерского 1981 года издания: 22.14, 22.15, 22.17, 23.31, 23.27, 23.41,
23.13,23.5,24.26.
127
ДОБАВЛЕНИЕ
КИНЕМАТИКА ПРОЦЕССА ФУГОВАНИЯ
ДРЕВЕСИНЫ*
Схема и расчетная модель процесса фугования
Строганная поверхность доски воспринимается на первый взгляд как
идеально плоская. Однако в действительности она имеет более сложную
форму. Причины этого кроются в самом характере процесса фугования.
На рис. 118 показана схема процесса фугования. На переднюю плиту 1
фуговального станка поступает заготовка, например, брусковая деталь 2,
которая перемещается со скоростью Vмеханизмом подачи. При прохожде-
нии над ножевой головкой 3, вращающейся с угловой скоростью о, проис-
ходит снятие стружки с заготовки, так что задняя плита 4 станка находится
в контакте с уже обработанной поверхностью.
Для определения
геометрической формы
обработанной поверхнос-
ти необходимо выяснить,
какой формы след остав-
ляют в геометрическом
теле заготовки точки
режущего лезвия - режу-
щие кромки ножей - в
процессе обработки. Для
этого требуется изучить
относительное движение
режущих кромок относительно заготовки и найти их относительные траек-
тории. В результате мы оказываемся в ситуации, в точности соответст-
вующей сложному движению- движение режущих кромок мы должны
рассматривать относительно двух систем координат - неподвижной (ста-
нина станка) и подвижной (движущаяся заготовка).
Вспоминая основные понятия и определения сложного движения,
заключаем, что движение режущих кромок относительно станины является
абсолютным движением, движение кромок относительно движущейся за-
готовки - относительным движением, а движение самой заготовки - пере-
носным движением. Абсолютное и переносное движения в данном случае
известны: абсолютное представляет собой вращательное движение кромок
* Более полно этот вопрос рассматривается в брошюре: В.В. Андронов. Матема-
тическая модель поверхности фугованной древесины. - М.: МЛТИ, 1992. - 24 с.
128
вместе с режущей головкой, переносное - поступательное прямолинейное
движение заготовки со скоростью V. Относительное движение неизвестно
и подлежит определению, причем основной интерес представляет опреде-
ление траекторий относительного движения кромок.
Для решения задачи выделим относительное движение, для чего сле-
дует условно остановить заготовку и рассмотреть движение ножевой голов-
ки при этом условии. С этой целью мысленно сообщим станине вместе с на-
ходящимися на ней предметами поступательное прямолинейное движение
со скоростью, равной и противоположно направленной скорости заготовки.
Теперь заготовка неподвижна, а ножевая головка вращается с угловой ско-
ростью со и одновременно перемещается поступательно вместе с центром А
со скоростью V противоположно направлению подачи (рис. 119). Это плос-
копараллельное движение и есть относительное движение головки, в ходе
которого происходит снятие стружки ножами и формирование обработан-
ной поверхности. Использованный здесь искусственный прием выделения
относительного движения называется методом обращенного движения и
широко применяется в теоретической и прикладной механике.
После выделения относительного движения заготовка и неизменно
связанные с ней оси Оху неподвижны, поэтому изучение относительного
движения осуществляется по обычным правилам кинематики точки (см.
лекцию 7). Прежде всего, получим уравнения движения какой-либо из
кромок. Будем при этом считать, что скорость подачи и угловая скорость
ножевой головки постоянны: К= const,
со = const.
Пусть в начальный момент
t = 0 кромка (точка М на рис. 119)
занимает свое наивысшее поло-
жение, совпадающее с началом О
осей Оху, связанных с заготовкой.
За промежуток времени t головка
повернется на угол ср = со/, а ее
центр А сместится вдоль заго-
товки на расстояние AqA = Vt,
При этом кромка ножа перейдет в
положение М.
В момент времени t коор-
динаты точки М
х = ОА' + А’М'= А^А +М"М,
у --М'М = ~{АА{ - АМп)
будут выражаться следующими функциями времени:
х = Vt + R sin со/,
у = 7? (cos со/-1),
(1)
129
где R - расстояние точки М до оси вращения ножевой головки. Это и есть
уравнения относительного движения ножевой кромки.
Полученные уравнения яв-
ляются параметрическими урав-
нениями циклоиды. Напомним,
что циклоидой называется кри-
вая 1 (рис. 120), которую описы-
вает любая точка М окружности
радиуса г при ее качении без
скольжения по данной прямой
(оси х на рис. 120). К циклоидам
также относятся траектории дру-
гих точек, неизменно связанных
с этой окружностью, называемой
производящей окружностью. Ли-
ния, описываемая какой-либо
точкой D, расположенной внутри
производящей окружности (AD <
Рис. 120
г), называется укороченной циклоидой (кривая 2 на рисунке). Траектория
точки N, лежащей вне производящей окружности (AN > г), называется уд-
линенной циклоидой (кривая 3). Из рисунка видно, что циклоиды являются
периодическими кривыми (с периодом I = 2лг). По этой причине для по-
строения всей бесконечной кривой достаточно изучить ее поведение на ка-
ком-либо отрезке оси х, соответствующем периоду.
Выясним, к какому типу циклоид относится траектория точки М при
фактических соотношениях между величинами R, V, со в процессе фугования.
Нетрудно установить, что мгновенный центр скоростей в относительном
плоскопараллельном движении головки находится строго под центром А (см.
рис. 119) на расстоянии АР = И/co (по этому поводу см. разъяснения на с. 108,
109). Проведем через точку Р окружность с центром в точке А и прямую PL
как показано на рис. 119. В силу постоянства величин И, со расстояние АР
также постоянно, из чего следует, что окружность имеет постоянный радиус
и все время касается прямой PL (в точке Р). По свойству мгновенного центра
скоростей точка Р в каждый момент неподвижна, поэтому окружность катит-
ся по прямой PL без проскальзывания. Следовательно, построенные окруж-
ность и прямая как раз и являются производящей окружностью и направ-
ляющей прямой циклоиды, задаваемой уравнениями (1).
В соответствии со сказанным радиус производящей окружности на-
шей циклоиды равен г = АР = VI®. При фуговании окружная скорость ре-
зания больше скорости подачи (R® > V), откуда следует неравенство R >
VI® = г или, иначе AM > г. Таким образом, траектории относительного
движения точек режущего лезвия являются удлиненными циклоидами.
130
Геометрические характеристики обработанной поверхности при
одном ноже в ножевой головке
Рис. 121
Если в головке имеется
только один нож, то обрабо-
танная поверхность имеет в про-
дольном сечении вид, показанный
на рис. 121. Первый случай (а)
имеет место, если толщина слоя
А, снимаемого за один проход,
превосходит расстояние |у*| до
£ точки самопересечения циклои-
ды. При этом обработанная по-
верхность имеет вид волнообраз-
ной цилиндрической поверхности
с длиной неровностей (волн) X,
равной периоду циклоиды:
(2)
Л , п 2лИ
Л - I = 2тгг =----
со
и высотой неровностей (гребней) h = |у*|, где у* (у* < 0) - ордината точек
самопересечения циклоиды. Во втором случае (б), когда А < |у*|, на обра-
ботанной поверхности цилиндрические участки чередуются с плоскими
участками. При этом период неровностей остается тем же, а высота неров-
ностей равна толщине снимаемого слоя: h = А. Чтобы определить, какой
формы поверхность соответствует принятому режиму обработки (приня-
тым значениям параметров R, о, V, А), требуется определить величину у*.
Величина у* может быть найдена как ордината графика циклоиды
у = /(х), соответствующая середине периода I (рис. 122). Как видно из ри-
сунка, для ее определения достаточно иметь в переменных х, у уравнение
куска циклоиды, соответствующего одному из следующих интервалов из-
менения переменной со/: 0 < (at < п/2 или Зп/2 < (at <2п.
Выберем интервал 0 < со/ < л/2. На нем справедливы следующие за-
висимости, вытекающие из уравнений (1):
у + R . у2 +2Ry z
cosco/ -----, sinco/ = J------—~ (у < 0),
R N R2
y + R 1 у + R
art = arccos -----, t = — arccos --------
R co R
131
Подставляя эти выражения в первое уравнение (1), приходим к ра-
венству
V y + R I у2 + ZRy
х = — arccos-—— + RJ- ------, (3)
со R N R 7
которое и определяет иско-
мую связь между коорди-
натами х, у текущей точки
рассматриваемого куска цик-
лоиды, показанного на
рис. 122 сплошной линией. I
Если теперь положить в \
I nV
этом равенстве х = — = —,
2 со
то получим уравнение для
определения значения у*.
Оно имеет следующий вид:
Рис. 122
nV
СО
V у*+ R I у2 + 2 Ry*
= — arccos --------+ R. - ---------—
со R \ R
Полученное трансцендентное уравнение в общем случае можно ре-
шить графическим способом либо численно. Однако при условии Rg)»V
(окружная скорость ножевых кромок много больше скорости подачи), что
характерно для работы фуговального станка, может'быть получено при-
ближенное аналитическое решение.
Введем для удобства новую переменную
z = — (у* < О, z < 0)
R
и запишем уравнение (3) в следующем виде
л - arccos(l + z) _ Асо
7-(z2 + 2z) V ’
Из него видно, что при Ясо / И —> оо имеем z —> 0. Следовательно, при
больших значениях параметра Лео / V неизвестная z по модулю мала, и по-
этому можно в этом случае приближенно принять
arccos(l + z) « arccos 1 = 0,
7” (z2 + 2z) « 4- 2z
132
и рассматривать следующее простое приближенное уравнение:
я _R®
4^Tz~~v~'
Решая его, находим
я2К2 л2К2
z =----y* = Rz =-----------
2Д2со2 27?со2
Теперь можно подвести итог. Если параметры режима обработки та-
ковы, что удовлетворяется неравенство
то высота неровностей обработки составляет h = |дл.|, если же Д > то
h - Д.
Геометрические характеристики поверхности в случае
многоножевой головки
При двух ножах в режущей головке и достаточной толщине снимае-
мого слоя продольное сечение формируемой поверхности имеет вид, пока-
занный на рис. 123. В этом случае период и высота гребней определяются
пересечением двух циклоид (А и 2?), служащих относительными траекто-
риями двух противоположно расположенных ножевых кромок. Видно, что
для периода имеет место формула
. _ I nV
Л — — —--,
2 со
х
Рис. 123
133
а высота гребней h = -у„ должна определяться из условия
(4)
где символом X*) обозначена та же неявная функция у = fix), которая зада-
ется равенством (3).
Условие (4) и равенство (3) приводят к следующему уравнению для
определения неизвестной z, связанной с у** равенством Rz:
тс / 2 - arccos(l + z) _
/-(Z2 + 2z) {5)
Полагая опять 7?co»K и рассматривая вместо (5) приближенное
уравнение
тс Rd)
находим
_2тл2 2tz2 2тх2
ТС у ТС V , I । ТС V
z------, У** —----------, > h = \yj =----.
8Я2<о2 8Ясо2 1 1 87?со2
Аналогичным образом можно получить характеристики поверхности
(период Хк, высоту hk) при произвольном числе к правильно расположен-
ных ножей в головке. Соответствующие формулы имеют вид:
Естественно, что при к = 1 и к - 2 приходим к ранее полученным
формулам.
Высота неровностей обратно пропорциональна Аг2, поэтому с увели-
чением числа ножей в головке она быстро убывает. Пусть, например, про-
цесс фугования характеризуется следующими условиями: радиус враще-
ния кромок R = 60 мм; число оборотов шпинделя п = 4500 об/мин
(со = тсп! 30= 150л 1/ с); скорость подачи V= 20 м/мин = 333,33 мм/с. То-
гда значения высоты неровностей для различных значений числа ножей в
головке, рассчитанные по приведенной формуле, представятся в виде сле-
дующего ряда (в мм):
= 0,04; Л2 = 0,01; h3 = 0,0025; h4 = 0,00062; ...
Видно, что начиная с к = 3 формируемая поверхность практически не
отличается от плоской поверхности.
134
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
Основные учебники и задачники
1. Тарг С.М. Краткий курс теоретической механики. - М.: Высшая школа,
2002.
2. Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики.
Т.1, Т.2.-М.: Наука, 1985.
3. Мещерский И.В. Сборник задач по теоретической механике. - М.: Нау-
ка, 1981.
4. Сборник заданий для курсовых работ по теоретической механике. Под
ред. А.А. Яблонского. - М.: Высшая школа, 1998.
Дополнительные учебные пособия
5. Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в
примерах и задачах. Т. 1. Статика и кинематика. - Санкт-Петербург: По-
литехника, 1995.
6. Андронов В.В. Механика в лесоинженерном деле. - М.: МГУ Л, 2000.
135
СОДЕРЖАНИЕ
Предисловие........................................... 3
Введение. Предмет и основные понятия теоретической механики. 4
СТАТИКА
Лекция 1. Задачи статики. Аксиомы статики. Связи и реакции
связей.............................................. 9
Аксиома 1 (9). Аксиома 2 (10). Теорема (о соответствии силы скользящему
вектору) (10). Момент силы относительно точки (12). Алгебраический момент
силы (12). Аксиома 3 (правило параллелограмма сил) (13). Аксиома 4 (о
равенстве действия и противодействия) (13). Аксиома 5 (о затвердевании) (14).
Аксиома 6 (освобождаемое™ от связей) (15). Основные типы связей и их
реакции (17). Вопросы для самопроверки (20). Упражнения (21).
Лекция 2. Сходящиеся силы и пары сил............................ 22
Сходящиеся силы. Приведение сходящихся сил к простейшему виду (22).
Вычисление и построение равнодействующей (23). Условия равновесия
сходящихся сил (24). Теорема о трех силах (28). Теорема Вариньона (29). Пара
сил и ее момент (29). Свойства пары сил (33). Приведение системы пар сил к
простейшему виду или сложение пар сил (34). Вопросы для самопроверки (36).
Упражнения (36).
Лекция 3. Преобразование и равновесие пространственной
произвольной системы сил...................................... 38
Момент силы относительно оси (38). Аналитический способ вычисления
момента (39). Геометрический способ вычисления момента (39).
Преобразование пространственной произвольной системы сил (42). Лемма о
параллельном переносе силы (42). Приведение пространственной
произвольной системы сил к данному центру. Главный вектор и главный
момент. Основная теорема статики (43). Вычисление и построение главного
вектора и главного момента (45). Перемена центра приведения (47). Вопросы
для самопроверки (48).
Лекция 4. Преобразование и равновесие пространственной
произвольной системы сил (продолжение). Частные случаи
системы сил..................................................... 49
Случаи приведения к простейшему виду (49). Приведение к паре (49).
Приведение к равнодействующей (49). Приведение к динаме (51). Условия
(уравнения) равновесия пространственной произвольной системы сил (51).
Частные случаи системы сил (54). Плоская система сил (54). Система
параллельных сил (56). Равновесие системы тел (58). Вопросы для
самопроверки (60). Упражнения (60).
Лекция 5. Центр параллельных сил и центр тяжести................ 61
Центр параллельных сил (61). Распределенные силы (63). Центр тяжести (64).
Интегральные формулы для координат центра тяжести (65). Метод разбиения
(67). Вопросы для самопроверки (69).
136
Лекция 6. Трение твердых тел................................ 70
Трение покоя и трение скольжения (70). Трение качения (72). Решение задач
статики при учете сил трения (74). Заклинивание (76). Вопросы для
самопроверки (77). Упражнения (77).
КИНЕМАТИКА
Лекция 7. Кинематика точки.................................. 81
Способы задания движения точки (81). Определение траектории, скорости и
ускорения точки при векторном способе задания движения (84). Определение
траектории, скорости и ускорения точки при координатном способе задания
движения (85). Определение скорости и ускорения точки при естественном
способе задания движения (89). Естественные координатные оси и их орты
(89). Определение скорости (91). Определение ускорения (92). Вопросы для
самопроверки (95). Упражнения (95).
Лекция 8. Простейшие движения твердого тела................. 96
Поступательное движение (97). Вращательное движение (99). Уравнение
вращательного движения. Угловая скорость и угловое ускорение тела (99).
Траектории, скорости и ускорения точек тела (100). Векторы угловой скорости
и углового ускорения тела (101). Векторные формулы для линейной скорости,
касательного и нормального ускорений точки тела (102). Вопросы для
самопроверки (103). Упражнения (103).
Лекция 9. Плоскопараллельное движение твердого тела........ 104
Уравнения движения (104). Угловая скорость и угловое ускорение тела при
плоскопараллельном движении (106). Определение скоростей точек тела.
Метод полюса (106). Мгновенный центр скоростей (108). Определение
скоростей точек плоской фигуры через мгновенный центр скоростей (109).
Различные случаи определения положения мгновенного центра скоростей
(НО). Определение ускорений точек тела (111). Вопросы для самопроверки
(116). Упражнения (116).
Лекция 10. Сложное движение точки.......................... 117
Основные понятия и определения (117). Теорема сложения скоростей (118).
Теорема сложения ускорений (120). Причины появления ускорения Кориолиса
(121). Вычисление и построение ускорения Кориолиса (122). Вопросы для
самопроверки (126). Упражнения (126).
ДОБАВЛЕНИЕ
Кинематика процесса фугования древесины.................... 127
Схема и расчетная модель процесса фугования (127). Геометрические
характеристики обработанной поверхности при одном ноже в ножевой головке
(130). Геометрические характеристики поверхности в случае многоножевой
головки (132).
Рекомендуемая литература................................... 134
Учебное издание
Вячеслав Васильевич Андронов
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
20 ЛЕКЦИЙ
Часть 1
СТАТИКА. КИНЕМАТИКА
Под редакцией автора
Оригинал-макет выполнен отделом компьютерного набора и верст-
ки издательства МГУ Л а
По тематическому плану внутривузовских изданий учебной лите-
ратуры на 2003 г., доп.
ЛР № 020718 от 02.02.1998 г.
ПД № 00326 от 14.02.2000 г.
Подписано к печати 20.01.03. Формат 60x88/16
Бумага 80 г/м2 "Снегурочка" Ризография
Объем 8,7£ п. л.____________Тираж 500 экз. Заказ № 3%Ч
Издательство Московского государственного университета леса.
141005. Мытищи-5, Московская обл., 1-я Институтская, 1, МГУЛ.
Телефоны: (095) 588-57-62, 588-53-48, 588-54-15. Факс: 588-51-09.
E-mail: izdat@mgul.ac.ru