Курс математического анализа. Том 1 - Бохан К.А., Егорова И.А., Лащенов К.В.

Автор: Бохан К.А. Егорова И.А. Лащенов К.В.
Теги: анализ математика математический анализ
Год: 1972
Похожие
Курс математического анализа. Том 2
Курс математического анализа. Том I.
Курс математического анализа. Том I
Курс математического анализа. Часть II. Книга 1.
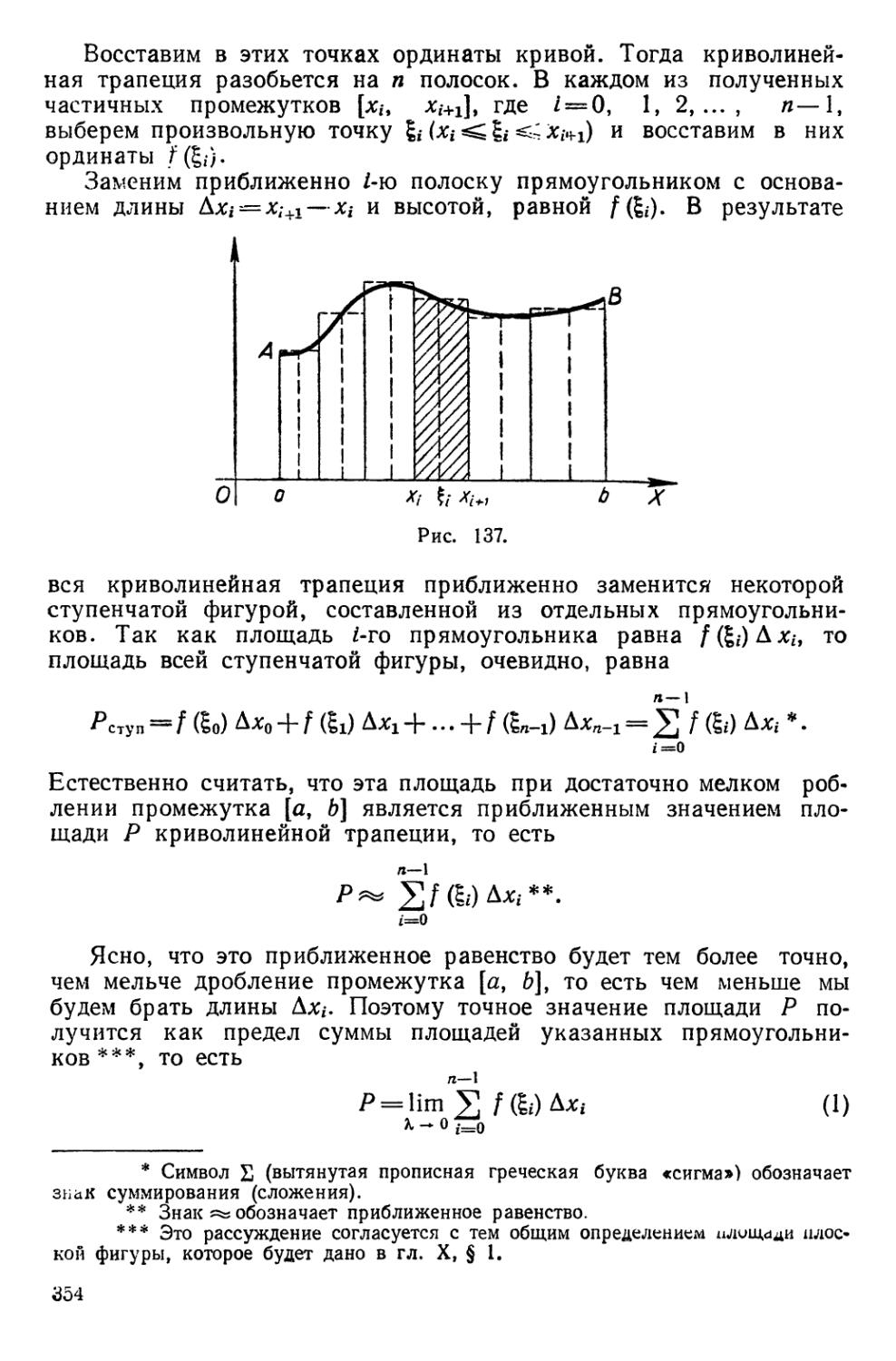
Текст
                    К. А. БОХАН,
И. А. ЕГОРОВА,
К. В. ЛАЩЕНОВ
КУРС
МАТЕМАТИЧЕСКОГО
АНАЛИЗА
ТОМ I
УЧЕБНОЕ ПОСОБИЕ
ДЛЯ СТУДЕНТОВ-ЗАОЧНИКОВ
ФИЗИКО-МАТЕМАТИЧЕСКИХ
ФАКУЛЬТЕТОВ
ПЕДАГОГИЧЕСКИХ ИНСТИТУТОВ
Под редакцией
проф. Б. 3. ВУЛИХА
Издание 2-е
ИЗДАТЕЛЬСТВО «ПРОСВЕЩЕНИЕ»
МОСКВА 1972

517.2
Б86
Бохан К. А. и др.
86 Курс математического анализа. Т. I. Учеб.
пособие для студентов-заочников физ.-мат. фак-тов пед.
ин-тов. Под ред. проф. Б. 3. Вулиха. Изд. 2-е. М.,
«Просвещение», 1972.
511 с.
Перед загл. авт.: К. А. Бохан, И. А. Егорова, К. В.
Лащено в.
4-6-4 517-2
БЗ №8—1972—№ 14

ПРЕДИСЛОВИЕ РЕДАКТОРА
Предлагаемый курс математического анализа рассчитан на
студентов-заочников. Хотя существует большое количество учебников по математическому анализу,
которыми пользуются студенты стационарных вузов, однако эти учебники
рассчитаны, как правило, на то, что студент изучает их параллельно со слушанием
лекций и имеет постоянный личный контакт с преподавателем. Заочник работает
в других, более трудных условиях, и поэтому он нуждается в таких
дополнительных пособиях, которые могли бы хоть частично облегчить его работу. К такому
типу пособий относится и этот курс, составленный сотрудниками кафедры
математического анализа Ленинградского педагогического института имени
А. И. Герцена.
В курсе особенно подробно рассматриваются основные понятия
математического анализа, приводится большое количество столь же подробно решенных
примеров, даются не только упражнения обычного типа для самостоятельной
работы студента, но также и вопросы для самопроверки, которые помогут
студенту-заочнику выяснить, насколько хорошо он разобрался в изучаемом
курсе. Если студент пожелает иметь дополнительный материал для упражнений
сверх того, который содержится в этой книге, ему можно рекомендовать как
различные общие задачники по математическому анализу, например Н. А.
Давыдова, П. П. Коровкина и В. Н. Никольского, или Г. Н. Бермана, или
Б. П. Демидовича, так и специальные задачники-практикумы, изданные
Московским заочным педагогическим институтом.
В процессе изучения курса студент должен глубоко вникать в сущность всех
новых понятий и формулировок всех теорем. При разборе каждой теоремы очень
полезно выяснить, где в доказательстве используется то или иное ее условие.
Изучение того или иного параграфа можно считать законченным лишь тогда,
когда студент может безошибочно воспроизвести все содержащиеся в этом
параграфе определения, теоремы с их доказательствами и ответить на вопросы,
поставленные для самопроверки. Только после этого рекомендуется переходить
к следующему параграфу.
При изложении материала в этом курсе иногда, по более сложным и тонким
вопросам, делаются ссылки на учебник Г. М. Фихтенгольца «Основы
математического анализа». При ссылках [1] означает том 1 этого учебника, а [2] — том 2.
Кроме книги Г. М. Фихтенгольца, студенты-заочники могут также использовать
учебники Н. А. Фролова «Дифференциальное и интегральное исчисление» и «Курс
математического анализа», часть 2, и И. Е. Жака «Дифференциальное исчисление».
При написалии книги авторы пользовались сборниками задач Г. Н. Бермана,
Б. П. Демидовича и других авторов.
Весь курс состоит из двух томов, содержащих десять разделов. Доцент
К. А. Бохан написал I и II разделы этого курса, главу девятнадцатую раздела VI,
а также § 4 главы шестнадцатой раздела V. Доцент И. А. Егорова написала
разделы V, VII, VIII, IX и X. Доцент К. В. Лащенов написал разделы
III и IV, а также семнадцатую и восемнадцатую главы раздела VI. В
согласовании глав и разделов между собой принимали участие все авторы.
Проф. Б. 3. By лих

ОТ АВТОРОВ
На кафедре математического анализа Ленинградского государственного
педагогического института имени А. И. Герцена авторы данного курса в течение
многих лет систематически работали над созданием специальных учебных
пособий для студентов-заочников педагогических институтов. Эти пособия
издавались Ленинградским педагогическим институтом имени Герцена, а также
большими тиражами Московским государственным заочным педагогическим
институтом. Длительное время пособия использовались в работе многих
пединститутов. При подготовке к печати данного курса авторы с благодарностью учли
полезные замечания и советы, высказанные рецензентами, а также лицами,
работавшими с этими пособиями. Поэтому можно сказать, что настоящее учебное
пособив является итогом многолетней работы авторов над созданием
специальных учебных пособий для студентов-заочников пединститутов.
В течение всех этих лет доктор физико-математических наук, профессор
Б. 3. Вулих неизменно оказывал нам большую помощь своими ценными
советами и замечаниями и проделал огромный труд по редактированию настоящего*
пособия. Мы выражаем ему особую благодарность.
Выражаем также глубокую благодарность доктору физико-математических
наук, профессору | И. П. Натансону 1, доктору физико-математических наук,
профессору С. Г. Михлину и доктору физико-математических наук, профессору
Н. Я. Виленкину, которые принимали участие в чтении рукописей и сделали
много ценных указаний.
Авторы просят присылать отзывы и отдельные, замечания по данному курсу
по адресу: Ленинград, Д-88, Мойка, 48, ЛГПИ, математический факультет,
кафедра магматического анализа.
авторы

Раздел 1
ВВЕДЕНИЕ В АНАЛИЗ
ГЛАВА I
ВЕЩЕСТВЕННЫЕ ЧИСЛА
Понятие вещественного числа принадлежит к основным
понятиям математического анализа. Средняя школа не дает учащимся
достаточного представления о вещественных числах и их
свойствах. Поэтому естественно было бы начинать изучение
математического анализа с расширения и углубления школьных знаний
о числе. Однако теория вещественных чисел сама по себе
является далеко не простой. Хотя существуют различные подходы
к построению теории вещественных чисел (метод сечений,
определение вещественных чисел как бесконечных десятичных дробей
и др.), но каждый из них на первых порах работы по
математическому анализу, притом заочно, может вызвать значительные
затруднения. Здесь для облегчения первоначального знакомства
с вещественными числами мы ограничимся краткими сведениями
о них, не претендуя на полноту и строгость. Считаем, что этих
кратких сведений достаточно для успешной работы над
последующими главами. Если же читатель пожелает изучить теорию
вещественных чисел более глубоко и полно, то это можно сделать,
например, по рекомендованной нами книге Г. М. Фихтен-
гольца [1].
Параграфы, посвященные свойствам абсолютных величин,
а также понятиям о границах множеств, о сегментах, интервалах
и окрестностях, следует рассматривать как вспомогательный
материал для последующих глав.
§ 1. ПОНЯТИЕ МНОЖЕСТВА
Понятие множества также принадлежит к числу основных
понятий математического анализа. Оно не поддается определению
через более простые понятия и может быть лишь описано или
пояснено на примерах.
Под множеством будем понимать собрание, совокупность,
коллекцию некоторых предметов, объединенных по какому-то
определенному признаку. Так, можно говорить о множестве всех
натуральных (целых положительных) чисел, о множестве только чет-
5

ных или только нечетных чисел. Все рыбы, находящиеся в вод-
ных бассейнах нашей планеты, также составляют определенное
множество. Можно, конечно, рассматривать множества рыб
определенного вида, возраста, размера и т. д. Примерами множеств
могут служить также множество корней данного уравнения,
множество всех многочленов, множество чисел, кратных 3, множество
целых чисел, больших числа 10 и меньших числа 100; множество
стульев в данной аудитории, множество букв данного алфавита
и т. п.
Предметы, составляющие данное множество, называют его
элементами.
Если имеем какое-то определенное множество, то относительно
любого предмета верно одно и только одно из двух утверждений:
либо этот предмет входит в данное множество в качестве его
элемента, либо не входит.
Символическая запись
М = {х}
означает, что множество М состоит из элементов х. В этом случае
под х понимают любой элемент множества М. В зависимости,
от того, что представляют собой элементы х, определяется и
природа самого множества М: то ли это будет множество рыб, то ли
стульев, чисел и т. д.
Если элементы множества можно обозначить отдельными
символами, то их выписывают подряд, заключая также в скобки,
например:
А = {а, Ь, с, d, еу /} или УУ = {1, 2, 3, ..., п, ...}.
В последнем множестве выписаны не все элементы. Однако
достаточно ясно показано, что N есть множество всех натуральных
чисел.
В дальнейшем будем пользоваться следующими обозначениями:
Запись х^М означает, что х является элементом множества М,
или х принадлежит множеству М (е —знак принадлежности).
Запись х EiW означает, что х не является элементом множества М,
или л: не принадлежит множеству М.
Так, например, если М есть множество четных чисел, то число
2^М, а число З^М.
Будем называть множество А подмножеством множества В или
его частью и записывать АаВ (или В zd Л), если каждый
элемент множества А является также элементом и множества В
(d — знак включения). Так, если А — множество четных
положительных чисел, а В —множество натуральных чисел, то Лей
(или В zd А). Заметим, что в определении подмножества не
исключается случай, когда А совпадает с В.
Множества А и В называются равными, А = В9 если
одновременно
AczB и ВсЛ,
б

то есть если множества А и В состоят из одних и тех же
элементов. Так, множество {2, 3} и множество корней уравнения
х2 — 5л:+ 6 = 0 равны.
Множество {х} называется конечным, если имеет смысл
говорить о числе его элементов, то есть если количество его элементов
можно выразить каким-то определенным числом. В противном
случае оно называется бесконечным множеством. Примерами
конечных множеств могут служить множество жителей какого-нибудь
города или множество всех людей на земном шаре. Совокупность
всех натуральных чисел есть бесконечное множество.
Если во множестве нет ни одного элемента, то оно называется
пустым множеством. Понятие пустого множества в ряде случаев
оказывается весьма удобным. Указывая способ образования того
или иного множества, мы заранее не всегда уверены, будет
ли это множество содержать хотя бы один элемент. Например,
решая задачу об отыскании множества целых корней уравнения
х2 + х+1=0, мы придем к ответу, что это множество пустое.
Пусть даны два множества А и В.
Если каждому элементу множества А поставлен в соответствие
один и только один Шемент множества В так, что каждый
элемент из В при этом окажется соответствующим одному и только
одному элементу из А, то говорят, что между множествами А и В
установлено взаимно однозначное соответствие.
Если, например, между студентами в аудитории распределены
стулья таким образом, что каждый студент имеет стул и больше
свободных стульев нет, то можно сказать, что между множеством
студентов и множеством стульев, находящихся в аудитории,
установлено взаимно однозначное соответствие.
При изучении математического анализа нам придется в
основном иметь дело с множествами чисел и множествами точек.
Введенные здесь определения и обозначения в дальнейшем окажутся
весьма полезными.
Вопросы для самопроверки и упражнения
1. Совпадают ли множества {а, 6, с, dy e} и {а, с, е, d, 6}?
Отв. Совпадают, так как они состоят из одинаковых элементов. Порядок
расположения элементов во множестве не имеет значения.
2. Во время игры назывались номера: 5, 2, 3, 4, 5, 3, 5 и 7. Укажите
то множество номеров, которое участвовало в игре.
Отв. {2, 3, 4, 5, 7}.
3. Укажите, какие из нижеперечисленных множеств будут конечными и какие —
бесконечными*
а) Множество студентов данного института.
б) Множество целых отрицательных чисел.
в) Множество натуральных чисел, кратных числу 7.
г) Множество маковых зерен данного урожая.
д) Множество корней данного многочлена.
е) Множество всех прямых, которые проходят через заданную точку.
4. Образуйте все возможные подмножества данного множества A = {at bf с, d}.
1

5. Дано два числовых множества: А = {2, 3, 5, 6, 7} и В —{1, 2, 3, 4, 5, 6, 7}.
Является ли множество А подмножеством множества В?
6. Тот же вопрос по отношению к множествам А — {2, 3, 5, 6, 7) и б =
= {1, 2, 3, 5, 6}.
7. Дано два множества: А = {8, 2, 1, 3, 6, 7} и ? = {2, 3, 7, 1, 8}. Которое
из них является подмножеством другого?
8. Почему про пустое множество можно сказать, что оно включается в любое
наперед данное множество?
9. Какими должны быть два конечных множества, чтобы между ними можно
было установить взаимно однозначное соответствие?
10. Даны два множества: Л —множество, состоящее из десяти стульев, и й-
множество, состоящее из десяти студентов.
Можно ли сказать, что А = 5? Можно ли установить между этими
множествами взаимно однозначное соответствие?
§ 2. МНОЖЕСТВО РАЦИОНАЛЬНЫХ ЧИСЕЛ
Будем исходить из того, что читатель знаком с натуральными
числами, любыми целыми числами (положительными,
отрицательными и числом нуль), а также с дробными числами, то есть
числами вида ±—, где т и я — натуральные. Все эти числа
объединяются под общим названием—рациональные числа.
Заметим, что целые числа также могут быть записаны в виде
дробей вида ±—, если положить п=1. При т — 0 и любом
натуральном п имеем: — = 0. Поэтому рациональные числа можно
определить как всевозможные числа, представимые в виде дроби — „
где т может быть любым целым числом (не исключая нуля), an —
по-прежнему натуральное.
Если у т и п есть общие делители, то дробь - - можно сокра-
тить. Например, -7-=~2"'
Таким образом, всякое рациональное число, отличное
от нуля, представило в виде несократимой дроби вида ± ~,
Будем считать также известными читателю правила
арифметических действий над рациональными числами. Множество всех
рациональных чисел условимся обозначать буквой R,
Каждое рациональное число можно изобразить определенной
точкой на прямой.
В самом деле, возьмем горизонтальную прямую и отметим на ней
произвольную точку. Она будет изображать число нуль и потому
обычно называется нулевой точкой. Возьмем затем еще какую-нибудь
точку на этой прямой справа от нулевой точки. Она будет
изображением единицы. Отрезок прямой с концами в точках 0 и 1 будет,
таким образом, единицей длины, или масштабом.
Прямую, на которой выбрана нулевая точка, определено
направление и указан масштаб, называют числовой прямой или числовой.
ь

3 1 1
-3 -2 "1 -1 О 1 f 2 1 У
1 1 I I II \i I I I I I to»»
Рис. 1.
осью (рис. 1). Чтобы изобразить точкой любое целое число ±/?,
нужно единицу длины отложить р раз от нулевой точки вправо
или влево в зависимости от знака этого числа. Числам + — и — —
п п
будут соответствовать точки на прямой, которые получатся, если
единицу длины разделить на п равных частей и одну часть
отложить т раз соответственно вправо или влево от нулевой точки
{рис. 1).
Точки прямой, соответствующие рациональным числам,
называются рациональными точками.
Если два рациональных числа а и Ь удовлетворяют неравенству
а < &, то точка Ь расположена на прямой правее точки а. Если
рациональное число с удовлетворяет неравенству а<с<^Ь, то точка
с находится между точками а и Ь. Соответственно говорят, что
число с находится между числами а и Ь.
Отметим основные свойства множества рациональных чисел R.
1. Для любых двух рациональных чисел а и b
справедливо одно и только одно из трех соотношений: либо а<Ь,
либо а>Ь, либо а = Ь. При этом, если a<cb и Ь<с, где
€ — также рациональное число, то a<ic.
Это свойство называется упорядоченностью множества R.
2. Если числа а и b—рациональные, то их сумма,
разность, произведение и частное (последнее при делителе,
отличном от нуля) являются также рациональными
числами.
3. Между любыми двумя различными рациональными
числами а и b существует промежуточное рациональное
число.
Так, например, число с= ^ (по свойству 2) будет рациональ-
ным, и если а<0, то а<^с<^Ьу так как а = —Т"^—к-"^—§—==
Между числами а и с, с и Ь таким же способом можно указать еще
по рациональному числу и т. д. Таким образом, между любыми
рациональными числами а и b содержится не только одно, а
бесконечное множество различных рациональных чисел. Это свойство
называется плотностью множества R.
Если последнее свойство множества рациональных чисел
перевести на геометрический язык, то оно означает, что между любыми
двумя различными рациональными точками на числовой прямой
содержится по крайней мере одна рациональная точка (а тогда
и бесконечное множество рациональных точек).
9

Можно доказать и более общее утверждение. Именно, между
любыми двумя различными точками на числовой прямой содержится
по крайней мере одна рациональная точка (а тогда и бесконечное
множество рациональных точек). Иными словами, любой участок
числовой прямой, каким бы малым он ни был, содержит
бесконечное множество рациональных точек.
Указанное свойство множества рациональных точек называют era
плотностью и говорят, что множество рациональных точек
расположено всюду плотно на числовой прямой.
При этом естественно возникает вопрос, а не будут ли
рациональные точки заполнять собой сплошь всю числовую прямую?
Другими словами: нельзя ли сказать, что каждой точке а на прямой
соответствует определенное рациональное число, указывающее на
длину отрезка от 0 до а?
Отрицательный ответ на этот вопрос
дается следующим примером.
Построим равнобедренный
прямоугольный треугольник с
катетом, равным единице длины (рис.2).
Откладывая гипотенузу на прямой,
получим точку М. Покажем, что
среди всех рациональных чисел не
найдется такого числа, которому
соответствовала бы эта точка,
Рис* 2- то есть что точка М не
является рациональной. Прежде всего
заметим, что (ОЛ)2=12 + 12 = 2. Следовательно, достаточно доказать,
что нет такого рационального числа, квадрат которого равнялся бы 2.
Допустим обратное: пусть такое число существует. Ясно, что оно
не может быть нулем. Остается предположить, что оно представима
в виде несократимой дроби —, где т и /: —натуральные числа,.
то есть ( —I =2. Тогда
т2 = 2п2. (1)
Отсюда следует, что т2 есть четное число. Но тогда четным будет
и число /я, так как в противном случае т2 было бы также
нечетным, поскольку квадрат любого нечетного числа есть число нечетное:
(2k + \)2 = 4k2 + 4k + 1 =2 (2k2 + 2k) + 1.
Пусть m = 2k, где k — каксе-то целое число. Тогда равенство (1)
примет вид: 4k2 = 2n2, или 2k2 = п2. Из последнего вытекает, что /г2,
а следовательно, и п есть также четные числа. Но тогда —
оказывается сократимой дробью, что противоречит нашему
предположению. Этим самым установлено, что на прямой, кроме рациональных
точек, есть еще и другие точки Одновременно доказано, что
уравнение х2 — 2 = 0 не может быть разрешено в рациональных числах.
J0

Таким образом, множества рациональных чисел R оказывается
недостаточно, чтобы решать даже такие простые задачи, как
измерение длин, решение уравнений, установление взаимно
однозначного соответствия между числами и точками прямой и т. д. Можно
было бы привести еще много примеров и задач, решение которых
невозможно, если иметь в обиходе только рациональные числа. Все
это привело к необходимости расширения множества R, к
пополнению его новыми, так называемыми иррациональными числами.
Вопросы для самопроверки и упражнения
1. Обладает ли свойством плотности множество всех целых чисел?
2. Может ли быть плотным конечное множество чисел или точек?
3. Доказать, что сумма двух рациональных чисел есть число рациональное.
4. Доказать, что число \ГЪ не является рациональным.
5. Доказать, что уравнение л:3 —2 = 0 не имеет рациональных корней.
§ 3. ВЕЩЕСТВЕННЫЕ ЧИСЛА
Решая задачу о расширении множества рациональных чисел,
будем исходить из необходимости создать такое множество чисел,
которое можно привести во взаимно однозначное соответствие с
множеством точек на прямой.
При рассмотрении прямой как множества точек существенную
роль играет следующая аксиома.
Аксиома (непрерывности прямой). Если
множество всех точек прямой разбито на два класса так, что
каждый из классов не пуст и все точки первого класса
расположены левее всех точек второго, то существует
пограничная точка, которая является либо самой правой
в первом классе, либо самой левой во втором классе.
Из этой аксиомы следует, что прямая является сплошной
линией, без «дырок». В каком бы месте мы ни разрезали прямую
на две части, разрез пройдет через одну из точек прямой. Это
соответствует и нашему наглядному представлению о прямой.
Займемся выяснением вопроса, нельзя ли положение
произвольной точки на числовой прямой определить с помощью одних лишь
рациональных точек. Если это можно каким-то образом сделать,
то, применяя аналогичную конструкцию к рациональным числам,
мы придем и к определению вещественного числа.
Пусть а — произвольная точка на числовой прямой. Тогда
множество всех рациональных точек можно разбить на два класса А
•и В следующим образом. К классу А отнесем все рациональные
точки, лежащие левее точки а, и будем называть его нижним
классом. К классу В отнесем все рациональные точки, лежащие правее
точки а, и будем называть его верхним классом. При этом оба
класса будут не пусты. В частности если окажется, что а является
также рациональной точкой, то ее можно включить в любой из клас-
11

сов. Для определенности в этих случаях будем точку а включать
в нижний класс А.
Такое разбиение множества рациональных точек называется
сечением и обозначается А/В.
Два сечения А /В и A' IB' будем считать тождественными, если
их соответствующие классы совпадают, то есть если А = А' и В=В'.
Легко показать, что различные точки а и р на прямой задают
различные сечения. Действительно, на участке прямой между
точками аир найдется по крайней мере одна рациональная точка г.
В соответствии с определением сечения она будет принадлежать
нижнему классу одного сечения и верхнему классу другого.
Следовательно, эти сечения не тождественны.
Таким образом, любая точка а на прямой определяет некоторое
сечение во множестве рациональных точек, причем различным
точкам соответствуют различные сечения. Точку а называют
пограничной точкой между классами сечения, определяемого ею.
Можно подойти к определению сечения во множестве
рациональных точек и с другой стороны, не оперируя точкой а.
Будем называть сечением такое разбиение множества
рациональных точек на два класса А и В, при котором:
\) А и В — непустые множества,
2) каждая рациональная точка принадлежит одному из классов
А или В,
3) каждая точка из А находится левее любой точки из В.
Из аксиомы непрерывности можно вывести, что при таком
определении сечения во множестве рациональных точек всякому сечению
также соответствует некоторая пограничная точка, которая
производит это сечение. Однако эта пограничная точка не обязательно
будет рациональной.
Итак, можно сказать, что между сечениями во множестве
рациональных точек и всеми точками прямой существует взаимно
однозначное соответствие.
Аналогичными построениями во множестве рациональных чисел R
можно определить вещественные числа как границы всевозможных
сечений во множестве R. Это делается следующим образом.
Разобьем множество всех рациональных чисел R на два класса
А и В так, что;
1) Л и В не пусты,
2) каждое рациональное число принадлежит одному из классов
А или Я,
3) каждое число из класса А меньше любого числа из класса В.
Такое разбиение будем называть сечением во множестве R
рациональных чисел и обозначать А!В.
В качестве примеров сечений в R рассмотрим следующие:
1. К классу А отнесем все рациональные числа г<5,ак
классу В — все остальные рациональные числа, то есть г>5.
2. К классу А отнесем все рациональные числа г<5, а к
классу В — все остальные рациональные числа, то есть rS^5.
12

3. К классу А отнесем все отрицательные рациональные числа,
нуль и все такие положительные рациональные числа, квадрат
которых меньше 2, а к классу В — все остальные рациональные числа.
В первых двух примерах рациональное число 5 является
«пограничным» числом между классами А и В. Оно будет либо
наибольшим в нижнем классе А (пример 1), либо наименьшим в верхнем
классе В (пример 2). Сечения такого вида называются рациональными.
Они всегда имеют в качестве «пограничных» рациональные числа.
Что же касается третьего примера сечения, то «пограничного»
числа среди рациональных чисел не найдется, так как можно
доказать, что в нижнем классе нет наибольшего числа, а в верхнем
классе нет наименьшего. Докажем, например, что в А нет
наибольшего числа, то есть, что, какое бы число а из этого класса мы
ни взяли, в нем найдется число а0>а. Пусть а—любое
положительное число из А (в случае, когда а<0, ясно, что оно не может
быть наибольшим, так как нуль и все положительные числа из А
будут больше а). Числа # + — будут больше а при любых п
(n=U 2, 3, ...). Подберем такое /г, чтобы было
(¦
Раскрывая скобки, получим:
. + !)¦<«.
а это неравенство равносильно неравенству
!(2fl+ij<2_a2.
Отсюда находим:
2а+±
и для выполнения последнего неравенства достаточно взять
^ 2а+1
Тогда
(*+ir<2
и, следовательно, число а0=а + — будет принадлежать классу А.
Поскольку пода мы понимали любое положительное число в классе А,
то этим и завершается доказательство. Совершенно аналогично
доказывается, что в классе В нет наименьшего числа.
Сечение во множестве рациональных чисел, обладающее тем
свойством, что в нижнем классе нет наибольшего числа, а в верхнем
классе нет наименьшего, называется иррациональным сечением.
13

Соотнесем каждому иррациональному сечению некоторый символ от
и будем называть его иррациональным числом.
Таким образом, иррациональное число определяется сечением
и возмещает недостающее «пограничное» число, как бы становясь
между всеми числами класса А и всеми числами класса В. В
примере 3 таким иррациональным числом является ]/~2.
Иррациональных чисел, очевидно, столько, сколько можно осуществить
иррациональных сечений во множестве R> то есть бесконечное множество.
В силу взаимно однозначного соответствия между множеством
всех рациональных чисел и множеством всех рациональных точек
прямой каждому сечению во множестве рациональных чисел будет
соответствовать определенное сечение во множестве рациональных
точек. Следовательно, каждому иррациональному числу будет
соответствовать определенная точка прямой.
Изложенный здесь способ введения иррациональных чисел с
помощью сечений в множестве рациональных чисел принадлежит
немецкому математику Р. Дедекинду (1831 — 1916).
Все рациональные и иррациональные числа в совокупности
образуют множество так называемых вещественных или действительных
чисел, которое условимся обозначать через W.
Из сказанного выше следует, что каждое вещественное число
изображается некоторой точкой на прямой. Можно доказать, что верно
и обратное, то есть что каждая точка на прямой является
геометрическим образом некоторого вещественного числа. При этом разные
вещественные числа имеют разные образы. Тем самым между
множеством W и множеством всех точек на прямой устанавливается
взаимно однозначное соответствие.
Точки числовой оси часто отождествляются с соответствующими
числами. Вместо того чтобы сказать: «Точка, соответствующая
числу а» — говорят коротко: «Точка а».
Отмеченным выше соответствием определяется и упорядочение
множества W. Вещественное число а считается меньшим, чем
вещественное число р, если точка прямой, соответствующая числу а,
находится левее точки, соответствующей числу р. Числа аир равны
между собой, если им соответствует одна и та же точка прямой.
Безотносительно к точкам прямой понятия «больше», «меньше»
и «равно» определяются для вещественных чисел следующим
образом.
Случай 1. Оба числа а и (3 — рациональные. Для них эти
понятия мы считаем уже известными из курса средней школы. Мы
пользовались ими при определении понятия сечения.
Случай 2. Одно из двух чисел а или Р, например а,
рациональное, а второе иррациональное. В этом случае число р, будучи
иррациональным, определяется некоторым иррациональным
сечением В/В' во множестве рациональных чисел. Число а, как
рациональное, должно по определению сечения принадлежать одному из
классов, В или Вг. Будем считать, что а больше, чем р, и
обозначать а> р, если а принадлежит верхнему классу В' сечения В/В'.
14

Рис. 3. Рис. 4.
Если же а принадлежит нижнему классу В, то оно считается
числом, меньшим, чем р, а<р (рис. 3).
Случай 3. Оба вещественных числа а и р —иррациональны.
Пусть а определяется сечением A /A', a P — сечением В/В'. Будем
считать, что а>р, если класс А больше класса В в том смысле,
что А целиком содержит в себе класс В, не совпадая с ним (рис. 4).
Если классы Л и В (а значит, А и В') совпадают, то числа аир
считаются равными, а = р (рис. 5).
Из этих определений можно вывести, что любые два
вещественных числа аир сравнимы между собой, то есть всегда имеет место
одно и только одно из соотношений: а>р, а<р, а = р. Это
свойство называется упорядоченностью
множества W. ¦ ^^а=^^^~~~
Можно показать, что из нера- д ^^\а/^^ 4f
венств а<р и р <у, где а, р и у — -?- »-
вещественные числа, следует нера- б ^^Ур^^. В X
венство a<Y- -——~-~^"^ —¦ .
Также нетрудно установить, что
среди вещественных чисел нет ни Рис* 5*
наибольшего, ни наименьшего.
Множество рациональных чисел всюду плотно в
множестве W всех вещественных чисел, то есть если а и р—
любые вещественные числа и а < р, то существует
рациональное число г, удовлетворяющее неравенству a<r<p.
Отсюда уже следует, что между а и Р содержится бесконечное
множество рациональных чисел.
Это свойство сразу вытекает из аналогичного свойства множества
рациональных точек, но оно может быть выведено и непосредственно
из определения иррациональных чисел с помощью сечений. Пусть,
например, числа а и р~-иррациональные и а<р. Предположим,
что число а определяется сечением А /А', а число р — сечением В/Вг
в множестве рациональных чисел R. Так как а<р, то класс А
входит в класс В, не совпадая с ним. Это значит, что существует
такое рациональнее число г, которое содержится в В и не
содержится в Л. Из последнего следует, что тогда г должно содержаться
в А. Так как re В, то г<р. Так как г(=А, то r>a.
Следовательно, a<r<p. Этим мы доказали, что между любыми двумя
различными иррациональными числами существует рациональное число.
Если же одно из чисел, например а, иррациональное, а другое, Р —
15

рациональное, то из неравенства а<р следует, что число р
принадлежит классу А' сечения А/А\ определяющего иррациональное
число а. Поскольку в Л' нет наименьшего числа, то в этом классе
найдется рациональное число г<р. Так как г^А\ то г>а.
Следовательно, снова получаем а<с/*<р. Случай, когда оба числа
а и р — рациональные, рассмотрен при изучении свойств множества
рациональных чисел R (§2).
Аналогично сечению во множестве рациональных чисе^, во
множестве вещественных чисел W можно так же ввести понятие сечения
как такое разбиение множества W на два класса X и К, при
котором выполняются следующие условия:
1) множества X и Y не пусты,
2) каждое вещественное число попадает в один ю классов,
X или У,
3) каждое число из класса X меньше любого чис^а из класса У.
При рассмотрении различных случаев сечений в R мы
встретились с таким сечением (иррациональное сечение), когда среди
рациональных чисел не оказалось числа, которое можно было бы считать
«пограничным» в этом сечении. Это было основанием для введения
новых, иррациональных чисел с целью пополнения множества /?.
После определения сечения в W естественно выяснить вопрос, нет ли
подобного случая и во множестве вещественных чисел. Иначе говоря,
не появляется ли необходимость пополнения тем же методом
множества W за счет введения еще каких-нибудь новых чисел.
Отрицательный ответ на этот вопрос дает следующая (основная в теории
вещественных чисел) теорема.
Теорема (Дедекинда). Для любого сечения X/Y во
множеств всех вещественных чисел W существует
вещественное число, которое производит это сечение, то есть
число, которое будет либо наибольшим в X, либо
наименьшим в Y.
Иначе говоря, во множестве W не существует такого сечения,
чтобы одновременно в нижнем классе не было наибольшего числа,
а в верхнем —наименьшего.
Это свойство множества W называется свойством полноты
или непрерывности. Из сказанного выше следует, что
множество R рациональных чисел этим свойством не обладает.
Теорему Дедекинда мы приводим без доказательства.
Метод сечений позволяет так же определить арифметические
действия над любыми вещественными числами. Эти действия являются
обобщением известных действий сложения, вычитания, умножения
и деления над рациональными числами и подчиняются основным
законам арифметики. На этих вопросах мы также не
останавливаемся и лишь в качестве примера наметим схему определения суммы
вещественных чисел.
Пусть а и р—два вещественных числа, определяемые
соответственно сечениями А /А' и В/В' во множестве рациональных чисел R.
Обозначим через а произвольное рациональное число из класса А,
16

через а'—-произвольное рациональное число из класса А'.
Рациональные числа классов В и Вг обозначим соответственно через Ь и Ъ'.
Тогда
a^a^d и 6^Р<&\
Определим сумму двух вещественных чисел а + Р как такое
вещественное число у, которое удовлетворяет неравенству а + Ь ^ у ^ а'+ Ь\
каковы бы ни были рациональные числа а, 6, d и Ь\ взятые из
соответствующих классов. Можно доказать, что такое число
существует и единственно.
В заключение коротко остановимся на представлении
вещественных чисел с помощью десятичных дробей. Покажем на примере
числа ~|/"2, как строится такое представление.
Так как 12=1 <2, а 22 = 4>2, то 1<]/"2<2 и число 1 можно
рассматривать как приближенное значение ]/"2 с недостатком, а
число 2 —как приближенное значение /2 с избытком. Допускаемая
погрешность такого приближенного представления, очевидно, меньше,
чем 2—1 = 1. Разделим отрезок с концами в точках 1 и 2 на 10
равных частей. Возводя в квадрат последовательно числа 1,1; 1,2;
1,3; ..., получим, что 1,42=1,96<2; 1,52 = 2,25>2. Следовательно,
1,4<]/2< 1,5. Дробь 1,4 является приближенным значением 1/2"
с недостатком, а 1,5 —с избытком. Допускаемая при этом
погрешность меньше, чем 1,5—1,4 = 0,1.
Разделив отрезок с концами 1,4 и 1,5 снова на 10 равных
частей и вычислив последовательно значения квадратов чисел 1,41; 1,42,
найдем, что 1,412= 1,9881 <2; 1,422 = 2,0164>2, то есть 1,41<
<1/2< 1,42, и погрешность приближения меньше, чем 1,42—1,41 =
= 0,01. Делим отрезок с концами 1,41 и 1,42 снова на 10 равных
частей и, действуя аналогичным образом, найдем, что 1,414 <
<1/"2< 1,415 с точностью приближения до 0,001, и т. д.
Очевидно, этот процесс приближения будет бесконечным, так как
в противном случае оказалось бы, что некоторая десятичная дробь
(рациональное число) равна иррациональному числу 1/"2. В связи
с этим говорят, что число "J/2 представимо бесконечной десятичной
дробью, и пишут: 1/2 = 1,414... . В общем случае можно доказать,
что всякое иррациональное число представимо в виде бесконечной
непериодической десятичной дроби, а всякое рациональное число —
в виде конечной или бесконечной периодической десятичной дроби.
Вопросы для самопроверки и упражнения
1. Отнесем к классу А все рациональные числа, квадрат которых меньше 2,
а к классу В — все остальные рациональные числа. Почему такое разбиение
множества R не является сечением?
2. Каким основным свойством отличается множество всех вещественных чисел W
от множества всех рациональных чисел R?
17

3. Чем объяснить, что множество всех рациональных чисел R не обладает
свойством полноты или непрерывности?
4. Доказать, что среди положительных рациональных чисел, квадрат которых
больше двух, нет наименьшего.
§ 4. АБСОЛЮТНАЯ ВЕЛИЧИНА ЧИСЛА
Понятием абсолютной величины и неравенствами, связанными с
абсолютными величинами, нам придется в дальнейшем пользоваться
очень часто как в теории математического анализа, так и в его
приложениях.
Определение. Абсолютной величиной вещественного
числа а называется само число а, если оно неотрицательное, или
число —а, если а отрицательное.
Пользуясь принятым обозначением |а| абсолютной величины
числа, можно записать:
, , ( а, если а^О,
а =<
{ —а, если а<0.
Очевидно, для любого вещественного числа а справедливо
— |а|^ок;|а| и | — а| = |а|.
Теорема 1. Неравенства |а|^р и — р^а^р
равносильны.
Доказательство. Пусть |а|^р. Тогда —|<х|^ — Р> и так
как —|а|<;а^|а|, то подавно — Р ^ а^ р.
Пусть справедливо неравенство—р^а^р. Это значит, что
одновременно выполняются неравенства а ^ Р и а^ — р. Из
последнего имеем: — а^р. Так как по определению |а| есть либо а,
либо — а, то | а|^р.
Теорема 2. Неравенства |а|<р и — Р<а<р
равносильны.
Аналогичное предыдущему доказательство этой теоремы
представляется читателю.
Теорема 3. Абсолютная величина суммы нескольких
чисел не превосходит суммы абсолютных величин этих
чисел, то есть для любого п справедливо неравенство
|c*i + a2+ ... +а„|<| аг \ + \ а2\+ ... + \ап |. (1)
Доказательство. Воспользуемся методом математической
индукции. В основе этого метода, как известно, лежит следующий
принцип:
Утверждение справедливо для всякого натурального числа п,
если:
1) оно справедливо для п=\ и
2) из справедливости утверждения для какого-либо
произвольного натурального n = k следует его справедливость для n = k+l.
18

Иногда по смыслу вопроса приходится проверять справедливость
утверждения не с /г=1, а с п = р. Так, в нашем случае установим
сначала справедливость неравенства (1) для п = 2.
Пусть аг и а2— любые вещественные числа. Для них
справедливы неравенства
— | ах | ^ аг ^ | аг | и — | а21 ^ а2 < | а21.
Складывая их почленно, получим:
— (| аг | +1 «21) < а1 + а2 < (| ах | +1 а21 )•
По теореме 1 это двойное неравенство равносильно неравенству
|ai + a2|<|ail + la2l- (2)
Предположим теперь, что неравенство (1) справедливо для n=kf
то есть
|а,+а2+ ... + «*!<!«! | +|а2|+ ... +|«ft|,
и докажем его справедливость для n = k+l. Действительно,
применяя неравенство, уже доказанное для двух слагаемых, получим:
! <*i + <*2 + ... + ak + ak+1 \ = \(a1 + a2+ ...+ak) + ak+1 | ^
^|а1 + а2 + а3+ ... + <** 1 + 1 a*+i1 <
< | а11 +1 а21 +1 а81 + ... +1 аА | +1 «*+i |.
Отсюда следует, что неравенство (1) справедливо для любого п.
Теорема доказана.
Если в неравенстве (2) заменить а2 на —а2, то получим:
l«i —a2l<|ail + |aa|. (3)
то есть абсолютная величина разности двух чисел не
превосходит суммы абсолютных величин этих чисел.
Далее, так как для любых чисел аг и а2 имеем:
а1 = (а1 + а2) — а2,
то из неравенства (3) получаем:
I «i | = | К + а2) — а21 < | ах + а2 \ + | а21.
Отсюда
|«! + оь21 ^= | схх | — |а2|.
Заменяя в последнем неравенстве а2 на —а2, получим:
lai — «21S^ | оьх | — |а2|.
Таким образом, абсолютная величина суммы и разности
двух чисел не меньше разности абсолютных величин этих
чисел.
Из определения действия умножения чисел следует, что
\*l'**\=\*l\'\*t\>
19

то есть абсолютная величина произведения равна
произведению абсолютных величин сомножителей. Это свойство
сохраняется и для любого числа сомножителей
1 ах • а2 • а8... ал | = | аг | ¦ | аа | • | а31... | ая |.
В частности, если в последнем равенстве положить а1 = а2 = а3 =•
= ... =ал = а, то получим:
|а»|-|а|»,
то есть абсолютная величина степени с целым
положительным показателем п некоторого числа а равна этой
же степени его абсолютной величины.
Из определения частного двух чисел следует, что
l«il
то есть абсолютная величина частного равна частному от
деления абсолютной величины делимого на абсолютную
величину делителя.
Заметим, наконец, что абсолютной величине разности двух ве-
щесгвенных чисел можно придать следующий геометрический смысл:
если а и р — какие-то точки прямой, то |а — Р| есть расстояние
между этими точками. Например, если а=—5, a р = 7, то
расстояние между этими точками равно |а — Р| = | — 5 — 7| = 12.
Рассмотрим несколько примеров, связанных с понятием
абсолютной величины.
Пример 1. Решить неравенство | 2х — 5 | ^ 3.
Заменим данное неравенство равносильными неравенствами: —3^ 2х — 5^3.
Прибавляя к каждой из частей этих неравенств число 5, получим: 2 ^ 2х ^ 8,
Поделив почленно эти неравенства на 2, найдем искомое решение: 1^д;^4.
Пример 2. Решить неравенство х2 — 9 < 0.
Данное неравенство можно записать так: х2 < 9. Так как Ух2 = | х |, то ! х | <
<3 или — 3<х<3. В общем случае неравенство х2 — а<0 при любом а>®
имеет решение: | х | < У а , а неравенство х2—а>0 имеет решение | х \ > У а •
Пример 3. Решить неравенство х2—5д:+6<0.
Зная корни трехчлена, стоящего в левой части данного неравенства (*i = 2;
х2 = 3), можем представить его в виде
(*_2)(*-3)<0.
Известно, что произведение двух множителей отрицательно лишь в том случае,
когда эти множители имеют разные знаки. Следовательно, возможны два случая:
либо х — 2<0, | либо х—2>0, ^
* —3>0, / х—3<0. J
Первая система неравенств не имеет решения (не совместна), а вторая имеет
решение 2<а:<3.
Заметим, что данное в этом примере неравенство можно решить и другим
способом. Действительно, представим левую часть неравенства в виде разности
квадратов:
!-<о.
(*-*)•-
20

Отсюда получаем:
I 5V> I
(х-т) <i
х~т
<т-
Последнее неравенство равносильно неравенствам:
1 5 1
""Т<*"Т<У
5
Прибавляя к каждой части этих неравенств число -^-, получим:
2 <х < 3.
Пример 4. Решить неравенство | х2 — Бх+6 | > я2-—5*+ 6.
Данное неравенство справедливо для тех значений х, при которых х2 — 5*+-
+ 6 < О (так как | а | > а только при а < 0). Как видно из примера 3,
решением такого неравенства будет 2 < х < 3.
Пример 5. Решить уравнение | 2х — 3 | = 2л: — 3.
По определению абсолютной величины имеем: |а| = а при а ^0.
Следовательно, в нашем уравнении должно быть
2х—3^0,
3
откуда 2*^3 и х^-у.
Пример 6. Решить уравнение \x\ = x+S.
По определению абсолютной величины имеем:
при x^0t
при х < 0.
Следовательно, при х^О данное уравнение представится в виде
х = х+3.
Оно, как легко видеть, не удовлетворяется никаким значением х. Если же х < 0,
то получаем уравнение:
-* = x+3.
Его решением будет единственное значение х = —^-.
Вопросы для самопроверки и упражнения
1. Доказать равносильность неравенств | а | < р и — Р < а < р.
2. Проверьте на npi ме ах справедливость неравенств, установленных для
абсолютных величин, взяв вместо букв числовые значения.
В задачах 3—12 решить неравенства и уравнения:
3. х2—25 <0. Отв. —5<*<5-
4. 16—x2^0. Отв. **$—4 и *^4.
5. |*-3|<2. Отв. 1<*<5.
6. |х|<*+1. Отв. х> — y-
и.;
*2-7|>3. Отв. М<2 и \x\>V\Q.
х2-2х-Ъ\>х* — 2х-3. Отв. —1<*<3.
х+5\ = х+5- Отв. x^z—b.
*+1| =-(*+!)• Отв. д:^— К
7.
8.
9.
М- . . .
11. |cosa:| = cos*. Ome. — -^ + 2&л ^ х^ -=- + 2&л, & = 0, ±1; ±:2; ...
12. | ^2 + jc — 2 | = 2 — л:—л:2. Отв. —2<л:<1.
21

13. Какие значения х удовлетворяют одновременно неравенствам \х — 2|<3
и \х — 6|<4? Отв. 2< х < 5.
14. Записать с помощью неравенства и знака абсолютной величины условие
того, что точка х отстоит от точки х0 на расстоянии, большем пяти. Отв. \х —
— А'о|>5.
15. Найти значения х, отстоящие от точки #0 = 3 на расстоянии, не
превосходящем 10. Отв. —7^ х ^13.
16. Отклонение температуры t от нормальной /0 не превышает 0,3°. Как это
записать с помощью неравенства и знака абсолютной величины? Отв. \t —10\^
^0,3.
17. Найти все значения х, при которых справедливы соотношения: a) /(x) = 0;
6) /М>0 и в) /(л')<0, если f(x)=x — x2.
Отв. а) л: = 0 и *=1, б) 0<*< 1, в) х<0 и х> 1.
§ 5. О ГРАНИЦАХ ЧИСЛОВЫХ МНОЖЕСТВ
Множество, элементами которого являются числа, называется
числовым множеством.
Определение. Числовое множество А = {х} называется
ограниченным сверху, если существует такое вещественное число М,
что все числа, являющиеся элементами данного множества, не
превосходят М, то есть х^М. Число М в этом случае называется
верхней границей множества А.
Если существует такое число т, что все элементы множества А
удовлетворяют неравенству х^т, то множество А называется
ограниченным снизу, а число т — его нижней границей.
Числовое Множество А называется ограниченным, если оно
ограничено как сверху, так и снизу, то есть если выполняется
неравенство т^х^М для всех xg/1. В этом случае множество А
лежит на отрезке прямой с концами т и М.
Если М — верхняя граница некоторого множества Л, то,
очевидно, всякое число М'', большее М, будет также верхней границей
этого множества. Если т — нижняя граница множества Л, то
всякое число т\ меньшее /л, будет также нижней границей этого
множества. Следовательно, можно сказать, что всякое ограниченное
множество имеет бесконечно много как верхних, так и нижних
границ.
Легко видеть, что множество, все элементы которого
удовлетворяют неравенству |лг|=^/(, будет ограниченным, так как в этом случае
— К^х^К и—К будет его нижней границей, а К — верхней
границей. Обратно, если множество А = {х\ ограничено, то есть
т^х^Му то всегда можно найти такое число /С, что |х]^/С.
Достаточно за число К взять наибольшую из абсолютных величин
\т\ и \М\. Тогда К^М (так как K^\M\^zM), a-—/C<m
(так как — /С^—\т\^т). Следовательно, для всех элементов
множества А справедливо неравенство — К^х^К, то есть
Если ограниченное числовое множество представить себе как
множество точек на числовой оси, то его границами будут концы
отрезков, содержащих все точки этого множества. Очевидно, таких
22

отрезков бесконечно много и по ним нельзя судить о
протяженности расположения точек множества по оси. Поэтому вводят по-
нятие точных границ множества, что соответствует концам
наименьшего отрезка, содержащего все точки данного множества.
Определение. Наименьшая из всех верхних границ
данного множества называется точной верхней границей или верх-
ней гранью этого множества. Наибольшая из всех нижних границ
множества называется точной нижней границей или нижней
гранью.
Точные границы множества А обозначаются:
sup А (точная верхняя граница) и inf А (точная нижняя
граница) (читается — супремум и инфимум).
Если множество А не ограничено сверху, условимся писать:
sup Л = + оо. Аналогично, если множество А не ограничено снизу,
пишем: inf А= — оо.
Рассмотрим несколько примеров множеств.
Множество всех натуральных чисел Л = {1, 2, 3,..., /г,...}
является бесконечным ограниченным снизу множеством. Числа m^l
будут его нижними границами, а число 1—его точной нижней
границей. Сверху это множество не ограничено, так как для него не
существует верхних границ. Какое бы число М мы ни взяли, в
множестве А всегда найдется число п>М.
Множество J5=={l»-9",y, ...,—, ...[является бесконечным
ограниченным множеством. Его точными границами являются числа
О и 1.
Рассмотрим множество С = {(—2)п]. Его элементами являются
различные степени числа —2. Это пример бесконечного множества,
не ограниченного как сверху, так и снизу.
Множество всех рациональных чисел R является также
бесконечным множеством, ке ограниченным как снизу, так и сверху.
Множество же положительных рациональных чисел /?f ограничено
снизу, а множество отрицательных рациональных чисел R_
ограничено сверху.
Легко видеть, что любсе конечное множество будет
ограниченным, так как среди чисел, составляющих это множество, всегда
найдутся наибольшее и наименьшее числа, которые и будут
точными границами этого множества. Обратное утверждение неверно.
Из ограниченности множества ке следует его конечность, как это
видно на пршере множества В.
Представляет интерес Еыяскекие вопроса о том, всегда ли у
ограниченного множества сушествуют точные границы. Иначе
говоря, всегда ли среди бесконечного множества верхних (нижних)
границ найдется наименьшая (наибольшая). Вообще говоря, среди
бесконечного множества чисел может и не быть наименьшего
(наибольшего) числа. Например, среди правильных положительных
дробей нет ни наименьшей, ни наибольшей дроби (см. ниже
пример 3). Что же касается существования точных границ у ограни-
23

ченного множества, то вопрос решается положительно следующей
теоремой.
Теорема. Всякое непустое ограниченное сверху
множество имеет точную верхнюю границу. Всякое непустое
ограниченное снизу множество имеет точную нижнюю границу.
Доказательство. Докажем существование точной верхней
границы. Вторая часть теоремы доказывается аналогично. Пусть
множество Л = {л:} ограничено сверху. Может оказаться, что среди
чисел х найдется наибольшее число х. Тогда оно и будет точной
верхней границей множества Л, так как, с одной стороны, число
х будет границей (выполняется условие х^х), с другой стороны,
любое число, меньшее ху уже не будет верхней границей.
Предположим теперь, что среди элементов множества А не
найдется наибольшего числа. Осуществим во множестве всех
вещественных чисел W сечение X/Y следующим образом. Отнесем к
классу Y все верхние границы множества Л, а к классу X — все
остальные вещественные числа. Проверим, что такое разбиение в W
есть действительно сечение.
В самом деле, класс Y не пуст, так как по условию теоремы
у множества А имеются верхние границы и они по условию
образования классов отнесены в класс Y. Класс X также не пуст: его
элементами будут, например, все элементы множества Л, то есть
А а X. Далее, каждое вещественное число принадлежит одному
из классов, поскольку оно либо является верхней границей
множества Л (в этом случае принадлежит У), либо не является
таковой (и, следовательно, принадлежит X). Наконец, каждое число
из класса X меньше любого числа из класса Y. Действительно,
пусть а — произвольное число из класса X, а |3—произвольное
число из класса Y. Тогда в Л найдется такое число х0, что а<.х0 (в
противном случае а было бы верхней границей для Л и находилось
бы в классе Y). С другой стороны, поскольку р —верхняя граница
множества Л, а х0 — элемент этого множества, то х0^р. Из двух
полученных нами неравенств следует, что а<Р-
Итак, мы доказали, что наше разбиение есть сечение.
Следовательно, существует «пограничное» вещественное число у. Оно по
теореме Дедекинда должно быть либо наибольшим числом в нижнем
классе X, либо наименьшим в верхнем классе У. Так как
множество Л содержится в классе X, то все его элементы х&^у.
Значит, у — верхняя граница множества Л. Но тогда у должно
принадлежать верхнему классу Y. Следовательно, у будет наименьшим
в У, а значит, будет наименьшей из всех верхних границ
множества Л или точной верхней границей для Л.
Точная верхняя граница у обладает следующим важным
свойством. Как бы мало ни было число е>0, у — г уже не будет
верхней границей и в множестве Л найдется число х>у — е. Если
бы такого числа х не нашлось, то у — г было бы также верхней
границей, и тогда у не было бы точной верхней границей.
Аналогичным свойством обладает и точная нижняя граница.
24

Пример 1. Числовое множество {х} состоит из всех чисел, для которых
|x|=sc3. Какие числа будут границами этого множества?
Заменим неравенство |#|=^3 ему равносильными неравенствами:
— З^х^З.
Отсюда видно, что число 3, а следовательно, и всякое большее число будет
верхней границей данного множества, а число -—3 и всякое меньшее число — его
нижней границей. Числа —3 и 3, очевидно, будут точными границами.
Пример 2. Числовое множество \х} состоит из всех чисел,
удовлетворяющих условию — 6 < л: г^4. Найти наименьшее число /С, удовлетворяющее
неравенству \х\ </С для всех х из данного множества. Какими границами этого
множества будут числа К и —Ю
Так как неравенство |*|</С равносильно неравенству — /С<*</С, то в
данном случае за К нужно взять такое положительное число, чтобы все
значения х, удовлетворяющие неравенству — 6<*^4, удовлетворяли и неравенству
— К < х < /С. Это, очевидно, будет при К, равном наибольшей из абсолютных
величин чисел -—6 и 4, то есть при К = 6. При этом число -—6 будет точной
нижней границей, а число 6 —верхней (неточной) границей данного множества.
Пример 3. Показать, что число 1 является точной верхней границей
множества всех положительных правильных дробей.
Так как по определению любая правильная дробь меньше 1, то 1 является
верхней границей данного множества. Остается доказать, что 1 наименьшая из
всех его верхних границ. Будем рассуждать от противного. Предположим, что
среди верхних границ данного множества есть число М<1; при этом М>0.
Как известно, между вещественными числами М и 1 найдется рациональное
число г (Л4<г<;1)» Но положительное рациональное число, меньшее 1, может быть
только правильной дробью. Таким образом, оказалось, что нашлась правильная
положительная дробь, которая больше М. А это значит, что М не может быть
верхней границей данного множества. Из доказанного следует, что среди верхних
границ множества наименьшей является 1, то есть 1 является точной верхней
границей.
Вопросы для самопроверки и упражнения
1. Докажите, что множество, ограниченное снизу, имеет точную нижнюкх
границу.
2. Приведите примеры ограниченных бесконечных множеств. Существуют ли
конечные неограниченные множества?
3. Приведите примеры множеств, которым принадлежат их точные границы.
4. Приведите примеры множеств, которым не принадлежат их точные границы.
5. Приведите пример множества, точная нижняя граница которого ему
принадлежит, а точная верхняя граница не принадлежит.
6. Можно ли утверждать, что в неограниченном множестве найдется
бесконечное множество элементов, больших, чем любое наперед заданное число М>0?
Рассмотреть возможные случаи.
7. Ограничено ли снизу множество всех отрицательных чисел? Ограничено
ли сверху это множество? Если да, то указать его точную верхнюю границу.
8. Может ли конечное числовое множество не иметь наибольшего числа?
Могут ли точные границы конечного числового множества не принадлежать этому
множеству?
9. Множество {х\ состоит из всех чисел, удовлетворяющих условию -— 2^л;<3.
Найти наименьшее число К такое, чтобы для всех х данного множества
выполнялось неравенство |*|</С. Какими границами этого множества будут числа
-К и К?
10. Доказать, что число 0 является точной нижней границей множества всех
положительных правильных дробей.
25.

§ 6. СЕГМЕНТ, ИНТЕРВАЛ, ОКРЕСТНОСТЬ
Определение. Множество вещественных чисел х,
удовлетворяющих неравенству а^х^Ь, называется сегментом или
отрезком и обозначается [а, Ь]. Множество вещественных чисел х,
удовлетворяющих неравенству а<сх<.Ь, называется интервалом и
обозначается (а, Ь). Числа а и b называются концами, а число
b — а — длиной как сегмента [а, Ь], так и интервала (а, Ь).
Так, например, сегмент [2, 5] и интервал (2, 5) с концами 2 и
5 имеют одинаковую длину, равную 3.
На числовой оси интервал (а, Ь) представляет собой множество
всех точек, содержащихся между точками а и b (рис. 6). Точки
а и b в это множество не входят. Если же к этому множеству
добавить точки а и Ьу то получим сегмент [а, Ь] (рис. 7). Таким обра-
а Ь a b
Рис. 6. Рис. 7.
зом, интервал (а, Ь) отличается от сегмента [а, Ь] лишь тем, что
ему не принадлежат концы а и Ь. Однако это малое отличие во
многих вопросах математического анализа играет существенную
роль. Множество (а, Ь) не содержит в себе ни наибольшего, ни
наименьшего числа, в то время как во множестве [а, Ь] такие
числа (а и Ь) имеются. На рисунках (см., например, рис. 6 и 7)
концы промежутков отмечаются жирными точками, если они
принадлежат промежутку, и остриями — в противном случае.
Определение. Множество вещественных чисел х,
удовлетворяющих неравенству а^х<.Ь или а<х^Ь, называется
полусегментом или полуинтервалом и обозначается соответственно
так: [а, Ь) или (а} Ь] (рис. 8 и 9). Интервалы и полуинтервалы
могут быть и бесконечными. Так, для обозначения множества
всех вещественных чисел пользуются символом (—оо, +оо) и это
множество называют бесконечным интервалом. Знаки —оо и +оо
не являются числами, и для них нельзя указать соответствующих
точек прямой. Поэтому в обозначениях интервалов и
полуинтервалов со стороны таких знаков квадратной скобки никогда не ставят.
Полуинтервал [0, +оо) есть множество всех вещественных чисел
х^О, а (—оо, а] есть множество всех вещественных чисел х^а.
Сегменты, интервалы и полуинтервалы (конечные и бесконечные)
условимся объединять под общим названием — промежутки.
й Ь ад
Рис. 8. Рис. 9.
26

Определение. Если а —
некоторое вещественное число, то интер- <>¦-<? а а+&
вал (а — б, а + 8), где б — любое * * *"
положительное вещественное число,
называется окрестностью точки Рис- 10-
а. Точка а лежит в середине
интервала и называется центром окрестности, а число б —радиусом
окрестности (рис. 10). Например, множество точек х, удовлетворяющих
неравенству \х — 5|<3, есть окрестность точки 5 радиуса 3. В
общем случае окрестность (а — б, а + б) может быть задана
неравенством \х—а|<б.
Вопросы для самопроверки и упражнения
1. Определить, какие множества заданы неравенствами \х—3|^2; |jc+2|^4;
|*-1 |<2; |*-5|>2.
Отв. [1, 5]; (—со, -6] и [2, +оо); (—1, 3); (— со, 3) и (7, +со).
2. Какая окрестность точки а определяется неравенством \х — а | < 5?
Отв. (а —5, а+ 5).
3. Из сегмента [— 3, 5] удален интервал (— 3, 5). Что осталось?
4. Из сегмента [2, 10] вырезан интервал (3, 8). Как записать множество
оставшихся точек сегмента с помощью промежутков?
5. Из интервала (—4, 5) вырезано два сегмента [—2, 0] и [1, 3]. Какие
промежутки остались?
6. Можно ли из конечного числа интервалов составить сегмент путем
склеивания?
7. Какова наибольшая окрестность нуля, содержащаяся в промежутке (— 6, 5] ?
§ 7. ДРУГОЙ ПОДХОД К ПОНЯТИЮ ВЕЩЕСТВЕННОГО ЧИСЛА*
В конце § 3 было упомянуто о возможности представления
любого вещественного числа с помощью бесконечной десятичной
дроби. Существует и такой подход к построению вещественных
чисел, при котором бесконечные десятичные дроби используются
для определения самого понятия вещественного числа.
Будем рассматривать всевозможные бесконечные десятичные дроби
как некоторые формальные символы. Каждую такую дробь
а, а^а? . лп...,
где а —любое целое число, а аъ а2, a3i..., ani... — «десятичные ?наки»,
принимающие определенные целые значения от 0 до 9
(включительно), будем называть вещественным числом. Число а называется
целой частью данного вещественного числа.
Два вещественных числа
а = а, ала<2аъ...ап.., и Р = 6, Ь1Ъфг...Ьп.,.
* Когда авторы уже полностью подготовили к печати рукопись этой книги,
была утверждена новая программа по математическому анализу для педагогических
институтов, которая вместо метода сечений рекомендует другие подходы к
понятию вещественного числа. При подготовке материала к экзамену студенты могут
опираться на этот параграф, ограничившись лишь прочтением § 3.
27

считаются равными, если прежде всего а = Ь и ап = Ьп при всех п,
то есть если равны их целые части и равны десятичные знаки,
стоящие на одинаковых местах. Кроме того, числа аир считаются
равными еще в одном случае. Именно, пусть а содержит девятку
в периоде, например, а = 2499,999..., а |3 получается из а заменой
всех девяток, стоящих в периоде, нулями и увеличением цифры,
непосредственно предшествующей этим девяткам, на одну единицу.
В нашем примере {5 = 2500,000... Тогда тоже а = (5.
Конечные десятичные дроби отождествляются с бесконечными
23
дробями, содержащими нуль в периоде. Например, ^ = 2,3 =
= 2,3000... Согласно сказанному выше о равенстве двух бесконеч-
23
ных десятичных дробей дробь -^ можно записать и с помощью
23
десятичной дроби с девяткой в периоде: т^ = 2,2999... Таким
образом, все конечные десятичные дроби также включаются в
множество вещественных чисел. Множество всех вещественных чисел
будем по-прежнему обозначать через W.
Из школьного курса известно, что всякое рациональное число
представимо в виде бесконечной периодической десятичной дроби
и, обратно, всякая бесконечная десятичная периодическая дробь
представляет собой рациональное число. Таким образом, множество
R всех рациональных чисел совпадает с множеством всех
бесконечных периодических десятичных дробей. Непериодические
бесконечные дроби составляют множество иррациональных чисел.
Заметим, что если целая часть вещественного числа а
отрицательна, например, а = 6,215000..., то есть
2 1 5
а = ~6 + Тб + НЮ + Т00б' W
то обычно пишут: а = -—5,785000..., что означает:
а = -(5 + Го + !|о + Тш)- (2)
Ясно, что выражения (1) и (2) равны между собой.
Исходя из понятия вещественного числа как бесконечной
десятичной дроби, можно определить, что означает неравенство а>р.
Именно, полагаем по определению а>(3, если аф§ и при этом
или Г) а > b (то есть целая часть числа а больше целой части
числа р),
или 2) а = Ь, но существует такое k, что ап = Ьп при /г<А, а
<Xk>bk*.
С помощью понятий равенства и неравенства между двумя
вещественными числами можно показать, что множество W вещест-
* Оговорка, что а^р, в этом определении существенна. Например, пусть
а = 3,000..., р =2,999... В этом случае целая часть числа а больше, чем целая
часть числа р- Однако эти числа равны между собой.
28

венных чисел обладает свойством упорядоченности, а множество R
рациональных чисел всюду плотно в W.
Если а = а, ага2а3... ап..., то числа
сп = а, a1a2a3..Mn=a+^+^2+^ + -- + w
называются десятичными приближениями к числу а с недостатком,
<а числа
Сп — Сп + Jon
— десятичными приближениями с избытком.
Рассмотрим все конечные дроби вида
S-//1.*-lAj.A4. -L drL
и "о т- ю ^ юз ^ 1аз ^ * • • "^ юл'
которые меньше а.
Если число а имеет вид: а = а, аха2.. л„000..., то сп = а и 8<Zcn,
Если же среди десятичных знаков числа а, стоящих после апу есть
хоть одна цифра, отличная от нуля, то среди всех конечных
дробей б дробь сп является наибольшей, то есть Ь^сп. Таким
образом, в любом из зтих двух случаев можно утверждать, что 8^сп.
Это замечание будет использовано в конце параграфа. Легко также
видеть, что между любыми двумя неравными вещественными
числами содержится некоторая конечная десятичная дробь. Например,
если а = 2,5314..., Р = 2,4832..., то между ними содержится число
2,5. Тем самым подтверждается свойство плотности множества R в
множестве W.
Наметим определение суммы двух вещественных чисел. Пусть
а и Р —некоторые вещественные числа, сп и с'п — десятичные
приближения к числу а соответственно с недостатком и с избытком
(сп^а^Сп), a dn и d'n—десятичные приближения к числу р
(dn ^ р ^ dn). Суммой а + р называется то вещественное число,
которое при любом п содержится между числами cn + dn и cn + d'*:
Cn + dn^a + fi^c'n + dn.
Не останавливаясь на доказательстве существования и
единственности такого числа, покажем на примере способ его получения.
Пусть а = 2,523523..., Р = 4,680808... Тогда q = 2,5; с[ =2,6; йг = 4,6;
d[ = 4J и потому 7,1 ^ct + P^ 7,3. Отсюда видно, что целая часть
числа а + р равна 7. Далее, с2 = 2,52; ^ = 2,53; d2 = 4,68; d.2 = 4,69
и потому
7,20 <а + р< 7,22.
Следовательно, первый десятичный знак числа а + р равен 2.
Таким же путем определяются и последующие десятичные знаки
числа а + р.
* Мы считаем, что сложение конечных десятичных дробей уже известно.
29

В заключение покажем, как с помощью десятичных дробей
можно доказать теорему из § 5 о существовании точной верхней
границы у ограниченного сверху числового множества.
Пусть непустое множество Л = {х} ограничено сверху, например,,
числом М. Не уменьшая общности, можно считать М целым числом,
так как в противном случае вместо М мы могли бы взять в
качестве верхней границы множества Л любое целое число, большее М.
Тогда существует лишь конечное множество целых чисел, которые
не превосходят М и являются верхними границами множества Л.
Среди них выберем наименьшее и обозначим его через cQ. Если
взять число Cq = c'0—1, то оно уже не будет верхней границей
множества Л. Далее, перебирая числа вида
, 1 ,2 , 9
найдем наименьшее из них, которое является верхней границей
множества А. Обозначим его через cj. Тогда число сх = с\—jx уже
не будет верхней границей множества Л. Аналогично, перебирая
числа вида
1 2 _9_ ,
Съ с1+юб' Cl+100' ", Cl_i~ 100' Си
найдем среди них с'% и сг = с\ — щ, где сг — верхняя граница
множества Л, а с2 уже не является верхней границей этого множества.
Продолжаем этот процесс до бесконечности. Ясно, что числа cw
получаются друг из друга по следующему закону:
^i = ^o + ^, где О^а^Э,
^2 = ^1 + ^-1 где 0^а2<9,
Сп = см + -^, где 0^ял^9,
а числа сп = сп+у^.
Образуем вещественное число
a = cQt а1а2а3...ап...
и покажем, что оно и есть точная верхняя граница множества Л.
Сначала установим, что а — какая-то верхняя граница
множества Л. Допустим противное. Пусть а не является верхней
границей множества Л. Тогда существует такое х^Л, что х>а»
Между а и х вставим некоторую конечную десятичную дробь:
30

Тогда тем более число
При этом р—сп ^ jq^ . Отсюда следует, что Р ^ Сл + j-^, то есть
Р>4- Таким образом, мы получили, что сп<.х. Это противоречит
построению, согласно которому сп было верхней границей
множества Л. Тем самым доказано, что а — верхняя граница
множества Л.
Теперь покажем, что а—точная верхняя граница. Рассуждая
снова от противного, предположим, что существует верхняя
граница у, меньшая, чем а. Между числами у и а вставляем конечную
десятичную дробь:
Тогда по сделанному выше замечанию 6^сп. Следовательно, сп>у
и потому сп тоже оказывается верхней границей множества Л,
вопреки построению. Полученное противоречие полностью завершает
доказательство теоремы.

ГЛАВА II
ФУНКЦИИ
Центральным вопросом данной главы является понятие функции.
Изучающему нужно глубоко осмыслить определение этого понятия
и различные способы задания функций. В дальнейшем сведения
о функциональных зависимостях будут постепенно расширяться.
Поэтому тем более необходимо, чтобы первоначальные исходные
понятия о них были усвоены безошибочно и прочно. Понятие
обратной функции, а также свойства четности и периодичности функции
используются при построении графиков. Кроме того, они будут
необходимы и при изучении последующих глав.
Рассмотрение элементарных функций продиктовано
необходимостью восполнения или закрепления знаний, полученных студентом
в средней школе, и подготовки его к успешной дальнейшей работе
по математическому анализу.
§ 1. ПОНЯТИЕ ФУНКЦИИ
Человеку, изучающему различные явления и процессы,
приходится иметь дело с различными величинами (длина, площадь, объем,
время, скорость, масса, вес, сила и т. п.). Для каждой величины
выбрана своя единица измерения. В результате сравнения
некоторой величины с ее единичной мерой получаем число или числовое
значение данной величины.
Величины, значения которых с течением изучаемого процесса
не меняются, то есть остаются одними и теми же, называются,
постоянными величинами. Те же величины, значения которых
меняются, называются переменными величинами или просто
переменными.
Так, например, при движении некоторого твердого тела его
масса, вообще говоря, остается величиной постоянной, а путь,
пройденный этим телом, в различные моменты времени будет
различным, то есть будет величиной переменной.
Далее, из формулы длины окружности l = nd следует, что при
изменении диаметра окружности d будет изменяться ее длина / и,
обратно, изменение длины окружности влечет за собой изменение
32

диаметра. Что же касается числа я, равного ~, то оно является
величиной постоянной, как бы ни менялись I и d.
Заметим, что некоторые величины остаются постоянными не все
время, а лишь в том или ином конкретном течении процесса, при
тех или иных условиях его осуществления. Так, число пассажиров
в поезде можно считать величиной постоянной, пока поезд
находится в движении. На остановках эта величина может измениться.
По закону Ома простейшая зависимость между силой тока /,
электродвижущей силой Е и сопротивлением R выражается
следующей формулой:
В этой формуле все три величины можно считать переменными.
Однако если хотят ее экспериментально проверить, то одну из
величин обычно сохраняют на некоторое время постоянной (не меняют)
и изучают зависимость между двумя остальными величинами.
Числовые значения величин являются абстракциями, они не
учитывают качественных свойств той или иной величины. Между тем
сами величины, отражая качество предмета, обычно конкретны. В
математике, таким образом, происходит отвлечение от конкретного
качественного содержания величины. Вместо нее рассматривается лишь
абстрактная величина, символически обозначенная какой-либо
буквой. Однако в этом следует усматривать не слабость, а силу
математики, не уход от действительности, а стремление сделать
математическую теорию более полной и всеобъемлющей, чтобы затем с ее
помощью обеспечить успешное исследование всего разнообразия
конкретных величин.
Множество значений, которые может принимать переменная
величина при своем изменении, называется областью изменения
этой переменной.
Так как на числовой прямой каждому вещественному числу
соответствует определенная точка, то каждое значение переменной
изображается некоторой точкой на прямой и, следовательно,
геометрическим изображением области изменения переменной является
определенное множество точек прямой.
Заметим, что постоянную величину можно рассматривать и как
частный случай переменной, множество значений которой состоит
всего из одного числа. Следовательно, областью изменения
постоянной величины в таком случае будет множество, состоящее из одной
точки.
Понятие переменной величины является основным понятием
математического анализа. Введение переменной в математику оказало
решающее влияние на дальнейшее развитие математической науки.
Увеличились познавательные возможности математики. Это привело
к значительному расширению области математических исследований.
Помимо установления количественных соотношений между постоян-
33

ными величинами, математика смогла изучать процессы, связанные
с изменением величин и движением вообще.
Все явления в окружающем нас мире находятся в постоянном
изменении и развитии. При этом изменение различных величин
протекает в определенной зависимости между ними. Математический
анализ и занимается изучением зависимостей между различными
переменными величинами.
Если две величины связаны между собой так, что каждому
значению одной из них соответствует определенное значение другой,
то будем говорить, что эти величины находятся в функциональной
зависимости. Примерами функциональных зависимостей могут
служить: зависимость длины окружности от ее радиуса, зависимость
пройденного пути от времени движения, зависимость площади
квадрата от длины его стороны, и т. д.
Переменные х и у, находящиеся в функциональной зависимости,
не могут одновременно принимать любые значения. Если одной из
них мы будем давать произвольные значения из области ее
изменения, то другая будет получать значения уже в зависимости от
первой. В этом случае первую переменную называют независимой
переменной, а вторую — зависимой переменной или функцией.
Пример 1. Формула длины окружности / = 2яг выражает зависимость
между радиусом г и длиной окружности /. Если г давать произвольные значения,
1 3
например —, 1, д-, то / будет принимать соответственно значения 2, 2я, 3.
В этом случае радиус окружности будет независимой переменной, а длина
окружности—зависимой переменной или функцией. Однако если эту формулу предста-
/
вить в виде г = ~-1 то получим зависимость радиуса от длины окружности.
Давая различные значения /, будем получать соответствующие значения г.
Переменные г и /, таким образом, поменялись ролями: / стала независимой
переменной, а г—функцией.
Дадим теперь более точное определение функции.
Определение*. Пусть даны две переменные х и у.
Переменная у называется функцией от переменной х, если каждому
значению х из области его изменения ставится в соответствие по
некоторому закону определенное значение у. Переменная х называется
в этом случае аргументом функции у.
Заметим, что аргумент не обязательно должен быть независимой
переменной. Он может, в свою очередь, находиться в зависимости
еще от одной или нескольких переменных.
Тот факт, что у есть функция от х, обычно обозначают
символом y=f(x), который читается так: «игрек равен эф от икс». Таксе
обозначение, однако, не раскрывает существа самого закона /
зависимости у от х. Если же функция представлена, например,
формулой у = х2 — 2л:+ 4, то здесь дается и закон зависимости у от х,
* Определение функции, близкое к данному, было высказано великим русским
математиком Н. И. Лобачевским (1793—1856) (см. [1], гл. II, п9 21).
34

так как указывается, какие действия и в каком порядке следует
произвести над значениями аргумента х, чтобы получить
соответствующие значения функции у. Так, при х — 0 получим: у=4, при
х=3 получим: (/ = 7, и т, д.
Обозначение функций при помощи различных букв, например:
y=f(x)f у=у(х), у = ^(х)у y=F(x) и т. д., используется лишь
для того, чтобы показать, что законы зависимостей у этих функций
различны.
Значение функции y=f(x) при х = х0 обозначается так: f(xQ).
x-i-2
Пример 2. Дана функция: f (х) = х3 — 2х-\-
Найти: /(-1), /(0), f (2) и }(a + b).
Вместо х подставим соответствующее значение и произведем подсчет.
Получим:
f(-l) = (-l)3_2(-l)+-7^1+2 = ^fe
К !-{-(— 1)2 J/2 '
/(0) = 2; f(2) = 4 + ^=;
f(a + b) = (a + b?-2(a + b) + a + b + 2
Пример 3. Дана функция: f(x) = \x\ — x. Найти значения: f(0), f(2) и
f(-3).
Имеем: f(0) = |0| — 0 = 0 — 0 = 0; f(2) = |2| — 2 = 2 — 2 = 0; f(-3) = | — 3|-
— (—3) = 3 + 3 = 6. Вообще для любого числа а^0
f (а) = [ а | — а = а — а = 0
и для любого числа а<0
f (а) = | а | — а = — а — а = — 2а.
Пример 4. Дана функция: ф (х)=х3 + 2х. Доказать, что ф (— х)= — ф (х).
Найдем значение ф(—х). Для этого достаточно в выражение ф(*)=х3+2л:
вместо х подставить — х. Получим:
ф (— *) = (— х)з+2 • (— х) = — л;3_2х = — (*з + 2х).
Сравнивая выражения для ф (— х) и для ф (х), заключаем, что ф(—*) =—Ф (*)•
Пример 5. Функция */=/(*) задана формулой f (x)=x3 — З^2 + 8лг +1.
Какими формулами заданы функции:
y = f(2x), y = f(j), y=lf(x)]2*y = 2f(x)7
Функция y = f(2x) отличается от функции y = f(x) лишь тем, что вместо
аргумента х подставлено 2х. Что же касается самого закона образования /, то он
не изменился. Следовательно, если в формулу для / (х) подставить 2х вместо х,
то получим формулу для функции y=f(2x):
f (2х) = (2х)3 — 3 (2*)2 + 8 (2х) +1 = 8л*_ 12x2+ 16л: +1.
Аналогично получаем:
85

Так как функция у = [/(*)]* есть квадрат функции y = f(x), то [f (л:)]2 = (д;3 —3^2 +
+ 8х+1)2= х* + 9х*+ б4х2+ 1 __ $хь + 1бх* + 2*з~ 48*» - 6Х*+ 16* = *« — 6** +
+ 25х4 —46*3 + 58*2+16*+1.
Аналогично,
2/(*) = 2(*з_ 3*2 + 8*+1) = 2*з-6*2+16* + 2.
Из определения функции не следует, что различным значениям
аргумента х должны соответствовать различные значения функции у.
Важно, чтобы каждому значению х соответствовало
определенное значение у. Например, f(x) = a тоже есть функция, хотя при
любых значениях х она принимает одно и то же значение а. Такие
функции называются постоянными функциями.
Понятие функции является основным понятием не только
математического анализа, но ц всей математики в целом. Специально
изучением функций занимается математический анализ.
Функция y = f(x) считается заданной, если:
а) указана область изменения аргумента х {ее обычно называют
областью определения или задания функции);
б) дан закон функциональной зависимости между х и у. При
этом не имеет значения, как этот закон зависимости представлен:
то ли формулой, то ли описан словами, то ли еще как-нибудь. Это
уже относится к способу задания функции.
Заметим, наконец, что мы будем все время рассматривать только
вещественные функции от вещественного аргумента, то есть будем
считать, что х и у принимают только вещественные значения.
Вопросы для самопроверки и упражнения
1. В чем состоит различие между понятиями «аргумент функции» и
«независимая переменная»?
2. Дана функция: f (х) = (* — 2)2 + Зх —г. Найти значения: /"(О), f(2),
/(-2)И/(3)- * Оше. 5, 5, Ю-*- и 4.
А
«*
п
К
В
_____*
X
>р
__Я.-_
1
Л
х if
—^
с
Рис. 11.
3. Дана функция:
Ф(*) = |* + 3|+2*.
Найти значения
Ф(0), <р(-4), q>(-3) и Ф(4).
Отв. 3, —7, —6 и 15.
4. Выразить радиус шара как
функцию его объема.
5. В треугольник ABC (рис. 11)
с основанием Ъ и высотой h вписан
прямоугольник КМРН, высота которого х. Выразить периметр L и площадь S
прямоугольника как функции от х.
Отв. L = 2b + 2(\--^\x, S = b(l~-~-\ где 0<*</z.
6. Дана функция: f (х) = *4 — cos х. Доказать, что f (—*) = f (x).
7. Дана функция: f (*) = -^ + sin 2x. Найти функции: /(За:), f (~
f(*+4.
fW и
36

§ 2. СПОСОБЫ ЗАДАНИЯ ФУНКЦИЙ
/. Аналитический способ. Существует несколько способов
задания функций. Среди них наиболее распространенным в
математическом анализе является так называемый аналитический способ.
Он состоит в том, что функциональная зависимость между
величинами изображается в виде формулы, указывающей, какие действия
(сложение, вычитание, умножение, деление, возведение в степень,
извлечение корня, логарифмирование, нахождение синуса, косинуса
и др.) нужно выполнить над аргументом, чтобы получить значение
функции. Примерами такого задания могут быть функции:
# = ^Z2> y=avcs\nx, y = \gx, S=%-
и другие встречавшиеся в курсе средней школы.
Определение. Множество всех значений аргумента, при
которых функция, заданная аналитически, имеет определенный
смысл, будем называть областью существования или областью
определения этой функции.
В соответствии с этим определением, функция у = ^Г2 сУЩест"
вует для всех хф2, так как только при х = 2 выражение -^
лишено числового смысла. Область существования в данном случае
складывается из двух интервалов: (— оо, 2) и (2, +оо).
Функция y = avcsmx существует для х, удовлетворяющих
неравенству — 1<;ж;1. Ее областью существования будет отрезок
[-1, +i].
Так как отрицательные числа и нуль логарифмов не имеют, то
функция y=\gx, очевидно, существует на (0, +оо).
Заметим, однако, что в тех случаях, когда функция y=f(x),
заданная некоторой формулой, отражает зависимость между
совершенно конкретными величинами (например, физическими,
геометрическими или еще какими-нибудь), область ее существования может
не совпадать с той областью, где формула имеет смысл. Так,
например, если рассматривать функцию S = ^-, не связывая ее
с какой-нибудь физической задачей, то областью ее существования
будет (—оо, +оо). Но, как известно, таким аналитическим
выражением в физике изображается закон свободного падения тела
в пустоте, где t — время, g — ускорение, 5 — пройденный путь. Если
это последнее учитывать, то бессмысленно было бы рассматривать
отрицательные значения t.
Точно так же сама по себе формула у = 2пх имеет смысл при
любых х (—oo<^< + co). Однако если этой формулой
представить длину окружности как функцию радиуса, то естественно
считать х положительным (0<х<С + со). В этом случае уже областью
существования будет (0, + оо). Таким образом, формулам, как
аппарату, созданному для описания функциональных зависимостей,
37

свойственны некоторые недостатки. Как видно из рассмотренных
примеров, бывают случаи, когда формула не может отразить всей
особенности нужной нам функциональной зависимости. В частности,
если по смыслу функция имеет более узкую область задания, чем
это следует из изображающей ее формулы, то нужно соответственно
указать и область рассмотрения формулы. Если же функция задана
формулой без каких бы то ни было дополнительных ограничений,
как это чаще всего и бывает, то областью задания будет считаться
вся область, где формула имеет смысл.
Пример 1. Определить область существования функции
Данная функция существует для таких значений х% при которых квадратный
корень принимает вещественные значения, то есть подкоренное выражение
неотрицательно: А — х^О. Отсюда получаем: *^4. Значит, данная функция
существует на промежутке (—со, 4] (рис. 12).
Пример 2. Определить область существования функции
•(х+\)(х-ЗУ
Очевидно, эта формула имеет смысл при любых значениях х, кроме х =— 1
и х = 3. В данном случае область существования функции складывается из трех
интервалов: (—со, —1), (—1, 3) и (3, + со) (рис. 13).
Пример 3. Определить область существования функции
ysssyV^?+\Tx-lg (*+1).
Данную функцию мы считаем существующей при всех тех
значениях х, при которых все три слагаемые имеют конечные
вещественные значения. Поэтому находим сначала область существования
для каждого слагаемого в отдельности.
Выражение У 4— х2 имеет смысл при 4 — х2^0; отсюда л:2^4
или |jc|^2. Область существования —отрезок [—2, +2].
Выражение -\/~х имеет смысл при любых значениях х.
Следовательно, его областью существования будет (—оо, +оо).
Выражение lg(#+l) имеет смысл при #+1>0, то есть при
*> —1. Область существования —интервал (—1, +оо).
Теперь остается определить область, представляющую собой общую
часть областей существования всех трех слагаемых. Ею будет
полуинтервал (—1, 2].
*r<-*f -1<х<3
ь X
Рис. 12,
за

Для того 1тобы легче найти область существования функции,
представленной в виде суммы нескольких слагаемых, прибегают
к геометрическому изображению областей существования всех
слагаемых на одной числовой оси. Тогда сразу видно, что следует
принять за область
существования всей функции. В нашем
примере такое геометрическое
изображение представлено на
рисунке 14.
Пример 4. Известно, что
lgx(x— 2) = lg* + lg (я — 2).
Одинаковы ли области существования
функций \gx(x — 2) и \gx + \g(x — 2)?
Область существования функции \gx(x—-2) определяется условием х(х — 2)>0.
Отсюда получаем, что либо х>0 и х — 2>0, либо #<0 и х — 2<0. Решая
системы неравенств
х>0\ х<0\
*-2>0J И *-2<0Г
находим, что \gx(x — 2) существует для #>2 и для *<0, то есть область
существования этой функции состоит из двух частей: (—оо, 0) и (2, +оо).
Для определения области существования функции \gx-\-\g(x— 2) следует, как
и в примере 3, найти сначала области существования для каждого слагаемого
в отдельности. Функция lg* существует для всех значений *>0, то есть на
(0, + оо). Функция lg(*—2) существует для*, удовлетворяющих неравенству
х—2>0, то есть на (2, + оо). Следовательно, функция lg* + lg(*—2) существует
на (2, +оо). Таким образом, получили, что области существования функций
lg*(# —2) и lgx + lg (x — 2) не совпадают. Поэтому равенство
lg*(*-2) = lg* + lg(*-2)
не является тождественным. Оно представляет тождество только на промежутке
(2, +оо).
Заметим, что функция может быть задана не одной, а
несколькими формулами. Если закон соответствия между аргументом и
функцией на всей области определения функции не удается
изобразить одной простой формулой, то иногда возможно изображение
его несколькими формулами, отображающими это соответствие на
отдельных ее участках.
Пример 5. Задание функции в виде
{*3 при —2=^*^ 1,
2х при 1 < х ==с 2,
4—* при 2<д:^3
следует понимать так: функция определена на отрезке [— 2, +3], причем на [—2, 1]
она изменяется по закону y — x3t на (1, 2] —по закону у = 2х и на (2, 3]— по
закону у = 4—х.
Пример 6. Задание функции в виде
( 1 для рациональных значений х,
ФМН Л • (-со<*< + оо)
I 0 для иррациональных значении х
39

следует понимать так: функция определена на всей числовой оси. В каждой
рациональной точке значение функции равно единице, а в каждой иррациональной
точке — нулю *.
Пример 7. Функция / (*) определена на отрезке [0, 1]. Каковы области
определения функций: /(*2), /(sin*), /(* — 2), /(*-)-2), / (2х) и / (-у)?
Под / (*2) мы понимаем функцию, получаемую из *2 по тому же закону, как
из х получается /(*). Например, если
/ (*) = 3*2 + 5*—1,
то
/ (*2) =3 (*2)2 + 5 (*2) - 1 =3r* + 5*2_ 1.
Так как по условию/(*) определена на отрезке [0, 1], то / (*2) имеет смысл для
всех тех *, для которых 0^*2^ 1, то есть при | * | ^ 1. Таким образом, областью
определения функции / (*2) является отрезок [—1, 1].
Функция /(sin*) определена для *, удовлетворяющих неравенству 0^sin*^1,
откуда
2&л^*^(2/г+1) л (6 = 0, ± 1, ±2, ±3, ...).
Область определения такой функции состоит, как выяснилось, из бесконечного
множества отрезков: [0, л], [2я, Зя], [—2я, —я], [4я, 5л], [—4л, —Зл] и т. д.
Область определения функции /(* —2) характеризуется неравенствами 0^* —
— 2^1, откуда 2^*^3, Функция определена на отрезке [2, 3].
Аналогичными рассуждениями легко установить, что функция /(*+2)
определена на отрезке [—2, —1], функция /(2*) —на отрезке 0, -~- и функция
f f-^-j —на отрезке [0, 2]. Читателю предлагается получить это самостоятельно.
В примере 7 мы, по существу, встретились с понятием
функции от функции или с так называемой сложной функцией. В
дальнейшем это понятие будет рассмотрено более подробно.
Познакомимся еще с двумя способами задания функции —
табличным и графическим.
2. Табличный способ. Если функция задана в виде таблицы, в
которой различным значениям аргумента сопоставлены
соответствующие значения функции, то такой способ называется
табличным способом задания функции.
Иногда в технике и естествознании сам факт зависимости между
некоторыми величинами не вызывает сомнения, а закон этой
зависимости не известен. Тогда проводят эксперимент, в результате
которого путем измерений получают ряд значений аргумента и
соответствующих значений функции в виде некоторой таблицы.
Так, например, известно, что рост любого растения является
функцией времени. Для того чтобы установить закономерность
изменения роста L при изменении времени t для конкретно выбранного
растения в определенных условиях, будем производить измерение
* Эта функция называется функцией Дирихле, по имени немецкого математика
Петера Густава Лежен а-Д и р и х л е (1805 — 1859).
40

высоты через определенные промежутки времени, начиная с
момента t0 = 0. В результате получим таблицу:
t
L
0
2
1
2,5
2
2,75
3
3
4
3,2
5
4
6
5
7
6,5
8
7
•
•
•
•
•
Конечно, эта таблица не является точным заданием исследуемой
функции, так как при измерении неминуемы погрешности,
зависящие как от качества измерительных приборов, так и от личных
качеств экспериментатора. Но тем не менее таблица будет отражать
зависимость величин L и /, характеризующую рост растения.
Таблицами можно задавать различные функциональные
зависимости. Так, если записывать пройденный путь автомобиля через
определенные промежутки времени, то получим таблицу
зависимости пути пробега от времени движения. Измеряя давление пара в
котле при различных температурах, можно получить таблицу,
отображающую закон зависимости давления от температуры при
постоянном объеме, и т. д.
Недостатком табличного способа задания функции является то,
что по таблице можно найти значения функции только для тех
значений аргумента, которые имеются в таблице. Однако у этого
способа имеется и ценное качество. Таблица позволяет
непосредственно, без всяких вычислений, получать значения функции,
соответствующие определенным значениям аргумента. Последнее
обстоятельство настолько важно, что иногда функции, заданные
другими способами, представляют в виде таблиц. Имеются,
например, готовые таблицы логарифмов, тригонометрических функций,
различных степеней натуральных чисел и др. Различные таблицы
широко используются и в производстве при технических расчетах.
При этом часто с помощью таблиц находят (хотя и приближенно)
те значения функции, которых в таблице нет. Например, существует
так называемый способ линейного интерполирования, с которым
знакомятся в школе при вычислении логарифмов.
3. Графический способ. Введем сначала понятие графика функции.
Определение. Графиком функции y=f(x), заданной в
некоторой области X, называется множество всех точек плоскости
(х, у), координаты которых х и у связаны соотношением y = f(x).
При этом х может иметь любое значение из X. Само равенство
y=f(x) называется уравнением этого графика (рис. 15).
Графики часто встречающихся функций представляют собой
некоторые сплошные кривые или, в частности, прямые линии. Однако
график может состоять и из отдельных изолированных точек;
например, график функции у = п, заданной на множестве натуральных
чисел {п} (рис. 16). Функция считается заданной графически, если
начерчен ее график. Например, для измерения давления атмосферы
41

0
M(x,yj/
и
к ^ s
>fM
—^
X
Рис. 15.
0| 1 2 3 U 5 6 7 S
Рис. 16c
на различных высотах пользуются специальным самопишущим
аппаратом—барографом, который на движущейся ленте записывает в
виде кривой линии изменение давления в зависимости от высоты.
В данном случае имеем графический способ задания функции.
Если функция задана графиком, то по нему можно получить
значения функции для любых значений аргумента. Значения функции
f(x), соответствующие различным значениям аргумента х, можно
получить измерением на чертеже соответствующих ординат (рис. 15).
Такая операция обычно называется «снятием» значений с графика.
Для того чтобы множество точек плоскости XOY могло служить
графиком некоторой функции, необходимо (и достаточно), чтобы
в нем не содержалось никаких двух различных точек с одинаковыми
абсциссами. Если это условие нарушено, то найдется значение х,
которому сопоставляется по крайней мере два различных значения
?/, что противоречит требованию однозначности в определении
функции (рис. 17). Например, парабола у2 = х не служит графиком
какой-нибудь одной функции вида y = f(x). Однако часть этой
параболы, лежащая в верхней полуплоскости, представляет график
функции у = ]/Гх, а другая ее часть, лежащая в нижней
полуплоскости,— график функции у =— У~х (рис. 18).
43

Легкая обозримость и наглядность
графического способа изображения
функций делают этот способ весьма удобным
при различного рода исследованиях. В
связи с этим часто прибегают к
графическому изображению даже функций,
которые заданы с помощью таблицы или
формулы.
Пусть функция y = f(x) задана
таблицей. Пользуясь тем, что на
плоскости с заданной системой координат
каждой паре чисел соответствует
определенная точка, отметим на плоскости
точки, соответствующие парам чисел, помещенным в таблице. Затем,
соединяя эти точки «плавной» кривой, получим графическое
изображение данной функции.
Если функция задана формулой, то для ее графического
изображения сначала нужно составить таблицу значений аргумента и
функции, а затем действовать указанным выше способом
Пример 8 Построить график функции, заданной формулой у = х2 — х-\-\.
Выбираем по нашему усмотрению несколько значений х и находим
соответствующие значения у. В результате получим таблицу:
X
У
•
— 4
21
— 3
13
— 2
7
— 1
3
0
1
1
1
2
3
3
7
4
13
. . .
На листе бумаги, лучше миллиметровой, строим систему координат и на
каждой из осей выбираем масштаб. В данном случае практически удобнее по оси
ординат взять более мелкий масштаб по сравнению с масштабом по оси абсцисс,
так как в таблице для у имеются существенно большие значения, чем для х.
Затем отмечаем точки, соответствующие парам чисел, указанным в таблице, и
соединяем эти точки «плавной» кривой.
Получим график, изображенный на
рисунке 19.
Заметим, наконец, что способ
задания функции формулой хотя
по наглядности и уступает
табличному и графическому способам,
но зато является более точным
по сравнению с ними. По
формуле можно найти значения
функции для любых значений
аргумента либо абсолютно точно, либо
с любой степенью точности.
-W*
43

Пример 9. Построить график функции у = х3 — 1.
Как легко видеть, эта функция существует при любом х, то есть на (— со,
+ со). Возьмем по своему усмотрению несколько значений аргумента и составим
таблицу:
X
У
...
— 4
— 65
— 3
— 28
— 2
— 9
— 1
— 2
0
— 1
1
0
2
7
3
26
4
63
...
...
В дальнейшем, поступая, как и в примере 8, получим график функции,
который изображен на рисунке 20. Естественно, в точках х, которые не входят
в таблицу значений, график может не отображать точных значений функции. Чтобы
график был более точным, нужно при составлении таблицы брать более частые
значения для х. Тогда получим больше пар чисел,
а следовательно, и больше точек на плоскости.
От этого график станет более точным. Иногда по
ходу исследования функции нужен более точный
график не на всей области, а в окрестности
некоторой точки. Тогда нужно брать больше значений
аргумента именно в окрестности этой точки.
Следует также заметить, что не
всякую функцию можно изобразить
графически одной или несколькими «плавными»
кривыми. Так, для функции Дирихле
(пример 6), как бы густо мы ни брали
Рис. 20. точки на числовой оси и сколько бы
точек на плоскости мы ни получили,
никакие две из них нельзя соединить «плавной» кривой, так как между
любыми двумя значениями х имеются в неограниченном количестве
как рациональные, так и
иррациональные значения и, следовательно, в любом
промежутке сколь угодно часто будут
встречаться значения функции, равные 0
и 1.
Пример 10. Построить график функции,
рассмотренной в примере 5.
График такой функции будет состоять из трех
графиков, построенных отдельно для каждой
частичной области задания функции. Каждый из
них строится обычным образом. Общий вид
графика показан на рисунке 21.
Если смотреть на график, состоящий
из нескольких частей, то иногда бывает
неясно, какое значение ординаты следует
считать значением функции в точке стыка Рис- 21.
между отдельными частями области
задания функции. В случае примера 10 такой точкой является
точка х=\. Если не иметь под руками аналитического
задания функции, то по графику неясно, считать ли /(1) = 1, или
44

f(l)=2, или, может быть, какое-нибудь промежуточное значение.
Чтобы избежать этой неясности условимся тот конец графика,
который соответствует точке стыка, отмечать более жирной точкой,
а другой конец —стрелкой, как это показано на рисунке 21.
Символом Е (х) условились обозначать функцию, значение
которой в каждой точке х равно целой части х, то есть
наибольшему целому числу, не превосходящему х *. Например, ?(2у) = 2,
Е(0)=0, ?(у) = 0,
Я(5)=5, Е(УЩ=4, ?(--^=-1
и т. д. График функции у=Е{х) изображен ниже, на рисунке 57
(стр. 112).
Две функции, f(x) и g(x), заданные на некотором промежутке,
называются тождественно равными на этом промежутке, f(x) =
=g(x), если их значения в каждой точке промежутка совпадают.
Так, например, функции f (х) = 1 и g (x) = sin2 x + cos2 x
тождественно равны на (— оо, +оо), так как для любого х справедливо
равенство sin2 х + cos2 х = 1. Функции f (х) = lg х2 и g (х) = 2 lg x
имеют разные области определения (первая определена для любых
х Ф О, а вторая—только для х>0). Однако эти функции
тождественно равны на промежутке (0, + оо).
Пример 11. Тождественны ли функции
f(x)=VxVx^2 и ф(х)= ]/¦*(* — 2)
на промежутке [2, +оо)?
Не выясняя, каковы области существования данных функций, заметим, что
обе функции, во всяком случае, определены в промежутке [2, + оо). Ясно, что
в этом промежутке значения / (х) и ср (х) совпадают, то есть в указанном
промежутке функции / (х) и ф (х) тождественно равны.
Пример 12. В каком промежутке тождественны функции
/(*) = * и у(х) = 10]*х?
Функция f(x) = x существует при любом значении х, то есть на промежутке
(—оо, -f-оэ)- Функция ф {x) = \0lgx существует лишь для значений #>0, то
есть на промежутке (0, +оо). Поскольку на (0, +оо) функции f (х) и ф (*)
совпадают (*=101**), то они тождественны на этом промежутке.
В заключение параграфа заметим, что иногда, определяя
функцию, не требуют, чтобы каждому значению аргумента
соответствовало только одно значение функции. В этом случае допускаются
многозначные функции—функции, у которых каждому значению
аргумента соответствует не одно, а два или несколько значений
функции. Например, функция у, определяемая из уравнения у2 = х,
* Обозначение Е (х) по начальной букве французского слова «entier», что
означает «целый» (читается «антье»).
45

двузначна, так как каждому значению х соответствуют два
значения у(у = ±У~х). Функция # = Arcsinjt является бесконечно-
значной, как хорошо известно читателю из школьного курса.
Вопросы для самопроверки и упражнения
1. Дана функция:
*/и —fsin* ПРИ —-!<*< О,
I W—\1+*2 при 0^*<2.
Найти /(1), /(- j),/(5) и/(0).
2. Функция y=f(x) определена на отрезке [а, Ь].
Каковы области определения функций:
f(x-a), f(x + a)9 f(3x) и / (j)?
В задачах 3 — 12 определить области существования функций.
3. f(x) = X3 + 5x2 — Зх+1. Отв. (—оо, +оо).
2х-\-1
4-/W = ^2_3^ + 2- °™- (-°°. Ч. С1» 2) и Р. +с°)-
5. f (*) = lgsin(jg —3)4-1^16 —jca. Отв. (3, 4] и (3 —2я, 3-я).
6. f (x) = \+x + Vx* — 9. Отв. (—оо, —3] и [3,+оо).
7. /(х) = arc cos ±^-?+ lg2*. Ome. [1, 4].
8. f(x)= Lfi±l, Отв. (—со, 0) и (0,+со).
9. f (x) =Ve (х) — х + 2х. Отв. При х = 0, ±1, ±2,...
10. f (х) = (х—3) l/"f=l?. Отв. (—оо, — 1) и [2,+оо).
V х+1
П. f(x) =У4х*-9х. Отв. (—оо,0] и L-, +оо].
12. /(^) = V2 + jc — х2. Ome. [ — 1, 2].
13. Дана функция: ф(х) = ]А — х2. Доказать, что ф[ф(*)] = |*|.
14. Дана функция: f (л:) = л:3+ — —За: . Доказать, что п—\ = f (х).
15. Тождественны ли функции:
а) f(x) = x и ф(*) = |*| на [ — 2, +2]. Отв. Нет.
б) f(x) = x и ф (*) = (!/*)* на [1, 3]. Отв. Да.
в) f(x) = x и ф(х) = }Лс2 на ( —оо, +оо). Отв. Нет.
16. Построить по точкам графики следующих функций:
а) у = х* + сх+\ при с = — 2, 0, 2.
б) у = -
1 * х—\
(х* при — 2^л:<2,
в) у = <4 при 2==сл:<3,
{4-х при 3^х^4.
§ 3. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ
Будем рассматривать функции, заданные на промежутках,
симметричных относительно начала координат: [ — а, +а], ( — я, +а)
или (— оо, +оо).
46

Рис. 22.
y=\x\
Определение. Функция y=f(x), заданная на симметричном
промежутке, называется четной, если для любых значений х из ее
области определения справедливо равенство
f(-x)=f(x).
Примерами четных функций являются: у = х2, y = cosx, y = \x\.
Они представляются графиками, изображенными на рисунке 22.
Как видно из определения и приведенных примеров, графики
всех четных функций симметричны относительно оси ординат.
Учитывая последнее, при построении графика четной функции нет
надобности строить ее по точкам для положительных и
отрицательных значений х. Достаточно построить график только для х^О
или л;^0, а затем зеркально отобразить полученную часть
графика относительно оси ординат.
Определение. Функция y = f (x), заданная на симметричном
промежутке, называется нечетной, если для любых значений х из
ее области определения справедливо равенство
f(-X)=-f(X).
В качестве примеров нечетных функций могут служить: у = л;3.
y = sinx и у= — . Их графики изображены на рисунке 23.
47

Особенностью нечетных функций является то, что их графики
симметричны относительно начала координат. Чтобы построить
график нечетной функции, достаточно сначала построить его часть
только для х^О или только для х^О. Затем двойным
отображением относительно осей координат (безразлично в каком порядке)
получается и вторая часть графика.
Неправильно было бы считать, что любая функция, заданная
на симметричном промежутке, непременно будет либо четной, либо
нечетной. Большинство функций не являются ни четными, ни
нечетными. Например, у=х+1, у = ах и у=х2 + 2х—3.
По отношению к четным и нечетным функциям справедливы
следующие утверждения:
Теорема 1. Сумма и разность двух четных (нечет-
ных) функций есть функция четная (нечетная).
Доказательство. Обозначим сумму f(x)+g(x) через F(x).
Тогда, если f(x) и g(x) четные, то
F(-x)=f(-x)+g(-x)=f(x)+g(x) = F(x).
Следовательно, F (х) по определению есть четная функция.
Если же f (x) и g{x) нечетные, то F(x) будет также нечетной,
так как
F(-x)=ft-x) + g(-x) = -f(x)-g(x) =
= -U(*) + g(*)] = -F(x)-
Совершенно аналогичное доказательство теоремы для случая
разности функций предоставляется читателю.
Теорема 2. Произведение двух четных или двух
нечетных функций есть функция четная. Произведение четной
функции на нечетную есть функция нечетная.
Доказательство. Введем обозначение F (x) = f (x) • g(x).
Тогда, если f(x) и g(x) четные, то
F{-x)=f(-x)-g(-x) = f(x)-g(x) = F(x)\
если f{x) и g(x) нечетные, то
F(-x)=f(-x).g(-x) = [-f(x)].[-g(x)] = F(x);
если, наконец, f(x) четная, a g(x) нечетная, то
F(-x)=f(-x).g(-x)=f(x)-[-g(x)] = -F(x).
Этим теорема доказана полностью.
Теорема 3. Всякая функция у =f(x), заданная на
некотором симметричном промежутке, может быть
представлена в виде суммы четной и нечетной функций,
заданных на этом owe промежутке.
Доказательство. Пусть на некотором симметричном
промежутке задана функция f(x). Рассмотрим функции:
ф(А;)--шу—- и Ц (х) = п } !2К '.
48

Первая из них будет четной, а вторая —нечетной, так как
f(_,)==/(z№)=(pW,
1>(-
¦ *)-'<-*>-'<*»-
f(x)-f(-x)
2 ~~
*W.
При этом
Пример 1. Представить функцию / (х) = 5* в виде суммы четной и нечетной
функций.
В данном случае
ф(*)=-2-[/(*)+/(-*>1=Т15*+5"*1'
Ч>М=у[/(*)-Д-*)]=-2-[5*-5-Ч.
Следовательно,
/м
5* + 5"
-5"*
В отдельных случаях функцию, заданную на [0, а], требуется
доопределить на [—а, 0) таким образом, чтобы она после этого стала
четной или нечетной на всем отрезке
[-—а, +д]. Это делается так. Пусть,
например, / (х) — любая функция,
заданная на [0, а]. Тогда функция
m/r\_J/(*) Для О^х^а,
4>(x)-\f(_x) для _а^х<0
будет четной на [—-а, +а], а функция
4\x) — \—f(—x) для — а^х<0
будет нечетной. Это легко проверить,
пользуясь определением четной и
нечетной функций. Во втором случае
доопределение возможно лишь для тех
функций f(x), для которых f(0) = 0 (иначе
не выполнится условие /(0)=—/(0)).
Заметим, что такому доопределению
функции геометрически соответствуют
рассмотренные выше способы
построения графиков четных и нечетных
функций на [ — а, +а], если они уже
построены на [0, а].
Операцию доопределения функции указанным способом иногда
называют четным или нечетным продолжением функции. На
рисунке 24 продолжения изображены пунктирными линиями.
Рис. 24.
49

Пример 2. Функцию / (х)=х2-\-х, заданную на отрезке [0, 3], продолжить
четным и нечетным образом на отрезок [—3, +3].
Очевидно, четная функция ср (х) запишется в виде
Ф(*) = {
а нечетная функция ар (л:) — в виде
х* + х
х2 — х
при
при
*(*:
'-{-:
1 + Х
х2 + х
при
при
0:
—3:
¦Х^З,
^*^3,
^х<0.
Вопросы для самопроверки и упражнения
1. Установить, какие из данных ниже функций f (х) являются четными,
а какие нечетными:
1+*
a) f{x)=x* + 3x*
Д) f М
-5хв, б) f (*) = * —*з, в) f(x)=ax + arx9 r)f(x) = \g
1-х*
х
2. Можно ли по графику функции судить о ее четности или нечетности?
3. Представить в виде суммы четной и нечетной следующие функции:
a) f(*) = *a + 3*a + 5* + 4, б) f(x)=2x, в) / (дг) = tg л:, г) /(*) = ^.
4. Выполнить четное и нечетное продолжение на всю ось функций, заданных
при х^О формулами:
а) /(*) = *, б) f (*) = sin*, в) f(x) = 3*—1.
Построить их графики.
§ 4. ПЕРИОДИЧЕСКИЕ ФУНКЦИИ
Определение. Функция у = f(x), заданная в некоторой
области, называется периодической с периодом I
(короче—Апериодической), где 1ф0, если для
любого х из этой области
числа х±1 тоже входят в
область задания функции и
при этом справедливо
равенство
f(x + l)=f(x).
Примерами периодических
функций могут служить три-
Рис. 25. гонометрические функции.
Так, sin а: и cos л: имеют
период / = 2я, a tgx и ctgA: — период 1 = п. Легко проверить, что
функция у = х — Е (х) будет также периодической с периодом /=1
(рис. 25).
Из определения периодической функции следует, что функция
периода / имеет также период — /, так как f(x—l)=f [(x — /) + /] =
= f(x). Более того, покажем, что числа вида ± /г/, где п — любое
натуральное число, также являются периодами /-периодической
функции. Действительно,
50

f(x + 2t)=f[(x + l)+l]=f(x + t)=f(x),
f(x + 3l)=f[(x + 2l) + l] = f(x + 2l) = f(x)t и т. д.,
f(x-2l)=f[(x-l)-l] = f(x-l)=f(x),
f(x-3l)=f[(x-2l)-l] = f(x-2l)=f(x), и т. д.
Часто периодом функции называют наименьший из всех
положительных периодов. Функция sin* называется 2я-периодической,
хотя ее периодами будут также числа 2&я, где k = ± 1, ±2, ± 3,—
Заметим, однако, что не всегда среди периодов функции можно
найти наименьший. Например, постоянная функция f(x)=c будет
периодической, и ее периодом можно считать любое вещественное
число аФО, так как / (х + a)=c = f (x).
Чтобы построить график l-периодической функции,
очевидно, достаточно его построить в пределах одного периода,
то есть от любого значения х до х + 1. Затем, сдвигая
построенный график вправо и влево на расстояние /, 2/,
3/,..., получим графическое представление функции на всем
желаемом промежутке.
Изучение периодической функции также достаточно ограничить
изучением ее на промежутке одного периода, так как особенности
в ее поведении будут также периодически повторяться.
Функцию f(x), заданную на некотором отрезке [а, Ь], можно
доопределить на всей числовой оси таким образом, чтобы она стала
периодической с любым наперед заданным периодом 1>Ь — а. Эта
операция называется периодическим продолжением функции.
Пример 1. Построить для функции / (х) = х2, заданной на
отрезке [—1, +1], периодическое продолжение с периодом 21 (1> 1).
Прежде всего данную функцию следует доопределить на
промежутках [—/, —1) и (1, /]. Это можно сделать различными
способами, однако с таким расчетом, чтобы ф(—/) = ф(/). Пусть,
например,
1 при —/^л:<[—1,
(f(x) = \x2 при — l^x^l,
1 при 1<л:^/ (рис. 26).
5!

Полагая для любого значения х из [—/, +/]
Ф (х ± 2/) = ф (х),
получим периодическое продолжение функции на [—3/, +3/].
Положив ф (л:±4/) = ф (х)у ф (х± 6/) = ф (х) и т. д., можем получить
периодическое продолжение (периода 21) функции ф (х) на всю
числовую ось. При этом на [—1, +1] будет ф (х) = / (*).
Заметим, что если функция f (x) первоначально задана на отрезке
[а, Ь] и при этом f(a)=f(b), то f(х) допускает /-периодическое
продолжение на всю ось и с периодом 1 = Ь — а. Предоставим
читателю самостоятельно убедиться в этом.
Пример 2. Функция f(х) с периодом 2/ задана на всей оси.
Какой период имеет функция ф (х) =/ (ах), где а > 0 —заданное
положительное число?
2/
Покажем, что функция ф (х) имеет период —. Действительно,
для любого х имеем:
Если, в частности, положить я = —, то ф (х) будет иметь период 2л.
Вопросы для самопроверки и упражнения
1. Определить, какие из данных функций являются периодическими, и
установить их наименьший положительный период:
X
а) f (x) = sin *+tg -=-. Отв. 2я-периодическая.
б) f (x)—cos2x. Отв. я-периодическая.
в) f (x)=cosx2. Отв. Непериодическая.
г) /(*) = |/tg;t. Отв. я-периодическая.
д) f(x)==sin2*. Отв. я-периодическая.
е) f (х) = A sin Хх + В cos Хх (X > 0). Отв. — -периодическая.
2. Доказать, что если f (x) есть /-периодическая функция, то функция ф (t) =
-'(f)
будет р-периодической.
3. Для функции
( л*, _1^д;^
/м- , 1
построить периодическое продолжение с периодом 2/ (/> 1).
4. Можно ли по графику функции судить о ее периодичности или
непериодичности?
§ 5. ПОНЯТИЕ ОБРАТНОЙ ФУНКЦИИ
В курсе средней школы рассматриваются конкретные примеры
обратных функций: логарифмическая функция как обратная
показательной функции и обратные тригонометрические функции. Здесь
рассмотрим понятие обратной функции в общем случае.
52

Пусть на некотором промежутке X* определена функция y = f (х),
значения которой сплошь заполняют некоторый промежуток Y на
оси ординат. Это значит, что для любого значения у = у0 из
промежутка Y существует такая точка х0 из промежутка X (одна или
несколько), что f(x0) = y0. Тем самым каждому значению у из Y
ставится в соответствие одно или несколько определенных значений
х из X. Значит, х можно рассматривать как функцию от г/,
определенную на промежутке Y, со значениями в Ху то есть х = ср(у).
Отыскание аналитического выражения функции х = ср (у) сводится
к решению уравнения y=f(x) относительно х.
Функция х = ф (у) называется обратной функцией по отношению
к функции y=f(x).
Пример 1. Функция у = 2* + 3 определена на (—оо, +оо). Областью ее
¦ У-3
" 2 '
значений будет также (—оо, +оо). Обратной функцией будет функция * =
определенная на (—оо, + оо).
Пример 2. Для функции у = х2 обратными будут две функции: х=Уу и
х——У у, или, как иногда говорят, двузначная функция х=± У у, существующая
только для у^О.
Перейдем теперь к выяснению вопроса о взаиморасположении
графиков прямой и обратной функций. Так как связь между
переменными х и у в прямой функции y=f(x) и обратной ей функции
* = ф(#) °Дна и та же> то графики
этих функций совпадают. Если же
обратную функцию представить в
обычно принятых обозначениях
(аргумент обозначить через х> а
функцию—через у, то есть записать
*/ = ф(х), при этом функцию у = ф (х)
мы по-прежнему будем называть
обратной по отношению к функции
y=f(x)) и если аргумент снова
откладывать на горизонтальной оси,
то график обратной функции
повернется. Чтобы получить его новое
расположение, нужно перегнуть
плоскость чертежа по биссектрисе первого
и третьего координатных углов. Можно сказать также, что график
обратной функции у = ср (л:) является зеркальным отображением
графика прямой функции y=f(x) в биссектрисе первого и третьего
координатных углов. Графическое изображение функций,
рассмотренных в примерах 1 и 2, а также им обратных функций, дано на
рисунках 27 и 28.
Рис. 27.
* Здесь X может обозначать промежуток любого типа: Х = [а? 6], Х = (а, Ь)
и пр. То же относится и к Y.
53

Рис. 28. Рис. 29.
Пример 3. Какая функция у = у(х) будет обратной для функции у=х2-\-
+ 4x7 Построить ее график.
Из уравнения х2 + 4х — # = 0 находим: х = —2 ± У4-{-у. Значит, обратных
функций две. Если обозначения х и у поменять местами, то эти две функции
примут вид:
г/ = -2 + УТ+Я у = — 2-/4 + *.
Так как графики прямой и обратной функций взаимно симметричны относительно
биссектрисы первого и третьего координатных углов, то, построив один из
графиков, легко получить и второй. Для построения графика прямой функции,
представляющего собой параболу, замечаем, что
л:2+4* = (л; + 2)2-4,
то есть вершина этой параболы находится в точке (—2; —4) и ветви направлены
вверх. Если еще учесть, что она проходит через начало координат, то построение
графика не вызовет затруднений (рис. 29).
Вопросы для самопроверки и упражнения
1. Для заданных ниже функций найти обратные. Построить графики тех и
других функций, используя свойства обратных функций:
а) у = 2х, б) у = х2-2, в) # = 2^> г) ^ = "7' Д) i^2*-1» е) У = ]о&х.
2. Возможен ли случай, когда графики прямой фрнкции y = f(x) и ей
обратной функции у = ц)(х) совпадают?
3. Найти обратную функцию для функции
1х при —оо < х<С 1,
х2 при 1 ^ х ^ 4,
2х при 4<*< + оо.
Построить графики прямой и обратной функций, расположив их на одном чертеже.
1 — х
4. Доказать, что функция у= 1 обратна сама себе, то есть что обратная
1 -\-х
функция для данной функции тождественна с ней,
U

5. На промежутке (0, +°°) задана функция у = хп (п — натуральное). Найти
обратную функцию на этом промежутке и установить, при каких значениях х
значения прямой функции больше значений обратной функции, а при каких —
меньше.
§ 6. ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
После введения понятия функции внимание математиков было
обращено на изучение большого количества различных
функциональных зависимостей. В результате непрерывного развития математики
и в настоящее время появляются все новые и новые классы
функций. Среди всего многообразия функций исторически выделились
функции, отличающиеся своей простотой и наиболее широкой
областью применения. Это так называемые простейшие элементарные
функции. Ссновное значение простейших элементарных функций
состоит в том, что они составляют базу для изучения более
сложных функций, являясь в большинстве своем составленными
элементами последних. Поэтому уже в средней школе первое знакомство с
функциями начинают с изучения простейших элементарных функций.
Поскольку в дальнейшем нам неоднократно придется прибегать
к иллюстрации многих математических понятий на простейших
элементарных функциях, то здесь мы дадим краткое описание
последних, оставаясь на «школьном уровне». В главе IV наши
сведения об элементарных функциях будут существенно дополнены.
К простейшим элементарным функциям обычно относят
следующие:
1. Степенная функция, то есть функция вида у = х1Х, где fx — любое
вещественное число. Зта функция имеет то или иное конкретное
содержание в зависимости от значений \i. Рассмотрим возможные случаи.
а) Пусть [х есть целое положительное число, \i = n. Тогда
функция у = хп существует на (—оо, +°°) при любом п и ее график
проходит через начало координат и точку (1,1)- При различных
значениях п получаются различные кривые (рис. 30). Среди них будут:
у=х (п=1) — прямая линия, проходящая через начало
координат и образующая с осью ОХ угол в 45°. Эта прямая является
биссектрисой первого и третьего координатных углов.
у = х2 (п = 2) — парабола. Проходит через начало координат,
симметрична относительно оси OY.
у=х3 (я = 3)-—кубическая парабола. Расположена в первой и
третьей четвертях симметрично относительно начала координат.
у^=хп (п — любое четное число) — кривая, расположенная в первой
и второй четвертях симметрично относительно оси OY (в силу
четности функции). По виду график напоминает график функции у = х2.
у = хп(п — любое нечетное число) —кривая, расположенная
впервой и третьей четвертях симметрично относительно начала
координат (в силу нечетности функции). По виду график напоминает
график функции у = хг.
б) Пусть [а — целое отрицательное число, [х = — /г. Тогда имеем
дробно рациональную функцию y = x~n=-li. Она существует для
?5

Рис. 30.
всех х ф0, то есть на промежутках (—оо, 0) и (0, +оо). Ее
графиками будут (рис. 31): г/ = 1(&=1)~гипербола. Расположена
в первой и третьей четвертях и в силу нечетности функции
симметрична относительно начала координат. Как видно из чертежа,
биссектрисы координатных углов у = х н у = — х будут также осями
симметрии.
У = ~& (п = 2) — кривая, расположенная в первой и второй
четвертях симметрично относительно оси OY.
Рис. 31,
56

у=—д (п = 3) — кривая, расположенная в первой и третьей
четвертях симметрично относительно начала координат.
у = ~п (п — любое четное число) —кривая, расположенная в первой и
второй четвертях симметрично относительно оси OY. По виду
график похож на график функции у=-^.
у = — (п — любое нечетное число) — кривая, расположенная в
первой и третьей четвертях симметрично относительно начала
координат. По виду график похож на график функции у = -^.
в) Пусть \i — положительное дробное число, то есть |л = —, где
т и п — натуральные числа, не имеющие общих множителей. Тогда
т
имеем функцию: у = хп = ухт. При этом будем считать, что при
извлечении корня четной степени из положительного числа берется
его арифметическое (положительное) значение. При нечетном п
подкоренное выражение может быть любого знака. Следовательно,
областью существования будет (—оо, +оо). При четном п число т
будет нечетным и корень будет иметь вещественные значения только
для лг^О. Следовательно, в этом случае областью существования
будет [0, +оо).
Рассмотрим частные случаи функции вида у = угхт.
Функция у=у х (т = 1) является обратной функцией по
отношению к функции у = хп. Следовательно, графики функций y = Vx
при различных п симметричны относительно биссектрисы у = х
графикам функции у = х? при соответствующих п. На рисунке 30 они
изображены пунктирными линиями.
Функция у = угхт при нечетных пит будет нечетной и ее
график расположится в первой и третьей четвертях симметрично
относительно начала координат. Если п нечетное, а т четное, то
функция будет четной и ее график будет симметричен относительно оси
OY, располагаясь в первой и второй четвертях. Наконец, если п
четное, а т нечетное, то функция определена только при лг^О,
а ее график расположится в первой четверти. Заметим также, что
поведение графика функции у=-\/~хт еще существенно зависит от
того, будет ли — >1 или — <1 (рис. 32).
г) Пусть \х—отрицательное дробное число, \х = . Тогда
функция представится в виде
-- 1
Ухт
Ы

Графики функции у=х п
У ¦
т и п - нечетн.
т-четм. , п-нечетн.
Рис. 32.
w - нечетн.
л -четн.
Задачу построения графиков таких функций при различных пит
можно значительно облегчить, используя построенные графики для
функций вида у = -\/'хт. В каждой точке х ордината функции
у=-^=. равна обратной величине ординаты функции у = у хт.
J~xm
\
Общий вид графиков функций у = л— Дан на рисунке 33.
В случае иррационального jx необходимо сначала определить,
что следует понимать под символом х11. Этим мы займемся несколько
позже, после ознакомления с понятием предела и непрерывности
функции (см. § 8, гл. IV).
Графики функции у=х~п
у A у\
en и п- нечетн.
О
У*
X О
т-четн., п -нечетн.
Рис. 33.
т-нечетн.;
п - четн.
53

2. Показательная функция
где а—любое положительное вещественное число (случай, когда
а=\, обычно не рассматривается, так как не представляет
никакого интереса).
Однако следует иметь в виду, что мы еще не дали определения
степени с иррациональным показателем. Когда это определение
будет дано (§ 8, гл. IV), мы увидим, что показательная функция
ах определена при всгх х, то есть областью существования
показательной функции является вся числовая ось (—оо, +оо). На рисунке
34 изображены графики показательной функции у = ах при
различных а.
Характерной особенностью показательной функции является то,
что она нигде не обращается в нуль, каково бы ни было число
а>0. Иначе говоря,
график показательной функ- У[
ции нигде не пересекает
ось ОХ.
3. Логарифмическая
функция
y = \ogax,
где а —любое
положительное число (отличное от 1).
Поскольку нуль и
отрицательные числа
логарифмов не имеют, то
областью существования
логарифмической функции
будет (0, +°°).
Логарифмическая функция по
определению является
обратной по отношению к
показательной функции.
Поэтому ее график легко представить по графику показательной
функции. На рисунке 34 график логарифмической функции изображен
пунктирной линией.
4. Тригонометрические функции
i/ = sina;, y = cosx, y = tgx, r/ = ctgA:, у = secх и у = cosecx.
Здесь аргумент х — числовая переменная, которую вовсе не
обязательно изображать в виде угла или дуги окружности. Однако под
значением тригонометрической функции от числовой переменной х
понимают значение той же тригонометрической функции от угла,
радианная мера которого равна х (рис. 35 и 36).
Характерной особенностью тригонометрических функций
является их периодичность. Функции tg* и ctg* имеют период я, а
Рис. 34.
59

Рис. 35.
остальные четыре функции — период 2я. Областью существования
для функций sin л: и cos л: является вся числовая ось (— оо, + оо).
Функции tg* = ^^ и secx = существуют для тех значений х,
при которых cosх Ф О, то есть для л;^ (& + у) я, а функции
ctgA:=^-^ и cosec;t = -:— существуют для хфктс(к = 0, ±1, ±2,
±3,..sjn*
5. Обратные тригонометрические функции
y = avcsinx1 r/ = arccosA:, r/ = arctgA; и y = arcctg.x;.
Рассмотрим функцию y = sinA\ Она определена на ( — оо, +оо),
и ее значения сплошь заполняют отрезок [—1, +1]. Это значит,
что для любого у0 из [—1, +1] найдется такое х0, что sinx0 = yQ.
В силу периодичности sinx множество значений х,
удовлетворяющих уравнению sinx = y0, будет бесконечным. Таким образом,
обратная функция для sin x является многозначной функцией с
областью определения [—1, +1] и областью значений (— оо, +оо).
Эту обратную функцию обозначают x = Arcsin# или в обычных
обозначениях аргумента и функции y = Arcsin.x;. Использование
такой функции затруднительно из-за ее многозначности, так как
Рис. 36.
60

неизвестно, какое из многих значений следует в том или ином
случае брать. Чтобы этого избежать, выберем такой промежуток
на оси OY, чтобы в этом промежутке каждому значению аргумента х
из [—1, +1] соответствовало одно и только одно значение у. Так
как при изменении х от —у до +-о~ Функция y — sinx по одному
разу принимает все значения от —1 до +1, то условились для
каждого значениях из [—1, +1] выделить то
значение y = Avcsmx, которое содержится в
промежутке —у, +-у • Такие значения Arcsinx
называются главными значениями и
обозначаются arcsinx.
Функция у = гхс$\х\х является однозначной
функцией на [—1, +1], обратной для функции
у = sin х, если последнюю считать заданной только
на —у, +-S- • Ее графиком является часть
кривой f/=Arcsinx, выделенная на рисунке 37
сплошной линией. Чтобы получить график
функции r/ = arcsinA:, достаточно зеркально отобразить
в биссектрисе первого и третьего координатных
углов график функции y=sinx,
рассматриваемый на отрезке —у, +-тН- Это достигается
поворотом чертежа на 180° вокруг вышеуказанной
биссектрисы.
Все остальные значения функции # = Arcsinx
можно получить с помощью формулы Arcsinx =
=Ая + (— l)*arcsin.x:, где k = 0, ± 1, ±2, ±3, ....
Аналогичным образом определяется
многозначная функция у = Arccos х как обратная по
отношению к функции у = cos х. Ее значения из
промежутка [0, я] называются главными
значениями и обозначаются arccos x. График функции
у=Arccos х изображен на рисунке 37. Его часть,
соответствующая функции у = arccos x, выделена
сплошной линией. Все остальные значения арккосинуса выражаются
через главные значения следующим образом:
Arccos х = 2kn±: arccos х, где k = 0, ± 1, ±2, ±3, ...
Функция y = krcigx является обратной по отношению к функции
y = igx. Так как последняя принимает все значения из ( — оо, + оо),
то и областью определения функции y=krctgx будет вся
ось (— со, +оо). В силу периодичности igx каждому значению у
соответствует бесконечное множество значений x=hxcigy.
Следовательно, функция y = krcigx является также многозначной. Ее
значения из промежутка (—у, +у) называются главными и обозначаются
6J

*/=arctg x. Все остальные значения Arctg* могут быть вычислены
по формуле
Arctg л; = arctg я + ^я, где 6 = 0, ±1, ±2, ±3, ...
График функции # = arctg x (рис. 38) получается уже известным
нам способом псстрсения графиков обратных функций. Областью
ее определения является (-—со, +оо), а областью значений
(-f +т)-
Аналогично, многозначная функция */ = Arcctg x определяется
как обратная по отношению к функции y = cigx. Ее главные
значения составляют интервал (0, я) (рис. 38). Все значения Arcctg x
выражаются через главные значения следующим образом:
Arcctg x = arcctg я+ foi, где & = 0, ±1, ±2, ±3, ...
Из определения обратных тригонометрических функций следует,
что
sin (arcsin х) = х, cos (arccos x) = х,
tg (arctg x) = х, ctg (arcctg x) = х.
И так как
cos f-о- — arcsin x) = sin arc sin x, 0 <: у — arcsin x^ я,
ctg (4 — arctg x) = tg arctg x = x, 0 < ~ — arctg л; < я,
то
arccos x = -о- — arcsin x и arcctg *=-o-—arctg a:.
2
Далее, пользуясь формулами связи между тригонометрическими
функциями, получим:
sin arccos л; = К1 — cos2 arccos x = V1 — *2,
cos arcsin x = Yl —sin2 arcsinx =V\ —x2y
sin arcsin x x
tg arcsin * =
cos arcsin x Y\ — x2'
Учитывая, в каких четвертях находятся главные значения
arcsin л: и arccos x, легко проверить, что во всех трех формулах
следует брать положительное значение радикала.
Если над простейшими элементарными функциями производить
различные арифметические действия, то будем получать новые
функции.
6. Целая рациональная функция, или многочлен,
у=а0хГ + а^-1 + а2хп~2 +... + ап_±х + ап,
где п — любое натуральное число, указывающее на степень много*
члена, a aQ, аъ а2, ..., ап — любые вещественные числа — коэффи-
62

циенты многочлена (а0 ^ь 0). Эта функция названа так потому, что
получается в результате только рациональных действий сложения
и умножения над аргументом х и постоянными а0, аг, а2, .. *, ап.
Как легко видеть, областью существования целой рациональной
функции является вся числовая ось (— оо, +оо).
Рассмотрим несколько частных случаев.
а) Если я=1, то имеем многочлен первой степени, или линейную
функцию: у = а0х-\-а1. При любых значениях коэффициентов а0 и аг
графиком этой функции будет прямая линия (рис. 39). В частности,
y = x(aQ=l, 0i = O) — уравнение биссектрисы первого и третьего
координатных углов.
График функции у = а0х(а1 = 0) — прямая, проходящая через
начало координат. Для каждой точки отношение ординаты к абсциссе
равно а0. Число а0 есть тангенс угла между этой прямой и
положительным направлением оси ОХ. Его иначе называют угловым
коэффициентом прямой.
График функции у = а0х-\-а1 — прямая с угловым
коэффициентом я0, пересекающая ось ординат в точке аг. Эту прямую можно
получить параллельным сдвигом на \аг\ единиц прямой у = а0х
вдоль оси OY вверх (при %>0) или вниз (при аг<с0).
б) Если я = 2, то имеем многочлен второй степени, или
квадратичную функцию:
у = а0х2 + агх + а2.
(1)
Покажем, что при любых значениях коэффициентов a0i аг и а2
графиком этой функции является парабола, но ее расположение
на плоскости зависит от
этих коэффициентов. Нач- у^
нем с более простых
случаев.
Рис. 38.
Рис. 39.
т

При а0=1 > а1 = а2 = 0 имеем степенную функцию: у = х2. Ее
графиком, как упомянуто выше, является парабола, симметричная
относительно оси OY, направленная вверх и проходящая через
начало координат (см. выше рис. 30). Точка (0, 0) пересечения
параболы с осью симметрии называется ее вершиной.
При произвольном а0 и а1 = а2 = 0 имеем функцию: у = а0х2. Ее
график есть также парабола, симметричная относительно оси OY,
проходящая через начало координат (рис. 40). Однако направление
ее зависит от знака а0. Парабола направлена своими ветвями вверх
при а0>0 и вниз при а0<.0. Абсолютная величина а0 сказывается
на степени «расхождения» ветвей. Чем меньше |а0|, тем ветви
больше «расходятся», как это видно из рисунка 40. Вершина
параболы у = а0х2 по-прежнему в точке (0, 0).
Рассмотрим функцию y = a0x2 + d (то есть полагаем в (1) а± = 0,
a2 = d). Ее графиком является парабола, получающаяся из графика
параболы у = а0х2 сдвигом на \d\ вверх (при d>0) или вниз (при
d<0) (рис. 41). Соответственно и вершина перемещена в точку
(0, d). Направление и ось симметрии остаются такими же, как и
у параболы y = aQx2.
Рассмотрим теперь функцию y = aQ(x-\-c)2-\-d. Легко убедиться,
что ее график получается из графика функции y = a0x2-\-d сдвигом
на |с| вправо (при с<0) или влево (при с>0) (рис. 42). Это есть
также парабола, симметричная относительно прямой х——с. Ее
вершина находится в точке (—с, d).
Возвратимся к общему выражению квадратичной функции (1).
Ее можно преобразовать к
виду
A y = a0(x + c)2 + d. (2)
Рис. 40. Рис. 41,
64

?яс. 42.
Действительно, так как пъ условию а0 ^ 0, то
у = а0х2 + а1х + а2 = а0{х2 + <^х+^.
К трехчлену, находящемуся в скобках, применим известный способ
выделения полного квадрата суммы двух членов. Рассматривая х2
как квадрат первого члена (отсюда вытекает, что первым членом
будет х), а — х как удвоенное произведение первого члена на вто-
рой (отсюда заключаем, что произведение первого члена на второй
равно ^-х и вторым членом будет —-], получим:
Положив в последнем выражении ^=^и -^^p^-==df получим (2).
Следовательно, можно утверждать, что квадратичная функция (1)
представляет собой параболу, симметричную относительно прямой
X==~~W и напРавленнУю вверх (при а0>0) или вниз (при а0<0).
Вершина этой параболы находится в точке (—-~-t а<>а*~~а^
в) Если /г = 3, то имеем многочлен третьей степени, или
кубическую функцию, у = а0л:3-)-а1х2 + а2л: + «з- В частности, график
у=х6 (а0=1» о1=а2 = а3=0) — кубическая парабола, рассмотренная
нами выше.
65

Можно было бы провести более глубокое исследование
многочленов различных степеней. Однако теми средствами, которыми мы
сейчас располагаем, это сделать затруднительно. Средства
математического анализа значительно облегчат эту работу.
7. Дробно-рациональная функция
= а°ХП + а1ХП1 "J" а2*П~2 + "' + дя-1* + а*
У Ь0хт + М"1"1 + Ь2хт-* + ...+ bm_lX + bm
(я0 ^ О, Ьо^?0), то есть функция, представляющая собой отношение
двух многочленов. Область существования ее составляют все точки х,
не являющиеся корнями знаменателя. Нами уже рассмотрен частный
случай дробно-рациональной функции у=-ц. К рассмотрению
остальных случаев вернемся также после изучения дифференциального
исчисления.
Рассмотренные нами элементарные функции будут неоднократно
встречаться в дальнейшем. Сведения о них, данные здесь в порядке
первого знакомства, будут постепенно пополняться новыми
результатами исследования.
Можно получать новые функции и так называемым способом
наложения (или суперпозиции). Этот способ состоит в том, что
вместо аргумента некоторой функции подставляется новая функция
от другого аргумента. Например, наложение функций z=y2 и
y = sinx дает функцию z = sin2A;. С другой стороны, функцию
у = lg3 (2л:2 + 5)1/» можно рассматривать как результат наложения
функций: r/ = z3, z = lgtt, u = Yv и v==2x2 + 5.
Функции, получаемые из более простых функций способом
наложения, обычно называют сложными функциями. В первом из наших
примеров z есть сложная функция от х. Переменная у в этом
примере играет роль промежуточной переменной, так как она
является функцией по отношению к х и аргументом по отношению
к z. Во втором нашем примере у есть сложная функция от х,
причем зависимость у от х осуществляется посредством уже трех
промежуточных переменных: z, и и v.
В общем виде, если на [а, Ь] определена некоторая функция
z = (f(x) с областью значений, составляющей [с, d] (то есть
c^z^d), и на [с, d] определена некоторая функция y = f(z), то у
будет сложной функцией от х, a z — промежуточной переменной.
Сложную функцию можно записать так: f[<p(x)]. Если y=f(x),
где я = <р(?) и t=ty(u), то сложная функция у от и запишется
в виде у=/{<р №(«)]}.
Заметим, что введение термина «сложная функция» относится
лишь к способу задания функции. С его помощью можно более
обозримо описать функциональную зависимость. К самой же
природе функциональной зависимости этот термин никакого отношения
•«.е имеет. Одну и ту же функцию можно рассматривать и как
непосредственно заданную, и как сложную. Например, функцию
y=ztg3x можно считать и сложной, полагая y = tgu, где и = 3х.
66

Все функции, получаемые из простейших элементарных функций
путем четырех арифметических действий или наложений,
последовательно примененных конечное число раз, составляют так
называемый класс элементарных функций. Например,
у = lg8 arctg 2VY + sin 3x.
8. Функция f (x) = \x\ (рис. 43) тоже относится к числу
элементарных. Она получается с помощью наложения простейших
элементарных функций по формуле
Если же воспользоваться
определением абсолютной величины, то можно
записать, что
| х при х^О,
' w—J _х при А:<о. о\ х~
Эта функция определена на всей оси |
(— оо, +оо).
Существуют также функции, кото- рис 43.
рые нельзя выразить через простейшие
элементарные функции вышеуказанным способом. Про такие
функции говорят, что они не выражаются через элементарные функции
в конечном виде. С ними мы познакомимся в дальнейшем при
изучении рядов и интегралов.
В заключение параграфа снова вернемся к вопросу о построении
графиков функций. Если дана какая-то функция y = f (x), то,
прежде чем приступить к построению ее графика, следует выяснить
вопрос о ее четности и периодичности. Как уже отмечалось раньше,
это может значительно сократить работу.
Иногда при построении графиков функций можно использовать
уже известные графики. Так, если график А функции y = f(x)
построен, то различными передвижениями и деформацией его можно
получить графики многих других функций (рис. 44).
а) График функции y = f(x + a) получается сдвигом графика А
параллельно оси ОХ на |я| единиц вправо (при а<0) или влево
(при а>0).
б) График функции y = f(x) + b получается движением графика А
параллельно оси OY на \Ь\ единиц вверх (при fc>0) или вниз
(при 6<0).
в) График функции y = kf(x) (k>0) получается из графика А
умножением ординат всех точек графика А на число k. Это будет
либо так называемое растяжение ординат в k раз (при k> X), либо
сжатие в -г- раз (при k<\).
г) График функции y=f(kx) (k>0) получается как бы сжатием
или растяжением (к оси OY) графика А в направлении,
параллельном оси ОХ. Абсциссы всех точек уменьшаются в k раз (при
67

i
\ 1
\
\
\ /
/ о
\ / /
/
' a
1
f
X
Рис. 44.
&>1) или увеличиваются в -г раз (при &<1)> а величины
соответствующих ординат сохраняются.
д) График функции f(x)+g(x) получается добавлением в каждой
точке к ординате функции f (x) соответствующей ординаты
функции g(x).
Пример 1. Построить график функции у = 3cos(2*4-1) путем движения
и деформаций графика функции r/ = cos*.
Предположим, что график функции у = cos х уже построен. Измеряя ординаты
отдельных точек графика этой функции и увеличивая их в три раза, получим точки
графика функции y — 3cosx. Если затем абсциссы всех точек полученного графика
уменьшить в два раза, не меняя ординат* то получим график функции у = 3 cos 2х. Так
как cos(2x+l)=cos2 (*+тг). то,
двигая график функции г/= 3 cos 2*
параллельно оси ОХ влево на
-^ единицы, получим искомый
график (рис. 45).
Пример 2. Построить на
одном чертеже графики следующих
функций:
f(*)«2*f ?(*) = 2-4л:, f(x)+
+*(*). f (*)-*(*). f(*+2).
y*3cos2x
(|)И?(2*).
Рис. 45.
8
Сначала строим обычным
способом по точкам'графики функций
f(x) = 2x и g(x) = 2 — 4x.
Для построения графиков
функций f(x)+g(x) uf(x)—g(x)
воспользуемся тем, что ординаты
последних в каждой точке х
равны соответственно сумме и
разности ординат графиков функций

f(x) и g (x) в той же точке. На чертеже точки
графиков функций P{x)-\-g{x) и f (*)— g (x),
соответствующие различным абсциссам х% могут быть
отмечены либо после вычисления соответствующих
ординат, либо непосредственно с помощью
чертежных инструментов.
График функции f{x+2) получается сдвигом
графика функции f (х) влево на две единицы.
Рис. 46.
Рис. 47.
График функции g(|-) получается «растяжением» графика функции g (*), то
есть если, сохраняя ординаты графика функции g (x)t абсциссы увеличить в два раза.
График функции g(2x) получается «сжатием» графика функции g (x), то есть
если, сохраняя ординаты графика функции g (x)t абсциссы^ уменьшить в два раза.
На рисунке 46 изображены графики всех этих функций.
Пример 3. Построить графики функций:
a) y = \g\x\; б) 0 = sin*+|sin*|; в) у = U+2 \.
а) Строим сначала график функции y = \gx. Так как для х>0 будет \х\=х
я \g\x\ = \gxt то график функции y = \g\x\ на положительной части оси (О, -fco)
совпадает с графиком функции y = [gx. Поскольку для любого хфО имеем
| — х | = |*1 и *g | — * I = *g I * I» т0 функция у = lg | х | является четной.
Следовательно, ее график симметричен относительно оси OY. Воспользовавшись этим,
достраиваем часть графика функции y = ig\x\t соответствующую
(рис. 47).
б) Строим сначала график функции y = sinx. Так как
{ sin х при sin х ^ О,
|sinx| = \ , ^л
(— sinx при sin *< О,
то
{2 sin х при sin х ^ О,
О при sinje<0.
значениям х <6
Рис 48.
69

Удваивая неотрицательные ординаты графика функции y = sinx и принимая # = 0
в точках, где sinx<0, получим график функции i/ = sin лс +1 sin д: | (рис. 48).
в) Строим график функции t/ = x + 2. Так как
\х+2
'-{-,
-(я+ 2) при
то график функции # = 1*4-21 на
у *
*4-2^0, т. е.
*4-2<0, т. е.
при
при
х^—2,
*<—2,
Рис. 49.
-2, 4-°°) совпадает с графиком функции
#=#+2, а на ( — оо, —2) получается
симметричным отображением последнего
относительно оси ОХ (рис. 49).
Вопросы для самопроверки
и упражнения
1. Построить графики степенной
функции у = хп при:
а) /1=1, 3, 5; б) л = 2, 4, 6.
2. Построить графики степенной
функции у — хп при:
а) л= —1, —3; б) л= — 2, —4.
3. Построить графики функции
т j—
# = у xk при:
а) /л = 2, &=1; б) т = 4, Л=1; в) т = 3, /г=1; г) т = 5, 6=1;
д) т = 2, ? = 3; е) т = 3, ? = 2; ж) т = 4, /г=*2; з) т = 3, /г = 4.
4. Построить графики функций: a) # = lg(— х); б) */= —Igx.
б. Построить графики функции у*=Асо&х при Л =2, —2, —1, 3.
6. Построить графики функций:
а) # = 21-*'; 6)# = |sinx|; в) г/ = sin | л; |; г) г/ = | х3 — 1 |.
7. Зная график функции # = /(*), построить графики функций:
а) */=-/(*); б) уН/(*)|; в) y=f(-*Y> г) у=/(|х|).
8. Построить графики следующих функций: f (я) = | * | — я, g (х) —| х 14- *,
¦2) и gf-o-). Построение выполнить на одном
чертеже.
9. Путем движения и деформации графика функции # = sm* получить
график функции у = 2 sin (3*4-2).
10. Можно ли из функций у= — и и sin а: составить функцию способом
у и2—2
наложения? Отв. Нет.
11. Определить целую рациональную функцию 2-й степени по условиям:
/(1) = 0,/(2) = Зи/(0) = 1.
Указание. Написать в общем виде целую рациональную функцию 2-й
степени f (x) = ax2-{-bx+c. Затем, используя условия задачи, найти а, Ь и с.
12. Из каких простейших элементарных функций с помощью наложения
могут быть получены следующие функции:
a) t/ = sin2 3*; б) */=У>4-2)3; в) у = а*ис ">***;
г) */= igз^тгг; д) #=cos2sin2*2; e) у^хП (Jg*+ *)3?
/M+sM. /(*)-*(*). /(*-

ГЛАВА Iff
ТЕОРИЯ ПРЕДЕЛОВ
Начало изучению понятия предела положено в средней школе.
Там с помощью предельных переходов определяется длина
окружности, площади боковых поверхностей и объемы цилиндра и
конуса, площадь поверхности и объем шара. Понятие предела
использовано также при определении суммы бесконечно убывающей
геометрической прогрессии. Здесь нам предстоит изучить теорию
предела на более общей основе, с необходимой глубиной и
строгостью, что позволит расширить круг приложений теории пределов
к решению теоретических и практических задач.
Понятие предела вместе с понятием функции составляют основу
математического анализа. Все остальные разделы курса так или
иначе используют теорию пределов.
§ 1. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ И ЕЕ ПРЕДЕЛ
Пусть каждому натуральному числу п сопоставлено
вещественное число, обозначенное хп. Тем самым нам заданы некоторые
вещественные числа, определенным образом перенумерованные: хг
имеет номер 1, х2 — номер 2, и т. д. Тогда говорят, что задана
последовательность чисел, или числовая последовательность:
%1* %2* *3» ' * * ¦ Xfit • • • ^1/
Числа, составляющие последовательность, называются ее
членами, а хп — общим или п-м членом последовательности.
Из способа образования числовой последовательности видно,
что характерным для каждой последовательности является
установление порядка следования чисел в ней: для любого п число xn+i
следует за числом хп, а хп предшествует хп+\. Что. же касается
значений этих чисел, то хп+\ может быть больше, меньше и
равно хп. Если в данной последовательности изменить порядок
следования членов, то получим уже другую последовательность. Так,
например, числовые последовательности
2, 4, 6, 8, 10, 12, ..., 2/z, 2п + 2, ...,
4, 2, 8, 6, 12, 10, ..., 2/1 + 2, 2/1, ...
являются различными, хотя и состоят из одинаковых чисел.
71

В отличие от числового множества, у которого все элементы
различны, числовая последовательность может иметь среди своих
членов и одинаковые. Иначе говоря, множество чисел, из которых
составлена та или иная последовательность, может быть
бесконечным, конечным и, в частности, может состоять даже из одного
элемента, например:
я, Ь, а, Ь, a, fe, ..., я, Ь, ..., (2)
я, а, а, а, а, а, ..., а, а, ... (3)
Числовая последовательность (1) считается заданной,
если указано правило или закон, с помощью которого по
номеру места в последовательности всегда можно назвать
число, стоящее на этом месте* Таким образом, числовое
значение члена последовательности хп зависит от п, то есть является
функцией от /г. Сама числовая последовательность может
рассматриваться как функция, заданная на совокупности всех
натуральных чисел (функция натурального аргумента). С другой стороны,
если задана функция натурального аргумента /(/г), то ее значения
#n = f (л) образуют числовую последовательность. Так, если / {п) =
=—г-г, то, давая в равенстве хп = , . переменной п натураль-
ные значения 1, 2, 3, ..., получим последовательность:
_ 1 __2^ __j^ _ п
xi 2 ' *2 3 ' *9 4 • *" ' Хп п -J-1 ' * * * ( '
Общим членом хп = ———— задается последовательность
О, 1, 0, i, О, I, 0, .... 1 + (~1)П, .... (5)
а последовательность
2, 4, 8, 16, 32, ..., (6)
состоящая из степеней числа 2 (с натуральным показателем), имеет
общий член хп = 2п. Последовательность (3) может быть задана
общим членом хп = а, а выражение общего члена последовательности
(2) может быть дано в виде
( а, если п — нечетное,
\ Ь, если п — четное
или
хя=±[а + Ь + (-1Г(Ь-а)].
Перейдем теперь к основному в математическом анализе понятию
предела числовой последовательности.
Определение. Число а называется пределом числовой
последовательности (1), если для любого сколь угодно малого
положительного числа е можно указать такое натуральное число N, что
72

для всех членов последовательности с номерами n>N выполняется
неравенство
\хп—а К е. (7)
Иначе говоря, число а будет называться пределом
последовательности (1) в том случае, если, какое бы малое положительное
число е мы ни взяли, абсолютная величина разности хп — а, начиная
с некоторого п, станет и при дальнейшем возрастании п останется
меньше этого е.
Тот факт, что последовательность (1) имеет своим пределом
число а, обозначается так:
limxn = a или хп-+а
(Urn есть сокращенное обозначение латинского слова limes,
означающего «предел»). Последовательность, имеющую пределом число а,
иначе называют последовательностью, сходящейся к а.
Остановимся подробнее на выяснении понятия предела, исходя
из его определения. Прежде всего заметим, что величина N
зависит от того, каково е, которое мы выбираем по произволу. Чем
меньше е, тем /V, вообще говоря, будет больше. Исключением
является случай, когда последовательность состоит из одинаковых
членов. Например, последовательность (3) имеет пределом число а, и
неравенство (7) выполняется для любого п, какое бы е>0 мы ни
взяли. Совершенно очевидно, что если Nt^>Nx и неравенство
\хп — а|<е выполняется при всех n>Nlf то оно подавно будет
выполняться и при n>N2.
Рассмотрим несколько примеров.
Пример L Показать, что последовательность (4), заданная общим членом
i
п ,
хп — - t , имеет своим пределом число 1.
Возьмем любое 8 > 0. Так как ( хп— i | =* —г-г— *
- , j, то для оты-
<: е, достаточно решить
екания значений я, удовлетворяющих неравенству \ кп—I
неравенство . <е. Получим: я> . Следовательно, за N можно взять
наибольшее целое число, содержащееся в , то есть ?( ). Тогда
неравенство \хп— 1|<е будет выполняться при всех n>N. Если окажется, что
Е[ )=^0, то N можно взять равным I. Поскольку е брали произвольно, то
этим и доказано, что I есть предел последовательности (4). В частности, если
в = 0,01, то #га?(н(ГоГ~I""99' если 8=а"2' то # = ? —Г~~ Н1, НТ* Д> Вы~
бранные таким образом N для различных значений е будут наименьшими из
возможных.
Пример 2. Показать, что числовая последовательность с общим членом
*„ = (— 1)" не имеет предела.
7а

Эта последовательность имеет вид:
-1, +1,-1, +1, ..., (-1)*, ... (8)
Будем вести рассуждение от противного. Предположим, что данная
последовательность имеет пределом некоторое число а. Это значит, что для любого s > 0, в
частности и для в=ол найдется такое N, что \хп — а \ <с ^ для n>N.
Поскольку хп принимает попеременно значения 1 и — 1, то должно быть
|1-о|<1 и |(-1)-а|<1.
Тогда получим:
2 = |1 —в + а—(—1)К|1 —а|Н-|а—(—l)|<i+-i = l,
то есть 2 <: 1, чего быть не может.
Для доказательства того, что некоторое число а не является
пределом заданной последовательности, достаточно убедиться, что
не все требования, сформулированные в определении предела,
выполнены. Действительно, по определению предела, как известно,
число а будет в том случае пределом последовательности xlt х2>
х3, ..., хп, .... если для любого е > 0 найдется такое N, что для
всех n>N выполняется неравенство \хп — а|<е. Допустим, что а
не является пределом данной последовательности. Выясним, что это
означает (обращаем внимание читателя на логическую цепь
последующих заключений). Из нашего допущения следует, что нельзя
для любого е >0 найти соответствующее N (to есть такое N>
чтобы при n>N выполнялось неравенство \хп — я|<е). Иначе
говоря, существует хоть одно такое е = е0>0, для которого
соответствующего N найти невозможно; какое бы натуральное число
за N мы ни взяли, неравенство \хп — а\<г0 не будет выполняться
для всех п>N'. Это в свою очередь означает, что найдется по
крайней мере хоть одно значение п = п0> N, для которого
\Хп0 — а\^г0.
В частности, если найдется такое число т>0, что \хп — а\^т
при всех /г, то а не может быть пределом данной
последовательности. Действительно, взяв е0=^т (е0>С), будем иметь \хп — aj^e0
не только для некоторых, но и для всех ч.
2
Пример 3. Доказать, что число ¦=• не является пределом последовательно-
. л 3/1 + 2
сти, заданной общим членом хп =
5/г— 1 *
Оценим снизу абсолютную величину разности -= т — -=. Имеем:
Зл + 2 2
5л—1 5
5/г +12
5(5л-1)
. Следов
3/1+2 2
_1_ 5/1+12 I
5 * 5л—1 > 5
(так как "^ . > 1 при любом п). Следовательно, если взять 80^-^, то
>е0
| 5/1—1 5|
при всех значениях /г, и уж, конечно, искать N в соответствии с определением
74

предела бессмысленно. Из полученного неравенства сразу следует, что число
не является пределом данной последовательности.
Пример 4. Показать, что последовательность
1 5 1 11 7 3/г — 1
3 MP 2 ' 21' 13'"" » 5/1+1'"'
(9)
имеет своим пределом число -=-.
о
Возьмем любое е;>0. Так как
I Зл—1
3
Хп~~~Ь
15/1+1
5(5/1+1)'
то из неравенства
взять N = Е [ rtr._ ) и тогда
8 _ 8 —5е
=-7^——гг < 8 получим, что п > ~н^—, то есть достаточно
0(0/1+1) Z06
то N = E
25е
8-0,5
2,5
*Я"~Т
<е при п>ЛЛ Если, например, 8 = 0,1,
(О Q О \
-—1—) = 7, и т. д.
Пример 5. Рассмотрим последовательность
1, q, q\ q*y ..., q*% ..
(10)
представляющую собой геометрическую прогрессию со знаменателем q. Покажем,
что эта последовательность сходится к 0 при | q \ <. 1.
Действительно, неравенство \qn—0|<e равносильно неравенству \q\n<ib.
Логарифмируя последнее, получим:
п lg | q ( < lg e или п >
(знак неравенства изменился на обратный из-за того, что мы делили на lg | q | <; 0).
Следовательно, для любого е соответствующее число N = E[—-—
сходится к нулю.
Эта последовательность имеет вид:
lg|?l.
1—(— i)n
Пример 6. Показать, что последовательность с общим членом хп = - '¦—
п
2. О, -*¦, 0, -f, О,
Так как
i-(-i)«
¦ о
1-
1)"
П
(11)
2 2 ^ /
— и неравенство —<е (где е
—произвольное сколь угодно малое положительное число) равносильно неравенству
2 /2 \
/г> —, то, взяв N — El —), мы получим: \хп — 0|<е при /г>ЛГ, то есть
Обратимся теперь к геометрическому истолкованию предела
числовой последовательности.
Числовую последовательность (1) можно рассматривать как
последовательность точек прямой. Точно так же и о пределе можно
говорить, как о точке на прямой. Так как неравенство \хп—а|<е
равносильно неравенству — г<С.хп—а<е, которое, в свою очередь,
равносильно такому:
а—-в<л;д<а + 8,
75

o-i o-?' a + e' a + i
I a
-4—* 1 1 i ! nijiii miii—j—4-—Y—i *—-**-
\/e \ x7 хл I xb i x3 ь x
Рис. 50.
то определение предела можно сформулировать и так: точка а будет
пределом последовательности то^ек (1), если, какую бы окрестность
(а — 8, а + е) точки а мы ни задали, найдется такое число N, что
все точки последовательности (1) с номерами n>N попадут в
заданную окрестность (рис. 50).
Вне этой окрестности может оказаться разве лишь конечное число
точек хъ лг2, xs,..., Xn. Если взять е' <8, то окрестность (а — е', а+г')
будет также меньше окрестности (а — е, а + г). Следовательно, в нее
попадут точки последовательности, вообще говоря, начиная с более
высокого номера.
Общий член хп последовательности (1) представляет переменную,
принимающую эту последовательность значений. Поэтому предел
последовательности (1) называют также и пределом переменной хп.
Выражение общего члена последовательности есть одновременно
и аналитическое представление переменной хп как функции от п.
2п
Так, например, хп= 2п\\ можно рассматривать и как переменную»
принимающую последовательно значения
2 4 8 16 2п
3 » б » 9 ' 17» '••» 2Л+1 » "•»
и как выражение общего члена этой последовательности. Отсюда
обозначение \\тхп=а можно рассматривать и как предел
переменной хпу и как предел последовательности значений этой переменной.
2п-\-\
Пример 7. Показать, что переменная *л = —~— имеет своим пределом К
Возьмем любое е > 0. Так как
2п II 2п | 2П1
12п -Ь1 1 1
—i~ 1 <8 равносильно неравенству ^ <с е. Отсюда 2Л ">
>-», /ilg2>lg — ип>-]Т2"- Если БЗЯТЬ N==E\WT^ T0
2п-\-\
для n>N. А это и значит, что lim—~—= 1.
76
_2« + 1 х
2п

Кроме рассмотренного, существуют и другие способы задания
последовательности, например способ рекуррентных зависимостей.
Последний состоит в том, что указывается, какие действия нужно
произвести над уже вычисленными членами последовательности
(всеми или несколькими), чтобы получить следующий член. Так,
если дана рекуррентная зависимость ал+1 = (/г + 1) ап, где /г=1, 2,
3, ... и начальный член at = l, то последовательными действиями
можем вычислить любой член:
(/1=1) а2 = 2-а1 = 2-1=2!,
(л = 2) я3 = 3-а2 = 3.21=3-2.1=3!,
(п = 3) а4 = 4.а3 = 4-3!=4!, и т. д.
Следовательно, можно сказать, что данная рекуррентная
зависимость определяет последовательность факториалов *:
1!, 2!, 3!, ..., /г!, ..., где ап = п\
В заключение параграфа заметим, что не все величины
изменяются таким образом, как рассмотренные нами переменные вида хп.
Окружающая нас действительность дает больше всего примеров
таких переменных, значения которых не могут быть занумерованы
и представлены в виде числовой последовательности. Они
изменяются непрерывно, без скачков, то есть при переходе от
одного своего значения к другому принимают и все промежуточные
числа. Например, такими переменными являются: высота растения,
атмосферное давление, скорость движения поезда, путь,
пройденный автомобилем, и другие. К изучению таких переменных мы
подойдем несколько позже, а пока ограничимся рассмотрением
переменных вида хп.
Вопросы для самопроверки и упражнения
1. Выпишите по пяти первых членов каждой из последовательностей,
заданных их общими членами:
а) *,г=-^ч, б) лс„ = л*+1. в) *Я=1+(~1)Л, г) *я = (-1)я-л.
2. Напишите общий член последовательности, состоящей из положительных
чисел, кратных трем и расположенных в порядке возрастания.
3. Составьте последовательность по следующему условию: an+i = an-\-d, где
di — a, /г = 1, 2, 3, ... Напишите выражение" общего члена этой
последовательности.
4. Составьте последовательность по следующему условию: n+1 = q, где at=
= а, /г=1, 2, 3, ... Напишите выражение общего члена этой последовательности.
5. Почему из определения последовательности следует, что она бесконечна,
то есть бесконечно множество ее членов?
6. Пользуясь определением предела числовой последовательности, доказать,
4 .2/i 2 | 1 2/г/2
что lim -—7-0 = —е". Начиная с какого п будет
5п + 3 5 ' I 5/Z + 3 \ 5
-?
* Напоминаем читателю, что факториал некоторого натурального числа /?,
то есть л!, есть произведение всех натуральных чисел от 1 до п включительно,
л! = 1 -2.3-..../1.
77

7. Пользуясь определением предела последовательности, доказать, что
.. Зя + 4 3 _. л
lim ^—Чг = тг. Начиная с какого /г будет
2л — 3 2
Зл + 4
2/г —3"
: 0,0001?
«. Пользуясь определением предела последовательности, доказать, что
дит
«Га ,а — ~о~» Для каких значений л величина
/г2 — 2
2я2 + 3
не превосхо-
19'
9. Определить площадь прямоугольного треугольника ОЛБ (рис. 51),
ограниченного прямой У = —- х, осью ОХ и прямой * = а, рассматривая ее как
предел суммы площадей вписанных прямоугольни-
а
ков с основаниями — при п — со.
п г
10. Определить площадь криволинейного
треугольника О AM, ограниченного параболой
у = ь[ —) , осью ОХ и прямой * = a,
рассматривая ее как предел суммы площадей впи-
а
санных прямоугольников с основаниями —
^ ab
при п —»со. Отв. -5-.
рис# 51. **• Составить такую ограниченную сверху
последовательность, чтобы точная верхняя
граница не была членом этой последовательности.
12. Составить последовательность сегментов, стягивающихся к какой-нибудь
заранее выбранной точке.
13. Привести пример ограниченной последовательности, не имеющей предела.
14. Дана последовательность точек хъ х2, х3, ..., хп,... Объяснить
геометрический смысл того факта, что точка х0 не является пределом этой
последовательности.
15. Доказать, что число 1 не является пределом переменной хп =
16. Дана последовательность точек 3, 2, 5, 4, 0, -д-, 0, -^-, 0, -„-,..., 0,
-„-, ... Все точки этой последовательности, начиная с пятой, находятся в
окрестности нуля (—1;+1). Почему из этого, однако, не следует, что точка нуль
является пределом данной последовательности?
4п + 3'
§ 2. БЕСКОНЕЧНО МАЛЫЕ И БЕСКОНЕЧНО БОЛЬШИЕ
ВЕЛИЧИНЫ
Определение. Переменная величина хп называется
бесконечно малой, если она имеет предел, равный нулю.
Следуя определению предела, можно сказать, что хп будет
бесконечно малой, если для любого сколь угодно малого е>0 найдется
такое N, что для всех я > N выполняется неравенство | хп | < е.
Иначе говоря, бесконечно малой называется такая переменная*
величина хп, которая при своем изменении, начиная с некоторого
номера я, становится и остается по абсолютной величине меньше
любого наперед заданного числа е>0.
78

Необходимо различать термин «бесконечно малая величина» от
выражения «сколь угодно малая величина». Бесконечно малая
величина по определению является величиной переменной. Когда же
мы говорим, что «е есть любое сколь угодно малое число», то под
этим понимаем, что е может быть выбрано произвольно, но после
того, как его выбрали, оно становится определенным
фиксированным числом.
Нельзя также думать, что все бесконечно малые величины
обязаны принимать только «очень малые» значения. Характерным
для бесконечно малой является не то, насколько малые значения
она принимает, а то, что она имеет своим пределом число нуль.
Так, например, переменная хп = 10010"2/г, принимающая значения
1008 1006 1004 1002 1 —— —— -^— ——
iuu , ши , ши , iuu , 1, 1002, Ю04, ШОб, 1008>...>
будет бесконечно малой, хотя ее отдельные значения сравнительно
велики.
Пусть переменная хп имеет своим пределом некоторое число а,
тогда разность хп—а = ап будет бесконечно малой величиной, так
как для любого е>0 найдется такое N, что для n>N
выполняется неравенство | ап \ = \ хп — а \ < е. Из последнего следует и
обратное утверждение: если ая —бесконечно малая, то число а
будет пределом переменной хп. Таким образом, можно сказать, что
всякую переменную хт имеющую предел, можно
представить в виде суммы этого предела и бесконечно малой
величины, хп=а + ап. Обратно, если переменную хп удается
представить в виде суммы некоторого числа и бесконечно
малой, то это число будет пределом переменной хг.
Отмеченная нами связь будет часто использоваться при доказательствах
многих теорем.
Примерами бесконечно малой могут служить переменные хп=
= —, хп= — — 1 хп=±—^-, xn = qn при |<7|<1, и др. Бесконечно
малыми также будут: амплитуда затухающего колебания маятника,
длина стороны правильного вписанного в окружность
многоугольника (а также разность между его периметром и длиной
окружности) при неограниченном удвоении сторон.
(— 1)п
Пример 1. Показать, что хп^=- — есть бесконечно малая.
Возьмем произвольное 8 > 0. Из неравенства | хп | =
(-i)"
п
1т. .г Г.М'
— <: е полу-
П
чаем/г>—. Если взять N = ?(-^-1, то для n>Af будет | хп | < е. При е=
1 4 /15\
= ут- получим: N = ? (10) = 10, при е = у= получим: N = El— 1 = 3, и т. д. А это
(-1)Л
и значит, что хл=- есть бесконечно малая.
Определение. Переменная хп называется бесконечно
большой величиной, если, какое бы сколь угодно большое число М мы
79

ни взяли, найдется такое натуральное число N, что \хп\>М для
всех n>N. Иначе говоря, хп есть бесконечно большая величина,
если при своем изменении, начиная с некоторого я, она становится
и остается по абсолютной величине больше любого наперед
заданного положительного числа М.
О бесконечно большой переменной хп говорят, что она стремится
к бесконечности или имеет бесконечный предел, и пишут: л:л-*оо
или Итл:Л = оо. Последнее обозначение бесконечного предела
условное, так как знак равенства можно ставить между числами. Вообще
в данном случае говорить о пределе в том смысле, как он
определен нами выше, нельзя, так как оо не представляет никакого
числа.
В связи с введением нового понятия —«бесконечный предел» —
условимся предел в ранее определенном смысле называть конечным
пределом.
Пример 2. Пользуясь определением бесконечно большой величины,
доказать, что хп = 2* п есть величина бесконечно большая.
Возьмем произвольное положительное число М и решим неравенство, j хп |>
> М, то есть неравенство 2V п > М.
Предварительно его следует прологарифмировать. Получим
Vnlg2>\gM и /л >^.
Возводя в квадрат обе части последнего неравенства, получим: п> ( f , 1 .
/lg Af\2
Если теперь взять N ^ {—.—=-] , то для всех п>Л/ будет выполняться
неравенство !#л|>М. Так как М может быть любым сколь угодно большим числом,
то согласно определению величина хп — Тп будет бесконечно большой.
Если бесконечно большая величина хп принимает- значения
одного знака (все или начиная с некоторого /г), то в зависимости
от знака ее называют положительной (и пишут: хп -> оо) или отри-
цательной (и пишут: хп->— оо) бесконечно большой. Так,
например, хп = п будет положительной, а хп = — п — отрицательной
бесконечно большой величиной. Переменная хп = (—1)Л-яесть бесконечно
большая величина, но ее нельзя назвать ни положительной, ни
отрицательной, так как ее значения все время меняют знак.
Укажем на важную связь между бесконечно малой и бесконечно
большой величинами.
Теорема. Пусть хп Ф 0*. Если хп — бесконечно большая,
то уп = бесконечно малая; если хп—бесконечно малая,
то уп = бесконечно большая.
* хпфО означает, что значения хп отличны от нуля при любом п. Таким
обозначением будем пользоваться и впредь.
80

Доказательство. Предположим, что хп — бесконечйо
большая. Возьмем произвольное е>0 и положим М =—. По этому М
найдется такое N, что для n>N будет \хп\>М. Тогда \уп\ —
1
= 1—; < j7 = е, то есть | уя | < е для п > ЛГ. А это значит, что
1*л|
#„ =— есть бесконечно малая. Аналогичное доказательство второго
хп
утверждения теоремы предоставляется читателю.
Вопросы для самопроверки и упражнения
/1-4-2
1. Доказать, что переменная величина *« = -2X— является бесконечно
малой. Для каких значений п будет | хп | < 10~3? Покажите, что величина —
является бесконечно большой.
2. Доказать, что переменная величина хп = 5п является бесконечно большой.
Для каких значений п будет | хп | > 5 000? Покажите, что величина — является
бесконечно малой.
0«e.„>E(l+iig).
3. Доказать, что переменная хп = пУ~х^ не ограничена, но не является
бесконечно большой. В чем различие между неограниченной и бесконечно
большой величинами?
4. Может ли переменная стремиться к нулю возрастая? Приведите пример.
5. Приведите пример бесконечно большой величины хп, значения которой
при возрастании п убывают. Как называется такая бесконечно большая?
6. Можно ли назвать бесконечно малой величину хп=0 при всех значениях /г?
7. Дана числовая последовательность 1,-77, ^, "о"» ^» Т~» 4, ...» п, —f ...
Почему нуль не является пределом этой последовательности, несмотря на то что
любая окрестность нуля содержит бесконечное множество членов
последовательности? Почему эта последовательность не имеет своим пределом со, несмотря на то
что, какое бы большое число М мы ни взяли, найдутся среди членов
последовательности большие по абсолютной величине, чем М7
§ 3. ОСНОВНЫЕ ТЕОРЕМЫ О ПРЕДЕЛАХ
Из определения предела и примеров следует, что хп может
различными способами стремиться к своему пределу. В примере 4
§ 1 все значения переменной хп = . { меньше ее предела -g-f
3/г—1 3/г 3 _ ^
так как 5 ^ <^Ъп==~Ъ' и Хп+1 ^Хп ПРИ ЛК)бом п, так
кяк г — г - 3* + 2 _ 3/г~1 - (5/»+1)(Зд + 2)-(5я + 6)(3||^1) _
л«ж *я+1 лл — 5л + 6 5л+1 — (5/1 + 6) (5я+1) ~
о
— /5/1-1-6) Г/г4-1) ^ ^* Следовательно, в данном случае переменная #л
стремится к пределу возрастая. В примере 7 § 1 все значения пе-
2п +1 2Л 4-1 2"
ременной х„= 2; больше ее предела 1, так как т ^> ==[>
$1

2Л+14-1 2п 4-Х
и хп+1<хп при всех п, так как хп+1 — хп = —^ ф- =
= 2^4-1 = — 2^+r<0. Следовательно, хл стремится к пре-
/ \\п
делу убывая. Переменная хп = -—— (пример 1, рассмотренный в § 2)
стремится к своему пределу 0 колеблясь (принимая поочередно по-
ложительные и отрицательные значения), а переменная хп=—-—'—
(пример 6, § 1) при своем изменении принимает наряду с другими
значениями и значения, совпадающие с пределом 0.
Однако во всех возможных случаях остается справедливым
следующее утверждение:
Теорема 1. Если переменная хп имеет пределом число а,
и а больше некоторого числа Ъ, то значения переменной,
начиная с некоторого п, будут также больше этого
числа Ь.
Доказательство. Пусть хп имеет пределом число а и а>Ь.
Возьмем окрестность (а — е, а + е) точки а, где е меньше расстояния
между точками а и Ь> то есть е<0 — Ь (а — 8>6). Такое е
желательно взять для того, чтобы точка Ь оказалась вне окрестности
(рис. 52). Тогда по определению предела для любого (а значит, и
для выбранного нами) е>0 найдется такое N, что \хп — а|<е
или
а — г<.хп<.а-\-г
для всех значений п> N. Следовательно, начиная с n = N+ 1, имеем
хп>а — е>Ь, то есть хп>Ь. Теорема доказана.
Геометрически данную теорему можно истолковать так: если
последовательность точек прямой {хп\ сходится к точке
а, и точка а лежит правее какой-то точки Ь, то и все
точки последовательности, начиная с некоторой, также
лежат правее этой точки Ь.
Теорема 2. Если переменная хп имеет пределом а, и а
меньше некоторого числа с, то значения этой переменной*
начиная с некоторого п, будут также меньше этого числа с.
Доказательство этой теоремы аналогично доказательству теоремы 1.
Предлагается провести его самостоятельно, сопровождая рисунком.
Теорема 3. Если переменная хп имеет пределом число
а > 0 (а < 0), то и все ее значения, начиная с некоторого пР
будут положительны (отрицательны).
а-е. а + с
ь ( ° \
—\—1 1 ( 1 1 II l]ll Mil)
Лъ Лч лк ля *7
Рис. 52.
82

Эта теорема непосредственно следует из теорем 1 и 2, если в них
положить Ь = 0 и с = 0.
Теорема 4 (о единственности предела). Если
переменная имеет предел, то он единственный. Иначе говоря,
переменная не может иметь двух различных пределов.
Доказательство. Допустим противное. Пусть хп имеет два
предела: \шхп = а и \imxn = b, где афЬ. Для определенности
будем считать а<Ь. Тогда между этими числами можно взять
некоторое число г (а </*<:&). Так как хп->а и а<.г, то по теореме 2
найдется такое натуральное число, которое в данном случае удобно
обозначить через Na, что хп<г для всех значений n>Na. Так
как хп-*Ь и b > г, то по теореме 1 найдется такое натуральное
число Nb (не обязательно совпадающее с Na), что хп> г для всех
значений n>Nb. Получили два неравенства:
хп<.г для n>Na,
хп> г для п> Nb.
Если же теперь взять за N наибольшее из чисел Na и Nb, то,
очевидно, для всех значений п> N выполняются одновременно оба
эти неравенства: xn<ir и хп>г, что невозможно. Полученное
противоречие и доказывает теорему.
Теорема 5 (о предельном переходе в равенствах).
Если имеем две переменные величины хп и уп, имеющие
пределами соответственно числа а и Ь, причем хп=уп для
всех п, то а = Ь.
Справедливость этой теоремы вытекает из того, что хп и уп по
существу обозначают одну переменную, а потому в силу
единственности предела а = Ь.
Теорема 6 (о предельном переходе в
неравенствах). Если переменные хп и уп имеют своими пределами
соответственно числа а и Ь, причем хп^уя для всех п, то
а^Ь.
Доказательство. Допустим противное. Пусть при
выполнении условий теоремы будет а> Ь. Возьмем какое-нибудь число г
между а и Ь (а> r>b). Так как хп-+а и а>г, то по теореме 1
найдется такое NX9 что хп> г для всех значений n>Nx. С другой
стороны, так как уп-+Ь и fe<r, то по теореме 2 найдется такое
Ny, что уп<г Для всех значений n>Ny. Если через N обозначить
наибольшее из чисел Nx и Ny, то для п> N будут одновременно
выполняться неравенства: хп> г и уп<г.
Отсюда получаем, что хп>уп для всех n>N. Это противоречит
условию теоремы. Теорема доказана.
Замечание. Из теорем 5 и 6 следует, что знаки равенства и
нестрогого неравенства сохраняются при переходе к пределу. Что
же касается предельного перехода в строгом неравенстве, хп<Суп,
то здесь в пределе может появиться и знак равенства, то есть можно
лишь утверждать, что lim xn ^ lim yn. В качестве примера рассмот-
83

рим переменные хп=— — и */п=—- Очевидно, хп<уп для всех пг
в то время как \\тхп = \\туп — 0.
Теорема 7 (о сжатой переменной). Пусть имеем три
переменные хп9 уп и zn, связанные неравенствами хп ^уп ^ zn
для всех п. Тогда если переменные хп и zn имеют один и
тот же предел а, то переменная уп также имеет предел
и этот предел равен а.
Доказательство. Возьмем любое е > 0. По этому е для
переменной хп найдется такое Nx, что | хп — а | < е для всех п > Nx, то
есть
а— г<схп<а + г. (1)
По этому же е для переменной гп найдется такое Nzr чта
12Л — а | < г для всех п > Nz, то есть
а-е<гп<а + г. (2)
Обозначим через N наибольшее из чисел Nx и N2. Тогда для п> N
будут выполняться одновременно неравенства (1) и (2). Используя
подчеркнутые их части, а также неравенства, данные в условий
теоремы, можем записать:
я — b<xn^yn^zn<Za + e для n>N.
Отсюда
я — г<суп<а + е для n>N.
Последнее означает, что Iim#/I = a. Теорема доказана.
Геометрически эту теорему можно пояснить следующим образом.
Возьмем произвольную окрестность (я — е, я + е) точки я. Так как
переменная хп-+ я, то все ее значения, начиная с некоторого,
находятся в этой окрестности. Аналогично, из zn->a следует, что и
значения z„, начиная с некоторого, находятся в этой же
окрестности. Так как xn^yn^zn для всех значений п, то и значения уп>
начиная с некоторого, будут в той же окрестности (а—е, я + е).
Поскольку окрестность выбиралась произвольно, то этим доказано,
что любая окрестность точки я содержит все значения уп, начиная
с некоторого. Последнее означает, что уп-+а.
Свойства предельного перехода в равенствах и неравенствах,
доказанные в теоремах 5, 6 и 7, наглядно могут быть представлены
следующими схемами:
Хп=Уп *п^Уп Хп<Уп Xn^yn^Zn.
Y Y Y Y Y Y Ч Y •
a =ft a ^b a ^b a
Определение. Переменную хп будем называть ограниченной,,
если ограничено множество всех ее значений, то есть если существует
такое положительное число К, что \хп\^К (— К ^ хп ^К) для
всех п.
84

Теорема 8. Если множество значений переменной хт
начиная с некоторого значения п, ограничено, то хп
является ограниченной величиной.
Доказательство. Пусть множество значений переменной хпу
начиная с хПо, то есть множество
\ Хп0> XnQ + \, X/Io-f-2, ..., Xno + k, ...},
ограничено. Это значит, что существует такое положительное число
А, что для всех значений п^п0 выполняется неравенство IXnl^A,
то есть — Л^л:п^Л. Иными словами, все значения хп для п>щ
находятся на отрезке [—А, А]. Вне этого отрезка могут
находиться лишь значения хп с номерами п<п0. Таких значений
конечное множество {хъ х2> ..., #n0-i }. Возьмем число/и, меньшее чисел
хг, х2, х3, ..., Хп0-\, — Л, и число М, большее чисел хг, х2, х3, ...,
Хп9-\, А. Тогда для всех значений п будет выполняться неравенство
т<хп<М. (3)
Действительно, если п^п0, то хп^А <сМ и хп^— А>т. Если
же п<п0, то по выбору т и М снова имеем: т<хп<М.
Неравенство (3), справедливое для всех значений п, означает, что
переменная хп ограничена (см. § 5, гл. I).
Теорема 9. Если переменная хп имеет конечный пределу
то она ограничена.
Доказательство. Пусть хп->я. По определению предела
это означает, что для любого 8 > О найдется такое Л/, что для п> N
(то есть начиная с nQ = N-\-l) выполняется неравенство \хп— а\<е
или а—8<Схл<С<2 + 8. Получили, что множество значений хп,
начиная с /i0 = JV+l» ограничено. Следовательно, по теореме 8
переменная хп является ограниченой.
Замечание. В данной теореме доказано, что из существования
конечного предела переменной следует ее ограниченность. Обратное
утверждение неверно. Из ограниченности переменной не следует
существование предела, так как существуют ограниченные
переменные, не имеющие предела. В качестве примера может служить
переменная *„==(— 1)л, рассмотренная в примере 2, § 1.
Вопросы для самопроверки и упражнения
1. Приведите примеры возрастающих, убывающих и колеблющихся перемен-
вых, имеющих конечные пределы.
2. Переменные хп и уп удовлетворяют неравенству 0 < хп < уп для всех
значений п. Известно, что уп есть бесконечно малая. Существует ли lim xn и если да,
то чему он равен?
3. Может ли положительная переменная иметь отрицательный предел, а
отрицательная переменная —положительный предел? Могут ли эти переменные иметь
пределом число нуль?
4. Докажите самостоятельно теорему 2.
5. Приведите пример, когда при предельном переходе строгое неравенство
сохраняется.
85

§ 4. АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ НАД ПЕРЕМЕННЫМИ
ВЕЛИЧИНАМИ
Докажем сначала два вспомогательных предложения.
Лемма 1. Сумма любого числа k бесконечно малых есть
величина бесконечно малая.
Доказательство. Рассмотрим случай двух бесконечно малых.
Для k бесконечно малых доказательство аналогично. Пусть ап и
Р„ — бесконечно малые. Возьмем любое е>0. Так как в определении
бесконечно малой величины е может быть любым положительным
числом, то по у для ап найдется такое Na, что j ап | < у для всех п > Nx.
По этому же у для $п найдется такое ДО р, что | Рл | < у для всех
n>N„. Возьмем за N наибольшее из чисел ДОа и ДО^. Тогда для
п> N будут выполняться одновременно оба неравенства: |ая|<у
и 1Рл|<у. Следовательно,
I «* + Р„ |< | *п I + I Р* I < ~ + | = в,
то есть
I а* + Рл I <e Для п> N.
А это и значит, что величина ая + рп есть бесконечно малая.
Замечание. Обращаем внимание читателя на то, что в лемме
речь идет о сумме хотя и любого, но вполне определенного числа
бесконечно малых ап, рл, уп, ..., цп.
Лемма 2. Произведение ограниченной переменной на
бесконечно малую есть величина бесконечно малая.
Доказательство. Пусть хп— ограниченная переменная
величина. Значит, существует такое число М, что \хп\< М аля всех д.
Пусть ап — бесконечно малая. Возьмем е>0. По тт Для ап найдется
такое ДО, что |ал|<д7Для n>N. Тогда для n>N получим:
I *>п • &n I = I *п I • I <*п | < М • |j = е, то есть | хп • ап | < е. Следовательно,
хп - <хп есть бесконечно малая величина.
Из доказанных лемм, в частности, следует, что:
1) произведение постоянной величины на бесконечно
малую есть величина бесконечно малая (так как постоянную
можно рассматривать как частный случай ограниченной переменной);
2) произведение двух бесконечно малых есть величина
бесконечно малая (так как любая бесконечно малая является
величиной ограниченной);
3) разность двух бесконечно малых ап — р„ есть
величина бесконечно малая (так как ап — рл = а/г + (~ 1) Рл, где
произведение (—1)Рл есть бесконечно малая).
86

Теорема 1. Если переменные хп и уп имеют конечные
пределы, то сумма и разность этих переменных также
имеют конечные пределы, причем
\\т{хп+уп) = \\тхп + \\туп.
\\т{хп—уп)=\\тхп — \\туп.
Другими словами, предел алгебраической суммы двух
переменных, имеющих конечные пределы, равен
алгебраической сумме пределов этих переменных.
Доказательство. Пусть хп-+а и г/Л->Ь. Тогда хп к уп
можно представить в виде
и.=ь + ря, J w
где ап и Р„ — бесконечно малые величины (см. § 2). В таком случае
и сумма хп + уп представима в виде
хя + Уп = (а + ап) + (Ь + $п) = (а + Ь) + (ая + $я).
На основании леммы 1 величина ал + рл является бесконечно
малой (как сумма бесконечно малых). Следовательно, переменную
величину хп + Уп удалось представить в виде суммы некоторого числа
а-\-Ь и бесконечно малой. А этого, как установлено в § 2, и
достаточно для того, чтобы число а+b было пределом переменной
Хп + Уп- То есть имеем:
l\m(xn + yn) = a + b = limxn + \imyn.
Аналогичное доказательство теоремы в случае разности хп — уп
предоставляем читателю.
Здесь же заметим, что доказанная теорема остается
справедливой и в случае алгебраической суммы любого, но вполне
определенного числа слагаемых. Доказательство теоремы в этом случае
совершенно аналогично только что проведенному доказательству.
Теорема 2. Если переменные хп и уп имеют конечные
пределы, то их произведение также имеет предел, причем
lim (хп уп) = lim xn • \\туп,
то есть предел произведения переменных, имеющих
конечные пределы, равен произведению пределов этих
переменных.
Доказательство. Пусть хп->а и уп-*Ь. Тогда,
воспользовавшись выражениями (4), можем записать:
хп • Уп = (а + ап) (b + $„) = ab + (а$п + Ьап + ап$п).
Величина а$п-\-Ьап-{-ап$п есть бесконечно малая (как сумма
бесконечно малых) (см. выводы из лемм 1 и 2). Следовательно,
lim (xn • уп) = ab = lim xn • lim yn
и теорема доказана.
8^

Заметим, что эта теорема также справедлива в случае любого,
но вполне определенного числа сомножителей и доказывается
методом математической индукции.
Теорема 3. Если переменные хп и уп имеют конечные
пределы, причем \\туп Ф О, то их частное ^ имеет также
Уп
предел и
Нт —=-*т Хп
Уп НтУя'
то есть предел частного двух переменных равен частному
их пределов, если предел знаменателя отличен от нуля *.
Доказательство. Пусть хп-*а и уп-+ЬфО. Для
доказательства теоремы достаточно установить, что разность ——-|- есть
величина бесконечно малая.
Представим — — -т-, используя (4) в виде
Уп &
хп а Ьхп-ауп_ Ь (а + ап)-а(Ь + $п) 1 ., ft
Легко видеть, что множитель (Ьап—а$п) есть бесконечно малая.
Покажем, что -.— есть величина ограниченная. Тогда с помощью
леммы 2 получим требуемое. Так как ря-*0, то найдется такое /V,
что |РЯ|<'-У Для всехм>ЛЛ Тогда \уп |==| Ь + $п\^\ Ь\ — \§п\>
Ь\ ~Ч Ч и, следовательно,
Ьуп
1 2 2
\<^\h\ ' I A I
Таким образом, установлена ограниченность переменной 7— для
УУп
n>Ny но тогда она будет и вообще ограниченной (см.
теорему 8, § 3).
Замечание. Обращаем внимание читателя на то, что во всех
трех теоремах этого параграфа условие существования конечных
пределов у переменных хп и уп является существенным. Без этого
условия, как будет показано в дальнейшем на отдельных примерах,
теоремы неверны, хотя предел суммы, разности, произведения и
частного все же может существовать.
* Поскольку ЬфО, то и упфО, по крайней мере начиная с некоторого
номера nQt а тогда и частное — имеет смысл при п ^ nQ. Следовательно, говоря
Уп
V
о lim —, мы рассматриваем предел последовательности
Уп
f«e *Л» + 1 **» + ! % **
88

Леммы и теоремы, установленные в этом параграфе, имеют очень
большое не только теоретическое, но и практическое значение. Если
до сих пор мы могли лишь проверять, пользуясь определением
предела, будет ли то или иное заранее угаданное число пределом
данной переменной величины, то теперь открывается возможность
и для вычисления предела переменной.
Пример 1. Переменная хп имеет предел а^?0. Найти предел переменной
х% — 2Ф
</* = ** +
х + а '
Воспользуемся теоремами о пределе суммы, разности, произведения и
частного. Получим:
л* — 2аа Y\mx* — \\m2cP а2 — 2а2 а
*п п ' хп + а п limx„ + lima а + а 2
Пример 2. Найти предел переменной
2/2 sin n
Так как предел суммы равен сумме пределов слагаемых, то
Ilm*.«llm-^+lim^.
Поделив в первом слагаемом числитель и знаменатель на п и применив теорему
о пределе частного, получим:
2п .. 2 2 2 0 / 1 л \
—r~r = lim г = -=—- = 2 так как >0 при л—*оо).
"+1 ,+± , + llml J \ 1
' п п
Нт-
sm/i
Второе слагаемое можно рассматривать как произведение ограниченной
величины sin п (| sin п | ^ 1) и бесконечно малой —. Следовательно, по лемме 2
второе слагаемое есть величина бесконечно малая и предел его равен нулю.
Таким образом, окончательно получаем, что lim хп = 2 + 0 = 2.
Пример 3. Пусть *„ = л-| , */„=—/*. Тогда ПтхЛ=*-т-ео, lim#n = -—oov
а У\т(хп + уп) = Пт— = 0.
Вопросы для самопроверки а упражнения
1. Где при доказательстве теоремы 3 использовано, что Ъф№
2. Переменная хп имеет предел афО. Чему равен предел Jim *wfl ? O/лв. Ifc
*л
3. Переменная хп имеет предел а ^ 0- Найти предел переменной */л =
хЪ + хп — 2 a2-fa —2
-? Отв.
2х*г+хп ' 2а2 + а -
5я
4. Найти предел переменной *я =
Указание. Предварительно числитель и знаменатель поделить на Бп. Отв. 1.
б. Доказать лемму 1 для случая любого* числа k бесконечно малых.
8S

§ 5. ОСОБЫЕ СЛУЧАИ ПРЕДЕЛОВ И НЕОПРЕДЕЛЕННОСТИ
В теоремах предыдущего параграфа указаны способы нахождения
пределов суммы, разности, произведения и частного двух
переменных, хп и уП1 имеющих соответственно конечные пределы а и Ь.
Остановимся теперь на рассмотрении отдельных возможных случаев
вычисления пределов, которые не охватываются указанными выше
способами.
I. Рассмотрим сначала частное — (у„^0).
Уп
1) Пусть хп-+а, а уп—бесконечно большая. Тогда — будет бес-
Уп
1
конечно малая, так как его можно представить в виде— -хп, где
1 Уп
бесконечно малая, а хп — ограниченная величина. Следовательно,
Уп
Уп
2) Пусть хп-+а^?0, а уп — бесконечно малая, не принимающая
нулевых значений. Тогда — будет бесконечно большой, так как
Уп
обратная величина — = уП'— есть бесконечно малая f > —).
хп хп \хп а ]
3) Пусть хп — бесконечно большая, а уп — бесконечно малая
(уп ф 0). Тогда —будет бесконечно большая, так как обратная вели-
Уп
U *
чина — может быть представлена в виде произведения двух беско-
хп
нечно малых ^=—-у„ и является, следовательно, бесконечно малой.
хп хп
4) Пусть л^ — бесконечно большая, а уп-*Ь^0. Тогда — будетг
Уп
бесконечно большая, так как обратная ей величина по
установленному в 1) есть бесконечно малая.
5) Пусть хп и (/„ — бесконечно малые величины. В этом случае
о пределе отношения — никакого общего заключения сделать нельзя,
Уп
так как в зависимости от характера изменения переменных хп и уп
возможны различные ответы. Так, например,
= 1-1;
= я->оо;
= 1-0;
П
г) если хп=^~ ' ->0, */* = — -> 0, то ~=(—1)* предела вовсе
71 ТЬ У П
не имеет.
а) если хп = — -»-0,
б) если х„= >-0,
в) если *п=^-»-0,
</„=4->0,
Уп = ^-*0,
У.-Т-0'
хп
ТО — ¦
Уп
Хп
ТО —
Уп
хп
ТО —
Уп
* Так как хп — бесконечно большая, то ее значения, начиная с некоторого,
отличны от нуля.
90

Таким образом, отношение двух бесконечно малых может быть
величиной бесконечно малой, бесконечно большой, может иметь
пределом число, отличное от нуля, а может и вовсе не иметь
предела. Следовательно, на вопрос о том, чему равен предел отношения
бесконечно малых, можно ответить только тогда, когда известны
законы изменения этих бесконечно малых, то есть если бесконечно
малые заданы. В связи с этим говорят, что отношение бесконечно
малых в общем случае представляет собой неопределенность, и этот
вид неопределенности обозначают символом -д- (говорят:
неопределенность вида -Q-]. Когда на основании исследования характеров
изменения данных бесконечно малых предел их отношения найден
или установлено, что его нет, то говорят, что неопределенность
раскрыта.
6) Пусть хп и уп — бесконечно большие величины. В этом случае
о пределе отношения — также никакого общего заключения сделать
нельзя. Так, например,
а) если хп = п2 -> оо, уп
б) если хп = п ->оо, уп
в) если хп = п -*со, уп
г) если хп = п(— 1)Л-*оо, уп
предела не имеет.
Из этих примеров следует, что отношение двух бесконечно
больших может быть величиной бесконечно большой, бесконечно малой,
может иметь пределом число, отличное от нуля, а также может
вовсе не иметь предела. Поэтому говорят, что отношение двух
бесконечно больших в общем случае представляет собой также
неопределенность, но уже вида —. Если бесконечно большие хп и уп
конкретно заданы и нам удалось найти предел их отношения или доказать,
что он не существует, то мы, так же как и выше, будем говорить,
что неопределенность раскрыта.
II. Рассмотрим сумму двух переменных хп + уп.
1) Пусть хп-*со, уп-^Ъ. Тогда (хп + уп) -^ со. Действительно,
величина уп будет ограниченной. Пусть \уп\<СМ для всех п.
Переменная хП1 начиная с некоторого /г, будет удовлетворять неравенству
\хп\> Р + Mt где Р—любое сколь угодно большое число. Тогда,
начиная с некоторого /г, получим:
\Хп + Уп\**\хя\-\уя\>(Р + М)-М = Р,
то есть | хп + уп \ > Р. В частности, если хп -^ -+- оо (— оо), то и
(Хп + Уп)-+ + оо(—оо).
= л2
-п
¦п
п -> оо, то — =* п
Уп
1
оо;
= л*->оо, то ^ = —-^0;
Уп
Хп
П
. оо, то — = 1 -> 1;
Уп
оо, то^ = (-1)я
91

2) Пусть хп-> + оо(— оо) и уп-+ + оэ(— оо). Тогда ** + #„-*-
-* + оо(—оо), так как сумма бесконечно больших одного знака
есть величина бесконечно большая.
3) Пусть хп и уп есть бесконечно большие разных знаков. Тогда
о пределе суммы хп + уп ничего определенного сказать нельзя до
тех пор, пока не будут известны законы изменения хп и уп. Этот
предел может быть равен нулю, бесконечности, числу, отличному
от нуля, а также может и вовсе не существовать. Например:
а) если хп = {^+^^ + <х>,уп = — п^ — оо,тохп + уп = — -+0:
б) если хп = 2п-+-\-со, уп= — я-* — оо, то хп + уп = п-+ + оэ;
в) если хп = (п + 2)-+ + оо, уп= - я-* — оо, то хп + уп = 2-+ 2;
г) если хп = п + (—1)Л-* + оо, ^=-^-^-00, то *„ + */„ =
= (—-1)" предела не имеет.
Таким образом, сумма двух бесконечно больших разных знаков
представляет собой в общем случае неопределенность, которая
обозначается символом оэ — оо.
III. Рассмотрим произведение двух переменных хп-уп.
1) Пусть хп и уп являются бесконечно большими. Тогда их
произведение будет также величиной бесконечно большой, так как в данном
случае — и —, а значит, и будут величинами бесконечно
J *п Уп хп'Уп J J
малыми.
2) Пусть одна из переменных имеет конечный предел, отличный
от нуля, а другая — бесконечно большая. Тогда их произведение
будет величиной бесконечно большой. Действительно, если хп->аФО,
а уп— бесконечно большая, то — будет бесконечно малой, а
Уп хп
величиной ограниченной (—>—(.Следовательно, их произведение
будет бесконечно малой, а тогда хп • уп будет бесконечно большой.
хп ' Уп
3) Пусть ^ — бесконечно малая, а */я — бесконечно большая.
Тогда имеем случай неопределенности, которая обозначается
символом О-оо. Например:
а) если *« = — ->0, уЛ = п2-*оо, то хпуп = п-+оо\
б) если хп = -^-+ О, yn = n-+oot то хпуп=— -*0;
о
в) если ** = — ->0, уп = п-+оо, то хпуп = Ъ-+Ъ\
г) если хя = (~~~п* -»0, Уп = п-+оо, то хпуп = (— 1)п предела не
имеет.
Кроме рассмотренных нами неопределенностей вида -д-, ^,
оо—оо и 0*оо, существуют еще другие случаи неопределенностей,
связанные с рассмотрением степеней. С ними мы познакомимся в
дальнейшем (см. § 10, гл. IV).
92

Раскрытие неопределенностей в некоторых случаях представляет
собой значительную трудность. В каждом отдельном случае
приходится изыскивать особый прием, позволяющий преобразовать
выражение к такому виду, когда о пределе возможно дать определенный
ответ.
Рассмотрим на примерах наиболее типичные приемы раскрытия
неопределенностей.
Пример 1. Пусть хп есть многочлен степени к относительно п:
xn = a0nk+alnk^ + a2nk^ + ...+ak_ln-\-ak (а0?ЬО).
"Как ведет себя этот многочлен при /i—*-f-oo?
Если бы все коэффициенты были одного знака, то, очевидно, хп была бы
бесконечно большой такого же знака. При разных знаках коэффициентов имеем
неопределенность вида оо —оо. Для раскрытия этой неопределенности вынесем за
скобки высшую степень п:
В скобках все слагаемые, кроме первого, являются бесконечно малыми.
Следовательно, предел выражения, стоящего в скобках, равен а0. Множитель пк есть
величина бесконечно большая. Отсюда заключаем, что хп стремится к -f-co или
— оо в зависимости от знака а0.
Пример 2. Пусть хп представляет собой частное двух многочленов:
_ aQnk + axnk-* + fl2ftfe-2 +•...+ аМ-гП + ak . ,n , , m
Xn ~~ Mm + Mm_1 + Mm"2 + — + bm-i"> + bm W^V'Oo^FV)-
Рассмотрим все возможные случаи поведения частного при л-^ + оо.
Как уже установлено в примере 1, числитель и знаменатель являются
величинам» бесконечно большими. Следовательно, имеем случай неопределенности
Бнда —. Вынося за скобки в числителе я*, а в знаменателе пт, получим:
. = «*""*
Предел второго множителя равен -j^zfiQ. Что же касается предела первого мно-
жителя, что он будет зависеть от соотношения чисел k ml т. Если к > т, то
nk~m—* со и, следовательно, хп—-:±:оо (знак совпадает со знаком -jrl- Если же
k = m, то /i*~m = n° = l и хп-+ —. Наконец, если &<т, то пк~т^= -0 и
bQ пп~к
Пример 3. Найти предел переменной хп~-—о«8-и1—•
Это частный случай предыдущего примера:
(n-l)(«-2) [ n)V a 1
n na
6, 62
, ak-i
• rtm-i i
rn'rt
ft*
93

Здесь для раскрытия неопределенности вида — мы поделили числитель и
знаменатель на п2.
Пример 4. Найти предел переменной хп = Yn2+2 — У2/г — 1.
Выражение переменной хп представляет собой неопределенность вида со—со.
Если правую часть умножить и разделить на сумму J^n2+ 2+ 1^2/1—1, то мы
со
придем к неопределенности вида —, которая раскрывается приемом, изложенным
в примере 3:
1^ + 2+ /2/1—1
Л2_2/1 + 3 ,. п ^л*
= lim -. ¦ >. = hm —,_ ,_ = со.
уП2+2 + у2п- 1 ЛГ\_ , J2, 1уГ2_ _ ^
Р Л* "Т" П4 "Г у nz П4
В этом примере мы использовали еще и теорему о пределе корня: если хп —•> а, то
У^—>-|/"а (при любом натуральном Р). Мы ее не формулировали отдельно,
поскольку она входит как частный случай в более общую теорему о пределе
степени с любым показателем (ср. также § б, гл. IV).
п с и «- „1 +2 + 3 + ... +Л
Пример 5. Найти предел переменной *я = ! 2 !
В данном случае имеем неопределенность вида —. Так как 1 + 2 + 3 +
+ ... + „- "fi-hil.,0
* + 7Г 1
¦+-Г8'
I+i+±+"
1+|+т+-
+ -!-
+ -!-
Пример 6. Найти предел переменной хп
Так как 1 + q + q2 + ... + qn есть сумма л + 1 членов геометрической
1 — <7Л+1
прогрессии со знаменателем ^ и она равна —=—- , то
1+4 + 4+-+ j» (i --^ (1 - ^
3J _ J. _ 4
Пример 7. Найти предел переменной хЛ = д (а > 0).
Если 0<а<1, то ап будет бесконечно малой и lim #„ = (). Если а =1,
то ап — 1 и \\тхп*= -у. Наконец, если а>1, то ап будет бесконечно боль-
со
шои и мы имеем неопределенность вида — ; раскрывая ее, получим:
lim xn = lim t = lim = 1.
1+а Л+i
94

Здесь неопределенность раскрылась путем предварительного деления числителя
и знаменателя на ап.
Приведем некоторые примеры, при решении которых используется формула
бинома Ньютона. Читатель, не знакомый с этой формулой, может примеры
-8—10 пропустить.
Пример 8. Доказать, что lim ^ = 0.
Знаменатель 2п с помощью формулы бинома Ньютона можно представить
ввиде2" = (1 + 1)* = 1+л4- П(ПХ~ 1) .+ ...+ 1 = 1+п+ (у~у) + - +
it,,, , /Л2 П\ , , t , , , /Л2 П\ П2
4- 1. Hol + n+fy—yj +...+ !> i + n+ hg— у)>у, так как все
пропущенные слагаемые из формулы бинома Ньютона положительны. Отсюда получаем,
1 2
что 0 < «^ <1 —2» или, умножая почленно на я, будем иметь:
^ 2" ^ п •
2 /г
Поскольку > 0, то по теореме о сжатой переменной и щ —* 0.
Пример 9. Показать, что lim
Для решения задачи достаточно установить, что переменную yfn можно
представить в виде суммы 1 + ая, где ап есть бесконечно малая при п -* оо.
Пусть угл~= 1 + аЛ. Очевидно, а- ^ 0 для любого п. Возводя обе части
последнего равенства в п-ю степень, получим:
n = (l+an)"=l+nan + n("-l) a2 + ... + a?.
Так как все члены справа неотрицательны, то для любого п > 1 справедливо
неравенство
п(п— 1) , , п(п— 1)
.2
п> Н—J >2 an» то есть ;г""1 > \ . 2 п
л 2
Сокращая на (л—1), получим: l>yaj. Отсюда следует, что —> а^ или
v
|->ал^0.
-i/"~2~
Так как I/ > () при п—*оо, то по теореме о сжатой переменной будет
стремиться к нулю и ал, то есть ап есть бесконечно малая.
Пример 10. Показать, что lim -/а = 1 при любом а > 0.
Для всех п, начиная с некоторого, будет выполняться неравенство — < а <
п Г~Т~ п
<: п. Тогда "1/ — < -|/а < -|//г *
Так как при п —> со будет j/n —* 1 и "|/ — = —-— —* 1 (см. пример 9)s то по
уп
теореме о сжатой переменной получаем, что и -|/а —>1.
Пример 11. Найти предел переменной:
Хп~~~ 1.9» 9 . Я "•" 3 . _. + • • • ~Г
1-21 2.31 3.4T,"T(fi-l)n'
95

т 1,1111111 1 1
Так как -.—~ = 1 •
1
2 '
1
2-3~
1
2
1
3 '
1 1
3-4~ 3
1-2 2*2-3 2 3*3.4 3 4 ' • ' * ' (л — \)п гг—1
1
, то
и
]\тхп= lim (1 ) = 1.
Вопросы для самопроверки и упражнения
1. Какой смысл придается слову «неопределенность» при вычислении пределов?
2. Что означают слова «неопределенность раскрыта»?
3. Подобрать две такие бесконечно малые величины, чтобы их частное было
величиной бесконечно большой.
4. Подобрать две такие бесконечно большие величины, чтобы их разность:
а) была величиной бесконечно малой,
б) имела предел, равный 5.
В задачах 5—17 найти пределы последовательностей.
2я cos n . 2
5- **в1?+Т ST- 0т*-Т-
6. *„ = sin/iH—. Отв. Предел не существует.
sinn , п+1 _
10. jc„ = //!» +2 — /n2 — 2. Oms. 0.
11. xn = 7=—. Отв. со.
f^T+T + l
(n+l)(n-2)(ii + 2)
13- *«- „з_„2+5и_2 • Um- '•
14 * 1+4 + 9 + ... + Я»
" — пЗ + Зп+2
Уназание. Предварительно преобразовать числитель, используя формулу
],+22 + г2 + ,.. + п^П^1^2п+1\ Отв. 1.
13 + 23 + 33 + ... + пЗ д
,5' *«- „а Т-
Указание. Воспользоваться сначала формулой суммы кубов натуральных
чисел: 13+2з + 33 + ... + л3 = (1+2 + 3 + ... + л)2, а затем —формулой суммы
натуральных чисел, приведенной в решении примера 5. Отв. ^-.
96
1
12. *„= V"t*- * ^ Отв. К

§ 6. МОНОТОННАЯ ПЕРЕМЕННАЯ И ЕЕ ПРЕДЕЛ
Определение. Если переменная хп изменяется так, что
х1 < х2 < х3 <С... <С хп <С ха+х <...,
то она называется возрастающей в узком (или строгом)
смысле. Если же
Xi > Х% ^> Х3 > . . . > Хп J> Xn+i Z> . . . ,
то переменная хп называется убывающей в узком (или
строгом) смысле.
Иногда переменную хп называют возрастающей и в том случае,
когда
Х]_ ^z X2 ^=z: Xg ^=~; . . . ^^ Хп ^^ -^/г+1 :^= • • • >
понимая под этим возрастание в широком смысле (неубывание).
Аналогично, если
Х\ ^^ Х% ^^ Х% ^^ . . . ^^ Хп ^: Xn+i ^^ . . . ,
то переменная хп называется убывающей в широком смысле (невоз-
растающей). Переменные, возрастающие и убывающие в узком и
в широком смысле, объединяются под общим названием
монотонных*.
Легко заметить, что возрастающая не ограниченная сверху
переменная будет положительной бесконечно большой, а убывающая не
ограниченная снизу переменная — отрицательной бесконечно
большой. Действительно, если, например, хп возрастает и не
ограничена сверху, то для любого числа УИ>0 найдется такое п0, что
хПо>М. А тогда для всех п> п0 и подавно хп>М.
Монотонные переменные по сравнению с другими переменными
обладают и той особенностью, что для них из ограниченности
следует существование конечного предела.
Теорема (о монотонной переменной). Любая
возрастающая переменная хп, ограниченная сверху, имеет
конечный предел. Любая убывающая переменная хп,
ограниченная снизу, имеет конечный предел.
Доказательство. Докажем теорему для случая возрастания
в широком смысле. Пусть хп возрастает и ограничена сверху.
Следовательно, на основании теоремы из § 5 главы I у множества
значений хп существует точная верхняя граница. Обозначим ее
через А и покажем, что А и будет пределом для хп. Действительно,
по определению верхней границы хп^А для всех п. Возьмем е>0.
По свойству точных границ, для этого е найдется такое N, что
xN> А—8. Тогда в силу возрастания хп для всех п> N будет
* Слово «монотонный» происходит от греческого слова «монотос», что
означает «однотонный». Здесь употребляется в смысле характеристики изменения
функции.
97

хп>А— е. Таким образом, для п> N получим: Л—8<л:л<Л+е.
А это и означает, что Птл:,1 = Л.
Вторая часть теоремы доказывается аналогично. Доказательство
ее рекомендуется провести самостоятельно.
В теореме о монотонной переменной устанавливается только
факт существования предела без указания способа для его
отыскания. Однако и это имеет очень важное значение в теории пределов.
Если по отношению к некоторой переменной уже известно, что
она имеет предел, то во многих случаях этим предрешается и
вопрос о его нахождении.
ап
Пример 1. Доказать, что переменная хп——г(а>0) имеет конечный
предел. Найти этот предел.
Докажем сначала существование конечного предела. Так как
_ аП+1 _ а ап _ап _ а
*/г+1~~ (л+1)! ~ТГр[ "п\ ~ ~п\ ~ п+\ ' *п*
то при п+1 > а, то есть при /г>а—1, переменная хп становится монотонно
убывающей. Кроме того, она ограничена снизу, например нулем. Следовательно,
по теореме о монотонной переменной хп имеет конечный предел. Теперь, опираясь
на факт существования предела, можно найти и его значение. Пусть Нт*я = Л.
Тогда и \imxn+1 — A, так как хп+1 пробегает ту же последовательность значений,
что и хп. Переходя в равенстве xn+i =—-т-тхп к пределу, получим. Л=0-Л,
ап
отсюда Л=0. Таким образом, lim —: = 0.
Пример 2. Доказать существование предела у переменной
1 ¦ ! +яАт+...+ !
~*-2+1 ^22 + 1^23+1 ^ "^ 2Я + Г
Переменная хп возрастает, так как хп+1 = хп+ „n+i \ \ » и» следовательно,
*/г+1>*я- Кроме того, она ограничена сверху, так как 2 < ^ ПРИ любом л,
и
1.1.1. .1 1.1.1. .1
^ О •" 92 ' 93 ' * * ' "• on
2+1 ' 22 + 1 ^ 23 + 1 ^ '"^ 2Л+1 ^ 2 ^ 22^ 23
I 1_
2 2w+i , 1
2
Следовательно, на основании теоремы о монотонной переменной заключаем, что
данная переменная имеет конечный предел. Относительно этого предела также
на основании упомянутой теоремы можно утверждать, что он не превосходит 1.
Пример 3. Последовательность задана рекуррентным соотношением
*Я+1 =
Л a + Vxn, Xt^Va,
где а > 0. Найти предел этой последовательности.
Заданная последовательность имеет вид:
Га, Va + Va, ]/ a + Va+fa, .... ]/ а + ]/ a + Va + ... + Va , ...
9&

Сравнивая значения для хп и хп+ъ легко заметить, что хп+1 > хп. Используя
последнее, получаем: хп~ Va-\-xn_i < Y~a + xn .
Отсюда х2п<а + хп и х% — хп — а<0. Решая последнее неравенство, найдем,
что хп<.-^-\- I/ -т- "Г" а для всех значени /г-
Таким образом, установлено, что данная последовательность возрастает и
ограничена сверху. Но тогда по теореме о монотонной переменной она имеет
конечный предел. Для определения предела будем рассуждать, как и в примере 1.
Пусть \\тхп — А. Тогда также Пт*/1_1 = Л (так как значения переменной хп_х
образуют ту же последовательность, что и хп) и, переходя к пределу в равенстве
*п-ъ получим А —Уа-\-А. Отсюда
А2 = а-\-А, или Л2 — Л— а = 0, откуда Л
-W-!¦+•¦
го до
Так как по условию а>0 и по доказанному хп возрастает, то должно быть Л>0,
то есть Л=—+1/ -д+а. Таким образом, Нтхя = -о-+1/ -г- + а.
Пример 4. Дана окружность. В нее вписываются последовательно
правильные многоугольники, каждый последующий из которых образуется удвоением
числа сторон предыдущего (рис. 53). Периметры этих п
многоугольников образуют числовую
последовательность:
Ръ Ра, Р*
0)
Рис. 53.
Доказать, что эта последовательность имеет конечный
предел.
Так как сторона треугольника меньше суммы
двух других сторон, то, как видно из обозначений
на рисунке 53, Рп < Рп+1 для всех значений /г, то
есть последовательность (1) возрастает. Кроме того,
периметр любого вписанного многоугольника меньше
периметра любого описанного многоугольника. Это
значит, что последовательность ограничена сверху.
В качестве верхней границы можно взять,
например, периметр описанного шестиугольника. По теореме о монотонной
переменной последовательность имеет конечный предел \\т Рп. Задача решена.
Загс-»-оо
метим, что предел lim Pn принимается за длину окружности. Именно так вво-
дится понятие длины окружности, известное читателю из элементарной геометрии.
Теоремой о монотонной переменной мы будем пользоваться еще
неоднократно, начиная со следующего параграфа.
Вопросы для самопроверки и упражнения
1. Доказать теорему о монотонной переменной для случая убывания.
2. Сформулировать теорему о монотонной переменной в терминах
последовательности.
3. Доказать, что последовательность, заданная рекуррентной зависимостью
х
xn+iz=zTrr—» где *i>0 — произвольное число, сходится. Найти предел этой
последовательности. Отв. 0.
1.1.1.
4. Доказать существование предела переменной хп--
+ ..+
1
3+1 ^ 32 + 2 ^Зз+З"1
99

5. Дана переменная хп — а" . Составить рекуррентную зависимость между
значениями хп+1 и хп, доказать существование предела и найти его. Оте. 1.
6. Дан равносторонний треугольник со стороной а\ из трб& высот его строится
новый равносторонний треугольник, и так п раз. Найти предел суммы площадей
всех треугольников при п —* со. Отв. a2 Y^ •
§ 7. ЧИСЛО е
Лемма (Бернулли)*. Для любого натурального числа т
и любого вещественного числа h> — \ справедливо
неравенство
(l+h)m^l+mh, (1)
называемое неравенством Бернулли.
Доказательство проведем методом математической
индукции. При т = 1 соотношение (1) очевидно (в этом случае оно
переходит в равенство). Предположим, что (1) справедливо при m=^ky
и докажем его справедливость при m = k+ 1. Учитывая, что 1+/г>
>0, имеем:
(l+h)k+1 = (l+h)k (l+h)^(l+kh)(l+h)=l+(k+l)h + kh2^
^l-\-(k+l)h (так как kh2^0). Лемма доказана.
Рассмотрим теперь переменную xn = (l-\—] . С первого взгляда
может показаться, что она имеет своим пределом единицу. Однако
это не так. Применяя только что доказанную демму Бернулли,
видим, что для любого п
(1+^1 + «4 = 2- (2)
С помощью этой леммы можно доказать существование конечного
предела переменной хп = [1+—Г.
Рассмотрим сначала переменную
1\л+1
+1\n+1
Покажем, что она монотонно убывает. Действительно, уп — {--^—}
ч г= ( П Y и Ъ=к — п"'пП+1 — ( п% Y*1 П~~[
^n_1 U—1/ уп ~~ (я— 1)я.(л+1)я+1 \/г2— 1 у " п •
Так как в силу неравенства (1) (при A = ^zn» т = /г+1]
п—1 п—Г
Уп-1 ¦
то ~=^^1, то есть Уп-г^Уп для всех п^=2. Ограниченность уп
Уч
* Якоб Бернулли (1654 — 1705) — швейцарский математик.
100

снизу очевидна, в силу (2) уп^2. Следовательно, уп имеет
конечный предел. Но тогда существует конечный предел и переменной хп,
так как
*Л = -^Т и Птхп = )тУп]\ =НтуЯт
Этот предел принято обозначать буквой е:
* = lim(l+-!Vl
Число е является иррациональным числом и, следовательно,
представляется в виде бесконечной непериодической дроби:
е = 2,718281828459045...
В качестве простейшего приближенного значения для числа е
полезно запомнить, что ?^2,7. Немного точнее: е = 2,72.
Подчеркиваем, что предыдущими рассуждениями мы не
доказывали равенство e = lim(l+ —J ; мы доказали, что указанный
предел существует, и назвали его числом е.
По мере изучения математического анализа будет
обнаруживаться все большее значение числа е во многих вопросах теории и
практики. Пока укажем лишь, что число е принято за основание
так называемых натуральных логарифмов, которые в силу особых
свойств числа е имеют 6oj.ee широкое применение в математическом
анализе, чем десятичные логарифмы. Натуральные логарифмы
имеют специальное обозначение: In x(\nx = \ogex).
Установим связь между lnx и \gx при любом значении х>0.
Для этого прологарифмируем тождество х=еХпх по основанию 10.
Получим:
ig а: = 1п д:- lge или lgx=M-lnx.
Число М называется модулем перехода:
M = lge = -n^ro = 0,434294...
Пример I. Доказать, что переменная хп= (1 -\ J стремится к своему
пределу е возрастая.
Для доказательства достаточно установить, что-^^>1 при любом п. Так
как
¦ыг-т^-ь+ъГ-ъ
+ч
<Cn+i (n+2V»i ( п у /д+2уч-1 / п уп д+1
х„ \n+l) '\n+lj \n+l) \n+l) ' n
_ f (n-j_2)j_n l"+i n+1
-[ (п-И)» J ' « •
101

Выражение, стоящее в квадратных скобках, преобразуем к виду
п(п + 2) =п*+2п =(п+1)2~ 1« 1
(Л+1)« (П+1)2 (Я+1)« (П+1)*'
Тогда с помощью леммы Бернулли получим:
Следовательно, -2±=- ^—г—г • —!—= 1-
хп ^ л+1 п
Заметим, что лемму Бернулли можно уточнить следующим образом: если
Л>—1, но Л^О, то при m^>2 (т— натуральное)
(l+/Om>l+m-/z.
Учитывая это замечание, легко видеть из предыдущего вывода, что -^^ > 1,
то есть что переменная хп = \Л-\ ] стремится к своему пределу строго
возрастая.
Пример 2. Найти предел переменной хп = п [In (п +1) — In л].
Воспользуемся пределом lim (1 Н ) =?• Получим:
limn [In (л+1) —lnrt] = lim л- In ¦ — lim In f 1 -\ ) = lne=l.
Пример З. Население страны ежегодно возрастает на 2%. Во сколько
раз оно увеличится за 200 лет?
Обозначим через /V первоначальное число жителей. Очевидно, через год будем
иметь:
«-^-"(Ч-И)-
через два года оно снова умножится на (1 +ёл), то есть будет равно
"(¦¦А) ('+¦)-»•№
через три года —
и т. д. Через 200 лет число жителей будет равно
*№-»[(¦+АП-
то есть увеличится в И 1 + ёл) раз. Чтобы легче представить себе это число,
выразим его приближенно. Так как lim (1 -j ] = е, то при больших значениях п
м _] j ^ву и, чем больше л, тем точнее это приближенное равенство. Так
/ 1 \50 / \ \П
как число U+eq) можно рассматривать как выражение вида (1 -| 1 при
/ 1 \50 Г/ Г\50]4
Л = 50, то (1 + кл) ***е и II1 + ел ^ **• Получили, что население страны
за 200 лет увеличится примерно в е* раз. Принимая ?^2,72, получим: ^^об.
102

Вопросы для самопроверки и упражнения
1. Почему выражение: «Мы доказали, что lim(l-J ]
правильное?
2. Найдите приближенное значение е из приближенного равенства (1 -\ )
е^е при я = 6.
/ 1 \п+4
3. Найти предел переменной хЛ = (1-| )
равен числу еъ — не-
Отв. 2,521.
Отв. е.
§ 8. ТЕОРЕМА О ВЛОЖЕННЫХ ОТРЕЗКАХ
Пусть имеем последовательность отрезков, вложенных друг
в друга таким образом, что каждый последующий содержится
в предыдущем:
[аъ bx] zd [a2, b2]zD[a3, b3\ =>...=> [ап, Ьп] =э ..., (1)
причем при возрастании п длина /г-го отрезка Ъп—ап-+0. Такую
последовательность отрезков называют стягивающейся.
Теорема. Для всякой стягивающейся
последовательности вложенных отрезков (1) существует точка с,
притом единственная, принадлежащая всем отрезкам этой
последовательности, то есть такая, что ап^с^Ьп для
всех п (рис. 54).
Доказательство. Левые концы отрезков
последовательности (1) образуют монотонно возрастающую последовательность:
аг ^ а2 ^ а3 ^... =^ ап ^..., (2)
а правые концы—монотонно убывающую последовательность:
(3)
При этом последовательность (2) ограничена сверху, а
последовательность (3) ограничена снизу, так как ап^Ьъ а Ьп^ах для всех п.
Следовательно, на основании теоремы о монотонной переменной эти
последовательности имеют пределы. Пусть lim an=crt a \\mbn=c".
Тогда из соотношения
0=lim (bn—an) = lim bn—lim an=c"— с'
получаем, что с'=с". Общее значение с'=с" обозначим через с,
*,
11 [§1 ]
Рис. 54.
к.
\
103

то есть с' =с" —с. И поскольку ап^с, а Ьп^с при всех п, то точка с
принадлежит всем отрезкам последовательности (1).
Остается показать, что точка с является единственной точкой,
удовлетворяющей этому условию. Допустим противное. Пусть
существует точка съ отличная от с и также принадлежащая всем
отрезкам последовательности (1). Тогда для любого п должно выполняться
неравенство Ъп — ап^\сг—-с|. Следовательно, Ъп — ал740 (не
стремится к нулю), что противоречит условию теоремы.
Заметим, что доказанная теорема становится неверной, если
в ней вместо отрезков рассматривать интервалы. Действительно,
возьмем, например, интервал (0, 1) и разделим его пополам.
Выберем в качестве второго интервала левую половину, то есть [О, -Л.
Делим (О, -Л снова пополам и выберем левую половину, то есть
(О, -]-V и т. д. Этот процесс деления и выбора интервалов
бесконечный. Следовательно, получится бесконечная последовательность
вложенных интервалов:
(О, 1)=>(0, 1)=>(0, |)=>...=>(о, ^г)=э... (4)
Интервалы этой последовательности не имеют ни одной общей
точки, так как, какую бы точку а на промежутке (0, 1) мы ни
взяли, найдется такое п0, что -щ^-<а> и интервалы
последовательности (4), начиная с (0, -угА, не содержат точку а. Точка нуль
является общим левым концом всех интервалов, но не принадлежит им.
Доказанная теорема будет в дальнейшем неоднократно
использована нами при доказательстве других весьма важных теорем.
Вопросы для самопроверки и упражнения
1. Построить последовательности вложенных отрезков, стягивающиеся:
а) к точке с = 5; б) к точке с=— 2.
2. К какой точке стягивается последовательность вложенных отрезков:
[т. ']• [т. ']. [4. ¦]• •••¦ Ыт- ']. ¦-'
§ 9. ЧАСТИЧНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
Пусть дана некоторая числовая последовательность
¦^1» -^2» -^3» •••» %ni ••• (1/
Если из этой последовательности выписывать не все члены подряд,
а с пропуском (например, брать члены через один, или каждый
пятый, или как-нибудь иначе), то получим новую
Последовательность:
«^nji Хп$> "^лз' " " * ^nk* '"'' ^ f
104

которая называется частичной последовательностью или
подпоследовательностью по отношению к последовательности (1). Здесь пх
означает номер первого из членов хп последовательности (1),
вошедших в (2), п2 — номер второго из членов хпу вошедших в (2), и т. д.
Например, если последовательность (2) состоит из х3, *8, лгп, ...,
то пг==3, /г2 = 8, п3=П и т. д. Порядковый номер члена xnk в (2)
определяется уже не числом п, а числом k, и /г1<я2</гз<"-<
<nk<.tik+i<••• Покажем, что для любого k справедливо nk^k,
то есть что при любом k член хПк есть либо xk, либо один из
членов, следующих за ним в (1). Воспользуемся методом математической
индукции. При k=l неравенство /гх^1 очевидно, так как лц есть
либо хъ либо один из последующих членов в (1). Предположим
теперь, что неравенство пт^т справедливо при k = m. Тогда
nm+iS?/im+l^m+l.
Из последовательности натуральных чисел 1, 2, 3, 4, ..., п, ...,
можно, например, выделить такие частичные последовательности:
1, 3, 5, 7, 9, ..., 2/i—lf ...,
2, 4, 6, 8, 10, ..., 2л, ...,
2, 5, 10, 17, 26, ..., /г2+1, ..., и др.
Заметим, что в частном случае последовательность (2) может
и совпадать с последовательностью (1), тогда xnk = xk, где &=1, 2,
3, ...
Теорема 1. Если последовательность (1) имеет своим
пределом число а, то выделенная из нее любым способом
подпоследовательность (2) будет такэ#е иметь предел,
равный а.
Доказательство. Пусть последовательность (1) сходится
к числу а. Это значит, что для любого е>0 найдется такое N,
что для n>N выполняется неравенство \хп—а|<е. Так как хп,а
либо совпадает с xk, либо правее его в последовательности (1),
то для k> N будет \xnk—а|<е, что и доказывает теорему.
Если последовательность (1) стремится к бесконечности, то легко
доказать, что любая ее подпоследовательность также стремится
к бесконечности. Предлагаем это сделать читателю.
Если же последовательность (1) не имеет предела, то из этого
еще не следует, что всякая ее подпоследовательность также не будет
иметь предела. Известно, например, что последовательность
+ 1, -1, +1, -1, +1, ..., (-1)», ...
не имеет предела (см. пример 2, § 1), в то время как ее
подпоследовательности
+ 1, +1, +1, +1, ..., +1. ...
-1, -1, -1, -1, ..., -1, ...
сходятся (первая к 1, вторая к —1).
105

Теорема 2 (Больцано — В ейер штр асса)*. Из всякой
ограниченной последовательности можно выделить
сходящуюся подпоследовательность.
Доказательство. Пусть последовательность (1) ограничена,
то есть существуют такие числа а и Ь, что а ^ хп ^ Ъ для всех п.
Это значит, что все члены последовательности находятся на отрезке
[а, Ь]. Разделим этот отрезок пополам точкой d = -^~—, тогда по
крайней мере одна из частей, [a, d] или [d, b], будет содержать
бесконечное множество членов последовательности (1). Обозначим
эту часть через [аъ Ьх]. Может оказаться, что обе части содержат
по бесконечному множеству членов последовательности (1), тогда
через [аъ Ь±] можно обозначить любую из них. Делим отрезок
[аъ Ьг] пополам точкой йг= а^ * и часть, содержащую
бесконечное множество членов последовательности (1), обозначим через [а2, Ь2].
Отрезок [а2, Ь2] делим в свою очередь пополам и часть, содержащую
бесконечное множество членов последовательности (1), обозначим
через [а3, Ь3] и т. д. Этот процесс деления никогда не закончится.
Получим последовательность вложенных отрезков:
[аъ Ьг\ zd [аз, 62]=)[оз, Ь3] =э ... =э [а„, Ьл]=э... (3)
При этом длина /г-го отрезка Ьп — ап = —^ *0 при я->оо.
Следовательно, по теореме о вложенных отрезках существует такая
точка с, что
lim #„ = lim bn=c. (4)
Возьмем какой-нибудь из членов последовательности (1),
содержащихся в [%, bj], и обозначим его через лц. Затем возьмем любой
из членов последовательности (1), содержащихся в [а2, Ь2] и
следующих за лц, и обозначим через хп^ и т. д. Такому выбору ничто
не препятствует, поскольку в каждом отрезке последовательности (3)
имеется бесконечное множество членов последовательности (1).
Выделенная таким образом последовательность лц, хп^ х„а, ..., xn/i, ...
будет сходиться к числу с, так как ak^xnk^bk для любого k»
и имеет место равенство (4).
Замечание. Условие ограниченности последовательности
является существенным, так как существуют неограниченные
последовательности (например, 1, 2, 3, ..., м, ...), из которых нельзя
выделить сходящуюся подпоследовательность. Однако отсюда не следует,
что только из ограниченных последовательностей возможно
выделение сходящихся подпоследовательностей. Например,
последовательность хп = п{~1)п является неограниченной, но из нее можно выделить
сходящуюся к конечному пределу подпоследовательность. Достаточно
придавать п только нечетные значения.
* Больцано Бернард (1781 —1848) — чешский математик. В ейер-
штрасс Карл Теодор Вильгельм (1815—1897)-—немецкий математик.
106

Вопросы для самопроверни и упражнения
1. Доказать, что если последовательность хп (я=1, 2, 3f ...) не ограничена,
то из нее можно выделить подпоследовательность xnk — оо.
2. Доказать, что монотонная последовательность сходится, если сходится
какая-нибудь ее подпоследовательность.
0 „ 1113 17 1 2я—1
3. Из последовательности ^, ^-, —, —, -, —, ..., уГ9 g/| , ...
выделить сходящиеся подпоследовательности.
4. Из данной последовательности выделено несколько подпоследовательностей,
сходящихся к одному и тому же пределу. Можно ли на этом основании
утверждать, что и сама последовательность также сходится?
5. Из данной последовательности выделена расходящаяся
подпоследовательность. Можно ли утверждать, что сама последовательность также расходится?
§ 10. ПРЕДЕЛ ФУНКЦИИ
Пусть функция y = f(x) задана на некотором промежутке X,
за исключением, может быть, точки х0 этого промежутка. Возьмем
из X последовательность точек, отличных от х0:
Xlf Х2, АГ3, ..., Хп, ..., (1)
сходящуюся к Xq. Значения функции в точках этой
последовательности также образуют числовую последовательность
f(*i), f(xj, f(xJ, ..., f(xn), ..., (2)
по отношению к которой можно ставить вопрос о существовании
и нахождении предела. Поскольку составление последовательности (1)
ничем не обусловлено, кроме того только, чтобы она сходилась
к точке х0, то ее можно составлять различными способами.
Соответственно будем получать и различные последовательности (2). Если
последовательности (2), соответствующие всевозможным
последовательностям (1), имеют один и тот же предел, например число Л,
то будем говорить, что функция y = f(x) имеет в точке х0 предел,
равный А, и обозначать: limf (x) = A.
х-+х0
Если же хотя бы для одной последовательности (1), сходящейся
к х0, последовательность (2) не имеет предела или имеет предел,
но отличный от предела другой последовательности (2), то говорят,
что в точке х0 функция y=f(x) предела не имеет.
Дадим теперь строгое определение предела функции в точке.
Определение 1. Число А называется пределом функции
f(x) в точке х0, если для любой последовательности точек (1) из
промежутка X, отличных от х0, сходящейся к точке xQj
последовательность соответствующих значений функции (2) сходится к числу А.
Существует и другое определение предела функции.
Определение 2. Число А называется пределом функции
f(x) в точке x0f если для любого сколь угодно малого числа е>0
найдется такое число б > 0, что для всех х ^ь х0, х<= X,
удовлетворяющих неравенству \х — #о|<6, выполняется неравенство \f(x)— Л|<е.
107

Первое определение основано на понятии предела числовой
последовательности, поэтому его часто называют определением «на языке
последовательностей». Определение же второе использует понятие
е-окрестности и б-окрестности и потому его называют определением
«на языке е— б».
Теорема 1. Первое и второе определения предела
функции эквивалентны, то есть если функция имеет предел в
точке х0 согласно одному из определений, то этот owe
предел функция будет иметь и по другому определению.
Доказательство. Пусть Л есть предел f (х) в точке х0 по
первому определению. Рассуждая от противного, предположим, что
А не является пределом этой функции по второму определению. Это
значит, что не для любого е > О можно найти такое б > О, чтобы
из неравенства \х—х0\ <6 следовало бы неравенство \f (х) — А |<?>
то есть существует такое е = е0, для которого нельзя подобрать б,
удовлетворяющего указанному условию. А это, в свою очередь,
означает, что для е0, какое бы б мы ни взяли, найдется хоть одна точка
хфх0 такая, что \f (х\—Л|^е0, хотя \х—л:0|<б. Возьмем в
качестве б последовательно числа:
iii 1
' 2 » 3 • "•, п* '•*
Для 6 = 1 в X найдется такая точка хг Ф х0, что |*i—*0|<1, а
\f(Xi) — A\^e0..
Для б=у в X найдется такая точка х2 Ф х0, что \х2—#ol<-o->
a \f(x2) — Л|^е0.
Для 6=у в X найдется такая точка х3 Ф х0, что \х3—-х0\ <-%>
а 1/(*з) — Л|^?0, и т- Д-
Для б=— в X найдется такая точка хп Ф х0, что \хп—х0!<—,
a \f(xn) — Л |з*е0, и т. д.
В результате выделится последовательность точек, отличных от xQi
Хъ Х2у «*з, • . • , Хп, . • • ,
сходящаяся к точке х0, так как \хп — х0|< >0 при п-+со. Тогда
согласно первому определению \\mf(xn) = A. Следовательно, по е0
найдется такое число N, что для п> N будет | f (хп)—А | <е0. Но
этого быть не может, так как для всех п выполняется неравенство
I/ (Хп) — А | ^ 80. Полученное противоречие и доказывает что число А
есть предел функции f(x) в точке х0 по второму определению.
Пусть теперь А есть предел / (х) в точке х0 в соответствии со
вторым определением. Возьмем любое &>0. По нему найдется такое
б>0, что из неравенства \х—л;0|<б будет следовать неравенство
| / (х)—А | <8. Возьмем последовательность точек хъ л*2, х3, •.., xnt...,
сходящуюся к точке х0(хпФ х0). Тогда по б найдется такое Л/, что
для п>N будет \хп—*0|<;6. Но вместе с этим будет выполняться
108

и неравенство \f (хп)—Л|<е. Следовательно, l\mf(xn) = A.
Поскольку последовательность точек, сходящаяся к х0, выбиралась
произвольно, то можно утверждать, что А будет пределом / (х) в точке х0
по первому определению.
После того как мы установили эквивалентность обоих определений
предела функции, можно пользоваться любым из них, в зависимости
от того, какое более удобно при решении той или иной задачи.
Следует заметить также, что оба, определения сами по себе еще
не дают способа отыскания предела данной функции. С их помощью
иногда можно лишь установить, будет ли то или иное число
пределом функции, или можно убедиться, что данная функция вовсе не
имеет предела.
Пример 1. Показать, что функция / (х) =х в любой точке х0 = а имеет
предел, равный а, то есть lim f(x)=a.
х-* а
Возьмем е > 0. Из неравенства \f(x) — а\ = \х—а I <С 8 заключаем, что б нужно
взять ^:в. Тогда, если | х — х0 | = | х—а\ <б, то \f(x) — a|<«.
Пример 2. Показать, что функция / (я) = 3# — 5 имеет в точке * = 2 предел,
равный 1. Каково должно быть б, если 8 равно 1, -~- и j^ ?
Возьмем любое е;>0. Задача состоит в том, чтобы по этому 8 найти такое
б>0, при котором из неравенства !л:—2;<б следовало бы неравенство
|(3х —5) — 1 |<е. Последнее преобразуется к виду \3 (х— 2) |<е или
\х — 2|<C-q-. Отсюда видно, что можно взять 6 = — # В частности, еслие=1,
О О
с 1 1 , 1 1 1
то о = -g-; если е = — ? то б = -g-; если е = -т™, то б = ggn .
Пример 3. Пользуясь определением предела функции в точке, доказать,
что функция f (х) = х2 — Зх — 1 имеет в точке х = 2 предел, равный —3, то
есть lim (х2 — Зх — 1) = — 3.
х-?2
Этот пример проще решить, используя определение предела функции «на
языке последовательностей». Пусть {хп} — произвольная последовательность
значений х, сходящихся к 2, то есть хп—* 2. Тогда, применив теорему о
пределе произведения (см. §4), получим: limx^= lim (xn • хп) = 2 • 2 = 4t
lim Зхп = 3 • 2 = 6.
По теореме о пределе суммы и разности получим:
m / (хп) = I i m (х\ — Зхп — 1) = 4 — 6 — 1 = — 3.
хп-+2 хп-+2 п
п п
Поскольку последовательность {хп} предполагалась произвольной (с одним
лишь требованием, чтобы хп—*2), то на основании определения предела
функции заключаем, что lim (х2 — Зх — 1) = — 3.
х->2
Таким образом, решение свелось к тому, что в выражение
данной функции мы подставили х = 2. Легко понять, что
проведенное рассуждение применимо к любому многочлену, и мы можем
сделать следующий общий вывод: для того чтобы найти
предел многочлена
109

а0хп + агх? г + ... + ап_хх + ап
при стремлении х к некоторому числу а, достаточно
подставить в выражение этого многочлена вместо х
число а, то есть
lim (а0хп + axxn~Y +... + ап-гх + ап) =
= а0ап + а^71-1 +... + ап-га + ап.
Для сравнения решим тот же пример 3, исходя из определения
предела функции «на языке е — б». Возьмем произвольное е>0и
найдем такое б>0, чтобы для всех точек х, удовлетворяющих
неравенству \х — 2 | < б, выполнялось неравенство
|(х2 — Зх— 1) —(—3)|<е.
Выражение, стоящее под знаком абсолютной величины, можно
преобразовать так:
(х*-Зх-1)-(-3) = х*-Зх + 2 = (х— -^J — -L =
-[(*-т)-т]-[(*-т)+т]-(*-?) С-1)-
Следовательно, должно выполняться неравенство
\(х—2) (х— 1)| <е или |х —2|.|*—1|<е. (1)
Пусть б пока еще не определено. Но если предположить
выполненным неравенство \х—2|<6, то \х— 1| = |(я—2) + 11^
^| х — 2|+ 1 <б + 1 и тогда
|х_2|.|х-1|<6 (6+1). (2)
Сравнивая (1) и (2), заключаем, что б достаточно взять таким,
чтобы б-(б+1) = е- Решая последнее равенство, получаем:
б2 + б = е, или 62 + 6— е = 0. Отсюда 6 = pdtl/ -^- + e.
У
Так как б должно быть положительным, то из двух возможных
решений берем:
б
=-4-+П+.
]Л +48—1
В частности, если е = 2, то 6=1, если е = щ, то 6 = 0,009, и т. д.
Заметим,что если для конкретных значений е нахождение
соответствующих значений б по полученной формуле затруднительно
(как в нашем примере при е = уоо), то можно вычислять его
приближенно. Однако округлять результат следует только в сторону
уменьшения.
ПО

Рис. 55.
П р и м е р 4. Показать, что функция / (х) — sin—, определенная для все х -ф. О,
в точке х — 0 не имеет предела (рис. 55).
Возьмем в качестве последовательностей значений хх сходящихся к нулю,
следующие последовательности:
D-L -Li- JL.
' л ' 2л* Зл ' ' пп '
' л ' 5л* 9л» *" (4л — 3) л»"*
Составим для них соответствующие последовательности значений данной
функции:
1#> К-н-)- /(к). Ki
^U^]''
'\5ЯГ '\9л),,"',Ч(4я — 3) л/'
Так как при любом п значения /(—) sin/ift = 0, а / {-п =т—] =
* ' \пл] ' \(4л —3) л /
. (4я — 3) л „ ,, v
= sm ^—-— = 1, то для первой последовательности lim/ (хп) = hm sinnrt = О,
а для второй — hm/ (хл) = hm sm —~— л = 1.
Оказалось, что для выбранных таким образом последовательностей значений
аргумента соответствующие последовательности значений функции имеют разные
пределы. А это и значит, что в точке х—0 функция sin—предела не имеет.
Кроме рассмотренного нами понятия предела функции в точке,
существуют также понятия предела в точке слева и предела в точке
справа.
Ill

Если в определении предела функции потребовать, чтобы х
стремилось к х0 не любым способом, а только слева (оставаясь все
время меньше х0), то получим определение предела слева в точке х0.
Аналогично, если существует предел функции f(x) в точке х0 при
условии, что х стремится к х0 только справа (оставаясь все время
больше jc0), то такой предел называется пределом справа. Пределы
слева и справа иначе называются односторонними пределами и
соответственно обозначаются так:
lim f(x) = f(x0-Q), lim f (x) = f (x0 + 0).
x-+xo — 0 x-*xo-\-0
Из определения предела следует, что если функция имеет в
какой-либо внутренней точке промежутка предел, то она имеет в этой
точке и односторонние пределы, причем
\[mf(x)=f(x0-0)=f(x0 + 0).
х-+х0
Но функция может иметь односторонние пределы и при отсутствии
предела в точке. Приведем пример такой функции.
( х2 при х^ 1,
Пример 5. г(х) = <
v F I x+\ при х>1.
В точке х—1 эта функция не имеет предела, но имеет предел слева, равный 1,
и предел справа, равный 2 (рис. 56).
Если же функция в некоторой точке имеет односторонние
пределы, равные между собой, то их общее значение будет пределом
функции в этой точке.
Пример 6. Вычислить односторонние пределы фу нкции у = Е (х) в точках,
соответствующих целочисленным значениям аргумента х. График этой функции
изображен на рисунке 57.
Рис. 56
112

Пусть х = п. На промежутках [я, п+1) и [п— 1, /г) функция постоянна,
причем Е (х) = п на [/г, п+1) и ?" (х) = /г — 1 на [л—1, л). Следовательно,
lim ?(х) = /г— 1, lim Е(х) = п.
х-+п — 0 х-+п-\-0
Аналогичная картина и в точках х=— п.
Для функции f (х), заданной в некотором промежутке X, можно
ввести также понятие бесконечного предела в точке х0 (при х-+х0).
По аналогии с двумя определениями конечного предела функции
в точке сформулируем два эквивалентных определения бесконечного
предела.
Определение 3. Если Yk
для любой последовательности д+е[
значений х:
А\
X±t -*2» "^3» * * *' ^я>* • •»
сходящейся к х0 (xn^x0),
lim/ (я„) = оо, то говорят, что
функция f (х) имеет в точке х0
бесконечный предел.
Определение 4.Функция
f (x) имеет в точке х0
бесконечный предел, если для любого сколь угодно большого положительного
числа М найдется такое число 6 > О, что для всех значений х из
X (х Ф х0), удовлетворяющих неравенству \х — х0 | < 8, выполняется
неравенство \ f (х) | > М.
Бесконечный предел функции / (х) в точке х0 записывается
следующим образом:
Нт/(л:) = оо или f(x)->oo при х-+х0.
х-+х0
Аналогичным образом определяются и соотношения
limf(x)= + оо и
х-+х0
lim f (х) = —оо.
Х-+Х0
Последнее, например, означает, что f(x) удовлетворяет условию
из определения 3 или 4, и, кроме того, известно, что в некоторой
окрестности точки х0 функция f(x) принимает отрицательные
значения.
Если бесконечный предел функции f(x) в точке х0 получается
при стремлении х к х0 только слева (х-+х0—0) или только справа
(л:->л:0 + 0), то в этом случае имеем дело с односторонними
бесконечными пределами.
Если функция f (x) задана в бесконечном промежутке, то для
нее имеет смысл вводить определение предела «на бесконечности».
Например, если[(х) задана в промежутке (а, +оо), то можно ввести
понятие lim f(x).
#->+00
Определение 5. Число А называется пределом функции
f(x) при х-* + оо, если для любого е>0 найдется такое
вещественное число К, что | f (х) — А | <е для всех значений х>К-
113

В этом случае число А называют пределом функции на
бесконечности и обозначают:
lim f(x) = A.
х—*--\-со
Неравенство | f (х) — А | < е равносильно неравенству А — е <
< / (а:) < Л + е. Учитывая последнее, можно дать следующее
геометрическое истолкование предела функции на бесконечности: lim f(x)=A
х-*-{-оо
геометрически означает, что кривая y = f(x) при х-^ + оо
неограниченно приближается к прямой у = А, то есть, какое бы е>0 мы
ни взяли, найдется такое /С, что для всех значений х>К кривая
y=f(x) будет находиться между пр ямыми у = А — е и у = А+е
(см. рис. 58).
Аналогично определяется и геометрически истолковывается предел
limf(x) = A.
Х-+— 00
Можно дать равносильное определение предела функции на
бесконечности «на языке последовательностей». Рекомендуем читателю
сделать это самостоятельно.
Пример 7. Используя определение предела функции на бесконечности, дока-
зать, что lim ех =1.
Х-++00
Возьмем произвольное е>0 и определим значения х, для которых
выполняется неравенство \ех — 1 | < е. Так как е х> 1 при любом х > 0, то наше
неравенство можно переписать так: е х—1<?, или ех <с 1+8. Логарифмируя обе
части последнего неравенства по основанию е> получим: —< 1п(1 + е), откуда
х > \—7Г-,—ч • Если за К взять число -.—тт—;—г- . то для всех значений к > К
In (1 + е) In (1 + e) '
JL _L
будет ] е х — 1 | < е. Следовательно, lim е х = 1.
Х—*--\-СО
Очевидно, график функции у = е х при х>К будет лежать в полосе между
прямыми #=1 + е и */=1 —е.
Предлагаем читателю самостоятельно сформулировать определение
«бесконечного» предела функции на бесконечности, то есть, например, соотношения
lim /(*) = + со.
X—ЮО
Пример 8. Используя определение предела функции на бесконечности,
доказать, что limaAr=+co (при а> 1).
*-»--|-оо
Покажем, что, какое бы большое положительное число М мы ни взяли,
начиная с некоторых значений х будет \ах |=а*> М. Возьмем любое число М>0
и будем искать значения х, при которых ах> М. Логарифмируя обе части
последнего неравенства по основанию а, получим:
х > loga M.
Итак, по М нашлось такое число K = \ogaM, что для всех значений я>/С
выполняется неравенство ах>М. Это и означает, что величина ах при х-+-{-со
является бесконечно большой, именно limaA" = +oo (см. рис. 34).
*-*-)-00
114

Вопросы для самопроверки и упражнения
1. Пользуясь определением предела функции, доказать, что в точке х = 2
функция f (х) = 3х2 — 2 имеет предел, равный 10. Каково должно быть 6, чтобы
из неравенства \х—2|<6 следовало неравенство | / (х) — 10 | <0,01?
2. Пользуясь определением предела функции, доказать, что lim —^~- = 2*.
3. Пользуясь определением предела функции, доказать, что lima* = 0 (a > 1).
х-+—оо
Зя 1
4. Пользуясь определением предела функции, доказать, что lim _ ¦ ф I.
лг-юо оХ-\-2
5. Показать, что функция у=х — Е (х) не имеет предела ни при каком целом
значении х. Чему равны односторонние пределы функции в этих точках?
§ 11. РАСПРОСТРАНЕНИЕ ТЕОРЕМ О ПРЕДЕЛАХ НА СЛУЧАЙ
ПРОИЗВОЛЬНЫХ ФУНКЦИЙ
Пользуясь определением предела функции / (х), можно было бы
доказать заново все теоремы о пределах. Однако в этом нет
необходимости. Если исходить из определения предела функции «на языке
последовательностей» и применить доказанные выше теоремы к
последовательностям типа f(xn), то легко получить соответствующие
теоремы для функций общего вида.
В качестве примера того, как можно доказанные теоремы
распространить на случай функций f(x), заданных в промежутке,
рассмотрим теорему о пределе суммы, разности, произведения и
частного.
Прежде всего заметим, что арифметические действия над
функциями можно производить только в общей части их областей
определения.
Теорема. Пусть функции f(x) и g(x), определенные
на некотором промежутке, в точке х0 этого промежутка
имеют конечные пределы, limf(x) = A и lim g(x) = B. Тогда
X—*-Xq X—+Xq
функции, представляющие собой сумму, разность,
произведение и частное этих функций (последнее при условии
ВФО**), имеют в точке х0 также конечные пределы, причем
\\m\f{x)±g{x)\ = A±B; Wm\t{x).g{x)\ = A-B;
X—*Xq X—+Xq
.. f(x) A
lim J\ \ = -p-.
x-*Xo gW в
Доказательство. Условия limf(x) = A и limg(x) = B на
X—+Xq X—+Xq
«языке последовательностей» означают, что для любой последов ате ль-
* Если функция f (х) имеет один и тот же предел при а:—>-{-оо и при х-*—оо,
то этот предел можно записать так: lim/(я).
Jt-fOO
** Из условия ВфО вытекает, что для х, достаточно близких к xQt будет
/ ч / л fix)
g (х) ф 0 и для этих х отношение \ \ не теряет числового смысла.
g О)
115

ности значений х: хъ х2, х3, ..., хп, ..., сходящейся к х0(хп^х0),
будет f(xn)-+A и g(xn)-+B. Если к этим двум функциям (уже от
натурального аргумента) применить теорему из § 4, то мы получим,
что f (хп) + g (хп)-> А + В. Отсюда вытекает (вследствие
произвольного выбора последовательности {хп}), что f(x)+g(x)-+ A H-B.
Другие случаи разбираются аналогично.
Таким же образом переносятся на случай функции, заданной
в промежутке, и все остальные теоремы о пределах (исключение
составляет теорема 8, § 3), а также все изложенное в § 5
относительно неопределенностей.
Определение. Функция f(x) называется бесконечно малой
при х-+х0, если Нт/(л:) = 0. Функция f(x) называется бесконечно
х-+х0
большой при x-+xQt если Нт/(л;) = оо.
х2 4
Например, функция f(x)= x__^ является бесконечно малой
х2 4
при х->2 (так как lim о~ = 0) и бесконечно большой при х-+3
х-+2 х 6
х2 4
(так как lim «-=оо).
х —3 Х~~ 6
Решим несколько примеров на вычисление пределов функций.
При этом в первых двух будут выведены весьма важные формулы,
которые необходимо запомнить.
Пример 1. Рассмотрим функцию / (х) = (1 + х)х. Она
существует для всех х>—1, кроме х = 0. Покажем, что
j_
\im(\ + x)x=e, (l)
л:-*0
пользуясь определением предела функции «на языке
последовательностей».
В параграфе 7 мы установили, что переменная яя = (1-|—J
имеет предел. Его мы назвали числом е:
Г
e = lim 1 +
п
Используем этот предел для доказательства равенства (1). Пусть
х стремится к нулю справа, пробегая любую последовательность
значений хъ хъ х3, ..., Xk,... Можно считать, что все xk<l*
Положим ?,(~)=nft. Тогда nk^^<nfc+l и -r4rr<*A^ ;г-
\xkj xk nk-\-\ nk
Поскольку xk -> 0, ясно, что nk -> оо. Следовательно,
(1+»-^тГ«1+^<(1+^Г+1- «
Пределы крайних выражений могут быть вычислены следующим
Иб

образом:
f1 +_J_ V* + ' 11m(l+ ' У» + '
,in41 + «ft + l) hm 1+ 1 lim(1+ ') ' ^
ft lim H —=-
„m(l +!)".+'= 1Ц(1 + ±)"..(, + ±)] =
= lim(l+i)"«lim(l+i-)=*.l=e.
Следовательно, применяя теорему о сжатой переменной к
неравенству (2), в пределе получим:
j_
\\m(l+xk)xk=e.
Поскольку последовательность xk-+0 (справа) выбиралась
произвольным образом, мы уже доказали формулу (1) «на языке
последовательностей», но лишь для предела справа:
j^
lim (l+x)x=e (3)
х-++0
(вместо *->0 + 0 пишут х-> + 0).
Пусть теперь xk стремится к нулю слева (xk> — 1). Положим
yk=—xk. Тогда 0<*/*<С1, yk будет стремиться к нулю справа и
<>+*.>*'-<'-*.>"МпУ'Ч'+А;)" -('+А
1-
Так как lim (1 4- . Ук ) Ук == е, a lim (1 + , Ук ) = 1, то
yk-+o\ 1—Ук/ &к-*° 1~~Уь;
\\m(l+Xk)Xk=e.
Как и выше, отсюда вытекает формула (1) для предела слева:
j_
lim (l+x)x=e. (4)
х-* —0
Из (3) и (4) следует, что рассматриваемая функция в точке нуль
имеет одинаковые односторонние пределы, что и завершает
доказательство нашего утверждения.
Пример 2. Рассмотрим функцию /(#) = . Она существует
для всех х^О. Покажем, что
hm—— = 1. (5)
С этой целью в окружности радиуса R построим острый централь-
ныи угол, радианную меру которого обозначим через х [0<:x<c-j .
117

С Построив затем хорду А В и линию тангенсов,
можем утверждать, что площадь Д АОВ <
площади сектора АОВ < площади ДАОС
(см. рис. 59). Пользуясь соответствующими
формулами для вычисления указанных
площадей, получим:
±-R*sinx<±-R2x<±-R4gx.
А Разделив все части неравенства на у Я2,
будем иметь:
sin*<A:<tgA;(o<*<y). (6)
Заметим, что соотношение (6) между
функциями sin х> tg х и их аргументом х
имеет самостоятельный интерес и будет использовано нами ниже.
Для решения данной задачи подвергнем неравенство (6)
некоторым преобразованиям. Разделим sin x на каждую из частей
неравенства. Получим:
, . sin х.
1 > > COS X.
Вычитая из единицы все части полученного неравенства, находимз
Рис. 59.
0<1
:< 1—cos*.
Так как sin-|-<l, то sin2-|-<sin-|-. Следовательно, в силу (6)
получим:
i—cos x = 2 sin2 Y<2sin-2-<2- -~=x.
Тогда
0<1
<*.
Возьмем е>0. Если за б взять наименьшее из чисел е и|,то
при 0<x<6 будем иметь *<е, а потому
sin х\
1
<е.
sin х
Тем самым доказано, что lim ——-= 1. Однако здесь мы предполагали,
лг — О *
что х-+0 справа (*>0). Но так как -— является функцией
четной (рис. 60), то есть не меняется при замене х на —х, то
предел ^— остается равным единице и при х-*0 слева (*<0). Таким
образом, равенство (5) доказано полностью.
118

Заметим, что из выведенной выше оценки для 1—cos х
следует, что
limcosA;=l.
Установим попутно еще один результат, который понадобится
нам в дальнейшем. Покажем, что для любого х справедливо
неравенство:
| sin х |
х\. (7)
Действительно, для 0 < х < ~ оно уже установлено выше (см.
неравенство (6)). При х = 0 оно очевидно. Пусть лг^-к-. Так как
у>1, a |sinj:|^l для всех х, то |sin*|<|*|. Остается доказать
неравенство (7) для х<сО. Пусть x<0, тогда —х>0 и по только
что доказанному имеем: | sin ( — х) | < | —х |. Таким образом, и
в этом случае | sin х | <; | х |.
Как уже отмечалось выше, для раскрытия неопределенностей
даже одного какого-нибудь вида нельзя указать единого способа.
В зависимости от конкретного примера неопределенность
раскрывается тем или иным способом. В дальнейшем с помощью
дифференциального исчисления будут получены некоторые общие способы
раскрытия неопределенностей (§ 2, гл. VI). Здесь же продолжим
рассмотрение некоторых наиболее употребляемых способов и
приемов раскрытия неопределенностей, начатое в конце § 5.
Пример 3. Найти предел многочлена я-й степени при х -+ + оо:
lim {clqX?1 + a^'1 + а2хп~2 + ... + ап_хх + ап) (а0 Ф 0).
х—*-}-оо
В данном случае можно повторить все рассуждения,
проведенные нами при решении примера 1, § 5. В случае коэффициентов
с разными знаками имеем неопределенность вида оо — оо. Для
раскрытия этой неопределенности вынесем за скобки высшую
степень х, получим:
Предел выражения в скобках, очевидно, будет равен первому
слагаемому а0 (так как остальные слагаемые являются бесконечно
-2л
Рис. 60.
119

малыми), а предел хп — бесконечности. Следовательно, все
выражение будет иметь своим пределом +°° или —сю, в зависимости от
знака aQ.
Пример 4. Найти предел lim — ——?—.
Имеем неопределенность вида —. Такие неопределенности, как уже показано
в примере 2, § 5, раскрываются делением числителя и знаменателя на высшую
степень х, в данном случае — на х3:
,. *3 + 5x2 + 3*-f 4
lim
-»оо 2*3 + 3*+ 8
^ X ^ X* ^ X3
х3 — а3
1
2 *
#-+оо
Пример 5. Найти предел Jim 3^—Зах+5х-5а
В данном случае имеем неопределенность вида j-. В подобных примерах
проще всего разделить предварительно числитель и знаменатель на х — а.
Деление всегда будет без остатка, так как х = а является корнем обоих этих
многочленов (вспомните следствие из теоремы Безу). Получим:
.. *3 — а3 .. х*-\-ах + а* За*
lim -^-г—^ = =—= lim —- '
c-+a 3*2— Зад: — 5* — Ъа х_+а Злг + б За + 5"
Пример 6. Найти предел lim (x — ]Ле2 —4).
Имеем неопределенность вида со —со. Решаем аналогично примеру 4, § 5.
Разделив и умножив на х-\-Ух2— 4, получим:
lim (* — у х2 — 4)= lim - /v ^r - = hm =0.
* — -foo * —+ oo AT + |/ JC2 — 4 Х-+ + ООХ+УХ2 — 4
Иногда при раскрытии неопределенностей бывает очень удобно
воспользоваться тем или иным уже вычисленным пределом. Так, например, с помощью
предела (5) можно найти многие другие пределы.
п _ .. tg* .. sin л: 1 .. sin а: .. 1 , , ,
Пример 7. lim -2— = lim == hm • hm = 1.1 = 1.
лг-*0 x x-+o x cos a: k^o x ^qCOSa:
« ,- l-cosx ,. 2si"2|- 1 .. f^iX 1 „ 1
Пример 8. Inn—9 hmo_™-Thm| -j- I =T-l8=y.
X
Пример 9. Найти предел lim 27l«sin^ (xzfiO — постоянная).
Имеем случай неопределенности вида со «О. Обычно такую неопределенность
О со d
сначала преобразуют к виду -^ или —, затем раскрывают. В данном случае выра-
sin|i О
жение —«— уже представляет собой неопределенность вида -^-. Следовательно,
2й
120

x Sin^ ATSin- Sin^
lim 2wsin^ = lim —:—= lim = x lim = x-l=x.
2« 2Л 2я
ях
Пример 10. Найти предел lim (1 —х) tg -~-.
Здесь также неопределенность вида О-со. Воспользуемся приемом решения
примера 9. Кроме того, полезно еще положить 1—x = z. Тбгда при х—*\ будет
г —0 и
1- /1 w пх 1- 4. я(1—-z) ,. , /я яг\
hm (1—л:) tg -^- = hm z-tg —^—* = lim г • tg -=- - -^ *
яг
. яг 2 .. Т 2,2
= hm г ctg -^ = — hm = — 1 = —,
2-»-о ^ я г-*о , яг я я
Пример 11. Найти предел hm -
л:—юо Л* *
Воспользуемся примером 1. Там установлено, что lim (l + (x)a =е. Попробуем
а-*0
представить ( __ .) в виде выражения (1 + а)а, предел которого при а — 0 нам
х-\-\
известен. Для этого положим = 1 + а. Тогда сс-*0 при я—оо и *
выразится через а в виде х = . Следовательно,
(х
lim
2-Нх г j_p
±IY*= lim(l+cc) а =lim [(l+a)aJ (1+а)=^2-Ь
— 1/ а_0 а —0
„ in и о 1- sm2x — cos2л:—1
Пример 12. Найти предел hm : .
v * л smx — cos^
0
Имеем неопределенность вида -=г9
sin2x — cos2# — 1 .. 2sinA:cosx — 2cos2* ,. Л |/2~ ,а^-
lim : —= hm -r——— = hm 2cos#=2 •-Ц-= j/2-
n smx-—cos* n sin л: — cos* л 2 r
*-*J *~*T x^l
Можно было также воспользоваться подстановкой х—j- = z (то есть х =.
я\
В заключение рекомендуем читателю при раскрытии неопределенностей
пользоваться и пределами, вычисленными в § 10 следующей главы:
jc-+0 -*
ах i
2) Hm = Iogae = lna;
3) lim ii+^lzzi = ^
121

Вопросы для самопроверки и упражнения
1. Функция y = f(x) имеет в точке хь конечный предел Л>0 (<0). Что
можно сказать о знаке этой функции в достаточно малой окрестности точки *0?
Указание. Сравните с теоремой 3 из § 3.
2. Сформулируйте основные теоремы о пределах из § 3 (кроме теоремы 8)
для случая произвольных функций f(x).
В задачах 3—26 вычислить пределы.
3 ь-™3*2-8* п 8 4 Пт а8-5*+6 1
5' 11ш %Г? + 1 • <*»• 3' 6- Ит ^Х?^. Ля., со.
лг_*оо *2+18* — 8 *-*оо я+1
7. Нш 8" + ?Г4 . Ом. 0. 8. lim (2-?±f)\ 0ш. е.
*—оо х3 + 8 *—оо\2*+1/ *
¦9. lim f-r-?—Y\ Отв.—. 10. lim (l+tgx)ctg*. Отв. е.
а:-^оо \1+х/ е лг^о
11. Нт (х-У* + Е?=Щ. Отв. -А. 12# Ит y*»+l-T/F=T отв. 0.
2
*о 1- ?х—2 л 1 ,. ,. tgmx л т
13. lim ¦*-= . Отв. —. 14. lim -? . Отв. —
x^iqYx— 4 4 *-.otg/i* /г'
sin2 (л: —а) л , «~ i- si" *—sin а ^
15. Пт 9 о , 9> 0тв- 1- 16- llm Z • Отв. cosa.
*-*а*2 — 2ах-\-а2 х-+а х~а
„~ 1. tg дс — sin jc ~ 1 «0 ,. /п ч . пх _ 4
17. lim -2 г . Отв.-jr. 18. lim (2— х) • tg —. Отв. —.
19. lim si"*7C°S* Owe. -^ 20. lim U^- tgf 1. Отв. *
21. limg * Г . Отв. 3. 22. lim n*~" . Ome.—m
x-+0 *2 *^e *"-* e
,. lhjc» —3 ,.3 OA ,. g*-e2
lim . Ome. —. 24. urn --—=:-.
K-+e x—e e x-+2 *—*
23. lim lh*3"3. Отв. —. 24. lim —?. О/пв. A
Указание. Предварительно в числителе вынести за скобки t?2.
25. lim ——*" ' а ~ . Указание. Обозначить дс+д:2 = 2. Отв. —.
х^о х + х* п
2* х2 2
26. lim тт. Указание. Обозначить х—2 = 2. Отв. 41п —.
*-2 * —2 *
27. Найти в точке * = 0 односторонние пределы функции
[х+
28. Найти в точке л;=1 односторонние пределы функции
f(Y\ — \ х* ПРИ *<1,
' w"~\ *+2 при jc^I.
Гдт+1 при х<0,
/(*)={ 0 при * = 0,
¦ 1 при *>0.
X-+QO
29. Вычислить предел lim {\/ (х+ I)2—jV(#— I)2).
122

а3 ?3
Указание. Предварительно воспользоваться формулой а — Ъ--
a2 + ab + b2
/х2 4-1
30. Найти постоянные а и Ъ из условия: lim —-Ц ах — 6=0.
Указание. Привести выражение к общему знаменателю х+\ и в
числителе коэффициенты при х и х2 приравнять к нулю.
31. Стеклянная пластинка поглощает 1% падающего на нее света. Какая часть
света будет пропускаться пачкой в 400 пластинок?
Указание. Воспользоваться решенной задачей (пример 3) из § 7 и
формулой (1) из § 11. Отв. ^е~4^-~
§ 12. МОНОТОННАЯ ФУНКЦИЯ И ЕЕ ПРЕДЕЛ
Понятие монотонной функции является аналогом понятия
монотонной переменной хп.
Определение. Функция f(x), заданная на некотором
промежутке, называется возрастающей (убывающей) на этом
промежутке в узком или строгом смысле, если для любой пары
точек промежутка х' и х"', удовлетворяющих неравенству х' <х", вы-
полняется соотношение
ftfXfW <f(*')>f (*"))•
Если при условии х' <*" выполняется соотношение
/(*')</(*") (/(*')^f (*"))>
то f(x) называется возрастающей (убывающей) в широком или
нестрогом смысле или неубывающей (невозрастающей).
Функции указанных в этом определении видов объединяются
под общим названием монотонных.
Для монотонных функций справедлива следующая теорема.
Теорема. Монотонно возрастающая или убывающая
в широком смысле функция f(x), заданная на некотором
промежутке, имеет конечные односторонние пределы в
каждой точке этого промежутка*.
Доказательство. Пусть f(x) монотонно возрастает в
широком смысле слова. Возьмем какую-нибудь точку с, не совпадающую
с левым концом промежутка. В силу монотонности функции
множество значений f (х) для всех х<С.с будет ограничено сверху.
Следовательно, по теореме из § 5 главы I существует точная верхняя
граница. Обозначим ее через А и покажем, что эта точная граница
будет пределом слева функции f(x) в точке х=с. Действительно,
f(x)^A для всех x<Zc По свойству точных границ для любого
е>0 найдется такое х' <с, что f(x')> А — е. Тогда для х'<.х<.с
и подавно f{x)>A—е. Итак, с одной стороны, для всех х<с
будет f(x)^A и тем самым / (х) <; Л + е> с другой стороны, для
* Ясно, что на конце промежутка можно рассматривать лишь один
односторонний предел.
12^

х' <х< с имеем: f (х) > Л — е. Следовательно, для а:' < х <с
выполняется неравенство
Л-е</(х)<Л+е.
Л это значит, что lim f(x) = A, так как если за б взять число,
Х-+С — О
не превосходящее с—х\ то |/(а:) — Л|<6 для всех л:<с,
удовлетворяющих неравенству \х—с|<6- Существование предела справа
в точке с доказывается аналогично. Доказательство же второй части
теоремы, когда f (x) монотонно убывает, очень напоминает только
что проведенное доказательство. Рекомендуется провести его
самостоятельно.
Если некоторая функция f(x) задана на отрезке [а, Ь] и
последний можно разбить на частичные промежутки так, что на каждом
из них f(x) будет монотонной, то такую функцию называют кусочно
монотонной. Из известных нам функций кусочно монотонными
являются: y = s\r\x (рис. 35), у=х2 (рис. 28), у = \х\ (рис. 43), у=
=х — Е(х) (рис. 25), функция, изображенная на рисунке 21, и
другие.
Пример 1. Определить промежутки монотонности функции f (x) = ax2-{-b.
Будем считать, что а > 0. Пусть хг и х2 — любые две точки на числовой оси,
удовлетворяющие неравенству хг<х2. Тогда
f (*2) — f{xi) = ax?2 + b — ax\ — b = a(xl — xi) = a-(x2 — xl)(x2-[-x1)
и из последнего можно заключить, что
а) f (*2> —f (*i)>0 при 0 ^ *!<*<,,
б) fW-ffe)<0 при *!<*2^0.
Таким образом, при а>0 функция f (x)=ax2 + b убывает на (—оо, 0] и
возрастает на [0, Н-оо).
Если же предположить, что а < 0, то легко обнаружить противоположную
картину: на (—оо, 0] функция будет возрастать, а на [0, 4-оо) — убывать.
Пример 2. Определить промежутки монотонности функции f (х)=ах*-{-
-j- bx-\-c.
Преобразуем квадратный трехчлен, дополняя его до полного квадрата:
-+to+.-.(-.+ i.+iH(.+?),+ l!S!:J.
Получим:
,, ч / , 6\2 , 4ас-Ь*
f(x) = a[x + -
2а] ' 4а '
И для дальнейшего исследования можно воспользоваться результатами
предыдущего примера, так как функция / (х) имеет такой же вид и лишь х заменено на
jc + s-. Следовательно, при а >0 функция возрастает, если jc + ^-^О (то есть
х^>—o~)i и убывает, если л:+^-<!0 (то есть л:^ — ^-]. Промежутком
возрастания функции будет —^-,+оэк а промежутком убывания будет (— оо,
--1
2аУ
Если считать, что а<0, то промежуток возрастания функции станет
промежутком убывания и наоборот.
124

Вопросы для самопроверки и упражнения
1. Доказать, что функция f(x) = x3 возрастает на (—оэ, + °°).
2. Доказать, что на отрезке 0, -^- функция sin х возрастает, а функция cos x
убывает.
3. Исследовать на монотонность следующие функции: а) {(х)=ах+Ь, б) f{x) =
= аЛ"(а>0).
Отв. а) На (—оо, +оо) возрастает при а>0 и убывает при а<0. б) На
(—со, -j-co) возрастает при а>1 и убывает при а< 1.
4. Следует ли из неравенства f(x)^g(x) неравенство / [f {x)] ^g [g (*)], если
функции / (х) и g (x) возрастающие?
5. Привести примеры монотонных и немонотонных бесконечно малых, а также
монотонных и немонотонных бесконечно больших величин.
6. Доказать, что монотонно убывающая функция, заданная на [а, Ь], имеет
в каждой точке односторонние пределы.
§ 13. СРАВНЕНИЕ БЕСКОНЕЧНО МАЛЫХ И БЕСКОНЕЧНО БОЛЬШИХ
При изучении различных вопросов, связанных с понятием
бесконечно малой величины, часто приходится различать бесконечно
малые по характеру их изменения. Одни бесконечно малые стремятся
к нулю «быстрее», другие «медленнее». Так, например, бесконечно
малая а = -у стремится к нулю при х ->- оо с «большей скоростью», чем
бесконечно малая Р = —. Действительно, если л: пробегает, например,
значения 1, 2, 3, ..., я,..., то
а
р
Определение. Бесконечно малая а называется бесконечно
малой высшего (низшего) порядка по отношению к бесконечно
малой р, если lim g- = 0(= оо).
В этом определении подразумевается, что аир суть функции
от одной и той же переменной (например, х) и а и Р стремятся
к нулю при одном и том же условии, накладываемом на аргумент
(например, при х, стремящемся к некоторому пределу).
В соответствии с определением -у при #->oo будет бесконечно
J_
малой более высокого порядка, чем —-, так как lim Л-= Нт4- ^
* лг-*оо _L *-*oo*
X
= lim * =о.
Определение. Две бесконечно малые а и р называются
бесконечно малыми одного порядка, если предел их отношения равен
=1 1
-.4
1
27'
1
' 3
1
64'
1
' 4
1
125' "
1
' 5 ' '
1
•' ' л3
1
" ' п
125

некоторому числу, отличному от нуля, то есть если \\т~=АфО.
Бесконечно малые одного порядка характеризуются как бы
«одинаковой скоростью» стремления к нулю.
В частности, если lim-o-=l, то а и р называются
эквивалентными бесконечно малыми, что обозначается так: а~р.
В отдельных случаях оказывается недостаточно знать, что из
двух данных бесконечно малых одна является бесконечно малой
высшего порядка, чем другая. Нужно еще как-то оценить, насколько
выше или как высок этот порядок. Последнее имеет немаловажное
значение при изучении характера изменения бесконечно малых.
Определение. Бесконечно малая а называется бесконечно
малой к-го порядка по отношению к бесконечно малой р, если а и
Р* будут бесконечно малыми одного порядка, то есть если lim p =
=АфО.
Так, например, 1 —cos* при х-^0 является бесконечно малой
второго порядка малости по отношению к бесконечно малой л:, по-
, 2 sm2 -7J- | sin -х- \ t .
,. 1— cos* *. 2 о i- 2 о * 1
скольку hm—g— =hm —-g— = 2 lim I —— J =2-T = T.
Пример 1. Функции sin x и х являются при * — О эквивалентными беско-
sin x
нечно малыми, так как hm =1.
х-+о х
Пример 2. Функции sin Зх и sin Ъх являются при х—* О бесконечно малыми
.. sin Зл; 3
одного порядка, так как hm ——— = -=-.
*-ooSin5x 5
Пример 3. Бесконечно малые х и х sin — будут несравнимыми бесконечно
. 1
х sm — .
х . 1 Л
малыми, поскольку их отношение = sin — при х — 0 не имеет предела
(см. пример 4, § 10).
Пример 4. Сравнить бесконечно малые: /х (х) = 2х, /2 (х) = sin Л'2, /3 (х) =.
= l^sin х, /4 (х) = У~\ +х-1 с бесконечно малой ф (х) = х.
2х
1) lim — = 2. Следовательно, 2х и х одного порядка,
х — о х
_Л ,. sin*2 .. Г sin х2 х2] .. Л .. sin*2
2) hm —-= hm —— • — = hm* = 0, hm-_=l.
*_>() x jc-+0L x XJ x-+0 X*
Следовательно, sin x2 является бесконечно малой высшего (второго) порядка.
.. УШИ ,.т\-ш/-ШГх 1] ^ lim Щ*= lim y^l= 1.
У* J „2
126

Значит, } sin x есть бесконечно малая низшего порядка. Ее порядок по
отношению к бесконечно малой х равен -^. В то же время х будет бесконечно малой
высшего (второго) порядка по отношению к бесконечно малой )/ sin х-
л цт ^Н1*-1 цт (VT+i-l)(VT+i+l) .. 1 1
4) hm =Iim . - = ит = -?г.
Следовательно, 1^1+а:—1 и х одного порядка.
Теорема 1. Для того чтобы бесконечно малые
величины а и р были эквивалентными, необходимо и
достаточно, чтобы их разность а —р представляла собой
бесконечно малую более высокого порядка, чем они сами.
Доказательство. Необходимость, Пусть а ~ р, то есть
а
lim -л- = 1. Тогда
06 — Р ig— /"i М_ i i;~ I
-!)¦
lim^-K = lim 1--К- =l-lim^=0.
a
Это значит, что бесконечно малая а — (5 имеет более высокий
порядок, чем а. Аналогично доказывается, что а — р— бесконечно
малая более высокого порядка, чем р.
Достаточность. Пусть \ima~^==0. Тогда lim f 1 Р-) = 0 и
получаем, что lim^-=l, то есть а^р.
Из этой теоремы следует, что при замене некоторой бесконечно
малой величины а эквивалентной ей величиной р допускаемая по
грешность не только абсолютная |а — Р |, но и относительная р—Ё
может быть сделана сколь угодно малой. Поэтому часто при
различных действиях над бесконечно малой прибегают к
приближенной замене одних бесконечно малых другими, им эквивалентными,
но имеющими более простой вид.
При раскрытии неопределенностей вида ту во многих случаях
полезно пользоваться следующей теоремой.
Теорема 2.Если имеем две пары величин а, р и а', Р'
бесконечно малых, причем а~а', Р~Р', то
,. а ,. а'
lim -5- = um 37
Р р
{предполагается, конечно, что хоть один из этих пределов
существует).
Доказательство. Отношение -g- можно представить в
следующем виде:
<^ _ _а а/_ &_
р - а' ' Р' * р
(здесь мы числитель и знаменатель первого отношения умножили на
одну и ту же величину а'Р'). Переходя в этом равенстве к пределу
127

и используя теорему о пределе произведения, получим:
t. а ,. /а а' В'\ ,. а ,. а' ,. В'
hm-p- = hm(^ • ? ¦ ILj^hm-. iim __ .i,m JL.
rt ft'
Так как по условию lim^7= 1 и lim^-=l, то получаем:
,. а ,. а'
Р Р
Эта теорема означает, что при нахождении предела отношения двух
бесконечно малых функций каждую из них можно заменить любой
эквивалентной бесконечно малой и от этого предел не изменится.
При удачно выбранной замене задача раскрытия неопределенности
может быть значительно упрощена.
Пример 5. Так как при х —*0 имеют место соотношения sin 2х -^ 2х и
1/-ТП г-i 1 * + ** ,. ]Л+л: + х2-1 .. ~2(* + х2) .. 1 + х 1
У 1+х + х2 —1~ —~—, то hm- L-r-7s = hm ~ = hm—j— = —
2 ' *-+0 sin 2л: x^0 2x x_+0 4 4
я* i
Пример 6. Так как при л:—- 0 будет tg*~ х и ах— 1 ~ л: In а, то lim ——г =
.. х • In а
= hm = 1па.
X2
Пример 7. Так как при х—*0 будет 1—cos-K^-^- и sin x ~ х, то
.. х3 ,. х3 cos л; ,. х3 cos л; п
hm -7 :— = hm —: - — = hm 5—= 2.
x^,q tgx—smx x-+o sm*(l—cosx) x^o x*
X"2
Замечание. В тех случаях, когда в числителе или
знаменателе стоит сумма, при раскрытии неопределенности нельзя заменять
отдельные слагаемые эквивалентными величинами, так как такая
замена может привести к неверному результату или вовсе к потере
смысла. В теореме 2 доказана возможность замены только всего
выражения, стоящего в числителе или знаменателе, на
эквивалентную ему величину.
Так, если бы в данном примере мы заменили слагаемые в
знаменателе на эквивалентные величины (tg х на х и — sinx на — х), то
Xs
в знаменателе получили бы нуль и выражение -^-не имело бы смысла.
В тех же случаях, когда числитель или знаменатель
представляют собой произведение нескольких бесконечно малых или
бесконечно больших, то каждую из них можно заменять эквивалентной
величиной, так как в этом случае и все произведение заменится
эквивалентной ему величиной.
Обычно при сравнении бесконечно малых одну из них условно
принимают за основную.
Пусть а—основная бесконечно малая. Тогда бесконечно малые
вида сак (где с—постоянный коэффициент и ?>0) естественно
считать простейшими бесконечно малыми.
128

Будем сравнивать различные бесконечно малые не с основной
бесконечно малой а, а с простейшими бесконечно малыми вида с-ак.
При этом для каждой бесконечно малой Р будем подбирать числа
с и k такие, чтобы с-ак<^§.
Определение. Простейшую бесконечно малую саЙ,
эквивалентную данной бесконечно малой р, называют ее главной частью.
Например, если х принять за основную бесконечно малую, то
главной частью бесконечно малой (1+х)*—1 будет \ix, так как
,|т(Н^Ь1_ь (1)
Термин «главная часть» имеет тот смысл, что после вычитания
из бесконечно малой Р ее главной части сак остается величина (5—сак,
являющаяся бесконечно малой более высокого порядка, чем Р и чем
c-ak (см. теорему 1). Следовательно, при замене бесконечно малой Р
ее главной частью с*а? допускаемая абсолютная погрешность jp —
— c-ak\ будет бесконечно малой высшего порядка по сравнению с р.
Р — c-ak
Р
будет величиной
Но тогда и относительная погрешность
бесконечно малой. Последнее означает, что относительная
погрешность приближенного равенства
р^с-а*
может быть сделана сколь угодно малой при а->0.
Из рассмотренных нами примеров известно, что если х считать
основной бесконечно малой, то:
а) для sinx главной частью будет х, то есть sin*^*,
б) для 1 —cos х главной частью будет у*2, то есть 1 —cos лг^-н-л;2,
в) для tgx главной частью будет х, то есть tgx^x, и т. д.
Заметим, что, выбрав основную бесконечно малую а, мы можем
находить главные части многих других бесконечно малых,
сравнимых с а. При этом для заданной бесконечно малой Р может
существовать много эквивалентных бесконечно малых, однако главная
часть у нее одна. Например, при х->0 функция sinx будет эквн-
• Л. t 1/1,4 (I+X)V-—I
валентной функциям: х, tgx, In (1 +л:), -—!— и др., но главной
частью будет только функция х\ все остальные не являются
простейшими.
Выделение главной части бесконечно малой величины можно
производить следующим образом. Пусть а — основная бесконечно малая.
Требуется выделить главную часть бесконечно малой р. Определим
сначала, если это возможно, порядок малости р по отношению к а,
то есть найдем такое число k > 0, при котором lim-^ = c=^=0. Тогда,
очевидно, величина сак и будет искомой главной частью, так как
lim—&-=1.
cak
129

Пример 8. Выделить главную часть вида схп бесконечно малой P = (l +
+ *W_1.
Так как lim —-—4 = 3, то величина Зх2 является главной частью
велико *2
чины (1+*2)»—1.
Формула (1) часто используется в приближенных вычислениях. Так,
например, для функции (1+*)^—-1 формула (1) принимает вид:
(\+х)* — \*** ii- х.
В частности (при натуральном /г),
1
и по этой формуле можно приближенно вычислять корни я-й
степени (где п—натуральное).
Пример 9. Найти приближенное значение корня 1^1051.
Сначала преобразуем корень таким образом, чтобы целая часть подкоренного
количества стала равной единице. Сделать это всегда возможно делением или
умножением на соответствующее число. В данном случае ]/ 1051 =^1000- 1,051 =
= 10VX05l= Ю \/ "1+0,051.
К. корню применим приближенное равенство (2), положив в нем я = 3 и
х = 0,051. Получим: \/ 1 +0,051 - 1 ъ^ -0,051. Отсюда 3/Т051^1+уХ
X 0,051 = 1,017, и окончательно имеем: ^/~Т0эТ = 10 3/Щ1 ^ 10 . 1,017= 10,17.
На вопросе об оценке погрешности нашего вычисления мы не останавливаемся.
Эквивалентность бесконечно малых ln(l+x) и х при х-+0
можно использовать для приближенного вычисления логарифмов
по формуле 1п(1+л:)^х (при малых значениях х).
Классификация бесконечно больших проводится на основании
следующих определений.
Если lim -тг =оо( = 0), то бесконечно большая а будет высшего
(низшего) порядка по отношению к бесконечно большой {3. Если
lim -q-=A 7^0 (А — число), то а и р будут бесконечно большими
одного порядка. В частности, если Л = 1, то бесконечно большие
эквивалентны, а~В. Если lim —^- = Л ^ 0, то бесконечно большая
а будет k-то порядка по отношению к бесконечно большой р.
Для бесконечно больших функций можно сформулировать
теорему, подобную теореме 2 об эквивалентных бесконечно малых.
Пример 10. При х-+ оо бесконечно большая /(х) = х2+5*+ 4 низшего
порядка по сравнению с бесконечно большой ф(д:) = л:3 — 2, так как
lIm Ц?= иш * + **+*- lim *+*2+*3_п
*з
130

Пример 11. При х —*оо бесконечно большая 2а;2+ 3 и бесконечно большая
(х—I)2 имеют одинаковый порядок, так как
.. 2*2 + 3 .. ^а:2 0
lim ; т^== lim - -— = 2.
лг^оо(*-1)2 *_>«> Л J_\2
Пример 12. При х-* со бесконечно большая Ух+а и бесконечно большая
У~х эквивалентны, так как
lim
УХ х-ьоо V х лг-юо V х
Пример 13. Определить порядок бесконечно большой л:4-|-5а:—1 по
отношению к бесконечно большой За:2+ 2 при а;—>со.
Решение сводится к отысканию такого числа /г, при котором многочлены
(3*2 + 2)/г и л:4+ 5* — 1 будут при * —со бесконечно большими одного порядка.
Из примера 2, §5, следует, что два многочлена при х—*со будут бесконечно
большими одного порядка в том случае, если они одинаковой степени. Предел их
отношения в этом случае равен отношению коэффициентов при высших степенях
х (см. также пример 4, § 11). Следовательно, многочлен За:2 + 2 нужно возвести
в квадрат (k = 2), чтобы получить многочлен как бесконечно большую величину
одного порядка с многочленом а:4 + 5л:—1. Действительно,
,. а:4 + 5а:—1 ,. *4 + 5х — 1 1
lim ¦ = lim ! = —
*->оо (За:2 + 2)2 *-оо 9а;4 + 12а:2 + 4 9 '
Итак, л:4 + 5х—1 есть бесконечно большая 2-го порядка по отношению к
бесконечно большой За:2 + 2.
Вопросы для самопроверки и упражнения
1. Доказать, что если бесконечно малые а, р и у удовлетворяют условию:
а^р и p~Y> то a^Y-
2. Будут ли объем и поверхность шара бесконечно малыми функциями его
радиуса, если последний стремится к нулю? Определяйте порядок малости этих
функций относительно радиуса.
Отв. Объем есть бесконечно малая 3-го порядка, а поверхность — бесконечно
малая 2-го порядка.
3. Сравнить следующие бесконечно малые функции в окрестности точки х = О
с функцией ф (а:) = х:
а) / (а:) = 5х; б) f (х) = |/ sin х ; в) f (х) = \ —cos 2л:; г) f (х) = х-\- sin x\
Д) / (*)= VT+lc-V\-x\ е) / (*) = tg*-sin*.
4. Определить при #—*2 порядок малости следующих функций по отношению
к функции ф(а:) = а;—2:
а) /(*) = а:3 — 8. Отв. Одного порядка, в) /(*) = tg (a:— 2). Отв. Эквивалентна.
б) f (х) = Ух—2. Отв. -?г. г) f (x) = Yx~~1 "-"!• 0тв- Одного порядка.
5. Считая х-+ +со, сравнить следующие бесконечно большие функции.
а) f(x) = A;2—Зх + 5 и <р(х)=х*+8х*~Зх + 2.
б) f(x) = x3 + 2x—\ и ф(а;) = (а;—1)з.
в) /(а:) = Т/"х2 + 5а;~-3 и ф(а;) = 2а: + 5.
г) /(*) = j/s=3 и <р(х) = Ух+\.
Д) / (*) = ]/* + V*+ Vх ИфМ = )/7.
131

Определить при х
шению к функции ср (х)
б) f(x) =
» 1 порядок роста бесконечно больших функций по отно-
Отв. Одного порядка.
1
в) f(x) =
Отв.
Отв.
3 '
2е
7. Считая центральный угол АОВ (рис. 61) основной бесконечно малой,
определить порядок малости следующих величин:
а) хорды АВ, б) стрелки CD, в) площади сектора АОВ, г) площади Д А ВС,
д) площади трапеции АВВХАЪ е) площади
сегмента ABC.
8. Используя эквивалентные бесконечно
малые, найти пределы:
а)
б)
lim
sin mx
х -* о sin пх
*_0 5х2-И*3*
в) lim
Отв.
О/яв.
.Отв.
т
~пт
\_
5е
_1
4/Г
>о 2л; • sin л:
9. Выделить главные части относительно
бесконечно малой х (вида cxk) следующих функций:
а) 2х — Зл:2 + л:3. Отв. 2л:.
б) Y\+x—YT^x. Отв. х.
10. Выделить главные части относительно бесконечно малой (х— 1) (вида
с(х — \)k) следующих функций:
а) л* — ЗХ+-2. Отв. 3(*—1)а.
б) In л:. Отв. х—1.
в) Vl—Vx
Отв.
3/2~
1
11. Использовать эквивалентность бесконечно малых ¦*/ \-{-х — 1 и—* по^
_____ 11 v'
х — 0 для приближенного вычисления корней: |/ 1018; JA0042; у^ТХ Найти
значения этих же корней с помощью логарифмических таблиц. Результаты сравнить.
12. Использовать эквивалентность 1п(1-}-л:) и х при х—>Ь для
приближенного вычисления натуральных логарифмов чисел: 1,01; 1,03; 1,1; 1,3.

ГЛАВА IV
НЕПРЕРЫВНОСТЬ И РАЗРЫВЫ ФУНКЦИИ
Понятие непрерывности функции является одним из основных
понятий математического анализа. Изучение этой главы следует
начинать только после изучения теории пределов, так как непрерывность
функции теснейшим образом связана с понятием предела функции.
Непрерывные функции обладают целым рядом важных свойств,
которых лишены функции разрывные. Эти свойства создают
большие удобства при использовании непрерывных функций в
различного рода исследованиях, имеющих огромное теоретическое и
практическое значение. Во многих случаях изучение функций более
сложной структуры удается свести к изучению непрерывных
функций, благодаря чему непрерывные функции составляют основной
и самый важный для анализа класс функций.
Понятие непрерывности позволяет более обстоятельно изучить
простейшие элементарные функции, в частности строго обосновать
введение таких функций, как показательная, логарифмическай,
степенная, обратные тригонометрические функции.
В некоторых случаях при изучении настоящей главы придется
заглядывать и в теорию пределов, что не только поможет лучше
разобраться в понятии и в свойствах непрерывной функции, но
будет также способствовать повторению и более глубокому
усвоению материала предыдущей главы.
§ 1. ОПРЕДЕЛЕНИЕ НЕПРЕРЫВНОСТИ ФУНКЦИИ.
ТОЧКИ РАЗРЫВА
Пусть на некотором промежутке определена функция f(x) и
jc0 — точка этого промежутка.
Определение. Если предел функции в точке х0 и значение
функции в этой точке равны, то есть
Hm/G*)=/(.*o). (1)
то функция f(x) называется непрерывной в точке х0.
Из этого определения прежде всего следует, что о
непрерывности функции можно говорить лишь по отношению к тем точкам,
в которых функция определена, то есть существует f(x0). Как
133

известно, при определении предела функции такого условия не
ставилось. Это объясняется тем, что значение /(х0) в определении
предела не участвовало.
Заметим также, что равенство (1), определяющее понятие
непрерывности функции в точке, можно представить в виде
lim f(x)=f(\im х)
X —*• Xq X •^ Xq
и словами можно сказать так: функция f(x) непрерывна в точке х0,
если предел функции в этой точке равен значению функции от
предела аргумента, то есть если возможен предельный переход под
знаком функции. Таким образом, если функция f(x) непрерывна
и нужно вычислить ее предел при x-*jc0, то достаточно в
выражение функции вместо х подставить х0 и подсчитать соответствующее
значение f\xQ). Это и будет искомый предел.
Соответственно двум определениям предела функции можно дать
два определения непрерывности функции: «на языке
последовательностей» и «на языке е — б».
Определение 1. Функция f(x) называется непрерывной в
точке х0, если для любой последовательности значений х:
*^1> -^2> -^8» • • • » ХП9 . . . ,
сходящейся к х0, последовательность соответствующих значений
функции /(хг), f(x2), f(x3)y...y /(*/*)>••• сходится к f(x0). При этом х,
стремясь к х0, может принимать, в частности, и значение х0.
Определение 2. Функция f (x) называется непрерывной в
точке х0, если для любого г > О найдется такое 6 > О, что для
всех х, удовлетворяющих неравенству \х—л:0|<6, выполняется
неравенство \/(х) —f(x0) | < е.
Эквивалентность этих определений нами уже доказана, поскольку
доказана эквивалентность соответствующих определений предела
функции (см. § 10, гл. III).
Наконец, дадим еще одно определение непрерывности функции,
которое по существу является перефразировкой первоначального
определения, но иногда оказывается более удобным для
практического использования.
Предположим, что аргумент х при своем изменении переходит
от значения х0 к новому значению хг. Величина хх — х0 называется
приращением аргумента х и обозначается Ах (читается: дельта х).
(Таким образом, х1 = х0-\-Ах.) Соответственно этому функция у =
=f(x) также изменит свое значение е/(х0) на /(л:0 + Д*)- Разность
f(x0 + Ax)—f(x0) называется приращением функции в точке дс0,
вызванным приращением аргумента Ал:, и обозначается А_у (читается:
дельта у).
Пусть дана, например, функция f (х) = х2 + 2х—3. Она
определена на всей числовой оси. Выберем некоторое значение х0
аргумента х и дадим этому значению приращение Ах, х = х0 + Кх. По-
134

лученную в результате точку вновь обозначим через х.
Приращение функции ку определится из соотношения:
&y=f(xQ + Ax)-f(x0) = l(x0 + Ax)* + 2(x0 + Ax)-3]-
—(xl + 2x0 — 3) = xl + 2x0kx + Ax2 + 2x0 + 2Ax—3-х] — 2д:0 + 3 =
= 2х0 А х + 2 Л х + Д хг = 2 (х0 +1) Д х + Д х2 *.
В частности,
если х0 = 2 и Дх = 0,1,то А у = 2 (2+1) .0,1+0,12 = 0,61;
если х0 = 2 и Дх = 0,01, то Д.у = 2 (2+ 1) -0,01 + 0,012 = 0,0601;
если х0 = 3 и Дх = 0,1,то &у = 2 (3+ 1) -0,1 +0,12 = 0,81.
Из этого примера уже видно, что величина приращения
функции ку зависит как от величины приращения аргумента Ах, так
и от точки х0, в которой это приращение функции вычисляется.
Геометрически приращение аргумента Ах представляет собой
изменение абсциссы точки кривой y=f(x) при переходе от
значения х0 к значению х0 + Д*, а приращение функции А у есть
изменение ординаты точки этой
кривой при переходе от
значения /(х0) к
значению/ (х0 + А х) (рис. 62).
Определение 3.
Функция f (x)
называется непрерывной
в точке х0, если
бесконечно малому
приращению аргумента в
этой точке
соответствует бесконечно малое
приращение функции,
то есть если из Ах —> 0
следует Ду->0.
Действительно, это условие означает, что lim |/(х) — f (х0)] = 0.
х-*х0
Последнее же равносильно равенству lim/(x) = /(x0), с помощью
х-^х0
которого мы и определили непрерывность функции.
Иногда приходится пользоваться понятием так называемой
односторонней непрерывности.
Определение. Функция f (x) называется непрерывной
в точке х0 справа (слева), если lim f(x) = f(x0) I lim f(x)=f(x0)\.
*-**o-f0 \x->x0-~ о /
Сравнивая это определение с определением непрерывности
в точке, можно убедиться в том, что функция, непрерывная во
внутренней точке, будет одновременно непрерывной справа и слева.
Справедливо и обратное утверждение: если функция непрерывна
AX)-f(*0)
* Обозначение Ах следует рассматривать как единый символ. Поэтому под
Ах2 понимают не Д • х2% а (Ах)2. То же относится к Ау.
135

в некоторой точке слева и справа, то она будет и непрерывной
в этой точке. Однако функция может быть непрерывной только
с одной стороны. Примером может служить функция у = Е (х}
(рис. 57), которая при каждом целом значении х непрерывна
только справа. Читатель легко может убедиться в этом
самостоятельно.
Определение. Функция f (x) называется непрерывной на
некотором промежутке, если она непрерывна в каждой точке
этого промежутка, В частности, если промежутком является отрезок
[я, Ь], то на его концах подразумевается односторонняя
непрерывность: в точке а — непрерывность справа, а в точке b —
непрерывность слева.
Определение. Точка х0, принадлежащая области
определения функции f(x), называется точкой разрыва функции f(x)>
если функция f (x) не обладает свойством непрерывности в ней.
Другими словами, функция f(x) имеет разрыв в точке х0^Х,
когда либо f (x) не имеет конечного предела в точке х0, либо
конечный предел в точке х0 существует, но не совпадает со
значением функции в этой точке, lim f (х) ^ь f (xQ).
Х-+ Х0
В соответствии с данным определением функция должна быть
определена в каждой точке разрыва. Однако часто к точкам
разрыва причисляют точки еще одного вида, в которых функция не
определена. Именно, рассмотрим случай, когда функция f (х)
определена в некоторой окрестности (х0 — б, х0 + б) точки x0i за
исключением самой точки х0. В этом случае говорить о непрерывности
функции в точке xQ нельзя, поскольку f (x) не определена в этой
точке. По той же причине х0 не подходит и под данное выше
определение точки разрыва. Тем не менее, если в точке х0 не
существует конечного предела f(x), то х0 тоже считают точкой
разрыва функции f(x). Например, говорят, что x = Q есть точка
разрыва функции у = — (здесь lim —= оо). Если же / (л:) имеет конечный
Х Х~*0 Х
предел в точке xQ, то достаточно дополнительно определить
функцию в этой точке, положив
f(x0) = limf(x),
Х-+Хй
и она становится непрерывной в точке х0. В этом случае точку х<>
не считают точкой разрыва первоначальной функции, а просто
говорят, что функция может быть доопределена в точке х0.
Например, функция f(x) = в точке х = 0 не определена (рис. 60). На
известно, что Нт-^-:- = 1 (см. пример 2, § И, гл. III). Если мы
х-+0 х
дополнительно примем, что /(0) = 1, то функция f (х) окажется
непрерывкой в точке х = 0. Ниже (§ 2) будет установлено, чта
эта функция непрерывна и во всех прочих точках.
136

Ясно, что при отсутствии конечного предела функции f(x) при
х -+ х0 доопределение ее в точке х0, после которого она стала бы
непрерывной в этой точке, невозможно.
Разрывы функций можно классифицировать следующим образом:
Определение. Если в точке разрыва х0 существуют
конечные односторонние пределы функции, то разрыв функции
называется разрывом первого рода.
К разрывам первого рода относятся так называемые
устранимые разрывы. Именно, если f(x0 — 0) = f (x0 + 0) ^ f(xQ), то разрыв
устраним в том смысле, что достаточно изменить значение
функции в точке х0, положив f(xQ) = lim f(x), и функция станет непре-
х-+х0
рывной в х0.
Определение. Если в точке х0 функция терпит разрыв,
причем хотя бы один из односторонних пределов бесконечен или
вовсе не существует, то разрыв функции называется разрывом
второго рода.
Различные случаи разрывов и характера непрерывности
функции для наглядности изображены на рисунке 63.
В точке а функция непрерывна справа, так как f(a + 0)=f(a).
В точке хх функция непрерывна, так как lim f(x) = f(x1).
x-*xt
В точке х2 функция имеет разрыв первого рода, так как
f (x2—0)=f(x2) 7^f(x2 + 0)» но непрерывность слева имеет место.
В точке х3 функция имеет устранимый разрыв первого рода,
так как существует lim f (х) Ф f(x3).
Х-+ Х%
В точке лг4 функция имеет разрыв второго рода, так как limf (л:) =
Х->ХА — 0
= —оо, lim /(*) = +00.
В точке хь функция имеет разрыв второго рода. Положение,
аналогичное точке х4, хотя и существует f (хь).
Рис. 63.
137

В точке хв функция имеет разрыв первого рода, так как
/ (хв — 0) =? f (xQ + 0) = f (л:6), но непрерывность справа имеет место.
В точке х7 функция не определена, однако предел функции
в зтой точке существует и конечен. Приняв этот предел за
значение fix?), получим функцию, доопределенную и непрерывную
в точке х7.
В точке Ь функция непрерывна слева, так как f (b — 0)=f(b).
Термин «непрерывная функция» связан с интуитивным
представлением о непрерывности (сплошности) кривой, то есть такой
кривой, которая может быть получена непрерывным движением
точки. Точно так же термин «разрывная функция» связывается
с представлением о разрывной (порванной) кривой. Поэтому
графики функций, как видно из рисунка 56 и многих других
рисунков, встречавшихся нам, наглядно показывают, где функция
непрерывна и где имеет разрыв.
Заметим, однако, что понятие непрерывности функции,
определенное нами выше, имеет более глубокий смысл и может быть
иллюстрировано графически лишь для сравнительно простых
функций. Вообще же существуют настолько сложные функции, что их
графическое изображение либо очень затруднительно, либо вовсе
невозможно; более того, нелегко даже мысленно представить себе
их графики. Тем не менее среди таких функций имеются как
разрывные, так и непрерывные функции в том смысле, как это
следует из принятых нами определений.
В математическом анализе чаще всего приходится встречаться
с функциями, допускающими графическое представление. Однако
нам уже встречались и такие функции, как функция Дирихле
(см. пример 6, §2, гл. II), график которой построить невозможно,
и функция y = sin— (см. пример 4, § 10, гл. III), график которой
можно построить лишь вне некоторой окрестности нуля (— б, +6).
В самой окрестности (— б, +6) график этой функции построить
невозможно, так как нельзя на ограниченном участке графически
воспроизвести бесконечное множество колебаний этой функции.
На рисунке 55 дано лишь очень приближенное графическое
изображение функции y = sin—.
Перейдем к рассмотрению некоторых свойств непрерывных
функций.
Теорема 1. Если функции f(x) и g(x), заданные на
некотором промежутке, непрерывны в точке х0 этого
промежутка, то в этой точке будут непрерывными также
функции: f(x)±g(x), f(x)g(x) и ^|~ (последняя при
g(x0) ф 0*).
Эта теорема непосредственно следует из теорем о пределе
суммы, разности, произведения и частного. Так, например, не-
* См. сноску на стр. 115.
138

D
lim f (x)
прерывность частного ' : : в точке х0 следует из того, что
11ГП —7~T*^~T- ГТ3**—Г"*"\.
x^XoS(x) Hm g (дс) g(x0)
x-+x0
Рассмотрим подробнее монотонные функции. Пусть на некотором
промежутке X определена возрастающая или убывающая в широком
смысле функция /(*).
Поскольку любая монотонная функция в каждой точке области
ее определения имеет конечные односторонние пределы (см. § 12,
гл. III), то она может иметь только разрывы первого рода.
Теорема 2. Монотонная функция у =/(-*:), заданная на
промежутке X, непрерывна на этом промежутке, если
множество всех ее значений Y заполняет некоторый
промежуток на оси ординат.
Доказательство. Пусть f (x) — возрастающая функция.
Предположим, что в некоторой точке х0 из X, не совпадающей с правым
концом промежутка Ху она имеет разрыв справа. Тогда / (x0) ^
^ / (*о + 0), точнее, f (х0) < / (х0 + 0).
В силу монотонности функции будет f(x)^f(xQ) для х<С.х0,
f(x)^f(x0 + Q) для х>х0.
Таким образом, получается, что функция f (x) не может иметь
значений между числами f (х0) и f(x0-\-0). Следовательно,
совокупность значений У функции f(x) не может состоять из одного
промежутка. Это противоречит условию теоремы.
Аналогичное доказательство теоремы для случая убывающей
функции предоставляется читателю.
Замечание. В данной теореме установлено достаточное
условие непрерывности монотонной функции. Из теоремы 2 § 5 будет
следовать, что это условие является и необходимым.
Пример 1. Пользуясь определением непрерывной функции, доказать, что
многочлен /(*}=» я3 — 3*2 + 5*—4 непрерывен на промежутке (—оо, +оо).
Возьмем любую точку *0 на числовой оси. Вычислим в этой точке предел
и значение функции. По теоремам из теории пределов находим:
lim/(*)== lim (*з — 3*2 + 5* — 4) = ** — 3*-* + 5*0 — 4,
А — Х0 X-~Xq
а подстановкой в f(x) значения * = *0 получаем: / (*0) = х% — 3*5 + 5*0 — 4.
Так как оказалось, что lim / (*)=/ (*0), т0 п0 определению непрерывности
*—*о
функция / (*) непрерывна в точке х0. Поскольку точка х0 выбиралась произвольно
на ( — сю, -}-со), то этим доказана непрерывность данной функции в каждой точке,
а следовательно, и на всей числовой оси (— оо, +оо).
Пример 2. Пользуясь определением непрерывности функции «на языке
е —6», доказать, что функция / (*) = * непрерывна в точке х — 1. В каких
границах должно изменяться*, чтобы выполнялось неравенство | f (*)—/(1)|<;
Показать, что эта функция имеет в точке х~-^- разрыв второго рода.
139

Возьмем произвольное 8>0и найдем окрестность точки я=1, для всех точек
которой будет выполняться неравенство | f (х) — /(1) | <; е. Так как /(1) = 5, то
*м *т 3* + 2 R Зх + 2-10* + 5 7(1—х) _ 7
1-х
_*
1
*~2
и неравенство запишется в виде
7
2
х— 1
1
Х~2
<С 8, ИЛИ
X—1
^ 7 •
что равносильно неравенствам
1
х —
х— 1
>^,или
(*-!) +
1 !
7
|>а-или
1
, , 2
'+5=1
7
>2е*
Так как абсолютная величина суммы не меньше разности абсолютных величин
слагаемых, то последнее неравенство будет выполнено, если выполнено неравенство
\х—1 _
Отсюда получаем, что ! х— 1 | <:
l>hHm2lir=T
>1 + Ъ-
то есть достаточно взять 6 =
2е + 7 ' 2е + 7
из неравенства \х—-1!<б получим, что | f (х) — f (1) | <8. В частности, если:
\_
1 .21
Т> то 6==iqi7-T6-
Таким образом, неравенство | / (x)—f (1) | < -^ будет выполнено во всяком слу-
1,1 15 17
чае, если | д:— 1 |< — то есть в интервале те<-х<
16*
Данная функция определена при всех хф-^-1 а прих=-х- знаменатель
обращается в нуль и функция не определена. Так как при этом lim / (х)— со (точнее „
lim /(#) = + оо, lim /(*) = —со), то мы говорим, что функция имеет в точке
J»'
1
х= -=- разрыв второго рода.
Пример 3. Доказать, что функция
/М =
sin — при х ф О ,
О при х = 0
разрывна в точке х = 0.
В примере 4, § 10, гл. III, нами установлено, что функция г/ = sin— в
точке х — 0 предела не имеет. Следовательно, остается заключить, что она не может
быть и непрерывной в этой точке. В точке х = 0 имеет место разрыв второго рода.
140

Вопросы для самопроверки и упражнения
1. Почему из непрерывности функции слева и справа в точке следует ее
обычная непрерывность, в то время как из существования односторонних пределов
функции в точке не следует существоЁание обычного предела?
2. Пользуясь определением непрерывности, доказать, что функция f(x)=x3 —
— 5х + 8 непрерывна на промежутке (— оо, +оо ).
3. Пользуясь определением непрерывности функции «на языке s — б», доказать,
х-}-3 1
что функция / (х) = Q о непрерывна в точке х = -^, В каких границах может
изменяться х, чтобы выполнялось неравенство
/(*)-/ (у
< -^-? Имеет ли эта
функция точки разрыва? Назвать их.
Примечание. Поскольку решение этой задачи проводится с помощью
некоторых приближенных вычислений, читатель может получить и несколько иную
оценку для искомых значений х. Поэтому данный ниже ответ следует
рассматривать как ориентировочный.
34 35 2
Отв. со^Жёд» разрыв при * = -«-.
4. Пользуясь определением непрерывности функции «на языке
последовательностей», доказать, что функция
| cos— при х ф О,
у 0 при х = 0
разрывна в точке х = 0.
5. В какой максимальной окрестности точки д:0 = 100 ордината графика
функции у —Ух отличается от ординаты у0 — Ю меньше, чем на в = 1ft п ?
Отв. (10 — 0,001)2 < х < (10+0,001)2.
6. Требуется изготовить металлическую квадратную пластинку со стороной
xQ ~ 10 см. В каких пределах допустимо изменять сторону пластинки х, чтобы ее
площадь отличалась от проектной площади у0 = 100 см2 не более, чем на
± 0,01 см2?
Отв. 1^99,99 ^*^с]Л00,01.
§ 2. НЕПРЕРЫВНОСТЬ НЕКОТОРЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
В этом параграфе мы проверим непрерывность некоторых
элементарных функций, пользуясь непосредственно определением
непрерывности функции. Другие элементарные функции будут рассмотрены
в § 6, 7 и 9.
1. Рассмотрим постоянную функцию f(x) = c на всей прямой
(—со, + оо). Так как равенство f(x0) = c выполняется в любой
точке х0, то при х-+х0 будет f (x)=c->c=f (х0), то есть Нт/(д:) =
х-+х0
= f(x0). Таким образом, постоянная функция непрерывна в каждой
точке прямой. Но тогда она непрерывна и на всей прямой (— со,
+ оо).
2. Функция f(x) = x непрерывна на (—оо, + со), так как для
любой точки х0 при x-^Xq имеем: f (x)=x-+x0=f (х0), то есть
lim/(*) = /(x0) (см. пример 1, § 10, гл. III).
х-*х0
141

3. Одночлен f(x) = axn (n — натуральное) есть непрерывная
функция на (—оо, 4- оо), так как его можно представить в виде
произведения функций, непрерывность которых уже доказана в пунктах
1 и 2:
ахп = а-х-х-х ... х.
п раз
4. Многочлен или целая рациональная функция f(x) = a0xn 4-
+ tfi*n-1 + tfoX71-2 +... + ап-лх + ап есть непрерывная функция на
(— оо, + оо), как сумма непрерывных функций.
5. Дробно-рациональная функция
f ( y\ = а°хП+aiXn~x+а2*п~2+ —+a*-ix+а*
непрерывна на (—оо, + оо), за исключением точек, в которых
знаменатель равен нулю, то есть кроме корней знаменателя, как
частное непрерывных функций.
6. Рассмотрим тригонометрические функции!
sin л:, cos a:, tgx, ctgx, secx, cosecx:.
Покажем, что функция sin* непрерывна в любой точке прямой.
Возьмем произвольную точку х0. Тогда
sin*— sin#ft =
2 sin ?=& • cos i±^L I = 21 sin ^^ J cos
* + *o
2
Заменяя
x4-x0
cos \ °
единицей, а
sin —
— числом
X— X(\
2 |
(на основании свойства, доказанного в конце § 11, гл. III), получим
неравенство:
| sin л: — sin х01 =^ |л: — л:01.
Для любого е>0 достаточно взять 6 = е, и тогда из неравенства
\х— х0\<8 будет следовать неравенство | sin л: — sin д:01 <с е. Это и
доказывает непрерывность sinx в произвольной точке х0.
Непрерывность функции cosx в любой точке прямой доказывается
совершенно аналогично.
Из непрерывности функций sin x и cos x по теореме о непрерывности
частного следует непрерывность функций tgx= и secx= во
COS X COS X
всех точках, где cosx^O, то есть везде, кроме точек x=(2k-\-
+ 1)-^, и функций ctgx=2^ и cosecx = -r—- во всех точках, кроме
jl sin х sin х
x = kn (k = 0, ±1, ±2, ±3, ± ...).
7. Функция f (x) = \x\ непрерывна на всей прямой. Действительно,
на (0, + оо) она непрерывна, так как /(л:) = |л:| = л' для x>0,
а непрерывность f(x)=x доказана в пункте 2. На (—оо, 0)
функция f (x) также непрерывна, так как для x<0 она принимает вид:
^(л:) = |д:| = — х, a f(x) = — х = (—1)-л: непрерывна на основании
доказанного в пунктах 1 и 2, а также на основании теоремы
о непрерывности произведения. Остается установить непрерывность
142

данной функции в точке х = 0. Для этого вычислим односторонние
пределы в этой точке:
lim |*|= lim (—х) = — lim x = Q, lim ]x\= lim x = 0.
x-+ — 0 X-+ — 0 x-* — 0 *->+() х-> + 0
Итак, lim f(x)= lim f(x) = Q = f(Q), то есть f (x) непрерывна и
х--*—0 л: —+ 0
в точке х = 0.
Таким образом, оказалось, что все рассмотренные здесь функции
непрерывны в областях их существования. Но тогда на основании
теоремы о непрерывности суммы, разности, произведения и частного
можно утверждать, что функции, получаемые из них при помощи
конечного числа арифметических действий, являются также
непрерывными функциями в областях их существования.
Пример 1. Исследовать на непрерывность функцию f (x)=x2~\-2 sin х.
Функция / (х) представляет собой сумму двух функций: х2 и 2 sin x. Поскольку
каждая из этих функций непрерывна на (— оо, + °°)> то и сумма их / (х)
является непрерывной на (—оо, + оо) (см. теорему 1, § 1).
х24-3
Пример 2. Исследовать на непрерывность функцию / (х) =-^—' fi .
Так как f(x) — дробно-рациональная функция, она непрерывна на (—оо, +оо),
за исключением точек, в которых знаменатель равен нулю, то есть за исключением
корней знаменателя. Для определения последних решаем уравнение х2-— 5л:+ 6=0
и получаем, что точками разрыва второго рода являются х = 2 и * = 3.
Пример 3. Исследовать на непрерывность функцию
,., ч cos л;
/(Х)-Т=Ж1-
Как частное двух непрерывных функций f(x) непрерывна на (—оо, +оо),
за исключением тех точек ху для которых sinx=l, то есть за исключением лишь
точек * = (4Jfe + l)y (&=0, ±1, ±2, ...).
Вопросы для самопроверки и упражнения
1. Пользуясь непосредственно определением непрерывности, доказать
непрерывность функции cos л:.
2. Почему можно утверждать, что функция
г/ ч х5 — 2jc3 + a:2 + 9a:— 17
/М- ^+з
непрерывна на (— оо, + оо)?
3. Непрерывна ли функция
, . ч хз + 5х2 — 9х+\
/« = ^Z9
на [— 2, + 2]? Отв. Да.
4. Непрерывна ли функция / (*) = (х2 + Ъх + 2) tg x на [0, я]?
Отв. Нет.
б. Сколько точек разрыва может иметь функция
/(*) = х+1
м ) ax* + b**+cx + d*
где а, Ь, с и d — вещественные числа?
Указание. Воспользоваться тем, что многочлен л-й степени может иметь
не больше чем п вещественных корней.
143

§ 3. ПРИМЕРЫ РАЗРЫВНЫХ ФУНКЦИЙ
Пример 1. Рассмотрим функцию, заданную следующим образом:
/(Ф
jc2 при х<2,
.х+1 при х^2.
Эта функция определена на (—со, +со). На промежутке (—со, 2) функция
f(x)=x2 всюду непрерывна, на промежутке [2, + со) f (х)=х+\ также всюду
непрерывна. В частности, в точке х--2 функция /(х) непрерывна справа.
Следовательно, разрыв функции f (х) возможен только в точке х — 2. Найдем
левосторонний предел функции в этой точке: lim f(x)= lim х2 = 4. Сравнивая этот
л-->2—о х-+2—о
предел со значением /(2) = 3, видим, что в точке х = 2 функция имеет разрыв
первого рода (рис. 64).
Пример 2. Установить, в каких точках и какого рода разрывы имеет
функция
[ х3 при х<0,
л
2х при Or^x^-s-,
/W =
\х при *>у.
На промежутке (—оо, 0) функция f(x)—x2 определена и всюду непрерывна.
На промежутке 0, -^-1 функция f(x)=2x также определена и всюду непрерывна.
На промежутке (-~-, +оо) функция f(x)=tgx определена и непрерывна всюду,
зх
за исключением точек x = (2k+\) -у (&=1, 2, 3, ...). Следовательно, можно
сказать, что данная функция f (х) определена на (—со, Ч-оо), за исключением точек
x = (2k + l) -у (k=\, 2, 3, ...). В точках jc = (2^-f-1) — функция f (х) имеет
разрывы второго рода, так как в них предел функции слева равен +оо, а справа
равен —оо. Остается еще исследовать точки стыка промежутков: х — 0 и .*;=—.
Поскольку
lim/(*)= lim л? = 0=/(0), lim/(*)=¦--= lim 2x = Q=--f(0),
x-+0 *-+ — 0 jc-v-j-0 x—-{-0
О
Lz_
Зтг
2
Рис. 64.
Рис. 65.
144

у*
Рис. 66.
U
-/ О
1 2 3
Рис. 67.
5 X
то в точке *=0 функция непрерывна слева и справа, а значит, и просто
непрерывна. Поскольку
lim /(*)= lim 2* = я =/(-=-), lim /(*) = lim tg*
—2-о
— 2-0
+ 0
*-j + 0
-°°*/(у),
то в точке ^ = -9" функция имеет разрыв второго рода (но непрерывна слева)
(рис. 65).
Пример 3. Функция f (х) = ^ (рис. 66) определена и непрерывна на
(—оо, +оо), за исключением точки дс = 2. Определим род разрыва.
1 / ,. 1 .. 1
lim - = — 00 и lim 5 =
Х-+2 — 0х —l x-+2+0x — z
Поскольку lim jr = oo (точнее,
= + оо], то в точке х = 2 имеем разрыв второго рода.
Пример 4. Установить, в каких точках и какого рода разрывы имеет
функция
х2 при — 2^*<0,
ЖН * при х-0.
— при 0<х^2.
Эта функция (рис. 67) определена на [—2, +2]. Так как х2 и — непрерывны
соответственно в промежутках [—2, 0] и (0, +2], то разрыв может быть только
на стыке этих промежутков, то есть в точке х = 0. Поскольку в этой точке
односторонние пределы равны 0 и +со:
lim f(x)= lim *2=0, lim f(x)= lim — = + oo,
X-+—0 at-»-—0 *-*-f0 X-+ + Q x
то jc = 0 является точкой разрыва второго рода.
Пример 5. Можно ли устранить разрывы функций:
а) /(*) = в точке х = а;
i \—х2 при х^2,
<9eW-{x_3 „ри*>2
д:2 при х^ 1,
ipn
в точке а: = 2;
f л;2 при х=± 1,
в) ф(л')=< л , в точке *=1.
' * w \ 2 при *=1
145

Как известно из определения, устранимыми могут быть разрывы только
первого рода и только в том случае, когда в точке разрыва существует конечный
предел (то есть существуют равные конечные односторонние пределы).
О примере а) сразу можно сказать, что разрыв функции f (х) в точке х = а
устранить невозможно, так как в этой точке односторонние пределы —бесконечные
[ lim = — со; lim = + оо]
\х-+а—о х—а х-»а+о х—а J-
Функция g (х) хотя имеет конечные односторонние пределы в точке разрыва
х = 2
(lim #(*)= lim (1— х2)=— 3, lim g(x)= lim (x — 3)= — 1),
X-+2—О Х-+2—0 л;—2+0 дг-2+О
но они не совпадают. Разрыв также неустранимый.
Функция ф (х) в точке разрыва х=\ имеет равные односторонние конечные
пределы ( lim ф(#) = Пт ф (*) = Нт х2— 1). Следовательно, разрыв может быть
л:_^1-_0 дг—1+0 х—1
устранен переопределением функции в точке я = 1. Для этого достаточно положить
/(1) = 1 вместо /(1)=-2.
tfi х
Пример 6. Доопределить функцию /(#) = -^— в точке х = 0 таким
образом, чтобы она стала непрерывной в этой точке.
В точке х = 0 эта функция не определена, но имеет конечный предел
ti? х
lim / (х) = lim ——=1. Следовательно, при определении значения функции в точ-
дт—О л:—0 х
ке х = 0 нужно исходить из того, что значение функции в этой точке должно
равняться пределу функции в этой же точке. Для этого достаточно положить /(0) = L
Тогда функция
( Mi при хфО,
/(*> = { *
[ 1 при х = 0
будет непрерывной в точке л: = 0.
Пример 7. Переопределить функцию
-х— при х ф 0,
2х ^~
2 при х = 0
в точке * = 0 таким образом, чтобы она стала непрерывной в этой точке.
Данная функция в точке * = 0 разрывна (разрыв первого рода), так как
lim/(*)=lim^ = W/(0) = 2
Переопределим ее в этой точке, положив f(0) = — вместо /(0) = 2. Тогда
получим, что функция
sin*
/мч
2^- при хфО,
-^ при х = 0
уже непрерывна в точке х = 0, так как выполняется равенство lim f(x)=f(0).
х-0
Строго говоря, изменив значение функции / (х) даже в одной точке, мы получаем
уже другую функцию, которую следовало бы обозначить другой буквой
(например» ё (*))• Однако, несколько нарушая эту строгость, мы обозначили измененную
функцию по-прежнему через / (х), чтобы подчеркнуть ее тесную связь с
первоначально заданной функцией.
146

при *> 2.
Пример 8. Функция
{1, если х—рационально,
О, если х—иррационально,
называемая функцией Дирихле, уже встречалась нам во второй главе (пример 6,
§ 2, гл. II). Показать, что она разрывна в каждой точке числовой оси.
Пусть х0 — любая точка из (—со, +оо). Будь она рациональной или
иррациональной, в любой ее окрестности найдутся как рациональные, так и
иррациональные точки. Следовательно, в любой окрестности точки х0 функция ф(л:) будет
иметь значения, равные 0 и 1. В таком случае не может существовать предела
функции в х0 ни слева, ни справа. Следовательно, функция Дирихле в каждой
точке числовой оси имеет разрывы второго рода.
Вопросы для самопроверки и упражнения
1. Установить, в каких точках и какого рода разрывы имеют следующие
функции:
|х2+1 при х^\, ( Е (х) при х^2,
I при х<1, б) /(*) = { _J_
х + 2 хф — 2. \ х — 2
, х прих^О, , х2 <0
1-х при 0<*^ 1, Л
в)/М= 1 г)/(*)= 1 прих = 0,
[ YZT^ ПРИ *> *• ( tgx+l при х>0.
Построить графики этих функций.
Отв. а) В точке х=\ разрыв первого рода, в точке х = —2 разрыв второго
рода, б) В точке х = 2 разрыв второго рода, в точках х=1, 0, — 1, —2, —3, ...
разрыв первого рода, в) В точке х = 0 разрыв первого рода, в точке л; =1 разрыв
л
второго рода, г) В точке х = 0 разрыв первого рода, в точках x = (2k-\-l) - (k =
= О, 1, 2, 3, ...) разрыв второго рода.
_ С х2 при х ^ 1
2. Будет ли функция /(*) = < непрерывна на [0, 2]? Отв. Да.
I х3 при х > I
1 cos х
3. Доопределить функцию /(#) = % в точке * = 0 таким образом, чтобы
она стала непрерывной в этой точке. Отв. /(0) = -=-.
4. Переопределить функцию
,м_рЕЕ! .*.*..
( — 1 при х = 0
в точке х = 0 таким образом, чтобы она стала непрерывной в этой точке.
I х |
5. Доказать, что разрыв функции / (*)=-—- в точке х = 0 устранить
невозможно. Построить график этой функции.
6. Можно ли утверждать, что квадрат разрывной функции есть также
разрывная функция? Проверить это на примере
/М=М пРри^§: О-Не,
7. Справедливо ли утверждение: «Если функции / (х) и g (x) имеют разрыв
в точке х0, то их сумма f(x)-{-g(x) есть также разрывная функция в точке х0»?
147

Проверьте это на примере, положив
( О при х^О,
/W== I 1 прих>0;
с I при х^О,
g('V)=l 0 при х>0.
7
Постройте графики. Отв. Нет.
8. Справедливо ли утверждение: «Если в некоторой точке х0 функция f (х)
непрерывна, а функция g (x) разрывна, то их сумма f(x)+g(x) является
разрывной функцией в этой точке»?
Отв. Да.
9. Если функция f (х) непрерывна в
интервале (аУЬ) и определена на его концах а
и Ь, то из зтого еще не следует, что она
непрерывка на отрезке [а, Ь\. Убедитесь в-
зтом на примере функции
/м-(тия0<ж<|'
10 для х = 0 и #=1.
I
JL
/ 2 3
Рис. 68.
Постройте график этой функции.
10. На -горизонтальной плоскости р
•*¦ стоят один над другим три цилиндра, ра-
Р диусы оснований и высоты которых
соответственно равны: нижнего 3 и 2, среднего 2
и 3, верхнего 1 и 1 м (рис. 68).
а) Выразить объем части тела,
заключенного между плоскостью р и плоскостью
горизонтального сечения, как функцию расстояния этого сечения от плоскости
р. Будет ли эта функция непрерывной? Построить график этой функции.
б) Выразить площадь горизонтального сечения тела, образованного этими
цилиндрами, как функцию расстояния сечения от плоскости Р (площадь сечения,
отделяющего один цилиндр от другого, считать равной площади сечения
нижнего цилиндра). Будет ли эта функция непрерывной? Построить ее график.
Отв. а) Объем б) Площадь
V(*) =
9ллг при 0 .-5
10л + 4л* при 2 г
25л -\-zix при 5^
31л при б г
~х^Ъ,
;*<оо,
5W =
9л
4л
л
0
при 0^*<^2,
при 2<д:<5,
при 5<#^6,
при 6<лс<оо
V (^ — непрерывная функция на [0, + со); 5 (*) —непрерывная функция на (0,2),
(2,5), (5,6), (6, + оо). В точках * = 2; 5; 6 имеет разрывы первого рода.
§ 4. НЕПРЕРЫВНОСТЬ СЛОЖНОЙ ФУНКЦИИ
С понятием сложной функции мы уже познакомились в конце
§ 6, гл. II. Здесь выясним вопрос об условиях, обеспечивающих
непрерывность сложной функции.
Теорема. Пусть на промежутке X задана функция z —
= ф (х), все значения которой содержатся в промежутке Z, а
на Z задана функция y=f(z). Тогда, если у(х) непрерывна
в точке х0, a f(z) непрерывна в точке z0, причем z0 = q> (x0),
то и сложная функция y—f[q>(x)]=F(x) непрерывна
в точке х0.
148

Доказательство. Воспользуемся определением непрерывности
функции «на языке последовательностей». Возьмем на промежутке X
любую последовательность точек
X\j %2> ^3» • • • » ХП9 • • • ,
сходящуюся к точке х0, и положим zn = q>(xn). Тогда по
непрерывности функции г = ф(х) в точке х0 имеем: lim zn = lim ф (хп) =
Ф (л:0) = z0, то есть последовательность точек гъ z2, z3, ... , zn, ...
промежутка Z сходится к точке z0. В силу же непрерывности функции
f(z) в точке z0 получаем: lim f(zn)=f(z0), то есть lim f[y(xn)] =
=/[ф(*о)1 или
lim F(xn)=F(x0),
что и доказывает непрерывность функции ^(л:) в точке х0.
Пример 1. Доказать непрерывность функции ^=sin x2.
Функцию 3> = sin х2 можно рассматривать как сложную функцию, считая у =
= sin 2, где 2 = *2. Тогда поскольку функция г = х2 определена и непрерывна при
любом значении х, то есть на ( — со, + со), а функция у — sin 2 определена и
непрерывна при любом значении 2, то на основании доказанной теоремы можно
утверждать, что функция ^ = sin x2 определена и непрерывна в любой точке, то
есть на ( — со, +оо).
Пример 2. Доказать непрерывность функции у — со& (*2-{-5*+8).
Функцию 3> = cos3 (x2 + 5* + 8), рассматривая как сложную, можно представить
через простейшие элементарные функции следующим образом: y = zd, где z=cosuy
a и = *2-|-5* + 8. Так как функция и = х2-{-Бх-\-8 определена и непрерывна
при любом значении *, а функция z = cos и определена и непрерывна при любом
значении н, то из теоремы о непрерывности сложной функции следует, что
функция z = cos (х2-\-5х-\-8) определена и непрерывна при любом значении х. Далее,.
так как функция у = г3 определена и непрерывна при любом значении 2, а
функция 2 = cos (*2 + 5* + 8), как мы только что доказали, определена и непрерывна
при любом значении *, то по той же теореме можно утверждать, что функция
jr = cos3 (*2 + 5*+8) также определена и непрерывна при любом значениие х, то
есть на ( — со, + оо).
Пример 3. Установить область существования и непрерывности функции
= 1
sin* Ф
Эту функцию можно рассматривать как сложную, если положить у= —, где
2 = sin*. Функция 2 = sin* определена и непрерывна всюду. Функция у =
= — определена и непрерывна при всех zz?0. Тогда по теореме о
непрерывности сложной функции функция у— —: определена и непрерывна на всей оси
(—оо, + оо), за исключением тех точек, где sin* = 0, то есть точек x — kK(k=Q>
± 1, ±2, ...).
Пример 4. Установить область существования и непрерывности функции
J> = tg2—Ц-.
^ х—\
Функцию у можно представить через простейшие элементарные функции
следующим образом: y = z2, где 2 = tg«, а н= г. Поскольку функция
и = , определена и непрерывна при всех значениях *, кроме х=1, а функция
2 = tg и определена и непрерывна при всех значениях и, кроме н = (2& + 1) -^- (? = 0,
149

±1, ±2, ...), то функция 2 = tg
для всех значений хф 1, при которых-
как сложная, определена и непрерывна
1
y^(2fc+l) —
можно преобразовать: -
1
*?*+!)»;,_,*
Последнее условие
2
(26 + 1)я
Таким образом, получаем, что функция z = tg
х—\
> *^1 + (2Л+1)я-
определена и
непрерывна для всех значений х, кроме х— 1 и *=1 +
(/г = 0, ±1, ±2, ...).
(2k + \)n
Далее, так как функция y = z2 определена и непрерывна для всех значений
1
г, а область существования и непрерывности для функции z = tg-
¦1
уже
установлена, то на основании теоремы о непрерывности сложной функции можно
утверждать, что данная функция существует и непрерывна на всей оси (— оо,+оо), за
2
исключением точек х=\ и *=14- /OL , t4— (6 = 0, н-1, ±2, ...).
(2^+1)я v » t » /
Вопросы для самопроверки и упражнения
1. Исследовать на непрерывность следующие функции, рассматривая их как
сложные:
а) f/ = sin3x. О/тгв. Непрерывна на (—со, -f-oo).
б) у=cos (1 — sin х). Отв. Непрерывна на (—со, +оо).
2
в) i/ = cos т. Отв. Непрерывна при х-ф\.
г) y = ctgn2n. Отв. Непрерывна при xzpb — (6 = 0, ±1, ±2,...).
2. Доказать теорему о непрерывности сложной функции, используя
определение непрерывности функции «на языке 8—6».
§ 5. СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ
Теорема. 1 (первая теорема Больцано-— Коши)*. Пусть на
отрезке [а, Ь\ определена функция f(x), непрерывная на
этом отрезке, причем на
концах отрезка она
имеет значения разных
знаков. Тогда на [а, Ь] найдет-
ся по крайней мере одна
точка с(а<.с<Ь),в
которой функция равна нулю.
Иначе говоря,
непрерывная функция при переходе от
значений одного знака к
значениям другого знака
проходит и через нулевое значение.
Доказательство.ТЛусть
для определенности / (а) < 0 и
f(b)>0 (рис. 69). Разделим отрезок [а, Ь] пополам точкой —^-.
Рис. 69.
Если окажется, что f/-^p-j = 0,
то точка
и будет искомой точ-
* Огюстен Луи Коши (1789—1857) —французский математик.
150

кой с. Если же /("-тг/^О» то на концах одной из частей отрезка
\а, ^-|- или г-тг-1 b\ функция будет иметь значения разных
знаков. Обозначим эту часть через [аъ 6J. Легко видеть, что / (а1)<0,
/ Фд > 0. В самом деле, если / (г-^-А >-0, то значения / (х) имеют
разные знаки на отрезке а, -—?— • В этом случае а1=ау 61==^±—
и f(tfi)<0, f(b1)>0. Точно так же разбирается случай, когда
f(^)<0.
Итак, мы получили отрезок [аъ 6J, на концах которого
значения функции имеют разные знаки. Разделим этот отрезок пополам
точкой ' .
Если f\2 ]=$> то Ql 2 * есть искомая точка. Пусть / Г ^ ЛфОг
тогда ту из частей, \аъ 2 или \ 2 , 6Х , на концах которой
функция имеет значения разных знаков, обозначим через [а2, Ь2Ь
При этом непременно снова будет /(а2)<0, a f(b2)>0. Делим
отрезок [а2, Ь2] пополам и повторяем такие же рассуждения.
Возможно, что на каком-то шагу точка деления окажется такой, что
в ней функция будет равна нулю. Тогда она и будет искомой
точкой с. Но возможно, что, как бы долго мы ни производили деление
отрезка [а, 6], f Г g )?=0 для всех п. Тогда получим такую
бесконечную последовательность вложенных отрезков
[аъ bx] zd [а2, Ь2] =э [а6, Ь3] =>... zd [an, bn] =э ...,
что при всех п
fW<0, f(bn)>0 (l)
и длина я-го отрезка Ьп—ап = -тш > 0- Следовательно, по теореме
о вложенных отрезках (см. § 8, гл. III) существует точка с и
притом единственная, принадлежащая всем отрезкам последовательности
lim an = limbn = c. В точке с, как точке отрезка [а, й], функция f (х)
П-+СО П—*СО
непрерывна. Следовательно, переходя к пределу в неравенствах (1),
получим, с одной стороны,
f(c) = limf(an)^0,
л-юэ
с другой стороны,
f(c) = limf(bn)^0.
я-»-со
Отсюда остается заключить, что /(с) = 0. Теорема доказана.
Геометрический смысл теоремы. Непрерывная
кривая при переходе с одной полуплоскости по отношению к оси
ОХ на другую непременно пересекает эту ось.
151

Теорема 2 (вторая теорема Больцано—Коши). Пусть на
отрезке [а, Ь\ определена непрерывная функция f{x),
принимающая на концах отрезка различные значения, например
f(a)=A, f(b)=B. Тогда, какое бы число С меэюду числами
А и В мы ни взяли, на отрезке [а, Ь] найдется такая
точка (#<г<&), что f{c) = C.
Иначе говоря, непрерывная функция при переходе от одного
значения к другому проходит и все промежуточные числа.
Доказательство. Пусть для определенности А <В (рис. 70).
Возьмем какое-нибудь промежуточное число C(A<.C<iB) и
рассмотрим вспомогательную функцию <p(x) = f(x) — С. Эта функция
непрерывна на [а, Ь], как разность непрерывных функций f (x) и
г|)(х) = С. Кроме того, ее значения на концах отрезка имеют разные
знаки:
(f(a)=f (а) — С=А — С<0,
<р (6) =/(&)_ С=В—С>0.
Следовательно, по 1-й теореме Больцано—Коши существует такая
= 0, то есть /(с)-— С=0. Отсюда
/(<?)--= С, что и требовалось
доказать.
Следствие- Если функция
f(x), заданная на промежутке
X, непрерывна на этом про-
Рис. 70.
межутке, то совокупность Y
ее значений тоже
представляет некоторый промежуток.
Доказательство. Положим
M=sup f(x), m=inff(x)t где обе
xgX xqX
точные границы вычисляются для
всего множества значений f(x)
(не исключено, что М = + оо или
т=—оо, см. § 5, гл. I). Тогда
в совокупности Y не может быть точек, расположенных ниже га
или выше М. Покажем, что интервал (га, М)сУ. Возьмем любое
у0 ? (m, M) и подберем два значения нашей функции уг и у2 так,
что т<у1<суо<у2<М. Существование таких значений вытекает
из определения точных границ. Пусть y1 = f(x1), yi = f{x2).
Применяя к функции / (х) на отрезке от х1 до х2 вторую теорему
Больцано — Коши, мы сразу заключаем, что у0 тоже встретится
среди значений функции f(x). Следовательно, справедливо
включение (m, M)czY. Концы интервала (m, M) могут как принадлежать,
так и не принадлежать совокупности Y, а потому Y может быть либо
интервалом (т, М)> либо отрезком [ту М>] либо полуинтервалом
(т, М] или [га, Af).
Заметим, что 1-я теорема Больцано — Коши является частным
случаем 2-й теоремы (достаточно по 2-й теореме считать Л<0,
152

В > 0 и С = 0). Однако из этого не следует, что 1- я теорема не нужна.
Она используется при доказательстве 2-й теоремы.
Доказанные теоремы Больцано— Коши имеют большое значение
для дальнейших теоретических исследований как в математическом,
анализе, так и в других смежных областях. Кроме того, они
имеют и непосредственные практические приложения. Рассмотрим,
несколько примеров.
Пример1. Доказать, что уравнение г* — 8л; + 4 = 0имеет корень
на отрезке [ — 2, +2].
Воспользуемся свойством непрерывной функции, отмеченным
в теореме 1. Для функции f(x)=-x* — 8x+4 имеем:
/( — 2) = — 32 + 16 + 4 =— 12<0,
/( + 2)= 32-16 + 4= 20>0.
Следовательно, существует такая точка с, что /(с) = 0. А эта
значит, что данное уравнение на указанном отрезке имеет, по
крайней мере, один корень с.
Пример 2. Показать, что любой многочлен нечетной степени
с вещественными коэффициентами имеет, по крайней мере, один
вещественный корень.
Рассмотрим многочлен нечетной степени с вещественными
коэффициентами
f(x) = a1rJ* + 1 + a2x2k + ... + a2k + 1x + a2k + 2.
Как следует из примера 3, § 11, гл. III, при достаточно больших
по абсолютной величине значениях х многочлен имеет знак высшего
члена агх2к + 1, то есть при достаточно больших х>0 — знак аг
и при х<0—противоположный знак. Таким образом, многочлен
нечетной степени, будучи непрерывной функцией, принимает
значения разных знаков. Следовательно, существует, по крайней мере,,
одна такая точка с, что f (с) = 0.
X3 X2
Пример 3. Доказать, что функция f(x) = -= ~- + 3 принимает значение*
равное 2-^-, внутри отрезка [ — 2, -}- 2].
Данная функция непрерывна на [ — 2, ~(- 2]. Кроме того,
/(_2) = -4-|+3=1, /ю-1-4 + 3-3*.
Следовательно, по второй теореме Больцано—Коши функция принимает
значение 2-~- в некоторой точке, лежащей внутри отрезка f — 2, -f- 2].
Пример 4. Найти приближенное значение какого-нибудь корня уравнения
х* + х* —5jc + 2 = 0.
Функция /(#) = хъ -\~х2 — Ъх + 2 непрерывна на всей оси. Будем вычислять
ее значение для целых значений х. Так как /(1)= — 1<0, а /(2) = 28>0, то
уравнение имеет между числами 1 и 2 хотя бы один корень. Разделим отрезок [1, 2]
на десять равных частей точками: 1,1; 1,2; 1,3;...; 1,9. Будем вычислять значения
функции в этих точках: /(1,1)=—0,68; /(1,2)=—0,08; /(1,3)= +0,87. На этом.
можно вычисление приостановить, так как уже между точками 1,2 и 1,3 меняется
знак функции и, следовательно, имеется хотя бы один корень уравнения. Делим:
отрезок [1,2; 1,3] на десять равных частей точками 1,21; 1,22; 1,23;...; 1,29 и снова
153

будем вычислять значения функции в этих точках: f(l,21)= —0,01, / (1,22)= +0,08.
Следовательно, между числами 1,21 и 1,22 находится хотя бы один корень нашего
уравнения. Таким образом, мы вычислили значение корня уравнения с точностью
до 0,01. Если бы мы продолжили аналогичные действия дальше, то точность можно
было бы довести до 0,001, 0,0001, 0,00001 и т. д.
Теорема 3 (первая теорема Вейерштрасса). Если функция
f(x) непрерывна на отрезке [а, Ь], то она ограничена на
этом отрезке, то есть существуют такие числа т и М,
что для всех х из [а, Ь] выполняется неравенство т^
^f(x)^M.
Доказательство. Докажем ограниченность функции f (х)
сверху (ограниченность снизу доказывается аналогично). Пусть / (х),
будучи непрерывной» не ограничена сверху на [а, Ь]. Это значит,
что нет такого числа М, чтобы f(x)^M для всех х из [а, &],
то есть, какое бы число мы ни взяли за М, найдется хоть одна
точка х из [а, Ь] такая. что f(x)>M. Будем давать М
последовательно значения: Л1 = 1, 2, 3,..., /г,...
Для М = \ найдется такая точка хг из [а &], что !(хг)>1;
» М==2 » » » х2 » [a, b], » f(x2)>2;
» М = 3 » » » х3 » [а, Ь], » /(#з)>3;
Для М = п » » » хп » [а, 6], » f(xn)>n\
В результате получим ограниченную последовательность точек xlt
x2i а:3,..., хп,— По теореме Больцано — Вейерштрасса (теорема 2,
§ 9, гл. III) из этой последовательности можно выделить сходящуюся
подпоследовательность xnk-+x0. Точка х0 будет принадлежать
отрезку [а, Ь] и, следовательно, в ней / (х) непрерывна. Тогда lim f (xnk) =
= f (x0). С другой стороны, точки хп выбирались так, что f (xnfi) > nk.
Значит, lim f (хп/г) = схэ . Полученное противоречие и доказывает
теорему.
3 а м е ч а н и е. Теорема становится неверной, если в ней отрезок
[а, Ь] заменить интервалом (а, Ь) Так, например, функция f(x) =
= - непрерывна на (Д1), но не ограничена: lim ~ = oo.
х х_+ + о х
Доказательство не проходит в том месте, где мы утверждали,
что в точке х0 функция непрерывна. Для интервала х0 может
совпасть с его концом и f (x0) не будет определено.
Пусть на некотором промежутке X определена функция f(x).
Будем говорить, что эта функция в точке х0 имеет наибольшее
(наименьшее) значение на X, если для всех остальных значений х
выполняется неравенство f (x)^ f (x0) (f (х) ^ / (лг0)).
Если рассматривать множество значений функции, то наибольшее
(наименьшее) значение функции (если оно существует) будет точной
верхней (нижней) границей этого множества (см. определение точных
границ множества на стр. 23). В случае, когда точные границы
функции являются ее значениями, говорят, что функция f (х)
154

Yl
^Z2
-8
Рис. 71.
достигает своих точных границ. Однако, как известно, не всякому
множеству принадлежат его точные границы. Если множество
всех значений некоторой функции, заданной на X, не включает
в себя своих точных границ, то такая функция не имеет на X
наибольшего и наименьшего значений.
Пример 5. Функция f(x) = x—Е(х)> заданная на [0, ft], где
ft ^ 1, не имеет наибольшего значения на этом отрезке, но имеет
наименьшее значение— нуль.
Множеством ее значений будет [0, 1],
а точными границами -- числа 0 и 1
(рис. 25). Следовательно, можно
сказать, что функция достигает
своей точной нижней и не достигает
своей точной верхней границы.
Пример 6, Функция/ (х) = х3,
заданная на (— 2, + 3), имеет
своими точными границами
числа— 8 и 27, но они не
достигаются функцией ни в одной точке
(-2, +3) (рис. 71).
Из этих примеров видно, что
ограниченные функции могут и
не достигать своих точных
границ. Это происходит из-за того, что
в рассмотренных примерах либо функции не были непрерывными
там, где они заданы, либо области их определения не являлись
отрезками.
Теорема4 (вторая теорема Вейерштрасса). Если функция f (х)
непрерывна на отрезке [а, Ь], то среди всех ее значений есть
наибольшее и наименьшее значения.
Иначе говоря, функция f (x), непрерывная на отрезке, достигает
на этом отрезке своих точных границ. Точная верхняя граница
является наибольшим значением функции, а точная нижняя
граница — наименьшим.
Доказательство. Пусть /(х) непрерывна на [я, ft]. Тогда по
теореме 3 она будет ограниченной на этом отрезке. Следовательно,
существуют точная верхняя и точная нижняя границы, которые
обозначим соответственно через Мит.
Покажем, что f (х) достигает М на [а, ft], то есть существует
такая точка xlt что f (x1) = M. Будем рассуждать от противного.
Пусть такой точки на [я, ft] нет. Тогда f(x)<M для всех х из [a, ft].
Рассмотрим вспомогательную функцию
Эта функция непрерывна на [a, ft] как частное двух
непрерывных функций (причем знаменатель отличен от нуля). Следовательно,
по теореме 3 она ограничена. Пусть ее верхней границей будет
155

некоторое число ц,>0, то есть м __ (х) <|Л. Тогда f(x)<M .
Получилось, что число М меньшее, чем М, является верхней
границей для /(л:). Но это противоречит тому, что М есть точная
верхняя граница функции f(x). Этим и доказано, что существует
точка х19 в которой f(x1) = M.
Аналогично доказывается, что / (х) достигает и своего
наименьшего значения, которое равно т.
Следствие. Если функция f(x) непрерывна на отрезке
{а, Ь], то совокупностью ее значений будет отрезок [т, М],
где т и М — точные границы функции.
Действительно, по только что доказанной теореме f (x)
ограничена на [а, b]> m^f (х)^М, а по второй теореме Больцано — Коши
любое число Р, взятое из отрезка [m, M], является значением
функции f (х) в некоторой точке хр из [a, b]9 f(xp) = P.
Обращаем внимание читателя на большое сходство данного
следствия со следствием из второй теоремы Больцано — Коши. Однако
там было доказано лишь то, что совокупность значений / (х) есть
какой-то промежуток с концами т и М. Сейчас, предполагая
функцию / (х) непрерывной на отрезке, мы доказали, что совокупность
значений f (х) есть также отрезок.
Вопросы для самопроверки и упражнения
1. Функция f (х) определена и непрерывна на отрезке [а, Ь] и на концах этого
-отрезка имеет значения одного знака. Можно ли утверждать, что на [а, Ь\ нет
такой точки, в которой функция обращается в нуль? Подобрать соответствующий
пример. Отв. Нет.
2. Имеет ли уравнение х8 + 1&*3 + 2 = 0 корни, принадлежащие отрезку
(—1, + 1]? Отв. Да.
3. Имеет ли функция х3 — 2х2 + х — 2 в какой-либо точке отрезка [1,3]
значение, равное нулю? Отв. Да.
4. Имеет ли. уравнение х1 — 2*3-|-*2 = 2 хотя бы один корень между числами
— 1 и 2? Отв. Да.
5. Принимает ли функция f (x)—2xQ — 4x8 + 5хъ + 7 значение, равное 7, в
какой-либо точке отрезка [ — 2, +2]? Отв. Да.
6. Имеет ли уравнение х7 — 4л:5 + х3— Зл'2 = 4 корень, больший 2?
Отв. Да.
7. Найти приближенное значение какого-нибудь корня уравнения х3 — 2х2—
— Ъх + 8 = 0 с точностью до 0,01.
8. Доказать, что функция
12х при — lsCx^O,
х+± при 0<*^1
разрывна в точке х = 0 и тем не менее имеет на [—1, + 1] как наибольшее, так
и наименьшее значения. Построить график этой функции.
9. Доказать, что функция / (*) = sin х на отрезке _ -^, -у имеет
единственную точку, в которой f(x)=c (где с — любое вещественное число,
удовлетворяющее условию | с | < 1.
156

10. Показать, что любой многочлен четной степени имеет по крайней мере два
вещественных корня, если он принимает хотя бы одно значение, имеющее знак,
яротивоположный знаку коэффициента при старшем члене.
11. Имеет ли уравнение sin х—х -j- 1=0 на отрезке [0, зт] хотя бы один корень?
12. Доказать, что функция
... sin jr- при хф2,
[ 0 при д;==2
лринп:лает на отрезке [2, Ь] (где Ь—любое вещественное число, большее 2) все
промежуточные числа между числами /(2) и f(b), однако не является
непрерывной на "этом отрезхе.
§ 6. СУЩЕСТВОВАНИЕ И НЕПРЕРЫВНОСТЬ ОБРАТНОЙ ФУНКЦИИ,
КОРНЯ И СТЕПЕНИ С РАЦИОНАЛЬНЫМ ПОКАЗАТЕЛЕМ
Понятие функции, обратной по отношению к некоторой
функции #=/(#), дако в главе II. Там же рассмотрен и вопрос о
графике обратной функции. Свойства непрерывной функции,
изученные в предыдущем параграфе, дают вйзможность доказать
следующую теорему.
Теорема. Пусть на некотором промежутке X
определена непрерывная строго возрастающая функция у =f(x) с
совокупностью значений Y. Тогда на Y существует обратная
функция х=у(у), также непрерывная и строго
возрастающая*
Аналогично, для непрерывной строго убывающей
функции y^f(x), заданной на X с совокупностью значений Y,
на Y существует обратная функция х=у(у), также
непрерывная и строго убывающая*
Доказательство. Пусть y=f(x) есть непрерывная строго
возрастающая функция на X. Как известно, областью значений
непрерывной функции будет некоторый промежуток У (см.
следствие из второй теоремы Больцано—Коши). По условию для
каждого значения у0 из У на промежутке X найдется такая
точка х0, что f (х0)=у0. Такая точка будет единственной, так как
в силу монотонности в строгом смысле f (xj Ф f (x2) при хх Ф х2.
Следовательно, каждому значению у0 из У соответствует
определенное единственное значение х0 из X. Таким образом, обратная
функция х = у(у) будет однозначной. Покажем, что х = у(у) строго
возрастает. Пусть yi<Cy2- Введем обозначения: (f(yi)=xlf <р(у2) =
=х2. Тогда #1=/!(х1), У2 = ?(х2). Если бы оказалось, что хг^х2,
то благодаря возрастанию функции y=f(x) мы имели бы y±^y2i
что противоречило бы предположению. Следовательно, х1<Сх2-
Непрерывность функции х=у(у) следует из того, что она
монотонна и ее значения сплошь заполняют промежуток X.
В случае строгого убывания функции доказательство
аналогично.
Замечание. Требование строгой монотонности функции /(х)
существенно. Если бы оно было нарушено, то x=q(y) могло бы
157

не удовлетворять определению функции, так как нарушилось бы
свойство однозначности. Немонотонную функцию нужно
постараться разбить на интервалы монотонности и на каждом
интервале строить обратную функцию.
С помощью доказанной теоремы легко доказать существование
арифметического корня п-й степени, где я —любое натуральное
число.
Рассмотрим функцию у = хп при некотором натуральном п. Она
непрерывна и строго возрастает на промежутке [0, +оо).
Непрерывность нами установлена в пункте 3, § 2, а строгое
возрастание можно доказать непосредственной проверкой условия
монотонности. Действительно, для любой пары значений хх и хг
из [0, +оо), удовлетворяющей неравенству хх<х2, имеем х*\<х*.
По следствию из второй теоремы Больцано — Коши множество
значений функции у=х?, рассматриваемой на промежутке Х =
= [0, +оо), представляет некоторый промежуток Y. Так как
наименьшее значение функции хп на промежутке X равно 0 (оно
получается при х = 0), то 0 и будет левым концом промежутка У.
С другой стороны, хп -+ +°° при х-> +оо, то есть справа
промежуток У не ограничен. Следовательно, К=[0, +оо). Тогда по
доказанной здесь теореме на [0, + оо) существует обратная
функция х = угу- Меняя обозначения, мы можем записать эту функцию
и как
y = Y~x.
Эта функция также непрерывна и строго возрастает на
промежутке [0, +оо).
Проведенным рассуждением мы доказали теорему о
существовании корня: для любого неотрицательного числа а и
любого натурального числа п существует такое
неотрицательное число р=уго^ что р* = а.
Число Р называют арифметическим корнем n-й степени
из числа а.
Полезно заметить, что если а ^=0, то у ал = а; в частности, }Лх2 =
= а. Однако если а< 0, то ]/~а2 =—а. Так как мы
рассматриваем арифметический корень из а2, то ]/"а2 = |а|.
Отметим еще, что если число п — нечетное, то функция y=j/rx
определена уже при всех значениях х из (— оо, -j-oo). Легко про-
верить, что и в этом случае функция ух непрерывна и строга
возрастает на всей оси.
С помощью корня вводится понятие степени с рациональным
показателем. Пусть х>0 и г — некоторое положительное
рациональное число.
Последнее можно представить в виде^, где т и п — начальные
158

числа (см. § 2, гл. I). Определим хгу то есть *пкак \fxn\
Легко проверить, что при таком определении степени с
рациональным показателем сохраняются все основные свойства
степеней с натуральным показателем. В частности,
хп,хт = хп+т^ {хп)т = хпт9 {ху)п = ^ g. j» = ^ И др.
Степень с отрицательным рациональным показателем — г
определяется равенством
х-'=Лг(*^0).
Вопросы для самопроверки и упражнения
1. Доказать теорему о существовании и непрерывности обратной функции для
случая строгого убывания.
2. Покажите на примере, прибегнув к графическому представлению функции,
что теорема о существовании и непрерывности функции становится неверной, если
в ней предположить вместо строгой нестрогую монотонность функции.
3. Найти обратную функцию для функции у=у^хт, заданной на [0, +оо).
Установить область существования и непрерывность обратной функции.
4. Доказать, что всякая функция вида y = a0x2n+1 -f- axx2n~Y + а2х2П~3-{- . . . +
+ апх-\-ап+1, где а0, аъ а2, . . . , ап — положительные числа, имеет обратную
функцию, непрерывную и возрастающую на (— оо, +°°)-
5. Дана функция f (х) — У a — х3. Показать, что f [f(x)] = x. Какая функция
будет для нее обратной?
Отв. f (х).
6. Найти обратную функцию для функции у = —~[~i(.acz? bd)- В каком
случае обратная функция совпадает с данной? Отв. При a — — d.
§ 7. СУЩЕСТВОВАНИЕ И НЕПРЕРЫВНОСТЬ ОБРАТНЫХ
ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
В главе II (§ 6, п. 5) мы уже познакомились с обратными
тригонометрическими функциями. Однако там не давалось строгого
доказательства их существования. Здесь же мы сможем легко
сделать это, опираясь на общую теорему о существовании и
непрерывности обратной функции.
1. Рассмотрим функцию y = sinx. Она непрерывна и строго
возрастает на отрезке —^ > + <г • Множество ее значений,
соответствующих этому отрезку, заполняет отрезок [ — 1, +1].
Следовательно, на основании теоремы о существовании обратной функции
можно утверждать, что для функции y = sinx, рассматриваемой на
— g , + ^ , существует на [ — 1, + 1 ] обратная функция у = arc sin x,
также непрерывная и строго возрастающая (см. рис. 37).
159

Выбор отрезка —у, +Y из все** области (—оо, +со)
существования функции y=sinx обусловлен тем, что нам нужен
был промежуток монотонного изменения этой функции, имеющий
максимальную длину. Таковым и является отрезок — 4^-, +4г .
Конечно можно было бы взять и другие промежутки монотон-
Г я Зя I I 3я 5л] ^
ности sin*, например у, -у или у, -у L но обычно принято
брать промежуток —у, +Т » так как он наиболее близко
расположен от начала координат.
2. Аналогичными рассуждениями можно доказать, что для
функции у = cos х, строго убывающей на [0, я], существует на [ — 1,
+1] обратная функция y = avccosx, непрерывная и строго
убывающая на этом промежутке (см. рис. 37).
3. Функция y = tgx непрерывна и строго возрастает на
интервале ( —4г» +1П- Множество ее значений на этом интервале
составляет всю ось (—со, +оо). Следовательно, на основании
теоремы о существовании обратной функции для нее существует на
(—оо, +оо) обратная функция r/ = arctgA:, изменяющаяся на
интервале (—-у, -^т)' также непрерывная и строго возрастающая
(рис. 38).
4. Аналогично устанавливается, что для функции y = ctgx,
убывающей на интервале (0, я), существует обратная функция
у = arcctg х на ( — оо, +оо), непрерывная и строго убывающая
на этом интервале (рис. 38).
Вопросы для самопроверки и упражнения
1. Докажите существование обратной функции у = arccosх на отрезке [—1,
+ 1].
2. Докажите существование обратной функции у = arcctg* на всей оси ( —оо,
+ оо).
3. Сопоставьте сведения об обратных тригонометрических функциях,
полученные здесь, с описанием обратных тригонометрических функций в п. 5, §6, гл. И.
4. Можно ли рассматривать функции sin *, cos xt tg x и ctg x как обратные
тригонометрическим функциям соответственно arcsin x, arccos x, arctg x, arcctg x?
Отв. Нет.
8. ОПРЕДЕЛЕНИЕ СТЕПЕНИ С ИРРАЦИОНАЛЬНЫМ
ПОКАЗАТЕЛЕМ
При рассмотрении элементарных функций (§ 6, гл. II)
значение символа а? при иррациональном \i и любом вещественном а>0
осталось нераскрытым. Иначе говоря, осталось неизвестным, что
следует понимать под степенью с иррациональным показателем.
Теперь этот символ можно определить, воспользовавшись понятием
предельного перехода. При этом мы будем исходить из уже
известного нам понятия степени с рациональным показателем.
160

Сформулируем сначала одно свойство иррациональных чисел,
которое может быть строго доказано в развернутой теории
вещественного числа: для каждого иррационального числа \i су-
ществует возрастающая последовательность
рациональных чисел
сходящаяся к \i.
Например, если число \л представлено в ви^е бесконечной
десятичной дроби с целой частью k и десятичными знаками сп
то можно принять rn = k1c1c2c3...cni то есть
•п I ш I 1С0 I Ш00 -т- ••• -г Шя .
Таким образом, в качестве гп мы берем «десятичные приближения
К|л» по недостатку. Так как при этом ц — r„ <-tqf» т° ясно, что ап - ^.
Кроме того, ал+1^/"л при всех п.
Лемма 1. Для любой последовательности
рациональных чисел rlf г2, г3, ..., /•„,.. м сходящейся к нулю,
последовательность аг\ аг\ аг\ ..., аг«, ... (где а>0) сходится к I,
lim а'л=1.
Доказательство. Ограничимся рассмотрением случая, когда
а> 1. Докажем заново, не опираясь на рассуждение из примера 10,
§ 5, гл. III, что у а — 1 при натуральном р—- со. Так как уа>\
при любом натуральном р, то можно положитьj/ra = 1 +h, где ft> .
Согласно неравенству Бернулли из § 7, гл. III, (1 +/г)р^ 1 -\-ph.
Р г~~ Р/—
Подставляя h=y а— 1, получим: а^1+р(у а— 1), откуда
1 р
По теореме о сжатой переменной отсюда следует, что ар =
= \/~а — 1. Но тогда и а р = —j > 1. Из доказанных соотношений
а*
вытекает, что для любогб е>0 найдется такое натуральное/?0, что
j_ i_
aKl+еий р°>1—е. (1)
Так как гя — 0, то для всех я, начиная с некоторого |гл|<—f
Ро
1 1 --
то есть < гп <—. Тогда, начиная с того же п, а я> < аГп <
Ро Ро
161

< а р° и в силу (1) имеем: 1 — е < аГп < 1 4- е, то есть | аГл — 1 1 < 8,
что и доказывает лемму.
Лемма 2. Пусть а>0 и \у, — какое-нибудь
иррациональное число. Тогда для любой последовательности
рациональных чисел
Pli f*2i f*3i • • • » Fm • • • » (^)
сходящейся к \i, последовательность ari, агъ, а% ..., аГп, ...
сходится к одному и тому же пределу А.
Доказательство, а) Если а=1, то лемма очевидна. В этом
случае А = \.
б) Пусть а>1. Рассмотрим сначала некоторую фиксированную
неубывающую последовательность рациональных чисел pi=^p2^
^Рз^...^Рл--.9 сходящуюся к |х. Тогда
а^ < а?* ^ ар» ^... ^ а9* ^... (3)
Возьмем рациональное число г>|х. Тогда для любого п будет
р„ < г. Следовательно, яРл <; аг, то есть последовательность (3)
ограничена сверху. По теореме о монотонной переменной она имеет
пределом некоторое число A; lim a?n=A. При этом Л >0, так
как aP/i>0 и последовательность (3) — неубывающая.
Возьмем теперь произвольную последовательность
рациональных чисел rn-+[i. Тогда последовательность рациональных чисел
ri — pu г*—Рз> г3—Рз»---. гл—Р«> ••• будет сходиться к нулю
и, по лемме 1, lim аГп~Рп=1. Но аГп = а?п-аГп~*п. Следовательно,
lim агл = lim др* • lim аг« " р« = Л.
в) Остается рассмотреть случай, когда 0<я<1. В этом
случае положим — = 6. Тогда 6>1 и по доказанному выше для
любой последовательности рациональных чисел гП9 сходящейся к \х,
существует один и тот же предел: lim ЬГл = ?;>0. Отсюда
lim аГп= lim —?-=ъ > 0.
Ьп °
Лемма доказана.
Таким образом, мы получили, что для любой
последовательности рациональных чисел гь г2, г3,..., /*„,..., сходящейся к jx,
последовательность аГ*9 аг*9 аг*,...9 аГл,... сходится к одному и тому
же пределу Л.
'/ысло A = lim аг« принимается за значение сРх
of = lim а7", если гя ->fi. (4)
Заметим, что формула (4), которую мы приняли за
определение а? в случае иррационального (х, может быть доказана и для
случая рационального fi. Действительно, в этом случае аГп = а*х
xar«"^. Но гп—(1->0, а по лемме ar«"~ll,-> 1 и по теореме о
пределе произведения lim аГп = а?*.
162

При а>\ легко проверить, что если г и г'— такие два
рациональных числа, для которых г<Ц1<г\ то аг<сР<сГ (прия< 1
получится противоположное неравенство: аг> а* > ап). Поэтому если
г иг' — рациональные приближения к jut с недостатком и с избытком
соответственно, то аг и ап будут приближениями (но уже не
обязательно рациональными) к а1Х тоже с недостатком и с избытком.
Нетрудно показать, что основное свойство степени, выражаемое
тождеством ах'+х" = ах' -ах'\ сохраняется и для любых вещественных
значений х! и ^'. Для этого достаточно взять последовательности
рациональных чисел г'п -+х' к ^'п -* х" и перейти к пределу в равенстве
Г' л." Г* Гк
Можно доказать и формулу
(а*у = ах§х"9 (5)
справедливую при любых вещественных значениях х' и х".
Вопросы для самопроверки и упражнения
1. Сформулируйте кратко, что понимается под степенью с иррациональным
показателем.
2. Докажите, что если r>jj, (r— рациональное, \i— иррациональное) иа>1,
то аг > а*\ а если г < ц, то аг < а*\
3. Докажите формулу (аа)^ = ааР, где а и (5 — любые вещественные числа.
§ 9. ПОКАЗАТЕЛЬНАЯ, ЛОГАРИФМИЧЕСКАЯ И СТЕПЕННАЯ ФУНКЦИИ
Возьмем некоторую постоянную величину я>0 в качестве
основания и переменную величину х в качестве показателя. Получим
функцию ах, которая теперь уже определена при всех
вещественных значениях х. Эта функция и называется показательной. Таким
образом, показательной функцией называется функция вида
у=ах{а>0>),
заданная на множестве всех вещественных чисел (— оо, +оо). Так
как при а=\ функция 1*=1 есть постоянная и ее свойства нами
изучены, мы будем в дальнейшем предполагать, что а^ь 1.
Выясним некоторые свойства показательной функции. Будем
предполагать для определенности, что а> 1. Докажем, что в этом
случае функция ах строго возрастающая. Пусть хх<Схг. Подберем
такое рациональное число г, чтобы х1<Сг<Сх2. Тогда, как
отмечено в предыдущем параграфе, ax*<iart ar<.aXz. Отсюда и следует,
что ах*<ах\ то есть ах возрастает.
Теперь докажем, что показательная функция ах непрерывна на
всей оси. Пусть х0 — произвольная точка на (—оо, + оо) и дана
некоторая последовательность точек хп->х0. При каждом значении п
подберем два рациональных числа г„ и г"п так, что г'„ <; лг„ < г„ и
гпп — г'п<—. Тогда хп — гп->0 и г"п — хя->0. Следовательно, гп->х0
163

и rnn-^XQ. По формуле (4) из предыдущего параграфа имеем:
агп -> ах° и агп -> ах°.
С другой стороны,
arn<zaXn<zarn.
Тогда по теореме о сжатой переменной аХп -> ах°. Тем самым мы
доказали, что limax = axo, а это и означает непрерывность функции а*
х—+х0
в точке х0.
Так как аг>0 при любом рациональном л, а для любого
вещественного значения х существует рациональное число г<л:, то
ах>0 на всей прямой (— оо, +оо) Последнее означает, что
график показательной функции у = ах расположен в верхней
полуплоскости и нигде не пересекает ось ОХ (см рис. 34).
Покажем, что совокупность значений функции ах состоит из
всех положительных чисел. Для ьтого благодаря следствию из
второй теоремы Больцано — Коши достаточно установить, что
supaA'=+oo, infa"* = 0. (1)
Представим величину а в виде a=\+h, где ft>0. По
неравенству Бернулли при любом натуральном значении п имеем: ап =
= (1 +h)n^l -\-nhy откуда сразу ясно, что ал-* + оо при /г->оо.
С другой стороны, а~п= -^-> 0. Отсюда и вытекают формулы (1).
Мы уже проверили, что для показательной функции ах
выполнены условия теоремы из § 6 о существовании и непрерывности
обратной функции. При этом областью задания функции будет
вся ось, а совокупностью ее значений — интервал (0, + оо).
Следовательно, на интервале (0,+ оо) существует непрерывная и строго
возрастающая обратная функция y=logax. Тем самым, в
частности, доказано существование логарифма для любого
положительного числа. Отрицательные числа не имеют логарифмов, так как
любая степень числа а(а>0) положительна Число нуль также
не имеет логарифма Таким образом, областью существования
логарифмической функции y=\ogax является промежуток (0,-f°°)-
Возьмем теперь в качестве показателя некоторую постоянную
величину (г, а в качестве основания — переменную величину х.
Получим функцию хУ-, определенную, во всяком случае, при всех
вещественных значениях х>0, которая называется степенной.
Из определения логарифма и из формулы (5) предыдущего
параграфа следует, что (например, при а>\)
# = (<№**)* =<?Ло**х.
А тогда из монотонности логарифмической и показательной
функций сразу вытекает, что & тоже монотонна: возрастает при |л>0
и убывает при |.i<0. При у, = 0 степенная функция обращается
в постоянную: х°=1.
164

Из непрерывности логарифмической и показательной функций
и из теоремы о непрерывности сложной функции (§ 4) вытекает,
что степенная функция также непрерывна. Действительно, х->х0,
тогда
logaX-^logaXo, \l logeX -> fl logaX0, (t l°8a* -> ct l°gaX°, TO eCTb & -> xg.
Вопросы для самопроверка и упражнения
1. Доказать, что показательная функция ах при а< 1 является строго
убывающей.
2. Откуда следует, что число нуль не имеет логарифма?
3. Построить графики функций у = ех и у = е~*.
§ 10. ИСПОЛЬЗОВАНИЕ НЕПРЕРЫВНОСТИ ФУНКЦИЙ
ПРИ ВЫЧИСЛЕНИИ ПРЕДЕЛОВ
При вычислении пределов функций фактически мы уже
неоднократно пользовались их непрерывностью. Так, например,
утверждая, что при х-> a sin x-> sin a, e?-+e?, х?-+ап, \Пс-+ jfa и т. д.,
мы были правы, поскольку эти функции непрерывны в точке х = а.
Как мы знаем, условие /(л:)->/(а) при х-+а и выражает
непрерывность функций f (x) в точке х=а.
Непрерывность элементарных функций позволяет нам найти
следующие важные пределы»
Пример 1. "т(1+тН =** ПРИ любом вещественном х.
Так как, считая jc^O, имеем:
.'i-l'+F-JL-U'+^n-U-J
l+i)*l -«¦
(последний предельный переход сделан на основании
непрерывности степенной функции*), а при х = 0 доказываемое
соотношение очевидно, то требуемое соотношение доказано.
Пример 2. lim ogg( "*"*' = logae. Доказать.
х -~ 0 х
Действительно, lim °ga(y= lim — loga (1 + x) = lim loga(l + л:)*
*: —0 * лг — 0 * *-*0
и в силу непрерывности логарифмической функции получаем
требуемое. В частности, при а=е имеем: lim Л* ~*~*' = 1, то есть
АГ — 0 Х
ln(l + x)~Jt.
Пример 3. lim =lna. Доказать.
а: -*0 *
Для доказательства этого равенства положим а*— 1=р. Тогда
а*=\ +р, x = \oga(\ +P)- При дс-*0 по непрерывности показатель-
* Переменным было /г, а показатель х считался постоянным.
165

ной функции а*-*1; следовательно, Р->0 и, пользуясь уже
решенным примером 2, получим:
1- 0*—\ ,. Р 1 1
Пример 4. lim v ' = ji. Доказать.
х - О *
Для доказательства положим (1+л:)^—1=р. Тогда (1+^ =
= 1 + Р и [х 1п(1 +Р)=1п (1 + Р). Из первого равенства при *-*0
по непрерывности степенной функции р -> 0. Переходя к пределу
в очевидном равенстве
(1+ДС)|*-1_ р Щ (1+дс)
л: In (1+р)" ^ * '
получим:
,. (1+*)Р—- 1 ,. Р ,. 1п(1+*) . .
(здесь мы дважды использовали предел, вычисленный в примере 2).
Вычисленные здесь пределы будут использованы в
дифференциальном исчислении. С их помощью легко решаются также
многие задачи на раскрытие неопределенностей.
1 —
п _ ,. In ^— 1 ,. In я— lne 1 .. е 1 .. 1п(г+1)
Пример 5. lim = lim = —lim =— lim—v ' '=¦
x-*e x & x -*• e x & e J^_ i e z -*¦ 0 2
=l.i=ip-,=2V
e e \e j
e
Примере. lim*/1 + sin*-Ulimcos*.(1+sin*> -'-l-l,!
* -* 0 tg * * — о sin д: п n'
ex ea ea (ex-a \\ ex~a 1
Пример 7. lim = lim — = ea lim == ea In e = ea.
x -*¦ a X Ct x-*¦ a X ^ x -* a % — Q,
1 1
„ Q f. (1+2jc)3 — 1 n .. (1 + 2*)3—1 0 1 2
Пример 8. lim^—I-—'- = 2 lim v ^ ' =2.- = --.
x-*o x x_q 2x 3 3
e~zx j з е-зх j з 3
Пример ^Um-g-^-^lta—^ T • In e— y.
Рассмотрим функцию y=u°t где и (w>0) и у — функции от
одной и той же переменной х. Функция uv в частном случае
может быть степенной (при постоянной v) или показательной (при
постоянной и). В общем случае она не будет ни той, ни другой,
это совсем новая функция. Мы назовем ее показательно-степенной
функцией.
Пусть и-* uQX) и v->v0 при стремлении х к некоторому
пределу. Найдем при этом условии предел uv. Выражение и° можно
представить в виде
uv=elnuV~eL'UiU.
166

В силу непрерывности логарифмической функции 1пи-+\пи0 при
и-*и0. Значит, lim (v- Inu)=v0lnuQ. А тогда по непрерывности по-
и — «о
С — С'о
казательной функции имеем:
lim и0 = lim е°1п " ^е*»1пи° = uv0°.
и -* и0 и — и0
V -* VQ V — С'в
В следующих трех случаях произведение t/-Inа представляет
собой неопределенность вида 0-оо: если и0 = 0 и т*0 = 0; и0=1 и
г/0 = ±оо; и0=+оо и i>0=0. Следовательно, в этих случаях и
выражение и0 будет также неопределенностью, вид которой
обозначается соответственно 0°, 1°°, оо°. Раскрытие этих неопределенностей
возможно только при наличии законов изменения переменных «иг/.
Способы раскрытия этих неопределенностей изложены в § 2, гл. VI.
Вопросы для самопроверки и упражнения
1. Какие функции f(x) для ограниченной последовательности хп обладают
свойством lim/(*„)=/(lim хп)?
2. Приведите пример функции f(x), для которой из х—*х0 не следует /(*) —
-/(*о).
3. Непрерывность каких функций использована в следующих соотношениях:
a) lim(jc + 3)2 = (a+ 3)2, б) lim arctg2jc = arctg l =?-?
х— а 1 4
4. Иногда говорят, что «если некоторое равенство f(x) = ф (х) справедливо для
любых значений переменной х, то оно сохранится и тогда, когда вместо х
подставим его предел (lim а:)». Произведя такую подстановку в тождестве
Е(2+1)-*(2-4) + И
при #—-со, показать, что это утверждение может привести к ошибке, если не
ограничиваться рассмотрением непрерывных функций.
§ 11. ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ И ИХ СВОЙСТВА
Частным случаем рассмотренной нами выше показательной
функции у = ах(0<ia^b\) (см. § 9) является функция у=ех, где за
основание взято число е. С помощью функции ех описываются многие
физические явления, такие, например, как радиоактивный распад,
изменение атмосферного давления в зависимости от высоты и др.
С помощью этой функции определяются также функции, имеющие
широкое применение как в самой математике, так и в ее
приложениях. Это так называемые гиперболические функции:
sh x=e ~~? (гиперболический синус),
qX I q-X
ch#=—-^—(гиперболический косинус).
* Определение функции вида Е (х) и ее свойства даны в § 2, гл. II и в
примере б, § 10, гл. Ш, а график—на рисунке 57.
167

th x== x. -x (гиперболический тангенс),
оХ\\х = ех_-х (гиперболический котангенс).
Из определения гиперболических функций следует, что все
они относятся к классу элементарных функций, так как являются
результатом арифметических действий над показательнььми
функциями вида у = ех и у = ех.
Название «гиперболических» эти функции получили потому,
что Х = сЬа:иК=5Ьл: удовлетворяют уравнению гиперболы X2—
_ у%=\
\[ex + e~x\* [ ех — е~х \ъ _е*х + 2 + е'** ё*х — 2 + е-*х , "|
[\~ J { 2 ) ~ 4 4 -1]'
подобно тому как тригонометрические функции X=cosx и Y = s\nx
носят название «круговых» в силу того, что удовлетворяют
уравнению окружности X2 -\-Y2=l.
Названия же гиперболических «синус», «косинус», «тангенс»
и «котангенс» происходят от того, что между ними имеют место
соотношения, во многом напоминающие или совпадающие с
соответствующими соотношениями между тригонометрическими
функциями: sinx, cosx, tgx, ctgx. Так, например, thx = -^, cthx —
= т~, th*-cth jt=l, ch2x — sh2A:=l, sh2 x = 2shx-chxt sh (x-\-y) =
==sh x-ch y-\-chx-sh у, и др.
В справедливости этих формул можно убедиться, если
воспользоваться определением гиперболических функций. Например,
ех е~х ех i е-х е2х е-%х
2shx-chx = 2 —2— —^— = 2— =sh2A\
Так как функции ех и е~* = — определены и непрерывны на
(—оо, +оо), то по теореме о непрерывности суммы, разности и
частного непрерывных функций следует, что гиперболические
функции shXy chx, thx и cthx так же определены и непрерывны
на ( —оо, +оо) (последняя за исключением точки х = 0).
Непосредственной проверкой условия четности и нечетности
функции легко устанавливается, что функции shx, thx и cthx
нечетные, а функция chx четная.
Так как е>1, то на промежутке [0, +оо) функция ех
возрастает от 1 до +оо, а функция ех = ~^ убывает от 1 до 0.
Следовательно, на этом промежутке разность ех — е~х возрастает от
0 до -j-оо. Можно доказать, что сумма ех-\-е~х также оказывается
возрастающей функцией и ее значения изменяются от 2 до+оо.
Отсюда заключаем, что на 10,+оо) функция shx возрастает от
0 до+оо, а функция chx возрастает от 1 до+оо. Из выражения
th — *•*-*"* _ I _ ^"^
ех+е~х ех-\-е~х
168

?'Ctb\
^ч-^' „
0 X
Рис. 72.
Рис. 73.
следует, что на [0,-{-°о) функция thjc также возрастает от О,
оставаясь меньше 1. Поскольку cthx =тт—, то, очевидно, функция
cthx убывает на (0,-j-oo) от +оо , оставаясь больше 1.
Полученные нами данные о поведении гиперболических
функций на (0,+оэ) дают возможность представить их графически на
этом промежутке. Используя же свойства четности и нечетности
функций, можно продолжить эти графики на всю числовую ось
{рис. 72 и 73). Заметим, что из всех гиперболических функций
только одна thx является ограниченной, так как |th*|<l или
— l<thA:<l- Отметим, что кривая y=chx или кривая более
обшего вида у--
еа + е
')
носит название цепной линии. Это
название кривая получила из-за того, что цепь или канат,
закрепленные с двух концов, принимают под действием собственного веса
такую форму прогиба.
Упражнения
Доказать справедливость следующих формул:
1. ch (х -\- у) = ch х • ch у -f- sh х • sh у. 4. th (x -\- у) =
ch2jc—1
2. sh2* =
3. ch2x =
ch 2x + I
5. I —th2* =
6. 1 — cth2* =
th x -f th у
1+thJcthy*
i
ch2*'
sh2*'
Сравнить эти формулы с соответствующими формулами из тригонометрии,
обратив особое внимание на знаки.
№

§ 12. РАВНОМЕРНАЯ НЕПРЕРЫВНОСТЬ ФУНКЦИИ
Пусть на некотором промежутке определена непрерывная
функция y=f(x). Как известно, непрерывность f(x) в точке х0
означает существование для
любого е>0 такого б>0, что
из неравенства \х—-х0|<б
следует неравенство \f(x)—
— / (*e) I < е.
Покажем, что величина б
может зависеть не только от
выбора е, но и от точки х0у
в которой определяется
непрерывность. Это легко
увидеть на графике конкретной
функции, например функции
/(#)=-, заданной на
промежутке (0, 1). На рисунке 74
показана зависимость б от е
(в одной и той же точке х0),
а на рисунке
75—зависимость 6 от л: (при одном и том же е). Но эту зависимость
для той же функции можно обнаружить и чисто аналитически.
Действительно, пусть 0<л:0<1. Возьмем 8>0и 6 = min<y, Щ\.
Покажем, что из неравенства \х—л:0|<;б следует неравенство
)/ (*) — f (*о) |<«- Так как \х—х0|<б, то — б<х—х0<б и, в
частности, х—xQ> —б или x>Xq — б. Поскольку б^*°
Рис. 74.
-, то х > х» —
— у, то есть #>у. С другой
стороны,
1_
"^0
. |*0 —*|
хх0
и в силу неравенства х>~-
I/W-/WK
<
)х0 — *
2
<
2
= 6.
Таким образом, мы нашли для
произвольного е>0
соответствующее ему б>0, причем из самого выражения б видно, что оно
зависит и от xQ.
Покажем теперь, что по е>0 невозможно подобрать
соответствующего б > 0, не зависящего от х0. Будем рассуждать от
противно

ного. Пусть е > 0, и допустим, чтое му соответствует некоторое б > О,
не зависящее от х0, такое, что из неравенства \х—л:0|<;б следует
неравенство \f (*) — f (х0) | <е. Возьмем на промежутке (0, 1) такую
точку х0, что х0<б, а затем возьмем х так, что Q<x<.jt—.
Тогда 0<#<#о> следовательно, \х—х0|<6. В то же время
tto-M-i-1^1-*?-*;-.
Полученное противор.ечие убеждает нас в невозможности выбора
б, общего для всех точек х0.
Из способа определения б через е и х0 по указанной выше
формуле можно находить и численные значения б в зависимости от е
или отх0. В частности, если х0 фиксировать, положив, например, х0 = ^,
то для ? = к) будет S = -gg, для ^ = ^ бУдет б==1бЬ» и т* д# Если
же фиксировать е, положив, например, е = -уд, то для ^о = е"
будет б = ^> для *o = uj- будет 6 = 2000' и т' д*
Полученные значения б можно, конечно, округлять в сторону
уменьшения.
Таким образом, 6 является функцией от е и л:, что обычно
обозначают так:
б = б (е, л:).
Поставим теперь вопрос, существуют ли непрерывные функции,
рассматриваемые на некоторых промежутках, для которых по
любому е>0 находилось бы соответствующее б>0, не зависящее
от х, то есть одно и то же для всех точек х из рассматриваемого
промежутка.
Ниже будет показано, что при некоторых условиях,
налагаемых на функцию /(#), выбор б зависит только от е, б = б(е).
Определение. Функция f(x), заданная на некотором
промежутке, называется равномерно непрерывной на этом
промежутке, если для любого е>0 найдется такое б>0, что
неравенство \f (xr) - ¦ f (х"); < е выполняется для любой пары точек х
и х" из данного поомежутка, удовлетворяющих неравенству
\х' — х"\<8.
Равномерная непрерывность функции на промежутке означает,
что в любом месте этого промежутка одна и та же степень
близости значений аргумента хг и х" обеспечивает заданную (выбором е)
близость соответствующих значений функции f (хг) и f{x").
Понятие равномерной непрерывности функции относится
к наиболее сложным и трудным для усвоения понятиям
математического анализа. Поясним равномерную непрерывность на
следующей модели. Представим себе, что график заданной
непрерывной функции y = f(x) есть некоторая тонкая, но жесткая
стальная нить. Задача состоит в том, чтобы изготовить такую муфту
171

Рис. 77.
длины б с цилиндрическим отверстием диаметра е (рис. 76),
которая могла бы свободно передвигаться вдоль этой нити от точки
A (a, f (а)) к точке В (6, / (&)), сохраняя при этом положение, при
котором ее ось параллельна оси ОХ. Очевидно, длина б такой
муфты будет зависеть только от величины диаметра ее отверстия
е: чем меньше диаметр отверстия е, тем короче должна быть
муфта (меньше б). Если для заданной кривой (нити) y = f(x)
такую муфту можно изготовить с любым сколь угодно малым
наперед заданным диаметром отверстия е, то функция f (х)
равномерно непрерывна на [а, Ь]. Действительно, в эгом случае для
любой пары точек х и х'\ удовлетворяющих неравенству \х' — х*\ < б,
будет выполняться неравенство \f (х') — /(х")|<е. Пытаясь
построить такую модель для функции f(x)=- на (0, 1), легко
убедиться, что она не является равномерно непрерывной на этом
интервале, так как по графику этой функции приблизить муфту
в крайнее левое положение невозможно, какой бы малой длины
б мы ее ни изготовили (рис. 77).
Теорема (Кантора*). Если функция f(x) непрерывна
на отрезке [а, Ь], то она и равномерно непрерывна на этом
отрезке.
Доказательство. Допустим противное функция f (*),
будучи непрерывной на отрезке [я, 6], не является на нем равномерно
непрерывной. Это значит, что не для всякого e>G найдется
таксе б > 0, чтобы для любых х' и х\ удовлетворяющих
неравенству ! х' — х" К б, выполнялось неравенство \f (x')—j (xff) |< е. А это,
в свою очередь, означает, что существует Такое е0, для которого
нельзя подобрать соответствующего б, то есть, какое бы б мы ни
взяли, найдется хоть одна пара точек х' и х" таких, что
|/-/|<6, в то время как |/(*')—•/(**) |^е0
* Георг Кангог (1845—1918) — известный немецкий математик,
основатель современной теории множеств.
172

Возьмем последовательность значений б, сходящуюся к нулю:
Х» 2 ' 3 » '•• » п • '•"
Для 6 = 1 найдутся такие точки х\ и jcJ, что \х[—х[\<\,
но |f (*,') — /«)|^е0.
Для 8 = V2 найдутся такие точки л:^ и л;*, что | jci—jc^ | -<C Va»
ко |/(*;>— f(xl)\^e0.
Для 6 = V3 найдутся такие точки хг и х"ъ, что | л:з — х"ъ \ < V3,
но |/(*;)— f(xZ)\^e0.
Для 6 = V^ найдутся такие точки х'п и д?, что |х'п—x'n\< г/П9
но \f(Xn) — f(xn)\^eQ.
Этот процесс бесконечно продолжаем.
В результате из [а, Ь] выделяется две ограниченные
последовательности:
Xif Хэ, Х3, ... , Хп, ••• (1)
Xit Xit Хг, ... , Хп, • •. (2)
Из последовательности (1) по теореме Больцано — Вейерштрасса
можно выделить сходящуюся подпоследовательность. Чтобы не
вводить новых обозначений, будем считать, что уже сама
последовательность (1) сходится к некоторой точке х0. Покажем, что тогда
последовательность (2) также сходится к х0. Действительно, из
очевидного равенства хп—х0 = х"п—х'п + х'п —х0 следует, что | х"а —
— х0\^\хп— х'п\ + \х'п — х0\, и так как при /г-^оо будет \х„—х'п\<с
< >О и х'п — x0->0, то х'п — х0->0.
Функция f (х) по условию непрерывна в точке х0.
Следовательно, при /г-кю будет / (х'п) -> / (х0) и f (x'n)-* f (х0). Это значит,
что разность \f(x'n)—f(Xn)\ должна стремиться к нулю при дг->оо.
Но это противоречит тому, что |/(хп) — f (х'п) !^е0 для всех п.
Обнаруженное противоречие и доказывает теорему.
Если в теореме Кантора вместо отрезка [а, Ь] рассматривать
ишервал (а, Ь), то теорема перестает быть верной. Это видно хотя
бы из примера функции f (x) == —, рассмотренной нами в начале
параграфа. Функция / (х) =— непрерывна на (0, 1), но не
является равномерно непрерывной на этом интервале.
Теорема Кантора дает возможность утверждать, что f (x)
равномерно непрерывна на [а, Ь], как только установлена ее
непрерывность на этом же отрезке. Однако иногда можно доказать
равномерную непрерывность функции и без теоремы Кантора.
Пример. Известно, что функция f(x)=x2 непрерывна на отрезке [0, 1].
Доказать ее равномерную непрерывность на этом отрезке, не ссылаясь на
теорему Кантора.
173

Возьмем любые две точки из [0, 1]: х' и х". Тогда /(*") — f (xf)—x'r — х'2==
= (я"-{-*') (л;'—л:'), и так как всегда х" + х'^2, то
|f(**)-f(*')l^2|**-x'|.
о
Если теперь взять любое е>0 и положить 6=-^-, то для любой пары точен
х' и х", взятых из [0, 1] и удовлетворяющих неравенству | х" — х' | <б, будет
выполняться неравенство | f (хп)—f (х') | < 8.
А это значит, что функция f(x)=x2 равномерно непрерывна на [0, 1].
В интегральном исчислении используется один факт, который
здесь легко получается в качестве следствия из только что
доказанной теоремы.
Введем понятие колебания функции.
Определение. Если функция f (x) определена и ограничена
на отрезке [а, Ь], то разность между ее точными границами на
этом отрезке называется колебанием функции на [а, Ь], то есть
колебание
(?> = М — т, где М= sup f(x), m= inf f(x).
Следствие из теоремы Кантора. Если функция f(x)
определена и непрерывна на отрезке [а, Ь], то по заданному е>0
можно разбить этот отрезок на конечное число частей так, что
на каждой из частей колебание функции не будет превышать е.
Действительно, по доказанной теореме f(x) будет равномерно
непрерывной на [а, Ь]. Следовательно, по заданному е найдется
такое б, что для любых точек х' и х\ удовлетворяющих
неравенству | х' — х" | < б, будет выполняться неравенство | f (x')~-f (х") | < е.
Если отрезок [а, Ь] разделить на такие части, чтобы длина каждой
из них была меньше б, то, очевидно, на каждой из отдельно
взятых частей разность значений функции в любых двух точках по
абсолютной величине будет меньше е. В частности, это справедливо
и для разности между наибольшим и наименьшим значениями
функции на каждой из частей, которая и составляет колебание
непрерывной функции на этом отрезке.
Вопросы для самопроверки и упражнения
1. Следует ли из равномерной непрерывности функции на промежутке
обычная непрерывность на этом промежутке? Отв. Да.
2. Доказать равномерную непрерывность функций: a) f(x)=x3 на [0, 1],
б) / (л-) = sin х на (—оо, +оо), не используя теорему Кантора.
3. Доказать, что непрерывная ограниченная функция у = sin — в интервале
(О, 1) не является равномерно непрерывной в этом интервале. Будет ли эта
функция равномерно непрерывной на [1, 2]? Отв. Да.
4. Доказать, что неограниченная функция f (x)=x-{-sm x равномерно
непрерывна на ( —оо, +оо).
5. Будет ли функция у = х2 — 3х равномерно непрерывной на интервале (1, 3)?
Отв. Да.

Раздел II
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ
ОДНОЙ ПЕРЕМЕННОЙ
ГЛАВА V
ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ
В этой главе центральное место занимают понятия производной
и дифференциала. Исторически эти понятия возникли из практики.
Скорость неравномерного движения, плотность неоднородной
материальной линии, а также тангенс угла наклона касательной
к кривой и другие величины явились прообразом понятия
производной. Возникнув из практики, понятие производной
получило обобщенный, абстрактный смысл, что еще более усилило
его прикладное значение. Создание дифференциального исчисления
чрезвычайно расширило возможности применения математических
методов в естествознании и технике. «Лишь дифференциальное
исчисление дает естествознанию возможность изображать
математически не только состояния, но и процессы: движение» (Ф. Энгельс.
Диалектика природы. К. Маркс и Ф. Энгельс. Соч., т. 20,
стр. 587). Таким образом, высшая математика существенно облегчает
диалектический подход к изучению различных явлений
действительности.
Кроме усвоения идейной стороны излагаемых вопросов, эта глава
требует от студента продолжительной работы по овладению
техникой дифференцирования. Нужно довести свое умение
дифференцировать до такой степени, чтобы дифференцирование элементарных
функций любой сложности не вызывало затруднений. Для этого
необходимо решить большое количество примеров. Помещенные
в конце каждого параграфа примеры для упражнения нужно
рассматривать лишь как небольшую часть всей работы по
практическому дифференцированию. Следует еще обратиться за примерами
к рекомендуемым сборникам задач (см. предисловие).
§ 1. ПОНЯТИЕ ПРОИЗВОДНОЙ
Исследование функций является одной из основных задач
математического анализа. Методы и средства исследования все время
развивались и совершенствовались вместе с развитием математики.
Как уже отмечалось, самым важным этапом в этом развитии яви-
175

лось создание дифференциального и интегрального исчисления
(XVII век), давшее в руки математиков совершеннейший аппарат
исследования.
В основе дифференциального исчисления лежит понятие
производной и дифференциала функций. Прежде чем перейти к
определению производной, рассмотрим
О М0 П задачу, решение которой под-
—I I 77J— ведет нас к этому понятию.
s Л5 Пусть некоторая
материальная точка М совершает прямо-
Рис- 78- линейное неравномерное
движение. Предположим, что за
время /0 пройден путь s0, а за время / — путь 5 (см. рис. 78). Тогда за
промежуток времени Д/=? —10 точка М пройдет отрезок пути &s = s — s0.
As
Отношение -т-. называется средней скоростью движения (оср) на
участке пути As, или за время от момента t0 до момента t = t0 + At.
Легко видеть, что с уменьшением At значение средней скорости иср
будет меняться, характеризуя движение на все меньшем и
меньшем участке пути As. Предел отношения -г- при Д/->*0 называют
скоростью v движения точки М в момент времени /0,
t. As ,, ч
hm t- = v. (I)
Заметим, что если бы движение предполагалось равномерным,
то величина -^ была бы постоянной и мы имели бы
А*
,. As As
Рассмотренное нами движение может быть задано некоторым
уравнением движения s = f(t). В этом случае, полагая /(/0) = <>0,
можно представить среднюю скорость уср и скорость v в данный
момент в виде
,. _f(t)-i(k). ri-\\mfJftdM
1—fo t-+tQ l—fo
Говоря о функции, обычно имеют в виду процесс изменения
одной величины в зависимости от изменения другой. При этом
изучение характера изменения неразрывно связано с вопросом
о том, с. какой скоростью (насколько быстро) происходит это
изменение
Понятие скорости, заимствованное из механики, успешно
применяется и к исследованию поведения произвольной функции,
приобретая при этом более общий характер. Для характеристики
изменения функций точно определяется, что понимать под
скоростью изменения функции при определенном значении аргумента,
176

то есть в определенный момент ее изменения, и как измерить эту
скорость.
Пусть на промежутке X определена некоторая функция y = f(x).
Возьмем какое-нибудь значение х0 из этого промежутка и придадим
ему приращение Дх. Это вызовет соответствующее приращение
функции &y = f (х0 + Ах) — f (x{)). Заметим, что приращение аргумента
может быть выбрано произвольно как по знаку, так и по величине,
однако с таким расчетом, чтобы значение х0-\-Ах не выходило
за границы промежутка X. В противном случае f(x0 + Ax) теряет
смысл, поскольку вне X функция не определена. Приращение Ау
есть величина, на которую изменилось значение функции y = f(x)
при изменении значения аргумента от х0 до х0 + Ах.
Отношение -г| будет средней скоростью изменения функции на
отрезке [х0, х0-\-Ах], а предел этого отношения lim -^-—скоростью
изменения функции при фиксированном значении х = х0.
Определяя скорость изменения функции, мы уже подошли, по
существу, к понятию производной. Дадим определение производной.
Определение. Производной функции y=f (x) в точке х0
называется предел отношения приращения функции в этой точке
к вызвавшему его приращению аргумента при условии, что
последнее стремится к нулю, то есть
l!m^= lim/(^?-fW,
Если такого предела не существует, то говорят, что данная
функция в точке х0 производной не имеет. Впрочем, в случае,
когда предел равен бесконечности определенного знака, условимся
говорить, что существует бесконечная производная.
Функция, имеющая конечную производную, называется
дифференцируемой, а действие нахождения производных называется
дифференцированием .
Для обозначения производных пользуются следующими
символами:
у' (читается: «игрек штрих»),
у'х (читается: «игрек штрих по икс»),
-У- (читается: «дэ игрек по дэ икс»),
f (x) (читается: «эф штрих от икс»).
В тех случаях, когда желают подчеркнуть, что производная
вычислена в какой-то фиксированной точке xQ, пользуются
обозначениями f (х0) или 'у" .
Рассмотренная нами задача о нахождении скорости движения
есть, таким образом, задача об отыскании производной от пути по
ds
времени: -^. Вообще, какую бы зависимость ни отражала функция
177

y = f(x), отношение -^ есть средняя скорость изменения у
относительно изменения х, а у' есть скорость изменения у при
некотором заданном значении х = х0. Например, если f(t), как функция
времени, отражает какой-либо процесс химического соединения или
распада, то производная будет скоростью течения этого процесса;
если f (t) описывает процесс какого-нибудь развития, то f (t) будет
характеризовать скорость этого развития в момент времени t; если
зависимость скорости некоторого движения от времени дана
формулой и = ф (/), то ф' (t) будет уже скоростью изменения скорости
или ускорением этого движения в момент времени t> и т. д.
Огромное значение производной состоит в том, что при
изучении любых процессов и явлений природы с ее помощью можно
оценить скорости изменения связанных между собой величин.
Поскольку производная в заданной точке есть предел, а предел, как
известно, есть число, то и производная в точке есть также число.
Однако в различных точках значения производной, ва&бще
говоря, будут раз яичными. Следовательно, производную можно
рассматривать снова как функцию точки.
Из определения производной функции вытекает и способ ее
вычисления. Чтобы вычислить производную функции y=f(x) в
некоторой точке х0, необходимо:
1) значению аргумента х = х0 дать некоторое приращение Дл: и
получить новое значение аргумента х = х0 + Ах;
2) найти соответствующее приращения функции
ky = f(x0 + Ax) — f(x0);
3) составить отношение -^ (приращение функции к вызвавшему
его приращению аргумента);
4) вычислить предел этого отношения при Дл;->*0, если он
существует.
Пример 1. Найти производную функции / (х) = угх в точке х0 = 1.
1) Дадим значению аргумента х0=\ приращение А*. Новым значением
аргумента будет 1 + А*.
2) Найдем соответствующее приращение функции:
Ду=/(1 + Д*)~/(1) = {ЛТДх-1.
3) Составим отношение -^-:
' Ах
At/ =8/"1 + А;с—1
Ах Ах
4) Вычислим предел этого отношения при Ах — 0:
.. Ау .. f/T+Ax-1 1
lim -r^- = lim - — = -х-
Дл:_+0 АХ ^x-+0 АХ 6
(здесь мы воспользовались известным пределом, вычисленным в примере 4, § 10,
гл. IV). Таким образом, получили, что /'(1) = —
178

Пример 2. Пользуясь определением производной, найти производную
функции */=х3 + Зх—4 в точке */=х0.
Дадим значению аргумента х = х0 приращение А*. Тогда функция у
получит приращение
Ay = [(xQ + Ax)^+3(x0 + Ax)-4]^(xl + 3x0-4)==xl + 3xlAx + 3x0Ax2 +
+ Дх3 + Зх0 + ЗДх—4 — 4 — 3x0 + 4 = 34 Дх + 3х0 Дх2 + Дх3 + 3 Ах.
Составим отношение -р и перейдем к пределу при Ах —* 0:
lim ^= lim (Зх§ + Зх0 Ах + Ах2 +3) = Щ + 3.
д*—0 АХ &х-*0
В точке х0 производная равна числу 3xJ + 3, что удобнее записать так:
П*о; = 34 + 3 = 3(4+1).
Если вместо х0 подставлять различные значения (то есть под х0 понимать
различные точки), то будем получать различные значения производной. В частности,
/'(2) = 3(2*+1) = 15; Г(1) = 6; /'(0) = 3; /'(я) = 3(я;*+1), и т. д.
Выражение f (*) = 3(х2+1) представляет собой значение производной в
произвольной точке х, являясь функцией от х.
Пример 3. Пользуясь определением производной, найти производную
функции j/ = cos5x в некоторой фиксированной точке х.
Дадим некоторому значению х приращение Ах, тогда функция у получит
приращение
A# = cos[5(x + Ax)] — cos5x= — 2sin (5xH—^-\ sin—^.
Aw
Составим отношение -—• и переидем в нем к пределу при Ах —- 0:
sin 5x -f
. 5Дх!
с . х sin —=¦
5 Ах\ 2
Ах
о • /е , 5ДХ\ . 5 АХ
-28Ш 5* + — 8Ш-3-
lim -г^= lim - т - = — 2 lim
Ддг-^ОДХ Д*-*0 А* Длг—0
. 5 Ах
= — 2 lim sin [5x + -7r—) • lim —т = — 2 sin Ъх--^- = — 5 sin 5x.
Л*—о \ 2 / Дд:_о Ax 2
Итак, получили: (cos 5х)' = — 5 sin 5x.
Пример 4. Закон свободного падения тела в пустоте определяется форму-
лой s=i>-, где g—постоянная величина. Найти скорость и ускорение этого
движения в некоторый фиксированной момент времени t.
Дадим некоторому значению t приращение At. За промежуток времени
[/, t + At] пройденный путь s получит приращение
A„_g(' + AQ2 gt*_2g.t.At+g.At*
as- ^ 2 2 "
Средняя скорость движения в течение промежутка [ty / + Дф
As , , А* /, . АЛ
v4 = Ai = gt+8-2=g(t+-2}-
Скорость движения в момент времени t:
то есть v=gt.
hm -г-= lim g[t+ -=-)= gt.
179

Найдем ускорение рассматриваемого движения, имея в виду, что ускорение
есть скорость изменения скорости v. Для этого некоторому значению t дадим
приращение At. Тогда v получит приращение
Среднее ускорение
Ускорение
Av = g{t + At)-gt=gAL
Av g At
то есть w=g.
Таким образом, постоянная g, участвующая в формуле свободного падения,,
и есть ускорение падения тела в пустоте (g^ 9,815 м/сек2).
Из того, что среднее ускорение wcp оказалось величиной постоянной (не
зависящей от At)у вытекает, что в данном случае скорость падения v изменяется
равномерно.
В заключение параграфа отметим, что иногда пользуются
понятием так называемой односторонней производной, понимая под этим
,. f(x)-f(xQ) ,. f(x) — f(x0) ~
односторонний предел hm -^—^-^-^или lim L^-L—-^-^. Односто-
х-+х0 — 0 X — Xq х-+х0+0 х~х0
ронние производные в точке х0 обычно обозначаются символами:
Г (хо — 0) — левосторонняя производная, f (x0 + 0) — правосторонняя
производная.
Из существования обычной производной /' (х0) следует
существование и равенство между собой односторонних производных f (лг0—0)
и f (х0 + 0). И обратно, если существуют f (х0 — 0) и f (х0-\-0),
равные между собой, то существует и f (x0), равная их общему
значению. Но и при отсутствии обычной производной
односторонние производные могут существовать. Например, функция f (х) =
= S sin л: | в точке х0 = 0 обычной производной не имеет, так как не
*. I sin х I — I sin л'о I ,. 1 sin я 1 T T
существует предела lim J ! — = lim L. Что же касается
х-* Xo X — Xq x_^q X
односторонних производных в этой точке, то они существуют:
/'(-0)= lim i™ii=_if f(+0)= lim ^^-=1.
*->—0 х jc-v+0 x
Вопросы для самопроверки и упражнения
1. Почему производная от функции есть, вообще говоря, некоторая функция,
в то время как по определению производная есть предел, а предел, как известно,
есть определенное число? Объяснить это на решенных примерах 1—4.
2. Пользуясь определением производной, найти производные следующих
функций:
а) у = sin (2х + 5). Отв. у' = 2 cos (2* + 5) •
б) # = )/*х2 + 3. Отв. у'--
У
в) у = е2Х+1. Отв. #' = 2е2л+1.
3. Определить среднюю скорость движения, заданного формулой
s = f2_5/ + 2
180

(где s—путь, a t — время), в течение времени: а) от момента t = B сек до момента
* = 15 сек\ б) от /=10 сек до / = 20 сек.
Отв. а) 1>Ср=15 ед. дл./сек, б) иср = 25 ед. дл./сек*
4. Закон некоторого движения определяется формулой s =/3-}-5/2-f-8/ — 4,
где s—путь в метрах, а /—-время в секундах. Пользуясь определением скорости
движения, найти скорость v и ускорение w этого движения в моменты времени:
а) / = 0; б) / = 2; в) / = /0.
Отв. а) и = 8 м/сек, ш = 10 м/сек2, б) у = 40 м/сек, w = 22 м/сек2,
в) о = (3fJ+ 10*о+ 8) л/сюс, ш = (6/0+10) ж/се/с2.
5. Можно ли определить Д#, зная только, что Дх = 2, если: а) у = Зд:+2;
б) */ = я:2; в) у=— ? Пояснить ответ чертежом.
Отв. В случае а) можно, Д# = 6. В случаях б) и в) нельзя.
§ 2. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
Истолкование производной с точки зрения механики как
скорости изменения функции не является единственной общей
иллюстрацией понятия производной. Можно дать и другое,
геометрическое толкование производной. Для этого достаточно проследить,
каким геометрическим операциям соответствует каждый этап
построения производной в данной точке, если следовать ее определению.
Но прежде чем это сделать, введем понятие касательной к кривой.
Возьмем на некоторой кривой две точки М и N (рис. 79, а)
и проведем секущую MN. Затем, оставляя точку М неподвижной,
будем ДБигать точку N вдоль по кривой в направлении к точке М.
Секущая MN при этом будет поворачиваться вокруг точки М. Если
она при MN-+0 стремится к некоторому предельному
положению MP, то это предельное положение секущей и называется
касательной к кривой в точке М.
Дадим более точное определение касательной.
Определение. Прямая MP (рис. 79, а) называется
касательной к кривой L в точке М, если угол ф между нею и секущей
стремится к нулю при неограниченном приближении по кривой точки N
к точке М.
181

В элементарной геометрии
обычно определяют касательную
к окружности как прямую,
имеющую с окружностью только одну
общую точку. Это определение
охватывает лишь частные
случаи кривых. В общем случае
оно не годится. Так, например,
на рисунке 79, б) касательная
имеет три общие точки с
кривой, а на рисунке 79, в)
прямая имеет одну общую точку
с кривой, но касательной не
является.
Перейдем к геометрическому
истолкованию производной.
Пусть функция f (х) имеет при
х = х0 производную /' (л;0). Покажем, что кривая y=f(x) имеет
в точке М {х0, f(x0)) касательную, причем угловой коэффициент
этой касательной равен значению производной f (xQ). С этой целью
дадим значению аргумента х0 приращение Ах и обозначим через N точку
(х0 + Ах, f(x0 + Ax)) (рис. 80). Секущая MN образует с
положительным направлением оси ОХ некоторый угол р. Как видно из чертежа,
/(*(> +Ах)—f(x0) Ay Q , Ay
/v — — v- -— * или p=arctg *
1
0
Ч:/^/
^Ла /
мА
Vi
*0
%
/h
/1 >
/ / •
>L
" !
>ьц.
1
i
*o +
йХ
X
Рис. 80.
tgP=^
К
Ал:
нулю,
Ах
то на графике
Ал:'
произойдет
следующее
Если Ах устремить
движение:
1) точка N будет неограниченно приближаться к точке Af,
двигаясь вдоль по кривой y^=f(x)y
2) секущая MN будет поворачиваться вокруг точки М,
3) соответственно будет изменяться и угол р.
Так как по условию производная /' (х0) существует, то,
пользуясь непрерывностью функции arctg x, можем записать:
Hm arctg ^ = arctg
lim|f)=arctgn*o).
Но тогда существует и предел lim jJ=arctg f (x0), то есть сущест-
вует предельное значение угла {}, которое мы обозначим через а.
А это значит, что существует предельное положение MP секущей MNt
то есть прямая MP является касательной к кривой y = f(x)
в точке М и
arctg f' (x0) = а или f (х0) = tg a.
Таким образом, производная функции f(x) в данной точке
х0 геометрически представляет собой угловой
коэффициент касательной к кривой y=f(x) в точке (xQ, f(x0))P
то есть тангенс угла между касательной и
положительным направлением оси ОХ.
182

Yk
a)
Ь)
Рис. 81.
Если в некоторой точке производная обращается в бесконечность,
то это значит, что касательная к кривой в этой точке параллельна
оси ординат. Если же производная в точке равна нулю, то
касательная к кривой в этой точке параллельна оси абсцисс (рис. 81).
Для того чтобы составить уравнение касательной к кривой y = f(x)
в некоторой точке (л:0, у0), достаточно написать известное из
аналитической геометрии уравнение пучка прямых, проходящих через
эту точку:
у—Уо = к(х—х0) (1)
и вместо k подставить значение углового коэффициента
касательной f (х0).
Получим:
У—Уо = Г(*о) (х — х0).
Прямая, проходящая через точку касания (xQi yQ)
перпендикулярно к касательной, называется нормалью к кривой в этой точке.
Из аналитической геометрии известно, что взаимно
перпендикулярные прямые обладают тем свойством, что их угловые коэффициенты
обратны по величине и противоположны по знаку. Следовательно,
/'(*(>)
, то получим уравнение нор-
1
(х - х0).
если в уравнении (1) принять k
мали:
Пример 1. Составить уравнение касательной и нормали к кривой у = х3 — Ь
в точке (2, 3).
Напишем уравнение пучка прямых, проходящих через данную точку (2, 3):
у— 3 = ?(*—2).
Чтобы определить, соответствующие значения k для касательной и нормали,
найдем производную ух при х=2:
ух = Ъх\ У[Л=2 = 3-22=12.
183

Следовательно, для касательной 6=12, для нормали к— — у^. Подставляя
эти значения в уравнение пучка прямых, получим:
уравнение касательной у — 3 — 12 (х — 2), или^=12а:—21,
о 1 / 1 19
уравнение нормали у — 3=—^(а: —2), или у = —• -^ х 4- -г--
IZ 12 ' о
Пусть производная /' (х0) не существует, а конечные односторонние
производные Г (х0 — 0) и /'(л:0 + 0) существуют (в этом случае
Г (х0 — 0) ^/' (х0 + 0)). Тогда к кривой y = f(x) в точке (х0, f (x0))
можно провести так
называемые односторонние
касательные, которые образуют между
собой некоторый угол.
Поэтому сама точка (х0, f(xQ))
в этом случае называется
«угловой» точкой кривой.
Так, на кривой y=\sinx\
(рис. 82) такой «угловой»
точкой является точка х = 0.
Левосторонней касательной
является прямая_у= —дс, а
правосторонней — прямая у = х.
Если же односторонние
производные в точке
бесконечны, то, хотя они и различны по знаку, в точке (х0% f (х0))
существует единственная касательная к кривой, параллельная оси OY
<рис. 81,6).
Пример 2. Определить угол между касательной к параболе у = ~х2 в точке
(l, -§-) и осью ОХ.
Поскольку угловой коэффициент касательной равен значению производной у'
в точке х—\, то задача и сводится к отысканию значения производной в этой
точке. Дадим значению *=1 приращение Да:. Тогда функция у получит
приращение
Рис. 82.
&У
1
Да:2
_(1+д*)2__.12==д*+ 2
Составим отношение -р- и перейдем к пределу при Ах —¦ 0:
Да:
^-14- — .
Да: г2'
,. Ьу
л*-о А*
:1.
Следовательно, угловой коэффициент касательной равен 1, или tga = l. Отсюда
получаем искомый угол
a = arctg 1 = -j-.
Условимся в дальнейшем под углом подъема кривой в некоторой точке
понимать угол между осью ОХ и касательной к кривой в этой точке.
Пример 3. Определить угол подъема логарифмической кривой ^ = logax
в любой точке х и исследовать зависимость этого угла от изменения х.
184

Для определения угла подъема кривой, то есть угла наклона касательной
к кривой, нужно сначала найти угловой коэффициент касательной, то есть
производную логарифмической функции. Дадим некоторому значению х
приращение Ах. Тогда функция у получит приращение
&У = ]oga (* + Ах) — log0 х = log0 ^—-^ = loga fl + -^
¦*('+?)
А</
Ах Ах
Поделим числитель и знаменатель этого отношения справа на постоянную
величину х (у нас x^tO, так как при х = 0 логарифмическая функция не
определена) и воспользуемся известным замечательным пределом:
lim ьа v—!—i = logae.
а-+о а
Получим
т'Ч + т) 1 Ч1 + т) 1
lim -г- = lim ^ - =— lim —. - ==—• logae,
д*-оА* Ах^о Ах х Ах_+о Ах х
то есть
X X
Из выражения производной видно, что угол подъема
логарифмической кривой обратно пропорционален значению х:
увеличивается при убывании и уменьшается при возрастании х. Можно
также сказать, что логарифмическая кривая по мере удаления х от
нуля вправо все более и более «медленно» поднимается вверх, так
как угол подъема постепенно убывает, приближаясь к нулю.
Вопросы для самопроверки и упражнения
1. Доказать, что производная строго возрастающей функции неотрицательна,
а строго убывающей функции — неположительна.
2. Какой смысл имеет знак минус у производной, если последнюю
рассматривать как скорость?
3. Под каким углом а кривая y = igx (см. рис. 36) пересекает ось ОХ?
Отв. а = 45°-.
х2
4. На параболе У—-г есть такая точка, в которой касательная наклонена
к оси ОХ под углом 60°. Найти эту точку. Составить уравнение касательной.
Отв. (2|/"з; 3), y = YJx — 3.
5. Определить угол подъема кривой у — х3 и исследовать зависимость этого»
угла от изменения х. При каком значении х угол подъема кривой равен: а) 0°,
б) 45°, в) 60°>
Отв. */' = 3*2. а) * = 0, 6)|*|e-Lf в) |x|=JL.
6. Найти углы наклона односторонних касательных к кривой
f(x) = i x при °^*=^2>
\ 4—д: при 2<*^с4
185

в точке (2, 2). Чему равен угол между этими касательными? Дифференцируема
ли функция в этой точке?
Отв. 45°- и 135-; 90s. Функция не дифференцируема, так как f (2 — 0)^6
=?/'(2 + 0).
§ 3. ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ ПРОСТЕЙШИХ
ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
В дальнейшем будет показано, что дифференцирование любой
элементарной функции сводится к дифференцированию простейших
элементарных функций. Поэтому естественно начать с вычисления
производных простейших элементарных функций.
1. Постоянная функция: y = f(x)=Cy где С—постоянное число.
В данном случае для любых а: и Ал: будет f(x-\-kx) = C и Ду =
= f(x + Ax) — f(#) = 0. Отсюда при любом АхфО будет ^- = 0 и,
следовательно, у' = 0. Таким образом, производная постоянной
функции равна нулю.
2, Степенная функция у = х^у где |х — любое вещественное число*.
Дадим некоторому значению х приращение Ах. Соответствующее
приращение у представится в виде
&у = (х + Ах)* — х?:
Сосчитаем
lim —¦ — hm * ^ ; = hm ^ 1^ ^ = л:|Х fy
X
(см. пример 4, § 10, гл. IV). Производная степенной функции х*
равна показателю степени fx, умноженному на степень
аргумента с показателем, меньшим на единицу, то есть
В частности, если у = х, то у'= 1 -х?= 1,
если (/=—, то у' = (х-1)' = — I • х-* = — -?,
если */ = !/"*, то у' = \х2) =Т-х 2 =—т=.
Заметим, что при выводе формулы производной от х*к мы
предполагали, что х>0 (вспомните область определения степенной
функции при произвольном |ы). Однако при некоторых значениях fi
функция х* имеет более широкую область определения. Например, если
(л равно натуральному /г, то область определения функции л/1
совпадает со всей осью. Можно доказать, что в этом случае формула
(хп)' == п^1'1 справедлива для всех х без исключения. Мы вернемся
к этому вопросу в § 5.
* Для функции xv- область изменения х определяется в зависимости от
значений \1 (СМ. § 6, ГЛ. II).
186

Пример 1. Найти производную функции у = х*.
По формуле дифференцирования степени имеем: у' = 3 • х2.
Пример 2. Найти производную функции */ = {Лс2.
_2
Представим функцию в виде у = хъ ' Тогда по формуле дифференцирования
степени получим:
2 -| 2
У --к'*
5
5 5>/Тз'
Пример 3. Найти производную функции у = х2 Yx-
Как и в примере 2, представим функцию в виде г/ = #3. Тогда у' =-^-*хъ «
7 8/г-
3. Показательная функция у = ах, где 0<я=И=1. Если
значению х дать приращение Ах, то Ar/ = a*+A*— ах^=ах(аАх—1) и
, ,. Ay ,. fl*(aAjr-l) *,. аА*-1
(/'= lim -p-= lim —^-г - = а hm —т—.
Пользуясь пределом, вычисленным в примере 3, § 10, гл. IV,
получим:
(ах)' = ах-\па,
то есть производная показательной функции равна самой
функции, умноженной на натуральный логарифм ее
основания.
В частности, если у = ех< то у' = ех.
4. Логарифмическая функция: y = \ogax, где 0<СаФ 1. Если
значению х дать приращение Ах, то Ay=\oga(x + Ax) — \ogax и
г &У v \ogQ(x + Ax)-\ogax 1 ,. loga\1 + T
hm -f- = lim Л ; =s_ = _ hm 1_
д*_>0Л* Д* — 0 A* *Дл' —0 t~
Пользуясь пределом, вычисленным в примере 2, § 10, гл. IV,
получим:
{\ogaxy = — \ogae.
Производная логарифмической функции равна обратной
величине аргумента, умноженной на логарифм числа е при
том же основании.
В частности, если у = 1пх, то у'= — .
5. Тригонометрические функции: sinx, cos*, tgx и ctgx. Пусть
y = s>iux. Для этой функции Ar/ = sin(x + Аде) — sin* и
Ах
t. Ay ,. sin (* + Ах) — sin л; ,. 2 / ДлЛ
hm f^ hm —^^ = hm ——cos * + T ).
2
187

Так как функция cos х непрерывна и lim =1, то получим:
*-о
X
(sin х)' = cos х.
Аналогичными рассуждениями устанавливается, что
(cos *)' = — sin л:
(см. пример 3, § 1).
Пусть y==tgx. Тогда
а 4.* i ! а \ 4.^ sin (а: + Дат) sin х
Ay = ig (х + Ах) — tg лг = —; ' : и
17 ь\ i / ь cos(*4-A*) cos*
,. Ац 1. sin (x -f- Да:) cos a: — cos (x -f- Ах) sm x
lim -r^ = hm —-—Чг-^—/ I а ч — =
Дл; ^o Ал: Дд. _^0 Ал: cos (л: -j- Дат) cos x
,. sin Ал: 1
= iim —-: ;—r—j—г .
д ^ ^ 0 Да: cos (a: + Да:) cos x
Отсюда, как и выше,
Аналогично доказывается, что
(ctg x)' = г-г—= —cosec* х.
v ь ' sm2 x
6. Производная обратной функции. Пусть функция у = f (x)
удовлетворяет условиям теоремы о существовании и непрерывности
обратной функции (§ 6, гл. IV) и функция х = у(у) является для нее
обратной.
Теорема. Если существует f (х0) Ф 0, то существует
производная обратной функции в точке y0=f(x0), причем
то есть производная обратной функции равна обратной
величине производной прямой функции.
Доказательство. Дадим значению аргумента у0 обратной
функции х = у(у) некоторое приращение АуфО- Тогда приращение
этой функции будет Ах. При этом АхфО, так как в противном
случае х0 + Ах = х0 и в силу однозначности прямой функции y = f(x)
мы имели бы f (xQ-\-Ax)=f (х0), то есть Ау = 0. Следовательно,
мода; 1
жем записать: -г— = -г-.
by Ду
Да:
Перейдем в этом равенстве к пределу при Ау-+0 (в силу
непрерывности функции х—у(у) будет также Дл;->0). В знаменателе правой
части получим: f (х0)ф0. Следовательно, существует предел и левой
части. Получим:
ф'<*/о>=гЬили x'^~h-
В качестве примера найдем производные обратных
тригонометрических функций.
188

Рассмотрим функцию у = arcsin л; на (— 1, +1). Она будет
обратной для функции x = sinyt рассматриваемой на ( — у, +у)« ^а
этом промежутке ху = cos у Ф 0. Следовательно,
(arcsin х)' = — = г , = п (— 1 <*<+ 1),
COS у у 1 __ 8Ш2 у у I __ ^2
то есть
(arcsin а:)' =:
W-
-ХА
Перед корнем берем знак плюс потому, что cos у > 0 на f — ~, + ^).
Функция r/ = arctgA: определена на (—оо, +оо) и является
обратной для функции x=tgy. Так как
ху = $ес*уф0 на (--J , + -J), то (агс1§*)'=^ = q— =
Цг2 (—оо<*< + оо).
1+*
То есть
(arctgx)' = *
Аналогично устанавливается, что
(arccosx)' = — •[ {— 1<х<+1),
К 1 —д:2
(arcctgx/ = — j-q^ (— оо < г/ < + оо).
Поскольку логарифмическая и показательная функции являются
взаимно обратными, то, зная производную одной из них, легко
получить производную другой. Так, например, производная
показательной функции у = ах может быть получена следующим образом:
(ах ' = 71 Г/ = —. = у In a = ах • In a.
У
Вопросы для самопроверки и упражнения
1. Найти производные следующих функций:
а)*/=^. Ото.у'=--. б) у=3/х*. 0тв.у' = -~.
в) у = хУх. Отв. у' = -у л: ]Л:. г) г/=к xyxY^ Отв. у'
I V я
2. Чему равна производная I 1/ ln cos2 J
8Vx"
т ?
Отв. Равна нулю, как производная постоянной.
3. Проверьте монотонность показательной функции ах, используя выражение
«е производной.
4. Получите самостоятельно формулы производных для следующих функций:
¦cos -v, ctg х, arccos jc, arcctg x.
5. Получите формулу для производной логарифмической функции, пользуясь
производной показательной функции.
189

§ 4. СВЯЗЬ МЕЖДУ ДИФФЕРЕНЦИРУЕМОСТЬЮ
И НЕПРЕРЫВНОСТЬЮ ФУНКЦИИ
Пусть на промежутке X определена некоторая функция y=f(x)y
имеющая в точке х0 этого промежутка конечную производную f (х0).
Так как число f (х0) является пределом переменной -^ при Дл;->0>
то последнюю можно представить в виде -^- = f (л:0) + а, где а —
бесконечно малая при А*-* О (см. § 2, гл. III). Умножая обе части
равенства на ?х, получим:
Ау=? (л:0) Ах + акх. (I)
Из этого равенства следует, что At/->0 при Дл:->0, то есть
бесконечно малому приращению аргумента соответствует бесконечно
малое приращение функции. А это
значит, что рассматриваемая функция
непрерывна в точке х0.
Отсюда заключаем, что из
существования конечной производной
(то есть из дифференцируемости
функции) следует непрерывность
функции в рассматриваемой точке.
Заметим, однако, что обратное
утверждение неверно. Функция может
быть непрерывной в точке, не
имея производной в этой точке.
В качестве примера такой функции может служить функция
f(x) = \x\, изображенная на рисунке 83. В точке х = 0 эта
функция непрерывна, так как limf(x) = f(0)=Q. Производной же
в этой точке не существует, так как
х—0 х »
hm ¦—1= lim —= — 1, hm L—1
х-* —О Х *-* —О х лг-^-fO Х
lim T= I,
и, следовательно, не существует lim / v ^_0
х-+0
Существуют непрерывные функции, которые не имеют
производных в нескольких и даже в каждой точке их области определения.
Первый пример непрерывной функции, не имеющей производной ни
в одной точке области определения, был построен Больцано. Ее
график не только нельзя построить, но и мысленно трудно
представить себе*.
Замечание. В выражении (1) а и Ау будут бесконечно
малыми только в том случае, если бесконечно мало Ал:. Если же Ал:
* О существовании непрерывных функций, нигде не имеющих производных,
можно прочесть, например, в учебнике Г. М. Фихтенгольца [2], гл. XVI, § 2.
190

придать некоторое постоянное значение, то и а, и Ау будут также
постоянными. Поясним это на примере.
Пример. Рассмотрим функцию у = х3. Ее приращение в точке х можно
выразить двумя способами:
Дг/ = (л: + Дх)3 — хз = Зл^Дя+ЗлгДл^ + Дхз,
Ау — у' • Дх+а- А* = 3л:2 Дл:+а- Ал:.
Приравнивая правые части и делая возможные упрощения, получим:
а = 3#- Длт+л:2.
Положим х=2. Тогда если Дл:=1, то а = 7; если Ах = 0,1, то а = 0,61; если
Дл: = 0,001, то а = 0,0601, и т. д.
§ 5. ПРАВИЛА ВЫЧИСЛЕНИЯ ПРОИЗВОДНЫХ
Чтобы вычислить производную от функции, составленной из
простейших элементарных функций, нужно знать не только способы
вычисления производных от этих простейших функций, но также
некоторые дополнительные правила, к установлению которых мы
и перейдем.
1. Постоянный множитель можно выносить за знак про-
изводной.
Пусть у = си, где с—постоянный множитель, а и — какая-то
функция от х, имеющая производную и' в некоторой точке х0.
Найдем if в этой точке. Для этого дадим значению х0
приращение Ах. Тогда и получит приращение Аи и, следовательно, у
получит приращение Ау=с{и-\-Аи) —си=сАи. Получим:
t/ = lim -^ = lim с*-^ = си\
Ах -> 0 **Х Ах -* 0 ^Х
то есть
(сиУ=си\
Пример 1. Найти производную функции г/ = 5л:2.
Имеем: у' = (5л:2)' = 5 • 2х = 10*.
2. Пусть uy v и w являются функциями от х и в некоторой
точке Xq имеют производные и\ vr и а/. Тогда их алгебраическая
сумма y = u + v—w также имеет производную в точке х0 и
справедлива формула
(u-\-v—w)' = u' + z/—uff
то есть производная алгебраической суммы равна
алгебраической сумме производных отдельных слагаемых.
Дадим значению х0 аргумента х некоторое приращение Да:. Тог-
да и, и и w получат соответственно приращения Аи, Av и Aw.
Последние в свою очередь вызовут приращение Ау функции у:
Ay=[(u + Au) + (v + Av) — (w + Aw)] — (u + v — w),
то есть
Ay = Au + Av—Aw.
191

Составим отношение -г^, поделив почленно последнее равенство
на Ах (Дх ^ 0):
Ау Аи . Av Aw ..
Ад: Да: ' Дл: Да: * *
Перейдем в этом равенстве к пределу при Дл:->0. Так как по
,. Аи г .. Av r ,. Aw ,
условию существуют lim — = и f lim = -г- = v , hm -- = w , то
существует предел всей правой части равенства (1). Но тогда
существует предел и левой его части. На основании теоремы о
пределе суммы получим:
,. Ay ,. iАи . Av Aw\ ,. Аи . ,. Av ,. Аш
lim д| = lim _+—-_ = hm — + hm ^ - lim s f
Д*—0А* Ддг—О^* ax ах/ Д*—0а* Дат —0а* Дд:— 0 ax
то есть
y' = u' + v'—w\
что и требовалось доказать. Как видно из хода наших
рассуждений, число членов алгебраической суммы и распределение знаков
в ней не играет в доказательстве существенной роли. Следовательно,
это правило остается в силе при любой комбинации знаков и любом
числе слагаемых.
Пример 2. Найти производную функции ?/ = Зл:2-f-8л: — 2cosх — ах.
Имеем: у' = (Зл:2 + 8*-2 cos х — ах)' = (Зл'2)' + (8х)' — (2 cos х)' — (ах)' = Ьх-{- 8 +
+2 sin л:—a* In а
3. Если и и v, являясь функциями от х, имеют производные
и! и if в некоторой точке дс0, то их произведение y = uv также имеет
производную в этой точке и справедлива формула
(и - v)' = и! • v + и - vr%
то есть производная произведения двух функций равна сум-
ме произведений производной первого сомножителя на
второй и производной второго сомножителя на первый.
Дадим значению х0 аргумента х приращение Да:. Тогда и и v
получат приращения соответственно Ах и Av. Но тогда и функция у
получит приращение Ау:
Ау = (и + Аи) (v + Av) — и - v = и - v + Аи - v + и • Av -\- Аи • Av — и-о,
то есть
Д у = А и • v + и • Av + Аи • Av.
Поделив почленно это равенство на Ах, получим:
&У А" . Av . Аи А ,_.
-* = -- v + и • -г + А- Av. (2)
Ах Ах Ах ' Ах v^;
По условию существуют lim -А- = и'и lim -г- = г;'. Кроме того,
из существования у' в точке х0, как известно, следует
непрерывность функции v в этой точке (см. § 4), то есть Ди->0 при Дл;-*>().
Следовательно, величина -г- • Av является бесконечно малой при
Дх->0 (как произведение величины, имеющей конечный предел,
192

на бесконечно малую) и ее предел равен нулю. Таким образом,
существует предел всей правой части равенства (2). Но тогда
существует предел и левой его части.
Получим:
,. Ау ,. Аи . ,. Av , ,. (Аа А \ г . ,
hm д| = 0 ltm -T- + W • hm д-+ lim -г- . Ad i = y.^ + a-y'
Дл:-*0АЛ: Длг—О^* Дл:-»Оа* Д*-*0 \^* '
{и и у в данном случае можно вынести за знак предела как
постоянные), то есть
t/=v-u' + u-v\
Пример 3. Найти производную функции у=х2 sin x.
Имеем:
у' == (х2)' • sin х + х2 (sin x)' = 2х • sin х+х2 cos #.
Заметим, что правило дифференцирования произведения двух
функций легко распространяется и на случай любого числа
сомножителей. Так, например,
(u-v-w)' = [(и • v) • w] = {и - v)' -w-\-(u-v)-w' = (u'v + и • v') w +
+ u-v-wr = u' -v-w + u-vr •w + u-v-xvf.
Пример 4. Найти производную функции у = ах • In x • tg x.
Имеем:
у' = (ах)' • In х • tg х + ах • (In*)' • tg x+ax In (tg x)f =
• . 'ix 4х , ax\nx „. /. . , I ,21nx\
x cos2 x \ x sm 2x)
4. Пусть ы и v—функции от х, имеющие в точке х0 производные
и' и и'. Кроме того, v ?ь 0. Тогда их частное у==— имеет также
производную в точке х0 и справедлива формула
1и\, у- и' — и-у'
\У ) ~~ V2
то есть производная дроби (частного) равна дроби, у которой
знаменатель есть квадрат знаменателя данной дроби, а
числитель — разность между произведением знаменателя
данной дроби на производную ее числителя и произведением
числителя на производную знаменателя.
Дадим значению х() приращение Дл;. Тогда и получит приращение
Аи, v получит приращение Av. Но тогда и у получит
соответствующее приращение Ау:
д и + Аи и v - Аи — и - Ау
J у-\-Ау у у (у^г &v)
Разделим обе части этого равенства на Ах:
Аи Ау (%\
Ау Ал: Ах
Ал: v (и + Ау)
перейдем к пределу при Ах -> 0. По условию существуют lim -?- = u'
и lim д- = у'. Из существования v' следует непрерывность и, то есть
193

Да-->О при Дл;-*0. Следовательно, существует предел всей правой
части равенства (3). Но тогда существует предел и левой части.
Получим:
..Дм .. Да
ahm- и hm -г— , , ,
.. &у Д* Д* v • и — U - Vе
д^о^- v-\\m(v + /Sv) ~~ и2
то есть
, о-а— u-v'
У =~
о*
х*±Ъх+1
Пример 5. Найти производную функции у —
X-f- 1
Имеем:
, (х+ 1) (х* + Зх+1)' - (х* + 3х+1) (*+!)' ^_ (*+ 1) (2*+3)-(*2+3* +1) - 1
* "" (*+1)2 (*+*)2
_ 2л:2 + 2^ + Зл: + 3 — лг2 — Зл: — 1 _х2+2*+2
~ (*+1)« — (х+1)2 *
Применим правило дифференцирования произведения к выводу
формулы для производной от хп при натуральном п. Рассмотрим
сначала функцию у=х. Так как при любом значении х и любом
Дл: приращение Ду = Дл:, то
у' = lim -г^=1 при всех л:.
При произвольном натуральном п представим у=хп в виде
произведения сомножителей х и найдем производную от этого
произведения,
у'=(*?)'= (х-х-х...х)'.
Очевидно, производная будет равна сумме /г слагаемых, в каждом
из которых все сомножители, кроме одного, остаются равными х,
а один сомножитель заменяется своей производной, то есть единицей.
Таким образом, получается сумма п одинаковых слагаемых хп~гу то
есть п • хп~г. Следовательно,
(*?)' = пх«-К
Пример 6. Правило дифференцирования частного можно использовать для
отыскания производных от функций igx и ctg*:
., w fsinxV cos2 x + sin2 x 1
(ctg*)' =
cos *; cos2 jc cos2 a: '
cos *\' — sin2 x—cos2 x 1
sin x sin2 x sin2 x
Пример 7*. Доказать, что если xt является корнем многочлена /(х)
кратности /г, то для производной /' (х) он будет корнем кратности к—1.
Пусть многочлен / (л:) имеет fc-кратный коре.нь xv Тогда, как известно из
алгебры, этот многочлен можно представить в виде
/M = (*-*i)*q>M.
* Эту задачу можно временно пропустить, если по высшей алгебре еще не
изучен вопрос о кратных корнях многочленов.
194

где Ц)(х) — многочлен, являющийся частным от деления / (х) на (*—Xi)k. Найдем
производную:
/' (*)«*(*-*!)*-! ф (*) + (*-*l)* ф' (*) = (* —Я1)*"1 [Аф M + (*-*l) Ф' (*)].
Из последнего легко видеть, что значение x=Xi является корнем уравнения
(*-**)*-i [*q> (*)+(*-*i) ф* (*)]=о
кратности /г—1, то есть ^ является (k—1)-кратным корнем для /' (х).
Пример 8. Пользуясь правилами вычисления производных,
найти производные гиперболических функций! shx, eh*, thx и cthx.
Найдем производную гиперболического синуса. Так как shx =
е-х—ё~х
= —*—•то
(sh*)' = \~^]-\ (ех-е-хУ = ±- (e* + e-x) = chx,
то есть
(sh A')'=chx.
(Здесь мы воспользовались правилом дифференцирования разности
и тем, что постоянный множитель можно выносить за знак
производной.)
Производная гиперболического косинуса получается совершенно
аналогично. Предлагаем самостоятельно получить формулу
(ch x)' = shA:.
Найдем производную гиперболического тангенса. Так как th x =
shx
ch*'
... у fshxV ch x (sh лс)/ — sh x (ch x)' ch2* — sh2* 1
(tn x) — \^j — ch2x — g^ ~ *HH2T>
то есть
(Здесь мы пользовались правилом дифференцирования частного.)
Аналогично получается формула
<cth*)' = -Sht
5. Производная сложной функции. Пусть дана функция у = Дх),
где x = y(t), и существуют конечные производные f (х0) и
<р'(*о) (*о = Ф &>))• Тогда y=f[q>(t)]=F(t), как сложная
функция от t, будет также иметь производную в точке t0, рае-
ную произведению ft (х0) на yi (t0), то есть
fi{t0)=fx(x0)-<pUt0), (4)
или, короче,
yi=y'x-x't
(здесь предполагается, что сложная функция F (t) имеет смысл, во
всяком случае, в некотором промежутке, содержащем /0).
195

Дадим значению /ft аргумента t некоторое приращение At. Тогда
соответствующее значение х0 переменной х получит приращение Дл;.
Это в свою очередь вызовет приращение Ау функции y=f(x). Его
можно представить в виде
Ay=f'x (*0). Да: + а - Да:, (5)
где а->0 при Да:-*0 (см. § 4). Заметим, однако, что если
приращение At мы выбирали по своему усмотрению (At^O), то
соответствующее приращение Ах получилось уже в зависимости от Д/ и
могло оказаться, в частности, равным нулю. В этом последнем
случае равенство (5) теряет смысл, так как а было определено только
при Дл:=И=0. Чтобы иметь право пользоваться равенством (5) и при
Д*=^0, условимся считать в данном случае и а = 0.
Тогда равенство (5) будет справедливо и при Дх = 0. Разделив
обе части этого равенства на At, получим:
Устремим в этом равенстве At к нулю. Так как по условию
функция x = q>(t} имеет в точке t0 конечную производную, то она
непрерывна в этой точке. Следовательно, вместе с At устремится к нулю
и Да:. Но тогда будет стремиться к нулю и а. В этом случае будем
иметь:
;™0(а-й)=°-«р'^)=о-
Таким образом, правая часть равенства (6) имеет конечный предел
fx(x0) Ф* (t0)- Но тогда имеет конечный предел и левая часть этого
равенства: lim -Jj = Fi (t0).
At-+0 ЛГ
Предельный переход в равенстве (6) даст равенство (4).
В данном случае переменная у зависела от t через посредство
одной переменной х, которую называют промежуточной переменной.
Возможна и более сложная зависимость—с двумя, тремя и
большим числом промежуточных переменных. Однако правило
дифференцирования и в этих случаях остается прежним.
Так, если y=f(x), где х=у(и), a u=$(v) и v = %(t)t то
производную yi следует искать по формуле
yi=yx'X'u-Uv-vi.
Приведем примеры дифференцирования сложных функций.
Пример 9. Найти производную функции у = е*2.
Данную функцию можно представить в виде у = еи1 где и = х2. Тогда у'х =
= у'и • их=еи - 2х. Заменив и на х2, окончательно получим: #'=е*2 -2х.
Пример 10. Найти производную функции # = tg2 |/ х2 + 1.
Данную функцию можно представить через простейшие элементарные
функции следующим образом: у = и2, где u = tgv, a v = Yw и w=x2+l. Тогда
. . - - о , 1 0 2dgV*P+l • sec2У** + 1
yr=y„ -^, • v„, ¦ т\= 2u -sec2v —t— 2x = — ' r -i—
** u u w A 2}'w V^+l
196

В дальнейшем, когда в практике дифференцирования накопится
достаточный опыт, можно будет обходиться и без записи сложной
функции в виде цепочки простейших элементарных, которую легко
держать в памяти, рассуждая следующим образом.
П^сть нужно найти производную От функции
у = In sin ]/arctg е5хЪ.
Замечаем, что эта функция представляет собой натуральный
логарифм некоторого выражения. Берем производную от
натурального логарифма по его аргументу, то есть так, как если бы все
выражение, стоящее под знаком логарифма, было независимой
переменной. После этого всматриваемся, что представляет собой
выражение под знаком логарифма. Это есть, оказывается, синус
некоторого выражения. Следовательно, нужно взять производную от синуса.
Выражение, стоящее под знаком синуса, есть квадратный корень
от нового выражения. Берем производную от корня. Подкоренное
выражение есть арктангенс—берем производную от арктангенса.
Под знаком арктангенса стоит показательная функция — находим
производную показательной функции. И, наконец, находим
производную от показателя по правилу дифференцирования степени.
Записав в виде произведения полученные результаты дифференцирования,
получим выражение искомой производной:
у' = —L==r • cos У arctg e3*5 * —е**1.15х*.
sin У arctg еЪх* 2 у arctg e**° I + е6*5
Такой способ дифференцирования более быстро приводит к цели
и по существу ничем не отличается от вышеизложенного способа.
6. Производная показательно-степенной функции. Пусть y = uv,
где и и v — некоторые функции от х(и>0), имеющие в данной
точке производные и' и v'. Эта функция не подходит" под известное
нам определение сложной функции (как функции от функции) и
поэтому к ней нельзя применить правило дифференцирования
сложной функции. Однако существование ее производной не вызывает
сомнения, так как возможно представление
y=uv=elnuV =ev]nu,
а производная показательной функции evlnu при наших
предположениях относительно и и v существует (см. п. 3, § 3).
Дифференцируя evl"u как сложную функцию от х, находим:
y' = (ev\nuy=ev\nu(vlnuy=evlnu!v' lnu + V^)=U*\v' In U •+ V »-) ,
то есть
(uvy = uv\nu-v, + vuu-1u\
Таким образом, можно высказать следующее мнемоническое
привило:
Чтобы найти производную показательно-степенной
функции, достаточно продифференцировать ее как пока-
зательную (то есть предполагая основание постоянным), а затем
197

как степенную функцию (предполагая показатель постоянным) и
полученные результаты сложить.
Пример 11. Найти производную функции y = (sin x)cosx.
Следуя выше указанному правилу, получим:
у' = (sin x)z°sx in sin x • (— sin x) +cos x (sin *)cos x — l • cos x =
= (sin x)cos*— l (cos2 x—sin2 x • In sin x).
Пример 12. Найти производную функции
у = Xх*.
Данную функцию можно представить в виде# = л:1\ где v = xx. К каждой из
этих функций применим правило дифференцирования показательно-степенной
функции. Получим:
у' =xv In x • v' + v • xv^^x°-1 (x.\nx-v' + v)y
v' = xx In x-\-x • хх~г = x* (In лг-f-1).
Подставляя в выражение для */' значения v и и', окончательно будем иметь:
у' = хх'х->> [х • In x . ** (In *+1) + **] :=***+*-1 [л: . In л: (In * +1) + 1].
Вопросы для самопроверки и упражнения
1. Пользуясь правилом дифференцирования дроби, вывести формулы:
(sec х)' = sec х • tg л$ (cosec л:)' = — cosec х • ctg *.,
2. Найти производную дроби —3~} и объяснить, почему эта производная
cx-f-d
будет тождественно равна нулю при ad*=bc.
3. Покажите, что производная от функции у=\пех тождественно равна
единице. Чем это объясняется?^ Отв. В силу тождества \пех = х.
4. Покажите, что производная четной функции есть функция нечетная, а
производная нечетной функции есть функция четная.
5. Найти производные следующих функций:
а) y = sinV~l+x2* Отв. у' = — ms |/~1 -f-*2«
б) y = (tgx)x. Отв. y> = (tgx)x(\ntgx + -^.
в) у = х]пх. Отв. у' = 2х1пх-{ \пх.
г) у = хх*. Отв. у'=хх2 + х (21пх+1).
д)* = Ш(1п*). Отв. у'=-^—у
§ 6. СВОДКА ФОРМУЛ ДИФФЕРЕНЦИРОВАНИЯ
Дадим сводку всех основных формул и правил
дифференцирования, полученных нами в предыдущих параграфах. Их нужно
обязательно запомнить, в особенности формулы, отмеченные
номерами.
1) Степенная функция:
(&у = 1иГ-1и (1)
В частности,
$'--*¦ <™--&
198

2) Показательная функция:
(ахУ=ах In a. (2)
В частности,
(«*)'=**• (3)
3) Логарифмическая функция:
(\ogax)'=±logae. (4)
В частности, (In л:)' =—. (5)
4) Тригонометрические функции:
(sin л:)'= cos л;, 6)
(cosa;)' = -— sin x9 (7)
(sec x)' = sec x • tg x,
(cosec x)' = — cosec jc • ctg л:.
5) Обратная функция: если функции y=f(x) и д:=ф(г/) взаимно
обратны, то
/'(•*)=^ или У;-Л. (Ю)
В частности:
Ф'(у) """ '* *;
(arcsin*)' = —1==, (И)
У 1—jc2
(arccosA;)' = —р=4=, (12)
(arc<g*)'=—^, (13)
(arcctg*)' = --r±^. (14)
6) Показательно-степенная функция:
(uv)'= uv In и v'+vu^u'. (15)
7) Сложная функция: если y=f(x), где л; = ф(<), то
y't=y'xx't. (16)
8) Гиперболические функции:
(sh*)'=ch*, (ch*)'=sh.*, (thjc)' = 5l1E, (сШлг)'=-д^.
Общие правила дифференцирования1
(с)'=0 (с = const), (17)
(си)' = св\ (18)
(и±г>)' = и'±г»', (19)
(иг>)'= «'*> + ««', (20)

Из правил дифференцирования и формул производных
простейших элементарных функций следует, что производная любой
элементарной функции есть также функция элементарная. Иначе говоря,
операция дифференцирования обладает тем свойством, что она не
выводит из класса элементарных функций. В дальнейшем будет
показано (см. раздел III), что операция интегрирования,
являющаяся обратной для операции дифференцирования, подобным
свойством не обладает.
Вопросы для самопроверки и упражнения
В задачах 1—24, пользуясь формулами и общими правилами
дифференцирования, найти производные следующих функций:
1. /(*) = *4-3*з + 5*2 + 3. Найти /'(0), р (— 1), р (л), р (а-Ь).
Отв. /'(*) = 4x3 — 9*2+ Ю*; р(0)=0; Р (—1)=—23; р (л) = 4я2 — 9п*+10щ
у (а—Ъ) = (а — Ь)[*(а — &)2-9(а — 6)+ 10].
*3 5*2
2. у=-~ о- +6*. При каких значениях *: а) #' = 0, б) у' =2, в) у'=— 2?
Отв. а) х — 2 и * = 3, б) *=1 и * = 4, в) нет таких значений *.
2* —1 Л , 1+2*—2*2
3- Уд«« „ , i- Отв.у'-
*2 —*+Г "' * (*2 —*+1)2-
*2)(3~*3) _ , 12-6*-6*2
(2-*2)(3—*з) _ , 12—6* — 6*2+2*3 + 5*4—3**
5. у= -L—=, Отв. (/'=-
6. (/=-7-111-2—у. 0/Лв- ^
4 *2+1 • ~ "* * **— Г
7. # = In (* • sin * j/"l — *2). Отв. #' = 1- ctg * — —
-*2-
* * 6* **
8. у = * arctg2 — + sin *2. 0/7ie. #' = arctg2— + 2 arctg —- + 2* cos *2.
l+*arctg* Л , arctg*
9. # = Л =^—. Отв. y'= ^-y-.
^l+*2 |.
(1+*2)2
10. # = 5arct^*(3/4*^ + l)2.
Отв. у> = (\Г&+\)\1пЪ(}^+1) +±l/l15^g/r
L 2/* (1+*) T3|/ *j
11. « = ln [In (In *)]. Отв. у' = —Л г—;—.
* i \ /j ^ * In**ln In*
12. */ = lntg-~—cos*lntg*. Отв. #' =—sin*lntg*.
— *
13. у = arcsin V1 — *2. Отв. #' =^ . .
|*|/l-*2
14. */ = *^. Отв. у' = х 2 (^+l).
15. у = (In *)*. Om«. y' = (In *)* /-L. + in In x).
200

16. y^V^+W- Отв. ^ = 2^(1нЛр[^
17. */ = *sin*. Отв. у' = х*[пх(^ + \пх.со*х\.
18. ^ = /r+^~In(l+]/"l+lj. Отв. y'^J-YY+T*.
19. */=,, о ,oarctg/j/ ^- tg ^-j. Ome. */' =
ya2_&2 &\r a_|_& &2y* " * a + bcosx
1 1 ^ + xV2+\ 1 . *]/1Г л , 1
20. у = —т= In — f—zr-1 j= arcctg — . Отв. у' =
4|/Т x2-jc/2+1 2>^2 1— *2* " x*+l '
21. */ = sh3x. Ome. i/' = 3 sh2 x ch л:.
22. y = ln(chx) + g^^. Отв. y' = th«*.
23. t/ = arctg (th ж). Ome. у'=—-.
24. */ = ech**. Отв. у'=е^х sh2x.
25. Написать уравнения касательной и нормали к кривой у — х*— 3 в точке
(1,-2). Отв. у = 4х-6, y = -^-L.
26. Написать уравнения касательной и нормали к кривой у = хъ-\-2х~ — 1 в
х 15
точке ее пересечения с параболой у = 2х2. Отв. # = 7* —5, у — =- + -=-.
27. На кривой г/ = х2— 6я + 3 найти точку, касательная в которой
параллельна прямой у = 2х — 3.
Указание. Воспользоваться тем, что у параллельных прямых угловые
эфициенты равны.
28. Под каким углом пересекаются кр|
а) у = х2 и у = Yx .
х — х2 х + х*
б) У—g- и ^ = -3—•
В) X2—1/2=12 и Л# = 8.
я вые;
Отв.
Отв.
Отв.
Отв.
(4, -5).
я
а = 0.
«=2".
Указание. Угол, под которым пересекаются кривые, измеряется углом
между касательными к кривым в точке их пересечения.
j_
29. Доказать, что для функции У = [ у ) выполнено условие 6х —
*-14де' = 5.
30. Дана кривая Зх2 + 4*/2 = 43. Выразить угол подъема этой кривой в любой
точке через координаты точки. Найти угол подъема в точке (3, 2).
Отв. а = arctg (—^- j.
31. Вращающееся маховое колесо, задерживаемое тормозом, са t секунд
поворачивается на угол q> = a-\-bt—ct2, где a, b и с—положительные постоянные.
Определить угловую скорость и ускорение вращения. Колесо останавливается,
когда угловая скорость оказывается равной нулю. Определить, когда это
произойдет?
Отв. v = b — 2ct, w = — 2с. Колесо остановится в момент *=о-.
201

32. Точка движется по параболе у = Ь-\-Зх2 так, что ее абсцисса х
изменяется с течением времени t по закону х = &. С какой скоростью изменяется
ордината? Отв. y't = 18 tb.
33. Закон движения тела дан формулой s = a-\-bt-\-ct2. Показать, что
действующая сила постоянна.
Указание. Иметь в виду, что ускорение пропорционально действующей
силе.
34. Лестница длиной а, прислоненная к вертикальной стене, падает, скользя
одним концом о стену, а другим о пол. С какой скоростью опускается верхний
конец лестницы в момент, когда нижний конец, отодвигающийся от стены с
постоянной скоростью и, отстоит от нее на расстоянии 6? Отв. -
у & — №
35. Распад радия происходит по закону R = RQ e~kty где R0 — количество
радия в начальный момент времени / = 0, a R— количество нераспавшегося радия
в момент времени t. Определить закон зависимости скорости распада радия от
времени. Показать, что скорость распада пропорциональна наличному количеству
радия.
36. Сила постоянного тока определяется как количество электричества,
протекшее через поперечное сечение проводника в единицу времени. Дать в
соответствии с этим определение силы переменного тока. Определить силу тока в конце
пятой секунды, если известно, что количество электричества, протекшее через
проводник, начиная с момента времени /=0, дается формулой Q = 2t2 -f- 2>t +1
(кулонов). Отв. / = 23а.
37. Точка движется по прямой у = 3*—4 так, что ее абсцисса возрастает
с постоянной скоростью у = 7. С какой скоростью изменяется ордината? Отв. 21.
а:3
38. Точка движется в первом квадранте по кубической параболе (/ = —
отправляясь от точки (0, 0). Какая из координат, х или г/, при этом изменяется
быстрее?
Отв. На промежутке (0, 4) быстрее изменяется х, на промежутке (4, -г со)
быстрее изменяется у, при х = 4 скорости изменения х и у одинаковы.
39. Канат висячего моста имеет вид параболы * и прикреплен к
вертикальным опорам, отстоящим одна от другой на 200 м. Самая нижняя точка каната
находится на 40 м ниже точек
подвеса. Найти угол между канатом и
опорными колоннами (рис. 84).
Указание. Сначала по
условию задачи составить уравнение
параболы, то есть определить величину
к в уравнении
Рис- 84« y = kx*. Отв. <* = -?- arctg -i
Z о
40. Колесо вращается так, что угол поворота пропорционален квадрату
времени. Первый оборот был сделан колесом за^ 8 сек. Определить угловую скорость
со через 32 сек после начала движения. Отв. со = 2я радиан/сек.
41. Два самолета вылетают (не одновременно) из пункта А и летят: один со
скоростью 850 км/час в южном направлении, другой — со скоростью 900 км/час
в западном направлении. С какой скоростью возрастает расстояние между
самолетами во время полета? Какова эта скорость в момент, когда расстояние первого
самолета от пункта А равно 75 км, а второго —180 км?
850а: + 900у .. -7 9 , _ , ол
Отв. v = ' у -¦ и = 1157— км час при л: = 75, #=180.
* Как известно (см. § И, гл. IV), тяжелая нерастяжимая нить, провисающая
под действием силы тяжести, имеет форму цепной линии. Но если провисание
невелико, то ее форма мало отличается от формы параболы.
202

42. Три измерения кристалла, имеющего форму прямоугольного
параллелепипеда, х, у и г (в сантиметрах) равномерно возрастают со скоростями 2 см/сек,
5 см/сек и 3 см/сек. С какой скоростью возрастают поверхность и объем кристалла?
Каковы будут эти скорости в момент /, когда измерения кристалла достигнут
величин: *=10, у = 4 и 2 = 7, если при *=0 л; = # = г=0? Будут ли поверхность
и объем возрастать также равномерно?
Отв. S'=121 см2/сек, V = 294 см?/сек. Поверхность S и объем V изменяются
неравномерно.
43. В уравнении параболы у = х2~{-Ьх-{-с определить числа бис так, чтобы
парабола касалась прямой г/ = 2л: — 1 при лг=1. Отв. 6 = с = 0.
§ 7. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ, ЗАДАННЫХ
ПАРАМЕТРИЧЕСКИ
Зависимость функции у от аргумента х не всегда выражается
формулой, связывающей непосредственно у и х. Связь между ними
может осуществляться и через посредство некоторой третьей
переменной t, называемой параметром:
;=;;;>} <-<'<»•
В этом случае говорят, что функция у от х задана
параметрически.
Если х и у рассматривать как прямоугольные координаты точки
на плоскости, то уравнения (1) ставят в соответствие каждому
значению t из некоторой области его изменения [a, PJ определенную
точку (jc, у) на плоскости. С изменением t точка (х, у) опишет
некоторую кривую на плоскости. Уравнения (1) называются
параметрическими уравнениями этой кривой. Так, например, уравнения
x = acost, \
y = bsint )
(O^t^ 2эт)
суть параметрические уравнения эллипса с полуосями а и &, а
уравнения
x = acost, 1 ,Л
= asmt }
У
суть параметрические уравнения окружности радиуса а.
Параметрическое задание функций удобно тем, что оно дает общую запись
для прямой и обратной функций.
Если в параметрическом задании функции (1) уравнение *=<р(0
решается относительно t, t = <D(x), то параметрическое задание
функции можно свести к явному: у=г|)[Ф (x)]=f (x).
Но и не решая первое из уравнений (1) относительно t, мы можем
все же рассматривать у как функцию от х, заданную через
посредство промежуточной переменной t. Предположим, что функции х =
= ф(0 и # = <Ф(0 имеют производные, причем q/ (t) -ф 0 (на
некотором промежутке). Кроме того, для x = y(t) существует обратная
203

функция t = %(x), имеющая конечную производную %' (л:)*. Тогда,,
применяя правила дифференцирования сложной и обратной
функций, находим:
. ,, , 1
yx=yt-tx = yf-r9
xt
то есть
yx = yjfy или, короче, yx = xj. {2)
Пример 1. Найти производную функции у от х, заданной параметрически
уравнениями:
= 2/ +/2,
* = 2/ + /2, л
у = Р-2Я )
Используя формулу (2), получим:
y't 2t—6P 2(t—3P) * (1 — 30
yx==xJ~* 2 + 2/ ^ 2(1+0 ^ 1+* "
Пример 2. Написать уравнение касательной и нормали к кривой
х = a cos3 /,
х = a cos3 /, |
# = a sin3 /, /
называемой астроидой, в точке Л, для которой t=-j- (рис. 85).
1) Находим координаты х и у точки А:
2) Составляем уравнение пучка прямых, проходящих через точку А:
„ а/2 ./ а 1/2"
¦(-•-?).
(2а>
3) Находим производную у'х в точке х =—-—•
4
y't За • sin2/ • cos ?
jcJ —3a • cos2/-sin/
= -tg/;
У
" 4
Отсюда заключаем, что для касательной угловой коэффициент k— — 1.
Нормаль к кривой есть прямая, перпендикулярная касательной и проходящая через
точку касания. Следовательно, искомой нормалью будет одна из построенного
нами пучка прямых (2а). Чтобы ее выделить, нужно воспользоваться тем
свойством, что угловые коэффициенты касательной и нормали обратны по величине и
противоположны по знаку. В данном случае для нормали /г = 1. Подставляя
в уравнения пучка прямых (2а) значения k для касательной и нормали, после
преобразования получим:
aV2
уравнение касательной у = — х-\ ^—, уравнение нормали у = х.
* Из условия <р'(tf)=?0 можно вывести, что функция x = <p(f) строго
монотонна. Тогда существование обратной функции t=%(x) вытекает из общей
теоремы (§ 8, гл. IV) и эта функция дифференцируема (по теореме о производной
обратной функции).
.204

К параметрическому представлению функции приводит решение
многих задач из механики, где координаты движущейся точки
М (х, у) рассматриваются как некоторые функции времени
движения t:
* = ф(*)> 0=<Ф(О-
В качестве примера рассмотрим задачу о траектории движения тела,
брошенного под углом.
Пример 3 Пусть некоторое тело М брошено под углом ср к горизонту
с начальной скоростью v0. Определить траекторию движения этого тела при
условии, что сила сопротивления воз-
у ^ духа не учитывается, то есть
движение происходит в пустоте.
Предположим, что в момент
времени ? = 0 тело М находилось
в начале координат (рис. 86).
Если бы на тело не действовала
сила притяжения Земли, то оно
Рис. 85.
Рис. 86.
перемещалось бы равномерно и прямолинейно по прямой ОР и через некоторое
время t находилось бы в точке М' (лс0, Уо)> Пройденный путь s определился бы
по формуле s = OM' = а0*> а координаты х0 и у0, точки Л4'--по формулам:
х0 = ОМ' cos ф = v0t cos ф,
у0 = ОМ' sin ф = v0 t sin ф.
Но под действием силы притяжения Земли тело М во время движения будет
несколько отклоняться вниз от прямолинейного пути ОР. Как известно из физики,
путь, пройденный падающим телом в пустоте под действием силы притяжения
at2
Земли за время t, равен ^- э где g— ускорение силы земного притяжения. Оче-
видно, за время t величина ~" н будет величиной отклонения движущегося тела
по вертикали вниз от точки М' Следовательно, в момент времени t тело М будет
находиться над горизонтом на высоте
gt* . . gt*
У=Уо — \==щПтЧ>~~2'
Таким образом, координаты движущегося тела выразятся уравнениями:
X = V0 t COS ф, ]
y = v0tshi(D — -_:-. I > '
¦и?, j
205

которые называются параметрическими уравнениями траектории движения.
Параметром является время L
Исключив t из уравнений (3), получим явное уравнение траектории:
/=-
gx*
то есть
1 У = Щ sin Ф — о о о— = х tg ф — 0 0 ь 0 я2.
СОЭф ^оСОБф т 2и|;С082ф т 2cJ§ COS2 ф
Исследование траектории движения можно проводить как по формулам (3),
так и по формуле (4).
Из (4) видим, что правая часть представляет собой многочлен второй степени.
Следовательно, траектория полета тела, брошенного б безвоздушном пространстве
под углом к горизонту, есть парабола.
Чтобы определить полное время полета Т (с момента вылета до падения;,
достаточно найти значение t, при котором г/=0. Из (3) получаем:
gt2
о018!11ф— ^г=°»
или
/ гг/\
l\v0smy—%A--
или
п * л л 2ра sin ш „
Решение 1Л = О соответствует началу полета, а /2 = — — — kohtiv полета Сле-
„ 2vQ sin ф
довательно, Г = —i~——#
Легко определить также и дальность полета X. Для этого достаточно найти
значение х, при котором #=0. Из (4) получаем:
Решение х-,=0 соответствует моменту вылета тела и нас не интересует. Второе
решение
tg ф «2^g cos2 ф vl 2 sin ф cos ф vg sin 2ф
*2= i i -J—
является искомым, то есть
v% sm 2ф
Как видно из полученных формул, полное время Т и дальность полета X
зависят- от начальной скорости vQ и угла бросания ф.
Опираясь на геометрический смысл производной, можно определить
направление движения тела в любой момент времени t. Для этого достаточно найти
выражение углового коэффициента касательной к траектории движения, то есть
выражение производной у'х. Получим:
у\ v0 sin ф—gt gt
уr = —т- = = tg ф -
V0 COS ф ° T V0 COS ф
Отсюда видно, что направление движения при заданных v0 и ф меняется
^ gt ,л 1 tgфг»oCosф
с течением времени t\ yr>0 при tg ф — > 0, то есть при t < ох -*¦ =
20b

vQ sin ф ~ л vл sin ф
e= — -. Это значит, что при 0^/< — - касательная к траектории полета
образует с осью ОХ острый угол. Следовательно, данному промежутку времени
Л , v0 sin ф
соответствует подъем тела: ух = и при /=— — и, следовательно, касательная
к траектории параллельна оси ОХ. Этому моменту, очевидно, соответствует наи-
. ^ Л ^о sin ф _ . ^ 2vQ sin ф / . 2v0 sin ф
больший подъем тела; ух<0 при — -<*<— (при / =—- -*- полет
заканчивается). Это указывает на то, что касательная к траектории полета
образует с осью ОХ тупой угол. Тело опускается.
Любопытно заметить, что, как видно из полученных формул, полное ъремя
полета Т поровну делится на время подъема и время спуска.
В дальнейшем мы снова вернемся к этой задаче (см. пример 15 из
упражнений к § 6 главы VII).
Мы видим, что все результаты исследования согласуются с тем, что
траектория полета есть парабола. Заметим, однако, что движущееся тело будет описывать
параболу лишь при условии, когда сопротивление воздуха отсутствует. В
пространстве, окружающем Землю, сопротивление воздуха оказывает существенное
влияние на полет тела, и поэтому траектория полета не является в точности
параболой. Например, задача внешней баллистики (науки о движении в воздухе
снаряда, ракеты и т. п.) и состоит в том, чтобы вычислить точную траекторию полета
с учетом сопротивления воздуха и многих других факторов, влияющих на полет.
Вопросы для самопроверки и упражнения
1. В каких случаях функцию, заданную параметрически, можно
преобразовать к явному виду?
2. Преобразовать функцию, заданную параметрически уравнениями д:='|/л/,
i/ = lnf, к явному виду. Отв. х = 21пх.
3. Показать, что астроида, заданная параметрически уравнениями х = a cos31,
Л А L
y = asm3t, может быть также представлена уравнением хг+уъ = а3, или у =
Л*3-*3]2.
4. Найти щ
а) x = ln (1 + tf2), y = t — arctg/. Отв. у'х
За* Ш* . , t(2-t*)
б) Х=Т+Г*> У=Т+Т*' 0тв' Ух= 1=2Г-
в) *=acos/, y = bsint> Отв. у'х = ctg/.
г) х = arc sin /, у = arc sin ^l — l2. Отв. yx = -j- Vl—t2.
\ t • j. t г ^ , sin 2* + 1
д) x = et smt, y=elcost. Отв. у' = ^—.
cos 2t
е) x=acht, y = bsht. Отв. y'x = —cth t.
5. Написать уравнение касательной к циклоиде х = а (t — sin *)» */ = « (1 —cos t)
» , n ~ а (л — 4)
в точке, для которой t — -^-. Отв. у = х Цг—'-в
/2
6. Определить угол наклона касательной и нормали к кривой х = —-1 y = Y^t
в точке, соответствующей значению /=1. Отв. 60q и 150°.
7. Найти точки кривой, заданной параметрически, x=^2fJi — ^t1-\-\2t—\1
2/ = /2 + /+1, в которых касательные параллельны оси OY> Ошз. *=1 и / = 2.
207
4. Найти производные следующих функций, заданных параметрически:
t_
2

§ 8. ДИФФЕРЕНЦИАЛ ФУНКЦИИ
Пусть функция y = f(x) имеет в точке х0 конечную производную
f (х()). В соответствии с выводом, полученным в § 4 этой главы, ее
прирашение Ау в этой точке можно записать в виде суммы двух
слагаемых:
Ay=f'(x0) Ах + а • Дл:,
где а->0 при Дл:-^0. Очевидно, если Дл: считать бесконечна малой,
то оба слагаемые справа будут также бесконечно малыми. Сравним
их с величиной Ау, при условии, что f (х0) Ф 0. Имеют место
следующие равенства:
Д*-0 ДУ Дх-0 *?
L Д* J
Длг-vO Щ А*—0 Щ_ I 1*0/
Ах
Из них видно, что второе слагаемое a-Дх представляет собой
бесконечно малую высшего порядка по сравнению с бесконечно
малой Ау, а первое слагаемое f (х0)-Ах эквивалентно Ау. Слагаемое
/' (х0)-Ах получило специальное название дифференциала функции
и специальное обозначение:
f'(x0)Ax = dy.
Таким образом, можно дать следующее определение дифференциала.
Определение. Дифференциалом функции в некоторой точке
называется произведение производной в этой точке на приращение
независимой переменной:
dy=f'(x0)-Ax. (1)
Здесь f (х0) может быть и нулем.
К понятию дифференциала можно подойти и несколько иначе.
Примем Дл: за основную бесконечно малую и сравним с ней Ау. Из
определения производной
П*о)-Пт/(*°+Ад*>-/('п)= Hmg
д*—о ^Х д*—оА*
(напоминаем, что f (xQ)=?0) сразу следует, что бесконечно малые Ау
и Дл: одного порядка, а бесконечно малая f'(x0) Ax представляет
главную и вместе с тем линейную часть бесконечно малой Ау (см.
§ 13, гл. III) (линейная — значит содержащая Дл: в первой степени).
Поэтому можно определить дифференциал функции dy и как
главную линейную часть приращения Ау.
Понятие дифференциала в некоторой точке, таким образом,
связано с существованием производной в этой точке.
Поскольку Ах можно брать произвольно, независимо от х, то
значение дифференциала dy будет также меняться, оставаясь про-
208

порциональным значению А*. Таким образом, дифференциал
функции есть некоторая часть приращения функции, линейно зависящая
от приращения аргумента Ах:
dy = A -Да:.
Дифференциал функции dy отличается от приращения Ау на
величину a Ax, которая при фиксированном Ах будет величиной
постоянной. Но если Дх-^О, то разность Ay—dy->0 и притом
«быстрее», чем Ах. Эту разность можно сделать сколь угодно малой.
Следовательно, приращение функции можно заменить
дифференциалом с любой степенью точности. Для этого нужно только взять
достаточно малое Ах.
Дифференциал функции dy линейно выражается через Ах, в то
время как приращение функции Ау находится, вообще говоря,
в более сложной зависимости от Дх. Покажем это на примере.
Пример 1. Пусть дана функция у = х3. Найдем выражения для Ау и dy
при некоторых значениях х и А*:
Ау = (х + Ах)3 — х3=^х3 + Зх2Ах+ЗхАх2 + Ах3 — *3 = 3л:2 Ах + Зх Ах2 + Ах3,
dy = y'- А* = 3л:2-Ах.
Из подчеркнутого видно, что вычисление Ау связано со значительно большим
числом действий над х и Ах (в том числе с возведением Ах во вторую и третью
степень), чем вычисление dy. Сравнивая правые части,
видим, что а • Ах=Ау — dy = ЗхДл:2 + Ах3, откуда
а = ЗхАх + Ах2. В частности, если дг=2, Ах = 0,1, то
Az/ = 1,261, dy=\,2 и Ay—dy = Q,06l.
Таким образом, с одной стороны, вычисление
дифференциала значительно проще, чем вычисление
приращения функции, с другой, dy^^Ay и
допускаемая погрешность при замене Ау на dy не только
абсолютная | Ау—dy\, но и относительная! — '
Рис. 87.
(последняя при условии, что /' (л:0) ^Ь 0, то есть dy^?0),
может быть сделана сколь угодно малой за счет
уменьшения Аде. Эти обстоятельства позволяют
заменять во многих случаях Ау величиной dy, что
создает большое практическое удобство.
Пример 2. Найти приращение и дифференциал функции у = х2 в
произвольной точке х при некотором значении Ад:. Дать им геометрическое
истолкование.
Дадим некоторому значению х приращение Ах. Тогда
Ау = (х-\гАх)2 — х2 = 2х- Ах+Ах2, dy = y' • Дх = 2л:• А*.
Пусть х">0 и Дх>0. Тогда, как видно из рисунка 87, приращение Ау есть
приращение площади квадрата со стороной х, если х увеличить на Ах (все
заштрихованное). Дифференциал dy есть часть приращения площади того же квадрата
(на рисунке покрыта одинарной штриховкой, то есть Ау без площади маленького
квадратика со стороной Ах).
Пример 3. Найти приращение и дифференциал функции у = х3-\-2х в точке
х = 2 при Ах = 0,1 и при Ал: = 0,01. Найти абсолютную и относительную
погрешности, допускаемые при замене приращения дифференциалом.
Ау = [(л: + Ах)3 + 2 (х + А*)] — (*3 + 2*) = Зх2 Ах + 3* Ах2 + Ах3 + 2Адг,
dy = (3x2 + 2)Ax.
При х = 2 и А* = 0,1 имеем:
Аг/ = 3-22.0,1 + 3-2-0,12 + 0,13 + 2-0,1 = 1,461,
ф = (3-22 + 2).0,1 = 1,4.
209

ky—dy
Ay
Абсолютная погрешность | Ay—dy\ =0,061, а относительная погрешность
= 7-7^7 (то есть относительная погрешность будет около 4%).
При х—2 и А* = 0,01 имеем:
Д*/ = 3 • 22 .0,01 + 3 • 2- 0,012 + 0,013 + 2 -0,01 =0,140601,
Ж/ = (3-22+2). 0,01 =0,14.
Абсолютная погрешность | Ay — dy [ = 0,000601, а относительная погрешность
Ay — dy \
At/
0,000601 , л n ,ft/4
(то есть будет уже около 0,4%).
0,140601
Пример 4. Пользуясь понятием дифференциала, вычислить приближенно
изменение, претерпеваемое функцией у = х3— 7х2 + 80 при переходе х от
значения 5 к значению 5,01.
В данном случае будем считать #=5, а Дх=0,01. Изменение функции Ау^^
«* dy' • Дх=(3*2— Нх) • Дх = (3 .52— 14 • 5) • 0,01 =0,05.
Пример 5. Пользуясь понятием дифференциала, найти приближенное зна-
в /"2 х
чение функции у— у » . при х = 0,15.
При х = 0 значение функции находится легко и равно I. Остается подсчитать,
насколько изменится значение у при переходе х от значения 0 к значению 0,15.
Произведем приближенный подсчет с помощью дифференциала. Для нахождения
дифференциала данной функции удобнее ее сначала прологарифмировать:
1П^Т1П2+^-
Дифференцируем это равенство, рассматривая In у как сложную функцию от *\
Получим:
I 1 2+х —4
—у =-*- - —
откуда
Таким образом, имеем:
у9 5 2-х (2+х)2
#' = -
Ay^dy = yf - Ах
5(4-*2)'
4t/ • А*
~5(*2_4)"
Подставляя * = 0, t/ = l и А* = 0,15, получим:
Следовательно,
У*-о.м = Ух-о + Ау^1- 0,03 = 0,97.
Если вычислить искомое значение с помощью четырехзначных таблиц, то оно
будет равно 0,9704. Как видим, сделанное нами вычисление достаточно точное.
Пример 6. Найти приближенно sin 60°3', если уже известно, что sin 60? =
= У^- = 0,866025, a cos 60°* = -1.
Решим эту задачу, также используя дифференциал. Пусть */ = sin#. Значение у
зх
при х=-х- (что соответствует 60°) нам известно. Изменению градусной меры угла
о
3 • п
от 60° до 60°3' соответствует в радианной мере Ал: = Q = 0,000872. Найдем
210

приближенное значение \у при * = — и Д* = 0,000872:
Ьу ^ у' • Ад: = cos х - Ах = у • 0,000872 = 0,000436
я, следовательно, sin 60^3' = sin 60^ +At/^0,866025+ 0,000436 = 0,866461.
Полученный результат имеет точность, которая обеспечивается только
семизначными таблицами тригонометрических функций.
Заметим, что для решения задач на приближенное нахождение
значений функции можно получить общую формулу. Пусть y=f{x)
есть функция, имеющая производную f (х) в точке х0. Тогда, если
х—л;0 = Дл:, то
by = f(x)—f(x0) и dy=f'(x0)(x—x0).
Так как ky^dy, то f(x)—f(x0)^f'(x0) (x—xQ),
или
f(*W(*o)+n*o)(*-*o).
Эта формула дает возможность приближенно заменять
произвольную функцию, имеющую производную, линейной функцией. При
этом точность при такой замене тем большая, чем ближе х к х0.
Геометрически эта замена означает, что участок кривой f (x) в
окрестности точки [х0, f(x0)] заменяется отрезком касательной к кривой
в этой точке: y — y{)=k(x—x0)9 где yo=f(x0), а угловой
коэффициент k = f (*(,)•
В частности, если xQ = 0, то приближенная формула запишется
в виде
f(x)**f(0)+r(0).x.
Подставляя вместо / (х) различные функции, получим, что для х,
достаточно близких к нулю,
sinx^&x, tgx^*, е*?*&1 + х9 1п(1+х)я«л;, (1 +х)|Х^ 1 + |uut и т. д.
Перейдем к выяснению геометрического смысла дифференциала.
Как уже известно, f (x0) есть угловой коэффициент касательной
PQ к кривой f(x) в точке (xQ, f (х0)) (рис. 88). Следовательно,
n*a) = tga = ^.
С другой стороны, dy = f (х0) Дл;. Значит, dy=BD.
Таким образом, если изменять аргумент от некоторого значения х0
к значению х0 + Да:, то дифференциал функции геометрически
представит собой приращение ординаты касательной PQ,
в то время как приращение функции ky = BC есть
приращение ординаты самой кривой y=f(x).
Из-за того, что дифференциал есть главная часть приращения
функции, можно подумать, что дифференциал всегда меньше
приращения. Однако это не так. Дифференциал может быть меньше
(рис. 88.), больше (рис. 89) и равен приращению функции.
Последнее, например, будет в случае, когда функция является линейной:
у = ах-\-Ь. Тогда dy = ky = a-Ах.
211

Рис. 88. Рис. 89.
Дифференциалу функции можно дать и механическое толкование.
Пусть у = Нх) есть закон прямолинейного движения некоторого
тела (х — время, у — путь). Тогда производная /'(х) еггь скорость
движения в момент времени х, а дифференциал dy = f (x) • Ах—путь,
который прошло бы тело в течение времени Ах, если бы оно
двигалось равномерно со скоростью, равной скорости в момент времени х.
Выясним, наконец, вопрос о дифференциале независимой
переменной х. Рассмотрим функцию у = х. В этом случае дифференциал
функции будет одновременно и дифференциалом независимой
переменной: dy=^dx. Поскольку dy=y' Ах=1 - Ах = Ах, то получаем:
dx=Ax.
Таким образом, если функция совпадает с независимой
переменной, то ее приращение и дифференциал равны между собой. В связи
с этим, говоря в дальнейшем о дифференциале независимой
переменной, будем считать его по определению равным приращению
этой переменной: dx = Ax.
Пользуясь последними соображениями, можно выражение
дифференциала функции представить в следующем окончательном виде:
dy = f'(x)dx. (2>
Отсюда ff(x) = ~1 то есть производную можно рассматривать и
как частное от деления дифференциала функции на дифференциал
аргумента. И несмотря на то, что dx можно брать произвольно
(dx = Ax), отношение * будет постоянным, равным f (x), так как
dy изменяется пропорционально dx и /' (х) является коэффициентом
пропорциональности.
Способ отыскания дифференциала функции непосредственно
следует из его определения. Чтобы найти дифференциал
некоторой функции, достаточно вычислить ее производную и
затем умножить на дифференциал аргумента. Все формулы
212

для отыскания производных легко преобразуются в формулы для
отыскания дифференциалов. Так, например:
1. d(c) = 0dx = 0 (c = const), 5. d(sinx) = cosxdx,
2. d{x*) = \kx*1dx, 6. d{<iTcs\r\x)= %,
3. d(ax) = ax In a dx,
4. d(\ogaX)=~-dx, 7. d(arctg*) = y^, и т. д.
Правила для отыскания дифференциалов будут выглядеть так:
1. d(cu) = cdu, так как d(cu) = (cu)' dx = c(u' dx) = cdu,
2. d(u±v) = du±dv,
так как d (и ± v) = (и ± v)' dx = u' dx± v' dx = du± dv,
3. d(uv)=vdu + udv,
так как
d(uv) = (uv)' dx = (u'v-\-uv')dx = vu' dx-\-uv' dx = vdu-\-udv,
- / a \ vdu — adv
4 -,. ¦ —
\ z> У я2
так как
j I u\ I u\r j vu' — uv' , vu' dx — uv' dx v du — и dv
d [ — )= [ — }dx= 5 dx = 5 = 5 .
\V J \V J V2 V2 V2
5. Пусть у есть сложная функция от /, то есть y=f(x), где х = <р (t).
Тогда ее дифференциал в случае существования производных у'х и xi
запишется в виде dy=y'tdt, где y't = y'x-x'ti то есть в виде dy=y'xx
xx'tdt. Но x'tdt есть dx и, следовательно, снова dy=y'xdx.
Таким образом, получили, что формула (2) верна как в случае,
когда х — независимая переменная, так и в случае, когда х —
функция от новой переменной t. В первом случае под dx понимается
дифференциал независимой переменной (dx=kx), а во втором
случае— дифференциал функции (и, как правило, dx ^ь Дх). Формула
(2) носит название инвариантной (неизменной) формы
дифференциала.
Заметим, что формула (1), также представляющая дифференциал
функция, свойством инвариантности не обладает. Действительно,
если х — функция, то Да:, как известно, вообще говоря, не
совпадает с dx и справедливость формулы (2) исключает справедливость
формулы (1).
Инвариантная форма дифференциала имеет существенные
преимущества при пользовании ею. Так, например, для функции t/=tg x
дифференциал запишется в виде dy=sec2 xdx независимо от того,
является ли х независимой переменной или функцией. В случае если
х — функция и конкретно задана, например x=t2, то вычисление
дифференциала dy можно продолжить. Находим дифференциал
функции х (dx=2tdt) и подставляем в ранее полученное выражение для
dy. Будем иметь:
d;c=sec2 х • 2/ • rf/=2/ sec2t2 dt.
213

Если бы мы пользовались при этом вместо формулы (2)
неинвариантной формой дифференциала (1), то в случае, когда х—
функция (x=t2)y мы не могли бы подобным образом продолжать
вычисление dy.
В заключение параграфа покажем еще одно применение
дифференциала функции. С помощью дифференциала можно оценивать
погрешности расчетов по точным формулам, в которые
подставляются неточные данные.
Пусть некоторая величина у определяется по формуле y=f (л*).
Если при измерении или неточном вычислении величины х
допускается погрешность Да:, то это, в свою очередь, повлечет за собой
погрешность Ду вычисления у по данной формуле. Так как при
малых значениях Да: дифференциал dy мало отличается от
приращения At/, то погрешность при вычислении у можно подсчитать по
\dy_'
I У
носительной погрешностью, допускаемой при определении у по
данной формуле.
Пример 7. Площадь круга вычисляется по формуле 5 = яг2. При
измерении радиус г оказался равным 5,2 см, причем допускаемая максимальная
возможная погрешность измерения Аг находится в пределах ± 0,05 см. Определить
абсолютную и относительную погрешности, допускаемые при вычислении площади
круга по указанной формуле.
Абсолютная погрешность:
\&S \ъ\ dS \ = \2лг dr \*^2п • 5,2 • 0,05 = 0,52л ^ 1,63.
Относительная погрешность:
формуле dy=y'-hx. Величина \dy\ будет абсолютной, а
от-
S
2 л г dr
лг-
Оказалось, что относительная погрешность равна удвоенной относительной
погрешности при измерении радиуса. В числах получим:
\dr\
dS\-9
~S\~
г
:2- °'°5- Х
5,2 52 '
то есть относительная погрешность не превосходит 2%.
Замечание. Понятия абсолютной и относительной
погрешности встретились в этом параграфе дважды — в данном примере и
в примере 3. Однако речь шла о разных вещах. Если в примере 3
мы находили абсолютную и относительную погрешности
приближенного равенства dy = ky, то в данном примере само AS представляет
собой величину погрешности при вычислении площади S, и мы
оцениваем эту погрешность приближенно с помощью дифференциала,
пользуясь тем, что dS^kS.
Вопросы для самопроверки и упражнения
1. Найти дифференциалы следующих функций:
а) у = д:3sin Зл\ Отв. dy = Зх2 (sin Ъх + х cos Зх) dx.
I х _ , dx
6)f/ = -arctg-. Ome.dy = -^-^.
B)y = -^*-t Отв. dy = tl^JLdx.
214

2. Известно, что и, v и ад — дифференцируемые функции от х. Найти
дифференциал функции у, если:
a) y = u-v-w. Отв. dy — v-w-du-\-u-w-dv-\-u-v- dw.
6)*/ = ^. Отв. dy=^-du-(^j dv.
i лг—г- ^ j du + dv
в) # = 1пУы + и. Отв. ф = 2(ц+а) -
3. Найти приращение и дифференциал функции у = 2х3 — Зх в точке #=1
при Ах = \, Лдс = 0,1 и Дя = 0,01. Найти для каждого из этих значений Ах абсо-
j I I Ay—dy
лютную погрешность \Ay — dy\ и относительную погрешность —^-т——
рые допускаются при замене приращения дифференциалом функции.
Отв. При Д#=1; А г/ = 11; dy = 3\ абсолютная погрешность 8; относитель-
о
ная уг. При Дх = 0,1; Д*/ = 0,362; ф = 0,3; абсолютная погрешность 0,062;
относительная ^з -—. При Ах = 0,01; Дг/ = 0,0306; dy = 0,03; абсолютная погрешность
0,0006; относительная =j.
51
4. Найти приближенно значения функций:
а) / (х) = (х — 3)2 (х--2)з (jc —4) прид; = 4,001; 6)/(*)=xln (л: — 2) прих = 3,015;
в) /(x) = -J^3a* + 2* — 4 при х=1,001.
Отв. а)/(4,001) ^0,008; б) /(3,015) ««0,045; в) /(1,001) ^ 1,0015.
5. Найти приращение и дифференциал площади круга 5 = яг2 при
некотором приращении радиуса. Дать им геометрическое истолкование.
Отв. AS = я (г + Дг)2 — яг2 = я(2г Дг + Дг2) = 2яг Дг + яДг2 — площадь кольца,
содержащегося между концентрическими окружностями радиусов г и r + Дг, dS =
= 2яг • Дг — площадь прямоугольника с основанием 2яг и высотой Дг.
6. Вычислить приближенно значения: У*27,0081, sin 299, cos 151° и tg48°41'.
Полученные результаты сравнить с табличными.
Отв. i/27,0081 ^ 3,0003, sin 29е* ^0,4849 (по табл. 0,4848), cos 151? ^
«~_0,8747 (по табл.—0,8746), tg44^ 41' «*0,9889 (по табл. 0,9890).
7. Цилиндр, диаметр которого был 10 см, высота — 20 см, при шлифовке
боковой поверхности потерял в весе 2 г. Насколько уменьшился его диаметр, если
удельный вес вещества цилиндра 2,5? Отв. Диаметр уменьшился на -т^=—.
8. На сколько уменьшится величина степени З4, если основание уменьшится
на 0,0063? Отв. Ау^ 0,6804.
9. Сила тока / определяется, как известно, по тангенсгальванометру из
формулы
/ = fc.tg<p.
Пусть dq>—ошибка, допущенная при отсчете угла ф. Найти абсолютную и
относительную погрешности при определении /. При каком значении угла <р
относительная погрешность будет минимальной?
Id/ I I k .112,1
,rf(P
Отв.
I
k COS2 ф • tg ф
dtp
Минимум при ф = 459.
| sin 2ф
10. Пользуясь понятием дифференциала, найти приближенное значение
функции у=хь — 2х4 +3*з — 4х2 + 6 при х= 1,001. Отв. #^3,998.
11. С какой относительной погрешностью допустимо измерить радиус R шара,
чтобы объем его можно было определить с точностью до одного процента?
|Д#| 1 \Av
0тв' I р |-з| с
(^0,ЗЗо/0).
215

12. Период качания маятника вычисляется по формуле T — zCy _. f где /—*
длина маятника, g—ускорение силы тяжести (g = 980 см/сек2). Какое влияние
на погрешность при вычислении периода Т окажет погрешность в один процент
при измерении: а) длины маятника /, б) ускорения g?
Отв. В обоих случаях относительная погрешность составляет
около 0,5 %.
13. Ход стенных часов регулируется маятником. Передвигая груз маятника,
можно изменять его «приведенную длину» / (см), от которой зависит период
качания Т (сек) маятника, согласно формуле, приведенной в задаче 12. Часы
спешат вследствие того, что маятник совершает одно качание в течение 0,499 сек
вместо того,, чтобы совершать его в течение 0,5 сек. На сколько должна быть
увеличена длина /, чтобы правильный ход часов был восстановлен?
Указание. Решение задачи сводится к нахождению дифференциала dl из
формулы / = —0- Отв. А/ »=: -Чг «« 0,1 см.
я* п*
14. По данному расстоянию d светящейся точки от оптического центра
двояковыпуклого стекла может быть вычислено расстояние ее изображения согласно
1 , 1 1 п
формуле —+ у=-тгтгде F — постоянная для данного стекла и данного сорта
лучей. Как влияет погрешность в измерении d на погрешность в вычислении /?
Отв. | Д/| = ^-| Ad |,
I
d
d
§ 9. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШЕГО ПОРЯДКА
Как уже выяснялось в § 1 этой главы, производная функции
г> некоторой точке является, в свою очередь, функцией этой точки.
Следовательно, по отнощению к ней можно снова ставить вопрос
о существовании и нахождении производной.
Определение. Производная от производной некоторой
функции называется производной второго порядка или второй
производной. Производная от второй производной называется
производной третьего порядка или третьей производной,
и т. д.
Производные, начиная со второй, называются производными
высшего порядка и обозначаются:
у", у'". у^\ у^, />,..., Г\ ... . *
или
d2y d?y dty d?y dfy d^y
dx*' dx*1 dx*' dx*' dx** '"> dxn '"
Производная /г-го порядка есть производная от производной
(п—1)-го порядка, то есть у{п) = (у{п~1]у. Заметим, что у', которое
раньше мы называли просто производной, называют также
производной первого порядка.
* Иногда при записи производных высших порядков пользуются
обозначением Ifxx , У'ххх И Т. Д.
216

Второй производной можно дать механическое толкование: f(x)
есть ускорение изменения функции по сравнению с изменением
аргумента. Выше мы фактически уже пользовались второй
производной при отыскании ускорения движения. В дальнейшем будет
показано, что вторую производную можно использовать и для
геометрической характеристики функции, например при определении
направления вогнутости кривой, ее кривизны и т. п.
Пример 1. Пусть дана функция у=х3. Ее производная у'=3х2
есть снова степенная функция, имеющая производные #" = 6л:, у"' =
=6, #<IV)=0. Все производные, начиная с четвертой, равны нулю.
Пример 2. Если у=±У 2х—х2, то
2 — 2х 1
У =
21/2* — х2 ]/~2х — х2'
(- 1) V2x— х* — (1-х) }~Х
т У2х — х2_—2х+х2 — (\ — х)2
У - 2х—х* ~~ ух — х2) ]^2х-х2
з
(2х — х2) 2
(/"' = — \(2х—х2) 2]'=-|- (2*-*2) 2 (2 — 3*) = -^—^ и т. д.
(2х —*«)"*
Пример 3. Рассмотрим многочлен п-и степени:
у = а^п + аххп-х + а2^~2 + ... + ап_2х2 + ап_гх + ап.
Последовательно дифференцируя, получим:
у1 = a<inxn-i + a1 (п— 1) хп~2 + а2 (л —2) п~3 + ... + ап_2 - 2х + ап_г.
у^^а0п(п^1)хп-2 + а1(п^1)(п — 2)хп-3 + а2(п—2)(п — 3)хп-^-\-
+ ... + art_2-2, и т. д.
Легко видеть, что на п-м шагу получим:
у{п) = а0п(п— 1)(л —2) (л — 3)...3-2-1, то есть
*/(/г) = а0 • п\ — постоянная.
Что же касается производных порядка выше /г, то вме они равны
нулю.
В некоторых случаях можно получить общий вид л-й производ-
н ой, по которому сразу записывается производная любого
порядка (предшествующие производные при этом не вычисляются).
Пример 4. Для функции у=ех имеем у1 =ех, у" = ех, ут—ех,....
Следовательно, можно сказать, что
(е*)<«> = 0*
для любого п.
Пример 5. Для функции y = s'mx имеем: у' = cosх, у" =
= — sin*, y"'=— cos*, yW=sinx, #(V) = cos;t, и т. д.
217

Эти производные можно представить также в виде:
0'=cosx = sin(* + -?), y" = cos l^x + ~^j = sin{x + 2'~Y
yin> = cos(x + (n—l)%) = sin(f + n~y
Таким образом, производную любого порядка от sin х можно
вычислять по формуле
(sinx)W = sin(x + n-?pj.
Например, (sin л:)(10> = sin f а: + 10- 4M = sin (х + л) = — sin x.
Аналогично получается формула для вычисления производной от
cos x:
(cos хУп>> = cos(x + n?
Пр и мер 6. у=\пх,
1 1 ,„ 2 ..(iv) б
У =-^> У = —*г. У = ^г> У =—1Г. и т- я.
Закон получения производных может быть представлен следующей
формулой:
Пример 7. у = х2 In лг.
#' = 2л:1пл:+л:, г/" = 2 Inx + 3, #f" = 2 (In *)' = — ,...
Дальнейшее дифференцирование можно производить по формуле
,2 (лг — 3)1
у(")д(-1)"-з * ' (я^3).
ЛГ
Пример 8. Выведем с помощью производных ф о р м у л у
бинома Ньютона:
+ ... + *".
Как известно, при натуральном /г выражение (a + x)'* есть
многочлен /г-й степени. Следовательно, его можно представить в виде
(a + x)n = A0 + A1x + A2x* + A3x* + .„ + An_1xn-i + Anxn, (1)
где коэффициенты Л0, Аъ А2, А3, ..., Ля_1, Ап пока неизвестны.
Для определения их поступим следующим образом. Положим в
тождестве (1) х = 0. Получим: ап = А0. Дифференцируя почленно
тождество (1), получим новое тождество:
n(a + x)n-1 = A1 + 2A2x + 3A3x2 + ... + {n — l)An_1xn-2 + nAnxni. (2)
218

Если в нем снова положить х = 0, то получим: пап 1 = Л1. Далее,
дифференцируя почленно тождество (2) и полагая х = 0, найдем:
п(п—1)(а + х)п-2 =
= 2-l-A2 + 3-2-A3-x + ... + (n--\)(n--2)An^-* + n(n--rl) X
х Апхп'2,
п(п—1)ап-2 = 21-А2, то есть А2 = п{"~1) ап~2 и т. д.
Мы видим, что при каждом дифференцировании степени к
коэффициенту добавляется новый множитель, равный показателю
степени, а сам показатель степени уменьшается на единицу.
Следовательно, после m-кратного дифференцирования тождества (1) (т^п)
получим:
п(п— 1)(/г — 2)...[/г — (т—1)](а + х)п-т =
=т(т— 1)(ш — 2)...3-2. ЬЛт + (т-И)т(т —1)...3-2Ат+гх + ...+
+ п{п—\){п — 2)...[п — {т — \)]Ап-хГт.
Полагая в этом тождестве л: = 0, получим:
п(п— l)(/i — 2) ... (п — т + 1) ап-т = т{т—\) (т — 2). ..3-2-1 • Ат>
откуда
Л^~ 1.2.3.../и й >ИТ'Д-
Подставляя вычисленные значения коэффициентов в (1), получим
формулу бинома Ньютона.
Взяв в формуле бинома Ньютона я=2 и 3, мы получим из нее
хорошо известные читателю формулы квадрата и куба суммы двух
чисел.
Пример 9. Пусть y = uv, где и и v — некоторые функции от х>
имеющие производные любого порядка. Тогда
y' = u'v + uv', y* = u'v + u'v' + u'v' + uv'' = u'v + 2u'v' + uv",
t/" = u'"v + mV + 2aV +2u'vm + u'v" + uvr" =
= u'"v + 3u"v' + 3u'v" + uv"\
Правые части разложений напоминают разложения различных
степеней бинома по формуле Ньютона, где вместо показателей
степени стоят числа, указывающие на порядок производных (и и и
можно рассматривать как «производные нулевого порядка» u{Q) и и(0)).
Учитывая это, запишем по аналогии общий вид производной п-го
порядка от произведения двух функций:
v(n) = (uvyn) = U(n)v + nu(n-\)V' + п{п2~г) и<"-2>гГ +
+ + Л(я-1)„.(В-Н») Uin-k)vW + _ + uvinh (3;
Эта формула носит название формулы Лейбница. Справедливость
ее доказывается методом математической индукции. Для п = 2 и 3
она уже проверена нами. Предположим теперь, что она верна для
21$

некоторога п, и докажем ее справедливость для п+l. С той целью
продифференцируем выражение (3), составленное для #(я):
у{п + 1) = u{n+l) v + u(n) v' + n ^(л) v> + u{n-D vr,^ +
+ n(n-\)...Jtl-k+l) jy „-*+l) v(k) + u(n-k) v(k+1) J + _ ^ + иг0 (Я) + tt0(irt-l)#
Раскрывая скобки и приводя подобные члены, получим:
y^^ = u^n^v + (n+l)u^v,+^n + n{n~l))^n-^v,, + ...+
, (п{п—1) ...(n-k-j-2) _^ п(п —1) ... (ft —fe-j-l)\ (л_Л+1) (Л) , .
~г\ (/г-1)! l к\ )и -Г.---Г
Но
я (/г— l)(ft-2) ... (ft — fe + 2) ft (ft — 1) (/г — 2) .-.. (n — k+l) __
(/г-1)! + k\ ~~
п\ й\ п\ I 1 , 1
+ Х =
~~ (? — 1)!(/г — Jfe + 1)! ^ /г! (/г — к)\ ~ (к- 1)! (/г — k)\ \n — k+l ^ к ;
_ д! ft-f 1 (я+1)! _ (ft-fl)ft(ft—1) ... (ft — k + 2)
~~ (A—1)! (ft — Аг)! " к(п — k+l)\ ~~ /г! (n — k + l)\ ~~ ft!
Пользуясь этим, можем записать:
+ (ft + l)/i(ft-n...(ft-fe + 2) u{n_k+1) v{k) +^ + (n+l) u,v{n) + uvin+1)m
Формула (З) доказана полностью.
x
Пример 10. Найти пятую производную от функции у= хъе2,
х
Полагая и — хъ и v — e2, найдем:
и' = Ьх*, ы" = 20л;3, ы'"=60л'2, tt<IV>=120xf «(V)=120,
XXX XX
, 1 2~ ,, 1 Т ,„ 1 2 (IV) 1 "2* (V) I Т
Подставляя в формулу (3) при п = 5, получим:
^0 = 120.Д+5.120х4^+Н60л2-Т^+гЙ20;с!,-Т-^ +
+ 5 • 5л* ~ е 2 + **• ~ е2 =е 2 f 120 + 300* + 150х* + 25** + ||** + ^ **) .
Пример 11. Пользуясь формулой Лейбница, написать выражение 25-й
производной от функции */ = *3cos#.
В данном случае и = х3, u' = 3jc2, и" = 6х, и'" =6, четвертая производная
u{iv^ и все последующие равны нулю. Далее, o = cos#, и для любого п имеем:
t;(/I) = cos Ix + n-jy]. Подставляя значения в формулу (3) при /г = 25, получим
220

справа только те слагаемые, у которых порядок производных от и ниже
четвертого (так как остальные слагаемые будут равны нулю):
,оь. 25-24...5-4 „, ,а_ , 25-24 ...4-3 „ ._ , 25 -24 ... 3 • 2 , ,911 ,
22! ^ 23! ^ 24!
+ 25-Заг2соз(лг+24. —W^cos [л: + 25~] =
= — 13800 cos х + 1800* sin x + 75а:2 cos х—х* sin *.
Пусть функция задана параметрически уравнениями1.
: = Ф<0. \
Ее производная при условиях, указанных в § 7, вычисляется пе
формуле
При отыскании второй производной ух следует исходить из
функции, заданной параметрически следующими уравнениями:
x=<f(t), }
. y't
xt
Применяя к ней ту же формулу (4) (и предполагая, что
производные второго порядка от х и от у существуют), получим:
Ухх = (Ух)х =
УЛ xryj-x1yt
$)t _ (x't)2 *iyi-*ivi
X,
W)3
(здесь нам пришлось пользоваться правилом дифференцирования
дроби).
Итак,
У** = (х;)з - (б)
Аналогичным образом можно получить производную от у по х
любого порядка.
Пример 12. Найти первую и вторую производные функции
x = cost, |
# = 3sin /. J
Находим по формуле (4) сначала первую производную:
y't 3 cos t
Й = 4 = г-7 = — 3ctg*.
Vx xt —smt ь
Теперь нужно продифференцировать по х уже найденную производную у'х. Но
221

она выражена через параметр t. Поэтому нужно еще раз воспользоваться
формулой (4), применив ее к функции
# = cos/, |
i/; = -3ctg*. J
Получим:
(у'х)' 3 cosec2 / 3
У"хх= х; = —sin/ """siiPl*
При решении этого примера мы повторили вывод формулы (5) для частного
случая. Но можно было бы получить как первую, так и вторую производные
путем непосредственного использования формул (4) и (5).
Перейдем теперь к определению дифференциалов высшего порядка.
Определение. Дифференциал от дифференциала функции у =
= f (х) в некоторой точке называется дифференциалом второго
порядка в этой точке и обозначается так: d (dy) = d2y.
Дифференциал от дифференциала второго порядка называется
дифференциалом третьего порядка и обозначается: d3y и т. д. Вообще
дифференциал от дифференциала (п— 1)-го порядка называется
дифференциалом /г-го порядка и обозначается: dny. При этом
дифференциал независимой переменной все время рассматривается кик
постоянная.
Из определения дифференциалов высшего порядка следует и
способ их вычисления. Пусть функция y = f(x) имеет в точке л*
производные любого порядка (х—независимая переменная). Тогда
dy = у' dx,
d2y = d(dy) = (у' dx)r dx = y" • dx-dx = y" dx2,
d3y = d(d2y) = (y" dx2)' dx=y'" dx2dx = y"' dx3,
dny = d (d^y) = (уп~г dx71-1)' dx=y(n) dx?-1 dx = y^ dxn.
Из этих выражений следует, что для любого п
то есть обозначение -г— можно рассматривать не только как символ,
обозначающий п-ю производную, но и как дробь.
Под обозначениями dx2, dx3, ..., dxn следует понимать степени
дифференциала dx, то есть (dx)2, (dx)3, ..., (dx)n. Чтобы не
смешивать их с дифференциалом от степени переменной х, последний
обозначается так: d(xn), например d(x2), d(x3).
Как для производных, так и для дифференциалов высшего
порядка справедливы следующие формулы:
(с«)(л) = с-^Л), dn(cu) = cdnu, (u±vYn^ = u^±v^n\
dn(u±v) = dnu=izdnv.
Если обе части формулы Лейбница (3) умножить на dxny
то получим формулу Лейбница для вычисления дифферен-
222

циалов высшего порядка от произведения двух функций:
Замечание. Формула
dny=y^dxn
при п>\ не обладает свойством инвариантности. Она верна, когда
х—независимая переменная, и перестает быть верной, когда х —
функция. Покажем это на примере дифференциала второго порядка.
Пусть х—независимая переменная, а функция y = f (x) имеет
первую и вторую производные. Тогда
dy=y'dx, (6)
d2y=y"dx2. (7)
Предположим теперь, что х не является независимой переменной,
а есть некоторая функция от t, x=q(t). Тогда у будет сложной
функцией от t. В силу инвариантности формы (6) первого
дифференциала, dy представится также в виде (6), хотя в этом случае
dx уже будет дифференциалом функции х=у (t). Так как dx=y' (t) dt
и q/ (t) — некоторая функция, то dx может не быть постоянной.
Дифференциал второго порядка
d2y = d(y' dx)=dy' -dx + y' -d(dx)=y" dx2 + y' d2x
или
d2y=y"dx2 + y'd2x. (8)
Сравнивая (7) и (8), видим, что форма (7) второго дифференциала
изменилась, прибавилось слагаемое у'd2x. Такого дополнительного
слагаемого нет (оно равно нулю), если х—независимая переменная,
так как в этом случае dx=Ax есть постоянная величина и,
следовательно, d2x = d(dx) = 0.
Пример 13. Найти дифференциалы dy, d2y и d3y от функции
у=х*—3*2 + 2
в случаях, когда:
1) х—независимая переменная,
2) л:—функция от другой независимой переменной.
Дифференциал первого порядка dy в силу свойства
инвариантности его формы представляется в обоих случаях одинаково:
dy=yr dx = (4x* — 6x) dx = 2(2x?—3x) dx.
В первом случае под dx понимается приращение независимой
переменной Ax(dx=Ax)i во втором случае—дифференциал от х как от
функции (dx Ф Ах).
Что же касается дифференциалов высшего порядка, то для них
при отыскании d2y и d3y приходится решать задачу для каждого
случая отдельно.
1) Пусть х—независимая переменная. Тогда, имея в виду, что
в этом случае dx является постоянной величиной и ее можно выно-
223

сить за знак дифференциала, получим:
d2y = d(dy) = d[2( x3 — 3x)ax\ = 2dx-d(2x3 — 3x) =
= 2dx • (6х2 — 3)dx = 6 (2x2 — 1) dx\
d*y = d(d2y) = d[6(2x2 — 1) dx2] = 6dx2• d (2x2 — 1) =
= Mx2 • 4x dx = 24x dx?.
2) Пусть x является в свою очередь функцией от некоторой
другой переменной. В этом случае величина dx уже не будет
постоянной и выносить ее за знак дифференциала, как мы это делали
в первом случае, нельзя. Нужно вычислить дифференциал от у' dx
как от произведения двух переменных. Получим:
d2y = d (dy) = d[2 (2x3 — 3x) dx] = 2d \(2x3 — 3x) dx] =
= 2 [d (2л:3 —3x) dx + (2x3 — 3x) d (dx)\=2 [3 (2x2 — 1) dxdx +
+ (2x3 — 3x) d2x\ = 6 (2x2 —l)dx2 + 2 (2x3 — 3x) d2x,
d3y==d(d2y) = d[6 (2л:2 — 1) dx2 + 2(2x3 — 3x) d2x] =
= 6d [(2x2 — l)dx2+2d [(2л:3 — 3*) d2x\ = 6 [d (2x2 —\)dx2 +
+ (2x2— 1) d {dx2)] + 2[d (2л:3 —Зл:) d2x + (2x3 — 3x) d (d2x)] =
= 5 [Ax dx dx2 + (2x2 —l)2dx d2x] + 2 [(6л:2—3) dx d2x +
+ (2x3 — 3x) d3x] = 2Ax dx3 + 18 (2л:2 — 1) dx d2x + 2 (2x3 — 3x) a3x.
Вопросы для самопроверки и упражнения
1. Продифференцировать следующие функции:
а) у = х]^\-\~х2. Найти у", б) у = е~*2. Найти у'".
в) у = уЦ*. Найти у'", г) у = хsin2 х. Найти */(IV). д) у = х2е2х. Найти у{20).
х2
е) У = -1 . Найти у(8).
Указание. При решении последних двух примеров воспользоваться
формулой Лейбница.
___12_
Отв. a) y>> = x^Jp2t б) у>"=Ае-*\Ъх-2х*), в) *'"=щ* 5 ,
г) t/(IV) = — 1б(у cos2*+sin2*V д) yVQ)=220<?x{x* + 20x + 9b)f
e)ifc8,e_8I_
(1-х)*'
2. Найти вторые производные у"хх функций у (л:), заданных в
параметрической форме:
х = a cos t, "i
у = a sin t. J
х = а (ф — sin ф)
' г/==а (1—совф).
x = a?cos /,
x = arcosr, \
y = at sin ?. J
Отв.
Отв.
Отв
— 1
у" —
Ухх asm4'
и- - "-1
*хх а(1—С08ф)2*
Jxx a (cos/ — ^ sin О3
224

1 х2
3. Найти d2y для функции j/ = ln 2 при условии, что: а) х—независимая
переменная, б) х—функция от другой переменной. Рассмотреть также частный
случай, когда x = tgt.
и d2x= — 4sec22tdt2.
4. Доказать, что для функции у = "J/ 2а; — л'2 справедливо равенство у3 * у"' +
+ 1=0.
5. Чему равна производная /г-го порядка от многочлена РЛ (л:) = «о*71 +
+ а1д;,г-1 + а2А:л-2 + ... + ая? Отв. а0п\.
6. Показать, что если тело движется по закону s = aet + be~l\ то его
ускорение численно равно пройденному пути.
7. Точка движется так, что скорость ее изменяется пропорционально
квадратному корню из пройденного пути (как это, например, имеет место при
свободном падении). Показать, что движение происходит под действием постоянной
силы.
Указание. Следует иметь в виду, что ускорение пропорционально
действующей силе.

ГЛАВА VI
ОСНОВНЫЕ ТЕОРЕМЫ
ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ.
ПРАВИЛО ЛОПИТАЛЯ. ФОРМУЛА ТЕЙЛОРА
В предыдущей главе мы учились находить производные и
дифференциалы функций. Теперь предстоит заняться более глубоким
анализом свойств функций и их производных. При этом будут вскрыты
связи между отдельными свойствами функций и их производных,
что составляет теоретическую основу приложений
дифференциального исчисления и открывает широкие возможности для различного
рода приложений.
Рассмотрим группу теорем, которые в силу своего большого
значения названы основными теоремами дифференциального
исчисления. На них и нужно обратить особое внимание при работе над
данной главой.
В качестве примеров приложения основных теорем рассмотрим
также вопрос о раскрытии неопределенностей и формулу Тейлора.
§ 1. ОСНОВНЫЕ ТЕОРЕМЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
Теорема 1 (Ферма)*. Пусть функция у =f(x) определена
на некотором промежутке X и во внутренней точке х0
этого промежутка имеет наибольшее или наименьшее
значение. Тогда если в точке х0 существует конечная
производная, то она равна нулю, то есть f (xQ) = 0.
Доказательство. Пусть f(xQ) есть наибольшее значение
функции f(x) на X. Это значит, что для всех х из X справедливо
неравенство f (x)^f (х0). По определению f (х0) = lim г^~~'(*<" f При-
х-*х0 х — *о
чем этот предел не зависит от того, каким способом х стремится
к х0. Однако если х приближать к х0 слева, то л:—х0 < 0 и'к _J v ^
^0. Если же х приближать к х0 справа, то х—х0>0 и LL^LzIiM^o.
X Xq
Осуществив в этих неравенствах предельный переход,
соответственно получим: f (х0)^0 и f'(x0)^0. Остается заключить, что
fW=o.
Пьер Ферма (1601 — 1665) — французский математик.
226

П
о"
,
^
_
1 i !
1 Л 1 1
л 1 J
1 '. ¦ -*—ч~-
<o *o X
Рис. 90.
Случай, когда f(x0) представляет собой наименьшее значение
функции на X, рассматривается аналогично.
Геометрический смысл теоремы Ферма состоит в том, что в точке
на кривой, имеющей абсциссу х0 (с указанным в теореме свойством),
касательная к кривой y=f(x)y если она существует, оказывается
параллельной оси ОХ (рис. 90).
Заметим, что теорема включает и те случаи, когда f (х) = f (x0)
для нескольких или даже для всех значений х из X. Так, на
рисунке 91 касательная параллельна оси ОХ в каждой точке, где
а<л:<6.
Теорема 2 (Ролля)*. Пусть на [а, Ь\ определена
функция у =f(x)> причем:
1) f(x) непрерывна на [а, Ь\;
2) на [а, Ь) существует конечная производная f (x);
3) /(а) =/(&).
Тогда внутри [а, Ь\ найдется такая точка с, что
f(c) = 0.
Доказательство. Положим \i=f(a)=f(b). Если окажется,
что f(x)=\i для всех х из [а, Ь], то f (х) = 0, как производная от
постоянной. В этом случае за точку с можно взять любую точку
внутри [а, Ь]. Пусть внутри [а, Ь] есть точки, в которых f(x)>\i
или /(x)<(i. Для определенности будем считать, что в некоторых
точках f(x)>\i. Так как функция f(x) по условию непрерывна на
[а, Ь], то по второй теореме Вейерштрасса она будет в некоторой
точке с иметь наибольшее значение. При этом, очевидно, /(с)>[г
и, следовательно, точка с лежит внутри [а, Ь]. На основании
теоремы Ферма получаем, что /'(с)=0.
Геометрически теорема Ролля означает, что если непрерывная
кривая изображает дифференцируемую функцию, то между двумя
точками, лежащими на одинаковой высоте, всегда имеется точка,
в которой касательная параллельна оси ОХ. Таких точек может
оказаться и несколько (рис. 92).
* Мишель Ролль (1652—1719)—французский математик.
227

Из последнего» в частности, следует, что между каждыми двумя
корнями дифференцируемой функции f(x) лежит корень (по
крайней мере один) ее производной /' (х).
Замечание. На первый взгляд может показаться, что первое
условие в теореме Ролля является лишним, поскольку
непрерывность функции f (х) на интервале (а, Ь) следует из второго условия
теоремы. Однако в теореме существенно необходима
непрерывность функции на отрезке [a, b], a из непрерывности на интервале
(а, Ь) не следует непрерывность
на его концах а и Ь. В
последнем читатель мог убедиться
на примере 3 из упражнений
к § 3, гл. IV.
Пример 1. Показать, что
уравнение л;3 + Зх — 6 = О имеет только
один вещественный корень.
Рассмотрим функцию f(x)=xz +
+ За: — 6. Она непрерывна на ( — оо,
4-оо) и имеет производную f (х) =
= 3^2 + 3 = 3(^+1). Легко видеть,
что f' (х) -? 0 при любых
вещественных значениях х. Но тогда
наше уравнение может иметь не
более одного вещественного корня, так как если бы оно имело, например, два
корня сг и с2, то f (ci)—f (c2) = 0 и по теореме Ролля между сх и с2 нашлась бы
такая точка с, что f (c) = 0. Последнее невозможно. Существование же одного
вещественного корня следует из того, что f(x)—^многочлен нечетной степени.
Теорема 3 (Лагранжа)*. Пусть на [а, Ь] определена
функция у =f(x), причем:
1) /0*0 непрерывна на [а, Ь],
2) на (а, Ь) существует конечная производная f (x).
Тогда внутри [а, Ь] найдется такая точка с, что
f{b)-f(a)_
-f'(c).
(1)
Доказательство. Рассмотрим на [а, Ь] вспомогательную
функцию
Ф {x)=f{x)-f (а)-?ф)~1{а) (х-а).
Эта функция удовлетворяет всем трем условиям теоремы Ролля.
Действительно, ср (х) непрерывна на [а, 6], так как она
представляет собой разность между непрерывной функцией f (х) и линейной
функцией. Внутри [at b\ она имеет конечную производную
<р'(*)=/'(*)-
f{b)-f(a)
Ъ — а ч '
* Жо зеф - Л у и
механик.
223
Л а г р а н ж (1736—1813) — французский математик и

Значения этой функции на концах отрезка [а, Ь] равны:
¦ "»>-'W(g-g),
о—a v '
ф(о)=/(а)—/(a)-
<p(&)=f(6)-f(a).
= 0,
¦M(ft_fl)=0,
то есть ф (а) = ф (6).
Следовательно, для функции ф(л;) справедливо утверждение
теоремы Ролля: внутри [a, b] существует такая точка с, что ф'(с) = 0.
Но ф'(с) =/'(*)¦
f(fr) —f(g)
значит, Г(Ф
,WW(«> = 0, Теорема до-
f(b)-fla)
казана.
Доказанное равенство (1) называют также формулой Лагранжа.
Ею иногда удобнее пользоваться в виде
f(b)—f(a)=f(c)(b — a), гдеа<с<&.
Выясним геометрический смысл теоремы Лагранжа (рис. 93).
Левая часть равенства (1) есть тангенс угла а между секущей АВ
и осью ОХ, то есть tga. Правая же часть, как известно, есть
тангенс угла а' между касательной
в точке (с, f (с)) и осью ОХ, то
есть /' (с) = tg a'. Следовательно,
tga = tga' или a = a'. Словами
это можно высказать так: на дуге АВ
найдется точка, в которой
касательная параллельна секущей АВ. Таких
точек может быть и несколько.
Замечание. Легко видеть, что
теорема Ролля является частным
случаем теоремы Лагранжа, когда
секущая АВ параллельна оси ОХ, то
есть когда f(b) = f(a).
Формулу Лагранжа можно применить и к части отрезка [а, Ь].
Возьмем на [a, b] некоторое значение х и дадим ему приращение
Да: такое, чтобы х + Ах оставалось в пределах этого отрезка. Тогда
получим:
1(х + Ах)-!(х)=Г(с)Ах,
где с есть определенное, хотя и неизвестное нам, значение между
х и х + Ах. Его можно представить так: с=а: + 8Дл:, где 0
—соответственно выбранное вещественное число между 0 и 1.
Представление формулы Лагранжа в виде
Ay=f'(x + bAx)Ax, 0<8<1, (2)
особенно наглядно показывает связь между приращением аргумента
и соответствующим приращением функции. Поэтому ее часто
называют формулой конечных приращений. Сравнив эту формулу с
известным выражением для приращения функции
ky=f'{x)Ax + aAx, (3)
Рис. 93.
229

видим, что при отбрасывании в (3) слагаемого аДх можно все же
сохранить равенство, но для этого нужно в производную /' (х)
подставить вместо х некоторое определенное значение Jt + бДл;,
заключенное между х и х-\-Ах. Правда, это значение в формуле остается
для нас неизвестным, в теореме утверждается только его
существование. Но несмотря на этот недостаток, формула Лагранжа имеет
очень широкое применение как в анализе, так и в других
смежных дисциплинах. Мы неоднократно будем пользоваться ею.
Теорема 4 (Коши). Пусть на [а, Ь] заданы функции
f(x) и g(x), причем:
!) /(¦*) и S (х) непрерывны на [а, Ь\,
2) на (а, Ь) существуют конечные производные f (x) и
g' (х) и, кроме того, g1 {х) ^ О.
Тогда внутри [а, Ь\ найдется такая точка с, что имеет
место следующее равенство:
f(b)-f(a)=f(c)
g(b)-g(a) g'(cy
Это равенство называют формулой Коти,
Доказательство. Прежде всего установим, что каждая из
частей формулы Коши имеет определенный числовой смысл.
Действительно, правая часть формулы имеет смысл, так как по условию
g' (ф^О. Левая часть потеряла бы смысл при g(b) = g(a). Однако
этого не случится, так как тогда к функции g(x) можно было бы
применить теорему Ролля и оказалось бы, что в некоторой точке с
из (а, Ь) производная g'{x) равна нулю. У нас же по условию
2) g' (x)^0 во всем интервале (а, Ь).
Чтобы доказать теорему, будем рассуждать аналогично
доказательству теоремы Лагранжа. В качестве вспомогательной возьмем
функцию
Ф (*) = /(*) -/ (а) - -Ш=Ш-Шх) -g(a)).
Функция Ф(х) удовлетворяет всем трем условиям теоремы
Ролля: она непрерывна на [a, &], имеет конечную производную
\ ) i \ 1 g(b)—g(a) s v '
на {а, Ь) и на концах отрезка [а, Ь] имеет одинаковые значения
Ф(а) = Ф(й) = 0. Следовательно, к ней можно применить теорему
Ролля, согласно которой внутри [а, Ь] найдется такая точка с>
что Ф'(с) = 0. Но 0'(c)=r(c)-f-?^^)gf(c). Значит,
ПС) g(b)~g(a)g(C) U' ИЛИ g(b)-g(a) g'(c)-
Теорема доказана.
Замечание 1. Теорема Лагранжа является частным случаем
теоремы Коши (при g(x)=x). Проверка этого утверждения
предоставляется читателю.
230

Замечание 2. Если в условиях теоремы Коши дополнительно
потребовать, чтобы / (a) = g (а) = 0, то формула Коши примет
следующий частный вид:
е(ь) g'W где а<с<°-
Теоремы Ролля, Лагранжа и Коши часто называют теоремами
о средних значениях. Такое название они получили потому, что в них
идет речь о производных при каких-то средних значениях
независимой переменной. Во всех трех теоремах устанавливается лишь
факт существования этих средних значений. Но в отдельных
случаях средние значения можно и вычислить.
Пример 2. Определить значение с из теоремы Лагранжа о среднем
значении для функции / (х) = 4а:3 — 5л:2 + х — 2 на отрезке [0, 2].
В данном случае /(6) = /(2) = 12, / (а) = / (0) = — 2 и f (*) = 12*2— 10*+ 1.
Подставляя полученные значения в формулу Лагранжа, будем иметь: 12 — (—2) =
= /' (с)-2, откуда р (с) = 7, то есть 12с2— Юс+ 1 = 7.
5-|-1/г97
Из последнего уравнения определяем значение с= .~ (второй корень
квадратного уравнения не принадлежит отрезку [0, 2] и потому мы его
отбрасываем).
Пример 3. Определить значение с в формуле Лагранжа для функции / (х) =
= 1п* на отрезке [1, а], а>1.
В данном случае f (a) — f(l) = f (с) (а — 1). Так как Р(*) =—, то Р(с) =—.
X С
Подставляя в формулу соответствующие значения, получим:
1 1 1 1 / i\ 1 а — 1 а — 1
In a — In 1 =—(а— 1) или 1па = f откуда с=-. .
С С 1П CL
Пример 4. Доказать, что уравнение я4— 4х—1=0 имеет в точности два
различных вещественных корня.
Рассмотрим функцию f(x) = x* — 4x— 1. Она непрерывна и на всей числовой
оси имеет конечную производную
Р(*) = 4*з — 4 = 4 (л*— 1) = 4(х—1)(*2 + л:+1),
которая обращается в нуль только в одной точке х=1. Следовательно,
непрерывная кривая y=f(x) может пересекать ось ОХ не более чем в двух точках,
так как в противном случае из теоремы Ролля следовало бы, что f'(x)
обращается в нуль более чем в одной точке. Тем самым мы установили, что данное
уравнение имеет не более двух вещественных корней. Покажем, что их и не менее
чем два. Действительно, f (х) меняет знак на отрезке [—1, -\-\] и на отрезке
{1, 2]: /(—1)>0, /(1)<0, /(2)>0. Следовательно, по теореме Больцано—Коши
функция / (х) обращается в нуль по крайней мере два раза. Итак, данное
уравнение имеет, с одной стороны, не менее двух вещественных корней, которые
находятся внутри отрезков [—1, 1] и [1, 2], а с другой стороны, не более двух
вещественных корней, то есть в точности два корня.
Примерь 5. На кривой у = 5—З*2 найти точку, в которой касательная
параллельна хорде, соединяющей точки А(—1, 2) и Б (0, 5).
Рассмотрим функцию /(*) = 5 — Зх2 на отрезке [—1, 0], концами которого
являются абсциссы точек А и В. На этом отрезке данная функция непрерывна
и имеет конечную производную f'(x) =—6*. Следовательно, к ней можно
применить теорему Лагранжа. Согласно последней на дуге АВ найдется по крайней
мере одна точка М, в которой касательная параллельна хорде АВ, причем
абсциссой точки М будет значение с, удовлетворяющее формуле Лагранжа: / (0) —
— f (— 1) = /'(с) (° — (— О) или 5 —2 = (—6с) • I. Отсюда с = — -~-. Подставляя это
231

значение в уравнение кривой, найдем у —4 —, то есть искомой является точка
Эту задачу можно решить и не используя теорему Лагранжа: составить
уравнение хорды как прямой, проходящей через две заданные точки, и по этому
уравнению найти точку на кривой, в которой касательная параллельна хорде.
Вопросы для самопроверки и упражнения
1. Доказать теорему Ферма для случая, когда в точке х0 функция имеет
наименьшее значение.
2. Показать, что теорема Лагранжа является частным случаем теоремы Коши.
3. Объяснить, почему теорема Коши неприменима для функций j(x) = x3-{-
-\-2x-\-3 и g(x) = x2 — х на отрезке [—1, +1]. Применима ли она на отрезке
[1, 2]? Отв. Да.
4. Определить значение с в формуле Лагранжа для функции f(x)=x2 на
отрезке [а, Ь]. Отв. с= "t" .
5. На кривой у — х* найти точку, в которой касательная параллельна хорде,
соединяющей точки А (—1; —1) и 5(2; 8). Отв. (—1, —1) и (1, 1).
6. Используя теорему Ролля, доказать, что производная у' функции у =
= х sin — обращается в нуль на беско-
у I jf\ Х
* " х нечном множестве точек промежутка (0, 1]
(рис. 94).
7. Определить значение с в формуле
Коши для функций:
а) /(л:)==д:3 и g(x) = x2+\ на [1, 2].
Отв. c = -q-.
: sin х и g (x) — 1 + cos x на
б) /(*) =
Отв. с = -
8. Доказать с помощью теоремы
Ролля, что уравнение х4 — 32*+9 = 0. не
может иметь более двух вещественных
корней, а с помощью теоремы Больца-
но—Коши установить, что два вещественных корня действительно существуют.
9. На кривой у = х2 + Зх + 1 найти точку, в которой касательная параллельна
хорде, соединяющей точки А (—1; —1) и В (А; 5).
10. Функция у— \—Ух2 обращается в нуль при х =—1 и * = + 1, а ее про-
2
изводная у' = —- не обращается в нуль ни в одной точке отрезка [—1, +1].
3 ух
Не противоречит ли это теореме Ролля?
11. Доказать, что все корни производной от многочлена / (#) = (д:-{-1) (х— 1)х
X (х — 2) (х — 3) действительны, и указать границы, между которыми они
заключены.
12. Обнаружить ошибку в следующем доказательстве теоремы Коши: пусть
f (x) и g (x) удовлетворяют всем условиям теоремы Коши. Тогда каждая из них
будет удовлетворять и условиям теоремы Лагранжа. Следовательно, можно для
232

каждой из них записать формулу Лагранжа.
f(b)-f{a) = f' (c)(b-a), где a<c<b,
?(6)—g(a)=g' (c)(b — а), где a<c<b.
Разделив первое равенство на второе и проведя сокращение, получим:
f(b)-f(a) _f'(c)
g(b)-g(a) g'(c)>
где а<Сс<b.
§ 2. РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ ПО ПРАВИЛУ ЛОПИТАЛЯ
Вернемся к вопросу о раскрытии неопределенностей, которым
мы занимались в главе III и который был наиболее трудным из
всей главы. Основная трудность заключалась в том, что мы не
могли указать общего способа решения задачи. В большинстве
случаев приходилось изыскивать различные способы и приемы
раскрытия неопределенностей в зависимости от вида неопределенности,
а также и от конкретного примера.
Дифференциальное исчисление значительно облегчает задачу
раскрытия неопределенностей, предоставляя в наше распоряжение
весьма мощный и в то же время простой метод. В основе этого
метода лежит использование доказанных выше теорем о средних
значениях. Начнем с отношения двух бесконечно малых функций,
о
то есть с неопределенности вида -д-.
Теорема 1. Пусть на (a, b) определены функции f(x) и
g(x)j причем:
1) lim f(x) = Q и lim g(x) = 0;
jc-wz-f-0 x-+ a 4- 0
2) на (а, Ь) существуют конечные производные f (л:),
g'(x) и, кроме того, ?(х)Ф0;
3) существует предел отношения производных
f'(x\
lim J, \ = ft (конечный или бесконечный).
f(x)
Тогда отношение функций 'L~Jr также имеет предел и
он равен ft, то есть
lim m Пт f±%=k.
Доказательство. Доопределим функции f (x) ng(x) в точке
х = а таким образом, чтобы они были непрерывными справа в этой
точке. Для этого достаточно положить f (a) = lim /(x) = 0 и g(a) =
х-+а + 0
= lim g(x)=0. Тогда f(x) и g(x) будут непрерывными на [a, b)
л- —а + 0
(непрерывность во внутренних точках следует из существования
конечных производных f'(x) и g'(x)).
Возьмем некоторую точку х из [a, b). На отрезке [а, х]
функции f(x) и g(x) удовлетворяют всем условиям теоремы Коши. Сле-
233

довательно, внутри [а, х] найдется такая точка с, что справедлива
равенство
f(x)-f(a) Г (с) _0 9СТ. Цх) _ Г (с)
8(*)-g{a) *'(')' g{*) g'(c)'
Если в последнем равенстве х устремить к я, то и с будет
стремиться к а (так как а<с<х). Получим:
Иш !М-= am 4?» =k,
x^a + 0g(x) e_a+0g'(c)
что и требовалось доказать.
В теореме точка а является левым концом промежутка и х
стремится к а справа. Аналогично рассматриваются случаи, когда а —
правый конец промежутка и х стремится к а слева или когда а —
внутренняя точка промежутка и х -+ а любым способом.
Доказанную теорему обычно называют правилом Лопиталя*
О ~
раскрытия неопределенностей вида -^-. Она дает возможность свести
предел отношения двух бесконечно малых функций к пределу
отношения их производных, который во многих случаях находится
значительно проще.
Иногда отношение производных оказывается снова отношением
бесконечно малых. В этих случаях теорему следует применить
повторно, производя попутно необходимые упрощения и сокращения
с применением уже известных пределов.
| COS X
Пример 1. Пользуясь правилом Лопиталя, найти lim —7 .
В данном случае f (х) = 1 — cos x, g(x) = tgx. Легко убедиться, что эти
функции удовлетворяют всем условиям теоремы 1. Действительно, обе функции
в окрестности нуля являются бесконечно малыми: lim (1 — cosjc) = 0. lim tg* = 0.
*->() x^>0
Их производные /'(*) = sin* и g' (x) = sec2x существуют и конечны, например,.
/ j? ЗХ \
в окрестности (—— —1 точки * = 0, причем g' (х)^Ь0. Предел отношения их
производных также существует:
.. f'(x) .. sin* 0 .
lim j-t7Jt= hm——= — = 0.
*-og'(*) *-*osec2* 1
Следовательно, на основании теоремы 1 можно утверждать, что предел отношения
данных функции -V^r также существует и равен пределу отношения их произ-
водных ¦' .) [ , то есть
яМ
.. 1— cos л: .. (1—cos*)' .. sin* 0 л
lim —г =hm -—-—гт-^—= hm —— =—- = 0.
х^о tg* *_о (tg*)' x_0sec2* l
В дальнейшем в тех случаях, когда непосредственно видно, что
функции, составляющие отношение ^\, удовлетворяют всем усло-
g Vе)
виям теоремы 1, мы будем располагать все вычисления в одну
* Гильом Франсуа де Л о п ита л ь (1661—1704)—французский
математик.
234

строку. Например, вместе с вычислением предела отношения произ-
водных J-rA мы будем убеждаться и в существовании этого предела.
л/~§ х 2
Пример 2. Пользуясь правилом Лопиталя, найти lim ¦ —.
х-+\ у2 — х—1
Имеем неопределенность вида-^r-. Применяя правило Лопиталя, получим:
.. /5^7-2 .. (]/"5=Т-2)' .. VT=~x~ 1
lim =hm v , fr=hm
с-пуЧПГх—1 *-i fl/^ —* — l)' *-vi}/*5 — * 2
Пример З. Пользуясь правилом Лопиталя, найти lim
Xх — X
_^i In x — #+1 *
Имеем неопределенность вида -^-. Применяя правило Лопиталя, получим
хх —х .. (хх—х)' ,. хх\г\х + хх—\ .. ж*+1(1п*+1)— л:
lim -. r-r = lim тт-^ T-Tw^hm i-^ = hm ~—!— .
x-+\\nx — x+\ x_+\ (lnx —*+l)' x^{ I l *_и 1-х
X
После первого применения правила Лопиталя мы снова получили
неопределенность вида -^-. Применим к полученному выражению еще раз правило
Лопиталя, то есть еще раз заменим отношение получившихся функций отношением их
производных. Но, прежде чем перейти к последующему дифференцированию,
полезно, как указывалось выше, произвести возможные упрощения, сокращение
общих множителей, использование уже известных пределов и т. п. В нашем
примере можно в числителе вынести х за скобки и, перейдя в этом множителе к
пределу, заменить его единицей *. Получим:
Пт **(1пх+1)-1 _{[т (хх In x + xx) (In x+ l) + x*-i_ 2
Покажем, что правило Лопиталя остается в силе и в случае,
когда аргумент х-^оо. Пусть f(x)-+Q и g(x)-+0 при х->оо и
-О и
lim Ц-у-(г-=?. Введем подстановку х = -г. Тогда при л:-^оо будет
f(*)=f[l)-+0' 2(x)=e(Jf)-+0-
Применим теорему 1 к функциям f[-f) и 8\-f)* считая их ПРИ
дифференцировании сложными функциями от t. Получим:
Ita т. = Нт Ж-Ит 11ЖЖ=Пт !Ж= iim Ш k.
ь(1+*)
Пример 4. Пользуясь правилом Лопиталя, найти lim ~ г--^-.
х -* оо я — * arctg х
Впрочем, это можно было сделать и раньше, начиная решение примера.
235

Имеем неопределенность вида -~-. Действуя по правилу Лопиталя, получим:
Ч1+?)_11мтЫ-?
Игл —^о—-г-— = Ит А ' —v ~ у = Нт — =0.
#—>00 Л- ^ arctg ДС #_>оо о * *-*оо *
1 + *2
Перейдем теперь к рассмотрению отношения двух бесконечно
больших функций. Оказывается, раскрытие неопределенности вида
— возможно по тому же правилу Лопиталя, то есть имеет место
теорема, аналогичная теореме 1.
Теорема 2. Пусть на (я, Ь) определены функции f(x)
и g(x), причем:
1) lim /(л:) = со и Hm g(x) = oo;
х-*а + 0 x-+a-\-Q
2) на {а, Ъ) существуют конечные производные f (х\
g'(х) и, кроме того, g'(x)=?0;
3) существует предел (конечный или бесконечный) отно-
тения производных lim J,) \=k.
Тогда существует предел отношения функций и также
равен k, то есть
x-+a+0 SW x^a + Qg \X)
Эту теорему мы сообщаем без доказательства. Читателя,
интересующегося ее доказательством, отсылаем к учебнику Г. М. Фихтен-
гольца [1].
т~1 с тт « л. In sin аде п
Пример 5. Найти предел функции у = -.—. , при х—*0.
Имеем неопределенность вида —. По правилу Лопиталя
.. In sin ах .. a ctg ах а .. tg bx
lim 1——- = lim , ,°, ==— hm ~— =
x^Qmsmbx jc-+obzigbx b x^0igax
(производим замену tg bx и igax эквивалентными величинами)
a f. bx a b
= — hm — ==— . — = 1.
b x-+oax b a
sec x I x л
Пример 6. Найти предел функции У = ~т —- при х—*-т-щ
i& * х ?
Имеем неопределенность вида —. По правилу Лопиталя
sin х
.. sec*-f* .. cos2* .. sm* + cos2*
hm t !—= hm — r= hm —;—*—- ==l.
„ tg* —* n sec2*—1 n l—cos2*
X _+• У —*¦ У —*¦
X 2 2 * 2
Пример 7. Найти предел функции # = —— при *-*оо.
236

Здесь также имеем неопределенность вида—. По правилу Лопиталя
j_
hm —5- = lim —?гт= lim —^ = 0.
Неопределенности вида О-оо и оо — оо легко преобразуется к не-
0 оо
определенности вида -^ или — и затем раскрываются по правилу
Лопиталя. Покажем это на примерах.
Пример 8. Найти lim (secx—tg#).
л
Я
При х—+ -~- выражение sec л;—-tg* представляет собой неопределенность вида
„ , 1 sin х 1 —• sin x
оо —оо. Но sec*—tg*= = и преобразованное выражение
cos л: cos a; cos л: г г г
л 0 ^
при том же условии х —> — есть уже неопределенность вида -р-. Применяя к
нему правило Лопиталя, получим:
.. 1 — sin х .. — cos x л
lim = lim :— = 0.
п cos х п — sin х
Х-+— Х-» —
Пример 9. Найти lim x2 • е1~х.
X2
Имеем неопределенность вида 0 ¦ оо. Но х2ел л:=—^=д-, и мы пришли к
неопределенности вида —. По правилу Лопиталя получим:
lim х2е1~х = lim -г^т = lim -==т = Hm —— = 0.
рХ 1 рХ 1 рХ~\
ЛГ-ч-ОО Х-»-ООе *-»-ООе Х-+СО^
Остановимся, наконец, на определенностях вида 0°, I00 и оо°
(см. § 10, гл. IV). Все они с помощью очевидного тождества
преобразуются к неопределенности вида 0-со, способ раскрытия
которой нам уже знаком.
Пример 10. Найти lim (x— 1)1п*.
х-+\
Имеем неопределенность вида 0°. Но (х—\)]пх = е1пх']п(х~~]К Получили в
показателе неопределенность вида 0 • оо. Раскрываем ее:
1
1-м 1 / 1М 1- 1п(Я--_1) ,. Х—1 ,. Х(\пх)2
hm [In a:- In (x— l)] = lim —^ = lim = = — hm —* r-=
x-*\ x-y\ _L x-y\ i x-+o x—1
\nx x(\nx)2
(\nx)2 + 2x\nx- —
= —lim = -= — lim [(In x)2 + 2 In x] = 0.
x-+\ * x-+\
Следовательно,
lim (x-l)lnx= Пте1пхЛа<х-1>=е» = 1.
*-*l x-*\
237

. ПК
Пример 11 Найти lim(2 — x) l .
X— \
. лх . тех, /0 ,
Имеем неопределенность вида 1°°. Так как (2—-х) " 2 = е 2
1
Hm ftg ™. In (2-x)l-lim ln(2~X)=^ lim
1
Ctg -7Г
s,n2T
2 г Sln2^ 2 ,- ,o **T I
= — lim -тс == —, то lim (2 — *) 2==ея.
Замечание 1. Предостерегаем читателя, что при
многократном применении правила Лопиталя необходимо каждый раз
проверять, не раскрылась ли уже неопределенность, иначе можно впасть
в ошибку. Если применить правило Лопиталя к выражению, не
представляющему никакой неопределенности, то можно получить
неверный ответ. Так, например,
х> + Бх+1 15
1хп^2Хз^2х+4 8*
Если же продифференцировать числитель и знаменатель, то по-
лучим: Hm2g±i=^.
Замечание 2. По правилу Лопиталя находится предел
отношения функций в том случае, если известно, что существует предел
отношения их производных. Если же последний не существует, то
из этого еще не следует, что не существует и предел отношения
функции. Так, например, lim—! =lim(l-| =1,втовремя
х-*оэ Х *-*оо \ х I
как отношение производных, равное 1+cosx, предела при х->оо
не имеет.
Воспользуемся правилом Лопиталя для сравнения роста
степенной, показательной и логарифмической функций.
Известно, что при л:->4-°° функции jf (|x>0), ах (а> 1) и logax
(а> 1) являются бесконечно большими величинами.
1. Покажем, что при л:->*оо любая показательная функция ах
(а>1) растет быстрее, чем лкэбая степенная функция х* (fi>0).
Ограничимся случаем, когда (х натуральное, \i = n. Применяя
п раз правило Лопиталя, получим:
,. ах 1. ах\па ,. a* (In a)2 ,. ах (In a)n
hm pj= hm ^t^ft= bm ,JnU = -= hm v =oo.
Следовательно, ах (а>\) при л;-^ + °° является бесконечно
большой более высокого порядка, чем бесконечно большая хп.
Случай, когда \i не натуральное, легко сводится к уже
разобранному, так как х[Х <л;Е(|х)-Н при х-+-\-оо.
238

2. Покажем, что при я-^ + оо любая степенная функция х*
(|х>0) растет быстрее, чем любая логарифмическая функция loga^
(а>1).
По правилу Лопиталя имеем:
lim "= lim -V?2-= Hm J^
*_+00 loga* x^ + o0 }_XQgae х-*-hoo loga*
= 00.
Следовательно, л;1* является бесконечно большой более высокого
порядка, чем бесконечно большая loga* (a>l).
Таким образом, показательная функция растет быстрее,
а логарифмическая медленнее, чем степенная*
Вопросы для самопроверки и упражнения
1. Доказать теорему 1 для случаев, когда х—*Ъ — 0 их-+с, где с —
внутренняя точка интервала (я, Ь).
2. Почему для раскрытия неопределенностей при х—+а правило Лопиталя не
требует, чтобы обязательно существовали производные /' (х) и g' (x) в самой
точке а?
Г М
3. Предел отношения производных , не существует. Можно ли утвер-
§ \х)
ждать, что предел отношения самих функции -*гт, представляющих неопреде-
0 оо
ленность вида -~- или —, также не существует?
В задачах 4—17 вычислить пределы с помощью правила Лопиталя.
In х ех еа I 1 \
4. lim -г—. Отв. 0. 5. lim . Отв. еа. 6. lim ctg* . Отв. 0.
*-octgx х_+а х — а х-+о\ *1
„ sin2©—?г*?Ф t / -/
7. lim г. Отв. —2. 8. lim —Г-1 - . Отв. — 9. hm
' X-+Q COS*—1' ' ' я 1+СОБ4ф ' 8' t^.Q \n(l+t)'
Отв. 2. 10. linw. Отв. 0. 11. lim arcsin (2-_fL Отв. 0.
а-оеа *-*21Леа —3* + 2
12. hm т-=^—. Отв. 1-^. 13. hm — . Отв. 1.
JK-1 1—|/х» 9 ^..оо X
I ! \ tgA. gX + sin*
14. lim — . Отв. 1. 15. lim —;—:—. Отв. оо.
. lim tg* — -Л :— . Отв. оо. 17. lim : -. . Отв. —-~-
16
Х-+
Замечание. Для приобретения навыка в раскрытии неопределенностей
по правилу Лопиталя желательно также использовать примеры, помещенные
в конце главы III.
% gjji ^
18. Убедиться, что lim —— существует и равен 1, но не может быть
х —*¦ оо X~(*COSX
вычислен с помощью правила Лопиталя.
239

§ 3. ФОРМУЛА ТЕЙЛОРА
Наиболее простой элементарной функцией является многочлен.
Его значения легко вычисляются, в то время как вычисление
значений других функций, например sin л:, In л:, ах, Ух, требует
определенных усилий. Над многочленами весьма просто выполняются
арифметические действия и операция дифференцирования.
Производная от многочлена есть снова многочлен; многочлен непрерывен
в любой точке. Кроме перечисленных, он обладает еще многими
другими «хорошими» свойствами.
Естественно поставить вопрос, нельзя ли другие более сложные
функции заменить многочленами, не допуская при этом больших
погрешностей. Решение этой задачи по отношению к некоторым
функциям оказывается практически возможным с помощью так
называемой формулы Тейлора*.
Пусть сначала треб}/ется многочлен п-й степени Рп (х),
расположенный по степеням х, представить в виде многочлена такой же
степени, но по степеням разности х—х0, где х0— некоторое
фиксированное число. В этом случае задача сводится к нахождению
коэффициентов Л0, Аг, Ао, ..., Ап, при которых выполняется тождество
Рп (х) ^А0 + А1(х-х0) + А2(х-х0)^ + .., + Ап(х-х0)п. (1)
Для этого продифференцируем наше тождество п раз:
Рп (х) =А1 + 2А2(х-х0) + ЗА3(х-х0)2 + ... + пАп(х-х0)п-\
Рп (х) =2А2 + 3.2-А3(х-х0) + ... + п(п-1)Ап(х-х0)п-\
Рп (х) =3! А3 + ... + п (л— 1) (л —2) Ап {х-Хь)п~\
РУ(х) = п\Ап
и в полученных равенствах примем х равным х0. Будем иметь:
Р п\Хо) = А0', Pn\Xo) = Ai\ Рп(х0) = 2А2\
Р;'(*о) = 3!Л3; ...; Р(?(х0)==/г!Л„.
Отсюда получаем искомые значения коэффициентов:
д —р /yv л _Pnjxp). А _Рп(х„)
А _Р"пЫ. . Л _Р^(Хо)
А,—^—, .... Лге-___.
Тождество (1) можно переписать в виде
Рп (X) = Рп (Х0) = ^Р~ (X - Х0) +
+ -^—(х—х0)2+ ...-] ш—(х—х0)п.
* Тейлор, Брук (1685—1731) — английский математик.
240

Коэффициенты нового многочлена оказались выраженными через
значения данного многочлена Рп (х) и его производных в точке х0.
Равенство (2) и называется формулой Тейлора для многочлена.
Возьмем теперь произвольную функцию f(x)y определенную на
[а, Ь] и имеющую в некоторой точке х0 этого отрезка производные
до п-то порядка включительно. Составим формально многочлен:
Pn(x) = f(x0) + ^-(x-x0) +
+ Ц^(х-х0)* + ... + 1^(х-х0)\ (3)
При х = х0 имеем: Pn(xQ)=f(x0). Представляя многочлен Рп(х) в виде
(2), получим в силу тождественности этих представлений:
Рп (Х0) =f'(*0), Рп (Х0)=Г(Хо), • • • , Р{п\Хо)=Г)(Х0).
Таким образом, мы получили, что построенный формально
многочлен Рп (х) и его производные в точке х0 совпадают со
значениями функции f(x) и ее производными в этой точке.
Если f (х) есть, в частности, многочлен степени /г, то Pn(x)=f(x^.
Если же f(x) — не многочлен или многочлен степени выше пу то
такое равенство не имеет места. В этом случае Рп(х) лишь
приближенно представляет функцию f (x) в окрестности точки х0. Разность
f(x) — Pn(x) = Rn(x), очевидно, будет погрешностью, допускаемой
при замене f (х) на Рп(х).
Подставляя в равенство f (x) = Pn(x)-\-Rn(x) вместо Рп(х) его
развернутое выражение, мы получим формулу, также называемую
формулой Тейлора:
f(x) = f(x0) + f-^(x-x0) +
+ ^(x-x0)' + ^.+ ^^(x--xor + Rn(x). (4)
В этой формуле Rn (x) называется остаточным или дополнительным
членом. Если f (х) — многочлен степени п, то Rn(x) = 0.
При х0 = 0 получим частный вид формулы Тейлора:
/М = «0)+^х + ах»+... + ^х» + Щ (5)
которую иногда называют формулой Маклорена.
При решении задачи о замене функции многочленом с помощью
формулы Тейлора особый интерес представляет вопрос об оценке
допускаемой погрешности и о возможностях ее уменьшения.
Поскольку отклонение Рп(х) от f(x) характеризуется функцией Rn(x),
то изучение последней позволит выяснить и вопрос о погрешности.
Но Rn (x) пока еще лишь символическое обозначение остатка в
формуле Тейлора. Прежде чем изучать его поведение, нужно раскрыть
этот символ, то есть выразить его через данную функцию и ее
производные. Существует несколько форм представления Rn(x). Их
241

можно найти, например, в учебнике Г. М. Фихтенгольца fl]. Здесь
мы ограничимся наиболее простой формой остаточного члена,
принадлежащей Лагранжу.
Пусть f(x) имеет в точке х0 и ее окрестности производные до
(л+1)-го порядка включительно. Тогда и Rn(x) = f (х) — Рп(х) тоже
имеет производные до (п+1)-го порядка включительно. Напишем
для f (x) формулу Тейлора (4). Если в ней положить х = х0, то
окажется, что
f (*о) = / (*о) + Rn (*o). то есть Rn (x0) = 0.
Последовательно дифференцируя равенство (4) и подставляя х0 вместо
х, будем получать:
/' (Хо) = F fa) + Rn (Xo), то есть Rn (x0) = 0;
Г (xo) = f"(xQ) + Rmn(xQ), то есть R'n(x0) = 0;
f"W=f"W + K'W, то есть /?;'(*0) = 0;
f{п) (хо) =f{n) (Хо) + R{n] (Хо), то есть Д(? (х0) = 0.
Таким образом, имеем:
Rn (хо)=Rk(хо)=Rn (хо) = R'n (xo)=...=R{'nl) (x0) = 0. (6)
Что же касается (п+ 1)-й производной, то от многочлена п-й степени
Рп(х) она будет равна нулю и, следовательно, получим равенство
K1)(x) = Rnn+X)(x), (7)
справедливое для всех х из окрестности точки х0.
R (х)
Если теперь к выражению . _J \п+1 многократно применить
формулу Коши с учетом свойств (6) (см. 2-е замечание к теореме 4
(Коши), §1), то будем иметь:
RnW = R'nfa) Rn(x2) __
(х-х0)ы (л + 1) (хг-ХоУ (п +1) /г(лг2-*0)"-1
Rn (xs) _ Rn (*n+i)
(n+l)n(n-l)(xs-x0)»-* ••• (n+1)! '
где х± лежит между х и x0, x2 — между хг и x0, а значит, между х
и х0 и т. д., ял+1 лежит между х и х0. Точку лгл+1 теперь уже
удобнее обозначить через с. Тогда из равенства
Rn(x) =R{nn+l)(c)
(x-xQr+i (я+1)!
получаем:
Ыл+О (С)
где с лежит между х и х0.
Так как в силу (7) Rnn+l) (c)=f(n+1) (c)t то остаточный член в
форме Лагранжа представится в следующем окончательном виде:
*"(*)=^тж(*~*оГ1 (8)
242

где с лежит между х и лг0. Последнее иногда отмечают и так:
с = х0 + Ъ(х—*о), где 0<8<1.
Формула Тейлора с остаточным членом в форме Лагранжа
имеет вид:
+ Т} (*-*°)" + ет$ t*-^1- <9)
В частном случае при х0 = 0 имеем формулу Маклорена:
f(x) = f(0) + ^x+^** + ...+
Как видно из (9) и (10), остаточный член тем и отличается от
предыдущих членов, что значение (/г+1)-й производной берется в
какой-то средней точке. И это не случайно. Легко показать, что
формула Тейлора (9) является обобщением известной нам формулы
Лагранжа о среднем значении. Действительно, если в формуле (9)
взять п = 0 и f(x0) перенести влево, то получим: f (х) — f(x0) =
= f (с)(х—х0) или Ay=f (с) Ад:, где е лежит между х и х0.
Рассмотрим несколько примеров приближенного представления
элементарных функций с помощью формулы Маклорена (10).
Пример 1. Пусть f(x) = ex. Тогда f{n) (х) = ех, где /z=l, 2,
3, ... и /(0) = 1, Г(0)=1, ..., fW(0) = l. Следовательно, по фор-
муле (10)
у Y2 уЗ уП рЪх
*-l+K + *+V+-+b+Wm**X- 0<в<1.
Если в этом разложении отбросить остаточный член, то получим:
<?*~1+тт+ш+1т+-+5- (»)
Можно подсчитать и погрешность, допущенную при тгком
представлении ех на некотором отрезке, например на отрезке [0, 1].
Тогда 0 <: х ^ 1 и
РЬх
\Rn(x)\ =
;ХП+1
(/1+1)!'
Из последнего видно, что погрешность стремится к нулю при
возрастании пу то есть если в формуле Тейлора брать все больше
и больше членов. Это значит, что функцию ех на данном отрезке
можно заменить многочленом с любой степенью точности. Так,
если м = 3, то | Rn (х) | <|j, если п = 5, то |#л (*) | < ^д, и т. д.
Можно поставить и обратную задачу: сколько нужно взять членов
разложения в формуле Тейлора для функции ех, заданной на [0, 1],
чтобы при этом погрешность не превышала 0,0001?
243

Для решения этой задачи достаточно решить неравенство
1п-4-1)\ <Q»QQ01- Последнее будет выполняться при п^7 (поскольку
8! > 40 000), а
е 3 3 1
| R1 (х) | < of < о? < Жппп <:
8! ^8! ^40000^10000*
Если в равенстве (11) положить х=1, то получим
приближенное значение числа е:
e^l=±l+^ + ±i + ...+^2,7182.
Пример 2< Пусть f (x) = sinx. Тогда f{n) (A:) = sin (x + n ~) для
п=1, 2, 3, ..., и /(0) = 0, Г(0) = 1, Г(0) = 0, ..., в общем виде
/<*»>(<)) = sin/пя = 0, f(2m-v (0) = sin (тп — ¦?-) = ( — l)m"\ где m =
2,
= 1, 2, 3,... Положив в формуле (10) п = 2т9 можно записать:
уЗ у 5 у2Ш~1
sinx = x-|i + ^-... + (-ir-1^:rnl + /?w.W, (12)
где остаточный член в форме Лагранжа имеет вид:
sin |e* + (2m + 1)^1
#2m (*) = L n , щ—— *2m+1 = ( — l)m cos 6* *,ni .
zm v ' (2m-}-1)! v ' (2m+l)!
Так как |cos6*|^l, то погрешность при отбрасывании
остаточного члена оценится следующим образом:
Формулой (12) можно пользоваться для нахождения
приближенных значений синуса любых углов с любой степенью точности,
так как при любом значении х имеем R2m(x)->0 при т->сх) (см.
пример 1 из § б, гл. III). Погрешность будет зависеть как от га,
так и от х.
Пример 3. Аналогичным образом для функции / (х) = cos x
разложение по формуле (10) при n = 2m+l даст
где
х2т+2
I ^2m+l (Х) |
cos[Qx + (m+\)n] 2m+2
(2m + 2)!
:(2/n + 2)! (2m + 2)!'
Пример 4. Указать некоторый промежуток значений х, при
которых имеет место приближенная формула
COSAT^l—2j + -jj,
с точностью до 0,00005.
Правая часть приближенного равенства составляет пять первых
членов в формуле Тейлора для функции cos x (члены с я и л?
244

равны нулю). Следовательно, должна иметь место следующая
оценка дополнительного члена:
\х\*__х*
|Яб(*)1
6! 61'
Чтобы погрешность была меньше 0,00005, достаточно потре-
бовать выполнения неравенства-^ <0,00005.
Решая это неравенство, получим: \х\ < 0,84. Оказалось, что
указанная точность приближения обеспечивается значениями х,
удовлетворяющими неравенству —0,84 <;*< 0,84.
Так как использованная нами опенка остаточного члена дана
«с запасом», то мы получили не наибольший промежуток, в
котором обеспечивается требуемая точность нашей приближенной
формулы для cos*. Эта точность может быть достигнута и в
несколько более широком промежутке.
Пример 5. С помощью формулы Тейлора вычислить sin 549 с точностью до
0,001.
54 • я. Зя
Градусной мере 549 соответствует —-—=— радиан. Если в формуле Тейлора
для функции sin х положить х = j~r, то для остаточного члена будем иметь
оценку:
/Зя_\2^+1
/Злу ' -1
%2т \ТК
Л(ЗУ___ 1 J Зя
< (2/п+1)1 <(2m+l)!VTaK КЙК Ю <l
Теперь для определения количества членов, которое нужно взять в формуле
Тейлора, чтобы погрешность осталась в заданных границах, решаем неравенства
/о *, 1ч, < 0,001. или (2/и+1)!> 1000.
(2яг+1)1 vi/
Так как уже 7! =5040 > 1000, то из предыдущего получаем: 2т +1 ^ 7, или т ^ 3*
Итак, достаточно положить га = 3, то есть воспользоваться формулой
х3 , хъ
3!+5!
Зя
Подставляя x = jx и производя вычисление с четырьмя знаками после запятой,
находим: sin 54° % 0,8100, или sin 54°^ 1,810. (Сохранять четвертый знак не имеет
смысла, так как мы обеспечили погрешность лишь меньшую 0,001.) По
пятизначным таблицам sin 54° = 0,80902.
Вопросы для самопроверка и упражнения
1. В каком случае остаточный член в формуле Тейлора (4) тождественно
обращается в нуль (при некотором л)?
Отв. Когда / (х) —- многочлен.
2. Почему правую часть в формуле Тейлора (10) нельзя назвать многочленом
(л+1)-й степени (если fix) не многочлен)?
/' (с)
Отв. Потому что коэффициент * Д- при хп+1 не является постоянной
величиной. Его значение зависит от х.
245

3. Разложить многочлен / (*) = *4 + 2л:3 — 8х2-|-4#+4 по степеням (*+!)»
пользуясь формулой Тейлора.
Отв. f (х) = — 9 + 22 (х + 1) + 4 (х + I)2 — 6 (х + l)3-f 2 (х+I)4.
4. Пользуясь формулой Тейлора, разложить функцию f(x) = x6 по степеням
(х+2).
Отв. *в = 64 — 192 (х+2) + 240 (*+2)2— 160 (л:+2)3 + 60 (* + 2)4 — 12(x+2)6 +
+ 2(л: + 2)в.
5. Определить погрешность, допускаемую в приближенном равенстве ех ^^ 1-J-
+А:+1г+*--+оТ на [0,1]- 0тв'0'0002-
6. Разложить по степеням х функцию /(а:) = 1п (1 +*). заданную на отрезке
{0, 1], с помощью формулы Тейлора. Оценить погрешность при отбрасывании
остаточного члена после пяти первых членов. Отв. -^-.
7. Определить значения х, при которых имеет место приближенная формула
х3
sin х*ы х— -57 , с точностью до 0,001.
Замечание. Смотрите примечание к примеру 3, помещенному в
упражнениях к § 1, гл. IV. То же относится и к примеру 9.
Отв. \х\<У0А2^0,65 = 37°\Ь'.
х3
8. Выяснить происхождение приближенного равенства arc sin Jt^»x + -^ и
оценить погрешность для О^х^-^-.
Отв. Приближенное представление arcsin x с помощью формулы Тейлора.
Погрешность меньше 0,03.
9. Определить, используя формулу Тейлора, значения х, для которых cos*^
«« 1 — у, с точностью до 0,0001. Отв. \х\<0,222^ 12°30\
10. Сколько нужно взять членов разложения функции f(x) = sinx в формуле
Тейлора, чтобы полученный многочлен отличался от sin x на отрезке [0, 1] меньше,
чем на 0,001? Отв. Три члена.
11. Вычислить tg46° с помощью формулы Тейлора, взяв три первых члена
разложения функции f(x) = tgx. Результат сравнить с табличным.
o™.,g,=,+2(,-i)+2(,-f)'+rf>(,-4)\
tg46° =1+2(^+2^^ =1,0355 (по табл. tg 46° = 1,0355).
12. Вычислить значение cos 32° с точностью до 0,0001, пользуясь разложением
функции /(a:) = cosa: по формуле Тейлора. Результат сравнить с табличным.
Отв. cos 32° ^ 0,8480 (по табл. 0,84805).

ГЛАВА VII
ИССЛЕДОВАНИЕ ФУНКЦИЙ И ПОСТРОЕНИЕ ГРАФИКОВ
Данная глава является последней и завершающей главой в курсе
дифференциального исчисления. Основным содержанием ее является
исследование функций и построение графиков. Это — важнейшие
практические результаты математической теории. Аппарат
дифференциального исчисления представляет возможность для создания
более совершенных методов исследования функций. С помощью
производных первого и второго порядка можно, оказывается,
достаточно быстро и полно выяснить все наиболее характерные особенности
в поведении той или иной функции.
Из самых различных областей науки и техники возникает большое
количество практических задач, решение которых связано с
исследованием функций и, в частности, с нахождением наибольших
и наименьших значений. Вместе с тем рассматриваемые в главе
вопросы будут неоднократно встречаться и при дальнейшем изучении
математического анализа.
В данной главе следует особое внимание обратить на
практическую сторону вопроса, то есть на методику исследования функций,
построения графиков и решения задач.
§ 1. УСЛОВИЯ ПОСТОЯНСТВА, ВОЗРАСТАНИЯ И УБЫВАНИЯ ФУНКЦИЙ
Теорема 1. Пусть на [а, Ь\ определена непрерывная
функция f(x), имеющая на (af Ь) конечную производную. Тогда:
(1) Для того чтобы f(x) была постоянной на [а, Ъ\,
необходимо и достаточно, чтобы f (х)=0 для всех х из (а, Ь).
(2) Для того чтобы f(x) была возрастающей
{убывающей) на [а, Ь] в широком смысле, необходимо и
достаточно, чтобы f (x)^0 (f (х)^0) для всех х из (а, Ь).
(3) Для того чтобы f (х) была возрастающей (убывающей)
на [а, Ь] в узком смысле, достаточно выполнения условия
f (x)>0 (/'С*0<°) для всех х из (а, Ь).
Доказательство (1). Необходимость условия очевидна,
так как известно, что производная от постоянной функции равна
нулю. Докажем достаточность. Из условия теоремы следует, что
функция f(x) удовлетворяет всем условиям теоремы Лагранжа
247

¦о конечном приращении. Следовательно, для нее можно написать
формулу Лагранжа на отрезке [а, х], где х—любая точка из [а, Ь]:
f(x) —f (a) =f' (с) (х—а) (а<с<х).
Так как по условию f (с) = 0, то получим, что f{x)=f{a) в любой
точке х из [а, Ь]. Справедливость утверждения (1) доказана.
(2). Докажем это утверждение для случая возрастающей
функции. Случай убывания рассматривается аналогично.
Необходимость условия. Пусть f (х) монотонно возрастает; тогда
для любых точек х и х0, удовлетворяющих условию а<С.х0<Сх<.Ьу
выполняется неравенство f (x) ^f(x0). Следовательно, _ ^0.
Переходя в последнем неравенстве к пределу при х->х0) получим:
f (х0)^0. Так как х0 — произвольная точка из (а, 6), то этим
необходимость условия доказана.
Достаточность условия. Пусть f (х) ^ 0 в каждой точке х из
(а, Ь). Воспользуемся формулой Лагранжа на произвольно
выбранном отрезке [х\ х"] из [а, 6]:
fW)—f (*') = !' {с)(хГ — х'), где х'<с<х\
Так как f (с)^0 и х" >х\ то и f (x") ^f(x'), что и требовалось
доказать.
(3). Пусть на (a, b) f (х)>0. Возьмем из отрезка [а, Ь] две
произвольные точки хх и х2 (x1<zx2). Применим к f (х) на [xl9 х2]
формулу Лагранжа. Получим:
f (х*) — / (*i) = Г (с) (*2 — *х), где хх < с < х2.
Так как f (с) >0 и х2>х1у то f (x2) —f(Xi) >0, то есть f (x2) >/ (%).
А это и значит, что f(x) на [а, Ь] строго возрастает. Случай,
когда /' (х) <С 0 рассматривается
ум* о аналогично.
— Заметим, что условие /' (х)>0
• A (f' (x) <. 0) не является необхо-
fMbO J/ Ч fbi^o димым для строгого возра-
/ ^/^ Ns^ л у стания (убывания) функций.
/^ ^V Строго монотонная
дифференту^ цируемая функция в отдельных
_ ' точках может иметь производ-
* ' *х ную, равную нулю (рис. 95).
р д5 В качестве конкретного
примера можно рассмотреть
функцию у = х3. Эта функция строго
возрастает на (— оо, +оо), так как при x1<zx2 имеем: х\<.х\. Но
ее производная у' =3х2 равна нулю при х=0.
Если вспомнить, что значение производной /' (х) в данной
точке х0 есть угловой коэффициент касательной к кривой y=f(x)
в точке (xQi f(x0)), то доказанные условия постоянства и
монотонности функции становятся еще более наглядными (рис. 95).
248

Замечание. Обращаем внимание читателя на то, что в
данной теореме доказана монотонность функции / (х) в некотором
промежутке [а, Ь] в предположении
f (х) ^ 0 (> 0) или f'(x)<:0 (< 0)
внутри всего этого промежутка. Если
же известно, что/'(л:0) >0{<0) в одной
точке х0) то отсюда нельзя заключить,
что / (х) монотонна хотя бы в малой
окрестности точки х0. В качестве
примера рассмотрим функцию
f(A;)==f T + *2sinT ПРИ х^°*
{ 0 при х = 0
(рис. 96). Ее производная f'(x) =-н- +
А Рис. 96.
+ 2х sin cos — . Значение /'(0) из
' X X I \ /
этой формулы получить нельзя, так как при х = 0 выражение
— теряет смысл. Найдем f'(0), исходя из определения производной:
f'(0) = Umnx)-ff>=lim
Х , 9 • 1
- =lim(-o- + x
*-*0 \'
Покажем, что, хотя f'(O)X), тем не менее ни в какой окрестности
нуля функция не монотонна. Действительно, если взять точки
1 = —у < 0. Если же взять точки xk
±2, ±3, ...), то f'{xk)=ff
1
(2?+1)я
(26 + 1) я (* —±1»
=1—cos {2k+\)n=\+ 1 =¦
= "2">0. Выбранные нами точки xk и x'k попадают в любую
окрестность нуля, так как xk->0 и 4->0 при &->оо. Следовательно,
производная функции меняет знак в любой окрестности нуля, что
и доказывает наше утверждение. Этот факт имеет место, очевидно,,
из-за того, что производная /' (х) в нуле имеет разрыв.
Пример 1. Определить промежутки, на которых функция / (х) — 3х2—2х
возрастает и убывает в строгом смысле.
Находим производную функции f'(x) = 6x — 2. Из неравенств 6л:—2 > 0 и
/ 1 \
6* — 2<0 получаем, что данная функция возрастает на (-_-, + оо) и убывает
/ Г
на ( — оо,
Пример 2. Определить промежутки возрастания и убывания функцир
у = ех + 5х*
Находим производную у' —ех+Ъ. Поскольку ех">0 при всех х, то и у' > 0-
на всей числовой оси. Следовательно, данная функция строго возрастает на всей
оси ( — оо, +оо).
249

Пример 3. Показать, что ех>1-\-х для всех вещественных значений
х^О.
Рассмотрим функцию f(x)=ex—х—1 (— оо<;е<;+оо). Ее производная
/' (х) — ех— 1 отрицательна при х<0, положительна при х>0 и равна нулю
в точке х = 0. Следовательно, данная функция слева от нуля строго убывает,
а справа —строго возрастает. Так как в точке # = 0 значение функции равно
нулю, то все остальные ее значения будут положительными, то есть ех—-х— 1 >0.
Отсюда получаем, что ех>х-\-\ при всех xzfiO.
Пример 4. Доказать тождество
1 х2
arccos 1 2 = 2 arctg х при 0 ^ х < + со.
\ х2
Рассмотрим функцию / (*) = arccos —2aEctg;t на промежутке (0, +оо).
1 -\- х
Ее производная на этом промежутке равна:
— 1 —4х 2
ПФ
VH&.
(1+*2)2 \+х2~
4х 2 2 2
/(l^Jt2)2 —(1 — Х2)2(1+Х2) 1-Х2 1+Х2 1+Х2
На основании теоремы о постоянстве функции заключаем, что / (х) является на
[0, +оо) постоянной, то есть
1-х2
f (х) = С или arccos . 2 — 2 arctg х = С, где С = const.
1 -\- х
Для определения постоянной С воспользуемся тем, что последнее равенство есть
тождество, то есть справедливо при любом х^О. Дадим переменной х какое-
нибудь значение, например х = 0. Тогда С = arccos 1—2 arctg 0 = 0.
Итак, мы доказали справедливость тождества
arccos -г—.—5- — 2 arctg x = 0
\+х2
на [0, +оо). Этим и завершено решение задачи.
Пример 5. Выяснить, существуют ли промежутки, на которых функция
2х
f (х) = arctg -: g — 2 arctg x равна постоянной, и найти эту постоянную.
Данная функция определена на промежутках ( — со, —1), (—1, 1) и (1, +оо).
Следовательно, сформулированный в теореме признак постоянства функции можно
применять лишь для каждого из этих промежутков в отдельности. Производная
функции в области ее существования:
Г ,,л * 2(1-*) + 2*.2* 2_ = _? 2_
1 1 / 2х V ' (1—^2)2 i+*2 i+*2 i+*2
Следовательно, на каждом из промежутков f (х) постоянна, f(x) = C. Однако
из этого не следует, что значения С на промежутках должны быть одинаковыми.
Для отыскания С достаточно (см. пример 4) взять по одной точке из каждого
промежутка и вычислить значения функции в этих точках. При этом
целесообразно выбрать такие точки, в которых значение f (х) вычисляется как можно
проще. Например, на промежутке (—1, 1) удобно взять точку #=0, на(1, -f-°°) —
точку л; = 1^3" и на ( — со, 1) —точку *=—1^3. Получим: /(0)=0,/(>^3) = —я
и /(—Уъ ) = зт. Следовательно, /(л:) = 0 на всем промежутке (—1, 1), /(*) = — я
на всем (1, +оо) и /(*) = я на всем (—со, — 1).
250

Для определения постоянных значений функции на двух последних
промежутках можно поступить и иначе. Именно, вычислим пределы: lim f(x)=n>
Х-*—СО
lim /(*) = —я.
х-*--\-оо
Так как f (х) на каждом из этих промежутков постоянна, /(*) = С, то можно
утверждать, что С = я на (— со, —1) и С = —я на (1, +оо).
Вопросы для самопроверки и упражнения
I. Доказать пункты (2) и (3) теоремы 1 для случая убывания функции.
В задачах 2 — 6 определить промежутки возрастания и убывания функций.
Отв. Возрастает на (—сю, —2) и (—2, 0), убывает на (0, 2) и (2, +оо).
3. /(*) = *)/ 4х—х2. Отв. Возрастает на (0, 3), убывает на (3, 4).
4. /(*) = 1п (х + У \+х2)- Отв. Возрастает на ( — со, + °°).
5. f (х)=2х2 — \пх. Отв. Возрастает на (-^-, со), убывает на (0, -^-\
6. /(х) = 3д: — х3. Отв. Убывает на (—со, —1) и (1, -f-co), возрастает на (—1,1).
7. Показать, что если /' (х) непрерывна в точке х = х0 и /' (х0) > 0, то f (х)
возрастает в некоторой окрестности этой точки.
8. Обязательно ли производная монотонной функции является функцией
монотонной? Рассмотреть примеры: а) / (х) = х + sin х\ б) /(*)=—; в) f(x)=ex.
Отв. Нет, не обязательно.
9. При каких значениях коэффициента а функция f(x)=x3 — ax возрастает
на всей числовой оси? Отв. а^0.
10. При каких значениях коэффициента Ь многочлен Р2 (х) = х2 — Ъх + 5
убывает на отрезке [ — 1, +1]? Отв. Ь^2.
II. Показать, что функция y = x — sinx нигде не убывает.
12. Показать, что функция y — arctgx — х нигде не возрастает.
§ 2. ЭКСТРЕМУМ ФУНКЦИИ. НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ
Одна из задач математического анализа состоит в том, чтобы
для каждой конкретно заданной функции f (х) установить: а) каковы
участки ее возрастания и убывания, б) имеет ли функция такую
точку х (одну или несколько), в которой ее значение является
наибольшим или наименьшим по отношению к значениям в достаточно
малой окрестности этой точки (х — б, х-\-д). Если в некоторой
окрестности точки х0(х0 — б, х0 + б) непрерывная функция f (х) слева от Хк
возрастает, а справа — убывает, то, как легко видеть, значение f (х0)
будет наибольшим в этой окрестности (рис. 97). В этом случае
говорят, что в точке х0 функция f (х) имеет максимум. Если же,
наоборот, в окрестности (х0 — б, х0 + 6) слева от х0 функция убывает,
а справа—возрастает, то/(л:0) будет наименьшим значением в
окрестности (рис 98). В этом случае говорят, что в точке х0 функция
имеет минимум.
Дадим строгое определение максимума и минимума функции.
Определение. Функция /(*), заданная на некотором
промежутке, имеет максимум (минимум) в некоторой внутренней точке х(
из этого промежутка, если существует такая окрестность (xQ — б, х0 + д)
251

Рис. 97.
VA
x-6 xQ x0 + 6
Рис. 98.
точки х0, что для всех х из этой окрестности (кроме х0) справедливо
неравенство
f(x)<f(x0) (f(x)>f(xQ)).
Значение f (x0) в этом случае называют значением максимума
(минимума) функции (рис. 97 и 98).
Заметим, что ради удобства часто слова «максимум» и «минимум»
заменяют одним словом «экстремум», а значения максимума и
минимума называют экстремальными значениями функции. Латинское
слово «extremum» означает «крайнее» значение.
В определении экстремума существенно, чтобы точка х0 была
внутренней точкой того промежутка, где функция задана, так как
требуется, чтобы функция имела смысл во всех точках некоторой
окрестности (х0 — б, лг0 + б).
Укажем в заключение, что понятие экстремального значения
функции нельзя смешивать с понятием наибольшего и наименьшего
значений функции на всем промежутке ее задания. Экстремальное
значение функции в точке есть максимальное или минимальное
значение по отношению к близлежащим значениям. Так, например, если
в некоторой точке х0 функция имеет максимум, то это значит, что
значение f(x0) является наибольшим по сравнению со значениями
в некоторой окрестности (х0 — б, х0 + б). По сравнению с другими
значениями f(xQ) может оказаться и не наибольшим. Когда же
говорят о наибольшем значении функции на отрезке [а, Ь], то под этим
понимают такое ее значение, больше которого нет ни в одной точке
этого отрезка, включая и концы. Отсюда получается, что
наибольшим значением функции на отрезке может быть либо одно из
максимальных значений, либо значение на одном из концов отрезка Так,
на рисунке 99 функция имеет максимум в точках л:2, л:4 и л:6, а
наибольшее значение — в точке х = Ьу минимум — в точках хъ х3, хъ и х7,
а наименьшее значение — в точке х3.
Чтобы найти наибольшее значение функции на [а, Ь] чисто
аналитическим путем, нужно, очевидно, отыскать все ее максимальные
значения и значения на концах отрезка. Затем, сравнив полученные
числа, выбрать наибольшее. Подобным образом определяется и
наименьшее значение функции.
152

После того как стала ясна идейная сторона вопроса, мы
постараемся найти практические способы обнаружения точек, в которых
данная функция имеет экстремум и какой именно — максимум или
минимум. Для этого займемся исследованием функций с помощью
дифференциального исчисления.
Пусть f (х) определена на [а, Ь] и в точке х0 этого отрезка имеет
экстремум (максимум или минимум). Это значит, что найдется такая
окрестность (х0 — б, х0 + 6), в которой f(x0) будет наибольшим или
наименьшим значением. Тогда по теореме Ферма, если в точке х0
существует конечная производная, то она должна быть равна нулю,
то есть /'(л:0) = 0.
Таким образом, необходимым условием существования
экстремума в точках, где существует конечная
производная, является обращение в нуль производной.
Чтобы найти точки, в которых производная равна нулю,
достаточно выражение производной приравнять нулю и решить
полученное уравнение. Предположим, что для некоторой функции
определены таким образом все точки,
где производная равна нулю. Можем
ли мы быть уверенными в том, что во
всех этих точках экстремум существует? Y J|t
Оказывается, нет. Производная может
равняться нулю и в точках, где
экстремума нет. Так, например, функция
f(x) = x? имеет производную f'(x) = 3x2,
которая при л: = 0 равна нулю, но в этой
точке, как легко видеть, экстремума
нет (рис. 100). Следовательно,
указанное условие не является достаточным
для существования экстремума.
Точки, в которых производная
равна нулю, называются
стационарными точками. В них изменение
функции как бы приостанавливается, скорость
изменения обращается в нуль. Мы в даль- Рис. 100.
Л
253

f'(x) несущ.
fU-Oh-
f'fxjHecyiM.
Рис. 101.
нейшем будем называть такие точки «подозрительными на
экстремум». Дальнейшее исследование должно подтвердить или
отвергнуть «подозрение», павшее на точку, где производная равна нулю.
Кроме стационарных, к числу «подозрительных» на экстремум
точек следует также отнести и точки, в которых производная
обращается в бесконечность или вовсе не существует. Среди них также
могут быть точки экстремальные, как это видно из рисунка 101.
Итак, представим себе, что все точки, «подозрительные» на
экстремум, нами определены. Чтобы решить вопрос до конца,будет ли в той
или иной из этих точек экстремум, следует подвергнуть каждую точку
в отдельности дополнительному исследованию.
Первый способ исследования. Пусть х0 — одна из
«подозрительных» точек. Предположим, что в некоторой окрестности этой
точки (х0— б, лг0 + б), за исключением, может быть, самой точки х0>
существует конечная производная, имеющая на (х0— б, л:0) и (х0, х0-\-8)
постоянные знаки. В зависимости от распределения знаков
производной слева и справа от х0 возможны следующие случаи:
1-й случай. /'(*):> 0 при х<.х0 и f'(x)<c0 при х>х0. По
теореме 1 из предыдущего параграфа это означает, что слева от Xq,
функция f (x) возрастает, а справа — убывает. Значение f(*0), таким
образом, является наибольшим в рассматриваемой окрестности, то
есть в точке х0 функция f(x) имеет максимум.
2-й случай. /'(*)<!0 при х<х0 и /'(#)>0 при х>х0.
Значит, f(x) слева от х0 убывает, а справа —возрастает; f(xQ) будет
наименьшим значением функции в некоторой окрестности точки х0, то
есть в точке х0 — минимум.
3-й случай. /'(*)> 0 при х<Сх0 и f'(x)>0 при х>х0 или
f'(x) <0 при х<х0 и f (х) <0 при х> х0. Это значит, что / (х) либо
всюду возрастает, либо всюду убывает. Следовательно, в любой
окрестности точки х0 найдутся значения как большие, так и
меньшие, чем /(х0),
мума (рис 102).
то есть в точке х0 нет ни максимума, ни мини-
254

\у'<о
\j'-0
</<
о\
/у
Ч'=0^у
•>о
0
/ ]
у'= -оо
h?P
, s&
Y
X
Рис. 102.
Итак, если производная функция при переходе через точку
х0 меняет знак, то в этой точке функция имеет экстремум.
Это условие является достаточным для существования
экстремума. При перемене знака производной с плюса на минус
в точке х0 функция имеет максимум, с минуса на плюс —
минимум. Если же при переходе через точку х0
производная знака не меняет, то в этой точке экстремума нет.
Полученные нами результаты для функции/(х), у которой
/7(л;0):=:0, можно свести в следующую таблицу:
Знак /' (х) при
х0 — 6 < х < х0
1+ 1 +
Знак /' (*) при
I++I
Заключение
Максимум
Минимум
) Экстремума
J нет
Пример 1. Исследовать на экстремум функцию у — -^ *3—^-х2~{-6х.
Находим производную: у' — х2—-Ъх-\- 6. Приравниваем ее нулю: х2— 5* +
-Ь 6 = 0. Корни этого уравнения хг = 2 и х2 = 3 определяют стационарные точки.
Поскольку производная всюду существует и конечна, то в данном случае других
точек, «подозрительных» на экстремум, нет. Проверим достаточные условия
экстремума. Для этого производную удобнее представить в следующем виде: у' =
=t*-2) (*-3).
1) Исследуем точку хг = 2. Если х < 2, то у' > 0; если 2 < х < 3,то у' < 0.
Следовательно, в точке хг функция имеет максимум. Значение функции в этой
точке ^2=i-23-A.22 + 6-2 = 4 -|.
2) Исследуем точку *2 = 3. Имеем: w'<G при 2<х<3 и г/'>0 при #>3.
1 5
Следовательно, в точке #2 —минимум. Значение функции у \х_2 = -«- • З3—— • 32-{-
О Z
+6.3-4.
Используя сведения, полученные о данной функции, и учитывая, что у = 0
при х=0г можно получить ее приближенное графическое изображение (рис. 103).
255

Рис. 104.
Замечание. Если функция имеет несколько точек,
«подозрительных» на экстремум, то при исследовании каждой из них
нужно проследить за знаком производной в непосредственной
близости слева и справа. Иначе исследование может дать неверный
ответ. Так, например, на рисунке 104 в точке х0 функция имеет
минимум. Но если взять слева от х0 точку х', а справа—точку х\
то в точке х0 экстремума не обнаружится, так как /'(л/)>0 и
f'(x")>0. Все это произойдет только потому, что точка х' взята
слишком далеко от ха, настолько далеко, что между х' и х0
оказалась вторая «подозрительная» на экстремум точка хг. Во избежание
подобных недоразумений рекомендуется поступать следующим
образом.
Пусть функция f(x) в области ее задания [а, Ь] имеет конечное
число точек, «подозрительных» на экстремум, а между ними f(x)
непрерывна. Расположим эти точки в порядке возрастания:
я < *i < х2 < xs <... < хп < Ь. (1)
В каждом из интервалов
, . . . ,
(*п, Ь)
существует конечная производная /' (х) Ф 0, так как точки, в
которых производная равна либо нулю, либо бесконечности, либо вовсе
не существует, включены в число точек (1). Кроме того, на каждом
из интервалов производная /' (х) имеет постоянный знак, так как
если бы на некотором из интервалов она меняла знак, то (в силу
непрерывности f (x) внутри этого интервала) нашлась бы точка,
в которой f (х) = 0, что невозможно. Следовательно, знак
производной /' (л:) в любой точке интервала будет знаком, соответствующим
всему интервалу. Взяв в качестве «пробы» по одной точке из
каждого интервала, получим некоторую последовательность знаков
f (x). Это позволит сразу решить вопрос об экстремуме функции
в каждой из точек, «подозрительных» на экстремум.
25G

П р и м е р 2. Исследовать на экстремум функцию у = (х—2)2 (х-\- I)3.
Функция определена и непрерывна на всей оси ( — оо, +оо). Ее производная
[/'=2(;с~2)(л:+1)з + 3(л:---2)2(л;+1)2==(а'--2)(д;+1)2(2л:+2 + Зд:--6) = 5(л:-2)х
X (*+1)2(*—=-) всюду конечна. Следовательно, «подозрительными» на экстремум
будут лишь стационарные точки. Решая уравнение
(х —2)(дс+1)*(х—-J-)—0t
получим: *х= — 1, ^2 — -^-, х3 = 2. Область определения функции разобьется этими
точками на следующие интервалы: ( —оо, —1), ( —1» -?-), (-*-, 21, (2, +со).
Определение знака производной в каждом из интервалов можно провести по
следующей условной схеме:
X
(х-2)
<*+1)2
К)
Знак у'
— оо<х< — 1
—
+
—
+
4
— 1 <*<1Г
о
—
+
—
+
А<*<2
—
+
+
—
2<х< + оэ
+
+
+
+
В этой схеме по строкам выписаны знаки каждого из переменных
сомножителей выражения у' в каждом из указанных интервалов. Положительный
коэффициент 5 на знак у' не влияет.
Распределение знаков у' по интервалам (нижняя строка) дает право заклю-
4
чить, что в точках хг = — 1 экстремума нет, в точке х2=-^—максимум: ух=0$ =
1244
= 8;jrxF%8,4, в точке х3 = 2 — минимум: ух=2 = 0.
Заметим также, что постоянство знака производной внутри
каждого из интервалов указывает на монотонность функции в каждом
интервале. Если учесть еще, ^что у = 0 при х = — 1 и у = 4 при
х = 0, то можно примерно представить себе график этой функции
(рис. 105).
Пример 3. Исследовать на экстремум функцию у = х
1
2 ~з 2
Производная у' =
-х =-
не обращается в нуль ни при каком конечном
3" ЪУх
значении х. В точке лс = 0 она не существует. Следовательно, единственной
точкой, «подозрительной» на экстремум, является точка х = 0. Так как г/'<0 при
х<0 и #'>0 при #>0, то в точке х = 0 функция имеет минимум, у\х==0 = 0.
График этой функции дан на рисунке 106.
257

Второй способ исследования. Пусть л;0—-точка,
«подозрительная» на экстремум, в которой f'(xo) = 0. Предположим,
что в этой точке существует вторая производная f"(x0)*?0. По
определению второй производной
rw-Hm f'(*>-n*o)=limm.
Х-+ХС Х Х<> Х-+Х9Х Х0
На основании теоремы 3 из § 3 главы III можем утверждать, что
для ху достаточно близких к х0, выражение
будет одного
знака с f"(x0).
1-й случай. /"(#0):>0. Тогда для х, достаточно близких к х0,
>0, то есть f'(x) и х—х0 будут одного знака. Значит, если
х<.х0, Tof (x)<0; если лг>л:0,
то f'(x) >0. Получили, что
первая производная при переходе
через точку х0 меняет знак с
минуса на плюс. Тогда, при-
Рис. 105.
Рис. 106.
меняя первый способ исследования, заключаем, что в точке х9
функция имеет минимум.
2-й случай. f"(x0)<0. Тогда для х, достаточно близких к х0,
Г (х)
—— <0, то есть ['(л;) и х—х0 будут разных знаков: если л;<х0,
X Xq
то f (л;) >0; если x>xQy то /'(х)<0. Оказалось, что первая
производная при переходе через точку х0 меняет знак с плюса на
минус. Значит, в точке х0 функция имеет максимум.
Полученные нами результаты исследования можно представить
в виде следующей таблицы:
гм
0
0
Знак /"(*о)
+
Заключение
В точке х0 минимум
В точке х0 максимум
Пример 4. Исследовать на экстремум функцию примера 1 вторым способом.
1 5
В примере 1 рассматривалась функция f(jc) = -x'3--x2 + 6^. Там же >ста-
258

новлено, что точки х1 = 2 и *2 = 3 являются «подозрительными» на экстремум.
Находим вторую производную: f" (х) = 2х—5.
Так как f" (2) = 2-2—5<0, то в точке %! —максимум.
Так как /" (3)==2« 3—5>0, то в точке х2 — минимум.
Замечание. Если сравнить между собой два рассмотренных
нами способа исследования функций, то второй способ оказывается
практически более удобным, так как он быстрее приводит к цели.
Но, к сожалению, он не всегда применим. Случаи, когда первой
производной в исследуемой точке не существует, а также когда
вторая производная равна нулю, этим способом исследования не
охватываются. Иногда и вычисление втррой производной настолько
громоздко, что проще воспользоваться первым способом
исследования.
Пример 5. Каковы должны быть коэффициенты р и q трехчлена х2-\-рх-\-
+ q, чтобы этот трехчлен имел при х = 3 минимум, равный 5?
Рассмотрим функцию f (x) = x2 + px-\-q. Ее производная /' (х) = 2х-\-р везде
имеет конечные значения. Следовательно, минимум функции в точке х = 3 будет
в том случае, если /'(3) = 0, то есть 2-3-}-/? = 0. Из последнего получаем, что
р = —6. Для определения коэффициента q воспользуемся тем условием, что
f (3) =5. Тогда З2 — 6-3 + q = 5, откуда 4=14. Задача решена: искомый трехчлен
имеет вид: х2 — 6х+14.
В заключение параграфа остановимся на задачах другого типа,
связанных с предыдущим. Пусть требуется найти наибольшее и
наименьшее значения функции /(л-), непрерывной на отрезке [а, Ь]. По
второй теореме Вейерштрасса такие значения существуют. При этом
они могут достигаться как во внутренних точках отрезка, так и на
его концах. Однако если наибольшее (наименьшее) значение функции
достигается в какой-нибудь внутренней точке xQ, то х0 обязательно
будет точкой максимума (минимума). Следовательно, чтобы найти
наибольшее и наименьшее значения функции f(x) на [я, 6], нужно:
1) найти все точки максимума и минимума, лежащие в интервале
(а, &);
2) вычислить значения функции во всех этих точках, а также
значения на концах отрезка, то есть f (а) и f (b)\
3) из всех полученных значений функции (как правило, их будет
конечное число) выбрать наибольшее и наименьшее.
Пример 6. Найти наименьшее и наибольшее значения функции у ==х* — 2х2 -J--5,
заданной на отрезке [ — 2,+2].
Исследуем функцию на экстремум. Находим первую производную: у'=4х3—
— 4х = 4х(х2— 1). Решаем уравнение 4х(х2— 1) = 0 и находим стационарные точки:
х1==0, х2— — 1, *з=1- Других «подозрительных» точек нет. Проверим вторым
способом достаточные условия экстремума в этих точках. Находим вторую
производную: #"=4 (Зл:2— 1). Так как у" \ _0= —4 <0, то в точке хг — максимум, у l^.o^
= 5; так как у" \x=s+ j = 8 >0, то в точках х2 и x3—MmmMyM,yXsss+l=4.
Определяем значения функции на концах отрезка: г/ |x 2 = г/Лг-2= 13.
Сравнивая экстремальные значения функции и значения на концах,
заключаем, что у = 4 является наименьшим, а #=13 — наибольшим значениями функции
на указанном отрезке.
Замечание. Решение данной задачи можно было бы упростить,
ограничившись только вычислением и сравнением значений функции
259

в стационарных точках и на концах отрезка, не проводя
исследования на экстремум в каждой из стационарных точек. Так как
наибольшее и наименьшее значения должны достигаться в одной из
перечисленных точек, то при сравнении значений функции в этих
точках они непременно будут обнаружены.
Сделанное замечание имеет общий характер. Именно, несколько
упрощая указанный выше способ отыскания наибольшего и
наименьшего значений функции, можно придать ему следующую форму.
Правило. Чтобы найти наибольшее и наименьшее
значения функции f(x) на отрезке [а, Ь\, нужно:
1) найти все точки, «подозрительные» на экстремум, то
есть стационарные и такие, в которых функция не
дифференцируема,
2) вычислить значения функции во всех этих точках, а
также значения на концах отрезков: f(a) и f(b),
3) из всех полученных значений выбрать наибольшее и
наименьшее.
Вопросы для самопроверки и упражнения
1. Может ли значение максимума некоторой функции оказаться меньше, чем
значение минимума этой же функции? Отв. Да.
2. Пользуясь второй теоремой Вейерштрасса, пока *ать, что между двумя
максимумами (минимумами) непрерывной функции имеется минимум (максимум) этой
функции.
3. Известно, что если функция f (х) слева от х0 возрастает, а справа убывает»
то в точке х0 имеет место максимум. Справедливо ли обратное утверждение? Отв. Нет.
4. Может ли монотонная функция иметь экстремум? Отв. Нет.
5. Исследовать на экстремум и построить графики следующих функций:
1) у=х2 — 6х-\-8. Отв. min при х = 3.
2) y — xz—12л;-f 1. Отв. max при х=—2, min при х — 2
о
3) у = х2 (х — 4). Отв. max при л: = 0, min при x — -^-t
,v ^ я . 5я п
4) у = smAT + cosA:. Отв. max при х = -т-, min ПРИ л:==~г» пеРи°А *п.
5) у = х2-е~х. Отв. min прил: = 0, max при х = 2.
6) у = ех-{-е~х. Отв. min при х=0.
х
7) г/= — . Отв. min прил: = е.
"In л:*
10л-
"4 + *8*
8) У = А, z* Отв. min при *= — 2, max при л; = 2.
лч , cos 2л:
9) y = cosx-i ?г-.
2я
Отв. max при x = kn, min при x = 2kn ±-~- (6 = 0, ± 1, ±2,...).
10) х=-.—,\ч , 1 , 1Ч. Отв. Экстремума нет.
' (*+1)(х2-}-1)
6. Может ли функция, имеющая максимум (минимум), не иметь наибольшего
(наименьшего) значения? Может ли функция, имеющая наибольшее (наименьшее)
значение, не иметь максимума (минимума)? Отв. Да (в обоих случаях).
260

7.Найти наибольшие и наименьшие значения на указанных промежутках
следующих функций:
1) у= \х\ при — 1 ^х^ 1. Отв. 1 и 0.
2) у = Е(х) при — 2^х*=с1. Отв. 1 и —2.
3) у = х3 — 6х при — 3^х^4. Отв. 40 и —9.
4) у = х + 2Ух при 0^д:^4. Отв. 8 и 0.
8. Существуют ли наибольшие и наименьшие значения на указанных
промежутках у следующих функций:
1) у = х2 при 0<:дс^ 1. Отв. Наименьшее не существует, наибольшее равно I.
2) t/ = cosjc при ~-=^:#<Ся.
Отв. Наименьшее не существует, наибольшее равно 1.
3) у = — при 0 < х ^4. Отв. Наибольшее не существует, наименьшее равно -j-.
4) у = arcsin х при — 1 < л: < 1 ?
Отв. Функция не имеет ни наибольшего, ни наименьшего значения.
я
9. Доказать, что функция /(*) = * sin— имеет бесконечное множество точек
максимума и бесконечное множество точек минимума в любой окрестности нуля.
Указание. Смотри задачу 6 из упражнений к § 1, гл. VI.
§ 3. ИССЛЕДОВАНИЕ ФУНКЦИЙ И ПОСТРОЕНИЕ ГРАФИКОВ
До сих пор мы строили графики функций примерно следующим
способом. Пусть требуется построить график функции у = f(x),
определенной на [a, b].
1. Строим оси координат и выбираем масштаб.
2. Выбираем произвольным образом некоторые точки из [а, Ь\:
*ъ хъ хз> •••» хп и вычисляем значения функции в этих точках:
tfi = f(*i). i/2=*f(*2)> 03 = f(*s)> ••> Уп = !(хп)-
3. На плоскости отмечаем точки, соответствующие парам чисел
(*ъ УгЪ fe Jfe). (*з> </з)> •¦•> (*п, Уп)-
4. С помощью лекала соединяем точки плавной кривой и
получаем приближенное графическое представление данной функции.
Изложенный способ обычно называют способом построения «по
точкам». Следует отметить, что он прост по идее и сравнительно
быстро приводит к цели. В случаях, когда функция непрерывна
и изменяется довольно плавно, такой способ может обеспечить и
необходимую степень точности графического представления. Для этого нужно
только брать побольше точек из [а, 6], чтобы достичь определенной
густоты их размещения.
Предположим теперь, что функция в отдельных местах имеет
особенности в своем «поведении»: либо ее значения где-то на малом
участке резко меняются, либо имеют место разрывы. В качестве
примера такой функции рассмотрим функцию, истинный график
которой дан на рисунке 107 сплошной линией. При построении графика
этой функции по точкам очень маловероятно, что он получится
таким, каким должен выглядеть фактически. Точки а, {} и у могут
не попасть в число произвольно выбираемых значений х, и график
окрестности этих точек может оказаться далеко не похожим на истин-
261

ный. Наиболее существенные части графика таким способом могут
и не быть обнаружены. Получим в качестве наиболее вероятного
график функции, отмеченный на чертеже пунктирной линией. Только
лишь по счастливой случайности выбор значений*может пасть,
например, на значение а. Тогда после вычисления значения функции в этой
точке и сравнения его с другими значениями будет обнаружен
сильный скачок функции в этом месте. Насторожившись, постараемся
путем добавления новых точек в окрестности точки а уточнить
положение графика в этом месте. Но разве можно рассчитывать на такую
случайную удачу. Это обстоятельство и снижает ценность способа
построения графика «по точкам».
Существует второй способ построения графиков, основанный на
аналитическом исследовании функций. Он выгодно отличается от
рассмотренного выше способа. Важной особенностью второго способа
является то, что в его основе лежит прежде всего обнаружение и
изучение характерных особенностей в поведении кривой. Только после
ьтого приступают к построению графика. Места, где функция
изменяется плавно, не изучаются особенно Подробно, да и нет
надобности- в таком изучении. Зато те места, где функция имеет какие-либо
особенности в поведении, подлежат полному исследованию и
максимально точному графическому изображению. Легко догадаться, что
этими особенностями и являются точки максимума, минимума, точки
разрыва функции и др.
Перейдем к изложению второго способа.
Исследование функций можно вести по следующей примерной схеме:
1. Выяснение области существования функции.
2. Вопрос о четности и нечетности функции.
3. Определение точек разрыва функции. Нахождение предельных
значений в точках разрыва слева и справа.
4. Исследование функции на экстремум и нахождение
экстремальных значений.
262

5. Нахождение точек пересечения кривой с осями координат.
Эту схему мы называем примерной потому, что она может быть
изменена и дополнена новыми пунктами в зависимости от характера
функции и целей исследования. Например, могут быть включены
такие вопросы, как периодичность функции, вопрос об асимптотах
и др., а вопрос о четности и нечетности функции становится
ненужным, если область задания несимметрична относительно л: = 0.
Сведения, полученные о функции в результате исследования по
предполагаемой схеме, будут настолько подробны и полны, что после
этого не составляет особого труда представить себе график функции
и сделать его набросок. При этом построенный таким образом
график будет отражать все особенности данной функции, несмотря на его
неполную точность. При необходимости уточнить отдельные места
кривой можно вычислить координаты нескольких дополнительных точек
Пример 1. Исследовать и построить график функции у = j-4*2.
Проведем исследование по предложенной нами схеме.
1. Функция существует для всех х-уЬО и только при * = 0 она теряет смысл
2. Функция не является ни четной, ни нечетной, так как f(—х) = {-4лГ-
« f(-x)^f(x), f(-x)jz-f(x).
3. В точке х — 0 функция имеет разрыв второго рода. При этом
Л + 4*2\=— со, lim (1 + 4a;2W+oo.
X ] х-+ + 0\Х J
3#з l 8*3 1
4. Находим производную (/' = г— и решаем уравнение —^— = 0. Точка
lim
л:-* —0
х*
1
х=-^г является стационарной точкой. Других «подозрительных» точек нет.
Проверим достаточные условия экстремума в точке * = —. Так как знаменатель
производной всегда положителен, то достаточно проследить за знаком числителя
Получаем: у' <0 при х < -~-, */'>0 при *>-~-. Следовательно, в точке х = -~
функция имеет минимум, ее значение в этой точке у. j =3.
5. Точек пересечения кривой с осью OY нет, так как данная функция не
определена при * = 0. Чтобы найти точки пересечения кривой с осью ОХ, нужно
решить уравнение \-4х2 = 0, откуда найдем, что 4л;3 = — 1 или х——^-
(остальные два корня мнимые).
Полученные результаты исследования можно собрать в следующую таблицу:
\\
У'
У
(-.-?)
—
Убывает
\Г2
2
—
у=о
№)
—
Убывает
0
х
Разрыв 2-го
рода
f(-0)=-oo
;/(+0)=+оо
К)
—
Убывает
1
2
0

Минимум
(W
+
Возрастает
26}

Заметим, что в верхней строке таблицы значения х, полученные при
исследовании, нужно располагать в порядке возрастания.
Переходя к построению графика, следует прежде всего выбрать удобное
расположение системы координат на чертеже. Так, например, если функция нигде
не имеет отрицательных значений и существует только для х>0, то естественно
ось OY сдвинуть несколько влево от центра, а ось ОХ —вниз. В нашем случае
функция существует всюду, кроме * = 0, и принимает как положительные, так и
отрицательные значения. Следовательно, начало координат можно расположить
в середине чертежа.
Масштаб по осям координат также желательно выбирать в зависимости от
того, насколько большие значения придется откладывать на той или другой оси.
Чем большие значения откладываются на оси, тем мельче должен быть масштаб.
В данном случае по оси ОХ следует взять масштаб покрупнее, так как на ней
будут только отметки х =
V2
По оси ОУ следует взять более мелкий
1
при x = -<j- значение
/
масштаб, так как
# = 3 является минимальным значением
функции и, следовательно, в окрестности
точки х = — будут значения функции,.
большие 3.
По составленное выше таблице строим
график функции. Сначала наносим
точки, отмеченные в таблице. Затем
делаем набросок кривой, исходя из
характеристики ее на каждом из участков. По-
^ лучим график, который изображен на ри-
X сунке 108. Заметим попутно, что
рассмотренная в этом примере кривая носит
специальное наименование — «трезубец
Ньютона».
Остановимся специально на характере
графика функции около значения * = 0,
которое представляет точку
«бесконечного» разрыва функции. Для любого Jt=?0
расстояние от точки М на кривой y = f(x) до прямой д; = 0 (то есть до оси Оу}
будет равно | х | (расстояние измеряется по перпендикуляру, проведенному к этой
прямой из точки М). Но когда х—+0, то точка М удаляется по кривой в
бесконечность, а расстояние от М до оси Оу стремится к нулю, то есть кривая
неограниченно приближается к оси Оу. В таком случае ось Оу называют
вертикальной асимптотой для данной кривой (сопоставьте с понятием асимптот
гиперболы из аналитической геометрии).
Вопросу об асимптотах кривых будет в дальнейшем посвящен отдельный
параграф (см. § 5 этой главы).
х2
Пример 2. Исследовать и построить график функции у== 2 .
1) Функция существует всюду, кроме точек х=±2.
2) Она является четной, так как f(—*)=/ (х). Следовательно, ее график
симметричен относительно оси Оу. Воспользуемся этим обстоятельством и
ограничимся исследованием и построением графика функции только для х^О.
Вторая часть графика для х<0 может быть достроена по симметрии.
3) В точке х = 2 функция имеет разрыв второго рода, причем:
Рис. 108.
lim
х2
2_-04—JC2
. = +00,
X2
hm ——=—со.
->2+о 4 — х2
Значит, прямая х = 2 является вертикальной асимптотой для данной кривой.
264

4) Находим производную у' =
(4 —л:2) 2л:+ 2*. *2
8х
и приравниваем
(4 — **)2 (4 — х2)2
ее нулю. Получим: 8х = 0 или л: = 0. Поскольку точка дс = 0 является
внутренней точкой области определения функции, то в ней может быть экстремум. Но
мы не будем проверять достаточные условия экстремума в этой точке, так как
при симметричном достраивании графика вопрос об экстремуме в этой точке будет
решен и без этого.
5) Кривая проходит через начало координат, так как у = 0 при х = 0.
Других точек пересечения кривой с осями координат нет.
х2
Исследуем поведение кривой при х—- + оо. Имеем: lim - =— 1. Та-
•X*
ким образом, расстояние от любой точки М на кривой до прямой у =— 1, изме-
I х2 I
ряемое величиной | f (jc) —(—1) |= 2 + И , ПРИ удалении М в бесконечность
(то есть при х —-со) стремится к нулю; иначе говоря, при х—*оо кривая
неограниченно приближается к прямой г/= — 1, то есть прямая г/= — 1 является
горизонтальной асимптотой для данной кривой.
Составим таблицу:
\ X
У'
У"
У
0
0
+
0
(0,2)
+
+
Возрастает
2
х^
^><с
Разрыв 2-го рода
f(2-0)=+co,
f(2+0)=-oo
(2, +оо)
+
—
Возрастает
График этой функции дан на рисунке 109. Как видим, в точке х = 0 функция
имеет минимум, f/|JC_0 = 0, а прямые х = 2 и х-
асимптотами.
-2 являются вертикальными
Вопросы для самопроверки
и упражнения
1. Почему при исследовании
знака производной слева и справа от
точки х0, «подозрительной» на
экстремум, нужно брать точки, близкие к
jc0? Чем определяется степень этой
близости?
2. Как исследуется поведение
кривой y = f (х) при х -* ± со?
3. Как используются свойства
четности, нечетности и периодичности
функций при исследовании последних
и построении их графиков?
4. Провести исследование и
построить графики функций:
е
О
-U-
-/
Рис. 109.
а) */ =
г) «/ = * +
*2'
1
б) (/ = Зл;4 —2jc2-
-1
д) у = \п
х+2'
в) У-т + з*.
е) у = sin х + х.
265

§ 4. НАПРАВЛЕНИЕ ВОГНУТОСТИ КРИВОЙ И ТОЧКИ ПЕРЕГИБА
Пусть функция f (x) имеет в точке х0 конечную производную.
Тогда касательная к кривой y = f(x) в точке М (х0, / (х0)) не будет
параллельна оси OY.
Определение. Будем говорить, что кривая в точке М
вогнута вниз (вверх), если в некоторой окрестности этой точки она
лежит ниже {выше) касательной. Точку М (х0, / (х0)) называют
точкой перегиба, если кривая переходит в точке М с одной стороны
касательной на другую, то есть если в некоторой окрестности
точки М все точки кривой с абсциссами х<х0 лежат по одну
сторону от касательной, а все точки с абсциссами х>х0 — по
другую. Если при х=х0 функция f(x) имеет с обеих сторон
бесконечную производную одного и того же знака, то точку
М (х0, f (х0)) также называют точкой перегиба кривой y=f(x) (рис. 110).
Выясним условия, при которых имеет место определенное
направление вогнутости, или перегиб кривой.
Пусть функция f (х) имеет вторую производную /" (х),
непрерывную в точке х0. Составим уравнение касательной к кривой
y = f(x) в точке М(х0, у0):
Здесь у0 = !(х0), а через Y обозначена текущая ордината
касательной в отличие от текущей ординаты у из уравнения кривой y = f (x).
Разность ординат у — Y, соответствующих одной и той же абсциссе*
будет:
r = y—Y = y—y0 — f'(x0)(x — xQ) = f(x) — f(xJ — f'(xQ)(x — x0).
С помощью формулы Тейлора с остаточным членом в форме
Лагранжа при п=\ можем записать:
f (*) = / (*о) + Г (*о) (x-xj + f^ (x-x0)\
Вогнутость
вниз
Вогнутость
вверх |
1 L
266

следовательно,
(см. § 3, гл. VI), где точка с находится между х и х0. Из этой
формулы следует, что г имеет такой же знак, что и f (с).
Возможны следующие случаи:
1-й случай. /*(х0):>0. Так как по условию f (х) непрерывна
в точке х0 и f* (xQ) > 0, то для всех точек х, достаточно близких
к х0, будет f(x)>0. Поскольку точка с находится между х и х0,
то за счет приближения х к х0 (как слева, так и справа от х0)
получим: f(c)>0. Но тогда будет и г>0 (то есть у—Y>0y
или y>Y). Тем самым мы доказали, что в некоторой окрестности
точки х^ кривая лежит над касательной, то есть в точке М кривая
направлена вогнутостью вверх.
2-й случай, f (х0) < 0. Совершенно аналогично доказывается,
что в этом случае в точке М (х0, у0) кривая вогнута вниз.
3-й случай. f"(x0) = 0. Если при этом f (x) слева и справа
от точки xQ имеет разные знаки, то это означает, что при переходе
через точку х0 разность г меняет знак, то есть кривая переходит
с одной стороны касательной на другую. В точке М имеется
перегиб, и эта точка отделяет участок, где кривая направлена
вогнутостью вверх, от участка, где кривая направлена вогнутостью вниз.
Обращаем внимание читателя на то, что наличие только
равенства f"(x0) = 0 еще не обеспечивает наличие перегиба у кривой
в точке х0. Например, если имеем функцию f(x) = x*, то /" (х) =
= 12л:2 и f(0) = 0. Однако, как легко видеть, кривая,
изображающая эту функцию, в точке х=0 перегиба не имеет.
Заметим также, что в точке х0 может быть перегиб и в том
случае, когда f (х0) не существует. Достаточно, чтобы f (x) меняла
знак при переходе через эту точку.
Полученные нами результаты можно представить в виде
следующей таблицы:
Г (х) при
1*о — &<х<х0
<о
>о
Г (*о)
>о
<о
= 0
или
не существ.
f" (x) при
х0<х<х0 + 6
>о
<о
Заключение о
кривой в точке х0
Вогнута вверх
Вогнута вниз
> Перегиб
Определение. Если кривая вогнута вверх (вниз) в каждой
точке некоторого промежутка, то она называется вогнутой вверх
(вниз) на этом промежутке*
267

Пример 1. Определить интервалы, в которых функция у = Здс4 — 8х* + б*2 +
4- 12 сохраняет направление вогнутости, и найти ее точки перегиба.
Находим производные: */' = 12х3 — 24х2 + 12*, //" = 36х2 — 48*-}- 12 = 36 (*— 1)х
X (х—5"). При этом у"—0 в точках х=1 и -~-. Вся область определения
функции разбивается этими точками на три интервала: (—оо, ~\ у (-«-» 1) и
(1, + со). На каждом из них*/" будет постоянного знака, причем знаки по
интервалам распределятся следующим образом:
(-"•т).(т'!)'(1'+00)-
+ — +
Значит, данная кривая на (— со, ~\ и на (1, +оо) вогнута вверх, а на
(-«-, 1] вогнута вниз. В точках * = -^- и *=1 она имеет перегиб.
Пример 2. Определить интервалы, в которых функция у^=\/^хъ сохраняет
направление вогнутости, и найти ее точки перегиба.
' 5\' 2 1
/ i з i 5 т „ 10 -т 10 „
Находим производные: у = \х°) =-5-х°, и"=—- х ° =—-—. В данном
<* 9 9ух
случае у" нигде в нуль не обращается. В точке х = 0 она не существует. Но так
как у" <0 при х<0 и г/">0 при л;>0, то в точке х = 0 кривая имеет
перегиб: вогнутость вниз сменяется на вогнутость вверх (см. рис. 32 на стр. 49).
Пример 3. Показать, что кривая у = \п(х2—1) везде вогнута вниз.
Данная функция определена при |*|> 1, то есть на (—оо, —1) и (1, -f-co).
Найдем ее первую и вторую производные:
аш,_ 1 _ 2х t„_(x2—l)-2 — 2x-2x 2(*2 + l)
* X2—1 X2— 1' V (jt2—1)2 (*2-1)2'
Поскольку г/"<0 при всех значениях х из области определения функции, то
кривая везде вогнута вниз.
Вопросы для самопроверка и упражнения
1. Доказать, что кривая y = f (х) вогнута вниз в точке М (х0, у0), если /" (лг0) < 0.
2. Какое условие является достаточным для наличия перегиба в точке?
3. Что можно сказать о поведении функции в точке, где она и ее первая
производная равны нулю, а вторая производная отлична от нуля?
4. При каком условии точка, в которой кривая вогнута вверх (вниз), будет
точкой экстремума и какого именно?
5. Может ля функция иметь экстремум в точке, в которой ее график имеет
перегиб?
6. Показать, что кривая у = х2-{-8х — 9 везде вогнута вверх.
7. Определить направление вогнутости кривой у = х8 — 9хъ + 6х3 — Ъх2 -f-1 в точке
х = 0 и лг = 2.
Отв. В точке х = 0 кривая вогнута вниз, в точке х = 2 вогнута вверх.
3
8. При каких значениях а кривая y = x8-\-ax3-\--ir-x2-\- 1 будет вогнута вверх
на всей числовой оси? Отв. При |а|^2.
9. При каких значениях а и b точка (1,3) является точкой перегиба кривой
3 9
у = ах3 + Ьл;2? Отв. При а = ^-, ^ = ~9~-
10. На примере функции у — хА-\-8х3+\8х2-\-8 проверить, что между
абсциссами точек перегиба кривой может и не быть точек экстремума.
268

§ 5. АСИМПТОТЫ КРИВОЙ
Понятие асимптот вводится для кривых, ветви которых уходят
в бесконечность, то есть если точка М, движущаяся по этой
кривой, может удалиться от начала координат как угодно далеко. Это
может быть в случаях, когда функция не ограничена или когда она
задана на неограниченном промежутке.
Определение. Прямая линия называется асимптотой для
кривой y=f{x), если расстояние точки М, лежаи^ей на кривой, от
ётой прямой стремится к нулю при движении точки М вдоль какой-
нибудь части кривой в бесконечность.
Различают три вида асимптот: вертикальные, горизонтальные
и наклонные.
Вертикальные асимптоты. Пусть lim f(x) = oo. В этом
х-+х0
случае расстояние d точки М на кривой y=f{x) от прямой х = х0
будет равно \х — х0\ (расстояние измеряется по перпендикуляру,
проведенному к асимптоте из точки М). Последнее стремится к нулю
при стремлении М в бесконечность (когда х->х0). Следовательно,
прямая х=х0 будет вертикальной асимптотой для данной кривой (рис. 111).
Примеры. Рассмотрим кривую у— г. Так как
hm —-х=-сои hm —* =+оо,
х-*2— о*—z x-+2-\-o* — ^
то прямая х = 2 является вертикальной асимптотой для данной кривой (см. рис. 66
на стр. 145). Все функции с бесконечными разрывами имеют вертикальные
асимптоты. Так, например, для функции r/ = tg x асимптотами будут прямые х=
л 1
= ± (2/г+1)^,где п = 0, 1, 2, 3, ... (см. рис. 36 на стр. 60); для функции г/ = -
вертикальной асимптотой будет ось ординат (см. рис. 23 на стр. 47); для кривой
y = \ogax вертикальной асимптотой будет также ось ординат (см. рис. 34 на стр. 59).
Рис. 111.
269

Горизонтальные асимптоты. Если lim f{x) = A (или
X -* -f СО
при х—*— оо), то прямая у = А будет горизонтальной асимптотой
для кривой у=/(х), так как d = \\m(f (х) — А) = 0 (рис. 111).
X -—-{- ОО
Примеры. Кривая r/ = arctg x имеет своими асимптотами горизонтальные
зх зх
прямые 1/ = — ^ и У = п (см- рис. 38 на стр. 63). Кривая у = ах имеет своей
асимптотой ось абсцисс (рис. 34). Ось абсцисс будет асимптотой и для кривой у =
= JZT2 (рис* 66)-
Наклонные асимптоты. Пусть некоторая кривая у=/(х)
имеет наклонную асимптоту У=ах-\-Ь (рис. 111). В данном случае
расстояние точки М на кривой от прямой будем измерять также по
перпендикуляру, опущенному из точки на прямую. Оно выразится
в виде d = (y—У) sin а, где угол а — постоянный. Отсюда
заключаем, что условие d—+ 0 равносильно условию ,у — К —0, то есть
условию
lim(y — ax—b) = 0. (1)
X -+ ОО
Таким образом, условие (1) является необходимым и достаточным
для того, чтобы прямая у = ах-\-Ь была асимптотой.
Покажем, как найти постоянные а и Ъ. Из соотношения (1)
следует,
что
,. и — ах — Ь
lim- =
*-»-оо х
= 0 или lim
X -» О
lim - = a
X -* ОО Х
(2)
Из условия (1) также следует, что
lim (у — ах) = Ь. (3)
X —> ОО
Обратно, если а и Ъ определены соотношениями (2) и (3), то
условие (1) будет выполнено. Таким образом, для нахождения
наклонной асимптоты сначала из (2) определяем ее угловой
коэффициент а, затем, подставляя значение а в (3), находим свободный
член Ь. Если оба предела (в формулах (2) и (3)) существуют и имеют
конечные значения, причем lim -9^0, то существует и наклонная
лг-юо х
асимптота.
Пример 1. Для кривой у = —L— ¦ f a= lim * = lim ' Т = 1;
х—1 х-*ооЛ- *-*оо Х(Х—I)
6= lim &-«*) = lim f^ + ^+l_,\ Um 3?±1 з
л:—> оо х -+ оо \ х—* / х -* оо *—*
Следовательно, уравнение наклонной асимптоты будет */ = *-{-3.
Пример 2. Кривая # = (*—1)2 (a:-j-3) асимптот не имеет, так как при
х—> оо не только у стремится к бесконечности, но и -.
270

X2 Ф
Пример 3. Гипербола — — —=] имеет своими асимптотами прямые
-*, так как
x-+mx х-+оэ\ о. У \xj J а' *-*оо\ a a J
= lim [± — (V x2-a2 -*)] = ± — lim ~"g2 =0.
jc-ooL a J a x-+ooyx2 — a2 + X*
Пример 4. Найти асимптоты кривой у =
2х2 + 3х — 5
л: (л: —4) '
Так как lim y= lim , .— =2, то прямая у = 2 является горизон-
тальной асимптотой данной кривой. Поскольку, как легко видеть, у —* со при
х — 0 и при л: — 4, то пря- .
мые * = 0 (ось Оу) и * = 4 У Д
является вертикальными
асимптотами.
Выясним вопрос о
существовании наклонных
асимптот, то есть асимптот
вида у — ах-\-Ь. Будем искать
угловой коэффициент а
наклонной асимптоты, то есть
у
предел отношения — при
lim 1L-
2*2-f3* — 5
= 0.
3 4
5 6 7 8 9
Так как a = 0, то данная рис> ц2.
кривая наклонных асимптот
не имеет.
При построении графика функции следует прежде всего нанести на чертеж ее
асимптоты, если таковые имеются. Это значительно облегчит построение графика
и даст представление о его поведении за пределами чертежа. График данной
функции изображен на рисунке 112.
Вопросы для самопроверки и упражнения
1. Почему график ограниченной функции, заданной на ограниченном
промежутке, не может иметь асимптот? Может ли иметь асимптоты и какие график
ограниченной функции? Может ли иметь асимптоты и какие график функции,
заданной на ограниченном промежутке?
2. Найти асимптоты следующих кривых:
ах+b . , , , .
6) у-
2л*—5*2 + 4*+1
в) у = хе
г) у = 2х
2х2—х—\
X
- arc cos —,
х
^ da
Отв. х = и у =—.
с * с
Отв. х=—-jr-, х=1 и у — х — 2.
Отв. х = 0 и j/=jt-)-l.
Отв. у = 2х—s-#
271

3. Будет ли прямая Y — ax+b наклонной асимптотой для кривой y=f(x),
если величина у — Y-~ О, колеблясь, то есть принимая как положительные, так
и отрицательные значения? Иначе говоря, может ли кривая, приближаясь к своей
асимптоте, бесконечно много раз пересекать ее? Отв. Да.
§ 6. РАЗЛИЧНЫЕ ПРИМЕРЫ И ЗАДАЧИ
Рассмотрим еще несколько примеров на исследование функций
и построение графиков. Прежде всего заметим, что определение
направления вогнутости и перегибов, а также указанный способ
нахождения асимптот дают возможность провести исследование
функций еще более детально и получить более точное представление об
их графиках. Примерную схему исследования функций, данную
в параграфе 3, можно дополнить пунктами:
6. Определение точек перегиба и интервалов, на которых
функция сохраняет направление вогнутости.
7. Отыскание асимптот кривой.
Соответственно дополнится и таблица, отмечающая основные черты
в поведении кривой.
*3
Пример 1. Исследовать и построить график функции у = -х «-.
о — х
1) Функция существует всюду, кроме точек х=±}^3.
2) Функция нечетная, так как f (—*)=—f (x). Следовательно, ее график
симметричен относительно начала координат. На этом основании можно ограничиться
исследованием и построением графика только для О^жС+оо. Затем, пользуясь
симметричностью, можно будет легко получить и остальную часть графика.
3) Функция имеет разрыв второго рода в точке х=У^З, причем
Iim Г^2== + °°' lim T^Ti^""00'
Следовательно, прямая я = 1^3 является вертикальной асимптотой кривой.
, (3 — х*)Ъх*+2х-х* 9**-*4 *2(3— *)(3+л:)
4) Находим производную: у'= к- (3-^)2 "ff-*»)»"8 (3-л*)« '
х2 (3 х) (3 -J- л:)
Приравниваем ее нулю: —~«— w~ =0, откуда х2 (3-х) (3+х)=0. По-
(о х)
следнее имеет место при дс = —3, х=0 и х = 3. Нам придется исследовать на экстремум
только точку х = 3 (точку х = 0 на экстремум не исследуем, так как она является
крайней точкой области [0, +оо)). Знак производной слева и справа от точки
# = 3, очевидно, будет зависеть от знака числителя в выражении производной,
так как знаменатель всегда положителен. В окрестности точки х = 3 имеем: f/'>0
при *<3 и г/'<0 при х>3. Следовательно, в точке * = 3 функция имеет мак-
I Л 1
симум, 1/1л.з = -4у.
5) Так как # = 0 только при * = 0, то пересечение с осями координат
происходит только в начале координат.
6) Определим точки перегиба и интервалы, на которых функция сохраняет
направление вогнутости. Находим вторую производную:
9*2— л* у (3 —*2)з (18* —4*8) + (9*2 — х?) (3 — *2). 4* 6* (9-f-*2)
У \(3 — *2)2j (3—JC2)4 (3-*2)3
Мы видим, что у" = 0 только при х=0. При этом в окрестности точки х — 0
будет у" <0 при *<0 и (/*>() при *>0. Следовательно, в начале координат
кривая имеет перегиб (впрочем, наличие перегиба в начале коордитат обнаружи-
272

лось бы и после симметричного продолжения графика налево от оси OY). Иногда
направление вогнутости может измениться при переходе через разрыв кривой,
поэтому следует выяснить знак у" и около точек разрыва функции. В данном
случае у' >0 на промежутке (0, 1^3 ) и у" <0 на промежутке (]/"3, +оо).
Следовательно, кривая вогнута вверх на (0, ]^3) и вогнута вниз на 0^3, +со).
Итак, исследуемая кривая характеризуется для х^>0 следующей таблицей:
|\* 1 о
I \ »
У'
У"
У
1
0
0
0
(0,^3)
+
+
Возрастает
Кривая
вогнута вверх
Кз
^х^
^х^
Разрыв 2-го
рода
/ (1^3-0) = +оо
/(У"3+0)=-со
(/3", 3)
+
—
3
0
—
Возрастает Максимум
Кривая вогнута
(3,+оо)
—
—
Убывает
вниз
7) Выясним вопрос об асимптотах.
а) Наличие вертикальной асимптоты x = Y^S уже установлено в пункте 3.
б) limj/= lim
л*
3-х2
= оо. Следовательно, горизонтальных асимптот нет.
и х2
в) a = lim-^= lim 0—2 =
: —1, 6= lim (у-(— х)) = lim .^—-^
ЛГ-+СЮ Х-*СО\° Л"
X*
f * =
= lim
Зд:
З-л?
Следовательно, прямая у =
= — д: является наклонной
асимптотой данной кривой. Так
как пределы найдены для х —* оо
(то есть они одинаковы и при
х—* + оо, и при *-^—оо), то
к асимптоте у = — х график
функции будет приближаться
как при удалении вправо, так и
при удалении влево (рис. 113).
Пример 2. Провести
исследования и построить график
функции
sin2*
2 -{- sin x
1) Функция существует для
всех х.
Рис. 113,
273

2) Функция не является ни четной, ни нечетной, так как
sin2 х
/(-*)«
и/(-*)^/(*),
2 — sinx
/ (— х)ф—[ (х) (при sin х ф 0).
3) Функция непрерывна на всей оси и имеет период 2л. Учитывая последнее,
будем исследовать ее и строить график только в пределах одного периода,
например на [0, 2л]. Затем, пользуясь периодичностью функции, продолжим график
на всю ось.
4) Находим производную
, (2 +sin х) 2 sin* cos*— sin2* cos* sin *• cos х- (4 +sin x)
У = (2 +sin*)* "" (2 +sin*)» и приравниваем ее
нулю:
sin x - cos x - (4-f sin x)
(2 +sin*)2
- = 0.
Отсюда следует, что sin*-cos* = 0 (так как A + sinx^bO). В пределах отрезка
[0, 2л] стационарными точками будут: * = 0, -^-, л, -^- и 2л. Других
«подозрительных» на экстремум точек нет. Знаки производной по интервалам
распределяются следующим образом:
(°- т). (т« *)• (*• I51)' (тя> 2л)-
+ - +
По чередованию
, =1
I Зл=1-
знаков заключаем, что в точке *=-« максимум:
3
в точке х — л — минимум: у\х-п = 0\ в точке * = -^-л—максимум;
sin2 *
5) Из уравнения 9 "". ~ = 0 находим, что кривая пересекает ось абсцисс
в точках * = 0, л и 2л. С осью ординат кривая пересекается в начале координат.
6) В исследовании функции на направление вогнутости и перегибы нет
особой надобности, так как кривая везде непрерывна и поведение ее между
экстремальными точками легко себе представить.
7) Легко проверить, что асимптот у данной кривой нет.
Составим таблицу:
\ х
У'
У
0
0
0
И)
+

Возрастает
л
~2
0
1
3

Максимум
(И
—
Убывает
л
0
0

Минимум
(- -?)
+

Возрастает
Зл
2
0
1

Максимум
(* *)
—
Убывает
1
2л
0
0
Поскольку функция отрицательных значений не имеет, то систему координат
можно сдвинуть на чертеже вниз. Так как по оси ординат максимальное из
откладываемых значений равно 1, то по этой оси следует взять масштаб крупнее,
чем по оси абсцисс.
274

После построения графика функции на отрезке [0, 2л] можно периодическим
продолжением получить график на сколь угодно большом участке и станет видно,
что в точках х = 0 и х = 2л
функция имеет минимум. На Vji
рисунке 114 изображен
график, соответствующий отрезку
[ — 2л, 2л].
Пример З.Приизменении
параметра / от —оо до -}-со
точка, определяемая
координатами
Sat За/2
x=irnw>y=-TTw{a:>0)>
описывает некоторую кривую,
которая носит специальное на- рис. Ц4.
звание — «лист Декарта».
Исследовать форму этой кривой.
Для решения задачи мы проведем исследование хну как функций от / с тем,
чтобы получить ответы на все те вопросы, которые фигурировали в предыдущих
примерах.
1) Функции х (/) и у (/) существуют на промежутках (— оо, — 1) и (— 1, +оо).
, _ (1+/3)* За — За/. З/2 _ За (l—2/з)
z> xt- (1-W3)2 ~~ (1-Ь/3)2 '
, _ (1 + /3) 6а/ — За/2 . 3/2 За/ (2 - /3)
у*~ (1-Й3)2 "" (1+/3)2 #
Следовательно, всюду, где х и у имеют смысл, то есть при всех t-ф —1,
производные х\ и у\ имеют конечные значения. Определим точки, в которых х\ и у\
обращаются в нуль или бесконечность:
х} = 0 при 1 — 2/3 = 0, то есть при /= ,,—.¦,
у 2
x't= + co при / = —1,
y't=Q при / = 0 и при 2 — /3 = 0, то есть при / = 0 и /=J/*2,
yj=—со при / =—1
Таким образом, если всю ось (—oo</<-f-oo) разбить на интервалы
(-со
,-1), Н.0,,(0^), (^/2-), № +»).
то внутри каждого из них производные х\ и у\ будут конечны и постоянного знака.
Это характеризует и монотонность поведения самих функций х (/) и у (/) в
указанных интервалах. В самом деле, #/>0 при /<g—-, x't <0 при />j7r^t
_ 3 _ л 2 ^ 2
y't>0 при 0</<|А2, y't<0 при /<0 и />|/"2. Составим таблицу:
/
х\
У)
1 х
1 у
(-00, -1)
+
(-1. 0)
+
Возрастает
Убывает
(°-w)
+
+
(W^)
+
(У 2, + оо)
—
Убывает
Возрастает 1 Убывает
275

3) Вычислим на концах интервалов значения х и у или, если таковые
отсутствуют, их предельные значения:
lim x(t) = \\m-^L-=:0t Hm *(/) = +оо, lim *(/) = — со, *(0) = 0,
f — oo f —ool+f3 t-+ -1-0 /—14-0
/ 1 \ 8/2 3fl 2а 8/-Т- /8/го-ч 3aJ/T Я/7Г
\V2
lim y(0= lim -^L=0, lim j/(0 = -oo, lim y(t)=* + co, y(0)=0r
/-.00 /-00 »+'3 /—1-0 <__l+0
Пункты 2 и З можно иллюстрировать следующей таблицей:
t
(-00, -1)
(-1, 0)
(°ф)
(w**)
(|/Т +оо)
X
Возрастает от 0 до + сю
Возрастает от —оо до 0
Возрастает от 0 до а \/~4
Убывает от а ']/~4 до a'j/^2
Убывает от а j/*2 до 0
У
Убывает от 0 до —со
Убывает от -|-со до 0
Возрастает от 0 до a j/~2
Возрастает от а j/"2 до aj/r4
Убывает от а У4 до 0
4) Так как х и у обращаются в нуль при / = 0 и / = оо (то есть lim *(/) =
t — OQ
= lim y(t)—0), то кривая пересекает сама себя в начале координат.
t-»oo
5) Так как при t —*—1 величины х и у стремятся к бесконечности, то
кривая имеет бесконечные ветви. Это значит, что она может иметь асимптоту. Найти
такую асимптоту можно тем способом, который был изложен в § 5 для кривых,
заданных явным уравнением:
,. У ,. 3a/2(i_M3
hm -^-= hm ; ' ' =— 1,
3at*+3at
lim (y + x) = lim —г-р
Ш+За
/_»_! 3t2
Следовательно, уравнением асимптоты является у=—-х—а.
276

Во второй и третьей колонках последней таблицы показано, как изменяются
абсцисса х и ордината у точек заданной кривой в зависимости от изменения
параметра /. Учитывая эту связь, а также пункты 4 и 5, можно построить
кривую (рис. 115).
Этот пример показывает, что метод
исследования функций одной переменной может
быть использован при исследовании и
построении кривых, заданных в
параметрической форме.
До сих пор нам задавалась
функция, описывающая ту или иную
зависимость между некоторыми
величинами. Наша задача состояла лишь
в ее исследовании и построении
графика.
В последующих примерах не
дается готовой функции для
исследования. Ее нужно сначала составить по
условию задачи. При этом важно
установить, какую величину выбрать
за независимую переменную. В задачах, где такой выбор можег
быть сделан не единственным образом, следует остановиться на том
из них, который делает функцию более простой для исследования.
Заметим также, что при решении многих задач практического
содержания не обязательно проверять аналитически достаточность
условий экстремума (с помощью первой или второй производной),
последнее оказывается иногда весьма сложным. Заключение о
наличии экстремума обычно легко сделать на основании условий за-
у///\ дачи. Это относится также и к отысканию
наибольших и наименьших значений.
Пример 4. Найти число, которое, будучи
сложено со своим квадратом, дает наименьшую сумму.
Обозначим искомое число через х. Сумма х2-\-
-\~x=f(x) будет, очевидно, функцией, подлежащей:
исследованию. Имеем: /' (*)=2л; + 1; решаем
уравнение 2д:+1=0 и получаем х=—-_-. Так как /* (х) =¦
Рис. 115.
= 2 > 0 для всех х, в том
= —~~, то f (х) в .точке х =-
числе
1
и для х =-
- имеет минимум:
/
Это значение, очевидно,
2
_1\ J 1__ 1_
2)~~ 4 2 ~~ 4
будет и наименьшим значением функции, так как на всей области своего
существования функция не имеет больше точек экстремума.
Пример 5. Построить прямоугольную площадку возле каменной стены
так, чтобы с трех сторон она была огорожена проволочной сеткой, а четвертой
стороной примыкала к стене. Для этого имеется а погонных метров сетки. При
каком соотношении сторон площадка будет иметь наибольшую площадь?
Обозначим стороны площадки через хну, как показано на рисунке 116.
Тогда площадь площадки будет равна S=x-y. Получили функцию от двух
переменных. Такие функции мы пока исследовать не умеем. Но в данном случае
эту функцию легко преобразовать к функции от одной переменной, если учесть,
что по условию, данному в задаче, должно выполняться равенство 2х-[-у = а.
277

Тогда у=а—2х и S = x(a —2л:), где 0^х^-~- (область существования функ*
ции S определяется из тех соображений, что размеры площадки не могут быть
отрицательными). Дальше решаем по обычной схеме:
S'=a — 4х) а — 4* = 0; х = -
о а а
Так как S" =
-4<0, то при х = — функция S имеет максимум. Ее значение
чЬ .__а="г(а~у)="я" (еДинии- площади).
Поскольку S (х) непрерывна на 0, -^- и ее значения на концах 5(0) и
З 1-у равны нулю, то найденное значение будет и наибольшим значением
функции. Таким образом, наиболее выгодным соотношением сторон площадки при
данных условиях задачи является — = 2.
Замечание. Хотя по смыслу задачи значения х = 0 и х = — (если л: = -~-,
то у = 0) нас не интересуют, так как в этих случаях не получится никакой
площадки, и, следовательно, х нужно было искать в открытом промежутке
0, -JT-), однако для решения задачи удобнее было перейти к замкнутому
промежутку и рассматривать функцию S (х) на 0, -^ .
Пример 6. Из круглого бревна данного диаметра d требуется вырезать
балку прямоугольного сечения так, чтобы она, находясь в горизонтальном
положении, обладала наибольшей прочностью * (известно, что прочность прямо
пропорциональна произведению ширины сечения на квадрат высоты сечения).
Обозначим ширину сечения через х, а высоту — через Л, как показано на
рисунке 117. Тогда сопротивление представится формулой <p = kxh2, где k —
коэффициент пропорциональности. Кроме того, как видно из чертежа, зависимость
между х и h определяется равенством x2-{-/i2 = d2, откуда h2 = d2 — х2. Подставляя
это значение, получим функцию одной переменной ф (x) = kx[d2 — х2], где 0^
^ х ^ d. Исследуем ее: ф' (*) = k(d2 — За:2), d2 — Зле2 = 0, откуда х = —~
у 3
* Под прочностью понимают способность балки выдерживать значительные
нагрузки не разрушаясь.
Рис. 117.
Рис. 118.
278

Так как ф (х) непрерывна на [0, d], неотрицательна и ф (0) = ф (d)=0, то
можно утверждать, что ф(--=] будет наибольшим значением функции, то есть
наибольшим сопротивлением. При этом h — Л/ d2 — — — dy -^- и отношение
h dV\-v*
— = -т = |/"2. Таким образом, максимальная сопротивляемость балки
на изгиб будет в том случае, когда высота поперечного сечения в У2 раз будет
больше ширины.
Пример 7. В данный шар вписать цилиндр, имеющий наибольшую боковую
поверхность.
Пусть радиус шара — /?, а радиус основания цилиндра —г (рис. 118). Тогда
высота цилиндра h определится по формуле h~2yrR2 — r2J и боковая
поверхность 5 —по формуле S = 2nr-2y R2 — г2, где 0<r<R. Отсюда 5' = 4л х
X (У R2 — r2 Г* )=4л. R2~2r2 . s'=0 при R2-2r2 = 0, откуда r = -^Lr
У R2 — r2
VH2^
12
Функция 5 (г) положительна и непрерывна на [О, R]. На концах отрезка она
равна нулю. Следовательно, внутри отрезка и именно при г = -т= она имеет
наибольшее значение. Цилиндр
такого радиуса будет искомым. У J
Пример 8. Через какую
х2 и2
точку эллипса -5- + 7Q = 1 следует
провести касательную, чтобы
площадь треугольника, составленного
этой касательной и осями
координат, была наименьшей? \^ 0\
Легко предвидеть, что если на
эллипсе найдетzy. одна точка,
удовлетворяющая условию задачи, то
в силу симметричности эллипса
таких точек будет по крайней
мере четыре. Симметричность эллипса позволяет ограничиться отысканием точек
только в первой четверти, то есть точек с положительными координатами (рис. 119).
Из уравнения эллипса находим: у = -^ У 8 — х2. Если абсциссу искомой точки
о
обозначить через *0, то ординатой будет: yQ = -^-/в —#$. Составим уравнение
касательной к эллипсу в точке (*0, #0), пользуясь известной формулой из снали-
Зх
тической геометрии: у—y0 = k (х — х0). В нашем случае у' = и fc =
Рис. 119.
= </'
3*п
2/8-
2 У 8 — х*
Следовательно, уравнением касательной будет:
Зато
— У8-^===-
2 2/8-д;2
(х — х0).
Найдем отрезки, отсекаемые касательной на осях координат:
* = 0; ye±V8-jcj
xl
.3(8—*a+3atj
12
2 V8-
2 2 V&-x% x0
279

Площадь прямоугольного треугольника будет:
1 8 12 = 48
2 " х0У8=1ё0 x0Vs^xJ/
Очевидно, она окажется наименьшей в том случае, когда выражение х0У8 — х\
будет иметь наибольшее значение. Поэтому достаточно исследовать функцию
p = jc]/8-x2 на предмет отыскания наибольшего значения. Имеем:
р' = ^8-*2-
д:2
8 — 2x2
У 8 — *2 У 8 — х*'
8 — 2л:2 = 0* х = 2.
Остается показать, что точка с абсциссой х0 = 2 будет искомой. Это вытекает,
например, из следующих соображений. Функция S — , изображающая
*оУ8 —*3
площадь треугольника, неотрицательна, а потому ограничена снизу, непрерывна
и имеет непрерывную производную на (0, У8). На концах интервала она
обращается в бесконечность. Следовательно, наименьшего значения она достигает
внутри интервала. Но внутри интервала производная от функции равна нулю
только в точке л:0 = 2. Отсюда заключаем, что точка х0 = 2 и будет точкой
наименьшего значения функции. Соответствующее значение у0 определится из урав-
нения эллипса Уо = -к-У8 — 22 = 3. Таким образом, искомой точкой на эллипсе
будет точка (2, 3). По симметрии определяются и остальные точки: (—2, 3),
<-2, -3) и (2, -3).
Пример 9. Консервная банка данного объема имеет форму цилиндра.
Каково должно быть соотношение ее размеров (высоты и диаметра), чтобы на
изготовление пошло минимальное количество жести?
Обозначим радиус банки через г, а высоту —через h (рис. 120). Полная
поверхность банки 5 = 2я r2-\-2n rh, а объем v — nr2h, откуда/г = ^^. Подставляя
яг2'
значение h в формулу для поверхности, получим:
5 =
2v
--2ЛГ- + -.
г
Задача сводится к исследованию S как функции от г. Имеем- S'=4ttr —
2v
2v
Приравнивая производную нулю, 4яг 2" = 0, найдем, что 4яг3 — 2и = 0, откуда
"2к И Г = \
V
2R'
'Ksl
Рис. 120.
Рис. 121.
280

Искомое соотношение размеров банки будет: /г = 2г.
Пример 10. На какой высоте следует повесить электрическую лампочку
в классе, чтобы в точке М пола, отстоящей на расстоянии / от вертикальной
проекции этой лампочки на пол, была наибольшая освещенность. (Освещенность /
cos ф
определяется по формуле I—с—~-^ где г—расстояние от источника света, ф —
угол падения луча, с — коэффициент пропорциональности, соответствующий данной
лампочке.)
Выберем за независимую переменную высоту лампочки над полом h (рис. 121).
Тогда г = ]Лг2-f/2 и coscp = — = -
Функция, подлежащая исследованию, представится в следующем виде:
, cos ф h Л ^ , ^ .
l-c-J?-c(ht+lt),/t, где 0<Л< + со.
Находим производную:
(Л2 + /2)V2 3А(Л! + /2) 1/, . 2Л
/1=с = с- V. 4 = 0 при /2-2/?а=:0,
п (Л2 + /2)3 (/г2 + /2) 2
то есть при h = -7=. Так как /' > 0 при h < -7= и /' < 0 при h > —7=,
j/2 1/2 /2 '
то наибольшая освещенность и будет при /г = -^=^0,7/.
Вопросы для самопроверки и упражнения
1. Провести исследование и построить графики функций:
\ 1 *\ x2-\-l ч sin х 8 Л—
д) х = г (2 cos/ —cos 2/), 1 е) х — а (/ — sin /), 1
i/ = г (2 sin/—sin 2/), J f/ = a (1—cos/). J
2. Данное положительное число с разложить на два слагаемых так, чтобы
произведение первого из них на квадрат второго было наибольшим. п с 2с
О о
3. В данный шар вписать конус наибольшего объема.
32
Отв. Максимальный объем вписанного конуса равен гт л а3, где а — радиус
а У 8"
шара; радиус основания вписанного конуса r = —^—
4. Показать, что из всех цилиндров данного объема наименьшую полную
поверхность имеет тот, у которого осевое сечение есть квадрат.
5. В данный конус вписать цилиндр наибольшего объема.
4
Отв. Наибольший объем вписанного цилиндра равен ^= лИа, где а — радиус
основания конуса, a h — его высота.
6. В прямоугольной системе координат дана точка (1, 2). Провести через
эту точку прямую линию так, чтобы она образовала вместе с положительными
полуосями координат треугольник наименьшей площади.
Отв. Прямая оказывается такой, что отрезок ее, заключенный между осями,.
х ц
делится в точке (1, 2) пополам, —+ -~=1 .
7. Окно имеет форму прямоугольника, завершенного полукругом. Периметр
задан. Каковы должны быть размеры окна, чтобы оно пропускало наибольшее
количество света? Отв. Высота прямоугольника должна равняться радиусу полукруга.
281

К r--i
I
\l/
s/s%//;s//////A
Рис. 123.
8. Определить отношение высоты конического шатра к радиусу основания при
условии, что его боковая поверхность наименьшая при заданной вместимости.
Отв. V2 .
9. На оси параболы у2 = 2рх дана точка М на расстоянии а от вершины.
Найти абсциссу ближайшей к ней точки кривой.
Отв. х = а — р при а>р и х = 0 при а^р.
10. Из круга радиуса R вырезан сектор с центральным углом а. Из сектора
сделана коническая поверхность. При каком <угле а объем полученного конуса
-будет наибольшим? Отв. а = 2jt V2U ^ 293° 56'.
11. Тело движется по закону s = 18^ + 9/2 — t3. Найти его максимальную
скорость. Отв. Максимальная скорость и = 45 при ? = 3.
12. Три пункта А, В и С расположены так, что L Л?С = 60°. Из Л в б
движется автомобиль со скоростью 80 км/час, из В в С —поезд со скоростью
50 км/час. Через сколько времени расстояние между поездом и автомобилем
будет наименьшим, если движение началось одновременно и А В = 200 км}
27
Отв. Через 1 j= часа =^ 1 час 39 минут.
13. Луч света, выходящий из точки Л, отражается в зеркале в точке В и
затем идет через точку С (рис. 122). Показать, что путь ABC будет кратчайшим
при условии, что угол падения а равен углу отражения р.
14. Определить, какой высоты следует поставить фонарные столбы для того,
чтобы в наименее освещенной точке между ними (посредине) освещение было
наилучшим. Расстояние между фонарями равно а (рис. 123).
Указание. Воспользоваться формулой для освещенности, данной в условии
решенного нами примера 10. Отв. Л = ——.
15. Тело брошено (в пустоте) под углом ср к горизонту с начальной
скоростью v0 (см. рис. 86 на стр. 176). Полное время полета определяется фор-
2v0 sin <p
мулои
-, а горизонтальная дальность — формулой X =
v% sin 2ф
где
g ' * ' ' ' ' g
ускорение силы тяжести (см. пример 3 из § 7, гл. V).
1) Под каким углом ф должно быть брошено тело, чтобы время полета Т
было наибольшим?
2) Под каким углом ф нужно бросить тело,
дальше?
16. От канала
ной Ь (рис. 124).
длину / бревна, которое
чтобы оно упало как можно
Отв. 1) ф = 90°, 2) ф = 45°.
шириной а под прямым углом к нему отходит канал шири-
Стенки каналов плоские вертикальные. Найти наибольшую
можно сплавлять по этим каналам из одного в другой.
/ * 2\3/2
Отв. / = Va3 + 6V
282

17. Завод А отстоит от железной дороги, идущей с юга на север и
проходящей через город В, считая по кратчайшему расстоянию, на а км. Под каким
углом ф к железной дороге следует построить подъездной путь от завода, чтобы
транспортировка грузов из А в В была наиболее экономичной, если стоимость
провоза одной тонны груза на расстояние 1 км составляет по подъездному пути
р руб., по железной дороге q руб. (p>q) и город В расположен на b км
севернее завода Л?
_ а а а
Отв. ф = arccos —, если arccos — ^ arctg -=-;
Р ' Р * Ь "
. а а . а
ф == arctg -г-, если arccos — < arctg -j-..
18. Из всех ваз одинаковой вместимости и имеющих форму усеченного конуса,.
в котором образующая составляет с основанием угол а, найти ту, у которой
полная поверхность была бы минимальной.
Указание. В обозначениях на рисунке 125 боковая поверхность вазы вместе
с площадью дна представится в виде
S = n (x—yctga)2-
Щ х2 — (х—j/ctga)*
cos
sin a y • ctg a
--n(x — #ctga)2 +
1 \ . x*
cos a
>a J
(¦
5s = nl (гг + r2) = л/ —
r\ — r2
Объем вазы V = -«- пу
и== —-i 1\ Откуда —г— = *3 — (х — i/ctga)8. Если постоянную величину
О /"i~"~^2/ 71 XgCC
-г обозначить через а3, то получим: (х—у ctga)3 = *3 — а3. Таким образом.
для решения задачи нужно исследовать функцию и — (х — у ctg a)2 (l i -j-
x2
cos a
cos a
при условии, что (x — #ctga)3 = *3 — a3, то есть функцию и = (х3 — я3)з х
х[1~шУ
cos a
Отв. х =
1
1 — cos a *
Рис. 124.
283

§ 7. ГРАФИЧЕСКОЕ РЕШЕНИЕ УРАВНЕНИЙ
Умение строить графики функций может быть с успехом
использовано для приближенного решения уравнений.
Если дано уравнение
f(x) = 0, (1)
то для определения его вещественных корней достаточно построить
график функции y = f(x) и найти абсциссы точек пересечения
графика с осью ОХ. Действительно, если х0 — абсцисса точки
пересечения графика функции y=f(x) с осью ОХ, то /(х0) = 0, а это
значит, что х0 есть корень уравнения (1). Погрешность, допускаемая
при таком решении уравнений, будет тем меньше, чем точнее
построен график и чем точнее измерена абсцисса х0. Разумеется, при
предварительном исследовании функции y=f(x) по предлагаемой
нами схеме (см. § 3 этой главы)
в пункте 5 следует ограничиться
только определением точек
пересечения кривой с осью 0Y.
Уравнение (1) можно графически
решать и другим способом.
Последний состоит в том, что функцию / (х)
представляют в виде разности двух
X функций: f(x) = f1(x) — f2(x). Тогда
*"" уравнение (1) представится в виде
fi (х) =/2 (х). Построение графика
Рис. 126. функции у =f (х) заменяется
построением графиков двух более простых
функций: y = fi{x) и y = f2{x). Абсциссы точек пересечения
графиков этих функций будут корнями уравнения (1). Действительно
(рис. 126), если х0 — абсцисса точки пересечения указанных
графиков, то М*о) = М*о) и получаем, что f(x0)=f1(x0) — f2(*0) = 0,
то есть х0 — корень уравнения (1). Если же графики функций у =
= f1(x) и y = f2{x) не пересекаются, то из только что проведенного
рассуждения следует, что уравнение (1) не имеет вещественных
корней.
Преимущество этого способа состоит в том, что представление
f(x) = f1(x)— f2(x) дает возможность выбрать функции f1(x) и f2(x)
так, чтобы их графики строились как можно проще. Так, при
решении квадратного уравнения ax2-\-bx-\-c = 0 удобно представить
его в виде ше2=—Ьх — с, или
Построение же графиков параболы f±(x) = x2 и прямой f2(x) =
= х — — не составляет особого труда.
284

Рис. 127.
Рис. 128.
Пример 1. Решить графически уравнение 2х2— 4х — 3 = 0.
Преобразуем уравнение к виду (2):
*2 = 2* +
2 '
Затем строим графики функций у-
•-х2 и у = 2х + -^-. Как видно из рисунка 127,
хх и х2 являются абсциссами точек пересечения графиков. Сняв эти значения
с чертежа с помощью измерительных приборов, получим приближенные решения
3 п 2
данного уравнения: xt — — х2 — 2-^-
5 о
Заметим, что поскольку любое уравнение вида ах2 + Ьх + с можно
привести к виду (2), то при графическом решении нескольких таких
уравнений нет необходимости для каждого уравнения строить
график параболы у = х2. Достаточно построить его один раз (но как
можно точнее!), а затем на этом чертеже строить графики прямых
У = —^х'
соответствующих различным уравнениям.
Пример 2. Решить графически уравнения:
а) 2*2_*_8 = 0, б) 3*2 + 6*+10=0.
Преобразуем данные уравнения к виду (2): а) *2 = —-* + 4, б) х2 = -—2*——¦
и строим на одном чертеже графики функций у = х2, */ = -~- х+4 и у = — 2х—^.
Получим, что (рис. 128) приближенными решениями первого уравнения будут
*i = —т- и *2=х» втоРое уравнение не имеет вещественных решений.
Изложенный здесь способ графического решения уравнений
применим также к решению кубических, показательно-степенных,
логарифмических и тригонометрических уравнений.
Пусть дано кубическое уравнение
ax2 + bx2 + cx + d = Q. (3)
285

С помощью замены переменной по формуле x = z—~- это уравнение
преобразуется к виду, не содержащему квадрата неизвестного,
az2 + c1z + d1 = Q,
или
а а
Построив на одном чертеже график кубической параболы y = z*
и график прямой у = — — z—-, находим корни преобразованного
уравнения. Для исходного же уравнения корни получим по фор-
муле х = г-±.
Заметим, что и здесь этот способ решения особенно выгоден,,
если решается несколько кубических уравнений. Строится график
кубической параболы y = z3 и на том же чертеже проводятся
прямые у = — — 2 —-, соответствующие различным заданным уравнениям.
Пример 3. Решить графически уравнение 54*3 + 54;с2 — 90* — 7 = 0.
Преобразуем это уравнение, заменив переменную х по формуле x=z—^-:
54(г-|)3 + 54(2-4)2-90(г-|)-7 = 0,
54z3 — 54z2 + 182 —2 + 5422 —362 + 6 —90z + 30 —7 = 0,54z3—1082 + 27 = 0.
Получим
г3 — 2г+у = 0, или 23 = 22 —i-.
Затем строим параболу y = z3 и прямую у = 2г—-=-, Из рисунка 129
получаем: 2Х = ^-, z2 = -=-, 2з = -с". Следовательно, приближенными корнями исход-
ного уравнения будут: Xi = — 2, х2 = -- *3 = tf.
Напоминаем читателю, что в тех случаях, когда при построении
графиков приходится по какой-либо из координатных осей
откладывать сравнительно большие значения, то по этой оси желательно
брать более мелкий маснтаб. Это улучшит расположение графиков
на чертеже. Кроме того, если уменьшается масштаб по оси 0Y
относительно оси ОХ, то графики функций будут пересекаться под
менее острым углом и становится легче определять правильное
положение точек пересечения их. На рисунке 129 масштаб по оси
0Y уменьшен в два раза по сравнению с масштабом по оси ОХ.
Заметим, наконец, что кубическое уравнение (3) можно
графически решать и с помощью преобразования к виду
ах2 + Ьх + с =
1 * X
(последнее получено почленным делением уравнения (3) на хк
переносом — в правую часть). В этом случае строятся графики пара-
286

болы y~ax2-{-bx-{-c и гиперболы {/ = ——, после чего находятся
абсциссы точек пересечения их.
Пример 4. Решить графически уравнение 2* —х —2 = 0.
Представим уравнение в виде 2* = л:+2. Из уравнения сразу видно, что хг = 2
является его корнем. Это уравнение может иметь не более двух вещественных
корней, так как график показательной
функции не имеет точек перегиба и
может пересечься с прямой не более
чем в двух точках. Выясним, имеется
ли второй корень, и если да, то
найдем его значение. Для этого построим
на одном чертеже графики
показательной функции у = 2* и линейной
функции у = х-\-2. Из рисунка 130
5
следует, что *2 =—о- является
приближенным значением второго корня
данного уравнения.
Рис. 129.
Рис. 130.
Упражнения
Решить графически следующие уравнения:
1. Зх2 — 5х—2 = 0.
2. *з —9*2-f 20*— 12 = 0.
3. х3 — 4х— 1=0.
4. ** — 4х+1=0.
5. х = 2-*.
6. x=2sirix.
7. e* = cosx.
§ 8. УТОЧНЕНИЕ КОРНЕЙ УРАВНЕНИЯ
Из первой теоремы Больцано — Коши (§ 5, гл. IV) следует, что
если непрерывная функция y = f(x) на концах отрезка [а, Ь] имеет
значения разных знаков, то внутри этого отрезка уравнение
/W=o (1)
287

Рис. 131. Рис. 132.
имеет по крайней мере один вещественный корень и число а можно
считать приближенным значением этого корня с недостатком, а число
b — его значением с избытком. Допускаемая при этом погрешность
будет, очевидно, меньше числа b — а. В решенном нами примере 4
(§ 5, гл. IV) показан метод, с помощью которого можно как угодно
уменьшать отрезок, заключающий искомый корень, иначе говоря,
показан метод приближенного вычисления корней с любой
степенью точности. Однако этот метод, хотя и прост по идее, связан
с большой вычислительной работой. Требуется вычислять
большое число значений функции f (х). Практически более удобными
и более быстро приводящими к цели являются так называемые
метод хорд и метод касательных. Перейдем к знакомству с этими
методами.
1. Метод хорд. Пусть уже известно, что вещественный корень
х = с уравнения (1) находится внутри отрезка [я, 6](а<с<Ь).
Предположим также, что на [а, Ь] функция f (х) имеет непрерывные
производные /' (х) и /" (х) постоянного знака, а ее значения f (а) и
f (b) -— противоположных знаков. Выполнение этих условий обычно
достигается за счет уменьшения отрезка [а, Ь]. Постоянство знака
/' (х) указывает на монотонность функции / (х) на [я, b] (либо только
возрастание, либо только убывание). Следовательно, в обоих
случаях кривая у = Г (х) на участке [а, Ь] пересекает ось ОХ только
один раз, то есть х = с будет единственным корнем на [а, Ь].
Постоянство же знака /* (х) на [а, Ь] указывает на то, что
направление вогнутости на этом отрезке не меняется.
Дугу кривой y=f{x) на [а, Ь] заменим хордой, соединяющей
точки А(а, /(a)) и B(b, f(b)) (рис. 131). Примем ^ — абсциссу точки
пересечения хорды с осью ОХ—за первое приближение корня.
Очевидно, \с—#i|<b — а. Точку х± можно найти и аналитически.
Для этого достаточно составить уравнение прямой, проходящей
через две точки A v В:
* — <* _ У — /(о) /9v
288 i

и подстановкой в это уравнение у = 0 найти точку пересечения
прямой (а значит, и хорды) с осью ОХ. Будем иметь:
х — а _ —/ (а)
Отсюда
*1=я-щЕщ/(а)- (3)
Эта формула, как ниже будет видно, является основной
расчетной формулой метода хорд. Случаи, отвечающие четырем
комбинациям знаков f (x) и /" (х) изображены на рисунке 132. Как видно
из чертежей, во всех четырех случаях хх лежит между а и b с той
стороны от корня с, где f{x) имеет знак, противоположный знаку
f" (x) (последнее можно доказать и аналитически).
Практически в каждом из случаев определяем знак 1(хх) и,
сравнив его со знаками f (а) и /(b), выберем тот из двух отрезков
[а, хг] и [хъ 6], на концах которого значения функции имеют
разные знаки. На нем и будет находиться искомый корень с.
Предположим для определенности, что на [а, Ь] производные
/' (х) и /" (х) положительны (в остальных случаях рассуждения
ведутся аналогично). Тогда х1 будет лежать между а и с.
Следовательно, корень с находится внутри отрезка [xub]. Применим
к этому отрезку снова формулу (3), положив в ней а = хг. Получим:
х*=хх- f{b)_f\Xl)
fОбозначение х2 оказывается между х± и с. Следовательно, с находится
внутри отрезка [х2, Ь). Применив к нему снова формулу (3), получим:
*з = *2— f(b)-f(x2) f (**)'
и т. д. На /г-м шагу (п>1) будем иметь:
хл=хп_г - f^^fl^) f (*«-i) • (4>
В результате получится последовательность все более и более
точных значений корня. При этом, как видно из рисунка 131, все
они будут лежать с той же стороны от корня с, что и хъ то есть
а < хг < х2 < *3 <... < хп <... < с. (5)
Заметим, что при сохранении знаков у /' (х) и /" (х) можно
сделать следующий вывод: если значение f (х±) оказалось
противоположного знака по сравнению с f{b), то f(xn) и при всех
последующих значениях п будет противоположного знака по сравнению
с f(b). Если же /(*i)—противоположного знака по сравнению
с f(a), то этим же свойством обладают и все последующие
значения f(xn).
Остается установить, что последовательность (5) сходится к с.
Действительно, эта последовательность возрастает и ограничена
289

сверху. Значит, она имеет конечный предел d^c. Переходя
в равенстве (4) к пределу с учетом непрерывности f(x), получим:
d = d-f(b)-df(d)-f{d)-
Отсюда заключаем, что f(d) = 0> то есть d —корень уравнения (1).
Но поскольку на [а, Ь] имеется только один корень, то d = c и
lim хп = с.
Оценку погрешности приближения хп корня с можно получить
с помощью формулы Лагранжа:
f(Xn)—f(c)=f'(x0)(xn — c), где xn<x0<c.
Так как с—корень уравнения (1), то f(c) = 0, и мы получим:
Обозначим через т наименьшее значение |f (*)1 на [хп, Ь]. Тогда
If (*о) \^т> и мы получим следующую формулу для оценки
отклонения приближенного значения корня хп от истинного значения с:
Замечание. Предупреждаем читателя, что хотя в остальных
трех случаях комбинаций знаков /'(*) и /" (х) (рис. 132)
рассуждения ведутся аналогично, но для них сохранится только
формула (3). Что же касается формулы (4), то она может измениться.
Именно, если предположить, что /' (х) и /" (х) имеют разные знаки
на [а, Ь], то для п>\ получим:
(вывод этой формулы предлагается сделать самостоятельно).
Сравнивая (4) и (4'), видим, что произошла замена хп_г на а, Ь на xn_v
Пример 1. Решить уравнение дс2 — 5 = 0 методом хорд.
Эта задача равносильна задаче об извлечении квадратного корня из 5.
Рассмотрим функцию f (х) = х2 — 5. Так как f(l) =—4, f (2) =— 1, f (3) = 4, то корень
уравнения находится внутри отрезка [2, 3]. Положив в формуле (3) а = 2 и & = 3,
получим первое приближение корня хг:
^=2-4-^1)' (-D = 2+i- = 2,2.
Поскольку f(x1)==f (2,2) = 4,84 — 5 < 0, а /:(3)>0, то корень находится внутри
отрезка [2,2; 3]. Применим к этому отрезку формулу (3), положив а=2,2 и Ь = Ъ.
Получим:
х2 = 2,2-4_(^80>16) . (-0,16) =2,23076.
В силу того что f (х) = 2х и f"(je)==2 постоянного знака на [2, 3],
нет-необходимости дальше определять знак }(хп)\ это значение будет отрицательным при
всех п.
290

Применим к отрезку [2,23076; 3] снова формулу (3). Получим:
3 — 2,23076
хо = 2,23076 -
4 + 0,02372
•0,02372 = 2,23529.
Подсчитаем, какова будет погрешность приближения, если остановиться на
значении хг Воспользуемся формулой (6). Производная f' (x)=2x есть
возрастающая функция. Следовательно, на рассматриваемом отрезке [х3, Ь] ее
наименьшее значение равно значению на левом конце, то есть m = f' (x3) =2 • *3 = 4,47058.
Найдем f(*3) = — 0,00348. Тогда
!*°-c|^S~°'ooo7<o'ool
Если по условию ^конкретной задачи такая точность вычисления корня достаточна,
то можно остановиться на х3. В противном случае процесс приближения следует
продолжить.
Рассмотренный нами метод хорд иначе называют методом
линейной интерполяции. Такое название метод получил из-за того, что
в его основе лежит замена данной функции / (х) на каком-то участке
[а, Ь] линейной функцией у =
= f(a)+^^(x-a), полу-
чаемой из равенства (2). При
этом ее значения на концах [а, Ь]
совпадают со значениями
функции f(x) (см. рис. 131).
2. Метод касательных.
Пусть на [ау Ь] находится только
один корень с уравнения (1).
Предположим также, что на
этом отрезке существуют
непрерывные производные f (x) и /" (х)
постоянного знака, а значения
функции f(a) и f (Ь) —
противоположных знаков.
Идея метода касательных
состоит в том, что дуга кривой
у = f(x) на [а, Ь] заменяется
касательной к этой кривой,
проведенной в одной из точек
Л (a,/(a)) и Б (6,/(6)) (рис. 133),
и после этого абсцисса х\
точки пересечения касательной
с осью ОХ принимается за
первое приближение корня с.
При этом касательную следует провести в той из точек Л и В,
чтобы она пересекалась с осью ОХ во внутренней точке [а, Ь], то
есть чтобы точка х\ оказалась ближе к корню с, чем точки а и Ь.
В зависимости от комбинаций знаков /' (х) и /" (х) возможны
четыре случая, изображенные на рисунке 134. Как видно из черте-
Рис. 133.
291

жей, касательную нужно проводить в той из точек А и В, ордината
которой одного знака с /" (х), так как в этом случае касательная
всегда будет пересекать ось QX во внутренней точке [а, Ь]. Если
же провести касательную в точке, ордината которой имеет
противоположный знак с f" (х)> то она может пересечь ось ОХ и вне
отрезка [а, Ь]
Для определенности рассмотрим снова случай, когда /' (х) > О
и/"(х)>0 (в других случаях рассуждения аналогичны). Тогда
касательную к кривой следует провести в точке В (6, f (b)).
Составим ее уравнение: y-f(b) =
= /' (b) • (х—b). Положив в этом
уравнении у = 0, найдем
абсциссу точки пересечения
касательной с осью ОХ:
f(b)
Рис. 135.
* = Ь-Щ. (7)
Эта формула является основ-
Т ной расчетной формулой метода
касательных.
Как видно из чертежа 135,
точка Xi лежит между с и Ь.
Следовательно, корень с
находится внутри отрезка [а, х\].
Кроме того, значение f (хгг) одного знака с /" (х). Применим к этому
отрезку формулу (7), приняв Ь = х[. Получим второе приближение
корня х'2:
• _ > f (*;>
Далее, точка х'2 лежит между с и х[, a f (x\) одного знака с /" (х).
Применим к отрезку [а, х2'} формулу (7), приняв Ь = х\. Получим:
хз — х* р(х'яУ
и т. д. На п-ы шагу {п>\) будем иметь:
/(*Vl)
X п — X п—1 •
(8)
В результате выделится последовательность все более и более
точных приближений корня с:
х/ > х2' > х3' > ... > Хп > • • - > с.
Эта последовательность убывает и ограничена снизу. Следовательно,
она имеет какой-то конечный предел d^c. Осуществив в равенстве
(8) предельный переход с учетом непрерывности f(x) и /' (х),
получим равенство:
d = d-
f'(d)'
292

Из последнего следует, что f(d) = 0, то есть d есть корень уравнения
(1), и, следовательно, c = d.
Формула (6), полученная нами для оценки погрешности
приближения методом хорд, применима также и при приближении методом
касательных.
При1иер 2. Решить уравнение х%— 5 = 0 методом касательных.
Положим f(x) = x2— 5. Как уже установлено в примере 1, эта функция на
отрезке [2, 3] меняет знак с минуса на плюс и имеет на этом отрезке
непрерывные положительные производные /' {*) = %х и /" (*) = 2. Следовательно,
касательную к кривой у — х2 — 5 нужно проводить в точке В (3; 4). Воспользуемся
формулой (7), положив в ней 6 = 3. Получим первое приближение корня, х\:
х'-З—1— 2 1
Применив к отрезку 2; 2-^- снова формулу (7), найдем второе приближение
корня, х2':
*'-2±—?-_2А
4 ~~Z 3 21 ~~Z21 •
Третье приближение корня получим, если применим формулу (7) к отрезку
"•'-2я~ш-2-23(й7-"т-д-
Определим с помощью формулы (6), какова будет погрешность вычисления
корня, если остановиться на х3'. Так как производная /' (х) = 2х есть
возрастающая функция, то наименьшим ее значением на отрезке 2; 2 щ-\ будет значение
/'(2)=4, то есть т = 4. Значение / (*3') = (2.23607)2 — 5=0,00001. Следовательно,
|*W|<°^ ===0.0000025.
Полученное нами приближенное значение корня является, как легко видеть,
значением с избытком, то есть с <С х3'= 2,23607, в то время как при решении
этого же уравнения методом хорд (пример 1) получено приближение с
недостатком х3 = 2,23529<с.
Заметим, что рассмотренные нами методы приближенного
решения уравнений обладают тем общим недостатком, что каждый из
них приводит к последовательности приближений только с одной
стороны от истинного значения корня с. Поэтому не представляется
возможным хорошо оценить допускаемую погрешность. Кстати
сказать, формула (6), которой мы пользовались при оценке
приближений в примерах 1 и 2, во многих случаях дает слишком грубую
оценку. Фактически погрешность часто оказывается гораздо меньше,
чем показывает формула (6).
Если же метод хорд объединить с методом касательных, то есть
приближаться к истинному значению корня с одновременно с двух
сторон (хорда и касательная пересекают ось ОХ по разные стороны
293

от корня), то на первом шагу (при f (x)>0 и f" (х)>0) получим:
х1<с<х1'.
На втором шагу вместо отрезка [а, Ь] уже рассматриваем
отрезок [х19 хг'\ (рис. 135). Для него найдем
по формуле (4):
"Xl~W7)4W)nXl)t
по формуле (8):
Х2 — Х\
Пч')
7(*i')
и снова х2<.с<С.х2. Затем рассматриваем отрезок \х2, х2] и т. д.
На п-и шагу будем иметь: хп<с<хп', где для п>\ значения
хп и xnf вычисляются по формулам:
Y у Х'п-1 ХП-1 f I \. Г / f (X'n-l)
Xn-Xn-i f(*^)-/(*w)eH*«-lJ. Ьп-Хп-1 f(x>n_iy
При этом lim x„ = lim x'n = c.
Оценивая разность хп' — хп> получаем возможность сразу судить
о степени точности сделанных приближений. При таком
комбинированном методе приближений нет надобности ни в каких
специальных формулах для оценки допускаемых погрешностей.
Пример 3. Найти все корни уравнения 2х—4л: = 0 с точностью до 0,0005.
Прежде всего заметим, что данное уравнение не имеет отрицательных корней,
так как при всех значениях *<0 будет 2х—4х>0.
Рассмотрим функцию f(x)=2x—4х. Она непрерывная и имеет производные:
/' (х) = 2*1п2 — 4, f"(*) = 2*(ln2)a.
Из выражения производных видно, что функция убывает до некоторого зна-
о*« , о л I In 4 —In In 2 \
чения аргумента *0, при котором 2Л° In 2 = 4 I х0 = 1—^ \ а потом
постоянно возрастает; ее график вогнут вверх. Отсюда заключаем, что в точке х0
функция имеет минимум и пересечение ее графика с осью ОХ возможно не более
чем в двух точках. Это значит, что данное уравнение имеет не более двух
вещественных корней.
Для определения промежутков, содержащих корни, произведем последовательно
вычисления: /(0) = 1, /(!)=—2, / (2) = —4,/(3) = —4,/(4) = 0,/(5) = 12.
Дальнейшие вычисления излишни, так как оба корня уравнения уже обнаружены:
один корень cY находится на отрезке [0, 1], а другой с2 = 4.
Найдем приближенное значение сх с требуемой точностью.
На отрезке [0, 1] /'(x)<0, а/"(*)> 0. Следовательно, функция на этом
отрезке убывает (от 1 до — 2) и ее график направлен вогнутостью вверх. В таком
случае (смотри соответствующий чертеж на рисунках 132 и 134) приближения по
методу хорд будут с избытком (справа от корня сг), а приближения по методу
касательных —с недостатком (слева от сх).
Положив в формуле (3) а = 0 и 6=1, получим:
*i=° д1р^5Г-/(0) = у=0,33333...^0,3334.
Формула же (7) при 6=0 дает:
^=0-/^=-Т^=4^693Т=0-30239--^0'3023-
294

При этом *! — #1 = 0,3334 — 0,3023 = 0,0311, то есть точность приближения
на первом шагу недостаточна.
Проделаем еще один шаг, применив методы хорд и касательных уже к отрезку
1*1! *ib Предварительно вычислим значения, которые будут нужны:
1
/(*i)=/(g) = 2*-4- g= 1,2600- 1,3333= -0,0733,
/ (х[) = г*'*03* — 4.0,3023 = 1,2045— 1,2092=0,0253,
/(х;) = 2°'302».1п2 — 4=1,2345-0,6931 — 4 =—3,1444.
По формуле (3) при а = х[ и b = xt находим:
, х- *!-*; f(xl Q3023I °'031Ь0'0253 0 3101
г~ ' /<*i)-/W) Hxi>-°'d0M+ 0,0733+0,0253 _0,31°4,
По формуле же (7) при 6 = *; будем иметь:
<-*'-^-ода+Ж-0'8108-
Разность *2--Х2 = 0,3104 — 0,3103=0,0001 показывает, что полученная точность
вычисления удовлетворяет заданной. Получили, что 0,3103 <сх < 0,3104. Любое
из чисел 0,3103 и 0,3104 можно взять за приближенное значение искомого корня
сг и допускаемая при этом ошибка не превзойдет 0,0001. Их среднее
арифметическое 0,31035 будет, очевидно, еще ближе к сг.
Вопросы для самопроверки и упражнения
1. Почему при последовательном уменьшении промежутка, содержащего корень
(при комбинированном методе хорд и касательных), можно нижнюю его границу
округлять только в сторону уменьшения, а верхнюю — только в сторону
увеличения?
2. Уточнить методом хорд корень уравнения х2—2=0, содержащийся на [1, 2].
Найти хъ х2 и х3. Отв. j^sl-p» 1,333; *2= 1,394; лг3= 1,412.
3. Уточнить методом касательных корень уравнения 3* = 3х, отличный от
единицы. Найти х[, х'2 и x'z. Отв. ^ = 0,53; #2 = 0,72, *J=0,79.
4. Уравнение #4+6#3+14#2 — 50 = 0 имеет два вещественных корня.
Вычислить их по комбинированному методу с точностью до 0,001.
Отв. хге=& — 3,155; х2«s 1,425.
5. Вычислить с точностью до 0,0005 единственный положительный корень
уравнения хъ—х = = у содержащийся на отрезке [1; 1,1]. Отв. c^s 1,04478.

Раздел III
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ
ОДНОЙ ПЕРЕМЕННОЙ
Г Л А В А VIII
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 1. ПЕРВООБРАЗНАЯ И НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Интегральное исчисление является второй частью курса
математического анализа, непосредственно следующей за дифференциальным
исчислением. Само понятие интеграла наряду с понятием
производной и дифференциала является фундаментальным понятием
математического анализа. Это понятие возникло, с одной стороны, из
потребности решать задачи на вычисление площади, длины
окружности, объема, работы переменной силы, центра тяжести и т. д.г
с другой — из необходимости находить функции по их производным.
В соответствии с этим возникли понятия определенного и
неопределенного интегралов.
Как известно, основная задача дифференциального исчисления
заключается в отыскании производной или дифференциала заданной
функции.
Можно поставить обратную задачу: по данной функции f(x) найти
такую функцию F (х), которая бы удовлетворяла условию F' (x)=f (x)
или dF(x) = f (x)dx. Отыскание функции по заданной ее производной
или дифференциалу и является одной из основных задач
интегрального исчисления.
К задаче восстановления функции по ее производной или
дифференциалу приводят самые разнообразные вопросы математического
анализа с его многочисленными приложениями в области геометрии,
механики, физики, техники.
Например, с такого рода задачей мы встречаемся, когда по
заданной скорости движения материальной точки v=f(t) требуется найти
закон движения этой точки, то есть зависимость пройденного
точкой пути s от времени /. В дифференциальном исчислении мы имели
дело с обратной задачей. Там по заданному закону движения s=s(t)
путем дифференцирования функции s(t) мы находили скорость v этого
296

движения, то есть v(t) = s' (t). Следовательно, в поставленной выше
задаче мы должны по данной функции v=f(t) восстановить функцию
s = s(t), для которой f(t) является производной.
Определение 1. Функция F(х) называется первообразной
(или примитивной) для функции f (х) на некотором промежутке,
если для всех значений х из этого промежутка выполняется равенство
F' (x) = f(x), или, что то же самое, dF (x)=f (x)dx.
Таким образом, функция s(t) — переменный путь — есть
первообразная для скорости v = f(t).
Пример 1. Функция sinx является первообразной для функции
cos л: на всей оси ОХ, так как при любом значении х мы будем
иметь: (sin х)' = cos x.
Пример 2. Аналогично, функция F(x)==x3 является
первообразной для f(x) = 3x2, так как (хд)' =3jc2.
Возвращаясь к примеру 1, важно заметить, что первообразной
для cos л: является не только sinx, но и функция sinx + C, где С —
любая постоянная, так как (sinx + C)'=cosx. To же самое можно
сказать относительно первообразной F(x)=x3 из примера 2.
Указанное обстоятельство справедливо для любой функции f{x),
имеющей первообразную. Именно справедлива следующая теорема.
Теорема 1. Пусть F {х)—какая-нибудь первообразная для
функции f(x) в некотором промежутке [а, Ь\; тогда функция
F(x) + C, где С — любая постоянная, также будет
первообразной для f(x).
Обратно, всякая первообразная для f(x) в указанном
промежутке может быть представлена в виде F{x)-±C.
Доказательство. Так как производная от произвольной
постоянной равна нулю, то
[F(x) + C}'=F'(x)=f(x),
то есть наряду с ^(л:) функция F(x)+C есть также первообразная
для /(*).
Покажем теперь, что любая первообразная для f(x) представима
в виде F(x) + C.
В самом деле, пусть Ф(х) — произвольная первообразная для f (х)
в рассматриваемом промежутке, так что в этом промежутке Ф' (х) =
= f(x). Значит, функции Ф(х) и F (х) в рассматриваемом промежутке
имеют одну и ту же производную. Тогда в этом промежутке разность
Ф(х) — F(x) имеет производную, тождественно равную нулю, то есть
[0{x)-F{x)\'=0f{x)-F'{x)=f{x)-f{x)==O.
Как известно из дифференциального исчисления (см. гл. VII, § I,
теорема 1), производная функции тождественно равна нулю тогда
и только тогда, когда эта функция есть постоянная и, следовательно,
разность Ф(х) — F (х) есть некоторая постоянная величина С0, то есть
0(x)-F(x)=CQ,
отсюда
297

Таким образом, первообразная Ф(х) получается из выражения
F(x) + C надлежащим выбором произвольной постоянной С — С0.
Этим теорема полностью доказана.
Из теоремы (1) следует, что любые две первообразные для одной
и той же функции могут отличаться друг от друга только на
постоянное слагаемое. Значит, если для данной функции f(x) известна
одна первообразная F(x), то совокупность всех ее первообразных
представляется выражением
F(x)+C, (1)
где С — произвольная постоянная. Иными словами, других
первообразных, не входящих в выражение (1), быть не может. В силу этого
выражение (1) исчерпывает все семейство первообразных функций для
f (x) и представляет собой самый общий вид функции, которая имеет
производную f(x) или дифференциал f(x)dx.
Определение 2. Если F(х) — первообразная функция для f (x),
то выражение F(x) + C, где С — произвольная постоянная, называется
неопределенным интегралом от функции f(x) и обозначается
символом ^f(x)dx*. Итак, по определению
\f(x)dx = F(x) + C (2)
Функция / (х) называется подынтегральной функцией, произведение
f (x) dx — подынтегральным выражением, а переменная х—переменной
интегрирования. Символ ^ представляет собой растянутую латинскую
букву S и называется знаком интеграла. Читается: «неопределенный
интеграл f (x) dx».
Таким образом, неопределенный интеграл от какой-нибудь
функции представляет собой общий вид всех первообразных для этой
функции.
Формула (2) показывает, что если известна какая-нибудь
первообразная функция для f(x), то тем самым известен ее
неопределенный интеграл, и, следовательно, задача отыскания какой-нибудь
определенной первообразной для f(x) равносильна задаче отыскания
ее неопределенного интеграла.
В этой связи естественно возникает вопрос: для всякой ли
функции f(x), заданной на некотором промежутке, существует
первообразная F (х) (а значит, и неопределенный интеграл)? Оказывается,
что не для всякой. Однако если \ (х) непрерывна на каком-нибудь
промежутке, то она имеет на нем первообразную (а следовательно,
и неопределенный интеграл). Это утверждение будет доказано позднее
(см. § 5, гл. IX), а пока примем его без доказательства и всюду
в данной главе будем говорить лишь об интегрировании
непрерывных функций. В случае разрывной функции речь будет идти лишь
об интегрировании ее в одном из промежутков непрерывности.
* Это обозначение впервые ввел в 1675 г. знаменитый немецкий философ
и математик Г. В. Лейбниц (1646—1716).
,298

Например, функция f(x) = — имеет разрыв только при х = 0.
Поэтому промежутками непрерывности для нее будут (0, +оо)
и (—со, 0). В первом из них одной из первообразных для —
является In л:. Следовательно,
\ — dx=\nx + C.
Однако для х из промежутка (—оо, 0) эта формула уже лишена
смысла (так как \пх при a:<0 не определен). В этом случае одной
из первообразных для — будет уже не 1пл:, a In (—л;), ибо
[ln(-x)]'=Tir.(-l)=-i
и, стало быть,
[ -dx = \nl—x) + C.
Объединяя оба случая, мы приходим к формуле:
5
?=1п|х| + С.
Восстановление функции по ее производной, или, что то же,
отыскание неопределенного интеграла по данной подынтегральной
функции, называют интегрированием.
Поскольку интегрирование — обратное действие по отношению
к дифференцированию, то благодаря этому проверка правильности
результата интегрирования осуществляется дифференцированием
последнего: дифференцирование должно дать подынтегральную функ-
дию.
С dx
Пример 3. V —-— — \gx-\-Cy то есть выражение tg* + C представляет
•собой совокупность всех первообразных для функции —, так как (tg# + C)'=
СОЬлХ
f *4
Пример 4. Проверить, что \ xz dx — — + C
Дифференцирование дает: (-7~ + С) = *3- Следовательно, интегрирование
выполнено верно.
Пример 5. Проверить, что ^ cos
(sin 2x У
—s \-С\ = cos2x. Следовательно, интеграл взят верно.
Вернемся теперь к поставленной вначале механической задаче:
к определению пройденного пути s по заданной скорости движения
v=f(t). Так как скорость движущейся точки есть производная от
299

пути по времени, то задача сводится к отысканию первообразной
для функции v = f(t). Следовательно,
s=\f(t)dt. (3)
Пусть для определенности нам дано, что скорость движения точки
пропорциональна времени t> то есть v = at, где а — коэффициент
пропорциональности. Тогда согласно формуле (3) мы имеем:
s= J atdt = ^ + C, (4)
где С — произвольная постоянная. Мы получили бесчисленное
множество решений, отличающихся друг от друга на постоянное
слагаемое. Эта неопределенность объясняется тем, что мы не фиксировали
того момента времени ty от которого отсчитывается пройденный путь 5.
Чтобы получить вполне определенное решение задачи, достаточно
знать величину s = s0 в какой-нибудь начальный момент времени
t = t0 — это так называемые начальные значения. Пусть, например,
нам известно, что в начальный момент времени / = 0 путь s = 0.
Тогда, полагая в равенстве (4) / = 0, s=0y находим 0 = 0 +С, откуда
С = 0. Следовательно, искомый закон движения точки выражается
at2
формулой s = -2~. В частности, если мы имеем дело с задачей о
падении тела в пустоте, то a=gy где g— ускорение силы тяжести. Тогда
путь, пройденный падающим телом и отсчитываемый от точки, в
которой тело выходит из состояния покоя, будет выражаться формулой
S"~ 2 •
Остановимся теперь на геометрическом смысле семейства
первообразных F(x) + C для f(x), а значит, и на геометрическом
истолковании неопределенного интеграла. Заметим, что график
первообразной обычно называют интегральной кривой. Поэтому
неопределенному интегралу соответствует совокупность интегральных
кривых.
Как расположена одна кривая по отношению к другой? На это
дает нам ответ доказанная выше теорема. Если построена какая-
нибудь интегральная кривая, то согласно этой теореме все другие
интегральные кривые получаются из нее параллельным переносом
в направлении оси ординат (рис. 136), то есть график построенной
первообразной надо передвигать параллельно самой себе в
направлении оси ординат, чтобы получить все остальные интегральные
кривые.
Если F (х) — первообразная для f(x), то есть F' (x)=f (jc), то,
вспоминая геометрический смысл производной, мы видим, что график
первообразной F (х) в каждой своей точке имеет касательную с
угловым коэффициентом, равным f(x).
Все другие интегральные кривые будут иметь при том же
значении х параллельные касательные с тем же угловым коэффициентом
f{x) (см. рис. 136).
300

§ 2. ОСНОВНЫЕ СВОЙСТВА НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Из определения неопределенного интеграла непосредственно
вытекают следующие его свойства.
Г. Производная от неопределенного интеграла равна
подынтегральной функции; дифференциал от
неопределенного интеграла равен подынтегральному выражению, то есть
(\f(x)dx)=f(x),
d^f(x)dx = f(x)dx.
Действительно, из самого определения неопределенного интеграла
имеем:
(\f(x)dx)'=
=(F(x) + C)'=F'(x)=f(x).
Отсюда согласно
определению дифференциала, в
частности, вытекает, что
d^ f (x)dx =
= (^f(x)dx)' dx = f (x)dx,
то есть символы d и §,
когда сначала стоит d, a
затем $, взаимно
уничтожаются.
2°. Неопределенный интеграл от дифференциала
некоторой функции равен сумме этой функции и произвольной
постоянной, то есть
Рис. 136.
\dF(x)=F(x)+C.
Если учесть, что dF(x) = F' (x)dxy то эту формулу можно
переписать так:
\F' {x)dx = F(x)+C.
Эта формула непосредственно вытекает из определения
неопределенного интеграла, если иметь в виду, что F (х) есть первообразная
для F'(х).
Отсюда видно, что символы \ и d также взаимно уничтожаются
и в том случае, когда d стоит после $, но только при этом к F (х)
надо прибавить произвольную постоянную С.
301

3°. Постоянный множитель можно вынести из-под знака
интеграла, то есть если а = const^0, то
^ af (x) dx = a § f (x) dx*.
Справедливость этой формулы вытекает из того, что обе части
этого равенства в силу свойства Iе имеют одну и ту же
производную af (х). Действительно,
(\a f (x) dx)'=af (х), (а $ / (х) dx) =a(\f (x) dx)' =af (x).
Поэтому правая и левая части последней формулы выражают собой
одно и то же семейство первообразных для функции af(x) и поэтому
могут отличаться друг от друга на постоянное слагаемое.
4°. Неопределенный интеграл от алгебраической суммы
функций равен алгебраической сумме интегралов от
каждой функции в отдельности, то есть
\[f{x)±g{x)\dx = \t(x)dx±\g{x)dx.
Это свойство доказывается точно так же, как и свойство 3°.
Достаточно продифференцировать обе части равенства и воспользоваться
тем, что они имеют одинаковые производные и, следовательно, могут
отличаться лишь на постоянное слагаемое.
Разумеется, это свойство справедливо для любого конечного числа
слагаемых функций.
§ 3. ТАБЛИЦА ОСНОВНЫХ ИНТЕГРАЛОВ
Результаты, полученные в дифференциальном исчислении,
позволяют непосредственно проинтегрировать некоторые простые функции;
другими словами, любая формула, дающая нам производную (или
дифференциал) какой-нибудь функции, приводит к соответствующей
формуле интегрирования.
Например, формула d tgx = -^Г дает интегРал ) C0S2X dx =
= tgx + C.
Таким образом, если подынтегральное выражение f{x)dx
совпадает с дифференциалом некоторой функции F(x), то есть f(x)dx =
= dF(x), то достаточно прибавить к этой функции произвольную
постоянную, чтобы получить неопределенный интеграл.
Применяя последнее замечание к таблице дифференциалов
простейших функций, мы получим следующую таблицу интегралов;
* Это равенство и последующие, содержащие неопределенные интегралы,
следует понимать в том смысле, что разность между левой и правой частью есть
постоянная.
302

I. \dx = x + C\
II. ^jfidx-^ + C Oi^-D;
III. [~ = ln\x\ + C (см. стр. 299);
!V. Jj-^^arctgx + C^-arcctgx + C*;
V. \ , * =arcsinx + C = — arccosx + C*;
VI. V axdx=-^-^ + Cy в частности, \ eA"d*=e*-fC;
VII. $sin.*:d# = -—cos# + C:
VIII. ^cosxdx = sinx-\-C\
ix- S^=^+c=
Мзэтш
#—a
x + a
+ C(a^0)**;
XII. ^ /* ^lnljc + V^Tgl + C»»,
Здесь число а может быть как положительным, так и
отрицательным.
Интегралы, содержащиеся в этой таблице, мы будем называть
табличными.
Приведенную таблицу, так же как и таблицу производных
основных элементарных функций, следует знать наизусть.
Вычисление интегралов путем непосредственного использования
таблицы простейших интегралов и их основных свойств называется
непосредственным интегрированием. Однако и этот способ требует
определенных навыков, связанных с преобразованием и
разложением подынтегральной функции на сумму легко интегрируемых
слагаемых. Приведем ряд примеров, где используется этот способ.
Пример 1. ^x* + ~Jdx=^x« + 3x* + 3 + ^dx==
= ix«dx + 3 \ x*dx + 2>\ dx+[ x~*dx = y + ^-х* + 3х — ~ + С.
При вычислении этого интеграла мы пользовались свойствами 3° и
4°, а также формулой II таблицы интегралов. Здесь же заметим,
что при вычислении отдельных интегралов нет надобности после
* Напомним, что arctg х = -^ arcctg x\ arcsin х = -=— arccos x.
** На выводе формул XI и XII мы остановимся ниже, а пока в
справедливости их легко убедиться непосредственным дифференцированием обеих частей
равенства.
303

каждого слагаемого писать произвольную постоянную, потому что
сумма произвольных постоянных есть также произвольная
постоянная, которую мы и пишем в конце всех выкладок.
С / х jc\2 С/ х хх х\
Пример 2. \ (sin -^ +cos-x-1 dx= V i sin2 -o-+2 sin "9"cos ~o~ + cos2 ~o" jdx==
= ? (1 + sin x) dx=\ dx+{ sin xdx = x—cosx + C.
Пример 3. Вычислить интеграл ^ tg2 x dx.
Так как tg2x=sec2*— 1, то, применяя свойство 4° и формулы IX, I таблицы
интегралов, получим:
Jtg2*d*=Jj (sec2*-l)<b:= J "да- J dx = tgx-x + C.
Пример 4. Вычислить интеграл \ . » — dx.
r r r J sin2 х cos2 л:
т t • 9 i «» С * j f sin2A-+cos8*:
Так как 1 = sin2 x+cos2 х, то \ —г-т г— ^*= \ —г-у—!—5— ^*=*
j sin2 jc cos 2 л: J sin2 a; cos2 л:
« \ (4_ + ^_U.f J*_+ С ^—tgx-ctfx+C.
J \cos2x ' sm2x/ J cos2 a: j sin2 a: to ь
Пример 5. Вычислить интеграл f |^1 + sin 2д: dx.
В этом примере мы также используем тригонометрическое тождество 1 =
= sin2 х + cos2 x:
\ уг\ 4-sin 2х <2х=Д j/4+2 sin x cos xdx— \ У sin2 x-{-2 sin a: cos a:-f-cos2 xdx~
= \ ^(sin x+cos a:)2 ^а:= f (sin x + cos *) <2x * =
= J sin a: <2a: -f С cos a: <2a: =—cos a:-|-sin x + C.
Замечание. Все формулы основной таблицы интегралов
остаются справедливыми и в том случае, когда переменная
интегрирования не является независимой, а представляет функцию от
некоторой другой переменной.
Действительно, пусть имеем формулу
\f(x)dx = F{x) + C, (1)
где переменная интегрирования х является независимой
переменной. В частности, под этой формулой можно понимать любую из
формул основной таблицы.
С другой стороны, пусть нам дан интеграл, в котором
подынтегральное выражение может быть записано в виде f(u)du, где
ы = ф(л;) — любая дифференцируемая функция и, следовательно, du =
= ф' (х) dx. Иными словами, подынтегральное выражение имеет вид:
f [ф (*)] ф' (х) dx. Образуем сложную функцию F(u) = F [ф (х)]. По
правилу дифференцирования сложной функции
F' [ф (x)]x = F' (и) Ф' (*)=/ (и) ф' (х) = / [ф (х)] Ф' (х).
* Здесь мы считаем, что интегрирование совершается е таком промежутке,
где sin х-j-cos x^0, и, следовательно, арифметическое значение корня равно siiiJt-f-
+ cos at.
304

Тогда
lf[<p(x)]y'(x)dx = F[<p(x)] + C,
что коротко может быть записано и так:
\f(u)du = F(u) + C. (2)
Таким образом, для интеграла ^f(u)du (где и—функция от
другой переменной) мы получили формулу, имеющую тот же вид,
что и формула (1). Благодаря этому область применения основной
таблицы интегралов значительно расширяется. Поясним это
несколькими примерами.
Пример 6. Вычислить интеграл \ sin3 х cos х dx.
С С sin4 х
Так как cos x dx = d sin х% то \ sin3 x cos x dx — \ sin3 x d sin x = —- \-С.
Здесь мы применили формулу II таблицы интегралов, предварительно заменив
в ней х на u = sinA;. Справедливость полученного результата легко проверяется
дифференцированием.
Пример 7. Вычислить интеграл \ 2 q.
Постараемся получить в числителе дифференциал знаменателя. Для этого
запишем интеграл так: \ 2 » я = Y \ 2<Ч * Замечая, что 2х dx = d (jc2 + 3),
-будем иметь:
Г xdx _ 1 ? 2xdx _ 1 С d(x* + 2,) 1 2
J?+3-l3lH:3~2"J"^+3_-2-In(x+3)+C-
В этом примере мы воспользовались формулой III, заменив в ней х на « = jt2-f-3.
Пример 8. Вычислить интеграл \ i . 2х*
Так как exdx = de*, то ^ ?р^* = \ 1+W " arctgg* + C-
В данном случае мы применили формулу IV, заменив в ней * на и — ех.
Отметим одно полезное следствие из формулы (2). Пусть и =
= ях+6 (а 9^0). Тогда du~adx, откуда dx = — du. Подставляя это
в формулу (2), мы немедленно получим:
^f(ax + b)dx = ±F(ax + b) + C. (3)
Часто встречаются случаи, когда а=1 или Ь = 0.
Из сказанного следует, что если мы умеем интегрировать
функцию f (х), то мы можем легко проинтегрировать и f(ax + b). Так,
например, если учесть, что \ — = 1п|*| + С, то согласно правилу,
выраженному формулой (3), находим:
i
^rj-^-ln\ax + b\ + C.
ax + b a ' ' ' '
Точно так же \ cos (ax+ b)dx=—sin (ах+ Ь) + С.
305

Пример 9. Вычислить интеграл $ ctg xdx.
Имеем.
[ ctgxdx= { c4^d*= [ *™1 e in| sin*| + C.
J to J smx j sm* ' '
Отсюда, в частности, в силу формулы (3) следует и более общий
результат:
\ ctg (ax+ b)dx = — \n\sm(ax + b)\ + C.
Несмотря на то, что применение обобщенной таблицы основных
интегралов значительно увеличивает класс функций, интегралы от
которых берутся непосредственно, однако существуют многие классы
функций, интегрирование которых не может быть выполнено только
с помощью этой таблицы. Наша ближайшая задача и будет состоять
в том, чтобы научиться интегрировать как можно более широкие
классы функций. Этому вопросу и будет посвящена остальная часть
настоящей главы.
Вопросы для самопроверки и упражнения
1. Объясните, почему функции arcsin* и — arccos* имеют одинаковые
производные (аналогично arctg* и —arcctg*).
Применяя метод непосредственного интегрирования, вычислите следующие
интегралы:
2. $(4*з — 3 sinx + 6Vx)dx. Отв. *4 + 3cos* + 4*Ух + С.
3. С 9~~*dx. Отв. 3* ——*}/"*+?• 4. \ *——<1х. Отв. х—4 arctg*+С,
5- \ }\\+х\ dx' 0тз' 1п'х'+2arctgх+а
6. $ ]Л + sin х dx. Отв. 2 ( sin у — cosy)+C.
- ^ cos2* -rf*. Om*. sin a;—cos*-f C.
cos*—sin x
8. $ cos3 д; sin x dx. Отв. — -?-cos4*+a
9. $esin*cos*d*. Ome. eeifl* + C.
10. [l-^dx. Ome.-J-In» * + C.
|2e С cos*rf* Ome. 2)/2 +sin*+ C.
j т^г+яп **
Ome. ln(l+e*)+C.
3
13. yyrfx^xdx. Отв. -g-y^(4 + *2)*+C.
I*-1|
•MS
+ 2d*. Ome. *+|-ln
*+1
+ C.
Y2 + x*-V2-&_ ^ 0niQ arcsin * _ ln | x + y2 + x2 , + a
yx=^ ' ' У2
306

§ 4. МЕТОД ПОДСТАНОВКИ
Метод подстановки, или замены переменной в неопределенном
интеграле, состоит в том, что при вычислении интеграла
\f{x)dx
вместо переменной х вводится новая переменная t, связанная с х
определенной зависимостью: л:=?ф(/). При этом функцию ф (t)
следует выбирать так, чтобы подынтегральная функция становилась
более удобной для интегрирования.
Пусть мы имеем интеграл
lf(x)dx. (1)
Введем новую переменную / вместо х, положив x — cp(t), где
функция ф(?) монотонна и дифференцируема*. Тогда будет
справедлива формула
$/(*)«** = $/[<р(0]ф'(ОЛ. (2)
Действительно, используя свойство 1° неопределенного интеграла,
продифференцируем обе части этого равенства. С одной стороны,
d\f(x)dx = f (x) dx, а с другой, d \ f [<р(/)] q>' (t) dt = f[y (t)] ф' (t) dt =
= / (x) dx (так как dx = q>' (t) dt). Таким образом, обе части формулы
(2) имеют один и тот же дифференциал и потому выражают собой
одно и то же семейство первообразных для функции f (х). Это и
доказывает равенство (2) в том смысле, что правая и левая части его
могут отличаться между собой разве лишь на постоянное слагаемое.
Таким образом, для вычисления интеграла (1) с помощью
подстановки л: = ф(/) надлежит не только в функции f (х) заменить х
через ф (/), но и dx выразить через t и dt, то есть положить dx =
= (f'(t)dt. При вычислении неопределенного интеграла с помощью
подстановки x = q>(t) мы получаем искомую функцию, выраженную
через t Чтобы возвратиться к прежней переменной х, достаточно
в полученной функции заменить t значением, которое находится из
соотношения x = y(t), то есть значением t=ty(x), где ty(x) —
обратная функция для ф(/)**.
Пример 1. Вычислить интеграл \\га2— х2 dx.
Здесь удобно применить подстановку x = asint и, значит, dx =
= acostdt. Эта подстановка освобождает нас от корня: "j/a2 — х2 =
= }/га2 — a2sm2t = ±a cost, и в этом, разумеется, весь смысл
данной подстановки. Можно считать, что / изменяется в промежутке
— у, + у . Тогда значения переменной х заполнят весь
промежуток [ — а, -\-а]. Кстати, в этом промежутке подынтегральная
функция определена и непрерывна. Так как cos^^O для всех t из
* Из дифференцируемое™ следует непрерывность.
** Заметим, что из монотонности функции x = q>(t) вытекает существование
обратной функции t = ty(x).
307

——, +y , то арифметическое значение корня Va2—x2 = acost
(а>0). Далее в промежутке — ^-, + у функция x = asinf
монотонно возрастает и имеет непрерывную производную xi=acost*
Следовательно, подстановка x = asint удовлетворяет всем
требованиям правила замены переменной в неопределенном интеграле и мы
вправе применить формулу (2). Согласно этой формуле в
подынтегральной функции переменную х надлежит заменить на a sin/, a dx
на a cos tdt. В результате подынтегральное выражение делается
более удобным для применения формул неопределенного
интегрирования: Va2—x2dx = a2 cos2 tdt.
Итак,
i Va2 — x2dx = a2 \ cos2tdt = ^{ (l+cos2t)dt =
= i[\dt+ \cos2tdt)=Y{t+Ys[u2i) + a
Заметим, что интеграл ^cos2(dt с помощью подстановки u = 2tT
du = 2dt приводится к табличному: \ cos 2t dt = -=- \ cos udu =
= у sin # + C=ysin2/-f С.
Выразим найденную первообразную через прежнюю
независимую переменную х. Для этого из равенства x = asin/ находим:
t= arcsin —. Затем у sin2/ = sin/cos/, а так как sin/=—, tocos/=
= —]/а2—х2 и у sin 2/ = -^- Va2—х2. Тогда окончательно получим:
§ Va2-*2 dx = ^Va2-x2 + yarcsin^ + C.
Предлагаем читателю проверить непосредственным
дифференцированием правильность этого результата, то есть что производная
правой части равна Va2—х2.
В последующих примерах мы не будем более столь подробно
останавливаться на обосновании законности применения той или
иной подстановки; предоставляем это сделать самостоятельно.
с V~x
Пример 2. Вычислить интеграл V ¦?--= dx.
Здесь полезно применить подстановку x = t6, освобождающую нас от
радикалов. Дифференцируем это равенство: dx = 6tbdt. Тогда
=6 (4- ^—§- *б+-|-'3-'+arctg *)+с*-
/8
* Целую часть дроби . выделяем делением.
308

Возвращаясь к старой переменной х, получим
Vx .^=e(l^-|v^+4-^-^+arctg^) + c.
Выбор подстановки (то есть выбор функции x = tp(t)) может быть
подсказан разнообразными соображениями. Так, в примере 1
подстановка приводит к тому, что корень извлекается и мы
освобождаемся от иррациональности. В примере 2 корни V х, V*>
фигурирующие в подынтегральном выражении, также наводят на мысль
подставить вместо х такую переменную /, чтобы оба корня
извлекались.
При замене переменной весьма часто бывает выгоднее задавать
не х как функцию /, а, наоборот, задавать t как функцию от х и
писать подстановку в виде t = ty(x).
Теоретически оба способа равнозначны, так как если функция
x=y(t) монотонна, то всегда можно выразить t как функцию от лг
и написать: t = ^(x). Однако при вычислении некоторых интегралов
подстановка t = ty(x) может оказаться более удобной. К сожалению,
нельзя дать общих правил, по которым следует выбирать ту или.
другую подстановку применительно к заданному интегралу; умение
разыскивать удачные подстановки достигается практикой. Отдельные
замечания, относящиеся к определенным типам подынтегральных
выражений, будут сделаны ниже вместе с указанием типичных
подстановок. Однако не следует слепо придерживаться какого-то раз
навсегда установившегося шаблона в выборе подстановки. Весьма
часто встречаются интегралы, которые могут быть вычислены с
помощью различных подстановок, и искусство вычислителя состоит
в том, чтобы применить ту из них, которая быстрее и проще ведет
к цели.
Рассмотрим ряд примеров на применение подстановки ( = ч\)(х)-
С 1 -
Пример 3. Вычислить интеграл 1 -^ех dx.
т л/Ч dx
1ак как а[ — ) = ^» то данный интеграл можно записать так:
Последний интеграл подстановкой / = — сразу приводится к табличному. Стала
быть
$^*--$Д*(1)_-$Ул_-.Ч.с.
Возвращаясь к переменной х, окончательно получим:
с 1 - 1
\^«* ?/* = -«*+С.
309

Прим ер 4. Вычислить интеграл \ (2х + З)8 <*х.
Этот интеграл можно было бы вычислить методом разложения
подынтегральной функции по формуле бинома Ньютона и затем
интегрировать сумму из 9-ти слагаемых. Но такой прием слишком
громоздок. Гораздо проще данный интеграл берется непосредственно
с помощью правила, выраженного формулой (3) из § 3, и табличной
формулы II:
J (2x + 3)*dx = ±(2x + 3)» + C.
Данный интеграл может быть легко вычислен и при помощи
подстановки t = 2x-\-3. Действительно, замечая, что d (2х + 3) = 2dxt
мы видим, что указанной подстановкой наш интеграл сводится к
интегралу от степенной функции; так что подстановка t = 2x4-3, dt =
= 2 dx дает:
J(2x + 3)8d* = y ^t*dt = ±t* + C=±(2x + 3)» + C.
Пример 5. Вычислить интеграл \ ]/' 1 — х dx.
Так как d(\— х)=—dx, то подстановкой t=\ — х этот интеграл сводится к
интегралу от степенной функции. Таким образом, подстановка ?=1 — х, dt=—dx
дает:
13 3
Пример 6. Вычислить интеграл ^ еах dx.
Как известно, если а постоянна, то d (ax:)=adx. Отсюда при а^ЬО dx=?
= — d {ax) и интегралу можно придать вид:
ieaxdx= — ieaxd(ax)*
Последний интеграл подстановкой t=ax сразу приводится к табличному (см.
формулу VI):
Г eaxdx=— $eaxd(ax)=^- ? е' dt = ^-e<+ C = ^-eax+C.
Пример 7. Вычислить интеграл \ cos m x dx.
Этот интеграл берется тем же приемом: под знак дифференциала подведем
постоянный множитель т и разделим на него интеграл. В результате получим:
\ cos mxdx = — у cos mxd (mx).
Здесь уже напрашивается подстановка 1 = тх, приводящая интеграл к табличному:
Jcosmxdx = — \ cosm*d(m*) = — l costdt = —sin/ + C = —sin mx4-C,
* Заметим, что таким же путем устанавливается и общая формула
J/(*)Ac = l ^f(x)d(ax),
то есть под знак дифференциала можно вводить постоянный множитель, разделив
при этом на него весь интеграл.
310

Отметим, что интегралы в примерах 5, б и 7 могут быть также вычислены
с помощью формулы (3) из $ 3, что и рекомендуется сделать самостоятельно.
Пример 8. Вычислить интеграл \ e~~x*xdx.
Замечая, что d (х2) = 2х dxt полагаем /=— х2. Отсюда dt~—2xdx. Тогда
С х2
Пример 9. Вычислить интеграл \ . „ dx.
Подстановка t = x3, dt = 3x2dx дает:
f ^ , 1 f ЗА? . 1 f dt 1 . . , . 1 . . , „
) T+*dx=T ) Т+Щ2ах—з ) TT^ = Tarctg/ + C = TarctgA:3 + c.
В этой связи заметим, что если подынтегральное выражение имеет
вид: f(x2)xdx, f(x?)x2dx и т. п., где f (t) — легко интегрируемая
функция, то следует соответственно применить подстановку # = /2,
x=t3 и т. д.
Пример 10. Вычислить интеграл \ tg x dx.
гг , sin х
Так как \gx = , то наш интеграл можно записать в виде
cos х' г
\ tg х dx = \ ^^ dx.
J J COS X
Теперь, замечая, что dcosx = — sin*d*, полагаем t = cosx. Это дает: dt= —slnxdxn
Пример 11. Вычислить интеграл V у—~—^dx.
х2
Подстановка / = *3 + 1, dt = 3x2dx дает:
$t?*4S^--H?->I<I-k:->I*+"-".
Вообще для интеграла, в котором числитель равен производной
знаменателя, будем иметь:
Действительно, подстановка t = f(x), dt = f (х) dx дает:
$7cf d*= Sf = lnl^+c=lnl/WI + c-
Пример 12. Вычислить интеграл \ -^—rdx.
Подстановка t = ex, x = \nt, dx — — дает:
= ^3+y^2 + / + ln|/~l| + C = ^^+l^+^+ln|^-l|+C.
311

Пример 13. Вычислить интеграл \ - dx.
J )/*+1-1
Подстановка t = Y x-{-1, л:=/2 — 1, dx = 2tdt дает:
-Ь21п I/ —1|) + С = /«-Ь4/ + 41п|/—1 |+C = jcH-4|/^+T+41nly'"i+l —I 1+Clt
где Ci = C+l — произвольная постоянная.
Пример 14. Вычислить интеграл V ,
Подстановка t = \/ х-\-2, *=/3 —2, djt=3/2 Л дает:
= |- »/(* + 2)»-3 ^ + 2)« +С.
Вообше, если подынтегральное выражение не содержит других
п *_
иррациональностей, кроме корня из линейной функции /ах-\-Ь, то
п
следует применять подстановку t = y ax + b.
С dx
Пример 15. Вычислить интеграл \ 2 2> azfiO.
Подстановка t ——- dt = — дает:
a r a
С dx = 1 I dT _^ 1 Р
)а* + х*- а \ { + {±_)2~ a J
Таким образом, мы получили формулу
^-i.def+C-l.rdgif+C.
5M^ = ^arctg^+c- (4)
Пример 16. Вычислить интеграл \ —7==l {a > 0).
J у а2 — *2
Применяя подстановку t — —, получим:
С dx — 1 a _ Г
Следовательно, мы пришли к следующей формуле:
= arcsin t + С = arcsin 1- С.
/l-/2 <*
*** arcsin—+C*. (5)
Ya* — x* <*
* Заметим, что формулы IV, V таблицы интегралов получаются из формул (4)
и (5) соответственно при а = 1.
312

С dx
Пример 17. Вычислить интеграл \ 2_ 2 (афЩ.
Имеем
{ _^?_ = 1 f (х+а)-(х-а) 1 Г /1 1_\
J л^-а* 2а J х2~а2 а 2а ) \х-а х+а)а
ш^{1п1х-а\-\п\х+4) + С-^1п\^
+ С
Здесь мы использовали формулу (3). Этим установлена формула XI таблицы
интегралов.
Пример 18. Вычислить интеграл V , .
J V# + a
Здесь удобно положить |/^х2-j- а=^ — х, где / — новая переменная *. Возводя
t2—a t24-a
в квадрат, получим: х= g , откуда dx=—^-dt. Так что
Окончательно получаем:
то есть получили формулу XII таблицы интегралов.
Замечание. В отдельных простейших случаях, когда после
несложных преобразований подынтегрального выражения становится
ясно, какая подстановка приводит данный интеграл к табличному»
само интегрирование целесообразнее осуществлять без введения новой
переменной (новой буквы) и подстановку при этом лучше
производить в уме, мысленно. Проиллюстрируем это замечание на примере:
С **±-1 С 3*Мх_1 Г d(l+x*) 1. с
J 1+л*~3 ) 1+хЗ-З ) l+хз —з ш I x-t-^H-°-
На последнем этапе мы мысленно применили подстановку t =
— 1+*3» после чего интеграл преобразуется в табличный: \ — =
= 1п|/| + С.
Таким же экономичным приемом можно было вычислить
примеры 4—10, что и предлагается сделать студенту.
Упражнения
1. icos(5x + Z)dx. Отв. у sin (5л:+ 3) +С. 2. i 2 ^ . Отв. - yln 12 — Зх | + С.
Г d* 1 С jc 1
5. С yos2jg rfx. 0me. — In (1 + sin 2x)+C. 6. [ X^rri- Отв. 2arctg]/7+C.
J 1-f-sin 2л: 2 x '' J л:(л:+1) ьг ^
* На этой подстановке мы остановимся ниже.
313

7. { Q0S}fj dx. Отв. 2 eta 1/*+С. 8. [ V2x-Zdx. Отв. i-(2x-3)2 +C.
dx
Ve*+\
10. С _ °* a. (l/>+l=f). Ome. In
yex+i__i
+ C.
"•St
yV+1 + 1
dx I 1\ л - . 1
—, я^т . Ome. С—arcsin—.
Ome. 2 [1/7+1 — In (1+1/7+1)]+С
+У7+Т
dx
13. J *з {/** + 1 dx. Отв. A (**+!) & +C.
14. ^ j^- (/ = Inir). Ome. ln|ln*|+C.
15. V , (* = asinf). Ome.-pr arcsin „-Va2- *2 + C.
3 1/а2_^2 v 2 a 2 ^
§ 5. МЕТОД ИНТЕГРИРОВАНИЯ ПО ЧАСТЯМ
Метод интегрирования по частям основан на обращении формулы
дифференцирования произведения двух функций.
Пусть и и v—дифференцируемые функции от х. Тогда d(uv) =
= udv + v du, откуда udv = d(uv) — v du. Проинтегрировав обе части
этого равенства, получим формулу:
\udv=zuv—\vdu. (1)
Эта формула называется формулой интегрирования по частям.
Она позволяет свести вычисление интеграла § и dv к вычислению
интеграла \^vduy который может оказаться более простым для
интегрирования.
Рассмотрим ряд примеров на применение формулы (1).
Пример 1. Вычислить интеграл $ arctg x dx.
Интересной особенностью данного примера является то, что
разложение на множители и и dv подынтегрального выражения
здесь как бы уже дано в готовом виде и нам остается положить
и = arctg х, dv = dx,
откуда
• dx
d*=J+*' » = *•
Применяя формулу (1), получим:
\ arctg #с(л: = х arctg x— \ х- yq-^^^arctgA:---^ \
1+*2
__ In /I _L v2\_L/r>
314
= х arctg x — 4- In (1 + x2) + С.

Далеко не всегда интегрирование по частям совершается так
относительно просто, как это было в примере 1. В более сложных
случаях все искусство применения формулы (1) заключается в том,
чтобы удачно разбить подынтегральное выражение на два
множителя: и и dv, что, разумеется, не всегда сразу удается. Например,
если бы мы, пытаясь применить формулу (1) к интегралу \^xexdx>
взяли и = ек, dv=xdx, откуда du = ex dx, v = -^x2, то получили бы
\ хех dx = -? х2ех — у \ х2ех dx,
то есть пришли бы к еще более сложному интегралу, нежели тот,
от которого отправлялись. То же самое получится и в случае, если
взять и = хех, dv = dx. Однако если принять и = х, dv = exdx и,
значит, du = dx, v = ex, то формула (1) быстро приводит к цели:
$ xe*dx = xe* — \ ex dx = xex — ex + С.
Таким образом, приведенный пример показывает, что и и dv
нельзя выбирать как попало. Только последний выбор оказался
удачным, и это не случайно. В самом деле, из двух множителей
подынтегральной функции второй множитель (то есть ех) при
дифференцировании и интегрировании не изменяется; первый же (то есть х)
при интегрировании повышает степень, а при дифференцировании
обращается в единицу — выражение более простое, чем он сам.
Поэтому выгоднее первый множитель дифференцировать, а второй
интегрировать, то есть положить и = х, dv = exdx, что и сделано выше-
Пример 2. Вычислить интеграл ^xlnxdx.
Этот интеграл отличается от предыдущего только тем, что вместо
ех стоит 1пх. Но если бы мы здесь за и взяли х, а \nxdx за dv,
то пришлось бы искать еще отдельно и v. Хотя таким путем задачу
все-таки можно было бы довести до конца, все же и здесь,
руководствуясь теми же соображениями, что и выше, можно указать
иной путь, более простой, а именно: положим и = \пх, dv=xdx.
dx х2
Отсюда du = — , v = y- Тогда
С 1 л *2 . С х2 dx х2, 1ft х2, х2 . ~
\x\nxdx = -^\nx— \у '— = -^\пх — у \ xdx = Y lnx — -т"
"Нечасто формулу интегрирования по частям приходится применять
последовательно несколько раз.
Пример 3. Вычислить интеграл § х2 sin x dx.
Пусть и--=х2, dv = sinxdx, тогда du = 2xdx, v=—cosx.
Следовательно, $ х2 sin xdx= — x2 cos x + 2 $ x cos x dx. К последнему
интегралу опять применим правило интегрирования по частям, полагая и = х>
dv = cosxdx, du = dx, у = sin #. Тогда §A;cos#dA;=#sin x —
315

— ^sinxdx = xs'u\x-\-cosx-{-C и окончательно получаем:
^ х2 sin х dx= —х2 cos x + 2 (х sin x + cos #) + С.
Таким же образом вычисляется и интеграл ^cos^djt.
Итак, разобранные примеры показывают, что применение метода
интегрирования по частям состоит в том, что подынтегральное
выражение f(x)dx представляется в виде произведения двух
множителей и и dv, причем последний содержит в себе и dx. Общих правил
для разложения подынтегрального выражения на указанные
множители, к сожалению, дать нельзя. Однако следует иметь в виду,
что разложение на множители подынтегрального выражения нужно
производить так, чтобы в результате дифференцирования одного
множителя (то есть и) и интегрирования другого множителя (то есть dv)
подынтегральное выражение vdu интеграла правой части формулы (1)
по возможности легко интегрировалось. Разумеется, не всегда за
счет указанной разбивки подынтегрального выражения на
множители и и dv формула интегрирования по частям приводит к
интегралу, более простому для интегрирования.
Иногда повторное интегрирование по частям приводит заданный
интеграл к самому себе. В этом случае может получиться или ничего
не дающее тождество (значит, интегрирование было проведено
нерационально), или такое уравнение первой степени относительно
искомого интеграла, из которого находится заданный интеграл.
Иллюстрируем сказанное двумя примерами.
Пример 4. Вычислить интеграл $ еах sin bx dx.
Положим u = smbx, dv=eaxdx, отсюда du = b cos bx dx, v =—eax
и, следовательно, по формуле (1) будем иметь:
\ eax sin bxdx = — eax sin bx V eax cos bx dx.
Полученный интеграл вычисляем снова интегрированием по
частям; полагая и = cos bxt dv = ef1* dx, откуда du = — b sin bx dx,
1 ax
v=— ea , так что
\ eax cos bxdx= — eax cos bx-\— \ eax s in bx dx, (2)
то есть мы пришли к исходному интегралу—это обычный камень
лреткновения для начинающих. Может показаться, что надо искать
другой способ; на самом же деле задача почти решена.
Действительно, подставляя значение этого интеграла в предыдущее
выражение, получим:
\ е"* sin bxdx = — eax sin bx——\ — eax cos bx -j— \ eax sin bx dx) =
= -je™ (a sin bx-— b cos bx) — -^ \ eax sin bx dx.
316

Перенося интеграл из правой части этого равенства в левую,
получим:
а2 + 62 С
e°*sinbxdx=asinbx-bcosbx g'* + C*
и окончательно
$ e°*smbxdx = asiab*^lcosbx e°* + C**. (3)
Заметим, что по ходу вычисления интеграла ^еах sin bxdx нами
по существу вычислен и интеграл \еах cos Ъх dx, так как из (2) и (3)
следует:
$ e°*cosЬхdx = aco%b^XbbrbX^+ С
Пример 5. Вычислить интеграл § ]/"х2+а d*.
Здесь так же, как и в примере 1, разбивка на множители и и dv
дана уже в готовом виде, и нам остается положить
u = Vx2+a, dv = dx.
Тогда
xdx
du = TT===i v=x.
Ух*+а
Применяя формулу интегрирования по частям, получим:
Но
[ 4=^= ={{x*+±I-adx=[V*T-adx--a[ r±_ =
= ^]/x2 — adx—aln\x + Y x2 + a\.
Подставляя последний результат в предыдущее равенство, находим:
\V~*!4^dx = xVlPTa — [
Объединяя оба интеграла в левой части, будем иметь:
2 \V'x2 + adx = xy x2 + a + aln \x + Vx* + a\ + C.
Отсюда
i Vx2Tadx = ±\/x2 + a +^ln| x + Vx2 + a \ + C.
* Появление произвольной постоянной С станет ясным, если учесть, что
неопределенный интеграл в левой части неявно содержит в себе слагаемым произвольно
постоянное число и, следовательно, его должна содержать и правая часть.
** Поскольку С —произвольная постоянная, то и kC—также произвольная
постоянная при k^O; при этом если учесть, что способ записи произвольной
постоянной несуществен, то при вычислении интегралов вместо kC пишут просто С.
317

Сходным образом вычисляется интеграл ^Т^я2 — х2 dx.
В заключение отметим, что этим способом, который естественно
назвать способом приведения интеграла к самому
себе, можно было бы вычислить интеграл, рассмотренный в
примере 2, положив при этом и = х In х, dv = dx.
Замечание. Правило интегрирования по частям имеет более
узкую область применения, чем метод замены переменной. Однако
следует иметь в виду, что есть интегралы, которые только и могут
быть вычислены с помощью метода интегрирования по частям,
например следующие:
$ хпеах dx, ^ sin ax dx, § х* cos ax dx, $ ** 'пШ * dx9
$ хп arctg x dx, ^x" arcsin x dx.
Пример б. В качестве еще одного примера применения
метода интегрирования по частям выведем рекуррентную*
формулу для вычисления интеграла
'«ЧтИ^ ("=1-2,3,...).
Применим к этому интегралу формулу (1), полагая
и = (х2 + а2)~п, dv = dx, отсюда du = — (jc2+fl2^-n> v = x>
и мы получим:
г х . р f x2dx
in~~ (x* + a*)n + J (x2 + a2)/i+i-
Последний интеграл преобразуем следующим образом:
С jfidx _ С х* + а* — сР . _
J (x* + a*)n+1 ~~ ) (*а + а2)л+1 ax —
С dx 2 ? dx . 2f
*= ] (Х2 + С2)П— d ^ (х2 + а2)11+1--'я —Д /Я+1.
Подставляя значение этого интеграла в предыдущее равенство,
получим:
^п — (д:2_|_а2)Я" + 2лг/ „ 2па21п+1,
откуда находим:
Эта формула позволяет свести вычисления интеграла /я+1 к
вычислению интеграла /л и, следовательно, дает возможность шаг за
шагом понизить значок п до 1 и в результате прийти к известному
интегралу
j С dx l *.~х
Ь= }* + * = ***& *
* От латинского слова recurrens — возвращающийся.
318

Такие формулы называют рекуррентными, то есть
«возвращающимися» к ранее полученным результатам.
Полагая в формуле (4) л=1, мы найдем:
/ _J i_4--Larcto*
Зная /2, по формуле (4) найдем при п==2:
. 1 ДС • о *< Л . оХ . О § гс
/з==4^'(А:2 + а2)2"Г4^2У2= 4а2(л:2 + а2)2"1 8а4 (*2-f а2) "*" 8а6 aFClgа
И Т. Д.
Замечание. При интегрировании часто приходится
последовательно применять метод подстановки и метод интегрирования по частям.
Покажем это на примере.
Пример 7. Вычислить интеграл ) e^xdx.
Положим здесь t = Yx* так что x = t2 и, значит, dx = 2tdt. Тогда получим
J eVxdx = 2 J fe'df.
Применяя интегрирование по частям к последнему интегралу, мы положим
u = t, dv = e( dt, так что du = dtt v = e(t откуда находим:
2 $ fe' Л = 2 (fe' — $ е' dt) = 2(tet-et) +C.
Наконец, возвращаясь к переменной л:, получаем:
J eV^cfjc = 2 fl/"i — 1) eV* + С.
В заключение коротко остановимся еще на одном методе
вычисления неопределенных интегралов специального вида, основанном
на многократном применении формулы интегрирования по частям.
Это так называемый метод неопределенных коэффициентов, суть
которого заключается в том, что вычисление интеграла определенного
вида производится по некоторой формуле, специально выбранной
для интеграла данного вида, в которой неизвестными являются
лишь некоторые буквенные коэффициенты. В качестве примера
рассмотрим интеграл вида
\P(x)eaxdx,
где постоянная а Ф О, а Р (х) — многочлен л-й степени. Применяя
формулу интегрирования по частям, приняв и = Р(х), dv = еах dxt
получим:
\ Р (х) eaxdx = l- Р (х) еах—\ \ Р' (х) e^dx.
Мы видим, что интеграл справа принадлежит к тому же
виду, что и интеграл слева, но степень многочлена Р' (х) на единицу
ниже степени многочлена Р(х). Применяя к нему снова
интегрирование по частям, мы придем опять к интегралу сходного
типа, то есть к интегралу J Р" {х) еах dx, где уже степень много-
319

члена Р" (х) на две единицы ниже степени многочлена Р(х). Так как
производная порядка п от многочлена /г-й степени есть
постоянная, то, применяя последовательно п раз формулу
интегрирования по частям и принимая каждый раз еах dx за dv, мы
придем к интегралу \ еах dx = -eax + C (см. § 4, пример 6).
Что касается всей алгебраической суммы, которая получается
в правой части после n-кратного интегрирования по частям
заданного произведения Р (х) еах, то ее можно представить в виде Q (х) еах + С,
где Q (х) — многочлен той же степени, что и Р(х), а
С—произвольная постоянная. Следовательно,
SP(x)eaxdx = Q(x)eax + C. (5)
Для определения неизвестных коэффициентов многочлена Q(x)
обычно прибегают к так называемому методу неопределенных
коэффициентов. С этой целью записывают формулу (5), причем
коэффициенты многочлена Q(x) рассматриваются как неизвестные, затем
дифференцируют обе части написанного равенства, сокращают
общий множитель еах ^0 и приравнивают коэффициенты при
одинаковых степенях х, стоящих в разных частях равенства. Из полученной
системы линейных уравнений и находят коэффициенты многочлена
Q(x). Проиллюстрируем изложенный метод конкретным примером.
Пример 8. Вычислить интеграл J(x2 — Зх+l) е2х dx.
В данном случае равенство (5) имеет вид:
J(x2 — 3x+l)e2xdx = e2x(ax2 + bx + c) + C.
Дифференцируя обе части этого равенства и затем сокращая на
общий множитель е2х ^ь 0, мы получим:
х%—3x+l=2(ax2 + bx + c) + 2ax+bt
или
х2 — 3x+l=2ax2 + 2(a + b)x + 2c + b.
Написанное равенство является тождеством. Поэтому, приравнивая
коэффициенты при одинаковых степенях х, получим систему из трех
уравнений для определения коэффициентов a, b и а
х2\ 1=2а,
х — З = 2(а + Ь),
хо\ \=2с + Ь.
1 3
Решая эту систему, находим: а = ^> Ь = — 2, с = 7>- Таким
образом, окончательно
[ (х2 — 3x+l)e2xdx = ^e2x(x2 — 4x + 3) + C.
Разумеется, двукратное интегрирование по частям приводит к тому
же результату, в чем мы рекомендуем читателю убедиться
самостоятельно.
320

Аналогичным способом могут быть вычислены и интегралы вида
J P (x) cos ax dx, J P (x) sin ax dx, где Р (х)—многочлен. Здесь также
путем многократного интегрирования по частям (принимая каждый
раз cosaxdx или siuaxdx за dv) можно показать, что указанные
интегралы могут быть вычислены по формулам:
\ Р (х) cos axdx = aQ (x) sin ax + Q' (x) cos ax + С,
J l (6)
$ Р (х) sin ax dx = aQ (x) cos ax — Q' (x) sin ах + С, j
где Q(at) — по-прежнему многочлен той же степени, что и Р{х)
Пример 9. Вычислить интеграл \ (х2 — 5*+6) cos Зх dx.
Согласно формуле (6) имеем:
$ (х2 — 5х + 6) cos Зх dx = 3 (ax2 + bx + c) sin 3x + (2ax+b) cos 3x + C.
Дифференцируя обе части этого равенства, получим:
(х2 — 5х + 6) cos Зх = 3 (2ох + 6) sin Зх+9 (ах2 + Ьх+с) cos Зх +
+2а cos Зх— 3 (2ах + &) sin Зх.
Стсюда
(х2— 5х + 6) cos Зх = (9ах2+96х + 9с+2а) cos Зх
и, значит,
х2 — 5х + 6 = 9ах2 + 9&х+9с+2а.
Сравнение коэффициентов при одинаковых степенях х дает:
х2
X
X»
1=9а,
-5 = 96,
6=9г+2а.
Решая эту систему, находим: a = -g-, 6 = — -q-, с==оТ« Следовательно,
V (л;2_5х + 6) cos3x dx = 2^ (9х2 —45х + 52) sin Зх+4- (2а:—5) cos3x+C.
Рекомендуем этот же интеграл вычислить с помощью формулы
интегрирования по частям.
Упражнения
1. ^Inxdx. Отв. xlnx —х+С.
г х2 4-1 х
2. J х arctg x dx, О/лв. ^ arctg х — ^- -f С.
3. ^arcsmxdx. Отв. xarcsinx + "Kl—х2 +С
с 111
4. $xln2xdx. Отв. -^ х2 1п2х — -о-*21п *+Т Х* + С-
б. ^ arctg Yx dx. Отв. х arctg У~х~—У~х~ + arctg j/4' + С.
6. С х arcte * ^ 0тв^ /r+F"arctgx-ln Ix+KlT^i + C.
J У 1+*2
7. ^ ^n l^x" dx. Отв. 2 (sin K* — Yx cos j/x ) + C.
321

8. ^ х cos2 x dx.
9. $ Vx In x dx.
X2 1 1
Ome. —+ —jcsin2x+—cos2*+C.
Отв. |)/? Л„*_|.) + с.
Отв.
2 sin2*
Указание. Положить и = -—, dv= . 9 dx.
sin jc ' sin2 л:
In
tg-
+ C.
Применяя метод неопределенных коэффициентов, вычислить следующие
интегралы:
11. $(*2 — 2x+5)e~xdx. Отв. е'х(х2 + 5) + С.
12. \{2x* — x2 + 2x — b)e2Xdx. Отв. (л? —2*2 + Зх—4) е2*+С.
г 1 1
13. ](x2 + 5x + 6)cos2xdx. Отв. -j(2*2 + 10лг+11) sin 2* + — (2*+5) cos 2x + C.
14. ? л: (х2 + 6) sin х dx. Отв. Зх2 sin х —- л;3 cos x + С.
15. ^(*2 + 2* + 3)cos*flfA;. Ome. (*+ l)2 sin х + 2 (*+1) cos x + C.
§ 6. СПЕЦИАЛЬНЫЕ ПРИЕМЫ ВЫЧИСЛЕНИЯ НЕКОТОРЫХ
ИНТЕГРАЛОВ
Рассмотрим некоторые типы интегралов, которые легко
вычисляются после несложных преобразований.
I. Интегралы типа
^ sin mx cos nx dx, § cos mx cos nxdx, $ sin nx sin mx dx,
где т и п—постоянные числа.
Подынтегральные функции легко приводятся к сумме первых
степеней синусов и косинусов с помощью известных формул
тригонометрии:
sin a cos p=y [sin (a + P) + sin(a —p)],
1
cos a cos p =—[cos (a + Р) + cos (a — Р)],
1
(1)
sin a sin р = у [cos (a — P) — cos (а + Р)].
Рассмотрим несколько примеров на применение этих формул.
Пример 1. V sin Зх sin 5x dx=-^- \ (cos 2л: —cos Sx) dx =
1С 1С 1 1
e~o" \ cos2xdx—s- I cos8xdx = -j- sin2* — y^ sin 8x-\-Ct
16'
Пример 2. V cos 2x sin 4x dx = -^- V (sin 6*+ sin 2x) dx —
\ s)n bx dx-\--х-\ sin2A;rf^ = —«.-г^созб^ —— cos 2^4-C.
322

Пример 3. \ sin x sin 2а sin За dx=-<y \ (cos х—cos Зд:) sin За dx =
= -9" \ cos x sin Зх dx —fT- V cos Зд: sin За: dx =
= — \ (sin 4a + sin 2x) dx—— \ sin 6л: <2a =
= H7 cos 6a:—-y^ cos 4a—— cos2a + C.
II. Интегралы видя \s'mm xzosnxdx, где т и п — любые целые
показатели.
1) Пусть хоть один из показателей т или п будет нечетным
положительным, например n = 2k+l. Полагая sin* = ^ получим:
cos xdx = dt и потому
^ sinm х cos" xdx = ^ sinm x cos2* a: cos x dx =
= \ sinmx(l—sin2 x)kd sin x=\tm (I—t*)kdt.
Этот интеграл после разложения (1—t2)k по формуле бинома
Ньютона вычисляется непосредственно.
Аналогично поступаем, если т — нечетное положительное.
Пример 4. \ sin2 a: cos3 a: dx — \ sin2A:(l — sin2 x) d sin x =
c f coss л: . f (1 - sin2 a)2 , . Г (1 -f2)2 .,
Пример 5. \—-dx-\ sin*x dmx-y-js-Ldt-
J '6 J '4 J *2 ^5 ^ З/з * ^° 5sin*A^3sin3A sin a"1"
2) Пусть оба показателя /л и /г—четные и положительные
числа, тогда указанный выше прием не приводит к цели, и в этом
случае предпочтительнее другой прием, основанный на
применении формул
.„ 1 —cos 2а о 1+cos2a /оч
sin2x= 2 ' cos2a:=--i--2 . (2)
Именно, пусть m = 2k, п — 21 и ?>/, ? = г + /, тогда
^ sin2* х cos2' л: dx = ^ sin2r x (sin л: cos x)2/ dx =
-ух \ sin2rx-sin2/2^dx=25?i7 \ (1 — cos2*)rsin2/2*dA;.
Применяя формулу бинома Ньютона и затем перемножая, мы
получим сумму интегралов того же вида: § cos* 2x sinp 2л; dx, но
с показателями степеней, меньшими первоначальных. Те из них,
в которых хотя бы один из показателей р или q оказывается
нечетным, вычисляются приемом, разобранным выше (первый
случай). Интегралы, в которых оба показателя р и q четные, могут
быть вычислены с помощью многократного применения формул (2).
323

Пример 6. \ sin6 х cos8 х dx = -j- \ sin2 2x sin4 xdx=*
= ~ \ sin22;t(l — cos2x?dx=jz \ sin2 2x (1—2 cos 2x + cos8 2x) dx=
e V sin22x dx—-g- \ sin22xcos2A:rfjc + ^ 1 sin22*cos22xdx =»
= 4Д (1 —cos4*)dA:—^ \ sin2 2x d sin 2*-fg^ \ sin24jc dx =
=i^-ii8sin4^-Asin32x+T58 J o-«»e*>*-
" I58*-S8sin ^"-й^^-Шsin 8x+C'
III. Интегралы вида \ ^4^4-0 ^ принадлежат к числу
основных интегралов, часто встречающихся на практике. В
числителе подынтегральной функции стоит линейный двучлен Ах-\-В,
а в знаменателе — квадратный трехчлен x2-\-px-\-q. Чтобы взять
этот интеграл, выделим из трехчлена в знаменателе полный
квадрат двучлена * + у:
x^px+q^+2^x+^)+{4-pi)={x+if+{q-piy
Это разложение подсказывает нам подстановку:
x + ~ = tt x=t — у, dx = dt.
р2
Положим далее q-7*— = ft, где ft может быть положительным или
отрицательным числом*. В результате наш интеграл
преобразуется к виду
г
At + B-A P
J /+*+/*= j fi+h 2dt.
Последний интеграл представим в виде суммы двух интегралов, тогда
Первый интеграл в правой части берется непосредственно, так
как у него в числителе стоит дифференциал знаменателя, и потому
он равен логарифму абсолютной величины знаменателя**.
* Мы считаем, что квадратный трехчлен x2-{-px-{-q не является полным
квадратом какого-нибудь двучлена, так что hzjtQ.
** См. формулу (3) § 4.
324

Второй интеграл вычисляется по формуле (4) § 4 или по формуле
XI таблицы основных интегралов, в зависимости от того, будет ли
разность ^—--^-=ft положительным или отрицательным числом.
Обратимся к примерам.
Пример 7. Вычислить интеграл V Т" Q dx.
Выделим в знаменателе полный квадрат двучлена: x2 + 4jc+9 = (jc+2)2 + 5.
Теперь прибегаем к подстановке x+2 = t (тогда x = t — 2, dx = dt), которая дает:
и
Ив_Л f в^Л гдм+б^
+ 4д:+9" J (Х+2Р+5 " J <*+5
- \ 1*+5 d' = 3 J 7^+5-7 S ?Н^=31П(< +5)-]71arct8|71+C-
Возвращаясь к переменной #, получим:
Пример 8. Вычислить интеграл \ 2__ J" ^ cU.
Так как х2 —6дс+5= (дс—З)2 — 4, то, полагая д^—3 = ^, откуда * = ?Ч-3.
dx=dt; находим:
С 3jc—2 . f 3(f + 3) —2 ., f 3* + 7 .,
= Y J 72ZI4 + 7 ) ^=4 = Т1п К2-41 + -1п|-7-Го-| + с =
= ~ln|^-6^+5|+-J-ln
4 I f + 2
jc—51
+ C.
IV. Интегралы вида ^
Yx*+px+qdx вычисляются точно таким
же приемом, что и интегралы вида III.
Как и в предыдущем случае, здесь также выделяем полный
квадрат из квадратного трехчлена х2 + рх + д = (х + -^Л +д—~~.
Затем прибегаем к той же подстановке x+-^- = t, которая
преобразует данный интеграл к виду
С Ах+В CAt+B~T
С Ах+В dx= \ —, 2 dt.
Отсюда
P Ax+B g^ACU g+UAAt* (4)
где по-прежнему h=q — -?-. Первый интеграл есть ишеграл вида
325

\-Д; = 21Л* + С, если положить u = t2 + ht и, следовательно,
J У и
S
2tdt
: = 2V~t2 + h + C = 2Vx2 + PX + <! + C.
Пример 9. Вычислить интеграл V ™ „ "—~ dx.
Vt*+h
Второй интеграл вычисляется непосредственно по формуле XII
таблицы основных интегралов.
(» Ах-\-Ь
Аналогичным приемом вычисляется интеграл вида \ г dx
ЭУ—xZ+px+q
при условии, что (7 + 4">0. Обратимся к примерам.
4х— 8
Vx* + 6x—2*
Выделим полный квадрат из подкоренного выражения: *2+6л:—2 = (# + 3)2—11.
Подставляя #+3 = *, x = t — 3, dx — dt, получим:
J Ул;2 + 6л:-2 J У**—11 J У Я- 11
= 2 \ —20 V =
J У/2—И J V/я—11
= 4 V/2_ii_20 In | /+у/2__ и | + C=
= 4^2 + 6jc—2—20 In |* + 3 + ]Лс* + 6* —2| + C.
r» x i 3
Пример 10. Вычислить интеграл V dx
J /5 + 2*-*2
Выделим полный квадрат: 5+2# —х2==6 —(*—I)2. Подстановка л:— l=tf
x = t-\-l, dx = dt дает:
[ , x+s - [ /+4 - Ч -**i't *
J -у5 + 2х-*2 J -Уб3?2 2 J /6-/2 J Уб^=72
= — "Уб=72 + 4 arcsin -L + C = — /5 + 2x^*2 + 4 arc sin ^J + C.
Уб /6
Заметим, что первый интеграл вычисляется с помощью подстановки u = Q — t2l
du=—2tdt, так что
}ут=^ Ъу и
а второй выражается через арксинус согласно формуле (5) § 4.
Замечание. Разобранные примеры показывают, что сущность
рассмотренного способа вычисления интегралов вида III и IV состоит
прежде всего в выделении полного квадрата двучлена из
квадратного трехчлена в знаменателе с последующим применением
подстановки t = x + Y и затем в представлении данного интеграла в виде
суммы двух интегралов, один из которых берется непосредственно
(так как числитель его есть дифференциал двучлена t2 + h в
знаменателе), а другой сразу приводится к одному из табличных
интегралов (в зависимости от знака числа К). На практике указанное
преобразование лучше производить без введения новой переменной
326

интегрирования t. В этом случае каждый из интегралов вида III
и IV в результате такого преобразования представится так:
? Ах+В А __Л ? 2х+р А [п Ар\ С dx /t-\
) x2 + px + qdX—2 ) x*+px+qdX + [* —T) ) x*+px+q W
С Ах + В А С 2*+P ^+(д_^) f _*_. (6)
J Ух^ + px + q 2 J ]Лс2 + р* + <7 'V 2 У J y& + px+q
Легко видеть, что эти формулы непосредственно следуют из
формул (3) и (4), если в последних перейти к первоначальным
обозначениям.
Интегралы в правых частях формул (5) и (6) вычисляются уже
непосредственно, если учесть, что в числителе каждого из первых
интегралов стоит дифференциал трехчлена в знаменателе, а вторые
интегралы после выделения из этого трехчлена полного квадрата
двучлена х+^ сразу приводятся к одному из табличных интегра-
лов (в зависимости от знака числа q — ^ч.
Проиллюстрируем указанный прием на конкретных примерах.
г» 4* 7
Пример 11. Вычислить интеграл /= V —— .^dx.
В числителе подынтегральной функции выделим производную знаменателя,
равную 2х—6. Для этого, как легко видеть, достаточно сначала из числителя
вынести за знак интеграла множитель 2, а затем вычесть и прибавить в
числителе 6. В результате получим:
' = 2 \ x2_6xll3dx = 2 \ ___i_^*B
Г^"^+(6-т),..
(2*~6)+^L о Г 2,-6 „ , . \ dx
*2 —6х + 13 \ Х2_бд:+13 ^ 1 *2 —6*+13*
Первый из интегралов правой части равен In (х2 — 6*+13) (см. формулу (3) § 4).
Второй интеграл, как видели выше, вычисляется путем выделения полного
квадрата двучлена из трехчлена в знаменателе:
t dA = [ rf(*-3) =J_arct
J *2_6* + 13 ) (*_3)2 + 4 2 arCXg
X-
Здесь мы использовали формулу (4) § 4.
Таким образом, окончательно будем иметь:
s
i?^1jft_21n(«.-e,-H3)+4arCtgi±2+C.
Пример 12. Вычислить интеграл /= \ ' dm.
J V2+4x-x*
Выделим в числителе производную подкоренного выражения, равную 4—2х.
Для этого числитель дроби сначала умножим на —2 и, следовательно, перед ин-
327

тегралом поставим множитель —o~t a затем в числителе прибавим и вычтем 4:
I
х+3
: d* =
V2 + 4x — х* ~~ 2
1 с (4 —2л:)—10
J /2 + 4*—х* 2 J К2 + 4х — л*
— _ JL С (4 —2л:)—10 1 Г 4 — 2х С dx
~~ 2 J У 2 +Ах — х* Х~ 2 ) У2 + Ах — х* * \ У2 + Ах — х**
Первый интеграл есть интеграл вида V -т= = 2Уи-{-С, где и = У 2 + 4л: — х*
а второй интеграл после выделения полного квадрата двучлена из подкоренного
выражения берется непосредственно:
С dx _ С d(x—2)
) У2 + 4х-х*~~ ) /6-(х-2)»"
= arc sin -—т=—|-С.
/6
Здесь мы воспользовались формулой (5) § 4.
Окончательно получаем:
С * + 3 ^в—/2 + 4^-^+5 arcrin ^-pJ + C.
V. Рассмотрим интеграл вида \ —т=
<ta
. =- (х>0). Этот ин-
одса + Ьдр+с
теграл легко берется с помощью простой подстановки *=у. Дей-
ствительно, ах= — -^, тогда
dx
tdt
dt
xYax* + bx+c
t2Ya^+b'T+c
Уа+bt+cP'
а последний вычисляется методом выделения полного квадрата из
подкоренного выражения.
С dx
Пример 13. Вычислить интеграл \ — —.
J xYx*-4x+l
Применим подстановку х=-— dx — — —, тогда
С dx
J xVW^4
4л:+1
Jl/>_4f + l J
в — in | / — 2 +"K/a — 4/+ 1 | + C = — In
1~2л: + Ул:2 —4л:+1
т-«+У>4+-
= —In
+ C==ln
-Лп
\—2x+Vx2 — 4x+l
l — 2x — Yx* — 4x+l I , ~
+^ii
4-C =
где С! = С—1пЗ.
328

Упражнения
с I 1
1. \ cos 2х sin 4x dx. Отв. — -^ cos бдс —— cos 2x + С.
2. \ cos2 a: sin4 x dx. Отв. -^ х—-^ sin 2* — ^ sin 4* + тр^г sin бдг -f С.
J 16 64 64 192 '
? sin3 * 1 1
J cos4 * 3 cos3 x cos д:
5. С /.3лГ~"1 :rfx. Отв. ЗУ*» + 2* + 2 — 41п|л:+1+угл:а4-2>;+2|+С.
J У х*-\-2х+2
Л О у 11 у 1
6. \ dr.. Отв. С — 8V5 + 2X—X* — 3arcsin^=i.
J )/5 + 2jc-jc2 /6
rfjc л 1 2-х
— —. Отв. -тг- arccos —^ -
* 1/^2^4*-4 2 х/2
§ 7. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ФУНКЦИЙ
Будем называть элементарной функцией любую функцию,
которая выражается через основные элементарные функции * с помощью
конечного числа арифметических действий и операций взятия
функции от функции. Например, функция
*/l + 8in3*
l/=arctgfi±5
-2с*
будет элементарной.
Самый важный класс функций, интегралы от которых всегда
выражаются через элементарные функции, представляют
рациональные функции:
р/х\-рМ
Н(Х)~Ш'
где Р(х), Q(x) — многочлены. Если эта рациональная дробь
неправильная**, то мы всегда с помощью деления Р (х) на Q(x) можем
выделить из нее целую часть (то есть многочлен), интегрирование
которой осуществляется непосредственно и приводит при этом снова
к целой рациональной функции. Например,
+ 1 In | х*-х+ 11 + J/3 arctg^- + C ***.
* Степенная, показательная, логарифмическая, тригонометрические,
обратные тригонометрические функции.
** То есть степень числителя Р (х) не ниже степени знаменателя Q(x)
*** См. § 6, интеграл вида III.
329

Поэтому мы сосредоточим внимание исключительно на
интегрировании правильных рациональных дробей, то есть дробей, у которых
степень числителя ниже степени знаменателя.
Интегрирование правильной рациональной дроби основано на
следующей теореме*.
Каждая правильная рациональная дробь может быть
представлена в виде суммы конечного числа простых
дробей следующих четырех типов:
I. —; И. гАл? (*=2, 3, 4, ...);
х—а* (х — а)п х ' ' п
Ш- x* + px + q; IV* (jfl + px + q)" (П = 2, 3' 4' '•")'
где A, B, C, D, M, N—числовые коэффициенты.
При этом предполагается, что трехчлен x2 + px-\-q,
фигурирующий в дробях III и IV типов, не имеет вещественных корней
(следовательно, ^-—<7<0].
Таким образом, для интегрирования правильных рациональных
дробей нужно прежде всего научиться представлять их в виде суммы
простых дробей и затем уметь интегрировать последние.
Остановимся сначала на интегрировании простых дробей. Дроби
I и II типов мы уже умеем интегрировать:
f JL-dx = Aln\x—a\ + C;
Интегрирование дроби III типа показано в § 6 (см. интеграл
вида III). Что касается вычисления интеграла от простой дроби IV
типа, то есть вычисления интеграла
Mx+N
I
(x2+px+q)
ndx,
то к нему применим тот же прием, который мы применяли при
вычислении интегралов вида III и IVb§6 (cm. замечание), то есть
метод выделения в числителе первого интеграла производной
трехчлена x2 + px-\-q9 а именно:
Г Mx+N . _М С 2х + р . . /д. Мр\ f dx
} (x* + px + q)* аХ~ 2 ) (x* + px + q)" ах+{" 2 ) } (tf + px + q)*-
Первый интеграл в правой части есть интеграл вида\-^ =
= 1__пц1~/г + С, где u=x2 + nx + q. Ко второму интегралу применим
* Доказательство этой теоремы можно найти, например, в кн.: Г. ГТ.
Толстое, Курс математического анализа, 1954, т. I, гл. VIII, § 8; Н. С. Писку-
ное, Дифференциальное и интегральное исчисления для втузов, 1963, гл. X, § 9.
330

подстановку #-f-y = f, в результате получим]
ln \ (*+px + q)" — J (*¦
dt
П2
где a2 = q —t-r-^-O. Последний интеграл может быть вычислен при
любом п по рекуррентной формуле*:
А О/! 1
/л+1 = 2па* (Р + а?)п + "2^2" /л (Л==1» 2» 3'*--)-
Если подставить сюда значения ? = л; + -^- и a2 = <?— ^-, то получим
для интеграла
(Х2+рх + д)П
следующую рекуррентную формулу:
* + ~2~ 2/г—1
/я+1= 7 JjSx 1 7 n2\^# М
2/г(? — ?-) (**-{-/>* + ?/* 2я^ — ^]
Итак, мы установили, что интеграл от каждой простой дроби
выражается через элементарные функции, или, как принято
говорить, каждая простая дробь может быть проинтегрирована в
конечном виде. Этим исчерпывается вопрос об интегрировании простых
дробей.
Таким образом, интегрирование любой рациональной дроби
приводится к интегрированию многочлена и конечного числа простых
дробей. Поэтому мы получаем следующую важную теорему:
Интеграл от любой рациональной дроби есть
элементарная функция, выражающаяся через рациональные
функции, логарифмы и арктангенсы.
Эта теорема имеет особо важное значение по той причине, что
далеко не всякая элементарная функция имеет интеграл,
выражающийся через элементарные же функции. Так, например, интегралы:
№**' \^lTdx> $E7> \Tdx> \е~"**, $sin*»d*f
\cosjc2dA:, \ У sinхdx, \ . , \ . * = ,.».
J J J V**+l J K2—sin**'
и ряд других не выражаются конечным числом элементарных
функций. О таких интегралах говорят, что они не берутся в конечном
виде. Однако это не значит, что эти интегралы не существуют; они
существуют**, но первообразные для их подынтегральных функций
не выражаются никакой конечной комбинацией элементарных функ-
* См. формулу (4) в § 5.
** В теории определенного интеграла мы докажем, что если подынтегральная
функция непрерывна в некотором промежутке, то она имеет первообразную в
этом промежутке.
331

ций и, следовательно, представляют собою функцию более сложной
природы. Это подобно тому, как мы иногда говорим, что «]/г2 не
извлекается», разумея под этим лишь то, что не существует
рационального числа, квадрат которого равнялся бы 2. Однако мы знаем,
что существует такое вещественное число—]/^2 -— иррациональное,
квадрат которого равен 2. То обстоятельство, что неопределенные
интегралы от некоторой части элементарных функций не
выражаются через элементарные функции, указывает на существенное
отличие операции интегрирования от обратной ей операции
дифференцирования, которая, как известно, замкнута относительно класса
элементарных функций (то есть производная любой элементарной
функции есть элементарная функция).
Перейдем теперь к вопросу о разложении рациональных дробей
на простые дроби. Мы не будем здесь излагать доказательство
теоремы о разложении рациональной дроби на простые, а ограничимся
лишь разъяснением этой теоремы, то есть дадим более точные
указания относительно числа и вида тех простых дробей, на которые
разлагается данная правильная рациональная дробь.
Из алгебры известно, что всякий многочлен с вещественными
коэффициентами степени выше второй разлагается единственным
образом на линейные и квадратичные множители с вещественными
коэффициентами. Таким образом, этими множителями являются
либо линейные функции вида х—а, где а—вещественное, либо
квадратичные множители вида x2 + px-\-q с вещественными
коэффициентами, но с комплексными корнями и, следовательно,
неразложимыми на вещественные линейные множители.
Например. 1) л?—1 = (*— 1) (х*+х+1);
2) x4-l = (x-l) (jc+1) (x*+2);
3) x*+l = (x*+V2x+l) (x* — V2x+h.
Некоторые из множителей, на которые разлагается данный
многочлен, могут входить в его разложение несколько раз. Объединяя
одинаковые множители (если они есть), разложение любого
многочлена Q (л:) можем представить в следующем виде:
Q (х) = а0(х—а±)^ (х — а2)** ...(*—as)ks x
X (х2 + qxx + qx)r* ... (х2 + ртх + qmym, (2)
где а0 — коэффициент при наивысшей степени х в многочлене, а
klt k2,..., kst rl9 r2,..., rm — натуральные числа*. Разложение (2)
знаменателя Q(x) рациональной дроби на множители теснейшим
образом связано с разложением самой дроби на простые дроби.
В алгебре устанавливается, что:
1. Каждому неповторяющемуся множителю вида х — а отвечает
в разложении одна простая дробь вида —з~-
* Заметим, что если степень многочлена Q (х) есть п> то k1-\-k2 + ••• +?$ +
+ 2(r1+r2+... +rm) = /i.
332

2. Каждому множителю вида (х—a)k отвечает сумма k
простых дробей вида -^+-^+...+_^.
3. Неповторяющемуся множителю x2-\-px + q отвечает одна
л - л Mx+N
простая дробь вида х2 ' —.
4. Каждому множителю вида (x2 + px + q)r отвечает сумма г
простых дппбей вида ЛМ+^i . M2x+N2 Mrx+Nr
стых брооеи виОа x2+px+q +{х*+рх+я)*+- +{*+рх+яу
Здесь А, М, N, А-и Mt, Л^-—числовые коэффициенты.
Таким образом, зная разложения (2), мы тем самым знаем
знаменатели всех тех простых дробей, на которые разлагается данная
рациональная дробь ~-7\• Остановимся на определении коэффици-
ентов Aiy Miy Ni\ при этом заметим, что если степень
многочлена Q (х) равна п, то и всех коэффициентов будет тоже п.
Для определения этих коэффициентов обычно прибегают к
знакомому нам методу неопределенных коэффициентов, который в
данном случае состоит в следующем: после того как правильная
рациональная дробь ^j~ записана в виде суммы простых дробей, в
числителях которых стоят неопределенные буквенные коэффициенты,
эти дроби приводим к общему знаменателю, которым, очевидно,
будет Q(x). Затем отбрасываем знаменатель в обеих частях равенства
и получаем равенство двух многочленов: слева — многочлен Р (х) с
известными коэффициентами, а справа — многочлен с неизвестными
буквенными коэффициентами (п — 1)-й степени. Так как это
равенство должно быть тождественным, то, приравнивая между собою
коэффициенты при одинаковых степенях х в левой и правой частях,
мы получим систему п линейных уравнений с п неизвестными, из
которой и определяются эти неизвестные коэффициенты. Как это
делается практически, мы разъясним на примерах.
2 #2 х «_ з 2х2 х 1 3
Пример 1. Пусть дана дробь xZ+x2J2x - x{x_l){J+2) . Разло-
жим ее на простые дроби.
Так как множители знаменателя все линейные и различны, то
разложение будет иметь вид:
2x2 —х+3 а В С
х(х—\)(х+2) х + *— 1 + х+2 '
где коэффициенты Л, 5, С нам пока неизвестны и их численные
значения требуется определить. Умножая обе части этого тождества
на общий знаменатель дробей, то есть на х(х— 1)(х + 2), и затем
отбросив его, мы получим тождество:
2х2—х + 3 = А(х—1)(х + 2) + Вх(х + 2) + Сх(х— 1), (3)
или, если раскрыть скобки и собрать члены, содержащие
одинаковые степени х, получим тождество:
2л:2— х + 3 = (А + В + С)х2 + {А + 2В — С)х — 2А.
333

Сравнивая коэффициенты при одинаковых степенях х в левой
и правой частях этого тождества, мы получим следующую систему
из трех уравнений относительно неизвестных А, В, С:
при х2\А + В + С = 2,
при х \А + 2В—С= — 1,
при х°\ —-2я = 3.
Решая эту систему, мы находим: А=—?", В = -^, C = -g-, так
что искомое разложение будет:
2*2 — л;-{-3 3 4 . 13
х(х—1)(л: + 2) 2х + 3 (л:— 1) ' 6 (х + 2)'
Замечание. В рассматриваемом примере коэффициенты А,
В, С можно было бы определить быстрее. Действительно, положим
в тождестве (3) х=0, тогда все слагаемые справа, кроме
первого, уничтожаются и мы сразу получим, что 3=—-2Л, откуда
Л=—3/2. Затем, полагая последовательно х=1, х=— 2, мы
аналогичным образом найдем: 4==ЗВ, 13 = 6С, откуда В=4/3> С = 13/б.
Такой способ нахождения коэффициентов обычно называют
методом частных значений. Как мы только что видели, этот способ
требует затраты значительно меньшего труда и потому заслуживает
особого внимания при интегрировании рациональных дробей. Если
корни многочлена в знаменателе только простые вещественные, то
для определения неизвестных коэффициентов целесообразно пользо-
ватья именно этим способом. В остальных случаях для определения
неизвестных коэффициентов можно комбинировать оба способа:
способ частных значений и способ неопределенных коэффициентов.
Как это делается, мы покажем ниже на примерах.
Пример 2. Разложить на простые дроби следующую дробь:
Зх+Ъ _ 3* + 5
х4—1 ~~ (х— \)(х+\)(х2+\)'
Здесь мы имеем:
Ъх+Ь^ А В Сх + Р
х*—1 х— 1+х+1 *2+1 '
откуда
Зх + 5 = Л (x+l)(x*+l) + B(x-\)(x*+l) + (Cx + D)(x*-l).
Для определения коэффициентов применим комбинированный прием:
при х= 1 I 8 = 4Л, Л =2,
при а:= — 1 I 2=—4В, Б=—V2-
Сравнивая коэффициенты при одинаковых степенях ху получим:
при х* I Л + В + С = 0,
при х2 \ Л— ? + D = 0.
3 5
Подставляя значения Л и В, находим: С=—^-, ?> =—^-. Так что
3* + 5 _ 2 1 Зх + 5
** — I""*— 1 2(jc+1) 2(*2+l)-
334

Пример 3. Разложить на простые дроби следующую дробь:
3*2-8л;+2
(х-2)2(х2 + х+\у
В данном случае будем иметь:
3*2—8*+2 А В Сх+Р
(х —2)2 (х2 + х+ 1) а:—2 + (х—2)2 + *2+*+1 •
Отсюда после приведения к общему знаменателю получим:
^х2 — 8х+2 = А (х—2)(x2 + x+\) + B(x2+x+l) + (Cx + D){x — 2)2.
2
Полагая х=2, получим: —2 = 7В, ? =—=-. Сравнивая коэффициенты при
одинаковых степенях х, находим:
при х8
при х2
при *0
л+с=о,
— A + B+D — 4C = 3,
— 2A + B + 4D = 2.
2 38 38
Подставляя значение В = —=-, из этой системы находим: Л=^, С = —tq»
47
D = -rm Тогда данная дробь представится в виде
Зх2 —8х + 2 38 2 38г — 47
(х — 2)2(л:2-+л:+1) 49 (л: —2) 7 (х — 2)2 49(х2 +х+1)'
После того как произведено фактическое разложение
рациональной дроби на простейшие, ее уже нетрудно проинтегрировать, что
и предлагается сделать студенту в разобранных выше примерах.
г» х* 2л:3 -4- Ъх -4- 4
Пример 4. Вычислить интеграл \ з~1Г\—^^ ^Хщ
Подынтегральная функция — неправильная рациональная дробь, поэтому
выделим ее целую часть делением числителя на знаменатель. В результате получим:
*4_2*3-i-3* + 4 0 , 2х+6 0 , 0 х+3
' ==х-—2-\- ==*-—2 + 2- '
*з+1 ' *з+1 * *з+Г
Полученную справа правильную дробь разложим на простые дроби:
х + 3 х + 3 А Вх + С
^з_|_1— (х+\)(х* — х+\)~~ x+l*^ я* — х+19
Отсюда х+3 = Л (х2 — х+\) + (Вх + С) (х+\).
2
Полагая х = —1, находим: 2 = ЗЛ, A = -q-. Сравнивая коэффициенты, полу-
Следовательно,
при х2
при х
л+в=о,
— Л+Я + С=1,
X
+ 3 2
2
отсюда Б = о-
отсюда C = -~-.
2д:—7
*з+1 3(*+1) 3(х2—х+1)'
335

и окончательно находим, что
? ** —2*» + 3* + 4
*з+1
dx
-и-
2-f
4
г2 4 2
e^_2*+-lln|*+l|---=-
3(*+1)
2д:—1
2 2а: —7 1.
х2 —л:+1
d*—6
dx
J (~tf
¦+4
v2 4 2 8 2л: 1
= \-2x+f In | x+11 —j In (*»-*+1)+ y= arctg-уТ+С-
Пример 5. Вычислить интеграл
Здесь
*2 + 2*+7 Л
+ 2д:+7
;dX.
2)(**+1)»
Ва:+С Da: + ?
Отсюда
(* —2)(х*+1)а a: — 2^ *«+1 ^(х»+1)а#
х2 + 2а: + 7==Л (а:2+1)2 + (Ва: + С)(а:—2)(a:2+1) + (Da^ + ?)(a:-2).
Полагая л: = 2, находим: 15 = 25Л, А = -^-.Сравнивая коэффициенты,получим:
при а;4
при х8
при х2
при х°
л+в=о,
— 2Я + С = 0,
отсюда В = —
отсюда С = —
2Л+Д — 2С + ?> = 1, отсюда D = —2,
Л— 2С —2? = 7, отсюда ? = — 2.
Тогда
С *2
+ 2л:+7
2)(а:2+1)2
dx*
JL5(*-
3 а:+2 2(jc+1)
2j" 5^+1
rf* =
1
Aln|x_2|_A in(^+l)_^ arctgx+^py
¦ 2 С **
J (*2+l)2
Применяя к последнему интегралу рекуррентную формулу*, найдем:
/ _С _J*L_—_JL_j.JL t
J (*2+l)2 ~2(л-2+1)~*~ 2 arctS*.
и окончательно получаем
С а:2 + 2а: + 7 ,.. 3
^-^^
Упражнения
Вычислить следующие интегралы:
.1 *3 —
+2
, dx.
-бж+5
С 2д;а— Плг—25 _,
См. формулу (4) в § 5.
336

.5 *3-*2-
2л:
rfjc. Ome. In1 * j \-С.
>з
3_ 61_
f хз__2х + 7 . л . (jc—I)4 (л: —5)20 . -
(лг—3)3лг15
^ С *4 ^ о ** о , 1 1 I X— l I • 16
жг—2
+ -^1п|дг+2|+С.
+С.
~6 л. От. \пШ-Ж+С.
6*+4 ' У*—1
Отв. -|- In (л:2 — 2а:-Ь5) — In | лг— 1 |-j-i-arctg^i + C.
13. [ Х{{7^) dx. Отв. i-arctgJc2-i-ln(j^+l)+C.
м- \x-^rwdx' 0mB- 51п\х'~ъ{п(х2+1)+ц^
i5' Jl*=3
-Х+1)2(л;_1)2
7—5л: 2 25 . 2х— 1
Отв. 0 . 9 г-тт г т= arctg —-==-
3(дс2~а:+1) *-1 3/3 /3
§ 8. ИНТЕГРИРОВАНИЕ ПРОСТЕЙШИХ ИРРАЦИОНАЛЬНЫХ
И ТРАНСЦЕНДЕНТНЫХ ФУНКЦИЙ
В этом параграфе мы рассмотрим вопрос об интегрировании
простейших иррациональных и трансцендентных (неалгебраических)
функций.
Выше мы установили важную теорему об интегрировании в конечг
ном виде любой рациональной функции. Эта теорема естественным
образом приводит к мысли: нельзя ли какой-либо подстановкой
свести интегралы от некоторых иррациональных и трансцендентных
функций к интегралам от рациональных функций? Если это
преобразование удастся осуществить, то тем самым будет положительно
337

решен вопрос об интегрировании в конечном виде этих функций»
Преобразование подынтегральной функции в рациональную
функцию с помощью надлежащим образом выбранной подстановки
называется рационализацией интеграла. Таким образом, рационализация
интеграла есть один из методов, с помощью которого
устанавливается интегрируемость в конечном виде некоторых классов
нерациональных функций.
В качестве примера применения этого способа рассмотрим
несколько простейших типов интегралов, допускающих указанную
рационализацию.
Предварительно введем одно обозначение, которое будет весьма
часто встречаться в этом параграфе. Речь идет о символе R(x, у).
Этим символом будем обозначать рациональную функцию своих
аргументов, то есть х и у. Другими словами, R(x,y)— это такая
функция, которая получается из х и у, а также некоторых
постоянных с помощью рациональных действий, то есть четырех
арифметических действий*. Такова, например, функция
п, ч з*2—хф
R(*> У) = —7=.
Если R (х, у) — рациональная функция от х и у и вместо у
подставлена какая-нибудь рациональная же функция от х, то полученная
сложная функция от одной переменной х будет то же
рациональной. Однако если вместо у подставить некоторую иррациональную
функцию от х, то сложная функция может уже не быть
рациональной. Например, R(x, у) = х-\-у — рациональная функция.
Подставим у=Ух. Получим: R (x, y) = x + ]fx, а это уже
иррациональная функция от х.
Остановимся на интегрировании некоторых простейших
иррациональных функций.
I. Интеграл вида
где подынтегральная функция есть сложная функция от xt полу-
т fax -4- Ь
ченная из рациональной функции R (х ,у) подстановкой у = ~\/ —-J—»
} CX-f-g
Иными словами, подынтегральная функция есть рациональная функ-
т ?ах-Х-Ъ
ция от х и 1 / —-J- • Здесь т — натуральное число, а, Ь, с, g —
постоянные коэффициенты.
Рационализация этого интеграла достигается с помощью под-
становки Т/ J. =t9 откуда
cx+g ' a — ctmi (a — ctmy
* К арифметическим действиям относят сложение1 вычитание, умножение и
деление.
338

Тогда для данного интеграла получим*:
где /?!(?) —рациональная функция от переменной t. Полученный
интеграл вычисляется по правилам интегрирования рациональных
функций. Переход к старой переменной х осуществляется с
помощью подстановки
У cx+g
Замечание. К интегралу вида I приводится интеграл
w*-mf ш^к
где символ R по-прежнему указывает, что над величинами,
стоящими в скобках, производятся лишь рациональные действия, а
k, п% ..., г, s — целые положительные числа. Действительно, пусть
т — общий знаменатель дробей —, ...,—. Тогда —=—. .... — =
г /I s n m s
= —. Отсюда
ах-\-Ь
то есть подынтегральная функция оказывается рациональной функ-
цией от л: и у
Пример 1. Вычислить интеграл \ -
3 Т/(х—1)3(jc—S
f—^—t-j/i^^^
Так как
3 ]/"(*-7)з(*~=^)=3 У *-1 (jc—1> (*—2)'
то положим t = ~i/ :. Тогда
2 х—2 _2 — Р _ 2tdt
x-V *TZf2» (1-^)3-
Поэтому
dx
w.
jc— 1 (x—l)(x-2)~
e=s-)s=s-»),,-")
f* о
Пример 2. Вычислить интеграл I —-. -
J *(2+i
21 ~ "<* --«/??+*
*-l
* Если вместо xt dx и радикала подставить их значения.
339

Положим t
-V
x—l 1
dx
3/2
* 2 +
И?) .
(l~/3)2
t*dt
(1-/з)(2 + /)'
rf/ и
К последнему интегралу применим известный метод интегрирования рациональных
дробей. Разложим на простые дроби подынтегральную функцию:
В
Ct+D
(1— /з) (2 + /) 1—/ ' 2+t ¦ *» + *+!•
откуда /2 = ^(2 + /)(/2 + /+l) + 5(l-/)(/2 + /+l) + (C/ + D)(l-/)(2 + /).
Для определения неизвестных коэффициентов применим комбинированный
способ:
1=&4, Л=-1
Следовательно,
при / = 1
при /= — 2
при /3
при /°
4 = 9В, В =
0 = Л-В-С, С=--1,
i
= 3
/2rf/
3 J 1-/+3 J/ + 2 } /2
lln|l-/| + i-ln|/ + 2bi-J
rf/
/ + 2 J/2 + /+1
2/+1
d/ =
/2+/+1 d/ 2
4 K)"+f
-|- In 11 —/1 + -|- In | * + 2 I—i- In (<¦ + <+1) — i arctg ^tJ:+C,
VT
VT
и, возвращаясь к старой переменной х, получим окончательно:
Jdx
ущ
т,п|1-"|/:
л:—1
+ТШ 2+
v^
-т,п1У Ч^+У — +1)-frarctg —FT—+
П. Рассмотрим интегралы вида
lxm(a+b^)pdx9
где a, b — любые постоянные, показатели т, п, р—рациональные
числа. Подынтегральное выражение хт (a-\-bx)p dx называется
340

биномиальным дифференциалом. Знаменитый русский математик
П. Л. Чебышев в 1853 г. доказал, что при интегрировании
биномиальных дифференциалов интеграл берется в конечном виде (та
есть выражается в элементарных функциях) только в следующих
трех случаях:
1) когда р—целое число,
т 1 1
2) когда —^ целое число,
3) когда ^1- + р—-целое число.
Если ни одно из этих условий не выполняется, то интеграл
не берется в конечном виде.
В первом случае, когда р—целое положительное,
интегрирование выполняется непосредственно. Для этого достаточно разложить
бином в сумму по формуле Ньютона.
Если р—целое отрицательное, то рационализация достигается
с помощью подстановки х = Р, где [х —общий знаменатель дробей
тип.
_J/ I\-2
Пример 3. Вычислить интеграл у а = у х \1+*3/ dx.
Здесь m=—=-, п=-~-, р=— 2. Применим подстановку x — t6, dx=6tbdt~
Тогда
С -* _eC-^-eC?±!=!*-ef *
-6S(T
*** 6arctgt — -^-T—3arctgt + C = 3 (arctgf—у-^ + С —
[+/2)2 ЬЬ t2+l &» i ^"-ь„ J+^
= 3(arctg|/r^ * - 1 + C; при этом заметим, что для вычисления интеграла
мы применили рекуррентную формулу (4) § 5.
Ь
+'2):
|2
т-1 т+1
Во втором случае, когда —! целое число, рационализация
интеграла осуществляется с помощью подстановки a-\-bxft = ts, где
s—знаменатель дроби р=—.
Пример 4. Вычислить интеграл ) \fx V~\ +2>Y& dx = ) *3(l+3*3)3 dx.
Здесь m = -~-, /i=— p=— отсюда =2. Поэтому применяем подста-
новку 1+3*3=^ откуда * = —;— (Р— 1)з и d*=-^—(*з_ 1)2/2 <#. Тогда
о у «3 2
I Vx~Vl + 3s/x^dx= I (/3TJ}% 1-1(/в-1)1^Л=± I p(p-i)dt=~
341

С dx (* _ 1
Пример 5. Вычислить интеграл V -= \ дг~1 (1 + лгб) я dx.
,1 х\/ 1-f*5 J
Здесь /п= — 1, п = 5, /?==—о-! отсюда = 0. Следовательно, применяем
3 ' п г
L 3 t2 dt
подстановку 1+д:5 = ^, откуда x = (?3_i)5 и dx = -= т. Тогда
о -
(/3-1)5
I 3 t2dt 3 Г tdt I Г dt
р rfx = р 1 J_ 3 *»#=3р/#1р
t—\
Р dt
J KM'
.i,„
<—i
VP+t+i
,Ц^Щ+С
где f = -J/T+75. Заметим, что для вычисления интеграла \ _ мы применили
известный нам метод интегрирования рациональных дробей.
В третьем случае, когда —^—\-р — целое число,
подынтегральное выражение преобразуется к рациональному виду с помощью
подстановки а + &л^ = ?У, где s — по-прежнему знаменатель дроби
*=т •
Пример 6. Вычислить интеграл ^дсУ^+я4 dx= \х (1 +Х4)2 dx.
Здесь т=1, л = 4, р = -^-и +р=\. Поэтому l+x4»*2^, отсюда
_JL —А/
x = (t2— 1) 4 и dx = s"(/2—l) 4 dt. Следовательно,
_ J. ___L _ 5
^уЧ+^л^-у §(/2_1) 4(/2_1) 2^^2-1) Т'Л—LJ-^2-^
^^\х2УТ+1^ + \п(х2 + У'\+х^)+С.
При этом последний интеграл вычисляется известным нам способом
интегрирования рациональных дробей
t2 t2 А , В , С , D
"г" /II "Г
(/2—1)2 (^ —1)2 (/_|_1)2 *—1 ^(f—l)*^ f+\ ^ (t+\)2'
отсюда t2 = A(t-l)(t+l)2 + B(t+l)2 + C(t+l)(t—\)2 + D(t-l)2.
* Более подробное изложение вопроса интегрирования биномиального
дифференциала см. в учебнике Г. М. Фихтенгольца [1], стр. 306.
342

Для определения коэффициентов применим комбинированный способ:
Следовательно,
С Pdt 1
J (*2-1)2 4
при t — l
при /=— 1
при *=0
при t3
ln| f-1
1-4D, D=-i,
0 = —Л+Д+С+?
0 = Л+С
С = -
л=-
1
1
4(*-1) 4
ln^+1
1
4(*+1)
-C=-f In
4
*-1
*+1
1
2(Р-1) +C = --^-[^/l+^ + in(^2 + /i+^)] + C<
Пример 7. Вычислить интеграл
Здесь /п=—11, л = 4, р= ^- и
tfx
/n+1
= ? x_11(l+*4) 2 dx.
p = — 3. Поэтому 1 + я4 = *»**„
отсюда x = (t2 — 1) 4 и<& = — -тг^2— 1) 4 *<#• Следовательно,
\
dx
= _JLC (^—i)4-(^-i)2 p
2 «2_
1)
5^
'«Л-
-is/m^vm
так как ? =
^-
III. Интегралы вида
где R — рациональная функция от х и от \rax2-\-bx-\-c. Этот
интеграл представляет интерес в том случае, когда квадратный
трехчлен не имеет равных корней, в противном случае мы придем
к рациональной функции, которую уже умеем интегрировать.
Казалось бы, по аналогии с интегралом вида I и здесь для
рационализации (а значит, и вычисления) данного интеграла
следовало бы применить подстановку ]/rax2 + bx + c =t. Однако, как
легко проверить, в этом случае х и, следовательно, dx не
выражаются рационально через t. Поэтому такая подстановка не
освобождает нас от иррациональности и тем самым не решает
поставленной задачи. Оказывается, рационализация данного интеграла
достигается с помощью одной из трех подстановок Эйлера
(1707—1783).
343

Первая подстановка Эйлера. Если а>0, то полагаем*
Vox2 + bx + c =t—V~ax.
Возводя в квадрат, получим: ax2 + bx + c=t2 — 2 Va tx + ax2, откуда
после уничтожения члена ах2 находим: bx+c=t2—2]/а tx, так что
b+2V<* t' (b+2Va tf
Vax2 + bx + c=V«t2 + bt+fV« .
b+2Va
Мы видим, что х, dx и радикал рационально выражаю-Гся через t.
Подставляя в данный интеграл вместо ху yrax*+bx + c и dx их
значения, получим:
С р( t2~c_ VZt* + bt+cVZ\ 2{Vat* + bt+cVa) ,
)«[b+2Vaf b+2Vat j (b+2Va tf
где уже под знаком интеграла стоит рациональная функция от пе-
веменной t.
f dx
Пример 8. Вычислить интеграл \ — yr a ==¦-
Воспользуемся первой подстановкой Эйлера. Положим ^дс2 — i = ^—л:, отсюда
1 j_ /2 /2 _ 1
.х2-—1 = /2—2tx+x2, —l = t2—2tx, х = 2 , dx = dt, при этом заметим,
что х + У х2 — 1 = /. Следовательно,
С dx 1
c + Yx2—l 2
SV^4HT~^)^4(ini^+i)+^
д-1-1п|дг+Т^ЗГ|+ , JL=rг+g-
2 4(л:+У*2 — О
Замечание. Формула X11 таблицы интегралов, то есть
In | х + Vx* + a \ + С, нами была как раз установлена
V'x*+a
с помощью первой подстановки Эйлера: ]/ х2 + а = t—х (см. § 4,
пример 18).
Вторая подстановка Эйлера. В случае если с>0, то
для рационализации интеграла можно применить вторую
подстановку Эйлера: _
Vax2 + bx + c=xt + Vc **.
* Можно было бы положить и Yax2 + bx-\-c=t-\-Yax.
** Можно было бы положить и Yax2 + bx-j-c = xt—Yc*
344

Возводя в квадрат обе части равенства, получим: ax-\-b = xt2-\~
+ 2l/c/, откуда х = vL/7 - Дифференцируя, находим: dx —
e— (a-?)* dt ПРИ этом
Va* + bx + c = ^*-?p]?.
Полученные выражения показывают, что х, dx и радикал
рационально выражаются через / и, следовательно, подынтегральное
выражение рассматриваемого интеграла преобразуется к
рациональному виду, а значит, интеграл берется в конечном виде.
? dx
Пример 9. Вычислить интеграл \ \ т/1 <- — 2 *
Пол а гаем Vl+x—x2 = tx —- 1; отсюда 1 + х — х2 == t2x2 — 2tx + 1 и, следова-
1+2* , 2(1-/-/2) /_ *2_|_/_i
(гельно, *e^—, ?fa= ^2+1)2 <К, У1+л:-х2= /2+1 . Тогда
{ * =-2 С —**— = -2 { dt — 2 arctg (*+1> +
х
Замечание 1. Рассмотренные выше два случая (а>0, с>0)
приводятся один к другому подстановкой х=—. Поэтому можно
ограничиться применением первой подстановки. Покажем это на
предыдущем примере.
dx 1
(*+l) Vl+x — x2
dz Г dx ? dz
Применяя к интегралу у -— ^ ,ГГ , подстановку лг=~э dx=-~-
dz С dx ? dz
- мы получим: \ г == — \ _ а к послед-
*2' J (x+l)Vl+x-x2 J (г+1)/г2 + г-Г
нему интегралу можно уже применить первую подстановку Эйлера.
Третья подстановка Эйлера. Если квадратный
трехчлен ах2 + Ьх + с имеет (различные) вещественные корни а и р„
то (считая х>а) мы получаем:
Уы* + Ьх + с =]/а(*-а)(*-р) = (*-а) |/"2^|1.
Следовательно, подынтегральная функция рационально зависит or
а(х— 6)
х и радикала __ , так что
$ Д U, l^ + foc + c) djc- J Дх (jc, ]Л^г) dx
и мы пришли к рассмотренному выше интегралу I типа, который
рационализируется с помощью подстановки 1/ а ^х~ ™ = t. Эта
подстановка и представляет собой третью подстановку Эйлера.
345

С dx
Пример 10. Вычислить интеграл \ ,
J (х—2) ]/ — 3+4*--*2
Так как ]/—3 + 4*-*2=}/(3-*)(*- 1) = (3-*) "I/ |=lf то,
^х~=Т .
j—- = *, найдем:
, W+1 х 9-^1 dx - 4tdt V-3+4X-* У-
x-TTtT^ x-z-t^+v dx-(t*+i)*> v 6+*x x - i+t
полагая
тогда
С dx = С l+fl # ЬН! . ** dY==2 С dt ^
) (л;_2) )Л=3 + 4* —** J ^_i 2/ " (1+/2)2 J *2-l
= ln
<-ll+c=i„l^-1-^3-^
/+l| |K*—f+]/"3 —*
+ C.
Замечание 2. Выше мы уже отмечали, что вторая
подстановка Эйлера с помощью замены переменной #=-- приводится
к первой подстановке, и потому уже с чисто формальной точки
зрения мы можем ограничиться применением первой и третьей
подстановки, чтобы любой интеграл рассматриваемого здесь вида
привести к интегралу от рациональной функции. Это замечание
справедливо не только формально, но и по существу. В самом деле,
«ели квадратный трехчлен ах2-\-Ьх-\-с имеет вещественные корни, то,
как мы только что установили, и подынтегральная функция
R(x, У ах2 + Ьх-\-с) преобразуется в рациональную функцию с
помощью третьей подстановки Зйлера. Если же корни этого трехчлена
не являются ЕешестЕенными, то при всех значениях х он имеет
тот же знак, что и его старший коэффициент а*. А так как в этом
случае Ь2~-4ас<0, то коэффициенты а и с имеют одинаковые
знаки. Следовательно, если с>0(применима вторая подстановка),
то и а>0 — значит, применима и первая подстановка. Если же
а < 0 (значит, и с < 0), то в этом случае трехчлен ах2 + Ьх + с
всегда отрицателен и радикал \/Гах2-\-Ьх + с имеет невещественные
значения, то есть этот случай выводит нас из области вещественных
чисел, а мы занимаемся интегрированием функций, принимающих
только вещественные значения. Поэтому при а<0 имеет смысл
рассматривать лишь случай, когда корни трехчлена вещественны,
и мы снова приходим к третьей подстановке.
Таким образом, двух подстановок Эйлера (первой и третьей)
достаточно для того, чтобы любой интеграл III типа свести к
интегралу от рациональной функции и, следовательно, вычислить в
конечном виде.
* + о~) "^ 4~2 ' еСЛИ Учесть»
что выражение в квадратных скобках положительно при всех значениях х.
346

Теоретическая ценность подстановок Эйлера очевидна, однако
следует отметить, что на практике они обычно приводят к сложным
и трудоемким выкладкам. Поэтому для вычисления интегралов Ш
типа следует прибегать по возможности к другим приемам. Так,
например, для вычисления интеграла \ — — целесообразнее
1
применить подстановку * = у, на которой мы уже останавливались
ранее.
До сих пор мы систематически изучали интегралы только от
алгебраических функций (рациональных и иррациональных). Ниже
мы рассмотрим интегралы от некоторых классов неалгебраических,,
в первую очередь тригонометрических, функций.
IV. Рассмотрим интеграл типа
$/?(sin;e, cosx)dx7
где, как и выше, R обозначает рациональную функцию своих
аргументов sin л; и cosx.
Например, интегралы
и
-dx, \s'm2 xcos*xdxt \ ——
sin2A: + 3 cos x
являются интегралами такого типа, но этого нельзя сказать,
например, об интегралах
С V—: j С sinx+1 ,
\ cos х у sin х ах, \ —г ах.
J J 2 J/ cos*— sin3*
Рационализация этого интеграла достигается с помощью так
называемой универсальной подстановка
tgy = /, —Я<*<Я.
2
Действительно, так как *=2arctgf, dx = YJ-^dt и sinA: =
2 ie — 1 — te2 —
Ig 2 2t Xg 2 1-/2
ТП2> cosx== zr = T~Г75» то> подставляя в данный
i+ttfy 1+' i+tg»^- 1+t
интеграл вместо sinx, cos* и dx значения, выраженные через t>
получим:
J R (sin*, cos*) dx=^R (—, I=g) . ^ dt,
где уже под знаком интеграла стоит рациональная функция от
переменной t и, следовательно, интегрирование совершается в
конечном виде.
dx
Пример 11. Вычислить интеграл V =—
4 sin # + 3 cos x4
347

Подстановка t
Несмотря на то что универсальная подстановка дает возможность
проинтегрировать всякую функцию вида R (sin#, cosx), однако
на практике она часто приводит к слишком сложным и трудоемким
выкладкам. Поэтому наряду с универсальной подстановкой полезно
знать и другие подстановки, которые во многих случаях быстрее
приводят к цели. На некоторых из них мы уже останавливались
в § 6 (специальные приемы интегрирования). Здесь укажем еще
ряд таких подстановок.
1. Если подынтегральную функцию R (sin*, cosx) можно
преобразовать в рациональную же функцию только от tgx, то есть
R(sinx, cosx) = R1 (tgx), то рационализация может быть достигнута
<: помощью подстановки t = \gx. Действительно, в этом случае х=
= arctg/, dx= 1 2, так что igx и dx рационально выражаются
через t и, следовательно, все подынтегральное выражение
приводится к рациональному виду:
\ R (sin л:, cos x) dx= \ R± (tgx)dx= \ R± (t)-j
dt
+t*
Замечание. Подстановку t = tgx целесообразно применять
и в том случае, когда выражение jR(sin#, cosjc) не меняется от
леремены знака одновременно перед sinx и cos#.
Пример 12. Вычислить интеграл \ —г-г .
r r J sm x cos x
Подынтегральная функция -г-= не изменится, если в ней заменить
r YJ sm5 x cos x
sin хна (—sin*) и одновременно cos а: на (—cosx). Поэтому полагаем tgx — t,
* * ; dt te* l l
откуда * = arctg t, dx = и sm *= to ™° v —
Тогда
'1+'2 j/l+tg2* |/"l+^, /T+tg27"
УТ+72
С dx f (1 + ^)2 i i
: — i- ctg4 x - ctg2 a: + In 1 tg x |+C.
Пример 13. Вычислить интеграл V
dx
sin4 x cos2 л: *
В этом случае также полагаем /=tg л:, отсюда, поступая аналогично, получим:
348

2. Если выражение i?(sinx, cosjc) при замене sin л: на (—sin*)
только меняет знак, то интеграл §#(sinx, cos x) dx легко
рационализируется подстановкой t = cosx.
COS2 X
Пример 14. Вычислить интеграл
При замене sin x на (-
sin3 х
dx.
¦ sin х) интеграл только меняет знак. Поэтому
полагаем cos х = t, отсюда sin x = У 1 —/2, dx = — ^ ^ . Следовательно,
) co*xdX- ) (1-
dt_
/2)2 :
COS*
уТ^Т2'
2(1 —*2)-г 4
In
1+f
+С =
1
Интеграл
s
2 sin2 х
In
tg
+ С.
Pdt
(1-в2
вычислен методом разложения на простые дроби. Именно,
Р А . В , С , D
+
(1-/2)2 1__/ I (1_/)2 ' 1+f » (1 + 02*
Отсюда *2 = Л (1— *)(l + f)a + fi(l + /)a + C(l+*)(I —*)« + D(l — 0а-
Для определения коэффициентов применим комбинированный способ:
1
*=1
*=—1
Так что
1=4Б, Я=-
t
1=4D, D=|,
о=—л+с,
о=л+в+с+о
} *-'--|.
-|[ш|«-
1
f
1
2(1 — t2)^ 4
In
(*-l)2
In | t+1
f+1
+C =
cos a:
f+1 ' J ('+1
1
t+
1
r]+c=
2 sin2 x
f-o-ln tg
fl+C
3. Точно так же, если функция /? (sin jc, cos*) при замене cos a:
на (—cosx) лишь меняет знак, то интеграл от этой функции
преобразуется в интеграл от рациональной функции при помощи
подстановки / = sinA;.
Пример 15. Вычислить интеграл \ — . _ = \ . . л .
r r J sin x sm 2x J 2 sin2 * cos jc
Подынтегральная функция только меняет знак при замене cos л: на (—cos*).
Поэтому целесообразно применить подстановку *=sin*, откуда x=arcsin?,
dx=
УТ^Т2'
dx
2 sin2 x cos
Следовательно,
__=_1_ С dt
x 2 ) P(l-P) "~
l + t
1 , l »
s-2?+TIn
1-f
+ C = -
J ^(i_^2) dU2 J/2+2 J i-**s
¦)|+c
2 sin jc
i.n|«(i+«
349

Пример 16. Вычислить интеграл \
dx
cos6 х'
В этом случае также целесообразно применить подстановку smx — t. Эта
подстановка дает:
+ 8" ) LF^^O + O"3] ^=Тб
+ i^(7r^2-(Tqbp)+c=4ln |tg (^+-J)
i—*| + i6\i-/ i+t) +
3 sin x , 1 sin x
{-С
8 cos2* 4 cos4 a:
Заметим, что для вычисления интеграла \ —л—-^- мы применили известный
J (1— г2)3
нам метод интегрирования рациональных дробей.
V, Интеграл вида
\R{ex)dx
рационализируется подстановкой ex = t. В самом деле, так как
x=\nt и dx=-j, то получим:
$Я(е*)Лг=$Я(0у,
то есть пришли к интегралу от рациональной функции относительно
переменной t.
f ex— 1
Пример 17. Вычислить интеграл \ ^ dx.
Полагаем е* = /, отсюда dx=-— и, следовательно,
= 2 In (1 +0 — In t+C = 2 In (1 +e*) — x + C.
Итак, мы рассмотрели ряд подстановок, с помощью которых
интегралы от некоторых иррациональных и трансцендентных
функций приводятся к интегралам от рациональных функций и потому
интегрируются в конечном виде. Однако в подобных случаях часто
интегрирование можно производить посредством других подстановок,
не приводящих подынтегральное выражение к рациональному виду.
Для этих подстановок нельзя дать никакого общего правила, а
изобретательность и навык приобретаются практикой в решении
достаточно большого числа примеров.
Упражнения
1. [ _*dX . Отв. ±:(6х-9а)%/ (х + а)*+С.
2# С х -\-\ А^ Пто _1_
\у\ Зх*** °тв' 405(286~24^ + 54^'/1 + ЗА;+а
350

3. Cl^lf+'dc
J уТ^М-i
U
От*. * + 4]/7^ + 41п|УТйЛ--11 + С.
Отв.
У 2-х
+С.
5,
6.
7.
8.
9.
10.
И.
-d*.
г «
Отв. у ах-{-х2 ~ ~2 \п
Уа + х—Ух
dx
^(лг-1)»(* + 2)*%
х^ dx
Отв
з V .
Va+x+V х
+с.
х—\
х+2~
/1+2*:
х* dx
0+2*»)
Отв. -g-(jc» —1)|/"1+2jc* + C.
. - a: (^2 — 3) 3
Отв. С v, —рг arcstn x.
2_
з
- dx.
dx
Отв. С-
2]/"1_a;2 2
(1+2jc3)3
x2dx
V\-2x — x~2'
l+T/T+x+x»
0//w. In
5л;5
Vl + jc + ^-j-jc
]Л+а; + а:2 + а: + 2
+ C.
5
i2. \ * '; ' * ~^-_ dx.
J xVl+x + x*
13. J/jc2 — 2x — Г dx. Отв.
14. \ sin3 x dx.
15. \ sir
t. С sin3*
16. \ г- d*.
J cos4 a:
17. ?-*-
J sin3 a:*
Отв. 4(3 — *)/l — 2jc — A;2 + 2arcsin^t-+C.
2 ч ]/^2
Отв. 1п|2]Л + а: + а:2 — а: — 2 | + C.
a:-1
]/x2_2a;-1 +in|x—i+]/"jc2_2jc—1|+C.
sin3 a: cos2 x dx.
Отв.
Отв.
1
3 cos3 x
r cos a:
1
cos a:
! Г
i u
In
18.
19
20.
21
[ 1+tj
J sin 1
•5
2a;
dx
dA\
5 + 4 sin a:'
dx
С d*
J l+sin2x
J si
sin a: cos x
-dx.
~ cos3 a: . n
Отв. —x cos x+С
Отв. j= cos3 a: (3 cos2 x — 5) + C,
Отв. y(tgx + ln|tgx|) + C.
2 5tg{ + 4
Отв. yarctg ^ bC.
Отв. -LarctgC^tgArJ+C.
Отв. 2/"tg^+C.
351

22
23,
24.
25.
С dx
s
x(l+xex)
dx
dx.
Отв. х- ln(l+e*)+C.
xex
Отв. In
\+xe*
+C.
Отв. С—У \+е~*х.
е*у\+е*х'
\y-&r=T\dx. Отв. l^lln(l + 0 + ^ln(^~^+l)~^arctg-?^ + Ct
где t — Ye**— 1.

ГЛАВА IX
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 1. ЗАДАЧИ, ПРИВОДЯЩИЕ К ПОНЯТИЮ
ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Понятие определенного интеграла наряду с понятием
неопределенного интеграла также является основным и даже более
фундаментальным понятием математического анализа.
Понятие определенного интеграла довольно сложное, и поэтому,
прежде чем его сформулировать, мы считаем целесообразным
разобрать две конкретные задачи, приводящие к понятию
определенного интеграла. К этому понятию приводят самые
разнообразные вопросы и задачи из области геометрии, механики, физики и
техники. Из всего многообразия задач мы рассмотрим только две
задачи, взятые из двух совершенно различных областей: одну —из
геометрии, другую — из механики, к решению которых, как мы
увидим, будет применен один и тот же метод.
1. Задача о площади криволинейной трапеции. В школьном
курсе элементарной геометрии вычисляются площади
прямолинейных фигур: прямоугольника, треугольника, трапеции,
многоугольника. Единственная криволинейная фигура, площадь которой там
вычисляется, — это круг.
Рассмотрим следующую геометрическую задачу.
Вычислить площадь плоской криволинейной фигуры достаточно
общего вида, а именно фигуры аАВЬ*, ограниченной сверху
кривой y = f(x)r a^x=^bt при этом/(х)^0, с боков—двумя
ординатами х = а и х = 6, а снизу — отрезком оси ОХ (рис. 137).
Такую фигуру принято называть криволинейной трапецией.
Требуется определить ее площадь. Для этого разделим основание
трапеции произвольным образом на конечное число частей, что
равносильно дроблению промежутка [а, 6], на котором задана
функция y = f(x), на п произвольных частей точками а=х0<Х\<
< хъ <... < xt < хм <... < хп-\ < хп = Ь.
* Понятие площади плоской фигуры будет дано и гл. X, а пока мы
пользуемся интуитивным представлением о площади плоской фигуры.
353

Восставим в этих точках ординаты кривой. Тогда
криволинейная трапеция разобьется на п полосок. В каждом из полученных
частичных промежутков [#,-, х,-+1]э где / = 0, 1, 2,..., п— 1,
выберем произвольную точку ?,• (я* < ?« <; йгч-i) и восставим в них
ординаты f (?,-).
Заменим приближенно /-ю полоску прямоугольником с
основанием длины Д*| = х;+1 —*| и высотой, равной f&i). В результате
Рис. 137.
вся криволинейная трапеция приближенно заменится некоторой
ступенчатой фигурой, составленной из отдельных
прямоугольников. Так как площадь /-го прямоугольника равна fdfiAxi, то
площадь всей ступенчатой фигуры, очевидно, равна
/>сту п = / (Бо) Л*о + / (Si) ИХг+... + f (tn-J Ах»-! = ? / (?0 Д*. *.
Естественно считать, что эта площадь при достаточно мелком роб-
лении промежутка [а, Ь] является приближенным значением
площади Р криволинейной трапеции, то есть
Ръ 2ШД*/**.
1=0
Ясно, что это приближенное равенство будет тем более точно,
чем мельче дробление промежутка [a, b], то есть чем меньше мы
будем брать длины Да:,-. Поэтому точное значение площади Р
получится как предел суммы площадей указанных
прямоугольников ***, то есть
/> = lim2 /<Ь)Д*| (1)
* Символ 2 (вытянутая прописная греческая буква «сигма») обозначает
знак суммирования (сложения).
** Знак ^- обозначает приближенное равенство.
*** Это рассуждение согласуется с тем общим определением площади
плоской фигуры, которое будет дано в гл. X, § 1.
354

при условии, что длина наибольшего частичного промежутка, то
есть K = max{Axi\y стремится к нулю*. Очевидно, если К — О,
то длины всех частичных промежутков будут стремиться к нулю,
то есть все Ал:,-—О**. Таким образом, задача о вычислении
площади криволинейной трапеции приводит нас к рассмотрению
предела суммы вида
л—1
а= 2ШД**- (2)
Мы видим, что эта сумма представляет собою некоторую
переменную величину, имеющую весьма специальный вид. Определение
предела такой переменной при X— *0 будет
дано ниже, в § 2 (см. замечание).
Таким образом, новое понятие площади
криволинейной трапеции вводится с помощью
операции предельного перехода, исходя уже
из известного понятия площади
прямоугольника. Как нам известно, в элементарной
геометрии площадь круга также определялась с
помощью операции предельного переходу—
как предел площадей вписанных и описанных
многоугольников.
Пример 1. Вычислить площадь
криволинейной трапеции, ограниченной сверху кривой
у = ех, O^x^l (рис. 138).
Разобьем промежуток [0, 1] на п равных
частей точками 0 = х0<Сх1<С.---<хп = 1, при
этом л:0 = 0, «i=-,x2=-, ...,xt= '-,... ,
хп=1 и все Ддс- = -, где ? = 0, 1, 2,..., п— 1. Выберем ?,==;?,= -;
следовательно, высота 1-го прямоугольника будет крайняя левая
i
ордината i-й полоски, равная f(li)=en. Тогда площадь
ступенчатой фигуры выразится следующей суммой:
Yl
0
1
г
1
fa
ШЁ
шИ
ш!*
' i
Рис. 138.
п-\
п—\
Li n
п—\ 1
:(1+*"+«"+... + * Я)_1.!^
1 е-!
i=0
1-е"
еп -1
Здесь пользуемся формулой суммы геометрической прогрессии. Эта
сумма выражает приближенно значение площади нашей фигуры.
* Величину X, характеризующую мелкость дробления промежутка [a, b]t
иногда называют рангом дробления.
** Вместо Л, — 0 было бы неправильно писать п—>оо, так как
увеличение числа точек дробления промежутка [а, Ь] еще не обязательно означает, что
дробление становится более мелким, то есть все Д^ неограниченно убывают; если
же I 0, то все А^ — 0 и обязательно п —¦ со.
355

Предел этой суммы, очевидно, дает точное значение искомой
площади, то есть
1_
1 е — 1 , 1Ч v n
- = (e—l) lim-j =
P = lim
я -•• оо " — п ->-оо
п 1
е — 1 е
1 *.
1
Рис. 139.
Замечание. Выше мы предполагали, что функция f (х)
принимает на промежутке [а, Ь] только положительные значения,
то есть график ее расположен целиком над осью ОХ. Рассмотрим
теперь случай, когда функция / (я) меняет свой знак на промежутке
[а, Ь], то есть некоторые части
V& л графика находятся над осью, а
другие под осью ОХ (рис. 139).
Если в этом случае
составим сумму (2), то слагаемые
/ (?;) А хи соответствующие
частям графика, лежащим под осью
ОХг будут отрицательными,
ибо Д#? > 0, а ордината / (Е,) —
отрицательна. Тогда предел
такой суммы даст величину, которая будет учитывать площади
частей фигуры, находящихся над осью ОХ, со знаком плюс и
под осью ОХ — со знаком минус. Следовательно, в этом общем
случае предел суммы (2) будет выражать алгебраическую сумму
площадей, заключенных между осью ОХ, графиком функции
y=f (х) и ординатами х = а и х = Ь. При этом площади над осью ОХ
будут получаться с положительным знаком, а под осью ОХ — с
отрицательным.
К отысканию предела суммы вида (2) приводит не только задача
вычисления площади криволинейной трапеции, но и многие другие
задачи физики, техники и естествознания.
2. Задача о пройденном пути. В качестве второй общей задачи
рассмотрим вопрос из механики.
Определить путь s0, пройденный материальной точкой за
промежуток времени от момента t0 до момента 7\ если известна скорость
движения точки как функция времени t, то есть задано v = f(t).
Разобьем промежуток времени [t0, T] на п произвольных частей
точками
В результате промежуток [t0, T] разобьется на частичные
промежутки вида [ti9 ti+1], где 1 = 0, 1, 2, . . . , п— 1. Величину i-ro
промежутка времени обозначим через Ati = ti+1 — tt. Затем в каждом из
них выберем произвольно момент времени xt, t[, ^т,<:^+1, и вычи-
* Здесь мы использовали формулу lim -
х -+о
1.
356

слим скорость в этот момент, то есть найдем У( = /(т|). Если
дробление промежутка [t0, T] достаточно мелко, то приближенно мы
можем считать, что в течение каждого частичного промежутка
времени движение происходит равномерно, то есть с постоянной
скоростью.
Для определенности будем считать, что в течение всего i-ro
промежутка времени точка движется с постоянной скоростью,
равной Vi = f(Ti). Тогда путь, пройденный точкой за /-й промежуток
времени, очевидно, будет приближенно равен Viktiy и, следовательно,
путь, пройденный за все время от t0 до Г, приближенно будет
равен- сумме этих величин, то есть
Это приближенное равенство будет тем точнее, чем мельче
дробление промежутка [t0, Г], то есть чем меньше частичные
промежутки [ti, ^-+1], и в пределе, когда величина наибольшего
частичного промежутка времен» (которую мы обозначим через А, = тах {А/;})
будет стремиться к нулю, получим точное равенство:
гс—I
s0 = lim 2 f (**)*'*•
Решение обеих задач, как мы видим, свелось к одному и тому же
вычислительному процессу. Можно было бы привести еще целый
ряд задач из других областей, которые решаются точно таким же
методом и в конечном итоге приводят к рассмотрению предела
суммы вида (2), то есть
Изучение предела такого рода суммы и приводит к понятию
определенного интеграла.
§ 2. ОПРЕДЕЛЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Дадим теперь строгое аналитическое определение определенного
интеграла, впервые данное для непрерывной функции в 1823 г.
французским математиком О. Коши (1789—1857). При этом Коши
дал первое аналитическое доказательство существования
определенного интеграла от непрерывной функции. Позднее немецкий
математик Б. Риман (1826—1866) показал, что определение, данное
Коши, применимо к более широкому классу функций. Это
позволило ему впервые высказать в общей форме определение интеграла
и установить условия его существования.
357

Определение. Пусть функция f (х) определена в промежутке
[а, Ь]. Разобьем этот промежуток на п произвольных частей
точками
а = х0 < хх < х2 <... <Xi < Xi + х <... < хп = b.
В каждом из полученных частичных промежутков [xiy xi+1]t где
i = 0, 1, 2,..., п — 1, выберем произвольно точку ?; (х-й ^ & ^ x-t +!).
Вычислим значение функции /(?,-) и умножим его на разность
Xi + 1 — Xt = &Xh после этого составим сумму*
а*2/(Ь)А^ь (1)
которая называется интегральной суммой для функции / (х) на
промежутке [a, ft]. Пусть к по-прежнему обозначает наибольшую
из разностей Дхг = д^ + 1— **» то есть длину наибольшего частичного
промежутка.
Если существует конечный предел интегральной суммы (1) при
Х—>0, не зависящий ни от способа дробления промежутка [а, Ь]
на части, ни от выбора точек %it то этот предел называется
определенным интегралом функции f (x) по промежутку [а, Ь]
и дбозначается символом**
ь
I = \f{x)dx. (2)
а
Таким образом,
Ъ я—1
$/(*)Лс = Нт2/(Ь)Л*«. (3)
Функция / (х) в этом случае называется интегрируемой в
промежутке [а, Ь\. Числа а и Ь называются соответственно нижним и
верхним пределами интеграла, f (x) — подынтегральной функцией,
х — переменной интегрирования.
Возвращаясь к задачам, рассмотренным в предыдущем
параграфе, мы можем полученные там формулы для площади Р
криволинейной трапеции и пройденного пути sQ записать в следующем
виде:
Ъ Т
P=$f{x)dx, *0 = $/(*)#.
a tQ
Замечание. Уточним понятие предела интегральной суммы а,
ибо это не совсем обычный предельный переход. В самом деле, до
сих пор когда мы говорили о пределе, то имели в виду предел
функции, зависящей только от рдной переменной. Теперь речь идет
* Сумму о иногда называют суммой Римана.
** Это обозначение было введено французским ученым Ж. Фурье (1768 -
— 1830).
358

о пределе интегральной суммы (1), которая не является функцией
в обычном смысле слова. Действительно, интегральная сумма о
зависит как от способа дробления, то есть от выбора точек xif так и
от выбора точек E,-f которые в каждом частичном промежутке
берутся произвольно, и, следовательно, не является функцией одной
переменной. Поэтому необходимо точно определить смысл предела
интегральной суммы, то есть предела (3). Предел (3) будем
понимать так, что каждому числу е>0 отвечает такое 6>0, что
при любом способе дробления, при котором А,<6, и при любом
выборе в соответствующих частичных промежутках точек & будет
выполнят ъся неравенство
2 f&)tei — \f(x)dx\<*.
\ 1=0 а I
Таково определение интеграла на языке «е — б».
Из определения определенного интеграла как предела
интегральной суммы непосредственно следует, что величина интеграла (2) (если
он существует) зависит только от вида функций / (х) и от чисел
а и Ь. Следовательно, если f (x) задана и пределы интегрирования
а и b закреплены, то интеграл (2) определяется однозначно и
представляет собой некоторое число. Отсюда, в частности» следует,
что определенный интеграл не зависит от переменной
интегрирования х. Поэтому букву х можно заменить любой другой буквой и
это не отразится на величине интеграла. Иными словами,
определенный интеграл не зависит от обозначения переменной
интегрирования, то есть
ь ь
yix)dx= \f(t)dt = ... = lf(u)du. (4)
а а а
Это свойство интеграла вполне аналогично тому, когда мы,
например, письем:
ю ю
1=1 fc=i
Здесь обе суммы выражают одно и то же число, а именно:
Значит, сумма не зависит от того, как мы обозначим индекс
суммирования. Для лучшего понимания сделанного замечания
рекомендуем читателю продумать, как строятся интегральные суммы
1 1
для интегралов ^x*dx u^t*dtf и убедиться, что это построение
о о
в обоих случаях одно и то же и никак не зависит от обозначения
переменных х и t.
359

Приведенное выше определение интеграла дано для случая а<&,
в соответствии с этим Xi<CXt+1 и, следовательно, Д^>0.
Аналогичным обрааом можно дать определение интеграла в том случае,
если а>Ъ (то есть если нижний предел больше верхнего), с той
лишь разницей, что интегральная сумма а в этом случае
составляется для дробления а = х0 > хг > х2 >.. • > хг > *1+1 >... > хп = Ьу
где уже все Axt = Xi+1 — Xi будут отрицательны.
Вопросы для самопроверки
1. Сколько интегральных сумм можно составить для заданного способа
разбиения промежутка [а, Ь]?
2. Приведите пример функции, для которой величина интегральной суммы не
зависит ни от способа разбиения промежутка [а, Ь] на части, ни от выбора
точек ?,- в этих частях.
3. Почему в определении определенного интеграла вместо л—>0 нельзя писать
п —> со (последнее означает неограниченное увеличение числа частичных
промежутков)?
§ 3. УСЛОВИЯ СУЩЕСТВОВАНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Существование конечного предела интегральной суммы а, а
следовательно, и существование определенного интеграла прежде всего
зависит от свойств подынтегральной функции /(х), заданной на
промежутке интегрирования [а, Ь]. Поэтому законно возникает вопрос:
для каких функций указанный
YJ^ предел (то есть определенный
интеграл) существует? Прежде
всего отметим, что имеются
функции, от которых
определенный интеграл заведомо не
существует. Такими функциями
являются, например, все
неограниченные функции.
Действительно, пусть функция f(x)
задана в промежутке [а, Ь] и
не ограничена в окрестности
^ некоторой точки с внутри этого
промежутка (рис. 140). Тогда,
если разбить этот промежуток
произвольным способом на
части, то функция f(x) будет неограниченной хотя бы в одной из них,
пусть, например, в [xi9 хм], содержащем точку с.
В этом случае за счет надлежащего выбора точки & в
промежутке [Xi, xi+i] слагаемое /(&)Дя,' интегральной суммы, а вместе
с ним и вся интегральная сумма о могут быть сделаны по
абсолютной величине сколь угодно большими Поэтому интегральная
сумма а не будет иметь конечного предела, а это означает, что
определенный интеграл от неограниченной функции не существует.
Таким образом, если функция f(x) интегрируема в [а, Ь], то она
необходимо ограничена в этом промежутке. Отсюда, конечно,
Н 1 1 V
Рис. 140.
360

не следует, что всякая ограниченная функция интегрируема
(установленное условие не является достаточным).
Поясним это на примере. Рассмотрим функцию Дирихле,
которая определяется на сегменте [0, 1] следующим образом:
. | 1, если х рационально,
\ 0, если х иррационально.
Как видим, эта функция ограничена на сегменте [0, 1], однако
она не интегрируема в нем. В самом деле, если мы, составляя
интегральные суммы а, в качестве точек & будем брать, например,
рациональные точки, то получим: ст = 1. Следовательно, и предел а
в этрм случае при Х->0 (где К по-прежнему длина наибольшего
частичного промежутка) будет тоже равен единице. Если же все &
брать иррациональными, то а обращается в нуль и, значит,
предел суммы о при К->0 в данном случае будет равен также нулю.
Таким образом, поведение интегральной суммы а существенным
образом зависит от выбора точек |t- и поэтому за счет одного лишь
уменьшения к интегральная сумма а не может приблизиться ни
к какому конечному пределу, а это значит, что функция г|)(х) не
интегрируема в промежутке [0, 1].
Таким образом, для существования определенного интеграла
от некоторой функции последняя, помимо ограниченности, очевидно,-
должна обладать дополнительными свойствами, обеспечивающими
ее интегрируемость. Как мы увидим ниже, таким свойством,
например, является непрерывность.
Пусть на сегменте [а, Ь] задана непрерывная функция f(x).
Тогда в силу первой теоремы Вейерштрасса* функция f (х)
ограничена на [а, Ь]. Следовательно, существуют такие постоянные
т и М, что
m^f(x)^M, a^x^b,
и поэтому условие, необходимое для интегрируемости функции
/ (х), выполнено. Числа т и М можно считать соответственно
точной нижней и точной верхней границами для значений функции
f (х) в промежутке [а, Ь]. Напомним, что наибольшая из всех
нижних границ некоторого множества называется точной нижней
границей этого множества, а наименьшая из всех верхних границ —
точной верхней границей множества.
Так как функция f(x) непрерывна на [а, Ь], то в силу
второй теоремы Вейерштрасса* эта функция достигает своих точных
границ, так что числа т и М можно просто считать соответственно
наименьшим и наибольшим значениями функции f(x) в промежутке
[а, Ь).
Суммы Дарбу. Разобьем промежуток [а, Ь] на п
произвольных частей. Так как функция f(x) непрерывна на [а, 61, то она
* См. гл. IV, j 5.
361

Рис. 141.
будет непрерывной и в любой его части. Через т,- и Mt обозначим
соответственно наименьшее и наибольшее значения функции fix)
в /-м промежутке [л;,-, xi+i] и составим следующие суммы:
п—\ п—\
s=^rriiAxh S = ^]MiAxi.
Эти суммы называются соответственно нижней и верхней
интегральными суммами или нижней и верхней суммами Дарбу*. Так
как mi и Mi являются значениями функции / (х) в частичном
промежутке [Xi, xi+i] (то есть в этом промежутке существуют такие
точки ?;, ?/, что / (li) = m* и / (?/) = Mt), то при заданном способе
дробления промежутка \а, Ь] суммы Дарбу являются просто
наименьшей и наибольшей из интегральных сумм о, так что
5^a^S. (1)
В случае, когда /(х)^0, всюду на промежутке [а, Ь] суммы
Дарбу s и S, как легко видеть, геометрически выражают собой
площади ступенчатых фигур, изображенных на рисунке 141.
Ступенчатая фигура, соответствующая нижней сумме Дарбу, входит
в криволинейную трапецию, ограниченную сверху кривой y = f(x),
a^x^b (см. рис. 141, а), ступенчатая фигура, соответствующая
верхней сумме Дарбу, выходит из указанной криволинейной
трапеции (см. рис. 141, б).
Важно отметить, что суммы s и S зависят только от способа
дробления промежутка [а, Ъ] и полностью им определяются, в то
время как интегральные суммы а зависят не только от способа
дробления данного промежутка, но и от выбора точек !¦,-.
Суммы Дарбу обладают следующими простыми свойствами.
Свойство 1. От добавления новых точек дробления
промежутка [а, Ь] нижняя сумма Дарбу не уменьшается,
а верхняя сумма Дарбу не увеличивается*
Доказательство. Мы остановимся на доказательстве этого
свойства лишь для верхних сумм Дарбу. Очевидно, для этого
достаточно рассмотреть тот случай, когда к имеющимся точкам дроб-
* Гастон Дарбу (1842—1917) —французский математик.
362

Рис 142.
ления промежутка fa, b] добавляется хотя бы одна новая точка
дробления х!.
Пусть промежуток [а, Ь\ разбит на части точками a = x0<*i<
<*2<...<**<л:ж <•••<*« = 6, и S —верхняя сумма Дарбу,
отвечающая данному дроблению.
Допустим, что новая точка /
окажется между точками хк и
xk+u то есть хк<х' < */ги (рис Л 42).
Обозначим через S' верхнюю
сумму Дарбу, отвечающую
полученному новому дроблению
промежутка [а, Ь]. Она, очевидно,
будет отличаться от прежней суммы
5 только тем, что в сумме S
промежутку \xk, xk+i] отвечало одно
слагаемое Mk (xk±i —xk), в то время
как в сумме 5' этому
промежутку (который уже разбит точкой х на два промежутка)
отвечает сумма двух слагаемых Mk (xr — xk) + Mk (xk+i — х'), где Mk и
Mk — наибольшие значения функции f (х) в промежутках [xk, x'] и
[х\ *fc+i]. Так как эти промежутки являются частями промежутка
[Xk, *k+i]> то Mk^Mky Mk^Mk. Тогда будем иметь:
Mk(xr — xk)^Mk (xf — xk), Mk (xk+i — x')^Mk {xk+i — x').
Складывая эти неравенства почленно, получим:
Mk (tf — xk) + Mk (xk+t — x')^Mk (xk+i — xk).
В случае неотрицательной функции это неравенство выражает
простой факт, заключающийся в том, что сумма площадей двух
прямоугольников с основаниями [xk, х'\ и [х, xk + i] не превосходит
площади прямоугольника с основанием [xk, xk+i\ (см. рис. 142).
Итак, сумма двух новых слагаемых, отвечающих промежуткам
[Xk, x']> [x\ xk+i], не превосходит одного слагаемого, отвечающего
Т,а
Т,а\
-ч«—?—?—*—¦*-
~Г*-
Ъа
"?¦
6^—А-чк-ч!) А к 6 ** &-4
Рис. 143.
363

промежутку [xk, xk+x]. Это и доказывает, что S'^S. Аналогично
этому доказывается данное свойство и для нижней суммы Дарбу.
Свойство 2. Каждая нижняя сумма Дарбу не больше,
чем каждая верхняя сумма Дарбу, хотя бы отвечающая
и другому дроблению промежутка.
Доказательство. Рассмотрим какие-нибудь два способа
7\ и Т2 дробления промежутка [а, Ь] на части, и пусть способу 7\
отвечают суммы Дарбу sx и Slf а способу Т2 отвечают суммы s2 и S2.
Составим новое дробление Тз путем объединения всех точек дробления
способов 7\ и Т2 (рис. 143). Пусть этому способу дробления отвечают
суммы Дарбу ss и Ss. Так как способ дробления Т3 получается из
способа 7\ или Т2 добавлением новых точек деления промежутка [а, Ь],
то в силу свойства 1 из сопоставления способов дробления 7\ и Тг
получим: Si^Sg, a из сопоставления способов Т2 и Т3 будем иметь:
S3^S2. Но s3^S3y тогда, сопоставляя последние три неравенства,
мы и получим: %^S2, что и доказывает свойство 2.
Замечание 1. Установленные свойства справедливы также и
для сумм Дарбу, составленных для любой ограниченной функции,
имеющей точки разрыва, и доказательство этих свойств проводится
аналогично.
Замечание 2. Свойство 2 показывает, что множество всех
нижних сумм Дарбу {s} ограничено сверху. В качестве верхней
границы может служить, например, какая-нибудь верхняя сумма S0.
Тогда по известной теореме множество нижних сумм {s}, отвечающих
всевозможным способам дробления промежутка [а, Ь], имеет конечную
точную верхнюю границу /=sup {s}, причем /^S0, ибо S0
является просто верхней границей для множества {$}, а /—точной
верхней границей этого множества. Так как SQ есть произвольная
верхняя сумма Дарбу, то постоянное число / будет удовлетворять
неравенству
5^/^S, (2)
где s и S — совершенно произвольные нижняя и верхняя суммы
Дарбу. Если интегральная сумма о и суммы Дарбу sn S отвечают
одному и тому же способу дробления, то из сопоставления
неравенств (1) и (2) сразу следует, что
•G —/|^S — 5. (3)
Это неравенство существенным образом нами будет использовано
при доказательстве теоремы о существовании определенного интеграла
от непрерывной функции.
Теорема (достаточное условие интегрируемости).
Если функция f (х) непрерывна в промежутке \а, Ь], то она
интегрируема в этом промежутке, то есть интеграл
ъ
)f(x)dx (4)
а
существует.
364

Рис. 144.
Доказательство. В силу теоремы Кантора * функция f(x),
непрерывная в промежутке [a. b]t равномерно непрерывна в этом
промежутке. Значит, каково бы ни было число е > 0, по числу
. _^ >0 найдется такое число 6>0, что неравенство \х"—*'|<6
влечет за собой новое неравенство ^j
i/(^)-f(^)l<^-, (5)
где бы в пределах
рассматриваемого промежутка [а, Ь] ни лежали
точки хг и х'\
Разобьем промежуток [af b]
произвольным образом на части
[*ь *i+i] (i = 0, 1, 2,..., п—\) с
длинами Д*?<;6. Пусть этому
дроблению промежутка отвечают
суммы Дарбу s и S. В частичном
промежутке [xt, xi+i] так выберем точки х\ и я",-, чтобы было /И/ =
= f(x'i) и Mi = f(x"i), где т,-, Мг по-прежнему обозначают
наименьшее и наибольшее значения f(x) на [л;*, *?+i] (рис. 144). Тогда
в силу неравенства (5) мы будем иметь:
Mi-mi<?1[(i = 0, 1, 2,..., п-1),
откуда получаем:
п—1 га—1
i=0 i=0
если ^<б, где ?i = max {Д Xi).
Пусть а — одна из интегральных сумм, отвечающая тому же
дроблению промежутка [а, Ь], что и суммы Дарбу s и S. Тогда из
последнего неравенства и Неравенства (3) непосредственно следует,
что |а —/|<е, если Я<6, а это и означает, что существует
предел
lima = /,
я-о
то есть существует интеграл (4). Теорема доказана.
Не следует думать, что определенный интеграл существует только
для непрерывных функций. Так, например, существует интеграл от
функций, имеющих конечное число точек разрыва первого рода**.
Таким образом, непрерывность функции является достаточным, но
необходимым условием ее интегрируемости.
Замечание. Выше мы рассмотрели задачу об определении
площади Р криволинейной трапеции, ограниченной сверху кривой
* См. гл. IV, § 12.
**" См. [1], стр. 327. Как указано в предисловии, символ [1] означает ссылку
на учебник Г. М. Фихтенгольца «Основы математического анализа», т. I, 1955.
365

y = f (x), где f (x) — положительная непрерывная функция, заданная в
промежутке [а, Ь[. Площадь Р этой трапеции была вычислена нами как
л—О
предел суммы а = ^/ (10 Д*ь то есть была получена формула
/>=$/(*)<**. (6)
Теперь мы видим, что в силу доказанной теоремы этот интеграл
существует, то есть формула (6) при этих условиях всегда имеет
смысл.
Таким образом, если f (х) — положительная, непрерывная в
промежутке [а, Ь] функция, то определенный интеграл от этой
функции выражает собой площадь указанной выше криволинейной
трапеции. В этом и заключается геометрический смысл
определенного интеграла
Вопросы для самопроверки
1. Сколько сумм Дарбу можно составить для данного фиксированного
разбиения промежутка fa, b]?
2. Проведите доказательство первого свойства сумм Дарбу для нижних сумм
Дарбу.
§ 4. ОСНОВНЫЕ СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Рассмотрим ряд свойств определенного интеграла, доказательство
которых, как Мы увидим, будет основано на его определении как
предела интегральной суммы.
Не делая каждый раз особых оговорок, ниже, при изложении
свойств определенного интеграла, мы будем считать все
рассматриваемые функции непрерывными, так что определенные интегралы
on них заведомо существуют.
Свойство 1. Если переставить между собой пределы
интегрирования, то определенный интеграл изменит только
знак, то есть
\f(x)dx=-]f(x)dx. (1)
а Ь
Доказательство. Пусть а<С.Ь. Составим интегральную
сумму
для дробления: a = x0<Zx1<x2<Z---<<Xi<ZXi+1<C..- • <xn = b.
Теперь поменяем ролями а и Ъ, то есть будем считать а верхним
пределом, а Ь — нижним, сохраняя при этом все прежние точки
дробления промежутка [а, Ь] и все выбранные ранее точки |/. Так
как нумерация точек дробления промежутка всегда ведется в на-
366

Х\° 1° ш1 I1 »2 t ш1 1' *?' \Л'1\П'1 *\
Ъп-1 1л-2 Хк+Ак *к xf \'0 г
Х'п *„'_, х'п-2 *о
Рис. 145.
правлении от нижнего предела к верхнему, то прежние точки
дробления Xi и точки It будут теперь занумерованы в обратном порядке
(рис. 145):
6 = лъ>х\>х2> ...>xi>*i+i> ...>х'п = а9 (2)
где уже Дл^ = л^+1 —xi <0(?=»=0, 1, 2,... f n— 1).
Легко видеть, что интегральная сумма of = 2^ (5i) A*i»
составило
ленная для точек дробления (2), отличается от прежней суммы
о только знаком:
а*=—<т\ (3)
Предел левой части этого равенства по условию существует и
ь
равен интегралу ^ / (х) dx, следовательно, существует предел
Прайс
вой части равенства (3) и по определению этот предел и есть
определенный интеграл:
а
\f (x) dx = lima\
ь * -о
Переходя к пределу в равенстве (3), мы и получим равенство (1).
Ясно, что это равенство справедливо при любом соотношении
между пределами а и Ь. Согласно доказанному свойству всякий
интеграл, нижний предел которого больше верхнего, всегда можно
свести к интегралу, нижний предел которого будет меньше
верхнего. Для этого достаточно переставить между собою пределы
интегрирования и изменить знак перед интегралом.
Свойство 2. Каковы бы ни были числа а, Ь, с, всегда
имеет место равенство
\f(x)dx = \f(x)dx + lf(x)dx. (4)
а а с
Доказательство. Допустим сначала, что а<1с<Ь. Так
как предел интегральной суммы не зависит от способа дробления
промежутка [а, Ь] на части, то будем дробить его так, чтобы точка
с всегда была бы точкой дробления промежутка. Если с — хт, то
интегральную сумму можно разбить на две суммы:
п—\ т—1 п—\
о = VI (|.) Axi = ? f (Ь) bXi + ^f (Si) A*i.
367

Каждая из этих сумм является интегральной суммой функции f(x)
соответственно для промежутков [а, Ь], [а, с], [с, Ь] *. Переходя
в последнем равенстве к пределу при Я->0, мы и получим
равенство (4).
Суть доказанного свойства состоит в том, что интеграл по всему
промежутку оказывается равным сумме интегралов по его частям.
Другое взаимное расположение точек а, 6, с легко приводится
к рассмотренному случаю. Пусть,
например, эти точки расположены так: а<Ь<.с.
Тогда по доказанному будем и?леть:
с !> с
\f(x)dx = lf(x)dx + \f(x)dx9
а а Ь
откуда
b с с
\f{x)dx=\f{x)dx-\f{x)dx\
Рис. 146.
переставив в последнем интеграле
пределы, мы опять придем к соотношению (4).
Установленное свойство интеграла в случае
неотрицательной функции выражает простой геометрический факт:
если криволинейная трапеция с основанием [а, Ь) разбита на две —с
основаниями [а, с] и [с, Ь] (рис. 146), то площадь данной трапеции
равна сумме площадей двух ее частей.
Свойство 3. Постоянный множитель можно вынести
за знак определенного интеграла, то есть
\ kf(x) dx=k \f(x) dx.
(5)
Доказательство. Разобьем промежуток [а, Ь] произвольно
на части и составим интегральную сумму для функции kf (x).
Очевидно, будем иметь:
2*/(b) А*, = *?/&)**«•
Переходя в этом равенстве к пределу при А,-* 0, мы и получим
формулу (5).
Свойство 4. Определенный интеграл от алгебраической
суммы функций равен алгебраической сумме их интегралов:
]\f(x)±g(x))dx = ]f{x)dx±]g(x)dx.
(6)
* Функция fix), непрерывная на [д, 6], будет непрерывной на любой егс
части, а следовательно, интегрируема на промежутках [а, с], |с, Ь].
368

Доказательство. Составим интегральную сумму для
функции f (x)±g(x). Очевидно, будем иметь:
"?if (Ь) ±g d,.)] д*,="f;'/ d») д*г ± 2« (Ь) д*.
/=0 f = 0 /=0
Остается в этом равенстве перейти к пределу при А,->0, чтобы
получить формулу (6).
Это свойство легко распространяется на случай любого
конечного числа слагаемых функций.
Свойство 5. Если^(х) — неотрицательная на [а, Ь]
функция и нижний предел интеграла меньше верхнего, то и
сам интеграл будет числом неотрицательным, то есть
ь
\f(x)dx^0. (7)
а
Доказательство. Пусть а < Ъ и / (х) ^ 0. Тогда при любом
дроблении промежутка [а, Ь] на части и каком угодно выборе
точек Е,-, очевидно, будем иметь:
так как f (Е/)^0, Длг,->0, и остается перейти здесь к пределу при
Я-^0, чтобы полу ить неравенство (7)*.
Замечание. Если функция f(х) неположительна на [а, Ь] и
ь
a<ib, то аналогичным образом можно показать, что J f (x) dx^Q,
а
что и предлагается сделать самостоятельно.
В этой связи также заметим, что при а>Ь будем иметь:
ь
\ f (x) dx^O, если f(x)^0 на [а, Ь],
а
ii
Ь
если f(x)^0 на [я, Ь].
а
Оба эти неравенства вытекают непосредственно из свойства 1
и из только что доказанного свойства.
Свойство 6. Если функции f(x) и g(x) заданы в про-
межутке [а, Ъ\, где а<Ь и всегда f(x)^g(x), то
ь ь
\f(x)dx^\g(x)dx, (8)
а а
то есть неравенства можно почленно интегрировать.
* Мы воспользовались теоремой о предельном переходе в неравенствах (см.
гл. ill, § 3).
369

Доказательство. Применяя предыдущее свойство к
разности g (x) — f(x) ^ 0, получим:
\\g{x)-fx))dx2*0.
а
Но в силу, свойства 4
ъ ь ь
\ [g (x)-f(x)] dx = \g(x) dx-\f(x) dx,
a a a
следовательно,
b b
\g(x)dx-\f(x)dx^Qt
a a
откуда и получаем неравенство (8).
Замечание. Несколько труднее доказывается более точный
результат, а именно: если функции f (x) и g(x) непрерывны в [а, 6}
и f (x)^g(x), причем f (x) не всюду равна g(x), то
ъ ъ
\f(x)dx<\g(x)dx
а а
(равенство исключается).
Свойство 7. Если функция f(x) задана в промежутке
[а, Ъ\ и а < Ъ, то
]f(x)dx
\\f{x)\dx, (9)
то есть абсолютная величина интеграла не превосходит
интеграла абсолютной величины подынтегральной функции.
Доказательство. Применяя предыдущее свойство,
проинтегрируем почленно очевидное неравенство
H/(*)l^/(*Xlf(*)l-
В результате получим:
ъ ь ь
— \\Пх)\ dx^\f(x) dx^\\f(x) | dx,
a a a
а это равносильно неравенству (9).
Свойство 8. Если т и М — соответственно наименьшее
и наибольшее значения функции f(x) в промежутке (а, Ь\,
где а<6, то
ь
m(b — a)^ ]f(x) dx^M(b — a). (10)
а
Доказательство. По условию для всех х из [а, Ь\ имеем:
m^i(x)<*M.
370

Проинтегрировав почленно эти неравенства (применяем свойство 6),
получим:
Ь Ь b
m^dx^^f (x)dx^M^dx.
а а а
Ь
Отсюда, замечая, что ^dx = b— а*, находим:
а
Ь
m{b — a)^\f (x) dx^ M(b — a),
а
что и требовалось доказать.
Следствие. Если во всем промежутке [a, b] (а<.Ь) имеет
место неравенство \f(x)\^K, то
jj f (х) dx
\К(Ь-а). (11)
Действительно, неравенство | f (x) | ^ К равносильно двойному
неравенству
Отсюда в силу свойства 8 находим:
ь
— K(b — a)^\f(x)dx^K(b — a),
а
а это равносильно неравенству (11).
Свойство 9 (теорема о среднем). Если функция f(x)
непрерывна на промежутке [а, Ь], то в этом промежутке
существует хотя бы одна точка с такая, что
]f(x)dx=f(c)(b-a)**. (12)
а
Доказательство. Пусть а<&. Так как функция f(x)
непрерывна на [а, 6], то по второй теореме Вейерштрасса *** она
принимает в этом промежутке как свое наибольшее значение М,
так и наименьшее значение /тг, так что для всех х из [а, Ь] будем
иметь: m^f(x)^M. Отсюда в силу свойства 8 находим:
ь
тф — а)^ \f (x)dx^M (b — a)t
b n — i
* Действительно, \dx = \im ^ l-A*/ = & — a.
a ^-*o /=0
** В формулировке этой теоремы условие непрерывности функции весьма
существенно.
*** См. гл. IV, § 5.
371

откуда
Положим
\f(x)dx
т^'^-г <Af.
о — а
ь
\f(x)dx
Гак как число \i заключено между наименьшим и наибольшим
значениями непрерывной функции f (х) на промежутке [а, 6], то
непрерывная функция f(x), принимающая значения т и М, по
второй теореме Больцано — Коши * должна принимать и все
промежуточные значения между ними. Следовательно, существует такая
точка с в промежутке [а, Ь], что f(c)=\iy или
]f(x)dx
= /(*).
а это равносильно равенству (12).
Величину / (с) принято называть средним значением функции f (x)
в промежутке [а, Ь].
Заметим, что формула (12) справедлива не только при а<Ж
но и при а>Ь. Этот случай легко приводится к рассмотренному.
В самом деле, если а> Ь, то в
силу формулы (12) будем иметь:
а
\f(x)dx = f (с) (а — Ь) (а^сЬ? Ь).
ь
Остается переставить пределы
интегрирования, чтобы получить
формулу (12) для этого случая.
Замечание. Формула (12)
имеет простой геометрический
смысл. Действительно, пусть
функция f (x) неотрицательна на [а, Ь]~
Тогда, как нам известно, интеграл слева формулы (12) выражает
площадь криволинейной трапеции, ограниченной сверху кривой y = f (x), a
правая часть этой формулы представляет площадь прямоугольника
с тем же основанием и высотой, равной f (с) (рис. 147). Таким
образом, формула (12) геометрически выражает тот факт, что для
площади криволинейной трапеции, ограниченной сверху непрерывной
кривой, всегда существует равновеликий ей прямоугольник с тем же
основанием и высота его равна одной из ординат этой кривой.
* См. гл. IV, § 5.
Рис. 147.
372

1
Пример 1. Оценить интеграл ^ х (1 — х) dx.
о
Вычисляя наименьшее и наибольшее значения подынтегральной функции
в промежутке [0, 1], легко убедимся в том, что 0^x(l—x)^— (O^x^l)-
Отсюда в силу свойства 8 будем иметь:
1
0< ? *(1—*)<fo<-L *.
о
Интересно заметить, что точное значение интеграла равно -^-.
1
J_
у 2 + х — х^
о
Так как подынтегральная функция непрерывна на [0, 1], то нетрудно
установить, что свое наименьшее значение эта функция принимает при * = -— а
наибольшее—на концах промежутка [0, 1], то есть при * = 0 и х=1. Этими
значениями будут: /(-—) = — ^0,67 и /(0)=/(1) = -—5^0,70. Следовательно, для
\ 2 / 3 \ 2
всех х из промежутка [0, 1] имеют место неравенства:
2 ^ 1 1
3 ^ У2 + Х — х* ^ /<Г
Отсюда согласно свойству 8 находим:
1
Пример 2. Оценить интеграл V —- dx.
\<\
1 J 1
У2 + х — х2 V2
о
Заметим, что точное значение интеграла равно:
1 г 1
Г» 1 . Г* 1 j 2д:— 1
dx = I , dx = arc sm —«—
/2 + *-** \ i/~A L_±\2
и
Пример 3. Оценить интеграл \ dx
= 2 arc sin -^-S3ss0,68.
л
х
5.
^ „ , ... sin х
Сначала исследуем поведение подынтегральной функции f (x)= на
промежутке \-у, -jr- . Для этого находим ее производную: f (х) =
xcosx—sinx
х2
cosx(x — tgx) _ __ я ^ _ д 14 ,. . . л
: ^—2—^-. Так как cosx>0 и х — tg*<0 для — <*<-^- , то/'(*)<().
* Равенство исключается — см. замечание к свойству 6.
я
** Напомним, что если 0<х<-^-, то sinx<*<tg* (см. гл. III, § 11,
пример 2).
Ъ1Ь

Значит, данная функция монотонно убывает на промежутке -j- , -5- . Тогда
1 -наибольшее значение, а м-^ = наименьшее ее значение
^ \ 4 / я — »-_»„.,, « » у 2 / я
ц указанном промежутке. Поэтому для всех к из — -^-\ будем
2 sin* 2]/"2" _ у
— ^ ^ . Отсюда по свойству 8 получаем;
иметь:
J_ С sin х
2 < J х
dx<LT
5.
4
В этом случае точное значение интеграла нельзя найти элементарным путем.
Пример 4. Найти среднее значение функции f(x) = cos2 к на промежутке
{О, я].
По формуле (12) имеем:
/(с) =— 1 cos8 х dx = у- V (I -\-cos2x)dx = ^- f а:Н—^- sin 2x
= 2 •
В заключение этого параграфа заметим, что свойства 1 — 8
определенного интеграла, установленные выше для непрерывных
функций, справедливы также и для любых интегрируемых функций,
причем доказываются они аналогичным способом *. По аналогии
с теоремой о среднем для непрерывной функции доказывается
подобная теорема для любой функции f(x), интегрируемой (и, значит,
ограниченной: m^f(x)^M) в промежутке [а, Ь]. В этом случае
вместо формулы (12) доказывается равенство
ь
$f (x)dx = [i (b — а),
а
где число [л содержится между границами т и М.
Вопросы для самопроверки и упражнения
\ш Почему в формуле (12) (см. теорему о среднем) точку с нельзя считать
произвольной точкой из промежутка [а, Ь]?
2. Приведите пример функции, для которой формула (12) справедлива для
любой точки промежутка [а, Ь].
3. Сформулируйте теорему о среднем для интегрируемой функции и
докажите ее.
4. Применяя теорему о среднем, найти средние значения следующих функций:
a) /(x) = jt2 на промежутке [0, 1]; б) /(*)=cosa; на промежутке 0, -^ ;
1 12 1
в) /(*) = — на промежутке [1, е]. Отв. а) ^-; б) —; в)-
х ив "F "*'' ~ 1 ' "|в ~ "' "' 3 ' "' я' "' в~Г
* См. [1], стр. 330 — 333.
374

б. Не вычисляя интегралов, установить, какой из интегралов больше:
2 2 1 1 II
а) \ xdx или V sin xdx; 6) у d\ или у у-^—; в) V е* dx или у е*г dx;
1С 71
2" 2"
г) у s\r\mxdx\um у sin xdx. Отв. а) первый; б) второй; в) первый; г) второй,
1 it
6. Доказать неравенства: а) 1 < у е*2 dx<: е\ б) -^ < Хтт:—2~<-зх"
7. Оценить интегралы:
7С
1
а) У- J j/T+rfdr, б) /= \ xVigxdx; в) /= ^ у^
dx.
Отв. а) 2 < / < Vb ; б) 0 < / < Ц; в) 0,51 < / < 0,85.
§ 5. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ КАК ФУНКЦИЯ ВЕРХНЕГО ПРЕДЕЛА.
СУЩЕСТВОВАНИЕ ПЕРВООБРАЗНОЙ ДЛЯ. НЕПРЕРЫВНОЙ ФУНКЦИИ
До сих пор мы рассматривали определенный интеграл с
постоянными пределами интегрирования. Как уже отмечали ранее,
величина такого интеграла для данной подынтегральной функции
зависит только от пределов интегрирования а и Ь. Следовательно, если
мы будем изменять, например, верхний предел 6, то величина
интеграла будет, вообще говоря, меняться. Другими словами,
интеграл с переменным верхним пределом представляет собой функцию
своего верхнего предела. Таким образом, если мы имеем интеграл
л-
^f(t)dt с постоянным нижним пределом а и переменным верхним
а
пределом х, то величина этого интеграла будет функцией верхнего
предела х. Обозначим эту функцию через Ф(х), то есть положим
Ф (*) = $/(/) Л. (1)
а
Здесь переменную интегрирования мы обозначили буквой t с тем,
чтобы не смешивать ее с верхним пределом х (это всегда возможно
сделать, если учесть, что величина определенного интеграла не
зависит от обозначения переменной интегрирования).
Заметим, что если функция f (t) непрерывна на [а, Ь], то она
будет также непрерывной и в промежутке [а, х], где a<ix^b;
так что интеграл (1) существует, и функцию Ф(л:) имеет смысл
375

ргссматривать для всех х из [я, 6], то есть для всех точек
замкнутого промежутка [а, 6], кроме точки х = а, в которой интеграл (1)
пока теряет смысл. В самом деле, определение определенного
интеграла мы дали только для случая, когда пределы интегрирования
не равны между собой, то есть когда афЪ. Чтобы не исключать
случая х = а, мы должны придать определенный смысл выражению
0(a)=\f(t)dt.
а
Применяя теорему о среднем к интегралу (1), находим:
<b(x)=\f(t)dt = f(c)(x-a),
а
где с содержится в промежутке [а, х]. Если теперь устремить х к
точке а (следовательно, и с-+а) и при этом учесть ограниченность
f(c), то в пределе мы получим:
ИтФ(х)--
х — а
Mmf(c)(x—a)=f(a) 0 = 0.
Отсюда естественно в качестве определения принять, что
O(a)=\f(t)dt = 0, (2)
а
и притом не только- для непрерывной, но и для любой
интегрируемой функции. Это дополнение к определению определенного
интеграла расширяет понятие
интеграла.
Замечание 1. Исходя из
геометрического смысла интеграла, мы
заключаем, что в случае
неотрицательной функции f (t) новая функция
Ф(х) (определенная равенством (1))
выражает собой площадь переменной
криволинейной трапеции с
основанием [а, х] (рис. 148). При х = а эта
функция согласно формуле (2)
принимает значение, равное нулю, что
естественно и с геометрической точки зрения. В самом деле, в
этом случае основание криволинейной трапеции стягивается в точку,
а ее боковые стороны х = а и х = Ь сливаются в одну линию х = а.
Значит, трапеция вырождается в прямолинейный отрезок, площадь
которого равна нулю.
Теперь остановимся на важной теореме, которую следует
считать одной из основных теорем математического анализа, а
именно на вопросе о производной от интеграла по переменному
376

верхнему пределу или на вопросе о существовании первообразной
для непрерывной функции.
Теорема. Производная определенного интеграла от
непрерывной функции по его верхнему пределу существует
и равна значению подынтегральной функции в верхнем
пределе, то есть
(1 f(0 dt \ =f(x) или Ф' (x)=f(x). (3)
Доказательство. Рассмотрим произвольное значение х из
[д, Ь] и придадим ему произвольное приращение А* ^ О, причем
так, чтобы точка х + Дх не вышла из [я, Ь], то есть a^x + kx^b»
Тогда функция (1) получит новое значение:
Ф(* + Д*)= \ f(t)dt=\f(t)dt+ $ /(0Л = Ф(х)+ $ f(t)dL
а а х х
Отсюда находим приращение функции Ф(х):
х-\-Ьх
Ф(х + Ах)—Ф(х)= $ f{t)dt.
X
Применяя к этому интегралу теорему о среднем (см. формулу (12),.
§ 4), получим:
Ф (х +Ах) —Ф (x) = f(c) Их,
где с находится между х и x-f Ах, так что если Ах—>(), то с->х~
Разделив обе части последнего равенства на Ах, получим:
Ф(*-М*)-Ф(*) _И/Л
Ах —1\ч-
Если теперь Ах устремить к нулю, то точка с будет стремиться
к точке х и тогда в силу непрерывности /(х) на [а, Ь] будет f (с}
стремиться к /(х). Поэтому в пределе получаем:
.. Ф (лг-f-Але) — Ф (х) ,. х/ч , , ч
lim —'—^ u- = hmf(c) = f(x),
*х->0 ах с-+х
или Ф'(х) = /(х). Теорема доказана.
Из этой теоремы вытекает, в частности, что Ф(х) — непрерывная
функция на [а, Ь]. В связи с этим отметим, что непрерывность
функции Ф(х) может быть установлена и при более широких
предположениях относительно подынтегральной функции /(х). Применяя
рассуждения, подобные тем, какими мы пользовались при
доказательстве последней теоремы, а также теорему о среднем для
интегрируемой функции (см. формулу (13), § 4), нетрудно доказать
непрерывность функции Ф(х) для любой интегрируемой на [а, Ь\
функции /(х).
377

Из доказанной теоремы следует, что если функция f{x)
непрерывна, то она имеет первообразную, которая равна определенному
X
интегралу ^f{t)dt.
а
Итак, мы установили, что всякая непрерывная функция имеет
первообразную. Случай, когда определенный интеграл имеет
переменный нижний предел и постоянный верхний предел, легко
приводится к рассмотренному, если воспользоваться свойством 1
определенного интеграла (см. формулу (1), § 4). Примерами,
иллюстрирующими доказанную теорему, могут служить следующие
равенства:
1) К cos3f?ft) =cos3x; 2) К«й ~;
3) (\Vsmtdt) = j/"sinx; 4) [\е<* dt) = — \\^dt) = — e*\
Замечание 2. Доказанной теореме можно дать
геометрическое толкование. Действительно, пусть функция fix) непрерывна и
А
положительна на [а, 6], тогда функция 0(x) = ^f (t)dt —
определенен
ный интеграл с переменным верхним пределом будет выражать
собой переменную площадь криволинейной трапеции, органиченной
кривой y = f(x)f начальной ординатой х=а, некоторой подвижной
ординатой, отвечающей переменному значению ху и отрезком оси ОХ
(см. рис. 148 — заштрихованная часть). В таком случае доказанную
теорему на геометрическом языке можно прочитать так:
производная от переменной площади Ф (х) по абсциссе х равна конечной
ординате f(x) Другими словами, переменная площадь Ф(л;)
является первообразной для данной ординаты f(x).
§ 6. ОПРЕДЕЛЕНИЕ ЛОГАРИФМИЧЕСКОЙ ФУНКЦИИ ЧЕРЕЗ ИНТЕГРАЛ
Обычно логарифмическая функция (или, коротко, логарифм)
определяется как функция, обратная показательной, и все свойства
логарифма вытекают из свойств показательной функции. Сейчас мы
укажем другой подход к определению логарифмической функции.
Из интегрального исчисления нам известна формула
In
х
Попробуем принять эту формулу за определение In я, то есть за
определение логарифмической функции, и, опираясь на свойства
определенного интеграла, вывести отсюда ряд свойств логарифма.
378

1°. Функция \пх определена только для #>0, ибо при х^О
интеграл (1) не существует.
2°. In 1 = 0 — очевидно.
3°. Логарифмическая функция непрерывна во всякой точке, где
она определена, то есть при всех х>0. Это сразу следует из того,
что интеграл является непрерывной функцией своего верхнего
предела. Кроме того, ясно, что \пх—возрастающая функция от х.
4°. Далее, (lnj*;)f = ( \ -у- = ->0. Отсюда также следует, что
\ 1 ' х
In л:—функция возрастающая.
5°. In— = lnjcx — Inхг. Действительно, с помощью подстановки
x2t = u находим:
1 х% лг8 1 1 1
В частности, In- = ln 1 — 1п* = 0 — 1пх =—\пх.
6°. In (хг х2) = \пх1+ In х2. В самом деле, In (хг х2) = In у = In хг —
— In — = ln^! + ln^2- Отсюда ]пх2 = \п(хх) = \пх + ]пх = 2\пх.
х2
Общая формула In хп = п In x легко доказывается методом
индукции.
7°. 1п?=1. Действительно,
ta(I + X)-_.ta(1+±)_.'+J>-
= (по теореме о среднем) = п
1
.1. -1 = .1
Сп ' П ~~ Сп
где \<сп<\ + — . В силу непрерывности логарифмической
функции предел левой части равенства равен In г, то есть
lim In f 1 +~Y = In lim (l +-Y = In*.
А правая часть -—> 1 при л->оо, так что в пределе получим:
Из свойств 6е и 7° сразу следует, что для любого натурального
п имеем: \пеп = п. Отсюда нетрудно вывести (используя 7° и 6°),
что и для любого рационального числа г выполняется равенство
\п(ег) = г. А тогда, используя непрерывность показательной
функции е* и логарифма, мы сразу видим, что \п(ех) = х для любого
37$

вещественного х. Таким образом, функция In л:, определенная
формулой (1), является обратной для функции ех, то есть совпадает
с обычной логарифмической функцией.
§ 7. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА.
ОСНОВНАЯ ФОРМУЛА ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
Вычисление определенных интегралов методом, основанным на
определении интеграла как предела интегральной суммы, как
правило, связано с большими трудностями даже в простейших случаях
(см. § 1, пример 1). Поэтому естественно возникает задача: найти
другой практически более удобный и легкий метод вычисления
определенных интегралов. Такой метод существует и, как мы увидим
ниже, основан на тесной связи, существующей между понятиями
неопределенного (первообразной) и определенного интегралов.
Пусть f(x) непрерывна в промежутке [а, Ь]. Тогда, как мы
только что установили, определенный интеграл с переменным
верхним пределом
\f{t)dt
а
является одной из первообразных для функции f(x). Допустим,
что нам известна еще какая-нибудь первообразная для f (х),
например F(x). Тогда эти первообразные, как известно, разнятся между
собой на определенное постоянное слагаемое С0 (см. теорему 1 из
§ 1, гл. I). Следовательно, мы будем иметь:
\f(t)dt = F(x)+C0.
а
Полагая здесь х = а (в силу формулы (2), § 5), мы находим: 0 =
к
= F(a) + C0, откуда C0 = — F(a) и, следовательно, $f (t) dt = F (х) —
а
— F(а). В частности, при х~Ь мы получим:
\f(x)dx = F(b)-F(a)> (1)
а
Это и есть основная формула интегрального исчисления, которую
также называют формулой Ньютона — Лейбница*.
Заметим, что правую часть этой формулы часто обозначают
символом F(x)\ba (знак двойной подстановки от а до Ь), и тогда
формула (1) при этом обозначении принимает вид:
\f{x)dx = F(x)\ba.
а
* Исаак Ньютон (1642—1727) — величайший английский физик и
математик.
380

При выводе этой формулы мы считали, что а<.Ь, однако это
ограничение легко устраняется. В самом деле, если а--=Ь> то формула
(1) очевидна, так как обе части ее обращаются в нуль. Случай,
когда а>Ь, легко приводится к рассмотренному. Действительно,
согласно формуле (1) для интеграла, у которого нижний предел
меньше верхнего, будем иметь:
\f{x)dx = F(a)-F{b),
а затем, переставив пределы, придем к прежней формуле (1).
Заметим, что здесь в качестве ^(л:) может быть выбрана любая
первообразная для fix) из семейства F(x)-\-C, и от этого разность
F(b) — F(a) не изменится (ведь все первообразные отличаются друг
от друга на постоянную величину, которая при вычитании все равно
уничтожается).
Итак, формула Ньютона—Лейбница, как мы видим, с одной
стороны, устанавливает связь между определенным и
неопределенным интегралами, с другой стороны, она дает простое,
эффективное средство для вычисления определенного интеграла, которое
можно сформулировать в виде следующего правила.
Правило. Значение определенного интеграла от
непрерывной функции равно разности значений любой
первообразной для нее при верхнем и нижнем пределах
интегрирования.
Приведем несколько примеров на применение формулы Ньютона —
Лейбница:
1) \ sin х
о
о
/2
dx--
-cos х
i Л \
= — (cos -^ cos 0) == 1;
2 ,r-t
Г—з-к-3*
2 2
y(1-2)=f;
xdx 1 . х2
r = -«г- arc sin -=-
V4-x* 2 2
о
V2
1 / • 1
= -~- f arcsm 1 — arcsm - , _ .
Z \ 2 J b
. 1\ я
4) { e*xdx=^e*x
= _(,2_,0)=_(,2__1)<
Таким образом, формула Ньютона — Лейбница дает практически
удобный способ вычисления определенных интегралов: она позволяет
трудоемкую задачу о вычислении предела интегральной суммы
свести к более легкой в ряде случаев задаче отыскания первообразной
лля подынтегральной функции. Эта формула, по существу,
устанавливает тесную связь между двумя фундаментальными разделами
математического анализа—дифференциальным исчислением (куда и
381

относится понятие первообразной) и интегральным исчислением. Эта
связь впервые была установлена Ньютоном и Лейбницем. Именно
поэтому формулу (1) связывают с именем Ньютона и Лейбница.
Только с открытием формулы (1) важнейшее в математическом
анализе понятие определенного интеграла нашло то большое значение
в математике и ее приложениях, какое оно имеет в настоящее время.
Эта формула значительно расширила область применения
определенного интеграла: благодаря этой формуле стало возможным решение
многих задач геометрии, механики, физики и техники единым
методом.
Замечание. При вычислении определенных интегралов с
помощью формулы Ньютона—Лейбница следует особое внимание
обращать на законность условий ее применения. Напомним, что
применение этой формулы для вычисления определенного интеграла от
непрерывной в [а, Ь] функции / (х) существенно предполагает для ее
первообразной F (х) выполнение равенства F' (x)=f(x) во всем
замкнутом промежутке [а, Ь]. Отсюда, в частности, следует
непрерывность первообразной F(x) в этом промежутке. Нарушение
непрерывности F (х) и f (х) хотя бы в одной точке промежутка [а, Ь] (конечно,
в этой точке уже не будет иметь смысла и равенство F'(x)=f{x))
может привести к ошибочному результату. Поясним это замечание
на примере.
1» 1
Рассмотрим интеграл \ . , 2dx. В данном случае
подынтегральная функция /(*)= 2 , Х2 непрерывна в промежутке [ —1, +1] и
ее первообразная F (х) нам хорошо известна: F (х) = arctg x.
Следовательно, по формуле Ньютона—Лейбница находим:
\ rh^dx=arctg x
= arctg 1—arctg (—1) = 2 arctg 1 = y
— l
Заметим, что функция F(x) = arctg x непрерывна в промежутке
[—1, +1] и во всех точках его выполняется равенство F' (x)---f{x).
Стало быть, применение формулы Ньютона—Лейбница обосновано
и получен верный результат. Если же для вычисления этого
интеграла в качестве первообразной взять функцию F (я) == arcctg —
(легко проверить, что (arcctg —) = 1 , х2 при хфОУ то формальное
применение формулы Ньютона—Лейбница дает:
-И
§ \Ц7#dxearcctgТ|~! = arcctg 1 — arcctg(~ 1) = Т'—ТЯ==~Т-
Пришли к абсурду, так как -9 ^~~T• Ошибка возникла потому,
382

что функция F (х) = arcctg — в точке * = 0, принадлежащей
промежутку [—1, +1], не имеет смысла, значит, равенство F'(x) = f(x)
при х = 0 тоже лишено смысла. Кроме того, при переходе череь
эту точку функция F (х) делает скачок, равный —п (действительно,
lim arcctg —= я и lim arcctg — =0). Наличие скачка (разрыва)
у функции F (х) = arcctg — в точке х = 0 и привело к тому, что
применение формулы Ньютона—Лейбница оказалось незаконным.
Далее необходимо отметить, что формула Ньютона—Лейбница
сохраняется для всякой интегрируемой в [аг Ь] функции f(x), если
последняя имеет в этом промежутке непрерывную первообразную
функцию F(x), удовлетворяющую условию
F'(x)=f(x) (2)
во всем промежутке [а, 6], за исключением разве лишь конечного
числа его точек. Говоря здесь о «первообразной» функции F(x), мы
понимаем ее в несколько более широком смысле: прежде мы
требовали, чтобы равенство (2) выполнялось для всех точек промежутка
[at b), а теперь F (х) должна иметь своей производной f (x) всюду
в этом промежутке, за исключением, может быть, конечного числа
его точек, лишь бы и в них не нарушалась непрерывность
функции F(x).
В заключение заметим, что теорема о среднем значении для
интеграла от непрерывной функции представляет частный случай
теоремы Лагранжа (см. гл. VI, § 1).
Действительно, пусть f(x) непрерывна на [а, 6], a F(x) — ее
первообразная. Тогда F'(x) = f(x) и по теореме Лагранжа
F(b)-F(a) = F' (c)(b-a)-f(c)(b-a)9
ТО есть
ь
[f(x)dx=f(c)(b — a), где а<с<Ь.
Вопросы для самопроверки и упражнения
2
1. Рассмотрим интеграл \ __ .2 dx. Непосредственно формула Ньютона—
о
2
гт -. Г dx 1
Лейбница дает: \ =
¦ 1)2 "~" 7=Т
2
= — 2<0.
о
Но это невозможно, так как определенный интеграл от неотрицательной
функции также неотрицателен (см. свойство 5f § 4). ОбъяснитеЁ почему произошла
ошибка.
383

п
2. Рассмотрим интеграл /=\у— -—dx. Здесь подынтегральная функция
о
f (х) = -гт—2— непрерывна в промежутке [0, я] и одной из ее первообразных
будет функция * F(х) = — arccos . Эта функция непрерывна в про-
у2 у 1 -f- cos2 л:
межутке [0, я] и во всех его точках выполняется равенство F' (*) = / (х). Значит,
формула Ньютона—Лейбница применима и мы будем иметь:
п г-
f dx 1 У 2 cos x
х — ; arccos
J 1+cos2* yr2 Y\ -f cos2*
я
7~r
Это верный результат. Если же в качестве первообразной взять функцию F (х)
I . igx ( / 1 . tg*y l , я
= --- arclg -^rrr- легко проверить, что -тг arctg -^=-,1 =т-т s— при хф-рг
V2 V2 V \/2 /2/ l+cos** K ^2
я л
то формула Ньютона—Лейбница дает: \ -г—г -— = -— arctg -^ = 0.
J 1+cos** i/2 l/2
о г г 'о
Объясните, почему в последнем случае применение формулы
Ньютона—Лейбница приводит к ошибке.
Вычислить с помощью формулы Ньютона—Лейбница следующие интегралы:
о
2
3. \x(3 — x)dx. Ошв 14. 6. [ , dx Отв. %-т
б 3 J У 16-*2 6
Я
"2 2
4. ( sm2xdx. Отв 1. 7. \ dx. Отв. ln(e-f-I).
я
5. С *L=. о™. 2. 8- \C^dx. On*. I.
1 я
sin3* ' ' 2
6
§ 8. ЗАМЕНА ПЕРЕМЕННОЙ В ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
Пусть f(x)— непрерывная функция, заданная в промежутке [а, Ь]9
ь
и требуется вычислить интеграл ^f(x)dx.
а
Предположим, что х есть некоторая функция от tf то есть х =
= ф(0> удовлетворяющая следующим условиям:
1) ф(0 — непрерывная однозначная функция, заданная в
промежутке [а, Р] и имеющая в нем непрерывную производную q/ (t)\
v2 cos jc
* Эта первообразная может быть найдена подстановкой 1=
У 1 -J- cos2 *
Предлагаем также непосредственным дифференцированием убедиться в том, что
F' (х) = , , * 0 .
v ' l + cos2*
384

2) значения функции x=(p(t) при изменении t в промежутке
[а, р] не выходят за пределы промежутка [а, Ь];
3) ф(а) = а и ф(Р) = 6.
Тогда справедлива формула
5/(*)Лг=Л/1чр(01ф'(0«*. (1)
а а
которая называется формулой замены переменной или подстановки
в определенном интеграле.
Действительно, прежде всего заметим, что в силу
непрерывности подынтегральных функций оба интеграла из формулы (1)
существуют; более того, существуют и соответствующие им
неопределенные интегралы, то есть первообразные функции для
подынтегральных функций. Теперь докажем равенство этих интегралов.
Для этого введем в рассмотрение функцию
F(x) = \f(t)dt9
а
которая является первообразной для функции f(x), то есть F (л:) =
= /(л:)*. Тогда по формуле Ньютона — Лейбница будем иметь:
\f(x)dx = F{d)-F(a).
а
С другой стороны, рассмотрим сложную функцию от переменной t:
Ф(0=Пф(0].
Согласно правилу дифференцирования сложной функции находим.
Ф'(0 = /7/[ф(0]ф'(0=^[ф(0]ф'(0-
Отсюда следует, что функция Ф (/) является первообразной для
функции /[ф(0]ф'(0 И потому по формуле Ньютона —Лейбница
получаем:
$/Гф(01ф'(0Л=ф(Р)-Ф(«) =
а
= F[ip(P)]-F[4(a)] = F(b)-F{a) = {f(x)dx.
а
Этим установлена справедливость формулы (1).
Замечание 1. Если при вычислении неопределенного
интеграла с помощью замены переменной мы должны были от новой
переменной / путем обратного преобразования возвращаться к
старой переменной х, то в этом нет необходимости при вычислении
определенного интеграла.
а
Пример 1. Вычислить интеграл \ yaz х* dx (a > 0).
* См. формулу (3) § 5, гл. IX.
385

Полагаем x = asinf9 откуда видно, что х = 0 при / = 0 и х = а
при t = ~; следовательно, t изменяется в пределах от 0 до у
^см. таблицу). Проверим законность такой подстановки.
Во-первых, подынтегральная функция /(л:) = |/а2 —л:2 непрерывна
в промежутке интегрирования; во-вторых, функция x = siut
непрерывна вместе со своей производной x't = a cos t в промежутке О,-^М
и, в-третьих, при изменении / от О до-^-функция x = <p(t) = asint
возрастает от 0 до а. При этом ф(0) = 0 и ср{-^-) = а. Таким
образом, данная подстановка действительно удовлетворяет всем
требованиям правила замены переменной в определенном интеграле и
потому мы вправе применить формулу (1). На основании этой
формулы указанная подстановка дает:
\ Va2 — x2dx = \Va* — a4m4acostdt = a2\zos2tdt =
X
0
а
t
0
л
2
г 2
а2
Т$ (l+cos2/)d/= Т(*+ —
п
sin 2Л ' 2
4
Замечание 2. Часто вместо подстановки x = y(t) применяют
обратную подстановку t = ty(x). В этом случае пределы а и Р для
переменой t определяются непосредственно: а=г|>(а), р = \|)(6).
Однако здесь следует иметь в виду, что функция x = y(f)
(которая получается из уравнения t = ty(x), если его решить
относительно х) должна по-прежнему удовлетворять всем указанным
выше условиям замены переменной в определенном интеграле, в
частности функция x = y(t) должна быть непрерывной однозначной
функцией от t в пределах интегрирования, и при непрерывном
изменении х от а до Ь переменная / также должна непрерывно
изменяться от а до (5.
Если хотя бы одно из этих условий не соблюдено, то формула
(1) может привести к ошибочному результату. Покажем это на
примерах.
4
Пример 2. Вычислим интеграл \ х2 dx.
—2
Непосредственное вычисление по формуле Ньютона—Лейбница дает:
4
x2dx--
= 3
—2
—2
= ^(64 + 8) =
= 24.
Применим теперь к этому интегралу подстановку t = x2, так что dx =
2Vt
¦dt.
386

Из соотношения t = x2 находим пределы интегрирования для t: если х — — 2, то
/ = 4, и если х = 4, то ?=16, следовательно, t изменяется в пределах от 4 до 16.
Тогда указанная подстановка приводит к результату:
4 16
I16 1 ,сл оч 56
\ x*dx=Y\ У1 dt = -gV&
= у(64-8) =
Получили другой результат. Полученная ошибка объясняется тем, что
функция x=±\^t не однозначна, а двузначна. Поэтому, если взять положительную
часть х= +Vt, то при / = 4 мы получим: х= -\-V^ = +2, а не —2, как должно
было быть; а если взять х— — Yt , то при /=16 мы получим: х = — Kl6 = — 4, а
не+ 4, как должно было быть. Следовательно, подстановка ( = х2 здесь
неприменима, так как обратная ей функция неоднозначна.
Пример 3. Рассмотрим еще пример, когда невыполнение указанных выше
условий замены переменной в интеграле также ведет к ошибке. Пусть мы имеем
интеграл
\ dx = x\ =зх.
о |о
С другой стороны,
я я я я
f С dx ? dx С dtgx
J J cos* x +sin2* Jcos2 x (I +tg2 x) ~* ) 1 +tg2 x *
0 0 0 0
К последнему интегралу естественно применить подстановку t — igx. При этом
если *=0, то t — О, и если х = л, то ?=0, то есть t изменяется от 0 до 0.
Применяя формально формулу (1), получим:
я я и
Как видим, пришли к абсурду, так как nzfiQ. Это произошло потому, что
уравнение t = \gx для О^х^п определяет функцию # = arctg/ как двузначную при
t=Q и, кроме того, при непрерывном изменении х от 0 до я переменная / = tg*
л
имеет разрыв при переходе х через-~-. Таким образом, функция x=arctg? не
удовлетворяет сформулированным выше условиям (см. замечание 2) и потому
применение формулы (1) не оправдано.
Замечание 3. На практике замену переменной обычно
производят с помощью монотонных непрерывных функций по той
причине, что, во-первых, с ними проще оперировать, во-вторых,
монотонность гарантирует однозначность как прямой, так и обратной
функции и, наконец, в-третьих, при изменении переменной / в
промежутке [а, Р] значения функции x = y(t) не выходят из
промежутка [а, Ь] (рис. 149).
В заключение этого параграфа остановимся на применении
правила подстановки при интегрировании четных и нечетных
функций. Как известно, функция f(x) называется четной, если
f(—x) = f(x), и нечетной, если /(—х) = — f(x). Геометрически это
значит, что график четной функции симметричен относительно
оси OY (рис. 150), а график нечетной функции симметричен
относительно начала координат (рис. 151).
387

Покажем, что
Л-а
\ f(x)dx^=2\f(x)dx,
если f(x) четная, и
если f(x) нечетная.
Если к интегралу подойти с геометрической точки зрения как
к площади криволинейной трапеции с учетом знаков площади, то
эти форхмулы вполне очевидны.
В первом случае фигура
симметрична относительно оси ординат,
и потому площадь ее равна
удвоенному интегралу по
половине промежутка, симметричного
относительно начала координат.
Во втором случае фигура,
ограниченная кривой, симметрична
относительно начала координат,
при этом площадь части ее,
расположенной в первой четверти над
осью ОХ, будет получаться со
знаком плюс, а площадь второй
равной части, расположенной в третьей четверти под осью ОХ, —
со знаком минус, и потому алгебраическая сумма площадей этих
|)игур равна нулю.
Дадим аналитическое доказательство указанных формул. Пусть
f(x) задана в симметричном относительно начала координат
промежутке [-—а, а]. Тогда, по свойству 2, §4, будем иметь:
-fa 0 а
J f(x)dx= $ f(x)dx + \f(x)dx.
— а —а О
Xj
b
Хо
а
О
1
\ /1
pi
i i
* tQ
fi
7
Рис. 149.
Рис. 151.
3S*

В первом интеграле справа произведем замену переменной
л; = — t и воспользуемся свойством 1, § 4:
О 0 а и
\ f{x)dx = —\f{—t)dt = \f(—t)dt = \f{—x)dx.
— а и О О
Тогда получим:
(f{x)dx=\f{—x)dx + lf{x)dx = l\f(—x) + f(x)]dx.
— a U 0 0
Если теперь f{x) — четная функция, то сумма /(— х)-{-\(х)
равна 2/(а:), и мы будем иметь:
-\-а а
\ f(x)dx = 2\f(x)dx9
— а О
а если f(x) — нечетная, то сумма f(—x)+f (x) равна нулю и потому
— а
что и требовалось доказать.
Это свойство часто бывает полезным на практике. Например,
+ i
интеграл $ sin a? rfjc = 0, ибо подынтегральная функция нечетная
и интеграл берется по симметричному относительно начала
координат промежутку [—1, +1]. При этом заметим, что
неопределенный интеграл от этой функции не берется в конечном виде.
Вопросы для самопроверки и упражнения
1 i -* Отв. 4-2 In3. 2. ( -*?=. Oms. ?.
о
n2 2
3.
2
{ у ex— i dx. Oms. 2 — -5-. 4. { — . Oms. 4=arctgl
J 2 J 3 + 2 cos* 1/5 &]
0 0 3 + 2 008*' ' Уъ W
1
dx _ я
Отв. —,
Ух*—I
6. Объяснить, почему формальная замена переменной х = — в интеграле
+ 1
Г dx я
\ . , а = -=- приводит к неверному результату.
7. Почему в интеграле \ху\ — х* dx нельзя положить x = sint?
383

7t 7C
T 2"
8. Доказать, что если /(/) непрерывна на [0, 1], то \ f (sinx) dx=\f(cosx)dx.
о 6
9. Доказать, что для непрерывной периодической с периодом са функции / (х)
справедливо равенство \ f (x) dx=\f (x) dx.
§ 9. ИНТЕГРИРОВАНИЕ ПО ЧАСТЯМ
Для определенных интегралов имеет место формула
интегрирования по частям, аналогичная той, которая ранее была установлена
нами- для неопределенных интегралов.
Теорема. Если функции и (х), v (х) — непрерывные
вместе со своими производными в промежутке [а, 6], то
имеет место формула
ь ь ь
^и dv = uv^ — ^vdu. (1)
а а
Формула (1) называется формулой интегрирования по частям
для определенного интеграла.
Доказательство. По условию функции и и v имеют
производные; следовательно, по правилу дифференцирования
произведения будем иметь:
(uv)' = u'v + uv'.
Отсюда следует, что функция uv будет первообразной для
функции u'v + uv' и ввиду непрерывности последней в промежутке [а, Ь]
интеграл от нее существует в этом промежутке. Тогда согласно
формуле Ньютона — Лейбница будем иметь:
ъ ь
$ (u'v + uv') dx = uv j ,
а
отсюда
ъ ь ь
^u'vdx+^uv' dx = uv\ ,
а а
или, что одно и то же,
ь ь ь
^ v du + § и dv = uv I ,
а а
откуда и следует формула (1).
е
Пример 1. Вычислить интеграл \ In x dx.
390

dx
Положим u = \nx, dv = dx, отсюда du = — f v = x, и поформуле(1) находим:
\ In x dx = x In x\ — %
dx
x — = e — x
x
[ ' Г
= 1.
l
2
Пример 2. Вычислить интеграл { x sin x dx.
о
Положим u = x, sin xdx = dv, отсюда du = dxt v = —cos x. Тогда
2 1 T
.2 г ,2
x sin x dx = — # cos * L + \ cos x dx = sin x\ = i.
? л: sin л: d* = — л: cos л: I 4- [
6 l0 6
Пример З. Вычислить интегралы
In = \ s'mnxdxt /* = 5 cosnxdx,
где n — целое неотрицательное число.
Предварительно покажем, что /„ = /*. Действительно,
/* = { cos" х dx = { sin" (-J — х) dx.
о о
Полагая у— x = t в последнем интеграле, получим:
тс
о F
/* = —5 8ШЛ*Л = $ 8тя/Л = /я.
Остановимся на вычислении первого интеграла. Легко видеть,
что /о = у> /i=l. Пусть теперь п>\. Полагаем u = sinn~1x, dv =
=-smxdx, отсюда v = — cos*, du = (n — 1) sin""2 л: cos xdx.
Тогда интегрирование по частям дает:
? |2
1п =} sin"-1 xd (— cos x) = — sin71"1 x cos jc +
0 °
тс тс
2" 2"
+ (л—1)5 sin"-2;tcos2A;dA;==(Az--l)5 sin"-2;t(l — sin2*) dx =
о о
тс тс
2" 2"
= (/г —1)5 s\nn-2xdx — (n—Y)\ sinnxdx.
о о
391

Если использовать введенное обозначение, последнее равенство
можно записать и так: 1п = (п—1) /я_а —(п—l) 1п> отсюда находим
рекуррентную формулу:
/п=^1/л-2, (2)
по которой интеграл 1п последовательно приводится к /0 или It
в зависимости от того, число п четное или нечетное.
Рассмотрим оба случая.
1. Пусть п = 2т\ тогда, применяя формулу (2) последовательно
т раз, получим:
/ _2т—1 j _2m — 1 2m—3 . __ __
/2m— 2m y2m-2— 2m ' 2m - 2 ' 2m'4 ~~
_ 2m—1 2m —3 2m —5 ? _1_ , _ (2m—l)(2m —3) ... 3-1 я_
~~ 2m ' 2m —2'2m —4 "*• 4 ' 2 ° 2m (2m — 2) ... 4 . 2 *2>
что сокращенно записывается так:
31
2
/ _С nin^,^_ (2m-l)ll л
2. Если n = 2/n+l, то аналогично предыдущему w^yottmm
f 2m(2m —2) ... 4-2 - T ,
Wi = (2m+ 1) (2m- 1) ... 3- 1 ' 7l' 3 TaK K8K /l==1, T0 B сращенном
виде получим:
2~
/ ^ __ С .;n2m-n ^ (2m) 11
/2*й-1— \ sin хах — (2т+1)|Г
Таким образом, объединяя полученные результаты, мы будем
иметь:
- * / (я—1)!1 л
2 2 -Ь—^ у, если п четное;
\ cosnxdx= \ s\nnxdx = l (n__nn (3)
о 6 [ -—г~—, если п нечетное.
Формула Валлиса. С помощью формулы (3) легко получить
знаменитую формулу Валлиса *, дающую простое выражение для
числа я через натуральные числа.
Легко видеть, что для всех х интервала (0, у J имеют место
неравенства:
sin2m+2 х < sin2""1 x < sin2m x.
* Д. Валлис (1616—1703) —английский математик.
392

Интегрируя эти неравенства в пределах от 0 до у, получим:
1С ТС ТС
2" 2" У
$ sin2m+2xdx<\ sm*m+lxdx<\ sir\2mxdx
0 0 0
или (если заменить интегралы их численными значениями по
формуле (3))
(2m+l)ll я (2т) II (2т — 1) 11 л_
(2m-f-2)!l * 2 ^ (2m+l)l! ^ (2т) И * 2'
Отсюда после несложных преобразований находим:
^Г (2т) 11 у _[_
2т-\-\ я ^\ (2т) 11 "[» 1 я
2/Л + 2" 2 ^L (2m—1)11 J '2т+\<2*
Так как lim 9mj"0= 1, то (по теореме о сжатой переменной*) из
последнего неравенства следует, что
I2 1
я г Г (2т) 11 ]2
2т+Г
Это и есть формула Валлиса. Эта формула мало пригодна для
приближенного вычисления числа я, но она имеет значение в
различных теоретических рассуждениях, например при выводе формулы
Стирлинга**:
П\п Пп
п\=У2ппЩе"\0<®<:\.
Упражнения
Вычислить интегралы:
1 1
1. $ xexdx. Отв. I. 2. $ x In (х* +1) d*- Ome. In 2 — I
о о
а л п
с г. ли- Г
3. \ У а2 — х2 dx. Отв. -j- . 4. ^ #2 cos * d*. Отв. — 2я.
о о
1 я
С /¦- я С х 35
5. \ arc tg у xdx. Отв. -^ — 1. 6. V cos8 ~ d*. Отв. ^ я.
о о
я
4 1
7.
о
С . »г* . ^4 Л С arcsin* . ,--
\ smB2*d*. Отв. г?. 8. \ d*. Отв. яК 2 — 4.
* См. гл. III, § 3, теорема 7.
** Д. Стирлинг (1692—1770) — шотландский математик. Вывод формулы
см. [2J, стр. 57.
393

§ 10. ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГО
ИНТЕГРАЛА
Вычисление определенного интеграла по формуле Ньютона —Лей-
бница не всегда возможно, ибо далеко не все функции
интегрируются в конечном виде, то есть первообразные таких функций не
выражаются через элементарные функции с помощью конечного
числа арифметических действий и операций взятия функции от
функции.
Даже если первообразная функция известна, но имеет весьма
сложный и неудобный для вычисления вид, то и в этом случае
применение формулы Ньютона — Лейбница крайне затруднительно.
В этих случаях прибегают к приближенным методам вычисления
определенного интеграла; на некоторых из них мы остановимся ниже.
Пусть требуется вычислить интеграл
l=J/(x)rf*, (1)
а
где f(x)— непрерывная функция в промежутке fa, ft].
Так как интеграл (1) представляет собой предел интегральной
суммы вида я_!
c=2ffo)A*i, (2)
(где Jti^ii^*i+i, Axt=X{+1—xt), то последняя может служить
аппаратом приближенного представления интеграла (1). Таким
образом, ь „_,
\Hx)dx** 2 /&)***• (3)
a i = o
Это приближенное равенство будет тем более точным, чем мельче
дробление промежутка [a, ft], и погрешность этого равенства
стремится к нулю, если все длины Дя/ стремятся к нулю. Как нам
известно, в случае интегрируемой функции предел соответствующей
интегральной суммы не зависит ни от способа дробления промежутка
[a, ft], ни от выбора точек ^ в частичных промежутках [л;,-, xi + 1].
Однако если мы будем рассматривать произвольные дробления
промежутка интегрирования и произвольно выбранные точки ?,
в частных промежутках, то практическая ценность приближенной
формулы (3) будет невелика. Поэтому на практике во многих
случаях при вычислении интеграла по формуле (3) промежуток
интегрирования [a, ft] делят на п равных частей длины Ах,-= ~а .
Рассмотрим три простейших способа приближенного вычисления
определенного интеграла.
1. Способ прямоугольников. Разобьем промежуток [a, ft] на п
равных частей точками x-t = a-\-i , i = 0, 1, 2, ..., п и
положим yi = f(xi), то есть г/; —значения функции в точках х-ь. Если
394

учесть, что здесь &Xi = Xi+1 — xr-
Ъ-а
, 1 = 0, 1, 2, ..., п- 1, то
формула (3) в данном случае приводит к двум приближенным
формулам:
ь
Ь — а
^f{x)dx
а
Ь
J f(x) йХ
(Уо+У1+--'+Уп-1)>
b—a
п
(У1+У2+--+Уп)
(4)
(5)
в зависимости от того, берем ли мы за ?г начальные точки
частичных промежутков [xif xi+1], то есть lt = xit или конечные точки их:
?f = *f+i- Формулы (4) и (5)
называются формулами
прямоугольников.
Замечание. Формулы
прямоугольников имеют простой
геометрический смысл. В самом деле,
если / (а:) — непрерывная
положительная функция на промежутке
[я, Ь], то интеграл, стоящий в
левой части формул (4) и (5),
выражает собой площадь криволинейной
трапеции аАВЬ (рис. 152). Правые
части этих формул представляют
собой площади ступенчатых фигур, составленных из
прямоугольников* с равными основаниями. Следовательно, формулы
прямоугольников геометрически выражают тот факт, что площадь
криволинейной трапеции приближенно заменяется площадью ступенчатой фигуры.
2. Способ трапеций. Если за приближенное значение интеграла (1)
принять среднее арифметическое правых частей приближенных
формул (4) и (5), то получим так называемую формулу трапеций:
Рис. 152.
^f(x)dxf
Ь — а
*?*-+У1+У*+---+Уп-1
(6)
Эта формула имеет простой геометрический смысл в случае
непрерывной и положительной на промежутке [я, Ь] функции f (x).
Действительно, в этом случае, как мы уже отмечали, левая часть
формулы (6) выражает собой площадь криволинейной трапеции,
ограниченной сверху кривой y = f(x). Правая часть этой формулы,
которую можно записать и так:
Ь — а/Уо + У! , У1 + У2
г + Уз
i Уп-1 + Уп
' + 2
* Этим и объясняется название этого способа.
395

представляет собой сумму площадей прямолинейных трапеций с
основаниями yi и i/,4-1 и высотой Дх, = —=^—, г = 0, 1, 2, ..., п—1
(рис. 153).
Таким образом, применение формулы (6) геометрически означает,
что площадь криволинейной трапеции приближенно заменяется
площадью фигуры, состоящей из прямолинейных трапеций. Этим и
объясняется название формулы
(6) — формула трапеций.
Вычисление по формуле
трапеций практически не сложнее,
чем по формуле
прямоугольников, однако формула трапеций
при равных условиях обычно
доставляет большую точность,
чем формула прямоугольников.
Этот факт геометрически
очевиден: сумма площадей
прямолинейных трапеций более точно
выражает площадь
криволинейной трапеции, чем площадь ступенчатой фигуры, составленной
из прямоугольников. Это обстоятельство также подтверждается
оценкой погрешности упомянутых выше приближенных формул.
Для функции f(x), имеющей в промежутке [а, Ь] непрерывную
производную первого порядка, доказывается, что абсолютная вели-
формулы прямоугольников имеет следующий
Vl
0
1
А\
Уо\
0
_^ и - pXi S
Ул У2!
к7
ц
*э
^>,8
%\
t> X
Рис. 153.
чина погрешности^
вид**:
|я»1
(Ь-а)-
2/J
1П81 (а *?!<*)•
(7)
Для формулы трапеций при условии, что f (х) имеет в этом
промежутке непрерывные производные первых двух порядков,
абсолютная величина погрешности выражается формулой***
ф-а}
|Я»Н-
12га*
|/"(Л)1 (а^ц^Ь).
(8)
Из сопоставления этих формул видно, что с увеличением п
погрешность формулы прямоугольников убывает примерно как —,
а погрешность формулы трапеций убывает как бесконечно малая
порядка -2, то есть значительно быстрее. Таким образом, мы видим,
что формула трапеций, вообще говоря, значительно точнее, чем
формула прямоугольников, то есть при одном и том же п погрешность,
* Абсолютная величина разности между точным и приближенным
значениями интеграла. Погрешность часто называют дополнительным членом
приближенной формулы.
** См. Г. П. То л сто в, Курс математического анализа, т. 1, 1954.
*** См. [1], стр. 351.
396

даваемая формулой трапеций, как правило, будет меньше, чем
погрешность формулы прямоугольников.
С dx
Пример 1. Пусть дан интеграл /=\-у-т-—= In 2 я^ 0,69315.
Найдем его приближенное значение по формуле прямоугольников
при п = 10.
Разобьем промежуток [0, 1] на 10 равных частей точками х0 = 0;
л:1 = 0,1; х2 = 0,2; ...; х9 = 0,9; *10=1, так что A*j = -jg-, i=0f l,
2, ..., 9. Вычислим значения функции у = . , в этих точках,
которые мы обозначим через r/0, уъ у2, ..., ухо. Значение этих
ординат мы должны записать с помощью десятичных дробей. Поэтому
возникает вопрос, с каким количеством десятичных знаков следует
записывать эти дроби, если промежуток разбит на 10 частей?
Очевидно, что число знаков при заданном п находится в прямой
зависимости от степени точности, которую доставляет та или другая
приближенная формула; при этом число знаков при записи дробей
имеет смысл брать тем больше, чем меньше погрешность
приближенной формулы. Чтобы установить это число знаков при записи
указанных выше ординат, произведем оценку погрешности, которую мы
делаем в нашем примере, применяя формулу прямоугольников (4)
или (5) при п= 10.
В нашем случае /' (х) = —п ,2 , 0 ^ х ^ 1, отсюда следует,
что j /' (л:) | ^ 1. Тогда формула (7) дает:
Таким образом, формула прямоугольников при п=10 гарантирует
нам погрешность, не превосходящую 0,05.
Вычислим ординаты y0t уъ у2, ..., у1(1 с тремя знаками после
запятой, то есть с точностью до 0,0005. Так как при вычислении
каждой ординаты с тремя знаками мы делаем ошибку, меньшую,
чем 0,0005, то при сложении всех этих 10 ординат мы можем
получить ошибку от округления, меньшую, чем 0,005*. Далее согласно
формуле прямоугольников мы должны эту сумму умножить на
= tq j в результате чего ошибка ее уменьшится в 10 раз, то есть
она будет опять не больше, чем 0,0005. Следовательно, общая ошибка,
возникающая от погрешности формулы прямоугольников и от
округления, будет все же меньше, чем 0,051.
Разумеется, мы могли бы вычислять ординаты и с большим
числом знаков, но при полученной оценке погрешности формулы такое
вычисление было бы совершенно бесполезным, потому что в нашем
* При сложении и умножении ошибка может возрасти в соответствующее число
раз, а при делении — уменьшиться в соответствующее число раз.
397

результате нет никакой уверенности за второй знак после запятой.
Вернемся к нашему примеру. Вычисляя ординаты у0, уъ у2, ..., у10
с тремя знаками после запятой, получим: г/0= 1,000; #1 = 0,909;
у2 = 0,833; Уз = 0,769; у4 = 0,714; */5 = 0,667; 0в = О,625; у7 = 0,588;
г/8 = 0,556; у9 = 0,526; */10=jO,500.
В этом случае формулы прямоугольников при д=10 дают:
"-ri_^=1L (у0 + У1 + ... + у9)=±.7,187 = 0,7187,
о
или
1 dx = -±r(yi + y2 + ... + y10)=~ -6,687 = 0,6687.
о
Мы видим, что эти значения отличаются от точного значения меньше,
чем на 0,03, то есть истинная погрешность меньше полученной
оценки (9).
Теперь вычислим этот интеграл по формуле трапеций при п =10.
1 2
Для подынтегральной функции У = -гт— имеем: у" = п , хз ,
O^x^l. Легко видеть, что \у"\^2. Отсюда по формуле (8)
находим:
l^io К 122102 =-В8Г<0'0018- (10>
Будем вычислять ординаты с четырьмя знаками после запятой;
при этом, как легко проверить, погрешность от округления ординат
может быть включена в приведенную выше оценку (10). В самом
деле, общая погрешность при округлении ординат согласно формуле
1Л 0,00005 /, • п iv
трапеции при я=10 не превосходит величины —гд—(1 +9• 1; =
= 0,00005, а если учесть, что ординаты у0, у10 точные, то эта по-
0,00005 п ~ ЛЛЛЛ/|С
грешность от округления не превзойдет величины -^-rg— 9 = 0,000045.
Следовательно, общая погрешность, возникшая от самой формулы
трапеций и от округления ординат, не превосходит величины 0,0018.
Итак, вернемся к вычислению интеграла по формуле трапеций
при /г=10. Так как г/0= 1,0000; г/х = 0,9091; у2 = 0,8333; у3 = 0,7692;
у4==0,7143; уб = 0,6667; г/6 = 0,6250; */7 = 0,5882; у8 = 0,5556;
^9 = 0,5263; #10 — 0,5000, то формула трапеций при /г=10 дает:
1
'- dx ~ 4г (И1* +й + й +•••+ </.) *» -Ь ¦ 6W - C69377.
{
о
Здесь уже верны три знака, результат отличается от точного
примерно на 0,0006, и истинная погрешность значительно меньше
приведенной выше оценки (10).
В этой связи заметим, что формула (8), служащая выражением
для погрешности формулы трапеций, имеет скорее теоретическое,
398

чем практическое, значение, так как эта формула обыкновенно
дает довольно грубую оценку погрешности. Такое же замечание
можно сделать о выражении погрешности у других приближенных
формул интегрирования.
Итак, разобранный пример подтверждает, что формула трапеций
дает более точный результат, чем формула прямоугольников.
3. Формула Симпсона. Предварительно нам потребуется
следующая лемма.
Лемма. Площадь S криволинейной трапеции, ограниченной
параболой
у = Ах2 + Вх + С, (11)
осью ОХ и двумя ординатами ее у0, у2, расстояние между которыми
равно h, выражается формулой
h
3 = -^(Уо + *У1+У2),
(12)
где у1 — ордината кривой,
равноотстоящая от крайних ординат у0 и у2
(рис. 154).
Доказательство. Для простоты
будем считать, что кривая лежит над
осью ОХ. Так как площадь трапеции
не изменится, если перенести ее
параллельно самой себе, то, не нарушая
общности, мы можем считать, что
основанием трапеции служит отрезок оси ОХ,
симметричный относительно начала координат (см. рис. 154). Тогда
для площади такой параболической трапеции мы получим:
А
Уо
~ г
Yk
с.
%
г о
Уг
2
В
?
X
Рис. 154.
+ -
+!
S= $ (Ax2 + Bx + C)dx= $ (Ax2 + C)dx + B $ xdx =
= 2{ (Ax2 + C)dx = 2(A^+Cx
0
Таким образом,
24"
= 2[Л? + С?Н?(Л'? + 6С
А*
2
s=iM?+6c
(13)
Вычислим значение ординат у0, уъ у2. Подставляя значение
абсцисс точек Л, В, С в уравнение (11), мы получим соответственно:
Отсюда находим, что у0 + 4у1~{-х2 = А у + 6С.
Сопоставляя это равенство с выражением (13), мы и получим
для искомой площади формулу (12).
399

VI
о
Vol
Уг<
Чи.
й = хп
Рис. 155.
b=xn
Вернемся опять к интегралу (1). Как и в первых двух случаях,
разобьем промежуток [я, Ь] на п равных частей, считая, однако,
п четным числом, то есть п = 2т. Здесь также лгг = а + i "^~~» * = 0,
1, 2, ..., 2т, суть точки дробления промежутка [а, Ь]. В этих
точках восставим ординаты yt=f (х{) (i = 0, l, 2, ..., 2т). В
результате криволинейная трапеция разобьется на 2т полосок.
Рассмотрим двойной частичный промежуток [x2it #21+2]» J=0, 1,
2, ..., т—\. Заменим дугу кривой y = f (x), соответствующую
этому промежутку дугой параболы с вертикальной осью, то есть
параболой (11), проходящей через вершины трех смежных ординат,
то есть через три точки (x2i, y2i), (x2i+1, t/2f+1), (х2Ц2, У*+%) (рис. 155).
Такую параболу можно провести единственным образом через
указанные выше точки. Действительно, если координаты этих трех точек
последовательно подставить в уравнение (11), то получим систему
из трех уравнений с тремя неизвестными коэффициентами А, В, С,
из которой определяются они однозначно, а значения этих
коэффициентов единственным образом определяют уравнение параболы.
В результате каждые две смежные полоски заменяются одной
соответствующей параболической трапецией. Тогда вся криволинейная
трапеция аАВЬ приближенно заменится фигурой, состоящей из т
параболических трапеций, а площадь криволинейной трапеции
приближенно заменится площадью этой фигуры.
Так как площадь полоски, соответствующей промежутку [x2i,
Xoi+ih приближенно равна площади соответствующей параболической
трапеции, то согласно формуле (12) будем иметь:
^ f (х) dx ъ* -g- (y2i + 4#2l4l 4- у2и2),
ъ b — a 2 (b — а) -/л1о 1
где Ъ = ——•= к „ , 1 = 0, 1, 2, ..., т— 1.
400

Сложив почленно все эти приближенные равенства, получим при
ближенную формулу:
Ъ т—\
jj f (x) dx w у J) (Уч + 4«/«+i + У-и+г)
а / — о
или (для п = 2т) в развернутом виде:
ь
^f(x)dx^^[yQ + yn + 2(y2 + y4 + ...+ yn_2) + 4(y1+ys + 1)],
а
которая и называется формулой Симпсона * (или параболической
формулой). При этом если функция f(x) имеет непрерывные
производные до четвертого порядка включительно, то можно установить,
что абсолютная величина погрешности формулы Симпсона (в
предположении, что промежуток разбит на п==2т частей) имеет
следующий вид **:
\Rn\=®m?\fw®\ (<*<&<*)• (14>
Эта формула показывает, что погрешность формулы Симпсона
убывает примерно как бесконечно малая порядка -j, то есть убывает
значительно быстрее, чем в случае формулы трапеций, не говоря
уже о погрешности формулы прямоугольников.
Для сравнения точности приближенных формул вычислим тот же
интеграл
/=^^- = 102^0,69315
о
по формуле Симпсона при л = 4.
Разобьем промежуток [0, 1] на четыре равные части точками
х0 = 0, *! = -?¦, л:2 = у, я8 = —f xA=\ и вычислим значение
функции y=Ti— в этих точках. Чтобы выяснить, с каким количеством
и 1 -\-х
десятичных знаков целесообразно записывать ординаты у09 yly y2f
у3, уь мы, как и выше, предварительно оценим погрешность
формулы Симпсона при п = \. Для подынтегральной функции г/ = гт—
24
мы имеем: г/(4) = (1 ,Б, откуда видно, что | у{4)(х) | ^24 при 0^
<х^1. Тогда согласно формуле (14) будем иметь:
1^1^180^-24= 11&< 0,00053 < 0,0006, (15)
что гарантирует нам погрешность, не превосходящую 0,0006.
* Т. Симпсон (1710—1761) —английский математик.
** См. [1], стр. 352.
401

Если вычислим ординаты с четырьмя знаками после запятой,
то, как легко проверить, погрешность от округления ординат может
быть включена в приведенную выше оценку (15). Действительно,
общая погрешность при округлении ординат согласно формуле
Симпсона при п = 4 не превосходит величины -^— (2 + 2 • 1 +4 • 2) =
= 0,00005, а если учесть, что три ординаты у0, уъ #4 точные, то
0,00005
эта погрешность от округления не превосходит величины -^—х
X (2 • 1 + 4 • 1) = -^2— < 0,00003. Следовательно, общая
погрешность, возникающая от погрешности формулы Симпсона и от
округления ординат, не превосходит величины 0,0006.
В нашем случае у0= 1,0000; #х = 0,8000; г/2 = 0,6667; г/3 = 0,5714;
уА = 0,5000. Тогда формула Симпсона при п = 4 дает:
1
\
у^^^[1,5 + 2-0,6667 + 4 (0,8+ 0,5714)]^1-8,3190 = 0,69325.
о
Получили верные три знака, и результат отличается от точного
примерно на 0,0001. Следовательно, истинная погрешность меньше
границы (15).
Если этот интеграл вычислить по формуле Симпсона при п=6г
1
то получили бы \ утг^^ 0,693169, то есть верны четыре знака и
о
результат отличается от точного не более чем на 0,00002.
Итак, мы видим, что формула Симпсона дает результат намного
точнее, чем формулы прямоугольников и трапеций, несмотря на то,
что здесь мы разбили промежуток [0, 1] всего на четыре части.
Иными словами, формула Симпсона часто может дать более точный
результат даже при меньшем количестве ординат по сравнению
с предыдущими двумя формулами.
Упражнения
1. Применяя формулу прямоугольников и трапеций для я =10, приближенно
4
Г 43
вычислить интеграл I—\ x2dx=-^-^z21,33.
о
Отв. По формуле прямоугольников / ^ 18,24; по формуле трапеций / =^21,44.
2. Применяя формулы трапеций и Симпсона для я = 6, вычислить интеграл
2
/= jj r^_. = arctg2^ 1,10714..
о
Отв. По формуле трапеций / =« 1,1057, по формуле Симпсона /^1,10704.
1
3. Вычислить по формуле Симпсона для п = 10 интеграл /= \ е х dx^&
м 0,74682. Отз. /^0,746325.
402

В примерах 4 — 6 при вычислении по формулам прямоугольников и
трапеций взять я =10, а по формуле Симпсона п = 4. Полученные результаты сравните
с точными.
о
4. { — =1п 2 ^0,6931472.
1
Отв. По формулам прямоугольников 0,71877 и 0,66877; по формуле трапеций
0,69377; по формуле Симпсона 0,69315.
я
5. ( sin * d* = 1.
о
Отв. По формулам прямоугольников 0,91941 и 1,07657; по формуле трапеций
0,997 95; по формуле Симпсона 1,00000.
2
6. \ 3^ 0,25436. Отв. По формулам прямоугольников 0,27580 и 0,23691;
1
по формуле трапеций 0,25486; по формуле Симпсона 0,25435.
7. Ширина реки 50 м. Промеры глубины в поперечном сечении реки через
каждые 5 м дали следующие результаты:
X
У
0
0,1
5
1,2
10
1,5
15
2,2
20
3,4
25
3,8
30
3,6
35
зд
40
2,4
45 1 50
1,6 1 0,3
где х означает расстояние от одного берега, а у— соответствующую глубину
в метрах. Определить площадь Р поперечного сечения реки и секундный расход
воды Q, зная, что средняя скорость течения 1,5 м/сек.
Замечание. С такими задачами приходиться встречатся при
строительстве гидростанций, плотин, дамб и т. п.
Отв. По формуле трапеций Р ^ 115 ж2, по формуле Симпсона Р к» 116,3 ж2.
Расход воды соответственно равен Q— 172,5 м3/сек и Q= 174,4 м3/сек.

ГЛАВА X
ГЕОМЕТРИЧЕСКИЕ И МЕХАНИЧЕСКИЕ ПРИЛОЖЕНИЯ
ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
§ 1. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ ПЛОСКИХ ФИГУР
1. Определение площади. С понятием площади простейших
плоских фигур (прямоугольников, многоугольников, круга и его частей)
мы уже встречались в школьном курсе элементарной геометрии;
там понятие площади для указанных фигур было достаточно хорошо
изучено, и мы знаем способы и формулы для ее вычисления. С
общим определением понятия площади произвольной плоской фигуры,
ограниченной замкнутой кривой, можно подробно ознакомиться,
например, в учебнике Г. М. Фихтенгольца «Основы математического
анализа», т. I, стр. 354. Здесь мы ограничимся лишь самыми общими
сведениями, касающимися понятия
площади произвольной плоской
фигуры. Как известно, в элементарной
геометрии площадь круга
определяется как предел площадей
вписанных и описанных многоугольников.
Оказывается, понятие площади
произвольной плоской фигуры,
ограниченной замкнутой кризойг может быть
введено также путем операции
предельного перехода.
Пусть дана произвольная
плоская фигура (Р), ограниченная
замкнутой кривой, которую называют границей или контуром
данной фигуры. Рассмотрим всевозможные многоугольники (А)
площади Л, целиком содержащиеся в (Р), и многоугольники (В)
площади В, целиком содержащие в себе (Р) (рис. 156).
Многоугольники (А) будем называть «входящими», а многоугольники (В) —
«выходящими». Для площадей этих многоугольников будем всегда
Рис 156.
404

иметь А^В. Отсюда следует, что множество чисел {Л} ограничено
сверху, например, любым числом В. Следовательно, это множество
имеет конечную точную верхнюю границу* P#=sup {А} и, кроме
того, Р*^В, где В — площадь любого выходящего
многоугольника (В). Так как множество чисел {В}, таким образом, оказывается
ограниченным снизу числом Р*, то оно имеет конечную, точную
нижнюю границу P* = inf{jB}, причем Р*^Р*. Это следует из
того, что Р* является просто нижней границей для множества {В},
а Р*—точной нижней границей этого множества, то есть
наибольшей из нижних границ.
Определение. Если обе границы Р* и Р* равны друг другу:
Р* = Р*=Р, (1)
то их общее значение Р называется площадью фигуры (Р), а саму
фигуру в этом случае называют квадрируемой.
Приведенное определение позволяет сформулировать условие
квадрируемости в виде следующей теоремы:
Теорема 1. Для того чтобы фигура (Р) была квадриру-
ема, необходимо и достаточно, чтобы существовали такие
две последовательности многоугольников {(Ап)} и {(Вп)\
содержащихся в (Р) и содержащих (Р) соответственно,
площади которых имели бы общий предел
\\т Ап = ПтВп = Р, (2)
тогда этот предел Р и будет площадью фигуры (Р).
Доказательство. Необходимость. Предположим, что
фигура (Р) имеет площадь Р (следовательно, имеет место равенство (1)).
Тогда по свойству точной верхней границы для любого п найдется
такой входящий многоугольник (Ап) площади Апу что будет
Р-\<Ап^Р.
Переходя к пределу в этом неравенстве при п->оо и используя
при этом теорему о сжатой переменной, получим: lim An = P.
Используя свойство точной нижней границы, аналогично можно построить
такую последовательность выходящих многоугольников {(Вп)}, что
Р ^В/г<Р + — и, следовательно, \\тВп = Р.
Достаточность. Пусть существуют две последовательности
многоугольников \{Ап)} и {(Вп)}, содержащихся в (Р) и содержащих (Р)
соответственно, такие, что имеет место условие (2). Так как
площади многоугольников (Ап) и (Вп) удовлетворяют, очевидно,
неравенствам Ап^Р*^Р* ^Вп, то из (2) сразу следует, что Р* =
= р* = р, то есть фигура (Р) квадрируема и площадь ее равна Р.
Следует заметить, что иногда вместо многоугольников целесооб-
* См. гл. ], § 5.
405

разнее рассматривать другие фигуры, квадрируемость которых уже
установлена. В этой связи имеет место следующая теорема.
Теорема 2. Если для фигуры (Р) можно построить
такие две последовательности квадрируемых фигур {{Qn)\ ti
{(Rn)}> содержащихся в (Р) и содержащих (Р)
соответственно, площади которых имеют обший предел
lim Qn = \\m Rn = P,
(3)
Рис. 157.
то фигура (Р) квадрируема и предел Р будет ее площадью.
Доказательство. Так* как фигура (Qn) квадрируема, то по
свойству точной верхней границы существует такой содержащийся
в ней многоугольник (Ап) площади Апу что будет Qn <.An^Qn.
Откуда в силу (3) и теоремы о сжатой переменной имеем: \\тАп —
= lim Qn = P- Аналогично по свойству точной нижней границы
существует такой многоугольник (Вп)
площади Впу содержащий в себе
фигуры (/?„), что Rn < Вп < Rn +
Н . Отсюда в силу (3) находим:
lim B„ = lim Rn = P. Таким
образом, мы имеем: lim An = Hm Вп = Р
и согласно теореме 1 фигура (Р)
квадрируема. Теорема доказана.
Итак, каждой квадрируемой
фигуре (Р) можно соотнести число Р, называемое площадью этой фигуры.
Отметим простейшие свойства площади, необходимые нам для
дальнейшего.
1°. Конгруэнтные (равные) фигуры имеют равные площади.
2°. Площадь части фигуры меньше, чем площадь всей фигуры.
3°. Если фигура (Р) разбита на две фигуры (Рх) и (Р2) (рис 157),
то квадрируемость двух из этих трех фигур (Р), (Рг). (Р2) влечет
за собой квадрируемость третьей, причем всегда Р = Рг-{-Р2у то есть
площадь обладает свойством аддитивности.
Если фигура (Р), лежащая в плоскости OXF, может быть
разбита с помощью прямых, параллельных осям координат, на такие
части, каждая из которых представляет собой квадрируемую
«криволинейную трапецию», то прежде всего по свойству 3° сама
фигура (Р) квадрируема и площадь ее равна сумме площадей
криволинейных трапеций, составляющих эту фигуру.
Плоские фигуры, встречающиеся на практике, как правило,
всегда могут быть разбиты на такие трапеции. Таким образом,
отправляясь от площади криволинейной трапеции, можно вычислять
площади практически любых плоских фигур.
2. Площадь криволинейной трапеции. Обратимся теперь к
вычислению площади криволинейной трапеции A BCD, ограниченной сверху
непрерывной кривой y = f(x), a-^x^b, где f (x) — положительная
и непрерывная в промежутке [а, Ь] функция, с боков —ординатами
406

Рис. 158.
AD и ВС и снизу —отрезком оси ОХ (рис. 158). При этом не
исключается и тот случай, когда любая из боковых сторон AD и ВС
стягиваются в точку.
Мы уже сталкивались с задачей о вычислении площади
криволинейной трапеции в главе IX § 1. Однако там мы, скорее, стояли
на интуитивной точке зрения, чем на строгом обосновании понятия
площади плоской фигуры.
Указанная задача, как мы
помним, рассматривалась как
задача, подводящая к
понятию определенного интеграла.
Поэтому и решение ее было
основано на рассмотрении
предела суммы, имеющей
весьма специальный вид (то есть
суммы, которая потом была
названа интегральной).
Теперь мы рассмотрим,
впервые в строгом
изложении, ту же задачу об
определении площади криволинейной трапеции, исходя из
сформулированного в этом параграфе определения площади плоской фигуры.
Итак, пусть нам дана криволинейная трапеция ABCD (см.
рис. 158). Разобьем промежуток [а, Ь] на п произвольных частей
точками а = х0 < хг < х2 < •.. < хп = Ь. Обозначим через /и*, Mi
соответственно наименьшее и наибольшее значения функции f (x) на
частичном промежутке [xtl Xi+1\ (i=0, 1, 2. ..., п—1). В силу
непрерывности / (х) по второй теореме Вейерштрасса такие значения
существуют.
Составим суммы Дарбу:
п— 1 п— 1
s= 2 mtAxi, S= 2 Mi Axh
t = 0 i = 0
где Axi = Xi+1—Xi. Сумма Дарбу s, очевидно, представляет собой
площадь ступенчатой фигуры (входящего многоугольника), целиком
содержащейся в криволинейной трапеции ABCD; сумма Дарбу S
выражает площадь ступенчатой фигуры (выходящего
многоугольника), содержащей эту криволинейную трапецию (см. рис. 158).
Так как для непрерывной функции / (х) суммы Дарбу s и S
являются просто наименьшей и наибольшей из интегральных сумм,
то по теореме о существовании определенного интеграла обе суммы
при k = max{Axi}->0 имеют своим общим пределом интеграл
\j{x)dx:
lim s= HmS = W (x)dx,
X -* О Л - О Г,
(4)
407

откуда и следует *, что площадь Р данной криволинейной трапеции
существует и равна этому же интегралу:
pJ\f{x)dx. (5)
а
Таким образом, если f(x) положительная и непрерывная
функция на [а, Ь]9 то площадь криволинейной трапеции, ограниченной
сверху кривой y = f (x), выражается определенным интегралом и
вычисляется по формуле (5). Итак, исходя из общего определения
площади, мы доказали квадрируемость криволинейной трапеции
указанного вида и снова получили для ее площади ту же формулу,
что и в главе IX (§ 3).
Таким же способом можно установить, что всякая
криволинейная трапеция, ограниченная непрерывной кривой x = g(y)^0
(c^y^d), двумя
горизонтальными отрезками прямых
у = с, y = d и отрезком оси
OY, квадрируема и ее
площадь Р выражается формулой
P = ]g(y)dy.
с
Пусть функция f(x)
непрерывна на [а, Ь] и / (л:) ^ О,
Рис. 159. то есть кривая y = f(x) и
криволинейная
трапеция,ограниченная снизу этой кривой, лежат под осью ОХ. Рассмотрим функцию
у = — f(x). Эта функция уже не отрицательна и, следовательно,
график ее лежит над осью ОХ и симметричен графику функции y=f(x)
относительно оси ОХ, а криволинейная трапеция, ограниченная
сверху кривой y=—f(x), представляет собой зеркальное отражение
первоначальной трапеции (рис. 159). Следовательно, фигуры ABCD
и ABCD' конгруэнтны (равны), и, следовательно, по свойству 1°
площади их равны. Так как площадь криволинейной трапеции
ABCD', лежащей над осью ОХ, выражается формулой
Р= \ l-/(*)l dx = -]f(x)dxf
(6)
или
р=
] fix) ах
то этой же формулой выражается площадь данной трапеции,
расположенной под осью ОХ.
В силу теоремы 1, § 1, гл. X.
408

Таким образом, если f(x)^0 на [я, ft], то определенный
интеграл (5) по абсолютной величине также дает площадь Р
криволинейной трапеции, расположенной под осью ОХ.
ь
Замечание. Формула (6), записанная в виде $/(х)dx =— Pt
а
Ь
показывает, что в случае f(x)^0 определенный интеграл ^f(x)dx
а
дает площадь криволинейной трапеции ABCD, лежащей под осью ОХ,
но взятую со знаком минус. Это совсем не означает, что площадь
отрицательна (площадь есть величина положительная), а говорит
лишь о том, что перед числом Р, выражающим площадь этой
трапеции, стоит знак минус.
3. Площадь фигуры в декартовых координатах. Рассмотрим
теперь общий случай, когда некоторые части кривой */*=/(*)
находятся над осью ОХ, а другие —под осью ОХ. В этом случае
интеграл (5) и по абсолютной величине не дает уже площади всей
заштрихованной фигуры (рис. 160), а
представляет собой алгебраическую сумму Vh
площадей тех частей фигуры,
которые расположены над осью ОХ
Рис. 160.
Рис. 161.
и тех ее частей, которые находятся под осью ОХ; причем первые
входят в сумму со знаком плюс, а вторые — со знаком минус
(см. предыдущее замечание). Поэтому площадь всей фигуры в дан-
ь
ном случае выразится формулой Р = $ | / (х) \ dx, или (в случае, изо-
а
браженном на рис. 160)
с й Ь
P = \f(x) dx—\f(x) dx + \f{x)dx. (7)
а с d
Пример 1. Найти площадь фигуры, ограниченной параболой у = х2 — 3х,
прямой *= —2 и осью ОХ (рис. 161).
Часть фигуры находится над осью ОХ, а часть —под осью ОХ, следовательно,
искомая площадь находится по формуле (7):
о з
Р=Л (*2_з*)<&- \ (х^~Ъх)йх^{^-~ х^
-2 6
^.-(М-
53
~~ 6 *
40S

Пусть фигура ограничена снизу и сверху кривыми yi=fi(x)t
y* = U{x) и fi(*XM*)> a^x^b (рис. 162), где /\ (х), f2(x) — две
непрерывные функции. Используя установленное выше, можно
доказать, что фигура такого вида квадрируема, но мы на этом не
останавливаемся. Если этот факт считать уже известным, то ясно,
что площадь такой фигуры находится как разность площадей двух
криволинейных трапеций:
P-=\f2(x)ax-\Mx)dx = \\Mx)-Mx)]dx. (8)
а а а
Заметим, что это формула справедлива и тогда, когда fx (x) и
/2 (х) принимают отрицательные значения.
Упомянем также, что можно доказать и более общий результат,
а именно: если контур фигуры (Р) состоит из нескольких
непрерывных кривых, каждая из которых задается уравнением вида у =
= / (х) или x = g(y), то эта фигура квадрируема.
Для вычисления площади такой фигуры рекомендуется с
помощью прямых, параллельных координатным осям, разбить ее на
части, представляющие либо криволинейные трапеции, либо такие
фигуры, площади которых вычисляются как разность площадей
криволинейных трапеций.
Пример 2. Вычислить площадь фигуры, ограниченной прямой у = 2* + 3
и параболой у = х2 (рис. 163).
Найдем точки пересечения прямой с параболой, решив совместно их уравнения
Г </ = *2,
\ у = 2х + 3.
Следовательно, *2 — 2х — 3 = 0, откуда находим: х1= — 1, лг2 = 3. Согласно
формуле (8) будем иметь:
3 3 3
р=С (2x + Z)dx-{ x*dx=i (2* + 3--x2) d* = fx* + 3*—у) Р =у.
Рис. 162.
Рис. 163.
410

0
1 I
I /ffify
'ШЖ
i
в
S
t
» X
Рис. 164.
Рис. 165.
Пример 3. Найти площадь фигуры, ограниченной параболой ^ = *з —3* и
прямой у + Зх—4 = 0 (рис. 164).
В данном случае заштрихованная фигура ограничена двумя линиями.
Следовательно, для вычисления площади этой фигуры надо применить формулу (8).
Для этого найдем точки пересечения параболы и прямой. Решая систему
iy = x*-3x,
1*/ = 4-3*,
2. Тогда для площади искомой фигуры согласно фор-
получим х1 = + 2, х2 =
муле (8) будем иметь:
Я» 5 (4
-2
-fc2
= 2
-3jc — *a+3*)d*:
+г2
= \ (4 — x*)dx =
-2
i (4-*2) dx = 2(4x-^\
= 2
-i
32
: 3 •
(а<*<Р)
•}
(9)
4. Случай параметрического задания кривой. Рассмотрим случай,
когда кривая АВ задана параметрическими уравнениями
У = ¦(').
причем точка А соответствует значению t = a, точка В — значению
/ = Р*. Когда t изменяется от а до (J, то точка описывает кривую
от Л до В (рис. 165), при этом a = cp(a), & = ф(р), где а и Ъ —
абсциссы точек А и В. Производя замену переменной в интеграле
(5) по формуле * = ф(/), мы, очевидно, получим:
Э
P~№(t)<p'(t)dt. (10)
a
В самом деле, для осуществления указанной замены функции
ф(0> ФО должны удовлетворять всем необходимым требованиям.
А именно, мы считаем, что <р(/), <р'(/), ф(0 непрерывны на [a, P],
кроме того, функция ф(^) монотонная на [a, Р]. Тогда по теореме
О параметрическом задании кривой см. гл. V, § 7.
411

об обратной функции (см. гл. IV, § 6) существует обратная
функция t = v(x), a^x^b. Подставляя это выражение для t в
уравнение у=\|) (0» получим:
0=Ф(О=ФИ*)]=/(*). **?*<*, (П)
где f(x) — непрерывная функция на [а, Ь[. Так как мы пришли
к явному способу задания кривой, то для вычисления площади
криволинейной трапеции мы можем воспользоваться формулой (5):
ь
P=\f(x)dx.
а
Производя замену переменкой в этом интеграле по формуле x = y(t)
и учитывая условие (11), получим:
P=\f(x)dx= $/[<р(0]ф'(t)dt = ]V[v (ф (/))] <р' V) Л-$¦ (<) ф' (0А.
а а а а
то есть формула (10) доказана.
Замечание. Формула (10) может быть также использована
для вычисления площади фигуры, ограниченной замкнутой кривой,
при условии, что вся кривая обходится один раз по направлению
вращения часовой стрелки, когда параметр t изменяется от а до р.
Пример 4. Вычислить площадь эллипса (рис. 166)
\y = b sin t.
Ввиду симметрии кривой относительно осей координат достаточно вычислить
площадь части эллипса, находящейся в первой четверти. Поэтому находим:
а и z
Р = 4 \ у dx = 4 \ b sin t • a (— sin t) dt = 4a6 \ sin2 t dt = 4a6 • -^- • — = яаб *.
о j^ о
2
Пример 5. Вычислить площадь фигуры (рис. 167), ограниченной
замкнутой кривой
* = a sin t,
у = b sin 2*.
{
Предварительно остановимся на описании формы кривой. Эта кривая
симметрична относительно осей координат. Действительно, из уравнений кривой видно,
что при замене t на к — t переменная х не меняется, а у изменяет только свой
знак. Это значит, кривая симметрична относительно оси ОХ, Точно так же при
замене t на n + t переменная у не меняется, а х изменяет только свой знак.
Следовательно, кривая симметрична относительно оси OY Этим установлена
симметрия кривой относительно обеих осей и, стало быть, относительно начала
* Воспользовались формулой (3), $ 9, гл. IX.
412

Рис. 166.
Рис. 167.
координат. Последнее можно также установить из следующих соображений: при
изменении знака t будут изменять свой знак х и г/, то есть точка кривой
переходит в положение, симметричное с первоначальным относительно начала
координат. Следует учесть, что все точки кривой в силу переодичности функций sin t
a siu 2t получаются уже при изменении t в промежутке [0, 2я]. Кусок кривой,
лежащей в первой четверти, получается при изменении параметра t в промежутке
JO, -^-1, так как только в этой части промежутка [0, 2я] выполняются оба
неравенства х^О, у^О. Поэтому для выяснения формы кривой достаточно построить
ее часть, лежащую в первой четверти, а затем воспользоваться симметрией. На
рисунке 167 изображена данная кривая и на ней отмечены точки,
соответствующие значениям t, приведенным в таблице 1.
Таблица 1
1
0
JX
1
я
2
X
0
а
W
а
У
0
ь
0
Итак, ввиду указанной симметрии кривой мы можем ограничиться
вычислением площади фигуры, расположенной в первой четверти, и результат умножить
на 4:
а 2 2
Р = 4 V ydx = 4: V Ъ sin 2t a cos t dt=—8ab \ cos2*dcos/ =
= —о- ab cos3 t
8 и
413

Пример 6. Вычислить площадь петли
* = у(2-'2),
у—|-/(/._3)f
где а и Ь — положительные постоянные.
Из уравнений кривой видно, что областью существования данных функций
является промежуток (— оо, + °°) и что с изменением только знака параметра
t функция х не изменяется, тогда как у лишь изменяет свой знак. Отсюда следует,
что данная кривая симметрична относительно оси ОХ. Найдем те значения
параметра t, при которых х и у обращаются в нуль—точки пересечения с осями
координат. Для этого сперва положим л; = 0, то есть 2 — /2 = 0, отсюда t—± \r2.
Подставляя эти значения во второе уравнение, получим две взаимно симметрич-
Ь Ъ
ные точки r/j= —, у2= -\—т=, в которых кривая пересекает ось OY. Затем,
полагая # = 0, найдем: t = ±V3, t = 0. Подставляя эти значения в первое урав-
а
нение, получим две точки хх =—~-, х2 = а пересечения кривой с осью ОХ; при-
а
чем через точку #х =—~- кривая проходит
дважды при / = ± КЗ, пересекая самое себя,
образуя петлю (рис. 168). Из уравнений
кривой следует, что х—* —оо при t —* ± оо,
а у-^+оо при t—* + oo и у—+ — оэ при
/ —* —оо. Отсюда ясно, что кривая имеет
две бесконечные ветви: одну — во второй
четверти, другую —в третьей.
Из всего сказанного нетрудно заметить,
что при возрастании параметра t от —со
до + оо точка М обходит кривую так, как
указано стрелкой на рисунке 168; при
этом петля обходится по часовой стрелке
при возрастании t в промежутке [—КЗ,
Учитывая симметрию фигуры
относительно оси ОХ, достаточно вычислить
половину искомой площади и результат удвоить.
Найдем, например, площадь верхней части
фигуры (над осью ОХ), которой, как это
следует из наших рассуждений, соответствует изменение параметра t от
— Уз до 0 —это и будут пределы интегрирования. Тогда, учитывая, что x't = — at,
по формуле (10) находим:
Рис. 168.
Р = 2 С yx}dt=*2 ^ у^(Я-3)(-af)dt =
—Ys —Ys
о
= ab [ (3t* — P)dt = ab(p — ^Af=-jySab.
-Y*
Отметим, что если интегрирование производить в пределах от —Уз до -\-УзУ
то формула (10) сразу даст площадь всей петли. Предлагаем в этом убедиться
непосредственно.
414

5. Площадь сектора в полярных координатах. Рае:.мотрим
случай, когда кривая АВ задана в полярных координатах:
г = ф(0), а^в^р,
где ф(0)~непрерывная в промежутке [а, Р] функция.
Вычислим площадь Р сектора, ограниченного данной кривой и
двумя полярными радиусами, соответствующими значениям 0 = а
и 0 = р (рис. 169). Для этого разобьем промежуток [а, р] на п
произвольных частей точками
a = 0o<01<...<0;<0M<...<0„ = p
и проведем соответствующие этим углам полярные радиусы, тогда
криволинейный сектор АОВ разобьется на п частичных
криволинейных секторов. Если через nit и Mi мы обозначим соответственно
наименьшее и наибольшее значения функции г=^ф(0) в /-ом
промежутке [0/, 0,-+1] (/ = 0, 1, 2, ..., п—1), то круговые секторы,
описанные радиусами, равными /Я/ и Mt, будут соответственно
«входящими» и «выходящими» для сектора АОВ.
Так как площадь /-го входящего кругового сектора радиуса rt =
~ trii равна у гщ Д0/, где А0? = 0/ч.1 — ©ь а площадь выходящего
z'-ro сектора радиуса rt = Mi равна y/WfA©;, то суммы
/1—1 Л—1
/ = 0 г = 0
выражают собой площади двух фигур: первая — площадь фигуры,
составленной из входящих круговых секторов, вторая—площадь
фигуры, составленной из выходящих круговых секторов для сектора
АОВ.
Суммы s и S, как легко видеть, представляют собой суммы Дарбу
для интеграла -2"\ф2(0)й0. Следовательно,
а
Hms = limS = 4- [ Ф2(0 d®>
я,-о х->о z .)
а
где A, = maxA0?. Отсюда в силу теоремы 2 §1 площадь Р
криволинейного сектора АОВ существует и равна этому же интегралу:
p=y^ Ф2(@)^а (12)
а
Пример 7. Вычислить площадь, ограниченную лемнискатой Бернулли
<рис. 170) г2 = a2 cos 26 (а>0).
415

в
Рис. 169.
Рис. 170.
Предварительно остановимся на описании формы кривой. При 0 =
—полярный радиус кривой обращается в нуль, следовательно, кривая проходит через
полюс.
Из уравнения кривой видно, что полярный радиус г принимает вещественные
значения, когда cos 20 ^ 0, то есть когда угол 20 удовлетворяет неравенствам *
-~^20^-5l; 4^^20^-|я, откуда _-J^e*ss?; А^в^^л.
2 ' 2
Заметим, что когда 0 изменяется от т до -f--r.
4 4 '
4 ' 4 " —~— 4
то полярный радиус г
описывает часть кривой, расположенной в первой и четвертой четвертях, а при
3 5
изменении 0 от -г я до —я он описывает часть кривой, расположенной во
второй и третьей четвертях. Если к тому же учесть, что период cos 20 равен л, то
при замене 0 на 0 + я (что равносильно повороту полярного радиуса г на
угол я) полярный радиус г не изменится, и поэтому кривая симметрична
относительно полюса О. Более того, эта кривая симметрична относительно полярной
оси, так как для значений 0, отличающихся только знаком, г не изменяется.
Этих соображений уже достаточно для того, чтобы построить всю кривую (см.
рис. 170).
Таким образом, вся кривая расположена в двух вертикальных углах между
л Л л 3
прямыми, проведенными под углами 0=-т- и 0 = -д-я к полярной оси, и
пересекает сама себя в полюсе О.
Перейдем к вычислению площади. Учитывая симметрию кривой относительно
полюса и полярной оси, мы можем ограничиться вычислением площади фигуры,
находящейся в первой четверти, а это соответствует тому, что 0^0^ — .
Следовательно, вся площадь фигуры согласно формуле (12) будет равна
Т
Р = 4
¦ц
4
г2 dB = 2а2 \ cos 20 dS = а2 sin 20
Значение cos 20 будет неотрицательным при
2*~т)я^20^(2*+1г)д' /г==0, ±1> ±2'
В нашем случае достаточно взять fc = 0 и Л==1.
416

Рис. 171.
Рис. 172.
Пример 8. Вычислить площадь, ограниченную кривой r = acos30 (a > 0).
Легко видеть, что кривая проходит через начало координат и симметрична
относительно полярной оси (в силу четности cos 0). Так как величина
полярного радиуса должна быть неотрицательна, то и cos 0^0, а это возможно только
в первой или четвертой четверти. Таким образом, кривая расположена в первой
и четвертой четвертях (рис. 171). Половина этой кривой, расположенной в первой
зх
четверти, получается при возрастании 0 от 0 до -^-. Поэтому вся площадь
фигуры равна:
> = 2-у { r2dS = a2 [
cos6 0 dS = <
ЬЗ-5
2.4.6
~2
h*
Полученная площадь составляет ~ площади круга радиуса -7Г.
о 1
Пример 9. Найти площадь кардиоиды (рис. 172) r = a(l+cos0).
Так как кривая симметрична относительно полярной оси (в силу четности
cos 0), то достаточно вычислить площадь верхней половины. Эту половину
полярный радиус г опишет при изменении 0 от 0 до к. Тогда по формуле (12) на
ходим:
я я
-4
i r2dB = a2i (l+cos0)2rf0 = a2 С (1+2 cos 0 + cosa 0) d0 =
о / 3 _ . 0 . _ , sin 20
--a2 i-^-Q + 2 sin 0H ~—
i™2-
Упражнения
1. Вычислить площадь фигуры, ограниченной параболой у = 6х—х2 и осью
ОХ. Отв. 36.
2. Найти площадь фигуры, ограниченную линиями у = х2-\-4х, j/ = x + 4.
Отв. 20 4-.
о
3. Найти площадь фигуры, ограниченной линиями {у — *)2 = *3, дс=1.
Отв. 0,8
* Воспользовались формулой (3) § 9, гл. IX.
417

4. Вычислить площадь фигуры, ограниченной осью ОХ и одной дугой
циклоиды x = a(t — sin/), y = a(l — cost). Отв. Зла2.
5. Найти площадь фигуры, ограниченной астроидой х = аcos3/, r/ = asin3/.
3
Отв. — па2.
о
6. Найти площадь петли x=2t — /2, # = 4/—/3.
Указание. Кривая имеет две бесконечные ветви, расположенные во второй
и третьей четвертях, дважды проходит через начало координат, образуя петлю
в первой четверти. Отв. у^.
15
7. Найти площадь петли x = 3tz, y = t—t3.
Указание. Кривая симметрична относительно оси ОХ, имеет две
бесконечные ветви, касается оси OY в начале координат и дважды проходит через
точку (3, 0), образуя петлю, расположенную в первой и четвертой четвертях
Отв. -=-.
о
8. Вычислить площадь одной петли кривой r = acos20. Отв. — па2.
о
9. Найти площадь, ограниченную замкнутой кривой л = a cos 36, а>0.
Указание. Кривая симметрична относительно полярной оси и образует
три одинаковые петли. Полная площадь равна шестикратной площади половины
Л 5
петли, соответствующей изменению угла 6 от 0 до -г- . Оте. — а2 .
10. Найти площадь фигуры, ограниченной улиткой Паскаля r = 2a (2 + cos 0),
а>0.
Указание Кривая замкнута и симметрична относительно полярной
оси. Отв. \8ла2.
11. Найти площадь фигуры, ограниченной замкнутой кривой r = a sin 0 cos20,
а>0.
Указание. Кривая проходит через полюс, образуя две петли в первой
и второй четвертях, симметрично расположенных относительно оси OY. Отв. -%=-.
12. Найти площадь фигуры, ограниченной замкнутой кривой r = a Kcos 4 в",
а>0.
Указание. Кривая проходит через полюс, образуя четыре петли,
симметрично расположенные относительно осей ОХ и OY Отв. а2.
13. Найти площадь фигуры, ограниченной замкнутой кривой (х2-{-у2)3 — а2х*.
Указание. Перейти к полярным координатам: x = r cos 0, # = r sin 0.
3
Отв. -q па*.
о
§ 2. ДЛИНА ДУГИ КРИВОЙ
С понятиями длины прямолинейного отрезка и длины
окружности мы уже сталкивались в школьном курсе элементарной
геометрии. Нам известны способы и формулы для вычисления длины
этих линий, а также линий, составленных из конечного числа
отрезков (ломаная линия) и конечного числа дуг окружностей. Если
понятие длины отрезка строилось с помощью сравнения его с
некоторым фиксированным отрезком, принятым за единицу масштаба,
то в случае кривой линии мы не можем использовать этот
элементарный способ измерения длины, так как никакая часть
прямолинейного отрезка не совмещается с кривой. Как нам известно,
понятие длины окружности уже требует довольно тонкого подхода,
418

Ук
0
1
1
1
i
i
а
Jh
Xi
V'*7
*i+j
Be
a\
b
X
Рис. 173.
связанного с операцией
предельного перехода, и это подавно
будет иметь место при
определении длины дуги произвольной
кривой. К точному выяснению
понятия длины дуги кривой мы
сейчас и перейдем.
Пусть плоская кривая АВ
(рис. 173) задана уравнением
y = f(x), a^x^b, где f(x) —
непрерывная функция на
промежутке [а, Ь]. Разобьем
кривую АВ на п произвольных частей точками А=М0, МЪМ2, ...,
Mi, Mf+1, ..., Мп = В (занумерованными по порядку от Л к В).
Соединив эти точки хордами, получим некоторую вписанную
ломаную линию, периметр которой обозначим через р.
Определение. Если существует конечный предел s периметра
р вписанной в кривую ломаной, когда наибольшее из ее звеньев
стремится к нулю, то этот предел и называется длиной дуги АВ:
s = limp,
IX-* о
где \i—длина наибольшего звена ломаной*.
Кривую, длина которой существует, называют спрямляемой. На
языке «е — б» это определение означает, что для каждого числа е>0
найдется такое число б > 0, что для любой вписанной ломаной, у
которой |i<6, будет выполняться неравенство |s—р|<е.
1. Длина дуги в прямоугольных координатах.
Теорема 1. Если функция f(x) непрерывна вместе со
своей производной f (х) на промежутке [а, Ь\, то кривая
А В спрямляема и длина ее выражается формулой
s =
\y\+f*(x)dx.
(1)
Доказательство. Разобьем кривую АВигп произвольных
частей точками А=М0У Мъ M2i ..., Mt M/+1,..., Мп = В и соединим
их попарно хордами. Координаты точки Mi обозначим через х{ и f(xi)
(1 = 0, 1, 2, ..., я), так что для абсцисс этих точек получим:
а = xQ < хх <х2 <... < Xi < xiJrl <...<*„ = &. Тогда длина // одного
звена MiMi+1 ломаной линии вычисляется по известной формуле
из аналитической геометрии:
U = V(xi+1 -хд2 + [f(xi+1)-/{х{)]\ i = 0, 1, 2,..., n-l.
По формуле Лагранжа f (xi+1) — f (х() = f (lt) (xi+1 — xi), где xt ^ & =
*i+l-
* В этом определении подразумевается, что предел s не зависит от способа
разбиения кривой на части.
419

Следовательно, U =У 1 + f'* (Ь) • А*/, где kXi = xi+1 — Xi. Таким
образом, периметр всей ломаной линии равен
п —1
п—1
/ = о / = о
Мы имеем здесь интегральную сумму для интеграла (1). Так
как функция У~1 +f'2 (x) непрерывна на [а, Ь], то предел этой
суммы существует, когда А,=тах {Ах,-} ->0, тем более, когда
тах/?->0, и равен соответствующему определенному интегралу, то
есть
s = limp = lim'5 Vl+f,%&)-bxi= \vi+f'%(x)dx,
при этом ^^(х, а при jll —> 0 и подавно Я->О. Теорема доказана.
Пример 1. Найти длину полукубической параболы ау2 = х*, а>0от* = 0
до х — Ба (рис. 174).
Эта кривая симметрична относительно оси ОХ. Мы вычислим длину дуги
одной ветви кривой (например, верхней).
з Л 1
1 Т 3 -
Из уравнения у = ——хг находим: #'=—— *
У а 2 у а
муле (1) получим:
5а Ьа
2. Следовательно, по фор-
Jio+f^-s/.+s—so+s
335
Рис. 174.
Пример. 2 Найти длину дуги цепной линии * у =—\еа -\-е а]отх=0до
х=а (рис. 4:75).
* Название цепная линия происходит от того, что такую форму принимает
гибкая и нерастяжимая тяжелая нить (например, цепь), подвешенная за оба
конца.
420

l(- --\
Из уравнений цепной линии находим: у' = -к-\еа — е а]. Поэтому
ласно формуле (1) будем иметь:
-i!^+«"^-f('5-"4)C-f(—f)-
cor-
,3 „3
Пример 3. Вычислить длину астроиды хъ +у6 = а6, а>0 (рис. 176).
Эта кривая симметрична относительно осей координат. Достаточно вычислить
длину дуги в первой четверти. Положив в уравнении у=0, найдем: х=± а. Из
з 1
уравнения астроиды находим: у
( 1 1\2 --/- -\2"
\а*—х*} , (/' = — х з\аг—хг) '
а а / 2/2 1
тогда
= 47а\х 3d* = 4^.4*3| =6a.
.1 ^Ь [О
Замечание. Пусть кривая
уравнениями
* = <р(0,
0 = Ф(<), *о<<
параметрическими
-.}
(2)
Предположим, что обе эти
функции имеют непрерывные
производные в промежутке [t0t
Т], при этом <р' (/) Ф 0. Тогда
лс=ф(0 монотонна в [tQ, T],
так что она имеет обратную
функцию t = v(x), также
монотонную, непрерывную в
промежутке [а, 6]* (где а = <р(г0),
й = ф(Т)) и имеющую
непрерывную производную tx= —
/ - m т> ** Рис- 176«
(л:/ Ф 0). В таком случае
переменная у определяется как функция от а; и уравнение кривой АВ
может быть записано в явном виде:
у=Ф(*)=ф И*)] = /(*),
а^х^Ь, где, как легко видеть, f (x) будет непрерывной функцией
на [а, Ъ\, для которой также существует непрерывная производная.
* См. гл. IV, & 6.
421

Вычисление этой производной может быть выполнено по известному
правилу (см. гл. V, § 7):
f.yt__V(t)
Итак, поскольку уравнение кривой А В может быть записано
явным уравнением y = f(x) и функция f(x), заданная на [а, Ь]у
удовлетворяет всем условиям доказанной выше теоремы, то длина
дуги А В может быть вычислена по формуле (1):
ь
s = \Vl+y'xadx.
а
Производя замену переменной в этом интеграле с помощью
формул (2), находим:
ь т , — т
s=\VT+tfdx=^y 1+g-j xtdt=\Vtf + y?dt.
a t0 t0
Таким образом, длина дуги АВ, заданной в параметрической
форме, выражается формулой
т
& = \Vx?+y?dt, (3)
to
где t0 и Т — значения параметра t, соответствующие начальной
точке А и конечной точке В дуги или значениям х = а, х = Ь.
Заметим, что формула (3) по сравнению с формулой (1) имеет то
большое преимущество, что она применима к более разнообразным
кривым, в частности к замкнутым.
Это замечание относительно применимости формулы (3) не
вытекает из наших рассуждений. Однако следует иметь в виду, что
формулу (3) можно было бы вывести не из формулы (1) (как это
мы сделали), а непосредственно, исходя сразу из задания кривой
параметрическими уравнениями (2), как это проводится во многих
учебниках по математическому анализу *. В этом случае уже
нетрудно распространить формулу (3) и на случай замкнутой кривой.
При этом если кривая задана параметрическими уравнениями (но
не замкнута), то определение ее длины ничем не отличается от того,
которое было сформулировано в начале этого параграфа. Если
кривая замкнута, то можно произвольным образом разбить ее на два
куска и определить длину всей кривой как сумму длин этих кусков.
Впрочем, в следующем параграфе будет указан другой подход
к понятию длины кривой, одинаково применяемый к любым кривым.
Пример 4. Вычислить длину дуги одной арки циклоиды * = a (t— sin t)y
y — a(l — cos t) (рис. 177).
В данном случае параметр / изменяется от 0 до 2я, так как точка М
описывает одну ветвь циклоиды при одном обороте круга Из уравнения циклоиды
* См. [1J, стр. 370 — 375.
422

находим, что х\ = а (1 —cos f), y'( -
Тогда по формуле (3) находим:
= asinf и, следовательно, x't2-{-y't2 = 4a2 sin2-
2я
2л
s= \ V xt*+yt* dt = 2a \ sin-s- dt — 4a I—cos-^-j = 8a.
Пример 5. Вычислить длину петли кривой д: = ]Аз t2, y = t—P.
Из уравнений кривой видно, что областью существования функций х и у
является промежуток (— со, + °°) и что с изменением только знака параметра t
переменная х не изменяется, тогда как у изменяет лишь свой знак. Отсюда
вытекает, что данная кривая симметрична относительно оси ОХ. Так как х^О при
всех /, то кривая расположена в первой и четвертой четвертях. Непосредственно
из уравнений кривой следует, что х—--{-со при t—+ ± со, а #-— + со при t ——со
к у—+ — со при /-^ + оо. Это значит, что кривая имеет две бесконечные ветви:
одну —в первой четверти, другую— в
четвертой.
Найдем теперь точки пересечения
кривой с осями координат. Из уравнения для
х сразу видно, что х = 0 только при
^ = 0. При этом значении параметра / пере-
Рис. 177.
менная у тоже равна нулю; значит, данная кривая имеет с осью OY
единственную общую точку в начале координат. Положив теперь # = 0, то есть t — t3=
= 0, найдем ? = 0 и t=± 1. Подставляя эти значения в первое уравнение,
получим две точки #! = (), *2 = "КЗ пересечения кривой с осью ОХ\ при этом через
точку #2 = +]/3 кривая проходит дважды (при ?=± 1), пересекая самое себя и
образуя петлю (рис. 178). Из всего сказанного легко вывести, что при
возрастании параметра t в промежутке (— со, + °°) точка М обходит кривую так, как
указано стрелкой на рисунке; при этом петля обходится по часовой стрелке при
возрастании t в промежутке [— 1, +1]. В силу симметрии кривой относительно
оси ОХ достаточно вычислить длину половины петли и результат удвоить. Найдем,
например, длину верхней части (над осью ОХ)у которой соответствует изменение
параметра t от 0 до + 1— это и будут пределы интегрирования Так как x't =
= 2]/3 t, y't — i — 3t2 и */,'~+^-> = (1+3/2)2, то согласно формуле (3) искомая
длина равна:
= 4.
о о
2. Длина дуги в полярных координатах. Наконец, рассмотрим
случай, когда кривая АВ задана в полярных координатах уравнением
г = /(в), а^в^р,
где / (0) имеет непрерывную производную f (0) на промежутке
[а, Р]; при этом точкам А и В соответствуют значения а и р.
423

Известно, что прямоугольные координаты хну связаны с
полярными г й G соотношениями
Ar = rcos6, y = rsmO. (4)
Если учесть, что r = f(@), то уравнения (4) можно
рассматривать как параметрическое задание кривой АВ с параметром ©.
Тогда
х'е = г'в cos 0 — г sin 6; ye = /'е sin в + г cos 0,
так что x'es + z'e2 = г2 + г'ей, и формула (3) дает
в
s=\Vr*+ri*ae. (5)
а
Пример 6. Вычислить длину кардиоиды г —а (1 -}-cos в) (см рис. 172 на
стр. 417).
Так как кривая симметрична относительно полярной оси, то при изменении
в от 0 до я полярный радиус г опишет половину кривой. Тогда, если учесть,
что Гд =—a sin О, формула (5) дает:
я л
s = 2!JK/'2H-'es d0=2^Ka2(l+cos0)2 + a2sin2e d0 =
о
п
г* (* ft ft 1я
= 2 Via V У 1+cos в dQ = 4a \ cos у d0 = 8a sin -=- =8a.
Вернемся снова к формуле (1) и найдем с помощью ее
выражение для: дифференциала дуги в прямоугольных координатах.
3. Дифференциал дуги. Возьмем на дуге АВ произвольную
точку М, отвечающую значению х из промежутка [а, Ь], и будем
считать ее переменной точкой кривой АВ. Тогда длина дуги AM
будет функцией от х и согласно формуле (1), если в последней
заменить верхний предел b переменной х, получим для длины дуги AM
формулу:
s(x) = lVl+r%V)dt. (6)
а
Так как здесь подынтегральная функция непрерывна, то, при
нимая во внимание правило дифференцирования интеграла по верх
нему пределу, из последней формулы находим: -?- = V\ -\-f 2(х)
отсюда получим формулу для дифференциала дуги:
ds = У1 + ($f dx или ds = Vdx* + dy2. (7)
Эта формула позволяет дать простое геометрическое истолкование
дифференциала дуги. Действительно, дифференциал дуги ds
численно равен длине отрезка MP касательной к кривой в точке М,
то есть является гипотенузой прямоугольного треугольника с
катетами \dx\ и \dy\ (рис. 179).
424

Рис. 179.
Рис. 180.
Остановимся еще на одном применении формулы (1) и с помощью
ее установим интересный результат, которым часто пользуются во
многих приложениях математического анализа, а именно:
эквивалентность бесконечно малой дуги и стягивающей ее хорды.
4. Эквивалентность бесконечно малой дуги и стягивающей ее хорды.
Пусть МгМ — какая-нибудь дуга кривой АВ (рис. 180). Точку М,
будем считать неподвижной.
Теорема 2. Если кривая А В задана уравнением у =f(x)
и функция f(x) удовлетворяет всем условиям теоремы 1,
то предел отношения длины дуги МгМ к длине
стягивающей ее хорды МгМ равен единице, когда точка М стремится
к М± то есть
дл. МгМ
lim тм-ал
AI-Aft Л"' М1М
¦=1.
Доказательство. Пусть координатами точек М1 и М
соответственно будут дс0, у0 и *о + Ах, у0+ Ау. Тогда длина хорды МгМ
равна VAx2 + Дг/т = "I/ 1 + (д|) -Да: (мы считаем, что Д*>0), а
длина дуги МХМ согласно формуле (1) равна интегралу
\ Vl+fix) dx.
Применяя к этому интегралу теорему о среднем *, получим!
M.MJU = Vl+f'*(c)-bx,
где с находится между х0 и х0 + Ах\ так что если М-+М1У или
(что равносильно) Дх->0, то с-+х0. Так как функция f(x) имеет
производную f (x) и эта производная непрерывна, то
by _ А/ (*0)
Дл;
Да:
-ГЫ иГ(^ГМ.
* См. гл. IX, § 4, свойство 9.
425

Поэтому
дл. МгМ
то есть получили требуемый результат.
Таким образом, при указанных выше условиях бесконечно малая
дуга и стягивающая ее хорда суть эквивалентные бесконечно малые.
Легко видеть, что это свойство
применительно к дуге окружности выражается
известным нам предельным равенством
sin х
X
X-+Q
• 1.
Действительно, для дуги МгМ
окружности радиуса R (рис. 181) имеем:
lim 5^1
м — м± дл. МгМ
t. 2R sin x ,. sin x ,
aim = lim = 1,
x-+o 2Rx x-+o x
Рис. 181.
где х — половина центрального угла дуги МгМ .
Упражнения
1. Вычислить длину дуги кривой #2 = (*+1)3, отсеченной прямой х=4.
п 670
Отв. Tf.
2. Вычислить длину дуги кривой 9у2 = х{х—3)а между точками пересечения
с осью ОХ. Отв. 4 /ЗТ
1 1
3. Вычислить длину дуги кривой г/ = In (1 — х2) от * =
2 Д° Х=~2
_ Отв. 2 1пЗ — К
4. Вычислить длину дуги кривой у = У~х — х2 + arcsin Yx .
Указание. Промежуток интегрирования определяется областью
существования функции. Отв. 2.
5. Найти длину петли кривой x = t2, у— -it {& — ?>). Отв. 4^3.
6. Вычислить длину дуги кривой * = 4j^2askU, у — a sin 2t.
Указание. График этой кривой примерно такой же, что и на рисунке 167.
Отв. 8яа.
д
7. Вычислить длину дуги кривой r=asin3-r-.
Указание. Полярный радиус опишет кривую при изменении 0 от 0 до Зя.
Отв. уяа.
8. Вычислить длину дуги кривой r = 2asin0. Отв. па.
9. Найти длину дуги кривой г = а sin4 —.
Указание. Эта кривая симметрична относительно полярной оси, и поляр-
1 fi
ный радиус опишет ее при изменении 0 от 0 до 4я. Отв. -$- а.
о
л 3
10. Вычислить длину дуги кривой г = 2а (sin в -f-cos0) ог0— — до 0=—л.
42(3

Указание. Уравнение г = 2а (sin в + cos 0) = 2)^2 a cos (в—j-)
представляет собой окружность. Оно легко преобразуется к прямоугольным координатам:
*2 + у2 = 2а (х + у). Отв. 2па VT.
§ 3. УСЛОВИЕ СПРЯМЛЯЕМОСТИ КРИВОЙ
Укажем несколько иной подход к определению длины кривой.
Для простоты начнем с кривой, заданной явным уравнением
y = f(x) (a^x^b), (l)
причем функция f (х) непрерывна. Как и в предыдущем параграфе,
впишем в эту кривую произвольную ломаную, периметр которой
по-прежнему обозначаем через р. Рассмотрим совокупность {/?}
периметров всевозможных ломаных, вписанных в данную кривую. Если
эта совокупность ограничена, то данная кривая называется
спрямляемой; ее длина s определяется как точная верхняя
граница множества чисел {/?}, то есть s = sup {p}.
Можно доказать, что это определение равносильно тому, которое
было дано в § 2.
Поставим вопрос: какое свойство функции f(x) необходимо и
достаточно для того, чтобы кривая (1) была спрямляемой? В
предыдущем параграфе мы видели, например, что наличие непрерывной
производной /' (х) достаточно для спрямляемости кривой. Чтобы
ответить на поставленный общий вопрос, нам нужно ввести один
важный класс функций, имеющий применение во многих вопросах
математического анализа.
Пусть в промежутке [а, Ь] задана функция f(x). Разобьем этот
промежуток произвольным образом на п частей точками х0 — а<С
<Cx1<Zx2<Z..-<iXi<iXi+1<z...<.xn = b и составим сумму:
o=Sl/(*+i)-/(*i)|. (2)
Эта сумма полностью определяется способом дробления промежутка
[а, Ь]. Различным способам дробления этого промежутка на части
отвечают, вообще говоря, различные значения суммы v.
Следовательно, если мы будем брать все возможные разбиения промежутка
[а, Ь , то получим множество чисел {v}.
Определение. Функция f(x) называется функцией с
ограниченным изменением (или ограниченной вариации) в
промежутке [а, 6], если совокупность всевозможных сумм v
ограничена. При этом точную верхнюю границу этого
множества называют полным изменением (или полной вариацией) *
функции f(x) в указанном промежутке и обозначают симво-
* Функции с ограниченным изменением введены французским матаматиком
К. Жор да ном (1838—1922).
427

b
лом V (/)• Таким образом,
а
Ь
V(/) = supM.
а
Покажем, что всякая монотонная функция будет функцией с
ограниченным изменением. Пусть для определенности f (х) не убывает
на промежутке [а, ft]. Тогда при любом дроблении промежутка
[а, Ь] на части и для любых двух соседних точек xt и xiJrl
\f(Xi^-f(Xi)\=f(Xi^-f(Xi).
Поэтому для каждой из сумм (2) имеем:
+ ...+ \f(b)-f(xa_1)]=f(b)-f(a).
Следовательно, суммы v не зависят от способа дробления
промежутка [a, ft], они все равны f(b)—f(a). Но множество, состоящее
из одного числа, ограничено, а потому f (х)—функция с
ограниченным изменением и
ь
V(f)=f(b)-f(a).
а
Известно, что монотонная функция может иметь точки разрыва.
Следовательно, функция с ограниченным изменением не обязана
быть непрерывной.
Немного сложнее доказывается, что если функция f (х) кусочно-
монотонна на [a, ftj, то есть если промежуток [a,ft] может быть
разбит на конечное число частей, на каждой из которых f (x)
монотонна, то f (x) — функция с ограниченным изменением.
Проверим еще, что если f (x) имеет в [a, ft] ограниченную
производную | /' (х) | ^ М, то f (x) — функция с ограниченным изменением.
Действительно, в этом случае каждое слагаемое из суммы
(2) легко оценивается с помощью теоремы Лагранжа:
I f(xi+d—f(Xi) \ = \f'(c)\ (xi+1—Xi) ^ M (xi+1—Xi),
где Xt < с < **+1. А тогда
/i-i
v^M 2 (**+i—Xt) = M (ft — a);
гем самым суммы v в совокупности ограничены.
Заметим, что функции с ограниченным изменением могут быть
охарактеризованы как такие, которые представимы в виде разности
двух возрастающих функций.
Перейдем к установлению условия спрямляемости кривой.
428

Теорема Жордана. Для того чтобы кривая (1) была
спрямляемой, необходимо и достаточно, чтобы f(x) была
функцией с ограниченным изменением*.
Доказательство. Необходимость. Пусть кривая (1)
спрямляема и имеет длину s. Тогда при любом дроблении промежутка
[а, Ь] с помощью точек x-t имеем: \f(xi+1)—f (*i) I <Uf» где U—длина
звена Mi Mz+1 вписанной ломаной (см. рис. 173 на стр. 419).
п — 1
Отсюда следует, что v^ /^ //==/?, где р — периметр ломаной. А так
/=о
как p^s, то суммы v в совокупности ограничены числом s. Таким
образом, f (x)—функция с ограниченным изменением.
Достаточность. Пусть f(x)— функция с ограниченным
изменением на [а, Ь\. При любом дроблении промежутка fa, b] для
периметра р вписанной ломаной имеем**:
р = % = 2 V(xi+1 -х,)* + [f (*м) -/(Xi)]^
<S [(*/-n-*) + lf (*i+i)-f(*) !]=
= 2 (xm—Jf,) + S \f(Xi+J-f(x,)\ = (b-a) + v^b-a + V(J).
i=0 i=0 n
Таким образом, периметры р в совокупности ограничены и потому
кривая спрямляема
Определение длины, данное в начале этого параграфа, без
всякого изменения переносится и на кривые, заданные
параметрическими уравнениями:
*=ф(0. у=+(0 (to^t^T), (3)
где функции <р(/)иф(1) непрерывны (кривая (3), в частности, может
быть замкнутой). В этом случае для построения вписанной ломаной
следует разбить промежуток [/0, Т] на конечное число участков. Если
t0<t1<i...<tri = T суть точки деления, то за вершины ломаной
берутся точки Mi9 соответствующие значениям параметра tif
располагаемые в порядке возрастания параметра: (М0, Mlf ..., М^)***.
Для кривой (3) также справедлива теорема Жордана.
Теорема Жордана. Для того чтобы кривая (3) была
спрямляемой, необходимо и достаточно, чтобы q(t) и ty(t)
были функциями с ограниченным изменением.
* Как всегда, при определении кривой функция / (х) предполагается
непрерывной.
** Мы пользуемся здесь очевидным неравенством }^а2-\-Ь2^ \ а | + | b |.
*** Легко показать, что периметр такой ломаной вычисляется по формуле
71—1

В частности, если функции ср (t) и я|) (t) имеют непрерывные
производные, то длина вычисляется по формуле (3) из предыдущего
параграфа:
т
s=fyxi2 + yi2dt. (4)
to
Сказанное сейчас о спрямляемости кривых, заданных
параметрическими уравнениями, переносится и на пространственные
кривые. Так как пространственным кривым специально посвящена
глава XIII, то здесь мы на этом понятии останавливаемся лишь
вкратце, в связи с вопросом о спрямляемости кривых.
Пространственные кривые, как и плоские, часто задаются
параметрическими уравнениями. Иными словами, координаты х, у, г
точки пространственной кривой задаются как непрерывные
функции некоторого параметра t:
* = ф(*), 0 = Ф(О. * = х(0 Vo^t^T). (5)
Для пространственной кривой определение длины дуги может
быть дано в таком же виде, как и для плоской кривой. Если эта
кривая задана параметрическими уравнениями (5) и все три
функции имеют непрерывные производные, то справедливо следующее
обобщение формулы (4):
т
s=fyx?+y? + z?dt.
to
При stom длина дуги, отвечающая произвольному значению
параметра t из промежутка [t09 T] выразится формулой
s = s(t) = \Vx? + y? + z?dt
to
и, следовательно,
st =s' (t) = Vx? + y? + tf. (6).
§ 4. ПЛОЩАДЬ ПОВЕРХНОСТИ ВРАЩЕНИЯ
Пусть в плоскости OXY дана спрямляемая кривая АВ длины
S, заданная уравнением y = f(x), a^x^b (ри<\ 182), где функция
f(x) непрерывна вместе со своей производной на сегменте [а, Ь].
Для простоты рассуждений будем считать, что кривая АВ
расположена над осью ОХ (см. рис. 182). Если кривую АВ вращать
вокруг оси ОХ, то она опишет некоторую поверхность, которую
будем называть поверхностью вращения. Требуется вычислить
площадь Р этой поверхности.
430

Предварительно дадим определение площади поверхности
вращения. С этой целью разобьем промежуток [а, Ь] на п
произвольных частей точками а = х0<х1 <х2<....<Xi<xiJrl <...<Схп = b,
затем впишем в нашу кривую ломаную линию с вершинами Mi (х/,
у.) i = 0, 1, 2,..., п. Вместе
с кривой будем вращать
вокруг оси ОХ и эту
ломаную, в результате она
опишет поверхность,
составленную из п усеченных конусов
(в частном случае
вырождающихся в цилиндры или
конусы), площадь боковой
поверхности которых вычисляется
по известным нам правилам
элементарной геометрии.
Пусть по-прежнему К =
= max {Axi}— длина
наибольшего частичного промежутка,
где Axt = xi+1—Xi. Под площадью поверхности вращения кривой
будем понимать конечный предел * площади поверхности
вращения ломаной при Х->0. Таким образом, если через Рп
обозначить площадь поверхности вращения ломаной, то согласно
определению площади поверхности вращения кривой будем иметь:
Площадь боковой поверхности усеченного конуса, образованного
вращением i-vo звена, равна ** 2л/ **" ^^*i+1'lh где/; —длина хор-
Рис. 182.
ды MiMi+v Эта длина (как нам известно, из аналитической
геометрии) выражается формулой /; = V(xi+i—*/)2 + [/(*/+i)—ft*;)]2-
Но по теореме Лагранжа f (xi+1)—f (xt) =/' (|,-) (х?+1—*,-), xt ^
^?f<*f+i- Тогда li = Vl+f'2(li) &xi9 где Axi = Xi+1—xi. Значит,
для площади поверхности вращения ломаной будем иметь:
п — \
Разобьем эту сумму на две суммы следующим образом:
Рп=2л 2 f (Ь) Vl+ГЧЫ Ьх, +
+ я 2 [f (xO + f(xUl)-2f (|,)J 1/1 +f (?,) Axt.
(2)
* Если этот предел существует.
** Легко видеть, что из этой формулы как частный случай получаются
формулы для боковой поверхности цилиндра или конуса.
431

Первая сумма в правой части этого равенства является интеграль-
ь
ной суммой для интеграла 2я ^ f (x) V\ -\-f'2 (x) dx, и при А, -* 0 в силу
а
непрерывности функции f (x)Yl+ff2(x) интегральная сумма имеет
своим пределом этот интеграл. Покажем, что вторая сумма в правой
части равенства (2) стремится к нулю при Х-*0. Действительно,
в силу равномерной непрерывности функции / (х) в промежутке [а, Ь]
по всякому сколь угодно малому числу s>0 всегда найдется такое
8>0, что если только промежуток [а, Ь] разбить на части с
длинами, меньшими б, то есть А,<б, то каждая из разностей \f{xi) —
— f(li)\, \f(xi+1)—f(li)\ будет меньше е. Тогда \f (xt) + f (xi+1) —
- 2f (&) | ^ |f (xi)-f (Ь) \ + \f (*,+1)-f (h) |<e + 8 = 28 и, следова-
гельно, | я 21 U № + f M - 2f &)] V \+ГЧЬ) ^\^п Д] | f (*,) +
-f f (xi+1) - 2f (b) | Vl+Hfc) A*, < 2я8 "j? К1+/'¦&) A^i = 2я8 х
n—l
X 2 **<2nSe.
/ = 0
Так как 2nS — постоянное число, а е произвольно мало, то отсюда
следует, что рассматриваемая сумма стремится к нулю при А,—>*0.
Таким образом, переходя в равенстве (2) к пределу при А,->0,
мы получим:
ь ь
P=2n\f{x)V\+f2(x)dx или P*=2n\yVl+y'*{x)dx. (3)
а а
Замечание. Если кривая АВ задана параметрическими
уравнениями x = <p(t), y=tty(t)9 t0^t^T, где обе функции имеют
непрерывные производные на промежутке [t0, Т], причем ф' (t) ^ О,
а = Ф(/0), 6 = ф(Г), и тогда ф(0 монотонна на [/0, Г], то прежде
всего в этом случае мы можем от параметрической формы задания
кривой АВ перейти к явной форме y = f(x) и вычислить площадь
поверхности вращения по формуле (3). Чтобы получить выражение
площади через первоначальные функции x = ip(t), y = ty(t) и
параметр t, достаточно в интеграле (3) произвести замену переменной
по формулам x = q>(t), y=ty(t):
ь т
2я $ у VTTy^dx = 2n J ф (О Y l + (то)* ф' W dt =
a t0
Т
= 2я$ я|> (t) V<p'2 (t) + ф'я (0 dt.
t9
432

Следовательно, для площади поверхности вращения кривой,
ной параметрическими уравнениями, получаем формулу
задан-
Р=2п\ 4(0W2(0 + *'a(0 dt-
(4)
Впрочем, эта формула может быть выведена и без предположения
о монотонности функции ф(/)-
Наконец, если кривая задана уравнением в полярных
координатах: г = /(в), а^0^Р, где/(G) имеет непрерывную
производную f (0), то этот случай задания
кривой, как мы уже отмечали, с
помощью формул перехода х = rcos0 =
= f (0) cos 0, y = rsin 0 = / (0) sin 0
приводится к параметрической форме
задания кривой, если параметром
считать 0.
Так как xQ2 + y'Q2 = r2 + re\
формулы (4) получаем:
то
P=2n\r sin 8 V~r2 + r'Q2d@,
Рис. 183.
где а и (5 —углы полярных радиусов,
соответствующих точкам А и В.
Пример 1. Определить площадь поверхности шарового пояса.
Пусть дуга А В полуокружности ij—Yr^ — x2 вращается вокруг оси ОХ (рис. 183).
Вычислим площадь поверхности, образованной вращением этой дуги. Пусть
абсциссы ее концов будут хг и х2 > хх. Из данного уравнения окружности находим:
х R
P = 2n]yV\+y'*dx*
Vr2-
-2п]
-JC2-
Тогда формула (3) дает:
!/> — **
¦dx = 2nR ^dx = 27iRhy
где h = х2 — хг — высота пояса. Следовательно, площадь поверхности шарового
пояса равна произведению длины окружности большого круга на высоту шарового
пояса. Заметим, что если хг = — R, х2 = R и, значит, h — 2R, то получим: Р = 4я/?2
— площадь поверхности шара.
Пример 2. Найти площадь поверхности, образуемой вращением астроиды
вокруг оси ОХ.
Уравнения астроиды в параметрической форме суть х = а sin31, xl=acosH
(а>0). Так как кривая симметрична относительно оси OY (см. рис. 176 на стр.
421), то достаточно вычислить площадь поверхности, образованной вращением
дуги астроиды, находящейся в первой четверти.
Из уравнения астроиды находим: xt = 3а sin21 cos t, yt = — За cos2 t sin t и
потому xt' +#*2 = 9а2 sin2 ? cos2 ?. Тогда по формуле (4) получим:
-^-Р = 2п^ yVxi*+yi*dt=s2n Г a cos3 *• За sin tcostdt**
~2
= — 6 яа2 \ cos4 td cos t = — бяа2 —=—
о 5
6 12
¦у л а2. Отсюда Р = -г яа2
433

Пример 3. Найти площадь поверхности, образованной вращением
кардиоиды r = a(l+cos0) вокруг полярной оси (см. рис 172).
Из уравнения кардиоиды находим: rj= —a sin 0, так что г2 + г^2 = 4а2 cos2 -^-.
Тогда по формуле (5) получим:
та 7г
Р = 2л $ г sin б |/>2 4-/-'2 dO = 4ла2 ? (1 +cos6) sin 6 cos i- d6 =
о о ^
= Шла2 ^ cos4 ~- sin ~ dQ = - 32да2 ^
= -=- ла2.
о 5
Упражнения
1. Определить площадь поверхности, образованной вращением дуги
кубической параболы у = х3 вокруг оси ОХ от начала координат до дс = 1.
Отв. ^(К10б0-1).
2. Вычислить площадь поверхности, образованной вращением параболы у2 =
56
= 4ах вокруг оси ОХ от начала координат до х = 3а. Отв. -^-ла2.
о
3. Найти площадь поверхности, образованной вращением вокруг оси ОХ
петли кривой 9ау2 = х (За — х)2. Отв. Зла2.
4. Найти площадь поверхности тора, образованного вращением круга
х2-\-(у — Ь)2 = а2 вокруг оси ОХ, Ь>а. Отв. bn2ab.
5. Вычислить площадь поверхности, образованной вращением вокруг оси ОХ
I ? _?\
цепной линии f/ = -y \?а+? / от д: = 0 до * = а. Отв. — (е2 — е"2 + 4).
6. Вычислить площадь поверхности, образованной вращением вокруг оси ОХ
дуги синусоиды г/ = sin а: от * = 0 до * = л. Отв. 2л []/^2 -{- In (l-f-)/^)].
7. Определить площадь поверхности, образованной вращением вокруг оси ОХ
СП
дуги г/2 = 4 —|— jc, отсеченной прямой х = 2. Отв. -^-л.
о
8. Определить площадь поверхности, образованной вращением вокруг оси ОХ
и вокруг оси OY одной арки циклоиды х = а (t — sin t), y = a(l— cost)
64
Отв. -ула2; 16л2а2.
9. Определить площадь поверхности, образованной вращением петли кривой
x = t2, y=—(t2 — 3) вокруг оси ОХ. Отв. Зл.
10. Найти площадь поверхности, образованной вращением вокруг оси ОХ и
л
OY кривой x = efsintf y = e(cost от / = 0 до * = -~-.
Отв. |-7/2л"(е*-2); Ц^-(2е*+1).
П. Определить площадь поверхности, образованной вращением лемнискаты
r2 = a2cos20 около полярной оси. Отв. 2л (2 — У2) а2.
12. Найти площадь поверхности, образованной вращением кривой r = a2cos0
около полярной оси. Отв. па2.
§ 5. ВЫЧИСЛЕНИЕ ОБЪЕМОВ ТЕЛ
Понятие объема тела произвольной формы вводится совершенно
аналогично понятию площади плоской фигуры. Разница будет
состоять только в том, что если определение площади произвольной
434

плоской фигуры строилось на основе понятия площади
многоугольника, то в определении понятия объема тела произвольной формы
за основу берется понятие объема многогранника.
Пусть дано тело (V) произвольной формы, ограниченное
замкнутой поверхностью. Рассмотрим всевозможные многогранники (X)
объема X, целиком содержащиеся в теле (V), и многогранники (Y)
объема У, содержащие в себе (V). Рассуждая так же, как и в
случае определения площади, мы здесь убеждаемся в существовании
точной Еерхней границы V* для множества чисел {X} и точной
нижней границы V* для множества чисел {Y}, причем V^^V*.
Определение. Если обе границы V* = sup {X} и У* = т! {Y}
совпадают, то их общее значение V называется объемом тела (V),
а само тело в этом случае называется кубируемым.
Для объема имеют место предложения, аналогичные теоремам
1 и 2, установленные в § 1 гл. X для площадей, которые мы здесь
сформулируем применительно к объему.
Теорема 1. Для того чтобы тело (V) имело объем,
необходимо и достаточно, чтобы существовали такие две
последовательности, соответственно входящих и
выходящих многогранников {(Хп)) и {(Кя)}, объемы которых имели
бы общий предел \\тХп = \\т Yn= V. Этот предел и будет
объемом тела (V).
Теорема 2. Если для тела (V) можно построить две
последовательности соответственно входящих и
выходящих кубируемых тел {(Тп)} и {(17л)}» объемы которых
имеют общий предел lim Tn = \\mUn= V, то этот предел и
будет объемом тела (V).
На свойствах объема мы не останавливаемся; они аналогичны
тем, какие имеют место для площади.
Допустим сначала, что данное тело (V) есть прямой цилиндр
высоты Я, основанием которого служит квадрируемая фигура (Р).
Докажем, что объем этого цилиндра, так же как и объем
прямого кругового цилиндра, равен произведению площади основания
на высоту: V = P-H.
В самом деле, пусть многоугольники {(Ап)} и {(Вп)},
содержащиеся в (Р) и содержащие (Р) соответственно, таковы, что их
площади Ап и Вп стремятся к Р. Построим на этих многоугольниках
прямые призмы {(Qn)} и {(Rn)} высотой Н. Так как объемы этих
призм Qn = An-H и Rn = Bn-H имеют общий предел V = P-Hy то
в силу теоремы 1 этот предел и будет объемом данного цилиндра и,
значит, цилиндр кубируем.
Рассмотрим теперь некоторое тело (V). Допустим, что нам
известна площгдь любого его сечения, произведенного плоскостью,
перпендикулярной к некоторой прямой, например к оси ОХ (рис. 184).
Абсциссы крайних сечений тела обозначим через а и Ь. Площадь
сечения, перпендикулярного к оси ОХ, будет меняться вместе
с перемещением секущей плоскости, то есть каждому х между а и b
будет отвечать некоторое сечение с определенной площадью; поэтому
435

площадь этого поперечного сечения будет некоторой функцией от х.
Обозначим эту функцию через S (х) и будем считать ее
непрерывной функцией на [а, Ь].
Допустим, что любая пара сечений, будучи ортогонально
спроектирована на плоскость, перпендикулярную к оси ОХ, дает проекции,
целиком лежащие одна в другой.
При этих условиях тело (V) имеет
объем V, который выражается
формулой
ь
V=\S(x)dx. (1)
а
Действительно, разобьем
промежуток [а, Ь] произвольно на п
частей точками a-=x()<ix1<c.x2<i
<.. • < xi < xi+1 <...<*„ = &.
Через эти точки проведем плоскости, перпендикулярные к оси ОХ. Эти
плоскости разобьют тело (V) на п тонких слоев, толщина каждого
из которых равна величине Дх; = хг-+1—xt- (i = 0, 1, 2, ..., п— 1).
Рассмотрим i-и слой, заключенный между плоскостями х = х; и
x = xi+1 (i = 0, 1, 2, ..., п—1). Обозначим через /п* и М-г
соответственно наименьшее и наибольшее значения функции S (х) в
частичном промежутке [х/, X/+i]— это будут площади наименьшего и
наибольшего сечения в /-м промежутке. Легко видеть, что i-й слой
содержится между двумя прямыми цилиндрами высоты Ах,-,
построенными на сечениях площади /П/ и Mt. Объемы этих цилиндров
равны соответственно mt-Ax; и MiAxi. Построив такие цилиндры
для каждого слоя, мы получим два ступенчатых тела, одно из
которых состоит из входящих цилиндров, а следовательно, содержится
в данном теле (V), а другое — из выходящих цилиндров и,
следовательно, содержит данное тело. Объемы этих тел соответственно равны:
п—\ п—\
тп= 2 mi А*ь tf«= 2 Mi Ax*.
i = 0 1 = 0
Поскольку эти суммы являются суммами Дарбу для
непрерывной функции S(x), то они являются просто наименьшей и
наибольшей из интегральных сумм. Тогда по теореме о существовании
определенного интеграла обе суммы при Я = тах Дх; -> 0 имеют своим
ь
общим пределом интеграл § S (x) dx, откуда и следует, в силу тео-
а
ремы 2, что этот интеграл и будет выражать собой объем
рассматриваемого тела (V); так что формула (1) доказана *.
В случае, когда рассматриваемое тело получено вращением
некоторой кривой y = f(x) вокруг оси ОХ (рис. 185), в сечении этого
* Формула (1) пригодна для вычисления объемов практически любых тел, а не
только тех, которые обладают указанным вначале условием.
436

тела плоскостями, перпендикулярными к оси ОХ, будут получаться
круги площади S (х) = яу2 = пр (х). Подставив это в формулу (1),
получим формулу для вычисления объема тела вращения:
(2)
Замечание. Если кривая, вращением которой образуется тело
вращения, задана параметрическими уравнениями
x=4>Vh 0 = Ф(О. а<г<р, (3)
где ф(/) и ty(t) удовлетворяют упоминавшимся ранее в аналогичных
случаях требованиям, то, производя замену переменной в
интеграле (2) по формулам (3), получим:
(4)
где а и Р таковы, что ср(а) = а и ц>ф) = Ь.
Иногда приходится вычислять объем тела, полученного
вращением кривой x=g(y)f c^y^d вокруг оси 0Y (рис. 186). Объем
этого тела вращения вычисляется по формуле
d
V = n^x2dyy
с
которая выводится аналогично формуле (2).
Подводя итог сказанному, заметим что аналогично результату,
указанному в параграфе о площади плоской фигуры, и здесь можно
доказать, что если тело (V)
ограничено несколькими поверхностями, VI
каждая из которых порознь задается
явным уравнением одного из трех
Рис. 185.
видов: 2 = f(x, у), y=g(z, x),x = h(y, z) (где /, g, А — непрерывные
функции в некоторых ограниченных областях), то это тело ку-
бируемо.
437

Замечание. Возвращаясь снова к основной формуле (1):
ъ
V =^ S(x) dx, мы видим, что для вычисления объема тела по этой фор-
а
муле важно знать только площади S(x) его поперечных сечений, форма
же этих сечений на играет при этом никакой роли. Поэтому из
этой формулы непосредственно вытекает так называемый принцип
Кавальер и, названный так по имени итальянского математика
XVII века Кавальер и.
Принцип Кавальери для объемов. Если два тела,
содержащиеся между двумя параллельными плоскостями Л и Б,
обладают тем свойством, что в сечении их любой плоскостью С,
параллельной А и В, получаются всегда равновеликие фигуры, то
объемы этих тел равны.
Исходя из формулы (8) § 1 этой главы, можно сформулировать
аналогичный принцип и для площадей плоских фигур.
С развитием дифференциального и интегрального исчисления
принцип Кавальери утратил свое былое значение, однако в
элементарной геометрии он и сейчас применяется для вычисления объемов.
Рассмотрим теперь ряд примеров на вычисление объемов.
Пример 1. Вычислить объем тела, отсеченного от прямого кругового
цилиндра плоскостью, проходящей через диаметр основания (рис. 187).
Пусть R— радиус основания цилиндра, а — угол между секущей плоскостью
и основанием цилиндра. В произвольной точке х производим сечение,
перпендикулярное к оси ОХ. Это сечение будет прямоугольным треугольником ABC,
площадь которого 5 (х) = 7г-ВС • АС. Но АС = у и ВС=у tga. Следовательно, ?(*) =
1
= jr-y2 tga, а так как y2 = R2 — х2, то площадь сечения запишется так: S (х) =
= -S (R2 — х2) tga, — R^x^-\-R. Тогда согласно формуле (1) находим:
R R
~3J|o
-R 0
= tg a (' R3-^] = 4" Я3 tgcc = -r R2h> где h = KL = Riga.
l/ = i_tga С (R2 — x2)dx = tga [ (R2 — x2)dx = \ga(R2x
Рис. 188.
438

Эту задачу можно решить иначе, если производить сечение тела плоскостями „
перпендикулярными к оси OY (рис. 188). В результате в сечении получим
прямоугольники с площадью
S(y) = AD.MN = 2VR*—y*ytga.
Тогда искомый объем будет:
R R R ]
V = \S(y)dy = 2iga\y R2-y2ydy = -tga$(R2-y2)2 d(-y2) =
= -tga|-(tf2-r/2)2
o*-Tt«a*,-T**
Пример 2. Вычислить объем тора (кольца), образуемого вращением круга
около непересекающей его прямой, лежащей в его-
плоскости (рис. 189).
Пусть расстояние центра круга от оси вращения
равно Ь. Приняв ось вращения за ось ОХ, а
прямую ОС за ось OY, получим уравнение окруж-
rk
Рис. 189. Рис. 190.
ности x2 + (y — b)2 — a2(b>a), где а —радиус круга. Из этого уравнения находим:
ух = Ъ + У а2 — х2 — для верхней части окружности,
у2 = Ь—У^а2 — х2 — для нижней части окружности.
Тогда объем тора определится как разность двух объемов, каждый из
которых вычисляется по формуле (2):
а а а а
1/ = 2я \у\ dx-2n\y\ dx = 2n \ (y\~y'i) dx = 2n fa+yj (У1-У2) dx =
0 0 0 0
а
= 8кЬ i Va2 — x2 dx = ЫЬ fy У а2 — х2 + у arcsin -j\
= 2n2a2b *.
о
Пример 3. Вычислить объем тела, образованного вращением одной арки
циклоиды
x = a(t— sin 0, y = a(l—cost)
вокруг ее основания (рис. 190).
* Вычисление \У а2 — х2 dx см. гл. VIII, § 4, пример 1.
439

Объем этого тела вычисляется по формуле (4). Следовательно
2я 2я 2л
я $ y2x'tdt=na* J (1— cos/)3<# = rca3 J (1— 3 cos* + 3cos2/—cos* t)dt=*
= яа3 fy t — 4 sin / + -|- sin 2/+ -^ sin3 A
2я
= 2я2а3.
о
Упражнения
1. Точка пересечения диагоналей квадрата перемещается вдоль диаметра
круга радиуса а; при этом плоскость, в которой лежит квадрат, все время
остается перпендикулярной к плоскости круга, а две противоположные вершины
квадрата перемещаются по окружности. Найти объем тела, образуемого
движущимся квадратом.
Отв.—а?.
х2 у2
2. Определить объем тела, полученного вращением эллипса -y + ih"313! вок_
4
руг оси ОХ. Отв. -5- nba2.
о
3. Определить объем тела, полученного вращением полуволны синусоиды
я2
у = sin х вокруг оси ОХ. Отв. -у.
4. Определить объем тела, полученного вращением астроиды Jt = acos3?,
32
y==asm3t вокруг осей ОХ и OY. Отв. у^= яа3.
5. Определить объем тела, образованного вращением фигуры, ограниченной
линиями:
а) х// = 4, *=1, х = 4, у —0 вокруг оси ОХ, Отв. 12я.
б) #2 = (*_(_ 4)з, х = 0 вокруг оси OY. Отв. 58,5я.
512
в) г/2 = 4 —х, х = 0 вокруг оси OY. Отв. -у=- я.
г) у = х2, у = 4 вокруг прямой *==2.
2
д) г/ = sin л:, # = —х вокруг оси ОХ, дг;>0.
е) г = a2 cos в вокруг полярной оси.
§ 6. СТАТИЧЕСКИЙ МОМЕНТ И ЦЕНТР ТЯЖЕСТИ
Рассмотренные выше задачи на геометрические приложения
определенного интеграла показывают, что для решения их применяется
один и тот же вычислительный метод: составляют интегральные
суммы, а затем предельным переходом получают интеграл,
выражающий искомую величину. Этим же методом решают целый ряд
других задач из механики, физики и техники. В качестве первого
примера приложения определенного интеграла к задачам из
указанных областей рассмотрим вопрос из механики—определение
статического момента и центра тяжести материальной кривой.
1. Статический момент и центр тяжести материальной кривой.
Пусть на плоскости OXY мы имеем материальную точку А массы
т (рис. 191). Тогда, как известно из механики, статическим моментом
материальной точки А (т) относительно какой-нибудь оси называ-
440
Отв.
Отв
Отв.
128
"з"л
я2
'• 12
яа6
~6~

Y| *
•
•
•
.
0
щ
•
•
•
• •
\A3
A
e
•
•
,C
•
•
•
о
e
•
*. •
• An
•
X
ется произведение массы этой точки на расстояние ее до этой оси;
при этом для точек, лежащих по одну сторону от оси, расстоянию
приписывается знак плюс, а по другую — знак минус. Таким
образом, произведения тх и ту суть статические моменты точки А
соответственно относительно осей 0Y и ОХ,
Если имеется система материальных точек,то статическим
моментом этой системы относительно некоторой оси называется
сумма статических моментов отдельных ее точек относительно
той же оси. Статические моменты системы материальных точек
относительно осей ОХ и 0Y будем соответственно обозначать через Мх и
Му, Таким образом,если мы имеем в плоскости OXY систему
материальных точек Аг(хъ уг)ч А2(х2, у2), ..., Ап(хп, уп) (рис. 192), в
которых сосредоточены соответственно массытг, т2,..., тп, то для
статических моментов Мх и Му этой системы относительно осей ОХ
и 0Y будем иметь:
п п
i=l i=l
Из механики также известно,что центр тяжести каждой системы
материальных точек можно определить как такую точку С, что
если в ней сосредоточить массы всех точек системы, то ее статический
момент относительно любой оси будет равен статическому
моменту всей системы точек относительно той же оси.
Следовательно, если мы имеем в плоскости OXY систему п материальных точек,
то согласно определению центра тяжести будем иметь:
п п п п
хс? /я* = 2 гпьхс, уС']? /га/ = 2 т*У*>
/=1 t = i i = i ,• = !
где хс, Ус—координаты центра тяжести данной системы. Отсюда
находим координаты центра тяжести рассматриваемой системы:
п
Д] miyi
Ус=~ . (2)
/=1
Yi
о\
1
Afm)
т
i у
>
X
К
Рис. 191.
Хс =
2] miXi
/=i
5>«
/=1
441

Рассмотрим теперь случай, когда система материальных точек
заполняет сплошь некоторую плоскую кривую АВ, то есть случай
плоской материальной кривой. Определим статические моменты этой
кривой относительно осей координат и ее центр тяжести (рис. 193).
Будем считать,что кривая АВ задана параметрическими
уравнениями * = ф (s), y=ty (s),0^s^S,
где параметром s является длина
дуги* кривой, отсчитываемая от
начальной точкиЛ до переменной
точки М с координатами х, у, a S
обозначает длину всей кривой А В.
Когда точка М описывает кривую
АВ, параметр s изменяется от О
до 5. Функции <p(s) и я|> (s) мы
полагаем непрерывными на [О, S].
При этом будем считать, что
материальная кривая однородна, то
есть вдоль по этой кривой непрерывным образом распределена масса
так, что ее линейная плотность р (то есть масса, приходящаяся на
единицу длины) постоянна.
Вычислим статические моменты Мх и Му этой материальной
кривой относительно осей ОХ и OY. Для этого кривую А В разделим на п
частей точками A = A0(x0i y0), Аг(хг, уг), ..., Ai(xh yt), ...
,.., Ап(хп, уп) = В.
Пусть эти точки соответствуют значениям s0 = О <С sx <C s2 <... <
< St < si+1 <... < sn = S переменной дуги s. Если длину дуги AiAi+i
обозначить через Asi = si+1 — s,-, а массу этой дуги — через ти то
mi = pAsi(i = 0, 1,2,... ,п—1). При достаточно мелком дроблении
кривой АВ на части приближенно можно считать, что вся масса r-й дуги
AiAi+1 сосредоточена в одной какой-нибудь ее точке, например в
начальной точке Ai(Xi, у,), где / = 0,1,2, ... уп—1. При таком
допущении вся наша материальная кривая АВ приближенно заменится
системой, состоящей из п материальных точек: Л0, А1} Л2, ... , Аи • • • ,Ап-\-
Тогда статический момент Мх кривой АВ приближенно будет равен
сумме статических моментов этих п материальных точек относительно
оси ОХ. Следовательно,
п— 1 п — \
I = 0 / = 0
Ясно, что это приближенное равенство будет тем более точным, чем
мельче дробление дуги АВ, то есть чем меньше A, = max {As,-} — длина
наибольшей частичной дуги. Поэтому естественно считать, что в
* Так как с изменением длины дуги AM изменяется положение точки М (*, у)
на кривой и, следовательно, изменяются ее координаты х и у, то последние
являются функциями от s: * = (p(s), y = ty(s).
442

пределе, когда А,-*0, мы получим точное значение статического
момента Мх:
п- 1
Мх = р lim У. ytAsi.
Так как мы имеем здесь предел интегральной суммы,
составленной для непрерывной функции y = ty(s) на сегменте [0, 5], то этот
s
предел существует и равен интегралу р^ yds. Следовательно, для
о
статического момента кривой АВ относительно оси ОХ мы будем
иметь:
Мх = р\ yds. (3)
о
Рассуждая аналогичным образом, мы получим выражение
статического момента кривой АВ относительно оси OY:
s
Му = р^ xds. (4)
о
Теперь найдем координаты хС1 ус центра тяжести кривой АВ.
Так как вся масса этой кривой равна /n = pS, то (согласно
определению центра тяжести) мы должны иметь: тхс = Му, тус = Мх.
му мх
Отсюда хс =—, ус = —.
Подставляя сюда значения Мх, Му и т, окончательно получаем:
5 S
J х (s) ds ^ у (s) ds
хс = °—ё—, ус = 0—^—. (5)
Эти формулы показывают, что в случае однородной кривой
координаты ее центра тяжести зависят не от плотности, а только от формы
кривой*.
Следует заметить, что если кривая симметрична относительно
какой-нибудь оси, то, как легко видеть, центр тяжести ее лежит на
этой оси.
При использовании формул (5) на практике параметр 5 обычно
заменяют через ту переменную интегрирования, которая играет роль
независимой переменной в уравнении кривой АВ. Так, например,
если кривая задана в явном виде уравнением у = у (х) (а^х^Ь),
для которой дифференциал дуги ds = \r\-\-y'2, dx (см. формулу (7)
* Для неоднородной кривой, то есть р ф const в формулах (3) и (4)
плотность будет под знаком интеграла, и формулы (5) принимают вид:
5 б'
\ р xds \ р у ds s
хс = - Ус = - , гДе т = \ Р (s) ds.
т ' т
о
443

§ 2), то формулы (5) в этом случае принимают вид:
\xV^+y'Ux
\yVl+y'ldx
Ус =
(6)
Пример 1. Найти центр тяжести дуги АВ окружности х2 + у2 =
-= г2, лежащей в первой четверти (рис. 194).
В качестве независимой переменной выберем х\ тогда у=УV2 — х2,
0:
; г. Отсюда у' =
/г2 — х*
и Vl+y'x2 =
У> —х2'
Так как длина
четверти окружности равна -у, то по формулам (6) находим:
г г 1
*С = М ?rdx =—[ (r2-x2)~^d{—x2) = --(r2-x2)
О О
#с =— \ V r2 — x2—F= = — \ d#=—.
*с яг J r )/г2 —л:2 я J я
2г#
Из второй формулы (6) мы получаем: yc-S = ^yV 1 + Ух2йх. Умно-
а
жая обе части равенства на 2я, будем иметь:
б
2пус • S = 2л; $ у ]Л + у/ d*.
Правая часть этого равенства есть площадь Р поверхности,
образованной вращением дуги АВ вокруг оси ОХ. В левой части
1 множитель 2пус—длина окружности, опи-
** санной центром тяжести кривой при
вращении ее вокруг оси OX, a S—длина дуги
АВ; так что
P = 2nyc.S (7)
О
В
Рис. 194.
и мы приходим к первой теореме
Гульдина*: площадь поверхности, по-
-*- лученной от вращения кривой вокруг оси,
X не пересекающей ее, равна произведению длины
дуги этой кривой на путь, описываемый
центром тяжести этой кривой.
Эта теорема позволяет найти площадь поверхности вращения,
если известно положение центра тяжести вращающейся кривой,
и обратно — определить центр тяжести кривой, если известна
площадь поверхности вращения ее вокруг оси.
2_ Я 2
Пример 2. Определить центр тяжести дуги астроиды xz +у* = а3,
лежащей в первой четверти (см. рис. 176 на стр. 421).
Пауль Гульдин (1577 — 1643) —швейцарский математик.
444

Так как величина площади поверхности, описанной этой дугой при вращении
вокруг любой из осей, равна -~-па2 (см. §4, пример 2), а длина этой дуги равна
3
— а (см. § 2, пример 3), то по первой теореме Гульдина сразу находим: хс = ус =
2
Пример 3. Найти площадь поверхности тора, образованного вращением
вокруг оси ОХ окружности х2-\-(у — 6)2 = а2, при этом а<.Ь (см. рис. 189 на
стр. 439).
Длина окружности равна s = 2na. Центр тяжести окружности, очевидно,
совпадает с ее центром, который отстоит от оси ОХ на расстоянии, равном Ь.
Следовательно, длина пути, описываемого центром тяжести при вращении вокруг
оси ОХ, равна 2nb. Тогда по формуле (7) Р = 2л6 • 2ла = 4л2аЬ.
2. Статический момент и центр тяжести плоской фигуры.
Перейдем теперь к определению статического момента и координат
центра тяжести плоской материальной фигуры — тонкой пластинки
постоянной толщины. Пусть эта
пластинка однородна, то есть Y[
по всей площади ее равномерно
распределена масса, так что
поверхностная плотность ее (то
есть масса, приходящаяся на
единицу площади) постоянна.
Пусть эта пластинка имеет
геометрическую форму фигуры
ABCD, ограниченной снизу и
сверху соответственно
непрерывными кривыми y=g(x),
y = f (x)(a^x^b) исбоковот- ~q\
резками прямых х = а, х = Ь
{ркс. 195). Вычислим
статические моменты этой пластинки
относительно осей ОХ и 0Y,
обозначив их соответственно через Мх и Мг Для этого разобьем сегмент
[а, Ь] на п частей точками a = x0<*i<*2<---<**<*t+i<-- <
<хп = Ь и пусть А, = тах {А*/}, где Axi = xi+1—xt. Прямыми x = xt
(i = 0y 1, 2,..., п) разобьем нашу фигуру ABCD на п узких полос.
Так как функции f (x) и g(x) непрерывны, то при достаточно
мелком дроблении промежутка [а, Ь\ они мало меняются в каждом
из полученных промежутков [лгь xi+1] (1 = 0, 1, 2,..., п — 1).
Поэтому без большой погрешности их можно считать на промежутке
[xi, xi+1] постоянными и равными значениям /(&) и gfe), где & —
средняя точка промежутка [xit xi+1]. Ясно, что сделанное
допущение равносильно тому, что мы заменяем приближенно упомянутые
выше полоски соответствующими прямоугольниками, а всю нашу
фигуру A BCD — ступенчатой фигурой, изображенной на рисунке 195.
В этом случае масса нашей фигуры приближенно заменится массой
ступенчатой фигуры.
Рис. 195.
445

Таким образом, если речь идет об /-й полоске, то она
приближенно заменяется прямоугольником с высотой, равной разности
ординат /(gf) — g(b)> и основанием, равным величине Дл;г.
Так как площадь такого прямоугольника равна [/(?*•)—g(%i)]&Xi>
то масса его равна р [f(li) — g(lt)] Ax? (/ = 0, 1, 2,..., п— 1).
Эта величина и будет приближенной массой i-й полоски. Из
механики известно, что центр тяжести прямоугольника лежит
в точке пересечения его диагоналей и, следовательно, координаты
центра тяжести i-го прямоугольника равны соответственно |,- и
Будем считать, что вся масса /-го прямоугольника сосредоточена
в его центре и, следовательно, статические моменты г'-й полоски
относительно осей ОХ и OY (соответственно) приближенно будут
равны:
р [/ &)-*&)] л*,-j и (id+g т=12 р [f2 do -s2 а*)] д*ь
р [/а.) -g(i,)]A^-1,-.
Просуммировав статические моменты всех прямоугольников
относительно осей ОХ и OY соответственно, мы получим приближенное
значение статических моментов Мх и Му всей фигуры ABCD:
м*^р2[/2&)-?2&)]л*< и My^pj^hudd-gdi)]^.
i=0 /=0
Эти приближенные равенства будут тем точнее, чем мельче дробление
промежутка [а, Ь], то есть чем меньше X. Поэтому естественно
считать, что в пределе, когда А,->0, мы получим точные равенства:
Мх = ±- р lim 2 [Г (h) -tf fc) ] Д*ь
My = p lim 2 b [/ &)-*&) ] A**.
Так как мы имеем здесь пределы интегральных сумм,
составленных соответственно для непрерывных на сегменте [а, Ь] функций
[/2 (х) — g2 (х) ] и х [f (х) — g (x) ], то эти пределы существуют и
равны соответственно интегралам:
1 b ь
у Р \ [f2 (х) -g2 (х)} dx и р \х [f (x) -g (x)] dx.
а а
Следовательно,
ь ь
Mx=±p\\f2{x)-g2(x)\dx и My = p{x{j(x)-g(x)]dx.
а и
446

Рис. 196.
Рис. 197.
Теперь найдем координаты хс, ус центра тяжести фигуры ABCD.
Так как масса всей фигуры равна
ь
т = р \[f(x)—g(x)] dx = pP,
а
где Р — площадь всей фигуры, то для определения координат центра
тяжести фигуры, как и в предыдущем случае, значение статических
моментов Мх и Му следует разделить на массу всей фигуры:
Л**
}xU(x)-g(*)\dx
Ус = -
М,
о
*(*)-«* Ml *с
(8)
Отсюда видно, что в случае однородной пластинки координаты
центра тяжести ее зависят не от плотности, а только от геометрической
формы пластинки.
Замечание. Если фигура ABCD есть криволинейная трапеция,
ограниченная сверху кривой y = f(x), a^x^b, с боков двумя
ординатами х = а, х = Ъ и снизу отрезком оси ОХ (рис. 196), то,
полагая в формулах (8) g(x) = 0, получим:
о
ь 1 с
]xydx J}»2**
Хг = -
-. Ус
(9)
где P = [ydx — площадь данной трапеции.
а
Пример 4. Найти центр тяжести фигуры (однородной пластинки)*, ограни-
2
ценной прямой у = —х, синусоидой y=sinx при *> 0 (см. рис. 197}
* Ниже, говоря о центре тяжести фигуры, мы будем всегда иметь в виду центр
тяжести однородной пластинки.
447

Легко видеть, что прямая и синусоида пересекаются в начале координат и при
я
#=-^-. Тогда по формулам (8) будем иметь:
2
/!
О ^0
1 Г, , . . |Т Я*"| 1 / Я*'
12 —я»
Ус
= w\{s™x-^x2)dx=5p[\sin2xdx-^-i
А
Так как
1 / 1 я л\ я
2Р \~2 2""~?J~"24P*
f> = V | sin x *j dx = — (cos л: -J
2 4 — я
_12 —я2 _ я
*c — 12 — Зя' Ус~2А— 6яв
Пример б. Найти координаты центра тяжести фигуры, ограниченной
кривой V^jc -\-Yy = Ya * и осями координат (рис. 198).
Из уравнения Yx+Yy=Ya находим. у=а+х—2]Лщ О^л^а.
Тогда формулы (9) дают:
а а
*с = -р \ xydx = — V x(a + x—2Yax) dx=^p-f
о 6
а а
Ус^~ \ У***=^р J (a+x-21^)2^=^.
а а
Поскольку P^\ydx=\{a+x—2Y~ax)dx==-?-, то хс = ус = ^ч то есть
о о
центр тяжести лежит на биссектрисе первого координатного угла. Это можно
было предвидеть, если учесть, что фигура симметрична относительно указанной
биссектрисы.
Перепишем формулу (8) для ус следующим образом:
2yc-P = \[P{x)-g*(x)]dx,
* Эта кривая является параболой, осью которой служит биссектриса первого
координатного угла.
448

Рис. 198.
R х
откуда (после умножения на я) получим:
ь
2nyc.P = n\[f*(x)-g*(x)]dx.
Правая часть этого равенства представляет собой объем V тела,
образованного вращением плоской фигуры ABCD (см. рис. 195)
вокруг оси ОХ. Объем этого тела равен разности объемов тел,
полученных при вращении вокруг оси ОХ криволинейной трапеции,
ограниченной сверху кривой y = f(x), и трапеции, ограниченной
сверху кривой y=g{x). Поэтому
V = P-2nye
(10)
Эта формула выражает собою вторую теорему Гуль-
дин а: объем тела, образованного вращением плоской фигуры вокруг
не пересекающей ее оси, равен произведению площади этой фигуры
на длину окружности, описываемой центром тяжести фигуры.
Вторая теорема Гульдина позволяет по двум из величин,
входящих в формулу (10), находить третью. Покажем это на примерах.
Пример 6. Вычислить объем тора, образованного вращением круга
*2-+-(*/ — Ь)2 = а2 вокруг оси ОХ, Ь>а (см. рис. 189).
Площадь данного круга равна Р — па2, центр тяжести круга совпадает с его
центром, то есть лежит в точке (0, 6), и, следовательно, путь, описываемый
центром тяжести круга при вращении его вокруг оси ОХ, равен 2nb. Тогда по
формуле (10) находим: V =2кЬ • ла2 = 2л2а26.
Пример 7. Найти центр тяжести однородного полукруга, ограниченного
осью ОХ и полуокружностью у = У R2 — х2 (рис. 199).
В силу симметрии хс = 0. Для отыскания ординаты центра тяжести восполь-
1 V
зуемся формулой (10), согласно которой ус = —— . —-. Но в нашем случае
1 4
P = —jiR2 и К = -5"Л/?3 как объем шара, полученного вращением полукруга
4
вокруг своего диаметра. Поэтому ус = ~— /? ^ 0,425/?.
449

Упражнения
1. Пользуясь первой теоремой Гульдина, определить центр тяжести
следующих кривых:
а) дуги АВ окружности радиуса R (рис. 183), используя результат примера 1
§ 4 для случая хх —— х2.
г/г
Отв. лгс«=0, ус = —, где s—длина дуги АВ, h— длина хорды А В.
б) одной арки циклоиды #=а (t — sin t), y~a(l—cost) (рис. 177).
4
Отв. xc = nat yc = ~a.
2. Найти координаты центра тяжести полуокружности радиуса г.
2г
Отв. *с = 0, ус = — .
я
3. Найти центр тяжести дуги окружности радиуса /?, стягивающей
центральный угол а. а
Отв. Центр тяжести лежит на биссектрисе угла а на расстоянии 2R от
центра.
4. Найти центр тяжести фигуры, расположенной в первой четверти и огра-
ниченной эллипсом *2-(-^-=1 и окружностью х2 + */2=1.
Отв. хс=±, ус = ±.
5. Определить положение центра тяжести фигуры, ограниченной синусоидой
y = smx и отрезком оси ОХ от х = 0 до # = я. Отв. л:с = 1г-т ус=~-ш
Z 8
6. Найти центр тяжести фигуры, ограниченной косинусоидой y = cosx от
ял „1 Л л 2л + 31ЛТ
д: = до х = — и прямой у =—. Отв. *с = 0, ус = ~ .
2.2 2 24V'3-8n
7. Найти центр тяжести фигуры, ограниченной параболами уг—2рх и
х2 = 2ру. Отв. хс^ус = 0,9р.
8. Найти центр тяжести фигуры, ограниченной полукубической параболой
ау2 = х3 и прямой х — а, а>0. Отв. хс — ~у ус = 0.
9. Найти центр тяжести параболического сегмента, отсекаемого от параболы
3
у2 = 2рх прямой x = h. Отв. *с = —/г, ус = 0.
10. Найти центр тяжести фигуры, ограниченной одной аркой циклоиды
5
х=а (t— sin t)f y = a(l—cost). Отв. хс = ла, yc = —aw
И. Пользуясь второй теоремой Гульдина, найти центр тяжести полукруга
радиуса а. Отв. хс = 0, ус= о—.
оя
§ 7. РАБОТА ПЕРЕМЕННОЙ СИЛЫ
Из механики известно, что если действующая на материальную
точку сила F сохраняет постоянную величину и постоянное
направление*, совпадающее с направлением движения, а само перемещение
* Всюду в тексте книги жирным шрифтом обозначены векторы. Если
а—вектор, то \а\ обозначает его длину. Иногда, чтобы отличать векторы от скаляров^
над буквами, обозначающими векторы, ставят черту или стрелку: а или Ъ. При
рукописной записи (когда «жирное написание» невозможно) необходимо
пользоваться одним из последних обозначений.
450

А " F В
5=S0 s s = S
Рис. 200.
точки происходит прямолинейно, то работа W этой силы на пути s
вычисляется по формуле
W = F-s. (1)
Пусть теперь материальная точка М движется по прямой линии
под действием переменной силы F, причем направление силы
совпадает с направлением движения. Требуется определить работу,
произведенную силой F при перемещении точки М из начального
положения А в конечное положение В (рис. 200). Длину пути s,
проходимого точкой М, будем отсчитывать от некоторой точки О
прямой (см. рис. 200).
Положение переменной точки М вполне определяется длиной
отрезка ОМ, то есть величиной s. Пусть начальная и конечная точки
пути (то есть А и В) отстоят от начала О соответственно на
расстоянии 50 и S. Тогда каждому значению s из промежутка [s0, S]
отвечает определенное положение точки М на пути АВ. Если к тому
же учесть, что сила F имеет определенную величину в каждой точке
пути АВ, то эту силу можно рассматривать как функцию
расстояния s: F=F(s).
Мы считаем, что F(s) является непрерывной функцией от s в
промежутке [s0, S]. Работу, произведенную этой силой при
перемещении точки М вдоль пути АВ, то есть на участке пути от s0 до S,
можно определить следующим образом.
Разобьем промежуток [s0, S] на п произвольных частей
точками s0<s1<s2<...<s/<s/+1<...<s/I = S и пусть A,=max{As?},
где Asi = sr+1 — Si— длина /-го участка пути (рис. 201). Выберем в
каждом из полученных промежутков [st, si+1], где / = 0, 1, 2,...
..., п— 1, произвольную точку li (Si^lf^Sf+i). Сила, действующая
в этой точке, равна F=F (&). Если дробление промежутка [s0, S]
достаточно мелко, то (в силу непрерывности) сила F (s) мало
изменяется при Si, ^s^si+1, и поэтому приближенно будем считать, что
сила F в каждом из промежутков [sb S;+1] не изменяется и
сохраняет величину, равную, например, значению F (?,-). Так как рабо-
А тт
(J • * • • * • I I Ш • % %В
5 = 0 So S, 52 5, 5,- SU, ^.7 Sn=S
Рис. 201.
451

та такой силы на каждом из промежутков [s/, s/+1] выражается в
силу формулы (1) произведением F (Ц) As,-, то работа этой силы
на всем промежутке пути [s0, S] будет равна сумме*
n^F(h)^sh (2)
/=о
Величина этой суммы является лишь приближенным значением
искомой работы W, причем тем более точным, чем короче участки
[s/, s/j-x], то есть чем меньше Я. Поэтому вполне естественно точнее
значение работы определить как предел суммы (2) при Х,->0:
п- 1
Так как мы имеем здесь предел интегральной суммы,
составленной для непрерывной функции F (s) на промежутке [s0, S], то
s
этот пгедел существует и равен интегралу $ F (s) as. Таким обра-
зом, для искомой работы мы будем иметь:
s
W = \F(s)ds. (3)
So
Пример 1. Вычислить работу, совершаемую при сжатии
пружины на 20 еж, если известно**, что сила пропорциональна сжатию
пружины и что для сжатия на 1 см необходима сила в 2 кГ.
Здесь мы имеем случай работы переменной силы: сила
возрастает пропорционально сжатию пружины. Если сжатие пружины
обозначить через s (рис. 202), то силу можно записать формулой
F = ks, (4)
где k — некоторая постоянная, зависящая от упругих свойств
пружины. Найдем работу этой силы, которую она производит при
сжатии пружины на 20 см, то есть на пути от s0 = 0 до S = 0,2 м.
Вычислим эту работу в технической системе единиц, то есть в
килограммометрах (сокращенно кГм).
Согласно формуле (3) будем иметь:
«н
S 0,2 0.2
Fds=\ ksds = ks-^\ =к^-^- кГм.
о о
* Из механики известно, что работа силы на некотором пути равна су>ше
ее работ, соответствующих отдельным участкам, на которые разбит весь путЪ.
** Закон Гука.
452

Численное значение k определим из формулы (4) при условии, что
F=2kC a s = 0,01 ж, то есть k = ?- = g-|j-=20G.
Подставляя это значение &, мы и получим искомую работу
w/ 200-(0,2)2
W = ^ ; кГм = 4 кГм.
Приведем еще один пример на вычисление работы, решение
которого не будет опираться на формулу (3).
Пример 2. Вычислить работу, необходимую для того, чтобы
выкачать воду из полусферического сосуда (котла), радиус которого
R (рис. 203).
Задача сводится к вычислению работы, которую следует
затратить для того, чтобы последовательно поднять все частицы воды
на уровень краев котла, так как дальше она уже под действием
собственной силы тяжести сама вытекает из него. При этом можно
считать, что каждая частица опишет путь, равный глубине ее
погружения в котле. Так как сила, которую надо прикладывать к
каждой частице при ее поднятии, равна Еесу частицы, то работа
поднятия одной частицы равна произведению веса частицы на глу-
€ину ее погружения. Для вычисления всей работы мы поступим
следующим образом. Разобьем промежуток [0, /?j оси ОХ на
«произвольных частей точками 0 = х0<х1 <л;2<;. ..<*;<*m-i<- ..<х„ =
= R и рассмотрим сечения сферического сосуда плоскостями,
проведенными через эти точки деления перпендикулярно оси ОХ\ тогда сосуд
разобьется на отдельные шаровые слои. Рассмотрим /-й слой воды,
содержащийся между плоскостями х = Х( и x = xi+1 (* = 0, 1, 2, ...
..., п— 1). Приближенно заменим r-й слой воды цилиндрическим слоем
той же высоты Д*/ = *,-+1 — хи основанием которого служит круг с
центром в средней ючке Е,- промежутка \хи л:/+1 (см.
заштрихованную часть на рис. 203); при этом, как легко видеть, площадь ука-
Рис. 202. Рис. 203.
453

занного круга равна пу\, где y\ = R2— Й- Значит, объем этого
цилиндрического слоя воды равен
n(R2 — Й)Д*1.
Поскольку речь идет о воде, удельный вес которой равен
единице, то Бес i-ro цилиндрического слоя воды численно равен его
объему. Так как сила, которую надо приложить к этому слою для
поднятия его до свободной поверхности жидкости, равна весу его,
то работа, которую совершает эта сила* при поднятии *-го слоя
воды на расстояние ?,-, приближенно равна л (R2—g?) Е,-Д^?. Так
как это рассуждение может быть проведено для Есех слоев воды*
то полная работа W, необходимая для выкачивания всей воды из
котла, выразится приближенным равенством!
W**n% n(R*-%)tiAXi.
Это приближенное равенство будет тем точнее, чем мельче
дробление промежутка [0, /?], и в пределе при Х-+0 (где, как обычно,
Я = тах {Ал:,}) получим, очевидно, точное равенство:
W = l\mn^ я(Д2 —Й)ЬД*,.
Так как мы имеем здесь предел интегральной суммы, составленной
для непрерывной в промежутке [О, R] функции F(x) = л (R2 — x2)x,
то этот предел существует и равен интегралу
R
n\(R2 — x2)xdx,
о
и, следовательно, для искомой работы бу#ем иметь:
О
В частности, если R = 4 м и работу мы желаем вычислить в
килограммометрах, то, как легко убедиться, искомая работа будет равна
103-64л кГм.
Упражнения
1. Вычислить работу, которую необходимо затратить для того, чтобы
выкачать воду, заполняющую цилиндрический сосуд высотой И = 5 м и радиусом
основания R = 3m. Отв. 353 250 кГм.
2. Какую работу надо затратить, чтобы растянуть упругую пружину на
10 см, если сила в 1 кГм растягивает эту пружину на 1 см? Отв. 0,5 кГм.
* Эту силу можно считать приложенной к центру тяжести указанного слоя.
454

3. Цилиндр диаметром 20 см и длиной 80 см заполнен паром под давлением
10 кг/см2. Какую работу надо затратить, чтобы уменьшить объем газа в два раза,
считая, что температура газа остается постоянной?
Указание. Использовать закон Бойля — Мариотта: pa = c==const. Легко
установить, что работа внешней силы (которая по величине равна давлению пара)
по сжатию пара от объема v2 до объема v^ (v\ < i>2) вычисляется по формуле
Ц7= \ — dv = c\n^-. Отв. 1740 кГн.
*1

ГЛАВА XI
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
ь
В определении определенного интеграла $ / (л:) dx мы считали
а
Пределы интегрирования конечными, а подынтегральную функцию
f(x) ограниченной в промежутке [а, Ь]. Поэтому приведенное ранее
определение интеграла теряет смысл, если не выполняется хотя бы
одно из указанных выше условий, то есть когда промежуток
интегрирования бесконечен или подынтегральная функция не ограничена
в промежутке интегрирования. Однако и в этих случаях иногда
удается обобщить понятие определенного интеграла. В результате
такого обобщения и возникает понятие о так называемых
несобственных интегралах.
§ 1. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ ПЕРВОГО РОДА — НЕСОБСТВЕННЫЕ
ИНТЕГРАЛЫ С БЕСКОНЕЧНЫМИ ПРЕДЕЛАМИ
Определение. Пусть функция f (x) задана в промежутке
[а, + оо) и интегрируема в любой его части [а, А], то есть суще-
А
ствует определенный интеграл J / (x) dx при любом А > а. Тогда*
а
если существует конечный предел
А
\\щ \f(x)dx=I, (1)
то его называют несобственным интегралом первого рода
пли несобственным интегралом функции f(x) в промежутке
[a, -f со) и обозначают символом
1= ff(x)dx. (2)
а
В этом случае говорят, что несобственный интеграл (2)
существует, или сходится. Если же предел (1) не существует или беско-
456

нечен, то говорят, что несобственный интеграл (2) не существует»
или расходится.
Аналогично интегралу (2) вводится несобственный интеграл
следующего вида:
а а
$ f(x)dx= lim lf(x)dx. (3)
Наконец, как сумму подобных интегралов можно определить
несобственный интеграл с обоими бесконечными пределами, то есть
определить его равенством
ff(x)dx = I f(x)dx+ ff(x)dx, (4)
— оо — оо а
где а — любое число; при этом предполагается существование обоих
интегралов справа. Можно доказать, что сумма двух, интегралов
в формуле (4) не зависит от выбора точки а.
Так как несобственный интеграл определяется как предел
определенного интеграла, то на несобственный интеграл переносятся
все те свойства определенного интеграла, которые сохраняются при
этом предельном переходе. Например, свойства 1—7 определенного
интеграла, установленные нами в § 4 гл. IX, без труда переносятся
на случай интеграла с бесконечными пределами. Свойство 9
(теорема о среднем) здесь, очевидно, теряет смысл.
Заметим, что само вычисление несобственного интеграла
основано на его определении. Действительно, если через F(х)
обозначить первообразную для функции f(x)y то из определения
несобственного интеграла (2) следует:
-{-оо А
С f(x)dx= lim \f(x)dx= lim [F(A) — F(a)] =
a A-' + cOa Л- + 00
= F(+oo)-F(a) = F(x)\?»,
где F (-г oo)= lim F (А) есть условное обозначение этого предела.
Последний предел существует одновременно с несобственным
интегралом (2). Следовательно, для вычисления несобственного
интеграла (2) мы получили следующую обобщенную формулу Ньютона—
Лейбница:
+ 0О
\ f(x)dx = F(+cn)-F{a). (5)
а
Аналогично,
а
\ f(x)dx*=*F(a)-F(-oo),
— ОО
$ f(x)dx = F(+oo) — F(—oo),
— оо
где F(—oo)= lim F(A).
А — —оо
457

Таким образом, несобственный интеграл (2) может быть
вычислен по формуле (5) как результат двойной подстановки; при этом
из самого доказательства видно, что несобственный интеграл (2)
существует в том и только в том случае, когда существует
конечный предел
lim F(A) = F (+oo).
А— + оо
Пример 1. Вычислить несобственный интеграл [ е~ахdx, a>0.
По определению имеем:
+ оо А
[ e-**dx= lim [e~axdx = lim Г— i-<r«*l \A =
J л-ч-оо ^ 4-*+ooL « J|o
--1 lim (.-^-1)=±;
а л-Н-оо а
интеграл сходится. Если учесть, что в данном случае существует конечный
предел lim e~aA = 0, то вычисление интеграла можно произвести непосредственно
А-+-\-оо
по формуле (5), то есть
+ 00
1 Н-°° 1 1
e-**dx = — — е~аХ \ = — — (0— 1) =—,
а |о a v а
о
+ оо
Пример 2. Исследовать интеграл
1- «
\
\+х*-
Согласно определению находим:
Н- оо А
С xdx .. С xdx ,. Г I . #| , ПМ
^ l + *2 л^+00 ^) 1+** Л-н-оо1.2 к ^ '\\\
= 4- Hm [In (1+Л2) — 1п2] = +оо,
1 А-» + оэ
следовательно, данный интеграл расходится.
Пример 3. Исследовать, при каких значениях показателя а
существует несобственный интеграл
+ оо
\ % (я>0). (6)
а
Нижний предел а с итается положительным, так как в
противном случае подынтегральная функция — вблизи точки нуль будет
неограниченной, то есть при х = 0 она побратается в бесконеч-
Понимать это надо так, что при х-*0 функция — стремится к бесконеч-
ха
ности.
458

Приступим к исследованию интеграла (6).
1. Пусть сначала аф\. Тогда по определению несобственного
интеграла имеем:
Н- оо А
\ g= lim \^ = j^ lim (^l^j-L- lim (Л^-а'-).
a a l
Если a>l, то lim Л1-а = 0 и мы получаем]
+ 00
a —1
интеграл сходится. Если же а<1, то lim A1
вательно,
\ ^ = +оо;
:+оо и, следо-
интеграл расходится.
2. Пусть теперь а=1, тогда по определению находим:
4-оо А
у — = Пт \ — = lim (In Л — lna) = + oo;
J * Д-^ + оо J * Л-^ + оо
a a
интеграл расходится.
Итак, мы установили, что несобственный интеграл (6) сходится
при а>1 и расходится при a^l.
Полученным результатам можно дать простое геометрическое
толкование, если предварительно ввести понятие площади для
бесконечной области (бесконечной
трапеции). На первый взгляд
кажется, что не имеет смысла
говорить о площади такой
области, которая простирается
в бесконечность. Однако, как
мы увидим ниже, с помощью
предельного перехода можно
ввести понятие площади и для
такой области.
Пусть a > 1. Рассмотрим
бесконечную область,
ограниченную сверху кривой у--
слева — прямой х=аи снизу —
осью ОХ (рис. 204). Эта область бесконечно простирается вправо,
а кривая, ограничивающая ее сверху, асимптотически приближается
к оси ОХ. Предварительно вычислим площадь переменной
криволинейной трапеции aMNA (см. на рис. 204 заштрихованную часть). Обозна-
459

чим площадь этой трапеции через Р (Л), величина которой зависит от
положения точки А и растет вместе с Л, так что
.1
Найдем предел этой величины при Л-> + оо, то есть
lim P(A)=T±-~ lim (Л1"»—а1-)=-а1"в
/4-*+оо 1—а ^.,^00 а—1*
так как ПтЛ1_а = 0 при а>1. Естественно найденную величину
——j а1'11 принять за площадь всей указанной выше бесконечной
области.
Если же верхнюю границу бесконечной области заменить
гиперболой у = — или кривой У = ^ при а<1, то площадь Р [А)
криволинейной трапеции в первом случае выразится величиной
А
Р (А)=^~ =\п А — 1па9
а
а во втором
А
а
где а<1. В обоих случаях предел площади переменной
криволинейной трапеции при Л -> + ос равен + оо, то есть lim Р (Л) = -+- оэ,
так что в этих случаях простирающаяся в бесконечность область
уже не имеет конечной площади.
Таким образом, сходимость интеграла (6) при а>1
геометрически означает, что площадь указанной выше бесконечной области
конечна, а расходимость его при а^1 означает, что упомянутая
площадь бесконечна.
Результатами этого примера мы воспользуемся при выводе
признака сходимости и расходимости несобственных интегралов
рассматриваемого типа.
Часто встречаются несобственные интегралы от функций,
первообразные которых неизвестны. В этих случаях приходится
прибегать к признакам, дающим возможность судить о сходимости или
расходимости интеграла без отыскания самой первообразной.
Используя результаты последнего примера, мы приведем простой
достаточный признак сходимости и расходимости несобственного интеграла
с бесконечными пределами в случае, когда подынтегральная
функция неотрицательна в промежутке интегрирования.
Признак сходимости. Пусть функция f(x) непрерывна и
неотрицательна, то есть f(x)^0 в промежутке [а, + со), а>0.
460

Тогда интеграл
$ f(x)dx (7)
а.
сходится, если при а ^ х < + со выполняется неравенство
где а > 1 и /И — некоторая положительная постоянная. Если же
при а^х<С + оо выполняется неравенство
f(x)2*?, (9)
где а^1, М>0, то интеграл (7) расходится.
Доказательство. Так как функция /(*) неотрицательна, то
определенный интеграл с переменным верхним пределом
А
<b(A) = [f(x)dx (10)
а
представляет собой монотонно возрастающую функцию от
переменной А *. Тогда для первого случая (когда выполняется неравенство
(8)) будем иметь:
а а а
то есть функция (10) ограничена и, будучи возрастающей, по
известной теореме из теории пределов** имеет конечный предел при
Л-* + оо. Таким образом, существует интеграл
Н-оо А
\ f (x)dx= I im \ f (x) dx.
Во втором случае (когда выполняется неравенство (9)) мы будем
иметь:
А А
dx
ха
а а
А
Sdx
— = + оо,
а
и из последнего неравенства вытекает, что
А
lim Ф(Л)= lim \ f(x)dx=+co9
А-+-\-ао А—» + оо q
* Это легко видеть из геометрических соображений.
** См. гл. III, § 6 и 12.
461

то есть интеграл (7) расходится. Этим признак полностью доказан.
Из доказанного признака вытекает другой весьма простой и
практически удобный достаточный признак, а именно: пусть
функция f (x) неотрицательна и непрерывна в промежутке [а, +сю);
тогда интеграл (7) сходится, если при а > 1 существует
конечный предел
lim *7 (*) = /, (11)
х-»-\-со
и тот же интеграл расходится, если при а^1 существует
конечный или бесконечный предел
lim x*f(x) = I^0, (12)
дг-*4-оо
отличный от нуля.
Рассмотрим первый случай. Пусть существует предел (11)
при ос>1. Тогда из определения предела следует, что по е>0
можно указать такое N, что как только x>N, то будет
выполняться неравенство x*f (х) < / + е. Отсюда f (х) < —, где М = I+е>
>0. Мы получили, таким образом, условие (8), из которого сле-
дует существование интеграла ^ f (x) dx. Из очевидного равенства
N
-f-oo N -J-°°
$ f (х) dx = $ f (x) dx + \ f (x) dx (13)
a a N
вытекает сходимость интеграла в левой части этого равенства, то
есть сходимость интеграла (7) (в правой части этого равенства оба
интеграла существуют).
Второй случай. Пусть существует предел (12) при а<;1.
В нашем случае/>0. Возьмем положительное число М, меньшее,
чем /. Тогда по выбранному М можно найти такое N, что при x>N
будет выполняться неравенство* x°f(x)>M, из которого получаем:
Мы получили условие (9) доказанного выше признака, из
которое
рого вытекает расходимость интеграла ^ f(x)dx, а за ним в силу
равенства (13) и расходимость интеграла (7).
Пример 4. Исследовать интеграл \ .,
) У* + * + 2
Представим подынтегральную функцию в следующем виде:
11 i «
f (у) = — - = — —. Произведение x2f(x) = -
/*»+*+2 \ Г ,1,2 " lA+U2
* Известно, что если хп-^Ь и Ь <г ф > г), то хп <г (х„ > г) начиная с
некоторого места (см. гл. III, § 3).
462

как легко видеть, стремится к 1 при #-* + оо. Так как показатель а=-^- > 1,
то данный интеграл по доказанному признаку сходится.
Пример 5. Исследовать интеграл \ ,. dx.
Подынтегральная функция имеет вид: f(x) =
Следовательно, произведение x3f(x) =
v
а = -~- < 1, то интеграл расходится.
-f со
Пример 6. Исследовать интеграл Пуассона \ е х% dx, имеющий важное
о
значение в теории вероятностей и математической статистике.
Полагаем / (х)—ё~~хг. Пользуясь правилом Лопиталя, легко показать, что при
любом положительном а произведение ха f (х) = ха • е — х2 стремится к нулю при
х—*-+оо*. В частности, это верно и при а > 1 (например, при а = 2); отсюда
по доказанному признаку данный интеграл сходится. Интересно заметить, что
значение этого интеграла равно
2 "
Упражнения
Вычислить следующие несобственные интегралы:
+ 00
¦• \
dx
О
+ 00
1+JC2
Отв.
2 "
+ СО
2. \ cos х dx.
2
+ 00
In х
+ оо
dx. Отв. Расходится.
dx
dx
V*
1
Отв.
2 '
" ) 'л* + 2х+2'
— со
+ оо
Отв. Расходится.
Отв. я.
„-VT
dx.
Исследовать на сходимость следующие интегралы:
+ СО +0О
С х2 С dx
7» \ —т~1 гт- ^х. Отв. Расходится. 8. 1 . ," t
J x* + x+\ J л?+1
О О
+ оо з +со
в. \ т~\—т. Отв. Расходится. 10. \ .
О 1 '
Отв. 2.
Отв. Сходится.
Отв. Сходится.
х2
* Действительно, при а = 2 имеем: lim —- = lim
2*
*->+оо е* х-++оо2хех
= lim —
Л-*+оэ ех
,=0.
463

4-оэ -f-oo
11. V —L^t—Ldx. Отв. Расходится. 12. \ - dx. От л. Сходится.
1 0 * *
13. ^ Ух e~x dx. Отв. Сходится.
о
Н-оо -}-оо
п ^. С . У я С sin х . л
Пользуясь формулами \ е—*• ^х== ' и 1 «* = -~-, вычислить
[уюшие интегралы
-\-&> Н-оо
14. { е-ах* dx(ar>0). Отв. i-l/~. t5. ? -^Ld*. Ome. j/JT.
J 2 Г 2 ^ /д,
4- oo
\ хге~~кг dx. У к a 3 а н и е. Применить интегрирование по частям.
16.
о
Отв. — |/"я.
17. V {/л:. Отв. -=-1 если а > 0, и —^-, если а<0.
б
+ оо
Г» s|f]2 х
18. \ 2—d*. Указание. Применить интегрирование по частям.
Отв. |.
+ 0О
? sin3* .
о
Указание. Воспользоваться формулой sin3 х = — (3 sin х — sin 3*). Отв. г .
§2. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ ВТОРОГО РОДА — НЕСОБСТВЕННЫЕ
ИНТЕГРАЛЫ ОТ НЕОГРАНИЧЕННЫХ ФУНКЦИЙ
Пусть f (х) задана в промежутке [а, 6], но не ограничена в нем,
например, вблизи точки b (см. рис. 205). Точку b при этом будем
называть особой точкой. Тогда, как бы ни было мало
положительное число е, функция f (х) заведомо неинтегрируема в каждом
промежутке [Ь — е, Ь] слева от точки ft. Однако будем
предполагать, что функция f (x) интегрируема (следовательно, ограничена)
в любом промежутке [a, b — е). Тогда, если существует конечный
предел
Ь — е
lim \ f(x)dx=I, (1)
464

то его называют несобственным
интегралом второго рода функции f(x)
ют а до Ь и обозначают
l=]f(x)dx,
(2)
а про интеграл (2) говорят, что
он существует, или сходится. Если
же предел (1) не существует или
бесконечен, то говорят, что
несобственный интеграл (2) не существует,
или расходится.
Аналогично, если а — особая точка
и функция / (х) интегрируема во вся- Рис. 205.
ком промежутке [а + е', 6], как бы
ни было мало положительное число е', то несобственный интеграл
в этом случае определяется так:
Ь-е Ь
\ f (x) dx = lim \ f (x) dx.
(3)
Если функция f(x) неограничена в окрестности какой-нибудь
промежуточной точки с промежутка [а, Ь], то есть если точка с
особая и а<с<;&, то по определению полагают
Ь с Ь
$/ (Х) dx = \f(х) dx + \f (x) dx,
а а с
при этом интеграл в левой части этого равенства существует, если
существуют интегралы в правой части его.
Наконец, если функция f (х) неограничена вблизи точек а и b
{то есть а и b — особые точки), то в этом случае несобственный
интеграл определяется как сумма
ь с ь
\f(x)dx = \f{x)dx+\f (x) dx
{где с —любая точка интервала (я, Ь)), если оба интеграла справа
существуют. При этом сумма не зависит от выбора точки с.
Пример 1. Вычислить несобственный интеграл \
Подынтегральная функция
г при х= 1 «обращается в
бесконечность», то есть точка х=1 особая; в остальных точках
промежутка интегрирования эта функция непрерывна и потому
интегрируема в любом промежутке [0, 1—е], где 0<е<1- Следовательно,
465

по определению имеем:
1 1-8
dx .. С dx ..
.»,.,¦¦¦ = am \ - , = limarcsin x
= lim arcsin (1-е)
2 "
Следовательно, интеграл существует.
Пример 2. Исследовать, при каких значениях показателя:
а>0 существует несобственный интеграл
\%. (4)
О
Подынтегральная функция обращается в бесконечность при х = 0г
в остальных точках промежутка она непрерывна и, следовательно,
интегрируема в любом промежутке [е, 1], как бы мало ни было
е>0.
Пусть сначала аф 1. Тогда согласно определению
несобственного интеграла 2-го рода имеем:
1
? dx ,. С dx 1 ,. ,
О е
1-а8-0
lim (1 — г1-*).
Этот предел будет равен , , если а<1, и он равен
бесконечности, если а>1, а это значит, что при а<1 интеграл (4)
сходится, а при а>1—расходится. Наконец, при а=1 имеем:
1
1
lim \ ~ = limine
?_>0 J х е-+0
= lim (In 1 — In e) = lim In — = + со,
«-¦0 e->0 8
то есть интеграл (4) расходится.
Итак, мы установили, что интеграл (4) сходится при а<1 и
расходится при а ^ 1.
Полученным результатам (так же, как и в примере 3, § 1) можно
дать простое геометрическое истолкование.
Действительно, для всякого сколько угодно малого е> 0 интеграл
Е
выражает собой площадь криволинейной трапеции, заштрихованной
на рисунке 206. Эту площадь мы обозначим через Р(е). Очевидно,
если е -> 0, то заштрихованная фигура неограниченно простирается
вверх, а площадь ее Р (г) непрестанно возрастает. Однако, если
а<1, то, как мы установили выше, интеграл (4) сходится и най-
"l
денную величину , естественно принять за величину площади
466

бесконечной трапеции, ограниченной сверху кривой у=~, справа —
прямой х=1, слева — осью OY и снизу — осью ОХ.
Если a^sl, то интеграл (4) расходится, то есть интеграл \
cti
а с ним и площадь Р (г) переменной криволинейной трапеции
с уменьшением е растет безгранично; так что вся бесконечная
трапеция в этом случае уже не имеет конечной площади.
Вычисление несобственного интеграла второго рода. Пусть
функция f{x) определена и
непрерывна в полусегменте [я, Ь) и
вблизи точки b функция неог-
раничена (точка b — особая
точка для нее). Тогда для f (x)
в этом промежутке существует
первообразная функция F (х)> и
по основной формуле
интегрального исчисления (формула
Ньютона — Лейбница) будем
иметь:
С f(x)dx = F(b — г)—F(a). (5)
Рис. 206.
Отсюда следует, что несобственный интеграл (2) существует тогда
и только тогда, когда существует конечный предел
Vim F(b — s) = F(b).
8^0
(6)
Иными словами, интеграл (2) существует тогда и только тогда,
когда функция F(х) имеет конечный предел в точке b и,
следовательно, может рассматриваться как непрерывная на всем промежутке
[a, ft]. Переходя к пределу в равенстве (5)*, мы и получим формулу
Ньютона — Лейбница:
\f(x)dx = F(b)-F{a).
(7)
Замечание. Эта же формула справедлива и в том случае,
если особая точка лежит внутри промежутка интегрирования. Важно
помнить, что формула (7) применима в том случае, если
первообразная функция F (х) для f (х) будет непрерывной на всем
промежутке интегрирования [а, 6], в том числе и в особых точках.
Существование такой первообразной обеспечивает и существование
несобственного интеграла. Если же первообразная F (х) имеет раз-
Мы воспользовались теоремой о предельном переходе в равенствах.
467

рыв второго рода, хотя бы в одной точке промежутка [а, 6"*, то
несобственный интеграл не существует.
Итак, для вычисления несобственных интегралов от
неограниченных функций можно использовать формулу Ньютона — Лейбница,
если только функция F (х) непрерывна на всем промежутке [а, Ь]
и F' (x)=f(x) во всех точках, где f(x) конечна.
27
Пример 3. Вычислить интеграл
и
27
= 3(3 + 1) ==12.
-1
В данном случае первообразная функция F (х) = з1/1с непрерывна во всем
промежутке [—1, +27], в том числе и в точке л: = 0, в котором подынтегральная
функция обращается в бесконечность. Следовательно, можно применить
формулу (7):
Пример 4. Исследовать на сходимость интеграл \ -^.
-1
В точке х — 0 подынтегральная функция обращается в бесконечность (jt = 0 —
особая точка). Так как не только подынтегральная функция, но и его
первообразная F(x) = имеет бесконечный разрыв в точке х = 0, то даннцй интеграл
расходится и равен бесконечности. Если бы мы, не обратив на это внимания,
формально применили формулу (7) к этому интегралу, то получили бы нелепый,
результат:
|>=К)|::=-2-
Пример 5. Доказать, что несобственный интеграл
ъ
dx
(8)
где р>0, сходится при р<1 и расходится при р^\.
Легко видеть, что подынтегральная функция в точке х = Ь имеет
бесконечный разрыв, то есть Ь — особая точка для нее. Пусть
сначала рФ 1. Тогда по определению несобственного интеграла имеем;
Ь Ь-г lb—e
С _^- = Hm [ 77^^ = -ЦПт(Ь-*)Н =
l(b-x)P e_0 J (Ь-х)Р р-\е_+0к '
а а \а
Отсюда видно, что при /?<1 существует конечный предел, равный
т^-(Ь-—а)1~р, и, следовательно, данный интеграл сходится, а при
468

р>1 этот предел равен бесконечности, следовательно, интеграл
расходится.
Если же р= 1, то
Ь-е
Vt—^- = lim \ т—— = — lim In (b— x)
\b-t
= lim[ln(& — a) — lne] =
= lim In—- = + со, то есть интеграл расходится. Таким образом,
мы доказали, что интеграл (8) сходится при р<(1 и расходится
при /7^1-
Аналогично доказывается, что интеграл
и
С dx
3 (х-а
сходится при р<1 и расходится при р^1.
Используя результаты этого примера, установим следующий
простой достаточный признак сходимости и расходимости
несобственного интеграла от неограниченной функции.
Пусть функция }(х) непрерывна и неотрицательна в
полусегменте [at Ь) и в точке b функция претерпевает бесконечный разрыв
lim /(jt) = + oo.
х-+ b— О
Тогда:
1) интеграл
ь
\f(x)dx (10)
а
сходится, если существуют такие постоянные М ^> 0 и р <^ 1,
что при а^х<^Ь выполняется неравенство
2) интеграл (10) расходится, если существуют такие
постоянные р^\ и М^>0, что при а^х<^Ь выполняется неравенство
Докажем сначала первую часть признака. В первом случае
согласно условию (11) мы будем иметь:
а а а
46?

Следовательно, функция Ф(е) ограничена сверху и, будучи
возрастающей*, имеет конечный предел при е-*0, то есть интеграл (10)
сходится.
Во втором случае в силу условия (12) имеем:
dx
Ф(е)= $ f(x)dx^M J (T
-х)Р'
а а
Ь-*
С dx
но lim \ ,ь__х)Р = +оо при р^ 1 (см. пример 5). Тогда и подавно,
как это следует из последнего неравенства, lim [ f (x) dx = + °°>
ь-
? —0
то есть интеграл (10) расходится. Этим признак полностью доказан.
Из этого признака следует весьма простой практически удобный
достаточный признак сходимости и расходимости
несобственного интеграла второго рода; а именно: пусть f (x)
неотрицательна и непрерывна в полусегменте [а, Ь) и lim f(x) =
= + °°, то есть Ь — особая точка для этой функции; тогда
интеграл (10) сходится, если при р<4 существует конечный предел
lim (b — x)pf{x) = I, и этот интеграл расходится, если при
х-+Ь-0
р^ 1 существует конечный или бесконечный предел lim (b— x)pf(x) =
x-+b — 0
= 1 ф 0, отличный от нуля.
Действительно, в первом случае предел произведения (b — x)pf(x)
при #->& равен /, при этом / может быть и нулем. Возьмем какое-
нибудь положительное число М^>1, тогда произведение (b—x)pf(x)
при х достаточно близких к Ь будет меньше М, то есть
(b — x)pf(x)<M, а<с<*<6,
где с выбрано столь близко к 6, чтобы для всех значений х из
промежутка [с, Ь] имело место последнее неравенство. Из этого
неравенства находим, что
то есть получили неравенство (11), из которого согласно локя^ан-
* Так как функция f (х) неотрицательна в промежутке [а, Ь), ю шпецмл
ф (е) = С f (х) dx возрастает с уменьшением е.
а
470

ному признаку и следует сходимость интеграла ^f(x)dx. Тогда из
с
равенства
ь с ъ
\f (х) dx=\f {х) dx+\f {х) dx
а а с
вытекает сходимость интеграла (10) *.
Во втором случае произведение (Ь—x)pf(x) при х -> Ъ стремится
к пределу / ^> 0. Выберем какое-нибудь положительное число М <^ I.
При х достаточно близких к Ь указанное произведение будет
больше М, то есть
(b — x)°f (х)^>М при а<^с^х<^Ь,
где с достаточно близко к Ь. Из этого неравенства следует, что на
всем промежутке [с, Ь]
(где /7^1), то есть получили неравенство (12), из которого
вытекает по ранее доказанному признаку расходимость интеграла
ь ъ с ь
^f (x) dx, а последний в силу равенства ^f(x)dx = ^f(x)dx + ^f(x)dx
с а а с
влечет за собой расходимость интеграла (10), что и требовалось
доказать.
Замечание. Полученный признак сохраняет силу и в том
случае, когда подынтегральная функция f (х) обращается в
бесконечность при приближении к нижнему пределу, то есть когда
точка а является особой точкой. В этом случае надо рассматривать
предел произведения (х—а)р f (х) при х-+ау и если это
произведение имеет конечный предел при р<С 1, то интеграл (10) сходится,
а если это произведение имеет конечный или бесконечный предел,
отличный от нуля при р^1, то этот интеграл расходится**,
1
f dx
Пример 6. Исследовать интеграл \ ,г
о
Подынтегральная функция / (х)=~-7= в точке д:=1 обращается в бесконеч-
]/1— х3
ность, то есть х=1 — особая точка. Представим эту функцию в следующем виде:
вательно, lim (1 — х) 2f (х) = lim у^ , х , х2 — у^~.
* Так как оба интеграла в правой части этого равенства существуют.
** Этот признак доказывается аналогичным образом, как и в первом случае,
с помощью интеграла (9).
471

Так как здесь показатель р = -^- < 1, то согласно доказанному признаку
данный интеграл сходится.
С Ух
Пример 7. Исследовать интеграл \ dx.
J у 1-х*
о
Легко видеть, что точка *=1 является особой точкой для подынтегральной
Ух Ух ±
функции. Так как /(*)- T^Vl i/-/i , wi . *ч ' то О-*)2/(*) =*
У*" I- /1 чТг/ Ч !• К* 1
— :» откуда находим: lim (1—х)г /(*)= нш
У(1+*)(1+*) *-! X-.l/(l+*)(l+tf) 2
Но р = -^-<:1, следовательно, интеграл сходится.
1
Пример 8. Исследовать интеграл V z g.
о
Точка *=1 является особой для функции /(*) = - -. Запишем эту
функцию так: f М = у_х) у+х + х2у откуда (1—х)/(д:)в—__. Следовательно,
Так как найденный предел отличен от нуля и показатель р = 1, то данный
интеграл по доказанному признаку расходится.
Пример 9. Исследовать интеграл ^ In x dx.
о
Точка л:=0, то есть нижний предел интеграла является особой точкой для
функции f(x) = \nx. В данном случае произведение (x-a)Pf(x), предел которого
мы должны найти в точке а = 0, принимает вид: хР In x. Рассмотрим предел этого
произведения, когда х — 0. Мы имеем здесь неопределенность вида 0 • со.
Применяя правило Лопиталя, убеждаемся в том, что при любом положительном р это
произведение стремится к нулю.
Действительно, пусть р > 0, тогда
J_
lim хР In x= lim —=-= = lim =г==т = lim *p = 0.
х-+о x-+qx р x-*o — Pxpl Р х-и
В частности, это будет иметь место, например, при всех значениях /?<1, а
следовательно, по установленному выше признаку данный интеграл сходится.
Пример 10. Исследовать интеграл \ —==
J Уд: —si
о г
Как легко видеть, нижний предел, то есть * = 0, является особой точкой для
подынтегральной функции. Здесь мы должны исследовать предел произведения
(x—-Q)Pf(x)~xPf(x), когда х—*0. Из равенства / (*) = -
Ух — sin х ух 11 sin* \
У
472

непосредственно находим, что У~х{(х) = ^т^. Следовательно, lim х2 f (х)
1
V*
1 1 1 • sin х л. -ш/—:— -ж F sin х
: lim «1, поскольку hm -7=- = lim у sin хЛ/ z!!Lz~Q. i =o
х^о sinx *—о у х х-+о У х
Ух
Так как показатель р = — < 1, то интеграл сходится.
Упражнения
Вычислить н
Вычислить несобственные интегралы (или установить расходимость):
2 i
1. \_?*L. Ome.l. 2. С
2 1
(* Их (*
3. \—s—л—гг. #>яв. Расходится. 4. \ \nxdx. Отв. — 1.
J л2 — 4х+3 Л
2
5. \ -in. Отв. Сходится при р < 1 и расходится при р^1.
1
Исследовать на сходимость следующие интегралы:
1 1
С dx С х* dx
6. \ . 0/7ie. Сходится. 7. \ —. Отв. Расходится.
I {/I-*4 I {/(1—**)«
1 1 А-
С dx С ух
8. \—— . Отв. Сходится. 9. \ —т- dx. Отв. Сходится.
С Ins
С 1 1
12. \ —-g— rfx. Указание. Следует записать / (х) ——-
1 1
10. \ —- . Отв. Расходится. 11. \ — dx. Отв. Сходится.
J ех — cos х а -, .
п
_ 1
sin3 I ~ — х)
г я -пЗ
2"-*
и рассмотреть предел произведения
л
sin ( у — х
Отв. Расходится.

Раздел IV
КРИВЫЕ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
ГЛАВА XII
КРИВЫЕ НА ПЛОСКОСТИ
§ 1. НЕКОТОРЫЕ ОБЩИЕ СВЕДЕНИЯ О КРИВЫХ
Мы уже неоднократно встречались с вопросами, относящимися
к изучению плоских кривых (задача о проведении касательной,
определение длины дуги кривой и др.). В частности, мы встречались
и с различными способами задания кривой: явным уравнением,
параметрическими уравнениями. В этом параграфе мы коротко
остановимся на некоторых понятиях и терминах, часто используемых при
рассмотрении кривых.
Пусть кривая задана параметрическими уравнениями
*=Ф(0> У=Ч>(0 (а<^Р).
Если двум различным значениям параметра t, из которых хоть
одно отлично от а и р, на кривой соответствует одна и та же
точка, то такая точка называется кратной. Это могут быть,
например, точки самопересечения или точки самоприкосновения кривой
(точки М на рис. 207).
При совпадении точек кривой, отвечающих двум крайним
значениям аир параметра t, кривая оказывается замкнутой, а точка Л4,
служащая одновременно ее началом и концом, уже не считается
кратной (рис. 208).
Будем далее предполагать, что на рассматриваемой нами кривой
нет кратных точек, так что различным значениям параметра t отве-
Рис. 207. Рис. 208.
474

чают различные точки кривой (кроме случая замкнутой кривой,
когда Ф(а) = ф(Р), ^(a) = i|>(P))- Кроме того, предположим, что
функции ф (t) и г|) (t) имеют непрерывные производные ф' (t) и я|/ (/).
Точка кривой, отвечающая значению параметра t, при котором
одновременно
x>t==y>t = 0y то есть <р' (t)=V (0 = 0, (1)
называется особой.
Это название связано с тем, что, как можно показать^ в
неособых (простых) точках (то есть таких, для которых не выполняются
условия (1)) кривая имеет касательную и угловой коэффициент
касательной находится по известному правилу дифференцирования
функции, заданной параметрически (см. гл. V, § 7):
. У\ . x't
Ух = -г ИЛИ Xy = -r.
xt yt
Определение. Кривая, заданная параметрическими
уравнениями
называется гладкой, если функции ф (/) и i|) (t) имеют непрерывные
производные ф' (t), i|/ (t), не обращающиеся одновременно в нуль
(последнее условие означает, что
на кривой нет особых точек). f\. s*—¦>. у^ч^__
Геометрически гладкость кри- ( X/ \/
вой означает, что кривая во всех
своих точках имеет касательную, Рис 209.
причем при непрерывном
перемещении точки касания вдоль кривой направление касательной
изменяется тоже непрерывно.
Если непрерывная кривая составлена из конечного числа
гладких кривых, то такая кривая называется кусочно-гладкой (рис. 209).
Например, всякая ломаная, состоящая из конечного числа
прямолинейных отрезков, будет кусочно-гладкой линией.
Всякая кусочно-гладкая кривая спрямляема. Это легко выводится
из спрямляемости гладких кривых.
Кривую, заданную явным уравнением y = f(x), a^x^b, всегда
можно рассматривать как частный скучай кривой, заданной
параметрическими уравнениями, поскольку вместо уравнения y = f (x) всегда
можно написать: х=х, y = f(x) (и считать, что х—параметр).
Поэтому, если кривая задана явным уравнением y = f (х) и функция f (х)
непрерывна вместе со своей производной /' (х), то такая кривая не
может иметь особых точек и, следовательно, всегда будет гладкой.
Действительно, в этом случае всегда х'х=\ (то есть
производная х'х всюду отлична от нуля) и, стало быть, условие (1)
не выполняется. Разумеется, все сказанное относится и к кривой,
заданной уравнением вида x=g(y).
Итак, на кривой, заданной явным уравнением (при выполнении
указанных выше условий), особых точек нет. Это обстоятельство
475

играет существенную роль в теореме об эквивалентности бесконечно
малой дуги и стягивающей ее хорде (см. гл. X, § 2, теорема 2).
Эту теорему можно доказать и в более общем случае, когда кривая
задана параметрически, но тогда нужно поставить дополнительное
условие, чтобы точка Мх не была особой.
§ 2. КРИВИЗНА И РАДИУС КРИВИЗНЫ ПЛОСКОЙ КРИВОЙ
Одним из элементов, характеризующих форму кривой, является
степень ее искривленности, изогнутости в различных точках.
Рассмотрим какую-нибудь плоскую спрямляемую кривую,
которая не содержит кратных точек и имеет в каждой точке
касательную. Возьмем на этой кривой какие-нибудь две близкие точки Мх
и М и проведем касательные к
кривой в этих точках. При этом точки
Мг и М выбираем настолько близко
друг к другу, чтобы касательная при А )ш
перемещении точки касания от М к Мх
Рис. 210.
Рис. 211.
поворачивалась в одном направлении (рис. 210). Через <о обозначим
угол между этими касательными, или, точнее, угол поворота
касательной при переходе отточки М к точке Мг. Этот угол, который мы всегда
считаем положительным, называется углом смежности дуги МХМ.
Угол смежности в некоторой степени дает представление об
искривленности, изогнутости, или «кривизне», дуги МгМ. Из двух дуг
одинаковой длины больше изогнута та дуга, у которой угол смежности
больше (ср. рис. 210 и 211).
Однако, рассматривая дуги различной длины, мы не можем
оценить степень их изогнутости, пользуясь только одним углом
смежности. Один и тот же угол смежности могут иметь две дуги с
заведомо различной изогнутостью. Поэтому изогнутость, кривизну дуги
естественно характеризовать углом смежности, рассчитанным на еди-
0)
ницу ее длины, то есть отношением -у, где угол со измеряется в
радианах, а / — длина дуги МгМ. Зто приводит к следующему
определению.
476

Определение. Отношение угла смежности дуги кривой к ее
длине называется средней кривизной дуги:
Поскольку енак угла со не учитывается (угол берется по
абсолютной величине), то средняя кривизна есть число неотрицательное.
Для одной и той же кривой средняя кривизна на различных ее
участках может быть различной. Естественно, чем меньше дуга МгМ,
тем средняя кривизна лучше характеризует изогнутость дуги вблизи
точки М1у и для того, чтобы охарактеризовать степень изогнутости
в непосредственной близости к точке Mlf вводят понятие кривизны
в данной точке.
Определение. Кривизной кривой в точке Мг называется
предел, к которому стремится средняя кривизна дуги МгМ, когда
точка М стремится по кривой к точке Мг.
Обозначая кривизну кривой в точке Мх буквой /С, по
определению имеем:
/C = lim /Ccp = liniy.
В частности, для любой дуги окружности радиуса R (рис. 212) имеем:
i(Cp = Y = -o— = -o- = const, и, следовательно,
K=i- (1)
Таким образом, кривизна окружности в любой ее точке есть вели-
чина постоянная и равна величине, обратной радиусу окружности.
Этого нельзя сказать о кривизне произвольной кривой. Для
произвольной кривой кривизна в различных ее точках, вообще
говоря, будет различная. В этом мы убедимся ниже.
Перейдем теперь к выводу формулы для вычисления кривизны
плоской кривой в любой ее точке.
Пусть кривая задана явным уравнением y=f(x), a^x^b,
и пусть функция / (х) имеет гервую и вторую производную на [а, Ь].
Отсюда, в частности, вытекает, что /' (х) всюду существует и
непрерывна, следовательно, кривая спрямляема и в каждой точке имеет
касательную. Возьмем на кривой точку Мг (ху у), и пусть ей
отвечает дуга s, отсчитываемая от некоторой закрепленной точки М0
(рис. 213). Точнее, дуга s — это длина дуги М0М1у которой приписан
<еще и знак; именно, если отсчет дуги от М0 к М± происходит в
направлении возрастания параметра (в данном случае параметр — х),
то дугу s считают положительной, а в противном случае ее считают
отрицательной.
Придадим s произвольное приращение As. Тогда дуга 5 + As
определит на кривой новую точку М. Проведем касательные к кривой
477

Рис. 212.
Рис. 213.
в точках Мг и М. Через а иа + Аа обозначим соответственно углы,
образуемые этими касательными с положительным направлением
оси ОХ (см. рис. 213). Непосредственно из рисунка видно, что угол
смежности со дуги МгМ равен |Да|*.
Так как в данном случае кривая задана в декартовых
координатах явным уравнением y = f (x), то величины а и s обе зависят от хг
а-
а (х), s = s (x).
Следовательно, а можно рассматривать и как функцию от s,
заданную параметрически, а, стало быть, можно ставить вопрос о
вычислении производной от а по s. Как известно (вспомните
геометрический смысл производной), у' = tga, отсюда a = arctgr/', и, значит,
da= 1^у*р > но dy'=y"dx. Тогда
da =
У"
1+У'2
dx.
(2)
С другой стороны, дифференциал дуги ds = Y\-\-y'2 dx.
Из последних двух равенств следует, что существует производная
от а по s и она равна
da
ds
(3)
О +У»)
24 а
Поскольку в нашем случае длина дуги / = |As| и угол смежности
<о = |Аа|, то по самому определению средней кривизны дуги МгМ
* Приращение Да может быть и положительным, и отрицательным, в
зависимости от направления вогнутости кривой, а угол смежности мы всегда считаем
положител ьным.
478

имеем: /(cp = -y- =
находим:
или в силу (3)
| Да
~ | As
К
Отсюда для кривизны кривой в точке Мг
1 • is 1 • I Да
= hm /CCp=lim л-
Af — Af t As — 0| ^S
da
К-—*±Г. (4)
O+y*)4
Из этой формулы, в частности, следует, что в точках перегиба
кривой, где (как известно) у" = 0, кривизна равна нулю. Здесь же
заметим, что в последней формуле значение корня в знаменателе
берется только арифметическое (то есть положительное), ибо
кривизна кривой по определению есть величина неотрицательная.
Введем еще одно определение.
Определение. Величина, обратная кривизне кривой в какой-
нибудь ее точке, называется радиусом кривизны (кривой в данной
точке).
Таким образом, если радиус кривизны обозначить через R, то
У?=дг, а из формулы (4) вытекает, что
«- ,У'| • (5>
Из формулы (1) следует, что радиус кривизны окружности
s любой ее точке равен радиусу окружности
Пример 1. Найти кривизну и радиус кривизны napauojiai у—х*.
Так как у' = 2х, у" = 2, то формула (4) дает:
К--
(1+4*2)*
Легко видеть, что эта величина будет наибольшей при * = 0, для которого К = 2.
Этот факт подтверждается и геометрически, так как при * = 0 парабола
действительно изогнута более всего.
1 1 »
Для радиуса кривизны в силу формулы (5) будем иметь: # = —= — (1 -\~4х2)ъ f
и, значит, при * = 0 радиус кривизны R = -t%—наименьший радиус кривизны
данной кривой.
Пусть теперь кривая задана параметрически: # = ф(/), y = ty(t)f
«причем ф(/) и г|)(?) имеют непрерывные производные 1-го и 2-го
порядков. Тогда, как известно (см. гл. V, § 7),
и-и'1 „'-W-M /д.
479

Подставляя эти выражения в формулы (4) и (5), получим
соответственно:
к^ЖпЩ^ (7>
R_ (Ф+у?У (8
\у1**—у'(*?\ '
Как видим, формула (7) теряет смысл в тех точках, где х,-
и y't обращаются одновременно в нуль*. В таких точках кривая
может и не иметь касательной, и, значит, не имеет смысла
говорить о кривизне кривой в таких точках.
Пример 2. Найти кривизну циклоиды х = а (/ — sin t)t у=а (1 —cost).
Вычислим производные: х\ = а (1 — cos t), x{ = a sin tt y't=a sin t, ynt = a cos t-
Подставив эти значения в формулу (7), найдем К=—j ГТ"« Отсюда видно,
. t
4а
что наименьшую кривизну циклоида имеет при / == (2/г-f-1) я (л = 0, zb 1, ±2,...).
Из формулы (7) легко получить формулу для вычисления
кривизны кривой, заданной уравнением в полярных координатах г =
= ф{0). Действительно, этот случай задания кривой приводится
к параметрическому с помощью обычных формул перехода: х =
= rcos0 = q)(0)cos0, f/ = rsin6 = (p(0)sin0; роль параметра здесь
играет угол 0. Для этого случая
х'в = г' cos 0 —г sin©, xe = f cos 0 — 2r' sin 0 —г cos 0;
у'ь = г' sin 0 + /-cos 0, у& = г" sin @ + 2r' cos0—r sin©;
так что x<i + y<$ = r2 + r8 и увх'в — y'eXe = r2 + 2r'2 — rr\ и в силу (7)
находим:
Пример 3. Найти кривизну кардиоиды (см. рис. 172 на стр. 417):
г— a(l+cos0) (a>0).
Находим производные: г' = — a sin в, /-" = — a cos 6. По формуле (9) после
несложных преобразований находим:
*=П в"
4a cos y
Отсюда видно, что в точке, где 9=0, кардиоида имеет наименьшую кризизну,
а в точке, где в=я, кривизна теряет смысл
* В особых точках (см. условия (1) из § 1).
480

Упражнения
1. Найти кривизну и радиус кривизны гиперболы ху = 4 в точке (2, 2)
V~2 4
и построить соответствующий круг кривизны. Отв. /( = - , R=—y=i.
2. Найти кривизну и радиус кривизны кривой y = smx в точке f-~-, lj и
построить круг кривизны в этой точке. Отв. /( = /? = 1.
3. Найти точку кривой у = \пх, в которой кривизна наибольшая.
Отв. (^, -±1п2
4. Найти кривизну эллипса * = acos/, y = bsint в точке, для которой ^ = -о~.
0тВ.К= 8аЬ
_з •
(За2+62)2
5. Найти кривизну и радиус кривизны кривой #=3/2, y = 3t—t3 при * = 1.
Указание. Вид этой кривой примерно такой же, что и на рисунке 178.
Отв. /С = 4", #=6.
6 '
4
6. Найти кривизну кривой r = a cos3 0 (а >0) при О=0 (см. рис. 171). Отв. —.
§ 3. СОПРИКАСАЮЩАЯСЯ ОКРУЖНОСТЬ И ЦЕНТР КРИВИЗНЫ
Рассмотрим некоторую кривую, имеющую в точке М кривизну /С.
В этой точке проведем нормаль к кривой, направленную в сторону
вогнутости кривой, и отложим на этой нормали отрезок МС,
равный величине -тт (рис. 214). Опишем из точки С окружность радиуса
R = Ym ^та 0КРУЖН0СТЬ имеет с данной
кривой в точке М общую касательную и
одинаковую кривизну. Эта окружность называется
соприкасающейся окружностью. Иными
словами, соприкасающаяся окружность (с
кривой в точке М) — это окружность,
проходящая через точку М, радиус которой равен
радиусу кривизны кривой в точке М и
которая имеет в точке М общую касательную
с кривой и одинаковые направления вогну- Рис 214.
тости. Соприкасающуюся окружность
называют также кругом кривизны (здесь слово «круг» употребляется в
смысле «окружность»).
Центр соприкасающейся окружности называется центром
кривизны данной кривой в точке М. Таким образом, центр кривизны
лежит всегда на нормали к кривой в данной точке со стороны
направления вогнутости кривой.
Соприкасающаяся окружность примыкает к кривой в
окрестности точки М наиболее тесным образом по сравнению с другими
481

Рис. 215.
окружностями, проходящими через точку М и имеющими в этой
точке общую касательную с кривой. Можно доказать, что эта
окружность представляет предельное положение окружности,
проведенной через три точки, взятые на кривой, которые стремятся
к совпадению с точкой М (рис. 215).
Выведем теперь формулы для координат центра кривизны в
любой точке М кривой y = f(x). Функция f (х) предполагается дважды
дифференцируемой. Координаты точки М обозначим через х и у,
а координаты соответствующего ей центра кривизны С—через | и т].
Напишем уравнение нормали к кривой в точке М (см. гл, V, § 2):
Y-y—^X-x),
(1)
где X, Y обозначают текущие координаты точки нормали, а х, у —
координаты точки касания, то есть точки М (рис. 216) *.
Так как точка С (центр кривизны) лежит на этой нормали, то
ее координаты удовлетворяют уравнению (1):
Л — У = — ^(1 — х).
(2)
Но поскольку точка С отстоит от М на расстояние, равное радиусу
кривизны R, то
(?-х)2 + (г)-у)2 = #2. (3)
Решая совместно уравнения (2) и (3), найдем значения ? и т|.
Действительно, подставляя значение разности г\—у из (2) в (3), получим:
(t-x)* + ± ?_*)« = /?»,
У*
* В процессе вывода мы считаем, что у'х^Ь0, но окончательные формулы
верны и без этого ограничения.
482

отсюда
/2
х'х
(S-*)2=-
и, значит,
Подставляя значение этой разности в правую часть уравнения (2),
найдем:
(1+у'Я2
Таким образом, для координат центра кривизны будем иметь:
l=x±—VjL-rR, 4=*/ + X—j:r>
(i+vD* 0+</'*)2
2
а так как (см. (5), § 2, гл. XII) R = (l+%*) , то
fe *_ |й| . г] Уч_ ^ . (4)
Вопрос о выборе знака перед дробью решается следующим
образом. Если у'х>0, то в точке М кривая вогнута вверх (см. гл. VII,
§ 4) и, значит, ц>у (см. рис. 216), и потому следует брать в
формулах (4) нижние знаки. Если к тому же учесть, что в этом
случае \у"х\ = Ух, то формулы (4) принимают вид:
6=ж_У0+?», w + l±*L. (5)
Ух Ух
Аналогичными рассуждениями можно показать, что эти формулы
остаются справедливыми и в том случае, когда ух<0, что
предлагается проверить самостоятельно. Следовательно, формулы (5) дают
нам координаты центра кривизны для любой точки кривой.
Если теперь кривая задана параметрическими уравнениями
* = ф(0> У = ,Ф(0> Т0> заменяя в формулах (5) ух и у"х их
выражениями по формулам (6) из предыдущего параграфа, получим:
-Уи *l = </ + r^—яг?**- (6)
xty; — x;yt '" ¦ ' ¦ xtyi — x*tyt
Так как xt у и их производные являются функциями параметра tf
то, как это видно из формул (6), и координаты центра кривизны
?, г\ являются функциями того же параметра t.
483

Пример. Найти координаты центра кривизны параболы у2 = 2рх в
произвольной ее точке М (х, у) и в точке Мг (О, 0).
,. Y2p р
Имеем: у = ±у 2рх, откуда ^ = ± -—^== —; далее, по правилу диффе-
2ух У
Р Р2
ренцирования сложной функции, находим: упх — ^ • у'х = ^. Подставляя эти
У У
значения в формулы (5), получим координаты центра кривизны в произвольной
Ф
точке М (*, у): ? = 3#-{-p, т]= — ~. Затем, заменяя х и у координатами точки
Mi (0, 0), найдем: § = р, т) = 0 —координаты центра кривизны кривой,
соответствующего точке Мг.
Упражнения
1. Найти координаты |, т| центра кривизны и построить соприкасающуюся
окружность гиперболы ху = А в точке (2, 2).
Отв. g = 4, т] = 4.
2. Найти координаты ?, т] центра кривизны и построить соприкасающуюся
окружность кривой у = \пх в точке пересечения ее с осью ОХ.
Отв. | = 3, т| = —2.
3. Найти координаты центра кривизны и построить соприкасающуюся
окружность полу кубической параболы у2 = х3 в точке (1, 1).
Отв. Е = -2,Л= у.
4. Найти координаты ?, т] центра кривизны и радиус кривизны для
произвольной точки синусоиды y=sinx.
^ * , + /, , У ч 2cos2* n (l+cos2*)2
Ome. ? = * + ctg*(l-f cos2*), ti = : R=z±—L *
1 sin x ' | sin л: |
5. Найти координаты ?, т] центра кривизны и радиус кривизны кардиоиды
х = 2acos t — a cos 2t, y = 2a sin t — a sin 2t.
л с. 2a a ол 2a . . , a . _. n 8a
Отв. ^ =-^-cost+ -^ cos 2t, r\ = -^- sint-+-_¦ sin 2^, R = ~o-
. t
sm-g
§ 4. ПОНЯТИЕ ЭВОЛЮТЫ И ЭВОЛЬВЕНТЫ
Выше мы видели, что для произвольной плоской кривой I
каждой ее точке отвечает свой центр кривизны. Поэтому, если точка
М (х, у) перемещается вдоль данной кривой, то соответствующий
ей центр кривизны С(|, т]), Еообще говоря, также перемещается,
описывая некоторую кривую, называемую эволютой данной кривой.
Иными словами, эволютой плоской кривой L называется
геометрическое место ее центров кривизны. При зтом сама исходная
кривая L по отношению к своей эволюте называется эвольвентой, или
разверткой.
Ясно, что прямая линия не имеет эволюты, а эволютой окружности
является одна точка — ее центр. В прочих случаях эволютой
служит, вообще говоря, некоторая линия. Нетрудно видеть , что
формулы (5) и (6) § 3, выражающие координаты | и г\ центра кривизны
С через параметр х или t, можно рассматривать как уже готовые
параметрические уравнения эволюты данной кривой. Исключая из
этих уравнений параметр х или t, мы получим для эволюты
уравнение, связывающее непосредственно координаты g и г).
484

Рис. 218.
Пример 1. Найти эволюту параболы у=ах2.
Так как у' = 2ах, у" = 2а, то по формулам (5) § 3 находим:
? = *- 1+4fl2*2 .2ax = -4aW,
Щ = У-
--ах2-
2а
\+4а2х2
2а ~~
= 1(1+6а2*2).
\+Аа2х2
2а
Таким образом, параметрические уравнения эволюты параболы будут: ? = —4а2х3.
1 1 fi
Г)= о- (1+6а2*2). Исключая из этих уравнений параметр *, получим: 12= — .
•а(г] — о~] .Мы видим, что эволютой параболы является по л у кубическая
парабола (рис. 217).
Пример 2. Найти эволюту эллипса х = а cos t, y = b sin t.
Так как x'f — — a sin t, x'{ = — a cos ?; ^ = b cos tf, */J' =— b sin /, то, подставляя
это в формулы (6) § 3, получим:
l = acost-
b.cos t (a2 sin2 t + b2 cos2 t) __a2-
ab <
- cos3 t,
f . , a sin * (a2 sin2 t + b2 cos2 ^) б2 —й2 . , .
r\ = b smt - г—! L=—г— sm31.
1 ab b
Исключая параметр t, получим уравнение этой эволюты в неявном виде:
№)3+(Ьл)3=с3, где c2 = a2 —Ь2.
Мы видим, что эволютой эллипса является астроида (рис. 218).
Отметим два важных свойства эволюты и эвольвенты,
устанавливающих связь между ними.
1°. Нормаль к данной кривой (то есть к эвольвенте) является
касательной (в центре кривизны) к ее эволюте.
485

Доказательство. Допустим, что кривая задана явным
уравнением y=f(x). Угловой коэффициент касательной к эволюте,
заданной параметрическими уравнениями (5) предыдущего параграфа
(причем параметром служит х), равен
ъ=г- (1)
Далее, введем обозначение v=-^%—, откуда vy" = l + у'2. Тогда
упомянутые уравнения (5) коротко запишутся так: ?> = х—y'v,
r\ — y-\-v. Отсюда дифференцируя по х, найдем: ?*=1—y"v — y'v'
HT|i=j/' + t»'. Но так $ак y"v = l +у'2, то ?i=—у'{у' +v').
Подставляя эти значения & и г\'х в формулу (1), получим:
Итак,
%=—
fc- */'
Слева стоит угловой коэффициент касательной к эволюте, а ух
есть угловой коэффициент касательной к данной кривой (эвольвенте)
в соответствующей точке. Поэтому последнее равенство означает,
что касательная к кривой в некоторой ее точке и касательная к
эволюте в соответствующей точке взаимно перпендикулярны, то есть
нормаль к данной кривой является касательной к ее эволюте, что
и требовалось доказать.
Замечание. Мы доказали приведенное выше свойство для
случая, когда кривая задана уравнением в явном виде y = f(x).
Однако это свойство остается справедливым и в том случае, если
кривая задана параметрическими уравнениями, причем
доказательство его проводится совершенно аналогично.
Второе свойство приведем без доказательства.
2°. Пусть радиус кривизны изменяется вдоль дуги эвольвенты
монотонно, то есть либо только возрастает, либо только убывает.
Тогда приращение радиуса кривизны эвольвенты равно (по
абсолютной величине) соответствующему приращению дуги эволюты.
Так, например (рис. 219),
С^С2 = Л1аСа —AfxCx, ^C3 = M3C3 — M2C2f Сз^4 = М4С4 — М3С3 и т.д.
Приведенные выше два свойства позволяют дать очень простой
механический способ построения эвольвенты по ее эволюте.
Предположим, что нам дана выпуклая кривая CD — эволюта. Представим
себе гибкую нерастяжимую нить, одним концом закрепленную
в точке С и натянутую на эту эволюту CD. Если мы станем эту
нить развертывать, сматывая с эволюты, сохраняя ее все время
натянутой, то второй конец нити опишет кривую АВ — эвольвенту
данной кривой CD (см. рис. 219). Следовательно, закрепив в конце
486

этой нити острие карандаша, мы сможем указанным способом
вычертить эвольвенту по известной ее эволюте.
Нетрудно видеть, что данная эволюта имеет бесчисленное
множество различных эвольвент.
Пример 3. Найти эвольвенту (развертку) круга.
Пусть мы имеем окружность радиуса а (рис. 220). Возьмем ту
из эвольвент этой окружности,
которая проходит через точку
А (а, 0). Учитывая, что ВМ =
= AB = att где / — угол АОВ,
Y,
С\
О
1
/С
'Т
в
^
°Уг
\"и
\М>
'м,
X
Рис. 219.
Рис. 220.
мы непосредственно из рисунка видим, что координаты х, у точки
М выразятся следующим образом:
x=OC = OD + DC = OD + FM=acost + BMsmt =
= a cos / -f- at sin t = a (cos t +/ sin /).
Далее,
y = CM = FD = DB — FB = asmt—BM cos t =
= a sin / — at cos t = a (sin / — / cos /).
Таким образом, эвольвента круга представляется следующими
параметрическими уравнениями:
x = a(cost-{-t sin/), у = a (sin/ — /cos/), причем 0^/< + оо.
Геометрически это будет некоторая спираль, которую нетрудно
себе представить.
Легко проверить, что исходная окружность, то есть 1 = a cost,
rj = asin/ является эволютой полученной только что развертки
окружности, что и предлагается сделать самостоятельно.
Упражнения
1. Найти эволюту гиперболы ху=*4.
2. Найти эволюту параболы х = 2t, y = t2 — 6.
Отв. (* + */Г-(*-*/Г=4.
Отв. р » (Ч+»У.
243 V1
487

3. Найти эволюту полукубической параболы у3 = ах2.
Отв. ^=±l|/"-|(3r/ + a), г\ = -±№ + 2ау).
4. Показать, что эволютой циклоиды x=a(t — sint), y = a(l—cost) является
смещенная циклоида.
Указание. Параметрические уравнения эволюты переходят в уравнения
первоначальной циклоиды после преобразования координат и параметра по
формулам ? = ?i-f-rca, i] = T1i — 2а, t = t\ + n.
5. Показать, что эволюта кардиоиды x = 2acost—acos2t, у = 2а sin t — a sin 2t
есть также кардиоида, подобная данной.
Указание. Полученные параметрические уравнения эволюты преобразовать
к новым координатам и параметру при помощи формул ?=—?ь г\=—%, t =
= ?1 + л. В результате получим параметрические уравнения эволюты ?i=2 — cos tx—
a nj 2a . . а . ПА _ _
— -~-cos2?b г|х =-^-sm ti— -»-sin2^1, которая будет подобна данной кривой с
отношением подобия 1 : 3.

Г Л А В А XIII
КРИВЫЕ В ПРОСТРАНСТВЕ
§ 1. ВЕКТОРНАЯ ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА.
УРАВНЕНИЕ КРИВОЙ В ПРОСТРАНСТВЕ
Известно, что одним из основных понятий математического
анализа, выражающим идею взаимной связи переменных величин,
является понятие функции. До сих пор мы изучали функциональную
зависимость между величинами, принимающими только численные
значения. Другими словами, если переменная величина х есть
функция переменной величины t, то есть x = x(t), то как значения
независимой переменной t, так и значения самой функции х суть
числа. Таким образом, t и х являются в этом случае
скалярными величинами, или просто скалярами; иными
словами, мы имеем скалярную функцию скалярного аргумента. По
аналогии со скалярной функцией можно ввести понятие векторной
функции скалярного аргумента.
Определение. Если каждому значению параметра t из
некоторого промежутка отвечает определенный вектор г (зависящий
от t), то вектор г называется векторной функцией от
скалярного аргумента t, ив этом случае пишут:
г=/•(*). (1)
При изменении аргумента t вектор г (t) изменяется, вообще говоря,
как по величине, так и по направлению.
Как и в векторной алгебре, мы здесь рассматриваем свободные
векторы, то есть такие векторы, которые считаются равными, если
они равны по величине и одинаково направлены, или, иначе говоря,
если они имеют равные проекции на оси координат. Свободные
векторы могут быть отложены от какой угодно точки. Будем считать,
что вектор r(f) исходит из начала координат, то есть вектор г—
радиус-вектор некоторой точки М. В этом случае при изменении
параметра t конец вектора r(t) опишет некоторую линию L, назы-
489

ваемую годографом векторной функции г (t) (рис. 221). Уравнение (1)
называют векторным уравнением этой кривой.
С векторной функцией скалярного аргумента весьма часто
приходится встречаться в кинематике при изучении движения-точки,
когда радиус-вектор r(t) движущейся точки является функцией
времени t. Годографом такой функции является траектория
движения точки.
Если через х, у и z мы обозначим проекции вектора r(t) на оси
прямоугольной системы координат в пространстве (рис. 222), то эти
величины для каждого значения параметра t в свою очередь
принимают определенные численные значения и потому являются
скалярными функциями скалярного аргумента t\
x = x(t), y = y(t), z = z(t).
(2)
Как известно из векторной алгебры, разложение вектора r{t)
по ортам прямоугольной системы координат имеет вид (рис. 222):
r(t) = x(t)i + y(t)j+z(t)k.
(3)
Таким образом, задание векторной функции скалярного аргумента
(то есть функции (1)) равносильно заданию трех скалярных функций
того же аргумента (то есть функций (2)).
Так как уравнение (1) является уравнением некоторой кривой в
пространстве, то ту же кривую задают и уравнения (2). Уравнения (2) —
обычные параметрические уравнения кривой в
пространстве. С помощью этих уравнений для каждого значения t
определяются координаты х, у и z соответствующей точки кривой,
а по координатам можно определить и радиус-вектор этой точки.
В качестве примера неплоской кривой рассмотрим винтовую
линию. Так называется линия, описываемая точкой М, которая
движется по какой-нибудь образующей прямого кругового цилиндра,
вращающегося в то же время около своей оси так, что путь,
проходимый точкой М по образующей, все время пропорционален углу
поворота цилиндра. Винтовую линию можно получить так. Пусть
нам дан прямой круговой цилиндр радиуса а, ось которого совпа-
'X
Рис. 222.
490

дает с осью OZ (рис. 223). На данный цилиндр будем навивать
прямоугольный треугольник ABC так, чтобы вершина его А лежала в
точке пересечения образующей цилиндра с осью ОХ, а катет АС
навивался на круг в основании цилиндра. Тогда гипотенуза образует
на цилиндре указанную выше винтовую линию. Выведем уравнение
винтовой линии.
Обозначим через х, у и г координаты ее переменной точки М
и через t угол AOD поворота цилиндра, то есть угол, образованный
проекцией радиуса-вектора точки М на плоскость XOY с осью ОХ.
Мы считаем, что в начальном положении точка М совпадает с А.
Тогда из рисунка видно, что x = acost, y = asint. Кроме того,
поскольку перемещение точки вдоль образующей пропорционально
углу /, координата z = ct, где с — коэффициент пропорциональности.
Значит, параметрические уравнения винтовой линии запишутся так:
x = acost, y = asint, z=ct (4)
или в векторной форме
r=a cos ti-\-a sin tj+ctk. (5)
§2. ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ ВЕКТОРНОЙ ФУНКЦИИ
СКАЛЯРНОГО АРГУМЕНТА
Рассмотрим векторную функцию r=r(t) скалярного аргумента ?.
Для этой функции можно ввести основные понятия математического
анализа аналогично тому, как это делается с обыкновенными
скалярными функциями.
Дадим прежде всего определение предела для векторной
функции r(t).
Пусть функция r(t) определена в окрестности точки /0> кроме, быть
может, самой точки tQ.
491

Определение. Вектор г0 называется пределом векторной
функции г (t) при стремлении t к t0 (или, короче, в точке t0),
если длина вектора г (t)—г0 стремится к нулю, то есть
lim|r(9-r0|=0. (1)
t-+t0
Если г0 есть предел функции r(t) при t->t0, то это записывается так:
\imr(t)=r0 или r(t)-+r0 при t->t0.
t-+t0
Итак, когда мы пишем: limr(/) = r0, то подразумеваем под этим
соотношение (1).
V\bi видим, что определение предела для векторной функции
сводится к понятию о стремлении к нулю скалярной величины —
понятию, уже известному нам из анализа.
Если мы запишем векторную функцию r(t) и вектор г0 в
проекциях (см. формулу (3), § 1):
r(f)=x(f)l + y(t)J+z(t)k,
r0 = x0i + y0j+z0k,
то получим:
I г (0 -го | =V\ * (t) -хо I2 + [ у (t) -Уо? + I z (*) -г012- (2)
Тогда из условия (1) сразу следует, что
lim *(/)=*<>, limt/(0 = r/0» \im z(t) = z0> (3)
t-+t0 f-*tQ t-+t0
то есть вычисление предела векторной функции можно производить
по каждой проекции в отдельности. Обратно, из формул (3) с
помощью (2) сразу вытекает соотношение (1). Таким образом,
соотношения (1) и (3) равносильны.
Далее непосредственно из определения следует, что если r(t)->r0,
то и | г (/) | ->|г0|. Это сразу вытекает из неравенства ||/*(01 — l^oll^
^\r(t)—r0\. В частности, г(/)->0 равносильно с |r(f)|->0.
Пользуясь определением предела векторной функции, нетрудно
доказать, что пределы суммы, разности двух векторных функций,
а также произведения скалярной функции на векторную существуют
и равны соответственно сумме, разности и произведению их пределов.
Дадим теперь (по аналогии со скалярной функцией) определение
непрерывности векторной функции r(t). Пусть функция r{t)
определена в точке t=*t0 и в некоторой ее окрестности.
Определение. Функция г(t) называется непрерывной в
точке t0, если выполняется условие
limr(0=r(/0). (4)
В случае нарушения этого условия говорят, что функция r(t) имеет
разрыв в точке tQ.
492

Мы уже знаем, что соотношение (4) равносильно следующим -трем
соотношениям для проекций вектора r(t):
\imx(t) = x(t0)9 Wmy(t)=y(t0)9 \\mz (t)=z(tQ)9
t^t0 t^t0 /-/o
а эти последние соотношения в свою очередь выражают
непрерывность функций x(t)> y{t)y z (t) в точке tQ.
Таким образом, для непрерывности векторной функции r(t)
необходимо и достаточно, чтобы все три ее проекции на
оси координат были непрерывны.
Как мы уже отмечали, из условия r(t)->r(t0) вытекает
соотношение \r(t)\->\r(tQ)\ при t->t0. Это значит, что непрерывность
векторной функции влечет за собой
непрерывность ее модуля*. Обратного
утверждения сделать нельзя. Существуют векторные
функции, модули которых непрерывны, а сами
они имеют точки разрыва. Примером такой
функции является любая векторная функция
r(t) с постоянным модулем \r(t)\9 но такая,
что направление вектора r(t) меняется
скачками. Действительно, иэ геометрических сообра- Рис 224.
жений легко понять, что при стремлении г(t)
к г (t0) направление вектора r(f) имеет своим предельным
положением направление вектора г(/0) (см. рис. 224). Таким образом,
можно говорить о «непрерывной зависимости» от t направления
вектора г (0 в случае, если векторная функция r(t) непрерывна.
Нарушение этой «непрерывной зависимости» направления (даже при
непрерывности ее модуля) приводит к разрывам векторной функции.
Нетрудно показать, что сумма, разность двух непрерывных
векторных функций, а также произведение непрерывной векторной
функции на непрерывную скалярную функцию являются
непрерывными функциями. В дальнейшем мы будем рассматривать только
непрерывные функции.
§ 3. ПРОИЗВОДНАЯ ВЕКТОРНОЙ ФУНКЦИИ ПО СКАЛЯРНОМУ
АРГУМЕНТУ, ЕЕ ГЕОМЕТРИЧЕСКИЙ И МЕХАНИЧЕСКИЙ СМЫСЛ
Перейдем теперь к вопросу о производной от векторной функции
по скалярному аргументу.
Пусть векторная функция
r=r(t) (1)
задана в промежутке [Т09 Т]. Исходя из некоторого произвольного,
но вполне определенного (фиксированного) значения скалярного
аргумента t9 придадим ему приращение At9 не выводящее его из
промежутка [Т09 Т]9 так что и новое значение t + kt принадлежит этому
* Мы называем длину вектора также его модулем.
493

промежутку. Тогда значение функции r(t) заменится новым
значением r(t-\-At), то есть получит приращение kr(t)=r(t-\-kt)— r(t).
Составим отношение:
Дг (t) r(t+M) — r(f)
\t м
Определение. Если существует предел отношения
приращения векторной функции к вызвавшему его приращению аргумента,
когда Д^-^0, то этот предел называется производной
векторной функции r(t) no скалярному аргументу t, а сама
функция r(t) называется дифференцируемой в точке t Производная
/it*
обозначается через г' (t) или -г..
Таким образом, по определению имеем:
Ясно, что производная г'
скалярного аргумента t
lim
(О
и
Аг(<)
-f"(t).
есть также векторная
ее производная по t,
(2)
функция того же
если она сущест-
Рис. 225.
вует, дает вторую производную г" (t)
и т. д.
Исходя из определения
производной, нетрудно показать, что функция
r(t), имеющая производную, будет
непрерывной в рассматриваемой
точке; предлагаем это проверить
самостоятельно
Дифференциал векторной
функции определяется, как
обычно, равенством
dr(t)=r'(t)dt.
Теперь выясним геометрический
смысл производной векторной
функции. Пусть задана дифференцируемая векторная функция r(t).
Мы знаем, что векторное уравнение (1) является уравнением
некоторой пространственной кривой L, являющейся годографом
векторной функции r(t). Пусть точка М этой кривой соответствует
какому-нибудь фиксированному значению /, а точка Л^ —значению
t-\-kt (рис. 225).Обозначим через ОМ и 0МХ радиусы-векторы точек
М и Мъ так что OM=r(t), OM1 = r(t-{-kt). Тогда разность этих
векторов даст новый вектор MM1 = OM[—OM==r(t + &t)--r(t)==
= Аг(/), выражающий приращение векторной функции r(f). Мы
видим, что вектор ММ± есть вектор-хорда кривой, соединяющий
исходную точку М с новой точкой Mv Разделив вектор Л r(t) =
= ММХ на Д?, мы получим новый вектор
.Дг(0
Я
м
494

кол линеарный* с вектором Аг (?), так как он получается из
Аг(0 умножением на скалярный множитель -г^. Если А^^>0, то при
умножении на гт направление вектора Лг(/) не изменится и
вектор ij, как и вектор Аг(/), будет направлен по секущей ММг в
сторону возрастания параметра t. Если же Д?<Т), то вектор Аг(/)
направлен в сторону убывания /, но при делении на отрицательное
число А/ направление вектора меняется на противоположное и,
следовательно, вектор q по-прежнему лежит на секущей и направлен
в сторону возрастания t.
Выясним направление векторной производной г' {t)\ при этом в
дальнейшем будем предполагать, что годограф функции r(t) во всех
своих точках имеет касательную.
Так как при Д^О точка Мг приближается к точке М, то
секущая ММг годографа в пределе превращается в касательную к
нему в точке М. Поэтому векторная производная г' (t) лежит на
касательной к годографу и направлена в сторону возрастания
параметра i (см. рис. 225).
Остановимся коротко на механическом смысле производной
векторной функции.
Пусть годограф векторной функции r=r(t) является
траекторией движущейся точки; уравнение r=r(t), где t—время,
является уравнением движения этой точки. Тогда вектор приращения
MM1 = kr(t) изображает перемещение точки М за время Д?, а
отношение .у выражает среднюю скорость перемещения ее за этот
промежуток времени. В пределе этот вектор средней скорости даст
вектор скорости v в момент t, то есть
v= lim ^Jp-=r'(t).
Таким образом, производная радиуса-вектора движущейся
точки по времени есть вектор скорости движения,
касательный к траектории в соответствующей точке и
направленный в сторону движения (то есть в сторону возрастания t).
Полученный выше вектор скорости v = r' (t) также зависит от
времени t, и, дифференцируя его, получим вектор ускорения:
Рассмотрим теперь единичный вектор а0(0>
изменяющийся при изменении t только по направлению, но сохраняющий
постоянную длину, равную единице: \aQ(t)\ = l при всех t.
* Векторы, лежащие на одной прямой или на параллельных прямых,
называются коллинеарными.
495

a'(t)
Ясно, что годограф такой векторной функции r=a0(t) есть
кривая, расположенная на единичной сфере. Но так как векторная
производная r'=a'0(t) направлена по
касательной к годографу, а а\ it)
лежит в касательной плоскости к сфере
и потому перпендикулярен к вектору
a0(t). Итак, производная от
единичного вектора a0(t) есть
вектор, перпендикулярный к нему
(рис. 226).
В заключение этого параграфа
заметим, что модуль производной от
векторной функции вообще не равен
производной от ее модуля, то есть | г' it) \ ^ь.
^t\r(t)\\ Примером может служить единичный вектор: производная
модуля такого вектора просто равна нулю как производная от
постоянной, а производная же самого единичного вектора есть
вектор, перпендикулярный к нему.
?ис. 226.
§ 4. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ ВЕКТОРОВ
(ВЕКТОРНЫХ ФУНКЦИЙ)
Теперь остановимся на вопросе практического вычисления
производной векторной функции.
Пусть векторная функция r(t) задана в проекциях на оси
координат (см. формулу (3), § 1). Тогда выбранному значению t будет
отвечать вектор r(f) = x(t)i + y(t)j+z(t)k, а значению ^ + А^ —вектор
r(t + At) = x(t + At)i + y(i + At)j+z(t + At)k.
Найдем приращение вектора r(t), то есть вектор Ar(t)=r (t + At) —
—г (i). Так как вектор Ar(t) представляет собой разность векторов
r(t + At) и г (f), то Ar(t) = Ax(t)i + Ay(t)j+Az(t)k, где
Ax(t) = x(t + At) — x(t)1
Ay(t)=y(t + At)-y(t),
Az(t) = z(t + At) — z(t).
Тогда, разделив на At ^ь О, получим:
Ar (t) = Ах (t)
~ At
At
Ay(t)j [ Azjf) к
At
At
Если функции x(t), y(t) и z(t) имеют производные при выбранном
значении t, то, переходя в последнем равенстве к пределу при
Д^->0, получим формулу
r'(t) = x'(t)i + y'(t)j+z'(t)k,
(1)
позволяющую фактически вычислять производную векторной функции.
Пользуясь выражением (1) для производной г' it), легко
показать, что все основные правила дифференцирования скалярных функ-
496

ций остаются в силе и для векторных функций. Перечислим эти
правила. Ниже будем рассматривать только такие функции,
которые имеют производные.
1°. Производная суммы двух векторов равна сумме
производных:
(/•i(0+/-a(0)f=ri(0+ri(0. (2)
2°. Если векторная функция r(t) умножается на
скалярную функцию ф(0, то
(4>(t)r(t)y = <p'(t)r(t) + <p(t)r'(t). (3)
Следствие. Постоянный числовой множитель можно
вынести за знак производной: (ar{t))' = ar(t).
3°. Производная от скалярного произведения векторов
выражается формулой
(гг (t) - r2 (*))' =r/ (0 • r2 (t) + гг (0 . г2 (/). (4)
4°. Производная векторного произведения векторов
выражается формулой
(П (О ХГ8 (*))' =Г\ (О ХГ2 (t)+rt (/) ХГ; (t). (5)
Последние три формулы показывают, что известное правило
дифференцирования произведения обобщается на случай произведения скаляра
на вектор, а также на случай скалярного и векторного произведений.
Отметим, что в левых частях формул (2), (3), (5) фигурируют
производные векторных функций; в левой части формулы (4)
—производная скалярной функции. В правых частях формул (2), (3), (5)
стоит сумма векторов, а в правой части формулы (4) — сумма
скаляров. При этом в формуле (5) нельзя переставлять сомножители,
ибо векторное произведение не обладает переместительным свойством
Выше мы отмечали, что вывод всех этих формул может быть
произведен с помощью формулы (1). Однако они могут быть также
установлены, если исходить из общего определения производной
векторной функции (см. (2), § 3); при этом доказательство всех этих
формул аналогично доказательству соответствующих формул
дифференциального исчисления. В качестве примера выведем таким способом
формулу (4); для краткости вместо ггф, r2(t) будем писать гг и г2.
Для приращения скалярного произведения гг-г2 при переходе
от точки t к точке t-\-M получим:
А(/-1-/*2) = (/в1 + Аг1).(га + Дга) — /vr2 =
=гг -г2 + гг- Дг2 + Arx • г2 + Дгх • Дг2—гг • г2 =
= Ari-r2 + r1-Ar2 + Ar1.Ara.
Пользуясь правилом внесения скалярного множителя под знак
скалярного произведения *, можно написать:
м ="АГГа + Г1'"АГ + АГ1в"АГ
Как известно, (та- Ь) — т(а- Ь)^ где а, Ь — векторы, яг —числовой множи-
497

Гереходя в этом равенстве к пределу при Д?->0, получим:
lim
Значит,
Д (гх • г2) _
М
2И.(&«)+2?№)+2?.№-
(/Vr2)'=/vr2 + /vr;f
что и требовалось доказать. Доказательство остальных формул мы
предоставляем читателю.
В заключение этого параграфа докажем еще раз, используя
теперь правило 3°, что производная от единичного вектора aQ(t}
есть вектор, перпендикулярный a0(t).
Имеем: а0-а0=1. Дифференцируя это скалярное произведение,
получим:
а'0-а0 + а0-а0 = 0,
то есть 2а'0-а0 = 0 или а'0-ао = 0. Но равенство скалярного
произведения нулю как раз и означает, что векторы а0 и а'0
перпендикулярны.
§ 5. КАСАТЕЛЬНАЯ К КРИВОЙ. НОРМАЛЬ И ЕДИНИЧНЫЙ
ВЕКТОР ГЛАВНОЙ НОРМАЛИ
Пусть точка М (х, у, г) описывает некоторую спрямляемую
пространственную кривую L (рис. 227). Параметром, определяющим
положение точки М на
кривой, будем считать длину s
дуги AM кривой,
отсчитываемую от определенной точки А
кривой до точки М. Так как
положение точки М (х, у, г)
на кривой определяется
значением дуги s, то координаты х, у
и 2, а также радиус-вектор г этой
точки можно рассматривать как
функции длины дуги s:
x = x(s), y = y(s), z = z{s)
и r=r(s) или в проекциях
r=x(s)i + y(s)j+z(s)k. (1)
Рис. 227.
Продифференцируем вектор r(s) no s (здесь и ниже мы
предполагаем, что все необходимые производные существуют); при этом мы
считаем, что на кривой нет особых точек, то есть точек, где одно-
* Нетрудно проверить, что предел скалярного произведения равен
скалярному произведению пределов сомножителей.
498

временно х'9=>*у'8 = х'8 = 0. Получим новый вектор
т=г;, (2)
направленный, как мы знаем, по касательной к кривой в сторону
возрастания s (см. рис. 227). Модуль этого вектора
\r's | = lim
As-*0
Дг
As
= 1. (3)
ибо отношение длины хорды \Аг\ = ММъ стягивающей дугу ММЪ
к длине As этой дуги при стягивании последней в точку стремится
к единице (см. гл. X, § 2, теорема 2*). Таким образом, вектор т
^сть единичный вектор, направленный по касательной к кривой
в точке М в сторону возрастания s. Положительным направлением
касательной будем считать то направление, которое совпадает с
направлением касательного вектора т. Если вектор г задан в
проекциях (см. (1)), то согласно формуле (1) § 4 имеем:
т (s) = r's = x'si + y'sJ + z'sk. (4)
,2
Его модуль l=\x\ = Vxs2-\-y's2 + z's
На основании полученных результатов легко написать
уравнение касательной к кривой L, заданной уравнением (1), в точке
М (х, у, г).
Из аналитической геометрии известно, что уравнения прямой,
проходящей через точку М (х, у, г), имеют вид:
х—х = У—у = Z—г
т п р *
где X, Y, Z — текущие координаты точки прямой, а т, п, р —
проекции направляющего вектора прямой, то есть числа,
пропорциональные направляющим косинусам той же прямой.
Так как единичный вектор т лежит на касательной к кривой
в точке М (х, у, z), то проекции этого вектора x's, y's, z's на оси
координат (см. (4)) могут быть приняты за т, п и р. Следовательно,
уравнения касательной к кривой в точке М (х, у, z) запишутся так:
X-x__Y-y__Z-z
xs Vs zs
где значения производных x'Sy y's, z's вычисляются в точке касания.
Если в уравнениях кривой вместо длины дуги s взять любой
другой параметр t, то, рассматривая длину дуги s как функцию
параметра t, получим: xi=x'ssi, yi=y'ssi, zi=zsst-
Следовательно, производные от х, у, z no t пропорциональны их
производным по s. Поэтому в уравнениях (5) производные x'Sl y's и z'?
можно заменить производными xi, y\ и г\ (соответственно).
Доказанная там теорема справедлива и для пространственной кривой.
499

Тем самым мы приходим и к такой форме уравнений касательной:
X-
Y-y = Z-z
(6)
Пример. Написать уравнения касательной к винтовой линии (см. (4), § 1)
x—azost, y = asintt z — ct для произвольного значения t и для t--
4 '
Так как х}=—a sin t, y't=acost, z't=c, то из формулы (6) получаем:
X — a cos t Y — asint Z — ct
— a sin t
a cost
В частности, при t = — касательная определяется уравнением:
X-
aV%
aV2
Z — c
aV2
a]/2
Рис. 228.
Плоскость, перпендикулярная касательной и проходящая через
точку касания, называется нормальной плоскостью (рис. 228).
Всякая прямая, лежащая в этой плоскости и пересекающая кривую
в точке касания М, называется
нормалью кривой, и, следовательно,
пространственная кривая в каждой точке
имеет бесчисленное множество
нормалей. Найдем уравнение нормальной
плоскости к кривой в точке М (л\ у,
г). Известно, что уравнение плоскости,
проходящей через точку М (х, у, г),
имеет вид:
А(Х — x) + B(Y— y) + C(Z — z) = 0.
Здесь коэффициенты А, В, С
пропорциональны направляющим косинусам
перпендикуляра к этой плоскости. Поскольку перпендикуляром к
нормальной плоскости служит касательная (6), то уравнение
нормальной плоскости имеет вид:
xi (X-x) + yi (Y-y)+z! (Z-z) = 0.
Рассмотрим теперь вторую производную r'i векторной функции г (s).
Из формулы (2) следует, что г1 = [г'5~\'5 = х'в. Так как вектор x(s)
единичный, то вектор производной xs перпендикулярен к нему (см. § 3).
Следовательно, вектор ts лежит в нормальной плоскости и
определяет некоторую нормаль. Эту нормаль называют главной.
Положительным направлением главной нормали будем считать то, которое
совпадает с направлением вектора %'s- Таким образом, вводится
следующее определение.
500

Определение. Главной нормалью кривой в данной ее
точке Л1 называется прямая, проходящая через точку М и
имеющая направление вектора t's.
Если кривая плоская, то главная нормаль кривой совпадает
с нормалью, лежащей в плоскости самой кривой.
Построим единичный вектор п этого направления, то есть
направления вектора x's. Для этого, как известно, нужно разделить
вектор Ts на его модуль, так что
отсюда
или
г;=|г,'|л.
(7)
Выясним геометрический смысл
модуля вектора t's. Из
равнобедренного треугольника, построенного на рисунке 229 (напоминаем,
что длины векторов t(s) и т^ + Дб) равны единице), видно, что
| At(s) 1 = 2 sin
2 *
(8)
Угол со — угол поворота касательной при переходе из точки М
в точку Мъ то есть угол смежности дуги MMV Из равенства (8)?
следует, что (при As>0)
1- |At(s)| ,.
= lim ' .w ' = lim
As—0 As As —0
о • °>
2smT
As "
Заменяя числитель на эквивалентную бесконечно малую со, получим;
I Ts I = lim
As—О
As*
Отношение -г-, стоящее справа, представляет среднюю кривизну
дуги MMV Поэтому, как и в случае плоской кривой, величину \т'8\г
естественно, назвать кривизной кривой в точке М. Обозначив ее, как
обычно, через /С, мы имеем:
/С = |т;|Нг,% (9)
Тогда формула (7) принимает вид:
x's = Kn. (10)
Так как
x's=r;=x^i+y;j+Zsk, (П)
то для вычисления кривизны пространственной кривой получаем
формулу:
(12}
501
к=VV+#¦+*;'.

Пример. Вычислить кривизну винтовой линии г = а cos ti + a sin tj-\-dk (см.
формулу (5) § 1).
Перейдем от параметра t к нужному нам параметру — длине дуги s. Из
формулы (см. формулу (6), гл. X, § 3) s't = ]/ xf+\)'t + zf находим:
st = ]/ a2 sin2 t + a2 cos2 t-\-c2 — ~\/~a2-\-c2. Обозначая у а2-{-с2 через m, получим:
¦^t — m или ds = mdt. Беря за начало отсчета точку Л (см. рис. 223), которой
отвечает ? = 0, получим:
t t
s=z^ds = m^dt = mt,
о о
g
откуда t — —, то есть параметр t пропорционален длине дуги s. Тогда
уравнение винтовой линии после замены параметра примет вид:
S S S
r = a cos — i + a sin —j + c — ft.
m /я т
Дифференцируя последнее равенство по s, получим:
а . s . , a s . , с «_
T=r_ = sm — i-\ cos — j-\—k.
s m mm mJ m
Дифференцируя еще раз, найдем:
a s . а . s .
Т0 = Г0 = 5 COS —I 5 Sin — У,
s s т2 т т2 т Jf
а . s
т2 ту т2 т'
r^cos —, ys = — — sm —, гс = 0.
Отсюда согласно формуле (12) находим кривизну винтовой линии:
^=l^(-^C0S^)2+(-^sini)2=^-
Величина, обратная кривизне, называется радиусом кривизны
кривой в данной ее точке. Обозначим радиус кривизны через R,
тогда R-=-E( и формула (10) принимает вид: xs = ~^n. Отсюда п =
= Rt's = Rr's. Так как вектор т^ лежит на главной нормали, то проекции
этого вектора (см. формулу (11)) пропорциональны направляющим
косинусам главной нормали к кривой в точке М (х, г/, z).
Следовательно, уравнения главной нормали кривой будут иметь вид:
Х — х _Y — y==Z — z
x"s ~ y's ~ z"s '
где X, У, Z—текущие координаты точки на главной нормали.
В частности, уравнение главной нормали к винтовой линии будет
таким:
S S S
X — acos— У —asin— 2-е—
т mm
s . s
cos — sm —
т т
502

или
X —a cost Y — a sin t Z — ct
cost
sin t
0
(так как — = t — см. выше).
Введем еще одно понятие, которым мы воспользуемся ниже.
Определение. Плоскость, проходящая через точку на кривой
и перпендикулярная главной нормали в этой точке, называется
спрямляющей плоскостью.
Исходя из этого определения, можно сразу написать уравнение
спрямляющей плоскости
Xs(X-x)-ys(Y-y) + z';(Z-z) = 0,
проходящей через точку М(х, у, -z) кривой.
§ 6. БИНОРМАЛЬ И КРУЧЕНИЕ. СОПРИКАСАЮЩАЯСЯ
ПЛОСКОСТЬ
Введем еще один вектор, тесно связанный с кривой, именно*
положим
Ь = т х п,
где по-прежнему т—единичный вектор касательной, а я — единичный
вектор главной нормали. Так как т и п взаимно перпендикулярны
и имеют длину, равную 1, то из определения векторного
произведения следует, что и вектор Ь имеет длину, равную 1, и что он
перпендикулярен векторам т и п. Тем самым вектор Ъ лежит в
пересечении нормальной и спрямляющей плоскостей и, значит, направлен
по одной из нормалей к кривой. Вектор Ь называется единичным
вектором бинормали.
Итак, векторы т, п и Ъ взаимно перпендикулярны, а их взаимная
ориентация совпадает со взаимной ориентацией координатных
ортов (рис. 230).
Если кривая — плоская, то векторы т и п находятся в плоскости
кривой, а потому вектор Ь, будучи перпендикулярным этой плоскости,
остается постоянным (рис. 231). Для неплоской кривой вектор
b—переменный. Рассмотрим его
производную. По формуле (5) из
Рис. 231.
503

§ 4 имеем: bs = rsxn + xxn's. Но вектор r's = Kn и потому т'5хя = 0.
Таким образом, b's = ixris. Из этой формулы следует, что вектор
b's перпендикулярен касательному вектору т и потому лежит в
нормальной плоскости. С другой стороны, вектор b's, как производная
от единичного вектора, перпендикулярен самому вектору Ь. Будучи
перпендикулярным к векторам ти&, вектор b's должен располагаться
по главной нормали, то есть лишь скалярным коэффициентом
отличается от единичного вектора п:
bs= — У*п
(о
(коэффициент к может быть как положительным, так и
отрицательным) *. Формула (1) — одна из так называемых формул Френе.
Другой формулой Френе называется соотношение т'8 = Кпу которое
мы получили в предыдущем параграфе. Еще одна формула Френе
представляет выражение для ris, а именно: п'8 = кЬ— /Ст.
Действительно, при указанной выше
ориентации единичных векторов т, п, b
имеет место следующая формула
векторного произведения: п = Ьхт. Найдем
производную вектора п. По формуле
(5) из § 4 имеем:
п5 = ЬэХг + Ьхт'8.
$ft Но bs =—xn,T's = Kn и потому ns =
= ( — кпхт) + (ЬхКп)= —к{пх хт) +
Кфхп), а так как пхт=—Ь, Ьх
хп= — т, то
Рис. 232. п; = тФ-Кт,
что и требовалось доказать.
Величина к имеет для каждой точки, вообще говоря, свое
значение и называется кручением кривой (2) (в соответствующей точке).
Для плоской кривой кручение во всех ее точках равно 0.
Три взаимно перпендикулярных вектора т, п и &, связанные
с каждой точкой кривой, составляют так называемый основной
триэдр (рис. 232). При движении точки вдоль кривой векторы
основного триэдра, вообще говоря, меняют свое направление, оставаясь
все время взаимно перпендикулярными.
Приведем без вывода формулу, по которой можно вычислить
кручение:
х =
/С2
%s,
Xs ,
Xs ,
Уз,
Уз,
Уз ,
Zs
zl
Zs
* В некоторых учебниках этот коэффициент обозначают через % (без минуса).
•504

где все производные, входящие в определитель, берутся по s, а К —
кривизна*. При переходе к произвольному параметру t формулы и
для кривизны, и для кручения усложняются. Так, например,
формула (12) из § 5 для кривизны К в этом случае принимает вид.
К= з- >
(*'Ч</'2+*'2)2
где все производные берутся по t. В частности, если кривая —
плоская и, значит, z = 0, то это выражение сильно упрощается, и мы
приходим к известной нам формуле (7) из § 2 гл. XII. По формуле (2)
легко подсчитать кручение винтовой линии:
fl2 + c2 •
Предлагаем это проверить самостоятельно.
Определение. Плоскость, проходящая через точку М на
кривой перпендикулярно ее бинормали в этой точке, называется
соприкасающейся плоскостью (к кривой в точке М).
Иными словами, соприкасающаяся плоскость — это плоскость,
проходящая через касательную к кривой и ее главную нормаль (рис. 232).
Для плоской кривой соприкасающаяся плоскость совпадает с той
плоскостью, в которой лежит кривая, и, следовательно, для всех
точек кривой будет одна и та же. Для неплоской кривой
соприкасающаяся плоскость меняет, вообще говоря, свое положение при
переходе из одной точки кривой в другую. В общем случае
соприкасающаяся плоскость в точке М представляет собой предельное
положение плоскости, проходящей через точку М и две другие
точки Мг и М.2 на кривой, при условии, что Мг и М2 стремятся к М.
Абсолютная величина кручения показывает, насколько быстро
кривая отходит от соприкасающейся плоскости.
В заключение приведем без вывода уравнение соприкасающейся
плоскости, проходящей через точку M(x,y,z) кривой, заданной
параметрическими уравнениями x = x(t), y=y(t), z = z(t). Это
уравнение имеет вид:
(y'tzt-ziy't) (X—x) + (zixmt—xiz?) (Y—y) + (xix!—yix!) (Z —z)=0. (3>
Его можно также записать с помощью определителя 3-го порядка:
\Х — х Y—y Z—z
Xt yt Zt
xt y'i z't
= 0.
* См., например: А. П. Норден, Дифференциальная геометрия, Учпедгиз,.
1948.
505

Пример. Написать уравнение соприкасающейся плоскости к винтовой линии
{см. (4), § 1] x = acostt y = asmt, z = ct яя произвольного значения t и для
Так как x't = — a sin t, x'j = — a cos t, y't = a cos t, y't' = — a sin t, z't = c,
2^=0, то согласно формуле (З) уравнение соприкасающейся плоскости к
винтовой линии принимает вид:
с sin t- (X—a cos f)— с cos t- (Y — a sin t)-\-a (Z~—ct) = 0.
В частности, при ' = -т- эта плоскость определяется уравнением
2 \ 2 / 2 \ 2 У ' V 4

ОГЛАВЛЕНИЕ
Предисловие редактора 3
От авторов . щ , 4
Раздел I
ВВЕДЕНИЕ В АНАЛИЗ
Глава I. Вещественные числа
§ 1. Понятие множества 5
§ 2. Множество рациональных чисел 8
§ 3. Вещественные числа 11
§ 4. Абсолютная величина числа 18
§ 5. О границах числовых множеств 22
§ 6. Сегмент, интервал, окрестность • 26
§ 7. Другой подход к понятию вещественного числа 27
Глава II. Функции
§ 1. Понятие функции 32
§ 2. Способы задания функций 37
§ 3. Четные и нечетные функции 46
§ 4. Периодические функции 50
§ 5. Понятие обратной функции 52
§ 6. Элементарные функции 55
Глава III. Теория пределов
§ 1. Числовая последовательность и ее предел 71
§ 2. Бесконечно малые и бесконечно большие величины 78
§ 3. Основные теоремы о пределах 81
§ 4. Арифметические действия над переменными величинами 86
§ 5. Особые случаи пределов и неопределенности 90
§ 6. Монотонная переменная и ее предел 97
507

•§ 7. Число е , 100
§ 8. Теорема о вложенных отрезках 103
§ 9. Частичные последовательности 104
§ 10. Предел функции 107
¦§11. Распространение теорем о пределах на случай произвольных функций 115
§ 12. Монотонная функция и ее предел 123
-§ 13. Сравнение бесконечно малых и бесконечно больших 125
Глава IV. Непрерывность и разрывы функции
§ 1. Определение непрерывности функции. Точки разрыва 133
§ 2. Непрерывность некоторых элементарных функций 141
§ 3. Примеры разрывных функций 144
§ 4. Непрерывность сложной функции 148
§ 5. Свойства непрерывных функций 150
§ 6. Существование и непрерывность обратной функции, корня и степени
с рациональным показателем 157
¦§ 7. Существование и непрерывность обратных тригонометрических функций 159
§ 8. Определение степени с иррациональным показателем 160
§ 9. Показательная, логарифмическая и степенная функции 163
§ 10. Использование непрерывности функций при вычислении пределов . . 165
§11. Гиперболические функции и их свойства 167
§ 12. Равномерная непрерывность функции 170
Раздел II
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ
ПЕРЕМЕННОЙ
Глава V. Производная и дифференциал
§ 1. Понятие производной 175
§ 2. Геометрический смысл производной 181
§ 3. Вычисление производных простейших элементарных функций .... 186
§ 4. Связь между дифференцируемостью и непрерывностью функции ... 190
§ 5. Правила вычисления производных 191
§ 6. Сводка формул дифференцирования 198
§ 7. Дифференцирование функций, заданных параметрически 203
§ 8. Дифференциал функции 203
§ 9. Производные и дифференциалы высшего порядка 216
Глава VI. Основные теоремы дифференциального исчисления.
Правило Лопиталя. Формула Тейлора
§ 1. Основные теоремы дифференциального исчисления 226
§ 2. Раскрытие неопределенностей по правилу Лопиталя 233
§ 3. Формула Тейлора 240
508

Глава VII. Исследование функций и построение графиков
=§ 1. Условия постоянства, возрастания и убывания функций 247
$ 2. Экстремум функции. Наибольшее и наименьшее значения 251
$ 3. Исследование функций и построение графиков 261
§ 4. Направление вогнутости кривой и точки перегиба 266
§ 5. Асимптоты кривой 269
§ 6. Различные примеры и задачи 272
§ 7. Графическое решение уравнений 284
§ 8. Уточнение корней уравнения 287
Раздел III.
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
Глава VIII. Неопределенный интеграл
§ 1. Первообразная и неопределенный интеграл 296
§ 2. Основные свойства неопределенного интеграла 301
§ 3. Таблица основных интегралов 302
§ 4. Метод подстановки 307
§ 5. Метод интегрирования по частям 314
§ 6. Специальные приемы вычисления некоторых интегралов 322
§ 7. Интегрирование рациональных функций 329
§ 8. Интегрирование простейших иррациональных и трансцендентных
функций 337
Глава IX. Определенный интеграл
§ 1: Задачи, приводящие к понятию определенного интеграла 353
1. Задача о площади криволинейной трапеции —
2. Задача о пройденном пути 356
§ 2. Определение определенного интеграла 357
§ 3. Условия существования определенного интеграла 360
§ 4. Основные свойства определенного интеграла 366
§ 5. Определенный интеграл как функция верхнего предела.
Существование первообразной для непрерывной функции # 375
§ 6. Определение логарифмической функции через интеграл ¦ 378
§ 7. Вычисление определенного интеграла. Основная формула
интегрального исчисления 380
§ 8. Замена переменной в определенном интеграле 384
§ 9. Интегрирование по частям 390
§ 10. Приближенное вычисление определенного интеграла 394
1. Способ прямоугольников —
2. Способ трапеций 395
3. Формула Симпсона 399
509

Глава X. Геометрические и механические приложения
определенного интеграла
§ 1. Вычисление площадей плоских фигур 404
1. Определение площади —
2. Площадь криволинейной трапеции 406
3. Площадь фигуры в декартовых координатах 409
4. Случай параметрического задания кривой 411
5. Площадь сектора в полярных координатах 415
§ 2. Длина дуги кривой 418
1. Длина дуги в прямоугольных координатах 419
2. Длина дуги в полярных координатах 423
3. Дифференциал дуги 424
4. Эквивалентность бесконечно малой дуги и стягивающей ее хорды 425
§ 3. Условие спрямляемости кривой t s * 427
§ 4. Площадь поверхности вращения 430
§ 5. Вычисление объемов тел 434
§ 6. Статический момент и центр тяжести 440
1. Статический момент и центр тяжести материальной кривой .... —
2. Статический момент и центр тяжести плоской фигуры 445
§ 7. Работа переменной силы 450
Глава XI. Несобственные интегралы
^ 1. Несобственные интегралы первого рода —несобственные интегралы с
бесконечными пределами 456
§ 2. Несобственные интегралы второго рода — несобственные интегралы
от неограниченных функций 464
Раздел IV.
КРИВЫЕ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
Глава XII. Кривые на плоскости
§ 1. Некоторые общие сведения о кривых 474
§ 2. Кривизна и радиус кривизны плоской кривой 476
§ 3. Соприкасающаяся окружность и центр кривизны 481
§ 4. Понятие эволюты и эвольвенты 484
Глава XIII. Кривые в пространстве
§ 1. Векторная функция скалярного аргумента. Уравнение кривой в
пространстве 489
§ 2. Предел и непрерывность векторной функции скалярного аргумента . 491
510

§ 3. Производная векторной функции по скалярному аргументу, ее
геометрический и механический смысл 493
§ 4. Правила дифференцирования векторов (векторных функций) 496
§ 5. Касательная к кривой. Нормаль и единичный вектор главной
нормали 498
§ 6. Бинормаль и кручение. Соприкасающаяся плоскость 503

Константин Алексеевич Бохан,
Ирина Александровна Егорова,
Константин Васильевич Лащенов
КУРС МАТЕМАТИЧЕСКОГО АНАЛИЗА
Том I
Редактор В. Г. Долгополое
Переплет художника /О. М. Сигова
Художественный редактор А. В. Сафонов
Технический редактор Я. Я. Цирульницкий
Корректор Г. Я. Смирнова
* * *
Сдано в набор 1/IV 1971 г. Подписано
к печати 5/1 1972 г. 60 X 90l/ie.
Типографская бум. № 3. Печ. л. 32. Уч.-изд. л. 32,19.
Тираж 40 тыс. экз.
Издательство «Просвещение» Комитета по
печати при Совете Министров РСФСР
Москва, 3-й проезд Марьиной рощи. 41
Отпечатано с матриц ордена Трудового
Красного Знамени Ленинградской
типографии № 1 «Печатный Двор» им.
А. М. Горького Главпслиграфпрома
Комитета по печати при Совете Министров
СССР, г. Ленинград, Гатчинская ул., 26,
в типографии им. Котлякова
издательства «Финансы» Комитета по печати при
Совете Министров СССР. Ленинград,
Садовая ул., 21. Заказ № 572.
Цена без переплета 90 к., переплет 11 к.