Автор: Араманович И.Г. Бермант А.Ф.
Теги: анализ математика математический анализ высшая математика издательство наука учебник для втузов
Год: 1967
Текст
А. Ф. БЕРМАНТ, И. Г. АРАМАНОВИЧ
КРАТКИЙ КУРС
МАТЕМАТИЧЕСКОГО
АНАЛИЗА
ДЛЯ ВТУЗОВ
ИЗДАНИЕ ПЯТОЕ,
СТЕРЕОТИПНОЕ
Допущено Министерством
высшего и среднего специального образования РСФСР
в качестве учебника для высших технических учебных заведений
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
MOCK В А 1967
517,2
Б 50
УДК 517.0 @75.8)
Анисим Федорович Бермант, Исаак Генрихович А Романович
Краткий курс математического анализа
для втузов
М., 1967 г., 736 стр с илл.
Редактор С. А. Широкова
Техн. редактор С Я- Шкляр Корректоры С. Д. Кайсер и Я. #. Кришталь
Печать с матриц. Подписано к печати 18/V 1967 г. Бумага 60x907ie- Физ. печ. л. 46.
Условн. печ. л. 46. Уч.-изд. л. 44,7. Тираж 200 000 экз. Цена книги 1 р. 35 к.
Заказ № 1889.
Издательство «Наука»
Главная редакция физико-математической литературы.
Москва, В-71, Ленинский проспект, 15.
Ордена Трудового Красного Знамени
Первая Образцовая типография имени А. А. Жданова
Главполиграфпрома Комитета по печати при Совете Министров СССР.
Москва, Ж-54, Валовая, 28.
ОГЛАВЛЕНИЕ
Предисловие 11
Введение 13
1. «Элементарная» и «высшая» математика A3). 2. Величина,
Переменная величина и функциональная зависимость A4). 3. Ма-
Математика и действительность A6).
глава I
ФУНКЦИЯ
§ 1. Действительные числа 18
4. Действительные числа и числовая ось. Интервал A8). 5. Аб-
Абсолютная величина B1). 6. О приближенных вычислениях B2).
§ 2. Первоначальные сведения о функции 25
7. Определение функции B5). 8. Способы задания функций B7).
9. Символика C0). 10. Основные элементарные функции. Слож-
Сложная функция C2). 11. Элементарные функции C3). 12. Неяв-
Неявные функции. Многозначные функции C6).
§ 3. Начало изучения функций. Простейшие функции 38
13. Основные характеристики поведения функции C8). 14. Гра-
Графическое изучение функции D1). 15. Прямая пропорциональная
зависимость и линейная функция. Приращение величины D3).
16. Квадратичная функция D6). 17. Обратная пропорциональная
зависимость и дробно-линейная функция D8).
§ 4. Обратная функция. Степенная, показательная и логарифмическая
функции 50
18. Обратная функция E0). 19. Степенная функция E4).
20. Показательная и логарифмическая функции E7).
§ 5. Тригонометрические, обратные тригонометрические, гиперболиче-
гиперболические и обратные гиперболические функции 60
21. Тригонометрические функции. Гармонические колебания F0).
22. Обратные тригонометрические функции F4). 23. Гиперболи-
Гиперболические и обратные гиперболические функции F8).
Вопросы и предложения для самопроверки 71
1*
4 ОГЛАВЛЕНИЕ
ГЛАВА И
ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ
§ 1. Предел функции. Бесконечные величины 73
24. Предел функции непрерывного аргумента G3). 25. Бесконечно
большой аргумент G6). 26. Последовательности и их Пре-
Пределы G9). 27. Бесконечно большие величины. Ограниченные
функции (81). 28. Бесконечно малые величины (85). 29. Пра-
Правила предельного перехода (86). 30. Один признак существова-
существования предела функции. Первый замечательный предел (93).
31. Один признак существования предела последовательности.
Второй замечательный предел (95).
§ 2. Непрерывные функции , . . . 98
32. Непрерывность функции (98). 33. Точки разрыва функ-
функции A00). 34. Действия над непрерывными функциями. Непрерыв-
Непрерывность элементарных функций A02). 35. Свойства непрерывных
функций A06).
§ 3. Сравнение бесконечно малых величин 108
36. Сравнение бесконечно малых величин. Эквивалентные беско-
бесконечно малые величины A08). 37. Примеры отношений бесконечно
малых величин. Натуральные логарифмы (ПО).
Вопросы и предложения для самопроверки 114
ГЛАВА III
ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ. ДИФФЕРЕНЦИАЛЬНОЕ
ИСЧИСЛЕНИЕ
§ 1. Производная 116
38. Некоторые задачи физики A16). 39. Скорость изменения
функции. Производная функция. Производная степенной функ-
функции A20). 40. Геометрический смысл производной A23).
§ 2. Дифференцирование функций 125
41. Дифференцирование результатов арифметических дейст-
действий A25). 42. Дифференцирование сложной и обратной функ-
функций A29). 43. Производные основных элементарных функ-
функций A33). 44. Дифференцирование элементарных функций. При-
Примеры A38). 45. Дополнительные замечания о дифференцировании
функций A39). 46. Параметрически заданные функции и их диф-
дифференцирование A41).
§ 3. Геометрические задачи. Графическое дифференцирование 146
47. Касательная и нормаль к линии A46). 48. Графическое диф-
дифференцирование A50). 49. Геометрический смысл производной
в системе полярных координат A52).
§ 4. Дифференциал 154
50. Дифференциал и его геометрический смысл A54). 51. Свойства
дифференциала A57). 52. Дифференцируемость функции A61).
ОГЛАВЛЕНИЕ 5
53. Применение дифференциала к приближенным вычисле-
вычислениям A63).
§ 5. Производные и дифференциалы высших порядков , . . 166
54. Производные высших порядков A66). 55. Дифференциалы
высших порядков A70).
Вопросы и предложения для самопроверки 172
ГЛАВА IV
ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
К ИССЛЕДОВАНИЮ ФУНКЦИЙ
§ 1. Теоремы Ферма, Ролля, Лагранжа и Коши 174
56. Теоремы Ферма и Ролля A74). 57. Теорема Лагранжа A77).
58*. Теорема Коши A79).
§ 2. Поведение функции в интервале 181
59. Признаки монотонности функции A81). 60. Экстремумы функ-
функции A83). 61. Схема исследования функций на экстремумы. Наи-
Наибольшее и наименьшее значения функции A87). 62. Применение
второй производной. Точки перегиба A95).
§ 3. Правило Лопиталя. Схема исследования функций 202
63. Правило Лопиталя B02). 64. Асимптоты линий B08). 65. Общая
схема исследования функций B13).
§ 4. Кривизна 216
66. Дифференциал длины дуги B16). 67. Кривизна B17).
§ 5. Пространственные линии. Векторная функция скалярного аргу-
аргумента 221
68. Пространственные линии B21). 69. Винтовая линия B24).
70. Векторная функция скалярного аргумента B26). 71*. Прило-
Приложения к механике B31).
§ 6. Комплексные функции действительного переменного 233
72. Комплексные числа B33). 73. Определение и дифференциро-
дифференцирование комплексных функций B36). 74. Показательная функция и
формулы Эйлера B37).
§ 7. Решение уравнений 240
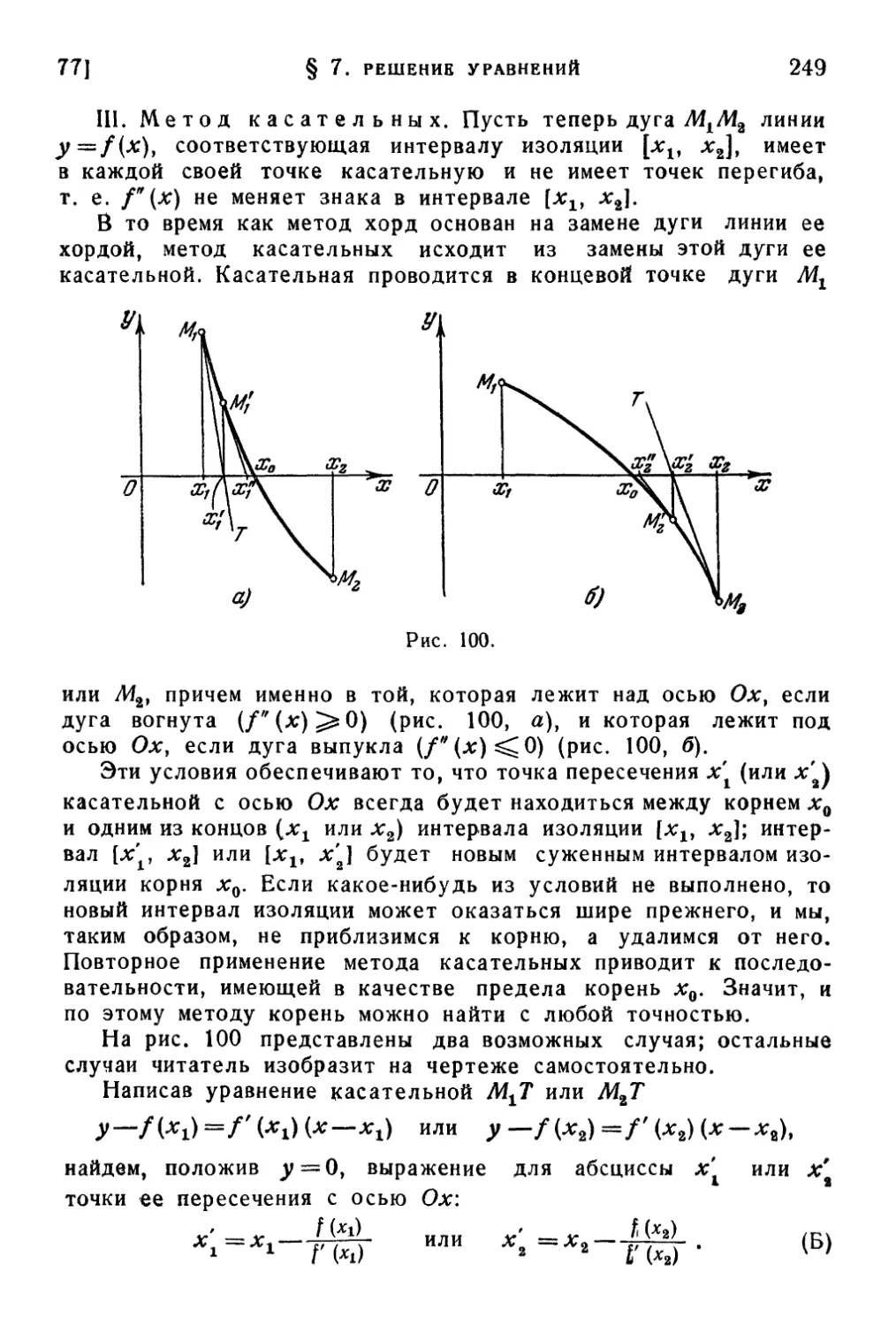
75. Общие сведения об уравнениях B40). 76. Признак кратности
корня B44). 77. Приближенное решение уравнений B45).
Вопросы и предложения для самопроверки 251
глава V
ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
§ 1. Неопределенный интеграл 253
78. Первообразная функция B53). 79. Неопределенный интеграл.
Основная таблица интегралов B56). 80. Простейшие правила
интегрирования. Примеры B59). 81. Интегрирование по частям
6 ОГЛАВЛЕНИЕ
и замена переменной B64). 82. Интегрирование рациональных
функций B70). 83. Интегрирование простейших иррациональных
функций B77). 84. Интегрирование тригонометрических функ-
функций B79). 85. Заключительные замечания. Использование таблиц
интегралов B83).
§ 2, Определенный интеграл , » . . 286
86. Некоторые задачи геометрии и физики B86). 87. Определен-
Определенный интеграл. Теорема существования B92). 88. Простейшие
свойства определенного интеграла B95). 89. Перестановка преде-
пределов и разбиение интервала интегрирования. Геометрический смысл
интеграла B96). 90. Оценка интеграла. Теорема о среднем. Сред-
Среднее значение функции C01) 91. Производная от интеграла по его
верхнему пределу C06). 92. Формула Ньютона — Лейбница C08).
93*. Интегрирование комплексных функций действительного пере-
переменного C11).
§ 3. Способы вычисления определенных интегралов 312
94. Интегрирование по частям и замена переменной в определен-
определенном интеграле C12). 95. Приближенные методы интегрирова-
интегрирования C17). 96. Графическое интегрирование C24).
§ 4. Несобственные интегралы 326
97. Интегралы с бесконечными пределами C26). 98*. Признаки
сходимости несобственных интегралов с бесконечными преде-
пределами C30). 99. Интегралы от разрывных функций C35).
Вопросы и предложения для самопроверки 338
ГЛАВА VI
ПРИМЕНЕНИЕ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
§ 1. Некоторые задачи геометрии и статики 340
100. Площадь фигуры C40). 101. Объем тела C43). 102. Длина
дуги C46). 103. Центр тяжести криволинейной трапеции C50).
§ 2. Общая схема применения интеграла 353
104. Схема решения задач C53). 105*. Площадь поверхности вра-
вращения C57). 106. Давление жидкости на стенку сосуда C59).
Вопросы и предложения для самопроверки 360
ГЛАВА VII
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ.
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
§ 1. Функции нескольких переменных 361
107. Функции двух и многих переменных C61). 108. Метод сече-
сечений. Предел и непрерывность C65).
§ 2. Производные и дифференциалы. Дифференциальное исчисление . ¦ 369
109. Частные производные и дифференциалы C69). НО. Полный
дифференциал C74). 111*. Дифференцируемость функций C77).
ОГЛАВЛЕНИЕ 7
112. Геометрический смысл полного дифференциала функции двух
переменных C80). 113. Применение полного дифференциала к при-
приближенным вычислениям C82). 114. Производные и дифферен-
дифференциалы высших порядков C85). 115. Отыскание функции по ее
полному дифференциалу C87). 116. Дифференцирование сложных
функций. Правила для отыскания дифференциала функций C93).
117. Теорема существования неявной функции C98). 118. Диф-
Дифференцирование неявных функций D01).
§ 3. Геометрические приложения дифференциального исчисления . . . 404
119. Поверхности D04). 120. Пространственные линии как пере-
пересечение двух поверхностей D07).
§ 4. Экстремумы функций нескольких переменных 410
121. Необходимые условия экстремума D10). 122. Достаточные
условия экстремума для функций двух переменных D12). 123. За-
Задачи о наибольших и наименьших значениях D14). 124*. Услов-
Условные экстремумы D16).
§ 5. Скалярное поле 422
125. Скалярное поле. Поверхности уровня D22). 126. Производ-
Производная по направлению D23). 127. Градиент D26).
Вопросы и предложения для самопроверки 430
Г ЛА ВА VIII
ДВОЙНЫЕ И ТРОЙНЫЕ ИНТЕГРАЛЫ
§ 1. Двойные интегралы 432
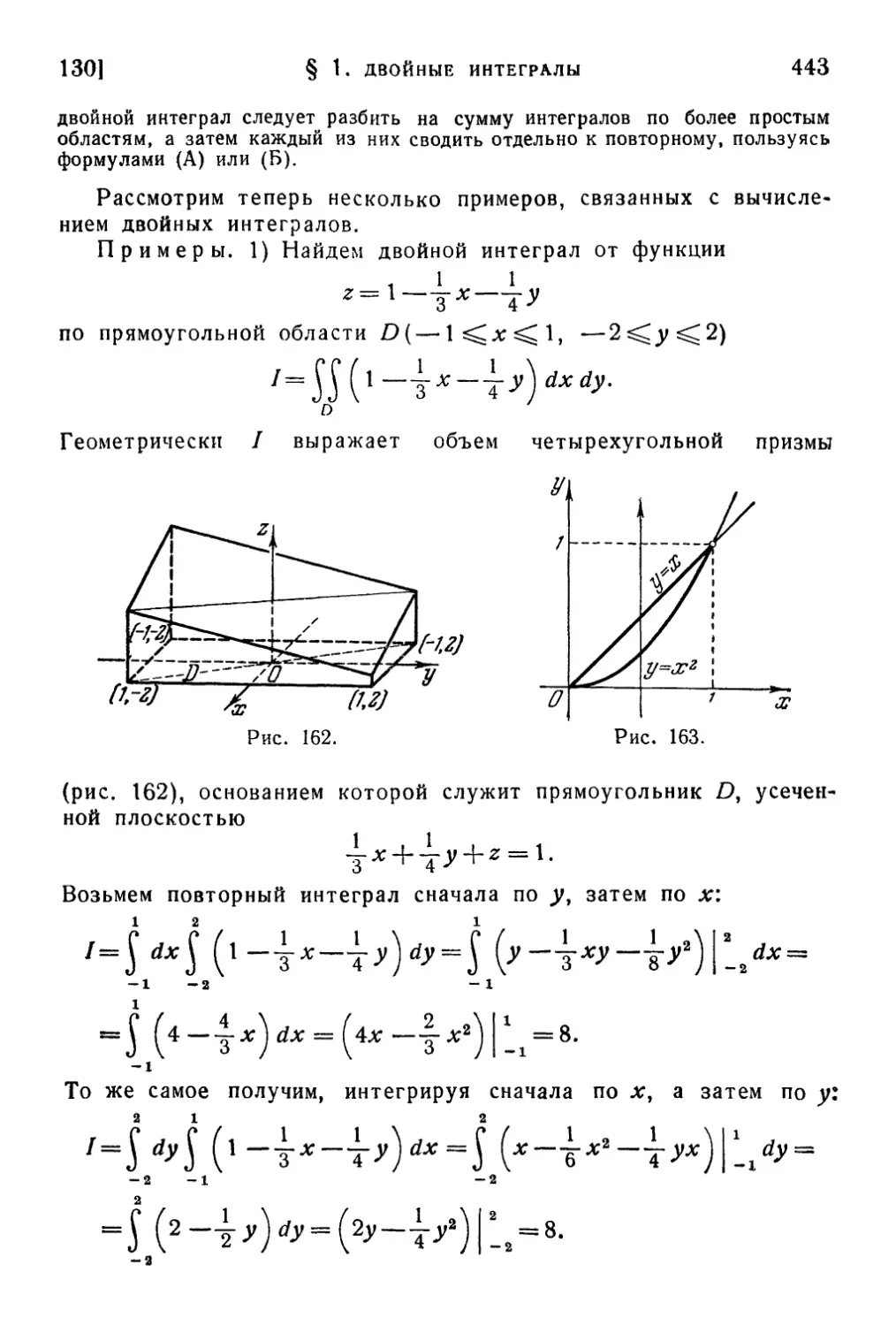
128. Объем цилиндрического тела. Двойной интеграл D32).
129. Свойства двойных интегралов D35). 130. Вычисление двой-
двойных интегралов D37). 131. Двойной интеграл в полярных коор-
координатах D46). 132. Приложения двойных интегралов к задачам
механики D51).
§ 2. Тройные интегралы 453
133. Масса неоднородного тела. Тройной интеграл D53). 134. Вы-
Вычисление тройных интегралов D55). 135. Применение тройных
интегралов D62).
§3*. Интегралы, зависящие от параметра 464
136*. Интегралы с конечными пределами D64). 137. Несобствен-
Несобственные интегралы, зависящие от параметра D69).
Вопросы и предложения для самопроверки 471
ГЛАВА IX
КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ.
ТЕОРИЯ ПОЛЯ
§ 1. Криволинейный интеграл 472
138. Задача о работе силового поля. Криволинейный интеграл D72).
139. Вычисление криволинейных интегралов. Интегралы по замк-
замкнутому контуру D75). 140. Формула Грина D81). 141. Условие
ОГЛАВЛЕНИЕ
8
независимости интеграла от линии интегрирования D83). 142. Ин-
Интегрирование полных дифференциалов. Первообразная функция D87).
143. Криволинейные интегралы по пространственным линиям D90).
144. Приложения криволинейных интегралов к задачам механики
и термодинамики D94). 145. Криволинейный интеграл по длине
(первого рода) D99).
§ 2*. Интегралы по поверхности 502
146*. Поток жидкости через поверхность. Интеграл по поверхно-
поверхности E02). 147*. Свойства интегралов по поверхности E05).
148*. Вычисление интегралов по поверхности E08). 149*. Формула
Стокса E14). 150*. Формула Остроградского E17).
§3*. Теория поля 519
151*. Векторное поле и векторные линии E19). 152*. Поток век-
вектора. Дивергенция E22). 153*. Циркуляция и ротор векторного
поля E28). 154*. Оператор Гамильтона и векторные дифферен-
дифференциальные операции второго порядка E33). 155*. Свойства про-
простейших векторных полей E35). 156*. Электромагнитное поле E38).
157*. Нестационарные поля E43).
Вопросы и предложения для самопроверки , 545
ГЛАВА X
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
§ 1. Дифференциальные уравнения первого порядка 547
158. Общие понятия. Теорема существования E47). 159. Уравне-
Уравнения с разделяющимися переменными E51). 160. Некоторые задачи
физики E54). 161. Однородные и линейные уравнения первого
порядка E58). 162. Уравнения в полных дифференциалах E64).
163. Приближенные методы решения уравнений первого поряд-
порядка E65). 164*. Особые точки дифференциальных уравнений пер-
первого порядка E69).
§ 2. Дифференциальные уравнения второго и высших порядков .... 572
165. Дифференциальные уравнения второго порядка E72).
166. Частные случаи уравнений второго порядка E74). 167. Прило-
Приложения к механике E76). 168. Дифференциальные уравнения высших
порядков E81).
§ 3. Линейные дифференциальные уравнения 582
169. Линейные уравнения второго порядка. Общие свойства E82).
170. Уравнения второго порядка с постоянными коэффициентами
без правой части E86). 171. Уравнения второго порядка с постоян-
постоянными коэффициентами с правой частью E91). 172. Метод вариации
произвольных постоянных E98). 173. Линейные дифференциальные
уравнения и-го порядка F00). 174. Линейные дифференциальные
уравнения /1-го порядка с постоянными коэффициентами F04).
175. Колебания. Резонанс F05).
§ 4. Системы дифференциальных уравнений 613
176. Общие определения. Нормальные системы уравнений F13).
177*. Геометрическая и механическая иллюстрации решений си-
системы дифференциальных уравнений. Фазовое пространство F17).
178. Системы линейных дифференциальных уравнений F20),
ОГЛАВЛЕНИЕ
179. Системы линейных дифференциальных уравнений с постоян-
постоянными коэффициентами F22). 180*. Случай кратных корней
характеристического уравнения F27). 181*. Матричная форма
записи системы линейных дифференциальных уравнений F30).
Вопросы и предложения для самопроверки 634
ГЛАВА XI
РЯДЫ
§ 1. Числовые ряды 636
182. Определение ряда и его суммы F36). 183. Необходимый при-
признак сходимости ряда. Гармонический ряд F40). 184. Ряды с по-
положительными членами. Достаточные признаки сходимости F42).
185. Интегральный признак Кош и F47). 186. Ряды с произволь-
произвольными членами. Абсолютная сходимость F49).
§ 2. Функциональные ряды 653
187. Общие определения F53). 188. Свойства правильно сходя-
сходящихся функциональных рядов F56).
§ 3. Степенные ряды 658
189. Теорема Абеля. Интервал и радиус сходимости F58).
190. Свойства степенных рядов F63).
§ 4. Разложение функций в степенные ряды 665
191. Ряд Тейлора F65). 192. Условие разложения функций в ряд
Тейлора F68). 193. Остаточный член ряда Тейлора. Формула
Тейлора F70). 194. Разложение функций в ряды Тейлора и
Маклорена F73).
§ 5. Некоторые применения рядов Тейлора 680
195. Приближенное вычисление значений функции F80). 196. Ин-
Интегрирование функций и дифференциальных уравнений F84).
§ 6*. Дополнительные вопросы теории степенных рядов 689
197*. Степенные ряды в комплексной области F89). 198*. Ряд и
формула Тейлора для функции двух переменных F92).
Вопросы и предложения для самопроверки , . . 694
ГЛАВА XII
РЯДЫ ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ
§ 1. Ряды Фурье 695
199. Гармонические колебания. Тригонометрические ряды F96).
200. Ряды Фурье G00). 201. Разложение в ряд Фурье четных и
нечетных функций. Ряд Фурье в произвольном интервале G05).
202. Примеры G07). F '
§ 2. Дополнительные вопросы теории рядов Фурье. Практический
гармонический анализ 714
Ю ОГЛАВЛЕНИЕ
203*. Равенство Парсеваля. Среднее значение квадрата периоди-
периодической функции G14). 204*. Ряды Фурье в комплексной фор-
форме G15) 205*, Ортогональные системы функций G17). 206. Прак-
Практический гармонический анализ. Шаблоны G19).
§3*. Интеграл Фурье 723
207*. Интеграл Фурье G23). 208*. Интеграл Фурье для четных и
нечетных функций G26). 209*. Интеграл Фурье в комплексной
форме. Преобразование Фурье G28).
Вопросы и предложения для самопроверки , 730
Таблица интегралов t 731
Литература 736
ПРЕДИСЛОВИЕ
Четвертое издание «Краткого курса математического анализа
для втузов» выпускается в значительно переработанном виде.
Главная цель переработки заключалась в том, чтобы привести
«Курс» в соответствие с программой по высшей математике для
инженерно-технических специальностей, утвержденной Министер-
Министерством высшего и среднего специального образования СССР в 1964 г.
Параграфы и пункты, относящиеся к той части программы,
которая может не изучаться во втузах с уменьшенным объемом
курса математики (это относится главным образом к специально-
специальностям технологического профиля), отмечены звездочками; читатель
может выпустить эти пункты без всякого ущерба для понимания
остального текста. Звездочками отмечены также относящиеся
к этим пунктам вопросы для самопроверки, помещенные в конце
каждой главы.
За последние годы в серии «Избранные главы высшей мате-
математики для инженеров и студентов втузов» вышел ряд книг
(см. перечень литературы), которые могут служить учебными
пособиями по изучению дополнительных разделов математики.
Именно поэтому в «Курсе» не отражены отдельные пункты общей
программы, относящиеся к уравнениям математической физики и
функциям комплексного переменного. Специального руководства
требует и раздел программы «Методы вычислений и программи-
программирование»; из него в «Курс» включены лишь отдельные вопросы
(применение дифференциала к теории ошибок, приближенное
решение уравнений, численное интегрирование).
Для лучшей фиксации внимания читателя формулировки важ-
важнейших определений и теорем даны жирным шрифтом. В книге
почти нет материала, выходящего за рамки программы; поэтому
мелким шрифтом набраны лишь отдельные замечания.
В «Курсе» разобрано много примеров и задач, относящихся
к различным разделам механики и физики. Изучение их безусловно
необходимо для овладения методами математического анализа и,
что особенно важно для будущих инженеров, методами примене-
применения анализа к решению конкретных физических задач.
12 предисловие
Книга ставит своей целью не просто сообщить читателю те
или иные необходимые ему сведения по математическому анализу.
Она предназначена и для того, чтобы развить у читателя логи-
логическое и математическое мышление, расширить его математиче-
математический кругозор. Поэтому большинство положений высказывается
с точным перечислением условий, при которых они справедливы.
Все места, где даются упрощенные доказательства, по возмож-
возможности оговариваются. Точно так же отмечаются все теоремы,
которые приводятся без доказательств.
Читатель, заинтересованный в более глубоком и детальном
изучении курса анализа, должен обратиться к более полным ру-
руководствам; некоторые из них приведены в списке литературы.
Включение в «Курс» ряда новых разделов потребовало в не-
некоторых случаях довольно существенной переработки старого
текста; при этом большое внимание было уделено упрощению и
уточнению формулировок определений и теорем. Писать об этих
изменениях вряд ли целесообразно: учащемуся, впервые читаю-
читающему книгу, они ничего не скажут; преподаватели, рекомендую-
рекомендующие этот курс студентам, легко обнаружат их сами1).
При изучении математики во втузах порядок прохождения
материала часто бывает связан не только внутренней логикой
курса, но и сроками прохождения дисциплин, опирающихся на
этот курс. Именно в связи с этим перенесен вперед (по сравне-
сравнению с предыдущими изданиями) параграф о векторной функции
скалярного аргумента, так как нужда в нем в курсе теоретиче-
теоретической механики возникает очень рано. Главы второй половины
книги образуют циклы (VIII и IX, X, XI и XII), которые могут
изучаться почти независимо друг от друга. При этом глава X —
дифференциальные уравнения — опирается лишь на самые простые
сведения о функциях многих переменных.
А. Ф. Бермант, создавший первоначальный вариант этого
«Курса», скоропостижно скончался 26 мая 1959 г. До сих пор
жива память о нем — талантливом ученом и педагоге, кипучем
организаторе, отдавшем очень много сил делу повышения мате-
математической культуры в нашей стране. Все изменения и дополне-
дополнения как в первое, так и в последующие издания внесены мною.
В процессе работы я часто пользовался советами моих това-
товарищей— математиков. Всем им выражаю свою искреннюю призна-
признательность.
#. Г. Лраманович
*) Отметим только, что в этом издании в определение функции вклю-
включается обязательное требование ее однозначности; в связи с этим
иначе трактуются вопросы о неявных и обратных функциях.
ВВЕДЕНИЕ
1. «Элементарная» и «высшая» математика. Говоря о курсе
математики, изучаемом в высших учебных заведениях, часто назы-
называют его «курс высшей математики». Соответственно те разделы
математики, которые изучают в школе, обычно объединяются
названием «курс элементарной математики». Сразу подчеркнем, что
это разделение математики на «высшую» и «элементарную» весьма
условно; нельзя указать никаких точных признаков, согласно ко-
которым такое разделение можно произвести.
Следует все же отметить, что те разделы математики, которые
мы относим к «элементарной», возникли и существуют уже очень
давно. Любому школьнику известны имена греческих ученых Пи-
Пифагора и Е в к л ид а, — первый из которых жил за пятьсот,
а второй за триста лет до нашей эры. Именно в то время была
создана та система элементарной геометрии, которая лишь с не-
небольшими изменениями изучается в школе и сейчас.
Несколько позже оформилась как самостоятельный раздел ма-
математики алгебра; ее рождение относят к VIII веку н.э., когда
хорезмский ученый Моххамед Аль-Хорезми изложил ее
основы в трактате «Альджебр аль-мукабала», из первого слова
названия которого и произошло само слово «алгебра». Разумеется,
правила арифметических и алгебраических действий, а также спо-
способы решения простейших уравнений были известны значительно
раньше.
Возникновение тригонометрии, связанное с астрономическими
исследованиями, также относится к античной древности. Конечно
и алгебра, и тригонометрия претерпели в своем развитии очень
большие изменения, прежде чем приняли свой современный вид.
Ведь алгебраической символикой начали пользоваться сравнительно
«недавно»: основу ее положил французский математик Ф. Виет
в книге, вышедшей в 1591 г.
Те же разделы математики, которые объединяются общим на-
названием «высшая математика», развились из учений, возникших
в XVII и XVIII веках в связи с прогрессом естествознания и
14 ВВЕДЕНИЕ
техники. Потребности науки и техники в более углубленном изуче-
изучении природы привели к учениям о процессах, явлениях, на-
наблюдаемых в окружающем нас мире. Это прежде всего коснулось фи-
физических явлений. Для того чтобы изучить их с количественной
стороны, стала нужна математика, которая была бы в силах иссле-
исследовать взаимные изменения различных величин, участвующих
в явлении.
Математический анализ — значительный раздел «высшей
математики» — как раз и занимается переменными величи-
величинами в их взаимозависимости.
Математический анализ основывается на тесной связи алгебра-
алгебраических и геометрических методов, впервые появившейся в анали-
аналитической геометрии, созданной знаменитым французским математи-
математиком и философом Рене Декартом A596—1650).
2. Величина. Переменная величина и функциональная зависи-
зависимость. Основное понятие, с которым мы встречаемся на каждом
шагу в любой естественнонаучной или технической области зна-
знания,— это понятие «величины». Под величиной понимают все
го, что может быть измерено и выражено числом (или числами).
В конкретных вопросах естественных и технических наук при-
приходится встречаться с величинами разнообразной природы. Приме-
Примерами величин служат: длина, площадь, объем, вес, температура,
скорость, сила и т. п. В математике же не участвуют конкретные
величины.
Математические положения и законы формулируют, абстра-
абстрагируясь от конкретной природы величин, принимая во внимание
лишь их численные значения. В соответствии с этим в ма-
математике рассматривают величину вообще, отвлекаясь от физического
смысла, который она может иметь. Именно поэтому математические
теории с одинаковым успехом могут быть применены к исследова-
исследованию любых конкретных величин. В этом, между прочим, выражается
та общность, универсальность математических теорий, которую
называют также абстрактностью, иногда неправильно пони-
понимая под этим оторванность от практики, от действительности.
Ф. Энгельс в таких словах подчеркивает эту особенность матема-
математики: «...чтобы быть в состоянии исследовать эти формы (прост-
(пространственные.— А. Б.) и отношения (количественные. — А. Б.) в чи-
чистом виде, необходимо совершенно отделить их от их содержания,
оставить это последнее в стороне как нечто безразличное; таким
путем мы получаем точки, лишенные измерений, линии, лишенные
толщины и ширины, разные а и b, x и у, постоянные и перемен-
переменные величины...»1).
1) Ф. Энгельс, Анти-Дюринг, Госполитиздат, 1952, стр. 37.
ВВЕДЕНИЕ 15
Среди совместно рассматриваемых величин обычно некоторые
изменяются, другие же остаются постоянными. Изменение,
движение есть первейший признак того, что мы называем
явлением, процессом. Явление, наблюдаемое в природе или технике,
и воспринимается нами как изменение одних величин, участвующих
в этом явлении, обусловленное изменением других. Например, на-
наблюдая некоторую массу газа при постоянной температуре, мы
отмечаем изменение упругости газа при изменении его объема.
Точно так же при рассмотрении падения тела (в пустоте) под воз-
воздействием силы тяжести мы отмечаем изменение скорости движе-
движения при изменении расстояния тела от точки, из которой началось
падение, а также изменение и этого расстояния и скорости дви-
движения с течением времени. Вместе с тем ускорение движения
остается постоянным и в любой момент времени, и на всем пути
падения.
Для изучения явлений необходимо ввести в математику понятие
переменной величины.
Переменной называют величину, принимающую различные числен-
численные значения; величина, которая сохраняет одно и то же численное
значение, называется постоянной.
Как уже было сказано, всякий процесс характеризуется (с ко-
количественной стороны) взаимоизменяемостью нескольких перемен-
переменных величин. Такое представление приводит к важнейшему в ма-
математике понятию функциональной зависимости, т.е.
связи между переменными величинами.
Установление и описание связи между величинами, участвую-
участвующими в данном процессе, есть первая и главная задача естествен-
естественных и технических наук. Законом процесса именно и называется
функциональная зависимость, проявляющаяся в этом процессе и ха-
характеризующая его; говорят еще, что эта зависимость описывает
процесс. Так, функциональная зависимость между упругостью
(р) и объемом (v) газа, состоящая в том, что при постоянной тем-
k
пературе р — — {k — постоянная), выражает закон, которому сле-
следуют газы при соответствующих условиях. Словесное выражение
функциональной зависимости — упругость газа обратно
пропорциональна объему (при постоянной температуре) —
есть обычная формулировка указанного закона. Аналогично функ-
функциональная зависимость между расстоянием (s), пройденным сво-
свободно падающим телом, и временем падения (*), состоящая в том,
что s = Y8t2 (?—Ускорение силы тяжести), выражает закон
свободного падения.
Важнейшей задачей математического анализа является всесто-
всестороннее изучение функциональных зависимостей.
16 ВВЕДЕНИЕ
3. Математика и действительность. Невозможно дать краткое
и исчерпывающее определение математики, Ф. Энгельсу при-
принадлежит суждение о предмете математической науки, которое
в силу своей глубины и лаконичности должно считаться наиболее
удачным и точным:
«Чистая математика имеет своим объектом пространственные фор-
формы и количественные отношения действительного мира...»1).
При этом Ф. Энгельс особо подчеркивает опытное происхож-
происхождение математики: «Как понятие числа, так и понятие фигуры
заимствованы исключительно из внешнего мира, а не возникли в
голове из чистого мышления»2).
Благодаря этому математика и оказывает существенную помощь
в изучении вещей и процессов, встречающихся как в различных
науках о природе, так и в различных науках об обществе, везде,
где есть необходимость рассматривать эти вещи и процессы с ко-
количественной стороны. Что же касается естествознания и техники,
то математика является для них чрезвычайно ценным методом тео-
теоретического исследования и практическим орудием. Без тех средств,
которые дает элементарная, а затем и высшая математика, невоз-
невозможен никакой технический расчет, а значит, без математики не-
невозможна и никакая серьезная инженерная и научно-техническая
работа. Это есть следствие того, что технические науки опираются
на физику, механику, химию и т. д., количественные закономер-
закономерности которых выражаются с помощью понятия функции и других
понятий математического анализа. Еще Галилей говорил, что
«законы природы записаны на языке математики».
Ярким подтверждением того, что и математическая наука рож-
рождается из объективной реальности, что и ее законы, соотношения
пра-вильно отражают в особой, присущей ей абстрактной форме
действительные соотношения материального мира, служит возмож-
возможность научного предвидения с помощью математики, т.е.
правильность выводов, получаемых математическим путем, согласие
«предсказанного» с реальностью, с тем, что фактически осущест-
осуществляется в дальнейшем.
В истории науки известно много ярких примеров предвидения.
Мы кратко коснемся здесь только некоторых примеров; они очень
выразительны по той роли, которую играет в них математика.
Как известно, основателем современного учения о полете тела
более тяжелого, чем воздух, является виднейший механик конца
XIX и начала XX вв. московский профессор Н. Е. Жуковский.
Он нашел математическим путем такие формулы и предложе-
предложения, которые легли в основу теории авиации. В частности,
!) Ф. Энгельс, Анти-Дюринг, Госполитиздат, 1952, стр. 37.
2) Там же.
ВВЕДЕНИЕ 17
Н. Е. Жуковский теоретически предсказал возможность «фигур
высшего пилотажа». Первая фигура — «мертвая петля» — в скором
времени была осуществлена капитаном русской армии П. Н. Н е-
стеровым. Итак, «мертвая петля», прежде чем она появилась
«физически», была открыта «математически»!
Французский ученый И. Леверье занимался вопросами дви-
движения планет солнечной системы. При этом он исходил из законов
классической механики, выраженных в виде известных функцио-
функциональных зависимостей. Леверье заметил, что некоторые его выводы
расходятся с имеющимися наблюдениями; он нашел также, что эти
расхождения могут быть устранены, если допустить существование
еще одной планеты с определенными массой и траекторией. На
основе его предположений новая планета, названная затем Непту-
Нептуном, действительно была вскоре обнаружена в том месте и в тот
момент, которые им были заранее указаны. Так за столом, на листе
бумаги, при помощи вычислений был для науки открыт новый мир!
Нас теперь не удивляет точнейшее знание будущих астрономи-
астрономических событий. Разумеется, оно возможно именно потому, что
употребляемые математические методы верно отражают объектив-
объективные закономерности.
Резко повысилась роль математики в последнее время, чему
во многом способствовало и расширение ее возможностей, связан-
связанное с созданием быстродействующих электронно-вычислительных
машин. Осуществление космических полетов, посылка ракет к дру-
другим планетам и телевизионная связь с ними — все это потребовало
необычайно сложных и точных математических расчетов. Матема-
Математические методы широко вторгаются в науки, еще недавно весьма
далекие от математики: в экономику, биологию, медицину. Можно
смело сказать, что ни один научно-технический замысел современ-
современности не обходится без участия математики.
ГЛАВА I
ФУНКЦИЯ
§ 1. Действительные числа
4. Действительные числа и числовая ось. Интервал. Мы начнем
изучение анализа с рассмотрения действительных чисел. Напомним
некоторые основные определения.
Целые положительные числа 1, 2, 3, ... называются нату-
натуральными.
Присоединяя к натуральным числам все дробные числа и нуль,
а также рассматривая не только положительные числа, но и отри-
отрицательные, мы получаем множествох) рациональных чисел. Любое
р
рациональное число имеет вид —, где р и q — целые числа.
Каждое рациональное число может быть записано в виде ко-
конечной десятичной или бесконечной периодической десятичной
дроби.
Иррациональными числами называются бесконечные непериоди-
непериодические десятичные дроби. Можно доказать, например, что У 2,
Y 3, lg 3, я, sin 20° и т.д. являются числами иррациональными.
Мы будем считать, что действия над иррациональными числами
читателю известны.
Все рациональные и иррациональные числа образуют множество
действительных чисел.
Перейдем теперь к геометрическому изображению чисел. Возь-
Возьмем прямую линию и на ней некоторую точку О, которую примем
за начало отсчета длин. Выберем масштаб, т.е. отрезок, прини-
принимаемый за единицу длины, и установим направление отсчета.
Определение. Прямая линия, на которой указаны начало
отсчета длин, масштаб и направление отсчета, называется число-
числовой осью.
1) Под термином множество здесь и в дальнейшем понимается некоторая
совокупность (конечная или бесконечная) чисел или точек.
4] § 1. ДЕйствитЕльные числа 19
Представим себе числовую ось в виде горизонтальной прямой;
положительное направление на ней установим слева направо. Будем
откладывать от начала отсчета все отрезки, соизмеримые
с единицей масштаба; длины таких отрезков, как известно из гео-
геометрии, выражаются рациональными числами. В соответствии с вы-
выбранным направлением отсчета отрезки, откладываемые вправо от
точки О, мы будем считать соответствующими положительным
числам, а отрезки, откладываемые влево от нее, — соответствую-
соответствующими отрицательным числам.
Пусть конец отрезка, соответствующего в выбранном масштабе
рациональному числу а, попал в точку М прямой. Тогда мы
скажем, что точка М изображает число а и что число а
есть координата точки Ж. Очевидно, точка О изображает чис-
число нуль.
Точки числовой оси, изображающие рациональные числа, назы-
называются рациональными точками.
Если мы будем изображать рациональные числа вида ±-^-,
±-^-, ...и все больше и больше увеличивать знаменатель N,
то точки, соответствующие этим рациональным числам, будут все
гуще и гуще покрывать числовую ось.
Более того, покажем, что, как бы близко друг к другу ни ле-
лежали две рациональные точки А и В, между ними обязательно
лежит еще бесконечно много рациональных точек. Пусть точки Л
и В имеют рациональные координаты а и Ь\ тогда середина от-
отрезка между ними, назовем ее точкой С, имеет координату ^i— ,
которая тоже является числом рациональным. В силу этого
же соображения точка Сг — середина отрезка АС—и точка С2 —
середина отрезка СВ—также будут рациональными точками. Но
так как этот процесс можно продолжать неограниченно, то мы и
получим бесконечно много рациональных точек, которые все лежат
на отрезке АВ.
И все же рациональные точки не исчерпывают всех точек чи-
числовой оси; на ней имеются и другие точки. В самом деле, так
как диагональ квадрата, стороны которого равны единице, несо-
несоизмерима с единицей масштаба, то ее длина не выражается
никаким рациональным числом. Поэтому, если отложить от точки О
отрезок, равный диагонали такого квадрата, то конец этого от-
отрезка попадет в точку, не являющуюся рациональной. Вообще,
концы всех отрезков, выходящих из начала отсчета и несоиз-
несоизмеримых с единицей масштаба (длины их выражаются иррацио-
иррациональными числами), попадут в нерациональные точки; такие точки
будем называть иррациональными.
20 гл. i. функция [4
Все рациональные и иррациональные точки уже полностью
исчерпывают прямую. Важно подчеркнуть, что между множеством
всех точек числовой оси и множеством всех действительных чисел
имеется взаимно однозначное соответствие. Это зна-
значит, что каждая точка числовой оси изображает какое-нибудь одно
число (рациональное или иррациональное), и обратно, каждое число
(рациональное или иррациональное) является координатой какой-
нибудь одной точки числовой оси.
На нашей числовой оси очень наглядно представляются раз-
различные соотношения между числами. Так, меньшему числу соот-
соответствует точка, лежащая левее точки, изображающей большее
число; числу, заключенному между двумя данными числами, соот-
соответствует точка, лежащая между точками, изображающими данные
числа.
В силу описанного соответствия между числами и точками чи-
числовой оси иногда будет удобно не делать различия между ними
и под точкой понимать число или под числом — точку.
Определение. Интервалом называется множество всех
чисел (точек), заключенных между двумя какими-нибудь числами
(точками), называемыми концами интервала.
Интервал с концами х == а и х — b, где а<СЬ, можно задать
неравенствами а < х < Ь; он обозначается еще так: (а, Ь). Если
вместе с множеством точек интервала рассматривать и его концы,
то получится замкнутый интервал. Замкнутый интервал с концами
х-=а и х = Ь задается неравенствами a^x^ib; его обозначают
так: [а, Ь]. В противоположность замкнутому интервалу интервал
(а, Ь) называется открытым или незамкнутым1). Если один конец
присоединяется к интервалу, а другой— нет, то получается интер-
интервал, открытый с одной стороны, или полуоткрытый интервал.
Полуоткрытый интервал задается неравенствами а^лг<?, если
присоединен конец лг = а, и a<ix^.b, если присоединен конец
х = Ь; записывают их соответственно так: [а, Ь), (а, Ь]. Таким
образом, присоединение конца к интервалу всегда обозначается
квадратной скобкой, а исключение —круглой.
В тех случаях, где нет нужды различать, причисляются ли
концы к рассматриваемому интервалу или нет, мы будем говорить
просто об интервале.
Кроме конечных интервалов, часто встречаются бесконечные
интервалы, т. е. либо множество всех чисел меньших, чем некото-
некоторое число с, либо множество всех чисел больших, чем число с,
либо, наконец, множество всех действительных чисел. Эти беско-
*) В математической литературе замкнутый интервал часто называют
отрезком, сохраняя термин «интервал» только для открытого ин-
интервала.
5] § 1. действительные числа 21
печные интервалы задаются соответственно условными неравенст-
неравенствами — оо < # < с, с < л; < -f оо и — оо < л: < + оо. Записывают:
( — 00, С), (С, + Оо) И ( —ОО, +ОО).
Если в первых двух случаях точку с причисляют к интервалу,
то это записывают в виде ( — оо, с] или [с, 4-оо).
Определение. Интервал длины 2/ с центром в точке а
называется /-окрестностью точки а.
Координаты х точек, принадлежащих /-окрестности точки а
(рис. 1), удовлетворяют, оче-
очевидно, неравенствам ^ о ^ о >—
Понятие окрестности точки Рис. 1.
часто используется в даль-
дальнейшем. Принадлежность точки х к данному интервалу будем
обозначать при помощи символа включения ?. Так, запись
х?[а, ft] означает, что точка х является одной из точек замкну-
замкнутого интервала [а> ft], т. е. что а^.х^Ь. Аналогично симво-
символическая запись х g (a, ft) означает, что а < х < ft, и т. д.
5. Абсолютная величина.
Определение. Абсолютной величиной (или модулем)
\А\ числа А называется число, равное самому Л, если А поло-
положительно или равно нулю, и равное — Д, если А отрицательно:
А, если
_Л, если Л<0.
Значит, |^| есть всегда неотрицательное число (положительное
или нуль). На числовой оси \А\ есть длина отрезка от начала
отсчета до точки, изображающей число А.
Соотношение
, где Д>0, (*)
равносильно двум таким соотношениям:
(**)
В самом деле, соотношение (*) означает, что точка А находится
от точки нуль на расстоянии, не большем В; а это возможно
только тогда, когда эта точка лежит в интервале [—В, В], т. е.
принадлежит ^-окрестности точки нуль, и значит, тогда имеют
место соотношения (#*); обратное также очевидно.
22 гл. i. функция [6
Установим следующие предложения об абсолютных величинах:
1) Абсолютная величина суммы не больше суммы абсолютных
величин слагаемых, т. е.
Возьмем сначала случай двух слагаемых. Непосредственной
проверкой легко убедиться, что если А и В имеют одинаковые
знаки, то левая и правая части соотношения (###) равны между
собой, а если разные знаки, то левая часть меньше правой.
Переходя последовательно от двух к трем, от трех к четырем и
т. д. слагаемым, легко доказать наше предложение в общем виде.
Равенство в соотношении (*#*) имеет место только в случае, когда
все слагаемые имеют один и тот же знак.
2) Абсолютная величина разности не меньше разности абсолют-
абсолютных величин уменьшаемого и вычитаемого:
\А—В\^\А\ — \В\.
Для доказательства положим А—В=С\ отсюда А = В-\-С и
по доказанному
[А-В\^\А\-\В\.
Что касается произведения и частного, то в силу определения
этих действий имеем:
3) абсолютная величина произведения равна произведению абсо-
абсолютных величин сомножителей:
\A.B-C...D\=^\A\.\B\.\C\...\D\;
4) абсолютная величина частного равна частному от деления
абсолютных величин делимого и делителя:
А
В
\В\
6. О приближенных вычислениях. В технических науках и в
практике почти всегда имеют дело с числами, выражающими при-
приближенные значения величин.
Известно, что произведенные подряд измерения одной и той
же величины приводят к числам, пусть даже еле заметно, но все
же отличающимся друг от друга. Когда говорят, что мера кон-
конкретной величины равна данному числу, то просто имеют в виду,
что в результате соответствующих измерений получаются числа,
настолько мало отличающиеся от данного, что этой разницей
можно пренебречь.
6] § 1. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА 23
Применения математического анализа в естествознании и инже-
инженерном деле всегда сопровождаются и заканчиваются вычислениями.
Поэтому совершенно необходимо научиться хорошо вычислять!
Какой же смысл придается понятию «хорошо вычислять»?
Первый признак хорошо выполненных вычислений состоит
в достаточной их точности. Вторым признаком следует
считать в известном смысле противоположное качество: вычисления
должны производиться в границах целесообразной точности,
без избыточной точности. Третьим признаком является
быстрота производства действий, экономия в труде и во времени.
Следует всегда производить вычисления в соответствии с
этими требованиями.
Дадим сейчас определения основных понятий, относящихся
к приближенным вычислениям.
Будем под Л понимать точное значение некоторой измеряемой
величины, или просто некоторое число.
Определение. Число а называется приближенным зна-
значением А с ошибкой а, если
А — а=а.
Для обозначения приближенного равенства служит символ »:
А & а.
Число а может быть меньше Л, а < Ау и больше Л, а > А.
В первом случае а>0 и а есть приближенное значение А с не-
недостатком.) во втором случае а < 0 и а есть приближенное
значение А с избытком. Чаще всего безразлично, какой именно
из этих случаев имеет место.
Ошибкаг) а, как и точное значение Л, обычно неизвестна, но
бывает известна та граница е, за которую заведомо не выхо-
выходит абсолютная величина ошибки: |а] не превосходит 8, т. е.
Определение. Абсолютная величина ошибки |а| назы-
называется абсолютной ошибкой. Если абсолютная ошибка | а | при-
приближенного значения а не превосходит положительного числа е,
то число е называется предельной абсолютной ошибкой при-
приближенного значения:
\А —
или
— е^Л—-а
Вместо слова «ошибка» иногда употребляют слово «погрешность».
24 гл. i. функция [6
Число е определяется не однозначно: всякое число, большее,
чем уже известная абсолютная ошибка, может быть также при-
принято в качестве предельной абсолютной ошибки, т. е. числа е.
Так, например, 3,24 есть приближенное значение числа 3,2447
с абсолютной ошибкой 0,0047 или числа 3,2447... с предельной
абсолютной ошибкой 0,005, ибо 0,0047...< 0,005. Впрочем, и тогда,
когда ошибка известна, часто вместо нее удобнее указать пре-
предельную ошибку; так, в данном примере вместо ошибки 0,0047
удобнее указать предельную ошибку 0,005.
Пусть производится какое-либо измерение с помощью простей-
простейших измерительных приборов. Тогда легко указать предельную
абсолютную ошибку. Если, например, мы измеряем длину при помощи
линейки, на которой деления нанесены через один сантиметр
(говорят: цена деления равна одному сантиметру), то ясно, что
ошибка не превысит 0,5 см. Разумеется, речь идет только об
ошибке, получающейся при снятии показания с линейки. Вообще
считают, что абсолютная ошибка при снятии показания с изме-
измерительного прибора не превосходит половины цены деления шкалы
прибора.
Обычно для краткости слово «предельная» опускают и под
абсолютной ошибкой понимают именно предельную абсолютную
ошибку е.
Приближенное равенство Д«а тем точнее, чем меньше е.
Важно заметить, что сама по себе абсолютная ошибка еще ни-
ничего не говорит о точности приближения; чтобы судить о точ-
точности, нужно обязательно знать, каково само значение А (хотя
бы приближенно). Так, например, одна и та же абсолютная ошибка
в 0,5 м свидетельствует о совершенно неудовлетворительной
точности при измерении высоты комнаты, о вполне удовлетвори-
удовлетворительной точности при измерении границ земельного участка и об
исключительной точности при определении, скажем, высоты
Эльбруса. Принято оценивать точность приближения по той доле,
которую составляет ошибка от измеряемой величины, т. е. по
относительной ошибке, которая определяется как абсолютная вели-
величина отношения ошибки а к точному значению А.
Так как фактически нам бывает известна только предельная
абсолютная ошибка е и приближенное значение а величины
А, то вместо относительной ошибки берут предельную относи-
относительную ошибку.
Определение. Предельной относительной ошибкой 6
называется отношение предельной абсолютной ошибки к абсолют-
абсолютной величине приближенного значения а:
а е
б=ргг
7J § 2. ПЕРВОНАЧАЛЬНЫЕ СВЕДЕНИЯ О ФУНКЦИИ 25
Как и раньше, слово «предельная» обычно опускают, понимая
иод относительной ошибкой именно предельную. Чем меньше
относительная ошибка б, тем приближение лучше, точнее.
Обычно относительные ошибки даются в процентах (т. е. в час-
частях от 100); они называются тогда процентными ошибками.
Чтобы получить процентную ошибку, нужно относительную ошибку
умножить на 100.
Говорят: а есть приближенное значение А с относительной
ошибкой 6; или, что то же, приближенное равенство А & а имеет
относительную ошибку 8.
В технических расчетах точность в пределах одного процента
обычно бывает достаточной, и лишь в особых случаях она дово-
доводится до десятых долей процента.
Вычисления, встречающиеся в математическом анализе, обычно
стараются привести к выполнению лишь арифметических
действий. Мы будем считать, что читатель знаком с простей-
простейшими правилами и приемами приближенных вычислений, относя-
относящимися к арифметическим действиям.
§ 2. Первоначальные сведения о функции
7. Определение функции. Возьмем некоторое множество значе-
значений величины х, т. е. некоторое множество точек на числовой
оси Ох, и обозначим его через D. Если каждому значению х из
множества D по какому-нибудь правилу поставлено в соответст-
соответствие одно определенное значение другой величины у> то говорят,
что эта величина у есть функция величины х или что величины
х и у связаны между собой функциональной зависимостью. При
этом величина х называется аргументом функции у, а множество
D — областью определения функции у. Значения аргумента х из
области D определения функции у мы можем выбирать по нашему
усмотрению произвольно; поэтому величина х называется неза-
независимой переменной. Значение же функции у, когда значение неза-
независимой переменной х уже назначено, мы выбрать произвольно не
можем; это значение будет строго определенным, именно тем,
которое соответствует выбранному значению независимой пере-
переменной. Значения функции зависят от значений, принимаемых
независимой переменной, и обычно изменяются при ее изменении.
Поэтому функцию называют еще зависимой переменной.
Определение. Величина у называется функцией перемен-
переменной величины х в области определения Z), если каждому значе-
значению х из этой области соответствует одно определенное значение
величины у.
Областью определения функции может быть любое множество
точек числовой оси, но чаще всего в математическом анализе и
26 гл. i. функция [7
в его применениях рассматривают лишь функции, областями
определения которых служат области таких двух типов:
1) множество целых неотрицательных точек числовой оси,т. е.
точек # = 0, лг=1, лг = 2, х — Зу ... (или некоторая часть этого
множества);
2) один или несколько интервалов (конечных или бесконечных)
числовой оси.
Говорят, что в первом случае мы имеем функцию целочисленного
аргумента, а во втором случае — функцию непрерывного аргумента.
В первом случае аргумент может пробегать ряд чисел: л; = 0, 1,
2, 3, ...; во втором случае аргумент пробегает один или не-
несколько интервалов числовой оси.
Множество значений, принимаемых функцией у, называется
областью значений функции.
Приведем простейшие примеры функций.
1. Температура т воздуха в данном месте, измеряемая
через каждый час в течение суток, является функцией целочислен-
целочисленного аргумента—времени t, принимающего значения ? = 0, 1,
2, 3, ..., 23. Действительно, каждому из этих значений величины
t соответствует вполне определенное значение величины т, и, зна-
значит, она, в согласии с данным определением, является функцией
величины t. Здесь область определения функции состоит из 24
«целых» точек. Если измерения производить не через каждый час,
а через каждую минуту, то температура будет функцией цело-
целочисленного аргумента, принимающего уже 24*60=1440 последова-
последовательных целых значений.
2. Периметр Р правильного многоугольника, вписанного
в данную окружность, есть функция целочисленного аргумента —
числа п сторон этого многоугольника. Здесь область определения
функции является множеством всех целых положительных чисел,
начиная с числа /z = 3. Другим примером функции этого же аргу-
аргумента может служить площадь S указанного правильного мно-
многоугольника.
3. Площадь S круга есть функция его радиуса г, ко-
который может принимать любое положительное значение. Каждому
значению г из интервала @, оо) соответствует определенное зна-
значение S, определяемое по формуле
S = яг2.
Областью определения функции служит множество всех поло-
положительных чисел, т. е. положительная полуось 0<г<°°-
4. Расстояние s, проходимое телом, свободно падающим в
пустоте, является функцией времени t падения тела. Каждому
значению t соответствует определенное значение s, находимое по
81 § 2. первоначальные сведения о функции 27
формуле {g—ускорение силы тяжести)
Областью определения этой функции является интервал [0, 7],
где 7 — время падения тела.
Обратим внимание на то, что зависимость расстояния от вре-
времени при свободном падении тела в пустоте имеет тот же характер,
что и зависимость площади круга от его радиуса, а именно: в
обоих случаях функция пропорциональна квадрату независи-
независимой переменной. С математической точки зрения только это и
важно: в самой математике интересуются тем, как зависит функция
от аргумента, и вовсе не интересуются тем, какое конкретное
физическое явление описывается данной функциональной зависи-
зависимостью. В математическом анализе указанные в примерах 3 и 4
функции суть просто частные случаи так называемой квадра-
квадратичной функции (см. п, 16).
В определении понятия функции не требуется, чтобы при изме-
изменении независимой переменной функция обязательно изменя-
изменялась. Так, в примере 1 может случиться, что температура т
воздуха в течение некоторого времени t остается постоянной; это
не мешает нам считать по-прежнему, что температура является
функцией времени. Рассмотрим еще один аналогичный пример.
Функция
у = a cos2 х + b sin2 х,
где а и b — постоянные, принимает различные значения в зави-
зависимости от величины л:, если афЬ. Если же а=Ь, то при всех
значениях х функция у является постоянной величиной1), равной а.
Не выделяя этого частного случая, мы говорим, что выраже-
выражение a cos2 х -f- b sin2 x при любых значениях постоянных а и b яв-
является функцией от х.
8. Способы задания функций. Задать функцию — это значит
указать область ее определения и правило, при помощи кото-
которого по данному значению независимой переменной находятся соот-
соответствующие ему значения функции. Важнейшими способами задания
функций в математике являются задания таблицей, формулой
и графиком.
х) В математике и других дисциплинах постоянную иногда называют
константой (const).
28
ГЛ. I. ФУНКЦИЯ
I. Табличное задание. При табличном задании просто
выписывается ряд значений независимой переменной и соответству-
соответствующих им значений функции. Этот способ часто употребляется.
Хорошо известны таблицы логарифмов, таблицы тригонометриче-
тригонометрических функций и их логарифмов и др.
Табличный способ задания функций особенно распространен
в естествознании и технике. Числовые результаты последователь-
последовательных наблюдений какого-нибудь процесса обычно группируются
в виде таблицы. Например, при изучении зависимости электриче-
электрического сопротивления г некоторого медного стержня от темпера-
температуры / была получена следующая таблица:
t
г
19
76,
,1
30
25
77,
,0
80
30
79,
,1
75
36
80,
,0
80
40
82,
,0
35
45
83,
,1
90
50
85,
,0
10
Сопротивление является функцией температуры, и приведенная
таблица дает значения этой функции для указанных значений
независимой переменной.
Преимуществом табличного задания функций является то, что
для каждого значения независимой переменной, помещенного в таб-
таблице, можно сразу, без всяких измерений и вычислений, найти
соответствующее значение функции.
Недостаток же табличного задания заключается в том, что при
нем обычно невозможно задать функцию полностью: найдутся
такие значения независимой переменной, которые не помещены
в таблице. Например, данная выше таблица не позволяет ответить
на вопрос о том, каковы сопротивления стержня при темпера-
температурах, меньших 19,1° или больших 50,0°. Точно так же по таблице
нельзя узнать значения сопротивления, например, при температурах
24,2° и 37,43°, прямо не указанных в числе значений температуры1).
Другим недостатком табличного задания, особенно ярко прояв-
проявляющимся при большом объеме таблицы, является отсутствие
наглядности. По таблице весьма трудно выявить характер
изменения функции при изменении независимой переменной.
II. Аналитическое задание (задание формулой).
Аналитическое задание функции состоит в том, что дается фор-
формула, с помощью которой по заданным значениям независи-
независимой переменной можно получать соответствующие им значения
*) Существуют специальные методы, позволяющие в известных случаях
приближенно находить значения функции, соответствующие значениям неза-
независимой переменной, не помещенным в таблице.
8] § 2. ПЕРВОНАЧАЛЬНЫЕ СВЕДЕНИЯ О ФУНКЦИИ 29
функции. Например, формулы
или З^
определяют у как функцию х.
При аналитическом задании функции под областью ее опреде-
определения (если только нет каких-нибудь дополнительных условий)
понимают множество значений а:, при которых формула, опреде-
определяющая функцию, имеет смысл. Это значит, что в результате
применения формулы мы получаем для у определенные дейст-
действительные значения.
Аналитическое задание функции — основной способ задания
в математическом анализе.
Преимущества аналитического способа заключаются:
а) в сжатости, компактности задания;
б) в возможности вычислить значение функции для любого
значения независимой переменной из области определения (значения
многих функций, например j/ = sin.xr, y — \gx, мы пока умеем нахо-
находить только при помощи таблиц);
в) наконец, и это самое главное, в возможности применить
к данной функции аппарат математического анализа, ибо он
наилучшим образом приспособлен как раз к аналитической форме
задания функций.
Если, например, мы хотим исследовать методами математиче-
математического анализа функциональную зависимость между температурой
и электрическим сопротивлением медного стержня, то нам нужна
именно формула, связывающая сопротивление и температуру, а не
отдельные (пусть даже известные в большом числе) соответствен-
соответственные значения функции и независимой переменной.
Неудобствами аналитического задания функции являются:
а) недостаточная наглядность;
б) необходимость производства вычислений, подчас очень гро-
громоздких.
III. Графическое задание. Прежде всего приведем сле-
следующее определение.
Определение. Графиком функции (в системе декартовых
прямоугольных координат) называется множество всех точек,
абсциссы которых являются значениями независимой переменной»
а ординаты — соответствующими значениями функции.
Иными словами, если взять абсциссу, равную некоторому значе-
значению независимой переменной, то ордината соответствующей точки
графика должна быть равна значению функции, соответствующему
данному значению независимой переменной. При этом масштабы
на обеих осях координат могут быть как одинаковыми, так и
различными.
30 гл. i. функция [9
Графиком функции обычно служит некоторая кривая (в част-
частности, и прямая) линия1). Так, графиком квадратичной функции
у = х2 является парабола, ось которой совпадает с положительной
полуосью ординат; графиком функции j> = — является равнобоч-
ная гипербола, для которой оси координат служат асимптотами, и
т. д. Графиком постоянной величины служит, очевидно, прямая,
параллельная оси абсцисс.
Обратно, если линия на координатной плоскости Оху такова,
что любая прямая, параллельная оси ординат, имеет с ней не
более одной общей точки, то эта линия изображает некоторую
функцию, именно ту, значения которой равны ординатам точек
линии при значениях независимой переменной, равных абс-
абсциссам.
Таким образом, понятия линии и функции тесно связаны.
Заданием функции порождается линия — ее график; заданием линии
порождается функция — та, для которой эта линия служит гра-
графиком. Графическое задание функции состоит в задании графика
этой функции.
В физике и технике функции нередко задаются графически,
причем иногда график является единственным доступным средством
задания функции. Чаще всего это бывает при употреблении само-
самопишущих приборов, автоматически записывающих изменение одной
величины в зависимости от изменения другой (например, времени).
В результате на ленте прибора получается линия, графически
задающая регистрируемую прибором функцию. К таким приборам
относятся, например, барограф, вычерчивающий барограмму — гра-
график атмосферного давления, и термограф, вычерчивающий термо-
термограмму— график температуры как функции времени.
К графику функции, как и к таблице, не может быть непосред-
непосредственно применен аппарат математического анализа, но график
функции наряду с этим недостатком обладает весьма важным преи-
преимуществом— наглядностью, что делает его чрезвычайно по-
полезным при изучении функции.
9. Символика. Для обозначения того, что величина у есть не-
некоторая функция переменной величины х, употребляется символи-
символическая запись
Латинская буква/—начальная буква слова functio (функция). Эту
запись читают так: «у есть функция от х» или короче:
г) Графиком функции целочисленного аргумента служит мно-
множество отдельных точек на плоскости с целыми абсциссами.
9] § 2, ПЕРВОНАЧАЛЬНЫЕ СВЕДЕНИЯ О ФУНКЦИИ 31
«jf есть эф от лг». Здесь буква / обозначает закон соответ-
соответствия между независимой переменной и функцией. Кроме буквы
/, в качестве символа функциональной зависимости используют и
другие буквы: F, ф, Ф и т. д. Иногда употребляюг и такую форму
записи: у=у(х). В скобках после символа функциональной зави-
зависимости ставится обозначение независимой переменной.
Для хорошо известных и наиболее часто встречающихся функ-
функций употребляют специальные символы: lg#, sin л:, arccosjc
и т. д.
Символ / при аналитическом задании функций указывает сово-
совокупность математических действий, которые нужно произвести над
ху чтобы получить у, а также порядок этих действий. Например,
символ / в равенстве
обозначает, что по значению х находятся его квадрат и его синус,
результаты складываются и из суммы извлекается квадратный
корень.
При одновременном рассмотрении двух функций употребляется
один и тот же символ, если функциональные зависимости одина-
одинаковы, и разные символы, если эти функциональные зависимости раз-
разные. Так, площадь круга ? зависит от радиуса г так же, как
поверхность шара Q — от его диаметра d\ поэтому мы можем записать:
и Q=
употребляя в обоих случаях один и тот же символ функции. Но,
желая записать, что и длина окружности / = 2яг, и площадь круга
S = nr2 являются функциями его радиуса г, мы не можем употре-
употребить один и тот же символ, а должны взять два различных
символа, например:
/-/(г) и. S = q>(r).
Частное значение функции можно найти, если подста-
подставить в выражение для функции вместо независимой переменной
соответствующее ее значение. Пусть частное значение функции
у=/(х) при лг = а равно Ь, Это записывают так:
Последнее равенство уже нельзя читать, как прежде: «д есть
функция от я», так как здесь и а и b являются постоянными
величинами. Его следовало бы читать так: «Ь равно значению
функции / при значении независимой переменной, равном я»,
но обычно читают коротко: «Ь равно эф от а», помня, какой смысл
32 гл. !. функция [10
вкладывается в эти слова. Часто употребляется и такая запись:
Точка М графика функции y=f(x), соответствующая абсциссе
х = а, имеет ординату /(а), что записывается так: М[а> /{а)]
(рис. 2).
Mfaffail ^^0 \-^^ *®# Основные элементарные
' — функции. Сложная функция.
Определение. Основны-
Sjaj ми элементарными функци-
функциями называются следующие
функции:
*5 1) степенная функция:
у = хп, где п — действительное
^ис. 2. число;
2) показательная функ-
функция: у = ах, где а — положительное число иа^1;
3) логарифмическая функция: ,y=logajt, где основание
логарифмов а — положительное число и a jtl;
4) тригонометрические функции: y=s'mx, y=cosx,
y=ztgx, а также реже встречаемые: у~\
0
5) обратные тригонометрические функции: д> == arcsin х,
; = arccosJt, j; = arctgA:, а также ^y^arcsecA:, у = arccosec лг,
Эти функции известны из курса средней школы; мы рас-
рассмотрим их вкратце в § 3.
Из основных элементарных функций можно строить другие
функции при помощи арифметических действий (сложения, вычита-
вычитания, умножения и деления) и новой операции взятия функции,
от функции, которую мы сейчас рассмотрим.
Пусть на некотором множестве D значений аргумента х задана
функция и = <р(лг) и G—область значений функции и. Пусть, далее,
на множестве G задана функция y—f(u). Тогда каждому значению
х из множества D соответствует одно определенное значение и
из множества G, которому в свою очередь соответствует одно
определенное значение у. Таким образом, в конечном итоге каждому
значению х из множества D соответствует одно определенное зна-
значение у, т. е. у есть некоторая функция от х; обозначим ее через
y^=F(x). Выражение для функции F(х) при помощи функций /и
Ф записывают так:
y = F{x)=f[<f{x)].
Говорят, что F(x) как функция х является сложной функ-
функцией, составленной из функций /и ф, или функцией / от функ-
11] § 2. ПЕРВОНАЧАЛЬНЫЕ СВЕДЕНИЯ О ФУНКЦИИ 33
ции ф^.Функция и = ц(х) называется при этом промежуточной пе-
переменной.
Таким образом, аргумент функции может быть независимой
переменной, а может быть промежуточной переменной, т. е. сам
может являться функцией независимой переменной. В последнем
случае и получается сложная функция. Например, функция у = sin2 x
есть сложная функция х, а именно у есть квадратичная
функция аргумента, который есть в свою очередь тригонометри-
тригонометрическая функция—-си н у с— независимой переменной х; обозначая
промежуточную переменную через и, можем записать: у = и2,
u~s\nx.
Задание сложной функции называют еще цепным заданием.
Цепь функций, с помощью которых строится сложная функция,
может состоять не только из двух, но из какого угодно числа
звеньев. Чем их больше, тем «сложнее» функция. Часто оказы-
оказывается полезным умение «расщеплять» заданную сложную функцию
на отдельные звенья.
11. Элементарные функции.
I. Функции, построенные из основных элементарных функций
и постоянных при помощи конечного числа арифметических дейст-
действий и конечного числа операций взятия функции от функции,
называются элементарными функциями.
Например, элементарными будут функции
У =
a2 2-\-\/Т
3 12
Важное значение элементарных функций видно из того,
что в математическом анализе, применяемом в основных задачах
физики и техники, употребляются чаще всего элементарные функции.
По формуле, определяющей элементарную функцию, важно
уметь находить область определения этой функции. Рассмотрим
с этой целью несколько примеров.
1. Областью определения функции у = хг +2лг — 5 служит вся
числовая ось.
2. Областью определения функции ^ = — является вся числовая
ось, кроме точки лг = О, в которой формула теряет смысл, ибо
1) Термин «сложная функция» указывает только на характерную осо-
особенность в аналитической конструкции функции и отнюдь не означает
какой-то особой ее сложности в обычном понимании этого слова.
2 Л. Ф. Бермант, И. Г. Араманович
34 гл. i. функция [И
делить на нуль нельзя; таким образом, область определения со-
состоит из двух открытых бесконечных интервалов:
— оо<лг<0 и 0<л:< + оо.
3. Областью определения функции j; = ]/l—х2 является
замкнутый интервал [—1, +!]> так как в каждой точке этого
интервала, т. е. при каждом х, удовлетворяющем неравенствам
—1 <!.*;<: 1, выражение ]/ 1 — х2 имеет действительное значение,
а в точке, лежащей вне интервала [—1, + 1]> т. е. при |аг|>1,
оно не имеет действительного значения.
4. Областью определения функции у = ]/гх2 — 1 служат два бес-
бесконечных интервала —оо<лг^—1 и +1 ^л: < + оо (в другой
записи: |л:|^1), т. е. вся числовая ось, за исключением интер-
интервала (—1, + 1).
5. Областью определения функции y = \gx является открытый
бесконечный интервал 0 < а: < + оо.
6. Областью определения функции у = ,- служит от-
\ О ~~~ X
крытый интервал (—5, 2), так как выражение lg(^ + 5) опреде-
определено при х >—5, а выражение |^8—л;3 при х ^2; точку х = 2
нужно исключить, так как в этой точке знаменатель дроби об-
обращается в нуль.
Конкретные задачи часто приводят к функциям, определенным в более
широкой области, чем допускает существо рассматриваемой задачи. На-
Например, площадь S круга выражается через его радиус г формулой
Хотя эта формула имеет смысл при всех значениях г, ясно, что прида-
придавать г отрицательные и нулевое значения лишено смысла; областью
определения данной функции служит только положительная полу-
полуось аргумента.
Основной закон теории упругости — закон Г у к а х) — утверждает, что
удлинение стержня прямо пропорционально величине растягивающей силы,
т. е. у = сх, где у— удлинение, х—растягивающая сила, с— постоянный
для данного стержня коэффициент пропорциональности. Эта функция, если
исходить только из формулы, определена при всех значениях х> однако
хорошо известно, что закон Гука справедлив лишь при небольших удлине-
удлинениях, что и ограничивает возможность применения приведенной формулы.
Иногда приходится иметь дело с функциями, которые на
разных интервалах имеют различные аналитические выра-
выражения. Зададим, например, функцию у =/(х) так:
/(je) = O, если #<0,
, если 0<лг<1,
/(лг) = 1+лг, если лг> 1.
Р. Гук A635—1703) —выдающийся английский физик.
11]
§ 2. ПЕРВОНАЧАЛЬНЫЕ СВЕДЕНИЯ О ФУНКЦИИ
35
Это — функция, определенная на всей числовой оси; график ее
показан на рис. 3.
С примерами неэлементарных функций мы встретимся
позднее.
II. Элементарные функции принято разделять на два класса:
алгебраические функции и трансцендентные функции.
Определение. Функция называется алгебраической, если
ее значения можно получить, производя над независимой пере-
переменной конечное число алгебраических действий: сложений, вы-
вычитаний, умножений, делений и возве-
возведений в степень с рациональным пока-
показателем.
Функция, не являющаяся алгебраи-
алгебраической, называется трансцендентной.
Например, алгебраическими являют-
являются следующие функции:
-*-И *' + >
Примеры трансцендентных функций:
X
Рис. 3.
Алгебраические функции в свою
очередь разделяются на рациональные и иррациональные.
Определение. Алгебраическая функция называется ра-
рациональной, если среди действий, которые производятся над
независимой переменной, отсутствует извлечение корней.
Алгебраическая функция, не являющаяся рациональной,
называется иррациональной.
Примеры рациональных функций:
1
— 5
+
(подкоренные выражения в последнем примере не содержат неза-
независимой переменной).
1"
Функции
~ 1" . служат примерами иррацио-
нальных функций.
Наиболее простыми рациональными функциями являются целые
рациональные функции или многочлены (при этом одночлен
2*
36 гл. i. функция [12
рассматривается как частный случай многочлена). Вот примеры
таких функций:
(среди производимых действий отсутствует деление на выражение,
содержащее независимую переменную).
Всякую рациональную функцию с помощью тождественных
преобразований можно представить в виде частного двух
многочленов, например:
у- 2 1 - л«-л« + д —2 •
Х~~х*+х*~1
Р (х)
Если рациональная функция R (х) записана в виде %(х)~тгг\>
где Р(х) и Q(x) — многочлены, то она называется дробно-рацио-
дробно-рациональной.
12. Неявные функции. Многозначные функции. До сих пор,
рассматривая функции, заданные аналитически, мы все время
предполагали, что в левой части равенства, определяющего функ-
функцию, стоит только у, а в правой — выражение, зависящее от х.
Такие функции мы будем называть явными. Например, явными
будут все функции, приведенные в начале п. 11.
Но и уравнение, связывающее две переменные, не разре-
разрешенное относительно какой-нибудь из них, может определять
одну из этих переменных как функцию другой.
Например, в уравнении прямой 2^ + 3^ = 6 ординатур можно
рассматривать как функцию абсциссы х, определенную на всей
числовой оси. Действительно, каждому значению х соответствует
одно значение у> находимое из уравнения прямой. Эта функция
задана в неявном виде. Чтобы перейти к ее явному заданию,
2
разрешаем уравнение относительно^ и получаем у = 2—-^ х.
Однако если мы возьмем уравнение окружности
то столкнемся с тем обстоятельством, что каждому значению хЛ
заключенному между —1 и +1, соответствует уже не одно, а
два значения у (рис. 4). В соответствии с этим мы скажем, что
уравнение jc2-)-j/2=1 представляет не одну, а две функции:
у=-\-\/~\—д-2 и у — —у"\—x2t каждая из которых определена
в интервале [—1, 1]; если х лежит вне этого интервала, то
уравнение, из которого находится у, не имеет действительных
решений.
12]
§ 2. ПЕРВОНАЧАЛЬНЫЕ СВЕДЕНИЯ О ФУНКЦИИ
37
Можно также сказать, что уравнение х2-\-у2=\ определяет^
как многозначную функцию от х. При этом функции у = -\- У\—хг
и у — — У\—х2 называют однозначными ветвями многозначной
функции1). С таким расширением толкования функции — именно
с введением многозначных функ-
функций, рассматриваемых как сово-
совокупность их однозначных ветвей,—
нам часто придется сталкиваться
в дальнейшем.
Пользуясь этим толкованием,
можно сказать, что неявной функ-
функцией у независимой переменной х
называется функция, значения кото-
которой находятся из уравнения, связы-
связывающего х и у и не разрешенного
относительно у. Чтобы перейти к
явному заданию функции, н}жно
разрешить данное уравнение от-
относительно у. Такой переход не
всегда легок, а иногда и вовсе невозможен. Так, уравнение
у3 — Зху + х* = О
определяет у как функцию дг, но выразить эту функцию в явном
виде труднее, чем в рассмотренных выше примерах, так как для
этого нужно решить уравнение третьей степени. А уравнение
Рис. 4.
вообще нельзя решить алгебраически относительно у, т. е. нельзя
явно выразить у через х. Разумеется при этом трудно установить
область определения функции у и выяснить, какие она имеет
однозначные ветви.
Способы численного решения таких уравнений, позволяю-
позволяющие для данного частного значения х находить соответствующие
ему значения у, будут рассмотрены в дальнейшем (см. п. 77).
Не следует думать, что любое уравнение, связывающее х и
у, обязательно определит некоторую функцию одной переменной.
Например, уравнение х2 +у2 + 1 — 0 не может быть удовлетворено
*) Мы не рассматриваем функций, которые при одних значениях х
задаются формулой у — + Y\ — х2, а при других значениях—формулой
у = — 1^1—х2. График любой такой функции нельзя нарисовать в виде
сплошной линии; советуем читателю для примера представить себе график
функции: у = + Y\—x2 при х? [—1, Oj и # = — V\— х2 при х? [0, 1].
38 гл. i. функция [13
никакими действительными значениями хну (сумма поло-
положительных чисел не может быть равна нулю1) и, значит, не
определяет никакой функции. К более детальному рассмотрению
неявных функций мы еще вернемся впоследствии (в п. 117).
§ 3. Начало изучения функций. Простейшие функции
13. Основные характеристики поведения функции. Изучить
заданную функцию — это значит охарактеризовать ход ее изме-
изменения (или, как говорят, ее поведение) при изменении неза-
независимой переменной. При этом мы всюду (где специально не
оговорено противное) будем предполагать, что независимая пере-
переменная изменяется возрастая,
У{ причем, переходя от меньших зна-
ffx)=O чений к большим, она проходит
~г ?/7 ^ через все свои промежуточные
$4^ значения.
4j\ . Постепенно, по мере расши-
/^. у —JLj_lt ^ рения средств исследования, мы
' \J / г будем в состоянии давать все
Vw/ более полное описание поведе-
поведения функции. Теперь же, имея
^ис- 5- в своем распоряжении лишь
средства элементарной матема-
математики и аналитической геометрии, мы будем характеризовать по-
поведение функции только по следующим простейшим ее особен-
особенностям:
I. Нули функции и знак функции в данном интервале. II. Чет-
Четность или нечетность. III. Периодичность. IV. Рост в данном ин-
интервале.
I. Определение. Значение х, при котором функция обра-
обращается в нуль, /(д:) = 0, называется нулем функции.
В интервале положительного знака функции график ее распо-
расположен над осью Ох, в интервале отрицательного знака —под осью
Ох, в нуле функции график имеет общую точку с осью Ох (рис. 5),
II. Определение. Функция у =f(x) называется четной,
если при изменении знака у любого значения аргумента значение
функции не изменяется:
Функция у =/(лг) называется нечетной, если при изменении
знака у любого значения аргумента изменяется только знак
значения функции, а абсолютная величина этого значения
остается без изменения:
13] § 3. КАЧАЛО ИЗУЧЕНИЯ ФУНКЦИЙ. ПРОСТЕЙШИЕ ФУНКЦИИ
39
В этом определении предполагается, что функции определены
в области, симметричной относительно начала координат.
Примерами четных функций могут служить у = х2, у = cosat,
примерами нечетных функций: у = л:3, j/ = sinx, y = tgx.
График четной функции симметричен относительно оси Оу;
график нечетной функции симметричен относительно начала коор-
координат. (Предоставляем читателю доказать это; см. рис. 6.)
Разумеется, функция может быть ни четной, ни нечетной;
например, таковы функции: y = x-\-l, j/ = 2*, y = 2 sinx
и т. п.
-я о *
Четная
-Д7
/Г
Мечетная
Рис. 6.
III. Определение. Функция у = f(x) называется периоди-
периодической, если существует такое положительное число а» что для
любого х справедливо равенство
+ a)=f(x).
(*)
Если функция периодическая, то имеют место также равенства:
f(x—a) =/(*), /(д? —2а)=/(дг)
и вообще
/(* + &*)=/(*)
при любом х и для произвольного целого (положительного или
отрицательного) числа k.
Наименьшее положительное число а, при котором условие
(*) соблюдается, называется периодом функции.
Примером периодической функции может служить функция
y — sinx; ее период равен 2я. Если периодическая функция не
определена в точке лг0, то она не определена и во всех точках
xo-{-kay где а — период. Например, функция y = tgx, период ко-
которой равен я, не определена в точках -^--|-&я.
40
ГЛ. I. ФУНКЦИЯ
[13
-га -«
2а За
Поведение периодической функции достаточно рассмотреть
в любом интервале, длина которого равна периоду функции,
например в интервале О^Сх^а, где а— период; в остальных
точках оси Ох значения функции получаются простым повторе-
повторением значений, принимаемых
ею в этом интервале. График
периодической функции полу-
получается путем повторения ча-
части графика, соответствующе-
соответствующего интервалу оси Ох, равно-
равному по длине периоду функ-
функции (рис. 7).
IV. Весьма важной особен-
особенностью в поведении функции
является возрастание и убывание.
Определение. Функция называется возрастающей в ин-
интервале, если большим значениям аргумента соответствуют
большие значения функции 1); она называется убывающей, если
большим значениям аргумента соответствуют меньшие значения
функции.
Таким образом, f(x) возрастает в интервале [а, Ь\%
Рис. 7.
если для любых значений хл. х9
У\
а\
О
В
«27
, удовлетворяющих условию
а^х1<х2<!?, имеет место
неравенство /(хх) </(х2), и
убывает, если для любых
значений хх, х2, удовлетво-
удовлетворяющих указанному усло-
условию, имеет место неравенство
Так, например,
у = 2* возрастает
числовой
Рис. 8.
функция
на всей
функция
Функция
интервале
тает в ин-
оси, а
у = 2~х убывает.
у = х2 убывает в
(— оо, 0] и возрас
тервале [0, оо).
Если рассматривать график функции слева направо (что соот-
соответствует возрастанию аргумента х), то для возрастающей функ-
функции график поднимается вверх (линия АВ на рис. 8), а для
убывающей функции опускается вниз (линия CD на рис. 8).
1) Когда говорят об изменении (увеличении, уменьшении) переменной
величины, имеют в виду алгебраическое изменение. Если речь
идетлэб ^зменеяяи абсолютной величины переменной, это особо ого-
оговаривается.
14] § 3. НАЧАЛО ИЗУЧЕНИЯ ФУНКЦИЙ. ПРОСТЕЙШИЕ ФУНКЦИИ
41
Определение. Интервал независимой переменной, в ко-
котором функция возрастает, называется интервалом возраста-
возрастания функции, а интервал, в котором функция убывает,— интер-
интервалом убывания. Как интервал возрастания, так и интервал
убывания называют интервалами монотонности функции,
а функцию в этом интервале — монотонной функцией.
Обычно, интервал, на котором рассматривается функция, можно
разбить на ряд интервалов, в каждом из которых функция моно-
монотонна. Так, например, для функции, график которой изображен
на рис.9, интервал[а,Ь] разби-
разбивается на интервалы [а, хх], У,
I •'V Л % J\r О I } I "^ О } *v Oil 1 *^ Q ) I ? "*
торых функция соответственно
убывает, возрастает, убывает,
возрастает.
Для простейших функций,
графики которых нам извест-
известны, интервалы монотонности
находятся легко; в дальней-
дальнейшем (п. 59) будет показано,
как можно отыскивать интер-
интервалы монотонности функции,
Приведем определение
стики поведения функции.
Определение. Значение функции, большее или меньшее
всех других ее значений в некотором интервале, называется
наибольшим или соответственно наименьшим значением функ-
функции в этом интервале.
Находить эти значения для любых функций мы научимся
в п. 61.
Исследование указанных в настоящем пункте особенностей
часто позволяет составить довольно ясное представление о пове-
поведении функции. Изучение функции следует начинать с отыскания
области ее определения. При этом некоторые вопросы исследова-
исследования могут отпасть сами собой; так, например, если функция опре-
определена только для положительных значений аргумента, то ее не
нужно исследовать на четность и нечетность, и т. д.
14. Графическое изучение функции. Когда известен график
функции, поведение ее может быть выяснено из рассмотрения
чертежа. По чертежу мы можем найти и интервалы монотонности
функции, и интервалы, где она сохраняет постоянный знак, и
нули функции, а также обнаружить, является ли функция четной
или нечетной или ни той, ни другой и имеет ли она период.
При этом, разумеется, точность ответов ограничена точностью
Рис. 9.
график которой нам неизвестен,
еще одной очень важной характери-
42 гл. I. функция [14
чертежа и тех измерений, которые приходится на нем произ-
производить.
Так, например, график функции у = /(х), приведенный на рис. 9,
показывает, что функция f(x) в точках av а2, а3, а4 обращается
в нуль: /(а1)=/(а2)=/(а3)=/(а4) = 0; что в интервалах (ax, a2),
(а3, а4) она отрицательна, а в интервалах [я, ах), (а2, а3) и
(а4, Ь) положительна; что в интервалах [х±, х2] и [х3, Ь] функ-
функция возрастает, а в интервалах [а, хг] и [л;2, л:3] убывает;
наконец, что наибольшее значение функции во всем интервале
[a, b] достигается в точке х~Ь:
а наименьшее — в точке х = хг:
f(x)>f(*i),
Пока мы можем строить график функции, или основываясь
на известных нам геометрических свойствах линии, изображающей
данную функцию, или, как говорят, «по точкам». Последний
хорошо известный способ состоит в том, что, выбрав какие-
нибудь п значений аргумента: лгх, лг2, ... хп, вычисляют соответ-
соответствующие им значения функции: /(хг), /(лг2), ..., f(xn) и
находят п точек на плоскости: Mx[xv /(хг)], М2 [х2, /(лг2)], ... ,
Ж„[лгп, /(^п)], принадлежащих графику функции. Проведя через
эти точки на глаз линию, мы получаем приближенное представле-
представление о графике функции, тем более точное, чем больше точек М
нанесено на координатную плоскость.
Зная график функции у=/(х), легко построить графики функ-
функций у=/(х) + Ь, y=f(x+a), y = Af{x) и y = f{kx), где 6, a, A
и к — заданные числа. Точки графика y=f(x)-{-b получаются
в результате переноса точек графика y=f(x) вдоль прямых,
параллельных оси Оу, на отрезок |?| вверх, если b > 0, и вниз,
если b < 0. Таким образом, весь график сдвигается вверх или
вниз.
Если y=f(x-{-a)) то график сдвигается вдоль оси Ох на
отрезок а влево при а>0 и на отрезок \а\ вправо при а < 0.
Это видно из того, что значения функций y=f(x) и y = f(x-\-a)
равны друг другу, когда значение х для первой функции равно х0,
а для второй х0 — а.
Чтобы построить график функции y~Af(x), если А > 0,
надо все ординаты исходного графика увеличить в А раз. Если
же Л<0, то строим график ^ = |Л|/(лг) и симметрично отра-
отражаем его относительно оси Ох. График функции y = f(kx) строим,
уменьшая в \k\ раз абсциссы всех точек графика у=/{х). Если
к < 0, то построенный график отражаем относительно оси Оу.
15] § 3. НАЧАЛО ИЗУЧЕНИЯ ФУНКЦИЙ. ПРОСТЕЙШИЕ ФУНКЦИИ
43
Для построения графика функции у = Af[k(x-{-a)]-\-b после-
последовательно строим графики функцийД (лг) =/(* + а), Д (лг) = Д (kx),
Д (x) = Af2 (х) и <У=/з(аг) + 6 (сдвиг и затем растяжение вдоль
оси ОХу растяжение и сдвиг вдоль оси Оу). На рис. 10 по гра-
графику у = sin х показано построение графиков у = 2 sin лг, у = sin 2x
и y = sin (x +^-) •
Зная графики функций y~fx {х) и^=/2(л;), легко построить
чисто геометрически график функции у = я^Д (лг) + а2/2 (#)> где
ах и а% — постоянные. Такое построение достигается умножением
ординат графиков каждой из функций Д (х)у Д (#) на соответ-
соответствующие постоянные av a% и сложением ординат полученных
Рис. 10.
линий. Выражение CL1f1(x)-{-a2f2(x) будем называть линейной
комбинацией данных функций. Можно также образовать линейную
комбинацию любого числа функций.
15. Прямая пропорциональная зависимость и линейная функ-
функция. Приращение величины. Прямой пропорциональной зависи-
зависимостью называется зависимость, выраженная формулой
где а — постоянная (афО).
Характерной особенностью этой зависимости является то,
что величина у пропорциональна величине х. Это значит, что
если хх и yv х2 и у2 — две пары соответственных значений х и
у, то Уъ'У 1 = Х2:х1* Постоянный коэффициент а называется
коэффициентом пропорциональности,
Еслку = аху то х=—у, и, значит, если у пропорциональ-
пропорционально л:, то и х пропорционально у, но с обратным коэффициен-
коэффициентом пропорциональности.
44 гл. I. функция [15
Прямая пропорциональная зависимость есть частный случай за-
зависимости, устанавливаемой линейной функцией, т. е. функцией
вида
где а, Ь — постоянные.
При 6 = 0 и аф§ отсюда получается прямая пропорциональная
зависимость; если же ЬФО, то у уже не будет пропорциональ-
пропорционально х.
Линейная функция определена на всей оси Ох. Как известно
из аналитической геометрии, графиком ее служит прямая ли-
линия. Постоянные коэффициенты а и Ь равны соответственно уг-
угловому коэффициенту прямой (т. е. тангенсу утла между прямой
и осью Ох) и ее начальной ординате (т. е. ординате точки пря-
прямой при л; = 0). При 6 = 0 график линейной функции (прямой про-
пропорциональной зависимости) есть прямая линия, проходящая через
начало координат. Ясно, что при положительном а линейная функ-
функция является на всей оси Ох возрастающей функцией, а
при отрицательном а—убывающей.
Введем одно простое, но важное понятие, а также обозначение,
которые постоянно будут употребляться и в дальнейшем.
Определение. Пусть некоторая величина и переходит от
одного своего (начального) значения U\ к другому (конечному) зна-
значению Иг . Разность конечного и начального значений называет-
называется приращением величины и; ее обозначают через Ли, т. е.
Приращение Аи может быть как положительным, так и отри-
отрицательным; в первом случае переменная величина и при переходе
от и1 к и2 = и1-\- Аи увеличилась, во втором уменьшилась. Если
Ди = 0, то щ = и1 и величина и не изменилась.
Подчеркнем, что Аи обозначает не произведение какой-то вели-
величины А на величину и, а является слитным символом, обозначаю-
обозначающим разность между наращенным значением величины и ее на-
начальным значением.
Когда независимая переменная х получает некоторое прираще-
приращение Дл:, то функция y=f(x) также получает приращение:
&у— f(x-\- Ах) — f(x). На графике приращение функции изобра-
изображается отрезком прямой, параллельной оси Оу, взятым со зна-
знаком + или— в зависимости от того, увеличилась или уменьшилась
ордината при переходе абсциссы из начального положения в ко-
конечное (на рис. 11 начальное положение абсциссы обозначено
через xlt а конечное через х2). Для произвольной функции ее
приращение зависит не только от приращения аргумента Ах, но и
от выбранного значения х; это наглядно видно на рис. 11.
Докажем теперь следующее важное свойство линейной функции.
15] § 3. НАЧАЛО ИЗУЧЕНИЯ ФУНКЦИЙ. ПРОСТЕЙШИЕ ФУНКЦИИ
45
Прямая теорема. Приращение линейной функции пропор-
пропорционально приращению аргумента и не зависит от начального
значения аргумента.
Доказательство. Пусть аргумент получил приращение Ах,
перейдя от значения х к значению х-\-Ах\ тогда функция полу-
получит некоторое приращение Ду, перейдя от значения у к значе-
значению у -+- Ау. Мы имеем
У{
Рис. 11.
Вычитая из второго равен-
равенства первое, найдем
Ау = аАХу
что и требовалось дока-
доказать.
Это соотношение выво-
выводится простои из геометри-
геометрических соображений. Из
рис. 12 видно, что Ау и Дл: являются катетами прямоугольного
треугольника ЛВС, причем tga = a. Значит,
\х = аАх.
Найденное свойство вполне характеризует линейную функ-
функцию; другими словами, нет никаких других функций, кроме линей-
линейных, которые обладали бы
тем же свойством. Докажем ~* q
это. ^
Обратная теорема.
Если приращение функции
пропорционально прираще-
приращению аргумента и не зависит
от его начального значения»
то эта функция — линейная.
Доказательство.
Действительно, допустим, что
для какой-нибудь функции
y=f(x) приращение Ау для
любого х пропорционально приращению независимой перемен-
переменит +Дх х
Рис. 12.
ной Ах:
Ау = аАху
где a — некоторая постоянная. Пусть прилг = О функция/(лг) рав-
равна Ьу т. е. /@) = &. Дадим теперь аргументу какое угодно новое
46
ГЛ. I. ФУНКЦИЯ
[16
значение х; функция получит тогда новое значение у=/(х)-
Приращение аргумента при этом будет равно Ах — х— 0 — х, а
приращение функции Ау=у— Ь. Следовательно, по условию должно
быть у — Ь~ах. Отсюда
у = ах + Ь
при любом л:, что и требовалось доказать.
Линейной функцией описывается всякий равномерный про-
процесс, т. е. такой процесс, в котором двум любым равным прира-
приращениям одной величины соответствуют равные между собой
приращения другой величины.
Например, движение — равномерное, если в любые равные про-
промежутки времени (t) проходятся равные пути (s); тогда As — vAt,
где v — постоянная скорость движения. Отсюда в силу свойства
линейной функции имеем: s = vt-\- sQ, где sQ— путь, пройденный
к моменту / = 0. Это — так называемое уравнение равномер-
равномерного движения.
Равномерные процессы — самые простые
и вместе с тем чрезвычайно важные.
16. Квадратичная функция. Квадратич-
Квадратичной функцией называется функция вида
Ьх + с,
у = ах2
где я, Ь, с — постоянные
на
Квадратичная функция определена
всей числовой оси.
В простейшем случае, когда ?=с = 0,
функция имеет вид у = ах2; ее графиком слу-
служит парабола с вершиной в начале коор-
координат и осью, совпадающей с положитель-
положительной полуосью Оу, когда а > 0, и с отри-
отрицательной полуосью Оу, когда а < 0. В
общем случае графиком функции у = ах2 +
+ Ьх + с является, как известно из ана-
аналитической геометрии, парабола, ось которой параллельна оси Оу,
b Ь2 — 4'
Рис. 13.
а вершина лежит в точке Мо
. Ветви параболы
°\ 2fl' 4a
направлены вверх или вниз в зависимости от того, будет ли а > О
или а < 0 (рис. 13).
Квадратичная функция только один раз меняет характер своего
изменения: она или сначала убывает, а затем возрастает, или на-
наоборот. А именно, если а > 0, то функция в интервале
(—оо, —— J убывает, достигая при х = — ^своего наименьшего
16] § 3. НАЧАЛО ИЗУЧЕНИЯ ФУНКЦИЙ. ПРОСТЕЙШИЕ ФУНКЦИИ 47
Ь2 — 4ас ( Ь . \
значения у — -г , а затем в интервале (—s~, + оо 1 воз-
возрастает; наибольшего же значения функция нигде не достигает.
Наоборот, при а<0 функция сначала в интервале (— оо, ——А
возрастает, достигая при х = — ^- своего наибольшего значения
у = 9 а затем в интервале (—~-, + оо) убывает; в этом
*тп \ ZCL J
случае функция нигде не достигает наименьшего значения.
Например, для квадратичной функции у=х2— 5лг + 4 имеем:
а =1 > 0; следовательно, эта функция имеет наименьшее значение.
Для его отыскания не нужно строить график функции; приведен-
приведенные выше формулы показывают, что наименьшее значение подуча-
подучается при лг = — 2^=2,5 и равно у = ^-^ = — 2,25. (Послед-
(Последнее значение можно получить не по готовой формуле, а подставив
в выражение функции лг = 2,5.)
Задачи отыскания наибольшего и наименьшего значений функции
возникают довольно часто в самых разнообразных вопросах.
Рассмотрим два примера.
1) Из всех прямоугольников с данным периметром Я найдем
прямоугольник, имеющий наибольшую площадь.
Обозначим одну из сторон прямоугольника через лг, тогда дру-
Р
гая сторона будет равна у — х. Следовательно, площадь прямо-
прямоугольника 5 равна
т. е. является квадратичной функцией от х. Так как а = —1 < 0,
то функция имеет наибольшее значение; оно достигается при
х= — w~==z~r и Равно
Но прямоугольник, периметр которого равен Я, а одна из сторон
р
имеет длину —, есть квадрат. Таким образом, из всех прямоуголь-
прямоугольников данного периметра наибольшую площадь имеет квадрат.
2) Найдем, через сколько секунд после выстрела поднимается
на наибольшую высоту над уровнем моря снаряд, выпущенный вер-
вертикально вверх из зенитного орудия, и какова будет эта наиболь-
наибольшая высота, если пренебречь сопротивлением воздуха; при этом
дано, что скорость снаряда при вылете из дула орудия v9 = 500 м/сек,
высота орудия над уровнем моря /го = 2ОО лс.
48 гл. i. функция [17
Пренебрегая сопротивлением воздуха, движение снаряда можно
считать равнозамедленным, с ускорением—g. Тогда, как известно,
высота h снаряда над уровнем моря в момент времени t будет равна
A = A0 + V—f *2.
Таким образом, h есть квадратичная функция от t, причем здесь
а = —т>-< 0. Наибольшее значение функции h (т. е. наибольшая
высота подъема снаряда) будет при
v0 500
7 =
Следовательно, через 51 сек после выстрела снаряд достигнет наи-
наибольшей высоты h — Н, причем
Я=200 + 500.51— ^.512 = 12 955л*^ 13 кн.
Вследствие наличия сопротивления воздуха практически И будет
значительно меньше.
17. Обратная пропорциональная зависимость и дробно-линейная
функция. Обратной пропорциональной зависимостью называется за-
зависимость, выраженная формулой
где а —постоянная ()
Ее характерной особенностью является то, что величина у об-
обратно пропорциональна величине л:, т. е. если хг и yv x2 и уг —
две пары соответственных значений х и у, то \у2:у1=х1:х2. По-
Постоянный коэффициент а называется коэффициентом обратной про-
пропорциональности.
Если j/ = —, то х = —; значит, если у обратно пропорцио-
х у
нально х, то и а: обратно пропорционально у, притом с тем же
коэффициентом обратной пропорциональности.
Обратная пропорциональная зависимость есть частный случай
зависимости, устанавливаемой дробно-линейной функцией, т. е. функ-
функцией вида
у cx + d > l ;
где a, ft, с, d—постоянные (с=^=0).
При а = 0, d = 0 отсюда получается обратная пропорциональ-
пропорциональная зависимость.
17] § 3. НАЧАЛО ИЗУЧЕНИЯ ФУНКЦИЙ. ПРОСТЕЙШИЕ ФУНКЦИИ 49
Дробно-линейная функция (*) определена на всей оси Ох, за
d ( ^ а\
исключением точки х=- точки х = 0 для функции у — ~
с \ х )
Будем предполагать, что be— ad=fcO, ибо в противном случае
функция вырождается в постоянную. В самом деле, пусть bc — ad\
обозначая отношение — через ту получаем: а = ст, b — -~ = dm
с с
и, следовательно,
„ ax + b __ cmx + dm _ cx + d _
-^ сл: + ^ eje + d cx + d
С помощью параллельного переноса системы координат дока-
доказывается, что графиком дробно-линейной функции служит равно-
равнобочная гипербола, асимптоты которой параллельны осям координат.
Именно, если параллельно перенести систему координат, взяв но-
новое начало в точке О' ( , — ), то уравнение графика дробно-
линейной функции (#) в системе О'х'у' будет иметь вид
, а' , be—ad
У 7> ГДе п ==~^~"
(так как по условию be — ad=^0, то а' ФО). Это — уравнение рав-
равнобочной гиперболы, асимптотами которой являются новые оси
координат, т. е. прямые
d a
Х У
Итак, для того чтобы построить график дробно-линейной функ-
/ d a\
ции, нужно через точку ( , —) провести прямые, параллель-
\ с с )
ные осям координат, и, приняв их за асимптоты, вычертить
равнобочную гиперболу с осями, равными 2 У 2 | а' |. В каких углах,
образованных асимптотами, расположена гипербола, зависит только
. , , be — ad
от знака коэффициента а =—%— » т« е* от знака выражения
be — ad: если be—ad > 0, то гипербола расположена в первом
и третьем углах, а если be — ad < 0, то—во втором и четвертом.
Пусть, например,
+ \
Здесь я=1, #=1, с=1, d = — 1, следовательно, асимптотами ги-
гиперболы являются прямые х — —1 и jj = —=1. Далее,
с с
a' =^^-z=2\ следовательно, оси гиперболы равны 2^2 | а' | = 4.
50
ГЛ. I. ФУНКЦИЯ
[18
На рис. 14 показан график этой функции; он расположен в пер-
первом и третьем углах, образованных асимптотами, так как здесь
bc—ad = 2>0.
В частном случае обратной пропорциональной зависимости
у = ~ асимптотами служат сами оси координат.
Ход изменения дробно-линейной функции легко усматривается
из графика, а именно:
Дробно-линейная функция (*) или только возрастает, или только
убывает в любом интервале оси Ох, не содержащем точки х== .
Тот или другой характер роста (возрастание или убывание) за-
зависит от знака выражения be — ad. Если be—ad > 0, то функция
убывает, если be — ad < 0,
то функция возрастает.
Рассмотрим поведение фун-
функции ^ = ^i—, график кото-
X— 1
рой изображен на рис. 14.
При значениях лг, меньших
единицы, эта функция остает-
ся постоянно меньше единицы
и убывает при приближении
¦*? лг к единице; при переходе
аргумента х от значений, мень-
меньших единицы, к значениям
большим единицы, функция
делает бесконечный скачок,
переходя от как угодно боль-
больших по абсолютной величине
отрицательных значений к как
угодно большим положитель-
положительным значениям; при дальнейшем росте х функция продолжает убы-
убывать, оставаясь больше единицы и неограниченно приближаясь
к ней, когда х неограниченно возрастает.
I/
Рис. 14.
§ 4. Обратная функция. Степенная, показательная
и логарифмическая функции
18. Обратная функция. Пусть задана какая-либо функция
yz=zf(x)\ D — область ее определения (т. е. множество значений л:),
a G—область значений функции (т. е. множество соответствующих
значений^). Будем говорить, что функция y=f(x) осуществляет
отображение множества D в множество G; из определения функции
следует, что каждой точке множества D ставится в соответствие
18] § 4. СТЕПЕННАЯ, ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ 51
одна-единственная точка множества G. Если при этом каждой точке
множества G соответствует опять-таки единственная точка множе-
множества Д то говорят, что отображение (соответствие) взаимно одно-
однозначное. При таком отображении различным точкам множества D
соответствуют различные точки множества G.
Например, функция у = х3 взаимно однозначно отображает всю
ось Ох в ось Оу, так как каждому значению х соответствует
одно-единственное значение у, и наоборот: каждому у соответ-
соответствует только один лг, равный ^/ у.
Функция у = х2 не осуществляет взаимно однозначного соот-
соответствия между осью Ох (область определения функции) и интер-
интервалом [0, оо) оси Оу (область значений функции), потому что любому
значению у > 0 соответствует не одно, а два значения х; это
х = + VУ и х = —Vy-
Функция у = sin х отображает всю ось Ох в интервал [—1, 1]
оси Оу. Ясно видно, что это отображение не взаимно однозначное:
каждому значению у из интервала [—1, 1] соответствует бесчис-
бесчисленное множество значений х.
Если функция y=f (x) осуществляет взаимно однозначное ото-
отображение множества D в множество G, то, согласно сказанному,
каждому значению у из множества G ставится в соответствие одно
определенное значение х из множества D. Поэтому можно сказать,
что определена функция х = ц>(у); О является ее областью опре-
определения, a D—областью значений. Мы замечаем, что величины х
и у как бы поменялись ролями: у стала независимой переменной,
а х—функцией. В этом случае функции y=f(x) и х = у(у) на-
называются взаимно обратными.
Если отображение множества D в множество G не взаимно
однозначно, то некоторым значениям у (а может быть, даже и всем)
будет соответствовать несколько различных значений х, и мы опять
сталкиваемся с той же трудностью, что и в п. 12 при рассмотре-
рассмотрении неявных функций, а именно с тем, что обратная функция
оказывается многозначной. Подробнее об этом будет сказано
дальше, а сейчас мы научимся по заданной функции находить ей
обратную и установим геометрическую связь между графиками
взаимно обратных функций.
Пусть величина у дана как явная функция от х:
Это же уравнение определяет х как неявную функцию от у.
Чтобы получить ее явное выражение, нужно, если это возможно,
разрешить данное уравнение относительно х:
Ясно, что функция y=f [x) и х = у(у) и будут взаимно обратными.
52
ГЛ. I. ФУНКЦИИ
[18
-х+1
Например, если у — хгу то x = i/yy или если j;=io*, то x = \gy
(заметим, что в обоих примерах соответствие между областями
значений лг и у взаимно однозначно). Легко непосредственно про-
проверить, что функция, обратная линейной, также линейна и что
функция, обратная дробно-линейной, также дробно-линейна.
Если функция с самого начала задана в неявном виде, т. е.
в виде уравнения, связывающего лг и у} то, разрешая данное урав-
уравнение сначала относительно у, а затем относительно лг, мы полу-
получим как раз пару взаимно обратных функций. Например, уравнение
ху + Зл:—у — 1 = 0 определяет взаимно обратные функции>> =
и лг = ^тто (обе они-
/ но-линейные).
\ / _ 3 В одной и той же сис-
/ °^JL теме осей Оху и уравне-
"^=.fe" ние (*), и уравнение (**)
выражают одну и ту же ли-
линию, но для функции/осью
аргумента является ось Ох,
*? а для функции ср — ось Оу.
Например, если у = хг,
то лг = \/у. Графиком этих
зависимостей будет так на-
называемая кубическая
парабола (рис. 15).
Если нужно построить
графики взаимно обратных
функций так, чтобы для
^ис 15* обеих функций осью аргу-
аргумента служила ось Олг, то
обозначим аргумент в формуле (**) через лг, а функцию — через у,
т. е. так же, как в формуле (#); тогда получим
В такой записи в обеих взаимно обратных функциях j;=)
и у = у(х) одна и та же буква (лг) обозначает независимую пере-
переменную и одна и та же буква (у)—функцию. Например, взаимно
обратными будут функции у ~хг и у = у лг, или у = 10* иу = \gx.
Заметим, что последовательное применение взаимно обратных функций
к любому значению х оставляет это значение неизменным, например:
?/*» = *, (У7у = х или lglO*=*, 10te* = *.
Символически это записывается так:
т. е. символы взаимно обратных функций как бы уничтожают друг друга.
О а N х
18] § 4. СТЕПЕННАЯ, ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ 53
При этом х должен быть таким, чтобы он находился в области определения
первой из применяемых функций. Так, тождество lg 10* = # справедливо
при всех х, а тождество 10lgA: = x — только при х > 0.
Если соответствие между областями значений х и у не взаимно одно-
однозначно, то указанные равенства не обязаны соблюдаться; например, У х2
имеет два значения: х и —х.
Между графиками функций y~f(x) и у = у(х) существует
простая связь:
График обратной функции у = ф {х) симметричен с графиком дан-
данной функции y~f{x) относительно биссектрисы первого и третьего
координатных углов.
Действительно, пусть при х = а Уи
ТочкаМ(а, Ь) принадлежит графику данной
функции. Тогда точка М с координатами (b, a)
принадлежит графику обратной функции, так
как а = у(Ь). Имеем (рис. 16): ДОЛГМ' —
= /\0NM, вследствие чего /_N'0M'=
= /_ N0M и ОМ = ОМ. Отсюда следует, во-
первых, что биссектриса OR координатного
угла будет и биссектрисой угла MOM, и, Рис. 16.
во-вторых, что Д MOM равнобедренный. По-
Поэтому биссектриса OR действительно является осью симметрии
треугольника MOM\ Итак, каждой точке на графике данной функ-
функции соответствует точка на графике обратной, расположенная сим-
симметрично с первой относительно биссектрисы первого и третьего
координатных углов. Так как верно и обратное, то наше предло-
предложение полностью доказано.
Имея график некоторой функции, можно, следовательно, полу-
получить график обратной ей функции с помощью простого перегибания
чертежа по биссектрисе первого и третьего координатных углов.
Именно так построен на рис. 15 график функции у = |/х по гра-
графику обратной ей функции у=х3.
Перейдем теперь к выяснению условий, при которых отобра-
отображение множества значений л: в множество значений^ будет взаимно
однозначным, т. е. условий, при соблюдении которых функция
У=/(х) будет иметь однозначную обратную функцию. Тот факт,
что значениям х соответствуют единственные значения^, означает,
что любая прямая, параллельная оси ординат, пересекает график
функции не более чем в одной точке. Чтобы значениям у соответ-
соответствовали также единственные значения х, нужно чтобы этим же
свойством обладали и прямые, параллельные оси абсцисс. Геометри-
Геометрически ясно, что это условие будет соблюдаться, если данная функ-
функция монотонна; при этом монотонной будет и обратная функция.
54
ГЛ. I. ФУНКЦИЯ
[19
Точное доказательство этого утверждения мы не приводим,
ссылаясь лишь на его геометрическую наглядность, вытекающую
из установленной связи между графиками взаимно обратных функ-
функций. Рекомендуем читателю самостоятельно проверить сделанное
утверждение, построив
19^й
чер-
*y=+V&
-*-&
Рис. 17.
соответствующие
тежи.
Если данная функ-
функция не монотонна, то
картина будет более
сложной. Пусть, напри-
например, дана функция^ = х2,
графиком которой явля-
является парабола (рис. 17).
Мы разобьем область
определения этой функ-
функции, т. е. всю числовую
ось, на интервалы, в ко-
которых функция монотон-
монотонна: (—оо, 0] и [0, оо).
В каждом из этих интер-
интервалов функция у = х2
имеет обратную: в ин-
интервале (—оо,0] это
будет функция j/ = — Ух (или в другой записи лг = —Уу)> а в
интервале [0, оо) — функция у=-\-Ух (рис. 17). При этом симво-
символом Ух обозначено арифметическое (положительное) значение корня.
Так же как в п. 12, можно сказать, что функция, обратная
к функции у — х2, многозначна, а функции у= + Ух и
у = — Ух—ее однозначные ветви. Заметим кстати, что
в дальнейшем для краткости функция у = + Ух будет обозна-
обозначаться просто через у = Ух.
Всюду в дальнейшем, говоря о взаимно обратных функциях,
мы подразумеваем, что в областях их определения они монотонны.
Если данная функция не монотонна, то мы, как в приведенном
примере, разбиваем область ее определения на интервалы моно-
монотонности и в каждом таком интервале берем соответствующую
однозначную ветвь обратной функции. Другие важные примеры мы
рассмотрим в п. 22 при изучении обратных тригонометрических
функций.
19. Степенная функция. Степенная функция
у=хп
19] § 4. СТЕПЕННАЯ, ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ 55
X
при целых и положительных значениях п определена на всей чис-
числовой оси. Вид графиков функций у = хп при различных целых
значениях п показан на рис. 18.
При четном п эти функции чет- ^.
н ы е, а при нечетном п — нечет-
н ы е; поэтому можно говорить об
их свойствах только для лг^О.
Чем больше п, тем ближе к оси
абсцисс лежат соответствующие
графики в интервале @,1) и тем
круче они поднимаются вверх при
приближении х к единице.
Пользуясь результатами п. 18,
можно сразу построить графики
функций у = \/х = X1/* , обратных
к функциям у=хп. Надо только
иметь в виду, что при нечетном п
обе функции определены и моно-
монотонны на всей числовой оси и гра-
графики их подобны графикам на
рис. 15 (/г = 3). Если же п — чет-
четное, то обратная функция состоит
из двух однозначных ветвей: у— Рис. 18.
= + Vх и J;==— Vх* область
определения каждой ветви—интервал [0, оо). Графики их анало-
аналогичны графикам, изображенным на рис. 17 (я = 2).
Пусть теперь п — любое положительное число. Если п рацио-
рациональное число: /г = ~, где дробь — несократима, то свойства
функции у = хп зависят от четности или нечетности чисел ряд
и указаны в следующей таблице.
Четное
Нечетное
Четное
Функция состоит из двух однознач-
однозначных ветвей, определенных в интер-
интервале [0, оо); графики их симметричны
относительно оси абсцисс
Нечетное
I
Функция определена на всей числовой оси
Четная I Нечетная
56
ГЛ. I. ФУНКЦИЯ
[19
При п иррациональном степенная функция рассматривается
только при х^О.
На рис. 19 в первом координатном угле представлены графи-
графики функций у-=хп для различных п > 0. Все эти функции воз-
возрастают в интервале @, оо); их графики проходят через точки
@,0) и A,1) и разделяются прямой у=х на два класса: обра-
обращенные своей выпуклостью вниз (я > 1) и обращенные своей
выпуклостью вверх (п < 1). Пользуясь приведенной таблицей,
легко построить полные графики этих функций.
Линии у = хп при п > 0 называются параболами соответ-
соответствующих порядков. Так, у = х2 (обыкновенная парабола) — пара-
парабола второго порядка, у— л:3 — парабола третьего порядка, или
кубическая парабола. Часто встречающаяся линия y=:x*i* (или
= л:3) — парабола порядка 3/2 — называется полукубиче-
полукубиче(рис. 20).
у = хп при я<0 являются линиями сущест-
сущестчем указанные параболы. Пусть п=—т,
21 в первом координатном угле представлены
графики функций у — -^ для различных т > 0. Все функции убы-
убывают в интервале @, оо). Когда х неограниченно возрастает,
у убывает, неограниченно приближаясь к нулю, и, наоборот, ког-
когда у неограниченно возрастает, х убывает, неограниченно при-
ской параболой
Графики функции
венно другого типа,
где т > 0. На рис.
201 § 4- СТЕПЕННАЯ, ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ 57
ближаясь к нулю. Отсюда мы заключаем, что при любом т > 0
положительные полуоси Ох и Оу являются асимптотами линий
у—-т> Так же, как у
и раньше, все линии „
проходят через точку
Рис. 20.
Рис. 21.
Линии у = —тл т > 0, называются гиперболами соответ-
соответствующих порядков; при т=\ получается обычная равнобочная
гипербола.
В заключение отметим, что линии у = хп в физике и технике
иногда называют политропными кривыми.
20. Показательная и логарифмическая функции.
I. Показательная функция. Показательная функция
у — а*
рассматривается только при а>0 и а^фХ1).
Эта функция определена на всей оси Ох и всюду положитель-
положительна: а* > 0 при всяком х\ это означает, что когда х — дробное
число, мы берем только арифметическое значение корня. По-
Поэтому график показательной функции расположен над осью Ох\
1) При а < 0 область определения функции состоит только из рацио-
р
нальных чисел # = ---, у которых знаменатель (/ — нечетное число, при
а=\ функция при всех к равна 1.
58
ГЛ. 1. ФУНКЦИЯ
[20
так как а°=1, то он проходит через точку @,1). Поведение по-
показательной функции существенно зависит от того, будет ли
а > 1 или а< 1.
Если а>1, то с увеличением показателя х увеличивается и
j/, причем неограниченное возрастание аргумента вызывает неогра-
неограниченное же возрастание и функции. Если а<1, то, наоборот,
при неограниченном возрастании аргумента функция убывает и
неограниченно приближается к нулю.
График показательной функции с основанием а симметричен
относительно оси Оу графику показательной функции с основанием
1 /1 \х
— . В самом деле, функцию у = ( — ) можно записать так: у = а~~х,
откуда видно, что для
положительных х она при-
принимает те же значения,
что и функция у = а* для
равных им по абсолют-
абсолютной величине отрицатель-
отрицательных л:, и наоборот. А это
и означает, что графики
функций
Уг
\
а</
а>1
1/3
\
1/10 %
\ \
\ \
\ \
ч
0
т
t
3 2
1/
а:
У =
симметричны относительно
оси ординат.
Рис 22. На рис. 22 показаны гра-
графики показательных функ-
функций при а =2, 3, 10, 7г> 7з> Vio- ^сь @х служит асимптотой
линий у** ах.
Похазательные функции встречаются в самых разнообразных
задачах. При этом чаще всего имеют дело с показательной функ-
функцией, в основании которой лежит специальное число е, играющее
очень важную роль в математике (см. п. 31); его приближенное
значение равно 2,718. Иногда функцию у = е* называют экспонен-
экспоненциальной, а ее график — экспонентой.
II. Логарифмическая функция. Логарифмическая
функция
обратна показательной функции у = ах, а > 0, аф\. Поэтому
легко построить график логарифмической функции. Именно, пе-
перегнув рис. 22 по биссектрисе первого и третьего координатных
20] § 4. СТЕПЕННАЯ, ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ 59
углов, мы и получим графики логарифмических функций при тех
же основаниях а (рис. 23).
Опишем, пользуясь этими графиками, поведение логарифми-
логарифмической функции. Прежде всего, мы видим, что логарифмическая
функция определена на всей положительной полуоси Ох и не оп-
определена для отрицательных и нулевого значений независимой
переменной. Все логарифмики
проходят через точку A,0), так
как логарифм единицы всегда ра-
равен нулю.
Поведение логарифмической
функции существенно зависит от
того, будет ли а > 1 или а <1.
В первом случае (а>1) лога-
логарифм во всем интервале @, оо) —
возрастающая функция,
притом отрицательная в интер-
интервале @, 1) и положительная в
интервале A, оо). Во втором
случае (а < 1) логарифм во всем
интервале @, оо) — убываю-
убывающая функция, притом положи-
положительная в интервале @, 1) и от-
отрицательная в интервале A, оо).
График логарифмической
функции с основанием а симмет-
симметричен относительно оси Ох с графиком логарифмической функции
с основанием —.
а
Принимая во внимание, что логарифмическая и показательная
функции взаимно обратны, имеем (см. п. 18)
\оёааХ==:Х и al°zax = x;
первое из этих равенств справедливо при любом л:, второе—при
х> 0.
Пользуясь последним соотношением, всякую степенную функ*
цию у — хп при х > 0 с любым показателем п можно представить
в виде сложной функции, составленной из показательной и лога-
логарифмической функций:
у —хп = (al°2aX)* = anXo%*x.
Возьмем логарифмические функции при двух разных основа-
основаниях ах и а2, т. е. ,Vi==logaiji; H^2 = loga2A;. Выражая х из
первого равенства через ух и подставляя во второе равенство»
Рис. 23.
60 гл. i. функция [21
пол)чим: у2 = \oga2 ofi=y1\ogaia1^ или, иначе,
Полагая л: — #2, получим соотношение \ogata2 = ~, .
Чтобы перейти от системы логарифмов при одном основании
(а2) к системе при другом основании (ах)у нужно логарифмы чисел
в первой системе умножить на постоянное число (-. ] —
так называемый модуль перехода от одной системы логарифмов к
другой. Следовательно, логарифмы чисел при разных основаниях
пропорциональны друг другу, т. е. одна логарифмика переходит
в другую посредством увеличения или уменьшения всех ее орди-
ординат в одно и то же число раз.
Логарифмы с основанием а = 10 обозначают через \gx и на-
называют десятичными, а с основанием а~е через lnjc и называют
натуральными (см. п. 37 II).
§ 5. Тригонометрические, обратные тригонометрические,
гиперболические и обратные гиперболические функции
21, Тригонометрические функции. Гармонические колебания.
I. Тригонометрические функции. В качестве незави-
независимой переменной тригонометрических функций
y^cosecx, y — ctgx
в математическом анализе всегда принимается радианная мера ду-
дуги или угла. Так, например, значение функции у = sinх при х = х0
равно синусу угла в х0 радианов.
Напомним, что радианной мерой дуги называется число, рав-
равное отношению длины этой дуги к радиусу окружности. Именно
при таком способе измерения аргумента делается понятным смысл
таких выражений, как x + sinjc, л: cos л; и т. п. Рекомендуем чита-
читателю вычислить с помощью таблиц значения написанных выраже-
выражений при л: —0,5, х-=\ и х — 2.
Между шестью тригонометрическими функциями: ^у = sin л:, у~
= cosat, y — tgx, ^y^secAT, y~ cosecx, y = ctgx — существуют пять
простых независимых алгебраических соотношений, выводимых на
основании определений этих фзнкций и позволяющих по одной
из них находить остальные.
Тригонометрические функции периодичны. Именно, функции
sin л: и cos л: (а потому и cosec х и sec л:) имеют период 2я, а функ-
функция tg* (а потому и ctgjc)— период я.
21]
§ 5. ТРИГОНОМЕТРИЧЕСКИЕ, ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
61
Перейдем к известным графическим изображениям тригоно-
тригонометрических функций. Начнем с функции y = smx. По ее графику
видно, что в интервале 0, -~- эта функция возрастает от нуля
до единицы, а затем в интервале у, -<Н убызает до — 1, про-
ГЗя о 1
ходя через нуль в точке дг = я, и, наконец, в интервале —, 2лс I
1
Зж
2
4L/
/2л
х
Рис. 24.
снова возрастает до нуля. Так как функция y = slnx имеет пери-
период 2я, то весь ее график (синусоида) получается передвиже-
передвижением вправо и влево интервала [0, 2я] вместе с соответствующей
ему частью графика на 2я, 4я, 6я, ... (рис. 24). Функции у ==
= sin^r нечетная; это хорошо видно на графике: он симметричен
относительно начала координат.
Так как
cos х = sin
то, согласно п. 14, графиком функции jj^
является рассмот-
рассмотренная выше синусоида, сдвинутая влево по оси Ох на -5- (рис. 25).
Рис. 25.
В интервале [0, я] функция j> = cos.*; убывает от 1 до —1,
проходя через О в точке # = у, и затем в интервале [я, 2я]
возрастает от —1 до 1, проходя через О в точке л; = ~; даль-
четная, ее
ше она изменяется периодически. Функция ^ =
график симметричен относительно оси ординат.
Функцию y^igx рассмотрим на интервале [0, я]. В точке
д; = ~она не определена; когда х неограниченно приближается к ^-
62
ГЛ. I. ФУНКЦИЯ
[21
слева (возрастая), J/, будучи положительным, неограниченно возраста-
возрастает, а когда х неограниченно приближается к ~ справа (убывая), у
неограниченно возрастает по абсолютной величине, оставаясь отри-
отрицательным. Так как функция y = tgx имеет период я, то анало-
аналогичная картина наблюдается в окрестности каждой точки лг =
= B&+1)-тг> где & — любое целое число. На всей оси Ох гра-
график функции у = tgх (тангенсоида) получается из графика в
интервале [0, п] простым по-
повторением на основании свой-
свойства периодичности (рис. 26).
В каждом интервале, где
функция y = tgx определена,
она возрастает. Так как
у = tg х — функция нечетная,
то график симметричен отно-
,^ сительно начала координат.
/ ^-jr1 / ° \~2 / \ Х Рекомендуем читателю
/ \ I \ I i представить себе графики
трех остальных тригономет-
тригонометрических функций (cosecAT,
sec дг, ctgA;) и затем описать
их особенности.
II. Гармонические
колебания. Тригономет-
Рис. 26. рические функции имеют важ-
важные применения в математике,
в естествознании и в технике. Они встречаются там, где приходится
иметь дело с периодическими явлениями, т. е. явлениями,
повторяющимися в одной и той же последовательности и в одном
и том же виде через определенные интервалы аргумента (чаще
всего — времени).
Простейшие из таких явлений — г а рмо нич е ски е колеба-
колебания, в которых расстояние s колеблющейся точки от положения
равновесия является функцией времени t:
5 = Л sin (с
Эту функцию называют синусоидальной. Постоянное число Л1)
называется амплитудой колебания. Число Л представляет собой
то наибольшее значение, которого может достигнуть 5 (размах
г) Мы всегда можем считать его положительным, так как если оно от-
отрицательно, то функцию можно записать в виде
s== —A sin
21]
§ 5. ТРИГОНОМЕТРИЧЕСКИЕ, ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
63
колебания). Аргумент синуса ш^ + ф0 называется фазой колебания,
а число ф0, равное значению фазы при ? = 0 — начальной фазой.
Наконец, н- называется частотой колебания.
Происхождение последнего термина делается ясным из связи
между ©и периодом Т нашей функции {периодом колебания).
Функция s = A sin (со^ + ф0) периодическая; ее период Т равен
—, так как для увеличения фазы на 2я нужно к независимой
переменной t прибавить —. Поэтому тг=^-> и значит, число
¦к- показывает, сколько периодов укладывается в единице вре-
времени, т. е. сколько раз данное периодическое явление повторя-
повторяется в течение единицы времени; это число дает, следовательно,
частоту явления. Число со показывает, сколько раз явление по-
повторится за 2я единиц; его называют круговой частотой, а иногда
и просто частотой.
Для того чтобы построить график синусоидальной функции
s = A sin
запишем эту функцию в виде s =
построения графика этой
функции методы, указан-
указанные в п. 14.
Рекомендуем читателю
самостоятельно построить
график функции
s = 3sin
этот график показан на
рис. 27.
Колебания,описываемые
уравнением
)»
-— ) и применим для
называются простыни гар-
гармоническими колебаниями, а их графики — простыми гармониками.
Часто встречаются суммы простых гармонических колебаний —
функции вида
= Ax sin
+ фа) + ... + Ап sin
<ря),
где Alt Л2, ..., An — постоянные.
64
ГЛ. !. ФУНКЦИЯ
[22
Колебания, получающиеся в результате сложения нескольких
простых гармонических колебаний, называются сложными гармо-
гармоническими колебаниями, а их графики— сложными гармониками.
Эти графики могут иметь очень сложную форму. На рис. 28 дан
график функции
5 ==2 sin 2t + sin Ы + ~
(пунктиром проведены графики слагаемых функций). Эта функ-
функция периодическая, с периодом 2п. График ее является сложной
Рис. 28.
гармоникой, получившейся в результате наложения двух простых
гармонических колебаний:
s — 2sm2t и ^ = sin
22. Обратные тригонометрические функции. Обратные триго-
тригонометрические функции определяются с помощью результатов
п. 18. Начнем с функции, обратной для функции ^у == sinлг. Об-
Область определения sin л; — всю числовую ось — разбиваем на интер-
интервалы монотонности, которых бесконечно много:
ГЗя _яП f_iL М \^_ Зя1
• • •' [ 2 э 2 J' [ 2 ' 2 J' [2 ' 2 J' ••*
Выберем в качестве основного интервал —~, у и функцию,
обратную к функции y = sinx на этом интервале, обозначим через
y = arcsmx. Так как область значений функции y = s\nx есть
интервал [—1, 1], то этот же интервал есть область опре-
определения функции y — arcsinx; областью ее значений явля-
[ я л!
—у, -у :
—2-^arcsin.xr ^ у .
Значение функции arcsin.*: есть радианная мера угла, синус
которого равен данному значению независимой переменной х; из
всех углов, удовлетворяющих этому условию, выбирается угол,
ется интервал
22]
§ 5. ТРИГОНОМЕТРИЧЕСКИЕ, ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
65
заключенный между —у и у • Таким образом, равенство у —
= arcsin лг эквивалентно двум следующим:
sin у — sin (arcsin x) = лг, — ^т^У ^ 4-.
Строя по обычному правилу график обратной функции, т. е.
перегибая рис. 24 по биссектрисе первого и третьего координат-
координатных углов, получим жирную линию на рис. 29. Сразу видно, что
функция у = arcsin лг возрастающая и не-
нечетная (arcsin (—х) = —arcsin л:).
Образуя в каждом из указанных выше интер-
интервалов монотонности соответствующую обратную
функцию, мы получим бесконечно много однознач-
однозначных ветвей; все они по-прежнему определены в ин-
интервале [ — 1, 1]. Графики двух из них, соответ-
Г Зя jt Г я Зя1
ствующих интервалам I j, — у и у, у ,
показаны на рис. 29. Рекомендуем читателю про-
проверить, что первая функция равна—я— arcsin л:, а
вторая я—arcsin лг, и написать выражения еще
для двух функций, соответствующих соседним ин-
интервалам. Всю совокупность однозначных ветвей
обозначают через
у = Arcsin х.
Пользуясь уже принятой терминологией, мож-
можно сказать, что функция Arcsinx бесконечно-
з н а ч н а, так как она состоит из бесконечного
числа однозначных ветвей. Изображая их все на
графике, мы, очевидно, получим ту же синусоиду, что и на рис*
24, только иначе расположенную относительно осей координат
(рис. 29).
Обычно приходится иметь дело только с ветвью y — atcsinx;
ее называют главным значением функции Arcsin x.
Совершенно аналогично определяется функция, обратная к
функции у — cos х. Интервалами монотонности созлг являются ин-
интервалы
• .., [—2я, —я], [—я, 0], [0, я], [я, 2л], •..
Функцию, обратную к функции y = cosx в интервале [0, я],
обозначим через ^ = arccosAr. График ее показан жирной линией
на рис. 30. Эта функция определена в интервале [—1, 1] и при-
принимает значения, заключенные между 0 и я:
Рис. 29.
А. Ф. Бермант, И. Г. Араманович
66
ГЛ. I. ФУНКЦИЯ
[22
Следовательно, равенство jj = arccos лг эквивалентно двум ра-
равенствам
cosy = cos (arccos х) = х, О ^jj <! я.
Функция у = arccos x у б ыв ающ а я, так как в интервале [0,я]
убывает и cos*. Для вычисления ее значений важно отметить
равенство
arccos (—х) = я— arccos лг,
которое немедленно вытекает из формулы приведе-
приведения cos (я—а) = —cos а.
Совокупность всех однозначных ветвей обрат-
обратной функции (их по-прежнему бесконечно много)
обозначим через j/ = Arccosx\ графики этих ветвей
изображены на рис. 30. Функция j/ = arccosx назы-
называется главным значением Arccos x.
Отметим следующие формулы, проверить ко-
которые предоставляем читателю:
sin (arccos x) —
cos(arcsinjc)=
arcsin x + arccos x = -—.
Перейдем к функции, обратной для функции
y = tgx. В интервале (—~, ^\ функция tgA; воз-
возрастает и, следовательно, имеет обратную, кото-
которую мы обозначим через j; = arctg.*;; графиком ее
служит жирная линия на рис. 31. Из свойств функции tgx сле-
следует, что функция у = arctgx определена на всей числовой оси
и является возрастающей и нечетной. Область ее зна-
Рис. 30.
чений — интервал —тт» -гг 1 , т» 6.
\ 1 *)
— у < arctg л: < у.
Совокупность остальных однозначных ветвей обозначается че-
через у = Arctgлг; графики их как бы «параллельны» графику arctgx
и получаются параллельным переносом этого графика вдоль оси
Оу на величину kn, где k — любое целое число (рис. 31).
Функция у~ arctgx называется главным значением Arctg x. Ре-
Рекомендуем читателю также исследовать функцию, обратную к
ctg*.
Всюду в дальнейшем, если не будет оговорено противополож-
противоположное, под обратными тригонометрическими функциями мы будем
понимать их главные значения.
221
§ 5. ТРИГОНОМЕТРИЧЕСКИЕ, ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ 67
Г п nl
Так как функции y = sinx и j/ = arcsin л взаимно обратны, то имеем
sin (arcsin x) = х, arcsin (sin x)=х.
Первое из этих равенств имеет место в интервале [—1, 1], так как функ*
ция arcsinx определена только в этом интервале. Второе равенство справед-
справедливо в интервале
ибо функция arcsln* обратна
функции sin х именно в интерва-
Если функцию
i/=*arcsin (sin х) рассматривать на
всей оси Ох, то тогда она уже
не всегда будет просто равна
аргументу х, как в интервале
ле
f_?L ill
—-jr-, — . Заметим прежде все-
- J л.
го, что это—периодическая функ-
функция с периодом, равным 2я:
arcsin [sin (х + 2я)] = arcsin (sinx).
Поэтому нам достаточно уз-
узнать, какова эта функция еще в
интервале
я Зя"|
чтобы знать
ее на всей оси Ох. Если -^ < х <
Зя я я
< ~y> то —^ <п—х < Y * и
мы имеем:
arcsin (sin x) = Рис. 31.
= arcsin [sin(ji— х)] =я—х,
[я Зя1
-jr-s -jr- служит отрезок пря-
z * J
мой у — п—х, пересекающейся под прямым углом с прямой у — х в точке
~ arcsin (si nv)
i
Рис. 32.
2
\
/
\о
\/
А
i
i
#
y=arccos(
1 |\
I
I
1
1
Рис. 33.
Му5у If)' Гра*ик ФУНКЦИИ У=* arcsin (sin x) в интервале Г — y
изображен на рис. 32; дальше он продолжается периодически.
68
ГЛ. I. ФУНКЦИЯ
[23
Рассуждая вполне аналогично, придем к следующим соотношениям:
cos (arccos *)=# для —1
arccos (cos x) = х для
Функция у = arccos (cos х) определена на всей оси Ох, имеет период,
равный 2я, причем в интервале [я, 2я] она равна 2я—х; графиком этой
функции служит та же линия, что и изображенная на рис. 32, только иначе
расположенная относительно осей ко-
координат (рис. 33).
Точно так же найдем
tg (arctg*)=* для — оо <*<<»,
-#-
т
2
для — ~
О
2,
х
arctg(tg*)=*
Функция # = arctg (tg x) опреде-
определена на всей оси Ох, кроме точек
я
*= B& + 1)-5-, где k—любое целое
Рис. 34.
число, и имеет период, равный я; гра-
график этой функции, показанный на
рис. 34, состоит из отрезков пря-
прямых линий, повторяющих через пе-
период, равный я, отрезок прямой у = х в интервале( —^-, -у) .
23. Гиперболические и обратные гиперболические функции.
Хотя функции, названные в заголовке пункта, не принадлежат к
числу основных элементарных функций, мы все же рассмотрим их
здесь, так как они могут быть исследованы самыми простыми сред-
средствами. Эти функции понадобятся нам в дальнейшем; кроме того,
они встречаются при решении различных прикладных задач (в
курсах электротехники, сопротивления материалов и др.).
I. Определение. Гиперболическими косинусом (chх)>
синусом (shjc) и тангенсом (thx) называются функции, опре-
определенные формулами
shjc=
— е
где е = 2,718... (см. п. 31).
Эти функции определены на всей числовой оси. Они связаны
рядом соотношений, аналогичных соотношениям между соответст-
соответствующими тригонометрическими функциями, что и объясняет их
названия. В частности, имеют место легко проверяемые формулы:
ch2 х—sh2 x = 1, ch 2x = ch2 x + sh2 x, sh 2x = 2 sh x ch xt
СП ^-1_th2JCt
sh2 x
23J
§ б. ТРИГОНОМЕТРИЧЕСКИЕ, ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
69
Графики функций chAr и
* х
легко построить по графикам фун-
фунф фу
кций е* и е~х (см. п. 20), используя метод, указанный в конце
Г ф
п. 14. График функции ^ = сЬлг (и его построение) показан на
рис. 35, а). Эта функция четная и положительная. Функ-
Функция у = shAr нечетная; при х > 0 она положительна, при
Рис. 35.
х < 0 отрицательна и при лг = О равна нулю. Ее график показан
на рис. 35, б).
Из графиков, да и прямо из определяющих формул видно,
что при больших положительных значениях х слагаемое е~*/2
роли не играет, и можно счи-
считать, что
&*-% и sh*« ст.
Уже при х > 4 абсолютная ошиб-|
ка этих приближенных равенств
меньше чем 0,01, а относитель-
относительная ошибка меньше чем 0,04%.
Отсюда ясно, что th* прий
больших положительных значе-
значениях х приближается к едини-
единице, оставаясь все время мень-
меньше единицы. Так как функция y^ihx нечетная и прилг^=О
равна нулю, то уже можно схематически построить ее график
(рис. 36). (По форме он очень похож на график arctg x (рис. 31); надо
только помнить, что его асимптотами являются прямые у = ±1>
а не прямые у = ± -к > как Для arctgx.)
70 гл. i. функция [23
II. Обратные гиперболические функции. Функции,
обратные к соответствующим гиперболическим функциям, обозна-
обозначаются через
Н y^Axshx, y — krthx
(читается: ареа-косинус гиперболический, ареа-синус гиперболи-
гиперболический, ареа-тангенс гиперболический).
Функция shjc определена и возрастает в интервале (— сю, оо);
область ее значений совпадает со всей осью Оу (рис. 35, б). По-
Поэтому функция j;==ArshA; также определена на всей числовой оси
и возрастает. Ее можно выразить при помощи логарифмической
функции. Для этого запишем равенство j; = ArshA; в виде
и разрешим полученное уравнение сначала относительно еу, а
затем и относительно у. После простых преобразований получаем
е2У—2хеу—1=0, откуда ey = л; + |/д;2 + 1. Второе решениеквад-
ратного уравнения х— ]/л;2+1 мы отбрасываем,таккаконопри всех
значениях х отрицательно и не может равняться положительной
величине еу. Вспоминая определение натуральных логарифмов
(п. 20, II), окончательно получаем
у = Arsh x = \n{x +Vx*+\). (*)
Функция ohx убывает в интервале (— оо, 0] и возрастает в
интервале [0, оо); область ее значений—интервал [1, оо). Сле-
Следовательно, функция у — Arch х состоит из двух однозначных
ветвей, определенных при х^\. Проводя такие же выкладки,
как при выводе формулы (*), получим два выражения:
(Arch х)г = In (x—Vx2— 1), (Arch xJ = In (x+Vx2 — 1).
Первая функция обратна к функции y = chx в интервале
(— оо, 0], а вторая — в интервале [0, оо). Легко заметить, что
т. е. что In (л:—Угх2 — 1)==—\п{х-\-Ухг — !)• Разумеется, так и
должно быть в силу четности функции у = ch x.
Функция у = Arth х определена в интервале (—1, 1)—это об-
область значений функции Шл;—и, как нетрудно проверить, равна
В заключение порекомендуем читателю построить графики всех
обратных гиперболических функций.
ВОПРОСЫ И ПРЕДЛОЖЕНИЯ 71
ВОПРОСЫ И ПРЕДЛОЖЕНИЯ ДЛЯ САМОПРОВЕРКИ
1. Какие числа образуют множество действительных чисел?
2. Что называется числовой осью?
3. Что называется интервалом?
4. Определить понятие окрестности точки.
5. Что называется абсолютной величиной числа?
6. Сформулировать основные предложения об абсолютных величинах.
7. Что называется абсолютной ошибкой и предельной абсолютной
ошибкой?
8. Что называется относительной ошибкой и предельной относительной
ошибкой?
9. Что называется функцией одной независимой переменной? областью
определения функции? областью значений функции?
10. Привести примеры функций целочисленного аргумента.
11. Что называется графиком функции в системе декартовых координат?
12. Что значит задать функцию? Определить табличное, аналитическое
и графическое задания функции. Описать особенности, достоинства и не-
недостатки каждого из этих способов.
13. Указать возможные способы обозначения функции.
14. Что такое частное значение функций? Как оно записывается?
15. Перечислить основные элементарные функции.
16. Какая функция называется сложной? Привести примеры сложных
функций.
17. Какая функция называется элементарной?
18. Дать определения алгебраической, рациональной, иррациональной
и трансцендентной функций.
19. Какая функция называется неявной? Привести примеры неявных
функций.
20. Что называется нулем функции?
21. Какая функция называется четной? нечетной?
22. Какая функция называется периодической? Что такое период
функции?
23. Какая функция называется возрастающей (убывающей) в интервале?
24. Что называется интервалом монотонности функции?
25. Что называется наибольшим (наименьшим) значением функции
в интервале?
26. Описать построение графика функции y^ajj (a2*+as) + a4» rAe ai>
а2у fls, a4—постоянные, если известен способ построения графика функции
* = /(*).
27. Определить линейную функцию, начертить ее график, сформулиро-
сформулировать и доказать ее основное свойство.
28. Определить квадратичную функцию, начертить ее график и описать
ее поведение.
29. Определить дробно-линейную функцию, начертить ее график и
описать ее поведение.
30. Какие функции называются взаимно обратными? Как построить
график обратной функции по графику данной функции в системе декарто-
декартовых координат?
31. Как определяются однозначные ветви функции, обратной для немо-
немонотонной функции?
32. Начертить графики степенных функций при различных показателях
степени и описать поведение этих функций.
33. Начертить графики показательных функций при различных осно-
основаниях и описать поведение этих функций.
72 гл. i. функция
34. Начертить графики логарифмических функций при различных ос-
основаниях и описать поведение этих функций.
35. Начертить графики тригонометрических функций и описать поведе-
поведение этих функций.
36. Что называется простым гармоническим колебанием, амплитудой»
фазой, начальной фазой, периодом, частотой, круговой частотой колебания?
37. Как построить простую гармонику?
38. Что называется сложным гармоническим колебанием? Как построить
сложную гармонику?
39. Начертить графики обратных тригонометрических функций и описать
поведение этих функций.
40. Определить гиперболические функции, начертить их графики и
описать поведение этих функций.
41. Описать свойства обратных гиперболических функций и начертить
их графики.
ГЛАВА II
ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ
§ 1. Предел функции. Бесконечные величины
24. Предел функции непрерывного аргумента. Рассмотрим функ-
функцию y~f{x) непрерывного аргумента х (см. п. 7) и введем важней-
важнейшее в математике понятие предела функции; это понятие играет
фундаментальную роль во всем математическом анализе.
Пусть независимая переменная х неограниченно прибли-
приближается к числу х0. Это означает, что мы придаем х значения,
сколь угодно приближающиеся к xQ, но не равные лг0. Запишем это
так: x-+xQ, и будем говорить, что х стремится к х0. Может ока-
оказаться при этом, что соответствующие значения f(x) н е о г р ан и-
ченно приближаются к некоторому числу А Тогда говорят,
что число Лесть предел функции у=/(х) при х -* х0 или что
функция у=/(х) стремится к числу А при х-+х0.
Определение. Число А называется пределом функции
y=f(x) при х—*л;0, если для всех значений л:, достаточно мало
отличающихся от числа х0, соответствующие значения функции
f(x) как угодно мало отличаются от числа Д.
Если А есть предел функции f(x) при х—> х0, то это записы-
записывают так:
Нт/(лс)==Л или f(x)—+A.
х-+х0 х-+х0
Символ lim составляется из первых трех букв латинского слова
limes (французского limite), означающего «предел».
Точка дг0, к которой стремится независимая переменная л;, назы-
называется ее предельной точкой.
Следует обратить внимание на то, что в этом определении не
требуется, чтобы функция была задана и в предельной точке; нужно
только, чтобы функция была определена в к а к о й-н и б у д ь окрест-
окрестности предельной точки, но не обязательно в самой точке. Так, на-
« sin х
пример, функция у = -у ие определена при лг = О, но, как это
будет доказано в п. 30, она стремится к 1 при лг, стремящемся к
74 гл. и. предел, непрерывность [24
нулю. Отыскание предела функции, определенной в некоторой окрест-
окрестности точки дг0, но не в ней самой, и будет составлять одну из
важнейших задач теории пределов.
Как же проверить вычислениями, что число А есть предел
функции/(дг) при дг—> лг0? Это делается так: задаем положительное
какугодномалое число е; если для него можно всегда подобрать
такое положительное число б, что для всех х (не равных х0), удов-
удовлетворяющих неравенству
\х-хо\<8
(т. е. для дг, принадлежащих б-окрестности точки дг0), будет спра-
справедливо также и неравенство
\f(x)—A\<B,
ю число А действительно есть предел функции /(дг)придг—>х0.
Мы увидим в дальнейшем, что подобную проверку, очель громозд-
громоздкую и затруднительную в конкретных случаях, с которыми нам
предстоит встречаться, не будет нужды производить, так как мы
укажем простые правила для отыскания пределов в этих случаях.
В качестве примера возьмем функцию J/ = Зле—1 и докажем, что
она имеет при х—* 1 предел, равный 2. Зададим положительное
число е. Для того чтобы имело место неравенство
\(Зх—\) — 2\<г
или, что то же, неравенство
нужно, чтобы было выполнено неравенство
Таким образом, для всех дг, отличающихся от 1 меньше чем на
<г-, наша функция будет отличаться от 2 меньше чем на е, где е—
произвольное положительное число, и следовательно, функцияу =
= 3дг—1 в самом деле стремится к 2 при х—>\. В этом примере
можно взять б = у .
Наличие у функции у=/(х) при х—>х0 предела, равного А,
геометрически иллюстрируется следующим образом (рис. 37): восста-
восставим к оси Ох в точке х0 и к оси Оу в точке А перпендикуляры,
продолжив их до пересечения в точке Ж, и произвольно зададим
положительное число е; тогда найдется такая б-окрестность точки
дг = дг0, что часть графика функции y=f (x), соответствующая этой
окрестности, будет содержаться в полосе, ограниченной прямыми
у = А—е и ^ =
24]
§ 1, ПРЕДЕЛ ФУНКЦИИ. БЕСКОНЕЧНЫЕ ВЕЛИЧИНЫ
75
Должно быть ясно, что если при х—>х0 функция имеет предел,
то только один, ибо значения функции для значений ху приближаю-
приближающихся к лг0, должны быть как
угодно близки к какому-то по-
постоянному числу и, следователь-
следовательно, не могут быть одновременно
близки кдвумразным посто-
постоянным числам.
Приближаясь к своему преде-
пределу, функция может оставаться
больше его или меньше его, а
может становиться, по мере при-
приближения аргумента к предельной
точке, то больше его, то мень-
меньше, т. е. колеблясь около своего
предела; при этом она может принимать и значения, равные пределу.
Примеры этого мы встретим дальше.
Рассматривая постоянную величину А как функцию, следует счи-
считать, что она имеет предел, равный ей самой:
lim A — A.
Х-+Хо
Действительно, разность Л—Л равна нулю и, значит, меньше любого
наперед заданного положительного числа.
Функция у — х при х—>х0 имеет, как легко видеть, предел,
равный х0) какова бы ни была точка х0:
Рис. 37.
В самом деле, неравенство
I*—*ol <е>
где 8—произвольное положительное число, будет справедливо для
всех х, принадлежащих е-окрестности точки xQi и значит, в данном
случае можно взять просто 8 = е.
Определение предела функции само по себе не дает еще спосо-
способов его отыскания; ниже мы выведем некоторые правила, при
помощи которых и будем отыскивать пределы функций.
Приведем теперь пример функции, не имеющей предела. Функция (п. 22)
t/ = arctg(tg x)
при
-к- не стремится ни к какому числу. Действительно, для значений
х в достаточно малой окрестности точки
и меньших -^- значения
76
ГЛ. И. ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ
125
функции будут как угодно близки к у (см. рис. 34), а для значений х в той же
окрестности, но больших -^-, значени я функции будут как угодно близки
к— i 9 и следовательно, нет такого числа, к которому значения функции были
бы как угодно близки для всех значений х в окрестности точки -^ •
25. Бесконечно большой аргумент. Пусть независимая перемен-
переменная х функции y = f(x) неограниченно возрастает. Это означает,
что мы придаем х любые значения, ббльшие всякого наперед за-
заданного положительного числа. Коротко говорят, что х стре-
стремится к положительной бесконечности, и записывают:
х—> 4-°°- Если х неограниченно убывает, т. е. становится меньше
всякого наперед заданного отрицательного числа, то говорят, что
N
Рис. 38.
х стремится к отрицательной бесконечности, и за-
записывают так: лг—>— сю. Аргумент функции, изменяющийся ука-
указанным образом, называется бесконечно большим аргументом.
Изучая функцию f(x) при бесконечно большом аргументе, мы
предполагаем, разумеется, что она определена при всех рассмат-
рассматриваемых значениях лг.
Может оказаться, что при бесконечно большом аргументе со-
соответствующие значения f(x) неограниченно приближаются к не-
некоторому числу А. Тогда говорят, что число А есть предел
функции у =/(лг) при х —> + оо или при х —> — со или что функция
y—f(x) стремится к числу А при лг—^ + сх) или х—> — оо.
Рассмотрим сначала детально случай, когда лг—*-|-оо.
Определение. Число А называется пределом функции
У=/(х) при л:—>-4"°°» если для всех достаточно больших зна-
значений х соответствующие значения функции f(x) как угодно мало
отличаются от числа Л.
25J
§ 1. ПРЕДЕЛ ФУНКЦИИ. БЕСКОНЕЧНЫЕ ВЕЛИЧИНЫ 77
¦foo, то это за-
Если А есть предел функции /(лг) при лг
писывают так:
Шп/(лг)=Л или /(лг)-* А
Наличие у функции y=f (х) при лг —* +оо предела, равного Л,
геометрически иллюстрируется следующим образом (рис. 38): восста-
восставим к оси Оу в точке А перпендикуляр и произвольно зададим
положительное числэ е; тогда
найдется такое число N, что часть
графика функции у=/ (лг), соот-
ветствующая значениям лг, ббль-
шим этого числа, будет содер-
содержаться в полосе, ограниченной
прямыми
у^А—е, у =
Л
Рис. 39.
Легко привести геометричес-
геометрические примеры функций, которые
приближаются к своему пределу,
убывая (рис. 39, /), возрастая
(рис. 39, //)и колеблясь (рис. 38). В последнем случае график может
любое число раз пересекать прямую^ = Л, т. е. функция может любое
число раз принимать значение, равное пределу.
Имея в виду геометрическую иллюстрацию предела функции при
лг—* + оо, часто говорят, что кривая y=f(x) при х—>-|-оо имеет
прямую у = А своей асимптотой.
Определение и геометрический смысл предела функции при
х—> —оо совершенно аналогичны только что рассмотренным, и мы
рекомендуем читателю сформулировать их самостоятельно.
Иногда бывает, что и при лг—* + оо и при лг—>—оо функция
/(лг) стремится к одному и тому же пределу А.
Это значит, что для всех значений х, достаточно больших по
абсолютной величине, соответствующие значения /(лг) как угодно
мало отличаются от числа А.
Записывают это так:
Нт/(д:) = Л или
А.
Геометрическая иллюстрация этого случая заключается в том, что
график функции^ =/ (х) будет находиться в полосе, ограниченной
прямыми у = А—е и j/ = /44-e, где 8 — сколь угодно малое поло-
положительное число, если только точки л; будут достаточно удалены от
точки х = 0 (рис. 40). Иначе говоря, прямая у = А будет являться
асимптотой графика функции^ =*/(#) и при* —* + оо и при х —*—оо.
78 гл. и, предел, непрерывность B5
Проверить вычислениями, что число А есть предел функции f(x)
ПрИ х—>4*оо(лг—>—оо), можно так: задаем положительное как
угодно малое число е; если для него всегда существует такое
положительное число ЛГ, что для всех дг, удовлетворяющих нера-
неравенству
x>N (х <—N),
будет справедливо также и неравенство
\/(х)-А\<г, (*)
то число А есть действительно предел функции/(х) при лг—*4~ °°
Рис. 40.
Если же неравенство (*) выполняется для всех лг, удовлетво-
удовлетворяющих условию
\x\>N9
то это будет означать, что х может стремиться к бесконечности
произвольным образом, т. е. что число А является пределом функции
и при х—>-J-00 и при х —*—оо, короче, —при х—>оо.
Примеры. 1) Функция
стремится к 1, если х произвольным образом стремится к оо, т.е.
Из рис. 14 ясно видно, что при неограниченном увеличении
JC-j- 1
абсциссы соответствующая точка равнобочной гиперболы jf = ^—у
действительно неограниченно приближается к прямой^у = 1. Убедимся
теперь и с помощью вычислений в справедливости этого заклю-
26] § 1. ПРЕДЕЛ ФУНКЦИИ. БЕСКОНЕЧНЫЕ ВЕЛИЧИНЫ 79
чения. Зададим е > 0. Для того чтобы выполнялось неравенство
т. е,
I —I I -
достаточно иметь
ибо \х—1|^|jc| — 1. Значит, для всякого дг, удовлетворяю-
удовлетворяющего неравенству
функция ^Ц- будет отличаться от 1 не больше чем на 8, а это
и доказывает, что lim^i-T = l; здесь в качестве указанного выше
*-><»х *
2
числа N можно взять —(-1.
6
2) Функция j> = arctg лг имеет различные пределы прид:—*-|-оэ
и х—>—оо. Из рис. 31 ясно, что
lim arctg x = -^- и Ит arctg х = — ~ .
26. Последовательности и их пределы. Рассмотрим теперь
функции целочисленного аргумента. Такой аргумент часто
обозначают буквой л, а значения функции — какой-нибудь буквой,
нижним индексом которой берется соответствующее значение це-
целочисленного аргумента. Так, если y=f(ri) есть функция цело-
целочисленного аргумента /г, то записывают: yn=f(n). Значения
принимаемые функцией целочисленного аргумента, образуют, как
говорят^ последовательность.
Определение. Последовательностью называется мно-
множество чисел, перенумерованных с помощью целых чисел и распо-
расположенных в порядке возрастания номеров.
Если дана последовательность уъ j>2, уг, ..., то тем самым
каждому целому неотрицательному значению п поставлено в со-
соответствие значение уп=/(п). Например, члены геометрической
1 1 1
прогрессии тг ,-г , -7г, ... являются последовательными значени-
? тс О
ями функции f(n) = 2».
80 гл. и. предел, непрерывность [26
Может случиться, что с увеличением п значения^ =/(п)
неограниченно приближаются к некоторому числу А.
Тогда говорят, что число А есть пр еде л функции/(л) цело-
целочисленного аргумента п или последовательности^,^, ...,>*„, ...
при /г—»-с», и записывают:
lim / (п) = А или lim уп = А.
п-+<х> /1-х»
Определение. Число А называется пределом функции
y=f(n) целочисленного аргумента п или последовательности
У\% Уъ> - - ч Уп> • • •» *сли Для всех достаточно больших целых зна-
значений п соответствующие значения уп как угодно мало отли-
отличаются от числа А.
Мы видим, что понятие предела функции целочисленного аргу-
аргумента можно считать частным случаем понятия предела функции
бесконечно большого аргумента, стремящегося к положительной
бесконечности, когда этот аргумент принимает только целые
значения. Значит, число А есть предел последовательности
УпУъ* • • • уУю • • • у если для всякого положительного числа е можно
указать такое положительное число N, что при всех я > N
справедливы неравенства
\Уп-А\<*-
Примеры. 1) Последовательность
_L .2 А п
2 > з ' 4 * *•• ' л + 1 ' •*•
имеет предел, равный 1. Действительно, для того чтобы модуль
разности
п
— 1 =
1
был меньше заранее данного положительного числа е, нужно только
выполнение неравенства л+ 1 > •—, т. е. я> 1. Таким обра-
образом, по заданному числу г всегда можно указать такое Af= — — 1,
что при всех я> N указанный модуль разности будет меньше е>
а это и означает, что 1 есть предел рассматриваемой последова-
последовательности.
2) Рассмотрим последовательность
. я 1 . Зя 1 . 5я 1 . Г/Г| „ч nl
smT» 2"smT' TSin T' "• '7Tsin [Bл—l)j, ...
Функция Уп = — sin |B/z— 1Lн стремится к нулю при п—+оо,
27] § 1. ПРЕДЕЛ ФУНКЦИИ. БЕСКОНЕЧНЫЕ ВЕЛИЧИНЫ 81
так как \уп—0| = — <е для всех п, удовлетворяющих условию
п > — . Разность
с
-0 =-j sin
будет положительной или отрицательной в зависимости от того,
нечетно или четно п. Значения ую неограниченно приближаясь
к нулю, становятся попеременно то больше нуля, то меньше нуля.
Переменная стремится к своему пределу, колеблясь вокруг него.
3) В элементарной геометрии доказывается, что периметр пра-
правильного вписанного в данную окружность я-угольника, как функция
целочисленного аргумента я, имеет предел, который и принимается
в качестве длины окружности. Аналогично и площадь этого я-уголь-
ника имеет предел, который и принимается за площадь круга.
4) Укажем примеры последовательностей, не имеющих предела.
а) Последовательность
. я . 2я . Зя . пп
sin у, sin -у, sin -у, .. . , sin^r, ...
не имеет предела, так как уп = sin-у при п = 1, 2, 3, 4, ... после-
последовательно принимает значения 1, 0, —1, 0 и затем опять те же
значения в том же порядке и т. д. Нет числа, к которому уп не-
неограниченно приближалось бы.
б) Функция уп = 2п-\- 1, значения которой при л = 1, 2, 3,...
составляют последовательность целых нечетных чисел 1, 3, 5, ... ,
не стремится к пределу, так как значения уп при п—юо неогра-
неограниченно увеличиваются.
27. Бесконечно большие величины. Ограниченные функции.
В дальнейшем для сокращения письма мы будем приводить опреде-
определения только для случая, когда х стремится к конечному пре-
пределу лг0. Необходимые изменения формулировок при стремлении х
к бесконечности предоставляем сделать читателю.
I. Бесконечно большие величины. Рассмотрим случаи
такого «предельного поведения» функции ^=/(лг), когда она при
х—>х0 неограниченно возрастает по абсолютной величине.В этих
случаях говорят, что функция f(x) является при х—*лг0 беско-
бесконечно большой величиной.
Определение. Функция y=f(x) называется бесконечно
большой величиной при x—*xQJ если для всех значений дг, до-
достаточно мало отличающихся от х0, соответствующие значения
функции f(x) по абсолютной величине превосходят любое наперед
заданное сколь угодно большое положительное число.
82
ГЛ. П. ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ
[27
Если функция/(лг)— бесконечно большая величина при*—*х0>
то это записывают так:
lim /(лг) = оо.
х-+х0
Наше определение бесконечно большой величины указывает,
что, как только аргумент х достаточно близко подойдет к лг0,
абсолютная величина функции f(x) станет как угодно большой.
Как же проверить вычислениями, что функция f(x) при х—>х0
является бесконечно большой величиной? Это делается так: задаем
положительное как угодно большое число М\ если для него можно
подобрать такое положительное число б, что для всех ху не
равных лг0, удовлетворяющих неравенству
будет справедливо также и неравенство
lf(x)\>M,
то функция f(x) будет действительно бесконечно большой величи-
величиной при х—>xQ. В случае х—> оо то же самое будет, если для
числа М можно подобрать такое положительное число N, что для
всех л;, удовлетворяющих неравенству |лг|>М, будет справед-
справедливо также и неравенство
||
Тот факт, что функция у =/(л?) при х—>х0 является бесконечно
большой величиной, геометрически иллюстрируется следующим
образом (рис. 41, а): произвольно зададим положительное число М;
м
О
-м
1
А
1
\
1
1
1
( х
а)
м
О/ N
X
6)
Рис. 41.
тогда найдется такая 8-окрестность точки дг = лг0, что часть графика
функции y=zf(x), соответствующая этой б-окрестности, будет
находиться вне полосы, ограниченной прямыми у — — Ж, у~М.
Случай, когда х—^ + °°» показан на рис, 41,6.
27J § 1. ПРЕДЕЛ ФУНКЦИИ. БЕСКОНЕЧНЫЕ ВЕЛИЧИНЫ 63
Функция y=zf(x), являющаяся при х-+х0 бесконечно большой
величиной, не имеет предела в обычном смысле. Желая, однако,
отобразить ту закономерность в ее предельном поведении, которая
заключается в неограниченном возрастании |/(лг)|, говорят, что
функция f(x) стремится к бесконечности или имеет своим
пределом бесконечность.
Допустим, что бесконечно большая величина у=* f(x) в некото-
некоторой окрестности точки х = х0 принимает либо только положитель-
положительные, либо только отрицательные значения. Эту особенность в пре-
предельном поведении функции /(х) выражают так:
Функция f(x) стремится к положительной или соответственно
к отрицательной бесконечности.
Записывают это следующим образом:
lim f(x) = + оо, lim f(x) = — оо.
X -> Хо X-*XQ
Условность этих выражений и записей необходимо всегда иметь
в виду и помнить, что бесконечность (оо) не есть число, поэтому
и говорить о каких-нибудь действиях над оо лишено всякого смысла.
Нельзя смешивать постоянное очень большое число с беско-
бесконечно большой величиной.
Примеры. 1) Функция у — —при х—+ О является бесконечно
большой величиной. Действительно, для справедливости неравенства
где М—любое положительное число, нужно только, чтобы выпол-
выполнялось неравенство
1 I <: —
т. е. чтобы значения х принадлежали ^-окрестности точки дг = О
(в данном примере о = т7Ь Итак,
lim — = оо.
х
Если х—^0 и х принимает только отрицательные значения, то
У~~ стремится к —оо, а если только положительные, то у =*
= — стремится к +оо:
lim Т = ~°°' lim Т= + °°-
Д?->0 Л х-± 0 Х
Х<.0 *> 0
84 гл. и. предел, непрерывность [27
Отмеченный сейчас характер предельного поведения функции
у = — можно отчетливо увидеть по ее графику—известной равно-
равнобочной гиперболе.
2) Функция y~^~^i — бесконечно большая величина при л;—> 1,
при этом она стремится к —оо, если х остается меньше 1, и
стремится к +°°, если х остается больше 1 (см. рис. 14).
3) Функция У = ~г при х—*0 имеет пределом +оо при любом
предельном изменении аргумента лг, стремящегося к нулю.
4) Функция у — ах, как легко убедиться, является положитель-
положительной бесконечно большой величиной при х—* + оо, если а>1:
lima*=+oo. При а<1 имеем lima* = + °° (см. рис. 22).
II. Ограниченные функции.
Определение. Функция y=f(x) называется ограниченной
в данном интервале, если существует такое положительное число Ж,
что при всех значениях х, принадлежащих этому интервалу,
выполняется соотношение \f(x)\^M. В противном случае функция
называется неограниченной.
График ограниченной функции целиком лежит между прямыми
у = — М и у = М. Иногда бывает удобнее говорить, что функция
ограничена, если ее значения заключены между какими-либо двумя
числами Л и В:
В этом случае ее график лежит между прямыми у = Л и у = В.
Например, функции у = sin х и у = cos x ограничены на всей
оси Ох, а функция у = ахне ограничена на оси Ох. Следует
подчеркнуть, что, говоря об ограниченности функции, необходимо
указывать интервал, в котором она рассматривается. Так, функция
jf=~ ограничена в интервале A, оо) и не ограничена в интервале
(О, 1); функция j; = tgx ограничена в интервале (о, ~j и не огра-
ограничена в интервале @, -5-). В связи со сказанным введем следую-
следующее определение.
Определение. Функция называется ограниченной при
х—+х0У если в некоторой окрестности точки х0 эта функция
ограничена.
Разумеется, всякая постоянная величина является ограниченной.
Точно так же и всякая функция у==/(лг), имеющая при х—*х0 пре-
предел, является ограниченной при х—*х0. В самом деле, если
28) § 1. ПРЕДЕЛ ФУНКЦИИ. БЕСКОНЕЧНЫЕ ВЕЛИЧИНЫ 85
то в некоторой окрестности точки лг0 значения функции / (х) как
угодно мало отличаются от числа А.
Величина, бесконечно большая при х—*лг0, является, конечно,
неограниченной функцией при х—>х0.
Заметим, что обратное заключение уже не обязательно справедливо,
а именно не всякая неограниченная функция является бесконечно большой
величиной. Например, функция y = xsinx принимает сколь угодно большие
значения I у х_п +2kn =-^- + 2^, где k — любое целое число J и, следова-
следовательно, не является ограниченной при х—> оо, в то же время она обра-
обращается в нуль при сколь угодно больших значениях x(yx=kn = 0) и, значит,
не может стремиться к бесконечности. Ведь последнее означает, что при
всех достаточно больших х значения у по абсолютной величине сколь угодно
велики и, разумеется, не могут равняться нулю. Рекомендуем читателю
выяснить геометрический смысл сделанного замечания, построив схемати-
схематический график функции y = xs\nx.
28. Бесконечно малые величины.
Определение. Функция, стремящаяся к нулю при х—>xOf
называется бесконечно малой величиной при х—*jc0.
Говорят также, что эта функция есть бесконечно малая вели-
величина в окрестности точки х0.
Примерами бесконечно малых величин могут служить функции:
у = х2 при х—> (), у = х—1 при х—> 1, у = — при х—> оо,
у = 2* при х—>—оо.
Нельзя смешивать постоянное очень малое число с бесконечно
малой величиной. Единственным числом, которое рассматривается
в качестве бесконечно малой величины, служит нуль (в силу того,
что предел постоянной равен ей самой).
Бесконечно малая величина есть, разумеется, величина огра-
ограниченная.
Бесконечно большие и бесконечно малые величины играют очень
важную роль в математическом анализе. Между ними существует
простая связь, хотя первые из них представляют собой функции,
не имеющие предела, а вторые—функции, имеющие предел.
Теорема. Если функция f(x)— бесконечно большая величина,
то ту-г — бесконечно малая величина; если ф (jc) — бесконечно
Т \Х)
малая величина, то —бесконечно большая величина.
Доказательство. Пусть/(х) —> оо при х —+ х0; нам нужно
убедиться в том, что тт^т—>0.
Зададим произвольное малое число 8 > 0 и возьмем число
М = -~. Так как f(x)—бесконечно большая величина, то для
86 гл. н. предел, непрерывность [29
всех х, достаточно близких к х0, будет
Но тогда
а это и означает, что lim гг-ч=0.
Аналогично доказывается и вторая часть теоремы; нужно
только считать, что в некоторой окрестности точки х0 функция
—т-г определена, т. е. что ф(лг)=^=О при хфх0.
Важными для дальнейшего являются следующие теоремы.
Прямая теорема. Если функция имеет предел, то ее можно
представить как сумму постоянной, равной ее пределу, и беско-
бесконечно малой величины.
Доказательство. Пусть limf(x) = А. Тогда, если е —
X-
произвольное малое положительное число, то \/(х) — Л|<е для
всех хл достаточно близких к х01 а это и означает, в соответ-
соответствии с определением, что f(x) — А есть бесконечно малая вели-
величина. Следовательно,
f(x)—A — a(x), или f(x) = А-\-<х(х),
где а (л:) — бесконечно малая величина при х—>х0. Разумеется,
а(лг) может принимать как положительные, так и отрицательные
значения, т. е. функция/(л:) может быть как больше, так и меньше
своего предела А,
Обратная теорема. Если функцию можно представить
как сумму постоянной и бесконечно малой величины, то постоянное
слагаемое есть предел функции.
Доказательство. Из равенства f(x) = A-\-a(x)y где А —
постоянная, а а(х) при х—>х0—бесконечно малая величина,
следует, что если е — произвольное малое положительное число, то
для всех х, достаточно близких к х0. Но это и означает, что
f(x) имеет своим пределом число Л, т. е.
lim f(x) = Ау
х-+х0
что и требовалось доказать.
29. Правила предельного перехода. Выведем сейчас простейшие
правила предельного перехода, т. е. правила, по кото-
которым можно находить пределы функций. Сначала мы будем рассмат.
291 § t- предел функции, бесконечные величины 87
ривать теоремы для бесконечно малых величин, а затем в качестве
следствий—теоремы для функций, стремящихся к пределам, не
обязательно равным нулю. Эти теоремы и будут давать нам пра-
правила предельного перехода в случаях, когда функция является
результатом арифметических действий над функциями, пределы
которых заранее известны.
Краткости ради будем обозначать здесь функции, имеющие
пределы, через и, и, f, а, Р и т. п. и писать Нтм, Нтг; и т. п.,
не указывая, при каком именно изменении независимой переменной х
рассматривается предел. При этом, однако, говоря о нескольких
функциях, мы будем предполагать, что они стремятся к своим пре-
пределам при одном и том же изменении независимой переменной
(т. е. при стремлении аргумента к одной и той же предельной
точке или к оо). Как и раньше, все доказательства будут про-
проводиться в предположении, что х—>xQ. Необходимые изменения
для случая х—> оо предоставляем сделать читателю.
Теорема I. Сумма двух, трех и вообще конечного числа
бесконечно малых величин есть бесконечно малая величина.
Доказательство. Возьмем две бесконечно малые величины а
и |3 и докажем, что их сумма со:
также бесконечно малая величина.
Зададим любое положительное число в. Существует такая
окрестность предельной точки, что для всех ее точек (кроме,
быть может, самой предельной) будем иметь1)
Так как модуль суммы не превосходит суммы модулей
MHa + P|<|
то в указанной окрестности будет
а это и доказывает, что со—бесконечно малая величина в окрест-
окрестности нашей предельной точки. Ясно, что доказательство полностью
сохраняется, если вместо суммы бесконечно малых величин рас-
рассматривать их разность.
О О
*) Если окрестности, в которых | а | < -^ и J Р | < -=¦, не совпадают, то
оба эти неравенства будут выполняться в наименьшей из них.
88 гл. и. предел, непрерывность [29
Пусть теперь дана сумма со трех бесконечно малых слагае-
слагаемых а, Р, Y:
Мы можем считать, что имеем сумму двух слагаемых (а+ P)+Y>
причем по доказанному (а+р)—величина бесконечно малая; на
основании того же соображения сумма двух бесконечно малых
(а+Р) и у также является бесконечно малой величиной и т. д.
Таким образом, последовательно теорема может быть доказана
для суммы любого постоянного числа слагаемых.
Специально сделанная оговорка о конечности числа сла-
слагаемых имеет существенное значение. Дело в том, что в анализе
приходится рассматривать особые суммы, в которых изменяются и
сами слагаемые, и их число. К таким суммам теорема не относится.
Если, например, допустить, что число слагаемых неограниченно
возрастает по мере стремления к нулю каждого из них, то утверж-
утверждение теоремы может оказаться неверным. Пусть
l ft 2 п
а Р т1
при п —у оо каждая из этих величин стремится к нулю, но вместе
с тем растет и их число. Сумма
1 + 2+...+я_я(я + 1)_ 1 1
W ~~ л2 "" 2л2 — 2 "*" 2п
при п—> оо — вовсе не бесконечно малая величина, а величина,
стремящаяся к -^ .
Из теоремы I непосредственно следует
Теорема Г. Предел суммы конечного числа слагаемых равен
сумме пределов этих слагаемых.
Доказательство. Пусть даны определенное число к слага-
слагаемых иу v, . .. , t, стремящихся соответственно к пределам а, Ьу ..., d,
и их сумма w:
Докажем, что
= lim и + \imv + ...
Имеем (см. прямую теорему в п. 28)
и = а + <х} г> = 6 + р, ...,t
где а, р, ...,т — бесконечно малые величины. Следовательно,
29] § 1. ПРЕДЕЛ ФУНКЦИИ. БЕСКОНЕЧНЫЕ ВЕЛИЧИНЫ 89
где <о = а-!-Р-}-...+<*> как сумма ft бесконечно малых слагаемых,
в силу теоремы I является бесконечно малой величиной. Так
как w равна сумме бесконечно малой величины со и постоянной
a + 6+...+cf, то последняя и является пределом для w (см. об-
обратную теорему п. 28).
Теорема II. Произведение ограниченной функции на беско-
бесконечно малую есть бесконечно малая величина.
Доказательство. Пусть а—бесконечно малая величина,
а и—функция, ограниченная в некоторой окрестности предельной
точки: |#|^Af. Докажем, что lim(#a) = 0.
Зададим произвольно малое положительное число е. Значения а
в некоторой окрестности предельной точки удовлетворяют нера-
неравенству lal<}j-f » следовательно,
откуда и вытекает справедливость теоремы.
В частности,
lim (ca) = 0,
если с — постоянная, а а—>-0.
Так как бесконечно малая величина — ограниченная, то произве-
произведение двух бесконечно малых есть также величина бесконечно малая.
Утверждение теоремы может стать неверным, если и не есть
ограниченная функция (пример: х2 > оо при X—> оо).
Из теорем I и II следует
Теорема 1Г. Предел произведения конечного числа множи-
множителей равен произведению пределов этих множителей.
Доказательство. Сохраняя обозначения теоремы Г, мы
докажем, что
lim w = lim (uv ... t) = lim и lim v ... lim t = ab ... d.
Возьмем сначала произведение двух множителей: и и v. Имеем
# = #-(-а, т; =
и, значит,
Величина, заключенная в скобки, вследствие теорем II и I беско-
бесконечно мала, и потому
lim w = ab.
Пусть дано три множителя: иу v, t. Тогда
lim w = lim (uvt) = lim [{uv) t] = lim (uv) lim t = lim и lim v lim U
90 гл. и. предел, непрерывность [29
Теорему легко последовательно распространить на любое ко-
конечное число множителей.
Из этой теоремы, в частности, следует, что:
1) постоянный множитель можно выносить за символ предела:
lim си = с lim и,
так как предел постоянной величины равен самой этой величине, и
2) предел целой положительной степени функции равен той же
степени предела этой функции:
lim un = lim (а - и.. .ы) = Пти Шли... lim и = (lim u)n.
Теорема III. Частное от деления бесконечно малой величины
на функцию, предел которой отличен от нуля, есть величина
бесконечно малая.
Доказательство. Пусть а — бесконечно малая величина,
а и — функция, предел которой отличен от нуля: \\ти — АфО.
Теорема утверждает, что — —*0.
Для доказательства убедимся в том, что ограниченная
функция. Пусть, например, А > 0. Значения функции а прибли-
приближаются к числу Лив некоторой окрестности предельной точки
А А
будут больше, например, чем -у , т. е. и>-х-\ тогда
Это и означает, что функция — ограничена в окрестности пре-
предельной точки.
Аналогично проводится доказательство и для случая А < 0.
(Рекомендуем читателю в качестве упражнения провести его само-
самостоятельно.)
В силу того, что частное — можно рассматривать как произве-
произведение ограниченной функции — на бесконечно малую а, по теореме II
Нш —= 0,
что и требовалось доказать.
Теорема ИГ. Предел частного равен частному от деления
пределов, если только предел знаменателя не равен нулю.
Доказательство. Пусть \imu = a и \\mv = b^Q. Тогда
v = b-\-p, где а и |5 — бесконечно малые величины.
29] § 1. ПРЕДЕЛ ФУНКЦИИ. БЕСКОНЕЧНЫЕ ВЕЛИЧИНЫ 91
Покажем, что
t. ,. и lim и a
Действительно,
и а-\~а а , Ъа—аВ
W ^
W v 6+р~ Ъ
но дробь . ?ГТgiv в силу теоремы III является бесконечно малой
величиной: числитель ее на основании предыдущих теорем беско-
бесконечно мал, а предел знаменателя, равный д2, по условию отличен
от нуля. Значит, \\mw--r.
Если ? = 0, то теорема теряет смысл.
Приведем пример, иллюстрирующий изложенные правила:
lim 3*3-~2х*+х+ 1 __ lim (Зх*-2х2+х+1)
х^2 х2—5* + 3 "~ lim (д:2 — 5*4-3) ~"
3 (lim jcK—
"™ 22 —5-2-fS ~~ b3*
В этом примере мы искали предел рациональной функции
при условии, что аргумент стремится к конечному значению (не
обращающему, однако, знаменатель дроби в нуль). Оказалось, как
легко заметить, что для того, чтобы найти такой предел, доста-
достаточно в выражение функции подставить вместо независимой пере-
переменной ее предельное значение1).
Перейдем теперь к рассмотрению случаев, когда теоремы о пре-
пределах неприменимы. Особенно часто это бывает при отыскании
и
предела отношения —, когда предел знаменателя равен нулю.
При этом, если предел числителя не равен нулю, то отношение
— является величиной бесконечно малой (см. теорему III), а отно-
отношение — является величиной бесконечно большой и Ига — = оо.
V V
Если же и числитель и знаменатель одновременно стремятся к нулю,
то для отыскания предела необходимы дополнительные преобразования'
или специальные рассмотрения.
Точно так же дополнительного исследования требуют и случаи,
когда функция не определена в предельной точке и когда аргу-
аргумент х стремится к бесконечности. Рассмотрим некоторые примеры,
иллюстрирующие эти случаи.
х) Далее, в § 2, мы увидим, что этот простой способ отыскания предела
относится ко всякой элементарной функции, если только пре-
предельная точка принадлежит области определения функции.
92 ГЛ. П. ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ [29
х 3
Примеры. 1) lim -^—й-
Х-+3 * **~^
При х—*3 знаменатель стремится к нулю, но к нулю стремится
и числитель. Но так как лг2 — 9 = (# — 3) (лг + 3), то 44
4—4 = —Г5
для всех значений х, отличных от л; = 3. Поэтому, в соответствии
с определением предела, получаем
2) lim 22*Г3
Эта функция стремится к оо, так как знаменатель дроби при
X—»1 есть бесконечно малая величина, а числитель при этом
к нулю не стремится. Действительно, lim (л:2 — 5лг4-4) = 0*
Ж-> 1
a lim Bл; — 3)=—1; поэтому в силу теоремы 111
Х-+ 1
hm
а так как величина, обратная бесконечно малой, есть бесконечно
большая, то
2*—3
3) h
Hm
2 — 4лг+ 1
Здесь и знаменатель и числитель —бесконечно малые величины.
Имеем
.. 4д;2 —4д;+1 ,. Bjc— IJ ,, 2x—l О
4) lim ^i_r. Деля числитель и знаменатель на х, будем иметь
ж-> <» х 1
. , 1+— 1+lim—
5) Если дг—*-оо, то дробно-рациональная функция стремится
либо к нулю, либо к бесконечности, либо к конечному числу,
отличному от нуля, в зависимости от того, будет ли степень
числители меньше степени знаменателя, больше ее или равна ей.
30] § 1. ПРЕДЕЛ ФУНКЦИИ. БЕСКОНЕЧНЫЕ ВЕЛИЧИНЫ 93
В самом деле, в рациональной дроби
разделим числитель и знаменатель на хп:
... +атх
при лг—> оо знаменатель стремится к #0, а числитель — к нулю,
если т<,п, к оо, если т > л, и к а0, если т = п. Ясно, что
предел будет один и тот же при произвольном стремлении х к оо.
Таким образом,
lim ^ = 0, если
lim y = ooy если /я > я,
*->- оо
lim v = -^-, если m = n.
30. Один признак существования предела функции. Первый
замечательный предел. Существуют различные признаки существо-
существования предела функции, которые приходится применять тогда,
когда непосредственно отыскать предел бывает затруднительно.
Приведем в виде теоремы один употребительный признак.
Теорема. Если значения функции f(x) заключены между
соответствующими значениями функций F(x) и Ф(л;), стремя-
стремящихся при х—+х0 к одному и тому же пределу А, то f(x) при
х—*х0 также имеет предел, равный числу А.
Доказательство. Пусть
lim F(x)= lim Ф(х) = А.
Докажем, что
lim f(x) = A.
Х-+ XQ
Возьмем произвольную е-окрестность числа А. По условию
существует такая fi-окрестность точки лг0, что соответствующие
значения ^(л:) и Ф (х) принадлежат е-окрестности числа А. Но тогда
в силу заданных неравенств значения /(#), соответствующие точкам
указанной б-окрестности точки лг0, также будут находиться в е-ок-
е-окрестности числа Л. Так как г — произвольно, то это и означает, что
lim
х-+ х9
что и требовалось доказать.
94
гл. и. предел, непрерывность
C0
Рекомендуем читателю рассмотреть геометрический смысл дока-
доказанной теоремы.
Применим теперь доказанный признак к выводу важного пре-
предельного соотношения
,. sin a i
lim = 1,
а-*о а
о котором мы уже упоминали в п. 24. Этот предел часто называется
первым замечательным пределом.
8
Теорема. Функция
имеет предел, равный 1:
При а
Рис. 42.
Доказательство. Будем исхо-
исходить из геометрического определения
синуса. Возьмем окружность радиуса 1 и
предположим, что угол <х, выраженный в
радианах, заключен в границах 0<а<-^ •
(Так как ^-^ является четной функцией, то достаточно рассмо-
рассмотреть случай, когда <х>0.) Из рис. 42 видно, что
площадь ДОЛС< площади сектора ОАС< площади
Так как указанные площади соответственно равны -^
•^а и
y то, следовательно,
sin а < а < tg a.
Деля все члены неравенства на sin а, получим
sin а
cos а
или
Из геометрического определения косинуса ясно, что
lim cos a = 1.
а-* о
Отсюда на основании признака существования предела заключаем,
что
t. sina 1
lim =• I.
a->o a
31] § 1. ПРЕДЕЛ ФУНКЦИИ. БЕСКОНЕЧНЫЕ ВЕЛИЧИНЫ 95
С помощью найденного предела вычисляются многие другие
пределы.
Примеры.
1) Urn iii=limsi^-L-==lims-^lin, -J 1.1 =
2) Hm s-i2^= lim
x
; . х
• ** dm -q* sin -jr-
3) Hm l"^cosx= lim - = lim lim sin -?=1- 0 = 0.
2
31. Один признак существования предела последовательности.
Второй замечательный предел. Рассмотрим функцию целочислен-
целочисленного аргумента п
или последовательность
Назовем эту последовательность ограниченной сверху, если суще-
существует такое число Ж, что для всех п
Аналогично последовательность называется ограниченной снизу,
если существует такое число т, что для всех п
Если последовательность ограничена и сверху, и снизу, то она
называется ограниченной.
Предположим, что последовательность уъ j/2, ... , ynf .. щ
монотонная, т. е. ее члены либо только возрастают, либо
только убывают.
Укажем, в виде теоремы, один простой признак существования
предела такой последовательности.
Теорема. Если последовательность у19 у^ ... , уп, .. • воз-
возрастает и ограничена сверху, то она имеет предел.
Пусть дана возрастающая последовательность
Поскольку она ограничена сверху, существует такое число Ж, что
уп < М при любом п. В теореме утверждается, что при этом
последовательность имеет предел — обозначим его через Л, — ко-
который, разумеется, не превосходит числа М, т. е. А^М. Действи-
Действительно, раз точка yn — f(n)y двигаясь в одном направлении — вверх
96 ГЛ. II. ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ [31
по оси Оу, — не переходит границы интервала [0, уМ], то она
должна неограниченно приближаться1) к некоторой
точке у = Л; ясно, что A^iM.
Если последовательность yn=f(n) монотонная, но неограничен-
неограниченная, то lim /(/*) = +00; точка уп, двигаясь вверх по оси Оу, вы-
ходит из любой окрестности точки j> = 0.
Аналогично обстоит дело и в случае убывающей последова-
последовательности
Если эта последовательность ограничена снизу: уп> т для лю-
любого л, то она имеет предел Л, не меньший числа /и, т. е. А^т.
Если же она не ограничена, то функция f(n) стремится к —оо:
lim f (п)= — оо.
П -> 00
Для немонотонной последовательности возможны не два,
а три случая:
1) последовательность имеет предел;
2) последовательностъ стремится к бесконечности;
3) последовательность не имеет предела ни конечного, ни бес-
бесконечного (например, последовательность уп = (—1)"); в этом
случае она называется колеблющейся.
Благодаря высказанному простому признаку можно иногда убе-
убедиться в наличии предела, хотя сам по себе признак и не указы-
указывает, чему равен этот предел.
Применим признак к доказательству существования важного
предела, который часто называется вторым замечательным пределом.
Сформулируем его в виде теоремы:
Теорема. Функция
имеет предел при п—+ оо.
Доказательство. По формуле Ньютона имеем
IIя1 1 п(п-\) 1 п(я--1)(я-2) 1
п(п— 1)...(я — k+\) 1 , п(п—
г) Строгое доказательство этого предложения мы опускаем.
31] § 1. ПРЕДЕЛ ФУНКЦИИ. БЕСКОНЕЧНЫЕ ВЕЛИЧИНЫ 97
С увеличением п каждое слагаемое (кроме первых двух), стоящее
на фиксированном k месте, увеличивается. Действительно,
становится больше с ростом я. Кроме того, при возрастании п
добавляются новые положительные слагаемые. Следовательно,
уп — возрастающая функция я. Но она ограничена; в самом деле,
заменив во всех членах правильные дроби, стоящие в скобках,
единицами, получим
Л<1 + 1+ + ++^
Мы еще больше увеличим правую часть, если произведем такие
заменц:
11 11
. — _,_____ |4Я ——— —•*
3)~~2-3 2-2 ~~22'
Следовательно,
1
41
1
л!
2
1
•3-4
1
•З...П
1-1 51
на
2
2
1
•2-2
1
•2..
.2
1
23
1
2"
.У» ^ * "г * ~т~ 2 '2а23 * " • » 2й ~" * '
тем более, дописав в правой ^астй члены прогрессии ^, птгп , .. •,
получим
Так как сумма бесконечно убывающей геометрической прогрес-
прогрессии, заключенной в скобках, равна 2, то
Итак, данная возрастающая последовательность ограничена
сверху, а значит, на основании изложенного в этом пункте приз-
признака имеет предел, который, очевидно, заключен между 2 и 3.
Этот предел называется числом е1).
1) Это обозначение, как и обозначение отношения длины окружности
к диаметру через л, введено Л. Эйлером.
Л. Эйлер A707—1783) — великий математик, физик и астроном. Ему
принадлежат важнейшие работы по Математическому анализу, небесной
механике, теории кораблестроения и другим разделам науки. Долгие годы
живя в России, он оказал большое влияние на развитие отечественной
математики.
4 А. Ф. Бермант, И. Г. Араманович
98 ГЛ. И. ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ [32
Определение. Числом е называется предел
Hm (l+ ?•)".
Число е иррациональное и поэтому не может быть точно выра-
выражено какой-нибудь конечной дробью. Приближенно оно равно
е« 2,718.
Число е играет очень важную роль в математическом анализе.
Оказывается, что функция
-ЫУ
имеет предел не только тогда, когда ее аргумент принимает цело-
целочисленные значения х = п, но и при непрерывном его изменении
и стремлении к +оо или к — оо; при этом пределом служит то же
самое число е. Итак,
lim
Чтобы не загромождать изложения, мы опускаем доказательство
этого предложения.
Отметим, что сформулированный в настоящем пункте признак
существования предела последовательности без всякого изменения
переносится и на функции непрерывного аргумента: если функция
f(x) возрастает и при х—> + 00 остается ограниченной (см. п. 27, II),
то она имеет предел. Предоставляем читателю подобрать примеры,
показывающие, что если отказаться хотя бы от одного из условий
(возрастания или ограниченности), то функция может предела и не
иметь.
Аналогичный признак имеет место для убывающей функции,
а также для случая х—> — оо.
§ 2. Непрерывные функции
32. Непрерывность функции. Напомним прежде всего, что
приращением функции y~f (x) в данной точке х0 называется
разность
где Ах — приращение аргумента (рис. 43). Введем теперь следу-
следующее определение.
Определение. Функция у =/(je) называется непрерыв-
непрерывной в точке х0У если эта функция определена в какой-нибудь
32]
§ 2. НЕПРЕРЫВНЫЕ ФУНКЦИИ
99
окрестности точки х0 и если
Нт Ду=0,
дкХ-± О
т. е. если бесконечно малому приращению аргумента соответст-
соответствует бесконечно малое приращение функции.
Например, функция у — х3 непрерывна в любой точке х0. Так
как
Ау = (*0 + Ах)*—х1 = 3x1 Ах + Заг0Да;2 + Да:3,
то ясно видно, что если Да:—> О, то и Ау —* 0, а это и означает
что функция непрерывна. (Рекомендуем читателю самостоятельно
доказать непрерывность в любой точ-
точке х0 функций sin а: и cos а:.)
Описательно можно сказать, что
функция непрерывна, если она изме-
изменяется постепенно, т. е. если ма-
малые изменения аргумента влекут за
собой малые же изменения функции.
Эта особенность выражает общую
характерную черту многих явлений и
процессов. Так, мы считаем, например,
что стержень при нагревании удлиняет-
удлиняется непрерывно, что рост организма про-
происходит непрерывно, что температура
воздуха изменяется непрерывной т. ть
Пользуясь выражением для Ау, можно записать также, что
Нт
Ах —> '
или, иначе,
Ит j
Если обозначить xQ-\-Ax через аг, то аг при Ах—> () будет
стремиться к х0 и последнее равенство можно переписать так:
X -+ХЛ
Таким образом, можно сказать:
Функция у =f(x) непрерывна в точке х0, если она опреде-
определена в какой-нибудь окрестности этой точки и если предел функ-
функции при стремлении независимой неременной х к лс0 существует
и равен значению функции при х = х0:
Hm f(x)=zf(x0). (*)
х-* х0
Заметим, что если значение функции /(аг) в точке аг0, в которой
она непрерывна, отлично от нуля, /(аго)=^О, то значения функции
Рис. 43.
100 ГЛ. И. ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ [33
f(x) в некоторой окрестности точки xQ имеют тот же знак, что
и f(x0). Действительно, вследствие непрерывности существует
окрестность точки лг0, в которой значения f(x) настолько мало
отличаются от своего предела, т. е. от f(xo)y что они остаются
положительными, если /(лг0) > 0, и остаются отрицательными,
если /(лг0) <0.
Определение. Функция называется непрерывной в интер-
интервале, если она непрерывна в каждой его точке.
Для концов интервала определения непрерывности функции
в точке надо несколько изменить. Именно, для левого конца
интервала приращению Дл; следует придавать только поло-
положительные значения, а для правого — только отрица-
отрицательные.
Геометрически непрерывность функции y=zf(x) в интервале
означает, что ординаты ее графика, соответствующие двум точкам
оси Ох, как угодно мало отличаются друг от друга, если расстоя-
расстояние между этими точками достаточно мало. Поэтому график непре-
непрерывной функции представляет собой сплошную линию без разрывов;
такую линию можно вычертить, двигаясь в одном направлении,
скажем слева направо, не отрывая карандаша от графика, так
сказать, «одним росчерком».
Собственно говоря, во всем предыдущем изложении, в частности
при описании свойств и графиков основных элементарных функций
в гл. I, мы уже предполагали, что эти функции непрерывны. Мы
опустим аналитическое доказательство этого факта и будем счи-
считать, что все основные элементарные функции непрерывны в тех
интервалах, В которых они определены. В п. 34 это общее поло-
положение будет распространено на все элементарные функции,
33. Точки разрыва функции. Если рассматривать график функ-
функции у =— в окрестности точки х=^0т то ясно видно, что он как
бы «разрывается» на отдельные кривые. То же самое можно ска-
сказать о графике функции у = igx в окрестностях точек х *= Bk -f-1) —
(см. п. 21, рис. 26). Говорят, что во всех указанных точках соот-
соответствующие функции становятся разрывными.
Определение. Если в какой-либо точке х0 функция не
является непрерывной, то точка х0 называется тонкой разрыва
функции, а сама функция—разрывной в этой точке.
При этом предполагается, что функция f(x) определена в не-
некоторой окрестности точки лг0; в самой же точке х0 функция
может быть как определена, так и не определена.
Наиболее характерными и часто встречающимися точками раз-
разрыва являются точки бесконечного разрыва, т. е. такие,
S3] §. 2. НЕПРЕРЫВНЫЕ ФУНКЦИИ 101
в окрестности которых функция является неограниченной; напри-
например, точка лг = О для функции <У = у, точки лг=B/г+1)-у для
функции y^tgx, точка л; = 0 для функции y = \gx (в последнем
примере функция jJ = lg x определена только с одной стороны от
точки разрыва л; = 0).
Важный класс точек разрыва образуют точки разрыва первого
рода. Для их определения введем понятие левого и правого
пределов функции.
Пусть х стремится к лг0, оставаясь все время слева от лг0,
т. е. будучи меньше х0. Если при этом условии значения функ-
функции f(x) стремятся к пределу, то он называется левым пределом
функции/(дг) в точке лг0; аналогично определяется и правый предел.
Левый и правый пределы обозначаются соответственно так: f(x0—0)
и /(#0 + 0). Значит,
Urn /<*) =/(*«-<>), Hm f{x)=f(xQ + 0).
Ясно, что если функция имеет предел при произвольном
стремлении х к л;0, то существуют ее левый и правый пределы и
они равны между собой. Обратное
тоже справедливо: если левый и пра- у
вый пределы существуют и равны '
между собой, то функция имеет тот
же предел при произвольном стрем-
стремлении X К XQ.
Определение. Точной разры- Q
ва первого рода функции f(x) назы-
вается такая точка xQ9 в которой
функция имеет левый и правый пре- Рис* 44>
делы, не равные между собой. Гео-
Геометрическая иллюстрация точки разрыва первого рода ясна из
рис. 44.
Все остальные точки разрыва называются точками разрыва вто-
второго рода.
Примером точки разрыва первого рода служит точка дс=-^- для функции
# = arctg(tgx) (см. рис. 34). Рассмотрим еще функцию # = arctg—. Эта
функция не определена в точке *=0. Если х -* 0, оставаясь отрицатель-
отрицательным, то *—оо и у-+ — тг (см. п. 22). Если же x-*0t будучи поло-
X ?>
жительным,то >-|-оо и у-+ ^- . Таким образом, точка jc = Q является
102
ГЛ. II. ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ
[34
точкой разрыва первого рода для функции y~arctg _ . График этой функ-
функции схематично изображен на рис. 45.
Не следует думать, что точки разрыва второго рода обязательно являют-
являются точками бесконечного разрыва. Существуют ограниченные функции,
которые при приближении аргу-
аргумента к точке разрыва не имеют ни
левого, ни правого пределов. При-
Примером служит функция y = sin —
X
при х -+- 0, в чем можно убедить-
убедиться, построив схематически ее гра-
график, придавая х значения -г— и
с27
В дальнейшем нам
яг
~2
Рис. 45.
такие точки разрыва встречаться
не будут. Мы также не рассмат-
рассматриваем случаи, когда один из
двух пределов существует, а дру-
другой нет.
Если в точке х0 левый и правый пределы функции f(x) равны
между собой и равны значению f(x0), то функция в этой точке
непрерывна. Если функция f(x) в точке х0 не определена, но
ее левый и правый пределы существуют и равны между собой, то
часто просто полагают f(x0) равной этому общему пределу; при
этом условии функция становится непрерывной в точке х0. Так,
например, функция ^ =
ТОчке х = 0 не определена. Но так
как
так:
lim
X-+Q
sin*
= 1, то можно рассмотреть функцию, определенную
sin*
если
Эта «доопределенная» функция уже будет непрерывной.
34. Действия над непрерывными функциями. Непрерывность
элементарных функций. Докажем сейчас, что если над непрерыв-
непрерывными функциями произвести конечное число арифметических дей-
действий или операций взятия функции от функции, то в результате
получится, как правило, также непрерывная функция. Все доказа-
доказательства совершенно однотипны; в каждом случае мы покажем, что
предел соответствующей функции будет равен ее значению в пре-
предельной точке, а это и означает непрерывность функции.
34] § 2. НЕПРЕРЫВНЫЕ ФУНКЦИИ 103
Теорема I. Сумма конечного числа функции, непрерывных
в некоторой точке, является функцией, непрерывной в той же точке.
Доказательство. Пусть дано определенное число функций
и, v, .. ., t9 непрерывных в точке лг=л;0. Требуется доказать, что
их сумма w — u-\-v-\~ . . . -\-t будет функцией, непрерывной в точке
х = х0. Так как слагаемые функции непрерывны, то
lim и = и0, lim v = % .. ., lim t = /0,
X-+Xo X-+Xo X-+Xq
где и0, v0, ..., tQ—значения соответственно функций и, v, ...
.. ., i в точке х — х0. В силу теоремы о пределе суммы (п. 29) имеем
lim w= lim (u-\~v-\- ... -\-t) = lim u-\- lim v+ . . . + lim t =
X -*¦ Xo X -*¦ X9 X -> Xo X -*¦ Xo X -> Xo
где w0—значение функции w при x = xQ. Итак, lim w = wQy что
x-+x0
и требовалось доказать.
Теорема П. Произведение конечного числа функций, непре-
непрерывных в некоторой точке, является функцией, непрерывной
в той же точке.
Доказательство. Сохраняя обозначения теоремы I при усло-
условии, что w = u-v.. .t, имеем в силу теоремы о пределе произведе-
произведения (п. 29)
lim w — lim (u-v. . J) =lim и» lim v.. . lim t~uovo.. J0~w0,
что и требовалось доказать.
Теорема III. Частное двух функций, непрерывных в некото-
некоторой точке, является функцией, непрерывной в той же точке, если
только знаменатель не обращается в ней в нуль.
Доказательство. Если а; = —, то по-прежнему в силу
теоремы о пределе частного (п. 29) при условии, что lim v = T>o=?Of
х-+х9
имеем
lim и
Нт<ш= lim ii=x-?x>-== —= ^п,
х^Хо х->Хо v lim v v0 °'
X -> Хо
что и требовалось доказать.
Теорема IV. Сложная функция, составленная из конечного
числа непрерывных функций, непрерывна.
Доказательство. Достаточно доказать эту теорему для
случая цепи функций из двух звеньев, потому что тогда последова-
104 ГЛ. II. ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ [34
тельно можно ее распространить на случай цепи из любого конечного
числа звеньев.
Пусть y=zf(z)y а <гг = ф(лг), так что
причем ф(лг) непрерывна при л: = л:0, a f(z) непрерывна при z = z0,
где zo~q>(xo). Утверждение теоремы состоит в том, что у, как
функция лг, т. е. функция F(x), непрерывна при х~х0.
Действительно, пусть х—>х0. Из непрерывности функции z =
я=ф(лг) следует, что при этом lim ф (л;) = ф (лг0) = z0, т. е. что
х-+х0
z—+z^ Так как f(z) непрерывна в точке z0, то lim f(z)=f(z0).
Ко ведь г = ф(лг) и с учетом только что сказанного последнему
равенству можно придать вид
или в другой записи
lim
х-+х
что и требовалось доказать.
Приведем еще без доказательства следующую теорему.
Теорема V. Функция, обратная к монотонной и непрерывной
функции, непрерывна.
Так как мы уже отмечали, что все основные элементарные
функции непрерывны в интервалах их определения (п. 32), то в силу
изложенных четырех теорем можно утверждать, что и любая эле-
элементарная функция непрерывна в тех интервалах, где она определена.
Точками разрыва элементарной функции могут быть только те
значения независимой переменной, при которых какие-нибудь из
составляющих функцию элементов делаются неопределенными или
при которых обращаются в нуль знаменатели участвующих в вы-
ражении функции дробей. Так, например, функция у==-^—-. раз-
рывна при лг = ±2 и непрерывна во всех остальных точках, а
функция j> = A:2tgх разрывна при х = B&+1) ~- (fc = 0, ± 1, ± 2,...).
Отметим, что предельное равенство lim f(x) =/(лг0), выражаю-
х-+х0
щее непрерывность функции при х = х0, можно переписать так:
lim /(*)=/( lim at).
X -»- Хо Х~+Хо
Значит, символ предела и символ непрерывной функции можно
переставлять между собой.
34] § 2. НЕПРЕРЫВНЫЕ ФУНКЦИИ 105
Отсюда следует простое, практически удобное правило пре-
предельного перехода:
Для того чтобы найти предел элементарной функции, когда
аргумент стремится к значению, принадлежащему области опре-
определения функции, нужно в выражение функции вместо аргумента
подставить его предельное значение.
Это правило очень важное, поскольку в применениях анализа
употребляются преимущественно элементарные функции.
Случаи, когда аргумент стремится к бесконечности или к какому-
нибудь значению, не принадлежащему области определения функ-
функции, требуют всегда специального рассмотрения.
х$ -L За:2 х 3
Примеры. 1) JJ = 2 ^— . Найдем lim у. Так как в трч-
ке лг = О заданная функция непрерывна (многочлен в знаменателе
не обращается в нуль), то
лЗ + з*2 — х—3 _03 + 3-02 — Q—3_— 3__ 1
™о *2-h*-6 ~~ 02 + 0 — 6 — — 6~~2*
Найдем lim у. При х = — 3 и знаменатель и числитель обра-
щаются в нуль; но х2 + х—6 = (л: + 3)(л;— 2), алг3 + 3лг2—х—3 =
= (л; + 3) (л;2—1). Сократив дробь на (лг-|-3), получим
8
Имеем также
lim g . ^— = оо, lim ¦ ^2 z— = 0,
х2 + ^-6 ' х* + х-6
,. х + 3д; — х—3
lim —-»-, ^— = сю.
х-+„ Х* + Х-6
Х2 4
2) у= . Найдем lim у. При лг = 1 заданная функция не-
cos -т-х х-*х
4
Х2 л I2 4 у—
прерывная и, значит, lim = = —Ъу 2. Предел этой
к~*х cos -т-х cos —1
4 4
функции при х—>-2 нельзя найти по общему правилу, так как при
х = 2 знаменатель обращается в нуль; но в точке х = 2 в нуль
обращается и числитель. Поступим следующим образом. Положим:
х—2 = 2г, т. е. x = z-\-2; тогда z при х—*2 будет стремиться
к 0. Имеем
иш _^!=1_= ,,„ »(«+«) , lim _?(?±iL.
106
ГЛ. 11. ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ
135
Далее находим
lim '
lim
n z-+o
n
sin—z
lim
Z->0
35. Свойства непрерывных функций. Непрерывность функции
в замкнутом интервале обусловливает наличие у этой функции
ряда важных свойств общего характера. Укажем (без доказатель-
доказательства) два из этих свойств.
Теорема I. Функция, непрерыв-
непрерывная в замкнутом интервале, хотя
бы в одной точке интервала принима-
принимает наибольшее значение и хотя бы
в одной—наименьшее.
Пусть функция у=/{х) непреры-
непрерывна в интервале [а, Ь] (рис. 46). Тео-
Теорема утверждает существование хотя
бы одной такой точки ?х ? [я, Ь\ *), и
хотя бы одной такой точки \г ?[а, Ь\%
что значения функции в этих точках являются соответственно наи-
наибольшим и наименьшим ее значениями во всем интервале [а, Ь]:
Рис. 46.
Разумеется, таких точек может быть и несколько; так на рис. 46
показано, что функция f(x) принимает наименьшее значение в двух
точках (они обозначены буквами ?2 и ?'а).
Это утверждение может стать неверным, если не предполагать
замкнутости интервала. В самом деле, например, функция у = х
непрерывна в любом открытом интервале (а, ?), но не достигает
в нем ни наибольшего, ни наименьшего значений: она достигает
этих значений как раз на концах интервала, но концы из интер-
интервала исключены. Точно так же теорема перестает быть верной
для разрывных функций. Читатель подумает над примером функ-
функции (заданной хотя бы графически), определенной и разрывной в
замкнутом интервале, не удовлетворяющей теореме I.
Теорема II. Функция, непрерывная в замкнутом интервале
я принимающая на концах этого интервала значения разных зна-
знаков, хотя бы один раз обращается в нуль внутри интервала.
Допустим, что функция у=1/{х) непрерывна в интервале [а, Ь\
и что /(я)<0, a f(b) > 0 (рис. 47). Теорема утверждает сущест-
существование хотя бы одной такой точки ? ? (а, Ь), что /(?) = 0. Гео-
Геометрически это означает тот очевидный факт, что непрерывная
1) Символ %i?[af b] означает (см. п. 4), что a^
35]
§ 2. НЕПРЕРЫВНЫЕ ФУНКЦИИ
107
линия — график непрерывной функции, — соединяя точку Л, лежа-
лежащую под осью Олг, с точкой В, лежащей над осью Олг, обязательно
пересечет ось Ох хотя бы в одной точке. Разрывные функции
этим свойством могут не обладать.
Теорему II можно формулировать в более общем виде:
Функция, непрерывная в замкнутом интервале, принимает внутри
интервала хотя бы один раз любое значение, заключенное между
ее значениями на концах интервала.
Пусть /(а) = /w, f{b) = Ж, и пусть,
например, m < Ж (предположение, что
/и>Ж, не вызовет никаких сущест-
существенных изменений в рассуждении).
Возьмем какое-нибудь число ц, заклю-
заключенное между m и Ж: m < \i < Ж.
Теорема утверждает существование
хотя бы одной такой точки 5 €(#> *)>
что /(?) = И" Это предложение не-
немедленно сводится к теореме II. В са-
самом деле, возьмем вспомогательную
функцию
ф (*)=/(*)—и;
«27
Рис. 47.
на концах интервала она принимает значения разных знаков:
<р(а)=/(а) — \i = m— \i <0 и <р (ft) =/(*) — [х = Ж— [i> 0. Так
как функция ф(лг) непрерывна в интервале [а, Ь], то в силу тео-
теоремы И она обращается в нуль при
некотором |?(я, Ь). Таким образом,
м
т
О
И г
Ъ as
Рис. 43.
откуда
Геометрически это предложение
означает, что любая прямая у = jx,
параллельная оси Ох и проходящая
между начальной и конечной точка-
точками непрерывной линии, пересечет ее
хотя бы один раз. Абсцисса точки
пересечения и будет тем значением
х = 1, при котором /(?)=ф (на
рис. 48 таких точек три). Это предложение показывает, что
Непрерывная функция, переходя от одного своего значения к дру-
другому, обязательно проходит через все промежуточные значения; в
частности,
Непрерывная в интервале функция принимает в этом интервале
хотя бы один раз любое значение, заключенное между ее наименьшим
и наибольшим значениями. Геометрически ясно, что если функция
108 ГЛ. II. ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ [36
в данном интервале монотонна и, скажем, для определен-
определенности, возрастает, то свое наименьшее значение она принимает
на левом конце интервала, а наибольшее — на правом; при этом
любое промежуточное значение функция принимает в точности
один раз.
§ 3. Сравнение бесконечно малых величин
36. Сравнение бесконечно малых величин. Эквивалентные бес-
бесконечно малые величины.
I. Порядок бесконечно малой величины. Для того
чтобы сравнить между собой две бесконечно малые величины, берут
предел их отношения.
В дальнейшем под аи Р мы будем понимать бесконечно малые
величины при одном и том же предельном изменении их общего
аргумента.
Определение. Сравнить две бесконечно малые величины
а и ($ — это значит найти предел их отношения.
При отыскании предела отношения бесконечно малых величин
могут возникать разные случаи.
а) Пусть lim-jr =0. Тогда а называется бесконечно малой вели-
величиной более высокого порядка, чем р. Можно сказать, что здесь а
стремится к нулю «быстрее», чем р, т. е. что при значениях аргу-
аргумента, достаточно близких к предельному, величина |а| будет «зна-
«значительно» меньше величины |Р|.
Пример. Пусть а = х2, Р=* (*—>()), тогда
Ит -? = lim x = 0.
Следовательно, а—бесконечно малая более высокого порядка, чем р.
Если а—бесконечно малая более высокого порядка, чем ($, то
говорят также, что Р — бесконечно малая более низкого порядка,
чем а. При этом
lim ?- = 00.
а
б) Пусть теперь предел отношения аир равен некоторому
числу, отличному от нуля, т. е.
lim~
В этом случае аир называются бесконечно малыми одного порядка.
36) § 3. СРАВНЕНИЕ БЕСКОНЕЧНО МАЛЫХ ВЕЛИЧИН 109
Пример, Если а = sin5л:, р = лг(лг—>О), то
^sinjk^g (CM. п.з0).
Следовательно, аир одного порядка малости.
С нулем, рассматриваемым как бесконечно малая величина, не
сравнивают никакую другую бесконечно малую величину, так как
на нуль делить нельзя. Мы также не сравниваем две бесконечно
малые величины аир, есяи их отношение не имеет предела (конеч-
(конечного или бесконечного).
II. Эквивалентность бесконечно малых величин.
Определение. Если аир — бесконечно малые величины
одного порядка, причем
lim f — U
то они называются эквивалентными или равносильными. В этом
случае также lim — = 1.
Эквивалентность бесконечно малых аир обозначается так: а ~ р.
Важным примером эквивалентных бесконечно малых величин яв-
являются sinx и х при лг—*-0.
Существует простой признак эквивалентности двух бесконеч-
бесконечно малых величин.
Теорема. Для того чтобы бесконечно малые величины аир
были эквивалентными, необходимо и достаточно, чтобы их разность
была бесконечно малой величиной более высокого порядка, чем а
и чем р.
Доказательство. Положим:а—Р = у. Необходимость
признака вытекает из того, что
? ^^ = lim(?— lWlinw —1=0,
V Р / р
ибо по условию lim -^ ^= 1. Точно так же убеждаемся, что lim — = 0.
Докажем достаточность признака. Пусть известно, что
lim X = q т. е. lim ~^=.Q. Имеем
а а
lim
(•-!)-»¦
откуда следует, что lim — = 1 ил и lim -^ = 1. Эти предельные равен-
равенства также легко получаются и в случае, если известно, что lim -5L = 0.
ПО ГЛ. II. ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ [37
Пример. При п —> сю бесконечно малая ап = -~- эквивалентна
бесконечно малой РЛ = —, так как они отличаются друг от друга
на бесконечно малую более высокого порядка: ап — рл = —^# Их
отношение стремится к единице:
Р* п
Во многих вопросах можно без всякой ошибки просто заменять
бесконечно малые им эквивалентными. Например, справедливо такое
предложение:
Предел отношения бесконечно малых не изменится, если заменить
их эквивалентными бесконечно малыми,
В самом деле, пусть а~а', |5 ~ |}\ Тогда
Следовательно, отыскивая предел отношения—бесконечно ма-
малых величин а и Р, можно отбрасывать и в числителе и в знаме-
знаменателе бесконечно малые слагаемые более высоких порядков, ибо
по доказанному выше это равносильно замене бесконечно малых
величин а и (J эквивалентными величинами.
37. Примеры отношений бесконечно малых величин. Натураль-
Натуральные логарифмы.
1. При отыскании пределов функции особое значение имеет
отыскание пределов отношений двух бесконечно малых величин.
Рассмотрим несколько важных примеров.
1) Л== lim -—J"*""" . Как видно, здесь требуется найти предел
2х
отношения двух бесконечно малых величин.
Умножим числитель и знаменатель данной дроби на V^
получим
Л= lim J/1+*"~1=s lim *-— = lim -
*-*° ±x x-*°jx(V\+x + l) х?о
Последняя функция непрерывна при лг = О, и значит,
37] § 3. СРАВНЕНИЕ БЕСКОНЕЧНО МАЛЫХ ВЕЛИЧИН 111
t
Следовательно, бесконечно малые величины /l+л: — 1 и -^
эквивалентны:
Поэтому при достаточно малых х можно считать, что
Это дает возможность вычислять значения функции y — Y\ + х
для различных малых значений х.
После простых преобразований с помощью этой формулы можно
приближенно вычислять и другие корни, например:
/627 = /625 + 2 = l/25 |/l +^g« 25 (l + 2^5) =25,040.
Этот результат — хорошей точности, так как /627 с тремя вер-
верными знаками равен именно 25,040.
Таким же образом легко показать, что вообще у а?-\-Ь можно
полагать приближенно равными +-о—, если Ь мало сравнительно с а2.
2) Л= lim . Выше (п. 30) уже было доказано, что Л = 1.
JC~*O Х
Таким образом, бесконечно малые величины situe и х эквивалентны:
sin л: -^ лг.
Из свойств эквивалентных бесконечно малых следует, что
lim sin*"~* = 0. Поэтому при достаточно малых х замена sinA: на х
приводит к очень малой относительной ошибке. Это дает возмож-
возможность вычислять значения функции y = sinx для малых значений jc
с очень большой точностью. Так, например, мы находим
т. е. приближенно
sinl° = 0,01728.
Абсолютная ошибка этого равенства оказывается равной 0,00001-
3) Л= lim 5 . Ясно, что мы имеем здесь предел от-
ношения двух бесконечно малых величин. С помощью простых
112 гл» н. предел, непрерывность [37
преобразований находим
2 2
Отсюда следует, что 1 — cos а при а—»-0 есть бесконечно малая
величина того же порядка, что и а2.
4) Л=Нт og*( +*). в этом примере требуется найти также
*-*о х
предел отношения двух бесконечно малых величин, ибо loga(\-\-x)
при х=*0 равен logel=0.
Выполним следующие преобразования:
А= Iim 1о*« <*+*>=: iim Uloge A+Jt)l = lim]og
Так как логарифмическая функция непрерывная, то можно пере-
переставить символы этой функции и предела при условии, конечно,
что предел аргумента существует:
Aoga 1\т(\+х)* \;
но предел в квадратных скобках действительно существует и равен
числу е, в чем можно убедиться, если положить х= —:
Iim A +х)х = Iim
(см. п. 34).
Итак,
Полученный результат показывает, что при х—^0 функции
а(^+А:) и х СУТЬ бесконечно малые величины одного порядка.
5) Л= Iim . Здесь дан снова предел отношения двух бес-
*-*о х
конечно малых величин, ибо в силу непрерывности показательной
функции а*—»1 при х—>().
Положим
тогда при х—>0 и z—>(). Логарифмируя обе части равенства
a*=\-\-z по основанию а, найдем
37] § 3. СРАВНЕНИЕ БЕСКОНЕЧНО МАЛЫХ ВЕЛИЧИН 113
и, значит,
А = lim » lim lim
2-)- О
что на основании примера 4 дает
А= lim- -=г-^-- ge
Таким образом, бесконечно малая при х—*0 величина а*—1
одного порядка малости с х.
II. Натуральные логарифмы. Из последних двух приме-
примеров отчетливо видно, что за основание а логарифмической функции
очень удобно взять число е. В самом деле, при а = е результаты
сильно упростятся и в обоих примерах D и 5) будут равны единице.
Следовательно, при х—^0 бесконечно малые величины loge (I -\-x)
и е*—1 эквивалентны лг. При достаточно малых значениях х и
l°geO+-*:)> и е*—* можно заменять через х со сколь угодно
малой относительной ошибкой:
log^(l +х) «л:, е*—1 жх.
Несомненно, это должно сильно способствовать упрощению вычи-
вычислений, и действительно, в анализе оказывается наиболее удобным
принимать за основание логарифмической функции число е. Лога-
Логарифмы по основанию е обозначают посредством символа In и на-
называют натуральными. Мы с ними уже имели дело в п. 23.
В новых обозначениях имеем
Так как логарифмы чисел при двух разных основаниях пропор-
пропорциональны друг другу (п. 20), то переход от натуральной системы
логарифмов к десятичной и обратно не представляет никакого труда.
Натуральные и десятичные лотарифмы связаны между собой
формулами
\gx-M\nx и Inx^-r^lgx,
где
М = lg е = jjlg » 0,434294 (-1 « 2,302585^ .
Число М называется модулем перехода от натуральных
логарифмов к десятичным. В практических расчетах всегда поль-
пользуются десятичными логарифмами, которые, не имея никаких
114 гл. н. предел, непрерывность [37
теоретических преимуществ перед любыми другими, удобнее в
вычислениях.
В этой книге мы везде употребляем натуральную систему
логарифмов.
ВОПРОСЫ И ПРЕДЛОЖЕНИЯ ДЛЯ САМОПРОВЕРКИ
1. Что такое предел функции y~f(x) при х—>х0? Дать определение с
помощью неравенств. Привести геометрическую иллюстрацию.
2. Дать пример функции y = f (х), имеющей предел при х—> хо\ не имею-
имеющей предела при х—> х0.
3. Что такое предел функции y = f(x) при х—^-foo? при х—>— оо?
Дать определение с помощью неравенств. Привести геометрическую иллю-
иллюстрацию.
4. Дать пример функции y — f(x), имеющей предел при х—> +<»,
х—>— оо; не имеющей предела при х—>+00» *—>— °°-
5. Определить предел последовательности (функции целочисленного аргу-
аргумента). Привести примеры последовательностей, имеющих и не имеющих
пределы.
6. Какая функция y — f(x) называется бесконечно большой величиной
при х—>х0, при х—> ± оо? Дать определения с помощью неравенств.
Привести геометрические иллюстрации.
7. Что означают записи:
lim
x-+x0
lim
lim
f (л:) =
/ (x) =
/(*> =
"T" °°>
+ 00,
— 00,
lim
*-¦•+
lim
x-+x(
lim
f (x)=s
>
Jt-+-06
"t" °°»
— 00,
— 00?
lim
х-*-— а
lim
*-> + <»
>
fW = -oo,
Дать словесные разъяснения и определения с помощью неравенств. При-
Привести геометрические иллюстрации.
8. Дать примеры функций, являющихся бесконечно большими величи-
величинами при различных предельных поведениях аргумента.
9. Какая функция называется ограниченной в интервале? при х—> х0?
при х—> ±оо?
10. Привести пример неограниченной, но не бесконечно большой вели-
величины.
11. Какая функция y = ft(x) называется бесконечно малой величиной при
х—>*(), при х—> ± оо? Дать определения с помощью неравенств. Приве-
Привести геометрические иллюстрации.
12. Какова простейшая связь между бесконечно большой и бесконечно
малой величинами? Доказать соответствующую теорему.
13. Какова простейшая связь между функцией, имеющей предел, и бес-
бесконечно малой величиной? Доказать соответствующие прямую и обратную
теоремы.
14. Сформулировать и доказать правила предельного перехода в случае
арифметических действий.
15. Сформулировать и доказать признак существования предела функции,
заключенной между двумя функциями, имеющими один и тот же предел.
16. Вывести первый замечательный предел.
17Ч Сформулировать и разъяснить признак существования предела моно-
монотонной последовательности.
18. Вывести второй замечательный предел.
ВОПРОСЫ И ПРЕДЛОЖЕНИЯ 115
19. Дать определение непрерывности функции y = f{x) в точке xQ и
иллюстрировать его геометрически.
20. Что называется точкой разрыва функции?
21. Привести примеры разрывных функций различного характера.
22. В чем состоит правило предельного перехода для непрерывной
функции?
23. Сформулировать и доказать теоремы об арифметических действиях
над непрерывными функциями.
24. Сформулировать и доказать теорему о непрерывности сложной
функции, составленной из непрерывных функций.
25. Что можно сказать об интервале непрерывности элементарной функ-
функции? Какие точки могут являться точками разрыва такой функции?
26. Сформулировать свойства функции, непрерывной на замкнутом
интервале. Дать геометрическую иллюстрацию этих свойств.
27. Что значит сравнить две бесконечно малые величины? В каком случае
одна из них будет более высокого порядка, чем другая?
28. Какие две бесконечно малые величины называются эквивалентными?
Привести необходимый и достаточный признак эквивалентности.
29. Привести примеры эквивалентных бесконечно малых величин.
30. Чему равны Km ^—! , lim 1о&*A+*> ?
X -> 0 Х Х-+0 *
31. Какая система логарифмов называется натуральной? Как перейти от
натуральной системы к десятичной и обратно? Чему равен модуль перехода Ш
ГЛАВА III
ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ. ДИФФЕРЕНЦИАЛЬНОЕ
ИСЧИСЛЕНИЕ
§ 1. Производная
38. Некоторые задачи физики. Рассмотрим простые физические
явления; прямолинейное движение и линейное распределение массы.
Для изучения их вводят соответственно скорость движения
и плотность.
Разберем каждое из указанных явлений и связанные с ними
понятия в отдельности.
I. Скорость прямолинейного движения. Пусть тело
совершает прямолинейное движение и нам известно расстояние s,
проходимое телом за каждое данное время ty т. е. нам известно
расстояние s как функция времени t\
Уравнение s = F(t) называется уравнением движения, а определяе-
определяемая им линия в системе осей Ots—графиком движения.
Рассмотрим движение тела в течение интервала времени А* от
некоторого момента t до момента t-\-At. За время t тело прошло
путь s^F{t), а за время t + At— путь s-f- As~F(t-{- At). Значит,
за At единиц времени оно прошло путь
Если движение равномерное, то s есть линейная функция t:
As
(п. 15). В этом случае As = v0At, и отношение ^( = ^0) показывает,
сколько единиц пути s приходится на единицу времени t; при этом
оно остается постоянным, не зависящим ни от того, какой
момент времени t берется, ни от того, какое взято приращение
38]
§ 1. ПРОИЗВОДНАЯ
117
времени At. Это постоянное отношение -? называют скоростью
равномерного движения*).
Но если движение неравномерное, то отношение -rj зависит и
от /, и от Д/. Оно называется средней скоростью движения
в интервале времени от /до t-\-Atи
обозначается через г>ср:
As
v
s
0
n
H
t
/
ct
г
At
к
va
t*
9
V.
/
Рис. 49.
В течение этого интервала времени при
одном и том же пройденном расстоянии
движение может происходить самым
различным образом; графически это
иллюстрируется тем, что между двумя
точками на плоскости Ots (точки А и В на рис. 49) можно про-
провести самые различные линии {АСХВ, АС2ВУ АС3В) — графики дви-
движений в данном интервале времени, причем всем этим разнообраз-
As
ным движениям соответствует одна и та же средняя скорость д-j •
В частности, между точками А и В проходит прямолинейный отре-
отрезок {АСВ)У являющийся графиком равномерного в интервале
As
(/,/ + At) движения. Значит, средняя скорость -гг показы-
показывает, с какой скоростью нужно двигаться равномерно для того,
чтобы пройти за этот же интервал времени (/, tf-j-Д/) то же рас-
расстояние As.
Оставляя прежним t, уменьшим At, Средняя скорость, подсчи-
подсчитанная для измененного интервала (t, t-\- Д^), Atx < At, лежащего
внутри данного интервала, может быть, разумеется, иной, чем во всем
интервале (t,t-\-At). Из этого следует, что среднюю скорость
нельзя рассматривать как удовлетворительную характеристику
движения: она (средняя скорость) зависит от интервала, для ко-
которого производится расчет. Исходя из того, что среднюю ско-
скорость в интервале (/, / + Д/) следует считать тем лучше характе-
характеризующей движение, чем меньше At, заставим At стремиться
к нулю. Если при этом существует предел средней скорости vcpi
то его и принимают в качестве скорости движения в данный момент/.
Определение. Скоростью v прямолинейного движения в
данный момент времени t называется предел средней скорости vcp,
*) Численно скорость равномерного движения равяа расстоянию,
проходимому за единицу времени; размерность скорости в единицах
СИ—м1 сек.
118 ГЛ. III. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ [38
соответствующей интервалу (t, t-\- At), при стремлении At к нулю:
Пример. Запишем закон свободного падения:
Для средней скорости падения в интервале времени (?, t + At) имеем
Ig(t + MY ~gt* о* А*-МАП" 1
а для скорости в момент t
w= lim 4-
Отсюда видно, что скорость свободного падения пропорцио-
пропорциональна времени движения (падения).
II. Плотность. Перейдем теперь к важному понятию из дру-
другой области физики, определяемому вполне аналогично скорости
движения, к понятию плотности.
Возьмем материальную линию (например, проволоку) и будем
двигаться от одного из ее концов к другому, измеряя длину s
пройденного куска, а также его массу /». Каждому значению s
соответствует определенная масса т> и поэтому последняя является
функцией s:
m = Q)(s).
Говорят, что материя распределена равномерно по всей линии и
что эта материальная линия однор одна, если два любых равных
по длине участка содержат равные же массы. В этом случае т
есть линейная функция s> точнее, т зависит прямо пропорционально
от s:
m = 60sy
где б0 — постоянный коэффициент пропорциональности, причем Am =
= 80As и отношение -^ ( = б0) показывает, сколько единиц массы т
1л S
приходится на единицу длины s. Это постоянное отношение назы-
называется плотностью (линейной) однородной линии.
Но пусть теперь материя распределена неравномерно. Рассмот-
Рассмотрим участок линии от s до s+As; масса Am этого участка выра-
выражается так:
38] § 1. производная 119
Отношение -~ массы к длине уже не будет постоянным, а будет
зависеть и от s, и от As; оно называется средней линейной
плотностью линии (проволоки):
гч Am
При одной и той же массе Am на данном интервале (sy s-\-As)
материя может быть распределена самым различным образом, и в
о km
частности равномерно. Значит, средняя плотность — равна плот-
плотности, с которой нужно распределить материю равномерно на
том же интервале (s, s-\- As), чтобы общая масса ее осталась той же
самой, равной Am. Таким образом, средняя плотность только, как
говорят, «в общем», «в среднем» характеризует распределение
материи на данном участке. Чтобы избежать такой неопределенно-
неопределенности, вводят плотность в данной точке линии (при данном s).
Эго понятие устанавливают, исходя из того соображения, что
средние плотности, соответствующие уменьшающимся участкам
длины As, все лучше характеризуют распределение материи.
В связи с этим мы скажем, что линейной плотностьюх) 6 материаль-
материальной линии в данной ее точке s называется предел средней линейной
плотности 6ср, соответствующей интервалу (s, s-\- As), при стремлении
As к нулю:
о »• с ,. Am t. Ф (s + As) — Ф (s)
б = hm бср = lim — = lim v } *-*-.
HI. Теплоемкость и скорость химической реак-
реакции. Рассмотрим коротко два других понятия, вводимых по тем
же соображениям и определяемых совершенно так же, как скорость
движения и плотность, а именно, понятия теплоемкости и скорости
химической реакции.
Теплоемкостью*) с тела при температуре х называется предел
средней теплоемкости сср, соответствующей интервалу (т,
при стремлении Ах к нулю:
дт-о Ат
где q = W(x) — количество тепла, сообщаемое телу при нагревании
его до температуры х.
1) Плотность равномерно распределенной материи численно равна
массе, заключенной в единице длины линии; размерность линейной плот-
плотности в единицах СИ — кг/м.
2) Единица измерения теплоемкости—джоуль на градус (дж/град)*
120 ГЛ. III. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ [39
Скоростью химической реакции у относительно участвующего в ней
вещества в данный момент времени t называется предел средней
скорости Ycpi соответствующей интервалу (t, t + At), при стремлении
At к нулю:
р Yc
At к нулю:
еде m = F(t) — количество вещества, вступившее в реакцию за время t*
39. Скорость изменения функции. Производная функция. Про-
Производная степенной функции.
I. Скорость изменения функции. Каждое из четырех
специальных понятий: скорость движения, плотность, теплоемкость,
скорость химической реакции, указанных в п. 38, несмотря на
существенное различие их физического смысла, является с мате-
математической точки зрения, как легко заметить, одной и той же
характеристикой соответствующей функции. Все они представляют
собой частные виды так называемой скорости изменения
функции, определяемой, так же как и перечисленные специ-
специальные понятия, с помощью понятия предела.
Разберем поэтому в общем виде вопрос о скорости изменения
функции у = / (а:), отвлекаясь от физического смысла переменных
х и у.
Пусть сначала f(x) — линейная функция:
Если независимая переменная х получает приращение Ах, то
функция у получает здесь приращение Ау = аАх. Отношение
Аи
-~=д остается постоянным, не зависящим ни от того, при
каком х функция рассматривается, ни от того, какое взято Дат.
Это отношение называется скоростью изменения линейной функции.
Но если функция y—f{x) не линейная, то отношение
Дд: Ах
зависит и от л;, и от Ах. Это отношение только «в среднем»
характеризует функцию при изменении независимой переменной
от данного х до х + Ах; оно равно скорости такой линейной
функции, которая при взятом Ах имеет то же приращение Дд>.
Определение. Отношение ^ называется средней ско-
скоростью vcp изменения функции в интервале (х, х-\- Ах).
Ясно, что чем меньше рассматриваемый интервал, тем лучше
средняя скорость характеризует изменение функции, поэтому мы
заставляем Дл; стремиться к нулю. Если при этом существует
39] § 1. производная 121
предел средней скорости, то он принимается в качестве меры,
измеряющей скорость изменения функции при данном х, и назы-
называется скоростью изменения функции.
Определение. Скоростью изменения функции в данной
точке х называется предел средней скорости изменения функции
в интервале (jc, x -j- Алг) при стремлении Ах к нулю:
9ШЯ {im «„-if ?.-if
II. Производная функция. Скорость изменения функции
yz=zf{x) определяется посредством такой последовательности
действий:
1) по приращению Длг, придаваемому данному значению х,
находится соответствующее приращение функции
2) составляется отношение -^-\
' Ад;'
3) находится предел этого отношения (если он существует)
при произвольном стремлении Ах к нулю.
Как уже отмечалось, если данная функция f(x) не линейная,
то отношение -^- зависит и от лг, и от Ах. Предел этого отно-
отношения зависит только от выбранного значения х и является,
следовательно, функцией от х. Если же функция f(x) линейная,
то рассматриваемый предел не зависит и от лт, т. е. будет вели-
величиной постоянной.
Указанный предел называется производной функцией от функ-
функции f (х) или просто производной от функции f (х) и обозначается
так: /' (лг). Читается: «эф штрих от Jt» или «эф п р и м о т л;».
Определение. Производной данной функции называется
предел отношения приращения функции к приращению независи-
независимой переменной при произвольном стремлении этого приращения
к нулю:
Значение производной функции в какой-либо данной точке х0
обозначается обычно /' (л:0) или у'х_х
Пользуясь введенным определением производной, можно ска-
сказать, что:
1) Скорость прямолинейного движения есть производная от
функции s = F(t) no t (производная от пути по времени).
2) Линейная платность есть производная от функции m = Ф ($)
по s (производная от массы по длине).
122 гл. ш. производная и дифференциал 139
3) Теплоемкость есть производная от функции q — Wit) по t
(производная от количества тепла по температуре).
4) Скорость химической реакции есть производная от функции
y=zF(t) no t (производная от количества вещества по
времени). И вообще скорость изменения функции y—f(x) есть
производная от у по х.
Понятие производной принадлежит к числу фундаментальных
понятий математического анализа. Один из основателей анализа —
И. Ньютон1) пришел к понятию производной, исходя из вопроса
о скорости движения.
IIL Пр о и з в о д н а я степенной функции.
Найдем производные от некоторых простейших функций.
Пусть у = х. Имеем
/ /ч/ 1- (х + Ах)—х ,. Ах л
/ = (*) =hm --^т-^ = lim Т=1,
т. е. производная (х)' есть постоянная величина, равная 1. Это
очевидно, ибо у = х—линейная функция и скорость ее изменения
постоянна.
Если у = х2, то
f*a ***+<**>'+A*)-to.
Пусть у = х2, тогда
АХ-+О
Легко заметить закономерность в выражениях производных
от степенной функции у = хп при /1=1, 2, 3. Докажем, что и
вообще производная от у = хп при любом целом положительном
показателе п равна пхп~х.
Имеем
—ха
Ах Ах
Выражение, стоящее в числителе, преобразуем по формуле бинома
Ньютона:
{х + Ах)п—хп = хп + пхп"г Ах + "(/^~]) хпАх2 + ... + Ахп—хп.
х) И. Ньютон A642—1727) — великий английский ученый (математик,
физик, астроном). Ньютон заложил основы многих разделов науки нового
времени, завершил создание основ математического анализа. Творения
Ньютона способствовали преодолению средневековой схоластики и внесли
неоценимый вклад в дело выработки подлинно научного материалистиче-
материалистического мировоззрения.
40] § 1. производная 123
Значит,
В правой части последнего равенства стоит сумма п слагаемых,
первое из которых не зависит от Дл:, а остальные стремятся
к нулю вместе с Ах. Поэтому
Urn %> = nxn-\
Итак, степенная функция у = хп при целом положительном п
имеет производную, равную пхп~х\
(xn)f = пхп.
При л=1, 2, 3 из найденной общей формулы следуют фор-
формулы, выведенные выше.
Позже (п. 45) мы докажем, что этот результат верен и для
любого показателя л, например:
Рассмотрим теперь отдельно производную от постоянной
величины
Так как эта функция не изменяется с изменением независимой
переменной, то Ду = О и -^ = — = 0. Следовательно,
т. е. производная постоянной равна нулю.
40. Геометрический смысл производной. Производная от
функции y=f(x) имеет очень простой и наглядный геометриче-
геометрический смысл, который тесно связан с понятием касательной к
линии.
Определение. Касательной М0Т к линии АВ в ее
точке Мо (рис. 50) называется предельное положение прямой»
проходящей через точку Мо и другую точку М линии, когда эта
точка М стремится слиться с данной точкой Мо.
Предельное положение прямой линии определяется тем, что
угол ТМ0М стремится к нулю вместе с хордой М0М.
124
ГЛ. Ш. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ
140
Геометрический смысл производной вытекает из следующего
предложения.
Теорема. Если значение производной от функции у =/(<*)
при
(х0, yQ)
равно /'(^оI)» т0 прямая, проведенная через точку
с угловым коэффициентом, равным /' (jt0), является
касательной к графику функции
в точке Мо.
Доказательство. Про-
Проведем через точку Жо (рис. 50)
прямую М0Т с угловым коэф-
коэффициентом f'(x0); это значит,
что/'(Aro) = tga, где a—угол
наклона прямой М0Т к оси абс-
абсцисс. Придадим затем х0 при-
приращение Длг, возьмем точку Ж,
лежащую на графике функции
и соответствующую значению
аргумента лго + Длг, и проведем
секущую М0М. Угловой коэффи-
коэффидо+Ах as
Рис. 50
циент этой секущей равен д^-^д*» где АУ==/(*о + Д*) — f(xo)-
Пусть теперь Ах—> (); тогда точка Ж будет стремиться по
линии АВ к точке Мо. Секущая МЬМ при этом поворачивается
вокруг точки М0У и ее угловой коэффициент стремится по усло-
условию теоремы к определенному пределу
lim ^-/'i
{*)
равному угловому коэффициенту прямой М0Т. По формуле для
тангенса угла между двумя прямыми (М6Т и МЬЩ
В силу равенства (*) при Длт-*О числитель дроби стремится к нулю,
а знаменатель — к числу 1 +[/' (хо)]2^О. Поэтому tg^ TM0M стре-
стремится к нулю, а значит, и сам 2i TMoM тоже стремится к нулю.
Таким образом, мы доказали, что прямая М0Т является касатель-
1) Подчеркнем, что значение производной /' (х0) отыскивается так:
сначала ищем производную /' (х), а потом в выражение для производ-
производной подставляем данное значение х0. Грубой ошибкой было бы сначала
найти /(х0) и потом дифференцировать; так как / (*о) — величина постоян-
постоянная, то мы всегда получали бы нуль!
41] § 2. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ 125
ной. Установленный геометрический смысл производной коротко
формулируют так:
Значение производной /' (лг0) равно угловому коэффициенту
касательной к графику функции y~f(x) в точке с абсциссой лг0.
Заметим здесь, что именно вопрос о точном определении и
построении касательных к линиям привел Г. Лейбница1) к
установлению (одновременно с И.Ньютоном) понятия производной.
§ 2. Дифференцирование функций
41. Дифференцирование результатов арифметических дейст-
действий. Действие отыскания производной называется дифферен-
дифференцированием (объяснение этого названия будет дано немного
дальше, в п. 50). «Продифференцировать функцию
f(x)» — значит найти ее производную f (х). Для этого нужно
найти
Такое непосредственное отыскание предела в большинстве
случаев представляет собой весьма громоздкое и трудное дейст-
действие. Но если знать—раз и навсегда — производные всех основных
элементарных функций (мы пока знаем только производную сте-
степенной функции у=*хп), а также правила, по которым следует
дифференцировать сложные функции, и результаты арифметиче-
арифметических действий, то можно находить производные любых эле-
элементарных функций, не выполняя всякий раз указанного
предельного перехода.
Выведем прежде всего правила дифференцирования арифмети-
арифметических действий. Мы будем предполагать, что функции-компоненты,
т. е. слагаемые, сомножители, делимое и делитель, непрерывны
и имеют производные при рассматриваемых значениях независимой
переменной. Из доказательств приводимых ниже теорем тогда
вытекает, что функции-результаты, т. е. сумма, произведение,
частное, также имеют производные при тех же значениях неза-
независимой переменной. Имея в виду это обстоятельство, мы не будем
всякий раз на него указывать, чтобы не загромождать формули-
формулировки теорем, а будем включать в эти формулировки только
вопрос о том, как найти производную результата, если известны
производные компонент.
г) Г. Лейбниц A646—1716)—-великий немецкий ученый, прославив-
прославивший свое имя э самых различных областях науки (математика, физика,
философия, история и т. д.). Он вместе с И. Ньютоном завершил создание основ
математического анализа; ему принадлежит большое число первоначальных
открытий в дифференциальном и интегральном исчислении.
126 ГЛ. Ш. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ {41
Теорема I. Производная суммы конечного числа функций
равна сумме производных слагаемых.
Доказательство. Пусть функция у задана как сумма
других функций и, v, ..., w той же независимой переменной х:
Докажем, что
/=z(u + v + ... 4-«>)' = и' + г>'+...-f w'.
Придадим независимой переменной х приращение Дл:; функ-
функции и, v, ..., w получат соответственно приращения
Ди, Av, ..., Д^, а функция у—приращение Ау. Ясно, что
у + Ау = (и + Аи) + (v + Av) + ... +(w-\-Aw).
Вычитая отсюда функцию у, получим
Ау г= Аи + Дг> + ... -f Aw>
откуда, деля обе части на Дат, найдем
Д^Аи Аи Aw
Переходя к пределу при Ах—>() и воспользовавшись теоремой
о пределе суммы (п. 29), будем иметь
,. Аи , t4 Av , , ,. Aw
hm -- + hm E+ ... + lim j-
так как
lim А?=у, lim ^ = «', Шп ?-*', .... II» g
то мы и приходим к доказываемому равенству.
Примеры. 1) jy = jc3—х2 + х—1. Имеем
)' — A)' = 3лг2 — 2х+\.
2) ху = х-\ . Имеем
~2
Теорема II. Производная произведения двух функций равна
сумме произведений производной первой функции на вторую и
производной второй на первую.
41] § 2. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ 127
Доказательство. Пусть функция у задана как произве-
произведение двух функций:
y = uv.
Докажем, что
у' = (uv)' = u'v + v'u.
В самом деле, придадим независимой переменной приращение
Ддг; при этом функции и, vy у получат соответствующие прира-
приращения Ди, Avy Ay, Наращенное значение функции будет
Аи) (v +
Отсюда
Ау в {у + Ау) —у = (и + Аи) (v + Av)—uv = Аи • v -f иAv + АиAv
Применяя известные правила предельного перехода и учиты-
учитывая, что при Ах—>-0 также и Av—*-0, как приращение непрерыв-
непрерывной функции, найдем
lim J2= lim pv + a lim ^+ lira ^ lim Av =
= u'v + uv' + u' -0 = a'
что и требовалось доказать.
Если один из множителей есть постоянная величина, например
v — Ct то получаем
у = (Си)' = C'w + Са' = Са',
ибо производная от постоянной равна нулю. Значит, постоянную
величину можно выносить за символ производной.
Правило дифференцирования произведения двух функций по-
последовательно распространяется на произведение какого угодно
конечного числа функций. Так, если y = uvw> то
у' — (uvw)'~ (uv)'w-\~uvw' = (u'v + uv') w + uvw' =
== u'vw + uv'w + uvw\
т. е. производная произведения трех функций равна сумме трех
слагаемых, причем каждое из них является произведением двух
из данных функций на производную третьей.
128 гл. ш. производная и дифференциал 141
Примеры. 1) у = 5х3—2х*-\-Ъх— 1. Имеем
у'^Ь(х*)' — 2{х*)' + Ъ{х)' — A)' = 15л:2 —
2) у==Bх + 3)(\—х)(х-\-2). Имеем:
Мы получим, разумеется, тот же ответ, если, раскрыв скобки
в заданном произведении, продифференцируем получающийся при
этом многочлен третьей степени.
Теорема III. Производная частного двух функций равна
дроби, знаменатель которой равен квадрату делителя, а числи-
числитель— разности между произведением производной делимого на
делитель и произведением делимого на производную делителя.
Доказательство. Пусть функция у задана как частное
двух функций и и v:
Докажем, что
Действительно,
и + Аи
Ay v+ Ау
У-
и
У
и'у—иу'
v
Аи-у — иАу
Аи
AxV
Ау
U Ах
Переходя к пределу при Ах—>0 и учитывая, что Av стремится
к 0, как приращение непрерывной функции, получаем
,. Аи ,. Ay
v lim -г и lim г—
* у (у+lim Ау)
что и требовалось доказать.
Примеры. 1; у = "Г х. Имеем
, B—За:)' B+д:) —B—Зл:) B + х)' —3 B + л:) — B—Зл)
у = -г м L = т ;:
2) д>=.лт~л, где п—целое положительное число. Имеем
42] § 2. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ 129
что подтверждает правило дифференцирования степенной функции
для случая целого отрицательного показателя.
Q
3) у~— , где С—постоянная, а и — функция от х. Имеем
, С'и — Си! ги^
этот результат следует запомнить; в частности, при и =
СУ С
)
4)^ = -^-, где С—постоянная. Для начинающего бывает
соблазнительным дифференцировать эту функцию по правилу
дифференцирования дроби. Этого делать не следует. Здесь дело
обстоит гораздо проще: нужно заметить, что эту функцию можно
представить как произведение постоянного множителя -^ на
функцию и:
поэтому
•-(И-¦*--?••
42. Дифференцирование сложной и обратной функций.
I. Дифференцирование сложной функции. Очень
важным является правило дифференцирования сложной функции5
указывающее выражение для ее производной через производные
функций, из которых она составлена.
Теорема. Производная сложной функции равна производной
заданной функции по промежуточному аргументу, умноженной
на производную этого аргумента по независимой переменной.
Доказательство. Пусть у =/(и)} н = ф (л:). Докажем, что
Придадим х приращение Ах\ оно вызовет приращение Аи
промежуточного аргумента и = (р(х), которое в свою очередь
повлечет изменение функции у на некоторую величину Д^/.
Для отыскания производной^' нужно найти lim -~ при Ах—*0.
Представим отношение д^ в виде
Aj/ __ At/ Дц
Ах ~~ Аи Д* '
5 А. Ф. Бермант, И. Г. Араманович
130 ГЛ. III. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ f42
Тогда в силу правила предельного перехода в произведении по-
получим
lim **- lim *У lim ^
(Ла—>О при Длг —* 0, так как и = ф(лг) — непрерывная функция).
Так как
lim |5=/'(«) и lim ?i«4>'(*),
то мы приходим к доказываемой формуле *).
Итак, для того чтобы продифференцировать сложную функцию
у =/[ф (л?)], нужно взять производную от «внешней» функции /,
рассматривая ее аргумент ф(лг) = а просто как переменную, по
которой совершается дифференцирование, и умножить на про-
производную от «внутренней» функции ф (х) по независимой пе-
переменной.
Примеры. 1) у = Bх2—IK. Эту функцию можно рассматри-
рассматривать как сложную функцию, составленную из кубической функции
у = и* и квадратичной и —2л;2 — 1. Имеем
Легко проверить правильность результата. Раскрывая куб раз-
разности, имеем: у — 8х6—12л:4 + 6л:2—1; дифференцируя этот мно-
многочлен, получим тот же ответ.
/ 1 \100
2) у=\х-\— ) . Здесь возводится в сотую степень функция
\ * J
и= х-\ . Имеем
х
1у= 100
Легко видеть все преимущества дифференцирования этой функ-
функции с помощью правила дифференцирования сложной функции по
сравнению с возможным дифференцированием ее как многочлена,
полученного от раскрытия бинома в сотой (!) степени по формуле
Ньютона.
г) Приведенное доказательство теряет силу, если Да будет обращаться
в нуль. Можно доказать (на этом мы не останавливаемся), что теорема и
в этом случае оказывается справедливой.
42] § 2. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ 131
3) у — У\ -\-х2. Полагая у — ]/*и , и=\-\-х2, имеем
Предположим теперь, что у, как функция независимой пере-
переменной л:, представляется посредством цепи, состоящей не из двух,
а из трех функций:
Согласно доказанному правилу имеем
где и'— производная от и, рассматриваемая как функция от неза-
независимой переменной х. На основании того же правила
и' = ц' (v)v' ^y'iv)^' (х).
Подставляя это выражение в предыдущее равенство, получаем
/=/'(и) ф» *'(*)•
Аналогично выводится формула при любом числе промежуточ-
промежуточных аргументов. Во всех случаях производная у' получается как
произведение производной по первому промежуточному аргументу
на производную от первого по второму, на производную от вто-
второго по третьему и т. д., наконец, на производную последнего
(считая от у к х) промежуточного аргумента по х.
Коротко можно сказать так:
Производная сложной функции равна произведению производ-
производных от функций, ее составляющих.
Пусть, например, у = A +1/х2+ IJ- Представляя эту функцию
в виде цепи, получим у = и2, #=1 -\~V~v, v = x2-\-\. Дифферен-
Дифференцируя, получим
II. Дифференцирование обратной функции. Пусть
y~f(x) и х = (р(у) — пара взаимно обратных функций (см. п. 18).
Покажем, что если известна производная от одной из этих функ-
функций, то легко получить выражение для производной другой. Допу-
Допустим, например, что нам известна производная /' (х) = lim -г-^ и
она не равна нулю. Чтобы найти производную ф' (у), нужно найти
предел lim ^-. Так как Ал;—>0 при Ду—>0 (мы рассматриваем
1Я2 ГЛ. HI. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ [42
только непрерывные функции), то из тождества д-^-т— получим
Ах
lim ?~_!¦
lim ±Ц
д* -* о Л*
т. e. что у'(y)=-p—r. Аналогично, если <p'(y)^O, то /'(#) =
= / / v. Коротко можно сказать, что производные от взаимно
обратных функций обратны по величине.
&k i/ Записывают это так:
V
=7 или *»в7
где индексы х и у показывают, по
какой переменной производится диффе-
дифференцирование, т. е.какая из переменных
принята за независимую.
Связь между производными взаимно об-
обратных функций весьма наглядно иллюстри-
иллюстрируется геометрически. В самом деле, пусть
линия LU является графиком функции
«/==? (jc) (рис. 51). Тогда
Уравнение линии LV можно записать и как х=ф(#). Производная
этой функции по переменной у, очевидно, равна угловому коэффициенту
той же касательной, но уже относительно оси Оу, т. е.
Но a-hP=-2", значит, tga = ctgP=-—^ , откуда
Таким образом, эта формула выражает собственно тот очевидный факт»
что углЫу образованные касательной к линии с осями координат, в сумме
дают -?? .
В качестве примера рассмотрим функцию y — \fx. Здесь х=у*
и х'у = Ъу*. Следовательно (мы опускаем индекс у у')9 -у'=^ •
Выразим теперь производную у' через независимую перемен-
переменную х. Для этого подставим в полученное равенство вместо у его
43] § 2, ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ 133
значение
3 \/ х2
Предоставляем читателю самому продифференцировать функцию
у = у//лг = лг1'3 по общей формуле дифференцирования степенной
функции и убедиться в том, что результат будет тот же.
43. Производные основных элементарных функций. В п. 39
мы нашли производную степенной функции у = хп:
У=пхп'К A)
Найдем теперь производные всех остальных основных элементар-
элементарных функций. Ради краткости приращение Ах будем обозначать
через h.
1. Производные тригонометрических функций.
Пусть
Придадим х приращение Ax = h. Тогда
v г» . x-\-h—х x-\-hA-x
) — sin л: = 2 sin--^-т: cos ^ ^ ¦-
Следовательно,
. h
sin -^r
. h
sin -^
у = lim ^= lim —r=- lim cos
2
По доказанному в п. 30 первый множитель равен единице, а
lim cos I лг -f — ) = cos (x + 0) = cos x,
так как cos л; — непрерывная функция.
В итоге
(sin л;)'= cos л:. B)
Формулу для производной функции y — zosx выведем на осно-
основании правила дифференцирования сложной функции. Так как
134 ГЛ. III. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ [43
= sin (х + yj, то,
' = (sin и)' и! = cos и» 1 ==cos
cosjn; = sin (х + yj, то, полагая л; + у = «1 находим
т. е.
(cosje)'= — sin*. C)
Рекомендуем читателю получить эту формулу иным путем —
отыскивая производную по общему правилу.
Производные для функций y — tgx и y — ctgx получим, приме-
применяя правило дифференцирования частного:
у. v/ /"sin* У (s'mxy cos *—(cos*)' sin x cos2* + sin2 x 1
^ ' \cos^y cos2* cos2* cos2*'
(cte xY — (COSXY — (c°s^)'sin*—(sin*)' cos * _
* * ' \sinл: У ~~ sin2* ~"
-sm* x—cos4*
sin4 * sin4 *
Итак,
(ctg*)' д^. E)
Примеры. 1) ^ = xsinAr. Имеем
у' == {x)'%\x\ x + x (sin x)' = sin x + дг cos дг.
cos*
m cos* f.
2) д; = . Имеем
, (cos*)'*—cos*(*)' *sin* + cos*
3) y = tg5x. Полагая y = \gu и и — 5х, получим
4) у =z sin3 2л;. Полагая y — tP, u = slnv и ^==2^, получим
у' = За2 cos v • 2 = 6 sin2 2x cos 2л:.
II. Производные обратных тригонометрических
функций. Производные обратных тригонометрических функций
легко получить, применяя правило дифференцирования обратной
функции (п. 42).
43] § 2. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ 135
Пусть у — arcsin х\ тогда х — sin у и a^ = cos^. Отсюда
' - -L— *
ху
Чтобы получить выражение для производной через независимую
переменную лг, надо вместо cos^y подставить его выражение
через лг, т. е.
= 1/^1 — sin2 у = 1/1 — х2.
Корень берется арифметический, потому что значения функции
yz=sncs\nx лежат в интервале (—-=-, -^ 1, a cos^r в этом интер-
интервале положителен.
Отсюда
(arcsinх)' = .-1—-^ . F)
Обращаем внимание читателя на то, что при #=±-п-, т. е. для дс =
= ± 1 производной не существует, хотя сама функция */ = arcsin# в этих
точках определена. Подробнее вопрос о дифференцируемости функций будет
рассмотрен в п. 52.
Совершенно аналогично получим, что функция у = arccos.? имеет
производную для всех значений х в интервале (—1, 1), причем
=-^JL=. G)
Теперь рассмотрим функцию у == arctg л:. Обратная ей функция
х =
У
У COS2 у '
Следовательно,
' « C0S2 _ 1 __ _J
Итак,
(arctg дг)'=г-^ (8)
и аналогично
(arcctg х)' = — , 2 • (9)
Примеры. 1)<у = Аг2 arcsin x. Имеем
j;' = 2л: arcsin л;
136
ГЛ. III. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ
[43
2)
1—X
. Имеем
Здесь производная выражается точно так же, как и производ-
производная от arctgjt. Это и не удивительно, ибо функции arctg-r-i^ и
arctgjc отличаются друг от друга на постоянное слагаемое: ~-,
если аг < 1, и ~, если х > 1.
III. Производные логарифмической и показа-
показательной функцией. Рассмотрим логарифмическую функцию
у = 1пх. Дадим х приращение h. Имеем
In
In
x + h
. ( , , h\
In \-\ }
\ */
Перепишем это так:
Отсюда
lim -т^= lim
= — lim
а это согласно пределу, найденному в п. 37, II, дает
lim -т^ = —.
/i-o h х
Итак, логарифмическая функция ^ = 1"^ имеет производную,
равную —:
(lnx)' = l. A0)
Теперь пусть y = \ogax. Известно (п. 20, II), что logaA: =
= \nx\ogae и, значит, (\ogax)' = loga e (In x)' =^^-
В частности,
/1 ч/ ^ 0,43429 . .. . .
(Ig^) ^^ (M=lg*)
43] § 2. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ 137
Для отыскания производной показательной функции восполь-
воспользуемся снова правилом дифференцирования обратной функции.
Если у~ах, то 1п^ = лг1па и лг = т^. Отсюда л;^=—г— и
у\—у 1п а — ах\па. Таким образом,
(ах)' = ах\па. (И)
В частности, если а = е, то
<**)'=**. A2)
Следовательно, функция у = ех при дифференцировании не
меняется.
Примеры. 1) у = х\пх, у' = (х)' In лг + лгAп л:)'= 1пл:4- 1.
2) у = (In л:K, у' = 3 (In лг)а (In л;)' = 3
3) jr-lnsln*, /«^
4) y = e~x. Полагая у = еа и и= —x, получим
у' = (еиУ и' = —е'х.
IV. Производные гиперболических и обратных
гиперболических функций. В соответствии с определе-
определениями, данными в п. 23, имеем:
)" chjc —sh ^(chA:)' ch2 x — sh2 jc 1
В этих формулах мы снова замечаем аналогию между гиперболи-
гиперболическими и тригонометрическими функциями.
Производные обратных гиперболических функций можно полу-
получить или по общему правилу дифференцирования обратных функ-
функций, или исходя из их выражений через логарифмическую
функцию (п. 23); мы предоставляем это сделать читателю и при-
приведем лишь окончательный результат:
(Arsh jc)' = (In (jc
(Arch x)f = (In (jc ± /jrZT))' = ±.
1
V*2 — l
(знаки ± соответствуют двум однозначным ветвям)
138 гл. т. производная и дифференциал [44
44. Дифференцирование элементарных функций. Примеры.
После того как мы вывели правила и формулы дифференцирова-
дифференцирования, мы в состоянии отыскивать производные любых элементар-
элементарных функций. При этом нам уже не приходится прибегать к оты-
отысканию пределов.
Для удобства выпишем таблицу основных правил и формул
дифференцирования, которую необходимо знать наизусть.
Правила дифференцирования:
ittVi —— It Ч) ~т— v t/
uV u'v— v'u
V
Формулы дифференцирования:
1) (хпу = пхп~1у 7) (arccos jc)' = — yL
2) (sin jc)' = cos jc, 8) (arctg x)r = 2,
3) (cosjc)' = — sinjc, 9) (arcctgjc)'=— !
7 x ъ ' cos2 jc ' ' y ' x
5) (Ctgjc)<= —sl~^, 1]) (a*)' = a* In a,
6) (arcsin jc)' = . ! , 12) (ex)' = e\
V \ — x2
Если у =/ (д), и = q> (jc), то у' —f {и) <р' (х).
Примеры. 1) ^ = gsinB«+i)e Полагая y — eat u — sinv,
v = 2x-\-\y получим
^у' = (ett)f (sini;)' Bjc+ 1)' = еи cos v• 2 = 2esin <2X+1> cos Bjc+ 1).
С накоплением опыта в дифференцировании отпадет необхо-
необходимость вводить специальные обозначения для промежуточных
аргументов. Обычно дифференцирование сложных функций произ-
производят, выделяя в уме простейшие звенья, ведущие от у к лг.
у' = sin Зх + х (sin Зл:)' = sin Зл: + Зл; cos Зл:.
45] § 2. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ 139
46. Дополнительные замечания о дифференцировании функций.
I. Логарифмическое дифференцирование. Функ-
Функцию вида
где и основание и показатель изменяются вместе с независимой
переменной, называют степенно-показательной. Простейшим при-
примером такой функции является функция
у = хху лг > 0.
Дифференцировать эту степенно-показательную функцию можно
как сложную функцию, записывая ее выражение так:
Xх = (б1п х)х = ех *п х.
Тогда
(Xх)' = ех1пх (х In х)' = Xх (In x +1).
Но можно поступить иначе, предварительно прологариф-
прологарифмировав эту функцию:
Дифференцируя это тождество по л; и помня, что в левой
части равенства стоит сложная функция от х> получим
откуда
у1 =у (In х+ 1) =хх (In х + 1).
Таким образом, мы получили то же выражение, что и найденное
другим путем.
Операция, состоящая в последовательном применении к функции
f(x) сначала логарифмирования (по основанию е), а затем диф-
дифференцирования, называется логарифмическим дифференцированием,
а ее результат
— логарифмической производной от функции f(x).
Логарифмическое дифференцирование может быть применено
для отыскания производных не только от функций степенно-по-
степенно-показательного типа. Так, например, для отыскания производной от
произведения
у = 2xVx2 + 4 sin2 x
удобно применить логарифмическое дифференцирование, что
140 гл. in. производная и дифференциал [45
позволяет быстрее найти результат. Имеем
In у = х In 2 + 2 In sin x + у In (л;2 + 4)
Пользуясь логарифмическим дифференцированием, можно доказать
справедливость формулы
*ля любого п. До сих пор она была доказана лишь для п целого
(п. 39, III). Логарифмируем функцию у=хп, считая х > 0:
\пу = п In х.
Дифференцируя, получим — = —, откуда
#'=— хп = пхп~1.
Если х < 0, то для тех показателей степени, при которых функция
определена, ее можно записать в виде у = (—\)п (—х)п\ дифференцируя
полученное выражение как сложную функцию, снова придем к доказывае-
доказываемой формуле.
II. Производные неявных функций. Допустим, что у
есть неявная функция х, т. е. она задается некоторым уравне-
уравнением, связывающим независимую переменную х с функцией уу
не разрешенным относительно у (см. п. 12). Тогда производную
от этой функции можно найти, дифференцируя по х обе части
уравнения с учетом того, что у есть функция от х (определяемая
этим уравнением). Выясним на примерах практический смысл этого
правила.
Найдем производную функции у, заданной уравнением
(уравнение окружности). Дифференцируя по х и имея в виду,
что у есть функция от х, получим
откуда
У
В этом примере нетрудно найти явное выражение для у,
именно yz=\f\—х2. Дифференцируя эту функцию, получаем:
у' — у —результат, как легко видеть, совпадающий
У 1 — х
46) § 2. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ 141
с только что найденным. (Если считать, что \^\—х% < 0, то
мы получим производную для ветви, определяемой условием
^<0.)
Возьмем еще неявную функцию y—f(x)y определяемую урав-
уравнением
у3—
Дифференцируя по лг, найдем
Зу2/ — Зау —
откуда
Здесь уже трудно выразить производную только через неза-
независимую переменную х. Иногда, пользуясь первоначальным урав-
уравнением, связывающим у и лг, удается упростить выражение для
производной. Например, возьмем неявную функцию ху2 ~ех+у.
Дифференцируя, получим у2-\-2xyy' — ех+у A +дО, откуда
У* = 5——Г^+у * Заменяя ех+у на ху2, придаем производной более
простой вид1):
У хB-у)-
Таким образом, всякую неявную функцию, заданную уравне-
уравнением, составленным из элементарных функций, легко продиффе-
продифференцировать по известным нам правилам независимо от того,
можем ли мы эту функцию представить в явном виде или нет.
Производная такой неявной функции выражается через незави-
независимую переменную и саму функцию.
46. Параметрически заданные функции и их дифференциро-
дифференцирование.
I. Параметрическое задание функций и линий.
Зададим две функции одной и той же переменной t\ обозначим
их через х и у\
Задание этих функций означает задание функциональной
зависимости между переменными х и у. В самом деле, для каждого
значения t (в некоторой области) из системы (*) находятся зна-
значения х и у, которые и являются соответствующими друг другу.
1) То же самое можно получить, если предварительно прологарифми-
прологарифмировать формулу, определяющую функцию.
142 гл. т. производная и дифференциал [46
Определение. Задание функциональной зависимости
между двумя переменными, состоящее в том, что обе перемен-
переменные определяются каждая в отдельности как функции одной и
той же вспомогательной переменной, называется параметри-
параметрическим, а вспомогательная переменная — параметром.
Отыскание по системе (#) непосредственной связи между
переменными х и у без участия переменной t называется исклю-
исключением параметра. В результате исключения параметра мы полу-
получаем уравнение между х и у, задающее одну из этих переменных
как явную или неявную функцию другой.
Прямой путь для исключения параметра таков: из первого,
например, равенства находим выражение для t через лг, т. е.
t=%(x), где % — функция, обратная функции ф, и подставляем
это выражение во второе равенство:
Таким образом мы получаем явное выражение для у как функции
от х. В конкретных случаях употребляются и другие приемы
исключения параметра (см. II, пример 1).
Рассматривая зависимость между хну как уравнение соот-
соответствующей линии, можно сказать, что линия задана парамет-
параметрически, или, точнее, параметрическими уравне-
уравнениями.
Параметрическое задание функций и линий часто имеет
преимущества по сравнению с другими формами их задания.
В то время как непосредственная связь между х и у может быть
весьма сложной, функции, определяющие хну через параметр,
могут оказаться простыми. Кроме того, при параметрическом
задании заранее не предусматривается, какая именно из перемен-
переменных принимается за независимую и какая —за функцию.
Заметим, что если хотя бы одна из функций системы (*)
постоянна, то исключить параметр t нельзя. Например, уравне-
уравнения аг=1, y = sint не дают возможности связать хну. Здесь
точки с координатами ху у, соответствующие различным значе-
значениям t, располагаются на отрезке прямой х ==¦¦!, заключенном
между точками A, —1) и A, 1).
Параметр может иметь различное истолкование в соответствии
с характером функциональной зависимости.
Параметрически заданные функции особенно часто встречаются
в механике при задании траектории движения. Параметром
служит при этом время t, а фукции х (t) и у (t) выражают законы
движения проекций движущейся точки на оси координат.
Исключая параметр t, мы получаем уравнение траектории
в виде связи между х и у — координатами движущейся точки.
461
§ 2. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
143
Приведем один простой пример, а именно рассмотрим траек-
траекторию тела, сброшенного с самолета, летящего горизонтально
на высоте Н со скоростью v0. Выберем систему координат, как
указано на рис. 52, и примем, что тело
было сброшено в момент ? = 0 (из точ-
точки Мо). Пусть в момент t тело нахо-
находится в точке М (х, у). Так как в гори-
горизонтальном направлении на тело никакие
силы не действуют (мы считаем, что
сопротивление воздуха отсутствует г)),
то его горизонтальная скорость по-
постоянна и равна v0. Тогда пройденный
по горизонтали путь x-=vQt. За то же
время t тело по вертикали пройдет
gt2 Рис. 52.
путь s = ~~, где g—ускорение силы
тяжести, и поэтому у~Н— ^- (см. рис. 52).Мы получили урав-
уравнение траектории в виде
y = H—SL, x = vQt.
Исключим параметр t:
О
X
х
Из этого уравнения видно, что траекторией служит парабола,
а точка Мо является ее вершиной.
II. Примеры. Приведем несколько примеров параметрического
задания линий.
1) Возьмем окружность с центром в начале координат и
радиусом, равным а. Обозначим через t дугу окружности (в ра-
радианах) от точки (я, 0) до текущей точки (л;, у).
Очевидно,
х —a cost, y — a$\nt.
Это и есть параметрические уравнения окружности. Для исклю-
исключения t возведем в квадрат оба уравнения и сложим их почленно.
Мы будем иметь
Когда t пробегает интервал [0, 2я], точка с координатами
лг, у один раз обегает всю окружность, начиная от точки (а, 0).
Проверим, что параметрическими уравнениями этой же окруж-
окружности будут и такие (геометрический смысл параметра указан
1) При учете этого сопротивления задача значительно усложняется.
И 4 ГЛ. Ш. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ [46
ниже):
Возводя обе части в квадрат и складывая, получаем снова
При изменении параметра t от 0 до оо переменная точка про-
пробегает верхнюю полуокружность от точки (я, 0) до точки
(—а, 0), а при изменении t от 0 до —оо — нижнюю полуокруж-
полуокружность. Таким образом, при непрерывном изменении /от — оо до
-\- оо переменная точка один раз пробегает всю окружность против
часовой стрелки, начиная от точки (—я, 0). Здесь параметром /
служит тангенс половины дуги окружности от точки (а, 0) до
текущей точки {х, у), т. е. как раз той дуги, которая являлась
параметром в первых уравнениях. Рекомендуем читателю дока-
доказать это.
Приведенный пример показывает, что одна и та же линия
может быть задана разными параметрическими уравнениями.
2) Около эллипса с центром в начале координат и с осями
а и Ь, лежащими на осях координат, опишем окружность с тем
же центром и с радиусом, равным а (если а > д). Тогда, прини-
принимая в качестве параметра / дугу этой окружности от точки
(я, 0) до точки с той же абсциссой, что и текущая точка (х, у)
эллипса, получим параметрические уравнения эллипса
х = a cost, y = bs\nt.
Действительно, исключая из этих уравнений параметр tf придем
к известному каноническому уравнению эллипса
При изменении / в интервале [0, 2л) точка (а:, у) движется
по указанному эллипсу.
Аналогично уравнения
х = a ch t, y = bs\\t и х = — a ch t, y — bsX\t
представляют параметрические уравнения соответственно правой
х2 и2
и левой ветвей гиперболы^-—й"^1- в обоих случаях пара-
параметр t изменяется в интервале (— оо, оо). В силу этого функиии
ch/, sh/ и были названы гиперболическими.
46)
§ 2. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
145
3) Циклоидой называется линия, описываемая какой-нибудь
точкой окружности, катящейся без скольжения1) по прямой линии
(рис. 53).
Прямая линия, по которой происходит качение, называется
прямой, а катящаяся окружность—про-
линия,
направляющей
изводящей окружностью, радиус ее обозначим через а.
Рис. 53.
Примем за ось Ох направляющую прямую, а за начало коор-
координат— точку прямой, с которой совпадает фиксированная точка Мо
производящей окружности.
Для составления параметрических уравнений циклоиды выберем
в качестве параметра угол /, на который поворачивается окруж-
окружность при переходе фиксированной точки окружности Мо в по-
положение М (рис. 53). Этот угол равен углу между радиусом
катящейся окружности, проведенным в точку Му и радиусом,
проведенным в точку Р ее касания с осью Ох. Найдем абсциссу х
точки М циклоиды:
x=ON=OP—NP,
но OP=MP=at (окружность катится без скольжения!), а
)=Ж, = a sin/,
где t — радианная мера ?МСР. Значит, x~a(t — sin/). Анало-
Аналогично находится ордината у точки М:
Таким образом, параметрические уравнения циклоиды таковы:
х = a (t — sin/), у — а A —cos t).
1) Говорят, что одна линия катится по другой без скольжения,
если длина дуги, на которую поворачивается подвижная линия, точно
равна длине пройденного куска неподвижной линии.
146 ГЛ. III. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ [47
Одна волна циклоиды получается при изменении t в интервале
[О, 2я].
Если исключить параметр t, то зависимость между хну
оказывается весьма сложной:
х4: Vy{2a— у)=: a arccos ?~^, 0 <х < 2па.
III. Производные параметрически заданных
функций. Укажем способ отыскания производной параметри-
параметрически заданной функции. Пусть у как функция х задана пара-
параметрическими уравнениями
Дифференцируя вторую из заданных функций по правилу
дифференцирования сложной функции, получим
(индекс показывает, какая переменная считается независимой; по
ней и производится дифференцирование). Производную tx найдем
по правилу дифференцирования обратной функции
Окончательно
что можно короче записать так: ух=—7.
xt
Например, для углового коэффициента касательной к окруж-
окружности x = acos/, y~asint находим выражение
у\ a cos t
4t^
xt —a sin t
Так как угловой коэффициент радиуса, проведенного в ту же
точку окружности, равен, очевидно, tg/, то это означает, что
касательная к окружности перпендикулярна к радиусу.
§ 3. Геометрические задачи. Графическое дифференцирование
47. Касательная и нормаль к линии. Из геометрического смысла
производной следует, что если нам известно уравнение y—f(x)
некоторой линии / в системе декартовых координат Оху на
плоскости, то мы можем аналитически (т. е. с помощью вычисле-
47]
§ 3. ГЕОМЕТРИЧЕСКИЕ ЗАДАЧИ
147
ний) решать геометрические задачи, относящиеся к касатель-
касательной к этой линии. Прежде всего составим уравнение касательной
к линии / в ее точке А10(лг0, у0), где
yo — f{xo). Так как касательная прямая "л
проходит через точку Мо (х0, у0) и имеет
угловой коэффициент, равный /' (л;0)
(п. 40), то ее уравнение таково:
У—
— хо
Далее, дадим определения трех про-
простых геометрических понятий, связан- •
ных с касательной; все обозначения
соответствуют рис. 54. Рис. 54.
Определение 1. Направлением
линии в ее точке MQ называется направление касательной
М07\ проведенной к линии в точке Мо.
Определение 2. Углом у между двумя пересекающи-
пересекающимися в точке Мо линиями называется угол ТМ0Т' между ка-
касательными, проведенными к линиям в точке их пересечения.
Определение 3. Нормалью к линии в ее точке Мо
называется прямая M0N, проходящая через точку Мо и перпен-
перпендикулярная к касательной М0Т в той же точке.
Так как нормаль к линии / в точке Жо проходит через точку
уИ0(лг0, у0) и имеет угловой коэффициент, равный —,, , то ее
уравнение таково:
У— У о = — Лг, (х — х0). (**)
Приведем примеры, показывающие, как применяется произ-
производная при решении геометрических задач.
Примеры. 1) Возьмем параболу у~ах2. Уравнение каса-
касательной в точке М0(х01 у0) этой параболы имеет вид
но уо =
или
У Уо — *u>Xq \Х Xq),
и, значит,
у — 2ах0х—ах\ — 2ах0 (х ——-
Из этого уравнения видно, что касательная пересекает ось Ох
при х = ^у т. е. в середине S отрезка ON (рис. 55).
148
ГЛ. Ш. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ
[47
Таким образом, мы получаем простой способ проведения каса-
касательной к параболе. Докажем также одно важное свойство пара-
параболы, заключающееся в том, что нормаль (M0Q) в любой точке
параболы делит пополам
угол,образованный фокаль-
фокальным радиусом FM0 и прямой
А10М1у параллельной оси
параболы, т. е. что
j/^QMqF = j/^QMqM^ (рис.
55).
Из аналитической гео-
геометрии известно, что рас-
расстояние OF =-г- . Угловой
У>
0
F
О
А
/1
г
м'\/
!/
коэффициент
1
Рис. 55.
равен-
1
2ахл
циент нормали M0Q по предыдущему равен —
для тангенса угла между двумя прямыми находим
1^
4а 1
хп 2ахл
прямой FMQ
Угловой коэффя
. По формуле
1 —
1
2ах0
равен углу наклона касательной M0S коси абс-
абсС другой стороны,
Заменяя у0 через ах*, после простых преобразований получим
Поэтому
цисс, т. е.
Следовательно,
что мы и хотели доказать.
Указанное сейчас свойство параболы широко используется в тех-
технике. Так, например, прожекторам, автомобильным фарам придают
обычно форму параболоида вращения, т. е. поверхности, получен-
полученной вращением параболы вокруг ее оси. Эта форма выбирается по
следующим соображениям. Если поместить источник света в фокус
47J § 3. ГЕОМЕТРИЧЕСКИЕ ЗАДАЧИ 149
параболы, то луч света, падая на гладко отполированную поверхность
рефлектора, после отражения от нее останется в одной плоскости
с падающим лучом и нормалью к поверхности, как это следует из
известного закона физики. В согласии с тем же законом угол паде-
падения луча должен быть равным углу отражения, что в силу указан-
указанного свойства параболы влечет за собой параллельность отраженного
луча оси рефлектора. Таким образом, после отражения все световые
лучи идут параллельным пучком, что и дает наибольшую силу осве-
освещения на больших расстояниях.
Аналогично этому придают параболическую форму различным
приспособлениям для наилучшего распространения или улавливания
звука (музыкальные эстрады, звукоуловители).
2) Найдем уравнение касательной к эллипсу в его точке Мо (лгО)-Уо)>
если эллипс задан своим каноническим уравнением
Дифференцируя неявную функцию, определенную данным уравне-
уравнением, находим
2х
откуда
и значит, угловой коэффициент касательной в точке Мо (лс0, у0) ра-
равен 2~ —. Уравнение касательной имеет вид
или, после преобразования,
1J2 V2
УоУ ^о_ ХрХ . *о
Ь2 Ь2 ~~ а2 ' а2 '
хо У2
Так как -у + тт=Ь т0 мы получаем такое уравнение искомой
касательной:
а2 "Г Ь2 — ' •
X2 И2
Аналогично уравнением касательной к гиперболе -у—•— = 1 в ее
точке Мо (х0, у0) является уравнение
ХоХ_УоУ_ 1
а2 Ь2 — 1'
150
ГЛ. III. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ
[48
3) Возьмем в качестве примера линии, заданной параметриче-
параметрическими уравнениями, циклоиду (п. 46, II)
х = a (t — sin t), y = a A —cos t).
Найдем угловой коэффициент касательной к циклоиде в точке
М0(х0,у0), которая соответствует
значению t0 параметра t:
У ^ а A — cosy ^ Ctg T #
Значит, уравнение касательной
имеет вид
У— J\) =
—др0).
Рис. 56.
1—
р
О
У
Q
X
м'
А/ Ъ
Пусть д; = л/0; это абсцисса точки
Р (рис. 56). Тогда
jF==a(l—cos*e)+ctg Ax
X [at0— a (t0—sin /0)] = 2л;
6
отсюда следует, что каса-
касательная к циклоиде прохо-
проходит через верхнюю точку
Т, а нормаль — через ниж-
нижнюю точку Р производящей
окружности в ее положе-
положении, соответствующем дан-
данной точке касания Мо.
Рис. 57.
48. Графическое диф-
дифференцирование. К графи-
графическому отысканию производной прибегают главным образом тогда,
когда аналитическое выражение для функции неизвестно и она
задается графически (например, посредством самопишущих при-
приборов).
Графическое отыскание производной называется графическим
дифференцированием.
Пусть АВ (рис. 57) есть график некоторой функции y=f(x).
Отложим на оси абсцисс влево от начала координат отрезок ОР,
равный единице масштаба.
Проведем на глаз касательную к линии АВ в точке М, соответ-
соответствующей данной абсциссе х\ из точки Р (иногда называемой
полюсом графика) проведем прямую, параллельную этой касатель-
касательной до пересечения в точке Q с осью ординат. Отрезок OQ будет
48]
§ 3. ГЕОМЕТРИЧЕСКИЕ ЗАДАЧИ
151
выражать значение производной f (х). В самом деле,
OQ = OPtg a = btg а = /' (х).
Операция проведения на глаз касательной является весьма не-
неточной. Ее можно уточнить, если воспользоваться специальным
прибором—зеркальным дериватором, служащим для проведения
нормали к линии.
Простейший зеркальный дериватор можно осуществить с по-
помощью обыкновенного зеркала прямоугольной формы.
Рис. 58.
Приложив зеркало ребром (перпендикулярно к плоскости чертежа)
к графику в точке М, нужно поворачивать его вокруг точки М до
тех пор, пока изображение линии в зеркале не будет без излома
продолжать саму линию. Тогда положение края зеркала будет
давать направление нормали в точке ЛТ, а перпендикуляр к нему—
касательную.
Проведем из точки Q прямую, параллельную осп Ох, до пересе-
пересечения с ординатой MN или ее продолжением в точке М'. Ордината
этой точки и даст значение производной f'(x) при данном значении
независимой переменной х. Для того чтобы вычертить график произ-
производной функции y=f'(x) по заданному графику функции y=zf(x)y
разобьем участок АБ линии y=f(x) (рис. 58), соответствующий
интересующему нас интервалу изменения независимой переменной х,
152 ГЛ. Ш. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ [49
на некоторое число частей прямыми x = xv х — х2У ... Найдем
графически значения производной функции в точках, делящих по-
пополам каждый частичный интервал. Средние точки интервалов
выгодны потому, что при этом в качестве касательных можно, как
правило, с достаточно большой точностью брать просто прямые,
параллельные хордам, соединяющим конечные точки каждой частич-
частичной дуги графика.
Далее, описанным уже приемом найдем точки графика производ-
производной Ми М2* ... Соединив эти точки непрерывной линией, мы и
получим приближенный график производной функции y=f(x). Он
будет тем точнее изображать производную функцию, чем больше
найдено точек М\ т. е. чем больше число частей, на которые раз-
разбивается весь интервал. Эти части не обязательно должны быть
равны между собой; их размеры нужно брать с таким расчетом,
чтобы соответствующие части линии как можно меньше уклонялись
от отрезков прямой. Интервал, в котором линия круто и часто
извивается, следует разбивать на большее число частей так, чтобы
каждая такая часть была достаточно малой.
Мы всюду предполагаем, что масштабы по оси абсцисс и по
оси ординат одинаковы. Именно при этом /'(.*;) =
49. Геометрический смысл производной в системе полярных
координат. До сих пор мы рассматривали уравнения линий в си-
системе декартовых координат, принимая независимую переменную
и функцию в качестве соответственно абсциссы и ординаты
точки на плоскости; при этом производная у' функции y=f(x)
оказалась равной угловому коэффициенту касательной к графику
функции.
Будем теперь считать, что независимая переменная и функция
являются соответственно полярным углом и полярным
радиусом точки на плоскости. Линия, определяемая уравнением,
связывающим между собой независимую переменную ф и функ-
функцию г,
называется графиком функции г=/(ф) в системе полярных коор-
координат.
Каков же геометрический смысл производной г'=/'(ф)? Ответ
на этот вопрос дает следующая теорема.
Теорема. Значение производной г' =/' (<р) равно длине поляр-
полярного радиуса, умноженной на котангенс угла в между полярным
радиусом и касательной, проведенными к графику функции г =/(<р)
в точке с полярным углом <р:
r'=rctg8.
49]
§ 3. ГЕОМЕТРИЧЕСКИЕ ЗАДАЧИ
153
Доказательство. Возьмем какое-нибудь значение ф и при-
придадим приращение Дф. Значениям ф и ф+Дф соответствуют
точки М и М на графике функции г=/(ф) (рис. 59). Полярный
радиус РМ изображает данное значение
функции, а полярный радиус РМ — на-
наращенное значение функции г-|-Дг = V\ IT
~/(ф+ Дф). Чтобы найти выражение для
Дг, применим к треугольнику РММ тео-
теорему синусов:
r-f Дг sin у sin [я—(Р+ Дф)]
г sin 8 sin В
"" sinp ;
далее находим, что
- Дл sin p cos Дф + cos P sin Д ф
1 +7~- ihTp ""
= cos Дф + ctg P sin Дф,
откуда
Рис. 59.
— = cos Дф — 1 + ctg P sin Дф = —2 sin2 ¦— -\- ctg P sin Дф.
Разделим обе части этого равенства на Дф:
1 a, sin2ir
1 ДА г» Z
ДФ
Дф
Заставляя Дф стремиться к нулю, замечаем, что в правой части
равенства первое слагаемое стремится к нулю, а второе слагае-
слагаемое—к lim ctg p и что левая часть стремится к —г'; таким об-
Лф -> о г
разом,
— г'= lim ctg p.
Дф ->-0
Но если Дф—> 0, то точка М неограниченно приближается
к точке /И, секущая ММ — к касательной МТ и, значит, угол р —
к углу 9; вследствие непрерывности ctgP мы и приходим к тре-
требуемому равенству
г' = г ctg 9.
Это соотношение дает возможность при помощи дифферен-
дифференциального исчисления решать задачи, связанные с касательными
и нормалями линий, заданных уравнениями в полярных координатах.
154
ГЛ. III. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ
[50
Заметим, что если с возрастанием угла ср радиус г возрастает,
то под 0 понимается острый угол (как на рис. 59), а если убы-
убывает,— то тупой.
Рис. 60.
Пример. Покажем, что так называемая логарифмическая спи-
спираль г — ает<* пересекается с любой прямой, проходящей через
полюс, под постоянным углом (рис. 60).
В самом деле,
г =
= тг,
и значит,
§ 4. Дифференциал
50. Дифференциал и его геометрический смысл. С понятием
производной теснейшим образом связано другое фундаментальное
понятие математического анализа — д ифференциал функции.
Пусть y=zf(x)—функция, непрерывная при рассматриваемых
значениях х и имеющая производную
50J § 4. дифференциал 155
Из этого равенства следует, что
где е—бесконечно малая величина при Длг—>-0. Отсюда находим,
что
где ос = еДлг.
Итак, бесконечно малое приращение &у дифференцируемой функций
y=f(x) может быть представлено в виде суммы двух слагаемых: 1)
величины, пропорциональной бесконечно малому приращению незави-
независимой переменной Д#, и 2) бесконечно малой величины более высо-
высокого порядка, чем Длг.
Действительно, первое слагаемое /' (лг) Длг при данном значе-
значении х пропорционально Длг, а второе слагаемое а таково, что
д* д*
при Длг —*0.
Только в одном случае, когда функция y=zf(x) линейная,
у = ах + Ь, приращение функции &у, как мы знаем, в точности
пропорционально приращению аргумента Длг:
Ьу = яДлг,
причем коэффициент пропорциональности а постоянен. Но вот
теперь оказывается, что если функция f(x) и не является линей-
линейной, то при условии, что она имеет производную, все же суще-
существует такой коэффициент пропорциональности /' (лг), что вели-
величина /' (х) Длг хотя и не равна точно приращению Д^у, но отли-
отличается от него на бесконечно малую величину более высокого
порядка, чем Длг; при этом коэффициент пропорциональности равен
/' (х), и значит, он зависит от значения х.
Справедливо и обратное предложение: если для данного значе-
значения х приращение ky=f(x+Ax)—f(x) можно представить в виде
где а—бесконечно малая величина более высокого порядка, чем.
Длг, то функция у =/(х) имеет производную и a—f'(x).
В самом деле, мы имеем
Д* ^Дх'
и так как -^ >§ при Длг—>(), то предел —^ существует и ра-
равен ау что и требовалось доказать.
Введем теперь следующее определение.
156 ГЛ. Ш ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ [50
Определение. Дифференциаломг) функции называется
величина, пропорциональная бесконечно малому приращению
аргумента &х и отличающаяся от соответствующего приращения
функции на бесконечно малую величину более высокого порядка,
чем Дл.
Дифференциал функции у обозначается через dy или df(x).
Мы видим, что необходимым и достаточным условием существо-
существования дифференциала функции у~/(х) служит существование про-
производной, и тогда
<*J =/'(*) А*-
Приращение Длг независимой переменной х называют ее диффе-
дифференциалом dxy т. е.
Дл: = dx.
Это согласуется с тем, что дифференциал функции у = х равен
dy = dx = (х)' Дл: = Длг,
т. е. й?лг = Длг.
Таким образом,
Дифференциал функции равен ее производной, умноженной
на дифференциал независимой переменной, т. е.
dy=f(x)dx.
Зная производную, легко найти дифференциал, и обратно. По-
Поэтому действия отыскания производной и дифференциала данной
функции носят общее название дифференцирование.
В общем виде (при произвольном лг) дифференциал dy=f'(x)dx
является функцией двух независимых друг от друга переменных:
х и dx.
Для производной мы имеем выражение 2)
1) Термин дифференциал происходит от латинского слова differentia*
означающего разность.
2) Из предыдущего следует, что
lim ** = &
дя^оД* dx
Нельзя понимать эту запись так, что Ьу при Дх-»-0 стремится к dy> a
&.х к dx. Верно здесь только то, что отношение приращений —- стремит-
Д х
du
ся к отношению дифференциалов ¦—, которое имеет смысл только в силу
данного нами определения дифференциала dy.
51]
§ 4. ДИФФЕРЕНЦИАЛ
157
Представление производной в виде отношения дифференциалов
оказывается весьма важным в анализе. В этом мы очень скоро
убедимся.
Рассмотрим геометрическую иллюстрацию дифференциала функ-
функции у=/ (х) (рис. 61). Так как /' (#) = tga, то дифференциал
dy=f'(x)dx измеряет отрезок /?Г, т. е.
Дифференциал dy функции y=zf(x) в точке х изображается
приращением ординаты точки касательной, проведенной к линии
в соответствующей ее точке (х, f(x)).
Рис. 61.
Приращение же функции Д/(-*г) изображается приращением орди-
ординаты точки линии (отрезок RM на рис. 61). Поэтому разность
между дифференциалом и приращением изображается отрезком МТ,
заключенным между линией и касательной к ней; этот отрезок яв-
является при dx —> 0 бесконечно малой более высокого порядка, чем.
отрезок MR.
Дифференциал функции в данной точке может быть как больше
приращения (рис. 61, а), так и меньше его (рис. 61,6).
51. Свойства дифференциала.
I. Дифференциалы основных элементарных функ-
функций. Так как дифференциал получается из производной умноже-
умножением ее на дифференциал независимой переменной, то, зная произ-
производные основных элементарных функций, можем составить без всяких
затруднений таблицу дифференциалов этих функций. Так, d(xn) =
= nxn~1dxy d(ax) = ax\n adx и т. д.
II. Дифференциалы результатов арифметических
действий. В соответствии с правилами отыскания производных,
158 ГЛ. Ш. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ [51
изложенными в п. 41, и принятыми там обозначениями придем к ана-
аналогичным правилам для отыскания дифференциалов,
а) Так как
(U + V+ ... + W)'=
то, умножая обе части равенства на dx, получим
d (и + v + ... + w) = du + dv -\- ... -\- dw.
б) Так как
(uv)' — u'v-\~uv'y
то, умножая обе части равенства на dx, получим
d (uv) = vdu + u dv,
в частности
d(Cu) = Cdu.
в) Так как
' уu'v — uv'
то, умножая обе части равенства на dx, получим
,/ u \ v du — и dv
а [ — == s •
\v J v*
III. Диффе р е нци а л сложной функции. Свойство
инвариантности. Рассмотрим свойство дифференциала функ-
функции, вытекающее из правила дифференцирования сложной функции.
Пусть y=f(u) и и = ц)(х) — непрерывные функции своих аргу-
аргументов, имеющие производные по этим аргументам /' (и) и ф' (лг).
Если обозначить F(x)=f[(f(x)], то, как было показано в п. 42, I,
/ = />'(*)==/'(«О Ф'(*)- (•)
Умножая обе части равенства на dx, получим
ио <р' (л:) dx = du, и значит,
dy=f'(u)du,
т. е. дифференциал dy имеет такой же вид, как если бы вели-
величина и была независимой переменной.
Итак,
Дифференциал функции у =/(») сохраняет одно и то же
выражение независимо от того, является ли ее аргумент и неза-
независимой переменной или функцией от независимой переменной.
511 §4. дифференциал 159
Это свойство называется инвариантностью (т. е. неизмен-
неизменностью) формы дифференциала. Всегда можно, не интересуясь
природой аргумента функции, записать ее дифференциал в одном
и том же виде.
Из равенства dy=f'(u)du следует:
/-*¦>-&
значит, во всех случаях
Скорость изменения функции относительно своего аргумента
равна отношению дифференциала функции к дифференциалу аргу-
аргумента.
Равенство (*) теперь можно переписать так:
dx ~"dudx' l '
Правая часть равенства (##) получается из левой просто умно-
умножением и делением на du (конечно, если du=^=0). Таким образом,
оказывается возможным производить арифметические действия над
дифференциалами, как над обыкновенными числами. Это и делает
очень часто выгодной запись производной в виде отношения диффе-
дифференциалов.
Вот, например, как просто при помощи такой записи выводится
правило дифференцирования обратной функции (ср. п. 42, II):
dy y
IV. Дифференциал как главная часть прираще-
приращения. Пусть в точке х производная функции у=/(х) отлична от
нуля: /'(х)фО. Тогда
где а—бесконечно малая величина более высокого порядка, чем dx.
Но при указанном условии она будет бесконечно малой величиной
более высокого порядка и чем dy и Д^. Действительно, при dx—*0
имеем
а а
dy~~ I' (x) dx ~~* '
ибо ^—>-0, a f (х)фО. Значит, Д^у и dy отличаются друг от
Друга на бесконечно малую величину более высокого порядка, чем
они сами, и следовательно, они эквивалентны:
dy ~ Д у.
160 ГЛ. Ш. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ [51
В дальнейшем приращение функции Ау будет очень часто за-
заменяться ее дифференциалом dy. В связи с этим коснемся общего
вопроса о приближенном выражении одной переменной величины
через другую при условии, что обе они стремятся к одному и
тому же пределу.
Пусть функции и(х) и v (х) при х—>х0 стремятся к одному и то-
тому же пределу Л, т. е. \imu — limv= Л. Тогда предел их, разнос-
разности равен нулю: \\т(и — v) = 0 и, следовательно, сама эта разность
и (х) —v (х) = а (х)
есть бесконечно малая величина при х—+ х0.
Если теперь в окрестности точки х0 заменять значения функции
и(х) значениями функции v(x)y то абсолютная ошибка a=\u-^v\
будет бесконечно малой.
Если предел АфО, то и относительная ошибка, по которой и
оценивается точность приближения, также является бесконечно
малой:
^ а и—v __ и 1 ^1 п
~~|и| v v Л
Но при Л = 0, т. е. когда обе функции и{х) и v (x) сами явля-
являются бесконечно малыми при х—*лг0, относительная ошибка может
и не быть бесконечно малой. Она будет бесконечно малой только
тогда, когда и(х) и v(x) — эквивалентные бесконечно малые. В са-
я и—v\
мом деле, из того, что о =
есть бесконечно малая более высокого порядка, чем v. Соглас-
Согласно теореме п. 36, II это и означает, что и и v эквивалентны.
Итак, если две бесконечно малые величины эквивалентны, то
значения одной из них являются приближенными значениями дру-
другой с бесконечно малой относительной ошибкой. Коротко говорят,
что каждая из двух бесконечно малых есть главная часть другой.
Вернемся теперь к вопросу о замене приращения функции ее
дифференциалом. При фиксированном значении х и приращение
Ay~f{x-\-Ax)—f(x), и дифференциал dy=f (x)Ax зависят толь-
только от Ах и при Дл:—^0 стремятся к нулю. Так как выше уже
было доказано, что Ау и dy эквивалентны, то замена Ау на dy
приводит к бесконечно малой относительной ошибке. Поэтому
можно сказать, что
Дифференциал функции есть главная часть приращения функ-
функции, пропорциональная дифференциалу (приращению) независимой
переменной.
Заметим только, что если в данной точке f'(x) = 0, то диф-
дифференциал dy = 0, и он не сравнивается ни с какой другой бес-
бесконечно малой величиной, в том числе и с приращением функции Д^.
'¦—- —* 0, следует, что разность u — v
52] § 4. ДИФФЕРЕНЦИАЛ 161
52. Дифференцируемость функции.
Определение. Функция у =/(х) называется дифференци-
дифференцируемой в точке jc, если она имеет в этой точке дифференциал.
При этом, как мы видели в п. 50, в точке х существует про-
производная /' {х) (и обратно). Таким образом, существование произ-
производной может быть принято в качестве условия дифференцируе-
мости функции, чему с геометрической точки зрения соответствует
существование у линии у=/(х) касательной, не перпендикуляр-
перпендикулярной к оси Ох.
Допустим, что функция f(x) дифференцируема при не-
некотором значении лг, т. е.
»m fx=f{x);
Длг-Х) &Х
тогда она обязательно непрерывна в этой точке. В са-
самом деле, при этом Ау = /' (х)Ах~±- а (см. п. 50), и при Ах—>0
приращение Ау также стремится к нулю, а это и является
условием непрерывности функции y=f(x) в точке х. Поэтому в
точках разрыва функция не может иметь производной.
Итак, если функция f(x) дифференцируема, то она обязательно
непрерывна. Обратное же не всегда справедливо, потому что мож-
можно указать примеры таких непрерывных функций, которые не во
всех точках имеют производную.
Например, функция д; = |л;|, непрерывная на всей оси Ох, не
имеет производной при д: = 0. В самом деле,
Ау = | х + Ад: | — | х |,
что при х = 0 дает
Ау = | Ах |
и, значит,
А* Л* •
приДл:>0 будет д|==д^=1»
а при А* < 0 » ^=^^= — 1.
Отсюда следует, что отношение -~ не имеет предела при Ал%
произвольно стремящемся к нулю, а это и означает, что произ-
производной не существует. Геометрически это также ясно: графиком
функции ^=[^1 служит ломаная линия (рис. 62), вершина кото-
которой находится в точке @,0), и, разумеется, в этой точке линия
не имеет касательной.
6 А, Ф. Бермант, И. Г. Араманович
162
ГЛ. III. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ
[52
Возможны случаи, когда график непрерывной функции имеет
в некоторой точке касательную, а функция в соответствующей
точке производной не имеет; это бывает тогда, когда касатель-
касательная перпендикулярна к оси Ох. Например, для функции у — у/х
имеем
/ !
У
При л;—> 0 значение производной стремится к бесконечности, т.е.
рассматриваемая функция в точке л; = 0 недифференцируема.
У\
О
Рис. 62.
«27
Рис. 63.
В точке @,0) линия y = j/x (кубическая парабола) касается оси Оу
(рис. 63).
В целях общности иногда говорят (несмотря на недифферен-
недифференцируемость функции), что в рассмотренном сейчас случае функ-
функция имеет бесконечную производную.
В анализе глубоко разработан вопрос о дифференцируемое™ функции
и о связи дифференцируемости с непрерывностью функции. Различие между
свойствами непрерывности и дифференцируемости функций изучалось
Н. И. Лобачевским1). Существуют любопытные примеры непрерывных функ-
функций, не дифференцируемых ни в одной точке; графики этих функций яв-
являются линиями, не имеющими касательной ни в одной своей точке.
Эти линии, конечно, невозможно вычертить и даже составить себе о них
сколько-нибудь отчетливое представление. Такие функции и линии обычно
в применениях математического анализа не встречаются, и мы их рассмат-
рассматривать не будем.
Заметим, что все элементарные функции дифференцируемы, всюду
в интервале, в котором они определены, за исключением, может
быть, лишь отдельных точек.
г) Н. И. Лобачевский A792—1856) — великий русский математик,
создатель неевклидовой геометрии. Ему принадлежит ряд фундаментальных
работ в области алгебры и анализа. Его работы оказали большое влияние
на дальнейшее развитие математики.
53] § 4. дифференциал 163
II. Односторонние производные. Вернемся еще раз
к функции у = | х |, график которой изображен на рис. 62. Как
мы уже видели, при х = 0 предела отношения -~ при произволь-
произвольном стремлении Длг к нулю не существует. Однако левый и
правый пределы этого отношения (см. п. 33) существуют:
Нш ^ = -1, lim ?Ul.
д* _* о А* д* _> о *Х
Дх < О Ах > О
Эти пределы называются соответственно левой и правой
производными в точке х = 0. Вообще, если функция y=f(x) в
точке х0 непрерывна и существуют левый и правый пределы
отношения -г^, то они называются односторонними производными
в точке х0; соответственно левая производная (/л'ев(#0)) и правая
производная (f'n (jc0)). Ясно, что если левая и правая производные
в данной точке совпадают, то функция дифференцируема.
Если функция определена на некотором замкнутом интервале,
то производные на концах интервала определяются именно как
односторонние: на левом конце интервала это будет правая
производная, а на правом — левая. Это совершенно аналогично оп-
определению непрерывности функции на концах интервала (см. п. 32).
53. Применение дифференциала к приближенным вычислениям.
Применение дифференциала к приближенному вычислению значений
функции основано на замене приращения Ду — f(xo-\-Ax)—f(x0),
которое может весьма сложным образом зависеть от Ах, чрезвы-
чрезвычайно простым выражением f'(xQ)dx, в отыскании которого и
состоит дифференцирование.
Итак, для малых dx
by = / (*о + dx) ~f (*o) » /' (*о) dx = dy (*)
с малой относительной ошибкой (см. п. 61, IV).
Приняв Ay = dy, мы заменяем данную функцию у =/(*) линей-
линейной функцией
У=/(хо)+/'(хо) (х—х0),
определяемой тем, что ее значение и значение ее производной
при х = х0 равны соответственно f(xQ) и /' (х0).
Геометрически это равносильно замене линии, являющейся
графиком функции y—f(x), касательной к ней в точке (лс0, /(#0)).
Такая замена только в достаточно малой окрестности точки х0
приводит к таким ошибкам, которыми можно пренебречь в изу-
изучаемом вопросе. Недостаток формулы (#) заключается в том,
что мы не умеем оценить погрешность при данном численном
164 ГЛ. Ш. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ [53
значении dx, хотя и знаем, что при dx-^О относительная ошибка
стремится к нулю х).
Приближенное равенство (#) практически используется прежде
всего для решения следующей задачи.
Известны значения f(xQ), /' (х0), dx; требуется вычислить при-
приближенное значение f{xQ-\-dx).
Из соотношения (•*) сразу получаем нужную формулу
Для иллюстрации приведем следующие примеры (ради сокра-
сокращения записей будем обозначать х0 через х и dx через Н):
1) у=г!/х. Имеем
dy = h
и, значит,
v ¦ m
в частности, при х—\
эта приближенная формула в случае w = 2 уже была нами полу-
получена раньше (п. 37).
2) j/ = sinAr. Имеем
dy = cos x • h
и, значит,
sin (л; + &)«sinx + cosx • h\
в частности, при х — 0 находим формулу sin htth, полученную
нами раньше (п. 37).
Положив, например, х = -^(^30°), h=-^x( = 1°), найдем
sin 31°»sin 30° + cos 30° . щ « 0,5 + ^- • 0,01745^0,5151;
с пятью верными знаками sin 31°я^0,51504. Читатель должен себе
объяснить, почему мы получили приближенное значение для sin 31°
с избытком.
3) ^ = 1пл;. Имеем
1) Этот недостаток будет устранен в гл. X.
53] § 4. ДИФФЕРЕНЦИАЛ 165
и, значит,
в частности, при х=\ приходим к формуле \п{\ -\-h)^h, полу-
полученной нами раньше (п. 37).
Пусть известно, что In 781^6,66058; вычислим In 782. Форму-
Формула дает
In 782^6,66058 + 4т ~ 6,66186.
/О!
По пятизначным таблицам находим In 782 = 6,66185. Как видим,
мы сделали незначительную ошибку, причем также в сторону пре-
превышения. И здесь читатель сообразит, почему так и должно быть.
Другой очень важной задачей является вычисление предель-
предельной абсолютной ошибки функции еу по заданной предельной
абсолютной ошибке аргумента гх. В практических задачах, как
правило, аргумент находится при помощи измерения, и его
абсолютная ошибка может считаться известной (п. 6).
Итак, пусть требуется вычислить значение данной функции
y=f(x) при некотором значении аргумента х, истинная величина
которого нам неизвестна, а известно лишь его приближенное зна-
значение х0 с предельной абсолютной ошибкой ех:
\dx\ < 6^.
Беря вместо истинного значения f(x) величину f(xo)> мы со-
совершаем некоторую ошибку, которую и должны оценить. Из со-
соотношения (#) имеем
Отсюда видно, что абсолютная ошибка, получающаяся в ре-
результате замены f(x) ее приближенным значением f(x0), меньше
чем \f (хо)\ех; эту последнюю величину мы и принимаем за пре-
предельную абсолютную ошибку функции е :
Предельная абсолютная ошибка функции равна произведению
абсолютной величины ее производной, взятой при приближенном
значении аргумента, на предельную абсолютную ошибку аргумента.
Предельная относительная ошибка функции бу равна
С Г/ / ч
у ~~ I i (*0) I
К*о)
т. е. произведению абсолютной величины логарифмической произ-,
водной на предельную абсолютную ошибку аргумента.
166 гл. ш. производная и дифференциал [54
Из полученных формул ясно, какова должна быть ошибка е^
в задании аргумента, чтобы была обеспечена заранее назначенная
допустимая ошибка значения функции:
«(*о)
П*оI
Ь' (ч
Разумеется, при вычислении гх нужно знать приближенное значе-
значение лг0, чтобы можно было найти соответствующие значения/(jc0)
и f'(x0) (см. пример 2).
Для иллюстрации приведем два примера.
1) В прямоугольном треугольнике даны гипотенуза с и при-
приближенное значение угла а с предельной абсолютной ошибкой еа.
Найдем относительные ошибки при вычислении катетов.
Имеем
а = с sin a, b = с cos а,
откуда
Если a>-j-, то a>? и ctga<tga; поэтому относительная
ошибка будет меньше для большего^ катета.
2) Нужно найти объем куба с относительной ошибкой 6 = 0,01 =
= 1%. Измерение ребра куба с помощью линейки, цена деления
которой равна 1 см, дало приближенный результат 20 ел*. Можно
ли считать, что приближенное значение v = S000 см3 обеспечивает
требуемую точность?
Обозначим ребро куба через х\ тогда v = x* и v' — Зх2. По
формуле для гх найдем
При произведенном же измерении ошибка составляет 0,5 см, что
значительно превышает найденную. Ясно, что нужный результат
мы получим, взяв линейку с ценой деления, равной 1 мм (тогда
ех== 0,05см), и заново произведя измерение ребра и вычи-
вычисление объема.
§ 5. Производные и дифференциалы высших порядков
54. Производные высших порядков.
I. Допустим, что функция y=f (x) имеет производную /' (х)
в некотором интервале независимой переменной х. Производная
от /' (л:) (если она существует) называется производной второго
порядка или второй производной от первоначальной функции f(x)
54] § 5. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 167
и обозначается через f"(x):
Да: -> о
Таким же образом производной третьего порядка или третьей производ-
производной /'" (л:) от функции у=/(х) называется производная от произ-
производной второго порядка. Дадим общее определение.
Определение. Производной л-го порядка /(/1) (л:) называется
производная от производной (л—1)-го порядка
Производные второго и вообще высших порядков оказываются
существенно необходимыми для определения важных понятий ма-
математики, механики, физики и для более полного исследования
функций, чем то, которое можно выполнить, применяя лишь пер-
первую производную.
Значение f"(x) в точке х определяет скорость изменения/' (х)
в этой точке, т. е. скорость изменения скорости изменения f(x).
Снова заимствуя термин из механики, можно назвать f"(x) уско-
ускорением изменения функции /(х) при данном х.
Вопрос о геометрическом смысле второй производной будет
рассмотрен в гл. IV (п. 62).
Производные от данной функции в данной точке могут суще-
существовать до некоторого определенного порядка, а производных
высшего порядка функция в этой точке может и не иметь» Однако
всякая элементарная функция, за исключением быть может отдель-
отдельных точек, имеет в своей области определения производные любых
порядков.
В целях единства терминологии производную данной функции
называют производной первого порядка или первой
производной. Умение дифференцировать всякую элементарную
функцию позволяет найти одну вслед за другой последовательные
производные данной элементарной функции до любого порядка.
Иногда удается просто указать общий вид производной й-го по-
порядка от данной функции для произвольного k. Коротко ее обозна-
обозначают y{k).
Примеры. 1) у=*хп, у' = пхп-\ у" = п(п— \)хп~*, ,..,
У*> = л(/1_ 1)(л — 2)... (я—k+\)xn~k\
если п—целое положительное число, то
/Я) = л! и /я+1) =ум+а)= ... =0.
168 гл. ш. производная и дифференциал [54
2) y — sinx, / = cosA; = sinf.x;-}- ~ч, у" = s\n(x-\-n)t ...
. . ., J/ = Stnl X+ -к- I .
3) у = Л уЛ) = е*.
4) j/ = ах, у' = ах In а, /' = a* (In аJ, ..., y{k) = а^ (In а)л.
5) jr =
II. Производные неявных функций. Если д; — неявная
функция, то для отыскания ее высшей производной нужно соответ-
соответствующее число раз дифференцировать заданное уравнение, свя-
связывающее х и у, помня всегда, что у и все ее производные суть
функции независимой переменной.
Так, вторую производную от функции уу заданной уравнением
найдем, дважды дифференцируя это уравнение. Получим последо-
последовательно
() + №) +/ +уУ = о.
Отсюда
В этом примере функцию и ее производную нетрудно явно
выразить через х. Тогда найдем
V = —
т. е. то же, что получается при двукратном дифференцировании
явного выражения функции. Вообще же производная какого-нибудь
порядка от неявной функции всегда может быть выражена, в конеч-
конечном счете, через независимую переменную и саму функцию.
Так, дифференцируя по х два раза подряд уравнение
определяющее неявным образом у как функцию х, получим
у%у' — ау — аху' + хг = 0
и
2у (/J +у*у" — 2а/— аху" + 2х = 0.
54] § 5. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 169
Находя из первого равенства у' и подставляя во второе, придем
к уравнению, из которого у" выразится через хну.
III. Пр о и зво д н ы е параметрически заданных функ-
функций. Для того чтобы найти производную высшего порядка от
параметрически заданной функции, нужно продифференцировать
выражение для предыдущей производной, как сложную функцию
независимой переменной. Пусть л: = ф(^), y=f(t). Имеем
У ~dx^yU) *
Далее,
ф'(О У *L = Г(Оф'(*)-/'@ф'@
у dx dt dx ф'2 (t) dx f
и так как
dt __ 1
то
п Г(Оф' (О-—/!' (Оф* (t)
У = /3/м •
Дифференцируя это выражение по х, найдем третью произ-
производную и т. д.
Пример. Найдем вторую производную у'\ если
a:— cos t, у =sint.
Здесь
, COS t . j
J —sin t &
dt
•^ —sin ^ sin3 ^ '
IV. Формула Лейбница. Укажем имеющее практическое
значение правило для отыскания производной п-го порядка от
произведения функций.
Пусть и и v — некоторые функции от л; и
выразим у(П) через производные функций а и v.
Имеем последовательно
у' ~u'v-\-uv\
170 ГЛ. III. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ [55
Легко подметить аналогию между выражениями для второй и
третьей производных и разложением биномов соответственно во
второй и в третьей степенях; эти выражения так сконструированы
из производных и и v (нулевого, первого, второго и третьего
порядков), как разложения для биномов — из последовательных
степеней и и v (нулевой, первой, второй и третьей). Оказывается,
эта аналогия справедлива в общем случае.
Формула Лейбница. При любом п справедливо равенство
-1 V + п{п2~1) я<" -2
... + /ш V* -
Эту формулу можно получить из разложения бинома (u-\-v)t\
если в нем заменить степени и и v соответствующими производ-
производными от и и v.
Доказательство этой формулы мы не приводим.
Пример. Найдем сотую производную от функции y = x2sinx.
Имеем
sin xyim = (
+ 100 (sin *)<"> (л:2)' + l^~ (sin x)m) (л;2)";
следующие слагаемые нет нужды выписывать, ибо все они равны
нулю: каждое из них содержит множителем производную выше
второго порядка от л:2. Следовательно (см. I),
/ни» ^ Х2 sin (х + ]00 . Л + 200л: sin (x + 99 • ~
+ 9900 sin (х + 98 • у W x2 sin х — 200* cos х — 9900 sin x.
55. Дифференциалы высших порядков. Дифференциал dy функ-
функции у=/(х) есть функция двух переменных (п. 50): независимой
переменной х и ее дифференциала dx. Дифференциал dx не-
независимой переменной х есть величина, не зависящая
от х: при заданном значении х значения dx могут выбираться
произвольно.
Рассматривая df(x) как функцию х, возьмем дифференциал
d[df(x)]. Если этот дифференциал существует, то он называется
дифференциалом второго порядка или вторым дифференциалом от
функции f(x) и обозначается через d2y:
Таким же образом дифференциалом третьего порядка или третьим
дифференциалом d3y от функции y=f(x) называется дифферен-
55] § 5. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 171
циал от дифференциала второго порядка как функции х. Дадим
общее определение.
Определение. Дифференциалом п-го порядка dny назы-
называется дифференциал от дифференциала (я—1)-го порядка как
функции х:
d
Найдем теперь выражения для дифференциалов высших по-
порядков от функции f(x)y причем предположим, что ее аргумент
есть независимая переменная. Имеем для дифференциала второго
порядка
d (dy) = (dy)f dx = [/' (х) dx]' dx,
и так как в силу сказанного dx следует считать при дифферен-
дифференцировании по х величиной постоянной, то
&у =f" (x) dx dx =/" (х) dx2.
Точно так же для дифференциала я-го порядка вообще найдем
dny = {d*-^)' dx = [У71-1 (x) dx"'1]' dx =/w (x) dxny
где под dxn понимается /2-я степень dx.
Итак,
Дифференциал п-го порядка равен произведению производной
п-го порядка по независимой переменной на п-ю степень диффе-
дифференциала независимой переменной.
Дифференциал df(x) функции f(x) называется, для общности
терминологии, дифференциалом первого порядка или первым диф-
дифференциалом.
Каждый дифференциал является бесконечно малой величиной
более высокого порядка, чем дифференциалы всех низших порядков:
d»y
dmy —
при dx—*0, если n>m и f(tn)(x)=fi0.
Последовательные дифференциалы
dy, d*y, d*y, ..., dny%
располагаются в порядке повышающейся малости.
Если у—/(х)у то dy=f (x)dx независимо от того, является
ли аргумент х независимой переменной или какой-нибудь функ-
функцией от нее (свойство инвариантности формы первого дифферен-
дифференциала, см. п. 51, III).
Дифференциалы высших порядков уже не обладают этим
свойством. В самом деле, предположим, что х есть не независимая
переменная, как мы допускали до сих пор, а функция от нее.
Тогда dx тоже будет зависеть от независимой переменной, и мы
172 ГЛ. III. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ [55
не сможем считать dx постоянным при дифференцировании пер-
первого дифференциала по независимой переменной. Таким образом,
выражение для d2y получится иным, чем указанное выше. Именно,
взяв дифференциал от dy, на основании правила дифференциро-
дифференцирования произведения получим
#У = d [/' (х) dx] = d [/' (x)] dx +/' (x) d (dx).
Ho
d[f(x)]=f(x)dx и d(dx) = d2x,
поэтому
d2y =f" (x) dx2 +/' (x) d2x.
Как видим, появился добавочный член f (x)d2x. Он обращается
в нуль, если х—независимая переменная:
d2x = (x)" dx2 = 0- dx2 = 0.
Еще более сложный вид имеет дифференциал третьего порядка:
d*y =/"' (х) dxs + 3/" (х) dx d2x +/' (x) d3x.
Итак, при нахождении дифференциалов высших порядков не-
необходимо строго учитывать природу аргумента дифференцируемой
функции: является ли этот аргумент зависимой или же независимой
переменной.
Из формул для дифференциалов получаем выражения для про-
производных в виде дробей:
v (») _ *<щ /х\ __ ii_y
У —J W ~~ dxn
Эти формулы, за исключением первой, верной всегда, спра-
справедливы лишь при условии, что х — независимая переменная.
dnu dn
Для удобства записи часто вместо j~ условно пишут j-н
Так, например, записывают: 2J8B#4—лг + 1)
ВОПРОСЫ И ПРЕДЛОЖЕНИЯ ДЛЯ САМОПРОВЕРКИ
1. Как определяется скорость движения? линейная плотность? тепло-
теплоемкость? скорость химической реакции?
2. Что называется скоростью изменения функции?
ВОПРОСЫ И ПРЕДЛОЖЕНИЯ 173
3. Дать определение производной данной функции. Выразить с помощью
производной понятия, указанные в вопросах 1 и 2.
4. Что называется касательной прямой к линии в данной ее точке?
5. Каков геометрический смысл производной отданной функции у = ^(х)
в системе декартовых координат?
6. Сформулировать правила дифференцирования результатов арифме-
арифметических действий. Привести примеры.
7. В чем заключается правило дифференцирования сложной функции?
обратной функции?
8. Вывести формулы для производных всех основных элементарных
функций.
9. В чем состоит прием логарифмического дифференцирования?
10. Как дифференцируют неявно заданные функции? Привести примеры.
И. В чем состоит способ параметрического задания функций и урав-
уравнений линий? Привести примеры.
12. Указать способ дифференцирования параметрически заданных
функций.
13. Что называется направлением линии в данной ее точке? углом
между двумя пересекающимися линиями? нормалью к линии в данной ее
точке?
14. Описать прием графического дифференцирования.
15. Каков геометрический смысл производной в системе полярных ко-
координат? Вывести соответствующую формулу.
16. Что называется дифференциалом функции? Как выражается диф-
дифференциал функции через ее производную?
17. Каков геометрический смысл дифференциала данной функции у = ? (х)?
18. Перечислить основные свойства дифференциала функции. В чем
состоит свойство инвариантности вида дифференциала функции?
19. Какая функция называется дифференцируемой? В чем состоит необ-
необходимое условие дифференцируемости функции?
20. Привести примеры непрерывных, но недифференцируемых функций.
21. Указать формулу для приближенного вычисления значений функции
с помощью дифференциала функции. Привести примеры.
22. Указать формулы для выражения абсолютной и относительной
предельных ошибок функции по заданной предельной абсолютной ошибке
аргумента.
23. Что называется производной п-го порядка данной функции?
24. Как находятся производные высших порядков от функций, задан-
заданных явно? неявно? параметрически?
25. Сформулировать правило Лейбница для дифференцирования произ-
произведения функций.
26. Что называется дифференциалом n-го порядка данной функции?
Как выражается дифференциал через соответствующую производную функ-
функции по независимой переменной?
ГЛАВА IV
ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
К ИССЛЕДОВАНИЮ ФУНКЦИЙ
§ 1. Теоремы Ферма, Ролля, Лагранжа и Кош и
56. Теоремы Ферма и Ролля. Изучение вопросов применения
дифференциального исчисления к исследованию функций мы начнем
с теоремы Ферма.
Теорема Ферма1). Пусть функция у=/(х), непрерывная
в некотором интервале [xv jc2], принимает свое наибольшее
(или наименьшее) значение во внутренней точке | этого интер-
интервала: хг^%<^х2. Если в точке | производная функции f(x)
существует, то она обязательно равна нулю: /'(|) = 0.
Доказательство. Если функция f(x) принимает в точке
? свое наибольшее значение, то это значит, что
/(*)</(?> (•)
для всех х ? [xv x2].
Производная /' (?) равна
AX-+Q
Так как I — внутренняя точка интервала, то приращение Ах
может принимать и положительные и отрицательные значения.
Рассмотрим отношение
А*
Числитель этого отношения, согласно условию (*), не может быть по-
положительным: f{l + Ax)—/(?)^0. Поэтому при Дл: > 0 отношение
х) П. Ферма A601—1665) —знаменитый французский математик, ра-
работы которого оказали очень большое влияние на развитие математики.
56]
§ 1. ТЕОРЕМЫ ФЕРМА, РОЛЛЯ, ЛАГРАНЖА И КОШИ
175
и предел его — правая производная (см. п. 52) — также
неположителен: /Пр(|)^0. Если же Ах < 0, то отношение
хг х
Да:
и, следовательно, /Лев(?)^0.
Так как по условию теоремы в точке ? производная функции
f(x) существует, то левая и правая производные должны быть
равны. Это возможно только в случае /Лев(?) =/пр(?) = 0. Но
тогда и /'(?•) = 0, что и требова-
требовалось доказать.
Рекомендуем читателю внести
соответствующие изменения в ход
рассуждений, если в точке ? функ-
функция принимает свое наименьшее
значение.
Геометрический смысл теоремы
Ферма ясен из рис. 64: касательная
к графику функции в его наивысшей
(или наинизшей) точке параллельна
оси абсцисс. Если наибольшее или
наименьшее значения функции принимаются ею на конце интервала
(например, на рис. 64 наименьшее значение принимается при х = хх
и х — х2), то касательная в соответствующей точке не обязана
быть параллельной оси абсцисс, т. е. производная может и не
равняться нулю.
Отметим, что возможны случаи, когда функция принимает свое
наибольшее или наименьшее значения в точках, в которых про-
производная не существует. Так, например, функция у = |дг| прини-
принимает свое наименьшее значение, равное нулю, в точке лг = О, где
она не имеет производной. Исследование поведения этой функции
и ее график приведены в п. 52.
Почти непосредственным следствием теоремы Ферма является
теорема Ролля.
Теорема Ролля1). Если функция f(x) непрерывна в замк-
замкнутом интервале [х1$ х2]9 дифференцируема во всех его внутрен-
внутренних точках и имеет на концах интервала равные значения, то
в этом интервале существует хотя бы одно значение jc=|, для
которого /'(|) = 0.
Доказательство. Если на концах интервала значения
функции равны между собой, /(хг) = /(лг2), то возможны два
случая.
х) М. Ролль A652—1719)—французский математик.
176
ГЛ. IV. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[56
1) Внутри интервала функция вовсе не изменяется и везде
f(x)=f(x1)=/(x2); тогда ее производная равна нулю при всех
значениях х.
2) Если функция изменяется, то, будучи непрерывной в замк-
замкнутом интервале, она принимает свое наибольшее и наименьшее
значения (п. 35), причем
хотя бы одно из этих
значений принимается ею
внутри интервала
[х1У х2]. Действительно,
если бы наибольшее и на-
наименьшее значения при-
принимались на концах ин-
интервала, то по условию
теоремы они были бы равны и функция была бы постоянной. На рис. 64
изображен случай, когда функция принимает н а и б о л ь ш е е зна-
значение внутри интервала в точке ?.
По условию теоремы производная существует во всех внут-
внутренних точках интервала, а значит и в точке, где функция
принимает свое наибольшее или наименьшее значение. По теореме
Ферма производная в такой точке равна нулю, а это как раз то,
что и требовалось доказать.
Геометрическое истолкование теоремы Ролля таково:
На линии y=f(x), где функция f(x) удовлетворяет условиям
теоремы Ролля, найдется точка, в которой касательная параллельна
оси абсцисс (рис. 64).
Если f(x1)=f(x2) = 0, то теорему Ролля можно формулиро-
формулировать следующим образом:
Между всякими двумя нулями функции лежит хотя бы один
нуль производной.
Именно так, причем лишь для многочленов, теорема впервые
была указана самим Роллем.
Утверждение теоремы Ролля перестает быгь верным, если не
требовать дифференцируемости функции во всех внутренних точках
интервала. Например, непрерывная функция у = ^/х2 на концах
интервала [—1, +1) имеет равные значения (=1), а вместе с тем
2
ее производная у' = ¦ э/— нигде в нуль не обращается. И дейст-
3 |/ х
вительно, в данном случае условия теоремы не выполнены: в точке
лг = О, лежащей внутри интервала (—1, +1), производной не су-
существует. Весьма характерен график этой функции (рис. 65).
В точке @, 0) имеется касательная, перпендикулярная к оси
абсцисс, причем кривая в этой точке как бы заостряется. Такие
точки будем называть точками возврата кривой.
57]
§ 1. ТЕОРЕМЫ ФЕРМА, РОЛЛЯ, ЛАГРАНЖА И КОШИ
177
Точно так же теорема может быть неверна, если функция не
является непрерывной в замкнутом интервале [хг, х2]. Например,
функция, заданная в интервале [0, 1] так:
у = х, если О^х < 1,
у = 0, если я=1,
удовлетворяет всем условиям теоремы Ролля, кроме одного: она
разрывна в правом конце интервала [0, 1] — в точке я=1. И за-
заключение теоремы не выполняется: как ясно видно, производная
tf
Рис. 67.
во всех точках интервала @, 1) равна 1, и, следовательно, нет
точки, в которой производная обращалась бы в нуль.
Если на концах интервала не существует производной, а сама
функция непрерывна, то теорема остается справедливой. Рекомен-
Рекомендуем проверить это на примере функции ^у = "|/"l —jc2, определен-
определенной и непрерывной в интервале [—1, 1].
57. Теорема Лагранжа 1)Л Вернемся снова к геометрическому
истолкованию теоремы Ролля. Так как хорда, стягивающая концы
дуги АВ (рис. 64), параллельна оси абсцисс, то касательная в
точке М будет параллельна этой хорде. Геометрически ясно, что
это последнее свойство сохранится и в том случае, когда хорда,
стягивающая концы дуги, не будет параллельна оси абсцисс.
Именно, пусть АВ — линия, имеющая в каждой точке касательную
и не имеющая точек возврата (рис. 66). Тогда на ней всегда най-
найдется точка, в которой касательная к линии будет параллельна
хорде, стягивающей линию.
Если условия, наложенные на линию АВ, не выполняются, то
такой точки может и не найтись (рис. 67).
*) Ж. Лагранж A736—1813) —знаменитый французский математик и
механик.
178
ГЛ. IV. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[57
Предположим теперь, что линия АВ задается уравнением
y=f(x), где /(*) — дифференцируемая функция, и абсциссы точек
А и В соответственно равны хх и х2 (рис. 66). Так как угловой
коэффициент хорды АВ равен *'*2^ ~~H*i) ,^ a уГЛОвой коэффици-
х2 хх
ент касательной в точке М (на рис. 66 их две) равен / (?), где
? — абсцисса точки М, то из условия параллельности касательной
и хорды следует равенство их угловых
коэффициентов. Таким образом, мы
приходим к следующему утверж-
утверждению.
Теорема Лагранжа. Если
функция f{x) непрерывна в замк-
замкнутом интервале [х19 х2] и диффе-
дифференцируема во всех его внутренних
точках, то в этом интервале су-
существует хотя бы одно значение
jc = |, для которого
Рис. 68.
— /(*i) _ p
—Xi
Приведем теперь аналитическое доказательство
этой теоремы. Для этого образуем вспомогательную функцию
F(x)=f(x)-Xx,
где А. — угловой коэффициент прямой Л^Л^ (рис. 68), равный угло-
угловому коэффициенту хорды М^^
^ = /i (**)—f (xi)
Функция F(x) удовлетворяет всем условиям теоремы Ролля:
в интервале [хг, х2] она непрерывна и в интервале (хг, х2) диф-
дифференцируема, ибо этими свойствами обладают и f(x) и Яле, а на
концах интервала ее значения равны между собой:
I (*а) — f (H) Y _
^з^ хг -
— xj (x2)
——
*«) «/(*.)-"^
х*—*
Ясен и геометрический смысл вспомогательной функции F(x). Ор-
Ордината точки ее графика будет изображаться отрезком PRy
(рис. 68), равным сумме постоянного отрезка
58] § 1. ТЕОРЕМЫ ФЕРМА, РОЛЛЯ, ЛАГРАНЖА И КОШИ 179
и отрезка QR. Значит, хорда, стягивающая конечные точки дуги,
соответствующей новой функции, будет параллельна оси Ох. По
теореме Ролля существует такая точка ?• ? {хъ х2), что f (§)«()•
Но F'(x) = f'(x) — k\ следовательно, /'(?) —Х = О, откуда
—у *• —I 'ь)>
что и требовалось доказать.
Разумеется, сама теорема Ролля получается из теоремы Лаг-
ранжа, когда f(x1)=f(x2).
По теореме Лагранжа имеем
Эта формула называется формулой Лагранжа, Она выражает
тот факт, что
Приращение функции на интервале равно произведению произ-
производной в некоторой промежуточной точке интервала на приращение
независимой переменной.
Формула Лагранжа позволяет дать точное выражение для при-
приращения функции через приращение аргумента и значение произ-
производной в некоторой точке интервала. Она имеет большое теоре-
теоретическое значение и будет в дальнейшем лежать в основе дока-
доказательств ряда важных теорем.
58*. Теорема Коши1). Теорема Коши является обобщением
теоремы Лагранжа. Приведем сначала ее аналитическую фор-
формулировку и доказательство.
Теорема Коши. Если функции f(x) и <p(Jt) непрерывны
в замкнутом интервале [х1$ х%\ и дифференцируемы во всех его
внутренних точках, причем <р'(*) в этих точках не обращается
в нуль, то в этом интервале существует хотя бы одно значение
х sss |, для которого
Ф'(!Г
Заметим, что <р (*а) — ф(л:г)=^=0, так как в противном случае по
теореме Ролля существовала бы внутри этого интервала точка,
в которой производная ср' (л:) обращалась бы в нуль,, что проти-
противоречит условиям теоремы.
Доказательство. Образуем вспомогательную функцию,
подобную той, которую мы строили, доказывая теорему Лагранжа.
L) О. Коши A789—1859) —знаменитый французский математик. Его вы-
выдающиеся труды лежат в основе многих разделов современной математики.
180 ГЛ. IV. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [58
Обозначим отношение '; 2(—- ¦,l\ через А. и положим
ф(*)—Ф(*0
Вспомогательная функция F(x) удовлетворяет всем условиям тео-
теоремы Ролля. Ее непрерывность и дифференцируемость следует из
того, что этими свойствами обладают функции f(x) и (р(х). Равен-
Равенство значений функции на концах интервала легко проверяется:
rn(r \ — f (*1)ф(*2>—f
следовательно, по теореме Ролля в интервале (jc1, jc2) существует
такая точка ?, что F'(%) = 0. Но F' (x)—f [х) — А.ф'(а:); следо-
следовательно, /'(?) —&<р'(g) = 0 и
Г F)
ф'E) '
Теорема доказана.
В частном случае при ф(х) = л: теорема Коши совпадает с тео-
теоремой Лагранжа.
Нельзя доказать теорему Коши, как это может показаться
с первого взгляда, простым почленным делением двух формул
Лагранжа, относящихся к функциям / и ф, потому что при этом
промежуточные значения g в первом и во втором случаях не обя-
обязаны совпадать.
Покажем, что теорема Коши с геометрической точки зрения
выражает тот же самый факт, что и теорема Лагранжа. Обозначим
для удобства независимую переменную через t и будем считать,
что функции f(t) и ф (t) являются параметрическими уравнениями
некоторой линии, причем у =/(/), x = y(t). Когда параметр t про-
пробегает интервал [tv t2]f переменная точка перемещается по ка-
какой-то дуге, начальная точка которой имеет координаты [ф (^i),/(^)],
а конечная [ф(?2)» /(^)]« Угловой коэффициент хорды, стя-
стягивающей эти точки, равен отношению ,A^Z \+\ * Производ-
Производная от функции, заданной параметрически, равна ^ = ^тУ • Сле-
Следовательно, формула
/(*»)-/(*!) = Г F) // ^р^м
опять-таки выражает равенство углового коэффициента хорды,
стягивающей концы дуги, и углового коэффициента касательной,
проведенной в некоторой промежуточной точке.
59] § 2. ПОВЕДЕНИЕ ФУНКЦИИ В ИНТЕРВАЛЕ 181
§ 2. Поведение функции в интервале
59. Признаки монотонности функции. Одно из самых важных
назначений дифференциального исчисления — это применение его
к исследованию функций (и линий), т. е. к характеристике пове-
поведения функции при изменении независимой переменной*).
Применение дифференциального исчисления к исследованию
функций опирается на весьма простую связь, существующую
между поведением функции и свойствами ее производных, прежде
всего ее первой производной.
Теорема (необходимый признак монотонности).
1) Если функция f(x) в интервале возрастает, то ее произ-
производная f (х) неотрицательна: /' (х) ^ 0;
2) если функция f(x) в интервале убывает, то ее производ-
производная /'(х) неположительна: /' (х)^0;
3) если функция f(x) в интервале не изменяется (есть кон-
константа), то ее производная /' (х) тождественно равна нулю.
Доказательство. 1) Пусть функция f(x) в данном интер-
интервале возрастает, т. е. f(x + Ах) >/(*), если Ах > 0, и /(*+ А*) <
</(*), если Ах < 0, для любого х в этой интервале. Но тогда
отношение
Ау_ f(x + Ax)-f(x) , .
будет величиной положительной независимо от знака Ал; и, зна-
значит, оно не может иметь в качестве своего предела, которым
является производная, отрицательное число; пределом может быть
или положительное число, или нуль: /' (х) ^ 0.
2) Если f(x) убывает, то отношение -^—величина отрицатель-
отрицательная и ее пределом, т. е. производной, может быть или отрица-
отрицательное число, или нуль: /' (х) ^0.
В пунктах 1) и 2) предполагается, что функция f(x) во всех
точках имеет производную. Предоставляем читателю нарисовать
график непрерывной монотонной функции, которая в отдельных
точках не имеет производной (см. п. 52).
3) Если f(x) — константа, то известно, что ее производная
равна нулю: f (х) = 0.
Геометрический смысл этой теоремы очевиден (рис. 69): если
подвижная точка М(х, у) при движении по графику функции слева
направо, т. е. при возрастании абсциссы, поднимается, то каса-
касательная к графику образует с осью Ох острый угол, тангенс
*) Рекомендуем перед чтением этого пункта еще раз внимательно про-
просмотреть п. 13.
182
ГЛ. IV. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[59
которого положителен; если же точка М(х, у) опускается, то
касательная образует с осью Ох тупой угол, тангенс которого
отрицателен.
Следует подчеркнуть, что производная монотонной функции
может в отдельных точках обращаться в нуль. Вот простой при-
пример; у = х3. Эта кубическая функция возрастает на всей оси Ох,
/
У,
0
\а
и
з)
Рис. 69.
но ее производная у' = 3х2 обращается в нуль в точке х = 0,
будучи положительной во всех остальных точках. Геометрический
смысл этого факта таков: касательная к графику монотонной
функции в отдельных точках может быть параллельна оси Ох.
Таким образом, в интервале монотонности функции знак ее про-
производной не может измениться на обратный.
Это предложение позволяет по характеру роста монотонной
функции в интервале установить знак ее производной в этом
интервале.
Однако когда мы только начинаем исследовать функцию, то ее
поведение обычно неизвестно, и поэтому значительно важнее
обратное предложение, сводящее вопрос о характере роста
функции в данном интервале к более простому вопросу о знаке
ее производной в этом интервале.
Теорема (достаточный признак монотонности).
1) Если производная /' (х) от функции f(x) всюду в интер-
интервале положительна, то функция f(x) в этом интервале возрастает;
2) если производная f (x) от функции f(x) всюду в интер-
интервале отрицательна, то функция f(x) в этом интервале убывает;
3) если производная f (х) от функции f(x) всюду в интер-
интервале равна нулю, то функция f(x) в этом интервале не изме-
изменяется (есть константа).
Доказательство. Возьмем в рассматриваемом интервале
две произвольные точки хх и лг2, причем пусть лс1<лг2. По фор-
формуле Лагранжа имеем:
-/(*i) =/' E) (*i -*i). *i < I < *2-
60]
§ 2. ПОВЕДЕНИЕ ФУНКЦИИ В ИНТЕРВАЛЕ
183
Так как хг<х2, то разность х2— хх положительна и знак
разности f(x2)—f{xx) полностью определяется знаком производ-
производной /'(?). Если производная f'(x) всюду положительна, то и
/' (I) > 0. Следовательно, f(x2) —/{х^ > 0, т. е.
при
ибо
при
но это и значит, что функция f(x) возрастает1).
Если производная всюду отрицательна, то и /' (?) < 0 и,
следовательно, f(x2)<if(x1) при х2 > хг, т.е. функция убывает.
Наконец, если производная всюду равна нулю, то и /'(?) = 0
и, следовательно, f(x2) =f(x1) при любых хх и лг2, т. е. функция
f(x) постоянна.
Это предложение дает нам простой и удобный аналитиче-
аналитический признак монотонности функции в интервале.
Так, например, для того чтобы убедиться, что функция
у= — хъ—2jc2 —6лг + 3 в интервале —1 < х < 3 убывает, доста-
достаточно удостовериться, что ее производная у'= 2лс2— 4л:—6
— 1 < х < 3 отрицательна. А это действительно так,
у' =z2(x+\) (*—-3), причем
множитель (лг-f-l) при всех
значениях х в данном ин-
интервале положителен, а мно-
житель (л:—3) отрицателен.
Геометрически ясно, что
функция будет монотонной
и в том случае, когда ее про-
изводная, сохраняя все время
постоянный заак, в отдель-
отдельных точках равна нулю. На-
пример, функция у = х—ыпх
возрастает в любом интервале, так как ее производная у' = 1 — cos x
все время положительна, кроме точек х = 2кя, где она равна нулю.
Заметим, что те значения х, в которых производная обращается
в нуль, называются стационарными точками функции.
60. Экстремумы функции. Особую роль в исследовании функций
играют значения х, отделяющие интервал возрастания от интер-
интервала убывания или интервал убывания от интервала возрастания
(рис. 70). В этих точках функция f(x) меняет характер своего
изменения; при переходе независимой переменной через эти точки
и
л
i
fjfy ft
I \
а?
к
РйС-
1) Из хода доказательства видно, что на концах интервала производная
может и не существовать.
184
ГЛ. IV. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[60
«27
(как всегда, слева направо) функция f(x) из возрастающей ста-
становится убывающей (график / на рис. 70) или, наоборот, из убы-
убывающей— возрастающей (график // на рис. 70). Если имеет место
первый случай (точка х'
на рис. 70 отделяет ин-
интервал возрастания от
интервала убывания), то
существует такая окре-
окрестность точки х\ что
значение f(x') является
наибольшим значе-
значением функции f(x) в
этой окрестности; если
имеет место второй слу-
случай (точка х" на рис. 70
Рис< 7l* отделяет интервал убы-
убывания от интервала воз-
возрастания), то существует такая окрестность точки х'\ что зна-
значение f(x") является наименьшим значением функции f(x) в
этой окрестности. Дадим общее определение.
Определение. Точка х0 называется точкой максимума
функции f(x), если f(x0) есть наибольшее значение функции f(x)
в некоторой окрестности точки xQ.
Аналогично
Точка х0 называется точкой минимума, если f(x0) есть наи-
наименьшее значение функции/(лс) в некоторой окрестности точки х0.
Точки максимума и минимума объединяются названием точки
экстремума. Если х0 — точка экстремума (или, как еще можно ска-
сказать, экстремальная точка) функции f(xI то говорят, что эта
функция достигает экстремума —соответственно максимума или
минимума—в точке х0 и что f(x0) есть экстремальное—соответ-
экстремальное—соответственно максимальное или минимальное — значение функции f(x).
Функция на данном интервале может иметь несколько экстре-
экстремумов, причем какой-нибудь минимум функции может оказаться
больше какого-нибудь максимума (рис. 71). Поэтому наиболь-
наибольшее и наименьшее значения функции в интервале в отличие
от экстремумов, носящих относительный характер, называют
иногда абсолютными максимумом и минимумом функции.
На графике функции точкам экстремума соответствуют вер-
вершины линии, обращенные соответственно вверх или вниз (на рис.
71 точки М' и М").
Обычно встречающиеся функции имеют на заданном конечном
интервале лишь конечное, определенное число точек экстрему-
экстремума; именно такие функции, как правило, и будут изучаться в даль-
дальнейшем*
60]
§ 2. ПОВЕДЕНИЕ ФУНКЦИИ В ИНТЕРВАЛЕ
185
Примером функции иного рода служит функция у = х sin — , которая
в любом интервале, содержащем точку 0, непрерывна, если считать «/*-<> = О»
но имеет бесконечное число точек экстремума. Ее схематический график
можно построить, воспользовавшись указанием к построению графика
функции у = sin— на стр, 102.
X
Установим теперь признак, дающий необходимое условие того,
чтобы данная точка являлась точкой экстремума.
Необходимый признак экстремума. Если в точке
х0 функция f(x) достигает экстремума, то ее производная в этой
точке либо равна нулю, либо не существует.
Если в точке х0 функция достигает экстремума, скажем мак-
максимума, то значение функции в этой точке является наиболь-
наибольшим ее значением в некоторой окрестности точки лг0. Но по
теореме Ферма в тех внутренних точках интервала, в которых
У\
О
А
Рис. 72.
дифференцируемая функция достигает своего наибольшего зна-
значения, ее производная равна нулю. Совершенно аналогично про-
проводится рассуждение и для точки минимума.
С геометрической точки зрения рассматриваемый признак озна-
означает, что касательная к графику функции в его вершине парал-
параллельна оси Ох (см. рис. 71).
Функция может также иметь экстремумы и в тех отдельных
точках, в которых она недифференцируема. Случаи эти изобра-
изображены на рис. 72. При этом в точках Мх и Мг график функции
имеет касательную, перпендикулярную к оси абсцисс. Такие
точки мы условились называть точками возврата. Характерным
их признаком является то, что производная f'(x) при стрем-
стремлении х к абсциссе любой такой точки стремится, с одной
стороны, к +оо, а с другой стороны, к —оо. В точках М3
и МА касательная переходит внезапно от одного наклона
к другому, т. е. в этих точках график не имеет определенной
186
ГЛ. IV. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[60
касательной; такие точки называются угловыми точками кривой.
При значениях х, равных абсциссам таких точек, левая и правая
производные функции f{x) (см. п. 52) различны.
Важно подчеркнуть, что необходимый признак экстремума не
является достаточным, т. е. из того, что производная в данной
б)
Рис. 73.
точке обращается в нуль (или ее не существует), еще не сле-
следует, что эта точка обязательно будет точкой экстремума. Так,
например, функция у = х* имеет производную у' = Зл:2, обращаю-
обращающуюся в нуль при лс = О. Однако точка дг = О вовсе не является
точкой экстремума (рис. 73, а).
Функция у = yfx, для которой у' = з/ —> не имеет произ-
производной при дг=О. Из рис. 73,6 ясно видно, что и здесь точка
jc = O не является экстремальной. Как легко заметить, в обоих
приведенных примерах точка jc = 0 не отделяет друг от друга
интервалы жжотояяостд противоположного смысла. И слева и
справа от этой точки производная имеет один и тот же знак.
Для того чтобы иметь возможность судить о том, когда же
данная точка будет являться точкой экстремума, мы перейдем
к установлению достаточного признака экстремума.
Первый достаточный признак экстремума1). Точ-
Точка х0 является точкой экстремума функции/(jc), если производная
f(x) при переходе х через х0 меняет знак; при перемене знака
+ на — точка х0 является точкой максимума; при перемене —
на 4* точка х0 является точкой минимума.
*) Позже, в п. 62, мы познакомимся с другим достаточным признаком
экстремума, который и будем называть вторым.
61J
§ 2. ПОВЕДЕНИЕ ФУНКЦИИ В ИНТЕРВАЛЕ
187
В самой точке х0 производная в силу необходимого признака
равна нулю или не существует.
Доказательство. Пусть при переходе х через х0 произ-
производная меняет знак с + на —; это значит, что слева от х0
находится какой-нибудь интервал возрастания функции, а справа —
какой-нибудь интервал убывания функции. Следовательно, точка
х0 есть точка максимума функции.
Так же убеждаемся, что при перемене знака производной с —
на +точка х0 есть точка минимума функции.
Замечание. Следует иметь в виду, что, основываясь только на пере-
перемене знака производной, нельзя еще заключить о наличии экстремума;
необходимо знать еще, что в самой точке функция непрерывна. Так, напри-
например, пусть t/ = —^-. Производная этой функции #'*= — меняет знак при
переходе х через точку х=0: слева от нуля у' > О и, значит, функция
возрастает, справа от нуля у' < О и, значит, функция убывает; сама же
точка * = 0 не является точкой максимума, ибо функция при * = 0 имеет
бесконечный разрыв.
На графике функции (рис. 74) это обстоятельство очевидно.
61. Схема исследования функций на экстремумы. Наибольшее
и наименьшее значения функции.
I. Схема исследования. Укажем последовательность
действий для изучения роста и отыскания экстремумов непрерыв-
непрерывной функции y—f(x) в заданном интервале, который может быть
как конечным, так и бесконечным. Будем считать, что функция
y=f(x) имеет производную всюду, за исключением, быть может,
отдельных точек.
1) Прежде всего нужно найти точки интервала, в которых
производная равна нулю (стационарные точки), т. е. действитель-
действительные корни уравнения /' (х) = 0, а также те точки, в которых
производная не существует. Обозначим все найденные точки
в порядке возрастания через х1} х21 ..., хп.
188 ГЛ. IV. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [61
Таким образом,
хг < х2 < ... < хп.
Это — те точки интервала, в которых функция f(x) может иметь
экстремумы. Их иногда называют критическими.
2) Затем разбиваем при помощи точек х{ весь заданный интер-
интервал [ау Ь]1) на частичные интервалы: (а, л^), (xv лг2), ...
. .., (•*:„_!, хп), {хп, Ь), в каждом из которых производная сохра-
сохраняет постоянный знак. В самом деле, в противном случае произ-
производная была бы равна нулю (или не существовала бы) еще
в точках, отличных от выделенных, а все такие точки мы уже
нашли в п. 1). Следовательно, эти интервалы являются интер-
интервалами монотонности функции.
3) Находим знак производной в каждом из частичных
интервалов, для чего достаточно узнать ее знак в какой-нибудь
одной точке интервала. По знаку производной определяем харак-
характер изменения функции в каждом интервале монотонности (воз-
(возрастает она или убывает). Следя за переменой знака производной
при переходе через границы интервалов монотонности — точки xi%
выясняем, какие из этих точек будут точками максимума и какие—¦
минимума. При этом может оказаться, что какая-нибудь точка х{
не служит точкой экстремума функции. Это случится, если в двух
соседних интервалах (х(_1} х{) и (xiy X(+1), разделяемых точкой
xh функция монотонна в одинаковом смысле, т. е. производная
в них имеет один и тот же знак. Тогда они объединяются в один
интервал монотонности функции. В этом случае точка хг не будет
точкой экстремума (пример: х = 0 для функции у = х3).
4) Подстановкой в выражение функции f(x) критических зна-
значений х = х( находим соответствующие значения функции:
Как уже отмечалось, не все из этих значений могут оказаться
экстремальными.
Если значения /*(лгх), /(х2), ..., f(xn) вычислены, а также
найдены значения функции на концах интервала f(a) и f{b), то
ход изменения функции легко представить и без исследования
знака производной. Так как нам уже известно, что в каждом из
интервалов (а, хх), (xv лг2), ..., (хп, Ь) функция не имеет точек
экстремума и, следовательно, монотонна, то, сравнивая между
собой значения функции на концах каждого такого интервала,
мы и определим, где функция возрастает и где убывает.
Какой из приемов следует употребить, зависит от конкретных
обстоятельств. Может быть, что удобнее и легче использовать
1) а и Ь могут быть равны соответственно — оо и + оо.
61]
§ 2. ПОВЕДЕНИЕ ФУНКЦИИ В ИНТЕРВАЛЕ
189
знаки производной, а может быть и так, что, нуждаясь все равно
в значениях функции в критических точках, проще использовать
эти значения и не выяснять знаки производной.
Результаты исследования целесообразно сводить в таблицу:
X
У
У
а
f(a)
а < х < хх
возрастает
+
f,(xi)
0
Хг < X < Х%
убывает
Ч
Ь(ч)
0
х2 < х < Ь
убывает
Ь
1(Ь)
На приведенной таблице (для простоты считаем, что в интер-
интервале [а} Ь] всего две критические точки) показана примерная
схема ее заполнения.
Знак производной в каждом из интервалов определяется путем
вычисления значения производной в одной из точек интервала
(безразлично какой). Если производная представлена в виде про-
произведения нескольких множителей, то достаточно найти знаки
этих множителей, не вычисляя их значений; по знакам множите-
множителей определится и знак произведения (см. ниже пример 2).
По такой таблице можно построить схематический график
функции.
II. Наибольшее и наименьшее значения функ-
функции. После того как все экстремальные значения функции най-
найдены, легко найти наибольшее Ми наименьшее т зна-
значения функции f(x) в интервале [а, Ь]. Для этого нужно сравнить
\т
М
Ь а.
Ь а Ь а
Рис. 75.
Ъ а
между собой значения функции в экстремальных точках и на кон-
цах интервала. Действительно, наибольшим значением функции
в интервале [а, Ь] может быть или одно какое-нибудь из макси-
максимальных ее значений, или значение на конце интервала. Анало-
Аналогично наименьшее значение функции следует искать или среди
минимальных ее значений, или среди значений на концах интер-
интервала. Некоторые из возможных случаев представлены на рис. 75.
190 ГЛ. IV. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [61
Ясно, что если функция в интервале [а, Ь] монотонно возрас-
возрастает, то ее наибольшее значение будет /F), а наименьшее /(а);
если функция монотонно убывает, то указанные значения просто
поменяются местами.
Часто встречается случай, когда функция в интервале имеет
только одну экстремальную точку. Если это точка макси-
максимума, то значение функции в ней, очевидно, будет наибольшим
значением функции в интервале, а если минимума, то наименьшим.
III. Примеры исследования функций. 1) Основ-
Основные элементарные функции. Хотя поведение каждой из
основных элементарных функций уже описано нами с помощью их
графических изображений в первой главе, однако применение
первой производной позволяет очень легко аналитически обнару-
обнаружить простейшие свойства этих функций.
Степенная функция: у = х*. Ее производная у'^пхп"г
при х > 0 положительна, если п > 0, и отрицательна, если п < 0.
Следовательно, на положительной полуоси Ох функция или везде
возрастает (п > 0), или везде убывает (я<0).
Показательная функция: у~ах. Знак ее производной
у'= ах1па совпадает со знаком In а, так как функция а* везде
положительна. Поэтому у' > 0, если а > 1, и у' < 0, если а < 1.
Показательная функция монотонна на всей оси Ох: возрастает
в первом случае, убывает во втором.
Логарифмическая функция: у = \пх. Ее производная
<У=— при дг>0 (а только для этих значений х функция опре-
определена) положительная, и значит, In jc везде возрастает.
Подобным образом, обращаясь к производным, нетрудно вос-
восстановить ход изменения и других основных элементарных функций.
2) Рассмотрим функцию
у = З*3 + 4,5л;2 — 4х + 1.
Эта функция имеет непрерывную производную на всей оси Ох.
Находим производную:
4 = Cлг— 1)(Злг + 4).
Отсюда видно, что производная равна нулю при Х«т ~ и
при а: = -о- .
Так как при х < — у °^а множителя отрицательны, то произ-
производная при этих значениях х положительна и, следовательно,
4 1
функция возрастает. При —-^ < х < -^ производная отрицательна
О о
611
§ 2. ПОВЕДЕНИЕ ФУНКЦИИ В ИНТЕРВАЛЕ
191
и функция убывает, а при х > у производная снова положи-
4
тельна и функция возрастает. Таким образом, х =— -^ есть точка
о
максимума, а х = -=—точка минимума, и мы имеем три интервала
4 4
монотонности: от —оо до ~-—интервал возрастания, от —--
1 л 1
до -х—интервал убывания и от -г до +°° — интервал возрас-
о о
тания.
Вычислим значения функции в точках экстремума и составим
таблицу поведения функции. При составлении таблицы учиты-
учитываем, что
lim у = lim *
X
У
У'
— 00
— 00
4
возрастает
4
3
4
max
0
~±<*<1
убывает
—
1
3
5
18
min
0
1
возрастает
+
+ оо
+00
По таблице легко построить схематический график функции
(рис. 76). Из графика ясно, между прочим, что уравнение
имеет только один действительный корень, т. е. остальные два
его корня1) — сопряженные комплексные числа.
3) Изучим функцию
в интервале [—2; 0,5]. В этом интервале функция непрерывна;
она будет положительна во всех точках, за исключением точки
лг = О, где она обращается в нуль. Возьмем производную
У -ТТ7=7е +
2+3*
J) Всякое алгебраическое уравнение имеет столько корней, какова его
степень (см, п. 75).
192
ГЛ. IV. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[61
Производная существует в каждой точке заданного интервала,
кроме точки х = 0. В этой же точке производная бесконечна,
причем если подходить к точке л: = 0 справа, то У—> + оо, а
если слева, то у'—^ — оо. Это указывает на наличие в точке
(О, 0) графика функции точки возврата в виде острия (рис. 77).
Рис. 76.
Рис. 77.
Производная равна нулю при х== «" . Следовательно, в данном
о
интервале есть две критические точки: стационарная точка
2
х =— -тг и точка х = 0, в которой функция недифференцируема.
о
[2 \
—2, 5" ) »
/ 2 \ J
( —^ , 0 ), @; 0,5]. Составляя таблицу поведения функции, видим,
что в первом интервале производная положительна — функция
в нем возрастает; во втором отрицательна — функция в нем убы-
убывает; в третьем снова положительна — функция в нем возрастает.
Впрочем, это ясно и из сравнения значений функции в критиче-
критических точках и на концах интервала:
X
У
У'
-2
=^0,21
—2 < х < —
возрастает
+
2
2
3
=^0,39
max
0
-1<х<
убывает
0
0
0
min
00
0 <х < 0,5
возрастает
+
0
,5
1,03
61] §2. ПОВЕДЕНИЕ ФУНКЦИИ В ИНТЕРВАЛЕ 193
Наибольшее значение функции в интервале [—2; 0,5] прибли-
приближенно равно 1,03 и достигается на правом конце интервала, а
наименьшее значение равно 0 и достигается в точке лг = О.
В дальнейшем (см. стр. 201) мы продолжим и уточним то
исследование заданной функции, которое было произведено здесь.
4) Методы исследования функций часто могут быть исполь-
использованы для доказательства неравенств.
Докажем, например, справедливость неравенств
9 тг
— х < sin х < х, если 0 < х < -у .
Рассмотрим функцию у = ^Ш. Так как ее производная
, cos х. , ч
в интервале @, -„-] отрицательна (х < tg лг), то у убывает и, значит,
функция 5HL^ меньше своего значения при лг = О (т. е. меньше 1) и
больше своего значения при # = — т. е. больше
2 . sin* . л
откуда и следуют наши неравенства.
IV. Задачи о наибольших и наименьших значе-
значениях. Предположим, что даны две величины, связанные функ-
функциональной зависимостью, и
требуется отыскать значение
одной из них (заключенное в
некотором интервале, который
может быть и неограниченным),
при котором другая принима- ° **
ет наименьшее или н а и- Рис. 78.
большее возможное значение.
Для решения такой задачи прежде всего следует составить
выражение для функции, с помощью которой одна величина вы-
выражается через другую, а затем найти наибольшее или наимень-
наименьшее значение полученной функции в данном интервале.
Примеры. 1) Найдем наименьшую длину / забора, с помощью
которого можно огородить участок в форме прямоугольника
с данной площадью s, примыкающий к стене (рис. 78).
7 А. Ф. Бермант, И. Г. Араманович
194 ГЛ. IV. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [61
Обозначим одну из сторон прямоугольника через х; тогда, как
легко видеть, будем иметь
s = x(l—2лг),
откуда
Наша задача сводится к отысканию наименьшего значения этой
функции при изменении х от 0 до оо. При х—*0 и при л: —* оо
функция /—^ оо. Следовательно, наименьшее значение следует
искать среди минимумов функции в интервале @, оо). Возьмем
производную
/' — о !L
В интересующем нас интервале имеем одну стационарную точку:
Лг = Т/ ~, которая является точкой минимума функции, ибо /' < О,
если х < l/-|-> и Г > 0, если х > 1/ -|-« Минимальное значение
У Т
здесь служит и наименьшим значением функции во всем интервале
(О, оо). Значит, какой бы забор, огораживающий прямоугольный
участок с площадью s и примыкающий к стене, мы ни взяли, его
длина не может быть меньше 2^2s и равна этому значению только
в том случае, когда меньшая сторона прямоугольника (равная
г Т^Т^^) в два Раза меньше ег0 большей стороны (рав-
(равной 2|/s—2~]/s = "|/2s] # в указанных условиях самый эко-
экономичный забор тот, у которого большая сторона в два раза
длиннее меньшей стороны.
2) Вычислим, через сколько секунд после начала падения под
действием силы тяжести (без учета сопротивления воздуха) кине-
кинетическая энергия дождевой капли будет наибольшей (и какова
она), если начальная масса капли т0 и капля равномерно испаряется,
так что убыль массы пропорциональна времени (коэффициент
пропорциональности обозначим через k).
Через t сек после начала падения кинетическая энергия а
будет равна
_ mv2 __ (mo — kt) (gtJ
где g—ускорение силы тяжести.
62] § 2. ПОВЕДЕНИЕ ФУНКЦИИ В ИНТЕРВАЛЕ 196
Вопрос сводится к отысканию наибольшего значения этой
функции при t > 0.
Имеем
Ясно, что ^ = 0 при * = 0 и при / = ||; если 0</<-|-^2,
то ~ > 0, а если t^>-^-~^ то ~ < 0. Отсюда следует, что при
ctt о к at
t = -r~ кинетическая энергия а достигает максимума, и так как
это единственный экстремум функции, то и наибольшего евоего
значения; оно равно
_ \ Ък ){ 3fe
Яшах-
Если же время падения капли на землю ^^-о?Г> то кинетическая
энергия все время возрастает и наибольшее ее значение будет
в момент падения капли на землю.
62. Применение второй производной. Точки перегиба.
I. Второй признак экстремума. С помощью второй
производной /" (х) исследуемой функции / (х) можно установить так
называемый второй достаточный признак экстремума, который иногда
оказывается более удобным и простым, чем первый.
Второй достаточный признак экстремума. Точка
xQ есть точка экстремума функции f(x), если /'(л:0)=:0, а
/'(хо)фО, причем, если /Чжв)>0, то х0 — точка минимума, а
если/"(xo)«<[O, то х0 — точка максимума.
Доказательство. Пусть f (x0) = 0 и /" (#0) > 0. Предполагая
вторую производную непрерывной, мы можем считать, что она
сохраняет свой знак в некоторой окрестности точки х0. Отсюда
следует, что функция /' (я) в этой окрестности будет возрастаю-
возрастающей, потому что ее производная /" (я) > 0. Так как /'(л:0) = 0, то
слева от точки х0 производная /' (л:), принимая меньшие значения,
будет отрицательной: /' (л:) < 0, а справа, — принимая большие значе-
значения,— положительной: f '(х) > 0. Итак, функция /' (л:) при переходе х
через х0 меняет свой знак с — на + , и, согласно известному нам
первому достаточному признаку, точка х0 является точкой ми-
минимума.
196 ГЛ. IV. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [62
Рассуждая аналогично, получим, что если /"(лго)<0, то f (х)
убывает и, переходя через точку лг0, меняет знак с + на — , т, е.
точка х0 является точкой максимума.
В том случае, когда f'[xQ) = 0 и f(xo) = Of а также в случае,
когда первой производной не существует, вторым признаком вос-
воспользоваться нельзя и нужно обратиться к первому признаку.
Так, например, обе первые производные функции у = х* равны
нулю при аг = О; вторым признаком воспользоваться нельзя, а по
первому мы устанавливаем, что,функция в этой точке достигает
минимума: производная */' = 4л;3 меняет знак с — на + при пере-
переходе х через нуль. Функция же д> = #3, хотя ее первые две
производные тоже равны нулю при лг = О, не имеет экстремума; дейст-
действительно, ее первая производная у'= 3х2 не меняет знака при
переходе х через нуль.
Однако в случае своей применимости второй признак оказы-
оказывается весьма удобным: вместо рассмотрения знака функции f (х)
в тощ^Ку отличных от предполагаемой точки экстремума, он позво-
позволяет дать ответ по знаку функции f (x) в той же точке.
Примеры. 1) у = ах2 + Ьх-{- с. Так как у' = 2ах-\-Ь равна
нулю при х=—гр, а У = 2а, то у имеет максимум в указанной
точке, если а < 0, и минимум, если а > 0.
Этот пример может наглядно убедить в большом значении
теории для математической практики. Он показывает, что с рас-
расширением средств анализа упрощаются и укорачиваются рассуж-
рассуждения и выкладки, необходимые для исследования конкретных
функций. В первой главе, где мы еще не владели дифференциальным
исчислением, изучение квадратичной функции потребовало от нас
довольно длинных и специальных рассмотрений, а здесь для этого
изучения нам понадобилось лишь три строки.
2) Вернемся к примеру 1) п. 61, IV. Мы выяснили, что функ-
функция / = 2лг-{- — имеет минимуме стационарной точке лг= у у:
производная /'=2—\ меняет свой знак при переходе х через
эту точку. Но проще заключить о наличии минимума в указанной
2s
точке просто из того факта, что /"=—>0 при всех положи-
положительных xf а значит, и при лс= у -^ .
II. Выпуклость и вогнутость линии. Точки пере-
перегиба.
Определение. Дуга называется выпуклой, если она пере-
пересекается с любой своей секущей не более чем в двух точках.
62]
§ 2. ПОВЕДЕНИЕ ФУНКЦИИ В ИНТЕРВАЛЕ
197
Дуга АВ на рис. 79 выпуклая, а на рис. 80 невыпуклая; у
дуги на рис. 80 есть секущие МхМг, которые, кроме точек Мх
и М2, пересекаются с дугой АВ еще в других, отличных от этих
точках Мъ.
в
Рис. 80
В,
Л
Если дуга выпуклая, то она целиком лежит по одну сторону
от касательной, проведенной в любой ее точке.
Будем теперь рассматривать линии, являющиеся графиками
непрерывных функций y=f(x). Если такая линия выпуклая, то ее
выпуклость обращена или вверх (рис. 81,/), или вниз (рис. 81,//).
Линии, обращенные
выпуклостью вверх, ус-
условились называть вы-
выпуклыми, а обращенные
выпуклостью вниз — во-
вогнутыми. Геометрически I /д /
ясно, что выпуклая дуга
лежит под любой своей
касательной, а вогнутая
дуга—н а д касательной.
Особую роль играют
точки на линии, отделя-
отделяющие выпуклую дугу от вогнутой; они называются точками
перегиба. На рис. 82 точка С отделяет выпуклую дугу АС
от вогнутой СВ.
Определение. Точкой перегиба называется такая точка
линии, которая отделяет выпуклую дугу от вогнутой.
При этом предполагается, что в этой точке к линии можно
провести касательную. Предоставляем читателю нарисовать линию
с угловой точкой, которая отделяла бы выпуклую дугу от вогну-
вогнутой; такие угловые точки мы не причисляем к точкам перегиба.
В точке перегиба касательная пересекает линию; в окрестности
этой точки линия лежит по обе стороны от касательной.
/ О
Рис. 81.
198
ГЛ. IV. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[62
В
Установление участков выпуклости и вогнутости и точек пере-
перегиба линии y=f(x) имеет важное значение для характеристики
этой линии, а значит, и для характеристики поведения функции/(л:).
III. Признаки выпуклости и вогнутости линии.
Связь между второй производной /" (х) и выпуклостью или вог-
вогнутостью линии y~f(x) мы установим, пользуясь лишь самыми
простыми геометрическими сооб-
соображениями. В основе лежит сле-
следующее предложение.
Интервалу убывания первой
производной соответствует учас-
участок выпуклости графика функ-
функции, а интервалу возрастания —
участок вогнутости.
В самом деле, если дуга вы-
выпуклая, то при перемещении
Рис. 82. точки касания слева направо
угловой коэффициент касатель-
касательной, т. е. /' (л;), как это видно из рис. 82, уменьшается: сначала
он принимает все меньшие положительные значения, потом ста-
становится равным нулю, а затем и отрицательным. (Особенно ясно это
видно на рис. 58 п. 48.) Таким образом, интервал [х19 х2] есть
интервал убывания функции /'(лг).
Верно и обратное: если функция f'{x) убывает, то убывает
и угловой коэффициент касательной к линии; при этом дуга кри-
кривой будет лежать под любой своей касательной, т. е. она вы-
выпуклая. (Это утверждение становится более наглядным, если
представить себе кривую, как бы построенную из «бесконечно
малых» отрезков касательных.)
Совершенно аналогично можно установить, что если дуга вог-
вогнутая, то функция /' (х) возрастает, и наоборот. Так, для графика
функции, изображенного на рис. 82, дуга СВ—вогнутая и [дг2, хг] —
интервал возрастания f'(x).
Воспользуемся теперь основной теоремой, устанавливающей
связь между характером изменения функции и знаком ее произ-
производной, приняв за функцию—f'(x) и за ее производную—f{x).
Если /"(*)> О, то f'(x) возрастает, а если /" (лг)< 0, то /' (лг)
убывает, В результате мы получаем следующую теорему.
Теорема. Если вторая производная /" (дг) всюду в интервале
отрицательна, то дуга линии y=f(x)> соответствующая этому
интервалу, выпуклая. Если вторая производная f (х) всюду
в интервале положительна, то дуга линии y—f(x), соответствую-
соответствующая этому интервалу, вогнутая.
Так же как и в конце п. 59, отметим, что если f"(x) сохра-
сохраняет постоянный знак, скажем положительный, и лишь в отдель-
62] § 2. ПОВЕДЕНИЕ ФУНКЦИИ В ИНТЕРВАЛЕ 199
ных точках обращается в нуль, то /' (х) остается возрастающей,
а соответствующая дуга графика функции y=f(x) вогнутой.
Например, для параболы четвертого порядка у=х* вторая про*
изводная У'= \2х2 всюду положительна, кроме точки л; = 0, где
она равна нулю; график же этой параболы всюду вогнутый.
Изложенная сейчас теорема делает особенно ясным второй
достаточный признак экстремума.
Если /' (х0) = 0и/" (х0) < 0, то вершина кривой, соответствую-
соответствующая точке лг0, лежит на выпуклой части линии у=/(х), и по-
поэтому точка х0 является точкой максимума. Если же /'(лг0) = О
и/"(.*го)>О, то соответствующая вершина лежит на вогнутой
части линии, и поэтому точка х0 является точкой минимума.
IV. Признаки точки перегиба. Мы определили точку
перегиба как такую точку графика, которая отделяет выпуклую
дугу от вогнутой. Из приведенного выше рассуждения следует,
что абсцисса точки перегиба (точка х% на рис. 82) разделяет два
интервала монотонности первой производной /' (х), т. е. является
точкой экстремума для первой производной. Применяя необходимый
признак экстремума, получаем:
Если х0 — абсцисса точки перегиба, то либо f'(xo) — O9 либо
f (х0) не существует.
Это и дает нам необходимый признак точки перегиба.
Однако не всякий корень уравнения /" (л;) = 0 является абсцис-
абсциссой точки перегиба. Например, функция у = х* имеет производные
у' == 4л:3 и у"=\2х2. Несмотря на то, что у"х=-0 = 0, точка @,0)
является вершиной кривой и не является точкой перегиба.
Для того чтобы выяснить, когда же точка х0 будет действи-
действительно являться абсциссой точки перегиба, нужно проследить еще,
меняет ли вторая производная свой знак при переходе через эту
точку. Таким образом, мы и приходим к достаточному при-
признаку точки перегиба:
Точка (*0, у0) есть точка перегиба линии j> =/(*), если/"С*)
меняет знак при переходе х через х0. При перемене знака с —
на 4" слева от нее лежит участок выпуклости, а справа —уча-
—участок вогнутости; при перемене знака с + на —, наоборот, уча-
участок вогнутости сменяется участком выпуклости.
Приведем еще второй достаточный признак точки
перегиба, аналогичный второму достаточному признаку экстре-
экстремума. Рекомендуем читателю доказать его самостоятельно.
Точка (х0, у0) есть точка перегиба линии y=f(x)f если
/"(л;0) = 0, a f'"(xQ)jk0; при /"' (д:0)>0 слева от нее лежит
участок выпуклости, справа—участок вогнутости, а при/ (лго)<О
слева лежит участок вогнутости, а справа — участок выпуклости.
В заключение отметим, что при отыскании точек перегиба
и интервалов выпуклости и вогнутости мы пользуемся теми же
200 ГЛ. IV. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [62
правилами, что и при отыскании точек экстремума, применяя, од-
однако, эти правила не к самой функции, а к ее первой производной.
При этом интервалу возрастания первой производной соответ-
соответствует участок вогнутости графика функции, интервалу убывания —
участок выпуклости и точке экстремума первой производной — аб-
абсцисса точки перегиба.
Примеры. 1) Линия у = л;4 + х6 в точке @,0) имеет точку
перегиба: действительно, у"хх=ь~(\2х*-\-&х)х_0 = 0 и J^'lo =
= B4лг + 6)л.=0 = 6 > 0. Слева от точки @,0) лежит участок вы-
выпуклости, а справа—вогнутости. Предоставляем читателю проверить,
что точка (—-?у —ygJ также является точкой перегиба.
2) Линия у = хъ-\-х в точке @, 0) имеет точку перегиба: прежде
всего, Ух=о = BОх*)х=о — ®> Далее, так как^10 = 0, то рассмат-
рассматриваем значения у" вблизи точки л; = 0 и замечаем, что у" при
переходе х через х = 0 меняет знак с — на +. Следовательно,
лг = О есть абсцисса точки перегиба, причем слева от этой точки
лежит участок выпуклости линии, а справа — участок вогнутости.
3) Линия у = х*-\-х в точке @,0) не имеет перегиба: здесь
также у'х=о = (^2л:2)д:=:0 = 0 и ^^0 = 0, однако при переходе х че-
через точку х = 0 производная у" знака не меняет.
Мы допускали, что функция f(x) во всем рассматриваемом ин-
интервале дважды дифференцируема. Если это не так, то нужно
исследовать f (x) и f"(x) в окрестностях тех отдельных точек,
в которых эти производные не существуют. В них также может
произойти смена участков выпуклости и вогнутости.
В качестве примера можно рассмотреть функцию у~%/х
(см. рис. 73, б), для которой точка @, 0) является точкой перегиба.
В обычно встречаемых случаях точки экстремума а, Ь, с, ... и
абсциссы точек перегиба а, C, у, ... чередуются (см. рис. 71).
Обратим внимание на разницу в характере терминов: точкой
экстремума функции называется точка на о с и независимой пере-
переменной, а точкой перегиба — точка самого графика. Это связано
с тем, что понятие экстремума относительное, зависящее от вы-
выбранной системы координат: точка на линии, соответствующая
точке экстремума, — вершина в одной системе координат может не
быть вершиной в какой-нибудь другой системе координат; опре-
определение же точки перегиба не зависит от системы координат,
а обусловлено свойствами, присущими самой линии: точка перегиба
остается таковой при всех перемещениях линии (как твердого тела)
на плоскости, т. е. в любой системе декартовых координат.
V. Примеры. 1) Характер графиков основных элементарных
функций в смысле их выпуклости теперь может быть очень легко
проверен.
62] § 2. ПОВЕДЕНИЕ ФУНКЦИИ В ИНТЕРВАЛЕ 201
Так, график степенной функции у~хп на положительной по
луоси Ох вогнутый при я<0 и л>1 и выпуклый при 0</г<1.
Действительно, вторая производная у" = п(п—\)хп~2 положи-
положительна в первых случаях и отрицательна во втором.
График показательной функции у = ах при любом а>0 вогнут
на всей оси Ох, так как у" = ах In2 a > 0.
Логарифмика^ = logaAr выпукла при а > 1 и вогнута при а < 1.
Действительно, вторая производная У' = — т г отрицательна в
первом случав и положительна во втором.
Так как
(sinAr)" = — sin a:,
то участки выпуклости синусоиды расположены выше оси абсцисс,
а участки вогнутости — ниже; точками перегиба синусоиды явля-
являются точки ее пересечения с осью Ох.
2) Дополним исследование функции
выполненное в п. 61 (III, пример 4). Произведенное уже изучение
интервалов монотонности и точек экстремума показывает, что наша
функция в интервале [ — 2; 0,5] имеет одну точку максимума:
2
х = —5" и °ДНУ точку минимума: х = 0. Найдем теперь участки
о
выпуклости и участки вогнутости графика функции и точки его пе-
перегиба. Для этого возьмем вторую производную
* , Хч/ 9x2+12* — 2
Так как множители ех и х\/х = \/х* положительны, то знак у"
совпадает со знаком квадратного трехчлена 9л:2 + 12лг—2. Этот
|/g_l_2
трехчлен имеет нули в точках хг***— » ^ —1,48 и
i/g 2
х2 = J—^— » 0,15. Легко видеть, чтоу > 0 в интервале (—2, хг)у
/'<0 в интервале (хг, 0), /<0в интервале @, ^2I)»-УЙГ>0 в
интервале (х2; 0,5); значит, в интервале (—2, хг) график функ-
функции вогнут, в интервалах (хи 0) и @„ х2) он выпуклый, в интер-
интервале (х2; 0,5) вогнутый (рис. 83).
х) Нельзя здесь рассматривать сразу весь интервал [лгх, дг2], так как
внутри него есть точка (х = 0) разрыва второй производной.
202
ГЛ. IV. ПРИМЕНеНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[63
Чтобы более точно построить теперь график функции, найдем
ординаты точек перегиба. Подставляя значения х± и х2 в выраже-
выражение функции, получим: jf*«_if48 « 0,30, уХъоль ^0,32. Как мы
видим, график функции, построенный на рис. 83, весьма значи-
значительно отличается от графика на рис. 77, построенного без долж-
должного анализа. В случае особо точного построения графика реко-
рекомендуется найти еще угловые коэффициенты касательных в точках
-2 -
Рис. 83.
%5
перегиба. Для этого нужно подставить значения хх и х2 в выра-
выражение для производной; произведя необходимые вычисления, по-
получим
yU-i.4e ~ 0,16, ^я0,15 « 1,80.
Заметим также, что вне рассматриваемого интервала функция не
имеет больше ни точек экстремума, ни точек перегиба.
§ 3. Правило Лопиталя. Схема исследования функций
63. Правило Лопиталя1).
I. Основные случаи. В дополнение к известным уже нам
правилам предельного перехода (гл. II) приведем здесь еще одно
очень удобное и простое правило, называемое правилом Лопиталя.
В дальнейшем мы его также будем применять к исследованию
функций. Оно может быть сформулировано в виде следующей тео-
теоремы.
Теорема Лопиталя. Пусть функции f{x) и <р(х) при
* ~> хо (или х ^> °°) совместно стремятся к нулю или к беско-
1)Лопиталь A661—1704) —французский математик, современник
Лейбница и Ньютона. Он написал первую книгу по дифференциальному
исчислению —«Анализ бесконечно малых», изданную в 1696 г.
63] § 3. ПРАВИЛО ЛОПИТАЛЯ. СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИЙ 203
. Если отношение их производных имеет предел, то от-
отношение самих функций также имеет предел, равный пределу
отношения производных, т. е.
Доказывать эту теорему в общем виде мы не будем, а ограни-
ограничимся лишь рассмотрением простейших случаев и примеров, разъяс-
разъясняющих суть дела.
Докажем прежде всего, что если при х—>х0 функции f(x) и
ф (л:) стремятся к нулю и их производные в точке х0 существуют,
причем ф' (л:0) Ф 0, то
Разумеется, здесь предполагается, что функции f(x) и ц>(х)
определены и непрерывны в некоторой окрестности точки х0 и зна-
знаменатель <р(х) не обращается в нуль в точках этой окрестности,
за исключением самой точки х0.
Поскольку/(лго) = ф(дго) = 0, то
Их) = f(*W(*o) ^ х-х0
ф (х) Ф (х) — ф (х0) Ф W
Переходя к пределу при х—>-х0 и используя теорему о пределе
дроби, получим
Х-*- Хо X Xq
что в силу определения производной дает
Km IS±-L
Alii* , . — /
x->x0V(x) Ф
Примеры.
sin л:
1) lim =
X-+Q Х
2) lim nA+A;)=il±
Мы видим, как просто отыскиваются теперь знакомые нам пре-
пределы. Конечно, простота эта в данном случае только кажущаяся,
204 ГЛ. IV. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [63
ибо мы пользуемся дифференцированием функций sin.*; и In (!+•*),
а оно само опирается на знание пределов отношений и
х
при х—> 0.
«\ «~ *2-5* + 6_2.2-5_ 1
*Т2 *2-3* + 2~~ 2-2-3 ~
sin 5л: 5 cos 5яЪ
4) ^
^ 2 cos 2я ~" ~ 2 *
Может случиться, что при лг = лг0 производная <р' (л:0) равна
нулю. Тогда, разумеется, формула (*) неприменима и приходится
пользоваться правилом Лопиталя в его общей форме:
(**)
Доказательство формулы (**) уже более сложно, чем формулы (*). Оно
будет опираться на теорему Коши (п. 58), и читатель, пропустивший
при чтении эту теорему, может пропустить приводимое доказательство
и прямо перейти к примерам.
Снова запишем отношение функций в виде
И*) = f W—<8(^о)
)—ф(*о)
и применим к правой части теорему Коши (при этом мы дополнительно
должны предположить, что производные f{ (x) и ф7 (д:) существуют в окрест-
окрестности точки х0 и ф' (х) не обращается в нуль нигде, за исключением самой
точки х0). Имеем
f{x)
Ф (х)
где ?—точка, лежащая в интервале между х0 и х. Если теперь х—у х0, то
и точка ?, заключенная между х0 и х, будет стремиться к точке х0. Так как
по условию теоремы предел отношения производных существует, то
Заменяя теперь переменную g переменной х, мы и получаем формулу (**).
Если заранее не оговорить существование предела отношения производ-
производных, то формула (*#) может не иметь места, хотя предел отношения самих
функций может существовать (примеры этого приведены ниже). Дело в том,
что из существования предела lim ( }х' при произвольном стремле-
нии х к х0 следует, конечно, существование предела lim LJl*L , однако
?-**рФ (б)
обратное неверно, так как точка {• может принимать только некоторые
избранные значения. Это аналогично тому, что lim sin JL не существует,
х-+ о х
в то время как для х = — предел lim sin—-— = limsin^n =
63J § 3. ПРАВИЛО ЛОПИТАЛЯ. СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИЙ 205
5) нш *-**** = lim 1-cosx + xslnx
' х^0 х —sinx x^0 l~cos*
Здесь производные числителя и знаменателя в свою очередь стре-
стремятся к нулю. Применяя правило Лопиталя повторно, а в случае
необходимости и далее, получим
,. 1 — cos* + *sin* ,. 2sin* + *cos* 3cos*—*sin* o
lim -. • = lim r = lim = 6.
x + 0 1-cos* ,^о sin* ^0 cos*
Заметим, что формула (##) остается справедливой и тогда, когда
отношение производных стремится к бесконечности; тогда и отно-
отношение самих функций тоже стремится к бесконечности.
~. ,. 1— cos* ,. sin л; ,. cos л;
6) lim —:—= lim -t = lim -:— = cx>.
x-+ 0 x— sin л: x_^0 1—cos* ^^QSinx
0
При повторном применении правила Лопиталя рекомендуется
сначала произвести все возможные упрощения, например сократить
общие множители и использовать уже знакомые пределы.
7) limarctg*-arcsin* = 1.m
' ТОГ Y — Qin *•
— COS*
COS2*
1—cos* (l+cos*+cos2*)(l+*2)
—*2
Ясно, что предел второго множителя равен г/3; продолжая при-
применять правило Лопиталя к первому множителю, получим
Докажем, что формула (**) остается справедливой при х—*оо,
предполагая, что функции f(x) и ф (х) определены и дифферен-
дифференцируемы для достаточно больших \х\. Полагая # = --, придем к
рассмотренному случаю, так как если х—>оо, то z—>0> Имеем
206 ГЛ. IV. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [63
сокращая на ( А и заменяя — снова на лг, получим
Отметим, что правило применимо во всех случаях стремления х
к бесконечности, т. е. при х—*+оо, х—>—оо и х—> оо (см.
п. 25).
Если при х—>х0 (или при х—> оо) обе функции f(x) и ц>{х)
совместно стремятся к бесконечности, то формула (*#) также ос-
остается справедливой. Доказательство более сложно, и мы его
спускаем.
J_
8) Hm~|- = lim —^^lim грг=0, /г > 0.
ЛЧ t. а* ,. ах\па ,. ах(\па)п
9) lim-pr = iim „.!=... =lim v =00,
если п—целое и положительное число и я> 1. Заметим, кстати,
что рассматриваемый предел равен оо при любом /z, если а > 1.
Примеры 8) и 9) показывают, что при х—*+°° логарифмиче-
логарифмическая функция 1плг возрастает медленнее, а показательная функ-
функция а* быстрее, чем любая степенная функция хп (при положитель-
положительном л).
Приведем пример, когда отношение функций имеет предел, а
отношение их производных не стремится ни к какому пределу.
Так,
lim
но вместе с тем
in*)' 1-f cos*
при х—> оо постоянно колеблется между 0 и 2 и, значит, не
имеет предела.
Этот пример не противоречит правилу Лопиталя — просто к
нему правило неприложимо.
II. Другие случаи. Первые рассмотренные нами примеры
отыскания предела отношения ¦ ?\-, когда и f(x)—*0иф(л;)—>0t
можно условно обозначить как случаи -^-; примеры же, ког-
когда и f(x)—*оо и ф(дг)—э-оо, — как случаи — .
63] § 3. ПРАВИЛО ЛОПИТАЛЯ. СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИЙ 207
С помощью правила Лопиталя очень часто удается находить
пределы функций и в других случаях, отличных от случаев -тг
и ~. Мы рассмотрим случаи: 1) 0«оо, 2) оо — оо, 3) 1°°, 4) оо°,
5) 0°. Разумеется, эти обозначения @«оо; оо — оо; I00; оо°; 0°,
как и -jr- и — 1 могут служить исключительно для наиболее крат-
краткого указания определенного случая при отыскании предела функ-
функции. Именно, они указывают, что при заданном изменении незави-
независимой переменной х (х—>х0 или х—* оо) функция представляет-
представляется выражением, являющимся соответственно:
1) произведением функции, стремящейся к нулю, и функции,
стремящейся к бесконечности; 2) разностью двух функций, стре-
стремящихся к положительной бесконечности; 3) степенью, основание
которой стремится к 1, а показатель — к бесконечности; 4) сте-
степенью, основание которой стремится к бесконечности, а показа-
показатель—к нулю; 5) степенью, и основание и показатель которой
стремятся к нулю1).
Нет нужды подробно описывать те приемы, которые позволят каж-
0 оо
дый из указанных случаев привести к основным случаям: -=г или — .
На разбираемых ниже примерах читатель ознакомится с этими при-
приемами.
Заметим только, что в случаях 3), 4), 5) функция предвари-
предварительно логарифмируется и, значит, сначала отыскивается предел
не заданной функции, а ее логарифма, а затем уже по пределу
логарифма находится предел функции (что допустимо вследствие
непрерывности логарифмической функции).
Примеры. 1) A = \imxn\nx, п > 0; случай 0» оо. Преобра-
зуя к виду
придем к случаю —. Применим правило Лопиталя:
-71-0'
х) В некоторых учебных руководствах сохраняется традиция называть
¦g-J — ; О-оо; оо —оо; I00; оо°; 0° неопределенными выражениями. Нахож-
Нахождение пределов этих выражений называют раскрытием неопределенностей,
почему и правило Лопиталя иначе называют правилом для раскры-
раскрытия неопределенностей.
208 ГЛ. IV. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [64
2) i4 = ]im(-^~T — -.—г); случай оо — оо. Преобразуя к виду
x-±i\х * \п X ;
А = lim —. тп »
х^г (х—\)\пх '
придем к случаю -д-. Применим правило Лопиталя:
л ,. In X .. X 1
4 = lim-—= = hm-j г = т .
8) A = lim (cos x)x%\ случай lw. Рассматриваем предел ^4j ==
= lim In (cos x)x* f который запишем в виде Лх = lim n c^s x ; это —
случай -^-. Применим правило Лопиталя:
— -—— 1
Но Лх = In lim (cos л:)*2 = In А, поэтому А = еА* = ^ 2 ~ -7= .
1
4) A = \im{ctgx)]nx; случай оо°. Рассматриваем предел
A1 = l\m\n(ctgx)lnx, или, иначе, Аг = lim l5L?*Sf; это — случай — .
Х->0 Х-+0 *ПХ °°
Применим правило Лопиталя:
1
А = lim ^ = lim :— = — 1,
Х-+0 * JC->0 C0S X S111 "^
откуда A = e^i = ^~1 = —.
5) i4 = limjt*; случай 0°. Рассматриваем предел A1 = lim\nxx9
или, иначе,
Аг = lim д: In лг = 0
(см. пример 1 при я=1), откуда Л=И» = е°=1.
64. Асимптоты линий. Когда мы хотим изучить функцию при
стремлении аргумента к бесконечности, нам приходится иметь
дело с частями графика, уходящими в бесконечность, так мазы-
64] § 3. ПРАВИЛО ЛОПИТАЛЯ. СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИЙ 209
ваемыми бесконечными ветвями графика. С бесконечными же вет-
ветвями нам приходится иметь дело и тогда, когда мы рассматрива-
рассматриваем функцию вблизи точек ее бесконечного разрыва (см. п. 33).
Знание бесконечных ветвей функции необходимо для того, чтобы
правильно представить себе форму всего графика и, следовательно,
характер изменения функции во всей области ее определения.
Подойдем к вопросу с геометрической точки зрения и введем в
связи с этим общее определение асимптоты линии (с частными
видами асимптот читатель уже встречался ранее).
Рис. 84.
Определение. Прямая линия Г называется асимптотой
линии L, если расстояние точки линии L от прямой Г стремится
к нулю при неограниченном удалении этой точки от начала коор-
координат.
Следует различать случаи вертикальной и наклонной
асимптот.
1) Пусть линия y — f(x) имеет вертикальную асимптоту.
Уравнение такой асимптоты будет х*=х0, а поэтому, согласно
определению асимптоты, обязательно f(x)—> оо при х—>х0; об-
обратно: если точка х0 есть точка бесконечного разрыва функции
/(лс), то прямая х = х0 служит асимптотой линии у=/(х).
Итак, если Hm/(je) = oot то линия y—f(x) имеет асимптоту
х->х0
Х = Х0.
Взаимное расположение бесконечной ветви линии и ее верти-
вертикальной асимптоты х = х0 обнаруживается исследованием знака
бесконечности (± оо), к которой стремится f(x), когда х стре-
стремится к лг0, оставаясь меньше лг0, т. е. слева, или оставаясь
больше х0, т. е. справа. Это ясно из рис. 84, где показаны воз-
возможные случаи. Может также быть, что график приближается к
210
ГЛ. IV. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[64
асимптоте только с одной ее стороны. Например, это будет для
функции у = In х,
2) Пусть линия у = f(х) имеет наклонную асимптоту.
Уравнением такой асимптоты будет у — ах-\-Ь. Согласно опреде-
определению асимптоты расстояние МЫг точки М на линии L от асимп-
асимптоты Г (рис. 85) стремится
к нулю при х—> оо. Удоб-
Удобнее вместо расстояния MN1
рассматривать расстояние
MN, т. е. разность ординат
точки М и точки Л/, лежа-
лежащей на прямой Г и имею-
имеющей ту же абсциссу, что и
точка М. Из рис. 85 имеем
Рис. 85.
cos а'
X = AWcosa,
где a—угол между асимптотой и осью Ох; поэтому расстояния
MN1 и MN стремятся к нулю одновременно.
Так как ордината точки М равна значению функции f(x), а
ордината точки N—значению линейной функции ах-\-Ь, то
MN=\f(x) — (
Это значит, что если
Нт[/(*) —(*
Х
= 0,
то линия y = f(x) имеет асимптоту у = ах-\-Ь\ при этом говорят,
что функция f(x) асимптотически стремится к функции ах-\-Ь.
Таким образом, вопрос о существовании и нахождении на-
наклонной асимптоты линии y==f(x) сводится к вопросу о су-
существовании и отыскании таких чисел а и ЬЛ что
lirn
Если это имеет место, то
— ах—?] =
(*)
где а(х) — величина бесконечно малая при х—юо. Разделим обе
части равенства на х и перейдем к пределу при х—> оо:
64] § 3. ПРАВИЛО ЛОПИТАЛЯ. СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИЙ 211
Так как — —*0 и ^^—>0, то
X X '
Из основного условия (*) находим теперь, что
lim [/ (х) —>ах] — Ь. (###)
Ясно, что верно и обратное: если пределы (**) и (###) су-
существуют и числа а и b найдены, то основное условие соблю-
соблюдается; таким образом,
Если 1-Ю- при х —> оо стремится к конечному пределу а и
если f(x)—ах при х—*оо стремится к конечному пределу 6,
то линия y=f(x) имеет асимптоту у=ах-\-Ь.
В частности, если функция f(x) стремится к конечному пре-
пределу при х—> оо:
Y\mf(x) = Ь,
то, очевидно, а = 0и линия y=f(x) имеет горизонтальную
асимптоту, параллельную оси Ох, именно у~Ъ. Если и а и b
равны нулю, то асимптотой служит сама ось Ох.
Если хотя бы один из указанных пределов не существует, то
линия у=/ (х) наклонных асимптот не имеет.
Например, для линии у = х + In x имеем
t. х + \пх / \пх\
lirn—1-—= limf 1 +—г 1= 1, т.е. в=1э
но
lim (л;-fin л;—1 .д;) = сх>
Х-*-со
и значит, асимптоты в данном случае не существует.
Асимптотическое изменение функции может быть
различным при стремлении х к положительной или к отри-
отрицательной бесконечности, и поэтому следует раздельно рас-
рассматривать случаи х—*+оо и х—> — оо.
Если существует асимптота в первом случае, то мы будем на-
называть ее правосторонней, а если во втором, то левосторонней.
Может случиться, что и при х—>-+оо, и при х—> — оо пределы
(##) и (*#*) одинаковы. Это означает, что правосторонняя и лево-
левосторонняя асимптоты являются частями одной и той же прямой.
Вслед за тем как найдена асимптота у — ах-\-Ь, исследованием
знака выражения а(х)=/(х) — ах — b при х—> оо можно устано-
установить взаимное расположение бесконечной ветви линии и ее асимп-
асимптоты. Ветвь линии находится, начиная с некоторого места, либо
212 ГЛ. IV. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [64
над асимптотой (а>0), либо под ней (ос<0), либо неограничен-
неограниченное число раз пересекает ее (а бесконечное число раз меняет знак).
Примеры. 1) Пусть у = а _. . График этой функции имеет
две вертикальные асимптоты: лг=—1 и л:=1. Чтобы найти на-
наклонную асимптоту, ищем пределы
Итак, наклонной асимптотой является биссектриса координат-
координатного угла у — х.
Вообще можно заметить, что если функция дробно-рациональная, то
при отыскании а и Ь можно сразу рассматривать произвольное стремление
х к бесконечности (см. пример 5 & п. 29).
2) Пусть у — хпе~х (/z>0). График не имеет вертикальных
асимптот. Из примера 9 п. 63, 1 следует, что lim xne~x — Q
и, следовательно, а = 0 и ? = 0, т, е. правосторонней асимптотой
является положительная полуось абсцисс. Левосторонней асимп-
хпе~х
тоты график не имеет, так как lim =оо. Наоборот, функ-
ция y=zxnex не имеет правосторонней асимптоты, а левосторон-
левосторонней является отрицательная полуось абсцисс.
Исследование функции у — j/x2ex, рассмотренной нами в п. 61,
III и в п. 62, V, можно теперь завершить во всей области ее су-
существования— на всей оси Ох. Так как отрицательная полуось Ох
является левосторонней асимптотой графика функции, а право-
правосторонних асимптот он не имеет, то окончательный вид графика
функции будет таким, как он изображен на рис. 83.
3) Линия у = ?1?Lj5 имеет асимптоту у = О, которую она пересекает
бесконечное число раз. Советуем читателю построить график этой
линии.
4) Найти асимптоты линии у = х arctgx. Так как — = arctgjt
зт к
при х —>-}- оо стремится к -~-, а при х —> — оо стремится к —-^ ,
то ищем пределы Ит (у — ^х) , lim
По правилу Лопиталя находим
л 1
arctgxTy ух
lim (уц:*х) =Hm = i = lim iX
X
65] § 3. ПРАВИЛО ЛОПИТАЛЯ. СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИЙ 213
Значит, имеем две асимптоты: правостороннюю у~~х—1 и ле-
левостороннюю у =—-?гх—1. Чтобы правильно представить себе
вид всей линии, рассмотрим первую и вторую производные от
данной функции.
Найдем первую производную
При х > 0 оба слагаемых положительны и, следовательно, У> О,
функция в интервале @, оо) возрастает. При х < 0 оба слагаемых
отрицательны и у' < 0, функция
в интервале ( — оо, 0) убывает
(это следует также из чет-
четности данной функции). Таким
образом, точка л: = 0 является
точкой минимума. Значение функ-
функции в этой точке yx=0 = Q.
Вторая производная
у"-.
О
все время положительна; это ук
значит, что кривая всюду вог-
вогнута. Пользуясь приведенными Рис. 86.
соображениями, можно схематич-
схематично начертить график функции у = х arctgx. Он изображен на рис. 86 1).
При достаточно больших |лг| функцию х arctg x можно считать
линейной, т. е.
х arctg х ж -у-х — 1
* arctg #» —|лг —
1
при х > О,
при х < 0.
65. Общая схема исследования функций. Теперь мы можем со-
составить схему, по которой удобно производить исследование
функций (и линий).
Пусть рассматривается функция у=/(х). Предлагаемая схема
состоит из четырех разделов, в которых устанавливаются:
I. 1) Область определения функции.
2) Точки разрыва и интервалы непрерывности.
3) Поведение функции в окрестностях точек разрыва; вер-
вертикальные асимптоты.
*) Предоставляем читателю проверить, что благодаря постоянной вог-
вогнутости линия не может пересекать ни одну из асимптот.
214 ГЛ. IV. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [65
4) Точки пересечения графика с осями координат.
5) Симметрия графика (четность или нечетность функции).
6) Периодичность графика.
(I. Интервалы монотонности функции; точки экстремума и
экстремальные значения.
Ш. Интервалы выпуклости и вогнутости; точки перегиба.
IV. Поведение функции в бесконечности. Наклонные (в част-
частности, горизонтальные) асимптоты.
В первом разделе дается в общих чертах описание особенностей
функции и ее графика. При этом нельзя забывать о существе той
конкретной задачи, которая привела к исследуемой функции.
Может, например, оказаться, что достаточно ограничиться более
узким интервалом изменения независимой переменной, чем область
определения функции.
Выполнение четвертого раздела иногда удобно производить вмес-
вместе с первым, когда выясняется общая картина поведения функции.
Можно, конечно, ограничиться словесным описанием поведения
заданной функции, но правильное, учитывающее все ее особенности,
графическое изображение является очень экономным и вырази-
выразительным средством для наглядного представления изучаемой
функциональной зависимости. Поэтому выполнение первых четырех
разделов следует сопровождать постепенным построением графика
функции. При этом прежде всего нужно на оси Ох выделить харак-
характерные точки, к которым относятся: точки разрыва, нули,
точки экстремума, абсциссы точек перегиба. На
плоскости Оху отмечаются точки графика, соответствующие атим
выделенным значениям аргумента.
В промежутках между характерными точками функция не меняет
резко своего поведения, ведет себя плавно, но для уточнения в иных
случаях следует брать в этих промежутках обыкновенные точки
и также вычислять соответствующие им значения функции, полу-
получая новые точки графика. Чем больше таких точек, тем точнее
линия, проведенная через все построенные точки, будет выражать
график функции.
Пример. Исследуем функцию
I» Функция определена и непрерывна на всей оси Oxf за исклю-
исключением точки х——1, где она терпит бесконечный разрыв. Следо-
Следовательно, прямая х =—I является вертикальной асимптотой, причем
lim y=—со, lim #y==+oo«
Нулем функции служит только точка х — 0.
65] § 3. ПРАВИЛО ЛОПИТАЛЯ. СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИЙ 215
II. Имеем
Производная обращается в нуль при х = 0 и х=—2; в интер-
интервале (— оо, —2) она положительна, в интервалах (—2, —1) и
(—1,0) отрицательна (в точке л; =—1 она не определена) и в
интервале @, оо) снова положительна. Значит, функция в первом
интервале возрастает, во втором и третьем убывает, в четвертом воз-
возрастает; х = —2 является точкой максимума, причем максимальное
значение функции равно —4, а х~0 является точкой минимума,
причем минимальное значение функции равно 0.
III. Имеем
Вторая производная в нуль нигде не обращается, но при пере-
переходе х через точку х = —1 меняет свой знак с минуса на плюс. Та-
Таким образом, в интервале (—оо, —1)
вторая производная отрицательна,
в интервале (—1, оо) положи-
положительна. В первом интервале график
функции выпуклый, во втором во-
вогнутый.
IV. Так как
— = lim
х „__
lim^—1
то существует наклонная асимптота
у = х—1. Вследствие того что
разность
Рис. 87.
положительна при х > — 1 и отрицательна при х < — 1, график
справа от прямой х=—1 находится над асимптотой jf = х—1, а
слева от прямой л:=—1 под асимптотой.
Приняв
216 ГЛ. IV. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [66
1
мы совершаем абсолютную ошибку а =
и относительную
8=-з; уже при |лг|>10 относительная ошибка меньше одного
процента. Практически функцию у = у— при \х\ > 10 можно счи-
считать линейной функцией у~х—1, что, конечно, значительно
упрощает ее использование.
Приняв во внимание полученные результаты, без труда построим
график (рис. 87), дающий правильное представление о ходе изме-
изменения функции на всей оси Ох. Методами аналитической геометрии
можно убедиться, что линия j/ = -^p- есть гипербола.
§ 4. Кривизна
66. Дифференциал длины дуги. Возьмем линию АВ—график
непрерывной функции у=/(х) — и примем точку А за начало
отсчета. Тогда длина дуги AM (рис. 88) будет являться функцией
абсциссы х точки М; обозначим
эту функцию s (х):
-1 ¦¦ 1.
и
Л9
x+dx ^х
Фактическое отыскание длины
дуги, т. е. функции s {х) по за-
заданному уравнению линии f(x)t
мы отложим до главы VI. Пока
же мы будем искать только
дифференциал этой функции,
который назовем дифференциалом
длины дуги. Так как
ds = s' (x) dx,
то сначала найдем производную функции s (x), т. е. предел от-
отношения длины дуги ММу соответствующей интервалу [лг, х + Длс],
к \х:
Рис. 88.
ММ'
(*)
Будем предполагать, что непрерывна не только сама функ-
функция /(лг), но и ее первая производная /' (х); тогда на ли-
линии АВ не будет ни угловых точек, ни точек возврата. Такие
линии условимся называть гладкими. Примем без доказательства
67] § 4. кривизна 217
следующий геометрический факт: предел отношения длины гладкой
дуги к длине стягивающей ее хорды при стремлении длины дуги
я ж д * f
к нулю равен единице: lim -=- = 1.
д*-*о ММ'
Применительно к окружности это свойство выражается первым
замечательным пределом
<. sin a *
hm == I.
а->о а
На основании свойства эквивалентных бесконечно малых величин
(см. п. 36, II) заменим при отыскании предела (*) дугу ММ'
эквивалентной ей хордой ММ = |/"Дл:2 -f- Ау2. Тогда
т- = lim
откуда
Внеся dx под знак радикала, получим простой, легко запоминаю-
запоминающийся вид формулы для дифференциала длины дуги:
Из последнего выражения следует, что
Дифференциал длины дуги можно представить длиной соот-
соответствующего отрезка касательной к линии в начальной точке
дуги (отрезок МТ на рис. 88).
Отметим, что хотя и длина хорды ММ', и длина отрезка ка-
касательной МТ эквивалентны бесконечно малой дуге ММ\ но отре-
отрезок МТ пропорционален dx, а отрезок ММ не является величиной,
пропорциональной dx, в силу чего дифференциалом длины дуги
и является длина отрезка касательной к дуге, а не длина стяги-
стягивающей ее хорды.
67. Кривизна. I. Первая производная f'{x) функции f(x) дает
нам простейшую характеристику линии y=f(x)y а именно ее
направление. Оказывается, что вторая производная /"(х) тесно
связана с другой количественной характеристикой этой линии,
с так называемой кривизной, устанавливающей меру изогнуто-
изогнутости, или искривленности, линии.
Предполагается, что рассматриваемая линия гладкая.
Назовем углом смежности дуги линии угол ф между касательными
в ее конечных точках Мо и ML (рис. 89).
Угол смежности ф в некоторой степени дает представление об
изогнутости дуги М0М1} так как он является тем углом, на который
поворачивается касательная при перемещении точки касания от
218
ГЛ. IV. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
167
начальной точки дуги Мо до конечной Мг; чем угол смежности
больше, тем, очевидно, больше изогнутость дуги. Но один и тот
же угол смежности могут иметь две дуги с явно различной
изогнутостью.
Так, на рис. 89, / этот угол приходится на большую дугу
(изогнутость меньше), а на рис. 89, II— на меньшую (изогну-
(изогнутость больше). В силу этого для характеристики изогнутости
угол смежности дуги рассчитывается на единицу ее длины.
Рис. 89.
Рис. 90.
Определение. Отношение угла смежности дуги к ее длине
называется средней кривизной дуги:
*- _ Ф
На отдельных участках той же дуги средняя кривизна мо-
может быть иной, чем та, которая соответствует всей дуге.
Чтобы избежать этой неопределенности, мы введем кривизну
в точке уИ0, основываясь на том, что чем меньше дуга М0М1у тем
лучше средняя кривизна характеризует изогнутость линии вблизи
точки М^.
Определение. Кривизной К линии в ее точке Мо называется
предел, к которому стремится средняя кривизна КСр дуги МОМХ
линии при стремлении конечной точки дуги Мх к ее начальной
точке М
о:
В частности,
'= Hm Kco= Hm
¦ •ЛТд
Ф
м0
для окружности радиуса г имеем (рис. 90)
К - ф - Ф -¦ ! -
как видим, средняя кривизна окружности — величина постоянная,
и значит, ее кривизна в любой точке также постоянна и обратна
радиусу. Эго вполне согласуется с нашим непосредственным пред-
представлением о характере изогнутости окружности.
671
§ 4. КРИВИЗНА
219
Найдем теперь выражение для кривизны линии, заданной урав-
уравнением у=/(х) в системе декартовых координат; мы предполагаем,
что функция f(x) дважды дифференцируема при рассматриваемых
значениях х. Возьмем на линии точки М и М с абсциссами соот-
соответственно х и х-\-Ах. Далее, обозначим через а и a-f-Да углы,
образованные с осью Ох касательными в точках М и М\ъ через
Д$-~-длину дуги ММ. Так как
угол смежности ф дуги ММ ра-
равен | Да| (рис. 91) 1)) то
Аа
As
Аа
Ах
As
Ах
При М —> М имеем Ах-
и искомая кривизна равна
¦о,
da
dx
ds
dx
da
dx
{см. п. 66). Из равенства tga=y, т. е.
da_ у"
dx~-l + (/'2'
и значит^
По формуле (*) кривизна определяется как функция абсциссы
точки линии. Если уравнение линии дано в параметрической форме:
*>Ф(;), y=f(t), то (см. п. 54, III)
или, в сокращенной записи,
К=
"х'—у'х"
{**)
*) Для вогнутой дуги Аа > 0, а для выпуклой Аа < 0. Поэтому мы и
пишем, что ф = | Да|.
220 ГЛ. IV. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [67
Здесь кривизна является функцией параметра /, соответствую-
соответствующего рассматриваемой точке линии. При t = x формула (**) прев-
превращается в формулу (*).
Только окружность (и прямая) имеют постоянную кривизну;
кривизна прямой линии, как видно, например, из формулы (*) равна
нулю, что опять-таки вполне согласуется с нашим непосредствен-
непосредственным представлением о неизогнутости прямой линии. У других
линий кривизна вообще меняется от точки к точке.
Пример. Найдем кривизну параболы у = х2 в любой ее точке.
2
Имеем: у = 2лг и /' = 2. Поэтому К= г .8 \ в частности,
кривизна параболы в ее вершине равна 2.
И. Радиус, центр и круг кривизны. Эволюта и
эвольвента. Проведем в точке М (рис. 91) нормаль к линии L
(в сторону ее вогнутости) и отложим на этой нормали от точки М
отрезок MN=py по величине обратный кривизне К:
р
Определение. Отрезок MN называется радиусом кривизны,
точка N—центром кривизны, а круг (и окружность) с центром
в точке N и радиусом MN — кругом (и окружностью) кривиз-
кривизны линии в ее точке М.
Окружность кривизны имеет, очевидно, ту же кривизну, что
и данная линия в точке М.
Для радиуса кривизны, имеем формулу
У"
В качестве меры изогнутости линии можно вместо кривизны
использовать радиус кривизны, причем линия тем больше изогнута
в данной точке, чем меньше радиус кривизны. Заметим, что радиус
кривизны прямой линии в любой ее точке условно считается беско-
бесконечным, так же как условно считают прямую линию окружностью
бесконечного радиуса. Роль радиуса кривизны линии в механике
при изучении криволинейного движения точки будет объяснена
позднее, в п. 71.
Замена бесконечно малой дуги линии вблизи данной точки
соответствующей дугой окружности кривизны сопровождается, как
можно показать, бесконечно малой ошибкой более высокого по-
порядка, чем при замене ее соответствующим отрезком касательной.
Следовательно, малую дугу линии мы можем считать дугой окруж-
окружности кривизны с большим правом (т. е. с меньшей ошибкой), чем
отрезком касательной.
68]
§ 5. ПРОСТРАНСТВЕННЫЕ ЛИНИИ
221
Каждой точке М на линии L соответствует точка N—центр
кривизны L в точке М.
Определение. Геометрическое место центров кривизны
линии L называется ее эволютой ?\ а сама линия L относи-
относительно своей эволюты 11 называется эвольвентой.
Укажем без доказательств приемы приближенных построений
эволюты по эвольвенте и эвольвенты по эволюте.
1) Каждая нормаль к эвольвенте является касательной к эво-
эволюте; эволюта как бы огибает все семейство нормалей эволь-
эвольвенты: Поэтому, если построить
достаточно большое число норма-
нормалей к эвольвенте L, то огибаю-
огибающая их линия и будет эволютой
V (рис. 92).
2) Если гибкую нерастяжимую
нить, обтягивающую заданную
выпуклую линию V (эволюту)
развертывать, сохраняя постоянно
натянутой, то каждая ее точка
опишет эвольвенту L (рис. 92).
Поэтому эвольвенту называют еще
разверткой. Эта операция
развертывания нити равносильна
качению без скольжения прямой
линии по данной линии L'\ каждая
точка такой прямой описывает эвольвенту L линии V'. Отсюда
ясно, что данная эволюта V имеет бесконечное число эвольвент L.
В тО же время любая данная линия, рассматриваемая как эволь-
эвольвента, имеет только одну эволюту.
Рис. 92.
§ 5. Пространственные линии. Векторная функция
скалярного аргумента1)
68. Пространственные линии. В п. 46 мы видели, что линия,
принадлежащая плоскости Оху, может быть задана параметриче-
параметрическими уравнениями х = х (t), у =у (t). Точно так же параметриче-
параметрическими уравнениями могут быть заданы и пространственные линии:
= z(t).
(*)
С изменением параметра t точка М(х, у, z), координаты которой
находятся по формулам (*), опишет некоторую линию.
1) Предполагается, что читатель уже знаком с векторной алгеброй
и аналитической геометрией в пространстве.
222 ГЛ. IV. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [68
Если все три уравнения (*•) линейны:
y y — nt-\-by z~
то получаются известные из аналитической геометрии парамет-
параметрические уравнения прямой. Исключая параметр i} получим ее
канонические уравнения
х—а у — b г—с
т п р
Касательная к пространственной линии определяется так же,
как и для плоской линии, т. е. как предельное положение секущей,
проходящей через данную точку М и близкую к ней точку М\ при
условии, что точка М стремится к данной точке М (см. п. 40),
Выведем уравнения касательной к линии, заданной параметри-
параметрическими уравнениями (*), в ее точке Мо(хОУу0, zo)y соответствующей
значению параметра t0.
Уравнения секущей прямой, проходящей через точки
о, У о, *о) и М'(хо+Аху
будут
х— х0 _у— у0 __z—z0
Ах At/ Az
Деля все знаменатели на соответствующее приращение Д/ па-
параметра и переходя к пределу при Д*—>(), получим искомые
уравнения
х— х0 у—у0 г— г0 , .
где д;0 = л;(^0), ^о=>>(*о)> 4 = z (*o)- При этом мы считаем,^ что
хотя бы одна из производных х' (?0), у' (^0), z' (t0) не равна нулю.
В противном случае точка (jc0, y0, z0) называется особой; такие
точки линии мы не рассматриваем.
Прямая, перпендикулярная к касательной и проходящая через
точку касания, так же как и в плоском случае, называется нор-
нормалью к линии в точке М0(х0, yQj z0). Линия в каждой своей
точке имеет, очевидно, бесконечно много нормалей; все они лежат
в одной плоскости, перпендикулярной к касательной и проходящей
через точку касания.
Определение. Плоскость, перпендикулярная к касательной
прямой в точке касания линии, называется нормальной плос-
плоскостью к линии в данной точке.
Согласно известному условию из аналитической геометрии
уравнением нормальной плоскости как плоскости, перпендикулярной
68] § 5. ПРОСТРАНСТВЕННЫЕ ЛИНИИ 223
к прямой (#*) и проходящей через точку MQ(x0, yQy z0), будет
х' (t0) (x-x0) -Ь/ (g (y-y0) +z' (t0) (z-zo) = O.
Пример, Пусть линия задана уравнениями
Составим уравнения касательной прямой и нормальной плоскости
к этой линии в точке Мо (О, 3, 2), соответствующей Значению
параметра * = 1. Так как лг^г=1 = 2, y^=i = 2, ^=i = 3, то уравнения
= 1. Так
будут
как
Х1ш1
х у
2 ~~
= 2,
-3
2
2—2
3 '
а нормальной плоскости
—12 = 0.
Для дальнейшего нам понадобится формула для дифференциала
длины дуги пространственной линии, заданной уравнениями (*);
она совершенно аналогична соответствующей формуле для плоской
кривой (см. п. 66), Как и раньше, будем рассматривать гладкие
линии; это значит, что функции (#) имеют непрерывные производ-
производные. Для таких линий отношение длины Д$ дуги, заключенной
между точками М(х, y7z) и М'(лг+Ал:, у+Ау, z+Az), к длине
хорды, соединяющей эти точки, стремится к единице при стрем-
стремлении точки ЛГ к точке М. Длина хорды равна VАх2 + &У2 + АЛ
поэтому
Деля числитель и знаменатель на приращение параметра Д?, са-
ответствующее приращениям координат Дат, Ду, Дг, получим
As
А*
1.
Переходя к пределу при Д*—> 0, находим
dt
1
т, е.
ds y~'z+'z + z'2dt или ds =
224
ГЛ. IV. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[69
Как показано выше, направляющий вектор Т касательной
к Линии в точке М имеет проекции [х\ у\ z'\, где для крат-
краткости х' обозначает x'(t) и т. д. Направляющие косинусы век-
вектора Т равны
cos р = -
cosy5
Воспользовавшись формулой для дифференциала длины дуги,
можно формулы для направляющих косинусов переписать в виде
dx
dy
dz
69. Винтовая линия. В качестве примера рассмотрим простран-
пространственную линию, определенную следующими кинематическими
условиями: точка М движется с постоянной
линейной скоростью <vx по окружности ра-
радиуса а, г сама окружность одновременно
поступательно перемещается в направлении,
перпендикулярном к ее плоскости с посто-
постоянной скоростью v2. При этом точка М
опишет линию, целиком лежащую на круг-
круглом цилиндре (рис. 93); она называется ци-
цилиндрической винтовой линией. В том случае,
когда точка М движется по окружности
против движения часовой стрелки, если смот-
смотреть со стороны, куда направлено поступа-
поступательное движение, винтовая линия называется
правой или просто правым винтом (как на
рис. 93). В противном случае она называется
левой винтовой линией или левым винтом.
Выведем уравнения винтовой линии в предположении, что осью
цилиндра служит ось Oz и поступательное движение происходит
в положительном направлении оси Oz, причем в момент / = 0
точка М находится в точке (я, О, 0).
Угловая скорость вращательного движения точки М равна — ,
поэтому ее абсцисса и ордината в момент t будут равны
а '' " а
равна высоте, на которую поднялась точка к моменту /, ,т, е,
z = v2t. Если в качестве параметра взять не время /, а полярный
и
х = a cos
/, jf*=asin— t. Что касается аппликаты г, то она
69) § 5. пространственные линии 225
угол ф точки Р—проекции точки Ж на плоскость Оху (у — — t) ,
то уравнения винтовой линии запишутся так:
х = a cos ф, у = a sin ф, г = сц>, где с = —— а.
Это —уравнения правого винта; уравнения левого винта отлича-
отличаются от них только знаком перед коэффициентом с.
После того как угол ф изменится на 2зх, точка М вернется
на ту же образующую цилиндра, поднявшись при этом на высоту Л,
равную 2яс. Эта величина называется шагом винта. Внося шаг h
в уравнения, получим практически удобный вид параметрических
уравнений винтовой линии:
h
X = CL COS ф, у = U Sin ф, Z = •*- ф.
Здесь оба коэффициента уравнения (а и h) имеют простой гео-
геометрический смысл.
Винтовая линия обладает рядом интересных свойств. Отметим
два из них:
1) Напишем уравнения касательной к винтовой линии в точке
Л/1 I v* \t ^ V
О \ 0» .• О» *^0/*
х — х0 у—г/0 z — г0
— asin<p0 acos90 h '
где ф0 — значение угла, соответствующее точке Мо. Отсюда
h к
cos у = —
т. е. косинус угла у, образованного касательной с осью Qz,
а значит, и сам угол у остаются постоянными во всех точках
винтовой линии. Но образующие цилиндра параллельны оси Oz,
поэтому винтовая линия пересекает образующие цилиндра под по-
постоянным углом, зависящим только от радиуса цилиндра и шага
винта:
2) Цилиндр, на котором начерчена винтовая линия, развернем
на плоскость вокруг какой-нибудь образующей и ограничимся
отрезком цилиндра, равным по высоте шагу винта (на нем нахо-
находится один виток винтовой линии) (рис. 94). Основание цилинд-
цилиндра и сечения цилиндра, параллельные основанию, перейдут в па-
параллельные отрезки длиной 2па, а образующие — в другие
отрезки, перпендикулярные к первым, длиной h. Указанное раз-
развертывание не исказит ни углов между линиями, проведенными
8 А. Ф. Бермант, И. Г. Араманович
226
ГЛ. IV. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[70
на цилиндре, ни длин линий. Вследствие этого винтовая линия
должна развернуться в такую линию, которая пересекает парал-
параллельные отрезки в одной плоскости под одним и тем же углом.
Но такой линией является только прямая. Итак, винтовая линия
при нашем построении перейдет в диагональ прямоугольника со
сторонами 2па и А. Рис. 94 наглядно демонстрирует найденную
Рис. 94.
выше величину косинуса угла у пересечения винтовой линии
с образующей цилиндра.
Возьмем какие-нибудь две точки винтовой линии Мх и М2. Расстоя-
Расстояние между ними, измеренное по винтовой линии, равно отрезку прямой
МгМ2, в который перейдет дуга винтовой линии, заключенная между
точками Мх и М2. Отсюда заключаем, что винтовая линия дает кратчай-
кратчайшее расстояние между двумя точками цилиндра.
Линия на поверхности, проходящая через две заданные точки и даю-
дающая кратчайшее расстояние между ними, называется геодезической. Так,
геодезической линией на плоскости служит прямая, на сфере—окруж-
сфере—окружность большого круга. На цилиндре геодезической линией оказывается
винтовая линия.
70. Векторная функция скалярного аргумента.
I. Векторная функция. Годограф. Как известно из
векторной алгебры, разложение любого вектора А, проекции
которого на оси координат равны лг, у и 2, имеет вид
где I, j и к—единичные векторы, направленные по осям коорди-
координат. Если проекции лг, у, z—постоянные числа (только такой
случай и рассматривается в векторной алгебре), то и вектор А
называется постоянным. Пусть теперь проекции вектора являются
функциями параметра /, изменяющегося в некотором интервале:
* = *{*), У=У(*)> z = z(t).
Тогда и сам вектор называется переменным; при этом каждому
значению параметра t будет соответствовать определенный вектор
70] § 5. пространственные линии 227
Определение. Если каждому значению параметра t соот-
соответствует определенный вектор A (t), то A (t) называется век-
векторной функцией скалярного аргумента.
Как и в векторной алгебре, мы рассматриваем свободные
векторы, т. е. такие векторы, которые считаются равными, если
они имеют равные модули и одинаковые направления, или, иначе
говоря, равные проекции на оси координат.
Мы будем представлять себе вектор A (t) исходящим из начала
координат; тогда при изменении t конец вектора А(/), имеющий
координаты x(t), y(t), z(t), будет описывать некоторую линию Z,,
уравнениями которой служат следующие параметрические урав-
уравнения:
* = *('), У=У(*)> z = z(t).
Так как вектор А (/) есть не что иное, как радиус-вектор
г точки М на линии I, то эту линию можно задать таким одним
векторным уравнением:
Определение. Линия L, описанная концом вектора А, на-
называется годографом векторной функции г = A (t).
Начало координат называют при этом полюсом годографа.
Если у вектора А (/) меняется только модуль, то годогра-
годографом его будет луч, исходящий из полюса, или некоторая часть
этого луча. Если модуль вектора A (t) постоянен (| A (t) | = const)
и меняется только его направление, то годограф есть линия,
лежащая на сфере с центром в полюсе и с радиусом, равным
модулю вектора А(^).
С векторной функцией скалярного аргумента особенно часто
приходится иметь дело в кинематике при изучении движения
точки. Радиус-вектор движущейся точки является функцией вре-
времени: r = A(tf); годограф этой функции есть траектория дви-
движения. При этом уравнение r = A(f) называют уравнением
движения (см. п. 71).
11. Предел и непрерывность векторной функции*
Для векторных функций A (t) скалярного аргумента вводятся ос*
новные понятия анализа аналогично тому, как это делается для
скалярных функций.
Определение. Вектор А называется пределом векторной
функции A (t) при t —* t0:
lim A it) = А,
если для всех значений t, достаточно мало отличающихся от tOf
модуль разности векторов |А(?) — А| будет как угодно мал.
228 ГЛ. IV. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
Если A(t)=x(t)i+y(t)} + z(t)k и \ = ai + bi + cky то
[70
Ясно, что из стремления к нулю |А(/) — А| при t—>t0 следует,
что x(t)—+ay y(t)—>by z(t)—+c; разумеется, верно и обратное.
Коротко это можно выразить в виде простого правила: проекции
предела векторной функции A (t) равны пределам ее проекций.
Определение. Векторная функция X(t) называется непре-
непрерывной при данном значении параметра I, если она определена
в окрестности точки t и если
— А@|= Ит
lim
При этом геометрический смысл разности ДА(/) ясен из рис. 95.
Это будет вектор ММ1 или вектор ММ'. Пусть вектор A (t) име-
имеет разложение
A(t) = x(t)l+y(t)l + z(t)k. (•)
Тогда
—x(t) и т. д.
В соответствии с правилами вектор-
векторной алгебры
где Ax = x(t
Так как
| Д А (О | =
то из условия |ДА(^)|—>0 следует, что и Дл;-^0, Ау^-к о,
Дг^О, Очевидно и обратное, т. е. из стремления к нулю Длг,
Ду, &z следует стремление к нулю |ДА(*)|. Это означает, что
если непрерывна векторная функция А(/), то непрерывны-
непрерывными будут и ее проекции на оси координат •?(/)* y{t), z(t), и
наоборот. Ясно, что годографом непрерывной векторной функции
г==А(^) будет непрерывная линия. Мы будем в дальнейшем
предполагать, что эта линия во всех точках имеет касатель-
касательную (см. п. 68).
III. Производная векторной функции. Чтобы оп-
определить производную векторной функции A (t) по скалярному
70] § 5. пространственные линии 229
аргументу /, составим прежде всего отношение
ДА @ _ A(* + AQ — A @
М """ А*
Геометрически это отношение изображается вектором, направлен-
направленным в сторону, соответствующую возрастанию t (направление от
М к М' на рис. 95). Действительно, если At > 0, то вектор
——±^ = MQ' имеет то же направление, что и вектор ДА (/) = ММ'У
т. е. он направлен в ту сторону годографа, которая соответст-
соответствует возрастанию параметра /. Если же Д^ < 0, то вектор
AA(t) = MM' направлен в противоположную сторону, и при де-
делении на отрицательное число At мы получим вектор MQ"} направ-
направленный снова в сторону возрастания /.
ДА(П А,
Рассмотрим теперь предел отношения —-г— при Лг—> 0.
Определение. Предел
lim
д/-> о
АА@
называется производной от векторной функции \(t) no ска-
скалярному аргументу t.
В силу определения предела (см. II) производная векторной
функции сама является вектором. Она обозначается A' (t) или
' '. Чтобы определить направление вектора А'(/), достаточно
заметить, что при А*—->О точка М'(М1) стремится к точке М, и
поэтому секущая ММ' (ММ") стремится к касательной в точ-
точке М. Поэтому производная A' (t) является вектором МТУ касатель-
касательным к годографу векторной функции А (/), направленным в сторону,
соответствующую возрастанию параметра t.
Если векторная функция А(/) имеет постоянный модуль, но
переменное направление, то ее производная функция А' (/) явля-
является вектором, перпендикулярным к вектору A(t). В самом деле,
годограф лежит на сфере, и поэтому производная А' (/), как век-
вектор, касательный к годографу, перпендикулярна к радиусу-век-
радиусу-вектору А(/).
Итак, производная вектора с постоянным модулем перпендику-
перпендикулярна к нему.
Перейдем теперь к фактическому отысканию производной А'(*).
Пусть векторная функция А(/) задана своим разложением
230 ГЛ. IV. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [70
Тогда, согласно (**),
AA(Q Ал: Дг/ Дг
м — At 1"t" м Ji~ мКш
Перейдя к пределу при Д^—>¦ 0 и воспользовавшись правилом
отыскания предела векторной функции, получим разложение про-
производной A' (t) по единичным векторам
Из этого разложения следует, что
Вспоминая выражение для дифференциала длины дуги ds (п. 68),
последнее равенство можно записать в виде
Таким образом, модуль производной векторной функции |А'@|
равен производной от длины годографа по аргументу t. Необходимо
подчеркнуть, что модуль производной |А'(^)| не равен произ-
производной от модуля (| А(^) |)'. Особенно наглядно это видно на при-
примере производной вектора с постоянным модулем: в этом случае
производная модуля вектора как постоянного числа просто
равна нулю; производная же самого вектора есть вектор, к нему
перпендикулярный.
Пользуясь выражением для A' (t)y легко показать, что все
основные правила дифференцирования переносятся почти без изме-
изменения на векторные функции:
1) [AxW + A.Wl^A^O + A.'W,
2) [f{t) A (*)]' =/' (t) A (t) +f(t) A' (t),
где f(t) — скалярная функция; в частности, [CA(tf)]' = CA'(tf), где
С—скаляр.
Правила дифференцирования скалярного и векторного произ-
произведений двух векторных функций также ничем не отличаются от
соответствующего правила в случае произведения скалярных
функций:
3) [AiW-AjW]' =А1'@-А2@+А1@'А2'@,
4) [Ах (t) X А2 (*)] - [A; (t) X А2 (t)} + [A± (t) X А2' (/)].
(В правиле 4 важен порядок перемножаемых векторов.)
Доказательства всех этих правил рекомендуем читателю про-
провести самостоятельно.
71]
§ 5. ПРОСТРАНСТВЕННЫЕ ЛИНИИ
231
Последовательным дифференцированием можно найти производ-
производные высших порядков от векторной функции. Так,
и т. д.
71*. Приложения к механике. Рассмотренное нами дифферен-
дифференцирование векторной функции скалярного аргумента имеет важное
применение в механике при определении скорости и ускорения
криволинейного движения. (В пп. 38, I и 54,1 был рассмот-
рассмотрен вопрос о скорости и ускорении прямолинейного движения.)
Пусть годограф векторной функции г = А(/) является траек-
траекторией движущейся точки, t—время. Тог-
Тогда вектор-производная
dv
называется скоростью движения.
Таким образом, скорость движения есть
вектор, касательный к траектории в соответ-
соответствующей точке и направленный в сторону
движения (т. е. в сторону возрастания t).
Модуль скорости равен (см.
п. 70, III)
Рис. 96.
ds
т. е. равен производной от пути по времени.
Если движение прямолинейное, то скалярная величина — вполне
характеризует скорость движения. Именно ее мы и называли ско-
скоростью прямолинейного движения. Вектор
dv
dt
d2r
di2
называется ускорением движения.
Представим ускорение w в несколько ином виде. Для этого
обозначим через хг единичный вектор касательной к годографу
(рис. 96). Тогда
i t ds
Дифференцируя это произведение (см. правило 2), получим
dt dt •
232 ГЛ. IV. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [71
Рассмотрим теперь производную ~ . Так как xt—единичный
вектор | тх | = 1, то производная его будет к нему перпендику-
перпендикулярна, т. е. направлена по некоторой нормали к кривой (эту
нормаль называют главной нормалью). Обозначив единичный вектор
этой нормали через v1? запишем
dt
dt
Из рис. 96 ясно, что |Дт1| есть хордаг стягивающая дугу
окружности QR — | хх | Дф = Дф, где Дф — угол смежности дуги ММХ
(см. п. 67). В силу эквивалентности бесконечно малой дуги и
хорды можно записать
dt
dt
Произведем еще следующее преобразование:
Ж
ds
где /С= -г-—предел отношения угла смежности к длине дуги.
Величину К, так же как и для плоской кривой, мы называем кри-
кривизной пространственной кривой, а величину, ей обратную, Р=-^- —
радиусом кривизны1). Подставляя выражение для -± в формулу
для ускорения, получим
/*у
\dt)
d2s
Первый составляющий вектор wt=^-^x1 называется тангенциаль-
тангенциальным ускорением; величина его равна второй производной от пути
по времени, и он направлен по касательной к траектории движе-
\dt I v |a
ния. Второй составляющий вектор \у„=^—— vt =-—'-v, называ-
Г П р 1 р 1
ется нормальным ускорением; он направлен по нормали к траек-
траектории, величина его равна квадрату величины скорости, делен-
деленному на радиус кривизны.
Если движение прямолинейное, то вектор хх постоян-
постоянный, его производная равна нулю и ускорение полностью ха-
а) Формулу для кривизны К пространственной линии мы не выводим.
72J § 6. КОМПЛЕКСНЫЙ ФУНКЦИИ ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО 233
рактеризуется величиной -^—ускорением прямолинейного дви-
движения.
Если движение равномерное, т.е. постоянна величина ско-
скорости |v|=^j, то первое слагаемое равно нулю и остается лишь
нормальное ускорение
|v I2
W = - -Vi.
В частности, когда точка равномерно движется по окружности
I V I2
радиуса /?, то р = /? и \^n\=zl—~-. Это ускорение направлено
к центру окружности и называется центростремительным.
§ 6. Комплексные функции действительного переменного
72. Комплексные числа. Предполагая, что читатель знаком
с комплексными числами из курса элементарной математики, на-
напомним лишь вкратце основные определения и правила арифмети-
арифметических действий.
Число
z = х + 1уу
где х и у— любые действительные числа, а / — так называемая
мнимая единица (i2 =—1), называется комплексным числом; х на-
называется действительной частью, а у—мнимой частью комплексного
числа z* Два комплексных числа считаются равными, если равны
порознь их действительные и мнимые части. Это значит, что ра-
равенство
равносильно двум равенствам
Равенство я = л: + /у = 0 имеет место, только если и лг = О
и jf = O.
Будем изображать комплексное число z = x-\-iy точкой плос-
плоскости Оху (рис. 97); абсциссой точки будет служить действитель-
действительная, а ординатой — мнимая части комплексного числа. Поэтому ось
абсцисс называют действительной осью, а ось ординат — мнимой
осью; плоскость же называют комплексной плоскостью. Если точка
изображает число г, то ее называют точкой z.
Можно изображением комплексного числа считать также вектор,
идущий из начала координат в указанную точку; его проекциями
на оси координат являются соответственно действительная и мни-
мнимая части комплексного числа. Этой геометрической иллюстрацией
комплексных чисел мы воспользуемся в следующем пункте.
234
ГЛ. IV. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[72
Если у = 0, то комплексное число z = x есть действительное
число, изображаемое точкой действительной оси, а если # = 0,
то z — iy называется чисто мнимым числом, изображаемым точкой
мнимой оси.
Положение точки, изображающей комплексное числом, можно оп-
определять также при помощи полярных координат г и ф(рис. 97). При
этом г =\гх%-\-у2 называется модулем, а ф — аргументом комплекс-
комплексного числа; они обозначаются так:
У
0
г = \z
= Argz.
3!
Величина Arg2 определена лишь
с точностью до слагаемого 2Ля, где
к — целое число. Если угол ф выб-
выбран в пределах от —я до я, то его
называют главным значением аргу-
аргумента и обозначают через atgz.
Если z = x-\-iy, то комплексное
число x — iy называется сопряжен-
сопряженным с z и обозначается через z.
Точка z симметрична точке z относительно действительной оси
(т.е. оси абсцисс). Ясно, что \z\ = \z | и arg z = —argz.
Пользуясь формулами перехода от декартовых координат к по-
полярным (д: = гсо5ф, ^ = гз1пф), можно любое комплексное число,
отличное от нуля, записать в тригонометрической форме
= r (cos ф + i sin ф).
рис 97
Действия над комплексными числами производят в соответствии
с формулами:
т. е. сумма двух комплексных чисел есть комплексное число, дей-
действительная и мнимая части которого равны сумме соответствующих
частей слагаемых. Геометрически этому соответствует известное
из векторной алгебры правило сложения векторов;
2) (X1
вычитание есть действие, обратное сложению, и аналитически
выражает обычное геометрическое вычитание векторов. Разность
двух комплексных чисел zx — z2 изображается вектором с началом
в точке z2 и концом в точке zx. Таким образом, \zx — z2\ есть
длина прямолинейного отрезка, соединяющего точки zx и z2;
3) (хг + 1уг) (х2 + iy2) - (хгх2 —Угу2) +1 (хху2 + хгУг).
Если сомножители взять в тригонометрической форме, то легко
72] § 6. КОМПЛЕКСНЫЕ ФУНКЦИИ ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО 235
вывести, что
гг (cos фх + / sin фх) г2 (cos ф2 +1 sin ф2) =
= /у2 [cos (ф1 + ф2) + i sin (фх + Ф2)Ь
т. е. при умножении модули чисел перемножаются, а аргументы
складываются.
Последовательно распространяя это правило на любое число п
сомножителей и считая их равными между собой, придем к правилу
возведения комплексного числа в целую степень
[г (cos ф -f- * sin ц>)]п = rn (cos лф -f- i sin /гф),
n—целое положительное число.
Это — так называемая формула Муавра1).
Произведение комплексного числа на сопряженное ему будет
действительным положительным числом, равным квадрату модуля
каждого из сомножителей zz = (х + iy) (х—iy) = х2 -\-у2 = | z\2 = jzj2;
при условии, что х2-\-1у2фО. Деление есть действие, обратное
умножению. Если делимое и делитель взять в тригонометрической
форме, то
гх (cos cpt + /sin фх) гх г . ч , • • /
^Ч— [ = -1-1 cos (фт —ш9) 4-1 sin (фт —
т. е. при делении модуль делимого делится на модуль делителя, а
аргумент делителя вычитается из аргумента делимого.
Внимательно рассмотрев вышеприведенные формулы, легко за-
заметить, что выражаемые ими правила можно объединить общим и
очень простым правилом:
Арифметические действия над комплексными числами производятся
по обычным правилам действий над обыкновенными двучленами (х + 1у)у
но в результате i2 везде заменяется на —1.
Известные в области действительных чисел законы и свойства
арифметических действий без изменения переносятся в область
комплексных чисел.
Отметим, что если в каком-нибудь арифметическом действии
вместо всех комплексных чисел взять их сопряженные, то и резуль-
результат получится сопряженный первоначальному. Действительно, изме-
изменив знаки у1 и у2 на обратные, мы увидим, что в правых частях
всех четырех формул 1), 2), 3) и 4) знак мнимой части также пере-
А. Муавр A667 —1754) — английский математик.
236 ГЛ. IV. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [73
менится на обратный. Но если это имеет место в каждом из четырех
арифметических действий, то, значит, имеет место и в любой их
совокупности.
73. Определение и дифференцирование комплексных функций,
I. Допустим, что мы рассматриваем векторную функцию скалярного
аргумента при условии, что ее проекция на ось Oz при всех зна-
значениях t равна нулю. Тогда
и линия г = А(/) — годограф этой функции —будет целиком лежать
в плоскости Оху. В этом случае часто оказывается удобным век-
вектор т = х\-\-у\ считать геометрическим изображением комплексного
числа z — x-\-iy и вместо векторной функции г (t) = x(t) i+y (t) j
говорить о комплексной функции действительного переменного *)
) y
Определение. Если каждому значению действительного
параметра t соответствует определенное комплексное число
z(t) = x(t) + iy(t), (**)
где x(t) и y(t) — функции, принимающие действительные значе-
значения, то z(t) называется комплексной функцией действительного
переменного.
Обычно параметр t изменяется в некотором интервале, конеч-
конечном или бесконечном.
Годографом функции z(t) называется линия с параметрическими
уравнениями х = х (t) и у ~у (/); таким образом, годографы векторной
функции (*) и комплексной функции (#*) есть одна и та же линия.
Определения предела и непрерывности комплексной функции
действительного переменного совершенно аналогичны соответ-
соответствующим определениям для векторной функции; предоставляем
их сформулировать читателю. Подчеркнем лишь, что непрерывность
комплексной функции z(t) эквивалентна непрерывности ее дейст-
действительной и мнимой частей х (t) и y(t). Годографом непрерывной
функции z(t), при изменении параметра t от tx до /2, служит
непрерывная линия, соединяющая точки z(t^) и z(t2).
Примеры. \) z(t) = t + it2 ( — оо<*< + оо).
Здесь x = t и y~t2; годографом служит парабола у = х2. При
изменении /от —оо до ~\- оо точка движется по параболе так,
что внутренность параболы остается слева.
2) z(t) = co
*) Комплексные функции комплексного переменного служат пред-
предметом изучения в теории функций комплексного переменного (см., напри-
например, [6]).
74] § 6. КОМПЛЕКСНЫЕ ФУНКЦИИ ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО 237
Так как | z (t) |=>l/*cos21-\- sin21 = \f годографом служит окруж-
окружность радиуса 1 с центром в начале координат; при изменении t
от 0 до 2л точка пробегает окружность против часовой стрелки.
Если бы параметр t изменялся в интервале [0, я], то годографом
быля бы верхняя половина окружности с начальной точкой z=\
и конечной точкой z-=.—1.
3) s@ = l+*cos* @<*<2я).
Годографом служит отрезок прямой, параллельной мнимой оси,
заключенный между точками 2^= I -f-* и 22= 1 — /; при изменении t
в заданнном интервале он пробегается дважды: сначала сверху
вниз, а потом снизу вверх.
И. Производная комплексной функции действи-
действительного переменного. Производная комплексной функции
z(t) определяется как обычно, т. е. как предел отношения прира-
приращения функции &z = z(t-\-At)—z(t) к приращению независимой
переменной Д?:
•'w-JS.-n-
Производная z' (t) в свою очередь является комплексной функцией.
Геометрически, вектор, изображающий комплексное число z' (/0),
параллелен касательной к годографу функции z(t)t проведенной
в точке, соответствующей значению параметра t0.
Дословно повторяя рассуждения, приведенные при выводе фор-
формулы для производной векторной функции скалярного аргумента,
получим
z'{t) = x'(t) + t/ (t).
Эта формула показывает, что комплексную функцию z(t) —
= х (t) ~\-iy (t) можно дифференцировать как обыкновенную сумму,
считая i просто постоянным. Разумеется, это правило приобретает
смысл только после введенных определений, Легко проверить, что
все правила дифференцирования действительных функций без
всяких изменений переносятся на комплексные функции.
Отметим, что произведение комплексных функций производится
по правилу умножения комплексных чисел и не связано ни со
скалярным ни с векторным произведениями векторных функций.
74. Показательная функция и формулы Эйлера. В этом пункте
мы дадим определение показательной функции с мнимым показа-
показателем степени z=^elt и изучим ее свойства. Эта функция в даль-
дальнейшем будет играть очень важную роль как в самой математике,
так и в ее приложениях к целому ряду конкретных дисциплин
(электротехнике, теории колебаний и др.).
238
ГЛ. IV. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
[74
Определение. Показательной функцией с мнимым показа-
показателем степени называется комплексная функция
где параметр t может принимать любые действительные значения.
Формула (*) называется форму-
формулой Эйлера.
Основанием для этого, может
быть, на первый взгляд несколько
странного определенияг) служит
то обстоятельство, что для функ-
функции elt оказываются справедливыми
все правила действий с обычной
показательной функцией у = е*,
включая формулу дифференциро-
дифференцирования.
Прежде чем проверить эти пра-
правила, остановимся на некоторых
свойствах функции eli, вытекающих
прямо из ее определения.
Как мы уже видели в примере
2 п. 73, модуль функции elt равен
единице; это следует так же из того, что правая часть формулы (*)
представляет тригонометрическую форму записи комплексного числа
с модулем, равным 1, и аргументом, равным /:
|*ft| = l, Arg *'* = *.
Годографом функции z=elt служит единичная окружность
(рис. 98). При t = 0 получим точку 2=1, при ^ = у—точку z = i9
при t = n — точку z — —1 и т. д. Таким образом,
-L
Рис. 98.
sin
:/, «'" = -1
1
При увеличении параметра t точка elt движется по окружности
против часовой стрелки и при t = 2it снова возвращается в исход-
исходное положение:
егН = cos 2л + i sin 2л = 1.
При дальнейшем увеличении t от 2л; до 4л точка eif снова обежит
окружность и т. д. Отсюда уже ясно, что функция elt периодичен
екая с периодом Т=2п. Действительно,
ei{i+*«> = cos (t + 2л) + i sin (t + 2л) = cos t + i sin t = en.
*) Позже, в гл. XI, мы придем к такому же определению, исходя из
совершенно других соображений.
74] § 6. КОМПЛЕКСНЫЕ ФУНКЦИИ ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО 239
Заметим, что если п—целое число, то
Основное правило действий с показательной функцией заклю-
заключается в том, что если хх и лг2—действительные числа, то
exiex2 _ ext+x2 проверим, что это правило соблюдается и для мни-
мнимых показателей степени. По правилу умножения комплексных чисел
в тригонометрической форме
eitteiti __ (cos f i _|_ I sjn f^ (cos f^ _|_ / s{n f^ -_
= cos (<x+ *,) + /sin (<1 + /,) = e'<'t+4
Здесь tx и /2 — любые действительные числа (положительные или
отрицательные).
Формула Эйлера позволяет записывать комплексные числа в
показательной форме. Если |z| = r и Arg2 = (p, то
z = г (cos ф + i sin ф) = ге1Ср.
Правило умножения показывает, что если z1 = r1ei^ и гг — г^\ то
Произведение числа z=reic? на е*л равно 2е1а=гех(ф+а). Геометричес-
Геометрически это означает, что вектор, изображающий комплексное число zy
поворачивается на угол а. Поэтому е1* иногда называют поворот-
поворотным множителем. В частности, если а = -^, то умножение на
е 2 =f приводит к повороту вектора против часовой стрелки на
угол 90°.
Требование сохранения правила умножения приводит к следую-
следующему определению:
i
Отсюда
Эти формулы определяют степень числа е с любым комплексным
показателем степени. Так, например, е2+*1 == е2 (cos 3 + / sin3).
Перейдем к дифференцированию функции в1*. По правилу
отыскания производной комплексной функции действительного пере-
переменного
(еа)' = —sin t + / cos t == / (cos / + / sin /) = ten.
Таким образом, комплексная функция elt дифференцируется так же,
как если бы I было просто постоянным числом.
Геометрически дифференцирование функции elt сводится к по-
повороту вектора z = elt на угол 90° против часовой стрелки.
240 ГЛ. IV. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [75
Пользуясь формулой (**), легко проверить, что вообще
Это значит, что всегда справедлива формула
где Я — любое число, действительное или комплексное.
Формула Эйлера
elt — cos
выражает показательную функцию с комплексным показателем сте-
степени через тригонометрические функции. Заменив в этой формуле
/ на —/, получим
e~il = cos (—t) + i sin (—t) = cos * — i sin t.
(Отметим, что elt и e"li—комплексно сопряженные выражения.)
Теперь легко выразить тригонометрические функции cos t и sint
через показательную
eit\_e-it pit e-it
cost=—-~—, sinf = -—к-.— . (**#)
Эти формулы также называются формулами Эйлера.
§ 7. Решение уравнений
76. Общие сведения об уравнениях. С решением уравнений
приходится сталкиваться в самых разных задачах, как чисто математи-
математического, так и прикладного характера. Например, при исследовании
функции y=f(x) для отыскания нулей функции, точек экстре-
экстремума и абсцисс точек перегиба требуется решить соответственно
уравнения /(л;) = 0, /'(лг) = О, /"(лс) = О. Далеко не всегда эти
уравнения удается решить точно, и приходится отыскивать их
корни приближенно. Однако, прежде чем переходить к приб-
приближенным методам решения, мы изложим вкратце некоторые общие
свойства уравнений, частично уже известных читателю.
1. Алгебраические уравнения и разложение
многочленов на множители. Пусть дан многочлен
Р (х) = аохп + аххп^ +...+ая
с действительными или комплексными коэффициентами, причем
aozjt=Q. Тогда уравнение
называется алгебраическим уравнением n-й степени.
75] »§ 7. решение уравнений 241
Основная теорема высшей алгебры утверждает, что всякое
алгебраическое уравнение степени п > О имеет хотя бы один корень,
действительный или комплексный. При этом, однако, теорема не
указывает способов фактического отыскания корня; она говорит
только об его существовании. Доказательство основной теоремы
алгебры далеко выходит за рамки книги.
При делении многочлена я-й степени Р(х) на двучлен х — а
мы получаем в частном многочлен Q(x) степени п—1 и в остатке
какое-то число R. Это можно записать в виде тождества
Подставляя в это тождество вместо х число а, получим, чтоР(а)~ R,
т. е. что остаток от деления многочлена на двучлен х—а равен
значению этого многочлена при л; = а (теорема Безу1)). Если а
является корнем многочлена Р(х), то R = P(a) = 0 и
P(x) = (x-a)Q(x).
Пусть х1 является корнем уравнения (*); тогда
где Qi(x)—многочлен степени п — 1. Легко заметить, что его
старший коэффициент (коэффициент при хп~г) равен старшему
коэффициенту многочлена Р(х), т. е. а0.
Если степень Qx(x) не равна нулю, т. е. он не сводится к
постоянной д0, то к нему можно снова применить основную теорему.
Пусть х2 — корень ^(л:); тогда Q1(x) = (x—x2)Q2(x), где степень
многочлена Q2 (x) равна /г —2, а старший коэффициент по-преж-
по-прежнему равен а0. Выражение для Р(х) примет вид
Р(х) = (х-хг) (х-х2) Q2 (х).
Ясно, что х2 тоже является корнем уравнения (*). Повторяя этот
процесс п раз, мы придем к разложению многочлена Р(х) на
линейные множители
Р(х) = а0(х—хг) (х—х2)... (х—хп).
При таком последовательном получении корней х1У х%, . . .хп
может оказаться, что некоторые из них будут совпадать. Если
какой-то корень встретился k раз> то он называется корнем крат-
кратности k. Если &=1, т. е. корень встретился только один раз,
то он называется простым.
Пусть корень xt имеет кратность &х, корень х2 — кратность k2
и т. д. Тогда разложение многочлена Р(х) можно записать так:
P(x) = <*o(x—Xi)*l(x—x2)k*.. .(x—xr)kr, (**)
2) Э. Безу A730—1783) —французский математик.
242 ГЛ. IV. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [75
где г — число различных корней, а сумма кратностей всех корней
равна п
Последнее равенство означает, что алгебраическое уравнение п-й
степени имеет п корней, если каждый корень считать столько раз,
какова его кратность.
Все сказанное до сих пор относилось к уравнениям (*) с лю-
любыми комплексными коэффициентами. Будем теперь считать, что
все коэффициенты aOt аъ ... ап — действительные числа.
Тогда комплексные корни уравнения (*) (если они есть) попарно
сопряжены. Это является следствием замечания, сделанного в са-
самом конце п. 72. Действительно, если коэффициенты многочлена
Р(х)— действительные числа, то, вычисляя его значения при
комплексно сопряженных значениях х, мы снова получим комплексно
сопряженные числа: Р(а—i$)=P(a + i$). Это и значит, что если
Р(а + /р) = 0, то и Р(а—/(}) = 0. Легко проверить,
что корни а + ф и а—/(J имеют одинаковую кратность.
Отсюда, кстати, следует, что любой многочлен нечетной степени
имеет хотя бы один действительный корень.
Объединим в разложении (**) множители, соответствующие
комплексно сопряженным корням кратности /; перемножая их,
получим
(x—a-i$I (х—а + фI =={х* — 2ах + а? + $2I = (х* +рх + q)\
где /? = — 2а и # = а2 + Р2- Дискриминант квадратного трехчлена
р2 — 4<7 < 0, так как его корни комплексные.
Проделав указанное преобразование со всеми множителями,
содержащими комплексные корни, получим разложение многочле-
многочлена Р(х) на линейные и квадратичные действительные мно-
множители
Р(х) = а0 (х-х^.. .(х* +p1x + q1Y>...,
где kt — кратности действительных корней, а I; — кратности комп-
комплексно сопряженных корней. Ясно, что (kx +...) + 2 Aг +...) = п.
Полученным разложением мы воспользуемся в следующей главе.
Из сказанного выше следуют простые, но важные для даль-
дальнейшего замечания.
1. Если многочлен Р(х) равен нулю при любых значениях х,
т. е. Р(х) = 0, то все его коэффициенты равны нулю
В самом деле, если бы аог^О, то Р(х) имел бы п корней, если
бы яо = О, а1ф0, то Р(х) имел бы п— 1 корень и т. д.; в уело-
75] § 7. РЕШЕНИЕ УРАВНЕНИЙ 243
вии же сказано, что многочлен имеет бесчисленное множество
корней.
Из приведенного рассуждения следует также, что если мно-
многочлен /г-й степени имеет больше чем п корней, то он тождествен-
тождественно равен нулю.
2. Если два многочлена равны друг другу при любых значениях х
а^+а^"-^ ... + an = boxm + b1xm-1+ ... +ЬтУ
то равны их степени и равны между собой коэффициенты при оди-
одинаковых степенях х.
Действительно, перенося все члены тождества в левую часть
и считая, например, что п > т, запишем
Но тогда из первого замечания следует, что во-первых
а0 = ах = ... = ап_т_1 = 0, т. е. что старший член первого мно-
многочлена есть an-mxmi а во-вторых, что ап_т = Ь0, ..., ап_г =
— bm-ъ ап — Ьт\ при этих условиях оба многочлена тождественны.
Алгебраические уравнения с произвольными коэффициентами
читатель умеет решать в двух случаях: п= 1 (линейное уравнение) и
п =2 (квадратное уравнение). Для случаев п = Ъ и п = 4 (куби-
(кубическое уравнение и уравнение четвертой степени) также имеются
общие формулы решения (формулы Кардано и Феррари1)),
однако ввиду их громоздкости пользование ими крайне затруд-
нитеяьно. Для уравнений же пятой степени и выше доказано,
что вообще не существует формул, пользуясь которыми можно
было бы при помощи конечного числа алгебраических действий
выразить корни через коэффициенты таких уравнений, или, как
еще говорят, решить уравнение в радикалах2); известны также
и конкретные примеры таких «нерешаемых» уравнений. Лишь
в отдельных частных случаях, в основном известных из школь-
школьного курса алгебры, возможно и алгебраическое решение; чаще
всего это бывает тогда, когда левую часть уравнения удается
разложить на произведение многочленов меньших степеней.
В силу сказанного ясно, почему так важно уметь решать
уравнения приближенно.
II. Уравнение /?(лг) = О, где R(x) — рациональная функ-
функция, всегда можно привести к виду 777^ = 0, где Р(х) и Q(x) —
*) Д. Кардано A501 —1576) —крупный итальянский ученый эпохи
Возрождения. Л. Феррари A522—1565) — итальянский математик.
2) Доказательство этого утверждения связано с именами двух замеча-
замечательных математиков: норвежца Н.Абеля A802—1829) и француза Э. Галуа
A811-1832).
244 ГЛ. IV. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [76
многочлены (см. п. Н), Для его решения нужно найти корни ал-
алгебраического уравнения Р(л:)=0 и взять из них те, при кото-
которых знаменатель Q(x) не равен нулю. Если при некотором зна-
значении л; = <х и Р(<х) = О и Q(oc) = O, то условимся а считать кор-
корнем R(x), если lim/?(#) = О, и не считать в противном случае.
Иррациональные уравнения, т.е. уравнения, содержащие х
под знаком корня, обычно удается свести к алгебраическим, возвы-
возвышая обе части уравнения в соответствующие степени. При этом,
однако, могут появиться посторонние корни, и поэтому, найдя
корни полученного алгебраического уравнения, нужно взять из
них только те, которые удовлетворяют исходному уравнению.
III. Трансцендентные уравнения. Уравнение f(x) = О
называется трансцендентным, если функция f(x) — трансцендентная
(п. 11). Примерами трансцендентных уравнений служат логарифми-
логарифмические, показательные и тригонометрические уравнения, изучаемые
в курсе элементарной математики. Другие типы трансцендентных
уравнений, как правило, алгебраическим путем решены быть не
могут. Более того, без специального исследования вообще нельзя
сказать, имеет ли данное трансцендентное уравнение корни и
в каком количестве.
76; Признак кратности корня. Чтобы перенести на трансцен-
трансцендентные уравнения определение кратности корня, рассмот-
рассмотрим подробнее свойства кратных корней алгебраических уравнений.
Пусть многочлен Р(х) имеет корень а кратности k. Тогда разло-
разложение (#*) из п. 75 можно записать в виде
= (x-a)kQ(x), где
Производная Р' (х) (это тоже многочлен) равна
Ясно видно, что Q1(a)=kQ (a)^=0. Поэтому производная Р'(х)
имеет число а корнем кратности k—1; если ft=l, то P'(a)^0
и а не является корнем производной. Рассуждая аналогично,
установим, что Р" (х) имеет а корнем кратности k — 2 и т. д.
Для производной Р(к~г)(х) корень а будет простым, а для &-й
производной P{k)(x) число а вообще не является корнем. Таким
образом, если а является корнем кратности & для многочлена Р(х), то
Р(<*) = 0, Р/(а) = 0) .... P(*)(a)=0, но Р(А)(а)=?0.
Именно это свойство кратных корней алгебраического уравне-
уравнения мы и примем за определение кратности корня любого урав-
уравнения.
77] § 7. РЕШЕНИЕ УРАВНЕНИЙ 245
Определение. Число а называется корнем кратности к
уравнения/(*) —О, или ^-кратным нулем функции/^I), если
= 0, но
При этом предполагается, что функция f(x) имеет k производных
в точке а.
Например, функция у — х— sin* имеет в точке л; = 0 трехкрат-
трехкратный нуль, так как д^=0 = 0, y'xst0 = A — cosat^^^O, yXSSQ =
но у'^0 = cos
Уравнение ^/лс2 = 0 имеет корень, равный нулю. Мы не гово-
говорим об его кратности, так как уже первая производная его ле-
левой чаати 3 '_^ не существует при л;=*0.
3 у/ х
Предоставляем читателю проверить, что если а — простой
корень уравнения f(x) = 0, то график функции у=/(х) пересе-
пересекает ось абсцисс; если а — двукратный корень, то график касается
оси абсцисс и в некоторой окрестности точки а целиком лежит
по одну сторону от оси абсцисс (т. е. точка а является точкой
экстремума функции f(x)). Когда а — трехкратный корень, то
точка (а, 0) оси абсцисс является точкой перегиба графика и
касательная в ней совпадает с осью абсцисс; нетрудно также
установить, что будет, если а—корень более высокой кратности.
77. Приближенное решение уравнений. Мы рассмотрим лишь
те способы приближенного решения уравнений, которые непосред-
непосредственно примыкают к содержанию настоящей главы — исследованию
функций. Заметим прежде всего, что знание хотя бы примерного
поведения функции у=^/(х) уже позволяет приблизительно уста-
установить, в каких интервалах график функции пересекает ось абс-
абсцисс, т. е. где уравнение /(д;) = 0 имеет корни. Функция /(л;)
предполагается непрерывной; поэтому если в точках хг и х2
функция имеет разные знаки, то из свойств непрерывных
функций (п. 36) сразу следует, что в интервале [х1у х2] имеются
нули функции.
Будем считать, что интервал [дг1, х2] удалось выбрать настолько
малым, что в нем лежит только один корень уравнения f(x) = Q;
такой интервал назовем интервалом изоляции корня. То, что
выбранный интервал является интервалом изоляции, обычно удается
проверить при помощи производной /' (л:): если она сохраняет
постоянный знак, то функция f(x) в этом интервале монотонна
и график ее пересекает ось абсцисс только один раз.
Говорят также нулем k-го порядка.
246 ГЛ. IV. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [77
Итак, мы исходим из того, что нам так или иначе удалось
изолировать корень х0 уравнения /(л:) = 0 в некотором интервале
[xlt х2], хг<х2. Каждое из чисел хг и х2 можно считать при-
приближенным значением корня х0: первое хх — с недостатком,
второе х2— с избытком, причем разность х2— хг является, оче-
очевидно, предельной абсолютной ошибкой этих приближенных зна-
значений. Излагаемые здесь методы приближенного решения уравнений
состоят в приемах, посредством которых по данному интервалу
изоляции [х1У х2] и по функции f(x) находится такой новый
интервал [x'v at'J, что
т. е, суживается интервал изоляции; значения х'х
и х'2 — лучшие, чем хх и х2, приближенные значения корня х0.
Применяя к интервалу [x'v x'2] тот же или другой метод, полу-
получаем еще лучшие приближенные значения x"v x корня х0.
Мы приводим три метода, самые простые и удобные: метод
проб, метод хорд и метод касательных, который известен
еще под названием метода Ньютона, а также комбинирование этих
трех методов.
Отметим еще, что иногда примерное положение корня уравне-
уравнения /(лг) = О удобнее находить, записав уравнение в виде
Ф1(л:) = ф2(лс), где фх (х) — ф2 (л:) =/(л:). Если графики функций
фх (х) и ф2 (х) известны, то абсциссы точек их пересечения и будут
являться корнями данного уравнения. Так, например, записав
уравнение 1п л: + лг — 2 = 0 в виде 1пд; = 2—х и построив соот-
соответствующие графики, легко заметить, что единственный корень
лежит между 1 и 2.
I. Метод проб. Этот метод является самым простым, но
не лучшим из методов последовательного приближения к корню
уравнения. Пусть интервал [хг, х2] есть интервал изоляции корня
уравнения f{x) = 0. Если корень простой, то значения функции
f(x) на концах интервала имеют разные знаки; допустим для
определенности, что /(а:1)<0, a f(x2)>0. Возьмем любое зна-
значение х = х' в интервале [х1У х2] и испробуем его, подставив
в функцию f(x); если /(л;')<0, то мы, заменяя хг на х\ полу-
получим суженный интервал изоляции [х\ х2]; если же /(#')>(), то
мы придем к суженному интервалу изоляции [х19 х'], заменив х2
через х\
Неограниченно применяя метод проб, мы получим последова-
последовательность точек х\ х'\ ..., которая, как это можно доказать,
имеет своим пределом корень х0. В' силу этого с помощью метода
проб можно найти приближенное значение корня с любой точностью.
77]
§ 7. РЕШЕНИЕ УРАВНЕНИЙ
247
Пример. Рассмотрим уравнение
f(x) = х* + 1,1
,9 х- 1,4 = 0.
Так как /' (х) = Зл;2 + 2,2л; + 0,9 > о для всех значений лг, то
функция f(x) монотонно возрастает иг значит, ее график лишь
один раз пересекает ось Ох; кроме того, /@) = — 1,4, а /A) = 1,6,
и значит, уравнение имеет единственный действительный корень,
лежащий в интервале [0,1].
Находим /@,5) = —0,55; затем вычисляем /@,7) = 0,112.
Это показывает, что интервал [0,5; 0,7] есть уменьшенный
интервал изоляции искомого корня. Далее мы имеем
/@,6)- —0,25, /@,65)- — 0,076, /@,67)- —0,002.
Ясно, что мы таким образом приближаемся к корню; он лежит
в интервале [0,67; 0,7]. Приблизим теперь к корню правую гра-
границу интервала изоляции. Испробуем 0,68; получим /@,68) =0,034,
Рис. 99.
Итак, мы нашли новый интервал изоляции [0,67; 0,68], кото-
который в 100 раз меньше первоначального [0,1]. Если взять в ка-
качестве значения корня число 0,675, то абсолютная ошибка будет
меньше 0,005.
Метод проб чаще всего требует более длинных вычислений,
чем излагаемые ниже методы хорд и касательных, ибо в этом ме-
методе выбор каждого следующего, более точного приближенного
значения корня в значительной мере случаен, тогда как в двух
следующих методах этот выбор производится целесообразно.
II. Метод хорд. Условия сохраняем те же, что и в методе
проб. Соединим концы дуги М1М2 (рис. 99) линии у=/(х), соот-
соответствующей интервалу [хг, х2], хордой МХМ%. Очевидно, что на
рис. 99, а точка х = х'% пересечения этой хорды с осью Ох лежит
248 ГЛ. IV. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [77
ближе к лс0, чем х^ исходя из нового суженного интервала [x'v лг2]»
получим точно так же точку x"v которая будет лежать еще ближе
к лг0, чем х'г. Таким образом, находим последовательность точек
х1У х'х , x"v ..., стремящуюся, возрастая, к неизвестному нам корню лг0.
Аналогично на рис. 99, б также получается последовательность
точек лг2, лг'2, х, ..., стремящаяся, убывая, к корню лг0.
Написав уравнение хорды М1М2
У—Нх)
(*«) —H*
найдем, положив у = О, выражение для абсциссы х' точки пере-
пересечения хорды с осью Ох:
или
Это выражение, верное для обоих случаев, изображенных на
рис. 99, а и б (а также и когда f(xx) > 0, /(л:2)<0), дает но-
новое приближение х' к корню х0 по двум предыдущим приближе-
приближениям хх и х2. Для того чтобы сузить интервал изоляции, нужно
заменить хг или х2 через х'. Какая именно из этих точек заме-
заменяется, можно установить сразу по известному нам поведению
функции f(x) или, когда это затруднительно, по знаку '
Пример. Применим метод хорд к тому же уравнению
/(лг) = лг3 + 1,1 а:2 + 0,9л:- 1,4 = 0.
Полагая а:1 = 0, л;2=1, находим по формуле (А)
и, далее, считая ^ = 0,467, дг2=1,
а:11» 0,617;
точно так же
л;111 » 0,660, jciv » 0,668, xv « 0,670, *VI » 0,670.
Устойчивость первых трех десятичных знаков в atv и xvi
указывает, как и почти всегда при подобных вычислениях,
на то, что мы подошли близко к истинному значению корня.
Испробуем для выяснения точности значение 0,671. Имеем:
/@,671)^0,0012, и так как /@,670)< 0, то новым интервалом
изоляции длиной всего в 0,001 будет интервал [0,670; 0,671].
Взяв за приближенное значение корня 0,6705, мы допускаем
ошибку, не превосходящую 0,0005, т. е. в 10 раз меньшую, чем
та, которая была допущена в методе проб при одном и том же
(примерно) объеме вычислений.
77]
§ 7. РЕШЕНИЕ УРАВНЕНИЙ
249
III. Метод касательных. Пусть теперь дуга MtM2 линии
у=/(х), соответствующая интервалу изоляции [xv x2], имеет
в каждой своей точке касательную и не имеет точек перегиба,
т. е. /"(лг) не меняет знака в интервале [х1у лг2].
В то время как метод хорд основан на замене дуги линии ее
хордой, метод касательных исходит из замены этой дуги ее
касательной. Касательная проводится в концевой точке дуги Мг
Рис. 100.
или М2, причем именно в той, которая лежит над осью Ох, если
дуга вогнута (/" {х)^0) (рис. 100, а)у и которая лежит под
осью Ох, если дуга выпукла (/"(л;)^0) (рис. 100, б).
Эти условия обеспечивают то, что точка пересечения х'х (или х'Л
касательной с осью Ох всегда будет находиться между корнем лг0
и одним из концов (xt или х2) интервала изоляции [хъ лг2]; интер-
интервал [x'v лг2] или [хг, х'2) будет новым суженным интервалом изо-
изоляции корня лг0. Если какое-нибудь из условий не выполнено, то
новый интервал изоляции может оказаться шире прежнего, и мы,
таким образом, не приблизимся к корню, а удалимся от него.
Повторное применение метода касательных приводит к последо-
последовательности, имеющей в качестве предела корень лг0. Значит, и
по этому методу корень можно найти с любой точностью.
На рис. 100 представлены два возможных случая; остальные
случаи читатель изобразит на чертеже самостоятельно.
Написав уравнение касательной МХТ или М%Т
=/'(*i)(*—*i) или jr—/(*,)=/'(*t) (*-*•).
найдем, положив JJ=O, выражение для абсциссы х или х'
О
точки ее пересечения с осью Ох:
или
(Б)
250 ГЛ. IV. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ [77
Пример. Снова вернемся к уравнению
/(*)=** +1,1*2 + 0,9*—1,4 = 0.
Так как /"(*) = 6* + 2,2 > 0 в интервале [0, 1], то касатель-
касательную проводим в точке с абсциссой, равной 1. По формуле (Б)
имеем последовательно
*! = 1 —fjjj" « 0,738, *" = о,738--?|?Щ- « 0,674,
*ш« 0,671, *IV« 0,671,
причем ясно из самого метода получения приближений, что
/@,671) > 0. Так как /@,670) < 0, то новым интервалом изоля-
изоляции будет интервал [0,670, 0,671]. Этот интервал по методу
касательных мы получили еще быстрее, чем по методу хорд.
IV. Комбинированные методы. Совместное использова-
использование различных методов для решения уравнений иногда называют
комбинированным методом.
Допустим сейчас, что,выполнены условия, указанные во всех
рассмотренных методах: дуга линии у=/(х), соответствующая
интервалу изоляции [xlt х2] корня х0 уравнения /(*)=0, в каж-
каждой своей точке имеет касательную, не имеет точек перегиба и
f(x1)f(x2)<i0. Если применять совместно, например, метод хорд
и метод касательных, то это приведет к двум последовательностям
точек, стремящихся к точке *0, с недостатком и с избытком.
В случае а на рис. 100 метод касательных дает приближенные
значения *A/|> к корню х0 с недостатком, а метод хорд—прибли-
хорд—приближенные значения х^ с избытком; в случае же б—наоборот.
Это и ускоряет процесс вычисления корня с данной точностью.
Разумеется, комбинированный метод можно также употреблять,
совмещая метод хорд или метод касательных с методом проб,
как фактически уже было сделано выше при решении уравнения
/(*)=*8 + 1,1*а + 0,9*—1,4 = 0.
Применим к этому уравнению комбинированный метод. Имеем
^«0,467 (см. II) и х'2& 0,738 (см. III).
По формулам (А) и (Б) находим
х" 0 Ifi7 m467) (°>7
Хх -0,467 J5 @,738)-
; @,467)
/@,658) @,674 —0,658)
I @,674) — i @,658)
0 671
ВОПРОСЫ И ПРЕДЛОЖЕНИЯ 251
Здесь мы уже на третьем шаге достигли интервала изоля-
изоляции [0,670; 0,671], в 1000 раз меньшего первоначального интер-
интервала [0, 1].
В настоящее время методы приближенного решения уравнений
составляют один из важнейших разделов вычислительной
математики или, как еще говорят, численного анализа.
Особенно подробно разработаны приемы решения алгебраических
уравнений, позволяющие находить не только действительные,
но и комплексные корни; один из наиболее употребительных таких
приемов носит имя Н. И. Лобачевского. Указания о книгах,
посвященных этому вопросу, читатель найдет в списке литера-
туры ([7], [8]).
ВОПРОСЫ И ПРЕДЛОЖЕНИЯ ДЛЯ САМОПРОВЕРКИ
1. Сформулировать и доказать теорему Ферма. В чем состоит ее геоме-
геометрический смысл?
2. Сформулировать и доказать теорему Ролля; указать ее геометри-
геометрический смысл.
3. Сформулировать теорему Лагранжа; объяснить ее геометрический
смысл и привести аналитическое доказательство.
4*. Сформулировать и доказать теорему Коши.
5. Сформулировать и доказать прямую и обратную теоремы о связи
между ростом функции и знаком ее производной. Каков геометрический
смысл этих теорем?
6. Определить точки экстремума (максимума и минимума) функции,
экстремальные значения функции, абсолютные экстремумы (наибольшие
и наименьшие значения).
7. Сформулировать необходимый признак экстремума. Привести при-
примеры, показывающие, что он не является достаточным.
8. В чем состоит первый достаточный признак экстремума?
9. Изложить схему исследования функции на экстремумы.
10. Как отыскиваются наибольшее и наименьшее значения функции
на данном интервале?
И. В чем состоит второй достаточный признак экстремума? Доказать его.
12. Дать определение выпуклости и вогнутости линии y = f(x) и точки
перегиба.
13. Сформулировать и доказать теорему о связи между характером
изогнутости линии y = f(x) и знаком второй производной от функции f (х).
14. В чем состоят первый и второй достаточные признаки для точек
перегиба?
15. Изложить теорему Лопиталя. Привести различные примеры при-
применения правила Лопиталя.
16. Что называется асимптотой данной линии?
17. Вывести аналитические признаки вертикальной и наклонной асимптот
линии y = f (х),
18. Описать общую схему исследования функций.
19. Вывести формулу для дифференциала длины дуги. На каком геоме-
геометрическом свойстве линии основывается этот вывод?
20. Что называется кривизной линии в данной ее точке? Вывести фор-
формулу для кривизны.
21. Определить радиус, центр и круг кривизны.
252 ГЛ. IV. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
22. Дать определение эволюты и эвольвенты. Указать приемы их
приближенного построения.
23. Вывести уравнения касательной прямой и нормальной плоскости
к пространственной линии.
24. Дать определение и вывести уравнения цилиндрической винтовой
линии.
25. Дать определения векторной функции скалярного аргумента и ее
годографа.
26. Дать определения предела и непрерывности векторной функции;
сформулировать правило отыскания ее предела.
27. Дать определение производной векторной функции скалярного
аргумента и указать ее геометрический смысл. Вывести формулу разложе-
разложения производной по единичным векторам.
28*. Что называется скоростью и ускорением криволинейного движе-
движения? Вывести выражения для тангенциального и нормального ускорений.
29. Дать определение комплексной функции действительного перемен-
переменного, ее предела и непрерывности.
30. Дать определение производной коплексной функции и указать пра-
правило ее отыскания.
31. Дать определение показательной функции с мнимым показателем
степени. Указать ее годограф, доказать периодичность и вывести формулу
для ее производной.
32. Что называется показательной формой комплексного числа?
33. Вывести формулы Эйлера, выражающие тригонометрические функ-
функции через показательную.
34. Описать процесс разложения многочлена на линейные и квадратич-
квадратичные действительные множители.
35. Дать определение кратного корня уравнения; придумать примеры
трансцендентных уравнений, имеющих простые и кратные корни.
36. Что называется интервалом изоляции корня уравнения? Описать
способы отыскания таких интервалов.
37. Изложить методы проб, хорд, касательных и комбинированные
методы для нахождения приближенного значения корня уравнения.
ГЛАВА V
ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
§ 1. Неопределенный интеграл1)
78. Первообразная функция. Занимаясь дифференцированием
функций, мы ставили перед собой следующую задачу: по данной
функции найти ее производную. Теперь перейдем к изучению об-
обратной задачи: найти функцию, зная ее производную. Как мы
вскоре увидим, решение этой обратной задачи имеет очень боль-
большое значение для дальнейшего изучения анализа и его приложе-
приложений. Начнем с определения первообразной функции.
Определение. Первообразной от функции f(x) назы-
называется функция F(x), производная которой равна данной функции:
Чтобы лучше отдать себе отчет о соотношении между первооб-
первообразной и данной функциями, рассмотрим примеры.
Пусть у = х2. Для какой функции х2 служит производной?
Очевидно, для -^ :
3
Поэтому первообразной от х2 является функция -^. Но не только
х3 г3
она. В самом деле, производной от -Q- + 5, V—100 и вообще от
о о
-j +C, где С —произвольная постоянная величина, будет также х2.
X3
Следовательно, любая функция -=- + С является первообразной отлг2.
1) В прежних изданиях Курса сначала изучался определенный
интеграл, а потом неопределенный. Так как чаще поступают наобо-
наоборот, то в настоящем издании соответствующие параграфы A и 2) перестав-
переставлены, но по-прежнему могут читаться в любой последовательности.
254 ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ [78
Две функции лс2 и j + C при любой постоянной С находятся
в таком соотношении друг к другу: первая является производ-
производной от второй, вторая — первообразной от первой.
Подобно этому любая функция 1пдг + С является первообразной
от —, любая функция sin л; + С является первообразной от cos х
и т. д.
При рассмотрении примеров бросается в глаза то обстоятель-
обстоятельство, что первообразных у данной функции не одна, а бесчислен-
бесчисленное множество, так как постоянная величина С может принимать
любые значения; производных же у данной функции, разумеется,
только одна.
Сформулируем теперь основную теорему о первообразных.
Теорема. Всякая непрерывная функция имеет бесчисленное
множество первообразных, причем любые две из них отличаются
друг от друга только постоянным слагаемым.
Наиболее трудным моментом доказательства является установ-
установление того, что данная непрерывная функция вообще имеет хоть
какую-нибудь первообразную. Этот факт мы доказывать не будем,
а несколько позже приведем его геометрическую иллюстрацию.
Пока же примем, что любая непрерывная функция f(x) имеет перво-
первообразную F(x).
Но тогда функция F(x)-\-C при всякой постоянной С будет
также первообразной, так как
Итак, функция f(x) имеет бесчисленное множество первооб-
первообразных.
Нам остается показать, что любые две первообразные от
функции f(x) отличаются друг от друга лишь постоянным сла-
слагаемым. Пусть F{х) и Ф(х)— две первообразные от /(л:), тож-
тождественно не равные между собой. Имеем
F'{x)=f(x), Ф'(х)=/{х).
Вычитая одно равенство из другого, получим F'(х)—Ф'(#) = 0,
т. е. [F (х)—Ф(лг)]'=0. Но если производная от некоторой функ-
функции (в нашем случае от F (х)—Ф(х)) тождественно равна нулю,
то сама функция есть постоянная (п. 59); следовательно, F (х) —
—Ф(х) = Сх (где Сх — вполне определенная постоянная), что и
требовалось доказать.
Таким образом, выражение F (х) + С, где F (х) — к ака я-нибу д ь
первообразная от /(#), а С—п роизвольная постоян-
постоянная, охватывает все без исключения первообразные от f(x). При-
78]
§ 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
255
давая различные численные значения С, мы будем получать раз-
различные первообразные.
Геометрическая иллюстрация существования
первообразной. Приведем теперь геометрическую иллюстра-
иллюстрацию того факта, что лю-
любая непрерывная функция
имеет первообразную.
Рассмотрим график
функции, изображенный на
рис. 101. Зафиксируем точ-
точку а и обозначим через
5 (л:) площадь криволиней-
криволинейной трапеции с основанием
[а, х]. Ясно, что, меняя л:,
мы как-то изменяем и пло- Рис. 101.
щадь криволинейной тра-
трапеции S (х). Найдем производную от функции S (л:), исходя из
определения производной
Пусть х получил приращение Ал:; площадь S(x) получает
при этом приращение AS (рис. 101). Геометрически ясно, что
тАх <AS< MAx,
где т и М — соответственно наименьшее и наибольшее значения
функции f(x) в интервале [лг, лг + Дл:]. Ведь тАх — это площадь
прямоугольника, целиком лежащего внутри фигуры, площадь ко-
которой обозначена AS, а МАх — площадь прямоугольника, содер-
содержащего эту фигуру внутри себя. Деля все части неравенства на
Ал:, получим
Так как f(x) — непрерывная функция, то при Ал:—^0 яти
Му являющиеся значениями функции в интервале [л:, лг + Дл:], бу-
будут стремиться к значению функции в точке л:, т. е. к /(*). По
признаку существования предела (п. 30) отношение -г— будет
стремиться к тому же пределу:
ltm ** =
Д
Таким образом, 5 (х) действительно является первообразной
от f(x).
256 ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ [79
Так же наглядно можно показать, что первообразных бесчис-
бесчисленное множество. Взяв за начальную не точку а, а какую-нибудь
другую точку а', мы получим новую функцию — площадь криволи-
криволинейной трапеции с основанием [а', л:], которая отличается от S(x)
на площадь трапеции с основанием [а' ,а], т. е. на постоянную
величину.
Разумеется, приведенное рассуждение, почти полностью осно-
основанное на геометрических представлениях, не может служить ана-
аналитическим доказательством теоремы. В то же время оно показы-
показывает, что отыскание первообразных, или, как мы будем говорить,
интегрирование функций, тесно связано с задачей отыс-
отыскания площадей фигур, ограниченных кривыми линиями.
79. Неопределенный интеграл. Основная таблица интегралов.
Введем название действия отыскания первообразных.
Определение. Отыскание первообразных называется неоп-
неопределенным интегрированием, а выражение, охватывающее мно-
множество всех первообразных от данной функции f(x), называется
неопределенным интегралом от f(x) и обозначается так:
jf(x)dx.
Функция f (х) называется подынтегральной функцией, выраже-
выражение f (x)dx—подынтегральным выражением, а переменная х—пере-
х—переменной интегрирования.
Предполагается, что подынтегральная функция f (х) при рас-
рассматриваемых значениях х непрерывна.
В п. 78 было установлено, что
где F(x) — какая-нибудь из первообразных от f (х), а С — произ-
произвольная постоянная.
Неопределенное интегрирование есть действие, обратное
дифференцированию. При помощи дифференцирования мы по дан-
данной функции находим ее производную, а при помощи неопреде-
неопределенного интегрирования мы по данной производной находим пер-
первообразную функцию. Правильность интегрирования всегда можно
проверить дифференцированием результата. Выбор символа для
обозначения результата операции, обратной дифференцированию,
будет оправдан в дальнейшем.
Найти неопределенный интеграл от функций—это значит най-
ги все первообразные от нее (для чего достаточно указать одну
из них). Потому и говорят неопределенное интегриро-
79]
§ 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
257
вание, что при этом не указывается, какая именно из первооб-
первообразных имеется в виду.
График первообразной от функции / (х) называется интегральной
кривой функции y = f(x). Очевидно, мы получим любую другую
интегральную кривую, если передвинем какую-нибудь интеграль-
интегральную кривую параллельно самой себе в направлении оси ординат.
Рис. 102.
Поэтому неопределенный интеграл геометрически представляется
множеством всех интегральных кривых, получаемых при непре-
непрерывном параллельном движении одной из них по направлению
оси Оу (рис. 102).
По самому определению неопределенного интеграла имеем
(ff(x)dx)' =
d$f (*) dx = / (х) dx
$f'(x)dx =
или
или
Символы дифференциала и неопределенного интеграла унич-
уничтожают друг друга, будучи примененными последовательно
(если отвлечься от постоянного слагаемого в двух последних
формулах).
В дальнейшем, говоря об интеграле и об интегрировании, мы
будем понимать неопределенный интеграл и неопреде-
неопределенное интегрирование.
Приведем прежде всего формулы интегрирования, прямо выте-
вытекающие из формул дифференцирования основных элементарных фун-
функций. Каждая из них легко проверяется дифференцированием.
^ А. Ф. Бермант, И. Г. Араманович
258 ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
Основная таблица интегралов.
+ c, кФ-\. 2) J^ = in
3) §axdx=j^ §
[79
5) Сcosjc dx = situ: + C. 6) [sinxdx =— cosjc
^ arctg* + C.
Добавим еще формулы интегрирования, связанные с гипербо-
гиперболическими и обратными гиперболическими функциями (см. п. 23):
~^ = thuc + С,
Г dx _
(Объединение двух последних формул приводит к формуле A1) ос-
основной таблицы.)
х) В этой формуле х может находиться в интервалах (—оо, 0) и @, оо);
изменяться в интервале, содержащем точку 0, он не может, так как в та-
таком интервале подынтегральная функция уже не является непрерывной.
Если х > 0, то In |*| = In* и производная равна —. Если же * < 0, то
In |*| = In (— *) и производная снова равна —.Таким образом, формула
охватывает оба случая.
2) * может находиться в трех интервалах: (—оо, —1), (— 1, 1), A, оо);
доказательство общности формулы аналогично приведенному в сноске 1).
80] § L НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 259
Последняя формула справедлива при —1<#<;1 (область опре-
определения Arthx); ее обобщением и незначительным видоизменением
является формула A2).
80. Простейшие правила интегрирования. Примеры.
Теорема I (об интеграле суммы). Интеграл от сум-
суммы конечного числа функций равен сумме интегралов от слагае-
слагаемых функций
где a, vy . . . , w — функции независимой переменной х.
Равенства, в обеих частях которых стоят неопределенные ин-
интегралы, означают, что левая и правая их части являются сово-
совокупностями первообразных от одной и той же функции. Следова-
Следовательно, для проверки таких равенств достаточно убедиться, что
производные обеих их частей равны между собой.
Производная левой части равенства (*) по определению интег-
интеграла равна u + v-^-.. ,-\-w. Применяя к правой части правило диф-
дифференцирования суммы, опять-таки получим
I и dx + I v dx + ... + I w dx\ =
= ([udx\ +([vdx\ +.
Теорема доказана.
Теорема II (о вынесении постоянного множите-
множителя). Постоянный множитель подынтегральной функции можно вы-
вынести за символ интеграла
где с — константа.
Действительно, производные обеих частей равенства равны
(fcf{x) dx)'= cf(x); (с ff(x) dx)'= c ($f(x) dx)'= cf(x)t
что и требовалось доказать.
Пример.
JB sin л;— 3 cos x) dx = 2 J sin x dx—3 Jcos x dx =
= — 2 cos л;—3s\nx + C.
Хотя каждое промежуточное интегрирование дает произвольное
постоянное слагаемое, в окончательном результате указывается
только одно слагаемое, так как сумма произвольных постоянных
будет также произвольной постоянной.
260 ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ [80
Теорема III (об инвариантности формул интег-
интегрирования). Всякая формула интегрирования сохраняет свой
вид при подстановке вместо независимой переменной любой диф-
дифференцируемой функции от нее, т. е. если
ff(x)dx=F(x) + C, то и $f(u)da = F(u) + C,
где # = ф (лг) — любая дифференцируемая функция от х.
Доказательство. Из того, что
ff(x)dx = F(x) + C, следует F'(x)=f(x).
Возьмем теперь функцию F (и) = F[(p (x)]; для ее дифференци-
дифференциала в силу теоремы об инвариантности вида первого дифферен-
дифференциала функции (п. 51, III) имеем
dF (и) = F' (и) du = f{u) du.
Отсюда
Это правило очень важно. Основная таблица интегралов в силу
этого правила оказывается справедливой независимо от того,
является ли переменная интегрирования независимой переменной
или любой дифференцируемой функцией ее; таким
образом, основная таблица сразу значительно расширяется.
Возьмем, например, интеграл \2хе dx. Замечая, что 2хdx
есть не что иное, как дифференциал d (л:2), перепишем интеграл так:
' dx =
где положено а = лг2. Последний интеграл, согласно формуле D)
основной таблицы и теореме III, равен еа4-С, значит,
2хе** dx = e* +C.
Как показывает этот пример, нужно стараться так преобразо-
преобразовать подынтегральное выражение, чтобы оно приняло вид по-
подынтегрального выражения известного нам интеграла, например
одного из интегралов основной таблицы.
Сразу предупредим читателя, что интегрирование значительно
сложнее дифференцирования. Дифференцирование функций (эле-
(элементарных) производится по раз и навсегда установленным пра-
правилам и формулам; интегрирование же требует, так сказать, ин-
индивидуального подхода к каждой функции. Нужен большой навык,
чтобы быстро и уверенно производить преобразования подынтеграль-
подынтегрального выражения для приведения интеграла к знакомому (табличному)
80] § 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 261
виду1). Приводимые ниже примеры должны помочь в приобрете-
приобретении такого навыка; мы настоятельно рекомендуем читателю после
разбора этих примеров самостоятельно решить побольше задач
из задачника. Лишь после этого стоит переходить к изучению
некоторых общих методов интегрирования, приведенных дальше.
Примеры. 1) fsin 5xdx. Умножим и разделим интеграл на 5
и внесем множитель 5 под символ интеграла:
I sin 5л: dx = у fsin 5л: • Ых = -^ \ sin 5л: d Eл:).
Полагая 5л: = а, придем к интегралу основной таблицы:
С If* 1 1
\ sin 5л: dx = -^- \ sin и du= —=- cos и + С= —^ cos 5л: + С
Подобным же образом найдем, например, что
2) /Bл:—1IООл?л;. Умножая и деля на 2 и замечая, что
2dx = dBx—1), получим
:— 1).
Полагая 2л:— 1 = и, находим
Легко видеть все преимущества такого интегрирования по
сравнению с интегрированием многочлена, полученного от раск-
раскрытия бинома в сотой (!) степени по формуле Ньютона.
3) Iх
dx. Преобразуем интеграл к виду
г) Заметим, что такое преобразование далеко не всегда удается выпол-
выполнить. Это связано с одной специфической трудностью интегрального исчис-
исчисления, заключающейся в том, что даже для сравнительно простых функций
первообразные не всегда выражаются при помощи элементарных функций,
т. е. являются функциями более сложного вида. Подробнее об этом будет
сказано в п. 85.
262 ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ [80
Мысленно полагая л;2-}-1=я, получим
С развитием навыка в интегрировании не будет нужды запи-
записывать все промежуточные выкладки и обозначения. Большая
часть их производится в уме.
4) \3 * .
Имеем
Вообще, если числитель подынтегральной функции является про-
производной знаменателя, то интеграл равен логарифму абсолютной
величины знаменателя.
В самом деле,
Например:
Jctg х dx = J^ dx = In | sin x | + C,
P ЛГ 1
5) \ t . xdx. Замечая, что xdx = у rf(а:2), получим
1Г d (a;2) 1 , .
2-jT+W=-2-arCtg
6) lo^ZT^' Разделив числитель на знаменатель, получим
в частном 1,5 и в остатке 3,5. Следовательно,
S d;e = J(!'5+гЙт) d;c = ]-5лг + 1,75 In 12л; -11 + С.
80]
7)
§ 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
dx ..
Имеем
dx 1
263
(*)"-¦"'Д*I-
1 1 I
=тт1п
a
1-й
+ C=^ln
2a
дс—a
лс+a
Совершенно аналогично найдем второй интеграл
dx 1 . х , ~
К этим интегралам легко преобразуются интегралы [-^т—ЦГ~ •
нужно только знаменатель представить в виде суммы или разности
квадратов. Например,
= f
C, dx =f
J*2 + 4*+l Ji
1
djc
+ C.
. 2 o"~- " этому интегралу применим комбинирован-
комбинированна -J- 4^ -j- о
ный прием. Замечая, что производная знаменателя равна 2л: + 4,
запишем числитель в виде -~-{2х-\~4:)'\-\ и разобьем интеграл на
сумму двух интегралов, каждый из которых находится уже из-
известными приемами:
_ ш _^х dx
=у In (*2 + 4л: + 8) + i arctg^±-2 + С.
9) i А г и 1 :. Аналогично примеру 7 получим
J К а2—*2 J У х2 ±а2
=arcsin -j + С
264 ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ [81
(При преобразовании логарифмического члена слагаемое — In a
отнесено к произвольной постоянной.)
10) С sin xcosxdx. По известной формуле тригонометрии имеем
f sin х cos x dx = -j(* sin 2xdx = ^- f sin 2x d Bx) = — j cos
Этот интеграл можно брать иначе:
I sin x cos x dx = \ sin x d (sin x) = у sin2 лс 4- С
или
I sin л: cos x dx — — I cos a: rf (cos x) = —x- cos2 x-\-C.
Может показаться, что для одного и того же интеграла мы по-
получили три существенно различных ответа:
—j cos 2x + С, у sin2 х + С, —у cos2 лг+ С.
Однако легко проверить, что разность любых двух из них есть
величина постоянная. Поэтому каждое из найденных нами выраже-
выражений дает все множество первообразных от sin л: cos л:.
11) \ sin2xdx и \cos2xdx легко находятся при пошщи фор-
. о 1 —cos 2х „ 1 -f cos 2x
мул smzjt = ^ и cos2a; = ——^ .
Например,
12) J cos3xdx. Последовательно находим
cos* xdx= J cos2 x d (sin x) = J A—sin2 a:) d (sin л;) =
= \d (sinx) — \ sin2 x d (sin x) = sinx — ysin3Ar + C*
81. Интегрирование по частям и замена переменной. Так как
интегрирование — действие, обратное дифференцированию, то каж-
каждому правилу дифференцирования должно соответствовать некото-
некоторое правило интегрирования. Доказанные в п. 80 три правила ин-
интегрирования соответствуют правилам дифференцирования суммы,
произведения функции на постоянную величину, сложной функции.
I. Интегрирование по частям. Метод интегрирования
по частям следует из формулы дифференцирования произведения
двух функций.
Пусть и(х) и v(x)—дифференцируемые функции от х. Имеем
d(uv) —
81] § 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 265
откуда
) — vdu.
Интегрируя обе части последнего равенства, получим
j и dv = \ d (uv) — j v du
или
Это и есть формула интегрирования по частям. Про-
Произвольную постоянную при интегрировании d (uv) мы не записываем,
присоединяя ее к произвольной постоянной второго, не завершен-
завершенного в общем виде интегрирования в правой части равенства (*).
Интегрирование по частям состоит в том, что подынтегральное
выражение f(x)dx представляется каким-либо образом в виде
произведения двух множителей и и dv (последний обязательно
содержит dx) и заменяется двумя интегрированиями: 1) при отыс-
отыскании v из выражения для dv; 2) при отыскании интеграла от vdu.
Может оказаться, что эти два интегрирования легко осуществля-
осуществляются, тогда как заданный интеграл непосредственно найти трудно.
Примеры. 1) \xexdx. Примем exdx за dv, х—за и, т. е.
положим
с = dv, \ I v = \ ех
> откуда i J
: — и> ) \ du = dx.
Получаем по формуле (*)
xdx = xex — e*+C=ex(x—
Мы видим, как незнакомый интеграл был приведен к хорошо
известным.
Неудачной была бы попытка представить подынтегральное выражение
иначе: xdx = dvt ex = u\ тогда v = y> du=*ex dx и
С хг \ С
J xe*dx=:-2 гх—^ \
хЧхdx.
Здесь интеграл в правой части равенства более сложный, чем в левой.
Легко заметить, что именно этот более трудный интеграл при помощи удач-
удачного применения метода (положить dv = exdx и и = х2) приводится к более
простому интегралу в левой части, который мы и нашли выше.
266 ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ [81
2) 5 х In х dx. Положим
Тогда
Здесь неудачей было бы положить \nxdx = dvt x = u, так как интеграл
\ \nxdx не проще исходного; его самого следует находить интегрированием
dx (*
по частям, положив dx = dv, lnx = u. Тогда v=x, du=-~ и I \nxdx = x\nx—
-х + С.
Иногда для получения результата нужно последовательно не-
несколько раз применить интегрирование по частям.
3) \ х2 cos х dx. Положим
cos xdx — dv, v = sin x,
Формула (#) дает
к2 cos x dx = x2 sin x—2 \x sin x dx.
Последний интеграл снова берется по частям. Окончательно полу-
получаем
\х2 cos х dx = х2 sin x + 2х cos x—2 sin x + С.
С развитием навыка отпадает необходимость подробно записы-
записывать все промежуточные выкладки и обозначения.
Многократным интегрированием по частям можно найти инте-
интегралы
\хт sin х dx, \xm cos x dx, \xm ex dx
(т—целое положительное число) и, значит, интегралы
i P (x) sin х dx, \ P (x) cos x dx, \P (x) ex dx,
где Р (х) — любой многочлен.
Повторное интегрирование по частям иногда приводит к пер-
первоначальному интегралу, и тогда получается или ничего не дающее
тождество (повторное интегрирование было произведено неудачно),
81] § 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 267
или же такое равенство, что из него удается найти выражение
для искомого интеграла. Рассмотрим пример
¦>*¦
ех cos х dx. Положим
ех dx = dv,
cos х = и,
= — sin x dx.
Отсюда
\ ex cos x dx — ex cos x + \ ex sin x dx.
Снова применим интегрирование по частям, положив
exdx = dv,
sin x = и,
du = cos xdx.
Тогда получим
fexsin xdx = exsinx —
и мы пришли к исходному интегралу. Подставив найденное выра-
выражение в результат первой операции, получим
JV*cos xdx = e*cos x + ?*sin x — J^^cos xdx;
перенося интеграл из правой части в левую, найдем
\ ?*cos xdx = y ex(zosx + sin л;) + С.
Умение правильно определять, когда и как следует применять
метод интегрирования по частям, вырабатывается практикой.
II. Замена переменной (метод подстановки). При отыска-
отыскании интегралов мы уже неоднократно пользовались теоремой III п. 80
об инвариантности формул интегрирования. Если подынтегральное
выражение удавалось записать в виде
fl<p(x)]<p'(x)dx=f(u)du,
где а = ф(лг) и интеграл от выражения справа известен:
ff(u)du =
то исходный интеграл был равен
Основную трудность как раз и представляет преобразование по-
подынтегрального выражения, так как заранее неизвестно к чему
*) Если здесь принять sin xdx за dv, то придем к тождеству
\ g*cos х dx == \ е
268 ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ [81
нужно придти и какой должна быть функция (р(х). В п. 80 мы
уже познакомились с самыми разнообразными примерами таких
преобразований; при этом в простейших случаях формула под-
подстановки и = ф(лг) не записывалась и окончательное выражение
для интеграла получалось сразу.
В более сложных случаях рекомендуется сначала выбрать ту
подстановку, которая представляется удачной, и лишь после пре-
преобразования подынтегрального выражения смотреть, добились ли
мы своей цели — упрощения интеграла. Может оказаться, что но-
новый интеграл еще не является табличным, но приводится к такому
проще чем исходный; это уже оправдывает сделанную подстановку.
u Г sin 2x .
Например, интеграл \ , 4 dx в результате подстановки
sinx = u, cosxdx = du приводится к интегралу \ %, ±du. Запи-
Записав последний в виде \ , f L2 (ПРИ этом подстановка u2 = v со-
совершается в уме), видим, что он равен arctg^2+C и значит
С sin 2x
(Более сложная подстановка sin2x = u сразу привела бы заданный
интеграл к табличному.)
До сих пор мы применяли метод подстановки, заменяя перемен-
переменную интегрирования х другой переменной и при помощи формулы
и — ц>{х). Можно производить замену, выражая не и через х, а
наоборот х через иу т. е. полагая
(предполагается, что tj) (и) и я|/(и) непрерывны). Тогда
Если последний интеграл удалось найти и он оказался равным
F(u) + Cy то заданный интеграл находится возвращением к пере-
переменной х. Для этого нужно из уравнения x—ty(u) выразить и
через х, т. е. найти обратную функцию и подставить ее вместо и
в выражение найденного интеграла.
Как и раньше, самое трудное—это удачно выбрать подстановку
x — ty (и). Приведем примеры, иллюстрирующие обе формы замены
переменной.
Примеры. 1) §х2У 4 — З*3 dx. Положим 4 — 3*3 = ы.
81]
§ 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
269
Дифференцируя, имеем: —9x2dx = du и xldx = —du. Поэтому
4
. Положим ye + 1=и, т. е.
Следовательно,
dx
""
"
Возвращаясь к переменной л:, окончательно получим
Нередко вместе с заменой переменной нужно применить дру-
другие методы (например, интегрирование по частям), для того
чтобы довести задачу до конца.
3) \ хъех* dx. Положим Xs = и. Имеем 3x2dx = du и, значит,
f
= ^[ ue
а этот интеграл, как мы знаем (I, пример 1), берется по частям.
Получаем
± ±ex*(x*— \) + С.
Пока мы пользовались подстановками типа и = у(х). Покажем
теперь применение подстановок типа x~ty(u) на примерах очень
часто встречающихся тригонометрических и гипербо-
гиперболических подстановок.
4) \ У 1 —х2 dx. Положим л; = sin и, dx = cos и du. Подставляя,
находим
Г У\—Х2 dx=[ cos2 и du = ~ ( и + у sin2w \+ С
(см. пример 11 п. 80). Возвращаясь к переменной х и замечая,
что sin 2и = 2 sin и cos и = 2х У 1 — х2, получим
Г ]/"Г3^2 dx = ±- (arcsin x + х ]/"l— x2) + С.
270 ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ [82
5) J У х2 + 1 dx. Здесь очень удобна подстановка1) x = shu,
dx = ch и du:
Так как u = Arshx = In (x + Vx2 +1) (см. п. 23, II), a
2xVx2+\, то
Аналогично при помощи подстановки x=chu найдем
Процесс интегрирования обычно состоит в целесообраз-
целесообразном применении изложенных выше приемов (алгебраические
преобразования подынтегрального выражения, интегрирование по
частям, интегрирование подстановкой), для того чтобы привести
заданный интеграл к интегралу, уже известному.
82. Интегрирование рациональных функций. Важнейшим клас-
классом элементарных функций, интегралы от которых находятся при
помощи достаточно простой последовательности действий2),
является класс рациональных функций (п. И). Всякая
рациональная функция R (х) может быть представлена в виде
Р (х)
дроби 0-Н, где Р(х) и Q(x) — многочлены:
Прежде всего заметим, что если степень т числителя Р(х)
больше или равна степени п знаменателя Q(x), то, разделив
многочлен Р(х) на многочлен Q(x), мы получим в частном неко-
некоторый многочлен N (х) и в остатке многочлен Рх (х) не выше
(п—1)-й степени. Следовательно,
1) Другая возможная подстановка * = tgw приводит к очень громозд-
громоздким преобразованиям. Введение гиперболических функций, хотя к ним
читатель, возможно, и менее привык, позволяет значительно упростить
производимые преобразования.
2) Последовательность действий называется алгоритмом.
82] § 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 271
Интегрирование многочлена N(x) не доставляет никаких за-
затруднений, и значит, весь вопрос заключается в интегрировании
дроби, степень числителя которой меньше степени знаменателя.
Итак, пусть степень числителя меньше степени знаменателя
(т<Сп). Такую рациональную дробь иногда называют правильной.
1. Разложение на простейшие дроби. Мы предпо-
предполагаем, что многочлены Р(х) и Q(x) имеют действительные
коэффициенты, причем коэффициент многочлена Q(x) при хп
равен 1 (этого всегда можно достигнуть делением числителя и
знаменателя на коэффициент при л:").
Многочлен Q(x) — знаменатель заданной подынтегральной
рациональной дроби— согласно п. 75, I, может быть представлен
в виде произведения линейных и квадратичных множителей с
действительными коэффициентами
гдеаесть&-кратный действительный корень уравнения Q(x) — 0,
а квадратное уравнение х2-\-рх + д = 0 имеет сопряженные комп-
комплексные корни (и значит, р2—4д < 0), которые служат /-крат-
/-кратными сопряженными комплексными корнями уравнения Q (х) = 0.
Р (х)
Интегрирование рациональной дроби -тА-{ мы основываем на зна-
нии разложения (#) многочлена Q(x) на действительные
множители (или, что равносильно этому, на знании всех корней
уравнения Q(x) = 0). Задачей отыскания корней алгебраического
уравнения Q(x) = 0 мы здесь специально заниматься не будем и
в последующем полагаем, что разложение (*) так или иначе
является известным. При этом оказывается, что дробь -Ти\ можно
представить в виде суммы так называемых простейших дробей
1-го и 2-го видов
где Ah Bh Сi — постоянные, а именно:
Каждому множителю (х — a)k в представлении (*) знамена-
теля Q (х) соответствует в разложении дроби ^— на слагаемые
сумма k простейших дробей 1-го вида
а каждому множителю (x2-\-px + q)f соответствует сумма t
272 ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ [82
простейших дробей 2-го вида
Доказывать это предложение в общем случае мы не будем;
на рассматриваемых подробно примерах будет видно, как можно
Р (х)
фактически осуществить разложение заданной дроби -^~\ на
простейшие дроби, т. е. найти все неизвестные коэффициенты Д-,
в„ с,..
Таким образом, при разложении (#) знаменателя Q(x) на мно-
. Р(х)
жители имеет место разложение дроби тгт-{ на слагаемые:
Р(х)_ Ak Ак_г Аг . Btx + Ct
Q(x) (* — a)k (x—a)* x—a " (x2 + px + q)t
Отсюда следует, что интеграл от всякой рациональной дроби
сводится к интегралам от простейших рациональных дробей 1-го
и 2-го видов, а эти интегралы находятся очень легко, что мы и
увидим опять-таки на нижеследующих примерах. Эти примеры
необходимо разобрать основательно, ибо на них мы демонстри-
демонстрируем, избегая общих рассмотрений, возможные случаи интегри-
интегрирования рациональных дробей.
Итак, предлагаемый метод интегрирования рациональных дро-
- „ Р (х)
беи -Q . ' состоит в том, что, зная разложение знаменателя на мно-
множители, мы составляем разложение (#*) и данный интеграл заме-
няем суммой интегралов от соответствующих простейших дробей,
II. Примеры.
1) \ 3_ dx. Разложение подынтегральной функции на про-
простейшие дроби должно иметь вид
х~-Ъ х—г А . В . С
*з—х~~х(х— 1)(л:+1) ~ х ~*~х— 1"*"х+\
(какими буквами обозначены коэффициенты, не имеет, конечно,
никакого значения). Прежде всего нам нужно найти коэффи-
коэффициенты Л, Ву С.
Освобождаясь от знаменателей, получим
х—3 = А (л:2 — 1) + Вх [х + 1) + Сх {х — 1).
Так как это —тождество, то, согласно замечанию на стр. 243,
коэффициенты при одинаковых степенях х должны быть равны
82] § 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 273
между собой:
0 = А + В+С, 1=5 —С, — 3 = — А.
Из этой системы трех уравнений с тремя неизвестными на-
находим
Л = 3, Я = — 1, С= — 2.
Еще проще для олределения коэффициентов И, Б и С посту-
поступить так: полагая последовательно л; —О, #=1, лг = —1, полу-
получим: — 3 = — Л, — 2 = 2В, — 4 = 2С, т. е. снова
Л = 3, Д=—1, С=—2.
Итак, тождественно
х—3 3 1 2
Л'3 — JC X Х—\ Х+ 1 '
поэтому
dx
= 3 In | x | — In | x— 1 I —21n|*+l|
= ln
t—5
з^-З 2 i 4 dx. Разложим знаменатель подынтегрдльной
дроби на множители. Замечая, что он обращается в нуль при
х = —1, разделим его на лг-j-l; в частном получится х2 — 4лг ~h
-)-4 = (лг — 2J и, значит, разложение дроби на простейшие должно
иметь вид
*_5 х—Ь ^JL-и В ' С
(jc —2J jc+1 *(* — 2J^х — 2 *
Найдем коэффициенты А, В, С. Приводя к общему знаменателю
и освобождаясь от него, получим
х — 5 = А(х — 2)* + В(х+\) + С(х+\)(х — 2).
Здесь удобно положить х = —1, лг = 2, х — 0\ получаем
— 6 = 9Д — 3 = 3?, — 5 = 4Л + Я— 2С.
Отсюда
л— —, #- 1, с— 3 .
Следовательно,
Г dx 2 г dx _
J (a:-^2*^ 3 J x-2 *~
274 ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ [82
Г 12
3) \ 4i rdx. Знаменатель легко раскладывается на
J X -\- X X 1
множители:
— л; — 1 = *3 (лг + 1) —(* + 1) = (х+ 1) (л:3 — 1) =
Разлагаем подынтегральную функцию на простейшие:
12 А ВCx + D
х+\ ^х-\^
Коэффициенты Л, Ву С, D находим из тождества
Подставляя сюда четыре различных численных значения дг, на-
например х = \, х = —1, х = 0, х = 2, получаем систему
12 = 65, 12 = — A + B-D,
12 = —2Л, 12 = 7Л+21?+3BС+?>),
из которой находим
Л = —6, В = 2, С=4, D== —4.
Следовательно,
x—\ ,
йх
\ -г-.—5 \ dx = — 6 \ —гт+ 2 \ —
Последний интеграл в правой части находим, выделяя в числи-
числителе производную знаменателя:
х-1 /§г 1 Г2у+1-3 ,
._?Г dx_
2 J („л. x\
V! V?
Окончательно имеем
1n (je« + jf+ l)_4/F arctg
82] § 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 275
С х2 1 х 1
4) \ / 2л.п2^' Знаменатель подынтегральной дроби уже дан
J X \Х -р 1)
своим разложением (#) на множители. Имеем
*2 + jc— 1 Л Bjc + C . Dx + E
где постоянные Л, Ву С, D, ? будут найдены из того условия,
что это равенство (разложение) тождественное. Освобождаемся
от знаменателей:
Здесь проще приравнять друг другу коэффициенты при одина-
одинаковых степенях х в левой и правой частях. Начиная с коэффи-
коэффициента при д;4, получим следующую систему:
С+Е=\, Л = —1.
Решая эту систему, находим
Л = — 1, В=2, C=l, D=l,
Значит, тождественно
jc(jc2+1J "" jc +(^2+1J + ^+1 '
и поэтому
2 + 1 С d Г 2+1 Г л:
Г» jc2 + ^—1 _ С dx Г
Первый и третий интегралы справа известны: они равны соот-
соответственно — 1пд; и ^1п(л;2+1)-
Займемся вторым интегралом:
Г Ъ*+\ d С 2х Г dx 1 , Г ^
J (j:l+1)l«* J (*2+1J«*-t-j (%2+lJ- X2+1 i-j (jC«+l)«e
Последний интеграл в правой части обозначим через /2:
dx
Применим здесь следующий прием. К числителю подынтег-
подынтегрального выражения прибавим и вычтем х2 и разобьем интеграл
на два интеграла:
рх2+1_Л.а с dx С
276 ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ [82
Применяя интегрирование по частям ко второму интегралу:
xd* ^dv
2xdx _J^
(JC2+1J Y
da = dx,
получим
Г х2 dx __ х 1 Г dx
J BflJ~~ 2(x* + l) + 2 J *2+l
J (*2-f-lJ
Подставляя в выражение для /2, найдем
/.=•-
2"j "^ТГ ^
Окончательно исходный интеграл равен
Легко проверить правильность ответа: производная правой
части равна подынтегральной функции.
Прием, указанный для отыскания /2, применим и для отыскания
интеграла
dx
при произвольном целом /г > 1. Если записать, что
1 1 х2
и преобразовать интеграл от второго слагаемого при помощи интегрирова-
интегрирования по частям, как это сделано выше, то получим равенство
7
2fe-3
2(k—
, 2fe-3 J
-1 2(k— 1) *"le
Это —так называемая формула приведения (рекуррентная формула) для
отыскания Ik. Заменив в ней k на k—1, получим выражение интеграла
lk-i через /л_2 и т. д. В конце концов мы придем к интегралу
dx
н интегрирование будет завершено. Предоставляем читателю проверить,
что, например,
83] § 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 277
В заключение еще раз подчеркнем, что если отвлечься от
чисто алгебраических трудностей, то интеграл от любой рацио-
рациональной функции всегда может быть найден. Из приведенных
примеров видно, что он выражается через рациональные функции,
логарифмы и арктангенсы, т. е. является элементарной функ-
функцией. Это замечание существенно, так как во многих случаях
интегралы даже от очень простых функций уже не будут функ-
функциями элементарными (см. п. 85, III), и мы, пытаясь привести их
к табличным интегралам, лишь понапрасну тратим время.
Поэтому очень часто при интегрировании главные усилия
направляются на отыскание такой замены переменной, которая
приводила бы данный интеграл к интегралу от рациональной функ-
функции; тогда дальнейший путь интегрирования ясен. О таких заме-
заменах говорят, что они рационализируют интеграл. Примеры общих
замен такого типа приведены в пп. 83 и 84.
Будем в дальнейшем символом /?(а, (J, у, ...) обозначать
выражение, рациональное относительно а, Р, у7 ..., т. е.
такое, в котором над а, |5, у> • • • производятся только рациональ-
рациональные действия. Ясно, что если каждая из величин а, Р, у, ...
является рациональной функцией некоторой переменной и, то и
все выражение R (а, Р, у, ...) будет тоже рациональной функ-
функцией от и.
83. Интегрирование простейших иррациональных функций.
I. Рассмотрим интегралы вида
где подынтегральная функция рациональна относительно
переменной интегрирования х и различных радикалов из х. Обо-
Обозначим через п наименьшее кратное всех показателей
ky ту ...; тогда все отношения -г==г1, — = /*о, •••—целые
числа.
Интеграл (*) заменой переменной
лг = ап, dx~ntin~1du
приводится к интегралу от рациональной функции (рационализи-
(рационализируется).
В самом деле, при указанной замене интеграл (#) принимает вид
!(и", иг\ иг\ .. .)nundu
и, согласно замечанию, сделанному в конце предыдущего пункта,
подынтегральное выражение есть рациональная функция от и.
278 ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ (83
Пример, i -_ * .__. Положим х = ие. Тогда Ух =и3,
J Vх +ух
jyr+Уг )и3+и
Дальнейшее просто: выделяя целую часть и интегрируя, получим
и, возвращаясь к старой переменной,
__dx ъ =2 Ух— 3 У~х +Ь yj—6\n\
Почти ничего не изменится, если все подкоренные выражения
ь одна и та
рал имеет вид
р
есть одна и та же дробно-линейная функция —^— , т. е. интег-
интегJ \ >
px+q '
В этом случае интеграл рационализируется заменой
ах + Ь ^ап х== qun — b
px+q ' а — рип '
Если р = 0, ?=1, т. е. подкоренное выражение — линейная функ-
функция, то все преобразования значительно упрощаются.
II. Рассмотрим несколько интегралов, зависящих от иррацио-
иррационального выражения Уа
1) I — . Вынося за символ интеграла —== (если а > 0)
J
или (если а < 0), приведем интеграл к виду
У —а
dx
С dx Г
\ г- ИЛИ \ г
J Vx* + px + q J V-x
Выделяя полные квадраты, получим
dx Г dx
— или I
84] § 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 2V9
Согласно решению примера 9 п. 80 первый интеграл выражается
через логарифмы, а второй при 4q+p2 >0 — через арксинус; если
же во втором интеграле 4<7 + Р2^0» то подынтегральная функция
принимает лишь мнимые значения.
2) I — . Легко проверить, что замена х—а=—
J (х—а) у ax2 + bx-\-c u
приводит этот интеграл к интегралу вида 1).
- dx. Этот интеграл можно разбить на два интег-
рала, выделив в числителе производную подкоренного выражения;
тогда один легко взять непосредственно (как интеграл от степен-
степенной функции), а второй является интегралом вида 1).
4) []/r
ax2 + bx + cdx. Выделением полного квадрата в подко-
подкоренном выражении интеграл сводится к одному из трех известных
интегралов (п. 81, II, примеры 4 и 5):
I— x*dxy
84. Интегрирование тригонометрических функций. Пусть дано
выражение, зависящее, и притом рационально, только от триго-
тригонометрических функций. Так как все тригонометрические функции
рационально определяются через sin л: и cos л;, то это выражение
можно считать рациональной функцией от sin л; и cosat, т. е. оно
имеет вид /? (sin лг, cosjc).
Интеграл \ R (sin лг, cos x) dx подстановкой и = tg ~ преобра-
преобразуется в интеграл от рациональной функции (рационализируется)»
По известным тригонометрическим формулам
sin x = 2 sin -к- cos -^ = 2 tg -=- cos2 -^ =
cos x - cos* 4—sin» ~ = cos* f A -tg2 -f =
2 2 2V 2J
т. e.
sin x = -t-t—t , cos x = \~u9
Наконец, из равенства x = 2aictgu имеем dx= 2 du. Итак,
Подынтегральная функция рациональна относительно и.
280
ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
[84
Примеры. I) ^~ и
dx f 1 + «а 2du
- Полагая « = tg-|, получим
du
- Полагаем и=
- Тогда
J
4—
2 — и
2 + tg-J
Вообще, с помощью указанного приема очень удобно вычислять
С dx
интегралы вида \ т—г~- ;— •
Метод интегрирования функций /?(sin.xr, cosat) с помощью
, X
подстановки tf^tg-^- всегда приводит к цели, но именно в силу
своей общности он часто является не наилучшим в смысле крат-
краткости и простоты необходимых преобразований.
Если, например, sin лг и cosat входят в выражение функции R
только в четных степенях, то гораздо быстрее ведет к цели
и2 1
подстановка u~tgx. Тогда sin2 л; = .- ---*--
du
dx =-r-j—г* э и интеграл рационализируется.
cos2a; =
3)
I
dx
sin2 x—3cos2jf
-1
du
In
In
+ C.
Такой же подстановкой берется интеграл вида J R(tgx)dx.
4) ? dx Г du
' J l+2tg* -J (l+tt«)(l+2«) *
84] § 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 281
Находя интеграл от рациональной дроби и возвращаясь к ста-
старой переменной, получим
Часто также бывает выгодным принять u = sinx или и = cos x.
Для иллюстрации рассмотрим интегралы типа
\ sinw х cosn x dx,
где т и п— целые числа. При их отыскании можно вообще избе-
избежать интегрирования рациональных дробей.
а) Если /»>0 и нечетное, то подстановка cos л; = и сразу
приводит интеграл к сумме интегралов от степенных функций;
если «>0 и нечетное, то к тому же приводит подстановка
— и2J
сч С sin6* , Г* sin4* . , С A — и
5) \—«—dx = \—о—smxdx =—V-—ir
1 J COS2 X J COS2 X J «2
где u = cosx. Разбивая интеграл на сумму интегралов, интегрируя
и возвращаясь к переменной х, получим
COS2 X COS *
б) Если оба показателя тип положительны и четны,
то с успехом применяются тригонометрические преобразования
с кратными аргументами.
6)
= 4- fsin2 2x 0 +cos 2x)dx = i f 1 cQos4*rf-* +
+ -^ f sin2 2л; cos 2л;с? Bл;) = -г^ х—ш sin 4л; + ^ sin3 2л; -f С.
(Подстановка tgл; = tt привела бы к более длинным выкладкам.)
в) Если оба показателя тип отрицательны и сумма их
четна, то подстановка u~tgx (или tf = ctgje) снова приводит
интеграл к сумме интегралов от степенных функций.
dx Г du
-ly-. + inlig
К тому же самому ведет применение искусственного приема: еди-
единица в числителе представляется как (sin2 x + cos2 л:)*, где
2k \ \—2.
282 ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ [84
dx p(sina* + cos2*)*
ш^—dx=s
+2 \dX
= — ctg x—j ctg3 л: — -i ctg5 л; + С.
г) Если один из показателей равен нулю, а второй есть
отрицательное нечетное число, то общая подстановка
u = tg-7r опять-таки приводит к интегрированию степенных функций.
m С dx С 2du 1 , 1 , , , , и
Легко заметить, что и при других показателях тип интег-
интеграл сводится к сумме интегралов рассмотренных типов; например
(т = — 2, /z = — 3):
J sin2 x cos3 x J sin2 x cos3 * X
f1 dx . С sin2 x + cos2 x , (* dx , С dx , f* cosa: ,
J cos3 x "•" J sin2 x cos x J cos3^ "*" J cosx ' J sin2x
Трудности, связанные с разнообразием применяемых приемов,
полностью искупаются легкостью заключительного интегрирования.
Интегралы \ sin** x cosn x dx очень удобно отыскивать при помощи
рекуррентных формул, позволяющих постепенно переходить от
больших показателей степеней т и п к меньшим. В таблице, приведенной
в конце книги, эти формулы значатся под номерами 64 и 65. Покажем на
одном примере метод их получения. Обозначим через
/„= \ cos* xdx.
Положим
dv = cos x dx, a = cosn~1x.
При этом
v = sinx, da = — (л— 1) cos
85] § 1. неопределенный интеграл 283
" x + (n — \) С cos"
x+{n — l) С cos" xdx—(n — 1) С cos" x dx,
откуда
п /„ = sin xcos"
и, следовательно,
1 . „_, , П 1
= —sinxcos" 1*Н——
Это и есть формула приведения, которую мы хотели получить.
Она позволяет легко довести задачу нахождения интеграла до конца.
Заметим, наконец, что к интегрированию функций R (sin x, cos x)
может быть приведено с помощью различных преобразований и под-
подстановок интегрирование целого ряда других функций, например
функций R (x, Y ах2-\- bx+с), т. е. функций, рациональных относи-
относительно х и Y ах2-{-Ьх-\-с. Но на этом вопросе мы задерживаться
не будем.
85. Заключительные замечания. Использование таблиц интег-
интегралов.
1. О технике интегрирования. Сравнительно в редких
случаях удается дать правила для интегрирования функций. Но и
тогда, когда имеется теоретическая схема для получения окончатель-
окончательного результата интегрирования, она вовсе не является наилучшим,
наиболее экономным путем. Интегрирование чаще всего может быть
выполнено не единственным способом. И всякий раз частные обстоя-
обстоятельства должны подсказать тот искусственный прием, который в
данном случае быстрее всех других приводит к цели. Владение опе-
операцией интегрирования (как и всякой математической операцией)
заключается не только в знании того, как можно в конце концов
найти данный интеграл, но и в умении взять его с минимумом
затраченного времени и труда.
Для характеристики этого приведем простой пример.
Возьмем интеграл
Было бы оплошностью применить здесь общее правило (разложить
данную дробь на простейшие). Можно заметить, что предваритель-
предварительная подстановка м = л:+1 значительно облегчает задачу:
284 ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ [85
Изобретательность и навык приобретаются практикой при ре-
решении достаточно большого числа примеров.
II. Использование таблиц интегралов. Изученные
нами методы интегрирования состоят в преобразованиях, приводящих
данный интеграл к интегралу, заранее известному, т. е. находяще-
находящемуся в известной таблице интегралов. До сих пор мы поль-
пользовались только самой краткой — основной таблицей интегра-
интегралов. Но ясно, что чем более полной таблицей интегралов мы имеем
возможность пользоваться, тем проще и короче делается само
интегрирование.
В практических целях часто употребляют различные справочники
и готовые таблицы особенно часто встречающихся интегралов. В кон-
конце книги имеется таблица интегралов, сравнительно небольшая, но
достаточная для нахождения интегралов в практически часто встре-
встречающихся случаях. Покажем на двух примерах ее применение.
* ~~ -dx. Этого интеграла нет в нашей таблице,
J
но его нетрудно привести к интегралам, находящимся в ней. Прежде
всего подкоренной квадратный трехчлен — 1 + Ах— 2х2 преобразуем
к виду квадратного двучлена:
__ 1 -j. 4х — 2х2 = — [ 1 + 2 (х2 — 2л;)] = 1 — 2 (х— 1 J.
В интеграле заменим переменную интегрирования по формуле
и = х—1, т. е. лг = и + 1; получим
J V — 1+4х — 2*2 J
J V i-2u2 J 1^1 —
«tof,.
2u2 J V\ — 2u*
Каждый из трех интегралов в правой части равенства имеется
в таблице — в формулах 33, 31, 29. Пользуясь этими формулами
а = |/2, Ь=\, находим
Г /x2
—2u2 + arcsin
= ~ B — и) V\—2u2 -^arcsinl/2u + C.
85] § 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 285
Возвращаясь к заданной переменной х, приходим к окончатель-
окончательному ответу
2) \ sin* xcos2 xdx. По формуле 70 при /ю = 4, /2 = 2 получаем
(по второй строке)
\ sin4 х cos2 x dx = -g- sin5 x cos x + -^ \ sin4 x dx.
Интеграл в правой части равенства находим снова по формуле 64
при /гс = 4, /z = 0 (по первой строке):
С 1 з Г
\ sin4 a: dx — —j sin3 x cos лс -f- -г- \ sin2 x dx
и далее (/я = 2, /г = 0):
Г* 1 1 С 1 1
\ sin2 аг^аг = —y sin л: cos x + -j \dx= —-j slnx cos л;-f у л; + C.
Значит, окончательно
f sin4 x cos2 лг rfAT =
= у sin5 лс cos x—g4 sin3 -^ cos x—j6*sin x cos x "^ Тб "^ ~^ ^'
III. Обинтегрировании в элементарных функциях.
В отличие от дифференцирования, интегрирование не есть действие,
всегда позволяющее найти элементарную функцию, являющуюся
первообразной от заданной элементарной функции. Строго
доказано, что во многих случаях и не существует такого эле-
элементарного выражения для первообразной. Другими словами,
можно указать элементарные функции, интегралы от которых не
выражаются никакими конечными комбинациями основных
элементарных функций. Про такие функции говорят, что они не
интегрируемы в элементарных функциях (или не ин-
интегрируемы в конечном виде).
Так, например, интегралы
С dx Сех - Г sin*, f cos х , С dx С *% ^
JFTT73 • J т**« 1 ~dx' 1 —"*• 3 пгз • 1е dx
нельзя представить никакими элементарными функциями.
Следует различать существование функции и возможность
ее выражения с помощью элементарных функций. Указанные
286 ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ [86
интегралы существуют, но наших средств—всех основных элемен-
элементарных функций —оказывается недостаточно для того, чтобы соста-
составить из них конечные выражения для этих интегралов.
Разъясним эту мысль. Допустим, что мы позволяем себе поль-
пользоваться всеми основными элементарными функциями, «роме логариф-
логарифмической. Тогда многие известные интегралы станут неберущи-
мися. Например, при этом нельзя будет выразить в конечном виде
\ ~ » \ ~~2~~Г и т. п. В самом деле, среди принятых функций (раз
нет в распоряжении логарифмической) не существует функции, про-
производная которой была бы равна — или -g—г и т. п. Включив в рас-
X X —- а
смотрение и логарифмическую функцию, мы сумеем выразить эти
интегралы в конечном виде, но не будет ничего удивительного, если
другие интегралы останутся еще не берущимися в конечном виде.
Для того чтобы сделать и их берущимися, нужно расширить
класс основных функций, которыми условились пользоваться.
Так в анализе и поступают. Среди неберущихся интегралов вы-
выделяют особенно простые и важные и детально изучают опреде-
определяемые ими неэлементарные функции. Эти новые функции
пополняют запас наших средств и делают доступным для интег-
интегрирования в конечном виде ряд не интегрируемых в старом смысле
функций.
§ 2. Определенный интеграл
86. Некоторые задачи геометрии и физики. К понятию опре-
определенного интеграла приводят самые разнообразные задачи
определение площади плоской фигуры, отыскание р або т ы пе-
переменной силы, нахождение пути по заданной переменной ско-
скорости и многие, многие другие. Разберем эти задачи по отдельности.
При этом сначала покажется, что методы их решения никак не
связаны с содержанием предыдущего параграфа—неопределенного
интегрирования. Лишь позже, установив свойства определенного
интеграла, мы обнаружим его тесную связь с неопределенным ин-
интегралом; именно эта связь и будет лежать в основе практического
решения поставленных задач.
I. Площадь криволинейной трапеции. Теория пло-
площадей исходит из двух положений:
1) площадь фигуры, составленной из нескольких фигур, равна
сумме площадей этих фигур;
2) площадь прямоугольника равна произведению его измерений.
В элементарной геометрии, опираясь на эти положения, находят
площадь треугольника, а также и площадь многоугольника, так
как всякий многоугольник может быть разбит на треугольники.
86]
§ 2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
287
С помощью предельного перехода по площадям правильных впи-
вписанных и описанных многоугольников определяется площадь круга.
Однако при этом используются особые геометрические свойства фи-
фигуры (круга), что в других случаях делается очень затруднительным.
Прежде всего определим площадь криволинейной трапеции, т.е.
фигуры, ограниченной осью Ох, графиком непрерывной функции
Рис. 103,
[=f(x) и двумя прямыми х = а и х = Ь (рис. 103); интервал
а, Ь] оси Ох назовем основанием трапеции1). Будем пока пред-
предполагать, что f{x) > 0 в интервале [а, Ь]9 т. е. что трапеция
расположена над осью Ох. Разделим основание трапеции—интер-
трапеции—интервал [а, Ь] — на п частичных интервалов
где а — л0 <^ х± <^ х2 <ч. . . . <^ хп_\ \ хп — о.
Проведя в точках деления интервала [я, Ь\ прямые,параллель-
прямые,параллельные оси ординат, мы разобьем рассматриваемую криволинейную
трапецию на п частичных трапеций (рис. 103).
Возьмем теперь в каждом из частичных интервалов по произ-
произвольной точке и обозначим их через \х, ?2, .,., ?я, так что
(Некоторые из выбранных точек |, или даже все, могут совпадать
с точками деления интервала [а, Ь] на частичные.)
В точках |х, §2, ..., \п проведем прямые, параллельные оси Оу,
до пересечения с линией у =/ (л:); отрезки этих прямых—орди-
прямых—ординаты точек графика — соответственно равны /(?,), /&2), ..., /(?„).
г) Эта терминология отличается от принятой в элементарной геометрии,
где интервал [а, Ь] называется высотой трапеции, а основаниями ее назы-
называются отрезки параллельных прямых х = а, х = Ь.
288 ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ [86
На частичных интервалах как на основаниях построим п пря-
прямоугольников с высотами, равными соответственно значениям
функции f(x) в точках ^ (рис. 103). Мы получили л-ступенча-
тую фигуру, которую также можно рассматривать как криволи-
криволинейную трапецию с основанием [а, Ь], но ограниченную не задан-
заданной линией А0А±А2. . .Ап_1Ап, а ломаной А^АхАхА2Аг. . ,Ап.
Площадь sn этой /г-ступенчатой фигуры мы будем считать
приближенным значением площади s заданной криволинейной
трапеции, тем более точным, чем больше пи чем меньше
длины частичных интервалов. Другими словами, мы исхо-
исходим из того естественного и наглядного представления, что чем
больше число прямоугольников и чем они уже, тем теснее пост-
построенная указанным сейчас способом ломаная линия Аоа'±.,. при-
примыкает к заданной линии А0Аг. . . и тем лучше площадь sn со-
соответствующей я-ступенчатой фигуры должна выражать площадью
заданной трапеции. Отсюда ясно, что площадью s криволинейной
трапеции, ограниченной линией А0АгА2. . . Ап следует назвать пре-
предел, к которому стремится переменная площадь п-ступенчатой фи-
фигуры, ограниченной ломаной линией AQA1A1A2.. .An при неогра-
неограниченном увеличении числа п и при стремлении к нулю наибольшей
длины частичных интервалов.
Следует иметь в виду, что точки хг, х2, ..., хп__1 могут быть
произвольными, но необходимо, чтобы при неограниченном увели-
увеличении числа п частичных интервалов длина наибольшего из них
действительно стремилась к нулю. Если этого не предусмотреть,
то может так случиться, что ступенчатая фигура не будет неог-
неограниченно приближаться к криволинейной трапеции. В самом деле,
будем увеличивать число точек деления основания так, например,
чтобы какой-нибудь частичный интервал, пусть (хп_1У Ь) (рис. 103),
оставался неизменным. Тогда ломаная может неограниченно при-
приближаться к дуге А0Ап_1 заданной линии y—f{x), но вовсе не
будет приближаться к дуге Ап_1Ап и постоянная часть трапеции
хп_хАп_хАпЬ не будет при этом процессе покрываться нашими
фигурами. Таким образом, по площадям этих фигур мы никак не
сможем определить площадь трапеции. Если же указать, что
длина наибольшего частичного интервала стремится к нулю, то
из этого следует, что число п частичных интервалов неограниченно
возрастает.
Напишем теперь выражение для sn. Вся фигура состоит из п
прямоугольников, а площадь прямоугольника, соответствующего
частичному интервалу [Х(„19 х{\, очевидно, равна /(?/)(•*:; — -*:,•_х).
Значит,
86]
§ 2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
289
Все слагаемые этой суммы имеют один и тот же вид: отличаются
они друг от друга только значениями индекса (указателя) при
независимой переменной.
Для сокращения записи вводят символ 2 (греческая прописная
буква «сигма») — символ суммы, именно пишут
(*)
Этот символ вообще означает, что нужно сложить выражения
данного вида, придавая индексу суммирования / все целые значения
от значения, указанного под символом «сигма», до значения,
указанного над символом «сигма».
В соответствии с определением площади s имеем
п
s = lim sn = lira У /(I;) [xi—xi_1).
Как указано выше, мы считаем, что переход к пределу совер-
совершается при условии, что длина наибольшего частичного интервала,
т. е. тах(лг?— ^_х), стремится к нулю.
Определив площадь криволинейной трапеции, мы в состоянии
находить площади и других фигур. Обычно их можно разбить
на некоторое число криволинейных тра-
трапеций и,таким образом, искомую площадь
определить как алгебраическую сум-
сумму площадей криволинейных трапеций,
составляющих эту фигуру. Так, напри-
например, площадь фигуры, изображенной
на рис. 104, может быть представле-
представлена в виде следующей алгебраической
суммы:
Рис. 104.
пл. ААСС — пл. ВВ'С' +
+ пл. BB'D'D — nn. AA'D'D.
II. Работа переменной силы. Перейдем теперь к важной
задаче физики — к определению работы. Мы увидим, что опре-
определение работы будет вполне аналогично определению площади
трапеции.
Пусть под действием некоторой силы тело движется по пря-
прямой линии, причем направление силы совпадает с направлением
движения.
Требуется определить работу, произведенную при переме-
перемещении тела из положения М в положение N (рис. 105).
Вели на протяжении всего пути от Ж к N сила остается пос-
постоянной, то, как известно, работа определяется как произведение
»0 А. ф. Бермант, И. Г. Араманович
290 ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ [86
силы на длину пути. Обозначим через А работу, через Р—силу,
через 5—длину пути A/IN. Тогда1)
A = PS.
Предположим, однако, что сила на пути от Ж к Afизменяется.
В каждой точке между М и N, находящейся на расстоянии s от
Рис. 105.
точки Ж, действующая сила принимает соответствующее значе-
значение Р. Это значит, что сила Р есть некоторая функция рассто-
расстояния 5, т. е. P = f(s). Как определить работу, совершенную при
перемещении тела из точки М в точку N в этом случае?
Разобьем весь путь MN, т.е. интервал изменения переменной s,
на п участков точками, находящимися на расстояниях
от точки М. Вместо действующей на пути MN переменной силы Я
возьмем другую силу Рп, сохраняющую постоянные значения на
каждом из наших участков, причем эти значения положим рав-
равными значениям действующей силы Р в каких-нибудь точках
участков. На первом участке [s0, Sj] эта сила равна Р1=/(а1),
где ах g (Уо> si]> Ha втором [^1Э s2] она равна P^~f{o2), где
<?2 € [^i» S2\> на участке [«у/_1, st] она равна />/=/(<t,-)i r^e
^/ € К-1, *,], и т. д.
Так как работа на всем пути равна сумме работ, соответст-
соответствующих отдельным участкам, на которые разбит путь, то для
работы Лд, произведенной силой Рю будем, очевидно, иметь
-*.-i)=;? /(a,) (*,-*/.!>.
Величину Ап мы принимаем за приближенное значение искомой
работы, тем более точное, чем больше число п и чем меньше
участки, на которые разбивается весь путь ММ. Работу Л опре-
определяют как предел Ап при п—*оо; при этом, как и раньше,
предполагается, что длина наибольшего из частичных участков
*) Если Р выражено в ньютонах и S в метрах, то А будет выражено
в джоулях.
86] § 2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 291
стремится к нулю:
п
A = llmAn = l\myg f{ot) (st—s^).
III. Путь и масса. Скажем кратко еще о двух других за-
задачах физики — об определении пути и массы. Решение этих
задач будет произведено совершенно так же, как и предыдущих.
1) Предположим, что точка совершает поступательное движе-
движение, причем известна величина скорости v в любой момент вре-
времени t в некотором промежутке \ТЪ 72], т. е. v—f(t).
Путь s, пройденный точкой за промежуток времени [7\, Г2],
определяется так:
п
s = lim sn = lim
где /0, /x> /2, . .., /я-1, /n — точки, разбивающие интервал [7\, Т2]
на /z частичных интервалов, причем
мы опять считаем, что тах(/,. — ^,--i)—^0. Каждое слагаемое
f(xi)(ti — ^i-i) суммы дает путь, который прошло бы тело за про-
промежуток времени [/;_!, /,-], если бы оно двигалось в это время
с постоянной скоростью, равной /(т,-).
Задача определения пути по скорости обратна задаче
определения скорости по пути (см. п. 38, I).
2) Возьмем отрезок материальной линии и предположим, что
известна плотность б в каждой ее точке 5, т. е. 6 = /($), причем
длина 5 изменяется на участке [0, S].
Масса m материальной линии на участке ее длины [0, S]
определяется так:
п
m = limmn = lim
где 50, sv $2, ..., sn_v sn—точки, делящие интервал [0, S]
на п частичных интервалов, причем
Si-i^Oi^St (/= 1, 2, ..., п) и тах(^— ^•_1)—>О.
Каждое слагаемое /(at-) (st — slmml) суммы дает массу, которую
содержал бы участок линии [s^^ s(], если бы плотность на этом
участке была постоянной, равной /(at) (т. е. если бы масса была
распределена равномерно).
Задача определения массы по плотности обратна задаче
определения плотности по массе (см. п. 38, II).
10*
292 ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ [87
87. Определенный интеграл. Теорема существования. В пре-
предыдущем пункте мы видели, что решение многих важных задач
геометрии и физики (определение площади, работы, пути, массы)
приводит к одной и той же последовательности действий над из-
известными функциями и их аргументами. Раз эта последовательность
действий применяется в различных случаях и имеет большое зна-
значение, то мы установим ее математически, независимо от конкрет-
конкретных условий той или иной задачи. Тогда и применение ее в каж-
каждом отдельном подходящем случае будет заранее узаконено
и не будет требовать специальных рассуждений.
Если отвлечься от физического смысла переменных и от их
обозначений, то указанная последовательность действий состоит
в следующем:
1) интервал [а, Ь], в котором задана непрерывная функция f(x)
(теперь мы отбросим предположение, что /(лс)>0 в интер-
интервале [я, ?]), разбивается на п частичных интервалов при помощи
точек
х0 = a, Xi, дг2, ..., xn_i, xn = ot
причем
а<хг<х2< ... <хп_х<Ь\
2) значение функции /(^) в какой-нибудь точке б/б^-ц xi\
умножается на длину этого интервала х{—х{_1% т. е. составляется
произведение f(it)(xi—x{^1);
3) берется сумма /п всех этих произведений
или, если обозначить х{ — xi_1 через Axiy
)А**; (А)
4) находится предел / суммы 1п при стремлении к нулю длины
наибольшего частичного интервала, и следовательно, при
п—> оо, т. е.
В рассмотренных выше четырех конкретных задачах этот пре-
предел / измеряет соответственно площадь, работу, путь, массу.
В общем случае он называется определенным интегралом или просто
87] § 2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 293
интегралом от функции f(x) в пределах от а до b и обозначается так:
ь
и читается: интеграл от а до b f (х) на dx. Следовательно,
по определению
Сумма (А) называется п-й интегральной суммой.
Определение. Определенным интегралом называется
предел, к которому стремится я-я интегральная сумма (А) при
стремлении к нулю длины наибольшего частичного интервала.
Символ интеграла указывает на его происхождение: \ является
как бы вытянутой буквой sy первой буквой слова «summa»; выраже-
выражение, стоящее за. (говорят также: под) символом интеграла,
показывает вид суммируемых слагаемых; индекс при переменной
в выражении под интегралом опущен, чем подчеркивается, что
в процессе суммирования, завершающегося предельным переходом,
переменная х принимает все значения в интервале [а, Ь\\ числа,
стоящие под и над символом интеграла, указывают концы интер-
вала^ на котором производилось суммирование.
Как и в неопределенном интеграле, функция f(x) называется
подынтегральной функцией, выражение f(x) dx — подынтегральным
выражением и переменная х — переменной интегрирования. Интер-
Интервал [а, Ь] называется интервалом интегрирования, число а — ниж-
нижним, а число b—верхним пределами^) интеграла.
Сам процесс образования определенного интеграла показывает,
ь
что символ \f(x)dx есть некоторое число. Величина его зависит
а
только от вида подынтегральной функции и от чисел а и Ь%
определяющих интервал интегрирования. Переменная интегрирова-
интегрирования х служит лишь для удобного обозначения определенного
интеграла; ничего не изменится, если переменную интегрирования
обозначить другой буквой, например t или и:
1) Здесь термин «предел» употребляется в смысле, не имеющем отноше-
отношения к понятию «предел функции».
294 ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ [87
Внешняя общность записи определенного и неопределенного
интегралов (в записи последнего отсутствуют лишь пределы ин-
интегрирования) подчеркивает тесную связь между ними, хотя оп-
определенный интеграл есть число, а неопределенный интеграл —
совокупность первообразных функций. Эту связь мы установим
позднее (в п. 92), а сейчас пока только отметим, что она позволит
вычислять определенные интегралы не при помощи построения
интегральных сумм с последующим переходом к пределу, а при по-
помощи неопределенного интегрирования. Именно поэтому мы не при-
приводим примеров вычисления определенных интегралов с помощью
суммирования; этот процесс вызывает серьезные затруднения
в самых, казалось бы, простых случаях.
Отметим только совершенно очевидный результат
который следует из того, что любая интегральная сумма для
функции f(x) = \ равна Ь — а:
п
У^Ах{ = х1—х0 + х2—х1 + ... +хп—хп_г = хп—xQ = b—a.
г = 1
Применяя определение интеграла к четырем конкретным вопро-
вопросам, разобранным в п. 86, можно полученные там выводы выразить
в таких словах:
1) площадь криволинейной трапеции равна интегралу от ординаты
линии, ограничивающей трапецию, взятому по основанию:
dx;
2) работа, произведенная силой, равна интегралу от силы, взя-
взятому по пути:
3) путь, пройденный телом, равен интегралу от скорости, взя-
взятому по времени:
88] § 2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 295
4) масса, распределенная на линии, равна интегралу от плот-
плотности, взятому по длине линии:
s
о
Говоря об определенном интеграле, мы еще не затрагивали
вопроса о том, для каких функций этот интеграл существует,
т. е. для каких функций существуют пределы их интегральных
сумм. Ответ дается следующей теоремой, которую мы приводим
без доказательства.
Теорема существования определенного интег-
интеграла. Если функция f(x) непрерывна в замкнутом интервале
[а9 6], то ее п-я интегральная сумма стремится к пределу при
стремлении к нулю длины наибольшего частичного интервала.
ь
Этот предел, т. е. определенный интеграл \f(x)dx, не зависит
а
от способа разбиения интервала интегрирования на частичные
интервалы и от выбора в них промежуточных точек.
Интегральные суммы, составленные при различных разбиениях
интервала интегрирования и различных выборах точек ?, могут
отличаться друг от друга весьма значительно. Сформулированная
выше замечательная теорема показывает, что для непрерывных
функций разница между этими суммами стирается по мере возра-
возрастания числа точек деления и убывания длины наибольшего
частичного интервала, совсем исчезая в пределе.
Далее везде предполагается, если не сказано противное, что
рассматриваемые функции — непрерывные.
88* Простейшие свойства определенного интеграла.
Теорема I (об интеграле суммы). Интеграл от суммы
конечного числа функций равен сумме интегралов от слагаемых
функций:
ь ь ь ь
wdx9
где a, vy ..., w—функции независимой переменной х.
Доказательство. Обозначим интеграл в левой части ра-
равенства через /. По определению интеграла имеем
п
I = lim 2 («/ + «V + • • • + wd &xi =
= lim
, ),
J
296 ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ [89
где иь vh . . ., w( — соответственно значения функций и, V, . . ., w
в какой-нибудь точке интервала [х(_19 х(], а IS.xi = xi—xi~i-
Воспользовавшись теоремой о пределе суммы, будем иметь
п п п.
/= lim 2«/Л*/ + lim 2*>А*ч + •. • + llm 2^Длг,,
( = 1 i = 1 i = 1
т. е.
ь ь ъ
I=\udx4-\vdx-\-...4-\ wdxt
a a a
что и требовалось доказать.
Теорема II (о вынесении постоянного множи-
множителя). Постоянный множитель подынтегральной функции можно
вынести за символ интеграла
ь ь
= с^ adxt
а
где а — функция аргумента х, с — константа.
Доказательство. Обозначим интеграл в левой части ра-
равенства через /. По определению интеграла имеем
Вынося постоянную с сначала за знак суммы, а потом за символ
предела, получим
п п b
I— lim c^uiHxi^= с lim 2^1*Д^ = с\ и<*Х1
i-l /=i a
что и требовалось доказать.
89. Перестановка пределов и разбиение интервала интегри-
интегрирования. Геометрический смысл интеграла. До сих пор мы пред-
предполагали, что нижний предел интеграла меньше верхнего, или,
как говорят, что интервал интегрирования направлен вправо.
Ничто не мешает, однако, в общем определении интеграла считать,
что а > Ь, т. е. что интервал интегрирования направлен влево.
При разбиении интервала интегрирования на части точками
*i. хг% ..., хп^х будем иметь (рис. 106)
89] § 2, определенный интеграл 297
и, следовательно, все разности х{—х(_х будут отрицатель-
отрицательными. Это значит, что при построении интегральной суммы раз-
разность х{— xi__1 уже не является длиной частичного интервала,
а отличается от нее знаком.
Если мы теперь рассмотрим два интеграла
\f{x)dx и \f(x)dx
и составим для них интегральные суммы при одном и том же раз-
разбиении интервала на частичные и при одном и том же выборе
1—I—I \3 \\ 1 li I *~
X
Рис. 106.
промежуточных точек, то ясно, что эти суммы будут отличаться
друг от друга только знаком. Таким образом, мы получаем
теорему:
Теорема III (о перестановке пределов). Если верх-
верхний и нижний пределы интеграла поменять местами, то интеграл
изменит только знак:
ь
Вследствие теоремы III мы в дальнейшем при изучении ин-
интеграла
ъ
]f(x)dx
а
будем считать, что а < ?, ибо если а > Ь, то с помощью измене-
изменения знака подынтегральной функции данный интеграл сводится
к интегралу, у которого нижний предел меньше верхнего.
Совершенно ясно также, что если верхний и нижний пределы
интегрирования совпадают, т. е. если Ь = а, то такой интеграл
нужно считать равным нулю:
С геометрической точки зрения это означает, что если конец
основания трапеции совместить с его началом, то трапеция превра-
298 ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ [89
тится в прямолинейный отрезок — ординату f(a)t площадь которого
нужно считать равной нулю.
Теорема IV (о разбиении интервала интегриро-
интегрирования). Если интервал интегрирования [а, Ь\ разбит на две
части [а, с\ и [с, b]f то
Ь с Ь
(x)dx. (*)
Доказательство. Так как предел интегральной суммы
не зависит от способа разбиения интервала [а, Ь] на части
(см. теорему существования, п. 87), будем дробить интервал так,
чтобы точка с всегда была точкой деления. При этом интегральную
сумму можно представить так:
2J/lg,) А*,-ЕхЛЫА*!+ 2»/(?*)***.
где в первой сумме в правой части собраны все элементы, соответ-
соответствующие точкам деления интервала [я, с], а во второй сумме—
элементы, соответствующие точкам деления интервала [с, Ь].
И первая и вторая суммы суть интегральные суммы для функ-
функции f(x), соответствующие интервалам [а, с] и [с, Ь]. Если число
точек деления неограниченно возрастает, а длина наибольшего
частичного интервала стремится к нулю для всего интервала [а, Ь],
то то же самое, очевидно, будет выполняться и для интервалов
[а, с] и [с, Ь\\ при этом первая сумма стремится к интегралу
в пределах от а до с, а вторая — к интегралу в пределах от с
до ?, и мы получаем требуемое равенство.
Равенство (*) справедливо и в том случае, когда точка с лежит
вне интервала [а, Ь], справа от него (а < 6 < с) или слева от него
(с<а<?) (при условии, конечно, что функция f(x) непрерывна
в [а, с] или в [с, Ь]).
Пусть а <Ь < с. По доказанному, так как Ь лежит между а и с,
a a
откуда
Ь с
а а Ь
Меняя местами пределы второго интеграла в правой части,
получим
ь ь
а а
что и требовалось доказать.
89] § 2. определенный интеграл 299
Аналогично доказывается, что равенство (#) имеет место и при
с< а <Ь.
Из доказанной теоремы непосредственно следует, что если
с1} с2, ..., ck — как угодно расположенные числа в интервале
непрерывности функции f(x), то
Ь Сх сг Ь
\f{x) dx = \f{x) dx + \f(x)dx + ... + \f(x)dx. (**)
a a cx cit
Теорема IV выражает так называемое свойство аддитивности
определенного интеграла.
Теорема V (о знаке интеграла). Если подынтеграль-
подынтегральная функция в интервале интегрирования не меняет знака, то
интеграл представляет собой число того же знака, что и функция.
Доказательство. Пусть f(x)^0 в интервале [#, Ь] [а
Тогда в интегральной сумме /„ = ^/E/) А*/ все слагаемые неот-
i = i
рицательны и, значит, /п^0, а предел неотрицательной величины
ъ
не может быть отрицателен, т. е. \ f(x) dx ^0.
а
Покажем теперь, что этот интеграл не может равняться нулю,
если только функция f(x) не равна нулю тождественно. Пусть
в какой-то точке с интервала
/(?)>0. Тогда вследствие непре- ' '—¦—¦—? *-
рывности функции f(x) сущест- а л G fi
вует такой интервал [а, Р](рис.
107), в котором функция остается Рис. 107.
положительной (см. п. 32). Обоз-
Обозначим через т ее наименьшее значение в интервале [a, PJ;
тогда /(дг)^т>0 для х ? [a, (J]. Любая интегральная сумма
для интервала [a, (J] удовлетворяет неравенству
2 f(lk)b*k ^ 2 %
ft=i k=i
э
Но тогда и ее предел )f(x) dx^ m(§— a) > 0. По теореме IV
a
a 3
Первый и третий интегралы в правой части равенства, по дока-
доказанному выше, неотрицательны, а второй, как мы только
300 ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ [89
что показали, положителен. Значит,
ъ
lf{x)d*>0,
а
что и требовалось доказать.
Если подынтегральная функция в интервале интегрирования
меняет знак, то интеграл от нее может быть и положительным
числом, и отрицательным, и равным нулю.
Свойство определенного интеграла, вытекающее из теоремы V,
следует иметь в виду при решении задач. Например, находя
с помощью интеграла площадь криволинейной трапеции, необхо-
необходимо учитывать ее расположение относительно основания. В слу-
случае, когда трапеция целиком лежит над осью Ох, интеграл
от ординаты выражает площадь; в случае, когда трапеция целиком
лежит под осью Ох, интеграл, будучи отрицательным, выражает
площадь трапеции, взятую с отрицательным знаком. Наконец,
в случае, когда трапеция лежит и над осью Ох, и под ней, для
отыскания ее площади нужно отдельно вычислить интегралы, выра-
выражающие площади ее частей, расположенных над осью абсцисс,
отдельно — интегралы, выражающие площади частей, расположен-
расположенных под осью абсцисс, и затем взять сумму их абсолютных величин.
Геометрический смысл интеграла. Условимся пло-
площади криволинейной трапеции, расположенной над осью Ох,
приписывать знак плюс, а расположенной под осью Ох — знак
минус. Тогда, очевидно, в силу теорем IV и V определенный
интеграл от функции f(x) будет суммой алгебраических
площадей (т. е. снабженных определенными знаками) криво-
криволинейных трапеций, расположенных над и под осью Ох, из кото-
которых составляется данная трапеция. Эту сумму и называют
алгебраической площадью всей криволинейной трапеции.
Имея это в виду, мы в дальнейшем определенный интеграл
ь
\f(x)dx
а
всегда можем рассматривать независимо от конкретного смысла
переменной интегрирования х и функции f(x) как алгебраическую
площадь криволинейной трапеции с основанием [а, Ь], ограниченной
линией y=f(x).
В соответствии с этой геометрической иллюстрацией интеграла
теорема IV (см. равенство (**)), выражающая свойство интеграла,
которое называется аддитивностью, означает тот наглядный факт,
что если основание криволинейной трапеции разбить на частичные
интервалы, то площадь всей трапеции будет равна сумме пло-
площадей трапеций, опирающихся на частичные интервалы.
90]
§ 2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
301
90. Оценка интеграла. Теорема о среднем. Среднее значение
функции.
1. Оценка интеграла. Укажем границы, между которыми
наверняка заключено значение интеграла.
Теорема VI (об оценке определенного интег-
интеграла). Значение определенного интеграла заключено между
произведениями наименьшего и наибольшего значений подынтег-
подынтегральной функции на длину интервала интегрирования, т. е.
a<b,
где т и М — соответственно наименьшее и наибольшее значения
функции f(x) в интервале [а, Ь\:
Доказательство. Возьмем две функции М—f(x) и
т—f(x). Первая из них в интервале [а, Ь\ неотрицательна, вто-
вторая неположительна. Значит, по теореме V (п. 89)
— f(x)]dx>0
Применяя теоремы п. 88 и формулу (*) п. 87, получим
ь ь
M(b — a)> \f{x)dx и т (д — а) <
что и требовалось доказать. Из доказательства теоремы V сле-
следует, что знаки неравенств могут перейти в знаки равенств
только в том случае, когда функция ^.
f(x) постоянна.
Геометрический смысл доказанных
неравенств таков: площадь криволиней-
криволинейной трапеции больше площади прямоу-
прямоугольника с основанием, равным основанию
трапеции, и высотой, равной наименьшей
ординате трапеции, и меньше площади
прямоугольника с тем же основанием и
высотой, равной наибольшей ординате
трапеции (рис. 108). Рис* 108*
Находя границы для интеграла, мы, как говорят, производим
его оценку. Может случиться, что весьма трудно или даже
невозможно найти точное значение интеграла, а оценивая его,
302 ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ [90
мы узнаем, хотя бы грубо, приближенное его значение. С такого
рода оценками приходится довольно часто встречаться в мате-
математике.
Указанные в теореме VI границы для интеграла тем более
точны, чем короче интервал интегрирования и чем меньше линия
у— f(x) отличается tio положению от прямой, параллельной
оси Ох.
Примеры. 1) Оценим интеграл
9—л
о
Известными методами дифференциального исчисления (гл. IV)
находим, что наибольшее и наименьшее значения подынтегральной
функции в интервале [0, 2] равны соответственно 0,6 и 0,5.
Значит,
2
0,5 B - 0)< J ^=^ dx < 0,6 B - 0),
0
т. е. интеграл заключен между 1 и 1,2. Если считать, что он
равен 1,1, то предельная абсолютная ошибка равна 0,1, а отно-
0,1-ЮО п0/ о „
сительная -———»9%. Позже мы сумеем найти точное значение
приведенного интеграла. Оно равно -5-In 5 — In 3^1,047.
о
2) Оценим интеграл
л
s-^-dx.
X
л
~Г
Легко проверить, что подынтегральная функция в интервале
"Г » "Т убывает и, следовательно,
Sin-тг Г •
я 4 ^i
• 51П-Т-
пХ<
X ^ Л
2 Т 4
т. е.
л
2
90] § 2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 303
Таким образом, интеграл заключен между 0,5 и 0,71, что дает
нам право считать его равным 0,6 с точностью до 0,1. Более
точные приемы показывают, что приближенно он равен 0,62.
И. Обобщение теоремы об оценке интеграла.
Интегрирование неравенств. Справедлива следующая
более общая теорема, чем теорема VI.
Теорема VII. Если в каждой точке х интервала [а, Ь\
то
ь ь ь
^^^(x)dx, а<Ь.
Это значит, что неравенство между функциями влечет нера-
неравенство того же смысла между их определенными интегралами,
или, говоря коротко, неравенства можно интегрировать. Читатель
должен понять, хотя бы из простых геометрических соображений,
что дифференцирование неравенства может привести к нелепым
результатам. Например, из неравенства f(x) < M9 конечно, не
следует, что /' (х) < 0.
Доказательство теоремы немедленно следует из применения
к неравенствам f(x) — ф(л:)^0 и f(x) — ty(x)^0 теоремы V
о знаке интеграла. Опять-таки знак неравенства между интегра-
интегралами переходит в знак равенства только тогда, когда функции
тождественно равны между собой.
В частном случае, когда <р(х) тождественно равно Ж, a ty(x)
тождественно равно т, получаем теорему VI.
С помощью теоремы VII легко получается важное неравенство,
которым мы воспользуемся в дальнейшем. При любом х
(Если /(#)>0, то правая часть неравенства превращается в ра-
равенство, а левая часть очевидна; если /(аг)<0, то наоборот.)
Тогда
ь ь ъ
- $ \f(x) | dx < \f{x) dx < J \/(x) | dx
или
[f{x)dx
Модуль интеграла не превосходит интеграла от модуля функции.
Предоставляем читателю выяснить геометрический смысл этого
304 ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ [90
неравенства. Напомним еще, что аналогичное неравенство имеет
место и для сумм: модуль суммы не превосходит суммы модулей.
III. Теорема о среднем. Определенный интеграл обладает
следующим важным свойством.
Теорема VIII (о среднем). Внутри интервала интегриро-
интегрирования [а, Ь\ существует хотя бы одно значение jc = |, для
которого
ь
[f(x)dx
•=/(?)• (•)
b — a
Доказательство. В силу теоремы VI имеем
ъ
Р (х) dx
и, значит,
где \х — некоторое число, заключенное между наименьшим (т) и
наибольшим (М) значениями функции f(x) в интервале [а, Ь],
т. е. т < [х < М. Но f{x), будучи непрерывной функцией,
обязательно принимает хотя бы один раз каждое значение, ле-
лежащее между т и М (см. п. 35). Следовательно, при некотором
?? (а, Ь) функция f(x) получит значение, равное (х, т. е./(?) = |1э
что и требовалось доказать.
Из равенства (*) находим
Эта формула позволяет теорему о среднем высказать в такой
форме:
Определенный интеграл от непрерывной функции равен произ-
произведению значения этой функции в некоторой промежуточной точке
интервала интегрирования на длину интервала.
Дадим наглядное пояснение теоремы. При движении прямой,
параллельной оси Ох (рис. 109), вверх от положения ВС площадь
прямоугольника АВСК будет непрерывно возрастать от величины,
меньшей площади трапеции, до величины, большей ее. Очевидно,
при некотором промежуточном положении прямой — обозначим его
90]
§ 2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
305
через FG—площадь прямоугольника AFGK окажется в точности
равной площади трапеции S. Так как при этом движении прямая
постоянно пересекает линию, ограничивающую трапецию, то
и в положении FG найдется одна
или несколько (на рис. 109 две)
точек пересечения Q; абсцисса
любой точки пересечения и
будет требуемым по теореме зна-
значением |.
IV. Среднее арифмети-
арифметическое значение функции.
Значение /(?), находимое по теоре-
теореме о среднем, называется средним
арифметическим значением
функции f(x) в интервале [а, Ь].
Определение. Средним арифметическим значением уср
непрерывной функции y=f(x) в интервале [а, Ь\ называется
отношение определенного интеграла от этой функции к длине
интервала:
\f(x)dx
** у о — а
Приведем некоторые соображения в обоснование этого определения.
Пусть некоторая величина у принимает п значений у1У у2, ....
•••> Уп- Средним арифметическим значением этой
величины называется частное . Так, если темпера-
температура воздуха в течение суток измеряется через каждый час, то
средней температурой будет частное от деления суммы
всех наблюденных температур на 24.
Но представим себе теперь, что величина изменяется непре-
непрерывно (например, температура воздуха известна в любой момент
суток) и мы хотим как-то в среднем охарактеризовать всю сово-
совокупность ее значений. Как в этом случае следует определить
среднюю температуру воздуха, принимая во внимание всю извест-
известную совокупность значений температуры? Вообще, чтб следует
принять в качестве среднего значения непрерывной функ-
функции y = f(x) в некотором интервале [а, #]?
Разобьем интервал [а, Ь] на п равных частичных интер-
интервалов и возьмем значения функции в серединах этих интервалов—•
точках ?,.:
/di), /(?,), ...,/(!„).
При таком выборе точек \t значения функции берутся через
306 ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ (91
равные промежутки; именно так обычно поступают при всякого
рода измерениях. Возьмем среднее арифметическое г\п указанных
значений:
Ясно, что чем больше п> тем больше значений функции учиты-
учитывается при отыскании среднего значения, и поэтому естественно
за среднее значение уср функции принять предел, к которому
стремится г)п при п—юо. Найдем этот предел.
Умножив и разделив выражение для х\п на b—а, получим
где Ах^ = Ах2= . . . = Ахп = -^^ . Переходя к пределу при
п—> оо (при этом Ах—> ()), получаем указанное выше выражение
для среднего значения
На основании теоремы о среднем (теорема VIII) заключаем,
что ,уСр =/(?)> где ? ? (a, ^). Среднее значение непрерывной
функции в интервале всегда (если только функция не постоянная)
меньше некоторых ее значений, больше других ее значений и
равно хотя бы одному ее значению.
Понятие среднего значения функции очень употребительно
в технике. Многие величины часто характеризуются своими сред-
средними значениями; таковы, например, давление пара, мощность
переменного тока, скорость химической реакции и т. п.
91. Производная от интеграла по его верхнему пределу.
I. Интеграл с переменным верхним пределом.
Будем считать нижний предел интеграла постоянным, а верхний
переменным. Придавая верхнему пределу различные значения,
будем получать соответствующие значения интеграла; следова-
следовательно, при рассматриваемом условии интеграл является функ-
функцией своего верхнего предела.
Остановимся на общепринятых обозначениях. Независимая пе-
переменная в верхнем пределе обычно обозначается той же буквой,
скажем хл что и переменная интегрирования. Таким образом,
например, записывают
91] § 2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 307
Однако переменная х в подынтегральном выражении служит
лишь вспомогательной переменной — переменной интег-
интегрирования, пробегающей в процессе составления интеграла (сум-
(суммирования) значения от а до х — верхнего предела интеграла.
Если нам нужно вычислить частное значение функции 1(х), на-
например при х = Ь, т. е. I(b), то мы подставим b вместо х в верхний
предел интеграла, но, разумеется, не будем подставлять b вместо
переменной интегрирования. Поэтому нагляднее было бы упо-
употреблять такую запись:
взяв для переменной интегрирования какую-нибудь другую букву
(здесь t). Мы, однако, будем часто обозначать одной буквой и
переменную интегрирования, и независимую переменную в верхнем
пределе, всегда помня их различный смысл в символе интеграла.
Свойства интеграла, изученные в предыдущем параграфе,
относятся и к интегралу с переменным верхним пределом.
II. Производная от интеграла1). Весьма важно изу-
изучить связь между функцией 1(х) и данной подынтегральной
функцией f(x).
Теорема IX (о производной интеграла по верх-
верхнему пределу). Производная от интеграла по его верхнему
пределу равна подынтегральной функции
Иными словами: интеграл с переменным верхним пределом яв-
является первообразной для подынтегральной функции.
Доказательство. Придадим аргументу х приращение Длг.
Тогда наращенное значение функции 1(х) будет
х+Ах
I(x + Ax)= J f(x)dx.
а
Значит,
х+Ах х
) — /(*)= J f(x)dx—\f(x)dx.
2) Если при прохождении курса сначала изучается определенный ин-
интеграл, то перед чтением этого пункта следует прочитать п. 78, где дано
определение первообразной функции и ее геометрическая иллюстрация.
308 ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ [91
Применяя к первому интегралу справа теорему IV, получим
х jc+Ajc х Х + &.Х
M=^f(x)dx + $ f(x) dx—^f(x)dx = \f{x)dx.
ахах
Последний интеграл по теореме о среднем равен
Д/=/(Б) (* + Ах—х) =/A) Ах,
где ?—точка, лежащая между х и х~\-кх.
По определению производной имеем
Но если Дат—>0, то at + Ajc стремится к х; поэтому и подавно
?—+х> а так как /(л:) — непрерывная функция, то
/
Ajc->o
что и требовалось доказать.
Из теоремы следует также, что
(*«)
Необходимо заметить, что результаты в формулах (*) и (#*) не
зависят от обозначения переменной интегрирования; имеют место,
например, такие равенства:
У^
4-$/О л=/(*>.
d \/(t)dt=f(x)dx.
а
Геометрический смысл тео-
теоремы был установлен в п. 78;
напомним его еще раз. Функция
1(х) выражает переменную
площадь криволинейной трапе-
трапеции с переменным основанием [а, л;], ограниченной линией y—f (x).
В теореме утверждается, что производная от площади трапеции по
абсциссе равна ординате линии, ограничивающей трапецию (отре-
(отрезок АВ*=/(х) на рис. 110), или что дифференциал площади тра-
трапеции равен площади прямоугольника ABDE со сторонами, рав-
Рис. 110.
92] § 2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 309
ными соответственно приращению основания трапеции и ординате
линии в крайней точке.
92. Формула Ньютона—Лейбница. Теперь мы подошли к завер-
завершающему этапу наших рассуждений, позволяющему установить
обходный путь для вычисления определенных интегралов.
Теорема X. Значение определенного интеграла равно разнос-
разности значений любой первообразной от подынтегральной функции,
взятых при верхнем и нижнем пределах интеграла:
-F(a), где F'(x)=f(x). (*)
Равенство (*) называется формулой Ньютона — Лейбница.
Другими словами:
Значение определенного интеграла равно приращению любой перво-
первообразной от подынтегральной функции в интервале интегрирования.
Доказательство. Рассмотрим функцию
так как она является первообразной от функции f(x), то в соот-
соответствии с теоремой п. 78 ее нужно искать среди функций F(x)-\-C,
где F(x)— какая-нибудь из первообразных от f(x).
Следовательно,
где Сг—некоторая определенная постоянная. Для отыскания ее
воспользуемся еще одним известным нам свойством функции 1 (х),
а именно тем, что
Отсюда /7(в) + С1 = 0> т. е. Сг=— F(a).
Итак,
при х = Ь получаем доказываемое равенство (*).
Разность значений функции записывают часто так:
Вертикальная черта с нижним и верхним индексами, стоящая
справа от символа функции и называемая знаком двойной подстанов-
подстановки^ указывает, что из значения функции, принимаемого ею при
310
ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
[92
верхнем индексе, нужно вычесть ее значение, принимаемое при
нижнем индексе.
Воспользовавшись этим обозначением, формуле (*) можно при-
придать вид
ь
причем Fr (x) —f (x).
Формула Ньютона — Лейбница дает нам основной способ вычи-
вычисления определенных интегралов. Она позволяет находить опре-
определенный интеграл, обходя суммирование, при помощи первообраз-
первообразных функций, т. е. при помощи неопределенного интегри-
интегрирования. Для иллюстрации возьмем несколько простых примеров:
\хЧх
SI
— dx = In x
X*
~~ 3
2
1
8
3
1
3
7
3 '
а
я
2
0);
cos xdx = sin x
= 1.
Если взять какие-нибудь другие первообразные от подынтег-
подынтегральных функций (т. е. отличающиеся от выше взятых на постоян-
постоянные величины), то, очевидно, получим те же результаты.
Заметим теперь, что так как F(x) есть первообразная от
F*(x), то
это можно записать так:
х
Мы пришли к несколько иному виду формулы Ньютона—Лейбница,
позволяющему основную теорему этого пункта выразить так:
Приращение функции в интервале равно определенному интегралу
по этому интервалу от дифференциала функции.
Замечание. Теперь очень легко показать, что путь s, найденный нами
в п. 87 при помощи интеграла (по скорости v), действительно совпадает с
тем путем, исходя из которого была определена скорость. Пусть путь s как
93] § 2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 311
функция времени t задан так: s — F(t). Тогда v~f(t) = F'(t) (см. п. 38, I).
Поэтому
8 = fF'(t)dt,
о
откуда по формуле Ньютона — Лейбница (считая, что F@) = 0) получаем
s^F(t).
что и требовалось доказать.
Аналогично в задаче о массе (п. 86, III) имеем
о
где /(s) = O'(s) (см. п. 38, II), причем m = O(s). Подставляя в интеграл
вместо f (s) функцию Ф' (s) (и считая Ф @) = 0), получим по формуле Ньюто-
Ньютона—Лейбница
что и требовалось доказать.
93*. Интегрирование комплексных функций действительного
переменного. Определенный интеграл от комплексной функции
действительного переменного (см. п. 73) определяется следующим
образом.
Если z(t) = x(t) + ly(t), to
Таким образом, вычисление интеграла от комплексной функции
сводится к вычислению интегралов от ее действительной и мни-
мнимой частей.
Если Z(t) = X(t) + iY(t)y где X(t) и Y(*) — какие-либо перво-
первообразные соответственно для x(t) и у (/), то по правилу вычисле-
вычисления производной комплексной функции
Комплексную функцию Z(t) естественно назвать первообразной
для комплексной функции z(t). Применяя формулу Ньютона —
Лейбница к интегралам в правой части равенства (*), получим
ь
b
а
Это—формула Ньютона — Лейбница для комплексных функций
действительного переменного.
действительного переменного
312 ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ [94
Примеры. 1) Если п — целое число (пфО), то
2JT
\ tn
о °
так как е*кЫ=\ (см. п. 74).
2)
§ 3. Способы вычисления определенных интегралов
94. Интегрирование по частям и замена переменной в опре-
определенном интеграле. Важнейшим результатом, устанавливающим
связь между определенным и неопределенным интегралами, является
формула Ньютона — Лейбница, согласно которой определенный инте-
интеграл вычисляется при помощи неопределенного интеграла
Так как в правой части равенства можно брать любую перво-
первообразную, то безразлично какую брать произвольную постоянную
при неопределенном интегрировании; поэтому ее вообще не пишут.
Простейшие правила интегрирования суммы и произведения
постоянной на функцию совершенно одинаковы для определенного
и неопределенного интегралов. Теперь мы рассмотрим правила
интегрирования по частям и замены переменной и укажем некоторые
особенности их применения для вычисления определенных инте-
интегралов.
I. Правило интегрирования по частям:
(A)
где и и v — функции независимой переменной.
Доказательство. Имеем
J и dv=\ и dv\x\ = (uv- J v du) \x[;
отсюда непосредственно и следует доказываемая формула.
941 § 3. способы вычисления определенных интегралов 313
Вместо того чтобы до конца довести неопределенное интегри-
интегрирование по частям, а затем выполнить двойную подстановку, можно
сразу воспользоваться формулой (А).
Рассмотрим в качестве примера интеграл
2
Jn = \ sinn х dx, n— целое положительное число.
о
Положим
dv = sin x dx, и = sin"'1.*;.
При этом
v = — cos лг, du = (n — 1) sin"~2 х cos х dx
L = — cos x sin" l x
С
-\-(n — 1) j sinn~2
Первое слагаемое в правой части: равно нулю; заменяя во
втором слагаемом cos2 л; через 1—sin2 л;, получим
откуда
Это — формула приведения (рекуррентная формула). С ее
помощью мы можем в конце концов снизить показатель степени
до 1, если п—нечетное число, или до 0, если п — четное число.
Но интегралы ft и /0 известны:
1Х = ] sin х dx = 1, /0 = ^dx = -5.,
о
и, таким образом, задача решается до конца. Например,
2 2
314 ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ [94
Предварительное полное отыскание неопределенного интеграла
потребовало бы более громоздких выкладок.
II. Правило замены переменной (подстановки).
Правило замены переменной в определенном интеграле требует
большого внимания.
Напомним (см. п. 81, II), что если x — ty (и), то
При этом, если известен один из интегралов, то известен и вто-
второй. Если первый равен F (х) (произвольную постоянную С не
пишем), то второй равен ^[^(и)]; если же известен второй инте-
интеграл, то чтобы найти первый, нужно вместо и подставить > его
выражение через х.
Теперь сформулируем правило.
Если в интервале [и19 и2] функции л; = г|>(я), if'(») и
непрерывны и q}(u1) — x1,tyiu2) = x2, то
Х2 И3
J f(x) dx = J /fo> («)] V (в) da. (Б)
ttt
Доказательство. Будем считать, что неопределенный
интеграл слева известен и равен F(x)\ тогда
Согласно сказанному выше неопределенный интеграл справа равен
] и поэтому
«а
S
Сравнивая полученные равенства, мы и приходим к формуле Б).
Из формулы (Б) видно, что подынтегральное выражение преоб-
преобразуется так же, как и в случае неопределенного интеграла.
Новые же пределы интегрирования их и и2 являются корнями
уравнений
Ф() и х2 = ^(и)
относительно неизвестной и.
Итак, вместо того чтобы, выполнив при помощи замены пере-
переменной неопределенное интегрирование, вернуться к первоначаль-
первоначальной переменной, а затем вычислить двойную подстановку вданных
пределах, можно сразу взять двойную подстановку в новых пре-
94] § 3. СПОСОБЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ 315
делах. Результат — значение определенного интеграла — получится
тот же, а выкладок потребуется меньше.
Часто замена переменной в определенном интеграле произво-
производится не по формуле лг = г|)(и), а по формуле и = Ц)(х)у выражающей
новую переменную через заданную. Тогда новые пределы и1ии2
сразу определяются по формулам
При этом иногда возникают затруднения, связанные с тем, что
если функция и~ц>{х) не монотонная, то обратная к ней функция
x = ty(u) будет не однозначной. Может даже оказаться, что раз-
различным значениям хг и х2 будут соответствовать одинаковые зна-
значения иг = и2 (например, при подстановке u = cosx в пределах от
— Y до -у) и интеграл справа в формуле (Б) будет равен нулю,
а слева нет. Поэтому, чтобы формула (Б) оставалась справедливой,
нужно на функцию м = ф(л:) наложить некоторые ограничения:
достаточно потребовать, чтобы ф (х) была в интервале (х1У х^)
монотонна и имела производную, не равную нулю ни в одной внут-
внутренней точке интервала (короче, производная ф' (лг) должна сохра-
сохранять постоянный знак). Тогда обратная функция x = ty(u) будет
удовлетворять всем требованиям, сформулированным в правиле
подстановки (см. теорему V п. 34 и п. 42).
г
Г хъ dx
Примеры. 1) \ у Положим x = sinu. Новые пределы
интегрирования их и и2 найдем из уравнений 0 = sina и -?~ыпи>
иг можно взять равным 0, а и2 — равным у. При изменении и от
О до ~ переменная x = sinu пробежит весь данный интервал
интегрирования 0,у . Таким образом,
2. ? —
2 6 в
f X**X sfsiP««CO8« f
J гГ\ v2 J cos a J
о V * * о е
-Lft, sin2u\\j_n V*
При выборе новых пределов интегрирования мог возникнуть вопрос:
почему взяты пределы их = 0 и иа=="б~» а не> скажем, ^ = 0 и
316 ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ [94
wa=-g- ? Ведь sin -7г- тоже равен у. Можно проверить, что и при этих пре-
пределах величина интеграла останется прежней, однако его вычисление услож-
усложнится. Дело в том, что теперь 1^1—яа= J^cos2 и уже не равно просто cosw.
Это имеет место только в интервале 0, -=¦ > где cosu^O; в интервале
же \-rj-> -g-1 корень будет равен — cosm, так как cosu^O. Поэтому
5JT
/г
** Л sif"cofUcfc=fsin*»d»-( sin» «da.
v2 J cos u\ J J
Произведя дальнейшие выкладки, получим тот же результат, что и раньше.
Чтобы избежать ненужных осложнений при вычислениях, всегда берут
наименьший возможный интервал изменения новой переменной интегри-
интегрирования.
2) \ 1_^1ПЛ2 dx. Полагая cos л: = и, будем иметь
я
2
J l + COS
г \+и2
4 '
3) ^„^j cosnxdx. Положим x==^ — u> торДа
0
я я_
To 2~
j cosnл:^л: = — J cosn Гу — u\du = J
sin"
а так как значение определенного интеграла не зависит от обо-
обозначения переменной интегрирования, то
я л
2 2~
Un = 5 cos" л: d* = J sinn л: dx.
Метод вычисления последнего интеграла с помощью формул при-
приведения указан на стр. 313,
95] § 3. СПОСОБЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ 317
4) Выведем формулу для интеграла, взятого по симметричному
интервалу [—а, а]:
а
l/(x)dx,
—а
в случаях, когда подынтегральная функция четна и нечетна.
Представим этот интеграл так:
а о а
(*)dx= I f(x)dx+\f(x)dx.
Заменив переменную интегрирования в первом интеграле в правой
части по формуле х ——и, получим
Обозначим в первом интеграле справа переменную интегрирования
снова через х\ тогда
а а
J f(x) dx = J [/(—*) +/(х)} ах.
—а о
Подынтегральная функция в, правой части равна нулю, если
f(x)—функция нечетная, и равна 2/(лс), если f(x)—функция
четная. Следовательно,
/О, если f(x) — нечетная функция,
S' I a
—а ~~ I ^ \ f(x)dxy если f(x) — четная функция.
V о
Эти формулы очень полезны. Например, сразу ясно, что
хъ ех* dx = 0, ^ sin3 x cos
—а
in3 x cos2 xdx
Рекомендуем читателю выяснить геометрический смысл выве-
выведенных формул.
95. Приближенные методы интегрирования. Перейдем теперь
к некоторым употребительным методам приближенного инте-
интегрирования, позволяющим находить приближенное значение
определенного интеграла от любой непрерывной функции с практи-
практически достаточной точностью. Потребность в приближенном вычис-
вычислении интеграла может возникнуть и тогда, когда не существует
318
ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
[95
или неизвестен метод отыскания точного значения интеграла, и
тогда, когда этот метод известен, но неудобен. Излагаемые при-
приближенные численные методы основаны на следующем: рас-
рассматривая интеграл как площадь криволинейной трапеции, мы
получим ее приближенное значение, т. е. приближенное значение
интеграла, если вычислим площадь другой трапеции, ограничиваю-
ограничивающая линия которой по возможно-
возможности мало отклоняется по положе-
положению от заданной линии. Вспомо-
Вспомогательную линию при этом про-
проводим так, чтобы получилась
фигура, площадь которой легко
вычисляется.
Мы дадим следующие пра-
правила численного интегрирования:
1) правило прямоугольников и
правило трапеций, 2) правило
параболических трапеций, назы-
называемое по имени его автора
Рис. 111.
правилом Симпсона1).
1. Правило прямоугольников и правило трапе-
трапеций. Разделим интервал интегрирования [я, Ь] на п равных
частей (частичных интервалов) и заменим данную трапецию сту-
ступенчатой фигурой, состоящей из п прямоугольников, опирающихся
на частичные интервалы, причем высоты этих прямоугольников
равны значениям функции y=f(x) в начальных или в конечных
точках частичных интервалов (рис. 111). Значение площади этой
фигуры и будет давать приближенное значение искомого интеграла
ь
I = \f(x) dx. Результат будет тем более точен, чем больше взято
число частичных интервалов.
Если обозначить значения
через у0,
где Длг
у±,
Ь
— а
> Уп-ъ Ут т- е- положитьyk =
a k принимает значения 0, 1,
функции f(x) в точках деления
%xk = a + kAx,
. . , я, то, оче-
очевидно, будем иметь следующие формулы:
= А*
или
/« /= &x(yt+y2+ ... +уп).
Эти формулы и называются формулами прямоугольников.
Х)Т. Симпсон A710—1761) —английский математик.
95] § 3. СПОСОБЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ 319
Оставим разбиение интервала [а, Ь] прежним, но заменим теперь
каждую дугу линии у=/(х), соответствующую частичному интер-
интервалу, хордой, соединяющей конечные точки этой дуги. Таким обра-
образом, мы заменяем данную криволинейную трапецию п прямолиней-
прямолинейными (рис. 111). Геометрически очевидно, что площадь такой
фигуры более точно выражает искомую площадь, чем площадь
я-ступенчатой фигуры, составленной из прямоугольников.
Ясно, что площадь каждой трапеции, построенной на частичном
интервале, равна полусумме площадей, соответствующих этому
интервалу прямоугольников. Суммируя все эти площади, получим
Эта формула и носит название формулы трапеций.
Если функция f(x) монотонна, то величины / и / дают оценку
интеграла значительно более точную, чем указанная в теореме VI
п. 90, При этом ясно, что если функция монотонно возра-
возрастает (этот случай как раз изображен на рис. 111), то
а если монотонно убывает, то, наоборот,
Беря в качестве приближенного значения интеграла значение,
получаемое по формуле трапеций
мы будем уверены, что абсолютная ошибка не превосходит абсо-
абсолютной величины полуразности / и /, т. е.
2
В качестве примера найдем приближенное значение интеграла
dx
и сравним найденные величины с его точным значением, равным
arctg l=^~»0,7S5. Пусть /г = 10. Тогда Ддг = 0,1; лгл = *.0,1
F = 0, 1, 2, ..., 10). Вычисляя значения функции (с точностью
320 ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ [95
до 0,001), получим
У о = * э Ух = 1 + @,1J ~ 0>990>
3;3 » 0,917, з>4^ 0,862, >fft = 0,8,
J>6-0,735,^,^0,671, j,8^0,610, у9 « 0,552, ^„=0,5.
Следовательно,
^/ = 0,1A+ 0,990 + 0,962 + 0,917 + 0,862 + 0,8 + 0,735 +
+ 0,671+0,610 + 0,552) « 0,810.
Аналогично вычислим /:
7« 0,755.
В этом примере J > /, так как функция убывающая. Таким образом,
0,755 <7< 0,810.
Возьмем в качестве / значение
0810^ 0,782.
При этом абсолютная ошибка не превосходит |ДУ|< 0,028, отно-
сительная ' _*о « 3,6%. Фактически же абсолютная ошибка со-
ставляет всего 0,003.
Вычислим еще приближенное значение интеграла
/= J s\nxdx = 2.
о
Пусть п = 6. Тогда по формуле трапеций
sin 0 + sinn , . я , . 2я . . Зя . . 4я
J jSiii + 8in + sm- + 8in
= Т @,5 + у/3+ 1 +1|/з + 0,5)« 1,9541.
Абсолютная ошибка равна 0,0459, а относительная — 2,5%.
В этом примере подынтегральная функция в интервале интегри-
интегрирования не монотонна и мы не можем дать оценку для вычис-
вычисляемого интеграла.
Действительно, здесь /=/=Утр, т. е. все эти значения дают
искомую величину интеграла с недостатком. Чтобы получить все-таки
оценку для вычисляемого интеграла, мы должны разбить интервал
95] § 3. способы вычисления определенных интегралов 321
интегрирования на части, в каждой из которых функция монотонна,
и рассмотреть интегралы по каждому частичному интервалу
отдельно.
II. Правило Симпсона. Это правило требует не на много
большей затраты труда, чем предыдущие, а приводит обычно к
более точным результатам (при
одном и том же разбиении ин-
интервала).
Как и раньше, разобьем ин-
интервал [a, b\ пап равных частей,
но предположим, что п—четное
число: л = 2/и. Заменим дугу линии
у=/(х)у соответствующую ин-
интервалу [лг0, лг2], дугой параболы,
ось которой параллельна оси
ординат и которая проходит через
следующие три точки дуги: на-
начальную точку дуги (хо,уо)у сред-
среднюю точку (хг, уг), конечную
точку (лг2, у2) (рис. 112). Аналитически это означает, что в ин-
интервале [лг0, х2] данная функция y = f (х) заменяется квадратичной
функцией y=px2-\-qx + r. Коэффициенты /?, q и г выбираются
так, чтобы значения обеих функций были равны при лг0, хг и х2
соответственно
Уо =
у2 =
Решая полученные уравнения, находим коэффициенты р, q и г.
Произведя подобные замены и в интервалах [лг2, лг4], [.x^^eL- • •>
[*л-2> хп\ будем считать, что площадь данной трапеции прибли-
приближенно равна сумме площадей получающихся параболических
трапеций. Докажем теперь, что площадь S трапеции, ограниченной
какой-нибудь параболой у = рх2-)-qx-}-г с осью, параллельной
оси ординат, будет выражаться формулой
(ДЛ. ОСН.)
S
(*)
гдед;н — ордината начальной, ус—ордината средней и ук — ордината
конечной точек дуги параболы.
Предположим сначала, что основанием трапеции служит интервал
оси Оху симметричный относительно начала координат, [—у, у].
Для площади такой параболической трапеции имеем выражение
Y Y Y
С [ §
Y
= С (px
-V
-V
-Y
11 А. Ф. Бермант, И. Г. Арамаиович
322 ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ [95
Так как здесь уя=Ух=-у=РУ2 qy + y ^c^
yK=yx=y—py2-\-qy~\-r и длина основания равна 2у, то непосред-
непосредственной подстановкой этих значений в формулу (*) убеждаемся
в ее справедливости.
Очевидно, что эта формула справедлива и для параболической
трапеции рассматриваемого вида с любым основанием. Действитель-
Действительно, площадь трапеции не изменится, если перенести ее параллельно
самой себе так, чтобы основание стало симметричным относительно
начала координат, и тогда искомая площадь выразится в согласии
с формулой (*).
Возвращаясь к первоначальной задаче, найдем по этой формуле
площадь Sx параболической трапеции, опирающейся на интервал
[ \
где Ах = -^-. Аналогично выразятся площади Sit S3, ..., S
последующих параболических трапеций:
$т = -J (Уп-t + 4Уп-1 +Уп)-
Сложив почленно все эти равенства, получим выражение, даю-
дающее приближенное значение искомого интеграла:
Т-г +Уп\-
Это и есть формула Симпсона.
По формуле Симпсона, например, для интеграла 1—
о
( = 0,2) при л=10 находим: /^0,200013; абсолютная ошибка со-
составляет всего 0,000013, а относительная — 0,01%.
Ясно, что для любого интеграла от квадратичной функции
у =px%-\-qx-\-r формула Симпсона должна, конечно, дать точное
значение. Заметим, что формула Симпсона дает также точное значе-
значение и для интеграла от кубической функции.
95] § 3. СПОСОБЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ 323
Применим формулу Симпсона к интегралу j sinxdx, вычислен-
ному раньше по формуле трапеций.
Простые подсчеты при # = 6 дают
-«¦
2,001.
Относительная ошибка результата равна 0,05%—очень хоро-
хорошая точность, достигнутая всего при шести точках деления интер-
интервала интегрирования.
1
Sdx
-г-.—5-по правилу Симпсона только при п = 4
о 1+Х
найдем 7^0,78539 со всеми верными знаками. Пользуясь правилом
трапеций, мы получили для величины этого интеграла худший ре-
результат при значительно большем объеме вычислений.
Приведенные правила приближенного численного интегрирования
позволяют находить интегралы не только от функций, заданных
формулами, но и от функций, заданных геометрическим или таб-
табличным способом.
Пример. Ширина реки равна 20м; промеры глубины в неко-
некотором поперечном ее сечении через каждые 2 м дали следующую
таблицу:
X
У
0 1 2
0,2 0,5
4
0,9
6
1,1
8
1,3
10
1,7
12
2,1
14 1 16
1,5 1,1
18
0,6
20
0,2
Здесь расстояние (в метрах) от одного из берегов обозначено
через х, соответствующая глубина реки (также в метрах) — через у.
Требуется найти площадь 5 поперечного сечения реки.
По формуле трапеций находим
5=!
по формуле Симпсона находим
+ 2,1 + 1,5 + 1,1 + 0,б)=22 ж2;
? = у [0,2 + 4-0,5 + 2-0,9 + ... + 4-0,6 + 0,2] = 21,9 м\
Результаты — весьма близкие. О точности их говорить не при-
приходится, так как по условию задачи точный профиль реки не задан.
11*
324
ГЛ. V. ИНТЕГРАЛ, ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
[96
96. Графическое интегрирование. Остановимся теперь на гра-
графическом методе отыскания значения интеграла. Пусть нам извес-
известен график функции y=*f (x). Поставим задачу: геометрическими
У\ ujr средствами, не прибегая к вычис-
вычислениям, найти приближенное зна-
значение интеграла
Будем предполагать, что масш-
масштаб по оси Ох равен масштабу по
Рис. 113. оси Оу и что полюс графика Р
находится на расстоянии единицы
масштаба от начала координат: ОР=1 (рис. 113). Проведем
прямую FG} параллельную оси Ох и пересекающую линию у=/(х)
так, чтобы площадь полученного прямоугольника как можно меньше
отличалась от площади нашей криволинейной трапеции. Для этого
нужно, чтобы площадь, заключенная между линией и прямой FG
и лежащая над прямой, по возможности точно равнялась площади,
заключенной между линией и прямой и лежащей под прямой. Про-
Продолжим прямую FG до пересечения с осью Оу в точке Т и соединим
эту точку с полюсом графика. Наконец, из точки А проведем пря-
прямую, параллельную РТ, до пересечения с прямой х = Ь в точке М'.
Легко убедиться в том, что отрезок МВ изображает искомую
площадь, т. е. отрезок MB содержит столько линейных масштаб-
масштабных единиц, сколько квадратных единиц содержит площадь криво-
криволинейной трапеции. В самом деле, из подобия треугольников РОТ
и АВМ' находим
ВМ1
~АВ
ОТ
ОР
откуда ВМ =
АВОТ
но ОР=1, а АВ*ОТ измеряет площадь трапеции.
Если интервал [а, Ь] недостаточно мал, то проведение прямой FG
на глаз может привести к ощутимой ошибке. Для того чтобы
уточнить построение, разобьем интервал интегрирования на частич-
частичные интервалы (не обязательно равные между собой) и всю трапе-
трапецию— на ряд трапеций, опирающихся на эти частичные интервалы.
Точки деления выберем таким образом, чтобы каждый частичный
интервал был интервалом монотонности подынтегральной функции
и чтобы в числе точек деления находились все точки пересечения
линии у=/(х) с осью Ох. Если в каждом интервале линия незна-
незначительно отличается от прямой, то в качестве средних линий частич-
частичных трапеций можно брать просто ординаты в средних точках ча-
частичных интервалов. Тогда отпадает необходимость проводить на
96] § 3. СПОСОБЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
325
глаз вспомогательные линии. Практически обычно так и по-
поступают.
Последовательно для каждой из частичных криволинейных тра-
трапеций построим указанным выше путем отрезок, изображающий ее
площадь. В целях ясности чертежа удобно откладывать этот отре-
отрезок не от данной оси Ох, а от другой оси Огху параллельной
первой (рис. 114). В точке х = а площадь трапеции, отсчитываемая
от прямой х=а, очевидно, равна нулю. Отметим на оси Охх
точку М'0(а, 0), она соответствует точке Мо линии у=/(х). До
прямой х~хг площадь трапеции равна площади первой частичной
ОСп «27
Рис. 114.
трапеции; она изобразится отрезком М'гхъ которой мы получим, если
из точки М'о проведем прямую, параллельную РТ1У до пересечения
с прямой х = хх в точке Мг. Эта точка соответствует точке Мх
на линии. Площадь трапеции до прямой х = х2 (т. е. значение ин-
интеграла, взятого от а до х2) равна сумме (в алгебраическом смысле)
площадей первой и второй частичных трапеций. Она изобразится
отрезком М'2х2, который получится, если из точки М'х провести
прямую, параллельную РГ2, до пересечения с прямой х = х2 в точке
М'2. Эта точка соответствует точке Мг на линии. Продолжая так же
326 ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ [97
дальше, построим последовательно точки М9 М^ ..., соответству-
соответствующие точкам Ж3, А14, ... линии. Ордината точки М\ соответствую-
соответствующей точке Mn[b, f(b)] линии, и даст нам искомое значение интег-
интеграла /. Ясно, что чем больше точек деления, тем точнее получится
построение.
Соединим полученные точки М'о, M'v M'^ ..., М'п плавной лини-
линией. Ординаты этой линии, очевидно, приближенно изображают зна-
значения интеграла, взятого от х = а до соответствующих точек
основания трапеции. Другими словами, эта линия является графиком
функции, определяемой нашим интегралом с переменным верхним
пределом:
Как известно (п. 79), линия у = ](х) называется интеграль-
интегральной кривой функции у=/(х). Рассмотренное нами геометриче-
геометрическое построение интегральной кривой по графику подынтегральной
функции называется графическим интегрированием.
Так же как и в случае графического дифференцирования, графи-
графическое интегрирование бывает наиболее удобным тогда, когда
подынтегральная функция задается графически, а аналитическое
ее выражение неизвестно. Это нередко встречается в практике,
например, когда функция определяется графиком, записываемым
самопишущим прибором.
§ 4. Несобственные интегралы
97. Интегралы с бесконечными пределами. Говоря об опреде-
определенных интегралах, мы всегда до сих пор подразумевали, что
интервал интегрирования конечен и подынтегральная функция
на нем непрерывна. Именно для этого случая и сформулирована
теорема существования определенного интеграла (п. 87). Довольно
часто, однако, возникает необходимость распространить определе-
определение определенного интеграла на случаи бесконечного интер-
интервала интегрирования и разрывной подынтегральной функции.
В этом пункте будут рассмотрены интегралы с бесконечными пре-
пределами; интегралы от разрывных функций будут изучаться в п. 99.
Пусть функция у — /(х) непрерывна в полу бесконечном интер-
интервале [а, оо). Тогда мы можем вычислить интеграл от функции f(x),
взятый по любому интерзалу [я, т)], г) > а. Интеграл
97] § 4. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 327
тем лучше выражает величину, которую следует принять в ка-
качестве интеграла от функции f (х) в интервале [а, оо), чем боль-
больше т]. Заставим г) неограниченно возрастать. Имеются две возмож-
возможности: или У(г)) при т]—> оо имеет предел, или 1(г\) предела не
имеет; последнее означает, что 1(ц) или стремится к бесконечности,
или колеблется и вообще не стремится ни к какому пределу.
Определение. Несобственным интегралом от функции
л
f(x) в интервале [а, оо) называется предел интеграла ^f(x)dx
а
при г]—*оо. Записывают это так:
[f(x)dx = \\m \f(x)dx.
Если указанный предел существует, то несобственный интег-
интеграл называется сходящимся* а если не существует, то расхо-
расходящимся.
Если первообразная функция F(x) для подынтегральной функ-
функции f(x) известна, то легко установить, сходится несобственный
интеграл или нет. С помощью формулы Ньютона — Лейбница по-
получаем
00
\f(x)dx= lira
Таким образом, если предел первообразной F(x) при х—> оо
существует (он обозначен через F(oo)), то несобственный интеграл
сходится, а если этот предел не существует, то интеграл расходится.
Примеры. 1) \^e~xdx = —е~*
==Ь Следовательно,
несобственный интеграл ^ е~х dx сходится и равен 1.
— = 1пл;
= оо. Интеграл расходится, так как первообраз-
первообразная In л: при х—> оо стремится к бесконечности.
3) Интеграл \ cos х dx расходится, так как величина \ cos x dx =з
о о
= sin т] не стремится к пределу при ц—> оо (колеблется).
о
328 ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ [97
Аналогично определяется несобственный интеграл и в интер-
интервале (—оо, а]:
а а
f(x)dx= lim \f(x)dx=*F(a)—F(—оо),
где F(—оо) — предел первообразной ^(л:) при х—>—оо.
Если функция f(x) определена и непрерывна на всей числовой
оси, то можно рассматривать и несобственный интеграл в интер-
интервале (—оо, +00)- По определению
+ 0О О + 00
f(x)dx = J f(x)dx + I f(x)dx.
Если оба интеграла в правой части сходятся, то интеграл ^ f(x)dx
— оо
называется сходящимся.
Если первообразная F(x) известна, то
где под символами /^(-(-оо) и F( — оо) понимают пределы, к
которым стремится F(x) соответственно при лг—^ + °° и х—> — оо.
Если хотя бы один из этих пределов не существует, то несобствен-
ный интеграл расходится.
+ 00
\ exdx~ex \ =оо—0 = оо. Интеграл расходится.
б) \
+ 0»
6)
Здесь и F( — оо) и F( + oo) равны бесконечности; интеграл
расходится.
Заметим, что на несобственные интегралы без всяких измене-
изменений переносятся простейшие свойства определенного интеграла,
сформулированные в п. 88, если только все интегралы, стоящие
в правых частях равенств, выделенных жирным шрифтом, схо-
сходятся. Справедливы также теоремы III—V п. 89.
Сходящимся несобственным интегралам можно придать опре-
определенный геометрический смысл. Пусть, например, график
97] § 4. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 329
функции у=/(х) ограничивает трапецию с бесконечным основа-
00
нием (рис. 115). Если несобственный интеграл j f(x)dx сходится,
а
то будем говорить, что заштрихованная фигура имеет площадь,
равную этому интегралу. Если интеграл расходится, то говорить
о площади фигуры нельзя.
Например, бесконечной трапеции, ограниченной положительной
полуосью Ох, прямой дг = а(а > 0) и ли-
1
= -5-, можно приписать площадь,
равную 2^, ибо
J x*aX-~2 l?\a ~
Рис. 115.
Бесконечной трапеции, ограниченной гиперболой j;= —, поло-
положительной полуосью Ох и прямой л; = а(а>0), нельзя при-
приписать площадь, так как
1 I <*>
X \а
Несобственные интегралы рассмотренного типа часто встре-
встречаются в задачах механики и электростатики в связи с опреде-
определением потенциала.
Пусть точка М массы т, находящаяся в начале координат,
притягивает свободную точку Мг массы 1, лежащую на расстоянии
X от М на оси Ох. Величина Р силы притяжения, как известно,
определяется по закону Ньютона
Р = & —t где к— константа,
а работа, произведенная при перемещении Mt из точки х — r в
точку лг = 6(?>г>0), — из формулы
Знак минус перед интегралом взят потому, что направление силы
противоположно направлению движения точки М (по той же
причине работа оказалась отрицательной).
330 ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ [98
Если точка удаляется в бесконечность (? = оо), то
—— ¦ \
а:2 г
Если точка Мг будет перемещаться из бесконечности в точку
дг = г, то сила притяжения произведет уже положительную
работу:
А — к т
Эта работа называется потенциалом, силы притяжения мате-
материальной точки М при Аг — г (или в точке л; = г).
98*. Признаки сходимости несобственных интегралов с бес-
бесконечными пределами. Выяснение вопроса о сходимости несобст-
несобственных интегралов значительно усложняется, если первообразная
функция неизвестна, В таких случаях иногда удается установить
сходится или расходится интеграл, пользуясь специальными
признаками, не требующими знания первообразной. Будем для
со
определенности говорить об интегралах вида \f(x) dx; признаки
а
а
сходимости для интегралов \ f(x) dx формулируются совершенно
— со
аналогично.
I. Начнем со случая, когда подынтегральная функция f(x)
во всех точках интервала [а, оо) неотрицательна: f(x)^Q. Гео-
г\
метрически ясно, что I(r\) = \f(x)dx с возрастанием ц будет
а
возрастать (если есть интервалы, в которых /(лг) = О, то в них
/(т)) постоянна). По признаку существования предела (см. конец
п. 31), если возрастающая функция ограничена, то она имеет
предел. Поэтому, если только нам известно, что 1(ц) ограничена:
М, где М—некоторая постоянная, то уже можно сказать,
что несобственный интеграл \f(x)dx сходится и его величина
а
не превосходит М. При этом, разумеется, мы еще не знаем, чему
этот интеграл равен; вычисление несобственных интегралов, когда
первообразная неизвестна, гораздо сложнее установления их
сходимости, и производится специальными приемами.
С помощью сказанного легко доказать следующий признак.
98] § 4. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 331
Признак сравнения. Пусть для всех значений х выпол-
выполняется неравенство
О </(*)< <р (ж). (*)
Тогда: 1) если сходится интеграл ^<p(x)dx, то сходится и
а
00
\f{x)dx;
а
00
2) если расходится интеграл ^f(x)dx, то расходится и
09
Доказательство. Предположим, что интеграл \(p(x)dx
а
Л
сходится и равен М; тогда J <р (лг) dx < М для любого rj. По
а
теореме об интегрировании неравенств (п. 90, II)
Это значит, что /(t]) = \ f{x)dx есть ограниченная функция и
а
оо
интеграл \f(x)dx сходится.
а
оо
Если дано, что интеграл ^f(x)dx расходится, то возраста-
а
ющая функция \f(x)dx стремится к бесконечности; но так как
а
л л л
\ ф (х) dx ^ \ f(x) dx} то и функция ^ ф (at) dx тоже стремится
а а а
00
к бесконечности, т, е. }y(x)dx расходится. Признак полностью
а
доказан,
332 гл. v. интеграл, интегральное исчисление [98
Предоставляем читателю выяснить геометрический смысл приз-
признака сравнения.
Совсем не обязательно считать, что неравенство (*) выпол-
выполняется во всем интервале [а, оо). Признак остается справедливым,
если это неравенство соблюдается для всех х^Ь>а. Тогда мы
с помощью признака сравнения исследуем интеграл в интервале
[Ь, оо). Добавление же затем постоянной величины — интеграла
в пределах от а до Ь, — очевидно, не нарушит сходимости или
расходимости интеграла.
Наибольшая трудность исследования данного несобственного
интеграла \/(лг)^лг с помощью признака сравнения заключается
а
в том, что нам заранее неизвестно, с чем же сравнивать подын-
подынтегральную функцию. Поэтому, чтобы применять признак, нужно
иметь некоторый запас функций, относительно интегралов от
которых было бы известно, сходятся они или расходятся. Легко,
например, проверить, что интегралы от функций y~e~kx при
&>0 сходятся в любом интервале [а, оо), а при k^O рас-
расходятся.
Так как при х^> \ имеет место неравенство е~~х* < в""*, то
оо
интеграл \ е~~х% dx сходится. Согласно замечанию, сделанному
1
ОС
чуть выше, сходится и интеграл \e—xidx, а так как подынтег-
о
о
ральная функция четная, то и интеграл \ e—x*dx.
Интеграл ^ e—x%dx называется интегралом Пуассона1) и играет
— 00
очень важную роль в теории вероятностей. Позже (в п. 131)
он будет вычислен специальным приемом; пока мы просто приведем
его значение
В качестве функций сравнения очень часто применяются сте-
*) С. Пуассон A781—1840)-~выдающийся французский математик,
физик и механик. Почетный член Петербургской академии наук.
98] § 4. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 333
пенные функции у = -^, относительно которых докажем сле-
следующее.
Несобственный интеграл \ -?, где а > О, сходится при m > 1
а
и расходится при m^l. (Ясно, что интересен только случай
m > 0, потому что при m < О подынтегральная функция стремится
к бесконечности при х—> оо и интеграл от нее заведомо рас-
расходится.)
При m=?\ имеем
00
J "^"""—m+1 а '
а
Если т>1, то показатель степени 1—т<0 и первообразная
стремится к нулю при х—*оо; интеграл сходится. Если же т< 1,
то 1—w>0 и первообразная стремится к бесконечности при
х—»-оо, т.е. интеграл расходится. Расходимость интеграла при
/я=1 установлена в примере 2 п. 97.
оо
Г dx
Примеры. 1) I — 3 сходится, так как неравенство
справедливо при всех х ^ 1 и
,,1/2,2/3
00
интеграл \ —^- сходится (т = -^-> 1).
J х1'9 b
i
00
dx расходится, потому что у-ц—>
1
со
при х > 1 и интеграл I —^L расходится (/»=-—< 1).
J V х *
1
II. Признак сравнения, сформулированный в п. I, относится
только к функциям, сохраняющим один и тот же знак в бес-
бесконечном интервале интегрирования (ясно, что исследование
интеграла от отрицательной функции сводится к предыдущему).
Более сложным оказывается исследование интегралов от функ-
функций, не сохраняющих постоянный знак, например таких, как
^-^ я Мы приведем сейчас один признак сходимости, позволяющий
X
иногда сводить исследование к случаю положительных функций.
334
ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
[98
Если сходится интеграл ]\f(x)\dx (интеграл от абсолютной
а
со
величины функции f(x))> то сходится и интеграл }f(x)dx. При
а
00
этом интеграл \f(x)dx называется абсолютно сходящимся.
а
Для доказательства образуем две вспомогательные функции
/+ (аг) и /" (л:), определив их следующим образом:
J Я*), если /(*)>(>,
f (х)-\ 0, если f{x)<Of
( 0, если /(*) > О,
ГМя8(/D если /W<0.
(Построение графиков функций /+ (х) и /" (а;) по заданной функ-
функции f(x) показано на рис. 116.)
Ясно, что функции /+ (л:) и
—/~(х) неотрицательны и
каждая из них не превосходит
[/(дг)|. Так как по условию ин-
интеграл от |/(аг)( сходится, то по
признаку сравнения заключаем,
¦&*&) что сходятся и интегралы
Рис. 116.
а а
нив в последнем интеграле знак
перед функцией, мы, очевидно,
не нарушим его сходимости.
Но Л*)=/+ (*)+/- W, и
раз сходятся интегралы от
/+(х) и f~(x), то согласно заме-
00
чанию на стр. 328 интеграл y(x)dx тоже сходится. Признак до-
казан.
Например, интегралы I *i 2 dx и I .s^ 2-д?лг абсолютно
о о
сходятся, так как подынтегральные функции по абсолютной
величине не превосходят положительной функции ^ . ^, интеграл
от которой сходится (пример 4 п. 97).
99] § 4. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 335
+ 00
Если сходится интеграл \ \f(x)\dxt то абсолютно сходятся
— 00
+ 00 +00
и интегралы ^ /(х) cos x dx и \ f(x) sin xdx, так как модули
CD 00
подынтегральных функций, очевидно, не превосходят |/(х) |. Этим
простым замечанием мы воспользуемся в дальнейшем.
Если интеграл от \f(x)\ расходится, то об интеграле от f(x)
на одном этом основании еще ничего сказать нельзя: он может
расходиться, а может и сходиться. В последнем случае (т. е.
когда интеграл от f(x) сходится, а интеграл от \f{x)\ расходится)
00
говорят, что \f(x)dx сходится условно (не абсолютно).
а
09
Примером этого служит интеграл Дирихле1) \ ^-2-^ dx. Можно
J х
о
доказать (мы этого делать не будем), что этот интеграл схо-
сходится, а интеграл оъмодуля подынтегральной функции расходится.
Таким образом, интеграл Дирихле сходится условно. Его величина
вычислена специальными приемами:
IL?dx- —
х йХ- 2
о
99. Интегралы от разрывных функций. Если в интервале
[а, Ь] функция f(x) имеет некоторое число точек разрыва пер-
первого рода, то дать определение интеграла для такой функции
не представляет никаких затруднений. В самом деле, при этом
естественно считать, что интеграл есть просто сумма обыкновен-
обыкновенных интегралов, взятых по частичным интервалам, на которые
разбивается интервал [а, Ь] всеми точками разрыва функции.
Обозначив их через cv с2, ..., ck1 где а < сг<с2<... •<с^<^,
будем иметь
Ъ С\ с2 Ь
$/(*) dx= $/(*) dx + ]f(x)dx+ .. . + $/(*) dx.
a a ct Cd
Этим самым дается и определение площади криволинейной
трапеции, соответствующей функции <у=/(лг) с конечным числом
Г. Дирихле A805—1859) —известный немецкий математик.
336
ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
[99
точек разрыва первого рода в интервале [ау Ь] (рис. 117): пло-
площадь такой трапеции есть сумма площадей трапеций, опирающихся
на частичные интервалы [а, сх], [сх, с2], ..., [ck, b]y заключенные
между последовательными точками разрыва.
Перейдем к распространению определения интеграла для
функций с бесконечными разрывами.
Пусть функция y~f(x) непрерывна для всех значений лг,
а^х<Ь, а в правом конце х=Ь интервала претерпевает бес-
бесконечный разрыв. Ясно, что
обычное определение интеграла
здесь теряет свой смысл. Но если
взять обыкновенный интеграл
Ь-е
1(г)= J f(x)dx, e>0,
Рис. 117.
то мы можем считать, что /(е)
с уменьшением е все лучше вы-
ражает ту величину, которую
следует принять в качестве ин-
интеграла от функции/(дг) в интервале [а, Ь]. Заставим е стремиться
к нулю. Тогда /(е) либо имеет предел, либо не имеет (стремясь
к бесконечности или вовсе не стремясь ни к какому пределу,
т. е. колеблясь).
Определение. Несобственным интегралом от функции
f{x)y непрерывной при а ^ х < Ь и неограниченной при х —±bf
Ъ—е
называется предел интеграла \ f(x)dx при 8—^0.
а
Записывают это так:
ь ъ—ъ
\ f(x)dx9 e>0.
Если указанный предел существует, то несобственный интеграл на-
называется сходящимся, а если не существует, то расходящимся.
Аналогично, если функция f(x) претерпевает бесконечный
разрыв только в левом конце лг=« интервала [а, Ь]у то
ь ь
= ton \ f(x)dx} 8>0.
Если первообразная функция F(x) известна, то в обоих слу-
случаях можно записать, что
ь
99] § 4. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 337
понимая под F(b) (или F(a)) предел, к которому стремится пер-
первообразная F(x) при х—>Ь (или при х—*а). Если этот предел
не существует, то интеграл расходится.
а
Пример ы. 1) f-^L:=!
о
1
. При х—> 1 предел In A—х) равен
о
о
бесконечности; интеграл расходится.
ь ь
dx
k
Вообще можно заметить, что интегралы \ и \
J (* —a)* J (Ь —дгI
а а
сходятся, если &<1, и расходятся, если k^\. Предоставляем
читателю доказать это.
3) \ * ... = ятг.ат*: = ~—(—-5.)= я. в этом примере
J у 1-х2 -1 ^ V г J
подынтегральная функция имеет бесконечный разрыв на обоих
концах интервала интегрирования.
Если функция f(x) имеет бесконечный разрыв в какой-нибудь
промежуточной точке х = с интервала [a, b], a < с < Ь, то по
определению
ь с ь
Если оба интеграла в правой части равенства сходятся, то схо-
ь
дится и интеграл \f(x)dx; этот интеграл расходится, если рас-
а
ходится хотя бы один из интегралов справа.
4)
10 1
еч С dx С dx . Г dx ~.
5) \—т= \~т+\—%- Оба интеграла справа расходятся, а
-1 -1 О
значит, расходится и данный интеграл.
Предположим, что линия y=f(x) имеет в точке х — b асимп-
асимптоту, перпендикулярную к оси Ох; тогда ограниченная ею
трапеция будет бесконечной (с бесконечными высотами)
(рис. 118). Если существует несобственный интеграл от функции/(л;),
338
ГЛ. V. ИНТЕГРАЛ. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
[99
то считают, что он измеряет площадь этой бесконечной трапеции;
в противном случае трапеция площади не имеет.
Например, бесконечной трапеции, ог-
ограниченной линией y~—==z и прямыми
\ х
лг = О, х = ау у = 0, можно приписать пло-
а
ибо [—?=: = 2j/a
J ух
о
(пример 1).
Бесконечной же трапеции, ограничен-
ограниченной гиперболой у =—и теми же прямыми
х = 0, х — а, у = 0, нельзя приписать
Рис. 118.
щадь, равную
площади, ибо
Г* A.Y. \л
\ — = 1плт
расходится.
На признаках сходимости интегралов от функций с бесконеч-
бесконечными разрывами мы останавливаться не будем, так как они
подобны рассмотренным в п. 98.
ВОПРОСЫ И ПРЕДЛОЖЕНИЯ ДЛЯ САМОПРОВЕРКИ
1. Что называется первообразной от данной функции? Привести примеры.
2. Доказать теорему о виде первообразной данной непрерывной функции.
3. Что называется неопределенным интегралом от данной функции?
интегральной кривой данной функции?
4. Сформулировать и доказать простейшие правила интегрирования.
Привести примеры.
5. В чём состоят методы интегрирования по частям и замены перемен-
переменной в неопределенном интеграле? Привести примеры.
6. Какая рациональная дробь называется правильной? Какие дроби
называются простейшими A-го и 2-го видов)?
7. Как производится разложение правильной рациональной дроби на
простейшие?
8. В чем состоит метод интегрирования рациональной функции?
9. Привести примеры интегрирования простейших иррациональных
функций.
10. Указать общий метод вычисления интеграла от функции, рацио-
рациональной относительно тригонометрических функций.
11. Описать методы вычисления интегралов вида \ sinn x cosm x dxt где
п и т—целые числа.
12. Когда говорят, что функция не интегрируется в элементарных функ-
функциях (в конечном виде)?
13. Как определяется площадь криволинейной трапеции? работа силы?
путь? масса?
14. Что называется определенным интегралом от данной функции в
данном интервале? Выразить с помощью интеграла понятия, перечисленные
в вопросе 13.
ВОПРОСЫ И ПРЕДЛОЖЕНИЯ 839
15. В чем состоит теорема существования определенного интеграла?
16. Сформулировать и доказать простейшие свойства определенного ин*
теграла.
17. В чем состоят свойства аддитивности и сохранения знака опреде-
определенного интеграла?
18. Каков геометрический смысл определенного интеграла от данной
функции (/=j5 (x) в данном интервале [а, Ь] в системе декартовых коорди-
координат?
19. Сформулировать, доказать и геометрически иллюстрировать теорему
об оценке интеграла. Доказать обобщение теоремы об оценке интеграла.
20. Сформулировать, доказать и геометрически иллюстрировать теорему
о среднем в интегральном исчислении.
21. Что такое среднее арифметическое значение функции у~1(х) в ин-
интервале [а, Ь]7
22. Чему равна производная от интеграла по его верхнему пределу?
Доказать соответствующую теорему и привести ее геометрическую иллю-
иллюстрацию.
23. Сформулировать и вывести формулу Ньютона—Лейбница.
24. В чем состоит метод интегрирования по частям в определенном ин-
интеграле?
25. В чем состоит метод замены переменной (подстановки) в определен-
определенном интеграле?
26. Вывести упрощающую формулу для интеграла, взятого по симмет-
симметричному интервалу [—а, а] от четной и нечетной функций.
27. Сформулировать ji вывести правила приближенного отыскания оп-
определенного интеграла: 1) правила прямоугольников и трапеций, 2) пра-
правило параболических трапеций (Симпсона).
28. Описать метод графического интегрирования.
29. Что называется несобственным интегралом от данной функции по
бесконечному интервалу? Дать геометрическую иллюстрацию и привести
примеры сходящихся и расходящихся интегралов.
30. Доказать признак сравнения для несобственных интегралов.
31. Какой несобственный интеграл называется абсолютно сходящимся
и какой условно сходящимся?
32. Что называется несобственным интегралом от разрывной функции
по данному конечному интервалу? Дать геометрическую иллюстрацию и
привести примеры сходящихся и расходящихся интегралов.
ГЛАВА VI
ПРИМЕНЕНИЕ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
§ 1. Некоторые задачи геометрии и статики
100. Площадь фигуры. Начнем с задачи о вычислении площади
плоской фигуры, или, как говорят еще, о квадратуре фи-
фигуры. Исторически эта задача так непосредственно связана с ин-
интегрированием, что часто само отыскание интеграла называют
квадратурой, и если какая-нибудь задача приводит к вычислению
интеграла, то говорят, что она сводится к квадратуре.
I. Система декартовых координат. В декартовой
системе координат за основную фигуру, площадь которой выра-
выражается одним интегралом, принимается криволинейная трапеция.
Если у=/(х) — уравнение линии, ограничивающей трапецию, то
площадь трапеции S (в предположении, что у^О) равна
ъ
где пределы интегрирования а и b (я < 6)— абсциссы начала и
конца линии.
Если линия задана параметрическими уравнениями
то, совершая подстановку в интеграле по формуле
получим
U
где tx и /2—значения, между которыми изменяется параметр t,
когда точка пробегает слева направо всю линию, ограничиваю-
ограничивающую трапецию сверху.
100]
§ 1. НЕКОТОРЫЕ ЗАДАЧИ ГЕОМЕТРИИ И СТАТИКИ
341
Пример. Найдем площадь S, ограниченную эллипсом —^~~
Ф
-~= 1. Имеем
Здесь удобно перейти к параметрическому заданию:
j; = ^sin / (см. п. 46).
Тогда
=— 2ab
Вычисление дает
II. Система полярных координат. Если линия, огра-
ограничивающая фигуру, задана уравнением в полярной системе коор-
координат, то в качестве основной фигу-
фигуры принимается криволинейный сектор
(рис. 119)—фигура, ограниченная ли-
линией г=/(ф), с которой любой луч,
исходящий из полюса Ру пересекается
не более чем в одной точке, и двумя
лучами ф = а и ф=($.
Покажем, что площадь такого
сектора выражается одним интегралом.
Разобьем весь сектор на п частичных
секторов при помощи лучей, накло-
наклоненных к полярной оси под углами
ф2,
Рис. 119.
Заменим каждый криволиней-
криволинейный сектор круговым, т. е. будем считать, что на каждом
из участков [фЛ, Ц>к+1] (& = 0, 1, ..., п—1) функция /(ф) по-
постоянна и равна значению ^—/(ф*)-
Напомним, что площадь кругового сектора радиуса г с цент-
ральным углом а равна -о-г2а. Поэтому площадь фигуры, со-
составленной из п круговых секторов, заменяющих криволинейные
342
ГЛ. VI. ПРИМЕНЕНИЕ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
[100
секторы (рис. 119), будет равна
Sn = т/2 (Фо) (Ф1— Фо) +т/2 (ФЛ (Ф2 —Фг)
где Аф(- = ф. + 1 — ф..
При образовании интегральной суммы для простоты приня-
принято, что все промежуточные точки |t- совпадают с левыми
концами частичных интервалов
[ф^, ф/ + 1]. Поэтому несколько из-
изменено обозначение для Дф,- и
суммирование ведется не от 1
до я, а от 0 до п — 1.
Рис. 120.
Рис. 121.
Предел суммы (*) при условии, что п—> оо и наибольший из
углов Ац>( стремится к нулю, как раз и даст искомую площадь
криволинейного сектора. Сумма (*) есть интегральная сумма для
функции /2 (ф) на интервале [а, Р], и поэтому
или, коротко,
где г=
Примеры. 1) Вычислим площадь 5 фигуры, ограниченной
первым витком спирали Архимеда г — ау и отрезком полярной
оси (рис. 120):
2Я
2) Вычислим площадь S фигуры, ограниченной линией г-
:асозЗф, которую называют трехлепестковой розой (рис. 121).
101]
§ 1. НЕКОТОРЫЕ ЗАДАЧИ ГЕОМЕТРИИ И СТАТИКИ
343
Площадь шестой части всей фигуры (половины одного лепест-
лепестка) выражается интегралом
у a2 f cos2 Зф Ар.
Действительно, конец полярного радиуса опишет всю огра-
ограничивающую сектор линию, когда полярный угол изменится от О
я
ДО -g-.
Следовательно, площадь розы равна
6 2
5 = 3а2 Г соБ2Зф^ф =а2 f cos2 \J> </г|5 == а2 ~-
о о
(мы заменили Зф = <ф), т. е. площади круга, диаметр которого
равен а.
101. Объем тела1). Пусть дано тело, ограниченное замкнутой
поверхностью, и пусть известна площадь любого его се-
сечения, произведенного плоскостью, перпендикулярной к неко-
некоторой прямой, например к оси абсцисс (рис. 122).
При этом можно считать, что площадь такого сечения явля-
является известной нам функцией S (х), где х— абсцисса точки пе-
пересечения указанной плоскости с осью а:.
Предположим далее, что все тело заключено между двумя
перпендикулярными к оси х плоскостями, пересекающими ее в
1) Общее определение объемов тел связано с изучением двойных ин-
интегралов и будет изложено в главе VIII. Сейчас мы рассматриваем один
важный частный случай этой задачи.
344 ГЛ. VI. ПРИМЕНЕНИЕ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ [101
точках а и Ь (а<#). Для определения объема такого тела ра-
разобьем его на слои с помощью секущих плоскостей, перпенди-
перпендикулярных к оси х и пересекающих ее в точках л;0 = a, xv лг2, ...
..., хп — Ь. Заменим каждый слой прямым цилиндром с той
же высотой и основанием, равным S(X;) (рис. 122); объем прямо-
прямого цилиндра равен произведению площади его основания на высоту.
Поэтому объем я-ступенчатого тела выразится суммой
= 2 ^ (*,) А*,.
1 = 0
Предел полученной суммы, а она является интегральной суммой
для функции S (х) на интервале [а, Ь], при п—»-оо и при стрем-
стремлении наибольшего Ajct. к нулю и даст нам искомый объем
ъ
V = J S (х) dx. (*)
Если рассматриваемое тело получается вращением криволиней-
криволинейной трапеции, ограниченной линией y=f(x), вокруг оси Ох, то
поперечным сечением с абсциссой х служит круг, радиус которого
равен соответствующей ординате линии y=f(x). (Если у < 0, то
радиус будет равен \у\.) В этом случае
и мы приходим к формуле для объема тела вращения
ь
V = n\y*dx, где y=f(x).
а
Примеры. 1) Найдем объем V трехосного эллипсоида1)
х% _|_ У* j_ *2 —
-&- + -Ьг~~г сз —Ь
Его плоскими сечениями, перпендикулярными, например, к оси Ох
(рис. 123), являются эллипсы с полуосями b Л/ 1 г и
с у 1—^г ,—«
х) Если читатель еще не знаком с поверхностями второго порядка, то
этот пример следует пропустить.
101]
§ 1. НЕКОТОРЫЕ ЗАДАЧИ ГЕОМЕТРИИ И СТАТИКИ
345
Площадь 5 (х) поперечного сечения в точке х нам известна
(см. п. 100):
поэтому
а а
С f X* \ С ( X* \
К= я?с \ ( 1 w-) dx = 2nbc \ [ 1 «- dx = 2nbc х — -
-а о
т. е.
Если две из полуосей равны между собой, например с = ?, то
для объема этого эллипсоида вращения получаем V=-^-
Если все три полуоси равны между собой,
т. е. а = ^=с, то эллипсоид превра-
превращается в шар объема V = -o-яа3.
2) Вычислим объем V тора («баран-
(«баранки»)— тела, полученного от вращения
круга около оси, лежащей в той же
Рис. 123.
Рис.
плоскости и не пересекающей круга. Пусть круг радиуса а враща-
вращается вокруг оси Ох, причем центр его лежит в точке @, b)}
(рис. 124). Уравнением вращающейся окружности будет
Мы, очевидно, найдем искомый объем, если из объема тела, образо-
образованного вращением верхней половины окружности (у = b + ]/ а2—л:2),
вычтем объем тела, образованного вращением нижней половины
346 гл. vi. применение интегрального исчисления
окружности (у = Ь—У а2— х2). Имеем
[102
—а
2л \ [(b + Va2—x2J — (b — V^—x2J] dx = ЪпЬ $ /a2 — x2 dx
и далее, полагая х = a sin ?,
4
102. Длина дуги. Пусть некоторая линия является графиком
непрерывной функции у=/(х), производная /' (х) которой тоже
непрерывна. Такие линии мы условились (см. п. 66) называть
гладкими. Определение длины дуги такой линии аналогично
определению длины окружности,
вводимому в геометрии.
Длиной дуги кривой линии
назовем предел, к которому
стремится длина вписанной в нее
ломаной при неограниченном
увеличении числа ее сторон и
при стремлении наибольшей из
этих сторон к нулю.
Итак, пусть линия АВ задана
«27
Рис. 125.
уравнением
у=/{х).
Будем предполагать, что во всем интервале изменения х функ-
ция, f(x) и ее первая производная /' (х) непрерывны. Разобьем
дугу АВ на п частей, и пусть точки деления имеют абсциссы
хо=а, xv х2У ...,Ь — хп (рис. 125). Проведя через каждые две
последовательные точки деления хорду, мы построим вписанную
ломаную, длина Ln которой равна
или
где
^*,—*^, Ду, =/(*,)— f(xt.x).
102] § 1. НЕКОТОРЫЕ ЗАДАЧИ ГЕОМЕТРИИ И СТАТИКИ 347
По формуле Лагранжа (см. п. 57) имеем
Ах, *
где gf g (Аг/в1, *,). Поэтому
Полученная сумма есть интегральная сумма для функции
V*l +/'2 (х)х) на интервале [а, Ь]. Переходя к пределу при п—^оо
и при условии, что длина наибольшего участка ломаной стремится
к нулю (при этом, разумеется, и наибольший из Алг,« стремится
к нулю), выразим длину L кривой при помощи интеграла:
или, коротко 2),
Ь
lVT^dx. (•)
Последнюю формулу, внося dx в подынтегральном выражении под
знак корня, удобно переписать в виде
(В)
(А)
где (А) и (В) условно обозначают начало и конец дуги АВ. Вместо
(А) и (В) нужно подставить соответствующие им значения выбран-
выбранной переменной интегрирования.
Если уравнение линии задано параметрически: лг = лг(^), y=y(t)
и tlt t2 — значения параметра t, соответствующие концам дуги,
причем tx < t2, то
xtM(t)+yft(t) dt. (••)
1) Так как в выражение функции, для которой составлена интеграль-
интегральная сумма, входит производная //(*), то f{ (x) должна быть непрерыв-
непрерывной, что и предположено с самого начала.
2) Заметим, что подынтегральное выражение является дифференциалом
длины дуги (см. п. 66). Иной метод получения формулы (*) будет указан
в п. 104.
348 ГЛ. VI. ПРИМЕНЕНИЕ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ [102
Пусть теперь линия задана уравнением в системе полярных коор-
координат: г = г(ф). Рассматривая в зависимостях
х = г cos ф, у — г sin ф
полярный угол ф в качестве параметра, получим
dx = (г' cos ф—г sin ф) dq>, dy — (/*' sin ф -f- r cos ф) </ф,
что дает
Vdx2 + dy2 = Vr2 + rf2 dtp
и, значит,
L =
а
где а и Р — значения полярного угла соответственно начала А и
конца Б дуги.
Вычисление длины линии называют спрямлением этой линии.
Примеры. 1) Спрямим одну арку циклоиды (п. 46)
х = а (t — sinf), y = a A—cos t).
Имеем
— cos tJ + sin2
т. е. искомая длина равна восьми радиусам производящего круга.
2) Вычислим периметр эллипса
х = a cos/, j; = #sintf (a > #).
Четверть эллипса, лежащая в первом квадранте, соответствует
изменению параметра ^ от 0 до -о-; поэтому
Л ?L
2 2
L = 4 С /a2 sin2 / + ?2 cos2 / d* = 4а С l/l— e2 cos2 tdiy
|/д2 fr2 jj
где е==-^ эксцентриситет эллипса. Подстановка / = -9- — ф
приводит нас к формуле
? = 4а J |/l —в2 sin2
о
Интеграл, стоящий справа, называется полным эллиптическим ин-
102] § 1. НЕКОТОРЫЕ ЗАДАЧИ ГЕОМЕТРИИ И СТАТИКИ 349
тегралом второго рода1); он не может быть вычислен обычными
приемами, так как первообразная подынтегральной функции не
выражается через элементарные функции. Поэтому длина эллипса
находится при помощи таблиц значений эллиптических интегралов,
которые приведены во многих справочниках, например в [13].
3) Вычислим длину логарифмической спирали r = aemcp от неко-
некоторой ее точки Ж0(г0, ф0) до переменной точки М(г, <р) (см.
п. 49, рис. 60). Имеем
ф ф
L = I Ya2e2m* + a2m2e*m<* dy = а ]Л+ш2 \ em* d<p =
Фо Фо
Здесь L дается как функция конечного полярного угла q>. Ее
можно представить как функцию конечного полярного радиуса г:
Это выражение показывает, что длина дуги логарифмической спи-
спирали пропорциональна приращению полярного радиуса дуги.
Если двигаться по спирали к полюсу, то полярный угол ф
стремится к —оо. Интеграл для длины становится несобственным,
и мы получаем
ф t
f « V^l + m2 mo Vl + m2
m
т. е. длина дуги логарифмической спирали от полюса до произ-
произвольной ее точки пропорциональна полярному радиусу этой точки.
Длина дуги пространственной линии, заданной уравнениями
x = x(t), y—y(t), z = z(t), вычисляется по формуле, аналогичной
формуле (#*):
где tx и t2 — значения параметра tt соответствующие концам дуги
х) Полным эллиптическим интегралом первого рода называется интеграл
г - . . Эллиптические интегралы встречаются при решении мно-
многих важных задач как в самой математике, так и в ее приложениях.
350 ГЛ. VI. ПРИМЕНЕНИЕ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ [103
103. Центр тяжести криволинейной трапеции. В аналитиче-
аналитической геометрии в качестве задачи на применение формул деления
отрезка в данном отношении обычно рассматривают задачу о
координатах центра тяжести системы материальных точек. Если
массы тъ /я2, ..., тп сосредоточены в точках M1(xv уг),
Ж2(дг2, у2), ..., Мп(хпУ уп) на плоскости, то координаты центра
тяжести М (?, ц) этой системы точек даются формулами
п п
2 */«* 2
2т'
Заметим, что для однородной системы материальных точек
(m1 = m2= ... =тп) координаты центра тяжести
п п
S */ % У1
не зависят от величины массы, а зависят исключительно от рас-
расположения точек.
Произведение массы точки на ее расстояние от какой-нибудь
оси называется статическим моментом этой точки отно-
относительно оси. При этом для точек, лежащих по одну сторону от
оси, расстояние берется со знаком плюс, а по другую—со знаком
минус. Поэтому произведения ximi и yimi суть статические мо-
моменты точки М{ относительно осей Оу и Ох. Сумма статических момен-
моментов точек называется статическим моментом системы.Сле-
системы.Следовательно, координаты центра тяжести системы точек М-х {хь у()
могут быть выражены так:
?=3 n=,ik
6 М ' ¦ М '
где Мх и My — статические моменты системы относительно осей
Ох и Оуу а М—сумма масс. Отсюда
Таким образом, центр тяжести можно определить как такую
точку, что если в ней сосредоточить всю массу системы, то ее ста-
статический момент относительно какой-нибудь оси будет равен соот-
соответствующему статическому моменту всей системы.
Рассмотрим теперь однородную пластинку постоянной
толщины. Поверхностную плотность ее, т. е. массу единицы пло-
площади пластинки, обозначим через б кг/м2. Центр тяжести такой
103]
§ 1. НЕКОТОРЫЕ ЗАДАЧИ ГЕОМЕТРИИ И СТАТИКИ
351
^
пластинки будет лежать в ее срединной плоскости, которую мы
примем за плоскость Оху. Ясно, что при наших условиях поло-
положение центра тяжести будет
зависеть только от г е омет- *| ^-—i r+**i0
рической формы плас-
пластинки. Мы примем сейчас, что
область, занимаемая пластин-
пластинкой в плоскости Оху, имеет
форму криволинейной трапе-
трапеции1), ограниченной дугой
A3 линии y~f{x) и с осно-
основанием [а, Ь] на оси Ох, Ра-
Разобьем эту трапецию на п
частичных трапеций с по-
помощью прямых, параллельных
оси ординат, пересекающих ось абсцисс в точках х0 = a, xv x2i ., ¦
хп = Ь. Заменим каждую частичную трапецию прямоугольником, высо-
высотой которого является значение функции/(х) в средней точке^,
частичного интервала: g. = ^bl^b?t (рИС. 126). Центр тяжести
каждого построенного прямоугольника известен: он лежит в
его центре, т. е. в точке М}[?,-,—/(?/) ); масса
хо=а $, х, ? х2
Рис. 126.
соответствующего
прямоугольника равна произведению его площади на плотность,
т. е. 6/E/) Д#/. Сосредоточим всю массу каждого прямоуголь-
прямоугольника в его центре тяжести и найдем координаты центра тяжести
полученной системы материальных точек:
24-им «ш
Так как плотность б — величина постоянная, то, вынося ее за
знак суммы и сокращая, получим
?<«) _
1) Отыскание центра тяжести пластинки произвольной формы и пере-
переменной плотности будет произведено в гл. VIII, п. 132, II.
ЗС2
ГЛ. VI. ПРИМЕНЕНИЕ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
[103
Геометрически ясно, что если, как обычно, стремить п к беско-
бесконечности и все Axi к нулю, то точки с координатами (?(и), ц(п))
будут стремиться к центру тяжести данной пластинки. В знаме-
знаменателях стоит интегральная сумма для функции y=f(x); преде-
ь
лом ее будет интеграл ^f(x)dx, т, е. площадь 5 пластинки.
а
В числителях стоят интегральные суммы соответственно для функ-
функций х/(х) и /2(х). Поэтому
\)xi(x)dx j\jti(x)dx
t в , *.__?
6- s » Л- s
Коротко эти формулы записывают так:
где y==
Пример. Найдем координаты центра тяжести однородного
полукруга радиуса R.
Выберем систему координат, как указано на рис. 127. Тогда
уравнение ограничивающей окружности будет y = YR2—х2.
В силу симметрии относительно оси ординат абсцисса \ центра
тяжести равна нулю: ? = 0. Най-
Найдем ординату центра тяжести:
R
у I {R*-x*)dx
Рис. 127.
Метод, примененный для отыскания координат центра тяжести
криволинейной трапеции, заключался в том, что трапеция разби-
разбивалась на части и положение центра тяжести каждой части отыс-
отыскивалось приближенно. Затем отыскивались координаты центра
тяжести системы точек с последующим переходом к пределу.
Этот же метод применим и для отыскания центра тяжести других
104] § 2. ОБЩАЯ СХЕМА ПРИМЕНЕНИЯ ИНТЕГРАЛА 353
тел. Найдем, например, центр тяжести тела, образованного враще-
вращением криволинейной трапеции вокруг оси абсцисс; объемную плот-
плотность тела обозначим череа б кг/мг. Пользуясь обозначениями
рис. 126, легко получим (рекомендуем читателю провести рассуж-
рассуждения самостоятельно)
2
Jk-л
Ясно, что центр тяжести лежит на оси вращения, и поэтому вели-
величина 2; полностью его определяет.
Пример. Найдем координаты центра тяжести полусферы,
образованной вращением четверти окружности jf = |//?2—х2
^/?) вокруг оси абсцисс:
;
Предоставляем читателю самостоятельно получить следующие
формулы для координат центра тяжести однородной линии,
заданной уравнением y=f(x), начальная точка А и конечная
точка В которой имеют абсциссы соответственно а и Ь\
ь ь ь ь
\xV\ + yt2dx lxd*
6 = *-
L ~~ L ' '— L L >
где L—длина дуги АВ, a ds—дифференциал длины дуги.
§ 2. Общая схема применения интеграла
104. Схема решения задач. Во всех рассмотренных нами зада-
задачах на применение определенного интеграла схема рассуждений
была одна и та же. Искомая величина (площадь, работа, путь,
объем и т. д.) соответствовала некоторому интервалу изменения
переменной величины, как раз той, которая в последующем слу-
служила переменной интегрирования. Так^ площадь трапеции соответ-
соответствовала интервалу [а, Ь] изменения абсциссы лг, работа — интер-
12 А. Ф. Бермант, И. Г. Араманович
354 ГЛ. VI. ПРИМЕНЕНИЕ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ [104
валу [s0, s] изменения пути s, путь — интервалу [Т0У Т] изменения
времени t и т. д.
Будем в дальнейшем предполагать, что эта переменная вели-
величина обозначена через х, а интервал ее изменения через [а, Ь].
Первым нашим шагом являлось разбиение интервала [а, Ь] на
частичные интервалы [xh xi+1], / = 0,l, ..., /z— 1, хо= ау хп = Ь.
При этом мы исходили из той существенной предпосылки, что опре-
определяемая величина, соответствующая всему интервалу, составляется
как сумма из таких же величин, соответствующих всем частичным
интервалам (свойство аддитивности). Так, площадь, работа, путь
аддитивны относительно интервалов, к которым они отнесены;
площадь криволинейной трапеции, имеющей основанием некоторый
интервал, равна сумме площадей криволинейных трапеций, имею-
имеющих основаниями все частичные интервалы; работа, произведенная
силой на некотором участке, равна сумме работ, произведенных
этой силой на всех частичных участках, и т. д.
Далее мы составляли сумму (интегральную сумму), выражающую
приближенное значение искомой величины, тем более точное,
чем меньше наибольший из частичных интервалов (и, значит, чем
больше п — число этих интервалов).
Переходя к пределу при п—*оо, мы находили искомую вели-
величину / в виде интеграла
ь
(*)
где f(x)—данная по условиям задачи функция (ордината линии,
ограничивающей трапецию, действующая сила, скорость движе-
движения и т. д.).
Точно также может быть решена и всякая другая задача анало-
аналогичного типа. Но мы сейчас покажем, что изложенный путь решения
(разбиение интервала на части, суммирование, переход к пределу)
эквивалентен более простому и единообразному пути, исходящему
из окончательного результата (искомая величина равна интегралу
от некоторой данной функции) и опирающемуся на теорию опре-
определенного интеграла.
Будем рассматривать интересующую нас величину (площадь,
работу, путь) на переменном интервале [а, л:] с фиксирован-
фиксированным левым концом а(а^а). Тогда эта величина будет какой-то
неизвестной функцией u — F(x) от абсциссы х правого конца
интервала. Если бы функция F(x) была известна, то лег-
легко было бы найти значение искомой величины, соответству-
соответствующее данному интервалу [а, Ь]; это значение мы обозна-
обозначим через Л Так как F(b) соответствует интервалу {а, Ь]у
/"(а)—интервалу [а, а] и /^-интервалу [a,b]t то в силу свойства
104] § 2. ОБЩАЯ СХЕМА ПРИМЕНЕНИЯ ИНТЕГРАЛА
аддитивности
т. е.
355
= F(b)-F(a).
(**)
Особенно наглядно это видно на примере площади криволинейной
трапеции (рис. 128). Здесь I = SaABb, F(a) = SaCAat F(b)=SaCBb и
равенство (**) очевидно.
Мы считаем функцию F(x) дифференцируемой; по формуле
Ньютона — Лейбница будем иметь
ь
т. е.
искомая величина I измеряется интегралом от дифференциала
функции u~F(x), взятым по интервалу [а, Ь], которому соответ-
соответствует эта величина.
Таким образом, подынтегральное выражение f(x)dx вформуле(*)
есть не что иное, как дифференциал du функции и = F (x), и стало
быть, для решения задачи доста-
достаточно знать даже не саму функ-
функцию F(x), а только ее диффе-
дифференциал; тогда искомая величина
выразится интегралом от этого
дифференциала, взятым по интер-
интервалу [а, Ь].
Теперь по аналогии с рассмотрен-
рассмотренными задачами можно дать общую
характеристику простейшей задачи,
решаемой с помощью определенного интеграла. Эта характеристи-
характеристика состоит в следующем:
1) В задаче ищется значение / некоторой величины и, соответ-
соответствующее данному интервалу [а, Ь] изменения независимой пере-
переменной х. Величина и обладает свойством аддитивности, т. е. при
разбиении интервала на части ее значение, соответствующее всему
интервалу, составляется как сумма ее значений, соответствующих
частичным интервалам.
2) Если величину и отнести к переменному интервалу с закреп-
закрепленным, например, левым концом а(сс^я) и переменным правым
концом х, то и можно рассматривать как функцию независимой
переменной х> т. е. u = F{x); функция F{x) предполагается диф-
дифференцируемой.
Рис. 128.
12*
356 ГЛ. Vi. ПРИМЕНЕНИЕ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ [104
При соблюдении обоих условий величина / будет равна
ь
х x+dx Ь
Рис. 129.
х
Это означает, что весь вопрос сводится к отысканию дифферен-
дифференциала du~dF(x).
Хотя функция u = F(x) и неизвестна, ее дифференциал часто
можно найти из условий задачи. Для этого в произвольной точке х
заданного интервала [at b] берется бесконечно малое приращение
dx и рассматривается соответст-
соответствующее ему приращение &F(x).
Та часть этого приращения, кото-
которая получилась бы, если бы все
другие величины, определяющие
образование ^(л:), сохранили в
интервале [xt x-\-dx) свои значе-
значения, принйтые в точке л:, обычно
и оказывается дифференциалом
dF(x). Всякий раз можно проверить,
что составленное выражение дейст-
действительно является дифференциа-
дифференциалом, убедившись в том, что оно,
во-первых, пропорционально dx,
а во-вторых^ отличается от kF(x) на бесконечно малую величину
более высокого порядка, чем dx.
Последнее требование эквивалентно тому, что предел отноше-
отношения полученного выражения к AF(x) при dx—> () равен единице.
Поясним сказанное на примере.
Рассмотрим простейшую задачу о площади криволинейной тра-
трапеции и получим ее решение новым, только что описанным мето-
методом. Пусть трапеция ограничена линией у=/(х); площадь ее,
соответствующую интервалу [а, Ь] изменения лг, обозначим через S.
Площадь трапеции аСМх будет функцией от X; обозначим ее S(x).
Выберем произвольное значение х и придадим ему приращение dx.
Тогда приращение Д5(лг) выразится площадью трапециилгЛШ'(лг + dx)
(рис. 129). Докажем, что дифференциалом функции S(х) будет
площадь прямоугольника xMN(x-\-dx), т. е. та часть прираще-
приращения Д5(аг), которая получается, когда мы считаем функцию f(x)
на интервале [х, x-{-dx] постоянной:
dS(x)=f(x)dx.
Так как написанное выражение для dS(x) пропорционально dx, то
остается проверить только, что оно эквивалентно &S(x). Из рис. 129
105]
§ 2. ОБЩАЯ СХЕМА ПРИМЕНЕНИЯ ИНТЕГРАЛА
357
видно, что их разность не превосходит площади прямоугольника
MAf'M'N, равной произведению АхАу:
AS(x) — dS(x)<AxAy.
Таким образом, эта разность является бесконечно малой величиной
более высокого порядка, чем Длг, что и доказывает справедливость
нашего утверждения (см. п. 51, IV).
Следовательно, в силу доказанного
Так как раньше, в п. 66 гл. IV, мы нашли, что дифференциал
длины дуги ds равен
то можно сразу написать (ср. с п. 102), что длина дуги L равна
ъ
105*. Площадь поверхности вращения. Выведем формулу для
поверхности тела вращения.
Пусть некоторая дуга АВ линии у = f(x) вращается вокруг
оси Ох (рис. 130). Требуется определить площадь Q поверхности
\
ч
й
йд
2
3
\
i
Рис. 130.
вращения в предположении, что функция f(X) HMeet непрерывную
производную.
358 ГЛ. VI. ПРИМЕНЕНИЕ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ [Ю5
Обозначим через Q(x) площадь, соответствующую интервалу
[а, х], и определим дифференциал площади. Поступим сле-
следующим образом. Проведем через произвольную точку лг, а < х <Д
плоскость, перпендикулярную к оси Ох. Придадим х прираще-
приращение dx; тогда площадь Q(x) поверхности получит приращение АС?,
равное площади поверхности, заключенной между плоскостями,
перпендикулярными к оси Ох и проходящими через точки х и
x-\-dx. Величина AQ удовлетворяет следующим неравенствам
(мы считаем, что Ay<dy, как это и изображено на рис. 130):
Действительно, выражение слева измеряет площадь поверхности
усеченного конуса, образующей которого служит хорда дуги,
а выражение справа дает площадь поверхности усеченного конуса,
образующей которого служит отрезок касательной. Деля все
члены неравенства на 2ny]/rdx2 + dy21 находим
4пу + 2лАу Yd* + Д У% < AQ
Так как при dx—*0 и левая и правая части стремятся к 1, той
2пу
Следовательно, выражение
2пу Vdx* + dy2 = 2nyV\ +y'2 dx
и является дифференциалом dQ(x). Отсюда
ь
или, сокращенно,
где ds — дифференциал длины дуги.
От этих формул легко перейти к случаям, когда вращающаяся
линия задала параметрическими уравнениями или уравнением в по-
полярной системе координат.
106]
§ 2. ОБЩАЯ СХЕМА ПРИМЕНЕНИЯ ИНТЕГРАЛА
359
Рекомендуем читателю самостоятельно написать соответствующие
формулы.
Пример. Вычислим площадь сферического пояса. Пусть дуга
окружности с центром в начале координат и радиусом г вращается
вокруг оси Ох.
Из уравнения окружности х2 + у2 = г2 имеем: 2 22
у у' = — х и, значит,
ь ь
— х2 I/ 1
= г2—х2,
**
т —
j
а
где Н—высота пояса. При Н = 2г получаем площадь сферы ф =
106. Давление жидкости на стенку сосуда. Пусть жидкость
(удельный вес ее обозначим через у н/м3) заполняет сосуд прямо-
прямоугольной формы. Подсчитаем давление Р этой жидкости на одну из
стенок сосуда, считая, что основание этой стенки равно а, а вы-
высота А. Здесь может быть применена общая схема, так как давление
на всю стенку складывается из суммы давлений на отдельных-ее
участках.
Обозначим давление на заштрихованную часть стенки (рис. 131)
через Р(х). Придадим х приращение dx. Мы найдем главную часть
приращения АР(х), пропорциональную dx, счи-
считая, что на выделенной полоске глубина жид-
жидкости не меняется и постоянно равна х.
Тогда
dP(x) = yax dx. (*)
Так как приращение АР(х) <ya(x-\-dx) dx,
то разность между АР(х) и dP(x) не превос-
превосходит
у а (х + dx) dx—у ах dx = у a dx'st
т. е. является бесконечно малой величиной бо- Рис. 131.
лее высокого порядка малости, чем dx.
Следовательно, мы доказали, что выражение (*) действительно
является дифференциалом функции Я(лг). Интегрируя в пределах
от 0 до А, получим
Интересно отметить, что это давление равно давлению жидкости
на площадку тех же размеров, погруженную горизонтально на глу-
глубину своего центра тяжести,
360 ВОПРОСЫ И ПРЕДЛОЖЕНИЯ
ВОПРОСЫ И ПРЕДЛОЖЕНИЯ ДЛЯ САМОПРОВЕРКИ
1. Как вычисляется площадь плоской фигуры в системе декартовых
координат? в системе полярных координат? в случае задания линии пара-
параметрическими уравнениями?
2. Вывести формулу для вычисления объема тела по площади его парал-
параллельных сечений.
3. Вывести формулу для объема тела вращения.
4. Дать определение длины кривой линии. Какова формула для вы-
вычисления длины линии в системе декартовых координат? в системе поляр-
полярных координат? в случае задания линии параметрическими уравнениями?
5. Вывести формулы для координат центра тяжести криволинейной
трапеции.
6. В чем состоит схема решения задач с помощью определенного инте-
интеграла и какова характеристика этих задач?
7. Привести примеры применения схемы.
8*. Какова формула для вычисления площади поверхности вращения
в системе декартовых координат? в случае задания вращающейся линии
параметрическими уравнениями?
ГЛАВА VII
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ.
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
§ 1. Функции нескольких переменных
107. Функции двух и многих переменных.
I. Случай двух независимых переменных. До сих
пор мы изучали функции одной независимой переменной. Но не-
нередко встречаются случаи, когда какая-нибудь величина зависит
не от одной независимой переменной, а от двух или большего
числа независимых переменных, т. е. когда значения первой ве-
величины находятся по значениям не одной, а двух или большего
числа других переменных величин. В этих случаях говорят, что
указанная величина является функцией двух или соответственно
ббльшего числа независимых переменных.
Например, площадь 5 прямоугольника есть функция двух не-
независимо друг от друга изменяющихся переменных—сторон пря-
прямоугольника а и Ь\ выражение для этой функции таково:
Объем V прямоугольного параллелепипеда является функцией
трех независимо друг от друга изменяющихся величин—ребер
параллелепипеда а, Ь% с:
V=abc.
Работа электрического тока А на участке цепи зависит от
разности потенциалов U на концах участка, силы тока / и вре-
времени t\ эта функциональная зависимость дается формулой
Остановимся сначала на случае двух независимых переменных,
которые будем обозначать буквами х и у.
Каждой паре значений х и у соответствует точка на плос-
плоскости Оху, координатами которой они служат. Возьмем некоторое
множество точек на плоскости Оху и обозначим его через D.
362
ГЛ. VII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[107
Определение. Величина z называется функцией перемен-
переменных величин х и у на множестве />, если каждой точке этого мно-
множества соответствует одно определенное значение величины г.
Множество точек D называется областью определения функции.
Обычно областью определения функции является некоторая часть
плоскости, ограниченная одной или несколькими линиями.
Тот факт, что величина z есть функция величин х и у, запи-
записывают так:
*=/(*, у).
В такой записи за символом функции (которым может быть не
только буква /, но и любая другая буква) указываются в скобках
те переменные (аргументы), от которых зависит функция.
II. Способы задания функции. Как и функции одной
переменной, функции двух переменных могут быть заданы табли-
таблицей, аналитически (формулой) и графиком (см. п. 8).
Табличное задание состоит в том, что для некоторого
количества пар значений независимых переменных указываются
соответствующие им значения функции. Осуществляется это обычно
посредством таблицы с двойным входом, устройство которой
должно быть понятно из рассмотрения, например, следующей таб-
таблицы для коэффициента полезного действия ц винтовой передачи
как функции от коэффициента трения \i и угла подъема а вин-
винтовой линии:
\
и-
0
0
0
\ а
,01
,02
,03
0
0
0
я
36
,897
,812
,743
0
0
0
я
18
,945
,895
,850
0
0
0
я
12
,961
,925
,892
Аналитическое задание функции означает, что дается
формула, при помощи которой по заданным значениям независимых
переменных отыскиваются значения функции.
Так, например, каждая из формул
sinB*+3|/)
задает z как функцию хну. При аналитическом задании функции
за область ее определения принимают (если нет дополнительных
условий) множество значений хну, для которых формула, опре-
определяющая функцию, имеет смысл, т. е. когда в результате ее
107] § 1. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 363
применения для z получаются определенные действительные зна-
значения. Так, например, областью определения функции
z = Vr2—х2— у2
является множество точек плоскости Оху, координаты которых
удовлетворяют соотношению
т. е. круг радиуса г с центром в начале координат. Для функции
—г2)
областью определения служат точки, координаты которых удов-
удовлетворяют условию
х2+у2>г2,
т. е. внешность круга.
Функция z = утг~Т1Г~2 определена на всей плоскости, а функ-
ция z =sin^' на всей плоскости, за исключением прямой у = х.
Так же как и для функций одной переменной, можно рассмат-
рассматривать неявные функции двух независимых переменных. Уравне-
Уравнение, связывающее три переменные величины:
F(x, у, *) = 0,
обычно определяет каждую из этих величин как неявную функцию
двух остальных; подробнее об этом будет сказано в п. 117.
Прежде чем перейти к графическому заданию, заметим, что
графиком функции z двух независимых переменных хну
(в системе декартовых прямоугольных координат) называется мно-
множество точек, абсциссы и ординаты которых являются значе-
значениями х и ул а аппликаты — соответствующими значениями z. Гра-
Графиком функции непрерывных аргументов обычно служит некоторая
поверхность.
Так как уравнение x2+y2-{-z2 = R2 есть уравнение сферы
радиуса R с центром в начале координат, то графиками функций
служат верхняя и нижняя половины этой сферы (рис, 132),
Графиком функции
является параболоид вращения (рис. 133), а графиком линейной
364
ГЛ. VII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
И 07
функции
z = ах + by + с
— плоскость; в частности, графиком константы, т. е. функции
z— С (С = const), служит плоскость, параллельная плоскости Оху.
Обратно, всякая поверхность в координатном пространстве Oxyz
изображает некоторую функцию двух независимых переменных,
именно ту, значения которой
равны аппликатам точек
Рис. 132.
Рис. 133.
поверхности при значениях независимых переменных, равных абс-
абсциссам и ординатам.
Графическое задание функции двух переменных как раз
состоит в задании графика этой функции.
III. Случай многих независимых переменных.
Распространим теперь данные выше определения на случай боль-
большего числа независимых переменных.
Пусть лг, у, z, . . . , /—независимые переменные, а и — вели-
величина, зависимая от них, т. е. их функция.
Определение. Величина и называется функцией перемен-
переменных величин xf y9 z, ... , t, если каждой рассматриваемой сово-
совокупности этих величин соответствует одно определенное значе-
значение величины а
То, что величина и и есть функция величин л:, у, г, . • • , *,
записывают так:
« = /(#, У, *, ... , ').
причем, разумеется, вместо буквы / в качестве символа функции
может быть употреблена любая другая буква.
Все другие определений, относящиеся к Случаю двух независи-
независимых переменных, без существенных изменений переносятся на
случай многих независимых переменных, и поэтому на них оста-
108J
§ 1. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
365
навливаться нет нужды. Заметим только, что геометрическая ил-
иллюстрация функций от п независимых переменных при п > 2 те-
теряет наглядность. Уже при/г = 3, т. е. для функции и=/(лг, у, z),
геометрически можно представить только область определения
функции в виде части трехмерного пространства. При п > 3 да-
даже области определения функции делаются геометрически нена-
ненаглядными.
Запись
F(xf у, z, ...,/, и) = 0 (*)
означает в общем виде наличие функциональной связи между ве-
величинами х, у, Z) . . . , t, и, т. е. тот факт, что какая-нибудь из
этих величин, например а, является неявной функцией остальных.
108. Метод сечений* Предел и непрерывность.
I. Метод сечений. Линии уровня. Как известно, в ана-
аналитической геометрии при изучении поверхностей второго порядка
обычно пользуются методом сечений, который заключается
в том, что определение вида поверхности по ее уравнению произ-
производится путем исследования кривых, образованных при пересече-
пересечении этой поверхности плоскостями, параллельными координатным
плоскостям. Этот же метод исследования применим и при изучении
любых функций двух переменных. Пусть, например, задана функция
* = /(*, У),
определяющая некоторую поверхность. Если мы придадим аргу-
аргументу у постоянное значение у0 и будем изменять только х, то
z станет функцией одной независимой пе-
переменной х:
*=/(*, Уо)-
Применив к этой функции известные методы
исследования функций одной переменной,
мы можем выяснить характер изменения
величины z в зависимости от изменения х.
Геометрически это означает, что мы рас-
рассматриваем линию пересечения поверхности
2:=/(лг, у) и плоскости у =j>0, параллель-
параллельной плоскости Oxz (линия CD на рис.
134). Придавая теперь^ другое постоянное значение^, получим
линию C1D1 и т. д.
Аналогично можно выяснить поведение z в зависимости от
изменения у при различных, но постоянных значениях лг. Так, на
рис. 134 изображена линия АВ пересечения поверхности z=f(x,y)
и плоскости л; = а:0. Чтобы представить себе эту линию, мы должны
366
ГЛ. VII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[108
исследовать функцию одной переменной z~f(xOy у). Зная харак-
характер расположения полученных линий, мы сможем составить себе
представление о всей поверхности, т. е. описать поведение функ-
функции z при произвольном изменении ее аргументов.
Но можно изучать функцию z = f(x, у) посредством того же
приема сведения функции двух переменных к функции одной пе-
переменной, придавая постоян-
постоянные значения не одной из не-
независимых переменных,а самой
функции. Именно положим
z = z0; тогда уравнение
дает зависимость между пе-
переменными х и у (т. е. функ-
функцию одной переменной), при
которой заданная функция z
сохраняет постоянное значе-
значение z0. Геометрически прида-
придание z постоянного значения z0
означает пересечение поверх-
поверхности z = f(x, у) плоскостью
z = zQi параллельной плоскос-
плоскости Оху.
На плоскости Оху уравнение (*) есть уравнение проекции /
линии пересечения L поверхности z=f(x, у) с плоскостью z = z0
(рис. 135)х). При перемещении точки с координатами х, у вдоль
линии / функция сохраняет постоянное значение, равное z0.
Определение. Линией уровня функции z =/(лг, у) назы-
называется линия на плоскости Оху, в точках которой функция со-
сохраняет постоянное значение.
Совокупность линий уровня, соответствующих различным зна-
значениям z, называется сетью линий уровня функции z = f(x, у).
Сеть эта, при условии, что она проведена для мало отличающихся
друг от друга значений z, довольно наглядно характеризует пове-
поведение функции.
Придадим z значения ... —ЗА, —2А, —А, О, А, 2А, ЗА, ... ,
где А—какое-нибудь положительное число. Сеть линий уровня
функции f(x, у) для этих значений назовем равномерной.
В тех участках плоскости Оху, где линии уровня равномерной сети
сгущаются, функция изменяется «быстро», а в тех, где они разре-
разрежаются, функция изменяется «медленно». Действительно, в первом
Рис. 135.
*) В пространстве уравнение f (х, #) = *0 определяет цилиндрическую
поверхность с образующими» параллельными оси#г, и направляющей / (или L).
108]
§ 1. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
367
случае небольшому, а во втором случае большому перемещению
точки Р(х, у) соответствует изменение функции на одну и ту же
величину А.
На рис. 136 изображена равномерная сеть (h=\) функции
z = x2-\-y2 (параболоид вращения). Этой сетью служит система
концентрических окружностей с цент-
центром в точке О@, 0) и сама эта точка.
Ясно видно, что по мере увеличения
А окружности сети сближаются, что
соответствует увеличению крутизны
поверхности.
В прикладных науках часто упот-
употребляют линии уровня для представ-
представления изучаемой функции двух неза-
независимых переменных. Так, например,
рассматривая высоту точки местности
над уровнем моря как функцию двух
переменных — координат точки, на
карты наносят линии уровня этой
функции. Они называются в топогра-
топографии горизонталями. С помощью
сети горизонталей удобно следить за
изменением высоты местности. В ме-
метеорологии пользуются сетями изотерм и изобар (линий оди-
одинаковых средних температур и линий равных средних давлений),
являющимися линиями уровня температуры и давления как
функций координат точки местности.
II. Предел функции. Перейдем теперь к определению пре-
предела функции двух переменных; оно будет совершенно аналогично
определению предела для функций одной переменной1).
Определение. Число А называется пределом функции
z=f(x,y) при х —>х0, у—+у0, если для всех значений х и у9
достаточно мало отличающихся соответственно от чисел х0 и у0,
соответствующие значения функции /(*, у) как угодно мало от-
отличаются от числа А.
Записывают
г-1
У
Рис. 136.
Hm f(x,y) = .
Х-*Хц
(*)
В этом определении не предполагается, что функция определена
в самой точке Р0(хь, yQ)t и поэтому мы считаем, что либо
либо
1) Читателю рекомендуется вспомнить содержание п. 24 гл. И.
368 ГЛ. VII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [108
Вполне аналогично определяется предел функции п независимых
переменных при п > 2.
Отметим также, что все правила предельного перехода, рассмот-
рассмотренные в п. 29 гл. II, без всяких изменений переносятся на случай
функций многих переменных.
III. Непрерывность функции. Пусть точка Я0(лг0, у0)
принадлежит области определения функции z = f (лг, у). Также
как и для функции одной переменной, приращением функции
z = f(x, у) в данной точке Ро называется разность
f(xo, у о),
где Ах и Ау — приращения аргументов.
Определение. Функция г =/(jc, у) называется непрерыв-
непрерывной в точке (jc0, y0), если она определена в некоторой окрестно-
окрестности этой точки и если бесконечно малым приращениям х и у
соответствует бесконечно малое приращение г, т. е.
lim Дг = 0.
Обозначив хо-\-Ах через х и yQ-}-Ay через у, мы можем условие
непрерывности функции f(x, у) записать в виде
lim [f(x,y)~/(лг0, >>в)] = 0 или 11т/(лг, у)=/(х
Последнее означает, что функция непрерывна в точке (лг0, у0), если
ее предел равен значению функции в предельной точке.
Определение. Функция, непрерывная в каждой точке об-
области, называется непрерывной в этой области.
Геометрически непрерывность функции z — f(x, у) означает,
что аппликаты точек ее графика, соответствующие двум точкам
плоскости Оху, как угодно мало отличаются друг от друга, если
расстояние между точками плоскости достаточно мало. Поэтому
график непрерывной функции представляет собой с п л ош н у ю
поверхность без разрывов.
Непрерывные функции двух независимых переменных обладают
теми же основными свойствами, что и непрерывные функции одной
независимой переменной (см. п. 35 гл. II).
Точка в плоскости Оху, в которой не выполняется условие
непрерывности функции, называется точкой разрыва функции. Точки
разрыва функции двух переменных могут образовывать целые линии.
Приведем примеры разрывных функций.
Функция ?= 2 з непрерывна всюду, кроме точки @, 0), кото-
рая является точкой разрыва. Ясно, что когда х—>0 и у—»0^ то
109] § 2. производные и дифференциалы 369
z—юо. Геометрически это означает, что в точке @, 0) поверхность
имеет бесконечный шпиль.
Воспользовавшись известным из аналитической геометрии общим
видом уравнения поверхности вращения, заметим, что уравнение
z~ 2 , % определяет поверхность, образованную вращением кри-
х "т~ У
вой z = -5, д> = 0, расположенной в плоскости Oxz, вокруг оси Oz.
Для функции г = й_ 2 точками разрыва являются все точки,
лежащие на биссектрисах координатных углов плоскости Оху, т. е.
точки, в которых у=х или у = —х.
Более сложный пример точки разрыва представляет точка @* 0) для
функции
*>У)-х2+у2-
В каждой точке прямой у — kx, где ft —любое число, функция принимает
постоянное значение
Если точка (*, у) стремится к точке @, 0) по прямой y = kx, то предел функ-
функции будет равен ¦ а . Придавая k различные значения, т. е. идя к на-
чалу координат по разным прямым, мы будем получать разные пределы
для функции I(xt у). Это и означает, что при произвольном стремле-
стремлении х и у к нулю функция не имеет предела и является, следовательно,
разрывной.
Совершенно аналогично определяется непрерывность функций
любого числа независимых переменных.
§ 2. Производные и дифференциалы. Дифференциальное
исчисление
109. Частные производные и дифференциалы.
I. Частные производные. Пусть z — f(x, у)—функция
двух независимых переменных х и у. Будем считать сейчас аргу-
аргумент у постоянным и рассмотрим получающуюся при этом функцию
одной переменной лг. Допустим, что эта функция / (лг, у) при дан-
данном значении х дифференцируема, т. е. имеет производную, равную
Этот предел мы обозначим через Д (лг, у), указывая нижним ин-
индексом х, что производная берется по переменной х при фикси-
фиксированном у.
370 ГЛ. VII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [109
Определение. Частной производной по х от функции
z=f(x, у) называется функция переменных х и у, получающаяся
при дифференцировании f(x, у) по х в предположении, что у
считается постоянным.
Для частной производной по х от функции z=f(x, у) употреб-
употребляют следующие обозначения:
дг ' df (*, у) ±rf( ч1
В отличие от обозначения обыкновенной производной, здесь
употребляется не прямое dy а круглое д и кроме верхнего штриха
нижним индексом указывается переменная х, по которой произво-
производится дифференцирование. (Иногда штрих сверху опускают и пи-
пишут просто zx или fx(xf у).) Обычно в тексте пишут z'x, а в фор-
дг
мулах Тх .
Обращаем внимание читателя на то, что у считается постоян-
постоянным только в процессе дифференцирования.. После того, как
выражение для /х (лг, у) найдено, хну могут принимать любые
значения. Это и означает, что Д(лг, у) является функцией обеих
переменных. Например, если z~x2y, то z'x = 2xy.
Разумеется, в частных случаях fx (лг, у) может оказаться зави-
зависящей от одной переменной или даже быть постоянной. Например,
если z = xy, то zx=y, а если z — 2x+y2, то zx = 2.
Совершенно аналогично определяется частная производная по
у от функции z—f(x% у):
Она обозначается еще так:
ду> Zy
Так как частная производная является обыкновенной про-
производной от данной функции, взятой в предположении, что изме-
изменяется только переменная, по которой производится дифференци-
дифференцирование, то фактическое отыскание частных производных
элементарных функций осуществляется по известным правилам
дифференцирования функций одной переменной.
Примеры. 1) Найдем гх и z'y от функции z — ЪаХу— х*— у9.
109] § 2. производные и дифференциалы 371
Считая у постоянной, имеем
g-Зоу-З*»;
считая х постоянной, имеем
2) Найдем zx и zy от функции z — xy.
При дифференцировании по х функция z является степенной,
а при дифференцировании по ^—-показательной. Находим
Значения частных производных при определенных значениях
лг0 и у=у0 обозначаются посредством символов
или
Например, если * = 3a.x:j;—х3—у9, то
Аналогично определяются частные производные от функции
любого числа независимых переменных.
Обозначения для частных производных такие же, как и в слу-
случае двух переменных, например:
дп- f (х v z t\- lim
Пусть r*=y x2-\-y2-\-z2. Эта функция выражает, между прочим,
расстояние точки Р(лг, уу z) от начала координат. Для ее частных
производных находим выражения
г- дох~у , \ *-*
дг
где cos a, cos p, cosy — направляющие косинусы полярного радиу-
радиуса точки P(xf y} z)i эти формулы нам встретятся в дальнейшем.
372
ГЛ. VII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[109
Абсолютная величина частной производной г'х=/х(х, у) или
z'y=zfy(x, у) дает величину скорости, с которой происходит из-
изменение функции z=f(x,y) при изменении только х или только
у, а знак частной производной Д или fy указывает характер этого
изменения (возрастание, убывание).
Геометрический смысл частных производных от функции
z = f(x, у) состоит в следующем: fx(xQ, yQ) есть угловой коэффи-
коэффициент относительно оси Ох, касательной в точке Л40(лг0, yOi z0) к се-
сечению поверхности z=f(x, у) плоскостью у =у0, т. е. fx (xOtyo) = tga
(рис. 137, а). (Видно, что на рисунке f'x(xQ, у0) < 0.)
У
Рис. 137.
Частная производная f? (х0> у^) есть угловой коэффициент отно-
относительно оси Оу, касательной в точке Мо (xQy yOt z0) к сечению по-
поверхности z=f(x, у) плоскостью лг = лг0, т. е. /у(х0, ^о)=^Р
(рис. 137,6). {Видно, что на рисунке /у (х0, у0) > 0.)
II. Частные дифференциалы. Приращение, которое по-
получает функция z=f(x, у), когда изменяется только одна из
переменных, называется частным приращением функции по соответ-
соответствующей переменной. Употребляются такие обозначения:
109] § 2. производные и дифференциалы 373
Определение. Частным дифференциалом по х функции
z=azf(x,y) называется главная часть частного приращения
А^г=/(л; + Ал:, у)—f(x,y)9 пропорциональная приращению Адг
независимой переменной х.
Аналогично определяется частный дифференциал по у.
Дифференциалы независимых переменных х и у просто равны
их приращениям, т. е.
Частные дифференциалы обозначаются так: dxz—частный диф-
дифференциал по х, dyz—частный дифференциал по у.
Так же, как для случая функции одной переменной, доказы-
доказывается, что если функция z — f(xy у) имеет частный дифферен-
дифференциал по лг, то она имеет и частную производную z'x, и обратно
(см. п. 60). При этом
Аналогично, если функция z=f(x, у) имеет частный диффе-
дифференциал по у, то она имеет и частную производную zy и обратно,
причем
i
Таким образом, частный дифференциал функции двух независи-
независимых перепенных равен произведению соответствующей частной про-
производной на дифференциал этой переменной.
Геометрический смысл частного приращения Axz состоит в том,
что оно выражает приращение аппликаты точки поверхности
при изменении аргумента х на Дат (рис. 137, а). На рисунке при-
приращение Axz < 0, оно изображено отрезком R0M0. Частный диф-
дифференциал dxz выражает приращение аппликаты точки касатель-
касательной Тх при том же изменении аргумента. В нашем случае dxz < 0,
он изображен отрезком /?вГв.
Точно так же частное приращение AyZ выражает приращение
аппликаты точки поверхности при изменении аргумента у на
Ау (рис. 137,6). На рисунке приращение Ayz > 0, оно изображено
отрезком R0MQ. Частный дифференциал dyz выражает приращение
аппликаты точки касательной Т . В нашем случае djc > 0,
он изображен отрезком RqT"q.
Из формул для частных дифференциалов находим
Ъх ах* ду dy '
Отсюда видно, что частные производные можно рассматривать
374 ГЛ. VH. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [110
подобно обыкновенным производным как дроби, если только в чис-
числителе каждой дроби записывать соответствующий частный диф-
дифференциал, а в знаменателе — дифференциал независимой перемен-
переменной. Единообразные же записи ^- и д- являются слитными, не-
расчленяемыми символами, и их ни в коем случае нельзя считать
дробями, ибо если даже условиться, что дх и ду обозначают dx
и dyy то dz в первом и во втором случаях должно обозначать
различные величины (dxz и dyz).
Возьмем, например, уравнение Менделеева — Клапейрона
ч dp dv дТ лл
и найдем из него ~ , ^=, ^- . Имеем
ov дТ ор
dv dv\ v J v2 •
д?~дТ \~у)===~~р~'
дТ д f pv \ v
dp dp \ R J R
Произведение этих трех частных производных дает важное в тер-
термодинамике соотношение
д±ди_дТ__ El A iLsa BL— 1
dvdT dp~~~ t>2 p R ~~ pv """
Если бы обозначения частных производных через круглое д были
действительно дробями, то в произведении слева мы получили бы
1, а не —1.
Таким же образом, как для функций двух переменных, опреде-
определяются частные приращения и частные дифференциалы функций
любого числа независимых переменных.
При этом, если и=/(х} у, zt ..., /), то, как и выше,
т. е. частный дифференциал функции нескольких независимых пе-
переменных по какой-нибудь из них равен произведению соответствую-
соответствующей частной производной на дифференциал этой переменной.
110. Полный дифференциал.
I. Полное приращение и полный дифференциал.
Пусть функция z—f\xf у) дифференцируема по х и по у; тогда
с помощью частных дифференциалов мы можем находить как угодна
ПО]
§ 2. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
375
точные выражения для приращений функции при достаточно малых
изменениях х и у в отдельности. Естественно постараться найти
выражение для приращения функции z=f(xy у) при произвольных
совместных изменениях ее обоих аргументов. В этом случае при-
приращение функции
Az=f(x+Ax, у + Ау) —
-/(*, У)
называют полным приращени-
приращением. Геометрически прираще-
приращение функции при переходе
от точки Р(х, у) к точке
Рх (лс + Длг, у + Ау) выразит-
выразится отрезком QMX (рис. 138).
Полное приращение функ-
функции весьма сложно выражается
через приращения независи-
независимых переменных; только в
одном случае эта зависимость
проста, именно в случае, когда функция f(x, у) линейная:
f(x, y) = ax + by + c; тогда, как легко видеть,
7
х
Рис. 138.
Но оказывается, что для данных значений хну обычно
можно подобрать такие коэффициенты а и bt что выражение
аАх + ЬАу хотя и не будет в точности равно Az, но будет отли-
отличаться от Az на величину бесконечно малую более высокого по-
порядка, чем расстояние р между точками Р и Рх (р = У^Ах2 + Ау2):
Az = а Ах + ЬАу + а,
причем
lira—= 0.
о-*о Р
Сумма аАх-\-ЬАу называется полным дифференциалом функции
я=/(л;, у); она обозначается через йг или df\x, у):
dz — adx + bdy (*)
(как и раньше, Ax = dx, Ay = dy).
Таким образом, при р—*0 разность между полным прираще-
приращением функции Az и ее полным дифференциалом dz есть величина
бесконечно малая более высокого порядка, чем р. Коротко будем
говорить, что dz есть главная часть приращения Az, В силу ска-
сказанного определение полного дифференциала можно сформулиро-
сформулировать так:
376 ГЛ. VH. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ПО
Определение. Полным дифференциалом функции двух
независимых переменных называется главная часть полного при-
приращения функции, линейная относительно приращений независи-
независимых переменных.
Докажем теорему.
Теорема. Полный дифференциал функции двух независимых
переменных равен сумме произведений частных производных
функции на дифференциалы соответствующих независимых пере-
переменных.
Д о к азат е л ь с тво. Формула (*) для дифференциала спра-
справедлива при произвольных dx и dy и, значит, в частности, при
dy — О. Но тогда полное приращение функции Az становится
частным приращением Axz и мы получаем
dxz = a dx%
откуда (см. п. 109, И)
Аналогично доказывается, что b=fy(x, у). Следовательно, выра-
выражение для дифференциала при данных значениях хну записы-
записывается так:
dz=/x{x, y)dx+/y(xfy)dy
или
что и требовалось доказать.
Так как
ТО
т. е. дифференциал функции двух независимых переменных равен
сумме ее частных дифференциалов.
Примеры. 1) Пусть z — Заху—Xs—у9. Тогда
dz = (Зау—Зх2) dx + {3ax — 3y*) dy.
2) Для функции z = xy имеем
dz =уху~х dx + xy In x dy.
Определение дифференциала переносится на функции любого
числа независимых переменных. Если и= f(x, у, z% ..., t)t то
Ill] § 2. производные и дифференциалы 377
полное приращение функции и равно
Au=rf(x + Ax, у + Ау, z + Az, ..., t + At)— /(#, у} zy •.., t)>
а полный дифференциал du равен
. ди . . ди . . ди . . , ди А.
Связь между приращением и дифференциалом выражается соот-
соотношением
Аи =
где а — бесконечно малая более высокого порядка, чем
Р =
Замечание. Пусть u=f(x, уу z, ..., t)—функция незави-
независимых переменных х, у, z, ..., t и полный дифференциал ее при
всех значениях переменных х, у, zf ..., t и произвольных dx,
dy, dz, ..., dt тождественно равен нулю:
Полагая все дифференциалы, кроме rfjc, равными нулю, полу-
получим, что ^ = 0. Точно так же установим, что тождественно равны
ди ди ~
нулю и все остальные частные производные ^-, ..., ^т. Следо-
Следовательно, и не зависит от х% у, z} ..., tt т. е. является величи-
величиной постоянной.
". Дифференцируемое™ функций.
Определение. Функция двух независимых переменных»
имеющая в некоторой точке дифференциал, называется диффе-
дифференцируемой в этой точке.
Для случая одной независимой переменной наличие у функции
дифференциала оказалось эквивалентным существованию у этой
функции производной (см. п. 52). Для случая двух независимых
переменных дело обстоит сложнее. Существование у функции
частных производных, как оказывается, еще не обеспечивает на-
наличия у этой функции дифференциала, т. е. дифференцируемости.
Поясним сказанное на примере. Возьмем функцию z = \/хъ +у*
и рассмотрим ее в точке @, 0). При у~0 функция z = x и
^=1. В частности, (~) =1, Аналогично найдем
ох \™}х=:ъ
378 ГЛ. VII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [111
V=o = l. Итак, обе частные производные в точке <0, 0)
ствуют и равны 1.
Вместе с тем функция z = j/x3-{-yd в начале координат не
имеет дифференциала. В самом деле, если бы дифференциал dz
существовал, то он был бы равен
и разность Az—(dx-\-dy) при любых dx и dy была бы беско-
бесконечно малой величиной более высокого порядка, чем р = jfdx2 + dy2.
Если взять, например, dy = dx, т. е. перемещаться из начала
координат по биссектрисе координатного угла, то Az
dx и разность Az—(dx-\-dy) = (\/2—2)dx. Величина
при этом же условии равна }/^2dx. Следова-
Следовательно, величины Az—(dx + dy) и р имеют тот же порядок ма-
малости, что и dx, т. е. обе эти величины одного порядка.
Полученное противоречие показывает, что рассматриваемая
функция в начале координат не имеет полного дифференциала,
т. е. недифференцируема. Причина этого, как оказывается, заклю-
заключается в том, что частные производные -? и ^ в окрестности
начала координат разрывны.
Действительно, производная
дг_ х*
Тх'
в начале координат не определена. Выражение для zx показывает
также, что она не стремится к определенному пределу при про-
произвольном стремлении х и у к нулю. Если, например, стре-
стремиться к началу координат по биссектрисе у = х, то (~) —
t \°xJy=x
с= __ и предел будет равен 3 __. Если идти по оси абсцисс,
У 4 У 4
т. е. при У = 0, то(^~) ==1, и т. д. При у=—х производная
\ox/y=i0
zx вообще не существует (обращается в бесконечность). Это и
говорит о том, что в окрестности начала координат производная
г'х разрывна (то же можно сказать и о производной г у).
Если, помимо существования всех частных производных, доба-
добавить еще требование их непрерывности, то из этого уже
будет вытекать дифференцируемость функции.
§ 2. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
379
Теорема. Если функция z=f(x, у) имеет в точке Р(х, у)
непрерывные частные производные fx(x9 у) и fy(x,y), то в этой
точке функция дифференцируема.
Доказательство. Рассмотрим полное приращение функ-
функции *=/(*, у):
Az=f(x + Ax, y + Ay)—f(xy у).
Если к правой части этого равенства прибавить и отнять вели-
величину f(x, у + Ау), то выражение для Az запишется в виде
Az=[f(x + Axt y + Ay)-f(x, y + Ay)] + [f(xy у + Ay)-f(xy у)].
Иными словами, приращение функции при переходе от точки Р
к точке Рг (рис. 139)
мы представили в виде
суммы двух прираще-
приращений: приращения, кото-
которое получает функция
при постоянном х, т. е.
при переходе от точки
Р к точке /V, и при-
ращеция при постоянном
уу т. е. при переходе
от точки N к точке /V).
Выражение в первой
скобке является прира-
приращением функции /(л:, у)
при постоянном втором
аргументе (;; + Ду), ко-
коРис. 139.
гда л: получает приращение Ах. Рассматривая это приращение
функции одного лг, применим формулу Лагранжа (п. 67). Будем
иметь
=fx(Zv у + Ay) Ax,
где положение точки Q(gXi y + Ay) показано на рис. 139.
Точно так же, применяя формулу Лагранжа к выражению во
второй скобке как к приращению функции одного у, получим
/(*, y + by)-f{x, y)=/y(x9 Z2)Ay,
где точка R{x, g2) лежит на отрезке PN.
Таким образом,
A*=/*Fi. У + Ьу)Ьх+/у(х, 12)Ау.
Но по условию производные fx и fy—функции непрерывные. Так
1) Рассуждение почти не изменится, если рассматривать пркращенля
функции на участках PNt и NiPx,
380 ГЛ. VII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [112
как при Р'-+Р точки Q и R также стремятся к точке Р, то
можно положить
где гх и е2 будут стремиться к нулю вместе с Длг и Ду, а сле-
следовательно, вместе с р = РР' == У Ах2 + Ду2. Подставляя эти вы-
выражения в формулу для Az, получим
А* = [/*(* /
или
А* = /
где а = е1Ах + е2Ау. В силу нерав^яств | Алг| ^р, [A^j^p имеем:
Следовательно,
так как гг и е2 при р —* 0 стремятся к нулю, то стремится
к нулю и отношение -—-, т. е. а является бесконечно малой
более высокого порядка, чем р. Поэтому сумма первых двух сла-
слагаемых в правой части равенства (*), линейная относительно Ах
и Ау, и представляет собой согласно определению дифференциал
функция в точке Р(х, у).
Аналогичная теорема имеет место и для случая большего числа
независимых переменных.
112. Геометрический смысл полного дифференциала функции
двух переменных. Так же как производная и дифференциал функ-
функции одной переменной связаны с касательной к линии — графику
функции, так и частные производные и полный дифференциал
функции двух переменных связаны с касательной пло-
плоскостью к поверхности — графику функции.
Пусть функция <гг = /(лг, у) дифференцируема при х = лг0,у =у0.
Рассмотрим сечения поверхности S, изображающей эту функцию,
плоскостями у=у0 и х~х0. К полученным плоским линиям на
поверхности (рис. 140) проведем касательные МОТХ и М0Ту в точке
Л*о (*о> J'o» ^о)- Эти две пересекающиеся в точке Мо прямые опре-
определяют плоскость Г, которая называется касательной плоскостью
1121
§ 2. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
381
к поверхности S в точке Мо. Точку Мо называют точкой касания
плоскости Т с поверхностью S. Найдем уравнение касательной
плоскости. Прямая МОТХ лежит в плоскости у~у0, параллельной
плоскости Oxz, причем ее угловой коэффициент относительно оси
Рис. 140.
Ох равен /х(х0, у0). Поэтому уравнениями прямой МОТХ являются
Подобным же образом находим уравнения прямой М0Т :
Так как плоскость Т проходит через точку М0(лг0, yOf zQ)} то
ее уравнение можно записать в форме
z—z0 = А (х—х0) + В (у —у0).
Прямые МОТХ и М9Ту лежат в плоскости Г, значит, координаты
точек, лежащих на этих прямых, должны удовлетворять уравне-
уравнению плоскости. Подставляя в это последнее выражения для z—zQ
и у—у0 из уравнений прямой М9ТХ, получим
откуда
= Д(*о, Уо)-
382 гл. vh. функции нескольких переменных [113
Точно так же найдем, что
в = /у(Хо, У о)-
Следовательно, искомое уравнение касательной плоскости есть
z—zo=fx(xo,yo)(x—xQ)+fy(xQ,
Позже, в п. 119, будет доказано, что касательная, проведен-
проведенная в точке M0(xQ, у0, zQ) к любой линии на поверхности 5,
проходящей через эту точку, лежит в касательной плоскости (*).
Геометрический смысл полного дифференциала функции двух не-
независимых переменных вытекает из следующего предложения.
Теорема. Полный дифференциал функции z=f(x, у) при
х = х0, у=у0 изображается приращением аппликаты точки ка-
касательной плоскости, проведенной к поверхности *=/(*, у)
в ее точке М0(х0, у0, г0).
Доказательство. Правая часть уравнения касательной
плоскости (*) является выражением для полного дифференциала
функции z=f(x, у). Поэтому уравнению касательной плоско-
плоскости можно придать вид
здесь г0 —аппликата точки касания, z — текущая аппликата точки
плоскости, a (dz)x=Xo— полный дифференциал функции
У=Уо
z = f(x,y), вычисленный при х = х0, у=у0.
Когда х получает приращение Аху а ^ — приращение Ау
(рис. 140) функция получает приращение Az, которое представ-
представляется отрезком R1M1 — приращением аппликаты точки поверх-
поверхности S, а дифференциал dz отрезком RXTX — приращением аппли-
аппликаты точки касательной плоскости Т.
Отклонение полного дифференциала от приращения функции,
т. е. разность^—Az, изображается отрезком МгТх, заключенным
между поверхностью 5 и касательной плоскостью.
113. Применение полного дифференциала к приближенным
вычислениям. В п. 5& мы видели, как применяется к приближен-
приближенным вычислениям дифференциал функции одной переменной. По-
Покажем теперь, как к решению аналогичных задач для функций
многих переменных применяется полный дифференциал. Будем для
простоты записи говорить о функциях двух переменных; все ска-
сказанное легко перенесется на функции большего числа переменных.
Исходным для дальнейшего является замена полного прираще-
приращения функции ее полным дифференциалом, т. е. приближенное ра-
равенство
118) § 2. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ 383
справедливое при малых Длг и Ду. Заменив dz его выражением,
придадим этому равенству вид
хо, уо)Ау.
Если положить л;0+Дл; = л;, уо + Ду=у, то это приближенное
равенство можно записать и так*
/(*» У)я*/(*о, Уо)+/х{*о, Уо)(х—хо)+Л(Хо> Уо)(у—Уо)- (*)
Последняя формула показывает, что замена полного прираще-
приращения функции ее полным дифференциалом привела к замене функ-
функции f(xy у) в окрестности точки (лс0, у0) линейной функцией.
Геометрически это значит, что участок поверхности z — f(x, у)
заменяется соответствующим участком касательной плоскости
к поверхности в точке Мо (х0, yQ, z0).
Формула (#) сразу позволяет по известным значениям f(xQy y0),
fx{xOf у о), fy(x0, yQ) приближенно вычислять значения функции
f(x, у) при условии, что х мало отличается от хо> а у от yQ.
Пример. Составим приближенную формулу для вычисления
значений функции
г = In (лгу+ 2^ — 2х)
в окрестности точки A, 1).
Здесь лго = 1,уо=1. Последовательно вычисляем:
±*в ! (У_2> (?\ ==—1
Эх ху + 2у*-2хкУ *h \дх)х=х
dz I
Так как zo — O, то
1п(ху + 2у* — 2х) « — (дг — 1) -Ь 5 (у — 1).
Советуем читателю вычислить значения данной функции в не-
некоторых точках по приближенной формуле и с помощью таблиц
и сравнить результаты.
Покажем теперь, как вычисляется предельная абсолютная
ошибка функции двух переменных по заданным предельным абсо-
абсолютным ошибкам аргументов. Мы сохраним те же обозначения,
что и в п. 53 (рекомендуем читателю перед чтением дальнейшего
еще раз обратиться к содержанию указанного пункта).
Пусть задана функция г=/(л:, у) и требуется вычислить ее
значение при условии, что известны лишь приближенные значения
аргументов х и у:
\dx\<*x; y=
384 гл. vii. функции нескольких переменных [ИЗ
где х0 и у0 приближенные значения, а ех и еу — предельные абсо-
абсолютные ошибки. Чтобы найти предельную абсолютную ошибку
функции ezy нужно оценить модуль разности между истинным зна-
значением f(x, у) и приближенным f(x0, y0). Из формулы (*) следует
\/(х, У)-/(*о
<\Мх09 yo)\\dx\ + \/y{xo, y,)\\dy\<
Таким образом, можно сказать, что
*г = \fx (хо> Уь) |«, + \/у С*о> Уо) I *у* (**)
Деля еж на /(аг0, ^о), получим предельную относительную ошиб-
ошибку 6Z.
В качестве примеров найдем относительные ошибки произведе-
произведения и частного.
1) Пусть z = xy и дг0, у0 — приближенные значения аргументов.
По формуле (**)
«,Чл|в* + |*о1«у
Деля на \z0 | = \хоуо\, находим 8г:
т. е. предельная относительная ошибка произведения равна сумме
предельных относительных ошибок сомножителей. Разумеется, &то
правило справедливо для любого числа сомножителей.
2) Пусть z = ~ и zQ = -?±-. Тогда
X Хл
вг= —
у»
т. е. предельная относительная ошибка частного равна сумме пре-
предельных относительных ошибок делимого и делителя. (Таким обра-
образом, предельные относительные ошибки, получающиеся при деле-
делении двух величин и при их произведении равны между собой.)
Формула (*¦) позволяет решать и обратную задачу: по известным при-
приближенным значениям *0, #0 и заданной допустимой ошибке вх в опре-
определении функции ? (х, у) рассчитать, каковы должны быть гх и ?<,. Поль-
Пользуясь неопределенностью задачи (две величины связаны ?олько одним со-
соотношением), мы можем подбирать величины ех и гу в зависимости от того,
114] § 2, ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ 385
какую из них легче сделать меньше, т. е. какую из величин х и у легче
измерить с большей точностью. Если при этом окажется, что приближен-
приближенные значения х0, у0 измерены с недостаточной точностью, то надо заново
произвести их измерения уже с требуемой точностью и затем снова вычис-
вычислить значение функции (см. пример 2 на стр. 166).
114. Производные и дифференциалы высших порядков.
I. Допустим, что функция z=f(xi у) имеет частные произ-
производные
? /;(* У) Г*х У)
эти производные в свою очередь являются функциями независи-
независимых переменных хну. Частные производные от этих функций
называются вторыми частными производными или частными про-
производными второго порядка от данной функции f(x, у). Каждая
производная первого порядка имеет две частные производные;
таким образом, мы получаем четыре частные производные вто-
второго порядка, которые обозначаются так:
дЧ г „ <L(
ду \дх) "~дхду
дх\ду) дудх~~ *yxzsslZyx> ду\
Производные f"x и fx называются смешанными] одна из них
получается дифференцированием функции сначала по х, затем
по у, другая, наоборот, — сначала по у, затем по х.
Пример. Для функции z = x3y2 — Злгу3 — ху-\-1 имеем:
Обращает на себя внимание тот факт, что смешанные производ-
производные оказались тождественными. Это обстоятельство не случайно.
Имеет место такая общая теорема, которую мы приводим без
доказательства:
Теорема. Если вторые смешанные производные функции
z=.f(x> у) непрерывны, то они равны между собой:
13 А. Ф. Бермант, И. Г. Араманович
386 ГЛ. VII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [114
Условие непрерывности частных производных является суще-
существенным; если оно не выполнено, теорема может оказаться не-
несправедливой.
Таким образом, функция двух переменных z=f(xy у) имеет
при указанных условиях фактически не четыре, а только три
частные производные второго порядка:
дЧ №г(Рг дЧ
дх2' дх ду ду дх ' ду2 '
Частные производные от частных производных второго порядка
называются частными производными третьего порядка (или третьими
частными производными) и т. д.
Теорема о равенстве вторых смешанных производных позво-
позволяет доказать общее предложение:
Результат повторного дифференцирования функции двух незави-
независимых переменных не зависит от порядка дифференцирования (пред-
(предполагается, что рассматриваемые частные производные непрерывны).
Докажем, например, что
дЧ _ дЧ
дх ду2 ~ ду дх ду *
Используя теорему о равенстве вторых смешанных производ-
производных, находим
д*у ^ д / дЧ \д f дЧ \ дЧ
дх ду2 ду \дхду) ду \ду дх) ду дх ду *
Точно так же сформулированное только что общее предложение
может быть доказано во всех других возможных случаях.
Легко проверить, что функция z=f(x, у) имеет л+1 частных
производных л-го порядка, которые можно обозначить так:
d2l d"z дпг дп2 дп2 д^г
*дхп' dxtldy1 dxtl~*dy2' **'* дх2дуп~2' дхдупУ дуп *
Элементарные функции двух независимых переменных, как
-правило (за исключением отдельных точек и отдельных линий),
имеют в своей области определения частные производные любых
порядков.
Частные производные высшего порядка для функций любого
числа независимых переменных определяются аналогично. Здесь
также имеет место теорема о независимости результата от поряд-
порядка дифференцирования. Так, например, если u—f(x, у, z)y то
д*и д3и д*и д*и д*и дЧ
дх ду дг дх дг ду ду дх дг ду дг дх дг дх ду дг ду дх *
115] § 2. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ 387
Повторное дифференцирование функции нескольких перемен-
переменных фактически производится последовательным нахождением
одной производной вслед за другой.
II. Полный дифференциал функции z = f{x, у)
зависит, во-первых, от независимых переменных х, у и, во-вто-
во-вторых, от их дифференциалов dx, dy. Дифференциалы dx и dy
являются величинами, не зависящими от х и у (аналогичное заме-
замечание для функций одной переменной сделано в п. 55).
Полным дифференциалом второго порядка называется полный
дифференциал от полного дифференциала первого порядка dz при
условии, что dx и dy считаются постоянными. Согласно этому
определению
Вычислим частные производные от выражений в круглых скобках
(напоминаем, что dx и dy считаются постоянными):
д (dz dz \__дЧ d4
dx[diaX +д~уйУ J ~"dx^UX + dx~dy йУ'
d (dz , , dz
Подставляя найденные выражения в формулу для d2z и приводя
подобные члены, окончательно получим
Совершенно аналогично последовательно определяются полные
дифференциалы высших порядков. Предоставляем читателю прове-
проверить, что полный дифференциал третьего порядка равен
и подумать над законом образования последующих полных диф-
дифференциалов.
115. Отыскание функции по ее полному дифференциалу.
I. Случай двух независимых переменных. Пусть х и
j/ — независимые переменные, а Р(лг, у) и Q(x, у) — функции от них,
непрерывные вместе со своими первыми частными производными.
13*
388 гл. vir. функции нескольких переменных [115
Говорят, что дифференциальное выражение Р(х, y)dx-\-
+ Q (х, У) dy является полным дифференциалом, если существует
такая функция и (л;, у), полный дифференциал которой равен дан-
ному выражению
du=P(x, y)dx + Q(x, y)dy. (*)
Выясним, в каком же случае выражение Р(х, у) dx-\-Q(x,y) dy
будет являться полным дифференциалом. Заметим, что для функ-
функций одной переменной аналогичный вопрос решался всегда утвер-
утвердительно. Именно, если имелось выражение f(x)dx, где f(x)—•
непрерывная функция, то всегда существовала функция у такая,
что dy=f(x)dx. Этой функцией была любая первообразная от
f(x): у =\ f(x) dx. Для функций двух переменных дело обстоит
иначе?. Оказывается, что выражение Р(х, y)dx-\-Q(x, y)dy далеко
не всегда является полным дифференциалом. Имеет место такая
тебрёма:
Т е о р е м а. Для того чтобы выражение Р{х, у)dx + Q (xf y)dy
было полным дифференциалом, необходимо и достаточно соблю-
соблюдение тождества
дР 0Q . ч
ду дх v ;
Доказательство. Докажем прежде всего необходи-
необходимость условия. Итак, предположим, что функция и (х7 у), для
которой имеет место равенство (*), существует.
Так как
то из равенства (*) получаем, что
Р(Х, Jf)=g И gy
Продифференцировав первое из этих соотношений по уу а второе
по х, будем иметь
дР дЧ dQ дЧ
ду дх ду • дх ду дх '
В силу теоремы о равенстве вторых смешанных производных
заключаем, что
ду~~дх '
что и требовалось доказать.
115] § 2. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ 389
Перейдем теперь к доказательству достаточности усло-
условия. При этом мы укажем путь фактического отыскания функции
и(х, у). Эта функция должна, как мы видели, удовлетворять
двум условиям:
*> ?=*(*.*>; 2) prQ(x,y).
Функций, удовлетворяющих первому условию, можно подобрать
бесчисленное множество. Все они заключаются в формуле
(***)
где <р (у) — произвольная функция от у, а интегрирование ведется
в предположении, что у — постоянная. В самом деле, дифферен-
дифференцируя полученную формулу по xt сразу получаем ^ = Я(аг, у)*
Постараемся подобрать теперь функцию у (у) так, чтобы выпол-
выполнялось второе условие. Дифференцируем найденное выражение
для и по у1) и приравниваем Q(x, у):
Ру Ту$ у),
откуда
<p'O0 = Q(*. у)—тУ1р(х> У)ах- (****)
Однако, чтобы последнее равенство было непротиворечиво и из
него действительно можно было интегрированием найти ф(у),
нужно, чтобы правая его часть не зависела от х. Докажем, что
при соблюдении условия (#*) так и будет. Дифференцируем пра-
правую часть (###*) по х:
_dQ дР
дх ду
Здесь мы снова воспользовались независимостью результата сме-
смешанного дифференцирования от его порядка2). Таким образом,
производная по х тождественно равна нулю, а это значит, что
г) Ясно, что поскольку интегрирование ведется по х> а дифференциро-
дифференцирование по у, то эти действия не уничтожают друг друга. Позже, в п. 136,
будет показано, что
2) Взамен этого можно было бы воспользоваться формулой сноски :).
390 ГЛ. VII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [115
правая часть равенства (***#) не зависит от х и является функ-
функцией только у. Следовательно, интегрированием можно найти (f(y)'
= J [Q(x> У)-§??/>(*, y)dx] dy;
в выражение для ф (у) войдет произвольное постоянное слагаемое.
Подынтегральное выражение представляет разность двух функций,
каждая из которых зависит от х. Поэтому перед интегрированием
необходимо произвести преобразования, в результате которых все
слагаемые, содержащие лг, должны уничтожиться.
Затем, подставив найденное для ц>(у) выражение в формулу (***),
мы получим функцию и(х, у), для которой данное дифференциальное
выражение Р(х, y)dx-{-Q(x, y)dy будет полным дифференциалом.
Теорема доказана.
Замечание. Ясно, что можно было бы обратить порядок дей-
действий и сначала подбирать функцию и (ху у) так, чтобы она удов-
удовлетворяла второму условию, а затем уже и первому.
Примеры. 1) Дано выражение
Проверим, что данное выражение является полным дифферен-
дифференциалом, и найдем функцию и(ху у). Здесь
Таким образом,
dP___dQ_
ду ~~ дх '
т. е. необходимое и достаточное условие существования функции
и(х, у) выполняется. Переходим к ее отысканию. Имеем
2) -— = хеУ 2ц
Из 1) интегрированием находим
Далее,
Члены, содержащие лг, уничтожаются и остается
115] § 2. производные и дифференциалы 391
откуда
ч(у)=-у
Следовательно,
Непосредственной проверкой можно убедиться в правильности
результата.
2) Выражение у dх — х dy не является полным дифференциа-
дифференциалом, потому что
^=1 а ?!=?!=—1
ду ' дх
II. Случай трех независимых переменных. Метод
отыскания функции двух независимых переменных по ее полному
дифференциалу почти без всяких изменений переносится на функ-
функции трех переменных. Мы поэтому ограничимся краткими указа-
указаниями. Пусть Р(х, у, z), Q(x, у, z) и R(xy у, г) — функции неза-
независимых переменных лг, у, z, непрерывные вместе со своими частными
производными. Имеет место теорема.
Теорема. Для того чтобы выражение
Р(х, у9 z)dx + Q(x, у, z)dy + R(x, у, z)dz (*)
было полным дифференциалом некоторой функции и{х, у, z)f
необходимо и достаточно соблюдение тождеств
дР _dQ dQ _dR dR _дР_ , .
W~'dxy mdz~Hyy дх~Ог' l**j
Действительно, если функция и (лг, у, z), для которой выраже-
выражение (*) является полным дифференциалом, существует, то
d dX+d+dz
Поэтому должны выполняться три равенства:
дх ' dy ^* дг
Отсюда сразу следуют тождества (**), как условия равенства вто-
вторых смешанных производных функции и (л:, у, z). Например,
d_Q_dJR
дг ~~ду > И
_J_ Jl_ _J
dz ~~dydz> ду дгду> Т$ е* дг ~~ду
Доказывать достаточность условия в общем виде мы не будем
(рассуждение аналогично соответствующему доказательству для
случая функций двух переменных), а просто приведем пример
392 гл. vii. функции нескольких переменных [115
отыскания функции трех переменных по ее полному дифферен-
дифференциалу.
Пример. Найдем функцию и (лг, у, z)y если
у) dx + (x2z + -\ dy + (x2y—2z) dz.
Здесь
—1 R = x2y—2z.
Выражение для du действительно является полным дифференциа-
дифференциалом, так как
дг —х ~~ду э
dR o дР
^ = 2ху = ^- .
дх * дг
Перейдем к отысканию функции и. Начнем с третьего из усло-
условий (#*#):
Функция и, удовлетворяющая этому условию, имеет вид
, у),
где при интегрировании х и у считаются постоянными; ф(лг, у)—
произвольная функция, которую мы будем подбирать так, чтобы
функция и удовлетворяла первым двум условиям (**#). Должно
быть
Отсюда
т. е.
Так как
да 9 . dcp 9 . х
— == x2z + -jr- = х г Н—
ду г ду ' у
\nydx-\—dy.
у
116] § 2. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ 393
то мы пришли к отысканию функции двух переменных ф(#, у)
по ее полному дифференциалу.
Поступаем далее, как указано в I:
Видно, что \|/ (у) = 0, т. е. г|э (j;) = С. Окончательно получаем
и = лг2^ — z2 + лг lnjf + С.
Предоставляем читателю произвести проверку правильности
результата.
116. Дифференцирование сложных функций. Правила для оты-
отыскания дифференциала функций.
I. Дифференцирование сложных функций. Пусть
задана дифференцируемая функция z~f(u, v). Тогда ее прира-
приращение Д2 можно представить в виде
где а — бесконечно малая более высокого порядка, чем
т. е.
lim r a =0.
Лу->- о
Предположим теперь, что и и v в свою очередь являются диф-
дифференцируемыми функциями независимой переменной лг, т. е,
и = у(х) и v = ty(x).
Таким образом,
т. е. z является сложной функцией переменной лг. Выразим теперь
производную j- через частные производные т-и j- и производ-
производные от функций и и т/ по лг. Придадим аргументу д; прираще-
приращение Длг. Тогда и и ^ получат соответственно приращения Аи и
Д^, через которые Az выразится по формуле (*). Разделим обе
части этой формулы на Длг:
Дг дг Лм , дг До , а
Дх ди Дл: *"«За Дл: ' Sc
394 ГЛ. VII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [116
и перейдем к пределу при Ах—> (). Согласно условию lim т^ = ;г
Av dv Ьх-+о*х ах
и lim x^^w"- Отношение -^- представим в виде
^* ах ьх
Первый множитель, согласно определению а, стремится к нулю,
а второй к определенному числу: |/(;г)+(;г) • Следова-
Следовательно, lim — = 0. Замечая еще, что значения ~ и ~ зависят
только от выбранного значения х, определяющего значения и
и v, и не зависят от Д.*, окончательно получим
dz dz da дг dv
dx dudx* dudx'
Ясно, что эта формула является обобщением правила дифферен-
дифференцирования сложной функции одной переменной.
Пример. Пусть
Положим tgx = u, slnx = v. Тогда y = uv. Имеем
dx dudx* dv dx cos2 x '
1 ' \nU'Cosx)=^{L~-^invf l
COS2* ' iW" —~y--^6~/ yCQSX
Раньше для отыскания производной от такой функции был рекомен-
рекомендован специальный прием — логарифмическое дифференцирование.
Пусть теперь z является сложной функцией двух независимых
переменных х и )i,t. e.
z=f(u, v),
где
и = ц)(х, у) и v = ^{x, у).
Таким образом,
*=/[ф(*, У), *Н*, У)] = Р(х, У)-
Все функции предполагаются дифференцируемыми.
Чтобы найти z'x, мы должны считать у постоянным, но тогда и
и и v становятся функциями только одной переменной х, и мы
приходим к уже рассмотренному случаю. Разница состоит только
1161 § 2. производные и дифференциалы 395
в том, что обыкновенные производные -^ и ~ заменятся частными
производными ч- и j-, и мы получим
дх ди дх * dv дх
и аналогично
dz dz да , dz dv
ду "~~ ди ду *^ dv ду
Итак,
Частная производная сложной функции равна сумме произведем
ний частных производных заданной функции по промежуточный
аргументам (и и v) на частные производные этих аргументов (и и v)
по соответствующей независимой переменной (х или у).
Пример. Возьмем функцию z= exys\n(x-{-y). Полагая ху = и9
x-\-y = v и, значит, z = easinv1 найдем
dz du . dz dv u . . a Л
z = -s- 3- + ^r- ¦=- = e sin а • у + e cos v • 1 =
x du dx dv dx 7
— exy [y sin (a: -\-y) + cos (a: +y)],
p dz da , dz dv u . , a i
i/ dudy x dvdy '
= e*y [д: sin (л; + j/) + cos
Сформулированное правило дифференцирования сложной функ-
функции остается справедливым для функций любого числа независи-
независимых переменных и при всяком числе промежуточных аргументов.
Пусть z задана как функция аргументов и, v, ..., w} кото-
которые являются функциями независимых переменных ху у> ..., t.
Тогда
dzdz du , dz dv , , dz dw
dz dz du ^dz dv , , dz dw
dy du dy ~* dv dy ' ' # 'дооду у
dzdz du .dz dv . , dz dw
В частном случае аргументы и, vy ..., w могут быть функ-
функциями одной независимой переменной х. Значит, фактически z
является функцией только х. При этом ее обыкновенная произ-
производная— ее называют в этом случае полной производной—•
имеет вид
dz dzdu _.dzdv dz dw
dx du dx ' 5y dx ' * ' # ' Ъхю dx~ *
396 ГЛ. VII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [116
Если в этой формуле положить и = х, то получим
dz dz , dz dv , dz dw
dx дх ' dv dx * ' ' * ' dw Zx *
Обращаем внимание читателя на различие между двумя произ-
производными по х, содержащимися в этой формуле. В то время как
-г? есть полная производная, т. е. обыкновенная производная от z
ах
dz
как функции х, ^- есть частная производная от z по аргументу х,
входящему в выражение функции непосредственно, значит, при
условии, что остальные аргументы, хотя они также зависят от х9
при дифференцировании остаются постоянными.
d2u д2и
Примеры. 1) Найдем вторые частные производные ^-g, ^ ,
jrj от функции
где г—полярный радиус точки в пространстве: г — Vx2-\-y2-]-z2.
Имеем:
да \ г ) __ \ г ) дг *•*__ ?.
дх
du
ду
и дальше:
d2u *
dx2
d2u }
ду2
dx
л —;
dr
У ди
г* ' дг
г*
Зу2 d2u
9 dz2
dx
z
г»
г8 — Ъгх
г2 — '
/•б
г2 г "^ г» •
/б
•
Можно заметить, что функция и = — удовлетворяет соотношению
д2и д2и д2и
2) Пусть г^гд;8^, где й = ф(лг). Тогда
^^Зл:2 "й а — =
116] § 2. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ 397
II. Инвариантность формы первого дифферен-
дифференциала и правила для отыскания дифференциала.
Теорема. Полный дифференциал функции z=f(afv) со-
сохраняет один и тот же вид независимо от того, являются ли
ее аргументы и и v независимыми переменными или функциями
от независимых переменных.
Если и и v — независимые переменные, то полный дифференциал
равен
, дг , . дг .
dz = v- du + з- dv.
ди ' dv
Пусть теперь и и vy а следовательно, и z являются функциями
независимых переменных х и у. По определению полного диф-
дифференциала имеем
Заменим j- и j~ по формулам, выведенным в I:
дгди .dzdv\*^ . (dz ди . dz dv
или перегруппировав члены:
. дг f ди . , ди , \ . дг
Выражения в скобках равны соответственно du и dv.
Следовательно,
что и требовалось доказать.
Таким образом, и для функций двух независимых переменных
имеет место свойство инвариантности формы первого
дифференциала функции (см. п. 51, III).
Совершенно аналогично, если z = f(u,v, ...,w), то всегда
независимо от того, являются ли непосредственные аргументы этой
функции независимыми переменными или нет. При нахождении диф-
дифференциала функции нескольких независимых переменных можно
также пользоваться простыми правилами, аналогичными правилам,
имеющим место в случае одной независимой переменной (п. 51).
Пусть и, v, . . ., w — функции любого числа независимых перемен-
переменных. Тогда имеют место правила, выраженные следующими фор-
формулами:
+ + + ... -\-dw;
398 гл. vii. функции нескольких переменных 1117
2) d(uv) = vdu + udv, в частности d(Cu) — Cdu, С — const;
и \ vdu — udv
)
55 *
Доказательства этих формул получаются сразу на основании
свойства инвариантности формы первого дифференциала.
Докажем для примера второе правило. Так как форма дифферен-
дифференциала не зависит от характера аргументов, предположим, что они—
независимые переменные. При этом
d (uv) = ч~ (uv) du-\--x- (uv) dv = vdu-\- и dv,
что и требовалось доказать.
Так же доказываются и остальные правила. Эти правила позво-
позволяют иногда значительно упростить выкладки.
Пример. Найдем <2 arctg ~. Полагая — = и, имеем
X X
d arctg -У- = (arctg и)' dii = -—-2 d ( -f
1 jlIL ^
Пользуясь третьим правилом, окончательно получаем
и 1 х dy — у dx ц , . х
= —г == Т d* +--:
-\-у
, , и 1 х dy — у dx ц , .
d arctg ~ = s —-—г == 9 Т 9 d* +-O
* ^ ^ * -\-у х
Отсюда, между прочим, сразу следует, что
д . w w д . у х
117. Теорема существования неявной функции. В нашем курсе
мы уже неоднократно встречались с неявными функциями, т. е.
функциями, определяемыми при помощи уравнений, связывающих
переменные величины. Напомним, что неявная функция одного
переменного определяется уравнением
В п. 12 было отмечено, что в некоторых случаях уравнение
(*) может и не определять функции: так, например, уравнение
д;2_|_уа_|_5 = 0 не имеет никаких действительных корней, и, зна-
значит, мы не можем рассматривать у как функцию от х. В более
сложных случаях вообще очень трудно установить, при каких
значениях х уравнение (*) имеет корни и в каком количестве;
при этом вопрос о том, определяет ли это уравнение некоторую
функцию, остается открытым.
117]
§ 2. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
399
Выясним сейчас, при каких условиях можно утверждать, что
заданное уравнение t (х, у)— О действительно определяет одну
из переменных как функцию другой. Имеет место теорема, кото-
которую мы приводим без доказательства.
Теорема существования неявной функции. Пусть
функция F(x,y) непрерывна вместе со своими частными произ-
производными в какой-нибудь окрестности точки М0(х0,у0). Если
F(xo,yo) = O и Fy(xo,yo)^Of
то уравнение
F(x,y) = 0
при значениях х, близких к xQf имеет единственное непрерывно
зависящее от х решение у = у(х) такое, что (р(хо)=уо* Функ-
Функция ф (х) имеет также непрерывную производную,.
Разъясним смысл этой теоремы на примерах.
1) Пусть F(x, у) = х2+у2 — R2.
Уравнение
является уравнением окружности. В любой точке окружности
М0(х0,у0), где у0ф0 (рис. 141), все условия теоремы выполнены:
l — Я2 = 0, Fy(xOiyo) = 2уоф0.
Функция y — YR2—х2, где знак у корня выбирается такой же,
как у у0, и является единственной
непрерывной функцией, удовлетворя-
удовлетворяющей заданному уравнению и такой,
что У R2—x\==yQ, Выбрав другой
знак у корня, мы получим другую
непрерывную функцию, также обра-
обращающую уравнение в тождество, но
уже не равную у0 при х — х0; она
будет равна —у0. Отметим также,
что если для разных значений х со-
соответствующие значения у брать
то положительными, то отрицатель-
отрицательными, то получающаяся функция бу-
будет разрывной (ср. со сноской на
стр. 37); в теореме же говорится о существовании единственной
непрерывной функции.
Иная картина будет в окрестности точек A(Ry 0) и В(—/?, 0).
В точке А при х > R мы вообще не получим действительного
значения для у, а при х < R оба непрерывных решения у =
c=+VR2—*2 и <У=—VR*—х2 обращаются в нуль при x = R.
Рис. 141.
400
ГЛ. VII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[117
Здесь F(x,y)=x*y + \ny — х. В
Частные производные Fx = 3x2y
окрестности этой точки и /^A,
теоремы существует функция у
Все дело в том, что частная производная /^у (/?, 0) = 0, т. е. ус-
условия теоремы нарушены. Так как в этой точке Fx (/?, 0) = 2R Ф 0,
то можно, наоборот, х выразить в виде единственной непрерыв-
непрерывной функции от у. Это опять-таки видно из рис. 141.
2) Пусть неявная функция определена уравнением
точке jW0A, 1) имеем F(\, 1) = 0.
— 1 и Fy — x3-\— непрерывны в
1)== 2Ф§. В силу приведенной
= ф(л:), обращающая данное урав-
уравнение в тождество и такая,
что фA)=1. Хотя мы и
установили существование
функции ф (а:), фактически
выразить ее в виде эле-
элементарной функции от
х нельзя, так как заданное
уравнение алгебраически
неразрешимо относительно
у. Частные значения функ-
функции ф(х) приходится оты-
отыскивать, задаваясь число-
числовыми значениями х и ре-
решая получающиеся уравне-
уравнения методами п. 77. Так
как функция у = ф (х)
соответствующее уравнение
Рис. 142.
к 1,
непрерывна, то при х, близком
имеет корень, близкий к 1.
В этом примере все высказанные утверждения легко проиллюстрировать
геометрически. Запишем уравнение (*) в виде
In у = х — х3у
и построим график его левой части: ы = 1п# — и графики правой части при
различных значениях х: это прямые и — х—хъу (рис. 142). Значения у
в точках пересечения этих прямых с логарифмикой и будут являться значе-
значениями функции у = (р(х). При я = 1 прямая и=1 — у пересекается с лога-
логарифмикой на оси Оу в точке у=\. Это соответствует начальной точке MQ.
Когда х возрастает, то точка пересечения прямой и*=х—хъу с осью Ои
поднимается вверх, а точка пересечения с осью Оу движется к началу ко-
координат. Поэтому искомое значение у непрерывно уменьшается и, как
легко заметить, стремится к нулю при *->-оо. Если же х уменьшать, то
опять-таки из рисунка усматриваем, что значения у будут уже больше 1,
причем сначала они увеличиваются, а затем начинают уменьшаться и при
# = 0 значение у снова равно 1. Пользуясь этим анализом, читатель сможет
118] § 2. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ 401
самостоятельно построить схематический график функции у = ц>(х) в интер-
интервале [0, оо) *).
Отметим еще, что в точке (—1, 1) также имеем F( — 1, 1) = 0, но здесь
7Г^(—1, 1) = 0 и условия теоремы не соблюдены. Рекомендуем читателю
графически установить, что когда х находится вблизи от— 1 слева (т.е. х < — 1),
то уравнение (*) не имеет действительных решений, а при — 1<я<0—
два непрерывных решения; одно из них непрерывно смыкается с уже иссле-
исследованным решением в интервале [0, оо), а другое стремится к оо при
х-+0.
Неявная функция двух переменных определяется уравнением
F(x, yy г) = 0,
связывающим три переменные величины. На вопрос о существова-
существовании такой функции отвечает следующая теорема, аналогичная
приведенной выше.
Теорема. Пусть функция F(x, у, z) непрерывна вместе
со своими частными производными в какой-нибудь окрестности
точки A!0(jc0, у0, z0). Если
^(*о» Уо> 2о) = О и K(xQf уOf *о)?*О»
то уравнение F(x, у, z) = Q в некоторой окрестности точки
(•Хс У о) имеет единственное, непрерывно зависящее от х и у
решение ? = <p(jt, у) такое, что ф(д:0, j;0) = ?0. Функция ф(лг, у)
имеет также непрерывные частные производные.
Отметим еще, что если в точке Жо производная /72 = ^> а, ска-
скажем, Fy^O, то уравнение F(x, у, z) = Q может не определять z
как функцию х и у, но определяет у как функцию х и z.
118. Дифференцирование неявных функций. Пусть условия
теоремы существования неявной функции, сформулированной в
предыдущем пункте, выполнены и уравнение
F{x, y) = 0
определяет у как некоторую функцию ^/ = ф(лг). Если в уравне-
уравнение подставить вместо у функцию ср (х), то получим тождество
F[x, <p(*)] = 0.
Следовательно, производная по х от функции ^(л:, у), где у =
= ф(лг), также должна быть равной нулю. Дифференцируя по
правилу дифференцирования сложной функции (п. 116), найдем
2) Положение точки экстремума (максимума) этой функции будет уточ-
уточнено в примере 2 п. 118.
402 гл. vii. функции нескольких переменных [118
откуда
* dx p
1 ч
Эта формула выражает производную неявной функции <у = ф(лг)
через частные производные заданной функции F(xy уI). Произ-
Производная у' не существует при тех значениях х и у, при кото-
которых /^ = 0. Но при этом, как было отмечено, мы и не можем
гарантировать существования самой функции ф (х).
Примеры. 1) F(x, у)==х2+у2 — 1 =0.
Имеем з— = 2лг, -з— = 2у; значит,
дх ' ду ' >
,2х ?
2) у у у
Согласно решению примера 2 п. 98
у —
Теперь можно продолжить решение указанного примера и найти точки
экстремума функции # = ф(х), определенной данным уравнением. В точках
экстремума «/' = 0; поэтому х и у связаны уравнением Зх2у—1 = 0, которое
нужно решить совместно с данным х3у + \пу—х = 0. Выражая у из первого
уравнения: у= , а и подставляя во второе, приходим к трансцендентному
.1 2х Л
уравнению In -5-3 о- = 0.
оХ о
Если а: > 0, то это уравнение записывается в виде In х =————-—>;
о Z
оно имеет единственное решение: х=^:0,49; при этом t/^rl,39. Анализ, про-
проведенный ранее, позволяет сразу сказать, что это максимум функции.
Если х < 0, то, полагая х=—z, приведем уравнение к виду In 2 =
=-5 ft • При 0<2< 1 оно имеет решение zs^0,74, т. е. *^—0,74 и
о 2,
I/ =^г 0,61. Предоставляем читателю проверить, что это минимум для той
ветви функции, которая ограничена в интервале [ — 1, 0].
II. Пусть теперь уравнение
F(x, у, г) = 0
определяет z как некоторую функцию 2=ф(лг, у) независи-
независимых переменных х и у. Если в уравнение подставить вместо z
х) Другой способ дифференцирования неявной функции одной перемен-
переменной был указан в п. 45, II.
+ F.
dz
дх~
дх и>
К
К'
Fy
dz
ду"
+ F',
dz
ду
К
= 0,
*
118] § 2. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ 403
функцию ф(лг, у)> то получим то>кдество
Fix* У, Ф(*, У)] = 0.
Следовательно, частные производные по х и по у от функции
F(x, у, z), где z = (p(x> у), также должны быть равны нулю.
Дифференцируя, найдем
откуда
Эти формулы выражают частные производные неявной функции
z = q>(x, у) через производные заданной функции F(x, y^ z). При
F2 = 0 эти формулы теряют смысл.
Примеры. 1) Найдем частные производные функции г, за-
заданной уравнением F(x, y} z) = х2 + у2 + z2—1=0 (уравнение
сферы). Имеем
dF o dF o OF o
^- = 2х, ^- = 2у, .г- = 2<г;
значит,
dz x дг у
дх z ' ду z
В этом примере можно найти явное выражение функции и прове-
проверить правильность полученных результатов.
2) F(x, у, z) = e~xy—2z + ez^Q. Находим
dF -д-v dF -xv dF
дх ^ * ду ' dz
Поэтому
дг_уе~*У dz _хе"х^
dx~~ez—2' dy~~~ez—2'
Здесь уже явного выражения для г мы получить не можем и
значения частных производных находятся по значениям независи-
независимых переменных х и у и самой функции z.
В общем случае, когда уравнение
F(x, у, z, . . ., и)^0
определяет и как некоторую функцию от х, у, z, ..., аналогично
404 гл. vu. функции нескольких переменных [П9
предыдущему найдем
ди__ ?* ди_ ?? ^f_,__^?
дх~~ р' ' ду~ р' ' dz ~~ Т7 » •••
и 1 и л м
§ 3. Геометрические приложения дифференциального исчисления
119. Поверхности. Если уравнение поверхности в пространстве
имеет вид
z = f (х v\
то уравнением касательной плоскости к поверхности в ее точке
ЛМ*о» ^о» 0о) служит (см. п. 112)
Рассмотрим поверхность S в пространства Oxyz, заданную
уравнением общего вида
F(xy y,z) = 0,
не разрешенным относительно какой-нибудь координаты. Предполо-
Предположим, что функция F{x, у, z) в окрестности точки Mo(xOiyo>zo)
удовлетворяет условиям теоремы существования неявной
функции и уравнение F(x, yy z) = 0 определяет z как функцию
х и у: z = f(x, у), причем f(xOy yo) = zo. Согласно п. 118, II
производные этой функции в точке (аг0, у0) будут равны
fix у) F'A*»y»**) /{x , ._ fy*» У»> U)
Jx \хо> Уо) — — / , Ту 1*о» У о) — р> . v-
Уравнение касательной плоскости можно переписать так:
К (хо> Уо> *о) . ч Fl (^e. Уо> го) . ч
z— zQ = т (х — л:0) т (V — Уо)
или
^o. Уо>
что короче записывают так:
Индекс 0 указывает, что частные производные берутся в точке
касания Мо(хОу yOt zo)} т. е. при лг = лг0, у=у0, z = z0.
119] § 3. ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ 405
Записанное в таком виде уравнение касательной плоскости
имеет смысл и тогда, когда [-з-i =0.Это будет просто означать,
V dzJo
что касательная плоскость в данной точке поверхности парал-
параллельна оси Oz. Если в точке Мо все три частные производ-
производные функции F(x, у, z) равны нулю: (^)os=(|^)o==r(-^)oss=o» T0
эта точка будет особой. Такие точки поверхности мы рассматривать
не будем.
Определение. Прямая, перпендикулярная к касательной
плоскости в точке касания, называется нормалью к поверхности
в этой точке.
Зная уравнение касательной плоскости к поверхности
F(x, у, z) = Q в ее точке М0(х0, yQi z0), можно на основании
известных из аналитической геометрии правил написать урав-
уравнения нормали к той же поверхности в той же точке. Они име-
имеют вид
х—х0 __ у — у0 ___ z—z0
(dF\ /3F\ -/dF\ •
\dxjo \ду Jo \dzjo
Если поверхность задана уравнением z—f(x, у), то уравнения
нормали к этой поверхности в точке MQ(xQi yQ) z0) запишутся
в виде
х—х0 __ у — Ур ___ z — Zq
f'x(x0,y0) t'y(x0,y0) ""l
Зная уравнение касательной плоскости, легко написать выра-
выражения для направляющих косинусов нормали; предоставляем это
сделать читателю для случаев задания уравнения поверхности в
явном и неявном виде (эти выражения понадобятся, в дальнейшем).
Примеры. 1) Найдем касательную плоскость и нормаль
к сфере
в ее точке Мо(хОУ у0У z0).
Имеем
и значит, уравнение касательной плоскости будет
(у —у0) + z0 (z — z0) = 0
или
406 ГЛ. VII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [119
Уравнения нормали имеют вид
Xq Уо го хо Уо zo
Отсюда следует, что нормаль к данной сфере проходит через на-
начало координат, т. е. что нормалью служит радиус сферы.
2) Составим уравнение касательной плоскости к эллипсоиду
вращения x2-\--~--\-z2 = 1, которая была бы параллельна плос-
плоскости лг + у—0 = 0.
Так как (ат)о = 2л:о' {%\=У°> (fH = 2^0( то уравнение
касательной плоскости в неизвестной пока точке Мо (хо> у0, z0)
имеет вид
2х0(* — лг0) +у0 (у—у0) + 2z0 {z — z0) = 0. (*)
Из условия параллельности плоскостей имеем
2^о = Уо _ 2*о
1 1 —1 '
Добавим к этим уравнениям еще одно уравнение, выражающее
условие, что точка MQ лежит на эллипсоиде:
Получаем систему трех уравнений с тремя неизвестными. Реше-
Решениями ее являются координаты двух точек: Мо (-к", 1, —о") и
• / 1 1 \
Мо (—y> —1» y)# Подставляя найденные координаты в урав-
уравнение (*), получим уравнения двух плоскостей, отвечающих ус-
условиям задачи:
х-\-у—2 = 2 и х-\-у—0=—2.
В п. 112 мы определили касательную плоскость к поверхности
как плоскость, проходящую через касательные прямые к двум
плоским сечениям поверхности, параллельным координатным плос-
плоскостям Oxz и Oyz. Докажем теперь следующее свойство касательной
плоскости, которое, по сути дела, и объясняет ее название.
Если линия L целиком лежит на поверхности, то касательная
прямая к этой линии в ее точке Мо лежит в касательной плоскости
к поверхности, проведенной через ту же точку. Иначе говоря, если
через точку Мо поверхности провести всевозможные линии, лежа-
лежащие на поверхности, то касательные к этим линиям в точке Мо
120] § 3. ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ 407
все лежат в одной плоскости — касательной плоскости к поверх-
поверхности.
Пусть поверхность задана уравнением F(x, уу z) =0, а линия ?
параметрическими уравнениями х = х (t),y =<y (t)y z~z (t)\ точке MQ
соответствует значение параметра t0. Условие, что линия целиком
лежит на поверхности, запишется так:
F[x[t), y(t), z(t)] = Q.
Дифференцируя это равенство, справедливое при всех значениях t,
по правилу дифференцирования сложной функции, получим
дх ' dys ' дг
Если обозначить индексом нуль значения производных в точке MQ>
то для этой точки последнее равенство примет вид
Значения частных производных (-^- ) , ( ^-) , ( ^- ) зависят
г \oxjo' \oyjo7 \dz Jo
только от уравнения самой поверхности и выбранной точки Жо;
значения же производных лг0', yQ, z0 зависят от выбора линии L
и представляют проекции направляющего вектора касательной к
линии L в точке MQ (см. п. 68). Равенство (**) показывает, что
любой такой касательный вектор перпендикулярен к одному
и тому же вектору {(/^о* (^)о> (^г)оЬ который мы назвали
нормальным вектором к поверхности. (Равенство (**) есть ра-
равенство нулю скалярного произведения этих векторов.) Но это и
означает, что все касательные прямые к линиям, лежащим на
поверхности и проходящим через точку Жо, лежат в одной плос-
плоскости— касательной плоскости к поверхности.
120, Пространственные линии как пересечение двух поверх-
поверхностей. В п. 68 мы изучали параметрические уравнения прост-
пространственных линий. Линия в пространстве может быть также
задана как линия пересечения двух поверхностей
Геометрически ясно, что касательной к этой линии в точке
ДОо^о» .Уо» ^о) будет линия пересечения касательных плоскостей
к данным поверхностям, проведенным в той же точке. Составляя
408 гл. vii. функции нескольких переменных
уравнение этих плоскостей
(?).<*-*j+C5).o-*>
[120
мы получим уравнение искомой касательной как линии пересечения
двух плоскостей. Направляющий вектор Т этой касательной можно
Рис. 143.
найти, взяв векторное произведение нормальных векторов к обеим
плоскостям (рис. 143):
Тогда
dF
dF
dF
дФ
алгД \ду}о \дг)о
дФ\ /ЭФ\ /аФ\
д J \ ду/о \дг /о
дх J
Зная направляющий вектор Т и точку касания Жо, можно пере-
переписать уравнения касательной в каноническом виде, а также
составить уравнение нормальной плоскости. Записывать эти урав-
уравнения в общем виде мы не будем.
Пример. Пусть кривая является линией пересечения двух
цилиндров
!=10 и у2 + г2 = 25.
120] § 3. ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ 409
Составим уравнения касательной прямой и нормальной плоскости
к этой линии в точке A, 3, 4).
Прежде всего находим проекции векторов Nx и N2:
dF\ л fdF\ . fdF\ =0
Вычислим теперь их векторное произведение:
i
2
0
j
6
6
k
0
8
Зная вектор Т и точку касания, составляем искомые уравнения:
л:— 1 у — 3 2 — 4 „
~—- = ?—?= ~ уравнение касательной,
\2х — 4^ + 3-г: — 12 = 0 — уравнение нормальной плоскости.
Чтобы найти длину дуги пространственной линии, заданной
уравнениями (*), постараемся разрешить их, например, относи-
относительно у и z\ тогда эти координаты будут являться некоторыми
функциями от х: у —у (х), z = z(x). После этого применим формулу
для длины дуги пространственной линии, заданной параметриче-
параметрическими уравнениями (см. п. 102), положив в ней i — x:
где хх и хъ — абсциссы начальной и конечной точек данной дуги.
Пример. Найти длину дуги линии, заданной уравнениями
л;2 — Зд> = 0,
(линия пересечения параболического цилиндра и гиперболического
параболоида), от точки Л@, 0, 0) до точки ?C, 3, 2).
Выражая из данных уравнений у и z через л;, получим j/= —э
410
ГЛ. VII, ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[121
§ 4. Экстремумы функций нескольких переменных
121. Необходимые условия экстремума. Начнем с рассмотрения
функций двух переменных и дадим определение точки экстремума;
оно совершенно аналогично соответствующему определению для
функций одной переменной (см. п. 60).
Определение. Точка Ро(х0, у0) называется тонкой экст-
экстремума (максимума или минимума) функции z=f(x, у), если
/С*о» У о) есть соответственно наибольшее или наименьшее
значение функции f(x,у) в некоторой окрестности точки Р0(х0,у0).
При этом значение f(x0, y0) называется экстремальным значе-
значением функции (соответственно максимальным или минимальным).
Говорят также,что функция f(x, у)
имеет в точке Яо(*о, у0) экстремум
(или достигает в точке Ро экстре-
экстремума).
Заметим, что в силу определения
точка экстремума функции обяза-
обязательно лежит внутри области опре-
определения функции, так что функция
определена в некоторой (хотя бы и
малой) области, содержащей эту
точку. Вид поверхностей, изображаю-
изображающих функции в окрестности точек экстремума, показан на
рис. 144.
Установим сначала необходимые условия, при которых функ-
функция z~f(x, у) достигает в точке Ро (х0, у0) экстремума; будем
пока рассматривать дифференцируемые функции.
Необходимый признак экстремума. Если в точке
Л> (•*<>»-Уо) Дифференцируемая функция z~f(x9y) имеет экстре-
экстремум» то ее частные производные в этой точке равны нулю:
Рис. 144.
дх)х=х0 f
У=Уо У=Уо
Доказательство. Допустим, что функция z=f(x, у) имеет
в точке Ро (лг0, у0) экстремум.
Согласно определению экстремума функция z=f(x, у) при
постоянном у =^0, как функция одного х, достигает экстремума
при х = х0. Как известно, необходимым условием этого является
обращение в нуль производной от функции f(x} у0) при x = xOi
т. е.
/х=
-о
121] § 4. ЭКСТРЕМУМЫ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 411
Аналогично функция z — f{x, у) при постоянном х = х0, как
функция одного у, достигает экстремума при у~у0. Значит,
У~Уо
что и требовалось доказать.
Точка Я0(лг0, у0), координаты которой обращают в нуль обе
частные производные функции z=f(xy y)y называется стационар-
стационарной точкой функции f(x, у).
Уравнение касательной плоскости к поверхности 2=/(лг, у):
*-г°=AH <*-*<>>+(Do {y-y°]
для стационарной точки Ро (лг0, ^0) принимает вид
Следовательно, необходимое условие достижения дифференцируемой
функцией z=f(x, у) экстремума в точке PQ(xOi yQ) геометрически
выражается в том, что касательная плоскость к поверхности—гра-
поверхности—графику функции в соответствующей ее точке—параллельна плоскости
независимых переменных.
Для отыскания стационарных точек функции z = f(x,y) нужно
приравнять нулю сбе ее частные производные
В-». %-" <•>
и решить полученную систему двух уравнений с двумя неиз-
неизвестными.
Пример. Найдем стационарные точки функции
z = 2л:3 + ху2 + 5*2 + у2.
Система уравнений (#) имеет вид
6*2 +у2 + юл: = 0, 2ху + 2у = 0.
Из второго уравнения следует, что или у = 09 или х=—1. Под-
Подставляя по очереди эти значения в первое уравнение, найдем
четыре стационарные точки:
М,@у 0), Ж2(-|, о), Ж3(-1, 2), ЛМ—1, —2).
Какие из найденных точек действительно являются точками
экстремума, мы установим в следующем пункте, где будет приве-
приведено достаточное условие экстремума.
412 ГЛ. VII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [122
Иногда удается, и не прибегая к достаточным условиям, вы-
выяснить характер стационарной точки функции. Так, если из усло-
условия задачи непосредственно следует, что рассматриваемая функ-
функция имеет где-то максимум или минимум и при этом системе урав-
уравнений (*) удовлетворяет только одна точка (т. е. одна пара
значений х, у), то ясно, что эта точка и будет искомой точкой
экстремума функции.
Заметим, наконец, что точками экстремума непрерывной функ-
функции двух переменных могут быть точки, в которых функция не-
дифференцируема (им соответствуют острия поверхности—графи-
поверхности—графика функции).
Так, например, функция z = ]/rx2-\-y2 имеет, очевидно, в начале
координат минимум, равный нулю, но в этой точке функция не-
дифференцируема; график этой функции есть круглый конус с вер-
вершиной в начале координат и осью, совпадающей с осью Oz.
Следовательно, если иметь в виду не только дифференцируе-
дифференцируемые, но и вообще непрерывные функции, то нужно сказать, что
Точками экстремума могут быть стационарные точки функции и
точки, в которых функция недифференцируема.
Вполне аналогично определяется понятие экстремума функции
любого числа независимых переменных
«=/(*. -V» г* • ••> О
и устанавливаются необходимые условия экстремума. Именно:
Дифференцируемая функция п переменных может иметь экстре-
экстремумы только при тех значениях х, у, z9 . . ., /, при которых равны
нулю все ее п частных производных первого порядка:
/Л*, У, z, ...,0 = 0, /у{х, у, г, ...,0 = 0,
/г (X, у, Z, . . ., 0 = 0, ... , f\ (X, у, Z, . . ., 0 = 0.
Эти равенства образуют систему п уравнений с п неизвестными.
122. Достаточные условия экстремума для функций двух пе-
переменных. Так же как и для функций одной переменной, необ-
необходимый признак экстремума в случае многих переменных не явля-
является достаточным. Это значит, что из равенства нулю частных
производных в данной точке вовсе не следует, что эта точка обя-
обязательно является точкой экстремума. Возьмем функцию z=txy.
Ее частные производные zx = y, zy = x равны нулю в начале коор-
координат, однако функция экстремума не достигает. В самом деле,
функция z = xy, будучи равной нулю в начале координат, имеет
в любой близости к началу координат как положительные значе-
значения (в первом и третьем координатных углах), так и отрица-
отрицательные (во втором и четвертом координатных углах), и значит,
122] § 4. ЭКСТРЕМУМЫ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 413
нуль не является ни наибольшим, ни наименьшим значением этой
функции.
Достаточные условия экстремума для функций нескольких
переменных носят значительно более сложный характер, чем для
функций одной переменной. Мы приведем эти условия без дока-
доказательства только для функций двух переменных.
Пусть точка Р0{х0, у0) является стационарной точкой функ-
функции z—f(xy у), т. е. ( ~] =0 и f~j =0. Вычислим в точке Ро
значения вторых частных производных функции f(xy у) и обозна-
обозначим их для краткости буквами Л, В и С:
С-(дЧ\
Если В2— ЛС<0, то функция f(x,y) имеет в точке Ро(хО9уо)
экстремум: максимум при Д<0 и С<0 и минимум при Л>0
и С>0 (из условия В2 — ЛС<0 следует, что А и С обязательно
имеют одинаковые знаки).
Если В2 — ЛС>0, то точка ЯО не является точкой экстре-
экстремума.
Если В2 — ЛС = 0, то никакого заключения о характере ста-
стационарной точки сделать нельзя и требуется дополнительное
исследование.
Примеры. 1) В примере п. 121 было установлено, что
функция
z = 2х3 + ху* + 5л;2 +у2
имеет четыре стационарные точки:
Af^O, O),Af, (—-§¦, о), Af,(—1, 2), AI4(—1, — 2).
Вторые частные производные данной функции равны
10, Й- = 2^, |Ч = 2
В точке Мх имеем: Л= 10, 5=0, С = 2. Здесь В2 — АС= —20 < 0;
значит, точка Л^ является точкой экстремума, и так как А и С
положительны, то точкой минимума.
В точке М2 соответственно будет Л=—10, В — 0, С=—^-;
это точка максимума. Предоставляем читателю проверить, что
точки М3 и Af4 не являются точками экстремума (в них В2 — АС> 0).
2) Найдем точки экстремума функции
z = х2— у2.
414 ГЛ. VII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Приравнивая частные производные нулю:
[123
дх-
ду'
Рис. 145.
находим одну стационарную точку — начало координат. Здесь
А = 2, ? = 0, С=—2. Следовательно, Б2 — ЛС>0 и точка @,0)
не является точкой экстремума.
Уравнением = х2—у2 есть урав-
уравнение гиперболического параболо-
параболоида; из рис. 145 ясно видно, что
стационарная точка @, 0) не яв-
является точкой экстремума.
123. Задачи о наибольших и
наименьших значениях. Пусть
требуется найти наибольшее и
наименьшее значение функции ? =
==f(x, у) в некоторой области
(рассматриваемой вместе со своей
границей). Если какое-либо из этих значений достигается функ-
функцией внутри области, то оно, очевидно, является экстремальным.
Нэ может случиться, что наибольшее или наименьшее значение
принимается функцией в некоторой точке, лежащей на границе
области.
Из сказанного следует правило:
Для того чтобы найти наибольшее или наименьшее значение
функции z=f(x, у) в замкнутой области, нужно найти все макси-
максимумы или минимумы функции, достигаемые внутри этой области,
а также наибольшее или наименьшее значение функции на границе
области. Наибольшее из всех этих чисел и будет искомым наиболь-
наибольшим значением, а наименьшее — наименьшим.
Пример. Найдем точку на плоскости Оху, сумма квадратов
расстояний которой до трех точек Рх @, 0), Р20> 0), Р5@у 1)
имеет наименьшее значение, и точку треугольника с вершинами
в Я1э Р2, Р3, сумма квадратов расстояний которой до вершин
имеет наибольшее значение.
Возьмем на плоскости какую-нибудь точку Р{х, у). Сумма
квадратов ее расстояний до заданных точек Pv P2, Рг (обозначим
эту сумму через z) выражается так:
— IJ
или
z = Зх2 + 3/ — 2х — 2у + 2.
Первая часть задачи сводится к нахождению наименьшего зна-
значения этой функции во всей плоскости, вторая часть — к нахож-
123] § 4. ЭКСТРЕМУМЫ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 415
дению наибольшего значения функции при условии, что точка
Р(х, у) принадлежит замкнутой области D, ограниченной тре-
треугольником PiP2Pz.
Найдем экстремумы функции z — 3x2 + 3y2— 2х—2j?-(-2. Из
уравнений
~ = 6х—2 = 0 и |? = 6j; —2 = 0
дх ду J
получаем
Значит, существует лишь одна стационарная точка
всей плоскости функция не имеет наибольшего значения, так как
ясно, что существуют точки, для которых указанная сумма больше
любого наперед заданного числа. А так как, с другой стороны,
очевидно, что эта сумма должна достигать наименьшего значения,
то именно стационарная точка Р только и может быть точкой,
в которой функция получает свое наименьшее значение ( = 1—J #
Между прочим, точка Я (-о-, -q-j служит центром тяжести тре-
угольника с вершинами в Р1У Я2, Я3.
Переходим ко второй части задачи. Вследствие того, что за-
заданная функция не имеет максимума, ее наибольшим значением
в области D является наибольшее из значений, принимаемых на
границе, т. е. на сторонах треугольника.
На стороне РгР2 имеем у — О и, значит,
эта функция достигает в интервале [0, 1] наибольшего значения
( = 3) при лг=1, т. е. в точке Я2.
На стороне РХР3 имеем х = 0 и, значит,
z = 3/ —2jr + 2;
наибольшее значение этой функции в интервале [0, 1] также
равно 3 и достигается при у=\, т. е. в точке Я3.
Наконец, на стороне Р2Р3 имеем х-\-у=\ и, значит,
z = З*2 + 3 A — л:J — 2х — 2 A — х) + 2 = 6л:2—6х + 3;
эта функция достигает в интервале [0, 1] наибольшего значения
( = 3) при лг = О и при х=\, т. е. наибольшее значение на сто-
стороне Р2Р9 функция z получает в тех же точках Я2 и Я3. Итак,
во второй части задачи искомых точек треугольника имеется две:
Я2 и Я3. Среди всех точек треугольника сумма квадратов расстоя-
расстояний этих точек от вершин Ях, Я2, Я3 имеет наибольшее значение.
416
ГЛ. VII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[124
124*. Условные экстремумы. При отыскании экстремумов функ-
функций нескольких переменных часто возникают задачи, связанные с
так называемым условным экстремумом. Разъясним это понятие на
примере функции двух переменных.
Пусть задана функция z=f(x,y) и линия L на плоскости Оху.
Задача состоит в том, чтобы на линии L найти такую точку
Рис. 146.
> >0> B которой значение функ-
функции f(x,y) является наибольшим
или наименьшим по сравнению
со значениями этой функции в
точках линии L, находящихся
вблизи точки Я. Такие точки Р
называются точками условного экст-
экстремума функции /\х,у) на ли-
линии L. В отличие от обычной точ-
точки экстремума значение функции
в точке условного экстремума срав-
сравнивается со значениями функции
не во всех точках некоторой ее окрестности, а только в тех,
которые лежат на линии L..
Совершенно ясно, что точка обычного экстремума (говорят
также безусловного экстремума) является и точкой условного
экстремума для любой линии, проходящей через эту точку. Об-
Обратное же, разумеется, неверно: точка условного экстремума мо-
может и не быть точкой обычного экстремума. Поясним сказанное
простым примером. Графиком функции z = Y^—х2—у2 являет-
является верхняя полусфера (рис. 146). Эта функция имеет максимум
в начале координат; ему соответствует вершина М полусферы.
Если линия L есть прямая, проходящая через точки А к В (ее
уравнение х-\-у—1=0), то геометрически ясно, что для точек
этой линии наибольшее значение функции достигается в точке
-, у], лежащей посередине между точками А я В. Это и
есть точка условного экстремума (максимума) функции
z = ]/r\—х2—у2 на данной линии; ей соответствует точка Мг на
полусфере, и из рисунка видно, что ни о каком обычном экстре-
экстремуме здесь не может быть речи.
Отметим, что в заключительной части задачи об отыскании
наибольшего и наименьшего значений функции в замкнутой об-
области (см. п. 123) нам приходится находить экстремальные зна-
значения функции на границе этой области, т. е. на какой-то линии,
и тем самым решать задачу на условный экстремум.
Приступим теперь к практическому отысканию точек услов-
условного экстремума функции z~f(x,у) при условии, что переменные
хну связаны уравнением <f(x,y) = Q. Это последнее соотноше-
124] § 4. экстремумы функций нескольких переменных 417
ние будем называть уравнением связи. Если из уравнения связи у
можно явно выразить через х\ y = ty (х), то, подставляя в выра-
выражение функции z~f(x, у) вместо у функцию ty(x), мы получим
функцию одной переменной
*=/[*, ч> (*)] = *(*)¦
Найдя значения х, при которых эта функция достигает эк-
экстремума, и определив затем из уравнения связи соответствующие
им значения у, мы и получим искомые точки условного экстре-
экстремума.
Так в вышеприведенном примере из уравнения связи х-\-у —
— 1=0 имеем у=\—х. Отсюда
г = ]Л — х2 — A— xJ
Легко проверить, что z достигает максимума при х = 0,5; но
тогда из уравнения связи j/ = 0,5, и мы получаем как раз точку
Я, найденную из геометрических соображений.
Очень просто решается задача на условный экстремум и тог-
тогда, когда уравнение связи можно представить параметрическими
уравнениями: x = x(t), y=y(t). Подставляя выражения для х и
у в данную функцию, снова приходим к задаче отыскания экстре-
экстремума функции одной переменной.
Если уравнение связи имеет более сложный вид и нам не уда-
удается ни явно выразить одну переменную через другую, ни заме-
заменить его параметрическими уравнениями, то задача отыскания
условного экстремума становится более трудной. Будем по-преж-
по-прежнему считать, что в выражении функции z=f(x,y) переменная
у является функцией от х, определенной неявно уравнением связи
ф(лг, j;) = 0. Полная производная от функции z = f(x,y) no x (см.
п. 116, 1) равна
где производная у' найдена по правилу дифференцирования не-
неявной функции (п. 118). В точках условного экстремума найденная
полная производная должна равняться нулю; это дает одно урав-
уравнение, связывающее хну. Так как они должны удовлетворять
еще и уравнению связи, то мы получаем систему двух уравнений
с двумя неизвестными
Л—^Л = 0, tp(x,y) = 0.
14 А. Ф. Бермант, И. Г. Арамановнч
418
ГЛ. VII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[124
Преобразуем эту систему к гораздо более удобной, записав
первое уравнение в виде пропорции и введя новую вспомогатель-
вспомогательную неизвестную к:
(*)
(знак минус перед к поставлен для удобства). От этих равенств
легко перейти к следующей системе:
/х(х,У) + Ь<Рх{х,У) = О, /„{х,у) + Кч'у(х,у)=0, (**)
которая вместе с уравнением связи <р (л:, у) = 0 образует систему
трех уравнений с неизвестными ху у и к.
Уравнения (**) легче всего запомнить при помощи следующего
правила: для того чтобы найти точки, которые могут быть точками
условного экстремума функции z=f(x,y) при уравнении связи
ф (лг, у)=0, нужно образовать вспомогательную функцию
где к — некоторая постоянная, и составить уравнения для отыскания
точек экстремума этой функции.
Указанная система уравнений доставляет, как обычно, только
необходимые условия, т. е. не всякая пара значений х и уу
удовлетворяющая этой системе,
обязательно является точкой ус-
ловногоэкстремума. Д ос т а т о ч-
н ы е условия для точек условного
экстремума мы приводить не бу-
будем; очень часто конкретное со-
содержание задачи само подсказы-
подсказывает, чем является найденная
точка. Описанный прием решения
задач на условный экстремум
называется методом множителей
Лагранжа.
Метод Лагранжа имеет на-
наглядный геометрический смысл,
который мы сейчас и выясним. Предположим, что на рис. 147 изоб-
изображены линии уровня функции z=zf(xyy) (см. п. 108) и линия L,
на которой отыскиваются точки условного экстремума. Если в
точке Q линия L пересекает линию уровня, то эта точка не может
быть точкой условного экстремума, так как по одну сторону от
линии уровня функция f(x, у) принимает большие значения, а по
другую —меньшие. Если же в точке Р линия L не пересекает
Рис. 147.
124] § 4. ЭКСТРЕМУМЫ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 419
соответстзующую линию уровня и, значит, в некоторой окрестности
этой точки лежит по одну сторону от линии уровня, то точка Р
будет как раз являться точкой условного экстремума. В такой точке
линия L и линия уровня f(x, «/) = С касаются друг друга (мы пред-
предполагаем, что линии гладкие) и угловые коэффициенты касательных
к ним должны быть равны. Из уравнения связи ф(л;, #) = 0 имеем
у' = — фУф^,, а из уравнения линии уровня у1 =—f'xlfy Приравни-
Приравнивая производные и произведя простейшее преобразование, мы и
получим уравнения (*).
Приведенное рассуждение может потерять силу, если линия уровня
такова, что во всех ее точках /* = 0, /^ = 0. Советуем рассмотреть,
например, функцию г = 4 — х2 и линию уровня л; = 0, отвечающую
значению 0 = 4.
Пример. Найти наибольшее значение функции z~xy, если х
х2 и2
и у положительны и подчиняются уравнению связи ~о~ + 4>~—1 = 0.
Здесь уравнение связи простое (оно представляет эллипс) и можно
было бы сразу прийти к отысканию экстремума функции одной пере-
переменной, выразив у через х или взяв параметрические уравнения
эллипса. Рекомендуем читателю сделать это самостоятельно; мы же
для иллюстрации решим пример методом Лагранжа.
Составим вспомогательную функцию
Ф(х, у)^Ху +
(Постоянное слагаемое в левой части уравнения связи при диффе-
дифференцировании дает нуль, и поэтому мы его просто не пидлем.)
приравнивая частные произзэдные пэ х и пэ у нулю, получим
дФ . Хх л дФ
J/+ 0
Исключая Я, приходим к уравнению 4у2 — лс2 = 0, решая которое
совместно с уравнением связи находим л; = 2 и у = \ (по условию
задачи х и у положительны).
Функция z = xy при рассматриваемых значениях х и у положи-
положительна и в точках пересечения эллипса с осями координат B У~2, 0)
и @, У~2) равна нулю. Поэтому найденная единственная точка РB, 1)
будет точкой условного максимума; в этой точке 2тах = 2. Легко
проверить, что в точке Р эллипс касается линии уровня функции
z = xy, проходящей через эту точку, т. е. гиперболы ху = 2.
Задачи на условный экстремум для функций трех переменных
допускают большее разнообразие. Пусть задана функция и =
= /(*> У> г) и переменные х, у и z связаны одним уравнением
420 гл. vii. функции нескольких переменных [124
ф(лг, у, 2) = 0; это есть уравнение некоторой поверхности. Тогда
точка условного экстремума является такой точкой поверхности,
в которой функция принимает наибольшее или наименьшее значе-
значение по сравнению с ее значениями во всех близлежащих точках
этой же поверхности.
Можно искать условный экстремум функции /(а:, у, z) и при
двух уравнениях связи: фх (лг, у} z) = 0 и <р2 (х, у, z) = 0l). Эти
уравнения определяют линию в пространстве. Таким образом, за-
задача сводится к отысканию такой точки линии, в которой функ-
функция принимает экстремальное значение, причем сравниваются зна-
значения функции только в точках рассматриваемой линии.
Метод множителей Лагранжа в случае двух уравнений связи
применяется следующим образом: строим вспомогательную функцию
где кг и Х2 — новые дополнительные неизвестные, и составляем
систему уравнений для отыскания экстремумов этой функции
дФ df , « д
ду ду ' х ду ~ 2 ду
дФ df л ^ , л ^ф2
Добавляя сюда два уравнения связи, получаем систему пяти урав-
уравнений с пятью неизвестными лг, у, z, Xv Я2. Искомыми точками
условного экстремума могут быть только те, координаты лг, уу
г которых являются решениями этой системы.
В самом общем виде задача ставится так: требуется найти экстремумы
функции п переменных u — f(x, у, г, .... t) при условии, что эти переменные
подчинены т уравнениям связи (т < п)
ф!(х, у, z, ..., 0 = 0, ф2(х, у, 2, ..., 0 = 0, .... фт(*, у, z, ..., 0 = 0.
Вспомогательная функция зависит от п переменных и содержит т до-
дополнительных неизвестных
Уравнения для отыскания точек экстремума этой функции и уравнения связи
составят систему т + п уравнений, из которой определяются координаты
х, у, z, ..., t возможных точек условного экстремума«
Примеры. 1) Найти прямоугольный параллелепипед наиболь-
наибольшего объема, если его полная поверхность равна заданной вели-
величине 5.
1) Рекомендуем читателю подумать, почему при большем числе уравне-
уравнений связи задача может потерять смысл.
124] § 4. экстремумы функций нескольких переменных 421
Обозначим стороны параллелепипеда через ху у, z. Тогда тре-
требуется найти наибольшее значение функции V—xyz при условии,
что xy+yz+zx
Вспомогательная функция Ф (лг, у, z) = xyz + k (xy+yz + zx).
Уравнения для отыскания точек экстремума этой функции имеют
вид
Вычитая эти уравнения друг из друга, получим
Отсюда ясно, что x=y = z, т. е. что искомый параллелепипед—
куб. Размеры его определим из уравнения связи:
x = y = z=yT и V-
2) Найти наибольшее расстояние от начала координат до то-
точек линии пересечения параболоида вращения z = x2-{-y2 с пло-
плоскостью х-\-2у—2 = 0. (Наименьшее расстояние равно нулю, так
как линия пересечения проходит через начало координат.)
Расстояние г от начала координат до точки (лг, у, z) равно
]/rx2+y2 + z2. Наибольшие значения корня и подкоренного выра-
выражения достигаются в одной и той же точке; поэтому будем ис-
искать условный максимум функции и = х2-\-у2-\-z2 при двух урав-
уравнениях связи
<Pi(*,>>, z)==ELX2+y2—z = 0 и q>2(x,y,
Составляя вспомогательную функцию
и приравнивая нулю ее частные производные, получим
2х + 2Кгх + А2 = 0, 2у + 2kty + 2Х2 = 0, 2z—k1 — X2 = 0.
Выразим отсюда координаты х, у, z через вспомогательные не-
неизвестные
2 "
Подставляя в уравнения связи
4
и приравнивая левые части обоих уравнений, получаем квадрат-
квадратное уравнение относительно t , V1" * Его первый корень приводит
422 гл. vii. функции нескольких переменных [125
к значениям Х2~0 и Х1 = 0; им соответствует начало координат —
точка минимума. Второй корень равен 2 ¦= —2. Даже не оты-
скивая Кг и Я2, находим дг=1, у —2 и 0 = 5. Ясно, что эта точка
наиболее удалена от начяла координат и /*тах = "|/30.
§ 5. Скалярное поле
125, Скалярное поле. Поверхности уровня. Предположим, что
в каждой точке Р некоторой области D нам задано значение
скалярной физической величины и, т. е. такой величины, ко-
которая полностью характеризуется своим числовым значением. На-
Например, это может быть температура точек неравномерно нагре-
нагретого тела, плотность распределения электрических зарядов в изо-
изолированном наэлектризованном теле, потенциал электрического поля
и т. д. При этом и называется скалярной функцией тонки; запи-
записывается это так: и = и(Р).
Область Д в которой определена функция и(Р), может сов-
совпадать со всем пространством, а может являться некоторой его
частью.
Определение. Если в области D задана скалярная функ-
функция точки и(Р), то говорят, что в этой области задано скаляр-
скалярное поле.
Мы будем счихать, что скалярное поле стационарное, т. е.
что величина и (Р) не зависит от времени t. Заметим, впрочем,
что в будущем (см. п. 157) читателю придется сталкиваться и с
нестационарными полями. Тогда величина и будет зависеть
не только от точки Р, но и от времени t.
Если физическая величина векторная, то ей будет соот-
соответствовать векторное поле, например силовое поле, электриче-
электрическое поле напряженности, магнитное поле и др. Векторные поля
будут изучаться в § 3 главы IX.
Если скалярное поле отнесено к системе координат Охуг, то
задание точки Р равносильно заданию ее координат лг, у, z\ и
тогда функцию и (Р) можно записать в обычном виде функции
трех переменных: u(xyy,z). Мы пришли, таким образом, к физиче-
физическому толкованию функций трех переменных.
Определение. Поверхностью уровня скалярного поля на-
называется геометрическое место точек, в которых функция и при-
принимает постоянное значение, т. е.
В курсе физики при рассмотрении поля потенциала поверхности
уровня называют обычно эквипотенциальными поверхностями (т. е.
поверхностями равного потенциала).
126]
§ 5. СКАЛЯРНОЕ ПОЛЕ
423
Уравнение поверхности уровня, проходящей через данную
точку Мо (xOi yQ, z0), записывается так:
и(х, у, г) = и(дг0, yQ, zQ).
Если в частном случае скалярное поле плоское, т. е. мы изу-
изучаем распределение значений физической величины в какой-то пло-
плоской области, то функция и за-
зависит от двух переменных, на-
например х и у. Линиями уровня
этого поля будут линии уровня
функции и {х, у) (см. п. 108, I):
и (*, у) = С.
126. Производная по на-
направлению. Важной характери-
характеристикой скалярного поля является
скорость изменения поля в за-
заданном направлении.
Пусть задано скалярное поле,
т. е. задана функция и (х, у, z).
Возьмем точку Р(х, у, z) и ка-
какой-нибудь луч Я, из нее выхо-
выходящий. Направление этого луча зададим углами а, Р, у> которые
он образует с направлениями осей Ox, Oy, Oz (рис. 148). Если
ех — единичный вектор, направленный по лучу Я, то его проекци-
проекциями будут направляющие косинусы
ex{cosa, cos|5, cosy}-
Пусть точка Рг(хг, yv zx) лежит на луче X; расстояние РРг
обозначим через р. Проекции вектора РРХ на оси координат будут,
с одной стороны, равны р cos a, p cos P, pcosy, а с другой сто-
стороны,— разностям хг — х, ух—у и гг—z. Следовательно,
хх = х + р cos a, yx^y + p cos p, zx = z+p cos у.
Рассмотрим теперь приращение функции и при переходе из
точки Р в точку Рг:
и(Рг) — и (Р) = и(л; + р cosa, jj + pcosp, z+pcosy) — u{xf y, z).
Рис. 148.
Если точка Рх будет изменять свое положение на луче Л, то
в выражении для разности и (Рг) — и (Р) будет меняться только
величина р. Составим отношение
9
424 гл. vii. функции нескольких переменных [126
и перейдем к пределу при р—> (), предполагая, что этот предел
существует.
Определение. Предел
Нш "~ и W = Нт и **+ р cos а> ^+р cos Р* * + Р cos V) — " (** У* *)
(•)
называется производной от функции и(х, у, z) по направлению X
в точке А
Этот предел будем обозначать символом хт- или и'к(х, yf z).
Величина его зависит от выбранной точки Я (л:, у, z) и от направ-
направления луча А, т. е. от a, (J и у-
Если точка Р фиксирована, то величина производной и'к будет
зависеть только от направления луча Л.
Из определения производной по направлению следует, что если
направление А. совпадает с положительным направлением оси Ох,
т. е. а = 0, р^у — тг» т0 предел (*) будет просто равен частной
производной от функции и (х, у% z) по х:
и(х+р, у, г) — и(х, у, г) _ди
Аналогичную картину мы получим, если направление X будет
совпадать с направлениями осей Оу и Oz.
Подобно тому как частные производные и'х, иу и и'г характери-
характеризуют скорость изменения функции и в направлении осей коорди-
координат (см. п. 109), так и производная по направлению и% будет
являться скоростью изменения функции и (лг, у, z) в точке Р
по направлению луча к. Абсолютная величина производ-
производной и'к по направлению Я определяет величину скорости, а знак
производной — характер изменения функции и (возрастание или
убывание).
Вычисление производной по направлению производится при по-
помощи следующей теоремы:
Теорема. Если функция и (х, у, z) дифференцируема, то ее
производная и[ по любому направлению к существует и равна
где cos a, cos E и cosy — направляющие косинусы луча *к.
Доказательство. Так как функция и(ху у, z) дифферен-
дифференцируема, то ее полное приращение можно записать в виде (см.
126] § 5. скалярное поле 425
п. 110, I)
Ди = и (л:-f Длг, у + ку, z+ Дг) — и(лг, у, z) =
ди А , ди А , ду
где е — бесконечно малая величина более высокого порядка, чем
P=VД*2' + ky2+kz2. Полагая A# = pcosa, Ajf^pcosJJ, Az =
-"pcosy, представим разность и (Рг) — и(Р) в виде
tt(P)«(^) pcosa + pcO8p + Pc
причем — —>() при р—>О. Отношение и ^""""^ будет равно
и(Р):=:ди ди р ди ±
р дх [ ду v [ dz r P
Так как значения частных производных j- , ^- и ^-в точке Я,
а также a, p и у от р не зависят, то, переходя к пределу при
р —*0, получим
что и требовалось доказать.
Из этой формулы непосредственно следует сделанное выше за-
замечание, что если направление к совпадает с положительным
направлением одной из осей координат, то производная по этому
направлению равна соответствующей частной производной, напри-
л о п ди ди
мер, если a = 0, P = Y = T, т0 Ж^дх '
Из формулы (#*) видно, что производная по направлению Я',
противоположному направлению X, равна производной по
направлению \, взятой с обратным знаком. Действительно, при пе-
перемене направления углы a, |J и у изменятся на я и
Это означает, что при перемене направления на противополож-
противоположное абсолютная величина скорости изменения функции и не ме-
меняется, а изменяется только характер ее изменения; если,
например, в направлении К функция возрастает, то в направле-
направлении X' она убывает, и наоборот.
Пример. Дана функция u = xyz. Найдем ее производную
в точке РE, 1, 2) в направлении, идущем от этой точки к точке
QG, -1, 3).
426 ГЛ. VII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [127
Находим частные производные функции u = xyz
ди ди ди
дх ^ > ду ' dz J
и вычисляем их значения в точке Р:
(ди\ о {ди\ лгу f ди
Так как проекции вектора PQ равны 2, —2 и 1, то его направ-
направляющими косинусами будут
2 2 2 1
cos а = , = -о- * cos В = —5-, cos у = -о- •
Следовательно,
Знак минус указывает, что в данном направлении функция и
убывает.
Если поле плоское, то направление луча Я вполне опреде-
определяется углом а его наклона к оси абсцисс. Формулу для произ-
производной по направлению в случае плоского поля можно получить
из общей формулы, положив у = 5- и Р = -о"—<*. Тогда
ди ди , ди .
— = _ cos a + тг sin a.
дХ дх ' ду
-, л ди ди п ди ди
Если а = 0, то^ = ^, а если а = т> то ^ = ^ .
127. Градиент. Рассмотрим снова формулу для производной по
направлению
ди ди , ди
cosa + co
Вторые множители в каждом слагаемом являются, как мы уже
отмечали, проекциями единичного вектора ех, направленного по
лучу X:
ex{cosa, cosp, cosy}.
Возьмем теперь вектор, проекциями которого на оси координат
будут служить значения частных производных -^ , ~ и ~ в вы"
бранной точке Р(х, у, z). Назовем этот вектор градиентом функ-
функции и(х, у, z) и будем обозначать его символами grad и или S/u.
127]
§ 5. СКАЛЯРНОЕ ПОЛЕ
427
Определение. Градиентом функции и(х, у, z) назы-
называется вектор, проекциями которого служат значения частных
производных этой функции, т. е.
Подчеркнем, что проекции градиента зависят от выбора точки
Р(ху у, z) и изменяются с изменением координат этой точки.
Таким образом, каждой точке скалярного поля, определяемого
функцией поля и (х, у, z), соответствует определенный вектор —
градиент этой функции. Отметим, что градиент линейной функции
и = ах + Ьу -\-cz-\-d есть постоянный вектор: grad u= а\-\-Ь]-\-ск.
Пользуясь определением градиента, формуле для производной
по направлению можно придать такой вид:
Следовательно:
Производная функции по данному направлению равна скаляр-
скалярному произведению градиента функции на единичный вектор
этого направления.
Так как скалярное произведение равно модулю одного вектора,
умноженному на проекцию другого вектора на направление перво-
первого, то можно еще сказать, что
Производная функции по дан-
данному направению равна проекции
градиента функции на направле-
направление дифференцирования, т. е.
да
cos ф,
О
Рис. 149.
где ф — угол между вектором
grad я и лучом X (рис. 149). От-
Отсюда сразу следует, что произ-
производная по направлению дости-
достигает наибольшего значения, когда созф=1,т. е. при ф = 0. Это
наибольшее значение равно |grad#|.
Итак, | grad и \ есть наибольшее возможное значение произ-
производной и^ в данной точке Р, а направление grad и совпадает
с направлением луча, выходящего из точки Р, вдоль которого
функция меняется быстрее всего, т. е. направление градиента есть
направление наискорейшего возрастания функции. Ясно, что в
противоположном направлении функция и будет быстрее всего
убывать.
428
ГЛ. VII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[127
Докажем теперь теорему, устанавливающую связь между на-
направлением градиента функции и поверхностями уровня скалярно-
скалярного поля.
Теорема. Направление градиента функции и (х, у, z) в каж-
каждой точке совпадает с направлением нормали к поверхности
уровня скалярного поля, про*
ходящей через эту точку (рис.
150).
Доказательство. Выберем
произвольную точку P0(xQiy0, z0).
Уравнение поверхности уров-
уровня, проходящей через точку Ро,
запишется в виде и (х, у, z) =
=*и0, где ио = и(хОУ у0, z0).
Составим уравнение нормали
D
У
Рис. 150.
к этой поверхности в точке Ро
(см. п. 119):
х — х0 ^у — уо z — z0
(ди\ /ди\ /ди\ '
\дх)о \дуH \dzjo
Отсюда и следует, что направляющий вектор нормали, имею-
имеющий проекции (Jfj f Is-} , (т) ? Я]вляется градиентом функ-
функции «(л:, у, z) в точке Яо, что и требовалось доказать.
Таким образом, градиент в каждой точке перпендикулярен каса-
касательной плоскости к поверхности уровня, проходящей через дан-
данную точку, т. е. его проекция на эту плоскость равна нулю. Сле-
Следовательно:
Производная по любому направлению, касательному w поверхно-
поверхности уровня, проходящей через данную точку, равна нулю.
Укажем теперь некоторые свойства градиента функции, часто
облегчающие его вычисление.
1 2) 1
2) gradC«1 = C gradw1? где С —постоянная.
Проверку этих свойств рекомендуем сделать читателю само-
самостоятельно.
3) gt2Ldu1u2 = u2gradu1-]-u1gradu2. В самом деле,
л д (ихи2)
grad ихи2 = -^р-;
, ^i •
ду
^ ду J ^ дг
= w2 grad ux + wx grad tt2.
127] § 5. СКАЛЯРНОЕ ПОЛЕ
4) grad/(tf) =/' (tf)grada. Действительно,
grad/<e)~?l/(e)]l + ?[/(B)lJ+!
429
Перечисленные свойства градиента показывают, что правила
его отыскания совпадают с правилами отыскания производной
функции.
Примеры. 1) Пусть г = \^х2 + у2 + -г2 — расстояние от точки
до начала координат. Тогда
gradr направлен по радиусу-вектору г, и модуль его равен
единице.
2) Пусть скалярное поле определено функцией --, где г опре-
определено в примере 1. Тогда по
свойству 4)
vu
У
a a Q v
7-=—72gradr==—7^7" •
В плоском поле и = и(ху у)
градиент
ди . , ди ,
Рис. 151.
лежит в плоскости Оху и пер-
перпендикулярен к линии уровня.
Если в плоском поле постро-
построена достаточно густая сетка
линий уровня (рис. 151), то
можно с некоторым приближе-
приближением графически определить мо-
модуль и направление градиента.
Направление градиента будет перпендикулярно к линии уровня*
Производная в этом направлении будет при достаточно малом h
приближенно равна
Р0Р >
Р0Р
где PQ — точка линии уровня и (ху у)=С, а Р— точка линии уровня
и(х} y) = C-\-h. Величина h известна, а длина отрезка Р0Р может
быть измерена на чертеже как расстояние по нормали между
430 ГЛ. VII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [127
соседними линиями уровня. Производная же по направлению гра-
градиента равна его модулю, и поэтому
| « -р-р .
Построение gradtf изображено на рис. 151.
ВОПРОСЫ И ПРЕДЛОЖЕНИЯ ДЛЯ САМОПРОВЕРКИ
1. Что называется функцией двух независимых переменных? областью
определения такой функции?
2. Описать табличный и аналитический способы задания функции двух
независимых переменных.
3. Что называется графиком функции двух независимых переменных?
Описать графическое задание такой функции.
4. Описать метод изучения функций двух и многих независимых пере-
переменных посредством функций одной независимой переменной. Что называется
линией уровня функции z = f{x, у)?
5. Что называется пределом функции z = f(x, у) при х—>-x0 и у—>у^>
6i Дать определение непрерывности функции двух независимых пере-
переменных в точке и в области. Привести примеры разрывных функций»
7. Дать определение частной производной функции двух независимых
переменных по одной из них. Распространить на функции многих незави-
независимых переменных.
8. Каков геометрический смысл частных производных функции z = j(x, у)
в системе декартовых координат?
9. Что называется частным приращением и частным дифференциалом по х
функции 2 = / (х, */)? Как выражается частный дифференциал функции через
ее частную производную?
10. Каков геометрический смысл частных дифференциалов функции
z = f(xf у) в системе декартовых координат?
11. Что называется полным приращением и полным дифференциалом
функции г=/(я, у)? Как выражается полный дифференциал функции через
ее частные производные?
12*. Какая функция нескольких переменных называется дифференци-
дифференцируемой? Сформулировать и доказать достаточное условие дифференцируе-
мости.
13. Что называется касательной плоскостью к поверхности в данной ее
точке? Вывести уравнение касательной плоскости.
14. Каков геометрический смысл полного дифференциала функции
z=z%(x, у) в системе декартовых координат?
15. Как применяется полный дифференциал функции для приближенного
вычисления ее значений?
16. Вывести формулу для предельной абсолютной ошибки функции
нескольких переменных.
17. Вывести формулы для предельных относительных ошибок произве-
произведения и частного.
18. Что называется частной производной л-го порядка функции двух
независимых переменных?
19. Сформулировать теорему о равенстве вторых смешанных произ-
производных.
20. Распространить определение частной производной п-го порядка и
теорему о независимости ее от порядка дифференцирования на функции
многих независимых переменных.
ВОПРОСЫ И ПРЕДЛОЖЕНИЯ 431
21. Дать определение полного дифференциала второго порядка функции
двух переменных и указать формулу для его отыскания.
22. Сформулировать необходимое и достаточное условия того, чтобы
выражение Р (х, y)dx-\-Q (х, у) dy было полным дифференциалом. Привести
доказательства этих условий^ Сформулировать соответствующие условия
для функции трех переменных.
23. Вывести правило дифференцирования сложной функции.
24. Что называется полной производной?
25. В чем состоит свойство инвариантности вида полного дифференциала
функции нескольких переменных?
26. Перечислить основные правила для отыскания дифференциала функ-
функции любого числа независимых переменных*'
27. Сформулировать теорему существования неявной функции.
28. В чем состоит правило дифференцирования неявно заданной
функции?
29. Записать уравнения касательной плоскости и нормали к поверхно-
поверхности, заданной уравнением в общем виде в системе декартовых координат.
30. Как составить уравнения касательной прямой и нормальной пло-
плоскости к кривой, заданной пересечением двух поверхностей?
31. Дать определение точки экстремума (максимума и минимума) функ-
функции двух переменных.
32. В чем состоит необходимый признак экстремума функции двух
независимых переменных? Каков его геометрический смысл?
33. Сформулировать достаточные условия экстремума для функции двух
переменных.
34. Описать способ отыскания наибольшего и наименьшего значений
функции двух переменных в заданной замкнутой области.
35*, Дать определение точки условного экстремума функции [(х, у)
на линии L.
36*. Указать способы отыскания точек условного экстремума. Сформу-
Сформулировать метод множителей Лагранжа и объяснить его геометрический
смыСл.
37*. Сформулировать задачи на условный экстремум для функций трех
и большего числа переменных.
38. Что называется скалярным полем? поверхностью уровня скаляр-
скалярного поля?
39. Вывести формулу для производной по направлению.
40. Дать определение градиента скалярного поля. Как выражается
производная по направлению через градиент?
41. Сформулировать и доказать свойства градиента.
ГЛАВА VIII
ДВОЙНЫЕ И ТРОЙНЫЕ ИНТЕГРАЛЫ
§ 1. Двойные интегралы
128. Объем цилиндрического тела. Двойной интеграл. Переходя
к изложению интегрального исчисления для функций двух неза-
независимых переменных, мы начнем, как обычно, с рассмотрения кон-
конкретной задачи — задачи об определении объема цилиндрического
тела.
Цилиндрическим телом называется тело, ограниченное плоско-
плоскостью Оху, поверхностью, с которой любая прямая, параллельная
оси Oz, пересекается не более чем в одной точке, и цилиндрической
поверхностью, образующая которой параллельна оси Oz,
Область Z), высекаемая в плоскости Оху цилиндрической по-
поверхностью, называется основанием цилиндрического тела
(рис. 152). В частных случаях боковая
цилиндрическая поверхность может и от-
отсутствовать; примером тому служит те-
тело, ограниченное плоскостью Оху и верх-
верхней полусферой z = Vr2 — х2— у2.
Обычно тело можно составить из
некоторого числа цилиндрических тел и
искомый объем определить как сумму
объемов цилиндрических тел, составляю-
составляющих это тело.
Прежде всего напомним два принци-
принципа, из которых мы исходим при опреде-
определении объема тела:
на части, то его объем будет равен
Рис. 152.
1) если разбить тело
сумме объемов всех частей;
2) объем прямого цилиндра, т. е. цилиндрического тела, огра-
ограниченного плоскостью, параллельной плоскости Оху, равен пло-
площади основания, умноженной на высоту тела.
128]
§ 1. ДВОЙНЫЕ ИНТЕГРАЛЫ
433
Пусть z = f(x,y) есть уравнение поверхности, ограничивающей
цилиндрическое тело. Будем считать функцию f(x, у) непрерыв-
непрерывной в области D и сначала предположим, что поверхность целиком
лежит над плоскостью Оху, т. е. что f(x, y)>0 всюду в об-
области D.
Обозначим искомый объем цилиндрического тела через V,
Разобьем основание цилиндрического тела— область D — на неко-
некоторое число п областей произвольной
формы; будем называть их частич-
частичными областями. Пронумеровав
частичные области в каком-нибудь
порядке, обозначим их через ах, а2,
. .., ап, а их площади — через Аа15
Да2, . . ., Дап. Через границу каждой
частичной области проведем цилинд-
цилиндрическую поверхность с образующей,
параллельной оси Oz. Эти цилиндри-
цилиндрические поверхности разрежут поверх-
поверхность на п кусков, соответствующих
п частичным областям. Таким образом,
цилиндрическое тело окажется разби-
разбитым на л частичных цилиндрических тел (рис. 153). Выберем в каждой
частичной области at- произвольную точку Pj (х^ у() и заменим
соответствующее частичное цилиндрическое тело прямым цилинд-
цилиндром с тем же основанием и высотой, равной zi=^f(xii y^. В ре-
результате получим /2-ступенчатое тело, объем которого равен
Рис. 153.
Уг)
, У*)
п
= 2/(*,-, Уд
Принимая объем V данного цилиндрического тела приближенно
равным объему построенного л-ступенчатого тела, будем считать,
что Vn тем точнее выражает К, чем больше п и чем меньше
каждая из частичных областей. Переходя к пределу при п—>оо,
мы будем требовать, чтобы не только площадь каждой частичной
области стремилась к нулю, но чтобы стремились к нулю все ее
размеры. Если назвать диаметром области наибольшее расстояние
между точками ее границы1), то высказанное требование будет
означать, что каждый из диаметров частичных областей должен
J) Например, диаметр прямоугольника равен его диагонали, диаметр
эллипса — его большой оси. Для круга приведенное определение диаметра
равносильно обычному.
434 гл. viii. двойные и тройные интегралы [128
стремиться к нулю; при этом сами области будут стягиваться
в точку *).
В соответствии со сказанным мы принимаем искомый объем V
равным пределу, к которому стремится Vn при стремлении к нулю
наибольшего диаметра частичных областей (при этом п—> оо):
К отысканию предела подобных сумм для функций двух перемен-
переменных приводят самые разнообразные задачи, а не только задача
об объеме.
Рассмотрим этот вопрос в общем виде. Пусть /(л:, у)— любая
функция двух переменных (не обязательно положительная), не-
непрерывная в некоторой области D, ограниченной замкнутой линией.
Разобьем область D на частичные, как указано выше, выберем
в каждой частичной области по произвольной точке Pt (х(, у^ и
составим сумму
п
2/(*f> Уд Л*/» (*)
1=1
где /(•?,-, у{) — значение функции в точке Р{ и АО; — площадь ча-
частичной области.
Сумма (*) называется п-й интегральной суммой для функции
f(xy у) в области D, соответствующей данному разбиению этой
области на п частичных областей.
Определение. Двойным интегралом от функции f (x,y)
по области D называется предел, к которому стремится п-п
интегральная сумма (#) при стремлении к нулю наибольшего
диаметра частичных областей.
Записывается это так:
lim J2/(*,, Л)Д<х? = $$/(*, у)da.
Читается: «двойной интеграл от f(x, у) на do по области D».
Выражение /(#, у) do, показывающее вид суммируемых слагаемых,
называется подынтегральным выражением; функция /(#, у) назы-
называется подынтегральной функцией, do — элементом площади, об-
область D — областью интегрирования, наконец, переменные х и у на-
называются переменными интегрирования.
г) Если известно только, что площадь области стремится к нулю, то
эта область может и не стягиваться в точку. Например, площадь прямо-
прямоугольника с постоянным основанием и высотой, стремящейся к нулю,
стремится к нулю, а прямоугольник стягивается к своему основанию*
т. е. к отрезку.
129] § 1. ДВОЙНЫЕ ИНТЕГРАЛЫ 435
Таким образом, можно сказать, что объем цилиндрического тела,
ограниченного плоскостью Оху, поверхностью <г=/(х,y){f(x,y)>0)
и цилиндрической поверхностью с образующей, параллельной
оси Oz, выражается двойным интегралом от функции /(лг, у),
взятым по области, являющейся основанием цилиндрического тела:
Аналогично теореме существования обыкновенного интеграла
(п. 87) имеет место следующая теорема.
Теорема существования двойного интеграла.
Если функция f(x> у) непрерывна в области Z>, ограниченной
замкнутой линией, то ее я-я интегральная сумма стремится к пре-
пределу при стремлении к нулю наибольшего диаметра частичных
областей. Этот предел, т. е. двойной интеграл \у(х9 y)da9
о
не зависит от способа разбиения области D на частичные об-
области ai и от выбора в них точек Р(.
Двойной интеграл, разумеется, представляет собой число, за-
зависящее только от подынтегральной функции и области интегри-
интегрирования и вовсе не зависящее от обозначений переменных инте-
интегрирования, так что, например,
SJ, v)da.
Далее мы убедимся в том, что вычисление двойного интеграла
может быть произведено посредством двух обыкновенных интегри-
интегрирований.
129. Свойства двойных интегралов. Читатель, наверное, уже
обратил внимание на то, что конструкции определенного интеграла
для функций одной переменной и двойного интеграла совершенно
аналогичны. Вследствие этого свойства двойного интеграла, а также
доказательства этих свойств почти повторяют соответствующие
свойства определенного интеграла. Мы приведем поэтому свойства
двойных интегралов без доказательств.
I. Двойной интеграл от суммы конечного числа функций
равен сумме двойных интегралов ст слагаемых функций:
436 ГЛ. VIU. ДВОЙНЫЕ И ТРОЙНЫЕ ИНТЕГРАЛЫ [129
И. Постоянный множитель подынтегральной функции можно
вынести за символ двойного интеграла:
, у)do.
III. Если область интегрирования D разбита на две части Dx
и ZJ, то
с, у) do.
d\ d2
IV. Если во всех точках области D функции f(x9у) и <р(лг, у)
удовлетворяют условию f{x9 y)^q>(x, у), то
г, у) do.
Знак неравенства может перейти в знак равенства только
тогда, когда обе функции совпадают.
Из свойства IV, в частности, следует, что
Если подынтегральная функция в области интегрирования не
меняет знака, то двойной интеграл есть число того же знака, что
и функция.
Свойство Ш и следствие из свойства IV позволяют уточнить
геометрический смысл двойного интеграла. Условимся объему ци-
цилиндрического тела, расположенного над плоскостью Оху, при-
приписывать знак плюс, а расположенного под плоскостью Оху —
знак минус. Тогда, если z~f(xf у) — уравнение ограничивающей
поверхности, то двойной интеграл jj/(#, у)do является алге-
D
браической суммой объемов тел, соответствующих положи-
положительным и отрицательным значениям функции f{xy у).
Если в двойном интеграле подынтегральная функция тождест-
тождественно равна 1, то двойной интеграл равен площади S области
интегрирования, т. е.
В этом случае двойной интеграл выражает объем прямого цилиндра
с высотой, равной единице; ясно, что этот объем численно равен
площади основания цилиндра.
V. Если функция f(x, у) во всех точках области интегриро-
интегрирования D удовлетворяет неравенствам
130] § 1. ДВОЙНЫЕ ИНТЕГРАЛЫ 437
то
JJ(jc, у) do < MS,
где S—площадь области D.
VI. Двойной интеграл равен произведению значения подын-
подынтегральной функции в некоторой точке области интегрирования
на площадь области интегрирования, т. е.
Значение/(I, г)), находимое из последнего равенства, называется
средним значением функции f(x, у) в области D (ср. с п. 90).
Геометрически теорему о среднем для двойного интеграла можно
сформулировать так: существует цилиндр, основание которого
совпадает с основанием D данного цилиндрического, тела, высота
равна аппликате поверхности z=f(x, у) в некоторой точке осно-
основания, а объем равен объему цилиндрического тела. Указанная
аппликата и изображает среднее значение функции f(x, у) в об-
области D.
130. Вычисление двойных интегралов. При вычислении двой-
двойного интеграла jj/(-#, у) do элемент площади da нам удобно пред-
D
ставить в ином виде. Будем разбивать область интегрирования D
в плоскости Оху на частичные области посредством двух систем
координатных линий: х = const, y = const. Этими линиями
служат прямые, параллельные соответственно оси Оу и оси Ох,
а частичными областями — прямоугольники со сторонами, парал-
параллельными осям координат. Ясно, что площадь каждой частичной
области Да будет равна произведению соответствующих Длг и Ау.
Поэтому элемент площади do мы запишем в виде
do = dx dy,
т. е. элемент площади в декартовых координатах является произве-
произведением дифференциалов независимых переменных. Мы имеем
D
При вычислении двойного интеграла (#) мы будем опираться на
тот факт, что он выражает объем V цилиндрического тела с осно-
основанием D, ограниченного поверхностью z = f(x, у). Напомним, что
мы уже занимались задачей об объеме тела, когда рассматривали
438
ГЛ. VIH. ДВОЙНЫЕ И ТРОЙНЫЕ ИНТЕГРАЛЫ
[130
применения определенного интеграла к задачам геометрии. В п. 101
была получена формула
ъ
V— j S (x) dx, (**)
а
где S(x) — площадь поперечного сечения тела плоскостью, пер-
перпендикулярной к оси аб-
абсцисс, а х — а и х — b—
уравнения плоскостей,
м У1 ограничивающих данное
Wrf^te^L/ тело (см. рис. 122 на стр.
343). Применим теперь эту
формулу к вычислению
двойного интеграла
Предположим сначала,
что область интегрирова-
интегрирования D удовлетворяет сле-
следующему условию: любая
прямая, параллельная оси
рис 154 Ох или оси Оуу пересекает
границу области не более
чем в двух точках. Соответствующее цилиндрическое тело изоб-
изображено на рис. 154.
Область D заключим внутрь прямоугольника
стороны которого касаются границы области в точках Л, В, С, Е.
Интервал [<z, b] является ортогональной проекцией области D
на ось Ох, а интервал [с, d] — ортогональной проекцией облас-
области D на ось Оу. На рис. 155 область D показана в плоско-
плоскости Оху.
Точками А и С граница разбивается на две линии: ЛВС и ЛЕС,
каждая из которых пересекается с любой прямой, параллельной
оси Оу, в одной точке. Поэтому их уравнения можно записать
в форме, разрешенной относительно у:
у=у^х) (ABC),
у = у2(х) (ЛЕС).
Аналогично точками В и Е граница разбивается на линии ВАЕ
130]
§ 1. ДВОЙНЫЕ ИНТЕГРАЛЫ
439
и ВСЕ, уравнения которых можно записать так:
х = хг{у) (ВАЕ),
х = х2(у) (ВСЕ).
Рассечем рассматриваемое цилиндрическое тело произвольной
плоскостью, параллельной плоскости Oyz, т. е. х = const,
a^x^.b (рис. 154). Б сечении мы получим криволинейную тра-
трапецию PMNR, плошадь которой выражается интегралом от
функции /(х,у), рассматри-
рассматриваемой как функция одной пе-
переменной уу причем у изменя-
изменяется от ординаты точки Р до
ординаты точки R. Точка Р
есть точка входа прямой
х = const (в плоскости Оху)
в область Z), а /? —точка
ее выхода из этой области.
Из уравнений линий ABC и
АЕС следует, что ординаты
этих точек при взятом х соот-
соответственно равны Ух(х) и
У2 (*)¦
Следовательно, интеграл ~"
R
х-х^у)
, y)dy
Рис. 155.
Ut(x)
дает выражение для площади плоского сечения PMNR. Ясно, что
величина этого интеграла зависит от выбранного значения х;
другими словами, площадь рассматриваемого поперечного сечения
является некоторой функцией от лг, мы обозначим ее через S(x);
Уг(х)
S(x)= J /(*, y)dy.
Согласно формуле (*#) объем всего тела будет равен интег-
интегралу от S (х) в интервале изменения х (а1
*) При выводе формулы (**) мы считали, что 5 (#) есть геометриче-
геометрическая площадь поперечного сечения. Поэтому дальнейшие рассуждения
справедливы, строго говоря, лишь для случая [ (*, у)^0- Основываясь
на уточненном геометрическом смысле двойного интеграла, нетрудно до-
доказать, на чем мы не будем останавливаться, что получающаяся формула
для вычисления двойного интеграла будет верна для любых функций.
440 ГЛ. VH[. ДВОЙНЫЕ И ТРОЙНЫЕ ИНТЕГРАЛЫ [130
Заменяя в этой формуле S {х) ее выражением, окончательно
получим
или в более удобной форме
Ь ГУг (X) -I
=U \f{xyy)dy\dx
a lyt(x) J
> = \dx J f(x, y)dy. (A)
о a yt (x)
Пределы внутреннего интеграла переменные; они указывают
границы изменения переменной интегрирования у при постоянном
значении второго аргумента лг. Пределы внешнего интеграла
постоянны; они указывают границы, в которых может изменяться
аргумент х.
Меняя роли л; и у, т. е. рассматривая сечения тела плоскостями
у== const (c^.y ^d), мы найдем сначала, что площадь Q(y) такого
сечения равна j /(•#, y)dx, где у при интегрировании считается
величиной постоянной. Интегрируя затем Q (у) в пределах измене-
изменения у, т. е. от с до d, мы придем ко второму выражению для
двойного интеграла
d xt (у)
с, у) dx dy = ^ dy $ fix, у) dx. (Б)
D с хх (у)
Здбсь интегрирование совершается сначала по л:, а потом по у.
Формулы (А) и (Б) показывают, что вычисление двойного ин-
интеграла сводится к последовательному вычислению двух обыкно-
обыкновенных определенных интегралов; нужно только помнить, что
во внутреннем интеграле одна из переменных принимается при
интегрировании за постоянную. Для краткости правые части фор-
формул (А) и (Б) называют повторными (или двукратными) интегра-
интегралами, а сам процесс расстановки пределов интегрирования—при-
интегрирования—приведением двойного интеграла к повторному.
Формулы приведения двойного интеграла к повторному приобре-
приобретают особенно простой вид, когда область D является прямоуголь-
прямоугольником со сторонами, параллельными осям координат (рис. 156).
В этом случае становятся постоянными пределы не только внеш-
внешнего, но и внутреннего интегралов:
Ъ 4 d Ь
\\f(x* y)do = ] dx] /(лг, у) dy = j dy } /(лг, у) dx.
D ас с а
13Q]
§ 1. ДВОЙНЫЕ ИНТЕГРАЛЫ
441
В других случаях для сведения двойного интетрала к повтор-
повторному необходимо прежде всего построить область интегрирования;
лучше всего изобразить эту область прямо в плоскости Оху,
как это сделано на рис. 155. Затем нужно установить порядок
интегрирования, т. е. наметить, по какой переменной будет про-
производиться внутреннее интегрирование, а по какой — внешнее,
и расставить пределы интегрирования.
Поясним на примерах, как производится расстановка пределов
интегрирования.
Примеры. 1) Приведем к повторному двойной интеграл
\ $/(•*' y)dxdy, если область D —треугольник, ограниченный
D
У
О\ а Ъ х
Рис. 156.
y=ff
О а, х
Рис. 157.
прямыми ^ = 0, у~х и х = а (рис. 157). Если интегрировать сна*
чала по у} а потом по х, то внутреннее интегрирование произво-
производится от линии ^ = 0 до ли ник у ~ху а внешнее — от точки
х = 0 до точки х — а. Поэтому
(x, y)dy.
Меняя порядок интегрирования, получим
а а
, y)dxdy=-\dylf(xry)dx.
2) Приведем к повторному интеграл $J/(*, y)dxdy> если
D
область D ограничена линиями у=*0, у=х2 и х-\-у — 2.
Область Д а также координаты крайних ее точек показаны на
рис. 158. Вид области указывает на то, что удобнее интегрировать
442 гл. viii. двойные и тройные интегралы
сначала по л;, а потом по у.
[130
\ 2-у
Если мы изменим порядок интегрирования, то результат уже
VI
ДB90) X
Рис. 158.
не удастся записать в виде одного повторного интеграла,
так как линия ОБА имеет на разных участках разные уравнения.
х О
л
Рис. 160.
Рис. 161.
Разбивая область D на две: ОВС и СВА, получим
D
-Х
J f(x, y)dy.
Этот пример показывает, как важно с самого начала продумать
порядок интегрирования.
Формулы (А) и (Б) сведения двойного интеграла к повторному справед-
справедливы и для случая областей более общего вида. Так, формула (А) приме-
применима к области, указанной на рис. 159, а формула (Б) —к области, изобра-
изображенной на рис. 160. В случае области еще более общего вида (рис. 161)
130]
§ 1. ДВОЙНЫЕ ИНТЕГРАЛЫ
443
двойной интеграл следует разбить на сумму интегралов по более простым
областям, а затем каждый из них сводить отдельно к повторному, пользуясь
формулами (А) или (Б).
Рассмотрим теперь несколько примеров, связанных с вычисле-
вычислением двойных интегралов.
Примеры. 1) Найдем двойной интеграл от функции
по прямоугольной области D( —
Геометрически / выражает объем четырехугольной призмы
fW
Рис. 162.
Рис. 163.
(рис. 162), основанием которой служит прямоугольник D, усечен-
усеченной плоскостью
Возьмем повторный интеграл сначала по у, затем по х:
То же самое получим, интегрируя сначала по дг, а затем по ух
-2 -1
444 гл. viii. двойные и тройные интегралы
2) Вычислим двойной интеграл
1130
по области ?>, ограниченной линиями у = х и у — х2. Область D
Рис. 164.
изображена на рис. 163. Интегрируя сначала по у, а потом по х,
получаем
ox'
?-V
О
Правильность результата можно проверить, изменив порядок
интегрирования:
20
3) Вычислим объем тела, ограниченного цилиндрическими по-
х2
верхностями 2 = 4—у2, <У = у и плоскостью 2 = 0 (рис. 164, а).
Поверхность, ограничивающая тело сверху, имеет уравнение
2 = 4—у2. Область интегрирования D получается в результате
1301
§ 1. ДВОЙНЫЕ ИНТЕГРАЛЫ
445
пересечения параболы у~-х- с линией пересечения цилиндра z =
= 4—у2 и плоскости г = 0, т. е. с прямой у = 2 (рис. 164, б).
Ввиду симметрии тела относительно плоскости Oyz вычисляем
половину искомого объема:
2
—f] dx =
128
Следовательно,
' = 9т ^12,2 куб. ед.
Рекомендуем читателю провести вычисления при измененном по-
порядке интегрирования.
4) Вычислим объем V тела, ограниченного поверхностью
г=1— 4лг2 — у2
и плоскостью Оху.
Заданное тело представляет собой сегмент эллиптического
параболоида, расположенный над плоскостью Оху (рис. 165).
Параболоид пересекается с плоско-
плоскостью Оху по эллипсу
Следовательно, задача состоит в
отысканий объема цилиндрического
тела, имеющего своим основанием
внутренность указанного эллипса и
ограниченного параболоидом
z= \ —4а;2—у2.
В силу симметрии тела относи-
относительно плоскостей Oxz и Oyz можно
вычислить объем четвертой его части,
заключенной в первом координатном угле. Этот объем равен
двойному интегралу, распространенному по области, заданной
условиями 4л:2 + У2 ^ 1, х ^0, у 2^0, т. е. по четверти эллипса.
Интегрируя сначала по у} затем по х> получим
Рис. 165.
_4x2_ /)^ = |.j(i_ 4x2)Tdx
446 ГЛ. VIII. ДВОЙНЫЕ И ТРОЙНЫЕ ИНТЕГРАЛЫ
Подстановка 2.x; = sm? дает (см. п. 94)
[Ш
1 т/ 2 If 4 , ,, 2 1 3
откуда К=^.
131. Двойной интеграл в полярных координатах. Для вычисле-
вычисления двойного интеграла
' У) da
мы пользовались до сих пор системой декартовых координат. От-
Отнесем теперь плоскость к системе
полярных координат г, ф и пред-
предположим, как обычно, что полюс
лежит в начале координат и по-
полярная ось совпадает с осью абс-
абсцисс. Тогда декартовы координаты
точки выражаются через полярные
по формулам
x — rcosq>y у—г sin у.
Разобьем область интегрирования
D на частичные области 0j двумя
системами координатных ли-
линий: г = const, ф == const. Этими
Рис. 166. линиями будут соответственно кон-
концентрические окружности с центром
в полюсе и лучи, исходящие из полюса (рис. 166). При этом час-
частичными областями Q; будут криволинейные четырехугольники,
ограниченные дугами концентрических окружностей и их радиусами.
Площадь Да,- области oL будет
ИЛИ
где
, = \ (г, + Аг,J ДФ, -~ rf ДФ/ = (г, + ^') Дг,
есть средний радиус между ri и г^Аг^
131] § 1. ДВОЙНЫЕ ИНТЕГРАЛЫ 447
Пусть дана функция /(лг, у), непрерывная в области ?>. Соста-
Составим для нее интегральную сумму, разбивая область D на частич-
частичные области а,- и выбирая в качестве произвольных точек Р4- (лг,-, у{)
областей а( точки, лежащие на средних окружностях радиуса rif
т. е. полагая
Тогда *)
п
. Ус) Д^= S/^'coscpf, r; sin ф;) г) Дг,- Дф?.
1=1 1=1
Так как в правой части стоит интегральная сумма для функции
/(гсоБф, г sin ф) г по переменным г и ф, то, переходя к пределу,
получим
/= Jj f{xy y)dxdy=]} /(гсоэф, г sinq>)rdrd<f.
D D
Это равенство является формулой преобразования двойного
интеграла от декартовых координат к полярным. Выражение
называется элементом площади в полярных координатах.
Правило преобразования двойного интеграла к
полярным координатам. Для того чтобы преобразовать
двойной интеграл в декартовых координатах в двойной интеграл
в полярных координатах, нужно х и у в подынтегральной функции
заменить соответственно через rcoscp и rsinq>, а произведение
dxdy заменить произведением rdrdy.
Вычисление двойного интеграла в полярной системе координат,
также как и в декартовой, сводится к последовательному интегриро-
интегрированию по переменным гиф. Укажем правила расстановки пределов.
1. Пусть полюс не содержится внутри области
интегрирования D, заключенной между лучами ф = фх и
ф = ф2, и координатные линии ф = const встречают ее границу не
более чем в двух точках (рис. 167, а. Область может также
иметь вид, изображенный на рис. 167,6.).
Полярные уравнения кривых ADC и ЛВС пусть будут г = гх(ф)
и г = г2(ф).
г) Следует заметить, что площади частичных областей о*;, примыкаю-
примыкающих к границе области D, могут быть и не равны /. Д/*; Аф/. Можно, од-
однако, доказать, что получающаяся при такой замене суммарная ошибка
стремится к нулю при последующем переходе к пределу.
448
ГЛ. VIII. ДВОЙНЫЕ И ТРОЙНЫЕ ИНТЕГРАЛЫ
[131
Интегрируя сначала по г в пределах его изменения при постоян-
постоянном ф, т. е. от гх(ф) до г2 (ф), а затем по ф от фх до ф2, получим
Ф2 Г2 (ф)
/(гсоБф, г sin ф) г dr.
Ф1 МФ)
Интегрирование в обратном порядке, т. е. сначала по ф, а потом
по г, обычно не встречается.
Рис. 167.
В частном случае, когда областью интегрирования служит
часть кругового кольца гх ^ г ^ г2, ф2 ^ ф ^ ф2, пределы интегри-
интегрирования постоянны по обеим переменным:
' 2
j f(r cos ф, г sin ф) г
2. Пусть полюс содержится внутри области
интегрирования и любой полярный радиус пересекает границу
в одной точке (так называемая звездная относительно полюса
область). Интегрируя сначала по г, а затем по ф, получим
, г sin ф) г dr,
где г = г(ф) есть полярное уравнение границы области.
В частности, при г = г (ф) = /? = const, т. е. когда область
интегрирования есть круг с центром в полюсе, будем иметь,
2Я R
г» г»
j= \ dtp \ f(r cos ф, г sin ф)
131]
§ 1. ДВОЙНЫЕ ИНТЕГРАЛЫ
449
Примеры. 1) Расставим пределы интегрирования в полярных
координатах, если область D — круг х2-\-у2^ах (рис. 168). Пере-
Переходя к полярным координатам, получим уравнение окружности в виде
г = a cos ф. Здесь гх (ф) = 0 и г2 (ф) = a cos ф. Пределы изменения по
от
—у Д° у- Поэтому
dq>
/(гсовф, r sin if) r dr.
2) Вычислим объем V общей части шара радиуса а и кругового
цилиндра радиуса -^ при условии, что центр шара лежит на
2
X
Рис. 168.
Рис. 169.
поверхности цилиндра. Систему координат расположим, как пока-
показано на рис.169. В силу симметрии измеряемого тела относительно
плоскостей. Оху и Oxz мы можем вычислить четвертую часть
объема, заключенную в первом координатном угле.
Имеем
— х2— y2dxdy,
где D — полукруг, являющийся половиной основания цилиндра.
Здесь очень удобно преобразовать двойной интеграл к поляр-
полярным координатам. В соответствии с правилом преобразования имеем
a2 — r2rdrdy.
15 А. Ф. Бермант, И. Г. Араманович
450 ГЛ. VIH. ДВОЙНЫЕ И ТРОЙНЫЕ ИНТЕГРАЛЫ [131
Так как полярное уравнение полуокружности, ограничивающей
область Д есть г = #со5ф (см. пример 1), то, интегрируя сначала
по г, а затем по ф, найдем
п
2 a cos ф
J
о о
Находя внутренний интеграл, получаем
•г"
о
Отсюда
Вычислим с помощью преобразования двойного интеграла к
полярным координатам один несобственный интеграл — интеграл
Пуассона (см. п. 98)
J «-*• <**.
(Этот интеграл играет важную роль в теории вероятностей.)
Для вычисления рассмотрим двойной интеграл
где D—четверть круга радиуса /?, расположенная в первом квад-
квадранте. Преобразуем этот интеграл к полярным координатам:
Предположим, что радиус R неограниченно увеличивается. Тогда
область Д расширяясь, будет стремиться заполнить весь первый
квадрант. По аналогии с несобственным интегралом от функции
одной переменной (см. п. 97) запишем это так:
со со
^^e-xi-yzdxdy==~ lim (I— e-RZ) = -j~. (*)
132] § 1. ДВОЙНЫЕ ИНТЕГРАЛЫ 451
Примем теперь в качестве области интегрирования D квадрат
-.а. Тогда
J ^*%-v% dxdy=\ dx ^е-*ш-Ул dy = \е~хг dx \ e~y2dy.
D oo oo
Так как величина определенного интеграла не зависит от обозна-
обозначения переменной интегрирования, то полученное выражение равно
Если а стремится к бесконечности, то квадрат D стремится
заполнить весь первый квадрант.
Оставляя без доказательства тот факт, что при любом рас-
расширении области D до полного квадранта интегралу у~хг-У* dx dy
D
будет стремиться к одному и тому, же пределу, запишем
а \ 2 /оо
\ (
= lira \\e"xtdx\ =(^e-**dxj . (**)
0 / \0
у со
у со \ 2
Сравнивая выражения (*) и (**), получаем f y~x*dx ) =-т-> т. е.
\o /
о
Так как подынтегральная функция четная, то
132. Приложения двойных интегралов к задачам механики.
I. Масса плоской пластинки переменной плот-
плотности. Рассмотрим тонкую пластинку, расположенную на плос-
плоскости Оху и занимающую область D. Толщину этой пластинки
считаем настолько малой, что изменением плотности по толщине
ее можно пренебречь.
Поверхностной плотностью такой пластинки в данной точке назы-
вается предел отношения массы площадки к ее площади при условии,
что площадка стягивается к данной точке.
Определенная таким образом поверхностная плотность будет
зависеть только от положения данной точки, т. е. являться функ-
функцией ее координат:
452
ГЛ. VIII. ДВОЙНЫЕ И ТРОЙНЫЕ ИНТЕГРАЛЫ
[132
Если бы плотность была постоянной (б— const), то масса всей
пластинки равнялась бы М =65, где S — площадь пластинки.
Найдем теперь массу неоднородной пластинки, считая, что ее
плотность является заданной функцией б (а:, у). Для этого разобьем
область, занимаемую пластинкой, на частичные области а1э а2, .. .,а„
с площадями Дах, Да2, ..., Да„
(рис. 170). Выбирая в каждой
частичной области произвольную
точку Pi(xh yt), будем считать, что
плотность во всех точках частичной
области постоянна и равна плотнос-
плотности б (xh у{) в выбранной точке.
Составим приближенное выражение
для массы пластинки в виде интег-
интегральной суммы
0
„¦5.
Уг
X
Рис. 170.
Для точного выражения массы следует найти предел суммы (#)
при условии, что л-^оо и каждая частичная область стягивается
к точке. Тогда
И. Статические моменты и центр тяжести плас-
пластинки. Перейдем теперь к вычислению статических моментов
рассматриваемой пластинки относительно осей координат. Для этого
сосредоточим в точках Р( (xh yt) массы соответствующих частич-
частичных областей и найдем статические моменты полученной сис-
системы материальных точек (см. п. 103):
> Уд
М{уп) - 2 х{8 (xi9 yt)
Переходя к пределу при обычных условиях и заменяя интеграль-
интегральные суммы интегралами, получим
х j j • V > У / > у j j V > У)
D D
Опираясь на результаты п. 103, находим координаты центра тяжести
\[хЬ (х, у) da
J J yt (x, у) da
133] § 2. ТРОЙНЫЕ ИНТЕГРАЛЫ 453
Если пластинка однородна, т. е. 6 (х, у) = const, то формулы
упрощаются:
xda
где S—площадь пластинки.
Предоставляем читателю проверить, что если пластинка имеет
форму криволинейной трапеции, то, приводя двойные интегралы,
стоящие в числителях, к повторным, мы получим формулы, выве-
выведенные в п. 103.
III. Моменты инерции пластинки.
Моментом инерции материальной точки Р с массой m относительно
какой-либо оси называется произведение массы на квадрат расстоя-
расстояния точки Р от этой оси.
Метод составления выражений для моментов инерции пластинки
относительно осей координат совершенно такой же, какой мы
применяли для вычисления статических моментов. Приведем поэтому
только окончательные результаты, считая, что 6(лг, j>)=1:
Отметим еще, что интеграл \\xydo называется центробежным
D
моментом инерции; он обозначается 1ху.
В механике часто рассматривают полярный момент инерции
точки, равный произведению массы точки на квадрат ее расстояния
до данной точки — полюса. Полярный момент инерции пластинки
относительно начала координат будет равен
§ 2. Тройные интегралы
133. Масса неоднородного тела. Тройной интеграл. К опре-
определению двойного интеграла нас привела задача отыскания объема
цилиндрического тела. В п. 132, I мы видели, что к этому же
самому определению можно прийти, отыскивая массу неоднородной
пластинки. В настоящем пункте мы дадим определение тройного
интеграла, исходя из задачи отыскания массы неоднород-
неоднородного тела1). Ввиду полной аналогии между определениями двой-
2) Мы уже отмечали (п. 107), что функция трех переменных не допускает
геометрического изображения. Потому мы и приходим к тройным
интегралам, исходя не из задачи геометрии, а из задачи механики.
454
ГЛ. VIII. ДВОЙНЫЕ И ТРОЙНЫЕ ИНТЕГРАЛЫ
[133
ного и тройного интегралов будем вести изложение по возможности
кратко. Рассмотрим тело, занимающее пространственную область Q
(рис. 171), и предположим, что плотность распределения массы
d этом теле является непрерывной функцией координат точек тела:
6 = б (х} у, z).
Единица измерения плотности—кг/мг.
Разобьем тело произволь-
произвольным образом на п частей;
объемы этих частей обозначим
Avu Av2i ..., Avn. Выберем
затем в каждой части по про-
произвольной точке P({xh у hZi).
Полагая, что в каждой час-
частичной области плотность по-
постоянна и равна ее значению
в точке Ph мы получим при-
приближенное выражение для
массы всего тела в виде
суммы
Рис. 171.
У о
(*)
Предел этой суммы при ус-
условии, что п—*оо и каждое частичное тело стягивается в точку
(т. е. что его диаметр х) стремится к нулю), и даст массу
М тела
, z)dv.
Сумма (*) называется я-й интегральной суммой, а ее предел —
тройным интегралом от функции 8 (л:, у, z) no пространственной
области Q.
К вычислению тройного интеграла, помимо определения массы
тела, приводят и другие задачи. Поэтому в дальнейшем мы будем
рассматривать тройной интеграл
У>
i, y?, zt)
где f(x, >y, z)—произвольная непрерывная в области Q функция.
г) Определение диаметра тела такое же, как и определение диаметра
плоской области (см. стр. 433). Если стремится к нулю диаметр тела, то
стремится к нулю и его объем.
134] § 2. тройные интегралы 455
Терминология для тройных интегралов совпадает с соответствую-
соответствующей терминологией для двойных интегралов. Точно так же формули-
формулируется и теорема существования тройного интеграла (предоставляем
это сделать читателю самостоятельно).
Свойства двойных интегралов, перечисленные в п. 129, полностью
переносятся на тройные интегралы. Заметим только, что если подын-
подынтегральная функция /(л:, у, z) тождественно равна 1, то тройной
интеграл выражает объем V области Q:
Потому свойства V и VI надо теперь сформулировать следующим
образом.
V'. Если функция f(x, у9 г) во всех точках области интегри-
интегрирования й удовлетворяет неравенствам
, у, z) < М,
то
$$$, у, z)dv<MV,
где V—объем области Й.
VI'. Тройной интеграл равен произведению значения подын-
подынтегральной функции в некоторой точке области интегрирования
на объем области интегрирования, т. е.
Ш/<*'¦?' *)А>=/E, ч,
Рекомендуем читателю самостоятельно сформулировать физический
смысл этого свойства.
134. Вычисление тройных интегралов. Вычисление тройного
интеграла м\/(^, у, z) dv, так же как и двойного, может быть
осуществлено посредством ряда последовательных интегрирований.
Мы ограничимся описанием соответствующих правил.
I. Декартовы координаты. Пусть дан тройной интеграл
от функции f(x, yt z)
причем область Q отнесена к системе декартовых координат Oxyz.
Разобьем область интегрирования Й плоскостями, параллельными
456 ГЛ. VIII. ДВОЙНЫЕ И ТРОЙНЫЕ ИНТЕГРАЛЫ [134
координатным плоскостям. Тогда частичными областями будут
параллелепипеды с гранями, параллельными плоскостям Оху, Oxzy
Oyz. Элемент объема будет равен произведению дифференциалов
переменных интегрирования
dv = dx dy dz.
В соо-тветствии с этим будем писать
Установим теперь правило для вычисления такого интеграла.
Будем считать, что область интегрирования Q имеет вид, изобра-
изображенный на рис, 1711).
Опишем около Q цилиндрическую поверхность с образующей,
перпендикулярной к плоскости Оху. Она касается области Q вдоль
некоторой линии I, которая делит поверхность, ограничивающую
область, на две части: верхнюю и нижнюю. Уравнением нижней
поверхности пусть будет z = z1{xty), уравнением верхней z = z%(x}y).
Построенная цилиндрическая поверхность высекает из плоскости
Оху плоскую область Di которая является ортогональной проек-
проекцией пространственной области й на плоскость Оху; при этом
линия L проектируется в границу области D.
Будем производить интегрирование сначала по направлению
оси Oz. Для этого функция f(xty, z) интегрируется по заключен-
заключенному в Q отрезку прямой, параллельной оси Oz и проходящей
через некоторую точку Р(х, у) области D (на рис. 171 отрезок ар).
При данных х и у переменная интегрирования z будет изменяться
от гг (лг> у) — аппликаты точки „входа" (а) прямой в область й,
до z2(x, у) — аппликаты точки „выхода" (($) прямой из области ?2.
Результат интегрирования представляет собой величину, зави-
зависящую от точки Р(х, у); обозначим ее через F(x, у):
г2(х, у)
2(
zx{x, у)
При интегрировании х и у рассматриваются здесь как постоян-
постоянные.
Мы получим значение искомого тройного интеграла, если возьмем
интеграл от функции F(x, у) при условии, что точка Р(х, у)
изменяется по области D, т. е. если возьмем двойной интеграл
с, y)dxdy.
1) Если область интегрирования Q более сложного вида, то ее надо
разбить на части указанного вида и вычислить данный интеграл как сум-
сумму интегралов, взятых по составляющим областям.
134]
§ 2. ТРОЙНЫЕ ИНТЕГРАЛЫ
457
Таким образом, тройной интеграл / может быть представлен
в виде
I=l\dxdy J f(x,y,z)dz.
D zt{x, у)
Приводя, далее, двойной интеграл по области D к повторному
и интегрируя сначала по у, а затем по х, получим
Ь yt(x) гг{х, у)
1=1 dx J dy J f(x, у, z)dz, (*)
a Ui(x) zt(x, y)
где уг(х) и у2 (х) — ординаты точек «входа» в область D и «выхо-
«выхода» из нее прямой х = const (в плоскости Оху), а а и b — абсциссы
конечных точек интервала
оси Ох, на который про-
проектируется область D.
Мы видим, что вычис-
вычисление тройного интеграла
по области Q производит-
производится посредством трех пос-
последовательных интегриро-
интегрирований.
Формула (*) сохраняет-
сохраняется и для областей, имею-
имеющих цилиндрическую фор-
форму, т. е. ограниченных
цилиндрической поверхно-
поверхностью с образующими, па-
параллельными оси Oz, а сни-
снизу и сверху поверхностями,
уравнения которых соот-
соответственно Z = ZX (X, у) рис# 172.
И 2Г = 2?а (ЛГ, у) (рИС. 172).
Если областью интегрирования служит внутренность парал-
параллелепипеда с гранями, параллельными координатным плоскостям
(рис. 173), то пределы интегрирования постоянны во всех трех
интегралах:
ь
*y> z)dxdydz=\dx
,y, z)dz.
В этом случае интегрирование можно производить в любом порядке,
пределы интегрирования будут при этом сохраняться.
458
ГЛ. VIII. ДВОЙНЫЕ И ТРОЙНЫЕ ИНТЕГРАЛЫ
[134
Если же в общем случае менять порядок интегрирования (т. е.,
скажем, интегрировать сначала по направлению оси Оуу а затем
по области плоскости Oxz), то это приведет к изменению порядка
/
а
У
г
/
0
/
л /\\
1
/
/
s
/
/
С
/
/
7
/
d
/ у
Рис. 173.
Рис. 174.
интегрирования в тройном интеграле и к изменению пределов
интегрирования по каждой переменной.
Пример. Вычислим тройной интеграл
где Q —область, ограниченная координатными плоскостями
и плоскостью х+у+г=\ (пирамида, изображенная на рис. 174).
Интегрирование по z совершается от 2 = 0 до 2=1—х—у.
Поэтому, обозначая проекцию области Й на плоскость Оху через
Д получим
1-х-У
J
dy.
Расставим теперь пределы интегрирования по области D—треуголь-
134]
§ 2. ТРОЙНЫЕ ИНТЕГРАЛЫ
459
нику, уравнения сторон которого л; = 0, у = 0, х-\-у —
\(x+y)-{x+y)*+
2 3 6
~J L2 2 3 "^ 3
II. Цилиндрические координаты. Отнесем область Q
к системе цилиндрических координат (г, ф, z), в ко-
которой положение точки М в
пространстве определяется
полярными координатами
(г, ф) ее проекции Р на плос-
плоскость Оху и ее аппликатой
(z). Выбирая взаимное распо-
расположение осей координат, как
указано на рис. 175, уста-
установим связь между декарто-
декартовыми и цилиндрическими ко-
координатами точки Ж, именно;
dz
х = г cos ф, y = r
Разобьем область
частичные области v
Q на
тремя
Рис. 175.
системами координатных
поверхностей: г = const, ф=соп8^ z— const, которыми буду!
соответственно круговые цилиндрические поверхности, осью кото-
которых является ось Oz, полуплоскости, проходящие через ось Ozy и
плоскости, параллельные плоскости Оху. Частичными областями v(
служат прямые цилиндры MN (рис. 175). Так как объем цилиндра
MN равен площади основания, умноженной на высоту, то для
элемента объема получаем выражение
dv = r dr с?ф dz.
Преобразование тройного интеграла \\\/(^, у, z)dv к цилиндри-
й
ческим координатам производится совершенно аналогично преобра-
преобразованию двойного интеграла к полярным. Для этого нужно в вы-
выражении подынтегральной функции f(x, у, z) переменные х> у, z
460
ГЛ. VIII. ДВОЙНЫЕ И ТРОЙНЫЕ ИНТЕГРАЛЫ
1134
заменить по формулам (*) и взять элемент объема равным г drdydz.
Получим
, у, z)dxdydz = 5j J/(rcos<p, rsincp, z)rdrdq>dz.
Q
Если, в частности, f(x, у, z)=l, то интеграл выражает объем V
области Q
Вычисление тройного интеграла в цилиндрических координатах
приводится к интегрированиям по г, по ф и по z на основании
тех же принципов, что и в случае декартовых координат. В част-
частности, если областью интегрирования служит внутренность ци-
цилиндра r^R, O^z^ih, то пределы трехкратного интеграла
постоянны и не меняются при перемене порядка интегрирования:
R
Jf(rcosф, г8И1ф, z)rdr.
3
III. Сферические координаты. Отнесем теперь область
интегрирования Q к системе сферических координат
(г, 0, ф). В этой системе координат
положение точки М в пространстве оп-
определяется ее расстоянием г от нача-
начала "координат (длина радиуса-вектора
точки), углом 0 между радиусом-векто-
радиусом-вектором точки и осью Oz и углом ф между
проекцией радиуса-вектора точки на
плоскость Оху и осью Ох (рис. 176).
При этом 0 может изменяться от 0 до
я, а ф — от 0 до 2л1).
Связь между сферическими и декар-
декартовыми координатами легко устанавли-
Рис. 176. вается. Из рис. 176 имеем
ОЯ = гcos (у— 0^=
и j/ =
Отсюда
х = г sin 0 cos ф, у = г sin 0 sin ф, z = rcos0.
(##)
*) В картографии положение точки на земной поверхности определяется
углом <р (долгота точки) и углом 6'==-^-—6 (широта точки). При этом дол-
долгота меняется от 0 до 2я (или от —л до я), а широта от —^ до
-у.
134]
§ 2. ТРОЙНЫЕ ИНТЕГРАЛЫ
461
Разобьем область Q на частичные области v{ тремя системами
координатных поверхностей: г = const, ф = const,
0 = const, которыми будут соответственно сферы с центром в на-
начале координат, полуплоскости,
проходящие через ось Oz, и
конусы с вершиной в начале
координат и с осями, совпада-
совпадающими с одной из полуосей Oz.
Частичными областями vi служат
«шестигранники» (рис. 177). От-
Отбросив бесконечно малые высших
порядков, будем рассматривать
шестигранник MN как прямоу-
прямоугольный параллелепипед с изме-
измерениями, равными: dr по направ-
направлению полярного радиуса, г dQ по
направлению меридиана, г sin 6 dq>
по направлению параллели. Для
элемента объема мы получим
тогда выражение рис |77
dv = г2 sin 0 dr dydQ.
Заменив в тройном интеграле ху у, z по формулам (##) и взяв
элемент объема равным полученному выражению, будем иметь
cos
r sm ® sin (P» r cos
sin
Особенно удобно применение сферических координат в случае,
когда область интегрирования Q — шар с центром в начале коор-
координат или шаровое кольцо. Например, в последнем случае, если
радиус внутреннего шара Rv а внешнего R2i пределы интегриро-
интегрирования следует расставить так:
2Л R2
sin 0 а?0 jj tf<p J f(r sin 0 cos ф, г sin 0 sin ф, г cos 0) r2 dr.
R
Если й — шар, то нужно положить /?1==0.
Пример. Вычислим объем шара радиуса R. В этом случае
подынтегральную функцию надо взять равной 1, и мы получим
= Csin0d0 f
462 ГЛ. VIII. ДВОЙНЫЕ И ТРОЙНЫЕ ИНТЕГРАЛЫ [135
В заключение отметим, что трудно дать общее указание, когда
следует применять ту или иную систему координат. Это зависит
и от области интегрирования, и от вида подынтегральной функции.
Иногда следует написать интеграл в разных системах координат
и только потом решить, в какой из них вычисление будет наи-
наиболее простым.
135. Применение тройных интегралов. Применение тройных
интегралов к вычислению статических моментов и моментов инер-
инерции пространственных тел основано на тех же принципах, что
и применение двойных интегралов к вычислению соответствующих
моментов плоских пластинок (.см. п. 132). Для вычисления коорди-
координат центра тяжести тела нужны статические моменты относительно
координатных плоскостей Оху, Oxz, Oyz; обозначим их соответ-
соответственно МхуУ Mxz, М . Повторяя-рассуждения п. 132, II (рекомен-
(рекомендуем читателю провести их самостоятельно), получим следующие
формулы для координат ?, т), ? центра тяжести неоднородного тела,
плотность которого задается функцией б (х, у, z), занимающего
область Q:
dv
~ j ~
Q
Q Q Q
Если тело однородно, т. е. 6 = const, то формулы упрощаются:
ш
j zdv
Л- у , t- у ,
где V—объем тела.
Пример. Найдем центр тяжести однородного полушара Q:
Две координаты центра тяжести (? и т]) равны нулю, ибо полу-
шар симметричен относительно оси Oz (тело вращения с осью Oz).
Интеграл jm^^ удобно вычислить, перейдя к сферическим
п
координатам:
2 2Я R
f f f z dv = Г Г С г cos 9 г2 sin 9 dr dy dQ = f sin 9 cos 9 dQ С dtp С
Q Й ooo
1 о /?4 1
1351 § 2. тройные интегралы 463
Так как объем полушара равен -|-Jt/?3, то
о
"8
Перейдем к вычислению моментов инерции тела относительно
координатных осей (см. п. 132, III). Так как квадраты расстояний
от точки P(xt у, z) до осей Ox, Oyy Oz соответственно равны
y2+z2, x2+z2, х2+у2у то полагая для простоты 6=1, получим
следующие формулы:
2
Аналогично плоскому случаю интегралы
называются центробежными моментами инерции.
Для полярного момента инерции формула имеет вид
Если тело неоднородное, то в каждой формуле под зна-
знаком интеграла будет находиться дополнительный множитель
6(лг, у, z) — плотность тела в точке Р.
Пример. Вычислим полярный момент инерции однородного
шара радиуса R. В этом случае очень удобно перейти к сфери-
сферическим координатам. Будем иметь
/0 = б f sin 9 rfG f d<?\ r*r* dr = ^??- = j MR\
0 0 0
где Ж—масса шара.
Так как для сферы моменты инерции относительно осей коор-
координат, очевидно, равны между собой, то, учитывая, что
/ + 4 = 2/0| получим
Моменты инерции тела относительно оси играют важную роль
при вычислении кинетической энергии тела при его вращении около
соответствующей оси. Пусть тело Q вращается около оси Oz
464 ГЛ. VIII. ДВОЙНЫЕ И ТРОЙНЫЕ ИНТЕГРАЛЫ [136
с постоянной угловой скоростью со. Найдем кинетическую энер-
энергию Jz тела. Как известно, кинетическая энергия точки измеря-
измеряется величиной -^ mv2> где т—масса точки, a v—величина ее
скорости. Кинетическая энергия системы точек определяется как
сумма кинетических энергий отдельных точек, а кинетическая
энергия тела — как сумма кинетических энергий всех частей, на
которые оно разбито. Это обстоятельство позволяет применить
для вычисления кинетической энергии интеграл.
Возьмем какую-нибудь окрестность dv точки Я (л?, у, z) тела Q.
Величина линейной скорости v точки Р при вращении около оси
О& равна © \/Гх2-{-у21 и значит, кинетическая энергия части dv
тела Q выразится так:
где б(Р) = б(лг, у, z) — плотность тела в точке Р. Для кинетиче-
кинетической энергии всего тела Q получаем
=Ш т ^{х*+ у2) ь (Р) dv=т юа Ш
v>
т. е.
Кинетическая энергия тела, вращающегося около некоторой оси
с постоянной угловой скоростью, равна половине квадрата угловой
скорости, умноженной на момент инерции тела относительно оси
вращения,
§ 3*. Интегралы, зависящие от параметра
136*. Интегралы с конечными пределами. Ранее нам уже
встречались интегралы, в которых подынтегральная функция за-
зависит от двух переменных, а интегрирование совершается по одной
из них в предположении, что вторая переменная считается посто-
постоянной. Так было в п. 115 при отыскании функции по ее полному
дифференциалу и в п. 130 при вычислении двойного интеграла
с помощью последовательного интегрирования. В виду того, что
такие интегралы встретятся и в дальнейшем, как в курсе анализа,
так и в различных дополнительных разделах (например, при изу-
изучении уравнений математической физики и операционного исчисле-
исчисления), рассмотрим их более подробно.
136] § 3. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА 465
Итак, пусть задана функция f(x, Я), которая определена и не-
непрерывна при всех значениях л; и Я, удовлетворяющих условиям
ъ
Если вычислять интеграл \/(#> h)dx при различных значе-
а
ниях Я ? [<*, Р], то каждому значению Я будет соответствовать свое
значение интеграла, являющегося, таким образом, некоторой функ-
функцией от Я; обозначим ее через /^(Я):
НЯ) =$/(*, k)dx. (*)
а
Интервал интегрирования [а, Ь] предполагается конечным
(случай бесконечного интервала интегрирования будет рассмотрен
позднее). Интервал [а, Р]— область определения функции ^(Я) —
может быть как конечным, так и бесконечным.
=i-=l!, еслиЯ=^0. ПриЯ = 0
Примеры. 1)
о
интеграл равен 1. Здесь функция /^(Я) определена и непрерывна
при всех значениях Я (проверить непрерывность при Я = 0 предо-
предоставляем читателю).
1
2) i - = ятс*\п^- =arcsinlr,k Интеграл определен, если
J у Я2—хй л I ° л
о
|Я|>1; приЯ = ±1 интеграл становится несобственным (подын-
(подынтегральная функция имеет бесконечный разрыв в точке л;=1), но
сходящимся.
2
3) j-^= = ln(* + l/^^ Интеграл
определен при Я?[—1, 1].
Лишний раз подчеркнем, что если функция f(x, Я) и интервал
интегрирования [а, Ь] заданы, то интеграл (*) зависит только от Я.
Наша ближайшая задача изучить свойства функции ^(Я) — интег-
интеграла, зависящего от параметра, В основе лежит следующая
Теорема I. Если функция /(*, Я) непрерывна при a<
ь
и а<Я<р, то функция /7(Я)=^/(др, l)dx непрерывна в ин-
а
тервале [а, Р].
466 ГЛ. VIII. ДВОЙНЫЕ И ТРОЙНЫЕ ИНТЕГРАЛЫ [136
Доказательство. Чтобы не усложнять доказательство,
дополнительно предположим, хотя это и не дано в условии тео-
теоремы, что функция f(xy к) имеет частную производную Д(лг, А.),
ограниченную при всех рассматриваемых значениях х и к:
\Мх, Я)|<Ж
Пусть к и к-\-Ак лежат в интервале [a, JJ]. По определению
ъ ь
F(^) = J/(at, k)dxy F(k + Ak) = ^f(x, k + Ak)dx.
a a
Приращение функции F (к) равно
ь
(x, k + Ak)-f(x, k)]dx. (**)
Подынтегральное выражение преобразуем по теореме Лагранжа
f(x, Х + ДЯ)— f(x, М=Д(*. &)ДЯ,
где ?€(^. А. + ДЯ)- Учитывая предполагаемое условие ограничен-
ограниченности производной Д, придем к неравенству
\f(x, X + AX)-f(x, k)\
Так как модуль интеграла не превосходит интеграла от модуля
подынтегральной функции (см. п. 90, II), то
- a)\Ak\.
Отсюда следует, что если Ак—>О, то и F(k + Ak)— F(k) —*0,
т. е. что функция F (к) непрерывна. Мы будем пользоваться тео-
теоремой в том виде, в каком она сформулирована, хотя ее доказа-
доказательство проведено в упрощающем предположении. Отметим еще,
что в ходе доказательства существенно использовалась конеч-
конечность интервала интегрирования [а, Ь].
Часто условие непрерывности интеграла, зависящего от пара-
параметра, записывают в виде
ь
lim J/(at, l)dx = ^f{x, k)dx, (***)
a a
выражающем тот факт, что предел непрерывной функции
при g—>к равен значению этой функции при % = к.
136] § 3. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА 467
При пользовании этой теоремой нужно внимательно следить за
выполнением всех ее условий. Так, например, пусть
F (Я) =
0
1 = arctg -r- ¦
о Л»
Эта функция непрерывна при всех значениях Я, кроме Я = 0; дело
в том, что подынтегральная функция /(дг, X) =-2ХТ2 РазРывна
при Х = 0 и лг = О.
Чтобы функция F Ск) была дифференцируемой, нужно предъявить
дополнительные требования к функции f(x, X).
Теорема II. Если функция/(jc, %) и ее частная производная
f'%(х9 к) непрерывны при a^x^Lb и а <[ ^ ^ Р, то функция F(k)
имеет непрерывную производную F'(к) и справедлива формула
ь ь
Доказательство. Вернемся к формуле (**), выражающей
приращение функции F(X)y и разделим обе ее части на АЛ; пре-
преобразовывая затем подынтегральное выражение по теореме Лаг-
ранжа, получим
\
Так как ? € (X, ^ + АЯ), то при ДЯ —> 0 значение g —> Я. Поэтому,
переходя к пределу при ДЯ—>0, запишем
ь
,7х(*, E)dx.
По условию теоремы производная Д(лг, Я) непрерывна; поэ-
поэтому предел правой части существует (см. формулу (***)); зна-
значит, существует предел и левой части равенства, а это и есть
как раз производная F' (Я), и эти пределы равны между собой:
Теорема доказана. Коротко ее формулируют так: производная от
интеграла по параметру равна интегралу от производной подынтег-
подынтегральной функции по этому параметру. Это предложение называется
правилом Лейбница; именно на него мы ссылались в сноске
на стр. 389.
468 гл. via. двойные и тройные интегралы [136
Правило Лейбница иногда применяется для отыскания сложных
определенных интегралов.
Пример.
dx
= — arctg —. Дифференцируя
о а ° а
о
обе части равенства по параметру а, причем дифференцирова-
дифференцирование интеграла совершается по правилу Лейбница, т. е. путем
дифференцирования подынтегрального выражения, получим
1,1 1
откуда
dx l arcte±
с
J
а ~*~2а2 (aa+
Продолжая дифференцирование, мы сможем вычислить интегралы
1
\гттг~ъуг Для я = 3, 4, ... Вычисление их без применения правила
о
Лейбница привело бы к гораздо более громоздким выкладкам.
До сих пор мы рассматривали интегралы, у которых пределы интегри-
интегрирования были постоянны. Встречаются, однако, и такие интегралы, у кото-
которых пределы интегрирования сами являются некоторыми функциями того
параметра, от которого зависит подынтегральная функция. Как раз это имеет
место при вычислении внутреннего интеграла при сведении двойного интег-
интеграла к повторному.
Пусть
а (К)
Будем считать, что подынтегральная функция I (х, к) и ее частная произ-
производная /^ (л:, X) непрерывны при всех рассматриваемых значениях х и А»,
и пределы интегрирования а(Х) и Ъ (к) вместе со своими производными—тоже
непрерывные функции от %. Тогда функция F (к) непрерывна, дифференци-
дифференцируема и ее производная равна
а (к)
(общее правило Лейбница).
Доказывать эту формулу мы не будем; отметим только, что приведенная
выше формула для случая постоянных пределов интегрирования, а также
теорема о дифференцировании интеграла по его верхнему пределу (см. п. 91)
являются ее частными случаями.
137] § 3. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА 469
137. Несобственные интегралы, зависящие от параметра.
Приведенные выше теоремы относятся, как уже было отмечено,
к интегралам с конечными пределами и с непрерывной подынтег-
подынтегральной функцией. Для несобственных интегралов дело обстоит
значительно сложнее. Мы ограничимся рассмотрением наиболее
часто встречающихся несобственных интегралов вида
00
/>(*)= $/(*, l)dx. (*)
а
Областью определения функции F(X) служит совокупность значе-
значений Я, при которых интеграл (#) сходится. Как правило, это
некоторый интервал, конечный или бесконечный.
Начнем с примера. Пусть
о
(е~х*х—у0 при х—>-f-o0)- Подынтегральная функция непрерывна
при всех значениях х и Я; функция же /^(Я) имеет бесконечный
разрыв при Я = 0.
Чтобы установить, при каких условиях теоремы п. 136 оста-
останутся справедливыми для несобственных интегралов вида (*), введем
следующее определение.
Определение. Несобственный интеграл \f(x, Я)rfjc, зави-
а
сящий от параметра Я, называется правильно сходящимся,
если можно указать такую положительную функцию <р(я)> что
при всех рассматриваемых значениях х и Я соблюдается нера-
00
венство |/(лг, Я)К<р(лг) и несобственный интеграл \)^{x)dx
а
СХОДИТСЯ1).
оо оо
гт ,. С sin Xx , С cos Kx j
Пример. Интегралы \ ——«dx и \ j—.—»dx сходятся пра-
о о
вильно при всех значениях Я, так как модули подынтегральных
функций не превосходят положительной функции - 2, интеграл
от которой сходится.
Для правильно сходящихся несобственных интегралов (*) имеют
место следующие свойства, которые мы приводим без доказа-
доказательства.
2) В более подробных курсах анализа вводится более общее, но и более
трудное понятие равномерной сходимости интегралов, зависящих от параметра.
470 гл. viii. двойные и тройные интегралы [137
\.Если функция f{xy X) непрерывна при х^а и X ?[Х1У Х2]
и интеграл F(X)=\^f(x, X)dx сходится правильно, то он является
а
непрерывной функцией параметра X.
2. Если при этом функция f(x> X) имеет непрерывную частную
производную fi (x, X) и интеграл от этой производной тоже схо-
сход ф X дфф д
у
дится правильно, то функция F (X) дифференцируема и справедлива
формула
В качестве примера применения указанных свойств вычислим один важ-
важный интеграл Пуассона, встречающийся при решении задач математической
физики
во
Заметим, что при Я, = 0 получаем интеграл /@)=\ e"xt dx——^- , вычис-
о
~*2 cos%x\*de~xZ
ленный в п. 131. Интеграл (#) правильно сходится, так как | е~*2 cos%x\*de
Дифференцируя интеграл (#), получим
о
Это действие законное, так как последний интеграл тоже сходится правильно.
00 \
Действительно \хе~~х2 smXx\^xe~x2t а интеграл \ хе"х2 dx = — ^—^~
2'
о
Интеграл, выражающий /' (X), проинтегрируем по частям, полагая
$се~х2dx = dv, sinXx — u. Тогда v = —о"*2» du = XcosXx и
оо оо
Г -*2 ! -Х2 °° X Г _х2
J 2 о 2 J
о о
Внеинтегральный член равен нулю и при х — 0, и при # = oo, а последний
интеграл есть снова / (X). В результате мы приходим к соотношению
X
Г(А,) = — / (%), которое перепишем в виде
ВОПРОСЫ И ПРЕДЛОЖЕНИЯ 471
Интегрируя, найдем, что 1п/(^) = — -j- +С. При ^ = 0 интеграл /@) равеа
; поэтому С = 1п-^—. Окончательно In/(л) = —-т- + 1п ~^—и
ВОПРОСЫ И ПРЕДЛОЖЕНИЯ ДЛЯ САМОПРОВЕРКИ
1. Как определяется объем цилиндрического тела?
2. Что называется двойным интегралом от данной функции по данной
области?
3. В чем состоит теорема существования двойного интеграла ?
4. Перечислить свойства двойного интеграла.
5. Вывести правило вычисления двойного интеграла в случае области,
ограниченной линией, пересекающейся с прямыми, параллельными осям
координат, не более чем в двух точках. Привести соответствующую формулу.
6. Как вычисляется двойной интеграл с помощью повторных в случае
произвольной области интегрирования в системе декартовых координат?
7. Как выражается элемент площади в полярных координатах?
8. Вывести правило преобразования двойного интеграла от декартовых
координат к полярным. Привести соответствующую формулу.
9. Как вычисляется двойной интеграл в полярных координатах с по-
помощью повторного интегрирования?
10. Как определяется масса неоднородной пластинки по заданной плот-
плотности?
11. Вывести формулы для вычисления статических моментов и моментов
инерции пластинки.
12. Как определяется масса неоднородного тела по заданной плотности?
13. Что называется тройным интегралом от данной функции по данной
области?
14. Перечислить свойства тройного интеграла.
15. Как вычисляются тройные интегралы в декартовой системе координат?
16. Как вычисляются тройные интегралы в цилиндрической системе
координат?
17. Как вычисляются тройные интегралы в сферических координатах?
18. Вывести формулы для вычисления координат центра тяжести про-
пространственного тела.
19. Вывести формулы для вычисления моментов инерции тел.
20*. Дать определение интеграла, зависящего от параметра. Привести
примеры.
21*. Сформулировать и доказать теорему о непрерывности интеграла,
зависящего от параметра.
22*. Сформулировать и доказать теорему о дифференцировании интеграла
по параметру (правило Лейбница).
23*. Дать определение правильно сходящихся интегралов и сформули-
сформулировать их свойства.
ГЛАВА IX
КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ
ПО ПОВЕРХНОСТИ. ТЕОРИЯ ПОЛЯ
§ 1. Криволинейный интеграл
138. Задача о работе силового поля. Криволинейный инте-
интеграл. В п. 86, II бтала рассмотрена задача о работе переменной
силы при движении тела по прямой линии, причем направление
силы совпадало с направлением движения. Мы рассмотрим сейчас
задачу, значительно более общую.
Предположим, что в области D плоскости Оху задано плоское
силовое поле. Это означает, что на материальную точку, по-
помещенную в области Д действует сила F1), определенная в каждой
точке D и расположенная в плоскости Оху2). Область D может
совпадать со всей плоскостью Оху или составлять некоторую
ее часть.
Тот факт, что сила F зависит от точки ее приложения, записы-
записывают в виде
F = F(*, У),
где х и у — координаты точки приложения силы. Чтобы задать
силу F(x, у), зададим ее проекции на оси координат, которые
будут также являться функциями переменных хну. Обозначим их
Р(ху у) и Q(x, у). Тогда
F = />(*
г) Часто в физике, чтобы охарактеризовать силовое поле, независимо от
помещенной в него материальной точки, вводят вектор напряженности
поля, понимая под ним силу взаимодействия поля с некоторым «единичным»
телом, т. е., например, с телом единичной массы, если речь идет о поле
тяготения, с единичным зарядом, если речь идет об электростатическом поле,
и т. д. В этом случае сила взаимодействия поля с данным телом будет равна
произведению вектора напряженности поля соответственно на массу или за-
заряд данного тела.
Отметим еще, что силовое поле является частным случаем векторного
поля (см. п. 151).
2) Пространственное силовое поле будет рассмотрено в п. 146.
138]
§ 1. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ
473
Пусть под действием сил поля материальная точка движется по
некоторой линии L, расположенной в области D и соединяющей
точки В и С (рис. 178). Найдем работу, совершаемую силами поля
F(#, у) при этом перемещении точки.
Разобьем линию L на п частей точками Bv В2, Вв, ... , Вп, Вп+г
(точка Вг совпадает с В, а Вп+1 — с С), координаты точек деления
Bk обозначим через xk и yk{k = \, 2, ... ,я+1). Заменим теперь
каждый криволинейный участок BkBk+1 прямолинейным вектором
перемещения BkBk+1. Условимся считать, что при движении мате-
материальной точки по отрезку BkBk+l на нее действует постоян-
постоянная сила, равная силе, приложенной в точке В^\
Тогда работа на этом участке будет равна
где ak — угол между векторами Fft и ВкВк+1. Написанное выра-
выражение представляет собой скалярное произведение векторов
и ВкВк+1) т.
е.
Так как проекции вектора BkBk+1 на оси координат равны соот-
соответственно xk+i-xk = Axk и ук+1-ук = Аук, то
В силу известной формулы для скалярного произведения работа
на рассматриваемом участке будет равна
ААк = Р (хк, Ук) Ахк + Q (хк, ук) Аук.
474 гл. ix. криволин. интегралы и интегралы по поверхности [138
Суммируя полученные выражения по всем участкам, найдем при-
приближенное значение искомой работы:
,= 2
k
9 yk)Ayk.
(*)
Переходя к пределу при п—> оо и считая, что длина наибольшего
участка стремится к нулю, мы и получим истинную величину работы.
К составлению сумм вида (*) с
последующим переходом к пределу
приводит не только задача о рабо-
работе, и поэтому совсем не обязатель-
обязательно всегда считать, чтоР(лг, у) и
Q(xj У) — проекции сил.
Рассмотрим этот вопрос в об-
общем виде. Пусть Р(х,у) nQ(x,y) —
функции двух переменных, не-
непрерывные в некоторой области
D, и L —гладкая линия, целиком
расположенная в этой области.
Разобьем линию L на п участков и в каждом таком участке вы-
выберем по произвольной точке Вк (?А, г\к) (в частности, эти точки
могут совпадать с концами участков, как на рис. 178). Обозначим
проекции &-го участка на оси координат через Ахк и Аук (рис. 179)
и составим сумму
Сумма (*#) называется п-й интегральной суммой по линии I,
а ее предел
ton 2 Р(xkJ ук) Ахк + Q(xk, yk)
лг, у) dy
— криволинейным интегралом по линии L1).
Определение. Криволинейным интегралом по линии L на-
называется предел п-й интегральной суммы (*) при стремлении к
нулю длины наибольшего частичного участка разбиения кривой L.
Линия L называется линией или контуром интегрирования.
Точка В называется начальной, а точка С—конечной точками
интегрирования.
J) Этот интеграл называют часто криволинейным интегралом по коорди-
координатам или второго рода. Криволинейный интеграл по длине кривой (первого
рода) будет рассмотрен в п. 145.
139] § 1. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ 475
В частности, если Q (х, у) = 0, то интеграл имеет вид
L
и называется криволинейным интегралом по координате х.
Аналогично, если Р(х, у)=0, то
5
L
называется криволинейным интегралом по координате у.
Возвращаясь к задаче о работе, можно сказать, что работа
силового поля при перемещении материальной точки по кривой L
выражается криволинейным интегралом
$ , y)dy,
где Р(х, у) и Q(x, у) — проекции сил поля на оси координат.
139. Вычисление криволинейных интегралов. Интегралы по
замкнутому контуру. Вычисление криволинейных интегралов, как мы
сейчас покажем, приводится к вычислению обыкновенных опреде-
определенных интегралов. Рассмотрим, например, интеграл
$, y)dx
L
и предположим, что уравнение линии интегрирования L дано в пара-
параметрическом виде:
x = x(t\ y=y(t).
Начальной точке линии (В) соответствует значение параметра tBt
а конечной (С) — tc. Возьмем интегральную сумму
пределом которой является данный криволинейный интеграл, и пре-
преобразуем ее к переменной /. Так как
&xk = xk+1 — xk = x (tk+1) —х (tk),
то, применяя формулу Лагранжа (см. п. 57, I), получим
где Э^ лежит в интервале [tk, /fe+1], a Atk~tk+1 — tk. В качестве
промежуточной точки (lk, v)k) выберем как раз ту, которая соот-
соответствует значению параметра Qk. Тогда
476 ГЛ. IX. КРИВОЛИН. ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ [139
Преобразованная сумма
будет обыкновенной интегральной суммой для функции одной пере-
переменной P[x(t), y(t)]xf(t), а ее предел — определенным интегралом
P[x(t),y(t))x'{t)dt.
tB
Таким образом,
*c
y)dx= J P[x(t)yy(t)]x'(t)dt.
tB
Совершенно аналогично получим, что
tc
S<3(*, y)dy= J Q[x(t),y(t)]y'(t)di.
L tB
Отсюда и вытекает правило вычисления криволиней-
криволинейного интеграла.
Для того чтобы криволинейный интеграл
С y)dy,
взятый по линии х = х (I), у =у (t), преобразовать в обыкновен-
обыкновенный, нужно в подынтегральном выражении заменить х, у, dx и
dy их выражениями через t и dt и вычислить получившийся
интеграл по интервалу изменения параметра t:
= \ {Р[х(О, у V)\х' (О + Q[х(О. у (t)\yf (')} dt,
'в
где гв и tc — значения параметра t9 соответствующие точкам В
и С линии L.
Из приведенного правила вытекает, что криволинейный интеграл
всегда существует, если функции Р(х, у) и Q{x, у) непрерывны,
а х (/) и у (/) непрерывны вместе со своими производными. Последнее
условие означает, что линия L гладкая, т. е. имеет непрерывно меняю-
меняющуюся касательную. Впрочем, линия L может состоять и из несколь-
139]
§ 1. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ
477
ких участков, на каждом из которых это условие выполняется.
Тогда при переходе к обыкновенному интегралу надо линию L
разбить на эти участки и рассматривать весь интеграл как сумму
интегралов по отдельным участкам.
if,
0
ИГ
!
X,
У~Уо> dy
mff
\c
1
1
1
y\
Уг
Уг
0
G
В
*x
Рис. 180.
Если уравнение линии L может быть задано в виде у=у(х),
то, полагая в общей формуле преобразования t = x, получим
хс
, y)dx + Q(x, y)dy= J {P[x, y{x)] + Q[x, y{x)]f {x)}dx,
XB
где хв и xc — абсциссы точек В и С.
Читателю предлагается записать самостоятельно формулу преоб-
преобразования криволинейного интеграла, если уравнение кривой задано
в виде х = х(у).
Если отдельные участки контура интегрирования заданы урав-
уравнениями различных видов, то этот контур нужно разбить на части
и интеграл вычислять как сумму интегралов по отдельным
участкам.
Отметим для дальнейшего важные частные случаи.
Если контур интегрирования L —отрезок прямой, параллель-
параллельной оси абсцисс (рис. 180, а), то криволинейный интеграл сразу
превращается в обыкновенный. Так как y~yQ и dy = 0, то
$ \y yo)dx.
L xx
Если L — отрезок прямой, параллельной оси ординат (рис. 180, б),
то л; =* дг0, с?лг = 0 и
J P{x, y)dx+Q (х, у) dy = \Q (*0, у) dy.
L yt
478 гл. ix. криволин. интегралы и интегралы по поверхности [139
Примеры. 1) Вычислим интеграл
(x+y)dy,
принимая за линию L (рис. 181):
а) отрезок прямой, соединяющий точки О@, 0) и ЛA, \)\
б) дугу параболы у = х2, соединяющую эти же точки;
в) ломаную ОБА.
В случае а) уравнение линии интегрирования у = х. Следова-
Следовательно, dy = dx и
в х
Рис. 181.
Рис. 182.
В случае б) у = х2, dy = 2xdx и
В случае в) контур интегрирования
разбиваем на два. На участке ОВу = 0
и dy = O, а на участке ЕЛ лг=1 и
dx = 0. Поэтому
3
У
Как видим, во всех трех случаях
мы получили различные значения ин-
интеграла, несмотря на то что начальная
и конечная точки контура интегрирова-
интегрирования были одни и те же. Это показы-
показывает, что криволинейный интеграл зави-
зависит не только от начальной и конечной
точек интегрирования, но и от линии, их
соединяющей. Подробно этот вопрос бу-
будет рассмотрен в п. 141.
2) Вычислим интеграл
/ = \ ху dx,
где L — дуга параболы х=у2 от ее точки А(\у —1) до точки
5A, 1) (рис. 182). Так как в уравнении контура х является
однозначной функцией от yf то, подставив в интеграл х=у2,
139]
§ 1. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ
479
получим
Если бы мы захотели уравнение контура записать в форме,
разрешенной относительно у :у = ±УхУ то для вычисления интег-
интеграла нам пришлось бы разбить контур L на две части: АО и
ОВ, уравнения которых суть у = —Ух и у = -\-ух. Тогда
= $ xydx+ ^
АО OB
3) Вычислим интеграл
где L — дуга циклоиды x = 2(t— sinf), jf = 2A — cos/) от точки
0@, 0) до точки ЛDя, 0). Пользуясь общим правилом, приходим
к интегралу (точке О соответствует значение ? = 0, а точке
А — значение t = 2я)
[4A— cos О2 — 4 (/ — sin t) sint] dt =
2Л
B — 2 cos t — t sin t)dt = 4: [2t
—2 sint
Интегрируя последний интеграл по частям, окончательно получим
/= 1бя—4( — t cos t-\- sin ;
2Л
о
До сих пор мы все время рассматривали случаи, когда контур
интегрирования был незамкнутым, т.е. когда его начальная
и конечная точки были различны. Заданием этих точек определя-
определялось и направление интегрирования. Ясно, что если
направление интегрирования изменить на противоположное, то
криволинейный интеграл изменит знаю на противоположный. Эю
следует хотя бы из общего правила приведения его к опреде-
определенному интегралу. Записывают это так (для сокращения записи
мы пишем Р и Q вместо Р(ху у) и Q (л;, у):
-L
dy,
480 ГЛ. IX. КРИВОЛИН. ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ [139
где через —L и -f- L обозначена линия L при двух ее взаимно
противоположных направлениях.
Очеш> часто встречаются случаи, когда криволинейный интег-
интеграл вычисляется по замкнутому контуру (рис. 183); часто
такие криволинейные интегралы обоз-
обозначают символом Ф • При этом, разу-
разумеется, выбор начальной точки интегри-
интегрирования (она же является и конечной)
на контуре интегрирования никакой ро-
роли не играет.
~~ ~*5 В случае замкнутого контура на
плоскости направление обхода,при кото-
Рис. 183 Pqm область, ограниченная контуром,
остается слева, называют положитель-
положительным. Перемещение в противоположном направлении называют
отрицательным. В первом случае обход контура совершается против
часовой стрелки, а во втором наоборот.
Условимся считать в дальнейшем, что если L — замкнутый
контур, то направление интегрирования в интеграле ^Pdx-\-Qdy
L
всегда будет положительным; интегрирование же в отрицательном
иаправлении будем обозначать так:
$ Pdx + Qdy.
В силу сказанного выше чЭти интегралы отличаются только
знаком.
Имеет место такое специфическое свойство криволинейных
интегралов:
Теорема. Если область D, ограниченную замкнутой
линией L, разбить на две части Dx и ?>2, то криволинейный
интеграл по всей линии L равен сумме интегралов, взятых в
том же направлении по линиям L1 и L2, ограничивающим об-
области Dx и D2.
Доказательство. Пусть область D ограничена замкнутой
линией L(AECBA), а области Dx и D2—соответственно линиями
LX(AECA) и L2(ACBA) (рис. 184). Имеем
^ J ^
Lt A EC С А
\ + Qy+\
АС СВА
140]
§ 1. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ
481
Интегралы по СА и АС берутся по одной и той же линии, но в
противоположных направлениях; поэтому их сумма равна нулю.
Складывая почленно два последних равенства, получим
ЛЕС
СВА
что и требовалось доказать.
Эта теорема, как читатель сам легко убедится, справедлива
при любом числе областей, на которые разбивается область D.
У\
О
Д
В
Ь х
Рис. 184.
Рис. 185.
140. Формула Грина1)* Важную роль в дальнейшем исследо-
исследовании будет играть формула, связывающая криволинейный интег-
интеграл по замкнутому контуру с двойным интегралом, распростра-
распространенным по области, ограниченной этим контуром.
Теорема. Если функции Р(х9 у) и Q(x, у) непрерывны
вместе со своими частными производными первого порядка в
области D, то имеет место формула
(*>
где L — граница области D и интегрирование вдоль L произ-
производится в положительном направлении.
Формула (*) называется формулой Грина.
Доказательство. Сначала возьмем в плоскости Оху
область Д ограниченную линией L, пересекающейся с прямыми,
параллельными осям координат, не более чем в двух точках
J) Д. Грин A793—1841)—известный английский физик и математик.
16 А. Ф. Бермант, И. Г. Араманович
482 гл. ix. криволин. интегралы и интегралы по поверхности [140
(рис. 185). Преобразуем двойной интеграл
ду
Интегрируя сначала по у, а потом по х, получим
ь у? (х)
a Ut {х)
где у~у^(х)— уравнение линии ABC, y=yi(x) — уравнение линии
ЛЕС. Выполнив внутреннее интегрирование, будем иметь
Ь
Во втором интеграле мы изменили пределы интегрирования, соот-
соответственно этому изменился и знак.
Первый интеграл есть не что иное, как криволинейный интег-
интеграл )Р(х, y)dxy а второй — криволинейный интеграл ^ Р{х, у) dx.
ABC CEA
Сумма этих интегралов будет криволинейным интегралом по всему
контуру L, обходимому в отрицательном направлении. Сле-
Следовательно,
D L
Совершенно аналогично
d x2 (у) d
jJ *Ldx dy = J dy J g-dx = I {Q {x2 (y), y]-Q [Xl (у), у]} dy,
%D с xt (у) с
где хг(у) и х2(у)—уравнения линий ЕАВ и ЕСВ в форме, раз-
разрешенной относительно х. Рассуждая так же, как и в первом
случае, получим
ЕСВ BAE
Сумму интегралов, стоящих в правой части последнего равенства,
заменим одним интегралом по всему контуру L, обходимому уже
141J § 1. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ
в положительном направлении:
483
Вычитая из равенства (*#*) почленно равенство (**), получим
L
что и требовалось доказать.
Пусть теперь область D, ограниченная контуром L, имеет более слож-
сложный вид. Разобьем ее предварительно на ряд областей, каждая из которых
удовлетворяет поставленным выше условиям, т.е.
пересекается с прямыми, параллельными осям
координат, не более чем в двух точках. Напри-
Например, область, изображенную на рис. 186, мы раз-
разбили пунктирными линиями на три области Db
D2 и DSt ограниченные соответственно контурами
/-!, L2 и L3. Для каждой из таких областей на-
напишем формулу Грина и сложим полученные
равенства. Сумма двойных интегралов по облас-
областям Z)b D2 и D3 даст двойной интеграл по всей
области D, а сумма криволинейных интегралов
по контурам Li, L2 и L3 в силу теоремы,
доказанной в п. 139, будет равна криволиней-
криволинейному интегралу по контуру L. Тем самым теоре-
ма Грина будет доказана для любой области D.
141. Условие независимости интеграла от линии интегриро-
интегрирования» Как мы уже отмечали при решении примера 1) в п. 139,
величина криволинейного интеграла
(*)
о
Рис-
J/>(*. y)dx + Q(x, y)dy
L
при заданном подынтегральном выражении и заданных начальной
и конечной точках линии интегрирования может зависеть от
линии, соединяющей эти точки.
Возникает вопрос: при каких условиях интеграл (*) не зависит
от линии, по которой производится интегрирование, а зависит
исключительно от начальной и конечной точек линии интегрирования?
С точки зрения механики независимость интеграла (*) от линии
интегрирования означает, что величина работы в силовом поле,
определяемом силой F = P(x, y)\ + Q(x, у)], не зависит от формы
пути, а зависит только от его начальной и конечной точек. То,
что работа в поле тяжести не зависит от формы пути, хорошо
известно из курса физики; решение же вопроса, поставленного
выше, позволит выяснить, как будет обстоять дело в других,
более сложных, силовых полях.
16*
484 гл. ix. криволин. интегралы и интегралы по поверхности [141
Прежде всего докажем простое вспомогательное предложение,
которое позволит нам заменить рассматриваемый вопрос другим,
решение которого мы получим, опираясь на результаты п. 140.
Для сокращения записи интеграл )Р(х, y)dx-\-Q(x, y)dy будем
L
обозначать символом IL.
Лемма. Для того чтобы криволинейный интеграл (*) не зависел
от линии интегрирования, необходимо и достаточно, чтобы этот
интеграл, взятый по любому замкнутому контуру, был равен нулю.
Доказательство. Пусть известно, что интеграл (*) не
зависит от линии интегрирования; покажем, что он равен нулю
по любому замкнутому контуру. Возь-
М^~—*Ч мем как0Й"нибуДь замкнутый контур L.
/г Л Отметим на нем две точки В и С
/ I (рис. 187). Так как по условию интег-
I у рал по линии ВМС равен интегралу по
#4^_^/ линии BNC:
О] Ъ
то интеграл по всему контуру L равен
Рис. 187.
Обратно, пусть известно, что интеграл (*) обращается в нуль
по всякому замкнутому контуру; покажем, что он не зависит от
линии интегрирования. Возьмем какие-нибудь две линии BNC и ВМС
(рис. 187), соединяющие две заданные точки В и С. Так как по
условию интеграл по замкнутому контуру BNCMB равен нулю:
bncmb Q* т' е-
то
Таким образом, лемма полностью доказана.
Для дальнейшего существенно уточнить, с какими областями
мы будем иметь дело. Условимся называть односвязной областью
часть плоскости, ограниченную одной замкнутой линией1). Напри-
Например, односвязными областями будут внутренности окружности,
эллипса, многоугольника и т. п. Примером неодносвязной области
служит кольцо; его граница состоит из двух непересекающихся
замкнутых линий.
Перейдем теперь к основной теореме нашего исследования.
х) Предполагается, что эта линия не имеет самопересечений, т. е. не
может, например, быть «восьмеркой».
141] § L КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ 485
Теорема. Пусть функции Р(х9 у) и Q(x, у) непрерывны
вместе со своими частными производными в односвяэной
области D. Тогда, для того чтобы криволинейный интеграл
$/>(*, y)dx + Q(x, y)dy (*)
L
не зависел от линии интегрирования, необходимо и достаточно,
чтобы во всех точках области D соблюдалось равенство
дР dQ t v
Если указанные свойства функций Р и Q соблюдаются при
любых хну, то область D совпадает со всей плоскостью Оху.
Так как равенство (**) является необходимым и достаточным
условием того, чтобы подынтегральное выражение
P(xt y)dx + Q(x, y)dy
было полным дифференциалом (см. п. 115, I), основную теорему
можно сформулировать в следующем виде.
Для того чтобы криволинейный интеграл (*) не зависел от
линии интегрирования, необходимо и достаточно, чтобы его
подынтегральное выражение было полным дифференциалом.
Доказательство. Как было отмечено в лемме, условие
независимости интеграла от линии интегрирования равносильно
равенству нулю интеграла (*) по любому замкнутому контуру,
содержащемуся целиком в области D. Докажем сначала доста-
достаточность условия (**) для равенства нулю интеграла по
любому замкнутому контуру. Возьмем произвольный замкнутый
контур L*, ограничивающий область D* и целиком лежащий внутри
области Д и применим к нему формулу Грина:
I
Так как по условию ^ = ^-, то двойной интеграл равен нулю.
Следовательно, равен нулю и криволинейный интеграл по контуру L*y
что и требовалось доказать.
Перейдем к доказательству необходимости условия (*#).
Так как нам дано теперь, что интеграл (*) по любому замкну-
замкнутому контуру равен нулю, то, опять-таки в силу формулы Грина,
заключаем, что равен нулю и двойной интеграл
•• с»)
486 ГЛ. IX. КРИВОЛИН. ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ [141
где О—любая область, заключенная внутри D. Допустим, что
равенство jr^ = ;r* не выполняется. Возьмем какую-либо точку М,
в которой это равенство нарушается, и вычислим разность
dQ дР
¦—-—-г- в этой точке.
дх ду
Допустим, что эта разность положительна1), т. е.
дх ду )м > U-
В силу предположенной непрерывности частных производных
dQ дР л
отсюда следует, что разность —^—-^- будет положительна в
некоторой достаточно малой области С, окружающей точку Ж, т. е.
дх ду > и
во всех точках области G. Но тогда по свойству двойных интег-
интегралов (п. 129)
и мы пришли к противоречию с равенством (**#). Это означает,
что наше предположение о несоблюдении условия (**) было не-
неверным, т. е. мы доказали, что д~ = ^- во всей области D. Тео-
Теорема полностью доказана.
Обращаем еще раз внимание читателя на то, что все условия теоремы
существенны. Возьмем, например, интеграл
—у dx-\-xdy
, *2+</а '
где I— окружность радиуса R с центром в начале координат. Здесь
у дР —х2—У2-\-2у2 у2—х2
Несмотря на то, что условия независимости интеграла от линии интег-
интегрирования выполнены, интеграл нулю не равен Действительно, взяв урав-
уравнение окружности в параметрическом виде x~Rcostt y = Rsmtt получим
2Я
С
23Т
( — R sin
*) Нетрудно убедиться в том, что если (-—- — ^- ] < 0, то ход до-
\ ох оу ) м
казательства не изменится.
142]
§ 1. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ
487
Никакого противоречия с доказанной теоремой здесь нет. Просто не выпол-
выполнены условия теоремы: функции Р (х, у) и Q (х, у) разрывны в начале ко-
координат, т. е. в точке, лежащей внутри контура интегрирования. Если
бы L был замкнутый контур, не содержащий внутри себя начала коор-
координат, то условия теоремы выполнялись бы и
тогда li был бы равен нулю.
Рассмотрим этот же пример еще и с другой
точки зрения. Возьмем кольцо, изображенное на
рис. 188. В этом кольце функции Р и Q, а также
их производные непрерывны, но несмотря на
это нельзя утверждать, что интегралы lix и Ii2
равны между собой. Так как 1^ + 1 „12 = 2п,
т. е. /it —/l3==2ji, to
Все дело в том, что кольцо ограничено двумя
контурами и не является односвязной об-
областью, как это требуется в основной теореме.
Рис. 188.
Подводя итоги нашего исследования, можно сказать, что если
область D односвязна и функции Р(х, у) и Q(x, у) вместе со
своими частными производными непрерывны в этой области, то
все четыре следующих утверждения равносильны, т. е. если
выполняется одно из них, то выполняются и все остальные.
1. Криволинейный интеграл j P dx -\- Q dy, взятый по любому
замкнутому контуру, целиком лежащему в области Д равен нулю.
2. Криволинейный интеграл \Pdx-\-Qdy не зависит от линии
интегрирования.
3. Выражение Р(х, y)dx-\-Q(xJ y)dy является полным диффе-
дифференциалом.
4. Во всех точках области D имеет место равенство ^— = ~? #
142. Интегрирование полных дифференциалов. Первообразная
функция. Если подынтегральное выражение в криволинейном ин-
интеграле
$ (x, y)dy (#)
является полным дифференциалом, то при соблюдении всех усло-
условий, сформулированных в основной теореме п. 141, величина этого
интеграла зависит исключительно от начальной и конечной точек
линии интегрирования. Поэтому интеграл (*) записывается обычно
в виде
U». Ух)
P{x,
, y)dy,
где (лг0, у0) — координаты начальной точки линии интегрирования,
488 гл. ix. криволин. интегралы и интегралы по поверхности A42
a (xv y±) — конечной. Каков же наиболее целесообразный способ
вычисления такого интеграла? Казалось бы, проще всего интег-
интегрировать по отрезку прямой, соединяющей данные точки. Однако
это не так. Мы воспользуемся замечанием, сделанным на стр. 477,
и будем интегрировать по ломаной М0М2Мг (или М0МвМг), звенья
которой параллельны осям координат (рис.189). Так как на
участке М0М2 у=у0 и dy—0} а на участке М2Мх х — хх и
dx = 0, то
<Jr».0t) Xt 0t
J P(x, y)dx + Q(x, y)dx=^P(xy yQ)dx+\Q{xvy)dy. (**)
(*<>¦ У о) xQ y9
Аналогичную формулу для интегрирования по ломаной MQMZM1
предоставляем написать читателю самостоятельно.
Рис. 189.
Рис. 190.
Если окажется, что ломаные М0М2М± и М0МгМ1 выходят из
области D, где выполняются условия основной теоремы (рис. 190),
то можно производить интегрирование, например, по ломаной
Пример. Вычислим интеграл
B, 1)
/== J
(о, о)
Здесь на звене ломаной, совпадающем с отрезком оси абсцисс, по-
подынтегральное выражение равно нулю и
/=
= 4.
Рассмотрим теперь интеграл с фиксированной начальной точкой
М0(х0> у0) и переменной конечной М(ху у):
x, у)
р (*.
> У)
142]
§ 1. криволинейный интеграл
489
Величина этого интеграла будет зависеть только от координат
конечной точки, т. е. являться функцией переменных х и у.
Выясним связь функции 1(х, у) с функцией и(х, у), для ко-
которой подынтегральное выражение является полным дифференциалом
du = P(xf y)dx + Q(x, y)dy.
Для этого будем вычислять интеграл (**#) по формуле (#*):
Q (х, у) dy,
= [Р (*, Уо)
причем во втором интеграле х считается в процессе интегрирования
постоянным. Так как P^-sr- и Q=~, то
= u(x, у0)
= u(xty0) — u(xQi y0)
= «(*. У)"«С*, <Уо)«
Уо
Следовательно,
(*. У)
5
и(х, уо)—и(хо, уо) + и(х, у)—и(х, у0),
= u(xy y)—u(xOi y9)
или
Если функцию и (лг, у) мы назовем первообразной для полного
дифференциала Pdx + Qdy, то полученная формула является фор-
мулой Ньютона — Лейбница для криволинейных интегралов.
Пользуясь полученными результатами, мы можем указать спо-
способ отыскания функции и (лг, у) по ее полному дифференциалу, во
многих случаях более удобный, чем рассмотренный в п. 115, а
именно:
(х,у)
и{х, у)=
, y)dx + Q(x,
о, У о)
x0, y0).
Величина и(х0, у0) играет роль произвольной постоянной. Это и по-
понятно, потому что сама функция и(ху у) определена с точностью
до постоянного слагаемого. Воспользовавшись способами вычисле-
вычисления криволинейного интеграла (***), указанными выше, и заменяя
490 ГЛ. IX. КРИВОЛИН. ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ [143
и(хо, У о) через С, получим две равносильные формулы для отыс-
отыскания м(дг, у):
( х у
и(х, у)-=
У
*, y)dy + C,
о, y)dy + C.
*о
Если в обоих формулах положить С — 0, то получим функцию
и(ху у), обращающуюся в нуль в точке (лс0, у0).
Начальную точку (л:0, у0) следует выбирать так, чтобы подын-
подынтегральные функции были по возможности более простыми.
Пример. Найдем первообразную функцию и (лг, у) для полного
дифференциала
{еу + х) dx + (хе? — 2у) dy.
Выбирая в качестве начальной точки начало координат, получим
Обозначив -9- + ^ одной буквой, получим окончательно
Этот пример был уже рассмотрен нами в п. 115, I. Рекоменду-
Рекомендуем читателю сравнить оба метода решения.
143. Криволинейные интегралы по пространственным линиям.
До сих пор мы рассматривали криволинейные интегралы от функции
двух независимых переменных х и у и линией интегрирования слу-
служила кривая, расположенная в плоскости .Оху.
Перейдем теперь к рассмотрению криволинейных интегралов от
функции трех переменных. С физической точки зрения это будет
означать, что материальная точка находится под действием сил
пространственного силового поля. Такое поле определяется
силой F(at, у, z) или, иначе, ее проекциями на оси координат, ко-
которые также будут являться функциями переменных х, у и z*
Запишем это так:
у, z)l + Q{x, у, z)) + R(xy yy z)к.
Рассуждая точно так же, как и в п. 138, мы придем к выражению
143] § 1. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ 491
работы в виде интеграла1)
$Р(х, У, z)dx + Q(x} у, z)dy + R(x1 у, z)dz, (*)
где L — пространственная линия, соединяющая начальную точку (В)
и конечную (С). В дальнейшем под функциями Ру Q и R мы будем
понимать любые непрерывные функции трех переменных. Интегралы
^Pdxy \Qdy и \Rdz называются соответственно интегралами
L L L
по координатам х, у и z.
Пусть линия L задана параметрическими уравнениями
x=*x(t), У=У(*) и z = z(t)9
причем начальной точке линии (В) соответствует значение пара-
параметра tBt а конечной (С) — tc. Тогда интеграл (*) преобразуется
в обыкновенный определенный интеграл по переменной t
x, у, z)dy + R(x, yt
= 5 {P[x(t), y(t), z{t)]x'{t)+Q[x(t)t y(t),
lB
+ R[x[t),y[t), z(t)}z'(t)\dt.
Рекомендуем читателю записать эту общую формулу для частных
случаев, когда линия L является отрезком прямой, параллельной
одной из координатных осей.
В случае интегралов по пространственным линиям также имеет
место основная теорема о независимости от пути интегрирования.
Теорема. Пусть функции Р(х, у, z)f Q(xf yf z) и R(xfyfz)
непрерывны вместе со своими частными производными в одно-
связной области Q. Тогда для того чтобы криволинейный ин-
интеграл
с, у, z)dz (*)
не зависел от линии интегрирования, необходимо и достаточно,
чтобы во всех точках области Q соблюдались равенства
JW^dQ ??_,?? dR дР
ду дх ' дг ду ' дх *** dF * ^**'
х) Рекомендуем читателю провести самостоятельно соответствующие
рассуждения.
492 ГЛ. IX. КРИВОЛИН. ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ [.143
Под односвязной областью в пространстве мы понимаем часть
пространства, ограниченную одной замкнутой поверхностью, при-
причем такую, что любая замкнутая линия в области может быть
стянута в точку, не выходя из области. Односвязными областями
будут, например, куб, шар, эллипсоид и т. д. Не является одно-
связной областью, например, тор («баранка») (см. рис. 124 на стр. 345),
ибо окружность, описанная любой точкой круга, вращением кото-
которого был образован тор, не может быть стянута в точку. Об-
Область Q может также совпадать со всем пространством или полу-
полупространством.
Доказательство теоремы отложим до п. 148, где оно явится
простым следствием формулы Стокса.
Согласно п. 115, II соотношения (##) являются необходимыми и
достаточными условиями того, чтобы подынтегральное выражение
Pdx-\-Qdy + Rdz являлось полным дифференциалом некоторой
функции и(х, у, z). Поэтому приведенную теорему можно сформу-
сформулировать так:
Для того чтобы криволинейный интеграл (*) не зависел от
линии интегрирования, необходимо и достаточно, чтобы его
подынтегральное выражение было полным дифференциалом.
Если условия независимости интеграла (*) от линии интегри-
интегрирования выполняются, то его обычно записывают в виде
J Pdx + Qdy + Rdz,
где (л:0, у0, z0) и (х^ yv zx) — координаты начальной и конечной
точек интегрирования.
Этот интеграл легко выразить через первообразную функ-
функцию и (лг, у, z), для которой подынтегральное выражение является
полным дифференциалом. Имеем1)
du(x, у, *) =
= u(xv yv Zl) — u(x0J y0, *e).
Фактическое отыскание функции по ее полному дифференциалу
при помощи криволинейных интегралов производится так же, как
и в плоском случае. Наиболее удобные формулы получаются при
интегрировании по ломаной, соединяющей начальную точку
ЛМ-^си <Уо> zo) c конечной точкой М{х, у, z) и имеющей звенья,
параллельные осям координат.
2) Доказательство полностью совпадает с соответствующим доказатель-
доказательством для плоского случая, и мы его повторять не будем.
143]
§ 1. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ
493
Примем за контур интегрирования, например, ломаную М0М1М2М
(рис. 191). Вдоль MQMX имеем: у=у0, z = z0 и dy = O, dz = 0;
вдоль МгМ2 имеем: z = z0 и dx — 0, dz~0; наконец, вдоль М2М
имеем: dx = 0, dy = O. Значит,
У, *) —
(*, fit г)
(х0,
x9
У
Уъ
z
Pdx + Qdy-
y, zQ)dy
y, z)dz.
7
e
/
у
to
/
/
7
/
У
/ 9
Рис. 191.
Мы придем к аналогичным формулам, если будем интегрировать
по другим ребрам параллелепипеда М0М, ведущим из точки Мо к
точке М.
Таким образом, если du = Pdx-\-Qdy -\-Rdz, то общее выра-
выражение для первообразной можно записать, например, так:
х у z
и(х, у, *) = $/>(*, у0, zo)dx+lQ(xty,zo)dy+lR{x,ytz)dz+C,
где Мо (х0, у0, zQ) — какая-нибудь точка области, С — произвольная
постоянная.
Пример. Найдем первообразную для полного дифференциала
Условия (**) здесь выполняются. Выбирая в качестве начальной
точки интегрирования, например, точку Afo(O, 1, 0), получим
Этот пример иным путем мы решили в п. 115, Н. Предложенный
здесь путь значительно короче и удобнее. Заметим, что нельзя
выбирать в качестве начальной точки @, 0, 0), так как Р и Q в
этой точке не определены.
494 гл. ix. криволин. интегралы и интегралы по поверхности [144
144. Приложения криволинейных интегралов к задачам меха-
механики и термодинамики.
I. Вернемся снова к задаче о работе силового поля, заданного
силой
с> У> z)\ + R(x, у, z)k.
Если проекции Я, Q, R силы F на оси координат удовлетво-
удовлетворяют условиям
dJ^_d_Q dJ}_dR_ dR__dP_
ду~дху дг ~~ ду ' дх ~~ дг > **'
то работа в этом силовом поле, выражаемая криволинейным
интегралом
$Р(лг, у, z)dx + Q(x, у, z)dy + R(x, у, z)dz9
не зависит от формы пути. Такое силовое поле называется потен-
потенциальным или консервативным. Функция и (лг, у, z)y для которой
>— выражение Pdx-\-Qdy-\-Rdz является пол-
полным дифференциалом, называется потенциалом
1(х,у) силового поля. В соответствии с результа-
результатами пп. 138 и 143 можно сказать, что ра-
бота в потенциальном силовом поле равна раз-
* ности потенциалов в конце и в начале пути.
У Рассмотрим два простых примера.
Рис. 192. 1)Поле тяжести. Выберем в плос-
плоскости движения материальной точки массы
m координатные оси, причем ось Оу направим вертикально вниз
(рис. 192). Проекции силы тяжести на оси координат будут равны
соответственно
где g—ускорение силы тяжести. Так как функции Р и Q посто-
постоянны, то они, очевидно, удовлетворяют условию (#) (и левая и
правая части его обращаются в нуль), и следовательно, работа
при перемещении материальной точки из точки Ж0(лг0, у0) в точку
М(ху у) выразится интегралом
(*. У) У
А= J mgdy = Mg} dy = mgy—mgyQ.
(Х9> У о) У о
Эта работа положительна, если у > yQ, т. е. если материальная
точка падает, и отрицательна, если точка поднимается.
Потенциальная функция и (лг, у) имеет вид
и (лг, у) = mgy + С.
144]
§ 1. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ
495
Обычно произвольную постоянную С выбирают так, чтобы
u(xj <У) = ^ ПРИ У~ 0. Тогда потенциалом поля тяжести будет
функция mgy.
2) Электрическое поле, создаваемое точечным
зарядом. Поместим заряд -\-q1 в начале координат. Тогда
сила Е, с которой этот заряд действует на единичный положитель-
положительный заряд, помещенный в точку M(xt уу z)t определится по
закону Кулона1):
где г—ух2-\-у2-\-z2 — расстояние точки М от начала координат
(закон Кулона записан в системе единиц CGSE для вакуума).
Направление силы Е совпадает с направлением радиуса-век-
радиуса-вектора 'ОМ. Поэтому (рис. 193)
R =
Учитывая,
дг
дх
Е|.
что
дг
cos y
X
У
' г >
г2
дг
дг
г
X
г '
г
г
Рис. 193.
легко найдем по правилу дифференцирования сложной функции
все частные производные функций Р% Q и R:
дР Ъдгх дг 3^1 ху
ду г* ду г* *
dQ 3qty дг 3^i xy
дх г4 дх г6
И Т. Д.
дР дО
Мы видим, что -J-— -з^ Читатель может проверить, что вы-
выполняются и остальные два условия (*). Следовательно, рас-
рассматриваемое поле потенциально. Найдем его потенциал
и{х, у, z). Чтобы избежать утомительного интегрирования,
г) IIL Кулон A736—1806) —выдающийся французский физик.
496 ГЛ. IX. КРИВОЛИЦ. ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ [144
заметим, что
Р(х, у, Z)dx + Q(x, у, z)dy + R(x, у,
дг . дг . . дг
dx + d+
Яг УТш = Яг-pr
Поэтому функция ~ + С и является потенциалом. Выбирая С
так, чтобы потенциал на бесконечности равнялся нулю, получим
«(*¦ У, <*) = ~ = ; Ч-
Следовательно, работа сил электрического поля при перемещении
единичного заряда из точки М0(х0, у0, zQ) в точку М(х, у, z) будет
равна
где г0 и г-—длины радиусов-векторов точек Мо и Ж. Так как заряды
одноименны, то работа положительна при их удалении друг от
друга (г > rQ) и отрицательна при их сближении (г<г0).
II. Рассмотрим теперь приложение криволинейных интегралов
к задачам термодинамики.
Будем под состоянием вещества понимать совокупность вели-
величин, характеризующих его физическое состояние. В термодинамике
обычно этими величинами служат: давление р, объем v и
абсолютная температура Т. Следовательно, состояние
задается указанием трех вел.ичин: р, v, Г. Но они связаны между
собой одним уравнением — так называемым уравнением состо-
состояния. Поэтому состояние фактически определяется двумя вели-
величинами, например р и v (третья, Г, есть функция р и v).
Геометрически каждому состоянию соответствует точка
М(р, v) в плоскости Opv, а каждому процессу (состоящему
в последовательном изменении состояния тела) — линия. Она
называется диаграммой процесса* В том случае, когда происходит
возвращение к исходному состоянию, процесс называют круговым
или циклическим', его диаграммой будет замкнутая линия.
Пусть дан идеальный газ, т. е. газ, который подчиняется
уравнению состояния Менделеева—-Клапейрона1):
pv = R7 (/? = const).
*) Д. И. Менделеев A834—1907) — великий русский ученый.
Клапейрон A799—1864) — французский физик и инженер.
Б.
144] § 1. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ 497
Поставим перед собой задачу — найти количество тепла Q,
поглощенного (или выделенного) газом при процессе, изображен-
изображенном данной диаграммой L. На линии L выделим произвольный ее
участок от точки М(р, v) до точки Мх(р-{-Aр, v + dv), представ-
представляющий «бесконечно малый процесс»; соответствующее ему коли-
количество тепла обозначим через AQ. Зто тепло идет на приращение
механической энергии частиц газа, т. е. в конечном счете на
приращение dT температуры, и на работу, производимую при
изменении объема dv. Мы найдем элемент dQ (главную часть AQ,
линейную относительно dT и dv), если допустим, что поглощаемое
тепло есть сумма двух количеств тепла: 1) затрачиваемого на
приращение температуры dT при постоянном объеме v, 2) затра-
затрачиваемого на работу расширения dv при постоянной температуре Т.
Первое равно cvdT, где cv—теплоемкость газа при постоянном
объеме, а второе р dv.
Следовательно, при соответствующем выборе единиц измерения
dQ = cvdT+pdv.
Согласно уравнению Менделеева — Клапейрона
±dv
внося это в выражение для dQ, получим
dQ=*vdp+b
Выясним смысл выражения cv -+-/?. Из двух последних формул
при постоянном давлении /?, dp = 0 находим
т. е.
откуда видно, что коэффициент при dT есть просто теплоемкость
с при постоянном давлении:
cv + R =
(ср и cv считаем постоянными).
Итак, окончательно:
498 гл. ix. криволин. интегралы и интегралы по поверхности [144
Для того чтобы найти искомое количество тепла Q, остается
проинтегрировать выражение для dQ по диаграмме процесса L:
Здесь условия независимости интеграла от пути интегрирова-
интегрирования не выполняются. Действительно,
а* V Л / я ' dp\R
но Ср-фс^ как это следует из соотношения (*). Таким образом»
величина Q существенно зависит от контура L, т. е. Q не является
функцией р и v. Наше рассуждение показывает, что количество
поглощаемого (выделяемого) тепла не есть функция состояния
газа, оно зависит не только от конечного состояния, но и о г
того, каким способом газ пришел к этому состоянию, другими
словами, от совокупности всех промежуточных состояний. В част-
частности, круговой процесс (цикл) может приводить к поглощению
или выделению тепла.
В термодинамике вводится величина S, характеризующая про-
процесс,— так называемая энтропия. Определяется энтропия интег-
интегралом
где L — диаграмма процесса.
Для идеального газа находим
и так как RT—pv, то
Подынтегральное выражение есть полный дифференциал, ибо
и, стало быть, энтропия является функцией состояния газа; ее
величина не зависит от того, как газ изменяется от начального
состояния к конечному.
Интегрируя, получаем
145] § 1. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ 499
Если процесс адиабатический (Q — const, dQ = 0, значит,
и dS = 0, т. е. 5 = const), то
pccvcp = const,
откуда
pvk = const,
где &=—>1, Это — уравнение диаграммы адиабатического про-
cv
цесса (так называемой адиабаты) в идеальном газе.
145. Криволинейный интеграл по длине (первого рода). Пусть
функция /(лг, у) непрерывна в некоторой области D и L — линия,
целиком расположенная в этой области. Разобьем кривую L на п
участков; возьмем на каждом из участков произвольную точку
(?А, г)Л) и построим следующую интегральную сумму:
где Ask — длина соответствующего участка линии L. Отличие
этой суммы от сумм, приводящих к криволинейным интегралам по
координатам (см. п. 138), состоит в том, что здесь значение
функции умножается на длину участка разбиения, а там на
проекцию этого участка на соответствующую ось координат.
Определение. Криволинейным интегралом по длине
называется предел я-й интегральной суммы (*) при условии»
что длина наибольшего участка разбиения стремится к нулю.
Записывается это так:
И» 2/E*, т|Л)Д*Л«С/<*, y)ds.
*=1 t
Свойства криволинейного интеграла по длине совершенно ана-
аналогичны свойствам определенного интеграла, и поэтому мы их
даже не формулируем. Вычисление криволинейных интегралов по
длине производится путем преобразования их в обыкновенные
определенные интегралы. Поскольку правила такого приведения
совершенно аналогичны приведенным в п. 139, мы сформулируем
только конечный результат.
Правило вычисления криволинейного интег-
интеграла по длине. Для того чтобы криволинейный интеграл
/(*, y)ds,
где линия L задана параметрическими уравнениями x = x(t) и
500 ГЛ. IX. КРИВОЛИН. ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ [145
y=y(t)f преобразовать в обыкновенный, нужно в подынтеграль-
подынтегральном выражении положить
и взять интеграл по интервалу изменения tf соответствующему
линии интегрирования.
Если параметрические уравнения различны для различных
участков контура интегрирования I, то его нужно разбить на
отдельные части и весь интеграл вычислить как сумму интегра-
интегралов, взятых по этим частям.
Из общего правила преобразования интеграла по длине линии
вытекают правила преобразования в частных случаях, когда урав-
уравнение линии задано в виде у=у(х) или в виде х = х(у). В пер-
первом случае в общем правиле надо положить t = x, а во вто-
втором t=y.
Пример. Вычислить интеграл
у ds,
где L—дуга параболы у2 = 2х от точки @, 0) до точки D, |/1Г).
Здесь линию удобно задать в форме, разрешенной относительно х:
л? = -|-, Тогда х'=у и интеграл преобразовывается к виду
VT
~J •
С помощью криволинейных интегралов по длине особенно
удобно решать задачу об отыскании массы материальной линии,
если линейная плотность б задана не как функция длины линии
(см. п. 78, III), а как функция координат хну точки М линии L:
6 = 6 (лг, у). Тогда масса линии равна J б(лг, y)ds (советуем чита-
L
телю самостоятельно это обосновать).
Укажем одну геометрическую задачу, просто решаемую с по-
помощью криволинейного интеграла по длине. Пусть дана цилиндри-
цилиндрическая поверхность G, направляющей которой служит линия L
в плоскости Оху и образующие которой перпендикулярны к этой
плоскости (рис. 194). Вычислим площадь Q части поверхности,
заключенной между линией L и какой-нибудь линией Lx на той
же поверхности, лежащей выше L. Аппликата точки М линии Lt
является функцией координат точки Р линии L:
* = /(*• Я
145]
§ 1. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ
501
В произвольной точке Р основания возьмем бесконечно малый
элемент дуги ds. Ему соответствует площадь поверхности Aq,
главной частью которой, пропорциональной ds, будет площадь
прямоугольника с основанием ds и
высотой, равной высоте поверхности
в точке Р. Следовательно, дифферен-
дифференциал dq искомой величины равен
dq=f(x, y)ds.
Интегрируя это выражение по линии
L, получим
Пример. Найдем площадь Q бо-
боковой поверхности половины эллип-
*2 , у2 1
тического цилиндра -=—(- ¦—- = 1,
плоскостью
Рис. 194.
j^, 2^0, усеченного
z=y (рис. 195).
Имеем
Q=\zds=\ yds,
L Г
i X2 . у2 л
где L — дуга эллипса -г + %- == 1
Вычислим интеграл. Параметрические
уравнения контура интегрирования:
s t, v = 3 sin t. Следовательно,
Q = J 3 sin * V9 cos2 / + 5 sin2 tdt=*3 I sin ^4 cos2 / + 5 dt.
Полагая costf = H, находим
1
Воспользовавшись табличным интегралом 34 (a =2,
получим
602 ГЛ. IX. КРИВОЛИН. ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ [146
Мы не будем останавливаться на определении интеграла по
длине для пространственной кривой
так как оно аналогично рассмотренному.
Отметим, что криволинейный интеграл, рассмотренный в п. 143»
^ + Qy + dz
L
всегда можно записать в виде интеграла по длине. Для этого
вспомним, что, согласно формулам, приведенным в конце п. 68,
dx — ds cos a, dy = ds cos |S, dz = ds cosy,
где cos a, cos p, cosy — направляющие косинусы вектора Т, каса-
касательного к линии L, a ds — дифференциал длины дуги; направле-
направление вектора Т определяется выбранным направлением интегриро-
интегрирования вдоль линии L. Заменяя dx, dy} dz их выражениями, мы
и производим преобразование интеграла:
= ^ (Р cos a + Q cos $ + R cos у) ds.
L
§ 2*. Интегралы по поверхности
146*. Поток жидкости через поверхность. Интеграл по
поверхности. Изучение интегралов по поверхности мы начнем
снова с физической задачи. Пусть имеется некоторое течение
жидкости. Говорят, что течение установилось, если скорость
частиц жидкости, протекающих через данную точку, зависит
только от этой точки и не зависит от времени. В каждой точке
М(х, у, z) области, в которой происходит течение, задан, сле-
следовательно, вектор v(x, у, г)-—скорость частицы жидкости
в этой точке. Таким образом, нам задано векторное поле —
поле скоростей жидкости1). Проекции вектора v на оси координат
будут являться функциями координат точки М. Запишем это так:
v = P(x, у, z)\ + Q(x, у, z)i + R(xy у, z)k.
Плотность жидкости считаем постоянной и равной единице. Будем
*) Поле скоростей текущей жидкости является конкретным примером
векторного поля; другой пример такого поля — силовое поле, ко-
которое мы рассматривали в п. 138 в связи с задачей о работе при движении
точки. Общей теорией векторных полей мы будем заниматься в § 3 этой
главы.
146]
§ 2. ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ
503
искать количество жидкости, протекающее за единицу времени че-
через заданную поверхность; разумеется, при этом считается, что
жидкость может свободно протекать через эту поверхность. Указан-
Указанное количество жидкости
назовем потоком жидко-
жидкости через поверхность.
Начнем с рассмотре- '
ния простейшего случая.
Пусть скорость течения —
жидкости во всех точках
одна и та же:
v = const.
Рис. 196.
Поток жидкости К через прямоугольник A^^D^ расположен-
расположенный в плоскости, перпендикулярной к скорости v (рис. 196),
будет равен произведению площади прямоугольника на величину
скорости:
К = Saxb1c1d1 Iv I •
Ясно, что это же количество жидкости К протекает и через
прямоугольник ABCD, расположенный в плоскости, нормаль к
которой п образует со скоростью v угол ф (рис. 196). Если обоз-
обозначить через 5 площадь прямоугольника ABCD, то из соотноше-
соотношений D^^DC и A1D1 = ADcos ф следует, что Sa^c^^S cos(f.
Поэтому можно записать:
где vn—проекция скорости v на нормаль п. Эта формула для
потока жидкости К верна не только для прямоугольника, но и
для любой площадки, расположенной в плоскости, нормаль к ко-
которой образует тот же угол ф со скоростью v (рис. 197). Если
площадь этой площадки равна а, то площадь ее проекции на
плоскость, перпендикулярную к скорости v, равна асоБф1). По-
Поток же жидкости через площадку, перпендикулярную к скорости
течения, равен произведению ее площади на величину скорости.
Перейдем теперь к общему случаю. Пусть в некоторой области за-
задано поле скоростей жидкости, определяемое векторной функцией
у, z)l + Q{x, у, z)} + R(x, у, z)k.
Возьмем некоторую поверхность S. Подсчитаем поток жидкости
через эту поверхность. Для этого разобьем данную поверхность
1) Эту площадку можно представить себе разбитой на маленькие прямо-
прямоугольники; так как для каждого такого прямоугольника формула верна, то
она верна и для всей площадки.
504 ГЛ. IX. КРИВОЛИН. ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ [146
произвольным образом на п частей; площади получившихся участ-
участков обозначим Дах, Да2, ... , Дап. На каждой площадке выберем
по произвольной точке М{(х{у yh z{) (рис. 198). Считая эти пло-
площадки плоскими и предполагая, что в пределах каждой площадки
скорость жидкости остается постоянной, а именно равной скорости
в точке Mh мы можем написать приближенное выражение
для потока жидкости
Кп = Дс^ | v± | cos (pi + kOz | v21 cos cp2 + ... + Да„ | vn | cos q>rt =
Здесь v,- — скорость в точке Mh a ф;— угол между нормалью щ
к поверхности S в точке Mt и скоростью v;.
Рис. 197
Чтобы преобразовать полученное выражение, заметим, что
| vj | cos ф^ есть скалярное произведение вектора v^ на
единичный вектор нормали.
Обозначим через а,, р/ и у( углы, образованные нормалью п?
с осями координат (величины этих углов зависят, конечно,
от точки Mi). Единичный вектор нормали имеет своими проекци-
проекциями направляющие косинусы cosotj, cos $h cosy** Поэтому
| V/1 cos ф, = Pt cos a, + Qi cos p; + Rt cos yh
где Pi% Qit R(—значения соответствующих функций в точке Mt.
Следовательно,
icos a/+Qicos P*+Rtcos Yt) д^. (•)
Перейдя к пределу при п—+оо и при условии, что каждая
площадка стягивается в точку, мы получим выражение для
потока жидкости К
п
/С=Urn Кп = Игл ^ (Р( cos о^ + Qt cos fy + Ricos Y^) Affj-
147) § 2. ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ 605
Этот предел запишем в виде
и будем называть интегралом по поверхности, В подынтегральном
выражении Р, Q, R и направляющие косинусы нормали cos a,
cosp, cosy являются функциями координат точки М(х, у, г)
поверхности S. В том частном случае, когда S — кусок плоскости,
направляющие косинусы будут постоянными.
В дальнейшем часто будем сокращенно обозначать
Pcos a + Q cos p + R cos у =/(M),
где f(M) — функция точки М поверхности S.
Дадим теперь общее определение интеграла по поверхности,
уже не связанное с рассматриваемой конкретной задачей. Пусть
S — некоторая поверхность и f(M)—непрерывная функция точки М
на поверхности S. Функцию f(M) можно записать в виде
f(x* Ур> z)y гДе ху У у 2 —координаты точки М. Разобьем по-
поверхность S на части, как указано выше, и образуем я-ю интег-
интегральную сумму
Определение. Интегралом по поверхности (или по-
поверхностным интегралом) называется предел ю-й интеграль-
интегральной суммы при стремлении к нулю диаметра каждой площадки
разбиения.
Записывается это так:
п
Ш X / Щд Да,- = J J / (М) da = J J / (*, у, г) da.
5
Если, например, функция f(x, yt z) является поверхностной
плотностью массы, распределенной по поверхности, то интеграл
выражает массу всей поверхности; если /(at, yt z) — плотность
распределения электрических зарядов, то интеграл выражает
суммарный заряд поверхности. В том частном случае, когда
/(лг, у, г) = 1, интеграл \\do просто равен площади поверх-
s
ности S.
147*. Свойства интегралов по поверхности. Определение
интеграла по поверхности, по сути дела, аналогично определению
двойного интеграла. Поэтому свойства двойных интегралов, пере-
506 ГЛ. IX. КРИВОЛИН. ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ [147
численные в п. 129, без всяких изменений переносятся на интег-
интегралы по поверхности.
Однако интегралы вида
$ (Яcosa + Qcos р + R cosу) dot (*)
s
где a, p и у— углы, образованные нормалью к поверхности S
с осями координат, обладают некоторыми специфическими особен-
, ностями, связанными с самой постановкой
физической задачи, и мы их рассмотрим
подробнее.
Дело в том, что нормаль к поверхности
имеет два направления (рис. 199). При
составлении приближенного выражения для
потока жидкости, в п. 146 мы считали,
впрочем точно не формулируя это, что все
нормали Hj- направлены в одну сторону
ис# * от поверхности S.
В дальнейшем всегда будем различать две стороны поверхно-
поверхности vS, скажем, представлять, что одна ее сторона закрашена
красной краской, а другая синей. В соответствии с этим будут
различаться два противоположных направления нормали (MN' и
MN" на рис. 199). Таким образом, мы должны различать поверх-
поверхностные интегралы (*) в зависимости от направления нормали;
как говорят, будем рассматривать поверхностные интегралы,
взятые по определенной стороне поверхности («красной» или
«синей»). Ясно, что с изменением направления нормали на противо-
противоположное направляющие косинусы (cos a, cos Р и cos y) переменят
знаки, а это повлечет за собой изменение знака всего интеграла.
Следовательно, интегралы (*), взятые по разным сторонам поверх-
поверхности, отличаются друг от друга только знаком. Сокращенно обо-
обозначая подынтегральное выражение в интеграле (#) через /(Af),
запишем последнее замечание так:
\[o, (**)
где через +5 и —5 обозначены две стороны поверхности S.
Отметим, что физические задачи, приводящие к интегралам по
поверхности, могут быть двух типов. В первом типе подынтеграль-
подынтегральная функция f(M) не связана с направлением нормали к поверх-
поверхности S, и поэтому выбор стороны поверхности интегрирования
роли не играет; таковы, например, задачи об отыскании массы или
заряда, распределенных по поверхности. Во втором типе задач
147] § 2. интегралы по поверхности 507
функция f(M) существенно зависит от направления нормали; так
в задаче об отыскании потока жидкости f(M) = Pcosa + Qcos |5 +
+ /?cosy является линейной функцией направляющих косинусов
нормали. Разумеется, при этом обязательно нужно указывать, по
какой стороне поверхности происходит интегрирование; изменение
этой стороны приводит к изменению знака интеграла1).
Остановимся еще на физическом смысле знака поверхностного
интеграла (#) с точки зрения задачи о вычислении потока жидко-
жидкости. На разных участках поверхности S жидкость может проте-
протекать как в направлении выбранной нормали, так и в противопо-
противоположном. Если поток К положителен, то в выбранном направлении
жидкости протекает больше, чем в противоположном, а если отри-
отрицателен, то наоборот.
Примечание. Мы все время рассматриваем поверхности,
у которых можно различить две стороны; такие поверхности на-
называются двусторонними. С одной сто-
стороны двусторонней поверхности можно
перейти на другую сторону, только
пройдя через ее край. Однако не всякая
поверхность является двусторонней. При-
Примером односторонней поверхности
может служить так называемый лист Рис.200.
Мёбиуса2). Модель его легко сделать
из прямоугольного листка бумаги. Для этого нужно полоску склеить
так же, как и при изготовлении модели цилиндра, только пред-
предварительно перекрутив бумагу (рис. 200). Выйдя из какой-нибудь
точки листа Мёбиуса с определенным направлением нормали,
можно непрерывным движением, нигде не пересекая границы листа,
прийти в ту же точку с противоположным направлением нормали.
Это значит, что, начав закрашивать лист Мёбиуса, скажем,
красной краской, мы закрасим его целиком, не оставив места для
синей. В дальнейшем мы будем иметь в виду исключительно
двусторонние поверхности.
Укажем, дополнительно, некоторые свойства интегралов, взя-
взятых по определенной стороне поверхности, т. е. удовлетворяющих
условию (*#). Теорема о разбиении поверхности интегрирования
на части должна для них, очевидно, формулироваться следующим
образом.
1) Советуем читателю обратить внимание, что подобное же обстоятельство
имело место и при изучении криволинейных интегралов. Задача о работе
при движении точки в силовом поле существенно связана с направлением
касательной к линии интегрирования, а задача об отыскании массы
линии или площади цилиндрической поверхности (п. 145) не связана.
2) Мёбиус A790—1868)—немецкий математик.
508 гл. ix. криволин. интегралы и интегралы по поверхности [148
Если поверхность S разбить на части Sly 52, . . . , Sn и направ-
направления нормалей на всех отдельных частях поверхности считать
совпадающими с направлением, выбранным на S, то интеграл по
всей поверхности будет равен сумме интегралов по отдельным ее
частям
В дальнейшем нам часто придется рассматривать поверхност-
поверхностные интегралы типа (*) по замкнутым поверхностям. В этом
случае различают внешнюю сторону поверхности и внут-
внутреннюю. Внешнюю сторону поверхности обычно называют по-
положительной стороной. Для интегралов по замкнутым поверхнос-
поверхностям имеет место теорема, аналогичная теореме о криволинейных
интегралах по замкнутым контурам, приведенной на стр. 480.
Теорема. Если область Й пространства, ограниченную замк-
замкнутой поверхностью S, разбить на части при помощи замкнутых
поверхностей Sv S2» ...» Snf то интеграл, взятый по всей по-
поверхности S (например, по положительной стороне), равен сумме
интегралов, взятых по соответствующим (положительным) сторо-
сторонам поверхностей S19 52> • • •» ?»:
5S SJ
s2 sn
Доказательство. В правой части равенства каждая ле-
лежащая внутри области Q часть поверхности проходится при ин-
интегрировании два раза по двум ее сторонам и сумма соответст-
соответствующих интегралов равна нулю. В результате останутся только
интегралы по частям границы области Q, в сумме дающие интег-
интеграл по всей поверхности 5, что и требовалось доказать.
148*. Вычисление интегралов по поверхности. Пусть дан по-
поверхностный интеграл
Предположим, что поверхность 5 такова, что она с любой пря-
прямой, параллельной оси Oz, пересекается не более чем в одной
точке; тогда ее уравнение можно записать в виде
z = z(x, у).
Покажем, что в этом случае вычисление интеграла по поверхности
S приводится к вычислению двойного интеграла по области D—
проекции поверхности S на плоскость Оху (рис. 201).
148]
§ 2. ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ
509
Возьмем элемент площади dxdy области D и проектирующийся
й него элемент площади da поверхности S. Проведем нормаль п
к площадке da так, чтобы она образовывала острый угол у с
осью Oz. Будем считать, что в
пределах площадки направление
нормали п не меняется; это зна-
значит, что площадка da считается
куском плоскости, касательной
к поверхности в точке проведе-
проведения нормали. Тогда, как уже от-
отмечалось в п. 146, при рассмот-
рассмотрении рис. 197
cos у da ^= dxdy.
Согласно результатам п. 119
нормаль к поверхности, задан-
заданной уравнением
z*=z(xt у), Рис. 201.
имеет проекции z'Xy zy, —1. Поэтому косинус острого угла у между
нормалью и осью Oz равен
cos V = -
Значит, da =
f(x,y,
+zy2dxdy и
, z(x,y)]y/~\+z'x+zfdxdy.
Из последнего равенства следует, что «суммирование» выражений,
стоящих слева, т. е. интегрирование по поверхности S, равно-
равносильно «суммированию» выражений справа, т. е. интегрированию
по области D:
$ S fix, У, z) da - J S f[x, у, z (xf у)]
S D
$ S J S iz* dx dy. (*)
S D
Может случиться, что уравнение поверхности нельзя записать
в виде, разрешенном относительно z, но можно записать в виде
y=y(x,z) или х = х(у, г). Тогда ход наших рассуждений будет
совершенно такой же, но только нужно будет проектировать по-
поверхность S соответственно на плоскость Oxz или Oyz. Если
обозначить через р и а острые углы, образованные нормалью
к поверхности с осями Оу и Ох, то получим формулы
cos $ da — dx dz и cos a da = dy dz.
Соответствующие формулы для приведения интеграла по поверх-
поверхности к двойным интегралам читатель напишет самостоятельно.
510 ГЛ. IX. КРИВОЛИН. ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ [148
Наконец, если уравнение всей поверхности 5 нельзя записать в
виде единой функции одного из указанных типов, то такую поверх-
поверхность нужно разбить на части, для которых ато сделать можно, и
вычислять интеграл как сумму интегралов по отдельным частям.
Если в равенстве (#) функция /(лг, у, z) тождественно равна 1,
то получается формула для вычисления площади поверхности
(обозначим эту площадь той же буквой S, что и саму поверхность)
В этой формуле z = z(x, у)— уравнение поверхности, а ?> — ее
проекция на плоскость Оху.
Пример. Найдем площадь части поверхности параболоида
вращения 2z~x2-\-y2 заключенной внутри цилиндра x2-\-y2 = R2.
Здесь zx — x и zy—y\ поэтому
где область D — проекция интересующей нас части поверхности
на плоскость Оху — есть круг радиуса R с центром в начале
координат. Переходя к полярным координатам, получим
Перейдем теперь к вычислению интегралов вида
, J>, z) cos a + Q (*, уу г) cos р + R (*, у, г) cos у] do,
s
где cos а, cosj), cosy — направляющие косинусы нормали, прове-
проведенной к той стороне поверхности, по какой происходит интег-
интегрирование.
Сама форма записи подынтегрального выражения подсказывает,
что этот интеграл удобно вычислять как сумму трех интегралов.
Начнем с интеграла от последнего слагаемого
х9у, г) cos у da.
Пусть поверхность 5 задана уравнением z~z(x,y), т. е. име-
имеет вид, изображенный на рис. 201. Тогда будем различать у этой
поверхности верхнюю сторону (именно к ней приведена нор-
нормаль п на рисунке) и нижнюю сторону. Для верхней стороны
148] § 2. интегралы по поверхности 511
поверхности угол y острый и, как уже отмечено выше, cos у da =
* Следовательно,
R (лг, у, z) cos yda = R [*, у, z (*, у)] dx dy,
и поэтому
/?<аг, у, z) cos у da = $ $ jR [лг, j>, г (а:, у)] dx dy, (**)
где D—по-прежнему проекция поверхности S на плоскость Оху.
Совершенно ясно, что, беря интеграл по нижней стороне по-
поверхности, мы придем к интегралу
Аналогично вычисляются и интегралы от остальных слагаемых.
Нужно только помнить, что в формулах
cos ado — dydz и cos {$ da = dx dz
под аир понимаются острые углы, образованные нормалью
к поверхности соответственно с осями Ох и Оу. Это означаем
что, разрешая уравнение поверхности относительно х или у:
х=х(у, z) или у=у(х, z) и записывая формулы, аналогичные
формуле (**),
Q(*f у, z) zos $ da = ^Q[xt у (ztx),z]dxdzt
P{x,y,
5
где Dx и D2 — проекции поверхности S соответственно на пло-
плоскости Oxz и Oyz, мы каждый раз берем интеграл по той сто-
стороне поверхности 5, которая обращена в сторону положительного
направления осей Оу или Ох. Если нам нужно взять интеграл по
противоположной стороне поверхности, то следует просто изме-
изменить знак у двойного интеграла.
Если при вычислении какого-либо из трех интегралов, уравнение по-
поверхности не удается записать в нужной форме, то предварительно разби-
разбиваем данную поверхность на части, для которых это сделать можно, и бе-
берем сумму интегралов по этим частям. Заметим только, что если в состав
поверхности S входит участок цилиндрической поверхности, образующие
которой параллельны, например, оси Ог, то интеграл \ V R cos у da, взятый
512 ГЛ. IX. КРИВОЛИН. ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ [148
по этому участку, равен нулю, так как нормаль будет перпендикулярна к
образующей, и поэтому У = -к и cosy = 0. В то же время для этого участка
будет равна нулю и правая часть формулы (##), так как проекция рассмат-
рассматриваемого участка на плоскость Оху является не областью, а линией. Ана-
Аналогичное замечание можно сделать, если образующие цилиндрического участ-
участка поверхности параллельны какой-либо дру-
другой оси;
В соответствии со сказанным интег-
интегралы по поверхности очень часто запи-
записывают так:
J (P cos a + Q cos p + R cos y) da =
5
В такой записи сразу видно, на какую
координатную плоскость производится
Рис. 202. проектирование поверхности $ при интег-
интегрировании каждого слагаемого.
Примеры: 1) Вычислим интеграл
х dy dz + dx dz + xz2 dx dy,
s
где «S — внешняя сторона части сферы x2+y2-\-z2— 1, заключен-
заключенной в первом октанте.
Обозначим проекции поверхности интегрирования на координат-
координатные плоскости соответственно через Du D2 и DB (рис. 202). Это
будут четверти кругов радиуса 1. Тогда
s
L = \ \ dx dz = \ \ dx dz,
S D>
/3 = J $ xz2 dx dy = JJ x A —x2 —y2) dx dy.
Второй интеграл равен просто площади области ?>2, т. е. —-.
Первый и третий интегралы вычислим, перейдя к полярным
*) В более подробных курсах интеграл, стоящий справа, определяется
при- помощи специальных интегральных сумм; тогда он называется интег-
интегралом по поверхности второго рода. Ради краткости изложения такие ин-
интегралы отдельно мы изучать не будем.
148] § 2. ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ 515
координатам:
a l
О
Итак,
/=
2) Вычислим интеграл
/ = Jj ^ cos Y^/a,
s
где S—внешняя сторона сферы х2-\-у2-\-z2 — 1.
Здесь аппликату 0 нельзя выразить однозначной функцией от
хну для всей поверхности интегрирования S. Разобьем поверх-
поверхность на две части: 3?ls лежащую над плоскостью Оху, и 52, ле-
лежащую под ней. Их уравнениями соответственно будут
z^V\—x2—y2 и z= —V\—x2—y2.
Имеем
/= \ j г cos y rfo> = \ \ z cos y d<5 + \ j -2: cos у do.
s st s2
Перейдем к двойным интегралам: S± — внешняя сторона части сфе-
сферы, расположенной над плоскостью Оху, — является верхней
стороной полусферы, и поэтому
^ \z cos y do = J ^ V\— х*1— y2dx dy,
Sx D
где D — круг х2-\-у2 ^1;
S2 — внешняя сторона полусферы, расположенной под плоско-
плоскостью Оху, — является, наоборот, ее нижней стороной, значит,
55 г cos y do= — J J — УХ ""х* "У2 dx
S2 D
где D—тот же круг.
В результате получаем
/ = \ J / \ — x2—y2 dxdy+\\ Y\—x2 — y2 dx dy =
D О
17 А. Ф. Бермант, И. Г. Араманович
14 ГЛ. IX. КРИВОЛИН. МНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ [149
Так как интеграл \\К 1—хг—у2 dx dy выражает объем полу-
о
сферы радиуса 1, то он равен 2/3 я. Поэтому /=4/Зя.
149*. Формула Стокса1). Для поверхностных интегралов имеет
место формула, аналогичная формуле Грина (см. п. 140), позво-
позволяющая свести вычисление интеграла по поверхности S к вычислению
криволинейного интеграла по контуру L, ограничивающему эту
поверхность (рис. 203).
Теорема. Если функции Р(х,у, г), Q(x, у, г), R(x,y, z)
непрерывны вместе со своими частными производными первого по-
порядка, то имеет место формула
= [Pdx+Qdy+Rdz,
(*)
где cos a, cosjJ и cosy — направляющие косинусы нормали к по-
поверхности S, a L — граница поверхности.
Формула (*) называется формулой Стокса.
Направление интегрирования по контуру L согласовывается с
выбранной стороной поверхности 5 при помощи следующего нагляд-
наглядного правила: если человек идет
по контуру L в направлении ин-
интегрирования и направление от его
ног к голове совпадает с на-
направлением нормали к выбранной
стороне поверхности, то эта по-
поверхность должна оставаться от
него слева.
Доказательство. Дока-
Доказательство теоремы производится
путем сведения интеграла по по-
поверхности сначала к двойному ин-
интегралу, а затем при помощи
формулы Грина к криволинейному.
Предположим сначала, что поверх-
поверхность 5 пересекается с любой прямой, параллельной оси Ог, не
более чем в одной точке, и пусть z = z(x, у) — уравнение этой поверх-
поверхности. Преобразуем поверхностный интеграл
Рис. 203.
Д. Стоке A819—1903) —английский математик и механик.
149] § 2. ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ 515
считая, что 5 — верхняя сторона поверхности; при этом условии
cosy>0. Нормальный вектор к верхней стороне поверхности имеет
проекции—^, —гУу 1. Так как направляющие косинусы пропор-
пропорциональны соответствующим проекциям, то
cos у 1
Поэтому cos p = — гц cos у, и
P , dP
Приведем этот поверхностный интеграл к двойному. Для этого
нужно в подынтегральной функции заменить переменную z ее вы-
выражением через х и у согласно уравнению поверхности z = z(x, у).
Но при этом подынтегральная функция окажется равной частной
производной по у от сложной функции, получающейся из Р{х,у> z)
после подстановки z{xyy) вместо z. Действительно,
Таким образом, интеграл / равен
Р [х, у, z(x, у)] , ,
ду йхйУ'
D
где D—проекция поверхности ? на плоскость Оху (рис. 203).
Применяя формулу Грина (п. 140), перейдем к криволинейному
интегралу по контуру L±—границе области D:
х, у, z(x, y)]dx.
Контур Lx является проекцией пространственной линии L—гра-
L—границы поверхности 5—на плоскость Оху, и интегрирование про-
производится в положительном направлении контура Lv Для завер-
завершения рассуждения осталось заметить, что так как контур L при-
принадлежит поверхности S, то координаты его точек удовлетворяют
уравнению z = z(x, у), и поэтому значения функции Р(х, у, z) в
точках контура L равны значениям Р[х, у, z (х, у)] в соответст-
соответствующих точках контура Lt. Проекции же соответствующих участ-
участков разбиения контуров L и Lx на ось Ох, очевидно, совпадают.
Значит, совпадают интегральные суммы, построенные для опреде-
определения криволинейных интегралов по координате х от функции Р
17*
516 ГЛ. IX. КРИВОЛИН. ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ [149
по контурам L и L1( а значит, равны интегралы
[р[х, у, г(х, y)]dx=^P(x, у, z)dx.
Итак,
Рассуждая точно так же, как и на стр. 483, можно показать, что по-
полученная формула верна и для поверхностей более сложного вида. Для
этого нужно разбить ее на более простые поверхности и к каждой из них
применить полученную формулу.
Аналогично доказывается справедливость еще двух соотноше-
соотношений (рекомендуем читателю доказать их самостоятельно, выбирая
каждый раз уравнение поверхности в подходящем виде):
1
Lt
Сложив почленно равенства (А), (Б) и (В), мы получим дока-
доказываемую формулу.
Формула Стокса позволяет интеграл по поверхности заменить
соответствующим криволинейным интегралом по границе поверхности
а, наоборот, криволинейный интеграл по замкнутой пространственной
линии заменить интегралом по поверхности, «натянутой» на контур
интегрирования.
Подобно тому как при помощи формулы Грина была доказана основная
теорема о независимости криволинейного интеграла в плоскости от пути
интегрирования (см. п. 141), так при помощи формулы Стокса можно дать
доказательство (пропущенное в п. 143) основной теоремы для криволинейных
интегралов по пространственным линиям.
Пусть мы имеем интеграл
С Pdx+Q dy+Rdz. (*)
Предположим, что равенства
d?___dQ_ _dQ___<^ dR __ дР
ду дх ' дг ду * дх дг
тождественно выполняются в односвязной области Q; тогда, натянув
на замкнутую линию L поверхность S, лежащую в области Q, в силу фор-
формулы Стокса заключаем, что криволинейный интеграл (#) равен нулю,
каков бы ни был этот замкнутый путь L.
Обратно, пусть криволинейный интеграл (*) обращается в нуль для
любого замкнутого контура, и пусть, однако, в какой-нибудь точке
150]
§ 2. ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ
517
*©) области Q указанные равенства не имеют места, скажем,
dQ дР
Проведем через точку Мо плоскость z — zQt параллельную плоскости Оху.
Тогда в этой плоскости можно взять такую окрестность точки Мо, что
dQ дР л о
в каждой ее точке будет -^ ^—> 0. В плоскости г = ?0 справедливы
равенства dz = 0, cosa = 0, cos E = 0, cosy=1- Рассуждая, как на стр. 486,
придем к выводу, что в противоречии с предположением в Q существу-
существует замкнутый путь, по которому интеграл (*) не равен нулю. Теорема
доказана.
150*. Формула Остроградского1). Рассмотрим теперь связь
между интегралом по замкнутой поверхности и некоторым
тройным интегралом по объему, ограниченному этой поверхностью.
Теорема. Если функции Р(х, у, z), Q(x, у, z), R(xf у, z)
непрерывны вместе со своими частными производными первого
порядка в области ft, то имеет место формула
dz=
<*)
где S — граница области Q и интегрирование по 5 производится
по ее внешней стороне.
Формула (*) называется формулой Остроградского.
Доказательство. Сначала
возьмем в пространстве Oxyz об-
область Q, ограниченную замкнутой
поверхностью S, пересекающейся
с любой координатной линией не
более чем в двух точках (рис. 204).
Преобразуем тройной интеграл
/ =
Рис. 204.
Для этого проведем цилиндричес-
цилиндрическую поверхность, ортогонально
проектирующую область Q на плос-
плоскость Оху; она касается пбверхности S по линии L, разбивающей
ее на две поверхности S2 и «S1? каждая из которых пересекается
с любой прямой, параллельной оси Oz, не более чем в одной
*) М. В. Остроградский A801—1861) —выдающийся русский мате-
математик и механик.
518 ГЛ. IX. КРИВО ЛИН. ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ [150
точке. Пусть область D есть проекция поверхностей S2 и Sx (и об-
области й) на плоскость Оху, a z = z2 (лг, у) и г = гг (х, у) суть урав-
уравнения поверхностей 52 и Sr Интегрируя сначала по z, получим
Q D zt {х, у)
Выполняя внутреннее интегрирование, получаем
y у, zx{x, y)]dxdy.
Так как плоская область D является проекцией на плоскость Оху
и поверхности S2, и поверхности Sx, то двойные интегралы в пра-
правой части служат выражениями для интегралов \ \ R (л:, уу z) cos у do,
взятых по верхним сторонам этих поверхностей (см. формулу
(**) п. 148). Значит,
/ = \ [ R cos у da — J [ R cos у d j = \ \ R cos у da + [\ R cos у da.
+S2 +St +S2 -Si
Так как верхняя сторона S2 и нижняя сторона St являются внеш-
внешними сторонами всей поверхности «S, то
Л'- (А)
Граница области Q — поверхность 5 — может содержать участки цилин-
цилиндрической поверхности с образующей, перпендикулярной к плоскости Оху\
формула остается при этом верной.
Как во всех предыдущих случаях, разбивая область Q на части и опи-
опираясь на свойства тройных и поверхностных интегралов, освобождаемся от
наложенного на поверхность ограничения встречать любую координатную
линию не более чем в двух точках.
Так же доказываются формулы
^do, (Б)
Складывая почленно равенства (А), (Б), (В), мы и приходим
к формуле Остроградского (#). Теорема доказана.
Формула Остроградского позволяет заменить тройной интеграл
соответствующим интегралом по поверхности, ограничивающей область
интегрирования, и, наоборот, интеграл по замкнутой поверхности
заменить тройным интегралом по области, ограниченной этой поверх-
поверхностью.
151] § 3. теория поля 519
Пример. Вычислим интеграл /= С \ {xcosa+y cos §+zcos у)do,
где S—-внешняя сторона сферы x2+y2 + z2 = R2.
По формуле Остроградского
4
так как объем шара V = -^
§ 3*. Теория поля
151*. Векторное поле и векторные линии.
I. Векторное поле. Определение векторного поля во мно-
многом напоминает определение скалярного поля, которое мы изучали
в п. 125 (кстати, советуем читателю вспомнить содержание всего
§ 4 гл. VII).
Определение. Если в каждой точке Р области D задан
определенный вектор, то будем говорить, что в этой области
задано векторное поле*
С конкретными физическими примерами векторных полей мы
уже встречались. Так, в § 1 было рассмотрено силовое поле
и решена задача о вычислении работы при движении материальной
точки под действием сил поля. В § 2 рассматривалось поле ско-
скоростей текущей жидкости и ставилась задача о вычислении
потока жидкости через заданную поверхность. В настоящем пара-
параграфе мы рассмотрим некоторые общие задачи, относящиеся к лю-
любым векторным полям. При этом в качестве примеров таких полей
чаще всего будут рассматриваться силовые поля (поле тяготения,
электрическое и электромагнитное поля) или поле скоростей
текущей жидкости. Рассмотрение этих полей придаст вводимым
математическим понятиям ясный физический смысл.
Векторное поле задано, если в каждой точке Я поля указан
соответствующий этой точке вектор А (Я). Мы будем сначала рас-
рассматривать стационарные поля, в которых вектор А (Я)
зависит только от точки Р и не зависит от времени. Проекции
вектора А (Я) на оси координат обозначим через Ах, Av, Аг% Если
точка Р имеет координаты х, у и z, то и сам вектор А (Я), и его
проекции будут функциями этих координат х), и мы можем записать
z(x, у, г)к.
Дальше всюду предполагается, что функции АХУ A Az непрерывны
вместе со своими частными производными.
!) В п. 70 рассматривалась векторная функция одного скалярного аргу-
аргумента. Здесь мы изучаем векторную функцию трех скалярных аргументов.
520 ГЛ. IX. КРИВОЛИН. ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ [151
Рассмотрим некоторые частные случаи векторных полей.
1. Однородное поле. Векторное поле называется одно-
однородный, если А (Я) — постоянный вектор, т.е. Ах> А и Аг—по-
Аг—постоянные величины.
Примером однородного поля может служить, например, поле
тяжести (см. пример 1 п. 144).
2. Плоские поля. Если в выбранной системе координат
проекции вектора не зависят от одной из трех переменных xt у, z
и одна из проекций равна нулю, например:
А (Р) = Ах {ху у) i + Ау (ху у) I
то поле называется плоским. С плоскими полями очень часто при-
приходится встречаться в гидродинамике при изучении плоских
течений жидкости, т.е. таких течений, когда все частицы
жидкости движутся параллельно некоторой плоскости, причем
скорости частиц, расположенных на од-
одной и той же прямой, перпендикулярной
к этой плоскости, одинаковы.
Рассмотрим еще один важный физи-
физический пример.
Пусть твердое тело вращается с
постоянной угловой скоростью <о. Най-
Найдем поле линейных скоростей точек
этого тела.
Как известно из кинематики, линей-
линейная скорость v равна векторному про-
произведению
Рис. 205. где со — вектор угловой скорости (т. е
вектор, отложенный на оси вращения
и численно равный величине угловой скорости; этот вектор направ-
направлен так, что если смотреть из его конца, вращение кажется про-
происходящим против часовой стрелки), а г — радиус-вектор точки
М вращающегося тела относительно какой-либо точки оси
вращения. Выбрав эту неподвижную точку за начало координат и
направив ось вращения по оси Oz (рис. 205), найдем проекции
вектора v.
Имеем
= G)k, r~х\-\-у]-{-zk,
тогда
i
0
X
j
0
У
k
со
z
151] § 3. теория поля 521
Таким образом,
т. е. поле является плоским.
II. Векторные линии.
Определение. Векторной линией векторного поля назы-
называется линия, в каждой точке которой направление касательной
совпадает с направлением вектора, соответствующего этой точке
(рис. 206).
Векторные линии в конкретных полях имеют ясный физический
смысл. Так, если мы рассматриваем поле скоростей текущей жидко-
жидкости, то векторные линии суть линии
тока этой жидкости, т. е. линии, по
которым движутся частицы жидкости.
В электрическом поле векторные
линии суть силовые линии этого
поля. Например, в поле точечного
заряда такими линиями будут лучи,
выходящие из заряда. Для магнит-
магнитного поля векторными (силовыми)
линиями будут линии, выходящие из
северного полюса и оканчивающие- Рис. 206.
ся в южном. Изучение расположения
силовых линий в электрических, магнитных и электромагнитных
подях очень важно в физике.
Выведем уравнения векторных линий.
Пусть векторное поле определено функцией
(для краткости аргументы функций АХ1 А А2 не выписаны). Если
векторная линия имеет параметрические уравнения
x = x(t), y=y(t), z = z(t),
то проекции направляющего вектора касательной к этой линии
пропорциональны производным xr (t), yf(t), z' (t), или, что то же
самое, дифференциалам dx, dy, dz (см. п. 68). Записывая условия
параллельности вектора А (Р) и вектора, направленного по каса-
касательной к векторной линии, получим
Система уравнений (*) представляет систему дифференци-
дифференциальных уравнений семейства векторных линий поля А(Р).
Такие системы уравнений будут рассмотрены позже (см. п. 176),
522 гл. ix. криволин. интегралы и интегралы по поверхности [152
а сейчас мы сможем определять векторные линии поля лишь в са-
самых простых случаях, опираясь на их физический смысл. Отметим
еще, что если поле плоское (см. I, 2), т. е. Az = 0y то вектор-
векторные линии лежат в плоскостях, параллельных плоскости Оху, и их
dx dy
уравнения имеют вид -j- = -r- .
Пример. Найдем векторные линии поля линейных скоростей
тела, вращающегося с постоянной угловой скоростью со вокруг
оси Oz.
Это поле определено функцией (см. пример 1)
А(Р) = —
На рис. 205 видно, что векторными линиями такого поля служат
окружности, лежащие в плоскостях, параллельных плоскости Оху
с центром на оси Oz. Уравнения таких окружностей имеют вид
х2-\-у2 = R, z = zQ = const.
Легко проверить, что равенство ¦ =—^- соблюдается. Продиффе-
Продифференцировав уравнение окружности, получим 2хdx + 2уdy = 0, т.е.
—^-=—. Умножив знаменатели этого равенства на со, мы и придем
к доказываемому равенству.
152*. Поток вектора. Дивергенция.
I. Поток вектора. Пусть векторное поле образовано век-
вектором
Возьмем в этом поле некоторую поверхность S и выберем на ней
определенную сторону1). Обозначим через п единичный вектор нор-
нормали к рассматриваемой стороне поверхности в произвольной ее
точке; проекциями вектора п служат направляющие косинусы нормали
nfcosa, cos p, cosy}. Рассмотрим интеграл по поверхности S от
скалярного произведения вектора поля А(Р) на единичный вектор
нормали п:
=^ {Ax cos a + Ay cos $ + A2 cos у) do. (*)
s
Если А(Р) — поле скоростей текущей жидкости, то интеграл (-*)
выражает поток жидкости через поверхность 5. В произволь-
произвольном векторном поле интеграл (*) будем называть потоком век-
вектора через поверхность S и обозначать буквой К.
1) Поверхность S предполагается двусторонней (см. стр. 507),
152]
§ 3. ТЕОРИЯ ПОЛЯ
323
Определение. Потоком вектора через поверхность на-
называется интеграл по поверхности от скалярного произведения
вектора поля на единичный вектор нормали к поверхности:
К— [[A(P)nda.
s
Таким образом, вычисление потока вектора сводится к вычислению
интеграла по поверхности. Из самого определения следует, что по-
поток вектора К—величина скалярная. Если изменить направление
нормали п на противоположное, т. е. переменить сторону поверхно-
поверхности S, то поток К изменит знак. Так как
скалярное произведение вектора А (Р) на г
единичный вектор нормали п равно Ап(Р) —
проекции вектора А (Р) на направление п,
то поток К можно представить в виде
Отсюда, в частности, следует, что если
на некотором участке поверхности проекция
вектора А(Р) на нормаль постоянна: Лп (Р) =
= ЛП = const, то поток через такой участок
просто равен AnQy где Q — площадь участка
поверхности.
Пример. Найдем поток радиуса-вектора
г через боковую поверхность Eг), верхнее Рис. 207.
основание (S2) и нижнее основание (S3)
прямого цилиндра радиуса jR и высоты Я, если начало координат
лежит в центре нижнего основания цилиндра, а ось цилиндра сов-
совпадает с осью Oz (рис. 207). На всех поверхностях п имеет
направление внешней нормали. На боковой поверхности St внешняя
нормаль п параллельна плоскости Оху и проекция гп равна R.
Поэтому
J J = 2nR2H.
На верхнем основании S2 нормаль п направлена параллельно оси Oz
и гп = Н. Следовательно,
Наконец, на нижнем основании S3 проекция гп — 0 и K3 = i
Особый интерес представляет случай, когда S—замкнутая по-
поверхность, ограничивающая некоторую область Q. Если берется
внешняя нормаль, то мы будем говорить о потоке изнутри
524 гл. ix. криволин. интегралы и интегралы vg поверхности [152
поверхности 5. Он обозначается так:
Вообще в векторном анализе и в его приложениях интегралы
по замкнутым поверхностям и по замкнутым контурам принято
обозначать соответственно символами (Ц) и Ф.
? if
Отметим также, что в курсах физики и прикладных дисциплин
интегралы по поверхности (в частности, двойные) и даже тройные
интегралы очень часто обозначают при помощи одного знака ин-
интеграла I При таком способе записи интегралы различаются по
обозначениям дифференциала и области интегрирования: \f(M)ds
означает интеграл по линии, \^f(M)do — интеграл по поверх-
s
ноет и, \f(M)dv—интеграл по объему.
п
Когда векторное поле А(Я) представляет поле скоростей
жидкости, величина потока К дает разность между количеством
жидкости, вытекающей из области Q, и количеством жидкости,
втекающей в эту область.
Если /С = 0, то в область Q жидкости втекает столько же,
сколько и вытекает. Так, например, будет для любой области, рас-
расположенной в потоке воды, текущей в реке.
Если же величина К отлична от нуля, например, положительна,
то из области Q жидкости вытекает больше, чем втекает. Это
означает, что в области Q имеются источники, питающие поток
жидкости. Наоборот, если величина К отрицательна, то это указы-
указывает на наличие стоков — мест, где жидкость удаляется из потока.
II. Дивергенция. Рассмотрим некоторую точку Р векторного
поля А (Р) и окружим ее замкнутой поверхностью S, целиком со-
содержащейся в поле. Вычислим поток вектора через поверхность 5
и возьмем отношение этого потока к объему V области Q, ограни-
ограниченной поверхностью S:
An (P) do
V
В поле скоростей жидкости это отношение определяет количество
жидкости, возникающее в единицу времени в области Q, отнесен-
отнесенное к единице объема, т. е., как говорят, среднюю объемную
мощность источника; если поток изнутри поверхности «S
меньше нуля, го соответственно говорят о мощности стока.
152] § 3. теория поля 525
Найдем теперь предел отношения
Ап (Р) da
lim— у
при условии, что область Q стягивается в точку Я, т. е. что V
стремится к нулю.
Если этот предел положителен, то точка Я называется источни-
источником,, а если отрицателен, то стоком. Сама величина предела харак-
характеризует мощность источника или стока. В первом случае в любом
бесконечно малом объеме, окружающем точку Я, жидкость возника-
возникает, а во втором случае исчезает. Предел этот называется дивер-
дивергенцией или расходимостью векторного поля в точке Я.
Определение. Дивергенцией, или расходимостью, вектор-
векторного поля А (Я) в точке Я называется предел отношения потока
вектора через поверхность, окружающую точку Я, к объему, ог-
ограниченному этой поверхностью, при условии, что вся поверх-
поверхность стягивается в точку Я.
Дивергенцию поля обозначают символом div А (Я). Таким образом,
An(P)do
div А (Я) = Ига — у ,
где предел вычисляется при условии, что поверхность S стягивает-
стягивается к точке Я.
Мы докажем сейчас, что при принятых нами условиях непре-
непрерывности функций Ах, А А2 и их производных дивергенция поля
существует в любой его точке (т. е. существует указанный
предел), а также найдем ее величину. Подчеркнем тут же, что
дивергенция векторного поля есть величина скалярная.
Теорема. Дивергенция векторного поля
выражается формулой
дАх , dAv
div X(P)—
дх ¦ ду ¦ dz '
где значения частных производных берутся в точке Я.
Доказательство. По формуле Остроградского (см. п. 150)
поток вектора К можно представить в виде
= $ (Лх C0S а + Ау C0S Р + Az C0S Y) d° =
526 ГЛ. IX. КРИВОЛИН. ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ [152
Тройной интеграл по теореме о среднем (см. п. 133) равен
произведению объема V на значение подынтегральной функции в
некоторой точке Р± области Q, т. е.
ШдАх дАу дАг\ /дАх дАу dAz\
дх ' ду ' dz J J \ дх ' ду ' dz J px
Если область Q стягивается в точку Р, то точка Рг стремится к
точке Р, и мы получаем
/дАх дАу_ ,
\ д ' ди '
\ дх ' ди
\ дх ди ^z /р ^^
div А (Я) = lim-^ %г; /Pl = —
' Р ^Р V дх
Р
-5-
ду
что и требовалось доказать.
Пользуясь выражением для дивергенции, теорему Остроградско-
Остроградского можно сформулировать в векторной форме:
An(P)da=\)\))uiV
Q
Поток вектора изнутри замкнутой поверхности равен тройно-
тройному интегралу по объему, ограниченному этой поверхностью, от
дивергенции поля.
Векторная форма теоремы Остроградского1) выражает в поле
текущей жидкости тот очевидный факт, что поток жидкости через
поверхность равен суммарной мощности всех источников и стоков,
т. е. количеству жидкости, возникающей в рассматриваемой облас-
области за единицу времени. (Если мощность стоков больше, чем источ-
источников, то жидкость в объеме исчезает.) Если, в частности, дивер-
дивергенция во всех точках равна нулю, то равен нулю и поток через
любую замкнутую поверхность.
Примеры. 1) Пусть дано однородное поле
где a, b и с — постоянные. Ясно, что дивергенция этого поля равна
нулю:
div A(P) = 0.
Если все частицы жидкости имеют одну и ту же скорость, т. е.
жидкость движется поступательно, как твердое тело, то в таком
потоке не должно быть ни источников, ни стоков. Поток такой
жидкости через любую замкнутую поверхность равен нулю.
х) Ее часто называют также теоремой Гаусса.
К. Гаусс A777—1855) — крупнейший немецкий математик, автор вы-
выдающихся работ по математике, астрономии и физике.
152] § 3. теория поля 527
2) Вычислим дивергенцию поля линейных скоростей вращающего-
вращающегося тела (см. пример 1 п. 151)
v== —coj/i-f- coatj.
Здесь
Если представить себе жидкость, вращающуюся, как твердое тело,
то ясно, что в таком потоке нет ни источников, ни стоков.
3) Вычислим дивергенцию поля радиуса-вектора г. Имеем
Поэтому
дх ' ду ' дг
Каждая точка поля является как бы источником постоянной мощнос-
мощности. Пользуясь векторной формой теоремы Остроградского, сразу
получаем, что поток радиуса-вектора через любую замкнутую поверх-
поверхность равен утроенному объему, ограниченному этой поверхностью:
III. Свойства дивергенции. При вычислении дивергенции
часто пользуются следующими ее свойствами:
1. div[C1A1(P) + C2A2(P)] = C1divA1(P) + C2divA2(P), где С,
и С2—скалярные постоянные.
В самом деле, если обозначить проекции вектора Аг(Р) через
Aix> Air Aiz и вектора А2 (Р) через А2х, А2у1 A2z, то
= (СгА1х + С2А2х) [ + (СгА1у + С2А2у) j + {СХА12 + С2Аи) к.
Поэтому
div [С1АХ (Р) + С2А2 (Р)] = С, ^ + С2 ^ + С, ^g-+
дА
2. Пусть А (Я) — функция, определяющая векторное поле, а
и(Р) — скалярное. Тогда
div [и (Р) А (Р)] = и (Р) div А (Я) + А (Я) grad и (Р).
Действительно,
и (Р) А (Р) = иАх\ + иАу] + uAzk.
528 ГЛ. IX. КРИВОЛИН. ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ [153
Значит,
, d(uAv) t d(uAz)
dz *~~
ди ди
дх ду дг
Поскольку grad u =-^—i + -^—j + -^—к, то выражение во второй
скобке есть скалярное произведение вектора поля А (Р) на градиент
функции и(Р); формула доказана.
В частности (см. пример 3),
div иг = Зи + г grad н.
153*. Циркуляция и ротор векторного поля.
I. Циркуляция. Пусть векторное поле образовано вектором
Возьмем в этом поле некоторую линию L и выберем на ней опреде-
определенное направление. Обозначим через ds вектор, имеющий направле-
направление касательной к линии и по модулю равный дифференциалу длины
дуги. Направление касательной считается совпадающим с выбранным
направлением на линии. Тогда (см. п. 68)
ds = dx\ + dyl + dzk.
Рассмотрим криволинейный интеграл по линии L от скалярного
произведения векторов А (Р) и ds:
J A (P) ds = J Axdx + Aydy + A2dz. (*)
L L
В силовом поле интеграл (*) выражает работу при перемещении
материальной точки вдоль линии L (см. п. 143).
Если А(Р) — произвольное векторное поле, a L — замкнутый
контур, то интеграл (•») носит специальное название—циркуля-
название—циркуляция вектора.
Определение. Циркуляцией вектора А(Р) вдоль замкну*
того контура L называется криволинейный интеграл по этому
контуру от скалярного произведения вектора А(Р) на вектор ds
касательной к контуру.
Так как скалярное произведение А (Р) ds = As (P) ds, где As (P) -—
проекция вектора поля на направление касательной, a ds—диф-
ds—дифференциал длины дуги, то циркуляцию можно записать в виде
криволинейного интеграла по длине дуги кривой (см. п. 145):
§As{P)ds.
153]
§ 3. ТЕОРИЯ ПОЛЯ
529
Напомним читателю, что если подынтегральное выражение ин-
интеграла (¦*) является полным дифференциалом и векторное поле
занимает односвязную область Q (см. стр. 492), то такой ин-
интеграл по любому замкнутому контуру равен нулю (см. п. 143).
Векторные поля, в которых это условие соблюдается, мы назвали
потенциальными. Следовательно, в потенциальном поле циркуляция
всегда равна нулю.
В произвольном векторном поле циркуляция есть некоторое
число, зависящее от контура L. Пусть, например, в поле имеются
замкнутые векторные линии (см. пример на стр. 522). Выберем
линию интегрирования, совпадающую с векторной линией. Тогда
As (Р) = | А (Р) | и, следовательно, циркуляция, т. е.
как интеграл от положительной функции, есть число заведомо
положительное. Если направление интегрирования изменить на
противоположное, то циркуляция ста-
станет отрицательной. Если L не явля-
является векторной линией, то циркуля-
циркуляция будет тем больше, чем ближе
направление векторов поля А (Р) к
направлениям соответствующих каса-
касательных.
Пример. Вычислим циркуляцию
вектора поля линейных скоростей вра-
вращающегося тела (см. п. 151)
V = — (?>у\ + COJCJ
вдоль контура L, лежащего целиком
в плоскости Я (рис. 208), нормаль п
к которой образует с осями координат
углы а, ($, у. Направление обхода контура L и направление нор-
нормали п согласованы между собой так же, как в теореме Стокса
(см. п. 148). Согласно определению циркуляция равна
Рис. 208.
(р •—-
coy
(x)X dy.
Применим для вычисления этого интеграла теорему Стокса
2dx dy,
где D — область, ограниченная контуром L. Интегрирование ведется
по верхней стороне плоскости Я, и поэтому dx dy = cos у do (см.
530 ГЛ. IX. КРИВОЛИН. ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ [153
п. 148). Так как cos у = const, то циркуляция равна
2со cos у \ \ da = 2со cos yS,
D
где S — площадь области, ограниченной контуром L. Заметим еще,
что G>cosY = u)rt — проекция вектора со на направление вектора п.
Поэтому окончательно выражение для циркуляции примет вид
(р — ay dx + сол: dy
(Если L — окружность радиуса /?, то циркуляция равна 2о)пя/?2.)
Из этой формулы вытекает, что если плоскость П поворачивать,
т. е. менять угол у, то величина циркуляции будет меняться.
Наибольшей она будет, когда у =¦ О, т. е. когда плоскость Я па-
параллельна плоскости Оху и нормаль п к ней параллельна вектору
угловой скорости со. Если же Y = ir, т. е. нормаль к плоскости
перпендикулярна к вектору со, то циркуляция равна нулю.
Ясно также, что если переменить сторону плоскости Я, то
вектор п переменит направление и проекция соп станет отрица-
отрицательной. Поэтому и циркуляция также будет величиной отрица-
отрицательной.
Установим теперь физический смысл циркуляции вектора в слу-
случае, когда А (Р) — поле скоростей текущей жидкости. Примем для
простоты, что контур L — окружность, расположенная в некоторой
плоскости. Предположим, что окружность является периферией
колесика с радиальными лопатками, могущего вращаться вокруг
оси, проходящей через его центр перпендикулярно к его плоскости.
Если циркуляция будет равна нулю, то колесико будет оставаться
неподвижным: силы, действующие на лопатки, уравновешивают
друг друга. Если циркуляция не равна нулю, то колесико будет
вращаться, причем тем быстрее, чем больше величина циркуляции.
Если, например, жидкость вращается, как твердое тело, вокруг
оси Oz и если ось колесика совпадает с направлением этой оси,
то, как мы только что видели, циркуляция равна 2со?, где 5 —
площадь колесика. Таким образом, отношение циркуляции к пло-
площади колесика равно удвоенной угловой скорости и не зависит от
размеров колесика.
Если ось колесика наклонить к оси Oz, то указанное отношение
уменьшится и станет равным 2о)л, где соп — проекция вектора со на
направление оси колесика. Наконец, если ось колесика станет
перпендикулярной к оси вращения жидкости, то, очевидно, коле-
колесико будет неподвижным.
В случае произвольного векторного поля отношение циркуля-
циркуляции по плоскому контуру L к площади 5, ограниченной этим кон-
153] § 3. теория поля 53f
туром, будет величиной переменной. Чтобы охарактеризо-
охарактеризовать вращательное свойство векторного поля в какой-либо его
точке Р, рассмотрим предел отношения циркуляции по плоскому
контуру /,, окружающему точку Р, к площади S, ограниченной
этим контуром, при условии, что контур L стягивается в точку Р,
оставаясь в одной и той же плоскости:
Ига —
§Asds
Как мы сейчас покажем, этот предел будет зависеть только
от выбранной точки Р и от направления нормали к плоскости,
в которой лежит контур L. После того как нормаль проведена
к определенной стороне плоскости, направление обхода контура L
вполне определено: именно обход совершается против часовой
стрелки, если смотреть из конца нормали. Чтобы вычислить ука-
указанный предел, преобразуем выражение для циркуляции, восполь-
воспользовавшись формулой Стокса:
(ft Asds = (f Axdx + Aydy + A2dz =
где cosa, cos p, cosy — направляющие косинусы нормали n, a D —
область, ограниченная контуром L. Последний интеграл по теореме
о среднем равен произведению значения подынтегральной функции
в некоторой точке Рг области D на величину ^ площади этой
области.
При стягивании контура L в точку Р значение подынтегральной
функции будет стремиться к ее значению в точке Р. Поэтому
где значения всех частных производных берутся в точке Р. Правая
часть равенства представляет собой как бы скалярное произведение
двух векторов: единичного вектора n {cos a, cos p, cos у} — норма-
нормали к плоскости, в которой лежит контур I, и вектора, проекции
532 ГЛ. IX. КРИВОЛИН. ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ A53
которого равны
dAz dAy dAx dAz дАу дАх
dy dz ' dz dx ' dx dy
Последний вектор называется ротором или вихрем векторного поля
и обозначается rot А (Я).
II. Ротор и его свойства.
Определение. Ротором векторного поля
называется вектор
Проекция wtn A (Я) этого вектора на любое направление дает предел
отношения циркуляции вектора поля по контуру, лежащему в пло-
плоскости, проходящей через точку Я, для которой вектор п является
нормалью, к площади, ограниченной этим контуром. Этот предел
будет наибольшим в том случае, когда направление нормали п
совпадает с направлением rot А (Я).
С помощью определения ротора теорему Стокса можно сфор-
сформулировать в векторной форме:
J J rotn А (Я) da = § As (P) ds.
s i
Поток ротора поля через поверхность 5 равен циркуляции
вектора по границе этой поверхности.
Направление интегрирования по контуру L и направление нор-
нормали п к поверхности S согласованы между собой так же, как
в теореме Стокса. Отсюда следует, что если две поверхности S
имеют одну и ту же границу L, то потоки ротора через эти по-
поверхности равны между собой.
Предоставляем читателю проверить следующее свойство ротора
поля:
rot [Сг\г (Р) + С2А2 (Р)] = Сх rot Ах (Я) + С2 rot А2 (Я),
где Сг и С2—-скалярные постоянные.
Докажем еще, что если и (Я) —скалярная функция, а А (Я) —
векторная, то
rot uX = и rot A + (grad и х А).
Чтобы избежать громоздкости выкладок, докажем только равен-
равенство проекций на ось Ох векторов в левой и правой частях фор-
формулы. Так как вектор ик имеет проекции аАХ1 иА , иАгУ то
диАг диАу /дА2 дЛу\ t { л ди л ди\
rot «А= -^ -~Z=zu[ -г ^ ) + [А?ъ А, -т- .
х ду dz \ ду dz J х \ г ду У dz)
154]
§ 3. ТЕОРИЯ ПОЛЯ
533
Первое слагаемое есть как раз и rot^A, Так как
i j k
да ди
grad и X А =
дх
ду
Л
ТО
ди
ди
дг
Л,
ди
А это и есть вторая пара слагаемых в доказываемой формуле.
Доказательство равенства проекций на остальные координатные
оси проводится аналогично.
4*. Оператор Гамильтона х) и векторные дифференциальные
операции второго порядка. Введенные нами основные понятия
векторного анализа: градиент, дивергенция, ротор—•
удобно представлять с помощью символического вектора V
(«набла-вектор»):
Перечислим правила действий с этим вектором:
1. Произведение набла-вектора V на скалярную функцию и(Р)
дает градиент этой функции:
д
д
ди. , ди . , ди
2. Скалярное произведение набла-вектора V на векторную функ-
функцию А (Р) дает дивергенцию этой функции:
дА7
3. Векторное произведение набла-вектора V на векюрную функ-
функцию А (Р) дает ротор этой функции:
i j к
дх
ду
дг
Аг
1) У. Гамильтон A805—1865) —английский математик.
534 ГЛ. IX. КРИВО ЛИН. ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ [154
Таким образом, действия с иабла-вектором производятся по
обычным правилам действий векторной алгебры, а затем умноже-
умножение, скажем, ^- на скалярную функцию заменяется производной этой
функции под;. Набла-вектор называют еще оператором Гамильтона.
Действия взятия градиента, дивергенции и ротора будут век-
векторными дифференциальными операциями первого порядка.
В них участвуют только первые производные от скалярных функций.
Перейдем теперь к векторным дифференциальным операциям
второго порядка.
Пусть имеется скалярное поле а (Р) и мы нашли градиент
этого поля gradи. Поле градиента является векторным полем,
и мы можем искать его дивергенцию и ротор: div grad и и rot grad и.
Если имеется векторное поле А(Р) = Лх[-\-АЛ-{-Azkf то
оно порождает два поля: скалярное поле div A (Р) и вектор-
векторное поле rotA(P). Следовательно, мы можем находить градиент
первого поля: grad div A (P) и дивергенцию и ротор второго поля:
div rot А (Я) и rot rot А (Я). Всего мы имеем пять векторных диф-
дифференциальных операций второго порядка. Особенно важными яв-
являются три из них, которые мы рассмотрим подробнее.
a) divgrad«=^ + ^ + 5jr.
Действительно, grad и = ^ '"т"д" Л~ 7Г^' Образуя дивергенцию
этого вектора, мы и получаем написанное равенство. Правая часть
его называется оператором Лапласах) от функции и и обозначается Аи:
Выражение div grad и можно с помощью набла-вектора записать
еще и так:
div grad и = V • (Vtf) = V2u.
Это обозначение оператора Лапласа тоже часто употребляется.
б) rot grad & = 0.
Соотношение это проверяется совсем просто. Каждая скобка
в выражении для ротора представляет в этом случае разность
вторых смешанных производных функции и, отличающихся лишь
порядком дифференцирования, например:
, А д (ди\ д {ди\ А
rot,, grad и = ^- -г- —^- К- =0.
хЬ ду\дг дг\ду
x) П. Лаплас A749—1827) —выдающийся французский математик
и физик.
155] § 3. теория поля 535
Это соотношение легко запоминается, если записать его с помощью
набла-вектора:
rot grad a = VX (Vtf) = (V X V) и = О,
так как векторное произведение одинаковых «векторов» равно нулю,
в) divrot А(Р) = 0.
Образуя дивергенцию от rot А (Я), получим
aiv rot л {П -д{д dz J^dy\dz дх ) + dz \ дх ду
у д*Ах дА2 у
' dz ду дх ду * дх dz
ду дх dz дх ' dz ду дх ду * дх dz ду dz '
что в силу равенства вторых смешанных производных равно нулю.
Если бы мы записали доказываемое соотношение с помощью
набла-вектора:
divrot A (P) = V-(VXA),
то получили бы смешанное произведение трех «векторов», из ко-
которых два вектора одинаковы. Но такое произведение равно нулю.
Остальные две векторные операции второго порядка:grad div A (Я)
и rot rot А (Я) — встречаются реже. Мы не будем записывать их
выражения через проекции вектора А (Я), а только укажем связь
между ними:
rot rot А (Р) = grad div A (P) — ДА (Я),
где ДА (Я) — AAxi-\- АЛ j+ AAzk (Д — оператор Лапласа).
155*. Свойства простейших векторных полей. Простейшими
векторными полями являются такие, для которых либо div А (Я) = О,
либо rot А (Я) = 0, либо, наконец, равны нулю и дивергенция и
ротор. Рассмотрим такие поля подробнее.
I. Трубчатое (соленоидальное1)) поле. Векторное
поле, для всех точек которого дивергенция равна нулю, называется
трубчатым или соленоидальным. Поясним смысл этого названия.
Возьмем в этом поле какую-нибудь площадку SQ и проведем через
каждую точку ее границы векторные линии (см. п. 151,11). Эти
линии ограничиваютчасть пространства, называемую векторной трубкой
(рис. 209). Жидкость при своем течении все время движется по
такой трубке, не пересекая ее стенок. Рассмотрим часть такой
трубки, ограниченную площадкой So и каким-нибудь сечением St
(рис. 209). Так как по условию div А (Я) = 0, то поток вектора
1) Термин «соленоидальное» происходит от латинского слова «solen»—
трубка.
536 ГЛ. IX. КРИЗОЛИН. ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ [155
через любую замкнутую поверхность равен нулю. Следовательно,
$S And°+ И Ando+ S$ Anda= SSS div A (P) dv = 0,
s
$S И Ando+ S$ Anda= SSS
s s0 sx я
где 5 — боковая поверхность трубки, а п — внешняя нормаль. Так
как на боковой поверхности трубки нормали п перпендикулярны
к векторам поля, то
Отсюда следует, что
Переменив направление нормали на площадке SOi т. е. взяв внутрен-
внутреннюю нормаль п', получим
Рис. 209.
SSSS
Это значит, что поток вектора в
направлении векторных линий через
каждое сечение векторной трубки
один и тот же, т. е. в поле без
источников через каждое сечение
векторной трубки протекает одно
и то же количество жидкости.
Согласно формуле в) п. 154
div rot А (Р) = О,
т. е. поле ротора любого векторного поля — трубчатое.
Справедливо и обратное предложение, которое мы приводим без
доказательства.
Каждое трубчатое поле является полем ротора некоторого век-
векторного поля, т. е. если div А (Я)—0, то существует такое вектор-
векторное поле В \Р), что
А (Я) = rot В (Р).
Вектор В(Р) называют вектором-потенциалом данного поля.
II. Потенциальное, или безвихревое, поле. Если
во всех точках поля ротор равен нулю: rot A (P) = 0, то поле на-
называется безвихревым или потенциальным. Из равенства нулю rot A (P)
вытекает, что
dAv дАь
ду
дх
дАу
дЛ2
дЛг
дг
155] § 3. теория поля 537
Написанные равенства представляют условие того, что выражение
Axdx -f- Aydy + Azdz
является полным дифференциалом некоторой функции и(х, у} г)
(см. п. 115,И).
При этом
л -- А -- А —
Это значит, что вектор А (Р) потенциального поля является градиен-
градиентом скалярного поля:
А (Р) = grad и.
Функция и называется потенциальной функцией векторного поля или,
коротко, потенциалом. Потенциал определяется с точностью до про-
произвольного постоянного слагаемого.
Из формулы б) и. 154 следует обратное предложение:
Поле градиента любой функции и (х, у, z) является потенциаль-
потенциальным, а сама функция и — его потенциалом.
В потенциальном поле циркуляция по любому контуру равна
нулю. При этом предполагается, что контур L можно заключить
в односвязную область, во всех точках которой функции
Ах, А , Az и их производные непрерывны. С точки зрения течения
жидкости равенство нулю циркуляции означает, что в потоке нет
замкнутых струек жидкости, т. е. нет водоворотов.
Работа в силовом потенциальном поле (см. п. 144) равна разности
потенциалов в конечной и начальной точках линии L, т. е.
(В)
\ Axdx + Aydy + Azdz = u(B) — u (Л).
(А)
Изучение потенциального поля значительно облегчается тем, что
это поле вполне определяется заданием одной скалярной функ-
функции— его потенциала. Проекции вектора поля А (Р) будут при этом
частными производными этой функции по соответствующим коорди-
координатам. Произвольное же векторное поле требует задания трех
скалярных функций — проекций вектора на оси координат.
III. Гармоническое поле. Векторное поле, являющееся
одновременно и потенциальным и трубчатым, называется
гармоническим. Поскольку поле потенциально, его можно записать
в виде
А (Р) = grad u}
где и — потенциал поля. Условие трубчатости поля означает, что
div А (Р) = div grad и = 0.
538 ГЛ. IX. КРИВОЛИН. ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ [156
Согласно формуле а) п. 154
А д2и , д*а . dhi _
Дц ——--U—--4- — = 0.
дх2 ' ду2 ' иг*
Функции и, подчиняющиеся этому условию, называются гармониче-
гармоническими. Они играют важную роль в различных разделах теоретиче-
теоретической физики. На их свойствах мы останавливаться не будем.
156*, Электромагнитное поле. Одним из важнейших приложений
введенных нами понятий векторного анализа является изучение
электромагнитных полей. Мы рассмотрим несколько простых
примеров.
I. Электрическое поле. Пусть Е—поле напряженности
точечного заряда q, помещенного в начало координат. Согласно при-
примеру 2 п. 144 напряженность поля в точке Р(х, у, z) равна
где г — у х2-\-y2-\-z2— расстояние от точки Р до начала координат.
Векторными линиями такого поля служат лучи, выходящие из на-
начала координат, т. е. из заряда.
Поле напряженности Е является полем потенциальным (см. п. 144,
пример 2). Обычно за потенциал ф поля Е берут найденную в п. 144
функцию и = —, взятую с противоположным знаком:
Таким образом, разность потенциалов между двумя точками поля
равна взятой о противоположным знаком работе, совершаемой си-
силами поля при перемещении единичного положительного заряда из
первой точки во вторую. Легко проверить, что
Е = grad ( — jr ) = — grad ф.
Это значит также, что rotE = — rot grad ф = 0.
Найдем дивергенцию поля напряженности. Имеем
дг __ _
Г ОХ "^—. о г\._о. и I о I .9 О ..9 v I .О \ 2 4^2
^л: ^ /-4 ч гь ' ду гъ ' dz r5
Отсюда
div Е = -^ [Зг2 — 3 (л:2 +у2 + z2)] = 0.
Следовательно,
Поток вектора Е через любую замкнутую поверхность, не содер-
содержащую внутри себя начала координат, равен нулю.
156] § 3. теория поля 539
Если же начало координат, т. е. заряд, содержится внутри по-
поверхности, то такого вывода сделать уже нельзя, так как в начале
координат поле не определено.
Вычислим поток вектора Е через сферу радиуса R с центром
в начале координат. На поверхности этой сферы направление век-
вектора Е совпадает с направлением нормали, т. е. радиуса-вектора.
Поэтому
p IP] q
Отсюда поток К равен
Мы видим, что величина потока не зависит от радиуса сферы /?.
Легко показать, что величина потока остается неизменной для л го-
гобой замкнутой поверхности, окружающей начало координат.
Возьмем такую произвольную поверхность1) и поместим внутрь
нее какую-либо сферу с центром в начале координат (рис. 210).
Разобьем теперь тело, ограниченное
поверхностью, на несколько конусов
с вершиной в начале координат. Каж-
Каждый такой конус имеет вид, изобра-
изобраРис. 210. Рис. 211.
женный на рис. 211. Так как часть конуса, заключенная между участ-
участком сферы и данной поверхностью, является векторной трубкой (см.
п. 155» I), а дивергенция поля равна нулю, то потоки через участки
сферы и поверхности равны между собой. Складывая потоки через
все такие участки поверхности, мы и получаем, что поток вектора
Е через любую поверхность, окружающую начало координат,
*) На рис. 210 изображена поверхность, звездная относительно начала
координат, т. е. пересекающаяся с любым радиусом-вектором только в
одной точке. Можно доказать, что рассуждение сохраняет силу для любой
поверхности.
540 ГЛ. IX. КРИВОЛИН. ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ [156
равен потоку через сферу, т. е. 4nq. Будем считать, что внутренняя
сфера имеет радиус, равный единице. Тогда поток через участок
поверхности Sx (рис. 211) будет равен #(о, где о> — площадь поверх-
поверхности сферы единичного радиуса, в которую проектируется участок
поверхности. Величину ю называют телесным углом, под которым
поверхность Sx видна из начала координат.
Пусть теперь поле создано системой электрических заря-
зарядов qx>q2, ••-, <?/»• Обозначим через Ех- напряженность поля, со-
создаваемого зарядом qh а через Е — результирующую напряженность.
Тогда
Проекция вектора Е на направление нормали п к любой поверх-
поверхности равна
Стало быть, поток через поверхность равен
причем последняя сумма распространена только на те заряды q-y
которые лежат внутри рассматриваемой поверхности.
Эта формула, играющая важную роль в изучении электрических
полей, называется электростатической теоремой Гаусса.
Пусть, наконец, мы имеем дело с непрерывным распределением
заряда. Обозначим через р плотность распределения заряда 1). Если плот-
плотность заряда непостоянна, то р является функцией точки поля Р, т. е. ее
координат. Суммарный заряд в данном объеме Q будет равен
Применив к этому заряду теорему Гаусса, мы получим
где S —граница области Q.
*) Определение плотности распределения электрического заряда анало-
аналогично определению обычной плотности (см. п. 133).
156] § 3. теория поля 541
Преобразуем первый интеграл, вводя div Ei
Отсюда
Поскольку интеграл равен нулю для любой области интегрирования Q, то
рассуждая так же, как на стр. 486, получим
divE = 4np. (#)
Примем без доказательства, что свойство электрического поля быть потен-
потенциальным сохраняется при непрерывном распределении зарядов.
Обозначим его потенциал через ф; тогда Е = — graci ф. Согласно фор-
формуле а) п. 154
div E = — div grad ф = — Дф. (**)
Из равенств (*) и (#*) получим
Полученное соотношение называется уравнением Пуассона. В тех точках
поля, где плотность заряда р равна нулю, оно превращается в уравнение
Лапласа: Дф = 0.
Изучением этих уравнений мы в нашем курсе заниматься не будем
II. Магнитное поле прямолинейного тока. Пусть
магнитное поле создано постоянным током /, текущим по бесконеч-
бесконечному прямолинейному проводнику. Найдем вектор напряженности
магнитного поля, создаваемого этим током. Согласно закону Био —
С а в а р аг) элемент тока создает в данной точке напряженность
магнитного поля, равную по величине k ^ , где / — ток, ds—
элемент длины проводника, г — расстояние от элемента тока до
рассматриваемой точки, а — угол между направлением тока и пря-
прямой, соединяющей точку, в которой ищется поле, и элемент тока,
&-—коэффициент пропорциональности, зависящий от выбора системы
единиц. Вектор напряженности направлен по нормали к плоскости,
содержащей элемент тока и точку наблюдения; направление напря-
напряженности устанавливается правилом Ампера2) (правило «бурав-
«буравчика»). В векторной форме закон Био—Савара записывается так:
!) Ж. Био A775—1862) и Ф. Савар A791 —1841) — французские
физики.
2) А. А м п е р A775—1836) —выдающийся французский физик и математик.
542 ГЛ. IX. КРИВОЛИН. ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ [156
где dH — вектор напряженности поля, создаваемого элементом тока,
ds — вектор, направленный по проводнику, а г —вектор, проведен-
проведенный из элемента тока в точку Ж, в которой ищется напряженность.
Пусть ток течет по проводу, совпадающему с осью Oz, в на-
направлении снизу вверх (рис. 212). Обозначим переменное расстоя-
расстояние от элемента тока до начала координат через |, а координаты
точки М через лг, у и z. Тогда
где р=ух2-\-у2 — расстояние от точки М до провода. Вычисляя
векторное произведение, находим dU:
1 J k
О 0 dl
х у z — l
Отсюда
klydl
-.J
Рис. 212.
dHx
klxdl
Чтобы найти Нх и Нуу проинтегрируем выражения для их диф-
дифференциалов в пределах от —оо до оо. Для этого вычислим не-
несобственный интеграл
Подстановка % — z=ptgt, dl =
pdt
__ Р
приводит к интегралу
я
-- Г
1 р2 1
costdt = ^.
2
я
Поэтому
2kly _ __ 2kly
2klx 2klx
В точках оси Oz поле не определено. Таким образом, вектор напря-
напряженности Н имеет то же направление, что и вектор линейной ско-
скорости при вращении тела вокруг оси Oz (см. п. 151, 1), если
направление тока совпадает с направлением вектора угловой
157] § 3. теория поля
скорости. Модуль вектора Н равен
543
Легко проверить, что дивергенция поля равна нулю. Имеем
дНх _ Мху
дх "" ' " ' ^
Мху
дг '
= 0.
Следовательно,
divH = 0.
Ротор этого поля также во всех точках равен нулю. Для этого
надо только проверить равенство
~ду ~дх
Имеем
дН*
ду
дх
Рис. 213.
Следовательно, циркуляция поля по
любому контуру, не окружаю-
окружающему ось Ozy равна нулю. Если же контур окружает ось Oz
(рис. 213), то такого вывода сделать нельзя, поскольку такой кон-
контур невозможно заключить в односвязную область, не содержащую
точек оси Oz, в которых поле не определено.
Вычислим циркуляцию по окружности радиуса /?, лежащей в пло-
плоскости Оху> с центром в начале координат
х = R cos t, y = R sin t.
Тогда
Величина циркуляции не зависит от радиуса окружности R. Можнэ
доказать, что она остается одной и той же для любого контура,
окружающего ось Oz.
157*. Нестационарные поля. В этом пункте мы сделаем несколько
кратких замечаний о нестационарных полях, т. е. о полях,
определяющие функции которых зависят не только от простран-
пространственных координат ху у, z, но и от времени t. Скалярное поле
544 гл. ix. криволин. интегралы и интегралы по поверхности [157
в этом случае определяется функцией и (х, у, z, t); частная произ-
ди „
водная -^ представляет скорость изменения величины и в данной
фиксированной точке М(х,у,г) с течением времени t.
Если поле векторное
А (х, у, z, t) = Ах (х, у, z, t) \ + А (л;, у, z, t) j + Аг (х, у, z, t) к,
то производной ^т- будет вектор
dt l"i" dt
дА
„ du dA
Производные jj И ^т называют частными или локальными про-
производными; они характеризуют изменение поля в данной точке.
Если скалярное поле нестационарное, то соответствующее ему
векторное иоле градиента также будет нестационарным. Так как
d (grad и) _ d [du\ . d (du\ . d (дил
dt dt\dx) dt \dyj** dt \i
С другой стороны, градиент скалярного поля -^- равен
i d /ди\ . , d (с
Из равенства вторых смешанных производных немедленно следует,
что
a (grad а) д ddu
dt s at
Аналогично, если векторное поле нестационарно, то его основ-
основные характеристики — дивергенция и ротор — зависят от t. Легко
проверить, что
А) ,дА
В первой формуле слева и справа стоят скалярные величины, а во
второй—векторные. При выводе этих формул, разумеется, пред-
предполагается, что выполнены условия равенства вторых смешанных
производных по пространственным координатам и по времени; сог-
согласно теореме, приведенной в п. 114, для этого требуется их
непрерывность.
Приведенные выше формулы играют важную роль при изучении пере-
переменных электромагнитных полей с помощью уравнений Максвелла J).
Д. Максвелл A831 —1879) —знаменитый английский физик.
ВОПРОСЫ И ПРЕДЛОЖЕНИЯ 545
Перейдем теперь к задачам, возникающим при изучении движущихся
сред. Пусть, например, рассматривается распределение температуры в дви-
движущейся жидкости. В нестационарном случае эта температура будет зависеть
от точки, в которой она измеряется, и от времени Т — Т(х, у, 2, t). Если
измерять температуру в фиксированной неподвижной точке М (х, у> г)> то
скорость изменения этой температуры со временем будет равна, как уже
сказано выше, частной производной ^—.
Если же следить за температурой движущейся частицы жидкости,
то она будет меняться еще и потому, что сама частица в своем движении
может попасть в более теплую или более холодную область течения. Пусть
x*=x(t), y = y(t), z = z(t) — уравнения траектории движущейся частицы;
тогда проекции скорости v этой частицы на оси координат равны
dx dif dz
v*~If vy=tf v*=If
Температура Т (х, у, z, t) является теперь сложной функцией от t и скорость
ее изменения равна полной производной по t (см. п. 116):
dTdT дТ дТ дТ
Сумма последних трех слагаемых в правой части равна скалярному произ-
произведению grad T и скорости v; поэтому
Таким образом, полная производная -тт (ее называют еще материальной про-
изводной) слагается из частной производной -^ и скалярного произведения
gradT-v, которое называют также производной переноса.
ВОПРОСЫ И ПРЕДЛОЖЕНИЯ ДЛЯ САМОПРОВЕРКИ
1. Как определяется работа при движении точки в силовом поле?
2. Что называется криволинейным интегралом I P (x, y)dx-\-Q (л-, y)dy
по данной линии?
3. Как вычисляется криволинейный интеграл с помощью обыкновенного
интеграла, если уравнение линии интегрирования дано в параметрическом
виде? Привести соответствующую формулу.
4. Как вычисляется криволинейный интеграл, если уравнение линии
интегрирования задано в виде у = у(х) или * = *(#)?
5. Как влияет направление интегрирования на величину криволинейного
интеграла? Как устанавливается положительное направление в случае замк-
замкнутого контура интегрирования?
6. Сформулировать и доказать теорему Грина.
7. Что означает независимость криволинейного интеграла от линии
интегрирования?
8. Показать, что независимость интеграла от контура интегрирования
эквивалентна равенству его нулю по любому замкнутому контуру.
18 А. Ф. Бермант, И. Г. Араманович
546 ГЛ. IX. КРИВОЛИН. ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ
9. Сформулировать и доказать теорему о необходимом и достаточном
условии независимости криволинейного интеграла от линии интегрирования.
10. Указать наиболее удобный способ вычисления криволинейного инте-
интеграла от полного дифференциала. Привести соответствующие формулы.
11. Что называется первообразной от полного дифференциала? Записать
общее выражение для первообразных.
12. Как определяется криволинейный интеграл по пространственной
линии?
13. Сформулировать теорему о независимости криволинейного интеграла
от линии интегрирования для пространственного случая.
14. Какое силовое поле называется потенциальным? Что называется потен-
потенциалом такого поля?
15. Дать определение криволинейного интеграла по длине и указать
способы его вычисления.
16*. Как определяется поток жидкости через заданную поверхность?
17*. Что называется интегралом по поверхности?
18*. Какие поверхности называются двусторонними? Привести пример
односторонней поверхности.
19*. Указать задачи, приводящие к интегралам по поверхности, у кото-
которых подынтегральная функция не связана с выбором направления нормали
к поверхности и у которых она связана. Что значит взять интеграл по опре-
определенной стороне поверхности?
20*. Как вычисляется интеграл по поверхности?
21*. Сформулировать и доказать теорему Стокса.
22*. Доказать, опираясь на формулу Стокса, теорему о необходимом и
достаточном условии независимости криволинейного интеграла по простран-
пространственной личии от линии интегрирования.
23*. Сформулировать и доказать теорему Остроградского.
24*. Что называется векторным полем? Привести конкретные примеры
векторных полей.
25*. Что называется векторной линией? Вывести уравнения (дифферен-
(дифференциальные) векторных линий.
26*. Что называется потоком вектора через поверхность?
27*. Дать определение дивергенции векторного поля. Вывести формулу
для выражения дивергенции.
28*. Сформулировать в векторной форме теорему Остроградского и ука-
указать ее физический смысл.
29*. Что называется циркуляцией вектора?
30*. Вывести формулу для предела отношения циркуляции вектора по
плоскому контуру L к площади, ограниченной этим контуром.
31*. Дать определение ротора векторного поля. Сформулировать в век-
векторной форме теорему Стокса.
32* ^ Указать правила действий с оператором Гамильтона.
33*. Перечислить все возможные дифференциальные векторные операции
второго порядка.
34*. Дать определение трубчатого поля и указать его основные свойства.
35*. Указать основные свойства потенциального поля.
36*. Какое поле называется гармоническим? Какому условию удовлет-
удовлетворяет потенциал такого поля?
ГЛАВА X
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
§ 1. Дифференциальные уравнения первого порядка
158. Общие понятия. Теорема существования. При изучении
интегрального исчисления функций одной переменной мы сталкива-
сталкивались с необходимостью отыскивать неизвестную функцию у по ее
производной или дифференциалу.
Уравнение
/=/(*) или dy=f(x)dx, (*)
где у — неизвестная функция от лг, a f(x) — заданная функция,
является простейшим дифференциальным уравнением. Для его реше-
решения, т. е. для отыскания неизвестной функции у, нужно проинтегри-
проинтегрировать данную функцию f(x). При этом, как известно, мы получим
бесчисленное множество функций, каждая из которых будет удов-
удовлетворять условию (*). В этой главе нам удобнее будет под интег-
интегралом \ / (л:) dx понимать какую-либо одну первообразную.
Тогда любое решение уравнения (*) запишется в виде
Вскоре мы увидим, что гораздо чаще приходится иметь дело
с уравнениями более сложного вида. Именно в эти уравнения, по-
помимо производной у' и независимой переменной лг, может входить
и сама неизвестная функция у. Примером тому служат уравнения
= 0, у''=4 , ху'=у+х и т. д.
X
Заменяя у через •—, можно эти самые уравнения переписать
в дифференциальной форме:
2ydx = 0, xdy—ydx = 0, xdy —
1С*
548 ГЛ. X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [158
Определение. Дифференциальным уравнением первого
порядка называется уравнение, связывающее независимую пере-
переменную, неизвестную функцию и ее производную.
Так как производную можно представить в виде отношения
дифференциалов, то уравнение может содержать не производную,
а дифференциалы неизвестной функции и независимой переменной.
Дифференциальные уравнения второго и высших порядков будут
рассмотрены в § 2.
Мы будем рассматривать только такие уравнения, в которых
неизвестная функция зависит от одного аргумента1).
Дифференциальное уравнение первого порядка в общем виде
записывается так:
В частных случаях в левую часть уравнения могут не входить
х или у, но всегда обязательно входит^'. Нам придется в основном
иметь дело с уравнениями, разрешенными относительно производ-
производной, т. е. вида
У'=/(х,У).
Определение. Решением дифференциального уравнения
называется функция, которая при подстановке ее вместе с про-
производной в это уравнение превращает его в тождество.
Простейшие примеры показывают, что дифференциальное урав-
уравнение может иметь бесчисленное множество решений. Мы наблюдали
это уже на примере уравнения (*). Простой проверкой легко убе-
убедиться также, что уравнение2) у'— У- имеет решениями функции
у~Сх, а уравнение у' = — ~ — функции у = —, где С—любое
число.
Уравнение у'=У^- имеет решениями функции у = х\пх-{-Сх.
В самом деле, найдя производную у' = In #4-1+С и подставив
ее в уравнение, получим тождество
1) Такие уравнения называются обыкновенными. Дифференциальные урав-
уравнения, в которых неизвестная функция зависит от нескольких аргументов,
называются уравнениями с частными производными. Они рассматриваются
в курсе уравнений математической физики.
2) Если нет опасности смешения, мы вместо «дифференциальное уравне-
уравнение» коротко будем говорить «уравнение».
158] § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 549
Как мы видим, в решения приведенных дифференциальных урав-
уравнений входит произвольная постоянная С; придавая ей
различные значения, мы будем получать разные решения.
Несмотря на то, что рассмотренные примеры носят частный ха-
характер, мы все-таки, не приводя доказательства, сделаем следующий
общий вывод.
Любое дифференциальное уравнение у' =f(x, у) имеет бесчис-
бесчисленное множество решений, которые определяются формулой,
содержащей одну произвольную постоянную; Эту совокупность
решений будем называть общим решением дифференциального
уравнения первого порядка и записывать так:
у = у(х, С).
Придавая произвольной постоянной С определенные числовые
значения, мы будем получать частные решения.
В дальнейшем при решении конкретных задач нас будут инте-
интересовать преимущественно частные решения. Необходимо выяснить,
каким же образом из общего решения можно выделить требуемое
решение. Зададим для этого начальное условие. Задать на-
начальное условие дифференциального уравнения первого порядка это
значит указать пару соответствующих друг другу значений незави-
независимой переменной (xQ) и функции (у0). Записывают это так:
Покажем на примере, как по общему решению и заданному
начальному условию можно отыскивать соответствующее этому
условию частное решение.
Выше мы видели, что уравнение у' = — имеет общее решение
у — Сх. Зададим начальное условие у |Xss2 = 6. Подставив эти зна-
значения х и у в общее решение, получим 6 = 2С, откуда С=3.
Следовательно, функция у = 3х удовлетворяет как дифференциаль-
дифференциальному уравнению, так и начальному условию.
Вопрос о том, в каком случае можно утверждать, что частное
решение дифференциального уравнения, удовлетворяющее данному
начальному условию, существует, а также что оно будет единствен-
единственным, выясняется теоремой, которую мы приведем без доказательства.
Теорема существования и единственности ре-
решения. Если функция f(x,y) непрерывна в области, содержа-
содержащей точку Р0(х0,у0), то уравнение yf =f(x9y) имеет решение
у =у (х) такое, что у (д:0) =yQ.
Если, кроме того, непрерывна и частная производная ^, то
это решение уравнения единственно*
550
ГЛ. X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
[158
Интересно отметить, что в условии теоремы не требуется сущест-
существования производной ~ .
Теорема эта впервые была сформулирована и доказана Коши.
Поэтому часто задачу отыскания частного решения по начальным
условиям называют задачей
Коши. у
Перейдем теперь к гео-
геометрической иллюстрации
введенных понятий.
Рис. 214.
Рис. 215.
График любого частного решения дифференциального уравнения
называется интегральной кривой. Общему решению соответствует
семейство интегральных кривых. Так как мы уже проверили, что
уравнение у' = ~ имеет общее решение у — Сх, то соответствующее
ему семейство интегральных кривых — пучок прямых, проходящих
через начало координат (рис. 214). Уравнение^' = —— имеет общее
Q
решение у= —. Ему соответствует семейство равнобочных гипер-
х
бол, асимптотами которых являются оси координат (рис. 215), а также
прямая у = 0.
Задание начального условия у \ x=Xo=yQ означает задание точки
Р0(х0, у0), через которую должна проходить интегральная кривая,
соответствующая искомому частному решению. Таким образом,
отыскание частного решения по начальному условию y\x=X(t=yQ
геометрически означает, что из семейства интегральных кривых мы
выбираем ту, которая проходит через точку Р0(х0Уу0). Согласно
теореме существования и единственности решения через каждую
точку, в которой функции /(а:, у) и ^непрерывны, проходит одна-
159] § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 551
единственная интегральная кривая. Вели в данной точке эти условия
нарушены, то это означает, что через эту точку либо вообще не
проходит ни одна интегральная кривая, либо проходит несколько.
Возьмем, например, уравнение У = —; из рис. 214 видно, что через
начало координат проходит бесчисленное множество его интеграль-
интегральных кривых. Это не противоречит теореме, так как в точке @, 0)
условия теоремы существования нарушены: правая часть уравнении
становится неопределенной.
Точки, в которых условия теоремы существования и единствен-
единственности решения нарушаются, называются особыми точками. Вопрос
о том, как ведут себя интегральные кривые в окрестности особой
точки, будет вкратце рассмотрен в п. 164; пока же предполагается,
что если мы отыскиваем частное решение уравнения у' ~f{xyy) по
заданному начальному условию у\х=х0=Уо, то в точке (лг0,у0)
выполняются условия теоремы существования и единственности.
Такие начальные условия будем называть возможными.
Теперь мы можем указать основное свойство общего решения:
Общее решение у = у(х, С) дифференциального уравнения
у' =/,(jcf у) обладает тем свойством, что из него по любому
заданному возможному начальному условию y\x==Xoi=yo может
быть найдено частное решение, удовлетворяющее этому условию.
Это означает, что, подставляя в общее решение значения х0 ну0,
мы получаем уравнение относительно С: <Уо==:ф(л'о> О> из которого
всегда может быть найдено одно-единственное значение С~С0.
Функция дг = ф(лг, Со) и будет искомым частным решением.
Отметим еще, что отыскание решения дифференциального уравне-
уравнения часто называют интегрированием уравнения. При этом
действие интегрирования функций называют квадратурой.
Перейдем теперь к приемам решения отдельных типов диффе-
дифференциальных уравнений.
159. Уравнения с разделяющимися переменными. Рассмотрим
уравнение вида
fi(y)dy=f2(x)dxy (•)
гДе /i (у) и/г(лг) — заданные функции. В этом дифференциальном
уравнении переменные разделены, т. е. каждая из перемен-
переменных содержится только в той части уравнения, где находится ее
дифференциал. Уравнение dy=f(x)dx является частным случаем
рассматриваемого уравнения.
В обеих частях уравнения (#) стоят дифференциалы некоторых
функций; справа этот дифференциал выражен прямо через незави-
независимую переменную лг, а слева через промежуточный аргумент у,
который является функцией от х. Именно эта зависимость у от х
552 ГЛ. X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [159
и является искомой. Произведя интегрирование, мы получим связь
между переменными х и у, освобожденную от ик дифференциалов:
\fi(y)dy = \ft(x)dx + C.
Напомним, что под символом V мы в этой главе условились по-
понимать какую-то одну первообразную. Ясно также, что произволь-
произвольную постоянную С можно писать в любой части равенства.
Если задано начальное условие у \ х=Хо=уо, то, определяя посто-
постоянную С, получим частное решение, удовлетворяющее данному усло-
условию. Воспользовавшись определенными интегралами, можно сразу
записать искомое частное решение:
У х
S А
Уо х0
При этом значения х0 и у0 действительно соответствуют друг другу,
так как обе части равенства обращаются в нуль при замене верхних
пределов у и х на у0 и х0.
Выполняя фактически интегрирование, мы обычно получаем неиз-
неизвестную функцию^ в неявном виде. Иногда, если решение уравнения
дано не в явном виде: у — ц>(х), а в неявном: Ф(лг, ^)=0, то
его называют интегралом уравнения.
Пример 1. Найдем решение уравнения
удовлетворяющее условию <у|л:=о = 2.
Интегрируя и записывая для удобства потенцирования произ-
произвольную постоянную в виде 1п|С|, получим In \у | =л;3 + 1п | С|,
откуда |j;| = |C|e*s или
у = Сех\
Если бы мы взяли произвольную постоянную в виде In С, то было
бы С> 0, и общее решение пришлось бы записать так: у = -^СесШ.
На вопрос, можно ли считать решением функцию у = 0, ответ
будет дан ниже (на стр. 554).
Подставляя в общее решение начальное условие, найдем С:
2 = С.
Таким образом, функция у = 2ех* является искомым частным решени-
решением данного уравнения. Если бы мы воспользовались определенными
159] § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 553
интегралами, то получили бы
У
г о
т. е.
\у = х3\* или lnv — In 2 = л;3.
Потенцируя, приходим к тому же частному решению
у = 2ех\
Очень часто встречаются уравнения, в которых переменные еще
не разделены, но их можно разделить, производя простые арифме-
арифметические операции.
Определение. Дифференциальные уравнения, в которых
переменные можно разделить посредством умножения обеих частей
уравнения на одно и то же выражение, называются дифферен-
дифференциальными уравнениями с разделяющимися переменными.
Таким будет, например, уравнение
dx f± (у) •
В нем переменные еще не разделены, однако, умножив обе его
части на /г (у) dx, мы приходим к уравнению с разделенными пе-
переменными.
Легко также разделить переменные, если уравнение записано
в дифференциальной форме и имеет вид
А (*)/2 (у) dx +/3 (х)/4 (у) dy = 0. (**)
Деля обе части уравнения на произведение /2 (у)/ъ (х), получим
hi*) U (У) У
Нам теперь даже не обязательно переносить одно из слагаемых
в правую часть. Интегрируя, запишем
v*/ J 12\У)
Следует заметить, что при делении на /2(y)fs(x) может прои-
произойти потеря некоторых частных решений. Пусть, например, при
у=Уо имеем /2(<Уо)=:О- Тогда функция у—у0 (постоянная)
является решением уравнения. Действительно, dy — 0 и подстановка в
уравнение (*#) приводит к тождеству. Считая х и у равноправными
554 ГЛ. X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [160
и рассуждая аналогично, получим, что если /3 (лг0) = 0, то х = х0
тоже является решением уравнения1).
В связи со сказанным сделаем еще такое замечание. Уравнение
у' =— имеет, как уже отмечено выше, общее решение у = Сх,
т. е. совокупность прямых, проходящих через начало координат,
за исключением прямой л; = 0 — оси ординат. Записав это же самое
уравнение в виде х dy—ydx = Q, мы получим и решение л; = 0.
Поэтому общим решением считают всю совокупность указанных
прямых, включая и ось ординат. Такое же замечание можно сделать
и при решении многих других примеров; например, уравнение
у' =—~, семейство интегральных кривых которого изображено
на рис. 215, имеет еще решения у = 0 и л; = 0, т. е. оси координат,
а уравнение примера 1—решение у = 0.
Пример 2. Найдем общее решение уравнения
х (у + \) dx — {x2 + \)y dy = 0.
Разделяя переменные, приведем его к виду
jcdx ydy n
х*+\ у+\ и'
Интегрируя, получим
т. е.
Итак, мы нашли общее решение, причем у является неявной
функцией от л;. Заменяя С на In | С|, мы можем представить решение
в таком виде:
Кроме этого, есть еще частное решение у——1, графиком
которого является горизонтальная прямая у = — 1. При С > 0 любая
интегральная кривая лежит выше прямой у——1, а при С<0—¦
ниже этой прямой (предоставляем читателю это проверить).
160. Некоторые задачи физики. Хотя дифференциальные урав-
уравнения с разделяющимися переменными являются весьма частными
случаями уравнений первого порядка, к ним приводят многие раз-
различные задачи из области физики и механики.
2) Обычно в ответах к задачам, приведенным в задачниках, указанные
частные решения не отмечаются.
160] § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 555
Заметим сразу же, что при решении задач физического характера!
приводящих к дифференциальным уравнениям, основную трудность
представляет, как правило, составление самих дифференциальных
уравнений. Здесь нет общего метода, и каждая задача требует
своего подхода, основанного на знании соответствующего закона
физики. Рассмотрим некоторые из этих задач, чтобы показать на при-
примерах, как составляются дифференциальные уравнения. Приведенные
примеры помогут читателю уяснить суть дела и перейти к самостоя-
самостоятельному решению подобных задач.
1)Радиоактивный распад. Экспериментальным путем уста-
установлено, что скорость радиоактивного распада пропорциональна ко-
количеству нераспавшегося вещества. Считая, что начальное количество
вещества равно Мо, найдем зависимость между количеством нерас-
нераспавшегося вещества М и временем t.
Скорость радиоактивного распада равна производной от количества
вещества М по времени t> т. е. —гт. Но по условию
_=
где k — коэффициент пропорциональности. Знак минус берется по-
потому, что с возрастанием t количество вещества М уменьшается.
Разделим переменные в полученном уравнении:
М ~~
Интегрируя, получим
1пМ= — Atf + lnC,
откуда
M=Ce~kt.
Обращаем внимание читателя на то, что в дифференциальное урав-
уравнение не входит величина MQ; она войдет в начальное условие,
которое имеет вид М\ Ыо = Мо, Из этого условия следует, что С = Мо.
Следовательно, частное решение, отвечающее условиям задачи,
имеет вид
ы
Константу k можно определить экспериментально, установив коли-
количество нераспавшегося вещества в какой-то момент времени1). Пусть,
например, половина начального количества Мо=1 г распадется
в течение 26,7 минуты. Здесь при ? = 26,7 М=0,5. Поэтому
0,5 = e*~26'7fe, откуда &= 6 ' ж 0,026» Следовательно, процесс
') Такой метод определения физических констант очень часто приме-
применяется в подобных случаях.
556 ГЛ. X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [160
распада протекает по формуле
Для того чтобы узнать, какое количество вещества осталось
нераспавшимся, например, через 10 минут после начала опыта, до-
достаточно в эту формулу подставить ?=10:
X = 6 w U,/ / с.
2) Охлаждение тела. Согласно закону, установленному
Ньютоном, скорость охлаждения тела пропорциональна разности между
температурой тела и температурой окружающей среды.
Пусть тело нагрето до температуры 70; температуру окружающей
среды будем считать постоянной1) и равной 7сGс<70). Найдем
зависимость между изменяющейся температурой 7 тела и временем
охлаждения /.
Пусть в момент времени t температура тела равна 7. Скорость
изменения температуры, т. е. -тг, по закону Ньютона пропорцио-
пропорциональна разности 7— 7С; следовательно,
dT __ ыт
Of— *\J 'с)-
Знак минус выбран потому, что с возрастанием t температура 7 тела
уменьшается. Коэффициент пропорциональности k зависит как от
физических свойств тела, так и от его геометрической формы (ясно,
что скорость охлаждения раскатанного листа стали больше, чем
первоначального стального слитка).
Разделяя переменные, получим -=—7Г"== — kdt. Отсюда
* * с
1пG— Гс) = — kt-\-\nC и 7=7С+С*~**.
Так как 7> 7С, то можно писать In G—7С), а не In | 7—7С|.
Рекомендуем читателю рассмотреть случай 7С > 70, т. е. когда
тело не остывает, а нагревается.
Подставляя начальное условие 7|1=0= 70, найдем С: 70= 7С + С,
т. е. С—То—7С. Окончательно закон охлаждения имеет вид
Коэффициент пропорциональности k должен быть либо задан, либо
установлен экспериментально путем измерения температуры 7
J) Мы считаем, что при охлаждении тела температура окружающей среды
не меняется. Если при охлаждении тела нужно учитывать повышение темпе-
температуры окружающей среды, то задача становится более сложной»
160] § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 557
в некоторый момент времени tl). Отметим, что теоретически темпе-
температура тела сравняется с температурой окружающей среды лишь
при t—>оо.
В обоих приведенных примерах соответствующий физический
закон непосредственно устанавливает связь между производной не-
неизвестной функции и самой функцией
(независимая переменная t в уравнение не
входит).
Рассмотрим теперь более сложный
пример.
3) Истечение жидкости из
цилиндра. Цилиндрический сосуд, в
дне которого имеется отверстие, наполнен
жидкостью. Найдем время Т, в течение
которого жидкость вытечет из сосуда,
если высота столба жидкости равна Н,
радиус цилиндра равен г, площадь отверстия равна 5 (рис. 216).
При решении задачи используем закон Торичелли2).
Скорость v истечения жидкости в случае отверстий, небольших
сравнительно с высотой столба жидкости, равна У 2gh, где h — вы-
высота уровня жидкости над отверстием, a g— ускорение силы тяжести 3).
(Эта скорость равна скорости при свободном падении тела с вы-
высоты А.)
Если бы убыль жидкости постоянно возмещалась, то скорость
истечения по закону Торичелли оставалась бы постоянной, и тогда
имевшееся вначале количество жидкости вытекло бы за - - сек.
Рис. 216.
Но без такого возмещения уровень жидкости все время понижается,
и скорость истечения уменьшается; задача оказывается более
сложной.
Пусть в момент времени t высота жидкости в цилиндре равна h
(рис. 216). Мы найдем связь между dt и dh, если предположим,
что за бесконечно малый промежуток времени dt скорость истечения
будет постоянной и равной \^2gh. Тогда объем dV жидкости, выте-
вытекающей из цилиндра за время dt, будет равен объему цилиндра
1) Если, например, известно, что при
температура Т
то
fe,n
h '1— 'с
2)Е. Торичелли A608—1647) — итальянский ученый, ученик и сотруд-
сотрудник Галилея.
8) В данной здесь форме закон Торичелли применим_только к идеальной
жидкости. Практически пользуются формулой v — \i V^2gh, где ^i — коэффи-
коэффициент, зависящий от вязкости жидкости и формы отверстия, из которого про-
происходит истечение. Для воды, например, в случае круглого отверстия ^^0,6.
558 ГЛ. X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [161
с основанием s и высотой vdt:
Предоставляем читателю проверить, что этот объем будет от-
отличаться от истинного объема вытекшей жидкости на величину
бесконечно малую более высокого порядка, чем Д*.
С другой стороны, поскольку уровень понизился на dh> этот
объем равен
dV = — nr2dh
(мы ставим знак минус, потому что dh < 0). Приравнивая оба най-
найденных выражения для dV, придем к дифференциальному уравнению
dt = — nr2dh.
Перепишем это уравнение в виде
Интегрируя, получим
Так как h
<=0
= //, то
Окончательно
В результате мы получили формулу, выражающую время истече-
истечения t как функцию высоты столба жидкости А. Полагая й = 0,
найдем полное время истечения
161. Однородные и линейные уравнения первого порядка.
Прежде всего рассмотрим простые и важные классы уравнений пер-
первого порядка, приводящихся к уравнениям с разделяющимися пере-
переменными.
I. Однородные уравнения.
Определение. Уравнение
называется однородным, если функция f(x, у) может быть
161] § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 559
представлена как функция отношения своих аргументов:
Например, уравнение
(ху —у2) dx — (лг2 — 2ху) dy = O
однородное, так как его можно записать в виде
dx х* — 2
В общем случае переменные в однородном уравнении не разде-
разделяются. Однако, вводя вспомогательную неизвестную функцию и
по формуле
— *=и или у = лги,
х ' •
мы сможем преобразовать однородное уравнение в уравнение с раз-
разделяющимися переменными.
Действительно, имеем
' \
и уравнение у' — у(У-\ принимает вид
= Ф(и), т. е. #т- = ф(и)—и.
Отсюда
du dx
ф {ц) —-U X
после интегрирования получаем
Найдя отсюда выражение для и как функции от лг и возвращаясь
к переменной у = хи, получим искомое решение однородного урав-
уравнения.
Чаще всего не удается просто найти явное выражение для и.
Тогда после интегрирования следует в левую часть вместо и подста-
подставить ~; в результате мы получим решение уравнения в неявном виде.
Разумеется, мы предполагаем, что ф (и) — ифО. Если ф(и)=и,
то ф(~]=- и не нужно делать никаких преобразований, ибо
\Х J X
само заданное уравнение у' = -У-—с разделяющимися переменными.
560 ГЛ. X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [161
Если же знаменатель ф(м) — и обращается в нуль лишь при
каком-то значении #0, то, как уже отмечено, функция и = и0 яв-
является решением преобразованного уравнения, а функция у ~и^ —
исходного.
Нет необходимости запоминать полученные выше формулы:
в каждом примере нетрудно проделать полностью указанное пре-
преобразование.
Пример. Найдем решение однородного уравнения
У —х2 — 2ху'
Замена у = хи приводит к уравнению
, и—и2 du 1 (и — и1 \ 1 и2
U4-XU =г; jr- ИЛИ -г = — \1 о U ===— •: гг-.
1 \—2и dx х \\-2u ) х 1 —2«
Разделяя переменные, находим
откуда |-21п|и|
— L ИЛИ
x у
-— , и значит,
» =~
Возвращаясь к переменной у, приходим к общему решению:
При С>0 интегральные кривые лежат в полуплоскости х > 0,
а при С<0— в полуплоскости х < 0.
И. Линейные уравнения. Вторым часто встречающимся
типом уравнений первого порядка является линейное уравнение.
Определение. Уравнение вида
т. е. линейное относительно искомой функции и ее производной»
называется линейным. Здесь р (х) и q (x) — известные функции
независимой переменной х.
Уравнение (#) сводится к двум уравнениям с разделяющимися
переменными путем следующего искусственного приема. Запишем
функцию у в виде произведения двух функций: y = uv. Одной из них
мы можем распорядиться совершенно произвольно; при этом вторая
должна быть определена в зависимости от первой таким образом,
161] § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 561
чтобы их произведение удовлетворяло данному линейному уравнению.
Свободой выбора одной из функций и и v мы воспользуемся для
максимального упрощения уравнения, получающегося после замены.
Из равенства y = uv находим производную у'\
у' — u'v + uv'.
Подставляя это выражение в уравнение (#), имеем
u'v + uv +p(x) uv = q(x), или u'v + u (v'+p(x)v) = q(x).
Выберем в качестве v какое-нибудь частное решение уравнения
v'+p(x)v = 0. (**)
Тогда для отыскания и получим уравнение
u'v = q(x). (***)
Сначала найдем v из уравнения (**). Разделяя переменные, имеем
dv
откуда
v = —\p{x)dx и v
Под неопределенным интегралом здесь понимается какая-нибудь одна
первообразная от функции р(х), т. е. v является вполне опре-
определенной функцией от х.
Зная vy находим далее и из уравнения (**#):
du a(x) [p(x)dx [p(x)dx
чкх) _,..x?j ? du = q(x)e* dx,
и значит,
f P(x) dx
dx-\-C.
Здесь мы уже берем для и все первообразные. По и и v найдем
искомую функцию у:
-\р(х) dx
dx +
Полученная формула дает общее решение линейного урав-
уравнения (#).
Положение не изменится, если мы прибавим произвольную постоянную
к интегралу в показателе. В самом деле, эта вторая произвольная постоянная
в конечном счете исчезнет, так как один множитель будет содержать ее
в знаменателе, а другой —в числителе.
562 ГЛ. X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [161
Можно решать задачу с помощью определенных интегралов
с переменным верхним пределом. При этом
X X
-\ p(x)dx * \ p(x)dx
v = е *• , и = J #(*) ех« + С,
[\q(x)ex° dx+C).
Частное решение, соответствующее начальному условию у\х-Хо=Уо%
получается отсюда при С = у0.
Как и раньше, мы не настаиваем на запоминании общей формулы.
Следует помнить лишь способ решения и применять его в каждом
конкретном случае.
Примеры. 1) Решим уравнение у'-\—« = ^2-?.
X * X
Положим y~uv, тогда у' = u'v + uv'. Имеем: u'v + uv'-\ uv =
sin х , . / , , v \ sin х г, * i v n r\
= , или uv+u[v-\— = . Пусть v H— = 0. Отсюда
X \ X J X X
dv dx , . I /-.
— = и, значит, In v = —1плг, т. е. v = —. Следовательно,
#'• — =: , откуда tt/ = sinAr и, значит, и = — cosa: + ^. Имеем
окончательно
у = uv = — (— cos х + С).
л
2) Найдем решение уравнения У — 2лгу= 1 при начальном условии
Здесь р(х) = — 2лг, q(x) = 1, лг0 == 0, у0 = 0. По общей формуле по-
получим
х
0
Несмотря на то, что интеграл в правой части не может быть выра-
выражен при помощи элементарных функций (см. п. 86), задача считается
решенной, так как функция у найдена. Ее значения можно вычислять
при помощи методов приближенного интегрирования. Впрочем, в дан-
данном конкретном случае прибегать к этим методам нет нужды, так
х
как для интеграла \ e~*zdx имеются готовые таблицы (точнее,
имеются таблицы для функции Ф(лг) = -т=\ е~х*dx).
У п J /
161] § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 563
К линейным уравнениям часто приводятся уравнения более слож-
сложного вида. Рассмотрим, например, так называемое уравнение
Бернулли1).
Если ввести вспомогательную неизвестную функцию у~п+1 =?,
(—п-\- l)y~ny' =z\ и уравнение примет вид
При п — О — это линейное уравнение, а при п = \ можно разделить
переменные. При других значениях п оно сводится к линейному при
помощи следующего приема: делим обе части уравнения на уп и
записываем его так:
то
Это линейное уравнение; решая его и переходя от z снова к у, мы
и получим решение исходного уравнения.
Рассмотрим одну важную задачу электротехники, которая при-
приведет нас к линейному дифференциальному уравнению первого по-
порядка. Пусть электрическая цепь имеет сопротивление R и само-
самоиндукцию L (рис. 217).
Если через / обозначить силу тока в цепи, а через Е электро-
электродвижущую силу, то, как известно из физики,
получаем
Считая, что Е является известной функцией времени,
линейное уравнение, которое запишем в виде ? .
di^T* -Г"
Проинтегрируем это уравнение в предполо-
предположении, что ?" = const при начальном условии
/|t=0 = 0. Это означает, что мы включаем в
цепь, в которой не было тока, постоянную
электродвижущую силу. Воспользовавшись
общей формулой, выраженной при помощи определенных интегра-
интегралов, получим
J=e
dt,
J)H. Бернулли A654—1705) и И. Берну л ли A667—1748) —швей-
—швейцарские математики, современники Лейбница и Ньютона. Своими работами
и широкой педагогической деятельностью они во многом способствовали раз-
развитию математического анализа.
564 ГЛ. X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [162
или, выполняя интегрирование,
/
-*(•-.-*>
Ток / слагается как бы из двух токов: тока -^ , соответствующего
А
Е 4<
закону Ома, и экстратока замыкания -^е , протекающего
а
в обратном направлении. Экстраток замыкания быстро стремится
к нулю, и поэтому в цепи довольно скоро устанавливается посто-
постоянный ток. Еще проще решается задача о размыкании цепи.
В этом случае мы считаем, что /1 <==0 = /0 и Е = 01). Тогда полу-
получается уравнение с разделяющимися переменными -г? =—у-/. Решая
-It
его, получим /=/ое L —экстраток размыкания. Скорость
стремления экстратока к нулю зависит от отношения -г : чем это
отношение больше, тем быстрее экстраток затухает.
Рекомендуем читателю самостоятельно решить задачу в случае,
когда электродвижущая сила Е синусоидальна, т. е. когда
162. Уравнения в полных дифференциалах. Возьмем уравнение
первого порядка, записанное в дифференциальной форме:
Р(х, y)dx + Q(xt y)dy = 0. (A)
Определение. Если левая часть уравнения (А) является
полным дифференциалом некоторой функции и (дг, у)9 то это урав-
уравнение называется уравнением в полных дифференциалах.
Выражение же Pdx-\-Qdy, как известно (п. 115,1), есть полный
дифференциал, если тр = -^«
Пользуясь ранее рассмотренными методами отыскания функции
по ее полному дифференциалу (см. п. 115,1 или п. 142), находим
такую функцию и(х, у), что
du(xt y) = P(x, y)dx + Q(x, y)dy.
Тогда уравнение (А) можно записать так:
du(x9 y) = 0.
1) Мы не останавливаемся на вопросе, как реализовать такую электри-
электрическую цепь.
163] § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 565
Последнее равенство означает, что между переменными хну суще-
существует зависимость вида
и (*, у) = С,
где С —произвольная постоянная. Полученная зависимость и дает
общее решение уравнения (А). Следовательно, интегрирование
уравнения (А) сводится к отысканию первообразной от левой
части. Воспользовавшись выражениями для этой первообразной, най-
найденными в п. 142 х), получаем общее решение уравнения (А) в виде
или в виде
*о Уо
Пример. Найдем общее решение уравнения
Bх +y)dx + (x — 4y) dy = O.
Так как
ду (
то левая часть уравнения является полным дифференциалом неко-
некоторой функции и(ху у). Беря за точку (лг0, у0) начало координат,
имеем
х у
и (х, у) = J Bлг +у) dx + $ (—Ay) dy=x* + xy—2y* = С.
О О
Решенное здесь дифференциальное уравнение является однородным,
поэтому его можно проинтегрировать и способом, описанным
в п. 161, I.
163. Приближенные методы решения уравнений первого по-
порядка.
I. Поле направлений. Если ни один из частных приемов
интегрирования уравнения первого порядка
y'=f(*,y) (•)
не приводит к цели или требует сложных выкладок, то можно
прибегнуть к приближенному решению. Мы изложим здесь графи-
графический способ Эйлера и вытекающий из него способ численного
х) Если изучение дифференциальных уравнений предшествует изучению
криволинейных интегралов, то читатель должен отыскивать функцию и (х, у)
методом п. 115, I.
566 ГЛ. X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [163
интегрирования. Прежде чем перейти к рассмотрению этих спосо-
способов, коснемся геометрического смысла уравнения первого порядка (*).
Уравнение (*) определяет в каждой точке Р{ху у) той области
плоскости Охуу в которой справедлива теорема существования и
единственности решения (п. 158), величину углового коэффициента
касательной (у') к интегральной кривой, проходящей через точку
Р(х, У)- Эту величину графически можно изобразить прямолинейной
стрелкой, исходящей из точки Р и имеющей угловой коэффициент,
равный f(xt у); при этом длина стрелки здесь не имеет никакого
значения. Таким образом, заданием уравнения (*) устанавливается,
как говорят, поле направлений в плоскости Оху.
Геометрическое место точек с одинаковым направлением поля
(у' = const) называется изоклиной (линией равных наклонов)
уравнения. Очевидно, мы получим уравнение изоклины, соответ-
соответствующей данному значения) у = С, если подставим это значение
в дифференциальное уравнение
С=/(*, у).
При произвольных, но постоянных С это есть уравнение семей-
семейства изоклин дифференциального уравнения (*).
Во всех точках одной изоклины, соответствующей одному С,
касательные к интегральным кривым имеют одинаковое направление.
Как видно, задачу интегрирования дифференциального уравнения
можно геометрически истолковать так: найти линии, удовлетворя-
удовлетворяющие тому условию, что касательные к ним имеют направления,
совпадающие с направлениями поля в точках касания.
Перейдем к изложению методов приближенного интегри-
интегрирования, причем здесь всюду предполагается, что теорема су-
существования и единственности решения справедлива.
II. Графический метод Эйлера. Рассмотрим метод
Эйлера построения интегральной кривой уравнения первого порядка
/=/(*, У)> (*)
проходящей через начальную точку М0(х0, у0), т. е. к графическому
отысканию частного решения с начальным условием
Приближенно это можно выполнить с помощью простых постро-
построений, вполне аналогичных тем, которые производятся при графиче-
графическом интегрировании функций, т. е. при решении уравнения (#)
в частном случае, когда f(x, у) является функцией только х
(см. п. 95).
Разобьем интервал [х0, х] на п частей точками хъ х2, .. ., xn_t
(рис. 218). Через точки деления проведем прямые, параллельные
163] § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 567
оси Оу, и последовательно проделаем следующие однотипные
операции.
Вычисляем значение /(#, у) в точке М0(х0, у0); /(лг0, j;0) изме-
измеряет согласно уравнению (*) угловой коэффициент интегральной
кривой в точке М0(х0, у0). Для построения направления, исходя-
исходящего из точки Af0, возьмем полюс Р графика на оси Ох слева от
начала координат на расстоянии, равном ОР — 1 (при этом мас-
масштаб ОР может быть отличным от масштаба, принятого по осям
координат); отложим по оси Оу отрезок ON0i равный в масштабе ОР
числу f(x0, у0), и соединим точку No прямой с полюсом Р. Направ-
Направление отрезка /Wo, очевидно, и будет искомым направлением кривой
в точке Мо. Проведем из Мо отрезок прямой, параллельной /Wo,
до пересечения с прямой х = хг. Мы получим точку Mv которую
и примем в качестве точки интегральной кривой, соответствующей
х = хг. Это построение означает замену дуги кривой в частичном
интервале [л:0, хх] отрезком ее касательной в начальной точке.
Далее, вычисляем значе-
значение f(x, у) в найденной
точкеМ1(х19у1);/(х1,у1)
измеряет угловой ко-
коэффициент кривой в точ-
точке Мг. Откладываем по
оси Оу отрезок ONly
равный в масштабе ОР
числу f(x±, уг), и сое-
соединяем прямой точку Nx
с полюсом Р. Затем из
точки Мх проводим от-
отрезок прямой, парал-
параллельной /Wx, до пере-
пересечения с прямой х = х2. В пересечении получаем точку М2, которую
принимаем за точку интегральной кривой, соответствующую х~х2.
Таким же образом и дальше находим одну вслед за другой
точки кривой, соответствующие точкам разбиения лг3, лг4, ...
интервала [лг0, х], пока не доходим до точки М (х1 у). Вычерченная
ломаная линия М0МхМ2.. ,Мп_1М и представляет приближенно ин-
интегральную кривую, проходящую через точку М0(х0, у0).
III. Численное интегрирование. Переведем на аналити-
аналитический язык прием Эйлера приближенного интегрирования диф-
дифференциального уравнения (*).
Первая операция дает такую связь между координатами точек
Р 0
Mi
MS
No
Ht
Nn-,
Уо
У,
Уг
X.
УзУг,
M
У
Xo X, Хг Ха XQ-1& X
Рис. 218.
Мо и г
вторая операция приводит к аналогичному соотношению
A)
568
ГЛ. X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
[163
и т. д.; наконец, п~я операция дает
У— Уп-1=/(*п-1> yn-i)(x—'xn-i)* (п)
Эти п равенств позволяют последовательно вычислить значения
неизвестной функции в точках делений интервала [х0, х]. Действи-
Действительно, из первого равен-
%М ства по заданным х0У у0
и выбранному хх находим
у1у из второго по извест-
известным х1у ух и выбранному
х2 находим соответствую-
соответствующее ему значение у2 и т. д.,
пока не дойдем до иско-
искомого значения у.
Чем меньше наибольший
из частичных интервалов
и, значит, больше число
п и чем х ближе к лг0, тем
точнее будет получаться
результат.
Итак, фактическое вычисление приближенного значения у можно
производить с помощью равенств A) — (л). Этот прием является
одним из методов численного интегрирования уравнения (*).
Пример. Рассмотрим уравнение
Рис. 219.
К нему не подходит ни один из изложенных способов решения
уравнений первого порядка. Найдем приближенное решение этого
уравнения на интервале [0, 1] с начальным условием у \х=0 = 0 и
вычислим у при лг=1.
Разделим интервал [0, 1] на четыре части точками хо = 0;
лгг = 0,25; *? = 0,5; лг3 = 0,75; лг4=1 (рис. 219). Обозначим через
•Уо» Ух* Угу Уз значения У' соответственно в точках лг0, хъ х%> лг3.
Так как лго = О, уо = Оу то /0 = 1 и, значит,
Л =И^1—^о) = 0,25; Ж! @,25; 0,25).
Далее,
У1 = 0,25-0,25я+1 = 1,016.
Поэтому
Л = 0э25+1,016-0,25 = 0,504; М2 @,5; 0,504).
Затем
/а = 0,5.0,504я + 1 = 1,127,
уг = 0,504 +1,127 -0,25 = 0,786; Мв @,75; 0,786).
164J § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 569
Наконец,
/3 = 0,75-0,7862+1 = 1,463
и
^=^4 = 0,786+1,463-0,25 = 1,152.
Следовательно, у = 1,152 является искомым приближенным значе-
значением при х=\ частного решения заданного уравнения, определен-
определенного начальным условием у | x=z 0 = 0. На рис. 219 в соответствии
с нашими подсчетами проведена интегральная криЕая уравнения,
проходящая через точку @, 0).
Существуют гораздо более точные методы приближенного ре-
решения дифференциальных уравнений; они излагаются в специаль-
специальных руководствах (см., например, [7], [8]).
164*. Особые точки дифференциальных уравнений первого
порядка. Пусть дано уравнение у=/(лг, у). Предположим, что
функция /(лг, у) удовлетворяет условиям теоремы существования
и единственности решения (см. п. 158) во всех точках некоторой
области, за исключением точки (лг0, у0); такие точки мы назвали
особыми. Через каждую точку области, кроме особой, проходит
одна-единственная интегральная кривая, и наша задача состоит
в том, чтобы выяснить, как ведут себя интегральные кривые, про-
проходящие через точки, близкие к особой. Мы не собираемся зани-
заниматься общими рассмотрениями и хотим лишь на некоторых
частных примерах выяснить суть дела.
Прежде всего условимся переменные хну считать равноправ-
равноправными; это значит, что с равным основанием можно рассматривать
у как функцию от х или х как функцию от у. При этом нам
придется уточнить определение особой точки. Возьмем уравнение
-7^ = — . Точка @, 0) является для него особой, так как правая
часть разрывна при у — 0. Если же считать х функцией, а у — не-
независимой переменной и переписать уравнение в виде ^-—у> то
точка @, 0) перестает быть особой, так как теперь правая часть,
разумеется, удовлетворяет всем условиям теоремы существования.
Единственным решением этого последнего уравнения при заданном
и2
начальном условии будет функция * = у. Интегральной кривой
является парабола, касающаяся оси ординат в начале координат.
Таким образом, через точку @, 0) проходит одна интегральная
кривая, и нам нет смысла считать эту точку особой. То же самое
можно сказать и о любой другой точке оси абсцисс.
570
ГЛ. X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
[164
Поэтому в дальнейшем будем считать особой только такую точку
(лг0, у0), в которой разрывны правые части обоих уравнений
dy j.. v dx
1
Именно такой случай имеет место для уравнений
dy __Ax+ By dx Cx + Dy
dx~~~Cx+Dy H dy~
(*)
в начале координат. Функции в правых частях не имеют предела
при произвольном стремлении х и у к
нулю (см. аналогичный пример на
стр. 369).
Приведем несколько примеров ис-
исследования уравнений типа (*).
Примеры. 1) ;/= — • Разделяя
переменные и интегрируя, получим
lnj> = 2 In л: + 1п С, откуда у = Сх2.
Это уравнение семейства парабол;
записав дифференциальное уравнение
в виде xdy — 2ydx = 0, найдем еще
два частных решения у = 0 и # = 0.
Рис. 220. Все интегральные кривые проходят
через особую точку — начало коор-
координат (рис. 220). Такая особая точка называется узлом.
Предоставляем читателю проверить, что для уравнения ;г ^ ^ ~
при К > 0 особая точка также является узлом; в частности, при
Х=\ семейством интегральных кривых служат прямые, проходящие
через начало координат.
2) т^=——. Общее решение имеет вид у — —. Это семейст-
во равнобочных гипербол; к нему следует добавить оси коорди-
координат: у = 0 и л; = 0 (рис. 221). Такая особая точка называется
седлом.
Аналогичная картина будет для уравнений ~ = —Л— и
i = bj при Я>0.
dy х
3)
. Общее решение х2-\-у2 — С; интегральные кри-
кривые—окружности с центром в начале координат (рис. 222). В этом
случае особая точка называется центром; через нее не проходит ни
164] § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 571
одна интегральная кривая. Для уравнения ~=—А,—-, где К > О,
особая точка также является центром; семейством интегральных
кривых будут эллипсы с центром в начале координат.
Рис. 221.
Рис. 222.
4) A — ^i-Ll . Замена у— их приводит после простых преобразо-
преобразований к уравнению с разделенными переменными "Г* 2 du = — . Ин-
тегрируя и возвращаясь к у, получим
или
-= г sin ф) уравнение
В системе полярных координат (je = rcos(p,
имеет гораздо более простой вид
г = Се*.
Это семейство логарифмических спиралей
(см. п. 49), изображенных на рис. 223.
Особая точка такого типа называется
фокусом.
Можно доказать, на чем мы не оста-
останавливаемся, что для уравнения (*) на-
начало координат при любых значениях
коэффициентов (если только AD—ВСфО)
является особой точкой одного из указанных четырех типов: узел,
седло, центр, фокус.
Исследование особых точек уравнений более сложного вида
представляет очень трудную задачу, далеко выходящую за рамки
курса.
Рис. 223.
572 ГЛ. X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [165
§ 2. Дифференциальные уравнения второго и высших порядков
165. Дифференциальные уравнения второго порядка. Мы перей-
перейдем теперь к изучению дифференциальных уравнений вида
Р(х, У, У\ /) = 0,
в левую часть которых входит вторая производная неизвест-
неизвестной функции. Мы будем называть их дифференциальными уравне-
уравнениями второго порядка.
Обычно рассматривают уравнения, разрешенные относительно
второй производной
/=/(*, у, у'). (*)
Начнем с простого примера:
Последовательно интегрирую, найдем сначала первую производную:
jf'=?- + Ci, а затем и саму функцию:
Так как мы интегрировали дважды, то и получили две произ-
произвольные постоянные, которые обозначили через Сг и С2.
Сформулируем общий вывод, доказательство которого мы прово-
проводить не будем.
Дифференциальное уравнение второго порядка у" =f(xf yf у')
имеет бесчисленное множество решений, которые даются форму-
формулой у = у(х, С1$ С2), содержащей две произвольные постоянные.
Эта совокупность решений называется общим решением.
Частное решение уравнения отыскивается при помощи задания
начальных условий
Например, найдем частное решение рассмотренного нами уравне-
уравнения у" = х при начальных условиях ^^-=2 = 2, у'1^=2 = 3. Подстав-
Подставляя эти условия в выражения для общего решения и его производ-
производной, получаем систему уравнений
откуда
С 1 vi С —
Следовательно, искомым частным решением будет
х3 , 4
У+х
165] § 2. УРАВНЕНИЯ ВТОРОГО И ВЫСШИХ ПОРЯДКОВ 573
Геометрический смысл начальных условий заключается в том, что
помимо точки (а:0, j/0), через которую должна проходить интеграль-
интегральная кривая, мы задаем еще угловой коэффициент касательной (у'о)
к этой кривой. Отметим, что так как общее решение уравнения вто-
второго порядка зависит от двух произвольных постоянных, то через
данную точку проходит бесчисленное множество интегральных кри-
кривых, лишь одна из которых имеет данный угловой коэффициент. Так,
например, легко проверить, что если в общем решении рассмотрен-
2
ного выше примера положить С2= -^ — 2СХ, то график функции
/ 2 \
+(-о- — 2СХ] при любом значении Сх пройдет через
заданную точку B, 2). Выбирая из всех этих кривых ту, для кото-
которой угловой коэффициент равен 3, мы и приходим к искомому част-
частному решению.
Чтобы сформулировать теорему существования решения для
уравнения второго порядка вида (*), будем считать, что правая
часть этого уравнения является функцией трех независимых пере-
переменных х, у и у\ так как при задании начальных условий коорди-
координаты лг0, у0 и угловой коэффициент касательной у'о ничем между
собой не связаны.
Теорема существования и единственности реше-
решения. Если функция f(x, у, у') непрерывна в окрестности зна-
значений xQt у о, у'0> то уравнение y"=f{x, у, у') имеет решение
у=у(х) такое, что у(хо)=уо пу'(хо)=у'о.
Если, кроме того, непрерывны и частные производные —-
и J-, t то это решение уравнения единственно. Доказывать тео-
теорему мы не будем.
Пользуясь приведенной теоремой, можно, например, сразу ска-
сказать, что уравнение у" = У--\-у имеет единственное решение при
начальных условиях y\x=i = 2, Уи=1 =—1; при этом, конечно,
открытым остается вопрос, как это решение найти. Если для этого
же уравнения задать начальные условия при л; —О, то теорема
существования никакого заключения сделать не позволит, так как
правая часть уравнения при этих начальных условиях будет не
определена.
Как и для уравнений первого порядка, задачу отыскания частного
решения по начальным условиям называют задачей Крили.
Для уравнений второго порядка выделение частного решения
можно производить и путем задания краевых условий] при этом
574 ГЛ. X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [166
задаются значения функции у в двух разных точках
С такой задачей читатель может столкнуться в курсе сопротивле-
сопротивления материалов при изучении уравнения прогиба балки. Еще более
общие задачи такого типа встречаются в курсе уравнений матема-
математической физики.
Найдем, например, решение уравнения у" = х при краевых усло-
условиях y\x=i = 0 и ^1^2 = 0. Выше было показано, что общее решение
хг
уравнения имеет вид у = -тг + Сгх-{-С2. Подставляя заданные усло-
условия, составим систему двух уравнений для отыскания произвольных
постоянных
-1 + Сх + С2 = 0, у
7 х3
Отсюда Сг~—-g-, С2=1 и частное решение таково: У = -б;—
В рассмотренном примере найдено единственное частное решение,
удовлетворяющее заданным краевым условиям. Однако так будет
далеко не всегда. Может оказаться, что уравнение второго порядка
совсем не имеет решения, удовлетворяющего заданным краевым
условиям; в других случаях оно может иметь бесчисленное мно-
множество таких решений. Примеры этого будут приведены позже
(пример 2 в п. 170). В сказанном и состоит коренное отличие зада-
задания краевых условий от задания начальных условий. Если заданы
начальные условия, то теорема существования (в случае ее приме-
применимости) сразу гарантирует, что поставленная задача имеет единст-
единственное решение. Если же заданы краевые условия, то, лишь найдя
общее решение, мы сможем установить, имеет ли задача решения и в
каком количестве.
166. Частные случаи уравнений второго порядка. Возьмем
дифференциальное уравнение второго порядка
и рассмотрим частные случаи, легко приводимые к уравнениям пер-
первого порядка.
I. Правая часть уравнения не содержит ^у и ji':
/' = /(*). (*)
Так как у" = (у')', то
166] § 2. УРАВНЕНИЯ ВТОРОГО И ВЫСШИХ ПОРЯДКОВ 575
Интегрируя еще раз, будем иметь
где Сх и С2 — произвольные постоянные. Пример такого уравнения
мы уже рассматривали в п. 165.
II. Правая часть уравнения не содержит у:
/«/(*• /)• (••)
Положим y' — z; тогда y" — z' и уравнение (##) преобразуется
в уравнение первого порядка относительно z:
*W(*. z).
Если мы найдем решение этого уравнения г = ср(лг, Сх), то искомое
решение получим интегрированием равенства у' = ?, т. е.
y = )V(x, CJdx + Cr
Пример. Решим уравнение
У х
Полагая /=ги y" = zr, приходим к уравнению первого порядка
z'-\— = лг, которое оказывается линейным. Решив его, найдем
х2 Ci r x2 Ci x3 Л •
г=-з—^"it* Тогда у т~^~х и ysss-^-+ci^nx+c2.
III. Правая часть уравнения не содержит х:
y"=:f(yy у'), (***)
Положим у' =рп будем считать р функцией от у. Дифференцируя
это равенство, получим у" — -Е-. Чтобы исключить лг, произведем
следующее преобразование:
dp dp dy dp r dp
llx dy dx dy У dy ^'
Таким образом,
>¦-'%¦
Подставив в уравнение, будем иметь
т. е. уравнение первого порядка относительно р как функции от у.
Если мы найдем его решение р ~ ф (у, Сг), то искомое решение получим
576 ГЛ. X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
из уравнения с разделяющимися переменными:
dy . ^ ч dy . С dy
-fL=p=zw(y С), т. е. . *п =dx и \ * =,
Пример. Решим уравнение
Полагая у'=р и y"—p-J--y получим
[167
Это уравнение первого порядка с разделяющимися переменными.
интегрируя, получим \пр =
_. dp du
Приведя епо к виду —^- = —~^-
1
и р = -
. Определив теперь^ из уравнения
dy =
, придем к искомому решению у2 ~Сгх-\-С2, или у =
x С2) 3 . При сокращении на /? было потеряно решение уравне-
уравнения р = у' — Оу т. е. у — const. В данном случае оно получается из
общего при С2 = 0.
В обоих последних случаях мы заменяли производную у' но-
новой вспомогательной функцией и приходили, таким образом, к урав-
уравнению первого порядка. Если уравнение
имеет вид у= /(/), т. е. если оно
одновременно относится и к типу
II и к типу III, то следует выбрать тот
ход решения, который окажется более
удобным.
167. Приложения к механике.
I. Цепная линия. Найдем форму
гибкой нерастяжимой однородной нити
(цепи), прикрепленной за два конца и
находящейся под действием собствен-
собственного веса (рис. 224).
За ось Оу примем вертикальную прямую, проходящую через
низшую точку iV линии; ось Ох проведем горизонтально, на не-
неопределенном пока расстоянии от точки 7V.
Возьмем произвольную точку М линии. В условиях равновесия
кусок нити NM можно рассматривать как твердое тело. Оно подвер-
подвержено действию трех сил: силы горизонтального натяжения /У, силы
натяжения Г, приложенной в точке М и направленной по касательной
О
Рис. 224.
X
167] § 2. УРАВНЕНИЯ ВТОРОГО И ВЫСШИХ ПОРЯДКОВ 577
к линии, и собственного веса Р, равного $8, где 5—длина дуги ЛШ>
а б — вес единицы длины нити.
Согласно условиям равновесия имеем
s8, Г cos а =/Л
Разделим почленно первое равенство на второе:
tg a = -?-,.
Следовательно, если у = ф (х) есть искомое уравнение линии ANB, то
у = ks, где & = — = const.
Продифференцируем это равенство по лг:
Будем решать это уравнение, как указано в п. 166, II. Положим
y'=zt тогда yw=:z'; следовательно, получаем
откуда
In @ + ]Л-Н2 ) = ^лг + Сх.
В точке Л^ имеем лг = О и должно быть z=y' = 0 (iV—низшая точ-
точка линии). Значит, Сх = 0 и 2+ ]/l+^2 = efeA;. Переносят в правую
часть и возводя в квадрат, приходим к равенству
Интегрируя, находим
у+^=i(gftx+e"ftX)=тch **•
Выберем теперь расстояние ОЛ^ равным -г-- Тогда С2 = 0, и мы
получаем искомое уравнение линии
В этом примере наглядно видно, как, пользуясь начальными
условиями задачи, удобно последовательно находить значения постоян-
постоянных интегрирования. Предварительное составление общего решения
привело бы к более громоздким выкладкам.
19 А. Ф. Бермант, И. Г. Араманович
578 гл. х. дифференциальные уравнения 1167
Обозначая -т- через а, запишем
Это — уравнение цепной линии, которая потому так и названа,
что ее форму, как мы видим, принимает свободно подвешенная цепь.
II. Задачи динамики материальной точки. Пусть мате-
материальная точка движется прямолинейно под действием некоторой
силы, направленной вдоль линии движения точки. Согласно второму
закону Ньютона произведение массы на ускорение равно действующей
d2s
силе: mw = F1). Так как ^ = -372*5 где t — время, а s—путь, то при
отыскании закона движения мы приходим к дифференциальному
уравнению второго порядка
В обычно встречающихся задачах сила F может зависеть от време-
времени t, расстояния ^ и скорости движения v = 7, т. е. F = FU,5, ^J .
В курсах механики принято производные по времени обозначать не
штрихами, а точками: v = st w — v = s. Поэтому дифференциальное
уравнение движения примет вид
ms = F(t9 s, i). (*)
Обычно задаваемые начальные условия s|f=0 = s0 и s|f=0 = s0 имеют
ясный механический смысл: это начальное положение точки и ее
начальная скорость. Рассмотрим теперь некоторые п р и м е р ы.
1) Равномерно ускоренное движение. Пусть сила F
р «4
постоянна; обозначим отношение—через а. Тогда 5 = а. Интегри-
руя, получим: ^=а^ + С1и $ = —-j-C^-l-Cj. Сразу видно, что
C1 = 5|t=;0 = <t;0 и C2 = s |*=о = $о- Таким образом, мы получили хоро-
хорошо известную формулу для пути при равномерно ускоренном движе-
at2
нии: s = —
г) Мы не рассматриваем ускорение w и силу F как векторы, так как
из условия задачи следует, что направление силы и ускорения определяется
их знаком, В самом общем случае уравнение движения имеет видт
где г (*) — радиус-вектор движущейся точки (см. п. 70). Проектируя это
равенство на оси координат, мы придем к системе трех дифференциальных
уравнений, решение которой в общем случае представляет большие матема-
математические трудности.
167] § 2. УРАВНЕНИЯ ВТОРОГО И ВЫСШИХ ПОРЯДКОВ 579
2) Движение точки в среде с сопротивлением. Как
показывает опыт, всякое тело испытывает при движении в среде
сопротивление со стороны этой среды. Сила сопротивления возрастает
со скоростью тела и зависит как от свойств среды (плотности, вяз-
вязкости и т. д.), так и от размеров и формы движущегося тела. Если
скорость движения невелика и тело имеет малые размеры, то силу
сопротивления можно считать пропорциональной скорости v:
Коэффициент пропорциональности k > 0, а знак минус указывает,
что сила сопротивления всегда направлена против движения1).
Если скорость движения велика, то сила сопротивления становится
пропорциональной квадрату скорости, т. е.
В этом случае коэффициент пропорциональности у рассчитывается
по формуле
где р — плотность среды, S — наибольшая площадь сечения тела,
перпендикулярного к направлению движения (миделево сечение),
а С—безразмерный коэффициент, определяемый опытным путем и
зависящий от формы движущегося тела 2).
Разумеется, установить, в каком случае можно принять тот
или иной закон сопротивления, можно только опытным путем.
В качестве примера рассмотрим падение тела на землю с учетом
сопротивления воздуха.
Будем считать, что масса тела равна т и начальная скорость
его равна нулю. На тело действуют две силы: сила тяжести mg и
сила сопротивления, которую мы примем пропорциональной квадрату
скорости движения. Дифференциальное уравнение примет вид
Применяя подстановку
do
s v *
придем к уравнению первого порядка
dv
m mg
г) Например, при движении шара радиуса R в жидкости, согласно зако-
закону Стокса, ? = 6я#г), где tj—вязкость среды.
2) Определение коэффициента С производится обычно при помощи
аэродинамических труб; при этом само тело неподвижно и на него
набегает воздушный поток.
19*
580 ГЛ. X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [167
Запишем его в виде
и введем обозначения: —• = « и ^§- = Ь2. Разделяя переменные,
получим
dv ,.
Hn=dr~adi
или после интегрирования (см. формулу A1) таблицы интегралов)
Так как f|t=0 = 0, то С=0. Тогда-^L = e*abt и
w о—v
Y=b\h{abt).
Из полученной формулы следует, что скорость v всегда меньше b
и стремится к этому значению при t—+ сю. Таким образом, скорость
вовсе не возрастает безгранично, как при свободном падении в без-
безвоздушной среде, а стремится к определенному пределу — предель-
предельной скорости:
*„,=*= Y
mg
Практически предельная скорость достигается довольно быстро;
величина предельной скорости (а также время ее наступления) уве-
увеличивается вместе с массой тела и с уменьшением коэффициента
сопротивления у, что хорошо согласуется с наглядными представ-
представлениями.
Перейдем теперь к установлению связи между скоростью паде-
падения и пройденным путем; для падения без учета сопротивления воз-
воздуха, как известно, v — Y%gs> где 5 — путь, пройденный при па-
падении. Для получения нужной зависимости можно было бы, зная
скорость, интегрированием найти путь и потом искать связь между
v и s. Мы, однако, поступим проще, исключив независимую пере-
менную t из самого дифференциального уравнения. Для этого при-
применим подстановку, указанную в п. 166, III:
dv dv ds dv
s==v' s-di==7sTt==vTs-
Дифференциальное уравнение с учетом введенных обозначений при-
примет тогда вид
168J § 2. УРАВНЕНИЯ ВТОРОГО И ВЫСШИХ ПОРЯДКОВ 581
Разделяя переменные и интегрируя, получим
\n(b2 v*) a
Так как t>|sss0 = 0, то С=—~о^п^2 и> следовательно,
1 , 6*
= у1пр—^, откуда v^by I — e~2av. Заменяя а и b их значе-
ниями, получим
V=V TV 1-е™-
Из этой формулы следует, что если отношение — велико (практи-
(практически это значит, что тело плохо обтекаемо), то уже при неболь-
2VS
ших s величиной е т можно пренебречь, и мы приходим опять
к предельной скорости у — . Если же отношение -^- очень ма-
мало, то, воспользовавшись приближенной формулой е*»1-|-лг, вер-
верной для малых х (см. п. 36), найдем, что при небольших 5
v я
т. е. что приближенно верна формула для скорости при падении
в безвоздушной среде.
Рекомендуем читателю самостоятельно проанализировать случай
свободного падения тела при условии, что сила сопротивления про-
пропорциональна скорости (например, это имеет место при опускании
тела в воде), и убедиться, что и в этом случае скорость v имеет
определенное предельное значение при возрастании t.
Несколько позже, в п. 175, мы вернемся к задачам динамики и
рассмотрим гармонические колебания точки.
168. Дифференциальные уравнения высших порядков. Решение
дифференциального уравнения становится более сложным по мере
того, как в левую часть его начинают входить производные более
высоких порядков. В этом пункте мы ограничимся только основными
определениями, относящимися к уравнениям любого порядка.
Определение. Порядком дифференциального уравнения
называют наивысший порядок производной, входящей в уравнение.
Обычно имеют дело с уравнениями, разрешенными относительно
старшей производной. Тогда уравнение #-го порядка запишется
в виде
582 ГЛ. X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [169
Общее решение такого уравнения зависит от п произвольных
постоянных: у = <р(х> С1У С2, ..., Сп). Чтобы выделить частное ре-
решение, отвечающее конкретным условиям задачи, нужно задать
начальные условия; они имеют следующий вид:
т. е. при х = х0 задаются значения самой функции и ее первых
(п — 1) производных. Дифференцируя (п—1) раз общее решение и
подставляя начальные условия, мы получаем систему п уравнений
с п неизвестными Сг, С2, ..., Сп.
На вопрос о существовании и единственности частного решения
отвечает теорема, совершенно аналогичная уже приведенным ранее
для случаев #=1 и п = 2. Формулируя ее, нужно считать, что пра-
правая часть уравнения (*) — функция /—зависит от п независимых
неременных лг, у, у', . * .У у{п~1}. Если эта функция непрерывна в
окрестности начальных значений х0, у$, у01 ..., у{(?~1} и имеет не-
непрерывные частные производные по всем переменным, начиная с у,
то уравнение (*) имеет единственное частное решение, удовлетво-
удовлетворяющее заданным начальным условиям.
Укажем один тип уравнений л-го порядка, которые легко реша-
решаются при любом пу а именно
Общее решение этого уравнения мы получим, произведя последо-
последовательно п интегрирований; при каждом таком интегрировании бу-
будет появляться новая произвольная постоянная.
Пример. Реший уравнение y(lY) = sin л;. Имеем:
yi»>=—cos*+Clf
Ciy + C,* +C3,
= sin х+Сг?
Изменяя обозначения произвольных постоянных, общее решение
можно записать в виде
у = sin х + Сгх* + С2х2 + Свх + С4.
§ 3. Линейные дифференциальные уравнения
169. Линейные уравнения второго порядка. Общие свойства.
Определение. Линейным дифференциальным уравне-
уравнением второго порядка называется уравнение первой степени
(линейное) относительно неизвестной функции и ее производных.
169] § 3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 583
Будем записывать его в виде
У" + Ч <*)/ + «2 (*)У —fix). (*)
Функция f(x) называется правой частью уравнения. Если функ-
функция f(x) тождественно равна нулю, то уравнение (*) называется
линейным уравнением без правой части (или однородным). В противном
случае уравнение (*) называют линейным уравнением с правой
частью (или неоднородным).
Если в некотором интервале а^.х^.Ь функции ах (х), аг(х)
и f(x) непрерывны, то уравнение (*) при любых начальных
условиях
У \х=х.=Уо, У' \х=Хо =/о, где х0 б (а, Ь)
имеет единственное решение, удовлетворяющее этим условиям. Это
следует из того, что к уравнению (*), записанному в виде у" =
= —0i(-*r)y — а2(х)У~Ь~/(х)у применима теорема существования
и единственности решения, сформулированная в п. 165; непрерывна
и сама правая часть, и ее частные производные по у (это —а% (х))
и по у' (это —ai(*)).
Заметим еще, что линейное уравнение
РО (*)/' +Pl (Х)У' +Р2 {Х)У =/(*)
можно привести к виду (*), деля обе его части на ро(х). При этом
в тех точках, где ро(х) = О, условия теоремы существования могут
нарушиться; такие точки называются особыми1).
I. Линейные уравнения без правой части. Рассмот-
Рассмотрим сначала уравнения без правой части, т. е.
где для краткости обозначено а1 = а1(х) и а2~а2(х). В частных
случаях ах и а2 могут быть просто постоянными.
Теорема. Если уг(х) и у2(х) — решения линейного уравне-
уравнения (**), то функция у(х) = С1у1(х)-\-С2у2(х) при любых по-
постоянных Сг и С2 также является решением уравнения.
Для краткости в дальнейшем мы будем записывать решения
в виде уг и y2t а выражение С1у1^С2у2 называть их линейной
комбинацией.
Доказательство. Продифференцируем дважды функцию
С
1) С такими случаями читатель может встретиться в дальнейшем при
изучении специальных типов линейных уравнений, играющих важную роль
при решении ряда задач математической физики.
584 ГЛ. X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [169
Подставим у% у' и у" в левую часть уравнения (**). Получим
СгУг + Сгу\ + ах (Сгу[ + С2у\) + а2(Схуг + С2у2) = ^
= Сх (у'[ + агу[ + а2уг) + С2 {у\ + аху\ + а2у2).
Выражения в скобках представляют собой результат подста-
подстановки в левую часть уравнения (**) соответственно функций ух и
y2t а так как они по условию суть решения уравнения, то оба
эти выражения тождественно равны нулю и, таким образом, функ-
функция у(х) действительно удовлетворяет уравнению (**).
На основе доказанной теоремы мы можем сделать следующий
вывод о структуре общего решения линейного уравнения без пра-
правой части:
Если ух и у2 — решения уравнения (**) такие, что их отно-
отношение не равно постоянной величине (¦?• ф const), то линейная
комбинация этих функций
является общим решением уравнения.
В предыдущей теореме мы доказали, что функция Схух-\-С2у2
является решением линейного уравнения без правой части. Следо-
Следовательно, она и будет общим решением, если только действительно
содержит две произвольные постоянные. Именно поэтому исключен
случай — = /5 = const, так как тогда У2==:^Уг и выражение Схух +
(
л = (С1 + кС2)у1 фактически содержит не две произвольные
постоянные, а только одну. Ясно также, что не может служить
для образования общего решения и такое очевидное частное реше-
решение уравнения (**), как у=^0. Отметим тут же, что это решение
называют нулевым или тривиальным.
Для линейных уравнений мы можем доказать основное свойство
общего решения, которое фактически все время применяется при
решении задач, а именно то, что из общего решения при любых
заданных возможных начальных условиях может быть найдено част-
частное решение, удовлетворяющее этим условиям.
Пусть заданы начальные условия у \x=Xo=yQy y'\XssXo=yOi при-
причем точка х0 принадлежит интервалу, где функции ах (х) и а2(х)
непрерывны, т. е. где выполнены условия теоремы существования
и единственности решения. В частности, если ах и а2 — постоянные,
то х0 может быть любым. Подставляя начальные значения в выра-
выражения для общего решения и его производной, получим систему
линейных алгебраических уравнений относительно Сх и С2:
Сху
169] § 3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 585
где у10 =ух (лг0), у{0 =у[ (лг0), у20 =у2 (х0), у'2О =у2 (х0) - извест-
известные числа.
Чтобы эта система имела решение при любых правых частях,
необходимо и достаточно, чтобы определитель системы был не раве-н
нулю
ФО. (***)
У10
Ую /го
(Если этот определитель равен нулю, то система имеет решение
только при условии -^.=-^ = ^5-, т. е. заведомо не при любых
У10 /20 У О
начальных условиях у0 и у0.)
Теперь докажем основную» завершающую часть рассуждения:
если ух и у2— такие решения, что ^-ф const (в частности, ни одно
из них не является нулевым), то определитель (***) не равен нулю
ни в одной точке х0.
Предположим противное, т. е. что этот определитель равен
нулю. Тогда система линейных однородных уравнений
СъУю + С2У20 = 0, Ci/ю + С2у go = 0,
получающаяся при нулевых начальных условиях jJq^O и jjo = O,
помимо нулевого решения Сх = 0, С2 = 0 имеет бесчисленное мно-
множество других ненулевых решений; пусть С10, С20 — одно из них.
Тогда функция С1Оуг + С20у2 является решением уравнения (**)
при нулевых начальных условиях. Но так как тривиальное решение
у^0у очевидно, также удовлетворяет этим условиям, а по теореме
единственности решение должно быть только одно, то
Отсюда—=—т^== const, что противоречит условию — =^=const
#1 С20 У\
(если С20 = 0, то-у1^0, что также невозможно по условию). Итак,
предположив, что определитель равен нулю в точке х0У мы пришли
к противоречию; тем самым наше заключительное утверждение, а
с ним и оснозное свойство общего решения доказаны.
И. Линейные уравнения с правой частью. Пусть
теперь лано линейное уравнение второго порядка с правой частью
Уравнение без правой части
/' / 0, (**)
586 гл. х. дифференциальные уравнения [170
получающееся из данного уравнения (#), если вместо свободного
члена f(x) взять нуль, назовем соответствующим уравнению (*).
Докажем теорему о структуре общего решения уравнения с
правой частью (*).
Теорема. Общее решение уравнения с правой частью (#)
можно составить как сумму общего решения соответствующего
уравнения без правой части (**) и какого-нибудь частного реше-
решения данного уравнения (*).
Доказательство. Обозначим через Ф(х) общее решение
уравнения (##), а через ф (х) — какое-нибудь частное решение урав-
уравнения (*). Возьмем функцию
Имеем
/ = ф' {х) + Ф' (*), /' = Ф" (х) + Ф" (х).
Подставляя выражения для уу у\ у" в левую часть заданного
уравнения (*), найдем:
Ф" (х) + Ф" (х) + аг [Ф* (х) + Ф' (х)] + а2 [Ф (х) + Ф (х)] =
= [Ф" (х) + ахФ' (х) + я2Ф (х)] + [ф" (х) + в1ф' (х) + я2ф (х)].
Выражение в первой квадратной скобке равно нулю, ибо Ф(л:) —
решение уравнения без правой части (**), а выражение во второй
квадратной скобке равно f(x), ибо ф(#) — решение уравнения с
правой частью (*). Следовательно, функция у — Ф(х) + Ц)(х) дейст-
действительно есть решение уравнения (*). Так как это решение зависит
от двух произвольных постоянных (от них зависит функция Ф(х)I
то оно и есть общее решение, что мы и хотели доказать.
Итак, для того чтобы найти общее решение уравнения с правой
частью, нужно найти общее решение соответствующего уравнения
без правой части и лишь одно какое-нибудь частное решение за-
заданного уравнения. Это можно записать так:
где уг и у2 — частные решения соответствующего уравнения без пра-
правой части, а <р(х) — частное решение уравнения с правой частью.
170. Уравнения второго порядка с постоянными коэффициен-
коэффициентами без правой части. Решением линейных уравнений второго по-
порядка с переменными коэффициентами аг и а2 мы заниматься не
будем; задача эта слишком сложна. Мы будем рассматривать толь-
только линейные уравнения с постоянными коэффициентами, т. е.
уравнения
170] § 3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 587
где ах и аг — постоянные величины. Как и раньше, начнем с урав-
уравнений без правой части.
Возьмем однородное линейное уравнение второго порядка
где ах и а2—постоянные. Поставим перед собой цель — найти об-
общее решение такого уравнения.
Попробуем удовлетворить уравнению (**) функцией вида у = егх
(г — константа). Читателя не должна смущать кажущаяся с первого
взгляда произвольность выбора этой функции. Внимательно просле-
проследив за простейшими выкладками, которые мы сейчас приведем, он
убедится, что особенности показательной функции действительно
дают повод ожидать, что при некотором определенном г функция
егх будет решением уравнения (##).
Имеем
Следовательно, должно иметь место тождество
erx{r* + axr+az) = 0
или, так как егхф0}
r* + air + at = 0. (A)
Отсюда видно, что функция егх будет решением дифференциаль-
дифференциального уравнения (**), если г будет корнем квадратного уравнения (А).
Уравнение (А) называется характеристическим.
Чтобы составить характеристическое уравнение, нужно в данном
дифференциальном уравнении (**) у заменить единицей, а каждую
производную искомой функции (у' и у") — величиной г в степени,
равной порядку производной (г и г2).
Следует различать три возможных случая для корней гх и г2
характеристического уравнения (здесь везде предполагается, что
коэффициенты ах и а2 — действительные числа):
1) ri и Г2 — Действительные и различные числа: гхфг2;
2) гх и г2 — действительные и равные числа: /*1 = г2(г1 — дву-
двукратный корень уравнения (А));
3) гх и г2 — комплексные сопряженные числа: г1 = а+р/, г2 =
Рассмотрим каждый из этих случаев в отдельности.
1) Корни характеристического уравнения дейст-
действительные и различные: ггфг2. При этом оба корня могут
быть взяты в качестве показателей г функции егху и мы сразу по-
получаем два решения уравнения (•**): ег*х и ег*х. Ясно, что их отно-
ег»х
шение не является постоянной величиной; =ze(rz~r*)x%
588 ГЛ. X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [170
Общее решение в случае действительных и разных корней
характеристического уравнения дается формулой
где Сг и С2— произвольные постоянные.
Легко проверить, что определитель (***) п. 169, I в данном слу-
случае не равен нулю.
Составим этот определитель, задаваясь каким-нибудь значением х0:
v 2 i;
Так как г2фг1У то этот определитель ни при каком значении х0
не равен нулю.
Пример. Решим уравнение
У*-/— 2у-0,
Составим характеристическое уравнение
г2—г-2 = 0.
Его корни суть
^ = 2, г2=-1.
Поэтому общим решением будет
Найдем частное решение по начальным условиям у\х~0~2>
^=о===—5. Составим систему уравнений относительно Сг и С2:
2СХ —С2=—5.
Отсюда Сг=—1, С2 = 3 и искомым частным решением будет
2) Корни характеристического уравнения дейст-
действительные и равные: г1 = г2. В этом случае мы непосредственно
получаем только одно решение ух = ет*кч Покажем, что в качестве
второго решения можно взять функцию
Продифференцируем дважды функцию у2:
170] § 3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 589
Подставим найденные выражения в левую часть уравнения (*#):
- е'« [x(rl + ахгх + а2) + Bгг + аг)].
Поскольку гх — корень характеристического уравнения, то г^-Ь
+ а1г1+а2 = 0; а так как гг—двукратный корень, то по формуле
Виета rl-\-rl——аъ т. е. 2г1 + ^1 = 0. Таким образом, выраже-
выражение, заключенное в квадратной скобке, равно нулю, и функция
у2 = хег*х действительно является решением уравнения (**).
Итак, в случае действительных равных корней характеристи-
характеристического уравнения общее решение уравнения (**) имеет вид
И здесь легко проверить, что определитель (*##) п. 169, I ни
при каком значении х0 не равен нулю:
Пример. Решим уравнение
/'_6/
Характеристическое уравнение
г2—
имеет один двукратный корень
^1 = ^ = 3,
значит, общее решение уравнения запишется так:
3) Корни характеристического уравнения — ком-
комплексные сопряженные числа: г1 = а + /р, г2 = а—гр,
р =7^= 0. Если допускать в качестве решений комплексные функции
действительного переменного (см. § 6 гл. 4I), то, как и выше,
получаем два решения уравнения (**): е{*+1&* и е{*~*$)х, причем их
отношение, равное «alFf не есть постоянное число. Общее решение
можно записать как
где Сх и С2—произвольные комплексные постоянные. Предо-
*) Если читатель не знаком с содержанием этого параграфа, то он мо-
может ограничиться запоминанием окончательного вывода, выделенного жир-
жирным шрифтом, и разбором примеров.
590 ГЛ. X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [170
ставляем читателю воспользоваться правилами дифференцирования
комплексных функций и проверить, что написанное выражение
является решением.
Для того чтобы получить решение в действительной
форме, воспользуемся следующим простым правилом: если уравне-
уравнение (**) с действительными коэффициентами имеет комплексное реше-
решение у — и (x)-\-iv(x), то каждая из функций и(х) и v(x) является
решением этого уравнения. В самом деле, дифференцируя функцию
у и подставляя результат в уравнение, получим
(„" + iv») + п1 (и' + iv') + а2 (и + iv) = 0,
или после перегруппировки слагаемых
{и" + аги' + а2и) + i (v" + ар' + a2v) = 0.
Так как комплексное выражение равно нулю только тогда, когда
равны нулю его действительная и мнимая части, то должно быть
и" + аги' + а2и = 0 и v" + axv' ¦+¦ a2v = 0,
но это и значит, что функции и (х) и v(x) являются решениями.
Так как по формуле Эйлера (см. п. 74)
х + ie«x sin рлг,
то в силу указанного правила функции е*х cos рл: и еах sin рл: явля-
являются решениями уравнения (**); ясно, что их отношение не есть
постоянная. Зная два частных решения, строим общее решение:
у = Схе*х cos рлг + С2е*х sin рлг = е*х (Сг cos рл: + С2 sin рл:),
где Сх и С2 — уже действительные постоянные. Второе решение
в комплексной форме е{Л~1&* нам даже не понадобилось; строя
общее решение по его действительной (е*х cos рл:) и мнимой
(— еа*зтРл:) частям, мы, очевидно, получим то же самое.
Итак, в случае комплексных сопряженных корней характерис-
характеристического уравнения общее решение имеет вид
у = е*х (Сх cos р* + С2 sin fix).
Предоставляем читателю лишний раз проверить, что и здесь
определитель (***) п. 169,1 не равен нулю.
Примеры. 1) у" — 4/+13j/ = 0.
Записываем характеристическое уравнение
Его корни суть
171] § 3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 591
Поэтому общее решение будет
у = е2Х (Сх cos Зл: + С2 sin Зх).
2) у" + ®*у = о (со = const).
Из характеристического уравнения
г2 + со2 = О
находим
/"! = ©*', Г2= —0)/.
Поэтому
у = сх cos сод; + С2 sin coat.
Полученное общее решение можно записать в несколько ином
виде, если ввести другие произвольные постоянные при помощи
условий
С1 — А sin ф, С2 = Л cos ф.
(Отсюда A = i/rC21 + Cl и tgq>=:?O Тогда
j; = Л (sin ф cos сод: -f- cos ф sin (ох) = Л sin (сад: + ф).
Задавая любые начальные условия, найдем единственные значе-
значения постоянных Сх и С2 или Л и ф.
Покажем, что при задании краевых условий (см. конец п. 165)
картина может быть иной. Пусть для определенности со = 1; тогда
общее решение у = Сг cos x + C2 sin x. Зададим условия ^|х=:0 = 0,
у | x=v.=y0. Из первого условия следует, что Сх = 0; из второго
условия C2sin:nc=^0 заключаем, что если у0ф0у то найти Сг
нельзя, т. е. что решения с заданными краевыми условиями не
существует. Если же уо = О, то любая функция y = C2sinx удов-
удовлетворяет и уравнению, и краевым условиям. Предоставляем чита-
читателю проверить, что если второе условие задать в любой точке
, то задача будет иметь единственное решение.
171. Уравнения второго порядка с постоянными коэффициен-
коэффициентами с правой частью. Рассмотрим теперь линейное уравнение
с постоянными коэффициентами а1 и а2 и с правой частью, т. е.
Нам уже известно (см. п. 169, II), что общее решение такого
уравнение слагается из общего решения соответствующего урав-
уравнения без правой части и какого-нибудь частного решения урав-
уравнения с правой частью.
Поскольку общее решение уравнения без правой части мы
находить умеем, то остается только найти частное решение дан-
данного уравнения (*). Сначала мы рассмотрим некоторые частные
592 ГЛ. X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ A71
случаи, в которых решение находится методом неопределенных
коэффициентов, а потом укажем и общий метод.
1. Пусть правая часть уравнения (*) имеет вид
где Р(х) — многочлен. Тогда уравнение (#) имеет частное реше-
решение вида
k
где Q(x)— многочлен той же степени, что и Р(х), причем если
число т не является корнем характеристического уравнения
г2 -|- axr -f- a2 as 0, то 6 = 0, а если является, то к — кратность
этого корня.
Принимая решение в указанной форме, мы находим неизвестные
коэффициенты многочлена Q(x) по методу неопределенных
коэффициентов.
Правило сохраняет свою силу и тогда, когда т = 0, т. е. в пра-
правой части стоит только многочлен; в этом случае надо проверить,
не является ли число 0 корнем характеристического уравнения.
В частных случаях многочлен Р{х) может быть нулевой степени,
т. е. постоянной величиной.
Приведем примеры, которые помогут читателю уяснить указан-
указанный прием отыскания частного решения.
Примеры. 1) у'—2у'+у=\+х; J>L=O = 2> /l*=o=—3-
Здесь характеристическое уравнение
Г2_2/-+1==О
имеет двукратный корень г=1. Значит, общее решение соответст-
соответствующего однородного уравнения будет равно
Правая часть уравнения имеет рассматриваемую форму, причем
/я = 0, Р(х) = \-\-х. Так как число 0 не является корнем характе-
характеристического уравнения, то частное решение ищем в виде
где Л, В—постоянные, подлежащие отысканию.
Дифференцируя и подставляя в дифференциальное уравнение,
находим
Приравнивая коэффициенты в обеих частях равенства
Л=1, — 2А+В=\,
получим А = 1, В »= 3. Итак, частным решением заданного
171] § 3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 593
уравнения является функция
а его общим решением—функция
После того, как найдено общее решение уравнения, находим по
начальным условиям частное1). Для этого найдем
/ A 2)
Тогда
2 = С1 + 3, —3 =
Отсюда Сг** — 1, С2=-—3. Искомым решением будет функция
2) /' — 4у у
Здесь характеристическое уравнение
г2 —
имеет корни r1=\i г2 = 3. Значит, общее решение соответствую-
соответствующего уравнения без правой части будет иметь вид
Правая часть имеет рассматриваемую форму, причем Р(х)~3ут. е#
является многочленом нулевой степени; число т — 2 не является
корнем характеристического уравнения, поэтому & = 0. Частное ре-
решение ищем в виде
у = Ае2Х,
где А — постоянная, подлежащая отысканию.
Тогда у' ~2Ае2Ху у" = 4Ае2Х. Подставляя значения у, у' к у" в
уравнение, получим
* =« Зе2Х,
откуда Л=—3. Следовательно, частным решением будет функция
у = — Зе2*, а общим
3) jr' —4у у
Здесь левая часть уравнения такая же, как в примере 2. По-
Поэтому общее решение соответствующего уравнения без правой части
J) Нами уже было найдено одно частное решение i/ = ^ + 3, но оно не
соответствует начальным условиям. Мы использовали это решение для на-
нахождения общего решения уравнения, а теперь из него получаем частное
решение, уже удовлетворяющее данным начальным условиям.
594 ГЛ. X, ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [171
запишем сразу:
Так как теперь /и=1, т.е. т является однократным корнем харак-
характеристического уравнения, то &=1; Р(х) = х— многочлен первой
степени. Поэтому частное решение ищем в виде
у = х (Ах + В) ех = (Ах2 + Вх) ех.
Дифференцируем дважды:
у1 = BАх + В)е* + (Ах2 + Вх) ех,
у" = 2Аех + 2 BАх + В) ех + (Ах2 + Вх) е*
и подставляем в уравнение:
2Аех + 2 BАх + В) ех + (Ах;2 + ^) ех — 4 [BЛл; + #) «* +
+ (Ах2 + Вх) е*] + 3 (Ах2 + Вх) ех = еЛ (— 4Лх + 2Л—2В) = лге*.
Отсюда
2Л — 2Я = 0, — 4Л=1,
т. е.
Итак, мы нашли частное решение ^=—-^ (х2 + х) е*, а следова-
следовательно, и общее:
2. Пусть правая часть уравнения (*) имеет вид
f(x) = a cos nx-\-b sin wjc.
Если числа +^ не являются корнями характеристического
уравнения, то уравнение имеет частное решение вида
у = A cos nx + В sin я*.
Если же числа +ш служат корнями характеристического
уравнения, то частное решение имеет вид
у = х (A cos /м; -j- #sin nx).
В частных случаях, когда а = 0 или 6 = 0, решение все равно
следует искать в указанном полном виде.
Примеры. 1) /' + 4/ + iay = 5sin2x.
Характеристическое уравнение г2 + 4г+13=*0 имеет корни
/•=—2±3*\ Значит, общее решение соответствующего уравнения
171] § 3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 595
без правой части запишется так:
у = е~2Х (Сх cos 3* + С2 sin Злг).
Так как числа ± 21 не являются корнями характеристического
уравнения, то частное решение неоднородного уравнения ищем в виде
у = A cos 2x + В sin 2x.
Дважды дифференцируем:
у' = — 2 A sin 2х + 2В cos 2лг,
у" = — 4A cos 2дг — 4? sin 2x
и подставляем в уравнение:
с — 4В sin 2х — 8Л sin 2дг + 8? cos 2дг + 1 ЗА cos 2дг +
Приравнивая друг другу коэффициенты при sin 2л; и cos 2л; в обеих
частях равенства (справа коэффициент при cos 2x равен нулю),
получим
8 9
Отсюда А=—7ю, Z? = kq, т. е. частным решением будет функция
о г\
, а общим
^к sin 2x.
2) у" y
Общее решение соответствующего уравнения без правой части
мы уже нашли на стр. 591:
у = Сг cos сол: + С2 sin солг.
Если /1=^@, то частное решение данного уравнения ищем в виде
у = A cos nx + B sin nx.
Дифференцируя и подставляя в уравнение, получим (рекомендуем
читателю проделать выкладки самостоятельно)
А (со2 — п2) cos пх + В (со2 — п2) sin nx = a sin ял;,
Отсюда
Л = 0 и 5=—?_.
(О2 — Л2
Поэтому общее решение неоднородного уравнения таково;
у = Сг cos сод: + С2 sin @* + ^^^ sinnx.
596 ГЛ. X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Если же /2 = со, то это решение не годится. В этом случае част-
частное решение ищем в виде
у = х (A cos сод: + В sin сод;).
Имеем
у = (A cos сод; + В sin сод;) -\- хсо (— A sin сод; + В cos сод;),
у" = 2со (— A sin оздг + В cos содг) — л;©2 (A cos co# + Л sin сод;).
Подставляя в уравнение, находим
2со (— A sin сод; + В cos сод:) — дгсо2 (A cos сод: + В sin co#) +
-f- jcco2 (A cos сод; -f В sin сод;) = a sin сод;,
т. е.
2со (— A sin сод: + В cos сод:) = a sin сод;,
откуда
Итак, функция
у— —— х cos сод;
является частным решением уравнения при л = <о.
Следовательно, общим решением будет
у = С1 cos сод: + С2 sin сод; — ^~ х cos сод;.
Перейдем теперь к самому общему виду правой части, при ко-
котором еще можно применять метод неопределенных коэффициентов.
3. Если в уравнении (*) правая часть имеет вид
f(x) = етх [Pt (x) cos nx + Р2 {х) sin nx],
где Рг(х) и Р2(х) — многочлены, а числа m-j-ш не являются
корнями характеристического уравнения, то ""частное решение
следует искать в виде
у ss етх [/?х (х) cos nx + /?2 (х) sin nx],
где /?х(л) и R2(x) — многочлены степени, равной высшей из сте-
степеней многочленов Рх(х) и Р2(х).
Если числа m~\-in являются корнями характеристического
уравнения, то указанную форму частного решения следует умно-
умножить на х.
Случай I получается из приведенного общего при # = 0, а слу-
случай 2 при /я = 0, Р1(х) = а, Р2(х)=Ь.
Заметим, что в результате решения может случиться, что сте-
степень одного из многочленов R± (x) и R2 (x) будет меньше взятой
первоначально, т. е. некоторые старшие коэффициенты этого мно-
многочлена окажутся равными нулю.
171] § 3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 597
Пример. /' +у s 4лг sin лг.
Здесь /я = 0, /г=1 и ±/ суть корни характеристического урав-
нения г2+1=0. Поэтому частное решение ищем в виде
у = х [(Ах + В) cos # + (А* + fii) sin ХЬ
Имеем
/«[ — А*»+ D^ — B)* + Bi4 + 2B1)Jcoe* +
+ [ — Агх2 - D А + ?а) л: + {2АХ — 2В)) sin x.
Подставляя в уравнение, находим
[2Агх + (А + ?х)] cos х + [ — 2Ах + (Лх—?)] sin х = 2^ sin *.
Это равенство будет тождественным только при
2Л1==0, Л + В1==О, -2Л = 2, Ах—Я=0,
Отсюда
Л=— 1, Я=0, Лх = 0, ^ = 1.
Следовательно, получаем частное решение
у = х (sin лг—х cos лг).
Общее решение дается формулой
у == С± cos л: + Q sin л: + л: (sin х — л: cos л:). %
Практически важно учесть следующее простое замечание.
Пусть правая часть уравнения у"-{-агу'-\-а2у ~f (х) равна
сумме двух функций: /(х)=/1(х)-\'/2(хI а ух и у2 суть решения
уравнений с той же левой частью, но с правыми частями, соответ*
ственно равными /г(Х) и /2 (х); тогда уг-\~у2 будет решением дан*
кого уравнения.
В самом деле,
+У2) = (yl
У + а2у2) = Д (х) + Д
Это значит, что если мы умеем найти решения уравнения, когда
правыми частями его являются отдельные слагаемые заданной пра-
правой части, то мы очень просто —в виде суммы решений —находим
и все искомое решение.
Например, в силу этого замечания уравнение (см. примеры 2 и 3
на стр. 593—594)
у _ 4/
имеет частное решение
598 ГЛ. X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ГД 72
Я, значит, такое общее решение:
у = Cte* + С2е3* - Зе2*—1 (*» + *) в*.
172. Метод вариации произвольных постоянных *)¦ Изложим
теперь метод, позволяющий отыскивать частное решение линейного
уравнения с правой частью
где /(#)-— любая функция.
При использовании этого метода нам нужно знать общее реше-
решение соответствующего уравнения без правой части. Метод вариации
постоянных в равной мере применим как к уравнениям с постоян-
постоянными коэффициентами, так и к уравнениям, в которых коэффициенты
ах и а2 являются функциями от х. Однако, так как мы умеем
решать лишь уравнения с постоянными коэффициентами, то и изла-
излагаемый метод практически мы сможем применять только к таким
уравнениям.
Пусть уравнение без правой части, соответствующее уравнению (*)
У" + аху' + <*>2у = 0 (**)
имеет общее решение
где Сх и С2 —произвольные постоянные.
Будем искать решение уравнения (•*) в виде
у = Сг (х) ух + С2 (х) у2, (***)
где Сх(х) и С2(х) — неизвестные функции, подлежащие определению,
а Ух и У г — известные частные решения уравнения без правой
части (**). Будем в дальнейшем для краткости вместо ^(л;) и
С2 (л:) писать просто Сх и С2, помня, что они являются функциями
от х. Поскольку определелию подлежат две функции Сх и С2, то
одним соотношением между ними мы можем распорядиться по про-
произволу. Продифференцируем равенство (***):
у=
Оказывается, что наиболее целесообразно подчинить Сг и С2 такому
условию, чтобы выражение для у' имело тот же самый вид, что и
при постоянных Сх и С2.
Для этого положим
2 = 0. (А)
Этот метод принадлежит Лагр-анжу.
172] § 3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 699
Тогда
Продифференцируем еще раз:
/' = С'гу'г + Сгу\ + С2у2
Подставим у, уг и у" в левую часть уравнения (*):
С\у\ + Ctyl + С2у2 + С2у + а^у'г + агС2у2 + а2Схуг + а2С2у2 =
= С[у\ + С2у2 + Сг (у[ + алу\ + а2уг) + С2 (у\ + aj2 + а2у2) = / (х).
Выражения в обеих скобках равны нулю, так как ^i и ^2
являются решениями уравнения без правой части (**). Значит,
чтобы функция у = Сгуг + С2у2 была решением уравнения (*), по*
мимо условия (А) должно еще соблюдаться условие
y (Б)
Таким образом, мы приходим к системе уравнений
Определитель этой системы, как мы уже отмечали в п. 169, I
в нуль не обращается:
и поэтому мы можем сначала найти Сх и С2, а затем интегрирова-
интегрированием и сами функции Сг и С2. Если при интегрировании произ-
производных С[ и С2 ввести произвольные постоянные, то мы сразу
получим общее решение неоднородного уравнения.
Пример. Решим уравнение
У"
Однородному уравнению У'+^==0 соответствует характеристиче-
характеристическое уравнение г2+1 = 0. Его корни г = ±*'. Поэтому ух = cosx
и y2 = s\nx.
Запишем решение данного уравнения в виде
у = Сг cos х + С2 sin х
и составим систему уравнений для отыскания С± и С2:
Cjcos х + С2 sin х = 0,
—С\ sin х + С2 cos at = tg x.
600 ГЛ. X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [173
Решив эту систему, найдем
Интегрирование дает
(см. формулу 69 таблицы интегралов),
С2 = J sin а; */л; = — cos x
где k% и &2—произвольные постоянные.
Теперь запишем общее решение заданного уравнения:
у = sin л;—In teff"+ -тг) +*i| cos* + [—cosAr + ^
= kx cos x + k2 sin x — cos л: In tg ( т + т) •
173. Линейные дифференциальные уравнения и-го порядка.
Изложенная в предыдущих пунктах теория линейных дифферен-
дифференциальных уравнений второго порядка легко переносится на линейные
уравнения я-го порядка (я>2).
Линейное уравнение /г-го порядка имеет вид
(•)
где коэффициенты av а2, . •., ап_19 ап—функции независимой
переменной х или постоянные величины.
Так же как и раньше, наряду с данным неоднородным
уравнением всегда будем рассматривать соответствующее ему
однородное уравнение (без правой части)
Чтобы сформулировать основную теорему о структуре общего реше-
решения такого уравнения, введем понятие линейной независи-
независимости системы функций.
Рассмотрим систему функций ф2 (л;), ф2 (л:), . . ., фл (л:), опре-
определенных в одном и том же интервале. Напомним, что линейной
комбинацией этих функций мы условились называть выражение
С1ф1 (х) + С2ф2 (*)+...+ Спуп (х),
где Cv С2, ..., Сп — постоянные величины.
Определение. Система функций срх(х), <р2(х), ..., срп(х)
называется линейно независимой, если ни одну из этих функ-
функций нельзя представить в виде линейной комбинации остальных.
173] § 3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 601
Это означает, например, что не может быть равенства
где ft2, ..., kn — постоянные величины.
Отсюда следует, что ни одна из линейно независимых функций
не может тождественно равняться нулю. Если, например, было бы
ф1(л:)^0, то указанное равенство выполнялось бы при &2 =
= ...=*„=<>.
В частности, две функции фг (л:) и ср2 (лг) линейно независимы,
если их отношение не есть константа: -^-т-т т? const.
Ф1W
Система функций, не являющаяся линейно независимой, назы-
называется линейно зависимой. Например, линейно зависимой будет
система
*• Ф2(*) = *2» Фз (*) = *3> Ф4и) = 2лг — х2.
Действительно, функция ф4 (х) является линейной комбинацией
остальных:
(При этом вовсе не обязательно, чтобы (рп(х) выражалось через
все остальные функции.)
Сформулируем теперь теорему о структуре общего решения
уравнения (**).
Теорема. Если yv у2, ..., уп суть п частных линейно неза-
независимых решений уравнения (**), то общим решением этого
уравнения является их линейная комбинация
У = С&ъ + С2;у2 +... + СпУп. (•#•)
Доказательство этой теоремы проводится так же, как и для
уравнений второго порядка (см. п. 169), и мы рекомендуем чита-
читателю провести его самостоятельно.
Если решения yv Уъ,...,Уп линейно зависимы, то по
крайней мере одно из них линейно выразится через остальные
п — 1 и функция (**#) будет фактически зависеть не от п, а от
меньшего числа произвольных постоянных. Она не будет доставлять
общего решения.
Существует простое условие линейной независимости частных
решений yv y2J ...,JV Именно, этим условием служит неравенст-
неравенство нулю так называемого определителя Вронского1) (или
вронскиана), составленного из функций yv y2, ...,уп и их
И. Гоэне-Вронский A778—1853) — известный польский математик.
602
производных!
ГЛ. X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
[173
У»
У2
У*
Уп
Уп
=7^0.
Знак неравенства означает, что определитель не может рав-
равняться нулю ни при каком значении х. Доказательство этого усло-
условия в общем случае мы не приводим; для п = 2 оно приведено
в п. 169, I. Этот определитель играет важную роль при отыскании
частного решения по заданным начальным условиям.
Действительно, если заданы начальные условия
то, чтобы из общего решения
получить частное, надо решить систему линейных алгебраических
уравнений относительно постоянных Cv C2, ..., Сп:
+...+ С„уп0=у0,
{п~1У>
Здесь через у$ обозначено значение k-Pi производной от частного
решения у( в точке х0. Определитель этой системы
У20 ... У по
Ухо Уъо • • • Упо
V" =
Ухо
У20
Упо
есть значение определителя Вронского в точке х = х0. Как мы
только что отметили, если система частных решений j^, y2i . ..,^л
линейно независима, то этот определитель в любой точке х0 отли-
отличен от нуля, если при этом значении х0 все коэффициенты урав-
уравнения (**) непрерывны. Следовательно, система линейных уравнений
относительно произвольных постоянных Сх, С2, ..., Сп всегда имеет
единственное решение. В частности, нулевым начальным условиям
(у0 =у0 = . #. r=^(ort") = 0) соответствует нулевое решение системы
Сх = С2 ==,..= Cw = 0,
т. е. функция, удовлетворяющая уравнению (#*) и нулевым началь-
начальным условиям, тождественно равна нулю.
173] § 3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 603
О линейно независимых решениях линейного уравнения п-го по-
порядка говорят еще, что они образуют фундаментальную
систему решений.
Общее решение линейного уравнения я-го порядка с правой
частью (*) слагается из общего решения соответствующего ему
уравнения без правой части (**) и какого-либо частного решения
самого уравнения. Доказательство этого проводится точно так же,
как и для уравнений второго порядка.
Метод вариации произвольных постоянных (см. п. 172) употреб-
употребляется и в случае линейных уравнений любого порядка я. Для его
применения нужно только знать фундаментальную систему решений
соответствующего уравнения без правой части.
Рекомендуем читателю самостоятельно придти к следующему
выводу.
Если yv у2) ..., уп— фундаментальная система решений урав-
уравнения
то решением уравнения
является функция
где С1У С2, ..., Сп—функции независимой переменной, производные
которых Си С2, ..., Сп удовлетворяют следующей системе п ли-t
нейных алгебраических уравнений:
+...+Спуа =0,
+ С2у2 +...+Спу'п =0,
(Первые (п—1) уравнений этой системы выбираются по нашему про-
произволу с таким расчетом, чтобы производные до (п — 1) порядка
включительно от функции С1у1 + С2у2 + ... + Спуп имели тот же
самый вид, что и при постоянных Сх, Са, ..., Сп. Если мы теперь
найдем п-ю производную и подставим выражения всех производных
в данное уравнение, то мы получим последнее уравнение системы.)
Чтобы лучше запомнить систему уравнений для отыскания
Си С2, ..., Сп, заметим, что определитель этой системы есть как
раз определитель Вронского (отсюда следует, что эта система имеет
единственное решение), а правые части уравнений все, кроме послед-
последней, равны нулю. В последнем уравнении правая часть равна /(#)-—
правой части данного неоднородного уравнения.
604 ГЛ. X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [174
174. Линейные дифференциальные уравнения я-го порядка
с постоянными коэффициентами. Решение линейных уравнений
с постоянными коэффициентами любого порядка производится совер-
совершенно аналогично решению уравнений второго порядка. Мы ограни-
ограничимся поэтому только самыми краткими указаниями. Начнем с урав-
уравнения /2-го порядка без правой части
-» + а,/»-» +...+*„_!/ + апу = О,
где av a2, ...уап„1У ап—действительные постоянные.
Характеристическим уравнением для него называется уравнение
л-й степени
Имеет место следующее предложение, обобщающее для любого
порядка п предложение, полученное нами для п = 2:
1) Каждому ^-кратному действительному корню г характери-
характеристического уравнения соответствует k частных решений вида
огх у-ргх yk — lprx
2) Каждой паре 1-кратных комплексно сопряженных корней
гг = a -f- р/, г2 = а — р/, характеристического уравнения соот-
соответствует 2t частных решений вида
e^cosp^, ^axcosP^f ..., хЫ1еяхсо8^х9
е*х sin Pjc, xe*x sin Рд:, ..., jc'-1*"* sin рл:.
Общая сумма кратностей всех корней должна равняться степени
характеристического уравнения п\ поэтому число всех частных ре-
решений будет в точности совпадать с порядком уравнения.
Доказательство того, что указанные частные решения линейно
независимы, т. е. образуют фУнд,аментальнУю систему решений,
мы не приводим.
Чтобы найти общее решение заданного уравнения, нужно взять
линейную комбинацию указанных частных решений.
Пример. ym+y{lV) + 2y'" '
Характеристическое уравнение
как легко заметить, имеет корень г = —1; после деления на
уравнение принимает вид
т. е.
Значит, имеем
175] § 3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 605
Поэтому общее решение заданного дифференциального уравнения
запишется так:
у = сге~х + (С, + Csx) cos x + (С4 + Сьх) sin x.
Отыскание частного решения уравнения с правой частью
где /(х) имеет вид
/ (х) =* етх [Рг (х) cos пх + Р2 {х)
производится по тем же правилам, что и для уравнений с правой
частью второго порядка (п. 171).
Оказывается, что уравнение имеет частное решение вида
у = xkemx [Rx (лг) cos пх + R2 (х) sin nx)y
где Ri(x), R2(x) — многочлены степени, равной высшей из степеней
многочленов Рх(х), Я2 (•*)> a k — кратность, с которой m±ni входят
в число корней характеристического уравнения. Если m±ni не
являются корнями характеристического уравнения, то k принимаем
равным нулю. Если правая часть уравнения f(x) не является
функцией указанного вида, то следует применить метод вариации
произвольных постоянных.
175. Колебания. Резонанс.
I. Механические колебания. Задачи о колебаниях
занимают значительное место в ряду важных задач современной
техники и физики. В большом числе случаев явления колебаний
описываются линейными дифференциальными уравнениями второго
порядка (линейные колебания), которые в простейших условиях
имеют постоянные коэффициенты. Рассмотрим сначала механи-
механические колебания.
Допустим, что на движущееся тело (массу для простоты будем
считать равной единице) действует сила, стремящаяся вернуть
тело в состояние равновесия, причем величина силы пропорциональна
отклонению от положения равновесия. Если обозначить через 5
расстояние тела от положения равновесия, а через со2 — коэффи-
коэффициент пропорциональности, то величина силы будет равна oJs.
Указанная сила называется восстанавливающей силой; со называется
коэффициентом восстановления.
Далее, пусть движение происходит при наличии сопротивления
среды. Силу, возникающую при этом, предположим пропорциональ-
пропорциональной скорости движения. Она направлена в сторону, обратную
направлению движения, а ее величина равна 2ks, если через 2й
обозначить коэффициент пропорциональности. Эта сила называется
силой сопротивления^ a k — коэффициентом сопротивления.
606 ГЛ. X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [175
Наконец, допустим, что на систему действует посторонняя
заданная сила /(*), выраженная как функция времени t. Ее назы-
называют возмущающей силой (точнее, внешней возмущающей силой).
Составим дифференциальное уравнение движения. Для получения
равнодействующей всех сил нужно, очевидно, восстанавливающую
силу и силу сопротивления взять со знаком минус, ибо первая
направлена в сторону, противоположную направлению отсчета s>
а вторая противоположна скорости. Таким образом, приходим
к уравнению
s = —2Ajs--
или
Итак, указанные явления механических колебаний описываются
линейными дифференциальными уравнениями второго порядка с по-
постоянными коэффициентами.
Если внешняя возмущающая сила отсутствует (/(^) = 0), то
колебание называется свободным или собственным, свободному коле-
колебанию отвечает однородное уравнение, соответствующее урав-
уравнению (*). При наличии возмущающей силы говорят, что колебание
вынужденное,— такое колебание описывается неоднородным урав-
уравнением (*), правая часть которого /(/) называется иногда возму-
возмущающим членом.
Восстанавливающей силой может быть сила упругости.
Реально такой случай осуществляется, например, при следующих
обстоятельствах. К вертикальной пружине подвешен груз, в точ-
точности уравновешивающийся силой упругости пружины. Если груз
выводится вертикальной силой из состояния равновесия, то в даль-
дальнейшем он будет совершать колебания — свободные при отсутствии
дополнительной силы, действующей на груз или на всю систему,
вынужденные при наличии ее (например, когда сама точка привеса
пружины по некоторому закону перемещается по вертикали). Сила
противодействия пружины (восстанавливающая сила) будет дейст-
действительно пропорциональна отклонениям (деформациям), как это
следует из закона Гука. Коэффициент восстановления есть
«жесткость» пружины.
II. Исследование свободных колебаний. Перейдем
к применениям известных нам решений линейных уравнений с посто-
постоянными коэффициентами к исследованию колебаний. Начнем со сво-
свободных колебаний
Характеристическое уравнение г2 + 2&г + <*>2= 0 имеет корни:
— k ± 1/^/52 — со2. Возможны три случая.
175] § 3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 607
1) Коэффициент сопротивления больше коэффициента восстанов-
восстановления: k > со.
При этом решением будет
где 6Х = Дг — V&—а>2>0, 82 = k + Vk2—со2>О.
Мы видим, что никакого колебания не происходит; с увеличе-
увеличением * отклонение s уменьшается, стремясь к нулю при /-»оо и
система стремится к равновесию (которое практически наступает
в конечный момент времени). Мы имеем дело с непериодически-
ми, как говорят, затухающими движениями. Наглядно
этот случай можно объяснить тем, что влияние силы сопротив-
сопротивления (тормозящей движение) настолько превосходит влияние силы
восстановления (вызывающей колебания), что движение затухает
до того, как система перейдет положение равновесия.
2) Коэффициент сопротивления равен коэффициенту восстанови
ления: & = <й.
При этом решением будет
Этот случай не отличается от предыдущего в том смысле, что s
является, начиная с некоторого t, убывающей функцией и s--*0
при t—+ оо.
3) Коэффициент сопротивления меньше коэффициента восстанови
ления: k < <о.
При этом решением будет
s^e"kt {Сг cos k{t + С2 sin ktt), где kx = Кю2 —ft*.
Совершив преобразование, указанное на стр. 591, запишем, что
где А и <р0—произвольные постоянные. Чтобы их определить нужно
задать начальные условия: начальное отклонение точки и ее скорость.
Теперь уже тело действительно совершает колебания — так на-
называемые затухающие гармонические колебания.
Если коэффициент сопротивления & = 0, то мы получим
т. е. обычное гармоническое колебание.
В том случае, когда кфО, амплитуда колебания Ae~"kt7 в отли-
отличие от случая чисто гармонических колебаний, не есть постоянная
величина, а зависит от времени; она стремится к нулю при t—>оо.
Следовательно, тело стремится к равновесию, но не монотонно, а
колеблясь около положения равновесия, с постепенно—по экспонен-
экспоненциальному закону—затухающими размахами (амплитудами). Как и
608 ГЛ. X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [175
для гармонических колебаний, величина kx = |/со2— &2 называется
частотой, величина ^=-т периодом, а ф0 — начальной фазой за-
затухающего гармонического колебания. Величина Ae"kt называется
амплитудой затухающего колебания. Логарифм амплитуды In A—kt
убывает с постоянной скоростью k. Чтобы найти максимальное от-
отклонение $, найдем производную s:
s = — kAe~kt sin (kxt + ф0) + Akxe"ki cos (kxt + <p0).
Приравнивая производную (т. е. скорость) нулю, получим уравнение
для определения экстремальных значений /:
Ясно, что максимумы и минимумы отклонений (с учетом знака) будут
Т л
чередоваться и следовать один за другим через полупериод — = — .
Отношение двух последовательных максимальных отклонений будет
равно1)
д=
Постоянная величина In Д = kT называется логарифмическим декре-
декрементом затухания.
Схематический график затухающего гармонического колебания
s = Ae"kt sink^ (при фо = О) указан на рис. 225. При построении
графика учтено, что в общих точках кривых Ae~ki и Ae"ki sin-k1t9
т. е. при kxt = -5- + 2/гя, они имеют общую касательную; прове-
проверить равенство производных в этих точках предоставляем читателю.
То же самое можно сказать и о кривых —Ae~hi и Ае~м sink^t.
Как уже отмечено, расстояние между соседними точками максимума
и минимума равно половине периода, т. е. —г .
III. Исс л ед ова ни е вынужденных колебаний. Ре-
Резонанс. Изучим теперь вынужденные колебания, которые описы-
описываются линейным уравнением с правой частью
Рассмотрим практически наиболее важный случай, когда коэф-
коэффициент сопротивления меньше коэффициента восстановления: k < со,
и внешняя сила —периодическая: f(t) = a sino^.
1) Через *о обозначено одно из значений t, при которых s достигает
максимума. На практике Л измеряется именно как отношение двух макси-
максимальных амплитуд, хотя ясно, что это число равно отношению любых
двух отклонений, отделенных интервалом времени Г.
175]
§ 3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
609
В силу свойств линейных неоднородных уравнений любое вынуж-
вынужденное колебание является результатом наложения собственного
колебания системы и какого-нибудь наперед выбранного вынужден-
вынужденного колебания. Найдем частное вынужденное колебание, т. е. част-
частное решение неоднородного уравнения
s + 2ks + (a2s = a sin (dxt.
Пусть ИфО\ тогда &-J, не есть корень характеристического
уравнения, и решение можно искать в виде
Л
Рис. 225.
Находя известным способом коэффициенты Ж и 7V, придем к реше-
решению (необходимые выкладки рекомендуем провести читателю само-
самостоятельно)
= 4! sin
где
M — 2/го)!
Таким образом, одно из вынужденных колебаний есть простое гар->
моническое колебание с амплитудой Аг, частотой сох и начальной
фазой фг Всякое другое получается наложением этого колебания на
20 А. Ф. Бермант, И. Г. Араманович
610
ГЛ. X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
[175
собственное колебание системы:
s = Ae~ki sin (ftj/ + ф0) + Ах sin (со^ -f фх).
Вследствие того, что первый член с возрастанием t довольно быстро
стремится к нулю, через некоторое время движение будет описы-
описываться в основном только вторым членом. С этим связано интересное
-
1
а
/
ь
\т
4
\1
о
у
а=О,50
\1
\
—
—
о
0,5
1,5
2,5
Рис. 226.
явление, возникающее при вынужденных колебаниях, так назызаемый
резонанс.
Рассмотрим амплитуду вынужденного колебания Аг и предположим,
что величины к и со неизменны, т. е. собственная частота системы
постоянна. Выражение для Ах запишем так:
а а
175] § 3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 611
где а = —, q = — . Амплитуда Ах пропорциональна величине
Характер изменения Я при изменении q виден на графиках функции
Я (q), соответствующих различным значениям а. На рис. 226 даны
графики Я = Я(?) при а = 0,50; 0,40; 0,30; 0,20; 0,15; 0,10; 0.
Как правило, а—величина небольшая, ибо коэффициент сопротив-
сопротивления к составляет обычно малую долю коэффициента восстановле-
восстановления со.
Исследование показывает, что с увеличением q, т. е. с увеличе-
увеличением возмущающей частоты <ov величина Я, а вместе с ней и ам-
амплитуда установившегося вынужденного колебания сначала возра-
возрастают до некоторого максимума, а затем быстро убывают, стремясь
к нулю при q—> оо (сох—>-оо). Этот максимум достигается при
q= у 1—у, т. е. при (olmax==yr(iJ — 2&L\ Легко проверить, что
при этом амплитуда Almax = -
2k у со2—?2
При близости частоты возмущающей силы к величине ю1тах и
при малом к (это значит, что colmax«со) тело будет совершать
через некоторый промежуток времени гармонические колебания
с очень большой амплитудой, которая может быть совершенно не-
несоразмерной с амплитудой синусоидальной силы, вызывающей само
колебание системы. Это явление резкого возрастания амплитуды
колебания под влиянием даже совсем малых внешних воздействий
и называется резонансом. Кривые на рис. 226 называются кривыми
резонанса.
Резонанс играет значительную роль в технике и физике. Каждое
упругое тело (например, любое сооружение) имеет свою опреде-
определенную собственную частоту колебания, зависящую только от свойств
тела. Представим себе, что это тело под действием внешней силы
выводится из состояния равновесия. Если частота внешней силы
близка к собственной частоте, то воздействие силы, как бы мала
она ни была, может оказаться огромным и разрушительным. При
проектировании различных сооружений (машин, мостов, кораблей,
самолетов и т. п.) особенно принимаются в расчет соображения
о прочности, связанные с резонансом. Резонансом объясняется хо-
хорошо известное из опыта явление, когда небольшая «раскачка»
упругого тела (скажем, моста) вызывает его поломку.
При отсутствии сопротивления, т. е. когда /5 = 0 (что на прак-
практике, однако, не может встретиться), амплитуда вынужденно-
вынужденного колебания равна .—^—jt и обращается в бесконечность при
20*
612 ГЛ. X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [175
совпадении возмущающей и собственной частот (оI = оо) (см. рис. 226,
кривая а~0). В том случае, когда с^^со, решение дифференциаль-
дифференциального уравнения колебания s +(o2s = asinco^ получается из общего
решения, найденного выше, приданием k значения 0. Но если оI = со,
то указанное решение не подходит, так как ш при этом становится
корнем характеристического уравнения г2 + со2 = 0. Решением, как
было показано в примере на стр. 596, будет функция
5 = A sin (со/ + ф0) — ^ t cos (at.
Второй член (так называемый «вековой член») показывает, что
с течением времени размахи колебания неограниченно возрастают,
что здесь и иллюстрирует резонанс.
IV. Колебания в электрической цепи. Картину, вполне
аналогичную механическим колебаниям, представляют процессы, про-
протекающие в электрической цепи, имеющей сопротивление /?, само-
самоиндукцию L, емкость С, если в ней действует напряжение v = v(/),
поступающее извне. Подобный вопрос мы уже рассматривали в п. 161,
где, однако, не принималась во внимание емкость. В общем случае
необходимо учесть, что часть полного напряжения обусловливается
наличием емкости. В физике показывается, что эта часть измеряется
величиной -7r\idtj где /—сила тока.
Таким образом, приходим к уравнению
откуда дифференцированием по t получаем линейное уравнение вто-
второго порядка с постоянными коэффициентами
г+
Это дифференциальное уравнение, описывающее явление течения
тока, аналогично уравнению, описывающему явление механических
колебаний.
Если внешняя электродвижущая сила постоянна (или вовсе от-
отсутствует), то уравнение будет однородным. Ему соответствует ток,
который в силу неравенства нулю сопротивления (ЯФ 0) неизбежно
будет затухающим. В электротехнике он называется переходным.
Распространяя и дальше аналогию с механическими колебаниями,
можно сказать, что этот ток ( при условии -^т < I/tv) дает
176] § 4. СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 613
ственные колебания цепи (контураI). Если существует внешнее
возмущающее напряжение, такое, что v' (t) не равно тождественно
нулю, то неоднородное уравнение имеет частное решение: / = /(/),
которое дает вынужденный ток, называемый установившимся.
Наконец, общее решение уравнения, т. е. зависимость тока от
времени при любых условиях, получается сложением переходного и
установившегося токов. Совершенно ясно, что, аналогично случаю
механических колебаний, по прошествии некоторого промежутка
времени переходный ток практически не будет влиять на течение
электричества. В случае, когда v(t) (а следовательно, и v' (t)) есть
синусоидальная функция времени, установившийся ток тоже будет
синусоидальным. Здесь мы опять можем столкнуться с явлением
резонанса, играющим особенно важную роль в колебательных кон-
контурах. В дальнейшие подробности входить нет нужды, так как
с математической стороны ход явления подобен случаю механиче-
механических колебаний.
§ 4. Системы дифференциальных уравнений
176. Общие определения. Нормальные системы уравнений.
С системами дифференциальных уравнений встречаются при изу-
изучении процессов, для описания которых одной функции недоста-
недостаточно. С примерами такого рода нам уже приходилось сталкиваться.
Так в п. 161 было отмечено, что отыскание векторных линий поля
требует решения системы дифференциальных уравнений. В сноске
на стр. 578 указано, что решение задач динамики криволинейного
движения приводит к системе трех дифференциальных уравнений,
в которых неизвестными функциями являются проекции движущейся
точки на оси координат, а независимой переменной — время. Позже
мы увидим, что решение задач электротехники для двух электри-
электрических цепей, находящихся в электромагнитной связи, потребует
решения системы двух дифференциальных уравнений. Количество
подобных примеров легко можно увеличить.
Начнем с определений. Будем всюду в этом параграфе неза-
независимую переменную обозначать буквой t, а неизвестные функции
этой переменной или через хгУ), #2(*)> • •> хпУ) или> если их
не больше трех, через x(t), y(t), z(t).
Определение. Системой дифференциальных уравнений
называется совокупность уравнений, в каждое из которых вхо-
входят независимая переменная, искомые функции и их производные.
*) Если от^ 1/ -тгг> то колебаний в цепи не будет, ток будет непе*
риодическим затухающим.
614 ГЛ. X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [176
Всегда предполагается, что число уравнений равно числу неиз-
неизвестных функций. Вот примеры таких систем (производные по /
обозначаем не штрихами, а точками):
I x = 2x+ y + t+l, (tx1 + x2 +2*1*3=0,
\ у = 3х — 2y + bt, I 2x2+'x3 — 2txx = 0,
{ + tx% = 0.
Решением, системы дифференциальных уравнений называется со-
совокупность функций
которая при подстановке в каждое из уравнений превращает его
в тождество. Вопрос об общем и частных решениях, а также об их
геометрическом смысле будет рассмотрен позднее.
Обычно приходится иметь дело не с произвольными системами
дифференциальных уравнений, а с так называемыми нормаль-
нормальными системами.
Определение. Нормальной системой дифференциальных
уравнений называется система уравнений вида
*1 ==У 1 (** Х^9 *2! • • • f Xn)f
*2 ==«/ ? (*» Х±9 *2* • • • t Xn),
(*)
Например, нормальной будет первая из приведенных выше систем.
Важность изучения именно нормальных систем следует из того,
что во многих случаях произвольно заданную систему дифферен-
дифференциальных уравнений удается привести к нормальной. Так, например,
система
/ * +
\ x-
приводится к нормальной, если разрешить данные уравнения отно-
относительно производных хну:
^{ х+ у- t).
Систему уравнений
176] § 4. СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 615
нельзя разрешить относительно х и уу и поэтому ее нельзя при-
привести к нормальной. Подобные системы мы рассматривать не будем.
Система уравнений
содержащая производные второго порядка приводится к нормаль-
нормальной при помощи введения новых вспомогательных неизвестных функ-
функций х1 = хг, х2 = х^. Тогда лг1 = лг3, л;2 = лг4, и заданная система
заменяется следующей нормальной системой:
Покажем теперь, что одно дифференциальное уравнение я*го
порядка, разрешенное относительно старшей производной, с помощью
введения новых вспомогательных функций всегда можно свести
к нормальной системе дифференциальных уравнений.
Возьмем, например, уравнение третьего порядка
*=/(*, ху ху х)
и введем две новые вспомогательные функции
у = ху z = y='x.
Тогда заданное уравнение заменится системой трех уравнений
которая является частным случаем нормальной системы (*). Ясно,
что так можно поступать в случае уравнения любого порядка п;
при этом число вспомогательных функций будет равно п — 1.
В обычно встречающихся случаях верно и обратное утверждение:
Нормальная система уравнений может быть заменена одним диф-
дифференциальным уравнением, порядок которого равен числу уравне-
уравнений системы. Эта замена часто позволяет решать такие системы.
Рассмотрим, например, систему уравнений
Продифференцируем первое уравнение по переменной t и заменим
производную у ее выражением из второго уравнения x=y = z.
Продифференцируем еще раз это уравнение и заменим произ-
производную z ее выражением из третьего уравнения x = z = x—y
Так как у = х, a z = xy то окончательно получим л: = лг —j
или
616 ГЛ. X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [176
т, е. линейное дифференциальное уравнение третьего порядка с по-
постоянными коэффициентами.
Обращаем внимание читателя, что в процессе исключения функ-
функций у и z мы выражаем их через функцию л: и ее производные.
Найдя общее решение полученного дифференциального уравнения
высшего порядка, мы получим выражение для функции х, завися-
зависящее от трех произвольных постоянных. Остальные неизвестные
функции (у и z) находятся уже не при помощи интегрирования, а
из их выражений через найденную функцию. Таким образом, общее
число произвольных постоянных не увеличится и будет равно порядку
системы.
Решим полученное уравнение третьего порядка. Характеристиче-
Характеристическое уравнение, ему соответствующее: г3 — г2-\-г—1 = (г2 ~f-1) X
Х(г—1) = 0, имеет корни г2 = 1, /*2 3 = ±/. Следовательно,
х = Схег + С2 cos t + C3 sin t.
Поскольку при исключении у и z мы получали у = х и z = дг, то
y = C1et — C2s\nt +C8cos*,
z = Схег — С2 cos t — С3 sin t.
В качестве примера, когда нормальную систему нельзя заменить
одним дифференциальным уравнением, рассмотрим следующую си-
систему:
Здесь указанным выше способом можно два последних уравнения
свести к одному уравнению второго порядка: у = г—у. Его общее
решение у=^С^ + С2е"г; тогда z=y = C^' —C2e""f. Первое же урав-
уравнение никак не связано с остальными и его приходится решать от-
отдельно: х = Сге*. Окончательно решение системы имеет вид
В него также входят три произвольные постоянные.
На основании рассмотренных примеров мы сделаем следующий
вывод (доказательство его мы опускаем).
Общее решение нормальной системы
п ~"~ fn
177] § 4. системы дифференциальных уравнений 617
имеет вид
где Сг, С2, ..., Ся — произвольные постоянные. Второй из приведен-
приведенных примеров показывает, что в выражения некоторых из xt могут
входить не все произвольные постоянные, а только часть из них..
Начальные условия, при помощи которых из общего решения
выделяется частное, задаются следующим образом:
Подставляя начальные условия в общее решение, получаем систему
алгебраических уравнений для определения произвольных постоян-
постоянных
Ф1 (*0» ^*1» ^2» • • • > Ц|) == -^10»
Cv C2, ..., Q=*20,
Для нормальных систем уравнений также имеет место теорема,
гарантирующая существование и единственность частного решения.
Теорема. Если правые части нормальной системы непре-
непрерывны вместе со своими частными производными в окрестности
значений tOf x1Q9 х20, ...,хп0, то существует единственная си-
система функций x1(t)9 x2(t), . •., xn(t), являющаяся решением
системы и удовлетворяющая заданным начальным условиям.
177*. Геометрическая и механическая иллюстрации решений
системы дифференциальных уравнений. Фазовое пространство.
Рассмотрим сначала для простоты нормальную систему двух диф-
дифференциальных уравнений
х =Д (t, х, у), у =/а {t, лг, у). (•)
Будем считать переменные хну независимо от их физического
смысла координатами точки на плоскости Оху\ саму эту плоскость
назовем фазовой плоскостью. Любое решение данной системы
* = *(/), y=y(t) (**)•
можно рассматривать как параметрическое задание линии на фазо-
фазовой плоскости. Пользуясь терминологией механики и считая, что
t — время, скажем, что функции х (t) и^(^) выражают законы дви-
движения проекций движущейся точки на оси координат, а линия (**)
является траекторией движения. Производные хну представляют
при этом проекции екорости движущейся точки на оси координат.
618 ГЛ. X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [177
Еще раз подчеркнем, что все сказанное является лишь удобной
геометрической, или вернее механической, иллюстрацией. В конкрет-
конкретных задачах переменные х и у могут обозначать величины, никак
не связанные с движением точки; например, это могут быть токи
в электрических цепях. Отметим также, что при указанной иллю-
иллюстрации решение x = x(t) одного дифференциального уравнения
x = f(tyx) является законом движения точки по оси абсцисс; раз-
различным частным решениям соответствуют при этом разные законы
движения. Участок оси Ох, по которому движется точка, может для
всех частных решений быть одним и тем же (например, если урав-
уравнение имеет общее решение х = sin Ct), а может быть и различным
(например, если x = Cs\nt). В первом из приведенных примеров мы
имеем гармонические колебания с одинаковой амплитудой, но с раз-
разной частотой, а во втором примере — наоборот.
Вернемся к системе двух дифференциальных уравнений (*) и
зададим начальные условия: х^^о = а, y\t=t = P> им соответствует
частное решение, xQ(t)y yo(t)y определяющее закон движения по
некоторой траектории Lo. Возьмем теперь новые начальные условия,
изменив начальный момент времени, но оставив прежними значения
фазовых координат хну: x\i=si = а, ^у|^=^=Р« Мы получим новое
решение x1(t),y1(t) и новую, соответствующую ему траекторию Ll7
которая, конечно, не обязана совпадать с Lo. Действительно, найдя
из уравнений (*) значения производных х и у в начальные моменты
времени t0 и tv мы получим разные величины. Это значит, что если
движение начиналось из точки (а, Р) в момент времени tQi то век-
вектор скорости был один, а если в момент времени tt — то другой;
при этом точки начнут двигаться по разным направлениям. Таким
образом, через одну и ту же точку фазовой плоскости могут про-
проходить разные траектории. Приведем один простой пример.
1) дг=1, y = 2t. Здесь оба уравнения не связаны друг с дру-
другом, и мы сразу получаем x = t-\-Cv y = t2 + C2. При начальных
условиях х |t=0 = 0, у |t=0 = 0 решением будут функции х = t, у = t2;
соответствующая траектория — парабола у = х2. Если взять те же
начальные значения х и у, но при t=\i то соответственно полу-
получим x~t—\,y = t2—1; исключая/, найдем уравнение новой траек-
траектории у = (х-{-\J—1—тоже параболы, но, разумеется, не совпа-
совпадающей с предыдущей.
Особенно важным для приложений является случай, когда в пра-
правые части уравнений (*) не входит независимая переменная t. Такая
система дифференциальных уравнений называется автономной; она
имеет вид
177] § 4. системы дифференциальных уравнений 619
Если движение описывается такими уравнениями, то, в какой бы
момент времени ни начинать движение из фиксированной точки (а, Р),
вектор скорости будет одним и тем же. Можно доказать, что все
движения, начинающиеся из точки (а, р), в разные моменты времени
будут проходить по одной и той же траектории (доказательства мы
не приводим, хотя механический смысл его довольно ясен). Пред-
Представляя себе движение в виде шарика, катящегося по траектории,
можно сказать, что шарики, выпущенные из данной точки в разные
моменты времени, будут двигаться по одной и той же траектории,
не сталкиваясь и не обгоняя друг друга (заметим только, что могут
быть и траектории в виде замкнутых линий, например окружностей
или эллипсов).
Можно также доказать, что для автономной системы через каждую
точку фазовой плоскости, в которой выполнены условия теоремы
существования решения, сформулированной в конце п. 176, проходит
одна-единственная траектория. Поясним сказанное примером.
2) -?-=у, -^ = —лг. Исключая функцию .у, получим х=у = —х,
т. е. х~\-х — 0. Запишем решение последнего уравнения в виде
х = As'm(t-\-(f); тогда .у =«= Лсоэ^ + ф). Траекториями служат окруж-
окружности х2 -\-у2 = А2 с центром в начале координат.
Уравнение семейства траекторий можно было бы получить и иначе,
исключив с самого начала дифференциал независимой переменной dt,
т. е. разделив второе из уравнений системы на первое з^= .
Решив это дифференциальное уравнение первого порядка, получим
общее решение в виде того же семейства окружностей.
Остановимся вкратце еще на одном вопросе. Рассмотрим снова
систему (#**) и предположим, что в точке (д:0, у0) обе правые части
равны нулю
Л (*о. .Уо) = 0, /2 = (лг0, у0) = 0.
Тогда функции х*=х0 и у=у0 (попросту говоря, постоянные)
являются решениями системы; это значит, что шарик, помещенный
в точку (х0Уу0), будет все время оставаться неподвижным. Такие
точки называются точками покоя. Например, для системы 2) точкой
покоя является начало координат.
Для уравнения ^ fu у) > полУченного исключением dty эти
точки будут особыми (см. п. 164). Отсюда ясно, что задача
о расположении интегральных кривых этого уравнения вблизи особой
точки тесно связана с задачей о расположении траекторий автономной
системы вблизи точки покоя. Читатели, которым в будущем над-
надлежит заниматься теорией, устойчивости, должны к рассмотренным
620 ГЛ. X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [178
вопросам отнестись с большой внимательностью. Продолжить изу-
изучение этих вопросов можно, например, по книге [6].
Все вышесказанное почти без всяких изменений переносится на
системы трех и более числа уравнений. При л = 3 у нас есть три
неизвестные функции: x(t)> y(t), z(t) и соответственно этому мы
рассматриваем траектории в фазовом пространстве Oxyz. Разумеется,
геометрическое их изображение в этом случае гораздо более сложно.
При п > 3 геометрическое изображение становится вообще невоз-
невозможным; сохраняя терминологию, мы говорим об п-мерном фазовом
пространстве.
Изложим еще гидродинамическую иллюстрацию решений системы диф-
дифференциальных уравнений. Рассмотрим стационарное поле скоростей текущей
жидкости V {vx, vr vz}> и пусть »* = fi (*, у, г), vy = f2 (х, у, z)f t>* = /3 (*, у, z).
Дифференциальные уравнения семейства линий тока (см. п. 151) имеют вид
dx dy dz
li(x, </, 2)~~M*> У. z)~~/3(*, У> г)
Если ввести параметр / и приравнять каждое из отношений dtf то получим
автономную систему дифференциальных уравнений
dx t , ч dy . . . dz , . v
27==fi(*, У* г), -? = Ы*> У> г), 4} = Гз(х>У*г)-
Решения x(t), y(t), z(t) этой системы и будут уравнениями линий тока.
Эти линии тока не изменяются во времени; частицы жидкости, текущие по
разным линиям тока, не перемешиваются друг с другом, так как эти линии
не пересекаются. В нестационарном случае картина течения жидкости ста-
становится более сложной.
178* Системы линейных дифференциальных уравнений. В при-
приложениях особенно часто встречаются системы линейных урав-
уравнений. Для большей краткости изложения ограничимся рассмотрением
нормальной системы трех уравнений с тремя неизвестными функциями
х (t), y(t) nz (t) и начнем с изучения свойств однородной системы
Функции at (t)y bx (t)y ct (t) предполагаются непрерывными.
Предлагаем читателю самостоятельно доказать следующие про-
простые свойства этой системы:
1) Если известно частное решение xx(t), jfx(O» ^i(^) системы
уравнений (*), то функции Cxv Cyv Czv где С—произвольная
постоянная, также образуют решение.
2) Если известны два решения xv yuzx и х2> д>2, z2, то и функции
Уг~\~У2> ^х + ^г также являются решением.
178J § 4. СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 621
Отсюда следует, что если известны три частных решения
(*i» Л. *i). (**У* **) и (*8, у3, z3)t то функции
У =
z =
представляют решение при любых постоянных Cv C2 и С3. Выясним,
в каком случае из него можно получить частное решение, удовлет-
удовлетворяющее любым заданным начальным условиям. Если эти условия
таковы:
то система уравнений для определения постоянных С1э С2, С3 при-
примет вид
^1^10 ~t~ ^2^20 I ^3^30 — ^0»
где xi09 yi0, zi0 — значения соответствующих функций при t = t0.
Для того чтобы эта система имела единственное решение при любых
начальных условиях, необходимо и достаточно, чтобы определитель
xi Уг <
Х2 Уг -
хз Уз -
ни при каком значении t — t0 не обращался в нуль. Мы, как и раньше,
будем говорить, что совокупность трех частных решений, удовлет-
удовлетворяющих этому условию, образует фундаментальную систему; ре-
решение (**) в этом случае является общим решением.
Общее решение неоднородной системы линейных уравнений
слагается из общего решения соответствующей однородной системы
(*) и какого-либо частного решения неоднородной системы. Доказа-
Доказательство этого утверждения схоже с доказательством аналогичной
теоремы для одного линейного уравнения (см. п. 169, II), и читатель
легко проведет его самостоятельно.
Задача решения системы линейных уравнений, по сути дела,
эквивалентна задаче решения одного линейного дифференциального
622 гл. х. дифференциальные уравнения [179
уравнения соответствующего порядка1), в рассматриваемом случае —
третьего. Действительно, чтобы свести систему (*) или (*#*) к одному
уравнению третьего порядка, мы должны, как указано выше, про-
продифференцировать одно из уравнений системы, например первое.
Заменяя каждый раз производные неизвестных функций в правой
части их выражениями, мы увидим, что все последовательные произ-
производные функции х будут линейно выражаться через функции х, у и z.
Поэтому и, наоборот, функции у к z линейно выразятся через х}
ху х. Отсюда следует, что в результате мы получим линейное диф-
дифференциальное уравнение. Ясно, что если исходной была однородная
система уравнений, то и полученное уравнение будет однородным;
в то же время неоднородная система может привестись как к неод-
неоднородному, так и к однородному уравнению. Примером последнего
t2
случая служит система х — х -\-y-\--x-, у = х— U приводящаяся к
уравнению х—х — лг = О.
Решением линейных дифференциальных уравнений с перемен-
переменными коэффициентами мы не занимались; поэтому не будем решать
системы таких уравнений и прямо перейдем к системам линейных
уравнений с постоянными коэффициентами.
179. Системы линейных дифференциальных уравнений с посто-
постоянными коэффициентами2). Пусть дана однородная система
где aiy bv ct — постоянные. Как отмечено в конце предыдущего
пункта, эту систему можно свести к одному однородному линейному
уравнению третьего порядка; нетрудно сообразить, что, как и в при-
примере на стр. 615, всегда будет получаться уравнение с постоян-
постоянными коэффициентами. Так как структуру решений такого уравнения
мы знаем, то практически целесообразно не сводить систему к одному
уравнению, а прямо искать частные решения системы в виде
x = kxer\ y = k2er\ z = k3er\ (**)
где kly kz, k3 и г — неопределенные постоянные, которые следует
найти.
х) Пример на стр. 616 показывает, что иногда может получиться не-
несколько таких уравнений; каждое из них содержит только одну неизвест-
неизвестную функцию.
2) Перед чтением этого пункта читатель должен вспомнить свойства
систем линейных однородных алгебраических уравнений. В учебниках [1] и [2]
они изложены для случая трех уравнений, в книге [10]—для любого их числа.
179]
§ 4. СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
623
Дифференцируя функции х, у и z и подставляя результаты в
систему (*), получим
kxrert = axkxe
k2rt
k2rert =
схкъет%,
х2 хъ
2k2ert + с2къег\
Сократив на ert и перенеся все члены в одну сторону, мы придем
к системе линейных однородных алгебраических уравнений относи-
относительно к±, к.г, к3:
(a1 — r)k1 + a2k2 + я3*з =0,
«2*1 + (*2— Г) *2 + *S*8 = 0, (*##)
«8*1 + ^3*2 + (С3 — ^) *3 = 0.
Чтобы эта система однородных уравнений имела ненулевые ре-
решения (только такие нас и интересуют), необходимо и достаточно,
чтобы ее определитель был равен нулю
а,—г
Ьг -г
= 0.
а А + (V-гг) *2 + с2кг
2 + (с3
Раскрыв этот определитель, мы получим уравнение третьей степени
относительно г. Это уравнение называется характеристическим..
Итак, для того чтобы существовало решение вида (**), нужно,
чтобы число г было корнем характеристического уравнения.
Предположим сначала, что все корни характеристического урав-
уравнения действительные и простые. Пусть один из таких
корней равен гг. Подставив это значение в систему уравнений (###),
получим
=0,
= 0,
с3—гг) к3 = 0.
Определитель этой системы по условию равен нулю. Примем без
доказательства, что если гх — простой корень характеристического
уравнения (а только такие корни мы сейчас и рассматриваем), то
по крайней мере один из миноров второго порядка этого определи-
определителя не равен нулю. Тогда одно из уравнений является следствием
двух остальных и система сводится к двум уравнениям с тремя
неизвестными. Решение такой системы будет зависеть от одной
произвольной постоянной. Если, например, система сводится к двум
первым уравнениям, то одним из решений будут числа
а2 02 —/
Ьх-
гх с2
A)
сх (
21 —
а2
>
A)
*з =
624 ГЛ. X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [179
(Эти формулы легко получаются, если перенести члены с k3 в правую
часть и решить получающуюся систему неоднородных уравнений.)
Все остальные решения получаются умножением чисел к[г\ k^ и k^}
на одну и ту же произвольную постоянную. Поступая так со всеми
корнями характеристического уравнения, мы найдем три системы
функций, каждая из которых является решением системы (*).
Эти системы функций таковы:
{%)РГг*
г е а ,
Доказательство того, что эти функции образуют фундаментальную
систему, мы опускаем. Общее решение системы (*) запишется в виде
х = C^i1 V.' + C2ftif
у = с^У»1 + С2/еB2)е
Примеры. 1) Решим систему
у— — 4х —у — 4z,
z= —у.
Система уравнений (***) имеет вид
Составим характеристическое уравнение:
-г О 1
-4 -A+г) ~4
О —1 —г
= — г3 — г2 + 4г + 4 = D — г2) (г + 1) = 0.
Его корни: гх= — 1, г2= —-2, г3 = 2. Здесь при отыскании kv k2i k3
удобнее взять первое и третье уравнения системы.
Для гг = — 1
Решением будут, например, числа ftj^=l, /j^ss—1, /531>==:
Следовательно, первое решение таково:
179] § 4. СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 625
Для г2=-2
Здесь можно положить k^—l, /гB2)=—4, /гC2)= ¦—2; тогда xz =
Наконец, для г3 = 2
Выбирая A?i3> = 1, /43)— — 4, &C3) = 2, получим
Окончательно общее решение системы таково:
Предоставляем читателю проверить, что найденная система частных
решений является фундаментальной.
Если среди простых корней характеристического уравнения
есть комплексные, то и решение получится в виде комплекс-
комплексных функций действительного переменного. Чтобы перейти к реше-
решению в действительной форме, следует воспользоваться предложе-
предложением, совершенно аналогичным доказанному на стр. 590. Если комп-
комплексные функции х1-\-1х2} Ух + 1у2у z1-\-iz2 являются решением
системы (*) с действительными коэффициентами, то их действитель-
действительные (xl7 y1% zx) и мнимые (лг2, у2, z2) части, взятые в отдельности,
сами являются решениями. При этом комплексно сопряженным корням
характеристического уравнения соответствуют одни и те же действи-
действительные решения.
Для большей краткости проиллюстрируем этот случай на примере
системы двух уравнений.
2)
\ у==
Характеристическое уравнение системы имеет вид
— 7 —г 1
-2 -5-
откуда гЬ2 = — 6±/. Система уравнений для отыскания кх и k2
сводится к одному уравнению с комплексными коэффициентами;
для корня гх=—6 + *' это уравнение таково:
626 ГЛ. X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [179
(Советуем лишний раз убедиться, что второе уравнение является
следствием первого.)
Можно принять, что ft1=l, k2=\-\-i] тогда решением данной
системы дифференциальных уравнений будут комплексные функции
х = e{~*+i) г = е-** cos t + ie'** sin t,
Беря отдельно действительные и мнимые части, получим два
решения в действительной форме:
хг = е~*г cos t, уг = е~*г (cos t — sin*);
х2 = e~Qt sin tt y2 = e~%t (cos t -f- sin t).
Как уже отмечено, комплексно сопряженный корень г=» —6 — /
приведет к этим же самым решениям.
Легко проверить, что найденные решения образуют фундамен-
фундаментальную систему и, следовательно, общим решением системы будет
лг = <?-«*(Схcos * + Ca sin*),
у = e~Qt [C1 (cos t — sin t) + C% (cost + sint)].
Подбор частного решения для системы неоднородных уравнений
можно производить, сведя эту систему к одному уравнению выс-
высшего порядка и пользуясь приемами, указанными в п. 174; оста-
останавливаться на этом детальнее мы не будем.
Рассмотрим в заключение одну задачу из электротехники, которая при-
приведет нас к системе линейных уравнений с постоянными коэффициентами.
Пусть даны две цепи; их сопротивление, самоиндукцию и емкость обоз-
обозначим соответственно через Rlt Llt Ci для первой цепи и через R2t L2, C2 —
для второй. Предположим, далее, что цепи находятся в электромагнитной
связи: каждая индуцирует электродвижущую силу другой. Если обозначить
через М постоянный коэффициент взаимной индукции, то оказывается, что
индуцированное напряжение первой цепи будет равно М — , второй —
М -гр , где *1 = *а@» *2 = *2@ обозначают силу тока соответственно в пер-
первой и во второй цепях.
Предположим, что в обеих цепях отсутствует внешняя электродвижу-
электродвижущая сила. При этом течение тока в цепях будет регулироваться следую-
следующими дифференциальными уравнениями (см. п. 175, IV):
180] § 4. СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
или, после дифференцирования по t,
627
Мы получили систему двух дифференциальных уравнений второго порядка;
ее можно решать и не приводя предварительно к нормальному виду. По-
Полагая /1 = fc1er*, i2 = k2ertt придем к системе однородных алгебраических
уравнений относительно kx и k2. Условием существования ненулевых ре-
решений будет равенство нулю определителя
¦77- Mr2
Mr2
= 0,
или
/ LJ LJ
На практике обычно оказывается, что это уравнение имеет две пары комп-
комплексно сопряженных корней, т. е. колебания тока в цепях будут склады-
складываться из двух гармонических колебаний. Подробный анализ всех встречаю-
встречающихся при этом случаев приводится в курсах электротехники. Отметим
еще, что если не учитывать емкостей в цепях, то течение тока будет опи-
описываться системой уравнений первого порядка; при этом процесс не будет
колебательным.
180*, Случай кратных корней характеристического уравнения.
Если характеристическое уравнение имеет кратные корни, то реше-
решение системы значительно усложняется. В то время как для одного
уравнения высшего порядка, зная кратности корней характеристи-
характеристического уравнения, мы всегда можем сразу написать фундаменталь-
фундаментальную систему (см. п. 174) и, следовательно, общее решение, здесь
дело обстоит иначе. Не вдаваясь в подробности, поясним на двух
примерах суть дела.
1) Решим систему
—г,
Характеристическое уравнение
2-г 1 -1
1 2-г -1
8 3 —2—г
628
ГЛ. X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
[180
имеет корни гг~0у г2>3=1. Для простого корня ^ = 0 можно
положить k[l) =-• /гB1) = 1, Лз1>==3. Решение будет состоять из пос-
постоянных: х1=\, ?y1=l, ^ = 3; понятно, их можно умножить на
произвольную постоянную Сх.
Для кратного корня г=1 система уравнений для kt
*1 + *2 —*8 = °» ^1 + ^2 — ^3 = °» 3^ +ЗА, —3ft8 = 0
сводится не к двум уравнениям, как для простого корня, а к од-
одному k1 + k2 — k3 = 0. Здесь можно произвольно задать уже две
величины, например, положить АХ = С2 и &2 = С3; тогда *3 = С2-{-С3,
и мы получим решение, зависящее от двух произвольных постоянных:
Легко заметить, что оно является линейной комбинацией двух част-
частных решений х% — ег, у2 — 0, z2 = ef и лг3 = 0, yz = el, zz = ei.
Фундаментальность полученной системы трех решений следует
из того, что определитель
= е*фО.
1
е*
0
1
0
ех
3
ех
,) е\
Окончательно, общее решение системы таково:
х = С1 + С2е\ У = С1 + С3е\ z==3C1 + (C2
2) Решим систему
х~х у,
у = 4х —у -f- 2г,
Корни характеристического уравнения
— г —1 О
4 _1— г 2 = — A — гJ A + О = О
О 2 1—г
равны: гг== —1, ^з^ 1. Простому корню соответствует решение xt =
= е~*, y1 = 2e~~t, zt= —2е~г.
Составляя же систему уравнений относительно А,- для кратного
корня
мы видим, что она снова сводится к двум уравнениям. В резуль-
результате мы найдем только одно решение; например, лга = е*, jr, = O,
180] § 4. СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 629
??2= —2^^. Третьего решения такого же вида, не являющегося
линейной комбинацией двух найденных, не существует. Оказывается,
что в этом случае можно найти решение вида
) «'. У = («2 + Р»<) «*. * = («.+ Рз') «'•
Постоянные aiy р,- определяются методом неопределенных коэффи-
коэффициентов. Дифференцируя х, у, z, подставляя результаты в уравне-
уравнения и сокращая на е*> получим тождества:
Осталось приравнять свободные члены (уравнения слева) и коэф-
коэффициенты при t (уравнения справа) в каждом тождестве:
1) Рх + сс^О, 4) Р2 = 0,
2) _4а1 + 2а2 + р2—2а3 = 0, 5) -4р1 + 2р2~2рз = 0,
3) р3-2а2 = 0, 6) -2р2 = 0„
Шестое уравнение равносильно четвертому, а пятое является
следствием первого, третьего и четвертого; всего остается четыре
уравнения с шестью неизвестными. Полагая, например, а1 = С2 и
а2 = С3, выразим через них остальные:
В итоге получим решение, зависящее от двух произвольных посто-
постоянных:
Решение, обозначенное выше индексом «2», получается при
С2==1 и С3 = 0. Если положить С2 = 0, С3=1, то получим третье
решение д;3=—teii ^3 = е/, г3 = A+2/) ef, образующее с первыми
двумя фундаментальную систему.
Как мы видим, несмотря на то, что в обоих последних примерах
был двукратный корень характеристического уравнения, решения,
соответствующие этому корню, имеют разную структуру: в пер-
первом случае решение содержит только функцию ef, а во втором
и е*, и te*.
При большом числе уравнений и более высокой кратности
корня алгебраические трудности резко возрастают, и без знания
специальных вычислительных приемов линейной алгебры решение
таких систем становится крайне затруднительным. Структура же
общего решения определяется следующим правилом.
Если характеристическое уравнение системы п уравнений имеет
корень г кратности т} то ему отвечает решение, зависящее от m
630 ГЛ. X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
произвольных постоянных, вида
где все P^t)—многочлены степени не выше m—1. При отыскании
коэффициентов этих многочленов ровно m из них можно принять
за произвольные постоянные; тогда остальные выразятся через них.
Может оказаться, что часть многочленов Pi (t) или даже все бу-
будут иметь степень, меньшую чем m—1. (В примере 1 при т = 2
все многочлены оказались нулевой степени, т. е. постоянными.)
В случае комплексных корней решения отыскиваются в виде
комплексных функций, а затем отделяются действительные и мни-
мнимые части; они будут состоять из функций вида tqe%i cos P* и
tfV'sinftt, где а-НР — корень характеристического уравнения крат-
кратности m и q^.m—1.
181 *• Матричная форма записи системы линейных дифферен-
дифференциальных уравнений. В этом пункте мы познакомим читателя,
знающего основы матричного исчисления, с очень удобной формой
записи системы линейных дифференциальных уравнений и ее ре-
решений. Эта форма записи в настоящее время широко применя-
применяется и в технической литературе.
Пусть дана нормальная система однородных линейных дифферен-
дифференциальных уравнений
(*)
Коэффициенты системы а^ могут быть функциями от t (непрерыв-
(непрерывными); в частном случае просто постоянными. Введем в рассмот-
рассмотрение матрицу коэффициентов системы
'я*
и матрицу-столбец Х(^), элементами которого являются неизвестные
функции x{{t), а также производную
Х(<) =
181] § 4. СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 631
Говорят также, что X (t) есть векторная функция скалярного аргу-
аргумента t с координатами хгУ), x2(t), ..., xn(t). В дальнейшем будем
матрицу-столбец Х(^) называть просто вектором и часто обозначать
коротко через X.
Произведение матрицы А на вектор X есть снова вектор
а21а22... а2п \ I х2 \ I а21х± + а22х2 +...+ а2пхп
1ап1.. .апп/ \хп
Элементы вектора справа есть как раз правые части системы
уравнений (*); поэтому ее кратко можно записать в виде одного
матричного дифференциального уравнения
Х = ЛХ. (**)
Частными решениями такого уравнения являются векторные
функции (коротко—векторы) X,- (t) с координатами хи (t), x2i (t)>.. .,
..., xni(t). Разумеется, уравнению (**) удовлетворяет нулевое,
или тривиальное, решение Х? = 0.
Основываясь на правилах действий с матрицами, легко прове-
проверить, что любая линейная комбинация частных решений
СА (t)+с2х2 (О +... + стхт (о,
где все Ct — постоянные, тоже является решением.
Введем определение линейной независимости системы векторных
функций. Система векторных функций называется линейно независи-
независимой, если тождество *)
ЯА (t)+я2х2 (t) +... + xmxm (t)=о (#*#)
при постоянных Kt возможно только при К1 = к2= ... = Xm = 0.
В противном случае, т. е. когда это тождество возможно не при
всех kif равных нулю, система называется линейно зависимой.
Иначе говоря, система векторных функций линейно независима,
если ни одну из функций нельзя представить в виде линейной
комбинации остальных, и линейно зависима в противном слу-
случае. Отметим еще, что одно написанное векторное тождество (*#*)
г) В этом определении совсем не обязательно считать, что Xj(/) яв-
являются решениями уравнения (##); они могут быть любыми векторными
rin/нкттиями
функциями
632
ГЛ. X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
A81
равносильно п координатным:
Vll С) + 4*1, 10 + • • • + K*lm it) = О,
:2да (<) = О,
@
= О-
Конечно, имеется в виду, что функции xif{t) определены и
непрерывны в одном и том же интервале изменения t.
Пусть теперь векторные функции Хх it), Х2 (t), ..., Х„ (t) явля-
являются решениями матричного дифференциального уравнения (**),
или, что то же самое, системы (*). Для того чтобы эти решения
были линейно независимы, необходимо и достаточно, чтобы опреде-
определитель
яе был paeew «рю ни при каком значении t из интервала, в кото-
котором коэффициенты системы a^it) непрерывны. В частности, если
рассматривается система с постоянными коффициентами, то это
должно иметь место при всех t. Доказательство этой теоремы мы
не приводим.
Любую линейно независимую систему п решений называют фун-
фундаментальной системой, а определитель W—определителем Врон-
Вронского. Если фундаментальная система известна, то общее решение
есть линейная комбинация функций, образующих эту систему:
X @ = СХХХ (t) + С2Х2 (/) + . .. + СпХп (/).
Предоставляем читателю записать общее решение в координатной
форме.
Частные решения системы (*) с постоянными коэффициентами,
как указано в п. 179, отыскиваются в виде krt
%
X(t) равны
— ь **
При этом векторные функции X(t) и
= е
rt
X [t) = rert
К
\к
181]
§ 4. СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
633
Обозначим вектор с координатами kv к2У ..., кп через К и
подставим выражения для X и X в матричное дифференциальное
уравнение (*#):
Сокращая на скалярный множитель е7**, получаем матричное алгеб-
алгебраическое уравнение
Нам требуется найти такой ненулевой вектор К (если К —нулевой
вектор, то получится нулевое решение), чтобы в результате
умножения матрицы А на этот вектор получился вектор гК, кол-
линеарный К. В матричном исчислении числа г, при которых
существует ненулевое решение уравнения (****), называются соб-
собственными числами, а сами векторы К — собственными векторами
матрицы А.
Отметим, что если К — собственный вектор, соответствующий
собственному числу г, то и любой вектор ЯК, ему коллинеарный,
тоже будет собственным. Действительно, из уравнения (##**) сле-
следует, что ЛХК = ХЛК=ЯгК = гЯК.
С точки зрения решения системы дифференциальных уравне-
уравнений это означает, что, умножая любое решение на числовой мно-
множитель, мы снова получаем решение.
Записав матричное уравнение в координатной форме и пере-
перенеся все члены в левую часть, получим однородную систему
линейных алгебраических уравнений
Ki -/•)*! + «и*. + • • • + <*i А = О,
«2А +(^22 — 0*2+ •' -+п2пК =°»
Ля1*1 + ^«2*2 + • •
Чтобы эта система имела ненулевые решения, т. е. чтобы г было
собственным числом, необходимо и достаточно, чтобы определитель
этой системы был равен нулю:
—г
"In
«2
= 0
Разворачивая определитель, получим уравнение я-й степени отно-
относительно г — характеристическое уравнение. Если все корни ха-
характеристического уравнения простые, то п различным собственным
634 ГЛ. X, ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
числам будут соответствовать п различных собственных векторов
(определенных с точностью до числовых множителей), и мы полу-
получим ровно п линейно независимых решений уравнения (**).
Трудности, возникающие в случае кратных корней характеристи-
характеристического уравнения, отмечены в п. 180.
ВОПРОСЫ И ПРЕДЛОЖЕНИЯ ДЛЯ САМОПРОВЕРКИ
1. Что называется дифференциальным уравнением первого порядка?
2. Что называется общим решением дифференциального уравнения
первого порядка?
3. Дать определение частного решения. В чем состоит начальное усло-
условие для уравнения первого порядка?
4. Сформулировать теорему существования и единственности решения
уравнения первого порядка.
5. Дать геометрическую иллюстрацию частного и общего решений
дифференциального уравнения первого порядка.
6. Дать определение дифференциального уравнения с разделяющимися
переменными и указать метод его интегрирования.
7. Какое уравнение первого порядка называется однородным? Как оно
решается?
8. Какое уравнение первого порядка называется линейным? Изложить
способ его решения.
9. Какое уравнение первого порядка называется уравнением в полных
дифференциалах? Описать способы его решения.
10. В чем состоит графический метод Эйлера построения интегральной
кривой уравнения первого порядка?
11. Описать метод Эйлера приближенного численного интегрирования
уравнения первого порядка.
12*. Какие точки являются особыми для дифференциального уравнения
первого порядка? Указать возможные типы особых точек и привести
примеры.
13. Что называется дифференциальным уравнением второго порядка?
14. Каков геометрический смысл начальных условий дифференциального
уравнения второго порядка?
15. Сформулировать теорему существования и единственности решения
для уравнений второго порядка.
16. Изложить способы приведения уравнений второго порядка
y" = fj(x, yt у') к уравнению первого порядка в случаях, когда правая
часть не содержит: 1) у и у'\ 2) у\ 3) х.
17. Дать определение дифференциального уравнения п-го порядка и
его общего решения, Указать, как задаются начальные условия для урав-
уравнения /1-го порядка.
18. Что называется линейным дифференциальным уравнением второго
порядка?
19. Какой вид имеет общее решение линейного уравнения без правой
части?
20. Доказать для линейных уравнений второго порядка основное
свойство общего решения.
21. Сформулировать и доказать теорему о структуре общего решения
линейного уравнения с правой частью.
22. Описать способ решения линейного уравнения второго порядка без
правой части с постоянными коэффициентами. Какое уравнение называется
характеристическим? Как оно составляется?
ВОПРОСЫ И ПРЕДЛОЖЕНИЯ 635
23. Какой вид имеет общее решение линейного уравнения второго
порядка без правой части с постоянными коэффициентами при действитель-
действительных и различных корнях характеристического уравнения? при равных
корнях?
24. Доказать, что если комплексная функция является решением ли-
линейного уравнения с действительными коэффициентами, то ее действительная
и мнимая части также являются решениями.
25. Указать вид решения в случае комплексных корней характеристи-
характеристического уравнения.
26. Разъяснить правило отыскания частного решения уравнения с пра-
правой частью вида
/ (х) = етх [Рг (х) cos nx + P2 (х) sin пх],
где Pi (я) и Р2 (х)-— многочлены. Привести примеры.
27. Как можно находить решение уравнения с правой частью, если
правая часть его представлена в виде суммы нескольких функций?
28. В чем заключается метод вариации произвольных постоянных?
29. Какая система функций называется линейно независимой? Какая —
линейно зависимой?
30. Сформулировать условие линейной независимости системы частных
решений линейного дифференциального уравнения n-го порядка.
31. Доказать теорему о структуре общего решения линейного уравнения
n-го порядка без правой части и с правой частью.
32. Как может быть составлено общее решение линейного уравнения
без правой части с постоянными коэффициентами порядка п в зависимости
от корней характеристического уравнения?
33. Что называется системой дифференциальных уравнений? Что назы-
называется решением такой системы?
34. Какая система дифференциальных уравнений называется нор-
нормальной?
35. Описать приемы сведения произвольной системы дифференциальных
уравнений к нормальной.
36. Описать приемы сведения нормальной системы к одному уравнению
высшего порядка.
37. Какой вид имеет общее решение нормальной системы дифферен-
дифференциальных уравнений? Сформулировать теорему существования решения
такой системы.
38*. Описать геометрическую иллюстрацию решения системы дифферен-
дифференциальных уравнений как траекторий на фазовой плоскости.
39*. Описать свойства решений автономной системы дифференциальных
уравнений.
40. Сформулировать свойства решений линейной системы дифферен-
дифференциальных уравнений.
41. Описать метод решения системы линейных уравнений с постоянными
коэффициентами с помощью характеристического уравнения. Рассмотреть
случай простых корней (действительных или комплексных).
42*. Указать вид решения в случае кратных корней характеристического
уравнения.
43*. Описать матричную форму записи системы линейных дифферен-
дифференциальных уравнений. Сформулировать определение линейно независимой
системы векторных функций и указать структуру общего решения системы.
44*. Установить связь между решением однородной системы линейных
дифференциальных уравнений с постоянными коэффициентами и задачей
отыскания собственных чисел и векторов матрицы коэффициентов системы.
ГЛАВА XI
РЯДЫ
§ 1. Числовые ряды1)
182. Определение ряда и его суммы. Пусть дана бесконечная
последовательность чисел и1У и2> • • • > ию
Определение. Выражение
называется рядом, а и1У и2, ... , »л, ... — членами ряда.
Коротко ряд записывается так:
Выражение для л-го члена ряда при произвольном п называется
общим членом ряда.
Ряд считается заданным, если известно правило, по которому для
любого номера п можно записать соответствующий член ряда.
Чаще всего общий член ряда задается формулой un = f (л), поль-
пользуясь которой можно сразу написать любой член ряда. Например,
если йп = ^, то ряд имеет вид
Если и„ = ^у, то ряд таков:
Иногда ряд задается при помощи рекуррентного соотно-
соотношения, связывающего последующий член ряда с предыдущими.
г) Перед чтением этого параграфа рекомендуем вспомнить содержание
пп. 26, II и 31.
182] § 1. числовые ряды 637
При этом задаются несколько первых членов ряда и формула, по
которой находятся следующие члены ряда. Например, пусть u1=\t
и2 = -2-, а рекуррентная формула такова: ип =-^ ип_г-\--^ып-.2.
Последовательно находим
11,1, 7 1 7,1 1 11
"з = -2 • 2" + '1==l2' tf*e#l5 + 'Т^й и т' А'
Таким образом, получаем ряд
Пусть дан ряд
«1 + М2 + • • • + «я + • • •
Сумму л первых его членов обозначим через sn:
и назовем /г-й частичной суммой ряда.
Образуем теперь последовательность частичных сумм ряда:
С неограниченным увеличением числа п в сумме sn учитывается
все большее и большее число членов ряда. Поэтому естественно дать
следующее определение.
Определение. Если при п—> оо существует предел после-
последовательности частичных сумм членов данного ряда
lim sn = s,
ft —>• 00
то ряд называется сходящимся, а число s — его суммой.
Записывают это так:
Если последовательность sn не стремится к пределу, то ряд
называется расходящимся.
Отметим, что ряд может расходиться в двух случаях: 1) если
последовательность sn будет стремиться к бесконечности и 2) если
последовательность $п колеблющаяся (см. п. 31). В обоих случаях
мы скажем, что ряд суммы не имеет.
638 гл. xi. ряды [182
В качестве простого примера рассмотрим сумму членов беско-
бесконечной геометрической прогрессии
a + aq+aq*+...+a<f-1+... (*)
Сумма п первых членов прогрессии равна
Если \q\ < 1, то lim qn — 0 и поэтому
П -> со
Hm*B = alim ?==
Следовательно, при |#|<1 бесконечная геометрическая прогрессия
образует сходящийся ряд, сумма которого равна
Если же |#|>1, то lim #" = оо, а поэтому и lim sn =
п -> оо л-* со
т. е. ряд расходится.
Пусть теперь 0=1. Ряд
имеет частичную сумму sn = na, которая стремится к бесконечности
вместе с п: lim sn= oo.
Я -> оо
Если же q = —1, то получается ряд
а — а + а — a -f- ...
Его частичные суммы принимают следующие значения: sx= a, s2—0,
s3 = a, 54 = 0 и т. д., т. е. sn — колеблющаяся последовательность,
не стремящаяся ни к какому пределу. Согласно определению этот
ряд расходится.
Таким образом, бесконечная геометрическая прогрессия пред-
представляет ряд, который сходится при |#|<1 и расходится при
M=>i.
В рассмотренном примере мы устанавливали сходимость или рас-
расходимость ряда, пользуясь непосредственно определением сходимости
и известной формулой для /г-й частичной суммы.
Однако в большинстве случаев этим путем идти нельзя, так как
очень трудно найти компактную формулу для sn> а значит, и пре-
предел sn. В дальнейшем мы будем выяснять сходимость ряда, не
находя фактически его суммы, а пользуясь признаками схо-
сходимости, к установлению которых мы вскоре и перейдем. Пояс-
Поясним предварительно, для чего важно знать, сходится ли ряд, даже
если мы не умеем находить его сумму.
182] § 1. числовые ряды 639
Рассмотрим сходящийся ряд
Разность между суммой ряда и его n-й частичной суммой называется
л-м остатком ряда. Остаток ряда есть в свою очередь сумма бес-
бесконечного ряда1); обозначим ее через гп. Имеем
Исходный ряд по предположению сходится, т. е. lim sn = s. Следо-
вательно, абсолютная величина остатка
будет как угодно мала, если только число п взято достаточно боль-
большим. Таким образом, мы всегда имеем возможность приближенно
подсчитать сумму сходящегося ряда, взяв достаточно большое число
первых его членов. Однако большую трудность представляет выясне-
выяснение величины возникающей ошибки. В дальнейшем на частных при-
примерах мы покажем, как иногда можно оценчвгть веи*«едгпу
ошибки и тем самым устанавливать, сколько нужно брать членов
ряда для получения его суммы с требуемой точностью. Напомним
еще раз, что расходящиеся ряды суммы не имеют.
Приведем теперь простейшие свойства сходящихся рядов.
1. Если ряд
сходится и имеет сумму s, то ряд, образованный из произведений
всех членов данного ряда на одно и то же число X:
тоже сходится и имеет сумму *ks.
Для доказательства обозначим п-ю частичную сумму первого
ряда через sny а второго через оп. Имеем
Следовательно,
lim on= lim (XsJ
я-* оо я-»- oo
Свойство доказано.
2. Если сходятся ряды
1) Сходимость его будет доказана чуть позднее (см. свойство 3),
640 гл. xi. ряды [183
то ряд, образованный сложением соответствующих членов данных
рядов:
тоже сходится и его сумма равна s' + $'•
Доказательство этого свойства также очень просто и опирается
на теорему о пределе суммы. Пусть $'п и s'n — соответственно #-е
частичные суммы данных рядов, а оп — частичная сумма получен-
полученного ряда. Тогда
Отсюда
lim а„ = lim (^ + ^) = lim s'n+ Urn s"n =
что и требовалось доказать.
Умножив члены второго ряда на — 1 (при этом по свойству 1
его сумма станет равной — s") и сложив с членами первого, полу-
получим, что
...=s'~ s".
3. Если ряд сходится, то сходится и ряд, полученный из
данного путем приписывания или отбрасывания любого конеч-
конечного числа членов.
Пусть ^:: сходящийся ряд
и мы выбросили из него конечное число членов, например члены #2,
1/8, и10 и и1Ь. Чтобы не менять нумерацию оставшихся членов, будем
считать, что на место выброшенных членов поставлены нули. Тогда
при п > 15 частичные суммы обоих рядов будут отличаться друг от
друга на постоянное слагаемое и2 + и8 + и104-и16- ^ если сУ1Дест"
вует предел одной из частичных сумм, то существует предел второй,
причем они отличаются друг от друга на то же постоянное сла-
слагаемое1).
Совершенно аналогичны рассуждения в случае приписывания
к ряду новых членов.
В качестве следствия из этого свойства получаем, что если схо-
сходится ряд, то сходится и любой его остаток, и наоборот.
183. Необходимый признак сходимости ряда. Гармонический
ряд. Как мы уже говорили, первый важнейший вопрос, относящийся
к данному ряду, заключается в выяснении его сходимости или рас-
*) Если сумма выброшенных членов окажется равной нулю, то суммы
обоих рядов будут совпадать.
183] § 1. числовые ряды 641
ходимости. Нашей ближайшей целью будет изложение признаков,
при помощи которых по общему члену ряда можно судить о сходи-
сходимости или расходимости ряда.
Необходимый признак сходимости ряда. Если ряд
сходится, то общий член стремится к нулю при неограниченном
возрастании его номера.
Доказательство. Имеем
если ряд сходится, то
Поскольку
то
lim un
П-> оо
lim sn_1--
П ->• оо
= lim (sn-
п -> оо
lim
я-> со
= S
-s
• и
lim sn =
П-+ CD
= lim 5Л —
Л-> со
— 5 = 0.
S.
- lim
Л-> с
Из доказанного необходимого признака сходимости вытекает до-
достаточный признак расходимости ряда.
Если ип не стремится к нулю, то ряд не может быть сходя-
сходящимся, т. е. он расходящийся.
Возьмем, например, ряд
111 п I
101^201 ^301 ^ ' •' ^ 100л+1
Этот ряд расходится, ибо его общий член мл = ТпТГТГТ ПРИ п—*°°
стремится к щ и, значит, не стремится к нулю.
Следует твердо помнить, что стремление я-го члена ряда к
нулю не является достаточным для сходимости ряда.
Рассмотрим ряд
1 ++"+- ..+-+...,
который называется гармоническим.
Здесь ип = >0, тем не менее ряд расходится, В самом деле,
сейчас мы докажем, что $п—> оо при п—юо.
Для доказательства заменим некоторые члены ряда меньшими
числами и убедимся, что даже сумма меньших слагаемых будет
стремиться к бесконечности. Выпишем несколько первых членов
гармонического ряда, разбив их на группы следующим образом:
21 А. Ф. Бермант, И. Г. Араманович
642 гл. хт. ряды [184
В каждой из круглых скобок заменим все слагаемые последним,
которое оставим без изменения. Получим (под каждой скобкой под-
подписано число слагаемых в ней)
Совершенно очевидно, что от такой замены сумма членов в каждой
скобке уменьшилась и стала равной у. Поскольку таких скобок
можно брать сколько угодно, сумма их будет стремиться к беско-
бесконечности.
Итак, мы доказали, что сумма меньших слагаемых будет стре-
стремиться к бесконечности, а следовательно, сумма ббльших слагаемых,
представляющих собой гармонический ряд, и подавно.
Еще проще доказать расходимость ряда 1 + --р= + -^=+...
...+—7=+.-., У которого п-й член также стремится к нулю. Здесь
Vn
sB = l+^+...+^>^ + -L.+ ...+-L=^==l0r. Следова-
V 2 у п у п у п у п у п
тельно, при п -+ оо и sn —* оо.
184. Ряды с положительными членами. Достаточные признаки
сходимости.
I. Признаки сравнения. Рассмотрим специально ряды,
все члены которых положительны:
Ul + u%+...+un+... (un>0).
Иногда в целях упрощения нумерации членов удобнее считать, что
ип ^ 0, т. е. что среди членов ряда есть равные нулю.
Исследование сходимости таких рядов значительно облегчается
следующим простым предложением:
Лемма. Если частичные суммы ряда с положительными чле-
членами ограничены сверху:
sn<M,
то ряд сходится1).
Доказательство. Так как все члены ряда положительны, то
частичные суммы его по мере возрастания числа членов тоже воз-
возрастают:
г) Для рядов с произвольными членами из приведенного условия вовсе
не следует сходимость ряда. Мы это видели на примере ряда а — а-\-а~—
— а+... , у которого все частичные суммы не превосходят числа а и ко-
который тем не менее расходится.
184] § 1. числовые ряды 643
Но если последовательность монотонно возрастает и ограничена
сверху, то по признаку сходимости Вейерштрасса (см. п. 31) она
имеет предел, также не превосходящий числа М. Следовательно,
lim sn = s ^ M.
П-+ СО
И обратно,
Если ряд с положительными членами сходится, то его частичные
суммы меньше суммы ряда: sn < s.
Из доказанной леммы немедленно следуют признаки сравнения
для рядов с положительными членами.
Признаки сравнения. Пусть даны два ряда с положи-
положительными членами:
i A)
2^ + B)
и пусть каждый член ряда A) не больше соответствующего
члена ряда B), т. е.
uk<vk (k=\f 2, ...)• (•)
Тогда:
1) Если сходится ряд B), то сходится и ряд A).
2) Если расходится ряд A), то расходится и ряд B).
Доказательство. Докажем сначала первую часть. Положим
п. п
fe=l /5 = 1
По условию ряд B) сходится, поэтому оп<Со, где а — сумма вто-
второго ряда. А из условия (*) следует, что
т. е. что частичные суммы ряда A) ограничены сверху. Но тогда
в силу только что доказанной леммы ряд A) сходится.
Для доказательства второй части достаточно заметить, что, по-
поскольку ряд A) расходится, его частичные суммы неограниченно
возрастают:
*»—>°°-
Так как on^srp то и оп—*оо. Следовательно, ряд B) расходится,
что и требовалось доказать.
Признаки сравнения применимы и в том случае, когда условию
(*) удовлетворяют члены рядов не при всех л, а лишь начиная
21*
644- гл. xi. ряды [1&4
с некоторого я = ЛЛ Это следует из третьего свойства сходящихся
рядов (см. п. 182).
Докажем, например, что ряд
будет расходящимся. Для этого достаточно сравнить данный ряд
с гармоническим рядом
Так как —^ > — при п > 1 и гармонический ряд расходится,
У п п
то и данный ряд расходится. (На стр. 642 мы доказали расходи-
расходимость данного ряда иным способом.)
Так же легко установить сходимость ряда
i._-L_i__L . 4--L-1-
2 "•" 2-22 '3-23 ' 1"тц.2''гТ'
члены которого меньше членов бесконечно убывающей геометриче-
геометрической прогрессии
1,1,1, ,1,
о * о2 ' 23 * ' ' 2п ' ' *
На практике признак сравнения наиболее удобно применять
в следующем виде: если предел отношения ип к vn существует
и не равен нулю
lim ?* = Л>0,
то ряды A) и B) или оба сходятся, или оба расходятся.
Докажем это. Из определения предела следует, что для любого
е > 0 можно указать такое число /V, что при всех я > N будет
е, или в развернутом виде
справедливо неравенство —- —
где е считаем настолько малым, что А — е > 0.
Предположим сначала, что ряд B) сходится; тогда по свойству
1 п. 182 сходится ряд с общим членом (A-^e)vn и по признаку
сравнения сходится ряд A), так как ип < (A + e)vn при всех п > N.
Наоборот, если ряд B) расходится, то из неравенства ип >
> (А — e)vn будет следовать, что расходится и ряд A). Например,
ряд с общим членом ип =^ 3 2 t расходится, так как предел отно-
1 2
шения ип к — равен -^-.
184] § 1. числовые ряды 645
Трудность применения признаков сравнения заключается в том,
что для данного ряда надо подбирать еще другой ряд, с которым
можно было бы его сравнивать. Очень часто в качестве «эталона»
расходящегося ряда принимают гармонический ряд, а в качестве
«эталона» сходящегося ряда или бесконечно убывающую геометри-
геометрическую прогрессию, или ряд из обратных квадратов
+ ++ + +
Доказать сходимость этого ряда можно следующим образом:
объединим его члены в группы, содержащие последовательно 1, 2,
4, 8, ... членов ряда, и заменим в каждой группе (начиная со вто-
второй) все слагаемые наибольшим из них, т. е. первым членом группы.
Тогда очевидны неравенства:
22 i за 22 ' 22 2 ' 42 ~*~ 52 б2 ' 72 42 4 22 '
1 1 1 ___ 1 1
g2-+.-.+j52<»-g2- — -g- — 23 И Т* Д*
Применяя теперь признак сравнения (с геометрической прогрес-
прогрессией), заключаем, что ряд из обратных квадратов сходится.
С помощью этого ряда легко установить сходимость, например,
ряда с общим членомип= 8 , . ; предел отношения ип к \/п2
равен 1. п
Перейдем теперь к признаку, который позволит в очень боль-
большом числе случаев устанавливать сходимость ряда, исходя только
из выражения для его членов.
II. Признак Даламбера1). Пусть дан ряд с положитель-
положительными членами
Если при п—> оо существует предел отношения последую-
последующего члена к предыдущему *~1, равный р:
Нт ^ = Р,
П-> СО иП
то при р < 1 ряд сходится, при р > 1 ряд расходится2).
При р = 1 ряд может быть как сходящимся, так и расхо-
расходящимся.
х) Ж. Даламбер A717—1783) —крупнейший французский математик,
механик и философ. Член Петербургской академии наук.'
2) Ряд также будет расходиться, если п+* -* оо при п -^ оо,
646 гл. xi. ряды [184
Доказательство. Пусть р < 1. В силу определения пре-
предела всегда можно выбрать такое число Л/", что при всех n^N
будет справедливо неравенство
^<p+e=pi.
где 8>0 берется настолько малым, чтобы р1 = р-}-8 еще остава-
оставалось меньшим 1. Тогда
M±l М±1р и т. д.
uN ^ ™ uN+1
Мы имеем
UN+1<
UN+2 <
Отсюда вытекает, что члены ряда
представляющего ЛЛй остаток данного ряда, меньше соответствую-
соответствующих членов бесконечно убывающей геометрической прогрессии
(знаменатель ее рх меньше 1). Следовательно, N-& остаток ряда
сходится, но тогда сходится и сам данный ряд.
Пусть р>1. Тогда можно выбрать такое N, что при n^N
будет справедливо неравенство
где е берется настолько малым, чтобы р1 = р^~е еще оставалось
большим 1. Но тогда каждый последующий член ряда будет больше
предыдущего и, поскольку все они положительны, не может выпол-
выполняться необходимый признак сходимости ряда, согласно которому
общий член должен стремиться к нулю. Значит, ряд расходится.
В том случае, когда предел р = 1, признак Даламбера непри-
неприменим: могут быть ряды как сходящиеся, так и расходящиеся.
Примеры. 1) Рассмотрим ряд ^ ~ . Здесь ил=трг, ип+1 *=
+1 п ,. Я+1 П 1 ,. П-\-\ 1 ^
9йтт- ПоэтомУ Р= hm штх'ш — 'о lim Чг^Т- Следова-
тельно, данный ряд сходится.
185]
§ 1. ЧИСЛОВЫЕ РЯДЫ
647
1
= ( *
2) Возьмем ряд^^. Для него -f^ = 7^+rp"
при п—* оо независимо от величины показателя р. При р=1 по-
получается гармонический ряд, который, как мы уже доказали, рас-
расходится. При р — 2 получается ряд обратных квадратов, который
сходится. Значит, когда р = 1, мы никакого заключения о ряде
сделать не можем. В этом случае приходится исследовать ряд с
помощью других признаков.
185. Интегральный признак Коши. Читатель, наверное, уже
давно обратил внимание на полную аналогию определений сходи-
сходимости ряда и сходимости несобственного интеграла с бесконечным
верхним пределом (см. п. 97). Точно так же много общего и в приз-
признаках сходимости рядов с положительными членами и интегралов
с положительной подынтегральной функцией. Сейчас мы приведем
признак, позволяющий в некоторых случаях сводить вопрос о схо-
сходимости ряда к вопросу о сходимости соответствующего несобст-
несобственного интеграла; может оказаться, что этот последний вопрос
будет более простым.
Интегральный признак Коши. Пусть дан ряд
члены которого являются значениями непрерывной функции/(jt)
при целых значениях аргумента х:
»i=/B), ...» un=j
и пусть/(лс) монотонно убывает в интервале A, оо). Тогда ряд схо-
сходится, если сходится несоб-
ственный интеграл § f(x)dxt
этот
и расходится, если
интеграл расходится.
Доказательство. Рас-
Рассмотрим криволинейную тра-
трапецию, ограниченную линией
y=zf(x), с основанием от
л; = 1 до х — п, где п —
произвольное целое положи-
положительное число (рис. 227). Площадь ее измеряется интегралом
О
3 4
Рис. 227.
/7-/ 71
Ia-=\f(x)dx.
648 гл. xi. ряды [185
Отметим целые точки основания л; = 1, х — 2у ..., л: = я — 1, лг = я.
Рассмотрим две ступенчатые фигуры: одна из них (входящая) имеет
площадь, равную /B) +/C)+ . .. +/(#) = $„ — иъ а вторая (вы-
(выходящая) — площадь, равную /О)+/B)+ .. . +/(л — 1) = вя — ип,
где $п = и1-{-и2+ . .. +ип. Площадь первой фигуры меньше пло-
площади данной криволинейной трапеции, площадь второй больше ее,
т. е. мы имеем
Отсюда получаем два неравенства:
*»<'„ + «!. (*)
Так как функция f(x) положительна, то интеграл 1п возрастает
вместе с п\ возможны два случая:
1) Несобственный интеграл сходится, т. е. /= lim ln сущест-
вует; тогда 1п < / и из неравенства (*) при всяком п находим
Следовательно, частичные суммы sn ограничены, и на основании
леммы ряд сходится.
2) Интеграл расходится; тогда 1п—> оо при п—> оо и на осно-
основании неравенства (**) заключаем, что sn также неограниченно
возрастает, т. е. ряд расходится.
Покажем на примере ряда
что интегральный признак иногда может с легкостью дать ответ
тогда, когда признак Даламбера неприменим. Для этого ряда, как
я
мы установили, -я+1—*1; применим к нему интегральный признак.
Очевидно, функцией f(x) является —р. Интеграл
)JP-dx=—f
lim (jc-'+i —1)
1—/
1 1
сходится, если р>1, так как в этом случае lim х~р+1 = 0
Х-+ оо
OS
и \-4 = ri если же р<1, то интеграл расходится, так как
J ху р— 1
теперь lim х"р+1= оо. При р=\ интеграл тоже расходится
186] § L числовые ряды 649
00 CD
\ — = In л: = оо. Поэтому рассматриваемый ряд сходится при р > 1
1 1
и расходится при р^1.
При р=1 получается гармонический ряд, и мы получаем еще
одно доказательство его расходимости. При р = 2 получается ряд
обратных квадратов; его сходимость уже была доказана раньше.
186. Ряды с произвольными членами. Абсолютная сходимость»
I. Знакочередующиеся ряды. Перейдем к рядам с чле-
членами, имеющими любой знак. Прежде всего остановимся на так
называемых знакочередующихся рядах. В таких рядах члены попе-
попеременно имеют то положительный, то отрицательный знак. Знако-
Знакочередующийся ряд можно записать так:
±(«i —«« + «8—•••)• (*)
где uv и2, и3, ...— положительные числа. Укажем простой
достаточный признак сходимости знакочередующегося ряда.
Теорема Лейбница. Если в знакочередующемся ряде аб-
абсолютные величины членов ряда убывают, т. е. в ряде (*)
иг > и2 > и3 >..., и общий член ип стремится к нулю, то ряд
сходится, причем его сумма по абсолютной величине меньше их;
остаток ряда гп по абсолютной величине меньше абсолютной ве-
величины первого из отбрасываемых членов: |гпК«п+1.
Доказательство. Возьмем для определенности перед всем
рядом (*) знак плюс
Рассмотрим сначала последовательность частичных сумм s2
с четными индексами и запишем их в виде
Так как по условию выражение в каждой скобке положительно
и число таких скобок растет вместе с т> то последовательность
s2m будет возрастающей. Наоборот, последовательность ча-
частичных сумм с нечетными индексами будет убывающей, так как
и сумма в квадратной скобке, на основании только что высказан-
высказанных соображений, будет возрастать вместе с т.
Таким образом,
650 гл. xi. ряды [186
Легко заметить, что любая сумма с четным индексом меньше
любой суммы с нечетным индексом
S2m ^ S
Действительно, если т < &, то
S2m < S2k ^
Если же т > k (или m=-k), то
На рис. 228 показано геометрическое изображение последова-
последовательности частичных сумм. Последовательность сумм с четными
Рис. 228.
индексами возрастает и ограничена сверху; значит, она имеет предел
inn s2m = s.
Так как s2m+1 = s2m + u2m + 1 и u2m+1-*0 при /я-*оо, то
т. е. суммы с нечетными индексами, убывая, стремятся к тому же
пределу s.
На рис. 228 ясно видно, что последовательность частичных
сумм приближается к своему пределу колеблясь; ясно также, что
сумма ряда 5 меньше любой суммы с нечетным индексом и, в ча-
частности, меньше uv
Если бы перед всем рядом (*) стоял знак минус, то рис. 228
надо было бы симметрично отобразить относительно начала коор-
координат; в этом случае было бы \s\<uv
Остаток ряда
представляет собой ряд, удовлетворяющий всем условиям признака
Лейбница. Поэтому его сумма гп по абсолютной величине меньше
первого члена в скобке, т. е. |гп|<ыл + 1, что и требовалось дока-
доказать. Теорема полностью доказана.
Теорема Лейбница позволяет в случаях, когда она применима,
установить не только сходимость ряда, но и оценить ошибку, до-
допускаемую при отбрасывании всех членов ряда, начиная с неко-
некоторого.
186] § 1. ЧИСЛОВЫЕ РЯДЫ 651
Например, по теореме Лейбница сразу видно, что ряд
сходится; мы увидим позже, в п. 194, что его сумма равна In 2.
Согласно доказанному предельная абсолютная ошибка приближен-
приближенного равенства 1п2^1—^"^Т—' " ^/Г^Т Равна7Г«
II. Абсолютная сходимость. Для рядов с произвольным
распределением зяаков их членов мы приведем только один важный
признак сходимости.
Достаточный признак сходимости. Если ряд, состав-
составленный из абсолютных величин членов данного ряда, сходится,
то сходится и данный ряд.
Доказательство. Обозначим через sn сумму п первых чле-
членов ряда
через s^ — сумму всех положительных членов^ а через s^— сумму
абсолютных величин всех отрицательных членов среди первых п
членов ряда. Тогда
= Sn— Sn И On =
где
Так как по условию оп имеет предел (обозначим его через а),
а^ и s^ — положительные и возрастающие функции от пу при-
причем Sn ^.on<o и Sn ^оп<,о, то и они имеют пределы. Вслед-
ВследS
ствие этого и sn = Sn—s^ при п—+оо стремится к пределу, что
и требовалось доказать.
Этот достаточный признак не является необходимым, т. е.
ряд 2^ ип может сходиться и тогда, когда ряд ^ \ип\ расходит-
/1=1 «я=1
ся. Например, ряд
как мы только что видели, сходится, а ряд (гармонический)
1+У + Т + Т+"-+7Г+--->
составленный из абсолютных величин его членов, как известно,
расходится.
652 гл. xi. ряды [186
Определение. Ряд, абсолютные величины членов которого
образуют сходящийся ряд, называется абсолютно сходящимся.
Если ряд сходится, а ряд, образованный из абсолютных ве-
величин его членов, расходится, то данный ряд называется неаб-
неабсолютно или условно сходящимся.
Например, ряд 1—у + у—"+ ••• ±—+ ••• условно сходя-
сходящийся.
Указанное разграничение абсолютной и неабсолютной сходимос-
тей рядов является весьма существенным. Оказывается, что неко-
некоторые свойства конечных сумм переносятся только на абсолютно
сходящиеся ряды; условно сходящиеся ряды этими свойствами не
обладают.
На этих вопросах мы подробно останавливаться не будем. Заме-
Заметим только, что абсолютно сходящиеся ряды обладают, как и обыч-
обычные суммы конечного числа слагаемых, переместителькым
свойством (при любой перемене мест членов абсолютно сходя-
сходящегося ряда он остается абсолютно сходящимся и с той же суммой).
Это свойство отсутствует у неабсолютно сходящихся рядов; оказы-
оказывается, переставляя члены такого ряда, можно добиться того, что
сумма ряда изменится.
Возьмем, например, условно сходящийся ряд
!__± .±_L + ±_±._L_±4-
и переставим его члены так, чтобы после каждого положительного члена
стояли два отрицательных:
2 4 "*" 3 6 8 ~Г'"
Сложим теперь каждый член с идущим после него отрицательным:
2 4^6 8 "г"*
В результате мы получили ряд, члены которого образованы произведе-
произведениями членов исходного ряда на -у . Но по свойству 1 п. 182 отсюда сле-
следует, что этот ряд тоже сходится и сумма его равна половине суммы
исходного ряда. Таким образом, изменив только порядок следования членов
ряда, мы уменьшили его сумму вдвое!
Абсолютно сходящиеся ряды обладают еще одним важным свой-
свойством: их можно перемножать.
Под произведением двух сходящихся рядов
' ..., A)
+... B)
187J § 2- функциональные ряды 653
будем, цдшимать ряд, образованный из всевозможных парных произ-
произведений членов данных рядов, расположенных в таком порядке:
(и{ох) + (utv2 -f u%vt) + {uhvs + u2v2 + u3vt) + ...
i-i + • • • + «„-Л +unvi) + • • • C)
В каждой группе членов этого ряда, объединенных скобками,
сумма индексов сомножителей (т. е. номеров мест, на которых они
находятся в своих рядах) постоянна: в 1-й скобке она равна 2, во
2-й. равна 3, в 3-й равна 4, ..., в #-й равна /г-f-l.
Имеет место теорема, которую мы приводим без доказательства:
Если ряды A) и B) абсолютно сходятся, то их произведение
есть также абсолютно сходящийся ряд, сумма s которого равна
произведению сумм рядов сомножителей:
§ 2. Функциональные ряды
187. Общие определения. Перейдем теперь к рассмотрению
рядов, членами которых являются не числа, а функции:
Такие ряды называются функциональными. Предполагается, что
все функции ип (х) определены и непрерывны в одном и том же
интервале, конечном или бесконечном.
Ряд (*) может для одних значений х сходиться, для других —
расходиться. Значение дс = л:0, при котором числовой ряд
сходится, называется точкой сходимости ряда (*). Совокупность
всех точек сходимости ряда называется областью сходимости ряда:
говорят, что ряд сходится в этой области. Областью сходимости
ряда обычно бывает какой-нибудь интервал оси Ох.
Пример 1. Ряд
1 + X + X2 + . . . + ХП + . . ,
сходится в интервале (—1, 1), так как при любом значении х из
этого интервала соответствующий числовой ряд представляет бес-
бесконечно убывающую геометрическую прогрессию. При |лг|^1 этот
ряд расходится.
Определение области сходимости более сложных функциональ-
функциональных рядов представляет весьма трудную задачу.
Сумма ряда является некоторой функцией от х, определенной
в области сходимости ряда; обозначим ее через
654 гл. xi. ряды [187
Так, в приведенном выше примере сумма ряда равна ; разу-
разумеется 31 а функция является суммой ряда только в интервале
(—1, 1)—области сходимости ряда.
Сумму п первых членов ряда (/z-ю частичную сумму) будем
обозначать через sn(x), а остаток ряда —через гп(х). Если ряд
сходится при некотором значении ху то
lim sn(x) = S {х) и lim rn{x) = 0.
п -*¦ оо
Хорошо известно, что сумма конечного числа непрерывных
функций есть функция непрерывная; далее, производная и интеграл
от суммы конечного числа функций равны соответственно сумме
производных и интегралов от этих функций. При изучении функ-
функциональных рядов сразу возникает вопрос: переносятся ли указанные
свойства на суммы бесконечного числа функций, т. е. на функцио-
функциональные ряды? Покажем на примере, что для произвольных функцио-
функциональных рядов эти свойства могут оказаться несправедливыми.
2. Рассмотрим ряд
У2 V2 У2
Л I Л I I
« Л I *-2\2 ~ •
2J^ '•" ^ A+х2)"^ "••
При лг = О все члены ряда равны нулю и сумма его равна нулю.
При х Ф- 0 ряд представляет сходящуюся геометрическую прогрес-
прогрессию, так как ее знаменатель д= у 2 < 1. Сумма ряда равна
1 -р X
Таким образом, сумма ряда S(x) оказалась разрывной функ-
функцией; она имеет разрыв в точке дг = О:
5(лг)=1, если хфОу и 5@) = 0.
Чтобы установить, в каких же случаях на функциональные ряды
можно перенести свойства конечных сумм функций, введем новое
определение.
Определение. Функциональный ряд
называется правильно сходящимся в области />, принадлежа-
принадлежащей области сходимости ряда, если в области D все члены его по
абсолютной величине не превосходят соответствующих членов
некоторого сходящегося числового ряда с положительными
членами.
187] § 2. функциональные ряды 655
Это значит, что во всех точках области D должно выполняться
неравенство \ип(х)\^Мп1 где Мп — член сходящегося ряда Мг +
+ Ж24-... + Afw+• ¦ •¦ этот последний ряд называется мажори-
мажорирующим (усиливающим) по отношению к ряду (*).
3. Ряд
sin 2а; , sin Зд; , , sin nx
sin nx
правильно сходится в любом интервале оси Ол:, так как
а ряд обратных квадратов сходится.
В более подробных курсах вводят более сложное определение равно-
равномерной сходимости ряда; поясним вкратце его смысл.
Пусть в точке хх ряд сходится. Это значит, что lim гп(хх) — 0\ по-
этому для любого числа е > О можно указать такое число Nl9 что при
всех п > Nx будет справедливо неравенство | гп (хг) | < е.
Возьмем в области сходимости другую точку х2; в ней тоже ряд схо-
сходится и lim rn(x2) = 0. Если взять то же самое число е, то, конечно, не-
П -*- со
равенство | гп (х2) \ < е будет выполняться, начиная с некоторого номера,
т. е. при п > /V2, однако может оказаться, что число iV2 будет больше Nx.
Именно поэтому мы обозначили числа Nx и iV2 разными индексами. Если
бы речь шла только о двух точках, то мы бы вышли из положения очень
просто: взяли бы из двух чисел Nx и iV2 наибольшее и обозначили его
через N\ тогда оба остатка были бы по абсолютной величине меньше 8
при всех п> N. Так же мы могли бы поступить, если бы у нас было не
две, а три, четыре или вообще любое конечное число точек. Но если
область сходимости интервал, то в нем бесконечное число точек, и
хотя каждой точке х соответствует свое число TV (e, х) (его обозначают
N (е, л:), подчеркивая, что оно зависит и от 8 и от х) такое, что при
п > N (е, я) остаток | гп (х) \ < в, но числа N общего для всех точек об-
области сходимости может и не найтись. В связи со сказанным становится
понятным следующее определение.
Определение. Функциональный ряд (*) называется равномерно
сходящимся в области Z), если для любого числа 8>0 можно указать
такое число /V(s), зависящее только от s и не зависящее от х, что при
всех /&>iV(e) неравенство |гм(дс)|<с справедливо для всех точек об-
области Z).
Легко показать, что если в области D функциональный ряд сходится
правильно, то он сходится и равномерно. Действительно, из определения
правильной сходимости ряда следует, что для любого х из области D
k»WI = l"«+iW+...K|«n+iWI+.-.<AIB+1+...=rJ|t
где гп — остаток сходящегося числового ряда М1 + М2 + ... + Мп-\- ... Ве-
Величина гп от х не зависит и будет меньше любого числа 8 > 0, если п > /V,
где N зависит только от е; но тогда при этих же значениях п и | rn (x) \ < 8,
что и означает равномерную сходимость ряда.
В то же время можно привести примеры (мы этого делать не будем)
таких равномерно сходящихся рядов, для которых нельзя подобрать мажо-
мажорирующие числовые ряды, т. е. такие, которые не являются правильно
сходящимися.
В дальнейшем мы для простоты будем говорить о правильно сходя-
сходящихся рядах, однако все сформулированные теоремы останутся справедли-
справедливыми и для рядов равномерно сходящихся.
656 гл. хк ряды [188
188. Свойства правильно сходящихся функциональных рядов.
В этом пункте мы сформулируем, не приводя доказательств, основ-
основные теоремы для правильно сходящихся рядов; они дадут ответы
на вопросы, поставленные в п. 187, о возможности переноса на
такие ряды свойств сумм конечного числа функций. Во всех теоре-
теоремах предполагается, что область правильной сходимости ряда есть
некоторый интервал оси Ох.
Теорема 1. Если ряд из непрерывных функций правильно
сходится в области />, то его сумма есть функция непрерывная
в этой области.
г, о . sin 2х , , sin nx ,
Пример. Ряд sin л;-}—п2~-+...Н ъ—h • • • сходится пра-
правильно в любом интервале (см. пример 3 п. 187); следовательно,
его сумма S (х) есть функция непрерывная.
Фактическое отыскание этой функции является задачей несрав-
несравненно более трудной; нам ведь даже неизвестно, будет ли эта
функция элементарной или нет. Разумеется, у нас всегда есть воз-
возможность приближенно подсчитать значения функции в различных
точках, беря некоторое количество членов ряда, т. е. Sn (х). Инте-
Интересно при этом отметить, что предельная абсолютная ошибка, воз-
возникающая при такой замене, может считаться одинаковой для всех
значений х, так как
!'.(*) Is
1 sin
"Г
• = rn,
где гп — остаток числового ряда — зависит только от п и не зависит
от х. Подобное же замечание относится, понятно, к любым пра-
правильно сходящимся рядам. (Читатель, познакомившийся с мелким
шрифтом в п. 187, может перенести это замечание на ряды равно-
равномерно сходящиеся.)
Итак, первая теорема утверждает, что сумма правильно сходя-
сходящегося ряда из непрерывных функций есть функция непрерывная.
Во второй теореме речь пойдет о перенесении на такие ряды про-
простейшего свойства интеграла: интеграл от суммы функций равен
сумме интегралов. Чтобы в дальнейшем не делать оговорок, усло-
условимся, что интервал интегрирования [я, Ь] всегда считается при-
принадлежащим области правильной сходимости ряда.
Теорема 2. Если ряд из непрерывных функций правильно
сходится, то интеграл от суммы ряда равен сумме ряда, состав-
составленного из интегралов от членов данного ряда:
ь ь ь ь
Коротко теорему формулируют так:
188] § 2. функциональные ряды 657
Правильно сходящийся ряд можно почленно интегрировать.
Сходимость числового ряда из интегралов доказывается очень
просто. Из определения правильной сходимости данного ряда сле-
следует, что | ип (х) | ^ Мп, где Мп — член сходящегося числового ряда;
по теореме об оценке интеграла (см. п. 90)
ь ъ
| \ ип (х) dx | < J ) ип (х) | dx < Мп (Ь - а).
а а
Так как по свойству 1 п. 182 ряд с общим членом Мп{Ь—а) схо-
сходится, то, согласно п. 186, И, сходится и ряд из интегралов
(и даже абсолютно). Доказательство второй части теоремы —равен-
—равенства левой и правой частей формулы (*) мы не приводим.
Теорема 2 применима и в том случае, когда берутся интегралы
с переменным верхним пределом:
XXX X
J 5 (х) dx = J Ul (x) dx-
а
где а^х ^Zb. Здесь справа стоит функциональный ряд; снова
X
пользуясь теоремой об оценке интеграла ( \ ип (х) dx ^ Мп(х—а) ^
а
^Мп(Ь—а)), устанавливаем, что он, как и данный ряд, сходится
правильно.
Теорема о возможности почленного дифференцирования ряда
более сложна, так как требует дополнительных предположений.
Теорема 3. Если ряд ttx{x)-{-u2{x)-{-...-^-un(x)-\-..m, состав-
составленный из функций, имеющих непрерывные производные, схо-
сходится в области D и его сумма равна S (х), а ряд из производных
и'п (х) сходится в этой области правильно, то производная суммы
ряда S' (х) равна сумме ряда из производных:
S' (ху=и\ (х)+и'2 (х) + ...+*; (х)+...
Говоря коротко: Если ряд, составленный из производных сходя-
сходящегося ряда, сходится правильно, то его можно почленно
дифференцировать.
Отметим, что правильная сходимость данного ряда, а также дифферен-
цируемость его суммы не предполагаются, а являются следствиями условий
теоремы. Однако проверка правильной сходимости ряда из производных
совершенно обязательна; при невыполнении этого условия теорема может
тт . . sin 23 х sin/г3 я
потерять смысл. Например, ряд sinxH щ Ь«««Н г !""••• пРа"
вильно сходится (он мажорируется рядом обратных квадратов) и его
сумма —непрерывная функция. Ряд ,же из производных cos л;+ 2 cos 23 я 4-
658 гл. xi. ряды [189
+ .. .-f-ncosn3х-\-... расходится, так как его общий член ни при
каком х не стремится к нулю. Следовательно, теорема неприменима, не-
несмотря на то, что сумма ряда, может быть, и имеет производную.
В настоящем курсе будут рассмотрены только важнейшие
классы функциональных рядов: степенные ряды и тригонометриче-
тригонометрические ряды.
§ 3. Степенные ряды
189. Теорема Абеля. Интервал и радиус сходимости. Начнем
с определения степенного ряда.
Определение. Степенным рядом называется функцио-
функциональный ряд
а0 + аг (х — х0) + а2 (л: — х0J + ... + «* (х — хо)п + ....
члены которого суть произведения постоянных а0, at,
а2» • • • f #„» • • • на степенные функции с целыми показателями
степеней от разности х — х0.
Постоянные а0, av а2, . .. , ап, ... называются коэффициен-
коэффициентами степенного ряда.
В частности, если хо = О, то мы будем иметь степенной ряд,
расположенный по степеням х:
а0 + ахх + а2х2 + ... + апхп + ...
В дальнейшем мы будем изучать именно такие степенные ряды,
потому что всякий степенной ряд подстановкой х—хо = х' пре-
преобразуется к ряду указанного вида.
Для удобства п-м членом степенного ряда называют член апхп
несмотря на то, что он стоит на (#-|-1)-м месте. Свободный член
ряда а0 считают нулевым членом ряда.
Степенные ряды обладают многими важными свойствами, к
рассмотрению которых мы и переходим.
Рассмотрим степенной ряд вида
и докажем очень важную теорему, на которой будет основано
изучение таких рядов.
Теорема Абеля. Если степенной ряд (*) сходится в точке
x0j&0, то он сходится и притом абсолютно в интервале
(— |*о I» 1*о1)» т-е- ПРИ всяком х> удовлетворяющем условию
М<1|
<1о|
Доказательство. Заметим, что вследствие сходимости ряда
апХо его общий член стремится к нулю: апх\—>0; поэтому
189]
§ 3. СТЕПЕННЫЕ РЯДЫ
659
все члены этого ряда ограничены, т. е. существует такое посто-
постоянное положительное число Ж, что при всяком п имеет место
неравенство |яп*2|<Л1 Запишем ряд (*) так:
и составим ряд из абсолютных величин членов этого ряда:
х
~Ч
f +-
В силу установленного неравенства каждый член здесь меньше
соответствующего члена геометрической прогрессии со знаменате-
х
лем
М+М
Если \х\ < \xQ
то
...+М
< 1 и прогрессия сходится; поэтому
сходится и ряд абсолютных величин, а значит, абсолютно сходится
сам ряд (*). Теорема доказана.
Несмотря на то, что | апхп | < | апх^ |, мы не можем сразу вос-
воспользоваться признаком сравнения, поскольку в условии теоремы
не сказано, что ряд в самой точке х0 сходится абсолютно.
Следствие. Если степенной ряд (#) расходится при лг = л:0,
то он расходится и при всяком х, большем по абсолютной вели-
величине, чем лг0, т.е. при \х\>\хо\.
В самом деле, если бы он сходился при каком-нибудь таком х,
то в силу теоремы Абеля он абсолютно сходился бы и при всех
меньших по абсолютной величине значениях лг, в частности при
х = х0, а это противоречит условию.
Перейдем к установлению области сходимости степенного ряда
(#). Здесь возможны три случая:
1) Область сходимости состоит только из одной точки х = 0,
другими словами, ряд расходится для всех значений лг, кроме
одного.
Этот случай может быть иллюстрирован рядом
действительно, если х фиксировано и хфО, то, начиная с доста-
достаточно большого я, будет |ллг|>1, откуда вытекает неравенство
|лил:п|>1, означающее, что общий член ряда не стремится к
нулю.
2) Область сходимости состоит из всех точек оси Ох, другими
словами, ряд сходится при всех х.
660
гл. xi. ряды
[189
Рассмотрим ряд
1 X
Для любого Ху начиная с достаточно большого п, будет —
Так как
< 1.
п+1
п + 2
П+2
П + 2
и т. д.,
то, начиная с номера п, члены ряда по абсолютной величине будут
меньше членов сходящейся геометрической прогрессии. Следова-
Следовательно, при любом х ряд сходится.
3) Область сходимости состоит больше чем из одной точки оси
Ох, причем есть точки оси, не принадлежащие области сходимости.
Например, ряд
представляющий геометрическую прогрессию со знаменателем х,
сходится при |лг|<1 и расходится при \х\^\.
В третьем случае на числовой оси наряду с точками
сходимости ряда имеются и точки его расходимости.
Из теоремы Абеля и ее следствия вытекает, что все точки
сходимости расположены от начала координат не дальше, чем
любая из точек расходимости. Совершенно ясно, что точки схо-
сходимости будут целиком заполнять некоторый интервал с центром
в начале координат.
Таким образом, можно сказать, что для каждого степенного
ряда, имеющего как точки сходимости, так и точки расходимости,
существует такое положительное число R, что для всех х, по
модулю меньших /?(|л;|</?), ряд абсолютно сходится, а для всех
х, по модулю больших R(\x\> R), ряд расходится.
Что касается значений x = R и лг =—R, то здесь могут осу-
осуществляться различные возможности: ряд может сходиться в обеих
точках, или только в одной из них, или ни в одной. При этом ряд
может сходиться как абсолютно, так и условно. Позже мы рассмот-
рассмотрим примеры, иллюстрирующие эти случаи.
Определение. Радиусом сходимости степенного ряда (#)
называется такое число /?, что для всех л\ |#!</?> степенной
ряд сходится, а для всех х, | *!>/?, расходится. Интервал
(— /?t JR) называется интервалом сходимости.
Условимся для рядов, расходящихся при всех х, кроме лг=*О,
считать /? = 0, а для рядов, сходящихся при всех х% считать
189] § 3. СТЕПЕННЫЕ РЯДЫ 661
Для степенных рядов вида
а0 + ах (х—х0) + а2 (х — л:0J +...+ап (х~хо)п + . ..
все сказанное выше остается в силе с той только разницей, что
теперь центр интервала сходимости будет лежать не в точкел; = 0,
а в точке лг = лг0. Следовательно, интервалом сходимости будет ин-
интервал (лг0—#, xo + R).
Укажем способ отыскания радиуса сходимости степенного ряда.
Прежде всего заметим, что для нахождения радиуса сходимости
мы можем исследовать ряд, составленный из абсолютных величин
членов данного ряда:
К1 + Ы1*1+---+К|1*Г+---> (**)
так как интервалы сходимости ряда (*) и ряда (**) совпадают.
К ряду (##), члены которого положительны, применим признак
Даламбера. Допустим^ что мы сумели найти предел отношения пос-
последующего члена ряда к предыдущему. В отличие от числового
ряда, этот предел будет содержать множителем или сам |д:|, или
некоторую его степень. Если, начиная с некоторого номера, члены
ряда идут без пропусков, т. е. коэффициенты ряда не обращаются
в нуль, то этот предел можно записать в виде
Если, например, ряд содержит только все четные степени х, т. е.
имеет вид а0 + а2х2 + . .. + #2n*2" + • • • > т0 этот предел равен
' (аналогично и в других слу-
2n
чаях). Для тех значений |дг|, при которых получаемый предел бу-
будет меньше 1, ряд сходится, а для тех, при которых больше 1,
ряд расходится. Отсюда следует, что то значение \х\, при котором
этот предел равен единице, и будет являться радиусом сходимости
ряда.
Может случиться, что найденный предел при любом \х\ будет
равен нулю. Это значит, что ряд (*) сходится при всех х и его
радиус сходимости равен бесконечности (#=оо).
Наоборот, если при всех |дг|^&=0 предел окажется равным бес-
бесконечности, то ряд будет всюду расходиться (кроме точки дгаяО)
и его радиус сходимости будет равен нулю.
Поясним сказанное на конкретных примерах.
Примеры. 1) Найдем радиус сходимости ряда
662
Имеем
ГЛ. XI. РЯДЫ
[189
"п + 1
О
при любом значении |лг|. Следовательно, ряд сходится при всех
значениях х, т. е. R=oo.
В силу необходимого признака сходимости общий член рассмат-
рассматриваемого ряда стремится к нулю:
хп
lim ~ = 0
при любом значении х. Это замечание будет существенным обра-
образом использовано в дальнейшем.
2) Возьмем ряд
Имеем
{П+\)Хп
= X
л+1
\х\
Следовательно, согласно признаку Даламбера ряд сходится, если
|лг|<1, и расходится, если |л:|>1. Итак, /?=1.
В этом примере нетрудно установить, что делается с рядом на
концах интервала сходимости. При х = 1 получаем расходящийся
1+L + L + ++
ряд
а при Xs=s ~"
1
1
2 -г з -г -.- -г я "г--
-1—^ ~ + ..., сходящийся неабсолютно.
Z о
Отметим, что при исследовании вопроса о сходимости ряда на
концах интервала сходимости признак Даламбера неприменим
(соответствующий предел здесь равен 1) и нужно применять дру-
другие признаки.
3) Исследуем ряд
х3
( ^)
Здесь
_. |2
Следовательно, радиус сходимости ряда равен 1; при |д;|<1 ряд
сходится, а при |л;|>1 расходится. Предоставляем читателю до-
доказать, что на обоих концах интервала ряд сходится абсолютно.
190] § 3. СТЕПЕННЫЕ РЯДЫ 663
4) Найдем интервал сходимости ряда
х-\ (х-1)* (х-1K (л-1)"
Ь2 »" 2-22 •" 3-23 "г • • • f rt.2" " • • •
Составим отношение:
1 I П4-1« ОП г>
= |дг —1
2// 4-1 I у 1 Iй
[Л 1 |
и найдем его предел:
«и4
lim
Согласно предыдущему ряд сходится, если i-^—-<1,т. е.
—2 < х— 1 < 2. Таким образом, интервалом сходимости ряда является
интервал (—1, 3) с центром в точке х=\. Предоставляем читателю
проверить, что на концах интервала ряд ведет себя так же, как
ряд примера 2.
190. Свойства степенных рядов. Рассмотрим степенной ряд
имеющий радиус сходимости R(R может равняться оо). Сумма
этого ряда — обозначим ее через S (х) — есть функция, определен-
определенная внутри интервала сходимости, а также в том из концов интер-
интервала, где ряд сходится.
Чтобы применить к степенным рядам результаты п. 188, дока-
докажем прежде всего следующие леммы1).
Лемма 1. Степенно» ряд правильно сходится в любом ин-
интервале [—bt b\, целиком лежащем внутри интервала сходимости.
Доказательство. Выберем точку х0 так, чтобы было
Ь<Хц<СИ.\ она лежит в интервале сходимости и по теореме Абеля
числовой ряд
сходится. Для любой точки х б [ —?, Ь] имеем |лг|<|л:0| и, сле-
следовательно, | апхп\ < ] аплго |. Последнее неравенство и означает,
что ряд (*) правильно сходится в интервале [—-b, b].
Лемма 2. Степенной ряд, составленный из производных
членов ряда (*), имеет тот же радиус сходимости, что и дан-
ный ряд.
1) Если п. 188 не изучался, то читатель должен прямо перейти к свой-
свойствам степенных рядов, сформулированным ниже.
664
ГЛ. XI. РЯДЫ
[190
Доказательство. Ряд из производных имеет вид
at + 2a2x+ ... +папхп~1+(п+ 1) ап+1ха+ ... (•*)
Предположим для простоты рассуждений, что предел отношения
существует1); тогда радиусы сходимости рядов (#) и (**)
можно отыскивать с помощью признака Даламбера:
Пт
/1-х»
апхп
Пт
папхп
— | X | Пт
= |лг| lim
П-*- CD
= | x I lim
art+l
lim
->00
a
Равенство пределов отношения последующего члена к предыдущему
для обоих рядов показывает, что радиусы их сходимости равны.
Заметим, что на конце интервала сходимости ряд (**) может рас-
расходиться и тогда, когда ряд (*) сходится; советуем читателю про-
х2 хп
верить это на примере ряда 1 +# + -оГ+ • • • +
•" "^"Ti2" *!"•••
Если теперь составить ряд из производных ряда (**), то он
опять будет иметь тот же радиус сходимости и т. д. Таким обра-
образом, все степенные ряды, получающиеся последовательным диффе-
дифференцированием ряда (*), имеют один и тот же радиус сходимости
и по лемме 1 правильно сходятся в любом интервале, целиком при-
принадлежащем интервалу сходимости.
Из доказанных лемм и общих свойств правильно сходящихся
рядов вытекают следующие свойства степенных рядов:
1. Сумма степенного ряда есть функция, непрерывная в интервале
сходимости ряда
5 (х) - ао
апхп+ ... (-
Дополнительно отметим, что в том конце интервала, где степен-
степенной ряд сходится, его сумма S (х) остается непрерывной.
Необходимо отметить одно обстоятельство, которое может иногда
привести к недоразумениям. Возьмем геометрическую прогрессию,
сходящуюся при |#1< 1:
Функция -j определена и непрерывна всюду, кроме точки #=1.
Тем не менее следует твердо помнить, что эта функция является
1) Если это не предполагать, то доказательство леммы усложняется.
191] § 4. разложение Функций в степенные ряды 665
суммой ряда только при |д:|<1; при [#|^1 ряд расходится и об
его сумме говорить нельзя.
2. Степенной ряд можно почленно интегрировать в интервале
сходимости
X X X X X
S(х) dx =5 aQdx +$ ахх dx + J a2x2dx + ...+$ anxndx+...=
о о о о
3. Степенной ряд можно почленно дифференцировать в ин-
интервале сходимости
Продолжая дифференцирование, последовательно получим
S"(x) = 2a2 + 3-2azx+...+n(n— \)anxn~2+ ...
S'"(x) = 3.2a3+...+n(n—\)(n-2)anxn~3+...
и таким же образом дальше. Итак,
Степенной ряд в интервале его сходимости можно почленно
дифференцировать любое число раз.
§ 4. Разложение функций в степенные ряды
191. Ряд Тейлора1). Мы знаем, что сумма степенного ряда в
интервале сходимости этого ряда является непрерывной и бесконеч-
бесконечное число раз дифференцируемой функцией (см. п. 190). Перейдем
теперь к выяснению обратного вопроса.
Когда можно утверждать, что заданная функция f(x) является
суммой некоторого степенного ряда?
Из свойств степенных рядов следует прежде всего, что эта
функция должна быть бесконечное число раз дифференцируема.
Однако, как мы вскоре увидим, это условие не является достаточным.
Наша ближайшая задача состоит в том, чтобы установить, какие
функции и в каких интервалах можно представить в виде сумм сте-
степенных рядов.
В дальнейшем, если заданную функцию f(x) мы представим в
виде суммы некоторого степенного ряда, то будем говорить, что
функция f(x) разложена в степенной ряд.
Важность такого разложения видна хотя бы из того, что мы
получаем возможность приближенно заменить функцию суммой
1) Б. Тейлор A685—1731) —английский математик, ученик Ньютона.
666 гл. xi. ряды [191
нескольких первых членов степенного ряда, т. е. многочленом. Вычис-
Вычисление значений функции при этом сводится к вычислению значений
многочлена, что можно сделать, производя только простейшие ариф-
арифметические действия. Особенно важно, что мы сумеем оценивать
точность получаемых приближенных значений.
Напомним читателю, что с частным случаем замены функции
многочленом мы уже встречались в п. 53, рассматривая применения
дифференциала к приближенным вычислениям. Именно там мы заме-
заменяли функцию в окрестности изучаемой точки многочленом первой
степени, т. е. линейной функцией. Однако полученные нами ре-
результаты носили весьма ограниченный характер; мы не умели оце-
оценивать точность такой замены и поэтому ничего не могли сказать
об интервале, в котором найденные приближенные формулы были
применимы.
Замена функции таким простым выражением, как многочлен,
оказывается очень удобной и в различных вопросах анализа: при
вычислении интегралов, решении дифференциальных уравнений и т. д.
Итак, предположим, что функция f(x) бесконечное число раз
дифференцируема в окрестности некоторой точки лг0. До-
Допустим, что ее можно представить в виде суммы степенного
ряда, сходящегося в каком-то интервале, содержащем точку х0:
где я0, av я2, . •., я„, ...—неопределенные пока коэффи-
коэффициенты.
Покажем, как, пользуясь свойствами степенных рядов, можно
найти коэффициенты а0, а1У а2, ... по известным значениям функ-
функции /(х) и ее производных в точке д:0.
Положим в равенстве (*) х — х0. Будем иметь
f(x0) = а0.
Продифференцируем степенной ряд
и снова положим х = х0. Тогда
/f(x0) = av
При следующем дифференцировании получим
f"(x)=:2a2+...+n(n-\)an(x-x0)n-*+...
Отсюда, полагая снова х — х0, найдем, что
f"(r\ — <2a т р а — LAtlL
191] § 4. РАЗЛОЖЕНИЕ ФУНКЦИЙ В СТЕПЕННЫЕ РЯДЫ 667
(Мы напишем для единообразия не 2, а 2!) После я-кратного диф-
дифференцирования получим
причем все остальные члены будут еще содержать множитель (х — х0)
и, следовательно, при х = х0 обратятся в нуль. Мы получим
= п\ап, т. е.
Таким образом находятся последовательно все коэффициенты а0, av
а2, ... разложения (*):
._„., а -fix) а - Г (*о) а - Г> (*о)
Подставляя найденные выражения в равенство (*), получим ряд
(**)
который называется рядом Тейлора функции f(x).
Определение. Рядом Тейлора функции f{x) в окрестности
точки х0 называется степенной ряд (**) относительно разности
х — д:0, коэффициенты которого а0, а19 а2, ..., а„, ... выражают-
выражаются через функцию f(x) и ее производные в точке х0 по формулам
— fix) a—fix) а — /Ч*о)
а
Эти коэффициенты называются коэффициентами Тейлора
функции f(x) в точке х0.
Таким образом, мы установили пока, что
Если функцию f(x) можно разложить в степенной ряд по степе-
ням разности (х — л:0), то этот ряд обязательно является рядом
Тейлора этой функции.
Обращаем особое внимание читателя на то, что все наши рас-
рассуждения были сделаны в предположении, что функция f(x) может
быть разложена в степенной ряд.
Если заранее этого не предположить, а просто считать функцию
f(x) бесконечное число раз дифференцируемой и составить для нее
ряд Тейлора, то ниоткуда не следует, что этот ряд сходится при
значениях дг, отличных от х0.
Более того, как это ни покажется странным читателю, могут
быть даже такие случаи, что ряд Тейлора, составленный для функ-
функции /(лг), сходится, а сумма его вовсе не равна f(x).
668 гл. xi. ряды [192
Примером может служить функция
i_
/(*) = * *г при х 5*0 и /@) = 0.
Это —бесконечное число раз дифференцируемая на всей оси Ох функция, причем
2 --
все ее производные в точке л: = 0 равны нулю. Действительно, /'(*) = ~"зв х*
при х ф 0 и Ц @) = 0, так как
=Il.m_L
(мы положили — = г J . Далее, Г'@)=0, так как
Иш
и т. д. Следовательно, все коэффициенты Тейлора функции i(x) при * = 0
равны нулю. Соответствующий ряд Тейлора состоит из членов, равных нулю,
и, значит, сходится, но не к функции /(*), а к функции, тождественно рав-
равной нулю.
192. Условие разложения функций в ряд Тейлора. Перейдем
теперь к выяснению условий, при которых можно утверждать, что
ряд Тейлора (**), составленный для функции f(x):
действительно сходится в некотором интервале и что его сумма в
точности равна f(x).
Обозначим через Тп(х) многочлен п-й степени, представляющий
/2-ю частичную сумму ряда Тейлора:
Tn(x)=f(x0)+f (х0) (x-xQ)+... +J^L (x-xQ)\
Назовем остаточным членом ряда Тейлора разность
Сходимость ряда Тейлора к функции f{x) в точке х означает, что
Я-> 00
или, что то же самое,
192] § 4. РАЗЛОЖЕНИЕ ФУНКЦИЙ В СТЕПЕННЫЕ РЯДЫ 669
Величина Rn{x) дает при этом как раз ту ошибку, которую мы
делаем, заменяя функцию f(x) многочленом Тп(х).
Прежде чем перейти к доказательству теоремы, которая позволит
нам оценивать величину остаточного члена, рассмотрим один частный
случай.
Предположим, что функция f(x) сама есть многочлен я-й
степени. Тогда при последовательном дифференцировании функции
f(x) мы будем каждый раз получать многочлен степени на единицу
меньше. После п дифференцирований мы получим постоянную вели-
величину и все последующие производные будут равны нулю. Таким
образом, от ряда Тейлора для многочлена f(x) останутся только
(я + 1) первых слагаемых, т. е. опять-таки многочлен /г-й степени.
Это, разумеется, можно было предвидеть и заранее, так как мы
попросту располагаем заданный многочлен по степеням разности х — л:0.
Полученное тождество
называется формулой Тейлора для многочленов.
Примеры. 1) Расположим многочлен / (х) = — 3 + лг — х2 -\- 2х3
по степеням разности х—1. Здесь л;0=1 и
=1= 10, /'"A) = 12.
Итак,
— 3 + х — х2 + 2х3 = — 1 + 5 (х — 1) + 5 (лг — 1 J + 2 (х — 1 K.
Раскрытая скобки в правой части и приводя подобные члены, чита-
читатель легко убедится в справедливости полученного тождества.
2) В качестве еще одного интересного примера расположим мно-
многочлен п-Pl степени f(x) = A -\-х)п по степеням х, т. е. по степеням
разности х — 0. Имеем
/10) = 1, /'@)=л, /*@) = л(я-1), ...
..., /t*> @) = л (л — 1).. . (я —
Формула Тейлора дает:
2!
, я (/г — 1) — (/t—ft + 1) ЛЛ
Мы получили известную формулу Ньютона для бинома в целой
положительной степени; она является, таким образом, частным случа-
случаем формулы Тейлора.
670 гл. xi. ряды [193
193. Остаточный член ряда Тейлора. Формула Тейлора. Пусть
f(x) — функция, относительно которой мы хотим выяснить, допускает
она разложение в ряд Тейлора в окрестности некоторой точки Хо
или нет. Запишем ее в виде (см. п. 192)
/ (х) = Тп (х) + Rn (х) =/ (х0) +/' (х0) (х-хо) + ...
где Rn(x) — остаточный член ряда Тейлора.
Докажем теорему относительно структуры Rn{x)9 которая в даль-
дальнейшем позволит нам устанавливать, стремится ли Rn(x) к нулю
при неограниченном возрастании п или нет, т. е. разлагается ли
функция / (х) в ряд Тейлора или нет.
Теорема. Если функция f(x) во всех точках некоторого
интервала, содержащего точку х09 имеет (/г+1)-ю производную
f{n+1)(x)9 то остаточный член Rn(x) для любой точки этого ин-
интервала имеет вид
где | заключено между х0 и х.
Доказательство. Запишем остаточный член Rn(x) в виде,
аналогичном формуле общего члена ряда (#), т. е.
о (х\-п
кп(х)-ип+1
и найдем такое выражение для De+1> чтобы равенство
1 (х х ) I D
было справедливо для любого х из интервала, указанного в условии
теоремы.
Зафиксируем независимую переменную х и положим ее равной
хх; тогда Dn+l станет равной
f{tl) (у \
/(%)-/(*,)-Г Uo) (*i-ч)- ¦ ¦ •- я," (н-ч)п
Г) lii
Наша задача придать теперь этому выражению вид, указанный в
условии теоремы, т. е. /(Л+1) (g), где ? € (х0' xi)- Заметим сначала,
193] § 4. РАЗЛОЖЕНИЕ ФУНКЦИЙ В СТЕПЕННЫЕ РЯДЫ 671
что при л = 0 это следует из теоремы Лагранжа (п. 57)
Доказательство для любого п проводится так же, как и доказа-
доказательство теоремы Лагранжа,—путем построения вспомогательной
функции ^(л;), удовлетворяющей условиям теоремы Ролля; только
теперь эта функция имеет более сложный вид. Именно, положим
F ('Ут\ -— ~Р ( v \ —— ~f (зс\ —— ~f (jc\ ( at —^— Jc"\ ——— ( v* —— д?^ ——
Г y\n Г)
(n+\)\
Из выражения для F(x) сразу видно, что /7(д:1)==0. Взяв
х = х0 и заменив Dn+1 его значением, убеждаемся, что и F(xo) = O.
Находим производную F' (х):
F' (х) = -/' (х)-Г(х) (Xl-x)+f (х)-
I \Х) ( Y у\2 ! f" I у\ (г У\ ^ ' (X Х\П 4*
Производная F' (х) существует во всех точках интервала, так
как по условию теоремы существует/(П+1) (л:), а следовательно, и
все производные низших порядков. В выражении для F' (х) уничто-
уничтожаются все слагаемые, кроме двух выделенных1); вынося еще общий
множитель за скобки, получим
F' (х) = ^^
[/ (*) +Z)n+1].
Итак, мы проверили, что функция ^(л:) удовлетворяет всем условиям
теоремы Ролля, и нашли ее производную. Подставим в выражение
для F' (х) то значение ? ? (л:0, л^), при котором производная равна
нулю (если значений ? несколько, то берем любое из них):
Первый множитель нулю не равен, потому что \:фхх) значит,
1) Рекомендуем читателю взять определенное значение п, скажем /i = 4fl
и привести полностью все выкладки. Тогда будет значительно понятнее рас-
рассуждение в тексте, проведенное для любого п.
672 гл. xi. ряды [193
должно быть Dn+1 =/(;а+1) (?), и
*¦ (*l) = /(Л + 1> (Б) (V+°1O1 ' ^ Е ^ (*«' *!>•
Так как aTj —любая точка интервала, то теорема доказана.
Найденное выражение для остаточного члена позволяет равенство
(*) переписать так:
В таком виде эту формулу называют формулой Тейлора п-го
порядка для функции f(x) в точке х0. Последний член в этой
формуле отличается от общего члена суммы только тем, что значе-
значение соответствующей производной берется не в точке х0> а в неко-
некоторой точке ?> лежащей между х0 и х.
При выводе формулы Тейлора мы предполагали только, что
функция f(x) имеет производные до (/г+ 1)-го порядка включительно,
где п — какое-то число. Последующие производные могут при этом
и не существовать.
Интересно отметить некоторые частные случаи этой формулы.
1) Пусть л = 0. Тогда
Мы получаем формулу Лагранжа, которая является, таким образом,
частным случаем формулы Тейлора.
2) Пусть /».-= 1. Тогда
Если в этой формуле отбросить остаточный член, то получим при-
приближенное значение функции, основанное на применении дифферен-
дифференциала (см. п. 53):
f(x)&f(xo)+f'(xQ)(x-xo).
При этом функция f(x) заменяется линейной функцией.
Само по себе выражение для остаточного члена Rn (x) не дает
возможности вычислять его величину, так как нам неизвестна
точка ?, в которой берется (/г+1)-я производная. Поэтому в даль-
дальнейшем мы ограничимся оценкой величины Rn(x). Это делается
на основании следующего замечания:
Пусть в интервале, в котором справедлива формула Тейлора,
/<п+*>(х) по абсолютной величине не превосходит числа Мп+\:
194] § 4. разложение функций в степенные ряды 673
Тогда для любого х из этого интервала остаточйый член Rn(x)
удовлетворяет неравенству
' , • (***)
Действительно, согласно доказанной теореме
у у |И
194. Разложение функций в ряды Тейлора и Маклорена1).
Разложение заданной функции f(x) в ряд Тейлора в окрестности
точки xQ распадается на два этапа.
1) Сначала мы вычисляем значения функции f(x) и ее производ-
производных в точке х0 и составляем ряд Тейлора для функции f{x). При
этом предполагается, что функция f(x) бесконечное число раз диф-
дифференцируема.
2) Находим интервал, в котором составленный ряд Тейлора схо-
сходится к функции f(x), т. е. устанавливаем, для каких значений х
остаточный член ряда Rn (х) будет стремиться к нулю при п —> оо.
При этом можно часто пользоваться следующей теоремой:
Теорема. Если в некотором интервале, окружающем точку
х0, абсолютные величины всех производных функции f(x) огра-
ограничены одним и тем же числом, то функция f(x) в этом интер-
интервале разлагается в ряд Тейлора.
Доказательство. Нам нужно установить, что для всех точек
интервала остаточный член Rn(x) стремится к нулю при п—> оо.
По условию теоремы во всех точках интервала
где М—достоянная, не зависящая от п. Тогда в силу неравенства
(***) п. 193
Но отношение ~->— стремится к нулю при п—> оо (см. п. 189,
пример 1). Следовательно,
lira Rn (x) = О
J) К. Маклорен A698—1746)—-шотландский математик; ученик и
последователь Ньютона.
22 д. Ф.Бермант, И. Г. Араманович
674 гл. xi. ряды [194
для всех точек х рассматриваемого интервала, что и требовалось
доказать.
Особенно часто используется разложение функции в ряд по сте-
степеням X. В этом случае мы, полагая лго = О, получаем ряд
)х"т 2j х + • • • Н п\ х + • • •
Этот ряд является частным случаем ряда Тейлора; по установив-
установившейся традиции его называют рядом Маклорена.
Перейдем теперь к разложению в ряды элементарных функций.
I. Показательная функция ех. Разложим в ряд Макло-
Маклорена функцию
Все производные от функции ех тоже равны ех и в точке х =
обращаются в 1. По формуле Тейлора
Рассмотрим интервал [ — Ny N], где N — любое фиксированное число.
Для всех значений х из этого интервала ех < eN=M. Следовательно,
все производные в этом интервале ограничены одним и тем же числом
М=е^ и по доказанной теореме lim Rn (x) = 0. По предположению
N—любое число, следовательно, функция ех разлагается в ряд
Маклорена при всех значениях х> г. в. на всей оси Ох.
Итак,
**«!+* + *!+*! + ... + ?+••• (_оо, оо). A)
То, что радиус сходимости ряда A) равен бесконечности, мы уже
доказали раньше (пример 1 п. 189). Здесь же мы установили, что
при любом х сумма этого ряда равна ех\
В частности, при лг=1 находим ряд для числа е:
II, Тригонометрические функции sinx и cosлг. Разло-
Разложим в ряд Маклорена функцию sinx. Для этого находим последова-
последовательно значения ее производных в точке лг = О:
/@) = (sin x)Xs0 = 0, /' @) = (cosx)Xsx0 - 1,
f*() (\)
0 = 0 и т. д.
Мы видим, что значения производных повторяются и образуют пери-
периодическую последовательность
О, 1, 0, -1, 0, 1, 0, -1, ...
194] § 4. РАЗЛОЖЕНИЕ ФУНКЦИЙ В СТЕПЕННЫЕ РЯДЫ 675
Любая производная функции sin.*; (т. е. icosjc или ±sinAr) по
абсолютной величине не превосходит единицы. Следовательно, ряд
Маклорена для функции sin x сходится к ней на всей числовой оси.
Итак,
g U lV-11^r+•.•(-«>> оо).B)
Совершенно аналогично получим разложение cos л; (оно также
справедливо на всей оси Од;):
|! jJ ^+... (-оо,оо). C)
Любопытно заметить, что нечетная функция sinx расклады-
раскладывается в ряд только по нечетным степеням лг, а четная функция
cosjc — только по четным.
Доказательство возможности разложения функций ех, sin лги
в ряд Маклорена было очень простым потому, что любая производ-
производная от соответствующей функции легко находилась. Все эти произ-
производные оказывались ограниченными в любом интервале оси Олг, поэтому
полученные ряды представляют разлагаемые функции на всей число-
числовой оси.
В тех случаях, когда исследование остаточного члена представ-
представляет затруднения (в частности, когда мы не можем пользоваться
доказанной выше теоремой), поступают иначе. Составив ряд Тейлора
для функции /(лг), определяют сначала интервал его сходимости
и лишь затем стараются доказать стремление остаточного члена
к нулю при значениях лг, принадлежащих интервалу сходимости.
Вне интервала сходимости ряда остаточный член можно не исследо-
исследовать, так как там он к нулю стремиться не может.
Для обычно встречающихся функций ряд Тейлора сходится
к функции f(x) во всей области его сходимости. Пример функции,
для которой это не так, приведен на стр. 668.
III. Биномиальный ряд. Разложим в ряд Маклорена
функцию
где т — любое действительное число1). Здесь
-1, f"(X) = m(m — 1)A+*Г"а, ...
/<»> (х) = т (т- 1). . .(да-л + 1) A +х)я~п, ,, *
х) Мы не берем просто степенную функцию хт потому, что если т не
целое положительное число (а только такой случай и интересен), to произ-
производные от хт, начиная с некоторой, в точке # —0 не существуют.
22*
G76 гл. xi. ряды [194
Поэтому /@) = 1, /'@) = m, /"@) = m(w-1), ..., /<">@) =
= /»(/»—1).. .(/и—л+1), ... Следовательно, ряд запишется
в виде
2! -* -г • • •
m (m—1
...н
Установим прежде всего область сходимости ряда. Найдем предел
абсолютной величины отношения последующего члена ряда к пре-
предыдущему:
iim
— п) п + 1ф т (/и—1).. .(т —
V ' ;
• X
/I _*. no V'v I A /* Л1
Согласно признаку Даламбера ряд сходится, если |лг|<1, и
расходится, если \х\ > 1.
Перейдем к исследованию остаточного члена, ограничившись слу-
случаем, когда 0<аг<1. В этом интервале для всех п > m — 1 мы
имеем
и поэтому
Здесь мы не можем воспользоваться теоремой, приведенной в начале
пункта, так как полученная граница для производной зависит от я.
Применим неравенство (**#) п. 193
— n)
*
Правая часть неравенства есть абсолютная величина (п + 1)-го члена
степенного ряда, сходящегося при |лг|<1 (как мы только что до-
доказали). Следовательно, Iim Rn (x) = 0. Соответствующее доказатель-
ство для интервала ( —1, 0) более сложно, и мы его не приводим.
Таким образом, биномиальный ряд представляет функцию (I
в интервале ( — 1, 1):
.., (-1, 1). D)
194] § 4. разложение функций в степенные ряды 67?
Разумеется, если т — целое положительное число, то ряд справа
содержит всего (т-\-1) слагаемых и превращается в формулу бинома
Ньютона (см. пример 2 п. 192). Исследование сходимости ряда D)
на концах интервала мы не приводим и заметим только, что если
т > О, то ряд сходится к функции (\*\-х)т во всем замкнутом ин-
интервале [ — 1, 1].
Приведем часто встречающиеся биномиальные ряды, соответству-
соответствующие значениям /я = —1, -д-» —"о" (спРава указаны интервалы^
в которых справедливы разложения):
(ряд справа представляет геометрическую прогрессию)
_ 1 _±х ¦ ЬЗ 1-3.5 ,, 1-3.5-7
~ 2Х^2ЦХ 2.4.6^ ^
Разложения отдельных функций в ряды могут быть получены и»
уже известных разложений с помощью свойств степенных рядов.
Покажем это на примерах.
IV. Функции InA +лг) и arctgA:. Для разложения в ряд Мак-
лорена функции f(x) = ln(\+xI) воспользуемся формулой для
суммы геометрической прогрессии
1)яхн+...{ — 1 <*<!)• (*)
Применим теорему об интегрировании степенных рядов и проинтегри»
руем ряд (*) в пределах от 0 до х. Поскольку
i
X
dx
то, интегрируя почленно правую часть ряда (*), получим
*) Функцию i/ = lnjc раскладывать в ряд Маклорена нельзя, так как
она разрывна при х = 0.
С78 гл. xi. ряды [194
При |дг|>1, а также при д; = —1 ряд E) расходится и по-
поэтому не может представлять функцию In A4-*). В точке л;=1
ряд сходится, и на основании дополнительного замечания к первому
свойству степенных рядов (см. п. 190) его сумма остается непре-
непрерывной. Поэтому разложение E) справедливо и при лс=1:
Вычислять значение In 2 с помощью этого ряда было бы крайне
затруднительно. Из теоремы Лейбница о знакочередующихся рядах
следует, что для вычисления In 2 с точностью до 0,00001 пришлось
бы взять 100 000 (I) членов ряда, что, разумеется, практически
неприемлемо. Позже, в п. 195, мы увидим, что, преобразовав полу-
полученный ряд, мы сумеем получить значение In 2 с такой же точностью
при несравненно меньшем объеме вычислений.
Совершенно аналогично получается разложение функции arctgjc
в ряд Маклорена. С этой целью заменим в формуле для суммы
членов геометрической прогрессии (*) х на л;2. Получим
^—л;в-Ь ...+( —1)^2"+ .. Л —1 <д:< 1). (**)
Интегрируя ряд (##) в пределах от 0 до л: и считая, что |л;|<< 1,
будем иметь
На концах интервала сходимости ряд сходится, и поэтому раз-
разложение F) остается справедливым и при х = ±\. Подставляя
в ряд значение лс=1, получим выражение для числа я в виде
числового ряда
я - 1,1 1 ,
l + +
Разложения A) — F), а также интервалы их применения следует
запомнить, так как многие другие функции могут быть разложены
в ряды при помощи этих разложений.
Приведем несколько примеров.
Примеры. 1) Разложим в ряд Маклорена гиперболические
функции eh* и shA:. Возьмем ряд A) для ех и заменим х на —х\
получим
Далее по правилу сложения и вычитания рядов находим искомые
194] § 4. разложение функций в степенные ряды 679
разложения, справедливые на всей числовой оси:
2
2) Разложим в ряд Маклорена функцию
Снова возьмем разложение функции у = е* и вместо х подставим
в него х2. Мы получим
Это разложение справедливо на всей числовой оси.
3) Разложим в ряд Маклорена функцию
Воспользуемся приведенным выше, в качестве примера биномиаль-
биномиального ряда при /я=—-х-, разложением функции ¦ и заменим
в нем х на —л;2:
Чтобы получить разложение заданной функции, нужно умножить обе
части равенства на л:3:
X3 з,1 511>3
__ з,1 5_1_1>3 7
4) Разложим в ряд Маклорена функцию
у = arcsin Хщ
Так как
Г dx —
arcsin х
• arcsin x,
О
то разложение arcsin x получается интегрированием ряда (***):
1 х* , ЬЗл:5 , Ь3.5л;7 ,
Это разложение справедливо в замкнутом интервале [—1, 1].
680 гл. xi. ряды [195
5) Разложим в ряд Маклорена функцию
у = e*sin х.
Так как ряды для ех и sin л: сходятся абсолютно, то, перемножая
их по правилу, указанному в конце п. 186, получим искомое раз-
разложение. Здесь общий закон образования коэффициентов подметить
трудно, и мы ограничимся вычислением нескольких первых коэффи-
коэффициентов ряда
§ 5. Некоторые применения рядов Тейлора
195, Приближенное вычисление значений функции. Допустим,
что нам известны значения самой функции f(x) и ее последователь-
последовательных производных в некоторой точке х0 и мы доказали, что функция
f (х) в окрестности точки х0 разлагается в ряд Тейлора. Тогда
точное значение функции f(x) в любой точке этой окрестности
может быть вычислено по ряду Тейлора, а приближенное ее значе-
значение— по частичной сумме этого ряда. Возникающую при этом ошибку
можно оценивать либо опираясь на теорему об оценке остаточного
члена, либо непосредственно оценивая остаток ряда. Если, например,
получающийся числовой ряд знакочередующийся, то это делается
при помощи теоремы Лейбница; в случае знакоположительного ряда
мы стараемся подобрать другой ряд (обычно геометрическую про-
прогрессию), члены которого больше членов остатка и сумму которого
мы можем найти.
На практике оценка остатка ряда оказывается более удобной,
так как оценка остаточного члена предполагает знание производной
нужного нам порядка во всем рассматриваемом интервале. Мы же
часто можем получать разложения функций в ряды, вообще не отыс-
отыскивая производных, а комбинируя известные нам ряды. Применение
указанных способов оценки ошибки станет более ясным после раз-
разбора приводимых примеров.
Примеры. 1) Мы имеем
**«!+* + *- + ...+?..
Производя вычисления по этой формуле в интервале [0, М], где
М — любое число, и учитывая, что наибольшее значение /*п+1)(х) = ех
в этом интервале равно ем, по теореме об оценке остаточного члена
поручим
195)
§ 5. НЕКОТОРЫЕ ПРИМЕНЕНИЯ РЯДОВ ТЕЙЛОРА
631
Эта оценка неудобна тем, что сюда входит величина ем. Кроме того,
она может оказаться слишком завышенной, так как установлена
сразу для всего интервала.
При Ж= 1 получим
Подсчитаем, например, сколько нужно взять членов ряда, чтобы
получить число е с точностью до 0,00001. Здесь лг=1 и должно
быть
< 10"
Легко проверить, что это неравенство справедливо при п = 8:
3 3
9"* ~ 362880 ^ Ю~6* Чтобы получить число е с этой точностью, надо
в сумме
i- + l
...+1^2,71828
все слагаемые брать с точностью до 10~"в во избежание накопления
ошибок при арифметических действиях. В результате мы нашли
число е с шестью верными знаками. L
Рекомендуем читателю проверить, что для вычисления у е = е%
с той же точностью понадобилось бы взять п = 6, т.е. семь слага-
слагаемых. Вообще, чем меньше будет показатель степени у е, тем мень-
меньше понадобится членов в приближенной формуле для достижения
одной и той же точности.
Покажем теперь, как можно оценить ошибку /?„A), пользуясь
всем рядом для ех:
-
' n\n
Итак, мы иолучили оценку ошибки -г-, т. е. почти в 3 раза бо-
-г
3
лее точную, чем найденную выше . ,, .
') Здесь мы намеренно увеличили правую часть для простоты вычислений.
682
ГЛ. XI. РЯДЫ
[195
2) Вычислим значения функций sin.*; и cos x при помощи их раз-
разложений в ряды. Приближенные формулы отличаются здесь очень
высокой точностью, а ошибка легко оценивается с помощью теоремы
Лейбница. Положим в разложении функции sinAT последовательно
л=1, 2, 3. Считая, что х > 0, получим
sinAT« ху
S\nX « X—-рг ,
Хъ
Первая и третья формулы дают значения sinx с избытком, а
вторая с недостатком. Рекомендуем читателю проверить, что для
получения значений sinx с точностью до 0,0001 следует пользоваться
первой формулой в интервале 0 < х < 0,08, второй в интервале
0,08 < х < 0,4 и третьей в интервале 0,4<х<0,91).
Рис. 229.
На рис. 229 сравнивается в окрестности точки х = 0 график
функции у = sinx с графиками приближающих многочленов
Аналогично получаем приближенные формулы для cos*:
cos x « 1, | R
cos л;:
X2 X*
~ X 2 + 24 '
720 *
x) Соответственно в градусной мере эти интервалы будут @,4°30'), D°30/,
23°), B3°, 52°). Все границы интервалов вычислены приближенно.
195]
§ 5. НЕКОТОРЫЕ ПРИМЕНЕНИЯ РЯДОВ ТЕЙЛОРЛ
683
Здесь первая и третья формулы дают значения cos* с избытком, а
вторая с недостатком.
На рис. 230 показано, как ведут себя графики функций j; = l,
У = 1— " 7 У = 1— у + || по сравнению с графиком функция
у =cosх в окрестности начала координат.
ч
Рис. 230.
3) Рассмотрим теперь известный ряд для 1пA+д:)!
2--г з" ••• ( —1 <^<1)«
х2 х3
In A -\-Х) = X о" г "о •
Коэффициенты этого ряда убывают несравненно медленнее, чем
коэффициенты рядов для ех, sin* и cosa;. Поэтому мы будем гово-
говорить, что этот ряд сходится медленно1).
Как мы уже отмечали, из теоремы Лейбница о знакопеременных
рядах следует, что для вычисления, например, 1п2 с точностью до
0,00001 нужно взять не меньше 100 000 (!) начальных членов ряда.
Такое суммирование практически невозможно.
Покажем, как здесь можно ускорить сходимость ряда. Заменим
х на —х и запишем ряд для 1п A—х). Вычитая из ряда для
1пA+л;) ряд для In A —л:), получим
По найденной формуле можно вычислять логарифмы любых по-
положительных чисел. В самом деле, когда х меняется в интервале
14- х
сходимости ряда ( —1, 1), непрерывная функция j— пробегает
J) Разумеется, это выражение чисто условное.
6?4 гл. хт. ряды [196
1 А-х
весь интервал @, ос). Вычислим по этой формуле In 2. Если т^^2»
то лг==-п-. Возьмем л-ю частичную сумму
о
Ошибку оценим так: 2 (^ +
2
Найдем л, при котором ошибка не превзойдет 0,00001. Должно быть
4Bл + 3)-32П+1>10б,
что уже имеет место при п = 4. Значит,
Итак, в новом ряде достаточно взять пять слагаемых (вместо
100 000 в исходном ряде), чтобы найти результат (In 2) с той же
точностью.
Полагая в полученном ряде х= ~N ¦ , где N — целое положи-
положительное число, придем к формуле
фактически служащей для вычисления логарифмов целых чиселэ
одного вслед за другим, с любой практически нужной точностью.
196. Интегрирование функций и дифференциальных уравнений.
I. Интегрирование функций. Допустим, что нужно най-
найти интеграл
причем известно разложение подынтегральной функции f(x) в ряд
Тейлора, а пределы интеграла лежат внутри интервала сходимости
ряда. Тогда мы имеем право интегрировать рад почленно. В резуль-
результате получится ряд Тейлора для функции ^(лг), имеющий тот же
радиус сходимости, что и ряд для подынтегральной функции f (х).
х
Если интеграл \^/{x)dx выражается через элементарную функцию
196] § 5, некоторые применения рядов тейлора 685
F(x), то мы тем самым находим ее разложение в ряд Тейлора.
Именно так мы поступали при разложении функций In (I -J-Jf), arctgA;
к
и arcsinjc. Если же интеграл \f(x)dx в элементарных функциях
а
не выражается (см. п. 85), то найденный ряд может служить выра-
выражением неэлементарной функции F(х) через самые простые
основные элементарные функции — степенные, правда, уже не конеч-
конечным выражением, а бесконечным. Однако мы уже убедились, что
такое представление функций с помощью бесконечных рядов отнюдь
не хуже, чем представление с помощью конечного числа основных
элементарных функций. Наоборот, оно в силу простоты членов ря-
ряда во многих отношениях значительно удобнее любой не степенной
функции.
Заметим, что, зная оценку остаточного члена ряда для подынтег-
подынтегральной функции f(x), мы можем на основании теоремы об оценке
интеграла оценить и остаточный член ряда для интеграла F(x).
Примеры. 1) Пусть дан интеграл
X
sin х
Г sir
J х
dx.
о
Деля ряд для sin л: на х, получим
sin* __t jc2 x*
Этот ряд, как и ряд для sin.*;, имеет своим интервалом сходимости
всю ось Ох. Интегрирование дает
sin х dx х * . х*
Этот ряд не сходится ни к какой элементарной функции;
он является аналитическим заданием новой функции, но посред-
посредством не конечного, а бесконечного числа операций. Между прочим,
X
« С sin х -
функция j ах часто встречается при изучении некоторых раз-
0
делов теоретической физики. С помощью приведенного ряда состаз-
лены ее подробные таблицы.
2) При изучении теории вероятностей важную роль играет
функция
686 гл. xi. ряды [196
называемая функцией Лапласа или интегралом вероят-
вероятностей. Вычислить интеграл в конечном виде нельзя, так как
\ е 2 dx не выражается в элементарных функциях. Разложим по-
подынтегральную функцию в ряд, для чего в разложение ех под-
ставим взамен х величину —^ :
2 ^22-2! 23-ЗМ * '
Тогда F(x) представится бесконечным рядом
1 / х3 хь х7
сходящимся на всей числовой оси. Вычислять значения функции
F(x) очень удобно, так как ряд быстро сходится.
3) Вычислим интеграл
2
dx
J
На первый взгляд раскладывать подынтегральную функцию в ряд ни
к чему, так как неопределенный интеграл выражается в элементар-
элементарных функциях. Однако его выражение очень сложно и мало удобно
для вычисления:
В то же время, разложив подынтегральную функцию в ряд
мы сразу получим
dx 1 л у
Р dx
JI + a:
Если ограничиться двумя первыми членами ряда (при этом ошибка
не превосходит f ^-l 'g-» 0,0002), то
2
dx
Xqrj? » 0,4938.
196] § 5. некоторые применения рядов тейлора 687
II. Интегрирование дифференциальных уравне-
уравнений. Рассмотрим теперь применение степенных рядов к решению
дифференциальных уравнений. Пусть задано дифференциальное урав-
уравнение и начальные условия, определяющие частное решение1). До-
Допустим, что решение уравнения в окрестности точки х0У в которой
заданы начальные условия, можно разложить в степенной ряд, рас-
расположенный по степеням разности х—л:0:
Продифференцируем этот ряд с неопределенными пока коэффици-
коэффициентами столько раз, каков порядок уравнения. Подставляя затем в
уравнение вместо неизвестной функции и ее производных соответ-
соответствующие ряды, мы получаем тождество, из которого и определяем
неизвестные коэффициенты ряда. При этом первые коэффициенты
ряда (в числе, равном порядку уравнения) определятся не из этого
тождества, а из начальных условий. Если, далее, доказать, что по-
полученный ряд сходится, то можно быть уверенным, что он выражает
искомое решение. Очень часто в обычно встречаемых случаях в та-
таком доказательстве и нет нужды.
Достаточно большое число членов ряда дает нам как угодно
хорошее приближенное выражение решения в виде многочлена.
Особенно удобно решать с помощью рядов линейные диффе-
дифференциальные уравнения.
Поясним на примерах указанный метод.
Примеры. 1) Решим линейное дифференциальное уравнение
второго порядка у"— ху—0 при начальных условиях y\Xz=Q = О,
У1*.о=1.
Решение ищем в виде ряда, расположенного по степеням х:
у = ао + агх + а2х2 + а3х3 -\ [-апхп-\ •
Коэффициенты а0 и ах находим из начальных условий:
Дважды дифференцируем ряд:
/' = 2а2 + 3 • 2а3х Н \- п (п — 1) апхп~* -\
Подставляя в уравнение вместо у и у" их разложения, получаем
тождество
azx+ ... +п{п- \)апхп~*-\ =
я
х) При помощи степенных рядов можно отыскивать и общие решения
дифференциальных уравнений, однако мы этим заниматься не будем и ото-
отошлем читателя, например, к книге [7].
688 гл. xi. ряды [195
Сравнивая коэффициенты при одинаковых степенях х% находим
я2 = °> <*з = °> 4-За4=1, ..., л (л— 1)ля = ая.8.
Поэтому
1
fll° "-4.6.7.9-10
и вообще
Значит,
*4 + *7 + +
T* + 3-4.6.7* + ' ' ' +3-4.6.7...3mCm + l)^ + ' ' '
С помощью признака Даламбера легко убедиться в том, что этот
ряд сходится на всей оси Ох и, следовательно, представляет иско-
искомое решение при всех х.
Заметим, что порядок уравнения нисколько не влияет на
метод решения его при помощи рядов.
2)у'=ху2 + \ при j/|*=1 = 0.
Это уравнение нелинейное, и поэтому подстановка вместо у
его разложения в ряд
J = 0o+«i(*-l) +a%{x—\)* + ...
привела бы к сложным уравнениям для определения коэффициентов.
Поэтому обычно поступают иначе.
Продифференцируем уравнение несколько раз подряд, рассмат-
рассматривая у как функцию от х;
v
'у» + 2хуу'".
Полагая в самом уравнении и во всех этих равенствах лг = 1 и
принимая во внимание, что y\x=i = 0, последовательно найдем
/L=i=i,/U=x = o,/"U=i = 2,yvU=1 = 6,...
Так как
ау\О a y'\ \ a " 1 0
то
197] § 6. ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ ТЕОРИИ СТЕПЕННЫХ РЯДОВ 689
§ 6*. Дополнительные вопросы теории степенных рядов
197*. Степенные ряды в комплексной области. Большинство
вопросов теории рядов почти без всяких изменений переносится
на ряды, членами которых являются комплексные числа. Пред-
Предварительно введем определение предела последовательности комп-
комплексных чисел; оно находится в той же связи с обычным опреде-
определением предела последовательности, в какой определение предела
комплексной функции действительного переменного (см. п. 73)
находится с обычным определением предела функции.
Определение. Комплексное число Z называется пределом
последовательности комплексных чисел zlf z2, ..., zn,...,
если для любого положительного числа & можно указать такое
число Nf что при всех # > N будут справедливы неравенства
Отсюда сразу следует (как и в п. 73), что существование предела
]\mzn = Z равносильно существованию двух пределов последователь-
ностей действительных чисел: \\тхп—а и \\туп = Ь.
Данное определение позволяет без всяких изменений перенести
на ряды с комплексными членами определение сходимости рада.
Ряд с комплексными членами
называется сходящимся, если существует предел последовательности
частичных сумм этого ряда.
Сходимость ряда (*) равносильна сходимости двух рядов с дейст-
действительными членами
где ип—действительные, a vn—мнимые части членов ряда:
Если сходится ряд, составленный из модулей членов ряда (*)
то сходится и сам ряд; в этом случае он называется абсолютно
сходящимся. Это немедленно следует из очевидных неравенств
KJ<W и KU<kJ-
Пусть теперь z — x-\-iy—переменная комплексная величи-
величина. Так как действие возвышения комплексного числа в целую поло-
положительную степень известно (см. п. 72), то можно рассматривать
690 гл. xi. ряды [197
степенные функции комплексного переменного:
w = zn9 n — целое положительное число.
В отличие от комплексных функций действительного перемен-
переменного здесь и независимая переменная, и функция принимают комп-
комплексные значения. Детальное изучение функций комплексного пе-
переменного не входит в задачу настоящей книги; читателей, кото-
которым оно предстоит, мы отсылаем, например, к книгам [6], [11]. При-
Приведем только определения простейших функций, основанные на
свойствах степенных рядов.
Для степенного ряда от комплексной переменной z
а0 + axz + a2z2 +... + anzn +..., (**)
где коэффициентами ряда я0, а15..., а„,... могут быть любые комплекс-
комплексные числа, оказывается справедливой теорема Абеля (п. 189), сог-
согласно которой из сходимости ряда (##) в точке z0 следует его абсо-
абсолютная сходимость при всех z, по модулю меньших z0 : \z\ < \zo\.
Из теоремы Абеля вытекает существование числа R такого, что
при всех z, удовлетворяющих неравенству \z\<cR, степенной ряд
абсолютно сходится, а при всех z таких, что \z\>R, ряд расходит-
расходится. Если | z | < /?, то точка комплексной плоскости z лежит в круге с
центром в начале координат и с радиусом, равным R; число R называ-
называется радиусом сходимости ряда, а круг \z\<R — кругом сходимости.
Радиус сходимости может быть равен нулю; тогда ряд сходится
только в одной точке — в начале координат. Может случиться, что
ряд сходится во всей комплексной плоскости; тогда говорят, что
его радиус сходимости равен бесконечности.
Сумма степенного ряда является в круге его сходимости неко-
некоторой функцией комплексного переменного; такие функции называ-
называются аналитическими.
Степенной ряд
\+z + f{ + ...+- + ... (**•)
сходится во всей комплексной плоскости. Это следует из того, что
он сходится при любом действительном значении z = N, а значит,
и внутри любого круга с центром в начале координат.
В точках действительной оси, когда z = x, ряд представляет по-
показательную функцию ех:
ех=\+х + ? + ... + %+...
Назовем теперь показательной функцией ег сумму ряда (**#);
эта функция определена во всей комплексной плоскости:
197] § 6. ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ ТЕОРИИ СТЕПЕННЫХ РЯДОВ 691
Для функции ez, определенной таким образом, остается справед-
справедливым основное свойство показательной функции
Действительно, перемножая по правилу, указанному в п. 186,
ряды для ezi и ez*t получим
В частности, если zx = x и *2 = /у, то ex+iy=e* eiy. Выразим с
помощью ряда второй множитель е1у:
Так как ха=—1, /3=—/, /4=1, /5 = / и т.д., то
Перегруппировав члены, что возможно в силу абсолютной сходимос-
сходимости ряда, запишем
@()
Ряды, стоящие в скобках, представляют соответственно cosjj и
. Поэтому
е*У = cos y~\-i sin у.
В результате мы пришли к уже известной формуле Эйлера,
получив ее из совершенно иных соображений, чем в п. 74 (см. снос-
сноску на стр. 238). Напомним, что с помощью формулы Эйлера мож-
можно вычислять значения ег для любого показателя степени z = x-\-iy.
ez=ex+iy = ех eiy = ех {cosy + i sinjf).
Через показательную функцию ег определяются тригонометри-
тригонометрические и гиперболические функции комплексного переменного:
COS Z — 75 , Sin Z = •
ch г = —^— , sh 2 = —s— ,
692 гл. xi. ряды [198
Все они определены во всей комплексной плоскости. Если z равно
действительному числу х, то получаются известные определения
гиперболических функций действительного переменного (п. 23) и
формулы Эйлера, выражающие косинус и синус через показатель-
показательную функцию с чисто мнимым показателем степени (п. 74).
Предоставляем читателю написать наосновании определений разло-
разложения в степенные ряды тригонометрических и гиперболических
функций и убедиться, что они могут быть получены из известных
разложений в действительной области путем замены х на z.
198*. Ряд и формула Тейлора для функции двух переменных*
Рассмотрим вкратце разложение в степенные ряды функций двух
переменных; при этом мы осветим только практическую сторону
дела и почти не будем касаться вопросов сходимости.
Определение. Степенным рядом по переменным х и у
называется ряд
апОхп + а„_ь ххп^у + ... + аОпу
Коэффициенты ряда нумеруются двойными индексами; перед про-
произведением степеней xkyl, где k и /—целые числа, стоит коэффи-
коэффициент аы. Для удобства члены ряда располагают так, чтобы в каж-
каждой скобке стояли члены одного измерения; тогда сумма индексов
у коэффициентов, стоящих в одной скобке, одна и та же.
Можно рассматривать степенные ряды по степеням разностей
х—*-лг0 и у—у0; для этого нужно в ряде (*) заменить х на х — х0
и у на у—у0.
Обычно ряд (*) сходится в некоторой области, содержащей точ-
КУ @, 0) и симметричной относительно осей координат (в частных
случаях — во всей плоскости). В любом прямоугольнике, цели-
целиком лежащем внутри этой области, ряд сходится правильно и его
сумма является непрерывной функцией переменных х и у. Эта фун-
функция имеет частные производные любых порядков и их можно нахо-
находить почленным дифференцированием ряда.
Пусть теперь f(x, у) — функция, имеющая в окрестности начала
координат частные производные любого порядка. Предположим, что
ее можно разложить в степенной ряд вида (*), и найдем коэффи-
коэффициенты ряда уже известным методом неопределенных коэффициентов.
Итак, пусть
/(*, У) = «оо + Ко* + *охУ) + Ко*2 + <*пхУ + ло«<У2) + • • •
Полагая л: = 0, y = 0t получим а00 — /@,0).
198] § 6. ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ ТЕОРИИ СТЕПЕННЫХ РЯДОВ 663
Найдем частные производные по л; и по у:
щ
щ = «ох + аих + 2ао*У + •. м
причем все последующие члены содержат множителями переменные
величины. Снова полагая л; = 0, у —0, найдем а10 и а01:
Совершенно аналогично получим
)
Во всех случаях индекс 0 показывает, что берутся значения произ-
производных в точке @, 0).
Итак, ряд Тейлора для функции двух переменных имеет вид
Закон образования последующих членов ряда ясен.
Беря разность между функцией f(x, у) и суммой членов ряда
до /1-го измерения включительно, получаем остаточный член ряда
Тейлора. Можно доказать, что он, как и в случае функции одной
переменной, образуется так: берется группа членов (л-)-1)-го из-
измерения и взамен значений производных в точке @, 0) подставля-
подставляются значения этих же производных в некоторой промежуточной
точке (|, г)), лежащей на отрезке, соединяющем начало координат
с точкой (лг, у).
Заменяя остаток ряда его выражением, получаем формулу Тей-
Тейлора с остаточным членом. Предоставляем читателю написать ее
при п = 2.
Ясно, что лишь при стремлении остаточного члена к нулю ряд
Тейлора будет сходиться к функции f(x, у).
Если раскладывать функцию f(x, у) в ряд Тейлора в окрест-
окрестности точки (лг0, у0), то значения частных производных берутся в
этой точке, а х иу заменяются соответственно на (л:—xQ) и {у—^о)-
При разложении в ряд Тейлора функции двух переменных очень
часто удается использовать уже известные разложения функций
одной переменной.
694 гл. xi. ряды [198]
Примеры. 1) Разложим в ряд Тейлора функцию exs\ny в окрест-
окрестности точки @, 0). Заменяя ех и siny их разложениями и перемно-
перемножая ряды, получаем
-J-+4-+(#-?
Разумеется, то же самое получится, если воспользоваться общей
формулой.
2) Разложим в ряд функцию ху в окрестности точки A, 1).
Находим частные производные
Найдя значения производных в точке A,1) и подставляя в общую
формулу, получим
Отсюда, например, следует, что A,04I|03«1 +0,04 + 0,04-0,03 =
= 1,0412.
ВОПРОСЫ И ПРЕДЛОЖЕНИЯ ДЛЯ САМОПРОВЕРКИ
1. Что называется числовым рядом? Что называется общим членом ряда?
2. Что называется суммой ряда? Дать определение сходящегося и рас-
расходящегося рядов. Привести примеры.
3. В чем состоит необходимый признак сходимости ряда? Привести
пример, показывающий, что он не является достаточным.
4. Указать простейший достаточный признак расходимости ряда.
5. Сформулировать и доказать теорему о сравнении двух рядов с поло-
положительными членами.
6. В чем состоит признак Даламбера? Доказать его.
7. В чем состоит интегральный признак Коши? Доказать его. Доказать
°° 1
сходимость ряда ^Г -^г • р>1.
8. Какой ряд называется знакочередующимся? В чем состоит признак
Лейбница для такого ряда? Доказать этот признак.
9. Привести общий достаточный признак сходимости ряда с произволь-
произвольными членами. Доказать его.
10. Что называется абсолютной сходимостью ряда? условной сходи-
сходимостью? Привести примеры абсолютно и не абсолютно сходящихся рядов.
11. Какой ряд называется функциональным? Что называется областью
сходимости функционального ряда?
12. Какой функциональный ряд называется правильно сходящимся?
ВОПРОСЫ И ПРЕДЛОЖЕНИЯ 695
13. Сформулировать и объяснить свойства правильно сходящихся рядов.
14. Какой ряд называется степенным?
15. Сформулировать и доказать теорему Абеля. Определить радиус схо-
сходимости и интервал сходимости степенного ряда.
16. Привести примеры степенных рядов, радиус сходимости которых
равен: 1) нулю, 2) бесконечности, 3) конечному числу, отличному от нуля.
17. Доказать леммы о степенных рядах и на их основании сформулиро-
сформулировать свойства степенных рядов.
18. В чем заключается задача разложения функции ?(х) в степенной ряд?
19. Что называется рядом Тейлора функции ?(*)? Как определяются
коэффициенты ряда Тейлора?
20. Что называется остаточным членом ряда Тейлора?
21. Сформулировать и доказать теорему об остаточном члене ряда Тейлора.
22. Что называется формулой Тейлора n-го порядка?
23. Какой ряд называется рядом Маклорена?
24. Вывести разложения в ряд Маклорена функций ех, sin*, cosx,
(\~\-х)т, ln(l + x), arctg х. Указать интервалу,- в которых полученные
разложения имеют место.
25. Указать способы оценки остаточного члена при приближенных вы-
вычислениях значений функций.
26. В чем состоит метод интегрирования функций с помощью степенных
рядов? Привести примеры.
27. В чем состоит метод интегрирования дифференциальных уравнений
с помощью степенных рядов? Привести примеры.
28*. Дать определение предела последовательности комплексных чисел
и сходящегося ряда с комплексными членами.
29*. Дать определение показательной функции ez с помощью стеленного
ряда и доказать ее основное свойство.
30*. Вывести с помощью степенных рядов формулу Эйлера.
31*. Дать определение тригонометрических и гиперболических функций
комплексного переменного.
32*. Дать определение степенного ряда по переменным х и у.
33*. Вывести методом неопределенных коэффициентов формулу разло-
разложения функции двух переменных в ряд Тейлора.
ГЛАВА XII
РЯДЫ ФУРЬЕ 1). ИНТЕГРАЛ ФУРЬЕ
§ 1. Ряды Фурье
199. Гармонические колебания. Тригонометрические ряды.
I. Как известно, простое гармоническое колебание описывается
функцией
где s—отклонение колеблющейся точки от положения равновесия,
t — время, Л—амплитуда колебания, со — круговая частота2) и ф0 —
начальная фаза (см. п. 21, II). Напомним еще, что период колеба-
ния Т равен —.
Функция A sin (Ы + ф0) (и ее график) называется простой гар-
гармоникой. Колебания, получающиеся в результате наложения не-
нескольких простых гармонических колебаний, называются сложными
гармоническими колебаниями. Например, в случае наложения двух
простых гармонических колебаний получаем
s = At sin (со^ + фх) + А2 sin ((o2t -f ф2).
Если, в частности, круговые частоты о^ и со2 равны между собой,
Oj = оJ, то результирующее движение оказывается снова простым
гармоническирл колебанием с той же частотой и тем же периодом3).
Пусть теперь о>1^= <о2. Периоды простых колебаний равны Тх = —
С02
1) Ш. Ф у р ь е A768—1830) —знаменитый французский математик и физик.
а) Для краткости мы ее в дальнейшем назовем просто частотой.
3\ Расгпллотл ntmiur интатапш пгппрпнтк итп ргпи ГЛ - = гл~ = гл тп
Для краткости мы ее в дальнейшем назовем просто частотой.
Рекомендуем читателю проверить, что если (ol = co2 = a>, то
A i(^4)
где b
199] § 1. ряды фурье 697
Результирующее колебание будет периодическим, если суще-
существует такое число Г, что имеют место равенства
Т = гхТх и T = r2T2f
где гх и г2 — целые числа. (Число Т будет наименьшим,
обладающим указанным свойством, если числа гх и г2 не имеют
общего делителя.) Отсюда вытекает, что отношение частот долж-
должно разняться отношению этих чисел
0)! Г/
Следовательно, частоты ю1 и со2 должны быть соизмеримы.
Если частоты несоизмеримы, результирующее колебание не является
периодическим. Если частоты соизмеримы, то можно положить
Сложное колебание
s =r. Ах sin (rx(ot + фх) + \ sin (r2a>t + фа)
будет периодическим с периодом
СО
Действительно, функция s не изменяет своего значения от
прибавления к любому значению t числа —; если, кроме того, гх иг2
не имеют общего делителя, то легко проверить, что это число
будет наименьшим положительным числом, обладающим указан-
указанным свойством.
В дальнейшем будем для простоты считать, что ю=1, т. е.
период Т=2л. (К этому всегда можно придти, изменив масштаб
по оси tt т. е. положив (at = tr.)
Периодическая функция
Ах sin (rxt 4- фх) + Л sin (r2t + ф2)
может иметь весьма своеобразный график, значительно отличающийся
от графиков простых гармоник (см., например, рис. 28 на стр. 64).
Было замечено, что вообще суммы простых гармоник
у = Ах sin (rxt + фх) + А2 sin (r2t + фа) + # ф . + Ап sin (rnt + фя)
при различных значениях параметров Ак1 фй и целых чисел rk и п
приводят к самым разнообразным периодическим функциям. В терми-
терминах механики это означает, что наложение простых гармонических
колебаний создает разнообразные периодические движения, отнюдь
не похожие на простые гармонические колебания.
698 ГЛ. XII. РЯДЫ ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ [199
Естественно, возникла обратная задача: нельзя ли так подобрать
простые гармонические колебания, чтобы их наложение вызвало
заранее данное периодическое движение, т. е. нельзя ли представить
всякое периодическое движение как сложное гармоническое колебание?
Оказалось, что этого, как правило, сделать нельзя, если
ограничиться конечной суммой простых гармоник. Если же
привлечь к рассмотрению бесконечные суммы простых гармоник,
т. е. ряды, то практически любую периодическую функцию можно
разложить на простые гармоники.
К рассмотрению этой задачи мы сейчас и приступим.
П. Тригонометрические ряды.
Определение. Тригонометрическим рядом называется
функциональный ряд
у + aicos х + *isln ^ + tt2cos2jc + ^2 sin 2* -f" • • •
... + «„ cos nx
членами которого являются синусы и косинусы от целых кратных
значений аргумента х.
Постоянные ai и Ь^ называются коэффициентами ряда. Мы пишем
свободный член ряда в виде -у для единообразия последующих
формул.
Коротко тригонометрический ряд будем записывать так:
j
^an cos nx + bn sin nx. (*)
Тригонометрический ряд (*) можно записать и в виде суммы
простых гармоник. Действительно, объединим слагаемые с одинако-
одинаковой частотой:
n sin nx.
Полагая an = An sin <pn и bn = An cos фп, получим
an cos nx + bn sin nx = An sin (nx + q>n).
Запись в таком виде удобна в тех случаях, когда нужно знать
амплитуду и начальную фазу /г-й гармоники. При этом
Тогда ряд (*) примет вид
199] § 1. ряды фурье 699
Иногда п-\о гармонику записывают в несколько ином виде:
ап cos пх + bn sin пх = Ап cos (пх — q>J,
Здесь по-прежнему амплитуда Ап~у а2п-\-Ьп^ но начальная
фаза ц>п определяется иначе:
Пусть теперь f(x) — произвольная периодическая функция с пе-
периодом 2л:1). Постараемся разложить эту функцию в тригонометри-
тригонометрический ряд, т. е. представить ее в виде суммы ряда
СО
/ (*) = Ц + 2 ап cos пх + Ьп sin пх. {*]
п = 1
В дальнейшем мы установим условия, при которых этб возможно.
Поскольку функция f(x) (а также ряд (*)) имеет период 2я, то
ее можно рассматривать в любом интервале длины 2я, Выберем
в качестве основного интервал (— я, я); на других участках оси Ох
функция f(x) (и ряд) будет повторять свои значения и свое поведе-
поведение в основном интервале (— я, я).
Выведем некоторые вспомогательные соотношения2), с помощью
которых будем отыскивать коэффициенты а^ и fy (в дальнейшей
k и р будут означать любые целые числа):
л
1) [ slnkxdx=aQ для любого к;
-я
2) f cos kx dx as 0, если
— n
Действительно,
я
\ sin kx dx =й» — -г cos kx > что в силу четности функции cos л
j ft — л
-я
равно нулю (cos kn = cos (— kn) )\
cos kx dx = -r- sin /?л;
= 0, так как sin feit = sin (
8) \ cos kx sin /?лг dx = 0 для любых /г и р.
х) Функции произвольного периода Т будут рассмотрены ниже, в п. 201.
*) Позднее, в п. 205, роль этих соотношений будет объяснена с более
Общей точки зрения.
700 гл. хп. ряды фурье. интеграл фурье {200
л\ С и /о»
4 \ coskxzospxdx^i
*-я ч
о) \ sinkxsinрлгrf# = 1 '
J ^ ^ я,
если
если к=
если
если к=
Эти соотношения легко доказываются с помощью известных формул
тригонометрии:
cos kx smpx = у [sin (Л+р) лг + sin (/?—/?) х],
cos ^x cos /?лг s= ~ [cos (/г+р) х + cos (/г —/?) *],
sin Ллт sin/>jkr = — [cos (Aj— /?)л: — cos (k +p) лг].
Если только k^py то, подставляя в интегралы 3), 4) и 5) вместо
произведений тригонометрических функций написанные выражения,
мы разобьем каждый из них на сумму двух интегралов. Эти послед-
последние будут равны нулю в силу формул 1) и 2), так как k-\-p и
k—p — целые числа, не равные нулю.
Если же ?=/?, то
я я
= ± f
(второй интеграл равен нулю тоже в силу формулы 2)),
Аналогично
я я
\ sin2 kx dx = у \ A — cos 2kx) dx = п.
-л —я
Таким образом, соотношения 1) — 5) полностью доказаны.
200. Ряды Фурье. Пусть f(x) — какая-нибудь функция, задан-
заданная в интервале (— я, я), относительно которой мы предполагаем,
что ее в этом интервале можно разложить в сходящийся тригономе-
тригонометрический ряд
со
°Ип cos пх+Ьп sin nx* (•)
Будем предполагать также, что ряд (*) можно почленно интегри-
интегрировать, т. е. интеграл от суммы ряда f(x) равен сумме интегралов
от членов ряда (достаточные условия возможности почленного
интегрирования ряда указаны в п. 188).
20TOJ § 1. ряды фурье 701
Интегрируя в пределах от —я до я обе части разложения (*),
получим
Интегралы от всех остальных членов ряда обратятся в нуль в силу
формул I) и 2) п. 199. Отсюда
A)
Чтобы найти коэффициент акУ где & — любое целое положитель-
положительное число, умножим обе части равенства (*) на cos kx и проинте-
проинтегрируем в пределах от — я до я:
я я
f {x) cos kx dx = ^- ^ coskxdx +
—я
qo Я
а«з cosnx cos kxdx + bn } smnx coskxdx) .
Все интегралы в правой части, кроме интеграла при коэффициенте
акУ равны нулю вследствие формул 2), 3) и 4) п. 199. Интеграл же
при ak равен я. Значит,
л
J / (#) cos kx dx = ak} cos2
— я —я
Отсюда находим я^:
я
a* = i- S f(x)coskxdx. B)
— Я
Формула A) получается из формулы B) при & = 0.
Чтобы найти коэффициент ЬкУ умножим обе части равенства (#)
на sinkx и проинтегрируем в пределах от —я до я:
я зт
^ /(х) sin&x d#= у ^ sinAjxt/jc +
— я —я
Я Я
a«0
sin nx sin
— я
В силу формул 1), 3) и 5) п. 199 все интегралы в правой части
равны нулю, кроме интеграла при коэффициенте bk. Этот интеграл
702 ГЛ. XII. РЯДЫ ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ [200
я
равен \ sin kx sin kxdx = n.Следовательно,
я я
J / (х) sin &х dx = я^ и 6Л = — \ / (лг) sin kx dx. C)
—л —я
Пусть теперь f(x) — произвольная функция, заданная в интер-
интервале (— Jt, я), относительно которой мы только предполагаем, что
л /\
-Зл
^0 Л
Рис. 231.
ЗЛ
существует интеграл от нее в интервале (—л;, я). При этом функ-
функция f(x) может иметь точки разрыва.
Определение. Коэффициентами Фурье функции /(^на-
/(^называются числа ап и Ьп, определяемые формулами
Ряд
) cos nx dXf
sin nx dx*
anC0S ПХ + *«SI11 ПХ
называется рядом Фурье функции f(x).
Мы уже отмечали, что сумма ряда Фурье функции f(x) есть
периодическая функция с периодом 2ит. Поэтому, если ряд сходится
в интервале (—я, зх), то
У
-Зк
Л А
0 л^ 1л
он сходится и при всех ос-
остальных значениях х и
сумма его периодически
повторяет те значения, ко-
~х торые она принимала в ос-
основном интервале (—я, п).
Таким образом, сумма ряда
Фурье будет представлять
функцию f(x), заданную в
интервале (—я, я) и периодически продолженную на всю число-
числовую ось.
Рис. 232.
200]
§ 1. РЯДЫ ФУРЬЕ
703
Рис. 233.
Поэтому, говоря в дальнейшем о разложении в ряд Фурье функ-
функции, заданной в интервале (— я, я), всегда будем считать, что
речь идет о периодической функции. Если при этом значения функ-
функции f(x) на концах основного интервала равны между собой:/(—я)«=»
=/(я), то функция продолжается
непрерывно (рис. 231), а если
/(—я)=т^=/(я), то при таком про-
продолжении концы основного интер-
интервала будут являться точками
разрыва функции (рис. 232).
Разумеется, еще нельзя утвер-
утверждать, что образованный ряд Фу-
Фурье сходится и что его сумма (если
он сходится) равна функции f(x).
Аналогичную картину мы наблюдали и при разложении функций в
ряд Тейлора (см. п. 191).
Сейчас мы сформулируем условия, при которых ряд Фурье функ-
функции f(x) сходится и имеет своей суммой именно функцию f(x).
Введем предварительно несколько определений.
Функция f(x) называется гладкой в интервале (а, Ь), если в
этом интервале она непрерывна вместе со своей первой производной
/' (*)•
Функция f (х) называется кусочно-гладкой в интервале (а> Ь),
если интервал (а, Ь) можно разбить на конечное число частичных
интервалов, в каждом из которых f (x) — гладкая функция.
Графиком гладкой функции является гладкая линия (см. п. 66);
на такой линии нет ни угловых точек, ни точек возврата. График
кусочно-гладкой функции состоит из конечного числа гладких дуг;
такая кривая линия называется кусочно-гладкой.
В силу данных определений кусочно-гладкая в интервале (а, Ь)
функция может иметь лишь конечное число точек разрыва 1-го рода
(см. п. 33). Например, функция, график которой изображен на рис. 233,
кусочно-гладкая в интервале (а, Ь).
Напомним, что в точке разрыва первого рода функция имеет
предельные значения слева и справа, которые мы условились обоз-
обозначать f(x — 0) и f(x + 0).
Сформулируем теперь основную теорему о возможности разложе-
разложения функции f(x) в ряд Фурье. Доказывать ее мы не будем.
Теорема. Если функция f(x) кусочно-гладкая в интервале
(—я, я), то ее ряд Фурье сходится к функции f(x) во всех
точках, в которых она непрерывна.
В точках разрыва функции f(x) ряд сходится к среднему
арифметическому ее предельных значений слева и справа, т. е.
к значению /(*<>— )+/(*о+ )¦ ГДе х^—ТОчка разрыва первого рода.
704 ГЛ. XII. РЯДЫ ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ [200
В обеих граничных точках интервала сумма ряда равна сред-
среднему арифметическому предельных значений функции при стрем-
стремлении независимой переменной к этим точкам изнутри интервала
В частности, если функция f(x) гладкая и ее значения на концах
интервала (—я, п) равны между собой, то разложение ее в ряд
Фурье справедливо во всем замкнутом интервале.
Условия основной теоремы могут быть несколько иными: можно
требовать, чтобы функция f(x) имела в интервале (—л, п) лишь
конечное число максимумов и минимумов и была непрерывной, за
исключением, быть может, конечного числа точек разрыва первого
рода (условия Дирихле1)). При соблюдении этих условий функция
также разлагается в ряд Фурье, сходящийся в точках непрерывности
функции к самой функции, а в точках ее разрыва (х0) — к значению
f(x o)-f/(*o+0) v
?-LJ?— о — • Условия основной теоремы, равно как и условия
Дирихле, относятся к очень широкому классу функций. В то время
как первые допускают у функции бесконечное множество точек
экстремумов,требуя существования непрерывной первой производной
(кроме, быть может, конечного числа точек), вторые ограничивают
число экстремумов, но зато не предъявляют никаких требований к су-
существованию производной. Любая из функций, употребляемых в ана-
анализе и в его применениях, удовлетворяет приведенным условиям.
Вместе же они, безусловно, охватывают все возможные функции,
какие только обычно могут встретиться, так что каждая такая функ-
функция представима своим рядом Фурье. Любопытно отметить, что для
справедливости предложения о разложимости функции в ряд Фурье
одной непрерывности недостаточно. Существуют примеры непрерыв-
непрерывных функций, ряды Фурье которых расходятся в некоторых точках.
Обратим внимание читателя на то, что условия, накладываемые
на функцию при разложении ее в ряд Фурье, значительно ме-
менее стеснительны, чем при разложении в степенной ряд. В самом
деле, если функция представлена рядом Тейлора, то она во всем
интервале сходимости ряда не только непрерывна, но и бесконеч-
бесконечное число раз дифференцируема. Для разложения же функции в
ряд Фурье этого вовсе не требуется; нужно только, чтобы суще-
существовала и была непрерывной (и то не всюду) первая производ-
производная рассматриваемой функции.
Если функция разлагается в ряд Фурье, то можно получить до-
достаточно хорошее ее приближение, взяв конечную сумму членов
*) Г. Дирихле A805 — 1859) — известный немецкий математик.
201] § 1. ряды фурье 705
ряда Фурье. По аналогии с рядом Тейлора эта конечная сумма чле-
членов называется многочленом Фурье:
к
f (х) « -J+X ап cos nx + Ъп sin nx.
Разумеется и здесь встает вопрос о величине ошибки этого при-
приближенного равенства. Однако эта задача более сложная, чем при
замене функции многочленом Тейлора, и мы касаться ее не будем.
Тригонометрические ряды находят важное применение в много-
многочисленных разделах математики и доставляют особенно удобные ме-
методы для решения трудных задач математической физики1). Теория
тригонометрических рядов возникла в результате постановки и ис-
исследования ряда конкретных проблем механики и физики. После-
Последующее развитие этого замечательного раздела анализа также про-
происходило в теснейшей связи с развитием математической физики.
Учение о разложении функций в тригонометрические ряды на-
называют гармоническим анализом.
201. Разложение в ряд Фурье четных и нечетных функций.
Ряд Фурье в произвольном интервале.
I. Разложение четных и нечетных функций. Допус-
Допустим, что разлагаемая в ряд Фурье функция f(x) — четная. Тог-
Тогда функции f(x)sinkx будут нечетными, и все коэффициенты bk9
как интегралы от нечетных функций по интервалу (—л, л), сим-
симметричному относительно начала координат, окажутся равными ну-
нулю (см. п. 94, пример 4). Следовательно, четная функция имеет
ряд Фурье, составленный ш одних косинусов:
00
1=1
где
я я
ап = ~ \ /(*) cos nxdx = ~ lf(x) cos nx dx,
—я о
ибо f{x) cos nx—четная функция.
Допустим теперь, что f(x)—нечетная функция. Тогда
f(x) cos kx будут нечетными функциями, и все коэффициенты ak
оказываются нулями. Следовательно, нечетная функция имеет ряд
х) Особенно велика роль тригонометрических рядов в электротехнике
при изучении периодических несинусоидальных токов.
23 А. Ф. Бермант, И. Г. Араманович
706 ГЛ. XII. РЯДЫ ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ [201
Фурье, составленный из одних синусов:
tsmnx>
где
чг X I /• / \ • » <W
)f(x) snxdx
—п о
ибо /(at) sinла:—четная функция.
II. Разложение функций с произвольным перио-
периодом. Рассмотрим теперь задачу о разложении в ряд Фурье функ-
функции, заданной в интервале (—/, /), где / — произвольное число.
Если в интервале (—/, /) функция f{x) удовлетворяет условиям
теоремы п. 200, то разложение может быть легко получено при
помощи замены независимой переменной по формуле х' = -у x. Тог-
Тогда функция f(x)=f(— xj , и когда х пробегает интервал (—/, /),
переменная х' изменяется в интервале (—л, п). Разложение этой
функции в ряд Фурье будет иметь вид
со
'--к+^4 (ancos nxf -\-bn sinnx')
или
CD
где
—Я
л I
bn-^\f{~x')sinnx'dx' = -Llf{x)zin^. dx.
(В интегралах слева произведена подстановка — х'~х.)
Здесь сумма ряда Фурье — периодическая функция с периодом
Т =2/.
Частоты последовательных гармоник, составляющих ряд, равны
пп я
(on=-j-; наименьшая частота со-^-^-,
III. Разложение функций, заданных на половине
периода. Пусть требуется разложить в тригонометрический ряд
202] § 1. ряды фурье 707
функцию f(x) в интервале @, я) (или, что сводится к этому, в ка-
каком-нибудь интервале @, /)). Мы можем по произволу продол-
продолжить функцию f(x) на интервал (—я, 0), но так, чтобы образо-
образовавшаяся в этом интервале функция F{x)y совпадающая с/(л;)в
интервале @, я), удовлетворяла условиям основной теоремы. Разло-
Разложив функцию F(x) в ряд Фурье, получим искомый ряд, представ-
представляющий функцию f(x) в интервале @, я); не имеет значения, что
он в интервале (—я, 0) представляет какую-то другую функцию,
по существу не связанную с данной функцией f(x).
В частности, f(x) можно продолжить четно на интервал (—я, 0);
значит, график функции f(x) продолжить симметрично относитель-
относительно оси Оу. При этом F(x) будет четной функцией и ряд будет
состоять только из косинусов. Если же f(x) продолжить нечетно
на интервал (—я, 0) значит, график продолжить симметрично отно-
относительно начала координат, то F(x) будет нечетной функцией и
ряд будет состоять из одних синусов.
Мы приходим к выводу, что если функцию f(x) можно
разложить в тригонометрический ряд, то в интервале @, я) таких
ее разложений существует бесчисленное множество. Значит, можно
составить сколько угодно сходящихся тригонометрических рядов,
представляющих в интервале @, я) одну и ту же функцию,
а в интервале (— я, 0) самые разнообразные функции,
202. Примеры. 1) Разложим в ряд Фурье функцию f(x)9
определенную в интервале (—я, я) так:
f i \ _ / — 1 ПРИ —п < х < 0,
^* \ 1 при 0 < х < я.
График этой функции, периодически продолженный на всю ось Олг,
изображен на рис. 234. Ясно, что эта функция удовлетворяет
условиям теоремы о разложении. Поскольку она нечетна, все
коэффициенты ап = 0.
Найдем коэффициенты Ьп. Согласно п. 201, I имеем
Ь
n
Ь
n л J
о
или
п
л
2 Г 2^2
=— \ \-sinnxdx = cosnx = (cos ля — 1),
л J nn о nn v "
о
^ = ^A—COS Я/2).
Так как cos nn = (—1)я, то, полагая последовательно я= 1,2, 3,...,
найдем
4 4 4
&1 ~—- ~~" . Un ~~~ 0 Un ~*~" —' Uл ~~" 0 Uп. "~~ i И Т Д
П оП оП
Таким образом,
/W==?(sinA:+"sin3A; + isin5A; + ---) •
23*
708 ГЛ. Xlt. РЯДЫ ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ {202
Согласно основной теореме сумма ряда в правой части равна 1
при 0 < л; < я и —1 при —я < х < 0. При лг = О, а также в
точках ± я сумма ряда, как это ясно видно, равна нулю, что
опять-таки соответствует теореме
о разложении. Аналогично ряд
ведет себя в любом интервале,
отличающемся от основного ин-
интервала (—я, я) целым числом
0
-1
\тс
периодов.
Интересно проследить, каким
рис 234 образом график функции прибли-
приближается графиками последовательных
частичных сумм полученного ряда.
На рис. 235 пунктиром показаны последовательные гармоники
ряда и сплошной линией — графики соответствующих частичных сумм.
Пользуясь найденным разложением функции /(#), легко написать
ряд Фурье для функции
ф(х) = 1а при —Д<Л;<°»
^ ' \b при 0 < х < я.
Для этого достаточно заметить, что
, ч а-\-Ь
2
(Указанная замена означает, что мы перенесли начало координат в
точку @, ^4—) и изменили масштаб по оси Оу.) Тогда
2) Разложим в ряд Фурье функцию
График этой функции, периодически продолженный на всю числовую
ось, изображен на рис. 236. Поскольку функция f(x) четная, то
все коэффициенты #„ = 0. По формулам п. 201, I имеем
я я
2 С
= я, я,, — — \xcosnx dx.
Интегрируя по частям, получим
«»=1
innx \n_Csmnx I =± х *=_2_ (сов „„_
§ 1. РЯДЫ ФУРЬЕ
709
J
——| 7
t
\ !
\ /
1 \ /
x—'
У
/
/
/
0
->
\ i
\ 1
\ 1
N
ЬУ
^-^ v^ -
f
:??
0
-i
?sw3x
031
J
L
h
6)
Рис. 235.
1
к
\
1
1
-Зл
\/
-Ел
\
j
!
-ft
1
ft
0
У
у
>
ft
\/
2a
At *
Рис. 236.
202}
710
Отсюда
ГЛ. XII. РЯДЫ ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ
[202
=—^1 и т.д.
Итак,
-
Приближение функции /(*) последовательными частичными сум-
суммами ряда Фурье показано на рис. 237.
Рис. 237.
При лг = О получается интересный числовой ряд для числа я.
Имеем
откуда
Из этой формулы получаются некоторые другие. Положим
22+33»" '•• J •
§ 1, РЯДЫ ФУРЬЕ
— — — — (
, = а1Э т. е. а2 = 24 .
я2 * , 1 , 1 , 1 , 1
202] § 1, ряды фурье 711
Мы имеем
или
Значит,
В п. 184 мы доказали, что ряд обратных квадратов сходится,
теперь же сумели найти его сумму.
3) Разложим в ряд Фурье функцию
f(x) = x, —я <х<п.
График этой функции, продолженной на всю числовую ось, состоит
из параллельных отрезков (рис. 238). Так как функция нечетна, то
находим только Ьп. Имеем
. 2 Р . . 2 Г х cos njc
bn=-\jxsmnxdx = -[
0
cos nx
2 Г—jtcosfttt , sinnx I я
о
2 cos nn
Полагая последовательно л = 1, 2, 3,..., получим Ьг = 29
- 1 /, -1
Итак,
-«-sin3jc—... ).
6 j
Это равенство справедливо при
—я<#<я. В точках х=±п
сумма ряда равна нулю.
Отметим, что в интервале @, я) —
функции примеров 2 и 3 представ-
представляют одну и ту же функцию. Обе
они в этом интервале просто рав-
равны х. Однако поскольку в интервал (— я, 0) они продолжены
по-разному: первая — четно, а вторая — нечетно, то и их разложения
в ряды Фурье получаются различными.
712
ГЛ. XII. РЯДЫ ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ
[202
4) Разложим в ряд Фурье функцию /(#), определенную в интер-
интервале (—я, я) так:
при
0<л;<я,
где а и Ь — постоянные. Графиком f(x) является ломаная, состоя-
состоящая из двух отрезков прямых:
у~ах пу~Ьх (на рис. 239
а<0 и Ь> 0).
\
/ •
J
1
\
-яг
bit
-an;
\
n
У
t
/
i
A
—
L- _ — _
\
1
1
I
1
+
1
t /
|/
y>
/
/
0
\
I
1
r
t /
i/
Рис. 240.
Рис. 239.
Вычислим коэффициенты Фурье функции f(x). При пфО имеем
аЛ = — f f(x)
о
ax
~ \ bx
a /^xsin/гд;
~"я V л
cos nx
b /xsi
x sin nx
cos nx
т. е.
a-
При л = 0 имеем
Далее,
x cos fix о
-n
sinnxj о
x cos nx
n
*"*
a —л о я
= cos nn
я n n n
—1)
7
2021
т. е.
§ 1- ряды фурье
713
Ь -а + ь и- a+b h _*±* Ь
Таким образом, ряд Фурье имеет вид
а+Ь
ИЛИ
(sin л;—-g- sin 2лг + у sin Зл;— ... J .
В интервале (— я, я) ряд представляет функцию f(x), а в точ-
точках х = ± я он равен *у
— а
Нетрудно заметить, что функции
примеров 2 и 3 являются частными случаями последнего примера.
Полагая а=—1, Ь=\, мы получим функцию примера 2, а при
а~Ь=\—функцию примера 3.
Пусть а = 1, ? = 0. Тогда
При -Ж*<°>
о при 0<лг <я
(рис. 240). В этом случае получаем ряд
nAr—ysin2х +-у-sin3#—...
Этот ряд в интервале (—я, 0) равен х, а в интервале @, я) схо-
сходится к нулю. При х = ±:п сумма его равна—-jr--
5) Найдем ряд Фурье функции f(x) = (sinx\ (рис- 241). Эта функ-
функция получается при «четном продолжении» функции sinx из интер-
интервала @, я) в интервал (—я, 0). Поэтому
4
714 ГЛ. XII. РЯДЫ ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ [203
я„ = — \sinx cos nxdx = — \ [sin (л+ \)х—sin (п—\)х]
о о
О, если п нечетное,
—4
—г-1—тт, если п четное.
Следовательно,
= 1_±(^-1 cos 2х + -1- cos Ах +... + BлI2_1 cos
Функция / (л:) = (cos дг| получается из предыдущей переносом
начала отсчета:
|cosa:| =
Поэтому
6) Разложим в ряд Фурье функцию f(x) = x2 при —1 <лг< 1.
Период этой функции, продолженной на всю числовую ось, ра-
равен 2. Пользуясь формулами п. 201, 11 и учитывая четность функ-
функции, имеем
а0 = 2 Г х2 dx=Y, ап == 2 Гл;2 cos ппх их =
о о
^ Г*2 sin ппх , 2х cos ппх
Отсюда
14/ 1 1
/(*) = Т~^2 ( C0S ПХ — 02 C0S 2ЯЛГ + ^2 C0S ЗЯ^— . . .
§ 2. Дополнительные вопросы теории рядов Фурье.
Практический гармонический анализ
203*. Равенство Парсеваля1). Среднее значение квадрата пе-
периодической функции. Пусть f(x) — функция, заданная в интервале
(—я, я) и удовлетворяющая условиям основной теоремы п. 200.
2) М. Парсеваль—французский математик первой половины
XIX века.
204} § 2. практический гармонический анализ 715
Разложим ее в ряд Фурье
00
f(x) = а-± + ? ап cos nx + bn sin nx.
Возведем теперь обе части равенства в квадрат и возьмем интег-
интеграл в пределах от —я до я. При этом мы не будем останавли-
останавливаться на доказательстве законности всех действий, производимых
над бесконечным рядом в правой части:
dx.
При возведении в квадрат суммы будут получаться квадраты сла-
слагаемых и удвоенные парные произведения. Интегралы от парных
произведений будут равны нулю в силу формул п. 199; по тем же
формулам интегралы от cos2nx и sln2nx равны я. Деля еще обе
части равенства (*) на я, окончательно получим
Это равенство называется формулой Парсе&аля; оно позволяет
найти среднее значение квадрата периодической функции за один
период.
204*. Ряды Фурье в комплексной форме. Используя комплекс-
комплексные числа и формулы Эйлера, можно придать ряду Фурье функции
f(x) в интервале (—я, я) удобную и легко запоминаемую форму.
Пусть
о»
/(х) = у а0 + ]? (an cos nx + bn sin nx).
Заменим по формулам Эйлера cos ял; и sin ял::
Jnx _|_0-И1д? pinx л—inx
cosnx — -~ , sinnx^
Тогда
n=l
716 ГЛ. XII. РЯДЫ ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ [204
Обозначим комплексное число ап—ibn через сп:
cn=an—ibn-
По формулам для ап и Ьп (см. п. 200)
я
= ±.§f(x)e-inxdx. (**)
—я
Комплексное число un-\-ibn является сопряженным к сп:
Формула для сп получается из формулы для спУ если в ней заме-
заменить п на—п. Поэтому мы обозначим
Я
Так как яо = — \ f(x)dx, то оно находится по формуле (**) при
— я
=0; поэтому можно считать, что ао = со.
С учетом введенных обозначений ряд (*) можно записать в виде
или еще короче:
00
/(*)-•5-S '»*'"* где cn=li
Здесь индекс суммирования п пробегает все целые значения от
— оо до +оо. Так как комплексное число е~1пх является сопря-
сопряженным к ein*y то члены ряда, отвечающие индексам ли —л,
представляют комплексные выражения
Сумма их дает действительную величину—п-ю гармонику. При этом
|сп| = т/ а%-\~Ьп является амплитудой этой гармоники1).
Формула (**) может служить и для вычисления коэффициентов
ряда Фурье, если воспользоваться правилом интегрирования комп-
2) В электротехнике при изучении несинусоидальных токов важ-
важную роль играет изучение амплитудного спектра функции, т. е. за-
зависимости | сп | от п.
205] § 2. практический гармонический анализ 717
лексных функций (см. п. 93). При подстановке пределов интегри-
интегрирования нужно помнить, что
е1пк = е~1пк = cos rrn = (— 1 )п.
Пример. Разложим в ряд Фурье функцию f(x) = ex в интер-
интервале (— л, л). Имеем
я я
ся = — \ exe~lnxdx = — \ еХ{-
п 1 — in
— я
Следовательно,
• Ae*e-inK—
Если мы хотим перейти к обычной форме ряда Фурье, то, как уже п>
ворилось, надо объединить слагаемые, отвечающие индексам л и —п:
1+д2 ~*
. vn 2соб пх — 2л sin nx
Тогда будем иметь:
1 , ^ч. Л,п/со$пх nsinn^\l
Рекомендуем читателю получить разложение ех обычным спосо-
способом и убедиться в тождественности результатов.
Комплексную форму ряда Фурье можно записать для любого ин-
интервала (—/, /):
^ где cn = 7
Читатель легко самостоятельно проверит правильность ре-
результата.
205*. Ортогональные системы функций. Рассмотрим сейчас
вкратце задачу более общую, чем разложение функций в ряды
Фурье. Именно рассмотрим задачу о разложении функций в ряды
по ортогональной системе функций. Будем в дальней-
дальнейшем считать, что функции ф^лг), ф2(лг), ... , ф„ (#), ... опре-
определены и непрерывны в некотором интервале [а, Ь\.
718 ГЛ. XII. РЯДЫ ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ [205
Оп р еде л е ни е. Система функций фх (л:), <р2(;с), ..., <р„ (лг),...
называется ортогональной в интервале [а, &], если интеграл от
произведения любых двух различных функций системы равен
нулю:
ь
l<pn(xL>m(x)dx = 0, пфт.
а
Обозначим через кп интеграл от квадрата функции <рп(л;):
ъ
а
Все числа kn положительны.
Если каждую из функций <рп(х) умножить на величину ,
то новые функции
M*) () M) W Ф()()
будут, разумеется, снова образовывать ортогональную систему. Кро-
Кроме того, интеграл от квадрата каждой из функций будет равен
единице:
ъ ь
Таким образом, функции <ф1(дг), ... , tyn(x), ... удовлетворяют
условиям
Такую систему функций будем называть ортогональной нор-
нормированной системой.
Примеры. 1) Система функций 1, cosat, sin а:, ... , cos/jjc,
sinnx, ... в интервале [ — я, л] будет ортогональной системой.
Это вытекает из формул 1)—5) п. 199. Из тех же формул следу-
следует, что система
1 cos х sin x cos nx sin nx
будет ортогональной и нормированной.
2) Система функций sin*, sin2Ar, ... , sinnx, ... будет орто-
ортогональной в интервале [0, я].
206J § 2. практический гармонический анализ 719
Действительно, если тфп} то
л ^ п
j Sin ШХ Sin ПХ dX = I 2 (/и —я) 2(m + n) J """*
о о
(см. формулу 62 таблицы интегралов). Так как
я п
С . 2 л [х sin 2пхI ?t_
jsm лл;^-^т 2T-J -2-
о о
то, чтобы эту систему нормировать, надо все функции разделить
¦¦
/I-
3) Система функций 1, cosat, cos 2jc, ... , cos/глт, ... будет
ортогональной в интервале [0, я]. Рекомендуем читателю прове-
проверить это самостоятельно.
Пусть теперь f(x)— некоторая функция, определенная в интер-
интервале [а, Ь]. Предположим, что ее можно представить в этом ин-
интервале в виде ряда, расположенного по функциям ^(л:), i|J(a:), ...
..., ^„(лг), ... , ортогональным и нормированным в этом интерва-
интервале, т. е.
/ (х) = с^ (х) + с2г|J (х)+...+ сп^п (*)+... (»*)
Чтобы найти коэффициенты разложения, умножим последователь-
последовательно обе части равенства (**) на функции г^ (х), if2 (л:), ... , t|)w (л:), ... и
проинтегрируем по интервалу [а, Ь]. При этом мы считаем, что ряд
справа можно интегрировать почленно. В силу соотношений (*)
получим
Ь оо Ь
J / (х) Ч>„ (х) dx - S с * S гЫ*) *в (х) dx - сп.
a fe==1 a
Коэффициенты сп, определяемые по этим формулам, называются
коэффициентами разложения функции f(x) относительно заданной
ортогональной системы. Мы не останавливаемся на вопросе а том,
когда разложение (#*) возможно.
Если, в частности, функций г|)п(х) суть тригонометрические функ-
функции примера 1, то ряд (##) будет просто рядом Фурье функции/(х).
Разложения в ряды по ортогональным системам функций встре-
встречаются при решении многих важных задач математической физи-
физики; некоторые из них приведены в книге [5].
206. Практический гармонический анализ. Шаблоны. Если
функция задана аналитическим выражением, то при помощи интег-
интегрирования можно вычислить ее коэффициенты Фурье и построить
720
ГЛ. XII. РЯДЫ ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ
[206
соответствующий тригонометрический ряд. Но в практике часто
встречаются случаи, когда функция задается графически или
таблично.
Так обычно получают функцию, описывающую исследуемый про-
процесс, в результате эксперимента. Данные этого эксперимента зано-
заносятся или в таблицу, или на график, который иногда образуется и
автоматически, в самопишущих приборах. Задача, возникающая пе-
перед исследователем,, состоит в отыскании соответствующего анали-
аналитического выражения для функции. Для этой цели могут быть упо-
употреблены тригонометрические ряды, поскольку есть уверенность, что
90
80
70
60
50
40
30
20
io
0f234
5 6 7 8 9 10 11 27t
Рис. 242.
эта функция приближенно и достаточно точно может быть выраже-
выражена суммой конечного числа первых членов ее ряда Фурье. Весь во-
вопрос заключается в нахождении коэффициентов Фурье функции. Он
может быть решен применением одного из способов приближенного
вычисления интегралов.
Методы приближенного разложения функции, заданной графи-
графически или таблично, в ряд Фурье составляют, как говорят, прак-
практический гармонический анализ.
Для упрощения вычислений коэффициентов Фурье разработаны
различные способы, учитывающие особенности подлежащих вычисле-
вычислению интегралов.
Эти способы схематизируют операцию приближенного вычис-
вычисления коэффициентов Фурье. Ниже мы вкратце даем представ-
представление об одном из этих способов, использующем так называемые
шаблоны.
Пусть в интервале @, 2я) задана функция y=f(x). Мы счита-
считаем, что при любом задании функции график ее нам известен. При
206]
§ 2. ПРАКТИЧЕСКИЙ ГАРМОНИЧЕСКИЙ АНАЛИЗ
721
этом в случае необходимости систему координат Оху следует па-
параллельным сдвигом перенести так, чтобы весь график был рас-
расположен над осью Ох и как можно ближе к ней (рис. 242). Это
скажется только на свободном члене в разложении Фурье, а вмес-
вместе с тем позволит избежать как отри-
отрицательных, так и слишком больших
положительных значений функции.
Приближенное представление функции
в виде многочлена Фурье требует отыска-
отыскания первых коэффициентов Фурье
ak = ~ \ / (х) cos kx dxy
о
2 Я
bk =—[ f(x) sin kx dx.
о
Для вычисления интегралов приме-
применяется одна из формул для численного
интегрирования, обычно самая простая из
них—формула прямоугольни-
прямоугольников. Интервал @, 2л) делится на п рав-
равных частей с помощью точек дго = О,
¦*1» **2> • • • > •* п
хп —
Алг==- . Тогда
п
я-1
п-\
(*)
0
1
2
3
4
5
6
7
8
9
10
11
44
46
76
88
86
63
24
20
26
40
58
65
_
40
66
—
75
55
—
17
22
—
50
51
—
23
38
—
43
35,5
—
10
13
—
29
32,5
Принимая во внимание особенности
множителей cos kx{ и sin kxh берут п
чаще всего равным 12 или 24 или, если есть надобность в боль-
большей точности, 48. Мы здесь возьмем п=> 12. Читатель легко прове-
проверит, что при этом в формулах (*) каждое из 12 учитываемых зна-
значений функции умножается лишь на одно из следующих чисел:
= sin^-=l, cos -|-= sin?. = 0,87,
- = sin -у = 0,50, cos ~- = sin 0 = 0,
cos -
взятое со знаком -J- или —.
722
ГЛ. XII. РЯДЫ ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ
[206
Укажем практически удобную схему вычислений с помощью
шаблонов (схема для 12 ординат).
Прежде всего составляется таблица из четырех столбцов и
12 строк. В первом столбце последовательно проставляются номера
точек деления интервала @, 2л); во втором — выписываются соот-
соответствующие этим точкам ординаты, снимаемые прямо с графика (если
функция задана графически), причем удобно выбрать столь мелкий
масштаб, чтобы ординаты могли быть выражены целыми числами;
в третьем столбце помещаются произведения соответствующих ор-
ординат на cos 30° = 0,87; в четвертом — произведения ординат на
cos 60° = 0,50 (кроме строк, отмеченных номерами 0, 3, 6, 9, клетки
которых прочеркиваются, так как они соответствуют произведению
ординат на косинусы дуг, кратных я или -^
0
f
г
3
4
5
6
7
8
9
Ю
ft
0
1
2
3
4
5
6
\ 7
8
9
Ю
11
0
1
2
3
5
6
7
8
9
10
11
0
1
2
3
4
S
6
7
8
9
Ю
11
Рис. 243.
После того как таблица оказалась заполненной (она приготавли-
приготавливается для каждой заданной функции), можно приступить с помощью
шаблонов к вычислению коэффициентов Фурье. Для коэффициента
а0, впрочем, не требуется шаблонов; он вычисляется как сумма чи-
чисел второго столбца, деленная на 6. Для вычисления других коэф-
коэффициентов (av bv a2i ?2, ... , а6, ?в) используются шаблоны из
прозрачного материала, являющиеся точной копией (только без чи-
чисел) приведенной выше таблицы и заготовленные раз и навсегда для
каждого коэффициента в отдельности. Те клетки данного шаблона,
которые соответствуют положительным слагаемым в формулах (*),
207] § 3. интеграл фурье 723
отмечаются иначе, чем те клетки, которые соответствуют отрица-
отрицательным слагаемым. (Первые можно, например, обвести одной краской
или жирной линией, а вторые — другой краской или тонкой линией.)
На рис. 243 даны шаблоны для первых четырех коэффициентов
ai> ^i> а2, Ъг (в схеме для 12 ординат). Рекомендуем читателю са-
самостоятельно разобрать их устройство, пользуясь формулами (*).
Накладывая шаблон, соответствующий коэффициенту ak или bkJ
на таблицу, мы выбираем из нее числа, занимающие клетки, обве-
обведенные жирной линией, а также числа, занимающие клетки, обведен-
обведенные тонкой линией. Складывая отдельно первую и вторую группы
чисел и вычитая из первой суммы вторую, получаем 6ал, так что
для вычисления ak остается только результат разделить на 6.
В приведенном примере находим:
636 лпс
= — = 106,
_ D4 + 40 + 38 + 29 + 51) — D3 + 55 + 24+17+ 13) 50 о
6 ~~"^ ' '
_ B3 + 66 + 88 + 75 + 36,5)-A0 + 22 + 40 + 50 + 32,5) = 134_о
D4 + 23 + 36,5 + 24+10 + 32,5) —C8 + 88 + 43+13 + 40 + 29)
6
ь ^D0 + 66+17 + 22) —G5 + 55+50 + 51)^ 86_ g
Таким образом получаем приближенное выражение функции в ви-
виде тригонометрического многочлена второго порядка
/(*)«53+• (8,3 cosх +22,3 sin*) — A3,5 cos 2лг+-14,3 sin 2дг).
§ 3*. Интеграл Фурье
207*. Интеграл Фурье. В п. 201, 11 мы видели, что разложе-
разложение функции f{x)y заданной в интервале (—/, /), в ряд Фурье
имеет вид
со
j \х) = -у + у. cin cos (on х + b sin cort лг, где сол = -т
п=1
I I
и ап = I J / (t) cos v>ntdt, bn = i. J / @ sin ©д< d<.
-/ -z
(Для удобства в интегралах, определяющих коэффициенты ап ц
/?я, переменная интегрирования обозначена буквой /.)
724 гл. хн. ряды фурье. интеграл фурье [207
Подставляя выражения для ап и Ьп в ряд Фурье, получим
-j V \ /(/) [cos a>nt cos ыпх + sin o)n/ sin <onx] dt =
Пусть теперь функция /(лг) определена на всей числовой оси
и не является периодической. Мы будем считать при этом, что она
в любом интервале (—/, /) может быть разложена в ряд Фурье
и что несобственный интеграл от абсолютной величины этой функ-
функции сходится:
Рассмотрим сначала функцию f(x) в интервале (—/, /); на
основании сделанных предположений ее можно разложить в ряд
Фурье, который мы запишем в виде (*). Будем теперь неограни-
неограниченно увеличивать / и посмотрим, во что при этом перейдет фор-
формула (*) для фиксированного значения х. Первое слагаемое фор-
формулы будет при /—*оо стремиться к нулю:
i$ \f(t)\dt <-|-0.
(Неравенство между интегралами доказано в п. 90.)
Введем обозначение:
До) = о)Л+1—o>n=--j (/г = 0, 1, 2, ...).
Тогда оставшаяся сумма перепишется так:
cos юя (/-
00
Заметим, что интеграл ф(о>)= \ f(t) cos <o(tf—x)dt сходится,
— GO
так как подынтегральная функция по абсолютной величине не
превосходит функции |/@|i интеграл от которой сходится. Более
§ 3. ИНТЕГРАЛ ФУРЬЕ 725
того, как функция параметра © он сходится правильно, и поэтому
<р (<*>)-—непрерывная функция, если только непрерывна f(t)
(см. п. 137). Когда / очень велико, можно считать, что интеграл
J/(/)cos(Dn(* — x)dt почти равен значению функции ф(со) при
со = (оп, т. е.
I cos <дп (t—л:) dt&y (o)n).
Написанная выше сумма перепишется теперь так:
я=1 -/ п=\
со
В сумме ^ф(а)/1)Д(о величина Ао) = -у стремится к нулю при
/->оо, а переменная о)л пробегает при этом все значения от 0 до оо.
Следовательно, можно считать, что эта сумма будет стремиться к
интегралу
СО ОО 00
\ <p(G))d(O= \ flf(O \ /(/)COS @ (t-X)dt.
О 0 —оо
Подставляя все в формулу для /(#)> получаем
() COS ©(*—
—оо
Интеграл, стоящий в правой части равенства, называется интегра-
интегралом Фурье.
Точное доказательство формулы (#*) требует более сложных
рассуждений, которые мы опускаем. Отметим только, что в тех точ-
точках, где функция f(x) имеет разрыв первого рода, интеграл Фурье
(так же, как и ряд Фурье) дает значение /**°~" J"twI*ot- ) ^ рде
х0 — точка разрыва.
Так как cos со (t — л:) = cos со/ cos со x + sinootf sinwjt, T0 фор-
формулу (**) можно переписать в виде
1С г*
О —во
00 00
Н— \ sinwAr^o) \ f(t) sincot dt. (***)
726 ГЛ. ХН. РЯДЫ ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ [208
Обозначим внутренние интегралы через Л (со) и Б (со);
00 00
А (со) = ~ С /(/) cos со/ dt, В (со) = i Г /(*) sin со* Л.
— 00 — О»
Тогда
00
/(¦*) = \ И(©) cos ю# + Я (со) sin coat] dсо.
о
В этой формуле мы имеем разложение функции f(x) в бесконечном
интервале (—оо, оо) на гармонические колебания, частоты которых со
непрерывно меняются от 0 до оо.
Когда функция была периодической, ее разложение в ряд Фурье
Zlfl
состояло из отдельных гармоник с частотами соЛ = -у-, отличающи-
отличающимися друг от друга на постоянное число Дсо=-у. Каждая такая
гармоника имела определенную амплитуду. Зависимость амплитуды
от частоты называется амплитудным спектром функции. Как говорят,
периодическая функция имеет дискретный спектр (т. е. она может
быть представлена в виде отдельных гармоник). Аналогично говорят,
что непериодическая функция имеет непрерывный спектр; частоты
образующих ее гармоник изменяются непрерывно. Функции А((о)
и В (со) дают закон распределения амплитуд (и начальных фаз) в
зависимости от частоты со.
Подробно на этом вопросе мы останавливаться не будем; отметим
только, что он играет большую роль в приложениях интеграла
Фурье к изучению непериодических процессов.
208*. Интеграл Фурье для четных и нечетных функций* Вернемся
снова к формуле (**#) п. 207
О> 09 СО Ю
/ (х) = -! Ccos со* dco С /(/) cos ®tdt+- Tsin cox da [f{t) sin cot dt.
0 — 09 0 -GO
Предположим, что функция / (x) — четная. Тогда функция
со
f(x) sinobx — нечетная и интеграл \ / (/) sin со/ dt будет равен
нулю. Кроме того,
Г f(t) cos (utdt = 2 \ f(t) cos со* dt.
§ 3. интеграл фурьё 727
Поэтому для четных функций
==— Г cosaxda § f(t) cos at dt.
о
Если же/(л:) —функция нечетная, то точно так же получим
у(л;)=— Г sin cox d(O \ f(t) sinat dt.
о о
Если функция f(x) определена только в интервале @, оо), то ее
можно продолжить в интервал (— оо, 0) как четным, так и нечетным
образом, т. е. представить ее различными интегралами Фурье. Очень
часто приходится также рассматривать функцию, равную f(x) при
дг> 0 и нулю при х <0. Ясно, что интеграл Фурье такой функции
будет равен полусумме ее интегралов Фурье, полученных при четном
и нечетном продолжении функции f(x). Действительно, при лг>0
оба эти интеграла, а также их полусумма будут равны f(x) (в точ-
ках разрыва: ~ ^ v ~ ¦ J . Если же х < 0, то первый из них
будет равен /(#), а второй будет равен —/(#), полусумма же их
будет равна нулю.
Примеры. 1) Представим в виде интеграла Фурье функцию
j 1 при 0 <[ х < 1,
/(*) = \ 0 при х> 1,
продолжив ее четным и нечетным образом.
Если продолжение четное, то
оо 1 ос
.С j. и. 2 f cos ©д; sin© ,
cos (ox d(x> \ cos at dt = — \ aw.
0 0 0
1 при —1 <л: < 1,
у при лг=±1,
О при х < — 1 и л:>1.
Если продолжение функции/(л:) нечетное, то
Отсюда, кстати, следует, что
f(x) = 1 С sin (ox d(o С sin at dt = A f sjru^X-c^sj^)
728 гл. xii. ряды фурье. интеграл фурье [209
Наконец, представление в виде интеграла Фурье функции, рав-
равной f(x) при лг> 0 и нулю при х < 0 (рис. 244), таково:
00
If/ sin© . . 1—cos со \.
— \ COS (дХ \- Sin (ОХ ] d(d.
Я J \ CD CO J
о
2) Представим в виде интеграла
Фурье функцию (Р > 0)
f(x) = е~$х при х > 0,
Рис. 244. продолжая ее на отрицательную по-
полуось так же, как в примере 1.
При четном продолжении (см. формулу 74 таблицы интегралов)
09 00 00
2 С С 2 Г* со
fix) =— \ cos солг rfco \ е~Р* cos at dt = — \ » , Q» cos оолг dco.
«J J Jijcoa + pa
0 0 0
При нечетном продолжении с помощью формулы 73 получим
00 00 00
f(x)=—\ SinCOATdcO \ в Р*81ПЮ/Л = — \ 2 , n2SinC0AT rfCO.
0 0 О
Так как /@) = 1, то при нечетном продолжении при л; = Обудет
точка разрыва. Поэтому интеграл Фурье при лг = О равен не/@)= 1,
а нулю — полусумме значений функции с обеих сторон точки раз-
разрыва. Наконец, функция
j e~$x при лг> О,
\ 0 при х < О
представится в виде
00
\ COS СОЛ' + СО SinCOJC .
о о» «со.
209*. Интеграл Фурье в комплексной форме. Преобразование
Фурье, Представление интеграла Фурье в комплексной форме совер-
совершенно аналогично комплексному представлению ряда Фурье. По фор-
формуле (**#) п. 207 имеем
о
где
со
f(x) = J [А (со) cos о>лг + В (со) sin <ox] tfco,
о
оо со
= -^ § f{t) cos at dt, ?(co) = -i- ^ f(t) sin at dL
§ 3 интеграл фурье 729
Заменим в интеграле Фурье coso>at и sin юл: по формулам
Эйлера. Получим
- J [А (в, ^±f^+B (со)
0
1 f { [Л(©)—/?(©) ] е*°* + [Л (ю) + Ю (со)] «-***} do.
о
Введем обозначение зх [Л (со) — /В (о) ] = F(<o). Согласно формулам
для Л (о>) и В (со) найдем
j(cos со*—/s
— 09
Далее,
я [Л (ю) +/В(ю) ] = ?(©)==
Если обозначить /7(со) = /?( — (о), то формула (*) будет опре-
определять F(&) при всех со, как положительных, так и отрицательных.
Подставив функцию F{co) в интеграл Фурье, получим
00
О
Интеграл от второго слагаемого можно записать так:
GO — GO О
f F(—со)е-'шхйсо= f F(co)e<4u*d( — co)= f F(co) e'^dco.
J J J
0 0 —oo
Поэтому окончательно
00
-^ J F(co) eI(B*dco, где F(co) =
Интересно сравнить полученный результат с рядом Фурье в ком-
комплексной форме (см. п. 204). Для функции f(x)> заданной в интерва-
интервале ( —/, /), мы имели
где с ==i ~i~ i f it) c~~ n dt и (оп ==
730 ГЛ. XII. РЯДЫ ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ [209
Здесь же числа сп заменяются функцией
непрерывно изменяющейся вместе с со, а сумма выражений сде1<л»* за-
заменяется интегралом.
Комплексная функция F(to) называется преобразованием Фурье
функции /(/). При этом модуль | /^(со) | называют амплитудной ха-
характеристикой функции (или амплитудным спектром), а — argF(o>) —
фазовым спектром.
Пример. Найдем преобразование Фурье функции
-{Г
f[t) = Г г ' (а>0).
у w ' п при t < О v '
Имеем
а+ 1ш
о
Следовательно,
0)
Дальнейшие сведения о преобразовании Фурье и его применени-
применениях к задачам электротехники читатель может найти в книгах [6], [12].
ВОПРОСЫ И ПРЕДЛОЖЕНИЯ ДЛЯ САМОПРОВЕРКИ
1. Какой ряд называется тригонометрическим? В чем состоит задача
разложения функции в тригонометрический ряд?
2. Вывести формулы для коэффициентов Фурье периодической функции
с периодом 2я.
3. Сформулировать условия разложения функции в ряд Фурье.
4. Указать особенности разложения в ряд Фурье четных и нечетных
функций.
5. Указать формулы для коэффициентов разложения функции с произ-
произвольным периодом.
6. Как можно раскладывать в ряд Фурье функции, заданные на поло-
половине периода?
7*. Вывести формулу Парсеваля.
8. Записать ряд Фурье в комплексной форме.
9%. Какая система функций называется ортогональной?
10*. В чем состоит задача разложения функции в ряд по ортогональной
системе? Как отыскиваются коэффициенты разложения?
11. Указать способы приближенного отыскания коэффициентов Фурье.
12*. Что называется интегралом Фурье?
13*. Указать условие представления функции интегралом Фурье.
14*. Как записывается интеграл Фурье для четных и нечетных функций?
15*. Записать интеграл Фурье в комплексной форме,
16*, Дать определение преобразования Фурье,
ТАБЛИЦА ИНТЕГРАЛОВ
(а, 6, m, n — постоянные)
I. Интегралы от рациональных функций
(ax+b)n + 1
Г (ax+b)n + 1
1. \ (ах + b)n dx~--—f ! 1ч—\-Ct л целое число, не равное — 1.
ax—b
ax+b
+C.
732
19.
20.
21.
22,
23.
ТАБЛИЦА ИНТЕГРАЛОВ
II. Интегралы от иррациональных функций
(a +
+C.
J У ах+b 6а
Г ^^_еи=г|-=Cаа^—
J К ax-\-b li)a
V
= у=* arctg
25.
26
27
Vax + b а Г dx
Г
J
х
Vax
ax + b+b \
dx
\ .
J х Vax + b
а Г dx
В формулах 28—47 считается, что а > 0, ?> 0
29-
32.
xdx
х2 dx
34
35
36.
37
. ГУа*х2±Ь2 dx=^~ х Va2x2± Ь2± ^ In | ax+ Va2x2± b* |j +C
. Г ^2 _ а2д:2 dx = ^. L j/-ft2_a2A:2 + Ь1 arcsin у + С.
\х У а2х2± b2 dx = Y^y(a*x2
ТАБЛИЦА ИНТЕГРАЛОВ
733
38.
-b4 In
39
40
• I"'»'
•F
•F
-aV+**arcsin
у 1
— b* +barcsin
ax
+ C.
42
43.
+ C.
45
46
•a)\~xV?
aarcsin?? +C.
6
dx 1
dx
¦' = —r arcsin
!:
dx 1
^ Ь 1п
+ C.
ь+у b*
+c
47 Г
dx
48
dx=
(b+x) + (a-b) In
arcsin
52. Г yAl±Jd* = -vru!
Г d?
64. |^=|=== =
(b-x)-(a+b)arcsin
_a_ Yx-Ъ
2 arcsin
734 ТАБЛИЦА ИНТЕГРАЛОВ
55
Sr/s
xm(axn + b) dx, где m, n, r, s — целые числа, s>l. Применяется
подстановка ox/I + 6 = wJl если —^ число целое, и подстановка
a+bx"n = ust если ———j число целое. В других случаях интеграл
не выражается при помощи элементарных функций (П. Л. Чебышев1)).
III. И нте г р а л ы от трансцендентных функций
6. \хпе
п — це
57. Г
56. \хпе* dx = ex[xn —пхп-1 + п(п — 1)х"~а— . . . + (— 1)п п
п — целое положительное число.
(In x)ndx = x [(In x)n— /i(ln x)n~l + n(n - 1) (In x)«-»_... + (—1)я
n—целое положительное число.
58.
59. filE^^fl^ + C. „#_h 60
J +1
0. f *L=in|ln
Г
J
4.Jsir
2(д-я)
• • j sin (m—n)x «in(m-j-n) x , ^
sin mxsin nx dx = —— [ ^п—~—?—\-Ct тфп,
2(m—n) 2(/7i + n) ^ ^
sin (m—n)jc , sin (m-\-n)x
^ + ^mJ sin—
64. \ sinmxcosnxdx в,ч,я+г„,^вя-1„ n_j Г
m-j-n +
m 96—n.
1 1 т + п — 2Г dx
/n— 1 sin'"' jccos"" x ' /n — 1 Jsinia~2jccosw jc '
Г J
' Jsi
sinm*cosw x\ _ _J 1 m+n—
I " n — 1 sin'" л cos"' л^ л —1
1) П. Л. Чебышев A821 — 1894) — великий русский математик. Для
его научной деятельности характерно стремление тесно связать решение ма-
математических проблем с принципиальными вопросами естествознания и тех-
техники. Работы П. Л. Чебышева оказали большое влияние на развитие сов-
современной математики вообще, русской —в особенности.
ТАБЛИЦА ИНТЕГРАЛОВ
733
66. jtg" *d*==
67. \ хп sinxdx=:
^— f tg"*^ Пф\.
—xncosx + n \ xn~1cosxdx.
—п Г xn
~1sinxdx.
+ C, a2 <
+ C,
71.
72.
73.
74.
75.
76,
77.
78.
79.
80.
81.
J ** sin nx dx д eaX (g Sin^~П C0S ПХ) + С
eax cos nx ?x === .
jcarcsinxdx~ (*- 1Л arcsinjc+ x*
2 4Tj
\ jc arccos x djc
arccosjc—.
ЛИТЕРАТУРА
КУРСЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
1. H. В. Ефимов, Краткий курс аналитической геометрии, «Наука»,
1965.
2. И. И. П р и в а л о в, Аналитическая геометрия, «Наука», 1966.
КУРСЫ АНАЛИЗА (более подробные)
3. В. И. Смирнов, Курс высшей математики, тт. I и II, «Наука», 1965.
4. Г. М. Фихтенгольц, Курс дифференциального и интегрального ис-
исчисления, тт. 1,11 и III, «Наука», 1966.
ЛИТЕРАТУРА ПО НЕКОТОРЫМ ДОПОЛНИТЕЛЬНЫМ
РАЗДЕЛАМ МАТЕМАТИКИ
5. И. Г. Араманович и В. И. Левин, Уравнения математической
физики, «Наука», 1964.
6. И. Г. Араманович, Г. Л. Лунц и Л. Э. Эльсгольц, Функции
комплексного переменного. Операционное исчисление. Теория устойчи-
устойчивости, «Наука», 1965.
7. Р. С. Г у тер и Б. В. О вч и некий, Элементы численного анализа
и математической обработки результатов опыта, Физматгиз, 1962.
8. 1) Б, П. Д е м и д о в и ч и И. А. Марон, Основы вычислительной ма-
математики, «Наука», 1966.
2) Б. П. Демидович, И. А. Марон, Э. 3. Шувалова, Числен-
Численные методы анализа, Физматгиз, 1963.
9. Н. В. Ефимов, Квадратичные формы и матрицы, «Наука», 1964.
10. Ф. И. Карпелевич и Л. Е. Садовский, Элементы линейной
алгебры и линейного программирования, «Наука», 1965.
11. П. И. Романовский, ряды Фурье. Теория поля. Аналитические
и специальные функции. Преобразование Лапласа, «Наука», 1964.
СПРАВОЧНАЯ ЛИТЕРАТУРА
12. А. А н г о, Математика для электро- и радиоинженеров, «Наука», 1965.
13. И. Н. Бронштейн и К. А. Се ме нд я ев, Справочник по математи-
математике для студентов втузов, «Наука», 1965.
14. М. Л. С м о л я н с к и й, Таблицы неопределенных интегралов, «Наука»,
1965.