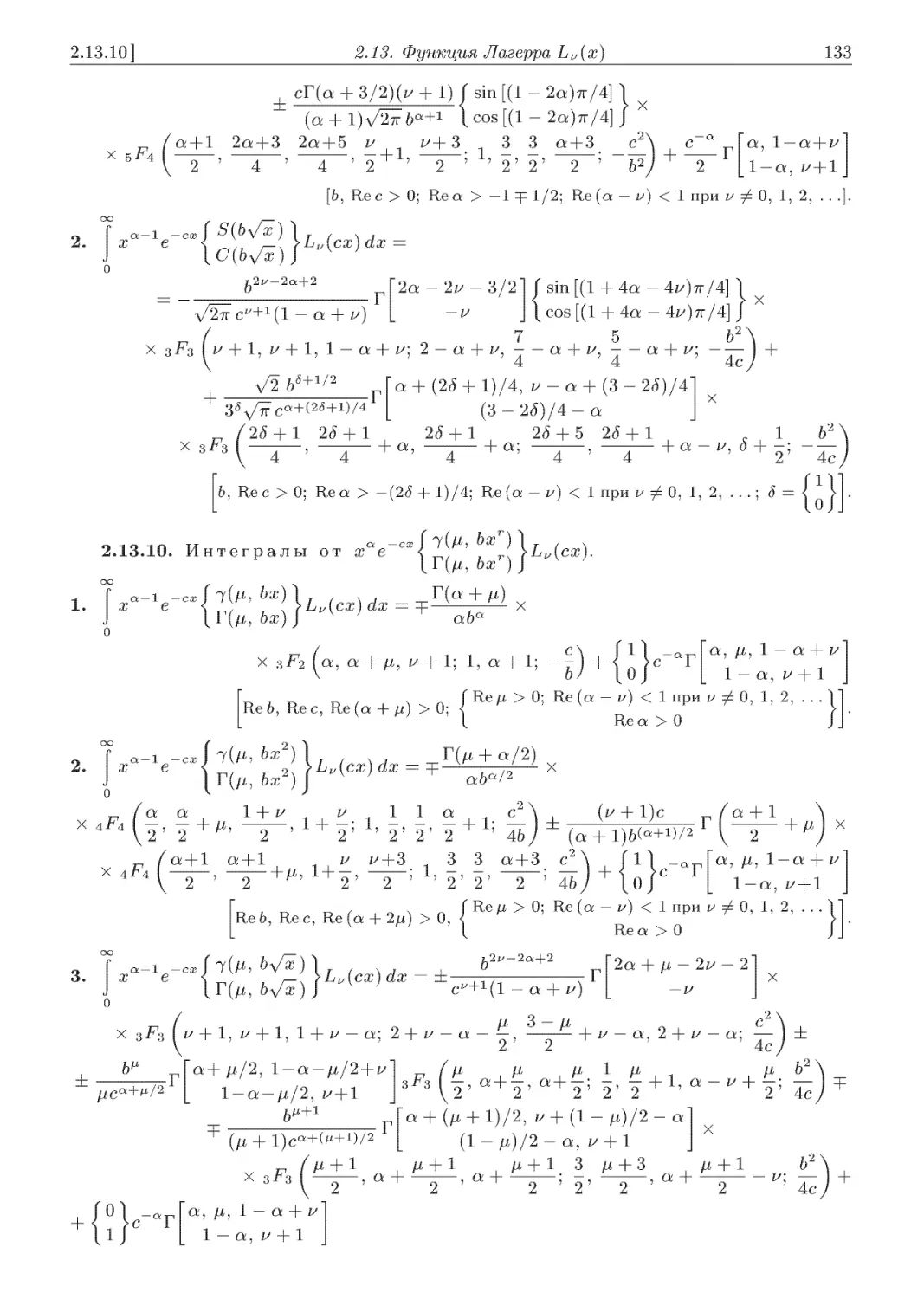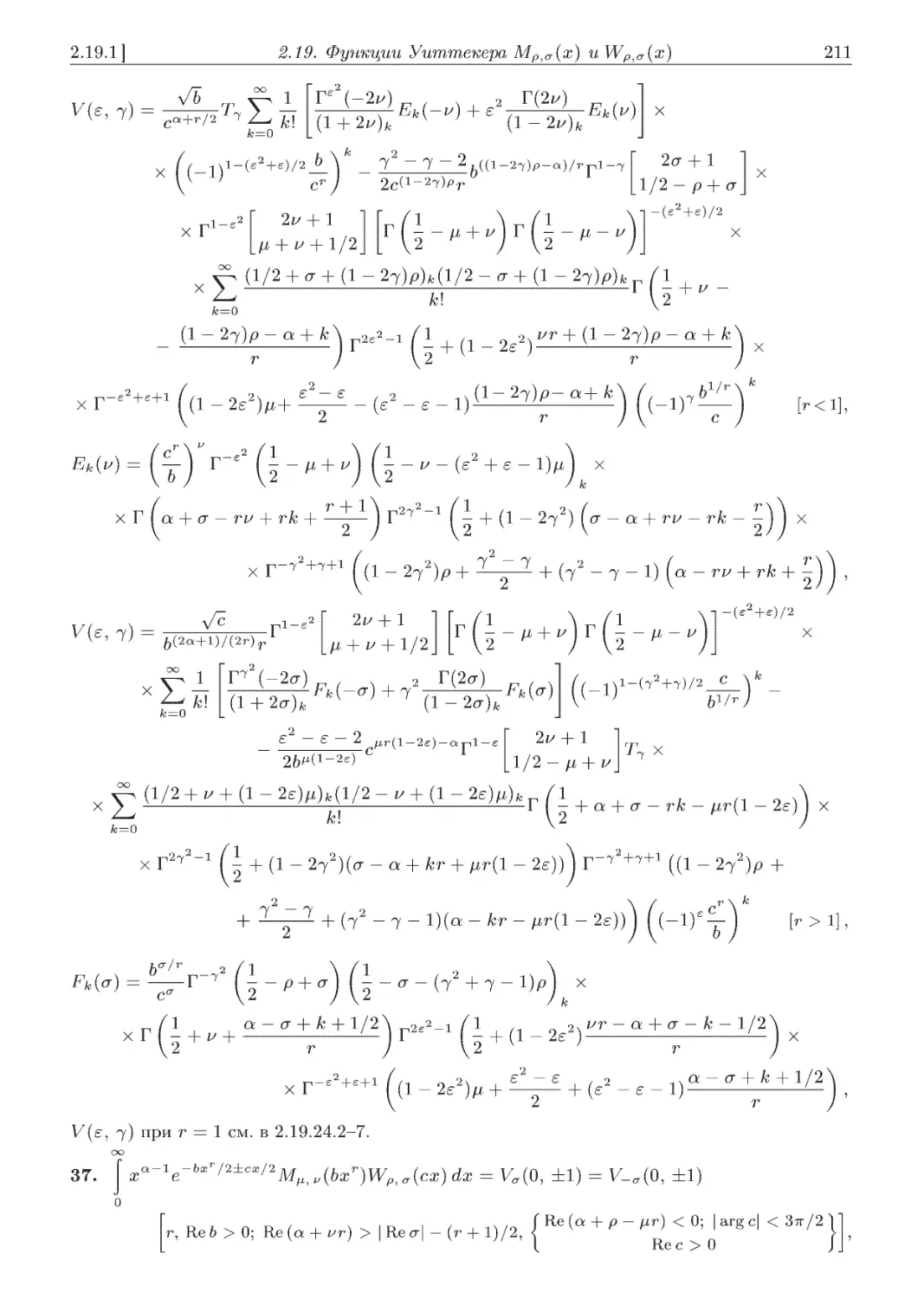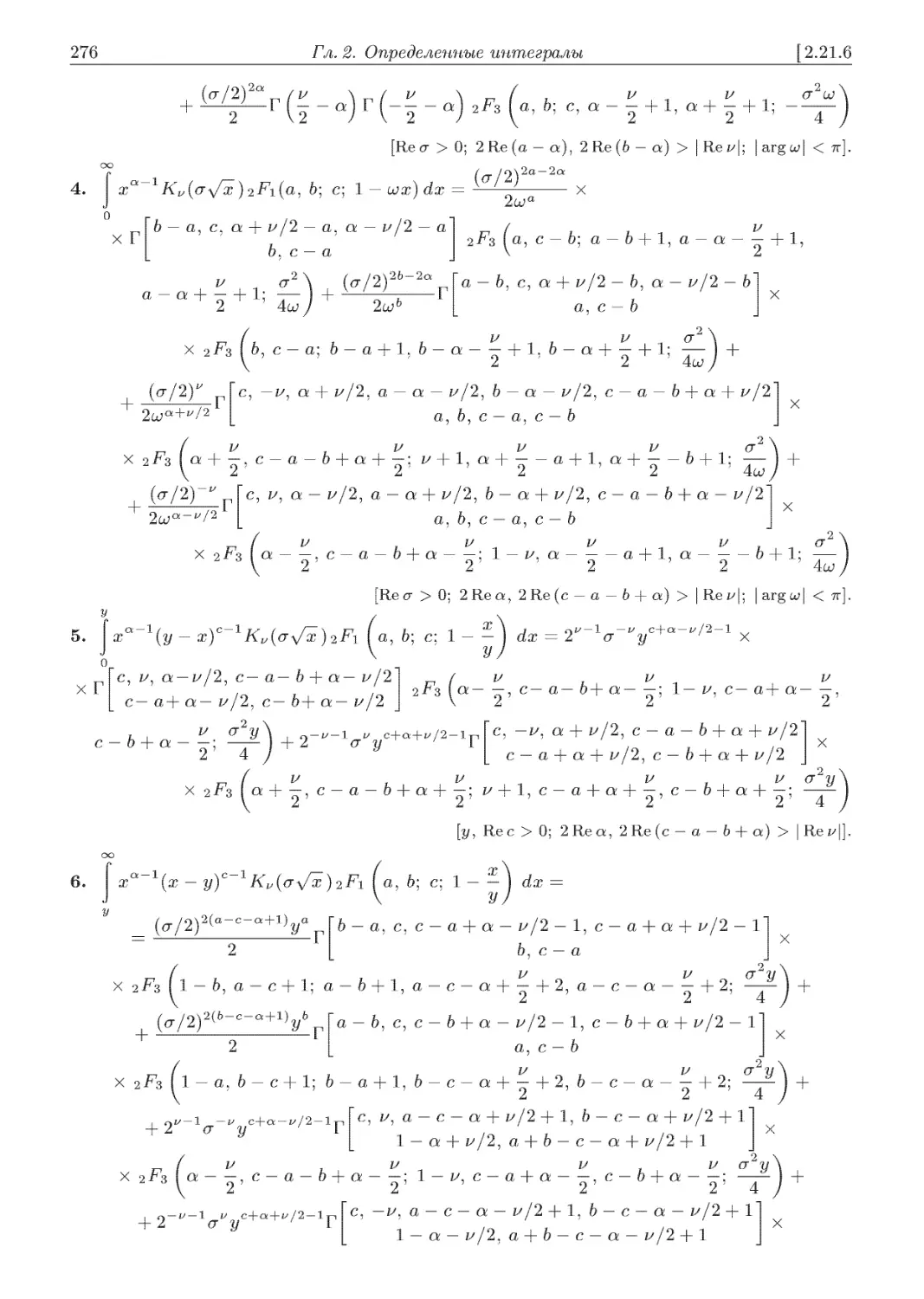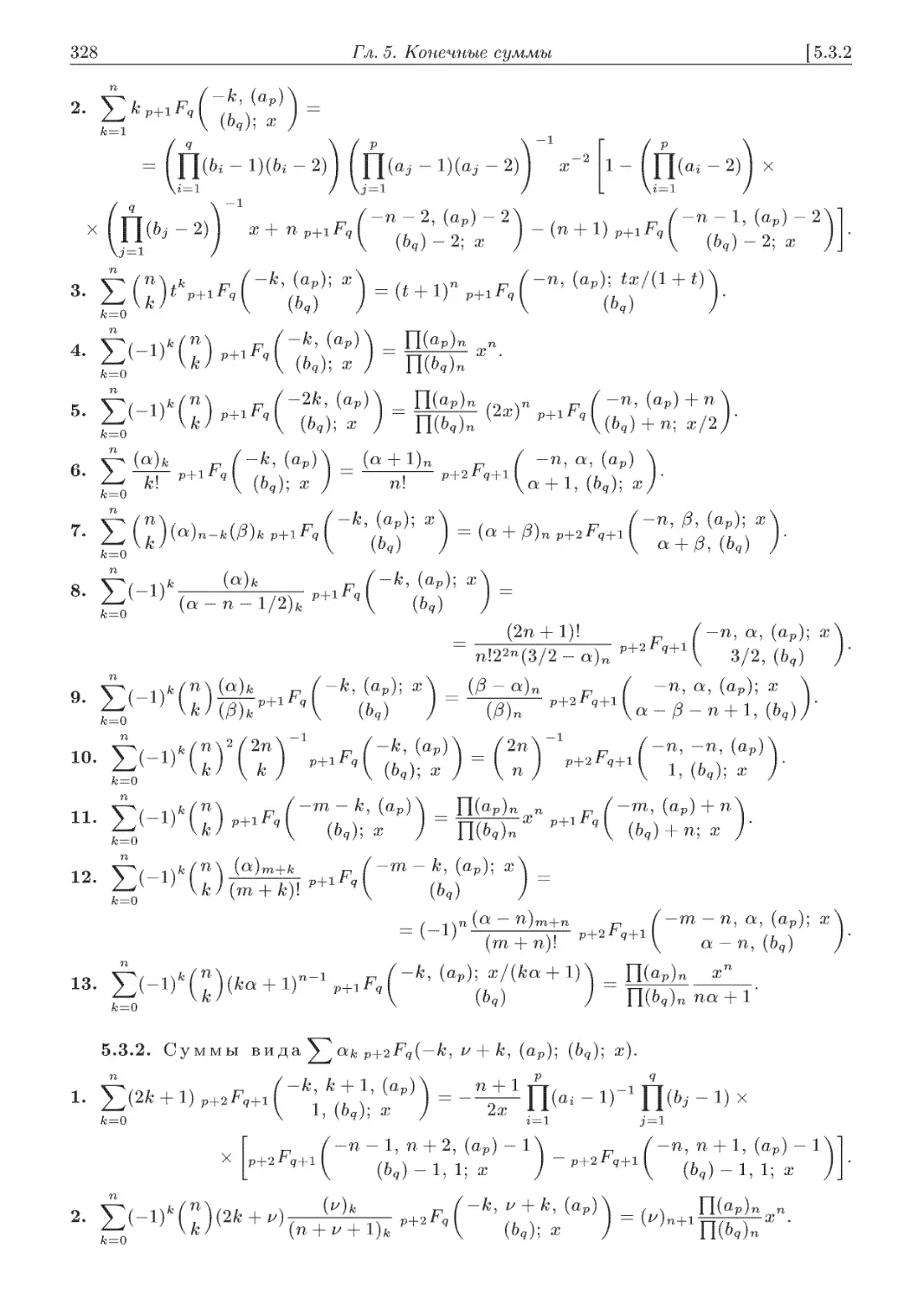УДК 519.6
ББК 22.194
П85
Прудников А. П., Б рынков Ю. А., Маричев О. И. Интегралы и
ряды. В 3 т. Т. 3. Специальные функции. Дополнительные главы. — 2-е изд.,
исправ. - М.: ФИЗМАТЛИТ, 2003. - 688 с. - ISBN 5-9221-0325-3.
Книга содержит неопределенные и определенные интегралы, суммы и ряды, не вошед-
вошедшие в предыдущие два тома. Приведены таблицы представлений обобщенных гипергеомет-
гипергеометрических функций, G-функции Мейера и их преобразований Меллина. Помещены разделы,
посвященные свойствам гипергеометрических функций, G-функции Мейера и //-функции
Фокса.
Первое издание — 1986 г.
Книга предназначена для широкого круга специалистов в различных областях, а также
для студентов высших учебных заведений.
ISBN 5-9221-0325-3 (Т. 3)
ISBN 5-9221-0322-9	© физматлит, 2003

ОГЛАВЛЕНИЕ
Предисловие ...................................................	21
Глава 1. НЕОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ .......................	23
1.1.	Введение. .................................................	23
1.2.	Обобщенная дзета-функция ^(s,sc), многочлены бернулли Вп(х), Эйлера
Еп{х) и полилогарифм Ыу(аз) .....................................	23
1.2.1.	Интегралы, содержащие ?(s,x),Bn(x) и Еп(х) .........................	23
1.2.2.	Интегралы вида ха Ып(ах) dx ..................................	23
1.2.3.	Интегралы вида /(ж) 1л2(ж) dx ..................................	23
1.3.	Обобщенные интегралы Френеля S(x^u) И С(ж,1/) ...................	23
1.3.1. Интегралы вида /(ж К	' > dx ..............................	23
J	lC(ax,i/))
1.4.	Функции Струве Н^(ж) И Liv(x) .................................	24
1.4.1.	Интегралы вида х Ии(ах) dx ...................................	24
1.4.2.	Интегралы вида xxelxHu(x) dx .................................	24
1.4.3.	Интегралы вида х Ш/л(ах)Ш1/(Ьх) dx ..............................	25
1.4.4.	Интегралы вида х JfJ,(ax)'H.i/(bx) dx ..............................	25
1.4.5.	Интегралы вида ххЪ1/(ах) dx ...................................	26
1.4.6.	Интегралы вида жАе Liu(x) dx .................................	26
1.5.	Функции Ангера Л1/(аз) и Вебера Ejy(a?) ............................	26
1.5.1. Интегралы вида ж < и	> dec ................................	26
J [Е^аж)]
1.6.	Функции Ломмеля з^^{х) Ш S^^ix) .............................	27
Г л Г 5м и (ах) 1
1.6.1.	Интегралы вида \ х <	> с!ж ...............................	27
J 1^^(аж) J
1.6.2.	Интегралы, содержащие Ju(x) и 5^,1/(ж) ............................	27
1.7.	Функции Кельвина Ьег^Дж), beliy(sc), keiv (ж) и ке1ц/(ж). ................	28

4	Оглавление
1.7.1.	Интегралы вида [ **( ^^ } dx и Ы ^<°ХН Ас	 28
J [ bei|/(aa;) J	J I keii/(aaj) J
1.7.2.	Интегралы, содержащие произведения функций Кельвина .................. 28
1.8.	Функции Эйри Ai (аз) И Bi (аз) .................................. 29
Г	f Ai(х) 1
1.8.1.	Интегралы вида /(жК ) Л dx ................................ 29
J	I Bi (as) J
1.8.2.	Интегралы, содержащие произведения функций Эйри ..................... 30
1.9.	Интегральные функции Бесселя «/^(аз), Неймана Yiv{x) и Макдональда
Къ„{х) ...................................................... 31
1.9.1.	Интегралы вида xaJil/(x) dx ................................... 31
г ( Yi (x) 1
1.9.2.	Интегралы вида ха < ^ > da; ................................ 31
1.10.	Неполные эллиптические интегралы jF(ae,fc), E(xyk) Ш II(аз, is, к) ........	31
1.10.1.	Интегралы по аргументу х .....................................	31
1.10.2.	Интегралы по модулю /	...................................	33
1.11.	Полные эллиптические интегралы K(fe),E(fe) И П(—?^5fe| .............	33
1.11.1.	Интегралы вида ка{1 — к ) s	\ dk ...........................	33
1.11.2.	Разные интегралы, содержащие K(fc),E(ib) иП(—,i/, к) ..................	33
1.12.	Функции Лежандра Р^(аз) И Q^(x) .............................	34
1.12.1.	Интегралы вида /(ж)Р^(ж) da;, f{x)Q%(x) dx .......................	34
1.12.2.	Интегралы, содержащие произведения функций Лежандра .................	35
1.13.	Функции Уиттекера Мр>о.(аз) И WPjO-{x) ..........................	35
1.13.1.	Интегралы вида \хае±ах^Мр^а{ах) dx ............................	35
1.13.2.	Интегралы вида I* xae±ax/2Wp,a(ax) dx ............................	36
1.13.3.	Интегралы, содержащие произведения функций Уиттекера .................	37
1.14.	Вырожденные гипергеометрические функции Куммера tF%(a;b;x) и Три-
коми Ф(а, Ь; аз) .................................................	38
1.14.1.	Интегралы, содерж:ащие 1^1@; 6; а;) ..............................	38
1.14.2.	Интегралы, содержащие Ф(а, 6; ж) ................................	38
1.15.	Гипергеометрическая функция Гаусса 2-Fi(ct, Ь; с; аз) . .................	39
1.15.1.	Интегралы вида a;Q2Fi(a,fe;c;ic) <1ж ..............................	39
1.15.2.	Интегралы вида A — х)@ 2^\(а5 Ь; с; х) dx ..........................	40
1.15.3.	Интегралы вида хаA ¦— х)^ 2^i(ct, 6; с; ж) da; ........................	40
1.16.	Обобщенная гипергеометрическая функция pFq((ap); (bq); ж), G-функция
Мейера, JE7— Функция Мак-Роберта И JEf-функция Фокса ..................	41
1.16.1.	Интегралы, содержащие pFq((ap); (bq); ж) ...........................	41
1.16.2.	Интегралы, содержащие (j-функцию Мейера .........................	41
1.16.3.	Интегралы, содержащие ^-функцию Мак-Роберта .....................	42
1.16.4.	Интегралы, содержащие Н-функцию Фокса ..........................	42
1.17.	Эллиптические функции Якоби и Вейерштрасса ...................	42

Оглавление
1.17.1.	Интегралы вида f(snu) du ...................................	42
1.17.2.	Интегралы вида /(спи) du ...................................	43
1.17.3.	Интегралы вида f(dnu) du ...................................	44
1.17.4.	Интегралы вида /(sntx, en и, dnu) du .............................	44
1.17.5.	Интегралы, содержащие эллиптические функции Вейерштрасса .............	46
Глава 2. ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ ..........................	47
2.1.	Введение. .................................................	47
2.2.	Гамма-функция Г(аз) .........................................	47
2.2.1. Интегралы по прямой (-у — гоо, "у + ioo) ..............................	47
2.3.	Обобщенная дзета-функция ?(в,аз) ...............................	48
2.3.1. Интегралы от f(x)?(s, a + bx) ...................................	48
2.4.	Многочлены Бернулли Вп(х) и Эйлера Еп(х) ......................	48
2.4.1.	Интегралы от f(x)Bn(x) .......................................	48
2.4.2.	Интегралы, содержащие произведения многочленов Бернулли ...............	49
2.4.3.	Интегралы от f(x)En(x) .......................................	50
2.4.4.	Интегралы от Ет(х)Еп(х + а), Вт(гх)Еп(х) .........................	50
2.5.	Полилогарифм Ы1/(ж) ........................................	50
2.5.1.	Интегралы общего вида ........................................	50
2.5.2.	Интегралы от А(х) Lin( —еж) .....................................	51
2.5.3.	Интегралы от А(х) Li2( —еж) .....................................	52
2.6.	Обобщенные интегралы Френеля S(x, и) И С(х, i/) ...................	52
2.6.1. Интегралы общего вида ........................................	52
{S(cx I/) 1
' > ...................................	57
С(сх, I/) J
±г ( S(CX I/) 1
2.6.3.	Интегралы от хаерх I к ' J } ................................	59
[ С(сх, и) J
2.6.4.	Интегралы от ха <	><	' >..............................	59
[ cos bx J {C(cx,v))
2.6.5. Интегралы от яа Пп(а: + z) 1 j 5(сЖ, i/
59
2.6.6. Интегралы от A S^x^\\{ ^*>*)\ ............................ 60
1СF) J 1С() J
{S(cx i/) 1
>......................... 60
_C(cx,i/) )
( si(bx) 1 f S(cx,u) 1
2.6.8.	Интегралы от ха {	\{	>.............................. 61
[ ci (bx) J [ С(сж, v) J
2.6.9.	Интегралыот x<*{ ^ ^ i} } { ^'^ }	 62
2.6.10. Интегра.ыот ,4 S^X\ }{ S?*' V\ }	 62
{C(bx)) {C(cx,v)}
2.6.11. Интегралы от ЖЛ т(м, M 1| 5(СЖ,
2.7. Функции Струве Н^аз) И L^ (аз) .................................	63
2.7.1.	Интегралы общего вида ........................................	63
2.7.2.	Интегралы от хаШ1/(сх) .......................................	69

6	Оглавление
2.7.3. Интегралы от xa(z ± xf I H"(ca;) I ................................ 69
I Меж) J
2.7.4. Интегралы от xa(z2 ± х2I3\ и^СХ' \ .............................. 70
2.7.5.	Интегралы от жае~раЧ "ч ; ^ .................................. 71
[ Ъи(сх) J
2.7.6.	Интегралы от хае^рх±2 I Н^СЖ^ 1 ................................ 72
I Меж) j
2.7.7.	Интегралы, содержащие тригонометрические функции и Ну (еж) .............. 72
{Ни(сх) 1
> ............ 73
Меж) J
2.7.9.	Интегралы, содержащие обратные тригонометрические функции и Н^ (еж) ....... 74
2.7.10.	Интегралы от хаШ,Л(Ьх±1)Ш1/(сх) ................................ 74
{Hjjicx) 1
> ......................... 74
Ьи(сХ) J
{Н (еж) 1
1/1 ' } .............................. 74
Li/(cx) J
2.7.13.	Интегралы, содержащие ^^(ба;)^ v	\ ........................... 74
[ liU(cx) J
2.7.14.	Интегралы, содержащие J^(bx г)Ши(сх) ............................	75
2.7.15.	Интегралы, содержащие YfJ,(ip(x))M.t/(cx) ............................	76
2.7.16.	Интегралы, содержащие произведения специальных функций на Yu(cx) ¦— Н|/(сж) . .	77
2.7.17.	Интегралы, содержащие произведения элементарных функций на /±у(сж) — L^(c?c) .	78
2.7.18.	Интегралы, содержащие произведения специальных функций на 1±и{сх) — Liu(cx) .	79
{Н^(сж) 1
> ......................... 80
Меж) J
2.8. Функции Ангера Jl/(a?) и Вебера "Еи(х) ........................... 82
2.8.1.	Интегралы общего вида ........................................ 82
2.8.2.	Интегралы от А(х)\ и^СХ* \ .................................... 84
[Ви(сх) J
хП { JlJ)CX\ I
1Е,(сж)/
2.8.3. Интегралы от хае^рхП { JlJ)CX\ I ................................. 85
1Е(сж)/
2.8.4. Интегралы от ж"/81116"}/^^} ............................... 85
[cosbx ) [Е1/(еж) J
{Jj/fcx) 1
> .......................... 86
Е(сж) J
2.9. Функции Ломмеля «/л,ь/(ж) И Sp,iV{x) ............................. 87
2.9.1. Интегралы общего вида ....................................... 87
[S^^(cx) j
2.9.2. Интегралы от А(х)\ ^'^СЖ^ 1 ................................... 89
[S(cx) j
хГ [ ^'"(сж) \
{Sp,v(cx))
2.9.3.	Интегралы от хае^рхГ [ ^'"(сж) \ ................................ 91
{Sp,v(cx))
2.9.4.	Интегралы, содерж;ащие тригонометрические или обратные тригонометрические функ»
f	\
.............................................. 92
2.9.5.	Интегралы от xaJx(bx±l)< M'	> ..............................	93
2.9.6.	Интегралы от xaY\(bx)sfJijl/(cx) .	.............................	94
Зц,и\сх) I .............................	94
2.9.8. Интегралы по индексу, содержащие Sn,nix(c) ..........................	94

Оглавление
2.10.	Функции Кельвина < v
{ beiz/(a;)
2.10.1.	Интегралы общего вида ....................................... 95
2.10.2.	Интегралы, содержащие алгебраические функции и функции Кельвина ......... 98
2.10.3.	Интегралы, содержащие е^рх и функции Кельвина ....................	99
2.10.4.	Интегралы, содержащие тригонометрические или логарифмическую функции и функ-
функции Кельвина ..................................................	100
2.10.5.	Интегралы, содержащие произведения двух функций Кельвина ..............	101
{l-»«|*	J л /у* \ I
"; !} ............................. Ю2
Ъе\и{сх) J
2.10.7.	Интегралы от ха Ju(bx){ кеГ" ^ 1 ............................... 102
[ keiu{cx) j
2.10.8.	Интегралы, содержащие Кц{Ъхп) и функции Кельвина .................. 102
2.11.	Функции Эйрж Ai (аз) ж Bi (аз) ................................. 103
2.11.1.	Интегралы общего вида ....................................... 103
Г Ai (еж) 1
2.11.2.	Интегралы от А(х){ ) {} ................................... 105
1В1(сж) J
г Г Ai (етI
2.11.3.	Интегралы от хае^рх I К } \ ................................. 105
I Bi (еж)J
2.11.4.	Интегралы от ха \ вШ Х > Ai (еж) ................................ 105
[ cos bx J
2.11.5.	Интегралы от ха Ju{bxr) AI (еж) .................................. 106
2.11.6.	Интегралы от Ai {ах + Ъ) Ai (еж + d) ............................... 106
2.12.	Интегральные функции Бесселм «/«^(х), Неймана Yijj{x) и Макдональда
Kiv(x) ...................................................... 106
2.12.1.	Интегралы общего вида ....................................... 106
2.12.2.	Интегралы от А{х)Ли{сх) и А(х)\ %1/^СХ^ I ......................... ИЗ
{ Kiy{cx) J
2.12.3.	Интегралы от хае^рх±П Jiv{cx) и хае^рх±П { Ytt/^x) X ................. Ц4
{ Kiv{cx) J
_, f sin bx 1 .	_, f sin bx 1 Г Уг„(еж) 1
2.12.4.	Интегралы от ж°	}Ли{сх) и ха{	\{	х ; ^ ............... 115
[ cos 6ж j	[ cos bx ) { Ki (еж) J
2.12.5. Интегралы от ха <	9 9 > Jiv{cx) и ж"<
(^ In |ж — z \ )	| In
2.12.5.	Интегралы от ха { ^ ^о ' V \ЛАсх)тха( "* ч"\ + V U * "иу""'' ^ ........ 116
, Kiv{cx) _
2.12.6.	Интегралы, содержащие Ei { — bx)Jii/ (еж) или Ei ( — bx)l v	> ............ 116
^Ьг.^и^!^;}!^}	 117
ciFaj)J	[ci {bx) ) [Kiu{cx)
(erf{bxr)} . .	f егГFжгI f Yiv{cx)\
2.12.8. Интегралы, содержащие ^ v /^^(сж) или <^ v \\\	) \\ ...... 118
[?F )J	[?F )j [^()]
)]
2.12.9.	Интегралы от A S(bx) }jiv(cx) и x~{ S(bx) U У^(сХ) )	 119
\c(bx)j "K '	\c(bx)j\Kiv(cx)j
2.12.10.	Интегралы от х° ( ^' Ьх) \jiv{cx) и ,./7(с.ИН^И| 	 120
{Yi (сжI
> .......... 120
Ki{cx)j
{Yi (ex) 1
>	121
Kiu{cx))
2.13. Функция Лагерра Lv(x) ......................................	122
2.13.1.	Интегралы общего вида .......................................	122
2.13.2.	Интегралы от А{х)е^рхLv{cx) ..................................	127
2.13.3.	Интегралы от жае??(ж)Ь1/(сж) ....................................	129

8	Оглавление
2.13.4.	Интегралы от хае^сх{	r }Lu(cx) ............................. 130
[cos bx J
2.13.5.	Интегралы от хае~сх [ Ы<кХ +^ *\ьу(сх) .......................... 130
! 1п|жп - zn\ J
2.13.6.	Интегралы от хае^ Ei(bxk)LIJ(cx) .............................. 131
2.13.7.	Интегралы от хае^сх {Sl)bX r{ \ь„(сх) ............................. 132
{ci(bxr) J
{erf (bxr) 1
1 ; \lu(cx) ............................ 132
erfc (bx ) J
Г S(bxr) 1
2.13.9.	Интегралы от жае^саЧ V ; }Lu(cx) ............................. 132
{C(bxr) j
2.13.10.	Интегралыотжае~сжG^'к Нь^сж) ........................... 133
1ГОЬжг) J
2.13.11.	Интегралы от xote~cxJIJb{bxr)LlJ(cx) .............................. 134
2.13.12.	Интегралы от хае^сх\ Y^bx ) Цлсж) ........................... 135
2.13.13.	Интегралы от хае^х)Lll(bxr)L1J{cx) .............................	135
2.13.14.	Интегралы от xae(p^Hm(bxr)LU(еж) .............................	136
2.13.15.	Интегралы от хае^ Lfi(bxk)Liy(cx) ..............................	136
2.14. Функция Бейтмена к^(х) .....................................	136
2.14.1.	Интегралы общего вида .......................................	136
2.14.2.	Интегралы от А(х)е^х)kv(cx) ..................................	142
2.14.3.	Интегралы от хае^рх\ 8Ш &Ж \kv{cx) ..............................	144
[cos bx J
2.14.4.	Интегралы от жае^ржAп^Ж + ^Н^1/(сж) ........................... 145
[ In |ж — z\ j
2.14.5.	Интегралы от хае~рх FA(±bx)kv(cx) .............................. 145
2.14.6.	Интегралы от жае"рж< ч 7 fcJca;) ............................. 146
[d(bx) )
2.14.7.	Интегралы от жае^рж{ erf Fж ) 1 ^/ч ............................ 147
[ erfc Fж ) J
2.14.8.	Интегралы от хае^рх\ S^bx\ \ku(cx) .............................. 147
[ С(Ьх) J
2.14.9.	Интегралы от хае^рх< J^jbX^\kl/(cx) ............................ 148
{Г(Ь)}
2.14.10. Интегралы от кц{Ъх)ку{сх) ....................................	148
2.15.	Неполные эллиптические интегралы F(x, fe), Е(х, к), П(ж, i/, fe) ..........	149
2.15.1.	Интегралы от /(ж)<	' > ...................................	149
[ Ej(ж, /г) J
2.15.2.	Интегралы по модулю А; .......................................	150
2.16.	Эллиптические интегралы К(ж), Е(ж) ............................	150
2.16.1.	Интегралы общего вида .......................................	150
Г Щсх) 1
2.16.2.	Интегралы отжа V ; \ .....................................	152
2.16.3.	Интегралы от (ж ± a)a(b ± ж)/3К(сж) ...............................	152
2.16.4.	Интегралы от (ж2 ± a2)a(b2 ± x2f { ; [ 1 .........................	153
[ Щсх) J
2.16.5.	Интегралы от жа(ж2 ± а2I3(Ь2 ± ж2O! ^СХ^ I ........................	154
I Щсх) J
2.16.6.	Интегралы от А(х)~К(сх) ......................................	156

Оглавление
2.16.7. Интегралы от А{х)\ К, , чч 1 .................................. 157
1
j
2.16.8. Интегралы от А(х)е^ [ К(сж^ 1 ................................ 158
1 Е(еж) j
} ............................	159
Е(сж) J
2.16.10.	Интегралы, содержащие In A(x)~K(cx) .............................	160
2.16.11.	Интегралы, содержащие Е1 (у?(ж)) или erfc (у?(аз)) и К(сж) ................	160
2.16.12.	Интегралы, содержащие Jt/(<f(x)) или ^(^(ж)) и К(сж) ................	160
Г К(сж) 1
2.16.13.	Интегралы, содержащие К~1,(у?(ж))<	> .........................	161
I Е(сж) J
2.16.14.	Интегралы от Д(ж)Н0О(ж))К(сж) ...............................	162
2.16.15.	Интегралы от Л(жMм^(^(ж))К(сж) ..............................	162
2.16.16. Интегралы от А (ж) /К^Ж))К(СЖН ..............................	162
1 Ч Е(??(ж))Е(сж) J
2.17. Функции Лежандра 1-го рода Р^ (х) j P^f (х) ........................	162
2.17.1.	Интегралы от (zm ± хт)^Р^(сх) .................................	162
2.17.2.	Интегралы от xa(z2 ± x2fpff{cx) ................................	163
2.17.3.	Интегралы от (ж ± a)a(b ± хI3 Р?((р(х)) ............................	164
2.17.4.	Интегралы от (хт ± am)a(fe2 ± ж2)^Р^(сж) ..........................	165
2.17.5.	Интегралы от (ж ± а)а(b ± x)^(d ± жOР^(сж) ........................	166
2.17.6.	Интегралы от Л(ж)[Р^(сж) + Р^(-сж)] .............................	168
2.17.7.	Интегралы от А(х)е^х) Pj?(x(x)) .................................	168
2.17.8.	Интегралы, содерж:ащие гиперболические функции и Pjf((p(x)) ..............	169
2.17.9.	Интегралы, содержащие тригонометрические функции и Р^((р(х)) ............	170
2.17.10.	Интегралы, содержащие erf (ip(x))P^(cx) ...........................	170
2.17.11.	Интегралы, содержащие е6^2'/4Dх(Ьх)РЦ1 (сх) ........................	171
2.17.12.	Интегралы, содержащие J\((p(x))Pjf(x(x)) ••••••••••••••••••••••••••	171
2.17.13.	Интегралы, содержащие Y\((p(x))P^(cx) ...........................	173
2.17.14.	Интегралы, содержащие 1\((р(х))Р^(сх) ...........................	174
2.17.15.	Интегралы, содержащие K\{(p{x))Pj^{cx) ...........................	174
2.17.16.	Интегралы, содержащие I Л^Ж^ 1р^(сж) ........................	175
[ L,x((p(x)) j
2.17.17.	Интегралы, содержащие SXj\((p(x))Pjf (еж) ..........................	175
2.17.18.	Интегралы, содержащие К(у?(ж))Р1/(сж) ............................	176
2.17.19.	Интегралы от Л(ж)Р^Fж)Р^(сж) ................................	176
2.17.20.	Интегралы от A(x)P}?i<p(x))Pg(x(x)) .............................	179
2.17.21.	Интегралы, содержащие показательную или тригонометрические функции
Р?(<р(х))Р?(х(х)) ...............................................	180
2.17.22.	Интегралы от жа«/Л(^(ж))Р^(сж)Р^(еж) ............................	180
2.17.23.	Интегралы, содержащие три функции P{f((p(x)) .......................	181
2.17.24.	Интегралы по индексу от произведений Рах+и(с) на элементарные функции ....	181
2.17.25.	Интегралы по индексу от произведений Р?х_1 /2^с) на элементарные функции . . .	182
2.17.26.	Интегралы по индексу от произведений Ргш^1/2(с) на специальные функции ....	182
2.17.27.	Интегралы по индексу от произведений Р?х+и (с) на специальные функции .....	184
2.17.28.	Интегралы по индексу от произведений Pjra._i/2(&)Aa;-i/2(c) на элементарные
функции .....................................................	187
2.17.29.	Интегралы по индексу от произведений Ргш-1/2(^)Аж-1/2(с) на специальные функ-
функции .........................................................	188
2.17.30.	Интегралы по индексу, содержащие Р^ГЖ_1/2F)Р^____1 ,2(с) ................	188
2.18. Функции Лежандра 2-го рода {^(ж), QjJ(as) .......................	190
2.18.1. Интегралы от (zm ± xm)PQ^{cx) .................................	190

10	Оглавление
2.18.2.	Интегралы от xa(z2 ± x2)@Q^(cx) ................................	191
2.18.3.	Интегралы от (ж ± a)a(b± x)^Q^((p(x)) ............................	191
2.18.4.	Интегралы от ха(хт ± amf(b2 ± x2OQ^(cx) ........................	192
2.18.5.	Интегралы от (ж - а)а(Ь ± х)@(хт ±dmIQ^(cx) ......................	193
2.18.6.	Интегралы от А(х)е^х)Q4(cx) ..................................	194
2.18.7.	Интегралы,содержащие гиперболические или тригонометрические функции и
QZ(<p(x)) .....................................................	194
2.18.8.	Интегралы от A(x)Jx(<p(x))Q%(x(x)) ..............................	195
2.18.9.	Интегралы от A(x)Kx((p(x))Q%(cx) ...............................	196
2.18.10.	Интегралы от A(x)K(ip(x))Qu(cx) ...............................	196
2.18.11.	Интегралы от Д(ж)^д(>(ж))^(сж) ..............................	196
2.18.12.	Интегралы от A(x)Jr]((p(x))Qxi(cx)Qti(cx) ..........................	198
2.18.13.	Интегралы от A(x)P^(ip(x))Q^(cx) ..............................	198
2.18.14.	Интегралы от А(х)\ sm(p)x\ XР^(сх)д^(сх) ........................	199
[cos^(x) J
2.18.15.	Интегралы от A(x)Jr,(<p(x))Px(cx)Q?(cx) ..........................	200
2.18.16.	Интегралы по индексу,содержащие Q±ix-i/2(c) •••••••••••••••••••••••	200
2.19. Функции Уиттекера MPjtT(x) И WPitT(x) ..........................	200
2.19.1.	Интегралы общего вида .......................................	201
2.19.2.	Интегралы от xaWPjCT(cx) .....................................	212
2.19.3.	Интегралы от хае^рх < р'а	У ................................	213
2.19.4.	Интегралы от хае^х' < р'а	> ...............................	214
2.19.5.	Интегралы от А(х)е±сх^21 7/^/^4 \ .............................	216
2.19.6.	Интегралы от х^е±сх/2 i smbx 1 Г—am>v~«v k ........................	220
2.19.7.	Интегралы от жае±сш/2 In (^(ж)|Мр)<т^СЖ^ I ..........................	222
2.19.8.	Интегралы от xae±cx/I Ei(-bx){ р' ) ' } .........................	223
2.19.9.	Интегралы оТ х-е"{ , V."^ Ц ™^^J ^ 	 224
2.19.10.	Интегралы от жогерж1)|/F(ж + z)±1/2)| „/'"",, } ..................... 226
2.19.11.	Интегралы, содержащие е±сх^А Jv(bx±r)l ±гж^ах-^^ {. ................... 227
2.19.12.	Интегралы, содерж;ащие /?/Fжг)<	[> ........................ 231
Г У (Ьжг) 1 Г М (сх) '
2.19.13.	Интегралы, содержащие < и\	\\ Pia) [ )> ...................... 233
[ Kv(bxr) J {WPya(cx) J
2.19.14.	Интегралы от жае±сж/2Н1/FЛ/^)(Мр'сг(СЖН ........................ 237
[ Wp,a(cx) J
2.19.15.	Интегралы от А(х)е±сх^2 Pn(ax±r ~ h){MpJ<T^X\X .................... 238
1 И^р,ст(сж) j
2.19.16.	Интегралы от Л(ж)ерж1„(а + Ьж)^ Pj	} ........................ 241
{WP}a(cx) )
2.19.17.	Интегралы от хае^рхНп(Ьу/х){ р^а^СХ^ I ......................... 242
{WPia(cx) )

Оглавление	11
2.19.18. Интегралы от A(x)e±cx^2C^{ax±r ^ b){Mp'a^X\\ .................... 242
2.19.19. Интегралыот Л(Ж)е±сж/2Р^'1/)(аЖ±1 ^1)(Мр'а^ЖН .................. 247
1 WPia(cx) J
2.19.20. Интегралы or^Je^/2/^^^ If М^(СЯI ..................... 249
2.19.21.	Интегралы от Л(ж)е±сж/2Р^(^(ж)IМр!<т^СЖН .......................	250
{WPj(T(cx) j
2.19.22.	Интегралы от ^(x)e±ca;/2Q{;(^(^))fMp'cr^a'H .......................	253
2.19.23.	Интегралы от А(х)\ М^Х + *\\{ М^х\ \ . .....................	254
2.19.24.	Интегралы от жае/(ж) f] М^.,^. (Ь^х±г) WPk^k (ckxTl) .................	257
2.19.25.	Интегралы от ха cos ахМ^^(Ьх)МРга- (еж) ...........................	259
2.19.26.	Интегралы от жа^Fж±г) f\ MPjj<Jj(bjx)WPkjCTk(ckx) ...................	260
2.19.27.	Интегралы от ха < v ±/ H	> .................	262
2.19.28.	Интегралы по индексу, содержащие MPjG(c) или WpitT(c) .................	262
2.20.	Вырожденные гипергеометрические функции Куммера iJPi(a;6;sc) и Три-
коми Ф(а, 6; as) .................................................	264
2.21.	Гипергеометрическая функция Гаусса 2-Fi(ci, Ь; с; аз) . .................	264
2.21.1.	Интегралы от Д(ж) 2^1 (а, 6; с; ж) .................................	264
2.21.2.	Интегралы от A(x)e^px±r 2F1(a1 b; с; <р(ж)) ...........................	268
Г з1п(ГЖ±1/2 1
2.21.3.	Интегралы от Д(ж)^	+1/9 > 2^1@, 6; с; <р(ж)) ......................	270
У cosax^ 1 J
2.21.4.	Интегралы от A(x)Jl/(ax±rJF1(a1 b; с; у>(ж)) .........................	272
2.21.5.	Интегралы от Л (ж) i ^l^V^j i 2^^^ 5; с; у?(ж)) .......................	274
2.21.6.	Интегралы от Д(ж)АГ1/(у?(ж)J^1(а, 6; с; х(ж)) .........................	275
2.21.7.	Интегралы от Л(ж)К(о-ж) 2Fi(a, b;c; у(ж)) ...........................	277
2.21.8.	Интегралы, содержащие функции Уиттекера и 2-Fi(a, 6; с; шх) ..............	277
2.21.9.	Интегралы, содерлеащие произведения двух функций 2-Fi(a, Ь; с; у?(ж)) .........	277
2.21.10.	Интегралы по параметрам, содержащие 2^1@., 6; с; ж) ...................	279
2.22.	Обобщенная: гипергеометрическая функция pFq((ap); (bq); ж) и гипергеомет-
гипергеометрические функции двух переменных ................................	280
2.22.1.	Интегралы общего вида .......................................	280
2.22.2.	Интегралы от А(х) pFq((ap); (bq); <p(x)) (см. также 2.23.1) ................	282
2.22.3.	Интегралы от ef^pFq((ap);(bq); ex) (см. также 2.23.2) ..................	282
2.22.4.	Интегралы, содержащие функции Бесселя и pFq((ap); (bq); сх) (см. также 2.23.3) . .	284
2.22.5.	Интегралы, содержащие различные специальные функции и pFq((ap); (bq);cx) (см.
также 2.23.4-6) .................................................	285
2.22.6.	Интегралы по параметрам, содержащие pFq((ap); (bq); ж) ..................	286
2.22.7.	Гипергеометрические функции двух переменных .......................	287
2.23.	?7-функция Мак-Роберта Е(р; ar : q; bs : ж) .........................	288
2.23.1.	Интегралы от A(x)E((ap);(bq); ср(х)) ..............................	288
2.23.2.	Интегралы, содержащие показательную или гиперболические функции и
Е((ар); (bq); еж) .................................................	288
2.23.3.	Интегралы, содержащие функции Бесселя и Е((ар); (bq); сх) ...............	289
2.23.4.	Интегралы, содержащие функции Лежандра и Е((ар);(bq);сх) ...............	290

12
Оглавление
2.23.5.	Интегралы, содержащие функции Уиттекера mE((ap);(bq);cx)
2.23.6.	Интегралы, содержащие произведения двух /^-функций ....
2.24. G-функция Мейера G™
2.24.1.	Интегралы общего вида ....
2.24.2.	Интегралы от A(x)G™qn (<p(x)
2.24.3.	Интегралы, содержащие показательную, гиперболическую или тригонометрическую
функции и G™qn
2.24.4.	Интегралы, содержащие функции Бесселя и G^J1 I шх '	1
2.24.5.	Интегралы, содержащие ортогональные многочлены и
2.24.6.	Интегралы, содержащие функции Лежандра и
(Ор)
(М
J/k
w\
(Ья) )
2.24.7. Интегралы, содержащие функции Уиттекера и
К)
(М
2.24.8.	Интегралы, содержащие функцию Гаусса 2-^1 (сь, 6; с; ж) и
2.24.9.	Интегралы, содержащие sF*((cs); (dt); -(ix)G™n (шх1/к
(М
290
290
291
291
293
295
296
297
297
297
298
299
299
299
300
300
2.25.	Ж-функцим Фокса ^VQ |W	.
[bq,Bq\ J
2.25.1.	Интегралы общего вида .........................
2.25.2.	Интегралы, содержащие элементарные функции и //-функцию
2.25.3.	Интегралы, содержащие специальные функции и //-функцию .
2.26.	Тэта-функции %(ж,д) .......................................	301
2.26.1.	Интегралы от /(ж)б^-(ж, q) .....................................	301
2.26.2.	Интегралы, содержащие произведения 0j{ax^q) ........................	302
2.26.3.	Интегралы, содержащие произведения 0j(x,aq) ........................	302
2.26.4.	Интегралы по <у,содержащие 0j(x,aq) ..............................	303
2.27.	Функции Матье ............................................	304
2.27.1.	Интегралы, содержащие элементарные функции и сете(ж, q) или sen(x,q) .......	304
2.27.2.	Интегралы, содержащие специальные функции и сеп(ж, q) илизеп(ж,д) ........	306
2.27.3.	Интегралы, содержащие Сеп(ж,д) или Sen(x,q) .......................	308
2.27.4.	Интегралы, содержащие fen(x,q) или gen(x,q) .......................	309
2.27.5.	Интегралы, содержащие Реп(ж,д) или Сеп(ж,д) .......................	309
2.27.6.	Интегралы, содержащие произведения функций Матье ...................	310
2.28.	Функции ъ'(аз), z/(as,p), /х(аз,Л), /х(аз, т, п), Л(аз,а) ...................	311
2.28.1.	Интегралы, содержащие i/(ex), v(сх, р) .............................	311
2.28.2.	Интегралы, содержащие /х(сж, А), /л(сх,т,п) .........................	311
2.28.3.	Интегралы, содержащие Л(сж, а) .................................	312
Глава 3. ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
ОТ СТУПЕНЧАТЫХ ФУНКЦИЙ ..................................	313
3.1. Введение.
313

Оглавление	13
3.2.	Кусочно постоянные функции ..................................	313
3.2.1.	Ограниченные функции ........................................	313
3.2.2.	Неограниченные функции ......................................	314
3.3.	Некоторые кусочно непрерывные функции ........................	315
3.3.1.	Степенные функции ..........................................	315
3.3.2.	Разные функции ............................................	317
Глава 4. КРАТНЫЕ ИНТЕГРАЛЫ ................................	319
4.1.	Введение. .................................................	319
4.2.	Двойные интегралы .........................................	319
4.2.1.	Интегралы, содержащие функции Hl/(x),Ju(x)iheru(x)ibeiu(x)iSfJltU(x) ..........	319
4.2.2.	Интегралы, содержащие iF\(a;b;x) ................................	320
4.2.3.	Интегралы, содержащие 2F\(a, b; с; х) ..............................	320
4.2.4.	Интегралы, содержащие pFq((ap); (bq)\ х) ............................	321
4.3.	Многомерные интегралы ......................................	322
4.3.1.	Интегралы, содержащие pFq((ap); (bq); x) ............................	322
4.3.2.	Интегралы по сфере ..........................................	322
4.3.3.	Разные интегралы ...........................................	323
Глава 5. КОНЕЧНЫЕ СУММЫ ..................................	324
5.1.	Числа и многочлены Бернулли ВП9 Вп(х) и Эйлера Еп, Еп(х) ..........	324
5.1.1.	Суммы, содержащие Вп ........................................	324
5.1.2.	Суммы, содержащие Вп(х) ......................................	324
5.1.3.	Суммы, содержащие Еп ........................................	325
5.1.4.	Суммы, содержащие Еп(х) ......................................	326
5.2.	Функции Лежандра Р?(х) и Q?(x) ..............................	326
5.2.1.	Суммы вида ]Г акр??к(х), "?а^±шк(х) .........................	326
5.2.2.	Суммы, содержащие произведения функций Лежандра ....................	327
5.3.	Обобщенная гипергеометрическая функция pFq((o>p)i (bq); ж) и G-функцим
Мейера. .....................................................	327
5.3.1.	Суммы вида ^afcP+iFg( —А; — га, (ар); Fд);ж) .........................	327
5.3.2.	Суммы вида Vj ак p+2Fq( — k, v + к, (ap); F9); x) .......................	328
5.3.3.	Суммы вида \J a^ p+iFg( —fe, (ap) + k; (bq) + k\ x) ......................	329
5.3.4.	Суммы вида V^ a^ p^-tFq(^k, (ap) — mk; (bq) — nk; x) ....................	329
5.3.5.	Суммы вида ]P ak pFq({ap) + k(cp);(bq) + k(dq); x) .....................	330
5.3.6.	Суммы вида ]Г ак pFq((ap) - k(cp); (bq) - k(dq); x) .....................	331
5.3.7.	Разные суммы, содержащие pFq((ap); (bq); x) ..........................	332
5.3.8.	Суммы, содержащие Gr-функцию ..................................	332
5.3.9.	Суммы, содержащие многочлены Неймана Оп(х) .......................	333
5.3.10.	Разные суммы .............................................	333
Глава 6. РЯДЫ. ..............................................	335
6.1.	ВВЕДЕНИЕ ...............................................	335
6.2.	Обобщенная дзета-функция C(s,v) ...............................	335
6.2.1. Ряды вида ^ aktk((s ±k,v) ....................................	335

14	Оглавление
6.3. Числа и многочлены Бернулли Bnj Вп(х) ш Эйлера Еп, Еп(х) ..........	335
6.3.1.	Ряды вида ^ акВк ..........................................	335
6.3.2.	Ряды вида ^ акВк(х + ку) .....................................	336
6.3.3.	Ряды вида ^акЕк ..........................................	336
6.3.4.	Ряды вида ^акЕк(х + ку) .....................................	337
6.4.	Функции Струве Н1/(х), Вебера Е1/(х) и Ангера «/^(ж) .................	337
6.4.1.	Ряды, содержащие Н1/(ж) .......................................	337
6.4.2.	Ряды,содержащие "E(k)u(x) .....................................	338
6.4.3.	Ряды,содерхашие Ли(х) ........................................	339
6.5.	Функции Лежандра Р?(х) и Q?(sc) ..............................	339
6.5.1.	Ряды вида J2a^Ktka(x) ......................................	339
6.5.2.	Ряды вида J2a^tta(x) .....................................	341
6.5.3.	Ряды вида J^ ак cos (ka + ьЖ+ка(х) ••••••••••••••••••••••••••••••	341
6.5.4.	Рядь, вида Е
6.5.5.	Ряды вида *? «ь Pfc&Hx)Р%#% (у) 		342
6.5.6.	Ряды вида ^a,Q^+^(x)Q^+^22(j/) 		342
6.5.7.	Ряды вида Еа*^Ж(»)^+^(«) 		343
6.5.8.	Ряды вида ? a* cos (Ы + Ь)Р?+*? (х)Р?+*?(у)		344
6.5.9.	Рядь, вида ? a* cos *aQ?+*? (Ж)С?^+^22(г/) 		344
6.5.10.	Ряды вида ? afc cos (ka + Ь)Р%+*? (x)Q^+^(y) 		345
6.6.	Вырожденная гипергеометрическая функция Куммера i-Fi(a; 5; ж) .......	345
6.6.1.	Ряды вида 2_^ ак l-^i (ctfc; ^fe5 ж) ...................................	345
6.6.2.	Ряды вида ^afeiFiCafe^fc^JiF^a;^;;!/) ..........................	346
6.6.3.	Разные ряды, содержащие iFi(a;b;x) ...............................	347
6.7.	Гипергеометрическая функция Гаусса 2-Fi(ct, ?»; с; ж) . ..................	347
6.7.1. Ряды вида У^ ад. 2^1 (од., бд.; сд.; ж) .................................	347
6.7.2.	Ряды вида ^М^") М^) ..........................	349
6.7.3.	Разные ряды, содерж:ащие 2^1(а,6;с;ж) .............................	350
6.8.	Обобщенная гипергеометрическая функция pFq((ap); (bq); ж) ...........	351
6.8.1.	Ряды вида ^aktkpFq((ap) ± k(cp);(bq) ± k(dq);x) .....................	351
6.8.2.	Ряды, содержащие тригонометрические функции и pFq((ap); (bq); x) ...........	354
6.8.3.	Ряды, содержащие специальные функции и pF<?((ap); F^); ж) ................	354
6.8.4.	Ряды, содержащие произведения pFq((ap); (bq); x) .......................	355
6.9.	Различные гипергеометрические функции .........................	355
6.9.1.	Ряды, содержащие 2^2(«, Ь\ с, d; x) ................................	355
6.9.2.	Ряды, соде ржащие 3^2@.1, «2, «з 5 bi, 62; ж) ...........................	356
6.9.3.	Ряды, содержащие разные гипергеометрические функции ..................	357
6.10.	Ж-функция Мак-Роберта E(p;ar : q; bs : z) .........................	358
6.10.1.	Ряды вида ^2акЕ((ар) ±mk;(bq) ± пк; z) ..........................	358
6.10.2.	Ряды, содержащие произведения ^-функций .........................	359

Оглавление	15
6.11. G-функция Мейера G^n ( z
6.11.1. Ряды вида V aktkG™n
(ар)±к(ср)\
(bq)±k(dq)J •••..•••.••••..••••••••...•
6.11.2. Ряды, содержащие тригонометрические функции и бг-функцию .............	360
6.12. Разные ряды ..............................................	361
6.12.1. Ряды, содержащие многочлены Неймана Оп(х) .......................	361
Глава 7. ГИПЕРГЕОМЕТРИЧЕСКИЕ ФУНКЦИИ:
СВОЙСТВА,ПРЕДСТАВЛЕНИЯ,ЧАСТНЬ1Е ЗНАЧЕНИЯ ...............	362
7.1.	Введение. .................................................	362
7.2.	Основные свойства гжпергеометрнческих функций ...................	362
7.2.1.	Гипергеометрическая функция Гаусса 2F\ (a, 6; с; z) ......................	362
7.2.2.	Вырожденные гипергеометрические функции Куммера
iFi(a; 6;^),Трикоми Ф(а, b; z) и Уиттекера MPj?J(z), WP}CT(z) ....................	365
7.2.3.	Обобщенная гипергеометрическая функция pFg((ap); Fg); z) ................	368
7.2.4.	Гипергеометрические функции нескольких переменных ....................	377
7.3.	Функции iF0(«;z) и 2-Fi(a,b;c; z) ................................	382
7.3.1.	Представления iFq(a; z) и 2Fi(a, 6; с; z) .............................	382
7.3.2.	Частные значения 2Fi(a, 6; с; z) ...................................	395
7.3.3.	Представления 2Fi(a, 6; с; —z) ....................................	410
7.3.4.	Частные значения 2Fi(a, b; с; —z) ..................................	411
7.3.5.	Значения 2Fi(a, 6; с; 1) ........................................	412
7.3.6.	Значения 2Fi(a, 6; с; -1) .......................................	412
7.3.7.	Значения 2F1 [ а, 6; с; - ] .......................................	414
7.3.8.	Значения 2Fi(-n, 6; с; 2) .......................................	415
7.3.9.	Значения 2Fi(o, 6; с; z0) при z® ф ±1,2±г ............................	416
7.4. Функция 3F2(ai,a2?a3;bi?b2;^) .................................	419
7.4.1.	Представления 3F2(ai, a2, аз; &1? &2 5 2) .••..•••..•.•...••...•.•.••••.	419
7.4.2.	Частные значения 3F2(ai, аг, аз; 6i, &2J ^) ............................	422
7.4.3.	Частные значения 3F2(ai, а2, аз; &i, &2J—я) ...........................	448
7.4.4.	Значения 3F2(ai, O2, аз; 6i, 62; 1) ..................................	449
7.4.5.	Значения 3F2(ai, аг, аз; 61, 62;—1) .................................	460
7.4.6.	Значения 3F2(ai, 0,2, о-з5 ^1 ? ^25 %о) при zq ф dbl .........................	464
7.5. Функция 4^з(«1, «2? «3,0,4; 61,62,63; z). ............................	465
7.5.1.	Представления 4F3(ai, аг, аз, 04; &i, &2> &з; 2) ••••••••••••••••••••••••••	465
7.5.2.	Частные значения 4F3(ai, аг, аз, а4; 6i, 6гj &з; з) ........................	467
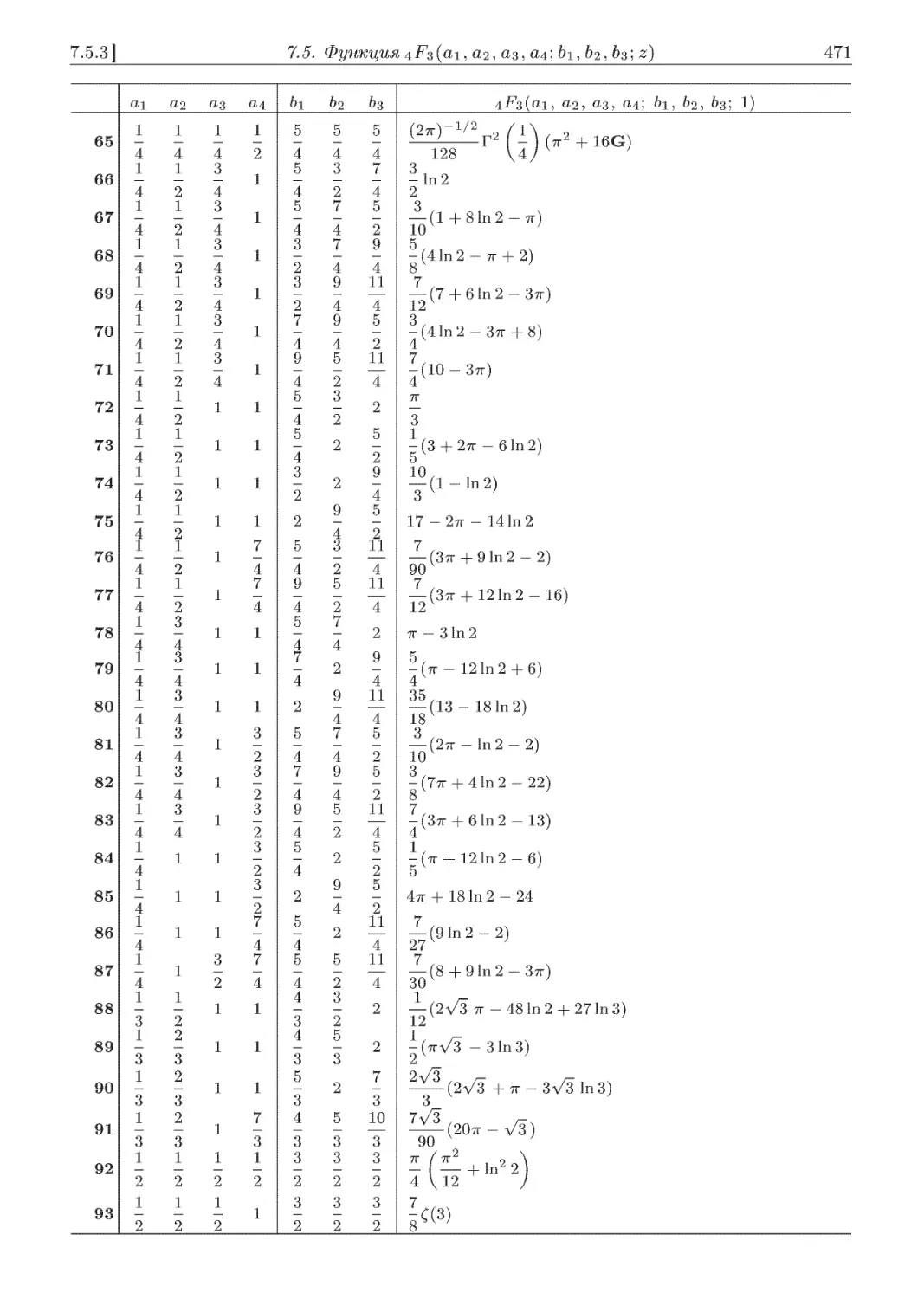
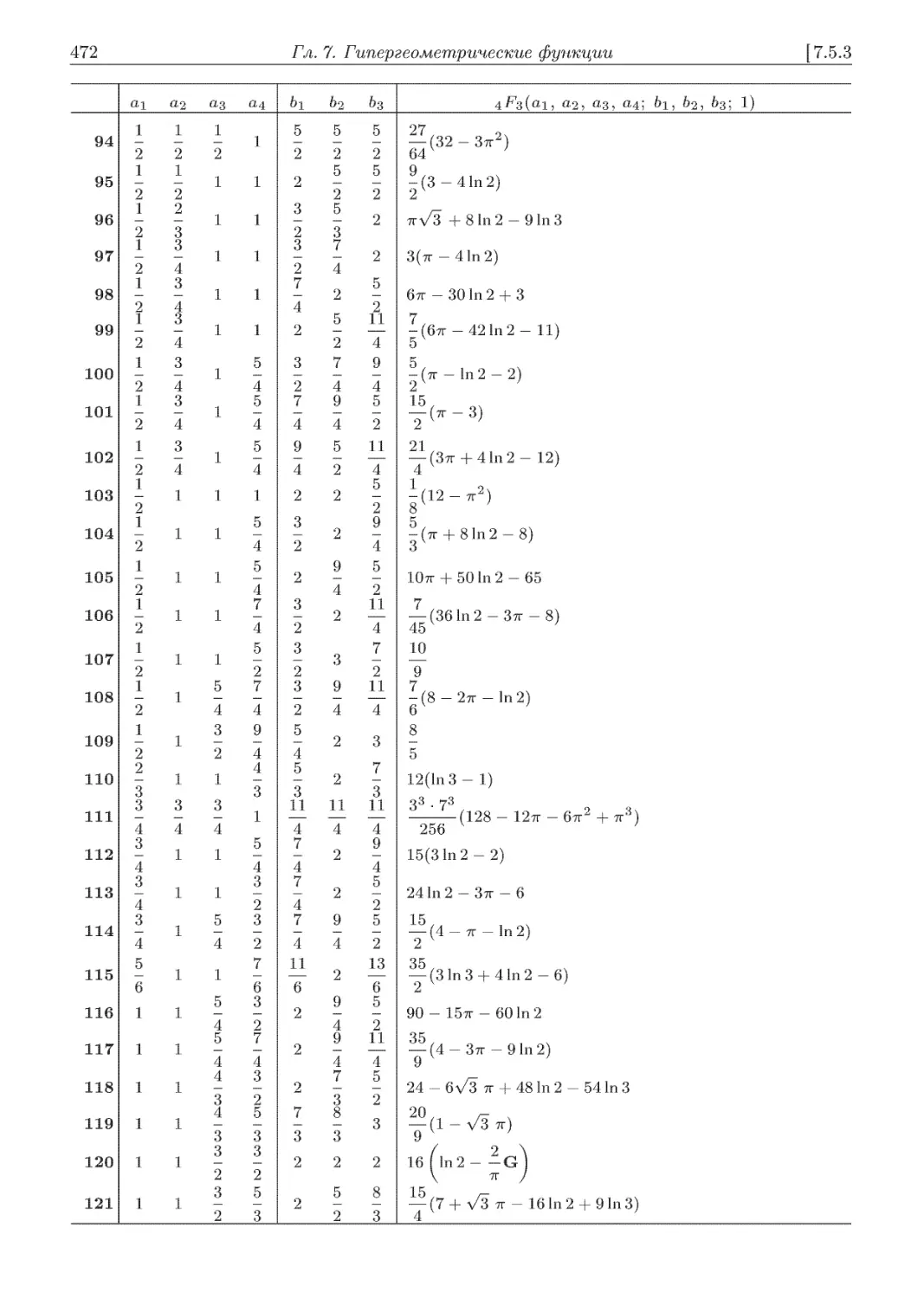
7.5.3.	Значения 4F3(ai, а2, «з5 а45 bi, 62, &з; 1) ..............................	467
7.5.4.	Значения 4F3(ai, аг, аз, a4j &i, 62, &з;—1) ••••••••••••••••••••••••••••	473
7.5.5.	Значения 4F3(ai, а2, «з5 а4 5 bi, 62, &з; ^о) при zo т^ il •••••.•.••.•••••.••••	475
7.6.	Функция 5-^4(cbi, ... ,as; bi, ... ,64; z) .............................	475
7.6.1.	Частные значения 5F4(ai, ..., 05; 61, ..., 64; iz) ........................	475
7.6.2.	Значения sF4(ai, . . . , 05; 61, . . . , 64; 1) ...............................	475
7.6.3.	Значения sF^ai, . . . , as; fei, . . . , 64; —1) .............................	478
7.6.4.	Значения 5Fi(ai, . . . , 05; 61, . . . , 64; zq) при zq 7^ dzl .....................	479
7.7.	Функция 6-F5(cti, ... ,ae; bi, • • • ,65; 2) .............................	479
7.7.1.	Представления 6F5(ai, ..., ae; bi, ..., 65; z) ...........................	479
7.7.2.	Значения 6F5(ai, . . . , a®] 61, . . . , 65; 1) ...............................	479
7.7.3.	Значения 6F5(ai,...,a6; 61,..., 65;-!) .............................	480

16	Оглавление
7.8. Функция 7-Fe(«i? • • • jO75 bi, ... ,6в» я) ............................. 480
7.8.1.	Значения т^бОъ • • • , «75 6Ь • • • , 66; 1) ............................... 480
7.8.2.	Значения 7^б(«1, . . . , а7; 6i, • • • , бе; -1) ............................. 481
7.9.	Функции 8F7(«i, ... ,as;bi9 ... ,b7;z) и g-Fefai» ... ,а9;Ьг, ... ,b&;z) . . . . . . . .	481
7.9.1.	Значения e^Mai, ... ,a8;6i, ... ,67; ±1) .............................	481
7.9.2.	Значения 9F8(ai, • • • , «g; &ъ • • • , Ь8; 1) ...............................	482
7.10.	Функция q+1Fq(oi, ..., aq+i; 61, ... ,bq; z) .........................	482
7.10.1.	Значения g+iF9(ai, ... ,a9+i;6i, ... ,6g; 2) ...........................	482
7.10.2.	Значения g+iF9(ai,...,a9+i; 61,..., 6g;±l) ..........................	483
7.11.	Функции Куммера %F±(a;b;z) ш Трикоми Ф(а, b; z) ..................	487
7.11.1.	Представления 0 Fq(z) и iFi(a;b; z) ................................	487
7.11.2.	Частные значения iFi(a;b; z) ...................................	488
7.11.3.	Представления iFi(a; 6; —2) ....................................	491
7.11.4.	Представления и частные значения Ф(а, 6; z) ..........................	491
7.12.	Функции 2^2(а1,а2;б1,Ь2;;г) и qFq(ai, ... ,og; bi, ... ,6q; г) .............	492
7.12.1.	Представления 2F2(ai, a2 5 6i, &2 5 ^) ................................	492
7.12.2.	Частные значения 2F2(ai, аг; &i, 62; z) ..............................	492
7.12.3.	Представления 3Fs(ai, a2, аз; 6i, 62, 63;—2) ..........................	499
7.12.4.	Представления qFq((aq); (bq); z) ..................................	499
7.13.	Функция 0Fi(fe;z) ..........................................	499
7.13.1. Представления и частные значения oFiF;diz) .........................	499
7.14.	Функция 1^2(a; bi,b2;z) ......................................	500
7.14.1.	Представления iF2(a; 61, 62; z) ...................................	500
7.14.2.	Частные значения 1F2 (a; fei, 62; z) .................................	501
7.14.3.	Представления iF2(a; 61, 62; —z) .................................	512
7.14.4.	Частные значения iF2(a; 61, 62; ^z2) ...............................	513
7.15.	Функция 2F3(ai,a2;bi,b2,b3;z) ................................	513
7.15.1.	Представления 2^3@1, a2; fc»i, 62, b%; z) .............................	513
7.15.2.	Частные значения 2Fs(ai, 02; 6i, 62, 63; z) ...........................	514
7.15.3.	Представления и частные значения 2^з(а1, «2; 6i, &2, bg; —z) ...............	514
7.16.	Функции вида 0Fq((bq); z), qr = 2, 3, ... ...........................	514
7.16.1.	Частные значения 0^2F1,6252:) ..................................	514
7.16.2.	Представления и частные значения о-^з(&1> &2> &з; z) •••••••••••••••••••••	514
7.16.3.	Представления и частные значения о-^з(&1> &2> &з; —г) ••••••••••••••••••••	515
7.16.4.	Представления 0^4F1,62563,64;^) и oFq—i((bq—i); z) ....................	516
7.17.	Функции видар-Ро(-п,(ар_1); 2), р = 2,3, ... .......................	516
7.17.1.	Представления 2^о(—n,a;z) ....................................	516
7.17.2.	Представления 2^Ь(—п, а; — z) ...................................	517
7.17.3.	Представления з^Ь(^?г, oi, «2; 2) .................................	517
7.18. Разные гипергеометрические функции ...........................	517
7.18.1.	Представления iFq(a;(bq); z) ....................................	517
7.18.2.	Представления 3Fg(ai, a2, аз; 61, •••, be; 2) ...........................	517
7.18.3.	Представления 4Fi(—n, ai, аг, аз; 6; г) .............................	517
Глава 8. G-ФУНКЦИЯ МЕЙЕРА И Я^ФУНКЦИЯ ФОКСА. .............	519
8.1. Введение. .................................................	519

Оглавление	17
8.2. G-функцжм Межера <
(ap)(bq) J ........................... 520
8.2.1.	Определение и обозначения ..................................... 520
8.2.2.	Основные свойства ........................................... 520
8.3. Ж-Функция Фокса Н,
¦тп
pq
ap,Ap][bq,Bq] 	 528
8.3.1.	Определение и обозначения .....................................	528
8.3.2.	Основные свойства ...........................................	529
8.4. Таблица преобразований Меллина ж представлений элементарных ж специ-
специальных функций через Gr-функцию Мейера ж JEf-функцжю Фокса ...........	531
8.4.1.	Формулы общего вида .........................................	531
8.4.2.	Степенная и алгебраическая функции ...............................	532
8.4.3.	Показательная функция ........................................	534
8.4.4.	Гиперболические функции ......................................	534
8.4.5.	Тригонометрические функции ....................................	535
8.4.6.	Логарифмическая функция ......................................	537
8.4.7.	Обратные тригонометрические функции .............................	539
8.4.8.	Обратные гиперболические функции ................................	540
8.4.9.	Полилогарифм Ып(ж) .........................................	541
8.4.10.	Функция Ф(ж, s, v) ..........................................	541
8.4.11.	Интегральная показательная функция Ei (ж) ..........................	541
8.4.12.	Интегральные синусы Si (a;),si (ж) и косинус с! (ж) .......................	542
8.4.13.	Интегральные гиперболические синус shi (ж) и косинус chi (ж) ...............	543
8.4.14.	Интегралы вероятности erf (ж),erfc (ж) и егп(ж) ........................	543
8.4.15.	Интегралы Френеля S(x) и С(х) .................................	544
8.4.16.	Неполные гамма-функции y(v, х) и ^(^j x) ...........................	546
8.4.17.	Обобщенные интегралы Френеля S(x,v) и С(х,и) ......................	548
8.4.18.	Функция параболического цилиндра Du(x) ...........................	548
8.4.19.	Функция Бесселя Ju(x) .......................................	549
8.4.20.	Функция Неймана Yu(x) .......................................	552
8.4.21.	Функции Ганкеля Я^1}(ж) и Я^2)(ж) ...............................	559
8.4.22.	Модифицированная функция Бесселя 1и(х) ..........................	559
8.4.23.	Функция Макдональда Ки(х) ...................................	563
8.4.24.	Интегральные функции Бесселя Jiu(x),Yiu(x) и Kiu(x) ..................	566
8.4.25.	Функции Струве Н^ж) и Ъи(х) ..................................	567
8.4.26.	Функции ВебераЕ„(ж),Е{;(ж) и Ангера JI/(x),J(J(aj) .....................	568
8.4.27.	Функции Ломмеля s^}u(x) и 5^,г/(ж) ...............................	569
8.4.28.	Функции Кельвина befi/(ж),beit/(ж),kerjy(ж) и keii/(aj) .....................	569
8.4.29.	Функции Эйри Ai (ж) и Bi (ж) ....................................	572
8.4.30.	Многочлены Лежандра Рп(х) ...................................	575
8.4.31.	Многочлены Чебышева 1-го рода Тп(х) .............................	577
8.4.32.	Многочлены Чебышева 2-го рода Un(x) .............................	579
8.4.33.	Многочлены Лагерра Ln(x) и Ln(x) ...............................	582
8.4.34.	Многочлены Эрмита Нп(х) .....................................	582
8.4.35.	Многочлены Гегенбауэра Сп(х) ..................................	583
8.4.36.	Многочлены Якоби Р^р'а\х) ....................................	586
8.4.37.	Функция Лагерра Lu{x) .......................................	587
8.4.38.	Функция Бейтмена ku(x) ......................................	588
8.4.39.	Функция Ломмеля Uu(x, z) .....................................	588
8.4.40.	Полные эллиптические интегралы К(ж),Е(ж),1Э(ж) ......................	588
8.4.41.	Функции Лежандра 1-го рода Pjf(x) и Ри(х) ..........................	592
8.4.42.	Функции Лежандра 2-го рода Q^(x) и Qv (ж) ..........................	599
8.4.43.	Функция Уиттекера МРуСТ(х) ....................................	607
8.4.44.	Функция Уиттекера Wp^a(x) ....................................	608
8.4.45.	Вырожденная гипергеометрическая функция Куммера 1^1@; 6; ж) ...........	609

18	Оглавление
8.4.46.	Вырожденная гипергеометрическая функция Трикоми Ф(а, Ь; х) .............	609
8.4.47.	Функция 0Fi(b; x) ..........................................	611
8.4.48.	Функция iF2(a; 6i, 62; ж) ......................................	612
8.4.49.	Гипергеометрическая функция Гаусса 2.Fi(a, 6; с; ж) .....................	612
8.4.50.	Функция 3-F2(ai, a2, аз; 6i, 62; ж) .................................	619
8.4.51.	Разные функции гипергеометрического типа ..........................	620
8.4.52.	Указатель частных случаев G-функции Мейера и /f-функции Фокса ..........	623
Приложение I. НЕКОТОРЫЕ СВОЙСТВА ИНТЕГРАЛОВ,
РЯДОВ,ПРОИЗВЕДЕНИЙ И ОПЕРАЦИИ С НИМИ ...................	626
1.1.	Введение ..................................................	626
1.2.	Сходимость интегралов и операции с ними .........................	626
1.2.1.	Интегралы по неограниченным кривым ..............................	626
1.2.2.	Признаки сходимости интегралов с бесконечными пределами от неотрицательных функ-
функций .........................................................	627
1.2.3.	Признаки сходимости интегралов с бесконечными пределами от произвольных функций	629
1.2.4.	Интегралы от неограниченных функций по ограниченным кривым .............	630
1.2.5.	Признаки сходимости интегралов от неотрицательных неограниченных функций . . .	631
1.2.6.	Равномерная сходимость функций и интегралов, зависящих от параметра ........	632
1.2.7.	Операции с интегралами, зависящими от параметра ......................	633
1.3.	Сходимость рядов и произведений и операции с ними ................	635
1.3.1.	Основные понятия ...........................................	635
1.3.2.	Признаки сходимости положительных рядов ...........................	635
1.3.3.	Признаки сходимости произвольных рядов ............................	640
1.3.4.	Признаки равномерной сходимости рядов, зависящих от параметра ............	641
1.3.5.	Операции с рядами ...........................................	641
1.3.6.	Степенные ряды .............................................	642
1.3.7.	Тригонометрические ряды ......................................	645
1.3.8.	Асимптотические ряды ........................................	645
1.3.9.	Бесконечные произведения ......................................	646
Приложение II. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ
ФУНКЦИИ И ИХ СВОЙСТВА ....................................	647
II. 1. Биномиальные коэффициенты ( ] .............................	647
v Ь'
11.2.	Символ Похгаммера(а)|{, ......................................	647
11.3.	Гамма-функция T(z) .........................................	648
11.4.	Пси-функция if>(z) ..........................................	650
11.5.	Полилогарифм LII/(z) ........................................	651
11.6.	Обобщенные интегралы Френеля S(z, и) Ш C(z, i/) ...................	653
11.7.	Обобщенная дзета-функция ^(z,t?) ..............................	653
11.8.	Многочлены Бернулли Bn(z) и числа Бернулли Вп . .................	653
11.9.	Многочлены Эйлера En(z) и числа Эйлера еп ......................	654
11.10.	Функции Струве Hiy(z) и L,y(js) ................................	655
11.11.	Функции Вебера E^(z), E^(z) и Ангера Jv(z), 3%(г) .................	656
11.12.	Функции Ломмеля sfJ,il/(z) ш S/J,ilJ(z) .............................	656
11.13.	Функции Кельвина beiv^), heiu(z), kerv(z) и kel^z) ................	657

Оглавление	19
11.14.	Функции Эйри AI(z), Bi(z) ................................... 658
11.15.	Интегральные функции Бесселя Jiv(z), Yiu(z), Kiv(z) .............. 659
11.16. Неполные эллиптические интегралы Р(ср^к), Е((р,к), ?)(y>,fe), П(<^, is, fe),
?/3?fe) и полные эллиптические интегралы K(fe), E(fe), D(fe) ............ 659
11.17.	Функция Бейтмена fel/(z) .....................................	661
11.18.	Функции Лежандра Pv(z), P?(z), Qv(z), Q?(z) ..................	661
11.19.	Ж-функция Мак-Роберта Е(р; ar : q;ba : z) ........................	667
11.20.	Эллиптические формулы Якоби cnw, dnw, snw ...................	667
11.21.	Эллиптические функции Вейерштрасса р(и), C(u)j ^i11) ¦¦-•--•-¦•¦¦¦-	668
11.22.	Тэта-функции 6j(z,q), j = 1, 2, 3, 4 .............................	668
11.23.	Функции Матье ...........................................	668
11.24.	Многочлены Неймана On(z) и Шлефли Sn(z) .....................	674
11.25.	Функции u(z), v(z,p), jla(z,A), /x(z,A,p). ........................	674
Список литературы ...............................................	675
Указатель обозначений функций и постоянных .............................	678
Указатель обозначений символов ......................................	686

20	Оглавление

ПРЕДИСЛОВИЕ
Решение многих задач, относящихся к различным областям науки и техники, приводит к
вычислению интегралов и суммированию рядов, содержащих элементарные и специальные
функции. Как известно, эта работа значительно упрощается с помощью соответствующей
справочной литературы, среди которой следует отметить серию книг Г. Бейтмена и А. Эр-
дейи «Высшие трансцендентные функции» и «Таблицы интегральных преобразований»,
пользующихся мировой известностью, и справочник И.С. Градштейна и И.М. Рыжика
«Таблицы интегралов, сумм, рядов и произведений».
Эти справочники на протяжении нескольких десятилетий являются настольными для
физиков-теоретиков и экспериментаторов, инженеров-исследователей, специалистов в об-
области прикладной математики и кибернетики. В них, однако, содержатся лишь формулы,
полученные до конца 40-х годов, что привело к необходимости издания более полного
справочного руководства, в котором были бы отражены новые результаты. В связи с этим
в издательстве «Наука» в 1981^1983 гг. вышли книги «Интегралы и ряды. Элементарные
функции» и «Интегралы и ряды. Специальные функции», которые включают результаты
в этой области математического анализа, опубликованные в последние годы.
Предлагаемая вниманию читателя третья книга включает в себя таблицы неопределен-
неопределенных и определенных интегралов, конечных сумм и рядов, содержащих функции Струве,
Вебера, Ангера, Ломмеля, Кельвина, Эйри, Лежандра, Уиттекера, гипергеометрические,
эллиптические, Матье, Мак-Роберта, Мейера, Фокса и некоторые другие. В нее также вошли
таблицы представлений обобщенных гипергеометрических функций и таблица преобразо-
преобразований Меллина широкого класса элементарных и специальных функций, объединенная с
таблицей частных случаев G-функции Мейера. Помещены разделы, посвященные свойствам
гипергеометрических функций, С-функции Мейера и Л-функции Фокса. В приложениях
содержится дополнительный материал, которых может быть использован при вычислении
интегралов и суммировании рядов.
Основному тексту предшествует достаточно подробное оглавление, с помощью которого
можно отыскать нужные формулы. Используемые обозначения, как правило, общеприняты
в математической литературе и приводятся в указателях в конце книги. При ссылках запись
ви да 2.17.9.1 обозначает формулу 1 из пункта 2.17.9. Во всех главах к, I, га, в = 1, 2, 3, ...,
если не указаны другие ограничения.
Для компактности изложения используется сокращенная запись.
Например, формула
(a2 -x2)^/2\cosbx j
м/ж
a )
Ь5Г
_, /a +1 a _ _ 1 l + a + <5^M^i/ 2 + a + <5 ™ /i
x 2F3 —-—, ^ + i5; <5 + ™,
2 ' 2 ' ' ' 2'	2	'	2	'4
a > 0; Re a > -5; Re/1 < 1; 5 = <

22	Оглавление
представляет собой сокращенную запись двух формул:
(х \
— ) dx =
а/
,а -
о
= л/i I ^ 1 ¦ ьт
\ А
"а + 1 а	3 2 + а- д- i/ 3 + a-/x + i/ а262
2 ' ?+ ' 2'	2	'	2	' 4
[а > 0; Re а > -1; Re jw < 1].
(берутся только верхние знаки и верхние выражения в фигурных скобках) и
(х \
а/
Г[A + о^ М-^)/2, B + a-/x + ^)/2j X
'а + 1 а 1 1 + а-/х-1/ 2 + a^ii + i/ a262
[a > 0; Re a > 0; Re д < 1].
(берутся только нижние знаки и ниж:ние выражения в фигурных скобках); по определению
[-1	771	П
ai	сЧ=ПГЫ/ПГF,).
k=l	1=1
Список основных литературных источников приведен в конце книги. Значительная
часть результатов получена авторами и публикуется впервые.
Мы надеемся, что три книги справочного руководства «Интегралы и ряды» будут
полезны научным работникам, инженерам и другим специалистам, использующим в своей
работе математические методы.
Авторы

Глава 1. НЕОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
1.1.	ВВЕДЕНИЕ
В этой главе содержатся неопределенные интегралы от специальных функций, а также
определенные интегралы, у которых один из пределов интегрирования является перемен-
переменным, в случаях, когда подынтегральная функция от него не зависит; постоянная интегри-
интегрирования для краткости опущена.
Некоторые формулы при определенных значениях параметров теряют смысл. Если эти
значения следуют из структуры формулы, то соответствующие разъяснения опускаются.
Выражения для интеграла при этих значениях параметров, как правило, даются в после-
последующих формулах.
1.2.	ОБОБЩЕННАЯ ДЗЕТА^ФУНКЦИЯ ?(в, ж),
МНОГОЧЛЕНЫ БЕРНУЛЛИ Вп(х),
ЭЙЛЕРА Еп(х) И ПОЛИЛОГАРИФМ Li „(а?)
1.2.1.	Интегралы, содержащие ((s, ж), Вп(ж) и 5п(ж).
Г	1
1.	C(sj x) dx = 	((s - 1, х)	[Res > 2].
J	-L s
2.	[ Bn(x) dx = -—Bn+1(x).
3.	[ En(x) dx = —J—?/те(ж).
1.2.2.	Интегралы вида /Уп(аж)Aж.
1 c^ir / 4i axa+1 _ /1, 1, . . . , 1, а + 1;-аж\
1. \x Lin(-ax) dx =	—-п+2^п+1	о i о	[Rea>-1; |arga|<7r].
J	ft~T"l	yZ, Z, . . . , Z, Q!t^	J
f 1
2. — h\n{—ax) dx = Ып+1(^аж)	[| arga| < тг].
J x
1.2.3. Интегралы вида /(жIл2(ж) dx.
-^v~j dx = -]
1 — ж
• I 	Г77 JLj121X J UX — 	 JLji21X J — — ill I JL — XI.
J ^ JL X j	JL X	Zi
3. 	\a2(x) dx = In ж Ыз(ж) — Ы4(ж).
J •?
4.	—	 Ы2(ж) dx =	In2(l — ж) Ы2(ж)	1п2A — ж) Ы2A — ж) +
J JL — X	A	A	I
+ 31пA - ж)Ы3A - ж) -3Li4(l - х)	1пж1п3A - ж).
1.3. ОБОБЩЕННЫЕ ИНТЕГРАЛЫ ФРЕНЕЛЯ 5(ж, и) И С(ж, и)
S(ax, p)
1.3.1. Интегралы вида f(x) 1 .
С (ах, и)
I, О. — 1 I О[AХ. Is) I I D\UJL. V) I .	XI ulttX, Is) I	tl	I OlttX, Ct "
X
С (ах, и) ) X С (ах, v) )	а \ С (ах, и) j а \ С (ах, а

24	Гл. 1. Неопределенные интегралы	[1.4.1
(ax,v)\ , ж1^" Г 5(аж, i/) 1 а^1 fcosax}
C(ax, is) )	1 — v X С{ах1 и) / 1 — i/I sinaa; /'
С(ах,и)ГХ- Ъ \C{ax,v)}
	-< >[(& + ъа)~и^({у^ ^ж + i^x) =р (& — ia)~u'y{y, ^ж ~ *аж)].
. Г . , Г S(ax, и) \	1	Г S(ax, v)
J	\C(ax,i>))	b
2b[\a-bJ \ C((a - Ь)ж, i/)J \a + bj \ С ((a + b)x, v) J J'
, f S(ax, v) 1 . 1 . . Г S(ax, v) 1
ysbxi _\	\ > dx = — 81пож< _\	' > =p
[G(аж, i/)J	6	[G(аж, и) )
J_ Г/ а V /С((а-6)ж, i/)l /_о_у ГС((а + Ь)ж, i/;
T 26 [\a - b) \S((a-b)x, v)f \a + b) \ S((a + b)x, v\
1.4. ФУНКЦИИ СТРУВЕ Н„(а;) И Lv(x)
1.4.1. Интегралы вида ж Н„(ах) dx.
Т л	а1/+1жЛ+|/+2
1. ж Н„(аж) с!ж = ±-	^т^	гт^т	^тгг X
| ^	^г|«^(А«й	«LJ1	«LJ1	^4|«^(-&.	1>€/ «АУ	а	^ 7Т оСЗО 1 /\ ~j| U \~ _L J 71 j Za\	1 U I
Г Г Ж1 = 0, ж2 = ж; Re (A + */) > -2
[ [ я?! = ж, Ж2 = оо; а > 0; R<
__ .-,_ ..,.., ., ReA< 1/2; Re (A + i/) <0
/,,\ -^ q /o
w	§ eyfy	JL JL|/ I U/eX/ I CXeAy 	 	I
\<
а	[[ж1=ж,Ж2:::::::::::сх),а>0; Re v < — 1
ail
.	,„	,-+3
3.
i/—l	l —i/
0(
О
Г22 /1, 1; -а2а2
к Т1
5. j-
1.4.2. Интегралы вида ж егжН|/(ж) с!ж.
±1/ «*	ж1±|Уе*ж
^^ж; ж^ 2г/ dz 1 ^^J^2 ^±il
°	A 11/2	f г^тг/2
т
+ 1±1/2Ц	егх-1
2. 1 ж^1/2егжН^1/2(ж) dx = 	Si Bж) -\	^=- [С + 1п2ж — ci Bж)].
Г Г 1/^-1/2; Rei/>-lll
LI ^^^i/2 IJ1
о
-1/2 г ж	1	Г	Ж
3. ж ' е Н1/2(ж) dx = 		2 ci (ж) — ci Bж) — С — In—Ь 2iSi (ж) — iSi Bж) .
J	V2tt	L	2	'
о

1.4.4]	1.4- Функции Струве Ми(х) uhv(x)	25
1.4.3. Интегралы вида жЛНм(аж)Н1/Fж) dx.
г iff
1. жлНм(ж)Н|/(ж) dx =	 I -(Л + /х + I/ - 1) жлНм^1(ж)Н?/^1(ж) с!ж +
J	Л — [A — V-\-l(	J
хх+^Ш^г{х) dx -
1/2)
2.
HA1(a;)Ht/(a;)da;=	{/
ax	o /оч ж	и^^ж; аж >	см. i.4.ij.
/tt V(u + 3/2) J	J
tt Г(/1 + 3/2) J	i/tt V(u + 3/2)
[см. 1.4.1].
Г	1 Г
J	ft2 - 62 { l
+ —=—;	™^ la17 x^Wvlbx) dx — 6	ж^Н^Гаж) <^ж >	[см. 1.4.1].
у7Г 1 ^
5. [Ih (,)HJx)i
J ж M
H (ж) dx —
[cm. 1.4.1].
f 1 и -— 1 Г 1 1
g# ¦—-Н^(ж) dx = 	 -~Н^__1(ж) da;	[Н^__1(ж) + Н^(жI +
H|/_i(a;) da;	[см. 1.4.1].
[см. 1.4.1].
f
1.4.4. Интегралы вида ж JM(aa;)H1/(fea;)
"+"+1^(х)-а^х) dx =
2(ax + i/ + 1
1	' IL™™ — — '	[CM. [i8]) 1.8.1].
. f a;-''-'+1^(a!)Hl,(a!) dx =
J
v I)
Г ж
3. a;JI/(aa;)HI/Fa;) da; = —	—[bJu(ax)'H.u-i(bx) — aJt/-i(ax)'H.u(bx)] —
л	"-"	Г » т /	\-wrt /J	\	т/ /	\ -Ш--Ш- /»	\1	ЯХ
^rг^[6Л(аж)Нг/(Ьж) аХ(аж)Н1/Fж)]ъг (
а1 — Ьл	а1 — о1 \а
х [^

26	Гл. 1. Неопределенные интегралы	[1.4.5
5. l-Jp{x)Hu{x) dx = Х_ 2[^(ж)Н1/_1(ж) - Jli-1{x)H.v{x)} -
X
1 Г 1 п~1
J x	2n \V? k=Q
- [Jo(x)Ho(x) - Jn(x)Mn(x)] - 2 2^ Jk(x)Mk(x) \	[см. [18], 1.8.1].
1.4.5. Интегралы вида жАЬ1/(аж) dx.
х и+1 x+v+2 / \ \	2 2\
о	[Re(A + ^>-2].
„ Г 1±„т , w ж1=с"
2. jx L,(ax) dx = —Ъи±1(ах) -
и — любое
о	Г Л ж'
1.4.6. Интегралы вида ж е жЬ|/(ж
~ Bi/ + l)r(i/ + 3/
[Re i/ > -1;
v + l ±х	2v (l±l)i/Wi
-^^-[L,^ Т L,+1(x)] - B|/ + 1)r(|/ + s/2)V?7B^ + 2,
2. f ж^1/2е±шЬ^1/2(ж) dx = ±-^=[Ei(±2:c) - С - 1п2ж].
J	у2тг
о
ж
4. жт1^2е жЬ!/2(ж) с!ж = .	 Ei (di2a;) — 2Ei (iba;) + С + In — .
о
X-2
5. f жЛ[/±г/(аж) - Jjv{ax)] dx =
3
/A=bi/ + 1 A±i/ + 3	а2ж2\	2Agcosj/7T	[A + A ib i/)/2]
X ' 2 V 2 ;	2 '	5 ^Г; ~ aA+! sin [(A + i/)tt/2] [A - A ± i/)/2j
[cci =0, Ж2 = ж; e = 0; Re (A ± i/) > —1] или [xi = ж, Ж2 = oo; e = 1; Re (A + i/) < 0].
1.5. ФУНКЦИИ АНГЕРА Jv(x) Ш ВЕБЕРА Е^(ш)
1.5.1. Интегралы вида хх< ^ ;
J
?
x
Ju(ax)\ _ 2(^1)ежЛ+1 . i/тг f cos (i/Tr/2) 1
\ _ 2(^1
/ rfiB" (I +
A + 1A + 3	и	и а2х2\ , 2(-1)?ажл+2	иж (sin (i/tt/2) 1
x2i^8 I 1,1+--; 2+^? 3 + I/ 3^l/- aV^	B/a)A+1e7rsecA7r	/sin[(A-i/Or/
2' 2' 2 ' 2 ' 4 у Г(A-А-1/)/2)Г(A-А + 1/)/2)\со8[(А-1/)тг/

1.6.2]	1.6. Функции Ломмеля 81Л^1/(х) и Б^^(х)	27
[xi = 0, х2 = х; е = 0; Re (Л) > -1] или [х\ = ж, ж2 = оо; е = 1; а > 0; Re (Л) < 0].
1.6. ФУНКЦИИ ЛОММЕЛЯ вд,.
1.6.1. Интегралы вида I xxI J*'v , \\ dx.
S(ax) J
?;й)}
- 2А+м~1тт~А~1 msec Л + /17Г^Г(^ ~ " + *) А (м + ^ + 1)/2] / О
2
Г Г
= О, Ж2 = ж; Re (Л + fi) > —2; | arg а\ < тг
= ж, ж2 = оо; Re Л < 1/2; Re (Л + ц) < 0; а > О
? л
2. j,
F (л A + At | i Л + М | о М^ + 3 М + ^ + 3 аж\.
1
2!
Л - и + 3
J1 Л	2	;1-"' 	2	;
= О, Ж2 = ж; Re (Л + /л) > —2; Re Л > | Re i/|; | arg a\ < тг '
Ж1 = ж, Ж2 = со; Re (Л + /л) < 0, а > О
3. \xS^u{x) dx 2^r(u+l
J	2
- (д + I/ - 1)жН4ж)^-1^-1(ж)] + I xfIMl/(x) dx
1.6.2. Интегралы, содержащие Ju(x) и з^1и(х) .
L. 1 — а2 Н	— ж J\(x)Sfj,}U(ax) dx = x[Ja(x)s^5 ^(аж) — J\(x)s^j u(ax)] —
о
x
.	-| \ т / \	/ \	J	/ \	/ \	/\
	M X'2/ \	^^	?il^	 dx = **'" .
0
3. I	—'/s т 7 ч	^^^	 dx = In I —-
4.
о
x^1 Ju(x) dx
(fJL + V - l)Ji/(x)sfJ,-lii/-i(x) - Ji/-l(x)sfjliU(x)
0

28	Гл. 1. Неопределенные интегралы	[1.7.1
1.7. ФУНКЦИИ КЕЛЬВИНА Ьег^аз), bei^sc), keiv (ж) И Ш„(х)
Обозначения:
I/„ = Ъети(х),	\fu = кег^ (ж),	\ f» = Ьеи,(ж),	\fu = ке^(ж),
u = he\u(x),	I gu = ке!1/(ж),	1 gv = — Ьег1/(ж),	1 #„ = — keiv (ж).
Далее jv, gV и /*, g-* — любая из этих четырех пар функций.
1 m 1 тж	Г л[Ьег1/(ажI	Г л ( keiv (аж) 1
1.7.1. Интегралы вида ж <	ч ? аж и ж <	> ах.
) { Ъе\и{ах) J	J I keiu(ax) J
, Г ЛГЬег1/(ажI ,	auxx+i/+1	f cos Ci/tt/4)
' J \Ъе\„(ах) ) ~ 2"(A + + l)r( + l\iC/4)
; 2' "^-' 2 +1'
аж	/ sin Ci/7t/4) \ /A+iz+3^ 3 v
I r» ,a4-9 / Л i . . i O\T-l/. . i O\ 1	/O	/yl\ П ^ I
2-+-2(A + i/ + 3)r(i/ + 2)\cosCi/7r/4)J 4\ 4 '2'2 ' 2 ' 4 ' 256
[Re(A + i/) > -1].
2» \^VZ::rJ}dx = UH	[ReX>\Re,\^l}.
cos Ci/7r/^
sin Ci/7r/^
1 4l ^ ' 4 ' 2 ' 2' 2' 256 ) 2^-i(A + i/ + l) l j1 sin f°— //l4 ^
A+iz+1^ A+I/ + 5 l + i/ i/	1# _o^4\ а2^"жл"г/+3
4 '	4 ' 2'2+'2'^25
cosCi/7r/4)
а4ж4
_ 2пжА"п+1 yJ (n-ife-1)! f cos [Cn - 2А;)тг/4] 1 / a2iL ,
in) -	1^	Z^ 1^7^ «юы i\ I sin [Cn _ 2^)тг/4] J V Г" '
cos [(n — 2k)ж/
2"+2	^ A;!(n + fe)!(A + n + Ik + 1) \ sin [(n - 2k)ir/4}
f ж+	Г	ж1м|/	^ = 0, 1, 2, . .
3. x1+u fv dx =	— (/„+i - gu+i)- 4. xX^v fv dx = -^^(/„_! - gu-г).
J	^	J	^
1.7.2. Интегралы, содержащие произведения функций Кельвина.
. Xlf^gv ^ gufu) dx = -X(fufu - fvfu + gugu - gvgv ).
Г	1
- I xtfvgt+gvfZ) dx = -^xIBflJgl-f1J~igZ+1-fi;+igl
. I x{fl + g-J) dx = x(fug'v - flgv).

1.8.1 ]	1.8. Функции Эйри At (ж) и BI (ж)	29
г	1
4.	I xfugu dx = -x2Bfl/gl/ - fv^1gy+1 - fv+igv-i).
5.	I x{fl - gl) dx = ^x2(fl - fu-ifu+i - gv + gv-igv+i).
f /ГЬегЦж)!2 |ЬеС(жI2\ _ Г Ьег^ж) ЪетЦх) + beiI/(x) ЬеС(ж) 1
J I \ кегЦж) / \ ке^(ж) /I	\ keiv (ж) кегЦж) + kei^sc) ке^(ж) /
7. ж[Ьег ;(ж) кег ;(ж) — bei '(ж) ке1;(ж)] dx = ж[Ьег1(ж) keri(a;) — beii(ic) keii(aj)].
1.8. ФУНКЦММ ЭЙРМ Ai(aj) И BI (ж)
Г	Г Ai (ж) 1
1.8.1. Интегралы вида f(x)< •) (\ ^х-
?
w
А+ 2 А + 5 4 х3
^ (А + 2)ГA/3)	V 3 ' 3 ' 3' 9
2. jV/2 Ai(x) dx = ^|^Г (^\ Ui(x)L_2/3 0ж3
О
Г	ч /9	<3™/^	/i9\J^919\J^Pi /1
I \ _L о ^^/""/^аз/ч	О	\ _±~ 1 ?_т # JL .4J /\ ~~f~~ ^ JL .u /\ "j" О	Tt Q / О
Р^	I /-V3 ^э	<	/л | I О^ 1 #у flf% ——— _______________^^	О^	^-- §~j л I „„„„„	____________________________ * __	___________________________ * 	1	 __ fY% I
J	l '	(А + 1)ГB/3) 2 Чб' 3 ' 3' 3 ' 3
3~1/3	л+2 „ (Ь 2А + 4 5 2А + 7 4 3/2\
~ (Х + 2)ГA/3)Х 2F2U'^; 3'^~;±3Ж J	[ReA>-l].
С	ч /9	Q~l/^	/i9\J-919\-l-.l:\ /I
6	Л ±2жл/2/3 ю- / N J	A+! n I	'	'	i
' J	u j (л + 1)гB/з) 22\6' з ' з' з ' з
31/6	л+2 „ /5 2Л + 4 5 2Л + 7 ,4
2 .... .
г- Г 1/2 ±2ж3/2/3 д./ \ j 2 з/2 ±2ж3/2/3 д.
7. ж ' е	' Ai (ж) аж = -ж ' е	' Ai
о	9
2ж^ ±2ж3/2/з
8. \х'е	' BI (ж) с!ж = -х ' е	; BI (ж) =р
J	5
°	/9 \	/9 \1 Ч1/3 /1
Г	I ^ 3/2 \ , г	( ^ S/2\\ _ О '	( I
V3 /	V3 /J 57Г V3
i# ж3/ 1 T1/3f з/2х f Ai(^) ^= uJZa\ г4/3/ 3/2xfAi^^T
3-^.4 3/2 [Л/з(ах3/2))	^2 з/Л _ 22/з . 35/V/3
Т7г(9^+4)Ж \/1/3(аЖ3/2);К4
J.U. X ii/з | ^л I ^i i^j ttJ" ~™ '77;х	\^x i 1jJl/3 | "^^ I ^-l X'1) ~
о

30	Гл. 1. Неопределенные интегралы	[1.8.2
2 3/2\ „, B 3/2
4V3*•
Ах
1	/2
I з/2 ^ I ~о	I А1{х) ах ^
4ж Г , . , B 3/2\ 1 /жч1/2 /2 3/2\ „/ /2 з/2
1 /жч
п (з)
dx	= 27T (х/3I/2/1/3BЖ3/2/3)
1(ж) ^/з П	тгА1(ж)
1.8.2. Интегралы, содержащие произведения функций Эйри.
Обозначения: у = аА1(х) + 6В1(ж), уп = ап Ai (ж) + 6пВ1(ж), га = 1, 2;
а,	6, ап, Ъп — комплексные постоянные.
tin	i	-*¦	Г п —1 / /	I	/ ч о то / / ,
I.	ж t/ii/2 аж = ———^[гаж B/i2/2 + 2/12/2) ^ ^ж 2/i2/2 +
J	2Bn + 1)
+ 2жп+ 1/12/2 — га(га — 1) жте~ B/i2/2 + 2/12/2) ^ж
г»	1	П —1/ /	,	/Ч	/	-1 Ч Г П — 2/ f	.	/Ч i	a f П —1 / / j	г \ -
2-	=9 ж B/i2/2+2/i2/2)-(^-1) ж (г/12/2+ 2/12/2) "Ж-2 ж 2/i2/2 «ж	[тг^.
L	J	J	J
« f n / j	1 Г -	Г n-1	Л .	г	n + 1, /	/J
J. ж 2/i2/2 dx = - ж 2/12/2 — га ж г/12/2 аж Н	—ж B/i2/2 — 2/12/2) •
J	2 [_	J	n + 1	J
4.	хпу[у2 dx = 2/2п + з\1 (n + 2) UnB/i2/2 + 2/12/2) -
5.	\vMdx = xyM-yW*.	^п\Х-\у'1У2 + У1У'2)
б.	2/i2/2 ^ = -B/12/2 + ^2/i2/2 ^
7.	2/i2/2 ^ж = -B/i2/2 + 2/12/2 ¦
Г	1 , ,	,	, ,	2	ч
8.	ж2/i2/2 «ж = -B/i2/2 + 2/12/2 - 2хугу2 + 2ж 2/12/2).
9.	^2/13/2 с!ж = -{2у[у2 + х2у[у2 - x2yiy2).
г	1 Гз
10.	«2/i2/2 dx = - -(ж2/i2/2 + ж2/12/2 - 2/12/2) + ж у[у2
II.	2/ dx = ху -у . 12. \yydx = -y.
I # *2	JL	#	#2	о о	I	о	X #	в
13. 2/ ^ж = ^B2/ 2/ + Ж2/ -жгу). 14. жгу dx = -(у у - ху
J	6	J	о
15. жгу 2/ ^ж = -гу .
1Й Г ,2	1 Г / ,	1 2\	2 ,2	'
16. ж г/ dx = - \3\xy у --у )+жг/ - ж ^
J	^	^	J
tn Г22,	1 Го Z' '	1 2Л	2/2. 32]
17. ж 2/ "Ж = - 2 I Ж2/ |/ - -2/ ) - х у + ж г/ •
J	ь L \	z /	J
. ж22/'|/
18. ж22/'|/ rfx = ™

1.10.1] 1.10. Неполные эллиптические интегралы F{x1 к), Е(х, к) и П(ж, i/, к) 31
-ил Г 2 /2 ,	1/. 2 /	j /2 . 3/2	4 2\
19.	ж у ах = — Dж |/ |/ — 4|/ -\- х у — ж у ).
о л Г 3 2 I	1 /о 2 /	о '2	3 /2 . 4 2\
20.	ж 2/ аж = -(Зж у у — Зу -ж у + ж 2/ )•
г»ч f 3 / i	1 / о / . 3 2 . 3 2 /2 . 3 21
21.	ж |/ у ах = - I -Зж2/ у + -у + -х у +х у \.
J	о V	z	А	1
1.9. ИНТЕГРАЛЬНЫЕ ФУНКЦИИ БЕССЕЛЯ Л„(х), НЕЙМАНА Yiu(x)
И МАКДОНАЛЬДА Kiv(x)
1.9.1. Интегралы вида \ xaJiu(x) dx.
\
dx =
«/г!,(ж)±
ztz I/	zl ztz
2.	ж ^Jiy(x)
J
Г i/	ж1/+1	217	/ 1\
3.	xv Jiv(x) dx = 	Jiu(x) H	^тг Г ( i/ H— J ж[^(ж)Н1/_1(ж) — ^_1(ж)Н1/(
4.	J*2n(^) dx = xJi2n(a:) + xJo(^) + —[^(ж)Но(ж) — Jq(x)H1(x)] — 2
J	n
5.	Ji2n+i(«) с?ж = xJi2n+i(x) — Jo(x) — 2 ^ J2k(%)-
iu(x) 1
Г f Yiu(x) 1
1.9.2. Интегралы вида ж°Ч ^ , ; > dx.
2±,
2. j ж1±1/Уг4ж) da; = j^YiAx) ±
. j ж1±1/Уг4ж)
. j x1±uKiv(
см. в 1.9.1.1].
3. j x1±uKiv(x) dx =
1.10. НЕПОЛНЫЕ ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ
F(x, к), Е(х, к) Ш П(ж, i/, fc)
1.10.1. Интегралы по аргументу х.
X
Г	1
1. sin xF(x, к) dx = — cos xF(x, к) -\	arcsln (A; sin ж).
J	к
Г	л/ i\ i • n/ i\ l*i /1 ~ k2 sin2 x 1 * i	/ 1
2.	cos xF(x, k) dx = sin xF(x, к) + у Arch W	—	 — — Arch	I ^^^
J	А;	у 1 — к	к	\ у 1 —
3.	\sm2xF{x, к) dx = -^[(A;2 sin2 ж - l)F(a;, Л) + ?(ж, Л)].
4. [iHLE^a,, fc)t/a: = itg2a;F(x, fc)
J cos ж	^
^a,, fc)t/a: = tga;F(x, fc)+
cos ж	^	л (l — Aj J
/	I
i sin x „, , ч ,	1 „, ,4	1 „/ /	7ТГ	vl-^2 sin^ x
5. 	F(x,k)dx= 	F(x, k)	p=rln Vb^tga: '	v
1 cos ж l ;	cos ж l ; J\ - k2 l
6. \^^LF(x,k)dx =	— F(a, A:)-ln ctg<c +
sin ж	sin ж	*

32
Гл. 1. Неопределенные интегралы
[1.10.1
7.
8.
9.
10.
11.
12.
14.
F(x, k) dx = tgxFix, k)
- к2 y/l - к2 sin2
- Jc2 sin2 ж
, *) d* =
1-А;
- Ш
yl-г sin ж
., Щ d<r.= -=-[*-
-
(ж, A;) dx =
\/l - A;2 sin2 ж
F(x, k) dx =
v 1 "~
F(ж5 к) -
— In | л/l — к2 tg ж -
Fix, к) + In ctg -.
2
sin 2ж
2ж
{x> к) dx = -FF^« k) ~
	—^rn;F(x. к) dx =
Fix, k)
arctg
X
15.	sin xE(x, k) dx = — cos xE(x, k) -\	-[A; sin ж у 1 — к2 sin2 ж + arcsln (A; sin ж)].
J	Jttb
о
x
16.	Ш8
ж, A;) dx = 81пж
Г	/2
— \k cosx^/l^k2sm2x -(I-k2) Arch \ Г ~ k* S1f X -k
2,k	у 1 л
Arch
1 —
17. [ %/l - к2 sin2 ж Е(ж, A;) dx = \e2{x, к).
, A;) dx	F2(ж, Jfe)E(Jfe) . во[Р(х, к)]
=	Ь in
in ¦
19.
у 1 — fe2 sin2 ж
= k-2[B - k2)x + k2 sinxcosx - 2E(x, k)y/l- A;2 sin2 ж].
|	1	( j
20. sin жП(ж, и.	к) dx = — созжП(ж, i/, A;) H	.	arctg I \
J	л/к2 -и	\ V 1
о	v	\
к2 - и
- к2 sinz ж
21.	= — cos жП(ж, i/, A;) H
Arth
1-A;2 sin2 ж
\v > к2}.
L	J
22. созжП(ж, и, к) dx = шжП(ж, и, к) - /(ж) - /@),
2A - и)(и - к2) + A - i/sln2 ж)BА;2 - v - ик2)
21/^A - i/)(i/ - Jfe2) cos ж д/l - к2 sin2 ж
П

1.11.2]	1.11. Полные эллиптические интегралы К(А;); Е(А;) и П ( —, г/, k J	33
[A -!/)(!/ -*2)<0].
1.10.2. Интегралы по модулю к.
1.	lkF(x, k)dk = Е(х, к) - A - k2)F(x, к) + (\/l - fc2sin2 ж - l)ctgx.
2.	1кЕ(х, k)dk = - [A + к2)Е(х, к) - (l-k2)F(x, к) + {л/l - к2 sin2 x -l)ctgar].
J	о
3.	[ш(ж, i/, k)dk = (к2 - 1/)П(ж, i/, А;) - F(x, к) + ?7(ж, А;) + {\/l - к2 sin2 х - l)ctga?.
1.11. ПОЛНЫЕ ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ K(fc),E(fc) И пГ-, i/, fe
k2f j K;f( 1
1.11.1. Интегралы ви д а [ jfca(l - k2f j K;f( 1 dk.
J	I E(A;) J
. lkaK(k)dk = Ja, Ja = -^2 {(a - IJ Ja^2 + A;a[E(A;) - a(l -
+1
2' 2' 2 ' ' 2
1 • fc2 1
 ^	,
Ji = E(A;) - A - ife2)K(^),	J3 = i[D + к2)Щк) - A - A;2)D + 3A;2)K(A;)],
J5 = —[F4 + 16k2 + 9fc4)E(ife) - A - jfe2)F4 + Ш2 + 45A;4)K(A;)].
2.
/« = —:	т{(а - 1J/«^2 - А;"^^ - Jfe2) - 2]Е(А;) - k^fl - fe2)K(ife)},
а(а + 2)
v2' 2' 2 ' ' 2 '
/5 = т^гг[F4 + 16fe2 + 9к4 + 22Бк6)Щк) - A - Jfe2)F4 + Ш2 + 45A;4)K(A;)],
1575
[A fe)K(^) 2Е(Л)],	/_4 ^l[2(^ 2)Е(Л) + A - k2)K{k)].
3.
J 1 — к
4. |
5. I Y^nk) dk = -±[(k2 - 4)K(fc) + (к
2
6-	J A _ fc2K/2K(fc)dk = 7=fr[R(fc) ~ E(fc)l-
7-	J (i -1K/2E<fc>dk = 7T=W[ik2 ~1)K(fc) + E(fc)]'
1.11.2. Разные интегралы, содержащие K(A;), E(A;) и П( —, i/, A;J.
2.
2 А. П. Прудников, Т. З

34	Гл. 1. Неопределенные интегралы	[1.12.1
Г	kK(k)dk
* J

[Е(к) - A - к2)Ж(к)]2 ~ A - к2)Щк) - Щк)'
5. [ш (-, I/, A;) dk = (fe2 -i/)n(-, i/, А;) -К(к)
1.12. ФУНКЦИИ ЛЕЖАНДРА РДж) И Q?(a?)
При вычислении интегралов, содержащих функции Лежандра, можно использовать
соотношения, приведенные в приложении 11.18, в частности
(г) —
sin (/i — i/)tt
1.12.1. Интегралы вида f(x)P^(x) dx, f(x)Q^(x) dx.
Обозначение:
ЛГA - ,
x
2.
о
4. J(l ± xT'\l T xy-^^RMx) dx = 2v^u)(l ± *)"/2(l T XT
x {(/x - i/ - 1)Я^+1(х) + [Bi/ + 1)Ж ±
5. J(l ± xyl\\ T x)-"/a-"-aR4{x) dx = 2( + 1)A + + 1)(l ± *)"/2(l =F
X [(l/ — fJL-\- l)R^+1(x) ± (fl + V -
T. ilia?) A ^ a?)	tijj(ж) йж = —-, • —гA ± a?) A ^ a?)	x
8. [A - x2)-»/2R4{x) dx = -A - х2у^
x) n(x)ax
Г	о /o i	fl - Ж2Г7
10. A - x Y' Ri(x) dx = ±	o ; o	\Bt/ -

1.13.1]
1.13. Функции Уиттекера MPi(T{x) и
35
12.
13.
dx =
-{[(i/i^ + V-:
—^{[B|/ + 1)Ж2^1]С(
14
15.
. f жA •
A^2)
2Ч-1//2-1
16. j,
17.
- О т М + 1)Д^
1 — ж
Pv[x)dx = -
v(y + 1)
in
1 — ж
1.12.2. Интегралы, содержащие произведения функций Лежандра.
Обозначения: Я?(ж), Я^(ж) = Р^(ж) или <Э^(ж).
. f жС(ж)С(ж) dx = г {[/i2 - (i/ + l)(i/ + жJ]С(ж)С(ж) -
(х) + Д^+1(х)Д^(х)] - (м - ^ - IJ Д^+1
- i/ - 1) х
R»+1(x)R?(x)\ + 2(p-v- IJR»
3.
(j/ + 1)(j/ + x2 ±
- i/ - 1)(г/ ± /х + 1) x [R*(
RSWRZix) dx =
- v - 1) ж [Д^
5.
1.13. ФУНКЦИИ УИТТЕКЕРА Mp>o.(as) И VFP)^
1.13.1. Интегралы вида \хае ах'2Мр,а(ах) dx.
a + (j + 3/2,
[ж, Re (с
1/2) > 0].

36
Гл. 1. Неопределенные интегралы
[1.13.2
оо
. \ха-1е-ах
2аа+1/2жа+<т+1/2 /g + G + l/2, p + G + l/2;-aa;
Х^	2а + 2G + 1 2 \	а + сг + 3/2, 2сг +1
+ e_ar^-^^+l,^+^+l/2J	[ш> Ree) Re(p_a) >0].
3.
4.
5.
6
7.
8.
dx =
. f
J
) dx = ^-jxa ex/2 Mp_
х) dx = 2g .^
das =	1	-
zp + la — 1
p_1/2,a+1/2
(x).
dx = ~
2р + 2G- :
1.13.2. Интегралы вида \хае ax'2WPj(T{ax) dx.
Я?	%J I  / О	I	I 1 / О	г™
. lxa~1e±ax/2Wp,a(ax)dx =
2а
2G
г. j x^e "
Ж
x 2F2
1/2 ^ р ^ сг
1, а + а+ 3/2
2а - 2а
Q . ,arga| <Зтг/2; Re (a + p) <0 . д	р
' 1	Re a > 0	' +
^ = Г
^ a-G+ 1/2, -a-p
f 1/2, 1/2- p-a j
-?T + 1/2, a - cj + 1/21
a — p + 1
. [
Bр + 2о- + 1)Bр -2G
2p
5.
6.
Т.
8.
х-'е^И^+х/а,^!

1.13.3]	1.13. Функции Уиттекера MPi(T{x) и Wp^{x)	37
1.13.3. Интегралы, содержащие произведения функций Уиттекера.
Обозначения: UPi(T(x), UPf(T(x) = Мр,а(х) или WPi(T{x).
/ cosp7r\A:Fi)/2 /(a + l)/2, 1/2+ p, 1/2- p; а2ж2/4\
V slncjTri	3 4 V I/2, (a + 3)/2, 1 - G, 1 + G )
2pa2s°+2	A±1)/2 Г 2<т
[
X
-2)(l-4G2)
, 1-p; aV/4
3/2, 2-a/2, 3/2-G, 3/2 + a/ ' a + 2a + l A [V^P"*7
„ /1/2 + p + <j, 1/2 - p + c, (J + (a + l)/2; aV/4
4 V	1 + G, 1 + 2G, 1/2 + G, G + (a + 3)/2
2G, 2cr	1 A/2 + p- a, 1/2 - p^ ^5 (l + a)/2 - а; а2ж2/4
'_l/2 - p + (J, 1/2 + p + d\ 3 4 V	1 - G, 1 - 2G, 1/2 - G, C + a)/2 - cj
. Re (a + 2a) > -1
ж > 0; Re a > -1; ^ v	;
[Rea > 2|Rea| - :
a+ 2a + l	[1/2-p-
o
/ l/z + p + o", 1/^ — p + cj, ^I + ftJ/z + crj —а ж /4 .
X 3^4	I /o _i_ 1_L	\( ¦  '-	' +
\	1 + ZG, 1/Z + G, 1 + G, (J + (tt
0 I а1^2<тжа^2<т+1 2 [ 2cr ] ^ (l/2 + p — cr, 1/2 — p — cr,
l| a^2<j + l [1/2"-P+"<TJ \	1-2G, l/2-G, 1-е, C + a)/2-G
тгаж
x
2(a + l)cjsIn<j7rr(l/2 - p + G)ГA/2 - p - a
+ a)/2, 1/2 + p, 1/2-p; ^а2Ж2
3
2тгра2жа+2	_ (a/2 + 1, 1 + p, 1-p; -а2
3/2, a/2 + 2, 3/2-G,3/2 + G
ж > 0; <
[Rea > 2|Recr| - ]
3. f -
J ж
t/P! ЛжHр,4Ж) ^ = ир,*(х)ир,а(х) + UPt<r(x)Up,
ж	c/p	c/p
4. [-И^><г(я;)Жр>0Г(я;) dx = ^^[WPja(x)Wfl,(T(x) - Шр,а(х)Ш
J x	p, — p
()^() d	U() U'()	U'{)
Г 1
5- J ^
—UPtU{x) — Up,a{
6.	f -^Wp, „(x)»Vp,r(x) dx = 2X 2[Wp,a{x)W'p,T(x) - W'Pta(x)Wa,T(
J X	TO"
f /' &2 — а2 но — pb i/2 — <j2
7.	+	^ +
8. | j i - IJ Up^(x)Up,4x) dx=U + ^^ - \ ) xUPitr(x)UPia(x) -
J x

38	Гл. 1. Неопределенные интегралы	[1.14.1
= (а-Ь)(ЛР-1/2) [^sjl*-(a+b)*/2MP+^-^)WP+,AbX) ~
1.14. ВЫРОЖДЕННЫЕ ГИПЕРГЕОМЕТРИЧЕСКИЕ ФУНКЦИИ
КУММЕРА iFi(a; Ь; ж) И ТРИКОМИ Ф(а, 6; ж)
1.14.1. Интегралы, содержащие iFi(a; 6; ж).
. [ xa^\F1(a; b; ±Xx) dx = ± — 2F2(a, a; a
xi = О, Х2 = х; Re a > О
= х, Х2 = оо; Re A, Re (а - а) > 0 j '
о Г п i-f / 1	\ j	I V (~1)	A ~~ Ь)кХП~	(	ill	ч
J	v	;	^ (l-a)fe(n-A; + l)!
3 1 /j»	- IT7-, ( /7 • /) • <7» I ft ф — TJ ! T*	> 	-	-	 i l^i I fl 	 I?' h' T 1
Г ¦¦¦/ (Л	п\ г ( ITt	JU _|_ 1 Л f	V	7
4.	f^-SFifo; 6; ж) dx = nlxb+n ^ ^^ 	4ji^i(a; 6 + А;; ж).
5.	fiFi(a; 6; ж) dx = ^^1F1(a^l; 6-1; ж).
6.	жа~ iFi(a; 6; ж) dx = 	жа~ iFi(a — 1; 6; ж).
7.	lxb^11F1(a; b; x) dx = ^xb1F1(a; 6 + 1; ж).
? _i _x	xa
8.	ж" e iFi(a; 6; Аж) dx = ±—2F2(a, 6 - a; a + 1, 6; -
J	a
^arJa, 6, 6^ a - aj f Ol	ГГ	xi = 0, ж2 = ж;
[ 6 — a, 6 — о J 11 J	[1ж1=:ж5ж2=:со5 Rg A, ]
Г	^-+3 /_-i\fc + l/-| __ »\ n —fe + l
= ж; Rea > 0	1	1
' Ж J
g
10
11
. Ub+n^1e^xiFi(a; 6; ж) dx = n!xb+ne^x V , ч ) }	rlFi(a + A;; b + А;; ж).
J	~i(b)k(n-k + l)\
. lxb^a^n^2e^x1F1(a; b; x) dx =
^ (a - 6 + l)fc(n- fe + 1)!
12.	f е~Ж1^(а; 6; ж) с!ж = 	^	eMjKiFi(a; 6-1; ж).
J	a — b + 1
13.	f^e^iFifo; 6; ж) dx = |хье"ж iFi(a + 1; 6 + 1; ж).
14.	(V^2e^iFi(a; 6; ж) rig = % _ xb^a^e^x iFi(a + 1; 6; ж).
1.14.2. Интегралы, содержащие Ф(л, 6; ж).
^	а Г 1 	 IjI
1. hca(a, 6; Лж) d» = ± —Г	2F2(a, a; a + 1; 6; Аж) ±

1.15.1]	1.15. Гипергеометрическая функция Гаусса 2Fi(a,b;c;x)	39
= 0, х2 = х: Re a, Re (а - b + 1) > О
= ж, Х2 = со;
\k+l7.n-k+l
/	^ n	' Ж>0;
= ж, Х2 = со; Re (а — а) > О J
к^	п + 1
J	^ (l-a)fe(b-a)fc(rc-A; + l)! l
4.	ж6^1^, 6; х) dx = п!Ж6+п V Т	 > ^^.^(a, 6 + Л; ж).
Г	1
5.	Ф(а, Ъ; х) dx = 	Ф(а -1,6-1; ж).
J	1 — а
1
6. (>^2Ф(а, 6; ж)с!Ж = 7	^1	-Ф(о-1, 6;
J	(а — 1)(а — 6)
ь
7. \xb~1V(a,b]x)dx=-	Ф(а, 6 + 1; ж).
. f жа^1е^ЛжФ(а, 6; Лж) dx = ± — Г Х^& 2F2(a, 6 - а; а + 1, 6; ^Лж) ±
J	а [1 + а - 6J
8
±
= 0, ж2 = ж; Re a, Re (а - b + 1) > 0; arg А < тг .	.
>, ж > 0
xi = ж, ж2 = оо; Re A > 0
Г J
г	^ тп-к+1
. жпе^шФ(а, 6; ж) dx = ~п\е~х ^ —^—	-Ф(а, 6 - А;; ж).
f Ь-а-п-2 -«	Ь-а-п-1 -»^	1
J	l	;	f-f (n-A; + l)! v	;
п+1 fe
11. жь+п^1е^шФ(а, 6; ж) da = ^п!жь+пе^ж V	-^(а + к,Ь + к; ж).
k=i
V 7
^ (п- к-\-1)\
1.15. ГМПЕРГЕОМЕТРМЧЕСКАЯ ФУНКЦИЯ ГАУССА 2Fi(a, Ь; с; ж)
1.15.1. Интегралы вида жа2^1(«, 6; с; ж) da;.
l
c;-xj	a \ c,a + l
xi = О, Х2 = x; Re a > 0
ж > 0
Ж1 = ж, Х2 = оо; Re (а ~~ a), Re F - а) > 0 / '	'
i ах = п\ } ( — 1) +1т	:—, i4t/	. ч /L	гт—2-гц	,	I-
с; ж/	^—J	(n - Л +1)!(а-A;)a,F-л)д. \ с - к; ж /
п + 1
о I а-п-2 о / «, О \ ^^ __,__a_n_i
О» IX
^ (n- ^
a,6\	c-1	/o-1,6-1
} dx =	^
6.
С* ^уэ I	f /1 	 I | / #1 	 ||	I	/S 	 1 * гр
5 JL /	I U JLJlt/ JL J	\ С JL 5 Jy
а^1,6л
c; x J	a — 1 \с;ж

40	Гл. 1. Неопределенные интегралы	[1.15.2
7. lxc~12F1( ttj Ь\ dx = —2Fi(a, b; с + 1; ж).
J	\c; xJ	с у
1.15.2. Интегралы вида \A — x) 2Fi(a, b; с; х) dx .
^стп[с, а + b — с] ^ fс — а, с — 6, /3 ~ а ^ 6 + с; 1-х
[ж < 1; Re^, Re(/3 - а - Ь + с) > б].
6J3 2\
+ 1, 6 - а + 1
ж < 1; Re (a-P), Re F - /3) > 0].
а — к, b — к
4. j()(::) +i
a,b
= n'fl - ж)а+ь-с+п+1 V
5. Kl-sy—W0'6
с; ж
. .а_та_! y^	(^l)fc(c "~ ^)fc	p (а — к, Ъ
^П	^(п-к + 1)\(а-к)к(с-Ь-к)к2 1\с-к;х
6.
Т.
)da;	7^Д^lxJF1(
c\xj	(c-a-l)(c-b-l)K	}	\c-l\x
1.15.3. Интегралы вида жаA — ж) iF\(a, b; с; ж) с!ж .
' Ц	( )^Г	б] //3, а-с+1, Ь-с+1; 1-ж
c\
Aж)	[с, a + 6cl
/З-а-6 + с [ a, b J3 2\ /З-а-Ь + с + 1, с-а-6
2 1 ' ¦; ж
n^^	/	i>\ n — fc + l	/	i i
__ ^	2_ "V ""^ / -| ч jfe~x~- \	I С^ гь } 1^ Ju	j—. $ (Jj Л/ • С/
n+i vc;ж
4. \x	(lж) F(	с!ж п!ж	>	y	F[
J
с!ж = п!ж	> ?Y^2F1[
c; ж/	-^ (п-к + 1)\(а-к)к \ c; x
5. [-1(Г^1(а
)	\c;x

1.16.2] 1.16. Обобщенная гипергеометрическая функция , G-функция Мейера и др. 41
6. \хс~1A-х)а+ъ~с+П2
с; х
= п\A — х
те+1
7.
8. \хс~1A-
9.
10.
11
c; x
е;
c; ж
(п-
а + k, b + к
^ fa + k, b
с; ж
= -xc(l-x)b-c2F1(a+l'b).
с	\с + 1; х)
a + 1, 6 +
с + 1; ж
I с+п —1/-I	\а —с —п —1 г-? I Q") О \ j
. ж	A — ж)	2-Г11	\ ах =
J	\с; х)	П4
-I о	с —а —п —2/-i	\а+Ь™с j-г / ""? " \ »
12. ж	A — ж)	2^11	I dx =
J	\c; ж/
= rj.lr
13.
14.
- х)
а+ь~с+п
a, b
n+l
а, „ ,
аж =
с; ж/	с — а — 1
a + k, b + k
a, 6 + A;
с + &; ж
a + A;, b
c; x
a + A;, b
l)\{c-a-k)k2ri\ с; х
с; ж
1.16. ОБОБЩЕННАЯ ГИПЕРГЕОМЕТРМЧЕСКАЯ ФУНКЦИЯ
pFq((ap); (bq); ж), G-ФУНКЦИЯ МЕЙЕРА, Е-ФУНКЦИЯ
МАК-РОБЕРТА И Ж^ФУНКЦИЯ ФОКСА
1.16.1. Интегралы, содержащие р^((%); (^д); ж).
2 1 /у7 Г/"л V (h V /^-7»^ /7'г — т» , -, Р * -, ((п \ 1 • (h \ 9- z1^^
J
fe=l	1=1
1.16.2. Интегралы, содержащие G-функцию Мейера.
II rna /^iTnn I _~, V Р/ I /7т» — т»а f~2-<m' ^"
\°ч)
1 — а, (ар\
{bq), -a
-Ъкф 1, 2, . . . ; к= 1, . . . , ш; 1= 1, . . . , щ Rea+ min Re Ьл > 0; 1) с*, ж > 0, | argc| < с*тг,
1 ^ j ^ m
или 2) с, ж > 0, с = 0, р= q, Re /j < 1, еж 7^ 1? или 3jc, ж > 0, с =0, р= qr, Re д < 2, еж = 1,

42
Гл. 1. Неопределенные интегралы
[1.16.3
или 4) с, х > 0, с* = О, р> q, Re [(p — д)а —/х] > -3/2; с* = га + те — (р +
9	Р
3=1	3=1
at + 1, п2, • . • , ар
с р Gpg I еж
3
4.
5. | x~bqG™qn I ex
p_i), ap
— 1, 62, • • • ,
[n < p].
[w ^ 1].
[m < q].
1.16.3. Интегралы, содержащие iiJ-функцию Мак-Роберта.
X
1. [ жаЕ((ар); Fq); еж) d» = -xaE((bq), -a; (ap), 1 - а; еж)
р	р+1
3, -1, -2, . . . ; j = 1, . . . , га; Re I 2а - Y] а^- + У] 6j
1)р + 1 > д, ж > 0, |argc| < (р - д + 1)тг/2, или 2) р + 1 = q, с, х > О .
Г	1-
2.	ж ар?/((ар); F9); ж) dx = —ж apiiJ((ap-i), ap — 1; F9); ж).
3.	ж ?/((<2р); (бд)^ ж) dx = ?J((a,p) — 1; Fд) — 1; ж).
1.16.4. Интегралы, содержащие Я-функцию Фокса.
1. /
о
, Ар]
[Ья,
— Ж Лр+1^
СЖ
[1 - a, 1], [ap, Ap
[Ья, Bq], ha, 1]
х > 0; |argc| <
p
q
E
i=m+i
>0 .
1.17. ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ ЯКОБИ И ВЕЙЕРШТРАССА
1.17.1. Интегралы вида \ f(snu) du .
г	1
1. snn и du = 7	ч—о en ii dn и snn™3 и +
J	(п — 1)^2
, (n^2)(l + fe2) Г п^2 п^8 Г п^4 ,
+ /—\\i2 \ш и du^	—ч sn и du.
f du _ -1 enwdnw (n - 2)A + Jfe2) f du	(n - 3)k2 Г dw
J snn г* n — 1 sn71^1 ii	n — 1	J snn^2 и	n — 1 J snn^4 и '
3.	sn гх dtx = -z- In (dn гх — к en гх) = — Arsh j к —	—^— j = — — In (dn и + к en гх).
4.	sn2 ti dix = — [гх — E(amu, k)].
f	1	1 + к2
5.	sn3 и du = —— en гх dn гх -\	of 3 In (dn гх — к en гх).
6.
ln
sn«	en ti + dn и
= ln
2k3
dn ix — en и

1.17.2]	1.17. Эллиптические функции Якоби и Вейерштрасса	43
_ Г du	cnndnn	_,	. ч
7.	—-— =	Ь и — Kfamn, k).
J sn^ и	sn n
8.	—-— = —rj[k сп и dn и + A + ^2) In (dn и — ken и)].
J SO U	An,
f dn	—1	en w dn
a + snn)n (n - 1)A - a2)(l - ife2a2) (a
Bn - 3)A + Jfe2 - 2Jfe2a2)a Г	dn	(n - 2)A + k2 - 6k2a2)
(n - 1)A - a2)(l - k2a2) J (a + snu)^1 (n ~ 1)A ~ a2)(l ~ k2a2) } (a
2Bп^Ъ)к2а	Г	dn	(n - 3)Jfe2	f	dn
(n- I)(l-a2)(l-ife2a2) J (a + snn)" (n - 1)A - a2)(l - k2a2) J (a
.' dn	q=l	enndnn (n™l)(l™5^2) [*	dn
I / -I	I	\ «-.	/^	-« \ / -I	I О 4 / -<	I	\ «-.	'
(lisnw)" Bn^l)(l^ife2) (lzbsnn)" Bn^l)(l^ife2) J (lisnn)"^1
dn	(n-2)^2 Г	du
Bп-1)A- к2)
du	dilc	cnndnn	(n ~~ 1)E — k2) [*	du
13.
1.17.2. Интегралы вида /(cnn)dn.
f 1
1. cnn и du = 7	г—г snndnncnn~ n^
cn n dn + -—;— ч, о— I cn n dn.
Г fJ/ll	1	ST1 11 Яп 11
2.
(n-l)ife2 J	(n-l)A;2
dn	1	sn n dn n
cnn n ~ (n -
2	dn	(n-3)Jfe2 Г dn
3.	cn и du = y- arccos (dn n) = — In (dn n — ik sn n) = — arcsln (A; sn n) = — arctg	.
J	к	к	к	к	dn и + 1
г	1
4.	сп2 и du = — [?J(amn, A;) — A — к2)и].
5.	сп3 и du =	— arcsln (A; sn n) -\	 sn и dn n.
J	An,	An,
Г du	1 . \/l — k2 sn n + dn n	1 . dn и + \/l — k2 sn n
6. 	 =	- In	 =	- In	r^=^=	.
J cnn y/\ — k2	cnn	y/l — k2 dnii- \/l-fc2 snw
f 4	1 snndnn	1 _.	I4
7.	—r— =	r^	И-	^^(amn, A;).
cn2 n 1-r спи	1 — Jfe^
dn	1 snndnn	1 — 2Ar , \/l — к2 snn + dn
I	%JSJ %JU	-ft-	KJ л. л. %JU \Л. л. J. %JU	-J-	AaA S ft/
' rf^ = 2A - ife2) cn2 n + 2A - ' оч° /о П '
П

44	Гл. 1. Неопределенные интегралы	[1.17.3
_ Г du	.	Л snudnu
9. 	 = и — Elamu, к) ±
J 1 ± сп гг
и Elamu, к) ±
1 ± сп гг	1 ± сп и
1.17.3. Интегралы вида \ f(dnu) du .
1.	dnn и du = 	sn и en и dnn^3 и +
J	п-1
(п-2)B^к2) Г , те^2 , (n-3)(l-fc2) f, п
+ ~	'- dnn 1udu-	 dnn
п-1	J	п-1	J
2.	dn и du = arcsln (sn it) = am u.
3.	dn2 и du = E(amu, k).
г	1
4.	dn3 и du = - [B — fe2) am w + fc2snucnw].
Г dи	1	cnu	1	. sn и
5.	 = /	arccos	 = t	arcsin	.
J dnu y/\ - k2	dnu Vl - k2	dnu
Г du	k2 snucnu	1 _.	. ч
6.	—г— =	7^—i	+	r^E(amu, k).
J dn и	1 — к2 dnu	1 — к2
m Г du	1	Г _2ч	л/1 — ^2 sniA — спи _2 /^
7. —5— = —;	очо /о B — А; ) arcter ,	к v 1 —
8. —j-^— = — L - E(am и, А;) - СП ^	 .
J 1 ± dnu k2 I	snu	J
1.17.4. Интегралы вида /(sn«, en и, dnu) du .
1. Я(зпп5 спи, dn и) du =
= Ri (sn и) du + Д2 (sn и) сп и du + Д3 (sn и) dn и du + Д4 (sn и) сп и dn и du
\R1 R\, R2, R3, Д4 — рациональные функции своих аргументов].
2.
г	Г / It \
3. Дз (sn и) dn и cin = Яз (	^ 1 —
2t	2
sn ад = 	—-, сп и du = —
2
2t 2
sn-u; = 	-, dn ад аи =	 at. t =
1 + t2	1 + t2	cnu
5.	| sn и сп и du =	-dnu.
к2
6.	I snu dnu du = — спи. 7. \ cnudnu du = snu.
4. Я4 (sn и) сп и dnu du = R4 (x) dx	[x = sn ад, dx = сп ад dn ад du].
Г
J
. sn и dn и du = — спи. 7.
8.	sn и сп2 и du = —-- A — fe2) Arch	+ A; en и dn и \.
9.	sn и сп и du = —^ [arcsln (ksnu) — к snu dnu].
10.	dn2 usnu du = — A — k2) Arch ,	— Аг сп и dn и .
г	1
11.	sn2 и en2 и du = ^r^r [B — fe2)?(am и, A;) — 2A — k2)u — k2 snucnu dn u].
J	OK

1.17.4]
1.17. Эллиптические функции Якоби и Вейерштрасса
45
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
28.
30.
31.
32.
33.
34.
35.
36.
37.
sn ixdn и du = ——г \{2к — 1)Е(ати, к) + A — к )и — к sn и сп и dn гх].
9	9
i cn и dn и du =
3k2
[A + fe2)iiJ(amt?, A;) — A — к2)и + 1г2 впгх cn tidn гх].
du =
спгь
впгх
dnu
¦In-
спи	2л/1 - к2
/1 — 1г2 — А; сп гх
dnti
- arctg ¦
к спи
¦ arctg -
k2
к2 — 1
спи . . 1 — dnu 1 . 1 — dn и . snu
	 аи = in	 = — In	 = in	.
snu	snu	2 1 + dn и	dnix + 1
спи .	1. 1 —A;snix 1, l-\-ksnu 1, 1 + ^ sn и
	 аи = ——in	 = — In	 = — In	.
dnu	к	dnu	2k 1 — ksnu к	dnu
dnu	li
	 du = - in
en и	2 1 — sn и
snu . 1 •
= In —
- sn и
dnu . 1 . 1 — спи
	 du = —in	 = In
sn и	2 1 + cnu	en и
спи
snu
спи
dn2 и
du =
du = In
1 — k2 snu + dntt 1 .
	— arcsin (A; sn u).
спи	к
snu
dn2 и
спи
sn и
dn2 и
en и
sn2 и
dnu
du = In
— к Arch
en и + dn и
snu	l*i
	 Arch
en и + dn и к
dnu
du = к arcsin (к sn гх) + \/l — Is2 In
1 dnit
du =
1 — к2 спи'
1 спи
1 — к2 dnu
dnu
du =	. 27.
du = —
snu
спи
спи	snu
аи =
29.
snz гх
cn гх dn и
sn гх
snu dnu
спи
snu спи
dn гх
спгх
snu dnu
snu
cn гх dn гх
dnu,
snix
du = In sntt.
1
dn2 и
dnu
du =
dnn,"
snu
du = In ¦
en ti
, = ^— In dnii.
TV
du = In ¦
1-k2
In
dnu,
du = In
sn it en ix	en ti
е/гх =
[sn гх dn и
du = —
1 JU2	r
JL — n> I I
cn и dn гх
sn tx
, k).

46	Гл. 1. Неопределенные интегралы	[1.17.5
n
sn и ,	1	Гж-,/	,ч / ,9ч , 9 sn и сп и 1
d	^(	fc) A fc2) А;2.
J
du= TVT\	Пп ^(атгл, fc) - A - fc2)u - А;
Г dn2 и ( 2\ cnudnu (	I4
39. —-— du = A- к )u	Eamu, k).
J SO2 U	EIIU
dnii J
СП U .	1 Г	_.	1Ч , 2 SI1 ti СП 111
40.	—~— du = —т \и — Е(ати. к) + к 	 .
J dn1 и	к2 L	dn^ J
Г dn2 и .	—.	1Ч snttdnti
41.	—-— aw = и — Е(ати, к) -\	.
J en2 и	спи
1.17.5. Интегралы, содержащие эллиптические функции
Вейерштрасса.
Обозначение: С (и) — эллиптическая функция Вейерштрасса.
f п/
1 JP {
4Bn-l)
3.
4.
,	^^	-1	р'{и)	Ц2п-3)а
5.
и) - p]» (n - 1N [p(«) - p]" 2(n - 1N J \p{u) - p]"
6Bn - 4)a f	dw	2Bn - 5) Г
J [p(«) - p]" ~ (n - 1N J '
(n - 1N J [p(u) - p]" (n - 1N J [р(м) - p]"
a = 4p2 - -g2, b = 4p3 - g2p - gz Ф 0 .
f du _ -2	p(u)	8(n - l)
- l)a [p(u) - e]n Bn - l)a J [p(u) - e]^1
du	Г	2 1
[ = ^--g2
du	-2 pf(u)	4
О	V	/
— e 3a р(ад) — e
. C(^)

Глава 2. ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
2.1.	ВВЕДЕНИЕ
В этой главе содержатся определенные интегралы от специальных функций, не вошед-
вошедшие в [17, 18].
Интегралы, у которых один из пределов интегрирования является переменным, в слу-
случаях, когда подынтегральная функция от него не зависит, помещены в главе 1. Отметим,
что многие интегралы, не вошедшие в эту книгу, могут быть вычислены с помощью метода,
изложенного в главе 8, или же получены как частные случаи интегралов общего вида из
разделов 2.24—2.25. Указанные в формулах условия сходимости интегралов обеспечивают их
существование либо в обычном смысле, либо как несобственных интегралов, либо в смысле
главного значения.
Некоторые формулы при частных значениях параметров теряют смысл, так как в пра-
правых частях возникают неопределенности; раскрытие неопределенностей позволяет получать
формулы, справедливые при этих значениях параметров.
В начале разделов, как правило, помещены интегралы общего вида, у которых аргумент
одной из подынтегральных функций зависит от параметра г > 0. При рациональных
значениях г правые части равенств выражаются через обобщенные гипергеометрические
функции. Пример такого преобразования приведен в [18], 2.1.1. Некоторые частные значения
интегралов общего вида помещены среди формул последующих пунктов.
2.2.	ГАММА^Ф?НКЦМЯ Г(ж)
(См. также [18], 2.2.)
2.2.1. Интегралы по пря мой G — *оо, j + гоо).
Другие интегралы вида
Г(ад-+ a,-a)r(bfc?„«)«
см. в 8.4.
Г тпг	11	п -п Ul "I" ^15 О\ Н~ ^2 j 0,2 ~~Ь Ь\. U2 '
1.	F[ai + s, «2 + s, oi — s, 02 — sj as = 2тггГ
[- Re ai, - Re a2 < 7 < Re 61, Re 62; см. также 8.4.49.20].
7+ioo
7+
f r\ai + S' tt2 + S' bl ~ S] J - -p[(ai + fol)A a2 + 6ll
J L ! + tti ^«2 -61 + s J	[l-a2 + (ai-b1)/2\
[-Reai, -Reo2 < 7 < Re 61].
7+ioo
3. f
J
-\-d — 1, с — a, d — b
7 —ioo
[- Rea < 7 < Reb; Re(a + 6 - с - d) < -1; см. также 8.4.49.19].
J |_	fti~h a,2И™ d3~\~bi~{-s	J	|_	/i — fti, /1 — 0-25 Л- — 0.3	J
7 —ioo
[h = a\ + u2 + «3 + bi; — Re ai, — Re «2, — Re аз < 7 < 0, Re h\].

48
Гл.2. Определенные интегралы
[2.3.1
7
Г гГа + з, 1 + а/2 + s, 6 + s, с + s, d + s, 6 — а — s,
J [	а/2 + s, 1 + a-c + s, 1 + a-rf+s
j _
Гб, с, rf, 6 + с - a, 6 + rf - a!
гГ
7+ioo
[-Re a, -Re a/2- 1, -Re 6, -Rec, -Red < 7 < Re F- a), 0].
_
7+
Г Га + s, 1 + a/2 + s, 6 + s, с + s, rf + s, e + s, / + s, b — a — s,
J [a/2 + s, 1 + a-c+s, 1 + a-ci+s, 1 + a-e + s, l + a™/
_ ._,
6, с, rf, e, /, 6 + с — a, & + rf — a, & + e — a, & + / — a
l + a — d^e,l + a — c — e,l + a — c — d,l + a — с — /, 1 + a — d— /, 1 + a — e^
7+ioo
-l; - Re a, - Re a/2 - 1, - Re 6, - Re c, - Re d,
- Re e, -Re/ < 7 < Re F- a), Ol.
J
7
7. f
J
s, C2 + s, . . . , cc + s, ai — s, с/2 — s, . . . , do — s\
А	В
min Re bk: A, B. C, D = 0, 1, 2, . . .;
0 ^ |argz| < —E (при ?J > 0) или | argz| = -^|при E > 0 м jA + Rei/	< -1
или arg z = 0 (при E = 0, А ф 0 и 7А + Re v < 1/2)
илиarg2; = 0 (при Ё = А = 0и Rei/<0,z^l или Re 1/ < — 1, z = 1)],
f 1 - fei, . . . , 1 - Ьв, ci, . . . , cc
j A+D K
[А > 0 (или А = 0, \z\ < 1)],
[А < О (или А = О, \z\ > 1)],
[z = (-1)А^С, А = О, А > С, Rei/ + С - Л + 1 < О].
2.3. ОБОБЩЕННАЯ ДЗЕТА^ФУНКЦИЯ ?(s, ж)
2.3.1. Интегралы от /(ж)?E, а + 6ж).
со
L. жа C(s? а Н~ ^ж) ^ж = ^ аВ(о!, s — q)^(s — о, а)	[а, 6 > 0; 0 < Rea < Res — 1].
1
2. [ ж
J
_¦/ \ cosec —
41 (s)	2
3. sin 2ttx((s, x) dx =
J
2.4. МНОГОЧЛЕНЫ БЕРНУЛЛ1 Bn(x) Ж ЭЙЛЕРА Еп(х)
2.4.1. Интегралы от f(x)Bn(x).
1	a+l
1. I Bn(x) dx = Sn,o. 2.	Bn(x)dx = an.
[0 < Rea < Ree - 1].
[1 < Re 5 < 2].
3.

2.4.2]	2.4- Многочлены Бернулли Вп{х) и Эйлера Еп{х)	49
о	\	k=o '
1/2
f Гзт2тшгж1	, ч , (/ 1ЧП Bn-J)!	Г
5. <	>B2n~s{x) dx = dz( —1) -у	 \2п~<5	га, п ф 0, 5 =
о
1
6.	<	}Вп(х) dx = О	К
J [ cos тжх J	LI ^t- + n — нечетное
о
l
_ Г f sin гитгж 1 _ / ч ,	, / - xn 1 + (™l)m Bn — ё"
7.	<	>152п^5(ж) dx = ±(—1) 	7:—-—7^	гтг^
J [СО8 1П7ГЖ]	2	(fTl7r)in"
0
1
0
1/2
9.
\cosBw
-1/2
2.4.2. Интегралы, содержащие произведения
многочленов Бернулли.
1/2
1. [ Вт{х)Вп{х) dx = (^l)m+1 m!w!. |oBm+n	[m, тг^О; m + n-четное].
J	(m + n)I2
о
1
2
. [ Вт(ж)Вп(Ж) da; = (^l)m+1 m'n' Bm+n
J	(m + n)!
о
n
3. Bm(x)Bn(x + a) dx = (-l)m+1anmln\ Y^ 7	—7	гтт^т+л	[т, п Ф 0].
J	^ (m + A;)!(n - A;)!
0	fc=i
4 }в2 (ж)В2 (х + -У) dx = 2(B2 (x)B2 (x^) dx= З2"^1-! Bт)!Bп)! ^ +2
о	о
1/2	[m, n^O].
5. В2то+1(ж)В2п+1 ( ж + - I б?ж = 2
ж + - I dx =
_ 1 - 22m+2n+1 Bm + l)!Bn + 1)? p
" 22-+2n+i ^Т2^Т2)Г 2
6. I Bm(x)Bn(x)Bp(x) dx =
.p+i |Г\-Гг /w\ /m\l (m + n-2.
P 7 w , + n\ , 1 7
/ ^	\*)Ь )	\9^/ (то 4- « 4- -n
L	\ dLifb /	\ jLa Fb / J \ i i I/ \^ § fa \^ U
U	A	\	l	l г
m n " ' - *	' m\~\ (m + n — 2k — 1)\
г m
7 1П
[nfc ^ 0; fe = 1, . . . , m].
г	m	1
pi, . . . , pm > 0 — целые попарно простые числа; N = FT Pk', Пк Ф 0; А; = 1, . . . , га .

50	Гл.2. Определенные интегралы	[2.4.3
2.4.3. Интегралы от f(x)En(x).
1
1. \хтЕп{х) dx = 4(^1)теBт+п+2 - 1) т1^1 Вт+п+2 +
о	т_Л
+ 2(^1)птЫ У 7	^——
Г	еа + 1 /	n+1 2к - 1
2.	еаш?/п(ж) с!ж = (™1)п	т^- I a*h — — а — 2 ^ ———акi
{	аП V 2 *=i Л-
1
f f sin ттгж ]Л/Ч1Л	ГГт + п^ четное
3.	<	>Еп(х) dx = 0	к
J [ cos гятгж J	|_ l ш + п — нечетное
о
2{^l)n+8Bn
i dx =
1 sin Bm + 1)*х )E^W dx = [Bm + l)vfn
0
5. sec7TxE2n^i{x) dx = (—1) ^ 2—2n | f ( 2n + 2, — J — Q ( 2n + 2, — ) |.
о
2.4.4. Интегралы
i
. J Em(x)En(z) ЙЖ = 4(
2. j B()B( + ) d 4AГ«Ы ^	~
. t^_-,v v " —-^о*(т + Л + 2)!(п-А)!
1
3. \ Bm(x)En(x) dx = 0	[ra + n — нечетное].
О
5. j B () E() d
0
2.5. ПОЛИЛОГАРИФМ Li^jc)
2.5.1. Интегралы общего вида.
' — г	°° / i\k Г /_ , i.\ /„ 1
к
(ас)
кп 1й + 1а + А;)/г I
fe=i
[г, Re^ > 0; Re a > -1; |ас| < 1].
[riRe/3>O;Re(a+/3r)<r;|argc!<7r;
_г_д.г^7Г
"Г^	^Г Lin(—еж) rfa; =	^> ^ ч 7 Г I 	 J Г ( р —
о	^=1
pr — а \~~^ (— 1) (p)fc(p^* — С^ Н~ ^^) П / \rfc
"" 7ГС	? 	гг^—т	;—\	\cz) [г > 0] —1

2.5.2]
2.5. Полилогарифм \ли{х)
51
а
(У 4- кг — а
(У 4- кг — а)п
Esin(Q_r_fcrOr(C2/)	Г»"' V > О; -KRea<r; |argc|<^; |cy|< 1].
J	v
00 / 1\fc
0; Re a > —1; | arg c\ < тг].
7 ce_1/sin6a;r\
J Ж \со56Жг/ nl
_
1
тг A/2 + 5) Д 2C
sin [(а- А;)тг/Bг)]1 / 6
f co
B, Bm)! I 2
sin[a7r/Br)]
if lnT' ±
fe! \lnT
_y-,(n-A;-2m-20 /^
!	\ r
(n - к ~~ 2m ~~ 21)
см. в 2.5.1.5; 6, r > 0; —1 — Sr < Re a < r; | arg c\ < ж, ё =
7.
— UJb j LiifiX—CXI (IX —
sin (a-\-kr)n \c'
. , , cosec	тг
kn \OL-kJ	r \cr
k/r
(=0
(-f)
^	A;! \ol) 4^ g!(n-p-ife-9-2/)!	V r,
[r > 0; -r-KRea <0; | argb|, | argc| < тг, \b\ < \c\r, At см. в 2.5.1.5 ].
2.5.2. Интегралы от А(х) Lin(—еж).
1. \ ха 1 Lin( — еж) с/ж = . 	с а	[-1 < Rea < 0; | argc| < тг].
о
а
0
X п+2^п+1(« + 15 1, 1, • • - , 1; « + /3 + 1, 2, . . . , 2; —ас) [а, Re/З > 0; Re а > -1; |argc| < тг].
со
Q	а — ~^-(	\@ — ^ Т * /	\ /-/

52
Гл.2. Определенные интегралы
[2.5.3
а, ЕеД > 0; Re (а + /3) < 1; |argc| < тг].
a + l, p-a-l)n+2Fn+i(a + l, 1, 1, . . . , 1; 2 - р + а, 2, . . . , 2; cz) +
n+iFn(p, р - а, • • • , р - а; 1 + р - а, . . . , 1 + р - a; cz)
< тг].
5.
(р - a)nsin(a - р)тг
[—1 < Re a < Rep; |argc
1лп(-сж) dx = 7rc|/Q:ctga7rn+iFn(l, 1, . . . , 1; 2, . . . , 2; -cj/) -
A — a)n sin an n
2.5.8. Интегралы от Л(х) Li2(—еж).
а
Г	/ Т
' J Х	12\а
аА I о
а
dx = —	> 7
п2	6 /-^i к
L	k=i
2.	\xn~1U2(-
J	va
о
а
Г	/ X \
3.	Ы2 ( — J <iiZ?
J Va/
о
. I 1 /ж\ 1 I тг'а
7	V2" Li2 ( — ) dx = — —т	:
о
5. f ^^ Li2
J ж + z
4тг
Jz
fl, 1 - a, . . . , 1 - a; 2 - a, . . . , 2 - a; -cj/)
[t/ > 0; | Rea| < 1; |arge| < тг].
[а > 0; Re a > -1].
[а > 0].
[а > 0].
[О < а < у].
| argc|, | argz\ < тг].
т ( а\ 1, 2/ а
- Li2 ( - ) - - In2 ( 1
2 V 2/
2.6. ОБОБЩЕННЫЕ ИНТЕГРАЛЫ ФРЕНЕЛЯ 5(ж, i/) И С(ж, i/)
При I/ = 0 обобщенные интегралы Френеля S(x, i/), С (ж, */) сводятся к интегральным
синусу и косинусу,
5(ж, 0) = -si (ж), С(ж, 0) = -с! (ж),
а при I/ = 1/2 — к интегралам Френеля,
s
соответствующие интегралы см. в [18].
2.6.1. Интегралы общего вида.
Обозначение: S =
xl
>.
(а + ^ + J + 2А)/г 1/ас
/ +
а ч	f sin (i/tt/2)
r'^ U)\cos(i/jr/2)
[a, r, Re a, Re/3 > 0; Re(a + г/) > -S].
(-1)"
\ 2
2k

2.6.1]
2.6. Обобщенные интегралы Френеля S(x, и) и С(х, v)
53
(ac)rk
(ac)rk(l - p)k^(a + v + r/3 - r - rk) f sin [(a + и + r/3 - r - гк)тг/2]
k\{r — r/3 — a + rk)
cos [(a + v + r/3 — r — г^)тг/
3.
о
X
S) и)
с, v)
гГ(р)
[а, с, г, Re^ > 0; Re (а + r/3 + i/) < г + 2].
X
\ fczx
)\2)
_сгр-а?
fc=O
(^l)fe(cz)rfc(p)fcr(a + i/ — rp — r&) J sin [{a + i/ — rp — гк)тг/2]
k\{rp — a + r&)	\ cos [(a + i/ — rp — гк)ж/2]
4.
xr - yr
r	\r ' ' r J ч ' [cos(i/7r/2)
[c, r, Re а > 0; ^<5 < Re (a + i/) < r Re p + 2; r| arg z\ < тг].
C g
r	^ «'A/2 + djfe(d + и + Zk)	r
^a V^ (c2/)rfcr(a + г/ - r - r&) / sin [(a + i/ - r - г^)тт/2]
cos [(a + и — r — гк)ж/2]
г/2) 1
r/2)J
J
С (ex, v)
[с, r, t/, Re a > 0; ™cf < Re (a + i/) < r + 2].
[c, r, Rep, Re a > 0; Re (a + v) > -S],
2fc
r(a/r)r(i/)fsin(i/7r/2)
\cos(i/7r/2)
(a/r)r(i/)fsi
rp«/^ \co
L Ь
U(r) = —
sin [(a +1/
17A) см. в 2.6.3.1.
6.
C(cx, v)
(
+
Г(
и)Г(-а/г) a/r f sin (i/tt/2) ] 1 у, Г(а + ^ - rfc) f sin [(a +/. - rfcOr/2] ]
r	P \cos(i/ir/2)J c"^ fcl(a-rfe) \ cos [(a + ^ - rfe)ir/2] J l
7.
[COS 0Ж
[c, r, Rep > 0; Re(a + ^) < 2].
[b, c, r > 0; Rea> -<5r; -?r - 1 < Re (a + i/) < 1 + max (r, 1)],

54
Гл. 2. Определенные интегралы
[2.6.1
2к)ж/Bг)]
2к Г(и)Г(а/г) i/-7 /sin[a7r/Br)]
Н	i 7	COS — "'"
cos [атг/Bг)]
2с"
U(j) при r = 1 см. в 2.6.4.1-2.
8. \ x <	r >СЧеж, i/j <
J	[ cos ож J
[6, с, г > 0; Re a > -<5r; -5r < Re (a + i/) < 1 + max (r, 1); [/G) см. в 2.6.1.7].
9.
с, г, Re а > 0; -1 < Re (a + i/) < 2,
argz < тг
z > 0
_k\(S-
cosec [(a + v + 7 + 2^)тг/г]
ctg[(a + i/ + 7 + 2feOr/r] J V 2
zr ~ (=pl)fcr(a -\-i/-r-rk)
л/ 4- 9&Vrv 4- i/ 4- л/ 4- 9^Л
z"w.,u™T-I'Jcosec(a'r/'')
2 [ ctg(air/r)
1 — a)
rF(a + 1/) 7 — a — i/
—	 cos J	тг
2aco;	2
-	^	^тг	2 In с
10.
• J
с, r, Re a > 0; 0 < Re (a + u) < 2,
5(сж, i/) dx = W(l)
z I < тг
z > 0
, 1/G) см. в 2.6.1.9 .
[6, c, r, Re a > 0; Re (a + /ir) > -5r; Re (a + 1/) > -1; Re (a + /zr + i/) > -1 - <5r;
Re (a + fir -\- v) < r + 1 + max (r, 1); при r < 1	замена х = t1' r]
l/-4-'Y	°°	/ -1 \ к
C^1	^"^	( —1)
i/2)fc(a + 1/ + 7 + 2A;)(i/ + 7 + 2k)
хГ /x
a + v + 7 + 2k\ ( sin [(/if + a + */ + 7 + 2А;)тг/Bг)] \ f с
cos [(/xr + a + 1/ + 7 + 2А;)тг/Bг)] J V261/
Г(|/)Г(/х + а/г) i/-7 f sin[(/xr + aOr/Br)]
7-7-7-	COS - TTs
при r = 1 см. в 2.6.6.1-2.
12.
13.
2 [ cos [(/xr + а)тг/Bг)]
[6, с, г, Re a, Re (a + v) > 0;
Re (a + fir) > -6r; -Sr < Re (a + /zr + v) < r + 1 + max (r, 1); ^G) см. в 2.6.1.11].
[с, r, Re 6, Re a > 0; Re (a + u) > -(!
(-1)*
pfr) = 	Г	 \
1 } fe(«+-+5)/r Z^ д.!^ + i/2)k(a + 1/ + S + 2ife)(i/ + <5 + 2Jfe)
r	/ \261/r/	a6a/r \ cos (i/ir/2) J

2.6.1]	2.6. Обобщенные интегралы Френеля S(x, и) и С(х, v)	55
, ,	b ул T{a + v + r + rk) / sin [(a + i/+ г + гА?)тг/2] 1 ( _Ъ\к
^ ~ са+г ^ kl(k + lJ(a + r + rk)\cos[(a + i/ + г + rk)n /2] j \ cr J
f i/) f sin \(a + и)ж/2] 1 Г_. г	. ,	ч . гж Ti a + i/ . c
^^Ч г,	ч , С	\-гф(а + 1>)±—tgT	тг - In —
•а X cos [(а + 1/)тг/2] / [ а ^	' 2 6	2	6
1 ас" I cos [(a + и)ж/2] j |_ a ' r v ' ; 2 °	2
P(l) см. в 2.6.7.1.
oo
14. [ ха~1е±ЬхГ Ei (т&жгM(сж, */) с!ж = Q(l),
c, r, Re а > 0; -1 < Re (a + i/) < r + 2, J ' аЩ ' <
L ь > о
J cosec [(a + i/ + 7 + 2к)ж/г] 1 / с \2fc ттГ (г/)Г (a / r) j~u ( cosec (атг/г) 1
r__a 00 . Iin/	. v	.	/ r \ fe
с ж~^ Аг!Г(а + г/ — г — rk) oi + u^r^rk^'y I с \
-\	— У, 	—7	 COS 	Ж 1	Г	Lr > 1],
1 ir^ Г(а + i/ + rJc) a + 1/ + rk — 7
ca ^^ k\(a + rk)
k=Q	l	;
1/+ rA) + — tg	t-ff + in —j \±—j [r < 1],
QG) при r = 1 см. в 2.6.7.3-4.
CO
15. [ ха^е±ЬхГ Ei (т&жг)С(сж, i/) fe = Q@)
c, r, Rea > 0; 0 < Re(a + i/) < r+ 2, i 'arg	i, ^G) см. в 2.6.1.14 .
l ь > 0 j	j
arg	i,
ь > 0 j
16. f ж"! Si ffH }s(cx7 u) dx = X(l)
J	I ci (bx ) J
0
x
[6, c, r, Re a > 0; -1 < Re (a + 1/) < r + 1 + max (r, 1)],
,(a+i/+7)/r Z-^ kl(j + 1/2)лA/ + 7 + 2A;)(a + и + 7 + 2A;)
sm[(a + i/ + 7 + 2JfeOr/Br)l 1 / с \2fe Г(г/)Г(а/г) v - 7 f sin [атг/Bг)] 1
afeQ;/r	2 [cos[o;7r/Br)] j
r(l + 2<5) ^ (A; + l)!C/2 + ё)к(а + Sr
x cos ¦
a + ?/ + or + lr + 2r« — 7 ( 0
.OJ 2ac« C°S 2 *	['
Л"G) при г = 1 см. в 2.6.8.1-2.
[6, c, r, Rea > 0; 0 < Re (a + u) < r + 1 + max (r, 1); ^G) см. в 2.6.1.16].

56
Гл.2. Определенные интегралы
[2.6.1
f Re a > -r; -r - 1 < Re (a + */) < 2] ,	,	1
c, r > 0, <	.	4V	;	L arg6 < тг/4
1	Re a > 0; Re (a + i/) > -1	j '	' 7 J
^ + 7
г ^ А;!G
хГ
и) а + I/ -
У G) при г = 1/2 см. в 2.6.9.3^4.
20.
1/+7
[6, с, г >0; Rea > -
> -
Re(a + i/) < 2],
^ к\A/2 + 7)fe(^ + 7 + 2А;)(а + i/ + 7 + 2А;)
2ife 1\ J sin[Ba + 2i/ +27+ 4ife+ г)тг/Dг)]
+ 2/ 1 cos [Bа + 2i/ + 27 + 4Jfe + г)тг/Dг)]
Or/Dr)]
)тг/Dг)]
а +1/- 7
{1) ~
(^l)fcr(o + 1/ + 6r + r/2
при г = 1 см. в 2.6.10.1-2.
DA; + 2J + \){Ark + r + 28r + 2a) X
	^	^тг f — J
21.
[r < 1],
[6, c, r > 0; Re a > -r(S + 1/2); -r(J + 1/2) < Re (a + v) < 2; ^G) см. в 2.6.1.20].
С' Г '	'
Re fj,, Re (a + /xr) > 0; -1 - г Re /x < Re (a + t/) < 2
Re a,
> 0; Re (a + i/), Re (a + /xr + 1/) > -
= ±-
v + 7
хГ
7 + 2k)
a

2.6.2]	2.6. Обобщенные интегралы Френеля S(x, и) и С(х, v)	57
Е kKlt + fc)(a + lir+rk) cos	г	4
R{"i) при г = 1 см. в 2.6.11.1-2.
zs. x ^ ^f^ ^_rx fLj{cx, и) ах — щи)
о
c,,,Re6>0,(
iR, Re(a + /xr), Re(a + i/), Re (a +/ir + и) > O
{S(CX h>) 1
C{cx,v)\
Обозначение: ё = < >.
1	\	(а + 1/) f sin [(a + 1/)тг/2] 1 г
4 \)	[ '*} c, Rea>0; -
C(cx,v)\	aca {cos (a + i/)tt/2
1- Jx<x *
о
2. \ха^г(а-xY^l	' \dx = -~
J	[С(сх, и) J
, ) J	i/ + d
о
2 ' 2	2 ' 2 ' А' 2 '^'	2	'u ' 2' 4
[a, Re а, Re^ > 0; Re (а + i/) > -E
B 0,
С(сж, i/)J 2(i/+ J) V	2
о
i/ + <5 a + i/ + ^ i/ + <5 . _ a + i/ + ^ . 1	а2 с2
x 2^'з I 	, 	;	\-l, 0 -\	, 8 + -;
2 2 '2 2 '2	4
! T a-V	ч/3-1
. жа1ж^«Г
J
i/ + о
, 1-a-^-i/-J) x
sin [(a + P + i^Ot/!
1-/3	/3 l-a-/3# 3-a-/3 3 - a - ^ - i/	a +'/3 + i/ 1ш а2 с2'
2 ' ~2"'	2 '	2 '	2	'	2 '2' 4~
ac2^a^/3(l -^)r/a , a , ^ _ 2ч f sin l(a + ^ + v)
2 — a — p	\ cos [(a + /3 + i/)
^ 3^/3	a + /0	« + /5	a + /3 + i/ З-а^/3-i/ 3_ a2c2
2 ' 2 '	2'	2'	2'	2	' 2' 4
, ... i	[a, c, Re^>0; Re(a + i9 + i/)<3].
ч cos (i/Tr/2) J
-, {is-\-S a + u + 8 у+ 8 . „ a + i/ + <5 _ 1 a2c2
x2F3f^-,^	;^- + l,/3+	j	'5+2;-^

58
Гл.2. Определенные интегралы
[2.6.2
I'1"*
6.
2'2^-
v+8 a+v+8-p
р 1 + р р —¦ ol	р -— а	а -\- и -— р \ — а. — v -\- p 1
1+р-а v
р 1 + р^а 3 + р^а 3 + p^a^i/ 1 а + i/^p З c^z
^'	2 '	2^ '
2z2
В (a, p-a)r(i/)
/-' f S(cx, v)
4
COS I UTT I ?)
,	, 1, ;
[c, Rea>0; -S < Re (a + u) < Rep + 2; |argz| <
p
x2F3
1	,
, 1- P+
5 . t 1
2	2
Ip — а
T{a+u-2p x
a	a
2' P; "+1" 2'
'
;
8.
ctg
2-1;
{sin [(a + и)ж
cos [(a + и)ж
/2]
2 ' 4
а л а + I/ 3^a^F
COS A/7Г/2)
2 '	2 '	2
[с, t/, Re а > (
9.
2	2
_ _, i; 2 - -, 2 -
ctg
атг , .Г sin(i/7r/2) 1
2 ^j\cos(i/7r/2) J
3 - a - и с2у2
	; - —
[с, У, Reo > 0; -tf < Re (a + v) < 4].

2.6.5]	2.6. Обобщенные интегралы Френеля S(x, и) и С(х, v)	59
2.6.3. Интегралы от хаерх
;}¦
С(сж, I/)
Обозначение: S = ,
jl. x e \ ^,	, / ax —	. . c / . ^ч x
J	Г
\с(сж, j/) j	?( )
0„ (v + 8 a + v + 1 a + v . v + 8 t . . 1 с2 \ , Г(аI» Г sin (un/2)
X 3F2 (^-,	, —j- -M; __ + 1, * + -; -_j +	{
[с, Rep, Re a > 0; Re (a + v) > -S].
¦ \xa~1(
¦"• \ X	G	\ „,	. / OiX — „ / ¦ , c\ in. /	r»\ A
2
+ 1 л+I. _C^ . r(i/)r(a/2)/sin(i/ff/2)
I Г sin (i/tt/2) 1
"\cos(i/tt/2) J
oo
2 '	2 ' 2 ' '" ' 2'
[c, Rep, Re a > 0; Re(a + v) > -S].
5(сж' v) V j™ _ - г	_Г | _
Г(а + i/) Г sin [(a + i/)tt/2]
2 ' " ! 2' 2 ! ' '	2 '4
a	a	a -\-1/ \ — a. — v <?%
2' x 2'A	2 '	2 ' 4 ;^ 2 Al^;A V 2У\со8(|/тг/2)
[с, Rep > 0; Re (a + v) < 2].
a Г Sin &Ж 1 f S(CX. u) 1
2.6.4. Интегралы от а;	><	ч>.
[ cos ox j i 6 (еж, v) J
Обозначение:
. f a-1 J 31П&Ж 1 ,	,	( ,
1. ж < , >Я(сж, I/) ^ж = 17A)
J	[cos Ьх J
о
[6, с > 0; —S - 1 < Re (а + i/) < 2 при 6 ^ с, -J - 1 < Re (a + i/) < 1 при 6 = с],
= crCa + iz + T)/ sin [(a + и + 7)^/
1 }	6a	\
= Ь*Г(а+ i/ + J)f sin [G - a - |/)тг/2] 1	[0 < с < Ц,
l7j c«+5(a + ^) \cos[G-a-i/Or/2]J
2
J
f r"^1) smox \п(гт v\ (It — U(ft)
J	[cos Ьх J
[6, с > 0; -5 < Re (a + v) < 2 при 6 ф с, -5 < Re (a + i/) < 1 при b = c; 17G) см. в 2.6.4.1].
S(cx, и)
it х- я	/я
I In .1! — Z 11
2.6.5. Интегралы от х л ,	n ^.	. r.
In |ж — z j { С (ex, v) J
111
Обозначение: S =
0
^-v /1 — -""V	IJ —4— <"\/	Ai —4— I J —4— -"V	#
cosec |(a + i^Ot|
VG) = -(Tl)^2 7^с"-|-уга+|<+1' f.
V" V ^ (»/ + 7)(a + i/ + 7)\

60	Гл.2. Определенные интегралы	[2.6.6
25 2 + lj	2+
1-а 1 3 3-а Ъ-ol-v
—- г' 1; 2' —' ~^—
с,1 с2г2>\ 2?Г(а + 1/-
М + 2; ^^rj T с«-1A-а
Г ' ' ' Г	2 '	2 ' 4
х
°?	МпГ-,+ ,П	x^na + ^-.tg	—--'
2.
атп/ ч I/— 7 fcosecaTr] Г(а + i/) a + i/ — 7
ГЫ cos —^тг<	> Н	~-	 cos	ltt
v ;	2 [ ctgaTT J	2aca	2
0
c, Rea > 0; 0 < Re (a + u) < 2, <j 'arg2:' K П\, V(j) см. в 2.6.5.ll.
2.6.6. Интегралы от ж ^ \ ^; H ^}	7, >.
Обозначение: S =
[6, с, Re a > 0; Re (a + v) > -1; Re (a + /1) > -5; Re (a + /z + 1/) > -5 - 1;
Re (a + /z + 1/) < 3 при b ф с, Re (a + 11 + 1/) < 2 при 6 = с],
а + /i + 1/ + 7) [ sin [(a + /i + 1/ + 7)тг/2]
1
(^ + 7) 1 cos [(a + \i + 1/ + 7)^/
a +/i + 1/+ 1 a + /i + v	a + j/ + 7
+7;
1 c\ ГA/)Г(а + /х) 1/-7 fsin[(a + /xOr/2]l
7 + -; 7^- M— ;	— cos	L?r< L_; ; ' \ \ о < с ^ ь ,
f 2' б2/	об"	2 \cos[(a + tiOr/2] J L	^ J'
br(a + ^ + i/ + ^) [sin [(a + /x + 1/ - 7)тг/2]
l7j	c«+M+5(a + fj + <5)(/i + 5) \ cos [(a + /i + и - 7)тг/2]
1 Л ВДГ(^ a+^ fSinH2)l
2' 62/	aca	2	\cos(/xtt/2) J	L	J
0
[b, c, Re a, Re (a + 1/) > 0; Re (a + ц) > -8; -S < Re (a + /л + v) < 3
при b ф с, —S < Re (a + /it + i/) < 2 при 6 = с; VVG) см. в 2.6.6.1].
2.6.7. Интегралы, содержащие EI (—Ьхпл J ^1^ '
. ж Ei( — Ъх){ „)	[ } dx =
Обозначение: 8 =
[ U J
1 с\ Г(а)Г(|/) / sin (i/tt/2)
' +2; ЬУ	\
2 ' 2 +; 2 + ' 2 + ' +2; ЬУ	аб" \ cos (i/tt/2)
/ sin (i/tt/2) |
\ cos (i/tt/2) J

2.6.8]	2.6. Обобщенные интегралы Френеля S(x, и) и С(х, v)	61
[с, Re b, Re a > 0; Re (a + v) > -S].
2
I	Л2
, + м + ;
0; Re(a + „) > -Я
[ (/) J
3. [ j'-'e* Ei (Tbx)S(cx, v) dx = Q(l)
[c,Rea>0;-KRe(a
+ t/ + 7) f cosec [(a + */)тг]
]
ctg[(a + i/Or] /
+fc(l-a)	"°^ff.F, ^1, 1, 5, ;
3-a 3-a-i/ , a + i/ c2\ с2"аГ(а + v - 2) а + гу-
1;J+C°S
'	2'1^;
3 . a _ а л a + i/ 3 —a —i/ с2 \ ттГ(а)Г(|/)
2' X" 2; 2" 2 ' ^^'	;	j^^
4. f ха^ге±Ьх EI (тбж)С(сж, i/) dx = Q@)
c, Re a > 0; 0 < Re (a + 1/) < 3, <j ' arg 6' "^ Ж }, Q(t) см. в 2.6.7.31.
Г si F3I Г,
\ciFx)/\.
OJ"
I	Q~l I ^ \"*^j I n/	\ J	v/i\
I	I Cl I UX II
2.6.8. Интегралы от х
Обозначение: 8 =
1.
о
[6, с, Re a > 0; -1 < Re (a + v) < 3 при b ф с, -1 < Re (а + i/) < 2 при 6 = с],
=	сГ(а + 1/+ 7)	f sin [(a + 1/ + 7)тг/2] 1
l7j 6(«+I/+^)A/ + 7)(a + v + 7) 1 cos [(a + 1/ + 7)тг/2] J
+ 7 a + 1/+ 7 a + 1/+ 1 a + 1/
1. с^ ГМПа)^^ Г«п(Г/2) [0<с,Ч,
2 ' 2	' ' 2' б2/ «^	2
65+2Г(а + 1/ + <5 + 2)	f sin [G - а - */)тг/2]
+ J + 2)B + 8)\ cos [G - а - ^)тг/2]
i/ + <5)J sin [G - а - 1/)тг/2] 1 J 11 тгГ(а + i/) а + 1/- 7
¦COS	7Г,
-a^i/Or/2]J Ц 0 J 2аса	2
i = С	h ^(ск + v)	tg	тг —- In —
ol	2	2	о

62	Гл.2. Определенные интегралы	[2.6.9
[b, c, Re a > 0; 0 < Re (a + v) < 3 при b ф с, 0 < Re (a + i/) < 2 при 6 = с; ХG) см. в 2.6.8.1].
2.6.9. Интегралы от х }	l)
\erfc (bxr)j\c(cx, и) У
fRea>-l; |Re(a + i/)| <21 . Ll	.1
> 0, <	к агеб < тг/4
3f3 (	V1
5—, -V1. ^ + 7; —5-^ + 1. -^ +
^г (SLtl) cos fll^, + ( ! }
OJ
л . Rea > -1/2; -3/2 < Re (a + i/) < 2 .	.
1	Rea > 0; Re (a + i/) > -1	Г	'
yG) = ±
Обозначение
Г	f Rea > -1/2; -1/2 < Re (a + i/) < 2] ,	,	, -/4	1
c>0J	oo/ , wn	[, arg6 <тг/4; УG cm.b2.6.9.3
L	I	Rea, Re (a + v) > 0	J	J
егралы
: ? = < >.
2.6.10. Интегралы от xa{ ) [ \{ ) ' ; \.
\C[bx) j [С7(сж, v) j
0
[6, c>0; Rea>^™l/2; -8 - 3/2 < Re {a+v) < 2 при b ф с, ™<f-3/2 < Re (a+i/) < 3/2 при 6 = с],
+ и + 7 + 1/2) /sin [Ba + 2i/ + 27 + 1)тг/4]
X 4'3 l^-' —г"' 	4	' 	4	+7; 7+2'

2.7.1]	2.7. Функции Струве Н„(х) uLu(x)	63
Г(|/)Г(а + 1/2) i/-7 f sin [Bа + 1)тг/4] 1 Г(а + i/) а + i/ - 7
= 23/У+1/2Г(а + ^ + ,5 + 1/2) Г sin [G - а - v - 1/2)тг/2] 1
Ш 3s0F с"+5+1/2Bа + 25 + 1) 1 cos [G - а - г/ - 1/2)тт/2] J
2a+2i/+3 2a+2i/+l . 2а + 2<5 + 1 . 1 5 + 25 2а + 28 + 5 Ь
[0<Ь<с].
[6, с > 0; Re а > -8 - 1/2; ^ - 1/2 < Re (а + и) < 2 при b ф с;
-Я - 1/2 < Re (а + и) < 3/2 при 6 = с; Z(j) см. в 2.6.10.1].
2.6.11. Интегралы от
( Re/i, Re(a + /x) > 0; -1 - Re/л < Re(a + и) < 2
'	' (Re a, Re (a + /x) > 0; Re (a + v), Re (a + /x + v) > -1
	c~f+lT(a + 7 + fji + г^)	/a + 7 + ^ 7 + ^ a+ fj,+ v+ 1 a+ /i+ v
" 6«+-r+-( + + )( + L/'3 V 2 ' ~2~'	2	' 2^ +7
0
f Re /1, Re (a + /x) > 0; Re ix < Re (a + u) < 2 ) , ч	1
с, Re6>0, <	P /	/	ч ,	Л	к ЯG) см. в 2.6.11.1 .
1 Rea, Re(a + i/), Re(a + /i), Re(a + /i + i/) > 0 J	J
Re /1, Re (а + и) > 0; - Re и < Re (а + и) < 2
2.7. ФУНКЦИИ СТРУВЕ Н„(х) Ш Ъ„
1 3
При и = ± —, dz —, . . . функция Н1/(ж) и прр
к функциям Неймана У^(ж) и Бесселя Ju(x), Iv{x):
13 13
При и = ± —, dz —, . . . функция НгДж) и при и =	,	, . . . функция I^(ж) сводятся
которые при этих значениях параметров являются элементарными функциями. Например,
~2~
тгж [ sin ж J "'"ч ' V тгж
Соответствующие интегралы см. в [17]. При вычислении интегралов от Ь|/(ж) можно
использовать формулу
2.7.1. Интегралы общего вида.
(сх)
о

64	Гл.2. Определенные интегралы	[2.7.1
a + v + r/3-r+l и
7	a + v + rP-r+l v + l Г	о "I
. J ,-V - а')""^^) d, =	y0Fr	Г„ /3/2
Г1
7г
a \^ A — /5)fc	sec [(а + г/ + г/3 — г — гк)ж/2]
k=o K' F(l + ' l " ~ '^ ' "» )r(l +
/ac\rk
\2/
Г ж
3.
2	у \	2
[а, с, г, Re/З > 0; Re (а + г/3) < г + 3/2, г- Rei/ + 1].
""
0	°°	/ 2 2/A4fc
\ ^ ( С Z /4J I **,v i ^ i «^ i j. i ,
X /	:—г	;	;—г—1 I 	 II \ О —
ж /c\rP~~a ir--\ (^l)fc(p)fc	sec [(ск-1-ь/ — гл — r'fcW/?/!	/^r\^fc
rk + rp + v-a\r	rk + rp-v-a\\2
2	/V	2
[c, r > 0; -1 < Re(a + i/) < r Rep + 1; Re (a - rp) < 3/2; r\ mgz\ < тг].
fc=O
/с\г™"^л	sec [(a + и — r — гк)ж/2]	/су\гк
1 2 127 ^^7 rfc + r + F^^| 7 rfc + r^i/^^\ vTJ
"= V +	2	J1 V +	2	J
[с, г, у > 0; -1 < Re (a + i/) < r + 1; Re a < r + 3/2].
T , _ г ГН (ex)}
5. жа e px < УК ; > dx = ?/±(r)	[c, r, Rep > 0; Re (a + v) > -1],
7Г
о
i/+i
1 j 2-^F p(«+"+i)/rrr(i/ + 3/2) ^ C/2)fc(i/ + 3/2)fc
, ±	тг y^ ii;	sec[^a + i/ + r/gj7r/zj	 / z^p_ \
1	г
C/±(l) см. в 2.7.5.2.
СХЭ
6. f ха^1е^рх^Ш1/{
^	3/2)fe
sec [(a + и - гк)ж/2]
ca ^ А?!ГA -{а-и- гк)/2)V{1 - (a + v - rk)/2) \ 2
[c, r, Rep > 0; Re (a + i/) < 1; Re a < 3/2]
oo	#	r
7. f ж"! smbx im Jcx) dx = UM к с, r>0; -1 - 5r < Re (a + i/) < r + 1; Re«<3/2
J	[ cos к J	L	fill
0	при r < 1, Re a < r + 1/2 при r > 1; <5 = < I ,

2.7.1]
2.1. Функции Струве Н„(ж) и ~Lv{x)
65
{Г) ~ 2
(-1)"
F гГ(|/ + 3/2) ^ C/2)*(i/ + 3/2)*
sin [(a + i/ - 2/c - 1)тг/Bг)] 1 /2b1/r\2k 2a+Sr-1nb5
cos [{a + v-2k- 1)тг/Bг)] /	+
J'
17A) см. в 2.7.7.4.
CO
8. [ xa~1J)>(bxr)Ilv(cx)dx = V(r)
0	[b, c,r>
> 0; Re (a + fir + u) > -1; Re (a + u) < r + 3/2; Re a < 2 при r < 1, Rea < r + 1 при г > 1],
(-1)*
•-«-"-2*-
V(l) см. в 2.7.14.1.
9.
a'
J'
[a, c, r, Re/3 > 0; Rea > |Rei/|]
/асч«_
V 2 /
r(^)[7cosi/7Ti4(i/) + 7Л(-1/) ± A - j) sin и ж A(±u)],
10.	[
0
oo
11.	| xa~1{xr - a
a
3 А. П. Прудников, Т. 3
) - bv{cx)] dx = W(Q)
L c, r, Re/3 > 0,
> 0
-Rea - 1 < Re i/ < Rea
dx =
r	1
W/	J
[a, r, Re /3 > 0; Re (a + r@ + u) < r + 1; | arg c\ < тг],

66
Гл.2. Определенные интегралы
[2.7.1
?SC/2)*(i/ + 3/2)*
Z\2k Cr~Cr~a(cOSU7T
A - /3)fer((a + 1/ + /3r - r - rk)/2) ('a - и - r + f3r -
1 + Я	frW/91
xsm
12
СХЭ
. f xa~1(xr - arf^[I±1J(cx) - Lu(cx)] dx = X@)
[a, r, Re/3, Re с > 0; Re (a + r/3 + i/) < r + 1; ^G) см. в 2.7.1.11].
13.
W;
+ 3/2)^-Q Wt)k
xnP--" + a^ + 1)(Ci)
[г > 0; | Re v\ < Re a < Re (rp — v) + 1; r| arg z\ < тг; | argc| < тг],
« (_1Ot
k\
[7 cos unD{u) + 7Z)(—!/¦) dz A — 7) sin i/7rD(zbi/)],
г ¦
r, Rec > 0; Re(a
L
15.
- L»(cx)} dx = Y(Q)
<1, '	Re(a + ,)>0
x у
dx =
< тг; У G) см. в 2.7.1.13 .
J
[r, 3/ > 0; I Re v\ < Re а < r — Re 1/ + 1; | argc| < тг],
k	2h
> + 3/2)
S
(cy\2h_
"" V 2 7
а - v - г - rk)/2)
х sin
2r-a+i7r
in1 ^	тг (^J
cos [(а + г/- г - гА:)тг/2]
fe=O

2.7.1]
2.7. Функции Струве Ми(х) и Ъи(х)
67
16.
;[1±и{сх) - Lu(cx)] dx =
г, у, Rec > 0; Re (a + i/) < r + 1, <|	"" v^ ' " ; " "	1;
V	;	\~Rea~ 1 < Rei/ < Rea j
см. в 2.7.1.151.
J
Re (a + и) > О
a - 1 < Re v <
17. (* ха~1е~рхГ[Уи(сх) -Н„(сж)] da = 17A)	[r, Rep > 0; Rea > |Rei/|; |argc| < тг],
о
Ufr) = -t
-y^ rT{u + 3/2) ^
n^c/r
"[7 cos utiF{u) + jF(—v) ± A — 7) sin i/7rF(±i/)],
> 1],
» (_!)* r((a + v + гА)/2)Г((а - v + rfe)/2)
2s k\	coSi(a + v + rk)n/2]
l-a-i/)/r
/тг Г(|/ + 1/2)
18.
19.
da; = {/@)
г, Re с, Rep > 0,
Re (a + v) > О
1	r	1
J V/	J
- Re a - 1 < Re v < Re a .
dx = V(l)	[r, Rep > 0; |argc| < тг; Re (a + v) < 1],
2fc
(-1Г
^ rV{u + 3/2) ^ C/2)fc(i/ + 3/2)fc
Г -
cp
(cosi/тг)
(l+7Tl±7)/2
?¦
A;!
cos [(a + i/ — г&)тг/2]
cp
2fe
20.
21.
r	/ \ 2
ж)] dx = V@)
[r, Rec, Rep > 0; Re (a + v) < 1; 1/G) см. в 2.7.1.19].
6, г > 0; | Re v\ - ёг < Re a < 1 + r - Re 1/; | arg c\ < тг, 5 =
0/ '
,*) = —.
(-1Г
3/2) ^ C/2)fe(i/
x cos ¦
2r
-[7 cos vttI{v) +7/(—i/)±(l —7) sin i/7r/(zbi/)],

68
Гл.2. Определенные интегралы
[2.7.1
х cos
Г((а + v + <5r)/2 + гк)Г((а - и + <5г)/2 -
cos [(а + и + г<5 ¦
22. I* Z sin 6жг
6, г, Rec > 0; Re(a + i/) < г + 1,
Re (a + z/) > -r
-1-r-Rea < Re i/ < Rea
rJ V ;	J
23. ха~ cos bxr[I±l/(cx) -Lu(cx)] dx = W@, 0)
о
6, r, Rec > 0; Re (a + i/) < r + 1, I	Re (a + i/) > 0	.	в 2.7.1.211.
V	;	Ч-1-Rea < Re i/ < Re a f l/ ;	'
24. f ж" ^(
[6, r > 0; | Re i/1 - r Re/i < Re a < 3r/2 + 1 - Rei/; |argc| < тг],
f?V+1	L
V27 r^AFrfi/-
3/2)
^ C/2)*(j/ + 3/2)* [l + (/xr - a - i/ - 2k - l)/Br) J V b1/r
2«/r-i
(-«/) ± A - j)si
2jk\2 )k
2 )k
ria + lir^jLt^l Lit
oo
25. xa^1
[б, г, Rec>0; Re (a+i/) < 3r/2 + 1,
dx = X@)
Re (a+i/+r/i) > 0
см. в 2.7.1.241.
wy	J

2.7.3]
2.7. Функции Струве Н„(а?) и Ь„(а?)
69
2.7.2. Интегралы от ж"Н|/(сж).
2
со
1. Н^(сж) dx = --ctg
J	с
[с > 0; -2 < Rev < 0].
[с > 0; Re а < 3/2; |Re(a + i/)| < 1].
[c>0;Rei/>-3/2].
2.7.3. Интегралы от xa(z ± ж)
3 3 а + /3 + f + 1 а
2> "+21 	 2	'
2 ха~~1(х — а)^~~1Ш
' J
а
I	гу -Х- и
х 3F4 1, 1 +
!
[а' Re/3>0; Re(a
2^V^	L^ + ^A -a - ^
2 ' 2
; 1 +
3	3 aV
-, -, i/ + -; --
+ Т7 «
2	2	' 2'	2' 4
cosec [(a + /3 + и)ж /2]
2 V27	Г(C - а - /3 + 1/)/2)Г(C - а - /3 - i/)/2)
~ "У V2/
2' 2'	2	'	2	'4
2^«^	A - /3) sec [(а + /3 + */)тг/2]
ГB - (а + ^ - ^)/2)ГB - (а + /3 + i/)/2)
/3 3-/3 3 о а + ^
2-
2' 2 ' 2'	2 ' "	2 ' 4
[а, с, Re /3 > 0; Re (a + C) < 5/2; Re (a + /3 + i/) < 2]
x 3F4 1,
2 ' 2
+ 1;
, 1 +
'-Р 3 3	c2z^
тг /су
X
2	' ~ '	2 ' 2' 2
sec [(a + ^ — р)тг/2]
ГA + (р + «/ - а)/2)ГA + (р - «/ - а)/2) ^
х 2F3 ( ^, ^; 1 + ? + р^, 1 + ^-^, i; -^
р cosec [(а + i/ — р)тг/2]
Г(C + р + у - а)/2)Г(C + р - i/ - а)/2) Х
>-г/-а 3 c2z:
' 25 4"
4.
2 ' 2 '	2	'	2
[с > 0; -1 < Re(a + i/) < Rep + 1; Re (a - р) < 3/2; |argz| < тг]
З + i/-а 3-1/-а с2|/2
1/ ^ а)/2)Г(C -u^ a)/2)
г 2\;

70 Гл.2. Определенные интегралы	[2.7.4
	8ес[(а + 1/)тг/2]	 Л • 9 - а ~ ^ 2 - а + ^ • с2|/2
ГB-(а-у)/2)ГB-(а + у)/2) 1 2 \ '	2 '	2 ' 4
[с, 2/ > 0; -1 < Re (a + i/) < 2; Re a < 5/2].
2.7.4. Интегралы от xa(z2 ±
2"+1>/5РГ(|/ + 3/2)
2.	х1~и(а2 — ж2)^3"
°	[а, Re^ > 0].
3.	ж17 (а — ж )
. .«/(ас)
[а, Re^ > 0; Re v > -3/2].
„+1, 2^ 2r,-l/2fH,fe)] ,	, C"^1 „/1	\ fl —
о
[a > 0; -3/2 < Re i/ < 1/2].
5. [ Х"+* (а2 - ,2)—
21/+1^тга [ shac
[a > 0; -3/2 < Re v < -1/2].
6. [ /"Ух2 а2)/3^1Н|/(сж) dx = Да+1/+2^-1' t/+1
x 2F3I1, 	^^; 	^^+/3, 77, ;
_^ 2^
2 "'	2
a, Re/3 > 0; Re (a + 2/3) < 7/2; Re (a + 2/3 + 1/) < 3].
-2^	„I/-2/3+1
sIn/Зтг ГC/2-^)ГC/2 + 1/-
_	Г	— I// 2	2 \y0 — 1тт /	\ j 	 -	«•	^
' • I	V	U j	МГЖ. 1/\^L,Ju J ttJL —	; ~	„ /„ m	^»ч Т-. /~ JTI '.	^»ч X
|	^	J)	Ia' c>0; 0<Re/3< 1; Re (i/ - 2/3) > -5/2].
[a, c> 0; 0 < Re^ < 1/2; Re B/3 - 1/) < 3/2].
i. ж (ж — a ) M.t/(cx) ax = —z	- [sinp7rJ_i/_/з(ас) + cosi/Trrl^+^g^ac)]
J	c^ cos (/3 + i/)tt
[a, c, Re^ >0; Re A/+/3) < 1/2; Re A/+ 2/3) < 3/2].
10. [ ж"+1(ж2 -
[а, с > 0; Re v < -2n - 1/2].

2.7.5]
2.7. Функции Струве Ми(х) и Ъи(х)
71
11.
dx =
"г- f1	\ г2 (аС\
[а, с > 0; |Rei/| < 1/2].
[с, Rez > 0].
= ^—cosec
л (-г
iF2 I 1;
3-i/
-, ——; —
?*&	dmi>	4k
[c, Rez > 0; |Rei/| < 2].
В
•I/ + 1. 3 3
' 2' 2
15.
16.
17.
18.
1 + P	2 '1 + Р	2 ' 4
[с, Rez > 0; -1 < Re (а + i/) < 2Rep + 1; Re (а - 2p) < 3/2].
тгс^1^1™^17	cI/+1z3^2p Г р — 3/2
Wl(^) +	2 + 2	Г
хЛA;^^+^
[с, Re z > 0; Re p > 1/2; Re Bp + и) > 1/2].
p-i i+i/-p
[с, Re z > 0; Re (i/ - р) < -1/2; Re i/ > -3/2; Re (у - 2p) < -1/2].
XlF2 1,2-—,2-—,
(rp I л/7.2
[с, у > 0; -1 < Re (а + i/) < 3; Re a < 7/2].
/7Г Z "•" ' Г Г2	/TZ\	Г2
-^—.	 sh^r ^+1/2 ( ^rHch^
/c sin 1/7Г L I	\ A J	A
2.7.5. Интегралы от xae
ae px< ^z
[c, Rez > 0; -2 < Re i/ < 0].
Л = In
. с
, В = arcsin -,
p {Rep> | Rec| jj'
=±
/ = 2 f 2 ±
2 7Г ^ С
2p2
c2Jp2±c2 \B)I '
13 =
4p2 2c2
с/ж =
i/+ 3/2

72
Гл. 2. Определенные интегралы
[2.7.6
1,
3 с2
-1].
3. - е р < ; ( } dx = Jn	\A = In -
J ж	I ьп(сх) J
/p2 + с2 + с D	. с fRep>|ImC|i]
	, В = arcsm —, <	> ,
р	р {Rep> ] Rec| J J
л = т- 11-
7Г
±с2
с2 ( А
со
ж «	I Ж С	1 i ?/ I CX J CX еД
п+1/2
п+1/2л/р2 ±с2
Р
[Rep > | Rec|; Re v > -1/2].
Г Г Rep > |Imc|11
LlRep> |Rec|jJ"
±2 f Н^(сж) 1
2.7.6. Интегралы от хае рх < ^	>
ж=AГ15—^
3 3
L ^ + 3/2 JX
[Rep > 0;
2.
3.
4.
5.
L,(cx)
^) erf
dx
2^+2р3/2Г(|/ + 3/2)
2
c»r(l/2 + v]
dx =
exp
/ 1
\ 2
> -1].
[Rep > 0; Re и > -3/2].
[Rep>0].
[Rep > 0].
^ + 3/2 J
1; 2'" ' 2'
3 a + i/ + 3> c2p
2 ' "T"
a — i/	a + is с р
[c, Rep > 0; Re a < 3/2; Re (a + v) < 1}
2.7.7. Интегралы, содержащие тригонометрические функции
и Ни(сх).
-1/2
Г	2	2
1.	81п6жНо(сж) с/ж = (с — h ) +
о
CO
2.	созбжНо(сж) с/ж =	(б2 — с
J	7Г
-/2 1,24-1/2 1 С + VC2 - б2
= г (с - И 1п	1
2
7Г
[6, с> 0; Ьф с].
[0 < с < 6],
[0 < 6 < с].

2.7.8]
2.7. Функции Струве Ми(х) и Ъи(х)
73
со
3. — cos Ъх Но (еж) dx = < > I
J X	v J V
о
оо	#
4 f та^1} Smbx Iff (гт) dr ~~ II
J	[ COS OX J
/с2 - Ь2
О < b < с
О < с < b
-1 - <5 < Re (a + u) < 2; Re a < 3/2 при 6 ф с, Re a < 1/2 при 6 = с; S =
и = ±-
a + i/ + 11 J cos [(a + i/)tt
i/+ 3/2 J \ sin [(a + i/)ir
/2]
/2]
1,1; -,*+-;
[0 < с < 6],
/тг V2
a + i/-l icos[(a + i/Or/2J
i/+ 1/2 J\sin[(a + i/Or/2]
1тг6д sec [(a + i/ + ^)тг
/i 	 а
I1
a + 8-v
1 b2
[0 < b < c].
5.	x v sin 6ж Н1/(сж) dx =
о
CO
f
л	—i/ —1	i тт / \ i	1 n / 2
6.	ж	созожН^Дсж) аж = \/ — (с —
о
7. ж/481п
о
[6, с> 0; Ьф с; Re i/ > -1/2].
8. ж
о
dx = -
4c
8c
9. | ж sin 6ж2Н0(еж) da = -r {sin
10.
S(ip)}
[6, с > 0; Ьф с; Re i/ > -3/2].
[6, с > 0].
[6, с > 0].
[(р = с2/D6); 6, с > 0].
[0 < 6 < с; Rei/ > -5/2].
2.7.8. Интегралы, содержащие логарифмическую функцию
L. ж In
о
со
a — л/а2 — х2 ГНо(сж)
{ ; !
Ьо(сж)
In
2: + л/х2 + z2
1 Г sin ac
sh ас
¦Но(сж) с/ж = —--- е
Ас
[а > 0].
[с, Re г > 0].

74	Гл.2. Определенные интегралы	[2.7.9
2.7.9. Интегралы, содержащие обратные тригонометрические
функции и Н1/(сж).
Г 1	Г/	ч	Ж1 тт / \ »	/ тг . ас т	/ас\
1.	— cos	(и + 1) arccos — Н^ (сх) dx = Л — sin — J^+i /2 —
J л/a2 - x2	V	}	a\ K )	У ас 2 "+1/2 V 2 /
0
[a > 0; Re и > -2].
2.7.10. Интегралы от ж"НмFж±1)Н1/(сж).
со
J	M
dx= ~	v" ^'	М
+ 1/2, I/ + 1/2, /X + I/ + 1/2
и
оо	[с, Re(^ + i/) > 0; Re/i, Rei/ > -3/2].
2.	Г Н^ ( — | Н„(сж) dx = -- J2vBy/bc)	[b, с > 0; Rei/ > -3/2].
J \xj
00
Г 1	fb\	1	^~
3.	-H,;-! — Ши(сх) dx =	-== J2U-iBvbc)	[b, с > 0; Rei/ > -1/2].
J ж	\ж/	V6c
0
2.7.11. Интегралы, содержащие Е1(^6ж2)< ^	>.
I Ь^(сж) J
х
и + 3/2 J
X3F3 A,	,	; -, - + и,	; T^j	[Re6>0; Re (a + 1/) > -1].
2. f жеЬж2Е1(-6ж2)Н0(сж) dx = -^- exp ( ^- ] erfc \-^=\	[c, Re 6 > 0].
J	2o	\4o/	\2vfe /
1. ж егГсFж)< т ; , > dx =
3	3a + i^ + 3 с
¦' 2' ^+ 2'	2 ' TiP
[Re(a + i/) > -1; |arg6| < тг/4].
2. J a* erfc (bv^)| ^gj } dx = ^^Г+Г) Г [ 1/+ 3/2 ' X
3 3
+
с2
; -, I/+-,
2.7.13. Интегралы, содержащие Du(bx){
1 L, (еж)
а +1/ + 1 а +1/ , 3 3	5=Ы ol + v±\l .ее2

2.7.14]	2.7. Функции Струве Н„(ж) и Ь„(ж)	75
Г11	2a+'i-17r6A'
+ l°iC^r(l-a + ^-t/)r(l-Q + /X +
, 1
iRe(<; + ''
|arg
0	[Re(a + i/) > -1; |argfe| < тг/4; |argc| < тг; U-(e) см. в 2.7.13.1].
. f жае^ь2ж2
0
^
X 1F1 I —	; 1+ i/+ —; ^^т^ )	[c, b > 0; Re^ > -1; Re (/x + v) > -3/2].
\	/
2.7.14. Интегралы, содержащие J^(bx r)Mv(cx).
oo
1. [ xa^1JfJ,(bx)Ml/(cx) dx = U
[b, с > 0; Re(a + /x + t/) > -1; Re (a + i/) < 5/2; Re a < 2 при с ф b, Re a < 1 при с = 6],
/-д 3 3
2c	Г (a + /i + i/ + l)/2 1 /
/5Рб°+"+1 L + 3/2 (l +	)/2j3 2 V
2	'	2	5 2'2+i/;
[0 < с < 6]
_2Г^_ \ (a + /x + i/l)/2 1 / 1 1_
^b^1 [i/ + l/2C + /iai/)/2j3 2V '2'2 l/'
2'2 l/' 2 ' 2
с«+м Г[М + 1,1-
[0 < 6 < с]
ею
f,,.._fll 4	/с - 6\	Г Г 0 < 6 < с
j	°	\о/тгF + с) \c + fe/	L10 < с < 6
о
со
3
о
. f х1/2Л+1/2Fж)Н1/(сж) da; = J-b~u~1/2cu(c2-b2)^1/2 [6, c>0,6 ^ c;-3
о
CO
. f жм+1/+1^(&ж)Н1/(сж) с!ж = /	[6, с > 0; -3/2 < Re (/x + i/) < 0; Re (//+ 2i/) < 1/2],
4
о
, ;
[0 < 6 < с],
3 3 2
1
, 1; ;^J	[0<c<6].
5. f жм/+1^Fж)Н1/(сж) dx = J	[6, с > 0; -3/2 < Re/i < min(l/2, Rei/)],
о
_ 2b sin /i7r(c б)	2V	/]
~	СГ()	+ бм+i	[z, + i/2J 2^x ^' 2 ^ 2

76
Гл.2. Определенные интегралы
[2.7.15
о
Т. [
J
. [ x
J
+ ;_
с \4с
da; =	 У^+i ( —
2^	4
9. [ J-v (- J Н„(са;) da; = ^ [si
j	L
10.
+
[с > 0; -1/2 < Re/ix < 1 - Ret/].
[6, с > О; |Rei/| < 1].
[6, О 0; -3/2 < Rei/ < 1/2].
+ - К2г,{2л/Ы:Ц
ж	J
[6, с > O; -7/2 < Re i/ < 0].
Г[/1 + 1, 1+ (il+v- a)/2, 1 + (/x- i/- a
x ,F4 (l
со
11. f
J
[6, с > 0; -5/2 < Re (a + v) < Re /i + 1; Re (a - /x) < 3/2].
2
~~ J0(ca;)Hi(ca;)] dx = — (p2 + c2)^3/2
тгр
12. [ же"рж[Л(сж)НЦсж) - Jl{cx)Wv{cx)] dx = — (p2 +
J	7ГР
[Rep > 2| Imc|].
[Re i/ > -1; Rep > 2|Imc|].
13.
[6, c> 0; -3/2 < Re и < 0].
2.7.15. Интегралы, содержащие YiJj((p(x))Miy(cx).
с < б
}'
СО
2. [ xti->+iYlt{bx)O.v{cx) dx
J
с2 -
3.	f У2„(Ьл/ж)Н„(са;) dx = - Jv [ — \	z— r(i/
J	с \4с/ тг2с
4.	[cos bxJy{bx) — sin 6жУ1/Fж)]Н|/(сж) da; = < >	P^
J [ 0 J v&c
CO
J	V	V	V	,
Г> - il)
[b, с > 0, Ьф с; Re (/х- i/) < 0; -3/2 < Re /lx < 1/2].
l	n/.. i i \ a	I ^__ I
Ac)
-1/2 (
V
[b, c> 0; -1 < Rei/ < 3/4].
с
V26y
26
3	с
X 2Fi ( 1, 2i/+-; I/ + 2; — )	[0 < с < 26; -3/4 < Rei/ < 1/2].

2.7.16]
2.7. Функции Струве Ни(х) и Ъ^{
77
6. x[Jfj,(bx)Jt/-fj.(bx) — У^(Ьх)Уи-1х(Ьх)]Н.и(сх) dx =
x[(c-
(с -
[b, с > 0, 26 ф с; -3/2 < Re i/ < 1; Re /i > -3/2; Re (/i - i/) < 3/2].
К (Ъж)У FжIН (еж) da; =
с
со
7. f
[6, с > 0, 26 ф с; Rei/ > -3/2;	-3/2 < Re/i < 1/2; -3/2 < Re (и + i/) < 1].
oo	2 —3i/ i/ —1
Г 1 —i/r т /i \ т /i \ i/- /i \л/- /i \itt /	\ i	AC	. 2	,,2\у-1/2
L^V / " V /	" V / ^V / J ^ V	/	/ЦГ L 9 fу "П /. . i 1 / О \ ^
oo	[b, c> 0, 26 7^ c; -1/2 < Re v < 3/2].
9. f x[Jl/2(bx) - y^/2(bx)]MlJ(cx) dx = — (c2 - 462)+1/2
о	[6, с > 0, 26 ^ с; -3/2 < Re v < 1].
10 т1/+1Г J2(hr) — Y2(br)]H (rr) dr —
0
[6, c> 0, 26 ф c; -3/4 < Rei/ < 1/2].
11.
= ±
-1/2 J exp(-zVc2 - 462 )
<	26 < с
<	с < 26
, -3/2 < Rei/ < 1 .
2.7.16. Интегралы, содержащие произведения специальных функ-
функций на Уи(сх)—Ни(сх).
г|> + 1/2, 1/2 +а*-1/1 х
1 1
1/2 + i/, 1 + д —
; |argc|<7r; -l/2<Re^ < 3/2; Re (/x-i/) > -1/2].
2^р ^ j fii^p^rv^ /z1»^^	"Н" (f*rriW
т I eiy С/ |/ | С/«Х/ J J |/ I IL-eX/ I	A JL |/ I О «Лу I
da; = —
3. | xJ-u(bx)[yu(cx) - П„(сх)] dx =
0
2cv cos viz
+
СХЭ
4.	J^^1+cr ( — J \Yu(cx) - Н|/(сж)] da; = -
J x1~f'a	\x J
[6, c> 0, 6^ c; |Rei/| < 2].
[6 > 0; |argc| < тг; Re v < 1/2].
4COSI/7T
2,+i^a B V&c)
. f
J
WjrTj^
)/2сA-<т)/2
¦<т = 0 или 1; 6 > 0; | arg c| < тг; а - 3/2 < Re и < а/2].
cos и-кКъи(V2ibc )Ж21/(V-2i6e )	[6 > 0; |argc| < тг; -1/2 < Rei/ < 1/3].
в.
-1 F fi- I I. 6
4 7 ' 2 I ' 4' 4' 64c2 7 c"u V 4c
[6>0; |argc|

78	Гл.2. Определенные интегралы	[2.7.17
2.7.17. Интегралы, содержащие произведения элементарных функ-
функций на I±u{cx)— Jju{cx).
1. ж [I±u(cx)-liU(cx)]dx = 	sec—-—тг^	>Г v	;/
J	са	2 [cosi/TTJ [I - (a=Fi/)/2j
[Re c> 0; -1 - Re и, T Re i/ < Re a < 1 - Re i/].
2	1 ™	/ /-$ ___ лр 1 ^	I jF [ i /** OP I — T I /"* ОГ9 I /^ r?9 —— — -
m § шЛу	I LI/	tX/ I	J. -4- f/ I L-'tX/ I	JLJ i/ 1 L-'fX' I 11/шАу —
л (ol±v л , _ adz i/ a2c2
J
\
1,
3 a2c2
;
a' Rec' Re/3 > 0; Re(«
4. ж + (ж ^a )p [I-u(cx)-bu(cx)]dx = 	ъ
J	€s
K ?
^ J
xsec
a + v -2p
,1;
1 3 3 3 + a + i/	с2
1; -ru + -r	p; -
(R Л	[I^p^v{ac) L^+V(ac)]
LOh I ID 	I	 /^ I #T
[a, Rec, Re/3 > 0; Re (C + i/) < 1/2].
В
.±1/) V 2 'F	2 У 1ЖА\ 2 ' A^"J ^ F ' 2 ' 4
^ -1 - Re a < Re и < Re a
6. —	 [I±v(cx) — Ъи(сх)] dx =	tg	жЪи(су) +
0
xsec^-l-iv	" il,F^l- 2-^-til о "~t/- ^^^l т ffy°^ etc a±"
X bCL л 7Г1 | л /	ч /л I 1-^2 IJ-i^1 ^i^1 ~5 ^ 1+ « ^1ь <j
X ¦— Re a — 1 < Re i/ < Re a
со	_^ ^^i	,	2
7 f т1^1/р™рж2[/ (rr) — L (гт^Ыт — 	-	—
IT» ж б [У i
J
о

2.7.18]	2.7. Функции СтрувеШ1/{х) иЪи(х)	79
[Rep > 0; Re и < 1].
8. ха 1 sin bx[I±u(cx) — Ъи{сх)\ dx = 17A)
. -2 - Re a < Re v < Re a + 1 J J'
[b,Rec>0;Re(a + ,)<2, {	Re(« + ")>-l
-3/2 f Sm " 7Гз 2*	" ' "	' '
3	3 c2\ c*" rftt±i/
2' ' 2' 6V ' 2±-b«±" \l±i/J	2
CO
9. ж"™1 cos 6ж[/±1/(сж) — Ъи(сх)\ dx = 17@)
о
I 6, Rec > 0; Re (a + i/) < 2, (	Re (a + i/J > 0	1	2.7.17.81.
2.7.18. Интегралы, содержащие произведения специальных функ-
функций на 1±и(сх) — 1ии(сх).
x^J (bx)\I+ (ex) L(cx)]dx- 2a°P+1 г
x J^bx)[l±^cx) - hv(cx)\ dx--^. ba+v+1 1
Д l + a + /i + J/ l + a + i/-/i 3	3 c2
fa±u-fi
2
2 '	2 '1=сгУ' 6
Ке(а + „ + и)>0
-1 - Re (a + ^) < Re v < Re (a + /i)
4
2.
0
2 '	2	' ^'	' fc
6 Rec>(M	-l/2<ReM<3/2
' eC ' ^ -1 < Re/i < 3/2, Re(/Lt-г/) > -1/2
oo
4
0
u + I) cos^1'/2 ^аЛ (l, 3-±^ + щ
O.)
lRe/i > -1, -3/2 - Re i/ < RejLi < 1/2-2 Re i/
СХЭ	-I _|_	I
- J а>1±1/""^(^)[/±„(са!) - Me*)] rf* =	7
i + ,) 2Fl (l, 1±^; ^|^ + W
[6, Re c> 0; ± Re v > -1; Re (^ - i/ =F ^) > -1/2].
6. f x1/2Jv+1/2{bx)[h{cx) - Lv(cx)] dx = J^ b-"-1/2c"(b2 + c2y1/2
0	[b, Rec> 0; |Rei/| < 1].

80
Гл. 2. Определенные интегралы
[2.7.19
оо
7. х~пJo(bx)[In(cx) — Ln(cx)] dx = Jn
[б, Re с > 0; z = с/л/b2 + с2 ],
Jo = — ВД,	Ji = — [K(z) - E(z)],	J2 = -^ [B + z2)K(z) - 2A + *2)E(*)],
7 C	7ТГ 2	^13
- (8 + 7z2 + 8z*)E(z)].
сю
n \
- [/.(еж) - ЬЛ
x J
23/2 ,_„_!
Г 4с	6
9. жНоFж)[/о(сж) — Ьо(еж)] dx =		— In -
J	ж1о{ол + с2) с
[6, Rec > 0; -1/2 < Re i/ < 1].
[6, Rec > 0].
. f же^рж[/1(сж)Ь0(сж) - 10(схIл(сх)] dx = — (р2 - с2)
J	¦тгр
о
J	тгр
о
{Н^(сж) 1
>
Jju(cx) J
[Rep> 2|Rec|].
[Rep > 2|Rec|; Re i/ > -1].
¦i/)/2,
3/2
1 + a
1 + a -
Imc|
Rec|
Re 6 >
|Rec|
3 3 cA
, Rei/>-3/2l.
J
3.
4
о
oo
'• J" e
[c, Re b > 0; Re i/ > -E ± l)/4].
1,(сж) йж = -—^ Г(|лНM_,/-2 u-i f — )	[c, Re6 > 0; Rei/ > -1].
7ГСГ	\4c/
arg6| < B=p 1)тг/2; Re (a + i/) > 2|Re/i| - 1,
| argc| < 7Г
c> 0; Re (a + v) < 2; Re a < 5/2 /J'
/zp (e) = =b (cos 11Ж cosec ¦
cosec [(a + i/)tt/2]
3/2
1	1
2	+M' 2'
^a + i/ 3 —a —i^ с
2 ' 2 ' 86

2.7.19]
2.7. Функции Струве Ни(х) и Ъ^{
81
6. [ ха~1е~Ьх2#А4(Ьж2)Ь„(сж) dx = /-(-1)
0	[Re 6 > 0; |argc| < тг; Re (a + v) > 21 Re /x| - 1; 1-(е) см. в 2.7.19.5].
7.
ехр
8.	f [2#2„(Ьл/я)
J
9.	[
J
da; = - Л ( —
с \4с
2тгс \4c/
[с>0; |arg6| < тг; -3/2 < Re i/ < 0].
[6, О 0; -К Re i/ < 1/4].
10.
11.
2c
[c> 0; | arg 6| < тг/4; | Re i/| < 3/2].
1	/ Ь2л
— exp -—) [0 0; |arg6| < тг/4; Re v > -3/2].
ЛС
?
12. x^V^iz
J
da; =
2-%/^c2-+1/2 ""-V^ ^2Cy
[c > 0; |arg6| < тг/4; Re i/ > -1/4].
oo
14. cos
о
/i - ^
2
1 „
sin
[c > 0; |argb| < тг/4; Re v > -3/4].
ca;) da; =
[c > 0; |arg6| < тг/4; Rei/ > | Re/x| -2].
15. f xYJbVx2 + z2 - bz)Kl/(bVx2 + z2 + bz)Uy{cx) dx = Дг exp ( ^cz - — )
J	2c2	\	2cJ
[c, Rez > 0; |arg6| < тг/4; -1 < Rei/ < 3].
..(еж) j	-^F6«+^+1 L ^ + 3/2, a + i/ + l J
-M + l a + iz-A + M + 1 a + i/-A-/i + l"
X 5^4 A
3 3
2' l/+2' 2
' +
|Rec|J
2	'	2
, Re (a + i/) > | Re A| + | Re /z| -
17.
x2Fi(l,2i/+|; 1/+ 2;
2 Re 6 >
Imc|l
Reel/
, Rei/ > -5/4 .

82
Гл. 2. Определенные интегралы
[2.8.1
18.
19. f
J
20.
21. f хК1(Ьх)Ш0(сх) dx
Jbt/(еж] J
dx =
3 c2
liV{cx)
2Re6>
Re c| J
dx =
v + 3/2)
2' 2' F+ 2' Т№
2 Re 6 >
2' F +
ImcMl
ReclJJ"
2
^-2/x-l^
62^CZ
| Rec| j'
z - (z + c) M - (z - c) M]
; 2Re6
22.
23.
dx = ^ [si
|Rec| J
cosy?si
|Re/x| < 3/21.
J
); 6, c>0].
24. f ж^
J
dx =
Ь0(сж)
cV4P±c2
0; Rei/ > -1/4].
ImcMl
Rec|/J
2.8. ФУНКЦИИ АНГЕРА ЛДж) И ВЕБЕРА
2.8.1. Интегралы общего вида.
.0_1 J Л„(сж)
L. [ж^^^-ж^
¦Г(/3)х
1г^гГ	(А; + а)/г	1 Г cos [(А; + ^)тг/2] 1 / ac\fe
Х ^ [/3 + (fe + a)/r, 1 + (k + i/)/2, 1 + (А; - v)/2\ \ sin [(A; + i/)tt/2] J I"T/
[a, r, Re a, Re/3 > 0].
2.
X > Г
cos [(к + 1/)тг/2] 1 /_ acf _
V
dx =
r
1- p - {k + a)/r
l^[k + a)/r, 1 + (A; + i/)/2, 1 + (A; - i/)/2 J \ sin [(A; + i/)tt/2] J V 2 У
3r~a ^^ [i _ ^jfe	cosec (r — '
^ k\ ГA + (r + v — a — rP
cos [(r + и — a — rP + rk)n/2] 1 /ac\rk
, sin [(r + i/ - a - r/3 + г^)тг/2] J VT/
гГ(р)

2.8.1]	2.8. Функции Лнгера Ju(x) и Вебера ~Еи(х)	83
( cz\k /с\гР~а
(~l)k(p)k	cosec (rp + г к — а) ж
^ Г (a + k)/r,p-(a + k)/r ]( coe[(v + к)п/2]\ / cz\»
x
Е
к=0
k\ ГA + (rp-a + u + гА;)/2)ГA + (rp - a - i/ + rife)/2)
{cos [(у — а + гр + гА;)тг/2] 1 /cz\гк
sin [(у - а + гр + гк)ж/2] j \~2 )	^' Г'
X Г:_ J.. _.,_., J.J Т	[с, г, Rea>0;Re(a-rp)<l;r|arg,|<7r].
Г ж™ х | Jjy(cx) 1	тг^/" т ^"^	1	к + си
J жг — iir 1 Е ("~х	=	~^	v т^/1 i /I. , .л /о\т-1/-1 ГТТ .л /о\ C^S I ^ х
		г <-^1'A+[к + 1')/2П'[1 + [к1-1/)/2) ~ г
о
cos [(i/ + A;Or/2] 1 / c|/\fc /с\г^а\Г^	cosec (г + г^™а)тг
2 /
.' cos \(i/ — а + г + г^)тг/2] 1 /су\гк
X \ г)	, ч / 1 М I	с, г, у > 0; 0 < Re а < 1 + г .
\ sin [(i/- а + г + гА;)тг/2] / \ 2 /
бЬ = t/(r)	[с, г, Rep, Re а > 0],
Г>1],
f cos [(i/-a-rifeOr/2] 1 / 2rp
\	J !F~
feOr/2] 1 /
;Or/2] J \
17A) см. в 2.8.3.1.	Ir "^ 4'
6. \ xa-1si
J
0
[6, c, r > 0; -r < Re a < r + 1/2 при r > 1, -r < Re a < min C/2, r + 1) при г < 1],
г<5 — а — к ( cos [(А; + и)ж/2] 1 / с \fc
Х €Ш 2^ ^t sin [{к + |/)тг/2] J l^^1^ '	[Г > Ч'
V(S)-±
r<f + l-a + ife f sin [(i/ — Aj)tt/2] \ / -„ ,	0 . - .
X COS 	 7T<	r/	; . , > I	+ 7Г& - I	X
2r	\cos[(i/-feOr/2]JV с J	\c)
E°°	(™l)fc cosec (a + rS + 2гк)ж
к\(8 + l/2)fcr(l - (a + i/ + <5r)/2 - гА;)ГA - (a - i/ + 5r)/2 - rife) X
cos[(i/^a^r^^2rifeOr/2]" ^ —i^2fe
= 1 см. в 2.8.4.1-2.	I sm L^ - a - ^ - ¦
о
[6, c, r, Re a > 0; Rea<r + 1/2 при r > 1, Rea < min C/2, r + 1) при г < 1; V(?) см. в 2.8.1.6].

84	Гл.2. Определенные интегралы	[2.8.2
о
Г	Зг + 1	min (Зг, 1 + г)	1
о, с, г > 0;	— г Не /z < Не а < 	 при г > 1, —г Не /х < Не а < 1 Н	при г < 1 ,
L	2	2	J
¦(ife + i/)/2, l + (A:-i/) '~' Х
w J	L \	'	/ / J ¦ ¦
\ sin [(A; + i/)tt/2]
ШтЛ = ±1-1	iVr	(»r + a k- ^j/x^.j	|
1 j	V2/	cr f^ [l + (/xr - a + fc + l)/Br), A + v - A;)/2, A - v - fe)/2j
sin [{и - к)ж/2]
cos [(i/- А;)тг/2] / \	с
E
cosec (a + /ir
qj A;!(l + /i)fcr(l - (a - i/ + /xr)/2 - гА;)ГA - (a + v + /xr)/2 -
X \ sin [(i/ - a - /xr - 2r^)?r/2] J \ cr
W(l) см. в 2.8.5.1.
2.8.2. Интегралы от /1(жК v	>.
Г a_i f Л и (сх) 1 .	2a7rc^a cosec an	( cos Г(г/ — а)тг/21 1
•J	lE^cx)/	r(l-(a-i/)/2)r(l-(a + i/)/2)\sin[(i/-a)ir/2]J
[c> 0; 0 < Rea < 1].
_ (a _ t/);2;;;;_ (tt+v)/2)
ec (ax/2
sin A/7Г/2) sec (атг/2)
x { C°S (^/2) -sec (ax/2) |	>	< Re q < ±
[ sin A/7Г/2) sec (атг/2) J
2/ 1^1 —cosi/ttJ
' 2' M 2'
a + 1 3 + f 3 - i/ a2c2
4. 7a!--V-oY-1f^Ca:J}da!=^^B(JS1l-^-^)f1Bin'/'r }x
J	^()]	2	V	2/ [ 1 - COSI/ТГ J
sin^TT | „ /, а + 1 я , a + 1
X
2 ' r ' 2 ' 2 ' 2 ' 4
/c\2—2/3—a	cosec (a + 2^)тг	f cos [(i/ — a —
' ^ V2/	ГB - /3 - (a - 1/)/2)ГB - /3 - (a + i/)/2) \ sin [(i/ - a - 2/3)тг/2]
	-, 2 - /3 - —	-; -^_E_ )	rtt5 C5 Re^ > 0; Re (a + 2/3) < 3].
2	2	4/

2.8.4]	2.8. Функции АнгераЗ„(х) и Вебера~Е„{х)	85
7	1 3„{сх)\ л za-2" D (a	a\(
сХI dX = ^ГВ B' Р~ 2) \
za-2?+1
а
"' 2"' ™Р+ 2"'
sini/тг ] „Л а + 1 3 + а	3 + */ 3 - i/
2F3 1, —— -
4	! —-"'—'—; "T
/сл2^™"	cosec Bp — а)тг	J cos [(i/ — а + 2р)тг/2]
~ Ж \2i	ГA + p - (a - */)/2)ГA + p - (a + i/)/2) \ sin [(i/ - a + 2р)тг/2]
2 2
. sini/тг 1 _ / 3 + 1/ 3 — 1
Ч , , 	> i^2 1; -^-, ^г-
ГB-(а-1/)/2)ГB-
{cos [(*/ —а)тг/21 1 _. / ol—v а + и с2у2\
г/	ч / 1 Ь^2 1; 2	,2	—;	^- )	с, у >0; 0 < Rea < 3.
sin[(i/-aOr/2] J V	2	2 ' 4 у	L'^ '	J
со
7. f ж"+1(ж2 - а2)/3^|/(сж) ± Л^^Ссж)] с/ж =
2,/з±Дас) -
- 2/3~1тг [tgT1^ J^-i/2(ac) + yTl/_i/2(ac)]}	[a, c, Re/3 > 0; Re (i/+ 2/3) < E ± l)/4].
2.8.8. Интегралы от ж
со
I. Jx^e"'
¦v(cx) j	иж \ 1 — cos иж
а а + 1 „ . I/ _ и с2
X
X 3F2 I 1, -^—, - + 1; -^—, ^^;	 1	[Rea > 0; Rep
00	f { х \	/	/	2
2. j Жа ге рх {vu{cx))dX= 2иж \l-coSI/7rJP ^V1' г"; 1 + ^' ^I5"^
о
	с	 /a + l\ f sini/тг
о о л тж	a ( Sin 6ж 1 f J^ (СЖ) 1
2.8.4. Интегралы от ж	Н^/ \ (•
{ cos ож J [ ЕДеж) J
. (V^sIn
J
2 ' 2 ' 2 '
[Rep, Re a > 0]
1
о
[6, с > 0; -KRea < 3/2 при 6 ^ с, -1 < Re a < 1/2 при 6 = с],
Г(а) <5-a f sini/TT 1	/ a a
^n/3 4' г'

86	Гл.2. Определенные интегралы	[2.8.5
сГ(а + 1) . 8 - а Г sini/тг ] ^ ( а + 1 а	3 + f 3 - i/ с2
-1) . а-fl / slni/тг I / 1-й l + i/ 3-а	а
1/62-°Т(а-2) a-J / sin i/тг \ „ Л п " -, , " 0 « 3-а &2
.« /2\a+5coSec(a + ^
W
W ГA - (a + i/ + <*)/2)ГA - (a - i/ +
1 I f"
J	\Eu(cx)
о
[6, с > 0; 0 < Re а < 3/2 при b ф с, 0 < Re a < 1/2 при 6 = с; V(S) см. в 2.8.4.1].
2.8.5. Интегралы, содержащие Jp,{bx)m
[b, с > 0; — Re /i < Re a < 2 при b ф с, ^Re/i<Rea<l при 6 = с],
rr -	i sin^ \ГГ (a + /x)/2 1	fa^M Q^ + Z1 i.i,17 i I/. c2>\_l
^ - 737^"i i «_..- Г I i , /.. Лл/о1 3J^2 1 ~~2~> 2 ' ' I' ' ft2/
2ac	f slnj7?r . ... , . . . ,, ,
A - |/2)тг6а+1 [I + cosi/tt j L(! + M- «)/2J
x 3f
Zi	Zi	Zi	Zi	I/
ч г / .	„ \ / ,-* n
Sin 1/7Г
I + cosi/ttJ^ LC + M^«)/2JX
1 —i/ l + i/ 3^/i^a 3 + /i^a b \ ub a J sin г/тг .
_ .. _	cosec (a + м)тг
ca+|i p[^ + 1? j _ (a + ^ _ ?/)/2, 1 - (a + /i + u)/2]
[(i/— a — д)тг/2] 1	f a + fi — is « + /1 + ^^ ,-•.&'
_sin[(i/^a^MOr/2] j z ' V 2 '	2 '	'
? a-irr/ ч т / м i 2asini/7rT,r (a + i/)/2 1
2. ж 1[Jt,(cx)-JJcx)]dx =	Г	, y/w
J	caslna7r 1 + (i/— a)/2
о
[Re(a + t/) > 0; 0 < Rea < 1; | argc| < тг].

2.9.1]
2.9. Функции Ломмеля sll^{x) и Б^^(
87
оо
. xJu{bx)\Ju{c
J
dx =
[a, Re^ > 0; Re v > -1; Re f> + 2C) < 1; |argc| < тг].
sin i/7T
[6 > 0; Rev > -1; |argc| < тг].
2.9. ФУНКЦИИ ЛОММЕЛЯ 8^„{х) И ^.„(
2.9.1. Интегралы общего вида.
1.
(-1)*
2 J
0 I z a
l}	г
A + /i + i/)/2, i
a, r, Re^ > 0, ^	F ,	, .
\Rea > -Re/x-1, Rei/ /J
,
l2i
A;!
7ГСа'
1 sec ¦
¦тгГ
„ . а — i/ — r(k — p + 1) \ Г	f cos (r — rp —
x Г [ 	\	*-	'- cos иж =p { v
2	/ [	[	cos fin
{cos (r — rp — a + г^)тг 11 / ac\rk
cosfin	j\ \~2~/
= (ас/2)- ГA + /i + i/)/2, i/l Г1 - BЛ + a - u)/r -
k{ } (li/)* L (l + )/2 J L
Г с > 0; Re (a + r/3) < r + 3/2 11
a, r, Re/3 > 0; Re (a +/i + r/3) < r + 1, ^	' V	P;	' \\.
CO
4
(ж- +
(}лс =
argc
; + 1J-^]Г(р)
x г p -
1 H
;(/*-!/ + з)/2)к
\ Z /	7Г С	^
E
fe=0
(—l)k(p)k oc + (j, — rp — rk ( a + v — rp — rk\ (a — v — rp —
S6C	—	7Г1 [	z	I I I	z	I X
A;!
X COS 1/7Г =F Л
2	V	2
cos (rp — a + г^)тг "[] ^ cz Yfc
COS/iTT
(?)'
+

Гл. 2. Определенные интегралы
[2.9.1
_ (cz/2)-"
2, 1/
f Re(a-rp) < 3/2; с > 0 11
[ Re а > | Re i/|; | arg e| < тг J J
J
fe=O
3)/2)fc((M-i/ + 3)/2)fc
+ /x-
/cgf
\ 2 /
_, /a + i/ - г - rfe\ _. /a - iv - r -
x Г 	 Г
2	у
7 fc=O
COS 1/7Г =F 1
cos (r — a + гк)ж 11 /су \гк
cos jtiTr
}](?)'
г, у > 0; -1 < Re (a + ^) < r + 1,
r, Rep > 0; Re (a + fi) > -1,
Rea < 3/2 + г; с > О
Re a > | Re v \; | arg с | < тг
c> 0
Re о > |Rei/|; |argc| < тг/J'
t/(r) =
x Г
r[(p +
Ik + a
r
/==0
2, ^1
/2
+
„ /а — и + rfc) \ I	I cos
х Г (	'- ) cos г/тг =р
о + г^)тг 11 /2гр
:os fiTi /J \ cr
2
17A) см. в 2.9.3.1.
. [ жа8т
J
6,
Г с > 0; Rea < max A, г)+ 1
[ I arg c\ < тг; Re а > Re v\ —
1/2 11
f
r J J
v / ~~
(-1)*
¦1J-1/ =
- /i — <5r -
^ + 3)/2)fc

2.9.2]
2.9. Функции Ломмеля sll^{x) и Б^^(
89
г[ VЖ
V-
•
x cos -
2b1/
г
1 + /1 — U
2	V 2
cos (a +
2 J \ 2
a — и + Sr
x cosi/tt
[
cos/iTr
2r-1b\2k
rk x
при r = 1 см. в 2.9.4.1, 2.9.4.3.
7. Г /ч cos bxr I */' v [CX
0
r > 0; -1< Re (a + ^) < r + 1, ( C > °; Rea < maxA' "} + 1/2 1; У(й) см. в 2.9.1.6] .
I ||	R	| R| J	J
|argc| < тг; Re a > | Ret/
1;
J
2
W(r)=(-
(\r
2k
(Ar + a -
2r-4\2k/r
A + ц. - и)/2, A + м + и)/2] ^ (_i)
Ar + 2rfc
х Г
г А; 1 Г
а - I/ + Лг
cos иж q=
см. в 2.9.5.1, 2.9.5.3.
{о I СЖ I 1
1. \ х { J: ) ; >
ь (	I cos аж
-тг cos иж =p л
\	[ COS jtiTT

90
Гл. 2. Определенные интегралы
[ 2.9.2
i/ 1+n-v a+v a-v
c>0;Rea<3/2
/ \
dx =
х Г
a, Re /3 > 0,
Re (a + fi) > -1; Re a > \Rei/\
cos P7r
2 ' 2 ' 2
' 2
2
2 ' 4
х
х
arg с < 7Г
4. ж1 ь'(ж2 — (
ч}
[с, Re/3 > 0; Re (i/ - 2/3) > -3/2, Re^- 1].
5.
"•
x 2F3 | 1
2[(АХ + 1)*-1/2]
'	о	Р»
< 7Г
1"

2.9.3]
2.9. Функции Ломмеля sll^{x) и Б^^(
91
¦тгГ
2	|2' 2 ' 2 r' 2
cos Bp — а)ж
-р х
x \cosu7T^i x ' ' }\ iF2 p;
COS /Х7Г	"	l
(l-Ax + i/)/2
;
,i,;
2 '
-i/)/2] /o+^
7.
8.
Rez > 0; -1 < Re(a +/x) < 2Rep + 1,
sec ^^ тг 2м Г
f . 2 '- ' -' 4
Re (a -2p) < 3/2; с > О
Re a > | Re v |; | arg с | < тг
2 / V 2
[с, Rez > 0; ^3 < Re (/x + i/) < 1; Re i/ < 3/2].
t
tg
7Г
2	2 ' 2 ' 2
/	(созатгП	t ч Г 01 2^тг2|/а
X COS 1/7Г =F 1	f Sl-a, I/(C1/) - Г, 	;
\	[ COS /17Г J /	[ 1 J	Sin 1/7Г
I/ > 0; -1 < Re (a + ^) < 3,
Re a < 7/2; с > 0
4
da; =
sin/хтг
Re a > | Re v \; | arg с | < тг
+ |/ + 1\„/АХ-|/ + 1
x
10.
[p = (/x + i/ + l)/2, o- = (^- i/ + l)/2; c, Rez > 0; -1 < Re ^ < 0].
2 ' 4 ' 2
2.9.3. Интегралы от ж1
, л(ас)	[а>0; |argc|<7r; | Re A| + Re/i < 1/2]
— a —/Lt —1
\A{?)
Rep > 0; Re(a + /t) > -1,
c> 0
Re a > iRefc1!; jargc| < n

92	Гл.2. Определенные интегралы	[2.9.4
2
Rep>0; Re(a + M)>-1, (D	„ ^	, }] •
I Re a > | Re i/|; j arg c| < 7r J J
9^	\	/ 2
3. j x~1/4e~p^Sfl,1/4(cx) dx = ^	[	|J	^
[c, Rep > 0; Re /1 > -7/4].
2.9.4. Интегралы, содержащие тригонометрические или обратные
,	( 3/х,*/(сж) 1
тригонометрические функции и < „ . . >.
Обозначение: 8 = < >.
1 ^tfs'mbx} t Ч1 , fc-«-M-icA*+i	fcos[(a + MOr/2]1
J	[cos&xj	(/i + IJ — i/2	[ sin [(a + jw)tt/2] J
a + /i + l a + /i + 2 3 + /x - 1/ 3 + /x + 1/ c2"
,	;	,	;
[0 < с < 6, Re a < 3/2 или 6 = с > 0, Re a < 1/2; -1 - 5 < Re (a + fi) < 2],
с
3- a -
2
-a- s
C
j cosec [(a + /i)ir/
\ sec[(a + AtOr/
Г (м - i/+ l)/2, (/* + " +l)/2 1 F /a + ^ + J a-tz + J	1 6^
U(" + " + *)/2 l + (va«)/2j 2 X V 2 '	2 ' +2'C2
[0 < b < c, Re a < 3/2 или с = 6 > 0, Re a < 1/2; -1 - 5 < Re (a + ц) < 2].
2. J^1
0	/ ь\
X (c2 - 62)?M+1)/4PJ^2/2 ( " )	[6, c> 0; Re/i > ^3/2 при 6 ф с, Re/x > -1/2 при b = с].
со
а-i f sin 6ж 1	f ч , _ , i-^-а «-1ГГ	Л cos [(а + /х)тг/2] 1
[cos&xj	[ sin [(а + д)тг/2] J
Г
о. ж
J
Л
[(а + /х)тг/2] 1
(а
2 Ч
2 '	2 ;д+2;
[6 > 0; -1-<У < Re(a + ^) < 2; Re a > |Rei/| -5; |argc| < тг].
^ f	!	Г/ , i\	Ж1	/ \ j	оМ-2 ^ /
4.	г- cos (/1 + 1) arccos — sM ^(сж) йж = 7r тгГ
J va2 — ж2	L	а\	\
х
т	/ас\ _	/flc\
X J(i+/i+I/)/2 — ^1+^-^/2 ( -^- )	[а > 0; Re /х > -2].
\ Z /	\ А У

2.9.5]
2.9. Функции Ломмеля sll^{x) и Б^^(
93
5.	— cos \(ll + 1) arccos — Su и (ex) dx =
J Vfl — ж2	L	a-I
= 	2^2n{ac)^1	 г fac\ /осл _ /осл /осчн
sin |/тгГ(A - i/ - /х)/2)Г(A + v - /i)/2) L p I 2 У " I 2 ) a V 2 J p V 2 Л
[p =
; a > 0;
1].
3.	.	^- cos l /x arccos — J 5» v (ex) dx =
a
2.9.5. Интегралы от xaJ\{bx
2^4
[a > 0; Re /x < 1; | argc| < тг].
x 3F2 1,
2	'	2	'	2 '	2 '
[0 < с < 6, Re a < 2 или 6 = с > 0, Re a < 1; - Re A - 1 < Re (a + /x) < 5/2],
Хз 2 ! '
хГ
^ A^jti^a 3
2	' <
[0 < b < c, Re a < 2 или b = с > 0, Re a < 1; - Re A - 1 < Re (a + ft) < 5/2]
00
[6, с > 0; Re (/i + i/) > -1 при 6 ^ с, Re (/x + i/) > 1 при 6 = с; -3 < Re (/x - i/) < 2].
oo
3. I xa^1Jx{bx)Sl,ylJ{cx) dx =
- c«+a sec 2 ^ [ A + 1, A - /x - i/)/2, A - /i + v)/2} X
+ A + i/ a + A-i/	ft2\, q«+m-2»i~«~m /x-i ^
-^	. 	2	'A + 1'^j+2	&	c x
X 1
4.
3^2 11
¦ i/ — /i 1 — i/ — /x 3™A™/i™a 3 + A^/i^a 6
5.
[6 > 0; Re(a +A) > |Rei/|; -1 - Re A < Re (a + fi) < 5/2; |argc| < тг].
(& — С )	/	\	P( 4- 1/2	1 ~~ I
[b > 0; Re(/x-3i/) < 4; Re (/x - i/) < 1; -6 < Re (/x + i/) < 4; |argc| < тг].
о
X Г

94
Гл. 2. Определенные интегралы
[2.9.6
в.
1 -
1 + \-\i
[6 > 0; -1 < Re A < 3/2; Re BA - /x) > |Rei/| - 1; |argc| < тг].
7.
[6 > 0; Re A > -1; -1 < Re (A + u) < 1/2- Re/z; Re (/z + i/ + 2A) > -3; |argc| < тг].
2.9.6. Интегралы от а
J х1-
х (с2 -
[6, с > 0, b ф с; ^3 < Re (/z - i/) < 1; Re (/x + i/) > 0].
Г ^ ^ 1
2.9.7. Интегралы от хаK\(bxr)< M;l/^ ^ i
х 3F2 1,
а + /х - А + 1 3 + /х - I/ 3 + /х +
[Re 6 > |Ime|; Re (а + и) > |ReA| - 1]
со
0
со
о
со
Ж	лд ^Oi
с!ж =
м, v{cx) dx =
5 —/х-1, v
[с, Re 6 > 0; Re/z > | Re ia| ^ 2].
- ЬГA + /х - 1/)ГA + /i + i/M^M^2 ^-i ( — |
[с, Re 6 > 0; Re (/х + i/) > -2; Re (/z - i/) > -4].
Г( • ' 	 ix
x 3F2
— /i — v З^А^а^
6
; -- ] +
;	,	;
Г-А, (a + A + i/)/2, (а + А-И
Vl[ A - ц + u)/2, A - y, - u)/2
Ь2\ 2а+"-3тг6"А а + ц - A
j+
2 '	2 ' ' ' с5
A, (a + i/-A)/2, (a-i/-A)/2l
nx
-A a -1/- A
[Re 6 > 0; |argc| < тг; Re (a + /1) > | Re A| - 1; Rea > | Re A| + |Rei/|]
2.9.8. Интегралы по индексу, содержащие Sn nix(c)-
CO	'
Kix(b)So7ix(c) dx = 2
xth7TxKix(b)So,2ix(c) dx = -|i/^- exp ( |- - 6 J El f-fr )•
J	о у ZO	\ou J \ 00J

2.10.11
5, in m	rx	(Ъети{х)\ Гкег1/(жI
2.10. Функции Кельвина <	; х > « <	, •! ?
95
оо
Ч
П^ + -
1пх{Ь)8ц,2гх(с) dx = /п
b2 + с2 "
2.10. ФУНКЦИИ КЕЛЬВИНА ( ^"^ } И ( ^
[ beiE/(a;) J [ kei^
2.10.1. Интегралы общего вида.
eiu(cx)
(х)
(х)
Z^v\ ^ix
cos[Ci/-2ifeOr/4]l
[a, r, Re/3, Re (a + i/) > 0].
oo
4
+ a
[r > 1; Rep, Re(a + i/) > 0; r = 1 см. в 2.10.3.2].
з.
X
oo
I. Jo—Eil
cos [Ci/ - 2^)тг/4]
sin[Ci/-2A;Or/4]
[r > 1; Re 6 > 0; Re (a + v) > r|Rejx|; r = 1 см. в 2.10.8.1].
()/	a + и)/г)
X
cos Ci/- 2А;)тг/4П / с \2к	t
. r;o on /j Uirr	r >1; Re6, Re(a + i/) >0; г = 1см. В2.10.6.1.
sin[Ci/-2А;)тг/4] J ^б1/^/	L	v	y	J
5. /"^/-ЖТ ! , l/; , > dx = U(is)	fa, r, Re^ > 0; Rea > Rei/П,
J	i keiI/(cx) j
" /a™)	[^ ^ • • • j -2, -1, 0, 1, 2, . . .],
fc=0
n —1
n)!
	^ I
Г \	Г
Ak{y) = У2], Г
СО
b. j ж (ж - a j <
fc=i
Bjfe + a + :
f BJfe + a -
4^
r
dx =
cos [(n — 2k)n/¦
sin [(n — 2к)ж f<
лл ас	±1 n — 2A; 1 /ac\2k r
- 4 In — =p 7Г tg±1 ^^ ttJ ^ — J [n = 0, 1, 2, . .
cos[Ci/-2A;Or/4]'
^)	[a, t, Re/? > 0; |argc| < тг/4],
-\ ± v{u) \v ф . . . , -2, -1, 0, 1,2,.. .],

96
Гл. 2. Определенные интегралы
[2.10.1
= ь^Ч^-ПР) Е ^ ch(n) (f f ±
fe=O
{cos [(n — 2^)тг/4] 1 Г
sin[(n-2A:Or/4] J [ t{
1
л 1 пС
- 4 In — :
1 + 1) + -'
Г
п _ 2к 1 /ас\2к
	тг — ± v(n) [п = 0, 1, 2, . . .],
(ос/г)-" f i/, 1 - /3 - BA + a - »/)/r
A-")*
1 f cos [C«/ - 2k)n/4] \
/\sin[Ci>-2fc)ir/4]J'
. и _ г _ r^ ^ / а _|_ гя _ |/ _ г — •
I
Г
7.
J
	i
+ zr)p { keljj(
cos [(a + r/3 + 2г/ — r — г^)тт/4] 1 /ac
sin [(a + rf3 + 2i/ - r - гк)
<7r;
тг/4] 1 /ac\rfc
тг/4] J IT/ "
[i/^..., -2, -1,0, 1,2, ...],
k=O
cos [(n - 2^)тг/4]
sin [(n — 2^)тг/4]
4 lf
Ah,	I LZ у
i-" (y)
2k
[n = 0, 1, 2, ...],
1 /cyp-<*
V) = 4 B)
- ol — v	2^ + а-^1 f cos [Ci> — 2А;)тг/4] 1
7	' P	r^ J \ sin [Ci/ ^ 2ifeOr/4] J '
-1/ — rp — rk ^ ( a — и — rp — rk
fe=0
cos [(a + 21/ — rp — г^)тг/4] 1 f cz\rk
sin [(a + 2i/ - rp - г^)тг/4] J V 2
r-
8.
яГ I ker^ (еж)
[r, t/ > 0; Re a > I Re i/|; | arg c| < тг/4],
fe=0
V.
rctg:
+ а + n J cos [G1 — 2Js)tt
sin [G1 — 2A;)
7Г/4] J L
8тг
+ 1)
n + 1) +

2.10.11
5, in m	rx	(Ъети{х)\ (keru(x)\
2.10. Функции Кельвина <	; х > « <	, •! ?
97
fe=O
oo
f a-i -Ржг J кегг/ (еж)
J	\ ке!1/(сж)
a — v J cos [Ci/ — 2к)ж /4\ 1
r	^1 sin [Ci/ - 2А;)тг/4] J '
a + ?/^r^rfc\ /a — i/ — r — rA;\
{cos [(a -
sin [(a -
' — r — гк)ж/4]
•-г- гк)тт/4] j К 2
r, Rep > 0; Re a > |Rei/|; |arge| < тг/4; r = 1 см. в 2.10.3.9],
+ гк)ж/4]
а — i/ + rfe \ J cos [(а -
2 / I sin [(а -
-а/г
-а/г
fc=0
[г > 1; I/ ^ ..., -2, -1, 0, 1, 2, . ..],
1	f 'УЬ 4- rv 4- 7i \ ( гпч ГГп 	 9&W /41 1
х
¦ тг — 4 In
2fe
[r > 1; n = 0, 1, 2, . . .],
(l-i/)*
sin [(Si/ - 2Л)тг/4] I'
СХЭ
in Г ol-i . и г J кег^ (еж) 1
10. ж sink < , , ч >
J	[ ке1х/(сж) J
l • i г I keiv (еж) §	ТХ7-/ i\
sinfea; ^ , , : > dx = Wiv, 1)
ке1|/(сж) '
[6, r > 0; Rea > | Rei/| - r; |argc| < тг/4; r = 1 см. в 2.10.4.2],
+ rS + у , Л „ ( a -
A
+rk x
, -a/r
+
n — l
> 1; v ф . . . , -2, -1, 0, 1, 2, . . .],
^	1
fc=0
Sr ~~ a — n — 2k ( cos [(гг^2^)тг/4]
X COS 	 7Г <
2r	\sin[(ra-2A;Or/4]
cos [Ci/ - 2^)т
sin (fc, - 2*K
4 А. П. Прудников, Т. З

98
Гл. 2. Определенные интегралы
[2.10.2
11.
оо
12. J x-
[b, г > 0; Re a > |Rei/|; |argc| < тг/4; г = 1 см. в 2.10.4.3; W(i/, ?) см. в 2.10.1.10]
eiv (еж)
dx = Z(y)
[b, r > 0; Re (a + /ir) > | Re u\; | arg c\ < тг/4; r = 1 см. в 2.10.7.1],
cos [(a + 2i/ + vii + 2rk)n/4] 1 /2Г~16\2*;
na/r-2 n —1 1
\r < 11
sin [(a + 2i/+ r/i + 2rifeOr/4] j V cr f	L J'
[r > 1; i/^..., -2, -1, 0, 1, 2, ...],
2fc/r
sin[(n-2A;Or/4] J [
2
2 , /. /xr-a-n-2A;\ 4 , c'
¦I---0I1 + -	I --ln:
/ r
4 "J V Ь
[r > 1; n = 0, 1, 2, ...],
2V-Vlvhvlr \ v, (fir + a - i/ + 2ife)/Br) ] / cos [Ci/ - 2^)тг
c"(l - i/)fe |_1 + (/xr - a + i/ - 2A;)/Br) J \ sin [Ci/ - 2^)тг
2.10.2. Интегралы, содержащие алгебраические функции и функ-
функции Кельвина.
' 2 Д sinCi/7r/4)
, - + l,
4 ' 4 ' 2' 2 ' 2
256
(iz + 2)
a + ^ , , 3
2
i/ + 3
' 2 '
cos Cf7t/4) J X
+ 2^ + 2 a + i/ + 2/9
a
f x i / ч »	1 f . ac . ac . ас	ас \
2.	— ber (еж) dx = —— ch ^^ sin ^^ + sh —^ cos ^^
J Va2 - x2 l ;	c^2 V V2 ^2	^2 лД J
a
3.	ber (-у/ж(a — ж))
4	' ' 256
[a, ЕеД, Re (a + v) > 0]
a > 0
dx = \Pl ( sh —=¦ cos —— + ch —— sin
V 2л/2 2^2	2i/2
^ Г	Ж	i • / \ i	^	-ac/y/2 I	ac
4.	/ ^ =r kei (еж) dx = — -—;=— e 7 ( cos —^ + sin ¦
/ x^ — >
[a > 0].
; /
J	[a > 0; |arge| < тг/4].

2.10.3]
* *п ^	^	(Ьеги(х)\ ( кет и (ж) 1
2.10. Функции Кельвина <	; х > « <	, •! ?
99
2.10.3. Интегралы, содержащие е рх и функции Кельвина.
э_рх ( Ьег(сж)
\ bei (еж)
dx =
/р^Гс^ ±р2
2(р4 + с4)
Rep > Ree
2. ж
Ьег1/(сж)
heltj(cx)
1	с" Га + i/l Г cos CI/7T/4) 1
J	2"р«+" L ^ + 1J I sm C1/7Г/4) /
1 и + 1 и	с ,
!2'—'2+1;)Т
4 '	4	4	4
<?\"+2 _а_„_2г Га + 1/ + 2] Г sin Ci/ir/4) \
i P	[ I/ + 2 J\cosC/,7r/4)/X
' d -\- и -\- 2 а -\- и + 3 си + ?^	o + iz + 5 3
4 ' А'	4 ' 2' 2 ' 2 +1; р4
Ые (а + I/) > 0; v^ Re p > Re с + | Im c|l
Г ™рж2 J Ьег^(еж) 1	1 /тГ	/ с2 \ J cos (p 1
J	\ Ье11/(сж) J	2yp ^^ \8p/\sin^J
[(р = с2/(8р) - 3A - 1/)тг/4; Rep > 0; Re i/ > -l]
no
1 _	^	г Г (а + i/)/2l f cos C1/7Г/4) 1
/ ^ " 2"+ip(«+")/2 l [ I/ + 1 J \sinCi/7r/4) JX
4 Г «-1
J
hel^cx)
1 i/ +1 v
' 2 ' 64p2
. 3 i/ + ;
ksinCi/7r/4)
+ 2
5.
6.
8.
9
sin (З^тг/4)
cos Ci/tt/4)
7 1	2	1 Г	c2	/ c2
- e^px [1 - ber (еж)] dx = - С + In — - ci ( —
J ж	2	4p	\4p
1 _ 2	1 /с
— e рж bei (еж) с?ж = — si I —
l ;	2 \4p
[Rep>0].
[Rep>0].
1
[y> = c2/(8p), ^ = c2/(8p) + 3i/tt/4; Rep > 0; Re i/ > -2].
2 f ЬеГ и (CX) I	ь	I tuisw I	о ,, ч
e "- <| , . ) !> dx = -r^TTTT< . !> Г^ = c2/Dp)+3i/7r/4; Rep>0;
J (
\ Ье1г/(
Bp)^i
и
oo	a^2
жа e pxI	} dx = ±	< r/	ч
J	{ ке^(сж) J	ea [ sin [(а + 2г/)тг
/4]J~ V	2	У^ V 2
a + i/ a + и + 2 а- и a - и + 2 1 1	3	p4'
4 ' 4 ' 4 ' 4 ' 4' 2'	4'	^c4
2^V/ cos [(a + 2i/ + 1)тг/4] "lr f ^ , ^ , ^ t p
sin [(a + 2i/+ 1)тг/4]
a + 1/ + 1 a + i/ + 3 a -
4 ' 2' 4' 4'
а + 2|/)тг/41 j V 2 + ^ ! V 2 +11 X
4 '	4 '	4
' sin [(a + 2i/)tt/4]
^cos[(a + 2i/)tt/4]
a — i/ + 2 a —
3 5 3 p4
1; 4' 4' 25 ^^

100
Гл. 2. Определенные интегралы
[2.10.4
^а 3
2 р
1 Зса+3
f sin [(а
\ cos [(а
/
+
2и
2и
4
+
+
1)тг/4]
1)тг/4]
1 <
4
V 2
+ 3^
4
he (л
1 г/
|1 |
V
а —
+ с)
2
4
>
J
+ 5
| Im с
5
4
3
' 2'
Re а
7
4'
>
<-;
Re «/П.
10.
2
= c2/(8p), ^ = c2/(8p) ^i/7r/4; Rep > 0; |Rei/| < 1].
СО
11. хе^рх
X kei (еж)
siny?
12.
tv (еж)
dx
= ±r'vr)/2(c-
Cv	[ SI
cos у?
cos Cftt/4)
sin Ci/tt/4)
x 2F3
а-i/ а - i/ + 2 1 1 - i/
'2' 2 ' 2'
2^3
cos Ci^tt/4)
sin Cj/tt/4)
5 2'
/с
l	j V
+ 1 X
2 3
! 3	v Ъ-v	c
5 2' J ^1T; ~ 6V
sin Ci/7r/4) 1 ^
cos Ci/7r/4) J
4 ^^' 2' 2^A' 2 ' 64p2
[Rep > 0; Rea> |Rei/|].
2.10.4. Интегралы, содержащие тригонометрические или логариф-
логарифмическую функции и функции Кельвина.
}	Пш		( с \ ( с \
1.	ber (су sin x) dx = ttJq i —=г 1 /о I ^^ 1.
J	\ у 2 / V V 2 /
СХЭ	.
Г	Г кег (ежI	Г	Г1
2.	\ха^ mnbxl^y^\dx = U(l) \b > 0; Rea > | Rei/| - 1; | argc| < тг/4, S = |
os [(а + <5 + 2i/Ot/4]
=
a + ё - i/ a + <5 - v + 2 13
X 4^3
+ 1,
2 a
-5-1/	3 5 3
1 +1; 2' 4' 4 '
Г ol-i , f кег^
. ж соз6ж< Л
J	[ ке^
^ (еж)
(сж)
с!ж = 1/@)
[b > 0; Re a > |Rei/|; |argc| < тг/4; U(S) см. в 2.10.4.2].
Г sin bx 1 .
1 sin ия i . . r /t	r^	5--, ,
4.	<	> kei \c\/(x — aJ + z2 } dx ¦
J [cos bx J
¦ е z<*+ х
/б4 + е4

2.10.5]
2.10. Функции Кельвина {	> и
Ъе\и(х)
кет и (ж)
101
Г sin ab 1	г 2
JicosaH	F± =
±Ъ2; а, 6, с,
5. xe-px
0
; Rep>0].
2.10.5. Интегралы, содержащие произведения двух функций
Кельвина.
f -рж2
J Ж<3
0
oo
I. \ ха~ге~рх1Ыт1{сх) + bell(cx)]
Ье1Лсж) dx = — sin — H	— Л —	[Rep > 0; Rei/ > -1].
4p \2p 2 / \2р/
с!ж =
4 '
. f жа^1е
. f
J
4 '	4 ' 2 ' 2 ' ' ' ' p
[Re(a + 2i/) > 0; Rep > лД (Rec+ |Imc|)l.
X
'
[Rep,
0].
^1
x dx J
-i /c2\
n /i/ —	[Rep > 0; Rei/ > n-1].
\2pJ
oo
5. f жа[кег^(сж) + ке^(сж)] da; =
a^4^ai^\a a + 2v a — 2u
' 4 ' 4
в.
о
x Г
[Re a > 2|Rei/|; |argc| < тг/4].
belt (еж) И ,	с2
7.	\ e px [hert/(cx)heiu(cx) -\-heiu(cx)her'l/(cx)] dx = —Iu [ — I
J	Ac \2pJ
о
o Г a_i -px2 L / ч f her'u(cx)\	. ( x f belt (еж) 11
8.	ж ep Ьег?/(сж)^ , v ( ^ ± Ье^сжК ,v /}\
[Rep, Rei/> 0].
daj =
9
° V 4	4	'	2	4
[Rep > 0; Re(a + 2i/) > ±1].
Г 2 ж2	/	/	с /с2 \
х2е^рх [her и (ex) belt (еж) — heiu(cx) ЬегЦсж)] dx = —- /j, I — 1 [Rep>0; Rei/>—2].
J	4»^ V 2p /
10.
dx =
[Rep, Rei/ > 0].

102	Гл.2. Определенные интегралы	[2.10.6
{Нрг ( f"V] 1
heiv(cx) J
T
(-
+
_ sin Ci/tt/4) J	V 4 '
-3 a +1/ a + i/ л 1 is -\-1 is „ i
4 ' 4 ' ' 2' 2 ' 2 ' ' 64
+ 2 a + г/+ 3
6-"-"-у+а ra + i/ + 2l/sinCi/7r/4)\	/а
2-+2(a + i/ + 2) L ^ + 2 RcosCi/7r/4)J 5 4\
a + i/	a + i/ + 5 a + i/ + 2 a + i/ + 6 3 i/	i/ + 3 c4
^^+ '	4 '	4 5	4 ' 2' 2 + ' ^^; ^F
[Re (a + u) > 0; Re (л/2 6 - с) > | Im c|l.
(сж)/	2I/(a + i/) [ ^ + l J \ sin Ci/7r/4)
+ v a + и + 2 a + i/	1 i/ +1 i/ . с4 \
+ 1	+1
'2' 2 ' 2
4I
x
3 i/ + 3
f sin Ci/tt/4) 1
\cosCi/tt/4) J
I (ex) j	c2 1 - cos [c /D6I
зг^ (еж)
[Re 6, Re (a + i/) > 0].
L	J
2.10.7. Интегралы от xaJn{bx
cos [(a + jti + 2i/)tt/4] 1 |"(a +/x + i/)/2, (a +/x - i/)/2l
sin [(a + /i + 2i/)tt/4]
i/ a + /i + i/ + 2 a + /x-i/ a + /i^i/ + 2 1 /x + 1
4'	4'	4'	45 2'^' 2+1;
2«-2fe/x+2 j gin [(a + ^ + 2i/)tt/4] 1 [(a + /x + i/)/2 + 1, (a + /x - i/)/2 + l
)тг/4П Г(а-
W4]J L
х
a+/i—i/ + 2 a+[jl—is . 3 /i	/i+ 3
+1, 	j	, 	j	+ 1; ^ 2 + 1, —; ^
[6 > 0; Re (a + /x) > I Re i/|; I arg c| < тг/4].
Г	Г крг Гг*^ I	1 I In 11 ~4~ be 1
2. JiFic)< .; 4W» = 77S	/,2/2ч^	[6>0; |argc| < тг/4].
I Lpi (/"I'll	4n	*?С1 rrfrr \ r\ n
0	lk-
2.10.8. Интегралы, содержащие K^(bxn) ж функции Кельвина.
'}
- sin (Sistt/4)
x 4F3 (	, 	i	, 	—, 	=	; -, -^-, - + 1; -Vi

2.11.1]	2.11. Функции Эйри Ai (х) и Bi (ж)	103
"(a + i/ + /x)/2 + l, (a + i/-/x)/2 + ll f sinCi/7r/4) I
и + 2	J [ cos Ci/7t/4) J X
a+F^ii+2 a+u—a	3 г/	i/+3 c4
, . а+*///+2 а+ */ /i	3 г/ , л
+1, 	j	, 	j	+ 1; -, -+1,
Re(a + i/) > |Re/i|; Re (л/2 6- c) > |Imc|l.
2fsinCi/7r/4)\]
[Re i/ > -1; Re(v/2 6- c) > |Imc|l.
«*• ж 1\|х10Ж Js , . , ч > ax ¦—- —,, , __w_— i	. ^	x
. f xa 1K^(bx2)\ ^T."(\ \ dx = — (a+|/)/2C Г ^
a + i/ - 2/x 1 i/ + 1
J cosCi/7r/4) 1	/
\ sin C1/7Г/4) J 2 3 V
4	'	4	5 2'
(a + i/ + 2/i + 2)/4, (a + i/ - 2/x + 2)/4l f sin Ci/tt/4) 1
^ + 2	J|cosCi/7r/4) J X
/ + ^/ + 2/1 + 2 a + i/- 2/1 + 2 3 и 1 i/+ 3 c4
;	+1;
4	'	4	' 2' 2 ' ' 2 '
[Re 6 > 0; Re (a + i/) >
4. Tx^1^ (barber2 (еж) 1 bci2 (ex)] dx = ^'^^ Г Г (^ + 2^ + 2^)/4, (a + 2i/-2M)/4
0
5 "^-. 2
[Re 6 > 0; Re(a + 2i/) > 2|Re/i|].
5. J y+^2l	2	^^	f |
. J xy+^aK{v+a)/2{bx2)[berl{cx) + bei2 (еж)] с!ж = ^^
°	[<j = 0 или 1; Re 6 > 0; Re v > -1].
oo	2
6. f x3Ko(bx2)[her2(cx) + Ье12(сжI dx = —7 ch ^-	[Re 6 > 0].
J	2o2 26
0
l fa + 2i/ + 2/x T 1 a + 2*/ - 2/x =F
Tn[(a + 2i/ + 2/i=Fl)/45 (a + 2i/2^Tl)/4l „
хГ[	+ iti^i	Г
0; Re (a + 2i/) > 2| Re д| ± 1].
2.11. ФУНКЦИИ ЭЙРМ А1(ж) И В! (ж)
Некоторые интегралы, содержащие функции AI (ж) и В1(ж), можно получить из [18],
2.15-16 с помощью соотношений
2.11.1. Интегралы общего вида.
3<l=F3)/12a«M
2тгг
(a + S*)/r 1/aVy 3<^V^c	/2

104
Гл.2. Определенные интегралы
[2.11.1
a3c3\k
J
оо
¦у	С? — 1 / Г	Т\0 — 1
-. j ж {х ^а ) ,
ж) с!ж =
2-31/е7ГГ
27ГГ
i	/2
ascs^k
jfe!
(a + rp-r-rk\
V	3
[a, r, Re^ > 0; |argc| < тг/3].
3.
AI (еж) dx =
2-
-p г2/з
2 .
k
+
[г, Re а > 0; I arg с| < тг/3; rl arg z| < тг]
a__r	/i\ °°	-1	i oi	/ 3 3\«
I/	/ 1 \ <г--л	1	Q + Oft Icy
rWV U/ ^0 *!B/3)* Ctg ~~Г~ П \T
fc=0
x^r(a~r."rMrr+Q~r~'
fe=0
cy
2 •
[r, t/, Rea>0; | argc| <тг/3].
Bi(ca!)
^ fc!B/3)fc V r
"
3Da-7)/6
[Rea, Rep > 0; r > 3/2; r = 3/2 см. в 2.11.3.1].
а + гА +
2тгс« ^^ A;!
fc=0
6.	j x e Ai(ex) с
0
oo	^	r
7.	f /-11 Sm bt Xr I Ai (еж) с/ж = С/(г)
J	[ cos 6ж J
ГA/3) ^ !	/a + 3fc\ fBin[(a + 3fcOr/Br)]\ / с3 ^
[Rea, Rep > 0; 0 < r < 3/2; |argcj < тг/3].
, r > 0; Re a > -rS, 5 = i i; | arg c| < тг/6 ,
{) 2
^0 fc!B/3)fc
31/6сГB/3)
1\ / sin
1)тг/Bг)]\ / c:
.3/2],

2.11.4]	2.11. Функции Эйри Ai(x) u Bi(x)	105
3Dа+4Дг-7)/бЬд ~ (-1)"	(a+5r+2rk\ (l+a+Sr+2rk	'2k
{Г)^ 2*0°+'* jLk\(s + l/2)\	3	) V	3
[г < 3/2],
С/C/2) см. в 2.11.4.1.
ОО
. f xa~1Jt/(bxr) Al(cx) dx = V(r)	[b, r, Re (a + vv) > 0; | arg c| < тг/6],
8
о
3i/6.2(a-H)/r-2crB/3)	!	(i/r+a+1+3fe)/Br) l/2^\
=
тгс«+-Г(|/ + 1) AjA;!(i/ + l)fc V	3	j \	3	/ \ 2c- У
[r < 3/2],
VC/2) см. в 2.11.5.1.
{Ai (еж) 1
В1(сж)J
°?	oDa —1)/6 —1 , N / _|_ 1 \
1. J ж"-1 Ai (ex) da; = ^ Г (|) Г (^^- j	[Re a > 0; | arg c\ < w/3].
2 L-Va3 xY^fА{(СЖ)] dx- ar(l/3) B U *\ Ы1
;' 9
23е3\
	 J	[a, Re а, Re/3 > 0].
3. 1 /_1_ Al(cx)dx = 2z/\l^ А1(^з )	[а>0; |argc| < тг/3].
"All
2.11.8. Интегралы от ^ ^ л _ , ч
[ Bi(еж)
о/о f Ai ( пф\ Л	ч("~1:Т:^)/12Р/'1 /Ч^ /е)т\	/ гу 'Угу 4~ Ч *)
^у 	 "I 	f%~. ^ о у xj a JIL J. I \^f еду J I	4L#	JL I -1- / t_# I	f ^J C^C. 1	f Ul,	^y f^^, |^ fj	^
0
r/2Q + 2\	/q + 1 2a+ 5 2 4c3
[Re a > 0; Re Cp ± 2c3/2) > 0; | arg c\ < тг/б].
2.11.4. Интегралы от xa^ """^¦"^ [-Ai (еж).
;}¦
a_i J sink3/2 1
Обозначение: S = <
Х- J X {
cos6х3/2 } Al (СЖ) ^ = 2.С^+з^/2 Г (б J Г (в
[6>0;2Rea>-3,;|argci<7r/6].

106
Гл. 2. Определенные интегралы
[2.11.5
2.11.5. Интегралы от ха Ju{bxr) Ai (еж).
. 7 х~*МЬх'») Ai (Сх) d, = 3D+
6
; i/ + l; -j-3 )	[6,
0; |argc| < тг/6].
2.11.6. Интегралы от Ai (аж + b) Ai (еж + d).
оо
1. Ai (аж + b) Ai (еж + d) dx = 	3^=
— 6c
[0 < с < а].
2.12. ИНТЕГРАЛЬНЫЕ ФУНКЦИИ БЕССЕЛЯ Л„(х),
НЕЙМАНА Yi^(x) И МАКДОНАЛЬДА Kiv{x)
Интегральные функции Jiu(x), Yiu(x), Кги(х) определяются формулами
2.12.1. Интегралы общего вида.
1. f ха^г(аг - x^^JiJcx) dx = -17A) + a"	В (-, р)
J	иг	V г /
[a, r, Rea, Re^, Re (a + v) > 0; U(e) см. в [18], 2.12.1.1].
2.
= -U и
2i/r \7rcosec(i/7r/2)J W
/а
. ха^(хг - ar
J
[а, г, Re/З > 0; Re a > |Rei/|; ^(e) см. в [18], 2.13.1.1].
3
dx = -
в A - ^ - -,
г
4.
[а, с, г, Re^ > 0; Re (a + /Зг) < г + 5/2; V(e) см. в [18], 2.12.1.2].
/3-^,/3)
Re с > 0
[c, r, Re a > 0; - Re v < Re a < r Rep+ 5/2; r|argz| < тг; W{e) см. в [18], 2.12.1.3].
6.
7.
8.
(жг + zr)p
z^^f 2ctg(i/7r/2) \_ /а
7rcosec(i/7r/2)
V г	г/
г > 0; Rea > |Rei/|; r|argz| < тг, I °	Г/? < 'С> }, Wv{e) см. в [18], 2.13.1.31.
^7 Jiv(cx) dx = —X(l)	ctg
xr - yr
иг	г
с, г, |/, Re а > 0; - Re и < Re а < г + 5/2; Х(е) см. в [18], 2.12.1.4].
тг cosec (i/tt/2) J & r

2.12.1]	2.12. Интегральные функции Бесселя, Неймана и Макдональда	107
\Г1 У > 0; Re а > | Re v
со
i. \ха~1е~рхГЛ1/(сх) dx = С/,
Re a < г+ 5/2; с > 0
Re с > 0
, Xv(e) см. в [18], 2.13.1.4 .
U при г = 1 см. в 2.12.3.5
[г, Rep, Re а, Re (a + */) > 0; с > О при г ^ 1, | argc| < тг при г > 1; У(е) см. в [18], 2.12.1.5].
ю.
dx = Ui,
2i/r \r/ X тг cosec (г/тг/2)
при г = 1 см. в 2.12.3.6
r, Re p > 0; Re a > | Re i/
с > О
' 1 Re c> 0
, У„(е) см. в [18], 2.13.1.5].
11. жа~ е рж Лу(сх) dx = -Z(l) ¦
о
= —Zu(l) ±
[с, r, Rep > 0; Re a < 5/2; Z(e) см. в [18], 2.12.1.6].
/	OL\{ 2ctg(l/7T/2) 1
I <	>
1I <
2ur \ г) \ 7Г cosec (W/2)
r, Rep > 0, (Rea < 5/2; C > °1, Z^e) см. в [18], 2Л3.1.б1.
I	Re с > 0	I	I
13.
C/2 = -
1 cos 6жг
а\ Г sin [атг/Bг)]
i/r \г/ \ cos [атг/Bг)]
С/2 при г = 1 см. в 2.12.4.1
6, с, г> 0; Rea > -5r; -6г - Re i/ < Rea <- + max (r, 1); 5= i 1, P(e) см. в [18], 2.12.1.7 .
,1),
14.
\cos6a;
V G, 1 = -^G, 1 +
&™а/г
Г(а/г) f sin[a7r/B
ur sin (ук/2) [cos [а7г/B
2r)] 1 y v-к
; } cos7 —
2г)] J	2
r
r > 1 ,
УG, 1) при г = 1 см. в 2.12.4.2-3
6, с, г > 0; |Rei/| - ^г < Rea < 3/2 +max (г, 1); ё = I I, С/х/G» г) см- в [18], 2.13.1.7 .
J \ cos 6жг /	2
о
[6, г, Re с > 0; |Rei/| < Rea + 5r; V(j, 1) см. в 2.12.1.14].
15

108
Гл. 2. Определенные интегралы
[2.12.1
16. J,-
-1e-p""lBmb.Xrr\jiv(cx)dx = Us,
I cos ox J
_, /a\ I дтт а
¦ Г ( — cos
\r/ \ 2 r
§tt a
	 arccos¦
r
[r > 1] или [r = 1; |c|2 < |62 +p2|],
[r < 1] или [r = 1; |c|2 > |fe2 +p2|]
6, r, Rep > 0; Re a, Re (a -f i/) > —<5r; с > 0 при г ^ 1, | arg c| < тг при г > 1;
S = | X 1, Q(e) см. в [18], 2.12.1.8J.
IT. j x-
0
- J sin bxr
I cos bxf
Wiu{cx)dx = W(l, 1),
, 1) = KG, 1)
— cos	arccos ¦ /
rJ I 2 r	Jb2-
X cos7	cosec	 [r > 1] или [r = 1; |c|2 < |fe2 + p2|],
[r < 1] или [r = 1; |c|2 > |fe2 + p2|]
6, c, r, Rep > 0; Re a > \Rev\ - Sr; S = I 1; К G, e) см. в [18], 2.13.1.8 .
с»
18. Jx-
19. f a"
J
20. f a;a
J
CO
21. |жа"
-l -p/ f sin 6жг
e 1
b, r, Re c, Re p > 0; Re a > | Re v
irza
S=i1\
loj'
In
— cosec —
а 1/	r
c, r, Re a, Re (a + v) > 0; Re a < 5/2,
argz < тг
z >0
i
ln
ln
c, r > 0; I Re v\ < Re a < 5/2,
аи sin {an/r)
r|argz| < тг'
z >0
WG, 1) см. в 2.12.1.17 .
см. в [18], 2.12.1.9 .
, e) см. в [18], 2.13.1.9 .
'ги (ex) dx =	Wi/@, 1)	cosec	cosec —
r, Rec > 0; Re a > | Re i/|, | Г' aFgZ' < ^ 1, ^G, e) см. в [18], 2.13.1.9 .
22. [ Z El (-6жг) Jiu(cx) dx = U4,
[/4 =
(/4 при r = 1 см. в 2.12.6.1
[r > 1],
[r < 1],
[c, r, Re 6, Re a, Re (a + u) > 0, X(e) см. в [18], 2.12.1.12].

2.12.1]	2.12. Интегральные функции Бесселя, Неймана и Макдональда
109
U5 = UV{1)
U5 при г = 1 см. в 2.12.6.2
{с > О 1	1
>, Uu(e) см. в [18], 2.13.1.12
со
24. f ха~1е±ЬхГ EI (=р&жг) ЛДсж) с!ж = G6,
тгб ~'' /а\ I cosec (
г/г V г У \ ctg(a?r/r)
'
|76 при г = 1 см. в 2.12.6.3
[с, г, Re 6, Rea > 0; - Re i/ < Rea < r + 5/2; У(е) см. в [18], 2.12.1.13].
со
25. [ ха^е±ЬхГ EI {^bxr)Yiv{cx) dx = ЛA, 1),
Л/	1 \	Г Г /	1 \
ЛG, 1) = -Uv(i, 1)
а\ Г cosec (an/г) 1 ~ i/тг	i/тг
2
Г ( —)< . / / ; > cos7 — cosec
иг \г/ { ctg (аж/г)
26
, 1) при г = 1 см. в 2.12.6.4-5
[с, г, Re b > 0; |Rei/| < Rea < г + 5/2; ^G, e) см. в [18], 2.13.1.13].
со
. [ /"'е^'' Ei (Tbxr)Ki,(cx) dx =-- А@, 1)
[г, Re 6, Re с > 0; Rea > |Rei/|; АG, 1) см. в 2.12.1.25].
27. [ ж"/ S! 5^} ) Jiv(cx) dx = U7,
J	1 ci (bx ) J
Ь~а/\Т(а\ \ sin [атг/Bг)]
а|/ \г/ \ cos [атг/Bг)]
U7 =
[г > 1],
[г < 1],
JJ7 при r = 1 см. в 2.12.7.1
[6, с, г, Re (a + и) > 0; 0 < Re a < 3/2 + r + max (r, 1); Z(e) см. в [18], 2.12.1.14].
r; }Yiu(cx) dx = GA, 1),
28.
сь, ц = -P.h, it - ^ г (?) {"'Г//^! /»" т— 2
GG, 1) при г = 1 см. в 2.12.7.2-3
[6, с, г > 0; |Rei/| < Rea < 3/2 + г + max (r, 1); КG, е) см. в [18], 2.13.1.14].
dx = ^l
2
[6, r, Re с > 0; Re a > |Rei/|; CG, 1) см. в 2.12.1.28].
со
Ч
Чп I Z! erf I— У I т- / ч » _ тт
ли. tx < ^^^}Jt,,(cx) dx - Us,
о

110
Гл. 2. Определенные интегралы
[2.12.1
Us = -
U8 =
U8 при г = 1/2 см. в 2.12.8.4
[	fi-i- iw
с, г > 0; Rea > --
31. f
J
" (
I eric (о
[г < 1/2],
тг | -г - Re г/ < Re a < - ,
arg6| < -, <	2 \, U(e) см. в [18], 2.12.1.15
44	Re(a + i/) >0	'	'
L, 1),
Ц- cosec ^
2	2
?>G, 1) = И/,G, 1)
DG, 1) при г = 1/2 см. в 2.12.8.5-6
г
arg 6| < тг/4; Re a > | Re */| - A ± ]
a_i/ erf Fжг)
> о
[г>1/2],
[г < 1/2],
1
, Wv(y, e) см. в [18], 2.13.1.15 .
32. \X
erfc I
iu{cx) dx =
•j
[r, Re с > 0; |arg6| < тг/4; Rea > | Rei/| - A ± l)r/2; D(j, 1) см. в 2.12.1.31].
oo	r
5. жа e	<	r > Jiv(cx) dx = f/9,
J	1 erfc 1 bx 1 1
( isec[a7r/Br)
	2x/	\ 2 cosec (атг/г) J	[^ > x/2],
f/9 = F(l)	t/9 при r = 1/2 см. в 2.12.8.7	[r < 1/2],
[c, r > 0; I arg 6| < тг/4; Re а > -A ± l)r/2; - Re 1/ - A ± l)r/2 < Re a < r + 5/2;
^	V(e) см. в [18], 2.12.1.16].
^a 1 a~i( S(bxr)\	JT
J	\C(bxr)j
0
/10 =
sin [(r + 2aOr/Dr)]
2r У \ cos [(r + 2а)тг/Dг)]
Uio = W(l)
С/ю при r = 1 см. в 2.12.9.1
[r>l],
[r < 1],
35.
[b, c, r > 0; Re(a + y) > -B±l)r/2; -B±l)r/2 < Rea < 5/2; W(e) см. в [18], 2.12.1.17].
dx = E(l, 1),
= -X1/G, 1)-
1/7Г	1/7Г
[r > 1],
[r < 1],
, 1) = Л-„G, 1)
, 1) при r = 1 см. в 2.12.9.2-3
[6, с, r > 0; | Re v| - B ± l)r/2 < Rea < 5/2; ЛГ„G, е) см. в [18], 2.13.1.16].
7 -1 f S(&*r
36- J^lc^'
'iv(cx) dx = --E@, 1)
[6, r, Re с > 0; Rea > | Re i/| - B ± l)r/2; E(j, 1) см. в 2.12.1.35].

2.12.1]	2.12. Интегральные функции Бесселя, Неймана и Макдональда	111
, Ьх )
ji*(cx) dx = Un,
С/и =
f/ц при г = 1 см. в 2.12.10.1
[с, r, Reb,
L
, Re (a + fir) > 0, /Re^>0- Rea < 5/2 \ X(e) см. в [18], 2.12.1.181.
I. Re (a + w), Re a > 0 J	J
Fij, 1) = —1^G, 1) Т
FG, 1) = ПG, 1)
FG, 1) при г = 1 см. в 2.12.10.2-3
с, г, Re 6 > 0; Re (а + fir) > | Rei/|,
~ 1/7Г	1У7Г
¦ — I cos ! — cosec —
г /	2	2
0! Rea <5/2\ УЛ
Rea > | Rej/| J
[г > 1],
[г < 1],
е) см. в [18], 2.13.1.17
r, Re 6, Re с > 0; Re (a + ttr) > Rei/|, <	G^ > , i, FG, 1) см. в 2.12.1.38 .
[ Rea > | Re i/1 J	J
40.
U12 = -
dx =
¦(?)
>Т[^)Т±\ л
/ж \ \г/	V 4
U12 при г = 1/2 см. в 2.12.11.1
с, г, Re а > 0; | arg 6| < B ± 1)тг/4,
Re (а + и) > 0
[г < 1/2],
L У{е) см. в [18], 2.12.1.19].
41. I xa^e±b2x2r/4D^bx^Yi^cx) dx = GA, 1),
а\ cos7(i/7r/2)
2r J sin(i/7r/2)
GG, 1) при г = 1/2 см. в 2.12.11.2-3
42
с, г > 0; | arg Ь| < B ± 1)тг/4,
со
Rei/| < Rea < 5/2 - rRe/ii
|Ret/| < Rea	J
^ ^y8 I /1 ^p 	 	 	 1 -J f П Si
jJU 1 U/JU —	vJTlUj II
, Zl/G, e) см. в [18], 2.13.1.18J.
[r, Re с > 0; Re a > |Rei/|; |argfe| < B ± 1)тг/4; GG, 1) см. в 2.12.1.41].

112
Гл. 2. Определенные интегралы
[2.12.1
43. [ Z Jll(bxr)Jil/{cx) dx = С/13,
- a)/Br)
1)к{а + fir + 2rk) [l - (а + fir - и)/2 - гк\ \ с
2Г-Ч
Ui3 при г = 1 см. в 2.12.12.1
[6, с, г, Яе(а + дг+ 1/), Re (а + fir) > 0; Re а < (г + 3)/2 + max (I, r); 5(е) см. в [18], 2.12.1.10].
w= i
при г = 1 см. в 2.12.12.2-3
(/xr-a)/Br) + lJ [ тг cosec
[г > 1],
[г < 1],
Re с > 0
ОО
45. I xa~1Ifx(bxr)Kit/(cx) dx = -- 17+@, 1)
[г ^ 1; | arg 6| < тг; Re с > 0 (Re (с - Ь) > 0 при г = 1); Re (а + fir) > | Re i/|;
1У+G, е) см. в [18], 2.13.1.10].
46.
6, с, г > 0; Re а > -Зг/2; -Зг/2 - Re v < Re а < 5/2 + г Re pt; T(e) см. в [18], 2.12.1.11].
'2cos[(a-/xrOr/Br)]
7Г
, 1) - ^^м, 47, 1) Т
2l/7rfea/rrsin(l/7r/2)
//G, 1) = U^^uljj 1)
#G, 1) при г = 1 см. в 2.12.12.4
Г6 > 0; Re а < (г + 3)/2 + тах (г, 1Y
ie 1/ /
c,r>0;
1
Re 6 > 0
,e) см. в [18], 2.13.1.11
| >
r, Rec > 0; Re а > r|Re/i| + Re 1/, | > 1, ЯG, 1) см. в 2.12.1.47

2.12.2]	2.12. Интегральные функции Бесселя, Неймана и Макдоналъда	113
'Yiu(cx)
2.12.2. Интегралы от A{x)Jiv{cx) и А(х)^	,
Р	2а^1 Г (ol + vMI Л
1. \ xa^1Jil/(cx) dx = 	Г К. )\.	[с, Rea >0, -Rei/ < Rea < 5/2].
J	aca I 1 — (a — &0/2J
о
? a-i(Yiu(cx)} _ 2a^2 Г (a + i/)/2 If 2ctg [(a - i/)tt/2] 1
J	[^«^(сж)/	aca [l — (a — i/)/2j \ Trcosec [(a — i/)tt/2] J
о
Г	п . (с> 0; Re a < 5/211
Re a > Rei/ , <	' } \.
^	'' I	Rec>0	JJ
3. \ ха~г(а2 - х2)^1 Л^(сх) dx = V-(v) + —	В (-,
[a, Rea, Re/3, Re (a + и) > 0],
2
f a-l/ 2	2чв^1 f Yiv(cx) 1 ,	.	1	ffcOSi/Trl,. ( ч	f 1 1., , Л
J	V	; \Kiv{cx))	sini/тг [I тг/2 J	I71"/2/	J
3^2
5. | /^(ж2 - а2)^1 Jiu(cx) dx = U-{и) + V^ + ^^— В (l - | - /3,
[а, с, Re^ > 0; Re (а + 2/3) < 9/2],
2 ' 2' F	2 '2
г
2з-а-2/з(а + 2/3 _ 2) L2 - /3 + (j/ - a)/2j
Г а-1/ 2	2ч/3^1 f Yiu
(a + 2/3 - i/)tt/2] 1 , ^+2^2 ( 2ctg(i/7r/2) 1вЛ_а*
: [(a + 2^ - i/)tt/2] J T	4i/ \ 7Г cosec (i^tt/2) J V 2 P'
2ctg[(
2 1 7Г cosec L v . ,
<9/2\
},J/tH,Vtcm.b2.12.2.5]
[с, Re z, Re a > 0; - Re i/ < Re a < 2 Rep+ 5/2],
2 ' 2" 2 ' ' ' ' r ' 2 ¦ ^ 4
Г|

114
Гл. 2. Определенные интегралы
[2.12.3
8.
{Yiu(cx)\ 	1 Ffcosi/Trl
Kiu(cx)} X^ sini/тг [\ тг/2 J
-v)\ ±
Trcosec [(i/ — а + 2р)тг/2]
^^ ( 2ctg(i/7r/2) 1 /a _a\
тг cosec (i/tt/2) J \2'P 2/
Rez > 0; Re a > |Rei/|, < ° > °J ^ (" " ^ < ^ }, W±(i/), X± см. в 2.12.2.71.
'	Rec > 0	j	l ;	J
9.
x2 — y2
	ctg — [c, 3/,Rea>0; -Rei/<Rea<9/2],
2a"
(a-:
{u - a)/2
a 1. 9 O + ?/ 9 tt^ 9 «. ^^V
2 ' '	2 '	2 ' 2 ' 4
2ctg[(a-i/Or/2]
2 [ тг cosec [(a — и)ж/2]
у > 0; Re a > | Rei/|,
ctff
8 2 \ ж cosec (j/tt/2) J
, YT(u), ZT см. в 2.12.2.э1.
>(Yiv(cx)}
X Kiu(cx) j *
2.12.3. Интегралы от жае рх Л^(сх)шхае
oo	i
е~рх Jio(cx) dx = - In	—		[с, Rep > 0].
о
oo	г /	\ 
f e^pxJiI/(c^) d» = — 1 - I 	 C^	J	[c, Rep > 0; Rei/ > -1; i/ ^ 0].
о	L\FVi^ /J
^^ тг2 Г 0] Г	Г c>0 11
-~Г< л \ Rep>0, {	И.
4p[lJ L	lRec>0jj
io(cx)
cos i/TT 1 / p +
ртг (тг/2 t
cosec i/TT f 1
i/p [тг/2
p+JP2± с2
J cos
1 1
с > 0
Г(а)
I a + i/	/a-
Rep > 0; |Rei/| < 1,
[c, Rep, Re a, Re (a + v) > 0],
Л2 -
f a_i ^„ж f Yi
жа e px{
J	[Ki
Yiv{cx)
Г(а) f 2ctg(i/7r/2)
'a \ тг cosec (i/tt/2)
Rep > 0; Rea > |Rei/|,
° 1,
Oj
см. в 2.12.3.5 .
J

2.12.4]	2.12. Интегральные функции Бесселя, Неймана и Макдоналъда	115
со
7. f ха~1е~рх2Л„(сх) dx = V-(v) + ^2	[Rep, Rea, Re (a + u) > 0; |argc| < тг],
о
. же рж2 Jio(ca^) с!ж = —Ei[-— |	[Rep >0; I argcl < тг].
J	4p V 4p/
9. Tx^e^l^^Hd^i^f/^^l^H^I 1 К(-„I±
J	\Kiu(cx))	sini/тг [I тг/2 J	\ тг/2 / Tl ;J
fReP>0;Rea>|Re,|; { C>° |, V^u) см. . 2.12.3.rl.
10. [ 1/2
. [ ха~1е~р/х2Л„(сх) dx = W+{u) + V+ +	Г (--)	[с, Rep > 0; Rea < 5/2],
11.
о
Р^1Г(--I 2cts(^/2) 1±I{ 2ctg[(a-i/Or/2] 1
41/ \ 2 / \ Trcosec (j/tt/2) J 2 \ тг cosec [(a — и)ж/2] j
kep > 0, {C > °; Rea < 5/2l IV±M, V± см. в 2.12.3.10l.
1	Re c> 0	J	J
n _. _ . тж	a f sin &ж 1 . . x a ( sin 6ж 1 f Yiu(ca
2.12.4. Интегралы от ж < f >Jiu(cx) и ж < , >< _, ,
[сойож]	[ cos bx J [^«^(сз
Обозначение: J = < >.
со
1. ж <	yJiyicx) dx = U
J	I cos bx J
0
[6, с > 0; Re (a + v) > -S; -S < Rea < 5/2 при 6 ^ с; -5 < Rea < 3/2 при b = c],
I \C6) I Sin^OJTT/zJ I
1/6" \ cos (сктг/2) J	"^
о	[0<6^c],
(а +
J
2
J
0
[6, с > 0; Rea > |Rei/| - <f; Rea < 5/2 при 6 ф с; Re a < 3/2 при Ь = с],
,) _ <,(_„)] + ЕМ ctg ^{sin ^ }	[о < с < 6],
i/6a	2 [cos(a7r/2)J

116
Гл. 2. Определенные интегралы
[2.12.5
W =	Г
ж
1 л (а + и + 8\ л fa-iz + tf^ / sin [A/-а)тг/2]
cos [(*/ —а)тг/2]
Fo[0<6 ^ с], [U(и), V1 см. в 2.12.4.1].
СО
Г а-1 I sin ^ж I
5» Ж \	/
J	[ COS ОЖ J
2.12.5. Интегралы от х
In
2 / V 2
[6, Re с > 0; Re а > |Rei/| - 5; V1 см. в 2.12.4.1].
In
OO	(
I \х^ЛЫ
" J	1 In
(и - а)/2
\ф (——-)+ф (-—— + l)	2 In - [с, Re а, Re (a + и) > 0; Re a < 5/2,
Rez > 0
z >0
cosec
ctg[(
"(a + i/)tt/2] 1
а + |/)тг/2] J
=±
x 2F3
-—^Г
— .2'
а Л а
2 -
a-i, (-1Г
2.
ln
a^^l^tg^^^21n^ ¦ -a^(W2)
3.
а-1[1п(^ + .
In
c> 0; |Rei/| < Re a < 5/2,
б!ж = -^
z > 0
2J ausin (атг/2)
, C/7(i/), V1 см. b2.12.5.i1.
) —L/o(—^jj— - Vo cosec —^~
Rec > 0; Rea
z > 0
атг	i/тг
cosec	cosec —
(i/), V1 см. в2.12.5.1|.
{Yiu(cx) 1
г ^^j^	Г(а)
L. xa Fii( — bx)Jil/(cx)dx = U^(u)	Ц-^-	[с, Re 6, Re a, Re (a + u) > 0].
avba
i/ a + i/ a + i/ + 1 a +
о T a-iP./ , ЛУг„(са!I 1 Г/cog
2. ж Ei (—6ж)< r^ ) {[} dx = ±	 <
J	I Klv{CX) J	Sin 177Г I 7Г
cosi/tt
г/2
U/2J Tl

2.12.7]	2.12. Интегральные функции Бесселя, Неймана и Макдоналъда	117
_ЦаЦ 2ctg(^/2) I	[Reb>0;Rea>|ReH,( с>° \,^W с. „2.12.6.11.
2avba \ ж cosec Отг/2) J	[_	iReoOJ T	J
3. ix-'e^EiiTbxVUcx) dx = Ui{u) ± Vx - W - Z[I>) J cosecQ7r \
J	i/6" [ CtgttTT J
+ i/l f cosec (a + ?/)тг 1 „ /^ a + is a
[c, Re 6, Re a > 0; - Re i/ < Re a < 7/2],
2
V	2"-2	Г(а + 1/-1)/2]	/1^-a 1	3-a-i/ 3- a+1/ 3-a. H)V
7 (ljft1 |(	3)/2j 4 3 V 2 '2' ' ' 2 ' 2 ' 2 ' ft2
4 3 lx 2 ' 2' "' "' 2 ' 2 ' 2 ' б2
W^ =	р (а + иI2
7	/г>	\U1 (У — 2	/	\ /О i
IZ — (ЖШ С	11^ — ^//^ I
"о"' ^) ' ' '	о '	^>
Л А	Л	Л
4. I жа^1е±6ж Ei (^fbx)Yiu(cx) dx = 	[cosi/7rt/i(i/) — Gi(—i/)l dz
J	Sin 1/7Г
J cosec атг 1
\ CtgttTT J
[c, Re 6 > 0; |Rei/| < Re a < 7/2; (/7(i/), V7, W7 см. в 2.12.6.3].
5. [ xa^1e±bx El {^hx)KilJ{cx) dx =	^	[[/0(i/) - ?/0(-^)] T
J	ii Sin 1/7Г
тг?Г a — i/	тгТжг	ol — v 7Г Г(а)
— Vo sec	7Г H	Wo cosec	тг -\	—- cosec
2	2	2	2	2uba
i/тг f cosec атг 1
2 \ ctgan j
Обозначение: S = I
[Re 6, Re с > 0; Re a > |Rei/|; I77(i/), V7, W1 см. в 2.12.6.3].
(cx) 1
(сх))
л^л^ „	a f si (&ж) 1 _. . ч a f si (&ж) 1 f Yiy
2.12.7. Интегралы от xai m) ! }J%v{ex и xaI .) ; H "
{ci(bx))	(ci{bx)) [Къи
. f x<--4slbx \jiu(cx)dx = U
J	[ cl bx J
[6, c, Re(a + i/) > 0; 0 < Re a < 7/2 при 6 ^ с; 0 < Re a < 5/2 при 6 = с],
Vo+
Г (^ + Q + 5)
[0<6,c]
=	^	U + ^1 Г sin [(a + V)ff/2] 1
v ; 2"^(a + v)ba+v L^ + lJ\cos[(a + j/Or/2] J
v a + v a + v a + f + 1 v	a + v	c2
(^ + 2)BJ + l)(a + J + 2)c«+'s+2	V'2

118
Гл. 2. Определенные интегралы
[2.12.8
3 (-
2.
[6, с > 0; Rea > | Reu\; Rea < 7/2 при b ф с; Re a < 5/2 при b = c],
sin(mr/2)^	[0<cO],
Г	г г/ \	ГГ/	\1	\ / x
	 COSI/TTt/fi/) — t/( —1/)|	^т^ Ctg 	 ж
sin 1/7Г	auba	2 [cos(a7r/2j
1 r(oL±Ji±S
(a + ё)жса+§ ~ V 2
r^a —2
¦ i/ + E \ J sin [(i/ — а)тг/2]
1 + J \cos[(i/-aOr/2l
/ a ~~ и + 8
Msin [(*/- а)тт/
5 cos [(i/ — а)тг
/2]
/2]
S = С + i
2
Г cv^i f si (bx) Л T~.
J [ciFx)J
2 7 -a"!46 —T"ln25
1 ^ /a
Г
[C/(i/M Vj см. в 2.12.7.1].
(a + S)ca+8
2
x —3
[6, Re с > 0; Re a > |Rei/|; V7 см. в 2.12.7.1],
f erf(&ж ) 1 т / \	f er
2.12.8. Интегралы, содержащие < . \ 'yJivlcx) или J
[erfc (bx
\/~ n ( p rn \ I
c> 0; Re a > -A ±l)/2; | arg b\ < тг/4,
-1 - Re i/ < Rea < 5/2
Re (a + и) > О
a + i/ + 1 a + i/
465
OG
Z r n \ }Yiv(cx) dx = ±-	[coeutiUi(u) - Ui(-v)] -
J	[erfcFx)j	sini/тг
f ll 2a-1 _ /a + i/\ _ (ol-v\ ol-v Г a + 1/2 ^ i/тг
- \ \	Г 	 Г 	 cos	7Г =p —^	^ ctg —
\0)ажса V 2 / V 2 /	2 ^ а1/у^г6"	2
I. J ^
arg6| < тг/4; Rea
Ee
2 sin i/тг
V 2 У V 2 )
см. b2.12.8.i|
Vtt	i/TT _, / a + 1
	— cosec — I
2auba	2 V 2
[Re с > 0; |argfe| < тг/4; Re a > | Re v\ - A ± l)/2; t/7(i/) см. в 2.12.8.1]

2.12.9]
2.12. Интегральные функции Бесселя, Неймана и Макдоналъда
119
J	\erfcFv^)i
Г(а
2"(а + i/)i/0Fb2e+2"
a +1/ v a + v	и
-^-, -; -^- + 1, - + 1,
5.
[erfcFv^)
dx =
ol-v Г(а + 1/2) i/тг
' 	 тг =1= —	¦	—- Ctg
B 2
|arg6| < тг/4; Re а > | Re i/| - A ± l)/4,
Re а "^ 5/2; C>0
с > 0
см. в 2.12.8.41.
J
J
! ^/t\ \к%и{сх) dx = Tt^
erfc(b^x) J	2sini/7r
^±^\ r f^
2 J \
,
2 / 2ai/62a sin (i/tt/2)
[Re с > 0; |arg6| < тг/4; Rea > |Rei/| - A ±l)/4; V7(i/) см. в 2.12.8.4].
7.
' "^—' 25 " + 1' 2 +1; ^
|"Ba + 2i/-l)/4l /l-2a 1 3 5 - 2a 5 - 2a - 2i/ 5 - 2a + 2i/ с2
Ba + 2I/ - 3)/4l
X
C-
'3-2a 3 5 л 7-2a-2i/	7 - 2a
X 4^'a I	, 7, 7, 1;	,		т
4 4' 4'	4	4
« + 7)/4J X
7-2а с2
ж ( secern ]
4'64/ 2ub2a 12 cosec 2атг I
[c > 0; |arg&| < тг/4; Re а > -A ± l)/4; -Rei/ - A± l)/4 < Re а < 3].
<
2.12.9. Интегралы от х < ГУ), { >Jiv(cx)nx < ry)L \ Н т,. ) \ >.
{G(bx)J v ;	{C(bx) J [ Kiy(cx) J
J	l
dx = U	[b, с > 0; Rea, Re (a + i/) > -B ±l)/2; Rea < 5/2],
X 4F3
+ l/2lfcos[(l-2a-2^Or/4]
+ \ J \ sin [A - 2a - 2^)?r/4]
v a + v	v	a +
, -, -^-; " + 1, 2+1, —г
c2
1; ^

120
Гл. 2. Определенные интегралы
[2.12.10
_
7 ~
2a + 2S - 2и
2а + 2E + 1 2<5 + 1 2<5 + 5 2а + 28 + 5	1 (^
4	' ^^5 ~~4~'	4	' 25
[Ь, с > 0; | Re z/| - B ± 1)/2 < Re a < 5/2],
С/ =
sini/тг
cos
ажса V 2 / V 2 /	2
Г(а + 1/2) Г sin [Bа + 1)тг/4] 1 i/тг
l\ fsin[Bi/-2a-lOr/4]l
4у 1 cos [Bi/ - 2а - 1)тг/4] J
[0 < 6 ^ с],
[<7(i/), V7 см. в 2.12.9.1].
со
Kiu(cx)
Q-I/
2	4/ V 2	4,
[6, Re с > 0; Rea > | Rei/| - B ± 1)/2; V1 см. в 2.12.9.1].
2.12.10. Интегралы от х
\Г(ц,Ьх)
\Г(/х, bx)){KilJ(cx)j
с, Re 6, Re (a + /x + i/), Re (a +/i) > 0,
J Rea < 5/2; Re^ > 0
\ Re a, Re (a + i/) > 0
i/ + 1
a +1/ i/ a + /i + i/ a + /i + i/ + l a
2 ' 2'	2 '	2	' ~~
1, -
7с2
CO
2. f х^Ч 1 /i? 6Ж Wi
J 1Г(/1, 6ж) J
Г /х,
2a^1
0 J атгса
с, Re b > 0; Re (a + /i) > |Rei/|,
-, bx)
cos
2 ' 2 J — 2
jRea < 5/2; Re/x >
1 Re a > Re v
(™1Oс
Г(а + ii) г/тг
7Г =p ——t^ ctg —
^ ai/6a & 2
°},ад
см. в 2.12.10.1 .
; = T:r^
2 sin i/TT
0 J acQ
2 ' 2
Re/i >
| Re
" 2ai/6a sin (i/tt/2)
[Re6, Rec> 0; Re(a + /x) > |Rei/|, ( Ее^ > ° \ ^ / ч см< b2.12.10.i1.
L	I Re a > |Rei/| j	J
'Bi/-2a-/x)/4+lJ	10
11 ГBа
Oj [{2v
¦ц-2)/4],

2.12.12]	2.12. Интегральные функции Бесселя, Неймана и Макдоналъда	121
-Rei/ < Rea < E-Re/z)/2ll
^	}j
c,Re«>0;|arg6|<B±l
, f
W4,{
ХГ
2a
¦¦^
7 ±1
4	' 8 '	4
A« 2-/i 3 -/* 2a +
2 '	4
, (^1O4с2^
S P
1	2a+ ii	2a + /i
2'	4 '	4
4' 4' 4' 4'
/	2a
w —
^- Bа + м-
/2-/x 3-/x	/x 5-
54\4'4' 4'
4'4' 4'4'	4 '
3 6-2a-/x-2i/ 6-2a-/x + 2i/ 6 - 2a -/x (-
oo
J
dx = -A— [cosi/7rt/i(i/) -
sin utt
1!1
0; | argfe| < B ±
СХЭ
J
dx =
2 sin
ГBа)
Ч4J^°^fe^\ 0F /sin(W2)r I4
[Re с > 0; Re a > |Rei/|; |arg6| < B ± 1)тг/4; U7(u), V1, W1 см. в 2.12.11.1].
2.12.12. Интегралы, содержащие произведения функций Бесселя
)
Kiu(cx)
со
1. [ xa^1JfI(bx)Jiiy(cx) dx = U
0	[6, с, Re (а + [1 + и), Re (а + /л) > 0; Re а < 3 при 6 ^ с; Re а < 2 при b = с],

122
Гл. 2. Определенные интегралы
[2.13.1
i/)/2
oo
•>	по01 — 1
2. jx .
) dx = W
[6, с > 0; Re(a + fi,) > | Rei/|; Rea < 3 при b ф с; Re a < 2 при b = c],
(i/), V7 см. в 2.12.12.1].
¦-")/2
Re (а + ^)> Re^|, j ,, - "" ' " ^ „ J,, Ут см. в 2.12.12.11
6, Re с > 0
arg&| < 7Г, Re(c - 6)
4. [ /"';(,((»
dx =
Re6>0,| C>° |, Rea
2.13. ФУНКЦИЯ ЛАГЕРРА Lv(x)
Некоторые интегралы, содержащие функцию Лагерра ЬхДж), можно получить такж:е из
формул раздела 2.19, поскольку
Lv{x) =
ex/2Mu+1/2t0(x).
u+1/2t0(
2.13.1.	Интегралы общего вида.
а,
1	I гп	(ft 	 <~т \Р	р	I I ргп | А <-п
L # 1 db I Uj	еду I О JLJ |у I С^ €А/ I IX еду
j ^	) \ ) г
оо
J
[а, г, Re а, Re/З > 0].
dx =
к
¦Е-
А;!
A;), 1 - a
-^ + *I(ас)"
[a, r, Rec, Re^ > 0; Re (a + r/3 - i/) < 1 + г при i/ ^ 0, 1, 2, . . .].
Ё <
г L -

2.13.1]
2.13. Функция Лагерра Lv(x)
123
)fc Ta-r(p+k), l-a + v
\ [
4-
[r, Re c, Re a > 0; r\ arg z\ < тг; Re (a — rp — i/) < 1 при t/ ^ 0, 1, 2, . . .].
ot — r °° / i -i \	i i
ч ,	7TV	\T~"^ [IS ~\- l)k	CX. + 1С /	ч ь
k=0
„r —ex
(су)гк
[г, у, Rec, Re a > 0; Re (a - i/) < 1 + г при i/ ^ 0, 1, 2, . . .].
CO
5. f ха~1е~рхГ~сх Lu(cx) dx = U	[r, Rec, Rep, Rea > 0],
_
[r>1J'
г, I — a + i/ —
17 при r = 1 см. в 2.13.2.2.
. 7 х*-*е-*"-г-"Ь„{
J
- rk, 1 -
7.
r, Rec, Rep > 0; Re (a - v) < 1 при i/ ф 0, 1, 2, . . .].
1 , г ^4СЖ'
[ cos ox J
6, r, Re с > 0; Re a > -<5r; Re (a - i/) < r + 1 при i/ ^ 0, 1, 2, . . . ; S =
v = b »<• y, (^+ l)k ^ / a + к \ j sin [(a + к)тг1
=
A;!
sin [(a - i/- jfe - 1)тг/Bг)]
cos [fa - i/- A; - 1)тг/BгI
1 fb1/r
o/J'
1],
+
- a - Jr - 2rA;
V при г = 1 см. в 2.13.4.1.
l
if, 1 — a + и
rk

124	Гл.2. Определенные интегралы	[2.13.1
г, Re с, Re а > 0, |rlargz' <Ж\; Re (а - i/) < 1 при и ф О, 1, 2, . . . 1.
со
9. f xa~1e~cx Ei(-bxr)Ll/(cx) dx = U	[r, Re 6, Rec, Re а > 0],
a-u-k-l
r	J \ с
1 ^\а -\- г -\- rk, 1 — а -\- is — г — rk~\ f b \
— а + и) + гфA — а) — In —	[г < 1],
U при г = 1 см. в 2.13.6.1.
со
). [ха~1е±ЬхГ~схЕЦ
JL \J # I еду	С-	1 JI | —j— U JU I JL/1/ \ C'sX/ / CXtX/ —— r
Lrg6
b > 0
[г, Rec, Rea > 0, ('arg6' "^ ^1; Re (а - i/) < г + 1 при i/ ^ 0, 1, 2, . . .1,
I ь > о J	J
v = -^^:
Е°° (i/+ l)fc /а + fc\ f cosec [(а + ^)тг
fc_n (fe!J V ^ У I ctg[(a + A:Or/
с
^>	q,	OO	г	1-1	I 1 /	V
i/ + l) ^ "Г[	1-a + r + rJb	J \ ^
a + rfc, 1 — a + г/ — rls
1 7 fc=o
i I / г \к
гфA — a + и — rk) — гфA — a — rk) — In — I ±— I —
к° -• - * -:»*/:1
k=0	-	v	¦	/v ~o l(" - J' - fc - !Wr] J V c
У при г = 1 см. в 2.13.6.2.
со
Г a_i ^сх Г si Fжг) 1
11. жа е сх< . /, г\ [>Ь1/(сж) с!ж = VF
о
[6, г, Rec, Re а > 0; Re (a - и) < 2г + 1 при и / 0, 1, 2, . . .], 8 = A ± 1/2),
_ /r ^ A/ + 1). /а^\ f sin [(a + *)тг/Bг)] 1 ,__с_\*
f^Q(klJ(a + k) V ^ / \cos[(a + ifeOr/Br)]J V feV-J	[r ^ iJ'
-i/-ife-l\f sin[(a-i/-ife-lOr/Br)]l Л
~~r	y\cos[(a-i/-ife-lOr/Br)]/ \
bV "¦ i *-) I ' _>	Ilr/Xll.r	/ /-»/	 i/	 ?•	 I \ I сшПл	 ii	 k>	 I \/ir/IVi»ll I / Л-"-/''
w =
у.
1 - a - §r - 2r - 2rk	\ \2c'

2.18.1]
2.13. Функция Лагерра Lv{x)
125
b5 \a + ёг, 1 - a + v - ёг
i/ + l, 1-a-Jr Ji^J [Oj2ca
R = С + r^(a) + гфA - a) - гфA - a + i/) - In —
при r = 1 см. в 2.13.7.1.
12. a;a"V
\егГсFжг)
dx = U
r, Re с > 0; | arg 6| < тг/4,
Re a > -r; Re (a - i/) < 1 при i/ ^ 0, 1, 2, .
Re a > 0
k fl] а
/7rcI/+1r(-i/) ^ A;!(l - a + i/ + A;)
6	^ (-l)k
1/2)
2r
гк, 1 — a + i/^ r^ '
— a — r — 2rlc
17 при г = 1/2 см. в 2.13.8.2.
О 1	Г 1	4-1
Иг-1"";;
1J	[l-a, J/ + 1J
OO
13. ха^ге^сх<
b, r, Re с > 0, Re a > -r(? + 1/2); Re (a - i/) < 1 при i/ 7^ 0, 1, 2, . . . , S = A ± l)/2],
cos[Ba
r	2
l(l^a + u + k)
+ 1, х
sin [(r + 2a - 2v ~~ 2к - 2)тг/Dг)] \ fb1/r
cos [(r + 2a - 2j7 - 2k - 2)тг/Dг)]
r/2+ 2rk, 1- a+ i/- r<5- r/2-
b
2(f
2k
[r<]
V при r = 1 см. в 2.13.9.1.
-, Re 6, Re c, Re (a + /xr) > 0,
f Re ^ > 0, Re (a - i/) < 1 при v ф 0, 1, 2,
I
Re a > 0
с \fc /ll _a Га, /x, 1
^) +\0/C Г[ l-a,
-1/) ^ A;!(l - a + i/ + A;)
1 r^^^i+P
±

126
Гл.2. Определенные интегралы
[2.13.1
?jj	к) [	1-a-fir-rk
+ сГаГ[а, /х, 1 - а + ИГ^A - а)Г^(> + 1)A Т 1)/2 [г < 1],
W при г = 1 см. в 2.13.10.1.
со
15. f xa~1e~cxJIJ,(bxr)Lu(cx) dx = U
°	[6, г, Re с, Re(a + ^r) > 0; Re (а - i/) < 3r/2 + 1 при i/ ^ 0, 1, 2, . . .],
r ^ n
2ст
2^1	*<*>
U при г = 1 см. в 2.13.11.1.
b > 0; Re (a - i/) < 3r/2 + 1 при v ф 0, 1, 2,
2r
2г
"
k\
x Г
2г
2r
[r < 1;
Um =
4c2
mr + 2rfe, 1 — a
+ 1) + ^/>(А; + га + 1) - 2гф(а + wr + 2rA?) + 2r0(l -
- 2r^(l -a-mr- 2rfe) + 2 In ^1 f Т А") Г + Vm
b J V 4c2V J
/^ при r = 1 см. в 2.13.12.1.
2cr
. . . , -2, -1, 0, 1, 2,
— 2rk
[r < 1; m = 0, 1, 2,

2.18.2]
2.13. Функция Лагерра Lv{x)
127
ею
17. [ ж«-1е-ь*г-с*LZl(bxr)L]y(
cx) dx = V
[г, Reb, Rec, Rea > 0],
1-a-rA;
V при r = 1 см. в 2.13.13.1.
18. lxa-1e-^
f ill
r, Re b > 0; Re a > -Sr; | arg c\ < тг/4, <5 = < > ,
W=
b2 \"
1 j
k\
—J	[r < 1/2],
при г = 1/2 см. в 2.13.14.2.
19. [ х*-1
°
f/ =
bx^L^cx) dx = U
[г, Re 6, Rec, Rea > 0; Re (a - jwr - v) < 1 + г при /x, i/ ^ 0, 1, 2, . . .],
+ Л)/г] /	c_\k
-(a + k)/r
	c_\k
17 при г = 1 см. в 2.13.15.1.
2.13.2. Интегралы от А(х)е^рхLu{cx).
^pxLv{cx) dx = ^P 7+f
2Fi (a,
CO
J
oo
. \ x
J
[Rep, Re(p-c), Rea>0].
о f ol-1 -ex T ( ч »	_a a, 1 +1/— a
3. \ x e Ljj(cx) dx = с Г
[Rec, Rea > 0; Re (a - i/) < 1 при i/ ^ 0, 1, 2, . . .].

128	Гл.2. Определенные интегралы	[2.13.2
а
4.	lxa~1(a-xf~1e~cxLl/(cx)dx = aa^~1B(a, /3) 2F2(a, i/+ 1; 1, а +/3; -ас)
о
оо	[a, Rea, ЕеД > 0].
5.	f ха~1(х - af^e'^L^cx) dx = а^ В A - а - /3, /3) х
х ^(a^ + ljl.a + Z»;^^
х 2F2(l-/3, 2 + i/-a-/3; 2 - а - /3, 2 - а - /3; -ас)
[a, Re с, Re/З > 0; Re (a + j3 - и) < 2 при и ф 0, 1, 2, . . .].
со	.,
Г Ж"
6.	у	г^ е cxLu(cx) dx = za р В (а, р - a) 2F2(a, i/ + 1; 1, 1 + а - р; ся) +
+ ср~аТ \а " Р'Х | Р + ^ " "I 2F2(p, 1 + р + i/ - а; 1 - а + р, 1 - а + р; с*)
|_ I/ + 1, 1 — а + р J
[Re с, Re а > 0; | arg2:| < тг; Re (а — р — i/) < 1 при v ф 0, 1, 2, . . .].
7.	[ ^^
X 2F2A, 2- а+ I/; 2- а, 2- а; -су) [у, Rec, Rea>0; Re (а- и) < 2 при i/ ф 0, 1, 2, . . .].
а
8. \xa-1(a2-x2)l3-1e-cxLI,(cx)dx =
В (|, /з) х
о
„	+ ^.,	а0^-^^ + 1) _ /а
2 ' I"' Х + 2 5 2' 2' Х' 2 +/3; —j
^1^)	[a,Rea,Re^>0].
9. [ ха^{х2 - a*f-^e-cxLv(cx) dx = ^ В (l - | - /3, ^) х
,	, 1 + ^ 2' 2' Х' 2
1 +	1	+ 5
2 '1+2' 2 Д'2'2' 2 +/^' 4
9 Я 9 Я Я Я
—; 2 — Р, 2 — Р, —	/3, —	Р; 	-
[a, Rec, Re^ > 0; Re (a + 2/3 - и) < 3 при и ф 0, 1, 2, . . .].
10.
о
3 3 3 + a c2z2\ 2р_а_Га-2р, l^a + i/ + 2p]
— ? -1"i—•> 	j -1? ~ч ~i	P5	I +c 1
\ — a + v	u — a I — a	1 —a	a	a	c2z2
'2	'	2 ' 2	'2	' 2 ' 2 ' 4
[Re c, Re z, Re a > 0; Re (a - 2p - i/) < 1 при i/ ^ 0, 1, 2, . . .].

2.18.3]
2.13. Функция Лагерра Lv(x)
129
аж
¦~2~
I/ + 3 3 3. c2y2
' *> o»
' 2' 2' 4
-2, 3-a
[y, Rec, Re a > 0; Re (a - 1/) < 3 при i/ ^ 0, 1, 2, . . .].
12.
13.
-,i/ + l; 1, a + ^, a+ _ ;
z	2	Z
[a, Re a, Re C > 0].
В A - ^ - 2a, ^) x
1-/3	/3 3-/3
1 3-/3	3-/3
a
; ,
a,
a; -ac
14.
j^=^
i.
[a, Rec, Re/3 > 0; Re Bа + C - 2i/) < 3 при и ф 0, 1, 2, . . .].
е'^Мсж) dx = 2za~p/2 В Bа, р - 2а) х
p + 1 P , , 3
2~' 2 '
p)/2-a
-a
3 3 +
/' 2' 2
оо
п1/2_ар[в-1/2,3/2-а + 1/
3/2-а, 1/ + 1
i 1 —ск /—
[Rec, Re а > 0; |argz| < 2тг; Re Bа - р - 2i/) < 2 при i/ ^ 0, 1, 2, . . .].
3
, з з
У'1; 2~а'2
:F2B - а + i/, 1; 2 - а, 2 - а; -с?/)
[у, Rec, Re а > 0; Re (а - и) < 3/2 при х/ ^ 0, 1, 2, . . .].
2.13.3. Интегралы от xae(fi^Lu(cx).
2' 2 ' ' 2' 2' 2' ' 4p
2 ' i+ 2' 2 ' ' 2' 2' 4р
[Rep, Rea>0].
5 А. П. Прудников, Т. З

130	Гл.2. Определенные интегралы	[2.13.4
X2F2 (u + 1, u + 1; 2-a + v; §-« + „; fW^' ^^j 2F
\	2	Ас)	[1 ai/ + lj
(а, а; \, а-,; ?
\	2	4с
р _Га + 1/2, l/2-a + i/l _ / , 1	13 1
1/2-a, I/ + 1 J '4 2'" ' 2' 2' 2 ' " "' 4с
[Re с, Rep, Re a > 0].
оо
J	"	?55	I 1 — QJ, i/ Ч- 1 I
о
X iF2(l ^ а + v; t- a, t- a; cp)	[Re с, Rep > 0; Re (а - i/) < 1 при v ф 0, 1, 2, . . .].
2"' 2' 2' ' + ?' ^^Г
о
	2	 \	2/ ^ + ' 2 4 I + 2"' ~~2~; ' 2' 2' 2 ^^™
а, 1 — а + г/] ^ /1 —а + г/	и —а 1 —а 1 —а	а	а с2р
[Re с, Rep > 0; Re (а - i/) < 1 при i/ ^ 0, 1, 2, . . .].
2
4. жа 1е р^ж схЬ^(сх) dx = 	Г(	)
. f xa~1e~p/V^~cxLl/(cx) dx = 2p2aF(~2a) 1F3 f 1 + i/; 1, 1 + a, ^ + a; -
- - 4)^ t'
x 1F3 f --a + i/; -, 2^a' 9^°' ~~4~) ^ReC' Rep>0; Re(«^l/)<1 ПРИ i/^0, 1, 2, . . .].
*^ t о ^ тж	« -ся Г S™ ^ж 1 r / \
2.13.4. Интегралы от же < , r }Lvlcx).
{ cosbx J
J
s'mbx
(a)/sin(a7r/2)l
b" Icos(a7r/2)J 4 3
Г(а)/8т(атг/2)\	/i/ + 1	i/ a a + 1 11 c2
4 3 I ~~2~> +2J I' ^^5 ' 2' 25 ^62
cF(a + l)(i/ + 1) / cos (атг/2) \	/a + 1 a	i/ i/+ 3 3 3 _c^
6«+1	\sin(a7r/2)J 4 4 2 '2+> +2' 2 5 '2'25 b^
[6, Rec > 0; Rea > -A ± l)/2; Re (a - i/) < 2 при i/ ^ 0, 1, 2, . . .].
? a-i ^сж f sinftv^ 1 r / ч,	262l/^2a+2 T,\2a-2v-2] ( sin (a-i/)tt\
J	^cosfev^J	c	L ^y J {cos(a - u)tt )
?• \ x с \ , ,— ? Liv\ cx i ax —	т™;	i I	\ \ ,	? x
0
/	3
x 2F2 fi/ + l, i/ + l; 2 - a + i/,	a ¦
Г[ i/ + l, 1-a-J/2 J2i?2 \ + 2' °+ 2; ^+ 2' a+ 2 ~ ^; ^IcJ
6, Re с > 0; Re a > -5/2; Re (a - i/) < 3/2 при i/ ^ 0, 1, 2, . . . ; S = \
2.13.5. Интегралы от /е"сТ/	j
f a_i ^сж f In (ж + z) 1 T f ч . 7tz f cosec атг 1 _ ,	., ^	ч .
. ж e < , v	; ^^(сж)^ = 	<	> 2F2(a, v + 1; 1, a + 1; ±cz) ±
J	I In ж - z I	a { ctg атг J
о
: - 1, 2 - a + i/] з|?зA^ 1? 2 ^ a + ^j 2 ^ a, 2 ^ a, 2; ±cz) +

2.18.6]
2.13. Функция Лагерра Lv(x)
Ш
[ф(а) + ^A ^ а) - фA - а + и) - In с]
Re с, Rea > 0, | 'arg2:' < ^1; Re (а - у) < 1 при и ф О, 1, 2, . . . .
2.
а \ ctg(a7r/2)
/а
X 3-Г4 I —
2' 2 ' 2 ' ' 2' 2' ' 2
2+1' ~2~' X) 2' 2'
sec(a7r/2)
i
, 1,
; 2,
4 Г[T'J	t
Rec, Rea > 0,
a + 1	{tg(aw/2)
с2^а^2рГ« - 2, 3 + U -
2 ' 2' 2' Т 4 J+
; Re (а - и) < 1 при i/ ^ О, 1, 2, . . . .
> 0
2.13.6. Интегралы от жо:
со
1. [ ха~1е~сх EI (^6ж)Ь4сж) dx
El
2.
^ з^2 fa, a, i/ + 1; 1, a + 1; --)
[Re 6, ReF + c), Re a > 0].
^ + 1; 1; ±|
b/
cigan
оо
J
EI (-
2'2' 2
' J
Rec, Rea > 0, { 'arg6' < ^1; Re (a - u) < 2 при и ф 0, 1, 2,
I b > 0 J
^Гсж) dx = -
Г(а/2)
i/	1 1	a	c2 \
' 2	2' 2'	2	4V
1 a + l^i/	i/ + 3	n 3 3
X +	l
5	> X + 2 ' ^5 lj 2' 2' ^5 46
^ /a\ f
coseC(a7r/2)
ctg(a7r/2)
! 2' 2' l!
sec(a7r/2)
tg(W2)
3 —
2 '
-2, 3-a
a 3 — a 3 — a c2
Rec, Rea > 0, { 'arg ' < ^ 1; Re (a - u) < 3 при и ф 0, 1, 2, . .
l о > 0 J

132
Гл.2. Определенные интегралы
[2.13.7
2.13.7. Интегралы от хае~сх\ &\ ),ХГ{ \hJcx).
\ ),Г{
ci(bxr)
J
~*е- \ Sl <**> \l4cx) dX = -Щ
fa a
5 4 VI' I'
\l4cx) dX = -Щ <?'] } x
ci(bx)) l ;	aba X cos (атг/2) J
i/	1 1 а	с2 \ cF(
' I+ 5 2' 2' ' I+;^pJ
a + 1
а + 1)(у + 1) Г cos (атг/2) 1 ,
а + 1NО:+1 \ sin (атг/2) J '
F + 3,3 3a + 3 с2'
, __, _ + i, - + i, __, i, _, _, __; ^
[b, Rec, Re a > 0; Re (a - i/) < 3 при i/ ^ 0, 1, 2, . . .].
ciFv^
cos (a — i/)tt
з	ь2У
I/ + 1, I/ + 1, 1 - а + I/; - - а + I/, 2 ^ а + i/, 2 ^ а + i/; ^^ ) -
bs+2
a
-a-J/2,
-,
-,
-; 2, 2+ -,
-, <5 + -; ^^
Я = С + l [ф(а) + ^A - a) - фA - a + и)] - In
6, Re c, Re a > 0; Re (a - i/) < 2 при и ф 0, 1, 2, . . . ; S =
( erf (bxr) 1
2.13.8. Интегралы от xae cx{ C\J r\}Lu(cx).
{ erfc (bx ) J
F4 -
1 -	i - -
"' 2" + ' ' 2' 2' ? +
. , I/ " + 3. - 3 3
ll _a [a, 1-a + i/l
2 ' ' 2 ' ' 2' 2 ' ' 2' 2' 2 ' 4&V
Re а > -1; Re (а - i/) < 1 при i/ ^ 0, 1, 2, . . .
J
2- Iх е uc\bW)}L"{cx)dx =
1,
Г(а
Re с > 0; | arg6| < тг/4,
2.13.9. Интегралы от жае~сж< ^ г^ ^^(сж).
Re а > -1/2; Re (а - i/) < 1 при i/ ^ 0, 1, 2, . . .
Re а > 0
J	\C6x)J r
0
a 2a+ 1 2a+ 3
6" \cos Bа + 1)тг/
1/ , . . 1 1 a
I + 1; lj 2' 2'?

2.18.10]	2.13. Функция Лагерра Lu(x)	133
Г(а + 3/2)A/ + 1) (sin [A - 2а)тг/4]
(а + 1)л/2^Ьа+1 I cos [A - 2а)тг/4]
/а + 1 2а + 3 2а + 5 i/	*/+3 3 3 а + 3 с2\ с~а Га, 1-
\ '	'	' + ' 5 ' ' ' 5 J +	[
/а + 1 2а + 3 2а + 5 i/	*/+3 3 3 а + 3 с\ с
Х54\ 2 ' 4 ' 4 ' 2+ ' 2 5 ' 2' 2' 2 5 62J + 2
[6, Re с > 0; Re а > -1 =р 1/2; Re (а - */) < 1 при и ф 0, 1, 2, . . .].
2.
j
^	г Г2а - 2i/ - 3/2] Г sin [A + 4а - 4i/)tt/4] 1
-а + i/) L	^v	J \ cos [A + 4а — 4|/)тг/4] /
л/2жс^ ^
х з^з [^ + 1, ^ + 1, 1 - а + I/; 2 - а + I/, - - а + i/, - - а + i/; - —
\	4	4	4с
_l л/2 6д+1/2	Га + B<5 + 1)/4, i/ - а + C - 2<5)/4
[	C-2Я)/4-а
2E + 1	2<5 + 1	2<5 + 5 2<5 +1 "	1^ б2
6, Re с > 0; Re а > -B8 + 1)/4; Re (а - i/) < 1 при i/ 7^ 0, 1, 2, . . . ; 5 = |
2.13.10. Интегралы от xae~cxi '^ r{ }L,,(cx).
aba
Г Reu > 0; Re(a-i/) < 1 при 1/7^0, 1, 2, .
Re 6, Re с, Re (a +/1) > 0; ^ P ' V	;	P ^ ' ' '
[	Re a > 0
2. I xa^Le^cxI ' vr~' """ 7 VL (еж) dx = Т^ vr" '" а х
о
^а а	l + i/	^ 11а
2' 2 ^' 2 ' 2' ' 2' 2' 2
/а + 1 а + 1	I/ I/ + 3 3 3 а + 3. с^ , /l^_eJa, /1, 1-
Х4^4 о , о -|-Д, 1-h ,	,1,,,
2 ' 2 ' ^' ' 2' 2 ' ' 2' 2' 2 ' <
Г Re и > 0; Re (а - и) < 1 при v ф 0, 1, 2, .
Re 6, Re с, Re (а + 2u) > 0, I	v	;
1	Re a > 0
tJU	f / 1 I—\ \	1 1v — 2ol4-2	Г	1
3. \x e^cx{ )	'\Lu(cx)dx = ±^^r?	гГ	p	x
J	\Г(/х, &v^)J	c^+^l-a + i/) [ -1/ J
0
u 3-
• - a - -, ^7-
дс«
'
|0|	Га,М, 1-а + И
\l/	L l-a, I' + l J

134
Гл.2. Определенные интегралы
[2.13.11
Re b, Re c, Re Ba + /x) > 0,
2.13.11. Интегралы от xae^cx J^(b
Г Re и > 0; Re (а - и) < 1 при и ф 0, 1, 2, . . .
[	Re а > 0
1' 1? 2' 2'
CO
4
2 ' ' 2' 2'
[6, Re c, Re (a + /x) > 0; Re (a - i/) < 5/2 при i/ ^ 0, 1, 2, . . .]
62
exp
J r +
[6, Rec > 0; Re v > -3/2 при v ф 0, 1, 2, . . .]
3.
oo
'•J
. J
-i/, 2~
2F2
[6, Rec, Re Ba + /x) > 0; Re (a - i/) < 7/4 при i/ ф 0, 1, 2, . . .].
b2"
x2,
62^
X M(l/_A,+i)/2, (/x+^/2 ( ^- )	[6, Re c> 0; Re (/x + 2i/) > -3/2 при и ф 0, 1, 2, . . .].
exp (-?) W/2 (^
[6, Rec > 0; Re i/ > -5/6 при v ф 0, 1, 2, . . .]
6.
сю
ч
0
х 1У(
oo
Ч
0
со
Ч
4с/ \4су
[6, Rec > 0; Re v > -3/2 при v ф 0, 1, 2, . . .]
exp
[6, Re с > 0; Re /x > -1; Re (/x - 2i/) < 3/2 при v ф 0, 1, 2, . . .]
6
ж] ах =	 exp I
[b, Rec > 0; Re v > -3/2; Rei/ > -1 при i/ ^ 0, 1, 2, . . .].
T^T	T™^	 exP
[6, Rec > 0; Re i/ > -1/2].
[6, Rec > 0; Re v < 0; Re i/ > -5/6 при i/ ф 0, 1, 2, . . .].

2.18.13]
2.13. Функция Лагерра Lv(x)
135
2.13.12. Интегралы от жае"са!( ^Ь,Х )А Ljcx).
(
У 2
v	1 1	,с\
, - + 1; -, -, 1; ±-j ±
3 3	,с2
1 ±
2 ' 2 ' 2 ' 2' 2' '
• О
2 cos мтг
— /х, а + /i/2, 1 + и — а — д/2
2 cos
- |, 2 - а
2.13.13. Интегралы от xaev(x)
оо
. \xa~1e~{b+c)xLll{bx)Lv{cx)dx =
= ^1 + 7^,7тГ^^ 3^2 fa, a-7, ^
(гт) Нт-
5 -?
9	-т.""
2. j.
О
[l-a,
, а,
7 -, , 7
1+5
а + 1/2, 1/2-а +1/
х 4F4
2 - a + i/,	a + i/,
2	2
- + 1/; -—
2 4c
[Re 6, Re c, Re a > 0].

136	Гл.2. Определенные интегралы	[2.13.14
2.13.14. Интегралы от хае<р{х)Hm(bxr)L1J(cx).
Обозначение: S = < >.
J	\ H2m(bx)
a a + 1 i> + l i>	11 1 + a - <5 - 2m c2
'^^'^^' 2+1; 2' 2'1'	2	! W
[Re с > 0; Re a > ^5; |argfe| < тг/4].
2. |Ж e
4 2/V 2
X 3F2 ( a, - + a, i/ + l; 1, —	ha-m; -™]	[Re c> 0; Re a > -<5/2; |arg6| < тг/4].
\ 2	Z	0 /
2.13.15. Интегралы от хае<р{х)Lfl(bxk)Ll/(cx).
00
J
г-, i	^ % -	_.jok — /x — 1, 2 — ок + д + i/l
X3F2 Q,q,i/ + 1; 1, 1 + a - /x: --r M	,. ¦, Г	л	.	. . x
3F2 (a, a, 1/ + I; 1, l + a-/x; --
V	6/
—M, 2 — a +/i,
x 3F2 (// + 1, /x + 1, 2 - a + /x + i/; 2 - a + /i, 2 - a + /i; -
[Re 6, Re c, Re a > 0; Re (a - /x - i/) < 2 при /z, v ф 0, 1, 2, . . .].
2 T,-^-^-L (br2)L (
X4^4t2'2' 2'2+I'2'2'2 M' 4feJ 26<«+4/' [ (l-a)/2,^+l, p + 1 '
_l_ о	ii	_i_ -1	_i_ -1	Ч Ч 2"
~2' 2 ' 2 ' 2 ' ~~2	^' ' 2' 2' 46
" ^\a - la- 2, 3- o:+ 2ii + i/l
¦Г	„	„	.	x
11 11^™а + |/, ^,i/^al 3 — a , 3 — a , _ a,
+ 1, /x + 1,	+ /i, 2+ ^—+ /i; ^^ +jti5 ^^ 4- /x, 2 —- — 4- /x,
2	h/i; 77	[Re 6, Re c, Re a > 0; Re (a - 2/x - i/) < 3 при д, i/ ^ 0, 1, 2, . . .].
2	4oy
2.14. ФУНКЦИЯ БЕЙТМЕНА kv(x)
Некоторые интегралы, содержащие ки(х), можно получить также из формул раздела
2.19, поскольку
М*) = ГA + |//2)Ж|//
2.14.1. Интегралы общего вида.
^ fc!(A +1)!
fe=0

2.14.1]
2.14- Функция Бейтмена kv{x)
137
± A; - In Bac) +
	Sin-— В (/3, -
жиг	2 V г
[a, r, Re a, Re/3 > 0].
2. \xa-1(xr-arf-1e±cxku(cx)dx =
а
_ 2аа+г/^г+1сГ(/3) . 1/тг ^ (IT W
^
k\(k
)^гГ1-/3-(* + а + 1)/г1х
2а°
-sin— В
+ Bс)г-^-° ул A^/3)^Га - гA - /3 + А;), 1 + а - гA - Р + к)
sm — cosec Irp — r — rk + a^	J тг	Bас)
( | arg c\ < it; Re (a + r/3 + i//2) <" r '
oo
4
a, r, Re^ > 0,
2cZa + 1^rp	1/7Г
тггГ(р) 81П^
Re c> 0
x Г [p
1
' k + )
Bc)rp~a ^ (-l)fc(p)fc
1 + a dz i//2 — rp — rk
x I sin -— cosec I a — rp — rk + —
/	I/\ l(l±l)/2
I a — rp — rAj + — 1 тг	Bcz)
V	А У j
r, Re a > 0,
arg c| < тг; Re (a — rp + ^/2) < 0
Re с > 0
, r|argz| < тг .
oo
'•J
\±\-v
± A; - In Bcy) -
22/°
УЖ	(ХЖ
1 ^T ctS
— r — rk
oo
. \xa^1e^pxr±c
Г . 1/7Г	/	.	l/\ 1
sm — cosec I а — rk — r -\	I тг
arg c\ < тг; Re Ba + v) < 2r
Re с > О
argc| < тг
', у, Rea > 0,
r, Rep, Re а > 0,
Re с > 0
17 =
2c

138
Гл. 2. Определенные интегралы
[2.14.1
, , 2с \к 2Г(а/г) . 1/тг
х ±^^ Н	l , J sin
pl/rj ^	«/r
и =
1 Га + rJc, a+l+rfe] [ .
Bс)"/2	^ (-
A;!
2r
2c
[г < 1] ,
U при г = 1 см. в 2.14.2.4.
со
6. f xa^1e^px~r±cxk1J{cx)
1) + j
ЖГ
lzbl - i/
к + а
1/r)k
\ .
sin
L
\ .	(
x sin — cosec а -
L 2	V
arg c\ < тг; Re Ba + v) < 0
. J/7T
sm —
г, Rep >
Л
Re с > О
7. \ха-1е-сх
J
, r }ky(cx) dx = 17A)	6, r, Re с > 0; Re a > ™^r: S = л , ,,
cosbx I	I	I 0 J j
2c	. 1/7Г
	:sm —
_ i
r
-(-iyy/2)kv(k + a-
2r
_ in
-\
2r
2 „;„ иж rfa\ fsin[air/Br)]
;Sln^~ V7/ \соа[аж/Bг)}
•A-7)-
Bc)-/
2a
^	A;!	V	2r
17G) при г = 1 см. в 2.14.3.1.
со	#
8. \х е I	r }k1/(cx)dx = 17@)
J	I cos bx I
о
sin [Ba + v - 2feOr/Dr)]
2c
Ь
6, r > 0; Rea> -?r; Re Ba + i/) < 2r; | argc| < тг; S = \ \] U(j) см. в 2.14.1.7|.
9.
= 1/A)
г, Re а, Re с > 0,
arg z | < тг
z >0

2.14.1]
2.Ц. Функция Бейтмена kv(x)
139
VM = 2cza+1 sin ™ V
Ш	2 ?-,
c [(к + а + 1)тг/г]
cosec(a7r/r)
a -r-rk + (-lO^/2J	V	2/ v ;
Bc)
a,a
sin(i/7r/2) I1
+ a)n
ctg ?
_ in Bc)] .
10. f xa-1ee"[X^ К + *Г) }kv(cx) dx = V{0)
J	[ in ж — z J
\r, Re a > 0; large! < тг; Re Ba + u) < 0, ( Г' Жё^ К Ж 1, У(т) см. в 2.14.1.91.
L	I z > о J	J
со
11. I ха^е±сх Ei(^bxr)kJcx) dx = U
J
Re fe, Re a >
0; f
^rg c| <C тг
Re с > 0
2 ^ k\(k
2c \к 2Г(а/г) 1/7Г
^n-l	l ' sin—
^ 2
Г .
[si
x[sin
(l±l)/2
Bc)
7/2
Г 1/7Г	(	V\ ]
sin -— cosec I a + — J тг
Q | fc(y+2a)
х
a ± 1//2
]\гж ctg
UJ
ж - In ^1 [r < 1],
U при г = 1 см. в 2.14.5.1.
со
19 /г»а"~^<о-*-°х ~~сх "с1, f~rh
J.J&. X С	JZLjI ^-f-f/
о
2с . 1/тг ^
Rec, Re« > 0,
argfe| < тг
b > 0
7^

140
Гл.2. Определенные интегралы
[2.14.1
тгГ
fe=O
a-r-rk,l + a-r-rk] . 7_
sin7
2с 1 / 2с
ЬГA - (-
sin7 а — г — гк Н— тг I q=
2J ^	2'
2rc
r\k
2Г(а/г) . i/it ( cosec (air/r)
2 \ ctg(a7r/r)
Bc)-asin1-T(i/7r/2) ^ 1 Г а + rfe, 1 + а + гк 1 . 7_i
= "	gr[	jSm
x ф(к + 1) — 2гф(а + г к) —
а + гк
f 1 + а
2rcr
tBc
/2
2	b
ги + 2а - 2к\ ( cosec [(и + 2а - 2А;)тг/Bг)]
k\
2c
17G) при г = 1 см. в 2.14.5.2-3.
оо
13. [ жае±6жГ+сж El {^bxr)K{cx) dx = 17@)
о
г, Re а > 0; Re Bа + и) < 2r, | arg с| < тт;
14. f xa~1e~cx
J
6ж )
, 17G) см. в 2.14.1.12 .
> 0
b,r, Rec, Rea>0; <5 =
2 ^ к\{к + 1)\{к + а ¦
2c
2Г(а/г) i/Trf sin [атг/Bг)] 1
- 2 \cos[a7r/Br)]J L Ь
=
1 U	*
а + <fr + 2r + 2rife, 1 + а + <5г + 2г + 2гк]
2r
a + rS, l^a
sin [Ba + 1/ - 2^)тг/
2c
sin (i/tt/2)
1 ^7 [ 1 ]
v
a
тг - In
1],

2.14.1]
2.Ц. Функция Бейтмена ku{x)
141
V(j) при г = 1 см. в 2.14.6.1-2.
15. [ xa-1ecxiS\ ffr\ \ku{cx) dx = V@)
J	[ Cl (OX ) J
[6, r, Rea> 0; Re Ba + u) < 4r; |argc| < тг; V(j) см. в 2.14.1.14].
16.
[r, Re с > 0; Re a > -A ± l)r/2; | arg fe| < тг/4],
'А; + г + а + 1%
2r
2r
+
2c 1 / 2c
х Г
KK GJ — =t
^ fc!(Jfe-a-i//2)
а, а -
2с
при г = 1/2 см. в 2.14.7.3-4.
0; Rea>-(l±lW2i | argc|< «,
I	|arg6| < тг/4
18.
0; Rea > -r(S + 1/2); «=
/2 + 2a + r + 2J^
¦Г| —	-^—— I х
2г
1 . B + 2a + r + 2Jfe\ тг Tl 2 + 2a + r + 2k
2c 1 / 2c
л/2	. 1/тг /2а + r\ f sin [Ba + г)тг/Dг)]
*-Sm 2 М, 2r / tcos[Ba + rOr/Dr)]
uh)=
ё + 1/2)

142
Гл.2. Определенные интегралы
[2.14.2
I	^ Г Л Г /9 ^к ^ v/f /9 Г Г™7 г (a + ^r + 2rk+ V 9 T)
2r+1cr
С/G) при г = 1 см. в 2.14.8.1-2.
19. J xa-1ec'
a^u/2 \
sin [Ba + i/ + r - 2А;)тг/Dг)] 1 / b1/r \k
cos [Ba + u + r- 2А;)тг/Dг)] J V ~2c"
= U@)
b, r > 0; -rE + 1/2) < Rea < -Rej//2; jargc| < n; S = I I; [/G) см. в 2.14.1.18 .
20
\Г(/х,
r, Reb, Rec, Re(a + rAt)>0)
(Re/'>0))
4Rea>0j'
2c
2c
sIn1^7(i/7r/2)
sin (a + i//2)tt
El	Га + fir + rA;, 1 + a + /xr + 7
v -;•-/-/ _ ife!(/x + A;) [ l + a + /ir + rife + (^lOi//2
А С
x Г
V(j) при r = 1 см. в 2.14.9.1-2.
21.
a, a + 1, /x
i//2, a + 1 +
sin(i/7r/2)
[r<l]
[	Re a > 0
2.14.2. Интегралы от A{x)ep^kv{cx).
2.
-i ±СЖ|
e
a, a + 1
2
Re a > 0,
[Rec, Rea > 0].
arg c| < тг; Re Ba + v) < 0
Re с > 0

2.14.2]
2.Ц. Функция Бейтмена ku(x)
143
ОС
aFlA|2; 2 _-;
[Re(c +
4.
5-
6. е^
о
Т. j х-
О
[Re(e + p), Rea> 0].
[Re(c + p) >0; n = 1, 2, 3, . . .].
[Rep > 0].
х sin ¦
утг	2а -
A±1)/2
a+ 1/2, a+ 3/2
33
. иж 2а + и
sin — sec	тг
2	2
1 ^/Л17/2
8.
^^cxk2n{cx) dx = (^1)-i2
X GXP
W/-
C+2n)/4,(i^2n)/4
OC--
[Re с, Rep > 0].
a-1e-p/x±cx
9 f xa-1e-p/x±cxk (cx)dx- 2C »a+1 sin ^ ГГ a
A T ^/
^(fc!JB + a)fc(Jb + l)
± к ) + ^(-А; - а - 1) - In Bрс) + Bс)
^-r(-a)sin^	|Rep>0,
Re с > 0
10. I xa~1{a-xf~1e±cxk4cx)dx =
K + L
(a + /3 + A; + 1) - ф(а + A;
± к I ~~ ln Bac) I x
X (±2ac)k + —	sin— В (a, /3)	[a, Rea, Re/5 > 0].
1/7Г	2

144
Гл.2. Определенные интегралы
[2.14.3
11. I ха~1{х - a)^1e±cxK{cx) dx =
х ^(А: + 1)
12.
Ч-
т
к+1
(-a - /3 - А:) - ^(-а - к) - ф
Л 1/тг	2а + 2/3 + ^
х I sin -— cosec	ж
2	2
х
	sin — В (a + 1, p — a —
ф(р — a — к — 1) — ф(а -
± А;) - In Bac)l x
c>0
-ф
± Л - Ы Bcz)\ x
/	J
а-р, 1 + а-
i/тг 2a^2
х I sin -— cosec
zl	A
Rea>0,
2^2 ( р, р — а Т ^ 1 + Р — aj Р — а5
argc| <7г, Re(a-p + i//2) < 0
к=0
2тг cosec 2атг -
; +1	\2
иж	t ч1_а Г а-1, а
tB) r^
	 ± к) -\пBсу)\ (±2су)к -
1/тг	2а + и
in — cosec ^—
A±1)/2
x 2F2A, 1-aT^i 1 - a, 2 - a; ±2c|/)	L Rea > 0, j
argc| < тг; Re Ba + i/) < 2
Rec > 0
2.14.3. Интегралы от xae px<
[cos ож
Обозначение: ? = < >.
1.
1 cos bx J
6d Г sin(i/7r/2) n1^7
&5 Rec>0;
-8],
Bc)«+'5
/a + 1 a , . n , a 1 + a
3 ( ^-' 2+5' 1+2 ' —
a+ 1, a+ 2,5

2.14.5]
2.14- Функция Бейтмена ku(x)
145
Г а-1 сх Г sin Ьх 1 , , ч .
2. ж е <	>«1/(сж)аж =
1 cos Ьх \
2-2a-i/ b2
[2сУ^г f a + I//2 - 1 ] Г cos [Bа + |/)тг/-
6«+"/2-i L "/2-1 Jlsin[Ba + i/Or/'
2-v	v	и б-i^ З 6- 2а -^	2а + и^
4 ' ~ I' ~ I' 4 ' 2'	4 '	4 '
[6 > 0; Re а > -ё; Re Bа + и) < 2; | arg с| < тг; ?/G) см. в 2.14.3.1].
2.14.4. Интегралы от хае
In
о:_1_1 . 1/7Г I cosec а тг
* + 81П-
In
Rec, Re a > 0,
arg z I < тг
z > 0
ctgaTr 1	1	1 / ч1
>Н	:	lnBez) х
2 cosec 2атг I а + А; + 1
д. 2za . i/тг J cosec атг
ai/	2 \ ctgair
a — 1, a
sin (viz/2)
sin (v/2 — а)ж
1-7
x 3F3 ^1, 1, 1 - a - (-1O-; 2, 1 - a, 2 - a; t(^1O2cz1 + Bc) a x
хГ,	a, a + 1	1 [ sin(i/7r/2) 1 ^7
x
a + l-lj'i/y
2.
иа-1Лс*/1п(ж
In
ku{cx)dx =
Re a >0; Re Ba + 1/) < 0; |argc| < тг;
Лагб*1 < ^
1 г > 0
2.14.5. Интегралы от xae^px El(±bx)klJ(cx) .
1. \xa-1e±cxm{-bx)kv(cx)dx = ±{2c)-a-1T\ " + 1',?*2 .
См. в 2.14.4.11.
o .	\(l±l)/2
. viz 2a + v у J/
x ( sin — cosec	тг I
F3A, 1, a + 1, a + 2; 2, 2,
a, a + 1
2a
sin —- cosec —
Л	Л

146
Гл. 2. Определенные интегралы
[2.14.6
2.
-1 (±Ь-с)х
= -BсГаГ
EI (^Ъх)ки{сх) dx = 17A)
Re с, Re a > 0, j
sin(i/7r/2) I1
6 > О
а, а + 1
1 + а + (^lOi//2, 1 - (-lOi//2 J [sin (а + *//2)тг
3. xa~1e{±b+c)x EI (=p &ж)^(сж) с!ж = 17@)
I Re a > 0; Re Ba + i/) < 2; |argc| < тг, ( ' arg6' < ^ 1, U{j) см. в 2.14.5.2
L	I b > 0 J
ku(cx) .
2.14.6. Интегралы от хае рх
dx = V(l)
r_sin(i/7r/2) т1
Z • О" у&С)~ ' " ' ~{О -f А) [
х Г
b, Rec, Re а > 0, S =
: + 2) L sin (а + 1//2)тг
-3, а+ 2<5+ 2
) . Л с . 3 2а + (-1
i
1,
' 2^' 2
+ d,
a + S + (-l)Ti^/2, 1 - (^l)°V/
т^-
= С
2а-
2c
2.
о
х Г
2a
sin [Ba + г/)тг/4]
2a
2a
2 - 2a -
2Bc)
и/2-1
cos [Ba + i/)tt/4] \ Га + i//2 - 1
4 ' 4c2 7 Ь^+^-^г-га-!/) \sin[Ba + i/Or/4]
/2-1/ 1 1/ 1 1/ 6-1/ 2^2a^i/ 3 6^2a^F 6^2a^i/
{Г> г - 4' г ~ 4' ~' 	4	5 2' 	4	' 	4	'
2a + v b2 \
1	;		[6, Re a > 0; Re Ba + u) < 4; largcl < тг; 1/G) см. в 2.14.6.1].
4	4c2 /

2.14.8]
2.14- Функция Бейтмена ku(x)
147
2.14.7. Интегралы от х
a-i ^cxf erf(bx)
са Le сх) v ;
[ erfc (bx)
ляг/ \	2С	. U7T
iyG) = T<,a/2l>tt+1sin —
r\ \кУ(сх).
) '
* ~РХ Г erf |
[ erfc Fжг
daj = W(l)	[Re с > 0; Rea > -A ± 1)/2; |arg6| < тг/4],
2
а + А;
х Г
а, а + 1	1 Г sin(i/7r/2)
- (-lOi//2, 1 + а + (-lOi//2j [sin(a + i//2Or
5- J e
Rea > -(
er:
erfc
argc
M
f Re Ba + v) < 0; | arg 6| < тг/4
I arg6| < tt/4
см. в 2.14.7.1 .
kv(cx)dx = (/A) [Rec > 0; Rea > -A ± l)/4; |arg6| < тг/4],
26
sin(i/7r/2) I1
а+ 1/2, а+ 3/2
/ -i \7 /о i_ /q _i / 1
2'UT2'UT2' 2'
x Г
а, а + 1
sin (|/тг/2)
1-7
4.
- (-lOi//2, 1 + a + (^lOi//2j [sin (а + ^/2)тг
i/(еж) dx = f/@) + —^=—2a + Jf	\ ^	X
Re а > -A ± 1)/4; | arg c\ < тг,
~Г ji" 2' A""
Г Re Ba + i/) < 0; | arg 6| < тг/4
I/	1 — I/	62\
см. в 2.14.7.3 .
2.14.8. Интегралы от
ею
1. j х-1*
0
V[l) =
\	| arg 61 < тг/4
Aii/(еж).
6, Re с > 0; Re a > -5 - 1/2, 8 =
\С{Ьх)
0/ '
a+ 3/2, a + 2E + 1/2
Oi//2, a + S + (^lOi//2 + 3/2
sin(i/7r/2) I1 _ /2E + 1 2a + 3 2a + 5 2a + 1 _	2a + 3 _
x 1Т„„„/. , .. /оч_ I 5^4 ( —-—,	—,	—,	ho,	—-.	ho;
cos (a + i//2)tt
2E 4
1
J 2'
4 ' 4 ' 4 ' 4

148	Гл.2. Определенные интегралы	[2.14.9
= у(п) _	(^У/2У2	Га + (i/ + 1)/2] | sin [Bа + i/ + 1)тг/4] 1
lj ^FB + i/N«+-/2 [ 1 + I//2 J \ cos [Ba + i/ + 1)тг/4] J
4'	^; 2'
4	4i
a + (i/-l)/2l f sin[B
a^y- 1)тг/4] 1
- 2a - u)ba+^/2-
2 — у	и	у 6 — у 2 — 2a — i/ 3 6 — 2a — у 5 — 2a — i/
4 ' ~4' ~ 4' 4 '	4 ' 2'	4 '	4 '
3 - 2a - v b2
4 ' 4c2
[b > 0; -B± l)/2 < Re a < -Rei//2; |argc| < тг; 1/G) см. в 2.14.8.1].
2.14.9. Интегралы от хае^рх{ 1^J ^l \к„(сх).
J	\(/, )
sin(i/7r/2)
^l}kl/(cx)dx = W(l)	[Re6,ReC,Re(« + /x)>0, (lL
\Г(/х, Ьж)/ l ;	W	L	lRea>0jJ'
0
= ±
x 3F2 /i, a + /i, a + /i + l; /x + 1, l + a + /x+ ^™—; (^lO^
\	2	2c
[	[
U " (-lO^/2, 1 + a + (-lO^/2j [sin (a + v/2)ir
2. ТУФ^ЖП
1-7
_. . i/	i/	1/	у	у b
x 3F2	,1	, —&	; 1 — a	, 1 — a — и	: —
!2' 2'	2'	2'	P2'2c
2
, bx)
0	x .. »	/
Г	,	x	,	f Re 11 > 0, Re Ba + 1/) < 0] , ч	1
Re 6, Re (a + ш > 0; arg с < тг, <	>, W(j) см. в 2.14.9.1 .
L	{	Re a > 0	J	J
2.14.10. Интегралы от kf?(bx)kt/(cx).
a-i, / ч, / ч , sin(i/7r/2) _[ a+ 1, a/2, a/2 + 1 1
жа fc-y(ex)K{ex)dx = \ ' 7Г	, \/9 , r	wo [Rec, Rea>0].
[1с)ауж [1 + (a + i/j/2, 1 + (a — i/j/zj
0
Г «.-i, 2_ 2^-1,	w	a-^-'c .	^a + l
J	0F	V 2
.^	Z	Z Z Z	Z
^o (a/2 + f3 + 1)кC/2)к(к\)Цк + 1)!
{ (^1-60-3^'^ +l) +
[a, Rea, Re/3 > 0].

2.15.1]	2.15. Неполные эллиптические интегралы F(x, k), Е(х, к), П(ж,1/, А;)	149
ci / \i / \ j 	 / \m+n—2	4С
3.
J ж
о
со
4. 1 ^е рш^2т(Ьж)^2п(сж) с?ж =
о
4C
1 — тп, 1 — n: 2; ——
p2
[Re Bc + p) >0; ra, n = 1, 2, 3, . . .].
n - l)!6eF - с + p)n^1(c - b + p)w^
X
. J x^
x 2-^1 1-m, 1-n; 1 — m — n;
(р + b + с)(р — 6 — с)
(р + 6 — с){р + с — Ъ)
[Re F + с + р) > 0; т, п = 1, 2, 3, . . .].
п
п<
.1=1
х FA ( п + а; -пы, . . . , -тп; 2, ... , 2; —-^-, . . . , 	:
с + р	с + р
, п = 1, 2, . . .; Rep, Re(n + a) > 0 .
2.15. НЕПОЛНЫЕ ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ
F(x, fe), ?7(я5, fc), П(ж, i/, fc)
2.15.1. Интегралы от /(
тг/2
ж)<	' ^ >.
[ К(ж, A;) J
1
ctg xF(Xj k)dx = - K(Vl - k2 ) + - In A;K(A;).
2.
3-
4.
5.
6.
г/2
0
tt/2
Sm2f
7Г/2
(x, А;') с!ж = —	7 In
l ' ;	2A-A;) A
о
тг/2
V 1 ^ ^ sin ж
™ fe2 sin2 a sin2 ж) \/l - ife2 sin2 ж
- \ In A -
dx = -
K(Vl - ^2 ) [A;' = VT^
sin2 x - sin2 o)(sin2 6 - sin2 x)
° I к 8mb
F(ai
, к) J
dx :=
secacosecft f K(A;) 1
2	\ E(fc) J
x K(ч/l - tg2 a ctg2 6 ) + I ° I к 8mbK(\/l- sin2 2a cosec2 2b )	[A; = л/l - ctg2 actg2 b].
[ 1J 2 cos a	L	J

150
Гл. 2. Определенные интегралы
[2.15.2
1.
2.15.2. Интегралы по модулю к.
Е(х, к)
sin ж	3
1/2
Г	т v '	1 4- v '" sin т
2. кЩх, и,	k)dk = tg	In	1/o	1/П(ж, I/, 0).
J	2 2	1 — и1'1 sin ж
о
2.16. ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ К(ж), Е(ж)
2.16.1. Интегралы общего вида.
Обозначение: 8 = < >.
		"" (l/2)*(±l/2)fc
Е(сж)/аХ	2г
х Г
nin(a,6)
2.
Oi — l fir	Г
(br - xrf
_! J Щу/1-х/а)
Щу/l-x/a)
(acfk	[a, r, Rea, Re/3 > 0; |ac| < 1].
dx = I [a, 6, r, Re a > 0 (и Re /3 > 0 при a ^ b)},
A;!
a + rfc, 1 + rk — 8 + a
^2	^ k! ж [l/2 + а + гк, 3/2 + a - <5 +
&a+/3r^r	Г 16fl 1	1 /O	\1
/ =	7	 В ( —, /3 In —	^ I — ) H— Ф \	Ь/3 ±
2dr	\r / [ 6 r \r / r \2 /J
AГ
2§r
^ ife!(A; + J-l)!
_ , /1 , \ 1 , (a + k\ 1 (a + k .
3.
(жг
Щу/1-х/а)
=
x Г
a + rfc, 1 + a — 8
.} (f Г
_l/2 + a + r^, 3/2 +a - 6 + rk\ \zj
[a, r, Re a > 0; |z| > a, r| argz| < тг; p = 1 при zr = ~~yr, у > a].
4.
/ж + b
2r
2s
dx =
^(l/2)fcC/2-.
^	(&!J
¦^ A — /3)fc [a + rfe,
(a- k-l/2)/r
(a-k-l/2)/r + ,
?
1/2 +a+ rk
[a, r, Rea, Re/3 > 0; |6| < a; |arg6| < тг].
5.
'(хг-ау-1 K(y/b/(x+b))\ , .ra
x Г
- (a-k- l/2)/r
2r
[a, r, Re/3>0; Re(a+ Дг
X
fe=0	V V
+ 1/2; |6|<o; |arg6|<7r].

2.16.1]
2.16. Эллиптические интегралы Ж(х), Е(ж)
151
6.
(xr
dx =
^a-pr-1/2
2гГ(р)
(kif
ba^1/2 у, (^l)fc(p)fc Га + rfc, 1+a-J+rfc, 1/2 ^ a ^ rfe
2**p' ?j k\	[	1/2 +a+ rk
[r > 0; 0<Rea<rRep+ 1/2; |6| < |z|; |arg6|, r|argz| < тг].
7.
о
X Ctg
(xr - уг)
2r
2V
fe, 1
(*!J
ife, 1/2 ^ a ^>
[г, у > 0; 0 < Re a < r + 1/2; |6| < y; |arg6| < тг].
8.
x Г
x Г
а + rfe, 1 + a — S + rk, 1/2 — а — rk
9.
Щл/l - x/a)
1/2 + a + rk
dx =
[r, Rep, Rea > 0; | arg6| < тг].
10. ж" sin bx1
/G) =
a
-1-1 Г a — 1
11. Ж
Щу/1-х/а)
\	1
[a, r, Rea > 0].
2rk
—h a + 7Г -
, 3
C' 2
I K(Jl-x/a
[a, r > 0; Rea > -r].
[a, r, Rea > 0; /G) см. в 2.16.1.10].
12.
_(l-2a)/Br)
= J(l),
2r
2r
+
a7 a+7r
2^
9t»^* 1 /9	 ry	 л/т- 	 9т»&1
[a, r > 0; -г < Rea < г + 1/2; |arg6| < тг].
1Q T
13.
J
[a, r > 0; 0 < Rea < r + 1/2; |arg6| < тг; J(j) см. в 2.16.1.12].

152
Гл. 2. Определенные интегралы
[2.16.2
14.
dx = —
4?
a ' b\ a b ^
Щ\/1 ~~ x/a]
, 1/2 — а — иг — 2гк~
\
[a, r, Re(a + i/r) > 0; Re a < Cr + l)/2; |arg6| < тг].
Ql^.y	OO
х Г
1/2 + а + иг + 2гА;, 3/2 + а - 5 + иг
К(сж
2.16.2. Интегралы от жс
1
(x/o
о [0
[а, г, Re (а + i/r) > 0].
[а > 0].
[а, Re а > 0].
. Т
J
К2' <J - «)
1-а/2
[Re с > 0; 0 < Re a < 1].
2.16.3. Интегралы от (ж ± а)а(Ъ ± ж)/3К(сж).
8
а
. [ 7Х
J х/а -
х V а
7
I 1^
тг 2 ' 2 ' 2 ' 2
/3)/2
[Re с > 0; -A ±1) < Re a < =pl].
[a > 0].
[a > 0].
[a > 0; 0 < Re/3 < 1].
[a, Re/5 > 0].
5.
y/(x-a)[b-x)
x } dx =
8z + 8
1/2

2.16.4]
2.16. Эллиптические интегралы Ж(х), Е(ж)
153
2(b2 -аЪ + а2) - 2y/abEab - 2а2 - 2Ь2)
Dab ~~ Ь2 - а2)
k± =
-	2а2 - 2Ь2)
-	2 + 2>/z +
±
1/2
2.16.4. Интегралы от (ж2 ± а2Г(Ь2 ±
	ix = — 2F2 i, i; 1; aV
,2 _ ^2	А г \4' 4' '
0
2. =:
/1 + ас — ^1 — ас
3.
1 /K(*/a)
/a2 - x2 \Щх/а)
[b ^ 2a ^ 26].
[a > 0].
[a > 0; \ac\ < 1].
[a > 0].
a
1 та~г(п2
JB (!¦")••
+ 2/3^2
zl Л Л	А
[a, Re a, Re/3 > 0; | arg A - aV)| < тг].
5.
dx =
|)/ A - a2c2f/2P_-f/2(l - 2а2с2)
[a, Re^ > 0; |arg(l - a2c2)| < тг].
7.
8.
9.
-=Fl/2
[a, Re/3 > 0].
[а > 0].
2 2
2 с
10
11.
f -2/3/ 2	2ч/3-1/
. ж (а — х ) <
J	l	} \
4acos/37r\2/3J [@ + 1/2
[0 < ac < 1; 0 < Re/3 < 1/2].
l\r2[ /3
/2
[a > 0; 0 < Re/3 < 1/2].
[a, Re/3>0].
/3
4, ? + 1/4
1О Г 2^4/3/ 2
12. ]Ж ^(а -
[a > 0; 0 < Re^ < 3/4]
13. [^(а2-
J v
?,/3,3/4-/3
3/4,3/4, 1/4+ y
Г (l + 2?)/4, E-2?)/4 1
In/Зтг A [3/4, 3/4, A + ?)/2, 1 - ?/2j
[a > 0; 0 < Re/3 < 1].

154
Гл. 2. Определенные интегралы
[2.16.5
14
15.
16.
17.
18.
19.
Е(г-
[3/4,3/4, (l + 2/3)/4j
[а > 0; 0 < ЕеД < 3/2].
I, C-а)/21
К(сж) с!ж =
1-а/2
2
¦ К
1 - а2с2
к± = ab~1(l±
К
Rea > 0; 0< Rea < 1 .
-а2^)'1; 0 < о < б].
[0 < а < 6].
г
а + b
[О < а < 6].
[a > 0; Re/3 > 2].
2.16.5. Интегралы от ж°
Обозначение: S =
< >.
-,2/3
, /3-е+ 3/2
, /3, /3 - e + 1; /3 + i; /3 - e + |;
а, ЕеД > 0,
Rez > 0
z > а
2.
4.
1/2
V - ж2) (б2 -
^){е(ж/Г)}'
_ГК(ж/а)
2&Vb2^
тга | K(a/Va2
6.
D(a/Va2 + z2;
]
J Л/(а2-ж2)F2-ж2) Va/
a __2 / / 2a
7
a + 6
a + Ь
[0 < а < b; Re/3 > 0].
[a, Rez > 0].
[а, Re/З > 0].
[О < а < 6].

2.16.5]	2.16. Эллиптические интегралы К(х), Е(ж)	155
9.
[a, Re^ > 0; 0 < Re/3 < Rep+ 1/2].
а
Г 2~2Я (а2 — Ж2)^ Г К(ж/а) 1 .	TTtg/Зж i_2/3/ 2	2\/3-1 Г КB//а) 1
J	^2~2/2 \Е(ж/а)ГЖ^	2 ^ (а 2/) \Е(г,/а)/ +
«	r[i9,l + /3-J, 1/2-01 о ^ ,,.,,.! , л 1 , л. 2/2
[0 < у < а; 0 < Re/З < 3/2].
12. Iх1 ]Р^~Х^ г к(-^] dx = ^a2f3~4pB (P-, l-p} x
о
X 3^2 (-, -, 1-р; 1, 1 + | -р; 1J	[а, Re/З > 0; Rep < 1].
is. -ж"л/о' °
Bа2 - ж2\B/з+з)/4 \ал/2/	2^+5/2а3 I C + 20)/4
о
[а > 0; 0 < Re/З < 1/2].
а
JL4. ж	(о. ж) (о ж] л ^- / ,,\ ^ яж = т я ft (f? а)	х
J
? 1 dx =
[ Mj[x/b) J	4
[Re/3 > 0; Re @ + 7) < 3/2; 0 < a < b].
b
i r f 2-2а-2Э/ 2	2\а —1/i2	2\/3-l I К(ж/6) 1	7Г 1-2/3 i 1 —2а /1 2	2
15. ж	(ж — а ) (о — ж ) < , ' > аж = — а о (о — а
J	|^ Лг^Ж/ Oj J	4
3 f 3
«2
Т~ х
2
1/2 +'/3	j sF2 ^/3, 1 + /3 - J, 1 - а; - + /9, - + /3; ^—j
[0 < а < Ь; Rea, Re/3 > 0].

156
Гл. 2. Определенные интегралы
[2.16.6
1.
2.16.6. Интегралы от Л(ж)К(сж).
ж
о
v/(e2 - х2) (х - у) W	2^/y(a - у)
2.
ж	а — b — х rr (х
/а? -х2 а2 + Ь2 - х2
«» i ,	жа	а
— ) dx =	у	К
¦Е
< у].
Kl-)dx =
2Ьх/а2 + б2
[а, 6 > 0].
4.
,/2
«3-3/4
-ж2)[а6^&2-ж2 -
б2 \ „ / б2
/-3/4
^3/4
а\/Ъ2 — а2
1
263/2F2-а:
Ь2
[0 < a < b].
-1/4
a\/b2 — a2
[0 < a < 6].
5.
ж (i/ж2 + z2 +
\а/
r^—i—7Г a/2
a2 + z2 - a) ' x
=2\fa2
6. (а2 — ж2) 1[(ж + Ьл/а2 — ж2 ) 2 + |ж — 6Va2 — ж2
о
-a)/s; a, Re z
7.
- bVa2 - x2
[0 < b < 1; |Re/3| < 1/2].
8. (a - ж ) 7 6ж + Va2 - ж2 7 + (-1)
6ж - V«2 ^
; К (-
= 0или1; а, 6>0].
9.
,-1/2
7.2 _
— Fж + у «2 —
sgn?(bx — л/а2 — х2 I /ж\
К. I — 1 аж =
&ж - Va2 - ж2 |i/2
а^&
> + 1
+ Г )	[е = 0 ИЛИ 1; а, 6 > 0].

2.16.7]
2.16. Эллиптические интегралы Ж(х), Е(ж)
157
2.16.7. Интегралы от А(х)
1.
2.
3.
4.
5.
6.
¦К
тг a_i I а/2, A-а)/2
''-+а)/2,1-а/
[Rez > 0; 0 < Re а < 1].
¦К
(Vx^T^ - zJ\ , _ z"-1 Ja/2, A - a)/2, A - a)/2
dx = 	Г
-К
l-a/2
[Rez > 0; 0 < Re a < 1].
2х/х2
Г '
Ba + 3)/4 J
[Rez > 0; 0 < Re a < 1].
^ Га/2, (l-a)/2, A - a)/2l
[Rez > 0; 0 < Re а < 1].
-К
1/2
К
/ж2 + а2 — а
ж2 + а2 + а/ л/х2 + а2 + а
X sech2 CK(sech ()K(th ()	[a, Re z > 0; ch С = (а +
[a, Rez > 0; 0 < Re a < 1].
- a2 I/2/BaI/2].
z2 + x	\	z	I
8.
¦E
-ж)
: + z2 — ж
a/2, E-2a)/4, A - 2a)/4
l-a/2
9.
10.
11.
~ ^2 +
_
[Rez > 0; 0 < Re a < 1/2].
Га/2, a/21
V а — \/я2 — ж2
( (aVa2 -х2 - а2 + ж2) \
¦ Е I 	 1 с!ж =
ж
,«/2
, (a 4
a+ 1/2
[a, Re a > 0].
[а > 0; Re a > 1].
¦Е
тш^ Г а/2+ 1, a/2-
4	(a + l)/2, (a-
[а > 0; Re a > 2].

158
Гл. 2. Определенные интегралы
[2.16.8
12.
/а2 — х2 + а
dx =
«/2
[а, Re а > 0].
2.16.8. Интегралы от А(х)е
Обозначение: S =
if{x) I
I Е(сж) J
/3, /3-5
, /3- «5 + 3/2
х 2F2 Г/3, /3 - 5 + 1; /3 + i, /3 - <5 + |; а2
[а, Re/З > 0].
 Г/3,/3-^ + 1,1/2-/3
/3 + 1/2
[a, Rep, Re/3 > 0].
4.
5.
(а2 - ж2K/2
1, 1
1/2-/3, 1/2, 1/2
[0 < Re/3 < 1/2].
6.
(a2 - ж2
Ь2 - ж2\ , /ж\ ,
ехр ( ^р^9	Г? * V J =
Т^2W2 еХР	РГ^22\
(а2 — ж2K/2	\ (а2- ж2)
ТТЛ V ^7
4р3/4 у 2
8.
1 г/
о К
2
<~ ( о )
12а/
[0 < a < 6; Rep > 0].
P \
8а2/
( Р \
-1/4, О I Т^ )
[а, Rep > 0].
[а, Rep > 0].
9.
10.
1	/	рх
ехр '
(а2 - ж2)
(а2 -
ехр —
К
(-) dx =
\а/

2.16.9]
2.16. Эллиптические интегралы Ж(х), Е(ж)
159
2.16.9. Интегралы от
A(x)iSin<P[X\}lKlCXl} .
{ cos(f(x) J { Е(сж) J
2 2
cos [о(а — ж )]
„ , ,J +1 /3 . . I 20 +2S + 3 2/3 + 25
x 2F3 ( —, j +*; «5+ 3,	j	,	-4
а > 0;
-5, 5 =
2. x(a - x
о
3.
dx =
Г2C/4)
(
\ 2
[a, 6 > 0].
[a > 0].
a
4 [ж-1/2а + ж fsin[by/x /(a - x)] \ /x\	л/а к f b
J	a — x \ cos [Ьл/х /(a — x)] J \a/	2	\4^a
тг /0F/Dv^)) 1
^)) J
[a, 6 > 0].
5.
J sin [b\fa + x /{a — x)\
6. \x(a2~xY~llsln{bVa2^X2
cos F\/a2 — x2 '
-	\ j	г и ( b \\ ж1°
—	) dx = .	 /Co —^^ H
^2a \2л/2а/\
= /A),
[a, b > 0].
Г ж	, ^^	9\т^ fx\j к а 2 {ab
7.	— cos ova — ж2 )K I — I dx = 	Jo —
J x/a2 ^ x2 K	} \aJ	4 ° I 2
8. l^-.Y-1'8111^2^2
cos (by a2 — ж2
9. |x-"'"'(oa-xy-18in-
[a > 0].
[a > 0; ЕеД > -5/2; I(e) см. в 2.16.9.6].
/3 + е/2, 1 + 0-S + e/2, A - e)/2 - /3
X2F3(/3 + ^l + /3-J + ^;
— 23/ 2	2\3 — l
^5 j) [«, b > 0; -1/2 < Re/3 < 1].
0
[a, b > 0; 0 < ЕеД < 1; J(e) см. в 2.16.9.9].

160
Гл. 2. Определенные интегралы
[2.16.10
11.
s!n(&/Va2 - ж2)
а2 -ж2 I cos {b/л/а2 - х2 ) j Va
К
[4(b/Ba))~Y02(b/Ba))]
12. |(a2 -/)/2sin
14.
15.
а2-
(а2 +
Ьх
iaz — xz x\
16.
cosbx
1.
2.
3.
4.
'	167Г
2.16.10. Интегралы, содержащие 1пА(ж)К(сж).
2 2	9
Ж	i	ft	У -rr ( &\ 1	Я
			 ln^~
/a2 — ж2 (ж2 — у2) а —
К ^
хл/а2 - х2 Bа2 -
In-
In (i-^-
T3/2
In A
12
?Г
8	L3/4
[a, b > 0].
[a, 6 > 0].
[a, 6 > 0].
[a, b > 0].
[a, 6 > 0].
[6 > 0].
[0 < у < a],
[a > 0].
[a > 0].
[a > 0].
2.16.11. Интегралы, содержащие El (ip(x)) или ег?с(^?(ж)) и К(еж).
2 fab\ (ab
= -тга2/о т Uo hr
[a, Re 6 > 0].
2.
(a2 - ж2K/2
exp
9	9 \ 2
erfc ( b
2.16.12. Интегралы, содержащие Ju((p(x)) или Yu(jp(x)) и К(сж).
Обозначение: 5 = < ?.
[a > 0].
л жг i <ju ,	7Г	a b , / a b ,
1 Ko ( 	^ ) ^ж = ^ ^ , sin -^- Jo ( -^- )	[a > 0].
sin
ab 2
ж(а" + ж") / 6ж \ /x\
(a2 - ж2M/2 la2-ж2 / Va/
63/2Г2A/4)
[a, b > 0].

2.16.13]
2.16. Эллиптические интегралы К(ж), Е(ж)
161
3.
/3 + 1//2, 1 + /9-J-
1,
[a, Re B/9 + iz) >0].
4.
/a2 - ж2 \ ГК(ж/аI ,
	 < ; ' ' > с!ж =
ж ){Щх/аI
13
3-1/
* iF, (,9 +^
[a, 6, ReB^ + и) > О;
/2а2 - х2
К
< 5/4].
[а, 6 > 0].
[а, Ь > 0].
I—9—I	о" I J TL/ ^ i 2\ / / 2	2\-\
х\/а2 + ж2 j Jo[o(a +ж )/(а — ж )J I /ж
(а2 - х2J \ Y0[b(a2 + ж2)/(а2 - ж2)] } ' "
sin F/2)
=	7|_ Г f COS F/2I /6
27/2afe [\ Sin F/2) j ° V2/ ^ 1 cos F/2)
|К(сж)
/6
° V2
2.16.18. Интегралы, содержащие
п.
2
Ж
О
(а2-
К - ) dx =
7Г
SVab
(a2 - ж2J
\a
[а,
[а,
ab
[a, b > 0].
Re 6 > 0].
Re 6 > 0].
Re 6 > 0].
ГК(ж/а)
}\Щх/а)
dx =
-i/, /3 + I//2,
а > 0; Re^ > Rev\, 5 =
хЗ/2
6 А. П. Прудников, Т. 3

162
Гл. 2. Определенные интегралы
[2.16.14
6.
7.
(п2 _ ™2\3/2
(a2 - ж2K/2
Ко
exp -
Ъх
'¦{-)
\а/
К - ) dx =
Aab
[а, Ее 6 > 0].
bx2
Ьа2
К ( - ) d» = -
2^26 а
Ei(-26)
2.16.14. Интегралы от А(х)Ш0((р(х))Щсх) .
Ъ
i. \x-^ib^EZ
о
к(-) dx = --Ко(Ь)
\а/	а
2.
1.
2.
3.
(ж2 - a2M/2
^^7 Ho bx
/2^^
К ( —^=- I dx = - M ' o /o e
/7Г	^6
2.16.15. Интегралы от А (ж) 5^, Ь/(^(ж))К(сж) .
x\J a? + ж2
(а2 -
(а2-ж2K/2
^м,о
¦5_i
к©
[a, Re 6 > 0].
[a, Re 6 > 0].
[a, Re 6 > 0].
i+i, oF)
[a, Re 6 > 0].
-///2, -/х/2
- сг.%
Va/
К - ) dx =
2.16.16. Интегралы от А(х)
[a, Re 6 > 0].
l)-"DcV + 1)К2(гсж) йж =
P, P
2. х
3.
К(с^а2-ж2)К(гсж)
E(cVa2 -ж2)Е(^сж)
[Re с > 0; 1/2 < Rep < 1].
> dx	[а, с > 0].
/^^^)Е(гсж) dx = ^4 [К(^с2) " Е(«2с2)]
[а, с > 0].
2.17. ФУНКЦИИ ЛЕЖАНДРА 1-ГО РОДА Р„(ж),
2.17.1. Интегралы от (zm ± жт) Pjf(cx).
г- I Р^ (-) dx = ZJ7Z	_ч /our/-', ^х /ои/1 ¦ i\i	[m = 0, 2, 4, . . . , п = 2, 4, . . .].
2. =
п[(п - ш)/2]![(п + т)/2]\(п + 1)!
i + п)\(п + 1)!?па7г
3. =0
4.
[т, тг = 1, 3, 5, . . .].
т + п = 1, 3, 5, . . .].
[a, Re a > 0].

2.17.2]
2.17. Функции Лемсандра 1-го рода Р1/(ж), Р^{х)
163
5.
6.
а/2
v I?
x3F2
Ъ
7. \{Ъ - x)a-xPv (-) dx = Г(а)(Ь2 - а2)а/2Р~а (-
J	Vа/	\а
8.
9.
10.
11.
12.
а + и + 1, а — и
[a, Re а > 0; Re и < 2].
[-b < а < b; Re a > 0].
[0 < а < 6; Re а > 0].
[а, Re а > 0].
[а > 0; тг - 7П = 1, 2, . . .].
^ - ) dx =
[a, Re (/3 + 1/) > 0; Re (/3 - i/) > 1; |arg(z + a)| < тг].
sin [(i/ + 1/2) arccos (г/а)]
7.2 - z2
sin(i/ + 1/2)тг
[а > 0; ^3/2 < Re v < 1/2; |arg(z + a)| < тг].
sin i/TT Га, 1 — a + i/5 —a — v
t — a
[a > 0; 0 < Re a < - Re i/, Re i/ + 1].
CO
I ^1	SI /y* 	 /1 1	1--^ I 	 1 лф 	 	 	 I /v 1 	 /v 	I	 f i 	/"y 	 I/ I /If 	 #1 i ' IP I 	 1
JLtJ. I 1 Л	(A I	1 у 111 yJuJLi 		1 I UK 5 -L	CJt n^ 	tJ-	J V	/	f III
о	[a > 6 > 0; 0 < Re a < - Re i/, Re v + 1].
14.
2a,
v
, a-/x/2, A +/x
a>0;2 Re a > Reu .
[a, Re Ba - д) > 0; Re Ba + 2/) < 1; Re Ba - u) < 2].
2.17.2. Интегралы от xa(z2 ± x2)CP{?(cx).
,0-?; 1-M, /3 + ^r^; 1	[o,Rea,ReB/3-A.)>0].
[a, Re B/3 - ц) > 0; Re(i/ -2/3) > -1].
/3-/U/2, -2/3-1/ 1
L-/3-M/2, -/x-i/J
[a > 0; Re/t/2 < Re/3 < -Re^/2].

164
Гл.2. Определенные интегралы
[2.17.3
4.
5.
{1+а-
X Г
i- i/)/2, 1+ (a- /i+i/)/2j
[a, Re a > 0; Re /x < 1]
fo, Rea > 0; m = 1, 2, ...1.
L'	'	' ' J
7. =0
8
S. J
[a > 0; I, 77i, n = 1, 2, . . . ; I + w + n = 2fe; As = 1, 2, ...; w.^n^l + ra].
[ при a > 0 и остальных значениях к, I, га, п = 1, 2, . . .].
ft I .tv, I I о Ж = A ft
oo
Г	1	О	О
Ц	т" ff — п
a
oo
L0. ж" ж2 — a
_1-р- /i/2, A - /х ± i/)/2, A =р 1 ~~ /х Т ^)/2j
[a > 0; Re/i/2 < Re/3 < (l±Rei/)/2, A T 1 =p Re i/)/2].
+ Ax + i/-a)/2, (M^^^a)/2]
1-a
[a > 0; Re^i < 1; Rea < 1 + Re(/x + v), Ке(ц - и)].
V/	2++!/^ [	l +	J
Va/
/х
[а > 0; 0 < Rea < 1 + Re (i/ - ^), -
2.17.3. Интегралы от (x ± a)a(b ± xf P^
Щ dx = BаГ	\
/x + 1, a + /3 + /x; 1)	[a, Re BД - /i) > 0; 2 Re a
. f (x + a)
J
3.
4. | (Ж + aj
)	()	[
a/	[ 1-/3—11/2, —и, —\i—v J
[a, ReB^ - /x) > 0; | Re^| + 2 Re {C + i/) < 0].
*\ dx = Ba)-^T \	J + ^ a ~ ^2,
a/	l ;	[a-fi/2 + u + l, ot-ii/2- v
[a >0; Re/ix < 1; 2Rea >
= 0
[a > 0; Re/x < 1; A; = 0, 1, 2, . . . ; A; < Re i/, Re (/x -
. [ (Ж + aY Pv (-
J x — у	va
— a
oo
. \{х-а)а^г{х + а
dx = -(a
^ dx =
[a > 0; Re/x/2 < Re a < 1 + Re (i/=F м/2), - Re (i/± |x/2)].

2.17.4]
2.17. Функции Лемсандра 1-го рода Р1/(ж), Р^{х)
165
7.
*) dx =
. f (ж + a)a"
Г W	;
[а > 0; Re/x < I; Re а < 1 + Re(/x/2 + i/), Re (/i/2 - v)\.
Bа)а+м/2 sin уж Га + /х/2, а - /i/2, 1 - а - /х/2 + 1/, -а - /х/2 - i/l
7Г	[	1 - /Х + I/, -/X - I/	J
[а > 0; |Re/x|/2 < Re a < 1 + Re {у - /х/2), - Re (i/+/х/2)].
9.
10. ж"?.
' DM
а + x
a — x
dx = aa+lJF
1 + i/, a - /i/2, -a - /i/2 - i/
-/x - i/, 1 + a - /i/2 + i/, 1 - a - /i/2
[а > 0; Re/i/2 < Re а < - Re (/i/2 + i/); Re v > -1].
аж + bx + с
с!ж = I —
COS О7Г Sin2 1/7Г
a/ sin (i/— aOrsin (i/+ а)тг
X Г(о — ^)Qi /о— ( v 1 ~h rf2 )Qi/
= b2d2; Re a, Re с > 0; | Rea| < - Rei/, Rei/+ l].
11.
CO
12. J«-
/x
[a > 0; Re/i < 1/2; Re a > Rei//2, -A + Rei/)/2)].
aa+Mcos/i7r r[/i + 1/2, a + (i/ + l)/2, a - и/2, -a - /x - i//2, A + i/)/2 - /x - a
13.
7Г3/2	'[	-/X-I/, 1-/X + I/
a > 0; Re*//2, -(Rei/ + l)/2 < Re a < - Re (/x + i//2), l/2 + Re(i//2- /x)].
diC= -	n|a-/x, -a-i/, 1/2-a]
[Re/i< Rea < 1/2, -Rei/; | argz| < тг].
2.17.4. Интегралы от (жт ± am)a(b2 ± x2f РЩсх).
\х = Г(а)(Ь2 -а2)(а~
2.
3.
4.
^PS (-) dx = Г(/3)F2 - а2
va/
-Ь < а < b; Rea > 0; Re/x < 1].
'ьл
[0 < a < 6; Re^ > 0; Re/x < 1].
(а2
(а2
х-
—
х ¦
/
х2)
-у
х2)
т/2
т/2
g (f
2(-1)
•¦©
(p — l)!(n —
[y > a > 0; re ^ m ^ 0].
> а > 0; n > m > 0; p = 1, 2, . . .].

166
Гл. 2. Определенные интегралы
[2.17.5
7. |(Ж - а)"" V - б2)"'^ (|) dx = (а2 - Ь2)(«+">/2 х
[у 0 [-а, о]; -га - 1 < Re/x < 1; га = 0, 1, 2, . . .].
x = (а2 - Ь2)(«+">/2
8.
хГ[1 "i -^ ++/-м -~/ ~ " Р"+" (?
[а > 6 > 0; Re а > 0; Re (а + jx) - 1 < Re i/ < -Re(a + /x)].
i/, 7 + /X —i/ —1
x 2F1 ( 7 + /x + i/, i/ + 1; 7 + jn;
z + a
9. = (z2 - а2
7
[a > 0; Re /x < 1; - Re G + /x) < Re i/ < Re G + д) - 1].
\ — il-\-v	1 a
[-6 < a < 6; Re a > 0].
11. |(x2 - a2)"" V -
(!)*¦ =
a, 1 — a + (i/ — /x)/2, A — /x — i^)/2 — a
x 2Fi
, 1 - a + —?-?; 1 - a - ц; 1 - —
[0 < b < a; Re a > 0; Re Ba + ц) - 2 < Rei/ < - Re Ba + fi) + 1].
2.17.5. Интегралы от (x ± a)a(b ± xH(d ± xI P^(ex).
/, a- ^; 1-
[0 < a < 6; ЕеД, Re Ba -/x) > 0].
2.
1; (-) dx =
Va
[0 < a < b; Re/x > -1/2].
3.
x k- j?
2a
2a
2a	M 2a
/ \	/ j
[0 < a < 6; RejLA > 1/2].
— I dx =

2.17.5]
2.17. Функции Лемсандра 1-го рода Р1/(ж), Р^{х)
167
[О < а < 6; Re/t < 1/2].
. [(ж - а)-("+1)/2F - Ж)-"-3/2(Ж + аГ/2Р1; (|
6.
• = (Ь-а)<*
х — у
8.
x - у
[-6 < а < 6; Re a, Re B/3 - /х) > 0].
Ж)-^ /хч ^ = _ + /2+ _ ^-^ /?ч
\а/	\а/
[у ? (-оо, a]; Re i/ > -1; - Rei/ - 1 < Re/x < 1].
>m f^\ J	( 1\тп-1от I/ 2	2\m/2 глт (У
n y-j dx = (-1) 2 2/B/ - a ) ' Qn ^-
9. j (a - x)
[y $. [—a, a]; m ^. n; I = 0, 1, . . . , n — m].
|) dx =
= ±2Aт1)/2-
п ч*1/2 .х
[a > 0; г 0 [-a, a]; -1/2 < Re/it < 1].
10.
-) dx =
,3+^2 \a - $ - ц/2, p - a - ц/2 - v, 1 - a + /3 - /x/2 + i/l
"l j	[	1-M + ", -А*-". 1-а + /3-м/2	J
Bа)"	Ja - М/2,/3 - а -
/3,1-м
х 3^2 lot	, —/х — i/, 1 — /х + i/; 1 + а^/З	, 1 — /х;
[а, Re Bа - /z) > 0; Re (а - /3 + /х/2) - 1 < Re i/ < Re (^ - а -
11.
, Д - a + /x/2 - i/, 1 - a + ^ + /x/2 + */
[a, Re Ba - /z) > 0; Re (a - /3 - /л/2) - 1 < Re v < Re (/3 - a

168
Гл. 2. Определенные интегралы
[2.17.6
12. Ux- а)
z)"-1±1/2P? (J) dx
1 -"± »>
13.
14.
2a J u \Ц 2а
[а > 0; Re/i < 1; Re (jtt =p ") < 1; Re (д =F ") < 1 Т 1; | arg (z + а)| < тг].
¦Bа)аГ ' ~	' ~ ~ X
/; 1 — а — /х; - )	[а > 0; 0 < Re а < Re i/ + 1, - Re i/].
4c(a - 6)™M / 4c2 + (a - bJ Г 1/2 -
тг	у 16аЬс2 — (а — ЬL \_1 — /i + i/j sin (jla + i/)tt sin (у — д)тг
Sin /17Г COS 1/7Г
(a -
1.
2.
2c
[а + 6 > 2c; а > 6; Re /x - 1 < Re i/ < - Re д].
2.17.6. Интегралы от Л(ж)[Р?(сж) + Р^(-сж)].
2\в-1
[a > 0; 2Re/3 > |Re/*|].
» + /х/2, /3-/х/2
(и-
-^ с!ж =
= T
Г[A - /x ± »/)/2, A T 1 - /i T v)/2, /3 + 1 ± 1/2]
2 '	2
2.17.7. Интегралы от A(x)eif{x)P^(
2.
3.
2ар
а - /х/2, 1 + I/, -I/
— ) dx =
[0 < a < |6|; Re/3 > 0].
[а, Rep > 0].
[a, Rep, Re Ba - fi) > 0].
-a-fx/2 ~a
5.
?[-\ dx =
а + /i/2, -I/, l + i/
Р
2а"
[а, Rep, Re Bа - /х) > 0].
jI/+i/2Bap)	[a, Rep > 0; Re /л < 1].
[a, Rep > 0; Re д < 1].

2.17.8]
2.17. Функции Лемсандра 1-го рода Р1/(ж), Р^{х)
169
= 2'4-1а-1/2рB№1)/4-1е-а2р/2^Bм±1)/4>B,+1)/4
-2(а2 " х2)-»/2е-рх-2Р!: (J) da; =
= Bр)<"+"-1>/2а-"е-р/Bв!'>?>„-1,-1
Р„ (^
^ПГ ^ (а)
6.
7.
8.
9.
10.
11.
12.
13.
14. ха~1(а2 — ж2)~(а+1/)/2
о
Bа)-" ^з
(а2р)	[а, Rep > 0; ReM < 1].
)
ft у
[а, Rep > 0; ReM < 1].
[а, Rep > 0; 2z± = р(л/г + а ± л/г - а)].
Pv (J
I [j
,+1/2
У,+1/2
> 0].
\ a/
-- dx = -
ж + а
а /	р
Р ^ W_^1/2t0 (-?=¦) [o,Rep>0].
Р U-_,-1/2,o(^=) [a,Rep>0].
г^/2е-р(«-»)/(а
" Va/
= Bа)>^-1)/2+"ер/2И/(м_1)/2_;,,м/2(р)	[a, Rep > 0].
7гГ(-д - ./) " 4
l-a/2, (l-a)/2
0, 1/2, -(a + /x + i/)/2, (/x - ^ - a)/2
15.
1
а тг
[a, Rep, Rea> 0].
[Rep > 0; 2az± = p(b ± \/b2 -2a)}.
16. х-"/а(х + а)"/2(Ж + Ь)-(и+1)'\х + а ¦
о
ab
[«. ^, Rep > 0; ReM < 1].
2.17.8. Интегралы, содержащие гиперболические функции
и Р^((р(х)).
ГЫ	sin2 иж cos an	„,	,^^^^1/2, ,
7Г3 sin (i/ + crjTrsm (г/ — а)тт
l + 62d2) = a2d2; Re b > 0; |Rea| - 1 < Re i/ < -
2.
i + (p_M + I/)/2, (i + p-^-^/2 J
[Re/i < 1/2; Re (p + ^ - i/) > 0; Re (p + /i + г/) > -1].

170
Гл. 2. Определенные интегралы
[2.17.9
оо
ч
[-1, -Rei/ -3/2 < Rep < - Re (/x + i/) - 1].
4. е рх sh1 ^ хPJ?(ch x) dx =
о
[Re/x < 3/2; Re (р +/х - i/) > 1; Re (р +/х + */) > 0].
2.17.9. Интегралы, содержащие тригонометрические функции
и Р?(ф)).
«.«-1
1.
(а2 — ж2)^/2 \ cos 6ж / \а
-) dx =
J
, а + 1 а , с С| 1 1 + а + д — fj, — is Л
х 2F3 ( —^—i ^ ' 2' 	2	'
оо
. f (ж2 - а2
[а > 0; Re а > -5; Rejx < 1; ? = A ± 1)/2].
Л- dx =
(i/ -
X 5'Ju+i/2,i/+i/2(tt6)	[а, 6 > 0; Re/x < 3/2; Re (/x + i/) < 1].
1 1 sin (Ьл/х + a) I _ /ж\ ,	/a fseci/7r"
ж + a I cos {b\fx + а ^
byj-
J-v-i/2(by/a/2)
[a, b > 0; -1 < Rei/ < 0].
4.
- a)Fl71 (-
Va
[a, 6 > 0; ^3/2 < Re i/ < 1/2].
5. | ^^^^^ cos (б^ж — a)Pu ( — ) <ix = — v ^^ sin
6. I 	cos ,	Pv [ — ) dx = - -
[a, 6 > 0; -1 < Re^ < 0].
ж + а i/ж + а Va
[a, 6 > 0; -1 < Rev < 0].
oo
4
2 '	2
[6 > 0; -1 < Rei/ < 0].
2.17.10. Интегралы, содержащие erf (ip(x))P^(cx).
^(^1 dx =
1 + (a - /x - i/)/2, C + a - /x + i/)/2
fI /1 a + 1 a , n 3 a — fi — i/ 3 + a —/x + i/ 2,2
x з*я i -, -^—, - + 1; -, 1 +	1	, 	2~^	; ~a h
[a > 0; Rea> -1; Re/x < 1].

2.17.12]	2.17. Функции Лежандра 1-го рода Ри{х), РЦ{х)	171
v - a) J2, {ц-у-а
2-а	Г
1	// + i/ — g [1 — и — а + 1 3	а 3 ^ а б2
1
1
2'
2'	2
[а > 0; Re/n < 1; Re (а - jti) - 2 < Rev < Re (jti - а) + 1]
3. jV^^V^
о
t* g + 1 \ + ol-\l-v 1 g-/x + i/ 2,2 1
' ~~2~; —"—' ^^; ' "
_, / g + 1 g , . 3 л x
x 3F3 A, -^-,2+1; 3, 1 +
3, 1 +2'	2! a
[a, Re a > 0; Re/i < 1; |arg6| < Зтг/4]
4. Т(Ж2 - a2)--/2ea=2 erfc (ЬЖ)^ (*\ dx =
J	V
\ dx = ^ b\T ()
a/	тгу a	\ 2 /
a
X W/(i^2ju)/4, (i+2i/)/4(a2b2)	[a > 0; |arg6| < Зтг/4; -1 - Re/i < Re i/ < Re и < 1].
2.17.11. Интегралы, содержащие е ж 'АD\{bx)P^{cx).
B)	[a>0;ReA<Rei/<-ReA-l; |arg6| < Зтг/4].
2. T2 ^vv^ (=)
(M-A + i/)/2, (M-A-i/-l)/2l	faV
»/»/C+2A~2M)/4,Bi/+l)/4
[a > 0; Re /x < 1; Re (A - /x) < Re i/ < Re (^ - A) - 1; | arg 6| < Зтг/4].
2.17.12. Интегралы, содержащие J\{ip{x))P^{x{x)).
PZ (^) dx =
\	a + X	1
LA + !,(! + « + A - M ^ ^)/2, l + (g + A-/x + v)/2\
; Л + 1,
^, 1 +^;
[a, Re(a + A) > 0; Re/i < 1]
2.	Ja^-^-*2)-"/2Л+хМЬаОР^ (f) ^ = /f a1"^"/2 J1/2_
[a > 0; Re/i < 1; Re (i/ - /x) > -2]
о Г Л" г	/l \o fx\ j	1 [п \ ab ix	/«6\ . . ab
3.	V^J,+l/2(^)P, ( -J dx = -T\ ~ COS — У^+1/2 — +8111 —
j	v a /	c?yz[z	\ л j	л
[a, 6 > 0; -1 < Re и < 0].

172
Гл. 2. Определенные интегралы
[2.17.12
4.
п 1
= —а — а
Т 1 ^ j dx =
'ab
Wl/2 I "ir I + «Л/+1/2 I ^ 1 ^-1/2
о5л
2; '^l/z v 2 У ' ^1/Z12 У '^1/z 12
a, 6 > 0; Re/x < 1; -2 Re /x - 1 < Re v < 2 Re /x].
5.
a
л Г /л-5/2/ 2
6.	аГ 7 (а
7.	(ж + а) ;
— а
со
8.	f(x + a)^M
a, 6 > 0; Re A < 5/2; Re (A + 2i/) < 3/2].
— | dx = i/ — 	 cos
7Г
— т)!
m)!
[a, b > 0; 0 < Re/x < 1].
— «/2n+i F V2a ) [a > 0].
9.
10.
11.
!ж =	л/а b^ sinu7rK2v+i(by2a)
ж
[a, 6 > 0; Re/x < 1; - Re /x - 3/2 < 2 Re 1/ < Re /x - 1/2].
		/_x	7М+2лB/1+3)/4	/ f—\
f^.)P» (-) dx = -=^	^	Kl+1/2 (bj± )
^a^	>/Ь^ГA-/х + 1/)Г(-/х-1/) +/ \ V 2 /
[a, 6 > 0; Re/i-3/2 < 2 Re 1/ < -Re/x - 1/2].
[a, b > 0; Re/x < 1; Re^ - 3/2 < 2 Re v < - Re ц - 1/2].
[2з± = с(л/а + 6 ±Vo- 6); a > 6 > 0; Re /x < 1/2; Re/i/2^ 1 < Re 1/ < -Re/x/2].
12. I (ж + а)/4(а-ж)
/	 t/z —1/2
3!	Л/2-^(Ьл/2а)Л_1/2(Ьл/2а)	[a > 0; -1/2 < Re/x < 1].
- dx = ^y
a/	2^ cos 1/7T
1 J - ^-^-1/2
[a, 6 > 0; Re/x < 1; -1 - ReM/2 < Re i/ < Re/x/2].
CO
"•I
oo
15. [(Ж-а)
J
x J
[a, 6 > 0; Re/i/2^ 1 < Re i/ < -Re/x/2].
х + a J ^a

2.17.13]
2.17. Функции Летсандра 1-го рода Ри(х), РЦ{х)
173
x iFi
I/; 1-2/х; -
16. j
[a > 0; Re и < 1; Re /x - 1 < Re i/ < - Re д].
[a, b > 0; Re i/ > -3/4].
it.
ЛЬ)
[a, 6 > 0; Re/x < 1; 2Rei/ < -|Re/x| - 1/2]
CO
18. [j_M(
-) dx =
19.
i/ I	I U/«Iy 		.—
РП - ) d x =
?)
a/
[a, 6 > 0; Refi < 1; -3/2 < Re i/ < 1/2].
oo	/	\
20. [ xlj/2Jl/(b%fx~)PIJ I Ж + 22; J
[a, b > 0; Re/Lt < 1; Re i/ > -1/2].
dx =
21.
22.
[6 > 0; -1 < Re i/ < -1/4; |argz| < тг].
dx =
1^^ ^/2
[b > 0; -1 < Re и < 0; |argz| < тг].
23. Je*.
a) X (n-m)!Bn + l)
[6 > 0; -1 < Re i/ < -1/6; |argz| < тг].
[а > 0; те ^ га].
24.
25.
shbx
Jr —
n \aJ
an+1bn
7ГТ7
(n-m)!Bn
f 1, 3, 5, ... 11
\o, 2, 4, .../J
1, Л
a/2, (a-
+ ж, 1 + Л, l + ж+Л, A + a — /x — i/)/
[a, Re (a ¦
2.17.13. Интегралы, содержащие Yx((f(x))P^(cx).
L. \x1/2Yv+li2{bx)P1J(^
a Г ab _	f ab\ . ab .
— сО8уЛ+1/2[Т)-81Пт
(а - /x + i/)
Л) > 0; Re/x < 1]
aft
[a, 6 > 0; -1 < Rei/ < 0].

174
Гл. 2. Определенные интегралы
[2.17.14
2.
Т [ - ) dx =
i/
/ ab
CO
. Ux + a
ab\	(ab\Y	fab^
2 J	\2 J	\2
[a, b > 0; -1 - 2Re/x < Rei/ < 2Re/z < 2].
-) dx =
2j~ YlJ+1/2 \b V 2 J y-"-1/2 V6 V 2
[a, 6 > 0; Re/i < 1; -Re/^/2- 1 < Re i/ < Re/i/2].
2.17.14. Интегралы, содержащие 1\(ф(х))Р„(сх).
. f (x - а)^/2(Ж + a)^
J
Z (-) dx =
V a J
оо
2. J (ж
2a
[a > 0; Re /x - 1 < Re i/ < - Re д].
-o))P^ - fe =
0/
[а, 6 > 0; (-l±Re/x)/2 < Re i/ < (-1 =р Re//)/2].
(n-m)!Bn
. 1, 3, 5, . . .
a>°5 n^m=^0, 2, 4, ...
2.17.15. Интегралы, содержащие К\((р(х))Р^(сх).
. J
= \^ e~abKv+1/2
2.
(f
4
a
oo
[a, Re 6 > 0].
[a, Re 6 > 0; Re/к < 1].
x W/M_C=Fi)/4,l,+C±i)/4(a6)	[a, Refe > 0; Re/i < 1].
2 / ^^1/2 V 2
5.
6.
[a, Refe > 0; Re/i < 1].
i(bV2a) [a,Re6>0; Re/i<l].
[a,Refe>0; Re/i<l].

2.17.17]
2.17. Функции Летсандра 1-го рода Ри(х), РЦ{х)
175
oo
}(x~a> (x + a
a
a
8. f (ж + а)м/4(о-
= )P?(Z)dx =
a J \aJ
oo
4
[a, Refe > 0; Re ц < 1].
[a, Re 6 > 0; Re /л < 1].
[a, Re 6 > 0; Re/z < 1].
10.
11.
1)] dx=
12. f (x + a)<"-3>/2(a - x)
J
[a, Re 6 > 0; |Rejx| < 2].
2/1-i,2V(bv^)
[a, Re 6 > 0; Re^ < 1].
-»'2e-p/{
2.17.16. Интегралы, содержащие
oo
. f (ж + а)/4(ж - a)"M/2[yM^1/2Fi/^T^)
J
oo
J
\x + a/ \a/
-г'^Г (M, |)	[a, Rep > 0; Reц < 1].
-) dx =
атг D^ ; smptir 2
sini/тг
[a > 0; Re ц < 1; -1 < Re i/ < 0; | arg 6| < тг].
sin2i/7r
[a, Re 6 > 0; Re/z < 1; -1 < Ret/ < 0].
2.17.17. Интегралы, содержащие
f) dx =
— cos jwttF
oo
2. f
J
[Re/x < 1; |Re(/z + i/)| < 1; Re (ц - и) < 2; |arg6| < тг]
(x2 - a2)-"/2S3€tl/2(bx)P!; (-) dx =
+ i/ - x)/2 + 1/4, (m - v - x)/2 - 1/4
1/2-x
[a > 0; Re/it < 1; Re {x - fi) - 1/2 < Re iv < Re (p - яг) - 1/2; |arg6| < тг]

176
Гл. 2. Определенные интегралы
[2.17.18
со
. [(ж - a)
^)P^ (-) dx =
[а > 0; Re/i < 1; Re (^ - ^) - 1 < 2 Re i/ < Re (д - ^) - 1; |arg6| < тг].
/х + а
'iH-l/2,/
[а > 0; Re i/ < 0; Re i/ < Re/i < 1].
2.17.18. Интегралы, содержащие
• [тг cos */7г + 2 sin i/tt(C + 2 In 2 + ^(i/ + 1))]
[a > 0; Re i/ 7^ -1/2].
[a >0; i/= -1/2].
x {Г
1/4,^/2 + 1 1^
з/4, {v + l)/2J 2 + [ 1/4
(f
4, „/2 + 1 J	2 /
[a > 0; i/ ^ -1/2].
[a > 0; i/ = -1/2].
Pv [-) Pa [-) dx =
\a/ \aJ	тг
[a > 0; Re i/ > -1/2].
2a A sin (сгтг/2) cos (i/tt/2) — Л^1 sin (i/tt/2) cos (сгтг/2)
2.17.19. Интегралы от A(x)P^{bx)P^{cx).
Условие: a > 0.
2. 1 РЛ-1РЛ-] <** =
3.
4.
2тг sin (cr — i/W + 4 sin
a > 0; Л = Г
¦(!/ + !)- ^(G + 1)]
2, O-/2
_ ТГ2 - 2 Sin2 <77Г^'(<7 + 1)
[о- - t/, сг + 1/ + 1 7^ 0].
^2	7x2BG + 1)
a
Г i / T \	/ T* \
P^ ( — ) P^ ( — ) dx = а!(к7 I, in, n),
J V a/	\a/
— a
/(ra, I, ra, n) = ^,„-— w
/(ra + 2, I, ra, n) = 0
[n > I или / — га = 1, 3, 5, . . .],
/(га + 2, n, га, n) = —
(n + ra)!
(n-m- 2)! 2n + 1'

2.17.19]
2.17. Функции Летсандра 1-го рода Ри(х), РЦ{х)
177
/(га+ 2, п + 2,т,п) =
4(w
(га-га)!
[те + к = 2, 4, 6, . . . , к > то].
5.
6.	f х'-пРГ(^)р^(^
J	\а/ \а
— а
7.	j хРГ (§) Р» (f) cte = 0
(Z-ra)I(ra-m)!'
(п — т)\ [1 + 3/2
[/ > п].
[1фп±1].
8.
9.
10
10.
— любой многочлен степени j; I + j < те; А; ^ те; / + п = 2, 4, 6, . . .].
рп2"г(^) dx = 0
[I + п = 2, 4, 6, . . .; / ^ п; к - р > т; (/ - п)/2 < р ^ fe].
)! Г
Г\
(п _ т)! Х [ / + 3/2
[i, гг ^ т; / > щ т = О, 1, 2, . . .].
11. [
J
а) \а
13.
2/ia
+ cj) > -1].
[ReM<0].
Г-)
— m ~ 2)\ma'
а
Г ^
J а2 ~~
—	а
а
15. [ -jJ—j P,m (-) Р™ (-) dx = О
—	а
а
¦ \~
J ал -
(п — тIта
16
17.
р? (?
-га)! "'
тA-т-2к- 1)! ПI 2fc X
а
19. [ Va2
[О ^ т ^ те; 0 ^ к ^ п].
[О ^ те ^ I ^ щ п - Z = 1, 3, . . .].
[п > I].
[те < I],
[fc = 0, 1, 2, ...; т^О].
[I + те = 2, 4, 6, . . . , I ^ те, Аг - р ^ то, I - 2р < те, р = 1, 2, . . .].
^ = 0	[те^1±1].
20. =

178
Гл. 2. Определенные интегралы
[2.17.19
а
21. [ _L_ Р? (-) Р™ (-) dx = I(k, I, m, n),
J у a2 — x2 va/ \aJ
I(m — 1, тг + 2k + 1, га, тг) = /(ттг — 1, тг + 2k + 1, m, тг) = /(га + 1, тг — 2/ + 1, га, тг) = О,
/(га + 1, тг + 2k + 1, га, п) =
(гг-ш)! '
/(га — 1, тг — 2k — 1, га, тг) =
22.
(п - т - 2к)\
= O, 1,2, ...].
—/3, 1—/3—д, 1 —/х + i/, I—/i—
[a > 0; Re/i < Re/3 < 1 - | Rei/|, 1/2].
-0, р-» + 1/2, 1/2 - р - I/, 3/2^/3 + i/l
3/2 - /3, 3/2 - /3 - /х, 2 - /х + I/, 1 - /х - и \
[а > 0; Re/i^ 1/2 < Re^ < 1/2-Re i/, 3/2 +Re i/].
1/2 - p, p - fj., 1 - p + i/, -is - 0 ~\
\- — 0, 1 — /x + г/, —/x — i/, 1 — /3 — /x J
[a > 0; Reju < Re/3 < -Ret/, 1 + Rei/].
25.
26.
хГ
a2/3 sin i/TT ^ [0, 1/2 - 0, -0 - i/, 1 - 0 + i/1
[a > 0; 0 < Re/3 < - Re i/, 1 + Rei/].
p — /x, —/x — i/, 1 — /x + i/
x 2Fl (^	2	; %P ; P-w i-
[Rep < 1; Re(p + cr + v - fi) > -1; Re (p + */ - <r - /x), Re (p + cr - pt - i/) > 0,
Re (p - /x - o- - i/) > 1; 0 < 6 < a ].
хГ
CO
• Jc
a
(p-
(f
(J, (p- /X- l)/2- G, (p-
[Rep < 1; Re(p- /х + 2<т), Re (p - /x - 2o-) > 1; Re (p - /x) > 0; 0 < b < a].
sin [A - 2(т)тг/4]
p - /x + Ba - l)/4, p - /x - B<7 + 3)/4
p^ 2^^1/2, 3/2 ^p
2b2 -a2
[0 < b < a; Re p < 1; -3/2 < Re <r < 1/2; 2 Re (/t - />) + 1/2 < Re <r < 2 Re (p - /it) - 3/2].

2.17.20]
2.17. Функции Летсандра 1-го рода Ри(х), РЦ{х)
179
2Q
29.
B|/ + 3)/4, A - 2i/)/4, р - II + B1/ - 1)/4, р - /i - Bi/ - 3)/4
2а2 - б2
[О < b < щ ^3/2 < Re v < 1/2; 2 Re (и - p) + 1/2 < Re v < 2 Re (p - /x) + 3/2].
1.
2.17.20. Интегралы от
хГ
r + A - ц + v)/2, г-(ц + v)/2, l-p,l-a + (p- /x)/2 j
/i + P 1 — p + С	Р + СГ
1 — р,
X 4i
1-I/-P
2 '	2
17 ^P ... l
2 '
.	. ,-i/2, a + (i/-p)/2,r + e-a + (l-i/ + G)/2,r + e-a-(i/ + G)/2
' " ¦ i/)/2, A-p + a)/2 + e, s- (p + cr)/2,1 + (i/ - /x)/2,1 + r- a - (i/ + p)/2
''/X — l/l — /X + I/	1 — I/ + G	1/ + СГ
2 '	2
p-i/
2^I/'1^°I 2
2 '
p + и b\
,1 + r-a--^-; -)
х Г
tin	1 + |/ + Pi,	,	^ + (J	. 1 + I/ - G
-1/2 - i/, a	, 1 + r + s-aH	—, r + s - a
1 —/х + I/ 1 — р + сг
p + cr 1 — ^x — i/ 3 + i/ — p
, г*-
2
/х
2 '	2
, i/ + cr
,
, г
1 - G + 1/
З-р + 1/
¦а; -)
с/
2	2	2	' c/
[r = 0 или 1/2; s = 0 или 1/2; Re (/x + p)/2 < Re a < r + s - Re (i/ + o-)/2,
¦|, |argc| < тг].
2.
о 1/2	2\—p/2/ 2
4. (ж — a j (ж ¦
a2/3 Г1/4 + /9, 1/4-/3, 1/4 + /9 -/x, -l/4-р-иЛ
тпЖ L	3/4-^-/x, l/4 + ^-i/, -/x-i/	J
[a > 0; -1/4, RejLi- 1/4 < Re^ < 1/4, -1/4-Rei/].
i/^/x + p + cr + l i/ — /x + p — a
2	'	2	'
[a > 0; Re (/x - i/ - p) - 1 < Re <7 < Re (p + i/ - /n);
a2
z| < тг;
x(x2
/ж2 + с2
dx =

180
Гл. 2. Определенные интегралы
[2.17.21
V + G
— fJL + 1/, 1 — /i + <X
[Re 6, Re с, Re (v + ст) > 0; Re p, < 1].
2.17.21. Интегралы, содержащие показательную
или тригонометрические функции Р^^
/ЖЛ р1/4 /Ж\
Va/ " Va/
/ар\ B) /ар\
2р 2 -+1/2 V 2 ) -+1/2 V 2 У
а (
2
2.
ч-1/4
cos F-^ж2 — a2
[a, Rep > 0].
ab
2тг Г(F ± l)/4 + u)V(B ± l)/4 - i/) Kl/+1/2 ^T
[a, 6 > 0; (=pl - 6)/4 < Re i/ < B ± l)/4].
3.
K	(ab\
"-1/2 VY;
л	/2	2\ —1/4
4. | ж(ж — a ) 7

cos (б^ж2 — a2
a
ab
[a, 6 > 0; |Rei/| < 1± 1/4].
0; -l=Fl/4<Rei/<±l/4].
5.
Г -
6. sin p(a —a;)sin IAxPy
о
L
В Q - /x, | - pj sin
2.17.22. Интегралы от жаJx((p(x))Pl?(cx)P?(cx).
in p aP^(cosa)
[a > 0; Re/i < Rep < 1/2].
[a > 0; Re/i, Re p < 1/2].
гГA - /х + 1/)ГA - /x - i/)
2.
afe\	/a6
K^+i/2 I
— ) da; =
2 /"^+1/2lT
) ? (
a / V a
[a, b > 0; Re^ < 1/2; |Rei/| < 3/4].
a
2
J. f xJo{by/x* - a2 JP"*4 (J) P^ (|)
-) dx = -
тгГB-/х + 1/
[a, 6 > 0; Re/x < 1, -5/4 < Re i/ < 1/4].
2 sin 1/7Г
тгб2 m
4.
2a sin i/TT
7Г26
[a, b > 0; -3/4 < Re i/ < -1/4].
ab"
Y
[a, 6 > 0; -3/4 < Re v < -1/4].

2.17.24]
2.17. Функции Летсандра 1-го рода Ри(х), РЦ{х)
181
5.
6.
[W,,,v+1/2(e"ab) - W^v
[a, b > 0; Re/i < 1; ^3/4 < Re v < -1/4].
2а	о fab^
¦ К
Va/J
[a, b > 0; Re/i < 1/2; ^3/4 < Re i/ < -1/4].
2.17.23. Интегралы, содержащие три функции Р„\
[2p ^
2.
-1/4
, — т — четные; I ^ га; га ^ /г — Z — тп ^ тг ^ А; + / + ?n].
-2 + z2 \ пи (л/х2 + ;
х
X
aX —
{2и + 3)/4 - /х, A - 2i/)/4 - /i
3/2 -2/х
[a, Re^ > 0; Re fi > 1/2; 2 Re ft - 3/2 < Re v < -2 Re/x + 1/2].
2.17.24. Интегралы по индексу от произведений Рах+^{с)
на элементарные функции.
Рх(с) dx =
2.
3.
1
/2A - с)
¦К
4« |^SP*e-i/2(c)da: = Q,-1/2(c)
5.
sh bx
сЬтгж
) dx =
2^3/2sinfe
(с + cos бK/2
_ . ch 6ж	. ч
6. | —^	Pix_1/2(c)dx =
СП 7ГЖ
arctg
1 + cos b
с — cos b
7.
8.
сЬтгж
dx =
тг V с + cos b
1
arctg
с + cos о
[|c| <	1].
[c >	1].
[c > 1; Rez >	0].
[6 > 0; -К с ^	1].
[c >	1].
[c >	1].
[6 > 0; |c| <	1].

182
Гл. 2. Определенные интегралы
[2.17.25
_ , cos Ьх	( .	1
9. I —2	Pix-i/2(c) dx= -
sh жх	~
10. =
[с > chb].
[c<chfe].
2.17.25. Интегралы по индексу от произведений -Р^в-1/2(с) на эле"
ментарные функции.
-I л —(м+1)/2
< 1/2].
2.
3.
dx = 2-
+ ch b)
2.17.26. Интегралы по индексу от произведений PiX-i/2(c) на специ-
специальные функции.
shTrx II ix	ix 1
thirx I Г + ~2~' ^~ 2 ' 2
2b /cos (be - Зтг/4) \
7Г \ sin (be-
shGrx/2) / Jia,(b)
thTra? J Jix(b)
8.
- J-ix(b)Yig,(b)]Pix-1/2(c) dx = ^
CO
9. J xthnx[jl(b)
dx = i
10.
1 ,/ 2 eibV*Z+2
ж V c + l
[с > 1].
[с > 1].
[с > -1].

2.17.26]
2.17. Функции Летсандра 1-го рода Ри(х), РЦ{х)
183
11.
о
12. ^ хеж
13.
14. ж
{a)H\2J
ч i	2^) ^iz
с) dx =	е
[z = у а2 + b2 + 2abc;
/2c- 2
[с > 1].
с\ < 1].
[с > 1].
сЬтгж
15.	iCth7TniC/<ri/a:F)Pia._i/2(c) dx = /П; I
1 /7Г
•1
16.	Ж
'~л	 лх%о
сп рттх
= 1Р
[с > 1],
1],
, /1;1 = -jA еЬс EI (-6 - 6с).
= 4/— [A + be - Ь)е~Ъ + 6Bс - 6 + 6с2)еЬс EI (-6 - 6с)]	[6 > 0; 1< с < 1].
V 2тг
18.
сЬтгж
19. ж
Re[Kix+1/2(b)Pix_1/2(c)}dx =
Г JisBF)
[Ь > 0; -1 < с ^ 1].
сЬтгж
20. J xthжx[Iix{a)Кix{b) - Kix(a)Iix(b)]Pix-1/2(c) dx =
о
21. (* xsh7TxKfx(b)Pix^1/2(c)dx =
22. [ xthTrxKix(a)Kix(b)Pix-1/2(c) dx = ^^
• — 2^
T 2a6c < a2 + b2 '
\ 2abc ^ a2 + 62 jj '
[c > 1].
23.
СП7ГЖ
[z = л/a2 + b2 + 2abc] a, b > 0; -1 < с ^ 1].
[ez EI (-2; - a - b) - e~z EI (z - a - b)}
[z = л/a2 + b2 + 2abc].
00
24. [ xth<irxKix(be"i/4)Kix(be-"i/4)Pix-1/2(c) dx = —^
2y^c

184
Гл. 2. Определенные интегралы
[2.17.27
25.
26.
(i/ -\- ix)r(u ~ i
S1/2,ix(b)Pix-i,2(c) dx =
= 4у6тг [sin Fс) с! Fс) — cos Fс) si Fс)].
[Rei/ > 0].
2.17.27. Интегралы по индексу от произведений
на специальные функции.
1	ffi чгф VI	„ i ,"т 1 г I	и 4v 1 Р^	(Л rlry —
Л.»	L.I1 7Гь6 II — — IJj "у" ь«1/ II I — — LL — IJu I 1 ¦ -I /nl LI С*Х —
J	\ ^	/ \ ^	/
2. ж вкттх Т(у + га
J
о
J l/2 + i/
[1/2-ц-и
(с-1)-"-
.
a
4.
5.
2 + Sh26)-
(с2 + Sh
сЬ7ГЖГ 2-^ + НГ 2-^-")^-/^^ =
Re i/ ^ 0; Re (/x + 2i/) < - .
[b > 0; с > 1; | Re/x| ^ 1/2].
chb
sh2 b
x [(с + 1)(C -
Г (I "
Г (I """'"
?_„ ch-
_
c2 -
c - ch 6\<
c-1 J
~" \ 2 V ch6-c
1/2 / b
^^2 \ 2
; с > 1; Re/i ^ 1/2J.
[1 < с < ch6; Re/z < 1/2].
[с > chb; Refi < 1/2].
.
	/i + ix j Г I	fi - ixj P^

2.17.27]
2.17. Функции Летсандра 1-го рода Ри(х), РЦ{х)
185
+ cos
М-1/2
¦ К-
ОО
9. ж sh тгпж Г
= л/1 - cos
_ рЦ-1/2 /_ ч|
^с; Re/x ^ 1/2].
+ гж,	/х — гж, г/
10
11. | хГ Q - М + ix^j Г Q - /х -
1/2].
. J
12. JxehTTxT Q -
[Jix(b)Y-ix(b) + J-i*(b)Yix(b)] x
13.
- l)->l/2Y1/2-lt(by/2T+2)
[| Re/xK 1/2].
14. J хГ Q -
15.
Г Г1 - /x
(Ь) - У^
Vi/2_^F>/2^T2)	[Re/x < 1/2].
/2(с) dx = гл/2тг A - с2)~м/2 х
= \/а2 + б2 + 2а6с; а, 6 > 0; |с| < 1; Re/х < 1/2].
. f
J
16. жяЬ
о
с) dx =
17.
Ei (-' - 4
> 0; -1 < с ^ 1].
b - be2 - 3c - 1 ,
+ 46c- Г + 2)e5c EI (~b - bc)\	[b > 0; -1< с < 1].

186
Гл. 2. Определенные интегралы
[2.17.27
19.
ж th тгж
(ж2 + 1/4) eh тгж
_ BжЬУ
20. xshwnxF I- — fi-\- гх\Г I- — fi — ixj ^Ux(b)P^x_1^2(c) dx = Jn,i,
Ji,2 =
еЬс EI (-Ъ - be) ~~ еЬ EI (-26) - e^b In ——	[b > 0; -1< с < 1].
[Re/i ^1/2],
1; Re/x<l/2],
[с > 1; Re/i ^ 1/2].
CO
г
L.
21. жяЬтгжГ
о
4	) \	4
= 2^1/27г2^6Fс)A±1)/2^
7 тгж /1	\ /1	\
22. ж sh — Г I	\i + ix ] Г I	/х - гж 1 Kix
Kix{b)P?x_1/2(c) dx =
± 1/2].
1/2].
23. f хЬЪтгхГ (- - ц, + ix) Г (-- /j, - ixj Kix(b)P?x_1/2(c) dx =
24. J Г Q - M + гх) Г Q - ц - гх) Re [AT
(-/х, 6c + 6)	[ReM ;C 1/2].
c)] dx = | Г Q - M) x
+ c)-1/2(l - с)^/2еь(с-1)/2И/м/2,м/2(Ьс + 6)	[6 > 0; -К с < 1].
X С
оо
25. [ ж sh ^f Г ( ± - /1 + гж ) Г j ± - м - ix ) [ Jix (b)
J	i \z
о
[Re/x ^ 1/2].
26. | zsh Ц- Г Q -
Г Q - M - г
27. (гж-
[Re/i ^ 1/2].
dx =

2.17.28]
2.17. Функции Летсандра 1-го рода Ри(х), РЦ{х)
187
2аЬ {с <
ix) Г Q - /i - гж) ^4«)^
28. ^ xshnxKtx(a)Kix(b)P?x_1/2(c)dx =
х (с2 -
29.
= \/a2 + 62 +2a6c; Re jla $C 1/2; |arga|, |arg6| < тг/2; | arg (с - 1)| < ?rl.
30. = 2Bм)/4тг3/2(с + 1У1/4(с - 1Г^/2К1/2^^(ЪлД^Т2)	[а = b; Re/x ^ 1/2].
'2с - 2 )	[Re/x^-1/2].
dx =
: /x± 1/2, I = 1; Re/i ^ 1/2].
[i/ = 2/i, I = 2; Re/i ^ 1/2].
*№P?_i/2(c)ds =
[Re/i < 1/2; Re v > 0].
32. жвЬтгжГ ( - -/х + гж ) Г ( - - fi - ix
33. =
34.
1
, -
A
/c- 1
- гж, i/ + —,
A
= 23/2^2|/тг3/2Г
^^^ (с2 -
2.17.28. Интегралы по индексу от произведений Pirx-i/2(p)Pix-i/2(c)
на элементарные функции.
1.
2.
3-
СП7ГЖ
th 7ГЖ
P(ix-i)/2(b)Pix-1/2(c) dx =
2Е
ch тгж
6-IX-1/2
7Г2(С^6)	6 + 1"
/2 =
4. | Ж , ^ P*a._i/2(b)Pi«-l/2(c) б!ж =
сЬттж
5. I ж (ж
4 / ch тгж
Pix-i/2(b)Pix-1/2(c) dx =
2(fec+l)
[-1 < b, с < 1].
[-1 < 6, с < 1].

188
Гл.2. Определенные интегралы
[2.17.29
2.17.29. Интегралы по индексу от произведений PiX-i/2(p)Pix-i/2(c)
на специальные функции.
J
3. | x sh ^
о
4.
OG
- J
da; =
da; = ^ Jo2 Q
dx =
dx =
- b).
с2 + 1
2с
0].
l<6<2c2-l
[6 > -1]-
8. =
9
ч
о
In
- 1 +
da; =
if	а + 6 + с а + 6 ¦
— — cos	 cos
4тг	2	2
^а + 6 + с
2	2
[О < а, 6, с < тг; 7г<а + 6 + с<3тг; правая часть — действительное число].
2.17.30. Интегралы по индексу, содержащие Pi"rx-i/2(b)PfIx_1,2(c).
[-1 <b, с < 1]
1/4)
1	/A-Ь)A-с)
с) •
. J xshnrxF Q - /* + гш) Г Q - /х - ix^J P^-1/2(fe)P^_1/2(c) do; =

2.17.30]
2.17. Функции Летсандра 1-го рода Ри(х), РЦ{х)
189
(с2 - 1)~м/2F - с)"	[г = 1; Л = 0; К b < с; 0 < Re/i <: 1/2].
6.	=0
7.	=2"
[г = 1; Л = 0; 1 < с < 6; 0 < Re и ^ 1/2].
lFr(|-Ax)F + i)^V-
• = 1/2; Re/i ^ 1/2].
8. хЬкжпхГ l--fi-\-ix)rl--fi-ix) Pinx-i/2(b)P?x_1/2(c) dx =
I	\Z	У \Л	У
[п = 1; Re^ ^ 1/2].
9.
10.
11.	=
со
12.	I x
о
B/л-3)/4
р?,<
[п = 2; Re^ ^ 1/2].
Hj Г ^ - H
F (с2 -
с2 -
(с2 -
[Re/it sC 1/2; v = A -
Ь2 + с - iys/2c[b + л/62+ c2-If F -
[Re^<;3/4; «/ = C-
вЬтгж
с+1
(A*-l)/2
OG
13. x sh 7гж Г
1/2].
,	\i — ix, и + ггж, v — irx Ptx-i
= ттГA - Л - fi)(b2 - 1ГА/2(с2 - l)-"/2(fe + c)x+»-\
[v = 1/2- Л; г = 1; Re A, Re/t < 1/2].
14.	=2A+V/2F(l^A^/i)(C2^
15.	= 2лтг3/2ГB - Л -
ос
•1
+ c2 -
V V 62 + c2 - 1
[1/ = A - 2Л)/4; г = 1/2; Re A, Re /x < 1/2].
c2 -
yb2 + c2 — 1
[1/ = C - ЗЛ)/4; r = 1/2; Re Л < 3/2; Re /x < 1/2].
16
1 л гж 1 л гж 1	.1
xp(i-i)/2Wd/2w^ = '
2 6-lV
^_2А-м)F + 1Гл/ах
[г = 1; Re A,
17. = 2FА+1)/4тг Г Q - Л Г Г| - 2А - д) (Ь - 1)"л/2F + 1)-1/4(с2 - 1)

190
Гл. 2. Определенные интегралы
[2.18.1
-* \ I/O I С
18.
19.
20.
21.
л^/2 V& + 1
nb т fb R	2Л r /fe Л	2
8 " V2 V	У " V2
[c > 1].
[-1 < с < 1].
[-1 < с < 1].
dx = /n
[с > 1; Re/x ^ 1/2],
-1I / = —— J2 I -
22'
(I) ^ (I)
(f) "-"/< (I)] [¦ -
23.
= Jn,
= F
2c2 -
/4 (f) ^1/4 (f
24.
P?x_1/2{c) dx =
2~^ Г Q - Л (b2 - l)-"(c - l)^/2(c + ^^"^^(гб2 + с - 1)^
2.18. ФУНКЦИИ ЛЕМСАНДРА 2^ГО РОДА Q»(x), Q^(x)
2.18.1. Интегралы от (zm ± xmf Q^(cx).
[Re/x < 1/2].
[a, Rei/ > 0].
2. I x^Qu (|) fe = eewT(a)(a2 - 62)a/2Q;a f^).
3.
J	\a
[a > 0; 0 < Rea < Rei/ + 1; |arg(a - Ь)| < тг].
Л	[a > 0; 0 < Rea < Rei/+ 1].
5.
= eeirir(a)(o2 -

2.18.3]
2.18. Функции Лежандра 2-го рода Qu{x), Q^{
191
6» = /f Г(а)ГA - а
7. J (
[а > 0; 0 < Rea < Rei/ + 1; | arg(a - Ь)| < тг].
Ж2 -
|) dx =
2.18.2. Интегралы от xa{z2 ±х2I3Q4{cx).
/3-P/2 1-2/3+,
[a > 0; |Re^|/2 < Re/3 < (l + Rei/)/2].
[М + i/ + 1, /3 - At/2, -/3 - i//2] x
Ц/2, (l-v)/2-
[a > 0; |Re/x|/2 < Re/3 < -Rei//2].
3. [ Ж
A±1)/2
(Ж2 - a2)^"^!; (J
4. ж
C ± 1 + 2/х + 2i/)/4, /3 + /х/2, /3 - /х/2, C =F 1 + 2i/)/4 - ,
[а > 0;
!ж =	—Г
, C ±1 + 2i/)/4 + /3	J
C =F l + 2Rei/)/4].
2P + I/ + 1
[а > 0; Rei/ > -3/2; Re^ > |Re/i|/2].
2.18.8. Интегралы от (ж±а)аF±;
а У	2sin/i7r
sin (/i — i/)tt
-i/, -ii-v
+ COS /Х7Г
[a > 0; |Re/x|/2 < Re^ < -|Re/x|/2- Ret/].
(\IS — в / \/3 — 1 f~\U ( \ J y^UJ
ж + a) la — ж) ц/jy I — J ax = 	 X
\a/ 2sm/i7r
x Г
[a > 0; |Re/i|/2 < Re/3 < 1 + Rer/- | Re/j|/2].
, \, M- Q. G) dx = Qv(z+)Qv(z-)
(ж — а)(ж — 6) ч с/
[Re и > -1; 2cz± = y/a{c- b) + c(c + b) ± y/c(c- b) - a(c + 6I.
Л/(ж-а)(ж-Ь) v«
f-a<6<al.

192
Гл. 2. Определенные интегралы
[2.18.4
5.
6.
7.
хГ
a + /x/2, a - /x/2, 1 - a ^ /x/2 + i/
[a > 0; |Re/x|/2 < Re a < 1 + Re (y =F /x/2)].
_ + /i + i/, l + i/, a + /x/2, a-/x/2l
1 + a + /x/2 + i/, 1 + a - /x/2 + i/ J
a + ж
[a > 0; Re i/ > -1; Re a > |Re/x|/2].
dx =
8.
s^a"""^1 Га +/x/2, a - /x/2, 1 - a + /x/2 + i/, I- a- /x/2 + i/l
2	L	1 +1/, 1 - /x +1/	J
[a > 0; |Re/x|/2 < Re a < 1 + Re (у ± /x/2)].
sin iVTr / e\a/2 .
sin (u
	г— ( —) r(l + a + i/)P_ _. 2 V1 + d2 ) x
— (iOT \a/	a I
= b2d2; Re a, Re с > 0; | Re a\ < Re v + l].
dx = 4^v
(а2 + 62)B^1)/4РаТ17/2
2V2-./ * V 2
6
10.
a2 + 62
dx = еМ7гг^тг aa+l//
[Re a, Re 6 > 0; |Rea| < Re 1/+ 1].
11 f т"
11. JЖ
[a > 0; Re i/ > -3/2; Re a > |Re/x|].
[a > 0; Re/x < 1/2; -(l + Rei/)/2 < Re a < 1/2 + Re (/x + i/)/2].
12
13.
00
. ж (z + x) ! QZ
J
COS jtiTTZ
x Г
¦ iv + 1, a + /x, a — /x, 1/2 — a
1 + a + i/
^ ' 2Z + X l с!ж =
|Re/i| < Re а < 1/2; |argz| < тг].
2^(^ + ж)
, OL — /i, 1 — O + l^
2.18.4. Интегралы от xa(xm ± amf (b2 ± ;
oo
1. f (ж - аУ3^2 - b2)~^/2Qi (y) da; =

2.18.5]
2.18. Функции Лежандра 2-го рода Qu{x), Q^{
193
2.	= e^
со
3.	J (ж2 - а2)"" V
[О < Ь < щ О < Re/3 < ReO + i/) + 1].
( J)
1/ 3
;
и + 3/2
[О < b < щ 0 <ReC < Re(/x + i/)/2 + l].
. J x1""-*-1^2 - а2)*-^
ofe-l|, k + l-v-2ul-m/ 2 ,2^-1/2^1	(a\	Го . , . D . o /ol
= 2 «!а	о (a — b ) ' Qv^u ( т )	[0 < 6 < a; Rei/ > —3/2].
2.18.5. Интегралы от (х - a)a(b ± xf (xm ± dmyQ4(cx).
^ (^) dx =
2.
iM —) dx =
a + 6
Q4
[0 < a < 6; Re/z < 1/2].
ja +
2a
[0 < a < b; RejLi < -1/2].
26
[a > 6 > 0; Re^ < 1/2; Re (fj, + i/) > -1].
oo
i. J(x-
26
5. I (x - a)a^(x -
26
— | dx =
[a>6>0; Re/i<^l/2; Re (u + i/) > -2].
i/+ 3/2
4c2
-6
- a, 2a + ^ + i/
^ + o/ ^
[a > b > 0; Re a > 0; Re Ba - /u - i/) < 2].
7 А. П. Прудников, Т. З

194
Гл. 2. Определенные интегралы
[2.18.6
6.
? (f
[(l + d2)Dc2 + d2(a-6J) = (a + bfd2; a + b > 2c > 0; a, b > 0; Re /x > -1/2; Re i/ > -l].
2.18.6. Интегралы от Л(ж)е^(ш)д^(сж).
CO
f x-a"e-»'Qn (*) dx = {-1Гп\Л О.п-
J	Va/	VP
о	f
j;^) dx =
ею
Г	-1
а + /i/2, и + 1, —I
[Re a, Rep > 0].
[а, Rep > 0; 2 Re а > |Re/j|]
a^ /i/2, i/ + 1, —v
a, Rep > 0; 2 Re a > |Re/i|].
0; Rei/>-3/2].
гр
[а, Rep > 0; Re v > -3/2].
[a, Rep > 0; Re i/ > -1].
[a, Rep > 0].
f(a2 - a,2)TB,
(x\
(-J
x
2.18.7. Интегралы, содержащие гиперболические
или тригонометрические функции и QjJ(y?(sc)).
4
осп ж) аж = у — ГA/ — <т + 1)
V 2	sm
2; Re 6 > 0; Re и > | Re cr| - 1

2.18.8]
2.18. Функции Лежандра 2-го рода Qu{x), Q^{
195
sin b\fx — a i (x
2.
Г cosb\/x — a _ fx\ .
3. 	Д— Qu [-) dx =
bJ-
2.18.8. Интегралы от A(x)Jx((p(x))Qii(x(x)).
oo
1 [(x^aT^ix + aT^^J (Ьх/я^а)О^ (-) dx =
J	v \a/
хГ'	- ¦ \ i^
¦ Л, 1 + a ¦
[a, b > 0; Re v > -3/2].
[a,
-i/, 1 + A,
Л — /j	a&
2 ' ' 2 ' ' 2
6	A| ^ + 3/2, 2 - a + (A + /x)/2 + i/
x 2F3 ( 1 + /i + i/, l + i/; 2-a+ ^^ + i/, 2i/ + 2, 2 - a + ^^ + v\ ^
oo
2. Ux- а
[a, 6 > 0; ReBo: + Л) > |Re/i|; Re Ba - д - 2i/) < 7/2].
{^j dx = 21-"ем"Л/?о b^1/2 x
2i/) > -2].
[a, 6>0; Re,к> -1/2;
3. | (x - a)B")/4(x2 -
/a + с — va —
/a + с + л/а —
I. \{x-a)a-1{x + a)
J
2	J "v^i* у	2
[a ^ с > 0; Re/i > -1/2; Re (/i + 2i/) > -2].
•(J [ - ) d» =
5. f (x - а)
J
a - /i/2 - i/, a - /i/2 + i/ + 1 \
a + /x/2, a - /i/2, A/2, -A/2 J
[a, 6 > 0; ReBa - А- д- 2i/) < 2; 2 Re a > |Re/i| -3/2].
ж -a/ Va
6.
a)-»'2J±M±1/2
[a, 6 > 0; Re/i > -1/4; Re i/ > -1].
[a, 6 > 0; Refi > -1/3].
7. f (x - аГ"-5/4(Ж + a)"/2JM_1/2 (-fJ=) Q4 (-) dx =
J	\ \/x — a J Va/
b \ cos/itt	/ 6
T-1/-1 I 7^ i "TV I/ + l/2,
7*

196
Гл. 2. Определенные интегралы
[2.18.9
со
i. \(x- o)-"-B/4(a! + а)м/2 J1/2_M
J
[a, b > 0; -Rei/ - 1, Re*/ < Re// < 1/3].
? (-) da; =
ж — а / V а
со
Г / 2	2\
. j (ж - а )
а
со
О. J(.'-.
^5/4 T
f J
+1/2
1-2/х J "^-" ^ VV2a
[а, 6 > 0; Re// < 1/3; Re i/ > -3/2; Re (//+ */) > -1].
[a, 6 > 0; |Re//| < 1; Rei/ > -3/2].
жл
oo
f
. J
Qn (f
0].
11
2.18.9. Интегралы от A(x)Kx((f(x))Q^(cx).
CO
1. [(ж - a)-"-5/4(x + a)"/2KM_1/2 ( 6 ) Q4, (-) dx =
J	\ у x — a, J V a /
[6, с, Rez > 0; Re i/ > -1].
[a, Refe > 0; Re v > -3/2; Re (//+ i/) > -1].
(f
1.
2.
2.18.10. Интегралы от А'
_J:	Kf / 2а "\п р
2V+1J
[a, Reb>0;
(^ + 1) + С + 2 In 2]
¦K I i/—¦— Qi/ - da =
x -\- a
[a > 0; Re i/ > -1/2].
	[ttcosutt - 2C ^41n2 - 2ф(у + 1)]	[a > 0; i/ ^ -1/2, -1, -2, . . .].
3. f г К (J^—^. ) Qv (-) dx = п П Bv + IJ	[a > 0; Rei/ > -1/2].
J V^ + a \V^ + a/\a/	16
2.18.11. Интегралы от
— (Л — Л ) Sin 	 7Г + (Л ¦
2l	;	2	v
Sin 	 7Г

2.18.11]
2.18. Функции Лемсандра 2~го рода Qv{x), Q^(
197
А = Г
(А +
А/2-
[о, Re A, Re 2/ > 0].
[а > 0; I > ?1; I + те — четное].
3. = -
4.
5.
r.
(Z-rc)(Z + n
х Л	п! [ A/2)! J
[а > 0; Z > n; Z = 2, 4, 6, . . . ; п = 1, 3, 5, . . .].
+ 1) — ф(и + 1)]A + cos Атг cos i/тг) — тг sin (А — 1/)тг
[Л + v = -1; A^i/; A, i/ 7^ -1, -2, -3, . . . ; a > 0],
+ cos2 f/тг)
2Bi/
2a
[Л = I/; I/ ^ -1, -2, -3, . . . ; а > 0],
[Л = -г/ - 1; I/ ф -1, -2, -3, . . . ; а > 0].
a > 0,
J [«-(!)]
!)]*=
> n; / + n = 2, 4, 6,
^n; Z + Ti = 1, 3, 5,
9.
10. =
11.
12.
13.
14.
oo
15. J
[a > 0].
[A = u; a > 0; Re i/ > -1/2].
+ i/, ^-/x + 1/2, ^ + /x-l/2, 3/2-/З + i/l
/3, 2-/x + i/, /3 + i/+ 1/2	J
[a > 0; 1/2, |Re/x- 1/2| < Re/3 < 3/2 +Re i/].
— j dx =
^ e2^ia2^ir Г/3, /3 + /i, /3 - /i, C ±
[a>0;
+ i/, /i + i/ + (l
, C±l)/2-/x + i/ J
C ±l)/2 + Rei/].
/3 + 1/2, /3 + I/ + 1, 1-/X
[a > 0;
COSjLJTT
*, /3 - /х, /3 + /х, 1/2 - /х, 1 + /х + i/, /x - i/l
1 + /3 + i/, /3 - i/	J
[a > 0; |Re/x| < Re/3 < 1/2].
— j dx =

198
Гл. 2. Определенные интегралы
[2.18.12
1/4 + /3, 1/4 - /3, /3 + /i + 1/4, 3/4 - /3 + is, /i + i/ + ll
3/4-/3 + /X, /3 + i/+ 5/4	J
[a > 0; -1/4, -Re//- 1/4 < Re^ < 1/4, 3/4 + Re is].
Ал/2
2.18.12. Интегралы от A(x)Jr]((p(x))Q^(cx)Qlt(cx).
1	( Ь \	f \ f \	2fl7ri Г +
1.	(ж2 - a2y1J2l, I	) Q?_i ( —) Q^ ( —) <^ж = ~~т;— Г
J	W^2 - a2 J	Va/ Va/	2a |_!~М~
a
[a, 6 > 0; | Re pt| < 3/4; Re i/ > -1/2].
oo
2.	J(,2-a2)-V.+1(-
e— Г1 + . + , 1
2a
— J Kp I — )	[a, b > 0; Re и > -1, -5/4 < Re /x < 1/4].
CO
[a, b > 0; Re i/ > -1; jRe/i| < 1/4].
2.18.13. Интегралы от A(x)Px((p(x))Q4(cx).
a
-t f о fx\ гл (x\ j	a
1. \px[-\Qv[-\dx
J Va/ Va/
A-i/ ГА/2 + 1, (i/-
(A-i/)(A + i/ + 1) 1	2
[a, Re A, Re и > 0].
a
Г /ж\ /х\	7Г — 7Г cos (A — i/)tt — 2 sin Attcos иж[ф{\ + 1) — ф{и + 1)]
J Va/ Va/	тг(А — г/)(А +1/+ 1)
3. = -
ttBi/ + 1)
a
4. f РГ f-) Q™ (-)
J	Va/ Va/
(I - n)(/ + n + l)(n - m)!
[А ф u; a, Re A, Re v > 0].
[A = 1/; a, Rei/ > 0].
[I ^ n; a > 0].
. J^(f)«.(f
[a, Re (t/ - A) > 0; Re (A + i/) > -1].
6.
7.
x Г
/3,
/3 + /i, 1-/3 +1/
/i, 1 + 1/ + /З
[a > 0; 0, ±Re^ < Re^ < 1/2, 1 + Rei/].
+
— a + к ~
и	3 /i + 1/ — a	3
5 1У+	+ '
и — a a1
8.
2	' ' 2'	2	' ^'	2
< a; Re^ < 1; Re (^ + A + ц + v - a) > -2; Re (ж - X + fj, + i/ - a) > -1].
ж
f) ^ (
3/2 + 1/

2.18.14]
2.18. Функции Лемсандра 2~го рода Qv{x), Q%(x)
199
2	'	2	' 2 +l/' \
< щ Re ж < 1; Re (ж + Л + /х + i/) > -1; Re (^ - Л + /i + i/) > 0].
9. =
^V^b (а2 -
X Р
10.
-«/-1/2
[Л = I/; |6| < a; Re^ < 1, Re (ж + ц + 2i/) > -1; Re {ж + *х) > 0].
М^1 /2а
/2
< а; Re^ < 1; Re i/ > -3/2; Re Bж + 2/i + i/) > 1/2].
гГ/3 + 1/4, , . . . , у , , . , , , . ,
[	/3+3/4, /3+1/+ 5/4, v~ /i+2	J [а
12. (^-аУ^р-Г,
< Re^ < 7/4 + Rei/].
13.
' - 1/4, /3 + /i + 3/4, /3 - /х - 1/4, 5/4 - ? + i/l
/3 + 1/4, /3 + i/ + 3/4, i/ - /x + 1	J
[a > 0; 1/4, -RejLA-3/4, Re fi + 1/4 < Re^ < 5/4 +Re i/].
¦Г
/3 + 3/4, /3 + i/ + 5/4, i/ - /x + 1	J
[a > 0; |Re/x| - 1/4 < Re/3 < Re ?/ + 3/4].
—- 1 dx =
V8 7Г
COS/iTTtt Г
/3 + 1/4, 1/4 - /3, /3 + /i + 1/4, /3 - /x + 1/4, /i + i/ + 11
/3 + i/+ 5/4,/3-i/+ 1/4	J
[a > 0; |Re/x| - 1/4 < Re/3 < 1/4].
2.18.14. Интегралы от А{х)[БШЧ)^Х\\рх (cx^Q^icx).
I cos <p(x) J
= e^ ' a*
1-/3, l-/3±/x, 1-/3TM
1/2 - /3, 1 - /3 + »/, A ± l)/4, -/3 - i/, A т l)/4
[a, 6 > 0; Re/3, Re (/3 q= A») > -A ± l)/4; Re/3 < 1; Re (/3 - i/) < 3/2].
^ + 5/4j "
^- )	[a, 6 > 0; Re и > -3/4].

200
Гл. 2. Определенные интегралы
[2.18.15
3.
26 '"
ab
к
v+1/*
ab
[a, b > 0; Re i/ > -3/4].
2.18.15. Интегралы от
со
. f
J
CO
2» JxJo(
/ la/	6
[a, b > 0; =pRe/i > -1/2; Re i/ > -3/4].
Va/ u \a)	b2 i 2i/+ 2
X MTM?I/+1/2(a6)VF±Mjl/+i/2(a6)	[a, 6 > 0; TRe/i> -1; Rei/ > -3/4].
CO
. f ж(Ж2 - oY-
J
oo
'•J
l/2-0,l-0 + v,Ti/2, -p-v, -r
a, b, Re B/3 + ?7), Re B/3 + 2^ + »j) > 0; Re/3 < 5/4; Re (/3 - i/) < 7/4].
[a, 6 > 0; Re v > -1; Re (/x + w) > -1].
2.18.16. Интегралы по индексу, содержащие Q±ia:-i/2(c).
2
-1/2(c) + Q-ix-1/2(c)]dx = ~^
о
[c > 1].
2.
i (z _ а _ 5) _ е^ El (-z - а -
= л/а2
2.19. ФУНКЦИИ УИТТЕКЕРА Мр?ст(ж) И WPjCT(x)
Функции Уиттекера Мр?сг(ж) и WPj(T{x) связаны с вырожденными гипергеометрически-
гипергеометрическими функциями\F\(a; b; х) и Ф(а; 6; х) соотношениями
MPia(x) =
^,.(Ж) Же(ст
\
При некоторых других значениях параметров функции MPi(T{x) и WPj(J(x) сводятся
к другим специальным функциям, например
-; 2G + 1; ж ),
^ 2G + 1; А
kJ
тг V 2
Соответствующие формулы см. в главе 7, а интегралы — в других разделах настоящей
главы и в [17, 18].

2.19.1]	2.19. Функции Уиттекера МР}(Т(х) и WPj(r(x)	201
2.19.1. Интегралы общего вида.
Обозначение:
1. xa^1(ar -xrf^1e±cx/2MPiCT(cx)dx = 17@)	[a, r, Re /3 > 0; Re (a + a) > -1/2],
о
fe=0 [1а^^;/й	v-1- *u)k
тр-Аг\
^	Л l
p
2.
0	[а, г, Re/З > 0; Re a > |Re<r| - 1/2],
Ua(j) = U(j) при а ф n/2, -n/2; 17G) см. в. 2.19.1.1;
fc=0
f)
[Лд.(о-)см. в 2.19.1.1].
3. [жа(жг ™аг)/3е^сж/2М/M<т(сж)с1ж = V@) [a, r, Rec, Re^>0; Re (a + r^ - p) < r],
"f)fc
х((-1Г v/ ' ?//^ac)fc + cr^r/3^aT7^ l Pjfc Г - + a + <j-(l-/j + fc)f) x
fc=O	"	^
2/1	\
x Г27 ч - + A - 272)(cr - a + r - rP + rife) 1 x
x Г^т2+7+1 ( A - 272)p + ^^ + G2 - 7 - l)(a - r + r/3 - rA;)) (ac)rfe
4.
'1	Rec > 0	JJ'
yCTG) = V(j) при «г ^ n/2, -n/2; ^G) см. в 2.19.1.3;

202
Гл. 2. Определенные интегралы
[2.19.1
" 1п (
.сг-г0-а|г('!+П _Wl-n
С»
ч
Е1^ТГЙГ ^ + «-A -" + ')¦¦ )г(^ + а-A-Ц + к
x Г±г ( —	p =p (a ^ r + r/3 - rk) ] (ac)rfe	[^fe(o-) см. в 2.19.1.3].
x-l
[r, Rec > 0; ™l/2^RecF < Re a < Re(r6> + p); r|arg^| < тг],
(l-2(j)fc
¦ Г -+а + а — гв — гк Г т —и1^27 ) х
х (а — а ¦
Ск((т) = (с;
G2 - 7 - l)(a - rO - rk) ) (cz)rk,
- p + a) Q - а - G2 + 7 - l)p
r /l/2 + а-
l
1/2 + a~
6.
г > 0; Re а > | Re a\ - 1/2; r| arg z\ < тг,
Г Re (а + р - гв) < 0; | arg c\ < Зтг/2 1
1	Re с > 0
= W{n) ПРИ о- ф п/2, -га/2; WG) см. в 2.19.1.5;
/Г
1) + V(n + fc + 1) - V ( ^^ - /9 ± fe ) -
2a + n + Ik
fe=0
х Г
7.
А;!
[Cfe(o-) см. в 2.19.1.5].
= Х@)	[г, у, Rec > 0; -1/2- Re a < Re а < Rep + r],

2.19.1]
2.19. Функции Уиттекера МР;СГ(х) и WPia(%)
203
)x
A272)p
^7 . / 2	1W
-z— + G ^7^ l)(a-r--
^и =
8.
\ + a - p\ f\ - a - G2 + 7 - l)p) ctg
r; iargcl < Зтг/21
= X{i) при о- / n/2, -n/2; XG) см. в 2.19.1.7;
r	\ *-^	k\
\k=0
lira , , 1 , -'•
	p ± к H	cosec -
2	It	r
¦ тг-\п(су)
- a — r — rAj I x
Dk(a) см. в 2.19.1.7.
CO
9. f xa-1e-pxr-cx/2WPi<T(cx) dx = У@)
[r, Rec, Rep > 0; Re (a + a) > -1/2],
Y(j) = c~ar*
1/1
Г
A - 272)p
(A_27)p_a)/r !_Л 2<т
+ G2 - 7 - l)(a-
A/2 + a + A - 27)p)t(l/2 - a + A - 27)p).
УG) =
pBa+l)/Br)r
[r < 1],
[r > 1],
УG) при r = 1 см. в 2.19.3.1-8.
10. I xa-le-r*r+c*/*}
. J я;в-1
V	r
[r > 1; Rep > 0; Re (a + o") > -1/2].

204	Гл.2. Определенные интегралы	[2.19.1
11 ra~1-e-Px ±cx'zw (cr)flr — Y (±1) — Y
[r, Rep > 0; Rea > |Reo-| - 1/2; |argc| < A±1/2)тг],
= Y(j) при r < 1 или при г>1иа/ ^/2, ^n/2; Y{^) см. в 2.19.1.9,
00
12. I xa^1e^px~r^cx/2MP;a(cx)dx = Z@)	[r, Rec, Rep, Re (p - a) > 0],
о
ZG) = c-aT7 ? 1 Г (i + а + a - rk\ Г2^-1 (| + A - 272)^ -a + rk)\ x
fc=0	^	^	^	^
2,	,
со
13. f /^^"^/2
со
. f /-^-^"^/2^^^) dx = Za(±l) = Z-a(±l)
L	I	Re c> 0
Za(j) = Z(j) при а ф n/2, -n/2; ^G) см. в 2.19.1.12;
2
xL]grl1f + a-r*lr|^ + a-
g
Fk(a) см. в 2.19.1.12.
CO
14. f xa-1e-cx/2l Sln t*r W, .(еж) da: = 1/@)
J	[ cosbx J
0	[6, r, Rec > 0; -1/2- ?r - Recr < Rea < Rep + r],
/I	\
Г (- + a + . + Sr + 2r*) x
хГ27 U + (l- 272)((j -a-Sr- 2rk) Г^7 +7+1 A - 272)p

2.19.1]
2.19. Функции Уиттекера МР;СГ(х) и WPi(J(%)
205
2/е	2	о	Toil
_ 7 -1-1 , ((i-27)p-a)/rrl-7	2G + 1
Ll/2-p + ff
^ A/2 + a + A - 27)p)fc(l/2 - o- + A - 27)p). /g - A - 27)p - k\
X L	ы	Г ^	r	' X
fc=O	x
к
X
sin [(a - A - 2j)p - А;)тг/Bг)]
cos [(a - A - 27)p - к)ж/Bг)]
ГBст)
} №
[г < 1],
¦Лк(а)
fe=O
1
2 ~
17G) при г = 1 см. в 2.19.6.1-3.
ч к I а —1 сж/2
15. \ х е ' {
x Г
[г > 1],
а - а + к + 1/2^ / sin [(а - а + к + 1/2)тг/Bг)]
cos [(а - <т + А; + 1/2)тг/Bг)] J'
[6, г > 0; | Recr| - ёг - 1/2 < Re а < г- Rep; |arge| < Зтг/2],
ПРИ г < 1 или при г > 1 и сг / п/2, —п/2; U(j) см. в 2.19.1.14;
и
(-1I* E fe,fc(i
2r
-^-^^^И'1^^I1}
16.
IT.
2r &	4г
[7 = 1 или -1; г > 1; Afe(<r) см. в 2.19.1.14].
[6, г, Re с > 0; Re а > | Re сг| - Sr - 1/2; 17СТG) см. в 2.19.1.15].
z| < 7Г
VG) = nz-
-, Re с > 0; -1/2- Re о- < Re a < Re p,
о / ч ¦ .2 ГBа)
z > 0
/	1 / 2 , ч /о \fe
zrT7 V ^^ Г ("i + а + а - г - г к) Г27" (- + A - 272)(ст - а + г + rfe)) x
х Г-72+7+1 f A _ 272)р + 71Z7 + G2 _ 7 _ 1)(а _ r _ rfc) j (M)r*
-272)р-

206
Гл. 2. Определенные интегралы
[2.19.1
ф ( | + A - 272)(<т -а))-ф (A - 272)р
G2 - 7 " 1)« ) "
Вк(<т) =
18. \xa-\^
- р + ffj Q - а - G2 + 7 "
cosec [(а - о + к + 1/2)тг/2]
r > 0; |Recr| - 1/2 < Re а < -Rep; |argc| < Зтг/2,
19. xa~1t
о
20.
1п
г, Rec> 0; Re а > |Re<j| - 1/2,
rl argzl < ^
^ > 0
, 1/G) см. в 2.19.1.17|
> в 2.19.1.17[
J
= W@)	[r, Re 6, Rec>0; Re (а + а) > -1/2],
-1) ^ + A^212){а^а^г^гк)\Г^
2cr + 1
х у, A/2 + а + A - 27)p)fc(l/2 - а + A - 27)p)fc р ^а - A - 27)р - fe\ u_^7c
- 7 - D(a + r + rk) ) ( - A) -
72 ^7
2 (\ + A - 272)(<т - a)
1
(l-272)p
и/G) = -
ЬBа+1)/Bг
L^272)p-
- 7 - 1)а - In -г	[г < 1]
A-2с7)л
| - Р
при г = 1 см. в 2.19.8.1-2.
21. \ ха^е±сх
El (^ter)
х = W(±l)
[г, Re 6 > 0; Re a > | Recr| - 1/2; |argc| < A ± 1/2)тг, 14^G) см. в 2.19.1.20].

2.19.1]
2.19. Функции Уиттекера MPt<r(x) и Wp,a(x)
207
22.
I erfc (bx
= X@)
2b
k=0
A/2 + a + A - 27)p)fc(l/2 -
+ a + a) Г2-2-1 Q
- 27>
G2 - 7 -
XG) при r = 1/2 см. в 2.19.9.2-6.
23.
x (a - о + к
2r
4)f
24.
erfc
argc| < Зтг/2	j
X(j) см. в 2.19.1.22 .
25
[r, Rec> 0; Rea > |Recr| - (r±r +l)/2; |arg6| < тг/4; ХG) см. в 2.19.1.22].
со
. f xa~1e~cx/2 J^(bxr)MPjG(cx) dx = Y@)
[b, r, Re с > 0; Re (a + i/r + cr) > -1/2; Re (a - p) < 3r/2],
V2
A7)""а)/г
1-7Г 2a+ 1 1 f, A/2 + a + A - 27)p)fc(l/2 - a + A -
2

208
Гл. 2. Определенные интегралы
[2.19.1
/r + a-(l-27)p-*)/Br)
- а + A - 27)р + fc)/Br) + 1
< 1],
2>iB« + l)/Br) ^ ~ ! I П(-2а)
2r
а/г
x Г
УG) при r = 1 см. в 2.19.11.1-2.
CO
6, r > 0; Re (a + i/r) > | Re <r| - 1/2, I Re ^
[Г > 1],
- а + <т - 1/2 - А;)/Bг) + 1J'
< 3r/2; |argc| < Зтг/2 11
Rec>0	/J'
Уо.G) = УG) при г < 1 или при г > 1ша ф п/2, -п/2; УG) см. в 2.19.1.25;
2a+1)/Br)
" k - 1)! о /п
^ (
(г)
fc=0
lzbn
27.
F/2)"
+ l|--ln-rM±-
[r > 1; ?Jfc(<r) см. в 2.19.1.25].
21/rf
;, 1/2 +a - a
[0 < г < 1; Re О 0; Re (а + иг) > |Re<r| - 1/2; |arg6| < тг].
СО
28. [ xa-1e-bxr-cx/2Il/(bxr)Mp,a{cx) dx = 17@, 0)
[г, Re 6, Re с > 0; - Re (ur + сг) - 1/2 < Re а < Rep + 1/2],
(^lI"
2 25
G2-7-2)тг(е -e)/
V+e)/2 ^ A/2 + a + A - 27)p)fc(l/2 - ct + A - 27)p)fc
A;!
(l-27)p-a
x Г"? +?+
2?lV2-3--r-
6 /	V2 ' -/ V2
- e2 + A - 2e
2ч i^r + A — 27)p - a + к
[r < 1],

2.19.1]
2.19. Функции Уиттекера МР;СГ(х) и WPi(J(%)
209
х Г1
(- - а + i/r - rk)
- 272)р
[г > 1],
= С/@, ±1)
29.
30.
31. 1 xa^1ebxr±cx/2KlJ(bxr)WPia(cx)dx = 17A, ±1)
о
г
г > 0; Re а > r| Re i/| + | Re a\ - 1/2; | arg 6| < Зтг/2,
= U(±l, 0)
Re с > 0; Re a > r\Rei/\ + | Re ст | — 1/2,
32.
33.
Re c> 0
'е, т) см. в 2.19.1.28 1 .
Re (а - р) < г/2; | arg 6| < Зтг/2
Refe > О
U(e, т) см. в 2.19.1.28 1 .
Re (а + р) < г/2; | arg c\ < Зтг/2
Re О О
U(e, т) см. в 2.19.1.28 1 .
= f/(-l, ±1)
[г, Re 6 > 0; Re а > r|Rei/| + |Re<j| - 1/2; |argc| < A ± 1/2)тг; С/(е, 7) см. в 2.19.1.28].
а-1 -сх/2
( ?„(Ьхг)
\Kv{bxr)
Mp,a(cx)dx = Uu<
72 -7-2 /-2
2,7
A/2 + a
x Г
2г
^2
2r
А1
7^M
A + 1/)* J V*C*r
[и ф т, -т; т = 0, 1, 2,

210
Гл. 2. Определенные интегралы
[2.19.1
1 \~2
(m-fc-1)!
Mm)
\
т).
Ак{и) = (Ц^
2 v
2 ^7 "
Г( -¦
(a - a - 2rk - rm) 1 + 2гф I A - 2j )p -
,ч\ , 2cH ( &2 X^
frm + 2r&)) + 2 In	 =p—^
7	о V 4cir
x Г-7"+7+1
'-2
[m = 0, 1, 2, ...],
')(<7 — a + ur — 2rk) J x
x (^lI^
[r > 1; 7 = 0 или 72 = 1 и (j 7^ n/2, -те/2],
2\	f ^2 1^ I V(^fc-l)!o n\ Л_пA+7)/2 2Дс
Ba + l)/Br)
6 /	1 7Г f 47ГГ
А;!
(-
,n^B*(-n/
-^ k\(k + n)!
ф(к
2r
_ J_
~ 2r
4-im^|((-D^a^
l/2\
[n = 0, 1, 2, ...; 72 =
2r
ХГ
35.
r > 0; Re а > |Reo-| +r|Rei/| - 1/2; |argc| < Зтг/2,
0;
3r/2
Re 6 > 0
Uv,<tW) cm- в 2.19.1.3:
|r, Re с > 0; Re а > |Re<r| + r|Rei/| - 1/2; |argc| < Зтг/2, { > \, Uv,cr{l) см. в 2.19.1.331
3. I xa^1e^(bxr+cx)/2M^4bxr)MPja(cx)dx = V@, 0)
[r, Re 6, Re с > 0; -Re(i/r + a) - (r + l)/2 < Re а < Re(/xr+ /э)],

2.19.1]
2.19. Функции Уиттекера МР}(Т(х) и WPj(r(x)
211
j
-(е2+е)/2
w ^ A/2 + а + A - 27)р)»A/2 - о- + A - 27)р)> ^ f ,
Х 2^	jfcj	' I 2 + " "
fe=O	V
1 - 27)р - а +
— а + гу — rk	) I x
2 /
G2 - 7 - 1) (а - ту + rk + ?)) ,
г A -
ГB
- ? - 2
х/2 -
A/2
_ 2e) x
- 272)(<т -a + kr + fir(l - 2e))\ Г4^1 (A -
G2 " 7 " 1)(« ~kr-
e, 7) при r = 1 см. в 2.19.24.2-7.
37.

212
Гл. 2. Определенные интегралы
[2.19.2
Va(e, 7) = V(e, 7) при г < 1 или при г > 1 и а / тг/2, ^п/2; V(e, 7) см- в 2.19.1.36,
2i/ + l
(I) foe;
1±п
~ g ~ 2
s2^s
jju.r(l — 2е)—- скр1—-е
х2а + п + 2к + 1
„гТ-'И^-'
x Г
38.
'
- а - rk - /xr(l - 2e)
- 2s))
[r > 1; Ffe(<j) см. в 2.19.1.36] .
39.
l/(bxr)Wp,a(cx)dx = Va(l1 ±1) = V-a(l, ±1)
\ r > 0; Re а > r\ Re i/| + | Re <r\ - (r + l)/2; | arg 6| < Зтг/2 ,
/Ее(а + р + |
I	Rec>0
4bxr)WP;a(cx)dx = W(-l, ±1) = VLff(-l, ±1)
0; |argc| < Зтг/2 1
), Me, 7) см. в 2.19.1.37
[г, Re 6 > 0; Re a > r\Rei/\ + |Recr| - (г + 1)/2; |argc| < A ± 1/2)тг; ^(е, 7) см. в 2.19.1.37].
2.19.2. Интегралы от xaWP} a(cx).
ею
L. [ xa~1WPf(r(cx)dx = Ap}(r	[Rec > 0; Rea > |Recr| - 1/2],
1	1'
а а, - а сг, ар,
Г(C - 2p + 2«т)/4)Г(C - 2p -
к Ф о],
[Re a > -1/2].

2.19.3]
2.19. Функции Уиттекера МР;СГ(х) и WPia(%)
213
2.19.3. Интегралы от хае
WPi<r(cx)f
L. [ xa~1e~pxMPta(cx)dx = Ia
0	[Re(a + a) > -1/2; 2 Rep > |Rec| или Re (p - a); 2 Rep = Re с > 0],
Bp - c)«
Г - + a
P/2
-+p + a,- + a-
2а + l)Dp2 -
P/2
[Recr >-l/2],
I-p-2a — •
_ p+5/4
- р)ГBа
Dр+1)тгг/2 1/4/2
-1],
[Re (cr - p) > 0] .
2.
3.
2c + l, p-a, l/2 + a + (jj
l/2 + p + (T, 1/2 - a + <j J
[Re с > 0; -1/2- Re cj < Re a < Rep].
cB±1)/4 x
. J
= 2Г
^
[2 Rep > |Rec|].
[2 Rep > |Rec|].
5.
Jo =
1 [1/2
<(J(cx)dx = Ja	[ReBp + c) > 0; |argc| = Зтг/2; Re a > |Re<r| - 1/2],
¦ a + c, 1/2 + a - cl ^ /^1 , л. , , 1 , л. _. , , Л. Л. с^ 2р^
1
- O--1/2
С / COSCT7T
P/2
X OIp-1/2
2p
/4р2 _ С2
2c
Recr| < 1/2]

214
Гл. 2. Определенные интегралы
[2.19.4
Ji/2-p =
- р + <т)ГA - р - (т)с1/4Bр - с)р~1/2Bр + с)~1/2 х
х Р;
2р-1/2
2с
J^p^l/2 — 2'
7. f /-V«
J
[|Re<j| - 1/2 < Re a < -Rep; |argc| < Зтг/2].
[Re а > |Re<r| - 1/2; Re с > 0].
8.
2.19.4. Интегралы от ж"е
"е/(
ж) (
[Re с, Rep > 0; Re (a + <т) > -1/2],
G - 7 - 1)<* х
а + а, | + а - а; |, 1 + а
1Ua:+1./JrA+<1+'>I*I(i+<1-JTl)('-<1-i
-7 +7+1
(/у2 _ 7 _ 1)а _ 1
a + l,a-a + l;^, | + а + G2 + 7 -
2a - 2A - 27)р) х
, I
; 1-а + A-27)р, 1-а

2.19.4]
2.19. Функции Уиттекера МР;СГ(х) и WPi(J(%)
215
2.
0 fp2
X GXP ( я~
г f T°-ip-v\f*-*
Чж e
о
со
*• J
0
oo
т It*	p
l-p-a-e)/2 p-a-1
i— [e = 0 или 1; Rec, Rep > 0; Re a > -(l + e)/4].
4 c/
ГDст + 1) a ^4a
[Rep, Rec> 0; Re a > -1/4].
(pt} (It = /4 f~ 11
[Rep > 0; Rea > \Ша\ - 1/2; |argc| < A ± 1/2)тг; A(j) см. в 2.19.4.1].
(cx)dx = Б@)	[Rec, Rep, Re (p - a) > 0].
xl1-" 4 2+A^272)(c7^a)
7 -
A-:
l
a' 2
72 ^7
x^a(§
G2 + 7 - l)p; 2*7 + 1, | + a + a; (-l)(^)/2cp ) ±
- -¦ I
CO
4
0
oo
4
= B(±l)
Re с > 0
J
[Rep > 0; |argcj < A±1/2)тг
8.
dx =
0
[Rep > 0; |argc| < Зтг/2].
oo
9. f X^
0
10.
11.
[Rep > 0; Recr > -1/4; |argc| < Зтг/2].
[Rec, Rep > 0].
4G
[Rep > 0; |argc| < Зтг/2].

216
Гл. 2. Определенные интегралы
[2.19.5
J
о
2.19.5. Интегралы от A{x)e±cx/2l ^ "^1.
1. {xa~1(a-xf~1e±cx/2MPi<r(cx)dx = 1/@)
[Re с, Rep > 0].
[a, Re/3 > 0; Re (а + а) > -1/2],
3, i
х 2F2 Q Т Р + (г, \ + а + а; 1а + 1, | + а + C + а; ±ас\ + 12аа
2.
[a, Re/3 > 0;
¦ 1)е±ас/2Мр±C/2}(Т+C/2{ас)	[а, Re/З > 0; Recr > -1/2].
4.
а
. l ха~г{а -
[а, Rep > 0; Re <т > -1/2].
(cx) dx = U(±l)
[a, Re^ > 0; Re а > |Retr| - 1/2; 17G) см. в 2.19.5.1].
6.
1/2- p + a, 1/2- p- a
[а, Re/3 > 0; Re (/3 + p) < l/2-|Re<r|].
7. ж
о
P-/3-1/
= V@)
c	x
— p + сг)тг
м^^^Сас) +со8(р-(тOг1Ур-^<г(ас)|
[a, Re/3 > 0; Re (/3 - p) < 1/2- |Reo-|].
[a, Re/3, Rec> 0; Re (a + /3 - p) < 1],
7 -
2 о
- 7 tt
^^ J В (/3, i - a - /3 - a ) x
/3, 2<j, 1/2- а - j3 + a
1/2-р + о-, 1/2-а+ (т
; | + а + /3 - G, 1 - 2ст; ±ас

2.19.5]
2.19. Функции Уиттекера MPt<r(x) и Wp,a(x)
217
2а+ 1
- 272)(<т - а - /3
-а- в-( 2 + -1)---а-в + а--а-в-а- (-1)^
9.
10.
11.
12.
13.
14.
) dx =
@-1)/2-<г ~C/2Г [Э, 2G + 1, р + (Т -/9 + 1/2] -ас/2.,-	/ ч
[а, Re^, Re с > 0; Re (р + ст - C) > -1/2].
= V(±l)
0Л
> 0
eac/2Wp+/3/2)CT±/3/2(ae)	[a, Re/5 > 0; Re (/3 + p ± a) < 1/2; |argc| < Зтг/2].
dx =
[x + z)
[а, Rec, Re/3>0].
[a, Rec, Re,0 > 0].
[Rec > 0; -1/2- Re a < Re a < ReF> + />); |argz| < тг],
В (I + a + *, в - a - o - I) x
x 2F2
- + а + a, - + a - G2 + 7 - l)p; 2a + 1, - + a - в + a; (-
+ 7v/2^
а а-9-а+1/2г [2<7, 1/2 + а - а, в - a + a - 1/2]
L	в,1/2-р + а	J
x 2F2 -Tp-ff, 7 + a-^; - + а - Й - <r, 1 - 2<т;
x ГA/2 + а - 0 + <т)Г2'у2^1A/2 + A - 272)((j - a + 0)) x
- 272)p
0, 0 - а - G2 + 7 ^ l)p; ^-а
• G2 -7 - !)(« -
1
+ сг, - - а +
\G^+7)/2^

218
Гл. 2. Определенные интегралы
[2.19.5
15.
16.
17.
{x + zf
dx = cV-Wz*-°/*r [2" + 1>° + Р-'- V2
x
a + n+1/2
X + Z
:)	[Re с > 0; -1/2 < Rea < Re (в + p) - 1/2; |arg^| < тг].
~cx/2Mp,a(cx) dx = (^1)п+1ГBст + 1)Г ( - + p - a) Z-+-+1/2 x
x e
-cz/2T^P;Cr(cz)	[Re с > 0; -те/2- 1 < Re <т < Re (p - те - 1/2); |arg^| < тг].
Ж" ге±сж/2РУр,<т(сж)с1х = И/(±1)
(ж + zH
18.
19.
X
——е~сж/2Мр Acx) dx = X@)
x - у
[ReOO; Re (в + p) >
2; |argz| < тг].
"^; 1^2ct; ±cy
[у, Re с > 0; -1/2- Re a < Rea < Rep + 1],
tg (a + а)ж х
2<т + 1
+ <J + l/2
1	\ /1
х\Г[--р-<т\г1--р + *
-l)p; |- a + a, |- a - <r; (_i
20.
21.
- у
„(еж) dx = X(±l)
• 0; Rea > | Rea| - 1/2,
TTz ±
Re с > 0
?Гсж/2МР5СТ(сж)б!ж = У@)
П
j
См. в 2.19.5.191
J
[г = 0 или 1/2; Re с > 0; - Re B<т + i/^ i/) - 1 < 2 Re a < Re Bp - i/) + 2r],
УG) = (±i/I^2rcA^l/)/2^o:z1/2^rr(a + i//2 + <т) x
2+G ^7^1)x
Dp) Г1
Г[|-р-(т] x

2.19.5]
2.19. Функции Уиттекера МРуГТ(х) и Wp,a{x)
219
/I \2г 2г —а —1//2 гщ I 1 + ^ ,	,	п
(±1/) с	; z Г I	Ь а + сг — 2г
I 27 — 1) х
V
х 3F3 \2г + |, 2г - |, 2г - а - | - G2 + 7 - 1)р; 2r + i, 2r - а
- а;
2Г ~~
i + G - G2 + 7 "
2г - 2а - I/ - 2G - 1, а + G +
7, -
2r- v-
l)/2l 7
\
-2г, 2G
X 1
A - i/ =F ")/2 - a + cr, 1/2 - p + cr
x з^зA/2 + a - G, 1/2 + a + i/ - <т, 1/2 - <j - jp;
l-2cr, 1 + a + - - cr, aH	cr -
22. Г яа-1
[r = 0 или 1/2; | arg c\ < Зтг/2; 2| Re a\ - Re A/ =p ") - 1 < 2 Re « < 2r - Re {u + 2p),
УG) см. в 2.19.5.21].
[r = О или 1/2; Re с > 0; Re Ba + v =p v) > 2|Re<j| - 1; У G) см. в 2.19.5.21].
24.
[г = 0 или 1/2; Rec > 0; -1/2 - Retr < Rea < Re (p =F "/2) + r],
ZG) = 2±ucr-a^v/

220
Гл.2. Определенные интегралы
[2.19.6
2а
-,
А
l/ 4l
1, г - a - G -	| ^
+ сг + 1, ™ + <т -	G2 + 7 ~ 1)р; —«
А	А
а + ff _ Г)
-* <н-(,,+1)/2-«7-ггГ2а-2<7 + 1, G -а - A ± 1/)/2 + Г, 2G
^	[ ")/2 + а-а-г, 1/2-р+а
- г;
- + а - а, - + а - а, - - <т - 7Р;
3-1/
а - сг - г,
25.
26.
[г = 0 или 1/2; |argc| < Зтг/2; j Recr| - 1/2 < Re а < г - Re(p± w/2); ^G) см. в 2.19.5.24].
г = 0 или 1/2; Re с > 0; Re а > | Recr| - 1/2; Z(j) см. в 2.19.5.24].
(ж +
О1ПС TI	ol ±cx/2 Г Sinbxr 1 f MP)G(CX) X
2.19.6. Интегралы от x e ' { , r >< Ж1Г ; : >.
[cosfex J [ Wp a(cx) J
cosbx
2p
2p
2a+ 2cr + l 2a
ir(a + cx+5l(COs[Ba + 2<J + 1Or/4]
1	1_ ^c^
2	' °" + ' 2 ' ~ 62
x
X 4F3
2a + 2G + 3 2a+ 2cr+ 5
2.
2G + 3 2p + 2G + 5	,	3 3 c2
,	,	,	; ,7 + 1, * + -, -; --
[6, Re с > 0; -1 =F 1/2 - Re a < Re a < 1 + Rep]
p „(ex) dx = U(l)
[6 > 0; | Re cj| ™ 1 =F 1/2 < Re a < 1 ™ Re p; | arg c\ < Зтг/2; S =
-G+l)/2
0fJ'
2	/ V 2
3 + 2a-2<7 l + 2a^2cr
3 +2a+ 2(j l + 2a + 2<r
4	'	4
1 + a + P7 r I
2ba+P
sin [(a + p)ff/
3 - 2p + 2a

2.19.6]
2.19. Функции Уиттекера МР;СГ(х) и WPia(%)
221
^ 2р ^ 2<т 3 - 2р ^ 2<т 1
+ Р 1-g-p, _\L_ . ,
2 ' 2 ' с2 '
±
G + 1)
3-
3 З^а^
'
4
-p 62
5. жа e cx/ <
J	\cc
CO
Чж e
0fJ'
хГ
x Г^
[6, Rec>0;Rea>|Reo-|- 1 + 1/2; U(j) см. в 2.19.6.2].
Мр,а(сж)с1ж = V@)
[b, Rec > 0; - Re cj - E + l)/2 < Re a < Rep + 1/2, S =
G2 - 7 - 1) (а + I
A - 272)p +
CA-27)P
x 2F2 ( -+o
5.
6.
oo
r. j x
8.
9.
, i
2a+1 1-Ba-2(i-27)p){8inja-;;-f^;>x
I. cos (a- A-27)р)тг
; l-a + (l-27)p, i-
6' Rec'
i2 \
[6, Rec > 0; Re cj > -1/4].
, ^ (еж) dx = y^ ( -
Л
p+o—1
V
^^J W(p_3or)/2,(p+<7)/2 ( ^J	[6, Rec>0; Re (p + ex) > -1/2].
wp
[b > 0; |Recx| - IT 1/2 < Rea < 1/2- Rep; |argc| < Зтг/2; VG) см. в 2.19.6.4].
[6, Rec > 0; Rea > |Recr| - l=p 1/2; VG) см. в 2.19.6.4].

222
Гл.2. Определенные интегралы
[2.19.7
10.
11 f та^г(
II. J X	t
)dx = 2
b > 0; Re <
= W@)
>'-{;}]
[6, Re с > 0; - Re a - 1 < Re a < Re p + 8/2, 8 =
- - G2 + 7 "
_l/2-p-<7
¦cr + l,a + crH—; (—1)
ч/2А2а-2^ + 1^1/2-с/ COS (« - аOГ 1 p Г 2G, 2d - 2tt - Г ^
H
a+ cr x
- 272) [a- a+
A-
¦G -7-1) «- о х
12.
13.
[6 > 0; \Rea\ - 1 < Re a < Rep+ 5/2; |argc| < Зтг/2; W(j) см. в 2.19.6.11].
°	[6, Rec > 0; Re a > |Re<r| - 1; 1^G) см. в 2.19.6.11].
2.19.7. Интегралы от хае±сх/2 In <p(x){ ™p1<rifX\\.
1. f xa~1e~cx/2\nxMpia(cx)dx = Л@)	[Rec > 0; ^l/2^Recj < Re a < Rep],
- 272)(<r - a
x 1-0 i -+Q+O-) +^ ( ™+A^272)(<j-a) )-t
2. f жа^1е±сж/2 1пжИ/Р!<т(сж) с!ж = A(±l)
0	Г R
[Re a >
Re с > 0
G2 - 7 - l)«) x
G2-7-1)а) -lncl
J
. [ x*-xe~cx
J
1 (
In \x — z
p,a(cx)dx = V@)

2.19.8]
2.19. Функции Уиттекера МР;СГ(х) и WPia(%)
223
Re с > 0; -1/2 - Re a < Re a < Re p,
= ±-
-2G
a + a + l/2	[1/2 — р —
1 Г sec (a + сг)тг1
¦<т\\ tg{a + a)n j
х 2F2 ( ^ + a - G2 + 7 - l)p, а + а + i; 2<r + 1, а
i;
z| < тг
>0
±
2<т 1 f sec (a -
c (a - <т)тг 1
, a - o- + |; a
1/2J L \2
x 3F3 Л l, l - а - G2 + 7 - l)p; 2, | - а + <т, | - а -
2G + 1
+ (т + 1/2
Г| ^
x Yl
- 272)(<т - a
x L Q + а + Л + ф Q + A -
Recr| - 1/2 < Rea < -Rep; |argc| < Зтг/2,
I
|Rec > 0; Rea > |Re«r| - 1/2, j
2.19.8. Интегралы от ж"е±сж/2 EI (-Ьж)( Мр! ^11.
см. в 2.19.7.3
см. в2.19.7.з|.
1. [ ха~1е~сх/2 EI (^6ж)МР)СТ(сж)с1ж = 14/@)	[Re 6, Re О 0; Re (a + a) > -1/2],
WG) = -1
* Г ^2а
x 3F2 B
(-1I
- p - «г
1
1/2-p +о-
1
, a -
±

224
Гл. 2. Определенные интегралы
[2.19.9
ею
2. f ха^е±сх/2 EI (-Ьх)Wp, a(cx) dx = W{±1)
3.
2.19.9. Интегралы от
[Re6 > 0; Rea > |Re<r| - 1/2; |argc| < A ± 1/2)тг; WG) см. в 2.19.8.1].
1	\	/	3	с
x В ( 2c- + 1, - + p - <т ) 2Fi ( 1, 2<т + 1; - + p + a; 1 - -
[Reс > 0; -1/2 < Rea < Rep+ 1/2; |arg6| < Зтг/2].
„I erf (by/a dz ж ) I f Mo о-(сж)
I erfc Fvа ± ж ) J [ И^р, ст (еж) J
2fe2 _
Х2^[1, j-p; ^;
462с
Ь2 -с)
[2 Rep > | Rec|; |argb| < тг/4].
2.
-,
) с!ж = —
1
+ 2' a"
+ 2^7
-, 2o
. f
4. j
с/ж =
[Re с, Recj > 0; |argb| < тг/4].
5.
Re (а + сг) > 1/2; | arg 6| < тг/4,
erfc
1)
J Re (fe2 - c) > 0 или 6 = л/с , Re (a - p) < 1/2
\	Re с > 0
J Re (a + p) < 0; | arg c| < Зтг/2
1	|argc| < Зтг/2
s
1-7
a + a, 1 + a - a, i;
, |
2^) ±
G
9'2~a~/9'

2.19.9]
2.19. Функции Уиттекера МР}(Т(х) и WPj(r(x)
225
[Re с > 0; Re а > |Recr| + (тЗ - 1)/4; jargfe| < тг/4; ХG) см. в 2.19.9.5]
7 7
7- J
erfc
[Re О 0; - Re a - C±l)/4 < Re a < Rep+ 1/2; |argfe| <
26
Г(а + a + 1)Г2"г2-1G2 + A - 272)(o- - а))
- 272)p + 72 - 7 - i + G2 - 7 - l)a) x
, a + <r + 1, a - a + 1; J4 + a + G2 + 7 - l)p; T(-l
x SF2 Q + a + A - 27)p, i - a + A - 27)p, i - a + A - 27)p;
1 - a + A - 27)p, I - a + A - 27)p; T(-lO^
| + A - 272)(^ - а)
OG
2 Г Ta~
1. jx
oo
- 272)p + 1-p- + G2 - 7 - l)a) x
a + G2 + 7 -
, p-<T + 1/2
[Reс > 0; -1/4 < Recj < Rep + 1/2; |arg6| < Зтг/4]
erfc (Ъу/х)Мр, а(сх) dx =
ca+1/2	[4G + 2 p-a] (	1 n 3	3 , с
[Re с > 0; -1/2 < Re ст < Rep; |arg6| < Зтг/4].
|Reo-| - C± l)/4 < Re а < 1/2 - Rep; |argb| < B =p l)?r/4; |argc| < Зтг/2; БG) см. в 2.19.9.7]
8 А. П. Прудников, Т. 3

226
Гл.2. Определенные интегралы
[2.19.10
¦{;
12
[Re с > 0; Re а > |Recr| - C ± 1)/4; |arg6| < B =р 1)?г/4; ?G) см. в 2.19.9.7].
/ /	\
Г <г-1/2 -я!/Bа) Л О-Ж	/Ж\
. ж ' е 'к ) erf \ 	 Мр а ( — ) аж =
J	\уа/^а/
а
13. i
[2<т + 5/2
2.19.10. Интегралы от жае
§=¦
2; ас-аб2)	[а > 0; Reo->-1/2].
1. [ xoc^1ei±b2^2c)x/4DlJ(bv^)MPja(cx) dx = 17@)
Re (а + (г) > -1/2; | arg 6|< B ± 1)тг/4,
Re с, ReBp- 2a - i/) > 0
Re с > 0
2. + 1) х
хГ7
х 3F2 ( - + <т - G2 + 7 ^ 1)Р, - + а + а, 1 + а + <т; 2G + 1,	 + а + ст;
А	4
(-„) х
а _ ст; ±(_
1/2-р+о-
- а - 7р, I + а - а, 1 + а - а; 1 - 2а, Ъ±1
0) 6" ы_72[ 2а+ 1
A - 27> + -L-^-L + (^ - 7 - 1) (a + '- ) ) x
. J
4<т
v	2с
1
[Re с > 0; Re ст > -1/2; Re Bp - 2сг - i/) > 1; | arg b\ < Зтг/4].

2.19.11]
2.19. Функции Уиттекера MPi(T{x) и
227
3.
р - сг -
4.
[Re с, ReBp-2(j- и) > 0; Re сг > -1/4; |arg6| < Зтг/4].
2+2c)x/4Dt/(b^)Wp,a(cx)dx = U(l).
Г Re Ba + 2p + v) < 0; | arg c| < Зтг/2 1
Re a > | Re a\ - 1/2; | arg 6| < B ± 1)тг/4,
I
oo
3. j Ж С
argc| < Зтг/2	/'
U(j) см. в 2.19.10.1
6. xp
0
7.
[Re с > 0; Re a > | Rea| - 1/2; |arg6| < B ± 1)тг/4; U(j) см. в 2.19.10.1].
b
2G + 1, 1/2- p-
[Re c, Re Bp + 2a - v) > 0;
Зтг/4].
1.
:)	[Re с > 0; Re v < -1; Re a > -1/2; |arg^| < тг].
2.19.11. Интегралы, содержащие е±сх/2Jv[bx±r^ Mp^^cx^
Bp+2cr + l 2p+2<j + 3
Ьа+а+1/2
i i	г
' 2' a+ 2' {J + 1' ™P
V+3/2Bp + 2g + 1) Г(t/ + a + <r + 3/2)/2l
X 4J
6a+a+i/2BCT + 1)	[(jy - a - a + l/2)/2J
2p + 2<t + 3 2p + 2<t + 5 2a + 2v + 2<r + 3 2a - 2v + 2<r + 3
3
-,
-;--
4	4	4
[6, Re с > 0; -1/2- Re (i/ + a) < Re a < Rep+ 3/2].
2.
2a
2a + 2i/ - 2a

228
Гл.2. Определенные интегралы
[2.19.11
5
'
а - v + р
2 '2' с2,
3-2р + 2<т 5-2р + 2<т
5-2р-2<7шЗ-а-1/-р ^-
3. [ xa~1e~cx/2 J4b^)Mp,a(cx) dx = У@)
[6, Rec> 0; -Re(i//2 + <r) - 1/2 < Re a < Rep+ 3/4],
G2 - 7 - 1) (а + V-
2 f
G2-7-2)
7 "
x 2F2 Q + ct + A - 27)p, i - ct + A - 27)p;
+ A - 27)p - ^ - a, 1 + A - 27)p + ? - a; (^1O+1 ^
4.
2G + 1
p - a + 1/2
5.
[6, Re с > 0; -1/2 < Re a < Re (p + i//2) + 1/4].
2a
6.
[6, Re с > 0; -1 < Re i/ < 2 Re (p + a) + 1/2].
exp I
[b, Rec > 0; Re p > 1/4; Re <r > -1/2].
X
<r) > 0].
8.
X exp ( -^- 1 D
c/
'а'-2' (^)
[b, Rec > 0; Re (/> + <r) > -1/2].

2.19.11]
2.19. Функции Уиттекера MPi(T(x) и WPi(T(x)
229
q [ B*-2р-3)/4-сх/2 j
9. j ж	е	Лзо
1/2
X ехр (-— ) /fp-<r ( — )	[6, Rec> 0; Re (За - р) > -1/2; Re (<т - Зр) < 1].
10.
X exp ( -— j Ip+a f — )	[6, Rec> 0; Reo- > -1/2; Re Cp + a) > -1].
[6, Re с, Recr > 0].
. erfc Mj
13. жа е сж J
о
\b > 0; Re(a + i//
14.
[6, Rec, Recr > 0].
- 1/2,
15. J
16.
Ь2
[6 > 0; |argc| < Зтг/2; Ret/ > -1; -1 < Re (i/ ± 2<r) < 1/2- 2 Rep].
-1/2
[6 > 0; ReO±3<r), Re (p ± <r) > -1/2; Re Cp ± <r) < 1; |argc| < Зтг/2]
/ b2\	/b2\
X exp I -— 1 M(I/+p±3<r+i/2)/2,(i/-p±<r+i/2)/2 I ^ J	[6, Rec> 0; Re i/, Re (i/ ± 2cx) > -1].
oo
17. f x(
X exp (-g-
[6, Rec > 0; Re(-p±3<r), Re(-p±a) > -1/2].
СХЭ
18. f xa~1e~cx/2Jv (-^ ) Mp Л
J	\V% J
0
[6, Rec> 0; ^5/4^Recr < Re a < Re(p + i//2)],
l/2-p-Gj
, a + a H	—, —	h a + a;

230
Гл.2. Определенные интегралы
[2.19.11
A - 27>
G2 - 7 -
(-l))
- - x
19. f жа^1е
J
f 4^
> 0
20. [ xOL~1e
0
[6, Re с > 0; -1 - Re (д + i/+ 2<т) < 2 Re a < 2 Re p + 1],
A -
x 4F4
+ 1
+ 1
;
(-1I
хГ
2p(l- -) - 2a,
7
+ 1 + G2 + 7 -
*а B7-1)p x_7
a - p(l - 27)
-a + p(l-27)
4F4 Q + p(l - 27) - a, 1 + p(l - 27) - a, i + a + p(l - 27), ^ - a + p{l - 27);
- 27) - a,
- 27) - a,
- 27) - a,
21.
) dx = W(±l)
Re с > 0

2.19.12]	2.19. Функции Уиттекера MPi(T(x) и WPi(T(x)	231
~	2\
22. f x~1/2ecx/2Ei(-cx)J2a(bVx)Mp a(cx) dx = - (\ j с х
о	'	^ '
хГ . °" +	exp ( — ) Г ( - + p - <r, ^O(-+p + <j, — ]
[l/2 + p + (jJ V4c/ V2	4c/ V2	4c/
[6, Rec> 0; Re p > -5/4; Re cr > -1/2].
{M a(CXI
1.
0
[Rec > 0; | Re a\ ~~ Re v ~~ 1/2 < Re a < 1/2- Rep],
^a / гзт^тгЧ1 Г-i/, l/2 + a + i/ + <7, 1/2 + a + i/ - cr, -a - i/ - pi
7Г У
- + 1/, -+а + гу + ст, - + a + v - <т; l + 2u, 1 +a +и + p; 1
zl	Л	А
c^a „ [i/, 1/2 + a - i/ + cr, 1/2 + a - i/ - cr, i/ - a - pi
4- "y	Г	x
72^2- L	1/2-p + cr, 1/2-p-cr	J
x 3^2 [- — ь?,- + а — и + а.^ + а — v-(i] 1 — 2i/, 1 + a — i/ + p; 1
7^1/2Г(а + i/ + p)Y2l-1{l- 7 + A- 27)(i/- a^ р))Г^2т Q- A- 27)(a
2. \xa~1e~cx/2IU'
-v -I- iy -I- /t 1 /9 4- a- 4- i/ - лг1
4F3
2.
о
-2a + 2i/ + 2cr 3 + 2a-
4	'	4	'	2	'	2	' ' ' ' <
[Rec > |Re6|; Re (a + i/) > |Recr| - 1/2].
oo
I. [ жае^F+с/2)ш/|/(&ж)М/))СТ(сж)с1ж = 17@, 0)
0	[Re 6, Rec > 0; - Re (y + cj) - 1/2 < Re a < Rep + 1/2],
ч	Г	( 2 . y-^.L^r 2G + 1
(e 7) = —	sini/тг	Г 7	/
+ A - 272)(. - a - 1/)) Г-2+7+1 (A - 272)p +
- + u, - + QL + U + ®, - + a +
A	A	A
с

232
Гл. 2. Определенные интегралы
[2.19.12
Q + A - 272)(сх + „ - а)) х
( - 272)р + ^р + G2 - 7 - 1)(а - *>)
х з^2 ( « — *Л - + а — v + а, - + а — и — а; 1 — 2i/, 1 + а — i/ + G2 + 7 — 1)р;
(~1)(
г 2b
с
-B6)
A-27)р-а
1/2 - p + <r
-*2+*-и A
- а) ) х
х з*2 Q + <т + A - 27)р, | - ^т + A - 27)р, A - 27)р - а + |;
4. ^a~V~6
о
5.
1 + v + A - 27)р - а, 1 - и + A - 27)р - a; (-lI"^* +е)/2^ ) .
(bx)Wp,a{cx)dx = 17@, ±1)
со
3. f xa^1e^cx
ею
7. f xOL~1e~b^E~cx/2h
1ш	26
2'	'	'с
[Re с, Re(c^ b) > 0; Re (а + i/) > |Re<r| - 1/2]
X
а -
1 +
[Re с > 0; Re (а + и/2) > |Reo-| - 1/2; |arg6| < тг].
(еж) dx = D@)
[Re 6, Ree > 0; -1/2 - Re (a + i//2) < Re а < Rep+ 1/4],
F/2)" _ Г A + i/)/2 + а + <rl _x_72 Г 2G
<J +1/2
x Г
-7+7+1
5	Л	5
' 2
- а — a;
1/2, 1/ + 1/2, и + 1, 1 + a + i//2 + G2 + 7 - l)p; (-
[l + i//2 + a + G] х_72Г 2.7
[	1	J

2.19.13]
2.19. Функции Уиттекера MPi(T(x) и WPi(T(x)
233
2-Р-
¦»
A - 272)р +
/2	^ f	У + 1
¦G -7-1) <* + —^— I 1 х
х 4F4
,	, 1 + + а + (т,1 + + а<т;
3/2, и + 1, и + 3/2, C + i/)/2 + а + G2 + 7 - 1)р; (-1)(t2+7)/V/c) -
G2 - 7 -
\
2 " * + A " 27)р, j + A " 2^р " а' 4 + A " 27)Р " а; ^^ "« + (!- 27)Р,
1 + ^-а + A- 27)р, ^у^ - а + A - 27)р, 1 - | - а + A - 27)р; (-1O^ ) •
rp,a(cx)dx = D(±l)
о. X
О
Re с > 0
2.19.18. Интегралы, содержащие
J
Лит	X
О
х Г
Ки(Ъх ) j [И/Р)<т
(СЖ)
—
\ A /
[Rec> 0; Rea > |Rei/| + |Re<r| - 1/2; 0G) см. в 2.19.12.1].
/2a - 2i/ + 2<r + l\ (i±i)/2 /2a - 2i/ +
,
c2\ [2
2'°^2'
, /2a + 2i/ + 2(j-
V	4
:F
X 4
О»	tl/	ti/
О
2а - 2i/ + 2(j + 1
2cr + 3 2p + 2cr + 5

234
Гл. 2. Определенные интегралы
[2.19.13
-p-7(a-i/)J \Г[2~Р + (Г)Г\2~Р~(Г
i + 2a-2u + 2a 3 + 2a - 2v + 2a 1 + 2a -:
- 2а
1 + а - 7 + 7Р	а -
5	'	2	' +
4
-IP.
1 -¦
2а + 2i/ - 2<т 3 + 2а + 2и - 2а
4тг [ тг 1 \6
X 4^3
- 2р - 2<т 3 - 2р -
1	а + и
Г	2
4
, 1-
Ь2
; Тс2)
-2) B
2% [ 7Г j \by
a^^ + P^)[A^2pJ^^
3-2p^2<j 5~2p~2(T
4.
5.
6. x-
4 ' 4
2'	2 ' ~
Rec > 0; Re a > |Rei/| + \Rea\ - 1/2; |argc| < Зтг/2, i "^^ |>, ^G) см. в 2.19.13.3|
,0)
Re 6 > 0
0].
7.
8.
х2*(р,р + 2<г;2* + 1;-^
са^1ж(ь±с/2)ж^Fж)И/Р!<т(сж)с1ж = С/A, ±1).
oo
f ха^гх^ъ±с/2)хKv{bx)Wp,(T{cx)dx = t/(-l, ±1)
3 /2 /Re(« + P) < V2; |argc| <Зтг/21
717 ' 1	Rec>0	J'
U(e, 7) см- в 2.19.12.3 .

2.19.13]
2.19. Функции Уиттекера MPi(T(x) и
235
[Re b > 0; Re a > | Re u\ + | Re<r| ~~ 1/2; |argc| < A ± 1/2)тг; U(e, 7) см. в 2.19.12.3].
СХЭ
9. I x^p^/2e{c/2^b)xKa(bx)Wp,(T(cx)dx =
0
-p, 2a-p; -2p; 1 - ^)
10.
—p, 2a — p, ^2cr — p
11	1
2 ^'2 °" ^'2
[Re 6 > 0; Rep < -2|Reo-|; |argc| < Зтг/2].
»..>ft,».(.+.)>,R.,i-..{'>^<;;."<}]-
FG) =
\ 7Г J 27ГСа
1-.2 Г 2а + 1
) + <7 + ly
'1 - I/
- x
x Г
-7+7+1
x 2F2
" 7 "
a- a; 1- „, 1 + a- "-+ G2 + 7- l)p; (-l
-a--||x
A -
a + a, -^- + Q-O-;
G2 - 7 - 1) (a + ?
&\ \ _ 72-7-2f-2cos(a - A - 27)p - i//2)ff
4c) j 4A^L
(a - A - 27)p - |) 2F2 (i
хГ tt-fl-
- 27)p, i - a + A - 27)p;
- 27)p + |; T(-lO^ ) •
"•I
, ф
(
7Г \ 2
COS I 2G 4	J 7Г
2 / ^'
sin \^(T - p
12.
[2v? = 3a ± i/ +p + 1/2, 2^ =
2<r + n-l/2
1/2; 6, Re с > 0; Re Ba ±v)> -1;
-1/2 < Re cj < 1/4 +Re (p =F i//2)]

236
Гл.2. Определенные интегралы
[2.19.13
13.
2cr+ 1
[6, Re с > 0; те > -1; Re <т > -1/2; Re p > -те/2].
(l-2n)/4(cx)dx =
"•¦;г[<,-агл>(-?)М?)
> = p + is	, 2ф = p - и + —	; 6, Re с > 0; Re v > —	; Re (y - 2p) < n \.
4	4	4
14.
2(р =	1/ - р - За, 2ф = - + v - р + <т; Re 6, Re с > 0; Re ст >	; Re (i/ + 2а) > -1 •
JLO. X t
0
Re i/| + 2| Re o-| - 1; |argc| < 3^;
°5 Re (a
:' L FG) см. в 2.19.13.10 .
16 I ха~ге~сх/
lb. j* e
17.
rLe о / U
[Re 6, Re с > 0; 2 Re a > | Re v\ + 2| Re a\ - 1; FG) см. в 2.19.13.10].
CO
18. f жае^сж/2/м
[6, Re с > 0; Re p > -1/4; Re <r, Re (v + <r) > -1/2].
г(сж)с1ж = G@)
[Rec> 0; (|Rei/| - Re (/x + 2<r) - l)/2 < Re a < Rep+ 1/2],
2(l-27)p-2a
г
Г(м + ^)/2 + a - A - 27)р, (М - «/)/2 + a - A - 27)р, 2A - 27)р - 2а + 1]
[	1 + (	)/2 + A 2) 1 + ( + )/2 + A 2)	J
1 + (/х - i/)/2 - а + A - 27)р, 1 + (ц + и)/2 - а + A - 27)р
х 4F4 Q + A - 27)р - а, 1 + A - 27)р - а, | + а + A - 27)р, | - о- + A - 27)р
1 + A - 27)р -а- ^±^, 1 + A - 27)р - а - ^у^, 1 + A - 27)р - а +
+ ^, 1 + A - 27)р - а + ^; (_1)(^

2.19.14]
2.19. Функции Уиттекера MPj(T(x) и Wp^{x)
237
19. [ жа~1
cx) dx =
2.19.14. Интегралы от xae±cx/2 Н„
1. f xa~1e~cx/2Hu(by/x)MPi<r(cx)dx = #@)
W
,a(cx) J
> 0	J
GG) см. в 2.19.13.18
[6, Rec> 0; -Re(a + u/2) ~~ 1 < Re a < Re(p - i//2) + 1/2, Rep+ 3/4],
l7j ~
1 G2 + A - 272) (a - a - U-))
-G2+7)/2
- 272)p + i + G2 - 7 - 1) x
^; |, | + 1/,
G2 + 7-
х Г
4с
i-Л 2а + 1
[1/2-р + а
| - а + A - 27)р) Г (l-¦?-« + (!- 27)р)]
2.
x 2F2 ( i + a + A - 27)p, 1 - ff + A - 27)p;
,2
1+ ^ + A - 27)p - a, 1 - V- + A - 27)p - a; (-lI^
dx =
3. x~1/2ecx/2M2a(bV^)Wp,a(cx)dx
#G) см. в 2.19.14.1 .
p ;_ f _
[b > 0; -3/4 < Recr < -Rep; Rep < 1/4; |argc| < Зтг/2]
oo
. J
+ 1)
> 0; Re. > -3/4; |argc| < 3./2]

238
Гл. 2. Определенные интегралы
[2.19.15
2.19.15. Интегралы от А{х)е±сх/2Рп{ах±г - b)\
а
1. \ха~1е~сх/2Рп (— -l) Mp a(cx)dx = (/@)	[а>0; Re (а + а) > -1/2],
1/2 ^p^J (а + ст
, ^ + а + <7, -+а + <т; 2<т + 1, -
A	A	A
A
(-1I-
-<гг
2<т
1/2 - р + о-J A/2 + а - G)п+1
1	1
~ 2а, ^ + а ~ а + п, - + а ~ а ~ щ (-
2.	\xa-1e±cx/2Pn(—-l)wp,tr(cx)dx =
°	[а > 0; Re а > |Recr| - 1/2; (/G) см. в 2.19.15.1].
а
3.	[^"^"^Рп ( — -1) MPj(T(cx)dx = У@)	[а>0; Re (а + ст) > п - 1/2],
1	1
X3F3 I - + a- (j2 +7- l)p, ™+a
\ z!	zl
(-1I
zl
3
cr, - + a + cr, 2<j+ 1;
zl
г!
1	1	3
- - cr - G2 + 7 - l)p, - + a - cr - n, - + a-<j
4.
- l
со
. f xa~1e~cx/2Pn f —
-1 ) Mp
/
dx = V(±l)
[a >0; Re a > \Re a\ + n ^ 1/2; V(j) см. в 2.19.15.3].
[a, Rec>0; Re (a - p) < -n],
x 3F3 j - + a+ a, - + a + a, - + <j^ (j2 + 7^ l)p; 1 + 2cr, - + a + a^ n, - + a + G + n;
(_1)
1-G2+7)/2
A/2 - a
- + а-G,- + а- cr, -- cr™ G +7 - l)p; 1- 2<7, - + a- cr - n, - + a- cr
(-1 \ С1 — 7) /2
~1)	ас
'Bп)!,
.1^т2Г
Ll/2

2.19.15]
2.19. Функции Уиттекера MPi(T(x) и WPi(T(x)
239
-а-п))х
A - 27> + -^ + (у _ 7 _ 1)(а + n) j х
, —гг,
у —1)р; ~2п, — — а~(т~п, — — а-\-о — щ (—1
А	Л
. J ха-1е±еи/2Р„ f ^ - 1J WP,.{cx) dx = W{±1)
Rec>0
7. f ха~1е~сх/2Рп (— - l) MPia(cx)dx = X@)	[a, Rec, Re (p - a) > 0],
a
C/2 + a + a)n ^
x
1/2 - p - o-J (-1/2 - a - cr)n+i
-I	<>	-I	О	О
x 3F3 f - + a + cr- n, - + a + cr + n, - + a- (j2 + 7- l)p; - + a+ a, - + a + a, 1+ 2cr;
a \ (_1}« 2a«-
3
W' 2
1	3
n' 2^ a~ ^2 +7 ~ 1^>Р; 2
3
' 2
1/2
^p + G2 - 7 - l)a) x
x SF3 (-n, n + 1, -a - G2 + 7 - l)p; 1, | - a - a, \ - a + a; (-lI-('y!'+'y)/2
8.
9.
<0; |argc
Rec > 0
[e = 0 или 1; а > 0; Re (а + <т) > -(e + l)/2],
(g/2-<*-g)n
^ |-n, 2<т + 1,
а Л + 2(_ 1}п ааа

240
Гл. 2. Определенные интегралы
[2.19.15
Ю.
11
1 - 2G, а - а + ^^ + щ {~lfl~1}/\
V (ет\ Нт — У(+Л\
" р, О" \'-'«-'/ t*X 	 1 ^_I_ JL^
[е = 0 или 1; а > 0; Re а > | Re<r| - (е + 1)/2; У G) см. в 2.19.15.9].
о
ZG) =
"caJ/ P2n+e (J- I МР)?Т(сж)с1ж = Z@)
? = 0 или 1; а > 0; Re (а + <т) > п + (е - 1)/2],
X
1/2 - р - а\ ((е - 1)/2 - а - ст)те+1
—^-,
- + а - G2 + 7 - 1)р, а
а + G + 1, а + <т + -, 2<т + 1; (-lI" т'?;/"ас ) +
а-.
„l/2^p + crj((s-l)/2^a + cj)n4
: — СГ — П -
Л
е
-;
Л
12.
13.
1 + а — сг, ™ + а^сг, 1 — 2сг; (—1) 7 ас
= Z{±1)
[е = 0 или 1; а > 0; Re а > | Re ст| + п + (в - 1)/2; Z(j) см. в 2.19.15.11].
/ж"
[е = 0 или 1; а, Re с > 0; Re (а — р) > —е/2 - п],
X
1/2 - р - cjJ (A + е)/2 + а + <j)n+i
., 1	.	. е
1_ гт -Х- п *?/т —I— 1 • / -| \ 1 —
? «
5 —«
*---<*-:
х Г-^+^+1 ( A - 27^)р + ^^ + Ga - 7 - 1) (а + п + ^
1
х
°	/2
-п, -- - а - п - G ¦

2.19.16]
2.19. Функции Уиттекера MPi(T(x) и WPi(T(x)
241
- — е — 2n5 —	а - а — п, —	а + <т — п; (—lI
14. f xa-1e±cx/2P2n+e (\ -) Wp,a(cx)dx =
15. | ха~1е~сх/2Р2п+е (J^) Mp,a(cx) dx = V@)
[e = Оили 1; a, Rec > 0; Re (a - p) < e/2],
-2a
a + a - n, -
a + a + 1, a + a + |, 2a + 1; (-lj^
2, nn a-a+l/2 l/2-.т
2G
(g/2 + a - G + 1)»
x 3F3 I —	ha-cr-n, ^^^^ ^^' 9 + a^ a+n + 1; a- cr + 1, a- cr + -, 1- 2cr;
A-7)/2 N
;	/
^. /а /а_ ,_,
2.
e
*' 2
i
9' 2
16.
± j Wp,«(cx)dx = V(±l)
g =: 0 или 1; a > 0, <
2.19.16. Интегралы отА(ж)ершЬп(а + к)
a
J	'	'
0
схэ
2. жа^ e^ +c' ^xLn{bx)MPi(J{cx) dx =
см. в 2.19.15.15]
(Л + 1)/2; а > 0; Re Л, 2 Re ст > -1].
[Re 6, Rec>0; Re (а + сг) > -1/2],
- п;

242
Гл.2. Определенные интегралы
[2.19.17
2 ( - +« - Х- а, - + а- о-, -- о- -7Р; 1^ 2ст, - + а - Л - а - га; (-lI^7^
г та^1е{^ь±с/2)/х Т,х(Ьт)\? (гт) Нт — W(+1)
J
[Re 6 > 0; Re a > \Recr\ - 1/2; |argc| < Зтг/2, И/G) см. в 2.19.16.2].
2.19.17. Интегралы от/е"Мгг 7* ^ч
[е = 0 или 1; Re с > 0; Re (а + а) > -(е + 1)/2; | arg 6| < тг/4]
П,
а- <т; -+е,
|+ G2- 7-
2.
! + о- + A - 27)р, | - о- + A - 27)/9, ^-^ - а + A - 27)р + п;
1±? - а + A - 27)р, 1 - а - | + A - 27)р; (-lI^
(cx) dx = Х(=Ы)
1.
[е = 0или 1; Rea > |Recr| - (е + l)/2; | arg 6| < тг/4; |argc| < A ± 1/2)тг, ХG) см. в 2.19.17.1].
2.19.18. Интегралы от Л(х)е±сх/2С^{ах±г - Ъ){ Мр>°^х\\,
{Wp,a(cx)j
р^{сх) dx =
\
-
-2а
[а > 0; Re A, Re (а + а) > -1/2],
А + 1/2, « +а+ 1/21
J Х
J
/1	9	1
х (Л - а - (т)п з^з ( « + °" - G + 7 - !)Р> 2
1/22-' \+ V2, а - . + 1/2
1/2 — р + сг, а + Л — сг + n + 1
+ g _

2.19.18]
2.19. Функции Уиттекера MPi(T{x) и
243
1	2	1
77 - <7 - G + 7 ~ 1)Р, - + а-<т51 + а-А^сг;
z	z
111 _|_ _|_ \	_|_	1 _|_	\	/" -| Ч 1 —
2.
3.
dx =
a > 0; ReA > -1/2; Rea > |Re<r| - 1/2; 1/G) см. в 2.19.18.1].
[a > 0; ReA > -1/2; Re (a + <x) > те - 1/2],
l
x BA)n3F3 j - + a -
4.
CO
. f
J
а+ А+ сг + 1
1	1
?, - + а + <т - п, -
1
-) x
- + а + 2А + <7, 1 + а + А + а, 2G + 1; (-1I (
2<7, Л+ 1/2, «^G^^ + 1/
1/2 — p + <7, a + A — cr + 1
x 3F3 I - - a - 7P, - + a - cr - n, -
BA)n а
1
- х
2
- + а + 2А - с, 1 + а + А - сг, 1-2G; (^1)A т)/2ас
Zi
Ж/2ОА — -1 Wp,CT(c^)dx = y(±l)
\ X	J
[а > 0; ReA > -1/2; Re а > | Re а\ + те - 1/2; V(j) см. в 2.19.18.3].
/2т \
'^ ( — - 1 ) Мр аГсж) Aж = W@)
\ a J
[а, Re с > 0; Re А > -1/2; Re (а + А - р) < 1/2 - п],
Г 'l/2-р-аП	1/2-а-сг	]BА)„(А-а-а)вх
1	1	2
'2	'2
ac +
1/2, <7-а-Л-
а-Л-<7, - + а - сг, --сг-
- 2<7, 1 + а-Л-G-п,
-G2+7)/2

244	Гл.2. Определенные интегралы	[2.19.18
1
2
-2Л-га, --Л-га, --а-Л-га-G + 7 -
1 — 2Л — 2га, 1 — а — Л — <х — п, 1 — а — Л + с
со
в. [ /-'(г - а)х-1/2е±сх/2С* ( — - 1 ) И/р,ст(сЖ) rfa; = W(±l)
7. f ха^1(Ж^а)л/2е"сж/2С^ ( — - 1) Mp,a(cx)dx = Х@)
[а, Re с > 0; Re Л > -1/2; Re (а + Л - р) < 1/2],
!	l [\/2-p-ay[ 1/2-a-a
x BЛ)„ (-+a+2\+a) 3F3 (-+a+a - n, -+a+2X+a + n, -+ a- (~y2 + 7 -
1 + а + Л + <т, - + а + 2Л + a, 1 + 2ст; (>1IЧт2+7)/2ас
п!	L1/2 - р + ^5 i/2 - а + {J +	п
-+«-^-«, -+а+2Л—сг + п, -— сг— 7Р5 1+а+А— <т, -+а+2Л— сг, 1— 2сг;
"G2+7)/2
г27
- 272)р + \ + G2 - 7 -
- Л - n, i + Л + п, ^а-Л^
. [ Xй-1 (х - а)х^1/2е±сх/2С^ (— - 1 ) Wp а{сх) dx = X(±l)
{	V ж / '
l/2{Ee(a + ^^
{
9. ^ха^(а - x)x^1/2e^cx/2GL+e ( J| J Mp> a{cx) dx = У@)
0	[е = 0 или 1; а > 0; Re Л > -1/2; Re (а + о-) > -{е + 1)/2],
Х Г[ V+л\" ^ га + e/t+ 1 |Г72 I 1/2 -2р - а I (I ~ " ~ ^п

2.19.18]
2.19. Функции Уиттекера MPi(T(x) и WPi(T(x)
245
1	_/ 2	_г)	1
2	17+7 Jp, « -+- ex -+- 2,
<7---га;
А
1/2-р + <7,а-
1
1 (? _ Q + <Л
lJ V2 а + <7)„
х з^з ( 2 ~ а - 7Р> а - а + -, 1 + а - а;
а-сг---п, 1 - 2<т,
10.
11.
/^ J Wp,a(cx) dx = Y(±l)
[e = 0 или 1; a > 0; Re Л > -1/2; Re a > \ Re a\ - (e + l)/2; УG) см. в 2.19.18.9].
p,a(cx) dx = Z@)
[e = 0 или 1; а > 0; Re Л > -1/2; Re (а + о-) > n + (e - l)/2].
Л
е +1
- + о- - G2 + 7 - 1)Р>
	-—;
А
Bп
а + А + <т + i, 2,7 + 1; (-lI-
«т, А+ 1/2, a-a-
1/2-р +a, l + a +
о ~ °" ~ 7Р5 « - сг - п
^,
;
12.
13.
а
Г 1а
° [е-
СО
J ж (ж-а
) dx = Z{±1)
[e = 0 или 1; a > 0; Re Л > -1/2; Re a > | Re <r\ + n + (e - l)/2; ^G) см. в 2.19.18.11].
p a(cx) dx = U@)
[e = 0 или 1; a, Re с > 0; Re Л > -1/2; Re (a + Л - p) < A - e)/2- n],
Л + 1/2, -е/г^а^А^^т^
| ^ « ^ <r) 3F3 Q + cj - G2 + 7 - i)p, ^ + « + ^,i + « + ^;
Л + 1/2, а-а- Х-е/2-п, 2a] (e

246
Гл.2. Определенные интегралы
[2.19.18
- — сг — 7Р, -
А	А
— 2сг,
l + a-a;l-- + a
?2n+e (l-e)/2-a-A-n
-G2+7)/2
^ (l - 72 + A - 272) (^ - | - a - A - n)) x
f A - 272)p +I + G2^7^l)(a + A + |+n
1	1-е	2
	A — n,	a ^ A — n — G + 7 — l)p, 1 — A — e — n;
1 - A - e - 2n, l-a-\-a---n, 1 - a - \ +a - - - щ (-if-^+^^t
14.
= 0 или 1; а > 0; Re Л > —1/2, <
I Re с > 0
15.
argcl < Зтг/21
>, t/G) см.
в2.19.18.1з]
'- ) MPj(J{cx)dx = V@)	J
[e = 0 или 1; a, Re с > 0; Re A > -1/2; Re (a + A - p) < (e + l)/2],
l/2,?/2-a-\
a + A - CTJ 3F3
— + a-G-n, --o--G +7-1)
-^ + a + A-<j + n; i+a + A-cj, l + a + A-^т, I - 2a; (-l)A^7)/2ac
Zi	A
- 272)p + \ + G2 - 7 - 1) (a + A - |)) x
- A - n,
- l)p, i + e + n;

2.19.19]	2.19. Функции Уиттекера MPi(T(x) и WPi(T(x)	247
16. | ха-\х - a)x-1/2e±cx/2cL+t (Jl J Wp,«{cx) dx =
Re с > 0	j '
V(j) см. b2.19.18.15J
2.19.19. Интегралы от Л(х)е±сх/2Р^ 1/)(аж±1 - 1I Мр' а^СХ\ 1.
[а > 0; Re/i > -1; Re (а + а) > -1/2],
-^a + i/^
2^7 + 1, | + а + /х + (т + п, i
Г	2G, /X + П + 1, а - G + 1/2	1
L1/2 - Р + ^5 « + j^ ^ <J + n + 3/2j
1	11
- - G - р7, - + « ™ ^, ^ + « ™ ^
Л	А	А
Ч,	1
1-2G, - + а + /х-G + га, -
2.
[a > 0; Re/z > -1; Re a > |Rea| - 1/2; ^/G) см. в 2.19.19.1].
3. [Жа(а^ж)^е"сж/2Р^'1/) f— -Л
J	\х J
[а > 0; Re^ > -I; Re (a + а) > те - 1/2],
п\Х
2 -J (а + ц + и + а+^Л В
/1	1	Ч
х з^з ( - + а - G2 + 7 - 1)Р> - + а + ст-п, -
а+м_<т+1/2с1/2_а г	l/2 + a-a-r.l /3
l	1	3
- - о- - 7Р? - + а - G - n, -
-G, | + а + /х - G, 1-2G; (-
4 \та~1(а — т^Р±сж/2рО'") [ _ _ 1 \ Ш (гт) dr — X(+l)
J	Vх
о

248
Гл.2. Определенные интегралы
[2.19.19
5.
УG) =
[а > 0; Re/i > -1; Re а > |Re<x| + n ~~ 1/2; X(j) см. в 2.19.19.3].
4P) a (ex) dx = Y@)
[a, Re с > 0; Re/i > -1; Re (a + /it - p) < -n],
гс!
1, - + а-
, -
2
1^^ +l)/2
2 „
- + a - i/ - <r, - + a - <t, -
_ a _ » _ n _
- cr - 7p; 1 - 2cr, -
n)n x
/1
x Г (± -
- a - м - n)J x
^^ "" nJ ^a — I1 — n — (l2 + 7 ~~
6. (^
7. [^(s-aJ
J
-1
Py(T(cx) dx =
[a, Re с > 0; Re/i > -1; Re (a + /x - p) < 0],
x Г7
-I	О
x з^з ( - + a + cr - n, -
1
о
, -i
1"^ +7)/2
2
7
n!
1/2 -

2.19.20]
2.19. Функции Уиттекера MPi(T{x) и
249
'3
х (-
- + а — а — п, -
I	A
1 - — сг — jp;
А
-+а + „-а,-
п!
¦ i/- <т, 1 - 2<т; (-lr-t'^ac
2<т +
G2 " 7 " 1)(а + ц) ) х
х з^з ( —М — п, 1 + г/ + п, ^а — /i — G2 + 7 — 1)р;
v, --a-fi-<T, - - а - ц + а; (-1I"
r,.2a_1
а
Г	fRe
а, Re и, > — 1, <
L	I
2.19.20. Интегралы от А(х)е
[а > 0, Re(a + cx) > -1/2],
+i 1 /О	I
cj + 1/2, а + (т-
2 Г ^2(j
J L1/2 - Р ~ °
/_ 1ч1
х з^з ( - ^ ^ ^ 7Р, « ^
Л*	X	С
о
а
Г
о. ж б
а - а + 1/2, а - G + 1
1	1
• 1, а - сг Н	—, 1 - 2сг; (-]
«,а-1
4. I
/ж + z
VM =
2 Г -2с
ХГ '.l/2-,-CT|3^V2
[а > 0; Re а > |Re<j| - 1/2; (/G) см. в 2.19.20.1].
[а > 0; Re а > |Recr| - 1/2; ?/G) см. в 2.19.20.1].
(nv\ tine — \/(п\
[Re с > 0; -1/2- Re a < Re а < Rep + 1/2; |arg^| < тг],
X
1
2'

250
Гл. 2. Определенные интегралы
[2.19.21
2а + 1, а + а + 1, а + а + 1; (^
9(=р1-1)/2 2 а^а 1/2^<х
i	1Z C
+l)/2c
'' Л	1
X3F3 ( --о—7Р, а-<т+-, a-<j
2G, G - а, « - G + 1/2, а - G + 1 =F V2
a-v + l,l/2-p + <r
1
l=F ^5 1-2с, а-с + 1, а-<т+1; (-l
2	/
• - а)) Г~7 +7+ ^
A -
¦ 2 + G -7-1)а) х
2 > х Т 2 ' 2 ~ G' + 7 ~ 1)Р " Щ 1? Х ~ а + {7> Х ~ а ~ а; (^1
5.
6.
-С^в-/2
Wp,(T{cx)dx = V{
Re<j| - 1/2 < Re а < 1/2™ Rep; |argc| < Зтг/2; |argz| < тг; 1/G) см. в 2.19.20.4].
[Re с > 0; Re а > |Re<r| - 1/2; |argz| < тг; V(j) см. в 2.19.20.4].
2.19.21. Интегралы от А(х)е±сх/2Р?(ф))\ ^р'а(;СХ\
{^ УУ р, сг \СХ)
1. J Xй-1 (х + 2z)±tl/2e-cx/2P? (| + l) Mp><7(cx) dx = W@)
[Rec>0; Re(jw/2™ о-)- 1/2 < Re а < Re (p- 2/=р^/2), Re (p + i/ =p /z/2) + 1; |argz| < тг/2],
Г тм -1	1 т м
\ flTii/2		 — П/ — 1J — /Т 	 — П/ -\- 1
Sin 1/7Г
u — 1	1 T M	1 — M
	a - i/ - <t, —	a + i/ - a, —	h a +
— а — а
+ 1,
a + i/
5i + .^7 + 7^)p5i±
+ a - i/ + <r; (^1)(
¦1/)Г(-/х-1/)]"
sin i/тг
2ст,
Г
1 —М
- a - */ + <t, A =F A*)/2 - a + i/ + G, A -
1/2-p +G, (l-/x)/2-a + o-
1	1+li	3 it ii	1 it м
r, -^<r-7p, ^-^+o:-(j; 1-2o-, ' +a + i/-a,	—
A	2,	A	A
0^
-, 2 ,--,-—, 2
„_а-^/2. -, гГ" + 1/2,а-
2. + 1	/1
'2 + р + сг 12
2^i Л

2.19.21]
2.19. Функции Уиттекера MPi(T{x) и
251
+ G — 7 —
± |
2
" "' 2
-i/-1/2, a-
j/ + 1, 1 =F | - а + i/ - G2 + 7 " 1)/»,
2. Ж"
О
—1/2 / Sln
2<т+1, l/
:G, р^1/Т^^1/21Aт1)/2Г	p
J	[2G- I/, 2G+ i/ + 1, p+ <7 + 1/2 J
[Re с > 0; Re a > -1/2; Re (p =F /x) > | Re i/ + 1/2|; |argz| < тг/2].
хГ
X
3. | ха-1(х + 2
0
[Re ^/2+ \Rea\- 1/2 < Re a < - Re(p + i/±/x/2), Re(i/- p =F м/2) + 1; |argc| < Зтг/2,
< тг; И/G) см. в 2.19.21.1] .
Cffi/2P^ (I + l) Wp,a(cx) dx = W(l)
4. f /^(ж + 2z)±tA/2e^cx/2P!; (| + l) Wp, a(cx) dx = W(-l)
о
[Re с > 0; Re (а - /i/2) > |Recj| - 1/2; |argz| < тг; И/(т) см. в 2.19.21.1].
2 ~сж/2
е
3/2 - /i - р - а
^
Г 1 3	1
\2(р =	р + а + /1 ± /i, 2^ = р + Зо-	Ь /х Т М; Rec > 0; Reft, Re (fj, + 2a) < 1; |argz| < тг .
6.
= 0или1/2; Rec>0; Re (д/2-сг)-1/2 < Rea <Re (p-i//2) + r, Re (p +
; |argz|<Tr],
, r
- а - ст, а + a
г - (/x + i/)/2, г + A - /i + i/)/2, A - /i)/2 - a ~~
[l/2 - p - ]
' 2

252
Гл. 2. Определенные интегралы
[2.19.21
, 2 1/2 —о- а —О- + 1/2 —гт-i
+ 7 С	Z	I
1-М	1 + М
V + \	У	1 — LL
2а, г - а + а	—, г - а + а + -, а - а -\	—
1	,	\i + v , 1-// + I/ 1-/х
2 ' ' 2 '2
3 + г
1
^сг — г,
г| I/ + 1/2, A + ^)/2 + а + а-г1 х
A - 272)р
г	^,^^«^^-^G +7-1)Р,
G2 ^ 7 - 1
1	1 —
(«+?-г))
-Г1"
- 272)р + \
г +
-I/-1/2, а + сг-г - -
I |	^
-/х - I/
X
Kf
т.
8.
?¦	, г - а + —	G + 7 - 1)р,
Х + Z
2ст + 1, p + iz/2, p-
p + ex + 1/2, a+{,
[Rec, ReBp + i/) > 0; Re Bp - i/) > -1;
^.„(ca;) d« = X(±l)
z/2
z| < тг].
r = 0 или 1/2; Re (а - /i/2) > |Re<r| - 1/2; |argz| < тг,
= /i - p + a + C ± l)/4, 2ф = /i + p + 3<j - G ±l)/4; Re с > 0,
fRe/x,
1 Re/i, Recr > О

2.19.22]
2.19. Функции Уиттекера MPi(T{x) и
253
2.19.22. Интегралы от A{x)e±cx
^/2e^c"/2Qe (| + l) Mp,a(cx) dx = Y@)
[Re c> 0; | Re/i|/2 - Re a - 1/2 < Re a < Re (p =F /x/2 + i/) + 1; |argz| < тг],
Г1
yG) = e
x Г
U-p + И
, а + а ¦
1/2-p-a
Г1 + M +
, a - a +
л /1 1 +д 1д 3±м 1±м
X3F3 ( --o"^7p, a- a H	^, a- cr H	—; 1 - 2a, a + v- а Л	—, ol-v-<t-\	—;
и + 3/2
?)¦»
x 3F3 (i/ + 1, 1 =F /i + 1/, 1 - a + 1/ T I - G2 + 7 - l)p;
1/ + 2, ^ - a + 1/ + a, ^ - a + 1/ - a; (^l)^
2 I ^ + (/*-1)/2/ , 2 чах/2 ^с
x B
3.
4.
5.
- 2<7, 2с + 1, р - о- - 1/2, р-а -1/2
р + сг + 1/2, р - <т - 2д - 1/2
= 1/2 - ц - р - <г, 2ф = р - ц - За - 3/2; Re с > 0; Re ст > -1/2; Re (p ^ cj) > 1/2;
Р; сг(сж) с?ж = V'(l)
| Re/i|/2 + | Recr| — 1/2 <Rea <Re(i/^ ft/2 - p) + 1; | argc| < Зтг/2; |argz| < тг;
Y(j) см. в 2.19.22.1].
Vo,a(cx)dx = Y(~l)
[Re с > 0; Re a > |Re/i|/2+ |Reo-| - 1/2; |argz| < тг; УG) см. в 2.19.22.1].

254
Гл. 2. Определенные интегралы
[2.19.23
= О или 1/2; Rec>0; | Re^|/2 - Re a - 1/2 < Re a < Re (р + у/2) + г + 1/2; |argz|<7r],
x Г
1, -
—	h r,	h <
2	'2
-2a
¦ p- a
3 +
L2
- a + a — r,
1 + 2a, 1 + a + a - r - |; {^l
+
- cr l/2 + a-cr-r
Г2о-, (/x + i/)/2 - r + 1, i//2 - a + G + r, A + /x)/2 + a - <r, A - /x)/2 + a - <rl
1/2 + 1 + /2 + 3 + /2 +	J
1/2 -
-(T, « - o- - 7P5
Л
l;
3/2-
272) (a + r + \ - а))
-7-1) x
r,
f a-l/ 1 \-r -e
3
2+"
— г -сш/2/-,2сг-2о
+ z
7.
Mpj a (CX) dx =
if, 2ct + 1, p+cj- 2a+l/2
[r = 0 или 1/2; 2y? = <т - p - 2r - 2a + 2, 2^ = p - о- + 2r - 2a - 1;
Re с > 0; 0 < Re a < Re p + r - 1/4; Re <r > -1/2; |argz| < тг].
wp,a(cx)dx =
fRe(a
2.19.23. Интегралы от А(х
r = 0 или 1/2; Re а > |Re/i|/2+ |Reo-| - 1/2;
+ p) < Re i//2 + r + 1/2; | arg c| < Зтг/2 1
Re с > 0	J '
argz| < тг, ^G) см. в 2.19.22.5
z)\(Mp,rT(cx)\
z)j\Mp,a(cx)j-
-21/ 1 M+a + ^ + ^l + e + iz-a.-l^-a-i/-.
111	l/2-p + ff, 1/2-p-a	'

2.19.23]
2.19. Функции Уиттекера MPi(T(x) и WPi(T(x)
255
_„Г< )/2
2i/, 1 + a ~ г/ + <т, 1 + a — i/ — <7, i/^a^p™ 1/2
1/2 - p + cr, 1/2 - p - a, 1/2 - /x + i/
3
1 + a - i/ + <7, 1 + a - i/ - <r; 1 - 2i/, - + a - i/ + p;
r (i +
± (/i - a - p)) 3F2 ( - - p + <r, -
/x ~~ a - p;
l< Rea < Re (/x - p)
Г 2ст+1 j cos(a/2-сг)тг\A±1)/2
[l/2- p+ a\ sin (a/2+ р)тг J
a/2-p, l + a/2 + p
-1,-1-2Reo-<Rea<-2Rep
oo
J,-,
0; |Re<j| < 1/2; [л ф р; а ф 0].
| < 1/2; cj^O].
[Re с > 0].
oo
Жа^1М|/+то+1/2!1/(сж)М(Т + п + 1/2,<т(сж)бгЖ =
/ ()	iF
? ^1
J
2cQ
Rec>0, Re(a + i/ + o-) > -1 .
L	v	; J
a)/2 + G, p-a/2,-p-a/2l
+ p+cj, (l-a)/2 + o-, ^: J
[c > 0; -l-2Recr < Rea < -2|Rep|].
* ' О О" \	^^ *^^ Iff /J ^T I €/ 1^- еДу I ЧЫ/ «АУ —	j_ j
0
[2|Recr| - 1 < Re a < -2 Rep; |argc| < тг].
Г а-1/ 2	2\C-
\ x [a — x )
¦ (
V
4a	V	2
'1	1
A±1)/2
Г
l 1 / с
+ crJ V si
Sin СГ7Г/
a + 1 a2c2
1/2-p + a\{ cosan

256
Гл.2. Определенные интегралы
[2.19.23
т,-
' 2
г, 1 +¦ 2ст, ^ + а + ^^^
1/2 - р + о-, 1/2 + р + ст
1	1 + а
х з*4 I ^ + Р - ^ 2 ~ Р ~ {J' ^^ ~ <J; Х ~ {7' г ~ 2(Т' § ^ {J' 2
/3^;
а, Re^ > 0; Rea > -1,
Re а > 2| Recr| -
10. ж (а -ж )р
J
' ;. : >
dx =
¦В (Д,^— )х
х 3F4 I - + р - сг, - - р - ег, —	ег; 1 - 2<т, - - ст, 1 - <т,
/3, (а
4 / \l/ 4<rsincT7r [/3 + (а + 1)/2, 1/2 - р + <т, 1/2 - р - а
1 1 1 + а 1 „1 + а а22
- + р, - - р, —?-; -, 1 - <т, 1 + а, /3 + —2~;
cosатгЧ/З + а/2 + 1, 1/2 - р + а, 1/2 - р -
3 3	3 , а , а , , а2
+	+ /3 + 1
11
. жа™ ' (а — х)и~ ' M^jtJ(ca — cx)Mpj(T(cx) dx =
= al/+<TBBi/ + 1, 2<т + 1)Мм+РI/+<т+1/2(ас)	[а > 0; Re и, Re a > -1/2].
а
12. f ж1/2^ст(а - жI/2^1/Мм,г/(са - сж)МР)<т(сж) da =
7
5. J x^1(
14. I" xv
? [1/2-р + (т, 1/2^р^<т
^^ 1^^ I_ +<Ji^ ^ 1 2 ¦ а'с2
[а, Re/З > 0; Re (/3 + 2р) < 1; |argc| < тг].
ix + ^)И/р,а(сж) daj =
[Re с > 0; Re v > |Recr|;

2.19.24]	2.19. Функции Уиттекера MPi(T(x) и WPi(T(x)	257
p,a{cz)
Rep -1/2 < Re. <0
^ 1/2 < Re. < 1/2 - Rep; Re. > 0
2.19.24. Интегралы от xaef(x) f\ MMj., ^. (bjX^) WPkjGk (ckxTl)
^е^М^, сгFж)Мр,сг(сж) dx = 22<T+1(bc)a+1/2FBa + l)Bp + b + с
о
x Bp + с - b)^a^1/2Bp + 6 - C)p-a-1/22Fi f I - ^ + ^, i - p + (j; 2a + 1;
46c	\
Bp + c-fe)Bp + fe_c)j	[R->-l/2;2ReP>|Re6|
OO
2. [жа^1е^(ь+с)ш/2ММ!1,Fж)Мр,С7(сж)Aж = V@, 0)
[Re6, Rec > 0; -Re(i/ + <r) - 1 < Rea < Re(/x
-2j/
72 - 7 - | + G2 - 7 - l)(a + ^)) 3F2 Q + ^ - (?2
a+ v+ a, 1 + a+ i/ - a; 1 + 2i/, | + a+ v + G2 + 7 -
^-(T2 + A - 272)(. - a + ,)) x
- 272)p + 72 " 7 " \ + G2 " 7 " 1)(« " i/
x 3F2 ( - — v — e/i, 1 + a — iv + <T, 1 + a — v — cr; 1 — 2f, - + a —
72-7-2 (i-27)p-ari-
? ?
+ A - 2?2)(^ + A -
x 3F2 (i + <r + A - 27)p, i - a + A - 27)p, A - 27)p - a - (e2 + e -
+ 1/ + A 27)p - a, \ - v + A - 27)p - a; (_i
9 А. П. Прудников, Т. З

258
Гл. 2. Определенные интегралы
[2.19.24
3.
dx = V@, ±1)
4. xoc^1e{b^e)x/2M^l/{bx)Wp^{cx)dx =
о
'--
3/2 + a + и - p
3
5.
1, - + a + i/ — p; -
[Rec, Re(c- 6) > 0; Re (a + i/) > |Recr| - 1].
1/2-p =f <T, 1+ [Л+ I/-p ± (Г
^ + /i + i/5l + 2i/±2(j; l + /x + i/-p±G; 1 - -
2	с
[Re 6 > 0; Re v > -1/2; -1/2 < Re (y ± a) < Re (/i - p); | arg c\ < Зтг/2].
. f жаеF±с)ж/2И/м, ^(Ьж)Жр, с (еж) dx = У A, ±1)
Rea
Recr| - 1; |argb| < Зтг/2,
Re (a + /i + p) < 0; | arg c\ < Зтг/2 )
Re с > 0	J '
V(e, 7) см. в 2.19.24.2] .
7. xa~1e{~b±c)x/2WIJttu(bx)WPia(cx) dx = V(-l, ±1)
0	[Re 6 > 0; Re а > |Rei/| + |Re<r| - 1; |argc| < A ± 1/2)тг, V(e, 7) см. в 2.19.24.2].
Pja(cx)dx = U@, 0)
[Re 6, Rec> 0; -1/2 - Re (jx + a) < Re а < Re A/ + p) + 1/2],
8.
1/2 -fi- и
Г(а -
- 272)p + i + G2 - 7 - l)(a - *
x (.7 - a -
?, - — ol — 1/ —
z
- 272)(^j - a + i/)) x
+ 1/ - (г2
2-P-
1/2 -p + i/
-272)p+^ + G2-7-
Ь 7 — l)p; 1 — 2i/, 1 — a — г/ — <т, 1 — a — 1/ + <т;
^
Г|2Г a + , + <T

2.19.25]
2.19. Функции Уиттекера MPi(T{x) и
259
х Г2
. -2е2)(а + 1/ + <7))Г"
- е~ \){а + а
2G
+ 7
2^
| - (s2 - e -
a - 7p,
9.
J-)WP a(cx)dx = U@, ±1)
ReOO
J
, Ще, 7) см. в 2.19.24.81
J
oo
10. \x«-\
11.
12.
13.
(cx) dx = U(l, ±1)
x = U(-l, ±1)
> 0	J
U(s, 7) см. в 2.19.24.8
= П 4&
^и(Ъа - bx)Mp,a{cx) dx =
{ Y+p В Bi/ + 1, 2a + l)eac/2Mp+l/+1/2tI/+a+1/2(ab - ac)
\lJ, + v + p + (T = -1; a > 0; Re z/, Retr > -1/2].
MPk^k(ckx)dx =
ol + R:	pi + <7i, —
'2 F	' 2
2o + 1, • • • 5 2<jn + 1; ¦
:> cfe,jR=> <jfe + -; Re(a + R) > 0; 2 Rep > >
fe=i	fe=i	fe=i
2.19.25. Интегралы от жа cosaa?MMj 1/(Ьж)Мр,о-(сж).
'He	„ /2c2
. ж^1
>
»-l/2
•1

260
Гл. 2. Определенные интегралы
[2.19.26
2.19.26. Интегралы от ха Jv(bx±r) f\ MPji a. (bjx)WPky(Tk(ckx).
оо	3, к
1. ж" Ju(bx)Mp,a(—icx)MPia(icx) dx = /
[b, с > 0; -1 - Re(и +2a) < Re a < 3/2™ 2|Rep| кроме того, Re a < 1/2 при 6 = с)],
1 + a - i/ , l + a + i/
"<J? 2 ~ P + {J'
1	1	c2\
- + p + cj; 2G + 1, G+ -, G + 1; ^1 [c< 6],
7 + 1, 2о- + 1, p-(a + i/)/2, -p-(a + i/)/2, A + а + i/)/2 +
1/2 - р + сг, 1/2 + р + <т5 -а - I/, A - а - i/)/2 + сг, i/ + 1
1 + а + i/	1 + а + I/	а + i/l + a + i/	а
+ 1 +	1 + +
2 ' 2
2 '
г, -
1 1 , о i а + i/
7, 1-p, - ^p; l-2p, 1-p	—,
	p; —
7, i
p, i
2p, !^^y
. J2CTFa?)
x [(c + Vc2 - 62 Jp + (c - Vc2 - b2 fp]
СХЭ
j f -O--1/2 т
2G + 1, 2G + 1
1/2-p +G, 1/2+ p +
7^ c; 6, c> 0; |Rep| < 1/4; Re a > -1/2].
ol/2 —о- /1ГЛ1 —о-
Z '	Л/7Г С	/9 , 9чя-/2
CO
. J2crFx)
5.
0
x Г
i/)/2 - p, 1 + a + 1/, A + a + i/)/2
[6 ^ с; 6, с > 0; Re a > -1/2, 2| Re p| - 1]
2G + 1
Г[1/2™р + ст](^2 + с2+С)
[6, Rec> 0; Rep < 1/4; Re a > -1/2].
X
(lTl)/2
sin (p + (a + i/)/2)tt
A - a - i/)/2 + G, 1 + (a + i/)/2 - p, v + 1 J [ cos (cr ^ (a +
+ a + i/	1 + a + 1/	1 + a + 1/	a + 1/
	G,	+G,	, !+^—; !
X
a + v
+
x 4F3 I - - p- <r, - - p + G, - - p, 1 - p; 1 - 2p, 1 - p	—, 1 - pH	—;
fRe(a + i/), Re(a
-1; Re(a + 2p) <3

2.19.26]
2.19. Функции Уиттекера MPi(T{x) и
261
6.
оо
Г. Jx
x3F2(--p+(j, - - р, 1 - р; 1 - 2р, - + V- р-(г\ —^
>, Rec > 0; Recr > -1/2; Re Bp + 2а - и) < 1/2].
'Ь2 + с2
/б2 + с2
с»
3.	Ж™ Jo(bx)W^p,
• 1/2J*'-1/2 \ 6
[6, Rec> 0; Re р < 3/4; Re a > -1/2].
2Ш8?Т7Г
р-а)
р
о--1/2
S-P-1/2
/б2 + С2
[6, Rec> 0; |Recr| < 1/2].
9.
х 4F3 I-- р, 1 р,
а, -- р-а\ 1- р
, 1 - рН	—, 1 - 2р; —
<T, (a + i/
(a + i/)/2-p, l/2-p + <7, 1/2-p-o-
и
2 ' 2	2
а + i/ 62
a;
10.
13
14.
сю
0
оо
0
оо
[6 > 0; 2|Recr| - Re и - 1 < Re a < -2 Rep; |argc| < тг].
<т - p + 1/2J J""p V^J K"+P V^cy
[6, Rec > 0; Rep < 3/8; Re<r > -1/4].
4c
'—^ W	(-
[6, Re с > 0; Re i/, Re (i/ + <j) > -1/2; Re (p - ц) < 3/4].
[6, Rec > 0; Rep < 1/2; Recr > -1/4].
+ cos (cr —
— ) WPi a(—icx)Wp, (r(icx) dx =
[6, Rec> 0; |Recr| < 1/4].
Ac
№A/2 - p + <т)ГA/2 - р-<т)

262
Гл. 2. Определенные интегралы
[2.19.27
15. f J2*{bx)M-Pi<r[c(Vx2
0
X K2a(V2ibc)K2a(V-2ibc)	[b > 0; |argc| < тг; Rep < 1/2; | Recr| < 1/4].
z)]dx =
,V\^2a + 1 I (/б2	+	с2
exp
/b2 + с2 L1/2-P + <7J
[6, Re с, Re^ > 0; Re p < 1/4; Re a > -1/2].
±r
i r ., i fi.T
2.19.27. Интегралы от хс
oo
'•J
0
oo
4
2с,
>, Re 6 > 0; Recj > -1/2].
[c, Re 6 > 0].
3.
4.
[6, Re с > 0; |Recj| < 1/4].
'	[Refe, Rec>0].
sln(p - a
2.19.28. Интегралы по индексу, содержащие MPi(T(c) или Wp, o-(c).
Условие: b, с > 0.
'1
ОС
2.
3.
| + сг + гж J Г Г | + сг - гж
ch(y/2)
1	1
2	M ^ Ж' 2
ch(y/2)J
1
[Recr > -1/2;
[Rea > -1/2; |Imy| < тг].
x Мм^Ж)<т(с)с1ж =
^+i/2 Г2<7 + l, 2<7 + 2/z + 1, 2G - 2д + 1
2G + 3/2
F +с)
[Re о- > | Re^| - 1/2].
4.
5.
¦2(т + 2ж)ГA + 2|/-2ж)
2G
[Re A/ + <т) > -1/2].
1Jтгж]
sin 2тгжГA + 2(j + 2ж)ГA + 2и - 2х)
M^X}1J~x(c)Mp+Xy(T+x(c) dx =
-1/2].

2.19.28]	2.19. Функции Уиттекера Мр,а(х) и Wp,a(x)	263
7.
8.
9.
10.
11.
оо
I
— оо
р+х,а + х{С)
чх „ р. 1 V ~ ^
X 2 " 2 1
оо
ж вЬптгжГ I	р-\
0
V 2 /
оо
J
0
оо
Г A
j xth2irxri--p +
о
оо
0
оо
Ж oil aj7T3;I I
0
«г2*
Ь2<т + 2Ж, 1/2-м-
Г1
2 [i/2-M + l/,
2 ' 2
\ / 1 Л
-гж)г( - ~ p~ix
0Г(-р-2гжM2р+1,
7ГСР /1 о \
• 1 г 1
' ) V2 Р у
С3/4р ^_ _ 2^j eF2
о 1 о • \ р (
Zp 1 Zi-Ж |1|
-|/-2ж, 1/2-р
I/-/X-
1/2^р+а, 1/2 +
— р + <т _ 1
2 **
1 '
, /2^2
2гжF)И//?,гж(с)с1ж
/62-2с2\
Слр (^ 4с J
9 9*1 P2
AjP AJ%X I J 2-
— <j — 2ж] м
P + СГ
2i/-p-<r, 1/2-
i/ + 2cr, +2j
[Re (i/ - (
\ jt _ г
7г261/)срехр f
=
J 1 b2\
V P+ 2' 4cJ
гж(с)с1ж =
'2c) [Re с >
(с) аж — ^ I
-p~v + 2o
; p -;
|Lt - p + О")
[Rep^
' 2c2 + 62
4c
[Rep
¦ 0; Re p <
— 1 / C
[Rep^
c) da? =
1
4c j
>0].
1/2],
<^ fll
1/2].
-bc/2
1/2].
СХЭ
12. I жвЬтгжГ --/i + ia;, - - /x - гж, - - р + гж, - - p - гж ^^1
/9ч (м-1)/2
x Wp, ix(c) dx=l±)	тгГA - р)ГA - /x - р)(Ь + 1
V
оо
13. ж зЬ2тгжГ — — /х + 2гж, — — /х — 2*ж, -^р + гж, -
J	I •"	^	^
X PL-l
[Re/i, Rep< 1/2].
14.	жзЬ2тгжГ 2р + 2гж, 2р - 2гж,	p + ix,	р - ix\ РЦ^1у2{Ь) х
«	L	J
о
х Wp,ix{c)dx = 2^-3/2^+1/2^2 _ 1}P-i/4exp (^_1±Л erfcF^)	[Rep > 0].
ОО
15.	ж sh 2тгжГ	р + 2гж,	р — 2*ж, 	— + гж, 	— — г
х М/Р!^(с)^ж = 2~p~Vc3/2~pF2 - 1)"р/2ехр f2& ~ гсЛ erfc (be)	[|Rep| < 1/2].

264
Гл.2. Определенные интегралы
[2.21.1
1С
16.
eh тгж

2Vbc
ехр
Ъ + С
оо
17. [ Г(гж)ГA-
— оо
da; =
оо
18.
19.
= 2тг*ГB<т
^р
^р - 2ix)Wp,iX(b)Wp+1/2jiX(c) dx =
20. f хsh2nxK2ix(b)Wp,iX(c)W-p,iX(c)dx =
е"(ь+с)/2
б РС
= 0
со
21. f
+ с2
[6 > с].
L
[b < с].
[Rep < 1/2].
2.20. ВЫРОЖДЕННЫЕ ГИПЕРГЕОМЕТРИЧЕСКИЕ ФУНКЦИИ
КУММЕРА iFi(a; Ь; ж) И ТРИКОМИ Ф(а, 6; ж)
Вырожденные гипергеометрические функции iFi(a; 6; ж) и Ф(а, 6; ж) связаны с
функциями Уиттекера МР}(Т(х) и WPjCr(x) соотношениями
Ф(а, Ь; ж) = ^b/2eK/V6/2-fl!F-i)/2W.
Для вычисления интегралов, содержащих функции \F\{a\ 6; ж) и Ф(а, 6; ж), следует
перейти к функциям Мр? ^(ж) и WP; «г (ж) и воспользоваться формулами раздела 2.19; см. так-
также формулы раздела 2.22 «Обобщенная гипергеометрическая функция pF9((ap), (^g)j ж)>;>
при р = q = 1.
2.21. ГИПЕРГЕОМЕТРИЧЕСКАЯ ФУНКЦИЯ ГАУССА 2Fi(a, Ь; с; ж)
2.21.1. Интегралы от A(xJFi(a, b; с; ж).
СХЭ
^аГ Г' "' " °' " [0<Rea<Rea, Re6; |argw| <тг].
. \xa^12F1(a, b; с; -wx)dx = шГ Г
J	[ a, 6, с— о;
CO
. ж 2^11«, 6; с; 1 — шх) dx = ш Г\
J	[
3.
а, Ь, с — а, с — b
[О, Re (а + b - с) < Re a < Re а, Re b; |argw| < тг].
с ~ а7 а — b + 1 '

2.21.1]
2.21. Гипергеометрическая функция Гаусса 2Fi(a,b;c; ж)
265
. 1
5.
6.
7.
8.
оо
х жa^a^12Fl (а, а - с+ 1; а - 6 + 1; - ) dx = уаГ\ ~
J	V	х/	[а, 1 — 6 +¦ ск, с — oj
2/
[у > 0; Re(c- о- 6) > -1; 0 < Rea < Rea; 6 ф 1, 2, . . .].
~г{у — х)^~г 2Fi(a, b; с; -шж) а*ж = В (а, ^)уа+^~1 3F2(a, 6, а; с, а + /3; ^шу)
[у, Rea, Re/3 > 0; | arg(l + a;t/)| < тг].
[2/, Rea, Re/3, Re (с - a - b + /3) > 0].
[a = c; Rea, Re/3, Re(a +/3 - a - 6) >0].
a, b; c; -
с, /3, c^a^
_ «
_ a
с, a, /3, с- a - a
c ~ a1 с — a, a + /3
[6 = a + /3; Rea, Re^, Re (c - a - a) > 0].
(с)те
1, а
[a = -тг, n = 0, 1, 2, . . .; /3 = 6-c-7i + l; Rea, Re/3 > 0].
c, a — с + 1, с — a/2 — 6
[a = a-c + l, /3 = c-6; Re 6 < Re с < Re a + 1; Re Bc - 26 ~~ a) > 0].
b; c; 1 - us) dx = i/^^F [ '	' ' ^4 x
— а, с —
a™6 + a; c^a™6 + l5 с™а^6 + а + Д; а;у)
[2/, Rea, Re/3, Re (c - a ~~ b + a) > 0; |arga;| < тг].
11	f CL-lf	NC-1 Tp (	U	Л	Х\ Л
11. ж B/ — ж) 2-ti I fl? о; с; 1	ах = |/
1	V	у)
с+а-1гГ с, а, с-а-6 + а
Г
12.
a, a + 1; 2; ^
[у, Re с, Rea, Re (с - а - b + а) > 0].
	г—х:г	[t/>0; Rea< 1].
13.
, 6; с; -
, 1 - a - /3) x
a, b, c^a^/3 + 1
[у, Re/3 > 0; Re (а +/3 - a), Re (а + /3 - 6) < 1; |argw| < тг].
14. I xa~1(x~yf~12F1(a, b; с; 1 - шх) dx = ш~ауа+C~а~1 х
' '	3F2(a, с — 6, а — а — /3 + 1;а — а + 1, а — 6 + 1; — I +
а, с^б, 6^а + 1
х 3F2 ( 6, с — а, 6 — а — у5 + 1; 6 — а + 1, 6 — а + 1;
а; у

266
Гл. 2. Определенные интегралы
[2.21.1
15.
[у, Re/3 > 0; Re (a + C - a), Re (a + C - b) < 1; |argw| < тг].
a, 6; c; —a; ж) с!ж = za p В (a, p — a) 3F2(a, 6, a; c, a — p + 1; шz) +
c, a — a + p, 6 — a + p, a — pi
?F2(a ^ а + р, 6 ^ а + р, р; с^а + р,
a, 6, с — a + p
p - a + 1; wz)	[Re a, Re (a - a + p), Re F - a + p) > 0;
16.
17.
х Г
2Fi(a, 6; с; -шх) dx =
а + Ъ — с + р; 1™
-ctJc, a^c+p, 6^
г:)^2 '
(a, 6; с; 1 - шх) dx = ш^а
^| < тг].
p, a + 6™ c+ p J
[Re (a + p), Re F + p) > Re с > 0; | argw|, | argz| < тг].
с, a, a — a, fe^a, c^a^fe + a]
а, Ь, с — а, с — Ъ
x 3F2 ( a, p, с ^ a ^ 6 + a; a — a + 1, a — 6 + 1;	— ) + a;
b — a^ c, a —a, a™
—a a—p—a
хГ
(	1 \ _ь аРъ
\ 3F2I а, с—Ъ, а-а + р; а—а + 1, а—6 + 1;	+а; z F x
а, р	J \	a;z/
а — 6, с, а — b, b — а
а, с - 6, р
[Re a, Re (с — а — b + a), Re (а — а + р), Re F — а + р) > 0; | arga;|, | arg2:| < тг].
F2 [ 6, с-а, Ь-а + р; Ь-а + 1, 6-а + 1;
ею
Г ж"™1 (	Ч1	!_а_Гс, а — а + 1, 6 — а + 1, а —
18. 	2Fi(a, 6; с;	-а;ж) dx = ш Г\	'
] х-у	I	а, 6, с - а + 1
о
х 3F2A, а™ а+ 1, 6™ а+ 1; 2 — а, с — а + 1; ~шу) — т?уа~ ctga7T2Fi(a, 6; с; ~
19.
х-у
2Fi(a, 6; с; 1 — а;ж)
[2/, Re a > 0; Re (a - a), Re (a - b) < 1; |arga;| < тг].
2/°
--^-^ctgfa-ajTrrr'
6, с — а
а, с - Ь; а - Ь + 1; —) + тгаГ V
W2/
(Ь - а
х 2Fi 6, с-а; Ь-а + 1;
V
Г	'	'	х
[	а, Ь, с-а, с-Ь	J
х 3F2 [ 1, а, с — а — b + а; а — а + 1, а — 6 + 1;
V
20.
x F3 ( p, a, P, 6,
г/
21. Ja;6-1^-^-"
[t/, Re a, Re (c - a - 6 + a) > 0; Re (a - a), Re (a - 6) < 1; |argw| < тт].
X
[у,
, | arg A - z)\ < тг].
z)^ хA — шх)а c /32Fi(a, 6; с; шх) dx = |/с+/3 X(l + шу)аA — шу) с х
X В (с, /3JFi(a, & + /3; с + /3; о;у)	[у, Rec, Re/3 > 0; | arg(l - шу)\ < тг].
22.
A-zx)
а, Ъ; с; - ) dx =
У

2.21.1]
2.21. Гипергеометрическая функция Гаусса 2Fi(a,b;c; x)
267
1/с+/3 \г\ с, р, с-а-,
A-2/2)"
3F2 [р, р, с-а-Ь + /3; с - а + /3, с- & + /3;
yz
Лп(у, z)
23
[у, Re с, Re^, Re (с - а - b + /3) > 0; |arg(l - yz)\ < ж].
I	Т*	I ^ 	 Ф I	17/ 	 1* 1	о /^i 1/7 h * Z1* * 1 	 — 1 /У 'T*
J	V	2//
c, a, /3, c — a — b
= У
+ ya
24.
25.
-а, с-Ь, а + 0\
С, а + 6 - С, /3, С - а -
а, 6, с™а™& + а +
с- а- 6 + 1, с-а-& + а+ Р) -
c
= 2/
I/
3-^2 \J- a5 i 05 с a o -p о5
)<z<2/; Re a, Re/3, Re(c- a- 6 + a)>0].
(a, 1 — P, с — a — b + a;
с— а + а, с— 6 + а; — )	[0 < у < z; Re с, Re а, Re (с - а - b + а) > 0].
у)
3-ip.T с, а, с- а- 6 + а
Г
с — а + а, с — b + а
х Г
с, с — а — Ъ. в, 1 — а —
с™ а, с™ 6, 1 - a
a, 6; c; 1--) ^ = y^z^^1 x
с, а + 6-с, /3, а
а, 6, а + 6
1 — а, 1 — 6, с — а — 6 + а; с — а — 6 + 1, с^а^
с+а+/з-2гГ с, а + /3-1, с-а-Ь + а + /3-
[0 < z < у; Re с, Re/З > 0].
26.
а, Ь; с; 1	rfa; =
= 1/
-i^-pp
c, a, c — a — 6
с — a + a, с — i
¦a	/	_ _	ш _	_	_y\
[y, Rec, Re a, Re (c — a — b + a) > 0; | argz| < тг].
у
27. [Ж" '(У^^H Х 2Fl ( ь с;1--} d^ = ^7T|/c^1ztt^1ctga7rr|"C' С ~ п ~ Ь] х
}	х - z	\	у J	[с- а, с- b\
L, б^с + 1; а + Ь^с
а,
ой
28.
- ^a + b-l^c-a-b+a-l ctg (а + 6^с^аOГ х
2//	|_с —а + а —1, с —
1, а — с — а + 2, 6 — с — а + 2; 2^а, а + 6^с-
[0 < z < у; Rec, Re a, Re (с- а- 6 + а) > 0].
.	3F2 A, а, с — а — 6 + а;
-а, с — о + ol\
2/

268
Гл. 2. Определенные интегралы
[2.21.2
29
с-а + а, с — 6 + а; — J	[0 < у < 2; Rec, Re а, Re (с - а - 6 + а) > 0].
. ж (у — х) 2Fi(a, 6; с; их (у — ж)) с!ж =
= гуа+/3В(а, /3LF3 fa, 6, а, /3; с, ^—,	; ^^)	[у, Rea, Re/3 > 0].
у	^
I T°L~1(ll — тЛС~а~1A — 1НТ — ?"]
• I tA/	It/	«A/ J	11	W Jb	/С J
30
2F1 а, а + -; с; —	г^
1	2 A — wx — zxJ
= у^1 В (a, e-a)F4Ba, а; с, с; угу, yz)	[у > 0; Rec > Rea > 0;
2.21.2. Интегралы от A(x)e~px±r2Fi(a, 6; с; <р(ж)).
oo
1. ж e 2^1 (a, 6; с; -шж dx = ш Y\	x
J	^	J
x
(	р х ра с
2F2 (а, а — с + 1;	а — а + 1, а — 6 + 1; — 1 Н
V	а; / uja
(	Р\ РЬ"°
(а, а — с + 1;	а — а + 1, а — 6 + 1; — 1 Н	г~
V	а; / ш°
x 2F2
_г|с,Ь-а,а-а| х
6, с — а
с, а — 6, а — b
а, с — b
F, 6 - c + 1; 6 - a + 1, b - a + 1; — )	[Rep, Rea > 0; |argw| < тг].
2.
3.
00
о
оо
,!-»; с; -
1	1; с; ^а;ж) da; = A/^
2	/	у ш
^A-а-Ь)/2, (а-Ь)/2
[Rec, Rep > 0; |argaj| < тг].
[Rec, Rep > 0; |argo;| < тг].
а; рс
[Rec, Rep > 0; |argw| < тг].
, а, а^а, 6 — а, с — а — 6 — а
а, Ъ; с; 1 - шх) dx = ш~а
х 2F2 ( а, с - а - 6 - а; а-а + 1, а-6 + 1; -—) +	Г
V	а;/ а;а [
х 2F2 (а, с-6; а-6 + 1, а-а + 1; --)
а, 6, с — а, с — 6
с, 6 — а, а — а
>, с — а
'ь"а гс, а -6, а-6
а, с — 6
2F2 F, с-а; 6 —а + 1, 6 —а + 1; —— )	[Rep, Rea, Re (с- a- b + а) >0; I argwl <тг].
оо
Г а_х ^р/х f	,	_а \с, а, а — а, о — а\
. \ х е Pl iF\{a, 6; с: —а;ж) rfx = w Г	,	х
J	[ a, b, с- а
х
7.
8.
2Fi(a, 6; с; ^d
а ^ а, 6 ^ а; 1 — а, с ^ а; а;р) + р"Г(^а) 2F2(a, 6; с, а + 1; шр)
[Rep, Re (a- a), Re F - а) > 0; | arg а; | < тг].
р
1 — а — b, а — Ь
^ fe _ fl^
[Rep > 0; |argw| <тг].
6, с — а
1;
2
а, с — 6

2.21.2]
2.21. Гипергеометрическая функция Гаусса 2Fi(a,b;c; x)
269
6,6 — I
- a, b -
a, 6, с — a
6 - а
;
_а Гс, а, а — а, 6 — а
1
' 2' 4u,
a, a — с + 1; a — a + 1, a — 6 + 1, ™; ^:
p Гс, a + 1/2, a - a - 1/2, 6 - a - 1/2]
X 2^3
9.
10
0
. \ x e
J
a, b, c-a- 1/2
3	13	3	, 3 i
2'a+2; 2'°^a+2'a^6+2; ~4
a, 6; J; -
2
a, 6; c: 1 —
[Rep, Re а > 0; |argw| < тг].
[Rep > 0; | argш\ < тг].
2a^2a Гс, 6-a, 2a
Г
I b, c- a
1	p2\ 2p2b~2a Гс, a ^6, 2a ^
a, с — 6; a — 6 + 1, a — a + 1, a — a + -; -r— I H	г—Г	,	I x
2	4cj/	ct;b [ a, c - 6
Х2^з[Ь, с —a;6 —a + 1, 6 —a + 1, 6 —a + -;—)+a;~ar ' ' *'	'
2 4ш/	[	a,6,c^a,c^6
x 2F3 fa, с - a - 6 + a; -,a-a + l, a-6 + 1; —
p _гГс, a+ 1/2, a^a^ 1/2, 6^ a -1/2, с -a- 6 + a + l/2l x
-,
a, 6, с — a, c — b
1# 3
3
3 p2
;
11.
6; с; -
6+-; —
[Rep, Re a, Re (c - a - 6 + a) > 0; |arga;| > тг].
a, b, c- a
2
_ a? c _ a; -
x 2F3 I a, 6; c, a + 1,
-;——
2 4
1
, a-1/2, a-a + 1/2, fe-a
7	^
13 3	1 р2ш
-; -, --a, c-a+-; - —
у	,
12. Ja;e-1(j/-a:)c-1e-f"I>2Fi f
[Rep, Re (a - a), Re F - a) > 0; |argw| < тг].
a, b; с; 1-- dx = ус+а-хГ
X 2-^2@, c--a--6 + a; c— a + a, c--6 + a; —py)	[y, Re c, Re a, Re (c — a — 6 + a)>0].
13.
а, 6; с; 1-^
с — а + а, с~
/	1
х 2^3 (а, с — а — 6 + а; с — а + а, с — 6 + а, -;
2F3 ( a + -, c-a-6 + a+-;
1 3
-,
-a + -, -; ^—^ ]	[2/, Rec, Rea, Re(c™a™6 + a) > 0].
, a, — с — a + 1, b — с — с
^^	/	\	г
14. f xa-1(x-j,)c-1e-f>Fi (a, 6; с; 1--) dx = ^""VГ' °~C"

270
Гл. 2. Определенные интегралы
[2.21.3
а^с^а+1 аг,Гс, 6-а, с-а + а - 1
X
X2F2A —6, a —c + 1; a —I
х 2F2(l^a, 6 — с + 1; 6 — а + 1, 6 ^ с ^ а -
о, с — а
а, с — Ъ
ty)	[у, Rec, Rep > 0].
X
15.
2Fi fa, 6; c; 1 -
V	у
= У
z, а — с ~~ а -
1 - а, аН
F3 a, c-a-6 + a; c-a
2(a-c-a + l) arfc, 6 - tt, 2(c - tt + Q -
x 2F3 [ 1 - 6, a -
3
2; ^-
»2F"
_с_а+1)^ьг[с, а- 6, 2(с^ & + а - 1)
с — Ъ1 а
x 2F3 ( 1 - a, 6- c + 1; 6-a + l, 6-c-a+-,6-c-a + 2; ^ ) -
oo
16. J"
17.
г, а-с-а + 1/2, 6 - с - а + 1/2
1/2 - а, а + b - с - а + 1/2
. .1 . . ¦ I. з. Л/
!' 2' 4
-, c-
A
2Fi ( а, с - а - -; с; 1 - —
1	, ,	1
[t/, Rec, Rep > 0].
[Rec, Rep > 0].
(ж-
о
Г(с)
Рс^а^ь
z)b
Fi a, 6; c;
1
18.
19.
(x + го)а(ж + z)
; pz)	[Rec, Rep > 0; | arg го |, | argz| < тг].
П /	-•	Ж(Ж + W + Z) \	I
— 2-Ti I л, «; 1; у—	w	^т I dx =
[Re p > 0; | arg ги |, | arg z | < тт].
pz
(ж
„ (	1
2F1 I a, c- a - -; c;
\	2
гКтг].
7+*оо
20
^2c+i(y2pz)	[Rec, Rep > 0; |argi
¦ p _ь	/	1\	Г с 1 ь_1
ж ер 2Fi а, 6; с; 1	da; = 2тг«Г f	р Ф(а, а + 6 - с + 1; р)
j_	\	ж/	l^5 c ~ aJ
7^*°°	[Re 6, Re(c^a) > 0; 7 > 1/2].
f •	±!/2 1
2.21.3. Интегралы от Л(а;)<	±1/2 /2Fi(a, b; с; (р(х)).
ycosax J
Обозначение: S = < >.
оо	^ ^
1. j8in^^2F1(a,6;|;-^jda: = ^^^rF)
ча + Ь-2.,-(о + Ь)/2
v/aJ

2.21.3]
2.21. Гипергеометрическая функция Гаусса 2Fi(a,b;c; х)
271
2. ж
[а > 0; Re a, Re b > 1/2; |argw| < тг].
^i(slna\/x\ t-i / i \ i 2а2а^2а _ [6 — а, с, 2а — 2а] Г sin (а — а)тг
1	V 2^а,1);с;-а;жс1ж=	Г	'	К } ; > х
[ cos cry ж J	иа [ о, с—a J [ cos (а — а)тт
1	гт2 \ 2<т2Ь"а:
а, а — с + 1; а — 6 + 1, а — аН—, а — а + 1; — j Н	г— х
2	4а; /	а;6
хГ
а-Ь, с, 2а-2Ь1 f sin (а-Ь)тг
а? с"" "
6, Ь-
1 ,	сг2
-, Ь-а + 1; ¦—
^	4а;
с, а + <5/25 а - а - ё/2, Ъ - а - 8/2
,a + --c + l;a+--a + l, а+--Ь + 1, J+|;
[о- > 0; Re а > -5/2; Re (а - а), Re (а - Ь) < 1/2; | arg ш| < тг].
Г	/	1
3. \ х^ ' cosсг^ж 2^1 [а, 6; —; ™с*
J	\ 2
22~а~
Г(а
00 f •
Г a_iJ Sir
J	1 со{
a, 6; с; —а;ж) dx =
[<j, Re a, Refe > 0; |arga;| < тг].
а" „Гс, a-<5/2, a - a + J/2, 6 - a + <5/2
a, 6, с — a + E/2
f ;
1.
> 0; Rea > -1/2; Re (a - a), Re (b - a) > -<*/2; |argw| < тг].
Г	Г * Г~ 1
5. ж"]	I— > 2Fi(a, 6; с; 1 — а;ж) <ia? =
J [ cos cry ж J
о
Гс, а + 8/2, а- а- 8/2, Ь-а- 8/2, с-а-
а7 b, с - а, с - b
+	+ 1 а+-
-; а+--а
+<5/2
-; ~
оа \ cos (а — а)тг
2ст
hft U, с-6; а-6 + 1; а-а+-,а-
6, с — а | \	2
,	,	1 ,	^т
6, с-а; Ь-а + 1, 6-а + -, 6-а + 1;--—
2	4ш
э Г а-i/	чс-1
. ж (j/ - ж)
J
— 6, с
cos (а— 6)тг j [а, с — b
[а > 0; Re a, Re (с- а- 6 + а) > -E/2; Re (а - a), Re (а - Ь) < 1/2; |argw| < тг].
^- >2^1 ( а, 6; с; 1	) dx =
^.с+а+д/2-iT, Г с. « + ^/2. с - а - 6 + а + с5/2
а + <5/2
-,
ё , 1 d2
[i/, Re с > 0; Re а, Re (с - а - b + а) > -8/2].
ж .
а? о; с; 1	аж =
у/

272
Гл. 2. Определенные интегралы
[2.21.4
_ 8 c+a+5/2-ir[c, а-с-а-6/2 + 1, Ь-с-а-8/2 + 1
= а у
г, i	S
х 2F3 [ а + -, с-а-
1 - а - 6/2, a + b^c^a^S/2 + 1
S 6 . S . 1 a'zy
Ь^ c-a + a+-,c-6 + a + -,J+-;	—
_ 2{j2(a^c^a + l) app-fl, cl f Sm (c - a + a)n
[б, с — aj \ cos (c — a + а)ж
, -	3
- 6, а -
-,
_ 2о.2
2(ь-с-«+1) bpU - Ь, cl f sin (с -
И sin (с — 6 + а)тг 1
cos (с — b + а)тг j
а, с — b\ X cos (с — b
- a, b - с + 1; Ь-а
-,
[у, о-, Re с > 0; Re (с - а + а), Re (с - 6 + а) < 3/2].
2.21.4. Интегралы от A(x)Ju((tx rJFt(a, b; с; ip(x)).
1 (a, 6; с; ™о;ж) <ix =
\с, а + и/2, a - a - i//2, 6 - а - и/2~
ш"^^/^ I	a, 6, i/+ 1, с — a — i//2
a + i//2, a + v/2 - с + 1; i/ + 1, a + i//2 - a + 1, a + v/2 -6 + 1;
I	i	/O
6, с — a, a — a + v/2 + 1
a, a— с + 1; a— 6+ 1, a^a	hi, a-aH	hi; -— 1 +
2	2	4ct?
f	b_	_v	_a+v
a, c — b^ b — a + и/2 + 1J \	2	2
[a, ReBa + i/) > 0; Re (a - a), Re (a - b) < 3/4; |argw| < тг].
2. j x(c-1)/2Jc-1(<T^JF1(a, 6; с; -и) dx = ^	(а+Ь)/2	Г
ш(а+Ь)/2ГL J
[0 < Rec < 2Rea+ 1/2, 2Re6 + 1/2; |argwi < тг].
oo
, f c-a/2-1
(a, Ь] С\ -
4.
i/trt [a, 6J
1 < ReBe^ a) < 2 Re a + 1/2, 2 Re 6 + 1/2; |arga?| < тг].
(с	X
I ft 	• /->• 	(tin1 1 /Ут* —
+ 1
Г (Зс —2а
э. ж1
—2а —3)/4
1-с)/2,а-с/2
5 -; с; -
2
<J
: — a) X
[Re а < Re с < 2 Re a + 2/3; | arg ш \ < ж].
[a > 0; -1 <Rec<2Rea + 2/3; |argw| < тг].

2.21.4]
2.21. Гипергеометрическая функция Гаусса 2Fi(a,b;c; х)
273
"(I)'
(a, Ь; с; -шж) dx =
/2-а
®\v f )V/2-ar[c) a — v/I, a - a + i//2, 6 — a + i//2
a, 6, v + 1, с — a + i//2
х
2
i/ .	v	и	и	аи)
o_a + _)b_a + _;j, + i)__a + i,__a + c;_
[о- > 0; -3/4 < Re a < Re(a + i//2), ReF + i//2); |argw| < тг].
с с -
-; ci ^ь
= А Шк
X
J
, a+ -¦ с; -
2
¦ = 2c<72a"c
2a
2 у"— V 2
i. Z Ju((i^/x JFi(a, b; c; 1 — шж) о?ж =
[Re a < Re с < 4 Re a + 1/2; |arga;| < тг].
5 c^ a^ a -
x 2^3 ( а, с — b; a — 6 + 1, a — a+ — + 1, a — a— — + 1; — -—
W2J6-2",
, c- a; 6-
c, a +
а, с — 6, 6 — a + и/2 +
v
^a+-+, ^«^
? ft — о — jz/2, 6 — en — jj/2j с —
a, 6, с — a, с — 6, i/ + 1
+ -5с-а-6 + а+-; i/ + l, a+ - -a + 1, a+ - -6 + 1; --
[o-, Re Ba + i/), Re(c-a-6 + a + t//2) > 0; Re (a - a), Re (a - b) < 3/4; |argw| < тг].
10.
\
a, b; с; 1- - ) dx =
-(!LY с+а+^/2~1гГ c1a + u/21c-a-b + a + u/2 j
12/ У	|_i/ + l, c-a + a + i//2, c-6 + a + i//2j
tt+2'C^a^'
-; 1/ + 1, c-a + a+
[1/, Rec, Re Ba + i/),
11.
/a\4a
V2"/
a, 6; c; 1	I dx =
2//
«^[c, 6 - a, c- a + a + и/2 - 1
c^a, 6, а™с^а + i//2 + 2
x 2^3 A — 6, a — с + 1; a — 6 + 1, a^c^a	h 2, a^c^aH	•
A	A
;
+ i//2) > 0].

274
Гл. 2. Определенные интегралы
[2.21.5
(!)s
a, с — 6, b — с — a + и/2 + 2
x 2^3 ( 1 — a, 6 — с + 1; 6 — a + 1, 6 — с — a	h 2, b — с — a -\	h 2;
A	A
z, a-c-a- и/2 + 1,6- с- а- и/2 + 1
. - a - i//2, a+6-e-a- i//2 + 1
/ол" c+a+I,/2-ir с7а~с~а
42/ *	U + 1, 1-а
p a2y
;
12.
а. -; с;
' 2' '
[у, сг, Re с > 0; Re (с - а + а), Re (с - b + а) < 7/4].
Г
х 2F3 а, а
2 ' 2
a.-\- v	и — a	cr i ,
-,«	s—+ i. e + —s—+ i; —r-1 +
a*z«+*-2* Г(с + 1)/2, (с + 1)/2-о, (a + i/)/2,a-(a + ^)/2l
a, I/ + 1, (с- а - I/
— с + 1 а + I/	^ а + I/
I/ + 1
а + i/ + с + 1
— a; —
' 2 ' ' ' 2	' '	2	-' 4
[c, Re (a + w) > 0; Re a - 3/2 < 2 Re a < Re с + 2; jargz| < тг].
13.
^J(c-1)/2(^JF1(a, |;c; ^^
¦ + l)/2, (c+l)/2-o
С1Ж — zl	(T	Z	X
Q.
[2Rea-2, -1< Rec<4Rea;
тг].
2.21.5. Интегралы от Л(ж){ Y^a^)\ 2F1(a1 b; с;
1.
0
(a, 6; с; -шж) с?ж = —
/2 - a,
6, с — a
¦ cos I a — a H	1 x
_. Гб — a, c, a + г//2 — a, a — i//2 — 6] _. /
x тгГ|	, ;	'	I2F3 (^a, a-
- cos o-aH	1 ttI
V	2/
hi; a - 6 + 1, a - a - - + 1,
a— 6, c, a— u/2— a, a+ u/2— b
а, с — b
6, 6 -
-
. J
а, 6, с -— а -- I//2
Гс, i/, a - j//2, a - a + i//2, & - a + i//2l
7 L	a, 6, c^o + f/2	J X
2
•	f	V	V	U	О"
x 2-^з I a	, a	c+1: 1 — 1/, a	a + 1, a	o + l: —
1	2	2	2	2	4ш
[a > 0; Re(a - a), Re (a - 6) < 3/4; 2 Re a > |Rei/|; |argw| < тг].
Pi I —, a; —; ^о;ж I dsc =
(а/2)
6-3/2
V^ra;r(a) a"
[а > 0; 1 < Re а < 2; |argw| < тг]

2.21.6]
2.21. Гипергеометрическая функция Гаусса 2Fi(a,b;c; x)
275
оо
О
оо
1, 2с	; с; — шх ) dx =
l, a; |; -w*j dx = ^g
> 0; -3/2 < Rei/ < 1/2; Re Bа - i/) > 3/2; |argw| < тг].
5.
(ELY с+а
\2/
a, b: с: 1	I dx =
У/
с, а + I//2, с — а — o + a + i//
—|— 15 с — л ~\- ct -\- и/2, с — о -j~ ct -
у	и	и	и а у
а + -,с-а-6 + а+-; I/ + 1, с-а + а+-,с-Ь + а+-; ^р
[у, Re с, ReBa + i/), Re (с - а - Ь + а + *//2) > 0].
2.21.6. Интегралы от Л (ж) ^(^(ж)) 2Fi (a, b; с; х(ж)).
J
Г
/2-a,a-v/2-a
Ь, с — а
а, a — с + 1; а — 6 + 1, а-аН	hi, а — а	Ь 1;	1 +
2	2	4ш/
Га - 6, с, а + I//2 - 6, а - I//2 - Ь]
[	Ь	\
+ 2шь
6, Ь-с + 1; Ь-а + 1, Ь-
^ + 1; ^^
2	4а;
(<т/2)" Гс, -I/, a + i//2, а-а-и/2, Ъ-а-и/2Л
«+-/2 [	6	/2	\
(	U	U
x2F3(a+-,a+--c
a,
a ¦
с
—
a —
— a
I//2
+ 1, a
и
+ 2
(<t/2)-%[c, ^, a - «//2, a - a + *//2, 6 - a + i//
a, о, с — CK + i//z
[Re<j > 0; 2 Re a > | Rei/|; | arg а;| < тг].
2.
(a1 b; с; ^шх) dx =
ш{а+ъ)/2
Г(сM1-а-ь,а-ь f -^
оо
. f Z^ f-^ ) 2Fi(a, 6; c; -wx) dx =
j v^;
[Rec, Re<r > 0; |argw| < тг].
Гс, -г/, а - г//2, a - a + i//2, 6 - a + i//2~
a, о, с — a + I//2
™, 6-a + ™; i/ + l, l-a+-,c-a+
Гс, i/, a + i//2, a - a ^ u/2, b^a^
i/	(J Ш
x 2F3 [ a - a - -, b - a - -; 1-й, l-a--,c-a--;
+

276
Гл. 2. Определенные интегралы
[2.21.6
(*/2f
v
2
и	а ш
+1;
4. f xa~1Kt/(ay/xJF1(a, b; с; 1 - шх) dx = ^^ °
[Re a > 0; 2 Re (a- a), 2 Re (b - a) > \Reu\; |argw| < тг].
2a-2a
X
хГ
— а, с, а + г//2 — а, а — W2 — а
6, с — a
2^з (а, с-6; а-
J V
v
1, a - a - - + 1,
2 + '
j a — 6, c, a + i//2 — 6, a — v/2 — bl
~A	,	x
а, с-6
b, с- а; 6-а + 1, 6-а-- + 1, 6 - а + - + 1;
2	2
+
Y ^[c, —i/, a + i//2, a — a — i//2, 6^a^ ^/2, c^a^6 + a + i//2l
—7^-1	.	X
а, Ь, с-а, с-
-,c-a-6 + a+-; I
Гс, i/, а - I//2, а - а
[
+ -
2
U	О"
--6 + 1; —
^6 + a^ и/2
а7 Ь, с- а, с- Ъ
z	z	z	4
[Recr > 0; 2 Re a, 2 Re (с - а - b + а) > | Rei/|; |arga;| < тг].
1/
5. f x^iy - x)c-1Kv(<tVx~JF1 (a, b; с; 1 - -) dx = 2»-1а-"ус+а-'//2-1
J	V	У)
хГ
с, и. а —и/2. с— a— b + a— v/2
c-a+a-i//2, c-b+a-i//2
	; 1- i/, с- а+ а	,
2'	'	2'
2'
с, -I/,
[у, Re с > 0; 2 Re а, 2 Re (с - а - 6 + а) > |Rei/|].
6.
а, 6; с; 1- -
У
- а, с, с-
6, с^а
l - 6, а - с + 1; а-Ь + 1, а-с-а+^ + 2, а-с-а-^ + 2; ^-
-65 с, с-
а, с — о
X
2
x 2F3 ( 1 - a, 6 - c + 1; 6-a + l, 6-c-a+- + 2, fe-c-a--+2; ^^¦
1	2	2	4
1 - a + i//2, a + &-c-a + i//2 + 1
ol — —, с — п — b + о, — — 5 I — v, с — fl + o; — —, с — b + ск — — 5
^^1 ь, c+Q^/2-infc, — *Л а — с — a — i//2 + 1, 6 — с — а — и/2 + 1
- а - и /2, а + 6-с-а- i//2 + 1

2.21.9]
2.21. Гипергеометрическая функция Гаусса 2Fi(a, 6; с; x)
277
х 2F3
[а, 6; с; --
V	.	U О"
--, с - 6 + а + -; ——
[Re с, Re«x > 0].
с-(а+Ь+1)/2
2(c+i
fc-g-c+
2	|_	2	'	2
[|/, Re с > 0; Re (a - b - c), Re (b - a - c) > -1; |argz| < Зтт/2].
2.21.7. Интегралы от Л(ж)К(<тжJ^1(а, b; с; (f(x)).
1	1	y2\	тг Г а, 1/2-a
a,	a; -; 1 — -^ <ix = —Г .
' 2 '2'	ж2/	2у [l/2 + a, 1-a
[у > 0; 0 < Re a < 1/2].
2.
3.
К(-
a,—; с;
2
^ с;
4с
dx =
1 2' 2'
> у > 0; Re с > 0].
2.
X 2Fi (i i; c + 1; /(a2 + ш - <r2a;?/2) )	[t/, Rec>0; | arg A - шУ2)\ < тг].
\Z I	/
2.21.8. Интегралы, содержащие функции Уиттекера и 2Fi(a, b; с; шх).
— ) 2Fi(a, b; с; —а;ж) с!ж =
Л5 ft "у" С zlO	J
' = 2a - a - 26 + 1, 2^ = a - 2a; Re cr, Rec, Re (a - a), Re (a + 6 - 2a) > 0; |arga;| < тг].
a, b; c; 1
у
(о+ь-1)/2
, (а - 6 ^ с + 1)/2 - р, (Ь - а - с + 1)/2 -
[j/, Re О 0; Re (с + 2р) < 1 - | Re (а - Ь)|; |arg<j| < Зтг/2].
2.21.9. Интегралы, содержащие произведения двух функций
2Fi(a, b; с; (р(х)).
. f 2Fi A - а, 1 - Ь; 2 - с; - ) 2Fi (а, Ь; с; -
J V	у) \	у
3.
4
(c — lJ/{[t/?(a) — ф(Ь)] sin атг sin Ъж + [t/>(c — a) — ^(c — b)] sin (с — а)ж sin (с — &)тг}
F — a) sin стг sin (c — a — Ь)ж
[с ф 1; а ф b; \Re(c - a - b)\ < 1].
[c = 1; a^ 6; 0 < Re(a + 6) < 2].
-[(B, a) - CB, 1 ~~ a)}	[c = 1, 6 = a; 0 < Rea < 1].
2тг
f	(
. 2Fi (l-a,
— a, 2 — b: 3 — c; — 1 2F1 f a, 6; c; — 1 dx =
2//	V	У/

278
Гл. 2. Определенные интегралы
[2.21.9
а(с — 1)(е — 2) sin (с — а)ж sin (с — 6)тг
F — 1)(с — а — 1) sin еж sin (с — а — 6)тг
5. хс (у-—х)а с 2F1 I а, 6; с; — I dx =
J	L V	У/1
о
7Г2/"
(а —6) sin (с —а —6)тг [а? ^? е —а, с —
с, с
X
-ф(с-Ь)]	[а ф b;
1].
6.
7,
7Г|/
2а
sin (с — 2а)тг [а^ с ~~ а]
оо
Г с^г п ( и	\ и1 f ' и' '
. х 2-^i(a? о; с; —ах) 2^i\Q> 5 о ; с ; —б
• = а; |Re(c- 2а)| < 1].
^а а^сГ\с, с,а + а-с,а + Ь'-с,а+Ь-с,Ь + Ь'-
Ш	'	а5 Ъ,а\ b'.a + a1 + b + h' ^2c
х iF\ (а + а —с, а + 6 ™ с; а + а +6 + 6 — 2с; 1
[Re с, Re(a + a' -с), Re (а + 6; - с), Re {а1 + 6 - с), Re (b + bf - с) > 0; | argo-|, | argw| < тг].
со
8. JoT
о
(а, Ь; с; -
(а, Ъ; с;
2, с
X
X 2FiBa- 1, 26- 1; 2с- 1; -д
а I а, 6, с - 1/2
[Re а, Re b > 1/2; |arg<x|, |arga;| < тг].
9. хс~г(у — х)с ml 2F1 (а, 6; с; — а;жJ^1(а, 6; с;; а;(у — ж)) rfa: =
а, 6, (а + Ь)/2, (а + 6 + 1)/2; ш2у2
а + 6,
10.
11. жс 1(у ~~ х)
[6^ ™а; 2/, Re с, Rec; > 0; | arg A - шу)\, \arg(l+ шу)\ < тг].
1/2, а, -а; ш2у2
[6 = —а, у, Re с, Re с' > 0; | arg(l — шу)\, | arg A + шу)\ < тг].
i (а, 6; с; стжJ^?1(с + с# — а, с + с# — 6; с;; а;(у — х)) dx =
= Ус+С'^ В (с, с;)A - шуJа~с~с' 2Fi(o, 6; с + с'; (а + а; - <та;)у)
[у, Re с, Rec; > 0; | arg A - <ry)\, |arg(l- шу)\ < тг].
12. xa~1(y-x)c~12Fi [a,b] с; 1- -) 2^1 (а', 6;; с'; 1 - иж) Же =
о
= У
, с;, с'-а'-Ь', а, с- а- 6 + а]	/ а;, 6;, а, с- а- 6+ а; шу
^ с —а , с —о J	\с—а+а, с—6 + а, а + о —с+1
a^i ^\ с, с, а!+ Ъ' - с, с - а'- У + а, с + с'- а - а'- 6 - 6' + а]
[	6+6+ +	66+ J
(с — а , с ^6, с ^а ^6 +а, с + с^а^а — 6 — 6 +а; ajf/
\с —а —6 +1,с + с — а — а —о +а,с + с —а —6 — 6 + а/
[у, Re с, Re а, Re (с- а- 6 +а), Re (с' ™ а' ™ 6' + а), Re(c + с' - а - а' - 6 - 6; + а) > 0;
|arg(l -wy)| < тг]
13
. f ха(х - а)с~г(ш - ж)с/т12^1 fa, 6; с; 1 - -) 2Fi fa', б'; с; 1 --) dx =
J	V	(Т /	\	и) /
= В(с, c/)(w-a)c+c^1Ha;B2Fi fc, D; c + c;; 1- -) [0<ст<ш; Rec, Rec'>0].

2.21.10]
2.21. Гипергеометрическая функция Гаусса 2Fi(a,b;c;x)
279
а -
а' -
b
+
b
+
b
+
b
+
a
0
0
0
f bf
— с -
a' -
a
-c
a -
- с
- с
f
- с
+
- с
-c +
a' -
^c
a' -
1
- с
+
- с
с
а
а
а
а
-Ь + а +
+ Ь' -с'
а
а — с'
а
Ь + а — b
-Ъ'
а
b
с — ft
с — а
с + с — а
b
c + b'
b
b
b
b
b
t
a
a
t
a
i
ft
/
a
ft
i
a
t
ft
a
a
t
ft
b'
c—a
c—a'
b'
b'
b'
b'
b'
b'
b'
b
A
a
a
с + с'—
с- b + a' +
+ b'-c'
-a'-b'
a' + b'
b-b'
A
b-b'
b + a — с
о -\- ft — с
В
— ft
— a
a +b' -
b-c
t
— с — с
— с
a +bf -
r
— с — с
В
a +b' -
— с — с
— с
— с
С
а + а'
а + а
с + с — а'
с — b + а'
с + Ь'
о + с — а
С
с- Ь+
+ с — а'
с + Ь'
с
а
с
с
b
b
D
с
+ с — а
с ~~ а+
-b + bf
fc'-6'
— a + ft'
- bf + с
D
-b' + c
b + a'
b + a'
14.
- wx)~a' 2F!(a, b; c; ujxJF1 (a\ b ~ c; c;
V
dx =
V	1- wx
= B(c, c)yc+c'~12F1(a + a, b; c + c; wy)	[y, Rec, Re с > 0; | arg A - шу)\ < тг].
2.21.10. Интегралы по параметрам, содержащие 2^1@, &; с; ж).
s + d
2F1(a, s; с; -х) ds = 0
7 —ioo
7+ioo
2. [ r\b^S}2F1(a1 s; c; ^x)ds = 27Tix^bFl C' п ~
[7, Red > 0; 0 < Rea < Rec; |argx| < тг].
7+ioo
7+	^
3.	Г \ S 2Fi(a, s; c; -x)ds =
J [s + d\
j — ioo
7+ioo
4.	[ r\b +
a, 1-6, c-bj
[7 < 1; 0 < 7 < Re6 < Rea < Rec; \mgx\ < тг].
0	[7, Red > 0; 0 < Rea < Rec; |ащж| < тг].
ft, S] с + S] —x) ds = 0
[Rea > 0; 7 > - Re b; Re (c ~~ a ~~ h) > 1; | arg (x + 1)| < тг].
5.
c+ s, 1 - s
7 — too
7+ioo
с, 1 — d, a
[Rea, Re (a - d) > 0; - Re b < 7 < Re d < 1; | arg (x + 1)| < тг].
. I zsTBc - 1 + s)r(-sJFiBc - 1 + s, -s; с; -ж) ds =
7го°	z2I/2"c	[l-2Rec < 7 < 0; |arg(» + l)| < тг].
7+гоо
7.

280	Гл.2. Определенные интегралы	[2.22.1
[, i -|
tt' Fi(a, 6, bf; с; го, г)	[^Rea, ^Rebf < 7 < О].
[
8. [ (z)\	f
J	L	с +
Га 6'1
= 2ттгГ а', F2(a, 6, b'; с, с;; го, z)	[-Re a, -Re 6' < 7 < 0].
7	/	/	L C J
. [ (^z)sr\a' + S"b' + S^SJF1(a,b; c + s; w)ds =
J	L	c + s	J
\ ' h'~\
= 2ттгГ ' F3(a, a\ b, b'; c; w, z)	[- Rea', - Re6; < 7 < 0].
L	J
7+ioo
9
7+ioo
10. Г (-2)'r|a + e^b+fe8> el2Fi(a + e, 6+s; c;
7 —*oo
= 2ттгГ Г*', \F4(a, b; с, с; w, z)	[-Rea, -Re6 < 7 < 0].
L c J
11. \ x sh27TxF(a + *ж)Г(а — ix)K2iX(b) 2F\{a + ix, a — ix; c; —z)dx =
[6 > 0; Rec > 2Rea > 0; |arg^| < тг].
12. [ (c - 1 + ix)V (\ - ix) Г ( 2c - I + гж ) /c-i+«(a)^c-i+«D x
о	-,	\	/ ,\c-l/2
x 2Fi ( 2c - I + to, I - to; c; ^zj <te = 2с^1/2^Г(с) Г^\	Kc_1/2(w)
\w = Ja2 + b2 + 2a6(l + 2z); | arg (z + 1)| < тг .
CO	L	J
f	SlnBn + 1OT3?	.	ч
-	F^—^=7^	r2Fi(a, 6; с + ж; z) x
J 81птгжГ(с +ж)Г(й — ж)
+ rf — a — 1, с-\- d — b — 1) d — x; z) dx =	^
jx
X 2Fi (a, 6; c + d^ 1; 4z(z - 1))	[Re (c + d) > 1; |z| < 1].
2.22. ОБОБЩЕННАЯ ГИПЕРГЕОМЕТР1ЧЕСКАЯ ФУНКЦИЯ
pFq((ap); (bq); x) Ш ГИПЕРГЕОМЕТРИЧЕСКИЕ ФУНКЦИИ ДВУХ
ПЕРЕМЕННЫХ
(см. также 2.23^24 и 2.19-21)
2.22.1. Интегралы общего вида.
Обозначения:
к, I, га, п, р, q = 0, 1, 2, ...; А;, I/O; тп^п + 1; р^^ + 1; г = 1/к
р	q	т	п	[к, I — взаимно простые],
EY^ , , q — p + 1	v-^	T^ j , ^^^, + 1
% " 2^6i + ^—^	'	P = Z^c^ Ъ^" + 	2
i=i	i=i	i=i	i=i
[aj, bj, Cj, dj — комплексные параметры, a.j, Cj 7^ 0, —1, —2, . . .],
(p = q-p-r(n-m+ 1) + 1, g = 2^1[A - l)(m - n + 1) + A - fc)(p - q + 1)],
cr, a; — комплексные переменные.
1°. Re (a - Cj - rai) < 0	[j = 1, 2, . . . , те; i = 1, 2, . . . , p];
2°. (ra- n^ l)Re(a - ra^-) - Rep > ^3/2	[i = 1, 2, ..., p];
3°. (p- q - l)Re(a - с,-) -rRe/x> ^3r/2	[j = 1, 2, ..., p];
4°. |y?| + 2Re[(g ^p+ l)(n - m + l)a + r(n - m + l)(/x - 1) + (q - p + l)(p - 1)] > 0;

2.22.1]	2.22. Гипергеометрические функции: обобщенная и двух переменных	281
5°. \<р\ - 2Re[(q - р + 1)(п - т + 1)а + г(п - т + 1)(/х - 1) + (д - р + 1)(р - 1)] > 0;
6°. Если A; = ra — га + 1, / = </ — р+1, то | arg A — zo<x™ а; )| < тг, где
q-p+1 m-n-1 _
кп — га + 1у
причем при Re [/х + р + (тг — га + 1)ск] < 1 допускается значение aq
7°. Re(a + ci) > 0	[j = 1, 2, . . . , m];
8°. Re (a - raj) < 0	[j = 1, 2, ..., p];
9°. Re [(p - g - 1) - r/x] > -3r/2;
10°. Re [(n - ra + l)a - p] > -3/2.
11°. Выполняется одно из следующих трех условий:
Ас > 0 или Ас = 0, As / 0, Re (a + /х) < 3/2 или Ас = As = 0, Re (a + /х) < 1/2,
¦ + |<71 cos (argcr),
где Ас = (д - р +
жа 1mFn((cm); (dn); -о-ж) pF9((ap);
q-p + 1
x G
<k + lm, kp+l
q^p+l
/k\ ^x —
(bq), (dn)
1,1 — a), A(A;, 1 — (aP)), A(/, (rfn) — «)
Д(Л, 0), Д(/, (cm) - a), A(k, 1 - F,))
0].
если выполняется любая из следующих четырех групп условий:
1)	тр /0; га = тг или п + 1; р = q или д + 1; | arg ст| < (га — тг + 1)тт/2;
|arga;| < (р - д + 1)тг/2; Re a > 0; 1°;
2)	771 > 0; га = тг или п + 1; р = д^1 или д; | arg <г\ < (ттг — тг + 1)тт/2;
|arg
)тг/2; Re а > 0; 1°, 3°;
|g| (рд )/
3)	га = п — 1 или п; р > 0; р = q или д + 1; | arg <т\ = (гм — п + 1)тг/2;
| arg ш| < (р-д + 1)тг/2; Re а > 0; 1°, 2°;
4)	га = п — 1 или тг; р = д — 1 или д; | arg <j\ = (га — п + 1)тг/2;
| arg
2.
1)тг/2; Re а > 0; 1°-3°, 5°, 6°
[ случаи m = п = 0 или р = q = 0 см. в 2.22.1.3].
); (dn); -.тх) PF,((op); F,); -uxl/k) dx =
	 /q \g-i д »р+а(п —т —1) —1 ар \"<?/? \"''«,
— \ /	/ \ /
|_ \^р/ ? V^m
АA, -а), А(к, 0), А(А;, 1 - (bq)), А(/, 1 - а - (dn))
если выполняется любая из следующих четырех групп условий:
1)	тр /0; т = п или га + 1; р = q или д + 1; | arg а\ < (га — га + 1)тг/2;
|arga;| < (р - 9 + 1)тг/2; 7°, 8°;
2)	тга = га или га + 1; р = </ — 1 или д; | arg сг| < (т — п + 1)тг/2;
|arg
3) 771 = тг — 1 или тг; р = д или д + 1; | arg <т| = (га — тг + 1)тт/2;
|argo;| <
)тг/2; 7°, 8°, 10°;

282
Гл. 2. Определенные интегралы
[2.22.2
4) т = п — 1 или п; р = q — 1 или g; | arg сг| = (га — п + 1)тг/2;
|argo;| = (p-qr +1)тг/2; 7°~10°
[случаи 77г = п = 0 или р = q = О см. в 2.22.1.4].
3.
[ap)] (bq); ^
(bq
A(Z, 1-a),
г, 1-(Ь,))
если выполняется любая из следующих пяти групп условий:
1)	q — р — г + 1 > 0; Re a, Re а > 0; arg ш — любой;
2)	р = q или q + 1; Re а, Recr > 0; | argw| < (p — q + 1)тг/2;
3)	А; = 1; I = q — р-\-1\ р < q — 1; Re а, Recr > 0; | argo;| < 2тг; 6° при m = п = 0 и 11°;
4)	А; = 1; I = г = 2; р = q - 1; Re а, Recr > 0; 0 < | argш| < 2тг; 6° при m = n = 0 и 11°;
5)	к = I = г = 1; р = q; Re а, Recr > 0; тг/2 < |argw| < Зтг/2; 6° при т = п = 0 и 11°.
4.
=
L К).
, (ар))
, -a), A(fe, 0),
¦ - • - I --г	I
кр, fcg + fe + l I	i|
р = q или д + 1; Re <т > 0; | argw| < (р — д + 1)тг/2; 0 < Re а < г min Re «j I.
2.22.2. Интегралы от А(х) pFq((ap); (bq); <р(х)) (см. также 2.23.1).
ip), a;
[a, Re а,
0; р
1].
2.
—n,
dx =
'— п, а, (ap_i); ш
Р, Fд)
[Re р > Re а > 0; | argz| < тг при р ^ д + 1; | arg z|, | arg (I — ш)\ < тг при р = q + 1].
iF2
1
; о, с;
dx =
C
[Reb,Rec>0].
2.22.3. Интегралы от ef{x)pFq((ap); (bq); ex) (см. также 2.23.2).
со	I
1- fx0"^"^' PFg((ap); Fg); -шж) с!ж = 1^т^1аГAа) l+pFg f(op), A(/, la); (bq); -^),
если выполняется любая из следующих пяти групп условий:
1)	I < q — р + 1; Re a, Re <т > 0; arg о; — любой;
2)	р = q или q + 1; Re a, Recr > 0; | argo;| < (p — q + 1)тг/2;
3)/ = qf — p + 1, p<qf — 1; Re а, Recr > 0; | argo;| < 2тг и 6° (при т = п = 0),
11° с заменой а на 1а;
4) I = 2; р = д + 1; Rea, Recr > 0; 0 < | arg о; | < 2тг и 6° (при m = п = 0),

2.22.3]	2.22. Гипергеометрические функции: обобщенная и двух переменных	283
11° с заменой а на 1а;
5) I = 1; р = q; Re a, Re a > 0; тг/2 < | arguj\ < Зтг/2 и 6° (при т = п = 0),
11° с заменой а на 1а
[ условия 6° и 11° см. в 2.22.1].
Г с^!
. ж
J
1? tt? ^5 ^^
с, с+1/2
йж = 21 {2с)о-	ш
_(а+Ь)/2
3.
4. I ж~ ^е
о
a + 6, с, с + 1/2
а+Ь — 2с — 1 A —а —Ь)/2тхт-
T	W1	Н/Aь)/2
a, 6, тг — a, n — b; -wi
n-1/2, с, с+ 1/2
тгГBс)
[Re с, Re<j > 0; |arga?| < тг].
[Rec, Recr > 0; |argw| < тг].
(n/2-bOrirr(l)
/ ^n (b-n/2Ort rr(i)
Л1
. [ ж^
J
c, d
[п = 1 или 2; Re с. Re <т > 0; | arg ш \ < тг].
dx = ^^-2Fi fa, b; d; —)	[Rec > 0; Re«r > Rew, 0].
6.
7.
8.
9.
r-cnd-l/2l1_2uA
l±l/2, с
—га, тг + 1; а;ж
1, с
d J
[Rec, Recr > 0].
[Rec > 0; Re «r > Rew, 0].
}
-p = arcsin у/ш/а ; Rec, Re a > 0].
dx = (J~cT{c)Pn ( 1 - — J	[Rec, Re<r > 0].
/d-3/2
dx =
_ Г(с) Г [sin Bn
oo
10. \xc~1t
с, с+1/2
[Rec, Rea, > 0].
CO
11. [ xc~1e~ax0F2(c, d; -wx) dx = F{c)F{d)a
о
. J ж е o^
12
13.
2, -, —j
2, 2c- 1; -u
(Jc I	cos{2y/a/u))
2ш3^\
[Rec, Recr > 0].
[Rec,
Г(с)ГBс -
[Rec > 1/2; Re a > 0].

284	Гл.2. Определенные интегралы	[2.22.4
14. Ixc-Ie-"^OF3 Uc+\, d; -wx} dx = 22
/П	\	[Rec, Re<r>0].
15. \1lj
= 2"-1Г(с)Г (±±±) Л^'-^-^е"'»"»/,.,/, ( —)	[Rec, Recr> 0].
OO	V	/
16.	f xc~1e~ax1F2(l\ c, d; шж) dx = (d - l)F(c)(id~c~1uj1~deaj/aj (d - 1, -)
?	[Rec, Retr > 0; Re d > 1].
17.	\xc~1e~<rx1F2(-n\ c, d; о;ж) dx = П;Г(С) L^-i /w\	jRec? Re(J>0]i
J	(tt)nCTc	Vcr/
о
oo
18.	\ хс^е^ал/Ш iF2(a; с, с + 1/2; ^о;ж) с!ж = 2ГBс)(т2а^2с(а2 + 4ш)"а
^	[Rec, Re(a±2y^) > 0].
19.	J *-e- " ,F, (с; с +а; А7+ 2/3) ^ = ЗГ(Зс)а,-«(.- + 27а,)-
^	[Rec, Re ha - 3w1/3l > 0].
20. JzV^fJ ,	;
J	\3/2, c, c + 1/2,
о
[Re^ Rea >
2.22.4. Интегралы, содержащие функции Бесселя и pFg((ap); (&g); еж)
(см. также 2.23.3).
/ + 1, (bq) + V/2- a,
, Т a-i , /
\p = q + 1; o-, Re Ba + i/) > 0, Rea < 3/4+ min Rea^; | argw| < тг, или [р = g; Rew > 0],
I + «//2 - а, ^ + 1, F,) + у 12 -а
2\ Г V/2a I
/ L + /2 1JP *
2\2а
p	g
или \p = q - 1; Re a < 3/4 + min Re ay ш > 0; Re ( 2a + ^ aj - ^ bk ] < 11 .
j=i	k=t
CO
2.
о
l
. \ xc^1//2^1Jl/((jy^JF2(aJ b; c, d] -шх) dx = Г^ °Г^Г^ [А(а, b) + A(b, a)],
oo
3.
о
A(a1b) = F\	b^a	.J2F2.
La^a,o,a^c + i/ + lJ \a — 0 + 1; a^c + i/ + l
[a, Rec, Rew > 0; Re Bc - 2a - u), Re Bc - 26 - 1/) < 3/2].

2.22.5]	2.22. Гипергеометрические функции: обобщенная и двух переменных	285
X W(a+b+3)/2^c,(a^b)/2 ( -;— I	к, Нес, Неш > 0; Re(e^2a), Re (с - 26) < 1/2].
\4а;у
t	{c+d)/2 — 1 т / /—\ rp l l.	j.	\ j 	 \^ / /	Г '
J	тгсхд	'/	[a,
° Г	/<T2\
x < Г(а)ГF — a) sin (c — a)?rM(a+5^i)/2 (a-6)/2 ( — I +ГF)Г(а^6) sin (c —6) x
/cj2\1
X тгМ(а+5^1)/2 F-a)/2 	 If	[Re c, a, Re a; > 0; Re(c+d-2a), Re (c + d - 26) <3/2].
CO
6.	f a;(c)/2Kc-i(fJv^)oF2(l, с; а;ж) с!ж = —^Y^e4w/cr2	[Rec, Reo-> 0].
о
СХЭ
7.	f жКо((туж)о^B, 2; а;ж) dx = ^^ El f -^ J - In -^ - С	[Rec>0].
о
oo	o	, _ ,
xc Jc-i(ay/x)Kc-i(ry/x)oF2(c, 2c — 1] —wx) dx =
J
[Rec > 1/2; Rer :
(ст2 + -
0
9. ]X^IA^)K4r^hF2 (?; c, d; -a,x
c + 1	4a2r2
4 '	2 '	' 2 ' (cj2 + r2 + 2a;J ' (ст2+т2 + 2ш
[Red, Re(d + i/) > 0; Rer > | Re<j| + | Im л/ш |].
10. [ ж"^^)^^^)!^ (-; с, d; -шх\ dx = 22dr(d)[AI/ + A-u],
4(j2r2
4 '	2 ' r ' 2 ' (cr2 + r2 + 2a;J ' (cr2 + r2 + 2a;J
[Re d > | Re i/|; Re (r + <r) > | Im
2.22.5. Интегралы, содержащие различные специальные функции
и p^q((ap)i (^9)? сж) (см- также 2.23.4-6).
. Ix^ia^xfpi7'^ A-—) PFq((ap); (bq); шх) dx =
J	\ a J
), a, a-j;
n\	\(o9), a+ p + n + 1, a — 7 — n
[a, Rea > 0; Re/3 > -1].
f 1/4	/ /^\	/7933	\	8^2 a5/4
j	^ j	( , ; , ;
a
3. Lbl+b2^"^1(a^a;)a+ai^bl^622Fi fa-6i, a - 62; a + «i - 61 - b2; 1 - -) x
nit	\ /L \	\ J	O1 -In Г ^1? ^2, CK + «1 — 6l — 62] ,-, /
x з^2((аз); (ог); wa; аж = a I	2^1@2, «3; a;
L	a ai	J
a,
[Re 61, Re 62, Re (a + ai - 61 - 62) > 0; |arg(l - aw)| < тг].
4.
о
^a-a;H^1-61-62-^^ (a-fti, a - 62; a + a2 - 61 - b2; 1 - |) x

286	Гл.2. Определенные интегралы	[2.22.6
[г 1	, 	г 	i и
iFi(a2; а; аи)
а, а\	\
[Re6i, Re62, Re (a + a2 - 6i - 62) > 0].
}	( 2x\	/	3	\
5. x n(a — xy Pn \ 1	1 iF2 I /3 — a + 1: n + /3 — a + 1, n + /3 H—; — a; ж 1 dж =
J	\ a) \	2	)
(/3 - a + 1)ПГ (	§)
[a > 0; Re^ > -1].
6. ^xb/^1e^ax/2W1+b/2^a,{1^b)/2((ixIF2(a; 1, b; шх) dx = г\Ь}а^Ь/2еш/а [a;, Re<r>0].
- 1 26-2 „i, , ,	ч , 22с-4Ьо/-2Ь Г26-1, с, с, 1/2-26 + с]
7- Г ^2(C-b;fe,C;-^)^= ^ г| с_26 + 1;2с_2Ь J
[Re 6 > 1/2; Re(c^26) > -1/2].
8. жь+6 ~2 iF2(a; 6,2a; —а;жI^2(а;; б', 2a;; — шх) dx = 0
о
[Re F + 6;) > 1; b-bf = ±1, ±3, ±5, . . . ; a; > 0].
_ w1^6^ Г6, 26 - 1, a + a; - 26 + 1, a + 1/2, a + 1/2]
~ л ч ""	a-6 + 1, a'-6 + 1, a + a'-6 + 1/2 J
[6; = 6; ш > 0; Re (a + a1 - 26) > -1; Re 6 > 1/2].
2.22.6. Интегралы по параметрам, содержащие pF9((ap); (°д); х)-
oo
— OO
a + ж, a — ж]	\(a + x)/2, (a + ж + l)/2y \(a — x)/2, (a — ж
a/2 + 3/4;
ГBа-1) \a/2-l/4, a + 1/2
I	1	F / a- I/2, a; ^ \
Г[а + ж, a - ж, 6 + ж, 6- ж] 2 \(а + ж)/2, (а + ж + l)/2y X
' 2a + 26 - 3 2a + 26 - 1 2a + 26 + 1 2a + 26 - 3 2a + 26 - 1 27ш2
6 '	6 '	6 '	4 '	4 ' T~
[Re (a+ 6) > 3/2].
_
J Г [a + x, 6 — ж, с + ж, d — x] X собжтг
(smxn\FJ(a + b)/2,a';u;\
X собжтг J \ а + ж, 6^ ж J
. ^ + d)/2,c; ш\ = 	1
X2 2| c + x, d-x ) X^ 2Г[(а + 6)/2, (c + d)/2, a + d - 1}
(sm[{b-a)n/2}\ (a' + c';w
rf = fc ^ ft c >

2.22.7]	2.22. Гипергеометрические функции: обобщенная и двух переменных	287
2.22.7. Гипергеометрические функции двух переменных.
оо
1.	ха~ е~рхФ\(а1 Ь; с; ш, zx) dx = Г(а)р~аF\ I a, b, а; с; ш, — 1
J	V	pJ
[Rep, Re(p- z), Re a > 0].
2.	f ^"^""^(б, 6'; с; шх, z) dx = r(a)p^"Si (b, 6;, a; c; -, zJ
[Re a, Rep, Re (p - w) > 0].
oo
3.	f жае^ржФ2F, Ь'; с; с^ж, *ж) с!ж = r(a)p~aFi [a, 6, &;; c; -, - )
J	\	p pJ
^	[Re a, Rep, Re(p^w), Re (p - z) > 0].
4.	f ж^^'^Фг^, 6;; с; шх, zx) dx = Г(с)рь+6^с(р - шуь(р - z)^
о
[Re с, Rep, Re (p - ш), Re (p - z) > 0].
5.	f ха~1е~рхФ3(Ь; с; w, ^ж) dx = Г(а)р~аФ2 (b, а; с; ш, - ] [Rea, Rep, Re(p-«)>0].
J	V	V)
oo
6.	f ха~ге~рхФз(Ь; с; шх, z) dx = F(a)p~aE2 (a, b; c; —, z) [Rea, Rep, Re(p-w)>0].
о
oo
7.	f жае"ря?Ф3F; с; шх, zx) dx = Г(а)р^аФ1 (a, b; c; —, - ) [Rea, Rep, Re(p-w)>0].
J	V	p p/
oo
8.	f хс^1е^рхФз(Ь; с; шх, zx) dx = Г(с)рЬ^с(р - ш)~ье*/р	[Re с, Rep, Re (p - ш) > О].
о
oo
9.	[ ха~1е~р^Ф3(Ь; с; ш, zx) dx = 2FBa)p~2a5i (а, Ъ,а+-; с; Щ,
о
^	[Re a > 3/4; Rep >
10.	[ жа^1е^ржФ1(а, 6; с, с; ш, zx) dx = F(a)p^aF2 (a, 6, а; с, с'; ш, - J
[Re а, Rep, Re (p - z) > 0].
oo	.	.
11.	ха^1е^рх^2(щ с, с: шх, z) dx = F(a)p^a4fi I а, а; с, с'; ^, z 1
[Re а, Rep, Re (p - ш) > 0].
7 а-1 -рхт /	/	ч ,	„,,-„„(	, Ш Z\
J	\	р pJ
[Re а, Rep, Re(p-w), Re (p - z) > 0].
7 а-l	(	I	Л
13.	ж e 2i(a, a , 6; с; а;, 2:ж) dsc = Г(а)р F3 a, a , 6, а; с: ш, — ]
J	V	pJ
[Re a, Rep, Re (p - z) > 0].
00	.	.
14.	жае^рж!Н2(а, b; с; ш, zx) dx = T(a)p~aE,i ( a, a, 6; с; ш, — )
[Re a, Rep, Re (p - 2) > 0].
12
15. жа e Py^x S2(a, 6; с; а;, ^ж) с!ж = 2ГBа)р aF% I a, a, 6, a -\—; с; ш, — I
J	V	2	p у
[Rea > 3/4; Rep > 2|Re-/?|].

288	Гл.2. Определенные интегралы	[2.23.1
2.23. Я-ФУНКЦИЯ МАК^РОБЕРТА Е(р; ar : q; bs : ж)
Соотношение
Е(р; ar:q; bs : ex) =
дает возможность получать интегралы, содержащие ^-функцию, также из формул раздела
2.22. При этом условие q ^ р — 1 для обобщенной гипергеометрической функции заменяется
условиями q ^ р + 1, | arg с| ^ (р^д + 1)тг/2 для iiJ-функции. Интегралы, содержащие Е-
функцию, можно также получать из раздела 2.24, поскольку она является частным случаем
(^-функции Мейера. Для J^-функции используются следующие обозначения:
E(p; ar : q; bs : x) = E((ap); (bq); x) = ^l v Ph X ~ ^' l p) ^
1. I xa-LE((av): (ba): ex) dx = Г I a + (%),\ "Ic^
2.23.1. Интегралы от Л(х)Е((ар); (bq); (fi(x)).
oo
ха^гE((ap); (bq); ex) <
о
10 ^ g < p + 1; — min Re a^ < Re a < 01 или
Р	р+1
L = р + 1; -1/4 + Re 5^ afc - 5Z &Z / 2, - min Re afe < Re a < 0 .
CO
. f жа(ж1/то^а1/т)/3^1Е'((ар); Fд); еж) dx =
X El (ap)'A4(m:,X ma ^; ^ I	[a,Re/3>0; Re(ma+/3)<l;m = l,2,...].
1 (y, A(m, 1- ma)
f
. j /"'(a - xf-'EiM; F,); ^""(o - a;)"') dz =
3 j
о
f(ap), A(k, a),
[a, Rea, Re/9>0; ib, / = 1, 2, ...].
L	И	J
/(ap) Д(„ -p-l/2); (b + 2V55)-\	c	R
5. \x1/2-p(a + bx + cx2yE((ap); F,);
[9 < p + l; Re a ^ 0; Re с > 0; Rep < -3/2].
2.23.2. Интегралы, содержащие показательную или гиперболиче-
гиперболические функции и Е((ар); (bg); еж).
1. жа 1e sxE((ap); (bq); ex) dx =
О	Г	//Л \. ±тгг / \	// ч , _. л±
Fq), 1-a J	\ (bq
I _a с,/ («р); е 7rtc/s\ _a /(ap) + a; e ^с/г
^тгеовесатг s ?J	' Л Fl

2.28.3]
2.23. Е~функция Мак-Роберта Е(р; ar : q;bs : ж)
289
q < p + 1; Re s > 0; | arg c\ < (p — q + 1)тг/2; Re a > — min Re a^ | или
p	p+i
г
= р + 1; с, Re s > 0; Re а > — min Re а&,	Ь Re
x^ 4
2 .
3.
Fg); c(s/m)r'
[я ^ P + I» F^e s > 0; I arg cl ^ (p ~~ 4 + lOr/2; Re a < 0].
ap); (b,); (a + bch x)n) dx = J^j (a + b)e+a/2 v
(ap), Д(п, -й-3/2); (a + 6]
(ap), A(n, -^-
2.23.8. Интегралы, содержащие функции Бесселя и Е((ар); (bq); еж).
; еж) dx =
2ma
Д
(ор), Д(т, J//2 - та), А(т, -и 12 - та); e"m7riBm)m62mc
ехр
г)Е
г,	ma), А (га,	ma); em7i
< р + 1; 6 > 0; | arg с\ < (р ~~ q + 1)тг/2; -3/Dт) - min Re afc < Re a < Re i//Bm) или
3
= p+ 1; 6, С > 0;
3 1 / <с—-\ ir—^ \ m + 1 i7
	min Re ад., Re — I > a^ — > 6|	< Re a < Re
4m l^fc^p	2 I j!i^	^-^ I 4m	2m
OG
. f
2mBa +
[q
3.
ap); (bq); ex) dx =
b \ 2ma /(ap), A(ra, i//2 — raa), A(ra, —u/2 — ma)
	 I	^ 1	—2m 1m
hi; Refe > 0; |argc| $C (p - q + 1)тг/2; Re а < -| Re i/|/Bm)].
; еж) с!ж =
ар), A(ra, i/ — ma), l
CO
l-m/2
), A(ra, —i/ — ma)
; Re b > 0; | arg c\ ^ (p - q + 1)тг/2; Rea<-
3/2-mL2ma
)Ки[Ьх~{2т) г)Е((ар); (bq); ex) dx =
ap), A(w, (y + /i)/2 — ma), A(m, (i/ — aO/2 - ma),
A(m, (/i — i/)/2 — ma), A(m, — (/x + г/)/2 — ma)
; (b/mJmc
10 А. П. Прудников, Т. З

290
Гл. 2. Определенные интегралы
[2.23.4
[q ^р + 1; Reb > 0; |argc| ^ (р - q + 1)тг/2; Re а < —(| Re/x| + | Rei/|)/Bm)].
2.23.4. Интегралы, содержащие функции Лежандра и i?((ap); Fд); еж).
_ @ ^ «
(aP), A(m, (// + i/ + l)/2), A(m, (/x —
(fcg), ABm, 1); ac
[q ^ p + 1; a > 0; |argc| ^ (p - g + 1)тг/2; Re/x, Re Braa - /x - i/) < 1; ReBma - ц + is) < 0].
CO
2. ж (ж — о, ) jP^ I 2 I — I — 11 E((ap); \bq)\ ex) dx =
a
(ap), A(m, fi — ma), A(m, —ma); ac
K(bq), A(m, 1-\- is — ma), A(m, — i/ — ma)
[q ^ p+ 1; a > 0; | argc| ^ (p - q + 1)тг/2; Re a, Re (ma + pt) < 1; Re /x < 1].
2.23.5. Интегралы, содержащие функции Уиттекера и ?J((ap); F9); еж).
na ('(ap), A(m, 1/2 + <7 - ma), A(m, 1/2-a- ma)
2.
(bq), A(m, 1 — p — гтга); (s/m)mc
; Res > 0; |argc| ^ (p - g + l)?r/2; m Re а + |Recr| < 1/2].
ар); (&д); еж) с!ж =
52maTOi/2-2ma /(др)? дBш, 1 - 2ma), A(m, ^ + <т - ma), A(m, i - (г - ша)\
	ill 1	-"	I
2тBа + 1)^17Гт^1/2 I ^^ д^^ 1 + р ^ таM Д(тj 1 _ р _ та). Bт)т&2тС I
[д ^ р + 1; Re b > 0; | arg с\ ^ (р - д + 1)тг/2; т Re а + | Re a\ < 1/2].
2.23.6. Интегралы, содержащие произведения двух IiJ-функций.
1. I xa^E((cm); (dn); ax)E((ap); (bq); шх1/к) dx = Bтг)
о
А| и, 11/-\-(тп — п — 1)о; — 1 —сх
k^l v	'ax
I, fc + lm
k + kq+lm, kp+l + ln I Ц(п-
A(k, 1), Д(/, l-a-{cm)), A(k, (fe,)) \
Д(/, -a), A(k, (ap)), Д(/, 1 - a - (dn)) /
A = (m - n - 1)A - 0/2 + (p~q- 1)A - fe)/2,
r	/ у J	/ j J ¦	л	'	/ .у J	/ у J '	q	'
условия см. в 2.24.1.1 при s = v = m, 5 t = n = l, it = n + l, m = q = Pj p = q-\-l] (cu) = l, (dn);
(dv) = (Cm)i (°>p) = li (bq)] (bq) = (d>p) •
со
n + l,kp+lm I	ll(m-n-l)
A(Aj, 1), A(l, 1 - a),
I, (dn) -a)
A(A;, (ap)), A(/, (cm) - a)
[Л, /i, i/ см. в 2.23.6.1; условия см. в 2.24.1.1 при s = n = l, t = u = m, v = n-\-l, m = q = p, p^^ + 1;

2.24.11
2.24- G-функция Мейера
(bq)
291
2.24. G-ФУНКЦИЯ МЕЙЕРА GZT (x
(ар) А
(bq)J
В разделе 2.24.1 приведен интеграл общего вида, который содержит в качестве част-
частных случаев при различных значениях параметров многие интегралы с элементарными и
специальными функциями; часть этих интегралов включена в настоящий справочник.
2.24.1. Интегралы общего вида.
Обозначения:
7П, га, р, д, з, t, и, v = 0, 1, 2, . . . ; k, I = 1, 2, 3, . . .
[к, I — взаимно простые числа],
b* =
p
¦t	—, с =т + п-
«2
¦ + 1
[aj, bj, Cj, dj — комплексные параметры
(p = g — p — r(v — u), 7] = 1 — ql(v — u) — /i — p	[a — комплексный параметр
с ш — комплексные переменные; сг, ш / 0.
1 . а» — bj, Cg- — dh ф 1, 2, . . .
2°. Re (a + с4 + rbj
0
[г = 1, 2, . . . , щ j = 1, 2, . . . , га; g = 1, 2, ,
[j = 1, 2, ..
3°. Re (a +
4°. (р- g)
5°. (р- g)
6°. (ад - v)
7°. (^-v)Re(a + r6i)-
8°. \<p\ + 2 Re [(g - p)(v -
9°. M - 2 Re [(g - p)(v -
10°. arga| < 6*тг;
11°. argcr| = 6*тг;
12°. argo;| < с*тг;
13°.
га*) < г + 1
+ c^ - 1) - rRe/i > -3r/2
+ d^) -rRe/x> ^3r/2
+ rai - r) - Rep > ^3/2
-3/2
[г = 1, 2,
т;
п;
h
h
g
Ы
[h
[*
U =
= 1,2,
= 1,2,
= I? 2,
= 1, 2,
= 1,2,
= 1, 2?
= 1. 2. .
. . . , s
. . . , 8
. . . , t
. . . , t
. . . , 8
. . . , 71
... 771
(v - u)(fi - 1) + (9 - p)(p - 1)] > 0;
- 1)] > 0;
= с*тг;
14°. Если ip = 0и c*+rF* -1)^0, то | arg A - госг~1шк)\ < тг5 где z0 = rl{v~u) exp [-A6* +
+ Агс*)тгг], причем при Re [/i + p + a(i; — ix)] < 1 допускается значение <т ш = zq.
15°. Выполняется одно из следующих трех условий:
Лс > 0 или Лс = 0, Л5 ф 0, Re ту > —1 или Лс = Xs = 0, Re 77 > 0,
где
Лс(д -	1/()	1/()
1
+ (q — in — га)тг], ^ =
g -p
As = (g — p)|cj| '{q~p> sgn (arga;) sini
при условии arg <т • arg cj / 0;
если arg <j = 0, arg w / 0, то As = A^
если arg а ф 07 arg cj = 0, то As = A^
если argcr = arg a; = 0, то As = Aj"+,
u* sgn (argo;) sin 0,
где A^ =
lim
s, As = lim As,
arg ш—->-d=O
I. T^-^^Jc
(d.)
(jrnn
M
= lim As.
org cu—->+0
гя<т^±0
10*

292
Гл. 2. Определенные интегралы
[2.24.1
lt, kn+ls
v, kq+lu
, ai),
an), A(/, 1 - a - di), . . . , A(Z, 1 - a - civM
6m), A(Z, 1 - a - a), . . . , A(I, 1 - a - cu),
ap)
bq)
если выполнено одно из следующих условий (если ms = 0 или nt = 0, то соответственно
2° или 3° опускаются):
1) mnsi ф 0; Ь*, с* > 0; 1°-3°, 10°, 12°;
2)u = v\ b* = 0; с*, а > 0; Rep < 1; 1°-3°, 12°;
3)	р = q; с* = 0; 6*, ш > 0; Re/x < 1; 1°^3°, 10°;
4)	р = д; гх = v; 6* = с* = 0; <т, о; > 0; Re/i, Rep < 1; cr1 7^ wfc; l°-3°;
5)	р = д; м = v; 6* = с* = 0; а, ш > 0; Re О + р) < 1; а1 = шк; 1°-3°;
6)	р > д; 8, Ъ* > 0; с* ^ 0; 1°-3°5 5°, 10°, 13°;
7)	р < q; t, 6* > 0; с* ^ 0; 1°^4°, 10°, 13°;
8)	и > V, т, с* > 0; 6* ^ 0; 1°^3°, 7°, 11°, 12°;
9)	и < v; n, с* > 0; b* ^ 0; 1°-3°, 6°, 11°, 12°;
10)p>g; u = v; Ъ* = 0; с* > 0; <т > 0; Rep < 1; 1°-3°, 5°, 13°;
11) p<q; u = v; 6*=0; с* ^ 0; <т > 0; Rep < 1; 1°^4°, 13°;
12)р = д; гх > v; &* ^ 0; с* = 0; о; > 0; Re/x < 1; 1°-3°, 7°, 11°;
lS)p = q; u<v; 6*^0; с* = 0; ш > 0; Re/x < 1; 1°-3°, 6°, 11°;
14)	р < g; w > г?; 6*, с* > 0; 1°^4°, 7°, 11°, 13°;
15)	р > g; tx < и; 6*, с* > 0; 1°^3°, 5°, 6°, 11°, 13°;
16)	р > д; и > v; b*, с* ^ 0; 1°-3°, 5°, 7°, 8°, 11°, 13°, 14°;
17)	р < д; и < v\ 6*, с* > 0; 1°™4°, 6°, 9°, 11°, 13°, 14°;
18)	t = 0; s, 6*, (^ > 0; 1°, 2°, 10°;
19)	s = 0; t, 6* > 0; у? < 0; 1°, 3°, 10°;
20)	п = 0; т, с* > 0; у> < 0; 1°, 2°, 12°;
21)	т = 0; п, с*, ^ > 0; 1°, 3°, 12°;
22)	st = 0; 6*, с* > 0; 1°-3°, 10°, 12°;
23)	тп = 0; Ь\ с* > 0; 1°-3°, 10°, 12°;
24)	w + п > р; t = ср = 0; я, 6* > 0; с* < 0; |arga;| < (т + п - р + 1)тт; 1°, 2°,
10°, 14°, 15°;
25)	m + п > д; s = (р = 0; t, 6* > 0; с* < 0; | arga;| < (т + п - д + 1)тг; 1°, 3°,
10°, 14°, 15°;
26)	р = д - 1; t = (р = 0; s, b* > 0; с* > 0; с*тг < |arga;| < (с* + 1)тг; 1°, 2°,
10°, 14°, 15°;
27)	р = д + 1; s = ip = 0; t, 6* > 0; с* ^ 0; с*тг < | argш| < (с* + 1)тг; 1°, 3°,
10°, 14°, 15°;
Щ Р < Ч - 1; t = if = 0; s, 6* > 0; с* ^ 0; с*тг < | arg о;| < (т + п - р + 1)тг;
1°, 2°, 10°, 14°, 15°;
29)	р > д + 1; s = у? = 0; t, 6* > 0; с* ^ 0; с*тг < | arg о;| < (т + п - д + 1)тг;
1°, 3°, 10°, 14°, 15°;
30)	п = (р = 0; в + t > и; т, с* > 0; 6* < 0; | argсг| < (в + ? - гх + 1)тт; 1°, 2°,
12°, 14°, 15°;
31)	т = (р = 0; в + t > v; п, с* > 0; b* < 0; | arg <т| < (s + t - v + 1)тг; 1°, 3°,
12°, 14°, 15°;
32)	n = (f = 0; гх = v - 1; m, c* > 0; 6* ^ 0; 6*тг < |arga| < F* + 1)тг; 1°, 2°,
12°, 14°, 15°;
33)	m = (p = 0; tx = v + 1; n, c* > 0; 6* ^ 0; 6*тг < |arg<r| < F* + 1)тг; 1°, 3°,
12°, 14°, 15°;
34)	n = (f = 0; и < v - 1; m, с* > 0; 6* ^ 0; 6*тг < | arg a\ < (s + t - и + 1)тг;
1°, 2°, 12°, 14°, 15°;
35)	m = <p = 0; и > v + 1; n, c* > 0; 6* ^ 0; 6*тг < | arga| < (s + t - v + 1)тг;
1°, 3°, 12°, 14°, 15°.

2.24.2]
2.24- G-функция Мейера
(bq)
293
-t, n+s
J. jx Guv[a
{1P) ) dx =
K)
[cm. 2.24.1.1 при к = I = a = 1].
(d«)
dx =
fc=O
1 — a, (an), 1 + к - a — (dv), an+i, . . . , ap
(bm), 1 + k- a- (cu), 1 + k- a, 6m+i, . . . , bq
b*, c* > 0; I arg <j| < тг; argcu < с*тг; — min bj < Re a < 2 — max Re бц — max Re сь .
4.
_, I	ap_i + ap — bq^i — bq — 1
=i	,	,	,	,
\_(lp — l — Oq — 1, ttp — 1 — Oq , ftp — Oq_i, flp — Og
c* > 0; | arg ш| < с*тг; Re
(«p-2)
2.24.2. Интегралы от А(х)
Обозначения см. в 2.24.1.
dx =
Jo	"" V	(Ьд) J
= аГ«гГ	Fm) + a, l-(an)-a	1
L«n+i + a, . . . , ap + a, 1 — 6m+i — a, . . . , 1 — 6^ — aj
Г71 + 7i Ф 0; c* > 0; |arga;| < с*тг; ш ^ 0; — min Re bj < Rea < 1 — max Re «j или
p^g; c* ^ 0; | arga;| = с*тг; — min Re 6j < Re a < 1 — max Recij, Re [ft + (q — p)a] < 3/2
или \p = q; c* = 0; w > 0; — min Re bj < Rea < 1 — max Reaj, Re у_Д^ — «j) < 0 .
a —1/
. Ж	(a
Ilk
^
, (ap))
, F,)), Д(/, l-a-/3
[условия см. в 2.24.1.1 при а = a 1, s = и = v = 1, t = rfi = 0, ci=/3].
CO
-C	T*	I 71 	 /7 1	It	I
4.
z)
Д(/, l-a-/3), Д(Л, F,)) )
[условия см. в 2.24.1.1 при <т = а^ , 5 = rfi = 0, t = и = v = 1, ci = /3].
/~imn I	Ilk
rGpq
я)

294
Гл. 2. Определенные интегралы
[2.24.2
А—1^а-Х
кПх~^%
G
/ к I
1,кп+1 I ш z
k+l I (
l,kq+l 1
[условия см. в 2.24.1.1 при а = z", s = t = u = v = l, ci = 1 — A, d\ = Ol.
A(f, 1-a), A(fc, (ap))
A(l, A-a),
5.
x-y
^mn I	Ilk
Gna ШХ '
dx =
A(J, 1-a), A(fc, (ap)), A(I, 1/2 - a)
A(Z, 1-a), A(fc, F,)), A(l, 1/2-a)
6.
[условия см. в 2.24.1.1 при cr = у , s = t = 1, и =¦ v =¦ 1, c\ = d\ = О, С2 ^ c?2 ^ 1 /2J.
^	r~imn
0
/ =
ш11 { z
, a),
0 < к < I; c* > 0; \arg(ujzl~k)\ < с*тт; (Z - ife) ( 1 - max Re aj ) + Re {C - a),
A; - fe max Re aj + Re a > 0 I ,
(A; -
~im-\-k, n-\-k — l
0< l< k; c* > 0;
^k-l
[ c*tt; (к—I) min Re bj
- I, a- /3 + 1), (ap), A(I, ^)
А(Л, a), (bq)
•¦— к max Re aj + Re a > 0 I,
Jp+fc,q+k
ife, a),
I = к > 0; с* > 0; | argw| < с*тг; Re(/3 - a), A; - A; max Re а^ + Re а > 0 .
7.
[1 + ax + 6A -
dx =
g:
•m, n + k + l
L^J^
\k+i
,1-/3), (aP)
, l-a-/3)
m > 0; p < q; Re a + I mln Reb,-, Re^ + к min Re69- > 0 I или I n > 0; p > q: c* > 0;
[	KjXm	J	l^jXm	J	J	[
|arga;| = с*тг; Re а + I min Re6.-5 Re/3 + A; min Re6?- > 0; Re((g - p)a + l/x) < 31/2;
8.
Ы
dx = J,
г
о \l — k — l 1 2a —1/2 a+jS —1/2
шк2
ABife, 1 - 2a), (ap)
с + /, 1/2 - a - /3), Fq), A(fe - I, 1/2 + /3 - a)

2.24.3]
2.24- G-функция Мейера
(bq)
295
_
Qtn+k + l,n+2k I ш^
ABfc, 1 - 2a), (ap), A(l - A;, 1/2 + a - ,
•I, 1/2 - a - P), (bq)
x G
J =
+ 2k, n + 2k
p+2k, q+2k
]
a-P-1/2 z<x+/3-l/2
ABk, l-2a), (ap)
ABk,l/2-a-0), (bq)
[I = к]
[mn ф 0; c* > 0; | arg(Wfc+l)| < с*тг; |argz| < тг; Re (a + kbj) > 0, j = 1, 2, . . . , m;
Re [a + /3 + (Jc + /)(сц - 1)] < 1/2, г = 1, 2, . . . , n] или [m > 0; q > p; c* ^ 0; | arg(wzfe+l)| = с*тт;
|argz| < тг; Re (a + kbj) > 0, j = 1, 2, . . . , m; Re [a +/3 + (fc + Z)(ai - 1)] < 1/2, г = 1, 2, . . . , n;
Re [(g - p)(a + $- 1/2) + (Aj + Z)/x] < 3(fe + Z)/2] или [те > 0; q < p; e* > 0; | arg(wzfc+l)| = с*тт;
| arg z\ < tt; Re (a + fe6j) > 0, j = 1, 2, . . . , m; Re [a + /3 + (k + Z)(ai - 1)] < 1/2, г = 1, 2, . . . , n;
Re [(q - p)a + fe/x] < 3A;/2].
9.
2(o/K/2
/, 3/2)
A(l,0),(bq
m+l,n
/, 1/2)
10.
[p^g; c*, Rea > 0; Re с > 0; Re [1A - a^-) + a] > 3; j = 1, 2, . . . , n; Z = 1, 2, . . .].
/ ax2 + 6ж + с
A(Z, 2-a), (ap)
Fg), A(Z, 3/2^ a)
[p ф q; c*, Rea, Re с > 0; Re(l6i + a) > 1; j = 1, 2, . . . , те; Z = 1, 2, . . .].
2.24.8. Интегралы, содержащие показательную, гиперболическую
или тригонометрическую функции и G^J1 ( шх
Обозначения см. в 2.24.1.
/k
(«р)
оо	/	\
I. \ x^e-^G™ (u>xl/h (йр)
п, kn+l I tJ
, (op))
[условия см. в 2.24.1.1 при s = v = I, t = и = di = 0].
2.
Gp"," f(a + 6cha;)'
(bq
¦g:
<m-\-l, n
2Ь3Р Р+1' y+l
(a+ 6)'
h 3/2)
I, 0),
2 61
, A(ra, 1/2)
I, 0), Fg) + B<9
g; c* > 0; Re 6 > 0; Re [1A -a,) - 0] > 3/2; j = 1, 2, . . . , n; Z = 1, 2, . . .].

296
Гл. 2. Определенные интегралы
[2.24.4
Г
J
Г
О. \ X
J
ex — 1 J SID OX I ^fjin
^ cos ox J
ш/к
(ap)
(M
A(l, C т 1 - 25)/4), A(fc, (ap)), A(/, C ±1 - 2a)/4)
[условия см. в 2.24.1.1 при а = a/2, a = 62/4, s = 1, t = и = 0, v = 2, d\ = 1/2, d2 = A T I)/4]-
7Г/2
1. [ Sin";
ше sin ж
da? =
[p < q; m > 0;
|argw| = с*тг;
тг/2
Г • a —1
э. sin
_ i7rcx/2 ?-/
Re(l6J- + a) > 0; j = 1, 2,
Re(lbj + a) > 0; j = 1, 2,
sin1
i-Kl/2
l, 1-a), (op)
2тг-
. . . , m ] или [ q < p; те > 0; с* ^ 0;
. . , m; Re[(p- g)a - /д] > -31/2].
^j ) ^ =
1A, 1-a), A(fc, 1-^), (ap) \
[p < g; m > 0; Re (a + /6^), Re (C + feb^) > 0; j = 1, 2, . . . , m ] или [ тг > 0; g < p; с* ^ 0;
arga;| = с*тт; Re (a + Ibj), Re (Д + kbj) > 0; j = 1, 2, . . . , те; Re[l/i + (g - p)a] < 31/2;
Re [fe/x + (g - p)/3] < Sk/2].
2.24.4. Интегралы, содержащие функции Бесселя и G™nn ( шх '
Обозначения см. в 2.24.1.
21/к
V
dx =
[условия см. в 2.24.1.1 при a = 5/2, а = 62/4, s = 1, t = и = 0, v = 2, rfi = i//2, d2 = -^/2].
2. х°
о
211k
, fcg+I
B/J
, (ap)), д (/,
3- a + i
[условия см. в 2.24.1.1 при a = a/2, ст = Ь2/4, s = 2, t = 0, it = l, v = 3, ci = с?з = A-1/)/2, di = -*//2;
3.
r~ikm, кп + 21
Х °"А!р+2/, feq
С?Ж =
, 1 - (a + i/)/2), A(l, 1 - E -
, (ap))
[условия см. в 2.24.1.1 при a = a/2, a = 62/4, 5 = v = 2, t = и = 0, d\ = -i^/2, d2 = ^/2].

2.24.7]
2.24- G-функция Мейера
(bq)
297
2.24.5. Интегралы, содержащие ортогональные многочлены и
1.
(Ья).
Обозначения см. в 2.24.1.
, kn-\-2l
kq+2l
2l/k
ы
dx =
(Ья)
ДB/, 1 - 5), A(fc, (ap))
, F,)), АA, A - 5 - г)/2 - А), Д(/, A - 5 + г)/2)
[условия см. в 2.24.1.1 при а = 5/2, сг = а™2, s = w = t; = 2, ? = 0, ci = А + A + г)/2, сг = A - г)/2,
di =0, d2 = 1/2; г = 0, 1, 2, . . .].
ab\3 n
p ^ g; a, c*, Re/3 > 0; |argu>| < с*тг; Rea + i min Re6i > 0 .
[	l^j^m	J
3.
2ж
¦укт, fen + 2I
Jfcp+2I, feg+2I
A n,
А(/, 1 - а), Д(/, 1 - а + I/), A(ife, (ар))
[условия см. в 2.24.1.1 при а = а *, s = it = v =2, t = 0, ci = А + г + 1, C2 = ^i^ ^ r, di =0, с^г^^^;
г = 0, 1, 2, ...].
2.24.6. Интегралы, содержащие функции Лежандра и
Обозначения см. в 2.24.1.
1.
(ap
Bтг)
/-ykm, fcn + 21
Х °"А!Р+2/, fcg+21
ДB/, 1-й), А(к, (ар))
е, F,)), Д(«, (А - 5 - «/)/2), Д(/, A + А - 5 + и)/2)
[условия см. в 2.24.1.1 при а = 5/2, <т = а~2, s = u = t» = 2, t = 0, ci = A- A- v)/2, c2 = l + (v- A)/2,
di = 0, d2 = 1/2].
СХЭ	/	\	1 1 ~ \
-^кт-\-21, кп
Ткр+21, кц+21
, (ар)), ABI, 1-5)
A(l, (A - 5 - i/)/2), A(Z, A + A - a + i/)/2), A(ife,
[условия см. в 2.24.1.1 при а = а/2, сг = а^2, t = ifc = v = 2, s = 0, ci = A-A-i/)/2, c2 = 1 + (у— А)/2,
di =0, d2 = 1/2].
2.24.7. Интегралы, содержащие функции Уиттекера и
Обозначения см. в 2.24.1.
a —1 —-ax
. \ x e
/2 n ж (
с/ж =

298
Гл. 2. Определенные интегралы
[2.24.8
гукт + l, kn+l
X ^kp+21, kq+l
-Р)
A(Z, 1/2 - a ~~ i/), A(fc, (ap)), A(Z, 1/2 - a + i/)
A(l, A — a), A(fc, Fq))
2.
[условия см. в 2.24.1.1 при s = t = и = 1, v = 2, c\ = 1 — A, d\ = 1/2 + i/, d2 = 1/2 — i/].
(ap)
(bq)
x G
¦km, kn + 2l
kp+2l,kq+l
A(Z, 1/2 - a - i/), A(l, 1/2 - a + i/), A(A:5 (ap))
Ь,)), А(/, A-a)
[условия см. в 2.24.1.1 при s = v = 2, t = 0, и = 1, c\ = 1 — A, d\ = 1/2 + u, d2 = 1/2 — i/].
(%)
km + l, fcn + 21
ГA/2 - A - |/)ГA/2 - A + i/)
A(Z, 1/2 - a - i/), A(Z, 1/2 - a + i/), A(ife, (ap))
A(I, -a - A), A(fe, (bq))
x О
[условия см. в 2.24.1.1 при s = v = 2, t = и = 1, ci = A + 1, d\ = 1/2 + u, d<i = 1/2 — v\.
2.24.8. Интегралы, содержащие функцию Гаусса 2^1(^,6; с; х) и
dx =
Обозначения см. в 2.24.1.
со	/	\
1. [ xa-\F1(a, b; с; 1 - <rx)G™n (uxl/k ^p) j
B7rJ(l-l) + c*(fe-
ГГ
x G'
fcm+2l,fen + 2l I 	^
-P)
/, 1 - a), A(Z, l + a + &-c^aM A(ife, (ap))
A(Z, a-a), A(l, 6-a), А(Л, F,))
[условия см. в 2.24.1.1 при s = ? = u = v = 2, ci = 1 — a, C2 = 1 — 6, di = 0, d,2 = с — a — b].
2.
a, 6; c; l-
(ap)
x G'
km, fcn+21
A(Z, 1 - a), A(Z, l + a + &™c-a), A(ife, (ap))
, Fg)), A(Z, 1 + a - с - a), A(Z, 1 + b - с - a)
[условия см. в 2.24.1.1 при a =d 1, s = u = v = 2, t =0, ci = с— a, C2 = c — b, d\ =0, б?2 = c — a — t
3.
, 6; c; l-
B7r)c*(fe-l)dl-c-a
чкт+21, кп
A(ife, (ap)), A(Z, 1 - a), A(Z, l + a + 6-c-a)
A(Z, 1 + a - с - a), A(Z, 1 + 6 - с - a), A(fc, (bq))
Л ^kp+2l,kq+2l I ^к(Ч~р)
[условия см. в 2.24.1.1 при а = d^1, ? = it = v = 2, s = 0, ci = с — a, C2 = с — 6, di = 0,
d<i = с — a — b].
4.
b; c; -
ja + b-c-l -а. Г
4, . , w, ., Г
x G
i,kn+i(«^
km-\
kp+2l, kq+21
Z, c-a)
A(Z, a - a), A(Z, b - a),
[условия см. в 2.24.1.1 при s = 1, ? = it = г; = 2, ci = 1 — a, C2 = 1 — 6, di = 0, cfo = 1 — с].

2.25.11
2.25. Н-функция Фокса Ы™п |ж[г/'
\bq,Bq]
299
а	/	\
5. \xa-1{a-x)a-c2F1 (b, 1-b; с; -) G™n [u(ax-x2)'/k ^p) 1
Jo	V	a>	V	(M /
р,кт, kn+-ll I *" ">	Д(^5 1 "" a)i ^(h c — a)i ^(^5 (ар))	1
;бд)), Д(/, A-Ь + с)/2-а), Д(/, (Ь + с)/2-а) /
[р < </; а, то >
> 0; Re (kа + Ibj), Re (к + ка - кс + Ibj) > 0; j = 1, 2, . . . , т ] или [ р > д; а, п > 0; с* > 0;
argw| = с*тг; Re (ка + Ibj), Re (A; + ка ~~ кс + Ibj) > 0; j = 1, 2, . . . , то; (р — </)А; Re а — I Re /i >
> -31/2; (р- g)lc(l + Rea - Re с) - / Re д > -31/2].
6.
а, 6;
-6+1 х . „
1	5 а » Gp
-ffcm, fcn+21
A(I, 1 - а), Д(/, (а + b + 1)/2 - а), Д(А;, (ар))
Д(А;, Fд)), Д(/, (а + 1)/2 - а), Д(/, F + 1)/2 - а)
[а, с* > 0; |argw| < с*тг; Re (ка + /&_,-) > 0; Re Blbj + 2ka - ка - kb) > -к; j = 1,2, . . . , то].
тг/2
7. sin" ж cosc жe^Q+c^ 2^1(^5 6; с; е*жсозж)С!
рд
Ы
dx =
+2fc
A(l, 1 - a), A(I, l + a + 6-c-a), (ap) 1
Fg), A(l, 1 + a - с ~~ a), A(l, 1 + b - с ~~ a) )
[p < q; Rec, Re (c - a - b), Re (a + Ibj) > 0; j = 1, 2, . . . , то ] или [ д < p; n > 0; с* ^ 0;
;| = c*7r; Rec, Re (c - а - 6), Re (« + %)> 0; j = 1, 2, . . . , то; Re [(p - q)a - l/x] > -3J/2].
2.24.9. Интегралы, содержащие sFt((cs); (dt); —«
Обозначения см. в 2.24.1.
/	, ,,	(г, \ \
dx = ,„ ч w,
J/fe
t. ja, .
sykm+sl, kn+l
^kp+tl + l, kq+sl
A(l, (c8)-ct), A(k, (bq))
[условия см. в 2.24.1.1 при s = 1, t = и = s, v = t + 1, (cu) = 1 — (cs), (dv) = 0, 1 — (dt)].
2.25. Я-ФУНКЦИЯ ФОКСА If™ \x^PJ Ap}]
I lbqj Вч\ J
Приведенные в этом разделе условия сходимости интегралов являются лишь достаточ-
достаточными; можно указать и другие условия сходимости.
2.25.1. Интегралы общего вида.
Обозначения:	р	т	q
* \ "^ л	\ "^ л	\ "^	\ "^
j=l	j=n+l	j=l	j=m+l
Ь*=\"Г7,^ V r7,4-VD,- V П,
1.
[Си, Си]
[dv, Dv]
К, Ap]
[bq, Bq]

300
Гл. 2. Определенные интегралы
[2.25.2
_ -a Tjm+t,n+s ш_ [a>n, Лп], [l — dv — aDVj rDv], (an+i, An+i), • • • , (aP, Лр)
[СгГ f^m' Вт], [1 — cu — aCu, rCu], Fm+i, Bm+i), • • • , F9, Bg) j
must Ф 0; a*, 6*, r > 0; |argcr| < Ь*ж/2; |argw| < а*тг/2; Rea + r min Re (bj/Bj)
+ min Re(dh/Dh) > 0; Rea + r max Re ((o^ - 1)^-) + max Re ((сл - 1)/Ch) < 0;
Aj-F/i, + к) Ф Bh{aj — I — 1); fe, I = 0, 1, . . . ; j = 1, 2, . . . , щ h = 1, 2, . . . , «г;
^¦(dfc + к) ф Dh(cj - I - 1); k, I = 0, 1, . . .; j = 1, 2, . . . , t; h = 1, 2, . . . , s j.
2.25.2. Интегралы, содержащие элементарные функции и
if-фу н кцию.
Обозначение:	п	р	т	q
j=l	i=n+l	j=l	j=m+l
К, ^Р]
dx =
= ш Г
1 — an — Лпа 1
, . . . , 1 — bq — Bqa\
2.
тпфО; a* > 0; | argw| < а*тг/2; -^ min Re (bj/Bj) < Re a < ^ mm Re (A - clj)/Aj) |.
к,
— a	^р+2)<?+1
Ql, T*J), ^ JL p , pj , [dp , Ут.р|
¦mn, ^ 0; r, p ^ 0; a, a* > 0; | arga;| < а*тг/2; Re a -+- r min Re (bj/Bj) > 0; Re a -
3 1 a —1 —ax jj-mn	r
. I x e Hpq \шх
[ap,
ax — о
(l-a, r), [ap, Лр]
тп ф0; a*, r.Recr > 0; |arga;| < а*тт/2; Rea + r min Re(bj/Bj) > 0
4.
я, Вя.
(C T 1 - 2a)/4, r/2), [ap, Лр], (C ±1 - 2a)/4, r/2) I
a*, r, o- > 0; |argw| < а*ж/2; Re a + r min Re (bj/Bj) > (-1 + l)/2; Re a+
+ r max Re ((clj - l)/Aj) < 1 .
2.25.8. Интегралы, содержащие специальные функции
и Я-функцию.
о
2, (а - г
= 2°
[ttp, ApJ
F + гж, r), F — гж, г), [6д, Бд]
[ap, Лр]
о + Ь, г), F + 1/2, r), [6,, Bg]
m+2,n
p» 9+2 I tz:

2.26.1]
2.26. Тэта-функции 0j(x, q)
301
а*, г, Re а > 0; |argw| < а*тг/2; Reb-r max Re((aJ- - l)Mj) > 0 .
2.
A - (a + i/)/2, r/2), [op, Ap], A - (a - i/)/2, r/2)
a*, r, a > 0; |argw| < а*тг/2; Re (а + i/) + r min Re (bj/Bj) > 0, Re a+
+ r max Re((aj - 1)/A/) < 3/2 .
3. xa~1Jli(ax)Jv((Tx)H.
mn
pq
Tj-m+l, n+1
"Лр+4,д+1
2
2, r/2), [op, Лр],
-a, r),
. - (a - /x - i/)/2, r/2), A - (a + /x - i/)/2, r/2), A - (a - /x + ^)/2, r/2)
a*, r, a > 0; |argw| < а*тг/2; Re (a + ^ + v) + r min Re(bj/Bj) > 0, Rea+
1
+ r max Re ((а^ — '.
4.
я, Bq]
ia-2
-Я,
то, n + 2
a JiP+2,g
- (a - i/)/2, r/2), A - (a + *)/2, r/2), [ор,
[Ья, Bq]
5.
a*, r, Recx > 0; |argw| < а*тг/2; Re а - | Rei/| + r min Re (bj/Bj) > 0|
a», A/
); -<rx)H
™
шж
dx =
= Г
(dt
s, n + 1
A - a, r), [ap, Лр], [rft - a, t]
a*, r > 0; s + 1 > t] |arga| < (s - t + 1)тг/2; |argw| < а*тг/2; Rea + r min ReFi/JBi) > 0;
Rea- min Re Cj + r max Re ((a,j — 1)/Aj) < 0 .
2.26. ТЭТА-ФУНКЦИИ %(ж,
2.26.1. Интегралы от f(xHj(x1q).
L. 0j(nx, q)
1 к
dx = 0
= l, 2; n = l, 2, ...]
rf
3.
(a:, g) rfaj = 0. 4. P2n(cosa?)^2(^, g) dx = 0.
J
7Г
5. 0j(nx, q) dx = ж
[j = 3, 4, . . . ; n = 1, 2, . . .].

302	Гл.2. Определенные интегралы	[2.26.2
7.
8.
9.
10.
0
7Г
jsin
0
{cos
0
= 0
АТГЬХ
\2mx
= 0
[в остальных случаях].
[j = 3, 4].
ч , „„ = (±l)m/n7rqm2/n2	[m/n = 0, 1, 2, . . .].
i(nx, q) l
[в остальных случаях].
Г
11.	cos Bm + l)x0j(nx, q) = 0	[j = 3, 4].
о
т/2	2
gcos2ж — g	t ч	тг _1/4Л
12. 	г-<7з(ж, q) dx = —g 02@, g).
о
13.
о
2.26.2. Интегралы, содержащие произведения 9j{ax1 q).
TV
1.	0i(mx, qH2(nx, q) dx = 0	[ra, n = 1, 2, . . .].
о
2.	|(9,-(Bт + 1)ж, р)^(Bш + 1)Bп + 1)ж, g) d^ = (^l)ni7T^2@, F4n2+4n+1g)	[j = i, 2].
о
3.	6>2(Bm + 1)ж, p)9j(nx, q) dx = 0	[j = 3, 4; n = 1, 2, . . .].
о
ТГ
4.	|"^-(Bт + 1)ж, р)^-(Bш + 1)ж, g) rfx = тг6>3@, pq)	[j = 3, 4].
о
ТГ
5.	|"^Bтж, рN>4(пж, q)dx = 0	[j = 1, 2; m = 1, 2, . . .].
о
ТГ
6.	l02Bmx, pHj(nx, q)dx = (^I)m(j)/n7rl92 (o, pq4m2/n2^	[j = 3, 4; m/n = 1, 2, . . .].
о
7.	[ 6>з(шж, рN>4(пж, g) dx = ж04 (о, pgm2/]	[m/n = 1,2,.. .].
о
2.26.3. Интегралы, содержащие произведения 0j(x, aq).
1 , ^«^xj -xV^5 ^, ^7 L л^ _ ..- ^ j shBv«^)
' J	\б»2(ж, <7/a)J 9 ch^Tr
0
	 . . . . ;^-2Ж)].
[Rea> 0; ^(тг±7г)/4 ^ ж ^ (Зтг =р тг)/4].
Г g-xfgsCic, q/a)\
' Jg \б/4(ж, q/a)j Ч
0
\
«) J
[Re a > 0; -(тгТтг)/4 ^ ж ^ (Зтг ± тг)/4].

2.26.4]
2.26. Тэта-функции 0j(x, q)
303
3.
4. [iln"-1^
Я	Я
5.
[Re a > -1/(/Зтг2); C > 0].
q/a)
2
?j B* + 1J« \ cos B*
)ж ]
)x J
[Re a > 0; Re a > 1/2; -A ± 1)тг/4 < ж < C Т 1)тг/4]
о 3±3^ ж
^'^+2^
л 5±1 ж
[Re a, Re a > 0; -A ± 1)тг/4 < x < C =F
J
q\e4(x,q/a)-
[Re a, Re a > 0; -A =p 1)тг/4 < x < C ± 1)тг/4].
о
2.26.4.
(тг/2, q/a) -
Интегралы по g, содержащие 0j(x7 aq).
[Re а > 0; Re а > 1/2; -A =F 1)тг/4 < ж < C ± 1)тг/4].
I	[Re а > 0; Re a > 1/2].
[Re а > 0; Re a > 1/2].
1.
01' 8 
[Re a > 0; Re a < 0; -(l±l)/4 < x < C=pl)/4]
2.
3.
4.
5.
1 - 2a, Ifl + x) - С f 1 - 2a,
4	/ V
[Re a > 0; Re a < 0; -A =F !)/4 < x < C ± l)/4].
62(х, aq)
dq =
а \ch[(l-2x)y/p/a]
[Re а, Rep > 0; -A ±1)/4 ^ ж ^С C=р1)/4].
0з(х, aq)\	±1
х > dq = —-=
, ,7/sh[(i-:
cosech 4 / — J
2-^ч	1
6 ^д19зFд5 ад) с?ж = -—:	 ( th
a | зЬBжур/а)
[Re a, Rep > 0; -A =F l)/4 ^ ж ^ C±l)/4].
-th^+2
[a, 6 > 0; Rep > 62/a2].

304	Гл.2. Определенные интегралы	[2.27.1
2.27. ФУНКЦИИ МАТЬЕ
В этом разделе содержатся интегралы, в подынтегральные выражения которых входят
функции Матье первого рода сеп(ж, g), sen(x7 g) и второго рода fen(x, g), gen(x1 g), моди-
модифицированные функции Матье первого рода Сете(ж, g), Sen(x, q) и второго рода Реп(ж, д),
Gen(x, q). Для краткости в некоторых формулах параметр q в обозначениях функций
Матье опущен; при этом к = 2\/q •
Определения и обозначения см. в приложении 11.24.
2.27.1. Интегралы, содержащие элементарные функции и сете(ж, д)
или sen(x, q).
V/ () \	жА / ce^@) \
>се2те(ж, q)dx = 	^—l _г	>ce2n(a).
J	7	2 I ce (тг/2) I
о
тг/2
ch(kmnamnx) \
n	>се2те(ж, q)dx = 	^—l _г
cos О cos a cos ж) J	7	2 I ce2n (тг/2)
f cos ж eh (fe sin a sin ж) 1	. ч	тг ,Bn+i) f sec a/ ce2n+i@) 1
• /i	\ >ce2n+i(^, q)dx = ±T^i	1f/ , / /o; ^ ce2n+i(a).
{ sin (A; cos a cos ж) J	4	[ k/ ce2n+iGr/2) J
о
тг/2
f sh (A; sin a sin x)
3. < .
J { sin ж cos (A; cos a cos ж)
0
/
[coseca/se2n+iGr/2)
1	. ч .
. . /f	> 8е2+2(ж q) dx =
sin x sin (A; cos a cos ж
Г f cos ж sh (A; sin a sin ж) 1	. ч .
4.	< . . /f	x> 8е2п+2(ж, q) dx =
J [ sin x sin (A; cos a cos ж) J
seca/se2n+2@)
8	[coseca/se2n+2GT/2)
7Г	/	1	Л
Г Г ch (lech a sin ж) 1	. x	/ -,\n ЛBп) I ce^n @, g)	,
5. \< )	/\ce2n(x1q)dx = (-lOrA}) 4 _x	V Се2п(тг, -q
J [ ch (kshacosx) J	1 се2те (тг/2, g) j
Г
6	1 § Ъии 1 II/ 4OJL JL 4JU V/V/kJ «4V I J	/	\ f	^^ ^^fl	I ^"^ 2 Tl \ ^ 1 ~f/ I
J \ cos (fe cos a cos ж) J n '	се2п(тг/2, g) [ ce2n(a5 g) j "
о
7.	sh (A; ch a cos ж) ce2n+i (ж, g) dx =	—	 Se2n+i (a, —q).
0	п
1	I sin (A; ch a cos ж) 1	тткА] } \ Ce2n+i(a, g) I
8.	< (	> се2п+1(ж, g) аж =	-;—-.	ri	/	>.
J [8ш(Лсо8асо8ж) J	2се2те+1(тг/2, g) [ ce2n+i(a, g) J
о
sh (A; chasm ж) 1	, ч .	жкВ\ п+ ' f f^l)n Ce2n+i(a, —q) 1
/* se9 -Li i ж о 1 аж =::::	я	/¦
sh (fe sin a sin ж) j n '	2se2n+1@, g) \ se2n+i(a, g) J*
со8(^8Ьаз1пж)се2п(ж, g) 1 _ тг J 2Л^2п)Се2п(а, g)/ce2n@, g)
sin(A;shasina;)se2n+i(ic, g) J X ~~ 2 1 ^,Bfn+1) Se2n+i(a, g)/se2n+1@, g) Г
о
Г	f cos (A; shasin ж) 1
11. со8ж<	.	>се2п+1(ж, д)с!ж =
J	[ ch (A; chasm ж) J
0	тгЛ^п+1) f	sechaCe2n+i(a, g)
i . j' cos (A; ch a cos ж) 1	. ч .
12. 8шж<	>8е2п+1(ж, д) йж =
1	' ch (А^пасозж) j
2ce2n+i@, g) \ (-1)та cosecha Se2n+i(a, -q) )'
О	_„Bп+1)
cosecha Se2n+i(a5 g)
2se2n+iGr/2, g) \ (-l)nsechaCe2n+i(a, -q) )

2.27.1]	2.27. Функции Матье	305
7Г
to Г	f sin (A; sh a sin ж) 1	/ ч
13. совж< \	. ' >se2n+2^, q) dx =
J	[ sh (A; chasm x) J
0	жкВ{^п+2) /	sechaSe2n+2(a, q)
4se2n+2(Q, q) \ (-l)n coseeh a Se2n+2(a, -q) )'
f . f sin(A;chacosa?)\
14. шж	> 8е2п+2(ж, q) dx =
J	[ sh(^shacosx) J
0	nkB^ n ' ( cosecha Se2n+2(a, q)
4se2n+2Gr/2, g) \(~l)nsechaSe2n+2(a, -q) )'
sin [z cos (ж - w)] 1	_ Г 0 1 Bn) се2та(ц)Се2пН
> се2тцж] ax — < >Z7rA0 	—	г——
[ cos [z cos (ж - w)J J	[1J	ce2n@)ce2nGr/2)
0
[z = kvch2 v — sin2 -и , tgw = tgиthv].
Г J sin [2 cos (ж--ш)Ц	/ ч. fl\ l /i Bn+i) ce2n+i (ц) Ce2n+i (^)
16. <	>се2те+1(ж)о5ж = ^ >7г/сЛ^ 	—	——
J [ cos [z cos (ж - w)] J	[OJ	ce2n+i@)ce^n+1Gr/2)
27r	[w, z см. в 2.27.1.15].
f
1 7
cos [z cos (ж — w)\ J	[OJ	se2n+H4uj se2n+ii
[w, z см. в 2.27.1.15].
• Г	/	Ml	f г\ Л i 2 oBn+2)	/ \ о	/ \
sin [2 cos (ж — wjj 1	/\»	I 0 1 ж к B%	SG2n+2(u)be2n+2(v)
г /	Ч-, f se2n+2 (ж j dx = — < >	j-t	-	z—j-rz
k cos [z cos (x-w)\)	{ 1 J	se 2n+2 @) se 2те+2 (тг/2)
о
2ж	[w, z см. в 2.27.1.15].
ю f /"i./ sin a sin я П ( w _ .Bn)/ ce^CO)
19.	exp ft .	> се2п(ж)аж = 27гЛй \ -\, /лЧ
J	\ [гсозасояж]/	I ce2n (тг/2)
о	v
2тг
^л Г Г cos ж ехр (A; sin a sin ж) 1	/ ч	Bте+1) f seca/ce2n+i@)
20.	\\	у	J }ce2п+1(x)dx = жA\ Ч ., ; , , ;'
J [ ехр (гк cos a cos ж) J	[ гк/ се2п+1(тг/2)
о
21 [/ ехр (Is sin a sin ж) 1	Гж) rfx - тгВBп+1) I ^/se2n+i@) 1	, ,
J \ sin ж ехр (гA; cos a cos ж) J п	1 \ coseca/ se2n+iGr/2) J
о
7Г
Г Г cos ж ехр (A; sin a sin ж) 1	/ ч .
22. N .	PV	\ Ue2n+2 ж)dx =
J [ sin ж ехр (гA; cos a cos ж) J
0	~и ¦ ¦ ( seca/se2n+2@)
г cosec a/ se2n+2 (тт/2)
n@) се2п(тг/2) \ i cef2n(u)
» = — еи cos (ж — и) -\— cos (ж + и) = — (ch v cos ж cos ад + sh v sin ж sin и) .
8	8	4	J
e <	yce2n+1(x)dx = -—	-^—		<	,	}Ce2n+i(v)
[dw/diij	^^се2п+1@)се2п+1(тг/2) ^ 2ce2n+1(ii)
[w см. в 2.27.1.23].
2тг
e
dw/ди j n	se2n+1(O)se2n+iGr/2)\ se2n+1(ii)
[w см. в 2.27.1.23].
2тг
26.	6* <	> Se2n-f 2 [X)CLX =	г—f"	z	:—г \
j	{dw/duj	к se2n+2@) se2n+2Gr/2) I 2se2n+2(ii)
[w см. в 2.27.1.23].

306	Гл.2. Определенные интегралы	[2.27.2
2.27.2. Интегралы, содержащие специальные функции и ееп(ж, q)
или sen(x, q).
1. Jo (к (cos а — cos ж) К	/\>ах = —
О
k2[A{2n+1)/ce'2n+1(n/2)]2fe2n+1(x)
[fe2nGr/2) = се2п(тг/2), fe2n+1Gr/2) = се2п+1(тг/2)].
о Г	SlUX	T/if	\\ \ se2n + l(x) \
2. 	Ji(«(cGsa — cos ж))<	; ; > ах =
J cos а — cos х	[se2n+2(^)J
о
cosec а Г 4тг1с2 [в[2п+1) / se2n+i (тг/2)]2 ge2n+1 (а) - 32 se'2n+1 (а)
32к \^тгк [В2п /se2n+2Gr/2)] ge2n+2(a)^:
7ГD2П)J
3. Jo A;W	 се2п(ж) dx = 	т^г	'	се2п(^).
J \ V	2	I	се2те@)се2п(тг/2)
о
cos ж
vcoS2,
4^2 cos z ce2n+i @) се 2та+1 (тг/2)
sin ж
sin^se2n+1(O)se2n+iGr/2)
cos22:
sin ж	v /,
4
0032,
sin2o;
ch2,
2тг
9.
_се2п+1(ж) j ^ "" |g[Afn+1)/ce2n+iGr/2)]2ce2n+i(z)
2тг
10. 	Ji(^(cosz — со8ж))<	; : > dx =
J cos z^ cos ж	[se2n+2(a?)J
Г 4[вBп+1)/8е2п+1Gг/2)]28е2п+1(Ж)

2.27.2]	2.27. Функции Матье	307
е/2т(^СО8ж)се2п(ж)
^2т+1 (k cos ж) ce2n+i (ж)
о
2тг
12. g2m()i
J	Lse2
^2п + 2(ж) /
T
8mBm
rV2
0	X
2тг
14.	I Щ3)(к(сЪг-со8х))сеп(х)Aх = ^^	{j) n v ;	[j = 1, 2].
о	Gn \ )
15.	| Я«(fc(sh г - г sin Ж)) се21г(Ж) dx = 4г^JJ^k^O) '
2тг	2
16.	^1}(fe(shz - ^8тж))8е2п+1(ж)с1ж = 4 2n+1—	2n+Lx •
J se 2n+1 @) Gek2n+i @)
2tt
"•f
4i(ce2n+iGr/2)JFek2n+i(z)
r^Я} (^(вЬ2:*81пж))се2п+1(ж)^ж =	/^ ^	77^
shz-tsma;	к ce2n+i@) Fek2n+1@)
Г сшж rr(i)/i/i	• • w	/ \j 4(se2n+2Gr/2)JGek2n+2(^)
18. —	r^	Я} )(k(shztsmx))se22(x)dx = ^+ ) '	^4
J h
Г
J
shz-tsma;	Is cos z se2n+2@) Gek2n+2@)
2tt
f
19.
о	-+2
2tt
СО8Ж	ГгA)Л..Ли2„ , ....,1 .Л __ /^ л	 4ice2n+1Gr/2)Fek2n+1(g)
fech«Fek^n+1@)
0
J
2 \се2пGг/
21.
22-
о
Ce2n+ll7r/
ш2ж rr(i)/, AT2 i^ч /41
24. —7j	H\ iky sh z + cos2 ж ) se2n(^) dx =
J h^ + 2
(),	i^	/	o
\ iky sh z + cos2 ж ) se2n(^) dx = —-r- cosech2z se2n
H\ iky sh z + cos ж ) se2n(^) dx r cosech2z se2n I I 7it
z + cos2 ж	fe2	\ 2 / Ne^ @)
25. h(k(smz + sin ж)) се2п(ж) dx = 2тг I —^--7—г 1
. /0 (A; (
жк
26. I Io(k(sinz + smx))se2n+i(x) dx = —

308	Гл.2. Определенные интегралы	[2.27.3
f cosx T t1t	чч , ч ,	TTifc3	/ Bi2n) V , ч
27.	;	/i fcsmz + sms se2n ж йж=-		—^77^ se2n(z).
J sin 2 +sin ж	Scosz	\ se2n@) I
о	v	/
7
28.	:	It(k(sinz+ sinx))ce2n^i{x)dx =	 —	— ce2n+i(z).
J sin 2 +sin ж	2cosz \ce2n+i@) I
0	V
2.27.3. Интегралы, содержащие Сете(ж, q) или Sen(x, q).
0
Се2п+1(Ж) j	2 } kAfn+1) Fek2n+1 (a
2 i „,	«cnacnn ~wm-r±v"/ j Jm ?ri [21?! n Gek2n+i(a)/ se2n+i(тг/2)
о
4 sh a } ЛB[2n+2) Gek2n+2 (a)/ se'2n+2 (тг/2) /'
. . .' sin (kch ach x) 1 _	, N ,	тгВ!2п+1^ cosecha f Se2n+i(a) 1
О	qU mJ	X	' l Цр	ITI ЛТ 		=	 <	>
4se2n+iGr/2) (Gey2n+1(a) J
>Se2n
[() J
0
sin (kch ach ж) 1 o	, ч .	жкВ^	cosecha f Gey2fX,2(a) 1
cos(fechachx) J	8se'2n+2Gr/2) [ Se2n+2(a) J
[() J	2n+2(
0
00	C2 \
f Ce2n(a)
-7ГГ
Г Г з!п(^сЬасЬж) 1
5. < ;	; >Се2те(ж)с1ж =
J [cos(fechach«) J
77ГГ p
[() J	2се2п(тг/2) { Fey2
0
n(a) 1
n(a) J
4ce2n+iGr/2) I Ce2n+i(a) j
о
CO
Г , / cos (A; cos ach ж) Се2п(ж)
J \ sin Aг cosach ж) Се2п+1(ж)
1 f ^ce2nGr/2)ce2n(a)/A^2n) 1 Г . f cos (A; cos a cos ж) се2п(ж) , f
fe2sina 1 2ce2n+1Gr/2)ce2n+i(a)/Afn+1) J J	\ sin (A; cos a cos ж) се2те+1(ж) _
о
Г f соз(^со8асЬж)8е2п+1(ж) 1 _
J X i (A	h ) 8() j
n Г , Г cos (A; chachx) Се2п(ж) 1 .	Г . f cos (A; ch a cos ж) се2п(ж) 1 .
8» I sn x л	/ аж ^^ 	 I sin x \	У dx
J	\ sin (A; ch ach ж) Се2п+1(ж) J	J	[ sin (k ch a cos ж) се2п+1(ж) J
sin (A; cos a ch ж) Se2n+2 (ж)
_ 4 J ^se2n+iGr/2)se2n+i(a)/Bfn+1) 1 f J cos (A; cosacosx) se2n+±VM,/ .
~ ^2|28е2п+2(тг/2)8е2п+2(а)/В^п+2) J J \ sin (k cos асоэж) зе2п+2(ж) j
со	тг/2
Г J cos (fcch ach ж) 8е2п+1(ж) 1	Г J cos (A; ch a cos ж) 8е2те+1(ж) 1
J X sin (A; ch ach x) 8е2п+2(ж) J	J \ sin (A; ch a cos ж) зе2п+2(ж) /
о	о
И81п(^со8аспж)Се2п(ж) 1	. ж ( 2A^2n)[ce2n(a) - fe2n(a)]/се2п(тг/2)
I	= — i	B 4-1)
cos (fc cos ach ж) Се2те+1(ж)]	4 l к A] jfce2n+i(a)^fe2n+i(a)l/се2те , 1(тг/2)
о '	^
[fe2nGr/2) = се2п(тг/2), Ге2п+1(тг/2) = се2п+1(тг/2)
со
Г	I sin I h. рпя л гЬ 1*1 Ярп„ i I i т* i I
12.
cos (A; cos a ch ж) Se2n+2 (ж)
о

2.27.5]	2.27. Функции Матье	309
тг
8 [ kВ{22n+2)
se2n+2 (a) ~~ ge2n+2 («)]/ se f2n+2 (тг/2)
= se2n+iGr/2), ge2n+2Gr/2) = se'2n+2Gr/2)].
2.27.4. Интегралы, содержащие fen(x, q) или gen(x, q).
тг/2
Г • Г sln(kcosacosx)[fe2n(x) — се2п(х)]
J	\ cos (A; cos a cos ж) [fe2n+i (ж) — ce2n+i (ж)
о
cos (A; ch а cos ж) [fe2n+i (%) — ce2n+i (ж)] J
. cosecha ( се2п(тг/2) Се2п(а)/Ло
dX	<	,	/о _!_¦
к \се2п+1(тг/2)Се2п+1(а)/4
[fe2n(Tr/2) = се2п(тг/2), к'2п+1{ж/2) = се^+1(тг/2)].
тт/2	со
Г Г sin (А;со8асо8ж)^е2та I-|(ж) — se2n+i^)]l	Г Г sin (A; cos ach ж) Se2n+i(x) 1
3. <	> аж = <	> аж
J [ cos (A; cos a cos ж) ge2п+2(ж) ~ 8е2п+2(ж) J	J { cos (A; cos ach ж) Se2n+2(a:) J
ж/2	[ge2n+i(^/2) = se2n+iGr/2), 8е2те+2(тг/2) = 8е2п+2(тг/2)].
" sin (A; ch a cos ж) [ge2n+1 (ж) - se2n+i (ж)]
COb ^Л CIl U Luo Л j Lon + 2 V / — ®^2n + 2 v^/J
1	/ se2n+iGr/2)Se2n+i(a)/Bfn+1)l
> «Ж Z<	ч / „B71 + 2) f
J	[8е2п+2Gг/2)8е2те+2(а)/^ ;j
ge2n+iGr/^) = se2n+iGr/z), ge2n+2Gr/^) = se2n+2Gr/2)j.
2.27.5. Интегралы, содержащие Fen(x, q) или Gen(x, q).
CO
sin (lech ach ж) 1	. .
ce2nGr/2)
, . , sin (kch ach ж) 1 .
Z. I ЬП Ж^	/II	i \ f ¦
cos (A; ch a ch ж) J
= ±-
k fe'2n+i @) Fey2n+1 (a) / ce2n+i @) J '
sin (А; сЬасЬж) 1
cos (A; ch ach ж) J
k2 ge2n+i @) Gey2n+1 (a) / se 2n+1 @)
8е2п+1(тг/2) I 1	452n+i(g) Se2n+i(a)
f f sin (А; сЬасЬж) 1 „	/ ч ,
4	I <	> (тРп i of /IT —
J [ cos (A; ch ach ж) J
ж I se2n+2(?r/
Г	252n+2(g)Se2n+2(a)
I ^ Se2n+2 (°) СеУ2п+2 (a) / se 2те4
4A.2 I BBn+2) I Uge2n+2@)Gey2n+2(a)/se2n+2@)

310	Гл.2. Определенные интегралы	[2.27.6
5.	[ sh х sin (к cos bch ж) Fe2n(x) dx = ce24^/2) \жС^(я) ce /fe) _ fe2n(fe)l [0<6<тг].
J	A;sin6i4^2n) L 2	J
CO
6.	fshscos(fccosbchg)Fe2n(s)<ftc = - ^"W^V71"/2) Реу2те@) ce2nF) [0<6<тг].
J	21s sin 6Aq П ce2n @)
7.	f sh ж sin (A; cos 6 ch ж) Fe2n+i (x) dx = 7rC>2w+1(^2"+iGr/2) Fey2n+1 @) ce2n+i F)
J	k2 sin ЪА\ п+ jce2n+i@)
^	[О<6<7Г].
8.	f sh я cos (к cos 6ch a) Fe2n+1 (ж) dx = 2C6'2w+1^ \*Cwb) ce2n+1 (b) - fe2n+1 FI
J	к2 sin ЬА\ } I A	J
[0 < 6 < 7Г].
oo
о f • /i l u \o	/ \j	2se2n+i(-7r/2) [7r52n+i(g)	,,ч	,,Л
9.	sin (A; cos bchx) Ge2n+i (x) dx =	Bn+i)— 	о	se2n+i (o) - ge2n+1 (o)
[0 < b < ж].
10.	[ cos (к cos 6ch x) Ge2n+1 (*) <te = - ff^"+i(g)8^"+i(T/2) Gey2tl+1 @) se2n+1 F)
J	kB\ 'se2n+i@)
[0 < 6 < тг].
OO	L	J
11.	[ sin (к cos 6 ch x) Ge2n+2 (x) d x = - SS2n+?}Q}™ 2n+2 (?г/2) Се2та+2 @) 8е2та+2 F)
J	^3^2 ;se'2+2@)
;se'2n+2@)
тг].
io f /i и и \п	f \j	4se2n+2Gr/2) 7го2п+2(д)	/ ч	/1Л
12. cos 0 cos b ch ж) Ge2n+2 (ж) dx =	|2n+2) 	? se2n+2 (b) - ge2n+2 F)
[0 < b < тг].
2.27.6. Интегралы, содержащие произведения функций Матье.
2тг
1. I сет(ж)сете(ж)с1ж = тг<5то,те.
[те, п ф 0].
[те, те ^ 0].
2.
3.
4.
5.
6.
7.
9.
0
2тг
J
J
0
2тг
Л
J
0
I
J
0
2тг
Г
I
0
2тг
|
J
0
7
0
2тг
0
8ет(ж)8ете(ж)^ж =
сет(ж)зеп(ж)с1ж =
\се2т(ж)8е2п(ж) j
( ( \ '
I ^m+ 2п+1
sin 2*/^J^}2 Л
cos 2ж се2п(ж) с!ж =
0
te = 0.
' ЙЖ :=:::: it
/ \ "\
( Т* ) 1
(х)
с = 0.
оо
27rS
8.
J
0
эBп)
ТГ >, •
1=0

2.28.2]	2.28. Функции v(x), */(ж,р), //(ж, А), /х(ж,ш,п), А(ж,а)	311
оо
cos2*ce2n+1(a0d* = y(A^
оо
0
. lcos2xsein+2(X)dx = ж
о
-I -I Г	о	2	/ \ i	Я" / г>Bп+1)\2 . V r>Bn + l) i-»Bn+l)
11. со8 2ж8е2п+1(ж)с1ж = --«(^	+7r2B	Б
0
2.28. ФУНКЦИИ 1/(ж), 1/(ж, р), /х(ж, А), //(ж, т, п), А(ж, а)
2.28.1. Интегралы, содержащие и(сх), v(cx, p).
1. [x^vi-} dx = aa\-,	Р-.	г	[a, Rea>0].
J	\а)	J а + ж Гж + 1	L	J
о	о
2.	[(а-ж)^1!/^ с/ж = а/3Г(/3)|/A, /3)	[а, Re/З > 0].
о
со
3.	f e~pxv{cx)dx= [pln^y1	[Rep>c].
о
оо	п
4.	f xne~pxv{cx)dx = -
fc=o
Rep > с; a/g — коэффициенты разложения (s + l)n = 2_j aks •
fe=o J
5.	е рх и(сх) dx = а — v \ —	[Rep > 01.
J	V Р \4р/
о
оо __	°°
6.	-^	v(cx) dx = - ? (ж + 1, 1 - -) dx	[Rep > 0].
о	о
оо
7.	е рж?/(сж, р) ^ж = —— (in — 1	[Rep > с; Rep > —1].
J р^ v с/
о
оо	п
8.	[ жпе^рж|/(сж, р)с!ж= те^+1 ^fefcfc? (ln^)"*
о	Р	fc=o
Г	п	1
Rep > с; Rep > —1; b^, — коэффициенты разложения (s + р + 1)п ^ Л b^s
оо	L			fc=0	J
Г -рх2	рК ( С р\
9.	е uicXjp) dx = 4 / — i7 I —, — I	[Rep > 0; Rep > — 1].
J У p \4p 2/
о
о
2
10. J xe-px\(cx, p) dx = -^^v (±-, B-^)	[Rep > 0; Rep > -1].
0
2.28.2. Интегралы, содержащие \l(cx, А), /х(сж, m, n).
. f е"р>(сж, А)сгж= Г(^ +1^ln^) A1	[Rep>c; ReA>-l].
о
. f хпе^рж/1(сж, A) dx = ^гт У" акГ(к + A + 1) fin ^) ~к~Х~г
J	pn+i ^^	V c/
о
2

312	Гл.2. Определенные интегралы	[2.28.3
1
Rep > с; Re А > —1; а^ — коэффициенты разложения (s + 1)п = 2_j aks
k=o J
?	л /F /с2 \
3.	\ e px fi(cx, X)dx = 2AJ- ц ( -—, A	[Rep > 0; Re A > -1].
J	r~v7/	у р \4p J
a
Г 1 n
4.	- W3 —fj,(cx, A) cfe = Г(/3 + l)/i(ac, A - /3 - 1)	[a > 0; Re A > -1].
J ж ж
о
7 _ x2	hf /с2 \
5.	\ e px fi(cx, m, 2n) dx = 2m J- /i —, m, n J	[Rep > 0].
J	у p \4p	J
2.28.8. Интегралы, содержащие А(сж, a).
oo	,
Г	1 /тг
1. \ x e p А (еж, a) о?ж = — д / — A By/cp , 2a)	[a, Rep > 0].
J	2 У Р
J
2VP
2.
о
. f аГ5/2е^р/жА(еж, a) с!ж = ^^[AB^^, 2a + 1) - AB^^, 1)]	[a, Rep > 0].

Глава 3. ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
ОТ СТУПЕНЧАТЫХ ФУНКЦИЙ
3.1.	ВВЕДЕНИЕ
В этой главе помещены преобразования Лапласа
оо
F(p) = \e~pxf(x)dx
о
некоторых кусочно непрерывных функций, заданных различными формулами на отдель-
отдельных интервалах действительной положительной полуоси.
3.2.	КУСОЧНО ПОСТОЯННЫЕ ФУНКЦИИ
3.2.1. Ограниченные функции.
/(а)
F(p)
Mi
О
о
1
1
1
Mo
Mi
М2
[па < ж < па + bi]
[па + Ь\ < ж < па + 62]
[па + bm < ж < (п + 1)а]
[6i < b2 < • • • < bm < а]
[2па < х < Bп + 1)о]
[Bп
<	ж < Bп + 2)а]
<	ж < Bте + 1)а]
[Bп + 1)а < ж < Bп + 2)а]
[BпJа < х < Bп + 1Jа]
[Bп + 1Jа < ж < Bп + 2Jа]
[О < х < fei]
[теа + 6i < ж < па + 62]
[па + &2 < х < па + &з]
[па + fem < ж < (n + 1)а]
[О < ж < а]
[Bп + 1)о < ж < Bп + 2)а]
Ml -
т6-ар .
m —1
Mo — (мо + Мт)е ар +
(Mfc+i - Mfc)e
т —1

314
Гл. 3. Определенные интегралы от ступенчатых функций
[3.2.2
7
Q
О
9
10
-1
0
1
0
-1
1
0
1
0
-1
0
1
0
-1
0
[Bn +
[Dm 4
[Dm 4
[Dn4
[Dn4
[0 < ж < а и
[Dп4
[Dтг4
[Dт 4
[0 < ж < а и
[(8п4
[(8п4
[(8п4
[(8п4
-2)а <
-1)о<
-3)а <
-1)а<
-3)а <
4тга <
-1)а<
-2)а<
-3)а <
8тга <
-1)а<
-3)о <
-5)а <
-7)а <
С ж <
С ж <
С ж <
С ж <
С ж <
С ж <
С ж <
С ж <
С ж <
С ж <
С ж <
С ж <
С ж <
С ж <
С Bте4
[0 < ж
С Dте4
С Dт 4
[0 <Г ж
С Dп +
; Dп +
С Dта +
; Dп +
С Dп +
С Dп +
С (8та +
С (8п +
С (8та +
; (8п +
; (8п +
3)а]
< а]
3)о]
5)а]
3)о]
5)а]
1)о]
2)а]
3)о]
4)о]
1)о]
3)о]
5)о]
7)а]
8)а]
F(p)
sech ар
2р
1 — sech ар
Р
1-е ар
р(е«Р _|_ е-ар)
sh ар
pch2ap
1
2
3
4
5
6
7
о
9
3.2.2.
п
п + 1
2п + 1
п(п
п*
пт
nflm
л
Неограниченные
/(ж)
[па
[па
[па
1) [па
[па
[па
[па
[па
[па 4 Ь\
[па 4 6т-1
[6i < Ь2 <
<
<
<
<
<
<
<
<
<
<
функции.
ж
ж
X
X
X
X
X
Z а.
С X
X
<
<
<
<
<
<
<
<
[о
(п 4 1)о
(п4 1)а]
(п 4 1)о]
(п 4 1)о]
(п 4 1)о]
(п 4 1)<х]
па 4 bi]
па 4 62]
(п4 1)а]
т-1 < «]
< ж < 6]
1
п(еаР —
1
рA- е
- cth —
ю 2
2
р2/еар
е°Р4
р(е«Р -
е2ар +
р(еР
т 1
{ '
рA - е
Р
F(p)
1)
-ар)
-1)
1
IJ
-1K
— е ар dm 1
р арт 1 — е^аР
р Г
т^2 -,
fe = l -"
"ЬрL

3.3.1]
3.3. Некоторые кусочно непрерывные функции
315
10
11
12
13
14
15
16
17
18
19
20
21
те/i + и
0
те + 1
МО
те/ii + 
те/12 + ^2
0
2те + 1
-2п-2
те
2те + 1
0
те + 1
)
[па + 6 < ж < (п + 1)а + 6]
[BпН
[па +
[DпЧ
[DпН
[(п + 1/2)
те/i + i/ [a In (теЬ + с) < ж
те/i + I/
те + 1
о
[0 < ж < а]
^1)а<ж<Bп + 3)а
[0 < ж < 6]
[теа + b < ж < теа + с]
с < ж < (те + 1)а + 6]
[0 < ж < а]
- 1)а < ж < Dп + 3)а
- 3)а < ж < (An + 5)о]
[те2а < ж < (те + 1Jа]
[те2а < ж < (те + 1Jа]
[0 < ж < а/4]
2а < ж < (те + 3/2Jа]
< а1п(те6 + 6 + с)]
[а In те < ж < а 1п (те + 1)]
[а!пBте +
1) < х < а1пBте + 3)]
[па < ж < (те + 1)а]
[па < ж < (те + 1)о]
1/e-0P_(t/_/L()e-Ba+6)P
cosech ар
2р
if 1
V(l с"Ьр) !
р 1^ик" " ; ' 1~е^аР
х [i/iep + (i/2 ^i/i)e"cp -
е~ар
^2С A - е™аРJ
x[me-bP + (№_m)e-cP_^
sh ар
2р ch2 ар
2р
— б^з @^ в )
р
2р
1(/1/ С\ /1 1/ |
р \baP \Pj b) caP ' F + c)aPJ
1 2_ар
р
A"е"прЧИ| ,1~е'ар)
р V 1-6е^аР/
1
р(еаР - 1)т
™"С(р + ?/) [Rep > — Re v + 1]
р
3.3. НЕКОТОРЫЕ КУСОЧНО НЕПРЕРЫВНЫЕ ФУНКЦИИ
3.3.1. Степенные функции.
1
Aijc
А2Ж
XjfiX
[па
[па + 6,
[теа
+ 6i
<
<
Ж
Ж
ж
< теа
< теа
< (пЛ
+
+
- 1
)а]
Р2A
1
- е~аР
т —1
+ J2
к=г
J
Г
- Ai +
-АО
т-1
- ^ (
fe = l
Пр)
(ар 1 ар т
Afe+i — Ад.) х

316
Гл. 3. Определенные интегралы от ступенчатых функций
[3.3.1
f(x)
F(p)
О
Аж + 71/i + У
\\Х + ГЦ11 +
Л2Ж + 71Д 2 +
X
X
0
ж
ж
— па
b
— па —
Ь-с
— 2па
Ъ
- Bп-
- с
10
6 — а
О
ж — 4тга
—	х + 4па + 2а
О
ж — па
—	х + тга + b
О
ж - Bп + 1)о
6
ж — 2тга
[па < ж < па + 6]
[па + 6 < ж < (тг + 1)а]
[тга < ж < (тг + 1)а]
[па < ж < па + Ь]
[па + 6 < ж < (тг + 1)а]
р2A -
А и
	1	I
2
а
_ е-ар)
Р2A_е-ар)
[па < ж < па + 6]
[тга + 6 < ж < па + с]
[?га + с < ж < (тг + 1)а]
[па < ж < па + 6]
[тга + 6 < ж < тга + с]
[па + с < ж < (тг + 1)а]
[2тш < ж < 2па + 6]
[2па + b < х < Bтг + 1)а]
[Bтг + 1)а < ж < Bп + 2)о]
[4па < ж < Dтг + 1)а]
[Dтг + 1)а < ж < Dтг + 2)о]
[Dтг + 2)а < х < Dтг + А)а]
[па < ж < па + Ь]
[па + 6 < х < па + 26]
[тга + 26 < ж < (тг + 1)а]
[тга < ж < Bтг + 1)а - 6]
[Bтг + 1)а - 6 < ж <
< Bп + 1)а + 6]
[Bтг + 1)а + 6 < ж < (тг + 1)а]
[2па < ж < 2па + Ь]
[2па + b < х < Bтг + 2) а - Ь]
p2(l - e~aP)
i	th^
Не"") 2
p2(l ^e^2ap

3.3.2]
3.3. Некоторые кусочно непрерывные функции
317
/(ж)
F(p)
12
-х + Bn + 2) a [Bn + 2)о - 6 < х < Bп + 2) а]
Лож	[0 < ж < 6i]
Л1Ж
[па + bi < ж < па + 62]
па + 6т < ж < (п + 1)а]
[6i < 62 < . . . < Ът < а]
х [Ао + (Ао — Аоа — Хта)р —
(Ао + Хт)(ар - р
13
14
15
16
[0 < ж < а и (An + 3)а < ж < Dп + 5)о]
1 + ар th ар
[Dn
ж < Dп + 3)о]
[0 < ж < а]
- 2па - 2а)	[Bп + 1)а < ж <
17
18
19
20
ж
О
ж + (-1
а- ж)	[2а < ж < Bп + 2)а]
О	[0 < ж < а]
(тг + 1)(ж — па — а)	[Bп + 1)а < ж <
пж - п(п + 1)а	[2па < ж < Bп + 2)о]
Bп + 1)ж - гг(п + 1)а	[па < ж < (п + 1)о]
2р2 ch ар
sech ар
th ар
Р и
coseco ар
2р2
р2(е2ар^;
-— cth —
р2	2
- а) +
[па <
¦1)
(ж — тга)
х < (п + 1)о]
[па < ж < (п + 1)а]
2	аBр + а)
^3" ~ п2(^ар __ 1\
3.3.2. Разные функции.
F(p)
[а(х — па) — (ж — паJ}1"	[па < ж < (п + 1)о]
тгГB?/ + 1)	ар / а X^+Va
cosech — ( — I	x
[Rei/ > -1
х
I/ + 1/2
±[2а(ж - 2па) -(х- 2naJf
2па < ж < Bп + 1)а
Bп + 1)а < ж < Bп + 2)а
ГГ21/
+1/2
(
V 2 /
, Rei/ > -1
: cosech ар Lv+1/2 (ар)

318
Гл. 3. Определенные интегралы от ступенчатых функций
[3.3.2
J2 (ж-In те)"
bn
[Rei/ > -1]
[па < ж < (п + 1)о]
[па < ж < (те + 1)а]
[па < ж < (те + 1)а]
A-62)
сте sin 6n
cn cos бте
[па < x < (те + l)o]
[na < ж < (те + l)o]
[па < ж < (n + l)a]
p(eap
fi-T_
1
1)
-1
-6)
^-6K
csinb(eap -
[Rep > Re In b]
[Rep > Re In b]
[Rep > Re In b]
p(e2ap _ 2ceaP COS 6 + C2)
[Rep > Re In с + |Im6|]
p(e2ap _ 2ce°P COS Ь + C2)
[Rep > Re In с + |Im6|]

Глава 4. КРАТНЫЕ ИНТЕГРАЛЫ
4.1.	ВВЕДЕНИЕ
В этой главе помещены двойные и многомерные интегралы, содержащие специальные
функции. Кратные интегралы с другими специальными функциями, а также ряд формул
общего характера, с помощью которых кратные интегралы сводятся к одномерным, приве-
приведены в [17, 18].
4.2.	ДВОЙНЫЕ ИНТЕГРАЛЫ
4.2.1. Интегралы, содержащие функции Н1/(ж), Л1/(ж), herl/(xI Ье11/(ж),
()
о о
2	3/2, i/ + 3/2
о о
X
Vl, a/2, /3/2; -с2/Dа6)\ 1 . ^ Г (а + 1)/2, (/3 + 1)/2] -(a+i)/2,-(/з+1)/2
Ч 1 +«//2, 1-^/2 j + 8Sm 2 LC + )/2 C)/2ja
3.	^-i^-ig-»* -ь» ber (СЖ|/) dx dy =
_ Г(а/2)Г(/3/2) ^ /a/4, (a + 2)/4, /3/4,
4:a-/-u^/-	\ i/z, l/z, i; ^c / {IDC L ч
OO OO
4aa/26/3/2 4^ 1/2, 1/2, 1; -с4/A6а262
[Rea, Re/3>0].
A I I a-i ^-i -а*2-ь„2к ./ ч , , с2Г(а/2 + 1)Г(/3/2 + 1)
4. \ \x yp e	bei (ежу) ^ж dy = 	ig^/o. т, д/о. 1	 x
(a + 4)/4, (/3 + 2)/4,
4	2 2
1, 3/2, 3/2; -c /A6a 6 )	/
CO OO
5. \\xa yp e	y \herl/(cxy)+heilJ(cxy)\ dx dy = ^/9 ¦ |У, д/9 , |У х
2-2i/-2J2i/
[a/2 + i/, /3/2 + 1/1 /(a+ 2i/)/4, (a + 2i/ + 2)/4, (/3
+ 1 + 1 J44	( l)/2 //2 + 1, i/ + l; c4/Da262)
[Re (a + 2i/), Re (/3 + 2i/) > 0].
-2i/-2^2i/-1
2-2^c-
6.	xay e ax by [her1/(cxy)her'l/(cxy)+ heiv(cxy) hei'v(cxy)] dx dy =
_ Г a/2 + i/, /3/2 + 1/1 _ /(a+ 2i/)/4, (a + 2i/ + 2)/4, (/3 + 2i/)/4, (/3 + 2i/ + 2)/4
2, i/ + 1; с /Dа о )
X
[Re i/, Re (a/2 + i/), Re(^/2 + i/) > 0].

320
Гл. 4-
интегралы
[4.2.2
т.
1, (а
4.2.2. Интегралы, содержащие iFi(a; 6; ж).
Fi(a; b; -cxy)dxdy =
, (/3 + /х + 1)/2; -c2/Dafe)
3)/2, (fi + v + 3)/2
[Re (a + /х), Re (/3 + ц) > -1].
2.
3.
4.
5.
в.
a + P + 7
a, 6^a, ДB, a), ДB,/3); e2/64\
1(a; b; x(l - y)) 1F1(af; bf; 1 - x) dx dy =
1
(ft, b1) Ul-tf^^fi^tFtia + a; b + b''; 1 - t) dt.
0
a; b';
= B
{щ b] xIF1(a; b'; y) dx dy =
= BF, bf
&;; t) dt.
ГF/2)Г(F + 1)/2) / a, 6 - a
2FiU
ГF)Г((Ь+1)/2)
a, 6 - a
4.2.8. Интегралы, содержащие 2^1(^5 b; с; ж).
l l
i I I/ \c —I/-»
. lUxy) A
x2F1[a,b;c;
1
-хГ ~ ^(l-y)a^d(l-uxya(l- vyya x
uv xy	\ , , „ [c, c, d — c, a — 6 — d + 1
— ux)(l — vy)
41
[Rec, Re(ci-c), Re (a - 6 - d + 1) > 0; |u| + \v\ < 1].
» ж 2/
a, a + 1; 6;
(I —
da; dj/ =
= Г ' / C,' . F4Ba, b;
[c + 0, d + oj
b, d + b; u, v)	[Re6, Rec, Red > 0; x/R + л/R < A •
L	J
3. \\{xy)c-1(l-x)d-1(l-y)a+b-2c-d{l-ux-vy)-a2F1 (a, b; c; - ^ Ж|/ ) rfx dy =
J J	V	1 — гхж — г;2//
о о
= 1
с, с, d, a + 6-2c-
a, a
— d + 1
4@,, с; c + d, a + o — с — d + 1; гх — wv, v — uv)

4.2.4]
(.2. Двойные интегралы
321
[Re с, Red, Re (a + b - 2c - d + 1) > 0; |it| + \v\ + \uv\ < 1].
4.2.4. Интегралы, содержащие pFq((ap); (bq); x).
dx dy =
Bl
K), A(m, a), A(n, /3);
, Д rn + n, a
2.
4.
dxdy =
_
— 1
a + 1, /3, 7, /3-
3 + 7, « + /3 + -
(ap), A(m, /3), A(n, 7), A(m + га, /3 + 7 + ^); см
[Re a > -1; Re/3, Re7, Re [f3 + 7 + 5) > 0, 11 = mmnn(m + n)^m^'
Rfn nJ^-'/W	P	/(ар),Д(т, а),Д(п,/3); cUim+rl\
D(a, p) t	j{t) p+m+ntq+m+n 1	I at
J	\	F9), A(m + n, a + p)	J
0
[Re a, Re/3 > Q; и = mmnn(m + n)"m"n].
к	т" <i/p p~
о.	ж I/ e
о о
с,
(ap), A(m, a), A(n, /3); сгь
р+то+тг^™
[Re a, Re^, Re7 > 0; и = mmnn(
J а*ж б?2/ :=
. Г(а)Г(/3)
(ap), Д(т, a), A{n, /3)
(bg); c(m/a)m(n/b)n
[Re a, Re b, Re a, Re /3 > 0; g > p + те + n — 1 или | arg(—c)| < (p — q + 1)тг/2 при р = q, q + 1].
6- J Jaje
0 0
(ар), а, а + 1/2, /3, /3 + 1/24
Fq); 16c2/(a262)	/
3; Rea, Re6, Rea,
7
8.
(bq
[p ^ q; Re a, Re 6, Re a > 0].
(ap);
dx dy =
, /3, a
(ap), A(m, a), A(n, ^), A(m + n, a + ^ + 7)
(bq), A(m-\-n, a + p); cm n
Re a, Re/3, Re (a + /3 + 7) > 0; q > p + m + те - 1 или |arg(-c)| < —	— при p = q, q + l\.
11 А. П. Прудников, Т. З

322
Гл. 4-
интегралы
[4.3.1
4.3. МНОГОМЕРНЫЕ ИНТЕГРАЛЫ
4.3.1. Интегралы, содержащие pFq((ap); (bq); ж).
Обозначение: dx = dx\ dx^ . . . dxn.
dx =
2 f
n); c/4
fe = 1
, a); cut
an, этг = mi + . . . + mn, it =
(%), A(mi, ai), . . . , A(mn, «n)
[га = rai + . . . + mn; Re ад., Re a^ > 0, A; = 1, 2, . . . , те].
CO	OO
c + с — га; ^
4.3.2. Интегралы по сфере.
c;-Xk
jr + ^a-^ (w + l
a, b\ [	(n + l)c - n
[Rea, Re6> n/(n + l); A > 0; n = l, 2, ...].
Обозначения: ж = (sci, . . . , жп), a = (ai, . . . , an), | ж | = у xf + . . . + х„ , a ж =
+ . . . + anxn; a = (<n, . . . , <rn), |cr| = 1, da — элемент площади на сфере \<т\ = 1; Дт(сг) —
(	^
сужение однородного гармонического I т.е. удовлетворяющего уравнению Лапласа
V
дх1
д2 \	\
+ . . . + ——— 1 Rm(x) = 0 1 многочлена порядка m от га переменных xi, . . . , жт на сферу
= 1.
'• J
(n-l)/2
¦±Л f /(M*)(i-t2)(n-3)/2^(*)
ж / j
dt
2.
m(i) = Tm(i) при n = 2,
(n-l)/2 I
f
при

4.3.3]
(.3. Многомерные интегралы
323
Г	•	а
4. | \xa\aRm(a)da= ^^\хГтГ^
а + 1, (га - а)/2
(т + п + а)/2
а + 1
-га + п)/2, 1 + (а - га)/2
5.
6.
Г?1... «Г*1
Г Г m = 2, 4, 6, . . . ; т ф а + 2, а + 4, . . . ; I
[ [ 771 = 1, 3, 5, ... или т = а + 2, а + 4, . . . ;
п 1
п —
Re а > -1
Re а > -
'• J
|сг| =
'• J
da
2	\ 2
[Q — положительно определенная квадратичная форма].
2тгп/2	?	tm~1dt
Г(га)Г(п/2 - га)
. . . (t + an)
[ak > 0, к = 1, 2, . . . , n; 0 < m < те/2].
4.3.8. Разные интегралы.
Обозначения: см. в 4.3.2.
оо	оо
L =
ПРИ <* * 2' 4' • " • 5 A =
2.
dx
	 ГПЧРГ
Г(п/2)	2
ка In к
при а = 2, 4, . . . ; 0 < а < 1 .
[|о| < г; 0 < а < 2].
ХA-
= гГ1'
ата, 7
_ «. \7-«1-...-ате-1
. . . |^1 ^C-j^Z^J Ct Ж =
l, . . . , ап, —y^i, . .
. -0п, 75 ^i, • • • , zn)
, Re G - «l - . • . - ап) > 0; | arg(l - zk)\ < тг; A; = 1, 2, . . . , n].
4.
i, ..., an, 75 ^l, • ••, zn)
an, 7 - ai - . . . - an
7	J
Re G ~~ a\ — ... — an) > 0; | arg(l — z^)\ < тг; к = 1, 2, . . . , n].
1 1
5. J . . . I x?
71"1 . . . A - Xn^-^-^l - xlZl - . . . - sn*n)*daj =
о о
= Г
ап, 7i
7i»
( — 0, «1, • • • , «и, 71? • • • 1 In', Zi, . . . , Zn)
[Re «fc, Re G^ — ад.) > 0; | arg A — zk)\ < тг; A; = 1, 2, . . . , n].
11*

Глава 5. КОНЕЧНЫЕ СУММЫ
5.1. ЧИСЛА И МНОГОЧЛЕНЫ ВЕРНУЛЛИ Вп, Вп(х) Ш ЭЙЛЕРА
Еп, Еп(х)
5.1.1. Суммы, содержащие Вп.
t t , (-l)-t
nt2n+1
3-
2n+4
'• E
2 b2	Bn)!2
= a|C(o + l)-i + (o + i;
n + k)\ D
B2n+1(r^[r})dT
1; a^O; Re a > -2n - 1].
= 0.
= 0.
*
"
2k
^ {2k + a)\{2n - 2k + \)\{2m + 2k + 2a + 2)\
[0 ^ 77i ^ n; <J = 0 или 1]
+122ra+"Bn+a)!
j D+2 + l)!
[0 ^ m ^ n; cr = 0 или 1].
9.
24n-l
Dn)!4
B2k - 1)B2' -
pt pt BA;)!B/)!Dn - 2k - 21 + 4)!
5.1.2. Суммы, содержащие Вп(х).
2.
x ±
2n
- n ± n) + Bm (x
1± 1

5.1.3]	5.1. Числа и многочлены Бернулли ВП1 Вп{х) и Эйлера ЕП1 Еп{х)	325
. ^—v „ / x + mk \ fmxp^1 ^—v / ж + n^ \
4. > i?D I 	 I — 1 —	У ^p 	 •
ip	I 1	7 р
m —1	/	о 7
n-l
та —1	/ kl\
6. ^ kB2m i — I :=: —(^ m — l)^2m	[^5 те взаимно простые].
fe=l Vn / 2
fe=
7.
k=Q
к—0
[n/2]
Г /ol
)t \Bk+n [x - -tj + (-1)	B*+B
fc=O	v	" 7
1
2n + 2 "	^ k\	|"»-r»-r-i- ¦ t iv -/	Bfc+n+1	^
max (to, n)
fc=O
= Вт(ж)Вп(ж) + (-1)т-т	:—^r~Bm+n	[m + n > 2].
max (rn, n)
12.	^
fc=O
13.	~~
= (±l)n \n j x ± у - ^^ } Bn-!(x ±y)-(n- l)Bn(x ± ;
14- Е(^)^В*(х)Вп-,B/) = ^(^)^^(^+ж)В"-*(«)	[а любое].
k=0	fe=O
5.1.3. Суммы, содержащие Еп.
fe=O
ХАгь n^ U I.\All Arvl.A	{An, T^ Alft> n^ /	V "^	^^ / \	"^	/
[0 ^ m ^C n; «г = 0 или 1].
П /
/I V4 I	1 D IP	/1 _L fJ^ O4n-1\ о
- /2n + l
/, I of. _l 1
fcO \Z^ + 1

326	Гл. 5. Конечные суммы	[5.1.4
5.1.4. Суммы, содержащие Еп(х).
k=0	fe=O
2
2. JT {-l)kEm (x ± ^py) = ±Bn + l)-mEm ({2n + l)x - Bn + lI^) =F
fe=O
n — 1	/	.
fe=O
2 /2m V ^ , ^kn (x + nk
2m
5. ^J(±l)fe ( 'I ) Ek(x)En^k(y) = 2(±l)n | ( ^^ Tx-y) En(x ±y)± En+1(x ±y)\.
k=0
6\. I	iK ел/Чел	/\ \. I i iK гр I i tf	\ tp	/ \	г	г ~\
^-^ \h /	*-^\kJ	\	t /
k=0	fe=O
(tj\1?	.Г	/ 'y* \	/ 'y -4- 1
I I 2^кЕьЕ л. -ъ(т) = 2m+n \E \-\E I
. ife УJ	m+n l ;	I m \2/ n V 2
8.
k=0
n	n
9. ^ (^)tfcBfe^)?Jn^fc(|/) = ^ (n)tkBk(x + a)?7n_fc(y + at)	[a любое].
5.2. ФУНКЦИИ ЛЕЖАНДРА РДж) Ж <Э^
(При /л = О, I/ = п см. также [18], 4.3)
5.2.1. Суммы
= ^— [(±1/ Т
-„+1W + I-IJ lM + ^ + ^ +
[Д^(^) = ^(z) или Q^{z)\.
fc=O
3. }^
fc=O
к=о	2	2 [ж-1 ж + l	J
fe=O
n
6. X"Dn-4k-
x)	[* > 1].

5.3.1]	5.3. Обобщенная гипергеометрическая функция и G-функция Мейера	327
(±l)k pfc-n/ ч
k=0
'•
8. ^
[п/2]
10 Y
1-
5.2.2. Суммы, содержащие произведения функций Лежандра.
т+п
2. ^ Bk + ljPr^)^"^) = л	-P?+n+1(tt)P?+w(s)	[-K Ж < 1; m ^ 1].
з. 2^(
k=0
[x > 1; те > 1].
5. ^[^S"fc	^ (V)
flfel	fsinna
[-1 < x, у < 1].
у/ .,tBn-<;)!fsiiibLIM M) _
^	kl [cosfcaj
= (^l)n( Slnna }pn (xy - v/(l^x2)(l^|/2) cosa)	[-1 < x, у < 1].
[ cos raa J V	/v^/	у
5.3. ОБОБЩЕННАЯ ГИПЕРГЕОМЕТРИЧЕСКАЯ ФУНКЦИЯ
pFq((ap); (bq); ж) И G-ФУНКЦИЯ МЕЙЕРА
5.3.1. Суммы ви да \J QLkP+iFq(—k — m, (ap); Fg); ж).
-i
—гг — 1,

328	Гл. 5. Конечные суммы	[5.3.2
2. 2kP+i
k=i	^ ^ q^
. V-, л\к(п\	(-к,{ар)
- ^, Л^к(п\	f-2k,(ap)\ ЩарУп ( ,n	( -n, (ap
а у^ (а)к F (-к, (ар)\ _ (а + 1)п _ ^ ( -п, а, (ар)
_ ^ /n\, ч /лч	_, f—k, (ap);
7. g(J(«)(^^( 'i
к=0
(a-n-l/2)k p+lF4 F
6,)
I / ffi 	1	 Ill	/ 	fi f~y in i • /ТЙ
n!22«C/2-a)n p^z 9""Ч 3/2, F,
a \4 iN<fe^\(«)fc p f-k, (ap); x\ _ @^аУп „ / -n, a, (ap); ж
\г р (	1 р -п, -п, (ар)\
—m — k1 (ар); ж
5.3.2. Суммы вида Л^ ак р+2^я(—к1 и + /г, (ftp);
¦	/-n-1, n + 2, (ap)-l\	/-п, п + 1, (ар)-1
П(^д)п

5.3.4]	5.3. Обобщенная гипергеометрическая функция и G-функция Мейера	329
5.3.3. Суммы вида V^a*. p+iFg(—A;, (ap) + k; (bq) + k; ж).
^-\ /ra\ Bа + 2n — lJfe , x
fc=o	^а П^
/-2n, 2а + 2п-1, (ар)
— р+2-Г g I	/, ч
fc=O
'—ra — n, (ap); ж
QL — ft, (bq)
5.3.4. Суммы вида \, ak p+iFq(—k, (clp) — rnk\ (bq) — nk\ ж).
—n, (ftp); ж
1
2n
/ ^ I i. /	TJ(~l	\ P+1 <? I /l \ ь
k=Q v « / IK1^*;	V l°gj "~ ^5 x
к V^	tfc	ПС1 - Mfc с, /"-^ ^ <r/2, -A; + A - <r)/2, (ap) - A;
*-* • • ~	* \ i /л i '. ГТ т—r / -.	\ p-|-2 ¦* qf I	/1 \ i
al ,	1	lOI 	 K* • T*
Bra + ст) ПA " aP)n	V	(^) - n; ж + 4/t
Д/п\ (-ж)"*	п_^_! ПA ~ Mfc	/-fc, a-fc, (aP)-fe
i^^^l")*	j	ПA«Р)*Р+2 q{(bq)-k; (ka + l)x
7 V l 'ь ]fk l ilx ~ Uq)k	F I ~^' ^ttp^ ~~ ^ 1 = tn
^k^ ПA-ар)* P+ V (&*)-*;; ^ /	ПA - aP)n Р^^\(&д)-п; ж-1/*
8. )_^(i 17т~ж~ ТТЛ	V" p+i^g
(Q)n ^nU(^-bq)n	( -n, (ap) - n, P - a
= TbVX TJ(l - a ) p+2 ^
^fc ori ^ ^	/-fe, (ap)-A;, a
fc n(i - ap
- 6g)n r f-n, (ap) -n, a-/3-n + l
(/3)n ПA - aP)n P+2 q
—A; — m, (aP); ж
^-A;, (bq)
~m — n, (ap); ж
Д, Fg)

330	Гл. 5. Конечные суммы	[5.3.5
5.3.5. Суммы ви да ^ «fc pFq((ap) + k(cp); (bq) + k{dq)\ ж).
4 (b у
\(	\	Г	/а + п, (ар)-1\	/а-1, (ар)-1
)_1x )	(ъ
(ар), Д(т, а), Д(т, а-/3 + 1
(b9), A(m, a-^-n-1); a
(Р - a)n	„ ( Op), A(m, /3 - a + n); x
f o\	p+m^ q+2n
л \Ч 1
h	^k)(P)k{ Fg),A(m,/3 +
_ (P - a)n	„ ( (%), A(m, а); ж
^ /n\ xk Шар)к *р (M + к] x\ _	((ap), р + щ x
+ CJ + 1/2, (ap);
		_	f(ap),a-n,
о V Ж ll(aP/fc 177 /	\ap) + »; Ж	\ _	^	|-r |-r !
о
1)
(ар) + 1;ж \ жп+1 ПЮп+i F
x PFq+11 /L x , 1 Q ,_ 2
:P^g+i
io. jr(n2-к){-^ггШь
); ж
, (ap)+ Л
1

5.3.6]	5.3. Обобщенная гипергеометрическая функция и G-функция Мейера	331
1 ( 2п\ Г	( (а ) 1/2" х \	((а ) 1/2*
= О\	I Р+1^ + 2( /L \ -I	III + P+l-^q + 2 I	/, ч 1
(op), (/3 -
bq), /3 - 1, (/3
; x
5.3.6. Суммы вида ^«fe pF4((ap) — fc(cp); (bq) — k(dq); x).
F9) - 1; ж
ч V^ l I? I v"p/' " "" л 1 I Or I \ / о\ 1 I On, i\^ o\ I w
2. > fep+ii^g . .	I = I Па* - l)(ai - 2)	I 1F^ - l)Fj - 2) х
2 Г	/(ap)-2, a-
i=i
p+2m J4 q+m
(ap) — 2, a — n — 1
Fq) -2; x
), A(m, a-n)
		/ (аР); ж
fc=O
? — а)п	р / (аР), A(m, y5 — а + гг); ж
. ^ a)n P+m 9+2mU^), A(m,/3), A(m, ^ - а)
ft j* Ж
(ар), А (га, а — &);
_ (Р — Ot)n
7- z^
- fa) Ж-"ПA-Цп	/ (ор) - п, 1 - а; ж
Jap), а — /г; ж\
(fe9),/3-fe ; =
(Р - а)пХп \\{ар)п

332
Гл. 5. Конечные суммы
[5.3.7
Q
(ap) ^k, a
\ ( Х) V
(
5.3.7. Разные суммы, содержащие pFq((ap); (bq); х).
те	т
П r(bi-bk) П Г(Ьк-сц + 1)
п	г=1	г=1
	z	 X к X
К) -п, а~
П 1
г=п+1
f[ Г(сч-Ьк)
i=m+l
— Gnm г
[р < q] или [р = д; |ж| < 1].
П T(afc - а^) Д r(bi ~
2.
*=i П r(ai -
5
П
¦ж * х
l-ak + (bq); (-
,. .. , од.-1-afc + l,
5.3.8. Суммы, содержащие G-функцию.
Обозначения: к, т, n, p, q, r, s = 0, 1, 2, ...
< р] или [^ = р; |ж| > 1].
к=0
_(«-,
^n+r
2-
тр+7% g + ?
A(r, a - /г), (op)
(Ь,), Д(г, /3-fe)
Д(г, a), (ap)
(Ь,), Д(г, /3 - 1)
[Re (а - C + s) > 0; т + те > (р + д)/2].
А(г, а + s), Fg), A(r, ^-s)
A(r, a-A;), (ap) \ _
A(r,a), Fg), A(r, /9-Л)
[Rea < 1; m + те > (p + g)/2].
(Ph
г, g+r
A(r, a), A(r, a + /3 - 1), (ap)
Fq), A(r, a + /3 + s — 1)
[Re (a + /3 + e) > 1; m + те > (p + g - r)/2].
r, g+r
(ap), A(r, a + fe) ^ _
F,), A(r, /3 + fe)
(ap), A(r, a + s
5
(ap), A(r, a-s)
(r, a), A(r, /3), F,
[Re (a- 13 + s) >0; m + те > (р+ g)/2+ r].
[Rea<s + 1; m+ те > (p + q-

5.3.10]	5.3. Обобщенная гипергеометрическая функция и G-функция Мейера	333
A(r, a). (av). А (г, в + k) \
i
A(r, а-в), (ap), A(r, /3 + s)
г, n+r
[Re a > 0; m + n >
7- ЕЧт
7)*
;)<w;
g + r
A(r, a — /г), (ap) \ _
(bq), A(r, a + k) J
A(r, a + 7), A(r5 a - 7 — s), (ap)
F9), A(r, a - 7), A(r, a + 7 + *)
(ap), A(r, a-/г) \ _
(ap), A(r, a — 7 — s), A(r, a + 7)
A(r, a — 7), A(r, a + 7 + s), Fg)
B/3).
rp+2r,g+2r
(ap), ABr, 2a -A;) \ _
ABr, 2a + fe), Fq) /
(ap), A(r, a + /3), A(r, a - /3 - e + 1/2)
A(r5 a + /3 + s), A(r5 a - /3 + 1/2), (bq)
^•E
Jp+r, q+?°
(ap), A(r, a + fe)
A(r, a + 2A;), (&g)
(ap), A(r, a-^-
A(r, a-/3), Fg)
_i), ap + A;
k, 62, • • • , bq
[m + n > (p + g)/2].
< p; q ^ m ^ 1; Re F1 — op) < n].
5.3.9. Суммы, содержащие многочлены Неймана Оп(х).
г„\ ^^ndnOm+n(x)
к=0
dxn
2.
3.
к=0
х
[<т = 0 или 1].
5.3.10. Разные суммы.
s . ( n =F п\ ,. (	1 =Ь 1 \
= п (h^nv	—) +С [в, v + —-—).
k=0
4 =n4(

334	Гл. 5. Конечные суммы	[5.3.10
n
) 2
~ 2-^F T(n + v + 3/2)
n
4. ^(-l'(")'/2
О („ - „ + 1/2). W'*k- -1"' '(,.-/+ 1/2).
./.,.-./. W-
(a)nxn fa + n; x
lF4
_ (^l)n(l — b)n ^ (a — n; x
2n\	(а)кBа~2п~1)к	к p f	a + к; х
к ) (а + 1/2)кBа)кBа-2п-1Jк	1 2 \a + к + 1/2, 2a - 2n
= r,a + l/2, 2al^_2ar2

Глава 6. РЯДЫ
6.1.	ВВЕДЕНИЕ
В этой главе приведены суммы рядов, содержащих некоторые специальные функции.
При преобразовании таких рядов, в частности при их приведении к форме, которая принята
в этой книге, можно воспользоваться формулами из приложения П. Формулы раздела 6.8
дают возможность находить суммы гипергеометрических функций и с помощью формул
раздела 7.3 — суммы рядов с различными элементарными и специальными функциями.
6.2.	ОБОБЩЕННАЯ ДЗЕТА-ФУНКЦМЯ ?(s, и)
6.2.1. Ряды вида y^afctfc((g ± к, у).
со
1. J2 **С(*> v) = *hH«) - iK» - *)]	[1*1 < f < i]-
k=2
oo
2-
k = 2
3.
4- Er
^, v) = -[2(T4p(v
_, /	\
l; a = 0 или 1].
5. V
f ^
+ 1)
6.
= 2 In r(v) + A -
In (г; - 1) - In Bтт) + 2v - 2
[arg |v - 1| < тг;
0, -1, -2, . . .].
[1*1 < Ml-
s, v) -
[-27Г < t < 0;
1, 2, . . .].
arg ( v - - ) < тг
6.3. ЧИСЛА И МНОГОЧЛЕНЫ БЕРНУЛЛМ
Еп, Еп(х)
6.3.1. Ряды вида Л
, Вп(х) Ш ЭЙЛЕРА

336	Гл. 6. Ряды	[6.3.2
°°	t2k	1	? 2
ЕС)* Bfc)!(fc + 1} В™+* =	2
00	f2fe	2
9. ^(^l)fc {2k + 1)!fe B2k = - Ch(t) + 2 In |t| - 2	[|*|<2тг].
k=l
6.3.2. Ряды вида y^j akBkjx + ,
00 4-к	п,„хи
k=0	v
00	лк
x) = (п — l)!(^t)~n — е1жФ(е*, 1 — га, ж)	[|t| < 2тг; п = 2, 3, . . .]
, _ t ( cosech (t/2) ch ?(ж - 1/2) 1
fc=O
4 Vf+-nfc t2fc+1 p , , t fcosechC^sh^- 1/2I	ri/1^2 1
* ^ } Bfc + l)! 2fe+H j 2\cosec(t/2)sint(aj-l/2) /	Ll '	J'
E\k/ \k ( ктг\
(—1) Bra) Bk(x) cos I 2пж H	1 = nctgn	[n = 1, 2, 3; 0 < x < 1].
6. YVl)feBri + l)fcBfe^)cos ГBп+1)ж+^1 =?2±lctg?2±l [n = 0,1,2; 0<«
fc=o	L	2 J 2	2
6.3.3. Ряды вида V^
S^y^fc =sech?	[\t\ <тг/2].

6.4.1]	6.4- Функции Струве Ну{х), Вебера Е^{х) и Ангера Jv{x)	337
6.3.4. Ряды вида ^^akEk(x + ку).
fsech(t/2)cht(a!-l/2)\
sech (t/2) sh t(x - 1/2) 
6.4. ФУНКЦИИ СТРУВЕ Н„(х), ВЕБЕРА Еи(х) Ш АНГЕРА Jv{x)
6.4.1. Ряды, содержащие Шу{х).
rHv(kx) = , y \	=BтгУп+1 - x
2пЧ
x >
Ж л \ —¦— -^ / -ш-т / »	\	\™^ I ** I	.	«I «л/	| -L
0Fr(^ + 3/2) + 2-+ir(i/ + 1) \ 0
[-A=р1)тг/2 < ж < C±1)тг/2; Rej/ > -3/2]
/, \ 7Г cosec ал- Г cos
( ) =I
fc	7Г cosec ал- Г cos air "I , . тг Г1
I	}H() + |
^GгТ7Г)/2 < ж < C±1)тг/2; Re и > -3/2].
а у тг i ^ -+- of z)	Ad ~
[0 < ж < тг; Re i/ > -7/2].
oo
E
Н^)	ЛМ [E()E()] +
2^)
00 /	l ЛЛ jt.	1
Е^ТН°(А:Ж) = 
[0<ж<2тг].
Bfe +1)	Bnl)!2^F V2J UJ ^ V fe
X ^n^fe^lF l	;/	[-тг/2<я; <тг/2; Re i/ > -1/2; n = 1, 2, . . .].
|_ /c/z + I/ + IJ
fc=0

338	Гл. 6. Ряды	[6.4.2
[-тг/2 < ж < тг/2; Re г/ > -1/2].
' 0 < х < а '
- а < ж ^ ^ -
is. Е^нЛм = - ' '^+1
(х/2)и+1 Г
14.=	л-w . » ^ч U- -1 !~ ^ 1	b^il	, q/o
- o/z
[О < а < ж < тг; Rei/ > -1].
6.4.2. Ряды, содержащие E(/c)i/(sc) .
2- g
\k
OO
I] w2 Е2те+1 ^Ж) = ^Г IctS a7rE2n+i (аж)+J2n+i (аж)]+
	 AC —ft	zlfl	(zI?l"T"iJlfl 7Г
[-(тг =F тг)/2 < ж < (Зтг ± тг)/2].
[О ^С ж ^С 2тг].
^ k2 — m2	ш2Bгг + 1)тг Am1
- -—[E2n(mx) -
6. 5] ^^Е2п+1(^ж) =	^ ^Е2п+1(ж)+ |[E2n(a
00 l^
7# S ^2	^2n(kx) = ^[ctga7TB2n(ax) - J2n(ax)]
ib=i Л а	J
00	,	-
8- У2 ТЪ	^2n(kx) = 7[E2n+i(ma;) - E2n-i(rax)] - -—E2n(mx) - ^-J2n(mx)
fe=i
fc^TO	[0 < ж < 2тг].
тг .
2m 2n
г—|—2 ^««ьЖ j J
4
ггж)-
[0 < x <
l-^x
[0 < ж <
С 2тг].
С 2тг].
00 / i \^
°° f-_i)fe	-2	/ o\ 2
2- E7irWE
	 sin i/тг
ж < C±1)тг/2].

6.5.1]	6.5. Функции Лежандра Р„(х) и Q${x)	339
^
6.4.8. Ряды, содерхашие Ju(x).
( 1 1 9	л 1У1Г
:C±1)тг/2].
Другие аналогичные ряды, содержащие Ju(zO мож:но получать из соответствующих
рядов для функций Вебера El/(z) с помощью соотношений:
Е,(^) + Е_„(*) = - ctg ^[J,W - J-,(z)].
6.5. ФУНКЦИИ ЛЕХСАНДРА РДж) И Q^(a?)
При суммировании рядов с функциями Лежандра могут оказаться полезными соотно-
соотнок(
(	j|g(	)|5 |g(
l j	LI z = ж, -к х
Г Г |
[{
<тг
тг
6.5.1. Ряды
/ГТо
=
1/2].
2- ? ^_1/2(«) = nffL(l - *)" 2 " 2 A + Ж)^2 - 1р-1/2(х)
\-\<х < 1; Re/x< 1/2].
3.	X](^l)fc^^i/2(cosa;) = -^Р-1/2(СО8Ж)	[0 < ж, 1/ж < тг; /i< 1/2].
4.	^A) JPfcl/^1/2(cosic)	^2 ( cosтгсо8ж1
[Bm - 1)тг < vx < Bm + 1)тг].
~	(Л _ т2чп/2
5.	g^^+nW = Bw - 1)!!AЛ^ + ^)^/2	[-K*< i; 1*1 < i]-
6.	f^l)fcB^ + l)P(fc+i/2),_i/2(cos x) = ^^ E ^1)fc+1 sin ^^^ x
k=Q	V V ^ fc=O	V
тг — cos x J	fBm — 1)тг < i/ж < Bm + 1)тг].
7* E 2l i jP(fc+i/2)^-i/2(cosa;) = — P_i/2(cosic)	[0 < x < тг; О ^ их < тг].
fc=o
00 / i \k
[-1 < x < 1; ii < 5/2; j/ ^ 0].

340
Гл. 6. Ряды
[6.5.1
9.
l;/i< 0].
"•E-
+ 1/2; ^t2(l - ж2)/4
l, (n + l)/2, 1/2
В формулах 6.5.1.12-14 для —1 ^ x ^ 1 следует заменить z —>- ж, л/z2 — 1 —^ Vl — ж2
J/2
[p = 1 - 2t cos x + t2, 0 < x < тг].
Е (
fc=o
Y^Bi/+l)fc y	2	(±zTl)
' 4^ fe'	*+"	T{v+l){l-2tz+fiY+1/2
t
rf|argB+l)|, |arg(*-l)|<,rV|
LI	г = ж,-Кж<1	JJ
18.
;,
<тг
= x, -1 < x < 1
21.
\Pu(z)
[Rez > 0].
[Re^ > 0].
r2 _ ¦
i
-/x-i/; l-/x; -A -
z
«>«1 \ ^ D^ /™\ 	 Г-1 О-/-/1

6.5.3]
6.5. Функции Лежандра Р?(х) и Q%(x)
341
6.5.2. Ряды вида
0е)'
!ln:
Jln
(«2-1I/2
x-t+(l-2tx + t2I/2
-1/2; |arg(z
4.
5.
6.
[-1 < x < 1].
2-1)|<7г].
[X > 1].
zp l)n
= ^те, ^?i + 1, . . . ; x > 1].
т + п + 1
n + 3/2
8-
n + 1
+ 3/2
1.
6, n + 3/2; 1/z1
6.5.3. Ряды вида У^ ak cos (к a + b)P?j
CO
Ы^1/2(СО8Ж) =
fl + 2)/2\
0 < ж < тг; Rcjla < 1/2; Re ^ < -1/2 при x = ±a/u] k± = ±[(ux =ро)/Bтг)], ak = 1 при А; 7^ fe±,
ak± = i при A/тгТа)/Bтг) = . . . , -2, -1, 0, 1, 2, . . . , afe± = 1 при A/тгТа)/Bтг) ^...,-2, -1,
О, 1, 2, ... .
2.
3. yj cos BА;
{;
	Рм1 /о(— cos ж)
2 ^/2l	;
2a — cos ж) м
ГГ0<2,
Ll 0 < ж
2a < x < n
<2а<тг
*(г) = |(г ± ^i?^T cosa)" - \
oo
5- E^
(г) = Uz ±
2
— I cos a
^	11
' F 2J
[Rez > 0].
[Rez > 0].

342	Гл. 6. Ряды	[6.5.4
вида
2. y^ cos kaQ^_1/2(z) =
k=i
[| arg (z + 1)|, | arg B — l)| < тг;
oo
о V^ i n	(	\ ж (	\-i/2 !^i /	\	г	i
о. у cos кп(о^k—1/2 (cos ж] = —т— (cos a — cos x) — --V —1/2(cos ж]	[а < ж].
		Zl '	Zi
fc = l
00
^*——'	2	2
fc=i
OO	г	~~
5. ^J(dzl) cos kaQ(k-i)/2(x) — Bж — 2cos2a)^ ' — ± arctg
k=i	L	^ж ~~
6.5.5. Ряды вида
~	- 1)"/2
D1* (fe - а)(Л а
[—тг < ж dz 1/ < тг; /х, i/ ^ 0].
sin атг
оо
4.	?(±1)*p;(«;)P-*(*) = -Р,(^ ± г/(«2-1)(г2-1)) - -P,(«)^ W
fe = l
[Re to, Rez > 0; | arg (го - 1)|, | arg(z - 1)| < тг].
оо	11
5.	^(±l)fcP*(cosa;)Pirib(cos2/) = -P^cos (x T y)) - « P./(cosж)Р„(cos?/)
[ — 7Г ^ X, y, X + у ^ ТГ].
6.	^(-l)*Pf(»)P;M(Z) = >„(«;*) - ±Pv{w)Pv(z)
k = l
[Reto, Re z > 0; | arg (ги — 1)|, | arg (z ¦— 1)| < тг] или [го = cos cp, z = cos 0; G<Cy?, 0, y> + ^ < тг].
°° (^1)к	1
^ E^^"(«)^"(«) = ^^)? - ^^гГ(Х)РГ»(х) to < , < i].
k=l
6.5.6. Ряды вида ^а^ЖЭД
2.
fc = 0
3. J2
k = n

6.5.7]
6.5. Функции Лежандра Р?(х) и Q%(x)
343
4. j^Bk + l)Qk(x)Qnk(x) =
5.
6.
Г.
Х"(
¦1)!'
[ж > 1].
[ж > 1; га = —п, — п + 1, . . .].
Г2"]	[ж > 1].
\k-n)V
Bn
= -n, -n
х (ж2-1)~(п
(ж)
10-
[х > 1; 7П = —тг, — тг + 1, . . .].
[ж > 1; 771 = —71, — 71 + 1, . . .].
[* > 1].
ъРт)'"--
+ 1
W + 2
6.5.7. Ряды вида
Re го, Re z, Re -
1; \w - \fw2 ~~ 1 |
2.
3.
4.
5.
6.
7.
8.
ж < у] к =
¦ х	1
l)PZ(x)Qk(y) = (-l)"n!
/у/(х
[-K ^ 1; у > 1].
[-1^Я!^1; у> 1].
[-1 ^ж ^ 1; |/ > 1].
E(
¦п)\-
B/ — x)m+n+1
[—1 ^ ж ^ 1; 3/ > 1; ra = —n, — n + 1, . . .]
k=i
?^B/) = -Qv(xy
2
[О < ж < 1; -1 < |/ < 1].
- -Р„(ж)<Э„B/)	[К ж <у].

344
Гл. 6. Ряды
[6.5.8
9.
(x)Q-2k{y) = \Qu
10.
п.
[1 < у < ж; i/ # -1, -2, -3, . ..]•
2Г(/х — i/) sin i/ж
Rew, Rez, Re WZ + X ^ 1;
- 1 |
I
r(-2i/-l)	(w
6.5.8. Ряды вида ? afe cos (fea
COS [Ш
2.
3.
4.
5.
0 < cosa
cos kaPy (cosx)PjJ' (cos y) = —Pu (cos ж cost/ ± sin ж sin у cosa) —
— ™i3i/(cosa?)Pl/(cos|/)	[0 ^ ж, t/ < тг; ж + у < тг].
Is
= 2P"(W ± ^(z2 ~ Х)(^2 - г) cosa) ~ 2()()
[Rew, Rez > 0; | arg (w - 1)|, | arg(z - 1)| < тг].
k^1/2(x) = -P^(x2 - A - x2) cos 2a)	[0 < x < 1].
7
- 1) cosa) -
- -Pu(w)P1/(z)	[Rew, Rez>0;
6.5.9. Ряды вида ]Г ак cos kaQ%+til(x)Q%+%l (у).
j

6.6.1]	6.6. Вырожденная гипергеометрическая функция Куммера iFi(a; b; х)	345
3.
*=1	_	,	____	ч ,
= ^{z -sin a) L-i r-2	r^— i 21
6.5.10. Ряды вида ?a* cos (ka + b)P%+*? (x) Q%#%(y).
J2.	.	(^ -«in2^/2
Г(Л + /л + 1/2) к~г/2К
_1/2	/2 cos2 о
fj)
3. ^(±1)к cos kaP-k(x)Qt(y) = |0,(^l/±V(^2
k=l
[1 < x < y; Imo = 0; i/ 7^ -1, -2, . . .].
• / \ / ^^^ "> "¦ -* t/ \^ )^ и\У) — — ^°C v\<^ У ^C \/ \-L — *L-i /\JL — I/ / Cub Uj — — Г и yX j\c^ и у у j
[-A± l)/2 < ж < 1; -(IT l)/2 < у < 1; Imo = 0].
6.6. ВЫРОЖДЕННАЯ ГИПЕРГЕОМЕТРИЧЕСКАЯ ФУНКЦИЯ
КУММЕРА iFi(a; 6; ж)
Для приведения рядов к виду, имеющемуся в справочнике, можно использовать соотно-
соотношение	(	, ж .	ч
iFi(a; о; ж) = е iFi(o —a; о; —ж).
Если ряд содержит только гипергеометрические функции вида iFi(—к\ 6; ж), то
соответствующие формулы после замены
см. в [18], гл. 5. Кроме того, можно воспользоваться рядами для обобщенной гипергеомет-
гипергеометрической функции pFq{{ap)] (bq); х) при р = q = 1 (см. 6.8).
6.6.1. Ряды вида ^«fc iFi(afc; 6^5 ж).
[0 < Rec < Re (b - 1)].
= e*iFi
lFl{b + k

346
Гл. 6. Ряды
[6.6.2
a; T
7- Ет^
Jc; ж
0;
(а + 6)/2, (а + 6-1)/2; 4ж
Зтг/4].
k\B-a)klFl{2-a
Q v\ 14fc
x y
= 1F2
a + k; x + y
6, а + 6 — 1
а/2; -ж2
1/2, C-а)/2
3/2; 2-a/2 )'
a; x\ (a; y
)lF{
"•Е
(а-с)к(с)к
kl(b)k(bJk l
a + 2A;; ж + 2/
2k; x
= #2(а' 6' 6' ж' У)-
C1 X
b
13
*
i) lFlia2a +
2а )'
а + к; х
a, 2a — b — с; х
6.6.2. Ряды вида \2akiF1(ak; bk; xIF1(a'k; bfk; y).
. ^ i .«,,«,. х I о а1 о а
¦ к J \ b + к )	\ 6, Ъ ; —х
: x
2fc о
1
1
a + k; x\ fa + k; x
_
~ 2
а/2, (а
6/2, (
; -ж2
, 6
; 4ж
&, 6', 6 + 6' -1
5.
кЩкB~Ь)к*
Ь + к
= F( a/2, (a + l)/2; -ж2 Л a(l - b)x /1 + a/2, A + a)/2; -ж2
2 4V2 CЬ)/2 A + Ь)/2/ ЬB6) 2 Ч
lj*!(a + 1/2)!
ЬB-6) 2 Ч 3/2,2-6/2,1 + 6/2
a; Ax

6.7.1]	6.7. Гипергеометрическая функция Гаусса 2.F1 (a, b; с; х)	347
^ (a)fc(fe- l)fc(fe- a)fc * fc (a + k;x\ {a + k; y\	f a; x + y
xy lFl{	)lFl{	) = 1Ч
- \^ (a)fc(fe- l)fc(fe- a)fc * fc (a + k;x\ {a + k; y\	f a; x + y\
8- L k\{b-iu{bu xy lFl{b + 2k )lFl{b + 2k ) = 1Ч ь )¦
_ОС'	(п\ , (nf\, (h Л\,	f п -Х- k>- т» \	/п1 -Х- k" 11 Ni
9» 2^ (-1) V,/l -.О Aл x У i^i l,9, bFi ,,0, =Фг(а, а; Ь; ж, 2/).
^	jfel @ — IJk(bJk	\ Ь + Ik J	\ Ь + Ik
6.6.3. Разные ряды, содержащие1^(а; b; x).
\ 2ife + 2c5" -
v^ (la)fe fc[sin(A; + l)y] (а + 25 + к; x
' ^Bk + S)l \	k J1
^coSexp^(l + cos
7Г	2	L 2 V	2
Sin |
^l x
2 J
'—¦(¦>
5- Ъттл:ьк (
E B6)ьD6-1)«
[-1 ^ x ^ 1].
^a; A + ж)з//2\ /a; (l-x)y/2\
26	/Ч	26	/
(a)fc(b - l)fcfe! 4fc p^-i.b-c-i)^^ p^-i^-c-i)^.^ „ /a + ife; ^
; c, fe^c; |A - ж)A - у), |A + ж)A +
6.7. ГИПЕРГЕОМЕТР1ЧЕСКАЯ ФУНКЦИЯ ГАУССА 2F1(a, 6; с; ж)
Для приведения рядов к виду, имеющемуся в справочнике, можно использовать соотно-
соотнония
2Fi(a, 6; с; ж) = A — х)с^а^ 2^1 (с — а, с — Ь; с; ж)
= {l-x)-%F1(a, с-Ь; с; -
= (l-a;)-!>2F1(c-a, 6; с; -?-).
V	ж — 1/
Если ряд содержит только гипергеометрические функции вида 2Fi(—k,b; с; ж), то соот-
соответствующие формулы после перехода к классическим многочленам согласно формулам
из 7.3.1 см. в [18], гл. 5. Кроме того, можно воспользоваться рядами для обобщенной
гипергеометрической функции PFq((ap); (bq); х) при р = 2, q = 1 (см. 6.8).
6.7.1. Ряды вида ^ttfc 2^1 (afe, fefc; Cfe; ж).

348
Гл. 6. Ряды
[6.7.1
*• e^
a — k, b
с; ж
a ~\~ Л'; о
с — а,
[И < 1; Re(l-i) > 1/2].
c; x
= F2{a1 b,b;c,c\x,t)
= F4(a, b; с, с ; ж, t)
(c-a)
2Fl(c+k x) =A"t)~a2Fl
a + A;, b
10.
12.
13.
k\(c)k
fc4fc
k=o
a, b
= 2Fl(c;a;+:
= FiF, b', a~b'; с; ж, ж —t)
[1*1.
, \t-
F (	2«, 2^
: + 1/2;ж/ 2 1 V« + 6 + l/2; ж/4
! , .^ ч	-xkyk2F1(	'	J = Fi(a, 6, 6; с; ж, у)
к\(сJк	"	\с + 2к; х + у - ху J
[\х\, \у\, \х + у - ху\ < 1]
(h\ . (г* 	 ft 	 h\ ,	/	rr 4- t Л 4- t	\
,., ч	^ж |/ 2F1	oI	= 1^з(а, a, 6, 6; с; ж, у)
ЩсJк	\c + 2k; х + у - xy J
15.
(a)feF)fe(c - a)fc(c - Ь)к 2k
Ы(с + 1/2)к(сJк Х
= 2Fi
k\{c)k{cJ
a + k,b
2a, 26
2c; ж
a
"У" 2*1 1 , ol ' ,	I = 2^1 I ' J2F1
\c + 2^; x + y - xy J	\c; xj \c; у
, \y\ < 1; ж + 2/| или х + у — xy\ < 1
a + k,2b + 2
c + 2k,x
a, b
18.
19.
a+k, b+2k
(a)fc(c - a)fcFJfc fe д.
2Fi
2^
= F2F, а, а; с, с; ж, -j
г; ж
с;
с; ж

6.7.2]
6.7. Гипергеометрическая функция Гаусса 2Fi(a, 6; с; ж)
349
22.
kl(cJk
2к
L^Jfe2Fi
a, b
с; 4ж — 4ж
а, 6
2
; x
с, 26 + 2АЛ „2fa,b
Ah	J = 2 I
25.
l)fc(c - a)fc(c - 6)fc(l/2)fc 2fc /2a + 2fc, 26
X 2 Ч
kl(c)k(c+k-l/2)k(cJ
6.7.2. Ряды вида ^ ак 2Fi f
ак, Ьк
ск; у
= F4(a5 6; с5 с;; х - ху, у - ху)
fc 2fc
Ж 2
] х
a, 6 + 1
к; x J	\ c; x
(а)к(Ь)к(Ь')к(с-а)к к к „ (a + к, 6 + k\ (a + k, b' + k
X У 2Fl{ c + 2k; x )>Fl{
- a)fc(c ~ ^)fc fe fe
1){с) X У
-2к; у
= Гг(а, 6, б'; с; ж, у)	[|*|, |у| < 1].
= 2F1
г(а)к(Ь)к(с)к 2к р
k\Ba)kBb)kX 2 г
+ 2к; ж
а, Ъ
с; ж + у - ху
2F]
4
»• Е^1)
, с/2, (с+1)/2\
а + 1/2, 6 + 1/2, а+ 6; ж2	/
a + /г, 6 + fc\ /ft + A;, 6 + Jb\
с + 1г;ж / \c + fc; —ж /
с, с/2, (с + 1)/2; ж2
a; + fc, 6; +
4 3
fc (a)fc(a/)fcF)fcF/)fc fc fc /a + A;, Ь + А;\
c + A:-l)fc(cJfciC У 2 Ч с + 2k; x J2 1\ с + 2k; у
2
2 X
= F3(a, а, 6, 6;; с; ж, у)	[\х\, \у\ < 1].
л, О + К \	I ZCL, Ли

350	Гл. 6. Ряды	[6.7.3
1П v^ (а)к(Ь + 1)к(с - а)к(с - Ь)к(-1/2)к 2к [а + к,
t" к\( + 1/2)( + к1)()	U
'2а, 26 +
2с; х
^ (aJk(b)k(b ~~ 1)к(с ~~ а - 6 + l/2)fc ^2fc ^
^ + ^,6 + ^-1\_ /2а, 26 - 1, а + 6 - 1
V	(Ш( )(/)	TFf
?^ А;!(а + 6 - l/2)fc(a + 6 + к - 2)к(а + b - 1Jк 2 г \а + Ъ + 2^ - 1; х
( а + к, Ь + к-1\_ / 2а, 26-1
х 2 1V + fe + 2^1 ~ 2
2fc F /a + fe, 6 + k
!(а + 6 - 1/2)ЛBа + A; - I)fcBaJfc	" \ 2a + 2k; x
a + k, b + k-l\ _ „ /26-1, а + 6-Г
J^2 4 2a + 26 - 2; x )'
a)l(b)k(b - l)feBa + 26-3)fc Jfe PY a + fc, 6 + fe; я
/a + A;, 6 + А;-1;ж\_ / 2a, 26 - 1, a + 6 - 1; ж
2 l! 2 + 26 + 2ife2 J^3 2
15. E
л; ж
' X
/a + A;, 6 + А;-1;ж\_ / 2a, 26 - 1, a + 6 - 1; ж
2 г\ 2 + 2Ъ + 2к1 )^3 2
1л V^ (a)fc(^)fcBa + 2^ "" l)fe 2fc „2 /a + 1г, 6 + ^; ж\	/ 2a, 26, a + 6; ж
16. 7	"	"—"	"	"—X 9Г1 I	I = Q^O
x—* л!1 za -г Au)t^T	\ za -г zo ~r AK, 1	\ Zfl -|- zo, zci -t- zo
17 у-	(flJW?	 2fe „2/ a + A:, 6 + fe; ж
• ? . , 1/л . л, . ,ч /л . л, . -ч 2i ^2а + 26 + 2А; + 1,
_, , 2а, 26, а + 6; ж
= 3^2
6.7.8. Разные ряды, содержащие 2Fi(a, 6; с; ж).
V"^ (a)fc fe/2 , „ /a + A;, a\ _ 1 .	i/2	v_a 1 „ /a, a
^ A;!	C°S ^ 2 ^l + A;; ^/ 2	Z €°S^ Z	22 ^l; z
fe5 c; 2/, -
^^
c; 2/
= 2"aF2 ( a, 6, fi + i/ + 1; c, /z;
к у^ (fl)fcF)fc ffcp(M,^)/^\
е( + 1Ы + 1)* * ()

6.8.1]	6.8. Обобщенная гипергеометрическая функция pFq((ap); (bq);x)	351
рЗ I	i	. .«	,.	Ж-1Ж + 1
= Fc ( а, 6; с, /х + 1, */ + 1; 2, —^~*» —^~*
x-1
2
а,
1/2
X + 1
1/2
<1 -
8.
a + /г, 6 + A;
*1; |arg(l-j/)| < тг].
10.
fc (Q)fc(Q;)fc(^)fc
(a)k(b)k(c-a)k к
а + к.Ъ
; у
= Si(a, a;, 6; с; |/, ж).
6.8. ОБОБЩЕННАЯ ГИПЕРГЕОМЕТРИЧЕСКАЯ ФУНКЦИЯ
aktkpFg((ap) ± к(ср); (bq) ± k(dq); ж).
6.8.1. Ряды вида
— А;, (ар)
'-А;, (ар)\ _ t
1, 1, (ар)
2,
.!._) - ь а -
з.
); х
(б,);
А;!
к=о
r
-А;, (ар)
-А;, (ар)
); (ka + 1)~ ж
-А;, (ар)
); ж
(Ья)
<1
k=0
k\
/l-4t \1 +
	1 p+l^g + 1
(ap); -
[1*1 < 1/4].
/3,
1 —
[t =

352
Гл. 6. Ряды
[6.8.1
j; x
X ю4
kl
p+2 ^
11
11-
k=0
h\
P+2^g
(bq); x
-k/2, A-A;)/2,
Fg); ж
, , 1 '/ 4A-;
L, 3/2, (ftp) -
1 + 1; t2(l-ty2xy
'(up); t х/4л
= A — Ц p
(ap), a/2, (a + l)/2\
yUg J j V у A.	LJ	th J
h X
F,);
k=0
00 ,k
t0 k] UMk
~k, 1 — к — (ap)
— k, a + k1 1 — A; — (ap)
1 — A; — (bq); x
v V 2
k[
16.
-к, A(r, A; + a), (ap)
A(r + 1, a), Fg); ггж
{а)к к	f(ap),
(dp)] t/ъ
(l + u)n = (-l)p+qtx; n ^ l]
(bq); A-
18.
A;!
< 1; \x\ < 1 при р ^ q].
-1
ПК).
XP+iFg(("P| f' ° )	[Re/3<0; Re 6,- > Re/5; j = 1, . . . , q].
\ \Pq) ~ P' x /
к; х\ = F f(ap); t + x
h ] X
(aP) + k; x
^ *!(/?)*
(ttp), (oL + fi —
(bq), a, /3,
(ap), /3 - a; ж
(Ьд), Р
[p ^ g] или [p = q + 1; |ж| < 1]

Z. B*)!
Bk)\
6.8.1]	6.8. Обобщенная гипергеометрическая функция pFq((ap); (bq);x)	353
ОО / п\	ГТ/	\	/ /	\ I I	\	/ / \	, л\
IPjfc fc I llapjfc j-, / io-pj -h ac, a \	/ yap), a -\- p
x yi(k \—p+1 q I (h \ h I = p+1 g I /l \
00 {о \	/ f \ i \	/ ( \
24. ~	Л	^
_ 1 - /Ю. (ж±ж)/2\ 1	/(ap); ж
~ 2 Р q+1 \ (Ь ) 1 /2 J~2 P 9+11
z	° i/z	z
^ ^fc E[(%)fc p / (ар) + ^;ж \	/" (ap); ж
[a = 0 или 1].
(ap); (х±х)/2л
); ж
. . _ г» _ 11 i
), a, 1/2 У 2
x ,	xk \\{ap)k „ (	(ap) + k;x	\_	( (ap); x
[<T = О ИЛИ 1].
(ap), 1; ж \
bq), 3/2, 3/2/
о JL» Jz
		I»	1 ff/i ^i	/ (n \ -4- Jt*• т* \	/ (n \* i*
ч*у \^	lllap;fc ci I iap) + л, ж \ _ I-, _ / i«Pj, x
9 p f(ap); x
= d/3 p*q+1{(bq), /3
B/3 — 2 — aJk fcEI(ap)fe Ei / (ap) + as; ж \ _	/ (ftp); ж
Bfc + <r)!(/3- 1JлЖ n(&g)fcP g+4(^) + ^5 2k + PJ~ P q+1\(bq), a + 1/2
[Re^ > 3/2; <j = 0 или 1].
12 А. П. Прудников, Т. З

354
Гл. 6. Ряды
[6.8.2
37.
(а)к(а-1)к
к; х
k; x
= pFq+i
(%), a; 2x
(ap); x
39.
B*)!
3/2;
(aP); ж/2
:ap); ж (г; + 1)
(A(p,kp + b); x
f A(p +1, b); x
[1, a+b)
6.8.2. Ряды, содержащие тригонометрические функции
и pFq((ap); (bq); x).
I/2; I sin (ж/2)
h A;, 2k
sin ж
COS Ж
К); г/
(o?), 1
{ '
F,),3/2; V\cosx
ap); 1 со82(ж/2)
(&,), 3/2; ""
/sinxl
\cosxfp*4+1
(ap); jcos
(bq),l/2;
6.8.3. Ряды, содержащие специальные функции и pFq((ap); (Ья); х).
2.
4
3.
, (ap)
(ap);-x2y/4

(-1) [к + - ) —/fc+l,
6.9.1]	6.9. Различные гипергеометрические функции	355
л, К + V, \0,р)
7.
^У J	l~xp+I q\(bq); 2A -х)^)'
-п, а, (ар)
); 2/
9.
а + 1 J	FTi " \^5 (bg); ж?/
'КО; ^1//ж
(У/4)* П(ар)
); (x + l)y/2\ 1	/(ap); j//2
(b,), 1/2 J " 2 P^+1 V F,), 1
(ap); A+a;)j//2\
J
[-l^x^l].
оо	г^з -, \	т-г/ \	/ / \ , i ф	\
1Р); A + х)у/2\
6.8.4. Ряды, содержащие произведения pFq((ap); (bq); x).
2- ^ШЖ+ТЖГ! p+2 П r& v ж )u(d u
к=0
ар), (cr); xy
(bq),(d8)
6.9. РАЗЛИЧНЫЕ ГИПЕРГЕОМЕТРИЧЕСКИЕ ФУНКЦИИ
6.9.1. Ряды, содержащие 2-^2К ^5 с? <^5 ж)-
I 2a, 26, a + 6; ж
= 3 3'
12*

356	Гл. 6. Ряды	[6.9.2
о v^/ -.xfc (a)fcF)fcF/)fc(c - l)fc(c - g)fc 2k fa + k, b + k;x
^ } к\BЬ)кBЬ')к(с-1Jк(сJк Х 2 2\2b + klC + 2k
(a + A;, b' + А;; -ж\ _ /a/2, (a + l)/2, F + 6;)/2, F + b' + l)/2; ж2/4
X22' rt" ' ' ' ftf '-4*б| 6 + 1/2, 6; + l/25 6 + 6;, c/2, (c
\ ^/ -j \k V^MV^feV"' — J-yfcV1* ~~ "jfe 2A; ^ift + K, 6 + Л;ж\	/ tt + К, О -
/ j\ )	i i / \ о / i -i \ /f\	2 ¦* 2 I	,i i , r» i I 2 -* 2 I
4
A;!(c)?(d-lJjfe(c02fc	\c + fe,d + 2^/ \ c + fc, d + 2fe
( a/2, (o + l)/2, 6, c~6; Ж
4 4c, c/2, (c + l)/2, d/2, (d+
-2A;/ \a + 6 + fe + l/2, c + 2ife_
_ /	2a, 26, a+ 6; ж
== 3-^3 I
\q. + 6 + 1/2, 2ft + 26 — 1, с
к v^/ 14fc(Q)fcF)fcF)fc(c^l)fc(c^a)fc 2fc F fa + k, 6 + А;; ж
^l j fe!B6)B6')(l)()	2 4 26 + fe, с + 2к
/o + fe, fe' + fe; -x\ = /a/2, (a + l)/2, (b + b')/2, (b + b1+ l)/2; x2/4
2 2\ 2b' + k, c + 2k J 4 5\ b + 1/2, b' + 1/2, b + b', c/2, (c + l)/2
y( 1)t(a)fc(b)fc(b-c-
2fc
a + fe, 6 + fc; x\ /a + fc, 6 — с + A; + 1; ^ж\
/a/2, (a + l)/2, 6 - c/2 + 1/2, c/2 - 6 + 1/2; ж2/4
4 5 V	(c + l)/2, C - c)/2, d/2, (d + l)/2, 1/2
aB6 - c)(l - c)	/a/2 + 1, (a + l)/2, 1 + 6 - c/25 1 - 6 + c/2; ж2/4
+ cdB - c) X4 5\ c/2 + 1, 2-c/2, l + d/2, (d + l)/2, 3/2
- v^/ -^xfc (a)fcF)fc(c - l)k(d - a-b)k 2k F f d - a - 6 + k\ ( a + k,b + k
?^0	k\(c - IJk{cJk(d)k	г \ с + 21c; ж / 2 \c + 2k, d + А;; ж
_, /d — a, d — 6
= 2^2	,
8 Vf 1xfc(a)fcF)fc(c^ l)fe(c-6)fc 2fc fb + k] -x/2\ (a + k, b + к; х\ =
	 I	1 F 1 I	J л П л J
fco	fc!Ba)fc(c-lJfc(cJA;	ХЧ c + 2fc / V 2a + к, с + 2k
„ / 6/2, F + l)/2; ж2/16
Va + !A c/2^
6.9.2. Ряды, содержащие 3^2(^1, «2, ^з; 6i, 62; ж).
k=0
3. у: ^"?,r;,"a;fc^a^(;_fcfca';:;) = m-c,a,i-d, bi /; *, -te).
Y^ (a)feWfc(c - a)k(c - b)k(c + l/2)fc(l/2)fe 2k /^2a + 2A;, 26 + 2A;, 2c + 2k
' f^Q	k\(c)k{cJk(c-l/2Jk	X 3 4 2c + 4^, 2c + 2* + 1; ж

6.9.3]	6.9. Различные гипергеометрические функции	357
= ,F1(a>b),F,(a'b'%+.}
\с; х) V с, с — 1/2;
2 гУР^(г ~ х + Р)> 2 *^~2(* ~ х
6- L^
_ аЬр2 [ - а, а + 6] ^(а + Ь)/2 ^ ~ yt\ n{a + b)/2 ( Ш + yt
-р г[ \с \)c \
= A - 2tx +12I'2, ш = (l - 2*жA - г/) + *2(i - г/JI/2] •
( k
-^ (с-1/2)* (с + l/2)fc V 4
7 х	(a)fcF)fc	(_Ш\к Гс~1/2( ) F (a + k, b + k, c + k; y\
0; -1 ,C ^ 1].
I - a)fc(e - 6 - c)fc 2fc „ /a +A;, e - 6-ь .
г з^ it	Ж2-*^11	. „>	JX
с, /fl + ^? b + А;, с + k\ _ fa.e — b.e
d + 2k, e + k] x J	\ d, e; x
^ (a)k(b)k(c - l)k(c - a)k(c - b)fc(-l/2)fc 2k /a + ^,fe + ^\
^	fe!(l/2)(l)()	Ж 2 Ч + 2^ J
_____ / 2a, 26
] x )^2 1
-I л X " 	V"Vfc V"/fc V^/rc V*" ^/fc	 zk
fri ^Ka + ^ ~ l/2)fe(a + 6 + l/2)k(d + A; — l)fe(d!Jfe
о jp о I	I gjpo
2a, 26, a + 6, с; х
^4 3
- c)fe2fc ^2 /" a + A;, b + /г, с + A;; x
X
+ 6 + Is + l/25 c/ + 21s
/ 2a, 26, a + 6, с; х
= 4 3\2a + 26, a+ 6 +1/2, d
6.9.3. Ряды, содержащие разные гипергеометрические функции.
а, а/2, (а + 1)/2, 6/2,
у, 	х^		х
' ^J!()B)(HfelbW° 2\ + ^^ + 2^/°
°П \1/2, A + а)/2, C - о)/2, 6/2, F + 1)/2
2A-a)» F
аB - а)Ь ° 5 V3/2, 1 + а/2, 2 - а/2, 1 + Ь/2, F + 1)/2

358
Гл. 6. Ряды
[6.10.1
] х \ f а + к; -х
)г 2
= 2F5
a, 6 — а; ж2/16
(а)к(Ъ)к
iF2
Ч6, 6/2, (Ь + 1)/2, с/2, (с + 1)/2У
а + Is; ж \ / Ъ + к; —х
~ 2
2fc „
г 2
(а + 6)/2, (а + b + 1)/2;
; ж \ / а + к] -х
I 2{
а/2, (а + 1)/2; -ж2/4
6,6/2, F + 1)/2, с/2, (с+1)/2/'
i-t
i-t
8-
'-А;/2, A-ife)/2, a
1/2; |/
а, а+ 1/2, 6, 6+ 1/2
lv26, 26-1/2, 3/2; l/k2
-к/2, A-к)/2, а/2, (а-
' 2'
а- 1)ГD6-2а- 1)
[26+1/2>2а>1].
'•Е-
(а)к(Ь)к
а, 6; с, d, /i + 1, v + 1; г/, у; —-—t, —-—t
2 ' 2
ж - 1
1/2
Ж + 1
1/2
<1 -
6.10. ?7-ФУНКЦИЯ МАК-РОБЕРТА ?J(p; аг : q; bs : z)
6.10.1. Ряды вида ^2акЕ((ар) ± mk; (bq) ± пк; z).
а{1) + к) = Е{{а"У' t!) " tZ))	[ltzl < 1; |argz/A -tz)l < *Ь
ap), a + 1г
00 j.fc
2. V^t
(bq):z-tz
g) + А;, с + ^
k\
(ap):
arg(l-t)z|<7r].
[Re с > 0; \argz\ < тг].
| < тг].

6.10.2]
6.10. Е-функция Мак-Роберта E(p;ar : q; bs : z)
359
5.
6.
7.
о©
о©
h
оо
V
,к
к\
,к
^Е
(ар), А(га, а -
(bq):z
(ар), А(га, а)
: га; |argz|, | arg((l - ¦
(ар), А(га, a):z
[Re F- a- c) > 0; |argz| < тг].
= / t_y
V	7
8.
; |argz|, | arg (A
2
а^тг/2; |argz| < тг].
9.
[0 ^ a ^ тг/2; |argz| < тг].
6.10.2. Ряды, содержащие произведения iiJ-функций.
1.
fc=O
a,b,c ] ( 2a, 26, a + 6, с
[Re a, Re b, Re с > 0; |argz| < Зтг/2].
;, c
2а, 26, а + 6, с
1/2J" \а + 6 + 1/2, 2а+ 26-1: г
[Rea, Re 6, Re с > 0; Re Ba + 26) > 1; |argz| < Зтг/2].
а + к, 6 + к, с + к\ j-,(а — 1 + к, 6 + к, с + к
a + b-l/2 + k:z
¦_,. а — 1, 6, с In/ 2а — 1, 26, а + 6 — 1, с
[Re 6, Re с > 0; Rea > 1; |argz| < Зтг/2].
a + k, 6 + к, с+ k\Ef 1/2 ^a + k, 1/2^6 + ^, c
+ b+ 1/2 +k:
cos (а- 6)тг Г 1
E
1/2 + а-Ь, 1/2-а + Ь, с, 1/2
[0 < Rea, Re b < 1/2; Re с > 0; |argz| < Зтг/2].
/ а + к, d — 6 — с + А; \ / а + А;, 6 + А;, с + к
W* \	х	)Е{	d + k:z
а, 6, с, d~6^c1 тр/я? d — b, d — с
d ^ 6, d ^ с	\	d: z
6.
[Rea > 0; |argz| < Зтг/2].

360
Гл. 6. Ряды
[6.11.1
6.11. С-ФУНКЦЖЯ МЕЖЕРА G™qn ( z
Т) ~\~ О
Обозначение: с* = m + п	.
2	/
6.11.1. Ряды вш да^2 aktk G^qn lz
(Ь,)
(ар)±/г(ср) \
{bq)±k(dq)J-
к=0
(%)
(&g-l), Ь + к
a — A;, {(ip—i)
{bq)
(ftp—i)j ft — A;
) G
(Op)
К)
a, (ap-i)
(ap_i), a
1; m
1; m
с*тг].
с*тг].
1; n
с*тг].
i,n + l
a - Л, (ap) \ _ a_i	i=i
[0 ^ m ^ g; 0 ^ n ^ p; |argz| < (с* + 1/2)тг].
a — и — к, (ap_2), a + i/ + ,
a — i/, (ap_2), a + i/ — 1
a,
[1 ^ n ^p- 1; |argz| < с*тг; i/ ^ 0, ±1, ±2, . . .].
a, (ap_i)
\а-1л»пп I ^
[|argz| < С*тг; |t| < 1; \tyfl -1/л/^| <с*тг/2].
6.11.2. Ряды, содержащие тригонометрические функции
и G-ф у н к ц и ю.
1 — к, (ар), 2 + А; \ _ i/a
3/2, (bq), I I " 
2,д+2
,9+1
k=0
a,
A;, a
2
arg z\ < с*тг; 0 ^ <p ^ тг].
с*тг; 0 ^ (p <C тг]
a, (flp-i) + A;, a
a + ife - 1/2, Fg)

6.12.1]
6.12. Разные ряды
361
а, (ар-i) \ 1
/l \ ' ~ ~ G
p+1, q+1
a, (ap_i), a
a-1/2, Fg)
[|argz| < с*тг; 0
6.12. РАЗНЫЕ РЯДЫ
6.12.1. Ряды, содержащие многочлены Неймана Оп(ж).
^	1	1
flJ Ж	~ %J Ж + 2(у-я?)
[Ы
2.
3.
4.
-«-XVI./J- (я._:
B/ - жK у - х'
1
ху\
тг].

Глава 7. ГИПЕРГЕОМЕТРИЧЕСКИЕ ФУНКЦИИ:
СВОЙСТВА, ПРЕДСТАВЛЕНИЯ, ЧАСТНЫЕ ЗНАЧЕНИЯ
7.1. ВВЕДЕНИЕ
В настоящей главе излагаются основные свойства, представления и частные значения
гипергеометрических функций одной или нескольких переменных. Ввиду важности для
приложений наибольшее внимание уделяется случаям p = q + lmp = q обобщенной
гипергеометрической функции PFq((ap); (bq); *), причем значительное место отводится
таблицам выражений этой функции через различные элементарные и специальные функции
при соответствующих соотношениях между параметрами (ар), (bq) с произвольным аргу-
аргументом z. Такие выражения в случаях, когда не все параметры фиксированы, называются
представлениями; если же все параметры принимают числовые значения, то эти выражения
называются частными значениями pFq((ap); (bq); *).
Отметим, что формулы представлений pFq((ap); (bq); — *) могут быть получены из
соответствующих формул для PFq((ap); (bq); z) путем замены z на ~z; однако в ря-
ряде случаев представляется целесообразным приводить выражения также и для функции
pFq((ap); (bq); -*).
Общая формула для вычисления значения g+iFg((ag+i); (bq); z®) в точке zq = 1 при
любых параметрах (ag+i) и (bq) известна только для случая q = 1 (см. 7.3.5). Аналогичные
формулы, выражающие значения g+i-Fg((ftg+i); (bq)] z) в других точках zo, получены лишь
при некоторых соотношениях между параметрами и для отдельных значений *о.
Таблицы 7.3—18 можно существенно расширить, если воспользоваться различными свой-
свойствами PFq((ap); (bq); z) из раздела 7.2.
Результаты, изложенные в этой главе, могут быть использованы для вычисления зна-
значений сумм и рядов после приведения их к виду V^ f z с помощью соотношений из
ЩЬ)
приложения II, а также для вычисления определенных и неопределенных интегралов на
основе формул из глав 1 и 2.
7.2. ОСНОВНЫЕ СВОЙСТВА ГМПЕРГЕОМЕТРИЧЕСКМХ ФУНКЦИЙ
7.2.1. Гипергеометрическая функция Гаусса 2Fi(a, Ъ; с; z).
Гипергеометрический ряд Гаусса определяется формулой
а> Ь' Z) ее F (а' Ь
(а, 6; с; z) ее F(a, Ь; с; z) ее 2fJа> Ь' Z)
V с )
с; zj f^Q (c)kk\
где с ^ 0, —1, —2, ... Он сходится, если выполнено одно из следующих условий:
1)И<1;
2)	|я| = 1, Re(c-a-b) > 0;
3)	|*| = 1, * ф 1, -1 < Re (с - а - b) ^ 0;
в остальных случаях ряд расходится.
Гипергеометрическая функция Гаусса определяется при |*| < 1 как сумма ряда Гаусса,
а при |*| ^ 1 — как его аналитическое продолжение. Для выделения главной ветви
аналитического продолжения, которая также обозначается символом 2F\(a, 6; с; *) и
удовлетворяет условию | arg A — *)| < тг, в комплексной z-плоскости проводят разрез
[1, оо).Аналитическое продолжение можно получить, в частности, с помощью интегральных
представлений Эйлера

7.2.1]
7.2. Основные свойства гипергеометрических функций
363
2. 2Fi(a, Ь; с; *) =
_
7+
3. 2Fl(a,b;c;z) = r\ C 1-L f Г [*' a " *>
[a, oj Z7T« J [ с — s
^{\ - t)c^\\ - tz)~a dt
0 [Reс > Re6 > 0; |arg(l — z)\ < тг], или Меллина-Барнса
7+гоо
(-*)
[0 < Res = 7 < Re a, Re 6; | arg(-z)| < тг].
7+ioo
7+
	 f Г[в, s + c-a-b, a- s, b - s](l -
27ri J
ds
[
a, b, с — а, с — bj
7^io° [0, Re(a + 6-c) < Res < Re a, Re 6; |arg(l-z)| < тг],
а также с помощью рядов Гаусса в окрестностях особых точек z = 1 и z = сю.
5. 2Fi(a, 6; с; z) =
6. 2Fi(a, b; c; z) = Г
'
с — a, с —
(a, b; I + a + b - с; 1 - z) +
с, 6 — a
6, с — а
Fi ( а, 1 + а - с;
1
г — а, с — 6; 1 + с ™ а ™ Ь; 1 — z)
[с — а — b ф din; | arg A — z)| < тг].
, 1%
+ Г1 '	l^J-^Fi F, 1 + 6-c; 1 + 6-a; - J	[a ™ 6 ^ ±n; |arg(-*)| <^]
[a, c^ 6J	\	z)
(случаи с- a-b = ±n, а-Ь±псм.в 7.2.3.14^23, 78^83 и 7.3.1).
Некоторые формулы замены параметров и аргумента:
7.	2Fi(a, 6; с; z) = 2FiF, a; с; z) = A^ zya2Ft (а, с - b; с; -^
= A - z)c~a~b2Fi(c -a, c-b; c; z).
Другие формулы преобразований функции 2Fi(a, b; c; z) см. в 7.3.1.
8.	2Fi@, b; с; z) = 2Fi(a, b; c; 0) = 1.
9. lim J-2Fi(a, 6; c; z) = (a),m+1 FO+1 zm+1
c->-m I ^cj	G72 + I)!
zm+1 2Fi(a + m + 1, 6 + m + 1; m + 2; z).
Формулы дифференцирования:
10.	-f^2F1{a,b; с; z) = (a)nW" 2Fi(a + n; 6 + n; с + n; г).
11.	¦?-[za+n-\F1(a, b; c; 2)] = (a)^ 2Fi(a + n, 6; c; 2).
12.	^-[^-^^(а, 6; c; z)] = (-l)n(l - c)nze-n-1iF1(a, b; с - n; z).
13.
14.
15.
16.
17.
18.
dzn
dznl
(с - а)п(с - 6)П/
2Fi(a5 b; c; z)\ =
)b"c+n2Fi(a, b; c; i
)a+b^c2F1(a, b; c; i
c —n —l/-i	\a+6 —c —n
A - z) T
-1) (l-c)nz	A-z)
)	2 -f^ 1 ^"-7 w, c,
, 6; c + n; z).
a, 6; с + тг; z).
c2Fi(a ^ n, 6; с ^ n; z).
(a - n, 0 - n; с - n; г).
\a-\-b — c —
w2Fi(a — 7i, 6; c; z).
dz
2F1 f a, 6; c; — j = (™l)n(a)nz a ^11 a + n, 6; c; -

364
Гл. 7. Гипергеометрические функции
[7.2.1
20.
21.
(а)п(с-6)п ^а^
	^
— 1) 2ft U + n, 6; с + га; -
V	2
23-
п \ / п
-, b; с-п;
I, fc; с - n - <Т;
= 0или1].
= 0или1].
[а = 0 или 1].
= О ИЛИ 1].
(с + п + a - |, 6; c;
29.
^2c^Vi _ 2^-c+n+ff-l/2 ^p
2c —2/1	2\b-c+n+l/2
--,b; с;
2' 6; C;
= (-1П2 - 2cJn+CJ2:2cn"
2ft ( —ra ~(jH—,6™n™cr;c^n^cr;
[<j = 0 или 1].
:	,6; с + га; 2
Г<7 = О ИЛИ 1
-п-1,Ь-щс- n;
[cr = 0 или 1
= 0 или 1].

7.2.2]	7.2. Основные свойства гипергеометрических функций	365
= 22n+2a(a)n+CJF)n+aza2Fi [а + п + а, Ъ + п + а; - + a; z2 )	[а = 0 или 1].
V	1	)
I. ^ [* a* (a, b; |; ,')] =
; - - a; zA \	[a = 0 или 1].
ча+Ь-1/2
)
a - n, 6 - n; a + -; zA	[a = 0 или 1]„
)a n a 2F1 I a,
v
_ n _ ff^ b _ n _ ff. 3
a+ a- |; i;
X z'T(l-z2)a-n-12F1 [a + a, a + a-\; a + i; 22 )	[o-= 0 или 1].
= (-4)n(a)n(l + <7-a)n x
[cr = 0 или 1].
X /2^1 I n + a + 1, a; a + -; z2 )	[a = 0 или 1].
Производные по параметрам см. в 7.2.3.57—62.
Дифференциальное уравнение Гаусса
37. гA - z)u" + [с - (а + Ъ + l)z]t/ - абгл = О
имеет общее решение
u(z) = Ciui(z) + G2tA2(zM
где Ci, Ci — произвольные постоянные, в качестве гц, и^ при с ф 0, ±1, ±2, . . . можно
взять функции ч?\(а, 6; с; z), zX^c^F\(\ + a — с, 1 + 6 — с; 2 — с; z) или любые из четырех
слагаемых правых частей формул 7.2.1.5—6, или же 12 функций, получаемых из 6 названных
с помощью формул 7.2.1.7.
7.2.2. Вырожденные гипергеометрические функции Куммера
iFi(a; b; z), Трикоми Ф(а, b; z) и Уиттекера MPj<J(z), WPi(T(z).
Вырожденные гипергеометрические функции Куммера iFi(a; b; z) и Трикоми
Ф(а, 6; z) определяются формулами
ОО / ч	fg
1. xFito; 6; «) = Е ёё^Г	П*1 < «>; Ь # 0, -1, -2, ...].
2.	Ф(а, 6; z) = T	" iFi(a; 6; *) + Г	F1- iFi(o-6 + l; 2 - b; z)
[\z\ < oo; 6^0, ±1, ±2, ...].
3.	Ф(а, n + 1; z) = lim Ф(а, 6; z) = ^	 x
(	°° / \	fe
x < iFi(a; n + 1; z)lnz + V /^ [ф(а + к) -ф(к + 1) -ф(п + к + Щ —

366	Гл. 7. Гипергеометрические функции	[7.2.2
Г(а) ?j(l-n)fc k\ '
4.	Ф(а, 1 - га; z) = zn#(a + n, n + 1; z)	[n = 0, 1,2,.. .].
Функции Уиттекера MPjCT(zM WPj(T(z) определяются формулами
5.	MPi<T{z) = гь/2е^г/\Рг(щ b; z), Wp,*{z) = zb/2e^z/2#(a, b; z)
[a = 1/2 - /o + o-, 6 = 2cr + 1; | argz| < тг].
Интегральные представления:
l
[h	1 Г
ta(l-tN"aeztdt	[Re6>Rea>0].
a, b- a\ J
о
oo
7.	Ф(а, 6; г) = —Ц [ t"^ + iN"""^"^ dt	[Rea, Rez > 0].
Г(о) J
Формулы преобразований:
8.	iFi(a; b; z) = ez iFiF - a; b; -z).
9.	iFi(a; Ь; ж) = г[ 6 j esa7ri^(a5 6; ж) + Г PI ее(а^ьOГ*е{ВФF- а, 6; -
[o^ aj	[aJ
10.	lim -j- tfifa; 6; z) = (a)n+^n+11Fi(o + n + 1; n + 2; г).
ь^-n Г(о)	(п + 1)!
11.	Ф(а, 6; z) = zlm4(a - 6 + 1, 2 - 6; z).
l-e-2mb'*)r[ ^^I,
[a — b + 1J
[m = 0, ±1, ±2, . ..].
12. Ф(а, Ь; е2т7гг2) = е-"т("ггФ(а, 6; г) + A - е"^-)Г	. J iFi(a; 6; г)
а — о + 1
13.	iFi(a; 6; z) = lim 2F1 (a, a; b; — J.
14.	Ф(а, 6; z) = z^a lim 2Fi fa, a - b + 1; a; 1 - -V
a—>oo	V	Z /
Формулы четности и симметрии:
Imz > О
Imz < О
16.	VF CT(z) = W -a(z) =
Формулы дифференцирования:
dn	(a)n
17.	-—- iFi(a; 6; z) = ^ ^n iFi(a + n; 6 + n; z).
18.	—- [za+n^11F1(a] b; z)} = (a)nza^1 iFi(a + n; 6; z).
19.	-^-[^-SFiCa; 6; z)l = (^l)n(l - b)nzb^n^ 1F1(a; Ь-щ
20.	-j^ [e"ziFi(a; 6; z)] = (^l)n F а)та e"ziFi(o; b + n; z).
21.	^ [^e^iFila; 6; z)] = (~l)n(l - b)nzb^n^e^z 1F1(a - n; b^n; z).
22.	^ [z6"a+ne"ziFi(a; b; z)] = F - a)nz6~a~Vz iFi(a - n; 6; z).
23. 	 z~aiFi(a;6; ^J= (^l)n (a)nz~a~n \F\ \ a + n; 6; — J.
dzn [	V	^/J	V	^/
24.	-^- La"be/ziFi fa; 6; i)l = (~l)n(b - a)nza~b~ne~1/z 1F1 fa - n; 6; ^V

7.2.2]
7.2. Основные свойства гипергеометрических функций
367
|2п+<т
1	2
x i^i [ n + а + -; c + n + сг; z
-;C;
4T
\С)П
28.
29.
30.
1;
с + i; с - щ
1
а+ 72+ сг;
2'
(а + ^5 2 -а>
с - 1; с + n + ff;
[а = 0 или 1].
= О„ли1].
= 0 или 1].
= 0 или 1].
[а = 0 или 1].
[а = 0 или 1].
/ 3	\
X iFi | с	; с + и; z2 J	[а = 0 или 1].
33.
«4.
= (-1)^B - 2cJn+CJz
2c^2n""e"z2
-п - I; с - п;
i; с - n - cj;
[<т = 0 или 1].
[a = 0 или
36-
z2	/	1 2\
lFl(a-n;<T+2;2J
a; |;
[a = 0 или 1].
[a = 0 или 1].
37. -f- Ф(а, 6; г) = (-1)п(а)пФ(а + n, 6 + n; г).
azn
38. -f- [гв+—1Ф(а, b; z)] = (a)n(a - b + l)n«<-1*(a + n, b; z).
azn
39.
^(а, b; z)] = (-l)n(a - b + l)n/-n"^(a, b - n; г).

368	Гл. 7. Гипергеометрические функции	[7.2.3
40.	?^ [е"*Ф(а, b; z)] = (^1)пе^Ф(а, b + щ z).
41.	-?L- [^а+п^е^Ф(а, b; z)] = (^l)nzb^a^e^z^(a - n, b; z).
J Г)
azn
Производные по параметрам см. в 7.2.3.57—61.
Дифференциальное уравнение Куммера
43. zu" + (b - z)u ~ au = 0
имеет общее решение
u(z) = d iFi(a; b; z) + С2Ф(а, 6; z),
где Ci, C2 — произвольные постоянные.
7.2.3. Обобщенная гипергеометрическая функция pFq((ap); (bq); z).
Обобщенный гипергеометрический ряд порядка (р, q), p, q = 0, 1, 2, . . . , определяется
формулой
_ у> (ai)fc(a2)fe ¦ • • (aP)fc ^fc
где 6j / 0, —1, —2, . . . , j = 1, 2, . . . , q; величины сц называются верхними, а bj -
нижними параметрами. Этот ряд сходится, если выполнено одно из следующих условий:
1) Р ^ Ч, \А < оо;
< 1;	j^	g+1
= 1, Re^ =
4) р = g + 1, |z| = 1, z ф\, — 1 < Re^g ^0;
в остальных случаях ряд расходится. Если один из верхних параметров равен нулю или
целому отрицательному числу, то ряд обрывается, превращаясь в гипергеометрический
многочлен (см. 7.2.3.4-5).
Обобщенная гипергеометрическая функция порядка (р, q) определяется как сумма обоб-
обобщенного гипергеометрического ряда в области его сходимости, а при р = g + I, \z\ j? 1 как
аналитическое продолжение этого ряда. Для выделения главной ветви этого продолжения,
которая также обозначается символом q-j-iFq((aq-j-t); (bq); z) и удовлетворяет условию
arg(l — z)\ < тг, в комплексной z-плоскости проводят разрез [1, оо). Аналитическое про-
долж:ение мож:но получить, в частности, с помощью интегрального представления 7.2.3.10,
интеграла Меллина-Барнса 7.2.3.13 или с помощью рядов в окрестностях особых точек z =
= 00 7.2.3.77-79 и z = 1 7.2.3.80-82, причем в окрестности z = 1 эти ряды для функции
q+iFq((aq+t); (bq); z) при q > 1 не являются гипергеометрическими.
2.	Функция pFq((ap)'j (bq); z) симметрична относительно верхних и относительно нижних
параметров, т.е. не зависит от порядка расположения ai, 0,2, . . . , ар в (ар) и 6i, 62, • • • , bq
в (bq).
3.	PFq((ap); (bq); 0) = pFq@, (ap_i); F,); z) = 1.
Если какой-либо верхний параметр равен — п, п = 0, 1, 2, ...,то функция
(bq); z) превращается в многочлен степени п, представимый в виде
л гр 1~пч (qp-i); z\ _ (-z)nH(ap^1)n	(-n,
p g| » /» \ I — /»\ T-r /» \ о+1-^ю—l
x
-n, (ap_i); Л (m^n)l пП(ар^)п	[D ^U
v и '	= -b	—z —^—^—~— x
-m, (bq-i) J	ml	U(bq-i)n
-n, 1 + m-n, 1-n- Fg-i)\ (/ -vm+n (w^?i)!n!
l ; m!(m + 1)!
m-n, 1 + 7П +(ap_i

7.2.3]	7.2. Основные свойства гипергеометрических функций	369
Если какой-либо нижний параметр равен ^m, m = 0,1,2, ..., а среди верхних нет
параметра —п^п = 0, 1, 2, ..., или такой параметр имеется, но n > m, то функция
pJFg((ap); Fg); z) не определена, но существует
6 Г	1 „ ( (ap); z \ = ^+1 П(ар)т+1
• ь^_тГF)р "\{bq-i),bj (m + l)\n(bq-1)m+1p
Если для г значений верхних параметров найдется г равных им значений нижних парамет-
параметров, то порядок функции pFq((ap); (bq); z) понижается до (р — г, q — г):
(аР-г), (сг); z
q-r), {Cr)
8.	При фиксированном значении аргумента z функция Г^ [(bq)] pFq((ap); (bq); z) являет-
является целой аналитической функцией параметров.
Интегральные представления:
1
9.	pFq((ap); (bq); z) = Г	Ь*	[^^(l - ^""""^-iF^-i^ap-i); (bg-i); tz) dt
[flp, bq — ap \ J
о
[p ^ 4 + 1; Re ^q > Re ap > 0; кроме того I arg A — z) \ < тг при р = g + 1].
io. ,+1FiW;^ =
Г	(i\ \	If	P ^
~	'	^	. . . . dta
0	0 Kml
[Re6fc > Reafc > 0; к = 1, 2, . .., q; |arg(l - z)| < тг].
(ap); ;
11. PFP.
V^pJ, {Cr)J
1	1 эт
Г	ГЛ ^	If	Г -T" a -1	Ь -a -1
I t^fe A — tfc) fe afe oFr((cr); ti . . . tpz) dt\ . . . dtp
~ ap) J J J fc=1
fefc > Reafc > 0; k = 1, 2, . . . , p].
Интегралы Меллина-Барнса:
^]^ J
[a,j ф 0, -1, -2, . . . ; j = 1, 2, . . . , p; 5 = —k G D+, s = a,j + A; G D~,
fe = 0, 1, 2, . . . ; L^oo см. в 8.4.51.1].
0 < Re s = 7 < min Re a,; | arg ( — z)| < тг
Представления через Gr-функцию Мейера см. в 8.4.51.1.
Некоторые случаи понижения порядка PFq((ap); (bq); z):
14.	pFJ1"'" ^
V
15.	pFg
16.	с |'(аР-2), Р + ™, <7 + п;
,=Ufc=o	i!*Kp)*(<Oi+*
X „ /.	ч	о —2-Го —2 i /,	\ , •

370
Гл. 7. Гипергеометрические функции
[7.2.3
18.
(ap_i), 1; г
q-1	p-1
3=1	k=l
[ai, . . . , op_i ^ 1].
-1 X
x o-
19.
20.
21
(aP-i),l; ^=f_ir(p-,)n!.
— X
1, 2; fei, . . . , feg^i ф 2].
(ap^2), p, cr; z \ = 1
(bg-2), p+ 1, cr + 1/ <j-p
ip-i) — ^; %
(bq-i) — n
(ap_2), p;
F9-2), P 4-
(ap_2), cr;
(bg-2), <r +
(p-^T)n1
P^ '"
aP-2), p\ z
00 p
-n), W; z
p-n), W; Z
(ap-n),
n mi —1
-E
A - mj)j|
(op_n),
гфк
24.
np+l t4 nq+n
[mn = 1, 2, ... и все <т^ различны; если <jj — сг^ = TV = 1, 2, . . . , то гад. < TV].
1, Д(га, (ар) + т); z
A(n, m + 1), A(n,
"П(ар)
(ap); (bq); n9
Функции pJF^((ap); F9); z), верхние параметры которых отличаются на целые числа от
нижних, связаны рекуррентными соотношениями типа
'(аР-2), Р,
25.
27.
= (<r - p)
1;
1, a,
*-2>
(аР-2),
o-(r - p) pFq
(ар_2), р, сг ¦
= 0.

7.2.3]	7.2. Основные свойства гипергеометрических функций	371
32- llfc-
3~	р —2
i=
(flp-2), P+ 1, О"
= 0.
+
-1 г /г ^
34. I | о,- I т vFal ,, '	..__...
" + 1; z
_(r_p) F / К-зЬР'^ + Л! , ЯЙПЯ. тг((а>Р-*)-
* P
3 = 1
(ар_2), /i + I, I/ + 1; z
¦ >-- м- -/у- -, ^ , («Р-г), /х,  * \ <tt(il- p)(v- р)
, CJ+1, Г, (bq-3)J ILV(<T- р)(т- р) ^ Ч\Р+1»<7»Г>
/(ap_3), /i, i/, p; 2:\ _ цу((т - р)(т - p) /(аР-з), /i + 1, i/+ 1, /?;
ир{(т - /х)(т - /х) ^ ((ар-з), /х, ^
<Т "f" 1 , Т ¦
37. \а + zV(aj - ЬМ q+1Fql(a'' '^ Z)+zJ2	^Zi
V Уч> ' i=i Ь,- П (
fe = l
V	I? I	(а9)? °"i Z	I _ _/-,	„\	177
\Ol, . . . , Uk-1, Ok + I, Ofc + 1, . . . , Oq
Соотношения специального вида:
r»Q	IP (	(%)? Z	1 1	I? I	(aP/5 Z	\ _ 9 /71 I	(ap)? Z
«JO. p^gl/,	ч	-	J+p^gi/,	ч	1	I — A pi
\\pq-2)', &, 1 — СГ/	\@g^2J, ^C", 1 + О"/
39. PFA „ ^>Г" "'/. )- 2 pF,L (°r,l)l CT; f 1 = -p-xF,-,

372	Гл. 7. Гипергеометрические функции	[7.2.3
); z J ' * \	[bq); z	J	' * \ (bq); z
Разбиение pFq на четную и нечетную части и его обобщение:
42. pFq((ap); (ft,); z) = А+(z) + A~(z),
A±(z) = -[pF,((op); F,); z) ± pFg((ap); (Ь,); -г)],
'(ар)/2,(Ы-
43. pFq((ap); (bq); z) =
l, Д(п, ai + fc), ..., A(n, ap + k); zn/nnA+q-p)
np+ q+n v A(n> k+1)j A(n'bi
Произведение функций pFg((ap); (bq)\ z):
oo
44. pFq((ap); F,); cz) rFs((ar); (&); d«) = ^cfc«fe
fc! П (/3.)* "+s+l/<'+'- ^	i _ (ap) _ kf (bq)
скП(ар)к	f-k,l-(bq)-k,(ar); (-i
f
kl 11 (bq)k	\	1 - (ap) - A;, (/5S)
когда р^д((ар); (bq); z) и rJFs((ar); (/3S); z) — не многочлены. Если PFq((ap); (bq); z) —
многочлен степени m (например, при ар = —тп), то при А; = 0, 1, . . . , тп значения си
определяются теми же формулами и
_ dkU(ar)k	f-m, I - A3s) - k, (ap_i), ^k; (^l)r+s
Если pFg((flp); F9); z) и rFs((ar); (/3S); z) — многочлены (например, при ар = — га, ar =
= —n, r?i ^ n), то при k = 0, 1, . . . , га и A; = m + 1, ?n + 2, . . . , n указанные выше
соответствующие формулы для с^ останутся справедливыми и
Сп+к = т к°к\	щьч)кПф,I " х
к - т, (ор-i) + к, -п, 1 - (/?,) - п \
(bq) + kj к + 1, 1 — (ttr__i) — fi; (—1)	c/d/
Формулы вырождения:
45.	lim pFq ((ap_i), <j; F9); — J = P-ii^((ap-i); (bq); z)	[g^p —1].
|<t|--»oo	\	G /
46.	iini prq((dpM Fg__]_M (jj dz) =:: p.rg—i((dpM lbq—i)] z)
|cr|—>oo
[<i ^ p + 1; lzl < °°] или [^ = P5 1^1 < i; R-e<t^o].
Дифференцирование по аргументу:
47.	-—- pFg((ap); (bg); ^) = —,hP!n pFq((ap) + n; (bq) + n; z).
48.	—;- [zCT pFq((ap); (bq); z)] = (—l)n(^o-)nza~np+iFq+i((j + 1, (ap); <r — n + 1, Fq); z)
[(r-n + 1^0,-1, -2, . ..].
n!II(ap)n^
49.	= у	, , ,	p+tPq+i{n + 1, (ap) + n^cr; n — <r + 1, (o9) + n — cr; z)

7.2.3]
7.2. Основные свойства гипергеометрических функций
373
50.	— [za+n^ PFg((ap-i), ст; (bq); z)] = (a)nZ^1 PFg((ap_i), ст + n; Fg); z).
51.	^^ [z"'1 р,Рд((ар); Fg-l), <Т; 2?)] = О - П)^/"" pFg((ttp); Fg-l), G - 7i;
52.	-— \z'" pt'q I -n,
dzn L	V
53.	-^
54.	—
55.	-^
56.	— [e~z pF,(-n, (ap_i); Fg);
= n!
—n, n ¦
= n! D-iFo.
p+m-*
(-?i, cr + 1, (ap_i); cr - n + 1, F9); z).
/A(r, -n), A(m, a + 1), (ap^r
l\ A(m, <7-n + l), Fg); zm
-p+iFq(-n, k — n, (ap_i) + Is; Fg) + A;; z).
Дифференцирование pFg((ap); F9); z) по параметрам в общем случае не приводит к
гипергеометрическим функциям:
); 2: J =
Y^ (ai + l)i . . . (ap_i + 1)
^ Fi + i)i...Fg + i)i V Р
58. ^
p	q — l
3 = 1 к=1
^ (Ъг + 1),.. . (Ь,_х + l),((a + i/)//? + 1), (/ + 1)!
Исключение составляют некоторые частные случаи:
д „ ( а + I/, (ap_i);
р-1	qf-l
¦ П «i П b^f
2, a
2,
a + ^ + 1, (ap_i);
p-l q-l
a + 1/, a + 1/, (ap_i) + 1; z
д zez
61. — iFi(l; a + 1/; z) = ^7	гт 2F2(a + 1/, a + 1/; a + 1/ + 1, a + 1/ + 1; -2).
aa	(a + i/J
62.	— 2
63.	|-l
64.	|.l
l, a;
; z) =
(a + i/)
(a + u)
; z).
;_?!
;_?!
= — [slnz cl (z) —cosz SI (z) —sin z (C + ln z — 1)].
= 2[cos z ci (z) + sin z Si (z) — cos z (C + In z)].

374
Гл. 7. Гипергеометрические функции
[7.2.3
65.
да
1; а
2
= »<(!
а=0
Дифференциальное уравнение, которому удовлетворяет PFq((ap); (bq); z), имеет вид
ee-
Это уравнение порядка max (p, q + 1) имеет две (z = 0, сю при р ^ q) или три (z = 0, 1, сю
при р = 9 + 1) особые точки. Если р ^ д, то особая точка z = 0 — правильная, a z =
= оо — неправильная (существенно особая) точка; если р = q + 1, то все три особые точки
z = 0, 1, сю — правильные.
Введем обозначения:
F*) = 6о, &i, • • . , Ьд — 9 + 1-мерный вектор, у которого bo = 1.
67.	и = 4(*) = z1^ pFq(l + (ар) - bk; I + F^; - bk; z)
[к = 0, 1, 2, . . . , q; bk - bt ф 0, ±1, ±2, . . . , к ф I].
68.	и = uf{z) = z~aiq+1Fp^(l + а3- - (bqy, 1 + aj - (ap)f; (~l)q~p+1 z^1)
[j = 1, 2, . . . , p; a3- -акфЪ,±\,±2,...,кф j],
где штрих в 1 + F*) - 6fc и 1 + а^ - (ар) означает, что члены 1 + 6^ — 6^ при h = к и
1 + aj — а л, при h = j отсутствуют.
1 - («g+l), I - 6j
О, 1 — fej, 1 — F,
[^g ^0, ±1, ±2, . ..].
69.	гл = Я,-д(;г
70.	и = ^g(z,
71.	u = ipq(z)
где функция ^
72.	?o(z, ^а)
или в виде ряда
У = 1, 2, ..., g].
[^д=0, ±1, ±2, ...],
может быть представлена через 6г-функцию Мейера.
1 _ /,
, 1	^Cig
0 < arg(l - z) < 7Г
9+1
k=l	3=1
Здесь coq = 1, Cfco = 0,^ = 1,2, . . ., а остальные коэффициенты
формулам
си = Я(^1), 2c2i = Я(^1 + 1)сц, . . .,
кск1 =
2с22 = [АЯ(^2) -
ксш = [АЕ(ф2 + А; - 2) -
+ А; -
Aq-2Q(t/>q -9 + 2)
k- 2)cfc_2;
А"-1 Я(фд -<? + 2) ^-2Я{фч - д + 3) 1
(9-1)!	(g-2)!	JCl9
А'-2Щфя-Я + 2)
определяются по
-9 + З)"

7.2.3]	7.2. Основные свойства гипергеометрических функций	375
Ck+j~q'
л	-
где А — разностный оператор вида
74.	Д°/(я) = f{x), Af(x) = /(я + 1) - f{x).
75,	Д"/(*)
9+1	9
76. Я(ж) = f](ж + a,-), Qix) = xY\ix + bj- 1),
причем справедливы соотношения
Cfcg = ?q(l, -A;),
к=о
1; m = 0, 1, 2, . . .].
Функция ipq(z) совпадает с правыми частями любой из соответствующих формул 7.2.3.81-
82, приведенных ниже.
Функции ?q(z, фц) и Lfq(z) в особой точке z = 1 имеют, вообще говоря, соответственно
степенную (при Кефч < 0, фч ф — 1, —2, . . .) и степенно-логарифмическую особенности, а
все функции Rjq(z) в этой точке непрерывны.
Тогда функции щ. (z), к = 0, 1, 2, . . . , q; uJ°(z)J j = 1, 2, . . . , р; Rjq (z), j = 1, 2, ...
• • • •> Чч ш ^q(zi Фч) (при фч ф 0, ±1, ±2, . . .) или (fq(z) (при фд = 0, ±1, ±2, . . .) образуют
три фундаментальные системы решений уравнения 7.2.3.66 соответственно в окрестностях
особых точек z = 0 при p^g + l,z = oo при p^q+lmz=t при р = q + 1.
В случае р = g + 1 это уравнение инвариантно при одновременной замене местами
z и z~x, bk и 1 — afc+i, а g + 2 его решений Uq(z) = q+i.Fg((ag+i); (bq); z) и u°°(z)^ или
Rjq(z), Cg(z? ^g) связаны между собой соответственно формулами 7.2.3.77-79 и 7.2.3.80-83.
Представления функции g+iFg((ag+i); Fg); 2:) в окрестностях особых точек z = 00 и
z = 1 имеют следующий вид.
Если clj - акф0, ±1, ±2, . . . ; j, А; = 1, 2, . . . , q + 1; j / A;; |arg(-z)| < тг, то
Fд) - afe
X (е71"*^ )в|гд+1^A + ак ^ (bq), flfc5 I + G>k ^ (ag+l) '¦> z )\
штрих означает, что слагаемое 1 + ак — aj при к = j отсутствует.
Если an+i — ап = mn, где mn = 0, 1, 2, . . . , п = 1, 2, . . . , г — 1, г = 2, 3, . . . , q +
+ 1, шг = 00 и aj - ак ф 0, =Ы, ±2, . . . , j, А; = г, г + 1, . . . , q + 1, j / A;, |arg(-^)| < тг,
то
78. g+1Fq((ag+i); Fg); z) =
Гап, (aq+i)' — anl /e7"^ та	(аП1 1 + ате —
II	/. ч	II 	 I a+l-Tg
9+1
fe=^+l	1 -	 1	J5^	I
»=i «=o nC + a.-aj)! П ГF*-а„-0
k=l	k=l
[n/2]
и
^	^	)J—Fn-m-i] Fk=Y^ (^1)тМ^тФт, Mo = Фо = 1,
m=0

376
Гл. 7. Гипергеометрические функции
[7.2.3
— числа Бернулли],
Е
Пр*fci'
2 Е
„_2то
Dk= Ъ
В ЧЕСТНОСТИ, При Г = 2, 7711 = П
79. g+1Fq(ai + ?i, (aq); Fq); z) =
(bq) l
+ n, K)J
- (a,)' + afc, 1 - ai - n
-а -I) '
=i	n j
7 (aq)'-ak, ai-afc
a1-(bq))k.k\a1,(aqy-a1
()')	L
з ~~ ai "~ n ~~ ^) ""
i=2
В окрестности точки z = 1 справедливы соотношения:
80. 9+1Fq(K+1); F,); z) = --r^r-
81.
(o,+i); F,); г) =
Ъ, ±1, ±2, ...;
*; F,) + fc; 1)(г - 1)"
<тг].
E
[фц = га; m = 0, 1, 2, . . .; |1 - з| < 1; | arg A - z)| < тг; Re a^ > -m; aj ф 0, -1, -2, . . . ; j
= 1, 2, ..., 9 + l].
82.
1
LK+i)
4,(^, -m) In A - z) + (^l
A - z)fc
J
[^q = -m; m = 1, 2, . . . ; |1 - z\ < 1; | arg A - 2?)| < тг; Oj ^ 0, -1, -2, . . . ; j = 1, 2, . . . , g + 1]
где функция Cg(z) представима в одной из следующих форм:

7.2.4]
7.2. Основные свойства гипергеометрических функций
377
7+*оо
2тгг
о, 1-0
	dt
_ nq+l,0
О, 1 - F,
[О < 7 < 1; z справа от G — гоо, j + too)].
. sln((ag+i) - 1
-Я;*(*);
функции Rjq(z) определяются равенством 7.2.3.69,
9
sin ((bq)f — bj)w = II sin I
Коэффициенты dk вычисляются по формуле
— bj)w.
7+гоо
Г
k
t, ±m)ln(l-t)
Если
= 0 m #A-6, - A;) = 0
[0 < 7 < 1].
[j = 0, 1, 2, . . . ,
где R(x) имеют вид 7.2.3.76, то коэффициент при In (I — z) в формуле 7.2.3.81 G.2.3.82)
обращается в нуль и эта формула не содержит логарифмического члена.
В частности, при q = 0 и q = 1 справедливы соотношения
?0B, ^0) =
r(l-ai)
(л _ И^1
- а2;
- 2:)
= 61 - ai - «2],
k\
); (bq);
fe-i,o = 0,
— ai, 61 — ft2, I — 1J A — фг)кк\
и равенства 7.2.3.80-82 преобразуются в формулы 7.2.1.5 и 7.3.1.29-31, 79-80. Если же q >
> 1, то функции Cg(z) Фя) и Ci(z) не выражаются через гипергеометрические функции
аргумента 1 — z, т. е. в окрестности точки z = 1 функция g+ii^g((ftg+i); (bq)] z) имеет
поведение не гипергеометрического типа, когда q ^ 2.
В заключение приведем представление обобщенной гипергеометрической функции в
виде ряда по гипергеометрическим многочленам, обобщающее формулу 7.2.1.7:
со / \ /	\к
84. ,+iF,((a,), ff; F,); »г) = A - to)-' ^ ^Г (^Т j "+lF^k' ^ ^ *)¦
Относительно других свойств и приложений обобщенной гипергеометрической
функции см. [1, 10, 11, 20, 21, 32, 33, 46, 49, 59].
7.2.4. Гипергеометрические функции нескольких переменных.
Определения:
л т? г и и'	\ \^ (a)k+i(b)k(bf)i wkzl
1.	Fi(a, b, b ; с; го, z) = 2_^
с
2.	Р2(а, 6, bf; с, с; w, z) = ^
(c)fe+l
fe, 1=0
(c)k(C)i k\l\

378
Гл. 7. Гипергеометрические функции
[7.2.4
3. Fs(a, а , b, bf; с; го, z) =
4. F^{a1 b; c, c; го, z) =
{a)k{a')i{b)k{b')iwkzl
)k+l
kill
(a)k+i(b)k+i w z
k J
— гипергеометрические функции Аппеля двух переменных.
5. ФЦа, Ь; с; w, z) = >
k\l\
6. Ф2F, 6'; с; w, г) =
% {c)k+l kill ¦
oo
9.	Ф2(а; с, c;; го, z) = ^ ]
с
10.	2i(a, a;, 6; с; го, z) = Л
fc, j
oo
11.	2г(а, 6; с; го, z) = \_. '
к, 1=0
Z
k\ll
— вырожденные гипергеометрические функции двух переменных.
12. FA (a, fei, . . . , fen; ci, ••• , сте; zi, . . . , zn) =
°° fa)	(b )	(b ) zkl
13.
k,	k -0	(Cl)*! • ¦ • (С„)*„
i, . . . , an, fei, . . . , &n; c; zi, . . . , zn) =
14. F^n)(a, 6; ci, . . . , cn; zi, . . . , zn) =
[\w\,\z\<l].
i=l
= l, 2, ...
15.	i^jrj (a, fei, . . . , bn] c; zi, . . . , zn) —
oo	/ ч	/| \	/| \	fei	к
= Z) a fcl+'fcTfe + +\' " " ^ fe^!.'''. fen!	[kil<i; i = i, 2, ...,n]
— гипергеометрические функции Лауричелла.
Относительно свойств других гипергеометрических функций нескольких переменных
см., например, [31, 40, 41].
Формулы симметрии:
16.	Fi(a, 6, b'; с; z, го) = Fi(a, 6', b; с; го, z).
17.	i*2(a, fe? fe'; с, c;; z, го) = Fi{a, bf', fe; с', с; го, z).
18.	Fs(a, a\ 6, fe;; c; z, го) = Fs(af, a, 6#, 6; с; ги, z).
~g rf^	I~7 /I	^	\	I~7 /I	/	\	I~7 /	I	/	\
JL CF # 141 *-*' 5  ^5 Оч Х>ч UL/ J — J. 41^5 ^ 5 l^« l^ « /О * UL/ | — 141 ^ 5 ^5 ^ 5 ^5 '-*-' 5 X^ I *
20.	Ф2(&, &'; c; z, го) = Ф2(&', 6; с; го, z).
21.	#i(a, 6; с, с; z, гу) = ^i(a, fe; c;, с; гу, z).
22.	#2(^5 с, с'; z, го) = ФгСа; с', с; го, z).
23.	2i(a, а\ Ъ; с; z, го) = Ea(a/, a, 6; с; го, z).

7.2.4]	7.2. Основные свойства гипергеометрических функций	379
24.	22(а, Ь; с; z, го) = 22F, а; с; z, го).
Формулы взаимосвязи:
25.	Fi(e, 6, 6'; с; «,, г) = A - w)-b(l - z)-*Vi (с - а, Ъ, У'¦ с; -^, -?-
?
26.	=(l-w)-aF1(a,c-b-b',b'; с;
\	го — 1 1 — го
27.	= A - го)с~а~ьA - 2)~bVi (с-а, с - Ь - bf, bf; с; го,
28.	lim F\ ( а, 6, —; с; го, ez ) = Ф](а, 6; с; го, z).
29.	lim Fi I —, 6, 6;; с; его, ez ) = #2F, bf; с; го, z).
30.	lim Fi I —, 6, —; с; его, e2z J = ФзF; с: го, z).
E"° , ?,	(
31.	F2(a, 6, 6'; с, с; го, z) = A - го) aF2 fa, с - 6, 6'; с, c';		-, —
32.	= (l^w^z)^aF2 fa, c^6, c;^6'; c, c;;	W	Z
— w
w + z — 1'
/ 1 . \
33.
I. lim F2 I a, 6, —; с, с'; го, ez J = #i(a, b; с, с;; го, z).
34.	lim F2 I a, —, —; с, с; его, ez I = Ф2(а; с, с; го, z).
е^о \ е е	У
35.	F3(a, а, 6, 6;; с; го, z) = Vr[C' P ~ М' <Т^1/](^го)-
^^ [р, a, c-/x-i/J
х
х F2 1 + Д + ^ - с, /i, 1/; 1 + /i — р, 1 + г/ — с; —, —
\	го z
[здесь сумма состоит из четырех слагаемых, в которых /х, i/, р, сг равны соответственно а, а', 6, 6;;
а, 6', 6, а'; 6, а;, a, bf и 6, 6;, а, о'].
36.	Fs(a, а , 6, 6;; а + а;; го, z) = A — z)~ F\ I a, 6, 6;; a + a;; го, 	J.
37.	lim F3 I a, a , 6, —; с; го, ez I = 2i(a, a;, b; с; го, z).
e^o \	e	У
38.	lim F3 ( a, —, 6, —; с; го, e2z | = 2г(а, 6; с; гу, z).
e^o \ e e	У
39.	F4(«, 6; c, c#; w, z) = г[С,' 6^?l(^^)^aF4 fa, 1 + a - c; c, 1 + a - b; —, i
[c — a,5fc>J	\	z z
\,
[c — b,
40.	F^(a, 61, 62; ci, c2; zi, z2) = F2(a, 61, 62; ci, c2; zi, z2).
41.	FJ?\a, b; a, c2; zi, z2) = F4(a, b; ci, c2; zi, z2).
Интегральные представления:
l
а~1
l
42. FUa, b, bf; c; w, z) = Г	U^	l 4li/ j	-jt du	[Rea, Re(c - a) > 0].
0
о
Г	с	1
43. Ftia, 6, 6'; с; w, z) = Г ,	, х
[о, о , с — 6 — 6 J
х
u+«|i	[Re 6, Re bf, Re (c - b - bf) > O].

380
Гл. 7. Гипергеометрические функции
[7.2.4
44.
b1bt; с, cf;
С' С
}х
J
45. F3(a, a\ 6, bf; с; го, z) = Г	,	, | x
[o, b , с — b — b
b, b , с ^ b, с — b
l l
x f Lb~ V^ - uH-**-1^ - vH'-**'-1^ ^uw^ vzya dudv
00	[Re b, Re6;, Re(c-b), Re (cf - bf) > 0].
6'^ - uw)~a(l - vz)~a> dudv
[Re 6, Re fe;, Re (c - 6 - bf) > 0].
u+Vv%°i
46.	Fs(a, a', 6, 6;; a + a'; w, z) = Г	, x
1	L «, a I
Г -i	'—i	—ь
x \u A — u) A — гхго) A — A — гх).
0	r	/
47.	F4(a, 6; с, с; w(l-z), z(l - w)) = Г , C? C , ,
[a, o, c-a, с — о
[Re a, Rea' > 0].
. — v)c b 1 dudv
48. <S>i(a, 6; с; го, z) = Г
a, c — a
X	ub-1vb'-1(l-u-v)c-b~b'-1euw+vzdudv	[Re 6, Re 6', Re (c - 6 - 6') > 0].
49.
so. *.(*;«; «»,*) = nb>1/2>c_b_1/2jx
1 1
[Rea, Re 6, Re (c-a), Re (cf - b) > 0].
a —l/i	\c —a —l/i	\—b uz j
и A — u)	A — гхгу) е aw
о	[Rea, Re(c- a) > 0].
,/ x
Яс-3/2 b —1/^	4—1/2/^	\c —6 —3/2 ««го i /o fT-%	\ \ j j
и ' v A — и) ' A — v)	7 e ch By A — u)z ) du dv
00	[Re b > 0; Re c, Re (c - 6) > 1/2].
A - u)c"b-V^ - vH' x
[с с	1
6, c~ 6, a, c - aj
и и
vz X
A - iiw)™aei^^ dudv	[Re 6, Re (c - 6), Rea, Re (cf - a) > 0].
r	c	i
52. 2i(a, a;, 6; c; w, z) = Г	,	,
[a, a , с — a — a j
x(l-uw) bevzdudv	[Rea, Rea', Re(c-a-a') > 0].
Г	C	Iff c-3 2 a-1	-1 2	е^а^З 2
53. 2г(а, 6; с; w, z) = Г	i /о -i /о	^C 3 va гA — и) 1/2A — v)c a 3/2 x
I a, c-a - 1/2, 1/2 1 JJ
о о
X A - uvwyb ch B^A - u)z ) du dv	[Rea > 0; Rec, Re (c - a) > 1/2].
54. F^\a, 6i, . . . , bn; a, . . . , cn; zi, . . . , zn) = Г
(Cn)
(bn), (cn ^ bn)

7.2.4]	7.2. Основные свойства гипергеометрических функций	381
1 1
x
00
[Rebi, ..., Re6n, Re (ci - 6i), . . . , Re (cn - fcn) > 0].
55. F^,n)(ai, • • • , fln, &i, • • • , 6те; с; zi, . . . , zn) = Г	х
[a, ... , an, с — ai — . . . — anj
-ui-...-«n^o [Reai, ..., Rean, Re(c-ai -...-an) >0; |arg(l-*i)|, ..., |arg(l-sn)| < тг].
56. ^V,bi,--.,6n;c;,1>...,,n) =
X
f wj1. . . U^i
[Re6i, . . . , Re6n, Re (c — 6i — . . . — 6n) > 0].
57.	F?°(a> bi, . . . , 6n; c; Zl, . . . , zn) = r[ C 1 f «"^(l - uH-^1 x
X A - uztyhl . . . A - uznybn du	[Re с > Re а > 0; |arg(l-zi)|, . .., |arg(l^zn)| < тг].
Представления через функциир]?д((ор); (^g)j z):
58.	Fi(a, 6, bf; c; w, 0) = Fi(a, 6, 0; с; го, z) = 2^i(a, 6; c; w).
59.	Fi(a, 6, 6;; c; 0, z) = Fi(a, 0, bf; с; го, z) = 2-^1 (a, &'; c; z).
C' C^a^ f, 2Fi(a, 6; с -Ь'; гу).
с — a, c — b J
61. Fi(a, b, bf; c; z, z) = 2Fi(a, 6 + 6'; c; z).
63. Fi(a, b, bf; b + bf; w, z) = A - z)^a2Fi fa, 6;
1 - z
64.	F2(a, 6, б'; с, с; го, 0) = F2(a, 6, 0; с, с'; го, z) = 2Fi(a, 6; с; го).
65.	F2(a, 6, 6;; c, c;; 0, z) = F2(a, 0, 6;; с, с;; го, z) = 2Fi(a, 6;; c; z).
68e ^/. , . ...... ^_n wr..PjWMa + l)/2,M-M2(l-^
с/2, (с + 1)/2, с
/л /О /'л _L
69. F2(a, 6, 6'; 26, 26'; z, z) = A - zya41
6 + 1/2, 6 + 1/2,
70.	F2(a, 6, 6': 6, с; го, z) = A — w)~a 2F1 ( a, I/: c; 	 I.
\	1-го/
71.	F2(a1 b, br; a, a; го, z) = A - го)~ьA - z)~b' 2Fi ( 6, 6'; a; —
72.	Рз(а, а\ 6, 6;; с; го, 0) = Fg(a, 0, 6, 6'; с; го, z) = Fs(a, a , 6, 0; с; го, z) =
= 2Fi(a, b; c; w).
73.	Fs(a, a , 6, 6;; c; 0, z) = ^з@, a , 6, 6;; с; го, z) = F3(a, a;, 0, bf; с; го, z) =
= 2Ft(af, 6'; c; z).
74.	F3 fa, a', 6, 6;; c; z, -iL-

382
Гл. 7. Гипергеометрические функции
[7.3.1
Гс, б' — а , с— а — Ь— а'Л /1 — 6', l + a' + a^c, l + a' + б^е; 1 —;
Lo,c^a^a,,e^o^aJ \	1+а^о,1+а+а+о^с
Гс, а'-fc', с-а-Ь-6'1 A-а, l+b'+a-c, l+b'+fc-c; 1-;
XI,	,	ii/ 3^2 I	i,i/	/ 1 i i/ , i ,
[а , с —a — b , c — b — b \ \ 1 + 6^а,1+о+6 + а^с
Гс, а' + а + 6 — с, У + а + 6 — с]
а/ + 6; + а + 6 — с, a, b
z^c(l^z)c^bx
l /l + e ^ a ^ 6 ^ a' ^ 6;, 1 — a, 1 — 6; 1 —
J \ 1 + c —a —6 —a', 1 + c —a —6 —6'
76.	Fs(a, с — a, 6, с — 6; с; ад, z) = A — z)a+ С2^1(«, 6; с; -ш + z — wz).
77.	F4(a, b; c, c;; w, 0) = 2Fi(a, Ь; с; w).
78.	F4(a, 6; c, c#; 0, z) = 2Fi(a, 6; c; z).
79. F4(a, 6; 6,6; w, z) = A - w - z)~a
; 6;
80. F4 (a, a + i; c, i; w, z ) = \{
a, a + |; c;
A
i; c;
81.	F4(a, 6; с, с'; z, z) = 4F3
82.	F4(a, 6; a, 6; z5 z) = —=
a, 6, (c + c/-l)/2, (c + c;)/2
с, с , с + с — 1; 4z
83. F^ia, b: с, с: z, —z) = 4F3
c/2,
, c; -4
85.	F4(a, 6; с, a + Ь —с+1; w(l — z), z(l — w)) = 2Fi(a, 6; с; wJFi(a, b; a + Ь —c+1; z).
86.	Fzi(a, с + с — a — 1; с, с'; гоA — z), z(l — w)) = 2Fi(a, с + c; — a — 1; с; го) х
x 2Fi(a, с + c; — a — 1; c;; z).
A- wf{l^ z)a
87.	F4 (a, 6; a, 6;
88.	F4 [a, 6; 6, 6;
1 — wi
= (l-w)a{l-z)a2F1
a, 1 + a — 6
6; wz
89. F4 a, 6; 1 + a - 6, b;
90.	Ф2F, 6'; 6 + 6#; го, z) = ez iFiF; 6 + 6;; го - z).
91.	Ф2(а; a, a; w, z) = T(a)(wz
= (l~z)a2Fi a, 6; l + a-6; --
1 — го
)A^a)/2ew+z
92.
с, с , с
7.3. ФУНКЦИИ iF0(a; z) И 2Fi(a, b; c; z)
7.3.1. Представления iFo(a; z) и 2Fi(a, 6; c; z).
1.	iF0(a; z) = A - ^)^a.
r-i /	\ r-i /	i	\ «6(a — c)F — c)
2.	2Fi(a, 6; c; z) 2Fi(-a, -6; -c; z) H	^	^	^<^
г2A^с2)
x 2Fi(l - a, 1 - 6; 2 - c; z) 2Fi(l + a, 1 + 6; 2 + c; z) = 1.

7.3.1]
7.3. Функции iFo(a; z) и 2 Ft (a, b; c; z)
383
2Fi(a, 6; с; z)
3
4
10
11
12
13
14
15
16
17
18
A-*Гв2*(а,с-Ь;с; —
A - z)M^6 2Ft(c - о, с - 6; с; z)
г[С' C~a~6l 2Fi(a, 6; 0 + 6-c+1; 1 - z)
\_c — а, с — 6J
L а, Ь J
x 2Fi(c-a, c-6; c-a-6 + 1; 1-я)	[|arg(l-z)| < тг]
"с, 6- al	/	1>
(-z) a 2F1 I a, 1 - с + a; 1-6 +a; -
6, с — aj	\
6; -
а, с — 6
с, 6 — a
ГГ'~ -|(l-z)-« 2Fx a, c-6; a - 6 + 1; —^- | +
,6, с — aj	V	1 —
.c а; 6 а
r|C^-u-«
,e -- а, с — 6
<тг]
x 2^1 [ o, 1 + a - c; a + 6 - с + 1; 1	) +
«=—"
(l-c)
x 2-^1 (с — a, 1 — a; 1 + с — a — 6; 1
[|arg(l - z)|, |argz| < тг]
х 2-^1@, 6 — к; с — m; z)
[Re (с — а) > га]
[c - 2a - F - a)z]^1[a(z - 1) 2Ft(a + 1, 6; c; z) +
+ (c — a) 2-Fi(a — 1, 6; c; z)]
(a - Ь)~г[а 2^i(a + 1, 6; c; z) - 6 2Fi(a, 6 + 1; c; z)]
(c - a - 6)^x[a(z - 1) 2Fi(a + 1, 6; c; z) +
+ (c — 6) 2-Fi(a, 6 — 1; c; z)]
[a - (c - 6)z]^1[a(l - z) 2Fi(a + 1, b; c; z) -
- zc^x{c- a)(c- 6) 2Fi(a, 6; c + 1; z)]
A + a- с)^х[а 2Fi(a + 1, 6; c; z) - (c - 1) 2Fi(a, 6; с-
[F - a)(l - z^Kc - a) 2Fi(a - 1, 6; c; z) +
+ F- c) 2Fi(o, 6-1; c; z)]
[c(l - z)]^x[c 2Fi(a^ 1, 6; c; z) + F - e)z 2Fi(a, 6; с +
+ i; ^)]
[a - 1 - (c - 6 - l)z][(a - c) 2Fi(a - 1, 6; c; z) +
	+ (c - 1)A - z) 2Fi(a, 6; с - 1; z)]

384
Гл. 7. Гипергеометрические функции
[7.3.1
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
а
а
а
а
а
а
а
а
а
а
6
6
сг-
6
6
6
6
6
6
6
С
с
тег -f
b
b
6 +
а + 6
а +
а + 6
а + 6
2
те
1
— тег
ь
+¦ тег
1
2
[^
С1
A
=
=
A
6z
Г1
A
-1 -
(т
-а)
-*)
(-1)
A +
A
A +
(а
A —
A-
"*)
тег, о
(
ln(l
а, «
-1п(
ы,
[а +
-.)
A-
2Fi(a, 6; с; z)
- Bс - а - 6 - l)zpx[(c - 1)A - z) 2Fi(a,
— 1; z) — с^г(с — а)(с — 6)z 2^1@, 6;
+ l)!z m
m+l(l — 6)m+l
x lim [Гт1(с) 2Fi(a — m — 1, 6 — m -
^a 2Fi
( к z \
\ z-lj
n (a)n ^ „\~a~n xx
x 2Fi(—те, 6 — а — те; 1 — а — те
a — 6)те
— 6)n
x 2Fi (—те, 1 — 6; 1 + a -
)n ,
х 2F1 | —те, а; 1 + а — 6;
)n(l - zYa^n х
x 2Fi (-те, 1-6; 1 - a- n;
-a
2F, 1 — ft)
ft 6
A -^-т*^ (а~т)к(Ь~т)к
k^o к\A-т)к
Г +6 1 °° ( ) (b)
[a — тег, 6 — тег] J^ k\{k + тег)!
- z) - ф(к + 1) - ф(к + тег + 1) + ф(а + А;) 4
[|arg(l-«)l < тг; |1
Aг!J ^?1" j V^ v) Vl
l^^)](l^^)fc [|arg(l-z)|<7r; |1
тег, 6 +
rU + 6
L а,
mlV W^6)^ (i -)*
тег] ^~** к\{\ — тгь)к
+ ТТ11/ 1\т\Г^ (« +'"^)feF + тег
b \ ~-^ к\(т + к)\
x(l^z)k[lп(l^z)^ф(k + l)^
- ф(к + тег + 1) + ф(а + к + тег) + г/>F + к +
[|arg(l-z)| < тг; 1
z)/2 |
/ о 1_ l-v7!77"
V а ' " ' а 2' 2
^ 2 ^ 11^
гГ1/2(у/Г^+л/^I^2ах
< 2FiBa - 1, а + 6 - 1; 2а + 26 - 2; 2\/z2
6; с-
с + 1; z)]
- 1; с; z)]
; 1- z) =
-Ъ\ - ) =
z /
i-J"
z)^5 x
-t/?F + A;)
-z|<l
-z\<\]
)k
m)

7.3.1]
7.3. Функции iFo(a; z) и 2 Ft (a, b; c; z)
385
2Fi(a, 6; c; 2)
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
.»_¦
а + Ь~ 2
a + b--\{->
„З/2-о-Ь/
[|arg(-z)|, arg(l-z)\ < тг; Re >/l - z > 0]
+ 6 _
1 1 - лД^^
2, 26; a + 6+™;
= Ж, 0 < Ж
2F1[2a, a-6+-;
a + 6+^;
,
l yl —
x 2FiBa, a + b; 2a + 26; 2^2 - ^ + 2z)
(
-г)|, | arg A -
Г(а + 6 + 3/2)/ Z4-Ba+2b+l)/4
Г(а +6 + 3/2) ^ж^-Bа+2Ь+1)/4
2a + 1
a + 6
a + 6
Г
2 V 2
/в 6
\2 2'
-zI/2 X
5 (--г)|, |arg(l - ,
—1/2 —а —Ь, /Z	Ч1
= ж, 0 < ж < 1]
A - 2x)
= x, 0 <
4гA Л_
> ' 2 '	2
а а + 1 а + 6 + 1
a + b
~ 5 а + 6;
13 А. П. Прудников, Т. 3

386
Гл. 7. Гипергеометрические функции
[7.3.1
50
51
52
53
54
55
57
58
59
60
61
62
??€>
64
а
а
а
а
а
а
а
а
а
а
а
b
b
b
b
b
b
b
b
6
6
и
6
a
a
a
a
a
a
a
a
a
+
+
+
2
+
2
с
6
о
6
2
6
6
6
6
ь
6
6
h
26
+ 1
+ 1
+ 1
+ 1
+ 1
+ 1
+ 1
+ 1
+ 2
_l_ 9
rffl
r(!
]
zF-
]
жF
(I
A
...
Г(а
Г(а
Г(о
(
Г(о
n
t + 6
, + 6
2
- a)
L
-a)
X
z)~'
1 +
— z
± V
Ы
-Ы
x
?- 1
- 6
6 —
\ — с
+ 1\ 2
)(* x
V 2 '
V 2 '
L^(o-b)/2
x i a a
tN.
to
z
ЕР ( а ~^~
-a Л«
I)- x2
x 2^1 (a
-1)( Z)(b-°
-1)(-Ж)F-°
/ЯГ[в"а4
<-2)г(Ь-а-1
К [
+ 2)( х)(ь-
[аР-ь 1
• /2 (а
2Fi{a,
г)A-а-Ь
2
2
1 а
а + 1
' 2
, а — b +
)/2(i z
[|
')/2A-а
J л
'z + 1\
2Vz /
VI - z/
-o-1)/2q
^1 + ж\
Vl - x)
a
2'
6; c; z)
[|argz ,
[|arg(-^|,
(а-Ь)/2-1
а
i
a-
. 9rt 9», _i_
v_6pb_a /1 -
arg(l - z)| <
) р-ь y1_
[z =
(Л
arg»
2' 4(^-1
= (a -1) <:
!A 2.)
arg (г — 1)| < 7г]
г = ж, 0 < х < 1]
arg A — г)| < 7г]
^ = ж, 0 < х < 1]
(i-*)V
iz ^~"J
h,JJ
1-х 4л/" "l
- z)
Щ z $ (-oo, 0)]
f ж^
-a/
ж, — сю < ж < 0]
\1/2 —Ь х
1 - v^J
2-v^
<•
i + A]
i-Jj
[|argz| <7г]
/1 + ж\1
ll-JJ
ж, —сю <
))
ж < 0]

7.3.1]
7.3. Функции iFo(a; z) и 2 Ft (a, b; c; z)
387
2Fi(a, b; c; z)
65
66
67
68
69
70
71
72
73
74
75
76
77
26
1 - a a + 1	1
2 ' 2 ' 2' 4(
o + l , , 1
2' 2 '
2' B-z)*
nl/2-6
X P 7
[	1	1
2F1 a,a-6+-; 6+-;
1 - V1 -
a-b-1/2
Ы/2
26-a
Re
>0|
226 r\b_+1/2]z-b(l-
x
x
/тг	a
arg(l=F«)|
r(a + ^rF + ^)(z-1)Aa6)/4
l/2-a-b
l/2-a-6/ /-4
а-Ь-1/2У VZ >
[\arg\
[z = x, 0 < x < 1]
+
X P
a + b — 1
Z-\
p6 —a
|argz
' Im;
*' llm;
-Г[а+-
x p;
a+b— 1
[z = ж, —00 < ж < 0]
13*

388
Гл. 7. Гипергеометрические функции
[7.3.1
2F1 (а, 6; с;
78
79
80
-2 ГЬ-2
а	а
а	а-\- т
[z = х,,0 < ж < 1]
X
х [In (-z) + 2ф(к + 1) - г/>(а + к) - ф{с - а - k)}z к
'-z)\ < тт; \z\ > 1; с - а ^ О, ±1, ±2, . . .]
а + га, с — а
+ те + 1) + ф(к + 1) - ф(а + к + те) - t/?(c - а - те -
81
а	а + то
а+то+1 + 1
; тг; И > 1; с-а^О, ±1, ±2, . . .]
(a)k+m(n + l-l)\ __k
+ ¦
Ы
- га) — ф(а + А; + га) — 1/^A + 1 — I
(-*)| <тг; \z\ S 1]
82
83
84
85
86
87
88
89
90
91
те
	Ь k —
то
— а
1-а
те \
— + 11 x
cos Bа arcsin
-Z) =
{l-z)e-\\-2z)
c 1 + с - a
-z)) а-
2 '
1 — с I?.
; с; 4z(l-
2 ' 2
-; с;
а + с - 1, с	;
1-а
1-а
1-а
1-а
<тг]
[z = x,
1
Ba —
cos [Bа — 1) arcsin л/z]
sin [Bа — 1) arcsin

7.3.1]
7.3. Функции iFo(a; z) и 2 Ft (a, b; c; z)
389
92
93
94
95
96
97
98
99
100
101
102
103
104
1 ПК
106
107
108
a
a
a
a
a
a
a
a
a
a
a
a
a
a
2
2
2
3
3
a
a
a
a
a
a
a
b
— a
— a
— a
— a
— a
1
+ 2
1
9
-1
1
9
1
1 2
1
2
+ 2
1
1 2
1
2
1
2
1
2
с
с
с
3
2
с
с
с
с
с
2а 1
2а
*?/7 1 1
1
2
3
2
4а+ 5
6
Г(с) /- z
1-aU
-(а+с-:
Г(с) / х
1-а VI-
- (а + с-
1
2(а^ 1)л/Г
Г(ф^2
2(а- 1)(а-
-
г(с)ж-2
2(о- 1)(а-
х Р
V 2
1 +v7!^7^
2с-1Г(с)(-г
х ^"-с
(с-2о-1/2)-
хA-г)
Гл. I О
L2/ 1 z
( 2
U + vr^i
1
2Bа- 1)ф
A^9z)a/
-*)
- 22
л
-2I1
[а + с-
/1
-2) U
1ЯГ.еA "
I
\
- (lit
У
-с)/2A.
с)A-с)У2
[A-х)-
L 2а -1
A-а)(У
2
•f л/Т^
ч 2а
-i + A
Г [A - v
2Fi(a, 6; с; z)
/2ff z V/apa-ea
^_J p_e A
^2z) [|arg(-^)|,
/2 [f ж V/2 P2^cn
|_Vl-aJ
ЕA^2ж) [;
[2(а — 1) arcsin \fz"\
¦i) {(a + c^3)I
-3 + 2z(l~a)]P12rac(l-
xc/2^2
- 1 1 {[a + c-3 +
/
2x) - (a + c-3)P2^c(
VT^^
1, c, 2^™^
2Fi|2a, 2a- c + 1;
A)- ,*(*,, с -
2c
^)(C)/2"a4"-CcP-
[|argz,
(l-aj)^)/2 x
/21 [^ = :
2c™1/2zAc)/4
-^1/a(^)
-2)]j/2aB-3/)-3
\2o-l
-.)
-Vi)-]
^I-2а-A + лЯI
а а 1 4а Н~ о 2
1
3' 3 ' 2' 6 '
^2z)^
arg(l-
-2Ж}-
у = ж, 0 <
э2^сA 2
-2,)}
2жA — а'
1^2ж)}
= ж, 0 < i
с;
2'
arg A-2
с, -оо<;
[
ж < 1]
'z;
I<т]
] Х
с < 1]
hy/z)
)|<7Г]
с < 0]
[V = 4(y-i)]
(l-9zJ
J

390
Гл. 7. Гипергеометрические функции
[7.3.1
2Fi(g, 6; с; z)
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
а	За
2
а	За
2
а	За
2
а	1-За
а	1-За
а	З-За
4а + 5
4а+ 2
3
3
2
4а
1
2
I-
1
2
3
2
З' 3 2' 3 6'
/ 1	1	1 _^r^
V 6	6	2 (z-4K
6' 3 '2'
12	3
тI У
- 3K
Л 1
6, с™ 6) V z
^Ь-п,с-Ь-п) ( 1 _ 2
1-c(l-z)c~b-1(c- l)Bz(c- 1, 6-c + l)
l^i j: (^:^b(i - г)-*-1 - (;:^)т
х (l^z)^TO 2Fi(l, 6^m; с; z) | =
~	' z -V
• - 1
A + 6-с)т
2Fi(l, 6; с- 771; z)
6 — 771
m
Ь-т- 1
A - ^)т+1 „ ^
6#(z, 1, h)
(m-lJK-sI"™-
то,—2 / L	1 ч
^ F — m + l)fe
: - 1
k / b + k-m-l
A-zf
[т = 1, 2, 3, . . . ; m-6^1, 2, 3, . . .]
' - 1

7.3.1]
7.3. Функции iFo(a; z) и 2 Ft (a, b; c; z)
391
2Fi(a, b; c; z)
127
128
129
130
131
132
133
134
135
136
137
1
--m
m
n
m + те
1
n — —
2
— + 1
те
Bm- 1)!! A-
Bm)!!
Bm-!)!!(&-1)!
Bi-i)H
(	1м fm-n-1 /	1 1 м
(m — 1)! J ^ (m — те — A; — 1)!
(m-n-l)\zy ^ (m — J« — 1)!
(n-1)!
(m - n)k
[m > n\
\m < те1
7
(ra-
/ ji-n
ifc!
n — l	/ e\ • 1	\	Г
El 2wikm\ Г	-, /
exp I	J In 1 - z1/n
k=o
[1 < n < m]
x exp
_ zl/n)
E
fe=i
/n I -2 sin
2wkm ( л /„ 2жк
cos	In 1- 2z1/n cos	+
\	n
¦ arctg ¦
[m, те = 1, 2, 3, . . . ;
x A -
(n)m
1
1, те; n+-; z
(l/2)n
n- l)\zn \~\ 1-z
2n-l
m-l
A/2)
¦s/z Arth л/z - ^
^—^ nm -
m — к
m-l
- 1
(m-l)!
[n = 1, 2, 3, ...]
ln(l-z)
[m = 2, 3, 4, . ..]
(Л-1)! / z
^ (l/2)fc

392
Гл. 7. Гипергеометрические функции
[7.3.1
2Fi(g, 6; с; z)
138
139
140
141
142
143
144
—п
¦—п
—п
--те
b
b
b
b
145
146
147
148
149
150
sin \fz +
2m ^ 1 /1-
m-3/2
Z
¦ m — 2
(_l)m^1arcsinA/^ -
~ V T^z ? WTl (l^l j	[m = 1, 2, 3, . . .
fc=O
2: =
? (c)fcfc! ~ (c)n
(C)n
n I i
-2n-2
(C)n
п!ГA-6)( ^)w.
[)9 = 6 - с - n]
[a = —те — 6, [3 = b — с — те]
[/3 = -n - 6]
_ ч-F+п+3)/2
2n + 2 -
x (F + 2n
- 2n + 2 -
-2n-
-2n-
п!ГA -i
Bn + 1)
fn+l
!)}
F + 2n
"!r(i-b), .„,
[z = ж, 1 < ж < oo]
<тг]
^+n+1 f 1 ^ -) + (b + 2n + l)P^n (l--
XT/	\	T
[z = ж, 1 < ж < oo]
Bn)!
Bn)!
[|arg(l-z)|<7r]
Л _ 1Л
^ 1
2B6- l)n
[z = ж, 1 < ж < oo]
")/2-1 \pb+n (i--
2
z
<7Г]

7.3.1]
7.3. Функции iFo(a; z) и 2 Ft (a, b; c; z)
393
151
152
153
154
155
1 Kfl
157
158
159
1 fift
161
162
163
164
165
166
1 ?*ff
1 ИЯ
169
a
—n
¦—n
¦—n
—те
—n
—n
—n
¦—n
¦—n
—n
—n
—те
-n
—те
—n
b
6
6
6
6
b
и
b
6
6
и
6
b
b
m
1
^2 ~ П
1
2
— 71
1
1
b
b
ь
b
с
26
26
и
-6
о
h
— те
— n
-n
— n
2
1
2
со I cm
7П 4
-1-
3
2
1
2
1
- те
— те
— те
1
2
1
2
1
1
' 2
+ 1
1
2те
1
2
2те
ГA-6) !_ь
2B6-1)ПЖ ^
+ РЬЬ+2Я (l - ^
n!2-2nzn A /
F+1/2)п п V
( +i)« L
(jb j J
(b)n ^n\2y^ J
n!(l - z)n A /
A^26^2n)n n \
nl „(n-i)/2
22та+!A/2 - b - n)<
Bn + 1)!
B-26Jп+1л/ЬГ
Bте)! b^n r
(l-2feJn ^
Bn)! /
(— 1) те! (h	«wo
те! П b^n /-
(l-6)n 2П
С
2A - 6)n+lv/^
¦* ТП, n ¦> -L 2, n /
Jo
13, n — ^
(ТП + l)(n + l)/m, n
j
(-l)n2n/(/n Л
(l-z)n т fl + z"
Tl+1 ^ VI -Z,
( i\n \^n ~\~ 1)'
rBn+3/2)v
* i3 I 1
( 1) Dn)! A-)
2^1@, 6;
;)]
!)
/z + 1\
'i + ,\
,i-J
>n + lVl - ^
/^b — n — 1 (
— °2n+l I
—)
4/ 2n
L)(n + 2)(n-
= (to + 1)/,
, 0 — lj ^"l, n
n
P2n{y z
c; z)
ГрЬ+n Л 2
1Л-1 v1 ^
[z = ж,
|л.
f 1\ 6 (Z -
-ь/'/*-1'\
-(l + z + nzH
)]A-г)"+1},
7lj n+i + z(ti +
71 + 1 "
( 1 ^l^1/2
X P2n + 1
r)
)+
1 <
1
2
Ml
-
z J\
1
2
f 1\
fz J
z —
/ z
1)toj
I1
f/
ж < 00'
[n^l]
/
1
771-|-1, П ?
Z) J

394
Гл. 7. Гипергеометрические функции
[7.3.1
2Fi(g, 6; с; z)
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
71+1
71+1
П + 1
71+1
71+1
3
П+2
3
+
3
П+2
тг + 2
1
2
1
3
2
1 - 2п
1
2
1
	71
2
п!
1 + z
A- z
-1
C/2)n4/i
2n+l
A- c)z1~c(z- l)n+c
. 1 m — n /	ч
771+1 ^ G1 — m)k
- с - n, n + 1)
(m)nzm^1
fe=0
k\ Xz^l
-m- 7i)fc
/1 - Z
2n
C/2)n
(n + l)v^

7.3.2]
7.3. Функции iFo(a; z) и 2 Ft (a, b; c; z)
395
2Fi(a, b; c; z)
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
n
2"
n

n

n

n
2
n
2
n
2
n

n
2
n

n
"
n
"
n

2(n
n
2"
n + 1
2
1-n
2
1-n
2
1-n
2
1-n
1-n
2
1-n
1-n
1
	n
2
(-l)"nl 6-П/2 /
—	гтт-Ь,, (
A - 2Ь)п
[AC — ljn
( i)n nl
( >
2-(l/2)n
1 \
7.3.2. Частные значения 2^i(a, Ь; с; z).
(См. также 7.3.3 при замене z на —z).
2Fi(a, 6; с; z)
2 2
1 — z + у z arcsin у z
1 ( arcsin yfz
2
16
- [B - 7z - 3z2
/1 Z
5 L /. . _ O\ arcsin л
128z2
- C - lOz - 8z2

396
Гл. 7. Гипергеометрические функции
[7.3.2
8
9
10
11
12
1 Ч
1 л
15
16
17
18
19
20
*>*?
*?Ч
24
25
26
27
*>я
29
30
32
33
34
а
1
2
1
2
1
2
-1
1
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
1
2
1
2
1
2
1
2
1
1
2
1
2
1
?
2
1
2
b
1
2
1
1
1
1
1
1
1
:i
?,
3
2
3
2
со | см
3
2
3
2
3
2
2
2
2
2
2
2
2
Б
2
Б
2
Б
I
_
2
5
2
с
4
1
2
3
2
2
5
2
О
7
2
4
1
2
1
2
5
2
3
7
2
1
2
1
3
2
5
2
3
7
2
4
1
2
3
2
2
3
2Fi(a, 6; с; z)
32
Г-dVi 4~ 1 1 Ч~^\ \С( \/~~ \ (Ч ЧЧ~ 1 ^Ч 1 1 ^ ~3\тг|/ /77 \]
1 - V^ Arth v^
1 Г Arth /г 1
2 L v^ J
^ t1 " (X " *K/2]
3 [ 2Arthv^l
8z[ лД J
8 Г 5 1
15z2 [l "j 2 J
5 Г о Arth л/^1 ol
o/i ^w v 9 i Q~ I *3~z
48z2 L yfz J
|Q OQ-v 1 Ч^-v2 ЯП -v^/2l
t5o^ L J
A — 2z)(l — z) '
2
— K(-\/z ) — 2,zT3(\/z )
7Г
4
— [K(\/z") -f- A — 2z)D(\/z"I
Зтг
3 farcsinv^ , o , q	r]
8z [ V^ ( ")V ~J
Г/1 | ~\TC( rZ \ o/i ~ i ~2\ тл/ /77 \1
j-. Г • у»	 -1
32z2 Iх } лД 1
32
105ttz2
fl - z)™1
Г"^ 4 " 4i/~Vi "^ Artb i Г~\
2
2
4 I A °~\ Artnyz
4 L v^ J
3 Г Arth -Jz 1
fl I Q«/1 ~\ V 1 I 9 ~
16z L л/z J
15z2 l J
5 Г Arth /z 1
32z2 Г "" ^^ " ~ v^ J
-^-3 [D + 3z)(l - zM/2 - 4 + 7z]
— C3	12z -f- 8z ) fl	z) '
3
2
\(o A~\\?( /~\ ~(r7 4.~\t'\( /~W
I
— C3	4z)fl	z) '
3
— [4K(\/^) + A - 8jz)D(v^I
9tt
ffo 1 9 ~ q~2\t->/ /77 \ /1 4~^"К"^ //Г-^" ^1

7.3.2]
7.3. Функции iFo(a; z) и 2 Ft (a, b; c; z)
397
2Fi(a, 6; c; z)
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
3
3
-T 3
3
7
2
-i 4
2
-i 4
2
-- 4
2
-- 4
2
-- 4
2
5 Г
48^ [
3-z-lGz2+8z"
[2B^z + 2z2)]
-{8-bz- 5z2 + 8z3
16
i E - 30z + 40z2 - 16z3) A - z
-^-A - z)^2 [A5 - 41* + 24z2)
15тгA — zj
[G -
32
525?rz2
[2(l + 4z^24z:
[(8 + 9z + 16z2 --
- 2z A9 - 44z + 24z2) Щу/z)]
.- 16z + 16z2)D(^)]
-(l-24z)K(v^)]
J)D(^) - D + 5z™24z2)]
35
- 105z3)	Jz Arth Jz
' 16
— A6 - 72z + 90z2 - 35z3
128z
3A + 3z + 15z2 ™
768z2
1 [ l+ж	^
— In	h 2 arctg x + V2 arctg
8ж[ 1ж	В	В
-3-W0z-10bz<
- 3 - lOz + 105zJ
1 + ж
2 In -^	In
1
2 In	In^
12а; [ 1 - ж	1 + ж + ж
+ 2^ arctg
1 - ж2 J
[х = z
г
[х =
L

398
Гл. 7. Гипергеометрические функции
[7.3.2
a b
2Fi(g, 6; с; z)
60
61
1
5
62
63
64
65
66
67
68
69
70
71
72
1
3
73
2
5
13
"б"
6
5
11
4
3
7
3
11
12
	— A^ж6) In —
6ж6 Збж7 1	' \ 1-
1 + ж 1
1
	in
2
in
ж 2 1 + ж + ж
20ж
2 ^	Зх/2ж]
^ + л/3 arctg
2	1 - ж2 J
[* = * ]
- (л/5 - 1) In [l - (л/5 - 1)| + ж2
2A0
arctg
4+(л/5 +1)ж
- -41пA-х)
[х = .
50ж6
+ 2A0 + 2л/5 )х/2 arctg
^ [A -	1/2
\/5 ) In
1)- + ж2] -
arctg-
4- (V5 - 1)ж
= B -
_ 4In A -
= z1'*]
1 Г 1 + ж	1
— In	h 2 arctg x
4 [ 1 - ж	J
¦]}
3 /3"
— д / —
2V z
г — средний действительный корень уравнения г — г -\	* — = О
3 V 3	I
— In (l+ж+ж2)™ 21пA-ж)+2\/3 arctg
™ In A + ж+ж2)- In A-оО + л/
arctg
3 Г 1 + ж	1/9 1 + 2!/2ж +
— In —— - 2 arctg a - 2"г/2 1„ , о1/9 „ ,
8ж3
Юж2
arctg
1-ж2
-2A0-
4-(ч/б -1)ж
- 2A0 +2л/5I/2 arctg-
7	7
5ж5 50ж7
A-ж5) In A-
¦ 51пA - ж) -
- V5In^

7.3.2]
7.3. Функции iFo(a; z) и 2 Ft (a, b; c; z)
399
2Fi(a, 6; c; z)
A0 + 2у/5I/2ж
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
2
2
1
2
1
2
1
2
1
2
1
2
1
2
2
2
2
2
2
2
1
1
3
2
2
5
2
3
7
2
4
1
2
3
2
2
5
2
3
7
2
4
1
~2
2
5
2
3
7
2
4
1
2
1
3
2
5
2
[D - llz + 15z2) K(y/z) -
75ttz
1 In1
1-V*
jlj [2A -,
¦»
[8 - 20z + 15z2 - 8A - гM/2]
тгA-
7Г
3
3ttz
15
16^2
32
157Г
B
1 Г 1
4 [(8 - 13z + 3z2) D
x arcsln y/z
¦ 2B - i
2 [Г^

400
Гл. 7. Гипергеометрические функции
[7.3.2
100
101
102
103
104
105
106
107
108
109
110
111
119
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
a
1
2
1
2
2
1
2
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
2
1
2
1
2
1
2
1
2
tol h
1
2
I
2
1
2
1
2
1
2
2
1
9
2
1
2
6
2
2
2
5
2
5
2
5
2
5
2
5
2
5
2
5
2
3
Q
-D CO CO CO
3
7
2
tO| -s
7
2
V
7
2
7
2
7
2
4
4
4
4
с
3
7
2
4
1
~2
1
3
2
2
3
7
2
4
1
~2
1
3
2
2
5
2
7
2
4
1
2
1
3
2
2
5
2
3
4
1
~2
1
3
2
2
JL[2_BH
5 Г
16z2 [
2^i(a, 6; c; 2)
-,)v^l]
ч Arth yfz 1
3A ")C 1 ")
^[D + *)(l-*K/'-4 + 5z]
— A - z)^2 [C - z)K(A/z") - 2zB - z)T>(y/z)]
3
4
5 [3arcsir
8z2 L v^
32 j.
157TZ2 ^
8
1 Г 5 - 3z
- D-3z)(l
4
з Г
2
15тг
15
— A-2;)^
5
45ttz
32 re i
75™* ^ '
A-92)A-
— A6 - 242
1 ГЗЗ-402
48 [ A -
8 ^
-—
(л^)]
2\ /-1 \—5/2
>z 1 \ — ")
Arth -y/z 1
^ Arth yfz 1 — З2]
' V~z 1-sJ
ox Arth л/z
h4z + 3z2)VT^7J
,)-/»
3 [A5 - llz + 4z2) K(v^) - z B3 - 23z + 8z2) Щу/z)]
+ Sz2)(l-z)-^
2 [2C - 2z)?L(^fz:) + C - 13z + 8z2) D(v^)]
-2)-/2
[B + 3« 8z2)D(/i:) A 4z)K(-v/z)]
7z + 8z2) T>(yfz) - 4A + z)K(yfz)]
zyb
+ 18z2^5z3)(l^z)/2
+ 15z2 f iKArthv^]
zK v^ J
5*2)A-*Гб/2

7.3.2]
7.3. Функции iFo(a; z) и 2 Ft (a, b; c; z)
401
2Fi(a, 6; c; z)
128
129
130
131
2
4
2
4
2
3
132
133
134
135
136
137
138
139
140
5
4
5
4
- 1
141
4
5
13
13
7
I
11
T
1
2
3
2
5
3
14
(л/5 + 1) In [l - (л/5 - 1)| + ж2] -
4 —
-2\/5I/2 arctg
4+(л/5
-(л/5 +1) In [1-
- 1 - + ж^
+
5 Г 1-
ln ¦
«In
8ж5 I 1-
4 - (л/5 - 1)ж
-1/2 i 1
; In —
21/2ж 1
- л/2 arctg	-
. - ж2]
3 Г 1 + ж
-—г- In	2 arctg ж
4ж3 1 — х
16ж7
1
1
^х^) |lnii^-2arctgJ|
1 — ж
In A - ж3) - 3 In A - ж) - 2\/3 arctg
2 + ж
3V2,
^j I In A - ж5) - 5 In A - ж) - л/5 In ¦
5ж
4 —
9
5^
25ж9
f
4+(л/5 +1)ж
5) (in A - ж5) - 5 In A - ж) -
[ж =

402
Гл. 7. Гипергеометрические функции
[7.3.2
142
143
144
1 лк
1 AR
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
a b
I >
5 i
6
8
i i
1 1
1 1
1 1
1 1
1 1
1 1
1 1
1 1
i 5
2
i 5
2
3
2
2
2
2
i »
2
1 2
1 2
1 2
с
11
6
17
6
15
8
1
2
1
2
3
2
2
5
2
3
7
2
4
5
1
2
2
2
5
2
3
7
2
4
1
2
1
2
3
2
2Fi(a, 6; с; z)
2A0 + 2
^I/2агс^A0 + 2^I/2ж
v5) arCtS 4^(л^^1)ж
2A0 2\/5I/2arct
A0-2л/5I/2ж
J
5 1 + ж 1 + ж + ж2 г- Зх/2ж
1 О/у>5 1 	 /v. I 	 /v. _|_ /T.Z 1 	 Т»^
JL xj «A/ I JL «д^ JL tJL/ | vU JL «X* I
-цд eg Г -|	д, 2	ж + ж2 3^/2ж
6ж® Збж11 1 + ж 1 + ж + ж2 1 — ж2
яС /¦*» I I "I 	 /у» "I 	 "ж Л. / JU гуъ 	[	 гъъ idi "I 	 /у» Л
\3 iAj |^ А «X/ А ^н^ * чау I еду А еДу
A z)^2
arcsin i/z
v/z(l-z)
z1//6l
¦1
3z3/2 arcsin y/l 1 [ж^г ]
\/г arcsin y7^ "j
J
-Iln(l-z)
" arcsin Л
J
z2
5 Г ,3/2 arcsin-х/г о 1
3z2 L"v ^; л/^ " ' ^J
^[zCz^2)^2(l^zJln(l^z)]
-^ [6A - zK In (i-z) + Gz- 15z2 + llz3]
2( г Л
3 [ArthV^ 1
« L л/г J
4A + л/l-z)™2
5 Г ^ Arth-v/г]
2z2 [ " л/г J
2 г i
z3 L J
(I-*)
2
(l^z)
2
2
2 14z 3z2
^ 1 ~ 1 4 ' ^
2+z+3Vi-
arcsin i/z
i/z(l^z)
15z3/2 arcsin i/z
л/Т^^
- arcsin \fz

7.3.2]
7.3. Функции iFo(a; z) и 2 Ft (a, b; c; z)
403
1 (\A
165
166
167
168
169
170
171
172
1 74
174
1 7K
176
1 77
178
179
1 ЯП
181
182
183
184
185
186
187
188
1 AQ
a
1
1
1
1
I
1
1
1
1
-1
1
1
1
1
1
1
1
1
1
1
1
1
b
2
2
2
2
2
2
5
2
5
2
2
2
2
3
3
3
3
3
0
3
7
2
7
2
7
2
7
2
7
2
7
2
2
7
2
с
5
2
3
7
2
4
1
2
1
2
3
2
2
3
7
2
4
1
2
1
2
3
2
2
to | сл
7
2
4
1
2
1
2
3
2
2
5
2
3
4
9
to
3 | arcsin yfz
2z |_,
2
/z(l^z)
z + ln(l~
5 3 z 3,
2z2 [ 1
Jf[*B-*) + 5
A _ gz _ 9z2 +
I C _|_ 6^ _ z2)
3 l ;
— C	z) A	z
3
2 г
3z L
4 Г 2
5 Г Arth xfz
z2 L V^
^ [8 " 4z " z2
8 ["
8 Г '
8 [
2
2Fi(a, 6; c; z)
/1-z ^_.^ /_
z
!(l-2)ln(l-2)]
A - z)^3
~
-¦
	 ]_
J
"I
2 z
1 *1
3j
^8л/Г^^]
о о 105z3/2 arcsin -%/z 1
92-
zx, | low arcsin ул.
3 arcsin д/z I
Z+ ^z{\ - z) J
3 f ,_! Г arcsin у^
5
8z2^
L v
3 arcsin y/
t(z + 2)
z
- 1
0 9~
i E - 60z - 90z2 + 20z3 - 3z4) A - z)^5
I
— /{5 _|_ j_5z	5z
5
	f 15	lOz -\-
15 l
2 г
/i \—5/2
5^iA)
— C5	3z)(l	a
5
4
2A - z)
2Z I"" 8
7 Г
15z3 L
^ _|_ 2; j A 	 z~)
3z ) A	z)~
/v
-1
1
-3/2 _ 2 _ 3Z
8 4z 3z2j
2 Arth •y/z" 1
лД J

404
Гл. 7. Гипергеометрические функции
[7.3.2
a b
2Fi(g, 6; с; z)
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
1	4
1	4
1	4
1	4
1	4
1	4
1	4
2
2
2
3
(i-*)
48 + 87z - 38z2 + 8z3 + 105
1A-*Г2[A-
3 Г _ ч-1/2 _
2 L
л/г
32
3ttz2
[D -
- 15z2) A -
3/1
¦-2 =
/T=z
4r [4 - 3z - D - z)VT^^] = 8A
[C
- zG

7.3.2]
7.3. Функции iFo(a; z) и 2 Ft (a, b; c; z)
405
217
91 Л
91 Q
221
222
223
224
225
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
a
3
2
3
CM
3
CM
3
2
-
3
2
?
3
2
2
2
3
2
3
2
3
2
3
2
3
2
3
9
со I cm
to | 00
3
2
2
со I cm
со I cm
3
9
2
2
2
2
6
5
2
Б
2
5
2
Б
см
3
3
3
3
3
7
2
7
2
7
2
7
2
7
2
7
2
7
2
4
4
4
4
4
4
4
2
2
2
с
2
*?
7
2
1
1
2
1
2
5
2
7
2
4
1
2
1
2
1
2
5
2
3
4
1
2
1
2
1
2
5
2
3
7
2
1
2
1
2
1
4
	М 	 ^
Зтг
16
37TZ
5/3
2z2 Vv^
32 j.
3ttz2 ^
A - 14z
(l + 5z)(
- (8 + 8^
-U-z)
A
3 Г Ц
8z [A-
15 ГЗ
16z2 [l
Ь \^~
(l — 16z
A + 6z)(
1^A~
— A-
15тг
\
- E - 2г
5
16 fi
15ttz V
32
15ttz2
A - 18z
(l + 7z)(
— A6 +
16 l
-(8-4i
8
1 \(s
16* L(
-B-z)
5 ГЗ
32z2 [
A-z)-
4
A-^)-
4
A + *)A
) 2
	2;
_ — 2
2К(\/г
Гтс/"Л/Z
arc
^35z2)(l^
|_	2
A —
- z
zJ
_ z
- z
Az~
— 48/
1 — z
zyA
')(l ~
)
г)"8/2
' ) I
"sin /~?
\fz
- z)^5
z)-7'2
Arth Vz 1
z2)(l
z ) A —
\ --9/2
[A5 +
[(9--
-2[(i +
"MD
^63z2)(l^
24z -
. + z^
f 8z
A -
™2z
A-
4
3
4
4-
"*)
ч-Б
-6z2 +
2)A-
3z2)
z)-5/2
+ 3z2
zJ
f Hz 4

z J
z)
34z-
2
z)KD
z)"e
z3)(l
-3A +
-61z2-
-3C +
2Fi(a, 6; c; z)
+ z\G(\fz I
; IV jj
у
v ;j
/i" 1
= J
/2-s]
In
1 2
z2) Щл/z) - 2z A9 + 6z - z2) D(v^)]
г) - C + 7z - 2z2) D(v^)]
/T\ 9/1 r 1
/zj z^l z +
./T\ (q Qy
\/Z) [Q 6Z
z2)D(v^)]
-2z2)D(v^)]
- z)"9/2
-3 „Arth^
л Arth v/z ]
"} Vi J
1чГг , о , г3/2 arcsin VI1
л/1 - -г |
—)у 1 _ ^ агс-
in -y/z

406
Гл. 7. Гипергеометрические функции
[7.3.2
245
246
247
9/|В
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
а
2
2
2
9
2
2
2
2
to to
2
2
2
2
2
to to to
2
2
2
2
2
2
2
6
2
2
2
9
2
5
2
2
2
2
5
2
2
2
2
7
9
7
2
7
2
7
2
7
2
2
7
2
3
3
3
3
3
с
3
2
5
2
3
7
2
4
1
1
2
1
3
2
3
7
2
4
5
1
9
1
2
1
3
2
5
2
3
4
1
2
1
2
1
3
2
5
2
A-
3
Az
2
z2
15
41
5
2z2
8
z3
(i-
4
1 "i
8
5z3
A -
A -
A4
A-
3
16z
4
A-z)
[ "
[l-z
г
s
Ш
-lbz-
^6z +
J + 3z)
/3-
V 1-
-20z~
I")
2 [
16
16
-2z)(l
~z)^3
16
h
-[
L
- 2z
\~i
ibz
*2)(
2 _____ ^
2z
z
\z
90z
(
16
16-
-z)
1"
>-
2Fi(a, b; c; z)
l + 2z
^(l-z)
1 ~~ z 11
"csin -y/i"
zY z J
2-5z3)(l^z)^5
l^z)^4
zy7/2
11-) 8 (i i T^)
-3
"L
2_20г3 + г4)A-г)-в
5z)(l z)/2]
4- 5z 1
l^zK/2J
170^ fi^q-2 40~3 10^ 1 A~\Z arcsmVz
f 83z + 6z2 + 15
- arcsin v^z
s J
, -- , ^1 + AZ
1 ^^ 1 ,—
— arcsin y/z
лА(ТL 2:)

7.3.2]
7.3. Функции iFo(a; z) и 2 Ft (a, b; c; z)
407
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
a
2
2
2
2
2
2
2
2
2
5
2
5
2
5
2
5
2
5
2
5
?
5
2
5
2
5
9
5
2
5
2
5
2
5
2
5
2
5
5
2
6
3
3
4
4
4
4
4
4
4
5
2
5
2
5
2
5
2
5
2
5
?
5
2
5
2
3
3
3
3
со со
3
7
9
7
2
с
7
2
4
1
2
1
2
1
со I cm
5
2
3
7
2
1
2
1
2
1
3
2
2
3
7
2
4
1
1
2
1
3
2
2
7
2
4
1
9
1
2
15 (i
з Г
z3 L
(i-*)~
A - z)~
32
(l + 3z)
A — z)~
96
(l-s)~
32z
1
5 A
- C + 2
3 v
3
9тг
16 a
5 ГЗз
32 A
3ttz2A
(l-2Lz
1
- (8 + 2
8 v
4
5 hfi
A - 24z
z)^1 3 2z
Z 1 oinh
i-z ' "lnA
49 704r
L
32 + 247z 4
-4
-3
[81 + 28г-
3 + Ш-4
)(l-s)-3
z)~2 [3 4z
4z + 8z2) A -
z)^4 [C + 10z
z) [E + 3z)I
-z)^2[2(l 2,
^z)^1[D^3,
- 105z2 - 35z
4z + 3z2) A -
L^z)^4
!lvT/23-
v^ A-
(8^12z + 3z2
- 144z2 - 64z
+ 8^A-,)
2Fi(a,
3-4z
-.]
6; c; z)
arcsin y/z
2553z2 260z3 + 20z4
- 40z2 4z3 4
4z2 + 15A + 1
2
Z
1 /1-2 0/1
+ 3z2)K(^
c(v^)-(i +
0K(v^)-(8
3) (l^z)^6
5z 1
)(l-2)-3/2]
3\ /-1 \ —13/
-315E
- 105A + 2z)J
z / arcsin V^
1 D^j
„ . arcsin д/z
arcsin i/z
V*(i-«).
o_ arcsin v^
Л/гA~г)
-I
)-8z(l + z)D(v^)]
- 7z)D(-^)]
2

408
Гл. 7. Гипергеометрические функции
[7.3.2
296
297
298
299
300
301
302
303
304
305
306
Qf|7
309
310
311
312
q-i q
Q1 Л
315
316
317
318
319
320
321
322
a
5
2
5
2
5
?
Ю I CM
5
2
5
2
5
2
5
2
5
2
5
2
5
k^
5
2
Q
3
3
3
3
Q
Q
3
3
3
3
3
3
b
7
2
7
2
7
?
7
7
2
4
4
4
4
4
4
Л
Q
3
3
3
3
Q
Q
3
7
7
7
2
7
2
7
2
7
2
7
2
с
1
3
2
2
3
4
1
2
1
2
1
3
2
2
3
7
2
1
2
1
2
1
3
2
2
5
2
7
2
4
1
9
9
1
3
2
2
5
2
4
15тг
— C -|- 4/
3
16
45?rz
32
15ttz2
A - 27z
— f 3 + 4'
3
— A6 +
— C + 5/
3
	B4 +
24 v
- F~zN
6
5 [3'
48z^ [3
(l-z)~
64
A-*)"
fi4
(l + 4zH
A — z)
64
9
3
64z^
15
A - 28z
(l + 15z
— E + 1'
5
- D + 3.
4
-|
~ E + z"
5
2 ¦-
	 fg .
5z3 L
z)-«[A5
уW|_ 	 z)
2)-4 [8A
-,)-3[B
-)[(
- 189z2 -
tz + 35z
72z + 18г
у)П 	z}~
ir-zy1
^rth-x/z
6 r
V
[б4 + 60
L
h2:2)(l^
5A1 +
A-z)^4
г
/y\ " 1 1
г
- 210z2 -
+ 15z2 +
b + 15,2)
z)(l - z)~
— 20z + 15
+ 74z +
9/2
+ Z)K(
8- 13z
-105z3)
П 	2;)
П 	 2,\
3-8z
A-
7z + 27^
zTb
lOz) + 3
Q ~ I
- 140г3 -
*3)A"
A-,)
	z\~
9/2
Z ) A —
2Fi(a, 6; c; z)
39z2)K (v^) - z D3 + 82z+ 3z2)D (д/^)]
v^) - (l + 14^ + z2) Щу/z)]
o«2\ тл/ /~Z \ A q«\1i/'/' /Z" \1
+ z J IV^ j ( ^J (У2 JJ
(i-,)-7
(l-z)-»/2
-—9/2
^3z2l
-K J
2 3
°~2) z3/2arCsin^l
iz2 + 15A5 + 40z + 8z2) x
V 1-* J
/9 1 ой-, 1 o~2\ arcsln yz 1
arcsln /z 1
"~ VZ(X^Z) -1
arcsin fz 1
-7^4)(l-2)
2)"e
-11/2
. %\ ^5/2 	 g

7.3.2]
7.3. Функции iFo(a; z) и 2 Ft (a, b; c; z)
409
323
324
325
326
327
328
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
a
3
3
3
3
3
3
Q
7
2
7
2
7
9
7
2
7
?
7
2
V
2
7
2
V
?
?,
?
7
2
7
2
2
7
2
4
4
4
4
6
4
4
4
4
4
4
Л
7
2
7
2
7
9
7
2
7
?
7
2
V
2
7
2
4
4
4
4
4
4
4
4
4
4
4
с
1
1
2
1
3
2
2
5
2
7
2
1
2
1
2
1
3
2
2
5
2
3
4
1
^2
2
1
3
2
2
5
2
3
1
2
1
9
1
3
2
(I-*)
128
A-z) 6
1 9Я
(l + 6z + ,
A - z)^5
128
(l + z)(l-
A - z)^4
128z
5
128z2
2Fi(a, 6; c; z)
128 3968z 26223z2 14702z3
1— -1
- 280z4 - 315C5 + 84z + 24z2) z3/
2 arcsin y/z 1
/1 _ z
[l28 + 1779z + 1518z2 + 40z3 +
+ 105E+ 20z + 8z2) J-
z
- arcsin л/z
0 / o\ arcsin л/z"
114 1 114.~ 1 4 ~ 1 I^ii 1 10 .v 1 Q~zi v
[ ^/z(l^z)
L , п.. | o.2 «/-, 1O- o. 24 arcsin^i
ч q / o\ arcsin л/z о
1 \ { ' JzJl^z)
- E - 160z - 1440z2 - 1280z3 - 128z4) A ~~ z)^15/2
1F + 90,
2
17Г
— A5 + 4
15 v
75тг
— E -\- 2z)
5 v ;
225ttz
32 fl
75tt*2A
A - 36z -
(l + 21z +
+120.»+ ie,»)(i-*)-»/»
)™6 [A5 + 113z + 113z2 + 15z3) K(y/z) -
- 2z B3 + 82z + 23z2) Щу/z)]
Q2; i. $z 1 A 	 z\~ '
Уъ [C9 + 74z + 15z2) K(v/z") - C + 82z + 43z2) T>(y/z)]
1 — z) '
- z)[2(l - 6z - 19z2)D(^) - A - 34z - 15z2)K(V^)]
^z)^3[D llz + 15z2)K(v^) (8 23z + 23z2)D(v/z")]
378z2 - 420z3 - 63z4)A - z)^8
35z2 + 7z3) A-z)^7
— A6 + 120z + 90z2 + 5z3) A - z)^13/2
16 l ;
~ (З ~f- lOz
3 l
8
- E + 3z)
5 K }
- F + z)(
6 V A
(l^z)^8
ОСИ
13628z4
/ -i \ 7
A-z) 7
9C|3
(l + 9z + <
A-^r6
256
_i_ 3z j A	z)
+ z2)(l-z)-11'2
A_z)-5
Г 2 „
256 10240z 99021z2 102592z3
П5Г105 1 -7°- ! П6-2 i 16~3) z3/2arcsin^
Ц
256 + 5175z + 8132z2 + 1452z3 +
I	 -1
+ 35C5 + 210z + 168z2 + 16z3) J-
- arcsin -\fz
?z2 + z3)(l^z) Vl^z J
7C3+104z + 28z2) +5E + 90z+120z2+16z3) -
L v
resin y/z ]
/z(l-z)\

410
Гл. 7. Гипергеометрические функции
[7.3.3
349
350
351
352
а
4
4
4
4
b
4
4
4
4
с
2
5
2
3
7
2
з
3
256z
JC + *)(l
5 „
768z2 ^
^)(l-,)-e
Г5 l + 68z +
— z)~5
z)^4|~3(l 6z
2Fi(a
36^- A
+ 24z2 +
, b; c;
- 18z
16z3)
*)
-72z2- 16z3
arcsin yfz
Vz(l-z)
)-
\
3 J
ircsinv^ 1
~16z + 92z2
7.3.8. Представления2^1(а, b; c; — z).
(См. также 7.3.1 при замене z на —z).
1
2
3
4
5
6
7
8
9
1 О
11
a
a
a
a
a
a
a
те
га
2
m
3
га
4
a
a
1
1
2
+
+
1
2
1
2
— a
1
1
1
1
a
a
a
с
1
2
со I cm
1
2
1
2
3
2
3
2
7i
ra
2 +
m
3
ra
4
A + z) a cos Ba arctg
A + zI/2^ . Urt
(ел -| \ /~ L\
H^ZCl — 1 j-y ^
1 Г, /
— H V 1 1 л- 1 s
1 [(/n^
1 r
4(o-l)^(l + ^) ' '
_™г-т/пПу\_
те z--' [
то _m/n/ (-l)m
те" 1 2
+ \^ cos BJb +
fc=o L L
- 2 sin |"BA; + 1
|ml(^)/Bl(-i
2F1 (a, 6
- 1) arctg \/^]
^ "a
те J
[1-(-I)»] Ь
i)ZL?Zll in |i_
те
^ Trmi +^
J arctg
n -I 1 -
\fe —1^ —A;
^—-' ra — kn
[(m-i)/a] (_1)к_1г
^ ra - 2fc
— cos
% ¦> (— 1J z
fc^l m ~ 4k
Зтятт
4
-k
¦ m^-m/2
| Ш „-m/3
¦ те ^-m/4
2
1/4 1
ч/^ Ч- z^/4 2
; с;
;J«
It
In-
(-
-2z
Z1! '
^Z1
sin
Г
r
sin
cos
+
_z)
]
hz1/-) +
!/- cos [BЛ +
lsin[BJfe + 1)ti
/ncos[Bfc + l
[ra, n - 1
ТП7Г r-
arctg у ^
-1
~ 2
гтетг z
4 arCtgv^
Ш7Г In Гл/I
4 ln Vz
1 Зттг 1
2C°" 4 Ы
"I
;BЛ+1
те
-/w] 1
OT/n]J,
, 2, 3, .
cos
2
^л/З
'""Mn (
zl/4
V^ +
(л/^ +
21
г2/"}-
. . ; га ^ n]
1
b(l-«)J
I
^4l + l)]

7.3.4]
7.3. Функции iFo(a; z) и 2 Ft (a, b; c; z)
411
7.3.4. Частные значения 2^i(a, b\ c; —z).
(См. также 7.3.2 при замене z на —z.)
a b
2i?i(a, b; c; — z)
- 1
7
8
9
10
11
12
13
14
15
16
- 1
I 1
- 1
- 1
- 1
1	1
2	2
\	x
3	5
4	4
3	5
4	4
5 1
4
» 1
4
5- 1
6
- 1
- 1
7
6
13
5
4
9
4
11
7
4
11
4
11
~6~
17
13
15
Iff . ax . 1 — аж
i a
L
2 arctg -
¦ -In
-62 arctg
1 + аж + ж2
6ж
— In
, о = B - л/2 )!/2, 6 = B + V^)V2]
1
12ж
7
72ж7'
4 arctg ж + 2 arctg -
х 14 arctg x + 2 arctg —^-^ - 3~1/2 In ¦
x 4 arc
8ж
5
П
- 2 arctg -
3 Г Г 1 -
	< о In —
16ж3 1 [ 1
[x = .
[x = .
16ж3 I L 1 - 6ж + ж2
1 + аж + ж2
- 2 arctg -
6 2 arctg ¦
-In-
1
1 — ах +
H	[x = ^/8, a = B-^I/2, 6 = B-
Arsh -y/z
—zr In (л/1 + Z
^^ arctg v^
2^/2A + z)^3/2 [(vThFI +1I/2 -
Зл/2
32ж7
5
12ж5
11 " 55
ln
ir
— 2 arctg -
[х =
¦ + 2 arctg	 + 4 arctg ж
¦ +
x arctg -
Збж11
x
(ж6 + 1) х
¦ + 2 arctg ж H	1
[ж = **/«]
16xs
аж 1 + аж + ж2]	Г , 6ж
2 arctg	 + In	¦—- - a 2 arctg :
+ In
1-х2	1 - ах +
' 1 -ж2
1 + 6ж + ж2
1 - 6ж + ж2
[x = z1/8, а = B - V2 I/2, b = B + л/2 I/2]
7 Г Г	ах	1 — ах + х2] Г	6ж
	 < а 2 arctff	 + In	 +62 arete
16ж7\ L	1-ж2	1 + аж + ж2]	[	В1-:
-In
. — 6ж + ж^
¦ iT6
ж2
[ж = z1/8, а = B - V2 I/2, 6 = B + л/2 I/2]

412
17
а
1
b
1
с
3
2
Гл. 7.
ln(Vz + 1
лАA-
Гипергеометрические функции
2i?i(a, 6; с; -z)
/1 + z ) Arsh V^
fz) Л/^A + ^)
[7.3.5
7.3.5. Значения 2Fi(a, 6; с; 1).
1. 2Fi(a, с; с; 1) = iF0(a; 1) = О
2. 2Fi(a, 6; с; 1) = Г
с, с — а — b
с — а, с — 6
3.	2F1{1, т; щ 1) = -±	-^—
\^1 ¦+ ТТЪ ТЪ j I
4.	2F1(-n, b; с; 1) = ^-=-^
7.3.6. Значения 2^1(а, 6; с; —1).
1. 2Fi(a, 6; а ^6; -1) =
[Re a < 0].
[Re(c-a-b) > 0].
[n > Z + m].
Г (а/2 - 6)Г [(а + 1)/2] 2Г [(а + 1)/2 - 6]Г (а/2 + 1)
2.	2Fi(a, 6; 1 + а - 6; -1) =
3.	2Fi(a,ft; 2 + а™6; -1) = -
6-1
A + а)/2, 1 + а/2 - b
П 2+a~h 1_г[ 2+а~Ь
' '¦ "	A + а)/2, 1 + а/2^
4. 2Fi(a, 6; 3 + а - 6; -1) =
2*A-Ь)B-Ь)\ [A + а)/2, l + a/2^6J
З + а-6	] ( а(а + 1)„Г	3 + а™6
а/2,
[4-1 Л 4- 1 1
а + b \
[a + 1,6+1^0, -1, -2, . . .]
6. A - a) 2Fi(l, а; 2 - 6; -1) + A - 6) 2Fi(l, 6; 2 - а; -1) = 21-а"ьг[ о ' , 1
[2- а, 2~ 6 ^0, -1, -2, . ..]•
7. 2F1(l,a;-a-n;-l) = 2-n-2e-2r[1 а' " а] + I ^(-1)
fc (a)fe
[n = -l, 0, 1, 2, ...].
8. 2Fi(l, a; ^a + щ -1) = 2п~
(l-o)fc
9. 2Fi(l, а; а + 1; -1) = аC(а).
Ю. 2Fl (l, ™ + /; ™ + / + 1; -1) = (-1)'™±»i{
- 2 ^ cos ГBЛг + 1)^^1 In [sin BA;
[те = 2, 3, 4, ...].
Til Г 7Г	1П7Г
— cosec
2	n
[n = 2, 3, 4, . . . ; ш = 1, 2, . . . , n - 1; Z = 0, 1, 2, . . .].
11. 2Fi(l, m; m + 1; -1) = (-l)"^^ In2+ ^ t^
12.	2Fi(l, a; a + 2; -1) = 2a(a + 1H(a) - a - 1.
13.	2Fi(l, a; a + 3; -1) = 2a(a + l)(a + 2)/9(a) - a2 - la/2 - 3.

7.3.6]
7.3. Функции iFo(a; z) и 2 Ft (a, b; c; z)
413
14.	aFl(i,a;a + 4;-l
15.	2FiB, a; b; -1) -
(a _|_ ь _ з) 2Fi(l, a - 1; 6-1; -1) =
16.	2FiB, a; a + 1; -1) = a(a - l)/3(a - 1) - a/2.
17.	aFaC-n, a; 6; -1) = ^Р,*6'«->-"> C)
{b)
2A - a)
[Re F-a) > 1].
18. =
(b)n
[0 < Reft < Rea - n + 1].
[Re6 > 0; Rea < 1-n].
19. 2Fi(-n, -ra; 1 - m; -1) = (-1)"
n!
(m-1)!
(m-n-l)!
fe=0
20.
21.
22.
(-n, m; 1 + m; -1) =
(ra + n)!
; -m; -1) = -
[to > n].
[m = 1, 2, 3, . ..].
f_ «„ 9- 1. „I1» — О71/
[e = 0 при 2тг ^ пг; е = 1 при 2те = этг + 1, т + 2, . . . , 2то + 1].
23
24
25
26
27
*>я
29
30
31
32
00
00
34
qc
oO
36
37
38
a
1
6
1
4
1
4
1
3
1
3
1
3
1
2
1
2
1
2
2
3
2
3
2
3
3
4
3
6
1
b
1
1
1
1
1
1
X
1
1
1
1
1
X
1
1
X
1
1
1
С
13
5
4
9
4
4
3
7
3
10
3
3
2
5
2
7
2
5
3
8
3
11
У
7
4
11
A
6
2
2Fi(a, 6; c; -1)
—^— [тгл/З - 6л/3 In B + л/3) - ЗлД]
54 L v ; J
л/2
	 тг -f- 2 In A -f- v 2 )
8 L J
5л/2 г i
	 тт -f- 2 In A -f- v2 )	2v2
16 L J
— (тг + л/3 In 2)
9 v ;
- C™21п2^3\/3тг)
7л/3
162 к
7Г
4
3
-(*-2)
5
- (Зтг - 8)
О
2л/3
	(тг - л/3 1п2)
9
5л/3 /—
^^ D0тг - 40л/3 In 2 - 39л/3 )
81
-7Г О ]rt ( ~\ 1 л/^ \
7Т Z ill IX "j" Л/ Л } \
7л/2 / \
	 I Зтг — 6 In A -|- v 2 ) — 2v 2 j
П6Г г г- 1
— 5тг - 5V3 In B + V3 ) - 3
18 L v ; J
In 2

414
Гл. 7. Гипергеометрические функции
[7.3.7
39
40
41
42
а
1
1
1
1
b
1
1
1
2
с
3
4
5
3
4 In 2 - 2
- (8 In 2-
— C1n2-
3
2A-In 2)
5)
-2)
2Fi(a, b; c;
-1)
7.3.7. Значения 2Fi a, 6; c; -I.
1. 2Fi [a, 6; c; - J = 2a 2Fi(a, с - 6; с; -1)
2. 2Fi a, 6;
a+b+l-m 1
' 2У
= 26~1I
[Re (b- a) > -1].
F + Jfe)/2 1
a, b
2 ' 2
5. 2Fi ( a, 6;
6.
7.	2Fi (a, -a; b; - 1 = -*-?-
8.	2Fi ( a, 1 - a; 6; - I = 21м6^тг
(<*+ «0/2
(а + 6)/2
6	1+rf	fe
, F-o + l)/2j |_(a + 6 + l)/2, F-a)/2_| J"
6	1
[l + b-a)/2y
9. 2Fi (a, 2-a; 6; - ) =
'2Ь-Ца-1)\ L(o + 6)/2-l, (l + 6-o)/2j [(a + b - l)/2, F - a)/2j j '
10. 2Fj (a, 3-a; 6; |j =
/тгГ(Ь)	f	6-2	2
а - 1)(а -2)\ Г[F - а + 1)/2] Г[(а + 6)/2 -
-о)/2]Г[(о + Ь-3)/2];-
11. 2Fi(a, 4-a; 6; -J =
26 - а - 3
Г[(а + 6)/2 - 2] Г[F - a + l)/2] Г[(а + fe - 3)/2] Г[F - a)/2] J "
4F - 3)
"•^i|a,5-a;6;-J = 26_B(o_1)(V_2)(a_3)(a_4)
2F-3J - (a-2)(a-3)
Г[(а + b)/2 - 2] Г[F - a + l)/2] Г[(а + 6 - 5)/2] Г[F - a)/2} j '
13. 2Fi ( a, 6 a; 6; 2 J _ 2b_e^ _ ^^ _ ^ _ ^ _ ^ _ g)
462 - 2a6 - a2 + 13a - 226 + 20 462 + 2a6 - a2 - a - 346 + 62
14. 2^1 I 1, а;
\
-—; -
11
(a + 6)/2 - 3] Г[F - a + l)/2] Г[(а + 6 - 5)/2] Г[F - a)/2] J '
=	 x
A — a)m-i

7.3.8]
7.3. Функции iFo(a; z) и 2 Ft (a, 6; с; z)
415
(a-m)/2l
(a-m)k _2~k
15. 2Fi 1, a;
16.	2Fi
IT.	2Fi
18.	2Fi
19.	2Fi
20.	2Fi
21.	2Fi
22.	2Fi
23.	2Fi
24.	2Fi
25.	2Fi
2 ; 2
[m = 1, 2, 3, . ..].
[m = 0, 1, 2, . . .].
I a, a; a + 1; — 1 = 2aa/3(a).
\	2/
l, 1; b;
l, 2; 6; I
l, 3; 6;
1, 4; 6; i
1
2, 2; 6; -
2, 3; 6; i
1
2, 4; 6; -
2
= 2(ft-lH(ft-l).
= 2(ft-l)[l-2(ft-2)/3(ft-l)].
= (ft - 1)[7 - 26 + 4F - 2)(ft - 3)/3F - 1)].
= I (ft - 1) [262 - 156 + 29 - 4F - 2)(ft - 3)(ft - 4)/3(ft - 1)].
= ^—^ [293 - 2086 + 5062 - 463 +
+ 8F - 2)(ft - 3)(ft - 4)(ft - 5)/3F - 1)].
= 4F - 1)[3 - 6 + F - 2)Bft - 5)/3F - 1)].
= 2F - l)(ft - 2) [7 - 26 + 4F - 3J/3F - 2)].
= - (ft - l)(ft - 2) [462 - 326 + 65 - 4F - 3)(ft - 4)Bft - 7)/3(ft - 2)].
6
f 3, 3; 6; - J = 2F - l)(ft - 2)(ft - 3) [7 - 26 + 2B62 - 146 + 25)^F - 3)].
26
27
28
29
30
31
32
a
1
3
1
1
1
1
1
1
b
со 1 to
4
3
4
4
5
5
с
1
2
2
2
3
2
3
2Fi(a, 6;
3^4 3 /1
8тг2 \3
8^2
3
14/3
8/3
15/2
11/3
c; 1/2)
)
33
34
35
36
37
38
39
a
1
2
2
2
2
3
3
6
5
2
3
4
4
3
3
с
4
1
1
1
3
1
2
2Fi(a, b; c; 1/2)
5/2
12
32
80
20/3
104
20
7.3.8. Значения 2Fi(-n, 6; c; 2).
1. 2Fi(-ra, a; 2a - 1; 2) =
= 7JFr(a~ 2I 2"
3. 2Fi(~n5 a; 2a + 1; 2) =
a + (n-l)/2
a+ 1/2
Hdfr[n/2
a + n/2
n/2

416
Гл. 7. Гипергеометрические функции
[7.3.9
4.	2Fi(-ra, a; -2ra - 2; 2) = 22n+2^^
5.	2Fi(-ra, a; -2ra - 1; 2) = 2 n4
(а + п
а + 1
n+2
2 /n+1 V27n+1
Bra-
6.	2F1(-n>a;-2n;2) = 2a»7^L'ra + 1
7.	2Fi(—ra, a; 1; 2) = (—l)n	2Fi(—n1 1 — a; 1 — a — ra; —1).
8.	2Fi(-ra, 1; rra; 2) = 2 m | (-
9.	2Fi(-ra, 1; -2ra - 1; 2) =
i!
m-2
(-1)*
Bn
fc=O
2zn+± - 1.
10.	2Fi(-ra, 1; ^2n; 2) = -^
11.	2Fi(-ra, 2; ^2n - 2; 2) = -^
!(ra + 1)?22п+1
2n
12.
(-n5 2; ™2n - 1; 2) =
-3-
2 1
7.3.9. Значения 2Fi(a, 6; c; z0) при z0 / ±1, 2 .
3 ' 3 ' 6	/	[ 2/3, a
. aFl ( a,
[Re a < 2].
2Fi(a, 6; c; -8)
8
9
10
11
	In
3
2
	2 n
3
-|-2n
1 n
— — —
3 2
1 те
6 " 2
	7i
2n-l	7i
6
2n- 1	7i
(-5/6)n + (n/3 ^ 3/4)(-l/2)n_i
2(-l/6)n + (-l/2)n
2(l/6)n-
1 (l/3)nB/3)n
[те = 2, 3, 4, ...]
[n = 1,2,3, ...]
[n = 1, 2, 3,
V ; C/2)n
(_l)[(" + l)/2]32n-[n/2]-l
i/2
(l/6)n/2
2тг-
\n+l_
+ 3
5 • 33n+2
Bте + 3)Bте +
12.	2jP
13.	2Fi ( 2, a;
14.	2JP
2' 2 ' '"
5 - a 1
2 ' ^2
Cn — числа Фибоначчи .
a+ 1/2

7.3.9]	7.3. Функции iF0(q; z) и 2Fi(g, ft; с; z)	417
15 F I	+-• --2 • --^ 2
' 2	2' 2	'3
29.
CO.
9\2a [4/3, 3/2-2al
8/ L 4/3-2a J'
2a + 3 l-V^^ 9-а/2^гГ Ba + 3)/4
;J=2 ^Г[
л_	/3 2a+ 5 1-
17. 2F, ^-, a; -j-; ^
= 22-а/2/-ГгГ Ba + 5)/4 1_ Г Ba + 5)/4
V 1 L(a + l)/4(a + 2)/4j [a/4, (a + 3)/4j J"
^ /	14
18. aF^+
/ 1-a 4a+ 5 1\ 9-a^r[ Da + 2)/3
19. 2F1^a;;J=2 ^ Г^
on F (n ^—^ 4a + 7 _1\ I!Vi f [ Da + 4)/3 1 Г Da + 4)/3
24 3 ' 6 ' 8J~ 2a-l Г [a, Ba + 5)/6j [a +1/2, (a + l)/3
/ 2-a 2a + 5, 4 - 3^2 \ _ B\a/2	Г Ba + 5)/6
22. 2FX ^a, ^-, -g-, ^^J - [z) ^Г[(а + 3)/6(а +
23. 2Fl(a,i^;^±Z;4-3^U
О	О	О	/
a - 1 1 [a/2, (« + 5)/6j [(a + l)/2, (a + 2)/6
24. 2JP
9^ р Л 9 Ч. 3 п 2~^	З3п/2 г[4/3, З/2-a
25.	2Fx \а, 2 - За, - - а, —г~ J = 22a_iy- Г[ 4/3 _ д
1-а За+ 5 1 /3\а/2 [2/3, (За + 5)/б1
26.	2^(а, -1-, -g-, д)=[) Г[	j
27 Л„1 on- 4 «• Л ч-аг[2/3-а, 4/3-а]
27.	2^^а,1-2а, --а, - J = 3 Г[ ^ 4/3 _ 2а J-
oo Ff * „. о„^7т2-М 26"	(GТ2)/4Jи
28.	2Fx (-n, --п,2п+-г-)=^
A/2)"
34. 2Fi fa, 1 - 2a; a + 2; i ) = j ^ ) (a + 1).
14 А. П. Прудников, Т. З
[аф\/2].
,2„ + 4)/3 1 Г р„+4,/3	^

418	Гл. 7. Гипергеометрические функции	[ 7.3.9
2a + 1 i1 9/9 9^ /2 + 72\° ,- Г Bа + 3)/4
37. 2^(а, ^±^; a + |; 2л^ - 2) =
[Г Bа + 5)/4 1 Г Bа + 5)/4
V | L(a + i)/4(a + 2)/4j L
4а + 2 8\ /3\2а ^^Г Dа + 2)/3
39.
-, т + 1, -J=2 3 ^
40. 2Fl(a,a+±;4a-l; ^U 22-ea32a^F (зг[ 4a ~ 2 7 1 -гГ 4? " X H
V	2	9/	I La, 3a-l/2j [«+ V2, 3a - lj J
An
2	/	(/)n/2
---12V2-iej = ^-5-j ^ Г[(а + 4)/6, (а
43. ^U^^U^-ieW^V^rr Ba + 2)/3
44.
2a/3 + l 1 _ Г 2а/3 + 1
a/2 + 1, (a + 3)/б] ~ L(a + l)/2, a/6 + 1
45. 2Fi ( a, 2a - -; 4a - 3; 12^2 - 16 j =
-I
[a/2, Ca-l)/2
47.	2Fi f-2n, n + i; n + 1; ™) = 3n.
48.	2^1 ( —n, —; пг; 4 J = Я(п, ?n), mS{n1 m) = (n + m)S{n1 m + 1) — nS(n -1, m + 1),
f 2n, n + |) = ^SW^SW , ^B^ + 1, n + 2) = 0, 5Bn, n) = 35
V	2/ E/6)nG/6)n
SBn + 1, n) = ^5n + 2, 5Bn5 n + 1) = 1, 5Bn + 1, n + 1) = -1,
n
n
) 5Bn + l, n + 2) = 0, SBn, n + 3) =
~2n + l' "v— • ->••.-;-"> "v—, ¦• i -y- 2Bn + l)Bn
Un + 3)= o"+,2oW SBn, n + 4) =
2Bn + 3)' v ' ' ' 4Bn + l)Bn + 3)Bn
5(n + 2)(n + 3)
8Bn + l)Bn + 3)Bn + 5)Bn + 7)'

7.4.1]
7.4- Функция 3F2(ai,a2, аз] bi,b2',z)
419
5Bn + l, n + 5) =
49. 2Fi I -2rc, -; n + 2; 4 1 = n + 1.
7.4. ФУНКЦИЯ 3F2(al9 a2, a3; 1ц, b2; z)
7.4.1. Представления 3^2@1, a2, аз; 6i, 62; z).
1
2
3
4
5
6
7
я
9
10
11
a\
a
a
a
a
a
a
1
1
a
a
a
a2
6
6
6
6
6
6
a
1
1
a +
a
a
1
9
аз
с
с
с
с
с
с
6
и
b
1
2
6
61
d
а —
а —
а +
а +
1 + а
2
те
1
1
1
Ь
а + 6+1
2
6
с
е
d
d
d
6 + 1
1 + а - с
с
6^а | 1
2 ' Х
2 6
2а+6-с+1
1
1^2
X
X
X
1 ^
A -
FЫ
(d)
2Fi(
о
1 + 0
1
b^c
A
(а -
(а-
п
2Fi
Г2
¦{[
3^
i-
[(d +
(d-i
c)fc
t
-[ь
z)-
с —
1)(
2(c
x [
a,
— л
-5
:; с
a*
2i
аз
1
ь
1
/г
С,
;jF2(ai, a2, аз;
d -+- e -— b ¦— с
1 — a
2 — 1, 6, c; d, e
e - 6 - c)(l + e
=)]3F2(a-l, 6,
(d- c)(l + d-
de(l - a)
6cz
(a — 1) d
x 2Fi(fc
2FiF, c; a1; z)
x з^2(а,
^i(a, c; a + 1;
/a a + 1
2 I 9 ' 9 '
1 + a 6, 1
r p, /„ i
[2-^1 (ft 1?
2J
\(a-2, 6-2;
(b 6 + 1
3 2\з' 3 '
a + 6 + 1 6 -
2 ' 2
x 2Fi fa, 1
	 l2a /
-z) 3F2 2a,
J \
2a + 6- c+ 1;
6]
¦]
z
c;
- с
¦x
+
b,
*)
+
6
с -
ь
- a
V J
9
с
1
, 62; z
x
) e(l
z
a) + (d - 6) x
d, e + 1; z) +
3 2{a
d+1,
; d+ A;
l,c +
a1 — 1
1 + a -
c] a +
— d 2J
r, ft
a — c;
1 • n
9* -r ^
2
f 2
3 '
L-z v
)
a; 6; I
-6,2a
X, I/,
e + 1; z
1; d + 1
1, d- 1
c-
4z
A — z
1 • •H
1, Z)
-1]-
(c- 1)
1)F- 1
27z
(l-4z
x
2
— с + 1;
J
;
;
6
\2
)^
K
Z
[
+
1
J
J
)
/
')
14*

420
Гл. 7. Гипергеометрические функции
[7.4.1
а2
62
, а2, аз; 6i, 62; z)
12
13
14
15
16
17
2а
18
19
20
21
. f*.
a b
a b
a b
1
6
2
22
23
24
25
а+6-1
а + 6
a- 1
a
a
~2
2a
а + 6 -
6- 1
6 + 1
6 +
а + 6 + 1
- b + 1
2
-A-
1 +
2Ь
2^11 М+ 26-2а; 6 + 1;
x 2Fi 6, 2a- 6; 6 + 1; 1 -
i	1	3
A-z) 2Fi (a + 1, 6+™; a- 6+™; z
(i-z)-2b-S
a - 1
-6-1;	6, a - 6 + 1; 2
a+ 26- 1
2а+ 26 + 1 2а+ 26 + 3	1 , 1
	, 	; а -\	, 6 Н	;
6	6	2	2
27z2
а + 6
а + 6 + 1
a 6 — 1 a + 6
~2' 2 ' ^~
; z X
а 6 + 1 а + 6
-, 	; 	;
2 2	2
а 6 а + 6 - 1
а - 1 6-1 а + 6 - 1
6 + 1 а + 6 + 1
-; 2
a 6
а + 6
а + 6
а + 6 -
а 6 а
а 6 а+6+1
a 6
а + 6
а + 6 + 1
а 6 а+6+1
= 2Fl (a, 6;
а + 6 + 1 1 - VI - z
2	2
a 6 a + 6 + 1
2"' 2'	2 '
^ /a + 1 6 + 1 a + 6 + 1
X 2Fi 	, 	; 	; z
1 2 ' 2 '	2
a 6
а + 6+1
а +6
а-6
2Fi
2 ' 2' 2 '
'a + 1 6 a + 6
~2~J 2' 2

7.4.1]
7.4- Функция 3F2(ai,a2, аз] bi,b2',z)
421
26
27
28
29
30
31
32
33
34
ai
a
a
a
a
a
a
a
771
j
1
1
a2
6
a +
a +
a +
a +
n
1
771
1
1
,4
1
3
1
3
1
3
a +
a +
2
a
a
a
a
a
13
6 + 1
2
+ 1
+ +
со | to со | to
со 1 to
со 1 to
2
+ 3
1
n
61
a + 6 + 1
a + 6
3a
2
3a+ 1
2
1
3
2
3
4
3
m
J
m + 1
тг + 2
a +
2
a +
3a
3a
2
n
n
n
b
6 + 1
2
+ 1
2
со | to
4
3
5
3
+i
+ 2
6
a-b
a
a-b ^
^a + b~
a + 1
a-*I
2Ж + 1
, Л
+ V1
ЗжCа -
Зж2Cа
+ e-2^
тп
nj - In
+ 1
mn
{fl — 771
3^2(«
F (°
2 1 ^
X
2 /a +
1 V 2
6
a - 6
- 1
?
V
a + 6
a,
a
E)a +
[fl
x(l
2
-l)Ca-
/зЛ
xln [l
z-m/j
x In 11
^ n -
p =
Г
zn [^
[(n + 1)!]2
Bn+l
)!(-z)»+
i, a,
i b-
2 1
i г
(->
Yb
2' 2
-2
, аз; 6i, 62;
f 1 a + 6
/a 6 + 1
\2' 2 '
i' 2
/a 6 + 1
\2' 2 '
6 a + 6 - 1
2' 2
а + 6 + l
2
[4A-
[4A-
же J
J J
o ./o\l —3a
- же27гг/3)
-2)
з Л
Z-l
E
fe=0
-
feZ"
0,1,
H
С.ф (^ ;
/1 f2wik
слр I ^
л ^
a +
2
г)
a +
2
; z
•)'
a +
+
X
+
^ 2wikm^
CXp I
V J
i B-Kik
слр I
k > [771
2, . . . , pi <
m) In A — z'
n —1 д.
)]-
тг $
+
2
6
_i_ 1
)x
6 + 1
2
z —
[x = .
[ж = >
X
f
:(p +
m —1
Л
"¦)
¦¦•)
¦ Л
'~)
27ж]
27ж]
si/3l
lm,
1I}
т1

422
Гл. 7. Гипергеометрические функции
[7.4.2
36
37
38
«l а2 аз
1 3+i $~'
2 2
--те а 2а + те
^те i n+1
6l &2
^ 2
2
ft -Ь — 2 я.
2
1 1
3F2(ai, a2, «з; 6i, 62; z)
^ (n + fc)!(^z)fc
1 ^ ch arcsin л/z ^ J
1 . 1 1
z V cos arcsin i/z /
Г n! ca(v/r_12
7.4.2. Частные значения 3F2(ai, a2, аз;
Обозначения:
/\	^ Гтг/ \l2
[K(x)--D(x)]2l
i, 62; z).
1-Ж2
х [2A - 2х2) В(х) - A - Зж2) К(ж)]2|5
1 -
а\
62
3F2(ai, O2,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
2 2
1 1
 2
1 1
 2
1 1
 2
1 1
 2
1 1
1 1
 2
1 1
 2
1 1
 2
1 1
 2
1	1
2	2
1 1
1	1
1	2
1	3
2	2
2	3
3	3
2	2
5	2
2
3	5
2	2
3
2
2	2
5
i [4A - z
^ [4B
i [4A -
z) + 2A + 2z)il>2(z) - zil>3(z)]
^ 9z2) ^i(z) - 2D - 19z^ 18z2)
z) + 2A + 2z)tM^) + C - z)^s(
[4A- z + 3z2) i/;2(z) - 4A- 4z + 3z2) ф
16
[2G - 22z + 6z
- 12B -
~~ z + Зл/z arcsin л/z -
~ 3z)i/;3(z)]
С1"-
- Li2(-
- 3
_L2-15Z-B-14Z-3*
15z3/2
arcsin v ^
1	1
2	2
1	1
'2	2
-- - 1
-- - 1
2 -
5 5
2 2
-ЫA3
8z L
- Зтг - 2zG
+ 3A + 4z)
32
45ttz
8A
- (l + 14z + z2)]
I - 4^ - z2) Arth %fz + 2A + 2
- 16
15tt

7.4.2]
7.4- Функция
,a2, аз] bi,b2',z)
423
«2 «3
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
1
2 2
1	1
2	2
2	2
1	1
2	2
1	1
2	2
1	1
2	2
1	1
1 1
	2
1	1
2	2
1	1
 2
1 1
 2
1 1
 2
1 1
 2
1 1
 2
1 1
 2
1	1
2	2
1 1
 2
	 2
2	2
1	1
--	- 2
2	2
-i	I 2
2	2
-I	I 2
2 2
-i 1 2
2 2
--	- 2
2	2
— -	- 2
2	2
-- - 2
-- - 2
3	3
1	1
1	2
1	3
2	2
2	3
3	3
1	1
1 5
2
I •
5 5
- 3
2
3 3
1 1
1 »
2
1	2
1	3
3	3
2	2
^	2
2
^	з
2
2	2
	 [A6 + 83z + 6z2)
C + 4z) arcsin y/I - 16 - 120z]
128
[A5 + 74z + 39z2) K(y/z) - z D3 + 82z + 3z2
16
z
z) + 2гф2(г) — — i/^3(z)
2
1
-	[4A - z)^i(z) - A - 4z)t/»2(z) - z^3(z)l
3
—	[8A - z + 3z2) i/J(z) - 8A - 4z + 3z2) фф) - z(l
-	[8A - z)tbi(z) + 4A + 2z)ib2(z) - C + 2z)t/?3(z)]
9
—	[4A + z - 2z2) ^i(z) - 2B - 7z - 4z2) t/?2(z) - zG +
-^- [2A3 -7z- 6z2) i^i(z) - A1 - 56z - 12z2) i/;2(z) -
675zL l	; V ; l	; V ;
D + 15z)
+ 3V1 - z
45тг
1
- [2A
- D + z + 9z2
32z3/2
2
[Зл/z +3A - z) ArthVz" +Li2(\/z) -
3z2) A
	 [D + 2z + 9z2) л/l- z - 4 + 15z3/2 arcsin y^
45z l	7
9
128z3/2
1
60z2
64
12
- A - 4z + 3z2) Arth л/z -
- 2A ^2z)[Li^
- C2 - 29z - 18z2) л/Т^ - 1ЪлД (З - 4z) i
zG1 ~~ 46z ~~ 9z2) Щу/z) ~~ 2A5 + 14z - 21z2
- [4C- 10z+ 8z2) i/>i(z) + 2zA3- 16z)i
15тг]
- zG -
i [2E - 8z)
[8A + llz - 12z
- 2D + llz - 48z2) i/>2(z
1 Г arcsin 1
з 17^
2л/1 - z
16
— [32A -
i - 2(l + 4z + 6z2)
(z) - 2A - 16z)i/>2(z) - C + 8z)il>3(z)

424
Гл. 7. Гипергеометрические функции
[7.4.2
«3
, «2, Q3; fei, b2; z)
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
1 1
~2 2
1 1
~2 2
-- - 3
-- - 3
1	1
'2	2
1	1
2	2
-i	- з
2	2
-i	i з
2	2
1	1
2	2
-- - 3
-\\ •
-1 1 з
2 2
-5 1 '
1	1
^2 2
--11
-- 1
--11
-- 1
--11
--11
--11
-- 1
-- 1
-- 1 -
-- 1 -
-- 1 -
-- 1 -
2	3
3	3
i I
2
1 -
-- 1 -
- 2
- 3
- 2
- 3
2 *
2
I >
^[B + 3, + ieO
16
2025z
(I-*)
4тг
[8A + 11 z - 12z2)
[(8 -
- 2A - 9z + 8z2) t/^ф)
(z) - 2A9 - 49z - 48z2)
16
128z
1
1 Г arcsin a/z
- |3	^^
128z3/2
64z
A1-
15z3/2 - A - 16z + 15z2) Arth
¦15*3/2-5(l-<
512z3/2
- 12A- v^ Arthv^) - -ln(l -.
о	Z
Arth
- л/z
Ibz
2E - z)^fz Arth
-2z+ ^	-\n(l-z)
z
1
4z~
4 Г
	 6 + 25z - 2C + 14z - 2z
45z2 L
\ Г	Л*.+-к FZ
—	A5 + lOz^z2)
5z [
16 Г
225z2 L +
Arth^
41n(l-z) -
30z In
1 + y/T^
-13 + Z+2A + 5z)In(l-,)
-15B + 5z)ln-
1-z
^[Зтг - 2C -
+ 4zB -

7.4.2]
7.4- Функция 3F2(ai,a2, аз] bi,b2',z)
425
67
68
«о
70
72
73
74
75
76
77
7й
79
ЯП
81
82
84
85
86
Я7
88
8»
90
91
92
oi
1
2
1
2
1
2
1
~2
1
2
1
~2
1
~2
1
2
1
2
1
2
1
2
1
2
1
~2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
«2
1
1
1
1
1
1
i
1
1
][
|
1
1
1
I
1
1
1
1
1
1
1
3
2
2
3
2
«3
3
3
T>
3
2
со I cm
3
2
2
2
2
5
2
5
2
5
2
5
2
5
2
5
2
5
2
5
to
5
2
5
2
3
q
3
3
3
2
3
2
3
2
2
2
Б
2
Ю | CM
1
2
3
2
5
2
3
1
2
1
2
1
2
1
2
3
2
_
2
3
2
9
2
3
1
2
2
2
1
2
1
2
1
2
5
9
3
Б
2
3
3
3
q
3
1
2
3
2
2
3
3
2
2
3
9
3
3
2
9
2
Б
2
1
2
1
'Л
1 [*
8 r
45-7TZ L
32z3/2
it»
64
i
2 '
5z [
1 Г
i ¦
lOz [
8
225z2
3 [ (
1 [3™
3 I 1-
2 ГЦ
9z[
"E-
15тг
+ 20z
16
3z
3F2(au a2, a3; bu 62; z)
•>-) /1	" „агс81пл^]
л/Z
- (8 + 92 - 2z2) л/1 - ^ - 15v^ arcsin л/2 ]
128 r/ 94 , ^4
2257rz" " ^ ^ V ~- 2z A9 + 6z - z2) ЩлД)}
(l-y/z Arth л/2) - 1	In A - 2)
z J
+ iin
4B3-
13z +
1-2)
4z
1 4^ __
A - 2) + 32 + E - 3z)V^ Arth л/z
4 Arth /zl
z Vz J
iu [ q^2\ Л ~ no 1 7K-v fifl In
2 J
1
U/r Arth ^/r"
J
1
z \
~^^ [2C + 4z + 8z2) л/T^z" - 6 - 5z]
1 Г
3 L
2
	 \ _
9z L
4 г
	 ^
45z^ l
4
27ttz
8
135ttz
16
675?rz2
1 r
8 Г '
1 Г
— 2-
6z L
3 [
32z [
fl — 6z
2
— A —
7Г
4 r
Зтг L
1
f ][ 	 /
j -f- 5z
v
[157Г
-[8A5
5z)(l
B-.
1 5z
-\- 4lZ
z~) \{
(\/~Z \
Arth /zl
VI J
\z\\I\	z
J
g/2]
J
q /i «v\?/"/ /" ^ 1 9~/ ч«-Л 1 W /" M
Я/"Ч c)v\\C(+Py\ А(Ч 1 ^-r 4- йг2^ ТП^/у" "ll
1 1 r -U 4r2^ TC(+/T \ Rr (94 94r -U kr2^ ПЛ/Г^
- 60тг + 75ttz]
— z) — 5л/2 Arth л/2 ]
Arth y/z 1
¦} v^ J
1
' J
, 2ч Arth i/z 1
v ^ J
1 — 2z)K(\/z") — 2C — 4z)D(\/z" I
	A -f- 4z)I3('\/z"I

426
Гл. 7. Гипергеометрические функции
[7.4.2
94
95
96
97
98
99
100
101
102
104
105
1 Пп
107
108
109
110
111
112
113
114
115
116
117
118
oi
1
2
1
2
1
2
1
^2
1
~2
1
^2
1
~2
1
2
1
2
1
2
1
2
1
~2
1
1
2
1
2
1
2
1
2
1
2
1
2
1
1
~2
1
2
1
2
1
1
~2
1
a2
3
2
3
2
3
о
4
to |
3
2
со 1 см
3
2
3
2
3
?,
2
3
2
со I cm
2
2
3
2
3
2
2
3
2
3
2
3
9
со I cm
3
2
3
9
3
to I to
со 1 см
«3
3
2
3
2
3
о
4
to |
3
2
со I cm
3
2
3
2
2
Я
2
2
2
2
2
2
5
2
b
to | сд
5
2
5
9
5
9
5
2
to | сд
bi
1
2
1
2
1
1
1
2
2
3
1
1
2
1
2
1
2
1
1
1
Б
2
5
2
3
1
2
1
9
1
2
1
2
1
1
1
2
62
5
2
3
1
2
3
2
3
3
1
1
Б
2
3
1
5
2
3
Б
2
3
3
1
2
1
2
3
1
2
3
2
3^2(^1, «22, «з; 6i, 625 2)
3 [1 + z —2z2 arcsin \fz 1
16 r/
15ttz
A — z)"
1 4
0
	[8A + z - 2z2) ^i(z) - 2D + z - 8z2) ф2(г) + z(l - 4z)t/?3(z)]
i [16A - z)^i(z) - 2E - 8z)^2(z) + C - 4z)il>3(z)]
J~- [F - llz + 8z2) фф) - 2C - 7z + 4z2) фф) + zC - 2z)^s(z)]
Г0/1 01^ [ Q-,2\ /, /^\ 1(\(^ 4" 1 ~2\ / /„\ |
225z L v ; v ;
(l - 5z + 3z2) A - z)^2 - Ъл/z Arth л/z
— B,	9z 4- 6z j fl	z)~~~ '
2
3 Г Arth -\/z" 1
8z [ \ ] °" ) ^ J
^[B + Z + 2^)vf=7-2]
3 Г /-	 arcsin y/z~\
16z [ " v^ J
8 0
Г//1 1 », й~^\ ТЛ( . /~Z\ @ 9.~\TC( . /^"\1
15ttz
9
64z3/2l- V- V- V-
/ic f „ | я~2\ /Я U | -I r /~Z ъггъгАхъ rZ 1 a
64
Г/9Г1 1 «I*?-, 1 Q~^\"K"/" /^ \ 1 Ктг
[^OU 1 _5Oa 1 Oa j 14.^Y^ J 107Г
— z F1 — llz + 6z ) D(yz ) I
_ C	30z -f- 40z 	16z 1 fl	z')~
3 V M
— A - z)^2 [C - 13z + 8z2) K(y/z) - 2z E - 14z + 8z2) T>(y/z)]
Зтг
4
— A - zY1 [E - 8z)K(y/z) - A + 12z - 16z2) В(^)]
16 r , ox
Гд^Ч 17~ 1 41 ~2 1 fi"^^ i/m f ~\ I
+ 2z A5 - 50z + 32z2) i/>2(z) - z A0 - 27z + 16z2) фф)]
^ ^ Г4/"_1 17~ I 1fi~2\ / /^\ 1 0/1 1 oo» q_i~2\ / ,o/^,\
18
-^A3-16г)^з(«)]
	[4B + 3z + 16z2) ^2B) - 4B - 3z + 16z2) ^i(z) -
45z L v ; v n . IK )w, f \]
^[4G - 16z)i/?i(z) - 4A - 162)^2B) + C - 16z)^3(z)]

7.4.2]
7.4- Функция
,a2, аз] bi,b2',z)
427
«2 «3
62
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
1 3
 2
1	3
2	2
1	3
2	2
3
2 2
5
2
5
2
-- - 3
2 2
-i ^ 3
-i ^ 3
2 2
1
2	2
1	3
'2	2
1	3
'2	2
I
2	2
-- - 3
-- - 3
-- - 3
-I » 3
2 2
1	3
2	2
1 3
 2
3
-- - 3
1
2 2
1
-I 2
2
-- 2 -
2
2
-т 2 т
2
2
2 3
1	1
2	2
1
2
1
2
1	5
2	2
- 1
- 2
1 1
1 I
2
2 2
2 "-
2
5 5
2 2
1
1 -
1 -
1
3
2
3 3
1	1
2	2
1
2
1	3
2	2
1 з
2
1 1
3
1 2
- 3
	[4C + 13* - 16z2) фг(г) - 4C + 7z - 16z2) '
16
675z
[2B9 - 34z +
- 4G - 23
- (8 - 56z + 75z2 - 30z3)
8
D
3
32;
2
15z
4тг
[(8 - 252
- [D^5z
2тг
3 n+21z-30z2
64z
/l -
- [D -
Arth
15z3/2}
— [l + 3* + ^ In A - *) - 3z3/2 Arth
5z L	*
-^-2 [D + 2z + 9z
1 Г	2
^ - 4
1 Г	2
	 -2 + 9z	In A - *) + E - 9z)V^ Arth y^ I
15* I	"
16
31 - C1 + 8z - 9z2) л/Г^^ + 30 In
225z2
-	C - 27z + 32z2 - 12z3) A -
-	B - 15* + 20z2 - 8z3) A - z
Arth -у/*"
4 Г 2 - * - 4z2 + 8z3
15z2
Зтг
[2C- 102
- * A7 - 43z + 24z2) D(>/* )]

428
Гл. 7. Гипергеометрические функции
[7.4.2
145
1 Аи
1 А7
148
149
150
151
152
1 КЧ
154
1 55
156
157
158
159
160
161
162
1 НН
164
165
166
1
2
1
2
1
2
1
2
1
2
1
2
1
^2
1
2
1
2
1
2
1
2
1
1
2
1
2
1
2
1
1
~2
1
2
1
2
1
~2
1
2
1
2
а2
2
2
9
2
2
2
2
2
2
5
5
2
5
VI
5
5
5
5
2
5
2
5
2
5
2
5
2
5
2
5
2
аз
5
2
5
2
5
2
2
5
2
3
3
3
1
5
2
5
2
5
2
5
5
5
?,
5
2
5
2
5
2
5
2
5
2
5
2
5
2
bi
1
3
2
3
2
Б
2
3
1
2
1
1
1
2
1
2
1
1
9
1
1
1
1
1
3
2
2
2
2
62
3
3
2
о
3
3
1
1
3
2
Б
2
1
2
I
3
2
3
1
2
2
3
3
2
2
3
2
8 IY14
45ttz LV"
1 Г
6 L
4 г
45z2 К~
1 Г/
20z L
64 п
675тг22 [1
32 L
3 Г1 +
128z [
3F2(ai,a2,a3; 6b 62; z)
9z 26z2)D(-x/z) B2 13z)K(V^)]
Arth /z 1
r _l_ io72\ д - ol
Arth /z 8
"\/ Z Z
5w 2A5+ 4z 6z2)K(v/z)+ z C1 + 19z
99z + 120z2 - 45z3) A - z)^3 - 45^ Arth y,
8z + 144z2 - 45z3) A - z)^5/2
2\ / ч-2 Arth^/zl
"\/Z J
36^ _ 45^2 Arth /-? 1
1-z l " " \/z \
- (9 - 144z + 280z2 - 224z3 + 64z4) A - z)~7/2
2
— A — z)
Этт
- (9 - 602
9 l
4
27тг
16A - z)~
135ttz
(l^z)^3
36
A - z)™2
54
& I(q — 69z Hr 84z — 32z ) K(-\/z") —
L V /
- z C3 - 153z + 176z2
+ 80z2 - 32z3) A - z)^5/2
У2 [2G - 26z + 16z2) K(y/z) -
- (l + 41z - 112z2
\(f\ 7~ 44~2 1 f\A~^\T\(,fZ\ (q on«
[4(9 70z + 186z2 186z3 + 64z4)^i(z) +
+ 2D4 - 249z + 324z2 - 128z3) ztjj2(z) -
- C3 - 142z + 170z2
[4A3 72z + 126z2 64z3) tjji(z) +
+ 2A + 66z - 204z2 + 128z3) t/?2(z) - D3 - llOz
2 ( ,
Этт1 ^
2A -z)~
135z
- (9 - 262
9 v
4
27тг
16 rri
135?rz LV"
A-z)^1
81
^2 [(9 - 27z + 16z2) K(y/z) - 2z A2 - 29z +
[4B + 15z 66z2 + 64z3) ^i(^)
24*2)D(^)]
/I]
-64z3)D(v/z)]
+ 64z3) D(v^)]
+ 32z2)K(V^)]
^64z3)z^3(z)]
+ 64z2)z^3(z)]
16z2)D(A/z)]
- 2D - 3z - 84z2 + 128z3) ip2(z) + z (l - 50z + 64z2) фз(г)]
-\- 16/2 ) A — z) '
j)™1 [A3 - 16z)K(v/z ) + A - 30z + 32z2) D(
+ 16z)K(v/z) 2A z +16z2)D(V^)]
[4A9 74z + 64z2) tpi{z) +
л/г)]
+ 2A + lOOz - 128z2) i/J(z) + C ~~ 58z + 64z2) ^з(^)]

7.4.2]
7.4- Функция
,a2, аз] bi,b2',z)
429
«2 «3
62
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
15	5
 2	2
15	5
2 2	2
1 5
1
2	2
I	«
2	2
I	«
2	2
i	^
1	5
~2 2
2	2
1 5
 2
1 5
 2
2 2
^-3 3
-- 3 3
2
--3 3
2
1
~2
1
^2
1
~2
1
2
1
^2
1
3	3
3	3
3	3
3	3
3	3
- 1
1 1
1 -
1 -
9 13
405z
32
2025,
[2C + 2z + 64z2) ip2(z) - 2C - 22z + 64z2) фг{
- [4A1 + 21z - 32z2) фф) - E9 + Mz - 128z2)
1
-	C - 42z + 73z2 - 55z3 + 15z4) A - z)
-	(8 - 88z + 175z2 - 140z3 + 40z4) A -
-33z + 40z2 - 15z3
Arth лД
— A2 - 75z + 100z2 - 40z3)
12 l	}
X~* [B4-131*+ 159*
127Г
- z G4 - 295z + 333z2 ~~
- (8 - 40z + 51z2 - 20z3) A -
8
[2F^17z + 10
67Г
- 73z
— A2 - 3
/1 _ \^1
^}
[A7 - 20z)K(v/i") + B - 39z + 40z
—	[F4 - 607z + 1095z2 - 825z3 + 225z4) A - z)^4 - 225-s/z Arth
—	[C2 - 165z + 200z2 - 75z3) A - z)™3 - 7Б-Д Arth yfl\
ЗА
—	F4 - 512z + lOOOz2 - 792z3 + 225z4
64
—	[A19 - 519z + 609z2^ 225z3)(l^z
128 L
—	C2 - 152z + 192z2 - 75z3) A - z)^5
3
_)
yz J
,^ , __~393z2+225z3) (I~z;r2~(l~18z + 225z^
— [E5 - 134z + 75z2) A - z)^2 + 3C - l-_;
64 [	л/z
Arth,
2562
3
l-z
2Ч Г
1 + ж2) 2 arctg x + 2
In
- A - ж2) I In	 + л/2 arctg
5 f 1/2
1-х
4\
1-х2
- 2 arctg x

430
Гл. 7. Гипергеометрические функции
[7.4.2
«3
, «2, Q3; fei, 62; z)
190
191
192
I I 1
- 1
- 1
193
- - 1
194
195
196
197
198
199
200
201
202
203
204
- 1
9 15
8 ~8~
7 4
6 3
7 5
6 3
5 13
3 T
5	7
4	4
7	9
4	4
5
4
4	5
3	3
4	11
з	Т
in
ln
1 ~ж "	1^21/^ж + ж
-1 - ln A - ж) - - ln (l + ж + ж2) - 3™1/2 arctg
ж
X [3
2 + x
х/ж~ Г 1 + V^ 1
H	ln	ln
3 L l-y/x 2
i /о	Л/Зж 1 1
+ 31/2 arctg	M> [ж =
1 — ж J J
/Ж\3/2	^Зж
ж+2 + Ы -«*em+
+ — [2A + ж3/2) In A + у/Б) + 2(l - ж3/2) In A -
18
54ж
, /i	24	Я/2 1 1 "~ V^ +
- In A + ж + ж2) - ж3/2 In	У—
Х	;	1 + л/^ +
l - ж3/2)' In [A + v^ + x)(l -
1 -
27
x arctg -
1 -ж 27
—- (l - ж2) in ^^ + 2A
ж arctg
14
2 + Jx~ 9ж3
7
[ж = .
- 2
15
32ж5
1
3z"
ж- 1
¦ 2A + ж2J arctg ж - 4ж
-z1/4
[In A-ж3) -31пA-ж)] + ¦
¦ arctg -
зж2 L*" ^ •" ; ""'Vi *^/J ' ж2л/з ""^г + ж
— - In (l + ж + ж2) - In A - ж) + 31/2 arctg
In
, 1.
Н— In
2
9ж5/2 1-х/ж 2 1-х/ж+ж
1/2
3 ' arctg
[х =
\/Зж
» I 1
111
2 2 2
111
2 2 2
111
2 2 2
1 2
3
11	13
~8~	У
11	15
~8~	~8~
1	1
1	2
1	3
15
2A-
™A^ж2) In
1 + ж
arctg	 — arctg ж
1 — crA
Чп-
21 Г 1/2/ 4, [ 2/Ж
	J 2-V2 A + ж4) 2 arctg	In
32ж7\	l	M	&1ж2
ФФ)
- A - ж4) | In ii5 _ 2 arctg ж
— [8A - г)фг{г) - 4B -
Al z

7.4.2]
7.4- Функция
,a2, аз] bi,b2',z)
431
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
oi
1
2
1
2
1
2
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
2
1
2
1
о
2
1
?
2
1
2
1
2
1
2
1
2
I
2
1
2
1
2
1
2
2
«2
1
2
1
2
1
2
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
2
1
2
1
9
2
1
?
2
1
2
1
2
1
2
1
2
I
2
1
2
1
2
1
2
2
«3
1
2
1
2
1
2
1
1
1
1
1
1
1
1
1
1
3
2
3
2
3
§
о
ico I cm
to to
2
2
2
2
CM CM
bl
2
2
3
3
2
3
2
3
2
3
2
2
2
2
5
2
b
2
3
1
1
1
to to
3
1
1
1
1
3
2
со | см
6
2
5
2
62
2
3
3
3
2
2
5
2
3
2
5
2
3
5
2
3
3
1
2
3
2
3
3
1
3
2
5
2
3
со I cm
Ю | CM
3
5
2
3-^2(^1) ^2 ? ^З? Oi, 625 Z)
Фз (z)
^ [2B - 5z)^2(z) - 4A - z)^(z) + 13^з(*)]
32
	[A - 4z)t/?2(z) - 2A - z)^i(z) +
27z
— л/1 — z + y/z arcsin y/z — 1
z L J
3 ^ A ^Аг*Ь^ j ! v/T[lj2(v/
D-Li2(-^)]}
—- h ~~ 9z + 6z3/2 arcsin y/z - 2A - Az)y/1 - z~\
4
4 Г2 j- / 2y^ \ 1
3 |"^ ^	 1 /1 1 0 \ arcsin y/z
g
9ttz l
9 ^A ^)Arthv^ o ! 1 + z[Li2(
/I)-Этт]
V^)-Li2(-v^)]}
-^2 [D + 11 z)\/T^z~ + 3C + 2z)y/z~ arcsin v^ - 4 - 18z]
1ч(Ч I 1П" I Ч~"*}ТС( v/~~\ (\A~(
ZI7TZ
1 H~ z JJL3 (у z J — Iztt — ЛЧжz
— [2D — z)%l>2(z) — 8A — z)ipi(z) — гфз(г)]
— [2A — z)ipi(z) — B — 5z)^>2(^) — %%Фз(%)}
	[8A - z)i/>i(z) - 2A - 7z)il>2(z) - F + 5z)i/?3(z)]
A - z)^1 j- ^ ^_ 1
7Г
1 / arcsin y/z 1 \
2\ y/z ' V/T^^ J
3 Г o arcsin лД /	1
8z I ' ^"^ V^ v 1 -J
— [B + 3z)K(A/z") - D + z)D(A/z")]
1 ы2ц_у л j ы2^ у-*'/ 1 ^-/vrtn \
4y z
3 f .xArthV^ /r . /
8z [_ y/z
—^- [B + z)^fY^^ - 2 + Зг3/2 arcsin
1бгз/2 l~v~ <¦ "•'I '4v~) 12
ГА
I)-Li2(-VI)]}

432
Гл. 7. Гипергеометрические функции
[7.4.2
«з
, «2, Q3; fei, 62; z)
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
- 2
- - 3
~~ ~~ 3
- - 3
- - 3
- - 3
- - 3
- - 3
- - 3
2
I I 3
2 2
11
1 1
1 1
1 1
3 3
1 1
2
1 2
1	3
3 3
2	2
* 2
2
i *
2 2
2	3
3	3
1 1
2
1 2
2
3
2
3
2
3
2
3
2
2
2 -
- 2
2
I •
—- [8 - (8 - 5z)Vl - 2 - 3C - 2z)^ arcsin
A3-5z)D(v^)]
arcsin ^
- A + v^)/2 In fz1/4 +
— [4-4/1 Arth V^ - 1 - - A - Sz) In A - z)
3 [

7.4.2]
7.4- Функция
,a2, аз] bi,b2',z)
433
«2 «3
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
1 1
1 1
-11
2
-11
- 1 -
- 1 -
- 1 -
- 1 -
2	™
3
2
3
2
3
2
3
2
3
2
I i 2
2	2
1
2
1
2
1
2
1
2
1
1
-1
1
- 1 -
2
1
- 1
3
2
3
- 1 -
- 1 -
2
2	~
1
2
1
2
1
2
1
2
1
2
1
- 1 -
-1
1
2 5
2
2 3
2 2
2	3
3	3
» 2
2
2 2
2 5
2
1 1
1 2
1	3
2	2
л/г
6z In
¦^ fll - A1
^ + 3B + Sz) In
3	Г arcsin y/z >
4	^
[Зтг -
+ 4A + z)T>(y/z)]
- A - «) Arth
^™ 2 + 3z - B +
z2 L
16
12тг + 9тг^ - 8C + bz)K{y/z)
Arth yfz
rth-v^l
л/г J
+ Ы2(-л/г)]
z)T>(y/z)]
— \l + -\n(l-z)
3z [ z
z L *
8 Г
7T 4D"
9z2 L
1 Г 1
9z- 12 In
1 + a/1^
3 [i —
3z
4
97Г
16
[Зтг^4К(л/^)^4A^:
[8C - z)K(y/z) - 16zB - z)T>(y/z) - 12тг + 9ttz]
27ttz2
1 Г 1	Arth.
4 U-
I
2z
8z
A-^)-
2
~[4(l^3z + z2)^
-[2(l + 2z)^2W-
z)tjj1(z) -4B + z]
2zE - 2z)il>2(z) - zB -

434
Гл. 7. Гипергеометрические функции
[7.4.2
<22 «3
, «2, Q3; fei, b2; z)
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
3
2
3
2
- - 2
2 2
- - 3
2
2
- - 2
- - 3
2
1
2
i - з
- - 3
- - 3
2	2
2	2
2	2
2	2
2	2
2	3
3	3
1 1
2
1	3
5 5
2	2
5
2
3	3
1 1
1 2
1	3
2	2
2	3
3	3
1	1
1	2
2
2	2
2 -
2
5 5
2 2
1 1
2
2
1	3
3
2	3
5
2
5 з
2
S[4A-
) - 4A -
- 4A - *)V>i(*) - 2A
4z
8
3ttz
9
- A - z)
^™ [D - z)y/l - z
z2 L
64
12
6_
9z
[2C
}-2
I-1
[4C - 10z + 6z2 - 2z
(
)
A6 - llz + 4z2)
2z2) tjj3(z)]
[2A+ 6z^ 4z2)
^ 4z+ 2z2)
[4D + z+ 4z2) tfj2(z) ^8B^ z+ 2z2) фф) - 2z(l
[4A -
- 2A -
- 2A + 2z)i/>2(z)
- 2z)tfj3(z)]
—	[2A + 2z)i
32
—	[G - 4г)^2(г) - 4A - *)i/.i(z) " C -
Z7T
[(8 - г
[2B -
-z(U-9z + 3z2
[B - 3z
3 [ arcsin i/z 1 — 3z
3z) Arth
Arth y/~z '
Arih-Jz
J
Sz \l-z
2
/1 -
¦ -4
2 Г	11
— v^ Arth yfl - 1 - - In A - z)\

7.4.2]
7.4- Функция
,a2, аз] bi,b2',z)
435
«2 «3
62
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
I 2 2
2
I 2 I
- 2 -
- 2 -
- 2 -
- 2 -
2
1
2
1
2
1
2
I 2 -
2
I 2
2
I 2
2
1
2
1
2
5 5
2 2
5 5
2 2
5	5
2	2
5	5
2	2
!	•
1
2
1
2
i - з
^ 2 3
- * 3
1 ^
2
3	3
2	2
5	2
2
»	3
2
3 3
1 1
1 5
2
Зтг
8A-z)
[F-
[B-
^) ^ z A1 - 5z + 2z
-D-:
1Г 2-2 Arth -y^
3 [	+
4
64
/1 - Z
¦7Г - F + ;
¦ - 2
Z < 7TZ
^ A6 - 8z + 10z2 - 3z3)
+
J
¦ [4(9 - 28z + 15z2 - 15z3 + 4z4) tpi(z) ¦
36
+ 2z E0 - 24z + 27z2 - 8z3) i/>2(z) -
- z B4 - 19z + 14z2 - 4z3) фз(г)]
— A - z)^3 [(9 - 3z + 2z2) K(-v/J) - z A5 - llz + 4z2)
. [4D - 15z + 12z2 - 4z3) фф) +
18
27z
+ 2A + 21z - 21z2 + 8z3) xjJ{z) - z A0 - llz + 4z2)
¦[8B ^9z2 +4z3) ipi{z) -
- 4D - 6z - 15z2 + 8z3) tjj2(z) + 2z (l - 8z -
^-A - z) [2B - z)K(Vi) + A - 7z + 4z2)
16A ~ "Г1 [A + 2*)K(Vz-) - B - 3z + 4z2)
iYTTZ
^	-^— [4B - 7z + 4z2) i/)i(z) + 2z(ll -
[8B - z + 8z2) ^2(z) - 16A - 2z + 4z2)
—
[2E
12тг
- (8 - 8z
67Г
-[B4 + 13z + 14z2 -3z3)
- 2z B5 - 9z + llz2 - 3z3) Щу/z)]
[A2 - 7z + 3z2) K(y/z) - z A9 - 17z + 6z2) Щу/z)]

436
Гл. 7. Гипергеометрические функции
[7.4.2
а\ „2 «3
Ъ\ 62
, «2, Q3; fei, b2; z)
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
2
з х '
1
5	з
2
3	3
3	3
3	3
3	3
3	3
3	3
3	3
4
3
¦ 5
1 '
5
5- 1 I
6 6
» 2
2
2 2
4
(i-*)
Зтг
[E - 3z)K(y/z~) + 2A - 5z + 3z2
—	F4 + 72z2 - 40z3 + 9z4)
| [E5 ~31z + 33,»- ^)
—	C2 - 40z + 32z2 - 9z3)
1
2 -
з 2
7
3
3
¦ arctg ¦
- 2
-z I In (!-
L
_ 2 arctg ZV4
9
4
9 11
15
1 I ж
15 Г	1 I
—- 4ж - 2A +ж2) arctg ж - (l - ж2) In
[x = _VS]
24
1A0 -
4V
2\/5 I/2ж
arctg
11 13
15 17
35 Г / оч Г 1 + ж + ж2 1 + ж]
--^Ых-A-х2) In-	^^+21П1	 -
- 2л/3 A + ж2) arctg ¦
63
16ж9
8ж
A - ж2) In	 + 2/2 In
l	; [ 1 + ж
ж2) arctg х + 2^1/2 arctg ——-
: + ж^
111
111
i 2
2
I 3
2
arcsin i/z
arcsin л/z	1 — z
arcsin \/z

7.4.2]
7.4- Функция
,a2, аз] bi,b2',z)
437
«2 «3
62
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
Ill
111
111
111
111
111
111
111
1
1
3
1 2
1 3-
2
i 3-
2
i 3-
2
11-
2
i »
2
11-
2
11-
2
¦ ¦ i
112
1 2
1 2
112
11-
2
- 2
2
3
2
2 2
2 5
2	3
5
2
3	3
4	4
1	1
2	2
1
2
1	5
2	2
1
2
2 2
- 2
- 3
2 -
2
2	3
i *
3	3
2	3
»	3
2
^	3
2
3	3
1	1
2	2
1	3
2	2
i	2
2
1 /1я . r- 1^2z . о л-
— I 2\/	 arcsin у z	arcsin у z —
z-1U2(z)
3 / 2 a- A -
— arcsin yz —2 + 24/	 arcsin <
ln(l-z)
arcsin \f z — 7
*-* / / -1- — z	i—
"" I "\/	 arcsin yz
— [A + z) U2(z) - 3z - 2A ~~ z) In A - z)]
^ [A + 2zf U2{z) - 4z - ^fz2 + 3A - z2) In (
1 -I- 9r
+ B+ *)(!-*;
r- 3	9 r-
arcsin s/z —6	arcsin у z
1 /	1	2 ,-	1-Z
— II H	arcsin -\/z — 2\l	 arcsin \/z
z \ z

438
Гл. 7. Гипергеометрические функции
[7.4.2
377
чтя
379
380
qo-i
382
384
385
387
9QQ
390
nm
392
qnq
one
396
398
400
401
oi
1
1
1
1
i
1
1
1
i
1
i
1
1
1
1
i
i
1
i
1
1
1
a2
1
1
1
1
i
1
1
1
i
1
i
1
1
5
4
?,
з
2
to
3
w to
_
2
3
2
3
2
3
2
3
2
3
2
a3
5
2
Б
2
f>
2
5
2
Б
2
Б
2
Б
2
Б
2
3
*э
3
3
4
7
4
2
2
3
to
3
ю to
_
2
3
2
Л
2
3
2
3
2
3
2
bi
1
2
3
2
2
2
9
2
2
3
1
2
3
2
2
9
2
2
•Л
1
Я
1
2
1
2
1
2
?,
9
2
5
2
ю | см
3
62
3
3
2
2
3
9
3
7
2
3
2
9
2
5
2
4
5
Б
2
1
?,
9
Б
2
о
?,
5
2
3
Б
2
3
2C
A -
1 Г
з L
2
3
4
3z
4
3z2
9z2
16
3z2
A-
A-
M
3
4z
3
4z3
2
8 г
(l -
2 Г
z L
3 Г
z L
4
Z

7TZ
6[
z\
H
TTZ
9
2z3
12
z^
7TZX
+ z) Г
iz [
>
з
2
l-z
-[-
Г 1
r
Г
[
г
fl-v
~zy2
4
4
1
l-z
Г ,
[
[2z +
[6z +
v 2 A -f-
- Q% _|_ jj
A -
2 — z
l-z
Г2C-
iv^V z
3F2(ai,
1 1 Чг
'(I-*)]
Г 2-,
1 ]
In (Л у
z ' \

1 + лД^
1 In
9
у 1
9л/1 Г 9r In
1 }
	 1
'\ - z + B
у 1 In
4 Z + (D ^Jy -,
ч arcsin х
1 I f4 *^~^
|П/1 у
z
>]
""\/z(l-z) \
z2 + 2A - z2) 1пA -
3z2 + 2z3 +6(l-z3
%/\ — z ) ' — 1
J
'¦^ j M 	2;)
— zz
Arth д/^ 1
" ^ j
2г) 6 + z
z
\
2 J
arcsln yfz 1]
\/^
[4К(д/
/2 L 2
[2^
1
z) — 4D(-\/z") — тг1
z + 2л/г arcsin -\/z -
,)K(VI)-16,DU
J
+ 1
V
4-1
z
— z
/z"
"^J
)ln
lv
- 2
rz)
«з; Ьи 62; z)
J
2 J
1 /71
V
^ J
2 J
arcsin л/г
I
J
1
a-*)]
4
— 4тг — ttz] =

7.4.2]
7.4- Функция
, аз] bi,b2',z)
439
402
403
404
405
406
лат
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
oi
1
1
1
1
i
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
«2
3
2
3
2
со 1 см
3
2
3
2
3
2
3
2
3
2
oto | со to I со
о
2
3
2
со 1 см
3
2
to | оо
со 1 см
3
2
2
2
2
2
2
2
2
«з
2
2
2
2
9
5
2
5
2
5
2
5
2
5
2
г
О
2
5
2
3
3
3
з
з
2
2
2
2
5
2
to I ел
5
2
1
2
1
2
1
2
2
о
1
2
1
2
1
to to
3
3
1
2
1
2
I
2
2
2
1
2
3
2
5
2
3
1
2
1
2
1
2
62
1
2
5
2
3
3
0
1
2
2
3
2
3
3
7
2
1
2
2
Ь
2
2
5
2
3
3
3
3
1
2
3
2
3
16 Г
7TZ2 ^ ^^
A-*)~3 Г
2 Г
2z [- -
2 ГЗ-z З ,
I In (Л
z [1 — z z
6 Г Arth^/i 1
z [ \/г ^
8 \а z aJ\—
2 4 a, 4V I
1 /о , оо7 i 1Чг2
- 1 О Т O«3Z -f- -LoZ
3z f (l~zM/2
4 Г 3'
3z2 L "A -
^ ~~ 2' Гоtv/ /"
3ttz L" U'
g
3?rz
1 л
Id г
37TZ2 [i7T *~ ~
3z2 V " "V
8 Г ' """
2 v )\
3A — z) 2 1
Q I "" ^
OZ
1 \ 2~z 0
2z[(l^zK/2 "
3 TArthv^z" 1-
4z [ л/^ 1
1 [3 2 ^
— — arcsin -\/z +
z U
1 1 o arcsin y^
z f ^A-^)
3/1 . 2 r-
— — arcsin уz ~~
z \z
^n{z)^z\
A-)[б|г„
(l^z)^3 Г
z [^
3F2(ai,a2,a3; 61, 62; z)
/r ( 2^
V \l+/i
2 \ / ~^~
2 - 3z ^
^(l^z)
")]
- arcsin y/z
% J
ln(l-^)-l]
^4z 1
zK/2 I
2 ) — 2zD(i/z ) — 7Г + ttz]
	 ( o arcsin д/z ^
+ 17z2 - 2z3 + 15B + bz)J-
"^~ arcsin Vll
-« J
-ra
i 0^2 2 ^ 5z
Vz(l-z)
in yfz
]
о/*з 4~Wi
)/2
arcsin y/z 1
L	arcsin2 V^"
0
-j" ZoZ Z -f- 010 -j" Z4tZ -f- OZ
2 / ^
" \1-Z
2\ / * • ^1
у 1 - z J
arcsin V^
iC~6z~z2)(l~zr2]

440
Гл. 7. Гипергеометрические функции
[7.4.2
«з
2, Q3;
2; z)
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
5
2
5
2
5
2
5
2
5
2
5
2
5
2
5
2
5
2
5
2
5
2
5
2
5
2
- 3
2 -
2 -
5
2
5
2
5
2
5 з
2
ъ- з
- 3
- 3
- 3
3 3
3 3
2 2
i *
1	1
2	2
I 2
2
5 2
2
-	(9 + 180z + 190z2 + 4z3
-	(9 + 39z - zA + z3) A -
9l	M
2 L l-8z-8z2l
2
9*
4
4A ~
~"~ (

1-2* 1
9wz
8A -z)-1
[2A-
[4K(y/z) -
- тгA - zJ
™ 7Г + 7TZ]
16
[8K(-v/z) -4тг - ttz]
24 + 480z + 440z2 - z3 + 2z4 +
24 + 84z - 5z2 +2z3 + 15D+ 3
32 + 85z - 16z2 + 4z3 - 15E + 2z)J	 arcsin
23- 12z + 4z2 +3C + 2z)
-A - z)-3 [A + 5, + 2z2) К(у^) - 2C + 52)D(v^)]

7.4.2]
7.4- Функция
,a2, аз] bi,b2',z)
441
452
454
455
456
457
458
45»
460
4tii
462
лач
4H4
465
zffifi
/ffi7
Ada
469
470
471
472
473
474
ATK
476
477
AT Л
a\
3
2
3
2
3
2
со I cm
3
2
2
3
2
3
2
3
2
3
3
2
3
2
3
2
3
2
3
2
2
3
2
3
2
3
2
со I cm
3
3
2
3
2
3
2
3
2
3
2
«2
3
2
3
2
3
2
со I cm
3
9
2
3
2
3
2
3
2
3
3
2
3
2
3
2
3
2
3
2
2
3
2
3
2
3
2
со I cm
3
2
3
2
3
2
3
2
3
2
3
2
«3
3
2
3
2
3
2
со I cm
3
9
3
tol
3
2
3
2
3
2
2
9
2
2
2
2
9
2
2
5
2
5
2
5
2
5
2
5
2
Ю | CM
5
2
5
2
6i
1
2
1
2
1
2
1
1
1
?,
2
3
1
?,
1
2
1
2
1
2
1
][
Б
2
5
2
3
1
2
1
2
1
2
1
2
i
1
1
9
2
Б
2
3
1
2
3
?,
3
3
1
•л
1
Б
2
3
1
5
2
q
Б
2
з
3
1
2
1
2
3
i
2
3
9
з^М«1, «2, «з; ^ь ^25 г)
4
— A — z) л [A — 3 z) D (\/~z ) -Ь 2zК(\/~z ) 1
7Г
3 Г arcsin \fz , . , . о /ol
z [ лД ">" J
16A — zi^1
[C о~)К(\/"~") F 5~)D(v/~)l
4 L v / J
2
z
A — ^)"[6i/'2(^) — 4i/ji(z) — 'фз(г)]
16
	[*01 (z) — '02(^I
z
32
	[t/?2\Z) — i/'3(z)|
Z
(l -f- 14z -f- 9z ) A — z)
-B + lU + 2Z2)(l-Z)-7/2
3 [Arth v'z 1 - 2z ]
z[ ^ " A^JJ
4 Г 6-9z + 2z21
z2 Г A - zfl^ J
A - z)™3 r/f> ( ^^ f ^2\ -c^/ /Г\ „/к i <з„\т^( /ГМ
7Г
3 1" arcsin i/z 1 — 2z ]
2z [ sfz A - zK/2J
8A — z)"
_^^ L^ ^/ \sr ~) \ ^) iv^jj
9
4<гз/2 \-"Л v " 2^v " > 2{- v " ^J
12 г ^^ ^ ^i
—г- 2 — 2vl — 2; — л/z arcsin vz
Z2 L J
64
	 [тг - B + z)K(v/z ) + 3zD(v/^)l
7TZ
A -f- 18z -|- 16z ) A — z\ 1
A(l - z)-* [C + 26, + 19,2) K(v^) - 2, E + 18, + ,2) D(^)]
±A _ г)-з [A + 7z)K(v^) + A - 7z - 2z*) D(Vi)]
Г4 (ч ^^ 17" I "»'^т/?1/'"»Л I
(l^z)^3, 2
6
HdV0 ^~ ~2^l i'ji (~\ ^(A A~ 4^\ ihnf "\ 1
(l-z;r2 + z(l - 2z)i/>3(z)]
3

442
Гл. 7. Гипергеометрические функции
[7.4.2
479
480
481
482
483
АЛЛ
485
486
488
ляа
лап
491
492
AQ4
АпА
495
Add
AQT
498
499
500
501
503
504
oi
3
2
3
2
3
2
3
2
3
2
3
2
3
2
3
2
3
to
3
2
3
2
3
2
2
3
2
2
3
2
3
2
3
2
3
2
3
2
3
2
3
9
3
2
3
2
3
2
3
2
а2
3
2
3
2
'Л
2
3
2
3
2
3
2
3
3
2
3
2
3
2
3
2
3
2
2
2
2
9
2
9
2
2
2
'Л
2
2
2
«з
5
2
5
2
3
3
3
Q
3
3
3
Q
Q
2
2
2
9
2
9
9
2
2
5
9
5
2
5
2
2
2
2
3
I
2
1
2
1
2
1
2
1
1
2
9
Б
2
1
9
1
2
1
2
2
1
Б
2
3
1
9
1
2
1
2
1
1
62
3
3
I
2
1
'Л
Б
2
1
2
5
2
2
Б
2
Б
2
1
9
1
Б
2
1
5
2
3
3
3
1
9
1
1
3
4A
3?

(и
3z
2i/>i (z
h22zH
-[2B
К25г2
^2 Сz) -f- 3 (x
- (8 + 72z + 27z2 ~2z3) A
_ (i
4 l
3
4z
A -
A-
3
8z
,4
4z
(
162
ti-
till -
3A
?
z
1 (<
4 v
3
4z
?
6
z
16
2
(H
!
_ (
2
4
z2
A -
8A
4 ~h 13/
Г Arth
4тг
2тг
2	2z
\fz
[(8 +
[D +
[arcsin л/г
1 V
7Г
г
(л
v ¦
3 Г'
3/2 []
4
_ g^; _|_
— z)~
4z
Г 3^
id-
4 + 10,
Г Arth
i ^
Г 4
Г "
L V
[^
h25zH
2 + 21,
Г2 — 5
- ZYA
Зтг
3?rz
z
2л/^
- z
h
3z ) (
2 Го
1 v
1
2 + г2
z
z
7-1
h35z2
^ -f- 12
- z) 1x
[2C
-[D
^ j /"]_ 	 %\
1 — 4z — z
A-zK
31z + 10z2
5z z2)K
l-5z +
A-zM/
z)K(v^)
> arcsin \/
\[z
T \n( * Py \
62z + 39z2
- 5z + 6z2
ai,a2,a3; bu 62; z)
01
\—9/2
z)
J
(a
/z) z\ z) Wz)\
г2]
2J
2D(Vi)l
J
1
+
1
fzJT^) J
3
z ПA
i 2 1
1
Z
+ 3z3) A-
2 ) A 	 z)~"
^2 1
-h 14z + 7z2
7z + z2)l
1
]\
2
:)
2 J
-9/2
) К(л/г) « A7 + 30z + z2) D(v^)]

7.4.2]
7.4- Функция 3F2(ai,a2, аз] bi,b2',z)
443
«2 «3
62
, «2, Q3; 61, fe2; z)
505
506
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
522
523
524
525
526
527
528
2 5-
2
2	3
2	3
2	3
2	3
- 2
2
3
5 5
2 2
* - 3
2
2
3
2
5 з
13
^ з
2
2
1	1
2	2
- 1
- 2
- 3
1 2
1 3
2 2
3- 3
2
3
1
2
1
2
i 2
2
1 1
1	2
2	2
1	1
2	2
1
_2
64
16
¦15F + 37z + 20z2
(l + 13z + 10z2)(l^z)
|г_ .- , _— , ^	, ~2 + llz + 6z'
^A6 + 72z + 18z2^z3)A^
3
16z"
1
^C + 96z-
32z3
9?rv
16A™.
[C + 46z
[4A + 8z
- z A1 + 82z + 35z2)
[C - 7z + 12z2) K(y/z) - F - 17z + 19z2) ]
36
-[4(9-
- 24z3
2z E3 + 237z + 27z2 - 2z3) t/j2(z) - z C3 + 83z - 10z2 - z3)
18
- 2A - 30z - 18z2 + 2z3) i/>2(z) - z A4 + 2z - z2) '
- [4D - 9z + 12z2 + 2z3) ^2(z) -
- 8B - 6z + 6z2 + z3) tbt(z) - 2z (l + z + z2) •¦
+ 2A + lOz - 2z2) ф2(г) ^ A + 3z -
[16A - z - z2) ^i(z) - 8B - 3z - 2z2) i/,2(z) - 4z2
16A ^ zy1
?z
[2E - 2z)^2(z) - 4B - z^tiz) - B - z)
A + 39z + 95z2 + 25z3) A - z)
- (8 + 136z + 159z2 + 12z3) A
8
4
A--
A
A
A
127Г
-*)
67Г
-*)
Зтг
- ^)
-4
-3
[B4 + 181z + 166z2 + 13z3)
- z G4 + 259z + 52z2 - z3) Щу/zj]
[4C + 8z + z2) K(v^) - z C1 + 18z - z2) T>(y/z)]
[G + z)K(v^) - B + 7z - z2) D
64
64 + 2622z + 6219z2 + 1490z3
15C0 + 295z + 328z2 + 40z3) J—^
+ 21z + 33z2 + 5z3) A -

444
Гл. 7. Гипергеометрические функции
[7.4.2
«3
, «2, Q3; fei, 62; z)
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
544
545
546
547
548
549
550
551
552
553
3 3
3 3
3 3
3 3
3 3
3 3
3 3
2
2	2	2
2	2	2
2	2	2
2	2	2
2 2 2
2 2 2
2 2 2
2 2 2
2 2 2
2 2 5-
2
2 2 «
2
2 2 ™
2
2 2-
2
2 2-
2
2 2 5
2
2 2 ^
2
2 2-
2
2 2-
- 2
5
2
2 3
1
2
- 3
1 -
1 -
- B + 17z + 5z2) A -
зA-*)-
64z
B - 9z + 72z2 + 40z3^ arcsin ^ о ¦ on- ¦ ™..2
— F4 + 512z + 360z2 + 8z3 + z4) A -
- 2 + 29z + 78z'
z L(i-^J ^
1	o ,
- arcsin2 лД - B - 3z)(l - z
12
12 + 76z +17z2 + 3A2 + 21 z + 2z2) J
— [3 In A - z) + z C - 6z + Hz2) A -
! 3
2

7.4.2]
7.4- Функция
,a2, аз] bi,b2',z)
445
«2 «3
62
554
555
556
557
558
559
560
561
562
563
564
565
566
567
568
569
570
571
572
573
574
575
576
577
578
579
2 5-
2
2 2
2 2
2 I 5-
2 - -
2 - -
2 - -
2 - -
2 - -
2 - -
2 - -
2 - -
2 - -
2 "
2 *
^	з
2
5	3
5	з
- 3
2
3 3
3 3
5 5
2 2
1
2
1 -
1
3
2
3
3
2
3
3
1
2
1
3
2
1
3
2
3
2
- 1
1
1
1 3
1
2
29 + 72z + 4z2 + 3A + lSz + 16
i C
о
-{2 + 39z + 56z2 + 8z3) A - z
A
- C + 35z + 25z2 + z3) A - z)
4 Г 2 - 7z + 8z2 - 8z3
3^2 L	(lO/2
Зтг
8A -
9ttz
[F + 53z + 60z2 + 9z3) К(л/г) - ^ A9 + 82z + 27z2) Щу/z)]
[B - 3z + 9z
- D - llz + 15z
¦ -2
64A - zY1
- 7TZ - B - 3z
16
A-z)
16 + 744z + 2040z2 + 659z3 + 6z
+ 15(8 + 88z + 115z2
+ 10z3)(l^z)^6
16+180z+117z2+2z3+15D + 13z+4z2) J—^— arcsin
42 + 61z + 2z2 + 3B + 21z
128 + 3165z + 5886z2 + 1216z
15D5 + 320z + 296z2 + 32z3) J—^
128z
- (9 + 504z + 1864z2 + 1024z3 + 64

446
Гл. 7. Гипергеометрические функции
[7.4.2
580
581
582
KflQ
584
585
586
588
589
кол
CQ1
592
593
594
595
596
597
598
599
600
601
«0*2
oi
5
?,
5
2
5
2
5
2
b
9
5
?
5
?
2
f»
2
b
2
5
2
2
5
2
5
2
5
2
b
2
5
9
5
2
5
?,
5
2
5
2
5
2
5
2
«2
5
5
2
5
2
5
2
b
9
5
?
5
?
2
f»
2
b
2
5
2
2
5
2
5
2
5
2
b
2
5
9
5
2
5
5
2
5
2
5
2
5
2
«3
5
5
2
5
2
5
2
b
b
?
5
?
2
f»
2
b
2
5
2
2
2
5
2
5
2
3
3
3
3
3
3
3
n
bi
l
?,
i
2
2
1
2
1
1
1
2
2
3
2
9
2
3
3
I
?
1
9
1
9,
1
1
1
1
3
2
b2
1
3
2
2
Q
1
2
Q
2
2
9
з
3
5
I
?
1
3
2
2
1
2
2
3
2
Этт [[° ' -1-
- (9 + 138z + 152z24
4A"z)~6rfi« 1 166
277Г Ll '
16A-z)^4 r ,
[°C 11
27ttz rv"
^ ~~ z' \л(ч i ^ч-
3F2(ai,a2,a3;
+ 663z2 + 341z3
- 2z A8
- 16zs) A - z)-11
z + 181z2 + 24z3)
+ (
z + z z j
-
6l , 62; Z)
¦f 24z4)K(V^)
+ 261z + 320z2 + 41z3) D(v^)]
/2
IVZ J "T"
1 - 52z - 259z2 - 74z3) D(v^)]
C - 14z - 13z2 - 24z3) K(y/z)]
~57z2 -72z3 -2z4)t/?i(z) +
+ 2z A7+ 174z + 126г2
Этт [[ ' '
^ ~~ Z' \Л(Л А 1 fi~
-2A-84*
A — z)"^4
27z L"^
-4D- 12
1 9
— (9 + 22z + 4z ) A —
9
4^ ~ Z' 1^G 1 14-
277Г K< ' И-
16A-z)™3 j-.
27ttz ^
A — z)"^4
27 L l
A A ^ 3
^ j fofo 4^
27z L"v^ *"
16A-^^rir i-i
256A-a2)"*
817Г2Ж4 И1
- C + 204z + 938z2 Л
- (8 + 248z + 643z2 Л
8
-
-53z2 +6z3)K(v
114z2 llz3)^
- 225z2 - 7z3) ф2
О I ] ljJ\y
-2z3)t/»2(z) -
z A2 + 74z + 26z2 - 7z3) ^з(з)]
Ъ) z B7+ 82z+ 19z2) Щу/z)]
1{Z)
(z) - z D7 + 71z - 13z2) ^з(^)]
z-9z2 - 28z3) *l>2(z) + 2z A - 14z - 2z2) фз(г)]
a /o
z) '
+ 3z2)K(^)^
6z2)K(v^) B
) Vl\ ) i-
+ 6zA3 + 2,
h llz2) t/?2(z) 4(
i/?i(z) 2G 10^
2ж2)В(ж) A
- 700z3 + 75z4) A
- 248z3 + 8z4)A -
- C + 57z + 85z2 + 15z3) A - z)™6
— A2 + I59z + I36z^
(Л y\ ~~®
+ 8z3)(l-z)
+ 663z2 + 243z3
-2zD1
- (8 + 56z + 39z2 + 2z3) A - z)™11/2
^ ~~ z' fh° i fi7~ i
67Г U ' ^ '
— C + lOz + 3z ) A —
3
46z2+3z3)K(V^
z)
(l + 30z + 17z2)D(v^)]
5z + llz2) "D(\/z)]
z)*l>2(z) - A + 16z - 2z2) фз&)]
1 4z + 6z2) ф\(z)
Зж2)К(ж)]2
[ж = 2™i/:"(l - Vl - ^I/:"]
_z)-13/2
1/2
+- yz j Jtv^yz j
+ 320z + 261z2 + 18z3) D(v^)]
0 z C5+ 82z+ llz2) D(-v/J)]

7.4.2]
7.4- Функция 3F2(ai,a2, аз] bi,b2',z)
447
603
604
605
606
RU7
608
609
610
611
612
613
614
615
616
617
618
619
620
621
622
623
oi
5
2
5
?,
2
2
tO | СЛ
5
2
5
9
5
2
Ю | CM
5
2
5
2
3
3
3
3
3
3
3
3
3
«2
5
2
5
2
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
з
3
3
3
1
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
3
bi
3
2
2
1
?,
1
2
1
2
I
2
1
1
1
3
2
3
2
2
1
2
1
1
1
1
1
2
2
2
2
2
1
Я
1
3
2
2
1
3
9
2
3
2
2
2
1
2
1
9
2
2
2
2
2
1
12
A
A
A
to | i—
1
l
(i
(i
(i
(i
(i
1
2
¦A2
-г)
Этт
- z)
64
-*)
64
B +
- F4
+ 9z
-C2
-*)
64
B +
-A6
-z)
512
- z)
3F2(ai,a2,a3; bu b
+ 21z + 2z2)(l- zY9/2
[/in | ой« | Q~2\ ту-/ /U \ o(-\ |
+ 15D0 + 680z + 1563z2 + 680z3
z + 126z2 + 70z3 + 5z4) A - zY7
-6 r
+ 15B0 + 115z + 88z
33z + 40z2 + 5z3) A - zY6
+ 1024z + 1864z2 + 504z3 + 9z4) A -
+ 9z2 + z3)(l^z)^
+ 184z + 96z2 + 3z3) A - zY11/2
\ KQ I inn* I KQ^ i o(o I QO~ I K
5, + z»)(l-,)-
+ 18* + Z2)A-*)-9/2
no i on «on» i ТГ» Q7Q ~2 | /jri i л
+ 15B25+ 2600z+ 4584z2+ 1536z3
-6 r
^fifi I 4OKI ~ i К*1О|1~-2 1 |R<RQ~3 I
+ 15G5 + 370z + 232z2
+ 20z + 48z2 + 20z3 + z4) A - z)~7
-*)
512
B +
3A-.
A
1
4
— о г
док ) ARIA'- I ДТ^^-2 I ^ДД-^ 1
+ 3(9 + 504z + 1864z2 +
15z + 12z2 + z3) A-z)^6
)-Б \(л t o^ t oGn^2 ( ciQ^3 ( aA_±
bl2z |_V" ' "~ ' """" ' """" ' ™
- z)
256
D +
^ '111 iRQ~ I «3(R~2 /-j 1Ол, f7f>.
256
z L
2; 2;)
18z + 5z2)D(A/z)]
+ 1690z4 +
! 4fl~4'l / Z irr—i
.^1
пл/il
V 1 — z j
-z)^13/2
^2 oJJ arcsin^
t4z3 + 2912z4 +
I f\A~ \ / ii^ir^ci
1 1 fi~^^l / IFfT1!
Х0^4~3 1 64~4)
1"" ; ^(i-^j
^ arcsin -/z
- 1 + 162z + 624z2 + 160z3
+ 152z2 + 16z3) x
arcsin x/z 1
V*A-«)J
2 3> arcsin VI
16" J y/t{l-z)
]

448
Гл. 7. Гипергеометрические функции
[7.4.3
7.4.3. Частные значенияз^(а1, аг, аз; bi, 62; — z).
(См. также 7.4.2.)
&1 &2
i, 62; —2
- - 1
- - 1
9 11
9 13
8 У
9 15
bx
Ч Г	h-
	 2(аж2 - 6) arctg	 + 2(бж2 + а) arctg	'¦
+ (Ьж2 - а) In г + 6Ж + Х1 + (аж2 + b) Ы * + аж + ^
х	' 1 - Ьх + ж2 v	; 1 - аж + хл
96ж7
[а = B - л/2 I/2, 6 = B + л/2 J1/2, ж = z1/8]
/ 4 ч	ах	/ а \	Ьх
{*Х< - 6) arctg —- + 2F^ + а) arctg —
1 — ах -
— (bx4 — a) In	 — (аж4 + b) In —
1 + bx + ж2	1 + аж + ж2 __
[а = B - л/2 )х/2, 6 = B + л/2 )х/2, ж =
а | A + ж6) In
1 — ах + ж2
- 2A - ж6) arctg
[а = B^л/2I/2,6 = B + л^2I/2,ж = ,
ЗУ2Ж
— ж
4 arctg \/ж + 2 arctg -
1 Г	31/2ж
— < In A - ж + ж2) - 2 In A + ж) - 2\/3 arctg	Ь
6ж I	°
In
1 Г q /о Г
^^ i ж3/2 4 arctg
9ж2 [ [
In
+ 2 arctg -
¦In-
1 — \/Зж + ж
1 + л/Зж + ж
arctg
4 4
4 4
+ ж
-2A - ж2) arctg
*V3]
15
2х -
21/2ж 1
+ 2л/2 (ж4 - 2ж2 - 1) arctg	 + 8ж
^	1	ж
/	Г ^
4
3 6
10
*	2
4
4	11
3	"б"
11 13
,^г Г.
z) H	=- in
' V2 [
— 2 arctg -
5
9ж
[1 Зх/2ж1
In A + ж)	In A - ж + ж2) + л/3 arctg	 -
._ .^ 3^1/2ln ~ х+х + 2 arctg ^—+4 arctg у,
18ж5/2
+ 2 arctg	h4 arctg i/ж
1 —ж
1 ^ Г Г	1 1 /iT9 1 'Т*	/iT9 1
	™< а A + ж2) In	 + 2A - ж2) arctg	-
32ж5\ L1	^ 1-бж + ж2 V	} &1-ж2]
^Ь [A + ж2) In 1 + ах + х2 + 2A _ Ж2} arctg а«^1 1
L	1 — аж + ж2	1 -— ж2 j J
[а = B- л/2I/2, 6 = B
, ж =
11
12
- - 1
11 15
21 /
	 <
64ж7\
аж +6) In
1	Ч 1-
- 6ж + х'
— 2 arctg -
Зл/З
/л \ Г 1 + ах + ж	<
- (Ьж - а) in	¦—- - 2 arctg ^~
L 1 — «ж + ж2	1 -
[а = B^л/2I/2, 6 = B +
= = z1/8]
arctg ж
[4z = 27ж2A-

7.4.4]
7.4- Функция 3F2(ai,a2, аз] bi,b2',z)
449
«2
Q2, «з;
13
14
15
16
17
2
3- i
4
* 1
4
- 1 -
3 3
2 2
I 2
4
7
2ж
9
4 4
11 13
15 17
15
2^4 ~
35
63
35
____ 2
: = z1/4]
-16ж + A - ж2) о In
1 + аж
1 + Ьж-
+ 2A +ж2) a arctg	¦
1 — ах + ж2
ах
' 1 - 6ж + ж2
[а = B - л/2 )х/2, 6 = B + л/2 )х/2, ж =
7.4.4. Значения 3-^2(^1, «,2, «з; 6i, 62; 1).
. а, 6, с; 1 I ц*,
1- з^2	.	1=11,
d, e
Ч JT 9
е — а, е — 6, с; 1
. а, 6, с; 1 ,
2. з^2	.	1=1
d, e
a,
3f2
[Re(d + e-a- 6-с), Re (d - с) > 0].
— а, е — a, s; 1
6 + s, с + s
[s = d + e — а — 6 — с; Re a. Re 5 > 0].
d,e,l-a,c-6 I _, /6, 1 + 6-d, 1 + 6-е; 1N
3. 3F2( a' 6' C' X I = Г1 ~7 "' ^ "~7 " " I 3F2( "' " " "  " " " "' " 1 +
l I, e /	Lrf^6? e^&. 1 + 6-a, cj3 V l + 6-a,l + 6-c '
¦ d,e,l-a,6-c 1 /c, 1 + c-d, 1 + c-e; 1
. — c, e — c, 1 + с — a, oj \ 1 + c — a, 1 + c — о
4.
a, 6, c; 1^ Ге-а-Ь,е] / a, 6, d - с; 1
\d, 1 + a + 6 — e
, e
e — a, e —
а + 6^е, d, e,
[Re(d + e - a- 6- с) > 0].
^a — fe^c
e — a, e — 6,
a, 6, c; 1
d,e
[Re(d + e - a- 6- c), Re(l + c- e) > 0].
l + a-d, 1 + 6-d, l + c-d5d, el
a,6,c,l + e-d,2-d	J
x 3F2
x 3F2
7.
1 + a — d,l + 6 — d, 1 + c — d;l\ Fl + a — d, 1 + c — dl / a, c, e — 6; 1
1+1	Ч jT 9 I
1 + e — a, I — a	J [1 — tt,l + a. + c — aj Yl + ft + c — a, (
[Re (d + e - a - 6 - c), Re A + 6 - d) > 0]
a, 6, c; l\	Fl + a — d, 1 + 6 — d, 1 + c — d, d, e
d, e /	[	a, 6, c, 1 + e — d, 2 — d
1 + a-d, 1 + 6-d, 1 + c-d; l\ |T,[ 1 + a-d, 1 + 6-d, 1 + c-d, e
1 + e - d, 2 - d
о, 1-f a — d, l + a. + 6 + c — d — e; 1
l + a + 6 — d, 1 + a + c — d
a, a + 6, a + c; 1
+ Г	'	'	'	'	I x
[l — d, l + a + 6 — d, 1 + a + c — d, e — aj
[Re (d + e - a - 6 - c), Re (e - a) > 0].
L + a - d)r(l -a-c)	\ a + 1, 1 + a-d ) ГA + 6- с)ГA - 6 - d)
15 А. П. Прудников, Т. 3

450	Гл. 7. Гипергеометрические функции	[ 7.4.4
6, 6 + а, b + d] 1\	Г а + 1,6 + 1
LT Л	=Г I
6 + 1, 1 + 6 — су	Lo,-+-I>, 1 — с, 1 — <
а + 6 If	6	/а + 6, а + с5а;1\	а
_а ~~ d, b - с] \ ГF + d)F(c - 6) 3 2\ 1 + a-d, 1 + а J + Г(а + c)r(d - a)
а + 6, b + d,b; 1\\ ,	Г c + d
-с)
, a + c, c; l\\ Г	a + 1, 6 + 1, с + 1, d + 1
+
Г(с + d)r(a -d)
[Re(a + 6 + c + cf) < 2].
g ^ /a, 6, c; 1\ = r\d~ b~ ci dl F( -n, 6, c; 1
\ d, a — n ) \_d^b,d^cj \t + b + с — d, a — n
[a ^ 0, -1, -2, . . . ; Re (d - 6 - c) > n].
/a, 6, c; 1\	\d, d-6-cl Г	6с
d, a-1/ L^ — b, c? — cj L (a-l)(l + 6 + c-d)_
[а ф 0, -1, -2, . . . ; Re (d - 6 - c) > 1].
а + 1, d у	{ [b, d — а, a — '
а	_ /6, 6 - d+ 1, 6 - а; 1
ГF - с + l)r(d - 6)F -а) V Ь - а + 1, 6 - с + 1
,	а, 6, с; 1	\	[l + a + 6 + c^d, 1 + c^d, d, d — а — b
12. 3^2 . .	.	. = 1
— dj [l + a + с — d, 1 + 6 + с — d, d — a, d —
a + с — d + 1, 6 + с — d + 1, 1;
1 I
3
d^e^ll	a, 6, с .
[Re(d~a-fe) > 0].
a, 6, c; 1 "\ __|r,[a + l, a-6-c-n ( ~
^	A;!(a - n)k
[Re a > те + 1; Re (a - 6 - с) > n - 1].
лл r-, i a, 6, c; 1 \	[1—c, 6+ml A + 6 —a)n	/l —m, 6, 1 + 6— a+ n; 1
14. 3^2 1	. . 1=11 . . .	I 7	ГТ771	г- 3^2 1 , ,	I.»
(m —1)!A— a)n	\ 1+6-a, 1 + 6-с
[Re с < т ¦— n].
[Rec< 1-n].
a-n,ft
[а ф b, с ф 1, Rec < 2].
. a, 6,c; 1 \	1 Га(а + 1) [2-с,2 + 6] , 6F + 1)
a + 2, 6 + 2/ a^6 [a^6^ 1 [ 2 + 6^c J a-6
[a t^ 6- 1, 6, 6 + 1, с t^ 1, 2, 3; Rec < 4].
a, 6, c; 1 \^	Г c + 1/2, (a + 6 + l)/2, (l-a-6)/2 + c 1
+ 6 + l)/2, 2c) ^	[(a + l)/2, F + l)/2, A - a)/2 + c, A - 6)/2 + c\
a, 6, c; 1 ^	/= Г. . i , . 1.1	[IUBc-a-b)>-l].
f Г	а/2 + 1-б-с	1 Г	(а + 1)/2-6-с	11
\ [a/2 -c,{a + l)/2, a/2 + 1 - 6J [(a + l)/2 - c, a/2, (a + l)/2 -b\\

7.4.4]	7.4- Функция 3F2(ai,a2, аз] bi,b2',z)	451
[Re (a -2b- 2c) > -1].
on „/	a, 6, c; 1	\ V^r ГГ	l + a-Ь, I + a - c, l + a/2-b-c	1
ZiU. Ч Г 9 I	I = 	 I
\l + a-6, 1 + a-c/ 2a [A + «)/2, 1 + a/2 - 6, l + a/2-c, 1 + a - 6 - cj
[Re (a -2b -2c) > -2].
a, 6, c] 1	\	1	2 + a — 6, 2 + a — с
" 3 2lv2 + a-6, 2 + a-c/ 2F-l)(c-l) [ a, 2 + a™6™e
-Ы a/2>2 + a/2-b-c 1_ [(a+l)/2, E + a)/2-6-cll	rR r - 2fe-2 ^>-4l
[ [l + a/2-6, l + a/2™cj [C + a)/2-b, C + a)/2-c\ J	L l	j J"
c, /a, « - n, 6; l\ _ (a- n)F- a)n(n - l)!r[c, c^ a^ 6 + l] ^ A - a)k(c - a)fe
a — n + 1, с / (a— b)(l— a)n(c — a)n \_ c~ a, c— b J ^-^ k\(b — a + 1)д.
[Re(a + b- c) < 1].
. a, 1 — a, 6;1\ ~i^2b ^ [	c, 1 + 26 — с
S. З.Г2 (	1 = 2	7Г1
[d = 1 + 6 - (а + с)/2, Re 6 > 0].
с - 6, с - 6 + 1/2, 2с - 2а - 6;
/ q, q, + 1/2, 6i 1 \ a4.c__5 2c, 2c — 2a — 6 ¦
24.	3F2	=4Г	| x
\ с, с+1/2 /	[6, 4c — 2a —
x 3F2
25.	= Г C? ^~ a ~ 2FiBa, 6; 2c™ 6; -1)	[0 < Re6 < 2 Re (c - a)].
/l,q,6;'l\ a6B + a + 6^c-a-)	/2,a + l,6 + l;l
\ c, d J cd[ab — (c — l)(d — 1)] \ c + 1, d + 1
[Re(a + 6-c™d) < -2].
a6 — (c — l)(d — 1)
27. 31
" (l + a-c)(l + 6-c) i	L	a' 6
1, a, 6; 1\	c-1	f^fc-1, l + c-a-6l
2, с / (a —1)F —1) [ L с — a, c — b
[a, 6, с ^ 1; Re (c - a - b) > -1].
2q F Л, a, 6; 1\	2(c^2J f Гс - 2, 2 + с - a - b] _ \
' 3 4 3, с 7 (a^2JF^2J \ [ c-a, c^6 J J (a ¦
[a, 6, c^l, 2; Re (c - a - b) > -2].
30. 3F2f -— j = -x^ 	(ф^	^ +
k — m — a, —ra — о/ 2 ^^ (—a — m)k{~b — m)k
A + m + 2a)m(l + m + 26)m [™a - b - m, 1/2 - a - m, 1/2 - b - m\
[Re (a + 6) < ~m - 1/2; m = -2, -1, 0, 1, . . .]•
31. 3f2( ^'^.U-^A + arm,)fc^! + frm)fc +
тг (m — 2а)т(тя — 26)m(m — a — 6)m	Г 1 — a, 1 — 6, 2m — a — b — 1/2 1
+ 22w+1(m-a-6^1/2)m	L1/2 + m - a, 1/2 + m - 6, 2m - a - б]
[Re (a + 6) < m - 1/2; m = 2, 3, 4, . . .].
32.	3F2( \а'Ь''*)=-^-[<ф(Ь)-ф(а)]	[Ъфа].
\1 + a, 1 + о/ о^а
33.	= а2ф'(а)	[b = a].
15*

452
Гл. 7. Гипергеометрические функции
[ 7.4.4
35.
2 + а, 2 +
2,e,i;l\ (аJFJ(а+6-1)
2 + а,2 + 6/	(о—6—1)з
3,а,6;1\ (а-1)»(Ь-1K
j= (a-6-l)8
2(а- 6)
[Ь ? а-1, а, а + 1].
а+6—1
(а - 6)(а + 6 - 3)
[Ъфа-1,а,а+1].
[Ь ф а - 1, а, а + 1].
а,
6-1
39.	s
40.	= F - 1)ф'{Ь - 1)
Л, 1, а; Л
о, о
42.	=2(Ь-2) + 2(Ъ-1Jф'(Ь)
43.	= 2F - 1)[1 - (Ъ - 2)ф'(Ь - 1)]
44.	з
[Re(a-2b)>-2].
I; ReF-o)>0].
[о = 1; Re Ь > 1].
[а — 2J
45. = 2F - 2J^#F - 2) - 2F - 1)
а, 6, (а + 6)/2;
[а^ 1, 2; Re F-а) > -1].
[a = l;Re6>0].
[а = 2; Re b > 1].
[а/1,2; Re(b-a)>0].
[а = 2; Re 6 > 2].
4fi
50.	3F2
51.	3F2
52.	3F2
DO.	3JT2
54.	3F2
a, a +1, &; l
a + 2, a + 3
a + 3, 1-6
2|a-o
[Re6<2]-
(l-6)(l-2a2)}	[6/1, 2, 3; Re 6 < 4].
a, a/2, 6, 1
a/2, 1 -f- a — 6
a+ 3/2, a + 2
a, a —- ra, a — 7г; 1
a —m-\-l, a —n-\-lJ A — a)n-i sin a?r
2 + a — b
о-Ы-1,1-6,0/2 + 1
(« + l)/2, a/2-6 + 1, a/2- 6 + l
a-6 + 1
n!(n — a)
[m = n, a / 1, 0, -1, -2, . . .; Re a < 2].

7.4.4]
7.4- Функция
,a2, аз] bi,b2',z)
453
55. =0
56.
а, а, а; 1
1, 1
m ф п, а ф 1, О, -1, -2, . . . ; Rea < 2; га, п = 1, 2, 3, . . .].
3S^~	[Rea < 2/3].
59.
60.
61.
62.
63.
64.
3F2
3F2
3F2
3F2
3^2
а, а + 1/3, а+ 2/3; 1
2/3, 4/3
а, а + 1/3, а+ 2/3; 1
4/3, 5/3
[Re а < 0].
[Re a < 1/3].
A-За)B-За)
з-За/2
cos (За + 2) —
1, а, -а; 1 \ 1 тга
=- + — ctgaTr.
1 + а, 1 — a/ z z
[о^ 1/3; Re a < 2/3].
1, a, 1 — a; 1
1 + a, 2 - a
1, a, a; 1
2 +a, 2 +a
1, a, a + 1/2; 1
- а)
ctgaTr.
1-2а
= (а + IJ [2а V(а) - 2а - 1].
2, a, a + 1/2; 1
a+ 3/2, a + 2
69.
70.
3, a, a; 1 "\ a2(a
a + 2, a + 2
-2a
/1/2, 1, a; l\ = 7Г Г 1 - a, 2 - a
' 3 2\3/2,2-а/ 4 [3/2-a, 3/2 ^ a
/1/2, 1/2, о; 1
Ч
C + 2а)/4, C - 2а)/4
73.
74.
75.
76.
1? ш'
' п; ! ) = тп V
1, п + 1/ т ~ п ^
k-
1, mfn7 m/n-\-l\ 1 ^ m(m
m/n + 1, m/n + l + 1
1-1
п/
кп
2, 771+ 1
1,1, m/n + I; l\	m + :
2, w/n + 1 + 1/ т + nl ~ n
[Re a < 1].
[Re a < 1].
[га > п].
[I = 0, 1, 2, . . . ; га = 1, 2, . . . , п - 1; п = 2, 3, 4, . . .].

454
Гл. 7. Гипергеометрические функции
[7.4.4
77 1-7 f 1/2, 1, 1; 1 \ n^sf x i,
77' sF2' n/9 (n « ^^ I	(n-1) |ln2-
78.
79.
Q^ (klf
2; 1
¦l)/2
2(n - 3)
11п2-
*-'?^i (•-»-'
[n = 3, 4, 5, . ..].
[те = 2, 3, 4, . ..].
[те = 4, 5, 6, . ..].
ол т? i ~n? a' ^5 ^Л (c "" a)n(d — a)n (-n, a, a + 6 — c — d — n + 1; 1
Oil. 3^2	,	I — 	-T^—73т	 3^21	,
c, rf /	(c)n(d)n	\ a —c —n + 1, a —a —n + 1
81.	=
82.	=
(a)n(c + d — a — 6)n
-n, с — a, d -— a; 1
1 — a. — n, e + d — ft — b
(c)n(d)n
I — ft — 6)n	f —n, d — ft, d — 6; 1
—n, 1 — с — n, 1 — d — n; 1
1 — a — n, 1 — 6 — n
84. = (-]
83 — ( i)n \Uj/n\l//n
(c)n(d)n
vn (d — a)n(d — 6)n	„ ('~ni 1 ~ d ~~ nJ a + b — c — d — n + 1;
(c)n(d)n	\	a —d —n + 1, b —d —n + 1
85	= (с^а)та 3Jp2 f ~n» a' rf ~ 6' X
(c)n 3 2 \d, a- c-n + 1
86	= (?^^L6)n F f-n,d-b,l-c-n; 1
87. 3F2
88.
(c)n(d)n °^ ^ ^1 - 6 - n, a-c —
—n, a, 6; 1 \ (c — ft)
c,
(c)n(c - a- b)n'
-Щ a, b; 1 \ = (c^a^l)n(c^b)n Г +
, 2 + a + b — с — n/ (c)n(c — a — b — l)n [ (c — a —
89.	3F2 -n'a'6;1 =0
\a — 1,0 — m J
90.	= R
91.	= R[(a - I + n)(l + ra) + m(b - a - m)
ГУ
92.	= —[ra(ra — 1)F — ra + n)F — ra + n 4
z!
. = 1, 2, 3, . . . , n- 1].
[I + m = n].
[I + m = n + 1].
x (a — I — m + n + 1) + 2lm(b — ra + n)(a — Z — ra + n + 1)]	[Z + m = n + 2],
93. 3F2
—n, a, b; 1
a + I, 6 + ra
- a)r,
1 — /, a, 1 + a ^ 6 ^ w;
l — ra, 6, 1 + 6 — a — Z; 1
[a 7^ 0, -1, . . . , -n - Z - 1; 6 7^ 0, -1, . . . ,	-n - m - 1; a + 6 7^ 1 - Z, 2 - Z, . . . , m - 1].
ал jp ( ~n" a' 6; г \ w!(l + a - b)m
94.	3^2. , , =7^™^—m	1^	ra = 0, 1, 2, ..., n .
\l + a, 6-ra/ (l + a)n(l-b)m
л- П-а Г'A + a — Ь)п + 1 -1	г л
95.	=—	7^	 I	^	II	[m = n + l].
96. 3F2
-n, a, b; 1 \ = f 1
l-a-n, 1-b-n) \0
0 J A - a - n)m(l - b - n)rt

7.4.4]	7.4- Функция 3F2(ai,a2, аз] bi,b2',z)	455
п Г n = 0, 2, 4, . . .
т = —, <
2 In = 1, 3, 5, . . .
—гг, а, 6; 1 \ Bа — 6 — 2п)(^а)пF — 2а)п
1 + 2a - n7 1 - a + bj Ba- 6)(-2a)n(l + b - a)n
-n, a, b; 1 \ A + a)n(l + a/2 - b)n
1 + a + n, 1 + a - 6/ ~ A + a/2)n(l + a - 6)n '
-n, a, 6;1
100. л, Zl
^-2га, (а
2а, A+ 6-70/2/ \ 0 j (A - 6)/2)т(а -
-п, а, 6; 1 \ _ ((а + 1)/2)п(F + 1)/2)п
n /n = 0, 2, 4, ...
a ф 0, m = —, <
2 \n = 1, 3, 5, ...
101. 3F2(	wjn^	,
(a - n)/2, A + a — n)
Ю2. = Bfe ~ a + l)n 2Fl(_n; 2b; 26 - a + 1; -1)	[о ф 0, -1, -2, . . .].
A - a)n
-n, a, 1-a; Л 22n+1 fa + b\ fb-a
104 3F2(
3 ' b,a-m
105.
b, l-b-2n J (ЬJп V 2 уп V 2
-т, 1, 2-6;
а/2,6	)~^	(Ь)п
106. 3i
107# . p. i	~п» а' «+ 1/2; 1
109.	3F2
110.	3F2
111.	3F2
[m = 1, 2, 3, . . . ; Z = 1, 2, 3, . . . или I = -n, -n - 1, -n - 2, . . .].
-n, 2, 2; 1\ _	A - a)B - a)(a - n - 3)
1, а / (п + а — 1)(тг + а ™ 2)(п + а — 3) *
—п, —тг, т; 1\ _ Bтг)!	/—Уг, —Уг, ш + 1; 1
1, m + 1 / (n!J	\ m + 2, —2n
-n, -n, 1; 1\ piJ	/-n, -n, m-l;l
3^2
— 2n, m / Bn)!	\	1, m
119 ^ /"-n/2, (l-n)/2, a; 1\	B6 - a)n
112. 3F2	=		 2i?i(^n5 a; 26 - a; -1).
\ o, 6 +1/2 /	B6)n
/-n/2, A - n)/2, a; l\ =	w B6 - 2a - l)nB6 + n - l)w
' 3 Ч 6, 3/2 + a^6^n J
=	[n 2m
a + 1, 1/2-m У (l/2)(l 2)	L
2a)n	2-
a-n)/2, l + (a-n)/2y l ; (-a)n'

456
Гл. 7. Гипергеометрические функции
[7.4.4
117.	3F2
118.	3F2
119.	=2n
120.	3F2
121.	3F2
122.	3F2
-ra/2, A - n)/2, a; 1
+ a — n)/3, B + a — n)/
= 2_w(Bq-2n)/3)w
A - a)n
-n,
:; 1-
2a + n
-n/2, A - n)/2, -m; l\ o^n _, ( -n, -n, m + 1; -1
= 2 3^21
1, —m — n	J	\ 1, ^n — ra
3F2I
n!	\ 1/2 — n, — n — m
-n/3, A - n)/3, B - n)/3; 1\ = (a - l/3)n Ff_ n !-!!_
a, a+ 1/3	/ Ca-l)n 2 1 \ 2' 2 '
_ m\ /4- 1 \	/	1
= 2-^1 I —w, л	; 2 — n — 2a;
(-n, 2 - 2n - 2a;
"n; 3
-2n/3, A ~~ 2n)/3, B - 2n)/3;
a, 1/2™ n
a; 4).
123
124
125
126
127
128
129
130
131
1 4*)
!..ZJ?,U!
133
134
135
136
137
138
139
140
141
1
g
1
8
1
g
1
8
1
g
1
8
1
Q
О
1
6
1
6
1
6
1
4
1
4
1
4
1
4
1
4
1
4
1
4
1
4
1
4
«2
1
3
8
1
2
5
8
3
4
7
8
1
1
3
2
3
5
6
1
4
1
4
3
g
1
2
1
2
1
2
1
2
5
8
3
4
«3
1
1
1
1
1
1
1
1
1
1
1
1
2
1
1
1
1
1
1
1
1
61
5
4
9
8
9
g
9
8
9
g
9
8
9
Q
О
7
6
7
6
7
6
5
4
5
I
5
4
5
4
—
4
3
2
9
I
5
4
5
I
62
9
g
11
3
2
13
8
7
4
15
8
2
4
3
5
3
11
6
5
4
5
4
11
g
3
2
—
2
9
4
5
2
13
8
7
4
5л/2 .
Гтг
7Г
32 L
3V2
40 K
	A -f-
48
3~ / (тт
4л/3
	(тг
27
5л/3
24
16^2
-Cf2,
16 Ч
1
-(тг + 2
4l
3
10
5
12 ^ +
— Bтг +
2
5л/2
7Г
24 L
Зтг
"в"
3-^2(tti, fl-2 5 СЕ.З5 ^i, 62; 1)
-л/2 1п2 + 21пA + л/2)]
2л/2 In A +л/2)]
л/2 )тг + 4 In 2 + 2л/2 In A + л/2 )]
+ л/2)тг + л/2 1п2 + 21пA + л/2)]
v2 )тг
л/2)тг + 81п2 + 2л/2 1пA + %/2)]
+ 2\/3 in 2)
-|- -у з In 2)
/1\
\4/
i j = 1, 07483307...
4/
^ - 1)тг^л/2 1п2 + 21пA + л/2)]
In 2)
2 In 2 — 1)
2 In 2 - 2)
4 In 2 — 7)
- л/2 1п2 + 21n(l + л/2I

7.4.4]
7.4- Функция
,a2, аз] bi,b2',z)
457
142
143
144
145
146
147
148
149
150
151
152
1 КЧ
J.Oo
1 КЛ
JLO44
155
156
1 КТ
JLO 1
158
159
160
161
162
163
164
165
166
167
168
ai
1
4
1
4
1
4
1
4
1
4
1
4
1
4
1
4
1
4
1
3
1
3
1
loo
1
3
1
3
1
3
1
3
3
8
3
8
3
8
3
8
3
8
1
2
1
2
1
2
1
2
1
2
1
2
«2
3
4
3
4
7
8
1
1
1
1
1
1
1
2
3
2
loo
2
3
5
6
1
1
X
1
2
5
8
3
4
7
8
1
1
2
1
2
1
2
1
2
1
2
1
2
«3
1
1
1
1
1
3
2
3
2
7
I
7
4
1
1
i
i
i
i
1
1
5
3
1
1
1
1
1
1
2
1
2
1
2
1
1
1
5
_
4
7
4
5
4
5
4
2
5
4
9
4
5
4
9
4
4
3
4
3
4
3
5
3
4
4
3
4
3
11
8
11
8
11
8
11
8
11
8
1
1
3
2
3
2
3
2
2
62
11
T
9
4
15
8
2
9
4
5
2
5
2
11
T
11
T
3
5
3
8
loo
7
3
11
6
2
8
3
3
2
13
8
7
4
15
8
2
1
3
2
3
2
3
2
5
2
2
3-^2(^1, «25 ^3; 61, 625 1)
7
	(Зтг	2)
48
15
16
7 /2
Г/1 I </о\-т. л/о1г|О О Ir» /1 1 л/^* M
1 i -\- vZITT vZloZ Z Ш 1 1 -\- v Z 1
40
7Г
6
^(тг + 61п2~6)
6
	D -f- тг -f- 2 In 2)
20
-F-тг-21п2)
4
	(Зтг -f- 4)
72
35
	A4 — Зтг)
144
— (тг - 4л/3 In 2 + Зл/3 In 3)
2тг
ЗУ^
5л/3
72 ^"
4л/3
9 v"
Ю^З г-
1 7Г Л/ Я In *"* J
27 v"
л/3 л-
-^—(тг + Зл/3 1пЗ)
5л/3
-[(л/2 - 1)тг + 41п2 - 2^2 1пA + л/2I
4LV ; \ /j
— (v 2 — 1) тг
16
Зл/2 г л- , ^Ч1
Гтг 1 л/0* In *"*• *? In 1 1 1 л/*) 11
17Г "Т" V Z ill ^ Z Ю IX ~т" v Z II
8
21-\/2г о. /^)}
32
10
1 л /1\
—^Г4 ( - ) = 1, 39320393...
4тг3 \4/
4
тг
тг
2
2
ТГ
~8~
3
	(тг 	8)
16
4
	/	тг)
тг

458
Гл. 7. Гипергеометрические функции
[7.4.4
169
170
171
172
173
174
175
1 7fi
ни
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
1 Oft
JL if О
«1
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
2
2
z
1
2
1
2
1
2
1
2
1
2
1
2
1
2
5
8
5
Q
О
2
3
2
3
«2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
5
8
2
3
3
4
3
4
3
4
7
g
1
1
1
1
1
1
1
1
1
1
7
8
1
1
X
«3
1
1
3
2
2
2
5
2
3
7
2
1
1
1
1
1
1
1
1
1
5
4
5
4
со I cm
7
4
7
4
2
7
2
1
1
1
4
3
bi
5
2
7
2
1
1
5
2
1
1
3
2
3
9
ico I cm
3
2
7
4
3
2
3
2
5
о
"Чсо I см
9
4
2
3
2
5
2
3
2
5
2
13
Y
13
Q
о
5
3
5
3
5
2
7
2
5
2
3
5
2
7
2
4
9
2
13
8
5
3
7
4
11
T
5
2
15
2
5
2
3
9
4
5
2
2
11
T
11
T
3
9
2
15
g
2
2
7
3
3-^2(^1, «25 ^3; 61, 625 1)
9
— (тг — 8)
16
225 / _ 256X
256 V 9/
— BG + 1)
2тг
40
Этт
9
8
	A8G + 13)
32тг
356
75^
7
128тг
-[(\/2 - 1)тг ^41n2 + 2\/2 In A + л/2)]
4
— (тг + 4л/з In 2 - Зл/З In 3)
^Gг~21п2)
4
7
— (Зтг — 6 In 2 — 2)
20
3
— (тг — 21п2 — 1)
2
— [A + л/2)тг - 4 In 2 - 2л/2 In A + л/2)]
2 In 2
3B In 2 - 1)
16 In 2 - 10
^-(8-тг -21n2)
12
5
— E — тг — 2 In 2)
2
-Or-2)
7Г
7
	fg _|_ Зтг	6 In 2)
60
— G — Зтг + 6 In 2)
10
-(l + 21n2)
77
60
35
— [тг — 2 л/2 In A + v 2 I
16
-[81n2 - (л/2 - 1)тг - 2л/2 In A + л/2)]
о
3 |п з
л/3
4л/3
9 v" v "

7.4.4]
7.4- Функция
,a2, аз] bi,b2',z)
459
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
«l
3
4
3
4
3
4
3
4
3
4
3
4
з
4
3
4
4
5
5
6
7
g
7
8
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
«2
3
4
7
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
«3
1
1
1
1
5
4
5
4
з
2
3
2
6
5
7
6
1
9
8
1
1
1
1
1
1
1
1
1
9
8
5
I
5
4
4
3
11
g
3
9
z
3
2
bi
11
T
7
4
7
4
2
7
4
9
4
7
4
5
2
9
5
11
6
15
g
15
Y
3
2
3
2
2
2
to | сд
3
7
2
4
5
2
2
9
4
7
3
2
2
2
b2
11
T
15
g
2
11
T
9
4
11
T
5
2
11
4
11
5
13
6
2
17
~8~
2
5
2
2
3
to | сд
3
7
2
4
5
17
Y
9
4
3
3
19
g
2
to | сд
3-^*2(^1» a2, «3; &i5 ^25 1)
441
	(тг -|- 2тг — 16)
32
21^2, /- , /-„
Г-тг л/о ]п о oinh 1 л/о \1
7Т V -" III Zi ли III 1 X jf" v *** I
5F1п2^тг)
2
-A81п2-3тг - 2)
6
— D — тг)
8
— A0-Зтг)
16l ;
з
-D-тг + 21п2)
21
— B — тг -f- 2 In 2)
4
12 / / ~^\
— 5 -тгу2 + л/5
5 V V У
	(Q — -j{- -у 3 )
12
^[8 In 2 - A + лД)ж + 2\/2 In A + л/2)]
63
— [8 — A Н~ V 2 )тг]
16
тг2
4
^GГ~2)
2
2
о
9(тг-3)
ч
о
25
6
9 2
8 о
™B0тг2 - 197)
3
9
-[16 - A + л/2 W - 81п2 - 2л/2 In A + л/2)]
2
5
-(8 - тг - 6 In 2)
2
— A5-27Г- 12 In 2)
32 - 2тгл/3 - 181пЗ
— [16-3(V^ - 1)тг-241п2 + 6л/2 In A +л/2)]
]_8
4 In 2
6A-In 2)

460
Гл. 7. Гипергеометрические функции
[7.4.5
225
226
227
228
*>*>€!
ZfZf О*
230
231
232
233
234
235
236
237
238
239
240
241
242
243
1
1
1
1
i
X
1
1
1
1
1
1
1
1
1
1
1
1
1
1
«2
1
1
1
1
i
X
1
1
1
1
1
1
1
1
1
1
1
1
3
2
2
«3
3
2
3
9
A
3
2
13
g
5
3
5
3
7
4
7
4
15
2
5
2
5
2
3
3
4
4
5
3
2
2
bi
2
5
9
A
3
2
9
zi
8
3
2
11
T
2
3
2
3
2
2
2
3
2
3
3
7
2
3
7
2
21
8
3
3
11
4
3
23
3
7
2
7
2
4
5
5
5
6
3
3
3-^2@1, a.2, «з; &i5 62; 1)
5
— (	6 In 2)
6
6- 12 In 2
— A7-24 In 2)
3 l ;
13
— [16 - 5(\/2 - 1)тг -40 In 2 + lOv^ in A + л/2)}
5л/3
12
-D + тгл/З -91пЗ)
-^(8 + Зтг ^ 18 In 2)
— G + бтг - 36 In 2)
9
— [32 + 7A + лД)ж - 112 In 2 - 28л/2 In A + лД)]
1
о
10
— D-31п2)
— A2 In 2 - 7)
9
9
4
ю I со
22
9
14
9
125
~48~
^A6™5тг)
7Г
2 о
— тг — 4
3
1.
7.4.5. Значения з^2(«15 «2, «з; &i? ^2; —1)-
а, а +
3F2
2.	3F2
3.	3F2
а, 6, с; -1
1+ а — cf, 1 + ci
a + 6, 1-c-d
= Г
с-Ь 1 /6, a + 6,
,l-b-d\sF2\ 1 + 6-c,
+ 1, 6 + 1, с
l + c-6, 1 + c /	[a + 6, a + c,l
a - 6, 1 + a - c] ^ /" 1/2, 6, c; 1
— d\
_1 + a, 1 + a -
1, a, 6; -1	\ _	(-1)"
. — 2n — a, 1 — 2n — b y
va/2 + l, (а + 1)/2У
1-a, 1-6
, а, 6; -
— fl)fc(l — 2 72 — 6)fe
¦ n — a)n(l + n — b)n
[Re (a+ 6) ^C 1/2-2n].

7.4.5] 7.4- Функция 3Fi{a\,a2,a3]b\,b2]z)	461
[	п	^
+	—— > — У ( —l) —-,	Г—-f	ГТ
l + 4n^a^oj A— а)пA— b)n J j^-J	A— а)д.A— b)k
[n = 1, 2, 3, . . . ; Re (а + 6) ^ 1/2 + 2n].
\a + 1,0 + 1/ a — b
к
		[n < m].
,^а,а/2 + 1,Ь; -1\ = у^ Г	1 + а^6
1 а/2, 1 + а^6 ) 2а [1 + а/2, (а + 1)/2 - b\'
8. 3F2(^ + 1^2;f 1) =|B—-bcoea.)	[Re a < 1/3].
9- 3
V4t	M = ^^
2/3, 4/3	/ 3A — 3a
1/3, a + 2/3; -l\	4
12.
1 + a, 1 — a / 2 2 sin атг
n,a,a/2 + l;l^	(a + l)n
17. 3^2	—
а/2, 1 + а + гг
—п. а, ^а — тг; —1\ 2(а + п) _. ,	ч
, -i 1	I = -^—;	" 2Fi(-n, а; а + 1; -1).
а + 1, 1 —а —71 / 2а+ п
—тг, —п, га; —1\ 9п с, [^п/^ч A ~ n)/2, — 7п;
1, 1 — тп — п /	\	1, ^?тг — п
20. = 22n
71!	\ 1/2 — 7i, ^m — 71
—тг, —71, ^п; —1\ 9п с, /'~^/2, A — п)/2, п + 1; 1
1,1 /= 3 Ч 1,1
-п, -п-1/2, 1/2; -1\ _ 2п + 1	/ 13
1/2 - п, 3/2	у ~ п + 1 2 J V "' 2' 2' ~
23.
4/3,5/3	) 3A-3о)B-3о) L	. — v- - —^ з_
[Re а < -1/3].
. 3F2[ 1>а'а; '1)=-+22a-1V^^ 1~п
— а, 1 — а/ 2
тга

462
Гл. 7. Гипергеометрические функции
[7.4.5
26.
0/2,C-0/2
+ *)/4, F-г)/4
1* 1 _ »• -1 \
=0,539222...
^--«¦¦¦
28
29
30
31
32
33
34
35
36
37
38
39
40
АЛ
49
43
44
АК
46
47
48
AQ
44 if
ai
1
6
1
6
1
6
1
4
1
4
1
1
4
1
I
1
4
1
4
1
4
1
4
1
1
4
1
4
1
3
1
з
1
3
1
3
1
3
1
3
1
loo
«2
1
Ч
со | toe
5
6
1
2
1
1
2
3
4
3
I
3
4
1
1
1
1
-i
1
1
tol
2
_
3
2
3
2
3
5
6
1
i
i
«3
1
1
1
1
1
1
1
1
1
1
1
3
2
3
2
7
4
7
4
i
i
1
i
i
1
1
1
5
loo
6i
7
6
7
6
7
6
5
4
5
4
3
2
5
4
5
4
7
4
5
4
2
5
4
9
5
4
9
4
4
loo
4
3
4
3
5
3
4
3
4
3
4
loo
4
3
5
3
11
~6~
3
2
5
9
7
4
11
T
9
4
2
9
4
5
5
2
11
4
11
4
3
2
5
_
3
8
3
7
3
11
2
8
loo
3
-[C- ^3)тг-31п2 +
^-[C-^3O1 + 3102 4
5л/3
	|д f 2 -f- v 3)
36
— f(v2 — 1)тг — 2v2 In (
4
20
—— [2л/2 + A-л/2)тг
z!4
2л/2
7 л/2
	[2v2 	Зтг -Ь 18 In
96
15v^ro /^ _|O|n/
[^V^ 7Г + ^1П(
— [21пA + ^) + тг-
r fK
* Г_ л/о In О I O 1^
7Г v -" Ш ^j ~t~ -" 1П
и
Зл/2
40 LV ;
^[C^V2).^6^
7 л/2
72
Ш\/2 r~
F2(ai, a2,
л/З In B +
л/З In B 4
1 + л/2)]
2 +201n(l
+ 21n(l +
'1 + v2 I
1 + л/2)]
V^ In 2]
A + л/2)]
+ 41n(l +
+ 61n(l +
« /1 1 */o
О7Г ' ±*±у? ~t~ loin ii ~T~ V ^
288
/л/З Л
^-r-2j' + l112
4
— In 2
3
5л/3
54 x"v "
4л/3
	Cv3 ~~ 2тг + 4V3
27
— [(л/З ™3)тг + л/3 1п(
27U ; l
7Г
2v?
5л/3 /—
72 l j
In 9^
> 111 Z I
In 2)
2 + V3)]
аз; 6i, 62J ~1)
-VE)]
V2)]
y/2)]
V2)]
1
J

7.4.5]
7.4- Функция
,a2, аз] bi,b2',z)
463
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
оо
66
67
оо
О «7
70
71
72
73
74
75
76
77
аг
1
2
1
2
1
2
1
1
2
1
1
2
1
2
1
?
2
1
1
2
1
2
1
2
2
3
2
3
3
4
3
4
3
4
3
4
3
4
3
4
4
5
6
7
8
1
1
1
«2
1
2
1
2
1
2
2
3
3
4
3
4
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
аз
1
1
1
1
1
1
1
1
1
1
5
4
5
4
2
7
2
1
4
3
1
1
5
4
5
4
3
2
3
6
5
7
6
9
8
1
1
1
з
_
2
5
2
9
2
3
3
2
7
4
3
2
3
2
2
5
2
3
9
4
3
2
5
2
5
3
5
3
7
4
2
7
4
9
4
7
4
5
9
11
6
15
У
2
2
3
ь2
з
_
2
2
9
2
5
3
7
4
5
3
2
2
5
2
3
9
4
5
2
3
9
2
2
7
3
2
11
4
9
4
11
4
5
2
11
X
11
13
—
6
17
—
8
2
3
3
3-^2(&1? ft2 5 Я-3) ^1, 62? ~1)
G
9
— C6757Г- 10976)
576 V ;
1 ,-
-[C- 2\/3)тг + 61п21
3
-[A - л/2 )тг - 2л/2 In A + лД)]
4
-[2 + A - 2^)^ + 4л/2 In A + л/2 )]
4
— Г-7Г — 4In A + v2 I
8
- -In2
2
3A-In 2)
10- 2тг -4 In 2
— [12(л/2 - 1) + 3B + лД)тг - 8л/2]
5 л/2
II О OV Z / /Г ZUy Z -р t:V Z Ш Z -р ID 1П 11 -p V Z II
16
_ /^j-	2 + 2 In 2)
— A57Г-32)
120V ;
2л/3 г-
/__ O-./Q In Q\
l 7Г Z V О Ш Z 1
3
4л/3
9 v
Зл/З
	r^j-	2 In A + л/2 )	v2 In 2l
2
7\/2
IzlV Z -p О7Г DV Z 1П Z О 1П 11 -p у Z II
15%Д о /^
8 v"
35л/2
ГЧ-тг Юл/^ I filnh I л/^^l
O7T ' IU v Zi "т~ О III 1 1- ~T"~ v ^j 1
32 L \ n
Зл/2
Г/1 I ^/n»"\_ /I1./0 /I In M I л/^>М
I I Z ~t" vZITT ^tA/Z ft 1П I 1 ~p v Z 1 I
8
21
^[A - л/2)тг -2 + 2V2 ln(l +V2)]
12
— ГтгE0 + Юл/5 I/2 - 251
25
35
6
63 /—1/0
— [tt^I _|_ д/2 J1/2 — 4]
8
2
-(тг2 + 12- 24 In 2)
12- 16 In 2

464
Гл. 7. Гипергеометрические функции
[7.4.6
78
79
80
O1
О JL
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
Q7
if I
98
аг
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
5
4
2
«2
1
1
1
1
A
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
7
4
2
«3
1
5
4
5
4
4
3
4
_
2
3
2
3
2
5
3
ю I co
7
4
7
4
2
5
2
5
2
3
4
5
9
A
2
6i
4
2
9
4
9
a
7
q
«3
2
2
5
9
A
3
2
8
3
2
11
T
3
2
3
2
2
2
9
4
3
4
9
4
3
7
3
3
5
2
7
9
A
3
7
2
8
3
3
11
T
3
3
7
2
7
2
4
5
6
11
4
3
3-^2(^1, «2 5 Я-3) ^1 , 62? ~1)
-F3-бтг2)
4
	[тг -4л/2 + л/2 1п2 + 21пA + л/2)]
— [2л/2 тг + 21п2 + л/2 In A +л/2) - 15]
4\/3
3
4л/3тг + 16 In 2 ^32
2
бтг - 15 In 2 - 5
бтг - 18
10
	(Зтг	6 In 2	5)
3
— Bтг^3г/3)
12
5 г-
-Bл/3 тг ^8 In 2 - 5)
7л/2
	[Зтг — 4л/2 + Зл/2 In 2 — 6 In A + л/2 I
18
- — [13 + 2 In 2 + \/2 In A + лД )]
о
-(тг2 +24In2 - 24)
	F In 2 + 8	Зтг)
18
^(Зтг + 12 In 2 - 17)
9 v ;
3
4
-A21п2 - 5)
9
35
48
35л/2
\Л In A 1 \/r) \ тг!
i/j. in 1 | | yj А \ 7Г1
32
2
— -41п2
3
7.4.6. Значения 3^2(^1, а2, ^з; &i? ^2; -2
/1/2,1/2,1/2; -1/4\ = тг^
3 2V	3/2, 3/2	у 10'
при zo / ±1.
3.
4. 3F2
5. 3F2
3/2, 3/2
а, 1-а, За-1; -1/8
2а, а+ 1/2
Га/2, а + 1/211 2
[ За/2 J/
-п, а, 2 - а; 3/4^ _ (D - а)/3)п(B + а)/3)г
3/2, -Зп- 1
-п, а, 2 - За; 3/4
1/2, -Зп
B/3)nD/3)n
(а)пA - а)п
A/3)пB/3)п'

7.5.1]
7.5. Функция 4 F3 (ai, a 2, аз, fl4; 6i, 62, fes; z)
465
6.
-n, a, 3a + ra - 1; 3/4
Ca - l)/2, 3a/2
7. 3F2
8. 3F2
9. 3F2
F(9 -
Ca-l)n '
(a)m/m\ \
A={ -(a)m/m\ [n = 3ra + l],
0 [n = 3m + 2].
-n, a, 3a+ n; 3/4 \ _ f l\ n!(a + l)w/3
3a/2, Ca + l)/2 J ~ \ 0 J (n/3)!Ca + l)n
-n, a, a+ 1/2; 4/3\ _ fl]	(l/3)mB/3)
n = 3, 6, 9, . .
n^3, 6, 9, ..
/ / = ]	(/)(/)
2a, B + 2a - n)/3 / \ 0 J (B + 2a)/3)m((l - 2a)/3)r
n = 3m, m = 1, 2, 3, . .
n 7^3, 6, 9, ...
—n, a, 3a + n; 3/2
3a/2, Ca + l)/2 J ~ 2Г(п/3 + 1)ГA - a - ra/3)Ca)n '"
1 3 3#
'2' ' 2' 2'
. /E" I О
-2)],	FC^:
24
16
-1)],
2 /	24
11. 3F2A, 1, 1; 2, 2; z) = i LI2(z) = Ф(*); Ф ( -
л/5 -1
2
1 +
Ф
+3
Н
2 / V5 -1
1
ф
л/5-1
л/5 +1 [тг2 о /л/5 -1
1п
10
п
7.5. ФУНКЦИЯ 4F3(ai, а2, а3, а4; bi9 62, Ь3; z)
7.5.1. Представления 4^3(^1, a2, аз, ла] bi, 62, 63; z).
6i 62
а + 1 6 + 1	е
о + 1 6 + 1 с + 1
Ь(о-е)
аб
(а, с, d; a + 1,
, с,
F —a)(c —a)
e(a^6)
d; 6 + 1, e + 1; z)
2Fi(c, d; c+1; z) +
a, d; a+1; z)+
2FiF, d; 6 + 1; z)
с а + 6 —с
а + 6 а + 6+1
а + 6
A - x)a 2Fi(o, с, а + 6; ж) х
x 2Fi(a, a + 6 — с; а + 6; ж)
[Ж2 = ±z(x - 1)]
1+a-6 1+
2	+a- с

466
Гл. 7. Гипергеометрические функции
[7.5.1
> Q2> Q3> «4; 61, 62, 63;
а + 6 а+6+1
2	2
а + 6
а а + -
10
11
12
1	1
—ha	а
2	2
—n	a
1 — а
2а -\- п
—те	— п	—те
13
—те	— п	—п
1
	п
2
1
2
2а
а + 1
1 + а - 6 - с; 1 + а - 6,
4z
1 + а - с; -
а + Ъ -
-с + 1
2F1 ( а, 6; с;
A-^J
X
х 2F1 ( а, 6; а + 6 — с + 1;
1 - л/1 -
- [2FiBa, 26, 2с;
+ 2FiBa, 26; 2с; -л/г)]
2с- 1
2Bа- 1)BЬ —
х [2FiBa-l, 26-1; 2с-1; y/z)-
- 2FiBa- I, 26- 1;
2с-1; -л
26	2а-
-26+1
3 '
а + 2 а	1
——, - + 1; 6+ -,
3 ' 3 '	2'
а- 6 + 1;
27z2
D-*)*
2Fi( а, а+ -; 6;
3 1 - л/Т^
P2a-l(Vl-Z - V3^) X
X P2a-l(Vl- 2:
6	2а-
-6 + ]
2п	2те
(Ь)пBа-Ь
/1- z - 1
2n
2
- 2n
{An-
х 1
^z + 1
X Р2п + 1
^ - 1

7.5.3]
7.5. Функция 4 F3 (ai, a 2, аз, fl4; 6i, 62, 63; z)
467
7.5.2. Частные значения 4Fs(ai, 0,2, «з, 04; 6i, 62, 63; z).
1
2
3
4
5
«1 «2 «3 «4
I I » 1
4 2 4
5 1 1 5
4 4
113 3
* 5 2 2
3 3
2 2 2 2
61 62 63
5 3 7
4 2 4
r- 2 »
4 4
2 I 4
2
I 5 3
3 3
111
4^з(сЫ» a2, «35 «45 61, 62, 63; z)
-z-3'4{(l + z1^f\n{l + z1^) -
A г1/4J1пA г1/4)] 2^lnA + v^) +
2"/4A+*1/я)ь;!:1/4+2*1/41-A-)+
+ 2(l-21/2)arctg2l/4_4zl/4
I^[13+ T" ^(l + 2^)v/l^arcsin^ - Aarcsin2 ^]
^[s«(^/._ 4) to (l-,i/») +
L + г2/3F + 4г1/3 _ 22/3} ,n A _ z) _
-2V3,(^/3+4)arctg||^]
(l-z)(^3 + llz2 + llz + l)
7.5.3. Значения 4-^з(а1, а25 аз, 04; &i, 62, 63; 1).
а, 6, с, d; 1
а6ГA - d)
1.
2 F 1 а^ «/2 + 1, 6, с; 1 \	ГA + а)/2, 1 + а - 6, 1 + а - с, A + а)/2 - 6 - с]
4 ча/2, 1 + а - 6, 1 + а- с/	[1 + а, A + а)/2 - 6, A + а)/2 - с, 1 + а - 6 - с\
[Re (а-26-2с) > -1].
ф[с)
_. i 1, а, 6, с: 1 .
3. 4F3	' ' ' '	1 =-а6с
4. =
iа 01	а о
5- =~f(«)
6. 4F3
1, a, 6, c; 1
7.	4F3
х {г
8.	4F3
9.	4F3
Ю. 4F3
3 - а, 3 - 6, 3 - с/ 2(а - 1)F - 1)(с - 1)
3- а, 3-6, 3-е, 4-а-6-
3 — а — 65 3 — п — с, 3 — 6 — с
1, а, 6, с; 1
-B-а)B-6)B-с)
+ а - с) w
2, 2 + а - 6, 2 + а - с) (а - 1)F - 1)(с - 1)
а + 1)/2, 1 + а-6, 1 + а-с, (а + 5)/2 - 6 - с
а, (а + 3)/2 - 6, (а + 3)/2 -с, 2 + а-6-с
1,	1, а, 6; 1\	а — п —
2,	2, а - п
]-}
[афЬ, Ьфс} афс].
[с = а, а^ 6].
[с = 6 = о].
4].
[Re (a- 26- 2c) > -5].
a, 2a + 1, a+ 3/2, b; 1
[ф(а> — п — 1) — ф(а -— 1) — i/?B — 6) — С]
[Re b < 2-те].
а3	2
= — В(а, 1— 6){^ (а)— ф A + а— 6) + [t/>(a)— t/>(l + a — 6)] }
[Re 6 < 3].
[Re6<0].
a + 1/2, a + 2, 2 + 2a - bj 22а+г [3/2 + a, l + a-6, 2 + a-6
2 +a, 1 - 6, 2 +2a- 6

468	Гл. 7. Гипергеометрические функции	[7.5.3
/а, а+ 1/2, 6, 6 + 1/2; 1
* 4 3\1/2, а-6 + 1/2, а-Ь + 1
_o_2a_lTj2a-26 + ll Г_Г 1/2-26
Г(а + 1/2)
=	2а
3/2, а-6 + 3/2, а-6+1/ Bа - 1)BЬ - 1) [а^
. а, а+ 1/2, 6, 6 + 1/2; 1 \ =	2^2а	Г 2а - 26 + 2 1
* 4 3/2	6 + 3/2	6+1/ B 1)BЬ 1) [26 + 3/2]
1, 1, а, 6; 1 \ _ аA + а - 6)
j	Х
(±±1 - bj ]	[Re (a - 26) > -3].
а, а + 1/4, а + 1/2, а + 3/4; 1
6i, 62, 63
П—1 / —4 —2 /2—2 —1 га + 4а
(А; — 4а) 2	+ 2 '	cos	тг
V	^
[вектор 6i, 62 ? 63 состоит из тех трех компонент вектора A + то)/4, B + то)/4, C + то)/4, D + те)/4,
которые не равны 1; п = 0, 1, 2, 3; Re a < то/4].
15. 4i	"^
17. =7СC)/8
18. 4F3 ( J1' f' 6' q X ) = О	[Л + / + m = 0, 1, 2, . . . , n - 1].
\a — A;, 6 — /, с — m/
19. =
n!
- a)k(l - b)i(l - c)
' 6' c; X ^ T(l + ao)i(l + Qc)m	г	1
= n!/ + m = 0, 1, 2, . . . , то .
a + 1, 6 - /, с - m/	A + a)n(l - 6)/(l - c)
21. 4F3
a — n + 1, 0 — n + 1, c + n —
n(n - l)(n + с - a - l)(ra + с - 6 - 1) _, / 2 - n, a + 1, 6 + 1, c; 1
(a - n + 1)F - n + l)(c + n - l)(c + n)	\a - n + 2, 6-n + 2, c + n
22 F- (
4 3
-а - п, а + 6 + 1/2, а + с + 1/2у
-га, 26, 2с;
_, )n	(a + l/2)n(a + 6 + c^fi + l/2Jn
^l j (a + 6 + l/2)(a + c+l/2)(l/2a6c) 3 2 \-2a - 2n, a + 6 + с
/ -n, 2c, с - 6 + 1/2; 1 ^ _
3 2 U
2Ч F (	^n, a, 6, c; 1
* 4 3V(-w)/2, (l + a-n)/2, 6 + с + 1/2
-n, 26, 2c; 1 \	~ (l-a)n 3 2 U + с + 1/2, 2c - a + 1
= (l/2 + 6 + c^a)n	/-n, b-c + 1/2, c-6 + 1/2; 1
* ~	(l)	3 2
-га, а, а/2 + 1, 6; 1"
а/2, 1 + а — 6, с
_ (с - 26 - 1)п	/-га, а - 26 - 1, (а + 1)/2 - 6, -6 - 1;
(c)n	V (a-l)/2-6, l + a-Ь, c-26-1

7.5.3]	7.5. Функция 4F3(at, п2, а%, 0,4; bi,b2]b%; z)	469
c+l,l + a-6
-n, a, 1 - a, 6; 1 \ ((a + с - l)/2)w((c - a)/2)wB6)w
/
" 4 3 VI " *> " "> c, 1 + 26 - C>/	F)nF + l/2)n(c)n
-ra, 1 + 6- (a + c)/2, 6+(l + a-c)/2, 1 - с - n; 1
X 4 3 V C - a - c)/2 - n, 1 + (a - e)/2 - ra, 1 + 2b - с
( -n, a, a/2 + 1, 6; 1 \ A + a)n((l + a)/2 - b)n
29. 4^3	~~
а/2, 1 + а + п, 1 + а - 6/ (A + а)/2)пA + а - 6)„ *
,)=
(а-26-1)п F f-n, (а + 1)/2, а - 26 + га - 1; 1
(-26-1)„ 3
. -n, a, a/2 + 1, 6; 1
* 4 3lva/2, l + a-6, 2 + 26-n
31 = (а - 26 - 1)п(-6 - 1)п(а - 26 + 2тг - 1)
~ A + а-6)п(-26-1)п(а-26-1)
/	-га, а,а + 1/2, 6; 1	\ Bа-6)пF-п)
о Л • д г ч I	I '^=-
\2а, F - гг + 1)/2, F - га)/2 + 1/ A - 6)пF + га)
-га, а, а + 1/2, 6; 1	\ _ A + 2а - 6)п
35.
чз
2а + 1, F-га)/2, F-га + 1)/2/	A - 6)п
-га, а, а + 1/2, 6; 1	\ _ A + 2а - 6
2а + 1, F - га + 1)/2, F - га)/2 + 1/ ~ A - 6)п(
-га, а, 6, -1/2 - а - 6 - га; 1\ _ Bа + 1)пB6 + 1)п(а -
.	-n, a, a + 1/2, 6; 1	\ _ A + 2a - 6)nBa - 6 - n)(b - n)
* 4 3\2a + l, F-n + l)/2, F-n)/2 + iy ~ A - 6)nBa - 6 + ra)F + n) '
-a - n, -6 - n5 a + 6 + 1/2 J (a + l)nF + l)nBa + 26 + l)n '
9?i „. -n, a, 6, 1/2-a-6-n; 1 \ Ba + l)nB6)n(a + 6)
3T.	4F3
38.	4F3
39.	4F3
40.	4F3
-n!l-6-n,a + 6 + 1/2/ (a + l)nF)nBa + 26)n "
-n, a, 6, 1/2 - a - 6 - n; 1 \	Ba)nB6)n(a + 6)n
1-a-n, 1-6-n, a + 6± 1/2 У (a)nF)nBa + 26 - A T l)/2)n *
-n, a, 6, 3/2 - a - 6 - n; 1 \ _	Ba)nB6)n(a + 6)nBa + 26-1)
1-a-n, 1-6-n, a + 6 + 1/2/ (a)nF)nBa + 26 - l)nBa + 26 + In - 1)"
-n, a, 6, 3/2 - a - 6 - n; 1 \ Ba)nB6 - l)n(a + 6 - l)n
1-a-n, 2-6- n5a + 6- 1/2/ (a)nF - l)nBa + 26 - 2)n '
—n, a, 6, 5/2 — a — 6 — n; 1
2-a-n,2-6-n,a + 6- 1/2 y
Ba - l)nB6 - l)n(a + 6 - l)nBa + 26-3)
(а - 1)„F - 1)пBа + 26 - 3)пBа + 26 + 2п - 3)'
„ /-га, 1 + га, а, а + 1/2; 1\	1	Г A - 6)n+i	F - 2а - l)n+i
41. 4^3	I _	I
1/2, 6, 2а-6 +2 / 2(а-6 + 1) |_Bа-6 + 2)„	F)п
—га, 2 + га, а, а + 1/2; 1"
3/2, 6, 2а-6 + 2
A-6)п+2 F-2а-1)п+2"
2(га + 1)(а - 6 + 1)A - 2а) [Bа - 6 + 2)п	F)п
—п, 1, 1, а; 1
2, 6, 1 + а — 6 — wy
1)--0(а-6-гаI.
(K)
44 F/-n,l,a,2-a;l\	n + 2	f [(n + 1)!]2	1
* 3\n + 3a + l3a) 2(n + l)(laJ \ C - o)n(l +o)n l	;J'

470	Гл. 7. Гипергеометрические функции	[7.5.3
[га = 2, 3, 4, . . . , п + 3].
_ /-п, 1, 1, 2га + п-1; 1\	2(т-1J	г//	ч .,	Ч1
46. 4F3	1=7	Ь	"	гШга + га)--0(т-1) .
V	2, т, т	у (n + l)B + 2)L^1	; ^1	л
1, 3/2, 3/2
Ж""? I	ff С/ •	S %J ft	ff в/ «	S %J щ -JL. I	I f С ] JL. I		 f	ft	JL «	#1/	JL ft	1С*	-1_ «	f|>	JL » JL
э# 4-ГЗ|	л л л	J ~~"	л	4JI	1 1 1
1
-n, -3/4, -1/4, 5/8; l\ _ n!(l/2 + n)n-i
-3/8, 1/2, 1/2-n ) ~	2Bn)! "
-n, -1/4, 1/4, 9/8; l\ _ n!(l/2 + n)n
-n,
-n,
-n,
2,
-n,
+ C^1
-n, -
2,2
1/2-
1, 1/2
;
n, 1/2
,1/2
Ь l)![(n + l)!
(n + 1)
2
-n; 1\
J"
51.	4F3
52.	4F3
1/8, 3/2, 1/2 -n J	Bn-
-n, 1/2, 1, 1; 1 \ _ 1 - 2n
1/2, 3/2, 3/2 - n/ ~ l + 2n"
. -n/2, A - n)/2, a, 6; 1 \ _ (a)n „ /-n, a - 2c - n + 1, 2c - a - 6; 1
4 3 vc, с + 1/2, a + 6-2e-n + l/ ~ Bc)n 3 \ ! ~ a ~ ni a + & ~ 2c ~ w + x
'-n/2, (l-n)/2, a, 6; 1\ = (c--o)n „/ -n, 2a, a + 6; 1
* 4 3l 1	+ 6 + 1/2/	() 3 2
c, 1 — с — n, a + 6 + 1/2/	(c)n	\2a + 26, a — с — n + 1 /
-n/2, (l-n)/2, a, a + 1/2; 1\ B6 - 2a)n _/ -n, 2a, с - 1/2
I :=:: 	 о fo
6, 6 + 1/2, с	у	B6)п	\2а^26^^ + !? 2l
-n/2, (l-n)/2, a, 6; 1\ _	n!	[a(l/2 + 6)m 6A/2 + a)
* 4 3| 1/2-m, a + 1, 6 + 1 )~ (a-6)(l/2)m [ A + 26)n	A + 2a)n
[те/2 <С т ^ n].
57. 4F3( -"A (l-")/2, a, 6; 1 \_ (a)n+1 - (b)n+1
58'
-n, (a + b + l)/2, (a + b)/2 + 1) (a - b)(a + b + l)n "
-n/2, A - n)/2, a, -a; 1\ _ F + a)n + F - a)n
1/2, 6,1-6-n	У	2F)n
2п~3Гп+ 4^
[n = 3, 4, 5, . ..].
1/2, -(n + l)/2, -(n + l)/2	у	n + 1
-n/3, A - n)/3, B - n)/3, a; 1
6, 6 + 1/3, 6 + 2/3
C6~3a)n	/	-n, a, 3a-36 + 1; 3/4
C6)n 3 2\Ca-36-n + l)/2, Ca^36-n)/2
/1/2,1, A + 0/2, A-0/2;	Л , nqc-,n9
61-	4^3 „,„ /о, л/о /о л/о 1=1,095402...
V 3/2. C + «)/2, C- г)/2 /
di p Л/2- !' B + 0Л, B-0/4;	Л , nfioo71Qo
62-	44 3/2,F + 0/4,F-0/4 J=1'06337193-

7.5.3]
7.5. Функция 4 F3 (ai, a 2, аз, a>4; 6i, 62, fes; z)
471
Ои
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
си
t7 JL
92
93
at
1
4
1
4
1
4
1
—
4
1
_
4
1
4
1
4
1
4
1
4
1
4
1
1
4
1
4
1
4
4
1
4
1
I
1
4
1
4
1
4
1
л
ч-
1
4
1
_
4
1
з
1
3
1
3
1
3
1
2
1
2
«2
1
4
1
2
1
2
1
—
2
1
_
2
1
2
1
2
1
2
1
2
1
2
1
о
А
_
2
1
2
3
4
3
4
3
4
3
4
3
4
1
1
1
1
1
2
2
3
2
3
2
3
1
2
1
2
«з
1
4
3
4
3
4
3
4
3
4
3
4
3
4
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
3
2
1
1
1
1
X
1
2
1
2
?14
1
2
1
1
1
1
1
1
1
1
1
1
7
4
7
4
1
1
1
3
2
3
2
3
2
3
2
3
о
А
7
4
7
_
4
1
1
1
7
loo
1
2
1
6i
5
4
5
4
5
4
3
2
3
2
7
4
9
4
5
4
5
4
3
2
2
5
4
9
4
5
f
4
2
5
I
7
4
9
4
5
4
2
5
4
5
4
4
з
4
3
5
3
4
ico
3
2
3
2
62
5
4
3
2
7
4
7
4
9
I
9
4
5
2
3
2
2
2
9
з
_
2
5
2
7
4
2
9
4
7
I
9
4
5
2
2
9
/i
4
2
5
2
3
2
5
3
2
5
Ico
3
2
3
2
63
5
4
7
4
5
2
9
4
11

4
5
2
11
T
2
5
2
9
4
5
2
11
T
11
T
2
9
4
11
4
5
2
5
2
11
T
Ю | CM
5
11
T
11

4
2
2
7
3
10
3
3
2
3
2
4-^з(а1) а2 5 Ct3, tt4; 61, 62, 63; 1)
B )-l/2 /]_\
Г2 1 1 (тг2 1 16CM
128 ^ \4JK }
3
-In 2
2
3
	(\ -(- 8 In 2	тг)
10
5
™D1п2-тг + 2)
8
7 ,
	G -f~ 6 In 2	Зтг)
12
3
— D In 2	Зтг + 8)
4
7
-A0-Зтг)
тг
I
1
5
10
— A — In 2)
3
17- 2тг - 14 In 2
7
	(Зтг + 9 In 2	2)
90
7 ,
^(Зтг + 12 In 2- 16)
12v ;
тг - 3 In 2
с
-(тг - 12 In 2+ 6)
4
35
— A3- 18 In 2)
18V ;
^-Bтг-1п2~2)
10l }
3
_(утг -1- 4 In 2	22)
8
-(Зтг+ 6 In 2 - 13)
4
-(тг + 121n2 -6)
5
4тг + 18 In 2- 24
7
— (9 In 2 - 2)
27V }
7
— (8 + 9 In 2 - Зтг)
— B\/3 тг - 48 In 2 + 27 In 3)
-(тгл/З - 31n3)
2
2л/3 /— /—
((У\/Ч 1 тг Ч-ч/Ч In Ч\
l^V «3 ~т~ ТГ о V о Ш о J
3
7\/3 /—
90
тг / тг2 \
	 I 	 _|_ \yi^ 2 1
4 \ 12 /
7
_ t( 3)
8

472
Гл. 7. Гипергеометрические функции
[7.5.3
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
ill
JL J. JL
112
113
114
115
116
117
118
119
120
121
at
1
2
1
2
1
9
A
1
2
1
2
1
2
1
toi i
1
2
1
2
1
9
A
1
2
1
9
A
1
2
1
_
2
1
2
1
2
2
3
4
3
4
3
I
3
4
5
6
1
1
1
1
1
1
«2
1
2
1
2
2
4
3
4
3
_
4
3
4
3
4
3
4
1
1
1
1
1
1
1
1
3
4
1
1
1
1
1
1
1
1
1
1
«3
1
2
1
1
1
1
1
1
1
1
1
1
1
1
1
5
4
3
2
1
3
4
1
1
5
4
1
5
/i
4
5
4
4
3
4
3
3
2
3
2
a4
1
1
1
1
1
1
5
4
5
4
5
4
1
5
4
5
7
4
5
2
7
I
9
4
4
i
i
5
4
3
2
3
2
7
6
3
7
4
3
9
Zj
5
3
3
2
5
3
6i
5
2
2
3
2
3
2
7
4
2
Я
toi (
7
4
9
4
2
3
2
2
3
2
3
2
3
2
5
4
5
3
11
4
7
4
7
I
7
4
11
2
2
2
7
3
2
2
62
5
2
5
2
5
3
I
2
5
2
7
4
9
4
5
toi -
2
2
9
4
2
3
9
4
2
2
11
4
2
2
9
4
2
9
4
9
4
7
g
_
3
2
5
2
5
2
5
2
2
2
5
2
11
T
9
4
5
2
11
T
5
9
A
9
4
5
9
z
11
T
7
2
11
T
3
7
3
11
4
9
4
5
2
5
2
13
5
2
11
T
5
9
z
3
2
8
3
4F3(ai, a2, «3,a4; 6b 62, 63; 1)
27 о
	C2	Зтг )
64
9
-C - 4 In 2)
ttv^ + 81n2-91n3
3(тг-41п2)
бтг - 30 In 2 + 3
7
-Fтг-421п2 - 11)
5V ;
5
-GГ-1П2-2)
15,
— (тг-3)
2 l ;
21,
— (Зтг + 4 In 2 - 12)
iA2-7T2)
1
_ (tj- -f- 8 In 2 — 8)
3
10тг + 501п2-65
7
— C6 In 2 — Зтг — 8)
45
10
?
7
— (8 — 2тг — In 2)
6
8
5
12(ln3- 1)
3З . 73
/1OQ 1OT fi-тг^ I тгЗ\
i jl^q JLZ7T O7T "T" 7Г 1
256
15C In 2-2)
24In2 -Зтг - 6
15
— D — тг — In 2)
2
35
— C In 3 H~ 4 In 2 — 6)
2
90- 15тг-601п2
^D^3тг^Э1п2)
9
24 - 6л/3 тг + 48 In 2 - 54 In 3
20
	(\	v3 тг)
9
( 2 \
16 In 2	G
V тг J
— G + л/3 тг - 16 In 2 + 9 In 3)
4

7.5.4]
7.5. Функция 4 F3 (ai, a 2, аз, fl4; 6i, bi, fes; z)
473
122
123
124
125
126
127
at
1
1
1
1
1
1
«2
1
1
1
1
1
1
«з
3
2
1
1
5
7
9
2
?14
7
I
1
1
5
7
9
2
6i
2
3
5
2
2
2
b2
to I сд
3
5
3
4
5
bS
11
T
3
5
3
4
5
4F3(ai, a2, «з, a4; &i, &2, 63; 1)
-A0 - Зтг)
8A0-тг2)
^(бЗОтг2 - 1)
27
32
4
25
21n2 + l- 1BG + 1I
7Г J
361n2 + 27- -A8G + 13)
64 Г 275 8 1
	 100 In 2 H	B5G + 19)
1225 L 3 тг J
, d; -1	\ ^fl+a-6, 1 + a-cl /l + a/2-rf, 6, c;
I :=:: *	3 -*z I
. — c, 1 + a — d J 11-}-а,1-{-а--Ь-—с} \l + a/2, 1 + a —
2.	4F3
3.	4F3
7.5.4. Значения 4F3(ai, 02, аз, a4; 61, 62, 63; —1)-
a, 6, c, d; -1	\ _Г1+а-6, 1 + a-cl _, (l + a/2-d, b, c; 1
1 + a -6, 1 + a
a, a/2 + 1, 6, c; —1
a/2, 1 + a — 6,
1, a, 6, c; -1
a + 1, *
=
1, с
1 — с
= abc
a - 6, 1 + a - с
[Re (a-26-2c) > -1].
F-a)(c-a)
¦
4. =
5. = —p (a)
a-6f
4
(a -
a, 2a+ 1, a+ 3/2, b; -1
_
2 + 2a - 6, 2 + a
a + l/2, a + 2, 2 + 2a-6
1,3/2, a, fe; -1\ _ Г2-а,2-Ь
[афЬ, Ьфс, афс].
[c = a, аф b].
[c = b = a].
[Re b < 1/2].
8.	4F3
9.	4F3
10.	4F3
11.	4F3
12.	4F3
13.	4F3
14.	4F3
15.	4F3
1, 3/2, a, 1 - a; -l\ _	тгаA - a)
1/2, 1 + a, 2 — a J	sin атг
/1/2, 1, a, 1 - a; -l\ _	тгаA - а)
)
V 3/2, 1 + a, 2™ a ) ~~ A - 2aJ
—n, a, a/2 + 1, 6; —1 \ _ A + a)n
[cosecaTr — 1].
a/2, 1 + a - 6, 1 + a + nj A + a - fe)n '
-n, 1, a, 1 - a; -l\	22n+2a(l - a)n\(n + 1)!
n + 2, a + 1, 2-a/ Bn + l)![Bn + IJ - A - 2aJ]"
-n, 1, a,2^a; -l\ = (n + 2)aBa) Г
n+3, a+ 1, 3- a/ 2(n + l)(l-aJ
—n/2, 1 + a, 1 — a — n
1, 1, 1
/1/2, 1, (l + t)/2, A-i)
I	Q/9 /Q I ^#Nl /9 /Q »
\ "/ 1 v ~r~ ill \ —
n2 + 7n + 4).
= 0, 94477614...

474
Гл. 7. Гипергеометрические функции
[7.5.4
IT. 4F3
1, 1, 1 + г, 1 - г; -1
2, 2 + г, 2 - г
= 0, 847134...
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
а\
1
4
1
4
1
4
1
4
1
4
1
4
1
4
1
4
1
3
1
3
1
3
1
3
1
2
1
2
1
2
1
2
2
1
2
1
2
1
2
1
2
2
3
3
4
3
4
3
4
5
6
1
«2
1
2
1
2
1
2
3
4
1
2
3
4
1
1
1
2
2
3
2
3
со | to
1
2
2
3
3
4
3
4
3
4
1
1
1
1
1
1
1
1
1
1
«3
3
4
3
4
1
1
1
1
1
3
2
1
1
1
1
1
2
1
1
1
1
1
1
1
1
1
1
1
5
4
1
1
«4
1
1
1
1
1
3
2
3
2
7
4
1
1
1
7
3
1
1
1
1
5
4
1
5
4
7
4
<ю 1 см
4
3
5
4
3
2
3
2
7
6
1
6i
5
4
5
4
5
4
5
4
5
4
5
4
5
4
5
4
4
3
4
3
5
3
4
3
to | сд
3
2
3
2
7
4
3
2
2
3
2
3
2
3
2
5
3
7
4
4
4
11
6
3
ъ2
3
2
7
4
со 1 см
7
4
2
7
4
2
to | сд
3
2
5
3
2
со | сд
to | сд
5
3
7
4
2
7
4
2
2
2
3
2
2
2
9
4
2
3
7
4
5
2
2
2
5
2
ito | сд
5
2
11
т
2
2
7
3
10
to | сд
2
2
5
2
9
4
to | сд,
9
4
11
4
7
2
7
3
9
4
5
2
5
2
13
6
3
4F3(ai, а2,«з, «45 6i, 62, 63; -1)
о
-(>/2 - 1)тг
— [(8>/2 - 7)тг - 2 - 30л/2 In A + лД)}
- [BлД - 3)тг + 2 In 2 + 4лД In A + лД)]
6
/2
— [2л/2 In 2 - ж + 6 In A + лД)}
4
— [5 In 2 -f- Bл/2 	3)тг -4- 4 л/2 In A -4- л/2 )	31
5
— [4 - A + лД )тг + 16 In A + л/2 )]
— [12 - C- 2л/2)тг - 101п2 + 4л/2 In A +л/2)]
— [3C - 2л/2)тг - 16 + 18>/2 In A + лД)]
( >fi\
2 In 2 - 1 - — ж
\ 2 )
4 In 9
V3
4
-C- л/Зтг+ 21п2)
3
— A61п2-3)
601 ;
— A27Г-7Г3 ^64)
128l ;
8 In 2 -j~ 2A — л/3 )тг
-[A - 2л/2)тг + 21п2 + 4^ In A +л/2)]
3A - 2л/2 )тг + 12л/2 In A + лД) - 3
-[4 - A - 2лД)тг + 2л/2 In A + л/2 )]
4
-[16 + A - 6л/2)тг - 61п2 - 12л/2 In A + лД)]
— [8 + 3C - л/2 )тг - 15 In 2 + 6^2 In A + лД)]
45
— E-61п2)
12 - 16 In 2
15[2- In2 - л/2 In A +л/2)]
6 + 3(л/2 - 1)тг - 91п2 + 6л/2 In A +л/2)
— [Bv^ - 1)тг - 8 + 4л/2 In A + л/2 )]
ГЧл^Ч л^Ч In ^ In Г*7* 1 л/ч М
[О V О V О ill Zi ill ^Zi "T" V «3 JJ
3
4CCC) + 24in2^20)

7.6.2]
7. 6. Функция 5 F4 (ai,. . . , as; 6i, • • • , &4; z)
475
45
46
47
48
49
50
а\
1
1
1
1
1
1
«2
1
1
1
1
1
1
аз
5
4
5
4
4
3
4
Q
dco | см
3
2
«4
3
2
7
4
3
2
5
Q
5
3
7
4
2
2
2
7
2
2
ь2
9
4
9
4
7
3
8
5
2
Ь
2
5
2
11
4
5
2
3
8
3
11
Т
4^3(
15
35л/2[<э
18 ^
12[41п2^ A -
160 In 2^ 110
15
— [2B- л/3)тг
4
-[21п2-3(\/2
а\, а.2, аз, а45 ^1 ?
+ 4лЯ 1пA + л/2) -
/2 6 In A +л/2)]
\/3)тг-5]
-г о in z — 1 j
- 1)тг - 4 + 6л/2 In
Ь2, Ь3; -1)
-12]
A + V2)]
2.
'.5.5. Значения 4-^3(^1, о>2, аз, 04; &i, 62, 63; 20) при zo 7^
'-п/2, A - п)/2, 1/3 - п, B2 - 9п)/21; -27\ _ (^8)та
5/6, 4/3, A - 9п)/21	) ~~ 1-9п'
l, 1, 1, 1; C-л/5)/2
2,2,2
=Ы-
3 -
6. ФУНКЦИЯ 5^4(ai, ..., a5; 6i, ..., b4; z)
6.1. Частные значения sF^ai, . . . , ав; 6i, . . . , 64; ±2;).
1
2
4
1
«2
2
1
аз
4
1
а4
3
а5
1
3
н
со I см
2
62
7
4
2
Ьз
2
4
9
4
4
5
м
yi{z
+ h
5F4(a
)Li2(z)
1, . . . , «5; 61
1) arctg z1/4 -
,..., 64; *)
I
1 + г1/4
S'.
1
3.
1/4, 1/2, 3/4, 1, 1; -z
3/2, 7/4, 25 9/4
Г
x \2(z
L
- 1) arctg
-Din-
fz + %74z + 1
/z - {Viz + 1
-10arctg^+5z 1[l-ln(l + ^)].
1.	5F4
= Г
2.	5F4
3.	5F4
7.6.2. Значения 5^4@1, . . . , a^; 61, . . . , 64; 1).
a, 6, c, d, e; 1
l + a/2-e, 6, c, d; 1
l + a/2, Ь+c+d-a, 1 + a-eJ'
п, п ^ 1/2, 6, c, d] 1
2a, e, e + 1/2, 6 + c + d^2e +
_ Г2е, 2e - b - c, 2e - b - d, 2e - с - dl / 2e - 2a, 6, c, d; 1
~ [2e - b, 2e - c, 2e - d, 2e - b - с - d\4 3\2e - b, 2e - c, 2e - d
a, a/2 + 1, 6, c, d; 1
a/2, 1 + a - 6, 1 + a - c, 1 + a - d

476	Гл. 7. Гипергеометрические функции	[7.6.2
1 + а-Ь, 1 + а^е, 1 + a^d, l + a^&^e^d]
,	.	.	Re (a — b — с — d) > —1].
1 + а, 1 + а-б-с, l + a-6-d, 1 + a-c-dJ
1, a, 6, e, d; 1
1Ф abcd\ (b _ а^с _ a}(d _ ^ + (a - b)(c - b)(d - b) + (a - c)(b - c)(d - с) +
ф{<1)
(a — d)(b — d)(c ~~ d)
fa, b, c, d не совпадают между собой],
= a2be	^	^ф(а) +
L( &) (	J
(a —6)(a —с) (a — bJ(b — c) (a — cJ(c — b)_
[a = d, a ^ 6, 6 ^ с, с ^ a],
[a = d, b = с, а ф 6],
a) — ф(Ь) — (a — Ь)ф'(а) +	— ф"(а)	[a = с = d, а Ф b],
f ^ = —^ (a)	[a = 6 = с = d].
5 5FJ	1, a, a+ 1/2, 6, 6 + 1/2; 1
\l/2 —- a — n, 1 -— a — n, 1/2 —- 6 — n, 1 —- b — n
Ln/2J	/o \ /m\	r-i . / i\m	i г -1 ii
l - ^a, l - .
-2a-26-2n
\ Da + 2nJnD6 + 2nJn L1/2 ~ 2a ~ 2n^ г/2 ~ 2b ~ 2n\ Ba + n)n(^b + n)n j
[Re (a+ 6) < 1/4-n].
1, a, a+ 1/2, 6, 6 + 1/2; 1	\ _
1/2 + n^a, 1 + n^a, 1/2 + n^6, l + n^6y
/1	О \ /1	OI\	L ' \	/ J Aft	П \ {Л	О1Л
A + 2п2а26Jп 12a,126 1 / 0FA + 2n - 4aJn(l + 2n - 46Jn
4	L1 + 4w - 2a - 2bl I 24n(l/2 + 2n - 2a - 26Jn
x Г
-]
[Re (a + 6) < те + 1/4, n = 1, 2, 3, . . .]•
7. 5F
/I Hi	1% U>	X
8. = — ctga7r+ ^	_ +^	[6 = a].
+ a, 1 — a, l + o, 1 — о J A{az — ол)	А
2 2	t
жа ж a	1
— ctg an + . 2	h -
4	4 81п2атг 2
1, a, a, 1 — a, 1 — a; 1 \ тга2A — аJ ГтгA — 2a)
1 + a, 1 + a, 2 - a, 2 - a J ~ A - 2aK [ sin2 атг
7Г	[a = 1/2].
11-
l + a, 1 + a, о — а, Л — a J 4A — a)
/1/2, 1/2, 1, a, 1-a; 1\ тгаA - а)
2, 2, 1 + a, 3 — a J 6A — a

7.6.2]
7. 6. Функция 5 F4 (ai,. . . , as; 6i, • • • , &4; z)
477
14.	5F4
15.	5F4
16.	5F4
IT.	5F4
18.	5F4
19.	5F4
20.	5F4
—n, a, 6, c, d; 1
1 + a — 6, 1 + a — c, 1 + a — d, 1 + a + в
—n, a, a + 1/2, b, c; 1
F - rc)/2, A + 6 - rc)/2, d, 1 + 2a + с - d
—n, a/2, 1 + a — 5 — c, d; 1
1 + a ^ 6, 1 + a^c, d — a/2 — n
A + 2a - 6)n / -n, 2a, d - c, 1 + 2a - d; 1
4 3
A — b)n	\ 1 + Aa — o, a, 1 + za + с — a
— ra, a, a + 1/2, 6, c; 1
2a, F + c)/2, F + с + l)/2, 1 + 2a - 6 -
(c)n(c + 2& - 2a)n _ ^ ( -ra, b/2, (b + l)/2, b + с - 2a, ra + с + 2b - 2a; 1
c + n, 1 - с - ra, 6 + c/2 - a, 6 + (c + l)/2 - a
_ (l + a)n(l + a-6-c)n
" F + c)nF + c^2a)n°
—7i, a, a/2 + 1, 6, c; 1
a/2, 1 + a ^ 6, 1 + a^c, l + a + nj A + a — 6)n(l + a — c)n '
-n, 1/2 -ra, -1/4, 1/4, 9/8;
1/4 -ra, 3/4 -ra, 1/8, 3/2
2,1 + г/2, 1 + г/2, 1 - г/2, 1 - г/2;
2 + г/2, 2 + г/2, 2 - г/2, 2 - г/2
2, 1 + г, 1 + г, 1-г, 1 - г;
2 + г, 2 + г, 2 - г, 2 - г
= 0
|=1, 289128...
= 1, 588468...
!n = 1, 2, 3, . ..].
91
Л JL
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
аг
1
8
4
1
_
4
1
4
1
4
1
4
1
4
1
4
1
4
1
4
1
4
1
4
1
4
1
4
1
4
1
4
1
4
3
1 00 г
4
1
_
4
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
«3
5
1 00 г
4
3
4
1
2
3
4
_
4
3
4
3
4
3
4
3
4
3
4
3
4
3
4
3
4
1
1
]_
а4
7
1 00 г
4
3
4
3
4
3
4
1
1
1
1
1
1
1
1
1
1
1
1
«5
1
1
2
1
1
1
1
1
1
1
1
1
1
1
7
4
7
4
7
4
7
4
6i
9
8
г
0
4
5
4
5
4
5
4
5
4
5
4
5
4
5
4
3
2
3
2
7
2
2
5
4
5
4
3
2
2
62
11
8
г
0
4
5
4
3
2
3
2
2
3
2
7
4
2
7
4
2
2
9
4
7
4
2
2
9
4
Ьз
13
8
г
0
4
7
_
4
3
2
7
4
7
4
2
2
5
2
2
9
4
9
4
5
2
5
2
5
2
9
4
5
2
64
15
8
г
0
4
7
_
4
7
4
7
4
2
11
4
2
11
т
9
4
11
т
5
2
11
т
11
т
11
т
11
4
11
т
5F4(ai, . . . , ав; fc»i, . . . , 64; 1)
35тт
32B +л/2)
/тг / 1 \
512V2 W ;
9тг .
— (тг - 2)
32 v ;
Зтг
8
1,014678...
6 In 2 — 7Г
7
^A441п2^27тг^2)
™B21п2^47г™ 1)
5V ;
7
^E41п2^9тг - 7)
15
5
— (8 In 2 — тг — 2)
2
7
	A08 In 2 — Этт — 44)
18
541п2-3тг - 27
7
3
7 ,
^D+ 12 In 2 -Зтг)
20V ;
^A9- 18 In 2)
45V ;
7
— (86 - 72 In 2 - 9тг)
54
7
-F7 — 9тг — 54 In 2)
9

478
Гл. 7. Гипергеометрические функции
[7.6.3
38
39
40
41
42
Л Q
4о
44
45
46
47
48
49
50
51
52
53
54
к к
оо
56
57
О1
1
4
1
4
1
4
1
4
1
4
1
2
1
1 ICM
1
2
1
2
1
2
1
2
1
2
1
2
1
_
2
2
3
3
4
3
4
1
1
«2
3
4
3
4
3
4
3
4
1
1
2
1
1 ICM
1
2
3
4
3
4
3
4
3
4
1
1
1
1
1
1
1
«з
1
1
1
1
1
1
2
1
1 ICM
1
1
1
1
1
1
1
1
1
1
1
1
?14
1
1
1
1
3
2
1
2
1
1 ICM
5
2
1
1
1
1
1
5
4
1
5
4
5
4
ч со 1 <м
3
«5
3
2
3
2
3
2
3
2
7
4
1
2
1
5
2
5
4
5
4
5
4
5
4
3
2
7
4
4
3
3
2
со 1 см
ч со 1 <м
3
6i
5
4
5
4
7
4
2
2
3
2
Б
» |см
3
2
3
2
3
2
7
4
2
2
2
5
3
7
4
2
Q
«5
5
2
2
&2
7
4
2
2
9
4
9
4
3
2
Б
» |см
3
2
7
4
2
2
9
4
2
9
4
2
2
9
4
Q
«5
5
2
2
6з
2
5
2
9
4
5
2
5
2
3
2
Б
> ICM
7
2
2
9
4
9
4
5
2
5
2
5
2
2
9
4
5
2
<э
О
3
4
ь4
5
2
11
4
5
2
11
т
11
4
3
2
Б
> ICM
7
2
9
4
11
т
5
2
11
т
5
2
11
—
4
7
3
5
2
11
т
О
3
4
5^4@.1, ... , «55 ^1} • • • » ^45 1)
3
-(Зтг - 141п2 + 2)
7
— (9тг — 72 In 2 + 26)
30
-B6 -тг- 32 In 2)
™A04-9тг - 108 In 2)
7
^B7тг + 144 In 2- 182)
18
ТГ 2 о
48
27 л 9
_GГ4+30^-384)
25 о
	(9тг2 -64)
576v ;
5тг	50 In 2 + 20
7
-(Зтг - 96 In 2 + 58)
6
135- 150 In 2
7D7-Зтг-54 In 2)
™(84-5тг2 -48 In 2)
7
-A2тг + 66 In 2 — 83)
3
— B7 — 3v 3 тг — тт )
27
15тг + 150 In 2 — 150
35
— (Зтг -24 In 2 - 26)
(тг + Лоитг ozo)
45
72тг4 + 12тг2 - 828
-^Dтг2 -33)
16V ;
7.6.8. Значения 5-^4(^1, . . . , as; 6i, . . . , 64; —1)-
1, а, 6, с, d; —1
1. 5-^4 1	'	I =—1я [1я см. в 7.6.2.4, где следует заменить ф(х) на /3(х)].
\а+ 1, о+ 1, с+ 1, а + 1/
/ 1, а, а, —а, — а; —1 \	тга	7r2a2cosa7r 1
\1 + а, 1 + а, 1 — а, 1 — a/ 4slna7r 4sln2 аж 2
/1/2, 1/2, 1, а, 1-а; -1\ _ тгаA - а) Г	2	1 - 2а , /
5 Л 3/2, 3/2, 1 +а, 2-a J ~ ~ A - 2аK [coseca7r ~ ^^^а^	^^^ \^2у
[а:
4.	5F4
5.	5F4
6.	5F4
A - 2а)
а(а - 2)
1, 1, 1, а, 2 — а; —]
2, 2, 1 + а, 3 - a J ~~ 12(а - IL
1/2, 1/2, 1, A + 0/2, A-0/2; -1
3/2, 3/2, C + 0/2, C-0/2
1/2, 1/2, 1, B + 0/4, B-0/4; -1
3/2, 3/2, F + 0/4, F-0/4
а , 2/,	ч2 67ГA - а
6 + тг A — а)
sin атг
= 0, 980248...
= 0, 986580...

7.7.2]
У. У. Функция
479
7
о
о
9
10
11
12
13
14
15
oi
1
4
1
I
1
4
1
4
1
2
1
2
2
3
1
1
«2
1
4
1
2
1
2
1
2
1
2
1
1
1
1
«з
3
4
1
2
3
4
3
4
1
3
2
1
1
1
?14
3
4
3
I
1
1
5
2
3
2
1
3
2
3
«5
1
i
1
1
1
5
2
9
4
4
3
3
2
3
6i
5
4
5
4
5
4
3
2
3
2
5
4
5
3
5
2
2
b2
5
4
3
2
3
2
7
4
3
2
2
2
5
2
2
63
7
4
3
2
7
4
2
7
2
2
2
3
4
64
7
4
7
I
2
9
4
7
2
3
7
3
3
4
5F4(ai, . . . , a5; fei, . . . , 64; -1)
0,99339507...
j[v2 ln(l + V2) - GJ
-[D\/2 - 3)тг - 21n2 - 4л/2 In A + л/2)]
^— [35тг - 72 In A + лД) + 2 - 2 In 2]
25
	A8G- 11)
144l }
16/4 \
— (	! 1
5 U у
2
— A2л/3 7Г-54-7Г2)
27
828-4321n2-576G
АB7Г2 _ 15)
16
7.6.4. Значения sF^ai, . . . , as; 61, . . . , 64; z®) при zo / ±1.
-n, a, a/3 + 1, 6, 1 - 6; 1/4	\ _	((a + l)/2)n(a/2 ¦
a/3, a + 2n + 1, (a - 6)/2 + 1, (a + 6 + l)/2/ ((a - 6)/2 + l)n((a + 6 + l)/2)n *
/-n, a, 2a/3 + l, 6, a - 6 + 1/2; 4\ _ 1 + (-1)та	2^nyi!(a + l)n/2
\2a/3, a + n/2 + 1, 26, 2a ^ 26 + l) ~ 2 (n/2)!F + l/2)n/2(a - 6 + l)n/2
7.7. ФУНКЦИЯ 6F5(ai, ..., a6; 61, ..., b5; z)
7.7.1. Представления qF^{u\1 . . . , ae; 6i, . . . , 65;
a, a + 1/3, a + 2/3, 6, 6 + 1/3, 6 + 2/3; z
[a,
1/3, 2/3, c,e+1/3, с+ 2/3
7.7.2. Значения 6F5(ai, . . . , a6; 61, . . . , b5; 1).
*», 3*. Зс,
/ 1, 3/2, a, a, 1 - a, 1 - a; 1 \ = aa(l-a)» , _ , _
\l/2,l + a,l + a,2-a,2-a/	1 - 2a L^ l ; ^l	л
2, 2, a, a, 2 - a, 2 - a; 1 \ тга2B - аJ Г	тгA - а)
6F5
6F5
-n, a, a + 1/3, a + 2/3, 6,6 + 1/2; 1
c, d, B6 - n)/3, A + 26 - ra)/3, B + 26 - n)/3y
Ca - 26 + l)n /-n, 3a, с - d + 1/2, d - с + 1/2; 1/4\
A - 26)n	3\	c, d, 3a -26 + 1	/
-n, a, a + 1/3, a + 2/3, 6, 6 + 1/2; 1
Ca + l)/2, 3a/2 + 1, B6 - n)/3, A + 26 - n)/3, B + 26 - n)/3/ ~ A - 26),
-n, 1, a, 2 - a, 6, 2 - 6; 1 \_	(n + 2)!n!	[	aB - a)
3/2].
n + 2, a + 1, 3 - a, 6 + 1, 3 - bj 2F - a)(a + 6 - 2) [F - 1JF + l)nC - 6)n
6B-6)	1 (n + 2)B-a)B-6)ab
2(n
(a - 1JF - IJ
' -n, 1- ra/3, a, 6, 1- 2a- 26- n, 1/2- a- 6- n; 1
—n/3, 1— 2a^ n, 1— 26^ n, 1— a— b— n, a+ 6+ 1/2
-n/2, A - ra)/2, a, a + 1/3, a + 2/3, 6; 1
F - n)/3, A + 6 - n)/3, B + 6 - n)/3, c, 3a - с + 3/2

480	Гл. 7. Гипергеометрические функции	[7.7.3
A + За-6)„ „ /-п, За, с-1/2, 1 + За-с; 4
—	4^3
A-Ь)„	\1 + За-Ь, 2с-1, 2 +6а-2с
1,3/2, A + 0/2, A + 0/2, A-0/2, A-0/2; Л _, 17,Q44
1/2, C + 0/2,C + 0/2, C-ОА C-г)/2 ) ~ '
1, 3/2, B + 0/4, B + 0/4, B - 0/4, B - 0/4; 1\
1/2,F + 0/4,F + 0/4,F-0/4,F-0/4 J-1'077536-
1 1 3 3 1 3- 1 5 5 7 7- Л V
г 4' 4' 4' 1; 2' 2' 4' 4' 4' 4' V " §
/1 3 3 3 9 5	Л 32 / 8
11. eF5 ^-, 1, -, -, -, i, ^ 2, 2, 2, 3, 1J = у ^1 - -
7.7.3. Значения 6^5(^1, • • • , «е; &i, • • • , ^5; — 1)-
_, / 1/2, 1, а, а, 1 - а, 1 - а; -1 \ тга2A - аJ Г А тгA - 2а)	1
1. 6^5 ( /	1 = —Г"^	гг- 4 - 4cosec а7г +—^-5	 cos атг
\3/2, 1 + а, 1 + а, 2-а, 2 - а/ A - 2аL [	sin2 атг	J
5	[а ^1/2
1, 3/2, а, а, 1 - а, 1 - а; -1 \ _ тг2а2A - аJ cos атг
J	2 атг	I" * 1/2].
1/2, 1 + а, 1 + а, 2 - а5 2 - а J " A - 2а) sin2 атг
2, 2, а, а, 2 - а, 2 - а; -1 \ тта2B^аJГ
1, 1 +а, 1 + а, 3 — а, 3 — а/	4A — а) [
fa,a + 1/3, а + 2/3, За - 1/3, За, За + 1/3; -1
* 6 5\	1/3, 2/3, 2а5 2а + 1/3, 2а + 2/3
_, / 2, 2, а, а, 2 - а, 2 - а; -1 \ тта2B^аJГ тгA - а)	1	.
\1, 1 +а, 1 + а, 3 — а, 3 — а/	4A — а) [ sm а7Г	J
9a -
1/2, 1/2, 1/2, 1/2, 1/2, 5/4; -1\	4 /3
]=2Г U
Г((За + 1)/2)Г(9а/2) Г[2/3, За, За + 1/3]	6
5/4; -Л=2Г-4^
i/4,1,1,1,1 ; V4,
7.8. ФУНКЦИЯ 7^6(ai, ..., а7; bi, ..., be; z)
7.8.1. Значения 7^б(«1, • • • , «75 &i, • • • , бе; 1).
L. 7 -^6 [	' /	' ' ' ' ? «/ 5
\а/2, 1 + а —6, 1 + а — с, 1 + а — а1, 1 + а — е, 1 + а — /у
1 + а — 6, 1 + а — с, 1 + а — а1, 1 + а — /, 1 + а — 6 — с — а1,
= Г|
1 + а, 1 + а — о — с, 1 + а — о — а, 1 + а — с — а,
1 + а — 6 — с — /, 1 + а — 6 — а1 — /, 1 + а — с — а1 — /
[е = 2а- 6- с- а1- / + 1].
• 1, а, а, а, 1 — а, 1 — а, 1 — а; 1
\1 + а, 1 + а, 1 + а, 2 — а, 2 — а, 2 — а
- ЗтгA - 2а) cosec2 атг + тг2A - 2аJ Т"^" I	[a ^ 1/2].
= Я^
A — 1а)ь
6 ч	у
3. = 		[a = 1/2].
960	l / J
/ 1/2, 1/2, 1, a, a, 1 - a, 1 - a; 1 \ _ тга2A - aJ
* 7 6\3/2, 3/2, 1 + a, 1 + a, 2- a, 2- a) ~~ A - 2aM X
x [2ttA - 2a) - 6 ctg атг + тгA - 2a) cosec2 атг]	[а 7^ 1/2].
5- = Wo	[a =1/2]-

7.9.1] 7.9. Функции sFjjai,. . . , as; fri, ¦ • • , 67; z) n 9-^8 (fli? • • • , «э; 61, • • • , bg; z) 481
_, / 1, 3/2, 3/2, a, a, 1 - a, 1 - a; 1 \ тта2A - 2aJ
6. 7/Vf	! —
7. 7F6
1/2, 1/2, 1 + а, 1 + а, 2 - а, 2 - а/	1 - 2а
х [2 ctg атг + тгA — 2а) cosec2 атг]	[а ф 1/2].
1, а, а, а, 2 - а, 2 - а, 2 - а; 1 \ _ а3B - аK
1 + a, 1 + a, 1 + a, 3 - a, 3 - a, 3 - a/ 16A - aN
x 1*8 - Зтг2A - af cosec2 атг + ЗтгA - a) ctg атг + 2тг3A - af cosa7T 1	[a ф ц.
/ 1, 1, 1, a, a, 2 - a, 2 - a; 1 \ _ a2B - aJ
7 6
, 2, 1 + a, 1 + a, 3-a, 3-a/ 12A - aN X
x [2тг2A - aJ ^12^ 9тгA - a) ctg атг + Зтт2A - aJ cosec2 атг]	[а ф 1].
,	—га, a, a/2 + 1, 6, c, d, 2a — 6 — с — d + n + 1; 1
11. 7-Г6 1	,	,
_ A + a)n(l + a - b - c)w(l + a - 6 - d)n(l + a - с - d)n
~ A + a - 6)n(l + a - c)n(l + a - d)n(l + a - 6 - с - d)n '
. -n, a, a/2 + 1, 6, b + 1/2, a - 26, 2a - 26 + n + 1; 1
7 6 va/2, 1 + a - 6, 1/2 + a - 6, 1 + 26, 26 - a - ra, 1 + a + ra
_ A + а)„A + 2а -46)„
. -n, 1,3/2, a, 1-a, 6, 1-6; 1
* 7 6lvl/2, n + 2, 1 + a, 2-a, 1 + 6, 2-.
(-l)nn!(n + I)!a6, Wi LX Г Г -га - a ] Г -n - 6
= -™—-—ту2	—r-(l — a)(l -— oj < I	— I
'1/4, 1/4, 1/4, 3/4, 3/4, 3/4, 1; l\ = 27тг _	^2
5/4, 5/4, 5/4, 7/4, 7/4, 7/4 J 256l	Ж h
7.8.2. Значения 7^б(а1, . . . , a^] 6i, . . . , &65 —1)-
/1, 3/2, 3/2, a, a, 1 - a, 1 - a; -1 \ _ a2(l - aJ
* 7 \l/2, 1/2, 1 + a, 1 + a, 2-a, 2 - a J ~ 1 - 2a X
x [4/3(a) - (l-2a)(^'(a)+^/(l-a)) - 2тг cosec атг]	[а ^ 1/2].
,1, 1, 1, a, a, 2-a, 2-a; -1^ _ a2B - aJ
Zi. 7Г -
2, 2, 1 + a, 1 + a, 3 - a, 3 - a) 12A - aN
x [tt2A - aJ + 12 - 9ttA - a) cosec атг + Зтг2A - aJ cos а7Г 1	[a ^ 1].
L	sin aTiJ
31тг6
'1, 3/2, 3/2, A + i)/2, A + i)/2, A - t)/2, A - t)/2; -1
1/2, 1/2, C + г)/2, C + г)/2, C - г)/2, C - г)/2
/1, 3/2, 3/2, B + i)/4, B + i)/4, B - i)/4, B - i)/4; -1
' 7 6 V 1/2, 1/2, F + i)/4, F + i)/4, F - t)/4, F - i)/4
6 7F6f1/4' 1/4' 3/4' 3/4' X' 3/2' 3/2; i-0 961977
7 6 V 1/2, 1/2, 5/4, 5/4, 7/4, 7/4 J ~ U' 9biy77-
7.9. ФУНКЦИИ 8^т(о1, ..., a8; bi, ..., Ьт; z) И 9F8(ai, ..., a9; bi, ..., b8;
7.9.1. Значения 8-^V(flij • • • ? ^g; 6i, . . . , 67; ±1).
2, 2, a, a, a, 2 — a, 2 — a, 2 — a; ±1
vl, 1 + a, 1 + a, 1 + a, 3 — a, 3 — a, 3^ay
16 А. П. Прудников, Т. З

482
Гл. 7. Гипергеометрические функции
[7.9.2
B-af ГГ ctgan 1 тгA - a) f 1 1 тг2A - аJ Г 2 cos атг 11
а — IK L\coseca7r/ sin2 атг \ cos атг/ sin3 атг \ 1 + cos2 атг j J
~Щ
1, 3/2, 3/2, 3/2, а, а, 1 - а, 1 - а; -1 \ _ тга2A - аJ
7.9.2. Значения gFs(ai, . . . , ag; 6i, . . . , 6g; 1).
1, 3/2, 3/2, a, a, a, 1 ~~ a, 1 - a, 1 - a; 1 \ _ тга3A - aK
vl/2, 1/2, 1 + a, 1 + a, 1 + a, 2 - a, 2 - a, 2 - a) ~ A - 2aK
x [тгA — 2a) cosec2 an + тг2A — 2aJ cosec2 атг ctga?r — 2ctga?r]	[а Ф 1/2].
2. 9F8
-n, 1, 3/2, 3/2, 3/2, a, 1 - a, 6, 1 - 6; 1
1/2, 1/2, 1/2, n +2, 1 +a, 2^ a, 1 + 6, 2^6
_ n!(n + l)!
Ba -
- 1)
3.
1.
b + l)nB-6)n
1/4, 1/4, 1/4, 1/4, 3/4, 3/4, 3/4, 3/4, 1; l\ _ 27rr 3 _ 2
5/4, 5/4, 5/4, 5/4, 7/4, 7/4, 7/4, 7/4 J ~~ 512 ^ ^
7.10. ФУНКЦИЯ ,+iFq(oi, ..., aq+1; bu ..., bq; z)
7.10.1. Значения q+iFq(all . . . , aq+1] bi, . . . , 6g; z).
a, 6i, . . . , bq;
о	с7
4.	9+1F,
5	С7
•	9+1 " Я
6	i i F
*-*•	9+1 9
[(9-l)/2]
1, a);
A(g, a)
1, a, . . . , a; z
a + 1, . . . , a + 1
1, m, . . . , m; z
A - x)a
1 + qx
=a Ф z' ^' a)"
T .
g
.-x)«+1z =-fr-
=-friz см. в 7.10.1.2].
, i);
(k~lq+l)/q
fc_i / m -
A;
z ^ . 21/f ч z1/gslnBl7r/g)
	h - > sln^(fe + lWarctg	^	^^»»
-^ + i q ?-f 9	i
i "У 2cos^(ife+lOrln f z2/q-2z1/q cos —+ 1V-
q j-^	qK	\	q J q
In
7.
8.
, l, ¦--, l;
2, . .., 2
9.
1, 1, . .. , 1, 2, . . . , 2; z
3, ...	. .., 3
= i(q - n, q)
[I(q, n) см. в 7.10.1.9].

7.10.2]
7.10. Функция
;6i, . . . jbq;z)
483
10.
2, 2, . . . , 2; z\ 1 ( ^V+1 1 _ ^ (k + l)(~zY
1, ...,1 )~z\dz) i-z~2^f h^z)k+2
'	>	/	V	7	fe=O l	;
1. lim
2.
7.10.2. Значения 9+iFg(ai, . . . , ag+i; 6i, . . . , 6g; ±1).
, 62, • • • , 6g, "~"C
a, 6i, &2, • • •
= rh - n^
с = \ Ffe - ak) - aq+i; Re с > 0 .
Rea < ^2 пк, rife = 0, 1, 2, . . . ; 6fc + nfc ^ 0, -1, -2, . . . при k = 1, 2, . . . , q;
bk — bi ^ 1 — rife, 2 - nfe, . . . , n/ - 1 при /г, I = 1, 2, . . . , q; k ф l\.
3.
4. q+iFq
5.
L, bi, ..., 6g; ±1
»1 + 1, • • • , bq + 1
1, a, a, &i, . . . , 6^-2; =Ы
a + 1, a + 1, bi + 1, ..., 6g^2
i; k, I = 1, 2, . .., g; fe ^ /,
= 2, 3, 4, ...
= 1, 2, 3, ...
9-2 9-2
9-2
[6fc ^ 6|5 fe, / = 1, 2, . . . , ^ - 2; Aj # /; q ^ 2].
1, a, a, a, 61, ... , Ьд^з; ±1
a + 1, a + 1, a + 1, 61 + 1, . . . , 6g^3 + :
9-3
9-3 9-3
Е
fe=i
9-3
n»
+
6. q+iFq
a, 6, . . ., 6; 1
6 + 1, ..., 6 + 1
j; fc, Z = l, 2, ..., g-3; fc^Z,
9-1
+ 6- aj
[Rea < q; q = 1, 2, 3,
16*

484	Гл. 7. Гипергеометрические функции	[7.10.2
7. о+-
,а + 1, ..., a + iy	(9-1)! ^-^(а) J	LU = 1,2,3,
/а, 2, 2, ..., 2; l\	(-l)gF - 1)(Ь - 2) ^ fc fe!(a - l)fc o(fc)
О. a+l-^al	|	I = -,	ГГ7	w	7	Г У.\ *-) 1	Г	Г"' *-}q
[Re (a -b) < -q- 1; q ^ 1].
— T? 01	fl * 1 \	I CT i — S i I I О i — fl I
9. o+l-^o ,	,	I :=: 	;	ч—T-,	ч	 x
FT \^
g_i, С /	(°"g-l — 5g)n@g^l)n	g
X	П (ai
fe	к	I
С = Sq - (Jq^l - П + 1, Sk = ^jP ttj, <Jk = ^ bj, ГГЦ = ^ Ukj TOQ = 0, q = 2, 3, 4, . . ¦
L	1
10. ,+i
ai — 7ii, • • • , aq — nq
9	fe-1
11. = Я — s(tti ^ 72i + 72
Пк(пк -
fe=i	i=o	L	j=o
Z-l
fe=i i=o	z=fe+i
L ^ 0, -1, -2, . . . ; j = 1, 2, . . . , q; в = ]Г njy R = n\ f\	^^; a0 = -n; n0 = 0;
14	/ -n, a, . . . , a; 1 \ ( ,
13. g+i^g	I = b(g, n),
\a- 1, . . . , a - 1/
n7- = 1, 2, 3, . . . при j = 1, 2, . . . , q .
3
5(g, n) = 0	[д = 0, 1, 2, ..., n - 1]
(n + 1, n) = A - a)^^^^ + l)! ^l - a - ^) ,
(n + 2, n) = ^~24	(n + 2)'[12(a + ^ - !)(a - 1) + ^C^ + 1)],
(a - l)S(q, n) = (a + n- l)S(q - 1, n) - nS{q - 1, ra - 1),
5(g, 0) = 1.
-gn-1, a, ..., a; 1\ Г. ,n (-a - gn)nlg Г n [a)qn+1
= A)	A)
ЛА	/-gn-1, a, ..., a; 1\ Г. ,
14. g + lFJ	= (-1)
a — 72, . . . , a — 72 / [	A — a)n J |_	(a — n)qn~\
5g
I, —72, . . . , —72, 1; 1 \	n\(a — 1) ^—\	Sq
-n-1, ..., -n-l,aj (n + l)^-1 ^ (n - k + l)!(n - A; + a)'
-n, A(g + 1, a), A(g, 6); 1 \ _ А (-п)л(а)дЛ!+л(Ь)дЛ!
16. 2g + 2F2g + 1| A/?ja+l)jA(9+lj6_
-n, A(g + 1, a), A(g, 6); l\ _ A + a - b)n
18	F / -n, A(g + 1, a), A(g, 6); 1 \ =	(a - 6)n
• 2g+2 2+l^	^
-n, 1,2,2, ...,2;

7.10.2]
7.10. Функция
;fei, . . . ,bq\z)
485
+ 1].
In + 2 —
20. 2q
21.
22.
Iq=0
In+3 =
= 2, 3, 4, . . . ,
2)!]2Bn
12
-n, 1, 3/2, 3/2, ..., 3/2; 1
-n, 1 - n/2, 1 - n/2, . . . , 1 - n/2;
-n/2, -n/2, . . . , -n/2
2n + l)Bn + 3).
(-n)k
[q = n, n + 2, n + 4, . . . ; n = 1, 3, 5, .
'-n, 1/2-n, l-n/2, l-n/2, . . . , l-n/2; ±l\ _	[J g = 2, 4, 6, .. .
9+1 ** f	1/2, -n/2, -n/2, . . . , -n/2	J ~ °	[U + n = 2, 4, 6, . . .
^-n, -1/2-n, l-n/2, l-n/2, . . . , l-n/2; ±Л_ 0	Г Г Ч = 2, 4, 6, . . .
3/2, -n/2, -n/2, . . . , -n/2	J ~	[\ q + n = 2, 4, 6, . .
1
-n, l-n/2, l-n/2, ..., l-n/2;
-n/2, -n/2, . . . , ^n/2
25.
26.
27.
/A(g, -n), 1; 1\ _ 2"
4
' ; J ч k=i
-n, 2, 2, ...,2; -1\	1
i,i,...,1 у n + i
1, 1, ..., 1; 1"
2fc-l
g = n + 2/ + l; / = 0, ±1, ±2, . ..
9 = 2/ + 1; / = 0, 1, 2, ...
52 = — = 1, 64493407...,
4
54 = — = 1, 08232323...,
6
S6 = — = 1, 01734306...,
= 2,3,4, ...],
[q = 1,2,3, ...],
53 = 1, 20205690...,
55 = 1, 03692776...,
57 = 1, 00834928...,
59 = 1, 00200839...,
28.
x" 93555
1, 1, ..., 1; -1
2, ..., 2
= 1, 00099458.
Ti =ln2 = 0, 69314718...,
T3 = 0, 90154268...,
T5 =0, 97211977...,
T2 = — =0, 82246703...,
JL.Z
T4 = ^ = 0,94703283...,
31тгь
30240
= 0, 98555109...,

486
Гл. 7. Гипергеометрические функции
[7.10.2
Т7 = 0, 99259382...,
Т9 = 0, 99809430...,
Т8 =
Т10 =
= 0, 99623300...,
7Чтг1
0O4Z05U
Bg - 2fc - l)!B7rJfc
= 0, 99903951...
30.
3i--iF"(\^7,43,:::;31;±1)=J(*'n)'
J(q, n) = ±{-lLn
- A) ±
k=o
32. q+iFq
o, о, . . .	. . . , о	y
~n, g)
, n) см. в 7.10.2.31].
a-"' 7"Bn
/"A) = j =0, 78539816...,
/"B) = G = 0, 91596559...,
3
J"C) = ^ = °5 96894615...,
/"D)
/"E)
/"F)
/"G)
/"(8) = 0, 99984999...,
0, 98894455...,
^^ = 0, 99615783...,
15оо
0, 99868522...,
= 0, 99955451...,
Щпу.
/+B) = — = 1, 23370055...,
8
/+C) = |(C) = 1, 05179979...,
8
/+D) = ^ = 1,01467803...,
/+E) = l, 00452376...,
/+F) = ^ = 1,00144708...,
/+G) = l, 00047155...,
/+(8) =
161280
= 1, 00015518...,
8257536
/-A0) = 0, 99998316...,
= °' 99994968...,
/+(9) = 1, 00005135...,
/+A0) =
О-1	1
= 1, 00001704...

7.11.1]
7.11. Функции Куммера \Р\{щ b; z) и Трикоми Ф(а, b; z)
487
34.
36.
A(q,
( LI/2,
V 5/2,
A.1/2,
I 5/2
f 1.1/2,
V 3/2,.
2<?+n
• • • i
— n
E
A
k
q-n
1/2; П .
5/2 )¦
1/2; -1>
,5/2 J
3/2, 5/2,
[q/2]
...,5/2 у
n
n
1
Bg - 2fe
(q-2k-
K(Q-k)-
- 2)\^
l)!Bfe)!J
g" /
fc=O ^
-zfc I 2 3 .
f Aj-l\2n-fe
А; у
47
37.
1,1/2, ...,1/2,3/2, ...,3/2; 1
, n) см. в 7.10.2.44].
(-D^3-7-
9-2
/ Д ч
fe=O
V *
-!Vfc-
J
39.
1, 1/2, ..., 1/2, 3/2, ..., 3/2; -1
5/2, ...
...,5/2
= C(q-n, q)	[C(q, n) см. в 7.10.2.38].
7.11. ФУНКЦИИ КУММЕРА гРг{щ Ъ; z) И ТРИКОМИ Ф(о, Ь; z)
7.11.1. Представления о^о(^) и iFi(a; 6; z).
. 0F0(z) = ez.
2
3
4
5
6
a
a
a
a
a
a
b
b
b
a
2a
2a-n
ez
z~~
ez
л
6/2
a -
a -
a;
Mp
(!
l
2
Ь; -г)
iFi(
»-l/2 ^J
2 n
a; 6; ,
X
Ba
f a + A;
[P = b/2
-n)kk\
- a, 2a =
— X
b-i]
-(I)

488
Гл. 7. Гипергеометрические функции
[7.11.2
7
8
9
10
11
12
13
14
15
16
17
18
а
а
а
те
те
те
1
1
2
—те
—те
—те
—те
b
2а + те
а — те
b
т
те + 1
b
т
т
b
2те
1
2
3
2
rH)(tI/a~V/a?-
(-1)пте! а„п„1г
A^а)пС n ^ "'
6-1 / д \n^ f^fl^b « /,
(п — II \dz ) C ^
(m-2)!(l-m)n 1_m[m^
(-1)тете! Г z ^p (-l)fezfc
zn c 2^ д.;
F- l)^1"bea!7F- 1, z)
L fc=o fe!J
/ im Г m—3
1 A/ lib 1 aj 1 С 7
(Ь)п П
'rl""z fz/2 ff f ^ 1
f2«V /тг n+l/^ \o/
(-1)тете! /_
2Bте+1)!лД 2n+1 V^
iFi(a; 6; z)
[-n)k{2a-l)k ( \\
[2a + n)kk\ V " 2)
>-l, z)]
(l+n-m)fc^ ^^
fc!B-m)fc " ^
24 (m-2)(m-l)
fe!J '
/a+*-l/2 B)
(!-»)* ( .)*]
fc!B-m)fc "[nJ<TO]
[m = 1, 2, 3, ...]
[m -2, 3, 4, ...]
; 2-6; *) = Г
Отметим, что при некоторых других значениях параметров а и 6 функция iFi(a; 6; z)
может быть выражена через указанные в п. 7.11.1-2 функции с помощью рекуррентных
формул
20. aiFi(a + l; 6; z) = (z + 2a - 6) iFi(a; 6; z) + F - a) iFi(a - 1; 6; z).
22. aiFi(a + l; 6 + 1; z) = (a — 6) iFi(a; 6 + 1; z) + 6iFi(a; 6; z).
7.11.2. Частные значения iFi(a; 6; z).
iFi(a; 6; z)
2
1
1
2
e~ - Vtt
- \e -\	\ — erfi
2	2
C-
16z
4
4z-4z
2,-
ff	Г -I	/
	 -C + 6z + 12z2 - 8z3)x — erfi (v^) - C + 4z - 4z2)e;
64z2 [2	у z
^ег/2 [2A + 102 - 422)/0 @ - D + 52 + 622 - 423)/! (J
(l-22)e*

7.11.2]
7.11. Функции Куммера \Р\{щ b; z) и Трикоми Ф(а, b; z)
489
10
11
12
1 Ч
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
47
О 1
38
а
1
2
1
—
2
1
2
1
2
1
2
1
2
1
2
1
1
1
1
1
1
1
1
3
_
2
3
2
3
2
3
2
3
2
3
2
3
Z
2
2
2
2
9
Z
2
6
1
3
2
2
5
2
3
7
2
4
1
1
2
3
2
2
5
2
3
7
2
4
1
1
2
1
2
5
2
3
7
2
4
1
~2
1
2
1
3
2
5
ICM
3
gZ/2 г / _
V
1 /тГ
—./— qy
г
€ Z' \ If)
L
3 Г1 +
4z [ 2
Ае^/2 г
3z L
15 [1
32z2 [2
5z2
l-2z-
1 /тГ
-\ — ez
2 у z
3 Г1 Г
2z [2 V
2z^2(ez
5 ГЗ
	 _
4z2 L2 V
3zBe2
A — 4z -
A -|- 2z)e
ez/2 ГA_
L
ez/2 Г/о
L
3 Г
	 €.Z —
2z [
ie«/27i
z
15 L*
8z2 Г
1 -4z-
1 + Z + -
4i+x
-L
2 L
3 г
1
4zP
2z^2[l^
iFi(a; 6; z)
~ 1
2/
i i\fz )
/^\ /z\1
	j 	j- I	j
^2/ V 2/J
2z рк 1
V z { ) J
V 2 / V 2 /-1
^«5 1 Д^ | Д~2\ / p-r.fi f /~~ \ (^ 1 r*~\/^'Z
Г / Z \ / Z\~\
z(l + 2z)/nl	I 	D + 3z + 2z2)/i [	j
L V 2 f V 2 / J
ezerf {лД)
erf (y/~z )
1)
^ezerf(v^)-l]
z J
-1-z)
Fiv 1
'— ez erf (л/z) - 3 - 2z
^ J
_ 2 — 2z — z2)
4z )ez
z
^z)lJ^)+zh(^\\
V 2 / V 2 / J
^) +/l (f)l
v 2' V 2 ^ J
1 /тг 1
— 4 / — erfi (\/~z )
2 V z J
(-)
\2/
3 + 23 /^crflf ^0
W ertnvzn
^ V ^ J
2z2 - z3/2E + 2z)v/7rezerf (л/z)
•/^^ /0 1 o«U2prfr/r\
2
+ 2z pr z f ( ^—^
2 V * J
1 — 2z /тГ 1
2 У z { }\
(l^z)ez\

490
Гл. 7. Гипергеометрические функции
[7.11.2
Ост
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
a
2
2
5
2
5
2
5
2
5
2
5
2
5
2
5
2
5
2
3
3
3
3
3
3
3
3
7
2
7
2
7
2
7
2
7
2
7
2
7
2
7
2
4
6
7
2
4
1
1
2
1
3
2
2
3
7
2
4
1
2
1
2
1
3
2
2
5
2
7
2
4
1
2
1
2
1
3
2
2
5
2
3
4
1
2
15 Г
8z2 L
6z~3[2
1
зC-
1
~ C -f-
3
з е
~~ C +
3
rz/2
4 /
	ez/
5 [J:

4z2 \_z
4
	gz /
z2
I [2_
2 [
1 Г
4 [ +
1B +
2
2
— [l
16z L
-A5
15 V
?A6
15 е
	A5
15
1
~ E +
5
4 ?
15^C
4l2
12 [
iFi(a; 6; *)
3~2z /? ]
2 V z J
+ z~B~z)ez]
18z^36z2^8z3)ez
12z + 4z2)ez
[C + 6. + 2.2)/0 (|) + 2.B + z)h (J)]
2z)ez
[C + 2г)/о(|)+A + 2^A)]
2 [./о (|) - A - z)h (|)]
> /тГ I
- 4 / — erfi (\/~z ) — C — 2z)ez
) у z I
Г /^\ /2\1
z/n 1	l 	D	z~)I\ I	I
L \2/ V2/J
12z - 13z2 - 2z3 - ^C5 + 28z + 4z2)i/^ ez erf (yfz)\
2 у z J
1 1
9z + 2z2 H—A5 + 20z + 4z2)-\/ttz ez erf (л/z)
2 J
2z H—C + 12z + 4z2)a ¦— ez erf (xfz)
2 у z J
z)ez
2 у 2 J
1 /тГ 1
2 у 2 J
2-2z + z2)ez -2]
- 120z - 360z2 - 160z3 - 16z4)ez
+ 90z + 60z2 + 8z3)ez
1 [A5 + 45z + 28z2 + 4z3)/0 (-) + ^B3 + 24z + 4z2)/i (-\]
+ 20z + 4z }€Z
1 [A5 + 18z + 4z2)/0 (-) + C + 14z + 4z2)/i (-}]
2z)ez
/2 [2.B + .)/„(§)- A-2,- 2s2)/! (|)]
/2[D-3. + 2.3)л(|НA-2.)/о(|)]
Ofi ~ 1|->P\~ Р»*^~3 /1~ /'^I^i 1 ЧТЧ~1 1ПЧ~ I Q~3\ /ZT ~z „„r / /77 \
yuZ iOOZ OZZ ^tZ l «ЗАО "T" «31 oZt IUoZ "T~ oZ ly 7Г 6 6П 1 у Z 1
2 J

7.11.4]
7.11. Функции Куммера \Р\{щ b; z) и Трикоми Ф(а, b; z)
491
66
67
68
69
70
71
72
а
4
4
4
4
4
4
4
6
1
2
1
3
2
2
5
2
3
7
2
1 I
1
-F
1
3
5
64z
24 + 87z + 40z2 + 4z3
+ 18z + 9z2 + z3)ez
33 + 28z + 4z2 + i(l{
+ 6z + z2K
Г 9 1
3 + 16z + 4z2 - -C
L 2
(о й„ I io ~2 |
\F\{_a] 6; z)
+ -A05 + 210z + 84
3 + 90z + 60z2 + 8z3)
^18z^36z2^8z3)^
з^ F* z r\
iz V z e
1
J
У|е*егГ(^)]
/- ezerf (v^)|
-3 + 4z + 4z2
7
1
2
3
4
.11.
a
a
a
a
a
3. П ре д став л ения iFi(a; b; —z).
b
a + 1
a + 2
1
2
3
2
iFi(a; 6; -z)
az""a'y(a, z)
2-0-1/2
_ ГA a)e~z/2{D2a i( v/2z) + ,D2a liVlz)]
2 — a — l
y	 ГA a)e^z/2[D2a г( л/2г) D2a 2(\/2z)]
7.11.4. Представления и частные значения Ф(а, 6; z).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
а
а
а
а
а
а
а
а
а
п
1
-п
1-71
2
1
2
1
6
6
6
6
а
2а
1
2
3
2
2
6
6
6
3
2
1
2
1
r[l!a-JlFl(a!b!
^-ьФA + а-6,2-Ь;
z^b/2e,/2^^(z)
егГA-а, z)
7r-l/2j2l/2-ae^/2/Ce_i/
= 	z1'2""a exp	h
2 [2
1 B — a) z^2 1 / z \
z C *-*-ла\2)
1 / d "
(n- 1)B- 6)n_i V^^,
z1~bezr(b- 1, z)
(-l)nn!L5;-1(«)
-e*Ei(-z)
Ф(а, 6; г)
,) + r[6e1]^lFlA +
2(f) =
«f«+ 1I^) f*i)
/ '
a-b; 2-6; г)
[х- = 6/2 - a, 2/t = b - 1]

492
Гл. 7. Гипергеометрические функции
[7.12.2
7.12. ФУНКЦИИ 2F2(ai, а2; Ьи Ъ2; z) Ш qFq(aij ..., aq; bly ..., bq; z)
7.12.1. Представления 2-^2(^1, Q>2] &i, 62; z).
1
2
3
4
5
а
at
а
а
а
1
1
1
2
«2
6
6
6
а
а
а
bi
«-1
а + те
а + 1
6 1
2
3
2
62
с
6 + 1
6 + 1
+ 2а^6
b
iFiF; с; z)
(«)п р
(а _ 5)n Il
а
а — b ±V"
F- 1)Bа-
— [iFi(a; 6
az
2а ^1 [V ^
i
1 («
tF;6
6 + 1
fe)(i
'erfi(,
2/^2@.1, a2;
6z
-l)c l '
_ч , v™^ (a
+ ' ^ 2^
L, л] 1 1-Г]
1]
bi, 62; 2)
c + l; z)
—¦ b)k-i , , J
(a)fc A a "' 1
(a; a + 1; z)
/2, l/2 + а-Ь yZj
. *I
11 }J
7. 2F2A, a; a + 1, 6; z) +
6-1
2F2A, a; a + 1, 2 + a - b; -z) =
a-b + l
7.12.2. Частные значения 2^2(^1, ^25 bi, 62;
iFi(a-6 + l; a -6 + 2; z) iFiF-l; 6; -2;).
62
1, 62; z)
2
-i 1
^^ 1
2
1
— [A + 2z)ez - 2^z3/2 erfi (y/I) - 1]
9
erfi
3 5z]
erfi
-- 1
2 -
2
1
A {3 -e'/» [C ^6z + 2z »)/0 (|) + 2zB - z)h (|)] }
^)y^erfi(v^)]
-1 - A5- 18z + 4z2:
J- [в - E - 2^)ez - 1C - 12*
8z L	2
10
11
12
13
14
-- 1
3
3
1
2
I 2
5
2
- 3
— \
45z I
10z^
_ Uz
D 9
X A5 20z + 4г2)Л/тт1 erfi (л/i) 4 + 20г
h^+'-

7.12.2]
7.12. Функции 2
и qFq{a1, . . . , aq;
. ,bq;z)
493
15
16
17
18
19
20
91
22
23
24
26
97
28
9Q
30
€»1
on
33
34
35
36
37
38
39
ai
1
2
1
~2
1
2

2
2
1
2
1
2
1
2
1
2
1
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
^2
1
2
1
2
1
2
«2
2
2
2
2
2
2
9
2
2
5
2
5
2
5
2
5
2
b
?
5
2
5
2
5
2
5
2
3
3
3
3
3
3
2
bi
1
2
1
2
1
1
1
1
3
2
5
2
3
1
2
1
2
1
2
1
2
I
?
i
3
2
3
to
3
2
1
2
_
2
1
1
1
1
3
2
1
3
1
,4
2
5
?
3
о
3
3
1
2
i
3
2
9
3
,4
2
3
2
9
1
2
1
,4
2
2
с
2
2
1
— \2,ez 	3v
2L
ez/2
2 Lx
If 1
_ 3ez -f- —
4 [ 2
2ег/2 г
15z
2
15z2
1
20z2
8
225z2
[zG
Ьо
3LV ;
ez/2
3 L
1
-[3e* -4V
3L
ez/2 г
9 Ll
4ez/
45z
[4C
ez/2 г
3 L
H2el+i
ez/2 г
9 L^
4ez/2 г
45z Ll
-[2D- z)c
8
— [4е'г 	5v
4
ez/2 r
/I
4A
i Г
16 [13ez +
ez/2 r
D
4 Ь
о Г
A +
If 1
_ 5ez 4- —
8 L 2
2^2@-1-. ^2; bi, 625 2)
'ttz erfi A/^ )]
- z- 2z2)ez - 2-s/^z5/2 erfi (y/z)]
3z)/0 ( - ) + 3z/i ( - J
\2/ \2/J
/tF 1
M 	Qz) a 	 erfi (\fz )
V z J
bz)l® M + {Z
z + 6z)IlKl)\
z3/2
2
« \/TTZ n I
О "T" • Z ¦ 1Эл J С 1
v (
15 Ч~ 20z 12z ) erfi [\/z J
<°z/2 f4O 1 ^r
34,2 + 12,3)/oQ +
/ 9ч /z \ I I
+ zC1 + 22z^12z2)/i (-)И'
3Z -8л/тг!егй(х/г)] V2/J j
/z\ /z\i
/7Г2 csrfi {\fz I
/ z \ / z \ 1
16z2)/i (-)]
/Z\ /Z\l
	 4* /7т-
/ f,rfi ( /~Z\
у сгп (v' * )
f Z\ /Z\l
' °\2/ X \2/J
/z\ /z\i
j °V2/ { } X V2/J
iz - ХЬл/тгх erfi(y/z)]
( z \ / 2: \ i
^^ ) -*0|J 1 ( ** 1 1
0
3 /tF
-(l-lOzJ^-erfi^)
V 2 / V 2 ^ -1
1 /it 1
40 "''Ij"'2 fi 1*?'
г+ 60;
у	 -i
C — 10z)a — erfi (л/z)

494
Гл. 7. Гипергеометрические функции
[7.12.2
40
41
42
43
44
лк
*±о
46
47
48
49
50
К1
О JL
52
53
54
55
56
57
58
ОУ
60
61
62
ОС»
64
65
1
1
~2
1
2
1
2
1
9
А
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
Z
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
9
,.;*,
1
2
1
2
1
2
«2
3
3
1
1
1
1
1
1
2
2
2
2
2
2
2
5
2
5
2
5
2
5
2
3
3
3
о
3
3
2
2
3
2
3
2
2
2
2
5
2
3
1
1
1
3
2
ю | см
3
1
3
2
3
2
3
2
1
1
1
_
2
2
ь2
2
5
2
2
3
2
5
2
3
3
3
1
з
2
5
2
3
3
3
3
3
2
3
2
2
о
1
3
2
2
2
2
2
-4V
64z [2
х ^_
— [\/тгг erfi
z
2 Г z/
\ г
2z L
— {з + е*
2 г
z2 L
8 г zj<
9z2 Г6
— [B +
2 L
1 Г 1
_ gz _|_ _
2 L 2
3 Г z 1
с
8z [
2ег/ г
2
	 М
3z2 L
«1 /О
^ h (
сГТ I6™ e
е^/2
	 (з +
1 Г /тГ
3 LV z
6 Г9/- /
3 L '
^ez/2 _
9z L
ezl \(л
4 L
_ _ /
8 [2 V z
ez/2 г
Л \
3 Г
32z L
1 ГЗ /тГ
— — \ — €
4 I 2 V z
2F2(ai, a2; Ьь 62; z)
5ж)/0 (?)_(!-5^A)]
Ь 12z ™ 20z2)i/^ erfi (v^) - A - 10z)ez
V« J
i\fz\ -\- 1 — ezl
- A + 2z)ez + 2^z3/2 erfi (v^)]
2 |^A - z)/0 ^-J + zh \^-jj 1
1 - 2z /тГ 1
2 У z ;J
/2 [A ^ 2*)/i (-) - C - 2z)/0 (-)] }
z Fk 1
)ez	C - 2z)x — erfi {л/z) - 1 + 3z
2 V 2: J
2 [C - 6z + 2z2)/0 (-) + 2zB - z)h (-)] - 6 + 9z|
V 2 / V 2 /-1
/~7г" 1
/- erfi(v^)
V 2; J
- 2z Гк 1
2 У z }\
(z\ , M (ZW
\ 9 / ^49/
j'jg2 	x _|_ x/ji z 1 erfi (\/~z )
J
"i~ 216 "i~ it) -p azj ern 1 -\/z )
Г (z\ /z\i1
z/2 |^F -Sz- 2z2)/0 (^-J + zE + 2z)/i (^-Jj j
/ z \ / z \ 1
1
i (\/z~) -f- ez
J
k2> h\2)\
/ z\ / z\~\
2\j(Z\ @ M- ^M
\2 / \ 2/-1
1
3rfi A/^) + E + 2z)ez
J
Z) 1Q \ J 1 A-i 1 1 1
l — QzHF 1
J 2 V ^ J
1
rfi Сл/z") -f- ez
J
:§)-ч§)]

7.12.2]
7.12. Функции 2
и qFq{a1, . . . , aq; fei, . . . ,bq;z)
495
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
аг
1
2
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
«2
3
1
1
1
3
2
3
2
3
2
3
2
3
о
q со 1 см <
'6
2
3
2
3
2
2
ю I см
5
2
5
2
5
2
5
2
ю | см
5
2
5
Z
5
2
5
2
3
2
2
2
3
1
2
1
2
1
2
1
2
2
2
2
5
2
3
3
1
2
1
2
1
2
1
2
со 1 см
со 1 см
to to | со
2
3
1
2
62
5
2
2
3
3
1
2
2
5
2
3
2
ю | см
3
3
3
3
1
2
3
9.
со to t
3
2
2
to со
3
3
2
2^2(«1, «2 5 &1, ^2 5 г)
3 [l + 6z /F^, /-^ ^]
4 / СГГ1 \ \/ a, ) G
16z L 2 V z J
z
-^{1 + z - ez - z[C + In {-z) - Ei (z)]}
-^{1 + 2z - ez + A - z)[C + In (-z) - Ei (z)]}
1 + 2z + 2v/7tz A + z)ez erf (y/z)
z
о Г 1 у / _. 
J- 4/6 erf ("\/z )
z L 2 У z K ;J
A[3 + Z-C-2^]
~z {?Z/2 [/0 (f) " h AI " Xl
l[l-.-e- + ^erii(^)]
j_{2-z-2e*/2[(l-*)Jo(§)+*/i(§)]}
^[EiW-z-C-ln(-z)]
3
-[3 + 2z + 2v/^B + z)ez erf (y^)]
3z
—^-[C -— 4z + 4z2)ez — 3 + z]
3 [ V z J
3z
^;;[;";;;)j)+,/i(f)]_1}
i[2e^/0(|)-2-,]
° I ~ 1 '^7rZ /к | о-Л~з f / /T\
2 L 2 J

496
Гл. 7. Гипергеометрические функции
[7.12.2
«21 «22
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
1	3
3	3
2	2
3	3
2	2
3
2
3
2
2
2
2
- 2
2
3- 2
2
^ 2
i 3
5
2
5
2
5
2
5
2
i 3
5 з
5 2
2
2
1
2
2
I 2
2
1 1
1 *
2
3
3
3
1
2
1
- 2
2
I з
1
2
1
1
2^
3
[A
o (f)-(l
§)- C-
B
[C-
(з-
20z2
|) + zG +
55z + 32z2
2
1
2
3 Г1-;
8^
[2B
10z + 2z2)h (J

7.12.2]
7.12. Функции 2
и qFq{a1, . . . , aq; fei, . . . ,bq;z)
497
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
1 ЧЧ
134
135
136
137
138
139
140
141
142
аг
3
2
3
2
to I со to I со
2
2
2
2
2
2
2
to to to to
2
2
2
2
2
2
2
CM CM
5
2
5
2
«2
3
3
со со
2
2
2
2
2
2
5
2
5
2
5
2
5
2
5
5
2
5
CM Ю I CM
5
2
b
2
3
3
со со
5
2
5
1
1
to to
1
2
1
1
1
1
3
1
9
1
1
2
1
2
1
1
3
2
3
2
3
1
2
1
1
1
1
2
1
62
2
5
2
2
5
2
1
1
3
2
Ю | CM
3
3
1
9
1
3
2
3
1
3
2
Q
3
2
3
3
1
1
3
2
5
1
2
1
	 D +
— A + 2,
- 2 + 7z -\
2 L
(l + 3z + z
1 Г
4 f + 2Z Ч
3 [l + 4z
8z [ 2
T [A ~~ ^ ~
Z
z2
i[3 + 36z-
3
VfF+
3
2ег/2 г
з[2 + г +
ii2+e
8L
2
— 13 + 21
16 L
9
ez/2 Г
CO 1
9 L(
7, + ;
,)/o (
-2,»-
>
2 /F
hz2)e
fC +
b28z2
27z +
+ 2^
*/2[г
+ 32z
-2г +
2^2(^1, a2; 61, 62; 2)
>z2)/0 (-) + zE + 2z)/i (-)}
y/z) - A -6z -4z2)ez
^ТГ^ /q lfi 2ч z r/ /~\\
+¦ 8z + 4z2)i/¦— ezerf(i/z)
ez erf (x/i") — 1 + 2z
*-i]
In(-*)-Ei(*)]
+ 4z3 +2F + 24z + 15z2 + 2z3)A/?fz ez erf {лД)\
F + 9z + 2z2)s/'kz ez erf {sfz)]
22z2 + 4z3)/0 (-) + z(ll + lSz + 4z2)/i (-)l
z
Г+223+/^ 2Z+f2Z-1
2 V z
л (?)-B-*)/„(?)]}
2 J
+ г3)ег
2 V z J
20z2 +8z3)x — ezerf (л/z) - 1 + 8z + 4z2
+ 392z2 + 160z3 + 16z4)ez
108z + 168z2 + 72z3 +8z4)/0 (*) +
+ 4zF + 27z + 16z2 + 2z3)/i (-)

498
Гл. 7. Гипергеометрические функции
[7.12.2
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
аг
to I ел
5
9
to i ел
ю | см
5
9
to I ел
ю | см
5
2
5
9
ю | см
to I ел
5
2
5
2
5
2
5
2
5
2
3
3
3
3
3
3
3
3
3
«2
to i ел
5
9
ю | ел
ю | см
5
9
ю I ел
3
3
3
3
3
3
3
со со
3
3
3
3
3
3
3
3
3
3
н
1
2
1
9
1
2
1
3
9
со 1 см
1
?,
1
2
1
9
1
2
1
1
1
3
2
3
2
2
1
9
1
2
1
1
1
1
со I см
2
2
со I см
2
3
со | см
2
3
1
1
3
9
2
1
3
2
2
to to | со
2
1
2
1
со I см
2
5
2
2
5
2
9
	[(9 + 52z +
4ег/2 г
9z И" ' "Л
9 L
	 [(9 + 14z
О ~ /1 I
- 3 + 60*+ 80
3 [
.2 + 8z3)c
44z2 + 8^
- + 4,Vo
2 ^2 (a
^3)/о (¦
/z\
+ 24г2 + 4г3)/0
+ 4г2)/о(
)/o (|) H
,2 + 25,3
iF + 84z + 123z2 +44z
- 6 + 3Qz + 17z2+2z3 +
6
-F + 39z + 28
6
	[A2 + 84*
12 [
-F + 24z + 15
6
	 [A2 + 392
— |9 + llz + 2
12 L
-F + 9z + 2z2
6
— 32 + 351z4
42
,2 + 4,3)e
+ 107z2 -
,' + 2,»)c
+ 26z2 +
z2 + -C
2
+ ^2)/o(-
-386z2 +
+ -B25 +
1 Г
— 16 + 69z +
16 L
iD + 32z + 38
4
1 Г
64 [55 + W2Z ^
4
(Л 1 Я ~
— Г 23 + 24z +
32 L
4
64z~ [ + Z +
36z2 +4z
z2 + 12z3
+ 2^
! + 4z4
2
f40z3
4z3)/0
+ 27z-
z\
2 /
108z3 H
lOOOz
• + if
+ г4)е
1
2
2 + z3K
+ 104z2 H
4z2 + i(c
zz
9 1
4z2 - -(]
h96,3
L, «2 5 6
D -y
E z
- 20z - 36z
( Z) +zA5 + 20z4
1 + lOz
AH (
+ ^C0
\-75z +
+ 4z2)/i (
I)]
2 _ 8^3)/i (|)]
/ZX1
XV2/J
-4^2)/i(|)]
1)]
+ 180z + 183z2 +
-i
+ ozz +
36z2+4z3)
+ 4zi)I0{^) +
-i
I — 1 +
Ь 24z2 H
+ 6z +
^8z4 +
¦f 872z2
75 + 17C
z
+ 392zs
/ 7l
XV7C
) + 66z
L - lOz
+ 52z2
- 28z2
~z{25 + 73z
zA9 + 22z
-4z3)^/| e
2z2)/1(Z)
+ 224z3 +
z + 76z2 +
+ 160,3 +
X
zerf (д/г) -
4z )y/izz ezerf(-\/z)\
1
+ 36г2 + 4г3)/1©1
+ 4^2)/i(|)]
z erf A/2)
i
J
1
L6z )v/7rz ez erf A/z )
j
8z3)v/^ezerf(A/z')
16z4)W- ezerf (y/z)\
1
ez erf (y/z)
ezerf(yfz~)j

7.18.1]
7.13. Функция оFi F;;
499
7.12.3. Представления;
'l, 1, a; — z\	a
г, аз;
С + In z -
1
2, 2, а + 1 ) " (a- \)z
7.12.4. Представления gFq((a,j);
а-1
); z).
2.
t
a — 1, . . . , a — 1
П ^
П
Многочлен Rq(z) удовлетворяет рекуррентному соотношению
Rq+1(z) = {z + a- l)Rq(z) + z^Rq{z), R0(z) = 1,
az
Ri(z) = z + a-l, R2(z) = (z + a - IJ + z, R3(z) = (z + a - if + 3z(
, ..., 2; ^
\Я+1к^
a - 1) +
d f d
/о = ez, /i = (z + l)ez, /2 = (z2 + 3z + l)ez, /3 = (z3 + 6z2 + 7z + l)ez,
h =
25z2
/5 =
15z4 + 65z3 + 90z2
/e =
- 21z5 + 140z4 + 350z3 + 301z2 + 63z
/7 = (z7 + 28z6 + 266z5 + 1050z4 + 1701z3 + 966z2 + 127z + l)ez.
7.13. ФУНКЦИЯ oiMb; z)
7.13.1. Представления и частные значения oFi(b;
1
2
3
4
5
а
7
8
9
b
5
^2
3
~2
1
9
1
2
3
2
5
2
7
2
9
2
г(фA-ь)/
Н-)с
Л 4 \
cos2Vz +:
sm2y/z
3 —3/2/ •
8
45 -б/2 Л
32 \
105 Г 3
64z3 [2лД
2Jb iB
2y/z sin ^
2VI-:
L 4 ^
E — о2
f
2у^СО82^)
г 45 г™
sin 2 VI-
- A5-42H08 2^ I
rF)^A)/
A+5ZJ€
сЬ2^ - 2
сЬ2у^
sh2-y/z
8
45 ^5/2 /
32Z V
105 Г
64z3 [(
oi^iF; z)
\fz sh2v/z
2ch2Vz -8Ь2л/^)
i „ 1 „u о f~Z ^.v. о /77
/~
3 ^_ 1

500
Гл. 7. Гипергеометрические функции
[7.14.1
Другие функции вида qFi I — ± щ z \ также являются элементарными и выражаются
\2	У
через вышеуказанные с помощью рекуррентных формул
10. 0FiF + 2; z) = ^-^[0*1F; z) - 0Fi(fc + 1; z)].
11.
-1; z) =
; z)
fe ^
0FiF + 1; z).
При Ъ ф — ±п функция oFi(b; z) через элементарные функции не выражается.
12.	oFl(b; z) +
13.	o^iF; -^)-c
14.	0FlF; -,)
-ьу
"A-6)
,14. ФУНКЦИЯ iF2(o; bi, Ь2; z)
,14.1. Представления iF2(a; 61, 62; z).
1
2
3
4
5
6
7
8
Q
1 О
11
12
13
a
a
a
a
a
a
a
a
a
1
2
3
2
1
1
61
a™
a —
a —
a —
a +
a +
L
U
3
2
2
1
2
1
I
2
1
2
2
1
2
1
2
1
0
1
0
n
62
6
2a 2
2a - 1
2a
2a + 1
2a™ 1
2a
2a+ 1
b
b
2n
1 h Г
ГГбЬ1^6 /b-i(
L
2 2 / 1
a - 1 Г 2
"И
2Г(«--
(§:
r(
т^2 / i 1 1 /2
I 1 <Х —|— — 1 II —
V 21Л 1
r2(a+i)(i!
тA-6)г ,
, -*! — b\z
Sin О7Г
7T(fe - 1)F - 2)
sin Ьж
z2
1 ^
{Bn)l}2 "
ii^2(ci; 615 Ъч\
z 1
a - 1 6 ^^ J
) Ы /e_,/aw_/e .
a- 1
1\/Zx2^2a
' ) *a — \l1\z) ~^~
Z2
1
' ~ I 177/ «--3/2v-2-J
' a —1/2 \^/
I-2a[/2_1/2(,)_/2+i/2
X3/2B(!) ч
z2)
IV 1\,гчЗ-2а/2
w]
¦(.^)(?)
\2/ a + l/2V^/ a-l/2lzJ
(«)]
14. 1F2[a; a^ i 2a - 1; z) +
	iF2 ( a - 1; a+ -, 2a - 1; z
, 1	\	2

7.14.2]
7.14- Функция 1F2(a; bi,b2; z)
501
15. 1F2 (а; а - -, 2а - 1; z J + iF2 ( а - 1; а - -, 2а - 1; 2 ) =
16. XF2 ( а; а - |, 2а - 1;
iF2 ( a — 1; a	, 2a — 1; z
(i2a — 2
IT. 1F2 U; а - |, 2а - 3; zj + ^^ iF2 U - 2; а - |, 2а - 3; z) =
- f) /а-5/2
18. iF2 (а; а-^,2а-3; z) + —Ц- iF2 (а - 2; а - i 2а - 4; z ] =
V	2	«1	V	2
19. XF2 ( 5; &? з - 6; z) + B6 - 3) xF2 Q; 6, 3 - b; z) =
2тг ,..
sin бтг
20. 1/
3sln бтг
7.14.2. Частные значения iF2(a; 61, Ь2; z).
Обозначение: U(z) = i J /0Bt) rft = /0Bz) + |[/0B^)LiBz) - /iBz)L0B
)].
61 62
iF2(a; 61,
9
10
11
ch2z-2zshiBz)
Io{2z) - 4z2U(z) + 2zhBz)
-\ch2z+	 - 2z shi Bz)
2	2z	l ;
- 2
2
1
2
1
2
1
2
1
2
3 2/oB,) ¦
- 8z2U(z)
5
2
т 3
7
2
- 4
3 Lf2,')«h2.-(l-2.»)^
;	V	; 2z
16z2
2
shi
C + 4z2)I0Bz) - C -
35z4
- 3z^ + 2z4) ^^ - C - z2 - 2z4) ch 2z - 4z5 shi Bz)
C0 + 9z2 + 4z4 + 16g6O1^ - 2A5 ~~ 3z2 - 4z4)/0Bz) - 32z6l/(z)l
1 1
i 3-
2
1 2
A - 2z2)/02(z) + 2z2/2(z) + 2zlo(z)h(z)
i[/oBz) + 2z/iBz) + A - 4z2)l7(z)]
i[C ^ 4z2)/2(z) - A - 4z2)/2(z) + 4zI0(z)h(z)]

502
Гл. 7. Гипергеометрические функции
[7.14.2
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
а
1
^2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
6i
1
1
1
1
3
2
2
3
2
3
3
?
2
2
2
2
2
2
5
2
Ь
ю | см
2
3
3
3
ь2
5
2
3
V
2
4
3
2
2
5
2
3
7
4
2
2
3
2
4
5
2
з
7
2
4
3
7
9
4
з^[A +
4 Г
15 [ V
5 rro
256 4
4
35z4
1 Г
з L
3 Га
32z2 L
2 fA
5 Г
I2gz4 ^
2 Г
5 [2C-2
1 [f* I
1 и 2 ^ '
4 Г
45 [ V"
5 rro
384z4 LV"
4 Hf
105z4^ ^
9 Г-
128z2 f
1 ГГ15
20z2 [(
15 Г
256z4 [
3 Г
Q Г
\(V
225z2 [(
1 1715
96z4 LA5
16 [-2
525z4 L"
4,2)/c
12Z2
- г2 Н
sh2z
2z
-u-
н„2)^
-4.24
*2)'o2(
9^.2 _
24Z2
iF2(a; 6i, fe2; ^2)
Bz) - 2z(l - 4z2)/iBz) - A -
о 2 4 '?(*)
-) 1 ( i - ) z2 (
+ 48z4 64z6)l7(z) (9 16 z
h2,<)/oW/lW-
-2z2(l-5z2+424)/2B)
, n о-2^ыBгI
2 j
0^2x^1 Bz) , /o 4^2xfr/ J
2z
1 4~4Wh-~ f- 4-41Sh2Z !
"jiZ Jiof-^zJ — @— Z + \AZ — OZ
z) - 4A - z2)I2(z) - C ~~ 4z2)
-16z4)l7(z) C 4z2)/0Bz)-
^ o^4 /2(z)
(л,) (О | л, ^^ ) Z2
-4.a№)]
2 /0(z)/i(^)]
1") z \
4)/oBz) +
+ 2,(9-8,2 + 16^)/1BZ)]
-(8-322 + б24-8г6)/2(г)]
22)shiBz)]
+ 222E-4г2)[/(г)|
4z3C 2z2)shiBz)
e hBz)
z
4
-2zE^4z2)/iBz)]
4C-2.2)^
ro(z)h(z)
z
}
+ 16z4)/0Bz) (9 36z2 144z4 + 64z6)l7(z)
3 + 48г2 16z4)/^(z) + A2 15z2
+ 40z2
-3z2-
-ш-
> + 56z
+ 180z
[45 + 7
о 4 8ЫB^) o o 2 .
Z
-16z4)«7(z)^G-4z2)/oBz)
о 4xSh2z 2 о 4^
1 ^ ^ 2z (" ' 5" "" )€
4 6xJlBz)
^(8 + llz2^4z4)/oBz)
2 16z4)/^(z) C1 + 48z2
2
2 + 240z4 64z6)C/(z) D5 +
6z2 - 16z4)/^(z) ~~ C0 + 71z2
+ 68z — 16z )I\ \z) — z
40z4 + 16z6)/f(z)
,-A-2,
24shZ2zl°
) 2z J
2D+ 9z2 4Z4I
lB*I
h2z +
z j
+ z2C5 + 56z2 - 16z4)l7(z)j
16z4)/2(z)
48z2 16z4)/0Bz)
- 2zE1 + 56z2 - 16z4)/iBz)j
75 + 64z2 - 16z4)/0(z)/i(z)j

7.14.2]
7.14- Функция 1F2(a; bi,b2; z)
503
iF2(a; bi, 62;
34
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
7 7
2 2
I 4
2
25
1 -
5
4
1
3
2
2
5
2
3
7
2
4
3
2
™ 2
5
2
3
7
2
4
2
2
2
2 -
2
5
2
5
2
1024z4 L
- A5 + 12z2 -^
- B1 + 16z2 - 4z4) ch2z]
2z	J
112z4
1225z4
C15 + 420z2 + 336z4 - Uz6)U(z) - A23 + 72z2 - 16z4)/0Bz) -
- 2(96 + 117z2 + 80z4 -
2A05 + 122z2 + 104z4 -
C89 + 324z2 + 192z4 -
- 2B10 + 173z2 + 92z4 - 16z6)
U(z)
3
8z2 °
ч/о2(г)„адвд+A„г2)%1
о [ z	z
^4 [(9 - 8z2 + 16z4)C/(z) - (9 + 4z2)/0Bz) + 2z(9 - 4z2)/!Bz)]
^j[2zD^z2)/0(z)
I$(z) - (8 - z2 + 2z4)/2(z)]
shiBz)
2z
2U(z)-
hBz)
2C™z2)/oBz)^F + z2+4z4
r2/ . Io(z)h(z)
— [A + 4z2)t/(z) - /0Bz) - 2zhBz)]
+ 8z4l7(z)
^[C ™ 4z2)/0Bz) - 2zC + 4z2)/!Bz) - C - 8z2 - 16z4)t/(z)]
^[z2(l + 4z2)/2(z) + D - 3z2 - 4z4)/2(z) - 4z(l + z2)/0(z)/1(z)]
16z2
1
2z

504
Гл. 7. Гипергеометрические функции
[7.14.2
КС
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
84
а
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
3
4
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
6i
2
[Г
5
3
3
3
7
2
'/
2
4
со | см
1
4
1
о,
1
-
1
2
1
2
I
2
1
2
1
?
3
4
5
4
3
2
3
3
2
2
3
2
3
2
7
4
2
62
7
2
4
3
7
2
4
7
2
4
4
7
4
3
4
1
3
2
2
5
2
3
7
2
4
5
4
7
4
3
-
2
5
2
3
'/
2
4
9
4
2
1/^2@.; 6i, 62; z )
45 Г sh2z ]
а Г т /о \ 1
/о 3 ^" ) (^ | ")/п|г>"'| | "E 1 4){/('*'1
5^4 |^v- ~~ "^ f z Х" ' ;*uv^ v" ' v-v-yj
О 9 9 9 9 9 ¦* 0 I ¦*•' J ¦» 1 \ % )
!YQ I ^4~2 I 1fi~44rr/ ч /0 ! 4~2ч тп(г>„\ ^~G 1 4~2чг /o^l
16 [o~2/o ^Jw2/ ч 0@ 4-2 Ow4v,2/.\ ^/n 4~2w /^\r /^\]
О ^Q 1 A~ 1 О "^ "\ ^ C. 1 0 ~^ "\ ^-.u o~ f7lr*~\
^16 Г / f )/ ( ) Z
ohc 1 1 1 ~2 | 4~4\r2/_\ л(-\ с | 7~2 | о~4ч 01 J 1 ч J
— ,f^- [erfi (v^I)- erf (л/2г)] 1 '
8z у 2z
1 + 4/—[e z erf (v2z ) — e"~ z erfi (v 2z )]
V 2
1 + 7tzL0Bz)
7Г
][ _l	j^i f2z)
2
1
2z2
Зтг
	[zLnBz) — LiBz)l
4z2
-^ [C + 4z2) ch 2z - 6z sh 2z - 3 + 2z2]
—-j-[8z2 - 6ttzL0Bz) + ЗтгB + z2)LiBz)]
-^ [2zA5 + 4z2) sh 2z - 3E + 8z2) ch 2z + 15 - 6z2 + 2z4]
4z"
_ /	Ге erf (v2z ) -f- e"~ erfi (v2z I
4 V 2z
J_ /il [e2- erf (v^)-ej8 erfi (v^I)]
16z V 2z
7Г
— Lq Bz)
4z
—^[ch2z - 1]
3-7Г
	Li Bz)
8z2
^^ A - 2z2 - ch 2z + 2z sh 2z)
2z4
	[3ttzL0Bz) - 3ttLiBz) - 4z2l
16z
-^ [C + 4z2) ch 2z - %z sh 2z - 3 + 2z2 - 2z4]
4zb
15 /тГ 	 /	 15
/ \ f erf (\/r> " \ 1 r» rrf! /л /о — \1
^[/oB*)-1]

7.14.2]
7.14- Функция 1F2(a; bi,b2; z)
505
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
а
1
1
1
1
1
1
1
1
1
1
1
1
1
1
со I смс
6
2
3
2
3
2
3
2
3
2
3
2
3
2
3
2
3
2
3
2
6i 62
2 *
2
2 3
2 I
2
2 4
5 5
2 2
- 3
2
5 7
2 2
- 4
2
со со
to | -я со
3 4
7 7
2 2
I 4
2
4 4
1 1
2 2
2
1
2
1 5
2 2
2 *
1 7
2 2
- 4
2
1 1
1 2
2
1 3
2
1-^2@4 fc»i, fc»2; z )
3 Tsh2z
2z2 [ 2z г\
1
z4 z
5 L 0 osh2z 21
8z4 Г° ° 2z J
±\2I0Bz)-h1{2z)-z2]
h ELoBz) -'}
JL[ch2z-l-2z2}
^[3.LlB,)-8,2]
-^ [2z sh 2z - ch 2z + 1 - 2z2 - 2z4]
4z"
z4
5 Lsh2z
2z4 Г 2z *
J 2z2]
*-\lhBz)-2-z2\
16z4 [4zLu(^
) 9 4z2j
— [4/0Bz) - 4 - 4z2 - z4]
ch2z + 2zsh2z
/0Bz) + 2z/iBz)
2IQ{2z)--hBz)
3 Г Оя,2ч8Ь2^ o 1
2z2 [^ ' "" ^ 2z ° " J
2 Г o 2,/iBz) o 1
Z2 [ " ^ - и — j
15 Г 2 2 sh2z1
°^ 1 ~2"iтп(^~\ fm 1 7~2>i ¦*¦ ^ '
z \_ z J
52j[2./1B*)-/oB«) + t/(,)]
z \ " z \
15 fro 1 °-2),
4 LlJ I 0^ л
foBz) (9 4z2)(/(z) 18z/iBz)]

506
Гл. 7. Гипергеометрические функции
[7.14.2
iF2(a; fei, fe2;
Ill
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
2
2
2
2
2
5
2
5
5
2
* 4
2
3 3
3 I
7
2
- 4
4
1
2
1
1
2
1
2
i 3
7
2
- 4
- 8z/0(z)/!(z)]
-Io(z)h(z)
z
^4 [C - 4z2)C/(z) - 3/0Bz) + 6z/!Bz)]
- z2/02(z) - D - z2)/2(z)]
6 \h{2z)
45
32z4
71
z)^C + 4z2)l7(z) + 2z/iBz)]
/1(z)^z2/o2(z) + B + z2)/12(z)
225
ch2z + 5	C + !
I - (9 + <
15
2^
16
z^
1 + 2z2 + tfz2L1Bz) + ^z
ch2z + z sh2z
• + 2D+;
¦G + 2z2)/2(z)j
г[тгA + 2z2)LiBz) - 7tzL0Bz) + 4z2]
- [3 - 3A + 2z2) ch 2z + 2zC + 2z2) sh 2z]
-ГотггC + z2)L0Bz) - тгF + 5z2)LiBz) - 8z2]
-^ [A5 + 27z2 + 4z4) ch 2z - 2zA5 + 7z2) sh 2z - 15 + 3z2]
/oBz) + z/iBz)
1 -

7.14.2]
7.14- Функция 1F2(a; bi,b2; z)
507
136
137
1 ЧЯ
139
140
141
142
143
144
145
146
147
148
149
1 КП
151
152
153
154
155
156
157
158
159
а
2
2
2
2
to to
to to
2
2
2
2
2
2
2
2
2
2
2
5
2
5
2
5
2
Ю | CM
ю I см
&1
1
1
]_
1
to | со to | со
to | со to | со
3
?
5
2
5
5
2
Ь
2
3
q
3
7
2
7
4
1
2
1
1
2
1
2
1
2
62
ю I см
3
7
2
4
3
2
5
2
3
7
2
4
5
2
3
7
2
4
3
7
2
4
7
2
4
4
1
2
1
3
2
2
3
1-^2 (a; bi, i>2; z )
Ц I 4~2) ch ^"
2 L , _2)'1Bг) т (о Л 2
z2 [V ' ~ ; 2: "V ^;J z 2V ^;
15 \(n 4~2ч i ^ /n 16~2)Sh2Zl
6 \a i -2u-r^-i n i 4-2i7l^l
z4 L ^ J
1 9
	 A + 2zz) ch 2z - 1 - 2z sh 2z
2z4
15 [л 2 ,, у 2w
322,4
-^ [2zC + z2) sh 2z - C + 5z2) ch 2z + 3 - z2}
^[l-Ch2z + ZSh2z]
45тг
64z4
-^ [A + z2) ch 2z - 2z sh 2z - 1 + z2]
4[l^/oBz)+z/1Bz)]
15 |"o <jsh2z "j
!Mi + /0B*)-H/lBJ
225 7г Зтг
—- [z sh 2z - 2 ch 2z + 2 + 2z2]
36 2
^ [C + 4Z2) ch 2z + 10z sh 2z]
о
3
2z
Z+ у S
1 Г 2 /iBzI
3 |^ o(-~) ( - J ^ J
2C+ 4z2) Г /iB^)l
3z2 [ u ~~ z \

508
Гл. 7. Гипергеометрические функции
[7.14.2
160
161
162
163
164
165
166
167
168
169
1 7П
171
172
173
174
175
176
177
178
179
180
181
182
183
а
5
2
ю I см
5
2
5
2
ю | см
5
2
ю | см
5
2
5
2
5
2
5
см ю | см
ю | см
ю | см
Ю I CMI
0
2
ю | см
5
2
5
2
5
2
5
2
5
2
5
2
3
6i
1
2
1
2
1
1
1
1
1
1
со | см
со I см
3
to | со to
3
2
2
2
2
2
3
3
3
7
2
7
2
4
1
2
7
2
4
1
3
2
2
3
7
2
4
со 1 см
2
Q
7
2
4
2
3
7
2
4
3
7
4
7
2
4
4
1
2
1-^2 (a; bi, i>2; ^ )
5 IV Ч 1 fi~2 I o~44sh2* ГЧ 1 °~2Wh°~l
9 Г / (e?9's\ 1
C0 1 <"*7"*2 I 4"'^) 6E 1 *"*"*2)/пB~н
3 °
3 ° 1
4 Г 2/ ч 1,ч,ч / 2чЛ2(^I
з L ^ z2 \
-^ [2zD + z2)/0(z)/i(z) - 2z2/^(z) - (8 + 3z2)/2(z)]
1
3z
1 T/iBz) o 1
3 [ z " J
2 Г о гч^С2^) /o J
8z4 p i — )c — ЗС1 2z J
ZiOi 1 a, IIQIAa,) 10 I OZ I
z4 L ^ J
3z2
-^[C + 4z2)/0Bz) - m(z) - 6z/iBz)]
^ [D + z2)ll{z) + z2/02(z) - 4zI0(z)h(z)}
^[/12(z) + /o2(z)^^/o(z)/1(z)j
?-[3U{z)-3IoBz) + 2zh{2z)]
^I1(z)[zI0(z)-2h(z)]
75 Г shiBz) sh2z 1
3 ^ 1 ch ^"
16z4 L" 2z z -"^^j
15 Г ^iBz)l
z4 [ ° " z J
— [8 + 36z2 + 16ttz2LiBz) + ?rzA5 + 4z2)LnBz)l
8

7.14.2]
7.14- Функция 1F2(a; bi,b2; z)
509
184
185
186
187
188
189
190
191
192
193
1 см
195
196
197
198
199
200
201
202
*?пч
204
205
206
207
208
209
а
3
3
3
3
3
3
3
3
3
3
Q
3
3
3
3
со со
3
3
Q
3
3
3
3
3
3
bi
1
2
1
2
1
2
1
2
1
2
1
2
1
1
1
1
]_
1
3
2
3
2
3
Я
3
3
2
2
2
2
5
2
Ь
2
5
7
2
7
2
1
со 1 см
2
ю | см
7
2
4
1
со 1 см
2
5
2
'/
2
4
со 1 см
2
ю I см
7
2
4
2
5
2
7
2
4
7
2
V
2
4
7
2
4
1/^2@.; 6i, &2J z )
— [2B + z ) ch 2z + 7z sh 2z]
4
— [16 + 8z2 + 12ttzL0Bz) + тгC + 4z2)LiBz)]
16
ch2z + - sh2z
2
Го~2 1 o^4 о „,/q | о~2\т /"o~\ | -тг/Л i 7~2 i /|~4\T /o~\l
64z4
-^ [2zA5 + 10z2 + 2z4) sh 2z - 5C + 6z2 + 2z4) ch 2z + 15]
i[B + z2)/oBz) + 3z/1Bz)]
I0Bz) + -h{2z)
3 Г о sh 2z о 1
32z2 L 2z V ; J
z4L ~ ~ z " ~~ J
1 Г 7Г 2\/\ / \1
1 Г sh2z 1
Q 1 A1"
4 L 2г J
^_[4T,L0B.) + 8,2 - .A - 4,2)LlB,)]
15 о О О
128z4
—- [C + 6z2 + 2z4) ch 2z - 2zC + 2z2) sh 2z ~~ 3]
1 Г JiBz)l
2 [ °^A'^ z J
3 Г 2 sh2^1
1Я 2 | ^ ^ 9
15 [ о 2 о о о 2 sh2z]
4 '" ' " j^ui^^j ^A 1 ^ )
32z2 L 4z^ ^ ] vK—)\
ГЧ~2 Атт "J г,(^ "\ 1 тг^Ч 1 4~2W -, Iе* ~Х\
-^[zB + z2) sh2z - A + 2z2) ch2z + 1]
225 г тг 2 i
128z4 Uz^3 ' " ^ u^"^ ^ l^^ J
45 ^2
16z6^ 1 - )c — -- J

510
Гл. 7. Гипергеометрические функции
[7.14.2
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
а
3
7
2
7
2
7
2
7
2
7
2
ь- | см
7
2
7
2
7
2
7
2
7
2
ь- 1 см
7
2
7
2
7
2
7
2
7
2
7
2
to | -я
7
2
7
2
7
2
7
2
7
2
&1
4
1
1
?
1
?
2
1
2
2
2
1
1
1
1
1
1
3
2
3
2
3
2
3
2
3
2
2
2
2
2
5
2
2
4
1
9
1
3
?
2
5
2
3
4
1
3
2
2
5
2
3
4
3
2
2
5
2
з
4
2
2
3
4
5
2
3
iF2(a; 6i, fe2; ^2)
18 2
z
— [3E + 16z2) ch 2z + 2zC3 + 4z2) sh 2z]
— [A5 + 44z2)/0Bz) + 2zB3 + 4z2)/iBz)]
— [A5 + 4z2) ch 2z + 18z sh 2z]
1 Г 2 ^ 2 /iBz)l
15 [ ; z J
Z + у S
p/ic 1 q-,2 | 4«4w /o«1 Qhn I 1 1 ~2 1 4-4'\ "^ '
5z |_ z J
-^ [A5 + 22z2)ll{z) + 18z2/!2(z) + 2zB3 + 4z2)/0(z)/i(z)]
— [A5 + 4z2)/0Bz) + 16z/iBz)]
15
^ [A5 + 4z2)/2(z) + C + 4z2)/2(z) + 28z/0(z)/i(z)]
/oB,) + |/lB,)
^ \aJ2(-\ A i~2\ -^1 (z) /-, л _2 \ -^0 (z)Il(z)~\
15 L ° ^2 " z J
^ [(8 + 5z2 + 2z4)/2(z) + 2z2(l + z2)/2(z) - 4zB + z2)I0(z)h(z)]
1 Г o o 2 sh2^1
15 L h^ !-(-'-) z j
15 L " °^"^ z J
1 Г sh2z 1
5 L z J
2 [ 2 hBz) 2 0 1
15z2 [ " z U "" J
2 [/л ( ^ 2 4^/iBz) o/o 2^r /o J
5z4 [ " " z u "" J
15 ^ ul-j il-j ! ( I - j ^ j
5 ГЫ-} ' ° z j
Г4~ Г- /-Ч Г, /~Л I o-,2i-2/ \ /-1 o^2\r2/ \1
2 L Ov^z-'lv'4'/ ' z^ ^0 \*) \l ^^ /il\^/J
^ [4z(l + z2)/0(z)/1(z) - z2li(z) - D + 3z2)/2(z)]
3 Г oJ2 sh2zl
10z2 L "" 2z J
5z2 [ u ^ ^ z \

7.14.2]
7.14- Функция 1F2(a; bi,b2; z)
511
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
а
7
2
7
2
7
2
7
2
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
4
6i
5
2
3
3
4
I
?
1
2
1
2
1
2
1
2
1
9
1
1
1
1
1
1
1
со | см
со | см
3
со I см
со I см
2
2
2
ь2
4
3
4
4
1
?
1
со I см
2
5
2
3
7
2
1
3
2
2
5
2
3
7
со 1 см
2
5
3
7
2
5
2
3
1F2 (a; bi, i>2; z )
6 Г ^ о_ о oJ2 /!Bz)]
5z4 [-A 1 - и(-~) (- 1 ^ ) ^ J
8 \т2(~} I2(~\ *4i о«2ч7о(^)^1(^I
^ [z2li(z) + B + z2)/i2(z) - Szlo(z)h(z)]
48 Г 2 Io(z)h(z) 2 9 2 1
5z4 [^v^ ; z ^oi*-/ "jn^/j
— [24 + 174z2 + 8z4 + ttz2G1 + 4z2)LiBz) + —A05 + 68z2)L0Bz)j
— [6D + 5z2) ch 2z + zE7 + 4z2) sh 2z]
— [96 + 112z2 + тгA5 + 52z2)LiBz) + 2ttzD5 + 4z2)L0Bz)]
— [2F + z2) ch 2z + llz sh 2z]
^^[wC + 18z2 + 8z4)LiBz) - 3ttzA - 12z2)L0Bz) + 68z2 + 16z4]
ch2z + - sh2z
3
[8~2 I 3^~4 °7г~C I 3~2 4~4)Ь1(О~) 1
128z4 L"" ' """ """\" ' "^ ~*" /^uv—;
-[F + 7z2)/0Bz) + z(ll + z2)/iBz)l
6
1 Г 2 o 2 sh2^1
96 L " z J
6
64z2 L ~ " 2z "" "\
/0Bz) + ^/iBz)
11D 1 O-,2 | i^w4\ /о | -10^2 i|3^4\ 1 ^^
— [бб + 8z2 + тгB3 + 4z2)LiBz) + —A5 + 44z2)L0Bz)j
1 Г 2 sh2z o 1
24 r- 2z Jc"^^I
1 [sSh2z ! ch-~l
5 2 2 4 2 4
1 9-*lBz)
1 Г 2 2xsh2^l
32z2 [I ! - )c — -I — ) 2^ J
i[f/lB,) + /oB,)]

512
Гл. 7. Гипергеометрические функции
[7.14.3
iF2(a; 6Ь b2; z2)
260
261
262
263
264
265
266
2	I
2
5	5
2	2
5	з
2
5	7
2	2
3	3
3 -
2
7 7
2 2
128z2
1
15
[б + 8z2 - — C - 20z2)L0Bz) - тгA - 4z2)LiBz)'
- 2?rzC - 4z2)L0Bz) + тгC +
^['o^-a-*2)- z j
* [3!^?-C-4*»)ch2*l
, ,„	C^4z2)ch2z,
32z4 L 2z V	;	J
r^ [^C - 4z2)L0Bz) - тгA - 4z2)LxBz) - 6 + 8z2
7.14.8. Представления iF2(a; bi, 62; —z).
2. i
, 6, 2 - 6; -,) -
1; - + 6, - -6;
' 2 ' 2
"'2
sln26?r
3
4
5
6
7
8
9
10
11
12
13
a
a
a
a
1
1
1
1
1
1
a + 1
1
2
3
2
6
6
6
6
6
Q
О
2
62
a + 1
a + 1
с
6
' + 3
2^6
3^6
6
i^2(ct; 6i, 625 —z )
21^2aaz^2a[rBa)cosa7r^CBz, 2a)]
-21™2aaza[rBa- l)cosa?r + SBz, 2a- 1)]
24-*-cF - l)(c - l)z2-b-ceb+c-3, b-cBz)
«r>5-26^2-26/L i\2e /ro«v\
2 Z @ - 1) 526-3,0(^2:) -
- r2F)z2b[sin 67ryoBz) + cos бтг J0Bz)]
TB6)BzIm26I72&-iD^, 0)
7r(fe^l)[E26-2B^) + ctg67rJ26^2Bz)] =
тгF — 1)
sin2fe7r
-A - 6)B - 6)[E3^26Bz) - ctg67rJ3^26Bz)] =
_ тгA-Ь)B-6)[л (o->) j (o^
z sln267r
^^-TF)Hb_]l/2Bz)

7.15.1]
7.15. Функция 2Fs(ai, Q2; 61, 62, 63; z)
513
7.14.4. Частные значения li^a; fc»i, 62; ^
62
iF2(a; 61, 62; -z
1 5
CBz)
^S B.)
4 4
1 - 2-s/^z[sin2zCBz) -cos2zSBz)} = 1 - л/2тгг C/3/2D;z, О)
[sin2zCBz) - cos2z5B^)]
д/2 - y/Tr[cos2zCBz) + 8in2zSBz)]}
8^72
15
7.15. ФУНКЦИЯ 2F3(ai, a2; bu b2j b3; z)
7.15.1. Представления 2^з(«1, «25 6i, 62, &з;
- -b; z = 1F1 (a + 6- 1;
1F1 (a - 6 + 1; 3-26;
2
3
4
5
6
7
8
9
10
11
ai
a 6
a a
a a
a a
a a
71 + 1 71
— 71 6
a2
+ 2
+ 2
+ 2
1
~ 2
+ n
a + b
2a
1
2
3
2
1
6
62
a + 6
2
6
6
2a
2a
6
2
a +
2a-
b
2a
2a
63
6 + 1
2
-6
+
+
+
2
+ 1
2
1
2
•
1
1F1 (a; a
0F1 (б; |
1 Г 26~
2 UBa-
chy^ 0F1
x Ыр1
v^ U l
= Г Г2a -
Bn-l)! (
V
L(b)nJ L
2F3(ai,
+ 6; 2y/z)
) 0F1 (l4
l)v^J
/ 1
f72
1 V
V 2'
/ 1
2/
2 \2n —1
a% 61, 62, 63
1F1 (a; a + 6
-2a- 6; -) =
x h-i {*
:l)/2
X
T 1 o, 1 T
2 ' " 2
2 ' "
- ) =Г|2а-
Д /20-1/2 (/
' z ' ~~~~a sh л/
r 6-1 / 0 ^\
Ln ( WZ)
^)/2а-ь(л^)
; 2^ ) ±
г)
Z X
X ha-3/2 (Vz)
17 А. П. Прудников, Т. З

514
Гл. 7. Гипергеометрические функции
[7.16.2
i, 62?
12
- 2n -2n
Bп)!
Dп + 1
7
1
2
3
4
5
6
7
.15.2.
ttl <22
1 3
4 4
1
2
1
2
3 5
4 4
3 5
4 4
1 1
5 7
4 4
Частные
6i 62 63
1 1 1
2 2
3 5 3
4 4 2
5 3 7
4 2 4
i » 2
2 2
1 3- 3-
2 2
3 2 2
2
» 2 5-
2 2
значения 2^?з(«1, «2; &i5 62, &з; 2;).
2-^"з(<21, С12? 01, 02, О35 Z)
См д/ Z /q yy Z J
3 / 4/ / 4/
—— erf ( y/4zj erfi f л/Жг) +
+ ^Dz)/4 [e^ erfi f #il) - e2^ erf f ^)]
V?r L \ / V /J
- [chi B-x/z) ™ In B-ч/г) - С]
2
z
7.15.3. Представления и частные значения
«2; 6i, 62, Ьз; —
1
2
3
ai
^те
те
2
1
a2
2
1
1
2
те
9-n 1
1
2
3
2
62
9-n
— те
2
3
2
Ьз
3
2
1
2
2F3(ai, 0
Bте + 2)!
Dте + 4)! v " v^v
x [— sin 1/
Bn)! "
X / f /*
,2; 61, 62j ^3j ™"^)
/j^n+3/2 x
z Y2n+5/2 W~z) +
+ СОБл/z J2n + 5/2 (V^)]
J ) - COS л/z Yn + 1/2 {Vz]\
- ci B\/Jz)]
7.16. ФУНКЦИИ ВИДА 0Fq((bq); z), q = 2, 3, ...
7.16.1. Частные значения о-^гС&ъ Ьг; г).
1
4Л
ii
61
1
3
?
3
4
3
62
со | to
4
3
5
3
H-
1 г
3y L
2 г
3l/2 L
0^2F1, 62; *) [3/ = 3^
+ 2е-/2сов(^|)]
/ 1/ 7Г \ 1
2/	2 2//2 ?Qg j Yo ~h 	 I
V 2 3 / J
g2/	2e 2//2 j»Qg j уз — 	 	j
V 2 3/J
7.16.2. Представления и частные значения oFs(bi, 62, 635 z)
1. 0F3 fi a, a+i; z) +^^0F3 f§, a + i a + 1; z) = 0^ Ba;

7.16.3]
7.16. Функции вида oFq((bq); z), q = 2, 3, . . .
515
62
63
6i
6з
Ьз
2а
2а- 1
2а + 1
1
1
з	,
[]Ffc-l) —0F3Fi-l, 62-1, 63 -1; *)
dz
61
Г2Bа) BV/^I 2а [ber2amlB/) + bei2a^i(l/)]
ГBа^1)ГBа)(|)^4ах
х [ber2a-2B/)bei2a_2B/) - ber 2а_2(з/) bei2a-2B/)]
x [Ьег2аB/)Ьег2а(у) + bei2a(y) bel 2a(y)]
10
11
12
13
14
15
16
17
18
19
20
21
1	1
n n — те — — n — m — l
2	2
(-l)'(n-l)!
t(l/2)n]
i {n-k)lzk
fc=O
— (ch ж + cos ж)
ber(t) = - [JoO
d
[n = 1, 2, 3,
fo(x) + /0(ж)
[t =
—jp:
8 у z
(sh ж + sin ж)
(ch ж — cos ж)
{beii(y)[berC/) - bei C/)] -
? -\/ Z
^л/z
2-\/z 1	X
	r-rrfsh z -— sin ж)
64z3/4l	;
-beri(j/)[ber(j/)
7.16.3. Представления и частные значения oi
1. 0F3
2, fe; ^
-, a, 2 - a; -;
'Ba-l;
C - 2a;
17*

516
Гл. 7. Гипергеометрические функции
[7.16.4
У =
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
а
1
	71
2
1
2а
3 — а
1
	те
2
Bа;
Bа; -
ГBа)
^ГBа) B
()
3Bа-1)
+ Sin
sin 2аж
тгA-о)B-о)
sln2a?r
[J2-2a(y)ha-2(y)
ber (ж) — 2 viz [beri(ж) + beii(ж)] — 4\/z bel (x)
= ber (ж) — ж berf (x) ¦— Ay/z bel (ж)
ch у cos t/
ber(ж)
1
4v/4i
[sh |/ cos t/ + ch t/ sin i/]
-bel'(ж)
ж
sht/sint/
64z3/2
[bei (ж) — x bei ;(ж) + Ay/z ber (ж)]
- [ch у sin у — shy cos у]
7.16.4. Представления oF^bi, 62, 63, 64; 2) и o^g-i
1.
2.
1234
-, -, -, -; z =
О D О О / О
2тг
I exp I у cos — I cos I y sin
5 I V	5 / V	5
4тг
. 4тг
exp [ 2/ cos — J cos I y sin —
5 / \	5
q q
;
; * =-
[у =
7.17. ФУНКЦИИ ВИДА pF0(-w, (aP-i); ^), p = 2, 3, ...
7
1
2
3
.17.1.
—те
—те
11
редставления 2
«2
a
t + 1
(a)n(-z)ni/
1 /F 1/B
2b6
F0(^n, a;
"i (-n; 1 -
Z) Mn+1/2
*)-
2F0(oi, a2; z)
a — те; —z"" ) =

7.18.3]
7.18. Разные гипергеометрические функции
517
л
к
«1
«2
e-l/Bz
1+^
2
2Fo(ai, a2; z
) / 1\
1	 /i\ / • \
) / Ж e~l/(%z) Н\У | q= )
V Z n + 1/2 I 2z /
ГГ 0 < argz ^ Зтг/2 11
[l-тг/2 <argz ^OjJ
7.17.2. Представления
~n, a; —z).
1
2
3
4
—те
-—те
те
2
—те
«2
те
n + 1
1 - те
2
2
«к-,»
2 1
2™nzn/
71 + 1
*.-е)
V г е [7-"-i/^
( l) J f l )}
[z(n + l) = -l
7.17.3. Представления 3Fo(~n, ai, «2; ^).
1,^1 =
1.
7.18. РАЗНЫЕ ГИПЕРГЕОМЕТРИЧЕСКИЕ ФУНКЦИИ
7.18.1. П ре д став л ения \Fq(a\ (bq); z).
ml
; z ==
|ГП + 1 У171/ Я
.fe=O
21гтг
q i—	AKTT	. ZIC7T
yfc = VI = cos	h i sin
g	g
2.
1; n, 61, 62,63; ^) = (n-
x 0F3Fi - n + 1, 62 - n + 1, 63 - n + 1; z) - Y^ ПA - 6i)fc^™
k=l1=1
7.18.2. Представления 3Fs(ai5 аг, аз; 61, . . . , og; 2;).
, 1 + 3a — 6,
,4
-k
n = 1, 2, 3, . . .].
1	2 , 6 b + 1 За За
l + 3a-6	3a - 6 \ - p (h л *
7.18.8. Представления 4.Fi(—n, ai, аг, аз; 6; z).
-За- 6; -8t
CL\	U2	Я3	CI4
4Fi(ai, 02, аз, «4; 6; —^
— те2а + те a a -j—
-—те 1 + Ti a 1 — a
2г
(-l)»(n!J2-2»(-*)»L-2-2» ^J L"a
Ja+n (a-Vi>) J_a+n+1 (z-
+ J-a-n (z-1/2) ¦
2г
2-v/z sin an

518
Гл. 7. Гипергеометрические функции
[7.18.3
3
4
5
ai
— те
те
2
те
2
2
1
1
a2
+ те
— те
2
— те
2
аз
а
1 + тг
2
3 + те
2
а4
2
1 +
2 +
а
те
2
те
2
6
3
2
1
2
3
2
4z(n + 1
X J-a
l) У <
*3/4(П +
4F1 (ai, a2,
[j +
)A — a) sin аж L
+ n + 2 (^^1/2) ^ •/-
Г _1/4 Г . / 1
+ cos 1
аз, «4;
„и
7ГП\
2 J
— -
тгте
2
Ь
/„
7Г?
~2
)
! X
/2) Л^п^2 (Z^1/2)j
( ^г/2\
+ 1/2 ^ J +
Лг+3/2 yz J ¦
г\ , v "I
™ 1 J—n — 3/2 \z )
/ V 7 J

Глава 8. G-ФУНКЦИЯ МЕЙЕРА И Я-ФУНКЦИЯ ФОКСА
8.1. ВВЕДЕНИЕ
В этой главе излагаются свойства Gr-функции Мейера и //-функции Фокса и приводится
таблица преобразований Меллина, объединенная с таблицей представлений через G- и
//-функции, для широкого класса элементарных и специальных функций. Эти функции
/(ж) обладают тем свойством, что их преобразования Меллина
со
/*(«) = \xs-1f{x)dx	A)
о
выражаются в виде отношения произведений гамма-функций
где dj, 6fc, ci, dm — комплексные, a Oj, /9д., 71, Sm — положительные постоянные. В неко-
некоторых случаях значениям f*(s) из таблицы 8.4 соответствуют функции /(ж), для которых
интеграл A) расходится, но сходится один из интегралов
*(8)x~ads = /(ж),
L
где L = L^oo или L+oo, L^(L+) — левая (правая) петля (см. 8.2); для обозначения этого
соответствия используется символ /(ж) <— /*(s).
Указатель частных случаев ^-функции Мейера и //-функции Фокса позволяет находить
их выражения через элементарные и специальные функции.
Использование преобразования Меллина дает возможность вычислять интегралы от
произведения функций, входящих в таблицу 8.4.
Пусть интеграл приведен к виду
dx
тогда в силу формулы 8.4.1.2 его преобразование Меллина /*(s) равно произведению
преобразований Меллина /*(s), /2 (s) функций fi(x), /2(ж) и, следовательно, также имеет
вид B). Воспользовавшись формулой обратного преобразования Меллина
7+гсхэ
1	f	*	—8
2ni J
7^*00
и формулой 2.2.1.7, можно найти значение /(?).
Пример. Вычислим интеграл ^
/@ =
о
Он представляет собой свертку (для преобразований Меллина) функций
Согласно формулам 8.4.3.1, 8.4.1.5, 8.4.3.2
fi{s) — Г(—s),	Re(s) < 0.
Преобразование Меллина /*(s) интеграла 1{з) имеет вид
/*(s) = Г(а + s)r(-s),	-Rea < Res = 7 < 0.

520
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.2.1
Воспользовавшись теперь формулами 8.4.2.5, 8.4.1.7 или 2.2.1.7, получим
a-1-x-x/t , _
dx = Г(а)
Rea,
Отметим также, что таблица 8.4 может быть расширена с помощью формул из раздела 7.3-
18, так как каждой из функций pFq((ap); (bq); z) таблицы 7.3-18 формула 8.4.51.1 ставит
в соответствие функцию f*(s) вида B).
8.2. G-ФУНКЦИЯ МЕЙЕРА G™ (z
8.2.1. Определение и обозначения.
С-функция Мейера порядка (in, n, p, q), где
формулой
ы \ =
(Ья)
определяетя
— fr
+ 8, . . . , Ьт + 8, 1 — tti — 8, . . . , 1 — пп — S
1 + S, . . . , ар + S, 1 - Ьт+1 - 8, . . . , l-bq - 8
? ds;
интеграл сходится, если выполнено одно из следующих условий:
1)	L = Lioo; с* > 0,
2)	L = Lioo; с*
argz\ < с ж;
arg z| = с*тг, (д — рO < — Re /x;
3) L = L^oo] p < g, 0 < \z\ < оо или р = д,
= 1, Re/i < 0;
или р = д, с*
0,
4) L = L+oo;
здесь
> д, 0 <
Р + q
< оо или р = д,
или р = д, с* ^ 0, |z| = I, Re/x < 0;
•1,
7 = lim Re s.
Контур Ь-оо (L+oo) представляет собой левую (правую) петлю, которая расположена в
некоторой горизонтальной полосе, начинается в точке ^оо + щ\ (+оо + i(pi), оставляет все
полюса подынтегральной функции вида s = — bj — к, j = 1, 2, . . . , га, слева, а все полюса
вида s = l — a/ + A;,/ = l,2, ...,n,fe = 0,l,2, ... — справа от контура и оканчивается
в точке — оо + i(f2 (+оо + i^>2)> где ip\ < ^2- Контур Ljqq начинается в точке 7 ~~ ^о0 и
оканчивается в точке 7 + *оо5 разделяя указанные полюса так же, как и L±oo.
Если в определении Gr-функции под знаком интеграла имеются только сомножите-
сомножители с параметрами bk (или только с а&), то в этом случае используется обозначение
~17П	' I соответственно
8.2.2. Основные свойства.
1. G-функция симметрична по параметрам ai, ..., ап из (ap), an+i5 . . . , ар из
(ар), 6i, . . . , &m из (&g) и 6m+i, . . . , bq из Fg) в отдельности.
2.
Представление в виде комбинации обобщенных гипергеометриче-
гипергеометрических функций:
к) \ _ 7 ..
— Ьт+1,
\ v' (=0 при выполнении условий 1), 3) или 2), 3) из 8.2.1.
3.
[р ^ q; условия 1)-3) и bj - Ьк ф 0, ±1, ±2, . . . ; j ф к; j, к = 1, 2, . . . , т].
(Л$g О/]_ • » # # * tt jg ^ть j -*- 	I	 ?^Х *жk j * * * 1 -*- 	I	 ^ттъ ^к
•к — Ьт+1, • • • j ttfc — 6g, 1 + ате+1 —- afe, ... , 1 + ftp — С

8.2.2]
8.2. G'-функция Мейера
521
. + (Ьд)-ал; IzU
. + (ар)г — ак
[р ^ <?5 условия 1), 2), 4) и a,j — ак ф О, ±1, ±2, . . . ; j ф к; j, к = 1, 2, . . . , п].
ОДеСЬ lfl.pl — flfc = tti — пк , . . . , Лк^ 1 — flfcj fl-fc + l — flfc, . . . , ftp — Qjk И 1 [111 — flfc5 •••) @>m — O-feJ =:::
= r(ai - afe) . . . r(afc^i - afe)r(afe+i - afe) . . . Г(ат - afc) (компонента ak - ak отсутствует).
Случаи, когда среди разностей bj — bkl clj — ak есть целые числа, приводят к более сложным
выражениям.
Разложения в суммы (j-функций:
sin (an+i — Ьк)ж ... sin (ap — Ък)ж
5. G™qn ( z
(ар) ] _ ^m + n^
п^р у^ Ш
^—^ sir
. * . Sin
x e
7ri(m+n —p —
Sin (ttfe ^ fem+lOT . . . SJn (flfc — Ьц)тг
— oi)tt . * . sin
x e
—i;
/ ]
p —m —n+1
, (ар)'к
[множители sin (bk — Ьк)тт и sin (ад. — «й)тг отсутствуют],
fe-l, 6fc + l, • • • , bq.
7. Функция
аналитична по z в секторе |argz| < с*тт. При с* > 0, р =
функции, удовлетворяющие условиям 3) и 4), аналитически продолжают друг друга через
окружность z = 1 в этом секторе. В случае с* ^ 0 сектор аналитичности отсутствует, но
при р = q две указанные аналитические при \z\ < 1 и \z\ > 1 функции имеют один и тот же
предел при z —У 1 вдоль луча argz = 0, если Re/i < 0, с* = 0. При \z\ > 1, р = q, с* = 1
для выделения главной ветви функции
проводят разрез (—оо, — !)• Если
> 1,р = дис* > 1, то при 0 ^ arg z ^ 2тг в проведении разреза необходимости нет.
Формулы понижения порядка и вырождения:
. Gpq
9/nfTTi
. (jp,
10.	Hm
11.	Hm
12- Hm
|bi|-»oo
13. Hm
I A —
/-iin, n — 1
_^ (dp)
(%) \] _
(flp)
. , ap
	 _<-fm, n — 1
	 /-ym-1, n
(Ья-i)
14. Gwpq I z
15.
Формулы симметрии и сдвига:
(ар) + a
(Ь,) J~"P" V (bq) + a
[arg(l/z) = -argz].
— Г*™

522
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.2.2
Соотношения специального вида:
16. G™" i z
17. Gpq
18.
19.
a, {ap~i)
(bq-г), п±1
( 1ur,m-\-i,n-i
(ap_i), a
a± /, Fq_i)
&±I5 (Op-i)
F^i), b
Л, Op)
A(k,b1),...,A(k,bq)
Соотношения между смежными функциями:
20.
21. (ap ^
22. G"
23.
Jpq
i
+
= G™\z
— 1, Q-2, . . . , ap
(aP-i), dp — 1
(ap_i),
m —1, n
a2, • • • , aP-i
— A;,
[те, те ^ 1].
[1 ^ n ^ p- 1].
[1 ^ n ^p- 1].
• , <xp_i
Формулы связи с функциями аргумента ze гж:
24.
25.
26. G
27.
= 1 UW.'G»
, П I	—«7Г
WLlU-r.»
о-гЪт+1тгпт+\,п [ zeiw
r^m, те-}
(bq)
(ap)
- 1].
(ap)
0, 1/2,
a + i&, a — ib, (ap—2) \
0, F9-2), 1/2
¦ iG™ali<nl ze%7X
1/2, (Ь,_2), 0
--гаж Ьж rim, n — 1
а + ib, (ap-2), a — ib
a — гб, (ap_2), a + i6

8.2.2]
8.2. G'-функция Мейера
523
28.
29. G"n
F,)
К)
(Ья)
m+n — q
П sir
, (ag),
sin(Fm)' - 6Л)тГ
8т(ан-Ьк)тг
\z
Здесь sin ((bmy - bh)w = f\ sin (bk - bh)w.
on
кфН
Формулы дифференцирования:
(ap) I _ ^^-l^m^ + l
, <?+2 I V /
V
0, ±1, ±2, ...;
-a, (op)
F,), \-a
фд
ahl (bq), ah
arg l-(-l
TP+l,qf+l
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
(bq),
F,
- - k, (ap)
dzk
d^
dzk
~dz
~dz
(ap)
(bq)
(ap)
(bq)
= (^l)kza^
^pq
CL\ — k, CL2, . . .
(aP-i), aP — к
(M
— 1, tt2, • • • , d
{b4
bi + k, 62, • • • , bq
<7Г .
[m > 1].
[те ^ g^ 1].
41 ^^
(%)
(bq)
(I, 61), ..., A(I, 6g), A(r, A;)
[I, r = 1, 2, . . .; с*, д см. в 8.2.1]

524
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.2.2
\(l, ai), ..., A(I, ap), A(r, 1 - k)
i(r, 1), A(I, 61), . . . , A(I, 6q)
[I, r = 1, 2, . . .; c*, /1 см. в 8.2.1].
Дифференцирование (^-функции по параметрам в общем случае не приводит к G-
функциям. Дифференциальное уравнение, которому удовлетворяет функция
, имеет вид
42. [(_
(Ья)
3=1 х	' к=1
Это уравнение порядка max(p, g) имеет две (z = 0, оо при р ф q) или три (z =
= 0, ^x)m+n^g, 00 при р = q) особые точки. Если р < g (р > д), то z = 0 (z = 00) —
правильная, a z = 00 (z = 0) — неправильная или существенно особая точка; если р = д, то
все три особые точки правильные.
43. u = ul{z) = e(m+n^1)bfe
[А; = 1, 2, . . . , q- bj - bk ф 0, ±1, ±2, . . . ; j ф к; j, к = 1, 2, . . . , q].
44.	.1 = u)[z) = R<?(z) =
45.	u = ul(z)
Zl
bhj bj, (aq)
bhj bj, (bq)
46. t* = ^(z) = <Mz)
я
[j = l, 2, ..., q; эфк].
[фч 7^0, ±1, ±2, ...].
№9 = 0, ±1, ±2, ...]•
где функция СдлС-2? д) мо^^ет быть представлена формулами
47.
48.
Здесь cogh = 1,
соотношениями
Cl2h = ЩФ2 + bh),
jCj2h = ЩФ2 +bh
zi) J^ TV/ Г^П^^	I'1
= 0, j = 1, 2, . . ., а остальные коэффициенты Cjqh определяются
bh),
bh) -
-2) -
bh - q + 2)
bh +
+ 3)
3)
)
6Л - g + 4)
3)
- g + 4)
(9-3)!
(9-4)!
9-2
X Cj + fe-, + 1,,,/» + (-1)"
где Д — разностный оператор 7.2.3.74-75.

8.2.2]
8.2. G'-функция Мейера
525
49. R(x) = f\(x + 1 ~~ aj), Q(x) = f\(x ^ bj),
3=1
причем справедливы соотношения
3=1
q, hf
k\
= 0, 1, 2,...].
Функция <pq(z) совпадает с правыми частями любой из соответствующих формул
8.2.2.53—56, приведенных ниже.
ФуНКЦИИ ?qh(z, фц) И (fq(z) В ОСОбоЙ ТОЧКв Z = (_1)ш + п~9 имеюТ5 вообще ГОВОрЯ,
соответственно степенную (при Иефд < 0; фч ф —1, —2, . . .) и степенно-логарифмическую
особенности с возможным разрывом при переходе через окружность \z\ = 1 (когда т + п ^
^ q), а все функции Щ4^ (z) в этой точке непрерывны.
Обозначим через u^(z) систему, получаемую из uk(z) одновременной заменой местами
z и z , m, fi, p, q, (ftp), (fe9) и и, in, (/, р, 1 — Fg), I — {о>р) соответственно.
Тогда функции u°k(z), k = 1, 2, . . . , q; uf(z),k = 1, 2, . . . , р; R$(z),j =
= 1, 2, . . . , q, j ф h, и Сд/г(^5 ^g) (ПРИ Фч Ф 0, ±1, ±2? • • •) или (fq(z) (при ^ =
= 0, ±1, ±2, . . .) образуют три фундаментальные системы решений дифференциального
уравнения 8.2.2.42 соответственно в окрестностях особых точек z = 0 при р ^. q, z = оо при
p^qmz = (^i)m+n^^ ПрИ р = д.
В случае р = q это уравнение инвариантно при указанной выше замене местами
переменных, a q + 1 его решений гс
О / \	со / \
и tfcfc(z) или ик (z), или
53-57).
), ?qh(z, фч), ^g(z) связаны между собой формулами 8.2.2.5 (или 8.2.2.6, или 8.2.2.50,
Представления функции С"
в окрестности особой точки z = (—1)г
имеют различный вид в зависимости от положения z (внутри или вне окружности \z\ = 1)
и от величины фд:
50. Gmn(- ^а<^ « —
П sln(afc -
sin^Tr ^	sm((bmy-bh)ir LV7"V '
т	[|arg(l-zi)| < тг; фч фО, ±1, ±2, ..., Сд/г(^) см. нас. 623].
где sin ((Ьщ)' — Ьн)тг = О sin (bk — 6/г)тг; в частности, формула 8.2.2.50 сводится
к соотношениям
(аа
51. G
¦тп
7Г
\q-m-n г
Ч
п
sm{{bmy-bh)ir
- 6,)тг
52.
(Ь.)
К)
0, ±1, ±2, ...].
П 8in(ah-bk)ir
= m+l
sin(ah - (an)f)w
/_^
3=1
ah, aj} (bq)
\z\ > 1;
0, ±1, ±2,
a при целых ^д она принимает вид

526
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.2.2
53. Ggq' I Z
^ = E
m	1-1
z h \.i
k=0
/ -t\l
-(-1) 7Г
l m-\-n — q — l
7Г
m
= /; | = 0, 1, 2, ...; |„| < 1].
54. G
h=l	fc=O	q
П
8т(ал-(ап)')тг ls**v~>v«^ -/
= /; / = 0, 1, 2, ...; |„| > 1; |arg(l-z2)| < тг; z2 = (-1)«
55. G"
E
^
i=o
^,o}
56. Ggq' I Z
(bq)
(-l)'^^, -I) In A - Zi) + (^lI!
[^- = -/; I = 1, 2, ...; \z\ < 1].
9
X i (/-1)!^2 afe(l-^2
- z2)j + (-l)'^^, -0 In A -
j=o [l 4j
[^ = -'5 / = 1,2, ...;
Функция Cg^(z) представима в любой из следующих форм:
7+гоо
f
i=o
(t -
!?
^1
[0 < 7 < 1],
< 1],
7+ioo
t — Z\
¦ dt [0 < 7 < 1; zi справа от G — ico, 7 + гею)].
57.
-щ
где функции R-fJ(z) определяются равенством 8.2.2.44. Остальные коэффициенты и
функции имеют представления
o>n+i — bhj • • • , aq — bh7
— bq + k
- aq)k
7+гоо
1- _
ln(l-t)-
, Q
dt

8.2.2]
8.2. G'-функция Мейера
527
[О < 7 < 1; zi справа от G — гоо, j + гоо); Re F^ — dj) > —(I ± 1)/2 — 1; j = 1, 2, . . . , q; 6/j, —
-a^O, -1, -2, ..., -(/±0/2],
l2^ *j — Zl \l —
ekqh\l — Zl
"Y — гоо
[О < 7 < 1; Re (bh - a,j) > -(I ± 0/2 -1; j = 1,2, ..., q; bh- a5 ф 0, -1, -2, . . . , -(/ ± 0/2],
причем ^(z, t/>g), efh (z, /), c*g/l, djg/l получаются из ?qh(z, фч), Ofh(z, I), cjqh, dkqh
одновременной заменой местами z и z~ , га и n, a^ и 1 — bh, bh и 1 — ah- Функции 0qh(z, I)
являются непрерывными в точке z = (—l)m n ч.
Значение G-функции в указанной точке выражается равенством
q
_l_ _ m	О Sin (ttfc — bh)il
58.
n-q)bhwi k = n
[m + n> q\ Кефч > О],
причем его правая часть лишь в частных случаях приводится к отношениям произведений
гамма-функций. Если выполняются условия
l-q+l
Ц
[h = l,2,...,q],
fe=l	x fe=l
где Я(ж) имют вид 8.2.2.49, то в формуле 8.2.2.53 (соответственно 8.2.2.54) второе слагае-
слагаемое, содержащее логарифмический член, отсутствует. Если же выполняется соотношение
(,qh(z, I) = 0, то Oqh(zj I) = 0 (а если (,^h(zj 0 — 0, то 0~h (z, I) = 0) и формула 8.2.2.55
(соответственно 8.2.2.56) не содержит логарифмического члена. Для выполнения последних
требований необходимо и достаточно, чтобы выполнялись соответственно условия
3=1
Если
0, то функция
= 1,2, ...,
аналитична в секторе | argz\ < (га +
+ п — д)тг, а правые части формул 8.2.2.51-52, 53-54, 55-56 соответственно аналитически
продолжают друг друга через окружность \z\ = 1. Если, кроме того, т + п — р ^ 2, то точки
z = =Ы при любом фд не являются особыми, если им приписывать аргументы жк, к =
= 0, =Ы, ±2, . . ., где |&| < т + n — q. Тогда коэффициенты при Gqqq- и G^-функциях из
формул 8.2.2.51-52 обращаются в нуль, т.е.
sln(afe -
kbhwik = n^
sm((bm)f - i
q
= 0
[|А;| < m + п - q; к = 0, ±1, ±2, . . .],
^ ЪкOГ
= 0
sm(ah -
PI
-n- g; Jfe = 0, ±1, ±2, . . .].
Если
argz| < 7Г, то в особой точке z = — 1 функция G«
(Ья)
при Re^g > 0 непрерывна, при Кефч = 0, фч ф 0 ограничена, при t/>g = 0, вообще говоря,
имеет логарифмическую особенность (см. 8.2.2.53-56), а при Retpq < 0 имеет степенную
особенность порядка —фч, к которой при целых фд может добавляться и логарифмическая
особенность, причем справедливо равенство	q
г	х	. , чп	m	П sinK -6*.W
59. Mm \(л -L~\-1>*nmnl * (ая)
z->-l

528
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.3.1
Если га + га — q ^ 0, то функция
-imn
является кусочно аналитической
функцией от z с разрывом на окружности \z\ = 1. Если га + га — q = 0, то эта функция
в особой точке z = 1 при Иефч > 0 непрерывна, при Кефя = 0, фч ф 0 ограничена,
при фч = 0, гага ф 0, вообще говоря, имеет логарифмическую особенность, а при Re фч < О
допускает степенную особенность порядка —фц1 к которой при целых фд может добавляться
и логарифмическая особенность. При этом асимптотика функции GJ
—>• 1 зависит от способа подхода z к 1 (извне или изнутри круга \z\
справедливы равенства
60. Mm
Z-H-1
при z —>
1). В частности,
sln(Fm); - ,
я
61. lim
|
'[l.oo)
^ sin (а/г - (an);Or
Относительно других свойств и приложений 6г-функции Мейера см. [1, 11, 13, 46].
8.3. М^ФУНКЩИЯ ФОКСА
8.3.1. Определение и обозначения.
//-функция Фокса порядка (га, га, р, q), где 0 ^ га-
формулой
1	Г
(ai, Ai), . . . , (ap, Ap) _
определяется
1. я:
	 ттТПП
g, Bq)
, P П
h J ^^
П
П
i = n+l	i = m+l
Ai? Б,- >0, г = 1, 2, ...,p, j = l, 2, ..., q,
[ap, Ap] = (ai, Ai), . . . , (ap, Ap), [6g, Bg] = Fi, Bi), . . . , (bq, Bq).
Интеграл сходится, если выполнено одно из следующих условий:
1)	L = Lioo; a* > О,
2)	L = Lioo; a* ^ 0,
argz| < а*ж/2;
argz\ = а*тг/2, 7Д < — Re/x;
3)	L = L^oo; A > 0, 0 < z < 00 или А = 0, 0 < \z\ < /3 или А = 0, а* ^ О,
= /3, Re/x < 0;
4)	L = L+oo; A < 0, 0 < \z\ < 00 или А = 0, \z\ > Р или А = 0, а* ^ 0, \z\ = /3, Re/x
здесь
Е
Е
с = га- + га —
П Аз АЗ П
М =
3=1
3=1
Контур L~oo (L+oo) представляет собой левую (правую) петлю, которая расположена
в некоторой горизонтальной полосе, начинается в точке ^oo + i<pi (+oo + iy?i), оставляет

8.3.2]
8.3. Н~ Функция Фокса
[аР1Лр]
[Ья,Вд]
529
все полюса функций T(bj + Bjs), j = 1, 2, . . . , га, слева, а функций ГA — clj — Ajs), j =
= 1, 2, . . . , n, — справа от контура, и оканчивается в точке ™оо + щч (+оо + i(fi2), где (р% <
< (f2- Контур Lioo начинается в точке 7 ~~ *оо и оканчивается в 7 + ъсю, разделяя указанные
полюса так же, как и L±oo-
8.3.2. Основные свойства.
1. Н-функция симметрична по парам (ai, Ai), • • • , (сь-п, Ап) из [ар, Ар], (ап+1, An-f-i, . . •
. . . , (ар, Ар)) из [ар, Ар], FЬ Вг), . . . , Fт, Бш) из [bq, Bq] и Fm+i, Bm+i), . . . , (bq, Bq)
из [6g, Bq] в отдельности.
2. Я,
•0,n
[ар,
= 0 при выполнении условий 1), 3) или 2), 3) из 8.3.1.
3.
Представление в виде ряда:
т
[ар, Ар] ______
г = 1 k=0 Ц ГA - i
[А ^ 0; условия 1)-3) и Bk(bj + I) ф Bj(bk + s), j ф к; j, к = 1, 2, . . . , m; I, s = 0, 1,2,.. .].
qq J~[ ГA — dj -— A — di ¦
4. я:
[ap, Ap] I _
v
П
m
П
(-1)*
g
.=n+i
[A ^ 0; условия 1), 2), 4) и Ak(l - a3- + l) Ф A3(l - ak + s), j ф к; j, к = 1, 2, . . . , щ I, s =
= 0, 1, 2, . ..].
5. Функция Яр
[ap, Ap]
аналитична по z в секторе | arg z
.Еслиа*
А =
= 0 , то функции, удовлетворяющие условиям 3), 4), аналитически продолжают друг друга
через окружность z = j3 в этом секторе. В случае а* ^ 0 сектор аналитичности отсутствует,
но, если А = 0, то две указанные аналитические при \z\ < f3 и \z\ > C функции имеют один
и тот же предел при z —У /3 вдоль луча arg z = 0, когда а* = 0, Re /i < 0.
Формулы понижения порядка, симметрии и сдвига:
в.
7. т
8.
[ар, Ар]
[bq-i, B
[ftp, Л.р\
[ъя,вя]
ар, Л
i, Аг)
j-m, n —1
(а2, А2), . . . , (аР5 Ар)
[bq-u Вд-г]
- ар, Ар
[ар + а Ар, Ар]
К, Bg]
Соотношения специального вида:
(a, A), [ap_i, Лр-i]
9ит-~ I у
10.
g-i, B9_i], (azb/, A)
/ -i\l rjTO + l, П —1
= l^1) HP,q
[Ор_1, /
F, В),
l, J5) _______
I
[ap_i, Ap-i], (a, A)
(a±/, A), [bq-i, Bq
(b±l, Б), [ap_i, Л
[6,_i, B,_i], F, Б)

530
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.3.2
(а, Л), [ар^2, Лр_2], (а±/, Л) | _
(a, Л), [bq-i, Вд-г]
—	( II f[m~ljn	7
-	\-Ч rip-iiq-i \z
1 « тттп
1A. Hpq I Z
[ap, A,] | = Ш]
[Ья, Вя
Mkp, kq
(•'-*)'
(а ± I, А), [ар_2,
, ар), Л
, 6,), В,
Соотношения между смежными функциями:
13. {ЬгАг - aiBi + Bi)#™
), (а2, Л2), • • • , (ар, Ар)
я, В„]
¦АЖ
[ар, Ар]
), F2,
[гм, те ^ 1].
14. Я^п U
i-ra —I, n
~ ^p-l>q-l
Формулы дифференцирования:
15 ^^ <f za H
а тттп
JP+1,<
— 1, п
р-1, д-1
)> («2, .
(-G, 1), [ap, Л
L тттп I _ —о-
[up,
я:
n —a
(ai — А;, Л1), (a2, Л2), • • • , (ap, Лр)
[n ^ 1; cr = Л1 для fc > 1].
17
mn cr
г	л i
[ap, Ap\
[Ья,вд]
[ap, Лр]
), F2,
18
jlo.
dz*
in
[6„ ^g
[ap, Л,
(cz + d)'
20. П(^-СЛ^ЯрТ
rjr'm, n-\
[т ^ 1; а = В\ для fe > 1].
@, a), [ap, Ap}
[bq, Bq], (k, a)
W > 0].
[ap, Лр]
**р+г, q+r
1
(cz + d)°
[ap, Лр], A-A;,
A, a), [&g, Бд]
[cr > 0].
[сг — a, cr], [ttp, Лр]
[6q, Bg], [cr - a + 1,
> 0].

8.4.1] 8.4- Таблица преобразований Меллина элементарных и специальных функций 531
Представления через G-функцию Мейера:
21. т
22. ЯГ
z
z
[up,
[Ья,
ч
Ар]
^ pq
I
(ap)
A(fcp, %
[Ai, . . . , Ар, Bi, . . . , Bq > 0— рациональные величины].
Здесь к — наименьшее общее кратное всех знаменателей величин А\, . . . , АР7 ?>i, . . . , Bqi
ki = kAi, i = l,2,...,p,lj = kBj, j = 1, 2, . . . , q,
p	q	m	n
i=i	i=i	[a*5 с*, /3, /i, А см. в 8.3.1].
Другие свойства //-функции и ее приложения см. в книгах [50, 61].
8.4. ТАБЛИЦА ПРЕОБРАЗОВАНИЙ МЕЛЛИНА И ПРЕДСТАВЛЕНИЙ
ЭЛЕМЕНТАРНЫХ И СПЕЦИАЛЬНЫХ ФУНКЦИЙ ЧЕРЕЗ
G-ФУНКЦИЮ МЕЙЕРА И М-ФУНКЦИЮ ФОКСА
В этом разделе приведены формулы преобразования Меллина
оо
/*(e) = \xa~1f(x)dx
о
для различных элементарных и специальных функций /(ж), для которых f*(s) имеет вид
I I т^Т	Г7^—vFTJ	F5	\ '	лз'1 вк, O|, JJm > 0.
A1 r(ci + Cls)T(dm - Dms)
j, к, I, m
В левом столбце таблиц указаны функции /(ж), в правом — их преобразования Меллина
f*(s). Символ /(ж) ^^ f*(s) означает, что существует интеграл 		f*(s)x^s ds,
2711 L
Г s-1
равный /(ж), причем интеграл ж f(x)dx в классическом смысле расходится; опреде-
о
ление преобразования Меллина в смысле теории обобщенных функций см., например, в
[36]. Контуры L±oo представляют собой петли (см. 8.2.1), разделяющие плоскость s на
области D и D (D слева, а D справа от L-t©©)- Условия представимости функций
/(ж) через G-функцию Мейера (//-функцию Фокса), указанные в правом столбце, могут
быть ослаблены; см. 8.2.1, 8.2.4A)-B)(8.3.1, 8.3.2).
8.4.1. Формулы общего вида.

532
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.2
8.4.2. Степенная и алгебраическая функции.
Обозначения: Аг = тт~1/2^/2I-2г, А2 = 22г^ иг^г\ А3 =
1
2
3
4
5
6
7
8
9
10
11
12
хи
xv
A
(X
A
1
11
A
xc
X
h
L
1
L
(v
H(\-x) G\\(x\
H(x 1) - Gi\ (x
V
- x)* = Г@)в\[
+ *)-' = -
1 /^n
I
Гж
— ж \
o,
0,
x ^p - Ж
I/
(•
(¦
1/2
1/2
+ 1
+ 1
0
/5
0
1 -
0
)
J
Г(р)соб(Р7т/2) '
ж)+ + -
Лп {(З -
sin 7'
7Г
sin77rF(
Г — 1 Sin С77Г
Goo
- 1 7Г
n -i —1
- ttG^ 1 ж
V
(тг + ]
(n + 1
2n
- ^(-l)fc™^fc/B
fe = l
rll (
- u\x
0 ^ 1
0 J '
/1 + x ±1)
(x
V
7O
т
1™
( x
\
:7ГГ
)~]
n+
1
0,
г
(
0, <
и, <
L, (n
-I
1 /
")/2, 1
)
)
)
)
-')
<
™P, A
C1 - P
-til Z'
7 J
f
\
0,]
0,]
- + 3)/
- + 3)/
=
Bn-
Bn -
- 2r -+
y ± ^)/
[r
-p)/2 \
)/2 /
/3, 7 \
0, 7 /
L/2 \
L/2 )
Bn + 2) \
Bтг + 2)/
Ы) J
,;/2)
= 0, 1/2]
r[ s + u '
[s + v + l
rr—•¦
Li - i/ - sj
Г s
-
1
1
Г (P)
J «, 1
тгГ
Le + 1/2,
7Г
Г(р) cos (ртг/
7Г
sin77rT(l —
sin aw
4s s
7Г
[|Re<7|<l;
L* + l/2,
-тгГ
s +
Г[в, 1 - «] +
г
+ r[s + (
Г V
s
Л\Г
1
1
s]
— s
1/2-
Г
r[
@,-
— s
1/2-
[He (s
+ 1/
[HC (S
[Res,
[Re /3 > 0; Re 5 <
[0 < Re
1 [o<
[e + (l-p)/2, A +
[0 < Re 5 <
S, 1 -)9 - S 1
s + 7, 1 - 7 - sj
[0 < Re s < 1 -
1~S,1~CT~5]
Re<j)<Res < A,'
1 _
j + Cn + l), n(n + l)"
(n +
2тг +
T ^
9. '
3)Bn + 2)~1, (n-
x Bn + 2)"
[0 < Re 5 < n(n
1) , 2тгBп + 1)
[0 < Res < 2теBп
1-1/ V
9 9
L
[-Re(i/=F^)/2 < Res < г
+ 1/) > 0]
+ 1/) < 0]
Re Д > 0]
С 1 - Re C}
s < Rep]
Re s < 1]
p)/2-*J
Re p < 1]
Re,e < 1]
L^Retr)]
 — s
-l)x
-1 - s
1 1
+ 1)™1]
1
J
-Rei//2]

8.4.2] 8.4- Таблица преобразований Меллина элементарных и специальных функций 533
13
14
15
16
 Т
17
18
19
20
21
22
(
(ж2 +
И
2 _|_ f
(ж2 +
A-5
(ж -
A-5
—
(ж-
—
A + V
Ьж ±у^У
1 + ж)г
21 (
^ „11
22
sm 7
-ЖСОБ7
!жсов7 +1
2ж cos 7 +
0+ [A + л
l-r±i/
0, 1/2
и
V
(о, i),
@, 1),
11 (
\
(
\ \
/i—^y _
-(-1)^A-^
/
\
+ LV
- (-1Jг
4 С02Гж
2 22 |^ж
]
(
or [ГУТ
(-1Jг (^1
/
22 V
or [G^
+ LVV
МJг (V \
/
4 q Ct oo I Ж
*-o ^-* 22 1
]
(
I _
(i/ + l)/2, i
0, i/
{y/x -Vi~
V-r- v/2
), 1/2
VT' л- Л
(^ + 2)/4,i
0, I//2
x + 1 + V л
V
/^ + 1 - ^/
L - r + ?//4
), 1/2
y/x\~p = 2P
(-i)'VT^
f ^v^ - (-
3/ ^n
22
- AA 1 ~
1 -
0, ]
"ж //A — ж^
-II y/x - 1
Гж
V
C+21
1/2, A
/2, 1-r
(-7Л,
ж; J -
//2 + 1 -
[r =
3T)T
1-Г +
[r =
—^^
1 — y/x
,/4+1-
[r =
/ «A/ -L
1 -r-
[r
sin —
P/2, A
-/2
+
H{x-
)/4, E-
-0/2
J
7/т) А
7/t) /
2,7/тг) \
)
= 0,1/2]
=
"/2 \
У
= 0, 1/2]
I/
-
)"]-
/ J
= 0, 1/2]
-
)>
/ J
v/A \
)
= 0, 1/2]
-ГA-р)х
"P)/2 \
)
1) =
20/4 \
J
1 = 0, 1]
fs, s + 1/2, r =F i//2- si
1 L s-r=F^/2 + l J
[0 < Res < rTRei//2]
sin Gs- 7)
sin 7
[0 < Res < 2; |7| < тг]
cosGs)T[s, 1-е] [0 < Res < 1; |7| < тг]
(s — 1) cos Gs — 27) sin 7 — sin Gs — 7]
2 sin3 7 sin stt
[0 < Res < 4; |7| < тг]
Г __i_ 1
2 U + (^ + l)/2, s + i//2 + 1 - 2r J
[Res > 0, -Re 1/]
Гг + ,/2-в,г-,/2-.1
L 1-е, 1/2-e J
[Res < r- |Rei/|/2]
Л r[ s,s + u/2 1
3 [e + A/ + 2)/4, e + i//4 + 1 - 2r J
[Res > 0, -Rei//2]
Гг + v/Al — s, r — j^/4- si
3 L 1-е, 1/2-s J
[Res < r- Re 1/1/4]
2^sin —ГA-/э)г[ s,p/2-s
2 [5 + A^р)/2,1/2 — s
[0 < Res < Rep/2 < 1/2]
2^з/2 /^г Г 5 + 1/2,A 20/4 s 1
[s + E - 20/4, A + 0/2 - s J
[-1/2 < Res < A-20/4]

534
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.4
8.4.3. Показательная функция.
o-V* -,
xk
n+1,
n+1, 0
-re, 1
— те,
О, 1-
1, С
С
71 + 1, 1 - С
n + 1, 1 - с, О
—n, c, 1
— n, с
Г(в)
Г(-в)
T(s)
Г(-8)
[Re s > 0]
[Re s < 0]
[-n - 1 < Res < -n]
[n < Re s < n + 1]
sincTr ~ Ls + 1-с, с-sj ""	ГA - 5)
[с - любое; s = -A; G D+, fc = 0, 1, 2, . . .]
, или
sincTr L^ + c, 1-е-s\	Г(в + 1)
[c - любое; s = fc G D^, fc = 0, 1, 2, . . .]
sin стг L	i]	()
[с —любое; 5 = — k G
G D~, k = 0, 1, 2, . . . , 71; s = -k E D+, fc =
= 71 + 1, 71 + 2, . . .]
sin стг [s + c, 1-— c--sj	F(s + 1)
[c —любое; s = k E D+, fc =
= 0, 1, 2, . . . , 71; s = A;Gl>~,A! = 7i + l, 71 +
+ 2,...]
8.4.4. Гиперболические функции.
3/2	nl-n 3/2
Обозначения: Л4 = —	, Лб
sin бтг
1
2
Г sh2y
Ich2y
Г sh (s
I \
^} =
/
G\i [x
\
)
(
g2J \x
i +
5/2
) =
)
1 -
с —
5/2-
, 1 +
5/2,
5/2
™ С
5/2-
с — ё /
L
)
с, A-5)/2/
2, A + 6)/2\
)
<
Л41
= 0,
А4Т
= 0,
л5
X
^ -
= 0
Г
L
1
[
L
1
(п
г
-
е
+
S +
, 2,
[с
, 2,
[
.«4
D'
при
11 п п
1 — любое; s
• ••]
Ч'-
5 1
2
^ 1 — любое;
¦••]
( 1] (fc)
- 7 ~~ ^ + 1? b
- 1 — любое;
fc G ,D+, fc
при 7i = 2,
7i = 1, 3, 5,
-5/2
5
2
= -5/2
1 — s
2 '
s = 5/2
( 2
Vn-2fc
s + 7
— 7 — s,
7 = A —
= 1, 2
4, 6, ..
1 + 5
2
-fcG
2
+ fcG
\ 2s
) X
1/2 +
( — l)n
,3,..
, s =
1
J
.1
J
D~, к =
1
7 - sj
) /4; e =
. ; s =
-1/2 G

8.4.5] 8.4- Таблица преобразований Меллина элементарных и специальных функций 535
4
к
о
*г
о
7
8
chn
= 2-
SO
r-hn
СП
= 2"
е-
\/х — с
[с = 0 при п = 1, 3,
"n I 1 при те = 2
W2/
1
1
[с = 0 при те = 1, 3,
-( ")прип = 2
п/
/B-) sh J_ = I Gii (
2ж 2 21^
5,
4
5,
4
1,
1,
f
X
\
. . . ; с = 1 или с =
,6,...]
L
. . . ; с = 1 или с =
,6,...]
о)
;¦¦)
G D~
eD+
[(г
5
х Г
= 7
?!
X
G
при
21 о ( 2 J
к \n-2kj
г[
Ls - 6 + 1, 6- s,
[6
D+, А; = 1, 2, 3
с=1ите = 2, 4
в остальных случаях]
1 — 1)/
fc 0
г
L^ +
+ к
= 0 G D'
G D^
[(г
5
= fe
G D+
G D"
1 Г.
2 L
1 Г,
2 L
при
i-l)/
\ ^
X
G j
при
2 /п\ ( 2
U/ U-
7^5
7 + 1/2, s + 6-7
1 — любое; 7 = A
G D~, fe = 1
"*" при п = 2, 4, 6
п = 1, 3, 5, ...]
2] , 9 \ "
ill i
V/fe/ \n^2fc/
Г о
Г
[s + 1/2, s + 6, ]
[Ь
D", Aj = 1, 2, 3,
с = 1ите = 2, 4
в остальных случаях]
5 + 1
5, 1 -
-Л
V]
S
X
1/2
7^ 1 "
6, .
\
1
2к)
, 1 +
2, 3
2s
X
— о
Ф1-
¦ ¦ ¦;
6, .
[-1
[0
1
-s\
— любое; s =
s = 0 G
. .; s = 0 G
-2s
X
1
7-6-eJ
-l)n) /4; s =
, . . . ; s =
s = 1/2 G
- J
- любое; s =
s = 0 G
..; s = 0 G
< Re s < 0]
< Re s < 1]
8.4.5. Тригонометрические функции.
Обозначение: S =
;}¦
1
2
Q
О
4
5
sin2v^=V^Gj§
cob2^=V5FG5S
J sln2\/« 1 y—
[ cos %/x J
fsln2^^1/2|
] СО8 2Ж™1/2 | ~
V /
—™: v 7Г Стоп 1
V 20^
f sin2-\/^" 1
13 ^
V
(¦
vlO
r02
Ж
сс
a
8
1/2, 0 /
0, 1/2 /
(x
Г
S/2, (l-S)/2 J
1 - 8/2, (l + 5)/2 \
L-oo
8 2-^ 1
^rh+1/2i
L 1-е J
^r[l/2e-J
j- Г s + 8/2
l{8 + \)/2- ь
Г <f/2 - s
V^r[e + (<J + l)/2
Г s _(_ a _(_ 1? s
[s^/2^
[И
[0<
1
[-5/2 <
"I
jj
[-1/2 <
+ 5/2 1
)/2- s\
к G D+, fe = 0
R,es| <
Res <
Res <
Res <
, 1, 2,
:i/2]
:i/2]
:i/2]
:*/2]
...]

536
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.5
10
11
12
13
14
15
fsin2x
[cos2x^1/2
sin By/x + 7тг)
cos
1-5/2, -а, E + 1)/2
1-а
7 + A-*)/2
О, 1/2, 7 + A
cos Bx~1/2 +7тг)
1, 1/2,
A + Я)/2-7
7 sin Bл/ж + уж) —
— л/ж cos Bл/ж + 771") =
7
/ 2
7 Sin —-=¦ + J7T
О, 1/2, 7-
1	/2
— cos -— + 7^ | =
l/Ж	\ л/Ж
1/2, 1, -7
cosn л/ж — с
[с = 0 при 71 = 1, 3, 5, . . . ; с = 1 или с :
= ci = 2~п ( П J при те = 2, 4,6,.. .]
\п/2)	J
. „ 1
cos	с
л/ж
[с = 0 при 71 = 1, 3, 5, . . . ; с = 1 или с :
при те = 2, 4, 6, . . .]
те/2
1 (ж S
з (ж sin 7) J
f а-e, <У/2-в
[в = 5/2 +fe G i^, Aj = 0, 1, 2,
в, в+ 1/2
[0 < Res < 1/2]
-s, 1/2- s
	7> 7+ —
[-1/2 < Re* < 0]
[в = -fe, -1/2 - к Е D+, к = 0, 1, 2, . . .]
[в = к, 1/2 + к E D~, к = 0, 1, 2, . . .]
[-п/2 < Re в < Т; 7 = A - МП /4]
[О < Re s < 1/2 при с = 0 и с = ci; -1 <
< Re s < 0 при с = 1]
fc=o
¦1/2
[-7 < Res < те/2; у = A - (-1)*
l2s Г -в 1
Г
[-1/2 < Re s < 0 при с = 0 и с = ci; 0<
< Re s < 1 при с = 1]
[|7| < тг/2; Res > -A ±1)/2]
[ COS75

8.4.6] 8.4- Таблица преобразований Меллина элементарных и специальных функций 537
1 R
17
1 Q
JLo
19
Ofl
zu
21
22
23
ж cos 7J ^
1sin7) 1 _
1 cos (ж" sin 7) [
/
A
((
о 3/7 /о Sin 1 3V
I cos f 3 -v"
^ V
1 cos C y/x
/
x Gq6 1 ж
V
e X 1 о 4/F~
cosz у4ж
V
1 /
= ^/2^: G04^
j sh 2 v4x sin 2 л/4ж
| ch 2 \/4x cos 2 у4ж
/
v /~tlO I
<J04 1
5/
j sh2 y/4/x sin 2
1 ch 2 yj4/x cos S
|sh2v/4^cos2
^ shz у 4/ж cos^
/
\
1/
1 -
,l),((l + «)/2,
l + <5)/2, 7/тг)
	 / \ I —
/ / ^
0, 1/3, 2/3, A
)\ ^
") j 4тг3/2 Х
5 112 5 1
V 6' 3' 3' 6'
}-
/2, 1/4, 3/4, A
r
2, 1/4, 3/4, A-
^5/2, 1/4, 3/4, (
У
™5)/2 )
¦-i \
i-s
2 J
\
-5)/2)
3 w
\
-5)/2 J
l + 5)/2 \
5/2 \
1/4, 3/4, 0, 1/2, E/2 /
J v 4/ж J
4 3/4, 1/2, 1,1-
^5/2
I
=ргг s)l8in75l
+ 1 V S)\ (
{ COS7S J
[1
T| < тг/2; Res < A ±l)/2]
лД Г s, s + 1/3, s + 2/3
2 |_e + (i-?)/
4^-3/2
1
6'
(
1 r/
	 I <
s + 1/4, s
Г
[l/4 — e, 2
[s = -S/2
,	 Г
Г[5 + 1/4, б
[s = 5/2
+V^r
5 1
z, (I + о)/*
1 2
3' 3'
+ 3/4, s +
s + 5/2
»/4- e, A-
- A; G D+,
5/2 ^s
+ 3/4, s +
1 3
4'5 4
[s = -1/4-A;, -3/4:-к Е D+,
г 1 .4
±\/2ж3 Г
1
sH—, s
[s = 1/4 +/5, 3/4
	8.	3
4 4
+ 1, s + 1 -
+ k E D~,
, 1
)	 с
[Res > -J/3]
5 0
6' 2
[Res > -5/6]
5/21
/
[Res > -5/4]
1
f J)/2- sj
к = 0, 1, 2, ...]
1
E + l)/2j
ife = 0, 1, 2, ...]
5
ife = 0, 1, 2, ...]
5 8
— ,	s
2 2 J
к = 0, 1, 2, . . .]
1
2
3
4
5
3.4.6. Логарифмическая
1пжЯA — ж) = — G
1пжЯ(ж — 1) = G%t
1ппжЯA^ж) =
ЫпхН(х- 1) = n!
ЫA + «) = Сй(«
15 (
(*
G°.
1,
1,
(
f 1
f 1
fl
1
0
1,
0,
3,0
0
fl
I
1
функция
;)
)
0, . . . , 0 /
i::::i)
-rf s
[5 + 1
[l-s,
(-1Гп!Г
Г[в+1-
,s + lj s2
-8 1 1
[5 + lj
[Res
[Res
[Res :
[Res
3] f-l<Re
>
<
> 0
<
0]
0]
]
0]
0]

538
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.6
In ( 1 + -
х
¦¦Gi\lx
-x\ =
In
1
X
О, 1
О, О
1, 0, 1/2
О, 1, 1/2
О, О, 1/2
In [ 1 + J^ ^±fe/(n+1)
fc=i
10
11
12
13
14
15
16
17
18
19
ln(l+
In ж
ж - 1
In ж
x-y у
In ж
О, О
О, О
ж + 1
In х
х + у
In ж
In2 ж
ж + 1
О, О
О, О
ж In у г
У
О, О, 1/2
О, О, 1/2
О, 1/2
О, 1/2
In (l + 2ж±х cos 7
1 + л/ж
1-у/Х
1/2, 1
1/2, О
[г = 0, 1/2]
тгГ
тгГ
тгГ
е+1/2,1/2-е,1-е
е, е, 1 — е
+ 1/2,е+1,1/2-
А(п + 1, (п
[0 < Re s < 1]
[-1 <Re 5 < 0]
[0 < Re 5 < 1]
(n + 1, - + (n + 1M),
A ( n + 1,	(n + l
е + 1/2, 1/2-
-(п + I) < Res < О
О < Res < (n + 1)™1
:п + 1, Bп + 1)е),
-Bn+ I)™1 < Res < 0
0 < Res < Bn + l)^
T[s, s, 1 - s, 1 - s]	[0 < Re s < 1]
1-е] х
х ( Г[е, 1 - е] -
[0 < Re s < 1]
х I lny — тгГ
Г[е, 2- е] х (in у -
Г[е + 1/2, 1/2-.
[у > 0; 0 < Re e < 1]
е, е, 1 — е, 1 — .
s + 1/2, 1/2- з _
4[s, 1-е] х
е, 1 - .
.е + 1/2, 1/2- sj
[у > 0; 0 < Re s < 1]
S
в, 1-в
в+ 1/2, 1/2- i
[у > 0; 0 < Re e < 2]
2Г[е, е, е, 1 - е, 1 - е, 1 - е] -
- 7r2r[s, 1-е]	[0 < Res < 1]
-1 < Res
О < Re e <
[|Res|
ТГГ
ItI < тг,
s + 1/2, 1/2- s
V}]
¦ 1, 1 - e
(~тгJг Ts +1/2, e + r, 1/2 - в, г - e
20F
-r, 1/2+ r - s
[-1/2 < Res < r]

8.4.7] 8.4- Таблица преобразований Меллина элементарных и специальных функций 539
20
21
22
23
24
25
26
/Т+~х ±1
[г = 0, 1/2]
In
у/х
In-
in-
In2(v^
In
-33 Ж
у/х
1, 1
О, 1/2
1/2, 1
0, 0
1, 1, 1/2
1, 0, 0
О, 1,1
0,0,1/2
1,1,1
1,0,1/2
О, 1, 1/2
О, О, О
х Г
2 Ll- в, 1/2-.
2 Le + 1/2, в + 1
j, s + 1/2 - r, 2r - s, 1/2 + r - s
s + 1/2, 1-е
[0 < Res < r + 1/2]
[Re s < 0]
[Re s > 0]
[-1 < Res < 0]
[0 < Re 5 < 1]
[-KReKO]
[0 < Re s < 1]
s + l, —s, —s, —s
l/2-в, 1-е
x/w Г s, s, s, 1 —
"T" [
8.4.7. Обратные тригонометрические функции.
Обозначение: S =
;}¦
arcsin-\
arccos-\
arcsin ж 1/2
агссозж^1/2
x	1
= arcsin ¦
arctg y/x = arccos _ = arcsin 4
arctg —=: = arccos
ч(«5-1)/2 Г sin (^arccos^/ж) I _
1 cos (i/ arccosi/ж ) J
4
0, 1/2
1/2, 1
0, 0
1/2, 1
1/2, 0
1/2, 1
0, 1/2
2 1 0J U + l	2 '
[Res > -(l±l)/4]
2\0J I 1-. ' ^
1/2 - s, -5
1 - s, 1 - s
[Res < (l±l)/4]
lrp + l/2, 1/2-e, -i
1 — s
[-1/2 < Res < 0]
in-
(г) ^X
x Г
2, 1/2- .
f- 1
[0 < Res < 1/2]
1
s? s + «
-1/ + S
[Re s > 0]

540
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.8
sin I v arccos ж
cos (i/ arccos ж"
1/2, 5
sin [i/ arctg V35 J I
cos (v arctg i
= T
Г(-1/)
8/2, {1-5)/2
sin ( и arctg ж 1/2 |
cos f i/arctg ж"'2
= +:
2
o —f
I//2-s, 1 - i//2-.
[Re s > 0]
5 ?/	1 — I/
- —,	S,
2 2	2
[-5/2 < Res < -Rei//2]
(	)
[0 < Res < (<5-Rei/)/2]
8.4.8. Обратные гиперболические функции.
1 /i/\i-2r Г cos (г - 1//2)тг 1 s A\
Обозначения: Л6 = —j= (-	< . )	7/о( к <5 = \ }.
л/ж V2/	[ sin (г — и/2)ж j	[0J
1
2
3
4
5
A + ^Гг
A + ^Гг
= Лз^
(l-x)^f-
(ж — i)Y
=^
11 — ж ^ <
J sh \y Arsh y/x j
1 ch (i/ Arsh -\/ж"]
G\l(x
V
1 + I//2
-5/2,A-
( ( 1
sh (i/Arsh ж
1 /
ch (i/Arshx"
\ V
-*21 f
22 1
} =
- r, 1
-5)/2
/O \ \
l-r-S/2, A
.. /o .. /o
w fsh f и Arth
-1)/2J V
1 ch (и Arth
v V
r /
[ ch fi/Arth
/
/ i/ \ 8 I
sh (i/Arth [2\
1
«
ch (i/Arth [2\/ж
Г ^П /
I/"'— 11 I
2 G22 \x
L -1 V
122 V
Vi —
+ 5^
(l + x
1 1 .,
1 + 1/
5 1
2'
—
_
+
ж
ж
ж
ж
i/
)~
—
2
1//2
[г
[г
)}
J >
1/2,
— \
1 1
/
14
-г \
)
= 0, 1/2]
"')
= 0,1/2]
=
-1//2 J
1
1
-5+1/ \
J
L + о \
Iff!
/
у—
у/к (
+л/^
[Rei/
['
['
„
i/
2
' Г
X
>
+ 5/2
, i//2 + r - t
A + 5)/2
?, r — i//2 — si
^ 8 J
[-5/2 < Res < r -
+ i//2, s - i//2, r
S Г
) Г[
\ S
) г
/
г
s -
-1/2
1 + A + д ) / А
[| Re 1/|/2
/2
s + 1/2, з
rl + v-8
s,
z
1-е,
[Re s < (
и J
5 8
S+ 2' 2
2 '
+ 5/2-
— r
< Res <
/21
[Res >
l-u-8
2
- - s
12-5-
1 + 5
2
, ^5/2 < Res < 5/2
Re i/|/2]
s
r + 5/2]
Re i/1/2]
-
s
Rei/|)/2]
-
s
^~Re i/]

8.4.11] 8.4- Таблица преобразований Меллина элементарных и специальных функций 541
8
1
2
.4.9
Lin
Lin
. Полилогарифм Li
1,
1,
n(x).
1, ...
0, ...
0, 1, .
0, 0, .
, 1
, о
• •,
)
:)
.i-r[., -.]
[0
<
<
Re*
Re*
<
<
0]
1]
8.4.10. Функция Ф(ж, s, v).
1
2
3
4
5
6
7
8
Ф(
/
*\
ф(
(i
(X
(x
A
ж,
' 1
ч ж
1-J
f
\
-*Y-
-i)
-i)'
-*)
те, v) —
| П-
= Gn'+1
\
5 715 V 1
= ^n+1
«,!,«)
1
Ж '
^ФA-х
/
+ Ф^"
-1 /
n + iy*
п + 1(Ж
1
) = Fi
,l,t,) =
1
-
,!,«) =
1
ж '
- гы
0, 1-
0, -v
1,H
1, V,
-G22(
)) 22 \
-r(v)G
G20(x
22 v
V
-1,
o,
o,
too
V
1,
V
1,
г
1
0
1,
1,
+
ь
X
+
_
1
V
0
1,
0
1,
1 -
V
v +
V +
,0 y
v +
V \
j
)
)
)
(-i)n
rfs +
(s 4
T>)r
^r
Г(«)
Г(«)Г
Г(«)Г
г»г
Г(«)Г
T[s, 1 - s]
(s — vj
[о
1, -5]
v)n
[-1 <
L+:::+.]
[Rev
r^v - s, -v -
[ -s, 1 - v - 5
[Re v > -
Г-s, 1 - v - s"
[ 1-е, 1-е .
[Rev > -1; v
Г s + 1, s +
[Rev > -1; v
< Res < 1; Res
Re s < 0; Re s >
] [0 < Re 5 <
1
< Rev]
-Rev]
l,Rev]
[-1, -Rev < Res < 0]
> -1; v ф 0; Re
1
1; v ф0; Re(s +
1
Ф 0; Res < 0, 1 -
I + l]
^0; Res > -1, -
s > 0]
v) <0]
- Rev]
-Ren]
8.4.11. Интегральная показательная функцияЕ1(я
Ei(-a;) =-G\l(x
1
1
0, 0
1, 1
0
0
о, о
е х Ei (ж) = —тг
О, 1/2
О, 0, 1/2
1, 1
1
1, 1, 1/2
1, 1/2
Ei \-2y/x I Ei [2у/х ) =
О, 1
О, 0, 0, 1/2
-Г
-Г
s, s 1 T(s)
— s, — s
. — s
-r[s, s, 1 - 5]
Г s, s, 1 — s
[e + 1/2, 1/2 -8
-r[s + 1, -s, -s]
-,rf
р 5, S, S, 1 - S
2 Le + 1, 1/2- s
[Re s > 0]
[Re s < 0]
[0 < Re s < 1]
[0 < Re s < 1]
[-1 < Res < 0]
[-KRee <0]
[0 < Re s < 1]

542
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.12
) \у/х J
1, 1, 1, 1/2
1, О
—5, —5, — S
5 + 1/2, 1-
[-1 < Res < О]
8.4.12. Интегральные синусы Si (ж), si (ж) и косинус с!(ж).
Обозначение: 6 =
;}¦
1
2
3
4
5
6
7
8
S
Si
si
ci
(
I
f
I
{
{
i (
/
\
B
si
ci
si
ci
2v
2
V
V
B
B
=
sin 2
CO
>
{
x
/ о 1»-
1 у ^ 1 '
iT J = "Г Сз1
2
л/ж) 1
уж j j
" 2 K
A \
f соэ2у/ж 1
1 э1п2у/ж J
/
I
1 -
2
1 -
2
т „-—1/2\ /
со5Bж^1/2))
з!пBж^1/2) J
/
/
12 I
G42 x
V
1 +
2
1 +
2
11 ж
/
\
L3 ^
coo
*{*
1 -
0
) -
i B-х
5
5
2
л/ж
. /
CI ^
5
5 ,
1
1/2,0
1/2, 1
0
1
,0 )
0, 1/2, 0
1
0, 0,
1
0, 5/2
-S/2, 1
1 M
2
1-8
2 '
)
2 "l
>r- 1
Vх J
1 + 5
2 '
35
2
1/2
, A-
,(*-
7Г3/2
2
5
2
5 i
1
2'
\
J
)
-<s)/2;
H)/2 ")
x
\
5
2 J
3/2
X
2
5 \
1 1
2
/
2 [l
2 [s
2 L
-irr[
у^рГ
^^™ L
2s
л/*7 Г
	Г
2 L
-^1
т3/2г
2
-г- Р
Т 2 Г
+ 1/2, -в"
- S, 1 - 5.
, 1/2-в 1
+ 1, s + lj
S, 5 + 1/2
5 + 1, 1 — .
5,5
5 + 1,1/2-
«s, s +
S + 1, A +
\ {л i г\ /
— s, 5/
s + E + l)
г 1-5
= -:
_ v^
2.
1=-
.]-
5/2
8)/2-
/2 1
2-sJ
2 — s
0 1
S + о |
35 5
е 4- 1	—
г» т^ А
е 1
5+ 2
5
. 5+ 2J ^
2 ' 2
1-й
2
5
+ 2 ^
[-1/2
n/tFjJs + 1/2-
2s [ 1 - s .
[-1/2 < Res
^ГГ1/2-5]
» L 5 +1 J
[0 < Re s <
V^r\s + 1/
2s [ 1 - 5
[0 < Re s
~^7 [1/2-e
[0 < Re
1 _
-s\ "
[0 < Re
1
=
[-1 < Re
-5 1 + 5
2 ' 2
— e	L 1 — e
< 0]
1/2]
J
< 1]
]
s < 1]
s < 1]
s < 0]
1
2
-l)/2 < Res < 1/21
1-5
5,
2
1,1	s
2
< Res < A -
5
<5)/2]

8.4.14] 8.4- Таблица преобразований Меллина элементарных и специальных функций 543
10
11
12
{::
\ si
? ci
О,
, 1/2
со8Bж^1/2
±
S1[^]±
COsBx^1^2) 1 / 2
1, C±1)/4, 1/2
C±1)/4
О, 1
О, О, О, 1/2
1, 1, 1, 1/2
1, 0
-rf-,- + i,
2 ' ~~2
[О < Res < 1/2]
х Г
1
2 ' '2 '2
[-1/2 < Res < 0]
1 Г	1
Г s, s, s Н—, — s
2
[О < Re s < 1]
[-1 < Res < 0]
8.4.13. Интегральные гиперболические синус shi (ж) и
косинус сЫ(ж).
shi
2 cos С7Г
Г3/2
2 COS С7Г
shi
shi
chi
chi
1, с
1/2, 0,0, с
1/2, 1, 1, 1 - с
0, 1-е
1/2, О, О
1/2, 1, 1
О
1
О, 0, 1/2
1,1,1/2
О
rS/2
s + 1/2, -s
2CQSC7T Ls + C? 1 ^ С — S, 1 — S, 1 — sj
[с ф 1/2 — любое; s = -1/2 - A; G D+, s =
= О G D~, А; = О, 1, 2, . . .]
r3/2
s, 1/2- .
2 cos стг Ls + l?s + l?s~~c + l5c"~"sJ
[с ф 1/2 — любое; s =
= 1/2 + к G D~, s = О G ?>+, А; = 0, 1, 2, . . .]
s + 1/2 —s
1 - s, 1 - s
s, 1/2- s
2 " I s + 1, s + 1
2s [ 1
[-1/2 < Res
s, s
¦1, 1/2- .
2s [ s + 1
[0 < Res < 1/2]
2s
у/тг ГГ ^«5 -s
2 [s + 1/2, 1 - sj	 2s
[0 < Re s < 1]
[-1 < Res < 0]
8.4.14. Интегралы вероятности erf (ж), erfc (ж) и егй(ж).
Обозначение: Aj =	.
erf
1
1/2, 0
[-1/2 < Res < 0]

544
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.15
2
3
4
5
6
7
8
9
10
11
_L J.
1 *>
JLZf
erfc (,
J erf
1 erfc
f erf
I erfc
V
е"жег
е^г/х
ex erfc
erf fv
V
evfft
\ v
ei i I *¦
л
er ^г
/
Gl2v
0, 1/2 J
'л/ж) 1
-/2 J
f (*^)=*<?й(*
1/2 \
1/2, 0 У
erf -— = iGji ж
VvW V
1/2, 1 \
1/2 У
1/2 \
0, 1/2 J
-fc ( —— J = - G\\(x
\%/x J ж V
1/2, 1 \
1/2 У
J \ J
л /~il2 1
= A7Gl3i(x
1/2, 1, с \
1/2, 1/4, 3/4, 0, с /
ж/ V V xj
/
1/2, 1/4, 3/4, 1, 1-е \
0, 1/2, 1-е J
\ / / \
/o /Y.l/4 1 prfr f л/о ^1/4 \
V ? JL I el 1С \y ? JL I —
9 /
- жлД G24l x
1/2, 1 \
1/4, 1/2, 3/4, 0 )
4 IT\ / 4 /4Л
V ж/ еГ \f ш/
i 13/
1/4, 1/2, 3/4, 1 \
1/2, 0 /
1
л/тг
= =F
1
ir\s
L
гг\°
L
G D4
Л7Г
G D"
i
жлД
i
тгл/2
r[s';
г s _
- 1
L
± 1
л/ж s
+ 1/2
1 -
+ 1/2
s -
s,s +
1
_s + c,
, s =
s + 1
, s =
г
г
L
I
+ 1
f 1/2
s + l
<-
1/2-
s + 1
rG
1/2
- s
1/2
f 1
1 1
2' 2
— s,
s +
1-е
2
1
, si
J =
4)[{
 =
J
J
J
-]
H
1/2, -e,
- e,l/4-
^ 1/2-л
0, 1/2 + fc G
s +
1
1 3
7' s + 7'
4 4
#1/2-
0, -1/2- к G
1
—, s
4'
1/2,
1
+ -, s +
2
s + 1, 1 -
1/4- e,
s + l,
-r(.+
-1/2 <
Re^
[Re
Res <
J > 0
s >0]
"}]
"JO < Res < 1/211
A Res<0 jj
[o<
Res| <
Res| <
Res <
1/2]
1/2]
1/2]
[-1/2 < Res < 0]
1/2- s
-«,3/4-
юбое; s =
D~' * =
1
2
s — с +
любое; t
D+, fc =
3 1
4' 2
s
[-1/4 <
1/2-s,
1-s
[-1/2 <
=S-l/2
= 0, 1,
1, c-
i = 1/2
= 0, 1,
1
s
j
Res <
3/4-
Res <
1
d
-k G
2,...]
-
s
+ fc G
2,...]
1/2]
J
1/4]
8.4.15. Интегралы Ф рене л я S(x) ж С(х).
Обозначение: 5 = < >.
1
2
SB^2
С Bу^
Ci 2 13 ^ж
3/4,
1
1/4,
о,
о,
1/4 J
3/4 J
2 [l-
2 [l-
h3/4, -s '
s, 3/4- s.
1-1/4, -5
s, 1/4- s.
2s L3/4-
[-3/4 <
~ 2s [1/4-
[-1/4 <
/41
- «J
Res <
Res <
со]
CO]

8.4.15] 8.4- Таблица преобразований Меллина элементарных и специальных функций 545
3
4
5
6
7
8
9
10
\c(;
is(
\c(
1 1
2 |
. i
5
2\/^) J
2 13V
1
(l + 25)/4, 0, C-
2Ж^/2) J
_lGll/
2 31 \
B
0
5 Bд/ж) 1 _
СBч/ж)/
= ^(ж
1
o,
5Bж-1/2)|
сBж-^)| =
_ iG02/
2 31V
B
0
[ COS 2л/X J
1 sin
cos
I sin
I cos
±
=
(/*-1/2)L(J
fcos hx^1^
±{ ) ;
\ sio BЖ^/2Л
= ±\ — G\\(x
V 2 3iv
+ l)/4, B +
B±l)/4, B
+ l)/4, 1, B
\ sin2i/aJ" J
/ c\ 	 t \ 1 Л
BТ1)/4
л /
)] / 2 ч
if ш
B±1)/4,
B±1)/4
± I cos АЛ» I 1
Isin2v/s J L2
= B,r)-3/2G?^;
Bж/2) 1 [1
BX-1/2) 1 L2
V J '
/ / i /o\ \
j cos [2x 1'2) 1
\ sin Ba;-1/2) J
-СB>/^)
к
BТ1)/4
BТ1)/4
/ 9 М
ч 1 +
Г1 /2
B±1)/4
_м)/4)
1)/4, 1 \
У
±1)/4 \
)
'B^) =
\
0, 1/2 J
=
1/2, 1 \
0, 1/2 )
\ 1
1/2, 1 J
2 Ll-e,
1рГ S,(
2 [s + 1
-г s's
2 L^ + l
1 Г A +
2 [s + A
±7ГГ[
±—г[
\/2 L
1
BтгK/2 Х
xr[s
1
BтгK/2 Х
Г
X S -
l + 25)/45
A + 25)/4
l + 25)/4-
s + (l + 2c
~~ 2s Is
+ A + 25)
(l + 25)/4
= — ri
2s [(I
25)/4- s,
+ 25)/4, 1
i p["(
2s [s
s + C - 25)
1/2
[B5-
s +
-s 1
-s\
l + 25)/4- s\
-A + 25)/4 < Res < 0]
5 j =
+ (l + 25)/4j
[0 < Res < (l + 25)/4]
[0 < Res < 3/4]
~s 1
+ A + 25)/4j
[-3/4 < Res < 0]
/4, (l + 25)/4- si
- s 1- s
3)/4 < Res < (l + 5)/4]
/4, C-25)/4- el
1/2, s + 1 J
[-A + 5)/4 < Re s < C - 25)/4]
1
1 + 25
3-25 1 + 25 1
4 ' 4 8\
[0 < Res < A + 25)/4]
1 3-25 1
S' 2 "' 4 j
-A + 25)/4 < Res < 0]
18 А. П. Прудников, Т. З

546
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.16
I	I	3 I
=Н ' 4' 2' 4' 2
8.4.16. Неполные гамма-функции 7(|Л х) и Г(^, ж).
Обозначения: As = 2й
'
пГ(у)
Лд =	:—-,	г—, Лю =
sin (у — с)тг
7A/, ж) =
Г(|/, ж)
1
i/, О
1
О, I/
7 [у, 2гух J — 7 (^5 —2г
2i\
1= ~
, i//2, О
(
\
±e^iv7X
" '-1 i
8 - i/
-, 1 -
exj(i/, x) =
is, с
v, 0, с
+ ^5 -
1- s
, S+ I/
s + 1
[- Re i/ < Re s < 0]
[Res >0, — Re v\
— Re v < Re s <
Res > 0, -
Л1
< Re i/11
Res < 0, Re v )\
J + l, 1- s
- Re i//2 < Re s < 1 - Re vj
s + 1, 1 - s
[Re i//2 - 1 < Re s < Re i//2]
s + 1, 1 - (8 + v)/2- s\
[0, (S - Re i/ - l)/2 < Re s < 1 - Re i//2]
л9г
-e, A + ^-
s + 1™ E + i/)/2, 1-eJ
[Rei//2- 1 < Res < 0, A + 1
+ 1/, 1 — 1/ — s
+ c, 1 — с — s, 1 — s J
[c t^ i/ — любое; s = — i/ — к G
G D+, s = 1 - i/ + A: G ?>~, & = 0, 1, 2, . . .]

8.4.16] 8.4- Таблица преобразований Меллина элементарных и специальных функций 547
10
11
12
13
14
15
16
17
18
19
/
е 'х "у I 1/
ежГA/, ж
i
xGf2
±
= у
eiv«/2-2
=
Г (i/, 2iV
"' W
л 1
1
Y Г'32
X Cj24
f
X
{
2
2
JL ^,
/
ЛцСЦ|
=
-i/
nfi
I (J
(¦
\
2г
/^
;(
b2i
Ж
1%
(.
\
f
X
\
1
1
¦rMO!i
-)оа(.
1 /
^i/J
1 + 1/
2 '
l + i/
2 '
Vх J
2г^) ±
^ Г (i/, 2
0, 1/2, A
2г \
T^i/,
1/2, 1,
A + 5-
i/, 1
0, i//2, (
- 1/, 1, 1
- 1/, 1 -
(¦
(•
i/, 0
1 -
" )
0, i/ /
1,1
\ 1 —
= Лю x
i/
1 l-S
2' 2
= Лю x
1
2 ' "
5J/Z
2i \
[1 + 5-.
i/)/2
v + l)/2
b + oo
с J
)
:¦')
"")
i/ /
•)
' 2 /
о \
1
2
/
/2)
/)/2 \
)
/
,J
Л9Г^
G D~
е-Г
1
ГA-
1

А10Г
A10T
s + 1
s + 1, s
, s = и -
•Mr[-
¦ 1/)
I
s + -
1
[
г 1
s + -
iRei/-
ЛюхГ L, s +
[0,E
ЛюГ
[(Rei/
- Rei/ -
f
1
— 1/, 1/ — s 1
+ 1 — с, с — s J
\c ф v — любое; s = j
- 1 - /г G jD+, к = 0, 1,
fi/, l-i/-el
1 — s J
[- Re и < Re s < 1 -
-l — i/, 1/ — si
[Re 1/ - 1 < Re s
s + 1/, 1 — 1/ — s]
[0, -Rei/ < Res < 1
1 — 1/, —s, v — s]
[Rei/ - 1 < Res < 0,
0 1 e I
2 ' 2' 2
— 1/ 1/
2 1 * 2
i---e
E - l)/2 < Res < A-Б
— 1/ 1/ 1/ + 1
ell
2 2 2
1/ 1 — 5
2 2
5 + 1^ 2
l)/2 < Res < A-S)/2,
1 ( l + i/ - 5 1 + 5
2' 5 2 2
^ +fe G
2,...]
Re i/]
< Rei/;
- Rei/]
Rei/]
f
s,
)/2]
72]
— 1/
5
l)/2 < Re s < A + 5 - Re i/)/2]
5 — 1/ 1 + 1/ — 5
2 ' 2
- 5 - l)/2 < Re e < 0, A + Re 1/
Г
[
i/ ( i/ + l
s + 1
[0, -Rei/ < Res < 1 -
s,	s
2
-5)/2]
Rei/]
18*

548
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.18
[Rei/ - 1 < Res < 0, Re v
1, 1 - и/2, A - и)/2, 1-й
8.4.17. Обобщенные интегралы Ф ренел я S(x, и) и С(х, и).
Обозначения: А\ъ = 21/™1^тг , 8 = < >.
Л12Г
5, S + ¦
2
' — v
А12Т
1 + 8 - и
2
[О, -F + Re i/)/2 < Re s < 1 - Re i//2]
-b(l + <J-i/)/2j
[Re i//2 - 1 < Re s < 0, (<J + Re i/)/2]
8.4.18. Функция параболического ци л и н д pa Du(x).
_	о1//2+1 f cos(i/tt/2) 1	тг3/2 fcoseccTri
Обозначения: Ai3 = 2 ; ^ <^ . ; . ( \,А14= О1//2Г,/	^1	Ь
[ sin (|/7г/2) J	21//2Г(—I/) I seccTr J
15 =
[Re s < 0]
[0 < Re 5 < -Rei//2]
[Re i//2 < Res < 0]
, 5 + 1/2, (!/
/2,
[0 < Re 5 < (Rei/ + l)/2]

8.4.19] 8.4- Таблица преобразований Меллина элементарных и специальных функций 549
10
11
12
13
14
15
16
± Dv (-
Ж21
±Du[-
{1-8I2,8/2
, 1 — <5/2
1 + i//2, с
A -8)/2, 8/2, с
2~\] ь+оо
A1AG\\[ x
2, 1 - 6/2, 1-е
- v /2, 1-е
Du
О, 1/4, 1/2, 3/4
Du
1/4, 1/2, 3/4, 1
1 + I//2, A - i/)/2
0, 1/4, 1/2, 3/4
1 _па/ 1/4, 1/2, 3/4, 1
¦Й!Ь
1/2
n- 1/2, 0
3/2 -n, 1
1/2
1-5/2- e
- l)/2 < Re 5 < (Re 1/ + l)/2]
/
[-(Re 1/ + l)/2 < Re e < A - <5)/2]
s + c, 1 — с — 5, I — J/2 —
с ф {1 ¦— 8)/2 — любое; s = (8 -— 1)/2 -— к ?
D+, s = -1//2 + A; G ?>~, А; = 0, 1, 2, . . .]
f 1 - <5/2, s + 1 - с, с - .
[с ^ A - 5)/2 - любое; s = A - 5)/2 + A; G
ED",s = i//2 - A; G 1^+, А; = 0, 1, 2, . . .]
1	1	3 I/
S, SH	, 8 -\	, 8 -\	,	S
4 2 4 2
[О < Res < -Rei//2]
i/113
[Rei//2 < Res < 0]
, в+ 1/4, в+ 1/2, s + 3/41
ж~ [ e + (l-i/)/2, e + l + iz/2 J
[Re s > 0]
-s, 1/4- в, 1/2- s, 3/4-s
20F ^ [ 1 + i//2 - в, A - i/)/2 - в
[Re в < 0]
(-1)п2тгг fs + n - 1/2, 1/2 - el
[(те-I)!]2 [	1-s	j
[1/2 - n < Re 8 < 1/2; n = 1, 2, 3, . . .]
(-1)п2тгг \s + 1/2, n - 1/2 - s
)]
[-1/2 < Re s < n - 1/2; n = 1, 2, 3, . . .]
8.4.19. Функция Бессе л я Jy{x).
_	л	2 f cos [(/x + i/)
Обозначения: t4i6 = ^^< 7 (
¦$}••-{;}¦

550
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.19
5+v и \-6+v \-v
inx~1/2\j (±
s:
COS X
5 +
1 -
i з :
4' 4
2 2
' 2
f Sin (л/ж +/17Г) 1
< ; ^_ ; > Ju (v ж) =
[ COS (л/Ж + /Х7Г) J
1/4, 3/4,
sin (ж ' + /1тг
COS (ж/2 + jttTT
^22
1 ¦— и	и
4' 4
-M,l+-,^
P	2 2
sin л/ж Jj/ (\/ж)
_j/ ("v/ж") =
л- 2i/=f 1
= — л/2 sin	7Г x
2 + 1 2 + 1
i/ i/ l — i/
"' ^' 2
1 \ ,	1	/ 1
± COS —=J — V
г- 2i/=p 1
= —V2 sin	тг x
4
1/I + 1/
s + ¦
5 + i/ Г
2 ' 4 '4
i+^-.
+i/
2	' 2
-E + Rei/)/2 < Res < 1/4]
1
I'
3 S + i
1+5- i/
2	2^J
[ - 1/4 < Re 5 < (Re 6 + i/)/2]
1/
2'
3
s, —
4
i/ + l
2	2
[-Rei//2 < Res < 1/4]
i/ 1 + 1/
	s,	s
2	2
1 + 5-i/
1-5 + i/
[-1/4 < Res < Re 1//2]
Л7 . 2i/=pl
— V^ sin	тг x
x Г
l + i/	i/ 2 + 1
s H	,	s	,	s
2	2 4
2 + 1	1/	l + i/
s H	, 1	s.
4	2	2
[Re i//2, -A + Re i/)/2 < Re s < B + l)/4]
x Г
11 + 1/
e + 1- ^5
	s,	s
2	2
1/ + 1 2 + 1
2	4
[(±1 - 2)/4 < Re s < - Re i//2, (Re 1/ + l)/2]

8.4.19] 8.4- Таблица преобразований Меллина элементарных и специальных функций 551
9
10
11
12
13
14
15
16
1 7
JL 1
1 Я
JLO
19
j2(^) = _LGii
J (\/x) J (\/x) =
j ( 1 \ j ( !
1
— X G11 (x\ °
~ V^ 13V i/
J f — 1 J f—
1 ruf
/
л/тг
\
1
2
L
V
1/2 \
v, -i/, 0 /
1 - i/, 1 + i/, 1 \
1/2 J
1 пг1(
V* 13 v
1/2 \
0, -i/, v J
\ _
у
1, l + i/, 1- i/ \
1/2 /
_
-1/2,-1/2,1/2-1/ У
^\ _
с /
З/2-i/, l/2 + i/, 3/2 \
i ;
о, i
2
ft + i/ /i + i/
2 ' 2 '
\
/1- I/ I/ - /Lt I
2 ' 2 /
"„^
2
,1-
f 2 '
"-1
1 M"7 i 1 ^ ~ ^ \
2 ' 2
/
2 COS 1/7Г 21 /
2 / 1 \ 2 /
2 COS 1/7Г
л/тг
24 v
1/2, 0 \
i/, -i/, 0, 0 /
1 \
fx J
Сж421 X
J—v (\/^) «^i/ (л/ж'
1 - i/, l + i/, 1, 1 \
1/2, 1 У
J —
2 sin i/тг ^20 /
1/2 \
v, -i/, 0 /
— К
fr[
^r[
1 r[
^ L
1 ГГ
v^ L
— r[
1 + 1/ - 8, 1 - S.
5 + 1/2, I/
[- Re i/< Re s< 1/21
[-l/2<Res<Rei/]
S [0<Res<l/2]
1 + 1/- S, 1 - I/- Sj
S + I/ + 1, 5-I/ + 1J
[-1/2 < Res < 0]
e + iz-1/2, 1-е 1
3/2-e, 1/2 + iz-sJ
[1/2-Re i/ < Res < 1]
5 + 3/2, 5 + I/ + 1/2J
[-1 < Res < Re i/ - 1/2]
Г ,. ^ + i/
+2^ '
2
	s, 1 - s
2
и — ц, и — и
1 ! ell e
1 ~т~ S , X "Т" S
2 2.
[- Re (/i + i/)/2 < Re s < 1/2]
1
2' ^
s
2
u, — i/ и -— и
с lie! 11
г> ¦ 1, г» -\- 1
2 2.
[-1/2 < Re s < Re (/i + i/)/2]
2 COS 1/7Г n [ 5 + 1/, 8 — V, 1/2 — S ]
L s, 1 - s, 1 - s J
[| Rei/ < Res < 1/2]
2 COS 1/7Г n [s + 1/2, V -— S, — I/ — s]
2 sin i/7i
у
Л/7Г
j.
о _|_ 1 о _|_ I _ e
[-
1/2 < Res < -
- Re i/|]
Г s -\-1/, s — i/ 1
-Г
[| Rei/| < Res < 1]

552
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.20
20
21
22
f—W2f—V
- sin итг G31 f x
i/, 1 - i/, 1,1
1/2
= ^16^24
2' 2
/Lt + I/
/Z — 1/
2	2
I/-//
J Jv
_
2'
2 sin итт [ i/ — s, — v — ,
[-1 < Res < -|Rei/[
E
,1	s
2
s+, s	,1
2	2	2
1 — d	и — v
s H	, 1 +	s,
2	2
1	s
Res < 1/2]
J + !^^
/1 + V
д + i/
2 2
¦ 1, s -
1-5
[-1/2 < Res < -|Re(/x + i/)|/2]
8.4.20. Функция Неймана Yu(x).
Обозначения: А17 =
K /o—-—, о = <
7Г5/2	I 0
у
1 - u/f,
C + iz)
-I//2, C + i/)/2
yfx
у
1 3
I' 4'
5 + i/ 5 — i/
2 ' 2 '
' — и — 1 1 — 5 — 1/ 1 — <
s + i//2, s - i//2
[|Rei/|/2 < Res < 3/4]
i//2- s, -1//2- ,
(i/ + 3)/2, -(i
[-3/4 < Res < -|Rei/|/2]
5 + i/	5 — i/
s + ¦
r-iz-1 3-5 +
1	3
1 ¦
	s,	s
4 4
/| -8)/2 < Res < 1/4]

8.4.20] 8.4- Таблица преобразований Меллина элементарных и специальных функций 553
Ш х-VI / 1
-1/2 ( J v I r~
os ж ; j \ л/ж
s:
cos ж
и +
1 3 '
4' 4'
( /-\ , [cos л/ж 1 , ^,
[ sin л/ж J
[ COS л/Ж
[sin л/ж
1/4,
3/4
A - и - S)/2, (S - и)/2
sin ж
cos ж"
G°A x
i--,
4'
1 — v 1 -\-1/ -\- S	v — 5
^"' 2 >1 + ~
4
cos л/ж
4'
3
I
l + i/ 1- i/-<* (У-,
2 '	2 ' 2
sin ж
COS X^
sin ж
COS 1/7Г
тг2л/2 l
"
/ ! X
^1"
1/4,
(i/ -
3/4
1 3
H—, 5 H—,
4 4
4 2
6-1/

2
3
s -\
5 - i/-
,	s
2	2
[-1/4 < Re s < (S - I Re i/|)/2]
l + i/	l-i/-6
12 3 2
+
iz/2
[(Re 1/ + ? - l)/2, - Re i//2 < Re s < 3/4]
^2
l, 1/4-e,
1//2- 5
3/4^5
[-3/4 < Re s < A - S - Re i/)/2, Re i//2]
1 - i/ -
2
5 + i//2, 1/4- 5, 3/4^ s
[(Re 1/ + ? - l)/2, - Re i//2 < Re 5 < 1/4]
cosi/tt	s + 1/4, s + 3/4, i//2 - s,
2Д [	()/
A + i/)/2 - s, A - 1/ - E)/2 - s
[-1/4 < Re s < A - 5 - Re i/)/2, Re i//2]

554
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.20
9
10
11
JL J.
12
13
14
15
16
17
18
j
j
=
(\/~X )
( —
( —
1
= ¦
( ]
+2 w
l
z—
( i
i
1
л/т7
Y (*/
\Y(_
j 1/ ^
1
- J
i
)Y (л
) ^V
11 (*
\
1С /
L \
_
Gil
-v -
\ i
H
1
22 I
3 + i/ -
3 + 3-
2
— l
1
^24
M
12(x
\
/x)
111
?-
У w
/
.'(
Уя)
r24 I *
/
1
f-
l)/2
1) /2
' 1
(
X
\
- ^
CQ2(
31 ^
1,
f
X
\
1/2
/
0. i/.
l-i/, 1
1/2
fa
V
, 4*, -
0, -i/,
л=
с/
1,1 + i/, 1
1/2,3/2-
_
, о
1/2, 1/2,-
^x ) ~
X
1
2 "^
2'
r»
0, 1/2
i/ + 1, 1
I \
42^
o,
1,
0, 1/2,
(/x + i/)/2,
/ _i_ W
\
) =
2 '
2' '
1
/i + ^
+ 2 '
i/ - 1/2
i/, —i/ —
-i/, 3/2
4/-
1 3
2' 2 +I/
, -i/ - 1,
-i/, 2, i/
1/2
i/-
1+ 2
1
4- ^
+ 2
-J
J
1/2 У
+ ^
3 \
1
-i)
+ 2 \
)/2 1
41 A /
/
i

Ф
i
!
л/тг
1
лАг
1
л/тг
1
л/тг
1
1
1
л/^
т
т
Г
г
г
Г
Г
г
г
5,5 + 1/
г
[5 + 1/2, 1 + I/-5J
[0, -Rei/
rf ^S'"^5 1
[S + i/ + l,l/2-sJ
[-1 < Re
.e-i/-l/2,l-i/-e,3/2+i/
[0, Re и <
[ s + 1/2, -i/-s,-s
L 5 +l-i/, e+ 1/4-3/2,-1
[-1/2 < Res
[5 + i/ + 1/2, 5 + 1/2, 1/2-
L 5, I/ + 3/2- 5, 3/2- 5
[-1/2, -1/2-Rei/ <
Г5 + 1/2, 1/2- 5, 1/2 + 1/-
L 5 +1/+ 3/2, 5 + 3/2, -^
[-1/2 < Res < 1/2
Г S + P + 1, 5 + 1, 1-5 1
[5 + 1/2, 2 + i/ - s, 2- sj
[-1, -1 - Rei/
Г S + l, 1 — S, l + i/ — 5 1
[s + 2, s + i/ + 2, 1/2-ej
[-1 < Re 5 <
S+ 2 ' " ' 2 "'
/1 — b> -— 1 3 + 2/ — p
s + ,
. 2 2
1
- - s, 1 - s
2
11 + V U, — V
11 ell
1 -r 5,1
2 ' ' 2
[(|Rei/|-Re/i)/2<
S 2' ' 2 S'
3 + i/ — /x /x + i-
S+ 2 ' " ' 2
JX - i/
u-I/ /X-1/-1
S "Г 1,
2 2
[-1/2 < Res < (Re/x
< Res
s < 0,
1
Res <
/2— i/ -
< 0, -
-1
J
Res <
"'1
» J
+ Rei/,
< Res
1, Re^
s,
— s
Res <
-
s
-Rei,
<1]
Rei/]
1/2]
]
-3 J
Re^]
1/2]
1/2]
<1]
' + 1]
1/2]
'l)/2]

8.4.20] 8.4- Таблица преобразований Меллина элементарных и специальных функций 555
19
20
21
22
23
24
25
Ju {у/х) Y~v {у/х) + J-u {у/х) x
пь-
1/2
и, -и, 0
\у/х
л/х
1 - I/, 1 + I/, 1
1/2
2
fJb — I/ V — /i /Lt +
2 ' 2 ' 2
—= G42 ж
1 -
1
2'
2 '
Jv{y/x~) Y^v
2 '	2 '	2
sin2i/7r
7Г5/2
sin2i/7r
7Г5/2
1/2
0, i/,
1, 1 - i/, 1 + i/
1/2
= A17GH x
2
ь + i/ /x - i/
~2 ' 2 '
/i +
s - i/, s +
Rei/|<Re5<l]
/i- I/
2 '
1
[(|Rei/| - Re/Lfc)/2, Re (д - i/)/2 < Re s < 1]
t + ь>
¦ — s, -
2
V — jJL
[-1 < Res < (Re/x- |Rei/|)/2, Re (i/ - /i)/2]
sln2i/7r
sin2i/7r Г 1
Г[+
1
[|Rei/| < Res < 1/2]
[-1/2 < Res <- |Rei/|]
A17V
(J, -\- V	fl — I/
2 ' ^ 2 '
2
is — fj, 1
2 2
1
,	S, 1 - .
2
[Re(/x- i/)
-Re/x)/2 < Re s < 1/2]

556
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.20
26
28
29
30
31
- J
= AitGJI
2( /~\ 2
( ~/= )
\Vx )
I
V
\
!
2'
i „
у Ш=
2
= ~^=" ^42
У (л/ж) У
=
V7T V
/ 1 \
У_„ -— У
VvW
2 03
~ л/тт 42
4
Vi/2-, (Л^)
2
= "Г11' ^24
+ ~^=" ^2
+ _
/
X
{
1, 1
1
2 +
-
2
"Г '
1/2
— u1
]
-^=G\\(x
(л/х') =z
2 ^3(
1/2
0, u, -
( ! >
rv —=
\л/^ )
(x
{
1, 1
1/2
1 t
.)
— и
2 '
2 ' ' 2 J
/
Д/2-i/ \ +
,-i/, l/2-i/ /
Gii(x
1/2 N
13 V i/, -i/, о /
i \
l +1/, - +1/ \
r
i -1/, i +1/, i \
1/2 /
1/2, 1/2 \ +
0, i/, -i/, 1/2 /
,1 + iz, 1/2 U
,1/2 У
<
X
{
' 2
1
4
/
A
1
0
1
—
\ 4
=
1
4

1, 1 - i/, 1 + i/ \
1/2 J
ii +
- i/, i/ — —, — I
4 4/
\
\
til
-, I/	,	U I
1 4 4 /
s + 1/2, s + 1, (/i + i/)/2 - s,
О - ?/)/2 - s, (i/ - /a)/2 - s 1
J
[-1/2 < Res < Re(u-n)/2, (Re/x-
2 r
1/2
1/2
2 [
— г
\/5F
2 [
-i-Г
+ -
Rei/|)/2]
s, s -j- I/, s — i/
I s + 1/2, s + 1/2-i/,
]+^rrS + ^,l/2-s]
+ i/-e J v^ Li + i/-e, i-sj
[|Rei/| < Res < 1/2]
[ -s, iz-s, -^-s
s + i/ + 1/2, 1/2- s,
-i
1 Г s + 1/2, i/ - s 1
- i/ - s J л/тг Ls + 1, s + iz + lj
[-1/2 < Res < -|Rei/|]
s, s -{- u, s -— и 1
+
.s + 1/2, s + 1/2, 1/2- s\
+ — г[ 5'Х/2^ 1
i/tF [I™7"? 1 + 1/ — SJ
[|Rei/ < Res < 1/2]
— s, i/ — s, —i/ — s 1
.s + 1/2, 1/2- s, 1/2- s\
1 Г s + 1/2, -s 1
+ 7^ [e + l-i/, e + l + i/J
[-1/2 < Res < -|Rei/|]
г 1 1 1-
S — — , S -^	— U. S -\- I/ — —
4 4 4
1 3
+
.11 . 1
1
S+-, ^7— S, I — S
5 5 3
	s,	i/ — s, —h ^ — s
L4 4 4 J
[1/4, |l/4-Rei/| < Res < 1/2]

8.4.20] 8.4- Таблица преобразований Меллина элементарных и специальных функций 557
32
33
34
35
Y" Ш =
¦Gttlx
5 3	5
I' 4 +I/' 4
1
2'
3 5 5
4' 4' 4 "
2'
3
Л —
4
Л —\- и
4
Ui -\- V LL — U
2 ' 2 '
— A \i-\- v 1 — [I — v
2 ' 2 ' 2
"•5
2 '
2 ' 2
2 ' ^ 2 '
1 - -
2'
2 '
2 COS 1/7Г
1/2
О, I/, ™2
2 „ I -1/4- s, 1/4- i/ - s,
5 + 3/4, -s,
^1/4-s] 1 Js + 1,
5 + 1/2, 1/4^5
5 + 5/4 - u, s + 3/4 + i/
[-1/2 < Re s < -1/4, -|l/4 - Re i/[
2
/—
л/тг
Г
S 2
1
о о J	«
г», г> ~r , -
Р — Ц
S+ 2
1-/X-Z/
' s
2 2
А* —
[(|Re/x|
; Res < 1/2]
— s,
1/2- s, A-
1
и — и
у —¦ и,
[-1/2 < Res < -(
2 cos i/тг
Rei/| < Res < 1/2]

558
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.20
38
39
40
41
42
' 1
17 \л/« / " \л/«
2 COS 1/7Г ]_
7Г5/2
J2 (V^) - Y$ (V
2 r
Jl (±=\ - У,2 (
= "^G42r
-I/ ^ ) u \
= COS 1/7Г
j- Ш j, (-
= -— G°
л/^ 4
2
COS иж ^32
7Г5/2 24
03
1/2
x±i,
И(
2
r
V
и
(
L
\
)
, i/
0,
1, 1 -
1/2
% 1/2
)-
,1/2 + v
'2)+
/
ljr24l "^
\
1/2
0,i/
—
1, 1-1/, 1
1/2, 1/2
•¦i
/i + I/ j
2 '
y-/i +
2 /
1
A* + ^ /
2 '
1/ — /1
2
1/, 1 + 1/ \
J
"" )
l/2-i/ /
l/2 + i/ \
J
^2 / ±1/2^1
1/2 \
-i/, 1/2 /
+ 1/, 1/2 \
v x )
u + v
2 '
1 + 1/
2 '
\
2 COS 1/7Г
2
2
2
2
1
1
j
— ?
+
s +
s +
¦]{¦
1
1/2,
s,
1/2,
— s, j
1/2,
(Lt + 1/
2
:os jd'
cos i/тгГ
[
(|Re
[-1/2 < Res
s, s + 1/, s — 1/
e+1/2-1/, 1/2 4
[|Rei/|
s7 и — s, —1/ — s
[-1 < Res
[cm. 8
s + 1/, s — 1/
s + 1/2, 1/2-5
[| Re i/l
/ — s, —1/ — s
1/2 - s, 1/2- s
[-1 < Res
/1 + 1/ 1
2 2
ггГ| s + (^i™1/)
M|+ Rei/|)/2<
¦•]
<-|Rei/|]
< Re s < 1]
<-|Rei/|]
.4.20.35-36]
]
< Re s < 1]
]
<-\Rbu\]
- s,
/2.1 +
1}
Res < 1/2]

8.4.22] 8.4- Таблица преобразований Меллина элементарных и специальных функций 559
43
44
45
cosi/tt 23
1 -
1
2'
1 - -
1
2'
/Lt +
- Y^ (у/Б) Yv (у/Б) =
2
2
У — jJL jJL -\- V 1-/1 —
2	2
Jx
1 -
1	1+p
2' '	2
2	2	2
1 + H +
Г (i/M)/2« 11
- COS 1/7Г1	>
[-1/2 < Res < -(|Re/x| + |Rei/|)/2]
21
2'
, s
2	2
[(|Re/i| + |Rei/|)/2 < Re s < 1]
/i -\- v	/J, — и
и - p,
2
2	2
[-1 < Res < -(|Rejx| + |Rei/|)/2]
8.4.21. Функции ГанкеляЯ^(ж)иЯ^(ж).
8.4.22. Модифицированная функция Бесселя ^(ж).
r^r>	л	\/^	л	(^1M7Г Г sec (с ^ |//2)тг
Обозначения: Aig = 	т^	г—, Aig = -—^—<	f,
sin (с — 1/)тг	у2 [ cosec (с — и/2)ж J
А^	л	г~	(	М + 17 \ а	-3/2 . / ,
	—5 Л22 = V ^ COSeC I СЖ	7Г 1 , Л23 = 7Г 7 Sin (fl +
— г/)тг	V	2 /
cos (с — и)
-W-

560
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.22
1-I//2, 1 + I//2,
1 - с- i//2
1-е- i//2
3
4
е1/(а-)/" Ш=
Г shv^ 1
[ ch уж J
= A19GU
1/2, с
I/, — i/, С
l-i/, l + i/, 1-е
1/2, 1-е
1 3
2 ' ~^'
1 + i/ —
2 ' 2
-, с
/ ! Л
i з 2' 2
1
1 + 1/
-, 1-е
sh y/x Iи
2 ' 2
, гл cosi/тг
1 3
4' 4
?/ + 1	V U 1 — 1/
2 ' 2' 2' 2
i/
Г| Ч
SinCTT I s + - + С, Ц	S,
- любое; s =
= -i//2 - A; G ?»+, A; = 0, 1, 2, . . .]
7Г
- I' | " ' ~ ,1
^ , 5 + 1 — С — j
[c^O- любое; s =
1//2 + C-.
= I//2 +A; G D~, fe = 0, 1, 2, ...]
T^1
А18Г
[-Rei/<Res<l/2]
[-l/2<Ree<Rei/]
S + U, 1/2 - 5
e, 1 - с - s, 1 + i/ - ,
? и - любое; s = -i/ - A; G i^+, s = 1/2 +
G D", A; = 0, 1, 2, ...]
+ i/ + 1, 5 + 1 — С, С — ,
[с ф и — любое; s = i/ + A; G i^"", s = —1/2 —
- A; G D+, A; = 0, 1, 2, ...]
А19Г
3
4 ~
5 + ¦
2 '4 ' „
c, 1 — e — s, 1 H	s,
2	'	2
+ 5)/2-любое; s = -{v + 8)/2-k G D+, s =
= 1/4 + A;, 3/4 + Jfe G D~, A; = 0, 1, 2, . . .]
1	3
^ 4
+ +1 +
Л19Г
8-i/
, s + 1 — e, e — s
\c ф (v + 8)/2 — любое; s =
= (y + 5)/2 + A; G D~, s = -1/4 - A;, -3/4 -
- к G D+, A; = 0, 1, 2, ...]
COS I/IT
	7=~ x
тгл/2
x Г
+
H	, S	,	5,	,
2	2 4	4
i/	l + i/
1	5,	S
2	2
[-(Re i/ + l)/2, Re i//2 < Re s < 1/4]

8.4.22] 8.4- Таблица преобразований Меллина элементарных и специальных функций 561
10
11
13
14
15
16
17
18
sh
x
J (
—
J — v
J-v
'2(
/2 /
1 V
I v
1 / i
ш Л
X
/
22 1
^42
24/?l
V xj
\/7Г Стл
/ 4/
BVi^
j_\
•у/ж1 /
— y4
f—)
— A2
/
1
n
1-й
Л
\
~»10
J'04
j 1
)'*
'.
V
Ли
r.
(
1
л/ж
1
)--
1 — 1/ 1/
2 Л ' 2
1 3
4' 4
4/^4 _
(
I//2, -x
'2 4/-l -
ч V ж/
и
1/
B^4^) =
/
V
1/ + I
2
0, 1/2,
= -Jtx x
1 I/
2' ' 2
1 — и
2
>Gl\(x
1/2
^42 ( x
V
l — i/
1/2,
— /-i20^jr24
(—) =
\y/x J
if
4x
	V
11 —
1/2, 1
X
COS 1/7Г
Try7!
I/
1
2'
1
//2, 0,
и
и и
2' 2'
i/
2'
-1/, 0, с
1-е
(
1/2
0, е
с 1 + i/
— с
1
4—
L4
1
ч—
v
j
1
)
. с
1
+ l/ \
2
/
1/2 )
-оо
л
2 /
— 1/ \
/
Ь + оо
)
\
-V V )
— ^ 1
COS I/
/?
х Г
^г|
L
[
[.=
Г
7Г
г- X
>
г 1
s+ 4's +
с 1 1
-1/4 < Res
s4
1 + и/2- 5,
[s = -v/2 -
s + i//2 + 1,
[. = ,/2-
1
Sj S+ 2
r> 1 " ' "*"
2
1
= -A;, -1/2-
1
^5' 2 ~ ^
1/
+ + 2'
1
[5 = A;, 1/2-
5 +
5 + e, 1 - c-
-ке D+, 8 = 1/2-
г
L
G D~,
АоПг\
[сфО
е d~ ,
А20Г
L-
5 +
5 + 1, 5 + I/ ~
[c
5 = -1/2 -
3 +c, 1 — с —
— любое; 5 =
к = 0, 1, 2, .
5
3 + 1 — С, 5 +
— любое; 5 -
к = 0, 1, 2, .
3 1/ 1 +
4' 2 °' 2
I/ 1/ + 1
е 1
2'°' 2
< (Rei/ + l)/2,
-I//2 1
1/2- 5, 1 - 5J
- A; G D+, А; = 0
2-5 1
5 + 1/2, 5 + 1J
f к Е D~, к = 0
4- в 1
— I/
2 J
- к G D+
2
, Jfe = 0
1/ 1-
1 1 el
2 2
+ i/
2
f A; G D~, к = 0
i/, 1/2 - 5
-5, 1 + U - 5, 1
[e ф и — любое;
f- A; G D~, A; = 0
1/2, и ^ s
hi, 5 + 1 — е, с
фи — любое; s
к G D+, А; = 0
з, 1/2- 5
5, 1 + V — 5, 1 —
= -A; G D+, 5 =
+ 1/2, -5
I/ + 1,5 -I/ + 1,
у
-Rei//2]
1, 2,
1, 2,
— 5,
1, 2,
1/
1,2,
-.1
5 = —
1, 2,
1
— 5 J
= ^ +
1, 2,
1/2 +
1
с — s\
= A; G D~, 5 = -1/2 -
1
¦ ¦ -1
...]
I/ —
...]
ке
A; G
A; G

562
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.22
19
20
21
22
23
24
25
Iv-l (\Я)
= A22G3
Чл/ж /
2 /" ! N
g22
24
/* (v^) =
/
ii /
I
0, с
i/ —
№)-
/
-19 I Ж
3
	i/,
2
1, 1 - с
/
4
I
\
1
' 2' ^
/x + ^
/
I
\
1
2J 1?
Ax-i/
2 '
1-е
j
sln2i/7r r
- ^3/2
1 \
Уж /
sin 2i/w /п12 (
жЗ/2 ^Х
1_и(у/Б) - i
' 2
/x + i/ /
2 '
1
2
1
Ь
>
1
, c,	,
2
3
-c, -,
2
M + ^
M
1 1 '
, н—
v- ц
2
¦v21 /
'm
1
8 Г
\
\
1
2 )
L + oo
1 \
2+U )
J
V - [I
9 '
\
2 >C /
b + oo
2 '
1 с \
,1 с
)
1/2 ^
1 - г/, 1
1/2
+ ^
2
У — 11
2 '
-и, О)
J
,-, )
2 /
А21Г
G D+,
л22г
= -(a^
G D~,
А22Г
+ i/)/2
s + с, 1-е -
С7^^-1/2-
5 = 1 + k G I
s +
3
s + -, s + 1/
2
1
^'
3
- sj	sj
2
любое; s =
J~, k = 0,'
1
2'
\сф v — 1/2 — любое;
1 2 '
L 5 + С, 1 - С
11
2
+ i/)/2- fc G
к = 0, 1, 2, .
Г 1
1 ft \ IS
I S ' 2
M + ^ „
2
1/ — д
0 1 1
2
— любое; s =
= -1/2 - k, -1 -
sin 2jy
7Г3/2
sin 21/
жЗ/2
л23г
Trj» + ",»-
". , M + ^ .
5 1 , S
2
- l f 20R
2 S'
1 1 ^
0, ± 1
oil
2
-
1
2
: 1/2-1/- fc G
L, 2, ...
5
— с, с — s
-
5 = 1/-1/2 +
= 0, 1, 2, ...]
1 и
2
_
2 — любое; s =
D+; s = 1/2 + A;, 1 + к G
..]
1 1 1 ^
1, s + 1 с
= (Ax + i/)/2
-v, 1/2-5
[| Re 1/
s + 1
1 1
2
, с — s
[сф{и +
+ A; G D ; s =
= 0, 1, 2, ...]
1
< Res < 1/2]
1
[-1/2 < Res < -
ft + 1/ 1
2 2
* (Ai + iO 1/2
ReH]
2 J
< Res <
1/21

8.4.23] 8.4- Таблица преобразований Меллина элементарных и специальных функций 563
8.4.23. Функция Макдональда^(ж).
„^	д	1 fcos(i/7r/2)
Обозначения: А24 =
1 J cos
2^тг \ sir
Kv Bv^) = i G%
Kv
и/2, -и/2
-Л\\=уГ*О&\х
1/2
i/, —v
,rm^)K(l\ = ^G
2x
ЖЛ COS™Gl\(x
V^
1/2 /
1/2
I/, —I/
е1/BжЧ^>
v^
-Gl x
ch л/х J	/
1
2у^
Glllx
"
-^Glllx
2лД 42
1-i/,1 + i/\
1/2 )
1/4, 3/4
E + i/ 8 — и
2 ' 2 '
l-5 + i/ l-5-i/
5 + i/	E — i/
4'
l + 5-i/ 1 + 5 +
/ 4у7г
x Cg2 I x
0, 1/2, i//2, -I//2
1/	1/
2 L2 ' 2
s + 1/, s ¦— i/
1/2-8
COS 1/7Г Г	1
—^r U + ^.s-,,--
[Res > |Rei/|/2]
[Ree<-|Rei/|/2]
[Res > |Rei/|]
[Ree<-|Rei/|]
COS 1/7Г I	1
Г |в + -, !/-*, -I/-*
Re 1/1 < Res < 1/2]
-i/ — s\
-1/2 < Res < -|Rei/|]
2д/2
x Г
2л/2
s H	, s H	,	s,	s
2	2 4 4
2	2
[(|Rei/| -<5)/2 < Res < 1/4]
s + 1/4, s + 3/4, E + j/)/2 - 8,
[-1/4 < Re s < (<5 - | Re i/|)/2]
, e
[Res > 0, -Rei//2]

564
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.23
10
11
х Ки
1/2, 1-I//2, 1 + I//2
+ J B\/2 ж1(//'
rV4A =
2' 2' 2' 2
12
/- I I x
Жу
х АГ„ ( 2 4/- 1 = Л24 х
ХОлп I X
6	и	1/1 +
1- -, 1 —, 1 + -, ^
2 2 2 2
13
14
113 1
I' I' I' ^I
15
16
17
Уи {2у/2 ж1/4) /С„
J	rm(^ 1/4, 3/4, 5/4, 5/4
0,	0, 1/2, 1/2
1,	1, 1/2, 1/2
1
1 и и \ -— ь>
' 2' ^' ~~2* 2
18
2	2 2 2
19
K
1/2
0,i/,-1/
iz/2
[Res < 0, Re 1//2]
[Res > |Rei/|/2]
- s,
[Res < -|Rei/|/2]
1 r[e-l/4, s + 1/4, s + 3/4
[Res > 1/4]
1 гГ-1/4-в, 1/4-e, 3/4-8
s + 5/4
ZLr
2 [
[Res < -1/4]
[0 < Re s < 3/8]
[-3/8 < Res < 0]
j + 1/2, s + iz/2, e-i//2l
[Res > | Rei/|/2]
x Г
-s, 1/2 - s, i//2 - s, -I//2 - s
[Res < -|Rei/|/2]
5, S + I/, 1/2 -Si
1 + iz-e J
[0, -Re i/ < Res < 1/2]

8.4.23] 8.4- Таблица преобразований Меллина элементарных и специальных функций 565
20
21
22
23
24
25
26
27
(у/х) Kv (у/Б) = ^^ X
1, 1 - I/,
1/2
V — /Lt	/Л +
2 '
2'
2 '
+ •
[/_„ (v^) +
¦ (jiq Ж
1/2
i/, -i/, 0
1 +1/, 1 - I/, 1
1/2
2' 2
jy U -— fl (J — U	/Lt
2 ' 2 ' 2 ' 2
A25GH I ж
+
2 '
5 1 +
2' 2
1/2
0,1/, -1
— s, i/ — s
[-1/2 < Res < 0, Re v\
- i/)/2, 1/2- s, 1 - s
|Rei/| -Re/x)/2 < Re s < 1/2]
[-1/2 < Res < (Re/x- |Rei/|)/2]
COS 1/7Г Г S + I/, S — I/, 1/2 — ,
/^F [
Rei/| < Res < 1/2]
cosi/tt [s + 1/2, i/ — s, —i/ — s
[-1/2 < Res < -|Rei/|]
и -
2 '	2 '	2 '
	, 1 Л	s
5
1	,
2
-i/)/2, (| Re i/|-
< Re s < 1 - . .
?// + */'"	v - г
+ 1	,	s,	s,
2' 2 '	2
2 ' ' 2
/1 — v
[6/2-
- 1 < Res < Re(i/ - ^)/2, (Re/x - |Rei/|)/2]
r|s,
s + i/, s - 1/
2 [ s + 1/2
[Res > |Rei/|]

566
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.24
28
29
30
31
32
33
34
к:
1, l-i/,
1/2
11	1
	, I/	, —I/ Н—
2	2	2
3/2, 3/2- i/, 1/2 + и
1
/1+1/ /1 — V I/ — /Л	/Л + I/
2 ' 2 ' 2 ' 2~
х G^ \х
1
I'1
,1 + ,
2	2
2 '
<v(y/i 2у/±х)Ки(у/-ъ 2
¦ GqI ( x
0, 1/2, i//2, -i//2
/civ7 2AVlV/V=l2^=^x
1/2, 1, 1-1//2, 1 + 1//2
7Г ^ -S,I/-S,-I/-J
[Ree<-|Rei/[
1/2-8
- i/ - 1/2, 5 - i/ + 1/2, s - 1/2
[Res > 1/2, |Rei/- 1/2|]
[Res < -1/2, -|Rei/ - 1/2|]
I/	/i-I/	1/-/X
[Res
u, — v	v — u,
¦ ~~ s, —:	s,
" ' 2
' ' 2
[Res < -(
2	2	2
[Res >
1 Г 1	i/	i/
Г — s,	s,	s,	s
|_ 2	2	2
[Re s < -
8.4.24. Интегральные функции Бесселя Jiu(x), Yiu(x) и Кги{х).
1
2
3
4
Ji B /?
T. ( 2 >
\УЖ )
Y%v By/x
= 2
/ 2
\-\/ж
x G
2
= Ig
\
/
\ l
/2
/
Si U
V
j20
fO2 /
q-i 1
31 \
1
o,
x
i
o,
\
1
o,
/
X
V
1,1
0
1//2,-
i
X
C + ^
u/2, -i//2 J
-1//2Д + 1//2 \
1) /2 \
^/2,-A + ^)/2 J
1+U 3 + 1У \
2' 2
)/2 /
M
2 L
Irf
2 L
Ir
2
Ir
2
.,, + •72
s + 1,1 + I//2 —
v/2-3,-3
s + iz/2 + 1,1-
s, s +
v/2-t
„s + (i/ + 3)/2,
1 J.J -+W
s\ 2s [1 + ^/2
[Res > 0,
1=--Lr[ "/2
sj 2s [s + u,
[Res <
i//2, s - v/2
f l)/2, C + i/)/2
j, —u/2 -— s, —s
— A + ^)/2 — s,
— s J
-Rez//2]
™S 1
'2 + lJ
0, Rei//2]
1
— s J
[Re s > 0]
1
i-*J
[Re * < 0]

8.4.25] 8.4- Таблица преобразований Меллина элементарных и специальных функций 567
5
6
' ( 2
X
)
0, i//2, — u/2 /
1,1-^/2,1 + ^/2 ^
-r s'
4 L
4 L
5 + i//2j e-i//2l
s + 1
[Re s > 0]
[Re s < 0]
8.4.25. Функции Струве Н1/(ж) и Li/(
„^	л	COSU7T .
Обозначения: A2q =	—, А27 =
[с- —)тг, А28 = —<	}.
V	2 /	7Г [ COS УТг )
31
ж) -Н
A -i/)/2, 1 + I//2, 1™ i//2
(l-i/)/2, 1 + 1//2, 1- I//2
й *
и -\- 1
1
' 2
2	2 2
= Л27 X
х GJJ ж
	, 1-е, 1	, 1+ -
2	2	2
1 + 1//2- s, 1 - i//2 - s
-A + Re i/)/2 < Re s < A - Re i/)/2, 3/4]
s + 1 + i//2, s + 1 - i//2
[-3/4, (Re 1/ - l)/2 < Re e < (Re 1/ + l)/2]
l-i/
i/ \ — v
Res < (
' 2 '
2 '2
A27F
2 2
[(Rei/- l)/2 < Res < -|Rei/|/2]
iz + 1 l-i/
* Н	1	s
2 2
I + С, 1 — С — 5,1	S,
[c ^ A/ + l)/2 — любое; s = -(v + l)/2 - A; G
G D+, s = (l-i/)/2+ife G D", ife = 0, 1, 2, . . .]
l-i/ 1 + и
s H	,	5
A21V I	2,.' 2
s + 1 — с, с — ,
[c^(i/ + l)/2 — любое; s = (y + l)/2 + Jc G
G D", s = (y-l)/2-k G D+, ife = 0, 1, 2, . . .]
I/ + 1	U 1 — 1/
» Н	, s ± —,
2	2 2
l±i//2-e
Re i/	л
^	1 - Re i
о .1 о ><Res<
Rei/ + 1 Rei/ [	2

568
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.26
1 —i/ i/ + 1	I/
H	,	s, ±
2	2	2
8.4.26. Функции Вебера Е|/(ж), Е^(ж) и Ангера Ли
cos (г/тг/2) I
sin (|/тг/2) у
Обозначения:
—,
2тг2
= 2
' 2' 2
1	i/ i/ l + 5 — i/
О, -, --, -,
2	2 2	2
1
2' '
- + 1, 1	>
2	2
l + i/ - 5
•¦з-
1 -
2 ' 2
/i + I/ V — Ц
0 —
2 ' 2 '
Е{?
2
l + i/ -
О, 1/2
О, 1/2, Z//2, -I//2
= A29Gli \x
и	и
-. 1, 1	, 1+ ~
2	2	2
1/2, 1
1 1
+ 5
	S,
2
[0 <Res < 1/2]
¦ -, 5 + 1, -S,	¦
Н
[-1/2 < Res < 0]
a — и	1 + i/ — 5
:!1	s,	s
2	2
[0 < Res < 3/4, (Re/i + l)/2]
Д	Д + 1
+1S+	'
LI
II — V
s, s +
l + i/ - 5 l + 5-i/
	2	' 	2	^
[-3/4, -(Re 11 + l)/2 < Re s < 0]
1/2, s + i//2, 1-5, 1/2 - si
[-Rei//2, 0 < Res < 1/2]
1	1/
1, ^5, - -5, - -
S + - + 1
[-1/2 < Res < 0,~Rei//2]

8.4.28] 8.4- Таблица преобразований Меллина элементарных и специальных функций 569
10
± Л_„
A - 8)/2, -и/2, i//2
= A30Gl\ x
,1-
2 2
2 cos — Iu Bл/ж) -Ju Bъ/х) -Ju (-2ц/х) =
sini/тг 21
	G13
i/тг / 2
2cos —/„
2
2г
О, i//2, -I//2
2г
и	и
1,1	, 1 + -
2	2
1 + у/2 -s,l- и/2 - s
[F-1)/2 < Res <
2, A-8)/2-8
+ i//2, e + l-i//2
[-B + <У)/4 < Re s < A -
sin 1У7Г Гз, s + I//2, 1 — .
[О, ^Rei//2 < Res
sin i/тг fs + 1, — s, v /2 — ,
I//2+1
[-1 < Res < 0, Re i//2]
8.4.27. Функции Ломмеля5М]Дж)и5й)Е/(ж).
1
2
3
4
, Bл/я") =
11 f
1
I
(/x + l)/5
(/x + l)/5
1-М х
2 '
A M)/
1-д
i-m'
2
>
V
1/
2'
J, ^/2 /
i/ \
1 + 1
I
/
;2, -i//2 J
i _i_ \
/
31 [ 1 + ?//2 - s, 1 -
[—A + Re /i)/2 < Re s
[S + A - М)/25 С/1
L 5 + 1 + ^/25 s ~
[-3/4, (Re/x-
^32r[s+i±^
[-A + R«m)/2,
Г 1 —/i
[(Re^-l)/2<
-l)/2<
Re^j/2
^i//2^s j
< (l-Re/x)/2, 3/4]
+ l)/2- si
Ы-1//2 J
Res < (l + Re/i)/2]
i/ 1-^ 1
< Res < A — Re/i)/2]
-i
if i/
Re s < (Re/i + l)/2, Rei/|/2]
8.4.28. Функции Кельвина Ьег|/(ж), Ье11/(ж), кег1/(ж) и
Обозначение: <5 = < >.
4
2+и и
	s, Ц	s,
4	'4
[з = -1//4-
- fe, -(i/ + 2)/4 - к Е D+, к = О, 1, 2, . .

570
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.28
Ьег„
bei,,
х СШ \х
и 2- и 2
4' 4
2
l-i/
2
ber D Щ 1
bei D Щ ]
ber
bei Ux
0, 1/2,
= ttGSJ I x
2 2
er;D^)l _
ei'D^) J ^T71
2^ 1	1 3-25
4 ' I' ~4'	4
3 5
4 ' I' I' 4
i/ i/ i i +
^' ~' ' 2' 2
17	I/	1	1 —
1		, 1+ -,	-,	1,
2	2	2	2
1 — и
и	и + 2
	s,	s
4	4
2 +
-и	, - + i/ ¦
2 2
[a = v/±
0, 1, 2, ...]
', k =
s +{1-8)/2
1/2- 5, 1 - s, 1 - 5/2- ,
[s = E - l)/2 -ke D+, к = 0, 1, 2,
тгГ
¦f 1/2, 5 + 1, S + 1-5/2J
s = A - 5)/2 + к G D~, A; = 0, 1, 2,
„3/4 - s, 5/4 - e, A + 25)/4 - s J
[s = -A + 25)/4 -ke D+, к = 0, 1, 2,
(l + 25)/4- s
i + 3/4, 5 + 5/4, s + A + 28)/A
s = (l + 25)/4 + fc G D~, к = 0, 1, 2, .
1
5 =
2 1
i/ + 1	v
Л	,	- + 1 - s, 1 - s,
2	2
1 - i/
	s,	i
2	2
[s = ~v/2 - к G D+, fe = 0, 1, 2, . .
i/
	h 1, s + 1, s + -,
2	2
1 - и и + 1
S H	,	8
2	2
= 1//2 + Aj G D", fe = 0, 1, 2, ..

8.4.28] 8.4- Таблица преобразований Меллина элементарных и специальных функций 571
10
11
12
13
beii
bei'
berj, B
г 1 1
, о — — , — ,
'44
ЬеМ2А/-) ,
ei, 2
ei^ B
er^ B
1 -
l-2i/-25
±ЪеЦ 2П-) x
V ж,
2i/=p
A '
26-2i/ 3 5
4	' 4' 4
ker
1	1
kei,/ D ^) j	4X
xGf
keri/
keii/ I
xG ж
2
1/ t/ + 2 1/ 2 — i/ 1/ +
I' 4 ' ~I' 4 ' 2
= ±- x
4
1	, 	, 1+ -,
4 4	4
5 + v
ker D \fx) 1
kei D^ж) j
о, i, i^, ^
2 22
1 + 25-21/	3	5
	л	S'7^S'7^^^
4	4 4
¦ = -Bi/ =p l)/4 - A; G ?>+, ife = 0, 1, 2,
Г3/2
2i/=p
l + 25-2i/
5 e
4
[s = Bi/=p l)/4 + ife G D~, A; = 0, 1, 2,
1/	1/ + 2	1/
4'	4	4'
t -\
+ i/	i/ + 5
, 1	s
2 '	2
1
4
Г
2 — i/
4
i/
— — 8 i
4
5 + 1-
[Res > |Rei/|/4]
1/ + 2
s,	s,
.4
2 ' 2
2 - 1/
[Res < -|Rei/|/4]
r\ 8 + 1/2, 8 + (l
4 [	1-8/2-8
[Re s > 0]

572
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.29
14
15
16
17
18
кег
kei
1
2'
i
Г sinCi/?r/4) 1 , 4—v
< > keiv 4va;
1 cos Ci/7t/4) j l ;
J cos (Зх/тг/4)
i sin Ci/tt/4)
Т1гзо /
= TiG04^x
i/
4'
/ sin (Зг/тг/4) \ /
tcosCW4)/ker4l
\sinC^7r/4)
4 40 I Ж
\
1 +
ker I B #4sc) + kei I B У
^8v^F 04
¦
Y
k)
1
±
Bi,(
+ 2
4
±
\ kei^ I
J V
1
4
o,
4'
25
=
I,
+ 5
2 '
2
2-
4 N
2 -
4
2-
i/
2
5
2
) =
5 — и
4 '
-28-и
4
)=
i/
V25 + v
4
i/
~*2
-keif
G4n ж
-, 1, 1--, 1 + -
±-Г
4
[Re s < 0]
i/ i/ + 2
7, s + ——,
4	4
2 + 25 + 1/
[Re s > - Re 1//4, (Re v - 2<*)/4]
	s,
[Re 5 < Re i//4, B5 - Re i/)/4]
1 Г	1	i/	i/
L	2'	2'	2
[Res > |Rei/|/2]
1 Г 1	v	и
Г — s,	5,	5,	s
L 2 '2 '2
[Res < -|Rei/|/2]
8.4.29. Функции Э й р и AI (ж) и BI (ж).

8.4.29] 8.4- Таблица преобразований Меллина элементарных и специальных функций 573
10
11
12
.2/3
e^2Ai |(^1
2/3
G?
.2/3
1/3, 1
1/6
5/6
0,2/3
1/3, 1
1/6
sh v^ 1
1
B/3I/6
4тг
5/12, 11/12
35 + 2 5 5 ™ 3<5 1-5
6 ' 2' 6 ' 2
x Gi ж
4тг
>	5 1 + 35
17
12' 12
2' 6 ' 2
B/3I/e
1/12, 7/12, 1/4, -1/12
4тг3/2
Y/~W П/12, 5/12, 3/4, 13/12
X (jr4n X
2/3
1/6, 1/2, -1/6
Gl? U
5/6, 1/2, 7/6
1/3
1 Г-s, 2/3-.
: 5/6-s
1	Г	2 1
Г с s + — — 	s
' 3' 6
[Re s < 0]
[0 < Res < 1/6]
B/3I/6
4тг
х Г
[-1/6 < Res < 0]
5 + 2	ё 1	7
, S Ч	,	5, 	 — 5
6 '	2' 12 '12
	S,	8
6	2
< Res < 1/12
¦'-{:}]
4тг
х Г
1	7 35 + 2	5
	, 8 Ч	,	5,	—
12	12 6	2
35 + 1	5 + 1
i-1/12 < Res < 5/2, 5 =
B/3I/6 \s + 1/12, a + 7/12, * + 1/4
4тг3/2
13/12-в
[Res > -1/12]
B/3I/6 Г1/12 - s, 7/12 - s, 1/4 - s
4тг3/2
2тг3/2Ш
5 + 13/12
[Res < 1/12]
1/6, s + 1/2, 1/3- s
7/6-в
[-1/6 < Res < 1/3]
1	Ts + 1/3, 1/6- s, 1/2-s
2тг3/2 ^12 L	s + 7/6
[-1/3 < Res < 1/6]

574
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.29
13
1/6, 2/3
3i/ + 2 v 2-3i/ v
6 ' ~2* 6 ' ~~2
14
4 -
6
1/3, 5/6
2тг3/2 ^/12
15
16
17
Ai^
5/6
0,1/3,2/3
1,1/3,2/3
1/6
1/6, 2/3
3v + 2 i/ 2 - 3i/ i/
6 ' 2' 6 ' 2
18
4 — 3t/
6
1/3, 5/6
4 + 3i/	i/
6 '	2"
19
20
21
Bi (
2тг
G24 I Ж
Bl
2тг
1/6, 2/3
0, 1/3, 1/6, 2/3
2/3, 1, 1/3, 5/6
1/3, 5/6
5/6, 1/3
0, 2/3, 1/3
2тг3/2
1 5
	s.	s
3 ' 6
[-Rei//2 < Res < 1/3]
1	5
3' 6'
25/331/3^3/2
' ' 2
[-1/3 < Res < Re i//2]
s, s + 1/3, s + 2/3]
1	Г-s, 1/3-s, 2/3-^
25/331/3^3/2 [	5/6-s
[Re s > 0]
"]
[Re s < 0]
, s + -,
2 2
2 - 3v	и
	, s
6	2
[Res > |Rei/|/2]
1/
s» ^ ~ e»
	s,	s
L 6	3
2-3i/	и
[Res < -|Rei/|/2]
2тг	в, e + 1/3
^Т7бГ	1 2 5 1
L	6 3 6 3
[s = -k,	-k - 1/3 G D+, fe = 0, 1, 2, . . .]
2тг
3i/6
11
= fc, 1/3 + Jfe G D~, к = 0, 1, 2, . . .]
s + 2/3, 1/6-si
? + 1/3, 2/3- s J
[0 < Res < 1/6]

8.4.30] 8.4- Таблица преобразований Меллина элементарных и специальных функций 575
22
23
24
25
26
2/3
1/3, 1, 2/3
1/6, 2/3
-y22
Ж24
1 2
6' 3
2 + 3i/ 2-3i/ +
6 ' 6 /
1 2
6' 3
Si/ + 2 2 —Si/
6 ' 6 ' ~^' 2"
Gil Ix
3' 6
A-Si/ 4 +Si/ \
4-3i/
з' 6
ai
и	и
1 + -, 1 —
2 2
2/3
1/2, -1/6, 1/6
1/2, 7/6, 5/6
1/3
1 [s + 1/6, -s, 2/3-s
s + 2/3, 1/3-s
[-1/6 < Res < 0]
x
I/	?/1	5
A-Si/	4 + 3i/
s Л	, s	,	5,	.
2 2 3 6
2-3i/
Ц	5, 1
2	2
1 5
	5,	6
3	6
|Rei/|/2 < Res < 1/3]
1	5 v	v
з's б' ^ ~5' ^^
l-3i/
1 + —,.-
1	5
3' 6'
3' ^ 6' 6
1+ 2' S + 1^
2-3i/
[-1/3 < Res < —| Rei/|/2]
1	^[s + 1/2, s- 1/6, 1/3-e
5/6- s
[1/6 < Res < 1/3]
3, 1/2-e, -1/6-
s + 5/6
[-1/3 < Res < -1/6]
8.4.30. Многочлены ЛежандраР„(ж).
Обозначения: Л3з = ГA/2 + n - I)

576
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.30
2
3
4
5
6
7
8
9
10
11
12
р
Рп
Рп
A
Рп
Рп
Рп
Рп
A
(х
(х
\х )
Bх-1)Н(х- 1) =
/ \
" \1 +
(y/Z)H(l-x) =
^20 /
\
(-^)я(ж-1)
_ ^02
"2
(л/ж) Я(ж- 1) -
1 ;
г*02 /
— ^22 1
f —) ЯA-ж)
\ л/ж' /
= ^22
- ж)?^1^2Р (\/Т
- (-1)'А33С?20
-l)e+-1/2Pn(\fl
+ IV
- (-1)'Л G02
22
-l)^/2Fn(i^
= ^34^
=G
= (
ж^
ж
)
1
ж
=
( X
V
ж

(ж
(ж
V
/
V
г^
02 /
22 1
22
8(.
1, 1
— ni
— те, те
0, 0
1,1
J 22^
\
п + 1 /
г, _|_1 /
t-T -L /
—п, —те ^
0,
A-п)/2, 1-
0, 1/2
1/2, 1
- те/2, (те4-
0, 1/2
1/2, 1
- те/2, (те4-
') =
-1, е + (те4-
0, 0
L^i =
с )
1/2+ е, 1/2
-п/2, A +
-1, 1/2 +
0. 0
0 /
hn/2 \
/
¦1)/2 /
hn/2 \
¦1)/2 /
1
У
+ е \
п)/2 У
п-/ \
Г
Г
Г
(?
г
г
г
г
л
Г -., - 1 =
_1 + те — s, —те — s J
"те + 1 — s, —те — si
1 - s, 1 - s J ~
=г[-;_7](-^
1 [s, те + 1 - s, те + 1 - si
Г1
г!J [ 1-s
J
Т1 Г 1-1 "I / -1
-(п!J11„,д|1 s](l
[0<
в, в+ 1/2 1 _
^ Г'" s + e ^1 /1
[Res > -е; / =
n/2]
-s, l/2-s 1
.l + n/2- s, (l-n)/2-eJ
Г е - s 1 /
~ [1 + ^/2 - sj \
[Res < е; 1 =
'-те/2- s, (n + l)/2- s
1/2 - s, 1 - s
n/2]
_
[l-e-sj V2
[Res < -те/2; I =
n/2]
"s - те/2, s + (те + l)/2l
/ =
s + 1/2, s + 1 J
=r[/;r_2e]('+^
[Res > те/2; 1 =
n/2]
33r[s + l/2+t-Vl-sJ =
Г П 's ^ 1
[s + 1/2 + n - IJ
[Re s > 0; 1 =
n/2]
Л
L s + e + 1/2, l + n/2 - s
Л г[1/2-е-П /1
= A334l + n/2^sJl24
[Res < 1/2-e; 1 = [те/2];
34Г ^ 5'
L 1- s, 1-s
= Лз4Г[1/2+1-"аП
Res < 1/2 + 1 -те; I = [те/2];
Re,<0
[Res < -те]
[Re s > те]
S)n
Re s < те + 1]
\
¦\- e - sj
; 2e = те - 21]
1 \
+?Jl
; 2e = те - 21]
-),
; 2e = те - 21]
-a
; 2e = n - 21]
Д - 5)i
; 2e = те - 21]
1 =
J
~e + s)
2e = n- 21]
1=
2e = n - 2fl

8.4.31] 8.4- Таблица преобразований Меллина элементарных и специальных функций 577
13
14
15
16
17
18
19
в+ 1/2, ? + 1/2
(п + 1)/2, -те/2
О, О
0,1/2
—»=
A -n)/2, l + n/2
-те/2, (те + 1)/2
те/2, A -п)/2
+ п)/2, -те/2
1/2, -те
О, О
те! л/ж
A-те)/2, A-те)/2
-те/2, (те + 1)/2
+ (те + 1)/2, s - те/2 1
г +? + •
[Re s > те/2; I = [те/2]; 2е = п - 21]
2п Is, (n + l)/2 -s, 1 + те/2 -j
те! л/ж	1 — s
те!^ L ' 2
[О < Re s < 1/2 + те - I; 1 = [п/2]]
2п |"s, s + 1/2, (l + 7i)/2- ,
те!^~ Г ¦  2 -JV 2
[-е < Res < (те + 1)/2; I = [те/2]; 2е = те -
s - те/2, s + (те + 1)/2
+ 1 + П/2, в + A-п)/2
ГГ -п/2-з, (п
1 + те/2 - s, A - те)/2-
[Re 5 > те/2]
1	[s, 1/2 - s, те + 1 - s
[Res < -те/2]
те!у^
[О < Res < 1/2]
Ti + 1	те 1 + п
з Н	, s	,	s
2	2 2
1-71
sH
1 Г те 1 + Ti 1 / 1-n
Г \s\ x H
J
,s\ x sH
2' 2 J V 2
[те/2 < Res < (n + l)/2J
8.4.31. Многочлены Чебышева 1-го родаГп(ж).
Обозначения
: Л35 = I — I у'ж , Л36 = (—1) I —- 1 у'к .
1
2
A
(ж
\-1/2пр /о 1\ __
— «*/^_|_ J п\^Ж — J-J —
— л/тг G20 f ж
- 22 v
1/2-те,
0, 1/2

/^ ^22 (x
V
1/2 +те \
;
0, 1/2 \
те, —те /
=
Д4
«.
-71 +
1/2-
- те —
\~Ч
?, s
1/2
r
" Г[
- s,
s, 1
n
ny/:
+
s
1
T
1/2
s + 1/2
s
+ те + "
~ 71 — S__
Г 1/2
Г
-]=
1 f1 ^
-/2]U"'>
[Re

г — si
[Res <
s"> 0]
1/2]
19 А. П. Прудников, Т. З

578
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.31
3
4
к
6
7
8
9
10
11
{х-1Г+^ТпBХ-1
Г™ ^02
1/2 /2
\ *^/+ п 1
/1-я;'
П \1 + жу
22п~1 г
Bте-1)!
A^ж);1/2тте(^)
/
rzz л/тГ Стоо I Ж
{х-1)+ in Н^
(ж- 1)^1/2Тп (у/х~)
+
/
22 V
(л Г1/^ f ! %
11 Ж J _|_ J fj, I
че^1/2т / rr-
X)+ n у
20 /
_ (-1) Л35С22 |
= (-!)'Л
0 =
(¦
\
/
tl2
22
=
(
0
)-
г 6

(
0
) =
/
- (
f
\
]
1/2 +те, 1/2- те \
0, 1/2 У
/z: r20f f
Л/Ж ix22l Ж
0, 1/2 \
те, —те /
^Ж
V
1 - те, 1/2- те \
0, 1/2 J
l + n)/2, (l-n)/2 \
, 1/2 /
i02(x
r22v
0, 1/2 \
те/2, -те/2 /
l + 7l)/2, A -7l)/2 \
, 1/2 /
-22 ^
2/1 I
0, 1/2 \
те/2, -те/2 /
\-
11 \
0, 1/2 /
1 |
x J
?22 *
V
те/2, -те/2 /
^- Г1/2 + 71 - S, 1/2- 71- Sl
1 ч 1 /*? ч
ri/2-n-s]/l \
[Res < 1/2-те]
у— fs — те, s + те!
L 5 + 1/2, S J ~
Г s - те 1
= л/тг Г (s)n [Res > те]
[s + l/2jl )n L J
22n^x Is, те- s, те + 1/2-sl
Bn-l)! [ 1/2-s J
^2ti — 1 /1 \
Ff 1 I 1
= 	 I [S, 71 — S] 1	SI
[0 < Re 5 < те; n = 1, 2, 3, . . .]
^Г=[в + (п + 1)/2+в1BA те)/2] =
Г '^s + e П]
= (-1) V^T^ + ^ + i^2j x
/1 \
x 1-+е-з)
V2 Л
[Re s > -e; I = [те/2]; 2е = те - 21]
^- [ 1/2- s, 1 - s 1
~ [l + n/2- s, 1 - те/2 - s\ ~
г i /2 _j_ e _ 5l
= (-lI^ Г^ + ^/2 _ s J (s + e),
[Re s < 1/2 + e; 1 = [те/2]; 2е = те - 21]
/ГГрГС1^^/2™ 5, (l + 7l)/2-el _
L 1/2- s, 1 - s J
ГA-п)/2- sl /1 \
= Л/^Г[ 1-е-* JU+e"Vi
[Re e < A - n)/2; I = [те/2]; 2e = n - 21]
Гв-„/2,, + п/21
L s, s + 1/2 J
Г s-те/2 1
= л/тг Г (s + e)i
Ls + 1/2- ej
[Re s > те/2; 1 = [те/2]; 2е = n - 21]
ГГ 5, 1/2 + 1- s 1
35 [e + l/2 + n-Z, 1/2- s\ ~~
[Re s > 0; I = [те/2]; 2e = n - 21]
Л35Г ' , =
L s + e, l + n/2- s J
= A36r[l + n/2-ee](e + e)l
[Re s < 1/2 - e; / = [те/2]; 2е = тг - 21]

8.4.32] 8.4- Таблица преобразований Меллина элементарных и специальных функций 579
12
13
1 Л
15
16
17
(х-
A-
A +
A +
(х-
A-
1)
х)
х)
х)
1)
х)
е-1/2
,-1/2
-п/2г
2п^
(п-
2те"
(п-
-1/2п
+ J
G02(
6 22v
^n Ну
/
1 12
1)! 22
г-Г/
1 21
1},^22
\ (8ж2
г- ^02
22
/т2
- (
1/2
1/2
X
I G20
22
1 \
Л
Iх
1
0,
-?¦
с +
Iх
1
0,
-8ж4
(т
V
1/
о,
-8ж4
ж2
+ 2е-
, 0
) =
/
(г
V
1
-п/2
1/2
-п/2
1/2
-1) =
2 + 2f
1/2
)
1 =
\
±1,1/2-1 \
)
/2 + е,е \
- п/2, п/2 J
A -n)/2 \
)
A -п)/2 \
J
г, 1/2-2n \
У
0, 1/2 \
— An, An J
Г1/2 + 1 - те - s, 1/2 + 1 - si
36 [ 1- s, 1/2- 5 J ~
Г1/2 + /-п-в] /1 \
~ ЛзбГ[ 1-5 J \2 /z
[Re s < 1/2 + 1 - те; 1 = [те/2]; 2е = те - 21]
Г s + те/2, s- те/2 1
Л36Г =
[s + в, s + е + 1/2j
Г 5-те/2 j
36 Ь + ? + 1/2Г +S^
[Re s > те/2; 1 = [те/2]; 2s = те - 21]
2n^ |"s, те/2 - s, (те + l)/2 - si
(n-1)! L 1/2-в J
2n^ r\ i ](г )
(те- 1)! h' П °J V2 ")t
[0 < Re 5 < те -
- I; I = [те/2]; 2е = те - 21; те = 1, 2, 3, . . .]
2п~г Гв, в+ 1/2, n/2-el
(n-1)! L e + (l-n)/2 J
(n-1)! L 2 J V 2 Jt
[-e < Re s < n/2; I = [те/2]; 2s = n - 21]
^- Г1/2 - 2n - s, 1/2 + 2те - si
L 1 - s, 1/2- s J ~
[1/2-2n- el /1 \
= ^ Г[ 1- s J \2 ~ SJn
[Res < 1/2- 2n]
r Is - 2n, s + 2nl
L в, в+ 1/2 J
= y^r\S~2n](sJn [Res>2«]
[s +1/2J
8.4.82. Многочлены Чебышева 2-го рода!7те(ж).
Обозначения: Л37 = —-—V^ ? -4з8
+ 1V Г A ( W(n + 1-\ Г
2-) ^,Дзв = (-1) 1^-*) V^F.
1
2
3
A
(x
(x
- i);/2t
- i)+/2t
=
M2.-l) =
Л G20(x
3/2 +те, -1/2-те \
0, -1/2 /
Jn {I ~ 0 =
02 /
- 37 22 (^
3/2, 2 \
- те, те + 2 /
/nB«-l) =
-1/2-те, 3/2 +те \
0, -1/2 )
Г 8, 8-1/2
[s + те + 3/2, 5 - те -
71 Г S
[s + те +
Г -1/2 - s, -1 - s
37 [l + те - s, -1 - те -
[-1/2
= (-1)тел37г| +^
ГЗ/2 + те- 5, -1/2-
37 [ 1-е, 3/2-в
Г-1/2-n-
- 1/2]
«J/^J \z / n
[Re s > 0]
.]=
-el
_JB + .)n
[Res < -1/2]
- n -— si
I(i-).
[Res < -1/2-те]
19*

580
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.32
4
к
о
6
7
8
9
10
11
12
(l-*I/2t/ (--l)-
\ж /
/
22 v
3/2, 2 \
те + 2, -те /
_п_2 г Л-жЧ
п \1 + х)
Г12 U
— tj"99 I Ж
Bп + 1)! V
-те- 1, -те- 1/2\
0, -1/2 )
A-х)^2ип(у/Б) =
-A G20(x
v
(те + 3)/2, (l-n)/2 \
0, 1/2 )
1I/2U ( М -
= M7Gll(x
V
1, 3/2 \
- те/2, 1 + те/2 /
(Ж^1)У21/те(у^) =
/
22 V
C + п)/2, A-те)/2 \
0, 1/2 )
(*-*)+2^« ("У =
- A G™[x
22 V
1, 3/2 \
- те/2, 1 + те/2 /
A - x)?+^1/2Un (л/Г^) = (-1)'Аз8 X
V
1
о, -1/2 ;
(x~l)?^1/2Un( fl^) =
+ \V ж )
/
22 ^ж
1/2 + s, 1 + s \
те/2 + 1, -те/2 /
(ж _ i)eml/2|7 ^л/ж - ll —
+ п v /
1/2 +Z + 2e, -1/2-I \
-1/2,0 )
г^	yi 5 + те + 21
Л37Г[ s + 3/2, 5 + 2 J ~
[ s - п 1
= Л37Г [ 5 + 3/2 J(S + 2)n [Re S > nl
1 fs, те + 2 - 5, те + 3/2 - s]
те!C/2)те [ 3/2-5 J
1 /3 \
	 ГГс П 1 1 cl I о
n!C/2)n L V2 Уп
[0 < Re 5 < n + 2]
Г 5, 5 + 1/2 1
5 + (те + 3)/2 s + (l-n)/2
= ^1УЛ^Г{3 + ^п + %у2\ X
/1 \
[Re s > -e; 1 = [те/2]; 2е = те - 21]
Г -1/2- в, -в 1
[l + те/2 - 5, -те/2 - s\ ~
t Ге-1/2-в]
= (-1) Аз7^^1 + п^2_ s^(s + e + l)i
[Re 5 < е - 1/2; 1 = [те/2]; 2е = п - 21]
Л Г-(те + 1)/2-5, (п + 1)/2-*1 =
Г (те + 1)/2 8\ A \
= Л37Г{ 1-е- JU+e"Vi
[Re в < -(те + 1)/2; 1 = [те/2]; 2е = п - 21]
г' 1 - те/2 I
= Аз7Г[з + 3/2 - е\ ^ + ? + Х^
[Re 5 > те/2; 1 = [те/2]; 2е = п - 21]
Аз8Г[в + 1/2 + п-Гз/2-в] =
Г 5 1 /3 \
38 [e + l/2 + n-/J \2~Ji
[Re s > 0; 1 = [те/2]; 2е = те - 21]
Гв + 1 + п/2,1/2-е—1
L s + e + l, l + n/2- s J
= ^з8г[1/2^в^51A + е + 5)|
[l + те/2 - sj
[Re 5 < 1/2 - e; I = [те/2]; 2e = n - 21]
[1/2 + 1 — те — 5, 3/2 + 1 — si
39 [ 1 - s, 3/2 - s J ~~
= -4з9Г П S f - - sj
[Re s < 1/2 + 1 - те; I = [те/2]; 2е = n - 21]

8.4.32] 8.4- Таблица преобразований Меллина элементарных и специальных функций 581
1 3
14
15
1 fi
1 7
18
1 Q
20
21
A
A
X
Bx-
X
A X
(x —
ж -
(я +
e_1/2{/ / fi—Л _
+ П\Уж /
/
22 V
1 + e, 1/2 + e \
-те/2, l + n/2 /
v_n/2-l,7 / 1 \
nwi + aJ
2n /
те! TI \
-те/2, -(п + 1)/2 \
0, -1/2 /
( 1—ж—\
) Lt4V^ + iJ
2n 21/
~ nf 22 \
-те/2, A-п)/2 \
0, 1/2 /
n! \
0, -те- 1 \
0. -1 /
/2 ! / 2i + l \
n\2Vx2 + x)
1 G21^
-те/2, l-n/2 \
-те/2, l + n/2 J
l)(z-l)^Vn(8z2-8z + l) =
/
-271-3/2, 2те + 5/2 \
0, -1/2 J
1/2 г /ж2 -8ж + 8\
)A Ж)+ Ln 1 2 I
\ x /
= Л37С20 (x
22 ^
2ч _. /ж2 +
\ 2ж
5/2, 3 \
2те + 4, -2n J
/
= 2(те + 1)^22 x
те + 3, 1 - те \
те + 2, -те у
/ж2 + 1\
- =
V 2x у
/
22 v
1 - те, 3 + п \
-71, 2 + те /
Ь2 /х2 + 2х + 2\
L)«+2 "V 2(^ + 1) J
1 ^12 /^
= 	Goo Ж
Bn + l)! 22 \
0, 2п 2 \
о, -1 у
те!
Г 5 + 1 + 7l/2, S - 7l/2 1
L + e + 1,
_ ЛздГг
[Re 5 > i
, те/2 + 1
= — Г\з, 1
те! L
[0 < Re s < 1 + те
2«
п!
[-е<
1 г[
п!Г[
1
= ^!
[
1
Г
те!
x(s^
Л37Г
=
А
= А3*
2(те +
-2(п
2(те +
1
{2пЛ
" s s _|_ 1/2
2n г
те! Г + е'
Res < те/2
s, 1 - s, 2-
2- ?
ГГ« 1 «К
1 [S, 1 ЗД
те
s + - + 1,
2
s -
1 „ г
71 \
Г-2те-3/2
L 1-
fs - 2те, s -\
[ s + 5/2,
L5 + 5/2J
x Г 5 +
1)Г
1 1)
4 Г П^
1)T
[те + 1
-2(n +
1
Bте + 1)
5 + 6 + 1/2J
s^n/2 L1 + ?+ ч
+ ? + 1/2J
a/2; 1 = [те/2]; 2е = те
- s, (n + 3)/2- si
3/2-5 J
{ + n-l-8\(--8\
V2 J i
-I; 1 = [те/2]; 2е = те
l + n/2- si
-n)/2 J
те 1 /1-n
I 1 el I
2 'X 5Ц 2 '
+ 1; / = [те/2]; 2е = те
f те — si
J
2-s)n [0<Res
n те i
s	, Ц	s
2 2
hi-те/2 j
те те 1
у	, 1 H	S X
2 2 J
-21]
-21]
л
"Л
-21]
<1]
[те/2 < Res < те/2 + 1]
s, 3/2- s J ~
-3/2-el /3 \
1-* J V2 72n+1
[Res < -2n-
-2те + 41
, + з J
(s + 3Jn+1 [Res
n + 2, s — те 1
+ 3, e + l-nj ~
1
+ 2)(s — n)
s, -2 - те- s 1
=
— s, —1 — те — s J
1
' (s _|_ n _(_ 2)(s - те)
[Res < -2
- s, 3 + 2те- si
2-s J
Tfs 1 el B eJ
[0 < Re
3/2]
> 2n]
>nj
-n]
»<1]

582
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.34
-Г[з — те, те + 1 — з] х
х (з + 1 — теJп+1	[те < Re s < те + 1]
8.4.33. Многочлены ЛагерраЬ^(ж)
1
2
4
5
6
-а
__]
А
п\ )
IXLX (
п (^
Ьп(х)
/х Т (
1~"п 1
= Г(А + п
= Г(А + те 4-
1 Gn/
те! 12V
1 i 2
ж/ те!
(™1)П ^2С
те!
ж / те!
/
12 ^
/
- l)GSi { ж
V
—те — А
0, -А
if.
ч
1, А
А +
i(.
—те
0,
11 ^
0
ж
1,
)
+ i
п +
)
1, 1
гг +
те -
0,
А
те
1
1
t-Г)
•7)
)
Г(А + те
Г(А + те
1 [з,
те! L
= —
1 г|-
n! L
1
1 Га,
те! L
те! Г[
Г
+ 1)Г
L
[
+ 1)Г
L
1 + теЧ
1 + А
rW(i
f А + те
s + A
г(-*H
1 - s
s + 1
5 +
S =
-Л-
- з
+ А
+ 1
+ 1
те + 1
-ке
А + 1
= Л G
J
^^)n
J
V + l)
1
те!
J 1
, 1 +
-s
r(.)
г!
Л-
ife =
к =
.]
0, 1, 2,
0
, 1,2,
[Res
[Res
[Res
[Res <
>0]
<o]
>0]
o]
8.4.34. Многочлены ЭрмитаЯп(ж)
1
2
3
4
/ i \[тг/2] г~ | f~i
— I — A. I "\/ 7Г WI ijr
Hn ( — ) =
/
V
-(¦
те/2 + 1 \
e, 1/2 -e J
Ь + оо
•(¦
-те/2
1/2 + e \
0, 1/2 J
(¦
1, 1/2 \
(n + l)/2 /
(_l)[n/2]
= e+ife G
"[,;¦
+ ,fe = 0,1,2, ..
у^те!Г ?~S
D^,k = 0, 1, 2,
[Res > -e; 1 =
,1/2-sl
-n)/2-eJ ~
[Res < e; 1 =
.; e =
1
. .; e =
= [n/2]
[n/2];
[3 =
n/2 -[
2 J
= n/2-[
; 2s = n
2e = n -
n/2]]
[* =
n/2]]
-21]
-21]

8.4.35] 8.4- Таблица преобразований Меллина элементарных и специальных функций 583
8.4.35. Многочлены Гегенбауэра С^(
Обозначения: А
ГA-2А)
BЛ)теГ(Л
, A4i =
(^l)nBA)n	=	1
п!ГA/2-А)' 42 п!(А + 1/2)пГBА)'
Л47 =
п!(А +
га!Г(А)'
И
^48 —
ГA - А)
п!Г(А)'
1
2
3
4
5
6
I
A - ж)+ (
А /~*2
(ж — 1)_|_ <
/ ^чА —1/2.
(ж — 1)_|_ ' (
- A G€
A - ж)+ <
^1 -|- л; 1
= A4iG^
/1 . \А —1/2,
A + ж) ' (
(Л 4- /тЛ~п~2А
= ^42^2^
7^Bж- 1) =
°(
2 И»
V
А + те
0, 1/2
7Л (- - А-
п \х J
/
7^Bж- 1) =
/
г •
\
1
2 +Л
=i(|-0-
/
= -А40<^22 I
V
7^Bж + 1) =
/
1
- - А
2
\х J
= A41Gi
/ -у 	 х\
п \1 + х)
А
{
1-2А
1
0, - -
2
1 1
2' 2
-А
ж
А +
— те
1
+ W'2
А
ж
А +
— те
1
— те, —
2
А
(ж
1/2
2А-
1
— те, —
2
А
-А^те \
I
/
1/2, 2А \
, 2А + те /
\
J
1/2, 2А \
, те + 2А )
+ А + п |
J
+ А, 2А \
f те, —те )
¦— X — те \
/
Ат Г
s, s
s + A + те +
( 1 \п 4 Г
40
\ / п
Г 1/2-А-в
[l + 71 - S, 1
= (-1)пл40г[
L
[Res <
Ат Г
г 1
^+те+А-
2
1 — sj
г 1
= АадГ 2 ~ П
L
[Res < 1/2
-A + 5 1
2
1 1
—, s ~\	те — А
2 2 J
=
"I
1 ^
s + A + те Н—
[Res > 0; Re A > -1/2]
, 1-2A- s 1
— 2A — те — s J
1/2^A^SlBA + s)n
1 + те — s J
1/2-Re A; Re A > -1/2]
1 I
' 2
1
-+A-s
=
2 -J
-eA~iG+A"*)n
-те- Re A; Re A > -1/2]
. „Г s — те, s + те + 2А 1
Ала 1 =
L^ + A + l/2, S + 2AJ
= Amv\
А41Г
s, - + A +те-
2
	l_
2
Г i
S^U l(s + 2A)
-A + 1/2J1
[Res > те; Re A > -1/2]
-s,	А —те —s
2
A-s
=
1 /1 \
= А41Г s,	A - 71 - si 1 - + A - s 1
[0
Fs + 2A + w,
41 [
= А41Г s — те
|"s, те + 2А-
[ АЧ
= Л42Г[5, те +
< Res < 1/2-71- Re A]
5-те, 1/2- A-sj
5 + 2A J ~
i-A-в] (s + 2A)n
[те < Res < 1/2- Re A]
s, те + A + 1/2 - si
-1/2-в J
2\-8](l + \-s)
V^ / n
[0 < Re s < те + 2 Re A]

584
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.35
8
Q
У
1 П
J.U
11
12
13
14
A
'
A
(ж
A
/1 1 ™ \
-*)+n-2A<tf(
02
^^п^2Лг
Ж L,
(-
22Л
X <^22 f
22 V
-ж)^1/2С
= А4
1)Л-1/2с
+
=
1/9
— 1)_1_~ С
= /14
-Ж)Л^1/2С
+
J- "Г «
-
\1 — Ж/
/
/
L
1
1-2А
1
0,--
V ' 2
^л /ж + 1\
I 1
ж
1-2А-
o,i-.
2
,А ( 1 + Ж ^
'п ^
1-ж|;
-lO1-^ ГA/
-1п!(А + 1/
X
1-2А-
0, 1/2-
n(v^) =
/
I
I
/~*20 I
3*^22 I ^
V
\
А
0
д/ 1 \ _
П 1 у— J
л /~*02 /
/140^22 1 ж
^ (\/ж) =
/
22
\
1
Af — 1-
Л G20 (х
22 V
—
А
- 71
\
'2-
2),
те,
А
1
т
2
А,
+
2
1
2
А,
-
1
те, -
2
1
' 2 "
-А)
гГ(А
1/2
те +
2
А +
те/2
п
А +
те/2
-А
- А-
- А
1 1
1/2
, А +
1
1/2
, А +
\
-те \
}
)
-га \
)
J
- га \
\
2
1
п/2 )
-га ч
2
/
)
п/2 )
А43Г
s. s ^	А
2
]_
s + 1 - 71 - 2А, sH	А-те
L 2
Г „ 1/1
= (-1)»Л4зГ| . . " .. | [-4
43
(-1)
22Л^1
L« + J- ^ ^ ^ ^AJ \2
[Re s > 0; Re A <
"n + 2A-s те + А + 1/2-sl
1- s, A + l/2-s J
Гте + 2A - si /1
[Re s < те + 2 Re A; Re A <
пУтг ГA/2- А)
	 X
Г s, 2A + те — s
[s + 1/2- А-те, А + 1/2-
[0 < Re s < те + 2 Re A; Re A <
Л 40 Г
> s;
40Г
= ("
-ReA
А 40 Г
-ReA
Г
[

> те/2
I
Sj S 2
те + 1 1 — те
s + A + , s +
=
-Г l)lA r\ S + ?
40 [^ + А + (те + 1)/^
/1 \
X V2 " V,
ReA > -1/2; 1 = [те/2]; 2е
1/2- A- s, 1- A- a
Д + те/2-s, 1-A-n/2- e.
[ 1 + те/2 — s J
[Res <
; ReA > -1/2; 1 = [те/2]; 2е
г 1 - 7i . 1 + те и
\ с с
А Ь, 6
2 '2 1 =
1/2- в, 1- e j
ГA - 7i)/2 - А - si /1
40 L 1 - е - s J \2 +
[Res < A
; ReA > -1/2; I = [те/2]; 2е
s-n/2, s + A + те/21
s + A, s + A+ 1/2 J ~
AJ ^-те/2 1(в + е
[s + 1/2 + A - e\
ReA > -1/2; I = [те/2]; 2е
„
\
- А- в I
Jn
1/2-те]
Jn
1/2-те]
1
-s\
1/2 - те]
>
X
[ReS>
= те - 21]
1/2 + E-
= n - 21]
e s)
)i
-n)/2-
= n-2Z]
+ A)l
[Res >
= те - 21]

8.4.35] 8.4- Таблица преобразований Меллина элементарных и специальных функций 585
15
16
17
18
19
20
21
(I-*)
1
2
1
IT
х
--Х-1
1/2+ е, А + е
- те/2, Л + те/2
-2е, - -Л-/
2
+ е, 1/2+ е
п/2, А + те/2
1 — п	п
— -А.1-А--
о,1-л
2
х-1
1- А ^ те/2, A-п)/2
О, 1/2
2' 2
О, - -А
2
Л 44 Г
s, 1/2 + \ + l - s
s + 1/2 +те- I, 1/2 + A - ,
S	1 f-4
? + 1/2 + те^|] \2
[Re s > 0; I = [те/2]; 2е = n - 21]
3 + ?г/2 +A, 1/2 - e - s
s + A + e, 1 + те/2 - s
[Re s < 1/2 - e; I = [те/2]; 2e = n - 21]
T\ + l-n-s,\ + X + l-.
l-s,\+X-s
1/2 + 1 -те - .
[Re a < 1/2 + I - те; 1 = [те/2]; 2е = те - 21]
+ A + те/2, s - те/2 1 _
+ A + e, s + e + l/2j ~
[Res > re/2; / = [n/2]; 2e = re -
1 — те
-те-А
[Res > 0; ReA<l-?i; l = [n/2\; 2e = n - 21]
'А + те/2^ в, (n + l)/2-e]
1/2- 8, 1-8
[Res < n/2 +
+ Re A; Re A < 1 - те; I = [те/2]; 2е = те - 21]
те	ж п + 1
1
[0 < Res < ReA + n-Z; I = [те/2]; 2е = n-2Z]

586
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.36
22
*?ч
24
25
26
97
28
/
п V
21/
22 V
2А-1 Л /^^
+ п \2у
— Л G20
48 22
(ж- lJ^^ (-
= Л48С02
/
Л S~4~\ 2
= Л49С?22
/
п у
/
22 v
Ап/2 А/
- f W A G2(
К ) 50 2!
^A-n/2 A /
+ п ^
= (-1)таЛ50^22
У x + l)
l-A-n/2, (l-n)/2 \
0, 1/2 /
Ъ )
(х
\
2А + п/2, A-n/2 \
-п/2, А + п/2 /
ч
-*-
Ж /
Г.
V
2А + те/2, А-те/2 \
-те/2, А + те/2 /
2 + ж \
2д/1 + ж у
1^Д51^2А^те \
0, 1-2Л )
2ж + 1 \
I ~"
2%/ж2 + ж /
1-А-те/2, А-те/2 \
А + те/2, -те/2 /
2- ж \
1
Ч
1-2А-П, 1-Л\
0, 1-2А /
2ж - 1 \
2л/ж2 - ж /
(
X
V
1- Л- -, Л- - \
те 2те 2
АН	,	 /
2' 2 /
Гв, в+ 1/2, А + те/2-s]
г те 1 / 1-п \
' 4' Г ' WJ 2 ' ' "Н 2 ' "Л
г _ <--
< Re s < те/2 + Re А; 1 = [те/2]; 2е = те - 21]
Г s - n/2J s + А + те/2 1
48 [s + 2А + те/2, 5 + А - те/2]
= л48г[ S^n'2 ](в + л-^)
[Res > те/2; Re A > 0]
л48г
1-2Л- - - в, 1+ - -Л- в
2 2
те те
Ц	s, 1 - А	s
L 2 ' 2 J
[1-2Л-П/2- в]
48 L 1 + тг/2 - 5 J X
х (А - | + в)
[Re s < 1 - те/2 - 2 Re A; Re A > 0]
\s. A - s, 2A + те - si
А4вГ[ 2X-s \
= Л4дГ[5, А — в]BА — s)n
[0 < Re 5 < Re A]
Г те те те 1
5 + АН	, s	, АН	s
s + А- -
= А,вг[в--,А + --в]х
[те/2 < Re 5 < те/2 + Re A]
Г s. 2A + те - s 1
ЛвоГ[, + 1_А,2А-,]
Г s 1
L s + 1 — A J
[Re s > 0; Re A < 1 - те]
fs + A + те/2, A + те/2 - si
50 [в + Л-п/2, l + n/2- s\
-A r\X + n/2^S] fs + A П)
50 [1 + ^/2- sj V 2/n
[Re s < те/2 + Re A; Re A < 1 - те]
8.4.86. Многочлены Якоби
л	Г(р + п + 1)
Обозначения: Л51 =
п\
Г(-р-а-п)
= 	j	•
п!Г(-(т-п)'	п!Г(р + (т + гг + 1)'

8.4.37] 8.4- Таблица преобразований Меллина элементарных и специальных функций 587
%
2
з
4
5
6
I
8
9
x)Pp(p,<r)Bx
{ X)+ n {
_ л p20 (
2 v
f a) /2
+ \ж
/
22 v
/ i^Pp(P'CT)f2
(Ж j+ n i
/
22 V
( ) /2
A — Ж) ^i i^n ' a 1 — —
+ \x
/
22 V
C1+ ^p^'CT)C2 +1)
n
= a52g122(
\
n \x
= Лб2б?|Цж
(I + Ж] j n
/
22 v
n cr 1 (
A — *^)-4- ^n
xA54Gl^
(Ж jJ-n-P^-lptP
xA54Gf2(x
p + 71
0, -cr
A =
j
p+1,
— 71, /C
— СГ —
0, -a
\
1 =
J
X
P + a
P + cr
X
cr + те
0, -p
)=
1
— 71, jC
«г) Л ~
Vi +
— p — с
0, -p
a^ /1 +
' i
VI -
-p-n
0, -p
о
) X +
1
V ж —
-p-a
-cr, 0
+ 1,
p + c
+ cr
n, p
+ 1,
+ те
+ 1,
+ <J
ж\
1 _
*)-
~ nJ
x\
— J ¦=.
xj
-p
l) =
1/
— 71,
— С — 71 \
)
r + l \
+ 71+1 /
+ П + 1 \
J
+ 1, -те J
-p-n \
J
r + l \
-p- те \
J
= (—l)n x
— С — 11 \
= (—l)n x
— сг — те \
Г
[s
= C^1
r
51 ^
- (-1
[
=
Ak\ V
= ,
a,As
52 [
=
A52r[S
А53Г
Г
/1 Г
= ^
A64r[e
s, s — cr 1
+ P + 71 + 1, S-CF-Wj ~
Г s 1
U + p + w + ij
[Res > 0; Re p > -1]
— p — s, — p — cr — s 1
+ те — s, — p — сг — те — sj
)те-^51Г A + P + <^ + 5)n
[1 + 71- Sj
[Res < -Rep; Re p > -1]
+ те + <r — s, — p —¦ n —¦ si
1 + cr-s, 1-s J
r_p_n_ si
^5lT^ i^5 J(l + cr-e)n
[Re s < -те - Re p; Re p > -1]
+ P + C + 71 + 1, S — 711
+ Р + СГ + 1, S + p + lJ
г -i
L «^ + p + 1J
[Res > те; Re p > -1]
, — cr — те — s, l + p + те — si
1 + p-e J ~
As2r[s, —<j — те — s](l + p — s)n
[0 < Res < -те- Re <r]
— 71, S + p +<T+ 71 + 1, — СГ— sl
JT[s -n, -a- s}(s + p + cr + l)n
[те < Re s < - Re cr]
s, n+p+cr + 1-s, p + n + 1—s
p + 1 — s
рГ _|_ _|_ _|_ 1 I f _|_ 1 ^
[0 < Re s < 7i + 1 + Re (p + cr)]
s, р + те + l — s 1
— n -— p -— <j, 1 + p — s J
[s — те — p — (jj
[Re s > 0; Re (p + сг) < -2те]
-cr, n + 1 + p + cr-sl ^ i^n x
[Re s < те +L1 + Re (p + a); Re\p + a) < -2n]
8.4.87. Функция ЛагерраЬ„(ж)
[0 < Re s < 1 + Re и, и ¦
0, 1, 2, . . .] или [Res > 0, i/ = 0, 1, 2, . .

588
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.40
2
Ф
i
I> + 1)
G\\(x
1,1 )
1 + 1/ /
1
+
1,
1)
2,
+ iM
или
-1, -
-1
-1 -
Res
1
Re i/ <
< 0, i/
Res
= o,
<
1,
0, ^
2,...]
8.4.38. Функция Бейтмена^(ж)-
Обозначения: Л55 =
-, Л56 = -
sin (i/tt/2)
2sin(i/7r/2)
1
2
3
4
5
6
e"'/2fc" (!
e*/2fc f^\
* V2/
fe_y (л/ж") &
*-* f г )
\л/х J
) = A5bG\l(X
1-1//2 \
0, 1 /
I
0,1 \
1
0. 1 /
0, 1 \
.. /0 1
v (л/ж) =
= A57GfJx
\
1 + I//2, 1-I//2 \
0, 1/2, 1, 1 /
К Ш =
_ л ^04 (
- 57 42^
0, 0, 1/2, 1 \
-I//2, i//2 /
Г s, s + 1 1
55 [s + 1 _ ul2\
Г -s, 1- s 1
55 [l-iz/2-eJ
Г ^
A^qT s, s + 1,
L '2
Г ^
Г s, s + 1/2, s 4
57 [s + 1 + I//2, s
^rf-'1"*'1-
[1 + I//2- S, 1
A
J
[0 < Re s
s]
[Rei//2
-1,5 + 1 1
s, 1/2- si
— i//2 — s J
[Re s > 0]
[Re s < 0]
< -Rei//2]
< Re s < 0]
[Re s > 0]
[Re s < 0]
8.4.39. Функция Л ом мел я СЛДж, z).
1
D-х/ж , 0) =
/ 4 \_^
/—¦ /-ill (
/^С1}Гж
"/2 A
i//2, 0, 1/2 /
1 - i//2, 1/2, 1 \
1-^/2 J
[-Rez//2 <
L s +1/
-I//2
s, 1 — s
Res <
2, i//2
2, s + 1
[-1/2, Rei//2- 1 <
1/2, 1
"'I
J
Res <
-Rei//2]
; Rei//2]
8.4.40. Полные эллиптические интегралы К(ж), Е(ж), ~D(x).
Обозначения: Л58 = ^^у А» = ^^у Лв0 = ^щ, Ав1
2Г2C/4)"
1
2
3
4
5
K(
K(
K(,
^(
V
A4
i \ 1 <¦
/T=x)H(l-i
Jl- -\н(а
V x )
""rl/2K(v
!(-
r) =
1
1/2,
0, 0
1, 1
1/2
- G2
= — С
7) =
--G
2
1/2 \
1/2 )
2 1 ж
1/2, 1
0, 0
~iO2 (
22 V
1,1
1/2,
21 (r
1/2,
0, 0
12)
)
1/2 J
1/2 \
J
H
2
2
2 [
s,l/2-s,l/2-sl
s + l/2,s + l/2,-sl
5 + 1 J
" -,. 1
5 + 1/2, S + 1/2J
¦ -, -
Ll/2-5, 1/2-sJ
5, s, 1/2- si
5 + 1/2 J
[0<Res<l/2]
[-l/2<Res<0]
[Re s > 0]
[Re s < 0]
[0< Res < 1/2]

8.4.40] 8.4- Таблица преобразований Меллина элементарных и специальных функций 589
6
7
8
9
10
11
12
13
14
15
16
17
18
1 + у/х
у/х + 1
К
IV
7Г 20
= — Gro9
1-л/Т+~аПК
; 4
i
4^
2 + ж^2л/ГТ1
1/2,1/2
0,0
1/2,1/2
0,0
1/2,1/2
0,0
1/2,1/2
0,0
s-vT^IK A + 2ж-2\/ж2
1 .
I :
ll-y/x \ 7Г 2U.
A	J A
\/ л/х — 1
ЯA-ж)К
Я(ж - 1)K
л/2 Ж1^
7Г
2"
= -^ с?5| {ж
3/2, 3/2
1, 1
1/2, 1/2
О, О
3/4,3/4
0,1/2
1/2, 1
1/4, 1/4
нA-х) у/ /i-v^N =
л/i + v^ чу 1 + л/^" /
2д/2
^1§(ж
Я(х-1)к/Л^1\ =
7Г
1/4, 3/4
О, О
3/4,3/4
1/2, О
- ж) х
хК| х1-
х
'1-х I =
3/4, 5/4
1/2, 1/2
ж - л/ж - 1 #(ж - 1) х
х К у 2A - ж + \/ж2 - ж ) =
+ 1)-1/2К
3/4, 3/4
О, 1/2
/1 + ж -
3/4, 3/4
О, О
1	Гв, 1/2-8,1/2-
2	[	1-8
4 [« + 1/2, s + 1/2
p
4 L 1 - s, 1 -
[О < Re 5 < 1/2]
[Re s > 0]
[Res < 1/2]
-^r[s,s 1-е i-e|	[0<Res<l/2]
-в, -1/2-.
[-1 < Res < -1/2]
-^["va + ri	[«<*-< V2]
w
2 [s + 3/4, s + 3/4
тггГ -a, 1/2-8
2 U/4- s, s + 1/4
S, S
2л/2 ' U + 3/4, s-
_ji_rri/4-e, l/4-el
2л/2 L 1- e, 1/2-e J
г + 1/2, e + 1/21
2 U + 5/4, S + 3/4J
L/4^ s, 1/4- s
2 " | 1 - s, 1/2- s
1-s
[Re s > 0]
[Re s < 0]
[Re s > 0]
[Res < 1/4]
[Res > -1/2]
[Res < 1/4]
[0<Res<l/4]

590
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.40
19
-1/2
х К
/1 + ж —
/1 + X + -
= Л58 G
3/4, 3/4
о, о
20
21
у/у/1 +
/ТТх -1
/1 + ж + 1
1/4, 1/4
О, О
уУ 1 + ж +
х К
22
1/2
1/4, 1/4
О, О
. + ж —
23
хк
3/4, 3/4
О, О
5/4, 5/4
1/2, 1/2
24
VI + ж
A JCV I JL
25
л/VI + х -
VI + ж
26
27
xKh/-
Ж
ГК
¦К
^^ + 1 I л/Т^х +1
1/4, 1/4
О, О
3/4, 3/4
1/2, 1/2
1/2, 1/2
О, О
1/2, 1/2
О, О
s, s, 1/4- .
s + 3/4
[О < Res < 1/4]
л59г
s, s, 3/4- s
в+ 1/4
[0<ReS<3/4]
[О < Re s < 3/4]
[0<ReS<l/4]
s + 1/2, s + 1/2, -1/4- si
s + 5/4	J
[-1/2 < Res < -1/4]
ЧЗ/4-..3/4-.
[0<Res<3/4]
¦ 1/2, s + 1/2, 1/4- si
s + 3/4	J
[-1/2 < Res < 1/4]
7Г Г S, 1/2- S
2" U + l/2, 1- .
s, s
s + 1/2, e-
Res < 1/2]
[Res

8.4.40] 8.4- Таблица преобразований Меллина элементарных и специальных функций 591
28
29
on
31
32
чч
ЧА
35
36
37
38
39
40
Я(ж-1)
у/х + л/ж - 1
(/1— 1)
(V + х )
A + жГ1/4к
A + Ж)-^К
к* №
к ^у
к |;v -
1 п
1 + ж \г^х
/7Г\A±1)/2^
V 2 /
/7Г\A±1)/2
V2"/ Ж
ЯA-ж)Е(\/
Я(ж-1)е(
\ 1
с)К
Л
1
(v
(v
"? -
2
_____ л
ж -
л
) =
V
/
д
/
:(
2
- 1
/тг
4
- v
/тг
4
)/4
F1)
_1
X
2^
/ж +
тг
2
2л^
Г7
ж2
\/1 + х
1
2
v^ll
~+~х
- - (
2
гт^
2гЯ
1
2\/'2
1 + ж
\л/Г^
1
2%/2
J
ъ \
I
j
31
21 L
V
-F,
/4 _
ТГ
~ 2
Л =
I
2 J
G
+
o21
JT2__
T"
-a
V
(
V
0
I
/
' \
2(
,{
- x
с — 1
/
^ V"
+ Ж
+ л/^
12 (r
22 V
1/2, 1/2 \
0, 0 /
\
1/2, 1/2 \
0, 0 /
ij
\
ж
3/2, 3/2 \
1,1 )
•¦)-
21 (
12 V
1
3/4, 3/4 \
0, 1/2 У
1-
12/
1/4, 3/4 \
0, 0 /
1/2, 1/2, 1/2 \
0, 0, 0 J
1,1,1 \
1/2, 1/2, 1/2 /
1/2,1/2 \
,0 J
1/2,1/2 J
—)
(¦
1/2,3/2 \
0,1 J
0,1 \
-1/2, i/2;
2
2 L
4
2Г|
1
2v^
1
2л/2
4
л^
4
L
1 r[
4 L
4 1
¦1/2-s, 1/2-«]
. 1-s, 1-s J
S,l/2-M/2-Sj
5 + 1, S + 1, -1/2-
5 + 3/2
Г[ ^ + 3/4 J
[5,1/4-5,3/4-5]
rL 1- J
гЬ, 1/2-s, 1/2-
L 1 - s, 1 -
Гя + 1/2, s + 1/2,
Ч - + 1,.-
1/2;!'s3/2"s]
-l/2,e + l/2,l-ej
s J
s, -1/2- s, 1/2 -i
1 — 5
[(-1 =p
5 - 1/2, s + 1/2, -*
5 + 1
[Res < 1/2]
[0<Res<l/2]
J
[-1 < Res < -1/2]
[0<Res<l/4]
[0<Res<l/4]
s, 1/2- si
J
[0 < Res < 1/2]
s + 1/2, -si
fl J
[-1/2 < Res < 0]
[0 < Res < 1/2]
[l/2<Res<l]
1
J
l)/2 < Res < +1/2]
1
[+1/2 < Res < (l±l)/2]
¦ ... + i 1
„5+1/2, S+3/2J
" ^s,l^s 1
„1/2-5, 3/2- S\
[Re s > 0]
[Re s < 0]

592
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.41
41
42
43
44
45
46
47
48
49
50
/1 + ж
1
/Т+ж
-Е
-Е
1/2,1/2
0,1
-1/2,1/2
0,0
х Е
2(l- VT^
1/2, 3/4
- 1/2, 1/2
х Е
-у/х-1)\ =
1/4, 5/4
0, 1/2
у/л/1 + X ~
х Е
2тг
4-1/2
/Г+~ж -1
Г2A/4)
¦Е
Gi2 ж
-1/4, 3/4
О, О
- \/л/1 + х -1 |
У
2тг
Г2A/4)
ЯA-ж) / 2^~?
1/4, 1/4
- 1/2, 1/2
¦Е
1 - v/1 - Ж	\ 1 + \Л - Ж
= ^G^[x
1/2, 1/2
- 1, 1
Я(Я5- 1)
-Е
2^ж2^ж
л/х + л/ж — ;
7Г
2"
— — ^22
-1/2, 3/2
О, О
D(i^) = iGjl
D
ж / 2
-1/2, 1/2
О, -1
1, 2
1/2, 3/2
5, 5 + 1, 1/2 -.
5, 1/2- s, 3/2
тг Гв- 1/2, s + 1/21
2	'	" '
[О < Res < 1/2]
[О < Res < 1/2]
[Res > 1/2]
^г[3/4-, -1/4-1	[Res<^1/4]
2 L 1- в, 1/2- 5 J
2тг Гв,
[
Г2A/4)
^ s, 1/4- s
[О < Res < 1/4]
2тг	[в+ 1/2, s - 1/2, 3/4^ s
Г2A/4)
5 + 1/4
тгГ
2 [в+ 1/2, S + 1/2J
тг ГЗ/2-в, -1/2-5
1- 5, 1-5
[1/2 < Res < 3/4]
[Re 5 > 1]
[Res < -1/2]
[0<Res<l/2]
[-l/2<Res<0]
8.4.41. Функции Лежандра 1-го рода Pjf(x) и Ри(х).
Обозначения: .	.
(-/х - I/)'
/W =
" ^ Г(-/х- I/)'

3.4.41] 8.4- Таблица преобразований Меллина элементарных и специальных функций 593
и) ,	2м+1тг	.	sin i/тг
Лея =
л72 =
тЗ/2
-1/2
2
3
4
5
6
7
8
9
10
11
1 —
M +
|/)Г(
i ^
-\L-V)
A хГ^/2Р^Bх 1)-
{ х)+ и { ) —
22 V
1 - /i/2 + i/, -ft/2 - i/ \
ft/2, -ft/2 /
(х-1)~^/2Р^(--1) =
= С5§| (х
АА 1
1, /x + 1 \
1
/i-^i + zi + i/ ;
(ж-1)+'х/2Р^Bж-1) =
/
221
1
/i/2, -ft/2 /
/2 \
A — ж) г Р^1 1 — — 1 I —
V ж ) /
22 V
1 1 /X \
|1-^/2рЛ2я!_1) =
22/
= Л.62^22 1 ж
i,/9 ^##/9 /
|1-ж|^/2Р^ (^--1^=^62^22^
\Ж / V !/+!,-!/ /
|1-ж^^2Р^Bж-1) =
/
	 z-y20 /
22 V
1-/X/2 + I/, -/x/2-i/ \ +
/х/2, ^/i/2 /
/
1 - /x/2 + i/, -/i/2 - i/ \
/i/2, -/x/2 /
|1^ж|^м/2рм f--l)=G^fa;
V ж ) 22\
02 /
i/ + l,-i/ /
1,1-ft \
i/ + 1, -i/ /
A + х)^/2 PjfBx + 1) =
/
63 22 ^
ft/2-i/, 1 + 1/ + /X/2 \
-/x/2, /x/2 /
/2 \
A + х)^'2Р^ (	hi) =
^ \ж /
= Д63^21/
V
/x + 1, 1 \
i/ + 1, -i/ /
A + х)-"/2Р^Bж + 1) =
/
64 22^
l + i/-/x/2, -i/-/x/2 \
1
ГA -/х-± */)ГA т 1 - M
Г s +/i/2, s-ft/2
Le + i/ + l-/x/2, s-i/-ft/2
~F |y)
[Res > Re/x|/2; Re/x < 1]
Л -."М-- 1
[l + i/- /x — s, — i/ — ft — sJ
[Re ft < 1; Res < 0, -Re/x]
r|"/x/2-i/-e, l + /x/2 + i/-el
[Res < l + Re(/x/2 + i/), Re (/x/2-
- i/); Reft < 1]
fs — i/, 5 + 1/ + 11
r »
Ls + 1- ft, s + lj
[Re /x < 1; Re s > Re 1/, -1 - Re 1/]
л62г
e + |,*-J,l + i/-J -*,
- i/- - -el [|Re/x|/2 < Res < 1 +
+ Re [u - /i/2), - Re A/ + ft/2)]
A62F[s + 1/ + 1, e - 1/, -e, -/x - s]
[Re 1/, -1 - Re 1/ < Re s < 0, - Re /x]
[e + l + i/-/x/2, e-i/-/x/2
+
_[/x/2-i/- s, l + i/ + /x/2-e]
+ Г 7 7
L 1 - /x/2- s, l + ft/2 - s j
[Reft < 1; |Re/x|/2 < Re s < l + Re(/x/2 +
+ i/),Re(Ai/2-i/)]
r|"e + i/ + l, e -i/j +
Ls + 1, s + 1 - /xj
+ Г1 ^ '
[l + 1/ - s, -1/ - sj
[Re /x < 1; Re 1/, -1 - Re 1/ < Re s < 0, Re /x]
г s _ M 1 + l/_^_s
ЛвзГ 2 ' 2
[ l-ft/2-s
[Reft/2 < Res < 1 +
+ Re A/ - ft/2), - Re A/ + /x/2)]
fs + 1/+ 1, 5 — 1/, —/x — si
[ 5 + 1 J
[Re 1/, -1 - Re и < Re s < - Re /x]
А64Г
MM 1/ l + i/+^
5 2 ' 2 ^ S' ^25
2
[Re/i/2 < Res < Re (/x/2-1/), 1 + Re (/x/2+i/)]

594
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.41
12
13
14
I/ +1, -I/
1 + ж
и	и
1 + 1/- -, 1 + I/ + -
_? ?2 2
2 ' 2
ж + 1
2' 2
15
1 + X
2 '
,t,-S
2
16
-Р^
1 - 6ж
17
;i +3/0/2,
-м/2, м/2
-1 + 6ж - ж2
-жJ
COS /А7Г	Г 1/2 + /1
2^2 [1/2 —
18
жJ
19
X G?99 I X
~~ /i/2, /i/2
- ж -^ .. /-1 + бж-ж2
¦у/тг sin f
s — г/, s + г/ + 1, —si
[Re i/, -1 - Re и < Re s < 0]
	,	1/ — 8,	i/ — .
2 2	2
-t-
[Rej^/2 < Res < - Re i/ - |Rejx|/2]
s - /i/2, s + /a/2, -/i/2 - и - ,
s + 1 + i/ - /a/2
[|Re/x|/2 < Res < - Re (/i/2 + i/)]
хГ
[Re /i/2 < Re s < - Re (i/ + /i/2); Re i/ > -1]
l
l/2 —/xj
хГГ e-M
[s + (l
[Re jla/2 < Re s < A - 3 Re /x)/2; Re /x > -1/2]
cos/itt _гГ 1/2 + j
¦ Д il 1
X Г 5 + -, S - -,
1 2' 2' 2
Re/i|/2 < Res
, (l-3Re/x)/2]
2 2
1 2 '	2
[Re/i/2 < Res < (l + Re/i)/2; Re/x < 1/2]
у/тг Sin /Х7Г

8.4.41] 8.4- Таблица преобразований Меллина элементарных и специальных функций 595
20
21
22
23
24
25
26
27
-/x/2, /х/2
1 - /х
/х _М
2 ' 2
1-ji-i
и — j
2
{1 X),	Гг
: АббСЦ Ж
1 + /A — V	[I + V
+
»
/x/2,
1-м-">1 + ^
2
2
l-fi/2, (l-/x)/2
2
2 2
< 1/2; |Re/x|/2 < Res < A +
3Re/x)/2]
[Re s > 0; Re /i < 1]
-i/;/2-e, i + i//2-ej
[Res < Re/i/2; Re/x < 1]
"(l + /x + i/)/2-e, (/x-i/)/2-el
1- e, 1/2-e	J
[Re /x < 1; Re s < A + Re (/x + i/))/2, Re (/x -
l-/x/2, s + (l-Ax)/2j
[Re/x < 1; Res > Ret//2, -(l + Rei/)/2]
1	1 + I/-/X
j, s H—,	s,
2	2
[0 < Re 8 < [1 + Re (i/ - /x)]/2, - Re (/x + i/)/2]
1 + и	и
\	, 8	,
2	2
/x	1 — /x
—	8.
2	2
[Re i//2, -A + Re v)/2 < Re s < - Re /x/2]
1-е, 1/2-e
[Re /i < 1; 0 < Re s < A + Re (/x +
()/2]
i//2-e
[Re i//2, -A + Re i/)/2 < Re 5 <
< Re/i/2; Re/x < 1]

596
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.41
28
= AQ7G22 x
1 — и и
	г, Ц	г
/X /X
2' 2
29
[г = 0, 1/2]
2 '	2
l +
30
31
2' 2
! \	[г = 0, 1/2]
/1
= ^69^1° Ж
и	1 — и
2 7J 2
l +
2' 2
33
и	1 —
2 .	2
34
J 2
COS/ХТГ Г	/Х+1/2
3/2 L"^17 "~ М? 1 + i/ —
35
sm(/i - i/)tt x
I/	1
+2^^'
i/ 1 + z/
^' 2
+
?1	I/ + 1	I/
j	, г Н	s, г	.
2	2	2
[Re /х/2 < Re s < r + A + Re ?/)/2, r - Re и/2]
Ъ>	Ь> + 1	II
'	, 5 Н	, Т
2	2	2
5 + 1	Г
[Re i//2, -(Re i/ + 1)/2 < Re s < г - Re i//2]
5-/X/2, -I//2-5, (l-z/)/2-5l
l-/x/2-e	J
[Re /x/2 < Res < -Rei//2]
e, e
[0 < Re 5 < - Re (y +
А69Г
+- i^/2 + 1 - jLA, e + (l-1/)/2-1
[Re /x < 1/2; Re s > Re i//2, -A + Re i/)/2]
1 + I//2- e, A -i/)/2-a
"Re/x < 1/2; Re 5 < Re(^-i//2), Re (д
2) + 1/2]
cos/iTT^r	^ + 1/2
7Г3/2 [-1/ - /X, 1 + U - t
_ Г I/ +1	I/	1/
XI 5 Н	, 3	, —/X	5,
2	2 Р 2
- /х - s	[Re i//2, -(I + Re и)/2 <
< Re s < - Re (jx + i//2), 1/2 + Re (i//2 - /x)]
f
/xj I
	 < sin (/x — i/)tt x
хГГ * - I//2, „ - «//2 - *
L (l)/2	A^/2J
+ sin (/x + 1/)тгГ

8.4.41] 8.4- Таблица преобразований Меллина элементарных и специальных функций 597
37
38
39
40
41
2 '
2 + x
2V/TT^
t-1/2
Г(-/х-1/)
1 + 2ж
G^K*
i/, 1/2
2y ж2 + ж
r-V2
(-М - I/)
GII х
3/2
, Fi/ + 5)/4
1-ж
.р2„Ч
cos2i/tt
2тг3/2
xG
|1±\/»J^ 2l/_!
ч	¦* I.
6i/ + 5)/4, A0i/ + 7)/4
5)/4, A0i/ + 7)/4
_ «. -2i/
TBi/ + 3/2)
2ТГ5/2 COS 1/7Г
xGiiU
7)/4,
+ sin is it G 22
5)/4
+ l
IOiz
[^ < 1/2; Rei//2, -(l + Rei/)/2 < Re 5 <
< 1/2 + Re (/x + i//2), Re (/z - i//2)]
^ Г(-^- v)
x Г
: — /1, -—I/ — 5, 1/2 —
f	J
[Re /i < Re s < 1/2, - Re i/]
x Г
2 ' 2' 2
[Re i//2; -A + Re i/)/2 < Re s < - Re (д +
^/2)]
3/2 + 2,
x Г
_-l-3i/, -i/J
4, -A0i/-3)/4-el
4, C-2i/)/4-e J
' [A + 2 Re i/)/4 < Re s < -C +
-10Rei/)/4; Rei/ > -3 ' "
cos2i/7r Г 2i/ + 3/2
" 2тг3/2 Г| -i/, -l-3i/
4	4
[Re i/ < -1/3; -(l + 2Rei/)/4, (l + 2Rei/)/4
< Res < -(l + 6Rei/)/4, -C + 10Rei/)/4]
x Г
+ A0i/ + 7)/4, E + 2i/)/4 - s .
[Re i/ > -3/4; -A + 2 Re i/)/4 < Re s < -A +
+ 6 Re u)/4]
rBi/
2тг5/2<
x Г
S 1/7Г I
, -C
s + Fi/ + 5)/4, C - 2i/)/4 - s
2t/ + 1 61/ + 1
¦ sin i/тгГ
4 ' 4
[-3/4 < Re i/ < -1/3; | Re Bi/ + l)|/4 <
< Re s < -A + 6 Re i/)/4, -C + 10 Re i/)/4]

598
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.41
42
\ =
)
I/ + 5/4,
О, 1/4
43
5/4, i/
О, 1/4
+ COSIU+-
4
44
45
46
47
48
49
50
51
-Vl-ж =
/х/2, -
x-l/2
_31 I
^33 1 х
-i/, l + i/, 1/2
-А*, 0, а*
1 + /х, 1, 1 - ах
l + i/, -i/, 1/2
-i/, i/ + l, 1/2
О, ~ax, А*
ж
1, 1 + /х, 1 - /х
1/2, l + i/, -1/
I/, -I/, 1/2
-//,0, /х
О, l/2 + i/, l/2-i/
х Г s, sH—, — i/	s, —и —
L	4'	4
[О < Res < -1/4- Rei/]
1П I I/ H	I 7Г X
4
хГ й'
i/ + 1, 3/4-
+ COS ( I/ H	) 7Г X
4,
x Г
s + 1/4, -v - s
¦i/+ 5/4, l-eJ
-I < Rei/ < -1/4; 0 < Re s < -1/4- Re i/]
¦Ax/2, e-Ax/2
[Res > I Re^l/2]
\/7Г
Л71Г
Л72Г
1 + I//2- e, (l-i/)/2-e
[Res < A- |Re/x|)/2]
s — /i, 1 + i/ — s, 1/2 — s, —i/ — .
1-s, 1 - ax- s
[Re ax < Re s < - Re i/, 1 + Re i/]
5 + i/ + 1, S + 1/2, S ™ ?/, —fJb — S
5 + 1, S + l-AX
[Re i/, -1 - Re i/ < Re s < - Re ax]
3, -I/ - S, 1 + I/ - 5, 1/2 - S
1 + A* — s, 1 — ax — s
[0 < Re s < - Re i/, 1 + Re v\
3-i/, s + i/ + 1, s + 1/2, -^
s + ax + 1, s — /i + l
[Re i/, -1-Rei/ < Res < 0]
5 —AX, 1/2—5, l + i/ — 5, 1 — i/ — sl
1 — s, 1 — a* — 5	J
[ReAx < Res < 1 - |Rei/|, 1/2]
1	11
1	1
S+2'5+2^M
[0, |Rei/| - 1/2 < Res < 1/2-Re ax]

8.4.42] 8.4- Таблица преобразований Меллина элементарных и специальных функций 599
52
53
54
55
56
/1 + х
1	1
О, - + */,	v
2 1 1 1
±
• + At, 1, —	/i
1
x
v,
3 3±2
4 4
11	1
4 4 P 4
- л/х)Р1/(л/1 + х +л/ж)
О, О, О,
1/2
Ри
1/2, 1, 1,
-«, - - I/ - 5,
[Re ц ±1/2 < Re s < 1/2 - Re i/, 3/2 + Re i/]
¦ X , i 1 1=FX
SH	, 5—1/, S+I/-+-1,	Д —
2	1=F1	2
[Re i/, -1 - Rei/ < Res < A=F l)/2 - Re/i]
x Г
111
7' s + 7 ~ ^' 7
4 4 4
3p	3
s H	-— =F ^j 7 - M - s
4	4
1T2
-1/4, RejLA- 1/4 <
< Re s < 1/4, A =p 2)/4 - Re u]
	s, 1 — s,
2
i/	1 — i/
S' 2
[0 < Re 5 < A + Re i/)/2, - Re i//2]
1/ + 1	1/
+++1
7
-,.+1,
[Re i//2, -A + Re i/)/2 < Re s < 0]
8.4.42. Функции Лежандра 2-го рода<3^(ж)и<
Обозначения:
2
1),
7Г COSeC /17T
тг cosec /хтг
(-ах - i/)'
2Г(>-
/х
sln/i7r
ГA - /х + I/)'

600
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.42
- cos /хтгГ(/х + и
л/2 ГA - /х + и)'
(/х + i/
= A74Gf2 х
2 ' 2
1, 1±
I/ + 1,
sin i/тг sin (/x — i/)tt
2тг sin/i7r
2' 2
2 sin /17Г
2' 2
2' 2
1 + ж
2' 2
ж + 1
ж- 1
A75Gf2
i/- -
2
_
2 ' 2
Л74Г
s + /i/2, s - /i/2, 1/ + 1 =F /x/2 - s
e + i/ + l±jx/2
[|Re/x|/2 < Res < 1 + Re A/ =F
s + i/ + 1, =F/x — s, —5
У + 1-8
[-1 - Re i/ < Re s < 0, =F Re /x]
sin i/TT sin (/i — i/)tt
27TSin /17Г
Д Д 1 7Г
— - i/ - s, — + 1/ + 1 - s
2	2	J 2sin^7r
x Г
— - i/ - s, 1 + г/ + — - s
2	2
1+--S, 1---S
2	2
- -ctg/хттГ
2 2
5---I/, 5-- + I/ + 1
2	2
[Re/z < 1; /x 7^ -1, -2, . . . , |Re/ix|/2 <
< Re s < Re (/x/2 - 1/), 1 + Re (/x/2 + 1/)]
5 +/i/2, e-jx/2
+ 1/ + 1 + /x/2, s + 1/ + 1 - /x/2j
[Re 1/ > -1; Res > |Re/x|/2]
1 + /x/2 - s, 1^/1/2 -
[Re i/ > -1; Res < - Re г/ - |Re/x|/2]

8.4.42] 8.4- Таблица преобразований Меллина элементарных и специальных функций 601
6
7
я
о
Q
if
10
11
\i-xuQ4(-r
VI
х {Gil U
1 V
/
\
"" \
1 + ж
1
A* P
2"' ~ 2
ж
I,
/X
1-ж|/
/
x G%%\ x
/1
/
x Gil \x
\
/
XG2\
/л \Vp)pb(X
\ +Ж) 4^^
21 /
x \
/
v ^21 I
X Goo 1
1
\
x Gil (x
AA 1
/
x O21 (
22 v
-G
V
-ж\
ft ft
2"' "
11 LL \
- — X -J— и — — \
, 2 2 +
/
JL4 /1 \ \
'+2'1 + I/
'I /J
2ГA + 1/)ГA-/х + 1/) Х
Ax/2-i/, -ax/2-1/ \
/x/2, —/i/2 /
f sin (д — i/)tt
2'1 + I/ 2 j +
/
+ COS /Х7Г X
Ж
A*
2
—1\
+1/
1 + 1/
/i /i
2 ' 2
M f
'I /J
f sin (/x —i/)tt
76 S —I	 X
[ sin (/x + i/)tt
M 1+ +M \
2' 2 +
/
+ COS /Х7Г X
Ж
1 +
_ (L
2
4 [
/*/2-
/
22^
/i
/i
M/2-
/x/2, -
21 f ж
22 v
/i
9 ' 9 11
'2 / J
= A77JcOSM7rX
1/, -/l/2 - I/ \
,M/2 /
/2-1/, -/x/2-i/ \1
/2, -,x/2 Л
|- 77|COS/i7TX
1/, -/x/2-i/ \ _
-/x/2 У
-/x/2-i/, /x/2-i/ \1
/2, -м/2 Л
f
^75 j Г
I
+ г
S+2'
^ + i/ + l+^,
U LL
	1/ — s.
2 2
1 . ^ 1 ^
1 H	s, 1
2 2
> -1; Re/x|/2 < Res <
г
e-|,l + I/+J-
[2i/ ф -2, -3, -4, ...,
ГР /x
w f sin(/x-i/Or r
\sin(/x + i/)tt
+ cos тггГ е
[l-
[/x^O, ±1, ±2, .
< -Rei/- |Re/x|/2]
Г /X /XI
76 [S + 2 , 5 2 j X
4, / sin (/x - 1/)тг ГГ
[ sin (/x + i/)tt [ s
6 — —
2
e + i/ + l-^
у — s
_s
_
+
1
J
-Rei/- Re/x|/2]
[•+?¦
s, 1 + t/ — — — s\
2 J
Re/x|/2 < Res < 1 +
1
¦ -+U 1
.l + /x/2-eJ +
5™^/2 11
- /x/2 — s J J
• • ?
Re/xl/2 < Res <
Ll/2 — I/ — 5 1
+
Г -/x/2- 1/ - s 11
Ls + i
[/a 7^ 0, ±1, ±2, .
< — Re v — Re/x 1/2]
Л77Г Г1 + 1/- ^ -e, 1
/ Л *
X < COS /Х7Г1
I 1 ~
V L -1-
Г О J-
h -1-1/.
[/x 7^ 0
+ Rei/ -
L 'I™
, ±1, ±2, ...;
ЛпГ[. + |,.-|]х
f [! + ^
x < cos/хтгГ
I L s^
L - + /1,
[/x ф 0, ±1, ±2, . . . ,
+ Rei/ -
Re/,|/2]
/ —- fJL/Z + 1 J J
• • 5
Re/xl/2 < Res <
-Ax/2 1
/2-J/
Re/x|/2 < Res < 1 +
-/x/2-i/ J
/x/2-ell
/2-1/ Л
Re/x|/2 < Res < 1 +

602
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.42
12
1-х»
- 6ж + ж2
cosec (dz/i — 1/4)тг х
/х/2, -/х/2
Л
13
1-х»
-1 + 6ж - ж
/i/2, -/
3/х)/2,
/2, /х/2
/х)/2
14
7Г Sin /17Г
М
' 2
Sin flTT
1- li-v	и -
о,!2 ' 2
2
- COS /Х7Г X
1 — и — i/
15
-, 1+ ¦
1 — i/	i/
. 2 . '2
[г = 0, 1/2]
16
0l ^^
2' 2
1 -Г- -, 1-Г+ -
2	2
I/ + 1 I/
2 7 2
[г = 0, 1/2]
-478
sin (di/x — 1/4)тг
xrf
х Г
¦ V2 COS /Х7Г X
/i l-3/i
~ 2"' 2
[-1/2 < Re/i < 1/4; |Rejx|/2 < Res
R)/2, (l-3Re/x)/2]
Ctg ( ±/i - - j Ж X
x Г
+
[-1/2 < Re/i < 1/4; |Re/i|/2 < Re s
-Re/x)/2, (l-3Re/z)/2]
sin(i/ - /i)tt
< A-
в-/х/2, A-3/х)/2-в
< A -
7T Sin/ITT
[i-v
x Г
2	2
1
1- s? g ^ S
+ COS /Х7Г X
1
2 '	2
[Re/i < 1; /x ^ 0, -1, -2, . . .; 0 < Res <
< A + Re (fi + i/))/2, Re (/x - i/)/2]
s + 1 H	r
|Re/i|/2 < Res < (Re и + l)/2 + r]
v -\- 1	/1	/i
s H	, r H	s, r	s
2	2	2
Rez/)/2 <Re5<r-

8.4.42] 8.4- Таблица преобразований Меллина элементарных и специальных функций 603
17
18
19
20
21
1 + ж
= Л80 х
2 ' 2 ' V 2
+ COS (/1 + V
2 ' 2
= ^80 X
2 ' ^ 2
. — и + cos (/i + и)ж x
1 — 1/ I/ 1 + /1
2"' ~2"' 2
1 — /i — I/ \ + [L — V
2
/i +
г
1 - v
/1	U
+ cos (/i + i/)tt x
x Г
u, v	I —
S — —,	5,
2 2	2
|Re//|/2 < Res < -Rei//2]
^80
1	[A — 1/
5, S H	,	5,
2	2
tt — 1/ и — и
+ 1+ ^^^
/i + I/
+ COS (fl + 1/)тГ X
х Г
2 2
ЛН1Г
5 + l + ^^
[0 < Res < -(
l + i/
ReM|)/2]
2 2 2
J + ¦
[| Re/x| < Res < (l + Rei/)/2]
1 1 + 1/ + Д
—, 	— — s.
2'	2
2 '	2
1 + V- fJL
[0 < Res < A + Rei/- |Re/x|)/2]
)/	/
[Re 1/ > -3/2; Re s > |Rejx|/2]

604
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.42
22
ж - 1
11 U
23
xGlUx
A- i/)/2-jx, 1 + 1//2- ц
24
25
2 + ж
1/2,
2ж + 1
2\/ж2 + ж
1+ 2 "^ 1+ 2 +i
l + i/ i/
2 '
26
27
-I/, 1/2
2ж
2л/х2 + ж
A84Gl22 х
2 ' 2
28
29
2 л/1 ^
1/2,
2ж - 1
2л/х2 ¦— х
l + i/ I/
2 ' 2
'2+^
(Ах - i/)/2 - в, -(ах + i/)/2 - .
1/2- s, 1 - s
[Re i/ > -3/2; Re a < -(Re и + | Re /x|)/2]
х Г
[Re /х < 1/2; -A + Re i/)/2 < Re s < 1/2 +
-/x, s -ax, 1/2- si
[|Re/x| < Res < 1/2]
i/ + 1	i/
-Re i/)/2 < Res < -Rei//2- |Re^|]
? + ax, s — fj,, v + 1 — s]
| ReA*| < Res < 1 + Rei/]
i/ + 1 i/ + 1
s H	5	Ь /x — s,
2	2
А84Г „ 2 ' 2
(l + Rei/)/2 < Res < l/2 + Rei//2- |
в + /х, в -/x
+ 1/2,5 + , +
[Re i/ > -3/2; Re s > | Re /x|]
Ax — i//2 — s, — ax — i//2 — .
A — i/)/2 — в, 1 + 1//2-* .
[Re i/ > -3/2; Re s < - Re i//2 - | Re /л|]

8.4.42] 8.4- Таблица преобразований Меллина элементарных и специальных функций 605
30
31
32
33
34
35
36
у/х
1 - ж
1-
~i22 ,
^22 1 x
-A0i/ + 3)/4, -Fi/
+ Ж
\4ж1/4
¦'(M + i/a)
x G\\ \x
4/i + 1 1 - 4/x
	 G33I X
1/2, -1/, l + i/
0, +|i, dbjti
1/2, 1 + i/, -i
1/4- i/, 5/4 + 1/, 3/4
1/4, 1/4 +д, 1/4-/x
3/4, 3/4-/x, 8/4+- j
3/4 + i/, 1/4, -1/4-
4 COS 1/7Г
x Г
f cos2i/7r
1 COS 1/7Г
s + Bi/ + l)/4, (lOi/ + 7)/4 - s
2i/ + 5)/4-S
4	4
Ю1/ + З 3-2i/
4	4
[-2/3 < Re 1/ < -1/4; |1 + 2 Re i/|/4 < Re s
< G + 10 Re i/)/4, E + 6 Re t/)/4]
П-2.--1Х
4тг3/2
x Г
10i/
4 7	4
62/+ 5
4	4
[-2/3 < Re 1/ < -1/4; |1 + 2 Re i/|/4 < Re 5
< G + 10 Re i/)/4, E + 6 Re i/)/4]
COS/17T
x Г
s + D/x
, C
s + E + 4/i)/8 ± 2/x, D/x + 7)/8 -
Н5ТГ1 <Re|i<CTl)-1;
+ 4Re/x)/8 < Res < 3/8 + A/2 + 2) Re ft]
Л74 fs, 5 =p /x, 1/2 — s, 1
-A +
s + 1/+ 1, 1 =|= jx — s
[0, ±Re^ < Res < 1/2, 1 + Re v\
A74
[-1/2, -1 - Re 1/ < Re s < 0, + Re u]
x, s + - - /x,
4"S'
1/ H	s
4
3
5 H—
4
- 1/4 < Res < Re и + 3/4]
3 1	1
4' 4 '4
j-^-e
[-3/4-Re 1/ < Re* < 1/4- |Re/ij]

606
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.42
37
/i + i
Ж
3/4, 5/4
1/4, 1/4
i/, l/4-i/
/i, 1/4- i/
38
40
41
42
43
44
^83 nl3
3	3 3
—, — — и,, —\- и,
4' 4 F 4 Р
11	3
—,	I/, —Ь
4	4 4
-1 + 2 3 3 + 2
	 — i/, —, v Л
4	4	4
11	1
^5 —1_ ^	^
4 4 4
i/ + C±2)/4, -1/4,
1/4 +А»
1	13
41
'•-4-"
41 3
3	1	3
4	4 Р 4
1 1
y, —,	1/
4 4
-г/, 1/2,1 + 1/
0, /1, —fj,
1, 1 - /х, 1 +/
1 + г/, 1/2, -I
4
+ -,
4
1
	s
4 1
s + - — и
Re s < 1/4]
в+ 1/4, 1/4- 5,
л/2тг	5/4 + и - s,
1
+ 7,
4
1/4 — лх — s
1/4- i/ - s
[-1/4 < Res < 1/4- |Re/i|]
1	1
4 ' 4
5 + 2
¦ + 1/ — s
3 + 2
Re /x| - 1/4 < Re s < E ± 2)/4 + Re v\
3 + 2 3	3
	, — — s, — -
4 4 4
4	^
5	+ 2
	h у — s
4
[-C±2)/4-Rei/ < Res < 3/4^ |Re/x|]
; - 1/4, s + /x + 3/4, s-/x-l/4,
; + 1/4,
5/4 + i/^s
s + iz + 3/4
- Re jw < Re s ~< 5/4 + Re v\
3 1	5
вз+1/+4'4"в'4-
	5,
4
[1/4, 1/4 + Re /x, ^3
	h v — s
4
[-3/4- Re и < Res <
< 1/4, 5/4 + Re /x, 1/4 - Re /x]
S, S + /LX, S - /X, l + I/ - SJ
в + 1/2, 8 + 1/ + 1	\
[|Re^| < Res < 1 + Re 1/]
s + 1/ + 1, — s, /x — s, —/x — si
1/2- s, l + i/ - s	J
[-1-Rei/ < Res < -|

8.4.43] 8.4- Таблица преобразований Меллина элементарных и специальных функций 607
45
46
47
48
49
50
51
1/2, i/ + I, -v
0, -/х, ц
1 + ж '
1, 1 + fJL, l-t
1/2, -i/, i/ +
/1 + ж
1 1± 1
¦ — J/, —,
2 2
О, /x, -/х
^±i
ж
1 1
-, О, Т^ ~"
IS*
1	1
	i/, 0, - + i/
\ 1 2 1
'  "^2+"
1? 1 + |1, -^
-I/, 1/2, -1/
т
2л/2
гAТ1)/2
3/4, l/4-i/, 5/4 + г/
1/4, 1/4 ±/i, 1/4 =р/х
s, s — /х, s + /x, 1/2 — ,
s + iz + 1, s — v
[|Re/x| < Res < 1/2]
s + 1/2, —5, --/i — s, /i — si
1 + I/ — 5, —I/ — 5	J
[-1/2 < Res < -|Re/x|]
s, s + pt, s - /x, C ± l)/2 + i/ - ,
s + 1/2, s + A ± l)/2 + i/
[| Re /i < Re s < C ± l)/2 + Re i/]
i- s, 1/2 - /x- .
1 ±1/2 + 1/ - s
[- Re i/ =F 1/2 - 1 < Re 5 < 1/2 - | Re /x|]
_л r
[|l/2 + Re/x| < Res < 3/2 +Re i/]
1
2^s, l + i/- s	J
[-1 < Re i/ < Res < 0, 1 + Re/z, -Re/^]
хГ e + l/4, s±/i +1/4, 1/4 -
L s + i/ + 5/4,
З/4 + i/- 5
3/4±|х- в
1/4, -l/4TRe/x < Res <l/4, 3/4 +Re i/]
8.4.43. Функция УиттекераМР)(Г(ж).
(См. также 8.4.45)
Обозначения:
[-1/2 - Re cr < Re s < + Re p; 2cf ф
-J- 1 Q *3	1
=FP, l/2 + o--.
s + cj + 1/2
< Re s < Re <j + 1/2; 2G^-1, -2, -3, . . .]

608
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.44
pja Biy/x)
1/2 +о-, 1/2- а, 1/2, 1
/ 2г \	/ 2г \ _
Р> \л/й/ Р> \ л/ж /
1/2-<7, 1/2+ <7, 0, 1/2
Р? -Р
s + <t + 1/2, p -— Sj —p ¦— ,
1/2 + ex - s, -s, 1/2- s
[-1/2- Recr < Res < -|Rep|]
s + p, s — p, 1/2 + cj — s
e, e + 1/2, 5 +a+ 1/2
[|Rep| < Res
8.4.44. Функция У иттекера WP) о-(ж).
(См. также 8.4.46)
Обозначения:	1
-1/2
1-р
1/2 + сг, l/2-o-
Wp
= A95GH(x
1 + р, 1-р
1/2, 1, 1/2+ G, 1/2 ^
0, 1/2, 1/2- <т, 1/2
1/2, 1, 1/2+ О-, 1/2 -а
0, 1/2, 1/2- а, 1/2
- Pi P
1 + Р, 1-Р
1/2, 1, 1/2+ G, 1/2 -а
s + cj + 1/2, s + l/2-cr]
e+1-p	J
[Res > |Re<r| - 1/2]
1/2 + сг- s, 1/2-cr- el
1-Р-8	J
[Res < 1/2 - |Recr|]
^94r|s+i-Cr, S+^
-p— S
[|Reo-| - 1/2 < Res < -Rep]
Л94Г I s — p,	cr — s,	her — .
[Rep < Res < 1/2 - |Re<r[
s H	, s + 1, s H	h cr, — p — s
1
e + l-p, - + er-s
[-1/2, -1/2- Recr < Res < -Rep]
1	1
s — p. — — s, 1 — s,	h cr — s
F' 2 '	'2
1
s + «tH—, 1 — p —¦ s
[Re p < Re s < 1/2, Re cr + 1/2]
i, S
-p, s + 1- p
[Res > |Recr| - 1/2]
p-8,
	a — s
2
1 — p — s
[Res < 1/2- |Re<r|]
p- s
1	1
•-, s+1, s + ^+cr, s + ^^cj,
I Re cr|- 1/2 < Re s < - Re p]

8.4.46] 8.4- Таблица преобразований Меллина элементарных и специальных функций 609
10
\уж у V <
_ 14/
о,
\/^ /
1/2,
=
1/2 +
ct, 1/2 ^ст \
J
s
1
- P
1
	s
2
— s
1
2
[Rep
1
<
— s,
Res
1
2
<
+ CT — Sj
1/2 - | Rea\]
8.4.45. Вырожденная гипергеометрическая функция Куммера
iFi(a; 6; ж).
(См. также 8.4.43)
Обозначения: Л97 = 2a
Н
а; 6; -
а; 6;
0, 1™ 6
1, b
а
[О < Re s < Re a; b ф О, -1, -2, . . .]
[- Re a < Re s < 0; 6 ^ О, -1, -2, . . .]
а+5	6	1+6
	hi,	s,	s
2	2	2	J
[О < Res < (l-? + Rea)/2, (l + ReF-a))/2]
Л97Г
1 + a- <f	1
s H	, — s,	s
2	2
6	6 + 1	a + S
s -\—, s ~\	, 1
2'	2	2
-Rea- l)/2, (Re (a - 6) - l)/2 < Re s < 0]
ГГ ь U-.»-
[b — a] L Ь — s
[0 < Re s < Re F - a); 6^0, -1, -2, . . .]
-a, -e
Г 6 U
L6^aJ L
[Re (a - 6) < Re s < 0; 6^0, -1, -2, . . .]
8.4.46. Вырожденная гипергеометрическая функция Трикоми
Ф(а, 6; ж).
(См. также 8.4.44)
Обозначения:	1	2а^ь
5	Л99 = ,— _,, V-,,	;—-
Г(а)Г(а-6
:}¦
2"°ГГЬ
/тг а
{;}¦
(а, 6; ж) =
1-а
0, 1-
, s + 1 — 6, а ¦— s]
[0, Re 6^ 1 < Res < Rea]
20 А. П. Прудников, Т. 3

610
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.46
6; -) =A98Gll[x
1, b
а
Ф (а, Ь] -2iy/x) ± Ф (а, 6; 2г
= A99GfJx (l-a)/2,l-a/2
л/ж/
= /199^42
1-6/2,
8 + 1 6 + 1 6	8
2 ' 2 ' 2' ~ 2
a + 1 a
2 ' 2
(а, 6; -
1 + 8 — а	8 + а
2 '	2~~
11
0, -,
2 2
6
, 1- -
2
a, 6; —) ±
1
2' '
1 -
6
' 2
<5 +
1
a
+
2
8
b
+ a
6; ж) =
a bi —
x
6; -
1 + а- I
=GfJx
0, 1 - 6
1, 6
6 — а
(a5 b.
— а — 6 а — 6
2 ' 2
6 1-6 1-8
2 2
8
2~' 2
Л98Г[5 + а, -в, 1 -6- в]
[- Re a < Re s < О, 1 - Re 6]
AmV
1-Я	1-6	6
s H	, s H	, s + 1	,
2 '	2 '	2'
о
1	s
2
1 + a	a
s.	.
2	2
[(Re 6 - l)/2, E - l)/2 < Re s < Re a/2]
a + 1	a 1 - 8
s + ¦
Л99Г
2<5'^2' 2
1-6	2-6
	 — " i
2	2
Re a/2 < Re s < A - Re 6)/2, A -
1	1-6	6
2' ^	2 ' ^	2'
A - <5 + a)/2 - s
[0, (Re 6- l)/2 < Res < A - <
1 - <f + a	1
Re a)/2]
АддГ
1 -
8 + 1

2
1-6
6
8, 1	.
2
5 - Re a - l)/2 < Re в < 0, A - Re 6)/2]
s, s + 1 — 6
s + a + 1 - 6
— 5, 1 — 6 — S
1+a-b-s
[Res > 0, Re 6- 1]
[Res < 0, 1-Re6]
6	1-6	1-8
1	, H	, s H
2	2	2
1 — a — 6	a ¦— b
[(Re 6 - l)/2, E - l)/2 < Re s < 1/2]

8.4.47] 8.4- Таблица преобразований Меллина элементарных и специальных функций 611
10
11
12
13
14
)
6/2, F
а + 6)/2,
(Ь-а)/2
(а; 6; -2-у/ж ) Ф (а, 6; 2л/ж) =
1 - а, 1 + а- 6
o,in,i-,
2	2
2
а; Ь;	^Л Ф fa, 6;
6O2,6/2,6
а, 6 — а
х Ф (а, 6; 2л/ж) = —= х
а — 6 + 1, 1 — а
О, A-Ь)/2, 1-6/2, 1-,
2 \ /	2
е -/v» ф( Ь-о, 6; —— ) Ф (а, 6; —— 1 =
а, 6 — tt
-6/2- 5, A - 6)/2- 5,
+ 1 - с5/2, A - а - 6)/2 - s,
Б2Г
1 + (а-6)/2- s
[-1/2 < Re 8 < A - Re 6)/2, A ¦
j, 8 + A - 6)/2, в + 1 - 6/2, а - в]
s + a-6 + 1, 6-s	J
[О, (Re 6 - 1)/2 < Re s < Re a]
- а, —s,
6	6
	s, 1	,
2	2
s + 6, 1 + а — 6 — s
[- Re a < Re в < 0, A - Re 6)/2]
s - 6 + 1
s + 1 — а
[Re в > 0, (Re Ь - 1)/2, Re 6 - 1]
1-6	6
s,	s, 1	s,
'2	2
+ a-6-s,
1-Ь-8
1 — а — 5
[Re в < 0, 1 - Re 6, A - Re 6)/2]
8.4.47. Функция о^(&; ж).
(См. также 8.4.19, 8.4.22)
2Ь+с-2
Обозначение: В3 = —г
0FiF; -l
О, 1-6
1, 6
3 - 6 - с 6 + с
2 '	2^
О, 2-6-с, 1-6, 1-е
М f • М -
4ж/ ° 1 \ 4ж/
1, 6 + с - 1, 6, с
F +с- 1)/2, F + с)/2
Г з 1
ГF)Г	[0<Res<(l + 2Re6)/4]
[6-sJ
ГF)г[
^Г:М
[-A + 2 Re 6)/4 < Res < 0]
s, F + с - 1)/2 - s, F + с)/2 - el
6 + С— 1 — 5,6- 5, С — 5	J
[0 < Res < (Re F +с) - 1)/2]
6 + C-1, 5 + 6, 5 + С
[(l-ReF + c))/2 < Res < 0]
20*

612
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.49
8.4.48. Функция iF2(a; 6i, 62; ж).
Обозначение: В4 = Г '
1
2
iF2(a;
iF2U;
61,
61,
62; -ж) =
i -j
62; -^\ =
/
X
V
1-е \
0, 1 - 61, 1 - 62 /
/ 1 1 h h \
31\\a )
Г s, a — s
L61 — s, 62 ~
[0 < Re.
-a)/2; 61, fe2 ^(
J54r[ s + a'^5
[s + bi, s +
[-Re a, Re (a
< 0; 61, 62 7^ 0, -
..]
? < Re
), -1,
62 J
-6i-
-1, -2
a, 1/4 +
-2, . ..]
-62)/2-
• • *J
Re F1
1/4 <
+ 62 -
Res <
8.4.49. Гипергеометрическая функция Гаусса 2fi(a, ft; с; ж).
Обозначения:
в, =
ГF-с
(«О»
r(i - 6)
(c)« '
ГA-а)
Г(а - с + 1)
в гГ	с	1 в гГ с 1 в г[с'са
[а, о, с — а, с — 6J	[а, с — oj	[2a
с,2о-с
¦1/2, 1/2-a + b
a
32a^F
В17 =
a + 6=pl/2, 1/2™ a + b
2a - (l±l)/2
6 + 1/2, 1/2 +a-b
2b-a
-багГ 4а+ 2/3
¦a-1)'	2ГD/3^а)Г(За^1)'
, _ 1 ^ [4a+ 2/3]
=
6a J'	ГA/3-а)Г(За)'
^r[a + 6 + l/2, a + 6 + 1/2]
: L 2«5 2b
-r\a + b-
2a + S,2b + l
A — 2a — 26) cos (a — 6)тг	^/тт Г	с7 с
2е™1 [а, 6, с — а, с — 6J '
1528 =
тг cos (а + 6)тг
1 ^[с, а + 6 - с-
а, 6
, (а
, О =
{;}¦
(с-Я)„
1 + О — С]
[Re F - с) > п - 1; Re s > 0]

8.4.49] 8.4- Таблица преобразований Меллина элементарных и специальных функций 613
2
3
4
5
6
7
8
9
10
(ж-
(ж-
A-
A-
(ж-
A-
(х-
иA
V
Н(х
1)
1)
х)
х)
1)
ж)
1)
-
-
b — c — n тр (
, 2^1 1 -П
+ V
02 /
= (-l)nB5G22\^
b — C — n тр /
+ 2^1 (-71,
--(-1ГВ5О°21(а
V
b^c^n2Fi f те
+ V
= BbG\l(x
— Ъ Тр I JL
, 2г 1 I —те, 01
-b2jPl / п 5.
+ V ' '
о ^02
— ?>бЬ22
+ &2^1 f-n, 6;
+ V
_ / 1\пв q20
~К ) 6 22
Ь (
+ V
— 1 ) 6
ж) 2^1 (а, с + те
_ , i\n d /-J20
7 22
6; с; -
с
1 + <
6; с; х)
1 + 6
6; с; -
6 — те
— те,
с;
1
1 _
20 (
с;
ж
ж —
L
\
1 -
0,
с;
ж
ж —
(х
V
1 -
0,
1
с;
1 -
с; ж)
(
\
1 -
о,
1) iF\ ( о, с + те; с; —
\ ж
— 1 ;
гВ G02
7 22
1\ =
с/
з — 6 — те,
6,
2с - 6 - те \
2с - 26 - те /
=
— с, 1 — с — те \
™) =
, 1 + 6-с-теЛ
6 )
х )
1 — 6, с — 6 \
0, те + с — 6 /
"\ _
1/
-с — те, 1 — 6 \
1-е /
^ _
1/
-с — те, 1 — 6 \
1-е /
х )
1 + 6, 6 +с \
6 + с + те, 26 /
=
-с — те, 1 — а \
1-е /
)-
(х
у
1, с \
с + те, а /
в5г[ - + 2с-6-
[ 5 + 2с - 6 - те,
-
6 + те — с — 5
1 + те + 26-2с-5 _
= (-1)ПМ14-6+Г2ЬС<
[ 1 + те + ЛЬ — .
=
о 1
2c- sj
х A + 6 — 2с — s)n
[Re F - с) > те - 1; Re s < п
Г s + 1 — с, с — 6 — s 1
[s + 1 -— с -— те, 1 — 5 j
[Re F- с) > те- 1; Res
„Г s — те, 1 + те — 6 — 5
I55I
Ls + 1 + б-с-те, 1 - 6 -
п Г s — те
[s + 1 + 6— с— те
[Re F - с) > п -
(-1)пв6г s'1 +
Г J 1
~ 6 [s + 1 - 6J
[Re 5 > 0;
5 + 1 — С, 6 — S
(— 1) Bq I
[s + 1 — с — те, 1 — s
= Я6г[6^5](с-5
[l — s J
[Res <
Г s, с -i- n — s 1
-^6 Г =
Ls + 1 - 6, с - sj
Г s 1
~ 6 [s + l-6j
[Re 6 < 1 -
fs + 6 + c + те, -6 - si
6 [s + Hc, 1-26-sj
-Ввг[ ™6^5 l(e +
[l - 26 - sj
[Re s < - Re 6;
Г s, с + n — s 1
[s + 1 — а, с — sJ
Г s 1
= В7Г[5 + 1-а]^^
[Re a < 1 -
Г s -\- с -{- n, —s 1
[s + c, 1 — a — s J
= БтГг -^ i
[1 — a — s J
[Re a < 1
+ Re F -
c-e)n
< Re (c -
=
8}
](l-6-s
- 1; Res >
-n-s] =
Re 6 < 1 -
1 =
J
)n
Re 6 < 1 -
- те; Re s >
b + c)
n
Re 6 < 1 -
-S)n
~ n\ Re s >
n
— те; Re s <
c)]
&)]
)n
те]
те]
те]
0]
те]
0]
- о]

614
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.49
11
12
13
14
15
16
17
18
19
20
21
(ж-1)
2Fi(a,
2F1 (a
v
A + ж)
A + ж)
A + ж)
=
A + ж)
2-Fi(a,
-с-
(-1
— с —
-|-
6; с
а+6-
а+о-
— а
2
(
V
\ те о /^2
1 J-58 t-J"*"
п тр (
V
: (-1)
—ж) —
с; _2Л
ж/
~ С 2 Fi (
2
2 1 |
Fi(o, 6
""а 2
6; с
х 2Fi
2^1 (о,
2F1 fa
V
6; с
(
F\ (a,
V
/
СШж
а, с + те^ с
of
1-е
0. 1
а, с -}- п; с
/
22 V
гГ с Ь15
La,6J 2i
= г с (
[a, 6J
я., 6; cj —ж
2 1*^
1 + а
0, 1-
(
(а, 6; с; -
ч
г(х
Ч
1 + а
а, 6
; 2а + 6 +
-2а-26
0, -2а-
6; 2а + 6 +
1 — а, а -
а, 6, а +
ж)ЯA-ж) + ж~аГ
(
а, 1 +
1-ж)
с; 1 -
= #1
а - с; 1 +
22 V
1^22 1 х
V
i
а
X \
I —
ж-1/
— те, 1 + а — с\
-с У
1
- =
1-ж/
1 — с — те, —те \
0, -а- те /
\(х
\
а, \
0,1-с У
V
а, 6 У
) =
-с, 1 + 6- с \
У
1 \
	1 гг
жУ
+ 6 - с, а + 6 \
У
1; -ж) =
1 — а — 6,
1 - 2а \
1 - 2а - 26 У
1 \
1*	) =
х у
f6 + I, a+ 26 \
26 + 1 У
Г с,1-6 1
X
_с-а, l + a-6J
1\
ж
1
?; жГ
- а, 1 - 6 \
0, 1-е У
1-а,1-6 \
0,с —а —6 /
,1 + а + о — с \
, 6 У
Г
Г
ф
Б
Ф
Б
ф
Б
<
Б
Ф
Г
Г 5,с + те-5 1
81 —
[s + 1 + a — с, с ¦— s\
= В8П S 1(с-в)„
[s + 1 + а - cJ
[Re (а- с) > те - 1; Res > (
Г s,c + n-s 1
[s — те, 1 + а + те — sj
-Г-1)пБ-г[ с + тг^5 1A-в)
[l + a + те — sj
[Re s < те + Re с; Re (а - с) > те -
Г 1 Г h 1
[а, б] L с- в J
[0 < Res < Re a, Re 6; с^ 0, -1, -2, .
Г с 1 Ts + a, s + 6, -sj
[a,b\ [ s + c J
[- Re a, - Re 6 < Re 5 < 0; с
0, -1, -2, ...]
fs, с — a — s« с — 6 — si
9r
L C-8 J
[0 < Res < Re(c- a), Re (c - 6); с
о, -l, -2, ...;
fs + a, s + 6, c — a — 6 — si
L s+a+6 J
[- Re a, - Re 6 < Re s < Re (c - a - 6); с
0, -1, -2, . ..]
Г
2a + 6 + 1 - s,
L
a + b-3,2a-s} [0<ReS
2a + 26-s
J
2Rea, Re(a + 6); 2a + 6 ф -1, -2, -3, .
[s + a, s + 6, s + a +26 + 1, a - si
10r
L s + a + 6 + l, s + a + 26 J
[- Re a, - Re 6 < Re s < Re a; 2a + 6
-1, -2, -3, . ..]
Гс, 1 — Ь1 Г s, a- s j
L a J U + l™6, c- sj
[Re (c - a - 6) > -1; 0 < Re s < Re a; 1
6, с фО, -1, -2, ...]
ВцГ[з, s + c — а — 6, а — s, 6 — s
ф
Б
-
[Re(a + 6- с), 0 < Res < Re a, Re 6; с
0, -1, -2, . ..]
цГ[в + a, s + 6, —s, с — a — 6 — s]
[- Re a, - Re 6 < Re s < 0, Re (с - а
6); c^O, -1, -2, . . :
1]
•]
Ф
Ф
<
Ф
—
Ф
—

8.4.49] 8.4- Таблица преобразований Меллина элементарных и специальных функций 615
22
23
24
25
26
27
28
29
30
31
32
A-ж)! 2Fi(a, 6; с; 1-х) =
с — а, с — 6
О, с - а - 6
а, 6; с; 1	=
жу
(ж- l)+~12Fi(a, 6; с; 1-ж) =
с, а + 6
а, 6
= Г(с)<?§2
с — а, с — Ь
О, с - а - 6
а, 6; с; 1 - - ) =
ж у
с, а + i
а, 6
а, 6; с;
а, 6; с;
1 - а, 1 + 6 - с
О, 1 - с
1 + ж
1 — а, с — а
О, с- а- 6
1 4ж
а, а-\	: с:
'	2' ' A + ж
1 — 2а, с — 2а
О, 1 - с
1	4ж
2 + 2а - 2с, 1 + 2а - с
О, 1-е
а, Ь; а
1
2' A-х)
3±1	1
	2а, - + b - а
2	'2
О, 1±	а- 6
2
- а, 1/2 + 6- а
О,
2Fi а, 6; 26; ±-
1 + а-26, 1/2 +а- 6
О, 1/2-6
Г(с)Г
s, s + с — а — 6
s + с — a, s + с — 6J
[Re 5 > 0, Re (a + b - с); Re с > 0]
1 — с — s, 1 — о — 6 — si
1 — a — s, 1 — 6 — s J
[Re с > 0; Re 5 < 1 - Re с, 1 - Re (a + 6)]
1 + а — с — 5, 1 + 6 — с — ,
Г(с)Г
Г(с)Г
L 1-5, l + a + 6-c-,
[Re с > 0; Re s < l + Re(a-c), 1 + Re F - с)]
Г(с)Г
s + a, s + 6
+ c, 5 + a + i
[Re с > 0; Re s > - Re a, - Re b]
, a-s, c-b-s
0
< Re s < Re a, Re (c - 6); сф О, -1, -2, . . .]
s -+¦ с — a
[0, Re(a +
+ 6 - c) < Re s < Re а; с ^ 0, -1, -2, . . .]
[Re (c - 2a) >
5, 2а- s
s + с — 2а, с — ,
> 0; 0 < Res < 2 Re а; с ф 0, -1, -2, . . .]
s, 2с- 2а- 1 - i
5 + 1 + 2а — с, с ¦— s \
[Re Bа- с) > -1; 0 <
< Re 5 < 2 Re (с - а) - 1; с ф 0, -1, -2, . . .]
5, 2а- A±1)/2- 5	1
+ 6-O + 1/2, а+ 6 +1/2- 5J
[Re (b - а) > -1/2; 0<Re5<2Rea-
- A ± 1)/2; а + 6 + 1/2 ^ 0, -1, -2, . . .]
s, a — s
5 + 6- a + 1/2, 6 + 1/2- sj
[Re F - a) > -1/2; 0 < Re s < Re a; 6 +
1/2^0, -1, -2, ...]
В17Г
s, 26 — a — s
a- 6 + 1/2, 6 + 1/2-5
[Re (a-6) > -1/2; 0 <
< Res < ReB6-a); 6 + 1/2 ф 0, -1, -2, . . .]

616
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.49
34
37
38
39
40
41
/T+x) a2Fi(a,6; а + 1;
2 у
1-a-b
1 - а,
z
О, 1-a-b,
а,6;а
а	а
2'	2'
a b
~2* 2'
3' 2' (ж-3K
5/6- а, 2 -За
О, -1/2
1 3 A + ЭжJ
3' 2' A-ЗжK
2 -За, 5/2- За
О, 7/6-2а
3'2' C+4ж)г
а- 1/3, 2 - За
О, -1/2
1 3
а,
2 - За, 5/2 - За
О, 7/3 - 4а
5 27ж2
б' D + ж'
5/6-а, 1-За
О, 1/3-4а
5 27ж
' A + 4жK
1 -За, 2/3 +а
О, 1/6-2а
5_ 27ж2A + ж)
6' (8 + 9жJ
1/2- За, 1 - За
О, 1/3-4а
2ь~1а
s, а — s,
Г | "' ~ '" 2
а + 6 — s,
2
а + 1-8
[О < Res < Re а, Re (а + 6)/2]
а	6
~2' S 2'
+ ? + 1,
в19г
В20Г
В21Г
а2 ' 2 ^
[- Re а/2, - Re 6/2 < Re s < Re а/2]
s, а + 1/6- s, За - 1 - si
3/2-e	J
[О < Re s < Re а + 1/6, 3 Re a - 1]
s, s+ 7/6-2а, За- 1 - .
s + 5/2-3a
[0, 2 Re a - 7/6 < Re s < 3 Re a - 1]
5, 4/3 — a — s, 3a — 1 — ,
3/2- s
[0 < Re s < 4/3 - Re a, 3 Re a - 1]
s, s+ 7/3-4a, 3a- 1 - .
5+ 5/2-3a
[0, 4 Re a - 7/3 < Re 5 < 3 Re a - 1]
3, a + 1/6 - 5, 3a - si
4a+ 2/3-5	J
[0 < Re s < Re a + 1/6, 3 Re a]
5, s + 1/6 - 2a, 3a - s
s + a + 2/3
[0, 2 Re a - 1/6 < Re s < 3 Re a]
s, 3a + 1/2 - s, 3a- s
4a+ 2/3-5
[0 < Re s < 3 Re a]

8.4.49] 8.4- Таблица преобразований Меллина элементарных и специальных функций 617
42
43
44
45
46
47
48
49
1	5 27A + ж)
= B21Gl\\x
ж(9 + 8жJ
1 -2а, 2/3 +2а
1/2
,жJ
а,
= ?22<322 (ж
2Fi а, 6
Fi а, 6; .
27A + ж)
2/3 +а, 1 -За
О, 1/2
1ш (8 + 9жJ
2' 27ж2A + ж
1-а, 1/2-а
2а, 1/3
а + 6+i; -я)] =
1 - 2а, 1 - 26, 1- а- 6
О, 1/2-а- 6, 1-2а-2Ь
а, 6; а + 6 Н	;
2 ж
1, 1/2 +а + 6, 2а+ 26
2а, 26, а + 6
1 + 1
: + Ь+-}-х) 2Fi
А
1-2а-6, -26,
О,	а-Ь-6,
а, 6;
i;-W
1 — а — 6 — ё
1-2а-26-<
1 + 1
2' ж/-Ча+' 2
1 1>
2' жу
1
2а+ 5, 26 + 1,
2а+ 26+
2Fi ( а, 6; а + 6 Н—; —ж J x
' 1 1 3
х 2Fi j — — а,	6;	а — 6; —ж ) =
О,\-а-Ь,а + Ь-\
s + а, s + а + 1/2, 2а - .
s + 2a + 2/3
[- Re a < Re s < 2 Re a]
s, 1/3 — a — 5, 3a — ,
1/2- s
[0 < Re s < 1/3 - Re a, 3 Re a]
s + 2a, s + 1/3, a - .
s + 1/2 - a
[-1/3, -2 Re a < Res < Re a]
s, 2a — s, 26 — s, a + 6 — ,
a + 6 + 1/2 - s, 2a + 26 -
[0 < Re s < 2 Re a, 2 Re 6, Re (a + b)}
s + 2a, s + 26, s + a + 6, -si
s + a + 6 + 1/2, s + 2a + 26 J
2 Re a, -2 Re 6, - Re (a + b) < Re s < 0]
В24П
[0 < Res
-s, 26 + 1-s,
5 + 1/2-5
, 2Reb + l,
- a + 6 + 5, -s
1
-a + 6 + 5 +-
[-2Rea~
-5, -2 Re 6 - 1, - Re (a + 6) - S < Re s < 0]
В25Г
1	1
 ~S' 2 +a~
+ a + 6 - 5,
1
2+6-a-.
— — a — 6 — .
2
[0 < Res < 1/2- | Re (a- 6)|]

618
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.49
50
а, 6; ft -
1
2'
1	1 , 3 Г.
	а,	о;	а — о:	=
2	2	2	х
' 2
Е>,	ft — i
2
-, - + а - 6, - + 6 - а
2 2	2
51
^25^33 I ж
а, 6; с; 1 — (л/1 + ж
а, 6; с; 1 — (-x/l
1 — а, 1 — 6, 1 + ft — с,
i526^44
О, 1 - С, 1	,
2
1 + 6- <
52
а, 6; с; 1 —
а, 6; с; 1 — ¦
1, с, с/2, (с +
а, 6, с — а, с — 6
53
а, 6; 1+а+6-
(
X 2^1 I «, 6; с;
„ — а — 6
1 -а, 1-6,
А
О, 1 - с, 1 - а - 6,
54
ft, 6; 1 + а + 6— с;
2
с — а —
i/ж — \/1 + х
55
х 2^1 ( а, 6; с;
= ^27^44 I ^
2Fi (о, 6;
у/х — ¦
1, с, а + 6, 1 + а + 6-с
а+6 а+6+1
а' о, —-—,
>-.1-=*щ'-
= B28G33 х
1 - о, 1 - 6, 1 -
а + 6
О, 1 - а- 6,
2
1 - а- i
1	1
s+ -, s + ^ + а-б,
1
2
S+2"
s+--а-6
2
[|Re(a- 6)| - 1/2 < Res < 0]
s, a— Sj 6-— s, с— a— s, с-— 6-— si
с- s, c/2 - s, (c + l)/2- s J
[0 < Res < Re a, Re 6, Re (c - a), Re (c - 6)]
[
< Res
s + a, s + 6, s + с — a,
s + c, s + c/2,
S + С — 6, —5
s + (c + l)/2
[-Re a, -Re 6, Re (a - c), Re F - «
; o]
ft + 6
S, ft -— S, 0 -— S,	S,
2
с — s, ft + 6 — s,
ft + 6 + 1
В27Г
l + a + 6-- с — ,
[0 < Re s < Re a, Re 6, Re (a + 6)/2]
; + c, s + a + 6,
s+l+a+6-c
¦Re a, -Re 6, -Re(a + 6)/2 < Re s
s, a -— s, 6 — s, (a + 6)/2 — s
a + 6-s, (a+ 6 + l)/2 - s
[0 < Re s < Re a, Re 6, Re (a + 6)/2]

8.4.50] 8.4- Таблица преобразований Меллина элементарных и специальных функций 619
56
а, о;
-6+1 у/х — у/1 + Ж
1, а+ 6, (а + 6 + 1)/2
а, 6, (а + Ь)/2
s + а, s + 6, s + (а + Ь)/2, -si
s + а + б, s + (a + 6 + l)/2 J
[-Re a, -Re 6, -Re(a + 6)/2 < Re s < 0]
8.4.50. Функция 3F2(ai, a2, аз; 6i, 62; x).
Обозначения:
2a - 6 - 1
2a-26-2, -6-1 I'
B _
a, a—6—c+1
= 25Г| C'
2a, 2a - c-
За
1
2
3
4
5
6
3F2(a!
- В G1
- 29 3
3^2 I «l, «2, «:
(l + жJ^1 3F2(c
= ^зо^зз ж
v
A + жJЬ+1зF2
a- 1
/
31 [
= ВзоОзз ^
(л/1 + ж - 1)аз
1 + a-c
= B3lG1?(
33^
(\/l + Ж — y/x^
1 + a-c;
/
6i, 625 —ж) —
3 I x
1 - ai, 1
0, 1 - 61
j; 01, 02; — I
Ж /
= 1?29^зз 1 a
i, 2a —2, 6; a — 1
6 + 2, 4 + 26-
5
0, - + 6-a, 2
A
(a, 2a-2, 6;
, 2a-6- 1; -
2 + 26, а + 1
6, 2а - 2, а
/
— а2 5 1 — аз |
1 - Ь2 /
=
1, 6Ь 62 \
«1, а2, аз /
,2о-6-1;-ж) =
3 \
2а, - + 6- а \
2
+ Ь- 2а I
/
1 \
Ж/ ~
1 \
?- -, 2а + 6 \
2 1
+ 6+^ J
F2 a, 6, c; l + a-6,
V
1+^A-лЯ
ж
а/2 + 1, (а
а, 6, с
n /
3F2 (^a, 6, с;
1 + 2(ж - л/ж"
l2 a2
-Ь 1)/2, 6 +с \
1 + а - 6,
-Ь,1 + --Л
2
Ь- с /
fs, ai —
L &i
Г 5 + Ol,
L s
["
5, —1
a-b
[0 < Re 5
^зо Г
5 + 6,
5 + a
5 + a -
[-Re 6, 2
531Ll-6-
s, a2 ™~ 5, аз — 51
- 5, 62 - 5 J
[0 < Re 5 < Re a,j,
s + 02, 5 + аз, —5
+ 6i, 5 + 62
Re aj < Re 5 < 0,
-6-5, 2a - 26 -
3
	s,
2
1 6 — 5
2
2a - 6- 1 - s
j =
1
J
j =
3-
< -Re 6- 1, 2 Re (a-
s + 2a-2,
1
2'
1
f 6+-, -26-1-
2
5 + 2a +
- 2 Re a < Re s <
a 1 — a
5,
2 2
-5, 1 — с — 5
1 - 6- С- 5
[-Re a < Res < -Re a/2, "l -
5, S +
L r
[0, Re F +
-,s + l + --6-
a
a
5 + Ц	С
с- а/2) - 1 <
Re
s
b
-21
s,
1, 2,
1, 2,
5,
-(.)-
Ie6-
- Re F +
_ c
s <
3]
3]
3]
1
Reo/2]

620
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.51
7
8
9
(8
*
с lTl I
с, 2 |
= B32GH
_ ж^A±1)/2^4
2
_ 8ж^A±1)/2^
2
41 /
— +^33^44 1
26 +
6 + <5
2а -
X
А /•• ^Ж 1
' A + хH
1 + 5-2а, - -а-
5 + с-2а, 1 + 6
5 + с — 6 — 2а
1 гр
(
{
Q / 1
) 3^2 1 а, а+ -
V 3
1 27ж2 л
1 + 5-За, - -6
0,	2а, 2 - 26
3
--2а-6,Ь + 6-
25+ 26-6а - 1
ч (
1 + 4ж) 3^2 а-, а +
V
1 27ж
Т 2' A + 4жK
(
X
\
1 + 5 — За, 8 -— а -
0, 25-а- -, 1-
5 -За- 1, За-26+ 2
-За-1
2
,ь,
)
)-
-За \
1 )
з'
J
2
ь,
\
1
J
^32
-*,
^3S
[0
-6)
+5
-6)
г
5, 2a — 5 — s, a + 5	s,
а- --в, c-8,
1 + 2а — с — 5 — s, с — 6 — s
[0 < Re s < 2 Re а - 5, Re Bа - с)
Re (с - 6)]
+ 1-
г
2
s, 3a — 5 — 5, 2a + 5	5,
2a	s, 26- 1 - s,
3
1 i
6 — — — «s, За — 6 — о + 1 — s
9
6а -26 + 2 - 25 - s
< Re s < 3 Re а - 5, Re 6 - 1/2, Re (За -
+ 1-5]
ззГ
Г 2
s,s + 25-a	, s + 1-6,
s + 5-a	,5 + 26+5- 3a-1,
s + 6 + 5 — За	, За — 5 — s
2
s +За-26+ 2-5
[0, ReCa-
+ 1/2 - 5, Re 6 - 1 < Re a < 3 Re a - 5]
8.4.51. Разные функции гипергеометрического типа.
1
q Fp\®>l 5 tt2 5 • • • ) dp?
Lai, a2
1
0
61, ..
- ai,
1 - fc
.,6,;
^ X
..., 1
-«) =
-ap \
l-bq J
Г
к
2)
Lai
0<
= 1
q =
, a2,
x
Res
2, .
P + -
. . . , ap.
X
rf S'ai^
[6i - s, 62
< min
s,
Re a j
. . , g и либо
L, Res <
1
4^
1)
1
2
S, . . . , bq
, Ькф0, -
о = p — ]
Reff>
s 1
-1, -2,
, 4 = P
k=i
• • • )
либо
')]

8.4.51] 8.4- Таблица преобразований Меллина элементарных и специальных функций 621
2
3
4
5
6
7
8
9
(l-a:)""
{х^1)с~
J^(x) =
H^B^
(">
V2
/ и
V2
#p(-a;;
E(p; ar
pq у
i /
F3 a,
V
3 \a,
Q
rrlO
02 *
i), (
M) = /
: q; bk :
at, . .
61, ..
= Hmn
X
а',Ь,Ь',с; 1-
3v
a +b'
а',Ь,Ь',с; 1-
a; + 6;
a;, 6;,
@, 1), (-
u
L3
X
V 2
*l + ")/2-
Ш
ж
\ О
1-
WA+i)
@,1)
en 11
|_ v"' -*-/'
ж\	qp>i (x
. , ap \ _
(ai, 1), ...
F1, 1), ...
[0 ^ m
ж/
с — а, с — 6 \
1
Ж/
с — а, с — 6 \
с -— а — b )
1 \
1 \
I/-1/2, /х)
ЬЛ,1)
/
+¦ A, l) ,
- А - 1/, /х)
1
1
I
ai,. . . , ар у
, («р, 1)
^ д, 0 ^ те ^ р
или ^ > р — 1; s = —-/е G i^ , s = a,j +
+ fc G D~, A; = 0, 1, 2, . . . , j = 1, 2, . . . , p;
-^ — 00-1
при знаке соответствия ^— I
Г(с)г[ S+,a 'j + 6 ' s + c^a^6 1
[s + a +o,s + c — a, s + c — 0]
[Res > -Rea', -Re6;, Re(a + 6-c); Re с > 0]
p/ чр Г 1 - a' - 6' - s, 1 + a - с - s,
[ l--a/--s, l--fe/--s,
1 ±1, 1
"*" [Rec>0;Ree<l-
l+a+6^c^s
j
— Re @/ + bf), 1 + Re (a — c), 1 + Re (b — c)]
r[ S ] [\fi\ < 1; Res >
[1 + 1/ — /is J
> 0 или fi = l; 0 < Re s < 3/4 + Re v/2]
[l - i//2 - s, 3/2 + i/ - /x(l + i/)/2 - fie]
[|/x| < 1; -(Re 1/ + l)/2 < Re s < A -
- Re i/)/2 или /i = l; -(Re 1/ + l)/2 < Re s <
< 3/4, A - Rei/)/2]
Г
и и
s H	hA, 1	Л - s
2 2
1 V s 1 +A + 1/ Га+П
L 2 * v 2^ ' j
[|/x| < 1; - Re (i//2 + A) < Re s <
< 1 - Re (i//2 + А) или /i = 1; - Re (v/2 + A) <
< Re s < 3/4, 1 - Re (v/2 + A)]
\_ и — p~~~ s
[p > 1/2; 0 < Res <
< 1 или p = 1/2; 0 < Res < 1, Re/x/2]
Г S + ab 5 + a2' •••, s + ap, -s
[ S + 01, . . . , S + Og J
r
— min Re ar < Re s < 0 и либо 1)
L
0 ^ q ^ p либо 2)g = p + 1, Res >	h
4
1 / P q \ 1
\r=l fc = l / J
P s + 61, . . . , s + bm, 1 — ai — s, ...
[ s + an+i, ..., s + ap, 1—6m+i—s, ...
. . . , 1 - an - s
. . . , 1 - 6g - s 1
-
— min Re bk < Re s < 1 — max Re a,j и

622
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.51
10
ЛА(х)НA - х) + Т>вA/х)Н(х - 1)
[А = 0],
[А <0]
[A = A^D^B^C]
1 	 ^1 ? • • • 5 1 	 feg)
CL\ , ... , tty4 ) ^1 , ...
_ ПЛ' B
— U B + C, A+D I x
• •• , со, •• • , 1 — do
[А, В, С, D = 0,1,2, ...
11
Я"
(ai, Ai), . . . , (ftp, Ap)
[0 ^C m ^C p, 0 ^C n ^ </]
либо 1) 2(ra + те) > p + q, либо 2) 2(ra + n) =
-Re
¦j=i	fe=i
p
либо
— 6j) > 0
«-::::::::::р, Я = P ~^ 1,
[2(ra + те) < p + q; s = —b^ —
- I e D+, к = 1, 2, . . . , m; s = 1 - ftj + I G
G D~, j = 1, 2, . . . , те; I = 0, 1, 2, . . . ; при
знаках соответствия <— (когда q > р, ж > 0
или д = р,0<ж<1)и
> 0 или q = р, ж > 1I
-. + (а),(Ь)-»"
- + (с), (d) - в
ь+а
(когда q < p, ж
S ~Ь ?11 , ••• , S -f СЬД, 01 — 5, ...
S + Cl, . . . , S + СО, rfl — S, ...
. . . , do — s
—¦ min Re a,- < Res < min Re бд, и либо 1)
Л + В > С + D, либо 2) Л + В = С + D,
^ 2, A Res < 1/2- Re i/,
А	В	С	D
либо 3) Л = С, в = D, Re i/ < 0
или [А + Б •
s = —djl G ,D+, j = 1, 2, . . . , Л; s
bk + I e D~, к = 1, 2, . . . , В; I = 0, 1, 2, . . .:
при знаках соответствия ^—^° (когда А > 0, ж
> 0 или А = 0, 0<ж<1)и ^° (когда А
< 0, х > 0 или А = 0, ж > 1)]
В\3 + 01, . . . , -вт^ + бтте,
1 — ai —
s, . . . , 1 — an — Ans
3, .7 = 1, 2, . . . , р; 5fc >0, к = 1, 2, ...
1 - Reft,-
q] — min
< Re s < min
и либо 1) a* > 0, либо 2) a* = 0, A Res
p	<?
- 1 + Re ( У^. a,- - У^. о*. 1 I или

8.4.52] 8.4- Таблица преобразований Меллина элементарных и специальных функций 623
г *
U* <0; s =-
1~аз+1
~ А ¦
при знаках
> 0, ж > 0
(когда А < 0
п
я
к=1
Ьк+1
-, j=l,
2,...,
соответствия
или А
, х > 0
р
? >
р
i=i
= 0, 0
или А =
га
п;
¦<—-
<
>
р
д
, 2, ...,
1-0, 1, 2
(когда
ж < /3)
я>/3)|
.- ?
я
тп; s
, . . .,
А >
I' + oo
и 4-—
. Здесь
1
к=1
8.4.52. Указатель частных случаев С-функции Мейера
и //-функции Фокса.
Ниже приведены номера пунктов и формул раздела 8.4, содержащих частные случаи
(^-функции Мейера G™qn{z) и //-функции Фокса H™qn(z) при соответствующих значениях
Г7г, тг, р, q. Поскольку G™q (z) преобразуется в G^^l(z) при замене z на 1/z, то указываются
только номера формул, где р ^ q (т ^ п при р = q). Соответствующие формулы, где р > q
(т < тг, р = </), мож:но найти в соседних строках. В столбце «тип» отмечены расположение
и знаки при s в гамма-функциях, находящихся в правых частях формул. Значения га, п, р,
g и тип связаны между собой: тип означают количество знаков + и — у s в числителе, а
q — mmp — n — количество знаков -и + у^в знаменателе. Полужирным шрифтом набраны
номера наиболее общих соотношений данного типа.
В заключение перечислены частные случаи //-функции Фокса.
Тип
(+)
/ i \
С)
(+-)
/ 1 \
(-)
++
(++-)
С:)
772
1
1
1
1
2
1
1
2
2
1
2
п
0
0
1
0
0
0
1
0
1
1
0
р
0
1
1
0
0
1
1
1
1
2
2
A
1
1
1
2
2
2
2
2
2
2
2
Номера формул
3.1,3
2.1-2, 3-4
2.5, 11
5.1-3, 11-12; 19.1; 47.1
23.1; 29.1
3.5
3.3; 4.7; 14.1, 5; 16.1, 11; 18.7; 43.1; 45.1, 5
11.1; 14.2; 16.2; 18.1; 23.3; 29.3; 44.1; 46.7
11.3; 14.7; 16.13; 18.3; 23.5; 29.5; 44.3; 46.1
2.6-8, 10, 21-23; 6.18; 8.5; 40.26; 41.15-16, 18-19, 35, 38
43; 42.12-13, 23, 30, 32; 49.19, 28-32
2.17-20; 6.1-2, 22; 7.1-2, 5-6; 8.3-4; 10.5-8; 30.1-4, 6-13
31.1-4, 6-13, 16-17; 32.1-4, 6-13, 18-21; 35.1-4, 8-9,
23-24, 27-28; 36.1-4, 8-9; 40.3-4, 7-8, 12-17, 27-28;
43-44, 47-48; 41.1-4, 7-8, 20-23, 26-27, 32-33, 44-45;
21-22, 28-29; 49.1-12, 22-25
, 40-41,
, 16-17;
11-20,
39-40,
42.4-6,

624
Гл. 8. G-функция Мейера и Н-функция Фокса
[8.4.52
Тип
(Г")
(++-
(++ +
(+ + +-}
(+--
(+-"
/+ + --
(---
(++
::~
+ + +
т
2
2
1
1
2
2
3
3
1
2
2
2
3
3
1
2
1
2
2
1
2
3
3
3
п
1
2
0
1
0
1
0
1
1
1
1
2
0
1
0
0
1
0
1
2
2
0
0
0
р
2
2
1
1
1
1
1
1
2
2
3
3
3
3
0
0
2
2
2
2
2
0
1
2
q
2
2
3
3
3
3
3
3
3
3
3
3
3
3
4
4
4
4
4
4
4
4
4
4
Номера формул
2.12-13; 6.5; 7.3-4, 7-8; 8.1-2; 30.5, 14-15, 18-19; 31.5, 14-15;
32.5, 14-15, 16-17, 22-23; 35.5-7, 21-22, 25-26; 36.5-7; 40.1-2,
5-6, 10-11, 18-25, 29-32, 35-38, 41-42, 45-46, 49-50; 41.9-14,
28-31, 36-37; 42.1-2, 8-11, 15-16, 24-27; 49.13-16, 26-27, 35-44
2.9; 6.11; 10.3-4; 40.9; 41.5-6, 17, 24-25, 34, 39, 42; 42.7, 31;
49.20-21
4.1, 3-4; 22.1
12.1; 13.3; 15.1-3, 7; 19.9, 11, 13; 25.1; 26.7; 27.1; 48.1
5.5, 7, 9; 12.3-5; 13.5; 15.5; 16.5, 7; 19.19; 20.1, 9, 19; 24.1
22.23; 23.19, 23; 25.7; 26.9; 29.11, 25
23.27, 29; 24.5; 29.15
12.9; 15.9; 16.17; 20.23, 35, 39; 21.1; 25.3; 27.3
3.7; 16.9; 18.9; 22.5
11.4; 18.5; 29.21
6.8
6.13; 41.54; 42.19-20,33-34, 51
51.2-3
6.23-26; 40.33-34; 41.46-53; 42.35-50; 49.17-18, 33-34, 45-50,
55-56; 50.1-2, 3-6
5.20; 22.11; 28.3, 5
23.15
13.1; 22.15-17, 19; 25.5
29.19
12.7; 19.7, 17, 21; 20.11, 13, 15; 45.3
19.3, 15; 43.3; 47.3
22.9, 25; 23.7, 21; 29.7, 13, 23
5.19; 23.9, 11, 13; 28.13, 15; 29.9
5.17
20.5, 21, 37, 40; 24.3; 46.9

8.4.52] 8.4- Таблица преобразований Меллина элементарных и специальных функций 625
Тип
(+-+~)
(++++)
С-—)
С--)
(+ + + + +)
//-функция
т
3
3
4
4
4
4
1
2
1
2
4
4
5
га
га
п
1
2
0
0
1
1
0
0
2
2
0
0
0
п
п
Р
2
2
0
2
2
4
1
1
3
3
1
3
0
q
р
q
4
4
4
4
4
4
5
5
5
5
5
5
6
Q
Q
Номера формул
11.7; 14.11; 23.25; 44.5; 46.11
16.15; 20.7, 25, 42;
23.33; 28.17
18.13; 23.31; 29.17;
12.11; 15.11; 16.19;
41.55-56; 49.51-54;
28.7, 9
5.22; 22.13; 28.1
14.9; 22.7, 21
19.5; 20.3, 17; 26.1,
23.17; 28.11
20.44
5.18
6.3, 4, 9-10; 9.1; 10
51.1, 8^10
2.14-16; 5.15-16; 6
26.5; 46.3
44.7; 46.13
18.11; 44.9; 46.5
50.7-9
3
.1
17; 51.4-7, 9-11
Поскольку G-функция Мейера является частным случаем /^-функции Фокса, то каждая
из формул таблицы 8.4 дает соответствующие частные значения //"-функции.

Приложение I. НЕКОТОРЫЕ СВОЙСТВА ИНТЕГРАЛОВ,
РЯДОВ, ПРОИЗВЕДЕНИЙ И ОПЕРАЦИИ С НИМИ
1.1. ВВЕДЕНИЕ
В этом приложении содержатся некоторые сведения о сходимости несобственных ин-
интегралов, рядов и произведений, а также формулы различных операций с интегралами
и рядами, которые могут быть полезны при вычислениях. Как известно, универсальных
признаков сходимости, дающих в применении к любому несобственному интегралу или
ряду исчерпывающую информацию, не существует. Все признаки сходимости имеют вполне
определенные сферы применения.
Для описания поведения функции <р(х) в терминах известной функции ф(х) использу-
используются следующие символы, определяющие отношения порядка.
Пусть на некотором множестве В заданы функции (р и ф переменной ж ? В и точка а
(конечная или бесконечная) — предельная для множества В.
Формулы
<р(х) ~ Ф(х)
(р(х) = о(ф(х))
<р(х) = ОШх))
(х-
(х-
(х-
-> а,
->¦ а,
-> а,
Ж
X
X
е
е
е
в),
в),
в)
означают соответственно, что:
1)	существует lim . , { =1, х ? В:
х^а ф(х)
2)	существует lim . , { = О, х G В:
х^а ф(х)
3)	существует постоянная М > 0, не зависящая от ж Е В, такая, что |у?(ж)| < М\ф{х)\
при х —> а, х (Е В. Например, sin х ~ х (ж —> 0); —- = о( — ) (х —> со); cos ж =
= ОA) (ж—юо).
Для любой последовательности действительных чисел ж д., А; = 1, 2, ..., множество всех
ее частичных пределов (конечных и бесконечных) имеет как наибольший так и наименьший
элементы. Наибольший элемент множества частичных пределов называется верхним преде-
пределом последовательности и обозначается lim ж д., наименьший элемент — нижним пределом
fc-->oo
и обозначается Mm ж д.. Например, если хи = (—1) , то lim жд. = —1, Mm xu = 1.
Относительно доказательств и примеров см., например, [9, 16, 19, 24, 26].
1.2. СХОДИМОСТЬ ИНТЕГРАЛОВ И ОПЕРАЦИИ С НИМИ
1.2.1. Интегралы по неограниченным кривым.
Ряд математических и прикладных задач приводит к интегралам по неограниченным
кривым, когда контур интегрирования имеет бесконечную длину.
Пусть задана комплексная функция f{z), z ? С, где С — некоторая простая кусочно
гладкая ориентированная неограниченная кривая; под кривой понимается множество точек
на расширенной плоскости, которое можно представить как образ отрезка а ^ t ^ b
действительной оси при соответствующем отображении z = z(t) [9].
Рассмотрим сначала случай, когда кривая С имеет одним своим концом точку а и
другой ее конец уходит в бесконечность. Обозначим через Ci часть кривой С, длина которой
отсчитывается от конца а. Пусть f(z) не имеет на С особых точек, т. е. точек z5 где f(z)

1.2.2]	1.2. Сходимость интегралов и операции с ними	627
обращается в бесконечность, и интегрируема на всех d. Если существует конечный предел
lim [ f{z)dz= \f{z)dz,
ct	с
то он называется значением несобственного интеграла от функции f(z) по неограниченному
контуру С.
В этом случае говорят, что интеграл сходится; если предел не существует или бесконечен,
то интеграл называется расходящимся.
Отметим, что если длина I каждого конечного участка Ci кривой С, лежащей внутри
круга радиуса R с центром в точке а, имеет оценку I = O(R) при г —у оо, а функция
f(z) интегрируема на Ci и \f{z)\ ^ B\z\~ ~~ , 8 > О, В — постоянная, для больших \z\, то
интеграл
\f{z)dz
сходится.
Если оба конца кривой С уходят в бесконечность, то несобственный интеграл по С
определяется по формуле
\f{z)dz= J f{z)dz- J f(z)dz,
где Са и Са — части кривой С, на которые она разбивается произвольной точкой а, причем
конец кривой С а уходит в бесконечность в направлении ориентации кривой С, а конец
кривой С а уходит в бесконечность против ориентации кривой С.
В частности, если кривая С совпадает с осью Ох и функция /(ж) интегрируема в любом
интервале (а, 6), ^оо < а < Ь < сю, то
со	Ь
/(ж) dx = lim f(x)dx.
Если этот предел не существует или бесконечен, но существует конечный предел
а	оо
lim f(x)dx= f(x)dx,
а^-оо J	J	oo
— a	—oo	r»
то он называется главным значением несобственного интеграла /(ж) dx и обозначается
тем же символом.
1.2.2. Признаки сходимости интегралов с бесконечными предела-
пределами от неотрицательных функций.
Рассмотрим интеграл
оо
\f(x)dx, /(ж) > 0, а > ^оо,	A)
а
где функция /(ж) интегрируема в любом интервале (а, 6), а < b < оо. Если в интеграле A)
а = ^оо, то этот интеграл можно разбить на сумму двух интегралов в пределах от ^оо до
О и от 0 до оо и исследовать сходимость каждого из них в отдельности.
Приведем некоторые признаки сходимости интеграла A).
1.	Если	,	v
/(ж) = о(х~1-5) , <5>0, ж^оо,
то интеграл A) сходится. Если
/(ж) ^ —, с > 0,	х —у оо,
то интеграл A) расходится. Если
/(ж) = О (х^11п^1^х х) ,	Л > 0, ж—> оо,
то интеграл A) сходится.
2.	Признак Коши. Пусть
Дж) ^ ^Л х—^°°-

628	Прил.1. Некоторые свойства интегралов, рядов, произведений	[1.2.2
Если Л > 0 и (р(х) ^ с < оо, то интеграл A) сходится. Если А ^ 1 и ^(ж) ^ с > 0, то
интеграл A) расходится.
3. Если при любом 6, а < b < оо,
ъ
/(ж) dx ^ М < оо,
где М — постоянная, то интеграл A) сходится.
оо
4. Если /(ж) ^ ^(ж), то из сходимости интеграла g(x) dx следует сходимость интегра -
"*	оо
а	г»
л а A), а из расходимости интеграла A) следует расходимость интеграла g(x)dx.
5.	Пусть существует предел	а
lim	= с, 0 ^ е ^ оо.
оо	х^°° g\x)
Если с < оо и интеграл g(x) dx сходится, то и интеграл A) сходится. Если с > 0 и
оо	^
л	а
интеграл g(x) dx расходится, то и интеграл A) расходится.
а
6.	Пусть /(ж) — дифференцируемая функция. Если
	 /'(ж)
то интеграл сходится. Если	;/ х
iim>0,
ж^оо /(Ж)
то интеграл A) расходится.
7. Пусть а > 0, а ^(ж) — дифференцируемая функция, такая, что lim <p(x) = оо. Если
х>оо
то интеграл A) сходится. Если а > 1 и
lim У v / 	 < оо,
то интеграл A) расходится.
8. Пусть <р(х) — дифференцируемая возрастающая на [а, оо) функция, такая, что а
^ ж < <р(х). Тогда интеграл A) сходится, если
X—^OQ	J \X J
и расходится, если	;
lim ^
9.	Если /(ж) дифференцируема и существует такая дифференцируемая функция g(x) <
< 0, что	/ ±( \ ( \м
Ш У > О,
аз—»-оо	J \^)
то интеграл A) сходится. Если
Б5Г <**)*('»' < о,
QQ	Ж^ОО	j\X)
Г 1
и интеграл —^^ б?ж расходится, то расходится и интеграл A).
J gix)
а
10.	Пусть /(ж) и (f(x) — дифференцируемые функции и

1.2.3]	1.2. Сходимость интегралов и операции с ними	629
= р + оA), ж —> оо,
где Р — постоянная, (р(х) < 0, ж > а. Тогда интеграл A) сходится при /3 > — 1 и расходится
при /3 < —1.
11. Пусть /(ж) — дифференцируемая функция и
Тогда интеграл A) сходится, если с < 0, а > — 1 или с < — 1, а = — 1. Интеграл A)
расходится, если с > 0 и а — любое, или а < -1ис — любое, или же с > —1 и а = —1.
12. Пусть /(ж) и ip(x) — дифференцируемые функции и
/(ж) ж ж
где а — постоянная, (р(х) < 0, ж > а. Тогда интеграл A) сходится при а > — 1 и расходится
при а < — 1.
13. Пусть /(ж) и <р(х) — дифференцируемые функции и
/'(ж) _ v^ 1 , ?>(ж) ,, , ,1U
\п(х)
Ло(ж) = ж, А^(ж) = ж In In . . . 1п^ж, <р(х) < 0, х > а.
к раз
Тогда интеграл A) сходится при а > -1и расходится при а < — 1.
14. Пусть /(ж) > 0 — дифференцируемая функция и для некоторого а > 0 существует
Km [Г(х)/'(Ж)] =-/3^0.
Тогда интеграл A) сходится при /3 > 0 и расходится при /3 < 0.
1.2.3. Признаки сходимости интегралов с бесконечными предела-
пределами от произвольных функций.
сю
1.	Если сходится интеграл |/(ж)| dx, то сходится и интеграл
(aO<*»>,	B)
который в этом случае называют абсолютно сходящимся.
оо
Если интеграл B) сходится, но интеграл \f(x)\dx расходится, то интеграл B) назы-
а
вается условно сходящимся.	оо
Относительно сходимости интегралов |/(ж)| dx см. 1.2.2.
а
2.	Пусть
Дж) = ^^ [1 + О(ж^е)] , ж^оо, ?>0.
Если Re Л > 0 и |^(ж)| ^ с < оо, то интеграл B) абсолютно сходится.
3.	Признак Абеля. Если интеграл B) сходится, а функция g(x) монотонна и ограниченна
на [а, оо), то интеграл
оо
jf(x)g(x)dx	C)
СХОДИТСЯ.
4. Признак Дирихле. Если в каждом конечном интервале (а, 6), а < Ъ < оо,

630	Прил.1. Некоторые свойства интегралов, рядов, произведений	[1.2.4
I dx
М,
где М не зависит от 6, а функция g(x) монотонно стремится к нулю при ж —у оо, то
интеграл C) сходится.
5. Пусть 7, A > 0 и
/(ж) = ж" cos hx1 \l
g(x) = cos cxx 1 + 0
где Si, E*2 > Re a + 1. Тогда интеграл (З) сходится при Re a < maxG. Л) — 1 (если j ф X
или b ф с) или же при Re а < —1 (если j = А и Ъ = с).
1.2.4. Интегралы от неограниченных функций по ограниченным
кривым.
Определение несобственного интеграла для случая, когда подынтегральная функция в
некоторых точках контура интегрирования обращается в бесконечность, достаточно дать
лишь в случае одной особенности, так как интеграл с несколькими особенностями можно
разбить на сумму конечного числа интегралов с одной особой точкой.
Пусть z = а — единственная особая точка функции f(z), z G С, где С — некоторая
простая гладкая ограниченная кривая.
Если существует конечный предел
{z)dz+ f(z)dz\,
с	-с	с»	J
где С\ С" — части кривой С, оставшиеся после удаления из С некоторой малой окрестности
точки a, a ?i, ?2 — длины удаленных частей С, отсчитываемые от точки а, то он называется
несобственным интегралом от f(z) по контуру С (с особенностью в точке а).
Если предел не существует или бесконечен при ei, si стремящихся к нулю независимо
друг от друга (т. е. интеграл расходится), но существует конечный предел при ei, €2 —У О,
связанных дополнительным условием, что удаленная окрестность точки а находится внутри
круга радиуса е с центром в точке а, то этот предел называется главным значением
несобственного интеграла и обозначается тем же символом.
Пусть, в частности, С совпадает с отрезком [а, Ь] оси Ох, функция /(ж) задана в
интервале [а, 6), интегрируема на любом отрезке [а, 6 — ?], ? > 0, но неограничена при
ж —у 6 — 0. Если существует конечный предел
Ь-е	Ь
lim /(ж) dx = /(ж) dx,
а	а
то он называется несобственным интегралом от функции /(ж) на [а, Ь]. В этом случае
говорят, что интеграл сходится. Если же предел не существует, то интеграл называется
расходящимся.
Аналогично определяется понятие сходимости несобственного интеграла в случае, когда
функция /(ж) неограниченна при ж —у а + 0.
Пусть функция /(ж) имеет в интервале (а, Ь) только одну особую точку с, а < с < 6,
в которой она неограниченна. Сходящийся несобственный интеграл от а до Ъ определяется
равенством
\ f{x)dx+ \ f(x)dx\,
J	J	J
О	?2^«	а	С+Е2
же этот предел не существует или бесконечен,
при е\ = 62 —У 0, то он называется главным значением несобственного интеграла /(ж) dx
а
и обозначается тем же символом.
О
где ?i, €2 > 0. Если же этот предел не существует или бесконечен, но существует предел
ь

1.2.5]	1.2. Сходимость интегралов и операции с ними	631
1.2.5. Признаки сходимости интегралов от неотрицательных не-
неограниченных функций.
Пусть неотрицательная функция /(ж) интегрируема на любом отрезке [а, с], а < с < Ъ
и /(ж) —у оо при ж —у 6^0. Рассмотрим несобственный интеграл
ь
jf(x)dx, f(xItO.	D)
а
1. Если при некотором S > 0
f[x) = О (F - ж)**) х —> b - 0,
то интеграл D) сходится. Если
/(Ж)~-^-, ж —>Ь-О,
О — Ж
где М > 0 — постоянная, то интеграл D) расходится.
Если	Г	ill	1
/(ж) = oUb- ху1 In"* F - ж) , ж —> 6 - 0, А > 0,
то интеграл D) расходится.
2.	Пусть (р(х) > 0. Если
Mm ^>o
b	x^b^O f{x)
и интеграл (f(x)dx сходится, то и интеграл D) сходится. Если
lim ^-f < оо
ь	ж^6^о /(ж)
и интеграл у?(ж) dx расходится, то и интеграл D) расходится.
а
3.	Если /(ж) дифференцируема и существует такая дифференцируемая функция g(x) <
< 0, что	(?( \ ( \м
(f(Xg(x)) >Q;
то интеграл D) сходится. Если
п^ (*«>*(«»' < о,
/(ж)
и интеграл —-.—г расходится, то расходится и интеграл D).
J §\Х)
а
4.	Если /(ж) дифференцируема и
lim		> —1,
то интеграл D) сходится. Если
Нт		< —1,
то интеграл D) расходится.
5.	Если /(ж) и (р(х) дифференцируемы и
где у5 постоянная, <р{х) > 0, а ^С ж < 6, то интеграл D) сходится при /3 < — 1 и расходится
при /3 > — 1.
6. Если /(ж) дифференцируема и
^ = с(Ь-х)аA + оA)), ж —>Ь-О,

632
Прил. I. Некоторые свойства интегралов, рядов, произведений
[1.2.6
где с — постоянная, то интеграл D) сходится при а = — 1, с < 1 или при — ]
и расходится при а = — 1, с > 1 или при а < —1, с > 0.
7. Если /(ж) и у?(ж) дифференцируемы и
A + оA)), ж —>&-¦
6 — ж b — x
<p(x)
b — x
где /3 постоянная, а <р(х) не меняет знака в [а, 6), то интеграл D) сходится при /3 <
< —1, ^?(ж) > 0 или при /3 > —1, (р(х) < 0 и расходится при /3 > —1, ^(ж) > 0 или
при /3 < —1, ^>(ж) < 0.
1.2.6. Равномерная сходимость функций и интегралов, зависящих
от параметра.
1.	Пусть функция /(?, ж) определена при t G D, ж ? A, a to — предельная точка D.
Если для любого ж Е А существует предел
lim /(t, ж) = <^(ж)
t—ytg
и для любого ? > 0 найдется такое не зависящее от ж число ё? > 0, что при |t — ?о| < <^е
неравенство \f(t, х) ~~ <р(х)\ < е выполняется сразу для всех ж Е А, то говорят, что /(?, ж)
стремится к (р{х) при t —> to равномерно относительно ж в А.
2.	Пусть функция /(?, ж) задана при всех ж ^ а и всех t из некоторой области в D и
при каждом t E D существует интеграл
сю
j f(t, ж) с/ж.	E)
а
Если для любого е > 0 найдется такое не зависящее от t число а? ^ а, что при всех
с > ае неравенство
г
t, x) dx <
выполняется для всех значений t E D, то интеграл называют равномерно сходящимся
относительно t в области D.
3.	Критерий Коши. Интеграл E) равномерно сходится в области D тогда и только тогда,
когда для любого ? > 0 существует не зависящее от t число а? ^ а, такое, что неравенство
f(t, ж) dx
< е
выполняется одновременно для всех t E D, лишь только а" > а ^ а?.
4.	Пусть функция /(?, ж) задана для всех ж? [а, 6), ^оо<а<5<оо,и?из некоторой
области D, и при каждом t E D существует интеграл (собственный или несобственный)
ъ
J/(t, ж) с/ж.	F)
а
Если для любого е > 0 найдется такое не зависящее от t число <5е > 0, что при всех
0 < rj < ё? неравенство
f /(t, x)dx < е
выполняется для всех значений t E D, то интеграл F) называется равномерно сходящимся
относительно t в области D.
Приведем некоторые признаки равномерной сходимости интеграла F).
Пусть функция /(?, ж) интегрируема по ж на любом отрезке [а, с], с > а при всех t из
области D.
5.	Признак Вейерштрасса. Если существует такая зависящая лишь от ж неотрицательная
функция (р(х), интегрируемая в [а, оо), что при всех t E D
\f(t, х)\ < <р(х)

1.2.7]	1.2. Сходимость интегралов и операции с ними	633
для ж ^ а, то интеграл F), Ъ = oo, сходится равномерно относительно t в области D.
6.	Признак Абеля. Если интеграл F), b = сю, сходится равномерно относительно t в
области D, а функция #(?, ж) равномерно ограничена, т. е.
\g(t, x)\^M,x^a,te D,
где М — постоянная, не зависящая от t и ж, то интеграл
Ж я)#(*, ж)йж	G)
сходится равномерно относительно t в D.
с
7.	Признак Дирихле. Если интеграл /(?, х) dx равномерно ограничен как функция t
с
\f(t,x)
dx
М, с ^ a, t G D,
где М — постоянная, не зависящая от t и с, a g(t, ж) —У 0 при ж —у оо равномерно
относительно t E D и монотонно по ж, то интеграл G) сходится равномерно относительно t
в D.
1.2.7. Операции с интегралами, зависящими от параметра.
Приведем некоторые свойства несобственных интегралов, зависящих от параметра.
1. Пусть функция /(t, ж) интегрируема по х (в собственном смысле) на отрезке [а, Ь]
при любом Ъ > а и при всех t из некоторого множества D, имеющего предельную точку to,
причем /(?, ж) —^ У (ж) при t —^ to равномерно относительно ж на [а, Ь].
Тогда справедливо равенство
ъ	ъ	ь
lim /(i, ж) dx = lim /(?, ж) dx =
*^t0 J	J t->-t0	J
Если, кроме того, интеграл E) сходится равномерно относительно ? ? D, то справедливо
равенство	оо	оо	оо
Mm /(?, х) dx = lim /(?, х) dx = ^р(х) dx.
а	а	а
Последняя формула верна также и при условии, что функция /(?, ж) ^ 0 непрерывна
по ж в [а, оо), а при t —у to монотонно возрастает и стремится к непрерывной интегрируе-
интегрируемой функции.
Если функция /(?, ж) удовлетворяет указанным в начале пункта условиям, а функция
g(x) абсолютно интегрируема (возможно, и в несобственном смысле) на отрезке [а, 6], то
имеет место формула
ь	ь
lim /(?, x)g(x)dx = lim /(?, x)g(x) dx.
t—Ho J	J t—tto
a	a
2.	Пусть дана последовательность функций Д(ж), к = 1, 2, . . ., интегрируемых (в соб-
собственном смысле) на отрезке [а, 6]. Если для всех ж ? [а, b] lim fk{x) = <^(ж) равномерно
fc-->oo
относительно ж из [а, 6], то функция (р(х) интегрируема на [а, Ъ] и
6	6	6
lim fk(x) dx = Mm fk(%) dx = ^(ж) с!ж.
fc^ooj	J k^i	J
а	а	а
3.	Пусть при ж ^ а и ? ? [а, /3] функция /(?, ж) непрерывна по ж и имеет частную
производную —f(t, ж), непрерывную или просто интегрируемую по ж и равномерно огра-
ничейную в области определения.
Тогда для любого t ? [а, /3]

634	Прил. I. Некоторые свойства интегралов, рядов, произведений	[1.2.7
h	Y г о
/(?, х) dx) = —/(?, ж) dx, a < b < оо.
У J ^*
1д
Если, кроме того, интеграл E) сходится для всех ? ? \ol, /3], а интеграл —/(?, ж) dx
сходится равномерно относительно ? в [а, /3], то для любого ? ? [а, /3]
f(t,x)dx\ = —f(t,x)dx.
а	а
Если функция /(?, ж) удовлетворяет указанным выше условиям, а функция g(x) абсо-
абсолютно интегрируема (возможно, и в несобственном смысле) на отрезке [а, 6], то справедлива
формула
А' ? д
f(t, x)g(x)dx) = \—f(t, x)g(x)dx.
/	J ^ ^
a
4. Пусть функция /(?, ж) непрерывна при ж ^ а и ? ? [а, /3]. Тогда
@ Л	.	ь 3	.
/(?, x)dx\ dt = UI /(?, ж) d? I dx, a < b < оо.
Если, кроме того, интеграл E) сходится равномерно относительно ? на [а, /3], то этот
интеграл непрерывен по ? из [а, /3] и справедливо равенство
/3
л
а
\fit,x)
а
\
йж] d?
/
сю
= J(
а
J
ск
\dt]
у
Последняя формула верна также и при условии, что функция /(?, х) ^ 0 непрерывна,
а интеграл E) непрерывен при ? ? [а, /3].
Если функция /(?, ж) удовлетворяет указанным выше условиям, а функция g(x) абсо-
абсолютно интегрируема (возможно и в несобственном смысле) на отрезке [а, 6], то имеет место
формула	г\ ь	б/з
\g(x)f(t, x)dx)dt= \g(x)(lf(t, x)dt)dx.
a a	a	ex
5.	Пусть функция /(?, ж) непрерывна при ж ^ a, t ^ а и интегралы
оо	оо
f /(t, ж)с!ж, f /(t, ж)Л
a	a
сходятся равномерно относительно t и х (соответственно) в любом конечном интервале.
Тогда, если существует хотя бы один из повторных интегралов
)	ОО ОО
\f(t,x)\dx\dt, Uj\f(t,x)\dt\dx,
а а	а а
то справедливо равенство
оо оо	оо оо
f | [ /(t, x)dxjdt= \ ( [ /(?, ж) dt) dx.
J\J	/ J\J	/
a a	a ex
Если /(?, ж) ^ 0,то эта формула справедлива при замене предположения о равномерной
сходимости предположением о непрерывности указанных в условии интегралов.
6.	Если функция /(?, ж) аналитична по ? и интегрируема по ж на [а, оо) для всех ?
из некоторой области D, а интеграл E) сходится равномерно в области D, то он является
аналитической в области D функцией.

1.3.2]	1.8. Сходимость рядов и произведений и операции с ними	635
1.3. СХОДИМОСТЬ РЯДОВ И ПРОИЗВЕДЕНИЙ И ОПЕРАЦИИ
С НИМИ
1.3.1. Основные понятия.
1. Пусть задана числовая или функциональная последовательность
{1 О©
Q>k}k=i — аЪ а2, аз,
Если существует конечный предел
п	со
lim У^ак = y^«fc,
k=l	k=l
то он называется суммой ряда. В этом случае говорят, что ряд
k=i
сходится. Если предел не существует или бесконечен, то ряд называется расходящимся; ак
со
называются членами ряда, a ^_J ак — п-м остатком ряда.
к=п+1
оо
2. Критерий Коши. Ряд \^ а к сходится тогда и только тогда, когда для любого е > О
k=i
существует целое Ne, такое, что
Е-
если т > п > N?.
ак
к = п
3.	Необходимое условие сходимости ряда. Если ряд ^J ак сходится, то ак —> 0 при
к —> оо.	k=i
4.	Числовой ряд с неотрицательными членами
оо
]Tafc, afc:>0,	A)
fe=i
называется пол общительным рядом.
Пусть такл^е заданы ряды	^
^Ьк, Ьк^0,	B)
53/(Л), /(fc)>o,	(з)
fe=l
где f(x) — монотонно убывающая при х > 1 функция.
Связь между сходимостью несобственных интегралов от неотрицательных функций
/(ж) и сходимостью соответствующих положительных рядов f(k) отражает следующий
результат (интегральный критерий).
5. Положительный ряд C) и интеграл f(x) dx сходятся или расходятся одновременно.
1
1.3.2. Признаки сходимости положительных рядов.
1.	Если ак = О ( к	1 при S > 0, к —> оо, то ряд A) сходится.
Если ак ^ ск~1+ при с > 0, 8 ^ 0, к —> оо, то ряд A) расходится.
2.	Признак сравнения. Если для всех достаточно больших к выполняется неравенство
а к ^ Ък и ряд B) сходится, то ряд A) также сходится.
Если для всех достаточно больших к выполняется неравенство ак ^ Ьк и ряд B)
расходится, то ряд A) также расходится.
3.	Признак сравнения. Пусть существует предел
11П1 —- = С, 0 ^ С ^ ОО.
fe^oo Ьк
Если с < оо и ряд B) сходится, то и ряд A) сходится. Если с > 0 и ряд B) расходится, то и
ряд A) расходится.

636	Прил.1. Некоторые свойства интегралов, рядов, произведений	[1.3.2
4. Если для всех достаточно больших к выполняется неравенство
	 ^ -г—, ®k T U,
ttfc	Ok
то из сходимости ряда B) вытекает сходимость ряда A), а из расходимости ряда A) —
расходимость ряда B).
5. Признак Куммера. Если существует такая последовательность положительных чисел
Ск, к = 1, 2, . . ., что для всех достаточно больших к
C > q > 0,
то ряд A) сходится. Если для всех достаточно больших к
О
и ряд ^J c^ расходится, то и ряд A) расходится.
к=1
Если существует такая последовательность положительных чисел с&, к = 1, 2, . . ., что
Mm ( ск—	Cfc+i 1 > О,
lim ( ck—	Cfc+i 1 < О
то ряд A) сходится.
Если
и ряд Л, ск расходится, то и ряд A) расходится.
к = 1
Если	i
Mm — (скак — Ck+iQ>k+i) > О,
то ряд A) сходится.
Если		 i
lim — (cfcflfc — Ck+i&k+i) ^ 0
сю	к—>оо ^к
и ряд YJ c^1 расходится, то и ряд A) расходится.
к=1
6.	Обобщенный признак Куммера. Если существует такая последовательность положи-
положительных чисел с^, к = 1, 2, . . ., что для некоторого фиксированного I
lim 	 1СД;-|-/с1д;-|-/ — Ск-\-1-\-1 u-fc+f + l J -^ U,
то ряд A) сходится. Если
I5S — (ск+1ак+1 - ск+1+1ак+1+1) < О
и ряд 2_^ ск расходится, то и ряд A) расходится.
к=1
7.	Признак Бертрана. Если
Г Г /	\ 1 1
lim «Пп A; U ( —	1 | - 1 \\ > 1,
{	L \ +	J J J
то ряд A) сходится.
Если	, г- ,	\ 1 1
П5Г hnA; hfe (-^--l) -l I < l,
fc^oo I L vafe+i / J J
то ряд A) расходится.
8. Признак Коши. Если для всех достаточно больших к
\f^k ^ q < 1,
то ряд A) сходится. Если для всех достаточно больших к
то ряд A) расходится.

1.3.2]	1.8. Сходимость рядов и произведений и операции с ними	637
Если
то ряд A) сходится.
Если
расходится.
Если для некоторого q < 1
то ряд A) сходится.
Если при q ^ I
Wk^oo ®к
расходится.
9. Признак Жамэ. Если для всех достаточно больших к
lim
lim
к—>оо
lim
\/ок
<
>
>с
<
1,
1,
оо,
то ряд A) сходится.
Если	l.
то ряд A) расходится.
10. Признак Даламбера. Если для всех достаточно больших к
то ряд A) сходится.
Если для всех достаточно больших к
а к
то ряд A) сходится.
Если	г— afe+i
lim —^ < 1,
СХОДИТСЯ.
Если	afc+i
lim —— > 1,
расходится.
11. Обобщенный признак Даламбера. Если для некоторого а > О
то ряд A) сходится.
Если
lim
то ряд A) расходится.
12. Признак Раабе. Если для всех достаточно больших к
(-
\ak+i !
то ряд A) сходится.
Если для всех достаточно больших к
то ряд A) расходится.
Если
то ряд A) сходится.
Если
то ряд A) расходится.

638	Прил.1. Некоторые свойства интегралов, рядов, произведений	[1.3.2
13. Пусть
^±i 1 + (fc)(l + A)) А оо,
где
оA), —
Если у?(А;) < 0 для всех достаточно больших к и а > — 1, то ряд A) сходится.
со
Если а < — 1 и ряд \^ ??(&) расходится, то и ряд A) расходится.
fe=l
14. Признак Гаусса. Если
0-fc+i к + рк
cik ка + qk0-"
то ряд A) сходится при д-р > 1 и расходится при q — р ^ 1.
Пусть
A;
Тогда ряд A) сходится, если Л > 1 или Л = 1, \i > 1, и расходится, если Л < 1 или Л = 1,
< 1.
15.	Пусть	xv
О5±1=	?+0A)
Если a < 1, с < 0 или а = 1, с < — 1, то ряд A) сходится.
Если с > 0, a — любое, или с > — 1, а = 1, или с — любое, а > 1, то ряд A) расходится.
16.	Пусть
1 <?(&)	i	1	1	a + o(l)
A;
afc	A; A;	y?(A;) <^(A; — 1)	A;
Если (p(k) < 0 для всех достаточно больших к и a > — 1, то ряд A) сходится.
оо
Если a < — 1 и ряд \^ к~гср(к) расходится, то и ряд A) расходится.
fe=i
17.	Пусть	/1Ч
afe	km k
Если с < 0, а < 0, то ряд A) сходится.
Если с > 0 и a — любое или а > 0 и с — любое, то ряд A) расходится.
18.	Пусть	„
4
а + оA) ,
	 = » /Д ? &	^ °°?
где Ло(А;) = A;, Xj(k) = A; In A; In In A;. . .In In . . . In^k.
j раз
Если (f(k) < 0 для всех достаточно больших к и а > — 1, то ряд A) сходится. Если
со
а < -—1 и ряд Л^ Лп (&)</?(A;) (In In . . . In m > 0) расходится, то и ряд A) расходится.
fc=m	n раз
19.	Логарифмический признак. Если для всех достаточно больших к
In к
то ряд A) сходится.
Если	In а к
Ink ^ ~1?
то ряд A) расходится.
20.	Если члены ряда A) монотонно убывают, то ряд A) сходится или расходится
одновременно с рядом

1.3.2]	1.8. Сходимость рядов и произведений и операции с ними	639
k=i
где га — любое натуральное число.
21. Признак Лобачевского. Если члены ряда A) монотонно стремятся к нулю, то ряд
A) сходится или расходится одновременно с рядом
m=0
где pm — наибольший номер членов ад., удовлетворяющий неравенству аи ^ 2^т, к =
= 1, 2, . . . , рт.	оо
22. Пусть ^(ж) > 0 — интегрируемая на A, оо) функция. Если интеграл F(x)dx
СХОДИТСЯ И	!
1 t . .
Mm —-г F(x)dx > О,
fe^oo f{k) J
к
где /(ж) > 0 — монотонно убывающая при ж ^ 1 функция, то ряд C) сходится.
Если	оо
1
расходится и
k+i
lim	F(x)dx < оо,
то и ряд C) расходится.
23. Если существует такая дифференцируемая при х > 1 функция F(x) < 0, что
inf hm —\	> О,
^0^1 L	f(k) J
где /(ж) — монотонно убывающая при х > 1 функция, то ряд A) сходится.
24.	Пусть /(ж) — монотонно убывающая при х ^ 1 функция и существует такая функция
g(x) < 0, что при ж ^ 1 функция ^(ж) = f(x)g(x) дважды дифференцируема и F"(х) =
= o(F'(ж)) при ж —^ оо.
Если	F,f ч
^Ты >0'
ж-->оо J \Х)
то ряд C) сходится.
lim %^ < О
ж^оо /(Ж)
оо
и ряд Л^ \/g(k) расходится, то и ряд C) расходится.
к = 1
25.	Пусть /(ж) — монотонно убывающая дважды дифференцируемая при ж ^ 1 функ-
ЦИЯ "	f'(r)
f"(x) = o(f'(x)), LL2 = 4)(x)(i + o(l)), Ж^оо,
Если <р(х) < 0 при ж > 1 и а > — 1, то ряд C) расходится.
оо
Если а < — 1 и ряд 2_J <р(к) расходится, то и ряд C) расходится.
к=1
26. Признак Ермакова. Пусть /(ж) > 0 — непрерывная монотонно убывающая при ж >
> 1 функция, а 7(ж) — некоторая дифференцируемая возрастающая функция, такая, что
7(ж) > ж.

640	Прил.1. Некоторые свойства интегралов, рядов, произведений	[1.3.3
ш Щ^ < 1.
то ряд C) сходится.
() р
27. Если /(ж) > 0 — непрерывная монотонно убывающая функция, lim /(ж) = 0, а
к—>оо
то ряд C) расходится.
27. Если /(ж) >
ё(ж) > 0 — непрерывная возрастающая при ж > 1 функция, причем 5(ж) —> оо при ж
и ?(ж + 1) > <5(жM
<*(ж + 2) - S(x + 1) ^ А[6{х + 1) - <5(ж)], Л > 0,
то положительные ряды
сходятся или расходятся одновременно.
28. Пусть /(ж) > 0 — непрерывная монотонно убывающая при ж > 1 функция, а ё(х) >
> 0 — непрерывная неограниченно возрастающая функция, lim ё(х) = оо, причем функция
ж-->оо
ё''(x)f(S(x)) при достаточно больших ж монотонно убывает.
Тогда положительные ряды
fe=l	fc=l
сходятся или расходятся одновременно.
1.3.3. Признаки сходимости произвольных рядов.
Пусть задан произвольный числовой ряд
1.	Если сходится ряд \^|afc|, то сходится и ряд D), причем последний называется
абсолютно сходящимся. fc=i	^
Если ряд D) сходится, но ряд \jlafc| расходится, то ряд D) называется
условно сходящимся.	^	k=i
Признаки сходимости ряда ^_^ \ак\ перечислены в 1.3.2.
2.	Пусть	k=i
ак = — [l + о (к^?)} , к —У оо, Ъ Ф 0, е > 0.
кх L	v /j
Если Re A > 1, то ряд D) абсолютно сходится. Если Re A ^ 1, то ряд D) абсолютно
расходится (но может сходиться условно).
3.	Признак Абеля. Если ряд D) сходится, а числа Ьк образуют монотонную ограниченную
последовательность,
\Ьк\ ^В, к = 1, 2, ...,
ТО РЯД	оо
/ пкЬк	E)
к = 1
СХОДИТСЯ.
4.	Признак Дирихле. Если частичные суммы ряда D) образуют ограниченную последо-
последовательность, т. е.
. = 1, 2, ...,
где В не зависит от п, а числа Ьк образуют монотонно убывающую последовательность,
причем Ьк —У 0, то ряд E) сходится.
5.	Признак Лейбница. Если члены знакочередующегося ряда

1.3.5]
1.8. Сходимость рядов и произведений и операции с ними
641
у ^(—1) ftfc, flfc > О,
fe=l
монотонно убывают по абсолютной величине (ак ^ o>k+i) и
lim ак = О,
к—-»оо
то этот ряд сходится. При этом имеет место следующая оценка остаточного члена:
оо
/ ( —1) flfc < ftn+1-
fc = n+l
1.3.4. Признаки равномерной сходимости рядов, зависящих
от параметра.
1. Пусть функции iik(z), к = 1, 2, . . ., определены на некотором множестве D. Функ-
Функциональный ряд	^
Е
Uk(z),
F)
сходящийся в каждой точке z ? D, называется равномерно сходящимся на множестве D,
если для любого е > 0 существует такой не зависящий от z номер Ne, что при всех N ^ N?
неравенство
]Р uk(z)
выполняется одновременно для всех z G D.
2. Критерий Коши. Ряд F) сходится равномерно на множестве D тогда и только тогда,
когда для любого е > 0 существует не зависящее от z целое N?, такое, что неравенство
к = п
имеет место для всех z ? D при т ^ п ^ N?.
Ниж:е приведены некоторые признаки сходимости рядов, зависящих от параметра.
3. Признак Вейерштрасса. Если функции Uk(z), к = 1, 2, . . ., на множестве D удовле-
удовлетворяют неравенствам
причем ряд
l ^ Ск, к = 1, 2, . . . ,
fc сходится, то ряд F) сходится на D равномерно.
к
4. Признак Абеля. Если ряд F) сходится равномерно на множестве D, а функции Vk{z)
при каждом z образуют монотонную последовательность и ограничены в совокупности, т. е.
\vk(z)\ ^ M5 к = 1, 2, ...,
где М не зависит от к и z G D, то ряд
СХЭ
G)
сходится равномерно в D.	1
5.	Признак Дирихле. Если частичные суммы ряда F) ограничены в совокупности,
:м, JV = 1, 2, ...,
где М не зависит от z ? D и N, a функции Vk(z) при каждом z образуют монотонную
последовательность, сходящуюся к нулю равномерно на D, то ряд G) сходится равномерно
на D.
6.	Признак Дини. Пусть члены ряда F) непрерывны и положительны при z ? [а, Ь].
Если сумма ряда также непрерывна на [а, 6], то ряд F) сходится на [а, Ь] равномерно.
1.3.5. Операции с рядами.
1. Сходящийся ряд D) обладает сочетательным свойством:
аПк) =
= О,
21 А. П. Прудников, Т. 3

642	Прил.1. Некоторые свойства интегралов, рядов, произведений	[1.3.6
rai, П2, • • • — подпоследовательность ряда натуральных чисел.
2.	Теорема Коши. Абсолютно сходящийся ряд D) обладает переместительным свойст-
свойством, т. е. всякий ряд, полученный из D) перестановкой членов, также сходится и имеет ту
же сумму.
3.	Теорема Римана. Условно сходящийся ряд D) не обладает переместительным свой-
свойством; для любого А существует такая перестановка членов ряда D), что полученный ряд
имеет сумму А.
4.	Сходящиеся ряды молено почленно складывать (вычитать) и умножать на постоянный
множитель:	о©	<х>	о©
c^afc ± d^bk = ^(cafc ± dbk).
fe = l	k = l	k = l
5.	Если два ряда сходятся абсолютно, то их можно перемножать и полученное произве-
произведение сходится абсолютно:
к, 1=1
6.	Если ряд F) сходится равномерно на некотором множестве D, имеющем предельную
точку а, и каждая из функций uk(z) при z —У а имеет конечный предел, то в ряде F)
возможен почленный предельный переход:
со	со
lim ^ uk(z) = ^^ om uk{z).
аk=l	k=\Z
7.	Если функции life (ж), к = 1, 2, . . ., интегрируемы на [а, 6], а < Ъ ^ оо, и ряд F)
сходится на [а, Ь] равномерно, то его сумма интегрируема на [а, 6], а ряд F) можно почленно
интегрировать:
Последняя формула сохраняет свою силу и в случаях, когда функции Uk(x),k = l, 2,...,
непрерывны и положительны на [а, 6], b ^ оо, а сумма ряда F) непрерывна и интегрируема
на этом интервале.
8. Пусть функции Uk{x), к = 1, 2, . . ., определены и имеют непрерывные производные
со
на [а, Ь]. Если ряд F) сходится, а ряд ^J uk{x) сходится на [а, Ь] равномерно, то ряд F) на
к=1
[а, Ъ] можно почленно дифференцировать:
9. Пусть функции life (ж), А; = 1, 2, . . ., определены и имеют конечные производные
оо
на [а, Ь]. Если ряд F) сходится хотя бы в одной точке, а ряд \^^ПЖ) сходится на [а, Ь]
равномерно, то и ряд F) сходится на [а, Ь] равномерно и	fe=i
4=1	' k=i
10. Если функции iifc(z), к = 1, 2, ..., аналитичны в области D, а ряд F) сходится на
D равномерно, то его сумма аналитична в D.
1.3.6. Степенные ряды.
Степенные ряды являются частными случаями функциональных рядов вида F) при
uk(z) = ak^t(z - zo)^1:
оо
f(z) = ^ ak(z - zo)k = a0 + at{z - z0) + a2(z - zof + . . .	(8)
fc=0
Для каж:дого степенного ряда (8), если только он не является всюду (кроме точки z =
= zq) расходящимся, область сходимости D состоит из точек некоторого круга \z — zq\ < R

1.3.6]
1.8. Сходимость рядов и произведений и операции с ними
643

с центром z = zq и с радиусом R = I lim
V
|а&
и, быть может, некоторого множества
точек, лежащих на окружности \z — z§\ = R. В каждой точке внутри указанного круга
степенной ряд (8) сходится абсолютно, а строго внутри круга (при \z — zq\ ^J г < R) и
равномерно. Вне этого круга ряд расходится. Если ряд сходится во всех точках комплексной
плоскости, то R = оо и его сумма f(z) является целой функцией. На границе круга
сходимости имеется хотя бы одна особая точка аналитической функции f{z), определяемой
суммой ряда (8).
Если функция /(ж) в окрестности U точки ж о имеет производные всех порядков и
удовлетворяет в U условию гп(х) —> 0 при п —> оо, где
г (т\ _ f(T\ _ X
к=0
то в этой окрестности она представима в виде следующего ряда Тейлора по степеням ж —:
k=0
Если функция разлагается в степенной ряд, то это разложение единственно и является
ее рядом Тейлора. Остаточный член гп(х) можно представить в форме Лагранжа
в форме Коши
гп(х) =
в форме Роше
гп(х) = 7,}
п\ [р + 1)
в интегральной форме
о)/(п+1)(жо + в(х - го)), 0 < в
1A - 0)nf(n+1\xo + в(х - х0)), 0
-'-1 f{n+1\x0 + в(х - х0)),	0<
х)=~. [ f{n+1\t){X-t)ndt,
п\ J
в форме Шлемильха
ф(Х-Хо)-ф@) {х-
_
(
ф'[{х - жо)A - в)]	п\	t (x° + ^x
здесь ф{х) произвольная функция, удовлетворяющая условиям:
1) ф{1) и ф''(t) непрерывны в @, х — Хо); ф'(х) не меняет знака в @, ж —
Пусть	оо
(9)
zl =T(z),
Я2,
1=0
г = mln (Ri, Я2).
Co степенными рядами можно производить следующие операции.
1. Внутри общего круга сходимости степенные ряды можно почленно складывать:
1=0 хк=0
к=0 х1=0
alzk
— радиус сходимости ряда У akz •
fc=0
2. Степенные ряды можно перемножать:
(
к=0 S'=0
3. Степенной ряд можно возводить в степень:
-J Z,	Z<r.
21*

644
Прил. I. Некоторые свойства интегралов, рядов, произведений
[1.3.6
5>*ч =
п	оо
со = «о 5 «о т^ 0, ск =
аок
га/ - А; + 1)сцск-1, к = 1, 2, . . .
4. Степенные ряды можно делить:
где
-ак =0
6о	0
... 0
... 0
... 0
— akbo bk—i Ьк-2 ••• <
5. Внутри круга сходимости \z — zq\ ^ R степенной ряд (8) можно почленно инте-
интегрировать и дифференцировать сколько угодно раз, при этом его радиус сходимости R
не изменяется. В частности, для ряда (9) при \z\ < Ri имеют место равенства
Е
ак	пк
- Z
пк + т
: \xm~1S(xn)dx,
о
Tifc + TO
dz
'¦makzh =[z-^) S(z).
6. Подстановка ряда в ряд:
о© / о©
<Ru
E
i, C2 = «162
сз = аз»1 ¦
С4 = CI461 '
7. Пусть п Ф 0 и I = 1, 2, . . . , п - 1.
ТогДа	™
k=0
n
< Ri
3=0
k=Q
8. Обращение степенного ряда. Пусть
w = f(z) = [
Тогда
0:2+20:3 + • • •-\
/0.
cmw ,
(m + ai + Q2 + ...lam -1)!,
га! «2? • • • «то? ft]71

1.3.8]	1.3. Сходимость рядов и произведений и операции с ними	645
G>2 \
суммирование ведется по всем целочисленным наборам «2, «з, • • • , Qm) удовлетворяющим
уравнению «2 + 2«з + • • • + (рь — 1)ат = т — 1.
9. Ряд Лагранжа. Если z = а + ^ф{х)^ то
00 /-к
10. Ряд Бюрмана^Лагранжа. Если w = f{z) = zф(z)) ф (а) ф 0, ф{сь) = 0, то
1.3.7. Тригонометрические ряды.
Ряд вида	оо
«о + ^(«fc соя^ж + ^fe sinfcsc),	A0)
где ад., /3^ — постоянные числа (коэффициенты ряда), называется тригонометрическим
рядом.
Рядом Фурье для функции /(ж), заданной и абсолютно интегрируемой в промежутке
(—/, I), называется ряд вида
ао , v^ / кжх	. Ажж\	/11Ч
— + > «л cos —	h bfc sin -— ,	A1)
^ ьЛ	l	l /
коэффициенты которого (коэффициенты Фурье) определяются по формулам
afe = у J f(t) cos ^ dt,	Ьк = j J /(t) sin ^ Л.	A2)
-Z	-I
1.	Если функция /(ж) на (—/, I) разлол^има в тригонометрический ряд A1), то этот ряд
является ее рядом Фурье, т.е. его коэффициенты ад., Ьк находятся по формулам A2).
2.	Если функция /(ж) кусочно дифференцируема в интервале (—/, I), то ее ряд Фурье
в каждой точке ж сходится и имеет сумму S(ж) = —	-, ж G (—/, I). Если,
кроме того, /(ж) непрерывна в точке ж, то S(x) = /(ж).
3.	Коэффициенты Фурье а^ и 6^ абсолютно интегрируемой функции / стремятся к нулю
при к —У сю:
4.	Функцию /(ж), определенную в промежутке @, I), молено разложить в ряд вида
оо
«о , v^	^ж	2
— + Уаксо®——,	ак = у
2 Г
у
6 J
или в ряд вида
Ss(x) = }_^Ьк sin ~т~> fc = 7 ^^ ^sm ^Г
к=1	0
В первом случае /(ж) доопределяется на (—/, 0) четным образом: /(—ж) = /(ж), а во
втором — нечетным: /(—ж) = —/(ж). Если /(ж) — кусочно-дифференцируемая функция,
то в точках непрерывности Sc{x) = /(ж) или Ss{x) = /(ж), — / < ж < I.
1.3.8. Асимптотические ряды.
Пусть {'0^(ж)}^=1, ж G D, — асимптотическая последовательность функций при ж —^
—^ жо, т. е. ^д.+1(ж) = о(^д.(ж)), ж —> жо, ж Е D, и функции <^(ж) определены на
оо
D. Формальный ряд У j <Pk(x) называется асимптотическим рядом (или разложением)
k=i
функции /(ж) относительно асимптотической последовательности {^(ж)}, если при любом
целом N ^ 1

646	Прил.1. Некоторые свойства интегралов, рядов, произведений	[1.3.9
N
/(ж) - ^^ 4>k(x) = о(фм(х)),	х —у х0.
k=l
В этом случае пишут
оо
f(x) ~^2(рк(х), {фк(х)},	х—> х®.
k = l
Если (fk(x) = afc^fe(dc), где пк — постоянные, то соотношение
оо
/(ж) ~ ^^ акфк(х),	х —у ж0,
k=i
называется асимптотическим рядом (или разложением) функции /(ж).
Важную роль играют асимптотические степенные ряды, для которых фк = х^ (ж —у
—> оо) или фи = (ж — жо) (ж —у жо). Асимптотические ряды допускают некоторые
операции алгебры и анализа. Соответствующие утверждения имеют место и для функций
комплексного переменного.
Примеры асимптотических рядов:
h (ж - т
-4)
к=0
Dill I %Ju	I 7 I II l^ Л |g-4-~ X ^	I 5 I ^	J 5 ^	/ I LAJ ^
г 2 4 / z—'	I».-»
fc=O
+oo.
1.3.9. Бесконечные произведения.
Пусть задана функциональная или числовая последовательность oi, аг, аз,
Если существует конечный отличный от нуля предел
п	оо
lim [lafc = Па^	A3)
fc=l	fe=l
то он называется значением бесконечного произведения. В этом случае говорят, что произ-
оо
ведение I I а к сходится. В противном случае произведение называют расходящимся.
к=1
1.	Необходимое условие сходимости произведения.
Если произведение A3) сходится, то а к —У 1 при к —у оо.
2.	Связь произведений с рядами. Произведение A3) сходится тогда и только тогда, когда
со
СХОДИТСЯ рЯД JJ In ttfc.
fe=l
При выполнении этого условия справедливо равенство
со	оо
у In аи = In I I ak •
к=1	к=1
3.	Если по крайней мере для больших к пк > 1 (или ак < 1), то произведение A3)
оо
сходится тогда и только тогда, когда сходится ряд Л> (ак — 1).
оо	сю	k = l
4.	Если ряды \^(а^ — 1), Yj(«fc — IJ сходятся, то произведение A3) также сходится.
к=1	к=1

Приложение II. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ
ФУНКЦИИ И ИХ СВОЙСТВА
II.1. БИНОМИАЛЬНЫЕ КОЭФФИЦИЕНТЫ
(а\_( ик(-а)к _ а(а - 1) ¦ ¦ ¦ (а - fc + 1)
f W] =0	[к = -1, -2, -3, . . .], или [fc > п], или [п = 0; Aj = 1, 2,
С)
Г(а
а \	а /а —1\ а — Ь/а\	/ а\ ( а \ f а-\-1
b + lj Ы-1 V	Ь ) Ь+1\Ь/' \bJ ' \b
/n + a\/ b \	f^\f^^n\ (' ^\ ('b ~ a\
V n ) \n-\-a J	\n J \ a J \aj\ n J
I	I = -—^— ( I = (™l)n-^™-— .
/1/2\ = (-^^/Зп-гЧ =	!
\п) 22n+1n\n-l) { }
» + l/2\ =(_i)-4"-1f2nY	p« + !/2N
2n + 1 /	\ n /'	\ n У " V 2ra
n \ 22n+1/2fi\^1	/ n \ 22n / - x^1
1/2; 7Г u; ' v^/2; ^
II.2. СИМВОЛ ПОХГАММЕРА (a)fc
I (aj	1 A — a — к)
(aH = 1,	(a)_fe = . , = j-	r-	[a Ф 1, 2, . . . , fc; fc = 1, 2, 3,
(a)fc = (a)n(a + n)k~n = (—1) A — a — k)k-
/M\ _____ \w ' "* ~~" ^-/-	/1 \ _____ m

648	Прил. П. Некоторые специальные функции и их свойства
= 2, C/2)л = 2.
(a)n+fc = (а)п(а + га)*.,	(a)n_fe = у^	 ^ .
A - a - n)fc
{a)nk = I —I 	 ••• 	 n ,	(aJfc=(-l —-—
Vn/fe V n Jk \ n Jk	\2Jk\ 2
2Jk
j=0
^л '	(a-
{a)m
(a - mk)nk = (-l)mfc(a)nfc~mfc(l - «)mfc	[те ^ ra],
/ -t\nk (J- (^)mk	г	п
= I1)	[n< m] .
~ y ' A- a)mk^nk
(a - k)k = (-1) A - a)k,	(a - m)k =	, _ _ j, / •
Ш	(a)mk	'	jn^fc^(a)fe"
(a-^)n±|fe=-T.	^ П^ч—^-^,	(a-
A - a - njmfezp/fe	A - a - ПJп
II.3. ГАММА-ФУНКЦИЯ
Определение:
CO
F(z)= lim Д^	[z^O, -1, -2, ...].
При He z ^ 0 функция F(z) может быть определена как аналитическое продолжение
приведенного интеграла или равенством
Y,k\ dt	[-n-1 <Rez < -n].
{	k=o ¦ J
F(z) — аналитическая функция во всей z-плоскости, за исключением точек z =
= 0, — 1, —2, . . ., в которых она имеет простые полюсы с вычетами
res V{z) = ^^	[к = 0, 1,2, ...].
= ГB) = 1.

II.8. Гамма-функция T(z)
649
) () (
) (
V п J
П У к
Г(*J"
2 '
Br»-l)!!'
3 '
¦Г(*)Г
|Г(гж)|2 =
.м2 ^
Г I \
Г(*)Г
2
fc=O
сЬтгж
(зд + s) = V{z0)
г j+« г |-
у + 0(?4)
/о
[ж2ф(к
chwx
[s -»¦ 0; го / 0, -1, -2, . . .].
[e -+ 0].
= 1 ±
61 = C, 6, = C@»' = 2, 3,4, ...
Ф
1 Л
к^
1) — 3^7 (А; Ч
* + !)]? + ¦
д —1) biak-i'
Ы)]
6
»}
InF(z
\z\ < l]

650	Прил. П. Некоторые специальные функции и их свойства
V{z) = у2тг zz~ ' e~z 1 + О ( — j	[z —»• оо; | argz| < тг].
\п —)> оо .
W(x + iy) = y/2w \y\*-4*e-*W\r* \l + o(-
1	\У
II.4. ПСМ-ФУНКЦМЯ
Определение:
ф^) — аналитическая функция во всей z-плоскости, за исключением точек z
: 0, — 1, —2, . . ., в которых она имеет простые полюсы с вычетами
res ф(г) = -1	[к = 0, 1, 2, . .
^ 1	— 1
i/j(z + п) = ^(^) + >•	,	ф(г — п) = ^(z) -
k=i z
ф(п + 1) = ^С + Y, Г
/ 1	\
C= Mm V- -Inn 1=0, 5772156649
) = -C - | - 31n2, ф 0) = ^C + | - 31n2.
\	[(9)/]
?1 ) = _C - In Bg)	ctg — + 2 > cos —— In sin —
q)	2	g	^	g	g
[p = 1, 2, . . . , ^ - 1; g = 2, 3, 4, . . .]
,	i/>(z) — Ф0- — z) = ^TrctgTrz.
¦ — j + Inn, фBz) = — (^) + ^^j-^+^ ) +ln2.
fe=0
2 '
х) = Ret/>(-ix) = КефA + ix) = КефA - ix) = -C + x2
1	1
+ | cthTT», Im^(l + ix) = ^
+ | cthTT», Im^(l + ix)	+ | cthTra x ^ fc2
fci

II.4- Пси-функция ф{г)
651
+ е) = -i (l - ^(fc + 1)е + |V(A; + 1) - ^-1 е
е I	L	^ J
fc=0
[е -+ 0].
m) = ф(п
1n! B^+1 - l)C(n
7Г2
II.5. ПОЛИЛОГАРИФМ Ll^C
Определение:	^
[n = l,2,...]
[n = 1, 2,
[n = 1, 2,
или \z\ = x' Rei/
При \z\ ^ 1 функция LIl/(z) определяется как аналитическое продолжение этого ряда.
Ее главная ветвь имеет представления
dt
[Re и
о
7+ioo
f
A + sI/slns7r
y — ioo
7+гсхэ
2тгг J
7 —too
' — дилогарифм Эйлера.
, i/, 1),
— числа Стирлинга 1-го рода].

652
Прил. П. Некоторые специальные функции и их свойства
Uv(z) - Liv(e2lriz) = —у In" z
e
(-1)" Li_n ( ^ ) = 0
LIn(» + (^l)nLIn ( - j = -
CO, те = —:,
6(n-2)!'
2Lia*(-l)
|arg(l - z)\ < тг]
[n = 1, 2, ...].
hin (iz) + hin (-iz) = 41 nLIn(z4)-21 nLln(z2).
'An(z) = \t 1LIn^i(t)dt
о
1 — z
[0 ^ p < 1; - тг < if ^ тг]
[n = 1, 2, . . .].
Li2(z) = -
) = -
J
dt =
lnt
t — 2:
dt =
[1 + >/i A -
L , , >-
1 — t\/ z
dt [arg(l -
^- -lnzln(l-z)
о
LI2(z) = -Li2 ( - ) ^ -
= Li2
- In\\ ^z)^ ln(-
[|arg(-z)
i2(wz) = hi2(w) + Li2(^) + Li2
yl — W
Li2
1 — Z
1 2
- In
7Г
IT'
12' Ll2UJ-12-
7Г
8

II.4- Пси-функция ф{г)	653
II.6. ОБОБЩЕННЫЕ ИНТЕГРАЛЫ ФРЕНЕЛЯ S(z, и) Ш C{z, и)
Определения:	^
S(x,i/) = \ t"'1 sin tdt	[Rei/<1],
X
oo
C(x,v)= \ t"'1 costdt	[Rei/<1].
X
Ha z-плоскости эти функции определяются как аналитические продолжения приведен-
приведенных интегралов.
¦?(*,*I Г sin (i/W/2)l гы_?^ F (§±Л. §±Л+1 Х + ----'\ 16 = 14}
'(z, и) \ 1 cos (i/tt/2) J ^ ' 5 + г/X 2\2' 2	2' 4 / L \ 0 /J '
u-i( slnz
cosz
5(z, 0I _ f si(*) 1 f 5(z5 1/2) 1 = ^ Г1 _ Г 5(z) 11 _
II.7. ОБОБЩЕННАЯ ДЗЕТА^ФУНКЦМЯ С(^, v)
Определение:
oo
C(z, v) = V jz	r-	[Rez>l;^ 0, -1, -2, . . .].
[Re,>l;Ret,>0].
0
При Rez ^ 1, z ф 1 функция ?B, v) определяется как аналитическое продолжение
приведенных представлений. В точке z = 1 функция {(z, -у) имеет простой полюс с
вычетом 1.
n-l	1
С@,«) |«,	C(n,«) ^IB»+i(«)- ^С@,») 1пГ(«IпB1г).
lim Jc(«. ») - J3l] =-V>(»)	[Ret,>0].
Частные значения f (z, v) см. в [17], пп. 5.1.3-5.
II.8. МНОГОЧЛЕНЫ БЕРНУЛЛИ Bn(z) Ш ЧИСЛА БЕРНУЛЛМ Вп
Определения:	то
< 2тг1
K -
\ i
3=0

654	Прил. П. Некоторые специальные функции и их свойства
Bn(z + 1) = Bn(z) + nzn~\ Bn(z + a) =
Bn(l -z) = (~l)nBn(z),	Bn(~z) = (~l)n[Bn(z) + nzn~\
m^1 / k \
Bn(mz) = mn^ Y^Bn[z+^\	[m = 1, 2,
fc=O	^	'
B'n{z) = nBn-!(z)	[n = l, 2,
n
Bn(z) = 2-n
k=0
m — 1
Bn(m) = Bn + n ^2 k71^1	[m, n = 1, 2, .
fe=i
Bn@) = (-l)nBn(l) = Bn. B2n (^j = B2n (^j = 1A - 21")A - 31-2n)B2n.
) A)nB () 2""A 21"n)
Bn (l) = ()n'B" (|) = -2""A " 21"n)Bn - 4-"n?n_1	[n = 1, 2, ..
- I = B2n I - I = -- A - 3 )B2n. Bnl-\=-(l-2 )Bn.
B0(z) = l,	B1(z) = z-±,	B2(z) = z2-z + ±,
B3(Z) = z*-3-z>+1-z,	B4(z) = z'-2zs + z2-^,
= z5-5-z*+5-z*-1-z,	Be(z) = ZS-Sz*+5-z*-1-z* + ±.
fc' Bn = Bn(O).
fc=O
B2n+1=Q [„ = 1,2,...],
-	X	R - 5	R - 691
—	^T^T?	?>10 — 7^7?	A512 — — "
30'	iU 66'	" 2730
II.9. МНОГОЧЛЕНЫ ЭЙЛЕРА En(z) Ш ЧИСЛА ЭЙЛЕРА Еп
Определения:
= 2ги - En(z), En(z + a) =
[m = 1, 3,

II.4- Пси-функция ф{г)	655
k=0
E'n{z) = nEn^1(z)	[n = l, 2, ...].
g
(„ + !)(„ +2) g I *
En@) = -En(l),
га + 1
E2n^i I - I = -E2n-i о
/	\ ^
[n = l,
[n = 1, 2,
E0(z) = l,	E1{z) = z-\,	E2(z) = z2-z,	E3(z) = z*-lz2 + \,
) = z4-2za + z,	Eh{z) = zb-\zA + \z2-\,	E6(z) = ze - 3z5 + 5zs -
A	A	A
Е2п+1=0	[n = l, 2,
E0 = l, E2 = -l, ^4 = 5,	E6 = -61, ^8 = 1385,
E10 = -50 521,	#i2 = 2 702 765.
11.10. ФУНКЦИИ СТРУВЕ Hu(z) Ш Lv(z)
Определение:
1	( 3	3 z^
X 4 2 + ' 2' T 4
]	(
\ Lv(z) / V5F Г> + 3/2) X 4 2 + ' 2' T 4
3/2)'
dz	7Г	dz	7Г
Hy fzem7ri] = em(l/+1OTiHI/(z)	[m = 0, ±1, ±2,
\jv\z) = —ге	м

656
Прил. П. Некоторые специальные функции и их свойства
}n-l/2 n
2 \ -к
= (—l)nJn+1/2(z),
2 / . cos z
smz -\
11.11. ФУНКЦИИ ВЕБЕРА E^(z), E?(z) И АНГЕРА J,,(z),
Определения:	ж
sin (i/t — z sin t)
cos (i/t — z&int)
dt =
1 fl —cosi/ttI _.
i/тг [ sini/7r J
Z	f 1 + COS 1/7Г
7ГA — i/^) [ Sin 1/7Г
1;
2 ' 2 ' 4
sin (yt — z sin t)
cos (yt — z sin t)
dt =
• fl/7T\
V 2
1,
/x-i/
+ 1
2 ' 2 + ; 4
1 t±
2' 2
f 008(^/2I
\sin(i/ir/2) J
3
2' 2~
l' 2 ' 4
2
J П si
2п-1)!!тг
fc=0
= -HoW,
J-^(^
-^) - (±l)"H±n(s).
2
7Г
[n = 0, ±1, ±2, ...
J±1/2(z) =
11.12. ФУНКЦИИ ЛОММЕЛЯ */*,.
Определения:
S(z)\ ± sin z[C(z) ±
— V+ 1
/^(z) — cos	ttYjj(z)

II.4- Пси-функция ip(z)	657
-j-sfJlil/(z) = =F-
(последние 4 формулы справедливы при замене всюду sfJ,jl/(z) на SfJ,iI/(z)).
Г
lim
м^^ Г(/1 — i/j
(±ll)/2
O2n + l(z), Si,2n{z) zO2n(z).
Sitl/(z) = l + v2S~i^{z)« S1/2,i/2(z) = -^,
EI/(z) =	[A + cos i/7r)so, 1/B)
7Г
11.13. ФУНКЦИИ КЕЛЬВИНА ber^(z), bel^z), ker^Cz) И keiI/(z)
Определения:
Ъет„(х)±1Ъе1„(х) = Ju (же±37гг/4) = e±uniJu
кег1/
(ж) iikel^C^c) = е^^/2Ки (xe±7Ti/4) =
f ber^z) 1/zyAf cos [Ci/ + 2^)тг/4] 1 (z/2Jk
\	\2 ^ \
fe=O
jker.(z) X + z"Y{-v) f, f cos[(i/ - 2feOr/4]) (z/2Jfc
sin [(i/-
±2"

658	Прил. П. Некоторые специальные функции и их свойства
kern(z) I	z^n ^—л ( cos [Cn + 2k)n/4] 1 (га — /г — 1)!
fe!	V27 "ln2\bein(^) }±
7Г f bein(^) 1
zn ^-^ J cos [Cn + 2/гOг/4] 1 ^(n + A; + 1) + ф(к + 1) /z\2k
^+i ^ [ sin [Cn + 2ifeOr/4] j	(n + ife)!ife!	12 J '
Г кег (г
= "lnf{bei(%)}± l{ ЬегЙ } + ]^-1)h № +t -"ЭД* (т)	Н {i}]
J ber^n(z) \ _ / bern(-z) \ _ . .n f bern(z)
= (-D"( !^g}	[« = 0,1, 2,...]
\kel
ил/2 (fv - gv) = -z[fv+i + U-i],
Д = Д+i Ч- йГж^+i - Л-i -5Г1/-1»	^^/^ = ±-Л ± -7=- (/«/±1 +^^±i)-
для любой пары функций
fv = ber,(z) 1	fy = heiu(z) 1	Д = keiv(z) 1	Д = kel^z)
gv = heiv(z) j ' gu = - beru(z) J '	g-,, = kell/(z) J ' g"i/ = - kerI/(z)
fber_I/(^)l	fcosi/7ri	f slni/тг I .	2 . (keiv(z)i
Dbei^i/(z)J	I sin wk J	[ cos 177Г J	7Г	[ Keiv(z) J
kei_i/(z) J I sin i/TT J	[cosi/ttJ
11.14. ФУНКЦИИ ЭЙРМ Al(z), B!(z)
Определения:
\
Ai(Z
Bi (г) / - ГB/3) j^UA C*)'
Ai(ez) = e[Ai(zL:iBi
Ai (г) 1 2.г/3 j Ai (e2-i/3,) 1	27гг/3 Г Ai
Bi (г) = е"/6 Ai (е2"/3г) + е"™/в Ai (е

II.4- Пси-функция ф(г)	659
11.15. ИНТЕГРАЛЬНЫЕ ФУНКЦИИ БЕССЕЛЯ Jiv(z), Yiv{z), Kiv(z)
Определения:
no	OO
rJt)) dt
Ли(х) = Jv(t) —,
J	t
Ha z-плоскости эти функции определяются как аналитические продолжения приведен-
приведенных интегралов с помощью рядов
/y*"(*)\=±J_/ ctg(i/7r/2) 1 _br(-i/)fcosi/7r-| fz\
\Kil/(z)}	2i/\7rcosec(i/7r/2) J 2tti/ l тг J 42/
x x
7Г I V2
^ k\{2k~n) V 4 /	2тг \тг/ V2/ ^ ife! (A; + n)\ Bk + n)
fe=O
И ( Yi G) 1	( Y G) 1
dz\K%v(z)\	\Kv{z)\
Ji±1/2(z) = ±Yhl/2(z) = f- { ^ Z\/V }. Ki±m(z) = /f Г (-1,
11.16. НЕПОЛНЫЕ ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ F(y>, fe), ^7(y>, Jfe),
D(y>, fc), П(у>, i/, fc), A0(y>, /3, fc) И ПОЛНЫЕ
ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ K(fe), E(fe), D(fc)
Обозначения:
0 < ife < 1, к' = Vl - k2 , At = \fl - k2 sin2 t,
/^-^2 f, _	/I ч Л к2
1 , .„ . . . ^, g = 4/A - ^) . ^
tg№ -<p) = к tgtp, smx =	2—.
1 + к sirr w

660
Прил. П. Некоторые специальные функции и их свойства
Определения:
<р	sin ц
F(<p, А) = J^= J
О	О
dt
E(<p,k) = ]Atdt= | ^
1 - k2t2
-t2
dt,
Ч>	о	simp
1 in2 tdt f
t2 dt
o
sin
, i/, A) =
dt
Ao(<p, /3, k) =
J
- t2)(l -
, и,
|, fc),
(-?3, fc) 1	f F(^, fc) 1	f F(mr ± V) fc)
] \E(V,k)f' \E(nn±V,k)
, fc) 1	f K(fc) 1
j+ \E(fc)J-
, k).
E
l~kf
l~kf .
E
Щ -
, к).
2^1-A* sin2
дк
, A)
') + E(A')K(A) - K(A)K(A') = -.
E
к
K
it*
*1Я
1 Г 1
K(A) = |
, I;
- *1Як(*)]' к
к (,„ J) = к
dE(A)
E(A) = |
Значения К(/г), Е(А;) и D(fc) при некоторых А; см. в гл. 7.
, i/i, A;) =
, fc) + arctg
, 1;
sm Jg
2^/1 - k2 sin2
; к2
0; к

11.4- Пси-функция ф{г)
661
П ( —, и, к) = sin2 фЖ(к) Н		х
У2' ' )	V K > 2^1-к'2 sin2 ф
!>, k')K(k) - S(V>, fc')K(fc) - F(i/>, fc')E(fe) + -l [г/ = ctg2 V; 0 < ¦</> ^ тг/2].
ли J
!>, Jfe;)K(ife) - E(^, ^;)к(^) - F(^? ЮЕЙ) + -I
[г/ ^ к' sin -0 — 1; ^l^Ci/^C —A; ; 0 ^ ф ^ тт /2].
A;)K(A;) - F(^>, A;)K(A;)]
[i/ = -fc2 sin2 ф; - к2 ^ i/ ^ 0; 0 ^ 0 ^ тг/2].
у 1 — fe2 sin ф
A:/2 sin*
= К(Л)-
, 0, A;) = F(tp, к).
; —1? A;) = F((p, к)	j ^(^? ^) "
; cosy?
^, k) = ± E(<p, к)
, i/, 0) =
arctg (л/1 - и tgv?)
1 ~
?, 0, 0) = <^,
|ЛО (|, /3, As) = K(k)E(/3, kf) - [K{k) - Щк)]Рф, kf).
[i/ < 1].
о (|, /3, 0) = sin/9, Ло (J, /3, l) = ^.
, k^J =2n±A0 (J^, /3,
11.17. ФУНКЦИЯ БЕЙТМЕНА ku(z)
Определение:
ф ("I'0;
- 17» 2' 2z) = -stn—e z x
7Г	Z
n±i//2 — 1 T-z
= (-1) {1±2JZ
[i/ 7^0, 2, 4,
11.18. ФУНКЦИИ ЛЕЖАНДРА
Определения:
), Qv{z), QZ
[| arg (z - 1)| < тг; [i ф m; m = 1, 2,
; m = 1, 2,
[-1 < ж < 1; fi ф m; m = 1, 2, . . .].

662
Прил. П. Некоторые специальные функции и их свойства
= P°{z) = 2Fi \-v,l + v; 1;
[-1 < x < 1; m = 1, 2,
[|arg(* + l)|
2"+3/2(n
2 , 2 +1, »+rz2
|argz|, |arg(z±l)| < тг; 1/+ 1/2, p + i/^-1, -2, -3, . .
2/j + 2n + 5	1
,	; n + 2; —
тг; ^ + и ф -1, -2, -3, . .
±
2sin/i7r
- Г
Формулы преобразований:
+ гО)
гО) =
^ J
^ (z2 - 1Г
-1 < х < 1; у, ф ±га; /л + v ф -1, -2, -3, . . .].
[jLt = га; i/ 7^ — га — 1, — га — 2, . . .].
[ц = ^m; i/ 7^ ra - 1, ra - 2, . . .].
fu{z)	[|arg(z-l)| <тг].
I	[-1 < Ж < 11.
[-1 < ж < 1].
[га > n].
[-1 < ж < 1].
[-1 < ж < 1].
[-1 < ж < 1].
[Imz ^ 0].
[-1 < ж < 1].
[Rez > 0].
[0 < у> < тг/2].
- гО)
¦Qiri

663
sin (fi + u)ttQ^(z) + sin (/i — i/OrQl^_1/_1(z) = тгегМ7Т cosцжР^(z).
Sin (/i + l/OrQZ(x) + Sin (/i — yOrQ^_l/_1(x) = 7Г COS fjLlT COS U7TP^ (x)	[—1 < Ж < 1].
[-1 < ж < 1].
[О < ж < 1].
[-1 < ж < 1].
(-ж) = - cos
- — sin
- гО) = iirettxirP?
{x ± iO) =
[-1 < ж < 11.
Рекуррентные формулы:
(если z ? [—1, 1], то А = В = С = D = 1; если z = ж ? [—1, 1], то следует положить
-/1 — х2
A = -D = -
-, G= -1 и заменить z на х после сокращения дробей):
f zP?(z) - P»+

664
Прил. П. Некоторые специальные функции и их свойства
Представления через гипергеометрическую функцию Гаусса:
Sin I/ТГ
—	<
sin /хтг
F1 -i/,
[-1 < x < 1].
^ 2
+ ^Or/2]J
\-\i-v	v-n 3
z-l
М/2
o^tl/7T
z + 1
В [1], гл. 3.2, указаны 72 представления вида
PZ(z) = A12F1(ai, 61; ci;
e-^QjJ^) = A32F1(a3, &з;
Частные случаи:
i(a2, 62; c2; ()•
2Fi(a4, b4; c4; ()•
[-1

665
2	/
I - х2 1 (i/
cos[(i/ + l/2)arccosa;]
+ 1/2) sin [(i/ + 1/2) arccos ж]
lz-1
1 + ж
hi < ж < 11.
[-1 < ж < 11.
[i/ 7^0; - 1 < ж < 1].
Z + 1
+ к
-D
-D
Pi1 (ж) = -л/1 - х2 ,	Ра1 (ж) = -Зжл/1 - ж2 ,	Р2(ж) = 3A - ж2).
^w = 4
- х2), Р!(х) = -15A -
2\3/2
Г» 1 '
Pt/{z)\u=n =: Рп(
[Рп(г) — многочлен Лежаыдра].
1 „ / lz-1
Bп + 1)тг"
¦E
-2K
in J±| - 2C -
2D
-к
¦K
in
111
- 2C
1-
- Wn-l(z),	Qn(x) = \ Pn(x) In
_ A, _

666
Прил. П. Некоторые специальные функции и их свойства
WQ(z) = l,
A Z — J.
Qo(x) = - In	 = Arth ж
A 1-х
( 1 ^n
В) + <Эп+1/2(-ж)<Эп-1/2(ж) = ^ ^ i .
[-1 < Ж < 1]
COS [
sin f
»/Oг/2]
= 2/x+(l±l)/27
Формулы дифференцирования:
' sin [(/л + i
^ COS [(/i + i
It)/2
-(" + 1)
J
= B-
Vz2-1
P^(xI-
Производные по индексу:
РГ
[В см. нас. 775????].
тгA — ж2) *
z = x E (-1
+ к + 1)-ф
= 0.
i/ = —1/2
- /i)
01/
1 ^ Ж
jv'o*:
2
-Р^(ж'
¦In-
Дифференциальное уравнение
у=~3/2
[и ф 0, ±1, ±2, . . .; Re/x < 1]
/l — ж	/l + ж 1 + ж
1 + ж ~ У 1-х	2
9 О / \1	! 1 + Ж
= -4^1-ж2Р^1/2(ж).
du
и = 0
имеет следующие фундаментальные системы решений при z 0 (^оо, 1] (z = ж G [—1, 1]):
, <Э^(ж))	Км^-М^О, ±1, ±2, . . .]
), РИW	(^W, РИ(^)) [i/ + |х, i/ - /х = 0, ±1, ±2, . . . ; М ^ 0, ±1, ±2, . . .].
P?(z), Qn{z) {Pn{x), Qn(x))	[^ = ±m, i/ = п или i/ = -n - 1, n ^ m].
nTOW, QnW	(Pnm(x), Qn{x))	[M = ±m, i/ = n или i/ = -n - 1, n< m].

II.4- Пси-функция ip(z)	667
11.19. ^-ФУНКЦИЯ МАК^РОБЕРТА Е(р; ar : q; bs : z)
Определение:
Е(р; ar :q; bs:z) = E((ap); (bq); z) = Е
; ar : g; bs : z) = ГК1' " " ' '
[Ol, . . . , uq J
[p ^ q; \z\ > 0] или [p = q + 1; |г| > 1],
рГ/\;	1	/ii	(и \ ( i\P-Q \
Ml	l	\Z g+l-^p —ll	- ,	/ \i	I
k=1 IA - ak, • • • , bq - ak\	\	l + ak-{ap)	J
[p > q + 1; \z\ < oo] или [p = q + 1; |z| < 1];
штрих ; означает, что из вектора (ap) — a^ удалена компонента а к — аи-
Е(р] аг : g; 6i, . . . , bq—i, ai : z) = E(p ~^ 1; a2, . . . , ap : g — 1; 6i, . . . , bq—\ : z).
E(p; ai, . . . , ap_i, 6i : g; 6S : z) = ?J(p — 1; ai, . . . , ap^i : g — 1; 62, . . . , 6g : z).
aizE(p; ar : q; bs : z) = zE(p; a\ + 1, a2, . . . , ap : g; 6S : z) + ?J(p; ar + 1 : g; 6S + 1 : z).
= zE(p; ar : g; &i — 1, 62, . . . , bq : z) + l^(p; ar + 1 : g; bs + 1 : z).
; _ Vio; ar : g; bs : z) = E(p; ar + n : g; bs + n : z).
~-—[z~aiE(p; ar : q; bs : z)} = (—l)nz~ai~nE(p; a\ + n, a2, . . . , ap : g; 6S : z).
——E(p; ar : g; bs : cz m) = mnz n?J(p + m; ar, A(m, 1) : g + m; 6S, A(m, 1 —n) : cz m)
[m = 1, 2, . . .].
Другие соотношения получаются из формул для С-функции Мейера (см. гл. 8).
11.20. ЭЛЛИПТИЧЕСКИЕ ФОРМУЛЫ ЯКОБИ спи, dnu, snii
Определения: пусть и = —	; тогда
J л/l ^ к2 sin2 t
am и = am (и, к) = (р^ snu = sin (p, спи = cos у?,
dn и = у 1 — ^2 sin2 <р , sn (—w) = — sn и, en (—и) = en гх, dn (—и) = dn гг.
/ , ч sn и en v dn t; ± sn v сп гл dn гг	, , ч сп гл en v =F sn ге sn v dn гг dn v
m (u±v) =	j^—	, cn(u±v) =	——	,
1 — k1 sn2 и sn1 v	1 — k1 sn2 и sn2 v
. , , ч dn и dn v =F k2 sn гх sn v en гг сп v
dn
аи

668	Прил. П. Некоторые специальные функции и их свойства
11.21. ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ ВЕЙЕРШТРАССА p(ti), СМ,
P{U) и2 2-" [(и- 2тил - 2пш2J	Bтшг + 2пш2J I '
га, п=0 L ч /	х / J
т+пфО
и	и
((и) = - - р(и) - — rfti,	(т(м) = гл ехр I С W ~ ~
о	о
р(--м) = р(г*), С(-^) = ~С(и),	^(^и) = -<г(ц)
оо	ею
gi = 60 ^ (mo;i + пс^г)^4, g = 140	^^
m,n=0	m,n=0
g-2 = -4(eie2 + e2e3 + e3ei),	g-3 = 4eie2e3, ei + e2 + e3 = 0,
где ei, ег, e3 — корни уравнения 4z3 — g*2^ — ,§ = 0.
11.22. ТЭТА-ФУНКЦИИ %(z, g), j = 1, 2, 3, 4
Определения (везде \q\ < 1):
0o(z, q) = 1 + 2 ^](-l)fcgfe2 cos 2^z. ^(z, g) = 2 ]Г(^1)У^+1/2J sin Bfe + \)z.
k=l	fc=0
(z, q) = 2^g(fc+1/2JcosBife + l)z. 6>3(z, g) = 1 + 2 ]P gfc" cos 2Jbz.
fc=0	fe=l
= eo(<J, г). 9i(-z, q) = 0i(z, q), i = 0, 2, 3,	вх(-г, 9) = -^B
i(г + тг, g)
f ^o(« + тт. <?) 1 f 0o(«, 9) 1 f
\0s(« + »r)9)/ les^.q-)/' 1
f ^o(^ + тг/2, g) 1 = f вз(^, g) 1	pi(^ + тг/2, g) 1=
\0s{z + ir/2,q)j \0o{z,q)f'	\ 02(z + тг/2, g) /
(z,Q)
^)\_^-i/4-iziO1(z,q)
2, g)
\ [(z7 g1/4)
, g) = lK(fe), g = exP U,r
7Г l/'^	Г|	K(ife)
11.23. ФУНКЦИИ МАТЬЕ
Функциями Матье cen(z, g), sen(z1 q) (периодическими или первого рода) называются
периодические решения уравнения Матье
—| + (a - 2g cos 2z)y = 0,	к = :
Если -^/g — действительное число, то существует бесконечное множество собственных
значений а и соответствующих им периодических решений y(z) = y(z + 2тг). Они могут
быть записаны в виде
оо
се2те(^, д) = /^ Ао" cos2rz,

11.4- Пси-функция ф{г)	669
се2п(тг/2, д) \^/ ^
се2те@5 д) ^^, xr a
оо
= У^ Л^Х1^ cos Br -
г=0
g) = ^ Bfr^t1} ™ BA;
r=0
Bn + l) Z^^1) B2r	/2r+l B^/9 Sin*).
1	r=0
2)z,
cos,),
/	/p. \	OO
= Se2;%T+'2) ctg^(-l)-Br
9^2	r=0
Собственные значения и коэффициенты рядов находятся из рекуррентных соотношений
[12]. Штрих обозначает дифференцирование по z.
Нормировка функций Матье:
у2(х) dx = тг.
о
Наряду с каждым периодическим решением уравнения Матье существует второе линей-
линейно независимое с ним непериодическое решение (функция Матье второго рода). Нечетное по
z непериодическое решение, соответствующее cen(z, qI обозначается через fen(z, g). Чет-
Четное по z непериодическое решение, соответствующее sen(z, g), обозначается через gen(z, g).
Они связаны соотношениями
fen(z, g) = Cn(q)[zcen(z, g) + fn(z, g)],
gen(z, g) = 5n(g)[2:sen(z, q) + qn(z, g)],
где fn(z, q), g-n(z, q) — некоторые функции, a Cn(q), Sn(g) не зависят от z.
Имеют место следующие разлож:ения:
\ ^V^ fe2n+i@, g) ^. r Bn+i) г / iz\ ( _iz\
ZCe2n + ll7r/Z5 ^J 0	L V	7	Ч	7

670	Прил. П. Некоторые специальные функции и их свойства
°5 Я)
EB^1)Re
r=0
- Jr+i {y/q eiz) Yr
iz) Yr
Модифицированные функции Матье первого рода
Cen(z, g) = cen(iz, g), Sen(z, g) = -isen(iz, g)
и второго рода
Fen(z, g) = -ifen(i2, g), GenB:, g) = gen(iz, g)
удовлетворяют уравнению
—| - (a - 2qch2z)y = 0, /г = 2-/g .
Это уравнение имеет, наряду с решением Се2П(^, д), допускающим представления
_ се2п(тг/2, д) ^к. .
~	4Bп)	2^^ Х^
л0	г=0
линейно независимое с ним решение
/А \ °°
Fe2/2n(^, q) = 2nBn?)— 5Z A^Y^B^/q shz)	[|shz| > 1; Re z > 0],
^0	r=0
Ё	1],
r=0
получающееся заменой J2r(^) на Y2r{z).
Аналогичное представление имеют также другие пары решений:
Се2п+1(г, Я) = _сек(тг/2 а) ^
/
Cth Z EB- + iMft-t^i B^ sh
r=0
и Fei/2n+i(^, g), получающееся заменой J2r+i(^) на Y2r+i(z);
= S62;+1ir/n2+'1f) * z f)(-l)'Br + DB^t4^! B^9 ch
и Gey2n+1(z, g), получающееся заменой J2r+i{z) на V2r+i(^);
n+2(Z, q) = Se2tI^2l+2)'?) cth г f>r + 2)В<2Д+2) J2r+2B^ sh г),
и Gey2n+2(z, g), получающееся заменой J2r+2{z) на У2г+г(^).
Модифицированные функции Матье третьего рода Ме„ B, g), Ne^'^z, g), j = 1, 2,
получаются при замене в приведенных выше рядах Jn(z) на Н^ (z).

II.4- Пси-функция ф{г)	671
Другие модифицированные
TTV=»L-n ( "у п\ —
A biV2n^ , Ц J ,
с 1 ( ) se2
7Г
Формулы связи:
Ce2n(^, q) -
Ce2n+1(Z, q) +
Se2n+i(z, g) + г
Se2n+2(z, g) + i
Cen(z, g)^iFeyn(z, q
функции
), g) v^.
2n) Z^^
r=0
дBп+1)
n + lGr/2,
A sPn+1
>п+2(тг/2,
^Fey2n+1(
Gey2n+1(
Gey2n+2(,
) = Mei2)(
Матье
я), ^
th ~
= ,?) =
*,9) =
?, ?) =
третьего
- K2r{ -
)
r=l
r=0
Ne«+2(a
Sen(«
рода
<?) =
^,9)
г, g)
,9) =
, <?)-
&hZ) °8Ьг>1;
[|shz| > 1;
->/Wl(-2^cM
+1 ^2r+2(^2i-^g ch z)
= -2Fek2n+1(a, g),
= -2Gek2n+1(ZjG),
= -2iGek2n+2(«, q),
- iGeyn(z, q) = Ne^2)(z
Re г
Rez
,9),
>0],
>0],
( )	( j
. Gey2n+1@, g) Gey2n+1@, g)
n+1(^z, g) = —	—— se2n+i(z, g) + —	—— ge2n+1(z, q).
selu 9J	ge^u gj
2n(z, ±g),	Me^+1(z, g) = ^2Fek2n+1(z, g),
Mei^fz, -9) = 2iFek2n(z, ^gM Ne^+1(^, g) = ^2Gek2n+1(z, g),
N4n+i(^» ~^) = 2iGek2n+iB;, -9),	Ne^+2(^, ±q) = -2i Gek2n+2B:, ±q).
Некоторые свойства:
ceo (ж, 0) = —=, сеп(ж, 0) = cosnx (n/0), sen(x, 0) = sin ж.
V2
Г сеп(штг + z, g) 1 _ f cen
\ sen(m7r + z, g) J	\ sen
(штг - z, g)
(ттт - z, g) у
enGr/2 + z, g) 1 = ± те Г сете(тг/2 - z, g) 1 ( cen(z + 7r, g) 1 =	n f cen(z, g)
enGr/2 + z, g) j	\ 8еп(тг/2 - z, g) j ' \ sen(z + тг, g) J	j\sen(z,g)J'
{/	\	Л	Г	/	Icy	\	\
ce2n+i(z, -g) J	\se2n+iGr/2 - z, q) у
se2n+i(z, -g)\ =	n Г се2„+1(тг/2 - z, q) 1
^l j \se2n+2Gr/2^z, g)J'
f fe2n(^, -9) \= / -jxnf feGr/2-2, g)
Ife2n+1(z, ^g)J Tl j 1
ge2n+1 {*/2-z,q)f'

672	Прил. П. Некоторые специальные функции и их свойства
(ge2n+1(z
i (
I &e2n+2\Z
f Fe2n(z, -
\Fe2n+1(z, ¦
¦ ,-я)
¦ ,-я)
<
¦q) 1
-я)}
\
} = (-D-{^
f Ce2n(z, -q) 1
[Ce2n+i(z, -9) J =
f S
f Fe2n(;
~ \-iGe2n4
fGe2n+1(z,^g)| =
i*/2-z,q))
(тг/2 - z, g) J '
= (_1}nf Ce2n(^ + W2,g) 1
)e2n+i(z, -^I +1J iCe2n+i(z +
)e2n+2(z, -q) J 1 Se2n+2(z + i
* + *i/2,q) 1
^(z + Tri/2, g)j'
_/ 1xn4-if *Fe2n+i(z + 7ri/2, g)l
^l } 1 Ge2n+2(z + 7ri/2, g) /'
В приведенных ниже формулах используются обозначения
^*2п4-1
оо
\"""Y
Z-Л
оо
оо
Е(-
се2п
.@, д)се2те(тг/2, д)
ce2n+i@, д)се2те+1(тг/2,
о л/Ч ^*-i
se2n+i@, g)se2n+iGr/2, g) se2n+2@, g) se2n+2Gr/2
ifB'
V " 1 ©о
n=0
oo
gBBn+2)
4Bn)^Bn) = 1^ r>
oo
V^ 4Bn) 4Bn) _ V^ 4Bп+1)лBп+1) _
/ j /~±2г+2/~±2я4-с2 — / , /±clr4-'\ -^2.4-1-1 —
?,	a/ ' 1
n=0
oo
\™~^ oBn + l) RB^
— / 2t*4-1 2s*
n=0
oo
r=0
,J^_1 cos Br + 1)го.
jBfi4~l) • /f) | i \
2r^2 sin Br + 2)w<
n=0
oo
re+!) _ \^ rB^+2) RBn+2) _ Л
I  _____ Jp Jf	Ji ^ - ^ ?	J л 1 л _____ fjl ^^ О »
T~j- ^	^ ZV~f-Z ZS~f~Z ' ? й
n=0
2rioJ2r(z) = 	се2п(гь) Ce2n(v).
P2n
1 -
}J2r+l{Z) — g2n+1 SG2n + 1\Ui 4)^e2n+l(Vj
J2r+2\Z) — SV2n+2\u>, C[)oe2n+2\V.
S2n+1
Я)
,я)
, я),
я),
.я),
i,Q)\
,я) У
где z = 2yg(ch2 v — sin2 гг) , tg го = tg и th v.
r+1 (y/q e) + Jr+1
се2п(тг/2, д)'
ДBп)
= —-— ce2n(z, g),
Jr
(у/Я etz) Jr+i (Vq e^z) - Jr+1 (jq e%z) Jr
.RBn+1)
= 	se2n+i(z, g),
S21
e"") - J.+2 (y/q e*z) Jr (y/q e~iz)
se2n+2(z, g),

II.4- Пси-функция ф(г)	673
?n)/r (y/q e-z) Ir (y/q eiz)
-I)"-*—се2„(г, -q),
Р2п
^(^l)r42rn) Jr (y/q e~z) Jr (y/q ez) = ^- Ce2n(z, g),
Jr+i (y/q ez) - Jr+i (y/q e^z) Jr (y/q ez)] =
	Se2n+i(z, g),
•2n+l
Jr+i (y/q ez) + Jr+i (y/q e^z) Jr (y/q ez)] =
Ce2n+i(^, g),
P2n+1
) Jr+2 (y/q e^z) - Jr+2 (y/q e^z) Jr (y/q ez)] =
oBn+2)
B2
, q),
2n(^, q) = cos2rz - -Sojr,	X 4r+i1) ce2n+i(^, 9) = cos Br
n=0
oo
e2n+i(^, 9) = sin Br + 1)г,	^ B^+t4 se2n+2B, g) = sin Br
П=0
1/1 \
n(^, q) = - cos B-^g cosucosz),
2
\ 	7^	rce2n(tA, g)ce2n(^, q) = -
^ се2п(тг/2, g)	2
oo	ABn)	г
/ 	7^	гсе2п(м, g)ce2n(^, q) = - ch By/q sln^slnz),
^ce2n@, q)	2
дBп+1)	^
+i(^, g)ce2n+iB;, g) = -^^310B^ cosucosz),
A4
те=0 ce2n+i
00	дB
/oT ce2n+i(^,
7r/z? Q)
+1)
ce2n+i('M, q) ce2n+i(^, q) = cos и cos z ch By/g slnnslnz),
^ ce2n+i@, q)
~	5Bn + l)	x
V ; x , —rse2n+i(>, g)se2n+iB:, g) = ^^ sh
Se2+llU 9J	^V^
n=0 Se2
^B
	^7
se2n+i(M, g)se2n+i(^, g) = sin и sin z cos B^g cos^cosz),
V77r
^ se2n+iGr/2, g)
00	BBn + 2)	1
2\. —~f—^7—/	г se2n+2(^fc, q) se2n+2(^,	g) =	— sin и sin 2; cos By/q cos и cos z),
f^Q se2n+2l7r/2? 9)	УЧ
oo	^Bn+2)	^
V] ; 2 , —rse2n+2(w, g)se2n+2(z,	q) = —— costicoszsh B^g sln^sinz),
Se	U ^j	/4
n=Q
\/4
1
g) ce2nfv, g) ce2n(^5 q) = - cos B^g a^cosz) cos (v/2^ |/sinz)
, g)	/
ce2+i(v g)ce2+i(^ q) = sin B^g ж cos z) cos
Еье2п+1 и, q	i .
	^ce2n+i(^, g)ce2n+i(^, q) = —sin
«2n+l	2
n=0
\~^ 8е2п+1(^? g)	/\	/ \ 1 /« /—	\ • / /7T~ • \
/	^se2n+i(v, g)se2n+i(^, q) = — cos B^g x cosz) sin [\/2q ysmz ,
^	S2n + 1	2
22 А. П. Прудников, Т. З

674	Прил. П. Некоторые специальные функции и их свойства
fc, q)
>	se2n+2(v, q)se2n+2(z, q) =
где ж = спи sin г; cos <z>, t/ = ch it sin v sin <p, e ^ =
n+2(v, q)se2n+2(z, q) = - cos B^ ж cos z) sin (y2g f/smz)?
ch (u — iv) — z
11.24. МНОГОЧЛЕНЫ НЕЙМАНА On(z) Ш ШЛЕФЛИ Sn(z)
kl
B)
Oo(z) = -Oi(z),	2О;(г) = О„_1(г)-Оп+1(г)	[n = 1, 2, ...]
(n - l)On+i(z) + (n + l)On-i(z) - 2(П -1)Оп(г) = — sin2 ^	[n = 1, 2, .. .]
2	Z	2
Z
nzOn±1(z) - (n2 - l)On(z) =
O2n+i0) = Bn-
[n/2]
"! '*'" "	[n = l,2, ...]
fc=O
50(z) = l, nSn(z) = 2zOn(z)^
11.25. ФУНКЦИИ i/(z), i/(z, p), /x(z, A), /x(z, A, p)
Определения:
t 2
г(ГГТ) dt'
' A) =
Г(А + m + 1) J	dtw Lr(^ + P + 1)
о
y-i —ш, p) = (—
[ReA>-m-l].
U{Z) = 1/B, 0) = /iB, 0) = /iB, 0, 0),	1/B, p) = /XB, 0, p),
r, A) = /xB, A, 0) = zfi(z, A - 1, -1), zi/(z, p - 1) - py{z, p) = /xB, 1, p),
/xB, A + 1, p) = z/i(z, A, p - 1) - p/xB, A, p).
in in
	 l/Bj = 1/B, —TlJ,		 ^(^j PJ =::: ^(^j P ~~ Щ-)
-r— fi(z, A) = /xB, A, -n), -v— /xB, A, p) = /xB, A, p - n).

СПИСОК ЛИТЕРАТУРЫ
1.	Бейтмен Г., Эрдейи А. Высшие трансцендентные функции. — М.: Наука, 1965, т. 1;
1966, т. 2; 1967, т. 3.
2.	Бейтмен Г., Эрдейи А. Таблицы интегральных преобразований. — М.: Наука, 1969,
т. 1; 1970, т. 2.
3.	Брычков Ю. А., Глеске X. Ю., Маричев О. И. Факторизация интегральных преобра-
преобразований типа свертки, Итоги науки и техн. ВИНИТИ. Мат. анализ, 1983, 21, 3-41.
4.	Ватсон Г. Н. Теория бесселевых функций, ч. 1. — М.: ИЛ, 1949.
5.	Виленкин Н. Я, Специальные функции и теория представления групп. — М.: Наука,
1965.
6.	Гобсон Е. В. Теория сферических и эллипсоидных функций. — М.: ИЛ, 1952.
7.	Градштейн И. С, Рыжик И. М. Таблицы интегралов, сумм, рядов и произведений. —
Изд. 5-е. — М.: Наука, 1971.
8.	Диткин В. А., Прудников А. П. Справочник по операционному исчислению. — М.:
Высшая школа, 1965.
9.	Кудрявцев Л. Д. Курс математического анализа. — М.: Высшая школа, 1981, т. 1, 1981,
т. 2.
10.	Лебедев Н. Н. Специальные функции и их приложения. — Изд. 2-е. — М.-Л.: Физмат-
гиз, 1963.
11.	Люк Ю. Специальные математические функции и их аппроксимации. — М.: Мир,
1980.
12.	Мак-Лахлан Н. В. Теория и приложения функций Матье. — М.: ИЛ, 1953.
13.	Маричев О. И. Метод вычисления интегралов от специальных функций (теория и
таблицы формул). — Минск: Наука и техника, 1978.
14.	Математические таблицы/Под ред. В. В. Карпенко, Е. Т. Колесова, Ю. С. Яковлева. —
Изд. 3-е. — Л., 1978.
15.	Никифоров А. Ф., Уваров В. Б. Специальные функции математической физики. —
М.: Наука, 1978.
16.	Никольский С. М. Курс математического анализа. — М.: Наука, 1975, т. 1; 1975, т. 2.
17.	Прудников А. П., Брычков Ю. А., Маричев О. И. Интегралы и ряды. Элементарные
функции. — М.: Наука, 1981.
18.	Прудников А. П., Брычков Ю. А., Маричев О. И. Интегралы и ряды. Специальные
функции. — М.: Наука, 1983.
19.	Салехов Г. С, Муратов Л. М., Поспеев В. Е. Вычисление рядов и несобственных
интегралов. — Казань: Изд. Казанск. ун-та, 1973.
20.	Слейтер Л. Дж. Вырожденные гипергеометрические функции. — М.: ВЦ АН СССР,
1966.
21.	Справочник по специальным функциям с формулами, графиками и математическими
таблицами/Под ред. М. Абрамовича и И. Стиган. — М.: Наука, 1979.
22.	Титчмарш Е. Введение в теорию интегралов Фурье. — М.: Гостехиздат, 1948.
22*

676	Список литературы
23.	Титчмарш Е. Теория дзета-функции Римана. — М.: ИЛ, 1953.
24.	Уиттекер Э. Т., Ватсон Г. Н. Курс современного анализа. — Изд. 2-е. — М.: Физ-
матгиз, 1962, т. 1: 1963 т. 2.
25.	Филиппов Ю. Ф. Таблицы неопределенных интегралов от высших трансцендентных
функций. — Харьков: Изд. Харьк. ун-та, 1983.
26.	Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, т. 1-3. —
М.: Наука, 1966.
27.	Хадтси П. И. Функция вероятности/Ин-т прикладной физики АН Молд. ССР. —
Кишинев, 1971.
28.	Янке Е., Эмде Ф., Леш Ф. Специальные функции. Формулы, графики, таблицы. —
Изд. 3-е. — М.: Наука, 1977.
29.	Agarwal R. P. Generalized hypergeometrlc series. — New York: Asia Publ. House, 1963.
30.	Appell P. Sur les fonctions hypergeometriques de plusleures variables. — P.: Gauthler-
Villars, 1925.
31.	Appell P., Kampe de Feriet J. Fonctions hypergeometriques et hyperspherlques. — P.:
Gauthier-Vlllars, 1926.
32.	Bailey W. N. Generalized hypergeometrlc series. — London and New York: Cambridge
Univ. Press, 1935.
33.	Buchholz H. The confluent hypergeometric function. With special emphasis on Its applica-
applications. — Berlin: Springer-Verlag, 1969.
34.	Byrd P. F,, Friedman M, D. Handbook of elliptic Integrals for engineers and scientists. —
Berlin: Springer-Verlag, 1971.
35.	Colombo S. Les transformations de Mellin et de Hankel, applications a la physique
mathematique. — P.: CNRS, 1959.
36.	Colombo S., Lavoine J. Transformation de Laplace et de Mellin. Formulaires. Mode
d'utilisation. — P.: Mem. Sci. Math., 1962.
37.	Doetsch G., Kniess H., Voelker D. Tabellen zur Laplace-Transformation. — Berlin;
Gottingen, Springer-Verlag, 1947.
38.	Doetsch G. Handbuch der Laplace-Transformation. — Basel, Birkhauser Verlag, 1950-
1956, Bd I-IV.
39.	Edwards U. M. Rjemann's zeta function. — New York: Academic Press, 1974.
40.	Exton H, Multiple hypergeometric functions and applications. — New York-London-
Sydney-Toronto: Chlchester, Ellis Horwood, 1976.
41.	Exton H. Handbook of hypergeometrlc integrals: theory, applications, tables, computer
programs. — New York-London-Sydney-Toronto: Chlchester, Ellis Horwood, 1978.
42.	Hansen Eldon R. A table of series and products. — Englewood Cliffs. — London: Prlntlce-
Hall, 1975.
43.	Igusa J. Theta functions. — Berlin: Springer-Verlag, 1972.
44.	Lang S. Elliptic functions. — New York: Adisson Wesley, 1973.
45.	Lewin L. Dllogarithms and associated functions. — London: MacDonald and Co., 1958.
46.	Luke Y. L. The special functions and their approximations. — New York: Academic Press,
1969, vol. 1, vol. 2.
47.	MacRobert Т. М. Functions of complex variable. — London-New York, MacMIllan, 1962.
48.	Magnus W., Oberhettinger F., Soni R. P. Formulas and theorems for the cpecial functions
of mathematical physics. — 3 ed. — New York-Berlin: Springer-Verlag, 1966.
49.	Mathai A. M., Saxena R. K. Generalized hypergeometric functions with applications in
statistics and physical sciences. — Lect. Notes Math., 348, Heidelberg-New York: Springer-
Verlag, 1973.

Список литературы	677
50.	Mathai A. M., Saxena R. К. The //-function with applications In statistics and other
disciplines. — New York-London-Sydney-Toronto: Halsted Press Book, 1978.
51.	Meixner J., Schotke F. W., Wolf G. Mathieu functions and spheroidal functions and their
mathematical foundations. — Berlin: Springer-Verlag, 1980.
52.	Oberhettinger F. Tabellen zur Fourier Transformation. — Berlin: Springer-Verlag, 1957.
53.	Oberhettinger F., Higgins T. P. Tables of Lebedev, Mehler and generalized Mehler trans-
transforms. Math. Note, №246, Boeing Scientific Research Laboratories, Seattle, Washington,
1961.
54.	Oberhettinger F. Tables of Bessel transforms. — New York-Heidelberg-Beriin: Springer-
Verlag, 1972.
55.	Oberhettinger F. Fourier expansions. A collection of formulas. — New York: Academic
Press, 1973.
56.	Oberhettinger F., Badii L. Tables of Laplace transforms. — Berlin-Heidelberg-New York:
Springer-Verlag, 1973.
57.	Oberhettinger F. Tables of Mellin transforms. — New York-Heidelberg-Berlin: Springer-
Verlag, 1974.
58.	Roberts G. E., Kaufman H. Table of Laplace transforms. — Toronto: McAinsh and Co.;
Philadelphia; London: W. B. Saunders Co., 1966.
59.	Slater L. J. Generalized hypergeometric functions. — London-New York: Cambridge Univ.
Press, 1966.
60.	Srivastava H. M., Buschman R. G. Convolution integral equations with special function
kernels. — New Delhi, Bangalore: Wiley Eastern Ltd., 1977.
61.	Srivastava H. M., Gupta K. C, Goyal S. P. The //-functions of one and two variables with
applications. — New Delhi, South Asian Publishers, 1982.
62.	Tricomi F. Elliptische Funktlonen: — Academische Verlagsgesellschaft, 1948.
63.	Tricomi F. Fonctlons hypergeometriques confluentes. — Mem. Sci. Math. Fasc, 140, Paris:
Gauthier^VIllars, 1960.
64.	Voelker D., Doetsch G. Die Zweidimensionale Laplace Transformation. — Basel: Birk-
hauser, 1950.
65.	Wheelon A. D. Tables of summable series and integrals Involving Bessel functions. — San
Francisco: Holden-Day Inc., 1968.

УКАЗАТЕЛЬ ОБОЗНАЧЕНИЙ ФУНКЦИЙ И ПОСТОЯННЫХ
А(х) — алгебраическая или степенная функция с постоянным показателем.
am i
am и = am (it, к) — эллиптическая функция Якоби, и =
dt
Ai (z) = -xl^ K1/3 (I z3/2) - функция Эйри.
л/l - k2 sin2 t
\	u
±	z3/2 1 — функция Эйри.
о	\ о	/
arccosz, arcctgz, arcsinz, arctgz — обратные тригонометрические функции.
Arch z, Arcth z, Arsh z, Arth z — обратные гиперболические функции,
arg z — аргумент комплексного числа z (z = z etargz) .
Bn — числа Бернулли.
Bn(z) — многочлены Бернулли.
Cz(a, b) = ж'а — 1'A — x) ~~1 dx — неполная бета-функция
о
bei^(z), beru(z), bei (z) = beio(z), ber (z) = bero(z) — функции Ке
Bi (z) = ,/f [/_1/3 (\ z3/2) + /1/3 (\ z3/2)] - функция Эйри.
С фA) 0 5772156649	ЭМ
С = — фA) = 0, 5772156649 ... — постоянная Эйлера-Маскерони.
X
If cos t
С(х) = 	 —— dt — косинус-интеграл Френеля.
у2тг J л/t
О
сю
С(х, v) = t1"^1 cos tdt [Re v < 1] — обобщенный косинус-интеграл Френеля.
X
С„ (z) = 	— 2-^1 I —п, те + 2А: АН	: 	 I — многочлены Гегенбауэра.
~ ^ ' —г/, 2А + и; АН	; 	 ) — функция Гегенбауэра.
^ i\ 2F1 ( I/, 2A + I/; А + ; ^
+ L)	\	АЛ
Cen(z, q) — модифицированная функция Матье 1-го рода.
cen(z, q) — периодическая функция Матье 1-го рода.
en z = 	 — гиперболическая функция.
2	х
chi (ж) ^ С + In ж + 	dt — интегральный гиперболический косинус.
ею	О
ci (ж) = — 	dt — интегральный косинус.
X
Ob (z) = — In I 2 sin — I dt — интеграл Клаузена.
о
о
спи = cos (am it) — эллиптическая функция Якоби.
cos z = ch (iz), cosec z =	тригонометрические функции.
sin z
cosech z =	гиперболическая функция.
shz
cos z
ctg z = 	 = г cth (iz) — тригонометрическая функция.
sin z
chz
cth z =	гиперболическая функция.
shz
+	— часть плоскости s, лежащая слева (справа) от контуров

Указатель обозначений функций и постоянных	679
. . f sin2 tdt	/тг \
~D(k) = —,	= D ( —, к) — полный эллиптический интеграл.
J x/l - к2 sin2 t	V2' /
, A;) =
J
f sin2 t dt
= —	— эллиптический интеграл.
J \/l - ^2 sin2 t
Dv{z) = 2v'2e~~z /4Ф I	, —; — J — функция параболического цилиндра.
dn г* = у 1 — k2 sin (am и) — эллиптическая функция .Якоби.
тт/2
Е(А;) = v 1 — /с2 sin t dt — полный эллиптический интеграл 2-го рода.
0 v
Е((р, k) = v 1 — к2 sin2 t dt — эллиптический интеграл 2-го рода.
о
о
Еп — числа Эйлера.
En(z) — многочлены Эйлера.
7Г
7Г
= — sin (yt — z sin t) dt — функция Вебера.
тг J
о
Ep(z; fi) = Л, 	;— [p > 0] — функция типа Миттаг-Леффлера.
Ei (ж) = — dt — интегральная показательная функция.
E(jp\ аг : q\ bs : z) = ?/((ар); {bq)] z) = E\
I — функция Мак-Роберта.
bq) J	\(bq); z
1, 61, ..., 6,
x 01, . .., ap
e = 2, 718281828459. . . — число е.
ez = exp z — показательная функция.
2 Г 2
erf (ж) = —=¦ e~~t dt — интеграл вероятности.
V« J
0
2 Г 2
erfc (ж) = 1 — erf (ж) = —=¦ e~* dt — дополнительный интеграл вероятности.
¦\/тг J
х	х
2 Г 2
егп(ж) = --— е* dt — интеграл вероятности мнимого аргумента.
У" J
О
•, fe) =	— эллиптический интеграл 1-го рода.
J у 1 — 1г2 sin2 t
fen(z, g), Fen(^, g), Feyn(z, g), Fekn(^, g) — вторые непериодические решения уравнения Матье.
2Рг(а, 6; с; 2) . F(a, 6; С; ,) . а^(в' ^ ') = ^ Ъ) ? ^f^^
= г[ С 1 \tb-1(l-t)c-b-1(\-tz)-adt	[Rec>Re6>0; I arg A - z)\ < ж]
L6, с — 6J j
о
— гипергеометрическая функция Гаусса.
pF,(oi,...,op; bi ,...,&,; г) = pF,((op); F,); z) = pF,fei' ' ' ' ' °p;
V 01, . . . , Oq
(bq) )-p^q\(bqy, z)-^Q(b1)k(b2)k...(bq)k k\
— обобщенная гипергеометрическая функция.

680
Указатель обозначений функций и постоянных
ОО / х	Д.
i-Fi(o; b; z) = \^ 	 — вырожденная гипергеометрическая функция Куммера.
(fe)fe!
^\a, 61, . . . , bn; ci, . . . , с„; zu ..., zn) =
k±,. kn=o
— функция Лауричелла.
¦j=i	J
— функция Лауричелла.
(. . . ; w, z) [j = 1, 2, 3, 4] — функции Аппеля:
.-.^. 1-
[\w
tp t и и' / ч V^ Ka)k+lWkKb )l ™ %
Г2\О", о, о : с, с : ги, z) = > 	!
fc^o (c)*(c')i Ш!
-°° {a)k{a')l{b)k{b!)lwkzl
F3(a, a;, 6, 6;; c; w, z)=
к, 1=0
(c)fe+,	A;!/!
G
^, -,_,_, ™, ^7 ^^ (c)fc(c0i kill
= 0, 9159655942 ... — постоянная Каталана
'i\<4
l + l^i <i],
al ? • • • ? a
01, . • . , 0q
= -Lfrf 6
6i + s, . . . , 6m + s, 1 - oi - s, . . . , 1 - on - s
гг + l + 5, . . . , ap + S, 1 — fem + 1 ~ 5, . . . , 1 — bq —
L
L = Ldbooj Liioo-)— G - функция Мейера.
gen(z, g), Gen(z, g), Geyn(z, g), Gekn(z, g) — вторые непериодические решения уравнения Матье.
I 1 х > О
Н(х) = < ' ^ ' — функция Хевисайда.
0, х < О
/^ ''(z) = Jl/(z)Jt-iYt/(z), Н„ (z) = Ju(z) — iYu(z) — функции Бесселя 3-го рода (функции Ганкеля
1-го и 2™го рода).
2 d	2
Hn(z) = ( — l)nez 	e""z — многочлены Эрмита.
dzn
+l
2; 2z
ttcos/itt
?(z) = J^ 1/2(z) (Hj(z) = Н„й) - обобщенная функция Струве.
,1/2
(oi, v4i), . . . , (op,
,2
*¦ p' p
— ЬГ-функция Фокса.
Iu(z) = —	-( — I o^i ( ^ + 1; — 1 = е ижг' Jv \e7V%' z) — модифицированная функция
Г(х/ + 1) \2/	V	4/	V	/
Бесселя 1-го рода (функция Бесселя мнимого аргумента).
Im z — мнимая часть комплексного числа z = х -\- iy (Im z = у)
1	/ а х ,у	/	Л N
./„(*) =
Г(|/ + 1) V2
Ji/(z) = — cos (yt — z sin i) dt — функция Ангера.
7Г J
Z\
+ l;	I — функция Бесселя 1-го рода.

Указатель обозначений функций и постоянных	681
Jjf(z) = /^ 	 [ц > — 1] — функция Бесселя-Мейтленда.
оо
Г	/-/¦/¦
Jiu(x) = Jv(t)	интегральная функция Бесселя 1-го рода.
X
X
J(Xj у) = 1 - е~у [ е~* Io By/jt) dt
о
тг/2
) = —,	= F I —, к
^ J у/1-к* sin21	l2'
/2
I	— полный эллиптический интеграл 1-го рода.
J у/1-к* sin21	l2 )
KAz) = ^-"W ~ M*)] [i/фп], Kn(z)= \im Ku(z) [n = 0, ±1, ±2, ...]—функция Мак-
2sini/7r	^^^
дональда (модифицированная функция Бесселя 3-го рода).
kv(z) =	,Wu/2,1/2B2:) — функция Бейтмена.
keix,(z), keru(z), kei (z) = keio(^), ker (z) = keroB:) — функции Кельвина.
оо
Kiu{x) = Kv(t)— — модифицированная интегральная функция Бесселя.
X
L±(x>, L>ioo — контуры в интегралах Меллина-Барнса для G- и //-функций.
Li/(z) = е"^"*^71"*/2HI/ (e7rt'2z) — модифицированная функция Струве.
Lu(z) = iFi(—i/; 1; z)—функция Лагерра.
Ln{z) = Ln(z) — многочлены Лагерра.
	|2:n+Ae™'z ) — обобщенные многочлены Лагерра.
п\ dzn V	/
00 fc
fc=l fe
00
= 	 	 [Re ^ > 0; I arg A — z)\ < тг] — полилогарифм порядка i/
Г(х/) J e* — z
0
Li2(z) — дилогарифм Эйлера.
ж
li (z) = Ei (In z), II (z) =	интегральный логарифм
J lot
0
Inz = \n\z\ + iargz — натуральный логарифм. \z = |z|ei(arg z+27rfc), к = 0, ±1, ±2, . . .1
Ми, fji(z) = •2;M+ е"~г/ \F\ ifi — ж -\	; 2/Lt + 1; z) — вырожденная гипергеометрическая функ -
ция Уиттекера.
п[^](п-Л-1)! /z\2fc-n-i
(jn(z) = — >^ 	 1 — 1	— многочлены Неймана.
fc=0
2~"""n dn
z2 l)n
Pn(z) =	(z — l)n — многочлены Лежандра.
тг! dzn
Pu(z) = P®(z) = 2Ft l — i/, l + i/; 1; 	J [| arg A + z)| < тг] — функции Лежандра 1-го рода.
,м/2
5 2
| < тг; ц ф т; т = 1, 2, .
(г-1)| <тг; т = 1, 2, ...].

682	Указатель обозначений функций и постоянных
/ d \ гп
Р™{х) = (^1)тоA - х2)т'2 — Pv{x)	[-1< х < 1; т = 1, 2,
\dxj
— присоединенная функция Лежандра 1-го рода.
Р"Р'ст)B) = SfA ~zyP{1 + zY°l^[A ~z)P+n{1 + zr+n] =
= 	— 2-^1 ( —п, р + о" + n + 1; /э + 1; 	 ) — многочлены Якоби
те!	V	2
Qu(z) = QQv{z) — функция Лежандра 2-го рода.
argz|, |arg(z±l)| < тг; i/+ 1/2, /x + i/^-1, -2, -3,
2
z
+ 5
Ъ {1'4^ -+2;
z±l)|, argz < тг; /i + i/ ф -1, -2, -3,
iO) + e*^/2Q{J(aj - iO)] =
2sin/i7r [	L !>• — /x + 1J
[-Kx <l; цф dim; /л + i/ 7^ -1, -2, -3,
— \ Qu(x)	[/x = m; 1/ 7^ -m - 1, -m - 2,
с1ж/
Г(^)	[At=-m; i/Z-m-1, -m - 2,
— присоединенная функция Лежандра 2-го рода.
2 \
х 2^1 (п + 1, р + п + 1; р + а + 2п + 2] 	 1	[|arg(z±l)| < тг]
— функция Якоби 2-го рода.
Re z — действительная часть комплексного числа z = х + iy (Re z = х)
res (f(z) — вычет функции (f(z) в точке а.
z = a
х
S(x) = 	 —-=- dt — синус-интеграл Френеля.
\/2тг J yt
о
оо
S(x, 1/) = t^^1 sin tdt [Re v < 1] — обобщенный синус-интеграл Френеля.
X
[^] (n- k - 1)! /z\2fe-n
Sn(z) = \ 	 I — ]	, Sq(z) = 1 — многочлены Шлефли.
fc=O	2
/m\	^-^	k I П + К -— 1\/ 2n — 771 \ jl
^n = > (-1)	, ,	i Fn-m+fe — ™сла Стерлинга 1-го рода.
f^	\n — m + k J \n — m — k J	^
j- f]	I — функция Ломмеля.
sen(z, q) — периодическая функция Матье.
Sen(z, q) — функция Матье мнимого аргумента.
, u(z) = 	1F2 I 1; 	, 	;	I — функция Ломмеля.
U ~т~ -L 1	\	zi	zi	*±
sec z =	тригонометрическая функция, sech z =	гиперболическая функция.
cos z	ch z

Указатель обозначений функций и постоянных	683
A, ж > О,
О, ж = О,
-1, ж < О.
sh z =	гиперболическая функция.
А
х
shi (ж) = 	dt = — г Si (ix) — интегральный гиперболический синус.
О
X
о. , ч f sint
hi (ж) = 	at — интегральный синус.
О	оо
si (ж) = Si (ж)	= — 	dt — интегральный синус.
2	J t
X
sin z = —г sh (iz) — тригонометрическая функция.
sn и = sin (am и) — эллиптическая функция Якоби.
(	\ \ — z\
Tn(z) = cos (narccosz) = F j —n, n; —; 	 I — многочлены Чебышева 1-го рода.
sin z
tgz = 	 = —ith (iz) — тригонометрическая функция.
cos z
sh z
th z =	гиперболическая функция.
chz
sin [(n + 1) arccos z] ( 3 l--z\
Un(z) = 			 = (n + 1) 2F1 I —n, n + 2; —; 	 J — многочлены Чебышева 2-го
рода.
Ut/(wj z) ~=- \ ( —1) ( — J	^2kJt-u(z) — функция Ломмеля двух переменных.
fe=O	Z
УУж, fi{z) = z^ ' eTz' Ф I fi — ж -\—, 2/i + 1; z\ — вырожденная гипергеометрическая функция
\	2	/
Уиттекера.
Yv(z) = cosl/7rJ^(z) J~v{z)	^	= Цт y^	[n = 0, ±1, ±2, ...1 - функция
Sin 1/7Г	i/->n
Неймана (функция Бесселя 2-го рода).
t/n(z, a, 6) = 2^0 (—71, а — 1 + п;	] — обобщенные многочлены Бесселя.
yn[z) = 2-^0 ( ~~ni 71 + 1;	1 — многочлены Бесселя.
оо
Yiv{x) = Yv(t)	интегральная функция Бесселя 2-го рода.
В (а, C) = —	бета-функция.
Г(а + /3)
X
Зх(а, /3) = ta~1(l - tI3^1 dt [Rea > 1; ж < 1].
о
xa
arg A — ж) I < тг] — неполная бета-фукнция.
P(z) = tz^1e^t dt [Re z > 0] — гамма-функция.
0 оо
r(i/, ж) = tI/™'1e""t dt = е~~~жФA — i/, 1 — i/; ж) — дополнительная неполная гамма-функция.
X
X
Г	Xv
7(^5 ж) = Г(г/) - ГA/, ж) = t1/~1e~*dt = — iFi(t/; 1/ + 1; -ж) [Re и > 0] — неполн,
;ая гамма-
функция.

684	Указатель обозначений функций и постоянных
П Г(ол)
1, ...,6,. =
3 = 1
a q + 1	g + fc^ 1	(ар) (ар) + 1	(ар) + fe - 1
, а) = —, 	, • • • , 	,	^(^j \ар)) '= 	)
!
fb	tb	ГЪ	fb	fb	№
т Ф п	JZ
%^п — ^	— символ Кронекера.
1, т = п
C(z) = \J — [Re z > 1] — дзета-функция Римана.
fe=i kZ
oo	i
C(z, v) = 2_j 7	r™" [Re z > 1; v Ф 0, —1, —2, . . .] — обобщенная дзета-функция Гурвица.
Oj(z, q) [j = 0, 1, 2, 3, 4] — тэта-функции:
CO
fe=l
oo
пЛ( у п\ — О \ Л f^i^/,(fe + l/2) cinf9k-l-iW
(/} 1 л^ C| J —— /л У I II C|	Dill I Zj Л/ "T~ 1 Ja* j
oo
fc=0
oo
^3(z, g) = 1 + 2 ^ qk cos2kz,
fe=i
5 /3, fe) — эллиптическая функция.
а	оо Л	oo
;	,(. A, ,) = J ^^Д [НеЛ > -1].
0
, i/, /e) =
J
о
A - v sin2 t) V1 - к2 sin2 t
p(ti) — функция Вейерштрасса.
а (и) — сигма-функция Вейерштрасса.
— эллиптический интеграл 3-го рода

Указатель обозначений функций и постоянных	685
., т
а™ = — V (-l)m-k (m)kn - числа Стерлинга 2-го рода.
fc=O
, S#(l/;z) (So B) = 0) — функции гипергеометрического типа.
= ? * L (c) - °/> (d) + °i J S+cF-4+D-1 {	1 + aj - (a)', (d) + Oi
[<ij —- а^ ф 0, dzl, db2, . . . ; j ф k] j, /e = 1, 2, .
/	(_л\О-В ¦
)'-^, (a)+ 6*1 „
\ a+dFb+c-i
[^ - bk ф 0, ±1, ±2, . . . ; j ф k] j, к = 1, 2, . . . , В].
00 zfe
Ф(*, s, v) = Y, f Mh,s	M < i; « # o, -l, -2, ...]
CO / \	/, \	hi
ж ( и	\	\^ ia)k + l(b)k WKZ"
Ф2F, 6 ; с; ги, z) = ^ —	——, Ф3F; с; ад, z) =
% ^)	kill
——,	Ф3F; с; ад, z) = ^ Т\	ГГ7
kill	k%Q(c)k+i kl11
[1 — с 1	Гс — ll
iFi(a; с; z) + Г	z1^0 iFi(l + a - с; 2-е; z) -- вырожденная
1 + a ~~ ej	L « J
гипергеометрическая функция Трикоми.
^пг	[N<4
Zl
= [lnr(z)]; = —у — пси~функция.

УКАЗАТЕЛЬ ОБОЗНАЧЕНИИ СИМВОЛОВ
(а) = а\, а2, . . • , а,_д; (ар) = aii а2? • • • •> о>р — специальные векторы.
(ар — Ьр) = а\ — 6i, «2 — ^2, ... , dp — Ьр
(а) + s = «1 + s, «2 + s, . . . , ад + s; (ар) + 5 = а\ + s, . . . , ар + 5;
(а)' — aj = а\ — «j, . . . , ttj-i — а^, aj_|_i — а^, . . . , ад — «j	[1 ^ i ^ ^]
(ар) — a,j = ai — a,j, . . . , aj_i — «j, a,j+i — aj, . . . , ap — «j	[1 ^C j <C. p]
(а)к = cl{cl + 1) . . . (a + A; — 1) [fe = 1, 2, 3, . . .], (a)o = 1 — символ Похгаммера.
[ap, Ар] = (ai, Ai), (a2, A2), . . . , (ap, Ap)
n! = 1 • 2 • 3 . . . (n - l)n = (l)n, 0! = 1! = (-1)! = 1
Bn)!! = 2 • 4 • 6 . . . Bn - 2Jте = 2теп!
ОН = (-!)!! =
n!
k\	k\(n-k)\	k\	' V0
циенты.
Re a, Re b > с означает Re a > с и Re 6 > с.
[ж] = n [n ^ x < n + 1, n = 0, ±1, dz2, . . .] — целая часть числа ж.
ж > 0,
= 1 — биномиальные коэффи-
-{Г
-{
— усеченная степенная функция,
ж < 0
I, i ж, ж > О,
|ж| = ^	— модуль числа ж.
— ж, ж < О
~z =¦ х — ъу [z = х + it/]
у?(ж) = О(%(ж)), ж —>¦ жо (у(ж) = о(%(ж)), ж —>¦ жо) — отношение 	 ограниченно (стремится к
нулю) при ж —> жо-
со
?>*(s) = Ж5^1у?(ж) с!ж — преобразование Меллина функции (р(х).
о
7+гоо
If	_
(р(х) = 	7	(p*(s)x s ds [ж > 0] — обратное преобразование Меллина.
ZTTt J
7 — гоо
<р(х) <—^° (f* (s) — символ соответствия (интеграл 	; cp*(s)z^s ds = (f(x) существует только
V	2?ri J
L
при L = L±oo; при L = Liqq он расходится J.
	 Г	'	\z~8 ds \L = L+oo, bjool — интеграл Меллина-Барнса
2ттг ] [(c) + 8,(d)-s\	L	J

Указатель обозначений символов	687
р	оо	п
3 = 1	k = l	fe = l
Р	п
( \ _|_ и\ — ГТ С - _|_ 6)	\^ — 4-	+ +	Г > 1
afc = amam+i . . . ап [п > т],	=0	[п < т]
i
оо	те
= 1	\п < т]	)> cife(z) = lim )> «fc(z)
^-—'	те—>оо ^—'
fe=l	fe=l

Научное издание
ПРУДНИКОВ Анатолий Платонович
БРЫЧКОВ Юрий Александрович
МАРИЧЕВ Олег Игоревич
ИНТЕГРАЛЫ И РЯДЫ
Том 3
СПЕЦИАЛЬНЫЕ ФУНКЦИИ. ДОПОЛНИТЕЛЬНЫЕ ГЛАВЫ
Редактор Е.Ю. Ходан
Корректор Т.С. Вайсберг
Оригинал-макет Т.Н. Савицкой
Оформление переплета А.Ю. Алехиной
ЛР №071930 от 06.07.99. Подписано в печать 06.02.03.
Формат 70x100/16. Бумага офсетная. Печать офсетная.
Усл. печ. л. 55,73. Уч.-изд. л. 76,82. Заказ №
Издательская фирма «Физико-математическая литература»
МАИК «Наука/Интерпериодика»
117997 Москва, Профсоюзная, 90
E-mail: fizmat@maik.ru
Отпечатано с готовых диапозитивов в ПФ «Полиграфист».
160001, г. Вологда, ул. Челюскинцев, 3.
Тел.: (8172) 72-55-31, 72-61-75, факс (8172) 72-60-72.
E-mail: form.pfp@votel.ru http://www.vologda/~pfpv
EBN 5-9221-0325-3
9 785922 103251