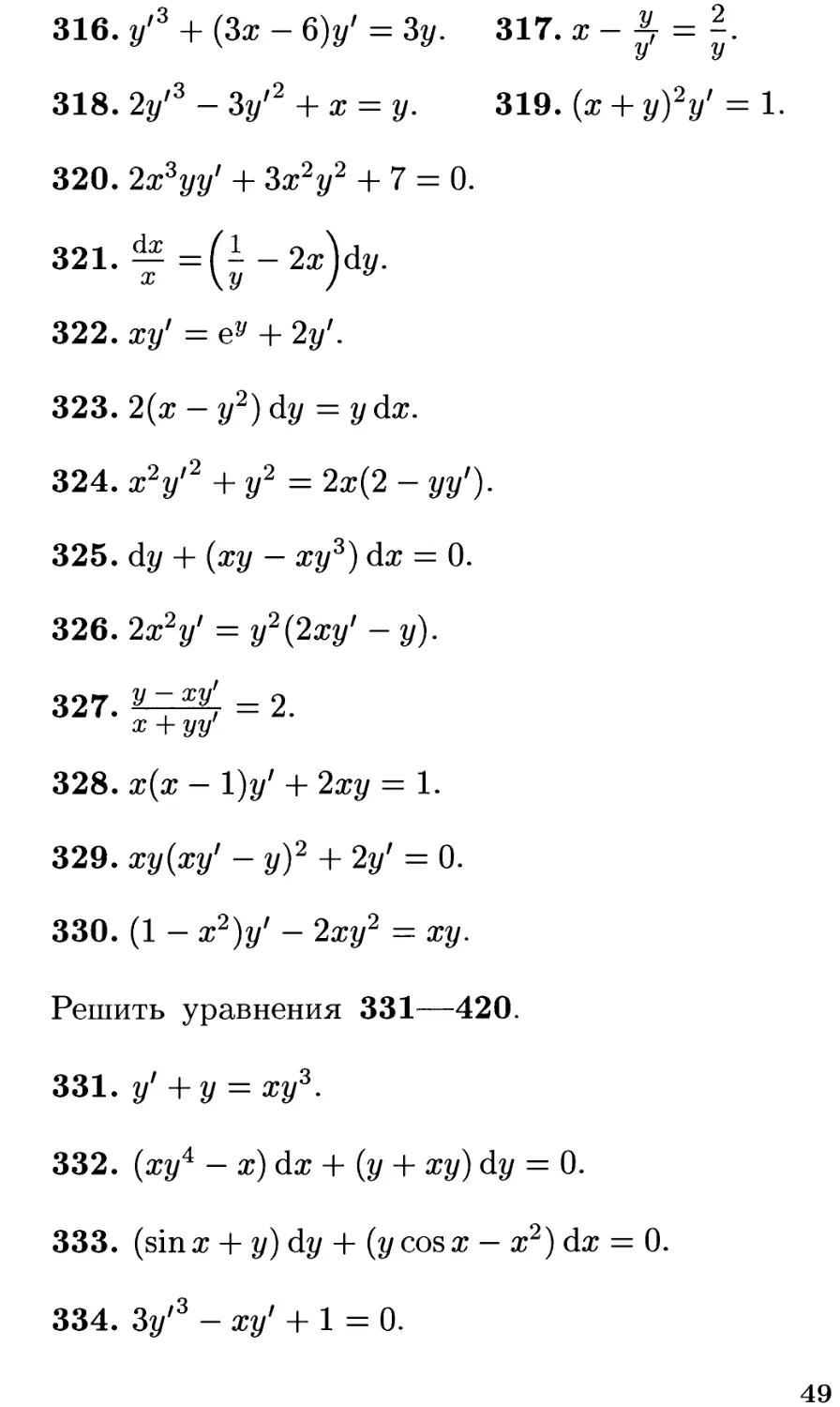А. Ф. ФИЛИППОВ
СБОРНИК ЗАДАЧ
ПО
ДИФФЕРЕНЦИАЛЬНЫМ
УРАВНЕНИЯМ
ИЗДАНИЕ ВОСЬМОЕ, ДОПОЛНЕННОЕ
МОСКВА
"ИНТЕГРАЛ-ПРЕСС"
1998
ББК 517.2
Ф 53
УДК 517.9
Филиппов А. Ф.
Сборник задач по дифференциальным уравне-
ниям: — М.: Интеграл-Пресс, 1998. — 208 с.
ISBN 5-89602-010-4
Сборник содержит материалы для упражнений по курсу диф-
ференциальных уравнений для университетов и технических вузов
с повышенной математической программой.
В настоящее издание добавлены задачи, предлагавшиеся на
письменных экзаменах на механико-математическом факультете
МГУ.
ISBN 5-89602-010-4
9 785896 020103
@ Издательство «Интеграл-Пресс», 1998
СОДЕРЖАНИЕ
Предисловие........................................ 5
§ 1.	Изоклины. Составление дифференциального урав-
нения семейства кривых............................. 7
§	2.	Уравнения с разделяющимися переменными.	11
§	3.	Геометрические и физические задачи..... 14
§	4.	Однородные уравнения................... 21
§	5.	Линейные уравнения первого порядка..... 25
§ 6.	Уравнения в полных дифференциалах. Интегриру-
ющий множитель.................................... 30
§	7.	Существование и единственность решения. 35
§	8.	Уравнения, не разрешенные относительно производ-
ной 	   42
§	9.	Разные уравнения первого порядка....... 48
§ 10.	Уравнения, допускающие понижение порядка....	54
§11.	Линейные уравнения с постоянными коэффициен-
тами ...........................................   60
§ 12.	Линейные уравнения с переменными коэффициен-
тами ............................................. 75
§ 13.	Краевые задачи.............................. 87
§ 14.	Линейные системы с постоянными коэффициентами 91
§ 15.	Устойчивость .............................. 105
§ 16.	Особые точки.............................   117
§17.	Фазовая плоскость.......................... 124
§ 18.	Зависимость решения от начальных условий и пара-
метров. Приближенное решение дифф, уравнений ..	130
§ 19.	Нелинейные системы......................... 142
§ 20.	Уравнения в частных производных первого порядка 146
Добавление....................................... 154
§ 21.	Существование и единственность решения..... 155
§ 22.	Общая теория линейных уравнений	и систем.... 159
§ 23.	Линейные уравнения и системы с постоянными
коэффициентами................................... 164
§ 24.	Устойчивость............................... 170
§ 25.	Фазовая плоскость.......................... 173
§ 26.	Дифференцирование решения по параметру и по на-
чальным условиям................................. 177
§ 27.	Уравнения с частными производными первого по-
рядка............................................ 179
Ответы........................................... 181
Ответы к добавлению.............................. 203
4
ПРЕДИСЛОВИЕ
Сборник содержит задачи по курсу обыкновен-
ных дифференциальных уравнений в соответствии
с программой, принятой на механико-математичес-
ком факультете МГУ. Часть задач взята из из-
вестных задачников Н. М. Гюнтера и Р. О. Кузьмина,
Г. Н. Бермана, М. Л. Краснова и Г. И. Макаренко,
учебников В. В. Степанова, Г. Филипса; большинство
задач составлено заново. Более трудные задачи от-
мечены звездочкой.
В начале каждого параграфа изложены основ-
ные методы, необходимые для решения задач этого
параграфа, или даны ссылки на учебники. В ря-
де случаев приведены подробные решения типовых
задач.
В это издание включено «Добавление» (§§ 21 —
27), содержащее задачи, предлагавшиеся на пись-
менных экзаменах и коллоквиумах на механико-
математическом факультете МГУ в 1992 —1996
годах. Задачи составлены преподавателями МГУ
Ю. С. Ильяшенко, В. А. Кондратьевым, В.М.Милли-
онщиковым, Н. X. Розовым, И. Н. Сергеевым, А. Ф. Фи-
липповым.
В книге приняты условные обозначения учебни-
ков:
[1]	В. В. Степанов. Курс дифференциальных урав-
нений.
[2]	И. Г. Петровский. Лекции по теории обыкно-
венных дифференциальных уравнений.
[3]	Л. С. Понтрягин. Обыкновенные дифференци-
альные уравнения.
[4]	Л. Э. Эльсгольц. Дифференциальные уравне-
ния и вариационное исчисление.
[5]	Б. П. Демидович. Лекции по математической
теории устойчивости.
5
6
§ 1.	изоклины.
СОСТАВЛЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО
УРАВНЕНИЯ СЕМЕЙСТВА КРИВЫХ
1.	Решение уравнения у’ — f(x, у), проходящее через точ-
ку (х, у) должно иметь в этой точке производную у', равную
f(x, у), т. е. оно должно касаться прямой, наклоненной под
углом а = arctg f(x, у) к оси Ох. Геометрическое место точек
плоскости (х, у), в которых наклон касательных к решениям
уравнения у' = f(x, у) один и тот же, называется изоклиной.
Следовательно, уравнение изоклины имеет вид /(х, у) = к, где
к — постоянная.
Чтобы приближенно построить решения уравнения у' =
= f(x, у), можно начертить достаточное число изоклин, а затем
провести решения, т. е. кривые, которые в точках пересечения
с изоклинами /(х, у) = к±, f(x, у) = к2, •.. имеют касательные
с угловыми коэффициентами соответственно fci, &2, ... Пример
применения этого метода см. [1], гл. I, § 1, п. 3, или [4], гл. I, § 1.
2.	Чтобы построить дифференциальное уравнение, которому
удовлетворяют кривые семейства
^(х, 7/, С1, ..., Сп) = 0,	(1)
надо продифференцировать равенство (1) п раз, считая у функ-
цией от х, а затем из полученных уравнений и уравнения (1)
исключить произвольные постоянные Ci, ..., Сп •
Пример. Составить дифференциальное уравнение семей-
ства кривых
Cix + (y-C2)2 = 0.	(2)
7
Так как уравнение семейства содержит два параметра, диф-
ференцируем его два раза, считая у = т/(т):
С1 + 2(?/ — С2)т/ = О,	(3)
2У,2+2(У-С2)У" =0.	(4)
Исключаем С\. Из уравнения (3) имеем Ci = —2(у — С2)у';
подставляя это в (2), получим
-2ху'(у-С2) + (у-С2)2 =0.	(5)
Исключаем С2. Из уравнения (4) имеем у — С2 = — у'2 /у", под-
ставляя это в (5), получим после упрощений дифференциаль-
ное уравнение
у' + 2ху" = 0.
3.	Линии, пересекающие все кривые данного семейства под
одним и тем же углом </?, называются изогональными траек-
ториями. Углы (3 и а наклона траектории и кривой к оси Ох
связаны соотношением (3 = а ± р. Пусть
у' = f(x, у)	(6)
— дифференциальное уравнение данного семейства кривых, а
y' = fi(x,y)	(7)
— уравнение семейства изогональных траекторий. Тогда tga =
= f(x, у), tg/3 = fi(x, у). Следовательно, если уравнение (6) на-
писано и угол р известен, то легко найти tg (3 и затем написать
дифференциальное уравнение траекторий (7).
Если уравнение данного семейства кривых написано в виде
Е(т, у, у') = 0,	(8)
то при составлении уравнения изогональных траекторий можно
обойтись без разрешения уравнения (8) относительно у'. В этом
случае в (8) надо заменить у' на tg а = tg(/3^p), где tg /3 = у' —
угловой коэффициент касательной к траектории.
Если же уравнение семейства кривых дано в виде ?/, С)=
= 0, то сначала нужно составить дифференциальное уравне-
ние этого семейства и только после этого — дифференциальное
уравнение траекторий.
8
В задачах 1—14 с помощью изоклин начертить
(приближенно) решения данных уравнений.
1-2/' = у-х2.	2. 2(у + у') =ж + 3.
3. у' =	~ 1.	4. (у2 + 1)у' = У~х.
5. уу' + х = 0.	6. ху' = 2у.
7. ху' + у = 0.	8.у' + у = (х-у')3.
9. у' = х — еу.	10. у(у' + х) = 1.
11. и' = т + Зт/-	12. у' = и	х + у
13. х2 + у2у' = 1.	14. (х2 + у2)уг = 4х.
15. Написать уравнение геометрического места
точек (х, у), являющихся точками максимума или
минимума решений уравнения у' = /(х, у). Как от-
личить точки максимума от точек минимума?
16. Написать уравнение геометрического места
точек перегиба графиков решений уравнений
а) у' = у - ж2;	б) у' = х - е27;
в) х2 + у2у' = 1;	г) у’ = f(x, у).
В задачах 17—29 составить дифференциальные
уравнения данных семейств линий.
17. у = еСх.
19. у = Сх3.
21. х2 + Су2 = 2у.
18. у = (ж-С)3.
20. у = sin(х + С).
22. у2 + Сх = х3.
9
24. Су = sinCa;.
26. (х — а)2 + by2 = 1.
28. у = ах3 + Ьх2 + сх.
23. у = С(х — С)2.
25. у = ах2 + Ьех.
27.	In у = ах + by.
29.	х = ay2 + by + с.
30.	Составить дифференциальное уравнение ок-
ружностей радиуса 1, центры которых лежат на
прямой у = 2х.
31.	Составить дифференциальное уравнение па-
рабол с осью, параллельной Оу, и касающихся од-
новременно прямых у = 0 и у = х.
32.	Составить дифференциальное уравнение ок-
ружностей, касающихся одновременно прямых у =
= 0 и х — 0 и расположенных в первой и третьей
четвертях.
33.	Составить дифференциальное уравнение всех
парабол с осью, параллельной Оу, и проходящих
через начало координат.
34.	Составить дифференциальное уравнение всех
окружностей, касающихся оси абсцисс.
В задачах 35—36 найти системы дифференци-
альных уравнений, которым удовлетворяют линии
данных семейств.
35.	ах + z — Ъ, y2+z2 = Ъ2.
36.	х2 + у2 = z2 — 2bz, у = ах + Ь.
В задачах 37—50 составить дифференциальные
уравнения1) траекторий, пересекающих линии дан-
ного семейства под данным углом
г) Уравнения, получаемые в задачах 37—50, могут быть
решены методами, излагаемыми в дальнейших параграфах.
10
З7.т/ = С^4,	<р = 90°.
38. у1 2 = х + С,	<р = 90°.
39. х2 = у + Сх,	V? = 90°.
40. х2 + у2 = а2,	V? = 45°.
41. у — кх,	<р = 60°.
42. Зж2 + у2 = С,	<р = 30°.
43. у2 = 2рх,	<р = 60°.
44. г = а + cos#,	tp = 90°.
45. г = а cos2 9,	V? = 90°.
46. г = а sin#,	V = 45°.
47. у = ж In ж + Сх,	<р = arctg2.
48. х2 + у2 = 2ах,	V = 45°.
49. х2 + С2 = 2Су,	ср = 90°.
5О.у = Сх + С3,	<р = 90°.
§ 2. УРАВНЕНИЯ С РАЗДЕЛЯЮЩИМИСЯ
ПЕРЕМЕННЫМИ
1. Уравнения с разделяющимися переменными могут быть
записаны в виде
у' =	(1)
а также в виде
M(x)N(y) dT + P(x)Q(y) dy = 0.	(2)
11
Для решения такого уравнения надо обе его части умножить
или разделить на такое выражение, чтобы в одну часть урав-
нения входило только т, в другую — только ?/, и затем проин-
тегрировать обе части.
При делении обеих частей уравнения на выражение, содер-
жащее неизвестные х и у, могут быть потеряны решения, обра-
щающие это выражение в нуль.
Пример. Решить уравнение
х2у2у' + 1 = ?/.	(3)
Приводим уравнение к виду (2):
ж2?/2	= У - 1; х2у2 dy = (у - 1) dT.
Делим обе части уравнения на х2(у — 1):
Переменные разделены. Интегрируем обе части уравнения:
/^Td» = /$; f +?/ + in|y-1| = -1 + с.
При делении на х2(у — 1) могли быть потеряны решения
ж = 0 и 2/- 1 = 0, т. е. у = 1. Очевидно, у = 1 — решение
уравнения (3), а х = 0 — нет.
2.	Уравнения вида у' = f(ax + by) приводятся к уравнени-
ям с разделяющимися переменными заменой z = ах + by (или
z = ах + by + с, где с любое).
В задачах 51—65 решить данные уравнения и
для каждого из них построить несколько интеграль-
ных кривых. Найти также решения, удовлетворяю-
щие начальным условиям (в тех задачах, где ука-
заны начальные условия).
51.	ху dx + (х + 1) dy = 0.
52.	д/т/2 + 1 dx — ху dy.
12
53.	(ж2 — 1)у' + 2ху2 = 0; 2/(0) = 1.
54.	у' ctga; + у = 2; у(х) -> — 1 при х -> 0.
55.	у' =	2/(2) = 0.
56.	ху' + у = у2; 2/(1) = 0,5.
57.	2х2ууг + у2 = 2.	58. у' — ху2 = 2ху.
59.	e~s (1 +	= 1-	60. z' = 10ж+г.
61.	+1 = 1.	62. у1 = cos(y — х).
63.	у' — у = 2х — 3.
64.	(х + 2у)у' = 1; 2/(0) = -1.
65.	у' = \J\x + 2т/ - 1.
В задачах 66—67 найти решения уравнений, удо-
влетворяющие указанным условиям при х —> +оо.
66.	х2у' — cos 2т/ = 1; т/(+оо) = 9тг/4.
67.	Зу2у' + 16ж = 2од3; у(х) ограничено при
х —> +оо.
68.	Найти ортогональные траектории к лини-
ям следующих семейств: а) у = Сх2] б) у = Сех;
в) Сх2 + у2 = 1.
В задачах 69* и 70* переменные разделяются,
но получаемые интегралы не могут быть выражены
через элементарные функции. Однако, исследовав
их сходимость, можно дать ответ на поставленные
вопросы.
13
69*. Показать, что каждая интегральная кривая
уравнения у' —	имеет Две горизонтальные
асимптоты.
70*. Исследовать поведение интегральных кри-
вых уравнения у' =	в окрестности начала
координат. Показать, что из каждой точки грани-
цы первого координатного угла выходит одна инте-
гральная кривая, проходящая внутри этого угла.
§ 3. ГЕОМЕТРИЧЕСКИЕ И ФИЗИЧЕСКИЕ
ЗАДАЧИ1)
1. Чтобы решить приведенные ниже геометрические зада-
чи, надо построить чертеж, обозначить искомую кривую через
у = у(х) (если задача решается в прямоугольных координатах)
и выразить все упоминаемые в задаче величины через х, у и у'.
Тогда данное в условии задачи соотношение превращается в
дифференциальное уравнение, из которого можно найти иско-
мую функцию ?/(т).
2. В физических задачах надо прежде всего решить, какую
из величин взять за независимое переменное, а какую — за ис-
комую функцию. Затем надо выразить, на сколько изменится
искомая функция т/, когда независимое переменное х получит
приращение Дт, т. е. выразить разность у(х + Дт) — у(х) через
величины, о которых говорится в задаче. Разделив эту разность
на Дт и перейдя к пределу при Дт —> 0, получим дифференци-
альное уравнение, из которого можно найти искомую функцию.
г) Все задачи этого параграфа сводятся к уравнениям с
разделяющимися переменными. Задачи, приводящиеся к урав-
нениям других типов, можно найти в соответствующих парагра-
фах. Необходимые для решения задач значения показательной
функции и логарифмов можно брать из таблицы в конце задач-
ника.
14
В большинстве задач содержатся условия, с помощью кото-
рых можно определить значения постоянных, входящих в общее
решение дифференциального уравнения. Иногда дифференци-
альное уравнение можно составить более простым путем, вос-
пользовавшись физическим смыслом производной (если неза-
висимое переменное — время t, то есть скорость изменения
величины у).
В некоторых задачах при составлении уравнения следует
использовать физические законы, сформулированные в тексте
перед задачей (или перед группой задач).
Пример. В сосуд, содержащий 10 л воды, непрерывно по-
ступает со скоростью 2 л в минуту раствор, в каждом литре
которого содержится 0,3 кг соли. Поступающий в сосуд рас-
твор перемешивается с водой, и смесь вытекает из сосуда с той
же скоростью. Сколько соли будет в сосуде через 5 минут?
Решение. Примем за независимое переменное время t, а
за искомую функцию y(t) — количество соли в сосуде через t
минут после начала опыта. Найдем, на сколько изменится ко-
личество соли за промежуток времени от момента £ до момента
£ + Д£. В одну минуту поступает 2 л раствора, а в Д£ минут —
2Д£ литров; в этих 2Д£ литрах содержится 0,3 • 2Д£ = 0,6Д£ кг
соли. С другой стороны, за время Д£ из сосуда вытекает 2Д£
литров раствора. В момент t во всем сосуде (10 л) содержится
y(t) кг соли, следовательно, в 2Д£ литрах вытекающего рас-
твора содержалось бы 0,2Д£ •?/(£) кг соли, если бы за время Д£
содержание соли в сосуде не менялось. Но так как оно за это
время меняется на величину, бесконечно малую при Д£ —> 0, то
в вытекающих 2Д£ литрах содержится 0,2Д£(?/(£) + а) кг соли,
где а -> 0 при Д£ -> 0.
Итак, в растворе, втекающем за промежуток времени
(£, t + Д£), содержится 0,6 Д£ кг соли, а в вытекающем —
0,2 Д£ • (?/(£) + а) кг. Приращение количества соли за это время
y(t + Д£) — у(t) равно разности найденных величин, т. е.
y(t + Д£) - у(€) = 0,6Д£ - 0,2Д£ • (?/(£) + а).
Разделим на Д£ и перейдем к пределу при Д£ —> 0. В ле-
вой части получится производная y'ft), а в правой получим
0,6 — 0,2?/(£), так как а -> 0 при Д£ 0.
15
Итак, имеем дифференциальное уравнение y'(t) = 0,6—
—0,2?/(£). Решая его, получим
i/(t) = 3 - Ce~°’2t.	(1)
Так как при t = 0 соли в сосуде не было, то ?/(0) = 0. Полагая
в (1) t = 0, найдем ?/(0) = 3 — С; 0 = 3 — С; С = 3. Подставляя
это значение С в (1), получим y(t) = 3 — 3e~0,2i. При t = 5 в
сосуде будет
?/(5) = 3 — Зе-0,2'5 = 3 — Зе-1 ~ 1,9 кг соли.
71.	Найти кривые, для которых площадь тре-
угольника, образованного касательной, ординатой
точки касания и осью абсцисс, есть величина по-
стоянная, равная а2.
72.	Найти кривые, для которых сумма катетов
треугольника, построенного как в предыдущей за-
даче, есть величина постоянная, равная Ь.
73.	Найти кривые, обладающие следующим свой-
ством: отрезок оси абсцисс, отсекаемый касательной
и нормалью, проведенными из произвольной точки
кривой, равен 2а.
74.	Найти кривые, у которых точка пересечения
любой касательной с осью абсцисс имеет абсциссу,
вдвое меньшую абсциссы точки касания.
75.	Найти кривые, обладающие следующим свой-
ством: если через любую точку кривой провести
прямые, параллельные осям координат, до встречи
с этими осями, то площадь полученного прямоуголь-
ника делится кривой в отношении 1:2.
76.	Найти кривые, касательные к которым в лю-
бой точке образуют равные углы с полярным ради-
усом и полярной осью.
В задачах 77—79 считать, что втекающий газ
(или жидкость) вследствие перемешивания распре-
деляется по всему объему вместилища равномерно.
16
77.	Сосуд объемом в 20 л содержит воздух (80%
азота и 20% кислорода). В сосуд втекает 0,1 л азота
в секунду, который непрерывно перемешивается, и
вытекает такое же количество смеси. Через сколько
времени в сосуде будет 99% азота?
78.	В баке находится 100 л раствора, содержащего
10 кг соли. В бак непрерывно подается вода (5 л
в минуту), которая перемешивается с имеющимся
раствором. Смесь вытекает с той же скоростью.
Сколько соли в баке останется через час?
79.	В воздухе комнаты объемом 200 м3 содержит-
ся 0,15% углекислого газа (СО2). Вентилятор подает
в минуту 20 м3 воздуха, содержащего 0,04% СО2.
Через какое время количество углекислого газа в
воздухе комнаты уменьшится втрое?
В задачах 80—82 принять, что скорость остыва-
ния (или нагревания) тела пропорциональна разно-
сти температур тела и окружающей среды.
80.	Тело охладилось за 10 мин от 100° до 60°.
Температура окружающего воздуха поддерживается
равной 20°. Когда тело остынет до 25°?
81.	В сосуд, содержащий 1 кг воды при темпе-
ратуре 20°, опущен алюминиевый предмет с массой
0,5 кг, удельной теплоемкостью 0,2 и температурой
75°. Через минуту вода нагрелась на 2°. Когда тем-
пература воды и предмета будет отличаться одна от
другой на 1°? Потерями тепла на нагревание сосуда
и прочими пренебречь.
82.	Кусок металла с температурой а градусов по-
мещен в печь, температура которой в течение часа
равномерно повышается от а градусов до b граду-
сов. При разности температур печи и металла в Т
градусов металл нагревается со скоростью кТ гра-
дусов в минуту. Найти температуру металла через
час.
17
83.	Лодка замедляет свое движение под дей-
ствием сопротивления воды, которое пропорцио-
нально скорости лодки. Начальная скорость лодки
1,5 м/сек, через 4 сек скорость ее 1 м/сек. Ко-
гда скорость уменьшится до 1 см/сек! Какой путь
может пройти лодка до остановки?
В задачах 84—86 использовать закон радиоак-
тивного распада: количество радиоактивного веще-
ства, распадающегося за единицу времени, пропор-
ционально количеству этого вещества, имеющемуся
в рассматриваемый момент.
84.	За 30 дней распалось 50% первоначального
количества радиоактивного вещества. Через сколько
времени останется 1% от первоначального количе-
ства?
85.	Согласно опытам, в течение года из каждо-
го грамма радия распадается 0,44 мг. Через сколь-
ко лет распадется половина имеющегося количества
радия?
86.	В исследованном куске горной породы содер-
жится 100 мг урана и 14 мг уранового свинца. Из-
вестно, что уран распадается наполовину за 4,5 • 109
лет и что при полном распаде 238 г урана обра-
зуется 206 г уранового свинца. Определить возраст
горной породы. Считать, что в момент образования
горная порода не содержала свинца, и пренебречь
наличием промежуточных радиоактивных продуктов
между ураном и свинцом (так как они распадаются
намного быстрее урана).
87.	Количество света, поглощаемое слоем воды
малой толщины, пропорционально количеству пада-
ющего на него света и толщине слоя. Слой воды
толщиной 35 см поглощает половину падающего на
него света. Какую часть света поглотит слой тол-
щиной в 2 м!
18
Для составления дифференциального уравнения
в задачах 88—90 за неизвестную функцию удобнее
взять скорость. Ускорение силы тяжести считать
равным 10 м/сек2.
88.	Парашютист прыгнул с высоты 1,5 км, а рас-
крыл парашют на высоте 0,5 км. Сколько времени
он падал до раскрытия парашюта? Известно, что
предельная скорость падения человека в воздухе
нормальной плотности составляет 50 м/сек. Изме-
нением плотности с высотой пренебречь. Сопроти-
вление воздуха пропорционально квадрату скорости.
89.	Футбольный мяч весом 0,4 кГ брошен вверх
со скоростью 20 м/сек. Сопротивление воздуха про-
порционально квадрату скорости и равно 0,48 Г при
скорости 1 м/сек. Вычислить время подъема мяча
и наибольшую высоту подъема. Как изменятся эти
результаты, если пренебречь сопротивлением воз-
духа?
90.	Вычислить время падения мяча с высоты
16,3 м без начальной скорости с учетом сопроти-
вления воздуха (см. задачу 89). Найти скорость в
конце падения.
В задачах 91—95 принять, что жидкость из со-
суда вытекает со скоростью, равной 0,6y/2gh, где
д = 10 м/сек2 — ускорение силы тяжести, h —
высота уровня воды над отверстием.
91.	За какое время вытечет вся вода из цилин-
дрического бака диаметром 2R = 1,8 м и высо-
той Н = 2,45 м через отверстие в дне диаметром
2г = 6 см? Ось цилиндра вертикальна.
92.	Решить предыдущую задачу в предположе-
нии, что ось цилиндра расположена горизонтально,
а отверстие находится в самой нижней части ци-
линдра.
19
93.	Цилиндрический бак поставлен вертикально
и имеет отверстие в дне. Половина воды из полного
бака вытекает за 5 минут. За какое время вытечет
вся вода?
94.	Воронка имеет форму конуса радиуса R =
= 6 см и высоты Н = 10 см, обращенного вершиной
вниз. За какое время вытечет вся вода из воронки
через круглое отверстие диаметра 0,5 см, сделанное
в вершине конуса?
95.	В прямоугольный бак размером 60 смх75 см
и высотой 80 см поступает 1,8 л воды в секунду.
В дне имеется отверстие площадью 2,5 см2. За ка-
кое время наполнится бак? Сравнить результат с
временем наполнения такого бака без отверстия в
дне.
96.	Резиновый шнур длиной в 1 м под действием
силы f кГ удлиняется на kf метров. На сколько
удлинится такой же шнур длины I и веса Р под
действием своего веса, если его подвесить за один
конец?
97.	Найти атмосферное давление на высоте h,
если на поверхности земли давление равно 1 кГ/см2
и плотность воздуха 0,0012 г/см3. Использовать за-
кон Бойля—Мариотта, в силу которого плотность
пропорциональна давлению (т. е. пренебречь изме-
нением температуры воздуха с высотой).
98.	Для остановки речных судов у пристани с
них бросают канат, который наматывают на столб,
стоящий на пристани. Какая сила будет тормозить
судно, если канат делает три витка вокруг стол-
ба, коэффициент трения каната о столб равен 1/3,
и рабочий на пристани тянет за свободный конец
каната с силой 10 кГ7
99.	В закрытом помещении объемом v м3 нахо-
дится открытый сосуд с водой. Скорость испарения
воды пропорциональна разности между количеством
20
Qi водяного пара, насыщающего 1 л*3 воздуха при
данной температуре, и количеством q водяного па-
ра, имеющемся в 1 м3 воздуха в рассматриваемый
момент (считаем, что температура воздуха и воды,
а также величина площади, с которой происходит
испарение, остаются неизменными). В начальный
момент в сосуде было то грамм воды, а в 1 м3
воздуха qo грамм пара. Сколько воды останется в
сосуде через промежуток времени tf
100.	Масса ракеты с полным запасом топлива
равна М, без топлива т, скорость истечения про-
дуктов горения из ракеты равна с, начальная ско-
рость ракеты равна нулю. Найти скорость ракеты
после сгорания топлива, пренебрегая силой тяжести
и сопротивлением воздуха (формула Циолковского).
§ 4.	ОДНОРОДНЫЕ УРАВНЕНИЯ
1.	Однородные уравнения могут быть записаны в виде
т/ = / а также в виде М(х, y)dx + N(x, y)dy = 0, где
М(х, у) и N(x, у) — однородные функции одной и той же сте-
пени1). Чтобы решить однородное уравнение, можно сделать
замену у = tx, после чего получается уравнение с разделяю-
щимися переменными.
Пример. Решить уравнение х dy = (а? + у) dx.
Это уравнение — однородное. Полагаем у = tx. Тогда dy =
= xdt + tdx. Подставляя в уравнение, получим
х(х dt + t da?) = (а? + tx) dx; xdt = da?.
Решаем полученное уравнение с разделяющимися переменны-
ми
dt = t = In |а?| + С. 2
2) Функция М(а?, у) называется однородной функцией сте-
пени п, если для всех к > 0 имеем М(кх, ку) = кпМ(х, у).
21
Возвращаясь к старому переменному у, получим у = х(1п |ж| +
+С). Кроме того, имеется решение х = 0, которое было поте-
ряно при делении на х.
2.	Уравнение вида у' = f (приводится к од-
нородному с помощью переноса начала координат в точку пе-
ресечения прямых ах + Ьу + с = 0 и aix + Ь\у + ci =0. Если
же эти прямые не пересекаются, то а±х + byy = k(ax + Ьу)\
следовательно, уравнение имеет вид у' = F(ax + by) и приво-
дится к уравнению с разделяющимися переменными заменой
z = ах + by (или z = ах + by + с), см. § 2, п. 2.
3.	Некоторые уравнения можно привести к однородным за-
меной у = zm. Число т обычно заранее не известно. Чтобы
его найти, надо в уравнении сделать замену у = zm. Требуя,
чтобы уравнение было однородным, найдем число т, если это
возможно. Если же этого сделать нельзя, то уравнение не при-
водится к однородному этим способом.
Пример. Дано уравнение 2х^уу' + у4 = 4ж6. После замены
у = zm уравнение примет вид 2mx42:2m_1? + z4m = 4ж6. Это
уравнение будет однородным в том случае, когда степени всех
его членов равны между собой, т. е. 4 + (2т — 1) = 4т = 6. Эти
равенства удовлетворяются одновременно, если т = 3/2. Сле-
довательно, уравнение можно привести к однородному заменой
у = z3/2.
Решить уравнения 101—129.
101.	(х + 21/) dx - xdy = 0.
102.	(х - у) dx + (х + у) dy = 0.
103.	(у2 — 2ху) dx + х2 dy = 0.
104.	2х3у' = у(2х2 - у2).
105.	у2 + х2у' = хуу'.
106.	(х2 + у2\у' = 2ху.
22
107.	ху' - у = rrtg|.
108.	ху1 = у — хеу!х.
109.	ху' - у = (х + у) In
110.	ху1 = у cos In
111.	(г/ + y/ху) dx = xdy.
112.	ху' = у/х2 — у2 + у.
113.	(2х - 4у + 6) dx + (х + у - 3) dy = 0.
114.	(2х + у + 1) dx - (4х + 2у - 3) dy = 0.
115.	х-у-1 + (у-х + 2)у' = 0.
116.	(х + 4у)у' = 2х + Зу - 5.
117.	(у + 2)dx = (2х + у — 4) dy.
118.	у' = 2( ^+2.)2.
119.	(у' + 1)1п^ = Щ.
120.	у' =	^—ГТ-
121.	х3(у' — х) = у2.
122.	2х2у' = у3 + ху.
123.	2х dy + (х2у4 + 1)у dx = 0.
124.	у dx + х(2ху + 1) ск/ = 0.
23
125.	2у' + х = 4у/у.
126.	у' = у2 -
127.	2хуг + у = у2у/х — х2у2.
128.	^хуу' = у/хе -у4 + у2.
129.	2у + (х2у + 1)ху' = 0.
130.	Найти траектории, пересекающие кривые
данного семейства под углом в 45°, причем этот
угол от касательной к кривой до касательной к
траектории отсчитывается в отрицательном напра-
влении.
а) у = хЛпСх; б) (х - З?/)4 = CxyQ.
131.	Найти кривую, у которой точка пересече-
ния любой касательной с осью абсцисс одинаково
удалена от точки касания и от начала координат.
132.	Найти кривую, у которой расстояние любой
касательной от начала координат равно абсциссе
точки касания.
133.	При каких а и (3 уравнение у' = аха +
+ЬуР приводится к однородному с помощью замены
у = zm7
134*	. Пусть ко — корень уравнения = к.
Показать, что:
1)	если f'(ko) < 1, то ни одно решение уравнения
Уг — f(y/x) не касается прямой у = кох в начале
координат;
2)	если f(ko) > 1, то этой прямой касается бес-
конечно много решений.
24
135. Начертить приближенно интегральные кри-
вые следующих уравнений (не решая уравнений):
а)9'=»ер£1;	б)9' = Ц^;
»)«' =	г‘> x‘J = y + у/»2 + £-
Указание. Тангенс угла между лучом у = кх и пересе-
кающей его интегральной кривой уравнения у' = f(y/x) равен
(/(&) — &) / (1 + &/(&)) (почему?). Для приближенного построе-
ния интегральных кривых надо исследовать знак этой дроби в
зависимости от к.
§ 5. ЛИНЕЙНЫЕ УРАВНЕНИЯ ПЕРВОГО
ПОРЯДКА
1.	Уравнение
у' + а(х)у = b(x)	(1)
называется линейным. Чтобы его решить, надо сначала решить
уравнение
у' + а(х)у = 0	(2)
(это делается путем разделения переменных, см. § 2) ив об-
щем решении последнего заменить произвольную постоянную
С на неизвестную функцию С(х). Затем выражение, получен-
ное для у, подставить в уравнение (1) и найти функцию С(х).
2.	Некоторые уравнения становятся линейными, если по-
менять местами искомую функцию и независимое переменное.
Например, уравнение у = (2х + у3)у', в котором у является
функцией от х, — нелинейное. Запишем его в дифференциа-
лах: ydx — (2х + у3) dy = 0. Так как в это уравнение х и da?
входят линейно, то уравнение будет линейным, если х считать
искомой функцией, а у — независимым переменным. Это урав-
нение может быть записано в виде
ds _ 2	2
dy УХ~У
и решается аналогично уравнению (1).
3.	Чтобы решить уравнение Бернулли, т. е. уравнение
у' + а(х)у = Ь(ж)?/П, (n # 1),
25
надо обе его части разделить на уп и сделать замену \/yn~x=z.
После замены получается линейное уравнение, которое можно
решить изложенным выше способом. (Пример см. в [1], гл. I,
§ 4, п. 2, пример 10.)
4.	Уравнение Риккати, т. е. уравнение
у' + а(х)у + Ь{х)у2 = с(ж),
в общем случае не решается в квадратурах. Если же известно
одно частное решение yi(x), то заменой у = yi(x) + z уравне-
ние Риккати сводится к уравнению Бернулли и таким образом
может быть решено в квадратурах.
Иногда частное решение удается подобрать, исходя из вида
свободного члена уравнения (члена, не содержащего у). Напри-
мер, для уравнения у' + у2 = х2 — 2х в левой части будут члены,
подобные членам правой части, если взять у = ах + Ъ. Подста-
вляя в уравнение и приравнивая коэффициенты при подобных
членах, найдем а и b (если частное решение указанного вида
существует, что вовсе не всегда бывает). Другой пример: для
уравнения у' + 2у2 = 6/ж2 те же рассуждения побуждают нас
искать частное решение в виде у = а/х. Подставляя у = а/х в
уравнение, найдем постоянную а.
Решить уравнения 136—160.
136.	ху'-2у = 2х4.
137.	(2х + 1)1/' = 4х + 2у.
138.	у' + у tg х = sec х.
139.	{ху + еж) dx - х dy = 0.
140.	х2у' + ху + 1 = 0.
141.	у — х{у' — х cos ж).
142.	2х{х2 + у) dx = dy.
26
143.	(ху1 - 1) In х = 2у.
144.	ху' + (х + 1)у = Зж2е“ж.
145.	(х + у2) dy = ydx.
146.	(2е^ - x)yf = 1.
147.	(sin2 у + х ctg у)у' = 1.
148.	(2х + у) dy = у dx + 4 In т/ dy-
150.	(1 - 2xy)yr = у(у - 1).
151.	у' + 2у = у2ех.
152.	(ж + 1)(у' + у2) = -у.
153.	у1 = у4 cos х + ytgx.
154.	ху2у' = х2 + у3-
155.	ху dy = (у2 + х) dx.
156.	ху' — 2х2у/у = dy.
157.	ху' + 2у + ж5?/3еж = 0.
158.	2у' — - =
V у X2 - 1
159.	у'х3 siny = ху' — 2у.
160.	(2х2у In 1/ ~ х)у' = у.
27
С помощью замены переменных или дифференци-
рования привести уравнения 161—166 к линейным
и решить их.
161.	х dx = (х2 - 2у + 1) dy.
162.	(х + 1)(уу' - 1) = у2.
163.	х(еу - у') = 2.
164.	(х2 — 1)у' sin у + 2#cos?/ = 2х - 2ж3.
165.	у(х) = f y(t) dt + х + 1.
о
166.	f(x- t)y(t) dt = 2x + f y(t) dt.
о	о
В задачах 167—171, найдя путем подбора част-
ное решение, привести данные уравнения Риккати
к уравнениям Бернулли и решить их.
167.	х2у' + ху + х2у2 = 4.
168.	Зу'+ у2+ ^ = 0.
169.	ху' — (2х + 1)у + у2 = — х2.
170.	у' — 2ху + у2 = 5 — х2.
171.	у' + 2уех - у2 = е2ж + еж.
172.	Найти траектории, ортогональные к линиям
семейства у2 = Сех + х + 1.
173.	Найти кривые, у которых площадь трапе-
ции, ограниченной осями координат, касательной и
ординатой точки касания, есть величина постоян-
ная, равная За2.
28
174.	Найти кривые, у которых площадь треуголь-
ника, ограниченного касательной, осью абсцисс и
отрезком от начала координат до точки касания,
9
есть величина постоянная, равная а.
175.	В баке находится 100 л раствора, содержа-
щего 10 кг соли. В бак втекает 5 л воды в минуту,
а смесь с той же скоростью переливается в дру-
гой 100-литровый бак, первоначально наполненный
чистой водой. Избыток жидкости из него вылива-
ется. Когда количество соли во втором баке будет
наибольшим? Чему оно равно?
176.	За время Af (где Af очень мало и выражено
в долях года) из каждого грамма радия распадается
0,00044 Af грамма и образуется 0,00043 Af грамма
радона. Из каждого грамма радона за время Af
распадается 70 Af грамма. В начале опыта име-
лось некоторое количество xq чистого радия. Когда
количество образовавшегося и еще не распавшегося
радона будет наибольшим?
177.	Даны два различных решения у± и у2 ли-
нейного уравнения первого порядка. Выразить через
них общее решение этого уравнения.
178.	Найти то решение уравнения
у' sin 2х = 2(у + cos х),
которое остается ограниченным при х —> тг/2.
179*. Пусть в уравнении ху' + ay = f(x) имеем
а = const > 0, f(x) —> b при х —> 0. Показать, что
только одно решение уравнения остается ограничен-
ным при х —> 0, и найти предел этого решения при
х —> 0.
180*. Пусть в уравнении предыдущей задачи
а = const < 0, f(x) b при х —> 0. Показать, что
все решения этого уравнения имеют один и тот же
конечный предел при х 0. Найти этот предел.
29
В задачах 181—183 искомое решение выражает-
ся через интеграл с бесконечным пределом.
181*. Показать, что уравнение ^+x = f(t), где
|/(f)| С М при -оо < t < +оо, имеет одно реше-
ние, ограниченное при —оо < t < +оо. Найти это
решение. Показать, что найденное решение перио-
дическое, если функция /(f) периодическая.
182*. Показать, что только одно решение урав-
нения ху' — (2ж2 + 1)у = х2 стремится к конечному
пределу при х —> +оо, и найти этот предел. Выра-
зить это решение через интеграл.
183*. Найти периодическое решение уравнения
у' = 21/cos2 х — sin х.
184*. Пусть в уравнении ^+a(t)x = f(t) a(t)
с > О, /(f) -> 0 при f —> +оо. Доказать, что
каждое решение этого уравнения стремится к нулю
при f —> +оо.
185*. Пусть в уравнении предыдущей задачи име-
ем a(f) с> 0 и пусть xo(t) — решение с началь-
ным условием Жо(0) — Ь. Показать, что для любого
е > 0 существует такое 6 > 0, что если изменить
функцию /(f) и число b меньше, чем на 6 (т. е.
заменить их на такую функцию /1(f) и число bi,
что |/i(f) - /(f)| < Ф |Ь1 ~ Ь\ < 5), то решение xo(t)
изменится при f О меньше, чем на е. Это свой-
ство решения называется устойчивостью по посто-
янно действующим возмущениям.
§ 6. УРАВНЕНИЯ В ПОЛНЫХ
ДИФФЕРЕНЦИАЛАХ.
ИНТЕГРИРУЮЩИЙ МНОЖИТЕЛЬ
1.	Уравнение
M(j;, у) da? + N(x, у) dy = О	(1)
называется уравнением в полных дифференциалах, если его
30
левая часть является полным дифференциалом некоторой
функции F(x, у). Это имеет место, если
дМ _ 9N и .
— = -о—. Чтобы ре-
ет?/ ох
шить уравнение (1), надо найти функцию F(x, у), от которой
полный дифференциал dF(x, у) = F'x dx+Fy dy равен левой ча-
сти уравнения (1). Тогда общее решение уравнения (1) можно
написать в виде F(x, у) = С, где С — произвольная постоян-
ная.
Пример. Решить уравнение
(2а? + За?2?/) da? + (ж3 — З?/2) dy = 0.	(2)
Так как J^(2a? + 3a?2?/) = За?2, ^(а?3 — З?/2) = За?2, то уравнение
(2) является уравнением в полных дифференциалах. Найдем
функцию F(a?, у), полный дифференциал которой dF = Fx da?+
+Fy dy был бы равен левой части уравнения (2), т. е. такую
функцию F, что
Fx = 2х + За:2?/, Fy = х3 — Зу2.	(3)
Интегрируем по а? первое из уравнений (3), считая у постоян-
ным; при этом вместо постоянной интегрирования надо поста-
вить <р(у) — неизвестную функцию от у:
F = J (2а? + За?2?/) da? = а?2 + а?3?/ + </?(?/).
Подставляя это выражение для F во второе из уравнений (3),
найдем </?(?/):
(а?2 + а?3?/+ </?(?/)) ^ = а?3 — З?/2; </(?/)=-З?/2; </>(?/)=-?/3 +const.
Следовательно, можно взять F(a?, у) = а?2 + а?3?/ — ?/3, и общее
решение уравнения (2) будет иметь вид
а?2 + а?3?/ - у3 = С.
2.	Интегрирующим множителем для уравнения
М(а?, ?/) da? + 7V(a?, ?/) dy - 0	(4)
называется такая функция т(а?, у) 0, после умножения на
которую уравнение (4) превращается в уравнение в полных
дифференциалах. Если функции М и N в уравнении (4) имеют
31
непрерывные частные производные и не обращаются в нуль од-
новременно, то интегрирующий множитель существует. Одна-
ко нет общего метода для его отыскания (когда общее решение
уравнения (4) неизвестно).
В некоторых случаях интегрирующий множитель можно
найти с помощью приемов, изложенных в [1], гл. II, § 3, п. 3
или в [4], гл. 1, § 5. Для решения некоторых уравнений можно
применять метод выделения полных дифференциалов, исполь-
зуя известные формулы:
d(xy) = ydx + xdy, d(y2) = 2ydy,
=	d(ln2/) = ^ И Т.П.
Пример. Решить уравнение
ydx — (4х2у + х) dy = 0.	(5)
Сначала выделяем группу членов, представляющую собой
полный дифференциал. Так как ydx — xdy = — x2d(y/x), то,
деля уравнение (5) на —ж2, имеем
d(|)+4ydj/ = 0, d (I) + d(2j/2) = 0.
Это — уравнение в полных дифференциалах. Интегрируя не-
посредственно (приводить к виду (1) не нужно), получаем ре-
шение
I + 2?/2 = с-
Кроме того, при делении на —х2 было потеряно решение х = 0.
Замечание. Так как после деления уравнения (5) на —ж2,
т. е. умножения на — 1/ж2, получилось уравнение в полных диф-
ференциалах, то интегрирующий множитель для уравнения (5)
равен — 1/ж2.
3.	Если в уравнении (4) можно выделить полный дифферен-
циал некоторой функции ^?(ж, ?/), то иногда уравнение упроща-
ется, если от переменных (ж, у) перейти к переменным (ж, z)
или (у, z), где z = (р(х, у).
Примеры. 1) Решить уравнение ydx — (х3у + x)dy = 0.
Выделив полный дифференциал как в предыдущем приме-
ре, получим
d (I) + ХУ^У = °-
32
Перейдя к переменным z = у/х и у, получим уравнение
dz + dy = О,
которое легко решается.
2)	Решить уравнение {ху + ?/4) da? + (х2 — ху3) dy = 0.
Сгруппируем члены так, чтобы выделить полные диффе-
ренциалы
х{у dx + х d?/) + у3{у dx — х d?/) = 0, х d{xy) + у3 d j = 0.
Разделив на х и сделав замену ху = и, х/у = v, получим урав-
и2
нение d?z Н—т dr = 0, которое легко решается.
В задачах 186—194 проверить, что данные урав-
нения являются уравнениями в полных дифферен-
циалах, и решить их.
186.	2ху dx + (х2 - у2) dy = 0.
187.	(2 - 9ху2) xdx + (4?/2 - 6ж3)у dy — 0.
188.	е~у dx — (2у + хе~у) dy = 0.
189.	dx + (?/3 + In х) dy = 0.
190.	^yldx- *!±p/dy = 0.
191.	+ yjx2 — y^dx — у/x2 — у dy = 0.
192.	(1 + у2 sin 2x) dx — 2y cos2 x dy = 0.
193.	Зж2(1 + In?/) dx = (%y — “)ф/.
194.	f^+2)dx + ^^^d?/ = 0.
\ sin у	/	cos 2y — 1 u
Решить уравнения 195—220, найдя каким-либо
способом интегрирующий множитель или сделав за-
мену переменных.
33
195.	(х2 + у2 + х) dx + у dy = 0.
196.	(х2 + у2 + у) dx - х dy = 0.
197.	у dy = (х dy + у dx)у/1 + у2.
198.	ху2(ху' + у) = 1.
199.	у2 dx - (ху + х3) dy = 0.
200.	(y-i)dx+f = 0.
201.	(х2 + 3 In у)у dx = х dy.
202.	у2 dx + (ху + tg ху) dy = 0.
203.	у(х + y)dx + (ху + 1) dy = 0.
204.	у(у2 + 1) dx + х(у2 - х + 1) dy = 0.
205.	(х2 + 2х + у) dx = (х - Зх2?/) dy.
206.	ydx - xdy = 2х3 tg | dx.
207.	у2 dx + (ех - у) dy = 0.
208.	ху dx = (у3 + х2у + х2) dy.
209.	х2у(у dx + х dy) = 2ydx + х dy.
210.	(x2 - у2 + y)dx + x(2y - 1) dy = 0.
211.	(2x2y2 + y)dx + (x3y - x)dy = 0.
212.	(2x2y2> - l)y dx + (4x2?/3 - l)xdi/ = 0.
34
213.	у(х + у2) dx + х2(у — 1) dy = 0.
214.	(s2 - sin2 у) dx + х sin 2у dy = 0.
215.	х(1п у + 2 In х - 1) dy = 2y dx.
216.	(s2 + l)(2xdx + cosy dy) = 2x sin yds.
217.	(2s3y2 - y) dx + (2x2y3 - s) dy = 0.
218.	s2y3 + у + (x3y2 - x)y’ = 0.
219.	(s2 - y) dx + x(y + 1) dy = 0.
220.	y2(yds - 2s dy) = s3(sdy - 2yds).
§ 7.	СУЩЕСТВОВАНИЕ
И ЕДИНСТВЕННОСТЬ РЕШЕНИЯ
1.	Теорема существования и единственности
решения уравнения
у' = f(x, у)	(1)
с начальным условием у(жо) = Уо>
Пусть в замкнутой области R (|ж — жо| С \У ~ 2/01 С &)
функции f и fy непрерывны1). Тогда на некотором отрезке
xq — d^x^XQ-\-d существует единственное решение урав-
нения (1), удовлетворяющее начальному условию у(хо) = уо.
При этом можно взять d = min {а;	где а и b указаны
выше, ат — любое такое, что \ f\ т в R.
L) Требование непрерывности f'(y) можно заменить требо-
ванием ее ограниченности или условием Липшица: |/(ж, yi) —
-f(x, У2)\	&|з/1 - 2/21, k = const.
35
Последовательные приближения, определяемые формулами
X
Уо(х) = УО, yk(x) -У° + f ^-1(5)) ds, k = 1, 2, ...,
Жо
равномерно сходятся к решению на указанном отрезке.
Замечание. Для существования решения достаточно толь-
ко непрерывности f(x, у) в области R, но при этом решение
может не быть единственным.
2.	Система уравнений
(у{ = А (ж, yi, Уп),
.................................. (2)
(Уп = Ых, У!, ..., уп)
в векторных обозначениях записывается так:
у' = f(x, у),	(3)
где у = (yi, уп) и f = (fi, ..., /„) — векторы. Непрерыв-
ность вектор-функции f означает непрерывность всех функций
е	р	df
ji, ..., jn, а вместо рассматривается матрица из частных
dfi . ,	1
производных	к = 1, ... ,п.
Теорема существования и единственности решения и все
утверждения п. 1 остаются справедливыми и для системы, за-
писанной в виде (3). При этом |?/| означает длину вектора у:
М =	+ +&
3.	Теорема существования и единственности
решения для уравнения n-го порядка
3/(п) = /(ж, у, у',	у(п~^).
(4)
Пусть в области D функция f и ее частные производ-
ные первого порядка по у, у', .. .,	непрерывны, и точка
(xq, уо, у'о, ..., Уц1 г)) лежит внутри D. Тогда при началь-
ных условиях
у(хо) = Уо, у'(х0) = у'о,	1 (х-0) = Уо'‘~1)
уравнение (4) имеет единственное решение.
Уравнение (4) можно свести к системе вида (2), если вве-
сти новые неизвестные функции по формулам у = у±, у' = у2,
36
у" ~Уз, •  -, У(п = Уп- Тогда уравнение (4) сводится к си-
стеме
У1 = У2, у'2 = уз, • y'n-i = Уп, у'п = Дж, 3/1,	, уп),
которая является частным случаем системы (2) и к которой
применимы все утверждения п. 2.
4.	Продолжение решений. Во многих случаях решение
уравнения (1) или системы (2) существует не только на отрезке,
указанном в п. 1, но и на большем отрезке.
Если уравнение (1) или система (2) удовлетворяет условиям
теоремы существования в замкнутой ограниченной области, то
всякое решение можно продолжить до выхода на границу этой
области.
Если правая часть уравнения (1) или системы (3) в обла-
сти а < х < /3, \у\ < oq (а и /3 могут быть конечными или
бесконечными) непрерывна и удовлетворяет неравенству
|/(х, 2/)|	а(х)|г/| + 6(х),
и функции а(х) и Ъ(х) непрерывны, то всякое решение можно
продолжить на весь интервал а < х < (3.
221.	Построить последовательные приближения
2/о? У1, У2 к решению данного уравнения с данными
начальными условиями:
а)	у1 = х - у2, 7/(0) = 0.
б)	у' = у2 + Зя2 - 1, 2/(1) = 1.
в)	у' = у + еу~1, 2/(0) = 1.
г)	у' = 1 + х sin у, у(л) = 2тг.
222.	Построить по два последовательных прибли-
жения (не считая исходного) к решениям следующих
уравнений и систем:
а)	у' = 2х + z, z1 = у; 2/(1) = 1, г(1) = 0.
37
б)	g = у, $ = а:2; ж(0) = 1, 2/(0) = 2.
в)	у" + у'2 -2у = О-,	7/(0) = 1, 2/'(0) = 0.
dF = 3te; = 2’ di|(=1= -1-
223.	Указать какой-нибудь отрезок, на котором
существует решение с данными начальными усло-
виями:
а)	у' = х + у3, т/(0) = 0.
б)	у' = 2у2 - х, 7/(1) = 1.
в)	=t + ex, ж(1) = 0.
г)	= У2,	= х2, ж(0) = 1, 2/(0) = 2.
224*. Для уравнения у' = х — у2 с начальным
условием 2/(0) = 0 построить третье приближение к
решению и оценить его ошибку при 0 х 0,5.
Указание. Оценить остаток ряда, сходимость которого до-
казывается в теореме существования решения, см. [1], гл. II, § 1;
[2], § 15.
225.	Пользуясь каким-либо достаточным услови-
ем единственности, выделить области на плоскости
ж, у, в которых через каждую точку проходит един-
ственное решение уравнения
а)	у' = 2ху + у2,
в) (х - 2)у' = у/у-х,
д) (У ~х)у' = т/In ж,
б)	у' = 2 + $у - 2ж,
г) у' = 1 + tgT/,
е) ху' = у+ х/т/2 - ж2.
38
226.	При каких неотрицательных а нарушается
единственность решений уравнения у' = \у\а и в
каких точках?
227.	С помощью необходимого и достаточно-
го условия единственности для уравнений вида
У' — f(y) (см- [1], гл. Ш? § 4, п. 1, мелкий шрифт
или [2], § 4) исследовать написанные ниже урав-
нения. Выделив области, где f(y) сохраняет знак,
приближенно изобразить на чертеже решения. Для
уравнений д) и е) правые части при у = 0 доопре-
деляются по непрерывности.
а) у' = Уу2,
в) у' = (у - l)v^,
д) У1 = У In у,
б) у' = у<Уу + 1,
г) у' = arccosi/,
е) у' = у In2 у.
228.	При каких начальных условиях существу-
ет единственное решение следующих уравнений и
систем?
а) у" = tg у +	б) (х + 1)1/" = у + у/У)
в) (х - у)у'у"' = 1пху,	г) у" - уу"' = Уу' - X,
д)	> =
е) = У3 + W + г)’ xdt = ^y-t-
229.	Могут ли графики двух решений данного
уравнения на плоскости х, у пересекаться в неко-
торой точке (жо5 У о)
а)	для уравнения у1 = х + у2?
б)	для уравнения у" = х + у2?
39
230.	Могут ли графики двух решений данного
уравнения на плоскости х, у касаться друг друга в
некоторой точке (жо, Уо)
а)	для уравнения у' = х + у2?
б)	для уравнения у" = х + у2?
в)	для уравнения уш = х + у2?
231.	Сколько существует решений уравнения
уМ — х +	5 удовлетворяющих одновременно двум
условиям: 2/(0) = 1, у'((f) = 2? Рассмотреть отдельно
случаи п = 1, 2, 3.
232.	Сколько решений уравнения у^ = f(x, у)
(f и fy непрерывны на всей плоскости х, у) прохо-
дит через точку (жо, Уо) по заданному направлению,
образующему угол а с осью Ох? Рассмотреть слу-
чаи п = 1, п = 2 и п 3.
233.	При каких п уравнение у^ = f(x, у) (f и
fy непрерывны) может иметь среди своих решений
две функции: ух = х, у2 = х + х4?
234.	При каких п уравнение у^ = f(x, у, у', ...
... .у^1^ с непрерывно дифференцируемой функ-
цией f может иметь среди своих решений две функ-
ции: yi = х, У2 = sin ж?
235*. Пусть /(ж, у) непрерывна по ж, у и при ка-
ждом ж не возрастает при возрастании у. Доказать,
что если два решения уравнения у' = f(x, у) удо-
влетворяют одному и тому же начальному условию
у(хо) ~ У о, то они совпадают при ж Xq.
236. Сколько производных имеют решения сле-
дующих уравнений и систем в окрестности начала
координат? (Теорему о гладкости решений см. [2],
§ 19 или [4], § 6, теорема 1.4.)
40
а)	у' = x + у7/3,
б)	у' =ф| - у2,
в) у" = |ж3| +у5/3, г) у'" = у - х^х,
+ й? = - + ‘2И,
С) £ = ./ + Ж * = №-
237*. При каких а каждое решение продолжается
на бесконечный интервал — оо < х < +оо
а)	для уравнения у' = \у\а?
б)	для уравнения у' = (у2 + еж)а?
в)	для уравнения у' =	+ \х^/у\2а?
г)	для системы у' = (у2 + z2 + 2)-а, z' = y(l + z2)a?
238*. Для следующих уравнений доказать, что
решение с произвольным начальным условием
у(хо) = у о существует при жо х < +оо:
а)	у' = х3 - у3,
б)	у' = ху + е у.
239*. Пусть на всей плоскости ж, у функции
/(ж, у) и f£(x, у) непрерывны и /'(ж, у) С k(x),
функция к(х) непрерывна. Доказать, что решение
уравнения у' = /(ж, у) с любым начальным услови-
ем ?/(жо) = у о существует при жо ж < +оо.
240*. Дана система в векторной записи у1 =
— /(ж, У\ удовлетворяющая условиям теоремы су-
ществования в окрестности каждой точки (ж, у).
Пусть в области \у\ > b при всех ж
У  f(x, у) С А;О)|г/|2,
41
где у • f — скалярное произведение, а функция
к(х) непрерывна. Доказать, что решение с любым
начальным условием у(хо) = у о существует при
хо х < +оо.
§ 8. УРАВНЕНИЯ, НЕ РАЗРЕШЕННЫЕ
ОТНОСИТЕЛЬНО ПРОИЗВОДНОЙ
1. Уравнения вида F(a?, у, у') = 0 можно решать следующи-
ми методами.
а)	Разрешить уравнение относительно у', т. е. из уравнения
F(a?, у, у') = 0 выразить у' через х и у. Получится одно или
несколько уравнений вида у' = f(x, у). Каждое из них надо
решить.
б)	Метод введения параметра1).
Пусть уравнение F(a?, у, у') = 0 можно разрешить относи-
тельно у, т. е. записать в виде у = f(x, у'). Введя параметр
получим
У = №, Р)-	(2)
Взяв полный дифференциал от обеих частей равенства (2) и
заменив dy через pdx (в силу (1)), получим уравнение вида
М(х, р) dx + N(x, р) dp = 0.
Если решение этого уравнения найдено в виде х = <р(р), то,
воспользовавшись равенством (2), получим решение исходного
уравнения в параметрической записи: х = <р(р), у = /((р(р), р).
Уравнения вида х = f(y, у') решаются тем же методом.
Пример. Решить уравнение у = х + у1 — In у'. Вводим пара-
метр р = у1:
р = т+р-1пр.	(3)
Берем полный дифференциал от обеих частей равенства и заме-
няем dy на pda? в силу (1): dy = da?+dp— pdx = da?+dp—
х) Здесь излагается простейший вариант этого метода. Бо-
лее общий вариант см. [1], гл. III, § 3, п. 1.
42
Решаем полученное уравнение. Переносим члены с dx влево, с
dp — вправо:
(р - l)d® =	(4)
а)	Если р ф 1, то сокращаем на р — 1:
, dp 1	. „
dx —	, х = In р + С.
Подставляя это в (3), получаем решение в параметрической за-
писи:
х = 1пр + С, у = р + С.	(5)
В данном случае можно исключить параметр р и получить
решение в явном виде. Для этого из первого из уравнений (5)
выражаем р через х, т. е. р = ех~с. Подставляя это во второе
уравнение, получаем искомое решение:
У = ех~с + С.	(6)
б)	Рассмотрим случай, когда в (4) имеем р = 1. Подставляя
р = 1 в (3), получаем еще решение
р = х + 1.	(7)
(Было бы ошибкой в равенстве р = 1 заменить р на у' и, про-
интегрировав, получить у = х + С.)
2. Решение у = <р(т) уравнения F(t, у, у'} = 0 называется
особым, если через каждую его точку, кроме этого решения,
проходит и другое решение, имеющее в этой точке ту же каса-
тельную, что и решение у = <р(т), но не совпадающее с ним в
сколь угодно малой окрестности этой точки1).
OF
Если функция F(x, у, у') и производные
рывны, то любое особое решение уравнения
dF
и тг-т непре-
F(t, у, у’) = О
удовлетворяет также уравнению
9F(x, у, у') _
ду'
(8)
(9)
х) Это определение взято из [1]. Есть и другие определения,
не равносильные этому.
43
Поэтому, чтобы отыскать особые решения уравнения (3), на-
до исключить у' из уравнений (8) и (9). Полученное уравнение
-0(т, т/) = 0 называется уравнением дискриминантной кривой.
Для каждой ветви дискриминантной кривой надо проверить,
является ли эта ветвь решением уравнения (8), и если явля-
ется, то будет ли это решение особым, т. е. касаются ли его в
каждой точке другие решения.
Пример. Найти особое решение уравнения
у = х + У - 1пт/.	(10)
Дифференцируем обе части равенства по у':
o = i-4-	(11)
У
Исключаем у’ из уравнений (10) и (11). Из (11) имеем у' = 1;
подставляя это в (10), получаем уравнение дискриминантной
кривой
У = х + Ъ	(12)
Проверим, будет ли кривая особым решением. Для этого
сначала проверяем, является ли она решением уравнения (10).
Подставляя (12) в (10), получаем тождество х + 1 = х + 1. Зна-
чит, кривая (12) — решение.
Теперь проверим, является ли это решение особым, т. е. ка-
саются ли его в каждой точке другие решения. В п. 1 было
найдено, что другие решения выражаются формулой (6). Пи-
шем условия касания кривых у = у\(х) и у = уъ^х) в точке с
абсциссой xq".
3/1(яо) = 2/2(^о), У1(яо) = 3/2(яо)-	(13)
Для решений (6) и (12) эти условия принимают вид ех°~с+С =
= xq + 1, ех°~с = 1. Из второго равенства имеем С = xq;
подставляя это в первое равенство, получаем 1 + xq = xq + 1.
Это равенство справедливо при всех xq. Значит, при каждом xq
решение (12) в точке с абсциссой xq касается одной из кривых
семейства (6), а именно той кривой, для которой С = xq.
Итак, в каждой точке решение (12) касается другого реше-
ния (6), не совпадающего с ним. Значит, решение (12) — особое.
Если семейство решений записано в параметрическом виде,
как в (5), то выполнение условий касания проверяется анало-
гично. При этом надо учесть, что у' = р.
44
3. Если семейство кривых Ф(т, у, С) = 0, являющихся реше-
ниями уравнения F(t, у, у') = 0, имеет огибающую у = то
эта огибающая является особым решением того же уравнения.
Если функция Ф имеет непрерывные первые производные, то
для отыскания огибающей надо исключить С из уравнений
Ф(х, у, С) = О, ^Ф( gj’ С) = О
и проверить, будет ли полученная кривая огибающей, т. е. ка-
саются ли ее в каждой точке кривые семейства. Эту проверку
можно провести изложенным в конце п. 2 методом, используя
условия касания (13).
В задачах 241—250 найти все решения дан-
ных уравнений; выделить особые решения (если они
есть); дать чертеж.
241.	у'2 - у2 = 0.	242. Sy'3 = 27у.
243.	(у' + 1)3 = 27(ж + у)2.
244.	у2(у'2 + 1) = 1.
245.	у'2 - 4у3 = 0.	246. у'2 = 4у3(1 - у).
247.	ху'2 = у.	248. уу'3 + х = 1.
249.	у'3 + у2 = уу'(у' + 1).
250.	4(1 - у) = (Зу - 2)2у'2.
Уравнения 251—266 разрешить относительно yf,
после этого общее решение искать обычными ме-
тодами (§§2,4,5,6). Найти также особые решения,
если они есть.
251.	у'2 + ху = у2 + ху'. 252. ху’^ху’ + у) = 2у2.
45
254. ху'2 = у(2у' - 1).
256. у'3 + (ж + 2)е» = 0.
258. (ху1 + З?/)2 = 7х.
253. ху'2 — 2уу' + х = 0.
255. у'2 + х = 2у.
257. у'2 - 2ху' = 8х2.
259.	у'2 -2уу' = у2(ех -1).
260.	у'(2у — у') = у2 sin2 х.
261.	у'4 + у2 = у4.
262.	х(у - ху')2 = ху'2 - 2уу'.
263.	у(ху' -у)2 = у - 2ху'.
264.	уу'(уу' - 2х) =х2 - 2у2.
265.	у'2 + 4ху' — у2 — 2х2у = х4 — 4ж2.
266.	у(у - 2ху')2 = 2у'.
Уравнения 267—286
параметра.
267. х = у'3 + у'.
269. х = у'у/у'2 + 1-
271. у = у'2 + 2у'3.
273. (у' + 1)2 = (у' -у)2.
275. у'4 — у'2 = у2.
277. у'4 =2уу' +у2.
решить методом введения
268.	х(у'2 - 1) = 2у'.
270.	у'(х — In у1) = 1.
272.	у = 1п(1 + у'2).
274.	у = (у' — 1)еу'.
276.	у'2 - у'3 = у2.
278.	у'2 — 2ху' = х2 — 4у.
46
279. ay + у'2 = х(х + у').
281. у'3 + у2 = хуу'.
283. у' = еху'/у.
285. у = 2ху' + у2у'3.
280. х2у'2 = хуу' + 1.
282. 2ху' — у = у'\п уу'
284. у = ху' — х2у'3.
286.	у(у - 2ху')3 = у'2.
Решить уравнения Лагранжа и Клеро (задачи
287—296).
287.	у = ху' - у'2.
289.	у = 2ху' - 4ц'3.
291. у'3 = 3(ху' - у).
293. ху' — у = kiy'.
295. 2у'2(у - ху') = 1.
288. у + ху' = 4^/у1.
290.7/ — ху' - (2 + з/').
292. у = ху'2 - 2у'3.
294. ху'(у' + 2) = у.
296. ‘Zxy’ — у = Iny1.
297.	Найти особое решение дифференциального
уравнения, если известно семейство решений этого
уравнения:
а) у = Сх2 - С2,	б) Су = (ж - С)2,
в) у = С(х - С)2,	г) ху = Су - С2.
298.	Найти кривую, каждая касательная к кото-
рой образует с осями координат треугольник пло-
щади 2а2.
299.	Найти кривую, каждая касательная к ко-
торой отсекает на осях координат такие отрезки,
что сумма величин, обратных квадратам длин этих
отрезков, равна 1.
47
300.	Найти кривую, проходящую через начало
координат и такую, что отрезок нормали к ней,
отсекаемый сторонами первого координатного угла,
имеет постоянную длину, равную 2.
§ 9.	РАЗНЫЕ УРАВНЕНИЯ
ПЕРВОГО ПОРЯДКА1)
Решить уравнения 301—330 и построить графи-
ки их решений.
301.	ху' + х2 + ху — у = 0. 302. Ъху' + у2 = 1.
303.	(2ху2 — у) ckr + xdy = 0.
304.	(ху' + у)2 = х2у1.	305. у — у' — у2 + ху'.
306.	(ж + 2у3)у' = у.	307. у'3 - у'е2х = 0.
308.	х2у' = у(х + у).
309.	(1 — х2) dy + ху da: = 0.
310.	у'2 + 2(х - 1)у' - 2у = 0.
311.	у + у' In2 у = (а: + 2 \пу)у'.
312.	х2у' — 2ху = Зу.
313.	х + уу' = з/2(1+ у'2).
314.	у = (ху1 + 2у)2.	315. у' = -±-~.
О/ у
-1) Все задачи § 9 решаются изложенными ранее методами.
48
316. у'3 + (3® - 6)у’ = 32/.	317.Ж-£ = 2.
318. 2у'3 - Зу'2 + х = у. 319. (х + у)2у' = 1.
320.	2х3уу’ + Зж2у2 + 7 = 0.
321-v=(;-2l)d»-
322.	ху' = еу + 2у'.
323.	2(ж — у2) dy = у скс.
324.	х2у'2 + у2 = 2ж(2 — уу').
325.	dy + {ху — ху3) d# = 0.
326.	2х2у' = у2{2ху' -у).
328.	х{х — 1)у' + 2ху = 1.
329.	ху{ху' — у)2 + 2у’ = 0.
330.	(1 — x2)yf — 2ху2 = ху.
Решить уравнения 331—420.
331.	у’ +у = ху3.
332.	(ж?/4 — x)dx + {у + ху) dy = 0.
333.	(sin х + у) dy + {у cos х — х2) dx = 0.
334.	Зт/'3 -ху1 + 1 = 0.
49
335.	уу' + у2 ctg х = cos х.
336.	(еу + 2ху) d# + (еу + х)х dy = 0.
337.	ху'2 = у-у'.
338.	ж(х + 1)(з/' - 1) = У-
339.	у(у - ху') = у/х4 + у4.
340.	ху' + у = In?/'.
341.	a;2 (ch/ — dec) = (ж + y)ydx.
342.	у' + х$у = Зу.
343.	(ж cos у + sin 2у)у' = 1.
344.	у'2 - уу' + ех = 0.
345.	у' = ^е2х + у.
346.	(ху' - у)3 = у'3 - 1.
347.	(4ху - 3)у' + у2 = 1.
348.	у'у/х = у/у - х + у/х.
349.	ху' = 2^/ycosa: — 2у.
350.	Зу'4 =у'+у.
351.	у2(у-ху') = х3у'.
352.	у' = (4х + у - З)2.
50
353.	(cos x — x sin x)y бж + (ж cos x — 2y) dy = 0.
354.	x2y'2 — 2xyy' = ж2 + 3y2.
355.	^+2ж?/1пж + 1 = 0.
356.	xyf = xy/у — ж2 + 2y.
357.	(1 — x2y) бж + x2(y — ж) dy = 0.
358.	(2же2/ + y4)y' = yey.
359.	ж2/'(1п1/ — In ж) = у.
360.	2у' = х + In у1.
361.	(2х2у - Зу2)у' = бж2 - 2ху2 + 1.
362.	уу' = 4ж + Зу - 2.
363.	у2у’ + ж2 sin3 ж = у3 ctg ж.
364.	2ху' — у = sin у'.
365.	(ж2?/2 + 1)у + {ху — l)2xyf = 0.
366.	у sin ж + у' cos ж = 1.
367.	xdy — ydx = ху/х2 + у2 бж.
368.	у2 + х2у'5 = ху(у'2 + у,3\
369.	у' = %2х-у + 2.
370.	(ж — у cos ) бж + ж cos dy = 0.
51
371.	2 ух2 у + у/1 + ж4 у2) d® + х3 dy = 0.
372.	(у1 - Xy/у) (х2 - 1) = ху.
373.	у'3 + (у'2 - 2у')х = Зу' - у.
374.	(2х + Зу — 1) dx + (4х + бу — 5) dy = 0.
375.	(2ху2 — y)dx + (у2 + х + у) dy = 0.
376.	у = y'Vl + У'2.
377.	у2 = (хуу' + 1) In х.
378.	4у = х2 + у’2.
379.	2xdy + у dx + ху2 (х dy + у dx) = 0.
380.	х dx + (х2 ctg у — 3 cos у) dy = 0.
381.	х2у'2 — 2(ху — 2)у' + у2 = 0.
382.	ху1 + 1 = ех~у.
383.	у' = tg(i/ - 2ж).
384.	Зх2 — у = у’\/х2 + 1.
385.	уу1 + ху = х3.
386.	х(х — 1)у' + у3 = ху.
387.	ху1 = 2у + Vl + У’2-
388.	(2х + у + 5)7/' = Зх + 6.
52
389.	у' + tg у = х sec у.
390. у'4 = 4у(ху' - 2у)2.
392.	ху' = х2е-у + 2.
393.	у' = За: + \/у - х2.
394.	х dy — 2у бж + ху2 (2ж dy + у drc) = 0.
395.	(ж3 — 2ху2) 4ж + Зж21/ dy = х dy — у 4ж.
396.	(уу')3 = 27х(у2 — 2ж2).
397.	у'-8х^у = ^-г.
398.	[2х - ln(y + 1)] da; - dy = 0.
399.	ху' = (а;2 + tgy) cos2 у.
400.	х2(у - ху') = уу'2.
401. у' =
Зх2
X3 + у + 1'
402. у' =
(1 + у)2
х(у + 1) - х2 '
403. (у - 2ху')2 = dyy'3.
404.	6х5у 4ж + (у4 In у — Зж6) dy = 0.
405.	у' = ^у/х + ^у.
406.	2ху' + 1 = у +
53
407.	О' + Ж = 1(^)2.
408.	у' = (Зж+у3~1)2~
409.	+ 1 + 1)(у2 + 1) d® = xydy.
410.	(ж2 + у2 + I)?/?/ + (ж2 + у2 — 1)ж = 0.
411.	у2(х — 1) бж = х(ху + ж — 2у) dy.
412.	(xyf — у)2 = х2у2 — х4.
413.	хуу' - х2у/у2 + 1 = (ж + 1)(?/2 + 1).
414.	(ж2 — 1)у' + у2 — 2ху + 1 = 0.
415.	у' tg у + 4ж3 cos у = 2ж.
416.	(ху' - у)2 = у'2 -	+ 1.
417.	(ж + т/)(1 — ху) бж + (ж + 2у) dy = 0.
418.	(Зжт/ + ж + у)у бж + (4ж1/ + ж + 2у)х dy = 0.
419.	(ж2 — 1) бж + (х2у2 + ж3 + ж) dy = 0.
420.	х(у'2 + е2«) = -2у'.
§ 10. УРАВНЕНИЯ, ДОПУСКАЮЩИЕ
ПОНИЖЕНИЕ ПОРЯДКА
1. Если в уравнение не входит искомая функция у, т. е. оно
имеет вид F(t, у(к\	у(п)) = 0, то порядок уравне-
ния можно понизить, взяв за новую неизвестную функцию низ-
шую из производных, входящих в уравнение, т. е. сделав замену
7/(fc) = Z.
54
2.	Если в уравнение не входит независимое переменное х,
т. е. уравнение имеет вид F(y, у', у", ..., у^) = 0, то порядок
уравнения можно понизить, взяв за новое независимое перемен-
ное у, а за неизвестную функцию у' = р(у\
Пример. Решить уравнение 2ууп = у'2 + 1.
В уравнение не входит х. Полагаем у' =р(у). Тогда
П _ d(y') _ dp(y) _ dp dy _ ,
dx dx dy dx ?
Подставляя у' = p и у" = pp' в уравнение, получим 2уррг = р2 +
+1. Порядок уравнения понижен. Решив полученное уравнение,
найдем р = ±у/Су — 1. Следовательно, у' = ±\/Су — 1. Из этого
уравнения получим 4(Ст/ — 1) = С2(т + С2).
3.	Если уравнение однородно относительно у и его производ-
ных, т. е. не меняется при одновременной замене т/, у1, уп, ...
на ку, ку', ку", ..., то порядок уравнения понижается подста-
новкой у' = yz, где z — новая неизвестная функция.
4.	Порядок уравнения понижается, если оно является од-
нородным относительно х и у в обобщенном смысле, т. е. не
меняется от замены х на кх, у на кту (при этом у' заменяется
на кт~1у', у" — на кт~2у" и т. д.). Чтобы узнать, будет ли
уравнение однородным, и найти число т, надо приравнять друг
другу показатели степеней, в которых число к будет входить в
каждый член уравнения после указанной выше замены. На-
пример, в первый член уравнения 2х4у" — Зу2 = а?4 после этой
замены число к будет входить в степени 4 + (ш — 2), во вто-
рой — в степени 2т, в третий — в степени 4. Следовательно,
т должно удовлетворять уравнениям
4 + (т — 2) = 2т = 4.
Отсюда т = 2. Если же полученные уравнения для т будут
несовместными, то дифференциальное уравнение не является
однородным в указанном смысле.
После того как число т найдено, надо сделать замену пе-
ременных х = еь, у = zem*, где z = z(t) — новая неизвестная
функция, at — новое независимое переменное. Получим урав-
нение, в которое не входит независимое переменное t. Порядок
такого уравнения понижается одним из ранее рассмотренных
способов.
55
5.	Порядок уравнения легко понижается, если удается пре-
образовать уравнение к такому виду, чтобы обе его части явля-
лись полными производными по х от каких-нибудь функций.
Например, пусть дано уравнение ууп = у'2. Деля обе части
на уу', получим ^7- =	(1пт/)' = (1пт/)'; In У = InT/H-lnC;
у' — уС. Порядок уравнения понижен.
Решить уравнения
421. х2у" = у'2.
423. у3у" = 1.
425. у" = 2уу'.
427. у"(ех + 1) + у’ = 0.
429. уу" = у'2 - у'3.
431. 2уу" = у2 + у'2.
433. у"2 + у' = ху".
435. ху'" = у" — ху".
437. у" = еу.
439. 2у'(у" + 2) = ху"2.
441. у'2 = (Зу - 2у')у".
443. у"2 - 2у'у'" + 1=0.
421—450.
422. 2ху'у" = у'2 - 1.
424. у'2 + 2уу" = 0.
426. уу" + 1 = у'2.
428. у'" = у"2.
430. у'" = 2(у" — 1) ctg#.
432. у"3 + ху" = 2у'.
434. у" + у'2 = 2е~».
436. у"2 = у'2 + 1.
438. у" — ху'" + у'"3 = 0.
440. у4 — у3у" = 1.
442.у"(2у' + х) = 1.
444.	(1 — х2\у" + ху' = 2.
445.	уу" - 2уу' In г/ = у'2.
56
446.	(у' + 2у)у" = у'2.	447. ху" = у' + xsin^.
448. у'"у'2 = у"3.	449. уу" + у = у’2.
450. ху" = yf + х(у'2 + ж2).
Решить уравнения 451—454, воспользовавшись
формулой, сводящей многократное интегрирование
к однократному (см. [1], гл. IV, § 2, п. 1).
451. ху™ ~ 1.	452. ху" = sin ж.
453. у’" = 2ху".	454. ху™ + у'" = еж.
Решить уравнения 455—462, преобразовав их к
такому виду, чтобы обе части уравнения являлись
полными производными.
455. уу"' + Зу'у" = 0.
457. уу" = у1 (у1 + 1).
459. уу" + у’2 = 1.
461. ху" = 2уу' — у'.
456. у'у1" = 2у"2.
458. 5у"'2 - 3y"ylv = 0.
460. у" = ху1 + у + 1.
462. ху" — у1 = х2уу'.
В задачах 463—480 понизить порядок данных
уравнений, пользуясь их однородностью, и решить
эти уравнения.
463. хуу" — ху'2 = уу'.	464. уу" = у’2 + 15т/2у/х.
465. (ж2 + 1)(у'2 - уу") = хуу1.
466. хуу" + ху'2 = 2уу'. 467. х2уу" = (у — ху')2.
57
468.	у" +	+ А = У~-
X xz у
469.	у(ху" + г/') = жг/'2(1 — х).
470.	х2уу" + у'2 = 0.
471.	ж2 (г/'2 - 2уу") = у2.
472.	хуу" = у'(у + у').
473.	4х2у3у" = х2 — у4.
474.	х3у" = (у - ху')(у - ху' - х).
475.	£ + у'2 = Зху" +
476.	у” = (2ху - у' + 4г/2 -
477.	х2(2уу" — г/'2) = 1 — 2жг/г/'.
478.	х2(уу" - у'2) + хуу' = (2ху' - Зуу/х3.
479.	х4 (у'2 — 2уу") = ^.х3уу' + 1.
480.	уу' + хуу" — ху'2 = х2.
В задачах 481—500, понизив порядок данных
уравнений, свести их к уравнениям первого порядка.
481.	г/"(3 + г/г/'2) = г/'4	482. у"2 - у'у'" =	
483. уу' + 2х2у" = ху'2. 484. у'2 + 2хуу" = 0.
485.	2ху2(ху" + у1) + 1 = 0.
58
486.	х(у" + г/'2) = у'2 + у'.
487.	у2 (у'у'" -2у"2)=у'4.
488.	у(2ху" + у') = ху'2 + 1.
489.	у" + 2уу'2 = (2х +	у1.
490.	у'у'" = у"2 + у'2у"	491. уу" = у'2 + 2ху2.
492. у"4 = у'5 - уу'3у".	493. 2уу'" = у'.
494. у'"у’2 = 1.	495. у2у’" = у'3.
496.	х2уу" + 1 = (1 — у)ху’.
497.	уу'у'" + 2у'2у" = Зуу"2.
498.	(у'у'" - Зу"2)у = у'5.
499.	у2 (у'у'" - 2у"2) = уу'2у" + 2у'4.
500.	х2(у2у'" - у'3) = 2у2у' - Зхуу'2.
В задачах 501—505 найти решения, удовлетво-
ряющие заданным начальным условиям.
501.	уу" = 2ху'2; у(2) = 2, у'(2) = 0,5.
502.	2у'" - Зу'2 = 0; у(0) = -3, у'(0) = 1,
J/"(0) = -1-
503.	х2у" - Зху' =	- 4у; у(1) = 1, у'(1) = 4.
504.	у'" = Зуу'; 7/(0) = —2, т/'(0) = 0, у"(0) = 4,5.
59
505.	у" cos у + у'2 sin у = у1; у(-1) = |, ?/'(—1) = 2.
506.	Найти кривые, у которых в любой точке
радиус кривизны вдвое больше отрезка нормали,
заключенного между этой точкой кривой и осью
абсцисс. Рассмотреть два случая: а) кривая обра-
щена выпуклостью к оси абсцисс; б) вогнутостью к
оси абсцисс.
507.	Найти кривые, у которых радиус кривиз-
ны обратно пропорционален косинусу угла между
касательной и осью абсцисс.
508.	Определить форму равновесия нерастяжи-
мой нити с закрепленными концами, на которую
действует нагрузка так, что на каждую единицу
длины горизонтальной проекции нагрузка одинакова
(цепи цепного моста). Весом самой нити пренебречь.
509.	Найти форму равновесия однородной нера-
стяжимой нити (с закрепленными концами) под дей-
ствием ее веса.
510*. Доказать, что уравнение движения маят-
ника у” + sin у = 0 имеет частное решение ?/(ж),
стремящееся к тг при х —>+оо.
§ 11.	ЛИНЕЙНЫЕ УРАВНЕНИЯ
С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
1. Чтобы решить линейное однородное уравнение с постоян-
ными коэффициентами
a0?/n) + ai2/(n-1) Н-h а>п-1у' + о>пУ = 0,	(1)
надо составить характеристическое уравнение
а>оХп + П1 Хп 1 + • • • + dn — iX + ап = 0	(2)
и найти все его корни Ai, ..., Хп.
Общее решение уравнения (1) есть сумма, состоящая из сла-
гаемых вида CiQXiX для каждого простого корня Xi уравнения
(2) и слагаемых вида
(Gn+i + С'т+зж + Сш+з^2 + • • • + Ст+кхк 1)еЛж (3)
60
для каждого кратного корня Л уравнения (2), где к — крат-
ность корня. Все Ci — произвольные постоянные. Коэффици-
енты уравнения (1) и корни А здесь могут быть вещественными
или комплексными.
Если же все коэффициенты уравнения (1) вещественные, то
решение можно написать в вещественной форме и в случае ком-
плексных корней А. Для каждой пары комплексных сопряжен-
ных корней А = а ± (3i в формулу общего решения включаются
слагаемые
Cm+ieax cos fix + Cm^2Qax sin/3x,
если эти корни простые, и слагаемые
Pk-i(x)eax cos/Зх + Qk-i(x)eax sin Де,
если каждый из корней a + [3i и a — (3i имеет кратность к. Здесь
Pk-i и Qk-i — многочлены степени к — 1, аналогичные много-
члену в (3), их коэффициенты — произвольные постоянные.
Пример. Решить уравнение yv — 2ylv — 16у' + 32т/ = 0.
Пишем характеристическое уравнение
А5 - 2А4 - 16А + 32 = 0.
Разлагая левую часть на множители, находим корни:
(А - 2)(А4 - 16) = 0, (А - 2)2(А + 2)(А2 + 4) = 0,
Ai = А2 = 2, Аз = —2, А4 = 2г, А5 = —2г.
По изложенным выше правилам пишем общее решение
у = (С1 + С2х)е2х + Сзе~2ж + С4 cos 2х + С5 sin 2х
(степень многочлена Ci + С2Х на 1 меньше кратности корня
А = 2).
2.	Для линейных неоднородных уравнений с постоянными
коэффициентами и с правой частью, состоящей из сумм и про-
изведений функций bo + bix + ••• + ЬтХ171, еах, cos/Зх, sin/Зх,
частное решение можно искать методом неопределенных коэф-
фициентов.
Для уравнений с правой частью Рт(а?)е7Ж, где Рт(х) = 6о +
+61 х +---И ЪтХ™') частное решение имеет вид
У1 = xsQm(x)efX,	(4)
61
где Qm(x) — многочлен той же степени тп. Число s = О, если
7 — не корень характеристического уравнения (2), а если 7 —
корень, то s равно кратности этого корня. Чтобы найти ко-
эффициенты многочлена	надо решение (4) подставить
в дифференциальное уравнение и приравнять коэффициенты
при подобных членах в левой и правой частях уравнения.
Если в правую часть уравнения входят синус и косинус, то
их можно выразить через показательную функцию по форму-
лам Эйлера
I i(3x	oi0x _ p—i/Зх
cos Де =-----------, sin/?a?= ---------- (5)
и свести задачу к уже рассмотренному случаю.
Если же коэффициенты левой части уравнения веществен-
ны, то можно обойтись без перехода к комплексным функци-
ям (5). Для уравнения с правой частью
еах cos Q(x) sin /Зх)	(6)
можно искать частное решение в виде
У1 = xseax(Rm(x) cos /Зх 4-Тт(т) sin/Зх),	(7)
где s = 0, если а + (Зг не корень характеристического урав-
нения, и s равно кратности корня а + (3i в противном случае,
a Rm и Тт — многочлены степени т, равной наибольшей из
степеней многочленов Р и Q. Чтобы найти коэффициенты мно-
гочленов Rm и Тт, надо подставить решение (7) в уравнение и
приравнять коэффициенты при подобных членах.
Еще один метод отыскания частного решения уравнения с
вещественными коэффициентами и правой частью вида (6) со-
стоит в следующем. Сначала решают уравнение с правой ча-
стью Р(х)е(а+Рг')х. Вещественная часть этого решения будет ре-
шением уравнения с правой частью Р(х)еах cos (Зх, а мнимая —
решением уравнения с правой частью Р(х)еах sin (Зх.
Если правая часть уравнения равна сумме нескольких функ-
ций вида Р(х)&х и вида (6), то частное решение отыскивается
по следующему правилу.
Частное решение линейного уравнения с правой частью Д +
+ ••• + /₽ равно сумме частных решений уравнений с той же
левой частью и правыми частями Д, ..., Д.
62
Общее решение линейного неоднородного уравнения во всех
случаях равно сумме частного решения этого уравнения и об-
щего решения однородного уравнения с той же левой частью.
Пример. Решить уравнение
у1" — бу" 4- 9у' = хе3х + е3ж cos 2т.	(8)
Характеристическое уравнение А3 — 6А2 + 9А = 0 име-
ет корень А = 3 кратности 2 и корень А = 0 кратности 1.
Поэтому общее решение однородного уравнения имеет вид
Уо = (Ci + С2х)е3х + с3.
Правая часть (8) состоит из двух слагаемых вида (6); для
первого 7 = а + (Зг = 3, а для второго а + (3i = 3 + 2г. Так как
эти числа различны, то надо искать отдельно частные решения
уравнений
у"’ - бу" + 9т/' = хе3х,	(9)
у"' — бу" 4- 9у' = е3ж cos 2т.	(10)
Число 7 = 3 является корнем кратности s = 2, поэтому част-
ное решение уравнения (9) согласно (4) имеет вид у± = т2(ат4-
4-Ь)е3ж. Подставив у = у\ в (9), найдем а = 1/18, Ъ = —1/18.
Далее, число а + /?г = 3 + 2г не является корнем характе-
ристического уравнения, поэтому частное решение уравнения
(10) согласно (7) имеет вид у2 = е3ж (с cos 2т 4- d sin 2т). Подста-
вив у = у2 в (10), найдем с = —3/52, d = —1/26.
Общее решение уравнения (8) равно у = уо + У1 + У2> где уо,
У1, у2 уже найдены.
3.	Линейное неоднородное уравнение
ao2/(n) + ai3/(n-1) +-И апу = /(т)	(11)
с любой правой частью /(т) решается методом вариации по-
стоянных. Пусть найдено общее решение у = С\у± 4-----F Спуп
линейного однородного уравнения с той же левой частью. Тогда
решение уравнения (11) ищется в виде
у = С1(т)?/1 4---И Сп(х)уп-
Функции Сг(т) определяются из системы
С'^ух 4- • • • 4- С'пуп = 0
С1У1 Н----Ь СпУп = 0
<л4п“2) + --- + с^п~2) = 0
ао(с'1?/^п_1) +  • • +	= f(x).
63
4.	Уравнение Эйлера
аохпу^ + aixn~1y^n~1>) +-----F an-ixy' + апу = f(x) (12)
сводится к линейному уравнению с постоянными коэффициен-
тами заменой независимого переменного х = е* при х > 0 (или
х = —е* при х < 0). Для полученного уравнения с постоянными
коэффициентами характеристическое уравнение имеет вид
аоА(А —1)(А —2)... (Л —7i + l) + ‘ •	2^(A —1)+ап—1 A-f-an = 0.
При составлении этого уравнения каждое произведение хку^
в (12) заменяется на произведение к убывающих на 1 чисел:
А(А — 1)(А — 2)... (А — А; + 1).
Пример. Решить уравнение
х3уш — х2у" + Ъху' —е2у = х3.	(13)
Сразу пишем характеристическое уравнение и решаем его:
А(А - 1)(А - 2) - А(А - 1) + 2А - 2 = 0,	(14)
(А - 1)(А2 - ЗА + 2) = 0, Ai = А2 = 1, Аз = 2.
При таких А общее решение однородного уравнения с постоян-
ными коэффициентами имеет вид (согласно п. 1)
Уо = (Ql + C2t)e^ + Сзе2*.
Чтобы решить неоднородное уравнение (13), сначала рас-
кроем скобки в (14): А3 — 4А2 -f- 5А — 2 — 0. По этому характери-
стическому уравнению составляем левую часть дифференци-
ального уравнения, а правую часть получаем из правой части
(13) заменой х = е*:
у"' - iy'l + by't -2у = e3t.
Так как число 3 не является корнем характеристического урав-
нения, то частное решение ищем в виде у± = ae3t. Подставляя
в уравнение, находим а = 1/4.
Следовательно, общее решение имеет вид
У — Уо + У1 — (Ci + С2/;)е^ + Сзе2* + ^е3* =
= (Ci + С2 1пт)х + Сзт2 + ^х3 (х > 0).
64
При х < 0 получается аналогичная формула, но с In |а?| вме-
сто 1пт.
5.	Для решения задач 635—640 и 879 можно пользоваться
следующими законами теории электрических цепей (см. также
[3], § 13).
Для каждого узла цепи сумма всех притекающих токов рав-
на сумме вытекающих токов.
Алгебраическая сумма напряжений источников тока, содер-
жащихся в любом замкнутом контуре цепи, равна алгебраиче-
ской сумме падений напряжений на всех остальных участках
этого контура.
Падение напряжения на сопротивлении R равно RI; падение
г	г
напряжения на самоиндукции L равно падение напряже-
ния на конденсаторе емкости С равно q/C, где q = q(t) — заряд
конденсатора в момент t; при этом = /; во всех трех случа-
ях I = I(t) — сила тока, протекающего через рассматриваемый
участок цепи в данный момент t. В этих формулах I выража-
ется в амперах, R — в омах, L — в генри, q — в кулонах, С —
в фарадах, t — в секундах, напряжение — в вольтах.
Пример. Последовательно включены: источник тока, на-
пряжение которого меняется по закону Е = VsincjZ, сопроти-
вление R и емкость С. Найти силу тока в цепи при установив-
шемся режиме1).
Решение. Сила тока I = I(t) на любом участке цепи од-
на и та же (по закону о последовательном соединении). Паде-
ние напряжения на сопротивлении равно RI, а на емкости q/C.
Следовательно, RI+^ = Vsmwt. Дифференцируя и пользуясь
тем, что = Z, получим уравнение
R — +	= VcjcoscjZ.	(15)
at о
Это — линейное уравнение с постоянными коэффициентами.
Для отыскания установившегося режима найдем периодиче-
ское решение этого уравнения. Исходя из вида правой части
уравнения, ищем решение в виде
Z = Al coscjZ + Bi sincjt	(16)
х) Установившимся режимом называется такой, при кото-
ром сила тока постоянна или меняется периодически.
65
Подставляя (16) в (15) и приравнивая коэффициенты при по-
добных членах, получим систему двух уравнений, из которой
можно найти Ai и В±. Но в электротехнике важнее знать не
коэффициенты и В±, а амплитуду изменения силы тока.
Поэтому выражение (16) переписывают в виде
I = Asin(cj£ — (/?).	(17)
Подставляя (17) в (15), переходя к тригонометрическим функ-
циям углов cut и (/?, приравнивая коэффициенты сначала при
sincjt, а затем при coscjZ, получим
RAcj sin ip + cos ip = 0, RAcj cos ip — sin ip = Vcu.
С	(у
Отсюда найдем
tg <р =-tTFt— 5 А = -/   . V 	.
RC(jJ	y/R2 +(шС)~2
Поясним, почему найденное периодическое решение называ-
ется установившимся режимом. Общее решение уравнения (15)
равно сумме найденного частного решения (17) и общего реше-
ния линейного однородного уравнения
+	=	(18)
Так как решение уравнения (18) I =	(здесь К —
произвольная постоянная) стремится к нулю при t —> +ос, то
любое решение уравнения (15) при t —> +оо неограниченно
приближается (и притом весьма быстро) к найденному перио-
дическому решению (17).
Решить уравнения 511—548.
511. у" + у' — 2у = 0.
513. у” - 2у' = 0.
515. у" - 4у' + 5у = 0.
517. у" + 4у = 0.
512. у" + 4у' + Зу = 0.
514. 2у" - 5у' + 2у = 0.
516. у" + 2у' + 10у = 0.
518. у"' -8у = 0.
66
519. yw - у = 0.	520. ylv + 4y = 0.
521. yvl + 64y = 0.	522. y" -2y' +y = Q.
523. 4y" + 4y' + у = 0.	524. yv - 6yIV + 9y'" = 0.
525. yv - 10y"' + 9y' = 0.
526. ylv + 2y" + у = 0.
527. у”' - Зу" + 3y' -у = 0.
528. у"' -у" -у1 + у = 0.
529. yIV - Зу" + 4у = 0. 530. yv + 8у"' + 16т/' = 0.
531. у'" - Зу' + 2у = 0.	532. у™ + 4г/" + Зу = 0.
533. у" - 2у' - Зу = е4х. 534. у" + у = 4хех.
535. у" -у = 2ех - х2.	536. у" + у' -2у = Зхех.
537. у" - Зу' + 2у = sin ж.
538. у" + у = 4 sin х.
539. у" — Зу' + 4у = 4х2е2х.
540. у" — Зу' + 2у = xcosx.
541. у" + Зу' — 4?у = е~4ж + хе~х.
542. у" + 2у' — Зу = х2ех.
543. у" — Ay' + 8у = е2х + sin 2х.
67
544.	у" — 9у = е3х cos х.
545.	у" — 2у' + у = 6хех.
546.	у" + у = х sin х.
547.	у" + 4?/' + 4?/ = хе2х.
548.	у” — Ъу' = Зж2 + sin 5#.
В задачах 549—574 для каждого из данных
уравнений написать его частное решение с неопреде-
ленными коэффициентами (числовых значений ко-
эффициентов не находить).
549.	у" — 2у' + 2у = еж + х cos х.
550.	у" + б?/' + 10?/ = Зже-3ж — 2е3ж cos х.
551.	у" — 8у' + 20?/ = 5же4ж sin 2х.
552.	у” + 7у' + 10?/ = хе~2х cos 5#.
553.	у” — 2у' + Ъу = 2хех + еж sin2#.
554.	у" — 2yf + у = 2хех + ех sin 2х.
555.	у” — 8у' + 17?/ = е4ж(ж2 — 3irsinir).
556.	у'" + у' = sin х + х cos х.
557.	ут - 2у" + 4?/' -Sy = е2х sin2ir + 2х2.
558.	у” — бу1 + 8у = 5же2ж + 2е4ж sin х.
559.	у" + 2у' + у = х(е~х — cos х).
68
560.	у'" — у" — у' + у = Зеж + 5irsinir.
561.	у" — бу' + 13?/ = ж2е3ж — 3cos2ir.
562.	у” — 9у = е~3х(х2 + sin3ir).
563.	у1У + у" = 7х — 3 cos х.
564.	у" + 4у = cos х • cos3ir.
565.	у'" — ±у" + З?/' = х2 + хе2х.
566.	у” — 4у' + Зу = е2ж sin2 х.
567.	у” + Зу' + 2у = е~х cos2 х.
568.	у" — 2у' + 2у — (х + еж) sinх.
569.	y1N + Зу" + 4у = sin ж • cos2ir.
570.	у" -Зу' + 2у = 2х.
571.	у" — у — 4shir.
572.	у" + 4?/' + Зу = chх.
573.	у" + 4?/ = shir • sin2ir.
574.	у" + 2у’ + 2у = ch х • sinir.
Решить уравнения 575—581 способом вариации
постоянных.
575.	у"-2у^у=
576.	у" + Зу' + 2у =
69
577.	у" + у =
578.	у” + Фу = 2tgx.
579.	у” + 2у' + у = Зе~ху/х+Т
580.	у" + у = 2 sec3 х.
581*. х3(у" - у) = х2 - 2.
Найти решения уравнений 582—588, удовлетво-
ряющие указанным начальным условиям.
582.	у" - 2у' + у = 0; у(2) = 1, у'(2) = -2.
583.	у" + у = 4ех; р(0) = 4, т/'(0) = -3.
584.	у" - 2у' = 2еж; у(Г) = -1, т/'(1) = 0.
585.	у” + 2у' + 2у = хе~х; y(Q) = т/'(0) = 0.
586.	у"' - у’ = 0; 7/(0) = 3, т/'(0) - -1, т/"(0) = 1.
587.	у’" - Зу' — 2у = 9е2ж; т/(0) = 0, т/'(0) = -3,
Л0) = 3.
588.	у1У + у" = 2 cos х, ?/(0) = —2, у1 (0) = 1,
7/"(0) = 7/"'(0) = 0.
В задачах 589—600 решить уравнения Эйлера
589.	х2у" — 4ху' + 6т/ = 0.
590.	х2у" — ху' — Зу = 0.
591.	хгу'" + ху' — у = 0.
70
592.	х2у"' = 2y'.
593.	x2y" — ху' + у = 8x3.
594.	x2y" + xy' + 4?/ = Юж.
595.	хгу" — 2xy = 6 In ж.
596.	x2y" - 3xy' + 5y = 3x2.
597.	x2y" — 6y = 5a;3 + 8a;2.
598.	x2y" — 2y = sin In a;.
599. (x - 2')2y" - 3(x - 2)y' + 4y = x.
600.	(2x + 3)3y"' + 3(2x + 3)y' -6y = 0.
Применяя различные методы, решить уравнения
601—611.
601.	у" + 2у’ +у = cos га;.
602.	у” — 2у‘ + у = хех sin2 ix.
603.	у" + 2iy = 8еж sin а;.
604.	у" + 2iy’ — у = 8 cos а;.
605.	у'" - 8iy = cos 2а;.
606.	у" -	= 31п(-х).
607.	у” + 2?/' +у = хех +
608.	у” + 2yf + Зу = е~ж(соз2а; + tga;).
71
609.	х2у" - 2у = -^-г.
у х + 1
л гч 2 //	/ I	In X । X
610.	xzy — ху +у =-------------Н :—.
у г/ г/ х	1П х
611*. у" +y = f(x).
612*. Какие условия достаточно наложить на
функцию /(ж), чтобы все решения уравнения за-
дачи 611 оставались ограниченными при х -> +оо?
В задачах 613—618 построить линейные одно-
родные дифференциальные уравнения с постоянны-
ми коэффициентами (возможно более низкого по-
рядка), имеющие данные частные решения.
613. yi = х2ех.	614.	yi	=	е2ж cos ж.
615. ух = х sin ж.	616.	ух	=	хех cos 2а;.
617. ух=хех, у2=е~х. 618. ух = х, у2 = sin#.
619.	При каких а и Ь все решения уравнения
у" + ay' + by = 0 ограничены на всей числовой оси
—оо < X < +оо?
620.	При каких а и b все решения уравнения
у" + ay' + by = 0 стремятся к нулю при х -> +оо?
621.	При каких а и b уравнение у" + ay' + Ьу — О
имеет хотя бы одно решение у(х) 0, стремящееся
к нулю при х -> +оо?
622.	При каких а и b каждое решение уравнения
y,f + ay' + by = 0, кроме решения у(х) = 0, монотон-
но возрастает по абсолютной величине, начиная с
некоторого х?
623.	При каких а и b каждое решение уравнения
у" + ay' + Ьу = 0 обращается в нуль на бесконечном
множестве точек х?
72
624*. При каких а и b все решения уравне-
ния у” + ay' + by = 0 удовлетворяют соотношению
у = о(е-ж) при х -> +оо?
625*. Для заданного b > 0 подобрать такое а,
при котором решение уравнения у" + ay' + by = 0 с
начальными условиями у(0) = 1, yf(0) = 0 возможно
быстрее стремится к нулю при х -> +оо.
626.	При каких к и ш уравнение у” + к2у = sintutf
имеет хотя бы одно периодическое решение?
627.	Найти периодическое решение уравнения
х + ах + bx = sintutf и нарисовать график зависи-
мости его амплитуды от величины
628.	Найти периодическое решение уравнения
х + х + 4а; = егсЛ и на комплексной плоскости начер-
тить кривую, которую пробегает амплитудный мно-
житель этого решения при изменении ш от 0 до +оо.
629*. Дано уравнение у" + ау' + Ъу = f(x), причем
|/(ж)| т (—ос < х < ос), а корни характеристиче-
ского уравнения А2 < Ai < 0. Найти решение, огра-
ниченное при — ос < х < ос. Показать, что а) все
остальные решения неограниченно приближаются к
этому решению при х -> +оо, б) если f(x) периоди-
ческая, то это решение тоже периодическое.
Указание. Применить метод вариации постоянных. Ниж-
ние пределы полученных интегралов взять бесконечными та-
кого знака, чтобы интегралы сходились.
В задачах 630—632 принять, что при отклоне-
нии груза от положения равновесия на расстояние х
пружина действует на него с силой кх, направлен-
ной к положению равновесия.
630.	Найти период свободных колебаний мас-
сы ш, подвешенной к пружине, если движение про-
исходит без сопротивления.
73
631.	Один конец пружины закреплен неподвиж-
но, а к другому прикреплен груз массы т. При
движении груза со скоростью v сила сопротивления
равна hv. При t = 0 грузу, находившемуся в положе-
нии равновесия, сообщена скорость vq. Исследовать
движение груза в случаях h2 < Акт и h2 > Акт.
632.	Решить предыдущую задачу при дополни-
тельном условии, что к грузу приложена еще пе-
риодическая внешняя сила f = b sin ait. Показать,
что при любых начальных условиях движение гру-
за будет приближаться к периодическому и найти
это периодическое движение (вынужденные колеба-
ния).
633.	На конце упругого стержня укреплена мас-
са т. Другой конец стержня вибрирует так, что его
смещение в момент t равно В sin cut Упругая си-
ла, возникающая в стержне, пропорциональна раз-
ности смещений его концов. Найти амплитуду А
вынужденных колебаний массы т. Может ли быть
А > В? (Массой стержня и трением пренебречь.)
634.	Частица массы т движется по оси Ох, от-
талкиваясь от точки х = 0 с силой Зтго и притя-
гиваясь к точке х = 1 с силой 4mri, где го и и —
расстояния до этих точек. Определить движение ча-
стицы с начальными условиями
я(0) = 2, ±(0) = 0.
635.	Электрическая цепь состоит из последова-
тельно включенных источника постоянного тока, да-
ющего напряжение V, сопротивления В, самоиндук-
ции L и выключателя, который включается при
t = 0. Найти зависимость силы тока от времени
(при t > 0).
636.	Решить предыдущую задачу, заменив само-
индукцию L конденсатором емкости С. Конденсатор
до замыкания цепи не заряжен.
74
637.	Последовательно включены сопротивление R
и конденсатор емкости (7, заряд которого при t = О
равен q. Цепь замыкается при t = 0. Найти силу
тока в цепи при t > 0.
638.	Последовательно включены самоиндукция L,
сопротивление R и конденсатор емкости С, заряд
которого при t = 0 равен q. Цепь замыкается при
t = 0. Найти силу тока в цепи и частоту колебаний
в том случае, когда разряд носит колебательный
характер.
639.	Последовательно включены источник тока,
напряжение которого меняется по закону Е=Vsin utf,
сопротивление R и самоиндукция L. Найти силу
тока в цепи (установившийся режим).
640.	Последовательно включены источник тока,
напряжение которого меняется по закону Е=Vsin wt,
сопротивление R, самоиндукция L и емкость С.
Найти силу тока в цепи (установившийся режим).
При какой частоте ш сила тока наибольшая?
§ 12.	ЛИНЕЙНЫЕ УРАВНЕНИЯ
С ПЕРЕМЕННЫМИ КОЭФФИЦИЕНТАМИ
1.	Большинство задач этого параграфа решается с помощью
методов общей теории линейных дифференциальных уравне-
ний (см. [1], гл. V, § 2, § 3 или [4], гл. 2, § 3, § 5) и методов
качественного исследования линейных уравнений второго по-
рядка (см. [1], гл. VI, § 2, п. 1, п. 3). К остальным задачам даны
указания или ссылки на литературу.
2.	Если известно частное решение у± линейного однородного
уравнения n-го порядка, то порядок уравнения можно пони-
зить, сохраняя линейность уравнения. Для этого в уравнение
надо подставить у = y\z и затем понизить порядок заменой
z' — и.
Чтобы найти общее решение линейного однородного уравне-
ния второго порядка аъ(х)уп + а\(х)у' + а>2(х)у = 0, у которо-
го известно одно частное решение j/i, можно понизить порядок
75
уравнения указанным выше способом. Однако удобнее восполь-
зоваться формулой Остроградского — Лиувилля:
Р,1 ^1 =Ce-fp(x>dX, Р(х) = ^4,
I У± У2 I	ао(ж)
где ?/1 и ?/2 — любые два решения данного уравнения.
Пример. Пусть известно частное решение у± = х уравне-
(а?2 + 1)2/,/ - 2ху' + 2у = 0.	(1)
По формуле Остроградского — Лиувилля получим
I I = Се ,f(??+T)da:; У1у'2-у'1У2 = С(х2+ 1).
12/1 2/2 I
Так как функция 2/1 известна, то мы получили линейное урав-
нение первого порядка относительно 2/2 - Проще всего оно реша-
ется следующим способом. Разделив обе части уравнения на 2/2,
получим слева производную от дроби 2/2/2/1
(У2 V 2/12/г - 2/'i2/2 С(х2 + 1)
UJ у2	у2
Так как 2/1 = х, то
|г = / c-^dx + C2 = c(x-^ + C2^
У2 = С(х2 - 1) + С2Х.
Это — общее решение уравнения (1).
3.	Общего метода для отыскания частного решения линей-
ного уравнения второго порядка не существует. В некоторых
случаях решение удается найти путем подбора.
Пример. Найти частное решение уравнения
(1 - 2х2)у" + 2у' + 4у = 0,	(2)
являющееся алгебраическим многочленом (если такое решение
существует).
Сначала найдем степень многочлена. Подставляя у =
= хп + ... в уравнение (2) и выписывая только члены с самой
старшей степенью буквы х, получим: —2т2 • п(п — 1)хп~2 Ч-F
Ч-4тп + • • • = 0. Приравнивая нулю коэффициент при старшей
76
степени х, получим: — 2п(п — 1) + 4 = 0; п2 — п — 2 = 0. Отсюда
ni = 2; корень П2 = —1 не годен (степень многочлена — це-
лое положительное число). Итак, многочлен может быть толь-
ко второй степени. Ищем его в виде у = х2 + ах + Ь. Подставляя
в уравнение (2), получим (4а + 4)ж + 2 + 2а + 46 = 0. Следова-
тельно, 4а + 4 = 0, 2 + 2а + 46 = 0. Отсюда а = -1, 6 = 0. Итак,
9
многочлен у = аг — х является частным решением.
4.	При решении задач 738—750 воспользоваться следую-
щими утверждениями, вытекающими, например, из § 7 гл. V
книги [5].
Пусть |/(«)|	ПРИ *0	< оо; с, « = const >0. Тогда
1) уравнение и" + (1 + /(t))u = 0 имеет два таких линейно
независимых решения, что при t —> +оо
ui(t) = cost	W2(t) = sint
2) уравнение и" — (1 — /(t))u = 0 имеет два таких линейно
независимых решения, что при t —> +оо
В задачах 641—662 исследовать, являются ли
данные функции линейно зависимыми. В каждой
задаче функции рассматриваются в той области, в
которой они все определены.
641. х + 2, х — 2.	642.6^ + 9, 8х + 12.
643. sin ж, cos ж.	644. 1, ж, х2.
645.	4 — ж, 2х + 3, 6х + 8.
646.	ж2 + 2, Зж2 - 1, х + 4.
647.	х2 — х + 3, 2х2 + х, 2х — 4.
648.	еж, е2ж, е3ж. 649. ж, еж, хех.
77
650.1, sin2x, cos2ir. 651. shir, chir, 2 + еж.
652.1n(ir2), ln3ir, 7.	653. x, 0, ex.
654. shir, chir, 2еж — 1, Зеж + 5.
655. 2Ж, Зж, 6х.	656. sinir, cosir, sin2ir.
657.	sinir, sin(ir + 2), cos(ir - 5).
658.	y/x, \Jx + 1, \/x + 2.
659.	arctgir, arcctgir, 1.
660. ir2, ir|ir|.
661. ir, |ir|, 2x + л/4ir2.
662. ir, ir3, |ir31.
663.	а) Являются ли линейно зависимыми на от-
резке [а, Ь] функции, графики которых изображены
на рис. 1? б) Тот же вопрос для рис. 2.
664.	Известно, что для функций ..., уп де-
терминант Вронского в точке хо равен нулю, а в
точке Xi не равен нулю. Можно ли что-нибудь ска-
зать о линейной зависимости (или независимости)
этих функций на отрезке [itq, #i]?
78
665.	Детерминант Вронского для функций т/i, ...
..., уп равен нулю при всех х. Могут ли быть эти
функции линейно зависимыми? Линейно независи-
мыми?
666.	Что можно сказать о детерминанте Вронско-
го функций т/1, ..., уП1 если только известно, а) что
они линейно зависимы? б) что они линейно незави-
симы?
667.	Функции yi = х, у2 = х5, Уз = |#5| удовле-
творяют уравнению х2у" — Ьху' + Бу = 0. Являются
ли они линейно зависимыми на интервале (—1, 1)?
Объяснить ответ.
668.	Доказать, что два решения уравнения у"+
+р(х)у' + q(x)y = 0 (с непрерывными коэффициен-
тами), имеющие максимум при одном и том же
значении ж, линейно зависимы.
669.	Даны 4 решения уравнения у"' + ху = 0, гра-
фики которых касаются друг друга в одной точке.
Сколько линейно независимых имеется среди этих
решений?
670.	Пользуясь известным утверждением об ин-
тервале существования решения линейного уравне-
ния ([1], гл. V, конец § 1), определить, на каком
интервале существует решение данного уравнения с
указанными начальными условиями (не решая урав-
нения): а) (х + 1)у" — 2у = 0, y(fl) = 0, т/'(0) = 2;
б) у” + ytgx = 0, 3/(5) = 1, з/'(5) = о.
671.	Могут ли графики двух решений уравнения
у(п) + pi(x)y^n~1^ + • —\-рп(х)у = 0 (с непрерывными
коэффициентами) на плоскости х,у а) пересекаться,
б) касаться друг друга?
672.	При каких п уравнение задачи 671 может
иметь частное решение у = х3?
673.	Линейное однородное уравнение какого по-
рядка на интервале (0, 1) может иметь такие четы-
ре частных решения: у± = х2 — 2х + 2, у2 = (х — 2)2,
у3 = х2 + х — 1, у^ — 1 — х?
79
В каждой из задач 674—680 составить линейное
однородное дифференциальное уравнение (возможно
меньшего порядка), имеющее данные частные реше-
ния.
67	4.1, cos#.	675. х, ех.
676.	Зж, х - 2, еж + 1.
677.	х2 - Зх, 2х2 + 9, 2х + 3.
678.	еж, shir, chir. 679. х, х2, ех.
680.	х, х3, |ж3|.
В задачах 681—701 найти общие решения дан-
ных уравнений, зная их частные решения. В тех за-
дачах, где частное решение не дано, можно искать
его путем подбора, например, в виде показательной
функции ух = еах или алгебраического многочлена
Ух = хп + ахп_1 + Ьхп~2 + ...
681.	(2х + 1)у" + 4ху' — 4?/ = 0.
682.	х2(х + 1)у" - 2у = 0; уг = 1 + Г
683.	ху" — (2х + 1\у' + (х + 1)у = 0.
684.	ху" + 2у' - ху = 0; У1 = ^-
685.	у" — 2(1 + tg2 х)у = 0; ух = tgx.
686.	х(х — \)у" — ху' + у = 0.
687.	(еж + 1)у" - 2у' - еху = 0; ух = ех - 1.
688.	х2у" 1п х — ху' + у = 0.
80
689.	у" — у' tg ж + 2у = 0; у± — sin х.
690.	(ж2 — 1)2/" + (х — З)?/' — у = 0.
691.	ху" — (х + 1)уг — 2 (ж — 1)у = 0.
692.	у" + 4яу' + (4ж2 + 2)у = 0; у\ = еах .
693.	ху" - (2х + 1)у' + 2у = 0.
694.	х(2х + 1)у" + 2(х + 1)у' - 2у = 0.
695.	х(х + 4)2/" - (2х + 4)2/' + 2у = 0.
696.	х[х2 + 6)2/" - 4(ж2 + 3)2/' + бед = 0.
697.	(ж2 + 1)2/" - 2у = 0.
698.	2х(х + 2)2/" + (2 - х)у' + у = 0.
699.	ху’" - у" - ху1 + 2/ = 0; 2/1 — х> Уъ =
700.	ж2(2ж - 1)2/"' + (4ж - i)xy" - 2ху' + 2у = 0;
Ух =х, У2 = 1/х-
701.	(х2 - 2х + 3)2/'" - (х2 + ^)УП + 2^2/' - 2у = 0;
Ух =х, У2= ех.
В задачах 702, 703 найти общее решение ли-
нейного неоднородного уравнения, если известно,
что частное решение соответствующего однородного
уравнения является многочленом.
702.	(ж + 1)ху" + (ж + 2)?/' - у = ж +
703.	(2ж + l)j/" + (2ж - I)?/' - 2у = ж2 + ж.
81
В задачах 704, 705, зная два частных решения
линейного неоднородного уравнения второго поряд-
ка, найти его общее решение.
704.	(х2 — 1)у" + 4ху' + 2у = бх; уг = х, у? =
— + # + 1
— х + 1
705.	(За;3 + х)у" + 2у' — бху = 4 — 12а;2; у^ = 2х,
У‘2 = (х + I)2.
В уравнениях 706—710 линейной заменой иско-
мой функции у = a(x)z уничтожить член с первой
производной.
706.	х2у" — 2ху‘ + (х2 + 2)у = 0.
707.	х2у" — 4ху' + (6 — х2)у = 0.
708.	(1 + х2)у" + 4ху' + 2у = 0.
709.	х2у" + 2х2у' + (х2 — 2)у = 0.
710.	ху" + у' + ху = 0.
В уравнениях 711—715 заменой независимого пе-
ременного t = <р(х) уничтожить член с первой про-
изводной.
711.	ху" — у1 — 4л3у = 0.
712.	(1 + х2)у" + хуг + у = 0.
713. а;2(1 - х2)у" + 2(х - х3)у' -2у = 0.
714.	у" -у' + е4ж?/ = 0.
715.	2ху" + у' + ху = 0.
82
716.	Зная три частных решения у± = 1, у 2 = х,
уз = х2 линейного неоднородного уравнения второго
порядка, написать его общее решение.
717.	Что можно сказать о функции р(х), если
известно, что все решения уравнения у” + р(хУу' +
+q(x)y = 0 при х -> оо стремятся к нулю вместе со
своими первыми производными?
Указание. Воспользоваться формулой Лиувилля.
718.	Доказать, что в случае q(x) < 0 решения
уравнения у" + р(х)у' + q(x)y = 0 не могут иметь
положительных максимумов.
719.	Где могут лежать точки перегиба графиков
решений уравнения у" + q(x)y = О?
720.	Могут ли графики двух решений уравнения
у” + q(x)y = 0 (функция q(x) непрерывна) распо-
лагаться так, как на рис. 3,а? рис. 3,6? рис. 3,в?
рис. 3,2?
83
721.	Доказать, что отношение двух любых ли-
нейно независимых решений уравнения 2/,,+ p(x)t/,+
+q(x)?/ = 0 (с непрерывными коэффициентами) не
может иметь точек локального максимума.
722.	Доказать, что в случае q(x) > 0 для лю-
бого решения уравнения у" + q(x)y = 0 отношение
у'(х)1у(х) убывает при возрастании х на интервале,
где у(х) 0.
723.	Доказать, что в случае q(x) 0 все реше-
ния уравнения у" + q(x)y = 0 с положительными
начальными условиями у(х$) > 0, у'{хо) > 0 остают-
ся положительными при всех х > х$.
724.	Доказать, что решение уравнения у" — х2у =
= 0 с начальными условиями у(0) = 1, у'(0) = 0 есть
четная функция, всюду положительная.
725*. Доказать, что в случае q(x) 0 краевая
задача
у" + q(x)y = 0, 3/(Ж1) = а, у(х2) = Ъ
при любых а, b и Xi х% имеет единственное ре-
шение. Доказать, что это решение — монотонная
функция, если b = 0.
726.	Найти расстояние между двумя соседни-
ми нулями любого (не тождественно равного нулю)
решения уравнения у" + ту = 0, где т = const > 0.
Сколько нулей может содержаться на отрезке
а С х Ь?
В задачах 727—730, используя результат преды-
дущей задачи и теорему сравнения (см. [1], гл. VI,
§ 2, п. 3), оценить сверху и снизу расстояние между
двумя соседними нулями любого (не тождественно
равного нулю) решения следующих уравнений на
заданном отрезке.
727.	у" + 2ху = 0, 20 О 45.
84
728.	ху" + у = 0, 25 < х 100.
729.	у" - 2ху' + (х + 1)2у = 0, 4 < х	19.
730. у" — 2еху' + е2ху = 0, 2	х 6.
731*. Доказать, что любое решение уравнения
у" + ху = 0 на отрезке —25 х 25 имеет не менее
15 нулей.
732. Пусть Xi, ^2, ... — расположенные в по-
рядке возрастания последовательные нули реше-
ния уравнения у" + q(x)y = 0, где q(x) > 0; при
яц х < оо функция q(x) непрерывна и возрастает.
Доказать, что хп+\— хп < хп — хп_\ (т. е. расстояние
между соседними нулями убывает).
733. В предыдущей задаче обозначим через с
конечный или бесконечный предел функции q(x)
при х -> оо. Доказать, что Иш (жп+1 — жп) = тг/у/с.
п—>оо
734*. Пусть у и z — решения уравнений у"+
+#(#)?/ = 0 и z" + Q(x)z = 0 с совпадающими на-
чальными условиями у(хо) = z(Xq), у1 (xq) = z’{xq) и
на интервале (ж0, #i) имеем Q(x) > q(x\ у(х) > О,
z(ж) > 0. Доказать, что на этом интервале отноше-
ние z(x))y(x) убывает.
735*. Пусть выполнены условия задачи 732 и
пусть bn— шах |?/(ж)|. Доказать, что Ъ\ > 62 >	> • • •
Хп^Я^Яп+1
736*. Пусть в задаче 733 предел с конечный. До-
казать, что Ъп —> В > 0 при п —> оо (в обозначениях
задачи 735).
737*. Заменой независимого переменного t = <р(х)
привести уравнение ± (^))4 = 0 к виду +
=Ь у = 0, затем избавиться от первой про-
изводной заменой у = a(t)u. (Это преобразование
85
называется преобразованием Лиувилля. Во мно-
гих случаях оно позволяет привести уравнение
у" + q(x)y = 0 к уравнению аналогичного вида, но с
«почти постоянным» (слабо меняющимися на интер-
вале (£о, ос)) коэффициентом при у. Это облегчает
исследование асимптотического поведения решения
при х —> ос.)
В задачах 738—748 исследовать асимптотическое
поведение при х -> +оо решений данных уравнений,
пользуясь преобразованием Лиувилля (см. задачу
737) и утверждениями п. 4 (стр. 77).
738. у" + х^у = 0.
740. у" + х2у = 0.
742. ху" — у = 0.
739. у" - х2у = 0.
741. у" + е2ху = 0.
743. у" -ху = 0.
744. ху" + 2у' + у = 0.
745. у" — 2(х — Х)у' + х2у = 0.
746*. у" + (ж4 + 1)у = 0.
747*. (х2 + 1)7/" - у = 0.
748*. х2у" + т/ln2 х = 0.
В задачах 749—750 получить более точное асим-
птотическое представление решений данных уравне-
ний, применяя два раза преобразование Лиувилля.
749*. у" -4х2у = 0.
750*. ху" + у = 0.
86
§ 13. КРАЕВЫЕ ЗАДАЧИ
1. Для отыскания решения краевой задачи
ао(х)у" + ai(x)y' + аз(х)у = /(ж), х0 х жь	(1)
ау'(хо) + /Зу(х0) = 0, уу' (д?1) + 8y(xi) = 0	(2)
надо подставить общее решение уравнения (1) в краевые усло-
вия (2) и из этих условий определить (если это возможно) зна-
чения произвольных постоянных, входящих в формулу общего
решения. В отличие от задачи с начальными условиями (задачи
Коши), краевая задача не всегда имеет решение.
2. Функцией Грина краевой задачи (1), (2) называется функ-
ция G(x, s), определенная при xq х xi, xq < s < xi, и при
каждом фиксированном 8 из отрезка [жо, ®1] обладающая свой-
ствами (как функция от х):
1)	при х ф s она удовлетворяет уравнению
«о (х)у" + ai (х)у' + а2 (х)у = 0;	(3)
2)	при х — xq и х — xi она удовлетворяет заданным краевым
условиям (2);
3)	при х = s она непрерывна по х, а ее производная по х
имеет скачок, равный 1/ао($)5 т. е.
G(s+o, 5) = G(S-O, «), G'J =G'J +-L (4)
|x=s+0	|ж=з — О	ОЩ5/
Чтобы найти функцию Грина краевой задачи (1), (2), надо
найти два решения yi(x) и уз(х) (отличных от у(х) = 0) уравне-
ния (3), удовлетворяющие соответственно первому и второму из
краевых условий (2). Если yi(x) не удовлетворяет сразу обоим
краевым условиям, то функция Грина существует и ее можно
искать в виде
Функции а и b зависят от 8 и определяются из требования, что-
бы функция (5) удовлетворяла условиям (4), т. е.
6т/2(«) = a?/l(s), Ьу'2(в) = ay'^s) + —1_.
87
3.	Если функция Грина С?(ж, s) существует, то решение кра-
евой задачи (1), (2) выражается формулой
J/(®) = У G(x, s)/(s)ds.
жо
4.	Собственным значением задачи
а0(ж)?/" + Л1(®)2/' + а2 (х)у = Ху,	(6)
ш/'(жо) + /Зу(х0) = 0, 72/'(ж1) +	= 0	(7)
называется такое число Л, при котором уравнение (6) имеет
решение у(х) 0, удовлетворяющее краевым условиям (7). Это
решение у(х) называется собственной функцией.
Найти решения уравнений 751—762, удовлетво-
ряющие указанным краевым условиям.
751.	у" - у = 2ж; у(0) = О, у(1) = -1.
752.	у" + у'= 1; т/'(0) = 0, у(1) = 1.
753.	у" - у' = 0; г/(0) = -1, т/'(1) - 7/(1) = 2.
754.	у" + у = 1; 2/(0) = 0, у (Д) = 0.
755.	у" + у = 1; 7/(0) = 0, т/(тг) = 0.
756.	у" + у = 2х — 7г; т/(0) = 0, 2/(тг) = 0.
757.	у" -у' -2у = 0; т/'(0) = 2, т/(+оо) = 0.
758.	у" — у = 1; 3/(0) = 0, у(х) ограничено при
х -> +оо.
759.	у" - 2гу = 0; т/(0) = -1, т/(+оо) = 0.
760.	х^у" — 6т/ = 0; 7/(0) ограничено, т/(1) = 2.
88
761.	х^у" — 2ху' + 2у = 0; у(х) = о(х) при х -> 0,
2/(1) = 3.
762.	х^у" + 5ху' + 3у = 0; ?/(1) = 3, у(х) = О(х~2)
при х -> +оо.
763*. При каких а краевая задача у" + ay = 1,
2/(0) = 0, 2/(1) = 0 не имеет решений?
Для каждой из краевых задач 764—779 постро-
ить функцию Грина.
764.	у" = f(x); 2/(0) = 0, 2/(1) = 0.
765.	y" + y = f(x); у'(0) = 0, 2/(0 = 0.
766.	у" +у' = f(x\, ?/(0) = 0, i/'(l) = 0.
767.	у" - у = /(ж); i/'(0) = 0, i/'(2) + 2/(2) = 0.
768*. 1/" +у = /(х); 2/(0) = 2/(0, 2/'(0) = 2/'(О-
769. х2у" + 2ху' = /(ж); 1/(1) = 0, i/'(3) = 0.
770.	ху" - у1 = f(x); i/'(l)=0, 1/(2) = 0.
771.	х2у" — 2у = f(x)-, 1/(1) = 0, 2/(2) + 2у'(2) = 0.
772.	у" = f(x)', 2/(0) = 0, i/(ar) ограничено при
X —> + 00.
773.	у” +у' = fix); i/'(0) = 0, у(+оо) = 0.
774.	ху" +у' = f(x); 2/(1) = 0, у(х) ограничено
при х -> +оо.
89
775.	у” + ±у' + ?>у =	у(0) = 0, у(х) = 0(е 2ж)
при х —> +оо.
776.	х^у" + ху' — у = /(ж); t/(l) = 0, у(х) ограни-
чено при х -> +оо.
777.	х^у" + 2ху' — 2у = /(х); t/(0) ограничено,
7/(1) = 0.
778.	у" — у = f(x), у(х) ограничено при х -> ±оо.
779.	х^у" — 2у = f(x), у(х) ограничено при х -> 0
и при х -> +оо.
780.	При каких а существует функция Грина
краевой задачи у" + ay = f(x)^ у(0) = 0, у(1) = 0?
781*. Оценить сверху и снизу решение задачи
х^у" + 2ху' — 2у — f(x), у(х) ограничено при х -> 0 и
х -> +оо, и его первую производную, если известно,
что 0	/(ж) тп.
Указание. Записать решение с помощью функции Грина.
В задачах 782—785 найти собственные значения
и собственные функции.
782.	у" = Ау;	у(о) = 0,	у(0 = о.
783.	У1' = Ау;	у'(0) = 0,	у'(0 = о.
784.	у" =	у(0) = 0,	у'(0 = о.
785.	х2у" = Ху,	2/(1) = 0,	у(а) = 0 (а > 1)
90
§ 14. ЛИНЕЙНЫЕ системы
С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
1. Путем исключения неизвестных систему, вообще говоря,
можно свести к уравнению более высокого порядка с одной не-
известной функцией (см. [1], гл. VII, § 1, п. 2 или [4], гл. 3, § 2).
Этот способ удобен для решения лишь несложных систем.
Пример. Решить систему х — у +1, у = 2е* — х. Исключаем
у. Из первого уравнения имеем у — х— 1. Подставляя во второе
уравнение, получаем х — 2е* — х. Решив это уравнение второго
порядка (методами § 11), найдем х = Cicost + C^sini + е*.
Значит, у — х — 1 = — Ci sin t + С2 cos t + e* — 1.
(dx \
где x означает
3?1 — «113?1 + * * ' 4"
Xn — CLnlXl + • • • + CbnnXm
(1)
или, в векторной записи, х = Ах, где х — вектор, А — матрица:
надо найти корни характеристического уравнения
«11 — A ai2 ... ain
«21	«22 — А . . .	«2п
(2)
«п1	«п2	•• • «пп А
Каждому простому корню Аг характеристического уравне-
ния соответствует решение С^цгел^, где Сг- — произвольная
постоянная, цг — собственный вектор матрицы А, соответству-
ющий этому Аг-.
Если для кратного корня А имеется столько линейно незави-
симых собственных векторов v1, ..., vk, какова его кратность,
то ему соответствует решение CiVxeXt + • • • + CkVkeXt.
Если для корня А кратности к имеется только т линей-
но независимых собственных векторов, и т < к, то решение,
91
соответствующее этому Л, можно искать в виде произведения
многочлена степени к — т на eXt, т. е. в виде*)
Xi = (а + bt + • • • + dtk~m) eXt,
----------------- (3)
sn=(p + ?tH------1- stk m)ext.
Чтобы найти коэффициенты a, b, ..., s, надо подставить ре-
шение (3) в систему (1). Приравняв коэффициенты подобных
членов в левой и правой частях уравнений, получим систему
линейных алгебраических уравнений относительно а, Ь, ..., s.
Надо найти общее решение этой системы. Коэффициенты
а, Ь, ..., 5 должны зависеть от к произвольных постоянных,
где к — кратность корня Л.
Найдя для каждого Л решения указанного вида и сложив
их, получим общее решение системы (1).
Пример. Решить систему
х = 2х У + z, у = —2х — z, z — 2х + у + 2г.	(4)
Составляем и решаем характеристическое уравнение
	2-Л 1	1 —2 -Л -1 2	1	2-Л	= 0,	(5)
А3 - 4А2 + 5А - 2 = 0, Ai =		2, Л2 = A3 = 1.	
Для простого корня Ai=2 находим собственный вектор (а, /3, 7),
решая систему
/3 + 7 = 0,
-2а - 2/3 - 7 = 0,	(6)
2а + /3 = 0
(коэффициенты этой системы равны элементам детерминанта
(5) при Л = 2). Из (6) находим 2а — —0 = у. Значит, вектор
(1, —2, 2) — собственный, и
x = e2t, у = —2e2t, z — 2e2t	(7)
— частное решение системы (4).
х) В случае к 3 число к — т нельзя уменьшить, а в случае
к 4 иногда можно, если известна жорданова форма матри-
цы А.
92
Для кратного корня Л = 1 сначала определим число линейно
независимых собственных векторов. При Л = 1 из (5) получаем
матрицу
1 1 1
—2 -1 -1
2 1 1
Ее порядок 71 — 3, ранг г = 2. Число линейно независимых
собственных векторов равно т — п — г = 1. Корень Л = 1 имеет
кратность к = 2. Так как к > т, то решение надо искать в виде
произведения многочлена степени к — т = 1 на еЛ*, т. е. в виде
х = (а, у = (с + dt)^, z = gt)^.
(8)
Чтобы найти коэффициенты а, 6, ..., подставляем (8) в систе-
му (4) и приравниваем коэффициенты при подобных членах.
Получаем систему
Ь + d + д — 0.
—26 — d — д — 0
2Ь Т d -Т д — 0.
Ъ— а + с + /,
d ——2а — с — /,
д = 2а + с + /.
(9)
Найдем общее решение этой системы. Из двух левых урав-
нений имеем b = 0, д = —d. Подставляя это в остальные урав-
нения, получаем
0 = а + с + /, d — —2а — с — f
(10)
(остальные уравнения будут следствиями написанных). Реша-
ем систему (10), например, относительно а и /:
а = —d, f = d — с.
Таким образом, все неизвестные выражены через с и d. Поло-
жив с — Ci, d = С2, имеем а = — С2, 6 = 0, f = С2 — С1, д = — С2.
Общее решение системы (9) найдено.
Подставив найденные значения а, 6, ... в (8) и прибавив
частное решение (7), умноженное на Сз, получим общее реше-
ние системы (4):
х — —С*2е^ + Сзе2*, у — (C*i 4- С*2^) е^ — 2Сзе2^,
Z = (С2 - Cl - C2t)e4 + 2C'3e2t.
93
3.	Другой способ решения системы (1). Для любой матрицы
существует базис, в котором матрица имеет жорданову фор-
му. Каждой клетке порядка р 1 жордановой формы соответ-
ствует серия hi, hz, ..., hp векторов базиса, удовлетворяющих
уравнениям
Ahi = A/ii,	hi ф О,
Ahz — Ahz + hi,
Ah3 = A/13 + A2,	(И)
Ahp — Ahp + hp—i.
Вектор hi называется собственным, a /12, h%, ..., hp — при-
соединенными. Каждой серии h\, hz, ..., hp соответствует p
линейно независимых решений ж1, х2, ..., хр системы х — Ах
(верхний индекс указывает номер решения):
х1 = eXthi,
х2 = eXt ^hi 4 Л2),
жз _ ext ^hi + j|/i2 + h^,	(12)
/ +p— 1	+p—2	t
xP =e У (p~zT)T^1 + (p - 2)!	-----+ hp
Общее число всех таких решений равно сумме порядков всех
клеток жордановой формы, т. е. порядку матрицы. Они соста-
вляют фундаментальную систему решений системы х = Ах.
Правило для запоминания формул (12). Соб-
ственному вектору hi, соответствует решение х1 — eXthi. Если
везде отбросить eXt, то каждая строка правой части (12) по-
лучится интегрированием по t предыдущей строки, причем по-
стоянную интегрирования надо взять равной следующему по
порядку вектору серии.
4.	В случае, когда имеются комплексные корни А, изло-
женные способы дают выражение решения через комплексные
функции. Если при этом коэффициенты системы (1) веществен-
ны, то можно выразить решение только через вещественные
функции. Для этого надо воспользоваться тем, что веществен-
ная и мнимая части комплексного решения, соответствующего
корню А = а + /3i (J3 ф 0), являются линейно независимыми
решениями.
94
Пример. Решить систему х — 4ж — у, у = Ьх + 2?/.
Составляем и решаем характеристическое уравнение
4TA.,-1J=0, А2- 6А+13 = 0, А = 3 ± 2г.
| 5	2 — А |
Для корня А = 3 + 2г находим собственный вектор (а, 6):
( (1 — 2г)а — 6 = О,
[ 5а - (1 + 2г)6 = 0.
Можно взять а = 1, b = 1 — 2г. Имеем частное решение
х = е(3+2г)*, у — (1 — 2г)е(3+2г)С
Так как данная система с вещественными коэффициента-
ми, то решение, соответствующее корню А = 3 — 2г, можно не
искать, оно будет комплексно сопряженным с найденным реше-
нием. Чтобы получить два вещественных решения, надо взять
вещественную и мнимую части найденного комплексного реше-
ния. Так как Ф3+2г^ = e3*(cos2£ + isin2Z), то
( Xi = Ree(3+21)*	= e3t cos2Z,
yi = Re(l — 2г)е(3+2г)* = e3?/(cos2Z + 2sin2Z),
f Х2 = 1ше(3+2г^	= е3* sin2Z,
?/2 = 1ш(1 — 2г)е(3+2г^ = e3*(sin2£ - 2cos2Z).
Общее решение выражается через два найденных линейно не-
зависимых решения:
х — CiXi + С2Х2 = Ci е3* cos 2t + С2 е3* sin 2£,
у — Ci2/1 + С2У2 = Ci e3f(cos 2t + 2sin2Z)+
+C2 e3t(sin2Z - 2cos2£).
5.	Чтобы решить систему
'	+ aux^-'1) H-----h aimx+
+ 6io2/(n) + ^112/(п-1) H-h biny = 0,
a2ox^ + a,2ix(p~1') +----h a2Px-\-
<	+ b2Gy^ + b2iy(q + • • ' + b2qy — 0,
не приведенную к нормальному виду, надо составить характе-
ристическое уравнение
I аюА™ + an А™"1 + • • • + aim 6wAn + Ьц An-1 + • • • + bin |	Q
I ^20	+ a21 A^9 1 + ’ ’ ’ + 0>2p	^20 A^ + 62I A9 + • • • + b2q I
95
и найти его корни. После этого решение отыскивается тем же
способом, как в п. 2.
Аналогично решаются системы трех и более уравнений.
6.	Частное решение линейной неоднородной системы с по-
стоянными коэффициентами
Xi = anXi-]---агпхп +	i = 1, ...,п	(13)
можно искать методом неопределенных коэффициентов в том
случае, когда функции fi(t) состоят из сумм и произведений
функций bo + bit + • • • + bmtm, eat, cos/3t, sin pt. Это делает-
ся по тем же правилам, что для одного линейного уравнения
с постоянными коэффициентами, см. п. 2 § 11, со следующим
изменением. Если fi(t) = Pnii(<t)e'yt, где Pmi (t) — многочлен
степени тг-, то частное решение системы (13) ищется не в виде
isQm(i)e7*, а в виде
= <Эк+Д*)еЛ г = 1,...,п,	(14)
где Q2m+s (£) — многочлены степени т + s с неизвестными ко-
эффициентами, т = maxm1; s = 0, если 7 — не корень харак-
теристического уравнения (2), а если 7 — корень, то s можно
взять равным кратности этого корня (или, точнее, s на 1 боль-
ше наибольшей из степеней многочленов, на которые умножа-
ется е7* в общем решении однородной системы). Неизвестные
коэффициенты многочленов определяются путем подстановки
выражений (14) в данную систему (13) и сравнения коэффици-
ентов подобных членов.
Аналогично определяются степени многочленов и в случае,
когда fi(t) содержат eai cos/3Z и eat sinа число 7 = a + pi
является корнем характеристического уравнения.
Пример. Решить систему
х = 4х — у + e3t(t + sin £),
у = х + 2у + t е3* cos t.
Сначала для однородной системы х = 4х — у,у = х-\-2у находим
корни Л1 = Л2 = 3 и как в п. 2 отыскиваем общее решение
хо = (Cit + C2)e3t, УО =(Cit + C2-Ci)e3t.
В системе (15) для функций t e3t, e3i sinZ, te3f cost числа а + /3г
соответственно равны 3, 3 + i, 3 + i. Поэтому надо отдельно
найти частные решения систем
х = 4х — у + t е3*, у — х + 2у,	(16)
96
х = 4х — у + e3t sin t, у — x + 2y + te3t cos t. (17)
Для системы (16) a + /3i — 3 = Ai = A2, s = 2, m = 1. Согласно
(14), частное решение можно искать в виде
Xi = (at3 + bt2 + ct + d) e3t, yi = (ft3 + gt2 + ht + j) e3*.
Для системы (17) а + /3г = 3 + г^ Ai?2, s = 0, m — 1. Частное
решение имеет вид
Х2 = (kt + I) e3t sin t + (mt + n) e3t cos t,
y2 = (pt + q) e3t sin t + (rt + s) e3t cos t.
Отыскав значения коэффициентов a, b, ..., общее решение си-
стемы (15) напишем в виде
X = Х0 + Xi + Х2, у = уо + yi + У2 •
7. Решение неоднородной системы
Xi = ац (t)xi н-\-ain (t)xn + Д (t), i = 1, п
можно найти методом вариации постоянных, если известно об-
щее решение однородной системы с теми же коэффициентами
aik(t). Для этого в формуле общего решения однородной систе-
мы надо заменить произвольные постоянные Сг- на неизвестные
функции Ci(t). Полученные выражения для Х{ надо подставить
в данную неоднородную систему, и из этой системы найти Ci(t).
8. Показательной функцией еА матрицы А называется сум-
ма ряда
eA=S+^ + ^ + ^ + ...,	(18)
где Е — единичная матрица. Ряд сходится для любой матри-
цы А.
Свойства еА:
а)	если А = СМС-1, то еА = С ем С"1;
б)	если АВ = В А, то еА+в = еА -ев = ев -еА;
в)	матрица X(t) = etA удовлетворяет уравнению = АХ;
Х(0) = Е.
Методы отыскания еА:
1) Путем решения системы дифференциальных уравнений.
В силу свойства в) г-й столбец матрицы etA есть решение си-
стемы уравнений (в векторной записи) х = Ах с начальными
условиями хДО) = 1, х^(0) = 0 при к ф i (xi — i-я координата
вектора х).
97
2) Путем приведения матрицы к жордановой форме. Пусть
известна такая матрица С, что матрица С-1 АС = М имеет
жорданову форму, т. е. состоит из клеток Ki. Каждая жорда-
нова клетка имеет вид К = ХЕ + F, у матрицы F все элементы
нули, кроме 1-го косого ряда над диагональю. Поэтому Fm = О,
где т — порядок матрицы F, и eF легко найти с помощью ря-
да (18). Так как еще еХЕ = еЛ F, то
еК = eXE+F =(AE.eF =eXE.eF = еХ QF
Составив из клеток eKi матрицу ем, найдем ел с помощью
свойства а). Доказательства и пример см. в [5], гл. 1, §§ 12-14.
В задачах 786—812 решить данные системы
уравнений (х означает и т. д.; для облегче-
ния работы в некоторых задачах указаны корни
характеристического уравнения).
786. ( х ~ Iх + у: [ у = Зж + 4у.	ятоят ( х = х — у, 787. [у = у-4х.
788 { х + х ~ 8у = °’ ' [у - х - у = 0.	789. | Х = 1 + У’ [у = 3у — 2ж.
790. ( Х = Х ~3у’ [у = 3х + у.	791. |Х + Х + 5у = °’ ' \ у ~ х ~ У = 0-
792.Р = 2ж + 2/’ [у = 4у-х.	793. ( х = Зх ~ 2/> [ у = 4ж - у.
794. { х = 2у ~ Зж’ [у = у-2х.	795. / Х ~ 5х ~ Зу = °’ ’ 1 у + Зж + у = 0.
' X = х + z — у, 796. < у = х + у — z, z = 2х — у (Ai=l, Л2=2, А3 = —1).	f х = х - 2у - г, 797. < у = у - х + г, Z — х - Z (Л1=0, Л2=2, Аз=-1).
98
х = 2х — у + г,
798. < у = х + 2у - г,
к z — х - у + 2г
(A1=l? Л2=2, А3=3).
х = Зх — у + г,
799. < у = х + у + г,
z — 4ж — у + 4г
(А].=1, А2=2, А3=5).
х = х — у — г,
801. < у = х + у,
^z = Зх + z
(А1=1, А2,3=1±2г).
х = 4у — 2г — Зж,
800. < у = г + ж,
z = бж — бу + 5г
(Ai=l, А2=2, Л3= — 1).
х = 2ж + у,
802. < у = х + Зу — г,
г = 2у + Зг — х
(Ai=2, Д2>3=3±г).
х = 2х + 2г - у,
803. < у = х + 2г,
г = у — 2ж — г
(Ai=l, Л2,3=±г).
х = 4ж — у — г,
804. < у = х + 2у — г,
г = х - у + 2г
(Ai =2, А2=А3=3).
х = 2ж — у — г,
805. < у = Зх - 2у - Зг,
к г = 2г - х + у
(Ai =0, Л2=Лз=1).
х = у — 2ж — 2г,
806. < у = х - 2у + 2г,
к г = Зх - Зу + 5г
(Ai =3, А2=Аз= — 1).
f х = Зх — 2у — г,
807. < у = Зх — 4?/ — Зг,
г = 2х — 4?/
(A1=A2=2, Аз=-5).
х = х — у + г,
808. < у = х + у - г,
г = 2г - у
(А1=А2=1, Аз=2).
х = у - 2г - х,
809. < у = 4ж + у,
^z = 2х + у - г
(Ai=l, А2=Аз= — 1).
х = 2х + у,
810. < у — 2у + 4г,
г = х - г
(А1=А2=0, Аз=3).
х = 2х — у — г,
811. < у = 2х — у — 2г,
г = 2г - х + у
(А1=А2=Аз = 1).
99
812. <
х = 4х — у,
у = 3х + у - z, (А1 = Л2 = Аз = 2).
z — х + Z
В задачах 813—825 решить системы, не приве-
денные к нормальному виду.
813.	\х = 2х — 3у,	8W 1 [у = х-2у.	|	х = 3х + 4г/, у = -х-у.
815. <	[ Х. = 2у'	816. < [ у = -2х.	f х = Зх — у — г, у = -X + Зу - г, z — —х — у + 3z.
817. <	f 2х - Зу = 4у - х, 81g 1 [ Зх — 4т/ = 2х — у.	* J	' х + х + у — 2г/= 0, х — у + х = 0.
819. <	f х - 2у + у + х - Зу = 0, [4г/ — 2х — х — 2х + Зу =	0.
820 f х ~ х+ 2У ~2У = °’
* \ х — х + у + у = 0.
Я21 f х~2У + 2х = °, о2о ( X + Зу - X = О,
\Зх + у-8у = 0. \х + Зу-2у = 0.
823 { £ + 5х + 2^ + У = °’
’	[ Зх + 5х + у + Зу = 0.
824 / +	~ 2ж - 2у ~ у = °’
'	[ х — 4х — у + 2у + 2у = 0.
825 f 2х + 2х + х + %У + У + У =
'	[ х + 4х — х + Зу + 2у — у = 0.
100
В задачах 826—845 решить				линейные неодно-
родные	системы.			
826.	( X \у	= у + 2е*, = х +t2.	827. <	f х = у — 5 cos t, [у = 2х + у.
828.	( X [у	= Зж+2т/+4е5^ = х + 2у.	829. <	[ х = 2х—4т/+4е-2^, [у = 2х-2у.
830.	( X \у	= 4х + у — е2*, = у-2х.	831. <	[х = 2у — х+1, (у = 3у-2х.
832.	( X \у--	= 5х—3y+2e3t, =х+у+5е~*.	833. <	[ х = 2х + у + е^, [ у = —2х + 2t.
834.	( X \у	= х + 2у, = х — 5sint.	835. <	f х = 2х — 4т/, [y = x-3y + 3et.
836.	( X \у	= 2х - у, = у — 2х + 18t.	837. <	f х = ж+2т/+16^е^, [у = 2х-2у.
838.	( X \у	— 2х + 4 т/ — 8, = Зх + бу.	839. <	f х = 2х — Зу, = х—2T/+2sint.
840.	( X \у	= х — у + 2 sin t, = 2х-у.	841. <	f х = 2х — у, у = х + 2 е^.
842.	( X \у	= 4х—37/+sint, = 2х—у—2 cost.	843. <	f х = 2х + у + 2е*, {у = х + 2у — 3 еЧ
844.	( X \у	= х - у + 8t, = 5х — у.		
845.	( X \у	= 2х-у, = 2у — х — 5 ef sin t.		
101
В задачах 846—850 данные системы решить ме-
тодом вариации постоянных.
846Ji = 2/+tg2/;1’
[ у = -х + tg t.
( х = 2у — х,
847. \ . л о e3t
[У = 4у-3х+^-^-.
{2
х = —4х — 2у + -т—г,
3
у = 6х + 3у- -гтр
Г •	,1
ОЛП I X = х — у-\-7,
849. < у cost’
[у = 2х-у.
х = Зх — 2у
у = 2x—y+15ety/t.
Решить системы 851—866, записанные в вектор-
ной форме: х = Ах, где х — вектор, А — данная
матрица.
851.	х = Ах,
852.	х = Ах,
853.	х = Ах,
854.	х = Ах,
О А
3 /
1\
0 /
-2\
-3 )
-2\
-1 J
/2 -1 -1\
855.	х = Ах, А =	1 0 -1 .
\3 -1 —2/
Zi —2 2\
856.	х = Ах, А= 1 4 -2 .
X1 5-3/
/-1 —2 2\
857.	х = Ах, А =	-2 -1 2 .
\-3 -2 3/
102
	- 3	2 2
858. х = Ах, А =	-3	-1 1
		2 0
	/ 3	-3 1
859. х = Ах, А =	3	—2 2
	\-1	2 0
	/ 2	1 -1
860. х = Ах, А =	-1	0 1
	\ 1	1 0
	/о 1	1\
861. х = Ах, А = |	1 0	1 Г
	\2 2	1)
	/ 0	1 Ц
862. х = Ах, А = |	1	1 0
	\-1	0 1 /
	/-2	1 2\
863. х = Ах, А = |	-1	0 2
	\—2	0 3/
	/0 1	
864. х = Ах, А = I	1 0	-i
	у 2 2	-3/
	/4 2	-2\
865. х = Ах, А = |	1 3	-i
	\3 3	-i /
	/2	0 -1
866. х — Ах, А = I	1 "	1 0
	\з -	i -i
В задачах 867—873 найти показательную функ-
цию ел данной матрицы А.
8в7'Мо
ЯЛЯ д_( ° 1 1
ооо. Л — I IQ;
103
869. А = (	2 1Л	870 А=Р~Ч 0 2/	87U. Л	0J. 	/0 1 0\
871. А = (	* .	872. А = 0 0 0. 1	\0 0 2/ '2 1 0\
873. А = 1	0 2 1. / ° 2/
В задачах матрицу еА.	874 и 875 найти deteA, не вычисляя ' 1 0 3\	/1 4 2\
874. А =	-1 2 0 .	875. А = 3 1-1. 0 1—1/	\ 2 1 - 3 /
876.	Тело массы т движется на плоскости ж, у,
притягиваясь к точке (0, 0) с силой o2mr, где г —
расстояние до этой точки. Найти движение тела при
начальных условиях ж(0) = d, 2/(0) = 0, ±(0) = 0,
3/(0) = v и траекторию этого движения.
877.	Один конец пружины закреплен неподвижно
в точке 0, а к другому прикреплен груз массы 3m,
соединенный другой пружиной с грузом массы 2m.
Оба груза двигаются без трения по одной прямой,
проходящей через точку 0. Каждая из пружин рас-
тягивается на величину х под действием силы а2тх.
Найти возможные периодические движения системы.
878.	На концах вала закреплены два шкива, мо-
менты инерции которых Ц и I2- При повороте од-
ного шкива относительно другого на любой угол
вследствие деформации вала возникают упругие си-
лы с крутящим моментом Кер. Найти частоту кру-
тильных колебаний вала при отсутствии внешних
сил.
104
L
£’=V'sinof
Рис. 4.
879.	К источнику тока с напря-
жением Е — V sin wt последователь-
но присоединено сопротивление R.
Далее цепь разветвляется на две
ветви, в одной из которых включе-
на самоиндукция L, а в другой —
емкость С (рис. 4). Найти силу
тока в цепи (установившийся ре-
жим), проходящего через сопроти-
вление R. При какой частоте cj си-
ла тока наибольшая? Наименьшая?
Указание. О составлении дифференциальных уравнений
в задачах об электрических цепях см. п. 5 § 11.
880*. Какое условие достаточно наложить на
собственные значения матрицы А, чтобы система
уравнений (в векторной записи) х = Ах + /(f) име-
ла периодическое решение при всякой непрерывной
вектор-функции /(f) периода cj?
Указание. Применив метод вариации постоянных в век-
торной форме, выразить общее решение через фундаменталь-
ную матрицу etA, функцию f(t) и начальные условия. Восполь-
зоваться условием периодичности.
§ 15.	УСТОЙЧИВОСТЬ
1.	Рассмотрим систему уравнений
= fi(t, Xi, хп), г = 1,	(1)
или, в векторной записи
ж), x = (xi, ...,хп).	(2)
Пусть все ft и
dft
дхк
непрерывны при to t < оо.
Решение х = <p(t) системы (2) называется устойчивым по
Ляпунову, если для любого е > 0 существует такое д > 0, что
105
для всякого решения x(t) той же системы, начальное значение
которого удовлетворяет неравенству
|ж(г0) - <р(*о)| < <*,	(з)
при всех t to выполняется неравенство
kW —¥’(<)! < г-
Если же для некоторого е > 0 такого 5 не существует, то
решение <p(t) называется неустойчивым.
Решение <p(t) называется асимптотически устойчивым, если
оно устойчиво по Ляпунову и, кроме того, все решения с до-
статочно близкими начальными условиями неограниченно при-
ближаются к kp(t) при t —> +оо, т. е. если из неравенства (3)
следует x(t) —	—> 0 (t —> +оо).
Наличие или отсутствие устойчивости не зависит от
выбора to-
Вопрос об устойчивости данного решения х = <£>(£) систе-
мы (2) сводится к вопросу об устойчивости нулевого решения
y(t) = 0 другой системы, получаемой из (2) заменой искомой
функции х — <p(t) = у.
2.	Исследование на устойчивость по первому
приближению. Пусть Xi(t) = 0 (г = 1, ...,п) — реше-
ние системы (1). Чтобы его исследовать на устойчивость, на-
до выделить из функций fi линейную часть вблизи точки
xi = • • • = хп = 0, например, по формуле Тейлора. Получен-
ную систему часто можно исследовать с помощью следующей
теоремы.
Теорема Ляпунова. Рассмотрим систему
=	----\-ainxn +^i(t, ®i, ..., хп), г = 1, ..., п, (4)
где aik — постоянные, a tpi — бесконечно малые выше первого
порядка, точнее, при |®| < £о
|^г|	?(®)|®|, i = 1, ..., п, у(х) —> 0 при |®| —> 0,	(5)
где |ж| = yixip Н---Н |жп|2.
Тогда если все собственные значения матрицы {а^), I,
k = 1,	имеют отрицательные вещественные части,
то нулевое решение системы (4) асимптотически устойчиво;
106
если же хоть одно собственное значение имеет положитель-
ную вещественную часть, то нулевое решение неустойчиво.
Пример. Исследовать на устойчивость нулевое решение си-
стемы
Г х = у/4 + 4у - 2 ех+у,
( у = sin ах + 1п(1 — 4у), а = const.
Выделяя линейную часть функций по формуле Тейлора, по-
лучаем
( х = —2х - у + ^i(x, у),
\у = ах - 4у + ^2(х, 2/),
где функции ipi и ?Д2 равны О(х2+у2) и, значит, удовлетворяют
условию (5). Находим собственные значения матрицы коэффи-
циентов
I 2 “ А ,	= О, А2 + 6А + 8 + а = О, А1,2 = -3 ±
I а -4 - АI
При а > 1 корни комплексные, ReAij2 = —3 < 0, а при
—8 < а	1 корни вещественные отрицательные, значит, в этих
случаях нулевое решение асимптотически устойчиво.
При а < — 8 один корень положителен, значит, нулевое ре-
шение неустойчиво.
При а = — 8 имеем Ai=0, Л2 = —би вопрос об устойчивости
не решается с помощью изложенной теоремы.
3.	Исследование на устойчивость с помощью
функции Ляпунова. Производной от функции v(t, Xi, ...
..., хп) в силу системы (1) называется функция
dv _ dv_ dv f । dv f
dt |(1) “	дхп
где Л, ..., fn — правые части системы (1).
Теорема Ляпунова. Если существует дифференци-
руемая функция v(x\, ...,Хп), удовлетворяющая в области
|х| < ео условиям
1)	v > 0 при х 0, v(0) = О,
2)	0 пРи И < со, t > to,
то нулевое решение системы (1) устойчиво по Ляпунову.
Если вместо условия 2) выполнено более сильное условие
107
3)	пт —w(x) < 0 при 0 < |®| < £0, t > to,
1(1)
а функция w(x) непрерывна при |®| < so, тпо нулевое решение
системы (1) асимптотически устойчиво.
Теорема Четаева. Пусти система (1) обладает нуле-
вым решением. Пусти в некоторой области V пространства
xi, ..., хп существует дифференцируемая функция v(xi, ...
..., хп), причем
1)	точка х = 0 принадлежит границе области V,
2)	v = 0 на границе области V при |х| < во,
3)	в области V при t > to имеем v > О, Ч? w(x) > О,
функция w(x) непрерывна.
Тогда нулевое решение системы (1) неустойчиво.
Не существует общего метода построения функции Ляпу-
нова v (когда решение системы (1) неизвестно). В ряде случа-
ев функцию Ляпунова удается построить в виде квадратичной
формы v = 52 bijXiXj или в виде суммы квадратичной формы и
i, j
интегралов от нелинейных функций, входящих в правую часть
данной системы.
4.	Условия отрицательности всех веществен-
ных частей корней уравнения
ао^1 + aiХп 1 + • * * + ап — 1А + ап — 0, ао > 0,	(6)
с вещественными коэффициентами.
а)	Необходимое условие: все ai > 0. В случае п 2
это условие является и достаточным.
б)	Условие Рауса — Гурвица: необходимо и достаточ-
но, чтобы были положителиными все главные диагоналиные
миноры матрицы Гурвица
(ai ао 0 0 0 0 ...0 \
«з «2 «1 «о 0 0 ... 0
as а4 аз а2 а± ао ... 0
\ 0 0 0 0 0 0 ... ап /
На главной диагонали этой матрицы стоят числа а±, 02, ...
..., ап. В каждой строке индекс каждого числа на 1 меньше
индекса предыдущего числа. Числа а^ с индексами i > п или
i < 0 заменяются нулями.
108
Главные диагональные миноры матрицы Гурвица:
А1 = ai,
A2 = h М
I «3 «2 I
Аз =
ai
аз
аз
ао О
(i2 ai
«4 аз
(7)
в)	Условия Льенара — Шипара. Необходимо и до-
статочно, чтобы все ai > 0 и чтобы An-i > 0, Ап~з > О,
Дп-5 >0, ..., где Ai те же, что в (7).
Эти условия равносильны условиям Рауса—Гурвица, но
удобнее, так как содержат меньше детерминантов.
Пример. При каких а и b корни уравнения А4 + 2А3 + аА2 +
+ЗА + 6 = 0 имеют отрицательные вещественные части?
Пишем условия Льенара—Шипара:
2 1 0
3 а 2
0 6 3
а > 0, b > 0, Аз =
= 6а — 46 — 9 > 0, Ai = 2 > 0.
Отсюда получаем условия 6 > 0, 6а > 46 + 9.
г)	Критерий Михайлова. Необходимо и достаточно,
чтобы на комплексной плоскости точка где f(X) — ле-
вая часть (6), при изменении от 0 до +оо не проходила через
начало координат и сделала поворот вокруг него на угол птг/2
в положительном направлении.
Другая (эквивалентная) формулировка критерия Михайло-
ва: Необходимо и достаточно, чтобы апап-\ > 0 и чтобы
корни многочленов
p(f) — ап — ап~2^ + ап~4^ — ...,
qM = an-i - ап-зр + ап-зТ]2 - ...
были все положительными, различными и чередующимися,
начиная с корня fi, т. е.
0 < fi < 771 < ?2 < ??2 < • • •
(Заметим, что многочлен (6) при А = ia> равен p(cv2) + zcjq(cj2).)
Пример. /(А) = А5 + 2А4 + 7А3 + 8А2 + 10А + 6. Здесь
ап = 6 > 0, an-i = 10 > 0, а многочлены p(f) = 6 — 8f + 2f 2,
(7(77) = 10 — 7?/ + p2 имеют корни fi = 1, f2 = 3, 771 = 2, 772 = 5.
Значит, 0 < fi <771 < f2 < 772- По критерию Михайлова все кор-
ни многочлена /(А) имеют отрицательные вещественные части.
109
5.	Условия устойчивости нулевого решения линейной систе-
мы с периодическими коэффициентами см. в [5], гл. III, § 16.
Задачи 881—898 решаются с помощью опреде-
ления устойчивости.
881. Пользуясь определением устойчивости по
Ляпунову, выяснить, устойчивы ли решения данных
уравнений с указанными начальными условиями
a) 3(f — 1)± — х, х(2) = 0. б) х = 4х — t2x, х(0) = 0.
в) х = t — ж, ж(0) = 1.
г) 2tx = х — х3, ж(1) = 0.
В задачах 882—888 начертить на плоскости ж, у
траектории данных систем вблизи точки (0, 0) и по
чертежу выяснить, устойчиво ли нулевое решение.
882. х = —х, у = —2у. 883. х = х, у = 2у.
884. х = —х, у = у. 885. х = — у, у = 2х3.
886. х = у, у = — sin#. 887. х = т/, у = ж3(1 + у2).
888.	х = — 7/cos ж, у = sin X.
Рис. 5.
889.	Траектории си-
стемы уравнений =
= Р(х, у),	= Q(x, у),
где функции Р, Р'х, Ру,
Q, Qx> Qy непрерывны,
изображены на фазовой
плоскости (рис. 5). Что
можно сказать о пове-
дении решений при
110
t —> +oo? Является ли нулевое решение асимпто-
тически устойчивым? Является ли оно устойчивым
по Ляпунову?
В задачах 890—892 выяснить, является ли устой-
чивым нулевое решение системы, если известно, что
общее решение этой системы имеет указанный вид.
890.	х = Ci cos2 t - С2 е-*, у = Cit4 e~b +2С2.
891.	х =	y = (C1t3+C2)e-t.
1 ~г t
892.	х = (G - Gt) е-4, у = lnggf)- + С2.
893.	Доказать, что для устойчивости по Ляпу-
нову нулевого решения уравнения = a(t)x (где
функция a(t) непрерывна) необходимо и достаточно,
чтобы
t
lim / a(s) ds < +00.
t->+oo J
0
894.	Доказать, что если какое-нибудь одно ре-
шение линейной системы дифференциальных урав-
нений устойчиво по Ляпунову, то устойчивы все
решения этой системы.
895.	Доказать, что если каждое решение линей-
ной однородной системы остается ограниченным при
t —> +00, то нулевое решение устойчиво по Ляпу-
нову.
896.	Доказать, что если каждое решение ли-
нейной однородной системы стремится к нулю при
t —> +00, то нулевое решение асимптотически устой-
чиво.
897.	Доказать, что если линейная однородная
система имеет хотя бы одно неограниченное при
t —> +00 решение, то нулевое решение неустойчиво.
111
898.	Устойчиво ли нулевое решение системы
±1 =	+ «12 (t)x2, %2 = «21(^)^1 + «22^)^2, ССЛИ
известно, что ац(£) + «22 (^) —> Ъ > 0 при t -> +00?
В задачах 899—906 с помощью теоремы Ля-
пунова об устойчивости по первому приближению
исследовать на устойчивость нулевое решение
х = 2ху — х + у
у = 5х4 + у3 + 2х — Зу
[ у = Зх — х + Зу.
( х = ех+2у — cos Зх,
9Ub [у = у/Т+~8х — 2еу.
ппо /я = 1п(4т/+ е"3ж),
\у = 2у-1 + ^Т—^.
( х — In^e27 —2 cos х),
9из* \ у = 2ех ~^/8+12у.
f х = tg(y-x),
904. < . nw о (А
1 у = 2У — 2 cos ( 3 — х 1.
905.
906.
f X = tg(z -у)- 2х,
< у = у/^ + ^х -Зеу,
. = -з?/.
' х = ех — e~3z,
< у =	— 3sin(a: + у),
z = 1п(1 + z — Зх).
112
В задачах 907—912 исследовать, при каких зна-
чениях параметров а и b асимптотически устойчиво
нулевое решение.
Г х = ах - 2у + х2, gag Г х = ах + у + х2,
\у = х + у + ху.	* [у = х + ау + у2.
(х = х + ау + у2,	Г х = у + sin ж,
[ у = Ьх — Зу — х2.	* [ у — ах + by.
Г х = 2е-ж—д/4+ш/,	Г х = 1п(е +ах)— еу,
[ у = 1п(1 + х + ау).	[ у = bx + tg т/.
913.	Исследовать, устойчиво ли решение х = —t2,
у = t системы
х = у2 — 2ty — 2у — х, у = 2х + 2t2 + e2t~2y.
914.	Исследовать, устойчиво ли решение х = cost,
у — 2 sin t системы
Г х = In (х + 2 sin2 — I,
[ у = (4 — х2) cos t — 2х sin2 t — cos3 t.
В задачах 915—922 для данных систем най-
ти все положения равновесия и исследовать их на
устойчивость.
915.	Р = У - х\~ х' 916. (	~ 1}’
[у = Зх — х — у. [у = ху — 2.
917.
х = у,
у = sin(® + у).
918.
( х = 1п(—х + у2),
(?/ = Ж-7/-1.
qi о Г ® = 3 - у/4 + х2 +у,
У1 \у = 1п(х2-3).
113
( nr>   (21У   p®
920. .	/.--S о
[y = y/3x + yz - 2.
921 Iх = ln^ +?/ + sina:)>
[ у = 2 + \/3 sin ж — 8.
922 p = -sin?/;________________
1 у = 2ж + у7! — Зх — siny.
В задачах 923—931 исследовать устойчивость
нулевого решения, построив функцию Ляпунова и
применив теоремы Ляпунова или Четаева.
923.
X = X3 — 7/,
у = х + у3.
924.[Х = У~Х + Х\
[у = х-у-хл-у6.
925. (Х 2у3 Хз’ 5
[у = -х -уА + уа.
926.(± = ^“Жз+2/3’
\у = хл - у6.
997 $Х=у-Зх-Х3,
927- i у = 6х — 2у.
928.(Х = 2у-Х-у3'
[у = х-2у.
929.
х = —х — ху^
у = уг -х\
эм.!х=х-у-ху3’
\у = 2х-у-ул.
(х = -/1(ж) - f2(y)
(у = /з(®) -
где sgn/,(;?) = sgnz, i = 1, 2, 3, 4.
В задачах 932—948 исследовать устойчивость
нулевого решения, пользуясь известными условиями
отрицательности вещественных частей всех корней
многочлена, например, условиями Рауса—Гурвица
или критерием Михайлова.
114
932.	у"' + у" + у' + 2у = 0.
933.	у"' + 2у" + 2у' + Зу = 0.
934.	ylv + 2у"' + 4у" + Зу' 4- 2у = 0.
935.	yw + 2у"' + Зу" + 7у' + 2у = 0.
936.	ylv + 2у"' + бу" + Зу' 4- бу = 0.
937.	ylv + 8у”' + 14?/" + 36?/' + 45?/ = 0.
938.	у™ + 13?/'" + 16?/" + 55?/' 4- 7бу = 0.
939.	ylv + Зу"' + 26?/" + 74?/' 4- 85?/ = 0.
940.	ylv + ЗДз/'" + 5,2?/" + 9,8?/' + 5,8?/ = 0.
941.	?/v	+ 2ylv +	4?/'" +	бу" + бу' + 4у	= 0.
942.	?/v	+ 2?/IV +	бу1" 4-	бу" + бу' + 2у	= 0.
943.	?/v	+ 3?/IV +	бу'" +	7у" + 4?/' 4- 4у	= 0.
944.	yv	+ 4?/IV +	9?/'" +	16?/" + 19?/' +	13?/ = 0.
945.	yv	+ 4?/IV +	16?/'"	+	25?/"	+	13?/' +	бу = 0.
946.	?/v	+ 3yIV +	10?/'"	+	22?/"	+	23y' +	12?/ =	0.
947.	yv	+ 5?/IV +	15?/'"	+	48?/"	+	44?/' +	74?/ =	0.
948.	yv	+ 2yIV +	14?/'"	+	36?/"	+	23?/' +	68?/ =	0.
В задачах 949—958 исследовать, при каких зна-
чениях параметров а и b нулевое решение асимпто-
тически устойчиво.
115
949.	у'" + ay" + by' + 2y = 0.
950.	у"' + 3y" + ay' + by = 0.
951.	?7IV + 2у"' + Зу‘	'' + 2у' +ау = 0.
952.	ylv + ay"1 + у"	+ 2у' + у = 0.
953.	aylv + у'" + у"	+ у' + by = 0.
954.	yiv + yin + ауп	+ У1 + by = 0.
955.	ylv + ay'" + 4у‘	7 + 2у' + by = 0.
956.	yw + 2у'" + ау‘	" + by'+y = O.
957.	ylv + ay1" + 4уJ	" + by' + y = O.
958.	7/IV + 2у"' + 4у'	'' + ay1 + by = 0.
Для исследования устойчивости уравнений с пе-
риодическими коэффициентами в задачах 959 и 960
надо найти матрицу монодромии и вычислить муль-
типликаторы, см. [5], гл. III, § 15, § 16.
959. Исследовать на устойчивость нулевое реше-
ние уравнения х + p(t)x = 0, p(t) = а2(0 < t < тг),
р (f) = b2 (тг < t < 2тг), р (f + 2тг) = р (f), при следующих
значениях параметров:
а)	а = 0,5, b = 0;
в) а = 0,5, Ь= 1,5;
д) а = 1, 6 = 0;
б)	а = 0,5, 6=1;
г) а = 0,75, 6 = 0;
е) а = 1,	6 = 1,5.
960. Исследовать, при каких а и 6 устойчиво
нулевое решение системы с периодическими коэф-
116
фициентами
= Ж*)(
+ 2) =.
х
У
Л(£) = f q q J ПРИ 0<t<l, A(t) = ( j q j ПРИ 1<^<2.
§ 16.	ОСОБЫЕ ТОЧКИ
1.	Особой точкой системы
= Р(х, у),	= Q(x, у)	(1)
или уравнения
dy _ Q&, У)	f9)
dx Р(х, у)’	' '
где функции Р и Q непрерывно дифференцируемы, называется
такая точка, в которой Р(х, у) = 0, Q(x, у) = 0.
2.	Для исследования особой точки системы
— ах by, -^ = cx + dy	(3)
или уравнения
dy _ cx + dy	,4)
dx ах + by	' '
надо найти корни характеристического уравнения
|а1\-лЬ°-	(5)
| О СЛ S\ |
Если корни вещественные, различные и одного знака, то особая
точка — узел (рис. 6,а), если разных знаков — седло (рис. 6,6),
если корни комплексные с вещественной частью, отличной от
нуля, то особая точка — фокус (рис. 6,в), если чисто мни-
мые, — центр (рис. 6,г); если корни равные и ненулевые (т. е.
A1=A27^0), то особая точка может быть вырожденным узлом
(рис. 6,ф или дикритическим узлом (рис. 6,е), причем дикри-
dx
тический узел имеет место только в случае системы = ах;
117
Рис. 6.
— ay (или уравнения = *0, а во всех остальных слу-
чаях при Ai = А2 Ф 0 особая точка является вырожденным
узлом.
Если же один или оба корня уравнения (5) равны нулю, то
а N = 0 и, следовательно, дробь в правой части уравнения (4)
| с а |
сокращается. Уравнение принимает вид — к, и решения на
плоскости х, у изображаются параллельными прямыми.
Чтобы начертить траектории (кривые, изображающие реше-
ния на плоскости х, у) в случае узла, седла и вырожденного
узла, надо прежде всего найти те решения, которые изобра-
жаются прямыми, проходящими через особую точку. Эти пря-
мые всегда направлены вдоль собственных векторов матрицы
\ а & ), составленной из коэффициентов данной системы (3). В
\с dj
случае узла кривые касаются той прямой, которая направлена
вдоль собственного вектора, соответствующего меньшему по
абсолютной величине значению А.
В случае особой точки типа фокус надо определить напра-
вление закручивания траекторий. Для этого надо, во-первых,
118
исследовать устойчивость этой точки по знаку Re А и, во-вто-
рых, определить, в каком направлении вокруг особой точки
происходит движение по траекториям. Для этого достаточно
построить в какой-нибудь точке (х, у) вектор скорости
определяемый по формулам (3).
Аналогично исследуется направление движения в случае
вырожденного узла.
Пример 1. Исследовать особую точку х = 0, у = 0 системы
х = 2х, у = х + у.	(6)
Составляем и решаем характеристическое уравнение
2 л А , ° . I = °, (2 — А)(1 — А) = О, Ai = 1, А2=2.
1	1 — Л
Корни вещественные, различные и одного знака. Следователь-
но, особая точка — узел (того же типа, что на рис. 6,а). Для
Ai = 1 находим собственный вектор (0, 1), а для Аг = 2 —
вектор (1, 1). На плоскости х, у
строим прямые, направленные
вдоль этих векторов, а затем
кривые, касающиеся в начале
координат первой из этих
прямых, так как |Ai | < |Аг|,
см. рис. 7.
Другой способ построения
интегральных кривых. Разде-
лив одно из уравнений (6) на
другое, получим уравнение ви-
да (4)
dy_x + y ( dx_ 2х \
d^-~2T“	Рис. 7.
Прямые, проходящие через особую точку, ищем в виде у = кх
(а также х = 0). Подставляя в написанные уравнения, находим
к = 1. Значит, у = х и х = 0 — искомые прямые. Остальные
интегральные кривые строятся с помощью изоклин (рис. 7).
Пример 2. Исследовать особую точку уравнения
dy _ 4х — Зу
dx ~ х — 2у
(7)
119
Находим корни характеристического уравнения
| 1 “ А л| = 0; А2 + 2А + 5 = 0; А = -1±2г.
Особая точка — фокус. Переходим от уравнения (7) к системе
= х - 2у,	^=4х-3у.	(8)
Строим в точке (1, 0) вектор скорости (^jj, 7u)- ® СИЛУ (8)
он равен (х — 2у, 4х — Зу). В точке х = 1, у = 0 получаем век-
тор (1, 4) (рис. 8,а). Следовательно, возрастанию t соответству-
ет движение по траекториям против часовой стрелки. Так как
вещественная часть корней А равна —1 < 0, то особая точка
асимптотически устойчива, следовательно, при возрастании t
решения неограниченно приближаются к особой точке. Итак,
при движении против часовой стрелки интегральные кривые
приближаются к началу координат (рис. 8,6).
Рис. 8.
3. Для исследования особой точки более общей системы (1)
или уравнения (2) надо перенести начало координат в исследу-
емую особую точку и разложить функции Р и Q в окрестности
этой точки по формуле Тейлора, ограничиваясь членами пер-
вого порядка. Тогда система (1) примет вид
= ах! +Ьуг +y?(®i, yi), = cXi+dyi+'iKxi, У1), (9)
где , 2/1 — новые координаты (после переноса), a, b, с, d —
постоянные. Предположим, что для некоторого е > 0
^1)^0,
р -L Iе-	р -L “ГС
120
где г = yjх? + Очевидно, это условие выполняется (при лю-
бом е < 1), если функции Р и Q в исследуемой точке дважды
дифференцируемы. Предположим еще, что вещественные части
всех корней характеристического уравнения (5) отличны от ну-
ля. Тогда особая точка х± = 0, yi =0 системы (9) будет того же
типа, что особая точка системы (3), получаемой отбрасыванием
функций (риф. Далее, угловые коэффициенты направлений,
по которым траектории входят в особую точку, для систем (3) и
(9) одни и те же (однако прямым у = кх для системы (3) могут
соответствовать кривые для системы (9)), а в случае фокуса —
направление закручивания траекторий одно и то же.
В том случае, когда для системы (3) особая точка — центр,
для системы (9) она может быть фокусом или центром. Для
наличия центра достаточно (но не необходимо), чтобы траек-
тории системы (9) имели ось симметрии, проходящую через ис-
следуемую точку. Ось симметрии, очевидно, существует, если
уравнение вида (2), к которому можно привести систему (9),
не меняется от замены х на —х (или у на —у). Для наличия
фокуса необходимо и достаточно, чтобы нулевое решение си-
стемы (9) было асимптотически устойчиво при t —> +оо или
при t —> — оо. Исследование на устойчивость можно провести с
помощью функции Ляпунова. Это сделать нелегко, так как в
рассматриваемом случае функцию Ляпунова часто приходится
брать в виде суммы членов второй, третьей и четвертой степе-
ней относительно х, у.
В задачах 961—978 исследовать особые точки
написанных ниже уравнений и систем. Дать чертеж
расположения интегральных кривых на плоскости
(ж, у)-
961.	у' =	2ж + т/ За? + 42/ ’	962. у'	_ х — 4у 2у — Зх
963.	у' =	У — 2х У	964. у'	_ х + 4у ~ 2х + 32/
965.	у' =	х — 2у Зх — 42/ ’	966. у'	— 2х~У х — у *
967.	у' =	У — 2х 2у — Зх'	968. у'	_ 42/ — 2х ~ х + у
121
969. у1	Г _ У х *	970. у‘	f — ^Х-у Зх — 2у‘
971. |	X = Зх, у = 2х + у.	972. |	х = 2х — у, у = х.
973. |	х = х + 3у, у = —6х — Зу.	974. |	X = X, у = 2х-у.
975. |	х = —2х — Зу, у = 2х + 2у.	976. |	х = Зх + у, у = у-х.
977. |	х = Зх — 2у, у = 4у — 6х.	978. |	х = у — 2х, у = 2у — 4х
В задачах 979—992
и систем.
найти и исследовать особые
точки данных уравнений
979. у' = ^4-
* Зх + 6
980. у' = J-2V-5-
JU — £у — О
981	=	4^2 ~ х2
* 2ху — 4у — 8 *
982. у' =
х2 — у2 — 1
983. у' =	?
* х - у
984. у' = у + '^1 + 2х2
Т -I- 1/ -I- 1
985 !х = х2-У>
[ у = 1п(1 — х + х2) — 1п 3.
986.	у2)’	987. /х~(2х У)(х 2)’
[ у = е — еу.	[ у = ху — 2.
988.
V^2 - г/ + 2 - 2,
arctgfa:2 + ху).
< •	2
989 )х = х -у’
989> \у = X2 — (у — 2)2.
122
990.
991.
A = in?/2	+1,
•	9	9
У = Ж - у 
X = 1п(1 -у + у2),
У = 3 - у/х2 + 8у.
х = у/(х - у)2 + 3 - 2,
у = еу2~х — е.
Для уравнений 993—997 дать чертеж располо-
жения интегральных кривых в окрестности начала
координат.
Указание. В задачах 993—997 особые точки не принад-
лежат к рассмотренным в начале § 16 типам. Для их исследова-
ния можно построить несколько изоклин. Затем надо выяснить,
с каких сторон интегральные кривые входят в особую точку.
993*.!/' =
* х + у
995*. у' =
У + х2
994*. у' =
У х2 + у
996*. у'=
998. Доказать, что если особая точка уравнения
(ах + by) бж + (тх + пу) dy = О
является центром, то это уравнение является уравне-
нием в полных дифференциалах. Обратное неверно.
999*. Доказать, что если уравнение предыдущей
задачи не является уравнением в полных дифферен-
циалах, но имеет интегрирующий множитель, непре-
рывный в окрестности начала координат, то особая
точка — седло (если ап ф Ьт).
123
1000*. Пусть в уравнении
/ _ аж + to/ + р(ж, у)	q ч
сх + dy + #(ж, у)	'
функции р и q определены и непрерывно диффе-
ренцируемы в некоторой окрестности точки (0,0), а
в самой точке (0, 0) р = рх = р'у = q = qx = qy = 0.
Доказать, что если уравнение (1) не меняется от
замены у на — у, а корни характеристического урав-
нения
с — A d _ п
а Ь-Х
чисто мнимы, то особая точка (0,0) — центр.
§ 17.	ФАЗОВАЯ ПЛОСКОСТЬ
1.	О понятиях фазового пространства, фазовой плоскости,
автономной системы, траектории см. [1], гл. VII, § 1, п. 4, или
[3], § 15, или [4], гл. 3, § 1.
2.	Чтобы построить траектории системы
X = fl(x, у), V = f2(x,y)	(1)
на фазовой плоскости ж, у, можно или исследовать непосред-
ственно эту систему, или, разделив одно уравнение на другое,
свести ее к уравнению первого порядка
dy _ /2 (ж, У)	/„ч
dx fi(x,yY
Траектории системы (1) будут интегральными кривыми урав-
нения (2). Их можно построить или решив уравнение (2) (часто
оно решается проще, чем система (1)), или с помощью метода
изоклин (§ 1), при этом необходимо исследовать особые точки
системы (методами § 16).
Для построения траекторий уравнения ж = /(ж, ж) на фазо-
вой плоскости надо от этого уравнения перейти к системе ж = у,
у = f(x, у), которая исследуется так же, как система (1).
124
3.	Предельным циклом называется замкнутая траектория,
у которой существует окрестность, целиком заполненная тра-
екториями, неограниченно приближающимися к этой замкну-
той траектории при t —> +оо или при t —> — оо. Предельный
цикл называется устойчивым, если траектории приближаются
к нему только при t —> +оо, неустойчивым — если только при
t —> — оо, полуустойчивым — если с одной стороны цикла тра-
ектории приближаются к нему при t —> +оо, а с другой стороны
при t —> — оо. О предельных циклах см. [3], § 28, [2], § 25.
В задачах 1001—1020 для данных уравнений
начертить траектории на фазовой плоскости. По
чертежу сделать выводы о поведении решений при
t —> +оо.
1001. х + 4х = 0.	1002. х -ж = 0.
1003. х — х 4- х2 = 0.	1004. х - Зх2 = 0.
1005. х + 2х3 = 0.	1006. х + 2ж3 - 2х = 0.
1007. х + ех-1 = 0.	1008. х - 2х + х + 1 = 0.
1009. х — sin# = 0.	1010. х + 2 cosx — 1 = 0.
1011. х — 44 4- З.т = 0.	1012. х + 2х + 5х = 0.
1013. x-x-2x = Q.	1014. х + 2х + х2+х = 0
1015. х 4- х 4- 2х - х2 =	--0.
1016. х 4- х2 — х2 4-1 =	0.
1017. х 4- 2* - х2 = 0.	1018. х + у/х2 + х2 — 1 =
1019. ж + 5ж-41п^	- = 0.
125
1020. х + х + arctg(#2 — 2x) = 0.
В задачах 1021—1034 начертить на фазовой
плоскости траектории данных систем и исследовать
особые точки.
1021.<	f х = 2х + у2 - 1, 1022 ( х = у2 — 4х2, ( у = 6ж - у2 + 1.	" [ у = 4у - 8.
1023.<	f х = 4 - 4х - 2у, 1024 Г х = 1 - х2 - у2, [у = ху.	’ [ у = 2х.
1025.<	\х = 2 + у-х2, 1026 Г х = ху - 4, ( у = 2х(х - у).	' \у = (х-4)(у-х).
1027.	( х = 1 — х2 — у2, 1У = 2ху.
1028.	(х = 2(х-1)(у-2), (у = у -X2.
1029.	f х = (х+у)2-1,	( х = (2х-у)2-9, [У = -у2-х+1.	’[у =9- (х -2у)2.
1031.	( х = (2ж — у)2 — 9, ( У = (ж - 2у)2 - 9.
1032.	f х = х2 + у2 — 6х - 8у, ( у = х(2у - х + 5).
1033. <	< •	2 ) X = х — у, (у = (х-з/)(ж-у + 2).
126
1034 р = х2+У2-^
iU44- |2/ = (Ж-1)(х + 32/-5).
1035.	Вывести уравнение движения маятника без
сопротивления. Для случая, когда все постоянные,
входящие в уравнение, равны 1, начертить траекто-
рии на фазовой плоскости. Дать физическое истол-
кование траекториям различных типов.
1036.	Вывести уравнение движения маятника с
сопротивлением, пропорциональным квадрату скоро-
сти. Дать чертеж траекторий на фазовой плоскости.
Указание. Воспользоваться чертежом, построенным для
задачи 1035.
1037.	Вывести уравнение движения маятника, на
который действует постоянная сила, равная поло-
вине веса маятника и направленная всегда в одну
сторону по касательной к дуге окружности, по ко-
торой движется маятник.
Приняв постоянные I и д равными 1, нарисо-
вать траектории полученного уравнения на фазовой
плоскости. Какие движения маятника изображаются
траекториями различных типов?
1038.	Груз массы т прикреплен к пружине. При
отклонении груза на расстояние х пружина действу-
ет на него с силой кх, направленной к положению
равновесия. Сила трения равна / = const и напра-
влена в сторону, противоположную скорости груза.
При t = 0 груз находится на расстоянии h от поло-
жения равновесия и имеет нулевую скорость.
Вывести уравнение движения груза. Приняв т=2,
к = 2, f = 1, h = 5, изобразить движение груза на
фазовой плоскости.
1039.	Изобразить на фазовой плоскости малые
колебания маятника переменной длины, считая, что
127
при движении маятника вверх его длина равна /,
а при движении вниз равна L > I. Во сколько раз
увеличится амплитуда за одно полное колебание?
(Пример: раскачка качелей.)
Указание. При малых колебаниях считать sin ж « т. Из-
менение длины маятника происходит мгновенно (скачком), при
этом угол отклонения маятника и его момент количества дви-
жения относительно оси не испытывают скачков.
Начертить на фазовой плоскости траектории си-
стем 1040—1046, записанных в полярных коорди-
натах, и исследовать, имеются ли предельные ци-
клы.
1040.	dr dt	= r(l-r2),	to = l.	
1041.	dr dt	= r(r - l)(r - 2),	= 1.	
1042.	dr dt	= ,.(1g =	
1043.	dr dt	= Sinr,	$ = 1.	
1044.	dr dt	= r(|r — 1| — \r — 2| — 2r + 3),	dy _ i dt — 1
1045.	dr	= r sin -,	= 1.	
	dt	r ’	dt	
1046.	dr dt	= dl-dsini47> S = l’	
1047*. При каких условиях система
= f(r\	dy
dt J[ h	dt	’
где функция /(г) непрерывна, имеет предельный
цикл? При каких условиях этот цикл устойчив?
Неустойчив? Полу устойчив?
128
1048*. При каких значениях постоянной а система
^ = 1,	= (г- 1)(а + sin2 </>)
имеет устойчивый предельный цикл? Неустойчи-
вый?
Для уравнений 1049—1052 с помощью изоклин
построить траектории на фазовой плоскости и ис-
следовать особые точки. По чертежу сделать за-
ключение о поведении решений при t —> +оо и о
возможности существования замкнутых траекторий.
1049.	х + х3 — х + х = 0.
1050.	х + (х2 - 1)£ + х = 0.
1051.	х + х — 2arctg± + х = 0.
1052.	х + 2* -х + х = 0.
1053*. Для уравнения х + 2ах — bsgnx + х = О
(О < а < 1, Ъ > 0) построить траектории на фазовой
плоскости и найти точки, в которых предельный
цикл пересекает ось Ох.
Указание. Найти зависимость между абсциссами двух по-
следовательных пересечений траектории с осью Ох.
1054. Показать, что уравнение х + F(x) + х = О,
где функция F непрерывна и F(y) > 0 при у > О,
F(y) < 0 при у < 0, не может иметь предельных
циклов на фазовой плоскости.
Указание. Исследовать знак полной производной
а^ + г/2).
129
1055*. Пусть f(x, у) и fy непрерывны,
/(О, 0) < 0, а при х2 + у2 > Ь2 имеем /(ж, у) > 0.
Доказать, что уравнение х + f(x, х)х + х = 0 имеет
периодическое решение x(t) 0.
Указание. Перейти на фазовую плоскость и исследовать
знак полной производной ^(т2 + у2). Построить кольцо, из ко-
торого не может выйти ни одна траектория. Применить теорему
21 из [3].
§ 18. ЗАВИСИМОСТЬ РЕШЕНИЯ
ОТ НАЧАЛЬНЫХ УСЛОВИЙ
И ПАРАМЕТРОВ. ПРИБЛИЖЕННОЕ
РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ
1.	Рассмотрим систему в векторной записи
= f(t, *).	(1)
где х = (а?1, ..., хп), f = (/i, ..., /п). Пусть в рассматриваемой
области вектор-функция f непрерывна по t, х и удовлетворяет
условию Липшица1) по х
НЖ ?/) - Ж ®)|| ОНз/-Ж!-	(2)
Через || || обозначается любая из обычно применяемых норм
вектора:
Ikll = 1/kil2 + •• + Ы2,
||х|| = [Ж1| + —I- |®п|
ИЛИ
||ж|| = шах |жг|.
г = 1, ..., хп
х) Если в выпуклой по х области имеем
(г, j = 1,	п), то в этой области выполнено условие
а
Лип-
шица с к = па.
130
Пусть x(t) — решение системы (1), a y(t) — вектор-функция,
удовлетворяющая неравенствам
-/(*, у)|| Нз/(о)-®(о)1Ю-
Тогда имеет место оценка
||^(0-y(0ll Oefc|i| +|(еад -1).
(3)
Это неравенство можно применять для грубой оценки ошиб-
ки приближенного решения y(t) системы (1), а также для оцен-
ки сверху разности решения x(t) системы (1) и решения y(t)
системы = g(t, у), если у) - f(t, т/)|| < у.
2.	Если в системе уравнений
^-=/i(t, Ж1,	«п, д), г = 1, ...,п	(4)
с начальными условиями
rq(O) = а;(/х), г = 1, ...,п	(5)
у является параметром, функции fi и ai (г = 1, п) не-
прерывны и имеют непрерывные производные по х±, ..., хп, у,
то решение имеет непрерывную производную по параметру у.
дх 
Производные = щ, i = 1, ..., п удовлетворяют линейной
системе уравнений
duj _	dfj
dt ~	dxj
Vi i = l...
ду ’	’
п,
(6)
и начальным условиям Ui(0) = а^(/х), * = 1, ...,п. Значе-
ния производных и в формуле (6) берутся при х± =
= rri(t), ..., хп = xn(t), где xi(t), ..., xn(t) — решение систе-
мы (4) с начальными условиями (5).
В частности, если положить = у, o>i(y) = const при
г ф к и считать, что все функции fi, ..., fn не зависят от у, то
из предыдущего утверждения будет следовать, что для системы
(4) с начальными условиями iq(0) = аг-, г = 1, ..., п производ-
Эх *
ные = щ (г — 1, ..., п) от компонент решения х±, ..., хп
131
по начальному условию ад. существуют и удовлетворяют систе-
ме уравнений
dt	dxi J
и начальным условиям Uj(0) = 0 при i 7^ к, iz^(O) = 1.
3.	Если в (4) и (5) функции /г- и ai имеют непрерывные про-
изводные по Xi, ..., хп, р, (вблизи значения р = 0) до порядка
т включительно, то решение тоже имеет непрерывные произ-
водные по р, до порядка т и, следовательно, разлагается по
степеням параметра р по формуле Тейлора:
x(t) = Vo(t) + pvi(t) + p2V2(t) -I-h	(7)
Здесь x и — n-мерные вектор-функции. Чтобы найти функ-
ции Vi^t), можно разложить правые части в (4) и (5) по степеням
д, подставить туда разложение (7) и приравнять коэффициен-
ты при одинаковых степенях р. Получим систему дифференци-
альных уравнений, из которой последовательно определяются
vo(t), m(t), ...
В случае, когда fi и ai — аналитические функции от х±, ...
..., хп, р, решение x(t) разлагается в сходящийся при малых р
степенной ряд по р (в силу теоремы об аналитической зависи-
мости решения от параметра, см. [4], гл. 1, § 6). Коэффициенты
этого ряда совпадают с коэффициентами разложения (7).
Изложенный метод можно использовать для отыскания ре-
шения дифференциального уравнения при малых р в тех случа-
ях, когда при р = 0 уравнение решается известными методами.
Пример. Разложить по степеням параметра р решение за-
дачи
х = х2 + 2pt~1, х(1) = —1.	(8)
Ищем решение в виде x(t) = vo(t) + pvi(t) + p2V2<t) + ...
Подставляя это в (8) и приравнивая коэффициенты при оди-
наковых степенях р, получаем систему
ц0=^,	ц0(1) =-1,
vi = 2г>о^1 + 2t~1, гц(1) = 0,
V2 = 2??о^2 + V2,	^2(1) = 0,
132
Из первого уравнения и начального условия находим vo(t) =
= —t-1. Подставляя это во второе уравнение, получаем
v1 = — 2t~1vi + 2t-1,	vi(l)=0.
Отсюда
vi(t) = 1 — t~2.
Подставляя найденные vq и vi в третье уравнение, получаем
V2 = — c2t~lV2 + (1 — t~2)2, ^2(1) = 0.
Решив это линейное уравнение и воспользовавшись начальным
t	2	8	1
условием, найдем V2(t) = л — т + тггт — 7Т- Следовательно,
'j	&	Зс	с
решение задачи (8) имеет вид
+М (1 “	+	~ Т + 3^2 ~	+°(м2)-
Это разложение можно продолжить дальше тем же способом.
Аналогичным методом можно получать разложения по сте-
пеням параметра периодических решений нелинейных уравне-
ний, в частности, уравнений вида
х + а2х = х, х, /1),	(9)
где функция f периодическая по t. Переходить от уравнения
2-го порядка к системе при этом не нужно. Произвольные по-
стоянные, возникающие при отыскании ^i(^), • ••, опре-
деляются уже не из начальных условий, а из условий перио-
дичности (см. [4], гл. 2, § 8).
В случае, когда правая часть (9) не зависит от t, период
решения x(f) заранее не известен. Тогда в уравнении (9) надо
перейти от t к новому независимому переменному т =
+^2М2 + • • •) и искать решения х(т) периода 2тг/а. Коэффициент
bi обычно определяется из условия существования периодиче-
ского решения для гц(т), и т. д. (см. [4], гл. 2, § 8).
4.	Если функция f(x, у) в окрестности точки (я?о, Уо) ана-
литическая, т. е. разлагается в ряд по степеням (х — xq) и
(у — Уо), т0 решение уравнения у' = f(x, у) с начальным усло-
вием у(хо) = уо тоже является аналитической функцией, т. е.
разлагается в степенной ряд в окрестности точки xq (см. [2],
133
§ 18	и [1], гл. II, § 1, п. 6). Аналогичное утверждение справедли-
во для уравнения y(n) = /(т, у, у',	у^п~1^) с начальными
условиями y(xQ) = Уо, 2/'(жо) = i/o, , 1/п-1)(т0) = 2/оП-1)-
Пример. Найти в виде ряда решение уравнения у"=ху2 —у'
с начальными условиями у(0) = 2, т/'(0) = 1.
Ищем решение в виде ряда
у = ад + aix + а2Х2 + • • • = 2 + х + а,2Х2 + а^х3 + ...,	(10)
так как из начальных условий следует, что clq = 2, ai = 1.
Подставляя ряд в дифференциальное уравнение, получаем
2а2+6азт+12а4Т2+. • • =х(2+х+а2Х2+... )2 — 1—2а,2Х—За^х2 —...
Представляя правую часть в виде степенного ряда и приравни-
вая коэффициенты при одинаковых степенях х в обеих частях
уравнения, получаем 2а,2 = — 1, баз = 4 —2а2, 12ад = 4 —Заз, • • •
Отсюда находим
15	1
а‘2 = - 2 ’ аз = 6 ’	0,4 = 8 ’ ' **
Следовательно,
у = 2 + х - |т2 + |т3 + |т4 + ...
5.	Для уравнения
ро(ж)т/(п) +Р1(ж)?/(п_1) +-\-рп(х)у = 0,	(11)
у которого все pi (х) аналитические в окрестности точки х = 0 и
ро(хо) = 0, т. е. коэффициент при старшей производной обраща-
ется в нуль в точке xq, решений в виде степенного ряда может
не существовать. В этом случае могут существовать решения в
виде обобщенных степенных рядов
ао(х — xo)r + ai(x - то)г+1 + а2(ж - то)г+2 + ...	(12)
где число г не обязательно целое (см. [1], гл. VI, § 2, п. 2, или [4],
гл. 2, § 7). Чтобы их найти, надо подставить ряд (12) в уравне-
ние (11) и, приравняв коэффициенты при наименьшей степени
(х — то), найти возможные значения показателя г, а затем для
каждого из этих значений г определить коэффициенты а^.
134
1056.	Оценить, на сколько может измениться при
О х 1 решение уравнения у1 — х + sin у с началь-
ным условием у (О) ~ ув == О, если число у о изменить
меньше, чем на 0,01.
1057.	Оценить, на сколько может измениться при
0 t Т решение уравнения маятника х + sin ж == 0
с начальными условиями #(0) = 0, £(0) = 0, если
в правую часть уравнения добавить такую функ-
цию </>(7), что |^)| С 0,1 (т. е. если приложить
некоторую внешнюю силу).
1058.	Чтобы приближенно найти решение уравне-
ния х + sin х — 0, его заменили уравнением х + х ~ 0.
Оценить при 0 t 2 возникающую от этого ошиб-
ку в решении с начальными условиями #(0) = 0,25,
£(0) = 0, если известно, что {х — sina?| < 0,003 при
и < 0,25.
В задачах 1059—1063 оценить ошибку прибли-
женного решения на указанном отрезке.
1059.	у' = I -	у(0) = 1; у = 1 - f, |х| j.
1060.	х -- х — у, у tx, #(0) == 1, у(0) == 0;
£ = !+/+у, У= у, И ^0,1.
1061.	у" - х2у = 0, у(0) = 1, г/'(0) = 0; у = е*4/12,
|ж| < 0,5.
1062.	у' = i + х, у(0) = 1; у = 1 + х, 0О^|-
1063.	у1 = 2ху2 + 1, 2/(0) = 1; у = jyy, |х|
Указание. Сначала выделить ограниченную область, в ко-
торой содержится приближенное решение у и, предположитель-
но, точное решение у. Ц<ля этой области оценить постоянную в
135
условии Липшица, затем оценить |з/ —#|. С помощью этой оцен-
ки проверить, содержится ли у в выделенной области.
В задачах 1064—1073 найти производные по па-
раметру или по начальным условиям от решений
данных уравнений и систем.
1064. у' -у + ц(х + у2), 1/(0) = 1; найти |	.
1065.	у' — 2х + цу2, у(0) = ц - 1;	найти	ду др,	। у=0
1066.	у' = У + У2 + ху3, у(2) = у0;	найти	ду дуо	। ?/о=О
1067.	g = |+^e-^a;(l) = l;	найти	дх ду,	। у=0
1068.	= x2+fi.tx3, х(0) = 1+ц;	найти	дх ду	। у=0
1069.	f х = 4ty2,	х(0) =- 0, [ у = 1 + 5/z#, 1/(0) = 0;	найти	дх I ду |	у=0
1070.	( х == ху + t2, ж(1) =- Xq, 121/ = -у2, 1/(1) = уо;	найти	дх дуо	жо=3 2/0=2
1071.	( х = х + у, #(0) == 1+/Z, [у = 2х+цу2, 1/(0) = —2;	найти	ду\ ду	)LZ=O
1072.	X — X = (ж+1)2— fix2; ж(0) :	= 1, х(0) =		= -1;
« дх I
найти
1д=1
1073.	х = 7 —	х(1) — 1, ж(1) = Ь; найти ^1
t х' v 7	’ v 7	’	db
Указание. При 6=1 решением служит функция х = t.
136
В задачах 1074—1078 найти 2-3 члена разло-
жения решения по степеням малого параметра ц,
1074.	у' — 4/j,x — у2, ?/(1) == 1.
1075.	у1 = | - 5цх, у(1) = 2.
1076.	ху1 = /ix2 + 1п у, ?/(1) = 1.
1077.	у1 = ^~У2, 2/(1) = 1 + Зд.
1078.	у’ = еУ-х +цу, г/(0) = -ц.
Для уравнений 1079-—1085 с помощью метода
малого параметра (см. [4], гл. 2, § 8) найти прибли-
женно периодические решения с периодом, равным
периоду правой части уравнения; /1 — малый пара-
метр.
1079.	х + Зх = 2sin£ + р,х2.
1080.	х + Ъх = cos 2t + /tx2.
1081.	х + Зх 4- х3 = 2/zcos t.
1082.	x + x2 = 1 + /i sin t.
1083.	x + sin x = /1 sin 2t.
1084*. x + x — sin3£ — sin2f + /ix2, найти лишь
нулевое приближение.
1085*. х + х = 6/zsinf — х3.
В задачах 1086—1090 с помощью метода малого
параметра (см. [4], гл. 2, § 8, п. 4) приближенно
найти периодические решения данных уравнений.
137
1086. х + х — х2 = 0.	1087. х + х + х3 == 0.
1088. х + sin ж = 0.	1089. х + х — //(1 — х2}х.
1090. х + х = ц(х — х3).
В каждой из задач 1091—1097 найти в виде
степенного ряда решение, удовлетворяющее данным
начальным условиям. Вычислить несколько пер-
вых коэффициентов ряда (до коэффициента при ж4
включительно).
1091. у' -- у2 — х; 1092. у' =х+~; У	у,		3/(0) = 1. 3/(0) = 1.		
1093. у'	-- у + хеу;	3/(0)	= 0.	
1094. у'	= 2х + cos?/;	3/(0)	= 0.	
1095. у'	== х2 + у3;	3/(1)	= 1.	
1096.у”	= ху' - у2-,	3/(0)	= 1,	3/'(0) = 2.
1097. у"	= у'2 +ху,	3/(0)	= 4,	3/'(0) = —2.
1098*. Построив мажорирующее уравнение (см.
[2], § 18), оценить снизу радиус сходимости сте-
пенного ряда, представляющего решение уравнения
у' — у2 — х с начальным условием у (О) ~ 1.
1099*. Оценить, с какой точностью можно полу-
чить при |ж|	0,2 решение уравнения у' — еу —х2у с
начальным условием ?/(0) == 0, если в степенном ря-
де, представляющем решение, взять только четыре
члена (до щ#4 включительно).
138
В задачах 1100—1109 найти линейно независи-
мые решения каждого из данных уравнений в виде
степенных рядов. В тех случаях, когда это легко
сделать, сумму полученного ряда выразить с помо-
щью элементарных функций.
1100.	у" — х2у - 0.
1101.	у" -ху1 — 2?/ = 0.
1102.	(1 — х2Уу" — 4ху' — 2у = 0.
1103.	(х2 + 1)у" + Зху1 + Зу = 0.
1104.	(1-х)у" -2у' + у = 0.
1105.	(х2 - х + \)у" + (4ж - 2)х/' Ч- 2^/ = 0.
1106.	у" — ху1 + ху == 0.
1107.	у" + ?/sina; = 0.
1108.	ху" + у 1п(1 — х) — 0.
1109.	у'" — ху" + (х — 2)у' + у — 0.
В задачах 1110—1116 найти те решения данных
уравнений, которые выражаются степенными (или
обобщенными степенными) рядами.
1110. ху" + 2у' + ху == 0.
1111. 2х2у" + (Зх - 2х2)у' - (х + 1)у = 0.
1112. 9х2у" - (х2 - 2)у - 0.
139
1113. х2у" — х2у' + (х — 2)у = 0.
1114. х2у" + 2ху' — (х2 + 2х + 2)у = 0.
1115. ху" — ху1 — у -- 0.
1116. ху" + у' — ху = 0.
1117*. Найти с точностью до О (ж5) при х -> 0
решение уравнения ху" + у1 — ху = 0, линейно
независимое с решением, указанным в ответе за-
дачи 1116.
В задачах 1118—1120 указать, имеют ли данные
уравнения решение в виде степенного ряда (или
обобщенного степенного ряда).
1118.	х2у" + ху' — (х + 2)у = 0.
1119.	х2у" + ху' + (1 - х)у = 0.
1120.	х2у" + (Зж — 1)у' + у — 0.
В задачах 1121—1125 найти в виде тригономе-
трических рядов (см. [1], гл. VI, § 1, п. 3 или [4],
гл. 2, § 7) периодические решения данных уравне-
ний.
1121.	у" -Зу = /(ж), /(ж) = |ж| при |ж| < 7Г,
/(ж + 2тг) = /(ж).
1122.	у" + у1 + у = | зтж|.
lion ///	/	2 sin х
1123.	у -У~ У -- н----л-----•
5 — 4 cos х
Указание. Разложение в ряд Фурье правой части уравне-
ос
ния 1123 имеет вид ^2 2-nsinnir.
п=1
140
1124. у"—it2y = /(ж), /(ж) = ж(1—х) при 0	х 1,
/(ж + 1) = /(ж).
лк // I	\ > SIH 2/ьЗ?
1125. у" + 9у = Е -^2—•
к=1
В задачах 1126—1129 с помощью метода лома-
ных Эйлера (с итерациями или без них, см. [4],
гл. 1, § 6, § 7) найти приближенно на указанном
отрезке решения данных уравнений с указанными
начальными условиями. Вычисления вести с двумя
или тремя десятичными знаками после запятой с
шагом h = 0,2 или h = 0,1.
1126. у' = у2 + х, 0 < х < 1;	?/(0) = 0,3.
1127.	у'= J+ж,
1128.	у' = - у,
1129.	у' =
* х + у’
0 <	х	1;
0 <	х	1;
1 <	х	2;
у(0) = 1.
у(0) = 1.
у(1) = 0.
В задачах ИЗО—1135 с помощью метода Адамса
или Штермера (см. [4], гл. 1, § 7) вычислить при-
ближенно решения написанных ниже уравнений на
указанном отрезке. Вычисления вести с тремя зна-
ками после запятой. Значения решения в начальных
точках вычислить с помощью степенного ряда.
ИЗО. у' = у,
0 < х 1;	2/(0) = 1.
1131. у' = у2 - х, 0 < х 1; 2/(0) — 0,5.
1132. у'-ж, 0 ж 1;	у(0) = 1.
1133. у' = х2 — 2/2, 1 С ж С 2;	2/(1) — 1-
141
1134.7/" = ху, 00^1; у(0) = 1, у'(0) = о.
1135. ху" + у' + ху = 0, 0 х 1; у(0) = 1,
у'(0) = 0.
Задачи 1136—1140 можно решить, сравнивая на-
клон поля направлений (определяемого уравнением
у1 — f(x, 2/)) в точках некоторых кривых у = (рг(х)
с наклоном этих кривых.
1136*. Оценить сверху и снизу решение урав-
нения у1 = 2 + sin ж — у2, 0 х < +оо, ?/(0) = 1.
(На плоскости ж, у построить полосу а у /3, из
которой не может выйти это решение.)
1137*. Оценить сверху и снизу решение уравне-
ния у' = + 2х, 0 х < +оо, 2/(0) = 1.
1138*. Доказать, что решение уравнения у'=х—у2
с начальным условием у (4) = 2 удовлетворяет не-
равенствам у/х — 0,07 < у(х) < у/х при 4 < х < оо.
1139*. Доказать, что для решения у(х) уравнения
у1 = х — у2 с начальным условием у(хо) = уо, где
х0 О, i/о 0, имеем
у(х) — у/х —> 0 при х —> +оо.
1140*. Оценить сверху и снизу то периодическое
решение уравнения у1 = 2у2 — cos2 5#, которое лежит
в области у < 0.
§ 19. НЕЛИНЕЙНЫЕ СИСТЕМЫ
1. Систему дифференциальных уравнений можно свести пу-
тем исключения неизвестных к одному уравнению (иногда к
нескольким уравнениям с одной неизвестной функцией в каж-
дом). Подробнее см. [1], гл. VII, § 1, п. 2, или [4], гл. 3, § 2.
142
Пример 1. Решить систему уравнений
„ = J,	(1)
Решение. Исключаем z из данных уравнений. Из перво-
го уравнения имеем z — ху'. Подставляя во второе уравнение,
получаем после упрощений
х3у" = (у-ху')* 2.
Данная система уравнений (1) приведена к одному уравнению
второго порядка. Это уравнение может быть решено методами,
изложенными в § 10 (путем понижения порядка). После того
как из этого уравнения будет найдено у, следует найти z, поль-
зуясь равенством z = ху'.
2. При решении системы уравнений путем исключения неиз-
вестных обычно получается уравнение более высокого поряд-
ка, поэтому во многих случаях удобнее решать систему путем
отыскания интегрируемых комбинаций (см. [1], гл. VII, § 5, п. 2).
Пример 2. Решить систему1)
dx _ dy _ dz	/q\
xz yz —ху'	' '
Первые две дроби образуют интегрируемую комбинацию.
Сокращая равенство	на и интегрируя, получаем
первый интеграл2)
(3)
Чтобы найти вторую интегрируемую комбинацию, воспользу-
емся следующим свойством равных дробей:
если =	=	то при любых ki, к2, ..•, кп
имеем
feiai -j- k2(i2 ~l~ • • • ~1~ кпап _
к1 Ь1 + /£2^2 + • • • + knbn
!) Система (2) записана в симметрической форме. О симме-
трической форме системы дифференциальных уравнений см. [1],
гл. VII, § 5, п. 1, или [4], гл. 3, § 3.
2) О первых интегралах см. [1], гл. VII, § 4 или [3], § 23.
143
Пользуясь этим свойством, получаем из (2)
y-dx + x-d^^	d(x^=^ а(хг/) = _2га2.
у • XZ + х • yz —ху1 2xyz —ху1 4 7
Следовательно,
xy + z2 = C2.	(4)
Очевидно, первый интеграл (3) и первый интеграл (4) незави-
симы. Система решена.
Вместо того чтобы искать вторую интегрируемую комбина-
цию, можно, воспользовавшись знанием первого интеграла (3),
исключить из системы (2) одно из неизвестных, например, х. Из
(3) имеем х = С\у. Подставляя во второе из уравнений (2), по-
лучаем	. Отсюда -Ciydy = zdz; z2 = -С^у2 + С2.
Подставляя сюда выражение для С\ из формулы (3), находим
еще один первый интеграл: z2 + ху = С2.
В задачах 1141—1160 решить данные системы
уравнений.
1141.	у' = -, z' =
* z’	у
1142.	у' = z' = у + 1.
1143.	у1 = z' = г^ + 2г~1\
X 1	х\у — 1)
1144. у' = y2z, z'=^--yz2.
1145. 2zy' = у2 — z2 + 1, z' = z + у.
1146 d:r _ <& _ dz
' 2y -z у z '
1147.	— = ll?/ = —
У X Z '
1148.	-d*_ = АУ = dz
У + z x + Z x + y’
1149.	drc = &У — dz
У -X x + y + Z X -y’
144
1150.	dr _ ф/ _ dz _ du Z	U	X	у '
1151.	dx _ dy 	 dz 	 du у — и ~ z — x ~ и — у ~ x — z'
1152.	dx __ dy _ dz z ~ xz ~ у '
1153.	dx _ di/ _ dz z2 -y2 ~ z ~ у *
1154.	dx _ dy_ _ dz x ~ у ~ xy + z'
1155.	dx _ di/ _	dz XZ	yz	xyx/z2 + 1 
1156.	dx	_ di/ _ dz X + y2 + z2 ~ у ~ z 
1157.	dx _ dy 	 dz x(y + z) ~ z(z-y) ~ y(y-zY
1158.	dx _ dy _ dz x2 xy ~ 2z2 xz ’
1159.	dx _ dy _ dz x(z -y) ~ y(y -x) ~ y2 - xz'
1160.	dx			dy	_	dz x(y2 - z2) ~~	y(z2+x2) ~ z(x2+y2Y
В задачах 1161—1163 для данных систем диф-
ференциальных уравнений и данных функций
проверить, являются ли соотношения <р = С пер-
выми интегралами этих систем.
1161- ё =	5 = -*; ^ = ^ + 2хУ-
<р2 = X2 - ty.
1162.	х = ху, у = х2+у2-, (pi = xlny — х2у,
V>2 = £ — 21ns.
145
1163.	d® = _dy = d£ = _du	ыж.
У	X и	Z 1 Г
1164.	Проверить, являются ли независимыми
первые интегралы = Ci,	системы
Z । X	X “г у
dx _ dy _ dz
х ~ у z '
1165*. Доказать, что в области, содержащей осо-
бую точку типа узла или фокуса, для системы
= Р(х, у),	= Q(x, у)
не может существовать первого интеграла вида
(р(х, у) = С с непрерывной функцией	const в
сколь угодно малой окрестности особой точки.
1166.	Пусть X, у) = С1, ^2^5 у) = С*2 ----
первые интегралы системы = /1(/, х, у),	—
= Л (А уУч функции /1, /2 и их первые произ-
водные по ж, у непрерывны. Пусть в пространстве
t. х, у поверхности х, у) = 1, (/>2 (Л ж, £/) = 2
имеют только одну общую линию (т. е. пересекают-
ся или касаются друг друга по этой линии). Дока-
зать, что эта линия является интегральной кривой
данной системы.
§ 20. УРАВНЕНИЯ В ЧАСТНЫХ
ПРОИЗВОДНЫХ
ПЕРВОГО ПОРЯДКА
1.	Чтобы решить уравнение в частных производных
где ai, ..., ап,Ь зависят от xi, ..., хп, z, надо написать систему
обыкновенных дифференциальных уравнений
_...__ б-Ттт, _ dz
ai ~	~ an ~ b	k '
146
и найти п независимых первых интегралов этой системы
(/?1(Т1, . . Хп, z) = Cl, 1
.................... >	(3)
Рп (^1 , • • • •> Хп, %) = Сп- J
Общее решение уравнения (1) в неявном виде записывается так:
F(pi, ..., рп) = 0,	(4)
где F — произвольная дифференцируемая функция.
В частности, если z входит только в один из первых ин-
тегралов (3), например в последний, то общее решение можно
написать и так:
Pn(xi, • хп, z) = f(pi, Рп-1),	(5)
где f — произвольная дифференцируемая функция. Разрешив
равенство (5) относительно z, получим общее решение уравне-
ния (1) в явном виде.
2.	Чтобы найти поверхность z = z(x, у), удовлетворяющую
дифференциальному уравнению
<и(®, У, + а2(х, у, z)^ = Ь(х, у, z)	(6)
и проходящую через данную линию
х — u(t), у = v(t), z = w(t),	(7)
надо найти два независимых первых интеграла системы
dx _ <ty _ dz	/g\
ai а2 b	' '
В эти первые интегралы
Р1(х, у, z) - Cl, ръ(х, у, z) = C2	(9)
надо подставить вместо x, у, z их выражения (7) через пара-
метр t. Получатся два уравнения вида
Ф1ад = С1, Ф2т = с2.	(ю)
Исключив из них t, получим соотношение F(Ci, С2) = 0. Под-
ставив сюда вместо Ci и С2 левые части первых интегралов (9),
получим искомое решение.
147
В том случае, когда в оба уравнения (10) не входит t, тогда
линия (7) является интегральной кривой системы (8), т. е. ха-
рактеристикой уравнения (6), и задача Коши имеет бесконечно
много решений (см. [1], гл. VIII, § 3, п. 4).
Пример. Найти общее решение уравнения
хгЭя +yz^ = ~ху’
а также интегральную поверхность, проходящую через кривую
у = х2, z — х3.	(12)
Решение. Составляем систему уравнений
dx _ d?/ _ dz
xz ~ yz ~ —ху
и находим ее первые интегралы (см. § 19, пример 2)
|=C1, z2 + ху = С2.	(13)
Следовательно, общее решение уравнения (11) можно написать
в неявном виде
F z2 + ху^ ~ 0,
где F — произвольная функция. Так как z входит только в
один из первых интегралов (13), то общее решение можно на-
писать и в явном виде. Мы получим
z2 + ху = f (^) ; z = ±ф (|) - ху,
где f — произвольная функция.
Чтобы найти интегральную поверхность, проходящую через
линию (12), запишем эту линию в параметрическом виде, на-
пример, взяв х в качестве параметра:
2	Ч
X = X, у — X , Z = X .
Подставив эти выражения в (13), получим
1=С1, хв+х3 = с2.
Исключив х, получим
1 . 1 _
С1 + С1 ~С2'
148
Подставив вместо Ci и С2 левые части первых интегралов (13),
найдем искомое решение
3.	О решении системы двух уравнений в частных производ-
ных первого порядка и о решении уравнения Пфаффа см. [1],
гл. IX, § 1 и § 2, пн. 1, 2, 3.
Для каждого из уравнений 1167—1188 найти
общее решение.
11в7-
1168. (l + 25)g-9g=O.
-1 -1 лл ди । ди । ди _
П69. ж_+2/_+г_=0.
1170. (Ж-г)^ + (у-г)|+2г£=0.
1171-у^+^ = х-у-
1172.	e-g+./'g^e-.
1173.	2j:g + (1/-i)g-i!=0.
1174.	ху^- — х2^- = yz.
1175.	^+2^ = ^ +г.
1176.	(ж2 + у2)	+ 2ху^ + z2 = 0.
1177.	2т/4 g - худ/у = xV^+1.
1178.	x2z^- + y2z^~ = х + у.
дх & ду *
149
1 1	OZ	OZ z
1179.	yz^--xz^- = ez.
1180.	{z-y)2^+xz^ =xy.
1181.	xyl^ + ^x~2z^ = yz-
1182.	y^+z^- = У-.
dx dy x
1183.	sin2 2:^ +tgz^ = cos2 z.
dx ° ay
1184.	(x + z)^ + (y + z)^ = x + y.
1185.	(xz + y)^ + (x + yz')^ = l-z2.
1186.	(y + z)^ + (z + x)%± + (x + y)^ = u.
1187.	x%± +y^ + (z + u)^ = xy.
dx v dy v 7 dz *
1188.	(u-x)^ + (u-y)^ -z^=x + y.
Найти решения уравнений 1189—1193, удовле-
творяющие указанным условиям.
1189.	х^- — у^- = 0; z — 2х при у = 1.
dx dy	г v
иэо. В + (2е* ~у^ = °’ z = y пРиа; = о.
1191.	2^g - у^ = 0;	z = у2 при х = 1.
1192.	+ 2$^ = 0; u = yz при х = 1.
dx dy dz ’	н
-в -в л о du । du । du _ г\ _ о ।	2	_
U93. x-^ + y-^ + xy-^ = 0; и = xz + у2 при z = 0.
В задачах 1194—1210 найти поверхность, удо-
влетворяющую данному уравнению и проходящую
через данную линию.
150
1194.	у2||+жу|| =ж; ж = О, г = у2.
1195.	- 2у^ = х2 + у2; у = 1, z = ж2.
1196.	ж||+у^ = z-xy; ж = 2, г = у2 + 1.
1197.	tgж^ + у^ = z; у = х, z=x3.
1198.	ж|| - у^ = z2(x - Зу); х = 1, yz + 1 = О.
1199.	ж^+у^ = z-x2-y2; у =—2, z = x-x2.
1200.	yz^ +xz^ = ху; х = a, y2+z2 = a2.
1201.	2^-жу|^ =2жг; х + у = 2, yz = 1.
1202.	2^ + (г2-ж2)^+ж = 0; у = ж2, z = 2ж.
1203.	(у - z)^ 4- (г - x)g = ж - у; z = у = -ж.
1204.	ж^| +	+ у)^| = г; ж 4- у = 2z, xz = 1.
12О5.	у2^+уг^+г2 = 0; ж - у = 0, ж - yz = 1.
12О6.	ж^+г^=у; у = 2z, x + 2y = z.
1207.	(y + 2z2)^ ~2x2z^ =x2; x = z, y = x2.
1208.	(x-z)^+(y-z)^ = 2z; x-y = 2, z+2x = 1.
1209.	жу3|^ 4-ж2г2^ = у3г; ж = -г3, y = z2.
1210*.ж^4-у^ = 2жу; у = х, z = x2.
151
1211.	Найти общее уравнение поверхностей, пере-
секающих под прямым углом поверхности семейства
г2 = Сху.
1212.	Найти поверхность, проходящую через пря-
мую
у = х, z — 1
и ортогональную к поверхностям
ж2 + у2 +	= Сх.
1213.	Написать уравнение в частных производ-
ных, которому удовлетворяют цилиндрические по-
верхности с образующими, параллельными вектору
(а, Ь, с). Найти общее решение этого уравнения.
1214.	Пользуясь результатом предыдущей зада-
чи, найти уравнение цилиндрической поверхности с
образующими, параллельными вектору (1,—1,1), и
направляющей
X + у + z — 0, х2 + ху + у2 = 1.
1215.	Написать уравнение в частных производ-
ных, которому удовлетворяют все конические по-
верхности с вершиной в данной точке (а, Ь, с), и
решить его.
1216.	Найти поверхности, у которых любая ка-
сательная плоскость пересекает ось Ох в точке с
абсциссой, вдвое меньшей абсциссы точки касания.
В задачах 1217—1219 решить данные системы
уравнений
{dz _ z
ду у ‘
{^=y~Z,
1218.	_
I ду - xz-
1219.	I 2yZ
= XZ.
v ду
152
В задачах 1220—1223 найти поверхности, удо-
влетворяющие данным уравнениям Пфаффа.
1220.	(х — у) cLr + z dy — х dz = 0.
1221.	3yz dx + 2xz dy + xydz = 0.
1222.	(z + xy) dx — (z + y2) dy + ydz = 0.
1223.	(2yz + 3x) ckr + xz dy + xy dz = 0.
153
ДОБАВЛЕНИЕ
Задачи, предлагавшиеся
на письменных экзаменах
В §§ 21—27 содержатся задачи, предлагавшиеся
на письменных экзаменах и коллоквиумах на 2-м
курсе механико-математического факультета МГУ в
1992—1996 годах, а также небольшое число задач,
дававшихся для подготовки к экзаменам. Исключе-
ны самые трудные задачи. Сокращено число задач
на решение уравнений стандартными методами (по-
добные задачи содержатся в предыдущих парагра-
фах этого сборника).
Ниже приводятся для примера три экзаменаци-
онные письменные работы (указаны номера задач
из §§ 21—27).
Работа 15.05.94 г. состояла из задач
17, 63, 81, 98, 170, 198.
Работа 4.06.94 г. состояла из задач
28, 51, 69, 122, 127, 148, 190.
Работа 18.05.95 г. состояла из задач
22, 56, 70, 129, 135, 194, 216.
На выполнение работы студентам давалось 3 ча-
са. Для получения оценки «отлично» требовалось
решить 5-6 задач.
154
§ 21. СУЩЕСТВОВАНИЕ
И ЕДИНСТВЕННОСТЬ РЕШЕНИЯ
1. Теоретические вопросы
Вопросы 1—5 рассчитаны на лиц, изучавших до-
казательство существования решения дифференци-
ального уравнения, основанное на переходе к инте-
гральному уравнению и построении последователь-
ных приближений [1], [2].
1.	Обосновать связь условия Липшица и диффе-
ренцируемости .
2.	Изложить общий план доказательства теоремы
существования и единственности.
3.	Сформулировать и доказать утверждение о
переходе от дифференциального уравнения к ин-
тегральному.
4.	Доказать, что последовательные приближения
сходятся к непрерывной функции.
5.	Доказать, что предел последовательных при-
ближений есть решение интегрального уравнения.
6.	Сформулировать и доказать утверждение о
единственности решения.
7.	Сформулировать теорему о существовании и
единственности решения дифференциального урав-
нения порядка п.
8.	Сформулировать и доказать лемму об интег-
ральном неравенстве.
2. Существование решения
и последовательные приближения
9.	Перейти от уравнения е£ у'" + ху = 2уу‘ к си-
стеме нормального вида и при начальных условиях
2/(0) = 1, 7/'(0) = 1, у"(О) = 0 построить два последо-
вательные приближения к решению.
155
10.	Построить три последовательные приближе-
ния 2/о5 2/1, У2 к решению задачи
y' = 2t + y2, 7/(0) =1.
11.	а) Задачу у1 = у2+х, у(1) = 0 свести к инте-
гральному уравнению и построить последовательные
приближения уо, у±, у%.
б) Указать какой-либо отрезок, на котором схо-
дятся последовательные приближения, и доказать
их равномерную сходимость.
12.	Существует ли решение задачи
у' = №), 2/(0) = о, где /(у)	у J °?
Обосновать ответ.
13.	а) Свести задачу
=	2/(1) =0, у'(1) = 1, у"(1) = 2
\У ч
к задаче для системы нормального вида.
б) При каких а существование и единственность
решения гарантируется теоремой?
14.	а) Указать все значения параметров а, а, А,
при которых теорема существования и единственно-
сти гарантирует однозначную разрешимость задачи
(ai + а)у'" + 2ау” - (a - l)i2y tgi = In |i|,
y(a) = 1, у'(a) = A, y"(a) = a.
б) На какой максимальный интервал можно про-
должить решение этой задачи в случае а = — 1,
а = —2, А = -3?
15.	Задачу ху1 = ----у(—2) =4 свести к инте-
Ху
тральному уравнению, построить последовательные
приближения и найти их предел.
156
16.	При каких начальных условиях существо-
вание единственного решения уравнения у,п sin х+
+х In ?/ + tg я; = 1 гарантируется теоремой?
3. Применение теоремы единственности
17.	Для уравнения у" =	— 1 известны два
/ Ух ч 2
решения: yi — 1 + sin ж, у% =	, проходящие
через точку (0,1). Как это согласуется с теоремой
единственности?
В задачах 18—22 требуется выяснить, при ка-
ких п наличие указанных решений у написанных
уравнений не противоречит теореме единственности.
18.	у"' = у, у', у"), f е С1, решения уг =
= 1 + t + nt2, у2 = 1/(1 - t) (-1 < t < 1/2).
19.	у^ = f (х, у, у', ..., ?/п-1)) , f G С1, решения
У1 = 2 cos х, у2 = 2 - х2.
20.	у^ +ai(x)y(n Ч------\-ап(х)у = 0, все аг(х)
непрерывны, решение yi = х(ех — 1).
21.	Уравнение то же, что в задаче 20, график
решения у^ указан на рис. 9
22.	Уравнение то же, что в задаче 20, график
решения yi указан на рис. 10.
157
23.	Сколько решений имеет задача
(а3 —4а)у"' + (а2+2а)у"+у' — 2у=х+а, у(1)=0, у'(1)=1
в зависимости от значений параметра а?
24.	Тот же вопрос для задачи
(1-а2)(ау'"-7/") = ау'+у2, 2/(0) = 2, у'(0) = 4.
25.	Сколько решений имеет задача
У^=х + у2, у(-1)=а, т/'(-1)=0
в зависимости от а и п?
26.	Тот же вопрос для задачи
У(п) = 2у2 - а2х, 7/(1) = 1, j/'(l) = а.
27.	Тот же вопрос для задачи
J/(n) =х + 2у' + у2, j/(-l) = ln(4 + a), у'(-1) = 1.
4. Продолжение решений
28.	Существует ли при — оо < х < оо решение
задачи у1 = е~у sin^), у(0) = О?
29.	Для задачи (2 - х2)у' - ху2 = 0, т/(ж0) = Уо,
где х0 = у/2 + Зе-1, у0 = -2,
а)	определить максимальный интервал существо-
вания решения:
б)	нарисовать график решения.
30.	а) Найти все решения уравнения
у' = жу2/(тг2 - ж2).
б) Найти непродолжаемое решение этого уравне-
ния с начальным условием у(—д/3) = 1/(1п х/я2—3—1)
и нарисовать его график.
31.	Доказать, что решение задачи у1 = х — у2,
2/(1) = 0 может быть продолжено на полуинтервал
1 X < 00.
158
32.	Имеет ли система Ах/At — sin?/, dy/At = x3
решение, которое нельзя продолжить на интервал
—оо < t < 00?
33*. Доказать, что решение задачи у' = х + у2,
т/(0)=0 не продолжается на полуинтервал 0^£<оо.
34*. На каком интервале можно гарантировать
существование решения задачи
/1
g = f(t, ж) (t е я, ж е Rn, f е С1), ж(0) =
\ о
если \f(t, ж)| С |#|2? Дать неулучшаемую оценку ин-
тервала, общую для всех таких f(t, х), и подтвер-
дить неулучшаемость примером.
§ 22. ОБЩАЯ ТЕОРИЯ
ЛИНЕЙНЫХ УРАВНЕНИЙ И СИСТЕМ
1. Теоретические вопросы
35.	Сформулировать теорему существования и
единственности решения линейного уравнения по-
рядка п на заданном интервале.
36.	Сформулировать и доказать теорему об общем
решении линейной однородной системы.
37.	Дать определение фундаментальной системы
решений для линейной системы уравнений и дока-
зать ее существование.
38.	а) Что называется общим решением линейного
неоднородного уравнения?
б) Сформулировать теорему об этом решении.
39.	а) Сформулировать основные свойства детер-
минанта Вронского.
б) Пусть W (t) — детерминант Вронского для
скалярных функций yi(t), ..., yn(t) класса Сп. Если
159
W (£) = О при a t Ь, то можно ли сделать вывод
о линейной зависимости данных функций на отрезке
[а, Ь]? Обосновать ответ.
40.	а) Дать определение фундаментальной мат-
рицы.
б) Написать фундаментальную матрицу для си-
стемы х = ?/, у = 0.
41.	Как из одной фундаментальной матрицы мож-
но получить другие?
42.	Сформулировать и доказать теорему об оцен-
ке решений системы
х = A(t)x
43. Сформулировать и
ствования периодического
нения первого порядка с
(х е Rn).
доказать теорему суще-
решения линейного урав-
периодическими коэффи-
циентами.
(Задачи 42 и 43 только для студентов, которым
читались эти теоремы.)
2. Линейные однородные уравнения
44.	а) Написать общий вид линейного однородного
уравнения порядка п с переменными коэффициен-
тами. При каких требованиях на коэффициенты это
уравнение имеет единственное решение, удовлетво-
ряющее заданным начальным условиям?
б) Пусть эти требования выполнены и извест-
но, что уравнение имеет частное решение yi = хк.
Каким может быть порядок уравнения?
45.	а) Сформулировать теорему существования и
единственности решения уравнения у'" + ai(x)y"+
+а2(х)у' + аз(х)у = 0 с начальными условиями.
б) Для какого наибольшего натурального числа
т наличие у этого уравнения решения у = (еж — 1)т
не противоречит сформулированной теореме?
160
46.	Найти два линейно независимых решения
уравнения х2у" — 2ху' 4- 2у — 0 и их детерминант
Вронского. Принимает ли он нулевое значение? Как
это согласуется с известными свойствами детерми-
нанта Вронского?
47.	Пусть yi(x\ У2(х) — решения уравнения
(х 4- 2)у" — Зу' 4- у\/1 — х = 0 с начальными усло-
виями ?/1(0) = 1, 2/1(0) = 0, 2/2(0) = 3, 2/2(0) = 2.
а)	Указать интервал, на который их можно про-
должить.
б)	Составляют ли они фундаментальную систему?
в)	Чему равен детерминант Вронского этих ре-
шений при х = — 1?
48. Пусть <pi(£), <^2^), ^з(^) — решения уравне-
ния — (f 4- 1)ут — 2у" 4- 2t2ytgt = 0 с начальными
условиями при t = 1:
epi = 2,	=	0,	= 0;
922 = -1,	v'2	=	1,	^2	= -1;
</>з = 0,	ср'3	=	0,	=	—2.
а)	Указать интервал, на который можно продол-
жить эти решения по известной теореме.
б)	Составляют ли они фундаментальную систему?
в)	Найти явное выражение для их детерминанта
Вронского на этом интервале.
г)	Решение y(t) с начальными условиями 2/(1) = а,
2/'(1) = 6, 2/,,(1) = с выразить через <^i(f), <^2(^)9 <^з(£)-
49. Существует ли такое значение параметра а,
при котором детерминант любой фундаментальной
матрицы системы
/ а 1 2\
^7 = Ах, xeR3, .4 =	3 2 0
ас	I	I
\-1 оз/
остается постоянным при изменении t?
161
50. Сколько линейно независимых решений, опре-
деленных при —оо < t < оо, имеет уравнение
t2x = 90а;? Обосновать ответ.
51*. Тот же вопрос для системы tx = 2а;, ty = Зу.
52.	Построить линейное однородное уравнение
возможно низшего порядка, имеющее на интерва-
ле (0,1) такие четыре решения:
У1 = 1-^, У2 = (а;-2)2, уз = х2+х-1, ?/4 = а;2-2а;+2.
53.	Известны два решения линейного однород-
ного уравнения 2-го порядка: ух — х, у2 = х2 — 1.
Найти решение с начальными условиями у (2) = 4,
т/'(2) = -3.
54.	Известны два частных решения ух = х2~2а;+3,
у2 = х ех +2 линейного однородного уравнения 3-го
порядка. Достаточно ли этого для отыскания реше-
ния с начальными условиями ?/(0) = 5, т/'(0) = —8,
т/"(0) = 2? Обосновать ответ.
55.	Для уравнения а;3(а;—1)?/,"+а;2(5—За;)?/"+а;(6а;—
—12)?/ + (12 — 6х)у = 0 известны два частных реше-
ния: yi = х, у2 = х3. Найти общее решение.
56.	Для линейного однородного уравнения 3-го
порядка известны два частных решения ух и ?/2-
Описать способ отыскания общего решения.
3.	Линейные неоднородные уравнения
57.	Известны два частных решения линейного не-
однородного уравнения первого порядка: ух = х,
У2 = ех. Найти решение с начальным условием
3/(1) = -1.
58.	Известны три частных решения линейного не-
однородного уравнения 2-го порядка: ух = х + 1,
у2 = х — 1, уз = 1 — х2. Найти общее решение этого
уравнения.
59.	Известны три частных решения линейного
неоднородного уравнения 2-го порядка: ух = а;2,
162
У2 = 1 — х, уз — 1 — За;. Найти решение с начальными
условиями ?/(0) = 2, y'(G) = 0.
60.	Даны три функции: у± = х + 1, у2 = 1 — 2а;,
Уз = х2 — 3. Составить линейное неоднородное урав-
нение 2-го порядка, которому они удовлетворяют.
61.	Известны два частных решения ух = х — 1 и
?/2 = (а;2 — х + 1)/х уравнения (а;2 — 2х)у" + 4(а; — 1)у'+
+2у — ба; — 6. Найти общее решение.
62.	Известны два частных решения ух = а;еж, у?, =
= (а; — 2) еж уравнения ху" — (а; + I)?/' + у — (х — 1) ех.
Найти общее решение.
4.	Краевые задачи
63.	Пусть известно, что уравнение у" + р(х)у'+
+q(x)y — 0 с непрерывными на [а, Ь] функциями
р(х) и q(x) не имеет решений у(х) 0, для которых
у (а) = у(Ь) = 0. Доказать, что для любых чисел
с, d существует единственное решение, для которого
3/(а) = с, y(b) = d.
64*. Найти наименьшее положительное число Т
такое, что для уравнения х — 2х = 8 sin2 t разрешима
краевая задача с условиями ±(0) = — 1, х(Т) = — 1.
65.	Известно, что при некоторой непрерывной
функции f(x) краевая задача
у” - 2у' + 2у = /(ж), 2/(0) = 2, з/(тг) = -2
имеет решение. Единственно ли это решение?
66.	Найти наименьшее положительное р, при ко-
тором краевая задача
у"+РУ = О, 3/(0) = 1, 3/(1) = 2
не имеет решений.
67.	Найти наибольшее из таких чисел а, что при
каждом р 6 (1, а) краевая задача
у" + 2у' + ру = 0, 2/(0) = 2, з/(тг) = 3
имеет решение.
163
§ 23. ЛИНЕЙНЫЕ УРАВНЕНИЯ
И СИСТЕМЫ С ПОСТОЯННЫМИ
КОЭФФИЦИЕНТАМИ
1. Отыскание решений
Найти все вещественные решения уравнений
68—71.
68.	х — 2х + х= + sin t.
69.	х + 4а;=(е2* +2) sin 2t.
70.	— 4а; cos х.
71.	у" + у = 5хе~2х +4 sin а;.
Указать вид общего решения (в задачах 72 и 73
общего вещественного решения) с неопределенными
коэффициентами. Не находить числовых значений
коэффициентов.
72.	у'" - 2у" + у1 = £е*(1 + cos£) + t.
73.	у" — 4у' + 4у = е2х(х + sin а;).
74.	у" — 2iy = 8 ех cos х.
75.	у" — 2iy' — у — 4 sin а;.
76.	у" + 4dyr — 5у = ех cos 2х.
77.	у'" + Siy = sin х cos х.
164
2. Периодические и ограниченные решения
Имеют ли уравнения 78—80 периодические ре-
шения?
78.	у1" +у — cost
80.	х — 2х = 8 sin2 t.
81.	При каких си G R существует периодическое
решение уравнения х + 4± = 2 cos cut?
82.	При каких целых b и с уравнение у'" + 62у' =
= sin х + с sin2 х не имеет периодических решений?
83.	а) При каких си 6 R уравнение у(^ +4у,п +4у' =
= coscut не имеет периодических решений?
б) Найти все периодические решения в случае
си = 3.
84.	Найти периодическое решение уравнения х+
+± + 25а; = sincjt Нарисовать график его амплитуды
как функцию от си.
85.	При каких целых а уравнение у" + а2у =
= sin 4х cos 2х
а) не имеет решений с периодом тг?
б)* имеет только одно решение с периодом тг?
86*. Те же вопросы для уравнения
у” + (а — 1)(а — 2)у' + а2 у = sin 2х.
Для каждого из уравнений 87 и 88 выяснить,
при каких а 6 R все решения этого уравнения не
ограничены при — оо < t < оо.
87. х + ах = sin2 t.
88. х + х = cosat.
165
89.	При каких а 6 R хотя бы одно решение урав-
нения
у'" + у" - 2у' = eat + sin 2at
ограничено при t О?
90.	Тот же вопрос для уравнения
у,п + а2 у1 = cos at cos 2t.
91.	Найти все значения а, а и /?, при которых
задача
х — 2х + 5х = а е* cos 2t — 17 sin 2t, x(fi) = a, x(0) = /3
имеет решение, ограниченное при t 0.
92.	Пусть х = <p(t) и х = ip(t) — решения урав-
нения х — х + 4х — 4а; = 0 с начальными условиями
</>(0) = а, </>'(0) = 6, </>"(0) = с; ^(тг) = а, = /3,
гр"(тг) = Указать какие-нибудь числовые значе-
ния а, Ь, с, а, /?, 7 так, чтобы ip(t) и 'ф($) были
периодическими и линейно независимыми.
3.	Системы уравнений
Решить системы 93—95.
х = у + х — 4,
у = Зу - х.
х = —5у.
у = 2x4- 2у.
93.
94.
95. <	II II II 1 1	1 1	1 w и 1! о 1 i—i
96.	При каких матрицах А все вещественные ре-
шения системы х = Ах выражаются только через
синусы, косинусы и константы?
97.	Для одного частного решения системы х = Ах
известна только первая координата: х^ = t2 +tsint.
Каким может быть порядок матрицы А?
166
98.	Найти фундаментальную матрицу системы
/О 1 0\
х = Ах, где А = [ООО, нормированную при
\1 0 1/
t = 0.
99.	Доказать, что для системы х = Ах с веще-
ственной кососимметрической матрицей А нормиро-
ванная при t = 0 фундаментальная матрица при
каждом t является ортогональной.
100.	Найти все вещественные периодические ре-
шения системы
х = 2у — х + 2 cos t, у = Ay — 2х + cos t.
101.	Найти решение с периодом тг системы
х = х — у, у = 2х — у + 6sin2 t.
102.	а) Найти все вещественные периодические
решения системы
х = х — у + 3 sin 2t, у = 2х — у.
б) Найти все решения с периодом тг.
103.	При каких а система
х = у + sin 2t, у = —4х + a cos 2t
имеет периодическое решение?
104.	Для каких вещественных чисел а и b все
решения системы
х = 2у — 4х + а, у = 2х — у + Ъ
ограничены при t О?
105.	Для каких матриц А каждое решение систе-
мы х = Ах ограничено при — оо < t < оо.
167
4.	Показательная функция матрицы
106. Сформулировать свойства показательной функ-
ции матрицы.
В задачах 107—110 найти etA.
107. А = 1	/—2 -4\	,ЛО . (-1 5\ 1 2/'	Ю8. Л - j 3J. /0 0 1\	/2 0 -1\
109. А =	0 0 0.	110. А = 0 2 0 . \ 1 0 0/	\0 0 2/
111. Найти вектор езлЬ, если
	л /1 -2\ ,	/2\ А ~ ( 1 -1 )’ Ь~ ( 4 )’
В задачах 112—114
а)	не вычисляя матрицу etA, найти ее детерми-
нант и собственные значения;
б)	найти etA.
112. А =	। ео i-н 1 II со 1-1 см 1 1 СМ Tt<
114. А =	/1 -2\ V -17 /1 0 0\	2
115. А =	10 0 11. Найти det J etA dt. \0 1 0/	0
116. При	каких матрицах А имеем efj4 —> 0 при
t -> +оо?
168
117. Найти фундаментальную матрицу системы
х = t~rAx.
118. Если А — такая матрица, что ел = Е, то
обязательно ли А = О?
119*. Что можно сказать о жордановой форме
матрицы А, если
5
etA = ^k\tkAkl
k=Q
120*. Если при всех t матрица etA симметриче-
ская, то обязательно ли матрица А симметрическая?
121*. Если etAetB =	то обязательно ли
АВ = В А?
122*. Если матрица etA ортогональная при ка-
ждом t 6 R, то обязательно ли А* = —А?
5. Линейные системы с периодическими
коэффициентами
123.	Что называется мультипликатором системы
х = A(t)x с периодической матрицей A(t)?
124.	Какому условию должны удовлетворять
мультипликаторы линейной системы для того, что-
бы все ее решения стремились к нулю при t -> +оо?
125.	Найти мультипликатор для уравнения х =
= (а + sin2 t)x.
126*. При каких значениях параметра a G R урав-
нение х = (а + sin2 t)x + 1 имеет ровно одно перио-
дическое решение?
127*. Пусть матрица A(t) имеет период Т, и
||А(/)|| а при всех t. Доказать, что для системы
х = A(t)x модули мультипликаторов не превосхо-
дят е.
169
§ 24. УСТОЙЧИВОСТЬ
1.	Теоретические вопросы
128.	Дать определение устойчивости по Ляпу-
нову.
129.	Сформулировать и доказать теорему об
устойчивости при наличии функции Ляпунова v(x).
130.	Сформулировать теорему об устойчивости по
первому приближению.
131.	Сформулировать необходимые и достаточ-
ные условия устойчивости по Ляпунову нулевого
решения системы х = Ах (х е Rn, матрица А посто-
янная) .
132.	Доказать, что если одно решение линейной
системы устойчиво, то устойчиво каждое решение
этой системы.
133.	Какому необходимому и достаточному
условию должна удовлетворять матрица Л, чтобы
для любой непрерывной функции h(t) каждое ре-
шение системы х = Ax + h(t) было устойчивым по
Ляпунову?
134.	а) При каких матрицах А система х = Ах
имеет более одного положения равновесия?
б) При каких дополнительных предположениях
все эти положения равновесия устойчивы?
135.	Система х = Ах, где х Е R3, А — посто-
янная матрица, имеет частное решение, у которого
известна только первая координата: х± = e~l + cos t.
Устойчиво ли нулевое решение?
136.	Система х = Ах (х е R4) имеет частное ре-
шение, у которого известны только две координаты:
Xi = sint + 2cost, Х2 =cos2t Устойчиво ли нулевое
решение?
170
137.	Если для системы х = Ах (х G Rn) нулевое
решение неустойчиво, то обязательно ли оно не-
устойчиво для каждой системы вида х = Ах + <р(х),
где <р(х) G С1, <р(х) = о(|х|) при х -> О?
138*. Пусть /(£, х) 6 С1, х G Rn и пусть разность
каждых двух решений уравнения х = /(£, х) стре-
мится к нулю при t -> +оо. Следует ли отсюда при
каком-либо п, что всякое решение этого уравнения
асимптотически устойчиво?
2.	Исследование устойчивости
конкретных систем
Для уравнений 139—144 и систем 145—147 най-
ти положения равновесия и исследовать их на устой-
чивость.
139. х= — х2.
140. i=sinrc — х.
141. х= — a; sin2 х.	142. х= — a; sin2 t.
143. х=х sin3 t.	т2 144.i=/+1.
145. х=у, у= — х3.	146. х=у, у=3х2 — 2х.
147. х=у — х + (у — х)2, у=0.
В задачах 148—155 выяснить, при каких значе-
ниях параметра а нулевое решение является
а)	асимптотически устойчивым;
б)	устойчивым, но не асимптотически;
в)	неустойчивым.
= у
•	Ч 9
у = —ау — х — ах
171
149 f % =	+ У + (а + 1)^2,
’ 1 у = х + ау.
чгл Г # — ах + a sin?/,
150. \	4	9
[ у = ах — а£у.
151. Н = У’
152 И =
' 1 У = ау-tgx.
, го Г х = Зу2 - ау,
lf>a'\y = 2x+(2-a)y.
1^4 f х = у-ах2 - у2,
’ {У = -(а+ 1)ж -ау.
155 I =-аа: + (а _
1 у = х + ау2.
156.	а) При каких а 6 R существуют ограничен-
ные при — оо < t < оо решения системы
х = 2у — 4х + 1, у = 2х — у + а.
Найти все такие решения.
б) Устойчивы ли они?
157.	Устойчиво ли решение системы
х = х — у, у = 2х — у + 6 sin2 t,
имеющее период тг?
В задачах 158—160
а)	найти все значения параметра a G R, при кото-
рых все решения уравнения неограничены при t О
(не требуется отыскивать решения);
б)	выяснить, являются ли эти решения устойчи-
выми или асимптотически устойчивыми.
158.	х + ах = sin2 t. 159. х + х = cos at.
160. х + ах = cos at.
172
§ 25. ФАЗОВАЯ ПЛОСКОСТЬ
1. Траектории линейных систем
161. При каких соотношениях между коэффици-
ентами а, 6, с, d особая точка системы х = ах + by,
у = сх + dy является
а) седлом,
б) узлом?
162. При каких a, b, с, d для каждого решения
системы х = ах + by, у — сх + dy полярный угол
точки (x(t), y(tY) возрастает при увеличении t?
В задачах 163—165 определить тип особой точки
и нарисовать траектории системы на плоскости х, у.
163.
( х = х + Зу,
[у = Ъу — х.
164. Р = Х ~ 5у’
±о*- \у = 5х-5у.
165.	Р = » + *-4.
[у = 3у-х.
166.	При каких а особая точка системы х=а(х+у),
у = а2 у является седлом?
167.	а) Может ли траектория системы
х = 2у — х, у = Зх — 2у
из точки {—а2 — 1, —1) попасть в точку (1, а2 + 1)?
б) Устойчиво ли положение равновесия?
168.	а) определить тип особой точки и нарисовать
траектории системы
х = ах — у, у = by + х
при а = —2, b = —3.
173
б) На плоскости параметров а, b указать такую
область, что при любых (а, Ь) из этой области вто-
рая компонента y(t) любого решения указанной вы-
ше системы имеет бесконечно много нулей при t 0.
169.	Рассматривается система
х = а2х — у, у = 5х — (3 + 2а)у.
а)	Будет ли нулевое решение системы при а = 1
асимптотически устойчивым? Обосновать ответ.
б)	Нарисовать траектории системы при а = — 3.
в)	Существует ли такое значение а 6 R, при
котором траектории — замкнутые кривые?
В задачах 170—173 исследовать
а)	при каких значениях параметра a G R нулевое
решение асимптотически устойчиво и при каких —
устойчиво;
б)	при каких значениях параметра а 6 R особая
точка — седло? узел? фокус?
в)	при указанном значении а дать чертеж траек-
торий.
170.	[ 4 = х +'« = 1
[ у = ах + у; 2
(х = ах + у,
\у = ау — {2а + 1)ж;
172.	(	+ »	„ =
[ у = ау — 2ах-
173.	/ ^ = ж + (2 - аЬ> а
' [у = ах - Зу,
174
2. Траектории нелинейных систем
174.	Найти и нарисовать траектории системы
х = х3 — За;?/2, у = Зх2у — у3.
175.	Имеет ли уравнение х + хь = 0 ненулевые
решения, определенные при — оо < t < оо?
176.	Имеются ли у уравнения х = 4х — 4а;3 не-
ограниченные решения?
177.	Перейти от уравнения х + ах + х — х3 = О
к автономной системе двух уравнений. Для этой
системы
а)	найти особые точки;
б)	указать значения а, при которых все эти точки
неустойчивы;
в)	существует ли значение а, при котором ровно
две особые точки устойчивы?
178.	Для уравнения х + 4а; — 6х2 = О
а)	найти уравнение у = ip(x) траектории, прохо-
дящей через точку (1,0);
б)	нарисовать эту траекторию, учитывая значение
предела lim ;
х—>оо х
в)	найти решение данного уравнения с начальны-
ми условиями а;(0) = 1, ±(0) = 0.
179.	Для уравнения х = —и'(х), где и(х) = — х4 +
+х2 — 1,
а)	дать чертеж траекторий на фазовой плоскости;
б)	найти особые точки и исследовать их на устой-
чивость;
в)	найти наклоны сепаратрис и периоды малых
колебаний;
г)	добавить +ах в левую часть уравнения и для
а > 0 исследовать типы особых точек полученного
уравнения.
180.	Для уравнения х — 2х — 2х3 провести такое
же исследование, как в предыдущей задаче.
175
181.	Для уравнения х + х = х2
а)	найти и исследовать особые точки на фазовой
плоскости;
б)	найти решение x(t), убывающее и стремящееся
к 1 при t -> +оо, а также его траекторию на фазовой
плоскости;
в)	выяснить, при каких а решение с начальными
условиями ж(0) = 0, ж(0) = а периодическое;
г)	указать на фазовой плоскости область, запол-
ненную замкнутыми траекториями;
д)	устойчиво ли решение с начальными условия-
ми х(0) = 0, ж(0) = --U?
V 3
В задачах 182 и 183
а)	дать чертеж траекторий на фазовой плоскости;
б)	найти особые точки и исследовать их на устой-
чивость;
в)	выяснить, определены ли все решения при
—оо < t < 00.
182. / Х ~ \ х2’
[У = У 
Г --- о» _
183. \	3 ’
[У = -у •
184*. Для системы
х = у — х2 у — у3. у = х* + х3 у2 — х3
а)	найти все особые точки;
б)	линеаризовать систему в каждой из точек
(О, 0), (1, 0), (J,. J,);
в)	исследовать устойчивость этих линеаризован-
ных систем;
г)	исследовать на устойчивость те же три особые
точки для исходной системы;
д)	дать чертеж траекторий на фазовой плоскости;
е)	выяснить, имеет ли данная система неограни-
ченные решения;
176
ж)	описать множество точек, через которые про-
ходят периодические решения.
§ 26. ДИФФЕРЕНЦИРОВАНИЕ РЕШЕНИЯ
ПО ПАРАМЕТРУ
И ПО НАЧАЛЬНЫМ УСЛОВИЯМ
1. Дифференцирование по параметру
185.	Сформулировать теорему о дифференцируе-
мости решения системы дифференциальных уравне-
ний по параметру. Написать систему дифференци-
альных уравнений в вариациях.
В задачах 186—194 найти производную от ре-
шения данного дифференциального уравнения (или
системы) по параметру /1 при // = 0.
186.	у' = fix + (ж > 0), у(1) = 1-2/1.
187.	у' — + уьхе~у (х > 0), у(1) = 1 + 2/1.
188.	у' = у — х + уьхе2у, у(1) = 2 — /1.
189.	у1 = ух + sin у, у(0) = 2/1.
190.	х = х sin ж + sin(a;2), а;(0) = /1, ж(0) =/1.
191.	х = х + sin(±2), х(0) = /1, х(0) = /12.
192.	х + х = 2/i sint + /1а;2, ят(О) = 0, i(0) = 0.
193.	х — 2х = /itx, x(G) = 4, х(0) = /i2 + 3/i.
194.	х = у, у = х + 3/i?/2, х(0) = 2 — 4/1, ?/(0) = 0.
177
2.	Дифференцирование
по начальным условиям
195.	Сформулировать теорему о дифференциру-
емости решения системы дифференциальных урав-
нений по начальным условиям. Написать систему
уравнений в вариациях и начальные условия для
нее.
196.	Доказать, что в случае у е R1 производная
по уо от решения задачи у' = f(x, у), у(х0) - у0
всегда положительна (предполагается f 6 С1).
В задачах 197—199 найти производную от ре-
шения по у о при у о = 0.
Указание. При уо = 0 каждая из этих задач имеет нулевое
решение.
197.	у' = 2xy + siny, у(1) = у0.
198.	у' = у3 sin а; + у cos ж, у(0) = уо-
С •	2
199-{^-^2ХУ -(°)=°5 2/(°)=2/о-
200*. х + sin# = 0, ж(0) = а, ж(0) = (3.
Найти при а = (3 = 0.
3.	Разложение решения по степеням параметра
В задачах 201 и 202 найти разложение решения
о
по степеням параметра у, до у включительно.
201.	у' = 5цх + ± (О 1), у(1) = 1-/2.
^У
202.	х = 2х — 2ж3, ж(0) = 1, ж(0) = /1.
178
§ 27.	УРАВНЕНИЯ С ЧАСТНЫМИ
ПРОИЗВОДНЫМИ ПЕРВОГО ПОРЯДКА
1.	Теоретические вопросы
203.	Написать общий вид квазилинейного урав-
нения с частными производными первого порядка.
Что называется характеристикой этого уравнения?
204.	Сформулировать и доказать утверждение о
связи решения уравнения с его характеристиками.
205.	Как можно использовать первые интегра-
лы некоторой вспомогательной системы дифферен-
циальных уравнений для получения решения дан-
ного уравнения с частными производными?
206.	Сформулировать постановку задачи Коши
для квазилинейного уравнения с частными произ-
водными и теорему существования ее решения.
207.	Сформулировать и доказать теорему о су-
ществовании решения задачи Коши для квазилиней-
ного уравнения с частными производными первого
порядка.
2. Задачи
208.	Найти общее решение уравнения
z^+xz^ = y.
дх ду &
Решить следующие задачи Коши (209—215).
209.	ху^ +xz^j = yz, z = 1 + у2 при х = 1.
210.	+ (z — х2)	= 2х, z = х2 +х при у = 2х2.
211,	+ xzWj = yz’ z = ~У2 при а: = 0-
212.	xz^+yz^ =х3 + у, z = 4у3 при х = Зу2.
179
213.	y2^ + xy^ =x3z, z = e«2?2 при x = 2y.
214.	x^ +z<~ = z + 2x2, z = x при у = | - x2.
215.	x^+y^ = x + y + z, z=x + y приу = х + 1.
Решить следующие задачи Коши (216—218) в
тех случаях, когда решение существует.
216.	+ 2^- = 5, z — 0 при у = кх.
дх ду 1	г &
217.	^+3^ = 2, а)г = у2 при х = 1;
б) z — 2х при у = За;.
218.	2	= 2, z = 2ау при х = (а2 + а - 2)у.
219.	Имеют ли решения в окрестности точки (1,0)
следующие задачи Коши:
а)	~	= °’ z = 2у при х = 1;
б)	~	= °’ z = 2у при х = 1 + у?
220*. Имеют ли решения в окрестности точки
(1,1) следующие задачи Коши для уравнения
(х3 - Зху2) + (Зж2у - у3)	= 0
a)	z — sin?/ при х2 + у2 = 2;
б)	z = sin?/ при х = 1?
221. Какому условию должна удовлетворять функ-
ция ip(x) 6 С1 для того, чтобы задача Коши
yB-a:t^=0’ z = (p(x>) при у = 0, -ОО < X <00,
имела решение на всей плоскости х, у?
180
ОТВЕТЫ
15. /(ж, 2/)=0; /'<0 (шах), /^>0 (min). 16. а) ?/=ж2+2ж;
б) ж=2сЬ?/; в) ж?у3=—(1—ж2)2;у=0; г) /'+/-/'=0. 17. у— еху>/у,
18. ?/=3?/2/3. 19. ху’=^у. 20. ?/2+?/,2=1. 21. х2у'—ху=уу'.
22. 2хуу’— ?у2=2ж3. 23. 2/,3=42/(ж2/л — 2?/). 24. у'= cos	— ♦
25. ж(ж-2)?/,,-(ж2-2)?/,+2(ж-1)?/=0. 26. (уу"+у,2)2=-уЗу".
27. у"у2(\пу—1)=у,2(ху' — у). 28. х^уш— Зх2у"-\-6ху' —6?/=0.
29. ynfyf=3yf,‘2. 30. (у-2хУ(у,2+1)=(2у'+1)2. 31. ху,2=у(2у'~
-1). 32. (ху'-у)2=2ху(у'2+1). 33. х2у"—2ху'+2у=0. 34. (у"у+
+?/,2+1)2=(?/,2+1)3. 35. yy'+zz'=0, y2+2xzz'=x2z'2 36. ж2+
+y2=z2—2z(y—xy'); x+yyf=zzf-zf(y-xyf). 37. 4yy'=-x.
38. y'=-2y. 39. (x2+y)y'=-x. 40. (x+y)y'=y-x; (x-y)y' =x+y.
41. (ж yV^)y'—y ± ж\/3. 42. (Зж ЯР уу/3>)у,=У ± Зж\/3. 43. (2ж^р
T?/v/3)?/,=?/ ± 2ж\/3. 44. rf sin 0=г2. 45. r'=^rctg0. 46. r' =
=r ctg(0 ± 45°). 47. (x+2y)y'=—Зж—у; (3x+2y)yf =y—x. 48. y'x
x[2xy ± (ж2— у2)]—у2 — ж2 ± 2ху. 49. ж(1+?/,2)=—2уу’. 50. уу,3+
+ху,2=—1. 51. у=С(х+1)е~х; ж=—1. 52. In |ж|=С*+	+ ж=0.
53. ?/(1п |ж2 —1|+С)=1, ?/=0; 2/[1п(1—ж2)+1]=1. 54. т/=2+Ссо8ж;
у=2—Зсозж. 55. у=(х—С)3; у=0; у=(х—2)3; у=0. 56. у(1 — Сх)=
=1; ?/=0; ?/(1+ж)=1. 57. ?/2-2=Се1/^. 58. (Се"*2-1)?/=2; у=0.
59. e-s=l+Ce*. 60. z=-IgfC-lO*). 61. x2+t2-2t=C.
62. ctg У-^-=х+С\ у—х=2тгк, fc=0, ±1, ... 63. 2ж+?/—l=Cex.
64. x+2y-\-2=Cey; ж+2?/+2=0. 65. г/4ж+2?/—1—21п(у/4ж+2?/—1 +
+2)=ж+С. 66. ?/= arctg^l —+2тг. 67. у=2. 68. а) 2у2+х2=С;
б) 7/2+2ж=С; в) у2=Сех2~^у2. 71. (С ± х)у=2а2. 72. Ь\пу—у=
181
= ±x+C, 0<y<b. 73. aln(a± \/ (i2—y2)^ y/a2—y2=x+C. 74. у=
=Сх2. 75. у=Сх2; у2=Сх. 76. r(l ±cos(/?)=C. 77. Количество
азота (в литрах) ж(£)=20—4е-*/200; ж(£)=19,8 при £=200In 20 «
« 600 сек=10 мин. 78. Количество соли я(£)=1Ое-*/20; ж(60)=
=10е-3 « 0,5 кг. 79. Объем СО2 (в л?) ж(£)=О,О8+О,22е“*/10;
ж(£)=0,1 при £=10 In 11 « 24 мин. 80. Температура тела ж(£)=
=20+80• 2“*/10; ж(£)=25 при £=40 мин. 81. Разность температур
воды и предмета ж(£)=55-(3/5)г; ж(£)=1 при £= In 55/(In 5— In 3)«
о or* гтп	/,ч	। b—a (.	1—е-/е/ А
« % мин. 82. Температура металла ж(£)=а+-^д- I £----------- I ;
ж(60)=6—1^(1-е 60/г). 83. Скорость (в м/сек) v(t)=
=(2/3/*/4)-1; 1?(£)=0,01 при £=4 Q 5+1) ~ 50 сек; путь s=
= lnl~5^15 м‘ 84* Оставшееся количество вещества ж(£)=ж(0)х
х2-*/30; ж(£)=0,01ж(0) при £=60/1g2 « 200 дней. 85. Остав-
шееся количество радия ж(£) = ж(0) • (1—0,00044)*; ж(£) = ^ж(0)
при £= In 0,5/ 1п(1 —0,00044) « 1600 лет. 86. Количество урана
®(<)=®(0)e-“‘ a=ln2/(4,5-109); x(t)=100, x(0)=100+14-|j| =
= 116,2; t=4,5-109-	970-10® лет. 87. Количество света,
прошедшего через слой в х см, y(x)=y(Q) - 2—*/35; ?/(200)=?/(0)х
х2-40/7 « 0,02 - ?/(0); поглощается 100%—2% = 98%. 88. Ско-
рость v(£)=50th^, путь (в метрах) s(£)=2501nch	s(£)=1000
при ch^=e4, £ « 5(4+1п2) « 23 сек. 89. Скорость v(£)=^j^x
xtgx/fcifC-t), д=10, fc=0,012, C=-^arctgy|v(0) « 1,75;
г>(£)=0 при £=С^1,75 сек; наибольшая высота ^-=2^ 1п^г’2(0)+
+1) ^16,3 м (без сопротивления воздуха £=2сек, Д=20л<).
90. Скорость г>(£)= th y/kgt, путь s(£)=-^ Inch \/kgt; s(t)=
=Д=16,Зл< при £=—X= 1п(е/г/г + А/е2/г/г —1)	1,87 сек, f(£)=
__________ vкд
= yj(l—e~2kfl) 16,4 м/сек. 91. Высота уровня воды Д(£);
г2	о2
у/Н—\/h—Q,3y/2g^t', h(t)=O при £=^-i
сек=
182
=17,5мин. 92. (2Я—/1(4))3/2=0,457Гг2у/2^-^, Л(4)=0 при t=
=	« 1040 сек-93-	^=kt’ k=^T 0"?г);
Д(4)=О при i=5(2+x/2)«17 мин. 94. Н5/2—[/i(4)]5/2 = ^^—
Д(4)=О при 4=(4Я2/3d2)у/2Н/д 27 сек. 95. Объем воды в баке
в литрах x(t);	In “—q	~ л/#, 9=1,8, а=10-3/2; ж(4)=360
при 4=260 сек (для бака без отверстия в дне 4=200 сек).
к Рх2
96. Удлинение нижнего куска длины х равно у(х)=—, а
кР1
всего шнура — у(1)= —. 97. На высоте h км давление p(h)=
=e-o,i2h (кг/см2). 98. Сила натяжения каната на расстоя-
нии ip (в радианной мере) по дуге от начальной точки равна
f (</?)=f (О)е^/3; /(6тг)=10е27Г « 5000 кГ. 99. Количество остав-
шейся воды m(4)=mo—v(qi —9о) (1—е“«*) , к — коэффициент
пропорциональности. 100. После сгорания массы х топлива
скорость ракеты 1?(ж)=с1п	v(M—т)=сIn	101. х+у=
=Сх2; х=0. 102. ln(x2-hy2)=C—2 arctg(?//a?). 103. х(у—х)=Су;
у=0. 104. х= ± ?/л/1п Сх; у=0. 105. у=Съу/х. 106. у2— х2=Су;
у=0. 107. sin^=Ca?. 108. у=—х Inin Сх. 109. In Х~^У =Сх.
110. lnCx=ctgQln|);y=a:e2’rA:, fc=0, ±1, ±2,... 111. 2^/ху=
=xlnCx; у=0; ж=0. 112. arcsin ^ = lnCx-sgnx; у=±х. 113. (у—
—2х)3=С(у—х—I)2; з/=а:+1. 114. 2х+у—1=Се2у~х. 115. (у—х+
+2)2+2х=С. 116. (у-х+5)5(х+2у-2)=С. 117. (у+2)2=С(х+у-
-1);2/=1-ж. 118. y+2=Ce~2&Icts^. 119. 1п|±|=1+^.
120. sin ^^=С(ж+1). 121. ж2=(ж2 — у) In Сх; у=х2. 122. х=
=—у2 In Сх; у=0. 123. х2у4 InСж2=1; у=0; х=0. 124. у2е~г/хУ =
=С; у=0; ж=0. 125. (2у/у-х) 1пС (2^-ж) =х; 2у/у=х. 126. 1-
—ху=Сх3(2+ху); ху = —2. 127. 2д/(1/ж?/2) —1=— In Сх; у=0;
ху2=1.
128.
arcsin т^от = In СXs;
|ж3|
|ж3|=?/2. 129. х2у In Су=\;
у=0. 130. а) у2=С(х+у); у=-х; б) (?/+ж)2(?/-2ж)4=С(?/-ж)3;
у=х. 131. у=С(х2+у2). 132. х2+у2=-Сх. 133. При д —^=1.
136. ?/=Сж2+ж4. 137. ?/=(2ж+1)(С+ In 12ж+11)+1. 138. у= sin ж+
183
+Ссозж. 139. ?у=еж (In |ж|+С*); ж=0. 140. xy=C— In |ж|. 141. y=
=a?(C+sina?). 142. ?y=Gex’2—ж2 —1. 143. ?/=dn2 x— In ж. 144. xy=
=(ж3+С)е“ж. 145. x=y2+Cy; y=0.146. ж=е^+Се“^. 147. ж=(С-
— cosy) sin?/. 148. ж=21п?/—?/+l+C?/2. 149. x=Cy3+y2; y=0.
150. (y—l)2x=y— In Cy; ?/=0; y=l. 151. y(ex+Ce2x)=l; y=0.
152. ?/(ж+1)(1п |ж+1|+С)=1; y=0. 153. ?/-3=Ccos3 a?-3sina?x
x cos2 x; y=0. 154. y3=Cx3 — Зж2. 155. y2=Cx2—2ж; ж=0. 156. y=
=ж4 In2 Сж; y=0. 157. ?у-2=ж4(2ex’+G); y=0. 158. y2=x2 — 1+
+С^/|ж2—1J. 159. ж2(С— cosy)=y; ?/=0. 160. xy(C— In2 y)=l.
161. x2=Ce2y+2y. 162. ?/2=С(ж+1)2-2(ж+1). 163. е~У=Сх2+х.
164. cos ?/=(ж2 — 1) In С*(ж2 — 1). 165. y=2ex — 1. 166. y=—2ex.
2	4	2	1	1	1
16r-y=l+c^^=l168-y=x+c^4i'y=x-169-y=x+
r	4	1
+s+u; y=x-170- y=x+2+c^~v y=x+2-171- y=eX~x+C'
y=ex. 172. 3x=Cy/\y\—y2; y=0. 173. xy=Cx3+2a2. 174. xy=a2 +
+Cy2. 175. Через 20 мищ 3,68 кГ. 176. Через 62 дня. 177. у=
=У1+С(у2—у1)- 178. ?/=tgж—зесж. 179. Ь/а. 180. Ь/а.
181. x(t)= f es-t/(s)ds= / ez f(z+t)dz. 182. y(x)=x f ex2~t2dt—>
— oo	— oo	+oo
oo
—> — i при ж —> +oo. 183. ?/(ж)= J e_s-sins'cos(s+2a:) зт(ж+в) ds.
2	о
186. 3x2y—y3=C. 187. ж2— Зж37/2+7/4=С. 188. xe~y —y2=C.
189. 4y 1пж+т/4=С. 190. ж+^- + ^-=С*. 191. ж2+|(ж2—т/)3/2=С.
192. ж—у2 cos2 х=С. 193. ж3+ж3 In?/—у2=С. 194. ж2+1=2(С—
—2ж)зт?/. 195. 2ж+1п(ж2+?/2)=С. 196. ж+arctg 197. ж?/+
+С=у/1+?/2. 198. 2ж3?/3—Зж2=С. 199. у2=х2(С—2у); ж=0.
200. (ж2—С)у=2х. 201. ж2+1п?/=С*ж3; ж=0. 202. уsinxy=C.
'Г2
203. -2~+ж?/+In |?/|=С; ?/=0. 204. — ж+1=ж?/ (arctg ?/+С); ж=0;
?у=0. 205. ж+21п |ж| + |?/2 —^=С; ж=0. 206. sin ^=Се~х2.
207. In \у\-уе~х=С-, у=0. 208.1п(^+1) =2у+С; у=0. 209. х2х
ху\пСху=—1; ж=0; ?/=0. 210. ж2+?/2=?/+С'ж: ж=0. 211. ж2?/+
+ In \х/у\=С] ж=0; ?/=0. 212. 2ж?/2+(1/ж?/)=С'; ж=0; ?/=0.
213. 1П |г±2/1 +у(1+^1=с- у=о- у=-х. 214. sin2 у=Сх—ж2;
ж=0.	215.	?/=С1пж2?/.	216.	sin?/=—(ж2+1) InС(ж2+1).
184
217. ху(С—ж2 — у2)=—1; ж=0; у=0. 218. у‘2=Сх‘2ех2у2. 219. хх
х д/1+(?/2/ж2)+ In (у/х+у/1+(?/2/ж2)^ =С; х=0. 220. ж3—4?/2=
=Cytyxy', ж=0; у=0. 221. а) ?/о=0,?/1=ж2/2, ?/2=(ж2/2)-(ж5/20).
б) ?/о = 1, ?/1 =ж3, ?/2=1+ж3—ж+(ж7 —1)/7. в) 2/о=1, yi=l+2x, у2=
= ^(е2ж + 1)+ж+ж2. г) 2/о=2тг, ?/1=7г+ж, ?/2=27г+ж+жсо8ж— sin ж.
222. а) 2/0=1, го=0; 2/1 =ж2, ^1=ж-1; ?/2=ж2+(ж-1)2/2, г2=(ж3-
—1)/3. б) ж0=1,2/0=2; Ж1=1+2*, 2/1=2+*; ж2=1+2*+(*2/2), 2/2=2+
+*+2*2+(4/3)*3. в) 2/0=1, 2/1=1, 2/2=1+ж2. г) ж0=2, Ж1=3-*,
ж2=5—4*+*3 223. а) -0,5^ж^0,5. б) 0,87^ж^1,13. в) 0,8^*^ 1,2.
г) -0,1^0,1. 224. 2/3=^-^ + ^-^, |г/—т/з|<0,00003.
225. а) Вся плоскость, б) ?/#2ж. в) ж#2, у>0. г) ?/#^+7гА;, к=
=0, ±1, ±2, ... д) ж>0, у^х. е) ж#0, |2/|>|ж|. 226. При 0<а<1
в точках оси Ох. 228. а) жо и у'о любые, у0^^-\-ттк, &=0, ±1,
±2, ... б) жо#-1, 2/о>0, 2/о любое, в) жо#2/о, ^о2/о>0, 2/о#0,
2/q любое, г) жо#2/о> 3/о#0, Уо любое, д) to и уо любые, жо#0.
е) *о>-1, ^о#0, 2/о#*о- 229. а) Нет. б) Да. 230. а) Нет. б) Нет.
в) Да. 231. В случае п=1 нет решений, при п=2 одно ре-
шение, при п=3 бесконечно много решений. 232. В случае
п=1 нет решений, если tga#/^o, 2/о), и одно решение, если
tgo=/^o, 2/о); в случае п=2 одно решение, а при п 3 бес-
конечно много. 233. п^5. 234. п^4. 236. а) 3. б) 2. в) 4. г) 4.
д) 3. е) 1. 237. а) 0^а^1. б) в)	г) -l^a^O.
241. у=Се±х. 242. т/2=(ж+С*)3; у=0. 243. т/+ж=(ж+С*)3; у=—х.
244. (ж+С)2+?/2 = 1; у= ± 1. 245. т/(ж+С)2=1; у=0. 246. т/[1+
+(ж-С)2]=1; у=0; у=1. 247. (?/-ж)2=2С(ж+?/)-С2; у=0.
248. (ж—1)4/3+2/4/3=С. 249. 47/=(ж+С)2; у=Сох. 250. ?/2(1—у)=
=(ж+С*)2; у=1. 251. у=Сех] у=Се~х+х—1. 252. х2у=С; у=Сх.
253. ж2+С2=2С?/; у= ± ж. 254. (ж+С)2=4С?/; ?/=0; у=х.
255. In |1 ± 2^/2?/—ж| =2 (ж+С ± \/2?/—ж); 8?/=4ж+1. 256. (ж+
+2)4/3+С=4е“^/3. 257. ?/=2ж2+С; ?/=-ж2+С. 258. ?/=Сж-3±
±2у/ж/7. 259. In Су=х ± 2еж/2; ?/=0. 260. In Су=х ± sin ж; ?/=0.
261. arctgu+| 1п|(и-1)/(и+1)|=±ж+С, где и= у/1-(1/у2); ?/=0;
у= ± 1. 262. ж2+(С?/+1)2=1; у=0. 263. (Сж+1)2=1-?/2; у= ± 1.
264. 2(ж-С)2+2?/2=С2; у=±х. 265. ?/=Се±а:-ж2. 266. у2=С2х-
185
-С] 4жр2=—1. 267. ж=р3+р, 4р=Зр4+2р2+С. 268. х=-^~,
2/=j^|-j--ln |р2- 1|+С. 269. ж=рд/р2+1, Зр=(2р2-1)>/р2 + 1+С.
270. ж=1пр+(1/р), у=р— Inр+С*. 271. ж=Зр2+2р+С, р=2р3+р2;
р=0. 272. ж=2 arctgp+G, р=1п(1+р2); р=0. 273. ж=1п|р|±
±3 In I	|±Зу^+Т+С, ?/=р±(р+1)3/2; у=±1. 274. х=ер+
z | vP+*-+*-1
+С, у=(р—1)ер; у=—1. 275. ж=± ^2^/р2 — 1 + arcsin	+С, у=
=±р\/р2-1; у=0. 276. х=± ^1п 1| + Зд/I-P ) +G У=±
ip^/l—р; р=0. 277. х= ± 2у/Т+р2—ln(y/p2+T ± 1)+С, У=~Р±
±Px/p2+i; У=в- 278. 4р=С2—2(ж—С)2; 2у=х2. 279. ж=-^+С,
5р=С2 —5^-; ж2=4р. 280. ±жр\/2 In Ср = 1, у =	л/21п Ср—
~ /о/	281‘ Рж2/=2/2+Р3) 2/2(2р+С)=р4; р=0. 282. р2 =
х/2 ш Ср /
=2Сх—С In С; 2ж=1+21п|р|. 283. Сж=1пСр; у=ех. 284. хр2 =
=С*д/|р| — 1, р=жр—ж2р3; у=0. 285. 2р2х=С—С2р2, ру=С; З2ж3 =
=-27р4; р=0. 286. у2=2С3х+С2; 27ж2р2=1. 287. у=Сх-С2;
4у=х2. 288. жу^=1пр+С, у=у/р(4— \пр—С); р=0. 289. ж=3р2 +
+Ср~2, р=2р3+2Ср“1; р=0. 290. у=Сх-С-2. 291. С3=3(Сж-
—у); 9р2=4ж3. 292. х=С(р—1)-2+2р+1, р=Ср2(р—1)-2+р2;
р=0; у=х—2. 293. у=Сх—\пС; р=1пж+1. 294. у= ± 2х/Сж+С;
у=—х. 295. 2С2(у—Сх)=1; 8р3=27ж2. 296. жр2=р+С, р=2+
+2Ср-1 —1пр. 297. а) 4р=ж4; б) р=0, у=—4ж; в) р=0, 27р=4ж3;
г) р=4ж. 298. жр=±а2 299. ж2+р2=1. 300. х=р (р2+2)/(\/р2+1)3
2/=Р2/(х/р2+!)3 и ж=р/(д/р2+1)35 р=(2р2+1)/(д/р2+1)3 301. у=
=х(Се~х — 1). 302. (Сх+1)у=Сх—1; у=1. 303. у(х2—С)=х; р=0.
304. ж(С—у)=С2; х=4у. 305. р(ж+С)=ж+1; р=0. 306. ж=Ср+р3;
р=0. 307. у=С; у=С±ех. 308. у\пСх=—х; р=0. 309. у2=С(х2 —
-1); х= ± 1. 310. 2р=2С(ж-1)+С2; 2у=-(х-1)2. 311. х=Су+
+ 1п2р. 312. р=Сж2е-3/ж. 313. (ж—С)2+р2=С; 4(р2— ж)=1.
314. 4ж2р=(ж+2С)2; р=0. 315. х=СеУ +р2+2р+2. 316. Зр=ЗСх
х(ж—2)+С3; 9р2=4(2—ж)3. 317. у2=С(ху—1); жр=1. 318. 4(ж—
—С)3=27(?у—С)2; р=ж—1. 319. ж+р= tg(p—С). 320. ж3р2+7ж=С.
321. у(ху-1)=Сх. 322. -е~У = In С(ж-2). 323. ж=р2(С-2 In \у|);
р=0. 324. Зху=С ± 4ж3/2. 325. у2{С^2 +1)=1; р=0. 326. у2 =
186
=2#lnC?y; y=0. 327. ln(#2+?y2)+arctg(?y/#)=C. 328. (#—l)2p=
=x- In |#|+C. 329. C2#2+2p2=2C; 2#2p2=l. 330. y(Cy/\x2-l\-
—2)=1; p=0. 331.p2(Ce2a+#+0,5)=l; p=0. 332. p2-l=C(#+l)4x
хе-4ж(р2+1); #=-l. 333. psin#-^- + ^-=C. 334. #=3p2+p-1,
p=2p3—In |p|+C. 335. 3p2=2sin#+Csin-2#. 336. x(ey +xy)=C.
337. x(p—1)2= In Cp—p, y=xp2+p-, p=0; y=x+l. 338. (#+l)p=
=#2+#lnC#. 339. y2 + \/x4+y4=C. 340. px=Cy/p—l, y=\np—
—Cy/p+1. 341. p=#tglnC#; #=0. 342. р2/3=Се2ж+(#/3)+(1/6);
y=0. 343. x=CeSiny —2(1+ sin?/). 344. Cy=C2ex+l; y=±2ex/2.
345. y2~(#2+С)е2ж. 346. y=Cx-tyCs-l; p3=(#3/2 ± I)2.
347. x(y2 —l)2=p3 —Зр+C; y= ± 1. 348. y/y—x—y/x=C; y=x.
349. Xy/y= sin#+C; p=0. 350. #=4p3—In Cp, y=3p4 — p; y=0.
351. p2+2#2 In Cp=0; y=0. 352. 4#+p—3=2 tg(2#+C). 353. xyx
x cos#—y2=C. 354. 4Cxy=C2x4 — 1. 355. #p(ln2 #+C)=l.
356. 2y/y—x2=x In Cx; y=x2. 357. (y2/2) — (1/#)—xy=C; #=0.
358. x=Cy2 — y2 (y+l)e~y; y=0. 359. p(lnp— ln#-l)=C. 360. #=
=2p—Inp, y=p2—p+C. 361. 2#3— #2p2+p3+#=C. 362. (p—4#+2)4x
x(2p+2#-l)=C. 363. y3=(C—#3)sin3 #. 364. p2#=psinp+cosp+
+C, pp=psinp+2cosp+2C; p=0. 365. x2y2 — l=#plnCy2; y=0.
366. 7/=Ccos#+sin#. 367. |#|=ln ^ + ^1+^-^ +C; #=0.
368. (?/-#)2=2C(#+?/)-C2; t/2/3-#2/3=C; y=0. 369. 27(?/-2#)2=
=(C—2#)3; y=2x. 370. sin(?//#)=— InCx. 371. #2 (>/l+#4?/2 +
+#27/)=С. 372. Зх/р=#2-1+С У|#2-1|; y=0. 373. x=^-p-
-|, y=C Q-l) y=x+2- y=0. 374. (2#+32/-7)3=Сеж+2^
375. (#2+p+ In Cy)y=x; y=0. 376. #=2д/р2+1— ln(l+д/р2+1)+
+ 1пС*р, р=рд/р2+1; ?/=0. 377. т/2=С1п2 #+21n#. 378. #=Cuew,
4y=C2e2u (2u2+2u+1); x2=2y. 379. #p2 In C#?/=l; #=0; y=0.
380. #2 sin2 y=2 sin3 y+C. 381. 1—xy=(Cx— I)2; #?/=l; ?/=0.
382. #е^=еж+С. 383. sin(?/-2#)-2cos(?/-2#)=Cea:+2^. 384. y=
=(2#+C)\/#2+l-#2-Cx-2. 385. (?/+#2)2(2?/—#2)=C*. 386. (#-
— l)2=p2(2#—21n C#); p=0. 387. #=р[1п(1+д/р2+1)— In Cp], 2y=
=#p—д/р2+1; 2p=—1. 388. (p+3#+7)(p—x—1)3=C. 389. sinp=
=Се-ж+#-1. 390. p=C2(#-C)2; 16p=#4 391. p2=#-(#+l)x
xlnC(#+l). 392. e^=#2ln Cx. 393. (y—2xy/y—x2)(2y/y—x2-\-x)=
187
=С. 394. ху2 = In ж2 — In Су, ж=0; г/=0. 395. ж(?/2+ж2)3 = |?/5 +
+ ^ж21/3+2ж41/+С'ж5; ж=0. 396. (it—1) In CxQ(u—l)5(it+2)4=3, где
it3=(i/2/ж2)—2; ?/2=Зж2. 397. х/^=(ж2 —1)(2In |ж2 —1|+С); ?у=0.
398. ж2 — (ж—1) ln(i/+l)—у=С. 399. tgl/=ж2+C'ж; з/=(2АгЧ-1)тг/2,
/с=0, ±1, ±2, ... 400. 1/2=Сж2+С2. 401. ж3=Се^-1/-2. 402. т/+
+1=ж1пС(1/+1); у=-1. 403. 1/2=2С2(ж-С); 8ж3=27?/2. 404. ж6 =
=у3(С—?/ In 2/Н-2/); i/=0. 405. lnC(it—i?)3^it2+iw+^-^=2arctg(l+
+2it/v), где it3=i/, и2=ж; 1/2=ж3. 406. (i/—1)2=ж2+Сж. 407. (ж2 +
+т/2)(Сж+1)=ж. 408. Зж+i/3— 1= tg(Зж^-C'). 409. (С—ж2)\/?/2+1 =
=2ж. 410. (ж2+т/2+1)2=4ж2+С. 411. ху—х=у(у—ж) ln|Ci//(i/—ж)|;
ж=0; ?/=0; у=х. 412. у= ± ж сЬ(ж+С); у= ± ж. 413. y/i/2+l =
=х(Сеж-1). 414. (у-х) In С=2; у=х. 415. (Ce*2+2i:2+2)x
х cosp=l. 416. (у2— Сх2+1)2=4(1—С)у2; у=±х. 417. у2+ху—1=
=Се*2/2. 418. 6х3у4+2х3у3+Зх2у4=С. 419. х+^+р2 —2у+2=
=Се~У; х=0. 420. е»(С2х2+1)=2С; x2=e~2v. 421. Cix-C12p=
= In |Ciх+11+C2; 2y=x2+C; y=C. 422.9C2(p-C2)2=4(Cix+l)3;
y=±x+C. 423. Cip2—l=(Cix+C2)2. 424. p3=Ci(x+C2)2; y=C.
425. y=Citg(Cix+C2); ln|	| = 2Cix+C2; y=(C-x)=l; y=C.
426. Cip=sin(Cix+C2); Ciy= ±sh(Cix+C2); y=C±x. 427. y=
=C1(x-e~x)+C2. 428. p=C3-(x+Ci) In C2(x+Ci); y=C1X+C2.
429. p+Ci In |p|=x+C2; y=C. 430. 2y=C± cos2x+(1+2Ci)x2 +
+C2x+Cz- 431. ?/=Ci[l ±ch(x+C2)]; y=Ce±x. 432. x=Cip+3p2,
P=^Ps + |Cip4+C12^+C2; p=C. 433. у=Сх ^-C2x+C2; y=
=(x3/12)+C. 434. e»+Ci=(x+C2)2. 435. y=Ci(x+2')e~x+C2x+
+C3. 436. y= ± ch(x+Ci)+C2. 437.	sin2(Cix+C2)=2C2; e» x
x sh2(Cix+C2)=2C12; e?'(x+C)2=2. 438. y=Ci ~-C3^-+C2x+
+Сз; y=j^x3V3x+Cix+C2. 439. 3Cip=(x-Ci)3+C2; y=C; y=
=C-2x2. 440. ln|p2+Ci±v/^4+2C'i^2+1|=2a;+C2; 2/=±l- 441. x=
=3C*ip2+In C*2P, т/=2С1р3+р; y=C. 442. x=Ciqp— 2p—2, y=Ci (p—
-l)eP-p2+C2. 443. 12(С!1/-ж)=С2(ж+С2)3+Сз. 444. т/=ж2+С1 +
+С2\/ж2 —1—In | ж+\/ж2 —11); у=ж2+ С1 + С2(хVT— ж2 + arcsiп ж).
445. lni/=Citg(C^+C2); In |(In 1/-C1 )/(ln 1/+C1)|=2Ciж+С2;
(С—ж) In2/=l; y=C. 446. x=u— In |l+it|+C2, где it= ± x/l+4C*ii/;
188
у=С; у=Се~х. 447. С22/=(С2ж2+1) arctg С1Ж-С1Ж+С2; 2у=
=кттх2+С, &=0, ±1, ±2, ... 448. х= ln|p|+2Cip—С*2, y=p+Cip2+
+С3; 2/=Cia?+C2.449. C2?/+l=±ch(C'ia?+C'2); С2у— l=sin(Cix+
+С2); 2т/=(ж+С)2; ?/=0. 450. ^=С2—ln|cos	451. 6?/=
=ж3 1п|ж|+С1Ж3+С'2Ж2+С'зж+С'4. 452. у=х J^-^di+cosa?+Cia?+
о 1
+С2. 453. ^CiL/e^dt-iCe^-ljI+^rr+Cs. 454. ?/=^-х
L о 2 J	2
х J ydi—^у^еж+С1Ж2 In |ж|+С2Ж2+Сзж+С4. 455. С2У2 —Ci =
=С2(х+С3)2; у=С. 456. С17/=1п|С1ж+С2|+Сз; 2/=C^+C2.
457. Cry— l=C2eCia:; у=С—х; у=0. 458. y=Cix2+C2x+C3; у=
= ± 7,С1ж+С2+Сзж+С4. 459. у2=х2+С1х+С2- 460. у=ех2/2х
х (Ci /е-ж2/24ж+С2) -1. 461. y=Ci tg(Ci 1пС2ж); у-Сг =
=C2(2/+Ci)|®|2C'1;	462. 2In |2=^| =С1Х2+С2-, у=
=4Citg(Cio:2+C2); у(С-х2)=4-, у=С. 463. у=С2еСх2. 464. С\х+
+4х5/2=1пС2у; у=0. 465. y=C2(x+Vx'i+l')C1- 466. y2=Cix3+
+С2. 467. у=С2хе~С1/х. 468. j/=C,2|x|c'i-(1/2)lnИ. 469. y=
=C2 ЫстГ/С'1; У=С' У=^~1/х- 470.	(я-^) к+
+Ci|ci; у=С. 471. т/=С2ж(1п Ci ж)2; у=Сх. 472.1п|?/|= 1п|ж2—2ж+
+C1I + L _п22^ _1+С2-> У=а 473. 4С1у2=4х+х(С1 In С2х)2.
уХ ly Tvl 1
474. у=—ж1п(С*2 In Cix); у=Сх. 475. ^=G2—31n | Ci |; у=Сх.
476. ж27/=С*1 tg(C*i InС*2ж), C2(x2y-\-Ci)\x\2C1 =х2у—Ci; х2ух
xln Сх=-1. 477. 4(Ci?/-l)=C2 1п2С2ж. 478. С2/=ж3/2(С2жс+2);
у—Сх2,!2\ у——2х3^2\пСх. 479. 2С2Х2у=(^С2Х—Ci)2 — 1; ж?/=±1.
480.	2С1С2у=С2\х\2+с^+\х\2-с^.	501.	(3-ж)?/5=8(ж+2).
502. ?/(ж+2)=-ж-6. 503. (1-1пж)2?/=ж2. 504. у=3th2 ^^-2.
505. Intg (f+ |) =2ж+2. 506. а) 4(С1^-1)=С2(ж+С2)2; б) ух
х y/(Ci/y)-l-\-Ci arccos y/y/Ci=C2±x. 507. у=С2-к In cos +
+Ci). 508. y=-^pX2-\-Cix-\-C2\ р — нагрузка на единицу дли-
ны горизонтальной проекции, Т — горизонтальная составля-
189
ющая силы натяжения нити. 509. ау= сЬ(аж+С1)+С2; a=q/T,
q — вес единицы длины нити, Т — см. ответ к задаче 508.
511.2/=С1еж+С2е-2а:. 512. ^Cie^C^e"3* 513. у=Сх+С2е2х
514. y=Cie2x +С2еж/2. 515. y=e2x(Ci со8ж+С*2 sin ж). 516. у=
=е-ж(С1 cos Зж+С*2 sin Зж). 517. y=Ci cos 2ж+С*2 sin 2ж. 518. у=
=С'1е2аЧ-е-ж(С'2 созжх/З+Сз зшж\/3). 519. у=С]ех+С2е~х+Сз х
х созж+С*4 sin ж. 520. y=ex(Ci со8ж+С'2Бшж)+е-а:(С'з собж+
+С*4 sin ж). 521.7/=еЖЛ//з(С1СО8 ж+С*2 8тж)+Сз cos 2ж + С*4 зт2ж+
_|_е-хл/3(^5 СО8Ж_|_(76 sin ж). 522. у=ех (Ci+C2x). 523. у=е~х/2х
х(С1+С2ж). 524. ?/=С1+С2ж+Сзж2+е3а:(С4+С5ж). 525. у=Сг +
+С2ех+С3е-х+С4е3х+С5е-3х. 526. y=(Ci+C2x) со8ж+(С3+
+С*4ж) sin ж. 527. ?/=еа:(С'1+С'2ж+С'зж2). 528. у=ъх (С\+С2х)+
+С3е-Ж. 529.2/=С1еж+С2е-ж+Сзе2а:+С4е-2а:. 530. т/=С1+(С2 +
+С*зж)cos2ж+(С*4+С*5ж)sin2ж. 531. y=ex(Ci+C2x)+Cze~2x.
532. У~С\ со8ж+С*2 зтж+Сз созжх/З+С^ зтж\/3.	533. у=
=С1е-ж+С2е3а:+(1/5)е4а:. 534. у=С\ со8ж+С*2 зтж+(2ж—2)еж.
535. г/=С1еж+С2е-а:+хеа:+а:2+2. 536. у=^-^ех + С1е~2х +
+С2ъх. 537. y=Ciex+C2 е2ж+0,18тж+0,3 cos ж. 538. ?у=С’1СО8ж+
+С2 sin ж—2ж cos ж. 539. у=С1ех+С2е4х— (2ж2—2ж+3)е2ж. 540. у=
=С'1еж+С'2е2ж+(0,1ж—0,12) cos ж—(О,3ж+О,34)зтж. 541. y=Ci х
хе-+С2е-^_2е-^_ (|+^)е-*. 542. у=(^-^+^ +
+Ciex+C2e~3x. 543. ?у=е2ж (Gicos 2ж+С*28т 2ж)+0,25е2ж+0,1х
За? । ^За?^
^)cosx+(c2 + ^Q sin®.
547. y=(Ci+C2x)e-2x+(^--^e2x 548. г/=С1+С2е5а,-0,2®3-
—0,12x2—0,048®+0,02(cos5®— sin 5®). 575. ?/=eI,(®ln|x|+Cix+
+C2). 576. у=(е-х+ё-2х)1п(ех+1')+С1ё-х+С2ё-2х. 577. y=(Ci+
+ ln | 8тж|) 8тж+(С*2— ж) cos Ж. 578. ?/=8т2ж1п | созж|— Ж COS 2ж+
+Ci sin 2ж+С*2 cos 2ж. 579. у=е~х ^(ж+1)5/2+С1+С2ж). 580. у=
=Cicosx+C2sinx-^^. 581. ?/=-^+С1еа’+С2е-Л 582. у=
=(7—Зж)еж-2. 583. ?/=2со8ж—5 8тж+2еж. 584. ?/=е2ж-1 —2еж +
+е—1. 585. у=е~х(х— sin ж). 586. у—2-\-е~х. 587. ?/=(ж—1)(е2ж —
—е-ж). 588. у=х—ж sin ж—2 cos ж. 589.7/=С1Ж2+С2Ж3 590. у=С\Х
хж3+С*2Ж-1. 591. y=x(Ci±C2 1п|ж|+Сз 1п2|ж|). 592. y=Ci+C2x
6 .	1	)
Sin ж— 37COS ж.
xcos 2ж+0,05зт 2ж. 544. y=Cie'5x+C2e
545. ?/=(С'1+С'2ж+ж3)еа:. 546. y=fci
190
х!п|ж|+Сзж3 593. y=x(Ci +С21п|ж|)+2ж3. 594. ?y=Gicos(21п|ж|) +
+C*2sin(2 In |ж|)+2ж. 595. y=Cix2+^ (с2 — | In ж— In2 xj. 596. у=
=a?2(Ci cosln|a?|+C*2 sin In |ж|+3). 597. г/=С1Ж3+С2Ж-2+ж3 1п|ж| —
—2ж2. 598. 2/=С1Т2+С2Ж-1+0,1 coslna?—0,3sinlna?. 599. у=(х—
-2)2(Ci+C2 In |«-2|)+ж-1,5. 600. 2/=Ci(®+|)+C2|a:+||3/2+
+С3р+111/2 601. у= (сг +С2х+ е-*+ . 602. y=^eix-
-^e~x+(^+Cix+C^ex. 603. y=Cie<-1+^x+[C2+(i-l)x]x
хе(1-г)ж_е(1+г)ж 6Q4. 2/=(2ж2+С1ж+С2)е-га:— егх. 605. y=Ci х
хе(Уз+г>+С2е(г-Уз)х+ (с^_ е~2гх ^2гх 606. у=О~ +
+ [с2-| 1п(-ж)+| 1п2(-ж)] х2. 607. у=(С1+С2х+х In |ж|)е-ж +
+ ех. 608. у= [ | + (Ci - cos 2ж+ (с2 + | In | cos х |) sin 2ж] х
хе-ж. 609. у=х2 In ^у-^-Ч-l-i 1пС2(ж+1). 610. y=x[Ci +
+(6*2+In 11пж|) 1пж]+611* ?/=Ci cosж+Сг sinж+
X	XX
+ / sin(a?-s)/(s) ds. 612. / /(s)cossds и / /(s) sins ds ограни-
o	oo
чены при ж->+оо. 613. у,п — 3у"+3у'— у=0. 614. у"— 4?/+5?/=0.
615.	yw+2y"+y=0.	616.	?/IV-4?/,,,+14?/,,-20?/,+25?/=0.
617.2/,,,-2/"-2/,+?/=O. 618. yw+y"=0, 619. а=0, 6>0. 620. а>0,
6>0. 621. 6<0 или 6^0, а>0. 622. 6>0, a^-2y/b. 623. а2<46.
624. а>2, b>a—1. 625. a=2y/b. 626.	± к\ ш=к=0. 627. х=
(Ь—си2) sinutf—аш cosut	л	1
(b-(v2)2-ha2cv2
а2
шах А достигается при ш2=Ь— -2~. 628. х=
д/(6—cj2)2+a2u’2 ’
nlUjt
Л 629.ж(*)=
4-аг+га>
—s) oAofi — s)	°? oAi z _oA2 z	, z 41 .
el(A;zV
630. 2тц/^Г 631. В случае h2>4km ж=^(е(-а+7^ —
2m~~' В случае h2<4km x=
V^km—h2
P~ 2m
кВ
b ’
_е(-«-7)<), а=^, -у=
= ^-e~at sin/ft,
= b(fc-7nu72)sinyt-&^coscut 633	. 634. ж=4-2cos t.
(Jt-mw2y+h2w2	к-тш7
h
2т ’
632.	a?(f)=
191
635. 7 = ^ (1- е_т‘\ 636. 7=Хе-‘/дсг. 637. 7=-Х е~Чкс.
К \	/	К	'
638. I=-^j-e-Ry2Lsinut, CR2<iL, и=^С2ЬС~^~- 639ф I=
=Asin(cut-<p),	’ ^=arctg 640. Z=Asin(cu£-^),
Ia)L	у
i/?=arctg---; max.4=^ при cu2 =
А=
=	641. Нет. 642. Да. 643. Нет. 644. Нет. 645. Да. 646. Нет.
647. Да. 648. Нет. 649. Нет. 650. Да. 651. Нет. 652. Да.
653. Да. 654. Да. 655. Нет. 656. Нет. 657. Да. 658. Нет.
659. Да. 660. Нет. 661. Да. 662. Нет. 663. а) Нет. б) Нет.
664. Линейно независимы. 665. Могут быть линейно зави-
симы или независимы. 666. a) IV=0; б) ничего нельзя ска-
зать. 667. Линейно независимы. Уравнение не удовлетворяет
3	5
условиям теоремы. 669. Два. 670. а) — 1<ж<ос. б) 27Г<Ж<27Г'
671. а) Могут при п^2. б) Могут при п^З. 672. п^4. 673. п^2.
674. у"— у' ctgrr=O. 675. (x—Y)y,,—xy,+y=Q. 676. у,п —у"=0.
677. (2ж2+6ж-9)?/"-(4ж+6)?/'+4?/=0. 678. у"-?/=0. 679. (ж2-
—2х+2')у'" — х2у" +2ху' —2у=0. 680. х2у"—Зху'+Зу=0. 681. у=
=Cix + C2e~2x. 682. У = С1(1+|) + С2(| + 1-^1п|х+1|).
683. т/=еж(С1Ж2-|-С2). 684. xy=Cie~x+C2ex - 685. ?/=Citga?-|-
+C2(l+a?tga?). 686. ?/=С1(1+ж1п |ж|)+С2Ж. 687. y=Ci (еж —1)+
+ eQi ’ 688* 2/=С1Ж-|-С2(1пж-|-1). 689. y=Ch sina?+C2 (2 — sin ж х
xln T-sinx)- 69°- У=с^х~^+^1- 691- г/=С1е2х+С2(Зх+
+ 1)е-*. 692. y=(Ci+C2x)e~x2 693. у=С1(2х+1)+С2е2х 694. ?/=
=Ci(x+l)+C2x-1. 695. у=С1(х+2)+С2х2. 696. г/=С1(х2+2)+
+С2х3. 697. y=Ci(x2+l)+C2[a:+(a:2+l) arctgx]. 698. ?/=С1д/[х|+
+С2(х-2). 699. y=Cix+C2ex+C3e~x. 700. ^Сц+Сгх-ЧСзХ
х(хIn |х|+1). 701. у=С1х+С2ех+С3(х2 — 1). 702. y=Ci(a:+2)+
+ ^- + (§+1)!п |я|+|. 703. у=С1(2х-1)+С2е~х+^±^. 704. у=
= -^ + -^+х- 705- y-Ci(<x2 + l')+C2x-1+2x. 706. z"+z=O.
707. z"-z=O. 708. z"=0. 709. x2z"-2z=0. 710. 4s2z"+(4x2 +
+l)z=0. 711. y'b-y=O. 712. у’Ь+у=О. 713. (t2-l)y't't-2y=0.
714. y't't +t2y=0. 715. 3y't't+t2y=0. 716. ?/=l+Ci(a:-l)+C2(a:2-l).
192
717. f p(ж)da?->+oo при ж->+оо. 719. На прямых у=0 и х=хг,
где д(хг)=О. 720. а) Нет. б) Да. в) Нет. г) Нет. 726. тг/^Дп;
[(6—а)у/т/тг] нулей или на один больше (квадратные скобки
означают целую часть числа). 727. 0,33<d<0,5. 728.15,7<d<32.
729. 0,49<d<l. 730. 0,15<d<l,2. 737. u"+(±1+^3<ж)и=0,
t= f 7 ;7^42 > y=^u.
В тех из ответов 738—750, где решение у2 не указано, оно
получается из yi заменой cos на sin.
738. 7/1 = ^ cos ^-+(Э(1/ж4). 739. т/ц 2=а?-1/2е±а;2/2(1+(2(ж_2)).
740. yi = -~ cos ^-+<Э(ж-5/2). 741. yi=e~x/2 cosex+O(e-3a:/2).
742. ?/i, 2=ж1/4е±2^(1+О(ж-1/2)). 743. ?/i, 2=ж-1/4е±
х(1+<Э(ж~3/2)). 744. 7/1=ж-3/4 cos2y/x+O(a?~5/4). 745. ?yi =
=е(ж-1)2/2 Г(2ж)-1/4 cos ^2ж^----Ю(ж~7/4)]. 746. ?/i = — cos ^- +
о	Ж о
+о(^). 747. 2/i,2=x<1±'/5V2(l+O(a;-2)). 748.	=
х |cos(Jj In2® — g Inina:) +O(ln-2x)j. 749. j/i, 2= [1 ± 32a:2
+ет+о(ж-в)]-vt-	750-^=ж1/4 О+бУ c°s (2^+
+ i6^/j)+ О(ж-5/4)- 751. ?/=(sh®/sh 1)—2x. 752. y=x+e~x— e-1.
753. y=ex —2. 754. ?/=l—sina?—cosa?. 755. Решений нет. 756. y=
=2ж—тг+тг cos x+C sin ж, C — произвольное. 757. y= —2е~ж.
758. 7/=е-ж-1. 759. y=-^-^x. 760. y=2x3. 761. y=3x2.
762. y=-x~3. 763. a=(2n—1)27t2, n=l, 2, 3, ... 764. <9=(з-1)ж
(О^ж^з), G=s(x—1) (з^ж^1). 765. G=sinscosa? (О^ж^з),
= cosssina? (з^ж^тг). 766. G=es(e~x — 1) (O^a?^s), G=l—es
(s^a?^l). 767. G=—e~schx (O^a?^s), G=—e-a:chs (s^a?^2).
768. G=2sin|®-s|. 769. G=|-l (l^x s), G=|-l
770. О=4Д (l^x^e), G=^|^ (s^x^2). 771. G=^^-
2sz	7 2sz	3s^x
(l^a<s),	(s^a<2). 772. G=-x (О^ж^з), G=-s
(з^ж<оо). 773. G=-l (О^ж^з), G=-es~x (з^ж<оо). 774. G=
=— 1пж (1^ж^з), G=— Ins (з^ж<оо). 775. G=^es(e-3a:— e~x)
(О^ж^з), G=^e-3a:(es—e3s) (з^ж<оо). 776. G=(l—ж2)/2з2ж
193
(l^x^s), G=(l —s2)/2s2t (s^t<oo). 777. G=x(s3 — l)/3s2
(O^x^s), G=s(t3-1)/3t2 (s^t^I). 778. C?=—(l/2)e“ 1Ж“51.
779. G=—x2/3s3 (O^x^s), G=—l/3x (s^x<oo). 780. а ф А;27г2,
k=l, 2, 3, ... 781.-™<^<C0,	782. Хк=-к2тг2/I2,
yk — sin(fc7nr/Z), k=l, 2, 3, ... 783. Xk=— к2тт2/12, yk — CQs(k'xx/l)')
A;=0, 1, 2, ... 784. Xk=-(k- j)2p-, yk=sin(k-^™, fc=l, 2,
о	к x ( kTV \2	1	r~ . /С7Г In T ,	. o o
3, ... 785. Afc=_ Q1-_J -^yk=^am^—-,k=l,2, 3, ...
786. x=Cief+C2e54, y=-Ci e* +3C2 e54. 787. z=Cie-4+C2e34,
y=2Cie-f-2C2e3t. 788. x=2Cie3t-4C2e~3t, y=Cie3t +C2e~3i.
789. x=e2t(Cicost+C2sint), ?/=e24[(Ci+C2)cost+(C2— Ci)sint].
790. x=e4(C'i cos3t+C2 sin3t), ?/=e4(Ci sin 3t—C2 cos3t). 791. x=
=(2C2 — Ci)cos2t— (2Ci+C2)sin2i, ?/=Cicos2t+C2sin2t. 792. x=
=(Ci+C2i)e3t, 7/=(Ci+C2+C2t)e3t. 793. a:=(Ci+C2t)e4, y=
=(2Ci-C2+2C2t)ef. 794. я=(С1+2С24)е-4, ?/=(Ci+C2+2C2t)e-‘
795. a:=(Ci+3C2t)e24, 2/=(C2-Ci-3C2t)e24. 796. x=Cief+C2x
xe2f+C3e-f, 2/=Cie4—3C3e_f, z=Cie4+C2e24-5C3e-4. 797. x=
=Ci+3C2e24,7/=-2C2e24+C3e-4, z=Ci+C2e24-2С3е“4 798. x=
=C2e24+C3e34, 7/=Cie4+C2e24, z=Cie4+C2e24+C3e34. 799. x=
=Cie4+C2e24+C3e54, y=Cie*-2C2e2t+C3e54 z=-Cie4-3C2e24+
+3C3e5t. 800. x=Cie4+C3e-4, у=Сге*+С2е2*, z=2C2e2t-С3е~*.
801. ж=е4(2С2sin2t+2C3cos2t), y=el(Ci— C2cos2t+C'3sin2t),
z=e4(—Ci—3C2cos2t+3C3 sin2t). 802. a:=Cie24+e34(C2 cost+
+C3sint), 2/=e3t[(C2+C3)cost+(C3—C2)sint], z=Cie24+e34x
x[(2C2—C3)cosi+(2C3+C2)sini]. 803. x=C2 cost+(C2+2C3)x
xsint, 3/=2Cie4+C2cost+(C2+2C3)sint, z=Cie4+C3cost— (C2+
+C3)sint. 804. a:=Cie24+(C2+C3)e34, y=Cie2t+C2e3t, z=CiX
хе24+С3е34.805.ж=С1+С2е4 y=3Ci+C3e4, z=-Ci+(C2-C3)e4.
806. a:=Cie34+C2e-f, y=-Cie34+(C2+2C3)e-f, z=-3Cie34 +
+C3e-f. 807. ж=С1е24+С3е“54, y=C2e2t+3C3e~5t, z=(Ci -2C2)x
xe24+2C3e-54. 808. x=(C1+C2t)et+C3e24, ?/=(C1-2C2+C2t)et,
z=(Ci-C2+C2t)e4+C3e24. 809. x=(C2+C3i)e-4, ?/=2Cie4-
—(2C2+C3+2C3t)e-4, z=Cief-(C2+C3+C3t)e-4. 810. x=Ci +
+C2i+4C3e3t, 2/=C2-2Ci-2C2t+4C3e34 z=Ci-C2+C2t+C3e34.
811. a:=(Ci+C3t)e4, г/=(С2+2С3<)е4, z=(Ci-C2-C3-C3t)e4.
812. x=(C1+C2i+C3t2)e24, j/=[2C! —C2+(2C2—2C3)t+2C3t2]e24,
z=[Ci-C2+2C3+(C2-2C3)i+C3t2]e24. 813. х=ЗС1е4+ЗС2е“4+
+C3 cos t+Ci sin t, y=Ci e4 + C2 e-4 + C3 cos t+C4 sin t. 814. x=
=-2e4(Ci+C2+C2t)-2e-4(C3-C4+C4t), 2/=e4(Ci+C2t)+e-4x
194
x(G3+C4). 815. я=е*(С1 cost+C*2 sin t)+e-i(C3 cost+C*4 sin t),
2/=е*(С1 sin£—C*2 cos t)+e-i(C*4 cost—C3 sint). 816. £=6444 x
хе^+Сзе^+Сбв-2*, ^СгеЧСге^+С^ЧСве-2*, z=Cie4
+С2е-*-(С3+С4)е2*-(C5+C6)e-2i. 817. ж^ЗСюЧСге"*, y=
=Cie4C2e4 818. x=Cle4C2e-t+2C3e-2t, y=2C1e4C3e~2t.
819. х=ЗСе~*,у=Се~\ 820. s=-2C2e34C3e<, y=Cie~4C2e3t.
821. ж=2С1е2Ч2С2е-2Ч2Сзсоз 2t+2C4 sin 2t, y=3Cie2t-3C2 x
xe~2t —C3 sin2f+C4 cos2t. 822. x=Cie^—4C2e~2t, y=Cie2 +
+C2e~2t. 823. ж=(С1+С2^еЧСзе-*, у=(-2С1-С2-2С^)е*-
—4С*зе_*. 824. х=С1е*+С2е~* +Cse2t+C4e~2t, 2/=С1еЧ5С2е-Ч
+2С'зе2*+2С'4е_Ч 825. ж=С1+С2еЧСз cost+C*4 sint, y=—Ci —
—С2с? + (|с*4 — ^C^cost — (|с*з+^6*4)sint 826. x=Ciet-\-C2x
xe-4te* — t2— 2, у=С1С* — C2e-4(t— 1)е* — 2t. 827. x=Cie2t+
+С2е~1 —2 sint— cost, y=2Cie2t—С2е~*+ sin t+3 cost. 828. x=
=С1еЧ2С2е4ЧЗе5*, з/^-СюЧС^ЧеЧ 829. z=Ci(cos2t-
— sin2t)+C'2(cos2t+sin2t), y=Ci cos 2t+C2 sin2t+e-2i. 830. x=
=Cie2t+C2e3t+(t+l)e2t, y=—2Cie2t—C2e3t —2te2t. 831. a;=(Ci +
+2C2t)e*-3,2/=(С1+С2+2С2^е*-2. 832. ^СЧ^+ЗСЧ^-е"*-
—4e3i, y=Cie2t+C2e4t —2e-i — 2e4 833. rc=Cief cost+C2ef sint+
+e4t+l, 2/=Cief(— cos t— sin	(cost— sint)—2ef—2t—1.
834. a?=C'ie_42C'2e2i—cost+3sint, y=—C'ie-4C'2e242cost—
— sint. 835. a?=4C'ie4C'2e-2i —4te*, ^СлеЧСЧ-2*—(t—l)e*.
836. rE=Cie343t2+2t+C2, ?/=-Cie346t2-2t+2C2-2. 837. x=
=2Cie24C2e-3i-(12t+13)ei,	2/=Cie2i-2C2e-3i-(8t+6)ei.
838. rr=2Cie8i-2C2-6t+l, 7/=3Cie84C2+3t. 839. a?=3Cie4
+C2e-43sint, ?y=Giet+C,2e_t—cost+2sint 840. x=Ci cost+
+C2 sint+tsint—tcos t, 2/=Ci(sint+cost)+C2(sint— cost)—2tx
x cost+ sint+ cost. 841. x=(Ci+C2t—t2)^, y=[Ci—C2+t(C2 +
+2)—t2]e*. 842. a?=Cie43C2e24cost—2sint, ?/=C'ie42C'2e24
+2cost—2sint. 843. a?=C'ie4C'2e3i+tei—e4i, ?/=—СлеЧС^е3* —
—(t+l)ef— 2e4 844. x=Ci cos2t—C2 sin2t+2t+2, y=(Ci+2C2)x
x cos2t+(2Ci— C2) sin2t+10t. 845. a?=C'iei+C'2e3i+ei(2 cos t—
— sint), y=C\et—C*2e34e*(3cost+ sint). 846. x=Ci cost+C2 x
xsint+tgt, y=—Ci sint+C2 cos t+2. 847. х=С1е*+2С2е2* —
—ef ln(e241)+2e2i arctge*, ^СлеЧЗСЧ2*—e* ln(e241)+3e2ix
xarctge*. 848. a?=C'i+2C'2e-i+2e_i ln|ef—11, у=—2С1—ЗС2е~* —
—3e-i ln|e* —1|. 849. x=Ci cost+C*2 sint+t(cos t+sint)+(cos t—
— sint) In I cos t|, y=(Ci—C2) cos t+(Ci+C2) sin t + 2 cos tln|cost| +
+2tsint. 850. rE=(Ci+2C2t-8t5/2)ei, y=(Ci+2C2t-C2-Mb/2 +
195
+10t3/2)ef. 851. x=Cie3tQj + C2e3(^J. 852. x=Cie2fQ j +
+С2е-^_0. 853. я^е-^^+С’ге-^-.Д 854- ж=с'1е'х
x(C0SqL • o/) + C2ef(Sm\ 855. а:=С1е4М+С2х
\cos 2f+ sin 2tJ	\sm2f— cos 2tJ	I /
/л	Л\	(°\	( Л	/ Л
X 1 1+Сзе 4 1 I. 856. a?=Cie2M 1 l+C^eM -1 1+Сзе 4 -1 I.
V/	W	V/	\-v	\-2/
0/ 2 cos t	\	/2 sin t \
+ <^21 2 cos t I + C'3i2sinf I.
\3 cos t — sin t/	\3 sin t+ cos t /
C0\	/ cos 2A	/sin2f\
1 j + Сге-*! —sin2f j + С*зе-Ч cos2f j.
1/	\ cos2f/	\sin2f/
196
S)- 87“-
2e2—e e—e2 \
2e2—2e 2e-e2J
A 1 o\	/e2 e2
872.	0 1 0 . 873. л o2 „2 .	874. e2.	875. e"1.
kooeM	^e0:2;
876. x=d cos at, y=^sinat; эллипс + (^F)	877- x=
—Ci sin (^=+Сг) , 3/=|^l sin (^j-*-^2) ’ X=C3 sin(at+C'4), y=
=—Сз sin(at+C4). 878.	^=j4sin(a;t—<p),
A=—.--------; шах	ПРИ 0 и cj=oo,
yfl2+(wL/(l-w2LC))2
min 4=0 при о>2 = -г7у- 880. Л	fc=0, ±1, ±2, ...
Х/О	си
881. а) неустойчиво; б) устойчиво; в) устойчиво; г) неустойчиво.
882. Асимптотически устойчиво. 883. Неустойчиво. 884. Не-
устойчиво. 885. Устойчиво. 886. Устойчиво. 887. Неустойчи-
во. 888. Устойчиво. 889. Все решения стремятся к нулю. Нет,
нет. 890. Устойчиво. 891. Асимптотически устойчиво. 892. Не-
устойчиво. 898. Нет. 899. Устойчиво. 900. Неустойчиво.
901. Неустойчиво. 902. Устойчиво. 903. Неустойчиво.
904. Устойчиво. 905. Устойчиво. 906. Неустойчиво.
907. —2<a< —1. 908. а<-1. 909. ab<-3. 910. а<Ь<-1.
911. 0<а<2. 912. — Ье<а<— е. 913. Устойчиво. 914. Неустойчи-
во. 915. (О, 0) неустойчиво, (1, 2) устойчиво. 916. (1, 2) и (2, 1)
неустойчивы. 917. (2&тг, 0) неустойчивы, ((2&-|-1)тг, 0) устой-
чивы. 918. (3,2) неустойчиво, (0,-1) устойчиво. 919. (2, 1)
устойчиво, (—2,1) неустойчиво. 920. (1,1) неустойчиво, (-4,-4)
устойчиво. 921. (2&7Г, 0) неустойчивы, ((2/сН-1)тг, 0) устойчи-
вы. 922. (—1, 2/стг) устойчивы, (—1, (2А?Н-1)тг) неустойчивы.
923. Неустойчиво. 924. Устойчиво. 925. Устойчиво. 926. Не-
устойчиво. 927. Устойчиво. 928. Устойчиво. 929. Неустойчиво.
930. Устойчиво. 931. Устойчиво. 932. Неустойчиво. 933. Устой-
чиво. 934. Устойчиво. 935. Неустойчиво. 936. Устойчиво.
937. Неустойчиво. 938. Неустойчиво. 939. Неустойчиво.
940. Устойчиво. 941. Неустойчиво. 942. Устойчиво. 943. Не-
устойчиво. 944. Неустойчиво. 945. Устойчиво. 946. Неустой-
чиво. 947. Устойчиво. 948. Неустойчиво. 949. a>0, 6>0, ab>2.
197
950. За>6>0. 951. 0<а<2. 952. Неустойчиво при всех а.
953. а>0, 6>0, а+Ь<1. 954. 6>0, а>Ь+1. 955. а>0, 6>0, 8а—а2Ь>
>4. 956. а>2, 6>0, 2а6-Ь2>4. 957. а>0, Ь>0, 2-х/3<^<2+\/3.
958. 0<а<8, 0<6<8а—а2.959. а) устойчиво; б) устойчиво; в) не-
устойчиво; г) неустойчиво; д) неустойчиво; е) устойчиво.
960. —4<а6<0 и а=6=0. 961. Седло. 962. Узел. 963. Фокус.
964. Узел. 965. Седло. 966. Центр. 967. Вырожденный узел.
968. Узел. 969. Особый узел. 970. Фокус. 971. Узел. 972. Вы-
рожденный узел. 973. Фокус. 974. Седло. 975. Центр. 976. Вы-
рожденный узел. 977 и 978. Особые точки заполняют пря-
мую линию. 979. (—2, —1) — узел. 980. (1, —2) — фокус.
981. (4, 2) узел, (—2, —1) фокус. 982. (1, 0) особый узел,
(—1, 0) седло. 983. (1, 1) фокус, (—1, —1) седло. 984. (О, —1) вы-
рожденный узел, (2, —3) седло. 985. (2, 4) узел, (—1, 1) сед-
ло. 986. (1, 1) фокус, ( — 1, —1) седло. 987. (2, 1) узел,
(1, 2) седло, (—1, —2) фокус. 988. (1, —1) фокус, (0, —2) сед-
ло, (—2, 2) узел. 989. (—2, 4) узел, (1, 1) фокус, (2, 4) и
(—1, 1) седла. 990. (—2, 2) вырожденный узел, (1, —1) фокус,
(2, 2) и (-1,-1) седла. 991. (—3, 0) фокус, (1,1) узел, ( — 1, 1)
и (3, 0) седла. 992. (О, 1) и (0, —1) седла, (—1, 0) фокус,
(3, 2) узел. 993. В области у>0 интегральные кривые распо-
ложены как у седла, в области у<0 — как у узла. 994. Че-
рез (0, 0) проходит одна кривая, имеющая там точку воз-
врата первого рода. Остальные кривые не заходят в особую
точку. 995. Из области у<0 все интегральные кривые обои-
ми концами входят в особую точку, а из области у>0 не вхо-
дит ни одна. 996. Две интегральные кривые проходят через
особую точку, касаясь друг друга. Остальные кривые распо-
ложены, как у седла. 997. Из области у>0 кривые не вхо-
дят в особую точку. В области ?/<0, ж<0 расположение кри-
вых напоминает вырожденный узел, а в области ?/<0, ж>0 —
седло. 1021. (О, 1) седло, (0, —1) фокус. 1022. (1, 2) сед-
ло, (—1, 2) узел. 1023. (1, 0) седло, (0, 2) вырожденный
узел. 1024. (0, 1) центр, (0, —1) седло. 1025. (2, 2) узел,
(О, —2) седло, (—1, —1) фокус. 1026. (2, 2) седло, (4, 1)
и (—2, —2) фокусы. 1027. (1, 0) и (—1, 0) седла, (0, 1) и
(О, —1) центры. 1028. (1, 1) седло, (1, —1) узел, (2, 2) и
(—2, 2) фокусы. 1029. (О, 1) и (0, —1) седла, (1, 0) фокус,
(—3, 2) узел. 1030. (1, —1) и (—1, 1) узлы, (3, 3) и (—3, —3)
198
седла. 1031. (1, —1) и ( — 1, 1) седла, (3, 3) и (—3, —3) узлы.
1032. (О, 0) фокус, (7, 1) узел, (0, 8) и (3, —1) седла. 1033. (О, 0)
фокус, (2, 4) узел, (1, 1) и (—1, 1) седла. 1034. (2, 1) узел,
( —1, 2) фокус, (1, 2) и (1, —2) седла. 1035. 1ф+д sin </?=0.
1036. ml(p+kl2fi\fi\+mgsincp=Q. 1037. <£+ sin1038. тх+
+/sgn±+/ca?=O. 1039. В раз. 1047. /(го)=О; при возра-
стании г функция /(г) меняет знак с + на — ; меняет знак с —
на + ; не меняет знака при переходе через нуль. 1048. а< —1/2;
а>—1/2. 1053. х— ± 6cth —Д2=_. 1054. х=у; 4(®2+у2)=
2vl—
=—2?yF(?y)<0 при у ф 0. 1056. Меньше, чем на 0,03. 1057. Мень-
ше, чем на 0,05(е2Т —1). 1058. Ошибка меньше 0,081.
1059. \у-2/|<О,О16. 1060. |ж-ж|+|^-2/|<0,0012. 1061. \у-у\<
<0,002. 1062. \у-?/|<0,015. 1063. \у-у\<0,034. 1064. е2ж-а?-1.
1065.	^-^+х+1.	1066.	ех~2.	1067.	t(e-1—е-4).
1068.	Ю69. t8. 1070. t2 lnt+2t2—2t. 1071. -e24-
-2e-4-3e-24.1072. -^-^ + (^-|)e-4+1. 1073.	A.
1074.	y=^ (x2-^) +/?	+	+0(^3).
1075.?/=2у/ж+2^(а?_1/2—a?2)+jit2^a?7/2—^a?+||a?-1/2—a?-3/2) +
+O(^3). 1076. 7/=1+^(ж2-Ж)+;/2ж^~ж)3 +O(m3). Ю77. 7/=| +
+3/z+/z2	3a?) +<9(/z3). 1078. ?/=a?—^(а?+1)+(^2/2)(еж —a?2 —
—2a?—l)+O(/z3).	1079. a?=sinf+jit^ — cos 2t) +/z2 sin t—
— sin3f) +<9(/z3). 1080. a? = cos2£+/z( — cos4f) +/z2 (yj[jX
xcos2£+6^2 cos6f) + O(/z3). 1081. a? =/zcos£-|-/z3(—cos£+
+ ^4 cos3t) +<9(/z5). 1082. a?i = l+/zsin£— ^-(1+ cos2£)+O(/z3),
a?2=—1— sint+ ^-(1 — i cos2^ +O(/z3). 1083. a?i=—sin2f-|-
+ ^g(sin2£--^ sin6f) + <9(jit5), a?2 = 7r-^sin2f-y^Q^Qsin2f-
— yL- sin 6t\ + O(f5)- 1084. a?=i sinf+i sin2f— i sin3t+O(jit).
Ill/	о	<5	о
1085. a? = 2\/Fsinf — sint+^sin3f)	1086. a?=
199
=Ccosr+C2 cost-cos2т) +<9(C3), r=t (1-^c<2 +
+<9(C3)) +C*2. 1087. #=Ccost+|^-(cos3t—cost)+<9(C5), t=
=t ^l+|c2+O(C4)) +C*2. 1088. ж=С cos т+^ту (cos t—cos 3t)+
+O(C5), r=t(1-y^+<9(C4)) +C2. 1089. rr=2cosT+|^sinT-
— sin3T+O(/z2), r=t ^1 — ^g+O(jit4)^ +C. 1090. ж=-^созт+
+ 12уз sin3t+<9(/z2), т= (1-^+O^t+C. 1091. т/=1+ж+
zr»2 ОлрЗ ,7™4	~»3	q,»4	~»2
+ ^- + ^f- + ^-+--- Ю92.т/=1+ж+|—1093.7/=^- +
/рЗ /y>4	/v»3	/p4
+ ^- + ^-+-- 1094.y=x+?-j-j-... 1О95.2/=1+2(ж-1)+
+4(x-l)2 + ^(x- 1)3 + ^(ж-1)4+ ... 1096. y=l+2x-^-^--
1097. y=4-2x+2x2-2x3+™x4+... 1098. K>0,73.
~4	™8
1099. Ошибка меньше 0,00024. 1100. yi = 1+ q—т+о—i—т—о +•••,
о  4 о • 4 • ( • о
~5	~9	~2	^.4 zr6
^=*+ф+4ТТ787э + -- - 1101.^=1+^ + ^3 + t^75+...1
7/2=^+^~ + 2^. 4 + 2 -4 • 6 ‘ ’ * ~x e 2 * 11^2. т/1=1+ж2-|-ж4-|- ... =
= -1..2> 2/2=ж+ж3+ж5+ ... = Ж 2 . 1103. t/i=1-| ж2 + |^Лж4-
1—хл	1—• 4
- . . . =(1+т2)“ I, ?У2=Ж-|ж3+|-^Т5-. . . 1104.7/1 = 1-^--^--
0	0’0	z z
11ж4	. 2 I 5ж3 . Зж4 .	11 ЛЕ II 3	4 I
---24--• • * ’ 2/2=я+я Н—6—1--4—Н • • • 1105. т/1 = 1+ж-ж3-ж4 +
+х6+х7-... = 12Дд2-; У2=ХУ1- 1106. 2/1=1-^--^+...,
2/2=ж+^— у2-+...	1107. 7/1=1-^- + ^о + ... , 7/2=Ж-~ +
+ Йо + --- 1108. 2/1=1+^- + ^2 + -ТТ+ •. • > ?/2=х+^ + ^+ ...
1109. 2/1=1-^.+ ... , У2=х+^--^+... , y3=x2 + ¥i-...
- - - л л х2 . ж4 sin ж 1 ж . ж3 cos ж
1110. 2,1=1-^г+^г	г/2 = __21 + ^г_... = —
ini 1 । 1 । ж । ж2 । еж I |1/2 А । 2ж . (2ж)2 .
ЫЫ. 2,1=-+l+2l + ^r+... = _	2/2=1x11/2 ^1+_ + ^ +
I (Зар3 . А 1112 ui— xl/3( 1 I х2_I___—_____I-
+ 5-7-9 + -J- 11 • У1~х +5-6 + 5- 6 • 11 • 12+-'J ’
200
^=ж2/3(1+Й + б"7~Г27Тз + "-)' 1113‘ ^4 + 1+?’
^2+т + Д + 4^б + ---=6(^1-1-Ю- 1114‘
_ 1 1 . 1 . ж2 . ж3 . 7ж4	_ . х2 । х3 । ж4
х + 2 + 8 + 40 + 720 + '" ’	У2-х+ 2 + 5 + 20 + ---
zv»3 ZV.4	Пг»2 гу»4
1115. 2/1=xW + ^r + |r+.. .=хех. 1116. ^=1+^ + ^^- +
/	‘2	™4	\	2
+ ^.62 + --- 1117. У2= ^+^+...Jln|x|-^—
Зж4
— у28 — • • • 1118. ?/1 и ?/2 — обобщенные степенные ряды с ир-
рациональными показателями. 1119. 2/1 и 2/2 — ряды с ком-
плексными показателями. 1120. Решений в виде обобщенных
степенных рядов нет, так как получаемый ряд 2/=1+1!ж+2!ж2-|-
+3!ж3-|- ... имеет нулевой радиус сходимости.
7Г . 1	cos(2fc- 1)ж
1121. У=-^ + ~ Z (^-^-fc+i)'
9 Л 00	1	/	9Ь	\
1122- У=п + п £ 16^-4F+1 (cos2^-4PTi sin2^J •
11 о о _ (fe3+fe) cos kx— sin кх
1123‘ 11 * * У~& 2*[(Р+^+1]	•
11 o .	1.1^ cos 2къх
1124^=-6^ + ^£p(4fe41)-
1125. у— £	+C1 cos3x+C2 sin Зх. 1136.
1137. 1+ж2<2/<1+ж2+arctg ж. 1141. y=C2e°lx2 z=2c±^e~Clx2
1142. y=C2eC1X, z=x+Q-ecix; y=0, z=x+C. 1143. 2/=^±^-,
z= (^2 ^'1^x. 1144. y=C2eClx2, z=^£±xe~Clx2; y=0, z=Cx.
(х-\-С2у	b2
1145. y=--Q^-\-^^-{x-\-C2}—(x-l~C2)2, z=-^-(x~l-C2)2-l--^-.
1146. y=C\z, x=2y—z+C2. 1147. x2—y2—Ci, x+y=C2z.
1148. x—y=Ci(y—z), (ж+2/+г)(ж—y)2=C2. 1149. x+z=C*i,
(ж+2/+г)(2/—Зж—z)=C2. 1150. ж2—z2=Ci, у2— u2=C2, (ж-|-г)=
=С3(гг+2/). 1151. ж+г=С1, у-{-и=С2, (ж-г)2+(2/-гг)2=Сз.
1152. ж2—2y=Ci, 6xy—2x3—3z2=C2. 1153. y2 + z2=Ci, x—yz=
—C2. 1154. ж=С*12/, xy—z=C2x. 1155. x—Ciy^ xy-2\/z2-\-\=C2.
1156. y=Ciz, x—y2-z2—C2z. 1157. 2/2+^2=C'i) x(y—z)=C2.
1158. Ж2=С1, xy+z2=C2. 1159. x+z— y=Ci, 1п|ж| + ^=С2.
201
1160. x2+y2+z2=Ci, yz=c2x. 1161. 1) да; 2) нет. 1162. 1) нет;
2) да. 1163. Да. 1164. Зависимы. 1167. z=f(x2+y2). 1168. z—
=f(xy+y2). 1169. u=fU, ^). 1170.
1171. F(x2—y2, x-y+z}=a. 1172. р(е~х-у-\ z+e-»^°J-Q =
=0. 1173. F(x2-4z, (ж+?/)2/ж)=0. 1174. F(x2+?/2, z/x)=0.
1175. F (— , xy- — '}=0. 1176. F	——1--)=0.
у у ' J X J	\x+y z' x—y z)
1177. F^+j/4, jz(z+v/z2+l))=0.1178.	ln|«jz|-^ =0.
1179. F(x2+?/2, arctg(x/?/) + (z+l)e z)=0.
1180. F(z2— ?/2, x2+(y—z)2)=0. 1181. F	2x—4z—?/2)=0.
1182. F(z—ln|®|,2x(z — 1)— ?/2)=0. 1183. F(tgz+ctgx, 2y—tg2z)=
=0. 1184.	(»-?/)(x+j/-2z))=0.
\ \x У)	J
1185.	F ((x-?/)(z+l), (x+?/)(z-l)) =0.
1186.	F(u(x—y), u(y—z), (x+y+z)/и2) =0.
1187.	F (ж/?/, xy—2u, (z+u—xy)/x)=0.
1188.	F((x—y}/z, (2u+x+y)z, (u—x—y)/z2) =0. 1189. z=2xy.
1190. г=2/еж-е2ж + 1. 1191. z=y2e2^~2. 1192. и=(1-ж+?/)(2-
-2ж+з). 1193. u=(xy—2z)	+	ll94* 2/2-^2- In \/y2—x2=
—z— In |з/|. 1195. 2x2(y+l)=y2+4z—l. 1196. (x+2y)2=2x(z+xy)-
1197. y/z/y^ sin x= siny/z/y. 1198. 2x?/+l=x+3?/+z_1. 1199. x—
—2y=x2+y2+z. 1200. 2x2— y2— z2=a2. 1201. [(y2z—2)2— x2+z]x
x?/22=1. 1202. x2+z2=5(xz—y). 1203. 3(x+?/+z)2=x2+?/2+z2.
1204. xz=(xz—y—x+2z)2. 1205. (l+yz)3=3yz(l+yz—x)+y3-
1206. x+y+z=0. 1207. 2(x3-4z3-3yz)2=9(y+z2')3 1208. (x-?/)x
x(3x4-y+4z')=4z. 1209. xz-l-y2=0- 1210. z=xy+f(y/x), где f —
произвольная дифференцируемая функция, для которой /(1)=
=0. 1211. F(x2— у2, 2x24~z2)=0. 1212. 2?/2+z2=z(x2+?/2+z2).
1213. F(bx—ay, cx—az)=0. 1214. x2 +3?/2 +z2 +3xy+xz+3yz=l.
1215. F((y—b)/(x—a), (z—c)/(x—a))=0. 1216. F(x2/?/, z/y)=Q.
1217. z=Cxy2. 1218. Решений нет. 1219. z=0. 1220. Решений
нет. 1221. x3y2z=C. 1222. z=y2— xy. 1223. x2yz=C—x3; x=Q.
202
ОТВЕТЫ К ДОБАВЛЕНИЮ
9. у'=и, u'=v, v' =у е~х (2и—х); 2/0=1, «0=1, «о=0; 2/1 = 1+ж,
«1 = 1, vi =1+(ж—1) е~х . 10.2/0=1,2/i=l+^+^2,2/2 = l+^+2i2+i3+
। +4 /о , .5 /к 11	\ л	Ж2 —1	X . Ж2 X3 . X5 19
+t /2+i5/5. 11. а) 2/о—0, 2/1 — —g—, 2/2— 4 + “^-6~"^20 —30’
б) например, |ж—1|^^. 12. При ж^О у=—х, при ж>0 решение
не существует. 13. б) При —1 и а=0. 14. а) При а^О,
требуется а#—1, ±3, (/г+1/2)тг (&=0, ±1, ±2, ...); при а=1 тре-
буется а^ — 1, ±3; при а=0 уравнение не дифференциальное;
б) —3<i<—7г/2. 15. уо=у1=у2= .. .=4, ^lim°ук =4. 16. 2/(жО)=2/О,
2/'(жо)=2/1, У,(жо)=2/2, где ж0#Ьг/2 (&=0, ±1,±2, ...), 2/о>0, 2/1
и 2/2 любые. 17. Начальные условия 2/1 (0)=1, у[ (0) = 1 и 2/2 (0)=1,
у'2(0)=у/2 различны. 18. п^1. 19. тг^5. 20. тг^З. 21. тг^4.
22. п^4. 23. а#0, ±2 бесконечно много решений, а=2 и а=0
одно решение, а=—2 нет решений. 24. а^О, ±1 бесконечно
много решений, а=0 и а=—1 одно решение, а=1 нет реше-
ний. 25. п 3 бесконечно много решений, п=2 одно решение,
при п=1 для а= ± 1 одно решение, для ± 1 нет решений.
26. тг^З бесконечно много решений, тг=2 одно решение, при
n=1 для а=1 и а=—2 одно решение, для а^1, а^—2 нет ре-
шений. 27. При 4 нет решений; при а> —4 для тг^З бес-
конечно много решений, для тг=2 одно решение; для тг=1 при
а=—3 одно решение, при аф—3 нет решений. 28. Да. 29. |«|<х/2.
30. a) y—\j (in л/|ж2—тг2 |'+с) , 2/—0; б) 2/=1 /1п (х/тг2—я2 —1) ,
|ж|<тг. 32. Нет. 34. |4|<1; для х’—х2 (жЕЯ1), ж(0)=1 имеем
ж=1/(1 —t) (4<1); для ж'=—ж2, ж(0)=1 имеем ж=1/(1+4) (t> —1).
40. б) Q . 44. б) тг^/г+1. 45. 771=2. 46. 2/1 =ж, У2=х2; W=x2.
47. а) —2^ж^1; б) да; в) 1/4. 48. а) — 1<4<тг/2; б) да; в) —16(4+
+1)-2; г) 2/=^"^^1(^)+^2(4)-^^^з(4)- 49. а=-5. 50. 2. 51. 4.
52. (ж2— 2х)у" — 2(ж—1)2/,+22/=О. 53. 2/=2+5ж—2ж2. 54. Да, у=
=3yi—2y2. 55. 2/=С'1ж+С'2Ж3+С'з(ж2+ж1п |ж—1|). 57. у=х—2(ех —
—ж)/(е —1). 58.2/=ж+С1+С2(ж+ж2). 59. у=2—ж2. 60. (ж2+4)2/,/—
-2ху'+2у=2. 61. ^=^- + ^+^-1- 62-
64. Т=Зтг/4. 65. Нет. 66. р=я2. 67. а=2. 68. х= (C'i+C2t+	е‘+
203
1	t
+ 2 cost 69. x=Ci cos2i+C2 sin2i+^g-(sin2i—cos2i)—2 cos2i.
70. т/=(С1+ж) cosx+(C2+x2) sin ж. 71. y=Ci cosx+C*2 зтж+(ж+
&2x~ 2#cosx. 72. 3/=(Ci+C2t) e* +C*3+£2 (at+b) +(ct+d)x
x eb cos t+(ft+g) sin t+ht2+kt. 73. ?y=(Gi+С*2ж) е2ж+(<2ж+6) x
хж2 е2ж + e2a:(ccosx+dsin х). 74. y=Ci е(1+г)ж +С*2 е~(1+г)х +
+аяе(1+г)ж+Ье(1-г)ж.	75. y=(Ci+C2x) егж + аж2 егх + Ье~гх.
76. у=С\ е(1-2г)ж +С*2 е(_1-2г)ж +ае(1+2г^ -^-Ьх е^~2г^х . 77. у=
=Ci е2гаЧ-С*2 е(''/з~г^х+Сз е(~^~г^х -j-ax е2гх+Ье~2гх. 78. Да.
79. Нет. 80. Нет. 81. cj#O, ±2. 82. с^О, b любое или с=0, 6=±1.
83. а) Ш#0, ±х/2; б)	=С+П7 sin3t
ол	(25—cj2)sincji—cjcoscji л	1	о_ ч о
84. х=-—-т—2—5Т2-;—2-------;	п—L охо 85. а) а=±2,
(25-cj2)2W	у/(25-и2)2+и2	7
а= ± 6; б) а нечетное. 86. а) а=2; б) а^2, а^О. 87. а=0, а=4.
88. а=0, а= zb 1. 89. а<0. 90. zb 1, аф i 2. 91. а=0, а=4,
/3=2. 92. а=1, 6=0, с=—4; а=0, /3=2, 7=0. 93. x=(Ci+C2i) e2t +
+3, ?/=(C'i+C'2+C'2i) e2t +1. 94. x=Ci e*(cos3£—2sin3£)+C*2 e* x
x(2cos3i+sin3i), y=Ci e*(cos 3i+ sin 3i)+C*2 e^(sin3i— cos3i).
95. x=Ci+ [C2+C3(t+1)] y= [C2+C3(i-1)] е-*,г=С1+(С2 +
+C3i) e-t. 96. Bee ReAi=O и в жордановой форме все клетки
/ i	t	0\
размера 1. 97. п^7. 98. I О	1	О I. 100. х=2С-\-2 sin i,
\е* —1 е^ — 1—t еу
у=С+ sin t. 101. х=—3— cos 2t, у=—3— cos 2t—2 sin 2t. 102. a) x=
=Ci cos t-\-C2 sin t— sin 2t—2 cos 2i, y=Ci (cos t+ sin t)+C2 (sin t—
— cosi)—2sin2t 6) x=— sin 2t—2 cos 2i, y=—2sin2i. 103. a=—2.
104. При a=—2b. 105. Тот же ответ, что в задаче 96.
/1—2t —4i \ iQg Zet(cos t—2 sin t) 5e*sin£
\ t l+2t/	\	— e^sini e^(cosi+2sini)
(ch t 0 sh A	/e2t
0 10. 110.	0
sh t 0 ch t/	\ 0
112. a) 1; Ai, 2=1; 6) (T2*
113‘ a) e2t’ А1.2=е‘;
e*(l+2£)	4£e* A
-te1 e*(l-2£)/
114. a) 1; Ai, 2 = cost±zsint;
204
6) (COsi+sint	—2sint A n5 2	_e_i 2 n6 Bce
\ sin t	cos t— sin tj
ReAi<0. 117. еЛ1п*. 118. Нет, например A=	)•
\ 0 2тггJ
119. A2=0, жорданова форма может содержать только клет-
ки вида (0) и	120. Да. 121. Да. 122. Да. 124. Все
|Л/г|<1. 125. е(«+1/2)7Г> 126. а/-1/2. 131. Все ReA^O и для
тех Xi, у которых ReAj=O, клетки в жордановой форме имеют
размер 1. 133. См. ответ задачи 131. 134. a) det 4=0; б) см. от-
вет задачи 131. 135. Да. 136. Да. 137. Нет. 138. При п=1 да,
при п^2 нет, см. рисунок к задаче 889. 139. ж=0 неустойчиво.
140. ж=0 асимптотически устойчиво. 141. ж=0 асимптотически
устойчиво, x=Tvk (&=±1, ±2, ...) неустойчивы. 142. ж=0 асим-
птотически устойчиво. 143. х=0 устойчиво. 144. х=0 устойчи-
во. 145. х=у=0 устойчиво. 146. (0, 0) устойчиво, (2/3, 0) не-
устойчиво. 147. (а, а) устойчиво, (а+1, а) неустойчиво (aER
любое). 148. а) а>0; б) а=0; в) а<0. 149. а) а< — 1; б) а= — 1;
в) а> — 1. 150. а) а<0; б) а=0; в) а>0. 151. а) а>0; б) а=0;
в) а<0. 152. а) а<0; б) а=0; в) а>0. 153. а) а>2; б) а=2; в) а<2.
154. а) а>0; б) а=0; в) а<0. 155. а) 0<а<1; б) а=0; в) а<0 и а^1.
156. а) а=—1/2; х=с, у=2с—1/2-, б) да. 157. Да. 158. а) а=0,
а=4; б) для а=4 устойчивы, для а=0 нет. 159. а) а=0, а= ± 1;
б) устойчивы. 160. а) а=0, а=1; б) для а=1 устойчивы, для
а=0 нет. 161. a) ad<bc; б) ad>bc, (a—d)2+4fec>0. 162. с>0,
(a—d)2+4bc<0. 163. (0, 0) узел. 164. (0, 0) фокус. 165. (3, 1)
вырожденный узел. 166. а<0. 167. а) нет; б) нет. 168. а) фо-
кус; б) |а—6|<2 169. а) нет; б) узел; в) а=—1. 170. а) все-
гда неустойчиво; б) |а|>1 седло, |а|<1 узел. 171. а) а< — 1 и
— 1<а<0 асимптотически устойчиво, а^0 устойчиво; б) а< — 1
и —1<а^ —1/2 узел (при а=—1/2 вырожденный); —1/2<а<0 и
а>0 фокус; а=0 центр. 172. а) а< — 1 асимптотически устойчи-
во, —1 устойчиво; б) —1<а<0 седло, а< —1 и а>8 узел, 0<а<8
фокус. 173. а) п< —1 и а>3 асимптотически устойчиво, —1
и а^З устойчиво; б) —1<а<3 седло, 1 — \/5<а< — 1 и 3<а<1+л/5
узел, а<1 —х/5 и а>1+х/б фокус. 174. ху=С(х2+у2)2. 175. Все
решения определены при —oo<t<oo. 176. Нет. 177. а) (0, 0),
(±1, 0); б) а<0; в) нет. 178. а) у= ± 2х\/х—\-, в) a?=cos-2^.
179. б) (0, 0) устойчиво, (=Ы/х/2, 0) неустойчивы; в) ^,2=42,
205
Т~тгх/2; г) (0, 0) устойчивый фокус (0<а<\/8), устойчивый
узел (а>\/8), (=Ы/л/2, 0) седла. 180. б) (0, 0) неустойчиво,
(±1, 0) устойчивы; в) A;i,2= ± х/2, Т~7г; г) (0,0) седло, (±1, 0)
устойчивые фокусы (0<а<4), устойчивые узлы (а>4). 181. а)
(0, 0) центр, (1, 0) седло; б) траектория у=—(ж— 1)-^/(2ж+1)/3,
решение x=^(cthi)2 —	(0<i<oo); в) |а|<1/\/3; г) — 1/2<ж<1,
3?/2<2ж3—Зж2 + 1; д) нет. 182. б) (±1, 0) неустойчивы; в) нет.
183. б) (0, 0) неустойчиво, (±1, 0) асимптотически устойчи-
вы; в) нет. 184. а) (0, 0) и все точки окружности ж2+?/2 = 1;
б) в (0, 0) ж=?/, ?/=0; в (1, 0) й=0, v=2u; в (1/х?2, 1/х/2) й=—и—v,
v=(u-\-v)/2\ в) неустойчиво, неустойчиво, устойчиво; г) устой-
чиво, неустойчиво, устойчиво; е) нет; ж) ж(^)=жо, ?/(io)=?/o, где
io, жо, ?/о любые такие, что Xq-|-2?/q<1 или Xq-|-2?/q>2.
186. (2ж2—12Д/ж)/5.187. (2+ q~1)x-xq~x. 188. (ж-1) е2ж+2-еж.
189. Зеж -ж-1. 190. 1+i. 191. chi. 192. sini-icosi. 193. 2e2t -
—2—t—t2. 194. дх/д[1=§+2 ch 2i—12 ch i, dy/8/1=4 sh2t— 12shi.
197. еж2+ж-2.198. esina:. 199. дх/ду$= sini, dy/dy$= cosi+ sin i.
200. 0. 201. ?/=ж1/2-|-^(2ж2—Зж-1/2)+^2 ^ж7/2—4ж+8ж-1/2 —
— ^ж-3/2) -f-O(^z3). 202. x=l-|-^sin2i-|-jLt2^cos2i—^cos4i—
—	+<9(/z3). 208. z2=2xy— ^x3+f(x2— 2y). 209. xz—y2 = l.
210. (z-x2)2+x(z-x2)=y. 211. z(e~x +2x-2)=y2. 212.	+
3	2	2	2
+ ^y~^—y+^-=0- 213. (ж2-?/2) In* ~y =y2+2(x2-y2} In |j/|-
-2 In |z|. 214. (2х+1)г=х(2х+1)2/2+2ху. 215. z=(ln |ж-?/|+1)х
х(ж+?/). 216. (к—2)z=5(kx—у) (/г#2). 217. a) z=2x—2+(у—Зж+
+3)2; б) z=2x+f(y—Зх), fEC1 произвольная функция с /(0)=0.
218. При а ф 0, а ф —1, г=(2ж+(4—2а)у)/а, при а= — 1 з=ж+
+/(ж+2?/), /ЕС1 произвольная функция с /(0)=0; при а=0
решений нет. 219. а) решений нет; б) единственное решение
Z-—1+д/2ж2+2?/2~1. 220. а) нет; б) да. 221. (р(х)=(р(—х).
206
ТАБЛИЦЫ ПОКАЗАТЕЛЬНОЙ ФУНКЦИИ И
ЛОГАРИФМОВ
Таблица!	Таблица2
X	ех	X	In X	1g х
0,00	1,000	1,0	0,000	0,000
0,05	1,051	1,1	0,095	0,041
0,10	1,105	1,2	0,182	0,079
0,15	1,162	1,3	0,262	0,114
0,20	1,221	1,4	0,336	0,146
0,25	1,284	1,5	0,405	0,176
0,30	1,350	1,6	0,470	0,204
0,35	1,419	1,7	0,531	0,230
0,40	1,492	1,8	0,588	0,255
0,45	1,568	1,9	0,642	0,279
0,50	1,649	2,0	0,693	0,301
X	ех	X	In X	1g х
-3	0,050	3	1,099	0,477
—2	0,135	4	1,386	0,602
-1	0,368	5	1,609	0,699
0	1,000	6	1,792	0,778
1	2,718	7	1,946	0,845
2	7,389	8	2,079	0,903
3	20,09	9	2,197	0,954
4	54,60	10	2,303	1,000
5	148,4	11	2,398	1,041
7Г	23,14	20	2,996	1,301
27Г	535,5	100	4,605	2,000
Для отыскания значений функций при промежуточных зна-
чениях аргумента в таблице 1 можно производить линейную
интерполяцию.
207
Филиппов Алексей Федорович
СБОРНИК ЗАДАЧ
ПО ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ
Формат 70 X КМР/зг. Объем 6,5 п.л. Тираж 2000 экз.
Издательство «Интеграл-Пресс». ЛР №065120 от 18.04.97.
125130. г. Москва, а/я 240. Integral.Press@g23.relcom.ru
Отпечатано с готовых диапозитивов в ПИП Типография
«Наука» Академиздатцентр РАН. Заказ № 3599